~<УГ 1АЯ

МАЕльяшевич
АТОМНАЯ
1/1 МОЛЕКУЛЯРНАЯ
СПЕКТРОСКОПИЯ
Издание второе
Эдиториал УРСС • Москва • 2001
ББК 22.344
Настоящее издание осуществлено при финансовой
поддержке Российского фонда фундаментальных
исследований (проект № 98-02-30058)
Ельяшевич Михаил Александрович
Атомная и молекулярная спектроскопия. Изд. 2-е. — М.: Эдиториал УРСС, 2001. — 896 с.
ISBN 5-8360-0177-4
Книга содержит последовательное изложение систематики атомных и молекулярных спектров.
В первой части рассматриваются общие вопросы спектроскопии, во второй — вопросы атомной
спектроскопии и в третьей — вопросы молекулярной спектроскопии.
Книга рассчитана на спектроскопистов и специалистов смежных специальностей — научных
работников, инженеров, студентов старших курсов.
Группа подготовки издания:
Директор — Доминго Марин Рикой
Заместители директора — Наталья Финогенова, Ирина Макеева
Администратор — Леонид Иосилевич
Компьютерный дизайн — Виктор Романов
Главный редактор — Елена Кудряшова
Верстка — Наталия Бекетова, Михаил Кириллов
Корректурные работы — Анна Шабалина
Обработка указателя — Андрей Стулов
Наборные работы — Анна Тюрина, Наталья Аринчева, Марина Круцко, Виктор Тарасов
Техническая поддержка — Наталья Аринчева
Менеджер по продажам — Алексей Петяев
Издательство «Эдиториал УРСС». 113208, г. Москва, ул. Чертановская, д. 2/11, к. п.
Лицензия ЛР №064418 от 24.01.96 г. Гигиенический сертификат на выпуск книжной
продукции № 77.ФЦ.8.953.П.270.3.99 от 30.03.99 г. Подписано к печати 18.09.2000 г.
Формат 70x100/16. Тираж 1000 экз. Печ. л. 56. Зак. №103
Отпечатано в АООТ «Политех-4». 129110, г. Москва, ул. Б. Переяславская, 46.
9
785 83 6»00 1 77 3»>
ISBN 5-8360-0177-4
© Эдиториал УРСС, 2000
ОГЛАВЛЕНИЕ
Предисловие............................................................. 10
Предисловие к первому изданию........................................... 12
ЧАСТЬ I
ОБЩИЕ ВОПРОСЫ СПЕКТРОСКОПИИ
Глава 1. Основные положения спектроскопии и ее разделы................... 15
§1.1.	Основные квантовые законы..................................... 15
§ 1.2.	Уровни энергии и переходы между ними.......................... 16
§ 1.3.	Спектры поглощения, испускания и рассеяния.................... 21
§ 1.4.	Деление спектроскопии по свойствам излучения............... 28
§ 1.5.	Деление спектроскопии по свойствам атомных систем.......... 32
§1.6.	Краткий исторический обзор развития атомной и молекулярной
спектроскопии.................................................... 35
Глава 2. Основные характеристики уровней энергии......................... 41
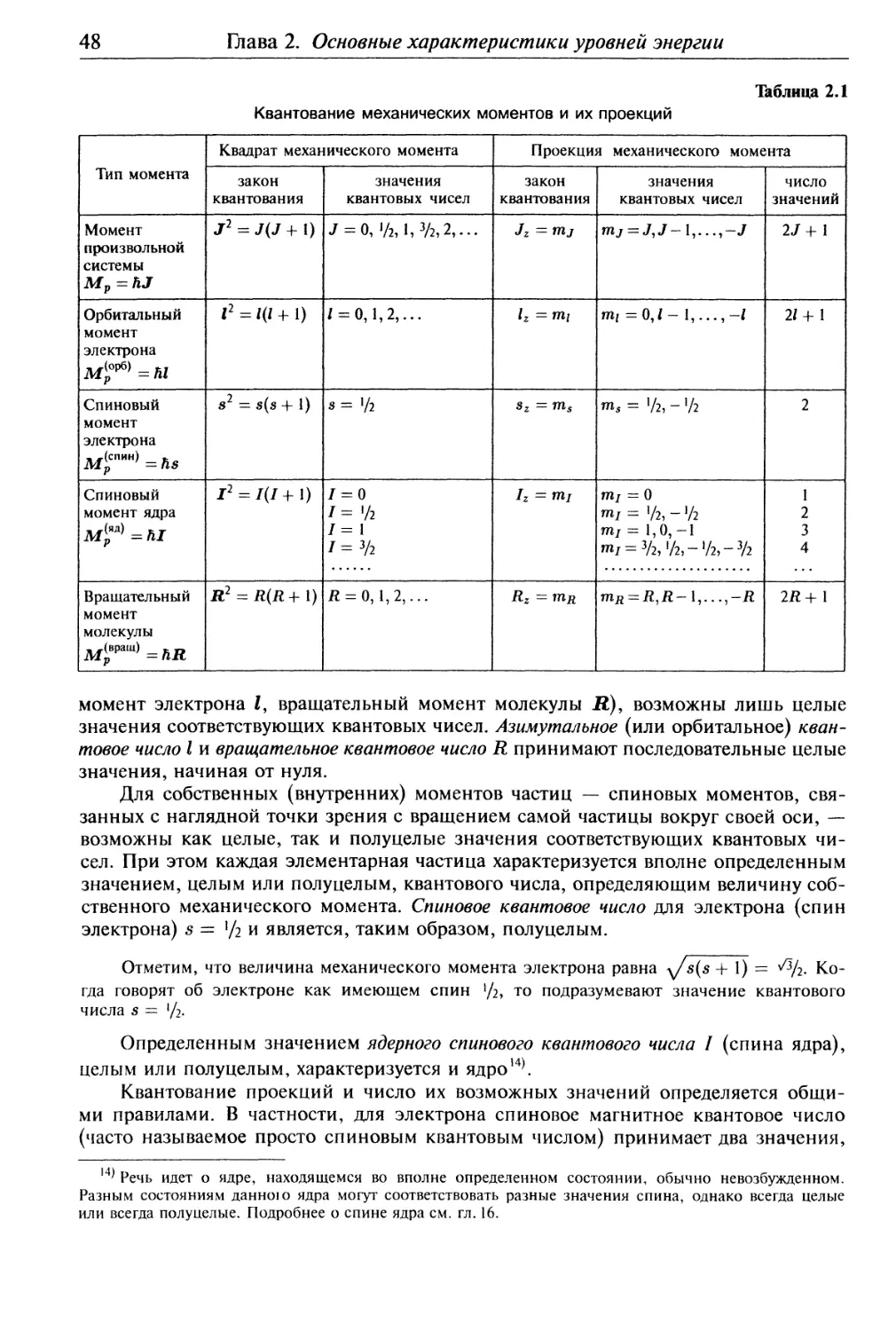
§2.1	. Невырожденные и вырожденные уровни энергии.................... 41
§2.2	. Значения физических величин в стационарных состояниях..	43
§2.3	. Квантование моментов количества движения и их проекций ....	45
§	2.4. Сложение моментов количества движения...................... 50
§2.5	. Магнитные моменты и их связь с механическими моментами ...	54
§	2.6. Прецессия и взаимодействие магнитных моментов.............. 57
Глава 3. Симметрия атомных систем и их уровней энергии................... 64
§3.1	. Общая характеристика симметрии атомных систем................. 64
§	3.2. Основные понятия теории групп и важнейшие группы........... 67
§3.3	. Невырожденные типы симметрии................................. 73
§	3.4. Вырожденные типы симметрии ................................ 77
Глава 4. Вероятности переходов и правила отбора.......................... 83
§4.1	.	Вероятности спонтанных и вынужденных переходов....... 83
§4.2	.	Время жизни возбужденных состояний................... 85
§4.3	.	Дипольное излучение.................................... 89
§	4.4.	Магнитное дипольное излучение и квадрупольное излучение	...	96
§4.5	.	Силы осцилляторов .......................................... 102
§4.6	.	Естественная ширина уровней энергии и спектральных линий	.	.	108
§4.7	.	Правила отбора для простейших видов симметрии ............... 113
§4.8	. Правила отбора для момента количества движения и его про-
екции .......................................................... 117
4
Оглавление
Глава 5. Интенсивности в спектрах ................................. 122
§5.1	. Мощности испускания и поглощения и заселенности уровней . .	122
§5.2	. Основные законы равновесного излучения................. 128
§5.3	. Коэффициенты поглощения..............................   136
§5.4	. Неравновесные спектры испускания и их интенсивности...	144
§	5.5. Контуры спектральных линий и полос.................... 150
§5.6	. Уширение спектральных линий, обусловленное тепловым движе-
нием и взаимодействиями частиц................................. 155
ЧАСТЬ II
АТОМНАЯ СПЕКТРОСКОПИЯ
Глава 6. Уровни энергии и спектры атома водорода и водородоподобных ионов 163
§6.1	. Квантовые числа одноэлектронного атома и степень вырождения
его уровней.................................................... 163
§	6.2. Зависимость спектров одноэлектронных атомов от заряда и массы
ядра........................................................... 166
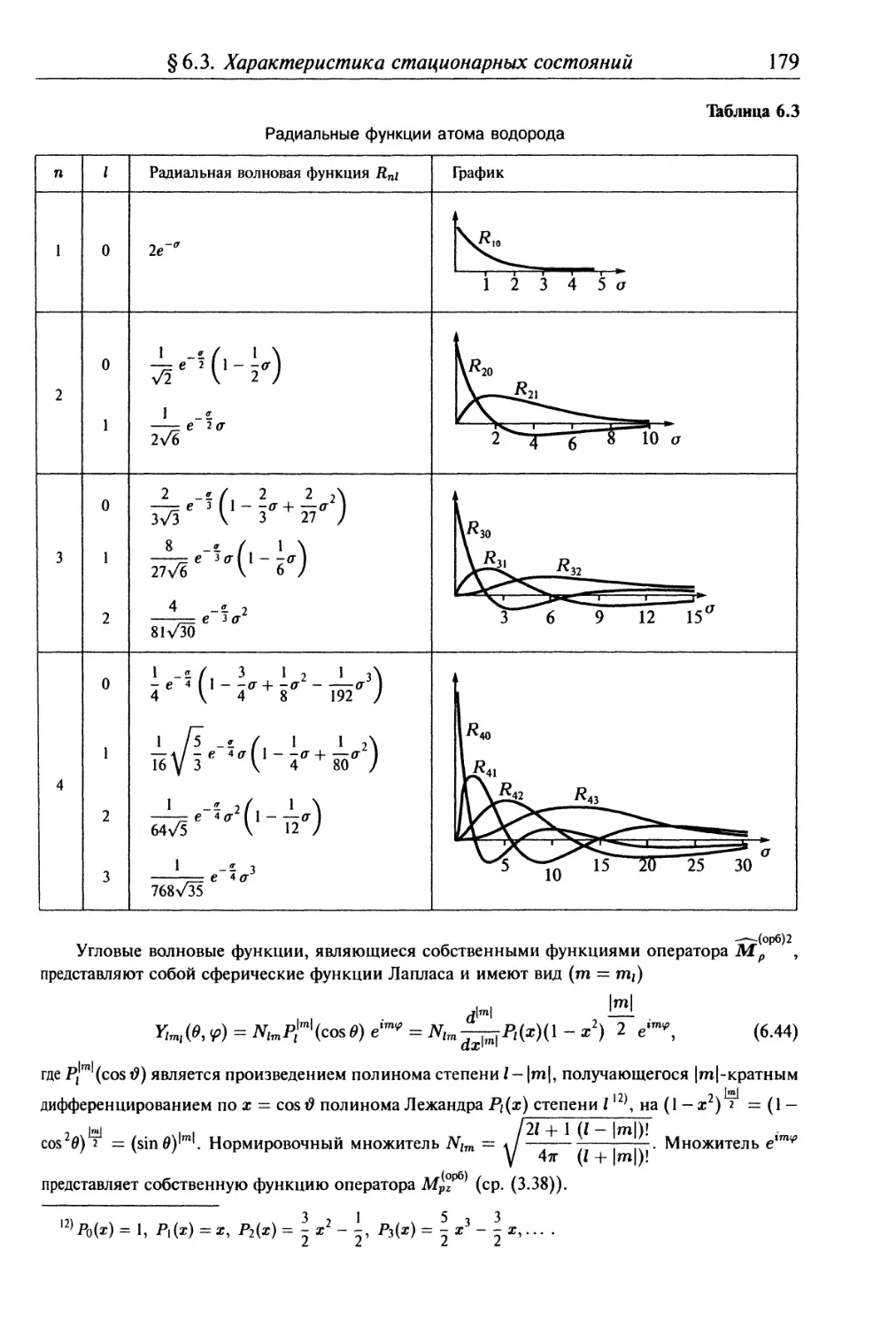
§	6.3.	Характеристика стационарных состояний одноэлектронного атома 170
§6.4	. Правила отбора и вероятности переходов для одноэлектронных
атомов......................................................... 180
§6.5	.	Тонкая структура уровней энергии и спектральных линий.	185
§6.6	.	Сдвиг уровней......................................... 192
Глава 7. Электронные оболочки атомов и периодическая система элементов . .	198
§7.1	. Квантовые числа электронов в сложном атоме и принцип Паули 198
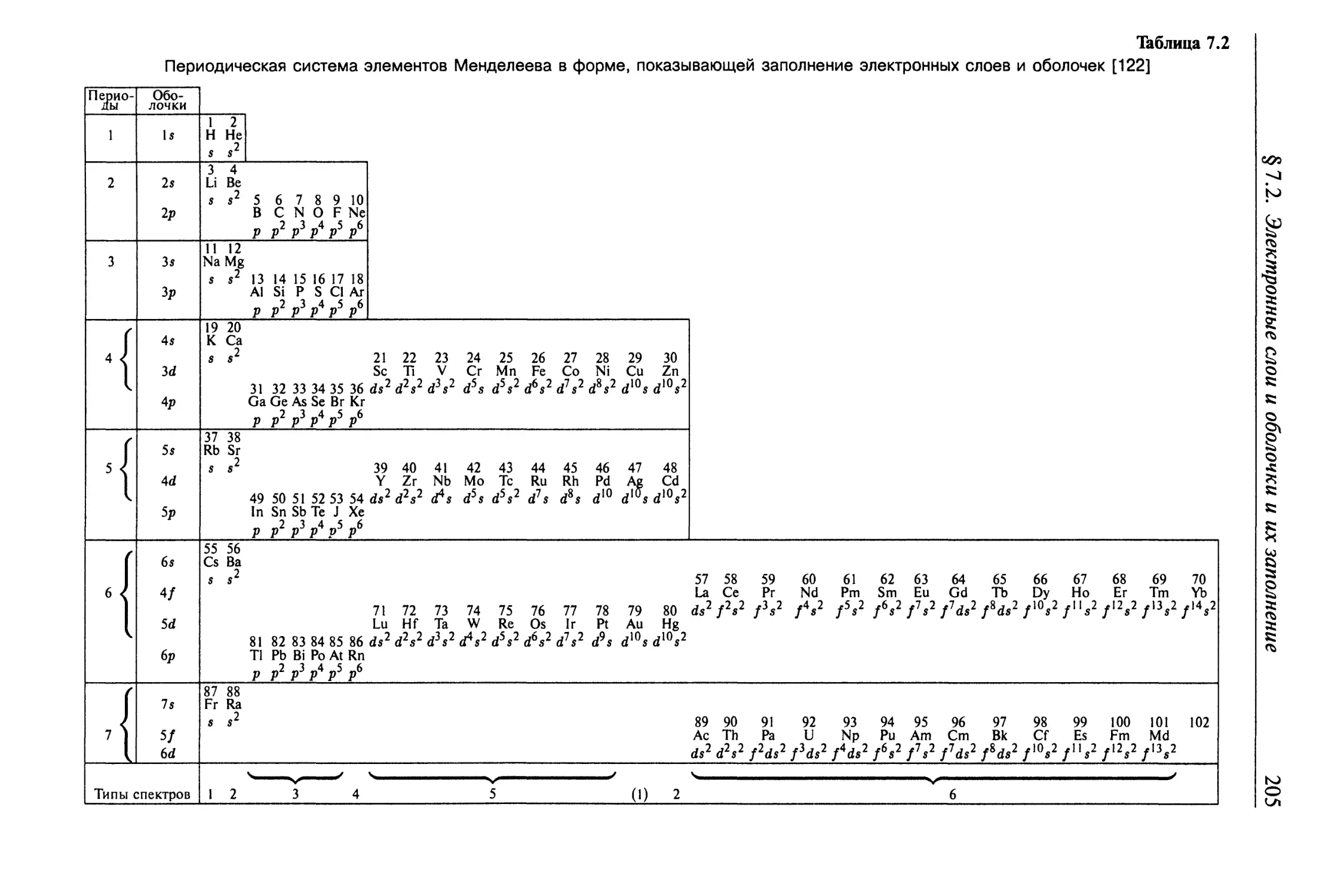
§	7.2. Электронные слои и оболочки и их заполнение........... 203
§7.3	. Зависимость энергии электронов от азимутального квантового
числа.......................................................... 206
§	7.4. Ход заполнения электронных слоев и оболочек........... 208
§7.5	. Свойства элементов с заполненными и незаполненными оболоч-
ками .......................................................... 210
§7.6	. Типы спектров различных элементов...................... 213
Глава 8. Одноэлектронные спектры атомов с одним внешним 5-электроном . .	216
§8.1	. Основной уровень атомов щелочных металлов............... 216
§8.2	. Возбужденные уровни и спектральные серии атомов щелочных
металлов....................................................... 218
§8.3	. Дублетная структура уровней атомов щелочных металлов..	223
§	8.4. Интенсивности в спектрах атомов щелочных металлов...	233
§8.5	. Спектры ионов, изоэлектронных с атомами щелочных металлов .	235
Глава 9. Основы общей систематики сложных спектров ................ 242
§9.1	. Сложение орбитальных и спиновых моментов и типы связи ....	242
§9.2	. Общая характеристика нормальной связи.................. 246
§9.3	. Термы конфигураций, состоящих из эквивалентных электронов .	254
§9.4	. Термы смешанных конфигураций, содержащих эквивалентные
электроны  .................................................... 259
§9.5	. Мультиплетное расщепление.............................. 261
Оглавление
5
§	9.6. Мультиплеты в спектрах...................................... 263
§9.7	. Случай связи (J,j)............................................ 273
Глава 10. Спектры атомов с двумя внешними s-электронами................... 276
§	10.1. Общая характеристика спектров атомов с двумя внешними элек-
тронами ......................................................... 276
§10.2	.	Спектр атома гелия................................ 278
§	10.3.	Спектры атомов щелочноземельных металлов.......... 284
§	10.4.	Спектры атомов цинка, кадмия и ртути.............. 288
§10.5	.	Смещенные термы...................................... 295
Глава 11.	Спектры атомов с заполняющимися и заполненными р-оболочками	.	301
§11.1	. Общая характеристика спектров атомов с заполняющимися p-обо-
лочками ......................................................... 301
§	11.2.	Спектры атомов с одним внешним р-электроном....... 304
§	11.3.	Спектры атомов с оболочками р2, р3 и р4........... 307
§11.4	.	Спектры атомов галоидов ................................... 312
§	11.5.	Спектры атомов инертных газов..................... 313
§	11.6.	Запрещенные линии в спектрах туманностей и солнечной короны	317
Глава 12.	Спектры атомов с достраивающимися d- и /-оболочками......	321
§12.1.	Особенности спектров атомов с достраивающимися оболочками	.	321
§ 12.2.	Общая характеристика спектров атомов с достраивающимися
d-оболочками..................................................... 323
§ 12.3.	Спектры атомов с d-оболочками, заполненными менее чем напо-
ловину .......................................................... 329
§12.4.	Спектры атомов с d-оболочками, заполненными наполовину ...	331
§ 12.5.	Спектры атомов с d-оболочками, заполненными более чем напо-
ловину .......................................................... 333
§ 12.6.	Спектры атомов с внешними s-электронами, помимо заполнен-
ной d-оболочки................................................... 336
§ 12.7.	Общая характеристика спектров атомов с достраивающимися
/-оболочками .................................................... 339
§ 12.8.	Спектры атомов с /-оболочками, заполненными менее чем напо-
ловину .......................................................... 344
§12.9.	Спектры атомов с /-оболочками, заполненными наполовину и
более............................................................ 347
Глава 13.	Рентгеновские спектры........................................... 350
§ 13.1.	Общая характеристика рентгеновских спектров поглощения и ис-
пускания ........................................................ 350
§ 13.2.	Регулярные и иррегулярные дублеты.............................. 356
§13.3.	Внутренняя конверсия рентгеновского излучения и недиаграмм-
ные линии........................................................ 361
§ 13.4.	Интенсивности в рентгеновских спектрах......................... 363
Глава 14.	Явление Зеемана и магнитный резонанс............................ 367
§ 14.1.	Расщепление уровней энергии в магнитном поле................... 367
§ 14.2.	Общая картина зеемановского расщепления спектральных линий
в слабом поле ................................................... 372
§ 14.3.	Множители д в случае слабого поля.............................. 378
6
Оглавление
§ 14.4.	Типы зеемановских расщеплений спектральных линий........ 383
§ 14.5.	Явление Зеемана в сильных и в промежуточных полях....... 389
§ 14.6.	Общая характеристика магнитного резонанса............... 395
§ 14.7.	Исследование электронного магнитного резонанса методом атом-
ных пучков...................................................... 399
§ 14.8.	Исследование электронного магнитного резонанса методом по-
глощения ....................................................... 402
Глава 15. Явление Штарка........................................... 407
§ 15.1.	Общая характеристика явления Штарка..................... 407
§ 15.2.	Явление Штарка для атомов в общем случае................ 411
§ 15.3.	Явление Штарка для атома водорода....................... 413
§15.4.	Штарковское уширение спектральных линий................. 417
Глава 16. Моменты ядер и их спектроскопическое исследование ....... 421
§16.1.	Общая характеристика моментов ядер...................... 421
§ 16.2.	Магнитные и электростатические взаимодействия ядерных мо-
ментов ......................................................... 424
§ 16.3.	Моменты протона, нейтрона и дейтрона и сверхтонкая структура
уровней атома водорода.......................................... 433
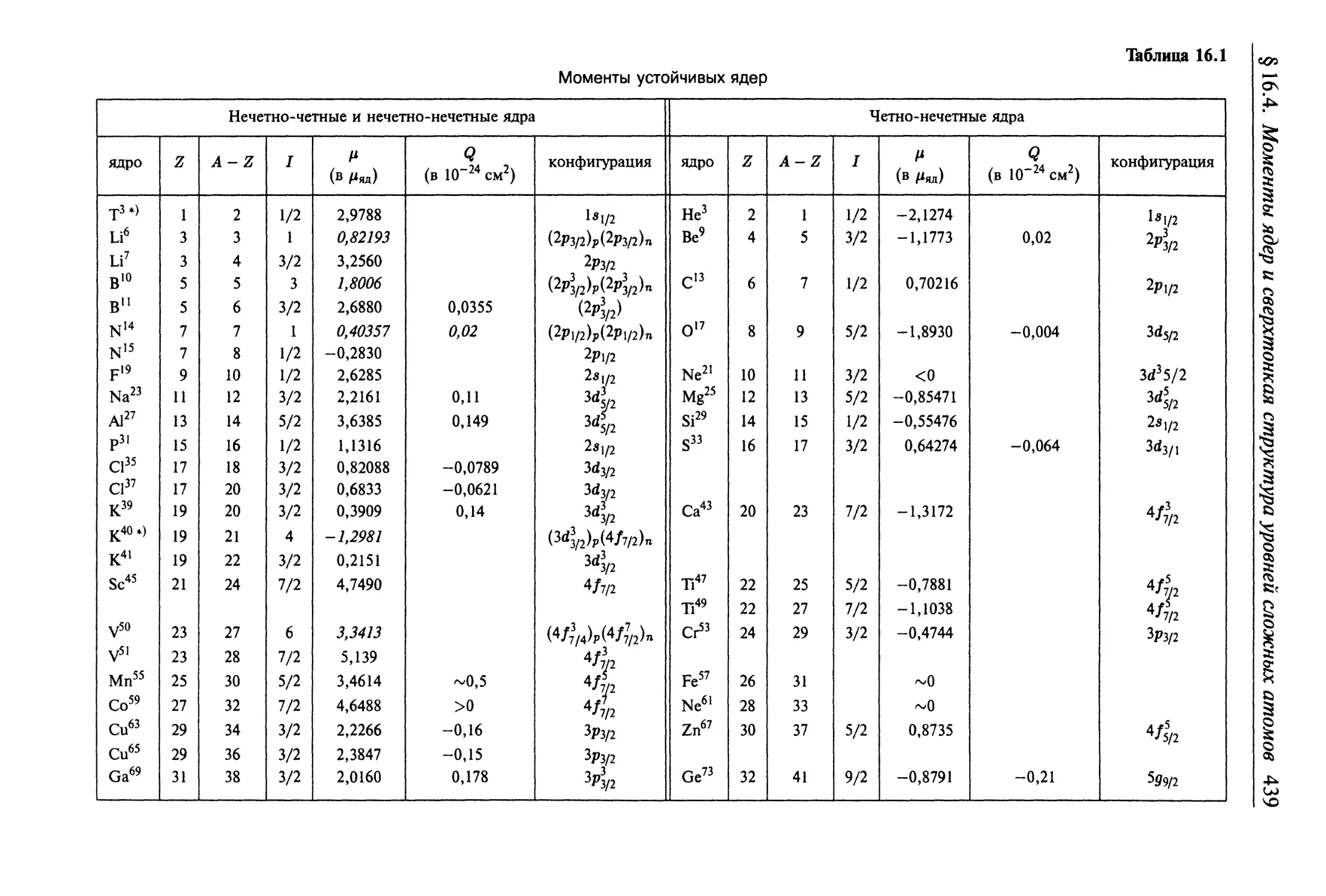
§ 16.4.	Моменты ядер и сверхтонкая структура уровней и спектральных
линий сложных атомов..........................................   438
§ 16.5.	Изотопическое смещение уровней энергии и спектральных линий 448
§ 16.6.	Модели ядра и теории моментов ядер...................... 453
ЧАСТЬ Ш
МОЛЕКУЛЯРНАЯ СПЕКТРОСКОПИЯ
Глава 17. Виды движения в молекуле и типы молекулярных спектров...	463
§ 17.1.	Разделение энергии молекулы на части и основные типы спектров 463
§17.2.	Порядок величин электронной, колебательной и вращательной
энергий.......................................................   467
§ 17.3.	Зависимость электронной энергии молекулы от расстояний между
ядрами.......................................................... 470
§17.4.	Колебательные и вращательные степени свободы и отделение
колебаний от вращения........................................... 476
§ 17.5.	Основные положения квантовомеханической теории молекул . . .	479
§17.6.	Характеристики переходов и интенсивности в случае спектров
поглощения и испускания......................................... 485
§17.7.	Характеристики переходов и интенсивности в случае спектров
комбинационного рассеяния....................................... 491
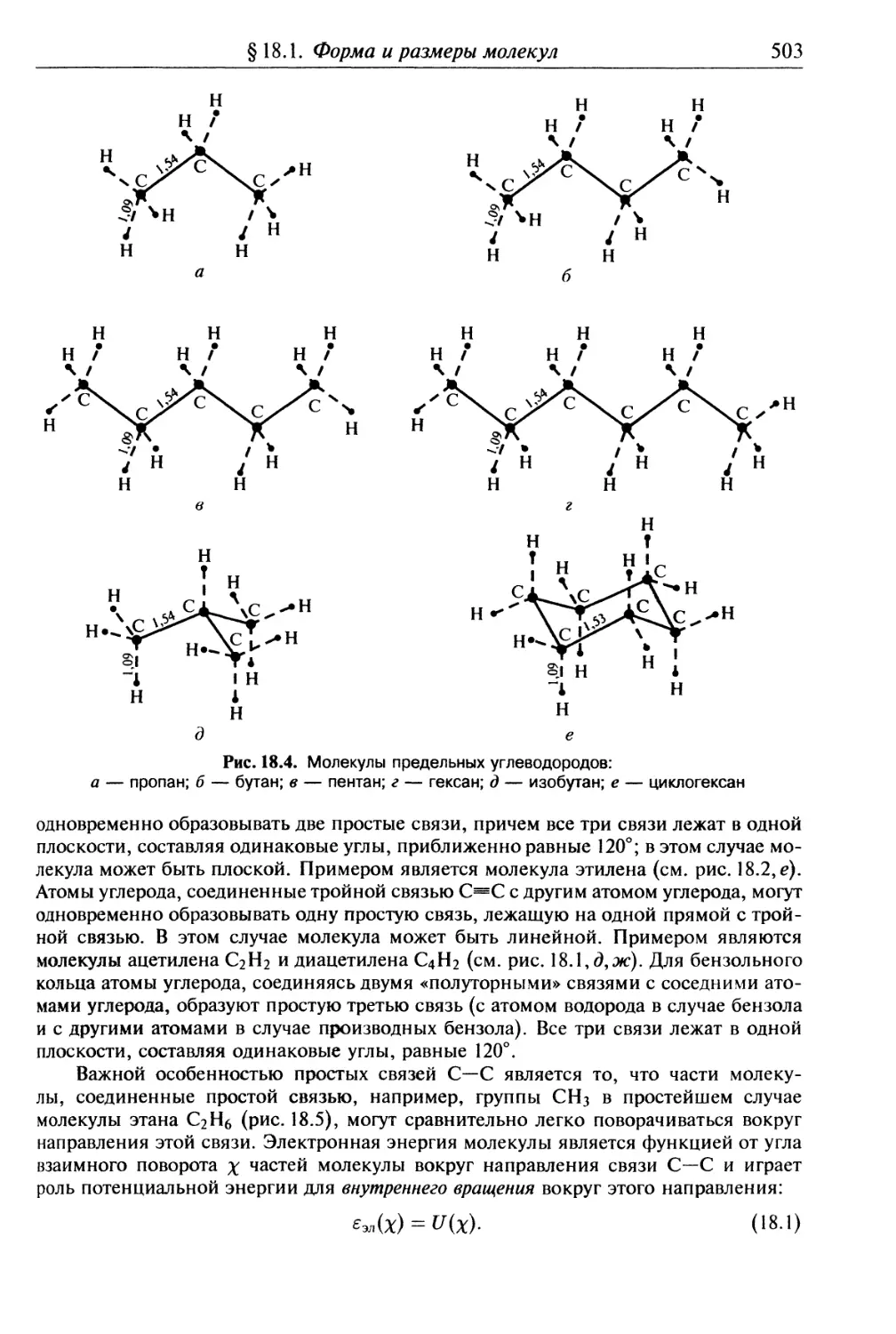
1лава 18. Равновесная конфигурация молекулы и ее свойства симметрии ....	499
§ 18.1.	Форма и размеры молекул................................. 499
§ 18.2.	Свойства симметрии равновесной конфигурации и точечные груп-
пы симметрии.................................................... 505
§ 18.3.	Точечные	группы низшей симметрии....................... 511
§ 18.4.	Точечные	группы средней симметрии....................... 515
§ 18.5.	Точечные	группы высшей симметрии ....................... 522
§18.6.	Общие выводы о симметрии молекул ........................ 525
Оглавление
7
Глава 19. Вращение молекул и вращательные спектры........................ 539
§19.1.	Общая характеристика вращения молекул.......................... 530
§ 19.2.	Вращательные уровни и вращательные переходы в случае линей-
ных молекул..................................................   536
§19.3.	Вращательные уровни молекул типа сферического волчка...	540
§ 19.4.	Моменты инерции и вращательные постоянные молекул типа
симметричных и асимметричных волчков........................... 543
§ 19.5.	Вращательные уровни и вращательные переходы в случае молекул
типа симметричного волчка...................................... 546
§ 19.6.	Вращательные уровни и вращательные переходы в случае молекул
типа асимметричного волчка..................................... 550
§ 19.7.	Вращательные спектры и структура молекул...................... 556
§ 19.8.	Действие внешних полей на вращательные уровни и вращательные
линии......................................................     559
§ 19.9.	Влияние ядерных моментов на вращательные уровни и на враща-
тельные линии.................................................. 565
Глава 20.	Колебания двухатомных молекул ................................  571
§20.1	. Колебания двухатомных молекул как частный случай колебаний
любых молекул.................................................. 571
§20.2	.	Гармонические колебания двухатомной молекулы.................. 572
§20.3	. Квантовомеханическая характеристика гармонического осцилля-
тора .......................................................... 580
§20.4	. Ангармоничность колебаний и схождение колебательных уровней
к границе диссоциации........................................   584
§	20.5. Построение кривых потенциальной энергии по опытным данным	592
§20.6	. Колебательно-вращательные спектры двухатомных молекул ....	594
§	20.7. Вращательная структура колебательно-вращательных полос ....	600
Глава 21. Колебания многоатомных молекул................................. 606
§21.1	. Общая характеристика нормальных колебаний многоатомных мо-
лекул ......................................................... 606
§21.2	. Классификация нормальных колебаний молекул по их форме . . .	609
§21.3	. Вид потенциальной энергии и выбор колебательных координат. .	615
§21.4	. Общий метод решения задачи о нормальных колебаниях молекул	620
§21.5	. Коэффициенты кинематического взаимодействия и составление
вековых уравнений.............................................. 628
§21.6	. Свойства векового уравнения и методы его решения.............. 635
§21.7	. Ангармоничность колебаний многоатомных молекул................ 638
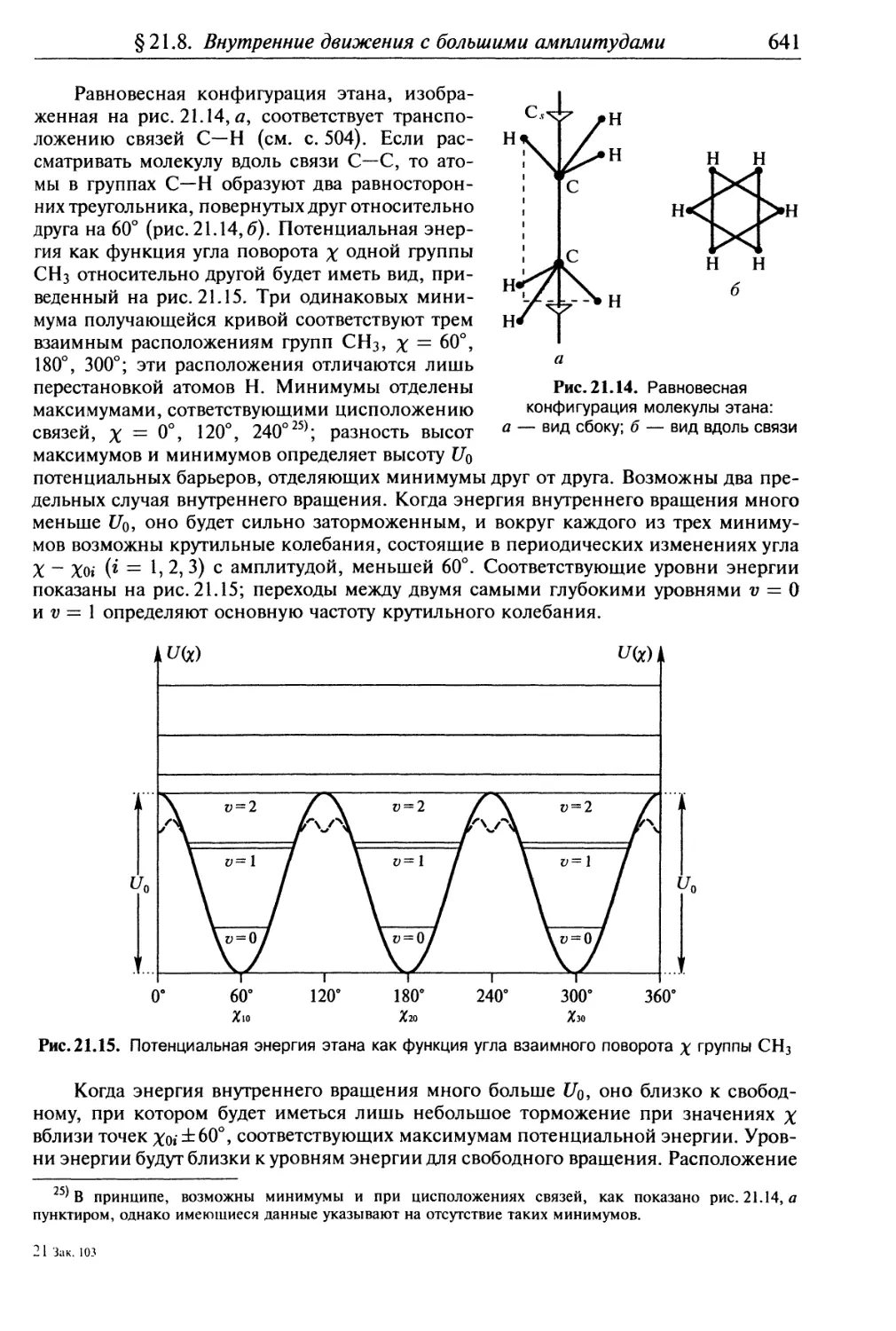
§21.8	. Внутренние движения с большими амплитудами в многоатомных
молекулах...................................................... 640
Глава 22. Симметрия колебаний многоатомных молекул . ..................   645
§22.1	. Общие принципы классификации колебаний по их симметрии
и координаты симметрии ............................	645
§22.2	. Типы симметрии для молекул, относящихся к точечным группам
низшей симметрии.............................................   649
§	22.3. Дважды и трижды вырожденные колебания...................... 654
§22.4	. Типы симметрии для молекул, относящихся к точечным группам
средней и высшей симметрии..................................... 661
8
Оглавление
§	22.5. Подсчет числа колебаний различных типов симметрии и нахожде-
ние коэффициентов симметрии....................................... 666
§	22.6. Решение задачи о колебаниях молекулы при учете свойств сим-
метрии ........................................................... 670
Епава 23. Колебательные спектры многоатомных молекул................... 676
§23.1	. Правила отбора в колебательных спектрах..................... 676
§	23.2. Интенсивности и поляризации в колебательных спектрах.	684
§	23.3. Колебательные спектры простейших многоатомных молекул ....	696
§	23.4. Вращательная структура колебательных полос.............. 702
§23.5	. Колебательные спектры органических молекул................. 706
§23.6	. Характеристичность в колебательных спектрах................ 713
Епава 24. Электронные состояния и химическая связь
в двухатомных молекулах................................................ 719
§24.1	. Свойства электронных состояний молекул и химическая связь . .	719
§24.2	. Классификация электронных состояний двухатомной молекулы
как целого........................................................ 721
§24.3	. Соответствие между электронными состояниями молекулы как
целого и образующих ее атомов..................................... 725
§	24.4. Характеристики отдельных электронов в молекуле и молекуляр-
ные электронные оболочки.......................................... 727
§	24.5. Возможные состояния молекулы с заданной электронной конфи-
гурацией ......................................................... 731
§24.6	. Электронные состояния и химическая связь в ионе молекулы
водорода.......................................................... 734
§24.7	. Электронные состояния	и химическая связь в молекуле водорода 740
§	24.8. Электронные оболочки и химическая связь в молекулах, состоя-
щих из двух одинаковых	атомов............................... 746
§	24.9. Электронные оболочки и химическая связь в молекулах, состоя-
щих из двух разных атомов ........................................ 750
Глава 25. Электронные спектры двухатомных молекул...................... 753
§25.1.	Колебательная структура электронных переходов................ 753
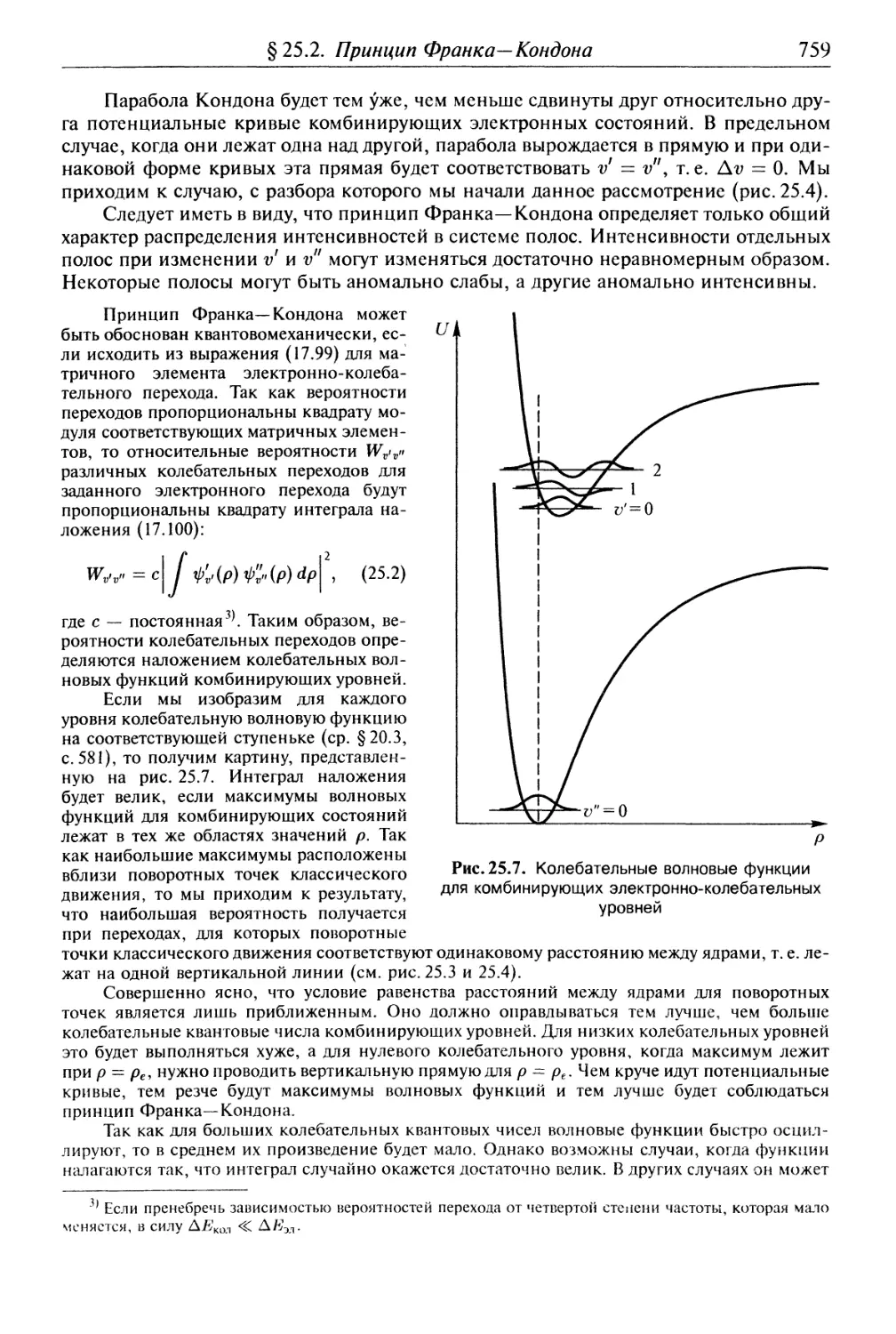
§25.2.	Принцип Франка—Кондона и относительные интенсивности
электронно-колебательных полос.................................... 756
§25.3.	Общая характеристика вращательной структуры электронно-ко-
лебательных полос................................................. 760
§ 25.4.	Взаимодействие электронного движения с вращательным......	763
§25.5.	Правила отбора и типы электронных переходов................. 771
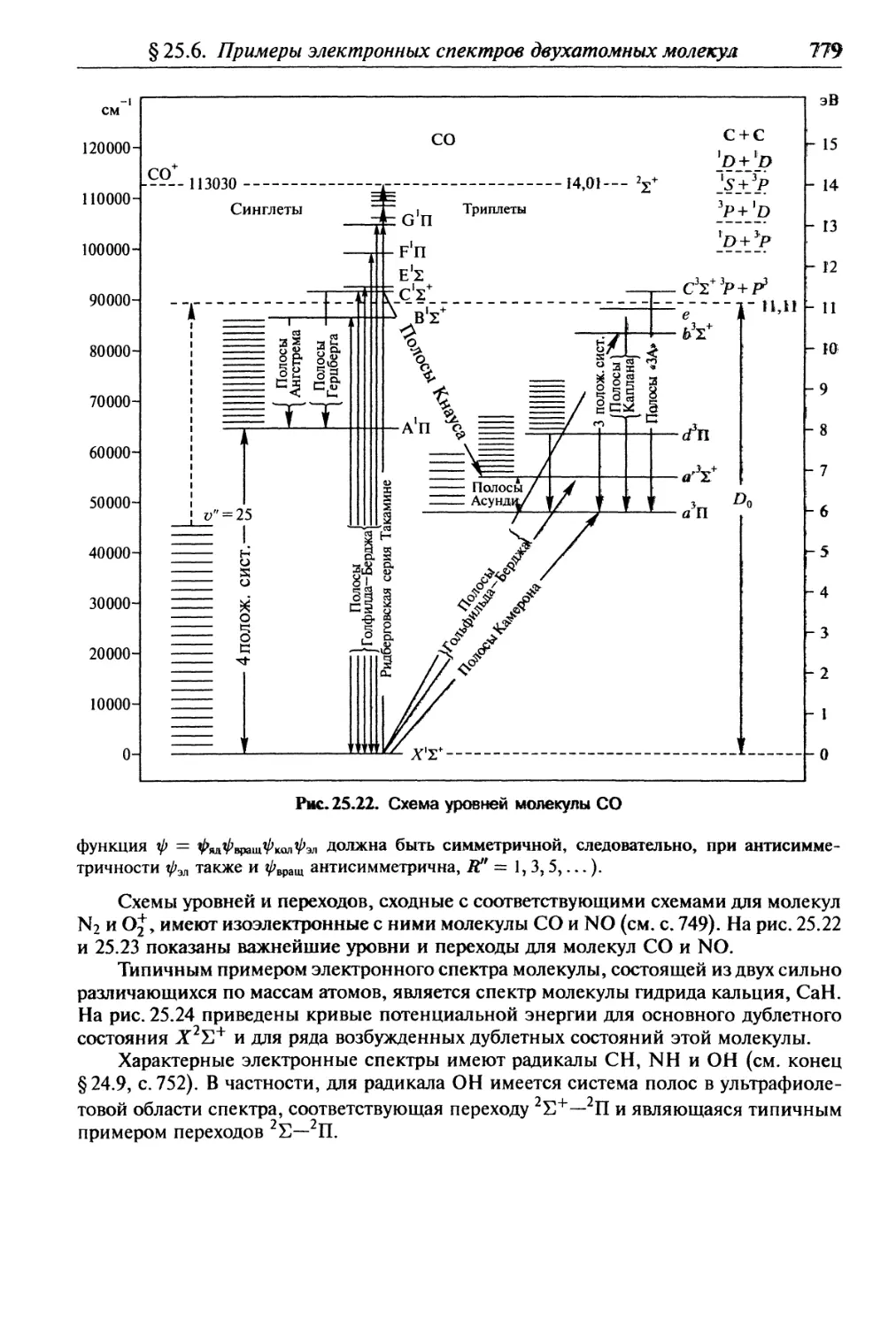
§ 25.6.	Примеры электронных спектров двухатомных молекул............ 775
§ 25.7.	Сплошные спектры поглощения и испускания двухатомных мо-
лекул ............................................................ 780
§25.8.	Возмущения и предиссоциация в спектрах двухатомных	молекул .	784
Глава 26.	Электронные состояния и химическая связь
в многоатомных	молекулах..................................... 788
§ 26.1.	Общая характеристика электронных состояний многоатомных мо-
лекул ............................................................ 788
§ 26.2.	Основы теории	направленной валентности...................... 794
Оглавление
9
§ 26.3.	Образование химических связей четырехвалентными атомами уг-
лерода ..................................................... 803
§ 26.4.	Нелокализованные электроны и методы их рассмотрения.	808
§26.5.	Электронные конфигурации и электронные состояния простей-
ших многоатомных молекул.................................... 816
Глава 27. Электронные спектры многоатомных молекул.............. 824
§27.1	. Общая характеристика электронно-колебательных переходов и ти-
пы электронных спектров..................................... 824
§27.2	. Принцип Франка—Кондона	для	многоатомных молекул.....	829
§27.3	. Примеры электронных спектров простейших многоатомных мо-
лекул ...................................................... 836
§	27.4. Полосы поглощения и испускания сложных	молекул.... 839
§27.5	. Квантовый выход и поляризация фотолюминесценции сложных
молекул..................................................... 848
ПРИЛОЖЕНИЯ
Литература...................................................... 857
Таблица волновых чисел, соответствующих энергиям, выраженным в электрон-
вольтах ....................................................... 874
Предметный указатель............................................ 876
ПРЕДИСЛОВИЕ
Эта книга была опубликована в 1962 году. Родилась она из цикла лекций,
которые автор читал еще в ГОИ им. С. И. Вавилова аспирантам и сотрудникам
этого Института. Разумеется, может возникнуть вопрос, а зачем переиздавать эту
книгу, да еще без каких-либо изменений, спустя столько лет? Область науки, ко-
торой эта работа посвящена, с тех пор необычайно продвинулась. Так стоит ли
возвращаться к старому? Чтобы ответить на этот вопрос вспомним, что как раз
в период от конца двадцатых до конца пятидесятых годов закладывались прин-
ципиальные основы базирующейся уже на квантовой базе современной теории
и методов расчета свойств объектов микромира. Эти основы не только не были
ревизованы в последующем, но как раз послужили тем фундаментом, на котором
и было построено громадное здание современной теоретической атомной и молеку-
лярной спектроскопии. Это привело не только к пониманию физики тех процессов,
которые происходят в результате взаимодействия электромагнитного поля с веще-
ством, но и к возможности предсказать на количественном уровне наблюдаемые
проявления такого взаимодействия для очень крупных систем, вплоть до полиме-
ров и кристаллов, с достоверностью, достаточной для оптимального выбора пути
исследования или создания «молекулярной машины» путем замены натурных экс-
периментов компьютерными. Весь опыт развития любой области науки показывает,
что сам этот процесс невозможен без постоянного обращения к исходным базовым
положениям, трактовкам тех или иных понятий и явлений. Это, в свою очередь,
требует обобщения и концентрирования соответствующих знаний. Лучшей формой
такого концентрирования были и остаются монографии. «Старение» монографий
происходит тем медленнее, чем более фундаментальные знания в них обобщаются.
Конечно, создать такой концентрат очень трудно. Подобно тому, как архивная полка
не есть еще наука и для превращения исходного материала в «Историю государства
Российского» нужна дополнительно голова Н. Карамзина, так и для того, чтобы раз-
бросанный по разным статьям материал многих авторов превратился в концентрат
знаний, нужна голова крупного исследователя, свободно ориентирующегося во всем
многообразии сведений и способного выделить в нем самое главное и подчерк-
нуть внутренние связи. Разумеется, это удается только ученым, широкая эрудиция
которых базируется не на чтении чужих публикаций или на их воспроизведении с не-
большими вариациями, а на собственной активной творческой работе, развивающей
данную область науки. Ученые необходимого для этого уровня составляют редкость.
Именно поэтому и монографии, подобные той, которая сейчас вновь предлагается
читателям, появляются также редко. В частности, в отечественной, да и зарубежной
литературе, монографии, подобной этой, так и не появилось. Надо еще учесть, что
само по себе написание книги такого большого объема требует громадного труда
и далеко не все даже выдающиеся ученые на это способны. Л. Ландау был блестя-
щим ученым, но здание «Теоретической физики» не было бы построено без «пера»
Е. Лифшица, который и выполнил всю практическую работу. Михаил Александро-
вич Ельяшевич принадлежал к той группе ученых, которые заложили самые основы
Предисловие
11
современной теории атомных и молекулярных спектров. Он автор ряда крупных
монографий по разным разделам теории оптических спектров, практически цели-
ком построенных на оригинальных материалах. Он одинаково свободно чувствовал
себя как в области атомной, так и молекулярной спектроскопии. Именно это позво-
лило ему создать уникальное научное произведение, пожалуй, не имеющее равных
по широте и уровню обсуждаемых вопросов и именно поэтому не потерявшее свое
значение и сейчас. Без всякого преувеличения можно сказать, что вся наша последу-
ющая теоретическая спектроскопия, подобно литературе, вышедшей из «Шинели»
Н. Гоголя, вышла из исследований М. Ельяшевича. Новые кадры спектроскопистов
учились по его книгам. Монография «Атомная и молекулярная спектроскопия» все-
гда рекомендовалась в качестве основного пособия при подготовке кандидатского
минимума по соответствующей специальности. К сожалению, она практически сразу
стала библиографической редкостью и сделалась недоступной. Надо поэтому при-
ветствовать повторное издание этой выдающейся монографии и принести глубокую
благодарность тем, кто сделал это повторное издание возможным. Книга оставле-
на без изменений так, как она была написана автором. Это сделано совершенно
сознательно. Основы теории атомных и молекулярных спектров, а именно этот-то
материал и составляет главное содержание монографии, не изменилось. Вводить же
отдельные вставки и пояснения, указывающие на дальнейшее развитие основопола-
гающих идей и методов расчетов, так же неразумно, как подправлять классическую
картину на том основании, что появились более выразительные краски. Кроме того,
любые такие замечания всегда отражали бы точку зрения их автора и, следовательно,
нарушали бы «авторскую чистоту» оригинала. К книге только добавлена в качестве
отдельной вставки дополнительная библиография, содержащая ссылки на неболь-
шое число достаточно крупных монографий по теории атомных и молекулярных
спектров, опубликованных как в отечественной, так и в зарубежной печати за годы
после выхода «Атомной и молекулярной спектроскопии». Заключая это краткое пре-
дисловие, считаю необходимым отметить, что Михаил Александрович был не только
выдающимся по всем меркам ученым, но и замечательным человеком по своим
душевным и нравственным качествам. У него было много учеников и друзей, ис-
пытавших на себе его благотворное влияние. Пусть это издание его капитального
труда послужит ему памятником и даст возможность новому поколению ученых
насладиться, пусть и заочно, общением с ним!
Чл.-корр. РАН
Л. А. Грибов
Москва
апрель 2000 года
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Данная книга содержит последовательное изложение систематики атомных
и молекулярных спектров. В основу книги положены лекции, прочитанные в Го-
сударственном оптическом институте имени С. И. Вавилова в 1956 г. для научных
сотрудников и аспирантов и прекрасно застенографированные О. В. Соколовой, ко-
торой я приношу мою глубокую благодарность. В книге также использован опыт
ведения курсов спектроскопии в ленинградских вузах и в Белорусском государствен-
ном университете имени В. И. Ленина.
Книга состоит из трех частей. Первая часть посвящена общим вопросам спектро-
скопии, ясное понимание которых является чрезвычайно важным. Во второй части
рассматриваются вопросы атомной спектроскопии, в третьей части — молекулярной
спектроскопии. Наряду с результатами исследований спектров в оптической области
уделено внимание результатам радиоспектроскопических исследований атомов и мо-
лекул. Разбирается ряд смежных вопросов, в частности вопросы химической связи
в двухатомных и многоатомных молекулах, весьма существенные при рассмотрении
электронных спектров молекул.
Книга рассчитана на широкие круги спектроскопистов и специалистов смежных
специальностей, как научных работников и инженеров, так и студентов старших кур-
сов. Более трудный материал, в частности материал, требующий знания квантовой
механики, напечатан мелким шрифтом и может быть опущен читателем, не имею-
щим соответствующей подготовки и знакомым лишь с общими основами квантовой
теории. В полном объеме книга примерно соответствует кандидатскому минимуму
по спектроскопии. Приведенный в конце книги список литературы не является
исчерпывающим. В него включены основные монографии, учебники и обзоры
по спектроскопии и смежным вопросам и ряд оригинальных исследований. В за-
ключение приношу искреннюю благодарность Э. В. Шпольскому, В. К. Прокофьеву
и Б. С. Непоренту, прочитавшим рукопись, за ценные замечания, Е. Е. Жаботинскому
и Л. Ф. Вересу за тщательное редактирование книги и всем товарищам, помогавшим
мне при подготовке и оформлении рукописи.
М. Елъяшевич
Минск
май 1961 года
ЧАСТЬ I
ОБЩИЕ ВОПРОСЫ
СПЕКТРОСКОПИИ

ГЛАВА 1
ОСНОВНЫЕ ПОЛОЖЕНИЯ СПЕКТРОСКОПИИ
И ЕЕ РАЗДЕЛЫ
§1.1. Основные квантовые законы
Все современное учение о спектрах электромагнитного излучения базируется
на квантовой теории, и поэтому естественно начать изложение атомной и молеку-
лярной спектроскопии с основных квантовых законов.
Квантовые представления были впервые введены в спектроскопию Нильсом
Бором, объяснившим в 1913 г. спектр простейшего атома — атома водорода [175] °.
Сформулированные Бором два постулата — о существовании стационарных состоя-
ний и о квантовых переходах с излучением — получили в дальнейшем всестороннее
экспериментальное подтверждение на огромном опытном материале атомной физи-
ки и нашли глубокое теоретическое обоснование в квантовой механике и в квантовой
электродинамике. Эти постулаты оказались справедливыми не только для простей-
ших, но и для самых сложных атомов, для молекул и для кристаллов, с одной
стороны, и для атомных ядер, с другой стороны. Для общности мы будем говорить
об атомных системах, подразумевая под ними любые микроскопические системы —
атомные ядра, атомы, молекулы, а также конденсированные макроскопические
системы, состоящие из сильно взаимодействующих атомов и молекул — твердые
и жидкие тела.
В настоящее время правильно рассматривать два постулата Бора как основные
квантовые законы, которым подчиняются любые атомные системы.
Согласно первому квантовому закону, атомная система является устойчивой
лишь в определенных — стационарных ~ состояниях, соответствующих некоторой
дискретной (прерывной) или непрерывной последовательности значений энергии Е
системы. Любое изменение этой энергии связано со скачкообразным переходом
системы из одного стационарного состояния в другое.
Весьма характерное отличие квантовой теории от классической состоит в воз-
можности дискретной последовательности значений энергии стационарных состоя-
ний
Е\, Е^, Е$, ... (Е\ < Е^ < Е$ <...).	(1.1)
Для конкретной системы последовательность значений Е может быть либо цели-
ком дискретной, либо целиком непрерывной, либо частично дискретной и частично
непрерывной (в различных интервалах изменения энергии).
Например, для гармонического осциллятора получается дискретная последова-
тельность, для движения свободной частицы — непрерывная последовательность,
9 Краткий исторический очерк развития спектроскопии читатель найдет в последнем параграфе
данной главы (см. с. 35).
16
Глава 1. Основные положения спектроскопии и ее разделы
для атома водорода — дискретная последовательность при энергиях, меньших энер-
гии ионизации, и непрерывная последовательность при энергиях, больших энергии
ионизации (см. ниже, с. 19).
Часто говорят о дискретном и о непрерывном (или сплошном) спектре значений энергии.
В дальнейшем термин «спектр» мы будем применять в первую очередь к спектрам электромаг-
нитного излучения — к спектрам испускания, поглощения и рассеяния. Для совокупностей
значений энергии при необходимости мы будем применять термин «энергетический спектр»
и говорить о дискретном или непрерывном энергетическом спектре.
В соответствии с законом сохранения энергии переходы атомной системы
из одного стационарного состояния в другое связаны с получением или отдачей
энергии системой. Ими могут быть либо переходы с излучением (оптические перехо-
ды), когда атомная система испускает или поглощает электромагнитное излучение,
либо переходы без излучения (безызлучательные или неоптические), когда происхо-
дит непосредственный обмен энергией между рассматриваемой атомной системой
и окружающими системами, с которыми она взаимодействует. К переходам по-
следнего типа относятся, в частности, возбуждение атомов и молекул электронным
ударом, передача энергии внутреннего движения при столкновениях между молеку-
лами от одной молекулы к другой. Нас в первую очередь будут интересовать переходы
с излучением; второй квантовый закон относится к переходам именно этого вида.
Согласно этому закону, электромагнитное излучение, связанное с переходом
атомной системы из стационарного состояния с энергией Ej в стационарное со-
стояние с энергией Ei, является монохроматическим, и его частота и определяется
соотношением
Ei-Ej = hv,	(1.2)
где h — постоянная Планка.
Электромагнитное излучение при этом поглощается (если Ej > Ej) или испус-
кается (если Ej < Ej) определенными порциями hi/ — квантами излучения, обычно
называемыми просто квантами2). Кванты можно рассматривать как особого рода
частицы, частицы света — фотоны, если говорить о свете в широком смысле слова,
подразумевая под ним электромагнитное излучение любой длины волны.
Закон (1.2) описывает квантовые переходы с излучением. Его часто называют
правилом, или условием, частот Бора (или условием частот излучения). Это есть за-
кон сохранения энергии для микроскопических процессов, связанных с излучением.
Приведенные формулировки двух основных квантовых законов близки к формулировкам
двух основных постулатов, данным самим Бором (см. [175] и особенно [6]). В литературе
встречаются весьма разнообразные формулировки основных постулатов Бора, причем обычно
в число их неправильно включается правило квантования движения электрона по круговым
орбитам в атоме водорода, связанное с конкретной формой теории Бора (см: ниже, с. 38).
§ 1.2. Уровни энергии и переходы между ними
Мы будем говорить в дальнейшем, по аналогии между энергиями стационарных
состояний и потенциальной энергией тела, поднятого на различные высоты (на раз-
личные уровни), и в соответствии с основанным на этой аналогии общепринятым
графическим изображением, об уровнях энергии и о переходах между уровнями энергии.
2> Для поглощения частоту можно условно считать положительной, лля испускания — отрицательной:
согласно (1.2), при Ei > Ej и > 0, при Ei < Ej и < 0.
§ 1.2. Уровни энергии и переходы между ними
17
На рис. 1.1 изображена простей-
шая диаграмма уровней энергии, образу-
ющих дискретную последовательность.
Горизонтальные линии проведены на
расстояниях, пропорциональных разно-
стям значений энергий Е\, Е2, Е$, Е^,
Е$ соответствующих стационарных со-
стояний. Слева дана шкала энергий.
Как и в случае потенциальной энергии
поднятого тела, начало отсчета энергии
является произвольным; за нуль может
быть принята энергия Е\ самого нижне-
го уровня или иная энергия, характери-
зующая определенное состояние систе-
мы, например для атома — энергия, соответствующая отрыву электрона, т. е. иониза-
ции атома, а для молекулы — энергия, соответствующая разрыву молекулы на части,
т. е. диссоциации молекулы. Переходы между стационарными состояниями — между
уровнями энергии — показаны вертикальными линиями, соединяющими соответ-
ствующие горизонтальные линии — комбинирующие уровни. Переходы могут быть
без излучения и с излучением. Для последних3* разность энергий комбинирующих
уровней, согласно (1.2), пропорциональна частоте перехода — частоте испускаемо-
го или поглощаемого кванта, поэтому шкала энергий Е пропорциональна шкале
частот и и шкале волновых чисел
и 1
— — - (где с — скорость света, а Л — длина
с Л
волны). При рассмотрении уровней энергии атомных систем можно пользоваться
любой из этих шкал, а также пропорциональной им шкалой абсолютных темпера-
тур Т согласно соотношению hv — кТ, где к — постоянная Больцмана; Т есть та
температура, при которой энергия hv фотона данной частоты и равна величине кТ,
являющейся мерой средней тепловой энергии.
1/1	h
Шкалы Е = hv, и, - = - и Т = —и связаны переводными множителями,
с Л	к
приведенными в табл. 1.1. Е дано как в эргах и электрон-вольтах (эВ) на частицу,
так и в калориях (грамм-калориях) на грамм-молекулу (моль). В таблице приведены
точные значения переводных множителей [124], от которых легко перейти к прибли-
женным их значениям (например 1 эВ ~ 8 000 см"1 « 23 000 кал/моль « 12 000 К).
Таблица 1.1
Переводные множители
Единицы	см 1	с-'(Гц)	эрг	эВ	К	кал/моль
1 см"1	1	2,99793 • 10ю	1,98618 -10’16	1,23977- Ю’4	1,4388	2,8584
1 с"1 = 1 Гц	3,33563- ЦТ”	1	6,6252 • 10’27	4,13541 • 10’15	4,7994-10"11	0,95447- 10"10
1 эрг	5,0348 • 1015	1,50940-1026	1	6,2414 -10"	7,2440-1015	1,4407- 1016
1 эВ	8066,0	2,41814 -1014	1,60221 • 10'12	1	11 605,4	23 082
1 К	0,69502	2,0836-1010	1,38044-10’16	0,86167-10’4	1	1,9888
1 кал/моль	0,34947	1,0477- Ю10	6,9412-10’17	4,3323 • 10’5	0,50282	1
3*В дальнейшем по всей книге мы будем говорить просто о переходах, подразумевая переходы
с излучением; при рассмотрении переходов без излучения это будет специально оговариваться.
18
Глава 1. Основные положения спектроскопии и ее разделы
В спектроскопии особенно широко пользуются волновыми числами (см"1)
и энергиями в эВ (согласно соотношению hv — eV, где е — заряд электрона, а V —
разность потенциалов в вольтах); в кал/моль часто выражают энергии ионизации и
особенно энергии диссоциации молекул. Согласно установившейся в спектроскопии
практике, частоты и волновые числа обозначают одной и той же буквой и\ при этом
нередко, приводя данные для переходов в волновых числах, говорят о частотах пере-
ходов. Аналогично говорят об энергиях переходов, энергиях ионизации и диссоциа-
ции и т. д., а данные приводят в волновых числах или в единицах частоты. В силу про-
порциональности друг другу шкал частот, волновых чисел и энергий фотонов подоб-
ная терминология не может привести к недоразумениям, и мы будем ею пользоваться.
Для единицы волновых чисел см-1 было предложено специальное название «кайзер»
(Kayser — по имени известного немецкого спектроскописта, автора многотомного Handbuch
der Spektroskopie) с обозначением К. Мы этим обозначением не будем пользоваться, чтобы
не смешивать его с обозначением К для абсолютной температуры. Для самих волновых чисел
было предложено обозначение а (вместо р), которое мы также не будем применять в этой
книге (см. протоколы объединенной комиссии по спектроскопии, J. Opt. Soc. 43, 410, 1953;
47, 1035, 1957).
Каждому возможному переходу между дискретными уровнями энергии соот-
ветствует определенная спектральная линия, характеризуемая в спектре значением
частоты (или волнового числа) монохроматического излучения (о термине «спек-
тральная линия» см. ниже, с. 31). Частоты спектральных линий на рис. 1.1 обозначены
Как Pj2, 1^13, ^23 и т.д.
Из основного соотношения (1.2) вытекает, что между частотами (и, следо-
вательно, волновыми числами) различных спектральных линий должны иметься
соотношения типа
Vik = Vij+Vjk,	(1.3)
например = ^12+^23, очевидные из диаграммы. Таким образом, могут наблюдаться
переходы с частотами, равными комбинациям — суммам и разностям — частот дру-
гих переходов. В этом состоит содержание комбинационного принципа, установленного
Ритцем в 1908 г. на основе обобщения опытного материала [170], еще до работ Бо-
ра. Комбинационный принцип представляет непосредственное следствие основного
квантового закона (1.2), выражающего, как мы уже подчеркивали, закон сохранения
энергии для микроскопических процессов, связанных с излучением, и являющегося
точным законом. Поэтому и комбинационный принцип является точным принци-
пом; он оправдывается на опыте тем точнее, чем выше точность измерений4).
Комбинационный принцип играет очень важную роль в спектроскопии. Его
соблюдение является критерием правильности схемы уровней, найденной исходя
из опытных значений частот спектральных линий. При интерпретации сложных
спектров отыскивают постоянные разности частот, соответствующие разностям
энергий пар уровней.
При переходах между уровнями г, j и уровнями к, I, т, ..., согласно комбинационному
принципу
Vik - fjk = t'ii - V)i = vm - vjm = ...	(1.4)
например в случае, изображенном на рис. 1.1, мы имеем
^13 ~ ^23 — ^14 ~ ^24 := ^15 — ^25 — ^12,	^13 — ^12 — ^24 ~ ^34 = ^25 ~ ^35 = ^23
и т.д., т.е. каждая разность повторяется по три раза. Зная совокупность частот наблюдаемых
спектральных линий, можно построить соответствующую схему уровней. Практически эта
4) Предел точности, с которой может быть проверен комбинационный принцип, определяется лишь
шириной спектральных линий.
§1.2. Уровни энергии и переходы между ними
19
задача тем сложнее, чем больше число спектральных линий, т. е. чем больше число возможных
переходов. Для очень сложных спектров нужно учитывать возможность случайного повторения
разностей частот (см. [15], § 16).
С помощью комбинационного принципа можно находить для спектральных ли-
ний, частоты которых известны с недостаточной точностью, более точные значения
по частотам двух или нескольких других линий (ср. с. 294).
Основной квантовый закон излучения (1.2) справедлив как в случае дискретных
уровней энергии, так и в случае, когда уровни энергии образуют непрерывную
последовательность (непрерывные уровни энергии). Возможны переходы как между
дискретными уровнями — переходы с дискретных уровней на дискретные, — сово-
купность которых дает дискретный спектр, состоящий из отдельных спектральных
линий, так и между дискретными и непрерывными уровнями, совокупность которых
дает сплошной спектр. Наконец, возможны и переходы между самими непрерывными
уровнями, совокупность которых также дает сплошной спектр.
Рассмотрим в качестве типичного примера общую схему уровней энергии и пе-
реходов между ними в случае атома водорода (рис. 1.2)5). Уровни энергии, начиная
с самого глубокого, образуют дискретную последовательность, соответствующую свя-
занным состояниям электрона и сходящуюся к границе ионизации, соответствующей
отрыву электрона от ядра. Выше границы ионизации получается непрерывная после-
довательность уровней энергии, соответствующая свободным состояниям электрона.
Дискретные уровни энергии атома водорода определяются известной формулой
Бора:
2‘7Г^9716’4 1	1
Еп =-------2-----2=-hcR- (п = 1,2,3,...),	(1.5)
hr nr	п
где п — главное квантовое число, а
2тг2те4	>
R =-----г— = 109 678 см 1	(1.6)
ch5
— постоянная Ридберга (тп — масса электрона6)).
Постоянная hcR, имеющая размерность энергии, равна энергии ионизации
И^ион = -Е] атома водорода
И^ион = hcR= 13,60 эВ,	(1.7)
т. е. R представляет энергию ионизации атома водорода, выраженную в см-1.
В дальнейшем мы будем обычно обозначать постоянные одной и той же буквой,
независимо от того, измеряются ли они в единицах энергии, в единицах частоты
и
или в волновых числах; это возможно в силу пропорциональности шкал Е, и, и -
с
и очень удобно, поскольку часто приходится применять по существу одни и те же
формулы, но выраженные в различных единицах. Поэтому мы будем обозначать
„	2тг2те4 W
через R и называть постоянной Ридберга не только постоянную -----------;— = —,
ch5 he
2тг2те4	W	2тг2те4
но и постоянные -----г— = — и -------х— = W; формула (1.5) при этом запишется
hr	h hr
R
просто в виде Еп = —
пг
5> Без учета тонкой структуры; см. с. 34 и подробнее с. 186.
6) Точнее, приведенная масса электрона и протона; подробнее о постоянной Ридберга см. § 6.2.
20
Глава 1. Основные положения спектроскопии и ее разделы
СМ4
о
-2238
-3047
-438Г
-6855
42786
-27420
409678 43,00
4,5!
-3,40
Эд
О>
-0,28-
-д,38'
-д.54'
эд
10,20
О
13,32
13.22
En~El
СМ4
709678
107740
706632
705292
702824
97492
Рис. 1.2. Уровни энергии атома водорода
82259
Дискретный спектр атома водорода получается при переходах между уровнями
энергии (1.5); для волновых чисел и спектральных линий получается, согласно
условию частот (1.2), общая формула
Еп2 _
he he
R	R	_	/ 1
2	2	I	2
П j	П2	\ nf
(П| < n2).
(1.8)
При переходах между определенным нижним уровнем (nj фиксировано) и по-
следовательными верхними уровнями (п2 меняется от п\ + 1 до оо) получаются
спектральные серии атома водорода (см. рис. 1.2):
Серия
Лаймана
П| = 1
п2 2
Серия
Бальмера
П| = 2
п2 3
Серия
Пашена
ni = 3
П2 4
Серия
Брекета
ni = 4
п2 5
Серия
Пфунда
nj — 5
п2 6
Серия
Хампфри
П\ — 6
П2 7
(1.9)
§ 1.3. Спектры поглощения, испускания и рассеяния
21
Волновое число каждой спектральной линии при этом является разностью двух
R	R	z ч
спектральных термов Т] = и Т2 = представляющих собой, согласно (1.5),
П|	nj
энергии, взятые с обратным знаком и выраженные в см”1.
Наряду с дискретным спектром для атома водорода получается и сплошной
спектр при переходах, показанных на диаграмме жирными линиями, — с дискретных
уровней на непрерывные (и обратно) и с непрерывных уровней на непрерывные.
Переходы последнего типа соответствуют изменению состояния «свободного» электрона,
движущегося в поле ядра с энергией, превышающей потенциальную энергию на бесконеч-
ности; их называют свободно-свободными, в отличие от свободносвязанных переходов
(переходов из свободных состояний в связанные и обратно) и от связанно-связанных пере-
ходов (переходов из связанных состояний в связанные). Следует подчеркнуть, что понятие
«свободного» электрона здесь не означает, что на электроны не действует никакое поле
(т. е. что потенциал, в котором движется электрон, постоянен); это понятие указывает лишь,
что полная энергия электрона больше его потенциальной энергии на бесконечности. Подоб-
ный электрон в поле ядра движется с ускорением, как и связанный электрон, что и делает
возможным переходы с излучением.
Для более сложных атомов, так же как и для атома водорода, характерными
являются дискретные спектры, состоящие из отдельных спектральных линий, —
линейчатые спектры. При этом с увеличением числа электронов в атоме услож-
няется и его спектр, увеличивается число спектральных линий, закономерности
в спектре становятся менее ясно выраженными, интерпретация спектра становится
все труднее. Для простейших молекул характерны дискретные полосатые спектры,
состоящие из более или менее узких полос со сложной линейчатой структурой.
Сложные молекулы дают спектры, состоящие из очень широких сплошных полос,
уже не обладающих линейчатой структурой. Интерпретация молекулярных спектров
представляет более трудную задачу, чем интерпретация атомных спектров.
§ 1.3. Спектры поглощения, испускания и рассеяния
В предыдущем параграфе мы рассматривали переходы между уровнями энергии
независимо от направления этих переходов, которое является весьма существенным.
Переход с некоторого нижнего уровня на какой-либо верхний соответствует увели-
чению энергии атомной системы, т. е. поглощению фотона, переход с некоторого
верхнего уровня на какой-либо нижний соответствует уменьшению ее энергии,
т. е. испусканию фотона. Совокупность переходов (с излучением) с нижних уров-
ней на верхние дает спектр поглощения, с верхних уровней на нижние — спектр
испускания.
В литературе часто пользуются термином «излучение» вместо термина «испускание» и со-
ответственно говорят о спектрах излучения, а не о спектрах испускания. Такая терминология
является неудачной. Слово «излучение» широко применяется в физике для сокращенного
обозначения электромагнитного излучения, т. е. электромагнитных волн (с волновой точки
зрения) или фотонов (с корпускулярной точки зрения); в теории излучения рассматривают
как процессы испускания фотонов, так и процессы их поглощения (а также процессы рас-
сеяния фотонов, см. ниже, с. 25). Именно в этом смысле мы будем говорить в данной книге
об излучении; процесс отдачи атомной системой энергии в виде фотона мы всегда будем
называть испусканием7).
Каждый отдельный переход характеризуется, наряду с частотой перехода и =
-(Ei - Ej) (см. (1.2)), вероятностью перехода — вероятностью поглощения при
Аналогично английским терминам, radiation (излучение) и emission (испускание).
22
Глава 1. Основные положения спектроскопии и ее разделы
переходе с нижнего уровня на верхний и вероятностью испускания при переходе
с верхнего уровня на нижний.
Спектр поглощения или испускания данной атомной системы, наблюдаемый
в определенных условиях, характеризуется заданием как совокупности значений
частот спектральных линий или полос, так и распределения интенсивностей. Интен-
сивности в спектрах зависят от вероятностей отдельных переходов и от числа атомных
систем в различных стационарных состояниях — от заселенностей различных уров-
ней энергии. При этом для спектров поглощения распределение интенсивностей
и соответственно вид спектров зависят от заселенностей нижних уровней (начальных
для процессов поглощения), а для спектров испускания — от заселенностей верхних
уровней (начальных для процессов испускания).
Для атомных систем данного рода, например атомов определенного элемента
или молекул определенного химического состава и строения, спектры, особенно
спектры испускания, могут быть весьма разнообразны, в зависимости от заселенно-
сти уровней.
Самым простым является случай, когда заселен только наиболее глубокий уро-
вень — основной, или нормальный, уровень, соответствующий минимуму энергии
атомной системы, т. е. когда все атомные системы данного рода находятся в устой-
чивом основном, или нормальном, состоянии. Из этого состояния, в котором система
при отсутствии внешних воздействий может находиться неограниченно долго, воз-
можны переходы лишь в состояния с большей энергией, следовательно, возможно
лишь поглощение фотонов, но не их испускание. При воздействии на атомные си-
стемы излучения различной частоты (обычно от источника излучения, обладающего
сплошным спектром испускания) получается спектр поглощения, соответствующий
совокупности переходов с самого глубокого нижнего уровня на различные верхние
уровни; для атома водорода, в частности, получается серия Лаймана в поглощении
(переходы п — 1 —> п = 2, 3, 4, ...; см. (1.9) и рис. 1.2).
В общем случае наряду с основным уровнем заселены и остальные — возбужден-
ные — уровни, соответствующие состояниям системы с энергией, превышающей
минимальную; для перевода системы в подобные состояния из нормального тре-
буется сообщить ей энергию — «возбудить» ее. Атомная система в возбужденном
состоянии обладает избытком энергии по сравнению с нормальным состоянием —
энергией возбуждения, — что делает ее неустойчивой. Она не может находиться
в возбужденном состоянии неограниченно долго, даже при отсутствии внешних воз-
действий, отдает энергию в виде испускаемых фотонов и поэтому обладает конечным
временем жизни. С каждого возбужденного уровня возможно как испускание, так
и поглощение, тем более интенсивные, чем больше заселенность данного уровня.
Чем больше число сильно заселенных возбужденных уровней, тем сложнее и спектры
испускания, и спектры поглощения.
Заселенность уровней и вид спектров зависят прежде всего от того, имеет ли
место термодинамическое равновесие. Если вещество находится в состоянии термо-
динамического равновесия, соответствующего определенной температуре, то засе-
ленность уровней закономерно убывает с увеличением их энергии (согласно закону
Максвелла—Больцмана, см. с. 124), и притом тем быстрее, чем ниже температура.
При достаточно низкой температуре практически заселен только основной уровень
и осуществляется случай, рассмотренный выше, когда возможно поглощение лишь
с основного уровня, а испускание вообще отсутствует. При повышении темпера-
туры, по мере заселения возбужденных уровней, появляется поглощение с этих
уровней, одновременно возникает тепловое, или температурное, испускание, тем
более интенсивное, чем выше температура. Спектр теплового испускания зависит
§ 1.3. Спектры поглощения, испускания и рассеяния
23
прежде всего от температуры, и в случае, если излучение находится в состоянии рав-
новесия с веществом (равновесное, или черное, излучение, когда каждый испущенный
веществом фотон поглощается им же, см. подробнее с. 128), этот спектр вообще
полностью определяется только температурой, не зависит от рода вещества и дается
известной формулой Планка. Если излучение не находится в равновесии с веществом
(нечерное излучение), то спектр теплового испускания, помимо температуры веще-
ства, зависит, в большей или меньшей степени, от рода вещества и его состояния;
температура, однако, остается при этом главным определяющим фактором.
Если вещество не находится в состоянии термодинамического равновесия, то за-
селенности уровней будут зависеть от конкретных условий возбуждения и могут очень
сильно отличаться от заселенностей при термодинамическом равновесии, соответ-
ствующем определенной температуре. В результате изменяются спектры поглощения
и спектры испускания. Действительное испускание при сильном возбуждении вы-
соких уровней может быть весьма интенсивным, даже при низких температурах
(холодное свечение), и во много раз превышать тепловое испускание, а значи-
тельное разнообразие возможных условий возбуждения приводит к исключительно
большому разнообразию спектров испускания, наблюдаемых в различных случаях.
Спектры поглощения обычно изучают при определенной температуре, когда
в исследуемом веществе имеет место термодинамическое равновесие. Спектры ис-
пускания, наоборот, чаще всего изучают в неравновесных условиях, применяя
различные способы возбуждения, оптические и электрические.
Условия возбуждения наиболее просты и определенны при оптическом возбу-
ждении — при возбуждении путем поглощения фотонов. Такое возбуждение можно
производить излучением известного спектрального состава и, в частности, моно-
хроматическим излучением, т. е. сообщая атомным системам вполне определенные
порции энергии hv. Оптическое возбуждение может быть прекращено в заданный
момент времени, что позволяет исследовать нетепловое испускание атомных систем
после прекращения возбуждения — послесвечение, — измерять его длительность
и законы затухания. При этом испускание, обладающее малой длительностью после-
свечения, называют флуоресценцией, а обладающее большой продолжительностью —
фосфоресценцией.
Флуоресценция и фосфоресценция представляют частные случаи фотолюминесценции —
нетеплового испускания при оптическом возбуждении (см. с. 27). Разделение фотолюминес-
ценции на флуоресценцию и фосфоресценцию по длительности послесвечения является лишь
качественным. Послесвечение газов, длящееся обычно доли секунды, и быстро затухающее
послесвечение жидких и твердых тел относят к флуоресценции, медленно затухающее после-
свечение жидких и твердых тел (в том числе кристаллофосфоров) относят к фосфоресценции.
Отметим, что термины «флуоресценция» и особенно «фосфоресценция» иногда применяют
для обозначения нетеплового испускания малой и соответственно большой длительностей
независимо от способа его возбуждения.
Простейшим и очень важным случаем оптического возбуждения является воз-
буждение одного определенного дискретного верхнего уровня энергии Ei атома
газа из основного состояния Е] поглощением фотона hv = Ег — Е\. Возбужденный
атом может отдать свою энергию возбуждения двумя способами: путем испускания
фотона, т. е. при переходе с излучением, и путем потери энергии при столкновении
с другой частицей, т. е. при безызлучательном переходе. Если атом возвращается
в основное состояние, испуская фотон hv той же частоты v, что и поглощенный
фотон, то мы имеем резонансное испускание, а соответствующее излучение назы-
вают резонансным. Явление резонансного испускания было впервые обнаружено
Вудом в 1905 г. [169] в парах натрия (для D-линий) и стало предметом большого
24	Глава 1. Основные положения спектроскопии и ее разделы
числа исследований8*; особенно подробно оно было изучено в парах ртути. Линии,
для которых наблюдается резонансное испускание, называют резонансными.
Рис. 1.3. Резонансные линии:
а — атома натрия; б — атома ртути
Обычно этот термин применя-
ется к одной или нескольким лини-
ям, наиболее интенсивным при резо-
нансном испускании. Подобные ли-
нии соответствуют переходам на ос-
новной уровень с наиболее глубоких
возбужденных уровней. Для атома
Na — это D-линии 5 890 А и 5 896 А
при переходе с первого возбужден-
ного уровня, являющегося двойным
(рис. 1.3, а), для атома Hg — это ли-
ния 2 537 А при переходе с одной
из составляющих первого возбужден-
ного уровня, являющегося тройным
(переходы с остальных составляющих
являются запрещенными), и линия
1 850 А при переходе со второго возбу-
жденного уровня (рис. 1.3, б). На диа-
граммах указаны обозначения уров-
ней; более подробно схемы уровней
атомов Na и Hg рассмотрены ниже
(см. с. 224 и 288).
Когда происходит оптическое возбуждение уровня, с которого возможны пе-
реходы не только обратно на основной уровень, но и на другие (более низкие)
возбужденные уровни, наряду с резонансным наблюдается испускание с частотами,
меньшими частоты резонансной линии. Изучение такого нерезонансного испуска-
ния атомов при их оптическом возбуждении позволяет непосредственно проверять
правильность схем уровней энергии.
Исследования спектров испускания ряда атомов при оптическом возбуждении были
выполнены в 1924-1926 гг. Терениным [194]. На рис. 1.4 приведены схемы уровней изученных
им атомов Т1 и Sb и показаны переходы в поглощении и испускании.
Для испускания, наблюдающегося при оптическом возбуждении атомных си-
стем с основного уровня, характерно то, что частоты линий испускания меньше
или равны частотам линий поглощения. Правило, что при оптическом возбужде-
нии частоты 1/исп испускаемого излучения меньше, чем частоты 1/погл поглощаемого
излучения, или равны им,
^ИСП ^ПОГЛ ? ^ИСП ^ПОГЛ >
было сформулировано Стоксом [158]; испускание, удовлетворяющее условию (1.10),
называют стоксовым, а линии испускания с частотой 1/исп < ^Погл — стоксовыми
линиями. Правило Стокса справедливо лишь для возбуждения с основного уровня.
При возбуждении с более высоких уровней (рис. 1.5) может получаться антистоксово
испускание, для которого частоты испускаемых фотонов больше частот поглощаемых,
^ИСП > Ц1ОГЛ 1 ^ИСП < ^ПОГЛ •	0* 11)
Соответствующие линии называют антистоксовыми.
При рассмотрении оптического возбуждения необходимо учитывать, что излу-
чение может не только поглощаться веществом, но и рассеиваться в нем, меняя
8) Обзор этих исследований до 1933 г. можно найти в монографии Митчелла и Земанского [22].
§ 1.3. Спектры поглощения, испускания и рассеяния
25
Рис. 1.4. Схема оптического возбуждения:
а — для атома таллия; б — для атома сурьмы
свое направление распространения. Различают рассея-
ние, при котором частота излучения не меняется, —
рэлеевское рассеяние в однородной среде, а также рассе-
яние в мутной среде (эффект Тиндаля) — и рассеяние,
при котором частота излучения изменяется, — комби-
национное рассеяние (эффект Рамана). В первом слу-
чае энергия рассеивающих систем остается неизменной,
во втором она меняется.
Рассеяние без изменения частоты является когерент-
ным — фаза рассеянного излучения определяется фазой па-
дающего излучения; рассеяние с изменением частоты являет-
ся некогерентным — фаза рассеянного излучения независима
от фазы падающего излучения.
Нас будет интересовать комбинационное рассеяние.
Для него частоты рассеянного излучения равны i/pacc =
Рис. 1.5. Схема
антистоксова испускания
1/пад Т 1х, гДе г'пад — частота падающего излучения, а и — частоты переходов
для рассеивающей атомной системы. Это соответствует тому, что энергия падающего
фотона /и/Пад уменьшается за счет поглощения энергии Ei - Ek = hv рассеивающей
системой (переход системы с более низкого уровня Ek на более высокий Ei)
или увеличивается за счет отдачи системой такой же энергии (обратный переход
с более высокого уровня Ei на более низкий Ek). В результате получаются фотоны
с энергией hupacc = hi/naA^hu = h(unaa^u). Совокупность линий с частотами ^ПадТ^
при заданной частоте 1/пад образует спектр комбинационного рассеяния; по аналогии
со стоксовым и антистоксовым испусканием мы имеем стоксовы линии с z/pacc =
^пад - у < и антистоксовы линии с ррасс =	+ у > 1/пад. Для атомных систем,
находящихся в основном состоянии, в комбинационном рассеянии получаются
только стоксовы линии, соответствующие различным переходам в рассматриваемой
системе с основного уровня на возбужденные. В дальнейшем, говоря о спектрах
рассеяния, мы обычно будем подразумевать спектры комбинационного рассеяния.
Весьма важную роль при спектроскопических исследованиях играют электри-
ческие способы возбуждения. В качестве источников света широко применяют-
ся различные типы газового разряда, в частности искровой и дуговой разряды.
26
Глава 1. Основные положения спектроскопии и ее разделы
При прохождении электрического тока через газы возбуждение происходит благо-
даря столкновениям между частицами, причем особенно существенным является
возбуждение электронным ударом. Электроны, ускоряясь в электрическом поле,
приобретают кинетическую энергию, которую они затем отдают при столкновени-
ях тяжелым частицам — атомам и молекулам, возбуждая их. Возбуждение может
происходить, когда кинетическая энергия электрона равна или больше энергии
возбуждения ДЕ. Вероятность возбуждения пропорциональна доле столкновений
(из общего числа столкновений
Рис. 1.6. Функция возбуждения
электрона с частицей), при которых происхо-
дит возбуждение. Эта вероятность представля-
ет функцию энергии электрона, как правило,
при увеличении энергии сперва возрастающую,
затем достигающую максимума и потом спада-
ющую (рис. 1.6). Соответствующую функцию
называют функцией возбуждения. Функции воз-
буждения являются важными характеристика-
ми состояний атомов и молекул и в простейших
случаях возбуждения атомов электронным уда-
ром могут быть рассчитаны (см., например, [23,
144, 219]).
В настоящее время метод электронного удара широко применяется для на-
хождения энергий возбуждения уровней атомов и молекул. Определяя на опыте
потенциалы возбуждения V, при которых электрон отдает частицам энергию
*	7
eVi = -mvi — kEi — Ei ~ E\,
2
(112)
находят соответствующие энергии возбуждения Ei~E\. Методом электронного удара
определяют на опыте и потенциалы ионизации атомов и молекул, а также потенциалы
диссоциации молекул, т. е. значения Vi в (1.12), при которых АТ?, = ТУИОН, где ТУИОН —
энергия отрыва электрона (энергия ионизации), или ДЕ, = 1РдИСС, где И^исс —
энергия разрыва молекулы на части (энергия диссоциации).
Исследование возбуждения атомов электронным ударом Франком и Герцем в 1913 г. [177]
явилось непосредственной проверкой существования уровней энергии атомов и наличия
квантовых переходов с излучением между уровнями. В этих классических опытах электроны
с энергией более 4,89 эВ теряли при столкновениях с атомами ртути энергию еК = 4,89 эВ,
возбуждая эти атомы, которые затем испускали линию 2 537 А, соответствующую переходу
с возбужденного уровня обратно на нормальный уровень, т. е. фотоны с энергией
hv = SEi = 4,89 эВ.
Следует подчеркнуть, что в электрических источниках света процессы возбужде-
ния атомов и молекул гораздо сложнее, чем при специально поставленных опытах
по нахождению потенциалов возбуждения методом электронного удара. Наряду с не-
посредственным возбуждением атомов и молекул при столкновениях с электронами
(притом различных скоростей) возбуждение происходит и при столкновениях тяже-
лых частиц друг с другом, и имеют место разнообразные процессы обмена энергией
при столкновениях; к этим вопросам мы еще вернемся в дальнейшем (см. с. 147).
В заключение остановимся на некоторых общих вопросах. Непосредственным
предметом спектроскопии является изучение спектров атомных систем — спектров
испускания, поглощения и рассеяния. Вместе с тем, более глубокая задача спектро-
скопии состоит в определении, на основе изучения спектров, характеристик уровней
энергии (т. е. стационарных состояний) атомных систем и характеристик переходов
с излучением между уровнями энергии.
§ 1.3. Спектры поглощения, испускания и рассеяния
27
В результате решения этой задачи получается исключительно ценная инфор-
мация как о строении микроскопических частиц — атомов и молекул, — так
и об агрегатных состояниях вещества. Как известно, спектроскопия сыграла очень
большую роль в развитии современной атомной физики, свидетельствующую об эф-
фективности ее методов. С другой стороны, спектроскопия, определяя для атомов
и молекул характеристики уровней энергии и оптических переходов между этими
уровнями, представляет теоретическую основу атомного и молекулярного спектраль-
ного анализа.
В настоящее время спектроскопические исследования охватывают весьма боль-
шой круг вопросов, и ряд разделов спектроскопии выделился в самостоятельные
направления. Это, прежде всего, относится к астрофизическим приложениям спек-
троскопии; современная астрофизика чрезвычайно широко пользуется спектроско-
пическими методами исследования, а ее результаты в значительной степени базиру-
ются на теории и систематике спектров. Вопросы спектроскопии астрономических
объектов в настоящей книге не разбираются и будут затрагиваться лишь в отдельных
случаях. В самостоятельную область исследований выделилось учение о люминес-
ценции. Люминесценцию определяют как избыток испускания тел над тепловым
испусканием', в зависимости от способа возбуждения различают фотолюминесценцию
(оптическое возбуждение), электролюминесценцию (возбуждение при прохождении
через вещество электрического тока)9), катодолюминесценцию (возбуждение потоком
электронов) и другие виды люминесценции. Наряду с общими характеристика-
ми спектров люминесценции, являющихся частным случаем спектров испускания,
в учении о люминесценции подробно рассматривается ряд специфических вопросов,
таких, как выход люминесценции, ее тушение, поляризация люминесценции; эти
вопросы представляют значительный интерес и с чисто спектроскопической точки
зрения; однако их подробный разбор выходит за рамки данной книги, и мы будем
их касаться лишь частично. Подробное изложение вопросов люминесценции можно
найти в специальных монографиях [102-104].
Приведенное выше определение люминесценции, данное еще Видеманом [163] в 1888 г.,
не является полным; оно не позволяет отделить люминесценцию от других видов нетеплового
свечения, в частности от свечения Черенкова (свечение вещества под действием электронов,
с
движущихся в среде со скоростью и, превышающей скорость света в данной среде: — < v < с,
п
где п — показатель преломления среды). Одним из важных признаков люминесценции
является, как подчеркивал Вавилов [370], ее конечная длительность (превышающая период
световых колебаний); по этому признаку можно отделить люминесценцию от свечения Черен-
кова, не обладающего конечной длительностью. Однако критерий длительности недостаточен
для полного решения вопроса о различии между фотолюминесценцией и рассеянием [371]. Не-
резонансное рассеяние (частота ипал падающего излучения не совпадает с частотами поглоще-
ния 1/погл рассеивающих систем) практически не обладает конечной длительностью и этим от-
личается от фотолюминесценции, однако при приближении к резонансу (1/пад = 1/погл) обычное
рэлеевское рассеяние непрерывно переходит в обладающее конечной длительностью послесве-
чения резонансное испускание, которое, таким образом, является предельным случаем рэлеев-
ского рассеяния; при этом обычное комбинационное рассеяние непрерывно переходит в также
обладающее конечной длительностью послесвечения нерезонансное испускание (i/Hcn Ф 1/погл,
см. выше, с. 24), которое, таким образом, является предельным случаем комбинационного
рассеяния. Эти предельные случаи рэлеевского и комбинационного рассеяния отличаются
от фотолюминесценции тесной связью процессов поглощения и испускания, которые не от-
делены друг от друга промежуточными процессами преобразования поглощенной энергии.
Для фотолюминесценции же как раз характерно наличие подобных промежуточных процессов.
Под это определение электролюминесценции подходит нетепловое испускание электрических ис-
точников света. Термин «электролюминесценция» в настоящее время применяют и в более узком смысле
для обозначения люминесценции кристаллофосфоров, помещенных в электрические поля [105].
28
Глава 1. Основные положения спектроскопии и ее разделы
Отметим, что наряду с обычной люминесценцией, определяемой как избыток испускания
над тепловым испусканием, возможна отрицательная люминесценция, определяемая, соглас-
но Степанову, как недостаток испускания по отношению к тепловому испусканию [372, 373].
§ 1.4. Деление спектроскопии по свойствам излучения
Изложенные в предыдущих параграфах общие положения справедливы для раз-
ных типов уровней энергии весьма различных атомных систем и для переходов,
для которых частоты излучения могут различаться на много порядков. Исходя
из этих различий, можно разбить спектроскопию на разделы. Подобное деление
можно произвести как в соответствии со свойствами электромагнитного излучения,
отличающимися для различных диапазонов длин волн и частот, так и в соответствии
со свойствами атомных систем, дающих спектры, в зависимости от природы этих
систем и от типов уровней энергии.
В этом параграфе мы рассмотрим деление спектроскопии по свойствам элек-
тромагнитного излучения, а в следующем — по свойствам атомных систем.
Частоты переходов с излучением могут относиться к любому диапазону шкалы
электромагнитных волн, изображенной на рис. 1.7, начиная от диапазона самых
медленных колебаний, соответствующих наиболее длинным радиоволнам, и кончая
диапазоном самых быстрых колебаний, соответствующих наиболее проникающему
гамма-излучению. Различают гамма-спектроскопию, рентгеновскую спектроскопию,
оптическую спектроскопию и радиоспектроскопию. В оптическую спектроскопию
входят ультрафиолетовая спектроскопия, спектроскопия видимого излучения и ин-
фракрасная спектроскопия, а в радиоспектроскопию — микроволновая спектро-
скопия и собственно радиочастотная спектроскопия. На рис. 1.7 показаны соответ-
ствующие диапазоны спектра электромагнитного излучения. Границы диапазонов,
разумеется, являются условными, поскольку свойства излучения постепенно изме-
няются с изменением длины волны, и произвести резкое разграничение различных
областей спектра невозможно.
В верхней части рисунка даны шкалы частот v (в Гц), волновых чисел - (в см ’)
с
с
и длин волн А = - (в см), а в нижней части — шкалы энергий фотонов hi/ (в эВ)
/гг/
и соответствующих температур Т — — (в К). Наряду с единицами, общими
к
для всей шкалы, указаны и единицы, практически применяемые для отдельных
областей спектра, например в случае шкалы длин волн — ангстремы (1А = 10-8 см)
и миллимикроны (1 ммк = 10-7 см).
Шкалы I/, -, hi/ п Т пропорциональны (см. с. 17); особенно существенно, что
увеличению частоты 1/ излучения при квантовом переходе соответствует увеличение
величины энергии hi/ поглощаемого или испускаемого фотона. Величина hi/ очень
мала в области радиочастот, составляя ничтожные доли электрон-вольта, увеличи-
вается в оптической области до нескольких электрон-вольт для видимого и уль-
трафиолетового излучения, достигает десятков тысяч электрон-вольт для жесткого
рентгеновского излучения и становится огромной для гамма-излучения, измеряясь
миллионами электрон-вольт. В то время как в области радиочастот мы имеем дело
с переходами между чрезвычайно близкими уровнями энергии, в области гамма-из-
лучения мы встречаемся, наоборот, с переходами между очень далеко отстоящими
уровнями.
область
инка-излучения
РенпшноОсш
область
Оптическая область
Радиочастотная область
К™*"**"	\ "^Z^		Ультрафиолет^.	X. тобоя область\^	\
Частота KHeu-lmu Ю'гц Ю3гц Ю9гц-1Мгц юЪи Ю9гц Ю9гц Ю"гц	10"гц	юаги юагц Ю*ги Юегц 10*гц Ю,ггц Ю^ец Ю*гц Юаеи Ю9,гц
Волновое число	КГ*с*-'	Ю^м4 Ю'*м-\ Ю'3^’ Ю^сн4 Ю^см'1 !снч Юсы-* Ю‘ог' Ю3см'< Ю'снг1 tfac* Xfor1 e'er* Ю9сег* ti'cer1 Юааг*
Лаона Волны	Hfcti Ю9см Ю3сн-1км Ю*си Ю3сн Ю9си*1м Юм 1сн Ю''см-Ihh Ю‘гсн Ю'гсн Ю^снЧнк КГ’см Ю'9сн Ю'Тсн-1мж ЮЫЛ Ю*ся Ю*см Ю^м
. <,,.. ..	|	.1	, »	.-.„..„Ь..... ।------------1,—.... „-1— -------1-..    4   ..J-.. ., ,.!-----,,i .. , ,1,	4 ...... и Г    Д
Вшктротые	| No | Hg |Н	J АЗ	AL	а	и	Рг	Rb	Т1	W R	о»	V
переходы	Резонансные линии атомЛ				&			!*		
Колебательные	'	‘	' |ttgJ JJtaCL |ман[со|ОН
переходы	частота основных колебаний
Вртцдтелъные	1 переходы	|		23ЙЯ231Э2ИЕ1Е2ЭИШ2		|на |аь//
Тонкая	1н сящш/ро			___sSm		|н	pio [к |иь |Сз Лублетиое растепление		
Сберхтшаюя стрцкттра	D |Н		Rb	
Магнитная	Аорнерпйа чистота для ядерн ногнетона Лорнорйа частота для ноемтона бора ав структура	№twec	{«юге fjXOoc 1Ю0Юас Электрическая	Частота резонанса ори p-iдебет и Л/ юрт*	\ю№б!м \шЮВ!сн фаЯ ВГпзв Ю"зб Ю’зб Ю’зб Ю’зб	Ю'взб Ю*зд Ю'зб Ю3зб Югзб Ю'зб	ив	ЮЛ	Югзб КУл^кзб Ю*зб Ю*зб Ю3збЧМ Ю’зб Темлературо Ю'’ъ Ю'виК Ю'9*К Ю'^Н Ю3*К Ю'гК Ю^	НТК	ЮгЪ Ю3'б ю*ъ Ю5Ъ Ю*'К Ю’ъ Ю*'б Ю9*л Ю**К юу				
Рис. 1.7. Шкала электромагнитных волн
§ 1.4. Деление спектроскопии по свойствам излучения
30
Глава 1. Основные положения спектроскопии и ее разделы
Практически широко применяется шкала длин волн, однако во всех вопро-
сах, связанных с расстояниями между уровнями энергии, основными являются
пропорциональные друг другу шкалы частот, волновых чисел и энергий фотонов.
Часто встречается необходимость перехода от одной шкалы к другой. Для шкал и,
и
-, Е и Т это производится с помощью табл. 1.1. Переход от шкалы длин волн А
с
и 1
к обратной ей шкале волновых чисел - = — легко производится при помощи таблиц
с А
обратных величин. При этом предполагается, что длина волны дана для вакуума.
Однако для оптической области (для А > 2 000 А) обычно приводят длины волн
в воздухе, Авозд, которые несколько отличаются от длин волн в вакууме, Авак. Так как
, Авак
Авозд =---, где пх — показатель преломления воздуха для данной длины волны, то
™А
^вак “ ^возд = <^возд(^А “О-	0*13)
Значения п\ - 1 равны (в единицах 10“4) [123а]
А= 8 000	7 000	6 000	5 000	4 000	3 000	2 000 1	,	к
2,7503	2,7579	2,7697	2,7896	2,8276	2,9156	3,2408 /	U	'
1 1
Для перевода длин волн в воздухе в волновые числа -— = —---------- имеются
'Авак	'Авозд
специальные таблицы [123, 123а].
Рассмотренное деление спектроскопии по диапазонам длин волн и частот излу-
чения определяется различием экспериментальных методов исследования отдельных
областей спектра. Для разных областей спектра применяются разные источники
и приемники излучения и разные способы спектрального разложения излучения,
не являющегося монохроматическим. Для оптической спектроскопии характерно
применение оптических методов, причем спектральное разложение производится
призмами и дифракционными решетками. В радиоспектроскопии применяются ра-
диотехнические методы, причем для микроволновой области используются методы,
разработанные в связи с радиолокацией. Специальные методы применяются в рент-
геновской спектроскопии: для спектрального разложения используется дифракция
рентгеновских лучей кристаллами, а также дифракционные решетки. В гамма-спек-
троскопии применяются специфические методы ядерных исследований.
Следует учитывать, что при изучении спектров испускания непосредственно
исследуется излучение, даваемое источником (например дугой или искрой в случае
спектров испускания в видимой и ультрафиолетовой областях), а в случае спектров
поглощения и рассеяния исследуется излучение, прошедшее через вещество или рас-
сеянное веществом, спектр которого изучается. В оптической и рентгеновской обла-
стях спектра для получения спектров поглощения обычно применяются источники,
обладающие сплошным спектром испускания; спектр поглощения вещества, че-
рез которое прошло излучение, получается на фоне спектра испускания источника
в виде темных линий или полос. В области радиочастот (включая микроволновую
область) для получения спектров поглощения применяют монохроматические ис-
точники излучения (в микроволновой области обычно клистроны) и для получения
спектров поглощения изменяют частоту излучения,0).
10) При применении методов магнитного резонанса и электрического резонанса, при помощи которых
исследуются частоты переходов, зависящие от напряженности поля, можно при неизменной частоте
источника излучения изменять поле, что обычно удобнее.
§ 1.4. Деление спектроскопии по свойствам излучения
31
В табл. 1.2 приведены некоторые данные, характеризующие экспериментальные
методы, применяемые для изучения различных областей спектра. В ней указаны
типы источников и приемников излучения и способы спектрального разложения.
Большое значение имеет разрешающая сила
А v
ДА “ Др
где ДА и Д1/ — соответственно разности длин волн и частот спектральных ли-
ний, которые еще разрешаются. В последнем столбце табл. 1.2 указаны примерные
значения разрешающей силы, достигаемые для исследуемой области наиболее точ-
ными методами. Разрешающая сила спектрального прибора зависит от ширины
спектральной линии, даваемой прибором и соответствующей строго монохрома-
тическому излучению (приборная ширина). Следует подчеркнуть, что сам термин
«спектральная линия» связан с тем, что оптический спектральный прибор дает
изображение в виде линии, входной щели прибора, на которую падает исследуемое
излучение; спектр получается как совокупность таких изображений щели в виде
линий, каждая из которых соответствует монохроматическому излучению. При дис-
кретной совокупности частот излучения отдельные изображения щели образуют
дискретный спектр, при непрерывной совокупности частот излучения эти изобра-
жения сливаются, образуя сплошной спектр.
Таблица 1.2
Экспериментальные методы изучения различных областей спектра
Область спектра		Источники излучения	Способ спектрального разложения	Приемники излучения	Разрешаю- щая сила
название	диапазон длин волн				
Радио- частотная	> 10 см	Излучающие радиоконтуры	Изменение частоты кон- тура	Приемная радиосхема	ю’
Микро- волновая	10 см - 1 мм	Клистроны	Изменение частоты кли- строна	Пьезокварц, болометры	ю6-ю’
Инфра- красная	1 мм - 0,75 мкм	Термо- излучатели	Эшелетты, призмы	Болометры, фотоэлемен- ты, фото- пластинки	1О3-1О5
Видимая	0,75 мкм - 0,40 мкм	Газовый разряд, дуга, искра, лю- 'минесцентные источники	Призмы, дифракцион- ные решетки	Фотопла- стинки, фо- тоэлементы	106
Ультра- фиолетовая	400 ммк - 10 ммк				
Рентге- новская	< 10 ммк	Рентгеновские трубки	Дифракцион- ные решетки, кристаллы	Фотоплас- тинки, фото- элементы, ионизацион- ные камеры	105
Более подробные сведения об экспериментальных методах спектроскопических
исследований для различных областей спектра можно найти в соответствующих
монографиях, обзорах и учебниках [111-119].
32
Глава 1. Основные положения спектроскопии и ее разделы
§ 1.5. Деление спектроскопии по свойствам атомных систем
С точки зрения строения вещества наиболее важно деление спектроскопии
по свойствам атомных систем, дающих спектры, прежде всего, в соответствии с их
природой — составом и строением. Различают ядерную спектроскопию, атомную
спектроскопию, молекулярную спектроскопию и спектроскопию конденсированных
систем.
Ядерная спектроскопия изучает уровни энергии атомных ядер и переходы между
этими уровнями. Наряду с переходами с электромагнитным излучением, дающими
гамма-спектры, возможны переходы, сопровождающиеся корпускулярным альфа-
и бета-излучением, т.е. испусканием альфа-частиц (ядер гелия) и бета-частиц (/Г",
т. е. электронов, и ^+, т. е. позитронов). Обычно в ядерную спектроскопию включают
как гамма-, так и альфа- и бета-спектроскопию. В настоящей книге ядерная
спектроскопия, в том числе и гамма-спектроскопия, не рассматривается1^ как
существенно отличающаяся от остальных разделов спектроскопии своей тесной
связью со специфической областью ядерной физики.
Атомная спектроскопия изучает электронные уровни энергии атомов и перехо-
ды между ними. Именно она сыграла особенно большую роль в развитии учения
о строении вещества. Для атомов были впервые сформулированы Бором его постула-
ты; объяснение спектра атома водорода, имевшее важнейшее значение для развития
всей атомной физики, указало пути объяснения спектров любых атомных систем.
В атомной спектроскопии очень ярко проявляется эффективность общих спектро-
скопических методов при изучении строения вещества.
Молекулярная спектроскопия изучает электронные, колебательные и враща-
тельные уровни молекул и переходы между ними. Так же как и в атомной, в мо-
лекулярной спектроскопии общие спектроскопические методы оказались весьма
эффективными; в настоящее время они являются одними из основных методов
исследования строения молекул. Следует подчеркнуть, что, в связи с большой слож-
ностью и разнообразием молекулярных спектров по сравнению с атомными, в мо-
лекулярной спектроскопии имеется гораздо больше нерешенных принципиальных
проблем, чем в атомной спектроскопии, основные проблемы которой уже решены.
Спектроскопия конденсированных систем — кристаллов, аморфных тел (напри-
мер стекол), жидкостей — изучает уровни энергии этих сложных систем и переходы
между ними. Число нерешенных проблем здесь еще больше, чем в молекулярной
спектроскопии; многие вопросы только начинают разрабатываться. Необходимо
отметить, что спектроскопия конденсированных систем тесно связана с атомной
и особенно с молекулярной спектроскопией, в значительной степени опираясь
на результаты этих разделов спектроскопии.
Данная книга посвящена атомной спектроскопии и молекулярной спектроско-
пии как важнейшим разделам спектроскопии, наиболее разработанным и предста-
вляющим теоретическую основу атомного и молекулярного спектрального анализа.
При изучении атомных систем различного рода мы имеем дело и с различными
типами уровней. Некоторые из типов уровней являются общими для разных атомных
систем, а некоторые — специфичными для атомных систем определенного рода.
Типы уровней отличаются как характером движения в изучаемых системах,
так и порядком величины разностей энергий Д.Е? соседних уровней данного типа,
составляющих от 106 до 10~11 эВ. Это соответствует в шкале частот изменениям
Изложение вопросов ядерной спектроскопии можно найти в монографии Грошева и Шапиро [143]
и в монографии под редакцией Зигбана [143а].
§ 1.5. Деление спектроскопии по свойствам атомных систем
33
частоты от 1О20 - 1021 Гц до 103 — 104 Гц, а в шкале длин волн — изменениям длины
волны от 10“10 до 107 см.
Рассмотрим подробнее различные типы уровней атомов и молекул. Уровни
энергии ядер, связанные с движением нуклонов — протонов и нейтронов —
в ядре и расположенные на расстояниях £±Е порядка сотен тысяч и миллионов эВ,
нас интересовать не будут, как являющиеся предметом изучения ядерной физики
и не имеющие непосредственного отношения к уровням энергии атомов и молекул.
Что касается уровней энергии конденсированных систем, то для последних получа-
ются те же основные типы уровней энергии, что и для атомов и молекул; отличие
состоит лишь в том, что преобладают совокупности непрерывных уровней и только
в предельных случаях получаются резко выраженные дискретные уровни, подобные
характерным дискретным уровням атомов и молекул, тогда как непрерывные уровни
для атомов и простейших молекул получаются лишь при сильных возбуждениях,
приводящих к ионизации и диссоциации.
Для атомов и молекул имеются следующие основные типы уровней и соответ-
ствующих переходов (см. также рис. 1.7).
1.	Уровни энергии, связанные с движением электронов относительно ядер12), —
электронные уровни энергии. Нужно различать уровни электронов внутренних оболо-
чек с энергиями связи от десятков до десятков тысяч эВ, переходы между которыми
дают рентгеновские спектры и изучаются методами рентгеновской спектроскопии,
и уровни внешних электронов в атомах и молекулах с энергиями связи порядка
немногих эВ (что соответствует волновым числам в несколько десятков тысяч см-1).
Переходы между уровнями энергии внешних (валентных) электронов дают опти-
ческие спектры в видимой и в ультрафиолетовой областях, которые и являются
основным источником сведений об этих уровнях.
2.	Колебательные уровни молекул, связанные с колебательными движениями
ядер в молекулах около некоторых равновесных положений с колебаниями мо-
лекул, приближенно являющимися гармоническими. Частоты этих гармонических
колебаний — нормальных колебаний молекул — отвечают энергиям примерно
от 0,025 до 0,5 эВ, т. е. волновым числам от 200 до 4 000 см-1. Соответствующие
переходы между колебательными уровнями молекул непосредственно изучаются ме-
тодами инфракрасной спектроскопии и методами комбинационного рассеяния света;
в последнем случае изменения Af частоты и рассеянного света равны частотам пе-
реходов между колебательными уровнями рассеивающих молекул. Наряду с этими
непосредственными методами колебательные уровни молекул можно определять
путем исследования электронно-колебательных спектров в видимой и в ультрафио-
летовой областях; электронные переходы в молекулах сопровождаются изменениями
колебательной энергии, что и приводит к возникновению электронно-колебательных
спектров.
3.	Вращательные уровни молекул, связанные с вращательным движением молеку-
лы как целого. Приближенно вращение молекулы рассматривают как свободное вра-
щение твердого тела с тремя моментами инерции вокруг трех взаимно перпендику-
лярных осей — сферического волчка (все три момента инерции одинаковы), симме-
тричного волчка (два момента инерции одинаковы, третий отличен от них) или асим-
метричного волчка (все три момента инерции различны). Разности энергий сосед-
них вращательных уровней составляют от сотых долей эВ для самых легких молекул
до стотысячных долей эВ для наиболее тяжелых молекул; им соответствуют волновые
,2^С точки зрения классических представлений связанные с движением электронов по некоторым
орбитам вокруг ядер — с орбитальным движением.
2 Зак 10'
34
Глава 1. Основные положения спектроскопии и ее разделы
числа от 100 до 0,1 см-1. Поэтому вращательные переходы непосредственно изучают-
ся методами инфракрасной спектроскопии (в далекой инфракрасной области спек-
тра) и комбинационного рассеяния света (по малым изменения Ai/ частоты и рассе-
янного молекулами света) и, в особенности, методами радиоспектроскопии (в микро-
волновой области спектра). Вращательные уровни молекул можно также определять
на основе изучения колебательно-вращательных спектров в близкой инфракрасной
области и электронно-колебательных спектров в видимой и ультрафиолетовой обла-
стях. Колебательно-вращательные спектры получаются в результате того, что измене-
ние колебательной энергии сопровождается одновременными изменениями враща-
тельной энергии. Последние происходят и при электронно-колебательных переходах,
что обусловливает вращательную структуру электронно-колебательных спектров.
4.	Близкорасположенные уровни энергии атомов и молекул, связанные с на-
личием у электрона собственного момента (спина), —- уровни тонкой структуры.
Разности энергий этих уровней составляют от стотысячных долей эВ (т. е. десятых
долей см”1) для атома водорода до десятых долей эВ (т. е. тысяч см”1) для самых тя-
желых атомов и для молекул, содержащих такие атомы. Соответствующие переходы
для наиболее легких атомов и молекул можно изучать радиоспектроскопическими
методами (в микроволновой области спектра). В видимой и ультрафиолетовой обла-
стях получается характерная, так называемая мультиплетная структура спектров,
причем для легких атомов наблюдаются совокупности близкорасположенных линий
(мультиплеты), откуда и происходит название «тонкая структура».
5.	Очень тесно расположенные уровни энергии атомов и молекул, связанные
с наличием у атомных ядер собственных моментов (ядерных спинов), — уровни
сверхтонкой структуры. Разности энергий этих уровней, появление которых обусло-
влено взаимодействием магнитных и электрических моментов ядер с электронными
оболочками атомов и молекул, очень малы, составляя от десяти миллионных до сто-
тысячных долей эВ (т. е. от тысячных до десятых долей см”1). Соответствующие пе-
реходы непосредственно изучаются радиоспектроскопическими методами ядерного
резонанса (магнитного и квадрупольного). В видимой и ультрафиолетовой областях
спектра наличие весьма близких уровней приводит к очень малому расщеплению
спектральных линий; отсюда термин «сверхтонкая структура». Расщепление линий,
обусловленное моментами ядер, наблюдается и в микроволновой области спектра
(при изучении вращательных микроволновых спектров поглощения газов и спектров
электронного парамагнитного резонанса).
Необходимо отметить, что поскольку наличие уровней сверхтонкой структуры определя-
ется свойствами ядер, то изучение этих уровней тесно связано с вопросами ядерной физики.
Однако они, в отличие от уровней энергии ядер, обусловленных движением нуклонов (и очень
далеко отстоящих друг от друга, см. выше, с. 33), имеют непосредственное отношение к во-
просам атомной и молекулярной спектроскопии и поэтому будут рассматриваться в книге
наравне с другими типами уровней атомов и молекул.
6.	Уровни энергии, получающиеся при расщеплении уровней энергии свобод-
ных атомов и молекул во внешнем магнитном поле, — уровни магнитной структуры.
Расщепляются как электронные уровни, так и вращательные уровни молекул и уров-
ни сверхтонкой структуры. Величина расщеплений электронных уровней энергии
в сильных полях составляет десятитысячные доли эВ (т. е. несколько см”1), вра-
щательных уровней и уровней сверхтонкой структуры — десятимиллионные до-
ли эВ (т. е. тысячные доли см”1). Непосредственное наблюдение переходов между
соседними уровнями магнитной структуры производится радиоспектроскопичес-
кими методами магнитного резонанса. В видимой и ультрафиолетовой областях
спектра изучается расщепление спектральных линий в магнитном поле — явление
§ 1.6. Краткий исторический обзор
35
(или эффект) Зеемана. Явление Зеемана наблюдается и в микроволновой области
спектра для вращательных линий.
В настоящее время термин «явление Зеемана» обычно применяют и к расщеп-
лению уровней энергии, а не только к расщеплению спектральных линий. В со-
ответствии с этим уровни магнитной структуры называют уровнями зеемановского
расщепления или просто зеемановскими уровнями.
7.	Уровни энергии, получающиеся при расщеплении уровней энергии свобод-
ных атомов и молекул во внешнем электрическом поле, — уровни электрической
структуры. Расщепляются как электронные уровни атомов и молекул, так и вра-
щательные уровни молекул, обладающих дипольным электрическим моментом.
Величина расщепления электронных уровней энергии в сильных полях в десятки
и сотни тысяч В/см достигает десятитысячных и тысячных долей эВ (т. е. от не-
скольких до десятков см”1), величина расщепления вращательных уровней энергии
в применяемых электрических полях порядка тысяч В/см составляет миллионные
доли эВ (т. е. сотые доли см"1). В видимой и в ультрафиолетовой областях спек-
тра наблюдается расщепление спектральных линий атомов в электрическом поле,
соответствующее расщеплению электронных уровней энергии, — явление Штарка.
Так же как и в случае явления Зеемана, термин «явление Штарка» применяют
к расщеплению уровней энергии в электрическом поле, в том числе и под действием
не только внешних, но и внутренних полей, и говорят об уровнях штарковского
расщепления.
Расщепление вращательных уровней дипольных молекул в электрическом поле
может изучаться непосредственно радиоспектроскопическим методом электричес-
кого резонанса. Его можно также определять путем изучения расщепления враща-
тельных линий в микроволновых спектрах поглощения газов.
Мы дали краткую характеристику основных типов уровней энергии атомов и мо-
лекул. Благодаря разнообразию этих типов может получаться весьма сложная струк-
тура уровней, особенно для молекул. При этом не всегда можно разделить различные
типы движения и отнести уровни к определенному типу. Возможны специальные
типы расщепления в результате взаимодействия различных типов движения.
Уровни энергии конкретных атомов и молекул, структура этих уровней и пере-
ходы между ними будут подробно рассмотрены в соответствующих главах, посвящен-
ных атомной спектроскопии (часть II) и молекулярной спектроскопии (часть III).
§ 1.6. Краткий исторический обзор развития
атомной и молекулярной спектроскопии
Развитие спектроскопии можно разделить на два периода: первый, с открытия
Ньютоном разложения белого света в спектр в 1666 г. [1] до введения Бором
в спектроскопию квантовых представлений в 1913 г., и второй, с 1913 г. по настоящее
время. В первый период спектроскопия развивалась прежде всего как эмпирическая
наука, не была вскрыта связь между спектрами и строением частиц вещества —
атомов и молекул; во второй период спектроскопия получила теоретическую базу
в виде квантовой теории и стала могучим средством изучения строения вещества.
Каждый из этих периодов можно разделить на отдельные этапы.
Первый этап развития спектроскопии, начавшийся с открытия Ньютона, про-
должался с 1666 г. до начала XIX века. Ньютон наблюдал сплошной спектр испуска-
ния Солнца и иных источников света; другие ученые, в том числе Ломоносов, вслед
за ним наблюдали также сплошные спектры испускания в видимой области; в самом
конце XVII1 века были открыты сначала инфракрасные, а затем ультрафиолетовые
36
Глава 1. Основные положения спектроскопии и ее разделы
лучи и, таким образом, область спектральных исследований была расширена. Однако
дискретные спектры еще не были известны.
Следующий этап развития спектроскопии характеризуется открытием и изуче-
нием дискретных спектров поглощения и испускания. В 1802 г. Волластон [156]
впервые наблюдал темные линии в солнечном спектре. Однако он рассматривал их
как «границы цветов». Основная заслуга открытия дискретных спектров принадле-
жит Фраунгоферу, который в 1814 г. обнаружил [157] много сотен темных линий
в солнечном спектре — линий поглощения, получивших название фраунгоферовых.
Наиболее интенсивные линии он обозначил латинскими буквами. Данные для этих
линий приведены в табл. 1.3. Длины волн их были измерены уже самим Фраунгофе-
ром, применившим для исследования спектров наряду с призмами дифракционные
решетки Фраунгофер наблюдал темные линии также в спектрах звезд и планет; им
были обнаружены светлые линии — линии испускания — в спектрах пламен и искр.
Фраунгофер, в частности, получил в спектрах пламен (при введении в них крупинок
соли) в желтой части спектра светлую линию натрия, совпадающую с темной лини-
ей D в солнечном спектре. Вслед за Фраунгофером ряд ученых исследовали спектры
испускания и поглощения различных источников света, в особенности пламен. Бы-
ли найдены многочисленные линии испускания и поглощения, и указывалось на их
принадлежность различным веществам.
Таблица 1.3
Наиболее интенсивные фраунгоферовы линии
Обозначе- ние линии	Длина волны, А	Элемент	Обозначе- ние линии	Длина волны, A	Элемент
В	6 869,96	О	F	4 861,33	
С	6 562,82	Н(Яа)	G'	4 340,47	Н(Я7)
D\	5 895,92	Na		Г 4 307,91	Fe
d2	5 889,95	Na	Cr	14 307,74	Ca
е2	5 269,54	Fe	9	4 226,73	Ca
Ь'	5 183,62	Mg	h	4 101,74	Н(Я.)
Ь2	5 172,70	Mg	H	3 968,47	Ca
h	Г 5 167,49	Fe	К	3 933,67	Ca
	<5 167,34	Mg	L	3 820,43	Fe
Началом нового этапа в развитии спектроскопии явилось установление Кирхго-
фом в 1859 г. соотношения между испускательной и поглощательной способностями
тел [159], получившего название закона Кирхгофа. На этой основе Кирхгофом
и Бунзеном был открыт [160] и стал развиваться спектральный анализ, давший
блестящие результаты, особенно в области астрофизики. С помощью спектрального
анализа впервые оказалось возможным определить состав небесных тел. За полве-
ка — с 1859 по 1913 г. — было исследовано очень большое число спектров самых
разнообразных веществ — линейчатых спектров, которые оказались принадлежащи-
ми атомам, и полосатых спектров, которые оказались принадлежащими молекулам.
С помощью спектрального анализа был открыт ряд новых элементов. Были составле-
ны обширные таблицы спектральных линий для большинства элементов; развитие
техники спектроскопии позволило получать весьма точные данные для длин волн
наблюдаемых линий и разрешать очень близкие линии.
Особенно важное значение имело установление закономерностей в расположе-
нии линий в атомных спектрах. В спектрах водорода и щелочных металлов были
открыты спектральные серии. В 1885 г. Бальмер показал [161], что длины волн
§ 1.6. Краткий исторический обзор
37
13 линий спектральной серии водорода, особенно хорошо наблюдавшейся в спек-
трах некоторых звезд, могут быть с очень большой точностью представлены общей
формулой; эта серия впоследствии получила название серии Бальмера.
ап1
Первоначальная формула Бальмера имела вид Л = —-----, где а — постоянная,
п2 - 4
а п = 3,4,5,... для последовательных членов серии; она совпадает с формулой (1.8),
1	4
если в последней положить и — -, R = -,	= 2 и п2 ~ п = 3,4, 5,... .
А	а
Ридбергом [164] были даны формулы для важнейших спектральных серий
щелочных металлов, причем ему удалось представить волновые числа спектральных
линий как разность двух спектральных термов (см. с. 21) вида Т\ — -----------г
(ni4-ai)2
R
иТ2 = --------гт, где Пу и п2 — целые числа, а Я] и а2 — постоянные, различные
(п2 4- а2У
для различных серий (для водорода а1 = а2 = 0),3).
Целый ряд формул для спектральных серий различных элементов был найден
Кайзером, Рунге и Пашеном [165]. Исходя из возможности представления волно-
вых чисел всех линий серий данного элемента в виде разности двух спектральных
термов, Ритц смог в 1908 г. сформулировать комбинационный принцип. Однако
физический смысл этого принципа (как и сущность спектральных термов и фор-
мул для спектральных серий) был выявлен лишь впоследствии Бором на основе
квантовых законов, непосредственным следствием которых он является (см. с. 18).
Параллельно с установлением закономерностей в атомных спектрах шло и уста-
новление закономерностей в молекулярных спектрах. Деландр [162] и другие ис-
следователи нашли формулы, определяющие расположение полос в молекулярных
спектрах и расположение линий, на которые эти полосы распадаются при достаточ-
ной дисперсии.
К концу первого периода развития спектроскопии, когда она уже накопила
огромный эмпирический материал о спектрах, были достигнуты очень большие
успехи в смежных со спектроскопией областях физики.
На основе электромагнитной теории света Максвелла, созданной им
в 1860-1865 гг., было показано, что свет представляет электромагнитное излу-
чение, и были открыты радиоволны, т. е. электромагнитное излучение большой
длины волны. Открытие рентгеновских и гамма-лучей расширило диапазон из-
вестных излучений в сторону малых длин волн. На основе электронной теории,
созданной в конце XIX века, была выяснена сущность дисперсии электромагнитных
волн в веществе и дана теория нормальной и аномальной дисперсии. Исследо-
вания Рождественского по аномальной дисперсии [171] подтвердили эту теорию.
Исходя из представлений электронной теории, Лоренц объяснил открытое в 1896 г.
Зееманом [167] явление расщепления спектральных линий в магнитном поле (в про-
стейшем случае расщепления линии на три составляющих, см. с. 376).
Наряду с волновыми свойствами электромагнитного излучения были открыты
его корпускулярные свойства. В 1900 г. Планк впервые выдвинул гипотезу квантов
излучения, а в 1905 г. Эйнштейн развил ее, введя представление о квантах как
частицах света (фотонах).
Открытие Менделеевым в 1869 г. периодического закона химических элементов
дало мощный толчок исследованиям строения вещества. Конкретно встала проблема
|3) См. подробнее с. 220.
38	Глава 1. Основные положения спектроскопии и ее разделы
строения атома. Изучение открытого в 1896 г. Беккерелем явления радиоактивности
в сочетании с результатами исследований свойств электронов привело Резерфорда
в 1911 г., на основе опытов по рассеянию альфа-частиц атомами, к носящей его имя
модели атома, состоящего из ядра и электронов.
Первый этап развития спектроскопии после 1913 г., уже на основе квантовых
представлений, связан с теорией Бора [175], подготовленной предыдущим развитием
спектроскопии и смежных с нею областей физики. Бор исходил из разработанной
Резерфордом ядерной модели атома и при помощи двух основных квантовых посту-
латов о существовании стационарных состояний и о переходах с излучением между
ними (см. § 1.1), что находилось в противоречии с законами классической меха-
ники и классической электродинамики, смог объяснить сущность закономерностей
в атомных спектрах и комбинационный принцип.
Для простейшего случая атома водорода как системы, состоящей из ядра (про-
тона) и электрона, Бор определил возможные значения энергии стационарных
состояний и получил общую формулу (1.8) для спектральных серий атома водорода.
При этом Бору пришлось ввести дополнительный постулат — правило кванто-
вания для круговых орбит, — состоящее в том, что при движении по круговой
h
орбите момент количества движения электрона равен Мр — п— (п — 1, 2, 3, ...),
2тг
т. е. является целым кратным постоянной Планка h, деленной на 2тг.
Правило квантования являлось искусственным условием, налагаемым на дви-
жение электрона в атоме, рассматривавшееся Бором согласно законам классической
механики. Правда, к правилам квантования можно было прийти из рассмотрения
соответствия между классической и квантовой теориями для больших значений
квантовых чисел п (на основе принципа соответствия), но главное противоречие
теории Бора с классической электродинамикой этим не устранялось: электрон,
движущийся внутри атома по законам классической механики с ускорением, дол-
жен был бы непрерывно излучать энергию, и частота соответствующего излучения
должна была бы равняться частоте обращения электрона по орбите вокруг ядра.
Поэтому теория Бора, хотя и представляла крупнейший шаг вперед в развитии
теории атома и явилась началом нового периода развития спектроскопии, не была
последовательной и давала лишь модель, хотя весьма наглядную, но заведомо огра-
ниченную и имеющую принципиальные недостатки|4). При применении наглядных
представлений Бора о движении электронов в атомах и молекулах по определенным
орбитам (что мы будем делать при изложении некоторых вопросов) следует иметь
в виду ограниченность и недостаточность этих представлений.
Все сказанное относится к связанной с правилами квантования конкретной
форме теории Бора, но не затрагивает справедливости двух основных постулатов,
в настоящее время полностью обоснованных как экспериментально, так и теорети-
чески (см. § 1.1).
Теория Бора сразу добилась крупных успехов в интерпретации накопленного
спектроскопией опытного материала и в раскрытии физического смысла сериальных
формул. Наряду с объяснением комбинационного принципа и спектральных серий
атома водорода Бор показал, что открытые Пикерингом [168] и Фаулером [173]
,4) Теорию Бора нельзя рассматривать как приближенно верную теорию, каковой является классическая
механика по отношению к механике теории относительности (классическая механика приближенно
справедлива при скоростях движения v, малых по сравнению со скоростью света с, т. е. при v/c < 1).
Классическая механика и классическая электродинамика к движению внутри микроскопических систем,
какими являются и атомы, неприменимы принципиально. Эти системы должны рассматриваться согласно
квантовой механике и квантовой электродинамике.
§ 1.6. Краткий исторический обзор
39
спектральные серии типа (1.8), но с полуцелыми квантовыми числами, которые
приписывались атому водорода, принадлежат ионизованному атому гелия (см. с. 169).
На основе теории Бора получили естественное объяснение установленные Моз-
ли в 1913-1914 гг. [176] закономерности в дискретных рентгеновских спектрах,
обусловленных переходами между уровнями энергии, соответствующими внутрен-
ним электронным оболочкам атомов.
Вслед за спектром водорода Зоммерфельдом [10, 178], Рождественским [184]
и другими были объяснены спектры атомов щелочных металлов и более сложных
атомов. Эти исследования привели к разработке в 1922-1925 гг. Ланде [17], Гун-
дом [12], Расселом [192] и другими систематики сложных спектров и завершились
открытием в 1925 г. спина электрона Уленбеком и Гаудсмитом [190].
Систематика атомных спектров развивалась в тесной связи с объяснением за-
кономерностей периодической системы элементов Менделеева, которое было дано
Бором на основе его теории атома [185]; эти закономерности оказались обусловлен-
ными заполнением электронных оболочек атома определенным числом электро-
нов. Число электронов в заполненных оболочках было окончательно установлено
на основе принципа Паули, сформулированного в 1925 г. [191].
Наряду с разработкой систематики и интерпретацией атомных спектров бы-
ли объяснены, исходя из теории Бора, и основные закономерности простейших
молекулярных спектров, в первую очередь спектров двухатомных молекул (Швар-
цшильд [180], Кратцер [188] и другие).
Одновременно с крупными успехами теории Бора выявились и ее слабости. Ряд
более тонких особенностей спектров не мог быть ею объяснен, многие формулы
теории оказались лишь приближенными, интенсивности в спектрах получались
лишь на основе принципа соответствия. Новый этап развития спектроскопии связан
с созданием в 1924-1926 гг. квантовой механики.
Являясь последовательной микроскопической теорией атомов и молекул, кван-
товая механика дает в принципе объяснение всех основных закономерностей атом-
ной и молекулярной спектроскопии. Простейшие системы, как атом водорода
и атом гелия, молекула водорода и ее ион, удалось полностью рассчитать квантово-
механически, для более сложных систем были разработаны приближенные методы
расчета. Однако главное значение квантовой механики как теоретической основы
спектроскопии состоит в том, что она приводит к правильной физической картине
и позволяет дать полную характеристику квантовых состояний атомов и молекул.
Важное значение для спектроскопии имеют результаты, к которым приводит и кван-
товая электродинамика, разработанная вслед за квантовой механикой. Она объясняет
законы излучения атомных систем и вместе с тем позволяет рассчитать такие весьма
тонкие эффекты, обнаруженные спектроскопическими методами за последние годы,
как сдвиг уровней (см. § 6.6) и аномалия магнитного момента электрона (см. § 14.7).
Развитие спектроскопии с 1926 г. характеризуется все возрастающим объемом
исследований. Значительно расширились экспериментальные возможности спек-
троскопии. Для молекулярной спектроскопии большое значение имело открытие
в 1928 г. одновременно и независимо Раманом в Индии и Мандельштамом и Ланд-
сбергом в СССР явления комбинационного рассеяния света [195, 196].
Весьма плодотворными оказались радиоспектроскопические методы исследо-
вания — разработанный Раби и его сотрудниками метод магнитного резонанса
в молекулярных пучках, метод микроволнового поглощения, методы магнитного
резонанса в твердых и жидких телах, основанные на открытом Завойским в 1944 г.
явлении парамагнитного резонанса, и другие. Особенно важное значение имеют
радиоспектроскопические методы для изучения уровней сверхтонкой структуры.
40	Глава 1. Основные положения спектроскопии и ее разделы
Значительно развилась техника спектроскопических исследований и в оптической
области спектра.
Дать даже самый краткий обзор многочисленных спектроскопических работ,
выполненных с 1926 г., не представляется возможным. Результаты некоторых наи-
более важных из них излагаются в соответствующих главах книги; там же даются
краткие сведения исторического характера.
ГЛАВА 2
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УРОВНЕЙ ЭНЕРГИИ
§2.1.	Невырожденные и вырожденные уровни энергии
В этой главе мы разберем общие характеристики уровней энергии и соответ-
ствующих им стационарных состояний атомных систем. Полная характеристика ста-
ционарных состояний дается квантовой механикой, и мы будем опираться в данной
и в дальнейших главах на основные ее положения и результаты. Сами квантовоме-
ханические методы, изложение которых можно найти в соответствующих учебниках
и монографиях, мы не будем рассматривать.
Элементарное изложение квантовой механики содержится в книге Шпольского «Атомная
физика» [129]. Можно рекомендовать книгу Шиффа по квантовой механике [132] и учебник
Компанейца по теоретической физике [125], в котором дано сжатое изложение квантовой ме-
ханики. На подготовленного читателя рассчитаны курсы квантовой механики Блохинцева [130]
и Ландау и Лифшица [131]. Подробные решения многих конкретных квантовомеханических
задач можно найти в монографиях Зоммерфельда [136] и Бете и Солпитера [134].
Понятие уровня энергии связано с постоянством энергии рассматриваемой
атомной системы в стационарных состояниях, и поэтому важнейшей характеристи-
кой уровня энергии является значение энергии.
Заданному значению энергии может соответствовать одно, вполне опреде-
ленное стационарное состояние или ряд (два и более) стационарных состояний,
отличающихся друг от друга какими-либо свойствами. Согласно общепринятой
терминологии, если имеется одно стационарное состояние с заданным значением
энергии, то уровень энергии называют невырожденным, если же имеется ряд таких
состояний, которым соответствует одно значение энергии, то уровень энергии на-
зывают вырожденным и говорят, что эти состояния вырождены. Число различных
независимых состояний атомной системы с одним и тем же значением энергии Ei
называют степенью, или кратностью, вырождения. Степень вырождения равна еди-
нице для невырожденных и больше единицы для вырожденных уровней.
Примером системы с невырожденными уровнями энергии является система
с одной степенью свободы, совершающая гармонические колебания около поло-
жения равновесия, — линейный гармоничс осциллятор. Таким осциллятором
можно приближенно считать двухатомную молекулу, в которой ядра колеблются друг
относительно друга по оси молекулы вокруг некоторого равновесного положения.
Согласно квантовой механике, для линейного гармонического осциллятора получа-
ются равноотстоящие невырожденные уровни энергии. Каждому значению энергии
осциллятора — энергии колебаний — соответствует одно, вполне определенное его
состояние (см. с. 575).
Примером системы с вырожденными уровнями энергии является электрон,
движущийся под действием электрических сил при отсутствии магнитных взаимо-
действий, например электрон в атоме водорода и в ионе молекулы водорода
42
Глава 2. Основные характеристики уровней энергии
или электрон в электрическом поле ионов кристаллической решеткиВ силу
наличия у электрона спина (собственного момента) уровни энергии электрона ока-
зываются дважды (двукратно) вырожденными.
Наглядно это объясняется тем, что спин электрона может ориентироваться,
при наличии некоторого выделенного направления, двумя способами — вдоль этого
направления (параллельно) и противоположно (антипараллельно) ему* 2). В электри-
ческом поле энергия электрона не будет зависеть от ориентации спина, и данному
значению энергии соответствуют два состояния, отличающиеся ориентацией спина.
В спектроскопии это двукратное вырождение играет очень важную роль. Именно
с ним связан тот факт, что для заполнения электронных оболочек атомов и молекул
всегда требуется четное число электронов (см. ниже, с. 203 и 792).
Важное отличие вырожденных уровней от невырожденных состоит в том, что
при наличии дополнительных взаимодействий первые могут расщепляться: значения
энергии для первоначально вырожденных состояний оказываются уже различными,
и вырождение исчезает, или, как говорят, происходит снятие вырождения.
Например, в только что рассмотренном случае электрона, движущегося под дей-
ствием электрических сил, двукратное вырождение снимается при приложении
внешнего магнитного поля3). Направление магнитного поля представляет выделен-
ное направление, вдоль которого ориентируется спин электрона, и энергия электрона
будет уже зависеть от того, ориентирован ли спин параллельно или антипараллельно
полю, поскольку магнитное поле действует на собственный момент электрона. Та-
ким образом, состояниям с параллельной и с антипараллельной ориентацией спина
будут соответствовать уже различные уровни энергии.
Степень вырождения является весьма существенной характеристикой уровней
энергии. В частности, при тепловом равновесии, согласно законам статистической
физики, заселенности уровней пропорциональны степени вырождения. Степень
вырождения поэтому называют статистическим весом (или просто весом) уровня.
Эту величину принято обозначать буквой д.
При квантовомеханической характеристике атомной системы при помощи волновой
функции («пси-функции»), зависящей от координат, степень вырождения определяется чи-
слом д независимых функций, соответствующих данному значению энергии Ек и являющихся
решениями волнового уравнения
Нгр = Егр,	(2.1)
где Н — оператор энергии, а Е — возможные значения энергии (собственные значения опе-
ратора энергии). Уровень энергии невырожден, если при Е = Ек уравнение (2.1) имеет одно
решение гр = грк (д = 1), и ^-кратно вырожден, если при Е = Ек уравнение (2.1) имеет
д независимых решений гркь грк2у ..., гркд (д 2). Отметим, что в последнем случае в выборе
независимых решений имеется известный произвол: значению энергии Ек соответствуют
не только д состояний, описываемых функциями грка (а — 1,2,3,...,^), но и любые
состояния, представляющие наложение (суперпозицию) этих состояний и описываемые
функциями, являющимися линейными комбинациями функции грка. Поэтому вместо д
Если пренебречь в первом случае магнитными взаимодействиями магнитного момента электрона
с орбитальным движением, а во втором — магнитными взаимодействиями электронов между собой.
2) Возможность двух ориентаций определяется квантованием проекции собственного момента элек-
трона, см. с. 48.
Мы пока считаем, что уровни энергии электрона вырождены только двукратно. Первоначальная
степень вырождения может быть и более высокой, поскольку к вырождению, обусловленному спином
электрона, может добавляться и вырождение, обусловленное другими причинами. Многочисленные
примеры этого будут рассмотрены ниже.
§ 2.2. Значения физических величин в стационарных состояниях
43
независимых функций ipka можно выбрать д других независимых функций
9
=	(£= 1, 2, 3,	5),	(2.2)
а=1
где Сра — постоянные коэффициенты 4\
Вырождение уровней энергии связано, как правило, со свойствами симме-
трии соответствующей атомной системы; снятие вырождения связано с изменением
ее симметрии; важный вопрос о свойствах симметрии будет рассмотрен позже
(см. гл. 3).
§ 2.2.	Значения физических величин в стационарных состояниях
Все физические величины, соответствующие состоянию атомной системы
с определенной энергией, т. е. стационарному состоянию, можно разделить, со-
гласно квантовой механике, на два рода. Одни из них могут иметь определенные
значения в этом состоянии, другие иметь их не могут. Для последних можно опре-
делить лишь вероятность различных значений в рассматриваемом состоянии, и они
нас сейчас интересовать не будут. Для величин, имеющих определенные значения
в стационарном состоянии, задание этих значений дает важную характеристику
соответствующего уровня энергии. Для свободной системы (например для атома
или молекулы в достаточно разреженном газе) наряду с энергией определенные
значения имеет величина момента количества движения. Однако в отличие от клас-
сической механики, согласно которой можно одновременно задать все три проекции
момента количества движения на три взаимно перпендикулярные оси, согласно
квантовой механике, любые две проекции момента количества движения не могут
одновременно иметь определенных значений. Однако и не требуется знать значения
всех трех проекций. Для полной характеристики состояния атомной системы, со-
гласно квантовой механике, достаточно знать значения лишь всех тех независимых
друг от друга величин, которые одновременно могут иметь определенные значения.
Число подобных величин равно числу степеней свободы системы. Таким образом,
полная характеристика системы с г степенями свободы дается заданием значений г
физических величин, обладающих тем свойством, что они могут одновременно
иметь определенные значения; при рассмотрении стационарных состояний одной
из этих величин является энергия системы5).
Одновременно могут иметь определенные значения те физические величины, операторы
которых А, В, С,... коммутируют друг с другом, см., например, [129], т. 2, и [130]. Для таких
величин можно найти общие волновые функции ip, являющиеся собственными функциями
одновременно всех коммутирующих операторов:
Aip = aip, Bip — bipу C ip = cip, ... .	(2.3)
Здесь а, Ь, с — собственные значения операторов А, В, С, ..., т. е. возможные значения
физических величин, которым соответствуют эти операторы.
Для свободной системы коммутируют между собой оператор энергии Н, оператор
--------------------------------2
квадрата момента количества движения Мр и оператор любой проекции момента количества
4) Обычно подчиняемые условию, чтобы функции ipka были ортогональны друг другу и нормированы,
как и исходные функции ipkp, см., например, [130].
Сформулированное свойство системы с г степенями свободы является общим, и можно было бы
выбрать такую совокупность величин, в которую не входила бы энергия; тогда энергия не имела бы
определенного значения, и состояние было бы нестационарным, т. е. менялось со временем.
44
Глава 2. Основные характеристики уровней энергии
движения, например проекции по оси z\ мы имеем, согласно (2.3),
= Ж =	Mpzi/> =	(2.4)
где Е, Мрь Mpz — возможные значения энергии, момента количества движения6) и его
проекции на ось z. Волновые функции ip характеризуют состояния свободной системы
с определенными значениями трех рассматриваемых физических величин.
Рассмотрим пример атома водорода. Движение электрона относительно ядра
(«орбитальное движение») определяется тремя независимыми координатами, и ему
соответствуют три степени свободы. Для характеристики состояния свободного атома
водорода, без учета спина электрона, необходимо задать значения трех независимых
величин7). Такими величинами являются энергия атома Е, его момент количества
движения м(орб)
относительно ядра (орбитальный момент) и одна из проекций
этого момента, за которую обычно принимается проекция Afj>op6^ по оси z.
Учет спина электрона означает введение четвертой степени свободы; соответ-
ствующей четвертой величиной, имеющей определенные значения наряду с Е, Мр°р^
и Мр°рб\ является проекция ЛГрСПИН> собственного момента количества движения
электрона (спинового момента) на ось z6 7 8) 9. Заданием значений четырех величин Е,
Мр , MpZ и Мр полностью характеризуются состояния атома водорода \
Другой пример, являющийся тривиальным, представляют системы с одной сте-
пенью свободы, к числу которых относится, в частности, линейный гармонический
осциллятор. В этом случае состояние полностью характеризуется заданием значения
одной физической величины, а именно энергии.
Возможные значения величин, характеризующих стационарное состояние, на-
ходятся путем решения квантовомеханической задачи для рассматриваемой системы.
Для энергии возможные значения оказываются дискретными — энергия квантует-
ся, если движение в системе является финитным (конечным), т. е. с классической
точки зрения происходит в ограниченном пространстве, как, например, связанное
движение электрона в атоме водорода; они оказываются непрерывными — энер-
гия не квантуется, если движение в системе является инфинитным (бесконечным),
т. е. с классической точки зрения происходит в неограниченном пространстве, как,
например, движение электрона в случае ионизованного атома водорода, когда элек-
трон может уходить на бесконечность (см. с. 19). Моменты количества движения
и их проекции (имеющие определенное значение) всегда квантуются — их возмож-
ные значения оказываются всегда дискретными (подробнее см. § 2.3). Существенно,
что квантование всех величин, могущих иметь определенные и притом дискретные
6) Являющегося вектором, квадрат которого может иметь определенные значения.
7) Если не рассматривать движения центра тяжести. Это движение, которому соответствует еще
три степени свободы, отделяется (в квантовой механике так же, как и в классической) и нас сейчас
не интересует.
8) Это справедливо, если пренебрегать магнитным взаимодействием спина с движением электрона
вокруг ядра — орбитальным движением, которому соответствует орбитальный магнитный момент,
-- 1Т	В,(СПИН)
см. с. 55. Что касается значения Мр самого спинового момента количества движения, то оно вполне
определенное и для всех состояний одинаковое (см. с. 48).
9) Если учитывать собственный момент только электрона и не принимать во внимание собственного
момента (спина) ядра (для обычного, легкого водорода спина протона), которому соответствует пятая
степень свободы.
§ 2.3. Квантование моментов количества движения и их проекций
45
значения, получается при решении квантовомеханической задачи автоматически,
без введения дополнительных условий10).
В результате квантования возможные значения ряда физических величин
для конкретных атомных систем выражаются через квантовые числа — целые
или полуцелые, образующие конечную или бесконечную последовательность. Ха-
рактеристика уровней энергии при помощи квантовых чисел — одна из основ
систематики спектров атомов и молекул. Например, для атома водорода важней-
шей характеристикой его уровней энергии является главное квантовое число п,
определяющее по формуле (1.5) возможные дискретные значения энергии; каждая
линия в спектре характеризуется заданием квантовых чисел п\ и П2 комбинирующих
уровней (см. (1.8) и рис. 1.2).
§ 2.3.	Квантование моментов количества движения
и их проекций
Исключительно большую роль в спектроскопии играет квантование моментов
количества движения и их проекций.
Для свободной системы квантуется квадрат М2р вектора момента количества
движения Мр. Он принимает вполне определенные дискретные значения согласно
закону квантования, к которому приводит квантовая механика:
М2 = h2J(J + 1),	(2.5)
где h — — — постоянная Планка, деленная на 2тг ’°, a J — квантовое число,
2тг
возможные значения которого равны последовательным целым и полуцелым числам:
1	3	5
J = 0,	1,	2, -, ... .	(2.6)
2	2	2	у 7
Для конкретных атомных систем значения J являются либо целыми, либо
полуцелыми в зависимости от числа частиц в системе и их свойств.
Момент количества движения мы для краткости будем часто называть механи-
ческим моментом^. Подобная терминология особенно удобна в связи с тем, что
наряду с моментами количества движения приходится рассматривать магнитные
моменты (см. § 2.5).
Формула (2.5) определяет величину квадрата вектора механического момента;
следовательно, абсолютная величина этого вектора равна
|Мр| =	= hy/j(J+\),	(2.7)
что при больших значениях J, значительно превосходящих единицу, дает
\Mp\^hJ (J>1).	(2.8) * В
10) В противоположность теории Бора, в которой правила квантования вводятся в качестве дополни-
тельных условий, см. с. 38.
В настоящее время часто (особенно в книгах по квантовой механике, см., например, [130] и [131])
обозначают через h и называют постоянной Планка величину, обозначенную в (2.5) через h (h пере-
черкнутое), и энергию фотона записывают в виде hw, где ш — круговая частота колебаний (о; = 2тп/).
В спектроскопии, однако, принято энергию фотона писать в виде hv, где v — обычная частота колебаний,
т. е. величина, обратная периоду колебаний Т, и мы сохраняем обозначение h и название «постоянная
Планка» для постоянной, входящей в основной закон (1.2) (h = 6,625- 10~27эрг-с). В наших обозначениях
h
энергия фотона hv = — • znv — hw.
2тг
12) Его называют также моментом импульса или угловым моментом.
46
Глава 2. Основные характеристики уровней энергии
В дальнейшем мы будем широко пользоваться представлением о векторах
момента количества движения как векторах величины hJ. Длина такого вектора Мр
пропорциональна значению соответствующего квантового числа.
Одновременно с величиной механического момента квантуется его проек-
ция Mpz по выбранному направлению, которое мы примем за ось z и будем
называть выделенным направлением.
Для свободной системы это направление является произвольным. Оно может быть
и выделенным физически, например в случае однородного магнитного или электрического
поля, однако при этом квантование величины самого механического момента не будет
нарушаться только в случае исчезающе слабого поля.
Закон квантования проекции механического момента имеет вид
Mpz = hmj,	(2.9)
где mj i магнитное квантовое число'3\ принимающее, при заданном J, 2J + 1
значений, от J до - J, отличающихся друг от друга на единицу,
mj = J, J - 1, ..., — J + 1, — J.
(2.Ю)
В зависимости от того, является ли J целым или полуцелым, mj будет целым
или полуцелым, а число 2J+1 возможных значений mj при заданном значении J бу-
дет нечетным или четным. Например, при J = 3 величина mj принимает 7 значений:
mj = 3, 2, 1, 0, -1, -2, -3,апри J = 5Д — 6 значений: mj = 5/2, 3Л, ’Л, -3Л, ~5/2-
Механические моменты и их проекции очень удобно измерять, в соответствии
h
с формулами (2.5) и (2.9), в единицах h = —. Вектор механического момента мы
2тг
будем обозначать при измерении в этих естественных единицах той же буквой, что
и квантовое число, в данном случае как J, а проекцию этого вектора — той же
буквой с индексом z, в данном случае как Jz Тогда (2.5) и (2.9) запишутся в виде
о	/	1	3	\
J2 = J(J+1) ( J = 0,	1, -,... ]	(2.11)
И
Jz—mj (mj = J, J - 1, ..., -J).	(2.12)
Абсолютная величина механического момента, согласно (2.7), равна
|J|= //(J+1),	(2.13)
что при больших J дает
\J\nJ (J»l).	(2.14)
Образно говоря, вектор J длиной J ориентируется относительно выделенного
направления 2J + 1 способами, давая проекции от J до -J, отличающиеся друг
от друга на единицу (рис. 2.1). При этом максимальное возможное значение проекции
равно J, т. е. длине вектора, в то время как, согласно точной квантовомеханической
формуле (2.14), максимальное возможное значение J проекции меньше величи-
ны д/7(7 + 1) и совпадает с ней лишь при J —> оо. Однако при решении многих
задач можно пользоваться наглядными представлениями и рассматривать векторы 13
13) Название «магнитное» связано с ролью этого квантового числа при квантовании энергии систем,
находящихся во внешнем магнитном поле.
§ 2.3. Квантование моментов количества движения и их проекций
47
длиной J, заменяя J2 на J(J + 1) лишь
в конечных формулах; результат при этом
получается правильный.
Возможность лишь вполне определен-
ных ориентаций механических моментов —
пространственное квантование — являет-
ся одним из отличий квантовой механики
от классической, играющим важную роль
в спектроскопии. Весьма существенно, что
для свободной системы, в силу произволь-
ности выбора выделенного направления,
энергия не должна зависеть от значения
проекции механического момента, и поэто-
му для уровня энергии с заданным зна-
чением J всегда имеет место вырождение
кратностью 2J 4-1. Иначе говоря, статисти-
ческий вес уровня с заданным значением J
равен
PJ-2J+1.	(2.15)
Следует отметить, что от величины ме-
ханического момента, определяемой значе-
нием квантового числа J, энергия, вообще
• /=0	ф/=7
Рис. 2.1. Проекция момента количества
движения
говоря, зависит.
Исключением являются уровни энергии атома водорода: в формулу (1.5) не вхо-
дят квантовые числа, определяющие значения механических моментов. Для орбитально-
го момента 2ИрОрб) это связано с кулоновским характером поля, а для полного момен-
та Мр = л4ор6) + М рпин) это имеет место лишь приближенно, если пренебречь магнитными
взаимодействиями. При учете магнитного взаимодействия орбитального и спинового момен-
тов друг с другом (см. §6.5) получается поправка к формуле (1.5), зависящая от значения
полного механического момента атома.
В основных формулах (2.11) и (2.12) содержатся правила квантования любых
типов моментов количества движения как отдельных элементарных частиц, так
и состоящих из них систем. При изучении состояний атомных систем нам будут
встречаться следующие основные типы моментов количества движения.
1.	Момент количества движения AfpOp6^ = hl электрона в атоме относительно
ядра — орбитальный механический момент электрона.
2.	Собственный момент количества движения МрПИН^ = hs электрона — спи-
новый механический момент электрона.
3.	Собственный момент количества движения МрЯд) = hJ ядра — спиновый
механический момент ядра.
4.	Вращательный момент количества движения ЛГрВраш^ = hR молекулы —
вращательный механический момент молекулы.
В табл. 2.1 приведена сводка формул для квантования механических моментов.
Важно подчеркнуть, что общая квантовомеханическая теория моментов ко-
личества движения приводит к любым целым и полуцелым значениям квантового
числа J и что для конкретных типов моментов оказываются возможными не все
значения этого числа. Для моментов, связанных, согласно наглядным представле-
ниям, с вращательным движением частиц по некоторым траекториям (орбитальный
48
Глава 2. Основные характеристики уровней энергии
Таблица 2.1
Квантование механических моментов и их проекций
Тип момента	Квадрат механического момента		Проекция механического момента		
	закон квантования	значения квантовых чисел	закон квантования	значения квантовых чисел	число значений
Момент произвольной системы Мр =hJ	J2 = J(J + 1)	J=0, 1/2, 1,3/2, 2,...	Jz ~ "Hlj	mj = J,J-1,...,-J	2J+ 1
Орбитальный момент электрона М рорб) = hl	Г = 1(1 + I)	/ = 0,1,2,...	lz =mi	=0,/- 1,...,-/	21-4-1
Спиновый момент электрона л4спин' = hs	s2 = s(s + 1)	s = ’/2	sz =ms	ms = ’/2, - ’/2	2
Спиновый момент ядра МрЛ) = hl	I2 = f(f + 1)	О	Jn" II II II II	Iz = ТП!	c- ~  0^ II II II II hshs	1 2 3 4
					
Вращательный момент молекулы 2И*в₽аш)=ЙЯ	R2 = R(R + 1)	Я = 0,1,2,...	Rz = mR	mR = R,R- 1,..Я	2Я+ 1
момент электрона Z, вращательный момент молекулы R), возможны лишь целые
значения соответствующих квантовых чисел. Азимутальное (или орбитальное) кван-
товое число I и вращательное квантовое число R принимают последовательные целые
значения, начиная от нуля.
Для собственных (внутренних) моментов частиц — спиновых моментов, свя-
занных с наглядной точки зрения с вращением самой частицы вокруг своей оси, —
возможны как целые, так и полуцелые значения соответствующих квантовых чи-
сел. При этом каждая элементарная частица характеризуется вполне определенным
значением, целым или полуцелым, квантового числа, определяющим величину соб-
ственного механического момента. Спиновое квантовое число для электрона (спин
электрона) s — ’Ди является, таким образом, полуцелым.
Отметим, что величина механического момента электрона равна y/s(s + 1) = ^Д. Ко-
гда говорят об электроне как имеющем спин ’Д, то подразумевают значение квантового
числа s = 'Д.
Определенным значением ядерного спинового квантового числа I (спина ядра),
целым или полуцелым, характеризуется и ядро14).
Квантование проекций и число их возможных значений определяется общи-
ми правилами. В частности, для электрона спиновое магнитное квантовое число
(часто называемое просто спиновым квантовым числом) принимает два значения,
,4> Речь идет о ядре, находящемся во вполне определенном состоянии, обычно невозбужденном.
Разным состояниям данною ядра могут соответствовать разные значения спина, однако всегда целые
или всегда полуцелые. Подробнее о спине ядра см. гл. 16.
§ 2.3. Квантование моментов количества движения и их проекций 49
равные по абсолютной величине, но противоположные по знаку и соответствую-
щие параллельной (ms — У2) и антипараллельной (ms — — '/2) ориентациям спина
(ср. выше, с. 42).
Квантовомеханический вывод законов квантования механических моментов и их проек-
ций сводится к нахождению собственных значений операторов квадрата механического мо-
мента и проекции этого момента. Согласно (2.4), мы имеем, полагая Мр = h2^2 и Mpz — hJz,
уравнения
J гр = a2гр, Jггр = Ьгр	(2.16)
2 Мр ъ Mpz
для нахождения собственных значении а = —5- и Ъ = —г— операторов J и Jz.
h	п
Применяя перестановочные соотношения для операторов J и Jx, Jy, Jz (операторы
проекций механического момента Jx, Jy, Jz не коммутируют друг с другом, но коммутируют
с оператором J ), можно определить а2 и Ъ (см., например, [131]); их значения получаются
равными а2 — J(J -Ь 1), где J = 0, ’/?, 1, 3А, •••? и b = rrtj, где mj = J, J — 1, ..., —J,
т. е. получаются основные формулы (2.11) и (2.12), в которых для квантовых чисел оказываются
возможными как целые, так и полуцелые значения.
В данном выводе не используется конкретный вид функции гр. Если операторы J
и Л, Jy, Jz непосредственно выразить через угловые координаты, характеризующие вра-
щение, и потребовать, чтобы волновые функции являлись однозначными функциями этих
координат, то при решении уравнений (2.16) получаются целочисленные значения квантовых
чисел J и mj. Это имеет место для орбитального движения электрона и для вращательного
движения молекулы; для характеристики движения в первом случае можно ввести углы в и tp
в сферической системе координат, во втором — эйлеровы углы у?, 0, гр. Для спиновых
моментов количества движения такие координаты ввести нельзя; приходится вводить особые
спиновые координаты, и квантовые числа не являются обязательно целыми. В соответствии
с общими формулами (2.11) и (2.12) квантования механических моментов квантовые числа
могут быть как целыми, так и полуцелыми. В последнем случае условия однозначности
волновых функций не выполняются; эти функции являются двузначными.
Легко вывести закон квантования проекции механического момента и одновременно
показать, что полуцелым квантовым числам соответствуют двузначные волновые функции.
Для этого достаточно решить второе уравнение (2.16). Оператор проекции механического
момента по оси z (оператор бесконечно малого поворота вокруг оси г), как известно, имеет вид
-	h ® д \ h д	z
Mpz — hJz — lx —	у —— J — — ——,	(2.17)
г \ ду дх/ г др
где — угловая координата, характеризующая поворот вокруг оси z. Мы получаем уравнение
Xv(v’) = T^-V’(v’) = Щф)-	(2.18)
Его решением является функция гр(<р) = гр$егЬ<р (где гр$ не зависит от <р), из условия од-
нозначности которой, гр(<р -Ь 2тг) = гр(<р), следует, что е?&^+27Г) = e^e2vtb _ егЬутак как
е2п6 = cos2?rb4- г sin 2тгЬ = 1. Отсюда Ь — т, где т — любое целое число, положительное
или отрицательное. Мы получаем закон квантования (2.12) с целыми значениями магнитного
квантового числа т = mj. Из целочисленности т следует и целочисленность J.
Полуцелые квантовые числа можно получить, если допустить, что функция гр(<р) дву-
значна, гр(<р + 2тг) = -гр(1р), гр(<р + 4тг) = гр(<р). При этом е27Гг6 = cos2tt6 4- isin2Tr& = -1,
b - т, где т — любое полуцелое число, положительное или отрицательное. Полуцелым
значениям т соответствуют и полуцелые значения J. Окончательно мы имеем
JzV(<p) = тф(<р),	(2.19)
где
= V’oe™*’	(2.20)
с целым т при однозначной функции и с полуцелым т при двузначной функции V’(V’)-
50
Глава 2. Основные характеристики уровней энергии
§ 2.4. Сложение моментов количества движения
Лишь в самых простейших случаях для характеристики состояния атомной си-
стемы достаточно задать значение одного момента количества движения. Обычно
можно характеризовать систему заданием значений ряда механических моментов от-
дельных частей системы, складывающихся в полный механический момент системы
в целом. Поэтому важное значение имеет закон сложения моментов количества дви-
жения. Квантовая механика приводит к очень простому и общему закону сложения
моментов.
Он состоит в следующем. Если две части системы характеризуются механиче-
скими моментами J\ и J2, значения квадратов которых определяются квантовыми
числами J] и J2, то значение квадрата J2 полного механического момента системы J
определяется квантовым числом J, последовательные значения которого отличаются
друг от друга на единицу и меняются от суммы J] 4- J2 до разности | J\ — «/21•
5/2 3/2
Таким образом, если
= + 1)
= J2V2 +1),
где J\ и J2 заданы, то
J2 = (J,+J2)2 = J(J + 1),
где
J — J\ 4“ J21 J2 ~ К «• ♦ ? |Т| — «^21 -
При Jx J2 это дает 2 J2 4- 1 значений
(2.21)
(2.22)
(2.23)
(2.24)
от Ji 4- Ji до Ji - J2,
а при J\ J2 дает 2J} 4- 1 значений
ОТ J\ J2 — J2 J\ до J2 — J\-
Рис. 2.2. Сложение моментов
количества движения: а — 2 4-2;
б - 2 4- 3/ъ в - 2 4- 1; г - 2 4- !/2
Квантовый закон сложения моментов имеет
весьма наглядный смысл. Складывая векторы дли-
ной J\ и J2, мы получаем, если они направлены
в одну сторону, их сумму — вектор ДЛИНОЙ J\ +J2,
если они направлены в разные стороны, их раз-
ность — вектор длиной |J] - J2|i если же они
составляют некоторый угол, — то вектор промежу-
точной длины. Для нескольких конкретных случа-
ев это показано на рис. 2.2. Отличие от обычного
закона векторного сложения моментов количества
движения, справедливого в классической механике, заключается в том, что значе-
ния полного момента квантуются и отличаются друг от друга на единицу. Моменты,
образно говоря, при векторном сложении могут составлять друг с другом не любые,
а лишь вполне определенные углы. Существенно, что моменты могут быть как парал-
лельными, так и антипараллельными. Если величина одного из слагаемых моментов,
скажем J2, равна !/2 (рис. 2.2, г), то J = J\ 4- ’/2, J\ - !/2, и получаются только две
взаимные ориентации моментов J \ и J2 — параллельная и антипараллельная. Если
слагаемые моменты имеют одинаковую величину (рис. 2.2, а), то минимальное значе-
ние J равно нулю, т. е. при антипараллельной ориентации моментов они в сумме дают
§ 2.4. Сложение моментов количества движения
51
момент, равный нулю. В частном случае Jx = J2— i/2> имеющем место при сложении
спиновых моментов двух электронов, J — 1, 0, т. е. при параллельной ориентации
получается момент, равный единице, а при антипараллельной — равный нулю.
Изменение длины полного вектора от суммы до разности получается, разумеется, лишь
когда длины векторов считаются равными (или пропорциональными) квантовым числам.
Согласно точным формулам (2.21), (2.22), (2.23), эти длины соответственно равны
а/ЛСЛ +1), аЛШ + 0 , a/j(J + 1),
и при J = J\ ± J2 J2)
+ 0 ± VJ2^2 + 9 * \/(Л ± J2)(J1 ± Л + 1) = 0.	(2.25)
Только когда J], J2 и J много больше единицы (см. (2.14)), соотношение (2.25) переходит
в равенство. Лишь в случае J\ — J2, J — J\ — J2 = 0 при любой величине J\ имеет место
равенство
/ЦЙО - аЛШ+0 = V(J1 - Л)(Л - Л + 1) = о. (2.26)
Из формулы (2.24) сразу видно, что если складываются два момента, характе-
ризующиеся оба целыми или оба полуцелыми квантовыми числами J\ и J2, то полу-
чается момент, для которого квантовое число J целое. Если J\ целое, a J2 полуцелое
или наоборот, то получается момент, для которого квантовое число J полуцелое.
Если производится сложение более чем двух моментов, что может быть лег-
ко выполнено многократным применением формул (2.21)-(2.24), то при четном
числе моментов с полуцелыми квантовыми числами получается полный момент
с целыми J, а при нечетном числе таких моментов — полный момент с полуцелы-
ми J. В частности, при сложении спиновых моментов двух или четырех электронов
(вообще — четного числа электронов) полный момент получается целым, при сло-
жении спиновых моментов трех или пяти электронов (вообще — нечетного числа
электронов) полный момент получается полуцелым.
Важное значение имеет вопрос о числе независимых состояний, соответству-
ющих исходным значениям J\ и Ji и получающимся значениям J. Заданному
значению J\ момента Jx соответствует 2JX 4-1 состояний, отличающихся значениями
mJ{ =т\ = J\, Ji-1, . •., -«71	(2.27)
проекции JXz этого момента. Аналогично, заданному значению J2 момента J2
соответствует 2J2 4- 1 состояний, отличающихся значениями
mj2 = rri2 = J2, «72-1, •. •, -J2	(2.28)
проекции J2z.
Общее число различных состояний, соответствующих различным парам значе-
ний mb т2, будет равно
(2Ji + 1)(2J2+1).	(2.29)
Значению J полного момента J = J \ + J2 будет соответствовать 2J 4- 1 состо-
яний, отличающихся значениями
=	m =	J-C ...,	-J	(2.30)
проекции Jz. Согласно формуле (2.24), получаем
при	J — J\	4- «72	2(J| 4- «72) 4-1	состояний,
при	J — Jx	4- J2 —	1	2(Jj 4-«72 - 1) 4-1	состояний,	(2 31)
при	J — |J| - J2|	2|J| - J2| 4-	1	состояний.
52
Глава 2. Основные характеристики уровней энергии
Полное число состояний системы, т. е. сумма чисел (2.31), равно (2/j4-l)(2/24-l),
что совпадает с (2.29), и, таким образом, не меняется при переходе от системы,
состоящей из двух независимых частей, характеризуемых заданными квантовыми
числами J\ и /2, к единой системе, характеризуемой квантовым числом /, меняю-
щимся от J| -h /2 ДО |<Л ~ ^21-
Величины 2J| -h 1 и 2/2 4- 1 определяют степени вырождения уровней энер-
гии Eji и Ej2 частей системы. При образовании полной системы, если не учитывать
взаимодействия ее частей, она будет обладать энергией
Я = 2^,4-^,	(2.32)
не зависящей от квантового числа /, и степень вырождения будет равна, со-
гласно (2.29), (2Jj 4- 1)(2<72 4- 0- Если учитывать взаимодействие частей системы,
то каждому значению J будет соответствовать своя энергия Ej, т. е. уровень энер-
гии (2.32) расщепится на 2J2 4-1 (при J\ /2) или на 2J\ 4-1 (при /|	/2) отдельных
уровней. Степени вырождения этих уровней будут определяться числами (2.31).
Например, при J\ = 2iaJ2 = 3/г мы имеем (2-24-1)( 3/2*24-1) = 5-4 = 20 состояний.
Полный момент характеризуется значениями J = 1/2, 5/г, 3/г, (см. рис. 2.2,0,
которым соответствует 2/4-1 = 8, 6, 4, 2 состояний, т. е. тоже 20 состояний.
В силу взаимодействия 20-кратно вырожденный уровень расщепится на 4 уровня
с кратностями вырождения от 8 до 2.
Следует иметь в виду, что характеристика отдельных частей системы при помощи
квантовых чисел является точной только при исчезающе малом взаимодействии этих частей.
Однако при слабом взаимодействии подобная характеристика будет иметь место с хорошей
степенью приближения; при этом объединение двух частей в единую систему является
реальным, а не носит чисто формальный характер, только при наличии взаимодействия
между ними, и именно подобный случай представляет физический интерес. При сильном
взаимодействии характеристика отдельных частей системы при помощи квантовых чисел уже
теряет смысл, но даже и в этом случае рассмотрение системы как образованной из двух частей,
характеризуемых определенными квантовыми числами, может применяться для определения
свойств полной системы, подсчета числа возможных уровней и их степеней вырождения.
С точки зрения квантовомеханического описания частей системы и системы в целом
квантовому закону сложения моментов соответствует переход от исходных волновых функций
к их линейным комбинациям, относящимся к тому же значению проекции Jz — Jiz 4- J2z
полного момента J = J\ 4-/2-
Невзаимодействующие части системы характеризуются волновыми функциями
(т\ — J\y / -I, . , -/1) и (т2 = J2, J2 — 1, - , -/?), являющимися собственными
функциями операторов Jiz и J2z,
— ТП\1рJ2tn2 ~ Hl21pj2m2.	(2.33)
Можно составить (2/ 4- 1)(2/2 4- 1) функций
J\m\;J2m2',	V,J2m2 ’	(2'54)
каждая из которых соответствует тому, что части системы находятся в определенных состоя-
ниях с квантовыми числами /ь ттц и /2, т2. Функция (2.34) является собственной функцией
оператора / = J\z 4- Аг, относящейся к собственному значению
т = т\ 4- т2.	(2.35)
Действительно, с учетом (2.33) мы имеем
Jz^Pj\m\;J2m2 — (/lz 4" Jiz')	= 'Ф Хг'Ф 4"	/2г^2т2 ~
(2.36)
= (mi 4-m2)V’j1m1V,J2Tn2 = (mi 4-m2)V’j17n1;j2m2-
Таким образом, в состоянии (2.34) проекция полного момента равна mi + m2. Переходу
к состояниям полной системы с квантовыми числами /, т соответствует образование
§ 2.4. Сложение моментов количества движения
53
линейных комбинаций функций (2.34), относящихся к тому же значению тп\ 4- т2 проекции
полного момента
'Фзт ~	2 ^Tnim2 V’Jimi ^2^2	(2.37)
mj .m2
(ГП]+702=ТП)
с вполне определенными, отличными от нуля лишь при тщ +т2 — т коэффициентами С^™т2,
которые могут быть найдены методами теории групп (см. с. 81).
Полное число функции (2.37) равно (2Jj + 1)(2J2 + !)•
При наличии взаимодействия частей системы энергия будет зависеть от квантового
числа J; функции при этом будут правильными функциями нулевого приближения.
Рассмотрение значений т], m2 и m проекций моментов позволяет получить
набор возможных значений квантового числа J при заданных значениях квантовых
чисел J| и Ji по методу сложения проекций, не применяя описанный в начале
параграфа наглядный метод векторного сложения. Первый из них является менее
наглядным и более громоздким, чем второй, однако он оказывается примени-
мым для определения возможных значений J, когда последний метод непригоден
(в случае, когда необходимо учитывать принцип Паули, см. с. 255).
По методу сложения проекций находятся, согласно формуле т = т\ 4- m2, воз-
можные значения т проекции Jz полного момента. Комбинируя всевозможными
способами значения 7П| и т2, мы получаем набор (2Jj 4- 1)(2^2 4- 1) значений т,
приведенный в табл. 2.2. Для определенности положено J| > J2. Из таблицы видно,
что получается набор значений т от J| 4- Ji до -(Ji 4- J2Y затем набор значений т
от J] 4- J2- 1 до -(</] 4- Л “О и т. д., до набора значений т от Jx -J2 до - J2)- Эти
наборы мы сокращенно обозначим как J\ 4- «/2, («7) 4- J2 ~ 1), • • •, («7) - Они со-
ответствуют значениям полного механического момента, даваемым формулой (2.24).
В таблице эти наборы отделены жирными линиями.
Сложение проекций двух моментов количества движения
Таблица 2.2
т\	J\	Jl -1		- Jl 4- 2J2	-Jl 4- 2J2 - 1		-Jl 4- 1	-Jl
h	J\ + J2	J\ 4- J2 - 1		-Jl 4- 3J2	-J] 4- 3J2 - 1		—J 1 4* J2 4* 1	-Jl 4- J2
j2-\	J\ + Ji - 1	J\ 4- J2 - 2		—J\ 4- 3J2 — 1	-Jl 4- 3J2 - 2		-Jl 4- J2	- Jl 4- J2 - 1
								
-h +1	J\ - J2 4- 1	Jl-J2		—J| 4- J2 4- 1	-Jl 4- J2		- Jl - J2 4- 2	- Jl - J2 4- 1
-J2	Jl-J2	- J2 - I		“Jl 4- J2	- Jl 4- J2 - 1		- Jl - J2 4- 1	-Jl - J2
Набор	(Jl - J2)				(Jl - J2 4- 1)		(Jl + J2 -1)	(Jl + J2)
Для частного случая сложения двух моментов, характеризуемых квантовыми
числами J| = 3 и J2 = 2, мы получаем табл. 2.3. Применяя введенные обозначения,
результат сложения моментов можно записать в виде
(3) х (2) = (5,4, 3,2,1).	(2.38)
Знак умножения здесь указывает на сочетание наборов (3) и (2).
Отметим, что каждому значению т в табл. 2.2 и 2.3 соответствует определенная волновая
функция (2.34). Волновые функции (2.37) являются линейными комбинациями функций
вида (2.34), соответствующих заданному значению т. Сразу видно, что максимальному
значению m — J{y-J2 соответствует одна волновая функция, значению т = Jj 4- Л - 1 — две
волновые функции и т.д. Наибольшее число волновых функций, равное 2J2 4- 1, получается
54
Глава 2. Основные характеристики уровней энергии
Таблица 2.3
Сложение проекций моментов количества движения
при Jj = 3 и J2 = 2
т2	3	2	1	0	-1	-2	-3
2	5	4	3	2	1	0	-1
1	4	3	2	1	0	-1	—2
0	3	2	1	0	-1	— 2	-3
-1	2	1	0	-1	-2	-3	-4
-2	1	0	-1	—2	-3	—4	-5
Набор		(О		(2)	(3)	(4)	(5)
при |m| < J\ - J2J в случае J\ = 3, J2 = 2 (табл. 2.3) оно равно 5 для значений |m| < 1,
т. е. для т — 1, 0, —1.
§ 2.5. Магнитные моменты и их связь с механическими моментами
Уровни энергии и соответствующие им состояния атомной системы характери-
зуются наряду со значениями механических моментов значениями магнитных мо-
ментов. Между магнитными и механическими моментами имеется непосредственная
связь. С определенным механическим моментом связан и определенный магнитный.
Магнитные моменты и их проекции квантуются, причем квантование определяется
квантованием соответствующих механических моментов и их проекций.
Значения магнитных моментов и их проекций определяются теми же кванто-
выми числами, что и значения механических моментов и их проекций; квантовое
число, определяющее квантование проекций как механического, так и магнитного
момента даже получило название магнитного квантового числа (см. с. 46).
Однако при заданном механическом моменте величина магнитного момента
для различных систем и для различных состояний рассматриваемой системы, во-
обще говоря, различна. Поэтому важнейшей характеристикой магнитного момента
является отношение его величины к величине соответствующего механического
момента, так называемое магнетомеханаческое {гиромагнитное) отношение.
Обозначим отношение магнитного момента р к механическому Мр через 7.
В этом отношении находятся величины моментов и величины их проекций
М Мг
7 = — =-------
^р Mpz
а отношение квадратов моментов будет равно
2 _
7 му
В векторном виде мы имеем
ц = уМр,
откуда следуют (2.39) и (2.40)15).
|5) Необходимо иметь в виду, что направление полного магнитного момента [Л системы может и не со-
впадать с направлением ее полного механического момента J (см. с.61). В этом случае в формуле (2.41)
нужно заменить д на его составляющую вдоль направления вектора Мр.
(2.39),
(2.40)
(2-41)
§ 2.5. Магнитные моменты и их связь с механическими моментами
55
В соответствии с (2.5) и (2.9) сразу получается закон квантования квадрата
магнитного момента
/	1	3	\
= 72^ = y2h2J(J +1) (у = 0, -, 1, -, .. J	(2.42)
и закон квантования проекции магнитного момента
fiz — 'yMpz = yhmj (mj — J, J - 1, ..., -J).	(2.43)
Согласно наглядным представлениям, магнитный момент, так же как и механичес-
кий, может ориентироваться 2J 4- 1 способом.
Если механический момент выражать в единицах h согласно формуле Мр — hJ
(см. с. 46), то (2.41)-(2.43) примут вид:
p = yhJ, /я2 = ^2h2 J2 = y2h2 J(J -hl), [iz = yhJz = yhmj. (2.44)
Входящий в эти выражения множитель yh имеет размерность магнитного
момента (эрг/Гс), и его величина определяет порядок величины магнитного момента
и его проекции, поскольку J и Jz имеют величину порядка единицы.
Для электронных магнитных моментов, с одной стороны, и для ядерных
и вращательных магнитных моментов, с другой стороны, yh имеет различный
порядок величины.
Для орбитального момента Мр*?® — hl электрона
ш	е
7' ~ М<орб> ~	(2'45)
где те — масса электрона16), и величина
eh eh
Мб =	-------------- (2.46)
2тес 4тгтес
представляет естественную единицу измерения электронных магнитных моментов,
называемую магнетоном Бора. Значение магнетона Бора равно, согласно наиболее
точным данным,
дБ = (0,92731 ± 0,00002) • 1 (Г20 эрг/Гс.	(2.47)
Согласно (2.44) и (2.46), орбитальный магнитный момент
Mz =	= -Мб^.	(2.48)
Знак минус связан с тем, что заряд электрона отрицателен (он равен — е, где е —
абсолютная величина элементарного заряда); магнетомеханическое отношение от-
рицательно и направление магнитного момента /// противоположно направлению
механического момента I.
Отношение (2.45) получается элементарно из наглядных представлений о движении
электрона в атоме по круговой орбите (рис. 2.3).
При движении электрона со скоростью v по круговой орбите радиусом а его момент
количества движения равен Мр = amev. С другой стороны, магнитный момент равен
произведению тока г, создаваемого движением электрона, на площадь орбиты S — 7га2;
если магнитный момент, как обычно, выражен в электромагнитных единицах, а ток —
16) Значение (2.45) относится к орбитальному движению электрона относительно ядра бесконечной
массы, ср. с. 167.
56
Глава 2. Основные характеристики уровней энергии
Отсюда
Рис. 2.3. Движение
электрона
по круговой орбите
согласно наглядным
представлениям
в электростатических, то /// — -iS. Ток г равен произведению заряда
электрона -е
v
времени, ----,
2тга
с
на число оборотов электрона по орбите в единицу
следовательно,
1 ev	2 eva
Hi = -- -—tv а = - —
c 2iva	2c
(2-49)
Pi = ~^—amev =
2mec	2mec
что и дает отношение (2.45).
Квантовая механика приводит к той же самой величине этого
отношения. Мы имеем соотношение
— е V^opG> eh
-ZVfp — ~~ I —
2тес	2тес
между операторами магнитного и механического моментов и аналогичное соотношение между
операторами их проекций
(2.50)
(2-51)
= -^-Tz = -р£.
2тес г 2тес
(2-52)
Учитывая законы квантования орбитального механического момента (табл. 2.1, с. 48),
мы, согласно (2.51) и (2.52), сразу находим и законы квантования орбитального магнитного
момента
= рШ +
И
/W =	= -рьГПгф.
(2.53)
Для спинового момента электрона МрПИН^ = hs отношение
us	е	,
7s - ----- =--------= 27z,	(2.54)
М^спин)	mec
т. е. вдвое больше, чем для орбитального момента, и соответственно спиновый
магнитный момент равен
ей
Мз = Ъ^з =--------s = -2дбз.	(2.55)
тес
Отметим, что проекция спинового магнитного момента равна (см. табл. 2.1)
HSz =	= -2ньт8 = Ч=2дб • ~	(2.56)
и что с наглядной точки зрения электрон обладает магнитным мс :ито?л, равным
по абсолютной величине одному магнетону Бора.
Различие в два раза значений ys и 7/, впервые установленное опытным путем,7\ обо-
сновывается релятивистской квантовой механикой. Из основного ее уравнения — уравнения
Дирака — автоматически вытекает наличие у электрона спина как релятивистского эффекта,
и для отношения 7s спинового магнитного момента к спиновому механическому моменту
получается значение (2.54), ровно вдвое большее, чем для отношения 7z соответствующих
орбитальных моментов. При учете взаимодействия электрона с электромагнитным полем,
17) В частности, вытекающее из опыта Эйнштейна и де Гааза, в котором одновременно измерялись
изменения магнитного и механического моментов намагниченного стержня при его перемагничивании.
§2.6. Прецессия и взаимодействие магнитных моментов	57
7^
согласно квантовой электродинамике, получается отклонение отношения —, от значения 2
7/
примерно на 0,1 % — аномалия магнитного момента электрона (|/xS2| # /1Б), что подтверждается
весьма точными радиоспектроскопическими измерениями (см. с. 448).
Мы рассмотрели случаи чисто орбитального и чисто спинового моментов элек-
трона. В общем случае, когда полный механический момент системы получается
в результате сложения механических моментов отдельных ее частей, складываются
и соответствующие им магнитные моменты. При этом отношение 7 для результи-
рующих моментов, магнитного и механического, может иметь различные значения
в зависимости от значений 7 для складываемых моментов и в зависимости от то-
го, как происходит сложение. При сложении электронных моментов, орбитальных
и спиновых, что имеет место в атомах и молекулах, получаются магнитные моменты,
е
для которых 7S будет порядка ---, а величина самих моментов и их проекций —
тес
порядка магнетона Бора р^- Количественно вопрос о величине результирующих
электронных магнитных моментов будет рассмотрен в § 14.3.
Значения 7 и р для ядерных и вращательных моментов гораздо меньше, чем
для электронных моментов. Правильный порядок величин 7 и р в этих случаях полу-
чается, если в формулах (2.45) и (2.46) заменить массу электрона те массой ядра, что
понятно физически, так как вместо движения электронов идет речь о гораздо более
медленном движении ядер. В качестве единицы измерения ядерных и вращательных
моментов вводят, по аналогии с магнетоном Бора (2.46), ядерный магнетон^
eh eh
Р'яц ~ 7яд^ — ~	— “j )
2трс 4ятрс
в выражение которого вместо массы электрона те входит масса протона тр
/ е \	тр
(7яД = ----1. Величина ядерного магнетона в — « 1836,5 раза меньше маг-
\ 2трс/	те
нетона Бора и, согласно наиболее точным данным, равна
/хяд = (0,505038 ± 0,000018) • 10~23 эрг/Гс.	(2.58)
Обычный порядок магнитных моментов ядер — от десятых долей до нескольких
ядерных магнетонов (подробнее см. гл. 16).
Можно было бы ожидать, что для спинового момента протона, по аналогии
рр	€
с (2.54), 7Р = —---г = ---- = 27яд и что соответственно протон (обладающий,
М^прот)	™рс
как и электрон, спином 1/2, s = ms — ± */2) имеет магнитный момент, равный
одному ядерному магнетону (рр = 2/хяд/, \ppz\ — /хяд, ср. (2.55) и (2.56)). Однако
действительная величина магнитного момента протона примерно в 2,8 раза больше
(см. (16.37)).
Обычный порядок вращательных магнитных моментов — сотые и десятые доли
ядерного магнетона (о вращательных магнитных моментах см. § 19.8).
§ 2.6. Прецессия и взаимодействие магнитных моментов
Весьма плодотворными при рассмотрении вопроса о действии магнитного поля
на атомные системы, обладающие магнитным моментом, и вопроса о магнит-
ных взаимодействиях внутри атомных систем являются наглядные представления
о прецессии магнитных моментов вокруг направления магнитного поля.
|8) Иногда говорят об электронном магнетоне Бора (2.46) и о ядерном магнетоне Бора (2.57).
58
Глава 2. Основные характеристики уровней энергии
Рис. 2.4. Прецессия
магнитного момента
в однородном
магнитном поле
С классической точки зрения магнитный момент в од-
нородном магнитном поле прецессирует вокруг направления
поля — равномерно вращается, сохраняя постоянным угол на-
клона 'О по отношению к направлению поля (рис. 2.4). Угловая
скорость щ подобного движения по классической теории равна
произведению напряженности магнитного поля на магнетоме-
ханическое отношение
ш = ——Н = -уН.	(2.59)
ЛГр
При положительном 7 угловая скорость прецессии напра-
влена противоположно магнитному полю, при отрицательном 7
(в частности, для электрона, см. (2.45) и (2.54)) — вдоль этого
поля.
Магнетомеханическое отношение 7 как определяющее
угловую скорость вращения магнитного момента вокруг на-
правления магнитного поля называют также гиромагнитным
отношением,9).
Формула (2.59) может быть выведена следующим образом [264]. Согласно закону изме-
нения момента количества движения,
dMv
= MF,	2.60
at
где MF — момент силы. Для свободной системы MF = 0 и момент количества движения
постоянен — имеет место закон сохранения
^=0.
dt
Сохраняется и соответствующий ему магнитный момент р.
Мр = const,
(2.61)
Рис. 2.5. Введение
подвижных координатных
осей
В магнитном поле Н на систему, обладающую магнитным
моментом д, действует момент силы [д-ff], следовательно,
= 1мЛГ]	(2-62)
at
Выражая магнитный момент через механический по фор-
муле (2.41), получим
= [уМрН].	(2.63)
Введем подвижные координатные оси, вращающиеся вокруг
некоторого направления с угловой скоростью о? (рис. 2.5). Тогда
согласно известной формуле преобразования вектора при пере-
ходе от неподвижных осей х, у, z к подвижным осям х, у',
z' — z (см., например, [126]),
(dMp\	(dMp\	г
\ dt )	\ dt )
X / неп	\	/	вращ
(2.64)
где I------ I — изменение вектора Мр относительно подвижных осей.
X dt / вращ
Из (2.63) и (2.64) следует:
(= Ь-Мр-Н! -	р].
\ dt /
X / вращ
(2.65)
|9) От греческого «гиро» ("рро) — вращение.
§2.6. Прецессия и взаимодействие магнитных моментов
59
dMp
dt
( &
уМр [Н + -
Это можно записать в виде
= ^МрЛэфф],	(2.66)
аналогичном (2.63), где
^эфф = Н + -	(2.67)
7
— эффективное магнитное поле, действующее по отношению к подвижным осям, вращаю-
щимся с угловой скоростью си.
В отсутствие поля момент количества движения сохранялся относительно неподвижных
осей, при наличии поля он будет сохраняться относительно подвижных осей20\ для которых
эффективное поле обращается в нуль,

т. е. относительно осей, вращающихся вокруг направления поля Н с угловой скоростью
си = ^Н.
Вместе с механическим моментом Мр будет сохранять свою величину и направление
относительно вращающихся осей и магнитный момент р. Это означает, что атомная система
вращается с угловой скоростью о? = — вокруг направления поля.
Действие магнитного поля на атомную систему, обладающую магнитным моментом р,
сводится, таким образом, к прецессии этой системы вокруг направления магнитного поля,
и мы приходим к формуле (2.59).
Изложенный вывод является чисто классическим, однако можно показать, что те же
результаты получаются и при квантовомеханическом рассмотрении [264], что делает законным
применение наглядных представлений о прецессии магнитных моментов к атомным системам.
Для орбитального момента электрона, соглас-
но (2.59) и (2.45), угловая скорость прецессии равна
еН
u =	,	(2.69)
2тес
и
что дает для частоты прецессии v — — величину
2тг
еН
4тгтс
Формула (2.69) является частным случаем общей
формулы (2.59). Образно говоря, происходит прецес-
сия орбитального магнитного момента и перпендику-
лярной этому магнитному моменту орбиты (рис. 2.6),
при движении по которой электрон создает магнит-
ный момент (см. с. 55). Эту прецессию называют
ларморовой, а частоту (2.70) — ларморовой частотой.
Рис. 2.6. Прецессия
электронной орбиты
Для движения электрона в магнитном поле можно сформулировать теорему Лармора
(доказанную им в 1897 г. [166]). Согласно этой теореме, действие магнитного поля на движение
электрона по орбите сводится к прецессии орбиты вокруг направления поля с угловой
скоростью (2.69). Этот результат, справедливый только для орбитальных моментов, может
быть легко получен методом, аналогичным использованному в выводе общей формулы (2.59).
Ввиду наглядности и простоты подобного вывода теоремы Лармора мы его приведем.
2°) При этом можно пренебречь, в силу малости угловой скорости си, различием между Мр и Мр, где
М'р — момент количества относительно подвижных осей.
60
Глава 2. Основные характеристики уровней энергии
Пусть электрон движется вокруг ядра по некоторой орбите под действием силы F.
е
В магнитном поле на него будет дополнительно действовать сила Лоренца —	, где v —
с
скорость движения электрона по орбите; полная сила относительно неподвижных осей х, у, z
(рис. 2.6) будет равна
Г--|»Я].	(2.71)
С
По отношению к подвижным осям х\ у', z' = г, вращающимся с угловой скоростью се
вокруг направления поля, будет действовать сила
r' = F--[®H’] + 2me[®w],	(2.72)
С
где 2me[vw] — сила Кориолиса2,). Формулу {2.72) можно переписать в виде
. е Г / 2тес \ 1 е _	,	,
Г' = F - - (к - -yy-oj] = F~ с	(2’73)
вводя аналогично (2.68) эффективное поле
2тес
7Тэфф = Н-	(2.74)
Приравнивание этого поля нулю и дает формулу (2.69).
Таким образом, в магнитном поле электрон движется под действием прежней силы F
по той же орбите, но только относительно подвижных осей, вращающихся с угловой скоро-
стью
Характерной особенностью прецессии магнитных моментов в магнитном поле
является независимость угловой скорости прецессии от остающегося постоянным
угла наклона магнитного момента по отношению к направлению поля.
В силу постоянства угла наклона остается постоянной и проекция магнитного
момента на направление поля. Сама величина угла наклона, согласно классической
теории, может быть любой. Согласно квантовой теории, как мы знаем (см. (2.43)),
проекция магнитного момента может принимать лишь определенные дискретные
значения. Поэтому дискретными являются и возможные углы наклона. Существенно,
что в магнитном поле сохраняется квантование проекции механического момента
и проекции соответствующего магнитного момента.
Отметим, что угол наклона вектора J, имеющего квантованную проекцию
Jz — т (т = J, J - 1, ..., -J), определяется, учитывая, что J2 = J(J + 1),
формулой
т т
cos 'О = —..==	—,
у/Щ + 1)
(2-75)
где J* = y/j(j + 1),
и,
таким образом, принимает значения от
J
— до
J*
J
~J*
т. е. при конечном значении J всегда | cos$| < 1. При рассмотрении проекций маг-
нитных моментов и переходе от классической теории к модельным представлениям
m
квантовой теории следует пользоваться формулой (2.75), а не формулой cos# — у.
До сих пор мы рассматривали прецессию заданного магнитного момента
во внешнем магнитном поле. Однако можно применить наглядные представления
о прецессии и к случаю магнитного взаимодействия моментов, характеризующих
части системы и складывающихся в полный момент.
21) Мы при этом считаем угловую скорость w малой, в соответствии с этим пренебрегаем центробежной
силой и заменяем в точном выражении для силы Кориолиса	скорость v' — v - [curj электрона
относительно подвижных осей его абсолютной скоростью v (г — радиус-вектор электрона).
§ 2.6. Прецессия и взаимодействие магнитных моментов	61
Рис. 2.7. Сложение магнитных
моментов:
а — при 71 / 72; б — при 7] = 72
Разберем вопрос о магнитном взаимодействии
двух моментов, характеризующих две части данной
атомной системы. Пусть имеются два механичес-
ких момента J\ и J2, которым, согласно (2.44),
соответствуют магнитные моменты
pii=7iAJb М2=72ЙЛ>-	(2.76)
При сложении J\ и J2 дают полный механический
момент
J = J1+J2	(2.77)
Магнитные моменты также складываются, давая
полный магнитный момент
д =	+^2 = ft(7iJi + 72^2),	(2.78)
который, вообще говоря (при 71 # 72), будет
иметь направление, отличное от направления век-
тора J. Мы получаем картину, изображенную
на рис. 2.7, а. Только в случае 71 = 72 = 7 име-
ет место р =	4- J2) и направления р и J
совпадают с точностью до знака (рис. 2.7,6). Рисунок соответствует сложению элек-
тронных моментов, для которых направление магнитных моментов противоположно
направлению механических (см. (2.48) и (2.55)).
Энергия взаимодействия двух магнитных моментов пропорциональна их ска-
лярному произведению р\Р2 = 7i72^2J]J2 (см. (2.44)), следовательно, пропорцио-
нальна величине J\ J2, и ее можно записать в виде
E = A(J}J2),	(2.79)
где А — постоянная, определяющая величину взаимодействия и зависящая от кон-
кретных свойств рассматриваемых моментов.
Для дальнейших применений мы преобразуем эту формулу. Произведение J\ J2
легко выразить через J\, J2 и J. Из (2.77) следует, что
J2 = (J, + J2)2 = J2 + J2 + 2(Ji J2),	(2.80)
откуда
. ч J2 - J? - J22
(J> Ji) =------------	(2.81)
Формула (2.79) тогда принимает вид
J2 - J] - J}
Е = А------------2-.	(2.82)
Замена J2, J2 и j\ на J(J+ 1), J|(Ji + 1) и + 1) (см. с. 46) дает окончательную
формулу для магнитного взаимодействия моментов:
р _ J(J+1)-Jl(j[ + 1)-J2U2 + 1)
Е 4	,	(2.83)
которой мы и будем пользоваться в дальнейшем.
Согласно квантовой механике, оператор энергии взаимодействия имеет вид
V = 4(ж)(«7|«72),	(2,84)
62
Глава 2. Основные характеристики уровней энергии
где Jj и J2 — операторы, соответствующие моментам частей атомной системы, а А(х) —
функция координат ж, описывающих систему, кроме тех координат, от которых зависят J\
и <72. Усреднение по координатам х дает среднее значение А = А(Х), которое и нужно
подставлять в (2.79) при наглядном рассмотрении.
Например, для взаимодействия орбитального и спинового моментов электрона опера-
тор V имеет вид
V = A(r)(fs),	(2.85)
где г — расстояние между электроном и ядром. К вопросу о спин-орбитальном взаимодействии
мы еще вернемся (см. с. 230).
Оператор («7| имеет в состоянии с заданными J, J\ и J2, как следует из справедливого
и для операторов соотношения (2.81) и из законов квантования (2.21)—(2.23), собственное
значение
j(j+i)-j,(j1 + i)-j2(j2 + i)
---------------2--------------,	(2-86)
откуда сразу вытекает формула (2.83).
Рис. 2.8. Прецессия двух взаимодействующих моментов:
а — вокруг момента Jy, б — вокруг момента J ц
в — вокруг результирующего момента J = J\ + J2
Согласно наглядным представлениям, энергию взаимодействия (2.79) можно
рассматривать как результат прецессии одного из моментов вокруг направления
другого момента. Моменту ц2 — 72^2 соответствует пропорциональное ему маг-
нитное поле Н2, в котором и прецессирует с некоторой угловой скоростью ш
момент = yihJi. Угловая скорость ш пропорциональна гиромагнитному отноше-
нию 71 и магнитному полю Н2 (см. (2.59)), следовательно, и произведению 7172;
энергия взаимодействия рь\рь2 пропорциональна этой угловой скорости. Мы имеем
картину, показанную на рис. 2.8, а: момент J\ прецессирует вокруг направления
момента J2. Однако можно с тем же правом рассматривать прецессию момен-
та J2 вокруг направления момента J\ (рис. 2.8,6); угловая скорость этой прецессии
по-прежнему пропорциональна 7172. Имеется произвол в выборе направления, во-
круг которого происходит прецессия; за такое направление можно выбрать любое
направление в плоскости моментов J\ и J2. При этом сохраняется пропорцио-
нальность энергии взаимодействия величине угловой скорости. Произвол в выборе
направления можно устранить, если принять во внимание, что имеется направле-
ние, фиксированное в пространстве, а именно направление полного механического
момента J, к которому и следует относить прецессию. Мы приходим к картине,
изображенной на рис. 2.8, в: моменты J\ и J2 прецессируют с определенной угловой
§2.6. Прецессия и взаимодействие магнитных моментов	63
скоростью о» вокруг направления момента J при неизменном взаимном расположе-
нии всех трех векторов. Вместе с моментами J\ и J2 прецессируют и моменты р\ и р,^
проекции всех этих моментов на направление J остаются неизменными.
Отметим, что полный магнитный момент (2.78), в общем случае (71 # 72)
не совпадающий по направлению с полным механическим моментом J, будет также
прецессировать вокруг направления последнего. К рассмотрению этого случая мы
вернемся позже (см. с. 381).
ГЛАВА 3
СИММЕТРИЯ АТОМНЫХ СИСТЕМ
И ИХ УРОВНЕЙ ЭНЕРГИИ
§3.1. Общая характеристика симметрии атомных систем
Исключительно важное значение для классификации уровней энергии и со-
ответствующих им состояний имеет симметрия рассматриваемой атомной системы.
Различные атомные системы обладают и различными свойствами симметрии. Вся
систематика как уровней энергии, так и переходов между ними основана в явном
или неявном виде именно на свойствах симметрии.
Для свободной системы все направления в пространстве являются равноправ-
ными. Если представить себе сферу, то равноправными являются все направления
из центра сферы наружу. Симметрия свободной системы является сферической сим-
метрией самого общего типа. Сферическая симметрия электрического поля ядра
имеет место для атома: потенциал действующего на электрон поля ядра зависит
только от расстояния г электрона от ядра и постоянен на любой сфере радиусом т.
Для системы, находящейся в однородном поле, магнитном или электрическом,
имеется выделенное направление — направление поля; однако остаются равноправ-
ными все направления, перпендикулярные направлению поля. Если провести ось,
параллельную направлению поля, то равноправными будут все направления в любой
перпендикулярной плоскости от этой оси наружу. Симметрия системы в однородном
поле является аксиальной (осевой) симметрией общего типа. Аксиальная симметрия
электрического поля ядер имеет место для линейной молекулы, ядра которой рас-
положены на одной прямой — на оси молекулы; примером этого являются все
двухатомные молекулы.
Сферическая и аксиальная симметрии являются частными случаями простран-
ственной симметрии.
Для систем, содержащих одинаковые частицы, например для атомов или мо-
лекул, содержащих не менее двух электронов, или для молекул, содержащих оди-
наковые ядра, имеет место перестановочная симметрия', одинаковые частицы, со-
гласно квантовой теории, являются неразличимыми, состояния атомной системы,
отличающиеся перестановками одинаковых частиц, являются тождественными
и получается симметрия относительно таких перестановок.
Наряду с пространственной и с перестановочной симметрией, представляющими два
основных вида симметрии атомных систем, возможна еще временная симметрия. Она связана
Это положение, как известно, лежит в основе квантовой статистики. В отличие от классической
статистики Больцмана—Гиббса, в которой состояния, отличающиеся перестановкой одинаковых частиц,
рассматриваются как различные, в квантовой статистике (как Бозе—Эйнштейна, так и Ферми—Дирака)
они считаются тождественными [125].
§3.1. Общая характеристика симметрии атомных систем
65
с обратимостью уравнений квантовой механики (как и классической механики) по отношению
к изменению знака времени на обратный [206].
Со свойствами симметрии атомных систем непосредственно связано вырожде-
ние их уровней (см. § 2.1). Как правило, вырожденные уровни получаются благодаря
наличию у системы определенной симметрии.
В отдельных случаях может иметься и вырождение, не связанное со свойства-
ми симметрии и получающееся вследствие совпадения значений энергии для двух
разных состояний, обусловленного частными свойствами этих состояний данной
системы. Такое вырождение называют случайным, в отличие от вырождения, обу-
словленного симметрией: симметрия представляет свойство системы в целом, опре-
деляющее свойства всех ее отдельных состояний. В частности, для электронных
состояний сложных атомов могут иметься несколько разных последовательностей
уровней, различающихся по своим свойствам, и случайно могут совпадать энергии
двух уровней различных последовательностей (см. с. 298). Для колебаний многоатом-
ных молекул возможны, например, случаи совпадения удвоенной частоты одного
нормального колебания с частотой другого нормального колебания, что приводит
к совпадению энергий двух колебательных уровней (см. с. 299).
Каждое состояние системы, обладающей симметрией, можно отнести к опреде-
ленному типу симметрии', возможны такие типы симметрии, для которых несколь-
ким состояниям с необходимостью соответствует одно и то же значение энергии,
т. е. имеет место вырождение. Если число подобных связанных друг с другом состоя-
ний, характерное для данного типа симметрии, равно д, то это означает, что уровень
энергии, которому они соответствуют, «/-кратно вырожден. Все типы симметрии
можно разделить на невырожденные (д = 1) и вырожденные (д > 1).
Примером вырожденных типов симметрии могут служить уровни свободной
системы, характеризующиеся определенным значением квантового числа J, т. е.
определенным значением величины механического момента. В силу наличия сфери-
ческой симметрии 2J 4- 1 состояний с разными значениями магнитного квантового
числа, определяющего величину проекции момента на произвольно выделенное
направление, оказываются между собой связанными и относятся к вполне опреде-
ленному типу симметрии, в данном случае «/-кратно вырожденному, где д = 2J 4- 1.
Возможные типы симметрии для системы, обладающей сферической симметри-
ей, различаются именно значением квантового числа J, определяющего величину
механического момента системы.
Квантование квадрата механического момента, вообще говоря, связано со сфе-
рической симметрией, а квантование его проекции — с аксиальной симметрией.
При наличии сферической симметрии имеется и аксиальная симметрия относитель-
но любой оси, проходящей через центр сферы: сферическая симметрия является
более высокой, чем аксиальная, и включает ее; поэтому квантуется как квадрат меха-
нического момента, так и проекция этого момента. При наличии только аксиальной
симметрии квантуется лишь проекция момента количества движения, а квантование
квадрата момента количества движения может быть только приближенным.
При аксиальной симметрии могут получаться лишь дважды вырожденные и не-
вырожденные типы симметрии, т. е. степень вырождения уровней энергии не может
превышать двух. При переходе от более высокой, сферической, симметрии к более
низкой, аксиальной, обязательно происходит расщепление всех уровней энергии,
первоначальная степень вырождения которых была больше двух. Это и имеет место
в случае однородного электрического поля, при включении которого вырожденные
уровни энергии с заданным значением J 1 (д = 2J 4- 1 > 3) расщепляют-
ся на дважды вырожденные подуровни с определенными значениями |mj| ]/г
66	Глава 3. Симметрия атомных систем и их уровней энергии
а	б
Рис. 3.1. Симметрия:
а — электрического поля
б — магнитного поля (Cxh)
и на невырожденный подуровень с mj = 02). В случае однородного магнитного
поля происходит полное расщепление всех вырожденных уровней, т. е. всех уровней
со значениями J */2 (9	2) на невырожденные подуровни.
Отличие магнитного поля от электрического
определяется тем, что наряду с аксиальной сим-
метрией оба эти поля обладают различной допол-
нительной симметрией. Электрическое поле обла-
дает симметрией относительно отражения в любой
плоскости av, параллельной полю (см. рис. 3.1, а):
оно не изменяется при отражении в этой плоско-
сти. Магнитное поле обладает симметрией отно-
сительно отражения в плоскости перпендику-
лярной полю: оно не изменяется при отражении
в такой плоскости; последнее связано с тем, что
магнитное поле характеризуется не направлени-
ем прямой в пространстве как электрическое по-
ле, а направлением обхода контура в перпендику-
лярной плоскости (направлением замкнутого тока,
создающего это поле, рис. 3.1,0. Напряженность
электрического поля представляет собой полярный
вектор, подобный направленному отрезку, и харак-
теризуется абсолютной величиной и направлением
в пространстве, а напряженность магнитного поля
представляет собой аксиальный вектор, или псевдо-
вектор, и характеризуется абсолютной величиной и направлением обхода некоторого контура,
которому лишь сопоставляется (обычно по правилу правого винта, как на рис. 3.1,0 напра-
вленный отрезок 3\
Свойства симметрии атомной системы определяются, во-первых, тем родом
симметрии, которым обладает рассматриваемая система, и, во-вторых, теми типами
симметрии, состояний системы, которые возможны для данного рода симметрии.
В разобранном примере свободной системы мы имели вполне определенный
род симметрии (сферическую симметрию) и для этого рода симметрии — различные
типы симметрии, характеризующиеся значением квантового числа J и различаю-
щиеся степенью вырождения уровней энергии. Особенно простой род симметрии
получается в случае системы, содержащей две одинаковые частицы. В этом случае
мы имеем только одну операцию симметрии — перестановку одинаковых частиц,
в результате которой система не изменяется, т. е переходит сама в себя. Для подоб-
ной системы, как можно показать (см. с. 74), получаются лишь два типа симметрии,
притом оба невырожденные, — симметричный и антисимметричный. Все состояния
системы соответственно разделяются на симметричные и антисимметричные.
Эти состояния различаются поведением описывающих их волновых функций "ф. Для пер-
вого типа симметрии волновые функции при перестановке одинаковых частиц не меняют
знака, для второго типа — меняют знак. Наличие такой симметрии не приводит к выро-
ждению уровней. Очень важный вопрос о симметрии по отношению к перестановкам двух
одинаковых частиц будет в дальнейшем разобран более подробно (см. §3.3).
Аналогичное разделение всех состояний на состояния двух типов симметрии получается
во всех случаях, когда имеется лишь одна возможная операция симметрии, в частности,
когда система имеет центр симметрии, при отражении в котором она переходит сама в себя.
При таком отражении волновые функции либо не меняют знака (четные состояния), либо
При полуцелом J — только на дважды вырожденные уровни. При J — */2 9 = 2; расщепления
в электрическом поле не происходит (ср. с. 409).
Аксиальный вектор представляет собою антисимметричный тензор второго ранга.
§3.2. Основные понятия теории групп и важнейшие группы
(Л
меняют знак (нечетные состояния). К вопросу о четности состояний систем с центром
симметрии мы также вернемся в дальнейшем (см. §3.3).
Математические методы исследования свойств симметрии атомных систем да-
ются теорией групп [137-139]. Теория групп позволяет произвести как классифи-
кацию различных атомных систем по родам симметрии — по их принадлежности
к различным группам, так и классификацию состояний данной атомной системы
по типам симметрии4), возможным для группы, к которой относится эта систе-
ма. Поскольку систематика спектров основана на свойствах симметрии, что уже
подчеркивалось в начале параграфа, то теория групп представляет естественный
математический аппарат для рассмотрения вопросов систематики спектров — си-
стематики уровней энергии и переходов между ними, и получаемые с ее помощью
результаты имеют важное значение для спектроскопии. Для понимания этих резуль-
татов требуется знакомство лишь с элементарными положениями теории групп.
§ 3.2. Основные понятия теории групп и важнейшие группы
Группой называется совокупность произвольных элементов (например поворо-
тов и отражений, перестановок, линейных преобразований и т.д.), удовлетворяющая
определенным условиям. Нас интересуют группы, представляющие совокупность
операций симметрии, переводящих рассматриваемую атомную систему саму в се-
бя. В случае пространственной симметрии такими операциями являются повороты
вокруг некоторой оси симметрии на определенный угол, отражение в центре сим-
метрии (инверсия), отражение в плоскости симметрии4 5^, в случае перестановочной
симметрии операциями симметрии являются перестановки одинаковых частиц.
Условия, которым должна удовлетворять рассматриваемая совокупность эле-
ментов, чтобы образовать группу (групповые постулаты), следующие.
1.	Произведение
с — Ьа	(3.1)
двух элементов а и Ъ группы есть тоже элемент группы.
Произведение при этом понимается в обобщенном смысле как сочетание
(композиция) двух элементов, дающее по определенному правилу третий эле-
мент. Для операций симметрии произведением является результат последовательного
применения, в определенном порядке, двух операций симметрии, что всегда дает воз-
можную операцию симметрии. Так, произведением двух поворотов CVx и С^2 вокруг
заданной оси на углы <р\ и является поворот вокруг той же оси на угол у>\ 4-
что можно записать в виде
= С(р2 С(рх	(3-2)
как частный случай общего правила (3.1).
Произведение а на b мы записываем как Ъа. Такой порядок применяется потому, что
приходится рассматривать действие элементов на другие величины, в нашем случае — действие
операции симметрии на волновые функции, aip означает результат применения операции а
к волновой функции ф, a Ъ(аф) = Ьаф — результат последующего применения операции Ь.
2.	Совокупность содержит единичный элемент е, для которого
ае — еа — а,	(33)
где а — любой элемент совокупности.
4) По неприводимым представлениям данной группы; см. § 3.3 и особенно § 3.4.
5) Для бесконечных систем, например, неограниченного кристалла, представляющего пространствен-
ную решетку, к этим операциям добавляется параллельный перенос на расстояния, кратные постоянной
решетки.
68
Глава 3. Симметрия атомных систем и их уровней энергии
Для операций симметрии таким элементом является тождественная операция,
когда система остается неизменной, например в случае поворотов вокруг оси —
поворот С\ на угол, равный нулю, а в случае перестановок — отсутствие перестановки
каких-либо одинаковых частиц. Очевидно, что для тождественной операции всегда
удовлетворяется условие типа (3.3).
3.	Совокупность содержит наряду с элементом а и обратный элемент а-1, для ко-
торого
а • а1 = а1 • а = е.	(3.4)
Для любой операции симметрии существует и обратная операция; например, опера-
цией, обратной повороту С^ на угол является поворот на угол -ip. Операции
отражения в плоскости и в центре, а также перестановка двух одинаковых частиц
обладают тем свойством, что повторение данной операции дает тождественную
операцию, т. е.
а • а = а2 = е,	(3.5)
или
а-1 = а.	(3.6)
Таким образом, если квадрат элемента группы равен единичному элементу, то обрат-
ный элемент совпадает с данным элементом. Операцией, обратной отражению
в плоскости, является это же отражение; операцией, обратной перестановке двух
элементов, является эта же перестановка и т. д.
4.	Выполняется так называемый ассоциативный закон
с(Ьа) — (сЬ)а,	(3.7)
т. е. безразлично, умножить ли сначала а на b и затем Ьа на с, или умножить а
сразу на произведение cb. Это условие всегда соблюдается для любой комбинации
последовательных операций симметрии. В силу (3.7) произведение трех элементов
группы можно записывать просто в виде cba.
С помощью перечисленных условий очень легко определить, представляет ли
рассматриваемая совокупность элементов группу. Следует подчеркнуть, что для то-
го, чтобы совокупность операций симметрии образовала группу, в нее обязательно
нужно включать, согласно условиям 2 и 3, тождественную и обратную опера-
ции. Например, в простейшем случае наличия одной плоскости симметрии, когда
имеется лишь единственная операция симметрии, отличная от тождественной, —
отражение а в плоскости, — необходимо, чтобы получить группу, включить и то-
ждественную операцию е. Что касается обратной операции, то в данном случае она
совпадает с операцией отражения. Всего группа отражения в плоскости содержит,
таким образом, две операции — е и а.
Все группы разделяются на конечные и бесконечные, по числу элементов,
которые они содержат. Число элементов в группе называют ее порядком. Группа,
состоящая из конечного числа элементов, представляет группу конечного поряд-
ка; группа, состоящая из бесконечного числа элементов, — группу бесконечного
порядка.
Простейшим примером групп конечного порядка являются группы отражения
в центре, отражения в плоскости, перестановки двух одинаковых частиц — все эти
группы состоят из двух операций, и следовательно, их порядок г = 2.
Примером группы n-го порядка является группа поворотов вокруг оси п-го
2тг
порядка Сп, т. е. такой оси, при повороте вокруг которой на угол — система
п
§3.2. Основные понятия теории групп и важнейшие группы
69
переходит сама в себя. Подобной осью обладают молеку-
лы циклических углеводородов, в которых атомы углерода
образуют правильный многоугольник (рис. 3.2)6). Опера-
циями, образующими группу поворотов вокруг оси п-го
2тг* 7)
порядка Сп, являются операция поворота Сп на угол —
п
и операции поворота на углы, кратные этому основному
углу. Общее число операций, включая поворот на угол
2тг
п • — = 2тг, т. е. поворот на угол нуль — тождественную
п
операцию, — действительно равно п. Мы имеем операции
cn,clcl...,cr\c",	(3.8)
где через обозначена тождественная операция.
При этом операцией, обратной повороту С*, явля-
ется поворот С”~к. Таким образом, совокупность пово-
ротов (3.8) содержит как тождественную операцию, так
и все обратные операции. Например, в случае оси шестого
порядка (оси Сб) мы имеем повороты:
в
Рис. 3.2. Симметрия
молекул циклических
углеводородов:
а — циклопропан С3Н6;
б — циклобутан С4Н8;
в — циклопентан С5Н10;
г — бензол С6Н6
Сб— поворот на 60°,
cl— поворот на 120°,
Cl— поворот на 180°,
С^— поворот на 240°, т. е. на —120°,
cl~ поворот на 300°, т. е. на —60°,
Cf— поворот на 360°, т. е. на 0°.
Эти шесть поворотов и образуют группу поворотов вокруг оси шестого порядка.
Порядок группы совпадает с порядком оси.
Предельный случай конечной группы поворотов вокруг оси Сп n-го порядка
представляет бесконечная группа поворотов вокруг оси бесконечного порядка —
группа вращений вокруг оси (группа Соо). Для этой группы возможны повороты
на любой угол р, что и имеет место при наличии аксиальной симметрии, рассмо-
тренной в предыдущем параграфе.
Группа вращений вокруг оси является не только бесконечной, но и непрерывной,
т. е. ее элементы зависят непрерывным образом от некоторого параметра, в данном
случае от угла р, принимающего любые значения от 0 до 2тг.
Важным понятием является подгруппа. Подгруппой называется часть элемен-
тов группы, образующая также группу, т. е. удовлетворяющая групповым условиям.
Например, подгруппами группы поворотов вокруг оси шестого порядка являются
группа поворотов вокруг оси третьего порядка, состоящая из трех операций:	,
С32 = С* и С3 = Cf = С\, т. е. поворотов на углы 120°, 240° и 360° = 0°, и группа
поворотов вокруг оси второго порядка, состоящая всего из двух операций: Сг =
Необходимо отметить, что правильный многоугольник переходит сам в себя не только при поворотах
вокруг оси n-го порядка, но и при других операциях симметрии, т. е. обладает более высокой симметрией.
Подробнее об этом см. гл. 18.
7^Эту операцию поворота принято обозначать, так же как и ось симметрии, символом Сп. Тем же
символом обозначают и саму группу поворотов.
70
Глава 3. Симметрия атомных систем и их уровней энергии
и с} = Cl — С\, т.е. поворотов на углы 180° и 360° = 0°. Для конечных групп по-
рядок подгруппы всегда является, как можно показать, делителем порядка группы.
Подгруппа соответствует более низкой симметрии, чем группа, частью которой она
является.
Основной характеристикой группы является закон, по которому произведение
двух элементов группы дает третий элемент, — закон сочетания элементов группы
(групповой закон). Группы, все элементы которых получаются умножением исход-
ного элемента на самого себя, как в случае группы поворотов вокруг оси (см. (3.8)),
называются циклическими. Простейший пример нециклической группы представляет
группа поворотов вокруг трех взаимно перпендикулярных осей на 180° (£>2). Ее эле-
ментами являются повороты С^\ С^ \ вокруг осей х, у, z и тождественная
операция С\. Очевидно,
(С*1*)2 = (С^)2 = (cj2))2 = С,.	(3.9)
Произведение двух разных операций дает третью:
______ л'Ау) <-ч(х)	^{у) __ Л<х)
v>2 — ^2 ^2 ’	^2 — ^2 ^2 >	^2 — '“'2 ^2
Рис. 3.3. Преобразование трех взаимно
перпендикулярных векторов:
й — первоначальная ориентация;
б — действие поворота
в — последующее действие поворота
В этом легко убедиться, если рассмотреть преобразование трех векторов 1, 2, 3,
направленных по осям х, у, z (рис. 3.3). Например, при повороте вокруг оси х
меняют направление на обратное
векторы 2 и 3, при последующем
повороте вокруг оси у — век-
торы 1 и 3; в результате изменяют
свое направление векторы 1 и 2,
т. е. получается поворот .
В общем случае результат пе-
ремножения двух элементов а и b
зависит от их порядка, т. е. Ьа Ф
ab. Однако в рассмотренных при-
мерах группы поворотов вокруг
оси любого порядка и группы по-
воротов вокруг трех взаимно пер-
пендикулярных осей на 180° результат двух последовательных операций поворота
не зависит от порядка их применения. Такие группы, для всех элементов которых
выполняется условие
ba = ab	(3.11)
(условие коммутативности), называют абелевыми (в честь норвежского математика
Абеля), или коммутативными. Группы, для которых условие (3.11) не выполняется,
называют неабелевыми, или некоммутативными.
Простейшим примером неабелевой группы является группа, получающаяся
из группы поворотов вокруг оси Сп (порядка п > 2), если присоединить к этой
оси п плоскостей симметрии crv, проходящих через нее8). Результат поворота Сп
и отражения ov в плоскости зависит от порядка применения этих операций:
&vCn Ф Cnav.
(3.12)
8) Данную группу обозначают Cnv (см. подробнее с. 517).
§ 3.2. Основные понятия теории групп и важнейшие группы
71
На рис. 3.4 это иллюстрируется для
оси С4 четвертого порядка; опе-
рации и C^(rv оказываются
различными9).
Весьма важным случаем неабе-
левой группы является группа трех-
мерных вращений — совокупность
всех возможных поворотов вокруг
неподвижной точки, т. е. поворо-
тов вокруг любой оси, проходящей
через точку, на любой угол. Имен-
но эта группа соответствует случаю
сферической симметрии * 10\ Приме-
ром операций группы трехмерных
вращений, для которых Ьа аЬ,
являются операции поворота на 90°
вокруг двух взаимно перпендику-
лярных осей; результат зависит от
Рис. 3.4. Преобразование трех взаимно
перпендикулярных векторов:
а — первоначальная ориентация;
б — действие отражения av в плоскости yz,
в — действие последующего поворота С4;
г — действие поворота С4;
д — действие последующего отражения av
в плоскости yz
порядка их применения.
При рассмотрении вопросов атомной и молекулярной спектроскопии прихо-
дится иметь дело, прежде всего, с точечными группами симметрии, т. е. с простран-
ственными группами, операции которых — повороты и отражения — оставляют
одну точку неподвижной в пространстве. Для атомов особенно характерна сфериче-
ская симметрия, которой соответствует, как мы указывали выше, трехмерная группа
вращений. При этом атомы обладают центром симметрии — ядром, рассматрива-
емым как силовой центр, в поле которого движутся электроны. Наличию центра
симметрии соответствует простейшая точечная группа симметрии второго порядка,
операциями которой являются отражение в центре i (инверсия) и тождественная
операция (отсутствие отражения). Для атомов и молекул, находящихся в одно-
родном внешнем магнитном или электрическом полях, т. е. в полях, обладающих
аксиальной симметрией, мы имеем группу поворотов вокруг оси симметрии
бесконечного порядка10. Для молекул характерна симметрия равновесного распо-
ложения ядер образующих ее атомов —- симметрия равновесной конфигурации,
которая определяет симметрию как колебательных, так и электронных состояний
молекулы. Симметрии равновесной конфигурации линейных молекул соответствует
точечная группа поворотов вокруг оси бесконечного порядка, а симметрии равновес-
ной конфигурации нелинейных молекул — конечные точечные группы симметрии,
классификация которых будет рассмотрена в гл. 18.
Наряду с пространственной симметрией весьма существенна, как для атомов,
так и для молекул, перестановочная симметрия, связанная с наличием одинаковых
частиц — электронов. Для молекул, содержащих одинаковые ядра, надо учитывать
также перестановочную симметрию по отношению к этим ядрам. Однако нет необ-
ходимости исследовать свойства состояний атомов и молекул при одновременных
Операция avC4 представляет отражение в плоскости, проходящей через ось и делящей пополам
угол между осями х и у\ операция C4av — отражение в плоскости, проходящей через ось и делящей
пополам угол между осями х и —у.
10) Если не учитывать отражений в плоскостях, проходящих через неподвижную точку, и отражений
в самой этой точке как центре, также возможных при сферической симметрии.
10 В магнитном поле дополнительно имеется плоскость симметрии перпендикулярная оси (груп-
па Cxh), в электрическом поле — плоскости симметрии av, проходящие через ось (группа Cxv),
см. выше, с. 66.
72
Глава 3. Симметрия атомных систем и их уровней энергии
перестановках нескольких одинаковых частиц; можно ограничиться рассмотрени-
ем перестановок только двух одинаковых частиц, что сводится к рассмотрению
простейшей группы перестановок — группы перестановок двух частиц, состоящей
из двух операций — из перестановки этих частиц и из тождественной операции
(отсутствие перестановки).
До сих пор, говоря о симметрии атомной системы и о переходе системы самой в себя
при операциях симметрии, мы не уточняли, какая именно величина, характеризующая систе-
му, переходит сама в себя. Такой величиной является с классической точки зрения энергия
системы как функция координат и скоростей (или импульсов), а с квантовомеханической
точки зрения — оператор энергии. Неизменность вида оператора энергии при преобразовани-
ях координат, соответствующих рассматриваемым операциям симметрии, — инвариантность
оператора энергии — и определяет как симметрию самой системы, так и возможные типы
симметрии ее состояний.
Например, для атома водорода оператор энергии (без учета спина) имеет вид
Н = Т+ и =
д1 2 д2	д2 \	е2
2т	ду2	dz2 у	г ’
(3.13)
где Т — оператор кинетической энергии, a U — потенциальная энергия, зависящая только
от расстояния г от электрона до ядра.
При любом ортогональном преобразовании координат
ж — аххх 4~ ахуу 4- axzz^
У = аухх 4- аууу 4- ayzz, >
z - azxx 4- azyy 4- azzz >
мы имеем
г'2
и
д2
дх'2
= x2 + у'2 + z'2 — x2 4- у2 + z2
д2	д2 _ д2	д2 д2
ду'2 + dz'2 дх2 ду2 dz2
Оператор энергии Н сохраняет свой вид:
2т у дх'2	ду'2 dz’2 J г'2 ’
(3-14)
(3-15)
(3.16)
(3-17)
т. е. является инвариантным по отношению к преобразованию координат (3.14). В этом
находит свое математическое отражение сферическая симметрия системы. Ортогональное
преобразование (3.14) включает как частные случаи любые вращения вокруг начала координат,
любые отражения в плоскостях, проходящих через начало, и отражение в начале. Таким
образом, оператор энергии в данном случае инвариантен по отношению ко всем операциям
трехмерной группы вращения, групп отражения в плоскости и группы отражения в центре.
Отметим, что и классическое выражение для энергии является инвариантным по отноше-
нию к преобразованию (3.14)12). В следующих параграфах нас будет интересовать поведение
волновых функций при операциях симметрии рассматриваемой группы, и поэтому существен-
ной является именно инвариантность оператора энергии. При классическом рассмотрении
симметрии колебаний молекулы в гл. 22 нам придется иметь дело и с инвариантностью
классического выражения для энергии. Свойства инвариантности классического выражения
для энергии и соответствующего ему квантовомеханического оператора энергии одинаковы:
инвариантность имеет место в обоих случаях по отношению к одной и той же совокупности
операций симметрии. Принадлежность к определенной группе есть свойство рассматриваемой
атомной системы, не зависимое от того, рассматривается ли она классически или квантово-
механически.
12) Кинетическая энергия Т —
1	2	1 2
-mv — -—р , где v — скорость, ар — импульс электрона, инвариантна,
2 2т
так же как и оператор кинетической энергии Т, по отношению к преобразованию (3.14).
§3.3. Невырожденные типы симметрии

§ 3.3. Невырожденные типы симметрии
Для атомной системы, обладающей определенной симметрией, получается
и вполне определенное деление состояний и соответствующих им уровней энергии
по типам симметрии. Каждую систему по ее симметрии можно отнести к некоторой
пространственной группе и к некоторой группе перестановок1^, а каждый уровень
энергии этой системы можно отнести к одному из возможных для данной группы
типов симметрии.
С математической точки зрения отнесение уровня энергии к определенному типу сим-
метрии означает его принадлежность к определенному неприводимому представлению данной
группы. Для понимания классификации состояний системы по типам симметрии нет не-
обходимости в подробном знакомстве с теорией представлений групп, являющейся одним
из хорошо разработанных разделов теории групп, детальное изложение которого можно найти
в книгах по теории групп и ее приложениям (см. [137], а также [55], т. I, с. 160). Основные
положения теории представлений групп будут кратко рассмотрены в следующем параграфе.
Для каждой группы получаются вполне определенные типы симметрии. Число
возможных типов симметрии и их основные свойства зависят от порядка группы
и от закона (3.1) умножения ее элементов — от структуры группы. Для групп одинако-
вого порядка и одинаковой структуры,4) получаются аналогичные типы симметрии.
Для конечных групп число типов симметрии конечно и не превышает порядка
группы, для бесконечных групп оно бесконечно.
Свойства типов симметрии существенным образом зависят от того, является
ли группа абелевой или неабелевой. Для абелевых групп, т. е. групп, все элементы
которых коммутируют (Ьа = ab, см. с. 70), получаются только невырожденные типы
симметрии. Поэтому для атомных систем, которые по своей симметрии относятся
к абелевым группам, уровни энергии являются невырожденными — каждому уровню
энергии соответствует одно вполне определенное состояние. Для неабелевых групп,
т. е. групп, не все элементы которых коммутируют, получаются как невырожденные,
так и вырожденные типы симметрии. Поэтому для атомных систем, относящихся
по своей симметрии к неабелевым группам, наряду с невырожденными имеются
вырожденные уровни, которым соответствуют по два или более состояний. Имеются
и такие атомные системы, относящиеся по своей симметрии к неабелевым группам,
для которых имеются только вырожденные уровни15).
Здесь мы рассмотрим невырожденные типы симметрии, получающиеся для абе-
левых групп. Для конечных абелевых групп число типов симметрии равно по-
рядку группы, и легко произвести классификацию этих типов симметрии, что
приводит к классификации уровней энергии систем, обладающих рассматриваемой
симметрией.
Простейший случай представляют собой группы второго порядка, содержащие
два элемента — единичный элемент е и элемент а, для которого ае — еа — а и а2 — е.
Такими группами являются: группа Q отражений в центре симметрии (а — i, где г —
операция инверсии), группа Cs отражений в плоскости симметрии (а = а, где а —
операция отражения в плоскости), группа поворотов вокруг оси симметрии С2
,3) Если система вообще не обладает никакой симметрией, ее можно отнести к тривиальной группе,
состоящей из одной операции — тождественной, — к группе первого порядка.
,4) Такие группы с точки зрения абстрактной теории групп являются тождественными. Они различаются
лишь природой элементов, которыми могут быть повороты и отражения, перестановки, линейные
преобразования и т. д.
,5) Такими системами являются свободные атомы и молекулы, содержащие нечетное число электронов.
Двукратное вырождение для них сохраняется и в однородном электрическом поле. В магнитном поле
оно снимается (см. с. 367).
74
Глава 3. Симметрия атомных систем и их уровней энергии
второго порядка (а — С2, где С2 — операция поворота на 180°), группа перестановок
двух одинаковых частиц (а = Р12, где Р\2 — операция перестановки частиц 1 и 2).
Для этих групп имеются два противоположных типа симметрии, различие которых
можно характеризовать, в общем виде, знаками + и
Различие типов симметрии 4- и - для состояний атомных систем определяется различным
поведением волновых функций, описывающих рассматриваемые состояния, при операции
симметрии а (см. с. 66): волновая функция либо сохраняет знак (тип симметрии 4-), либо
меняет его (тип симметрии -).
Данное свойство непосредственно вытекает из неизменности квадрата модуля |^>|2 вол-
новой функции, определяющего вероятность различных значений координат х, от которых
зависит эта волновая функция16^. При операции симметрии а волновая функция, вообще
говоря, изменяется и переходит в новую функцию , однако |^'|2 = |^|2, следовательно,
ip* = С$, где |С| = 1. Повторяя операцию симметрии, мы, в силу а2 = е, должны получить
систему в неизменном состоянии например, два последовательных отражения системы
в центре симметрии или в плоскости симметрии, естественно, ничего не могут изменить.
При этом мы получаем волновую функцию ip" = С ip' = C2tp = ip, откуда С2 — 1 и С = ±1;
следовательно,
=	(3.18)
Таким образом, действительно, волновая функция либо сохраняет знак, либо меняет его.
Два типа состояний для атомных систем, относящихся по своей симметрии
к перечисленным группам, принято называть:
четными и нечетными — для группы отражения в центре симметрии (С,);
положительными и отрицательными — для группы отражения в плоскости
симметрии (Cs);
симметричными и антисимметричными по отношению к оси — для группы
поворотов на 180° вокруг оси симметрии (С2);
симметричными и антисимметричными — для группы перестановок двух одина-
ковых частиц (Р).
Существенно, что деление состояний на четные и нечетные по отноше-
нию к отражению в центре и на симметричные и антисимметричные по отношению
к перестановке двух одинаковых частиц сохраняется и при наличии у системы,
наряду с данной симметрией, и других видов симметрии, например симметрии
по отношению к поворотам вокруг оси (группа вращений вокруг оси) или вокруг
неподвижной точки (трехмерная группа вращений).
Особенно важное значение имеет деление состояний на симметричные и ан-
тисимметричные по отношению к перестановкам одинаковых частиц. При наличии
в системе нескольких или многих одинаковых частиц данного рода все состояния
системы должны быть либо симметричными, либо антисимметричными по отно-
шению к перестановке любых двух частиц этого рода. Как можно показать [142],
если частицы имеют целый спин (ядра, для которых I = 0, I — 1, 1 — 2, ...;
см. табл. 2.1, с. 48), то все состояния системы симметричны по отношению к пе-
рестановке двух таких частиц; если же частицы имеют полуцелый спин (электрон,
для которого s = у2, и ядра, для которых I ~ */2, 3/г, • • •), то все состояния
антисимметричны по отношению к перестановке двух таких частиц17).
Легко найти вид симметричных и антисимметричных волновых функций для систем, со-
держащих две одинаковые частицы. Примерами таких систем являются атом гелия и молекула
,6) Под х подразумевается совокупность всех координат, описывающих систему.
,7) Первый случай соответствует квантовой статистике Бозе—Эйнштейна, второй случай — квантовой
статистике Ферми—Дирака (ср. примечание на с. 64).
§ 3.3. Невырожденные типы симметрии
75
водорода, содержащие по два электрона, движущихся в первом случае в поле ядра гелия,
а во втором — в поле двух протонов.
Пренебрежем сперва взаимодействием частиц. Если первая частица находится в со-
стоянии I, описываемом волновой функцией ^1(^1)? а вторая частица — в состоянии II,
описываемом волновой функцией V’n(a;2), где Z] и х2 — совокупности координат первой
и второй частицы соответственно, то полная волновая функция системы
^(11,2:2) = ^|(х,)^1|(а:2).	(3.19)
При перестановке частиц мы получаем волновую функцию
V>(Z2, Х|) = ^|(X2)’/’I1(®1),	(3.20)
которая будет соответствовать той же самой энергии.
Однако обе эти функции не удовлетворяют условию неизменности |^|2 (см. с. 74): вообще
говоря,
|^i(z1)V’ii(2:2)|2 # l^i(®2)^it(a;i)|2-	(3.21)
Правильными свойствами симметрии (3.18) будут обладать функции18^
V’s = CsM»i> ®г) + ^(®2, *1)1 = С>М(Я|)1М®2) + (®2)^n(«i)]	(3.22)
И
l/’s = СА[^(Х|, z2) - ^(®2, *1)] = САЬМ®|)1Ма:2) - Ф\(Х2)*МХ1)]-	(3.23)
Сразу видно, что при перестановке частиц, т. е. при замене з?| на х2 и обратно, первая
функция сохраняет свой знак, а вторая меняет его. Таким образом, функция является
симметричной, а функция — антисимметричной.
Свойства симметрии сохраняются и в том случае, если между частицами имеется взаимо-
действие; только тогда уже нельзя представить полную функцию xi) как произведение
и V’n(a;2)- При наличии взаимодействия энергии симметричного и антисимметричного
состояний будут, вообще говоря, различны, и эти состояния уже не будут вырождены.
Если состояния обеих частиц одинаковы, то, как следует из (3.23), антисимметрич-
ная функция тождественно обращается в нуль, откуда вытекает, что частицы, описываемые
антисимметричными функциями, не могут находиться в одинаковых состояниях. Это поло-
жение представляет общую формулировку принципа Паули, который мы будем применять
в дальнейшем (см. §7.1 и § 10.2).
Отметим, что антисимметричная функция (3.23) может быть записана в виде определи-
теля
=r I	1М*2) I	,	.
A|^ll(l|) ^и(*2) Г
Это выражение может быть обобщено и на случай нескольких или многих одинаковых
частиц. Мы получаем антисимметричную функцию в виде определителя

^i(®i)	^|(®г)
^ч(®1) •’Mzi) •••
Фл = Са
(3.25)
который меняет знак при перестановке двух частиц, т. е. двух его столбцов, и обращается
в нуль, если две частицы находятся в одинаковых состояниях, так как тогда две его строки
одинаковы.
Для абелевых групп конечного порядка г > 2 классификация получающихся
г типов симметрии будет различной в зависимости от структуры группы, которая
может быть разной. Например, группы четвертого порядка могут быть двух типов —
циклические и нециклические.
Примером циклической группы является группа поворотов Сд вокруг оси
симметрии четвертого порядка, включающая операции
а = СА, b = CA =C2 = b~', с=СА=а~\ e = CA=Ct. (3.26)
,8) Cs и Сд — нормировочные множители.
76
Глава 3. Симметрия атомных систем и их уровней энергии
В этом случае получаются четыре типа симметрии, один из которых является
симметричным по отношению к оси, другой — антисимметричным (см. с. 73),
а остальные два обладают более сложными свойствами.
Для циклической группы порядка п имеем ап = е, и волновая функция остается
неизменной при r-кратном повторении операции а, т. е. если при операции а имеет место
ip1 = Cip, то Cnip = ip и Сп = 1, С = д/Т (ср. с. 73). Так как 1 = ехр {2тггтп}, где т — целое
ш ]
2тгг— >, и мы имеем п различных возможных значений С:
п )
(	1
ехр < 2тгг —
I	п
ехр < 2тгг — >,
I nJ
Г п - 1 3
..., ехр < 27гг->,
I nJ
{п 3
2тгг — > — 1.
n J
(3-27)
Получаются п различных типов симметрии, для которых волновые функции при опе-
рации а умножаются на множители (3.27). Для циклической группы четвертого порядка
значения С равны
ехр
7Г
2
— г>
ехр {гтг} — -1,
ехр {г2тг} = 1. (3.28)
Помимо симметричной функции (С = 1, гр1 — ip) и антисимметричной функции (С = -1, ip' =
-ip) получаются функции, умножающиеся при операции а на i (ip1 — iip) и на -г (ip1 = -ity).
Примером нециклической группы четвертого порядка является группа Т>2 по-
воротов на 180° вокруг трех взаимно перпендикулярных осей (см. с. 70), для которой
а2 = Ь2 — с2 = ab = Ьа — с, Ьс — cb — а, са — ас = Ь. (3.29)
Каждый из четырех возможных типов симметрии можно характеризовать зна-
ками + и - по отношению к двум операциям, например к а и Ь; тогда свойства
по отношению к третьей операции определяются законом умножения (3.1).
Мы получаем следующие четыре комбинации свойств 4- и
операция операция	операция
а = С{2} Ъ = С[у) с = С(2} = С2^С2^ = Ьа
4-4-	4-
4-
4-
-	-	4-
(3.30)
Волновая функция для первого типа симметрии является симметричной по отношению
ко всем операциям, волновые функции для остальных трех типов симметричны по отношению
к одному из поворотов и антисимметричны по отношению к двум другим. Например,
для функции, соответствующей четвертой строке (3.30), можно написать
c*I,v = -V’,	=	(3.31)
Абелевой группой бесконечного порядка является группа вращений вокруг
оси, т. е. группа всех возможных поворотов вокруг оси Сж бесконечного порядка.
Для нее получается бесконечное число невырожденных типов симметрии, которые
соответствуют различным возможным значениям проекции момента количества
движения: либо целым
m = Q, ±1, ±2, ±3, ... ,	(3.32а)
либо полуцелым
13	5	7
т = ±-, ±-, ±-, ±-, ....	(3.326)
2	2	2	2
§ 3.4. Вырожденные типы симметрии
77
Соответствующие волновые функции умножаются при операции Cipx поворота на угол
на e2Wi. Для полуцелых т волновые функции при уч = 2тг умножаются на —1 и при = 4тг
умножаются на 4-1, т. е. являются двузначными.
Рассмотренное в § 2.3 квантование проекции момента количества движения, включая
случай полуцелых т, можно получить, исходя из рассмотрения группы поворотов вокруг оси
симметрии Сх. Тогда можно доказать, что волновые функции умножаются при повороте С\1
на eim<pi с целыми или полуцелыми т, откуда следует, что они должны иметь вид егт<р, а это
приводит к возможным значениям проекции момента количества движения, равным hm.
Случай оси симметрии Сп конечного порядка может быть получен из общего
случая оси симметрии бесконечного порядка (подробнее о связи этих случаев
см. [15], с. 115).
Существенно, что группа вращений вокруг оси остается абелевой и при присо-
единении к поворотам вокруг оси отражения в плоскости, перпендикулярной этой
оси. Типы симметрии по-прежнему являются невырожденными и характеризуются
квантовым числом т. Подобной симметрией (С^д) обладают атомные системы,
находящиеся в однородном магнитном поле, что приводит к полному расщеплению
уровней энергии, вырожденных (по т) в отсутствие поля (см. с. 66).
§ 3.4.	Вырожденные типы симметрии
Рассмотрим теперь вырожденные типы симметрии. Они получаются для неабе-
левых групп (см. с. 73).
Для неабелевых групп конечного порядка получаются вырожденные типы сим-
метрии, для которых в важнейших для спектроскопии случаях степень вырождения
равна двум и трем, — дважды (двукратно) и трижды (трехкратно) вырожденные
типы симметрии. Эти случаи имеют место для нелинейных многоатомных моле-
кул, равновесные конфигурации которых относятся к точечным группам симметрии
с осями симметрии порядка выше двух и будут подробно рассмотрены в гл. 22 в связи
с симметрией колебаний молекул.
Для неабелевых групп бесконечного порядка в случае группы вращений во-
круг оси с отражениями в плоскостях симметрии av, проходящих через эту ось,
получаются дважды вырожденные типы симметрии. Каждый такой тип симме-
трии соответствует определенному абсолютному значению |т| проекции момента
количества движения. Подобной симметрией (С^) обладают атомные системы,
находящиеся в однородном электрическом поле.
В случае трехмерной группы вращений, т. е. при наличии сферической симме-
трии, получаются, как уже отмечалось в §3.1 (см. с. 73), вырожденные типы сим-
метрии, соответствующие различным возможным значениям квантового числа J,
и степень вырождения g = 2J 4- 1 в принципе может быть сколь угодно большой.
К закону квантования квадрата момента количества движения можно прийти,
если исходить из наличия сферической симметрии, и методами теории групп найти
все возможные для трехмерной группы вращений типы симметрии. Получаются
типы симметрии, для которых число g связанных между собой состояний может
равняться любому целому числу:
# = 1, 2, 3, 4, 5, ... .	(3.33)
Для совокупности g таких состояний можно показать, что она соответствует
значению квадрата момента количества движения, определяемому формулой J2 =
J(J4-1), т. е. законом квантования (2.11). При этом квантовое число J определяется
числом g связанных между собой состояний при помощи соотношения g = 2J 4- 1,
78
Глава 3. Симметрия атомных систем и их уровней энергии
следовательно, принимает любые положительные значения, целые (при нечетном д)
и полуцелые (при четном #)19).
Методами теории групп можно также вывести квантовый закон (2.21)—(2.24)
сложения моментов количества движения. С точки зрения свойств симметрии этот
закон связывает вырожденные типы симметрии системы в целом с исходными
вырожденными типами симметрии частей системы. При этом сумма степеней выро-
ждения для получающихся типов симметрии системы в целом равна произведению
степеней вырождения для исходных типов симметрии частей системы:
52 9j = 9Ji9j2	(3.34)
^=|Л-Л|
ИЛИ
«Л+Л
52 (2J+1) = (2Ji + 1)(2J2 + 1),	(3.35)
как было уже рассмотрено выше (см. с. 52).
Наличие вырожденных типов симметрии для неабелевых групп обусловлено тем, что
среди операций симметрии, образующих неабелеву группу, всегда имеются такие, кото-
рые преобразуют волновые функции не самих в себя (с точностью до множителя), а друг
в друга или более сложным образом. Благодаря этому волновые функции двух или несколь-
ких (а иногда и многих) состояний оказываются неразрывным образом связанными между
Рис. 3.5. Атом водорода
в однородном электрическом поле
собой, и подобным состояниям с необходимостью со-
ответствует одна и та же энергия, т. е. имеет место
вырождение.
Поясним сказанное на конкретном примере ато-
ма водорода, находящегося в однородном электри-
ческом поле напряженностью Оператор энергии
имеет вид
h2 ( д2	д2	д2 \	е2	, х
я = -^-Н-5+т-5 + -^5 --+е^г 3-36)
2m \дх2 ду2	dz2 J	г
и отличается от оператора энергии (3.13) добавлени-
ем потенциальной энергии eJz электрона в электри-
ческом поле, направление которого мы принимаем
за направление оси z (рис. 3.5). В отличие от опера-
тора (3.13), оператор (3.36) сохраняет свой вид только
при ортогональных преобразованиях типа
Д' — ^хх^ ~Ь ^хуУу
У ~ Gyi’E 4" &ууУ)
z' = z,
(3-37)
включающих повороты вокруг оси z на любой угол и отражения в любой плоскости,
проходящей через ось z, в частности в плоскости xz (для этого отражения х1 = х, у' — —у,
z' — z). Таким образом, оператор энергии инвариантен по отношению ко всем операциям
группы вращения вокруг оси с отражениями в плоскостях, проходящих через ось (группы C^v).
,9) Будет ли J целым или полуцелым, связано уже не со свойствами трехмерной группы вращений,
а со свойствами рассматриваемых атомных систем. Целые значения получаются для атомных систем,
содержащих четное число частиц с полуцелым спином (электронов и ядер с полуцелым спином).
Полуцелые значения получаются для атомных систем, содержащих нечетное число подобных частиц.
§ 3.4. Вырожденные типы симметрии
79
(3.39)
Волновые функции оператора энергии, соответствующие определенным значениям про-
екции орбитального момента количества движения, имеют вид (см. (2.20)):
(3.38)
где т — магнитное орбитальное квантовое число и не зависит от <р20\
Рассмотрим преобразование функций фт и ф-т, соответствующих заданному |т|.
При операции поворота Ctpi на угол т. е. при замене угла р углом р' = ф- функция фт
умножается на e-tWl, а функция ф_т — на etWl, и мы получаем функции
Ф-т =
При операции отражения av в плоскости xz угол р меняет знак на обратный (см. рис. 3.5),
функция фт = фоегт<р превращается в ^oe~tw, т.е- в Ф-т, и, наоборот, функция ф_т = ф^е~гт<р
превращается в фт = фое'т<р. Мы получаем функции
Фт = Ф-т, 1
Ф-т = Фт- J
Волновое уравнение
Нфт = Ефт	(3.41)
преобразуется в уравнение
Ниф1 = Еф^.	(3.42)
В силу инвариантности оператора энергии
Н" = Н	(3.43)
и, согласно первому соотношению (3.40), уравнение (3.42) принимает вид
Н"ф-т =	(3.44)
следовательно, функция ф_т относится к тому же значению энергии Е, что и фт, т. е. должно
иметь место двукратное вырождение.
Мы видим, что при операциях симметрии функции фт и ф_т преобразуются линейно,
причем таким образом, что их нельзя отделить друг от друга. Действительно, если бы мы
вместо функций фт и ф_т взяли их линейные комбинации
Ф+ = ^(фт + Ф-т) = ~Фо(е,тр + е"’”**’) = фо cos ту, 1
1	1	?	(3-45)
Ф- =	~= Т^°(е'т’’ “ е “ Фо^птр, I
2г	2г	7	/
то при отражении в плоскости xz функции ф+ и ф_ переходили бы сами в себя, зато
7Г / ,	7Г \
при повороте на угол -— I <р — <р - -— | они переходили бы друг в друга.
2m \	2m /
Линейные преобразования функций фт и ф_т при операциях симметрии и av
образуют группу, каждый элемент которой соответствует определенной операции исходной
группы Cxv. Группу линейных преобразований, соответствующую (гомоморфную) данной
группе, называют представлением этой группы. Мы нашли представление группы C^v.
Число функций, преобразующихся друг в друга, определяет размерность представления.
В данном случае она равна двум — представление является двумерным. Если функция
переходит сама в себя при всех операциях симметрии (с точностью до множителя), то мы имеем
одномерное представление.
Представление, для которого нельзя выбрать функции так, чтобы они преобразовы-
вались раздельно, а не друг в друга, называется неприводимым. Примером неприводимого
представления группы Cxv и являются линейные преобразования функций фт и ф_т.
20) Она зависит от координат т и 0 (см. рис. 3.5, а также с. 177).
80
[лава 3. Симметрия атомных систем и их уровней энергии
Представление, для которого можно выбрать функции так, чтобы они преобразовыва-
лись раздельно, называется приводимым. Примером является представление, образованное
функциями (3.19) и (3.20) в случае группы перестановок. Эти функции переходят друг в друга
при операции перестановки, но их линейные комбинации (3.22) и (3.23), в отличие от ли-
нейных комбинаций (3.45), преобразуются раздельно. При помощи перехода от (3.19) и (3.20)
к (3.22) и (3.23) удается привести представление.
Для каждой группы можно найти все неприводимые представления. Они и определяют
возможные типы симметрии, а размерность каждого представления дает степень вырождения
соответствующего типа симметрии.
В общем случае r-мерного представления линейное преобразование г собственных
функций оператора энергии при операции симметрии а можно записать в виде
= (^=’> 2> ••>’)•
(3.46)
При операции симметрии Ъ мы получим преобразование
= Г (7 = 1, 2, ..., г).	(3.47)
/3=1
Операции симметрии с — Ьа будет соответствовать, согласно (3.46) и (3.47), линейное
преобразование
^7 ~ Ь-у/З'Фр ~	“2 ^‘у^а/За'Фа ^3	(3.48)
Р=\	р,а=\	а=1
где
•	(3*49)
0=1
Формула (3.49) представляет закон умножения матриц линейных преобразований (3.46)
и (3.47). Мы видим, что каждой операции симметрии соответствует определенная матрица
представления, причем произведению операций симметрии соответствует произведение ма-
триц. Легко видеть, что тождественной операции соответствует единичная матрица и обратной
операции — обратная матрица. Ассоциативный закон (3.7) для линейных преобразований
также выполняется, т. е. совокупность матриц линейных преобразований волновых функций
при операциях симметрии действительно образует группу, соответствующую группе операций
симметрии, относительно которых оператор энергии инвариантен.
Простейший случай представлений — это одномерные представления. Для них каждая
матрица сводится к одному коэффициенту, на который умножается волновая функция
при соответствующей операции симметрии. Например, для группы поворотов на 180° вокруг
трех взаимно перпендикулярных осей (см. с. 76), Ь2, четыре возможных типа симметрии (3.30)
характеризуются следующими коэффициентами:
Тип симметрии	Операция симметрии			
	е — С|	а _ £•(*)	ь = с{2у}	с = с'г>
А Ва Вь вс	1 1 1 1	1 1 -1 -1	1 -1 1 -1	1 -1 -1 1
Каждая строка дает одномерное представление рассматриваемой группы, причем стоящие
в данной строке коэффициенты 1 и -1 удовлетворяют групповому закону (3.29).
§ 3.4. Вырожденные типы симметрии
81
Для рассмотренной группы вращений вокруг оси, Cxv, мы имеем двухмерные неприво-
димые представления, которые характеризуются следующими матрицами21);
Операции симметрии
е =	(7^!	<rv
(3.51)
110 1 I e",W1	0(|01|
|01| I 0 e‘W1 I |10|
Различные представления отличаются значениями |пг|.
Для трехмерной группы вращений получаются неприводимые представления Dj раз-
мерности g = 2J 4- 122\ согласно которым преобразуются 2J 4- 1 собственных функций
операторов J2 и Jz (J задано, т — J, J - 1, ..., -J; см. с. 49). Эти функции переходят
сами в себя (с точностью до множителя е*”1*’1) при поворотах вокруг оси z на любой угол <рх,
но при других поворотах рассматриваемой группы (например вокруг осей х или у) преобра-
зуются друг в друга и оказываются связанными неразрывным образом, образуя неприводимое
представление. Иначе говоря, нельзя найти такие линейные комбинации функций ipJm,
которые преобразовывались бы каждая сама в себя или хотя бы согласно представлениям
размерности д’ < д, т. е. приводимым образом.
Рассмотрим сложение моментов количества движения. Пусть две части сложной систе-
мы описываются волновыми функциями (mi = Л, Л — 1,	— Ji), преобразующи-
мися, согласно неприводимому представлению DJ} размерности д} — 2J\ 4- 1, и волновыми
функциями ^j2m2 (m2 — Jz? Jz — 1, ♦ • —J2), преобразующимися, согласно неприводи-
мому представлению Z>j2 размерности д2 = 2J2 4- 1. Волновые функции полной систе-
мы ^jimi;j2m2 =	(см. (2.34)), число которых равно (2J, 4- 1)(2J2 4-1), будут преобра-
зовываться, согласно представлению размерности (2J, 4- 1)(2J2 4-1), которое называют прямым
произведением представлений DJ{ и Dj2 и обозначают DJ{ х Dj2 . Это представление оказывает-
ся приводимым23^. Можно найти такие линейные комбинации волновых функций ^jimi;j2Zn2,
которые будут преобразовываться между собой уже неприводимым образом, согласно пред-
ставлениям Z>j1+j2, Z>j1+j2-i, ...,	сумма размерностей определяется формулой (3.35).
Получающиеся линейные комбинации имеют вид (2.37), причем коэффициенты С^т2 в этой
формуле (коэффициенты Клебша—Гордана) могут быть найдены в явном виде [137, 138].
Окончательный результат приведения представления Djt х Dj2 можно записать в краткой
форме:
Dj{ х Dj2 = DJ}+j2 4- Z>j1+j2-i 4-	4-	(3.52)
Приводимое представление распадается на неприводимые. Это и есть закон сложения
моментов количества движения.
Разложение приводимых представлений на неприводимые как в рассматриваемом случае,
так и в других случаях производится с помощью использования свойств характеров, т. е. сумм
диагональных коэффициентов24) матриц представления. Для преобразовании (3.46)-(3.48)
характеры соответствующих матриц равны
г	г	г
Ха — aaai Xb ~ ^ДД> Хс ~	С77*	(3.53)
а=1	Д=1	7=1
21)Для получения (3.51) надо записать (3.33) и (3.40) в виде (3.46), например для операции av:
Фт ~ ’ Фт 4" 1 * Ф—тч 1
Ф—т ~ 1 ' Фт 4* 0 • 1p—m. )
Для тождественной операции е имеем V’m — Фт и V’-m — Ф-т, что дает единичную матрицу.
22) Представления группы трехмерных вращений, соответствующие заданному значению J, принято
обозначать символом Dj.
23) За исключением того случая, когда одно из представлений Dj} или Dj2 (или оба) является
одномерным.
24) Сумму диагональных коэффициентов матрицы называют также ее следом, или шпуром.
82
Глава 3. Симметрия атомных систем и их уровней энергии
В частном случае представления (3.51) мы имеем
Хс, = 2, хсп = е *W| + e,mv' = 2 cos , х°, - О-
(3-54)
Важнейшим свойством характеров является их неизменность при переходе от исходных
волновых функций к линейным комбинациям этих функций25). Мы не будем здесь более
подробно рассматривать свойства характеров; с ними мы встретимся в гл. 22 при разборе
вопроса о симметрии колебаний молекул.
25) Отсюда сразу вытекает, что характеры матриц приводимого представления равны суммам характеров
матриц неприводимых представлений, на которые распадается данное приводимое представление.
ГЛАВА 4
ВЕРОЯТНОСТИ ПЕРЕХОДОВ И ПРАВИЛА ОТБОРА
§4.1. Вероятности спонтанных и вынужденных переходов
Важнейшими квантовыми характеристиками процессов испускания и погло-
щения являются вероятности соответствующих переходов (см. § 1.3). Испускание
может быть спонтанным (самопроизвольным), т. е. происходящим при отсутствии
воздействий внешнего излучения (фотонов), в силу присущих атомной системе
внутренних закономерностей, и вынужденным — происходящим в результате воз-
действия внешнего излучения; поглощение всегда является вынужденным. Поэтому
переходы с излучением между двумя заданными уровнями энергии, верхним Ej
и нижним Ек, характеризуются вероятностью спонтанного испускания, вероятностью
вынужденного испускания и вероятностью поглощения.
Вероятностная трактовка процессов испускания и поглощения была впервые дана Эйн-
штейном в 1916 г. [182] при рассмотрении равновесия излучения с веществом с квантовой
точки зрения (см. вывод формулы Планка по Эйнштейну в § 5.2). Для характеристики вероят-
ностей переходов он ввел коэффициенты, получившие название коэффициентов Эйнштейна
(см. ниже).
Понятия соответствующих вероятностей переходов могут быть определены,
если рассматривать элементарные процессы изменения энергии атомных систем как
мгновенные и считать, что каждый процесс может произойти в любой момент време-
ни, независимо от остальных процессов того же типа (статистическая независимость
случайных процессов).
Пусть имеется совокупность одинаковых частиц — атомов или молекул0,
1 {
которые могут испускать и поглощать фотоны частоты и — игк = —\Ei — Ек).
h
Число спонтанно испущенных за единицу времени фотонов будет про-
порционально заселенности Ni верхнего уровня — числу возбужденных частиц
с энергией 1%; можно положить:
Z^^AikNi.	(4.1)
При этом предполагается независимость элементарного процесса испускания фотона
от концентрации частиц, что справедливо, в частности, для случая газа не очень высокой
плотности, в котором частицы взаимодействуют слабо.
Отметим, что формула (4.1) применима как к случаю, когда заселенность не изменяется
со временем (установившиеся процессы), так и к случаю, когда она переменна. В последнем
случае и будет функцией времени (см. с. 86).
° Это могут быть также ядра. В случае конденсированных систем можно рассматривать вместо ре-
альной совокупности частиц мысленную совокупность экземпляров данной системы — статистический
ансамбль; ряд результатов, изложенных в этой и в следующей главах, справедлив и для конденсированных
систем.
84
Глава 4. Вероятности переходов и правила отбора
Постоянный коэффициент пропорциональности
у(сп)
А* =	(4.2)
равен числу спонтанно испускаемых в единицу времени фотонов частоты и в расчете
на одну возбужденную частицу с энергией Ei, или, иначе говоря, равен доле частиц,
спонтанно испускающих такие фотоны в единицу времени. Его называют вероят-
ностью спонтанного испускания, или коэффициентом Эйнштейна для спонтанного
испускания (коэффициентом А). Это есть величина, отнесенная к единице времени
и имеющая размерность, обратную размерности времени. При измерении времени
в секундах выражается вс-1.
Число поглощенных за единицу времени фотонов пропорционально
заселенности Nk нижнего уровня — числу частиц с энергией Ek — и в соответствии
с тем, что поглощение является вынужденным процессом, плотности излучения р(и)
данной частоты, т. е. энергии фотонов в единице объема р(и) = n(v) hu, где п(у) —
число фотонов частоты и = Vik в единице объема2). Можно положить
^°ГЛ) = BkiNkp(v).	(4.3)
Замечания, сделанные выше относительно формулы (4.1), справедливы и в отношении
формулы (4.3).
Постоянный коэффициент пропорциональности
Eki —
1 £<?огл)
Nk
(4-4)
равен числу поглощенных в единицу времени фотонов частоты и = i^k, рассчи-
танному на одну частицу с энергией Ek и на единицу плотности излучения. Его
называют коэффициентом Эйнштейна для поглощения (коэффициентом В). Произве-
^(погл)
дение Bkip(v) — ——, имеющее, как и коэффициент размерность, обратную
Як
размерности времени, равно доле частиц, поглощающих фотоны частоты и = Vik
в единицу времени, и представляет собой вероятность поглощения. Поэтому коэф-
фициент Bki есть вероятность поглощения, рассчитанная на единицу плотности р(у)
излучения, обусловливающего вынужденные переходы.
Наконец, число фотонов частоты и — vik, испускаемых за единицу
времени в результате воздействия излучения плотности р(у), т. е. при вынужденных
переходах с верхнего уровня В, на нижний уровень Ek, будет пропорционально 7VZ-
и р(и). Можно положить, аналогично (4.3),
4ВЫН) = BikNiP(v).
Постоянный коэффициент пропорциональности
1 е»>
tk р(у) К
(4-5)
(4-6)
2) Величины р(у) и n(i/) можно относить к строго монохроматическому излучению частоты и или рас-
считывать на единицу интервала частот; подробнее см. § 5.5.
§ 4.2. Время жизни возбужденных состояний
85
называют коэффициентом Эйнштейна для вынужденного испускания, a Bikp(y) =
г(вын)
Чк___
Ni
представляет собой вероятность вынужденного испускания.
Отметим, что важное отличие вынужденного от спонтанного испускания со-
стоит (помимо его обусловленности излучением) в том, что тогда как спонтанное
испускание фотона может происходить в любом направлении, вынужденное испус-
кание происходит в направлении распространения падающего на частицу излучения;
если это излучение поляризовано, то поляризация при вынужденном испускании
совпадает с поляризацией падающего излучения.
Следует подчеркнуть, что именно вынужденное испускание представляет про-
цесс, обратный поглощению; его можно рассматривать как отрицательное погло-
щение. Хотя направление процесса спонтанного испускания и является обратным
направлению процесса поглощения, но они существенно различаются тем, что спон-
танное испускание не зависит от воздействия внешнего излучения, а поглощение
определяется именно этим воздействием. Поглощение и вынужденное испуска-
ние оба являются вынужденными процессами^; их отличие состоит в том, что
под воздействием излучения при элементарном процессе поглощения число фото-
нов частоты и уменьшается на единицу, а при элементарном процессе вынужденного
испускания — увеличивается на единицу. Коэффициенты Bki и В^ и соответству-
ющие им вероятности В^р(у) и Bikp(v) связаны между собой, как показывает
квантовая теория, очень просто:
9k^ki — 9i^ikt
(4-7)
где gk и gi — степени вырождения (статистические веса) уровней Ек и Ei. Для пере-
ходов между невырожденными уровнями (рг — gk = 1) Bki = Bik, что представляет
частный случай общего соотношения между вероятностями прямого и обратного
элементарных процессов при переходах между двумя квантовыми состояниями,
согласно которому эти вероятности равны друг другу.
Между коэффициентами Эйнштейна Aik и Bik существует весьма важное соот-
ношение
8тг/ш3 дк
Aik = -Y-^Bki.
с3 gi
Оно позволяет вычислить вероятность спонтанного испускания, если известна
вероятность поглощения4), и наоборот.
Соотношение (4.8) было впервые установлено Эйнштейном [182] и может быть строго
обосновано методами квантовой электродинамики [140].
(4-8)
§ 4.2. Время жизни возбужденных состояний
С вероятностями переходов связана одна из важнейших характеристик возбу-
жденных состояний — их время жизни, определяющее, в частности, длительность
послесвечения после прекращения возбуждения (см. с. 23). Время жизни непосред-
ственно зависит от вероятностей спонтанного испускания Эту зависимость
легко получить, исходя из соотношения (4.1).
^Термин «вынужденное» не применяют, говоря о поглощении, лишь потому, что оно всегда является
вынужденным.
4> Отнесенная к единице плотности р(и) излучения. При этом плотность излучения рассчитывается
на единицу интервала частот, см. с. 134.
86
Глава 4. Вероятности переходов и правила отбора
Рассмотрим убыль числа 7V, возбужденных частиц со временем вследствие по-
тери ими энергии при спонтанном испускании фотонов, считая, что в начальный
момент времени t = 0 заселенность уровня энергии Ei равнялась и что в даль-
нейшем возбуждение не производится. В силу (4.1) убыль — (dNi)k числа Ni за счет
спонтанных переходов Ei Ek будет равна за время от t до t + dt:
~(dNi)k = Z%n)dt = AikNidt,	(4.9)
где Ni — заселенность уровня Ej в момент t.
Отметим, что, согласно (4.9),
т. е. вероятность спонтанного перехода равна относительной убыли числа возбужден-
ных частиц в единицу времени за счет этого же перехода. Рассматривая состояние
возбужденной частицы как стационарное, т. е. не изменяющееся с течением вре-
мени, вплоть до момента испускания фотона, мы вводим вероятность спонтанного
испускания, определяющуюся свойствами этого состояния, как величину, не за-
висящую от времени. В любой заданный момент времени вероятность испускания
возбужденной частицей фотона одна и та же, независимо от того, когда эта частица
была возбуждена.
Уменьшение заселенности Ni уровня Ei будет происходить независимо за счет
каждого возможного перехода, и полная ее убыль —dNi за счет всех возможных спон-
танных переходов с данного верхнего уровня Ei на различные нижние уровни Ek
будет равна
-dNi = - ^(dNi)k = 52 AikN{dt = (52 A,*) Nidt.	(4.11)
к	к	к
Вводя полную вероятность спонтанных переходов с уровня Ei на все уровни Е*,
равную сумме вероятностей отдельных переходов,
1 dNi
к
мы получим уравнение
-dNi =AiNidt,	(4.13)
решение которого дает закон убывания числа возбужденных частиц со временем5):
Ni = NiQe~Att.	(4.14)
Таким образом, заселенность уровня Ei убывает со временем по показательному
закону.
Различные частицы существуют в возбужденном состоянии различное время.
Можно определить время жизни возбужденного состояния как среднюю продолжи-
тельность нахождения частицы в возбужденном состоянии. Время жизни выражается
dN-
Закон (4.14) выводится элементарным образом. Уравнение (4.13) можно переписать в виде —
-Aidt, и его интегрирование дает In Ni — -Ad + С, где С — постоянная интегрирования, которая
Ni
определяется из условия, что Ni = при t — 0. Мы получаем С — In и In- = —Ad, что
NiQ
и приводит к (4.14).
§4.2. Время жизни возбужденных состояний
87
через Ai простой формулой
1 _ 1
а, 52 ’
k
(4-15)
т. е. является величиной, обратной полной
кания. Согласно (4.14), это есть то время,
/	Ni	1
убывает в е раз ( при t = т имеем-= - =
V	Nio	е
вероятности (4.12) спонтанного испус-
за которое число возбужденных частиц
1	ч
=------= 0,368) .
2,718	’	)
Формула (4.15) может быть выведена следующим образом. Продолжительность суще-
ствования в возбужденном состоянии частиц, испустивших фотоны за время от t до t 4- dt,
можно считать равной t. Число этих частиц равно, согласно (4.13) и (4.14),
-dNi = AiNidt = AiNi0e~Attdt,	(4.16)
а их доля, по отношению к начальному числу возбужденных атомов Nt0, составляет
dNi	a t
-zz-= A^dt.	(4.17)
^vt0
Среднюю продолжительность жизни мы получим, умножая t на (4.17) и интегрируя по всем
возможным значениям t от 0 до оо:
00	00
r = t = J tA,e~A'‘dt = у J Axte~A'ld(A,t).
О	о
(4-18)
Учитывая, что J* Aite~Ait d(Ait) — f ze~zdz = I (z = Ait), мы получаем (4.15).
о	о
Отметим, что под знаком интеграла (4.18) стоит произведение продолжительности t
существования частицы в возбужденном состоянии на вероятность (4.17) этого значения t.
Таким образом, т представляет среднее, образованное с помощью вероятности — среднее
,	dNi
вероятное, или математическое ожидание. Отметим также, что в (4.17) берется доля-
NiQ
возбужденных частиц, испустивших фотоны, по отношению к числу возбужденных частиц
в начальный момент времени tQ, тогда как при определении вероятности спонтанного испус-
/ ч	dNi
кания с помощью формулы (4.12) берется доля возбужденных частиц, испустивших
фотоны, по отношению к числу возбужденных частиц в рассматриваемый момент времени t.
1 dNi —a t
При отнесении этих долей к единице времени первая доля равна----= Л,е ‘и убывает
NiQ dt
1 dN> А
со временем, а вторая доля равна - — —— = Лг и постоянна.
Ni dt
Из (4.15) следует, что
Л =	=	(4‘9)
к	Ti
Так как г, — средняя продолжительность существования частицы в возбужденном
состоянии, т. е. среднее время, спустя которое частица испустит фотон, то Л, = —
Ъ
есть среднее число фотонов, испускаемых частицей за единицу времени, если ее
О Оно больше «времени полураспада» Т\/2 возбужденного состояния ^ехр{ —— -J в —
1,443 раза.
88	Глава 4. Вероятности переходов и правила отбора
каждый раз возбуждать вновь сразу после момента испускания фотона. При малых
значениях ъ это может быть очень большим числом. Обычно времена жизни элек-
тронных состояний атомов и молекул с энергиями возбуждения порядка нескольких
электронвольт (испускание в видимой и близкой ультрафиолетовой области) имеют
порядок 10~8 с, что дает Л, = 108 с“\
Необходимо подчеркнуть, что время жизни в общем случае определяет, соглас-
но (4.19), полную вероятность спонтанных переходов с данного верхнего уровня
на все нижние и является характеристикой этого уровня, а не отдельного перехода.
Только в частном случае, когда возможен лишь один спонтанный переход (напри-
мер, с самого нижнего возбужденного уровня Е2 возможен спонтанный переход
только на основной уровень j^i), время жизни есть величина, обратная вероятности
отдельного перехода, и может служить его характеристикой.
Особым является случай, когда вероятности всех спонтанных переходов с дан-
ного возбужденного уровня равны нулю или очень малы (запрещенные переходы,
см. с. 114). Атомная система при отсутствии внешних воздействий может находиться
на таком метастабильном уровне — в метастабильном состоянии — неограниченно
или весьма долгое время (т = оо или очень велико). Метастабильные состояния
играют в ряде случаев важную роль, создавая возможность накопления энергии
возбуждения (см. пример атома ртути, с. 288).
Выше мы рассматривали убыль числа возбужденных частиц только за счет
спонтанных переходов. Однако в реальных условиях возбужденные частицы могут
терять энергию возбуждения также за счет безызлучательных переходов, в частности
частицы газа могут отдавать ее при столкновениях. Если убыль числа Ni за счет
безызлучательных переходов положить равной
-dN[ = CiNidt,	(4.20)
где
1 dNi
С =_________-
1 Ni dt
— вероятность безызлучательных переходов, то полная убыль —dNi числа 7V, будет
определяться уравнением
-dNi = AiNidt + CiNidt = (Д + CiNidt,
откуда получается закон изменения 7V,:
Ni = Moe"(A+C,)i •
Этому закону соответствует время жизни
, _	1	_ 1 Aj	_ Tj _ ъ
Ai 4- Ci	Ai Ai ~i~ Cj 1 4- 7i
Ci
меньшее, чем время жизни г,, в 7, = 1 4- — раз; таким образом, при наличии
Ai
безызлучательных переходов сокращается длительность существования возбужден-
ных состояний, что будет проявляться в уменьшении длительности послесвечения.
Наряду с уменьшением времени жизни происходит и уменьшение числа испускае-
мых фотонов, следовательно, происходит уменьшение интенсивности испускания —
его тушение. Число испускаемых фотонов уменьшается также в 7, раз и равно
N'M =	= -Ni0.	(4.25)
А,- + С, у,-
(4-22)
(4-23)
(4-24)
§4.3. Дипольное излучение
89
Действительно, при отсутствии тушения испустят фотоны — «высветятся» — все возбу-
жденные частицы, а при его наличии «высветится» число частиц, равное
ос	ОС
= / A(Nt dt = AiNi0 [ e-(A<+Ci}t dt = -j—rNio =
J	J	Ai + Ci
0	0
что дает (4.25).
Если ввести для случая оптического возбуждения (см. с. 23) уровня Ei понятие
о квантовом выходе испускания, как об отношении числа испущенных фотонов N-Q
к числу поглощенных фотонов (которому равно число возбужденных атомов Мо), то
^0 А 1
NiQ	Ai 4~ Ci	yi
т. e. квантовый выход уменьшается при тушении в соответствии с уменьшением
длительности.
Отметим, что для метастабильных состояний (Л, = 0 или очень мало) время
жизни (4.24) будет определяться вероятностью безызлучательных переходов, а кван-
товый выход (4.26) будет равен нулю или очень мал (при Л 0 и Д 0;
в предельном случае Д = 0 и будет отсутствовать и поглощение, т. е. оптическое
возбуждение вообще невозможно).
§ 4.3. Дипольное излучение
Вероятности спонтанного испускания и поглощения, связанные между собой
соотношением (4.8), могут быть выражены через величину, характеризующую пе-
реход и определяющуюся свойствами комбинирующих уровней рассматриваемой
атомной системы. Такой величиной является электрический или магнитный момент
перехода — величина, соответствующая, с классической точки зрения, амплитуде
изменения электрического или магнитного момента системы. Как известно, соглас-
но классической электродинамике, испускание и поглощение связаны с изменением
этих моментов во времени. В зависимости от типа изменяющегося момента получа-
ются различные типы испускаемого и поглощаемого излучения, деление на которые
сохраняется и в квантовой теории.
Здесь мы рассмотрим важнейший тип излучения — дипольное излучение (элек-
трическое), связанное с изменением дипольного момента системы.
Мы будем исходить из результатов классической теории излучения и перейдем
от них, на основе принципа соответствия между классической и квантовой теорией,
к вероятностям квантовых переходов.
Согласно классической электродинамике, свободная система электрических
зарядов, движущихся с ускорением, непрерывно теряет энергию в виде излучения.
В простейшем случае колеблющегося заряда потеря энергии в единицу времени
пропорциональна квадрату его ускорения. Разберем этот случай подробнее.
Пусть заряд ±е (е — абсолютная величина заряда) совершает линейные гармо-
нические колебания с амплитудой а и круговой частотой ш = 2ки вокруг положения
равновесия г о (рис. 4.1):
q = a cos (wt 4- р\	(4.27)
где р — начальная фаза. Соответствующий дипольный момент равен
Р = ±eq = ±еа cos (wt -у р) = PQ cos (ivt 4- р)-	(4.28)
90
Глава 4. Вероятности переходов и правила отбора
Энергия излучения осциллятора — полная
энергия излучения, испускаемого при гармониче-
ском колебании заряда во всех направлениях в еди-
ницу времени, —определяется известной формулой
классической теории излучения:
2 d2P 2 _ 2е2 d2q 2
3? ~d?	~ 3? di7
(4-29)
Отметим, что излучение заряда при дипольном мо-
менте (4.28) совпадает с излучением диполя — нейтраль-
ной системы, состоящей из зарядов +е и -е на рассто-
янии г, — при условии, что изменение г происходит
по закону (4.27). Считая для простоты, что колеблется
один из зарядов (рис. 4.1), мы имеем для диполя полный
момент Pr = er = er0 ± eq, отличающийся от момента
Р = ±eq лишь постоянным членом его ег0, а изменения
d2PT d2P
обоих моментов совпадают: -	= -г-.
at1 at1
Подстановка ускорения q = —из1 a cos (wt +	— -u^q (см. (4.27)) и усреднение
по времени дают (среднее значение cos2(o>f + р) равно, как известно, 1/2):
—	2е2о>4	2---77------г е2о>4	2
W = -^j-|a|2cos2(a>t + <р) =	.
(4.30)
Таким образом, энергия излучения осциллятора пропорциональна, согласно клас-
сической теории, четвертой степени частоты и квадрату амплитуды колебаний.
Формула (4.30) дает энергию излучения, испускаемого во всех направлениях. Под углом д
к направлению колебаний в телесном угле dQ (рис. 4.1) излучение равно
__	е2о>4	?	9
dW = —7|a|2sin2t>dfi,	(4.31)
8ТГС3
т. е. пропорционально sin 2d. Излучение классического осциллятора равно нулю в направлении
колебаний и максимально в перпендикулярном направлении.
Интегрирование sin 2д в выражении (4.31) по полному телесному углу дает множитель
sin 2д dQ =
2	8тг
sin и sin д dd — —,
3
о о
что и приводит к формуле (4.30).
Если ввести амплитуду Ро = ±еа колебаний дипольного момента соглас-
но (4.28), то (4.30) запишется в виде
__	о?4	9	1 бтг4 Л ч
РУ =	|Р0|2 =	p4|P0|2.	(4.32)
Зе-3	Зе-3
Выражение (4.32) справедливо не только для одного заряда, колеблющегося
с частотой и, но и для произвольной системы таких зарядов, характеризуемой
дипольным моментом
р = 52e,ri’
(4.33)
§ 4.3. Дипольное излучение
91
где ri — радиус-вектор г-го заряда. Для атома (4.33) сводится к Р = -е	rt (rt — ра-
i
диус-вектор г-го электрона относительно ядра, считаемого неподвижным), а для мо-
лекулы — к Р = е ^xRx ~e^rk (Rx иг* — радиусы-векторы ядер и электронов
А	к
относительно центра тяжести молекулы, a Z\ — порядковые номера ядер).
С точки зрения квантовой теории число испускаемых фотонов при энергии
излучения (4.32) равно
W _ 2тга?
hv 3hc?
16тг4
37г с3
(4-34)
Правильная формула для числа фотонов частоты Vik, испускаемых в единицу
времени при переходе с уровня Ei на уровень Ek, получается, если в (4.34) заме-
нить классическую амплитуду Ро колебаний дипольного момента величиной 2Pik,
где Pik — дипольный момент перехода — характеризует данный переход и зависит
от свойств комбинирующих уровней. Квантовая механика позволяет вычислить эту
величину.
Число фотонов частоты и — Vik, испускаемых свободной системой в единицу
времени (число фотонов на одну возбужденную частицу), согласно (4.2), представля-
ет вероятность Aik спонтанного перехода с уровня Д на уровень Ek. Мы получаем,
заменяя в (4.34) Ро через 2Pt* и приравнивая полученный результат вероятности
перехода:
Aik = = ^1/3|Р,л|2’ (435)
где через Wik обозначена энергия фотонов частоты v = Vik, испускаемых в единицу
времени.
Формула (4.35) является основной формулой, определяющей вероятность спон-
танных переходов.
Самую грубую оценку порядка величины этой вероятности для электронных
переходов мы можем произвести, полагая Pt* = еа, где е — заряд электрона, и взяв
для а значение 1 А = 10-8 см. Подстановка в (4.35) значений постоянных е и h
v	-1
и значения волнового числа — = 25 000 см для фиолетовой границы видимой
с
области спектра (А = 4 000 А) дает для Aik значение
Aik к 1,15- 108 с-1,
(4.36)
т. е. значение порядка 108 с *, что соответствует времени жизни т порядка 108 с
(ср. с. 87).
Дипольный момент перехода представляет с точки зрения квантовой механики амплитуду
матричного элемента дипольного момента, взятого по волновым функциям начального
и конечного состояний, зависящим от времени. Этот матричный элемент равен
J tj)*(ж, 7)Р(я)^.(я, t) dx,
(4.37)
где через х обозначена совокупность координат, от которых зависят волновые функции
и дипольный момент. Представляя волновые функции стационарных состояний в виде
Г	Q
i/>i(x, t) = ^(x) exp < — 2тгг—t
I	h
(	Pfc 1
г/>ь(х, t) = фк(х) exp < -Ini —t >,
I	h	I
(4-38)
92
Глава 4. Вероятности переходов и правила отбора
мы получаем
f - Ек ] Г
ехр
^*(ж)Р(ж)^А.(ж) dxy
(4-39)
т. е. матричный элемент дипольного момента изменяется со временем с частотой v — vik —
Ei — Ек
------- перехода, а его амплитуда равна
h
Pik= / ^(x)P(x)^k(x)dx.
(4.40)
Эта величина — матричный элемент дипольного момента, взятый по волновым функциям
стационарных состояний, — и входит в фо^ лулу (4.35) в том случае, когда комбинирующие
уровни Ei и Ек являются невырожденными. Можно сказать, что классическая амплитуда Ро
дипольного момента заменяется значением дипольного момента, усредненным по начальному
и конечному состояниям.
Следует отметить, что множитель 2, который мы ввели при переходе от Ро к Pik, связан
с тем, что
рпР'Ч> Рпг~'*
Р = Р0 cosM + V) = Р0е--+ ^|-е-
(4.41)
Поэтому квантовая амплитуда Ptfc, на которую в (4.39) множится экспоненциальный фактор
ехр	— ехР {Этггц^} — ехр
(4.42)
PoetV
соответствует не Ро, а —-—, т. е. по абсолютному значению вдвое меньше, чем Ро.
Расчет матричных элементов (4.40) и, следовательно, вероятностей перехода сравнитель-
но прост лишь в случае атома с одним электроном, когда момент (4.33), входящий в (4.40),
сводится к Р — -ег (результаты подобного расчета для атома водорода см. в §6.4). Расчет
для сложных атомов и для молекул хотя в принципе и возможен, но практически представляет
очень большие математические трудности. Можно полагать, что применение электронных
вычислительных машин лишь частично устранит эти трудности, и поэтому большое значение
имеет определение вероятностей перехода опытным путем.
Основная формула (4.35) применима в случае перехода между невырожденными
уровнями. В случае вырожденных уровней Ei и Ek спонтанные переходы ia —* k/3
между отдельными состояниями, соответствующими этим уровням (а = 1, 2, ..., gi
и /3 = 1, 2, ..., дк, где gi и дк — степени вырождения), характеризуются, аналогич-
но (4.35), вероятностями
64тг4 7,
-4га, к(3 — - 1 з |Р/а, fc/?l >	(4-43)
где Pia^k/з — дипольный момент отдельного перехода га —> fc/З. Для переходов между
вырожденными уровнями можно ввести [14] так называемую силу перехода1"1
Bik — 2 l-Pш, fc/?l ,	(4.44)
а,Д
получаемую суммированием |Ршдд|2 по всем вырожденным состояниям, соответ
ствующим как верхнему уровню (суммирование по а), так и нижнему (суммирование
по р). Вероятность спонтанного испускания выражается через 5^ по формуле
647Г4 3Sik 1	647Г4 з, 2	1 V.
Aik ~	7	3h^	~ ~а 52	<4'45>
уг уг a	Уг а р
7> Ее не следует смешивать с силой осциллятора, которую мы рассмотрим в §4.5
§4.3. Дипольное излучение
93
Отсюда для вероятности поглощения получается, согласно (4.8), формула
Qi с
Bki = ------------Ж =
дк 8tt/ii/3
Stt3 Sik _ 1 8тг3
(4.46)
Для вероятности вынужденного испускания это дает (см. (4.7)):
_ 9к _ 8тг3 Sik 1 8тг3 2
Otfc — —&ki — —у-------------- — — > ттт	•
9i 3/i2 gi gi 3h2
(4-47)
В (4.45) и (4.47) Sik делится на степень вырождения gi верхнего уровня, с ко-
торого происходит испускание, спонтанное или вынужденное, в (4.46) Sik делится
на степень вырождения дк нижнего уровня, с которого происходит поглощение.
Таким образом, Sik всегда делится на степень вырождения начального уровня.
Существенно, что сила перехода 5^ дает его характеристику, симметричную от-
носительно комбинирующих уровней, верхнего и нижнего. Для невырожденных
уровней Sik — 1-Pjfcl2, т. е. равно просто квадрату абсолютной величины момента
перехода, (4.45) сводится к (4.35), а (4.46) и (4.47) совпадают, давая
8тг3 7
Bki = Bik = ^\Pik\2.	(4.48)
Входящие в (4.45)-(4.47) величины представляют матричные элементы, взятые
по волновым функциям комбинирующих состояний ia и kfl:
Pia,k0 = J Ф{а(х)р(х)Фк^(х) dx.	(4.49)
Для невырожденных состояний (4.49) сводится к формуле (4.40), справедливой только в этом
случае.
Соотношения (4.45)-(4.48) имеют простой смысл. Так как 52 Aia,kp в (4-45)
Р
представляет полную вероятность спонтанных переходов из состояния ia во все
состояния kfl {fl — 1, 2, ..., дк), то Aik = “ 52 ^52 Да,*/?) равно средней вероятно-
сти спонтанных переходов из состояний ia (а = 1, 2, ..., gfl во все состояния к fl.
Аналогичный результат получается и для вероятностей
Bki —	Bk/3 ia И Bik —	Bia kfh
9к ^Р 9i
где
8тг3 2
Bk/3,ia — Biakp —	1^*», к(з\	(4.50)
— вероятность отдельного вынужденного перехода; Bki — средняя вероятность пере-
ходов из состояний kfl во все состояния ia при поглощении, Вгк — средняя вероят-
ность переходов из состояний ia во все состояния kfl при вынужденном испускании.
Дипольный момент Pia,kp является вектором, характеризующим, согласно на-
глядным представлениям, гармонический осциллятор, который можно сопоставить
данному переходу. Этот осциллятор колеблется вдоль направления Pia,kp с часто-
Ei — Ек
той vik — —~— и с амплитудой, равной абсолютной величине \Pictiк/з\- Через
94
Глава 4. Вероятности переходов и правила отбора
квадраты \Pl(l^kp\2 амплитуд колебаний осцилляторов определяются, согласно фор-
мулам (4.45)-(4.47), вероятности переходов в испускании и в поглощении. В случае
невырожденных уровней переходу i —> к соответствует один вполне определен-
ный осциллятор, в случае вырожденных уровней — совокупность осцилляторов
для отдельных переходов га —► kfl.
Если выбрать определенную прямоугольную систему координат ж, у, z, то век-
тор Pic^kp можно разложить на составляющие (Px)ia,kp (А = #, у, z), и тогда
|Р<О,кРI2 = |(Л)1а,А/з|2 + 1(Р,).а,^|2 + l(P; W2 = Е	(4-51)
Л
Рассмотрение составляющих дипольного момента перехода является существен-
ным, когда имеется выделенное направление. В процессах испускания таким может
являться направление внешнего поля, электрического или магнитного, а в процессах
поглощения — направление электрического вектора падающей электромагнитной
волны. Для молекул дипольный момент перехода будет определенным образом
ориентирован относительно равновесной конфигурации молекулы, и испускание
и поглощение можно представлять как обусловленные осцилляторами, твердо свя-
занными с молекулой; при этом каждому переходу между невырожденными уровня-
ми будет соответствовать свой осциллятор8).
Через составляющие (Рл)ш, кр можно выразить силу перехода 5^. Согласно (4.44)
и (4.51),
^ = ЕЕкл).«,^12.	(4.52)
а,/? А
Составляющие (Рд)^,^ в формулах (4.51) и (4.52) представляют матричные элементы
составляющих Рх дипольного момента Р:
(Рх)ш,1Ф= I tfa(x)Px(x)i/>kl}(x)dx.	(4.53)
Очень важным является частный случай переходов между состояниями, соответ-
ствующими заданным значениям квантовых чисел J и т, определяющих значения
квадрата и проекции момента количества движения (см. § 2.3). Полагая i = J',
а = т и к — J", /3 = т", получим
\Pj'm'.J"m"\ = \(Px)j,m',J"m"\	|(Ру) J'm', J"m" I 4~ l(^z) J'm', J"m" I —
= E j»™»!2	(4-54)
A
И
Sj'j" ~	l^7'm',J"m"|2 — У2 У2 ICP-Oj'm', J"m"|2 =
m'm"	m'm" A	, x
Л	(4.55)
—	2	J"m" I 4“	2	J'm',J"m"\ + E	i2-
m'm"	m'm"	m'm"
8) При оптическом возбуждении молекулы путем поглощения фотона определенной частоты и при по-
следующем испускании возбужденной молекулой фотона другой частоты поглощению и испусканию будут
соответствовать различные осцилляторы; см. подробнее §27.5.
§ 4.3. Дипольное излучение
95
Согласно (4.45)-(4.47), вероятности будут равны (г — J', к — J",	— 2J' + 1,
9k - 2J" + О
64тг4	-j Sj>j"	8тг3 Sj<j»	8тг3 Sj>j»
J J 3hc3	2J1 + 1	’	3h2	2J" + 1	3h2 2J1 +	1 V
Для переходов, соответствующих разным значениям Am — т' - т", отличны
от нуля разные составляющие	в выражении (4.54) (см. §4.8), т. е. различ-
ным переходам J'm' - J"m" можно сопоставить различным образом ориентирован-
ные осцилляторы. Реальный физический смысл это приобретает при наличии внеш-
него магнитного поля, когда происходит расщепление уровней с заданными значе-
ниями f и J" на подуровни, между которыми и происходят переходы (см. § 14.2).
Аналогичным образом для молекул при переходах между разными уровнями Ei
и Ek в выражении (4.48) могут быть отличны от нуля, в координатной системе ж, у, z,
связанной с молекулой, разные составляющие (Ра)ш,*/з (А — ж, у, z). Следователь-
но, и в этом случае различным переходам будут соответствовать осцилляторы,
различающиеся своей ориентацией.
Необходимо отметить, что для свободного атома в силу его сферической сим-
метрии по отношению к ядру (см. с. 64) любые три взаимно перпендикулярные
направления являются равноправными. Поэтому в выражении (4.55) для силы пе-
рехода между двумя уровнями J' и J" все три суммы одинаковы, и мы имеем
~	1(A) J'm', J"m"|2 — ~Sj' J", (4.57)
m',m"	m',m"	m' ,m"
что может быть проверено в конкретных случаях непосредственным вычислени-
ем [134]. Соотношения (4.57) означают, что вероятности переходов, соответствую-
щих, согласно наглядным представлениям, совокупностям осцилляторов, ориенти-
рованных по осям ж, у, z, одинаковы.
Для каждой составляющей дипольного момента отдельного перехода ш —* кр распре-
деление излучения по направлениям при спонтанном испускании определяется формулой,
аналогичной формуле (4.31):
е2о>4	э э
dWia,k/3 = t-^|(Pa).o,H sin 2«?Л dSi,	(4.58)
Z7TC
где — угол между направлением распространения излучения и направлением колебаний
соответствующего осциллятора (Ра)^^.
В случае поглощения вероятность перехода кр —* ш, согласно квантовой теории излу-
чения, будет определяться величиной
8тг3
cos20a,	(4.59)
где — угол между направлением колебаний электрического вектора в падающей электро-
магнитной волне и направлением колебаний осциллятора. Для случая изотропного излучения
усреднение этой величины по всем возможным направлениям в пространстве дает, при учете,
=	(4-60)
где ia — вероятность поглощения для изотропного излучения, соответствующая осцил-
лятору (Pa):Q)^. Для перехода с уровня Ек на уровень Ei получаем суммированием по а
96
Глава 4. Вероятности переходов и правила отбора
и р и делением на gk (ср. с. 93) вероятность поглощения, соответствующего совокупности
составляющих (Рд)1а,*д дипольных моментов отдельных переходов к ft —> ia:
В« =	В^° =	(4.61)
У*	г/fc
а,(}	аЛ
Суммирование по А дает с учетом (4.51) формулу (4.46). При этом для свободного атома
в силу его сферической симметрии имеет место (4.57) и
= В% = B^J, = Х-Ву.у = 1—(4.62)
J J J J J J 3	3 2J" + 1 3h2
§ 4.4. Магнитное дипольное излучение и квадрупольное излучение
Основная формула (4.29) для дипольного излучения является приближенной
и получается, если пренебречь амплитудой а колебаний излучающего заряда или,
иначе говоря, размерами излучающей системы по сравнению с длиной волны.
Для атомов и молекул всегда
А » а.	(4.63)
В частности, для видимой и ультрафиолетовой областей спектра длины волн имеют
порядок тысяч ангстрем, т. е. 10“5 см, тогда как а — порядка ангстрем, т. е. 10“8 см;
а
следовательно, — имеет порядок
А
10"3 =0,001.
Если принять во внимание, что размеры излучающей системы не бесконечно
малы по сравнению с длиной волны, то получаются, помимо рассмотренного на-
ми электрического дипольного излучения, магнитное и электрическое излучения
высших порядков (квадрупольное, октупольное и т. д.). Дипольное излучение соот-
ветствует нулевому приближению теории. В следующем — первом — приближении
к нему добавляется магнитное дипольное излучение и электрическое квадрупольное излу-
чение. Несмотря на то, что они значительно слабее обычного дипольного излучения,
в ряде случаев они играют существенную роль9). С излучениями, соответствующими
следующим приближениям теории и еще более слабыми, в атомной и молеку-
лярной спектроскопии практически не приходится встречаться, и мы не будем их
рассматривать.
Рис. 4.2. Колебания
излучающего заряда
С физической точки зрения нулевое приближение со-
ответствует пренебрежению запаздыванием электромагнитной
волны на протяжении излучающей системы. В этом при-
ближении мы считаем, что излучение движущегося заряда
доходит до рассматриваемой точки с одной и той же фазой
независимо от того, в какой части излучающей системы он на-
ходится. Для системы, размеры которой не бесконечно малы
по сравнению с длиной волны, необходимо учитывать изме-
нение фазы волны — запаздывание. Фаза электромагнитной
волны на большом расстоянии R от центра, вокруг которого
колеблется излучающий заряд (рис. 4.2), равна
( R — q cos д
2тг I ut----------------
\
{ R\ q- cos д , , х
= 2тг I ut-------I + 2тг~---------, (4.64)
\ А / А
Когда дипольное излучение запрещено правилами отбора; см. §4.7.
§ 4.4. Магнитное дипольное излучение и квадрупольное излучение 97
q • cos t?	а
где величина 2тг------, имеющая порядок 2тг—, определяет запаздывание. Представляя
Л	Л
волновой процесс в экспоненциальном виде:
ехр
2тгг I vt -
R - q cos t? \ 1 f (	R\\ f Q cos t?1
------------- I > = exp < 2тгг I vt - — I > exp < 2тгг —-— >,
(4.65)
мы можем разложить второй множитель при условии
а
27Г- < 1
Л
в ряд
,	х	/	\ 2
I q cos t? I	q cos t? 1 / q cos t? \
exp < 2тгг--------- > = 1 4- 2тп------------F - ( 2тгг--------- )
I A J	A 2 \ A /
(4.66)
(4-67)
Постоянный член в этом разложении, т. е. единица, определяет электрическое дипольное
а
излучение, рассмотренное в предыдущем параграфе; член первой степени, порядка 2тг-, дает
магнитное дипольное и электрическое квадрупольное излучения, член второй степени, по-
/ а\2
рядка ^2тг- ) , дает магнитное квадрупольное и электрическое октупольное излучение и т.д.
Вводя понятие о 2/-польном излучении, мы в i-м приближении получаем магнитное 2/-польное
и электрическое 2/+1-польное излучение. Само понятие 2*-поля взято из теории электричества,
в которой вводятся диполь — совокупность 21 = 2 зарядов, положительного и отрицатель-
ного, квадруполь — совокупность двух противоположно направленных диполей (см. с. 99),
т. е. 22 = 4 зарядов, октуполь — совокупность 23 = 8 зарядов и т. д.
Условие (4.66) является уточнением условия (4.63), от которого оно отличается множи-
телем 2тг. Если заменить А на сТ, где с — скорость света, а Т — период колебаний, и учесть,
2тга
что —- имеет порядок скорости v излучающего заряда,
v — q = —2nva cos (licvt 4- у?) =-----------cos (wt 4- <р)
(см. (4.27)), условие (4.66) можно представить в виде
v
- < 1,	(4.68)
т.е. разложение (4.67) есть разложение по степеням отношения скорости движения излучаю-
щего заряда к скорости света.
Магнитное дипольное излучение обусловлено изменением со временем магнит-
ного дипольного момента системы, т. е. обычного магнитного момента (магнитного
диполя)10).
Согласно классической электродинамике, энергия излучения магнитного дипо-
ля определяется формулами, совершенно аналогичными формулам (4.29) и (4.32)
для излучения электрического диполя. В единицу времени во всех направлениях
испускается энергия
Ж<магн) =		(4.69)
Зе3 dt2	'	’
|0) То есть системы, состоящей, с точки зрения формальных элементарных представлений о магнетизме,
из двух магнитных зарядов противоположного знака (полюсов), расположенных на некотором расстоянии
друг от друга.
4 3.1 к. 103
98
Глава 4. Вероятности переходов и правила отбора
Если ввести амплитуду д0 изменения магнитного момента,
Р — До COS (wt + (р),
то средняя энергия магнитного дипольного излучения составит
—;—г 16тг4 41	>2
W<MarH) =	4|	2;
3<г
а соответствующее число испускаемых квантов будет равно
17<магн> 16тг4 31	,2
~ 3h?l/ lMo1 •
(4-70)
(4-71)
(4-72)
(4.73)
Замена д0 удвоенным магнитным моментом перехода, 2p,ik, приводит к выражению
для вероятности спонтанного перехода между невырожденными уровнями Ei и Ек
при магнитном дипольном излучении, аналогичному (4.35):
ТЛ7(магн)	, Л 4
Лмагн) _ Wik	647Г з 2
ik ~ ~ •
Все другие формулы имеют также аналогичный вид, отличаясь лишь заменой Р на д.
Матричные элементы дипольного момента Р заменяются матричными элементами маг-
нитного момента д. Мы увидим в дальнейшем (см. §4.7), что свойства симметрии последних
существенно отличаются от свойств симметрии первых. Это связано с тем, что магнитный
момент является не полярным вектором, как дипольный момент, а аксиальным (ср. с. 66).
Отношение вероятностей магнитного и электрического дипольных излучений
равно
47H)
л!”"’ iw
Легко определить порядок величины этого отношения. Для электронных маг-
нитных моментов pik имеет порядок магнетона Бора, равного, согласно (2.47),
0,93 • 1О“20 эрг/Гс. Считая по-прежнему (см. с. 91), что Pik = еа, где а — 10“8 см,
т. е. = 4,8 • 10“18 ед. СГСЭ, мы получаем:
Лмагн)
-И 4- 10“б.
л(дип)
Aik
(4-74)
(4-75)
Таким образом, магнитное дипольное излучение примерно в миллион раз слабее
обычного электрического дипольного излучения.
р	v
Легко видеть, что отношение — имеет порядок - в соответствии с тем, что в раз-
Р	с
V
ложении (4.67) второй член — порядка - (ср. (4.68)).
с
Действительно, если исходить из наглядных представлений о движении электрона в атоме
/ х	eav
по круговой орбите, то, согласно (2.49), магнитный момент равен ------. Электрический
2с
р	V	V
дипольный момент имеет порядок еа и — — —, т. е. порядка -.
Р	2с	с
”1 Величины, относящиеся к последнему, мы будет обозначать индексом «дип».
§ 4.4. Магнитное дипольное излучение и квадрупольное излучение
99
Напряженности электромагнитных полей магнитного и электрического диполей отно-
сятся как ~ а энергии излучения (пропорциональные квадратам напряженностей)
//i\2	(v\2
и вероятности перехода — как I — ) = I - ) . Так как скорости электронов в атоме —
порядка тысячных долей скорости света, то
с непосредственной оценкой (4.75).
р\2
— порядка миллионных долей в согласии
Согласно наглядным представлениям, магнитное излучение при определенном
переходе связано с магнитными осцилляторами которые, так же как и электри-
ческие осцилляторы, характеризуются определенным направлением и определенной
М
величиной; последняя, однако, в — раз меньше.
Угловое распределение излучения для магнитного осциллятора — магнитного диполя —
такое же, что и для электрического осциллятора — обычного диполя, т. е. определяется
формулой (4.58), в которой (Рд)ш,^ заменено через	Разница состоит лишь в том,
что направления электрического и магнитного векторов в электромагнитной волне меняются
местами (см. рис. 4.3).
Рис. 4.3. Угловое распределение излучения:
а — для электрического диполя; б — для магнитного диполя
Электрическое квадрупольное излуче-
ние обусловлено изменением со временем
квадрупольного момента системы. Как из-
вестно, квадруполем называют совокупность
двух противоположно ориентированных ди-
полей одинаковой величины (рис. 4.4). Ве-
личина квадрупольного момента пропорцио-
нальна произведению заряда на квадрат дли-
ны: для квадруполей, изображенных на ри-
сунке, этот момент равен ez' z" для диполей
с моментом ez', смещенных на расстояние z"
по оси z (случай а), и ez'x’ для таких же ди-
полей, смещенных на расстояние х' по оси х
(случай б).
Для системы зарядов квадрупольный мо-
мент, как можно показать (см. [128], с. 122;
Рис. 4.4. Электрический квадруполь:
а — с моментом ez'z"\
б — с моментом ez'x'
100
Глава 4. Вероятности переходов и правила отбора
1
Qa/}~ 3
Dap 1, характеризуется совокупностью величин
Qxx	= Eed i	fxl-	-rA 3 J’	Qxy	— Qyx	= E i	^yi,
Qyy	= Ee‘l i	[vl -	Я'	Qyz	— Qzy	= E i	
Qzz	= Ee«l i		И)'	Qzx	= Qxz	= E i	
(4-76)
аналогично тому, как дипольный момент характеризуется совокупностью величин
(см. (4.33))
Рх —	Ру ~	Pz ~ ejZj.	(4.77)
i	i	i
Подобно величине квадрата вектора дипольного момента, равной сумме ква-
дратов его составляющих |Р|2 = ^2 1-РдI2	У> z), квадрат квадрупольного
А
момента равен
IQI2 = Е W2’	078)
А,/х
т. е. сумме квадратов всех девяти его составляющих (4.76).
С математической точки зрения квадрупольный момент представляет собой тензор вто-
рого ранга — совокупность 3-3 = 9 составляющих, преобразующихся как произведения
составляющих двух векторов Л. и В. В данном случае тензор является симметричным,
т. е. Qx^ = и число различных составляющих равно 6 (три диагональных составляю-
щих Qxx, Qyy, Qzz и три недиагональных составляющих Qxy = Qyx, Qyz - Qzy, Qzx = Qxz),2).
Величина (4.78) представляет инвариант тензора, не зависящий от поворота осей коорди-
нат х, у, z, подобно тому, как для вектора инвариантом является квадрат его длины.
Энергия квадрупольного излучения, в отличие от энергий электрического и маг-
нитного дипольных излучений, даваемых формулами (4.29) и (4.69), содержит
не вторые, а третьи производные квадрупольного момента, и поэтому при перио-
дическом изменении квадрупольного момента пропорциональна не i/4, a iA Число
испускаемых квантов пропорционально р5, и для вероятности спонтанного перехода
при квадрупольном излучении между невырожденными уровнями Ei и Ek получается
выражение
47й = ^-’№7,
где Qik — квадрупольный момент перехода. Зависимость от и5 вместо зависимости
от I/3 в формулах (4.35) и (4.73) для дипольного и магнитного излучений приводит
к более быстрому убыванию вероятности с уменьшением частоты перехода.
12)Для квадрупольного момента имеется еще дополнительное соотношение Qxx + Qyy + Qzz = 0,
вытекающее из (4.76). Тензор (4.76) можно представить как разность тензора Q'x^ = etajjA •
(xix — Xi, yi, Zi) и тензора
(j 52e»ri)^A/*’ ГДО 6xx = 1 И ^Ад=° (А#Д).
§ 4.4. Магнитное дипольное излучение и квадрупольное излучение
101
Квадрат квадрупольного момента перехода выражается через составляющие
(Qx^)ik этого момента по формуле, аналогичной (4.78):
1^2 = ЕК<2аД*12.
Ар
(4.80)
Величины (Q^)ik представляют собой матричные элементы составляющих тензора (4.76):
V’.’C'O Qx^x) dx.
(4-81)
По своим свойствам симметрии они во многом схожи с матричными элементами
составляющих магнитного момента (см. §4.7).
Так же как и магнитное излучение, квадрупольное излучение много слабее
дипольного. Отношение вероятности квадрупольного излучения к вероятности ди-
польного, согласно (4.79) и (4.35), равно
л<”">	10 \с) |Р„|
гк
В отличие от отношения (4.74), оно зависит от частоты. Для определения порядка
величины отношения (4.82) мы положим = еа2 и Р^ = еа, где а — размер
1	Зтг2
А------------- 10	4
(4.82)
излучающей системы. Тогда, если заменить — на — и положить-« 3, получим
л(квадр) / \ 2
_iL—_ — 7 I _ |
Лдип) - уду
Aik	х 7
При А = 5 000 А = 5 • 10-5 см и а — 1 А = 10-8 см находим
(4.83)
Лквадр)
____________in-?
(4.84)
Лдип)
Aik
т. е. по порядку величины несколько меньше, чем для магнитного излучения
(см. (4.75)). Так как речь идет об оценке порядка отношений вероятности, то можно
грубо считать, что для переходов, соответствующих видимой и ультрафиолетовой
областям спектра, вероятности магнитного и квадрупольного излучений в милли-
он раз меньше вероятностей дипольного излучения. Однако для других областей
^(магн)
спектра это будет уже неверно. Отношение —-—- как не зависящее от длины
Л \ДИП^
^(квадр)
волны, сохранит свое значение порядка 10-6, а отношение — будет изменяться
при неизменных размерах излучающей системы обратно пропорционально квадрату
длины волны. В частности, в области радиочастот оно будет чрезвычайно мало;
при Л — 1 см и а — 10~8 см мы получим отношение порядка 10 .
Следует подчеркнуть, что произведенные оценки справедливы как для от-
ношений вероятностей испускания, так и для отношений пропорциональных им
вероятностей поглощения.
102
Глава 4. Вероятности переходов и правила отбора
Согласно наглядным представлениям, квадрупольному излучению соответству-
ют для определенного перехода совокупности пар осцилляторов с квадруполь-
ными моментами (Qx^ik, ориентированных вдоль оси А и смещенных друг от-
носительно друга вдоль оси д13). Например, составляющей (Qzz)ik соответствует
пара осцилляторов, расположение которых показано на рис. 4.4, а, а составля-
ющей {Qzx)ik — (Qxz)ik — пара осцилляторов, расположение которых показано
на рис. 4.4, б.
Исходя из ориентаций пар осцилляторов, соответствующих различным составляющим
квадрупольного момента, можно определить угловое распределение квадрупольного излучения
для этих составляющих, отличающееся от углового распределения для дипольного излучения
(подробнее см. [2], [108] и [15], с. 180).
В заключение сопоставим вероятности спонтанных дипольных, магнитных
и квадрупольных переходов. Согласно (4.35), (4.73) и (4.79), мы получим, подставляя
численные значения всех постоянных и опуская индексы ink,
Л(дип) = 3 1029f-) |Р|2,
ус/
А(магн) = 3. 1{)29/^\ । |2^ >
ус/
Л(квадр) = 9.1029^\5|q|2
ус/
(С	1 л _1 \
и = ~ = 6 • 10 с ) это дает
л	/
Л(дип) = 2,5 • 10421Р\\	Л(магн) = 2,5 • 1042|д|2,	Л(квадр) = 3 • 105' |Q|2.
Полагая
Р = еа = 5 • 10-18, д = дБ = 10~2° и Q = еа = 5 • 10-26,
получаем
А(лип) « 6 • 107 с-1, Л(магн) « 2,5- 102 с-1, Л(квадр) « 8 с~',
(4.85)
(4.86)
(4-87)
в согласии с произведенными выше оценками.
§ 4.5. Силы осцилляторов
Соответствие, существующее между излучением классического осциллятора
и вероятностями квантовых переходов, позволяет ввести для характеристики пере-
ходов особую величину — силу осциллятора. Через силы осцилляторов могут быть
выражены вероятности переходов, и они же определяют связанную с вероятностью
переходов естественную ширину уровней энергии и спектральных линий, которая
будет рассмотрена в следующем параграфе.
Свободный классический осциллятор непрерывно теряет энергию путем излуче-
ния, и его колебания затухают. Затуханию классического осциллятора определенной
частоты и соответствует вполне определенная вероятность перехода До- Действи-
тельная вероятность перехода А зависит не только от частоты, но и от свойств
|3) Что эквивалентно ориентации вдоль оси д и смещению вдоль оси А, см. рис. 4.4, б (пунктир).
§ 4.5. Силы осцилляторов
103
А
комбинирующих уровней. Силу осциллятора можно ввести как отношение —
действительной вероятности перехода к соответствующей затуханию классического
осциллятора данной частоты.
Рассмотрим это подробнее. Если имеется осциллятор с начальной энергией
1	2 2
/То — dQ,
где ао — начальная амплитуда колебаний, то вследствие потери энергии на излучение
его амплитуда а будет со временем убывать по показательному закону
а = аце 2 ,
(4.88)
(4.89)
(4.90)
(4-91)
где 7о — коэффициент затухания.
Энергия осциллятора в момент времени t будет равна
U = ^тси2а2 = ^тпо;2 аое~7о< — ^ое~7о\
т. е. будет убывать также по показательному закону.
Коэффициент затухания 7о не зависит от начальной амплитуды и начальной
энергии колебаний. Как показывает расчет, для частицы с зарядом е и с массой тпе,
совершающей линейные гармонические колебания, он равен
2е2щ2 8тг2е2р2
7о г	—z	? j
Зтес3 Зтес
т. е. пропорционален квадрату частоты колебаний. В дальнейшем мы всегда бу-
дем сравнивать действительные вероятности перехода с вероятностями переходов
для колеблющегося электрона и под е и те в формуле (4.91) будем подразумевать
заряд и массу электрона. При определенной частоте колебаний v коэффициент
затухания 70 имеет вполне определенное значение. Он имеет размерность, обратную
размерности времени (см. (4.90)), и равен
/ \ 2
7о = 0,22 ( - | с-1 = 2,45 • 10~22и2с~1
\ с )
(4-92)
Для видимой области спектра (А == 5 000 А, —
\	с
70 = 0,88- 108 с-1.
1	-А
- = 20000 см ')
л	/
(4-93)
(4.94)
Формула (4.91) выводится следующим образом. Уменьшение со временем энергии
осциллятора, согласно (4.30), равно
dU — е1 . ,
------ = W =
dt----Зс3
Это можно представить, учитывая (4.90), в виде
d ( 1	2 2\	2 е2 о;2 1	2 2
dt\2 )	3 с3 тпе 2
(4-95)
ИЛИ
dU _
dt 3 с3 те
(4.96)
104
Глава 4. Вероятности переходов и правила отбора
Интегрирование этого уравнения дает
U = иое~Ъ\	(4.97)
где 7о определяется формулой (4.91).
Если в начальный момент времени имелось Nq осцилляторов, то их полная
энергия NqU будет убывать, согласно (4.90), по закону
N0U = NoUoe^1.	(4.98)
Сопоставим этот результат с потерей энергии, по квантовой теории, Nq воз-
бужденными частицами. Для случая, когда имеется лишь один возможный переход
с уровня Е2 на уровень Е\, число Nq возбужденных частиц будет, согласно (4.14),
убывать по закону (N = Ni, Nq = NiQ, A = Ai — A2\)
N = Noe~At,	(4.99)
а их полная энергия Nhv будет уменьшаться по аналогичному закону
Nhv = Nohve~At.	(4.100)
Сравнение (4.100) и (4.98) показывает, что оба закона дают одинаковое убывание
полной энергии со временем, если положить
А = 7о,	(4.101)
и при
Uq = hv	(4.102)
в точности совпадут. Различие классической картины и действительно наблю-
дающихся квантовых процессов состоит в том, что классические осцилляторы
с начальной энергией hv будут терять ее постепенно, все одинаковым образом,
а действительное испускание будет происходить квантовым образом порциями hv,
отдаваемыми целиком разными частицами в различные моменты времени.
Коэффициент затухания 70 с квантовой точки зрения, подтвержденной опытом,
Е2 — Е\
определяет вероятность перехода с данной частотой v — -------. Значение веро-
h
ятности перехода, соответствующее, согласно (4.101), коэффициенту затухания 70
классического осциллятора, мы обозначим через Л о (ср. с. 102). Таким образом,
4) = 7о =
о_2 2 2
о7г е v
Зт€с3
(4.103)
Действительная вероятность Ац. перехода с частотой = v, вообще гово-
ря, отличается от Aq. В частности, для дипольного излучения она определяется
не формулой (4.34), соответствующей коэффициенту затухания 70 = Ло14), а фор-
мулой (4.35), в которой амплитуда Ро дипольного момента заменена дипольным
моментом Pjfc перехода.
14> Полагая в (4.34) |Ро|2 — к«о|2 и определяя 0$ из условия Uq = hv = — = ^mea>2al, получаем
2w3 2 2	2тгй>3е2 hw	_ 2e2w2 _ 8тг2е2р2 _
ЗЛс3 6 °0 ЗЛс3 тгтеш2 Зт€с3 Зтес3
§ 4.5. Силы осцилляторов
105
Определим силу осциллятора для данного перехода как отношение действи-
тельной вероятности перехода к Aq:
fik = ^ = — = ~,	(4.104)
Ло 7о 7о
или
А* = fikAo = fiklo = 1-	(4.105)
При fik = 1 получаем вероятность перехода Aik = Ло = 7о. Величина Ло = 7о
представляет естественную единицу для измерения вероятностей спонтанных пере-
ходов.
Согласно (4.104) (4.105) и (4.103),
Зтес3
= <4106>
и, обратно,
8тг2е2р2
= <4407>
В отличие от Л^ величина является безразмерной.
В численном виде мы получаем, согласно (4.92),
с2
fik = 4,5^Aik = 4,5А2 Aik	(4.108)
и
/^\2	1
Aik = 0,22 -	= 0,22—^fa.	(4.109)
\ C }	Л
Если выбрать излучение с определенной частотой ио и длиной волны Ао = —, то
Ц)
можно выразить (4.108) и (4.109) в соответствующих единицах.
Полагая
i/0 = 6- 1014с-1,	— = 2 - 104 см-1 = 20000см-1,
С
Ао = — = 5 • 10-5 см = 5 000 А,
"о
получим
fik = 1,13 10-8( - ) A,t = l,13 10-8( A) Aik	(4.110)
\ у /	X А0 /
и
я /	2	о / А \ 2
А{к = 0,88 • 10s	- ]	-- 6.88 108 - Aik.	(4.111)
\voj	\A0/
В табл. 4.1 приведены значения вероятностей, соответствующие силам осцил-
лятора от 1 до 10-10, для различных длин волн.
Вероятности переходов измеряют в единицах Ло = 7о как для дипольных пере-
ходов, для которых силы осциллятора имеют наглядный смысл, так и для магнитных
и квадрупольных переходов. Силы осцилляторов для дипольного, магнитного и ква-
друпольного излучений, согласно (4.106) и (4.35), (4.73), (4.79), равны
.(дип) _ 8тг2те .2 .(магн) _ 8тг2те 2 -(квадр) _ 12тг4те 3	2	(4П2)
106
Глава 4. Вероятности переходов и правила отбора
Таблица 4.1
Значения вероятностей для различных сил осциллятора при различных длинах волн
Сила осцил- лятора	Длина волны (см)					
	100	10	1	10'1	10'2	10'3
1	2,2 • 10’5	2,2- 10“3	2,2- 10'1	2,2-10	2,2 • 103	2,2  105
10'1	2,2  10’6	2,2-10-4	2,2 • 10'2	2,2	2,2 • 102	2,2 • 104
10'2	2,2 • 10“7	2,2 • 10“5	2,2 • 10'3	2,2- 10'1	2,2-10	2,2 • 103
10'3	2,2 • 10“8	2,2 • 10“6	2,2 • 10'4	2,2 • 10'2	2,2	2,2- 102
ю*4	2,2-10-9	2,2  Ю'7	2,2 • 10'5	2,2 • 10'3	2,2- 10'1	2,2  10
10'5	2,2-10“’°	2,2- 10“8	2,2 • 10'6	2,2 • 10'4	2,2- 10'2	2,2
ю-6	2,2-10“"	2,2- 10-9	2,2 • 10'7	2,2 • 10'5	2,2- 10'3	2,2-10'1
10'7	2,2- I0’12	2,2- 10"'°	2,2 • 10'8	2,2 • 10'6	2,2 • 10'4	2,2- 10'2
10'8	2,2-10“13	2,2-10'"	2,2 • 10'9	2,2- 10'7	2,2 • 10'5	2,2 • 10'3
10'9	2,2- 10“14	2,2-10'12	2,2-10'10	2,2- 10'8	2,2 • 10'6	2,2 • 10'4
10-'°	2,2- I0’15	2,2- 10'13	2,2-10“"	2,2 • 10'9	2,2 • 10'7	2,2 • 10'5
Сила	Длина волны (см)					
осцил-						
лятора	10“4	5-10'5	10'5	10'6	10'7	10'8
1	2,2  107	0,88 • 108	2,2 • 109	2,2- 10"	2,2 - 1013	2,2-1015
10“'	2,2 - 106	0,88 • 107	2,2-108	2,2- 1О10	2,2- 1012	2,2-1014
10"2	2,2-105	0,88 • 106	2,2-107	2,2 • 109	2,2- 10"	2,2-1013
10'3	2,2 • 104	0,88  105	2,2 • 106	2,2- 108	2,2- 1010	2,2 -1012
10'4	2,2 • 103	0,88 • 104	2,2- 105	2,2 • 107	2,2 • 109	2,2- 10"
10'5	2,2 • 102	0,88 • 103	2,2 • 104	2,2 • 106	2,2 • 108	2,2- Ю10
10'6	2,2- 10	0,88 • 102	2,2 • Ю3	2,2- 105	2,2  107	2,2- 109
ю-7	2,2	0,88- 10	2,2 • 102	2,2 • 104	2,2 • 106	2,2  108
10'8	2,2- 10"'	0,88	2,2 • 10	2,2 • 103	2,2 • 105	2,2 • 107
10'9	2,2 • 10“2	0,88-10'1	2,2	2,2- 102	2,2  104	2,2  106
10’10	2,2 • 10“3	0,88 • 10'2	2,2- 10'1	2,2 • 10	2,2 • 103	2,2  105
^д(магн)
ветствии с отношениями вероятностей —и
(см. с. 98 и 101) имеют
При электронных переходах силы осцилляторов для дипольного излучения полу-
чаются порядка 10" \ для магнитного и квадрупольного излучений они в соот-
^(квадр)
у^(дип)
порядок 10~6-10~8.
Формулы (4.112) применимы для переходов между невырожденными уровнями.
В случае переходов между вырожденными уровнями вместо величин |Р^|2, |д,&|2
и \Qik|2 будут фигурировать силы переходов
= s'r1 = Е 1м„.вд|! " 5Г’' = Е№...«/
а,/3	а,Д
(ср. (4.44)), и надо различать силы осцилляторов для испускания fik, для которых
делится на дг, и силы осцилляторов для поглощения fki, для которых Slk — Ski делится
на gk. Первые считаются отрицательными (/^ < 0), а вторые — положитель-
ными (fki > 0).
Для правильного определения силы осцилляторов для поглощения, с учетом
степени вырождения и знака, мы выразим, согласно (4.106) и (4.8), Вкг через
§4.5. Силы осцилляторов
107
причем будем считать < 0:
с3 gi	с3 8тг2е2р2 #	тге2 gi
&кг ^ivhu3 д^гк	&xhv3 Зтес3 дк^гк	3hm€v gjJ'k
(4.113)
Полагая для поглощения	fki = ~~fik,	(4.114) 9k
получим	ive2 Bki = -	fki	(4.115) 3hmey
и, обратно,	3hmey _ fki =	^-Bki.	(4.116)
Силы осцилляторов для испускания и поглощения выражаются через силу перехода
симметричным образом. Для случая дипольного излучения они равны (см. (4.106),
(4.45) и (4.116), (4.46))
(4.117)
.(дяп) 8?ггте s';""1
Л‘ =
причем знаки сил осцилляторов получаются автоматически при определении частоты
Ei — Ej	Ek — Ei
по формуле (1.2), у = Уц = —-----------; так как Ei > Ek, то = ---------------- < 0
П	ГЬ
Ei — Ek	(магн)
и yki = —-— > 0. Совершенно аналогичный вид имеют формулы для f-k '
и /^агн\ а для /^вадр) и fk*™^ получается лишь другой коэффициент (см. (4.112)).
Для дипольного излучения, обусловленного электрическими переходами, можно
доказать очень важное правило сумм сил осцилляторов [134]. Сумма сил осцилляторов,
соответствующих всем возможным переходам с заданного уровня Ej на другие
уровни Ei, рассчитанная на одну степень свободы электрона, равна единице:
I
(4.118)
При Ei > Ej (поглощение, Ei = Ei, Ej = Ek) fji > 0, при Ei < Ej (испускание,
Ei = Ek, Ej =. Ei) fji < 0. В частности, при переходе с основного уровня мы
получаем
=	(4-119)
I
где все /ц > 0.
С конкретным примером применения правила сумм мы встретимся в гл. 6
при рассмотрении вероятностей переходов для атома водорода (см. с. 184).
Существенно, что равенство сумм сил осцилляторов единице относится к линейно-
му осциллятору, имеющему одну степень свободы. При применении правила сумм (4.118)
необходимо это учитывать. В частности, для электронных переходов в свободном атоме,
соответствующих движению электрона с тремя степенями свободы, вводят, с учетом соотно-
шения (4.57), средние силы осцилляторов
7(лип) ___ £ Длин) т(дип) _________ £ Лдип)
J ik	ik "> J ki 3 J ki >
(4.120)
108
Глава 4. Вероятности переходов и правила отбора
в три раза меньшие полных сил осцилляторов (4.117) и соответствующие одной степени
свободы движения электрона, что следует учитывать при расчете вероятностей перехода
по силам осцилляторов (см. [134], с. 402, и [15], с. 158). В формулах (4.107) и (4.115)
, 7 f	1
при замене f на f = — пропадает множитель -.
Для молекул в случае, когда вероятность электронного перехода данного рода определя-
ется линейными осцилляторами, ориентированными вдоль некоторой оси, что соответствует
одной степени свободы движения электрона, правило сумм можно непосредственно приме-
нять к силам осцилляторов для этих переходов.
Силу осциллятора можно связать с так называемым числом дисперсионных электронов.
В теории дисперсии отличие показателя преломления от единицы определяется суммой
членов, зависящих от частот возможных переходов и пропорциональных произведениям N fji,
где N — число электронов в единице объема, участвующих в дисперсии, a fji — сила
осциллятора для соответствующего перехода частоты
Произведение Nfji определяет число Nji дисперсионных электронов — эффективное
число электронов с частотой колебаний и fji можно определить как отношение числа
дисперсионных электронов к полному числу электронов. Сумма всех чисел дисперсионных
электронов равна
I	I	I
(4.121)
и равенство = 1 означает, что сумма чисел дисперсионных электронов совпадает
i
с полным числом электронов, участвующих в дисперсии.
Когда на каждый атом или молекулу приходится по одному электрону, совершающему,
с классической точки зрения, линейные колебания, то сумма У2 fji — Г Если таких элек-
тронов имеется п, то эта сумма должна равняться п. Отметим, что для свободного атома
в дисперсионные формулы входит средняя сила осциллятора (4.120), а не сила осцилля-
тора, вычисляемая по формуле (4.106) из полной вероятности перехода и соответствующая
колебаниям трех взаимно перпендикулярных линейных осцилляторов.
Числа дисперсионных электронов, а следовательно, силы осцилляторов и вероятности
переходов могут быть определены путем исследования аномальной дисперсии. Разработанный
Рождественским [171] метод крюков в настоящее время является наиболее точным методом
определения вероятностей переходов.
§4.6. Естественная ширина уровней энергии
и спектральных линий
До сих пор мы рассматривали уровни энергии как соответствующие строго
определенным значениям энергии системы Ei, а переходы между ними — как соот-
ветствующие строго определенным разностям энергии Ei — Ej, т. е. строго опреде-
Ei~Ei D -
ленным частотам уц —-------. В действительности каждый уровень энергии харак-
h
теризуется некоторым интервалом Д7?г- энергий — шириной уровня, и соответственно
каждый переход — некоторым интервалом AEij разностей энергии — шириной линии.
Ширина линии Д£^ равна сумме ширин комбинирующих уровней (рис. 4.5)
&Eij = ДД-4-Д^-.	(4.122)
Ширину уровней и ширину линий для покоящейся свободной атомной системы
называют естественной шириной. Она связана только с вероятностями спонтанного
испускания.
Сначала мы оценим порядок величины естественной ширины уровней энергии,
а затем уже разберем вопрос о контуре спектральной линии (о распределении
интенсивности внутри линии) и дадим точное определение естественной ширины.
§4.6. Естественная ширина уровней энергии и спектральных линий
109
Эта оценка может быть произведена на основе
квантовомеханического соотношения неопределен-
ности для времени и энергии.
Если продолжительность существования некото-
рой системы равна Д£, то неопределенность в энергии
этой системы будет ДЕ?, причем
ДЕ-Д^Л.	(4.123)
Величина ДЕ? и представляет ширину уровня, для ко-
торого время жизни т = Ы. Уровень будет беско-
нечно узким только в том случае, если продолжи-
тельность существования данной системы в соответ-
ствующем состоянии будет бесконечно большой; это
будет иметь место для нормального уровня системы,
для которого время жизни бесконечно. Напротив, рис 45 Ширина уровней
ширина возбужденного уровня с малым временем энергии и спектральной линии
жизни будет значительной.
Полагая Д£ = тг, получаем, согласно (4.123), для определенного уровня Ei
&Ei ~
(4.124)
В единицах частоты имеем
Эта формула определяет неопределенность в частоте через посредство времени
жизни. Для обычных времен жизни возбужденных электронных состояний порядка
10~8 с мы получаем
Лр~ 2ГЛ(РС ' ~ 10? с(4126)
что дает при частоте и — 1015 с-1 (А = 3 000А) отношение порядка 10~8,
и
т. е. чрезвычайно малую ширину уровней и спектральных линий.
Существенно, что величина Др не зависит от и. При определенных временах
жизни Ti и Tj комбинирующих уровней Ei и Ej, согласно (4.122) и (4.125),
Дц7 = Дц 4- Д^ ~
1/1	1 \
— I I---)
2тг \ Ti	Tj )
(4.127)
и определяется только этими временами жизни.
В основной формуле (4.125) мы можем выразить время жизни через обратную
ему величину Д — полную вероятность спонтанных переходов с данного уровня Ei
на все более глубокие уровни (см. (4.15)). Это дает:
Дц-^Д,	(4.128)
т. е. ширина уровня пропорциональна полной вероятности спонтанных переходов
с рассматриваемого уровня вниз и имеет тот же порядок величины, что и эта
вероятность15).
15) Если вместо обычной частоты ввести круговую частоту а> = 2тгр, то множитель 1/2тг сократится
и (4.128) запишется в виде
А^г-Лг.	(4.128а)
но
Глава 4. Вероятности переходов и правила отбора
Для спектральной линии, соответствующей переходу с верхнего уровня Ei
на нижний уровень Ej, мы получаем
Дц-7 = Дц + Д^7 ~	+ Aj),	(4.129)
2тг
Если нижний уровень является основным, то для него в силу т = оо А}; = 0 и ширина
линии совпадает с шириной верхнего уровня, с которого происходит переход.
Следует подчеркнуть, что даже в случае, когда Aj = 0, ширина спектральной
линии определяется не вероятностью A,j данного перехода, а полной вероятно-
стью Aj = 52 Aik всех переходов с верхнего уровня, являющегося для них начальным.
к
Только когда переход с верхнего уровня на нижний, для которого Aj = 0, является
единственно возможным, получается
А{ = Ац, ^Vij ~ 2-Л0-.	(4.130)
27Г
Такой случай представляет переход с первого возбужденного уровня Е2 на основной
уровень Е\. Существенно, что в случае (4.130) при одинаковых значениях вероят-
ности переходов ширины линий Др являются одинаковыми. В общем случае это
не имеет места.
Проведенное общее рассмотрение не позволяет определить контур спектраль-
ной линии, обусловленный естественной ее шириной. Это может быть выполнено
при помощи строгих методов квантовой электродинамики. Однако те же результаты
могут быть очень просто получены при классическом рассмотрении вопроса и при-
менении принципа соответствия. При этом определяется и естественная единица
измерения ширин уровней энергии и спектральных линий.
Как мы видели в предыдущем параграфе, классический осциллятор затухает
по показательному закону (4.90) с коэффициентом затухания (4.91). Отклонение
колеблющегося заряда от положения равновесия определяется формулой
Рис. 4.6. Контур спектральной
линии
q = a cos = аое 2 cos 27rz/0Z,	(4.131)
в которой амплитуда колебаний убывает по зако-
ну (4.89). Значение частоты колебаний мы обозна-
чили через Ро-
Затухающее колебание уже не является строго
монохроматическим и может быть представлено
как наложение колебаний различных частот I/,
близких к частоте i/0, с амплитудами, являющи-
мися функциями I/ и убывающими с увеличени-
ем |i/ - i/q|. На рис. 4.6 показано получающееся
распределение амплитуд, причем по оси ординат
отложена не сама амплитуда, а ее квадрат, опреде-
ляющий энергию W(u) излучения соответствую-
щей частоты и, следовательно, распределение ин-
тенсивностей испускаемой спектральной линии —
ее контур. Квадрат а2(и) амплитуды как функция
от частоты выражается формулой
а2^) = а2ы(^У—----------1	(4.132)
' 2 ' 4тг4(г/-1/0)2+ (-f)
где a(i/o) — максимальная амплитуда, соответствующая частоте и —
§ 4.6. Естественная ширина уровней энергии и спектральных линий
111
Формула (4.132) получается разложением координаты (4.131) затухающего осциллятора,
которую можно представить в виде
где
q =
Qq	\
у, о>о = 2тп/0), в интеграл Фурье
eMdu>,
qdt=^r j	dt-
о
«М = - / е-^
2Я J
о
Интегрирование выражения (4.135) дает
/\9°
~ 2тг ,(Wo - cu) -	’
откуда
2
1?И12 = 90
- ^о)2 + (^)
(4.133)
(4.134)
(4.135)
(4.136)
(4.137)
Q
1

что и дает (4.132).
Распределению квадратов амплитуд затухающего осциллятора соответствует
распределение энергии излучения по частотам
w(y) = wVo) (v)2-----------------------7;	(4.138)
V 2 / 47r2(J/ _ j/q)2 + (^)
W(y) уменьшается вдвое по сравнению с ее максимальным значением Ж(^о)
(см. рис. 4.6) при
4tt2(i/-^o)2= (у)2,	(4.139)
т. е. при v-Vq = ±-^-. Величина Ai/0 = 2~ = (часто называемая полушириной)
4тг	4тг 2тг
характеризует ширину испускаемой спектральной линии.
В квантовой теории 70 — Л), т. е. равно вероятности спонтанного перехода
с частотой и при силе осциллятора, равной 1 (см. с. 105), и, таким образом, ширина
спектральной линии равна
М) = у- =	(4.140)
27Г Z7T
в полном согласии с формулой (4.128).
Подстановка значения (4.91) для 70 дает
А^о =
4тге2г/2
ЗтНеС3 ’
(4.141)
т. е. естественная ширина возрастает пропорционально квадрату частоты.
112
Глава 4. Вероятности переходов и правила отбора
Если перейти от шкалы частот к шкале длин волн, то получим, в силу
ДЛ = Д- = -4д^	(4.142)
V VL
значение
4тге2
ДА0=--------j,	(4.143)
Зтес2
которое не зависит от длины волны и является постоянным. Таким образом, со-
гласно классической теории, естественная ширина линии, выраженная в длинах волн,
не зависит от длины, волны.
Следует подчеркнуть, что полученные результаты не находятся в противоречии со сде-
ланными выше выводами о независимости ширины Ai/ спектральной линии от частоты и о ее
неизменности при неизменности вероятности перехода в случае (4.130). Ai/ растет, соглас-
но (4.141), пропорционально квадрату частоты, а АЛ остается, согласно (4.143), постоянным
в класическом случае, т. е. при силе осциллятора, равной 1.
Величина ДЛо очень мала:
ДА0 = 1,16- 10,2см = 0,000116 А.
(4.144)
Так как формула (4.143) определяет постоянство абсолютного значения ширины
ДА0
спектральной линии, то относительная ширина ——- будет изменяться обратно
Л
пропорционально длине волны. Она будет очень малой уже в оптической области
спектра и совершенно ничтожной в радиочастотной области.
Чтобы перейти от классических формул к соответствующим квантовым форму-
лам, надо заменить 7о — Д действительными вероятностями перехода А. В простей-
шем случае, когда рассматривается переход с первого возбужденного на нормальный
уровень, ширины возбужденного уровня и соответствующей спектральной линии
будут одинаковы и равны
Др = — Д| = — /21 Aq,
2тг 2тг
(4.145)
где /21 — сила осциллятора для перехода Е2—*Е\. Контур линии будет определяться
формулой (4.138), в которой 70 = Д заменится величиной 721 = А2\ = /21Д = Л17о-
Однако в общем случае ширина спектральной линии будет определяться не толь-
ко вероятностью Лг; перехода между комбинирующими уровнями Ei и Ej, но будет
зависеть и от ширины обоих комбинирующих уровней в соответствии с форму-
лой (4.127). Полная ширина каждого уровня определяется полной вероятностью
всех спонтанных переходов с данного уровня Ei на все более низкие уровни Ek,
т. е. величиной 7, = Аг\ = ^2 Дь а ширина спектральной линии находится по фор-
k
муле (см. [140], с. 217)
2тгД1/0 =70 =7<+7; =	+	(4.146)
к	к
Контур линии будет определяться формулой (4.138), в которой 70 = Д заменяется
на7у. Вообще говоря,
Щ = У? Aik + 57 Aik > An	(4.147)
к	к
§ 4.7. Правила отбора для простейших видов симметрии	113
Рис. 4.7. Ширина спектральных линии
для переходов между тремя уровнями
т. е. линия будет шире, чем это соответствует вероятности Время жизни возбу-
жденного состояния равно, согласно (4.15),
1 1
52 Aik Aij
к
Знак равенства может стоять лишь в том случае, если с уровня Ei невозможны
переходы на какие-либо уровни Ek < Ei, помимо уровня Ej.
Таким образом, в общем случае
ширина линии больше, а время жизни
меньше, чем это соответствует веро-
ятности перехода между комбинирую-
щими уровнями.
Примером может служить случай
трех уровней Е\, Ei и Ез (рис. 4.7),
для которых велика вероятность пе-
рехода Е2 —> Е\ и малы вероятно-
сти переходов Ез —> Е2 и Ез —> Е\.
Уровень Е\, как основной, есть бес-
конечно узкий, уровень Е2 — широ-
кий (А21 = А2 велико), а уровень Е3 —
узкий (Л32 + А31 = A3 мало). Сильная
линия i>2i будет широкой, а из слабых
линий 1/32 и 1/31 первая будет широ-
кой, а вторая — узкой. Получающаяся
в спектре картина схематически по-
казана в нижней части рис. 4.7. Вре-
мя жизни на уровне Е2 будет мало,
а время жизни на уровне Ез — ве-
лико, причем обеим линиям 1/32 и из\
будет соответствовать одинаковое вре-
1
мя жизни Тз = ------------, меньшее,
1	।	^32	^31	различной ширины
чем — и------.
4*2	>1з1
До сих пор мы рассматривали ширину уровней энергии, связанную со спонтанным ис-
пусканием. Когда на атомную систему действует излучение, то длительность существования
системы в заданном состоянии уменьшается вследствие вынужденных переходов (поглоще-
ния и вынужденного испускания) из этого состояния, что приводит к дополнительному
уширению 7ВЫН уровней энергии. В частности, из-за поглощения основной уровень энергии
перестает быть бесконечно узким. Однако, если только плотности энергии излучения не чрез-
вычайно велики, ширина 7ВЫН мала по сравнению с шириной 7ИСП, определяемой спонтанным
испусканием, и обычно ею можно пренебречь. Другие причины уширения спектральных
линий, приводящие к ширинам, гораздо большим естественной ширины, мы рассмотрим
позже (см. §5.6, 13.4 и 15.4).
§4.7. Правила отбора для простейших видов симметрии
Как мы видели в §4.3 и 4.4, вероятности переходов определяются величинами
электрического или магнитного момента соответствующего перехода: для обычно-
го дипольного излучения — величиной электрического дипольного момента,
114
Глава 4. Вероятности переходов и правила отбора
для квадрупольного и магнитного излучений — соответственно величиной Qik
электрического квадрупольного и величиной p,ik магнитного дипольного моментов.
Однако эти величины отличны от нуля не для всех переходов. Обычно для рас-
сматриваемой атомной системы при данном виде излучения возможна, или, как
говорят, разрешена лишь часть переходов; моменты остальных переходов обращают-
ся в нуль и, следовательно, вероятности этих переходов равны нулю — переходы
являются невозможными, они запрещены. Условия, определяющие, какие переходы
разрешены и какие запрещены, носят название правил отбора. Вид спектров в зна-
чительной степени зависит от правил отбора, которые, сокращая число возможных
переходов, делают спектр более простым и более характерным и играют важную
роль при интерпретации спектров.
Правила отбора связаны, в первую очередь, со свойствами симметрии системы.
Зная симметрию данной системы и типы симметрии ее уровней, можно для данного
вида излучения (дипольного, квадрупольного, магнитного) найти правила отбора,
не производя расчета величин моментов перехода и пользуясь только методами
теории групп. В простейших случаях правила отбора получаются совершенно эле-
ментарно, даже без явного применения теории групп,6).
Для атомной системы, относящейся по своей симметрии к определенной группе,
получаются определенные правила отбора. Эти правила, вообще говоря, различны
для различных видов излучения — дипольного, квадрупольного и магнитного.
Особенно важное значение имеют правила отбора для дипольного излучения,
для которого разрешенным переходам соответствуют большие, по сравнению с ква-
друпольным и магнитным излучениями, вероятности (см. оценки в §4.4). Переходы
в оптической области, запрещенные для дипольного излучения, обычно называют
просто запрещенными переходами, хотя они и могут быть разрешенными (а в неко-
торых случаях обязательно разрешены) для квадрупольного и магнитного излучений.
Учет последних существен именно потому, что в ряде случаев наблюдаются слабые
линии, запрещенные для дипольного излучения и обязанные своему появлению
магнитному или квадрупольному излучениям.
Здесь будут разобраны правила отбора для простейших видов симметрии атом-
ных систем, соответствующих группам второго порядка, когда имеется лишь одна
операция симметрии, отличная от тождественной: отражение i в центре, или отраже-
ние ст в плоскости, или поворот С*2 вокруг оси симметрии второго порядка (т. е. по-
ворот на 180°) — в случае пространственной симметрии, или перестановка Р двух
одинаковых частиц — в случае перестановочной симметрии. В этих случаях, как
было показано выше (с. 74-74), имеются два противоположных по своим свойствам
типа симметрии.
При данной операции симметрии каждая составляющая дипольного момента
(электрического), магнитного момента или квадрупольного момента системы будет
либо сохранять свой знак, либо менять его,7\ Например, при отражении в начале ко-
ординат как центре симметрии дипольный момент системы Р = 52 eiri (см- (4.33))
i
и, следовательно, каждая его составляющая меняют знаки, а при отражении в плос-
кости симметрии перпендикулярной оси z, меняет знак его составляющая
Pz — 52 eizi И сохраняют знаки составляющие Рх — 52 eixi И = 52
16) Однако при этом в неявном виде используются основные положения теории трупп в применении
к свойствам симметрии атомных систем.
17) В случае операций а и — при надлежащем выборе ориентации осей х, у, z прямоугольной
системы координат.
§ 4.7. Правила отбора для простейших видов симметрии
115
Правила отбора зависят от поведения составляющей момента системы при опе-
рации симметрии и от типов симметрии уровней энергии Ei и Ek, переход между
которыми рассматривается: если составляющая не меняет знака при операции
симметрии, то разрешены соответствующие переходы между уровнями одного ти-
па симметрии; в противном случае разрешены соответствующие переходы между
уровнями противоположных типов симметрии.
Эти правила отбора получаются очень просто из рассмотрения свойств моментов перехода
или их составляющих, т. е. величин Pik, pik, Qik или (Ра),-*, (да),ь (Qx)ik Для дипольного,
магнитного и квадрупольного моментов, через которые выражаются вероятности переходов
согласно формулам (4.35), (4.73) и (4.79). Соответствующие величины представляют собой
матричные элементы вида (см., например, (4.40) и (4.81))
Mtk = J tfMifadx,	(4.149)
где М — рассматриваемый момент или его составляющая, а и tpk — волновые функции
состояний с энергией Ei и Ек. Матричный элемент есть постоянная величина, которая
не должна меняться, т. е. должна быть инвариантной, при любых возможных для данной
системы операциях симметрии. Если же матричный элемент меняет знак при операции сим-
метрии, то это означает, что = -Mik, т. е. Mik = 0, а следовательно, переход Ei —► Ек
запрещен. Из инвариантности матричного элемента (4.149) следует, что если М не меняет
знака при операции симметрии, то обе волновые функции должны при этом либо сохранять
знак, либо менять его на обратный, если же, наоборот, М меняет знак, то одна из волновых
функций должна сохранять, а другая менять знак. В первом случае, согласно (3.18), комбини-
руют уровни энергии одного типа симметрии, во втором случае — противоположных типов
симметрии, что и доказывает сформулированные правила отбора.
Поведение составляющих дипольного, магнитного и квадрупольного моментов при опе-
рациях симметрии легко определить, если учесть, что составляющие дипольного момента Рх,
Ру, Pz ведут себя, как координаты х, у, z\ составляющие квадрупольного момента Qxx,
Qyy, Qzz, Qxy, Qyz, Qzx — как произведения координат x2, у2, z2, xy, yz, zx (cm. (4.76))
и составляющие магнитного момента рх, ру, pz — как произведения координат yz, zx и ху.
Последнее вытекает из того, что магнитный момент пропорционален механическому моменту,
имеющему составляющие типа
Мх — m(yz - zy), Му = m{zx - xz) и Mz = т(ху - ух)
(т — масса частицы) 18\
Отражение в центре равносильно преобразованию координат
х =-х, у = -у, z — ~z,	(4.150)
при котором все составляющие дипольного момента меняют знак, а все составляющие
квадрупольного и магнитного моментов сохраняют его.
При отражении в плоскости симметрии, перпендикулярной оси z,
х = х, у=у, z=-z,	(4.151)
следовательно, сохраняют знак Рх, Ру, Qxx, Qyy, Qzz, Qxy, Mz и меняют его Pz, Qxz, Qyz,
Mx, My.
При повороте вокруг оси симметрии второго порядка, совпадающей с осью z, наоборот,
х = -х, у = -у, z = z,	(4.152)
так что сохраняют знак Pz, Qxx, Qyy, Qzz, Qxy, Mz и меняют его Px, Py, Qxz, Qyz, Mx, My.
В отличие от случаев отражения (4.150) и (4.151), при поворотах (4.152) векторы Рид ведут
себя одинаковым образом.
18) Механический момент есть аксиальный вектор или, иначе говоря, антисимметрический тензор
второго ранга с составляющими Myz = -Mzy, Mzx = -Mxz, Mxy = -Myx, которые мы записали,
как Мх, Му, Mz.
116
Глава 4. Вероятности переходов и правила отбора
Таблица 4.2
Поведение составляющих моментов для простейших пространственных групп
Группа	Операция симметрии	Поведение составляющих											
		Рх	Ру	Pz	Дх	Дг/	Дг	Qxx	Qyy	Qzz	Qyz	Qzx	Qxi/
Отражение в цен- тре симметрии (инверсия), Ci	i	-			+			+					
Отражение в плоскости симметрии, Cs	<Г<*>	-	+	+	+	-	-	+			+	-	-
	<Г<»>	+	-	+	-	+	-	+			-	+	-
		+	+	-	-	-	+	+			-	-	+
Поворот на 180° вокруг оси симметрии, С2	С(2Х)	+	-	-	+	-	-	+			+	-	-
	г(у) с2	-	+	-	-	+	-	+			-	+	-
	с'г)	-	-	+	-	-	+	+			-	-	+
При перестановках одинаковых частиц все моменты остаются неизменными, поскольку
зависят одинаковым образом от координат таких частиц (см., например, (4.33) и (4.76)).
В табл. 4.2 показано поведение составляющих дипольного, магнитного и ква-
друпольного моментов при отражениях в центре и в плоскости симметрии и при по-
вороте на 180° вокруг оси второго порядка. В тех случаях, когда в таблице стоит знак
плюс, комбинируют состояния одинаковой симметрии, когда стоит знак минус, —
противоположной симметрии.
Очень важным является правило отбора для группы отражения в центре —
для инверсии. Так как дипольный момент Р при инверсии г меняет знак, а маг-
нитный момент р и квадрупольный момент Q не меняют его, то при дипольном
излучении четные уровни комбинируют с нечетными, а при магнитном и квадруполь-
ном излучениях — четные с четными и нечетные с нечетными. Введя обозначения g
ддя четных состояний и и для нечетных19), это можно записать в виде:
дипольное излучение	g <—> и	(4.153)
магнитное излучение 1	{А
}g<—'	—fU	(4.154)
квадрупольное излучение J и	v	'
Приведенное правило отбора является альтернативным', переходы, разрешенные
для дипольного излучения, запрещены для магнитного и квадрупольного излуче-
ний, и наоборот — получается альтернативный запрет. Деление уровней энергии
на четные и нечетные имеет место для всех атомов, так как они всегда имеют
центр симметрии — ядро (см. с. 64), и поэтому для атомов магнитное и квадру-
польное излучения получаются именно тогда, когда дипольное излучение запрещено
(для запрещенных переходов). То же самое справедливо и для молекул, равновесная
конфигурация которых имеет центр симметрии.
В случае группы перестановок одинаковых частиц все моменты остаются неиз-
менными, поэтому симметричные уровни комбинируют с симметричными, а анти-
симметричные с антисимметричными — симметрия при переходе всегда сохраняется.
19) От немецкого «gerade» (четный) и «ungerade» (нечетный).
§ 4.8. Правила отбора для момента количества движения и его проекции 117
Мы имеем:
s<—> s,	а<—> а,	(4.155)
где s — симметричные, а а — антисимметричные уровни.
Как мы видели в § 3.3, полные волновые функции системы в целом являются, при на-
личии одинаковых частиц, либо симметричными, либо антисимметричными по отношению
к перестановке частиц (в зависимости от того, имеют ли частицы целый или полуцелый спин),
и в этом случае правила отбора являются тривиальными. Однако отдельные сомножители,
на которые разбивается волновая функция, в ряде случаев (например, когда ее можно прибли-
женно представить в виде произведения функции только от пространственных на функцию
только от спиновых координат) могут быть как симметричными, так и антисимметричными,
и тогда существенны правила отбора (4.153).
Мы не будем здесь останавливаться на правилах отбора для конечных точечных
групп порядка выше второго. Этот вопрос будет разобран в гл. 23.
§ 4.8. Правила отбора для момента
количества движения и его проекции
Очень важное значение для спектроскопии имеют правила отбора для квантовых
чисел J и т, определяющих величину момента количества движения и его проекции.
Эти правила связаны со сферической симметрией (трехмерная группа вращений)
и с аксиальной симметрией (группа вращений вокруг оси) рассматриваемой системы.
Для дипольного и магнитного излучений правила отбора одинаковы и имеют вид
A J = О, ±1	(4.156)
и
Ат = 0, ±1,	(4.157)
т. е. как J, так и т могут изменяться на нуль или на ±1.
Для квадрупольного излучения правила отбора отличаются от (4.156) и (4.157) тем,
что возможны также изменения J и т на ±2, и имеют вид:
AJ = 0, ±1, ±2	(4.158)
и
Ат = 0, ±1, ±2.	(4.159)
Правила отбора (4.156)-(4.159) соответствуют закону сохранения момента ко-
личества движения. При дипольных и магнитных переходах происходит испускание
или поглощение фотона с моментом, равным 1, а при квадрупольных переходах —
с моментом, равным 2. В силу упомянутого закона для поглощения имеем J\ +1 = J2
и для испускания J] — J2+I, где J] и J2 — начальный и конечный моменты
атомной системы, а I — момент фотона. Значения AJ = 0, ±1 и AJ = 0, ±1, ±2
зависят от взаимной ориентации моментов системы и момента фотона (рис. 4.8).
Из этих наглядных представлений сразу вытекает, что имеются дополнительные
правила запрета:
дипольное
и магнитное
излучения
квадрупольное
излучение
запрещены
J = 1/2 J = »/2 >
J =	> J= 1
z
запрещены
(4.160)
(4.161)
J = —>J = 0
118
Глава 4. Вероятности переходов и правила отбора
Рис. 4.8. Изменение момента количества движения
при различных переходах:
а — при дипольных и магнитных переходах;
б — при квадрупольных переходах
Действительно, в случае (4.160) изменение J\ — J2 момента системы при пере-
ходе равно нулю, а в случае (4.161) — нулю или единице, что делает невозможным
испускание или поглощение фотона с моментом 1 или 2.
Можно показать в общем виде [141], что 2/-польное излучение (см. с. 97) обладает
моментом количества движения, равным Z, причем независимо от того, является ли это излу-
чение электрическим или магнитным 20\ Отсюда следует, что момент равен 1 для дипольного
(электрического и магнитного) излучения (I = 1) и 2 для квадрупольного излучения (1 = 2).
Существенно, что при различных изменениях магнитного квантового числа т
ОТЛИЧНЫ ОТ нуля различные составляющие (P\)j'm',j"m", (px)j'm',J"m" И (Qx)j'm't J"m"
моментов перехода, т. е. различным Дт = т! - т" соответствуют, согласно нагляд-
ным представлениям, различным образом ориентированные осцилляторы. В част-
ности, для дипольного и магнитного излучений переходам Дт — 0 соответствуют
осцилляторы, ориентированные по выделенному направлению z((Pz)j'm? / 0,
(Pz)j'm,j"m # О), а переходам Дт = ±1 — осцилляторы, ориентированные перпен-
дикулярно этому направлению ((Pz)j'm,j'm±i#0, (px)j' /0) и ((Py)j-mij-m±1/o,
5^0). Это определяет поляризацию излучения. При Лт = 0 получается
линейная поляризация вдоль оси z, а при Дт — ±1, как можно показать, — круговая
поляризация в плоскости ху.
Правила отбора для квантовых чисел J и т и поляризацию соответствующего излучения
можно найти, рассматривая инвариантность составляющих матричных элементов вектора
(в случае дипольного и магнитного излучений) и составляющих матричных элементов тен-
зора (в случае квадрупольного излучения) по отношению к операциям симметрии группы
трехмерных вращений и группы вращений вокруг оси. При этом отличие вектора магнит-
ного момента р как аксиального от полярного вектора дипольного момента Р является
несущественным, оно проявляется только при операциях отражения (ср. табл. 4.2).
20) Электрическое и магнитное излучения отличаются четностью.
§ 4.8. Правила отбора для момента количества движения и его проекции 119
Матричные элементы для составляющих Ах вектора А имеют вид (ср. (4.53), i = J',
а = т', k = J", р = т").

J	dx,
(4.162)
а для составляющих TXfl тензора — вид
— I IpjimiTX^1pj'iт" dx.
(4.163)
Рассмотрим сначала поведение матричных элементов при операциях поворота вокруг
оси. Волновые функции при повороте на угол t/, согласно (3.39) 2|\ преобразуются по зако-
ну
= e~tm 1
J
Составляющая Az вектора по оси z при повороте не меняется, и мы получаем
CM/W./W = [	= f	e'{m ~т"*' dx
J	J	(4.165)
Из инвариантности матричного элемента следует, что
= j,	(4 д66)
откуда
т=т" для Az..	(4.167)
Этот же результат получится для составляющей Tzz тензора, преобразующейся как z2.
Другие составляющие Ах и Ау вектора и остальные составляющие тензора будут преобра-
зовываться не сами в себя, а более сложным образом, в соответствии с законом (3.37)
преобразования координат (где ахх = ауу = cos 92, -аух — аху = sin 92). Однако можно соста-
вить из них линейные комбинации, преобразующиеся, с точностью до множителя, сами в себя.
Такими комбинациями являются Ах ± iAy лля вектора и Тхх + Туу, Txz ± iTyz, Тхх - Туу ± гТху
для тензора. Они преобразуются по закону:
А!х ± iAy = Ах cos 921 -|- Ау sin у>\ ± i(-Ax sin 4- Ау cos 921) =
(4.168)
= AJcos^i =F i sin 920 ± iA^cos^i =F i sin = (A^ ± iAy) eWl,
Txx + Tyy = (Txx + Tyy) • 1,	(4.169)
T'z ± «X, = (Txz ± iTyz) e^',	(4.170)
± iTxy = (Txx - Tyy ± iTxy) e’2**’1.	(4.171)
При поворотах соответствующие матричные элементы будут умножаться на экспоненты
et(m -тп , €i(m -m Tl)^i и ег(т -т	отдичные от нуля лишь при т> _ т" — (),	_ т" — ± ,
т' - т" = ±2.
Окончательно мы получаем для составляющих вектора
/	//
т = т
f	Ч \ л
т = т ± 1
для
для
Аг
Ах i iAy
(4-172)
21) Мы рассматривали закон преобразования для орбитального момента; в общем случае любого
механического момента закон преобразования имеет тот же вид.
120
Глава 4. Вероятности переходов и правила отбора
для составляющих тензора
т	= т”	для	Tzz	и Тхх 4- Туу22\	'
тп	= тп” ± 1	для	Txz	± iTyz,	>
тп	= m ± 2	для	Тхх	- Туу ± iTxy.
(4.173)
Таким образом, мы получили правила отбора (4.157) и (4.159) и, более того, определили,
какие именно составляющие отличны от нуля при данном изменении магнитного кванто-
вого числа. Иначе говоря, мы нашли, какие именно осцилляторы соответствуют переходам
с различными значениями Am. Это дает нам поляризацию рассматриваемого излучения.
Например, в случае (4.172), т. е для дипольного и магнитного излучений, правилу отбора
Лги — тп1 - тп” = 0 соответствует линейный осциллятор, ориентированный вдоль оси z, а пра-
вилу отбора Ат = тп' - тп” = ±1 — совокупность двух одинаковых линейных осцилляторов,
7Г
ориентированных по осям х и у и колеблющихся с разностью фаз ± —, что дает враще-
ние по кругу вокруг оси z23\ Излучение в первом случае будет линейно поляризованным,
а во втором случае — поляризованным по кругу.
Сложнее закон преобразования волновых функции при операциях трехмерной группы
вращения. Волновые функции преобразуются совместно (см. с. 81), образуя неприводи-
мое представление Dj< размерности 2J' 4- 1; волновые функции также преобразуются
совместно, образуя неприводимое представление Dj„ размерности 2J” 4- 124\ Три составля-
ющие Ах (Л = ж, у, z) вектора А будут также преобразовываться согласно неприводимому
представлению группы вращения, а именно — согласно трехмерному представлению D],
Аналогично пять независимых составляющих тензора будут преобразовываться согласно не-
приводимому пятимерному представлению D2 25 26\
Матричные элементы (4.162) будут преобразовываться согласно прямому произведению
(см. с. 81) представлений Dj>, D{ и Dj", а матричные элементы (4.163) — по произведению
представлений Dj>, D2 и Dj<, т. е. согласно Dj> х D\ х Dj« и Dj> х D2x Dj«.
Можно показать (см., например, [55], т. II, с. 69), что матричные элементы будут отличны
от нуля, лишь если тройное прямое произведение, согласно которому они преобразуются
для рассматриваемого перехода, содержит тождественное представление Dq. Разлагая прямые
произведения Dj< х D{ и Dj< х D2 согласно (3.52), получим26)
Djt х D] — Dj>+\ 4- Dji 4- Dj'-x
(4.174)
и
Dj< x D2 — Dji+2 4-	4- Dji 4- Dji_\ 4- Dj<~2.	(4.175)
Тождественное представление Z>0 может получиться при перемножении двух неприводи-
мых представлений, только если они одинаковы (ср. (3.52), только при = J2 мы получим
J =	- J2 = 0; во всех других случаях (Ji / J2) значение нуль невозможно). Отсюда
вытекает, что в произведении
(Dji х Z>|) х Djn — (Dji+\ 4- Dji 4- Dj>_]) x Dju
тождественное представление получится лишь в случаях J” = J' 4- 1, J” = J' и J” = J' — 1,
т. е. мы получаем правило отбора (4.156).
22) Для квадрупольного момента, согласно условию Тхх 4- Туу 4- Tzz — 0 (см. примечание на с. 100,
Тур = Qxph мы имеем Тхх 4- Туу = -TZZ1 и тп' = тп” соответствует лишь одной составляющей.
23) В силу симметрии |AJ = |Ау\ = Ао и для гармонического колебания мы имеем по оси х
колебание Aqc1^1 и по оси у колебание :Аое,<л = Аце^ш1+2\ что и соответствует вращению по кругу
вокруг оси z.
24^ Представление В*,, образованное сопряженными волновыми функциями, совпадает с представле-
нием Dji (их характеры одинаковы).
25) Это будет иметь место при Тхх 4- Туу 4- Tzz - 0. Если сумма Тхх 4- Туу 4- Tzz не равна нулю, то она
является инвариантом тензора и преобразуется согласно одномерному тождественному представлению Dq.
26> Перемножать неприводимые представления можно в любой последовательности.
§ 4.8. Правила отбора для момента количества движения и его проекции 121
Аналогичным образом получается и правило отбора (4.158). Легко видеть, что дополни-
тельные правила запрета (4.160) и (4.161) вытекают из того, что (Z>0 х D}) х Dq = D} х Dq —
D\ / Dq, (D{/2 x D2) x D\f2 = -Ь Z>3/2) x = D3 4- 2D2 4- и т.д.
Метод вывода правил отбора путем разложения тройного прямого произведения пред-
ставлений, согласно которым преобразуются волновые функциирассматриваемых уровней
и составляющие моментов, является общим и может применяться во всех случаях. Для невы-
рожденных уровней и для составляющих моментов, преобразующихся сами в себя, его при-
менение сводится к исследованию инвариантности одного матричного элемента типа (4.149),
поскольку тройное прямое произведение трех одномерных представлений есть произведение
трех множителей, на которые при операциях симметрии умножаются фк, М. Примерами
этого являются выводы правил отбора (4.153), (4.154) и (4.172), (4.173).
ГЛАВА 5
ИНТЕНСИВНОСТИ В СПЕКТРАХ
§5.1. Мощности испускания и поглощения
и заселенности уровней
Основной экспериментальной характеристикой спектров атомов и молекул, на-
ряду с частотами спектральных линий и полос, являются интенсивности. Чаще всего
измеряются относительные интенсивности различных полос и линий, распределе-
ние интенсивностей в сплошном фоне, в полосах и внутри спектральных линий
(контуры полос и линий).
Интенсивности в спектрах испускания непосредственно связаны с энергией,
испускаемой возбужденными частицами в источниках излучения, интенсивности
в спектрах поглощения связаны с коэффициентами поглощения исследуемого ве-
щества, которые, в свою очередь, зависят от энергии, поглощаемой частицами этого
вещества.
Энергия излучения, испускаемого и поглощаемого частицами в виде фотонов
различной частоты, и соответствующие интенсивности в спектрах испускания и по-
глощения зависят от вероятностей переходов и от заселенностей уровней, начальных
для этих переходов (см. гл. 1).
Число процессов испускания и поглощения в заданном объеме в единицу
времени определяется формулами, приведенными в §4.1. Согласно (4.1), (4.3)
и (4.5) для спонтанного испускания, поглощения и вынужденного испускания чйсла
rz(cn) гх(пОГл) гх(вын)
соответствующих процессов Zik , Zki и Zik равны произведениям вероятностей
переходов Д*, Bkip(y) и Bikp(y) на заселенности уровней. Мы в дальнейшем
будем рассчитывать число процессов и энергию испускаемого и поглощаемого
излучения на единицу объема, и поэтому заселенности уровней будем относить
также к единице объема. Обозначая чйсла частиц в единице объема на верхнем
уровне Ei и на нижнем уровне Ек ~ заселенности этих уровней — через п, и пк,
мы можем записать (4.1), (4.3) и (4.5) в виде
4СП) = Aikni, Z{™™} = Bkip(v)nk, = Bikp(u)m. (5.1)
Мощности испускания и поглощения — энергии, испускаемые и поглощаемые
в единице объема в единицу времени, — мы получим, умножая числа (5.1) на энергию
фотона hv = Ei - Ек:
и,^п> - hvAikm, и£огл) = hvBkip(v)nk, 4ЫН) = hvBitp^m. (5.2)
г-1	тг(сп)	гг(погл)
Здесь Utk — мощность спонтанного испускания, Uki ' — мощность поглощения
и — мощность вынужденного испускания.
В силу того, что вынужденное испускание фотонов происходит в направлении
распространения падающего излучения той же частоты при сохранении поляризации
§5.1. Мощности испускания и поглощения и заселенности уровней
123
(см. с. 85), его роль сводится к тому, что фактически убыль числа фотонов и мощность
поглощения оказываются меньше, чем Я^огл^ и Ц*"огл\ Поглощение, наблюдающееся
на опыте, всегда является разностью собственно поглощения и вынужденного
испускания, т. е. результатом обоих вынужденных переходов — переходов с нижнего
уровня Ek на верхний уровень Ei и переходов с верхнего уровня Ei на нижний
уровень Ек. Убыль 7^ОГЛ^ числа фотонов в результате вынужденных переходов равна
= z<""’ - z‘r> =	(5.3)
Разность nkBki ~ niBik в (5.3), согласно (4.7), можно представить в виде
(	Tlfi Bjk	(	Tl>i Qk	/ \
nkBki - mBik = nkBki 1 - —	= nkBki 1 - — - ,	(5.4)
\	nk Bki /	\	flk pi /
и, учитывая, что
<ГЛ)' =	- СИ) = hv(nkBki - niBik)p(u),
мы получаем
^•огл)'=p(v)nkBki (i -	= 4огл) (i - Y
X nk 9г /	\ пк Pi /
(поглу = с;(погл)Л _ П£М	(5 5)
\ пк Pi )
Таким образом, из-за вынужденного испускания реально происходит относи-
щ Рк
тельное уменьшение поглощения, равное-------.В дальнейшем нас будут интересо-
пк Pi
вать именно величины, полученные путем приведения к реальным условиям погло-
щения, — приведенные величины, которые мы обозначаем штрихом: Я^огл^ — приве-
денное число поглощенных фотонов и и^огл^ — приведенная мощность поглощения.
Заселенности п, и пк, входящие в (5.1)—(5.5), зависят от распределения частиц
по уровням энергии. Заселенность п7 заданного уровня энергии Ej пропорциональна
общему числу по частиц в единице объема и числу pj состояний с заданной энергией,
т.е. степени вырождения (статистическому весу) этого уровня энергии^. Поэтому
nj можно представить в виде
п, = gjiwpj,	(5.6)
где
1 п,
= —-
Pj По
— доля всех частиц, находящихся в каждом из состояний с энергией Ej, <pj — функция
распределения частиц по дискретным состояниям^. Для отдельной частицы <pj дает
вероятность ее нахождения в каждом из состояний с энергией Ej, a pjipj —
вероятность ее нахождения на pj-кратно вырожденном уровне Ej.
Как правило, заселенность всех вырожденных состояний с энергией Ej одинакова.
У Случая распределения частиц по состояниям непрерывного энергетического спектра (см. с. 16) мы
рассматривать не будем. Нетрудно написать, как это обычно делается в статистической физике, функцию
распределения и для него, введя в качестве непрерывно меняющихся параметров энергию или другие
переменные.
124
Глава 5. Интенсивности в спектрах
Общее число частиц равно
»о = 52 П3 = га»52 9^’	(5-8)
}	j
откуда
52^ = L	(5-9>
j
Формула (5.9) представляет очевидное условие, что сумма вероятностей нахождения
частицы во всех возможных квантовых состояниях равна единице.
Понятие о функции распределения, как определяющей вероятности нахождения си-
стемы в различных состояниях, применимо и к конденсированным системам (например,
к кристаллам), когда уже нельзя говорить о реальном числе систем в заданном состоянии
и сохраняет свой смысл лишь понятие о числе систем в заданном состоянии для воображаемого
статистического ансамбля.
Заселенности уровней и вид функции распределения зависят прежде всего
от того, находится ли вещество в состоянии термодинамического равновесия. В тех
случаях, когда термодинамическое равновесие нарушается, существенно, как про-
исходит это нарушение и какие факторы влияют на заселенность уровней. Такими
факторами являются условия возбуждения уровней энергии и разного рода взаимо-
действия между частицами.
Мы рассмотрим подробнее заселенность уровней при наличии термодинамиче-
ского равновесия, когда заселенность полностью определяется температурой вещества.
Это послужит нам основой для разбора интенсивностей в спектрах испускания
и поглощения как при наличии равновесия, так и при его нарушениях.
Для вещества, находящегося в состоянии термодинамического равновесия, рас-
пределение частиц по уровням является вполне определенным и дается законом
Максвелла—Больцмана. Этот закон можно для дискретных уровней Ej записать
в виде
nj = gjTtoAe kT,	(5.10)
где А — одинаковый для всех уровней множитель, зависящий от абсолютной
температуры Т.
Формула (5.10) представляет собой частный случай формулы (5.6), когда
Ej
Pj = Ae~kT.	(5.11)
Согласно закону (5.10), заселенность уровня nj пропорциональна общему числу
частиц по, статистическому весу gj уровня и, что самое существенное и характеризует
наличие равновесия, — показательному множителю (экспоненте) e~Ej^kT.
Множитель А можно найти, если просуммировать (5.11) по всем уровням
энергии и учесть условие (5.9). Мы имеем
52 ям = 52	= А 52	= ь
3	3	3
откуда
е
з
§5.1. Мощности испускания и поглощения и заселенности уровней
125
где Z — статистическая сумма (сумма по состояниям),
з
которую можно также представить в виде
Е^	Е^	Еу
Z = д\е~^ + д2е~^ + д2е~^ + ...=
(	92	е2~е\	93 ^з--5!	\	_£1 9i Ej~E[
= д\е w (1 Н-----е Н---------е & +... ) = д\е & У —е ,
v 9\	9\	7	* 9\
(5.13)
(5.14)
выделив множитель, зависящий от характеристик основного уровня энергии Е\.
Закон (5.10) определяет абсолютную заселенность уровня Ej при наличии термоди-
намического равновесия. От абсолютной заселенности легко перейти к относительной
заселенности. Для двух уровней Ej и Ek отношение заселенностей, согласно (5.10),
равно
п,	q-j Ej~Ek
— — ~le кт .	(5.15)
пк 9к
Оно не зависит от общего числа частиц и от значения множителя А и определяется,
9j
с точностью до множителя — (т. е. отношения статистических весов рассматри-
вал
ваемых уровней), отношением разности Ej — Ek энергий двух рассматриваемых
уровней к тепловой энергии кТ, где Т — абсолютная температура, а к — постоянная
Больцмана.
Заселенность уровня Ej по отношению к основному уровню Е\, согласно (5.15),
будет равна
=	(5.16)
П\ 9\
откуда
- Ej~E\
nj — —ще .	(5.17)
9\
Формула (5.17) определяет абсолютную заселенность уровня Ej, выраженную через
заселенность п\ основного уровня. В этой формуле п\ зависит от температуры. Эту
зависимость легко найти, если учесть, что, согласно (5.10) и (5.12), П| = д\пое~Е^кт j,
и подставить выражение (5.14) для Z:
__	п0
П1 — (Й Ey-Ei (ft Е3-Ё,
1 +	+ ш е—V1 +. . .
д\ д\
п0
п •	Е,-Е\ *
j 9\
(5.18)
Формула (5.17) тогда принимает вид
Ej-E\	Ej-Ei
_ gj	пое йг~	_ gj noe~ №
nj ~ „ q2 bj-b, n-,	b,-b,	~ ~ л- B,-Bt 
5i	j g\
(5-19)
В формулах для заселенности уровней энергии, как абсолютной (см. (5.17)),
так и относительной (см. (5.15) и (5.16)), показательный множитель различным
126
Глава 5. Интенсивности в спектрах
образом зависит от температуры, смотря по тому, мала или велика разность энергии
А В1 = Ej - Ek по сравнению с кТ. Если мало по сравнению с кТ, т. е.
ЛЕ
—«1,	(5.20)
n>-L
то экспонента близка к единице, и приближенно
_ дя ЛЕ
е’- ~ 1 - —•	(5.21)
Заселенность в данном случае мало зависит от температуры; небольшое ее изменение
1
с температурой пропорционально —.
Если ЛЕ велико по сравнению с кТ, т. е.
ЛЕ
« = VF » ’>	<5-22)
KJ.
то экспонента весьма резко зависит от температуры: при увеличении температуры
в два раза она увеличивается в
. дд
е ^кт
(5.23)
е кг
раз, что при условии (5.22) может оказаться очень большим числом.
Отметим, что когда ЛЕ^ = Ej - Е\ велико по сравнению с кТ для всех
возбужденных уровней энергии, то их заселенности будут малы по сравнению
с заселенностью основного уровня (в (5.17) ехр	<С 1) и в (5.18) и в (5.19)
знаменатель можно положить равным единице, т. е.
п\ ~ п0	(5.24)
Пх Е]~Е\
nj « —пое~ ,	(5.25)
9\
где по — общее число частиц данного рода.
Ввиду того, что часто приходится оценивать заселенности уровней, абсолютные
и относительные, мы приводим в табл. 5.1 значения множителей е~а и еа =
а также 1 - е~а и еа - 1, которые встречаются в применяемых формулах. Таблица
составлена для значений а 0,1; при меньших значениях можно приближенно
полагать (ср. (5.21))
е~а я 1 - а, еа « 1 + а, 1 - е~а я еа - 1 « а.	(5.26)
Для грубых оценок полезно пользоваться округленными значениями:
е-3 я	1 S 20’	е-6 я	1 " 400’	е-'° я	1	1	
					" 20 000’	(5-27)
е-20 я	а 2- 10~9,	е-мя	з 10~13,	е"40я	а 4 - 10-18. J	
может принимать самые разнообразные значения, в зависимости от порядка вели-
чины разностей энергии и значений температуры.
§5.1. Мощности испускания и поглощения и заселенности уровней
127
Таблица 5.1
Значения множителей е~а, 1 — е~а, еа, еа - 1
а		1 — е’“		еа — 1	а	е~а	1 - е~а	еа	а	е~а	еа
0,1	0,905	0,095	1,105	0,105	2,2	0,1108	0,8892	9,02	6,5	1,50- 10’	6,65 • 107
0,2	0,819	0,181	1,221	0,221	2,4	0,0907	0,9093	11,02	7,0	9,12 -10—4	1,10- 103
0,3	0,741	0,259	1,350	0,350	2,6	0,0743	0,9257	13,46	7,5	5,53- 10’4	1,81 • 103
0,4	0,670	0,330	1,492	0,492	2,8	0,0608	0,9392	16,44	8,0	3,35  10’4	2,98 • 103
0,5	0,606	0,394	1,649	0,649	3,0	0,0498	0,9502	20,09	8,5	2,03 • 10’4	4,91 • 103
0,6	0,549	0,451	1,822	0,822	3,2	0,0408	0,9592	24,53	9,0	1,23- 10’4	8,10- 103
0,7	0,497	0,503	2,014	1,014	3,4	0,0334	0,9666	29,96	9,5	7,42 • 10’5	1,34- 104
0,8	0,449	0,551	2,226	1,126	3,6	0,0273	0,9727	36,60	10,0	4,53 • 10’5	2,20- 104
0,9	0,407	0,593	2,460	1,460	3,8	0,0224	0,9776	44,70	11,0	1,66- 105	5,98 • 104
1,0	0,368	0,632	2,718	1,718	4,0	0,0183	0,9817	54,60	12,0	6,15- 10~6	1,63-105
1,1	0,333	0,667	3,004	2,004	4,2	0,0150	0,9850	66,69	13,0	2,26 • 10’6	4,52 • 105
1,2	0,301	0,699	3,320	2,320	4,4	0,0123	0,9877	81,45	14,0	8,30- 10’7	1,10-105
1,3	0,272	0,728	3,669	2,669	4,6	0,0100	0,9900	99,48	15,0	3,06 • 10’7	3,27 • 106
1,4	0,247	0,753	4,055	3,055	4,8	0,00823	0,99177	121,5	16,0	1,16 -10’7	9,20 • 106
1,5	0,223	0,777	4,482	3,482	5,0	0,00674	0,99326	148,4	18,0	1,52- 10’8	6,55  107
1,6	0,202	0,798	4,953	3,953	5,2	0,00552	0,99448	181,3	20,0	2,06 • 10’9	4,84-108
1,7	0,183	0,817	5,474	4,474	5,4	0,00452	0,99548	221,4	25,0	1,38-10’"	7,24- 1О'°
1,8	0,165	0,835	6,050	5,050	5,6	0,00370	0,99630	270,4	30,0	9,25-10’14	1,08- 1013
1,9	0,150	0,850	6,686	5,686	5,8	0,00303	0,99697	303,3	35,0	6,30-10’16	1,59- 1015
2,0	0,135	0,865	7,389	6,389	6,0	0,00248	0,99752	403,4	40,0	4,28-10’18	2,34- 10'7
Тепловая энергия кТ, выраженная в электронвольтах, равна (ср. табл. 1.1. с. 17):
16	1,38-10’16	.
кТ = 1,38 • 10 6Тэрг =  - ,,ТэВ = 0,86 • 10-4ТэВ.	(5.29)
1,60 • 10 2
Величина кТ равна 1 эВ при Т = 11 600 К. Для грубых оценок можно положить
кТ » 10’4Т эВ, т. е. кТ » 1 эВ при Т = 10 000 К.
При комнатной температуре 15° С = 288 К мы имеем
кТ = 0,86 • 288 • 10“4 = 2,48 • 10-2 эВ,	(5.30)
поэтому приближенно можно считать, что при Т = 288 К ~ 300 К (или, тоже
приближенно, при 0° С)
кТа 0,025 эВ» 200 см-1.	(5.31)
При разности энергий 0,5 эВ » 4 000 см-1 (длина волны А = 2,5 мкм) мы
получаем для обычных температур а ~ 20, т. е. число частиц на возбужденном уровне,
лежащем выше основного на 0,5 эВ, составляет, согласно (5.27), всего лишь 2 • 10“9
от числа частиц на основном уровне. Как известно, для газа при нормальных
условиях число частиц в 1 см3 равно 2,7-1019 3), и поэтому число возбужденных частиц
в 1 см3 будет равно примерно 5 • Ю10. Уже при разности энергий 1эВ « 8 000 см”1
(длина волны Л = 1,25 мкм) а = 40, и мы получаем число возбужденных частиц
2,7 -1019 • 4 • 10~18 « 102, т. е. в 1 см3 будет содержаться всего лишь 100 возбужденных
частиц — совершенно ничтожное число.
Число Лошмидта £, равное отношению числа Авогадро N — 6,02 • 1023 к объему V — 22,4 л —
2,24- 104см3 одного моля газа.
128
Глава 5. Интенсивности в спектрах
При температуре 6 000 К положение будет совершенно иным. Величина кТ
равна
fcT«0,5 эВ « 4 000 см"1.	(5.32)
Даже при значительной разности энергий 5 эВ ~ 40 000 см 1 (что соответствует
ультрафиолетовой области спектра, А = 2 500 А) а ~ 10, е~а =	•, и число
возбужденных частиц будет весьма значительным, при атмосферном давлении оно
1	19	1	14 4)
будет иметь порядок — • 2,7 ♦ 10	« 10
В противоположность оптической области, для радиочастот не только при обыч-
ных, но даже при довольно низких температурах отношение а весьма мало и лишь
при самых низких температурах становится порядка единицы и больше. Например,
для излучения с длиной волны А = 1 см, что соответствует ДЕ = 1см-1, при обыч-
ных температурах, согласно (5.31), а имеет порядок и достигает значения 1
лишь при Т = 1,5К.
§ 5.2. Основные законы равновесного излучения
Мы рассмотрели заселенности уровней энергии для вещества, находящего-
ся в термодинамическом равновесии. При полном термодинамическом равновесии
в нем участвуют не только частицы вещества, но и излучение. Частицы излучают
и поглощают кванты излучения — фотоны, и если имеет место полное термодина-
мическое равновесие при определенной температуре, то излучение будет обладать
вполне определенными свойствами. Мы разберем основные законы такого излуче-
ния, находящегося в равновесии с веществом, — равновесного излучения или, иначе
говоря, излучения абсолютно черного тела (черного излучения). Хотя равновес-
ное излучение обладает сплошным спектром, зависящим только от температуры,
но не от рода вещества, а спектры, зависящие от рода вещества, в том числе дис-
кретные спектры, получаются лишь при отсутствии полного термодинамического
равновесия, законы равновесного излучения играют в спектроскопии важную роль.
Многие вопросы спектроскопии, касающиеся интенсивностей в спектрах, нельзя
понять без отчетливых представлений об условиях равновесия излучения. Вместе
с тем, изложение всей совокупности вопросов, связанных с неравновесными процес-
сами испускания и поглощения, естественно начинать с рассмотрения равновесных
процессов как предельного случая.
Равновесие вещества и излучения всегда осуществляется в некотором объеме.
Им может быть замкнутая полость, стенки которой, нагретые до определенной
температуры, испускают и поглощают фотоны, как это обычно рассматривается
в теории теплового излучения [3]. Им может быть заполненный веществом объем,
внутри которого частицы испускают и поглощают фотоны; именно этот случай
особенно важен для спектроскопии, так как внутри различных источников света
происходят процессы испускания и поглощения фотонов и, в большей или меньшей
степени, может устанавливаться равновесие между частицами вещества и излучени-
ем. Фотон, испущенный некоторой частицей, поглощается другой частицей, причем,
если средний пробег фотонов мал по сравнению с размерами объема, то излучение
будет в основном оставаться внутри этого объема и может считаться равновесным.
4) Учитывая, что увеличению температуры в 20 раз при постоянном давлении соответствует уменьше-
ние плотности и числа частиц в 20 раз.
§5.2. Основные законы равновесного излучения
129
Излучение, распределенное по объему, можно характеризовать полной плотно-
стью р — полной энергией излучения в единице объема — и определяющей его
спектральный состав спектральной плотностью р„ — энергией излучения в единице
объема, рассчитанной на единицу интервала частот. Тогда плотность излучения
с частотами от и до и -f- du равна pv du и полная плотность излучения
оо
р- J Pvdv.	(5.33)
О
Наряду с ру часто пользуются рх — спектральной плотностью излучения, рассчитанной
на единицу интервала длин волн; для данного интервала рх dX — —pv du, откуда
di/ d (с\	с	.	.
^ = -р^-рхТх\.хГр^-	(534)
ос
Формула (5.33) при этом заменяется формулой р = f Рх dX. Применение рх, как и других
о
величин, рассчитанных на единицу интервала длин волн, связано с традицией и при рас-
смотрении уровней энергии и переходов между ними нерационально; основными для нас
являются шкала частот и пропорциональные ей шкалы волновых чисел и энергии фотонов
(см. с. 17) 5\
Равновесное излучение при заданной температуре равномерно распределяется
по объему6) и характеризуется вполне определенной полной плотностью р, ко-
торая дается законом Стефана—Больцмана, и вполне определенной спектральной
плотностью р„, которая дается законом Планка (формулой Планка).
Согласно закону Стефана—Больцмана,
р = аТ4,	(5.35)
т. е. полная плотность равновесного излучения пропорциональна четвертой степени
абсолютной температуры.
Постоянная а равна
а = 7,564 • 10-15 эрг/см3 град4,	(5.36)
и из-за ее малости энергия, приходящаяся на излучение, даже при высоких тем-
пературах мала по сравнению с энергией вещества. Для газа кинетическая энергия
движения частиц в 1 см3 равна
3
Якин = Щ — кТ,	(5.37)
где По — число частиц в единице объема. В отличие от (5.35) она возрастает
пропорционально абсолютной температуре, т. е. гораздо медленнее. Если положить
по = 2,7 ♦ 1019 (число частиц в 1 см3 при нормальных условиях, ср. с. 127), то
#кин — 5,6- 103Т эрг/см3 и сравнение (5.35) и (5.37) при различных температурах дает
Т 1	10	1 02	103	104	1 05	106	107
Дин 5,6 103 5,6 104 5,6 105 5,6 106 5,6 • 107 5,6 • 108 5,6 • 109 5,6 • Ю10
р 7,5 - 10"15 7,5- 10~п 7,5 Ю"7 7,5 • 10~3 7,5-10 7,5 • 105 7,5 -109 7,5- 1013 ,
(5.38)
5) Спектральную плотность излучения в оптической области очень удобно рассчитывать на единицу
интервала волновых чисел (на 1 см-1), а в рентгеновской области — на единицу интервала энергий
фотонов (на 1 эВ).
6) Если не учитывать флуктуаций излучения, которые нас интересовать не будут.
5 Зак.103
130
Глава 5. Интенсивности в спектрах
Рис. 5.1. Поток излучения через единичную
площадку
Таким образом, только при темпе-
ратурах порядка миллиона градусов
энергия излучения становится срав-
нимой с энергией вещества.
Характеристикой излучения, на-
ряду с плотностью энергии, является
поток энергии излучения; на опыте
измеряются потоки, идущие от ис-
точников излучения; от потоков лег-
ко перейти и к плотностям излуче-
ния.
При плотности р излучения, рав-
номерно распределенного по всем
направлениям, на единицу полно-
го телесного угла, 4тг, приходится
Р
плотность —, а на телесный угол
47Г
р
dQ — плотность — dQ. При ско-
4тг
рости распространения с через еди-
ничную площадку с нормалью, образующей угол $ с направлением распростране-
ср
ния (рис. 5.1), будет проходить поток dQ cos ti. Полный поток через эту площадку
4тг
по всем направлениям в пределах телесного угла 2тг получится интегрированием по $
от 0 до тг/2 и по азимуту р — от 0 до 2тг:
2	2тг
ср f	Г	ср с
— / cos sin d'O / dp — — 7Г — - p,
4тг J	J 4тг 4
о	о
(5.39)
т. e. отличается от p множителем с/4.
Если излучение в некоторой замкнутой полости находится в равновесии со стен-
ками этой полости, нагретыми до определенной температуры, то поток через любую
единичную площадку, в том числе и с единицы поверхности полости, т. е. с по-
верхности абсолютного черного тела, должен определяться формулой (5.39), которая,
таким образом, дает поток излучения с единицы поверхности абсолютно черного
тела — его полную испускательную способность е. Согласно (5.39) и (5.35),
е=^р=™Т4 = аТ4.	(5.40)
Мы получили закон Стефана—Больцмана для полной испускательной способно-
сти, отличающийся от закона Стефана—Больцмана (5.35) для полной плотности
излучения значением постоянной. Постоянная
а = ? а = (5,6687 ± 0,0010) • 10~5 эрг/см2 • с • град4	(5.41)
и потоки энергии излучения становятся весьма значительными уже при температурах,
для которых р еще очень мало по сравнению с ЕКИИ (см. (5.38)). Например,
при 10 000 К
£ — 5,67 -10й эрг/см2 • с = 1,36 • 104 кал/см2 • с.
§5.2. Основные законы равновесного излучения
131
При применении законов равновесного излучения следует всегда учитывать,
для каких величин они даются — для плотностей излучения или для потоков.
Согласно формуле Планка, спектральная плотность равновесного излучения
равна
8тг/ш3 1
Р* ~ “7з аё 7
с	е*т — 1
(5-42)
В этой формуле содержатся все основные законы равновесного излучения. В пре-
дельном случае малых частот hv <С кТ в знаменателе ehu^kT - 1 « —, и получается
формула Рэлея—Джинса
8тп/2
Р„ =	(5.43)
(У
т. е. при малых частотах ри возрастает от нуля пропорционально i/2; существен-
но, что при заданной частоте р„ пропорционально Т и сравнительно медленно
увеличивается с повышением Т. В предельном случае больших частот, hv кТ,
в знаменателе ehu^kT 1 и при пренебрежении единицей получается формула Вина
8л hv3 _h»
Pv = ——е кт>
с5
(5.44)
т. е. при больших частотах pv убывает до нуля по показательному закону; в этой
области частот зависимость от Т получается очень резкой; pv при заданной частоте
весьма быстро увеличивается с повышением температуры.
Наиболее важно относительное распределение энергии излучения по часто-
там, которое лучше всего выявляется, если ввести безразмерную переменную
hv
а = -— (ср. (5.28)). Мы получаем
KI.
А — А
pudv — pada —	.
С2
a3 da С\ТА
------— —' J («) da,
еа - 1 с4 м 7	’
(5.45)
где
и
С| = 8тгЛс = (4,9918 ± 0,0002)1 (Г12 эрг • см
he
с2 = — = 1,43880 ± 0,0007 см • град
к
(5.46)
а3
— постоянные излучения, а /(а) = ----- — универсальная функция, максимум
еа — 1
которой лежит при значении а — «м = 2,8214 (т. е. при hvM ~ 2,8кТ). Максимуму
соответствует длина волны, обратно пропорциональная Т,
с ch с2 1 b 0,5081
Дм — — —----------------------—-------— — —--------см • град,
vM ам кТ Т Т Т Р ’
(5.47)
что представляет закон смещения Вина. Относительные значения------= —-------- функ-
Р«м /(<*м)
ции ра приведены в табл. 5.2. Полная плотность излучения, согласно (5.45) и (5.33),
равна
ОО	ОО	00
f	f	с\ f a5 da 4 с\ тг4 4	4
] —Т4	-Т- = «Т\	(5.48)
о
О
о
132
Глава 5. Интенсивности в спектрах,
Таблица 5.2
Распределение энергии равновесного излучения по частотам
а	/	Ра Ра = 		 Р<*м	и S ю	/	Pin а Pin а — ~ Pin ам	In а	а	/ _ Ра Ра — Р(*м	7(“) = у~ В %	/	Pin а Pin а ~ ~ Р\пам	In а
0,2	0,0254	0,047	0,00151	-1,620	5,8	0,416	84,2	0,719	1,76
0,4	0,0914	0,470	0,0109	-0,916	6,0	0,377	86,0	0,674	1,79
0,6	0,185	0,890	0,0330	-0,511	6,2	0,340	87,6	0,628	1,82
0,8	0,293	1,95	0,0699	-0,223	6,4	0,306	89,0	0,584	1,86
1,0	0,409	3,48	0,122	0,000	6,6	0,275	90,0	0,541	1,89
1,2	0,528	5,63	0,187	0,182	6,8	0,246	91,5	0,499	1,92
1,4	0,631	8,03	0,263	0,337	7,0	0,220	92,5	0,458	1,95
1,6	0,728	11,07	0,347	0,470	7,2	0,196	93,3	0,420	1,97
1,8	0,811	14,42	0,435	0,588	7,4	0,174	94,2	0,384	2,00
2,0	0,880	18,18	0,524	0,693	7,6	0,154	94,9	0,349	2,03
2,2	0,932	22,08	0,611	0,789	7,8	0,137	95,5	0,317	2,05
2,4	0,969	27,87	0,681	0,876	8,0	0,121	96,1	0,288	2,08
2,6	0,991	30,79	0,764	0,956	8,2	0,106	96,6	0,259	2,10
2,8	0,998	35,05	0,833	1,03	8,4	0,093	97,0	0,234	2,13
3,0	0,993	39,30	0,888	1,10	8,6	0,082	97,4	0,211	2,15
3,2	0,978	43,70	0,933	1,16	8,8	0,072	97,8	0,189	2,17
3,4	0,953	47,9	0,965	1,22	9,0	0,063	98,02	0,169	2,20
3,6	0,921	52,9	0,987	1,28	9,2	0,055	98,29	0,154	2,22
3,8	0,882	54,7	0,998	1,34	9,4	0,048	98,52	0,135	2,24
4,0	0,839	59,8	0,999	1,39	9,6	0,042	98,72	0,120	2,26
4,2	0,792	63,4	0,991	1,44	9,8	0,037	98,88	0,107	2,28
4,4	0,743	66,7	0,975	1,48	10,0	0,032	99,00	0,0950	2,30
4,6	0,694	69,8	0,951	1,53	12,0	0,00745	99,9978	0,0265	2,49
4,8	0,645	72,7	0,921	1,57	14,0	0,00160	99,99954	0,00748	2,64
5,0	0,596	75,4	0,887	1,61	16,0	0,000324	100,00000	0,00154	2,77
5,2	0,548	77,9	0,849	1,65	18,0	0,0000624	100,00000	0,000335	2,84
5,4	0,502	80,2	0,807	1,69	20,0	0,0000116	100,00000	0,0000690	3,00
5,6	0,458	82,5	0,764	1,72					
™ a3 da
где учтено, что - J ——- - —.
О е«- 1	15
С| я4
с постоянной а = -т—. Доля энергии излучения, приходящаяся на область спектра
с2
от 0 до «], равна 7(«i) = —, где
-*ОО
%4
Мы получаем закон Стефана—Больцмана
С2
С|
т.е.
7(«i) =
a3 da
еа ~ 1
«1
о
da.
a3 da
еа — 1
a3 da
еа -7’
(5.49)
Д)
1
Значения у(а) приведены в табл. 5.2 и позволяют получить долю энергии излучения
hv\	hv2
в интервале от = ------- до а2 = ----
кТ	кТ
как разность 7(^2) ~7(ai) [5]. Величина
{7(^2) “ ?(«I)} аТ4 дает абсолютную энергию излучения в этом интервале.
§ 5.2. Основные законы равновесного излучения
133
(5.50)
В выборе спектральной плотности имеется произвол, от которого зависит конкретный
вид функции и положение ее максимума. Функция рА, согласно (5.34) и (5.42), имеет вид
8тгЛс 1 С| 1
~ ~ТЕ 7 =	~ ’
Л еллт — 1 л — 1
содержит 1/А5, и ее максимум лежит при а'м = 4,9651 (т. е. при hi/M ~ 5кТ), что дает
с2
обычный коэффициент Ьх = -т- = 0,2898 см • град в законе смещения Вина (5.47). Можно
«м
ввести [120], записав соотношение pxdX = -pudv (см. с. 129) в виде рхХ d(ln А) = -pvu
где d(lnA) = -d(lni/), функцию
8тг/»/4	1
Pin а = Ри» - р\Х - —---------
с са-т — 1
8тгЛс 1	_ с,Т4 а4
\4	_*£.	, ~~ r4 _ 1 ’
Л ekxr — 1 с2 с 1
d(ln i/),
(5.51)
hv
отнесенную к единице интервала в логарифмической шкале, одинаковой для Л, v и а — — =
кТ
he
—- (InА отличается от -Ini/ и - Ina только постоянными); максимум функции (5.51)
kJ л
лежит при а'м = 3,9207 (т. е. при ~ 3,9кТ), что дает коэффициент Ь|Па = 0,3670 см • град
в (5.47). В (5.51) вместо универсальной функции /(а) входит универсальная функция 9?(а) =
а4
еа - 1
*/ \ л с	Pin а	.
= af(ay в табл. 5.2 даны относительные значения --------- = ——- функции р!п
Р|п«м Р(ам)
--------------1	1-----1---1--1--1--Г~Г~]-1 ~ГГ 1~Г1ТТТр1ТГ[ПТТ]ППрП1|П1фП^	1------►
0,4	0,6 0,8 1,0--2,0	3,0 4,0 5,0 7Д 9,0	14,0
Рис. 5.2. Универсальная кривая распределения интенсивности в спектре
равновесного излучения
а на графике рис. 5.2 приведен ее вид. Логарифмический масштаб по оси абсцисс делает этот
график весьма удобным; площадь, заключенная между двумя ординатами, пропорциональна
энергии излучения в данном интервале7).
Отметим, что переход к часто применяемым формулам для спектральных испускательных
способностей черного тела ер, сх и т.п. производится просто умножением соответствующих
7) Мы имеем
О]	О|
-/	[ У^-da = - 1 - f f(a)da =	- - ^-7(«i) = l,377(ai)
^(«м) J a y?(aM) J	15
о	о
(cm. (5.49)).
134
Глава 5. Интенсивности в спектрах
формул для спектральных плотностей равновесного излучения на с/4 (ср. (5.39)). Универ-
сальные функции остаются теми же самыми.
Ввиду большой важности формулы Планка (5.42), чтобы раскрыть ее физи-
ческий смысл, мы приведем вывод этой формулы по Эйнштейну [182], исходя
из квантовых представлений о вероятностях переходов.
При равновесии вещества с излучением процессы испускания фотонов ча-
стицами должны полностью компенсироваться процессами поглощения фотонов
частицами. При этом полное равновесие должно быть детальным, т. е. каждый
тип прямых процессов должен компенсироваться соответствующим типом обратных
процессов. Рассмотрим переходы между уровнями Ei и Ek (Ei > Ек). Испускание
фотонов с частотой и — —(Ei — Ек) должно компенсироваться поглощением фо-
h
тонов той же частоты. Приравнивая число Z-kn> спонтанно испущенных фотонов
приведенному числу Z^orJI^ поглощенных фотонов (см. (5.1) и (5.3)), получаем
niAik = (nkBki - щВ{к)р(1/).	(5.52)
Таким образом, в единице объема за единицу времени число спонтанных процес-
сов испускания равно числу процессов поглощения за вычетом числа процессов
вынужденного испускания. Отметим, что если перейти, путем умножения на hv,
к мощностям испускания и поглощения, то (5.52) дает, при учете (5.2), усло-
гг(сп) гг(погл) гг(вын) гг(поглУ
вие и-к — Uki - U-k = Uki , т. е. при равновесии мощность спонтанного
испускания должна равняться приведенной мощности поглощения.
Плотность излучения частоты v мы будем рассчитывать на единицу интервала
частот, т. е. положим р(и) — ри. Вероятности Aik, Bki и Bik можно также рассчитывать
на единицу интервала частот, что является наиболее общим случаем, так как
в действительности уровни энергии и спектральные линии имеют определенную
ширину (подробнее об отнесении вероятностей к единице интервала частот см. § 5.5).
Вместе с тем вывод становится применимым и к случаю состояний, принадлежащих
к непрерывному энергетическому спектру.
Согласно (5.52), мы имеем
- Р(0 -	_ дх •	(  )
\ nt Bki J
При термодинамическом равновесии отношение — определяется формулой (5.15),
'U'i
gk Е,-Ек gk hu
т. е. равно — е кТ = — екТ, следовательно,
9i	9i
__ Aik 1	__ Alk	1
? Bki (9k	Bik\	—П.( bi	9iBik
[ — ekT------j	±>кг I gkT------
\9i BkiJ 9i \ gkBki
(5-54)
9k	8тг/ш3 8>
Отношение Aik к —Bki, согласно (4.8), равно —-— , а отношение giBik к gkBki
9i	c
no (4.7) равно 1, и мы получаем формулу Планка (5.42).
Подстановка в (5.54) значения (4.8) отношения Aik/Вкг находится в соответствии с тем, что
плотность излучения рассчитывается на единицу интервала частот. Мы при этом получаем правильный
8тгй1/3
множитель -----— в формуле Планка для плотности излучения pv.
§5.2. Основные законы равновесного излучения
135
Из приведенного вывода сразу следует (ср. (5.53) и (5.54) с (5.42)), что еди-
ница в знаменателе формулы Планка соответствует вынужденному испусканию.
Когда вынужденным испусканием можно пренебречь по сравнению с поглощением
(nkBki > n{Bik и ehv!kT 1), мы получаем закон Вина (5.44). Показательный множи-
П;
тель в этом законе определяется малым отношением — заселенностей уровней Ег
пк
и Ek. Наоборот, когда ehv^kT близко к единице, что имеет место при hi/ < кТ,
т. е. в случае закона Рэлея—Джинса (5.43), вынужденное испускание почти пол-
ностью компенсирует поглощение и их малая разность, пропорциональная hv/kTb
определяет появление множителя Т в выражении для этого закона.
В приведенном выводе мы использовали значения входящих в выражение (5.54) отно-
шений AiklBki и В{к/Вы' получающихся строго на основе квантовой электродинамики. Эти
отношения можно получить, как это было сделано Эйнштейном, который впервые вывел их,
если исследовать формулу (5.54) при высоких температурах с учетом закона Рэлея—Джинса,
который может быть выведен чисто классически. При стремлении Т к бесконечности pv
должно также стремиться к бесконечности, что возможно лишь при
9i Bik
9к Bki
(5-55)
(так как ehvfkT —► 1, а знаменатель должен стремиться к нулю). Мы получаем соотноше-
ние (4.7). Формула (5.54) принимает вид
Aik 1
Qk	1
—Bki - 1
9i
что при hv «С кТ дает
Aik кТ
—t>ki
9i
и из сравнения с законом Рэлея—Джинса (5.43) получается соотношение (4.8).
(5.56)
(5.57)
Из вывода формулы Планка следует, что при равновесии плотность излучения
частоты и равна (см. (5.53))
^iAik	hi/niAik	. v
Pv ~	-------— - 7~7 ~---------—r.	(5.58)
nkBki - niBik hi/(nkBki - niBik)
Выражение, стоящее в числителе, представляет мощность U-k^ спонтанного испус-
кания, а выражение, стоящее в знаменателе, — отношение приведенной мощности
тг(погл)' гг(погл) тг(вын)
поглощения Uki — Uki - U-k к плотности излучения, т. е. равно энергии,
фактически поглощаемой в единице объема за единицу времени при плотности
излучения, равной единице.
Мощности испускания и поглощения так же, как и вероятности Aik, Bki и Bik,
можно рассчитывать на единицу интервала частот и обозначить их через U„
и 17^погл). Тогда (5.58) запишется в форме
= Е7,5сп> = hvmAikiy}
и^0Гл)’ hv(nkBki(v) -
pv
136
Глава 5. Интенсивности в спектрах
Если ввести понятие об объемной поглощательной способности, как отношении
гг(погл)
мощности поглощения Uy к плотности излучения ри,
^погл) hvnkBki(i/)p„
av —------=----------------— hi/nkBki(i/),	(5.60)
Pv	Pu
TO
, £/<погл) hv(nkBki(v) - niBik(v))pv	R / \\
av =--------=---------------------------= hv(nkBki(y) - niBik(i/)) (5.61)
Pv	Pv
можно назвать приведенной объемной поглощательной способностью. Формула (5.61)
тогда примет вид
тт(сп)
=	(5.62)
0>у
Мы получили закон Кирхгофа для объемных величин, характеризующих равно-
весное излучение: отношение мощности спонтанного испускания к приведенной объем-
ной поглощательной способности равно объемной плотности равновесного излучения^.
Следует подчеркнуть, что понятие поглощательной способности вещества при-
менимо и при отсутствии равновесия между частицами вещества, когда заселенно-
сти пк и ni уровней энергии отличаются от равновесных. В этих случаях, однако,
закон Кирхгофа уже не будет иметь места. На опыте определяется не объемная по-
глощательная способность, а связанные с ней коэффициенты поглощения излучения
веществом, которые будут рассмотрены в следующем параграфе.
§ 5.3. Коэффициенты поглощения
Коэффициент поглощения характеризует ослабление направленного потока
излучения с расстоянием за счет поглощения,0). Пусть имеется поток излучения ча-
Рис. 5.3. Поглощение в единичном объеме
стоты и, падающий на единичную
площадку перпендикулярно к ней
в направлении х (рис. 5.3). Обозна-
чим через Ту величину потока через
эту площадку, т. е. энергию излуче-
ния, падающего на нее за единицу
времени, равную
Ту = cuy(x), (5.63)
где Uy(x)— объемная плотность этого излучения, а с — скорость его распростране-
ния, т. е. скорость света.
Ослабление потока -dlv на расстоянии от х до х 4- dx за счет поглощения
пропорционально величине Ти потока и расстоянию dx:
dly — KylydXy
(5-64)
где
Ту dx
(5.65)
9) Закон (5.62) для величин, отнесенных к единице объема, отличается от закона Кирхгофа, свя-
зывающего испускательную и поглощательную способности тела, отнесенные к единице поверхности,
и является более общим.
|0) Направленный поток излучения может ослабляться и за счет рассеяния, которое мы сейчас рассмат-
ривать не будем.
§5.3. Коэффициенты поглощения
137
dlu
представляет коэффициент поглощения. Он равен относительному уменьшению-----
Л/
потока излучения на единице длины, т. е. доле энергии, которая поглощается
в единицу времени в единице объема (см. рис. 5.3; мы имеем кубик с гранью,
равной единице, и ребром, также равным единице). Иначе говоря, коэффициент
поглощения дает отношение энергии, поглощаемой в единицу времени в единице
.	(	~ dIA
объема I и равной------, к потоку излучения 1и через единичную площадку
\	dx /
(к плотности потока излучения). Отношение этой энергии к плотности излучения
будет равно, согласно (5.63) и (5.65),
1 / dlu\	с dlv
= aiv' (5-66)
Uy(x) \ dx /	ly dx
Если коэффициент поглощения не зависит от направления распространения излу-
чения, как это обычно имеет место для изотропной среды, то отношение (5.66)
равно поглощательной способности, определяемой формулами (5.60) и (5.61). Мы
получаем выражение
1	hvnkBki(y)
Ху -- Оу --
с	с
(5.67)
для коэффициента поглощения без учета вынужденного испускания, и выражение
,	1 , hv(nkBki(v) ~ щВЛ(у))
Ку -- Оу ---
с	с
(5.68)
для приведенного коэффициента поглощения, учитывающего вынужденное испус-
кание. На опыте всегда наблюдается приведенный коэффициент поглощения Ху. Разуме-
ется, когда вынужденным испусканием можно пренебречь, (5.68) сводится к (5.67).
В дальнейшем мы не будем писать штриха, и хи будет всегда обозначать, если не будет
сделано соответствующих оговорок, приведенный коэффициент поглощения.
Соотношения (5.67) и (5.68) можно получить из (5.60) и (5.61), если от объемной
Сру
плотности излучения ри перейти (ср. с. 130) к спектральной интенсивности излучения Kv = —
4тг
т.е. к потоку излучения, рассчитанному на единицу телесного угла и на единицу интервала
частот. Для этого а„ мы представим в виде
— [/<no,Jl)dQ с — [/*nora)dQ с — ^nora)dQ
_ 4тг_________________ 4тг________________ 4тг
"	1 ЛГ>	— О dQ
— p„dti 4?r
(5.69)
KydQ представляет поток излучения в направлении телесного угла dQ (которое можно выбрать
за направление х на рис. 5.3), а —L^norj,)dQ — энергию этого излучения, поглощенную
4тг
в единицу времени в единице объема с гранью, равной единице, т. е. на единице длины. Если
положить Kydft = 1у и	= Ху, то — L^norj,)dQ = - —, а„ =	= схи, т.е. мы
1у ах	4тг	ах	Iv ах
приходим к (5.67).
Закон Кирхгофа (5.62) для объемных величин можно представить в несколько иной фор-
ме, если ввести вместо поглощательной способности а„ коэффициент поглощения xv и вместо „
объемной плотности р„ интенсивность^ (штрихи мы везде опускаем). Умножая (5.62) справа
138
Глава 5. Интенсивности в спектрах
с
и слева на —, получим
4тг
—и(а,)
=	(5.70)
С
Заменяя avlc, согласно (5.68), через х„, и вводя коэффициент испускания
(5.71)
47Г
представляющий мощность спонтанного испускания в заданном направлении, отнесенную
к единице телесного угла, получаем закон Кирхгофа в виде
— = к,.	(5.72)
Таким образом, отношение коэффициента испускания к коэффициенту поглощения (приве-
денному) равно интенсивности равновесного излучения. В отличие от (5.62), соотношение (5.72)
относится к излучению, распространяющемуся в заданном направлении, и может быть
обобщено на случаи, когда имеется перенос энергии излучением.
Вопросы переноса энергии излучением играют очень важную роль в астрофизике,
и им посвящено огромное количество исследовании, обзор которых можно найти в ряде
монографий [149-152]. Эти вопросы являются существенными для источников света, особенно
высокотемпературных, однако в применении к последним недостаточно разработаны. Мы
не имеем возможности здесь рассмотреть их даже вкратце.
Рис. 5.4. Закон
ослабления потока
Из основной формулы (5.64) для ослабления потока
излучения на отрезке длины dx вытекает закон м)
4 - IuQe~^x	(5.73)
ослабления первоначального потока с расстоянием. Здесь
4о — значение потока при х = 0. Закон (5.73) является
показательным (рис. 5.4).
Быстрота ослабления потока будет тем больше, чем
больше коэффициент поглощения Необходимо под-
излучения с расстоянием черкнуть, что поскольку коэффициент поглощения явля-
ется, как правило, функцией частоты (и длины волны,
Хд — иД то излучение различной частоты будет ослабляться по-разному; показа-
тельный закон имеет место только для монохроматического излучения.
Следует также отметить, что ослабление прямого потока излучения происходит не только
вследствие поглощения, но и вследствие рассеяния. Полное ослабление -dlu потока излучения
равно —</4 = -(</4)погл - (^4) расе, где (-</4)погл определяется формулой (5.64), a -(^4)Расс =
puIydx, где ру —------—17— коэффициент рассеяния. В результате имеем -dlv =
Iv dx
(xv + py)Iydx и
ly = IyQe~^+Mx = 1у^х.	(5.74)
где
ау-Ху+Ру	(5.75)
— полный коэффициент ослабления.
Согласно (5.73), поток излучения ослабляется в е раз на расстоянии С, для ко-
торого
хЛ=1.	(5.76)
1 Вывод его является элементарным и совершенно аналогичен выводу формулы (4.14), см. примечание
на с. 86.
§5.3. Коэффициенты поглощения
139
Это расстояние
С =	(5.77)
Ку
называют пробегом излучения. Пробег излучения характеризует путь, который про-
летают фотоны до их поглощения, и является величиной, аналогичной длине
свободного пробега для частиц газа. Закон (5.73) можно записать, вводя 1у, в виде
1у =1уОе-г,.	(5.78)
Пробег излучения является средним значением пути, проходимого фотонами до их
поглощения. Доля фотонов, поглощаемая на расстоянии от х до х + dx, иначе говоря,
вероятность поглощения отдельного фотона на отрезке dx, согласно (5.64) и (5.73), равна
=^e-Xl'xdx.	(5.79)
Эти фотоны проходят путь х. Среднее значение пути (ср. (4.18))
ос
х = J xxve~KvX dx = — = ly.	(5.80)
о
Величина пробега излучения является весьма существенной характеристикой
взаимодействия излучения с веществом, находящимся при определенной температу-
ре и испускающим и поглощающим фотоны. Если эта величина мала по сравнению
с размерами L области, занимаемой веществом, то внутри области все испускаемые
фотоны будут поглощаться и установится равновесие излучения с веществом. Если,
наоборот, величина пробега велика по сравнению с размерами области, заполненной
веществом, то испускаемые фотоны будут выходить наружу, не успев поглотиться,
и излучение не будет находиться в равновесии с веществом. Таким образом, мы
имеем два предельных случая:
1
—	= iu L — имеется равновесие излучения с веществом. (5.81)
ки
—	— lu L — равновесие излучения с веществом отсутствует. (5.82)
Ку
Ввиду зависимости коэффициента поглощения и, следовательно, пробега излу-
чения от частоты, условие (5.81) может выполняться для некоторых частот и не вы-
полняться для других. Мы будем иметь частичное равновесие излучения с веществом;
например, в источниках излучения равновесие может иметься для фотонов, соот-
ветствующих сильно поглощаемым спектральным линиям, и может отсутствовать
для фотонов всех других частот.
Отметим, что в формулы (5.81), (5.82) входит коэффициент поглощения х„, а не х„ <хи,
так как существенно действительное расстояние lv, проходимое фотонами до момента погло-
, 1 1
щения, а не эффективное расстояние - -т >> —. Поскольку речь идет лишь о порядке
Ку Ку
величин, то эго соображение имеет шачение, только когда х'и < хи, т. е. когда вынужденное
испускание почти полностью компенсирует поглощение.
В формулу (5.73) в показатель экспоненты входит произведение D = КуХ,
и относительное ослабление потока излучения, прошедшего расстояние ж, равно
'.-ХуХ -D
— = е = е
Л,0
(5.83)
140
Глава 5. Интенсивности в спектрах
т. е. зависит от этого произведения, а не от коэффициента поглощения хи и рассто-
яния ж в отдельности. D называют оптической толщиной, или оптической глубиной.
Рис. 5.5. Ослабление излучения
с расстоянием:
а — при прохождении
поглощающего слоя;
б — для излучения, приходящего
с некоторой глубины
Первый термин (или менее удачный термин «опти-
ческая плотность») обычно применяется, когда рассма-
тривается поглощение в слое определенной толщины х
при экспериментальном измерении ослабления излуче-
ния (рис. 5.5, а). Второй термин употребляют, когда рас-
сматривается излучение, приходящее в данную точку
из других точек (в частности, в точки элемента поверх-
ности светящегося тела с некоторого расстояния от этой
поверхности — с некоторой глубины; рис. 5.5, б); подоб-
ное рассмотрение широко применяется при изучении
вопросов переноса излучения в астрофизике (см. с. 138).
При этом оптическую глубину общепринято обозначать
через г.
Для определения значений оптической тол-
щины D по значениям величины — = e~D (про-
4о
пускания) или величины 1 -	= 1 - e~D может
применяться табл. 5.1 (при а = D).
Рассмотрим теперь зависимость коэффициента поглощения от различных фак-
торов, исходя из основной формулы (5.68), которую мы запишем, учитывая (5.4),
в виде
= - hvnk ( 1--------]Bki(y).
С ' ^kdi'
(5.84)
Подставляя отношение заселенностей п, и nk уровней энергии Ei и Ек, равное --,
9k Pk
и заменяя пк через п$дкРк, получим (см. (5.6)):
1	(	Pi \	1	(	Pi \
- hvnk 11-------) Bki(v) = - hvnogk<pk 11-----Bki(v),
C	\	Pk /	C	\	Pk /
(5.85)
где pi и pk — доли частиц в отдельных состояниях с энергиями Ei и Ек.
Формула (5.85) показывает, что коэффициент поглощения пропорционален
концентрации п0 поглощающих частиц. Эту формулу можно записать и в виде

(5.86)
где
1	(	Pi \
<yv=z- hvgk>pk I 1------) Bki(y)
C	\	Pk /
(5.87)
— величина, в обычных условиях не зависящая от концентрации. При подстановке
в (5.73) мы получаем
4 = 40e’<M,°z.	(5.88)
Таким образом, ослабление излучения зависит от произведения пож, но не
от концентрации и толщины поглощающего слоя в отдельности, т. е. для слоев
различной толщины ж и с различной концентрацией По поглощающих частиц
§5.3. Коэффициенты поглощения
141
поглощение будет одинаковым при одном и том же общем числе частиц (на единицу
поперечного сечения) п$х в поглощающем слое (закон Беера)пК
Так как п0 имеет размерность, обратную размерности Объема,
то произведение п$х имеет размерность, обратную размерности
площади, следовательно av имеет размерность площади и в систе-	:
ме СГС измеряется в см2. Величина av имеет простой наглядный -.......
смысл. Согласно (5.65) и (5.86),	а
(5.89)
CLX —
4
есть доля излучения, поглощаемая в слое толщины dx и по-
перечного сечения, равного единице (рис. 5.6, а), т. е. вероят-
ность поглощения фотона одной из n$dx частиц, находящих-
ся в этом слое. Считая, что частицы имеют поперечное сече-
ние и что фотон, попадающий на частицу с этим поперечным
сечением, поглощается, мы получаем вероятность поглощения
—-- = crvnQ dx (рис. 5.6,6), т. е. формулу (5.89). Таким обра-
зом, представляет эффективное поперечное сечение для поглоще-
ния фотона. Величиной иногда пользуются для характеристики
поглощения как величиной, пропорциональной вероятности по-
глощения (см. (5.87)).
Рассмотрим теперь зависимость коэффициента поглоще-
r*—1 -*н
б
Рис. 5.6.
Ослабление
потока излучения:
а — поглощение
квантов в слое
толщины dx\
б — поперечные
сечения частиц
ния (5.85) от относительной заселенности уровней, определяемой множителем
для начального состояния и отношением ipkl^i, входящим в выражение 1-------.
Для поглощения особенно важен случай, когда вещество находится в равновесии,
так как обычно поглощение исследуется в условиях, когда излучение, которое на-
правляется на вещество и ослабление которого измеряется, не меняет заметным
образом заселенностей нижних уровней, являющихся начальными.
При равновесии, согласно (5.11), отношение
Ei~Et
— — е = е кТ,
(5.90)
и коэффициент поглощения (5.85) будет равен, если еще подставить равновесную
заселенность nk уровня Ek как функцию температуры (см. (5.19)),
xv = - hunk (1-е кТ ) Bki(u) = - hunQ
С \	/	С
9\
(	91	, S3
(14----е Ч--------е
\	9\	9\
(5-91)
Для поглощения с основного уровня это выражение сводится к
1-е ‘t)Bh(iz)
Ъ = - '“"‘1 I ‘ ~ “ I	---а7—«7^7------•	(5-92)
с V	'	с 1 + — е~ + — е~^ +...
9\	9\
12^ При очень больших концентрациях поглощающих частиц и сильном взаимодействии между ними
может изменяться вероятность переходов, будет зависеть от концентрации, и пропорциональность
и по может нарушаться; закон Беера уже не будет соблюдаться.
142
Глава 5. Интенсивности в спектрах
Если все разности Ei - Е} кТ (а Э> 1, см. (5.22)), что является обычным случаем
для электронных уровней атомов при не очень высоких температурах, то знаменатель
в (5.91) и (5.92) приближенно равен 1, заселенность п1 основного уровня практически
остается постоянной (п\ ~ п0, ср. (5.18) и (5.24)), 1 - e~hu^kT « 1 и коэффициент
поглощения определяется формулой
Мн = - hunoBuM-
с
Поглощение с основного уровня будет велико
бужденных уровней, для которых (см. (5.16))
дк
— — е кТ
д\
(5.93)
по сравнению с поглощением с воз-
пк
П\
пк
По
(5-94)
и коэффициент поглощения
1 . _ 1 .
1 D / \	1 г 9к
— - hvnkBki(v) = - hvn} — е
9\
Bki(y) - hvno — е Bki(v). (5.95)
с gi
с	с
При возрастании температуры будет появляться заметное поглощение сперва
с уровня Е^ затем с уровня Е$ и т. д. Заселенности уровней, для которых Ек - Е\
меньше или порядка кТ,
Ек — Е\< кТ,	(5.96)
при достаточно высокой температуре будут одного порядка и со всех них будет
наблюдаться поглощение (разумеется, если переходы разрешены правилами отбора).
Примером появления поглощения при возрастании температуры является серия
Бальмера (см. (1.9) и рис. 1.2). Энергия возбуждения Е2 -Е\ уровня п — 2, начально-
го для поглощения, равна примерно 10 эВ и при обычной температуре (Т ~ 300 К,
кТ = 0,025 эВ, см. (5.31))
Е2 — Е\
~ кТ
10
---- = 40,
0,25
~ = 400, е а практически равно
а « 10"18 и все еще мало. Наконец,
2 • 10 9, и заселенность уровня п = 2 стано-
а
е
нулю; при Т = 3 000 К а
10
при Т = 6 000 К а ~ — = 20, е
вится достаточной для наблюдения серии Бальмера в спектре поглощения Солнца
(температура поглощающего слоя солнечной атмосферы порядка 6 000 К, а толщина
этого слоя весьма велика). Изменение заселенности при переходе от Т = 3 000 К
к Т = 6 000 К составляет е~|0/е“20 = е10 « 2 • 109 раз (ср. (5.23)), т. е. является весьма
резким, что характерно для значений а Э* 1.
В случае, когда переход происходит между близкими уровнями, для которых
hv кТ (а 1, см. (5.20)), в выражении (5.91) для коэффициента поглощения
существенную роль играет множитель 1 - e~hv/kT. Вынужденное испускание почти
полностью компенсирует поглощение, и мы имеем
_лр	/ hv\ hv
1-е кт 1 - I 1------— •
V	кТJ	кТ
(5.97)
отсюда
(5.98)
1	hv	\ (hv)2 * * * * *
*v = - hvnk Bki(v) =--------—— nkBkl(v).
C	rbJ-	C h-1
Коэффициент поглощения даже при переходах между самыми нижними уровня-
hv
ми, для которых пк порядка п0, будет мал за счет наличия малого множителя а = —.
кТ
§5.3. Коэффициенты поглощения
143
Этот случай является типичным при исследовании поглощения в области радиоча-
стот, в которой при обычных температурах (кТ « 200 см-1, см. с. 127) мы имеем
значения
Л	100 м Юм 1м 10 см 1 см 1 мм 1
hv 1 he 7 Л с д ,	7 > . (5.99)
а= —	=----5-КГ7	5-Ю"6	5-10~5	5-10~4	5 • 10”3	5 - 10-2 f V '
кТ ХкТ	'
Формула (5.98) является основной, определяющей значения коэффициентов
поглощения при радиоспектроскопических исследованиях поглощения вещества,
находящегося в состоянии термодинамического равновесия.
К числу их относятся исследования поглощения в газах в микроволновой
области, исследования парамагнитного резонанса в твердых телах и жидкостях (пе-
реходов между уровнями магнитной структуры, связанной с электронными магнит-
ными моментами) в той же области, исследования ядерного магнитного резонанса
в твердых телах и жидкостях (переходов между уровнями магнитной структуры,
связанной с ядерными магнитными моментами) и квадрупольного резонанса в кри-
сталлах (переходов между уровнями электрической структуры, связанной с ядерными
квадрупольными моментами) в области коротких радиоволн.
В принципе, при очень интенсивных потоках излучения может существенно
нарушаться термодинамическое равновесие в веществе, и заселенность уровней
будет отличаться от равновесной, определяемой законом Максвелла—Больцмана.
Такое явление наблюдается в микроволновой области, где благодаря некоторому
преобладанию процессов поглощения над процессами вынужденного испускания
происходит выравнивание заселенностей комбинирующих состояний, при равно-
весии относящихся как e~hu^kT ~ 1-----. В результате мощность поглощения
кТ
стремится к пределу — к насыщению [247]. Значительное увеличение заселенности
верхних уровней, которая при температурном равновесии очень мала, наблюдается
при оптическом возбуждении атомов и молекул в видимой и ультрафиолетовой
областях спектра, что приводит к интенсивному испусканию (см. § 1.3).
Коэффициент поглощения, согласно формуле (5.84), пропорционален вероят-
ности поглощения	Это позволяет в случае, когда известны заселенности
комбинирующих уровней, по коэффициенту поглощения определять вероятность
поглощения. В обычном случае, когда имеет место равновесие, а вынужденное
испускание мало по сравнению с поглощением, для нахождения Bki(u) по коэф-
фициенту поглощения достаточно знать: для переходов с основного уровня, соглас-
но (5.93), общую концентрацию поглощающих частиц (т. е. заселенность основного
уровня п\ « п0), а для переходов с возбужденных уровней, согласно (5.95), —
заселенности этих уровней.
Так как вероятность поглощения Bkl(u) связана с силой осциллятора fki(v)
для поглощения, согласно (4.115), соотношением
тге2
Bki^ =
3 hTibg и
(5.100)
то коэффициент поглощения можно выразить через силу осциллятора. Для перехода
с основного уровня при наличии теплового равновесия и при малости вынужденного
испускания мы получаем из (5.100) и (5.93)
3hmev
= -у-
?rez
с 3hmev, ч
т--------— («<z)u- =
hvn$ 7ге2
1 3cme z 4
------
n0 ire2
(5.101)
144
Глава 5. Интенсивности в спектрах
В отличие от соотношения, связывающего коэффициент поглощения с веро-
ятностью перехода (формула (5.93) или более общая формула (5.95)), в соотноше-
ние (5.101) не входит частота перехода. Если для некоторой полосы или линии
измерить коэффициент поглощения как функцию частоты и определить f xvdu
по всему контуру полосы или линии, то, найдя при помощи соотношения (5.101)
силу осциллятора рассчитанную на единицу интервала частот, можно полу-
чить полную силу осциллятора
1 Зсте
По 7ге2
Miidv.
(5.102)
Эта формула, впервые полученная Кравцом в 1912 г. [172], позволяет характеризо-
вать полное поглощение для рассматриваемой полосы или линии величиной силы
осциллятора.
При применении формулы (5.102) к опытным данным удобно вводить коэффициент
поглощения, отнесенный к молярной концентрации С поглощающих частиц, равный
С ’
(5.103)
где С = — (N — число Авогадро).
N
Если рассчитывать коэффициент поглощения на единицу интервала волновых чисел
то мы получаем формулу Кравца (5.102) в виде
и
с ’
1 Зс2те
N зге2
(5.104)
В формулу (5.104) входит скорость света. Можно показать [230], что для среды с показа-
(п2 + 2)2 п(п2 + 2)2
гелем преломления п в эту формулу еще нужно ввести множители —--------, п и ---------
для дипольного, магнитного и квадрупольного излучений соответственно.
§ 5.4. Неравновесные спектры испускания и их интенсивности
Как правило, спектры испускания, исследование которых играет в спектроско-
пии важнейшую роль, являются неравновесными: наблюдаемое излучение не на-
ходится в термодинамическом равновесии с веществом. В отличие от спектров
поглощения, при изучении которых обычно наблюдается ослабление излучения,
проходящего через вещество, находящееся в равновесии, при изучении спектров
испускания очень часто приходится иметь дело с источниками излучения, в кото-
рых не только отсутствует равновесие излучения с веществом, но и само вещество
находится в неравновесных состояниях. Заселенность уровней энергии для частиц
такого вещества может очень сильно отличаться от равновесной; весьма важны
случаи, когда в самом веществе имеется лишь частичное равновесие (равновесие
для определенных степеней свободы).
Процессы, в результате которых возникают спектры испускания, могут быть
стационарными и нестационарными.
В первом случае излучение, испускаемое источником, является постоянным
во времени по интенсивности и спектральному составу; потери энергии на излу-
чение непрерывно пополняются при помощи возбуждения вещества в источнике
какими-либо способами — путем теплового (термического), оптического, элек-
трического возбуждения. Ни в коем случае не следует смешивать стационарные
§ 5.4. Неравновесные спектры испускания и их интенсивности 145
неравновесные процессы с равновесными, когда потери энергии путем испуска-
ния компенсируются поглощением излучения той же интенсивности и того же
спектрального состава, причем осуществляется детальное равновесие для всех ти-
пов происходящих процессов излучения, как это было рассмотрено в § 5.2 (вывод
формулы Планка по Эйнштейну, с. 134). Примером стационарных спектров ис-
пускания могут служить спектры, даваемые различными типами дугового разряда,
особенно на постоянном токе, спектры, получаемые путем оптического возбужде-
ния постоянными источниками излучения, наконец, спектры, возникающие за счет
термического возбуждения при нагреве вещества.
Во втором случае — нестационарных спектров испускания — сами спектры ме-
няются во времени. При этом, вообще говоря, может изменяться как спектральный
состав, так и интенсивности, абсолютные и относительные. Примерами типично
нестационарных спектров могут служить спектры импульсного разряда, спектры
вспышек и взрывов.
Многочисленные примеры как стационарных, так и нестационарных спек-
тров испускания (а также поглощения) можно привести из области астрофизики.
Обычные спектры Солнца и звезд представляют типичные примеры стационарных
спектров. Нестационарными спектрами являются спектры переменных звезд, новых
и особенно сверхновых, спектры солнечных пятен и протуберанцев и т. д.
С экспериментальной точки зрения проще изучение стационарных спектров
испускания, для которых в случае необходимости могут применяться, при фотогра-
фическом методе исследования, длительные экспозиции. Для изучения же неста-
ционарных спектров испускания приходится применять, особенно в случае быстро
протекающих процессов, разного рода развертки во времени, либо регистрировать
спектры с малыми экспозициями через короткие промежутки времени.
По отношению к состоянию равновесия вещества спектры испускания можно
разделить на три основных типа.
Спектры первого типа получаются, когда в источнике излучения вещество
находится в термодинамическом равновесии по отношению ко всем степеням сво-
боды и может быть охарактеризовано, как находящееся при вполне определенной
температуре. Распределение частиц по уровням определяется законом Максвелла—
Больцмана (5.10), и мы имеем равновесное тепловое, или температурное, испуска-
ние (см. § 1.3). При этом, однако, излучение не находится в термодинамическом
равновесии с веществом, и термин «равновесное» относится к состоянию излучаю-
щего вещества, в котором, благодаря подводу энергии извне и столкновениям между
частицами, сохраняется равновесное распределение частиц по уровням.
Энергия излучения, испускаемого в единице объема в единицу времени,
т.е. мощность испускания (см. (5.2)), пропорциональна заселенности п, начального
уровня, являющегося возбужденным (г 2), и вероятности спонтанного перехода.
Эта мощность определяется, с учетом (5.17) и (5.18), формулой
Et-E\
(сп)	9i Е'Е'	9ie ™
U,k = hvniAik = hvnx —e ” Aik = hvn0 —------5------------°-------------Л,*,
51	5i(l + —e « + — e tr+...j
v	9\	9\	/
(5.105)
которая, когда все разности Ej - Е\^ кТ, сводится к формуле
и%п) = кищ e-^Aik	(5.106)
(ср. (5.95)).
146
Глава 5. Интенсивности в спектрах
Наличие показательного множителя е ю приводит к резкой зависимости
Ei — Е\
испускания от температуры, особенно когда а — —--------- не менее 5-10. Бла-
К1
годаря тому, что метод спектров испускания является весьма чувствительным,
даже при а — 15-20 (что, согласно табл. 5.1, соответствует значениям е~а поряд-
ка 10~9 - 10~6, т. е. относительным заселенностям от миллиардных до миллионных
долей), можно хорошо наблюдать свечение. Для переходов в оптической области
спектра, соответствующих энергии возбуждения Ei — Е\ порядка 2,5 эВ (т. е. при-
о.	hv
мерно волновому числу 20 000 см и длине волны 5 000 А), а — — = 20
при кТ — 0,125 эВ (1 000 см-1), что дает Т & 1 500 К « 1 200° С; при этом
может наблюдаться испускание. При вдвое более высокой температуре (а = 10,
кТ — 0,250 эВ (2 000 см-1), Т = 3 000 К = 2 700° С) испускание будет уже весьма
интенсивным. Вообще, для наблюдения спектров испускания в видимой и ультрафи-
олетовой областях необходимы температуры в несколько тысяч градусов. Равновес-
ное распределение частиц по уровням, соответствующее таким температурам, может
осуществляться путем чисто термического возбуждения в высокотемпературных
электрических печах и путем возбуждения в электрическом разряде, в особенности
дуговом.
Высокотемпературная печь, дающая температуры до 2 800° С, была сконструирована
Кингом [227]. Она применяется для классификации спектральных линий атомов различ-
ных элементов по их энергиям возбуждения. С повышением температуры возбуждаются все
более высокие уровни, и появляются линии с этих уровней. Соответственно линии делят
на температурные классы: наиболее легко возбуждаемые линии относят к классу I, труднее
возбуждаемые — к классу И и т.д.; начиная со II и III классов наряду с линиями нейтраль-
ных атомов начинают появляться линии ионов (подробнее см. [15], с. 258). В печи Кинга
распределение атомов по уровням является равновесным, и приближенно может иметь место,
для сильно поглощаемых линий, равновесие вещества с излучением.
В дуговом разряде (например, в воздухе при нормальном давлении) между электродами,
угольными или металлическими, — в обычной электрической дуге — также может, при опре-
деленных электрических режимах, осуществляться, хотя бы и приближенно, равновесное
распределение частиц по уровням. Следует, однако, иметь в виду, что условия возбуждения
в дуге являются весьма сложными и в каждом конкретном случае требуется анализ того,
в какой степени заселенность уровней соответствует равновесному распределению.
Формулы (5.105) и (5.106) определяют абсолютные интенсивности в спектрах
теплового испускания. Особенно важное значение имеют относительные интенсив-
ности, которые обычно и измеряются на опыте. Относительная интенсивность lik/Iji
двух линий испускания i —> к и j —> I данного атома или молекулы, согласно (5.105),
равна
и™

Uik Щ Aik	Vik Qi	Aik
	—	g kr -
Uji Ttj Aji--------------------------Vji Qj-Aji
(5.107)
и изменяется с температурой тем сильнее, чем больше разность энергий АЕ = Ei~Ej
верхних уровней, начальных для испускания. Для перехода с того же верхнего уров-
ня (Ei — Ej = 0) отношение (5.107) не зависит от температуры, для переходов
с близких верхних уровней (Ei - Ej = &Е «С кТ) оно будет мало зависеть от темпе-
ратуры. В этих случаях по относительным интенсивностям линий можно определять
отношения вероятностей спонтанных переходов. Для относительной интенсивности
§ 5.4. Неравновесные спектры испускания и их интенсивности 147
двух линий различных атомов или молекул получается формула
АУ	Ь j
которая дает ту же зависимость от температуры, что и (5.107), однако содержит
еще отношение п\ /п\ заселенностей п\ и п\ основных уровней частиц типа а
и частиц типа 6; при малых заселенностях возбужденных уровней это отношение
можно заменить отношением п^/п^ (см. (5.24)). Формулы (5.107) и (5.108) явля-
ются основными в изучении интенсивностей в спектрах испускания при различных
температурах и имеют важное значение для эмиссионного спектрального анализа
(см., например, [111] и [112]); однако мы не имеем возможности останавливать-
ся на их приложениях. Необходимо только подчеркнуть, что по распределению
интенсивностей в спектре могут определяться температуры, в частности по форму-
ле (5.107), если известны разности Ei — Ej уровней энергии и отношения Aik/Aji
вероятностей переходов.
Спектры второго типа получаются, когда в источнике излучения вещество
находится в частичном тепловом равновесии, т. е. равновесное распределение частиц
по энергиям осуществляется для некоторых степеней свободы. Это распределение
будет соответствовать некоторой эффективной температуре, которую, однако, нельзя
рассматривать как температуру вещества в целом.
Например, равновесное распределение может иметь место по поступательным
степеням свободы и отсутствовать по электронным уровням. Может осуществляться
случай, когда для разных степеней свободы приближенно имеется равновесное рас-
пределение, соответствующее разным температурам. Типичным примером является
плазма электрического разряда, которая может характеризоваться определенной
электронной температурой Тэ (соответствующей максвелловскому распределению
электронов по скоростям) порядка десятков тысяч градусов, значительно превыша-
ющей температуры атомов Та и ионов Ти, которые также могут иметь определенные,
однако значительно меньшие значения, порядка тысяч градусов, а в случае тлеющего
разряда порядка нескольких сот градусов. Возбуждение электронных уровней атомов
в плазме будет происходить при электронном ударе, и заселенности этих уровней бу-
дут соответствовать электронной температуре. Различие температур электронов и тя-
желых частиц (атомов и ионов) определяется тем, что электроны хорошо обменива-
ются кинетической энергией между собой, а тяжелые частицы — между собой, одна-
ко обмен кинетической энергией между электронами и тяжелыми частицами проис-
ходит медленно из-за большой разницы в массах. В случае молекул может устанавли-
ваться распределение по колебательным и вращательным уровням, соответствующее
различным колебательной температуре Ткоя и вращательной температуре Твр.
В случае спектров второго типа формулы (5.105) и (5.106) для абсолютных ин-
тенсивностей и формулы (5.107) и (5.108) для относительных интенсивностей могут
применяться к переходам между уровнями энергии, соответствующим степеням сво-
боды, для которых приближенно устанавливается равновесие; в эти формулы надо
подставлять разные температуры для разных степеней свободы (например, Т ~ Т3
для электронных уровней атомов в плазме). Эти температуры могу г быть определены
по распределению интенсивностей, как и в случае спектров первого типа.
Спектры испускания рассматриваемого типа, соответствующие неполному рав-
новесию в веществе, являются переходными к неравновесным спектрам третьего
типа, когда в источнике излучения вещество не находится в тепловом равновесии
в силу условий возбуждения. К таким спектрам испускания относятся различного
148
Глава 5. Интенсивности в спектрах
рода спектры люминесценции (см. § 1.3), когда при возбуждении возникает неравно-
весное распределение частиц по уровням энергии. Характерными являются, в частно-
сти, спектры фотолюминесценции, когда при оптическом возбуждении получаются
значительные заселенности высоких уровней (для которых Д2? = Ei — Е\ kT),
что обусловливает большие интенсивности испускания. Интенсивности в спектрах
третьего типа уже не определяются температурой и могут очень сильно зависеть
от условий возбуждения.
При рассмотрении интенсивностей спектров испускания очень важными явля-
ются вопросы механизма возбуждения уровней энергии. За исключением случая
оптического возбуждения, происходящего благодаря поглощению фотонов, все
остальные способы возбуждения уровней энергии частиц сводятся к безызлуча-
тельным процессам обмена энергией. В газе такие процессы происходят при столк-
новениях (ударах) между данной частицей и другими частицами. Именно благодаря
столкновениям частиц устанавливается равновесие, характеризующееся определен-
ным распределением частиц по уровням, нормальному и возбужденным13).
Мы вкратце рассмотрим некоторые вопросы возбуждения при столкновениях,
важные для спектроскопии.
Столкновения частиц разделяют на упругие, при которых частицы обменивают-
ся кинетической энергией поступательного движения, сохраняя неизменной свою
внутреннюю энергию, и на неупругие, при которых происходит переход кинети-
ческой энергии относительного поступательного движения частиц во внутреннюю
энергию (одной из этих частиц или обеих) и обратно14). Именно неупругие столк-
новения определяют распределение частиц по уровням энергии. Распределение же
частиц по скоростям (при наличии равновесия — максвелловское распределение)
определяется как упругими, так и неупругими столкновениями.
Неупругие столкновения можно разделить на столкновения двух типов, на-
зываемые ударами первого и второго родов. При первых кинетическая энергия
относительного движения переходит во внутреннюю энергию, при вторых, наобо-
рот, внутренняя энергия переходит в кинетическую.
Представление об ударах первого и второго родов было введено Клейном и Рос-
селандом [186], рассмотревшими детальное равновесие, осуществляемое благодаря
компенсации прямых процессов возбуждения атомов при столкновениях с электро-
нами путем перехода кинетической энергии электрона во внутреннюю энергию
атома (т. е. ударов первого рода) обратными процессами отдачи энергии возбуждения
при столкновениях путем перехода внутренней энергии атома в кинетическую энер-
гию электрона (т. е. ударами второго рода). Это рассмотрение применимо и в общем
случае любых неупругих столкновений. Оно приводит к определенному соотноше-
нию между вероятностями ударов первого и второго родов как частному случаю
соотношений между вероятностями прямых и обратных процессов.
Удары первого рода между тяжелыми частицами-атомами, молекулами, их
ионами — и электронами, т. е. возбуждение тяжелых частиц электронным уда-
ром (см. § 1.3), являются основным процессом, приводящим к возбуждению этих
частиц в электрическом разряде. Возбуждение частиц может также происходить
при ионном ударе, т. е. при столкновениях с ионами, ускоренными электрическим
полем.
13) Только при очень высоких температурах в десятки и сотни тысяч градусов начинает играть
существенную роль и затем становится решающим взаимодействие излучения и вещества. При этом
обмен энергией между областями с различной температурой и установление равновесия осуществляются
лучистой теплопроводностью, т. е. переносом энергии излучением, а не частицами.
14) Возможен и переход внутренней энергии во внутреннюю (см. ниже).
§ 5.4. Неравновесные спектры испускания и их интенсивности
149
Следует иметь в виду, что хотя возбуждение электронным ударом в электричес-
ких источниках света является неравновесным процессом, обеспечивающим подвод
энергии к частицам и компенсирующим потери на излучение, но благодаря разного
рода другим столкновениям, в том числе ударам второго рода, может с большей
или меньшей степенью приближения устанавливаться тепловое равновесие, о кото-
ром говорилось выше (с. 145).
При неупругих столкновениях между частицами возможен не только переход
энергии возбуждения в кинетическую и обратно, но и передача энергии возбуждения,
полностью или частично, от одной частицы к другой, т. е. переход внутренней энер-
гии во внутреннюю. При этом в кинетическую энергию переходит лишь некоторая
доля энергии возбуждения. Вероятность передачи энергии возбуждения от одной
частицы к другой тем больше, чем меньше доля, превращающаяся в кинетическую
энергию. Наиболее вероятными являются резонансные переходы, когда энергия воз-
буждения одной частицы полностью передается другой частице, возбуждая ее. Это
возможно в столкновениях между одинаковыми частицами, или в столкновениях
между разными частицами, при наличии одинаковых разностей уровней энергии.
Когда рассматривается возбуждение частиц и вообще неупругие столкновения,
необходимо учитывать вид внутренней энергии. Ею могут быть электронная энергия
атомов и молекул и, в случае молекул, колебательная и вращательная энергии.
Вероятности передачи энергии зависят как от величины передаваемой энергии, так
и от ее вида. Расчету этих вероятностей посвящен ряд работ (см., например, список
литературы в [109]), результаты которых представляют значительный интерес; однако
они не могут быть рассмотрены здесь за недостатком места.
Примером передачи электронной энергии возбуждения является, в случае опти-
ческого возбуждения, передача этой энергии от атомов одного рода атомам другого
рода, сопровождающаяся высвечиванием, — сенсибилизированная флуоресценция. Ти-
пичный пример этого явления представляет флуоресценция таллия в смеси паров
ртути и таллия при возбуждении резонансной линией ртути 2 537 А [187].
На рис. 5.7 показана схема возникновения
во флуоресценции линий таллия 2 768 и 3 529 А.
Возбужденный атом ртути с энергией 4,89 эВ
при столкновении с атомом таллия теряет свою
энергию, за счет чего возбуждается уровень тал-
лия с энергией 4,45 эВ, который является началь-
ным для испускания указанных линий таллия.
Исключительно сложный характер име-
ют процессы возбуждения частиц в та-
ких широко применяемых в спектроскопии
Рис. 5.7. Схема сенсибилизированной
флуоресценции таллия
источниках света, как электрическая дуга
и электрическая искра. Наряду с процессами возбуждения электронным ударом
важнейшую роль играют различные другие процессы обмена энергии при столкно-
вениях. В зависимости от того, является ли разряд дуговым или искровым, процессы
обмена энергией протекают по-разному и получаются сильно отличающиеся друг
от друга спектры. Для дугового разряда характерно возбуждение уровней энергии
нейтральных атомов при сравнительно слабой ионизации газа, а для искрового
разряда — сильная ионизация газа и соответственно возбуждение уровней энергии
ионизованных атомов. Преобладание в спектре дуги линий нейтральных атомов,
а в спектре искры линий однократно ионизованных атомов нашло свое отражение
в том, что спектры нейтральных атомов называют дуговыми, а спектры ионизо-
ванных атомов — искровыми. Следует, однако, иметь в виду, что в спектре дуги
150
Глава 5. Интенсивности в спектрах
может иметься большое число линий однократно ионизованных атомов, особенно
атомов с низкими потенциалами ионизации, а в спектре искры могут наблюдаться
и интенсивные линии нейтральных атомов|5).
Спектры разных типов как дугового, так и искрового разряда могут быть
также весьма различными. В частности, при мощных искровых разрядах получаются
ионы высокой кратности ионизации, и в зависимости от условий этого разряда
в спектрах могут преобладать линии двукратно, трехкратно или даже более высоко
ионизованных атомов.
До сих пор мы рассматривали исключительно спектры спонтанного испуска-
ния. Вынужденное испускание в оптической области непосредственно наблюдать
не удается. Однако подобное испускание можно наблюдать в области радиоча-
стот, в частности в молекулярном генераторе [256, 257]. В нем создаются такие
условия, когда для некоторого перехода заселен только более высокий уровень мо-
лекул, при свободном более низком уровне, и начавшееся под действием излучения
небольшой интенсивности вынужденное испускание фотонов одними молекулами
стимулирует испускание фотонов другими молекулами — происходит генерация
радиочастотного излучения определенной частоты (подробнее о молекулярном ге-
нераторе см. § 19.8). На том же принципе основаны парамагнитные усилители
для микроволновой области [258] и усилители и генераторы излучения для оптичес-
кой области [258а], в которых используется вынужденное испускание при переходах
между уровнями энергии ионов в кристаллах; за последнее время разработке таких
усилителей (так называемых «мазеров» и «лазеров») уделяется большое внимание.
Впервые принцип молекулярного усиления был сформулирован Фабрикантом (см. сб.
«Электронные и ионные приборы». Труды ВЭИ, вып. 41, 1940, с. 236, 254, а также статью
Бутаевой и Фабриканта о среде с отрицательным коэффициентом поглощения в Сб. памяти
Ландсберга, изд. АН СССР, 1959, с. 62).
Рис. 5.8. Распределение
интенсивности в линии
§ 5.5. Контуры спектральных линий и полос
Все реальные спектральные линии обладают определенной шириной. Наряду
с естественным уширением спектральных линий, рассмотренным в §4.6, имеются
другие причины уширения (см. §5.6). Совместное действие всех причин уширения
приводит к определенному контуру спектральной линии, т. е. к определенному рас-
пределению в линии интенсивности как непрерывной функции частоты (см. рис. 5.8).
Контур спектральной линии характеризуется
некоторой формой; область частот, соответству-
ющая данной линии, — ее ширина — может быть
при этом весьма различной, как очень малой, так
и достаточно значительной. Для сложных атом-
ных систем — многоатомных молекул, состоящих
из большого числа атомов, и для конденсирован-
ных систем — вместо более или менее узких
линий обычно получаются сплошные полосы* 16),
которые также характеризуются определенным
контуром; в соответствии с большой шириной
мы говорим уже не о линиях, а о полосах.
около катода и в центральной части плазмы; в искре линии
нейтральных атомов возбуждаются в средней части искрового промежутка и при послесвечении.
16) Речь идет именно о сплошных полосах, а не о полосах, распадающихся при большой дисперсии
на отдельные линии, как это имеет место для простейших молекул (см. гл. 17).
15) В дуге линии ионов возбуждаются
§ 5.5. Контуры спектральных линий и полос
151
При рассмотрении вопроса о контурах спектральных линий и полос необхо-
димо, прежде всего, более точно определить, что следует понимать под контуром,
и выяснить, как понятие контура связано с характеристикой переходов в поглоще-
нии и в испускании при помощи вероятностей перехода, мощностей поглощения
и испускания и связанных с ними величин.
Так как при учете конечной ширины линий уже нельзя говорить о строгой
определенности частоты перехода и вероятности поглощения и испускания являют-
ся непрерывными функциями частоты, то их следует относить не к данной частоте,
а рассчитывать на единицу интервала частот (ср. замечание при выводе формулы
Планка, с. 133). Поэтому для перехода между уровнями Ei и Ek {Ei > Ek) конечной
ширины следует вводить вероятность спонтанного испускания Л^(р), вероятность
вынужденного испускания Bik(v) и вероятность поглощения Bki(u), рассчитанные
на единицу интервала частот. Соответственно мощности испускания и поглоще-
ния, испускательные и поглощательные способности, коэффициенты испускания
и поглощения, пропорциональные произведениям вероятностей на частоту и испус-
каемого или поглощаемого кванта, также следует рассчитывать на единицу интервала
частот. Это относится к силам осцилляторов, пропорциональным коэффициентам
поглощения (см. (5.100)). Для полос тем более надо вводить величины, рассчитанные
на единицу интервала частот.
Величины, отнесенные к единице интервала частот, мы будем называть, по ана-
логии со спектральной плотностью излучения, спектральной вероятностью, спек-
тральной мощностью и т. д. Зависимость любой из перечисленных выше спектраль-
ных величин от частоты можно представить в виде
F(v) - F(p0)^M	(5.109)
где F(vq) — максимальное значение величины F(v), достигаемое где-то в середине
линии, a (Pf(v) — функция, равная единице при и = uq,
Ы^о) = 1,	(5.110)
и спадающая к краям линии (рис. 5.8). Закон спадания будет зависеть от причины
уширения.
Для спектральной вероятности спонтанного испускания мы можем написать:
Aik(u) = Aik(v0)ipA(p);	(5.111)
функция <Pa(v) определяет контур линии испускания, если рассматривать зависи-
мость от частоты числа фотонов, испущенных за единицу интервала частот.
Для спектральной вероятности поглощения соответственно
Bki(v) = Bki(uQ)(pB{y),	(5.112)
где <Pb(v) определяет контур линии поглощения. Основное соотношение Эйнштей-
на (4.8) между вероятностью спонтанного испускания и вероятностью поглощения
остается справедливым, т.е.
Aik(y) = ^-^-Bki(u).	(5.113)
£ 9i
Так как ширина Др спектральных линий всегда мала по сравнению с частотой и
(А	ч
— <С 1 ), даже для широких линий, то величину и можно считать постоянной
\ и J
152
Глава 5. Интенсивности в спектрах
и заменить значением куба частоты для середины линии. Представляя (5.113),
согласно (5.111) и (5.112), в виде
Aik{v^tpA(y) =	(5-Н4)
с3 gi
и учитывая, что
8тгЛ^ дк
Aik{y^ = —----------Bki(v0),	(5.115)
с gi
получаем
<Pa{v) = ч>в(у),	(5.116)
т. е. совпадение контуров линий испускания и поглощения. Аналогичные рассуж-
дения применимы также к спектральным мощностям испускания и поглощения
и к соответствующим коэффициентам, отличающимся от вероятностей множите-
лем и (помимо постоянных множителей). Функция <p(i/) определяет контур линии,
независимо от того, какую величину рассматривать. Поэтому можно говорить о рас-
пределении интенсивностей в общем виде, положив
(5.117)
Для случая естественного уширения спектральной линии функция <р(у) определяет-
ся, согласно (4.132), формулой
/7\2 1
<рИ = у --------------------~—2,	(5.Н8)
у Z /	f У \
4тг2(1/- i/0)2 + ( -}
где 7 — коэффициент затухания осциллятора, сопоставляемого данному переходу.
Следует подчеркнуть, что совпадение контуров линии поглощения и линии спонтанного
испускания имеет место, когда поглощается излучение, имеющее постоянную интенсивность
в пределах линии. Если возбуждение производится узкой линией, ширина которой сравнима
с шириной линии спонтанного испускания и, тем более, если возбуждающая линия зна-
чительно уже этой линии, то совпадение не имеет места. Подобное положение получается
для резонансного испускания, возбуждаемого узкой линией: линия испускания также являет-
ся узкой, ее контур совпадает с контуром поглощаемой линии и резко отличается от контура
более широкой линии спонтанного испускания [140].
Для широких полос р3 в соотношении (5.113) уже нельзя считать постоянным,
и контур полосы поглощения будет отличаться от контура полосы испускания за счет
изменения этого множителя в зависимости от v — у§. Чтобы получить из контура
полосы испускания контур соответствующей полосы поглощения, надо, соглас-
Atfc(^) (v\3	( у \ 3
но (5.113), разделить значения <Ра(у) — ~—г на I — I • Функция <рд(р) ( — )
АцдУц)	\уо/
совпадает с функцией (рв(у) в (5.112)|7). Некоторое различие в контурах будет полу-
чаться и при переходе от вероятностей к мощностям, в связи с умножением на и.
|7) Если можно пренебречь сдвигом максимума функции —по сравнению с максимумом
функции Когда этим сдвигом пренебречь нельзя, то надо еще изменить масштаб так, чтобы
максимум функции	равнялся единице, как и максимум функции Pa(v).
§ 5.5. Контуры спектральных линий и полос
153
Наряду со спектральными величинами, рассчитанными на единицу интервала
частот, переход можно охарактеризовать интегральными величинами — полными,
или интегральными, вероятностями испускания и поглощения
Aik = J Aik(v)dv, Bik = J Bik(u) du, Bki = J Bkt(u) du (5.119)
и полными, или интегральными, мощностями испускания и поглощения
u^n) = J ^сп)du,	U^b,H) = J U^H)du, С^погл) = у ^<погл)du.	(5.120)
Аналогичные выражения можно написать для испускательной и поглощательной
способностей, для коэффициентов испускания и поглощения и для сил осцилляторов
(ср. (5.102)). В соответствии с общей формулой (5.109) мы получим
F = J F(u)du — F(uQ) J (pF(u)du,	(5.121)
т. е. максимальное значение функции
(5,22)
Для вероятности спонтанного испускания мы найдем формулу
Aik(u) = Aik ,	(5.123)
J <рА(и) du
которая выражает максимальное значение спектральной вероятности через полную
вероятность перехода.
Интеграл Др' = J du в (5.121) и (5.122) имеет порядок Др, где Др —
ширина линии или полосы (см. рис. 5.8); так как <р(ро) = 1, то площадь кривой —
порядка Др • 1. Следовательно,
F = Г(р0)Др',	(5.124)
где Др' = f 99f(p) du — порядка ширины линии Др, в частности
Aik = Aik(uQ)&u.	(5.125)
Аналогично,
Bki =Вк{(ио)Аи'.	(5.126)
Существенно, что полные вероятности для линий и узких полос, для кото-
рых р«ро, связаны так же, как и спектральные вероятности Aik(u) и Bki(u),
соотношением
Aik = Aik(u) = ivhul gk
Bki Bki(u) c3 gi-
Отметим, что при выводе формулы Планка (см. с. 134) соотношение (5.52) можно писать
при ри, равном спектральной плотности излучения, как для спектральных вероятностей, так
и для пропорциональных им полных вероятностей. Можно также, написав соотношение (5.52)
для максимальных значений вероятностей,
[nkBki(uQ) - niBik(uQ)]pu = п{А{к(и0),	(5.128)
умножить его на Др'. Тогда, согласно (5.125),
[nkBki(uQ) - niBik(uQ)]py^u = п<А<к,	(5.129)
154
Глава 5. Интенсивности в спектрах
где руАи' — плотность энергии излучения в интервале Ai/, a Bki(i/Q) и Bik(vo) — максимальные
значения спектральных вероятностей поглощения, в то время как Aik — полная вероятность
спонтанного испускания, связанная со временем жизни. При малом Ai/ можно говорить
о риАи' как плотности излучения частоты i/0.
Следует подчеркнуть, что все приведенные в гл. 4 формулы для вероятностей
дипольных, магнитных и квадрупольных переходов, согласно которым они выража-
ются через соответствующие моменты переходов, относятся к полным вероятностям.
Для нахождения спектральных вероятностей, рассчитанных на единицу интервала
частот, надо знать контур (р(у) линии или полосы, и тогда, согласно (5.109) и (5.122),
FM = F(n)Vpl») = fvpFMdl, ₽,(-)•
Для случая естественного уширения спектральных линий при спонтанном испуска-
нии, согласно (5.130) и (5.118), получается
/ х 2
(5.130)
__________________ 7 А2
Л 2/	/¥’(»')*'W
4тг2(р — р0)2+ 1-1
Aik
Входящий в (5.131) интеграл равен,8)
/7\2‘
4тг2(1/-1/0)2+ ( - J
(5.131)
(5.132)
В результате подстановки имеем формулу
-4jfc(^) — -4tfc7	z \ 2’
4тг2(р - р0)2 + (^)
(5.133)
интегральную вероят-
выражающую спектральную вероятность испускания через
ность.
Для спектральной вероятности поглощения получается контур, совпадающий
с (5.133),
1
(5.134)
2 *
Bki(v) = ВН7
4тг2(р - Ро)2 + ( 2 )
При этом 7 в (5.131) и (5.133), согласно (4.146), равна сумме естественных ши-
рин 7i и 7j комбинирующих уровней. Напомним, что в рассматриваемом случае
IS) Результат (5.132) получается при интегрировании по переменной v - i/g в пределах от -оо до +оо:
Это является законным, когда функция достаточно быстро спадает при увеличении (и — i<o)2
Последнее и имеет место для спектральных линий; для них всегда 7 щ и функция (р(и) становится
ничтожно малой задолго до того, как 1/ - i/g становится равным ~i/q.
§ 5.6. Уширение спектральных линий
155
естественного уширения значение \и — при котором F(y) уменьшается вдвое,
7
по сравнению с F(uq), равно —, а ширина линии
4тг
Др = 2|р - р0| = ~г
2тг
(см. с. 111, а также рис. 4.6). Таким образом, величина Др' интеграла (5.132)
7Г
равна у Ар, т.е. порядка Др, в согласии с оценкой, сделанной на с. 153.
В следующем параграфе мы разберем вопрос о контуре спектральных линий
при их уширении, обусловленном тепловым движением и разного рода взаимодей-
ствиями частиц. Вопроса о контуре широких полос испускания и поглощения мы
сейчас разбирать не будем и вернемся к нему в гл. 27, посвященной электронным
спектрам многоатомных молекул.
Сделаем замечание о наиболее рациональном выборе величины, характеризующей кон-
тур, для широких полос, с точки зрения связи этой величины с моментами перехода,
т. е. с матричными элементами, определяющими абсолютные значения полных вероятностей.
В случае дипольного излучения вероятность поглощения выражается, согласно (4.46),
только через дипольный момент перехода и не зависит от частоты, тогда как вероятность
спонтанного перехода Aik пропорциональна еще, согласно (4.45), и3. Поэтому для широких
полос рационально исходить из вероятности Bki То же справедливо и для магнитного
излучения. Для квадрупольного излучения сама Bki пропорциональна и2 (см. (4.79) и (4.8)),
ж	Вк^
и поэтому для характеристики контура лучше всего исходить из функции --—.
§ 5.6. Уширение спектральных линий, обусловленное
тепловым движением и взаимодействиями частиц
Контуры спектральных линий, получающиеся при их уширении, мы будем
характеризовать распределением интенсивностей (5.117), общим для поглощения
и испускания, которое мы запишем в виде
<5|35>
В рассмотренном выше случае естественного уширения эта функция равна, соглас-
но (5.118),
Рее#) = ,Л . 2-----------•	(5.136)
/4тг\ ,
( — ) (у ~ Vo) + 1
\ 7 /
Она убывает с увеличением \v - давая симметричный относительно значе-
7
ния и — Uq контур, характеризующийся шириной Az/ — 2\и - р0| = —• При боль-
2тг
2	<7\2
ших \и — Uq\, при которых (у — z/о) 7"	’ функция (р(у) спадает обратно про-
\4тг/
порционально \у — р0) • Если выражать и — Uq в единицах 7/4тг и обозначить —-—
7/4тг
через <5, то (5.136) запишется в виде
Pec#)--j-^;	(5.137)
156
Глава 5. Интенсивности в спектрах
оно принимает следующие значения:
б	0,5	1	2	3	4	6	8	10	15	20 1
<Рест(<5)	0,80	0,50	0,20	0,10	0,059	0,027	0,0154	0,0099	0,0044	0,0025 J	’
(5.138)
Как мы видели в §4.5, естественная ширина спектральных линий очень мала.
Однако обычно спектральные линии обладают гораздо большей шириной. При-
чинами такого уширения являются тепловое движение и взаимодействия между
частицами, т. е. факторы, зависящие от условий, в которых находится рассматрива-
емый атом или молекула.
Тепловое движение приводит к уширению спектральных линий, связанному
с явлением Допплера, т. е. с изменением частоты испускаемого или поглощаемого
частицей света в зависимости от скорости поступательного движения частицы.
Как известно, если частица движется со скоростью v, составляющей угол д с на-
правлением z распространения излучения (см. рис. 5.9), то допплеровское изменение
частоты равно
v	vz
и - д/о = ^о~ cos# = i/0—,	(5.139)
z	где i/о — частота излучения, испускаемого или поглощаемого
неподвижной частицей, a vcostf = vz— проекция ее скоро-
сти на направление z. Вследствие того, что частицы движутся
в различных направлениях и с различными скоростями, вместо
и	одной частоты iz0 получается совокупность частот в некотором
интервале, т. е. спектральная линия уширяется — получается
допплеровское уширение спектральной линии.
При наличии теплового равновесия распределение частиц
____________ по их скоростям определяется законом Максвелла, учет кото-
рого приводит к следующему контуру линии:
V1 1	Ж = РдопплМ =	(5.140)
Л/	где
Рис. 5.9. Схема	М(? 1
для явления	2кТ7	р.141)
Допплера	0
(М — масса частицы).
Таким образом, интенсивность убывает к краям линии по показательному
закону. Ширина линии Ai/ определяется из условия	= -, что дает
p(v - i/o)2 = In 2, откуда
/1п2 [1кТ
ки = 2|1/ - 1/0| = 2 J — = 2i/0y ^2 In 2.	(5.142)
По сравнению с естественным контуром (5.136), для допплеровского контура (5.141)
убывание интенсивности к краям при той же полуширине происходит гораздо
I/ - У Q
быстрее. Если положить б — —-==, то (5.140) запишется в виде
^o,UO = e^2|n2;	(5.143)
§ 5.6. Уширение спектральных линий
157
^доппл(^) принимает следующие значения:
<5	0,5	1	2	3	1
^доппл(<5)	0,84	0,50	0,063	0,0020 J	'
(5.144)
Формула (5.140) для допплеровского уширения выводится следующим образом. Макс-
велловское распределение частиц по составляющей скорости vz имеет вид
f \Mv2z}
dnVz = Л exp < ~2~j^ (dv^	(5.145)
где dnVz — число частиц из общего числа частиц п, скорости которых при данной температу-
ре Т лежат в пределах от vz до vz + dvz, а А — постоянная. Согласно (5.139),
с f 1 Me2 (и -1/0)21,ч
dnV! = А - ехр < —- — ------г----- Уф - Vo).	(5.146)
И)	Z Л2	UQ	J
Это есть число частиц, которые могут при данном переходе испускать или поглощать
частоту от и до и + du. Ему пропорциональна спектральная интенсивность 1(и), умноженная
на du = d(u — uq). Следовательно,
,4 fl Мс2 (и - u0)21
<5j47)
и так как при и = и0 экспонента равна 1, то приходим к (5.140).
Согласно (5.142), допплеровская ширина прямо пропорциональна квадратному
корню из абсолютной температуры Т и обратно пропорциональна массе частицы М.
Если вместо массы частицы ввести молекулярный вес р = NM, где N — число
Авогадро, и подставить численные значения постоянных, то для допплеровской
ширины получим формулу
2 /----- Т	6
Av = i/0 - ^2kN In 2 J - = 0,71 • 10 %
c	V Д
Т с
(5.148)
или, в волновых числах,
=0,71 • 10-6	у^см-1.	(5.149)
При обычных температурах допплеровская ширина значительно превосходит есте-
ственную. В качестве примера можно привести данные для 12-линий натрия.
При температуре Т = 300 К мы получаем (д = 23)
/ Др\
\ С / Na
0,044 см-1,
(5.150)
т.е. около 1/20 см ’. Естественная ширина для Л-линий, имеющих время жизни
т - 1,6 • 10-8 с, составляет, согласно формуле (4.125),
Др 1	.
— = ------=0,00033 см-’,	(5.151)
с 2яст	'
т.е. примерно в 100 раз меньше.
Допплеровское уширение играет основную роль в случае достаточно разрежен-
ных газов, когда число столкновений мало и уширение вследствие взаимодействий
158
Глава 5. Интенсивности в спектрах
между частицами, которое будет рассмотрено ниже, не является существенным.
Такие условия обычно имеются в лампах, например ртутных, применяемых при изу-
чении резонансного испускания. Для уменьшения допплеровской ширины источ-
ники света и поглощающие сосуды охлаждают; при этом, согласно (5.148), ширина
уменьшается как \/Т.
Для легких атомов допплеровская ширина, как это вытекает из ее пропорцио-
нальности \ХТ7Д, особенно велика. Для атома водорода {р = 1) она в л/2ОЬ « 14 раз
больше, чем для атома ртути (р — 200).
Существенно, что допплеровское смещение частоты зависит от угла 'О меж-
ду направлением распространения излучения и направлением движения частицы
и обращается в нуль, когда эти направления взаимно перпендикулярны,9). Поэтому
в случае молекулярного пучка, при его наблюдении перпендикулярно направлению
полета частиц, допплеровское смещение отсутствует и ширина линий соответственно
уменьшается до естественной.
Следует подчеркнуть, что даже когда допплеровская ширина значительно превосходит
естественную ширину, интенсивность в линии при достаточно больших значениях и - i/0 —
в крыльях линии — будет определяться естественным уширением, так как функция (5.137)
спадает с увеличением |i/ - iz0| гораздо медленнее, чем функция (5.143). Это обстоятельство не-
обходимо учитывать при наличии так называемого самообращения линий в источниках света,
когда середина линий испускания, особенно резонансных, сильно поглощается, а менее ин-
тенсивные крылья линий, которые поглощаются слабее, играют основную роль. Учет эффек-
тов, связанных с краями линии, очень важен при изучении резонансного испускания (см. [22]).
Допплеровское уширение спектральных линий имеет место как для атомов, так
и для молекул. Для последних, кроме того, приводить к расширению линий может
не только поступательное, но и вращательное движение (см. [234]).
Очень важное значение имеет уширение спектральных линий, связанное со вза-
имодействиями между частицами. За исключением случая достаточно разреженного
газа, именно этот тип уширения определяет значение ширины спектральных ли-
ний. При этом в зависимости от рода взаимодействующих частиц и от условий,
в которых они находятся, могут наблюдаться разнообразные эффекты уширения,
которым посвящены многочисленные экспериментальные и теоретические исследо-
вания (см., например, обзоры [24-26)).
В случае неупругих столкновений, когда в результате частица переходит без из-
лучения на другой уровень энергии, действие столкновений сводится к укорочению
времени жизни т возбужденного состояния, как мы видели в §4.2 (формула (4.24)).
1
Соответственно ширина уровня будет определяться не величиной 7, = Аг\ = —,
а величиной 7' = Дг + Сг = Д, а контур линии будет даваться формулой (5.118)
Ti
или (5.136), с заменой 7 = 7? +7j на 7' — 7«-Т7ь линия уширяется в отношении 7'/7-
В случае упругих столкновений, когда атом сохраняет после столкновения свою
внутреннюю энергию, уровни энергии в результате взаимодействия частиц также
уширяются. Теоретическая трактовка этого уширения представляет значительные
трудности из-за сложности процессов взаимодействия, меняющегося во времени
при столкновении. Приходится применять приближенные методы решения задачи.
Имеются две основные теории уширения спектральных линий — ударная теория
,9) Поперечный эффект Допплера
^при -0 =
существует, но очень мал; он порядка (v/с)2, в то
время как обычный эффект Допплера — порядка и/с.
§ 5.6. Уширение спектральных линий
159
и статистическая теория. Обе они взаимно дополняют друг друга и соответству-
ют двум предельным случаям взаимодействия при столкновениях — мгновенному
(ударная теория) и квазистатическому (статистическая теория).
Согласно ударной теории, с классической точки зрения, частица представляет
собой осциллятор, колеблющийся с частотой х/о> и при столкновениях с другой
частицей происходит скачкообразное изменение фазы колебаний. Получаются не-
зависимые колебания с частотой в течение времени тст между столкновениями,
и излучение в течение этого времени происходит также независимым образом20).
Времени испускания тст соответствует вместо строго определенной частоты i/0,
получаемой при бесконечной длительности колебаний, интервал частот Ах/ поряд-
ка ----аналогично случаю затухающего колебания (см. с. 111), когда вместо одной
2тгтст
7
частоты i/о получаются частоты, лежащие в диапазоне Ах/ — —, где 7 — постоянная
2тг
затухания ( ат =----время затухания в е раз, ср., например, (4.90), т. е. Ах/ =-).
\	7	2тгт /
Так же, как и в случае естественного уширения и уширения при неупругих ударах,
контур линии будет определяться формулой (5.118) или (5.136), где 7 = —. Линия
тст
будет уширяться тем сильнее, чем меньше время между столкновениями.
Квантовомеханическая теория в том же приближении, т. е. для случая очень
малого времени взаимодействия между частицами при столкновении (а именно
при этом условии можно считать, что происходит, с классической точки зрения,
внезапное изменение фазы колебаний), приводит к такому же результату. Мы имеем
еще один пример соответствия между классической и квантовой теориями.
Вследствие того, что время между столкновениями может быть очень малым,
уширение может быть весьма значительным. Например, при времени между столк-
новениями г = 10~11 с получается
что в видимой области спектра дает уширение линий порядка десятых долей анг-
стрема.
Время между столкновениями есть величина, обратная числу столкновений N
данной частицы в единицу времени, которое равно
N = nva,	(5.152)
где v — скорость частицы, п — число частиц в единице объема, а а — поперечное
сечение частиц.
Следует, однако, иметь в виду, что а не есть обычное поперечное сечение, которое
входит в формулы кинетической теории газов (газокинетическое сечение). Это — эффективное
сечение, которому соответствуют скачкообразные изменения фазы, в результате столкновения,
на величины, сравнимые с 2тг. Для нахождения значений а требуется специальный расчет.
Они зависят от характера взаимодействий между частицами, в частности от того, обладают
ли частицы электрическим зарядом, и от скорости частиц.
Предположение ударной теории о малой продолжительности столкновений бу-
дет справедливым при большой относительной скорости сталкивающихся частиц,
20) Получаются неинтерферирующие некогерентные цуги колебаний.
160
Глава 5. Интенсивности в спектрах
когда продолжительность удара мала, так что мы имеем, с классической точки
зрения, внезапное изменение фазы колебаний, а с квантовомеханической точки
зрения — сильное взаимодействие в течение очень малого времени. Условия при-
менимости ударной теории практически всегда выполняются для столкновений
тяжелых частиц с электронами; последние в силу их малой массы движутся, при той
же кинетической энергии, с гораздо большими скоростями. Поэтому уширение
спектральных линий в результате столкновений с электронами правильно описы-
вается ударной теорией, и на опыте получается характерный для ударной теории
контур спектральных линий.
Наоборот, при большой продолжительности столкновений между тяжелыми ча-
стицами, движущимися со сравнительно малыми скоростями, ударная теория может
оказаться совершенно неприменимой, и следует рассматривать взаимодействие ква-
зистатически, т. е. применять статистическую теорию. Идея ее состоит в следующем.
Рассматриваемая частица взаимодействует с окружающими ее частицами, которые
распределены вокруг нее по какому-то статистическому закону. Вследствие этих вза-
имодействий будут изменяться частоты колебаний I/, с классической точки зрения,
и положения уровней энергии Д, с квантовой точки зрения; в результате вместо
строго определенных значений и или Ei, будут получаться значения, лежащие в не-
котором интервале Ai/ или /\Ег. Чем больше плотность вещества, тем ближе будут
другие частицы к данной и тем большими будут Ai/ или ДД-. При этом рассматри-
вается взаимодействие неподвижных частиц и их движение учитывается лишь путем
усреднения взаимодействия по различным возможным расположениям частиц.
Так как силы взаимодействия частиц являются в основном электрическими
(магнитные силы взаимодействия обычно играют малую роль), то задача об изме-
нении АЕг положения уровней энергии есть по существу задача о явлении Штарка
под действием молекулярных электрических полей, в которых находится данная
частица. Ограничимся пока этим замечанием; к вопросам статистической теории
уширения спектральных линий мы вернемся в гл. 15. Отметим лишь, что уширение
существенно зависит от характера взаимодействия частиц и будет различным для за-
ряженных частиц, для частиц, обладающих дипольным моментом, и для частиц,
не обладающих им. Для последних уширение будет зависеть от их поляризуемости.
Взаимодействие может происходить как между различными, так и между оди-
наковыми частицами. В последнем случае, наряду со взаимодействием типа явления
Штарка, возможно взаимодействие резонансного типа для одинаковых частиц, нахо-
дящихся в одинаковых состояниях. При этом может получаться не только уширение
спектральных линий вследствие взаимодействия, но и их сужение [232].
Необходимо отметить, что когда уширение при столкновениях играет существенную
роль, т. е. при достаточно малых промежутках времени между столкновениями, допплеровское
уширение следует рассматривать совместно с уширением вследствие столкновений, поскольку
уже нельзя считать скорость движения частиц постоянной, как это делалось в изложенной
теории допплеровского уширения (см. [234]).
ЧАСТЬ II
АТОМНАЯ СПЕКТРОСКОПИЯ
6 Зак. 103

ГЛАВА 6
УРОВНИ ЭНЕРГИИ И СПЕКТРЫ АТОМА ВОДОРОДА
И ВОДОРОДОПОДОБНЫХ ИОНОВ
§6.1. Квантовые числа одноэлектронного атома
и степень вырождения его уровней
Рассмотрение спектров атомов всегда начинают с рассмотрения спектра атома
водорода. Этот спектр является простейшим атомным спектром, что обусловлено
простотой строения атома водорода, состоящего из протона с зарядом -1-е и одного
электрона с зарядом — е представляющего, таким образом, одноэлектронную систему.
Систематика спектров более сложных атомов и ионов, состоящих из ядра и двух
или более электронов, основана на приближенном рассмотрении многоэлектронной
системы, исходя из свойств одноэлектронной системы. Поэтому рассмотрение од-
ноэлектронного спектра атома водорода важно не только само по себе, но и для всей
атомной спектроскопии.
Уровнями энергии и спектрами, аналогичными уровням энергии и спектру
атома водорода, обладают все ионы — Не+, Li++, Ве+++ и т.д., состоящие из ядра
и также из одного электрона. Поэтому наше рассмотрение будет относиться и к ним.
Соответственно мы будем считать заряд ядра равным 4-^е, где Z — 1 для Н,
Z — 1 для Не+, Z — 3 для Li++ и т.д., и будем говорить об одноэлектронном
атоме, подразумевая нейтральный атом водорода и ионизованные атомы с одним
электроном — водородоподобные ионы. Они вместе с атомом водорода образуют
изоэлектронный ряд — ряд атомов с одинаковым числом электронов. Обозначая, как
принято в спектроскопии, последовательные члены ряда римскими цифрами I, II,
III, IV, ... °, мы получаем простейший изоэлектронный ряд
Н I, Не II, Li III, Be IV, ...,	(6.1)
состоящий из атомов с одним электроном, обладающих закономерно изменяющи-
мися свойствами. Атом водорода является первым членом этого ряда.
Водородоподобными системами являются и все микроскопические системы, состоящие
из двух частиц с зарядами противоположных знаков. Такими системами являются мезоатомы,
представляющие совокупность положительного ядра и одного отрицательного мезона 2\ и по-
зитроний — совокупность электрона и позитрона. Эти системы отличаются от атома водорода
и водородоподобных ионов приведенной массой (о приведенной массе и ее роли см. ниже,
§6.2, с. 167); их уровни энергии и спектры также аналогичны уровням энергии и спектру
атома водорода, отличаясь лишь масштабом шкалы энергий и шкалы частот.
Отметим, что значение цифры на единицу больше кратности ионизации.
Это есть одномезонные мезоатомы. В принципе возможны и многомезонные мезоатомы, содержа-
щие два или несколько мезонов.
6*
164
Глава 6. Спектры атома водорода и водородоподобных ионов
Состояние одноэлектронного атома характеризуется, если не учитывать маг-
нитного взаимодействия орбитального и спинового моментов электрона — спин-
орбитального взаимодействия (об его учете см. §6.5, с. 186), — четырьмя квантовы-
п лгМ) щ-(орб) , ,(спин)
ми числами, определяющими значения четырех величин Е, Мр , Mpz и Mpz
(см. § 2.2, с. 44). Эти квантовые числа следующие:
1.	Главное квантовое число п, принимающее целые значения
п = 1,2,3,...	(6.2)
и определяющее энергию стационарного состояния по формуле Бора (см. ниже
формула (6.13)3*).
2.	Азимутальное {или орбитальное) квантовое число I, определяющее значение
квадрата орбитального механического момента Afj>op6^2 = h2l2 по формуле М^р^2 =
h2l(l + 1) (см. табл. 2.1, с. 48) и принимающее, при заданном п, целые значения
1=0,1,2,..., п- 1,	(6.3)
т. е. п значений. Состояния с последовательными значениями I принято обозначать
буквами
I = 0 1 2 3 4 5 6 7 8 9 10	11	12	13	14	,64)
spdfghiklmn	о	q	г	t	' * '
и соответственно называть 5-состояниями, p-состояниями и т. д. Обозначения пер-
вых четырех состояний возникли исторически (при изучении спектральных серий
щелочных металлов, см. §8.2, с. 221); начиная с I =4, применяются последователь-
ные буквы латинского алфавита.
3.	Орбитальное магнитное квантовое число определяющее значение проек-
ции — hlz орбитального момента М<р£® по формуле Mpz^ — hmi и прини-
мающее, при заданном I, целые значения
mi =1.1- 1,...,-1,	(6.5)
т е. 214-1 значений.
4.	Спиновое магнитное квантовое число ms, определяющее значение проекции
= hsz спинового момента по формуле Mpz™® = hms и принимающее
два полуцелых значения
т’ = 2’ ~2	<6
Таким образом, характеристика стационарного электронного состояния атома
водорода или водородоподобного иона дается набором четырех квантовых чисел
n, 1, гпц ms.	(6.7)
С наглядной точки зрения I и mi определяют величину и ориентацию (по от-
ношению к произвольно выделенному направлению) орбитального момента I, a ms
определяет ориентацию (по отношению к тому же направлению) спинового мо-
мента s (равного по величине ’Д, см. с. 48). Векторы I и в при этом считаются
независимыми.
При наличии у ядра атома спина (см. с. 44) необходимо, в принципе, вводить, для полной
характеристики состояний одноэлектронного атома, не четыре, а пять квантовых чисел, однако
3) Для атома водорода эта формула была приведена в § 1.2 (формула (1.5)),
§6.1. Квантовые числа одноэлектронного атома
165
мы в данной и последующих главах не будем учитывать спина ядра, обусловливающего лишь
очень малые расщепления электронных уровней — их сверхтонкую структуру (ср. с. 34
и см. подробнее гл. 16).
Весьма важным свойством одноэлектронного атома является вырождение его
уровней энергии. Энергия одноэлектронного атома, согласно формуле Бора, зави-
сит только от п и не зависит от I, mi и ms, т. е. существует вырождение по I,
по mi и по ms. При этом вырождение по mi и по ms связано с независимостью
энергии свободного атома от ориентации его механического момента (благодаря
независимости моментов /из, это справедливо для каждого из моментов в отдель-
ности), что имеет место для любого свободного атома, а вырождение по I является
характерным именно для одноэлектронного атома, в котором электрон движется
в кулоновском поле ядра — в электрическом поле, потенциал которого убывает
обратно пропорционально расстоянию г электрона от ядра.
Как мы видели в гл. 3, вырождение уровней энергии, как правило, связано со свойствами
симметрии. Вырождение по I для атома водорода тоже связано, как показал Фок [212],
с симметрией. Если в волновом уравнении для одноэлектронного атома ввести в качестве
независимых переменных, вместо координат электрона х, у, z, его импульсы рх, ру, pz
(перейти к другому представлению, по терминологии квантовой механики), то получившееся
уравнение обладает четырехмерной симметрией; это и приводит к вырождению не только
ПО Ш/, но и по I.
Найдем степень вырождения уровней энергии одноэлектронного атома, исходя
из характеристики его состояний при помощи набора (6.7) квантовых чисел. Сте-
пень вырождения определяется числом независимых состояний с данной энергией
(см. §2.1, с. 41).
Рассмотрим сперва число независимых состояний при заданном значении ази-
мутального квантового числа I.
Согласно (6.5), при заданном значении I мы имеем 21 + 1 различных состояний,
отличающихся значениями тп/; с наглядной точки зрения вектор I может быть ориен-
тирован 21+1 способами. При заданных I и тп/ возможны 2 состояния, отличающихся
значениями ms (см. (6.6)); с наглядной точки зрения вектор з ориентируется двумя
способами (параллельная и антипараллельная ориентация по отношению к выде-
ленному направлению). Всего при заданном I мы получаем 2(21 + 1) независимых
состояний, отличающихся парами значений тп/, ms, т. е. степень вырождения по mi
и ms уровня энергии с определенным I равна
= 2(2Л-1);	(6.8)
при последовательных значениях I это дает
I =	012345678...
gi=2(2l+\)=2 6 10 14 18 22 26 30 34 ...
Для s-, р-, d- и /-уровней (I = 0,1,2,3) мы имеем независимые состояния,
приведенные в табл. 6.1; значения mi и ms для состояний будут нам нужны
в дальнейшем.
Теперь легко определить степени вырождения уровней с заданным значением
главного квантового числа п, если учесть, что при этом I принимает значение от 0
до п - 1 (см. (6.3)). Суммируя величину gi = 2(21 + 1) от 0 до п — 1, мы получаем
степень вырождения
п-1	п-1
5n = 52fl/ = 522(2/+i) = 2n2.	(6.10)
1=0	1=0
166
Глава 6. Спектры атома водорода и водородоподобных ионов
Таблица 6.1
Число независимых состояний при различных значениях азимутального квантового числа I
1	Название состояния с заданным 1	Число не- зависимых состояний 9< = 2(2/+1)	Квантовые числа независимых состояний при заданном 1
0	s -состояние	2	mi —	0 0 т>~	I
1	р-оостояние	6	mi=	110	0-1-1 _ _	iiiiii ms -	2	2	2	2	2	2
2	d-состояние	10	mt=	2	2 1	1 0	0 -1	-1 -2	-2 _	iiiiiiiiii ms ~	2	22	22	22	22	2
3	f -состояние	14	mi — 3	3 2	2	1	1	0	0	-1	-1	-2	-2	-3	-3 _ 1	11	1	1	_1	1	_1	1	_1	1	__1	1	1 — 2	2	2	2	2	2	2	2	2	2	2	2	2	2
Для последовательных значений п находим
п=1	2 = 2 • I2'
п = 2	2 + 6 = 8 = 2-22
п = 3	2 + 6+ 10= 18 = 2• З2 ►
п = 4	2 + 6+10+ 14= 32 = 2-42
п = 5 2+6+ 10 + 14+ 18 = 50 = 2- 52 ,
(6.Н)
Число независимых состояний при заданном I, равное 2(2/ + 1), и число
независимых состояний яри заданном п, равное 2п2, играют основную роль в теории
периодической системы элементов Менделеева, рассмотренной в гл. 7.
В дальнейшем мы будем пользоваться общепринятым обозначением состояний
электрона с заданными пи/, при котором цифра указывает п, а следующая за ней
буква s, р, d, /, ... — соответствующее значение I.
Таким образом, мы имеем состояния
1з	п — 1,	1 = 0	
2з, 2р	п = 2,	/ = 0,	1
3s, Зр, 3d	п = 3,	1 = 0,	1, 2
4s, 4р, 4d,	4/ п = 4,	1 =0,	1, 2, 3 ,
(6.12)
§ 6.2. Зависимость спектров одноэлектронных атомов
от заряда и массы ядра
Формулы (1.5) для уровней энергии и (1.8) для спектральных линий атома во-
дорода, рассмотренные в § 1.2 и иллюстрированные рис. 1.2, представляют частные
случаи общих формул для уровней энергии и спектральных линий одноэлектронных
атомов. Эти формулы были впервые получены Бором в 1913 г. на основе модельных
представлений его теории, а затем и выведены последовательным квантовомехани-
ческим методом Шредингером в 1926 г. Они имеют вид
RZ2
EnZ =----г (п= 1,2,3,...)	(6.13)
nz
§ 6.2. Зависимость спектров от заряда и массы ядра
167
где постоянная Ридберга
2тг27пе4 2тг27пе4 2тг2тпе4
s=__эрг=__с- =__
т~ М + те~ . , те
М
(6-14)
(6.15)
(6.16)
— приведенная масса электрона и ядра (те — масса электрона, М — масса ядра).
Введением приведенной массы учитывается тот факт, что в атоме движется не только
электрон,, но и ядро (хотя и гораздо более медленно); движение электрона и ядра
происходит вокруг общего центра тяжести.
Классическое выражение (6.16) для приведенной массы системы, состоящей из двух
частиц е массами М и те, сохраняется и в квантовой механике. Это связано с тем, что кван-
товомеханический оператор энергии («гамильтониан Я»), аналогичен классической функции
Гамильтона Н, в результате чего относительное движение частиц отделяется от движения
центра тяжести так же, как и в классической механике.
Уровни энергии и частоты переходов для членов изоэлектронного ряда (6.1)
отличаются масштабом, который увеличивается пропорционально RZ2, Так как.
постоянная Ридберга, согласно (6.16), лишь незначительно изменяется с массой
/ те	\	2
ядра I — < 1 I, то этот масштаб определяется множителем Z , т. е. возрастает
\ М	/
пропорционально квадрату заряда ядра. Для иона Не+ он больше, чем для атома
в 4 раза, для иона Li++ - в 9 раз и т. д. Соответственно увеличиваются энергии
ионизации, они равны (в эВ)
I II III IV V VI VII VIII
13,595 54,403 122,419 217,657 340,127 489,84 666,83 871,12
Спектральные серии для водородоподобных ионов аналогичны спектральным сери-
ям (1.9) атома Н, только смещены в коротковолновую область. В частности, для Не+
серии1 Лаймана (переходы п\ = 1, П2 = 2, 3,4, 5,..., линии Д*, Дд, Д, Д,...,
см. рис. 1.2) соответствуют линии 303,78 А, 256,31 А, 243,02 А, 237,33 А, ...
с границей при 227,85 А и серии Бальмера (п} = 2,	~ 3,4,5,6,... ли-
нии На, Нр, Hv Н6,...) - линии 1640,41 А, 1215,13 А, 1084,94 А, 1 025,27 А, ...
с границей при 911,40 А.
Несмотря на малость отличия приведенной массы т от массы электрона,
все же необходимо учитывать зависимость т от массы ядра М, определяемую фор-
/	/ те \2
мулой (6.16) I которую с очень малой ошибкой I — ) можно заменить формулой
\	\М J
/ тпе\ \
т — те 1-------) I. Значения постоянной Ридберга несколько отличаются как
\ м J J
для разных элементов, так и для изотопов одного элемента.
168
Глава 6. Спектры атома водорода и водородоподобных ионов
Если обозначить постоянную Ридберга для бесконечно большой массы ядра
через Rqq, то постоянная Ридберга для ядра с массой М будет равна
(617)
' + М
Численное значение постоянной Ридберга для бесконечно большой массы ядра
равно
Яоо = 109 737,309 ±0,012 см-1,	(6.18)
в то время как для атома водорода, в котором ядром является протон, она имеет
значение, примерно на 60 см-1 меньшее,
Ян = 109 677,576 ±0,012 см"1.	(6.19)
Для всех остальных одноэлектронных атомов постоянная Ридберга меньше, чем Яоо,
и больше, чем Ян. В частности, для дейтерия она равна
rd = Ю9 707,419 ± 0,012 см"1	(6.20)
и для гелия (Не4)
ЯНе = 109 722,267 ±0,012 см"1.	(6.21)
Мы видим, что отличия получаются не очень большие, порядка десятитысячных
долей, т. е. сотых процента. Однако эти отличия достаточны для того, чтобы
не только их обнаружить, но и измерить. Дважды в истории развития физики они
сыграли существенную роль: в первый раз, когда Бору в 1913 г. удалось истолковать
некоторые спектральные серии, приписываемые водороду, как серии ионизованного
гелия, и во второй раз в 1932 г., когда по наличию слабых спутников линий серии
Бальмера был открыт тяжелый водород — дейтерий.
История открытия и объяснения серий ионизованного гелия весьма интересна.
Наряду с серией Бальмера, Пикерингу в 1897 г. [168] удалось обнаружить в спектрах
звезд новую серию, линии которой выражаются формулой
(6-22)
5	7
где т = -, 3, -,4.
. . Сравнение этой серии, получившей название серии Пикеринга,
с серией Бальмера показано на рис. 6.1. Серия Пикеринга была истолкована Ридбергом как
Серия
Бальмера
Серия
Пикеринга
1.... i .	_I_I_I_I	t 1-1-X U-l.-l 1-1	t  L
3500	4000	4500	5000	5500	6000	6500 A
Рис. 6.1. Сравнение серий Бальмера и Пикеринга
§ 6.2. Зависимость спектров от заряда и массы ядра
169
принадлежащая также водороду; по аналогии Ридберг предсказал существование других серий
с полуцелыми квантовыми числами. Фаулером была действительно обнаружена серия
m = 2,	3,
2
(6.23)
которая была также приписана водороду. Вопрос о принадлежности серии Пикеринга и Фау-
лера был выяснен Бором [175, 185]. Эти серии принадлежат ионизованному гелию и должны
быть записаны в виде:
( 1
серия Пикеринга и = 47? [ —
\ 42
“7 ) > п2 = 5,6,7,...
"г/
(6.24)
/ 1
серия Фаулера и = 47? I —
X ) , п2 = 4, 5,6,...
niJ
Данные формулы получаются из (6.22) и (6.23) умножением числителя и знаменателя на 4 = 22,
/з\2	2
т. е. заменой 7? через 47?, 22 через (2 • 2)2 = 42, ( - ) через = З2 и т через (2m)2 = п2-
Давая эту интерпретацию, Бор ее убедительно доказал. В формулы (6.24) и (6.25) должна
входить умноженная на 4 (т.е. на Z2 = 22, см. (6.14)) постоянная Ридберга для гелия 7?Не,
отличающаяся от постоянной Ридберга для водорода 7?н (ср. (6.21) и (6.19)). На основе точных
данных Фаулера для длин волн увиденных линий Бор вычислил отношение 47?Не к 7?н- Оно
оказалось равным 4,0016, что полностью совпало с теоретическим отношением, вытекающим
из формулы (6.17):
(6.25)
47?Не
7?н
4
те
Мне
те те \
-4,00163.
МН МНе /
(6.26)
Принадлежность серий Пикеринга и Фаулера гелию была затем доказана и экспериментально;
они были получены в разряде с чистым гелием. Объяснение Бором серий Пикеринга и Фаулера
явилось блестящим успехом его теории (ср. с. 38).
Очень интересна и история открытия тяжелого водорода. После обнаружения в 1929 г.
изотопов кислорода О17
и О18, примешанных в отношениях
1
~2 500
1
и к основному
изотопу О16, выяснилось отличие в массе водорода при химических определениях и при фи-
зических определениях (при помощи масс-спектрографа). Химические определения дали
.6	1,00799
отношение массы водорода к массе изотопа кислорода О , равное ---------—, тогда как это
16
1,00778
отношение, согласно масс-спектрографическим данным Астона, оказалось равным -----.
16
Бердж и Менцель в 1931 г. предположили [199] для объяснения этого расхождения, что
водород имеет более тяжелый изотоп с массой 2, примешанный к основному изотопу с мас-
сой 1 в отношении ----; при химическом определении находилось отношение средней
4 000
массы водорода в смеси изотопов Н1 + Н2 к массе О16, а при физическом определении —
непосредственно отношение массы Н1 к О16. Они указали на возможность спектрального
обнаружения тяжелого изотопа водорода путем наблюдения слабых спутников линий серии
Бальмера. Юри, Брикуэдде и Мерфи в 1932 г. действительно обнаружили в спектре, снятом
во втором порядке при помощи вогнутой дифракционной решетки с радиусом 3 м (дисперсия
во втором порядке 1,3 А на 1 мм), спутники для линии 77а, 77^, Т77, серии Бальмера [200].
Положения этих спутников хорошо совпали с положениями, вычисленными по формуле (1.8),
со значением постоянной Ридберга для изотопа с массой 2.
В табл. 6.2 приведены данные, показывающие это совпадение. Так как данные для есте-
ственного водорода были недостаточно убедительными, ввиду слабости линий, то были

и
170 Глава 6. Спектры атома водорода и водородоподобных ионов
Таблица 6.2
Сравнение теоретических и наблюденных смещений линий
серии Бальмера для изотопа Н2 (D)
Линии		На		я7	н6
Вычисленное смещение AHi — Анг (в А)		1,793	1,326	1,185	1,119
Среднее наблюден- ное смещение (в А)	обыкновенный водород	—	1,346	1,206	1,145
	образец*) 1	—	1,330	1,199	1,103
	образцы**) 2 и 3	1,791	1,313	1,176	1,088
*) Водород, обогащенный путем испарения жидкого водорода при атмосферном давлении.
**) Образцы, обогащенные путем испарения жидкого водорода при атмосферном давлении в несколь-
ко мм Hg.
применены образцы, обогащенные тяжелым водородом путем испарения жидкого водорода4).
В остатке можно было ожидать большей концентрации тяжелого водорода; это и получилось
на опыте.
В заключение данного параграфа следует отметить, что для водородоподобных систем,
содержащих неустойчивые частицы, — для мезоатомов и позитрония, о которых упоминалось
в начале §6.1 (с. 163), — уровни энергии и возможные переходы определяются формула-
ми (6.13) и (6.14). В постоянную Ридберга, входящую в эти формулы, нужно подставлять
в качестве массы т приведенную массу
М,М2
m =---------,
М\ + 'М2
где М\ и М2 — массы двух частиц, образующих водородоподобную систему.
Для мезоатомов М\ равно массе мезона, а М2 — массе ядра. Так как массы мезонов
в несколько сот раз больше массы электрона (для /х-мезона — в 208 раз, для яг-мезона —
в 276 раз), то и масштаб энергий и частот увеличивается в несколько сот раз. Вместо разностей
энергий порядка эВ получаются разности энергий порядка тысяч эВ: им соответствуют
переходы в области мягких рентгеновских лучей, которые удается наблюдать [45]. Возможность
существования мезоатомов и наблюдения их спектров определяется тем, что время жизни
мезонов много больше периода колебаний при соответствующих частотах переходов.
Для позитрония, как системы, состоящей из частиц одинаковой массы те, приведенная
масса равна т — — и масштабы энергий и частот уменьшаются вдвое, т. е. в формулы входит
постоянная R^/2. Для перехода, соответствующего первому члену серии Лаймана (ni = 1,
п = 2), длина волны должна равняться А = 2431 A (Z нужно положить равным 1).
§ 6.3.	Характеристика стационарных состояний одноэлектронного атома
Мы рассмотрим характеристику стационарных состояний одноэлектронного
атома, соответствующих, если не учитывать спин-орбитального взаимодействия,
вырожденным уровням энергии (6.13).
С точки зрения модельных представлений теории Бора, на основе которых
им и была впервые получена формула (6.13) стационарные состояния соответству-
ют движению электрона по определенным орбитам. Несмотря на принципиальные
недостатки подобной классической модели (ср. § 1.6, с. 39), ее наглядными предста-
влениями широко пользуются и в настоящее время, и можно установить соответствие
между строгим квантовомеханическим описанием атома и его описанием на основе
4)Лишь впоследствии был открыт способ получения тяжелой воды в больших количествах путем
электролиза обычной воды.
§ 6.3. Характеристика стационарных состояний
171
этой модели. Поэтому мы вкратце разберем модельные представления о круговых
и эллиптических орбитах электрона в одноэлектронном атоме5).
Подробнее эти вопросы изложены в монографии Зоммерфельда «Строение атома и спек-
тры», т. 1 [10], первое издание которой, в одном томе, вышло в 1919 г. и явилось первой
книгой по квантовой теории атома и спектров; впоследствии монография была разделена
на два тома, причем в первом томе осталось изложение боровской теории, а второй том [136]
был посвящен квантовой механике.
При движении со скоростью v по круговой орбите радиусом а вокруг ядра
с зарядом Ze электрон обладает механическим моментом Мр = const, кинетической
1	2 M2V	Ze1
энергией Т = -mv = --------и потенциальной энергией U =----------. Учитывая,
2 2та2	а
mv1	2Т	Ze2	U
что центростремительная сила-------=-------равна силе притяжения------— = —
а	а	а2	а
электрона ядром, мы имеем Мр = m2a2v2 = а2т • mv2 = amZe2, U = —2Т
U М2Р	Ze2
и Е = Т 4- U = —Т = — ~ --------г = - ——. Применяя введенное Бором условие
2	2та2	2а
квантования механического момента
h
Мр =—п 1’2’3’ • )’	(6.28)
мы получаем радиус круговой орбиты
М2 _ h2n2	_ п2е2
anZ mZe2 4n2mZe2 2RZ'	(6.29)
Ze2
подстановка которого в выражение Е — - —— для энергии дает основную форму-
2а
2я2тпе4
лу (6.13) (где, согласно (6.15), R = —-=— эрг).
пг
Каждому уровню энергии EnZ соответствует круговая орбита радиуса (6.29),
причем постоянная
h2 h2	8
а0 = ан = —г = —-------г = (0,529172 ± 0,000002) 10"8 см (6.30)
те	4тгхте2
представляет радиус первой боровской орбиты (п = 1) для атома водорода (2=1)
и является очень удобной естественной единицей для измерения атомных размеров6).
Величина 2ао = 2а ц — 1,058 А ~ 1А дает диаметр атома водорода в основном
состоянии по теории Бора. Согласно (6.29), радиусы орбит пропорциональны п2,
т.е. быстро возрастают для возбужденных состояний, и обратно пропорциональны Z,
т.е. убывают для членов изоэлектронного ряда (6.1); это находится в соответствии
с тем, что энергия связи электрона WnZ — -EnZ, согласно (6.13), уменьшается
/ 1 \ э
при возбуждении f WnZ ~ — J и увеличивается с увеличением Z (WnZ ~ Z ).
5) Соответствующих связанным состояниям электрона (Е < 0); свободным его состояниям (Е > 0)
соответствуют гиперболические орбиты.
® Ее точное значение (6.30) соответствует т = те, т. е. бесконечной массе ядра, см. (6.16).
172
Глава 6. Спектры атома водорода и водородоподобных ионов
Рис. 6.2. Движение электрона
по наклонной орбите
Отметим, что для круговой орбиты отношение ско-
рости vn движения электрона по орбите к скорости света
равно, согласно (6.28) и (6.29),
Vnz Мр	2тге2 Z	Z
— =---------= —-------= а—,	(6.31)
с	cmanZ	ch п	п
2тге2 1
где а = -----~--------безразмерная постоянная, и граю-
ch	137
щая важную роль в теории тонкой структуры (постоянная
тонкой структуры, см. ниже, §6.5, с. 189). Относитель-
ная скорость на первой боровской орбите, как раз
равна а. Величина отношения (6.31) определяет величину
релятивистских поправок к формулам нерелятивистской
v /	2
теории; эти поправки могут быть порядка -, ( -j и т.д.,
aZ /aZ\2
т.е. порядка —, | — | и т.д.
п \ п J
71 = 1
(1 (1й
п = 2
а = 4а0
71 = 3
а = 9а0
b = j;a
b = ja
b = ^a
b = a
Рис. 6.3. Орбиты электронов при значении главного
квантового числа п от 1 до 4
При наиболее общем ре-
шении задачи об одноэлектрон-
ном атоме, на основе модель-
ных представлений теории Бора,
получается движение по элли-
птическим орбитам. В соответ-
ствии с тремя степенями сво-
боды состояния электрона ха-
рактеризуются тремя квантовы-
ми числами: п, определяющим
энергию по формуле (6.13),
как и в случае круговых орбит,
к, определяющим механический
,	Луг(°рб)
момент по формуле Мр = —
2тг
(к = 1, 2,..., п) и отличающим-
ся от I (см. (1.3)) на единицу
(к = I + 1)7), и тк, определя-
ющим проекцию механического
момента по формуле MpQ^ =
hmk, где m* = &, fc - 1,..., -к,
аналогично формуле Мр?® =
hmi, где тщ = I, I — 1,..., —I. За-
данным значениям п и к соот-
ветствует движение по эллипсу
с большой полуосью, даваемой
формулой (6.29), и малой полу-
осью, равной
&
bnz — a>nz—•	(6.32)
к = 4 а = Ь
к = 1 Ь = у а
к = 2 Ь = а
к = 1 Ь = у а
к = 2 Ь = у а
к = 3 Ь = а
Квантовомеханическая формула
1(1 + 1) =. (к - l)fc через к2.
= h y/l(l -I- 1) переходит в формулу МрОр^ = hk при замене
§ 6.3. Характеристика стационарных состояний
173
В частном случае к = п получаются круговые орбиты, рассмотренные выше и соот-
ветствующие, таким образом, максимально возможному, при данном п, значению
I = к — 1 = п - 1. Ядро атома находится в фокусе эллипса, а угол наклона d орбиты
эллипса (рис. 6.2) определяется формулой пространственного квантования.
д^-(орб)
C0S =	=	(™k=k,k-l,...,-k).	(6.33)
Эллиптические орбиты, соответствующие значениям п = I,2, 3 и 4, показаны
на рис. 6.3. При п = 1 возможна лишь одна орбита — круговая, при п — 2 возможна
Ь 1
эллиптическая орбита с отношением — = - и круговая орбита и т. д. На рисунке
а 2
приведены обозначения орбит при помощи символа (например, З2 означает п = 3,
к — 2), а также символов ns, пр, nd, nf (см. (6.12)), где s, р, d, f соответствуют
1 = 0,1,2,3, т.е. к = 1,2, 3,4.
Чем меньше к, т. е. чем меньше орбитальный механический момент, тем эллипс
более вытянут и тем меньше минимальное расстояние, на которое электрон подходит
к ядру, и тем больше максимальное расстояние, на которое он удаляется от ядра.
Для эллиптических орбит наименьшие расстояния от ядра составляют8)
2! (2s)	31(3s)	32(3р)	4|(4s)	42(4р)	43(4d)
0,134а2г =	0,057аз^ —	0,255аз^ =	0,0318а4г =	0,132^4^ —	0,338а4Я =
= 0,532^	= 0,513—	= 2,30— 7	Г7	= 0,509—	= 2,12— ’	Г7	= 5,42—
(634)
Мы видим, что, согласно модельным представлениям, электроны, движущиеся
по эллиптическим орбитам, особенно сильно вытянутым, подходят очень близко
к ядру. В частности, для орбит с к = 1 минимальное расстояние с увеличением п
anZ ао п	_
стремится к —у = —. Вырождение связано, согласно теории Бора, с тем, что
2n2 2Z
энергия зависит только от величины anz большой полуоси, но не зависит от его
/	/	ТПк\
формы I т. е. отношения — I и от наклона его плоскости I т. е. от cos d = — I.
\	nJ	\	к J
Возможные эллиптические орбиты находятся при помощи квантовых условий общего
вида, справедливых для периодических движений и имеющих форму
j Pi dqi = щй,	(6.35)
где qi — обобщенная координата, р: — сопряженный с ней импульс, и интегрирование
производится по всей области изменения переменной gt ; щ — квантовое число, принимающее
8) Они равны, согласно свойству эллипса (см. рис. 6.4),
а -
у/а2 - Ь2 = а
С помощью (6.32) и (6.29) получаем формулу
по которой и вычислены значения (6.34).
174
Глава 6. Спектры атома водорода и водородоподобных ионов
Рис. 6.4. Эллиптическая орбита электрона
целые значения9). Для движения электрона во-
круг ядра при введении полярных координат г
и ip в плоскости орбиты (рис. 6.4) и азиму-
та (/> относительно оси z (рис. 6.2) квантовые
условия имеют вид
prdr = nrh (пТ — 0, 1, 2,...),
p^dip — kh (k = 1, 2, 3,...),
> (6.36)
(j) p^dip = mkh (mk = 0, ± 1,...).
Здесь nr — радиальное, k — азимутальное и mk — магнитное квантовое число.
pr = mr — y/2m(E — U) =
a = MpOp6\ и p^ = что дает, в силу постоянства Мр°^ и Мр^ = МрОр6) cos 0,
при интегрировании по и 92 от 0 до 2тг, правила квантования, приведенные выше
(м(ор6) = — М(ор6) = —
\ ”	2х’ pz 2тг ) ’
Энергия выражается через главное квантовое число п = пг Ч- к, где & = / 4- 1 = п, п~ 1,..., 1
и соответственно пТ = 0, 1, 2,..., п - 1.
Отметим, что существенное отличие квантового числа к от квантового числа I состоит
в том, что оно не может принимать значения, равные нулю; это значение соответствовало бы,
согласно (6.32), вырождению эллипса в отрезок прямой длины 2anZl проходящий через ядро,
что в модельной теории исключается. Так как при п = 1 к = 1, то для основного состояния
атома водорода МрОр6) / 0 и соответствующий орбитальный магнитный момент должен был
бы быть равным не нулю, а -рв (см. §2.5, с. 55).
В действительности атом водорода в основном состоянии обладает магнитным моментом,
равным -рБ, однако не орбитальным, а спиновым (см. (2.56)), орбитальный же момент равен
нулю.
Перейдем теперь к квантовомеханической характеристике стационарных состо-
яний одноэлектронного атома.
Решение квантовомеханической задачи приводит к формуле (6.13) для уров-
ней энергии и одновременно позволяет определенным образом характеризовать
вырожденные состояния с различными значениями I и mi (при заданном п) нагляд-
ным образом при помощи распределения электронной плотности. Заряд электрона
при этом рассматривается как непрерывно распределенный по объему атома с не-
которой плотностью р(ж, г/, z) таким образом, что полный заряд равен е, т. е.
J pdV = J р(х, у, z) dx dy dz ~ e.
(6.37)
В отличие от наглядных представлений боровской теории, согласно которым элек-
трон движется по определенной орбите, в наглядной картине, иллюстрирующей
квантовомеханическое рассмотрение, электрон нельзя локализовать и каждому со-
стоянию сопоставляется пространственное распределение электронной плотности,
9) Квантовые условия (6.35) могут быть получены из квантовой механики в так называемом квазиклас-
сическом приближении (см. 1131], с. 193, и [132], с. 221) и при этом в них входят полуцелые квантовые
числа. Полуцелые квантовые числа вводились в отдельных случаях и до квантовой механики.
§6.3. Характеристика стационарных состояний
175
характеризующее это состояние. При-
меняя эту наглядную картину распре-
деления электронной плотности, часто
говорят об электронном облаке.
Следует подчеркнуть, что нагляд-
ные представления о распределении эле-
ктронной плотности — об электронном
облаке атома — правильнее отражают
свойства электрона в атоме, чем модель-
ные представления теории Бора, и на-
ходятся в соответствии со строгим кван-
товомеханическим описанием движения
электрона в поле ядра. Они примени-
мы также и для электронов в молекулах
и в конденсированных системах.
Для состояний одноэлектронного
атома сп — 1,2 и 3 общее распределение
электронной плотности (сфотографиро-
ванное с помощью специальной моде-
ли [13]) показано на рис. 6.5. Это рас-
пределение в первую очередь зависит
от Z; при I = 0 оно является сферически
симметричным и имеет максимум в на-
чале координат (где находится ядро),
для значений I > 0 электронная плот-
ность в начале координат равна нулю.
С увеличением п плотность электрон-
ного облака уменьшается и оно зани-
3s m = Q
Рис. 6.5. Распределение электронной
плотности для состояний атома водорода
мает все большую область; его размеры
увеличиваются пропорционально п2, в соответствии с увеличением размеров орбит
электрона в теории Бора (см. (6.29)). При заданных п и I распределение зависит
от mi, причем только от его абсолютного значения \mi|.
Благодаря сферической симметрии поля ядра,
в котором движется электрон, заряд в объеме dV
можно представить в сферической системе координат
г, 0 и <р (см. рис. 6.6) в виде
pdV — р(г, 0, <р) г2dr dQ. —
2	(6.38)
= Pni(r)r drpimi(0,(p)
где dQ = sin 0 dO dp — элемент телесного угла. Пол-
ная электронная плотность р представляет произ-
ведение двух множителей — рп/(г), являющегося
функцией только от расстояния г электрона от ядра
и зависящего от квантовых чисел п и I, и
являющегося функцией только от углов 0 и р и за-
висящего от квантовых чисел I и ттц. Первый мно-
Рис.6.6. Сферические
координаты для атома водорода
житель не зависит от ш/, а второй — от п. Необходимо отметить, что формула (6.38)
справедлива для любого сферически симметричного электрического поля и вто-
рой множитель pimi(0) р) имеет вполне определенный вид и не зависит от закона,
176
Глава 6. Спектры атома водорода и водородоподобных ионов
те© оэлорому ^потенциальная энергия U => U{r) изменяется как функция г; напротив,
первый множитель ^(г) зависит от этого закона.
Радиаль1^р&тределение электронной плотности в атоме можно характеризовать
функцией — pniirjr2- если проинтегрировать (6.38) по углам, что дает посто-
янный множитель f ^>)<Ш — С, то полный заряд, заключенный между двумя
сферами радиусов г и r + dr (рис. 6.6), получается равным Cpni(r)r2dr = CDni(r)dr.
Рис. 6.7. Радиальное распределение электронной плотности
для состояний атома водорода
На рис. 6.7 даны графики функции Dni(r) для одноэлектронного атома при значени-
г	г
ях п от 1 до 3, причем вместо г введена безразмерная переменная а = —— = Z—,
ао/Z	ао
т. е. г выражается в единицах a$/Z (в частном случае атома водорода — в радиу-
сах первой боровской круговой орбиты). Функция Dni(r) равна нулю при г — О,
в том числе и для 5-состояний (для них рпо(О) / 0 и р (0, 0, <р) = Рпо(О)Роо(0, <р) / О,
но pnQ-r2 = Рпо(О)О = 0)» и имеетп-Z максимумов, между которыми она обращается
в нуль. При I = п - 1, т. е. для состояний 1s, 2р, 3d получается лишь один максимум
ао 2
при г = —п , т. е. в точности равном радиусу (6.29) соответствующей круговой
Z
орбиты (k = I + 1 = п). С уменьшением I число максимумов, при заданном п, увели-
чивается, причем первый максимум приближается к ядру, а последний, наибольший
по величине, удаляется от него, т. е. распределение электронной плотности растя-
гивается вдоль радиуса. Это соответствует переходу от круговых орбит ко все более
вытянутым эллиптическим орбитам, при движении по которым электрон подходит
близко к ядру, а затем сильно удаляется от него (см. рис. 6.3). При этом время пре-
бывания электрона вблизи ядра, где он движется быстро, мало, а вдали от ядра, где
он движется медленно, велико, чему соответствует наименьшая величина первого
максимума и наибольшая величина последнего максимума.
Следует подчеркнуть, что соответствие между распределением электронной плотности
и боровскими орбитами не является однозначным. Состояниям Is, 2р, 3d с I = п - 1,
т. е. с моментом 4- 1) = hy/п(п - 1) и максимальной проекцией момента hl — h(n - 1),
§6.3. Характеристика стационарных состояний
177
мы сопоставляем круговые орбиты (к = п) с моментом hk = hn\ 5-состояниям (I = 0) мы
сопоставляем наиболее вытянутые орбиты с fc = 1, т.е. с моментом, отличным от нуля. Мы,
с другой стороны, могли бы 5-состояниям сопоставить исключаемый в боровской теории
предельный случаи к = 0, когда эллипс вырождается в отрезок прямой длины 2anZ\ при таком
сопоставлении момент равен нулю и с точки зрения модельных представлений теории Бора,0).
Угловое распределение электронной плотности, характеризующееся функци-
ей <р), показано на рис. 6.8. На нем даны, для значений I от 0 до 3, графики,
на которых в каждом направлении откладывается соответствующая величина функ-
ции. При этом для сферически симметричных «-состояний (I = 0) роо(0, <р) — const
и изображается сферой, а для остальных состояний (I > 0) pimi зависит только
от угла 0, но не от угла <р, благодаря чему распределение обладает аксиальной
симметрией относительно оси z, концентрируясь в направлениях, соответствующих
определенным значениям угла 0 (на рис. 6.8 показано распределение в одной верти-
кальной плоскости). При заданном I распределение зависит только от |тп/| и число
максимумов функции pimi, при изменении в от 0 до тг, равно I —	+ 1.
Р
электроны
s
электроны
d
электроны
т = — 1 т = — 2	/ = 2
Рис. 6.8. Угловое распределение электронной плотности
для сферически симметричного поля
f
электроны
Отметим, что распределение электронной плотности играет важную роль
при рассмотрении вопросов взаимодействия атомов, в особенности вопросов обра-
зования химической связи между атомами в молекуле (см. гл. 24 и 26). В теории
направленной валентности, в частности, существенно угловое распределение элек-
тронной плотности, ее концентрация в некоторых направлениях.
Вырожденные состояния одноэлектронного атома различаются волновыми функциями,
характеризующими эти состояния. Знание вида волновых функций существенно не только
для конкретных расчетов, но и для ряда качественных выводов; именно с видом волновых
функций связана наглядная картина распределения электронной плотности.
Волновые функции одноэлектронного атома являются решениями уравнения Шредин-
гера (ср. (2.1) и (3.13))
( h2 Ze21	,
Hip = 4-----—Д--------W = W,	(6.39)
I 8тг2пг r I
10) Разумеется, делаемое иногда сопоставление сферически симметричным s-состояниям круговых ор-
бит является неправильным (за исключением случая п = 1,1 = 0); круговая орбита может соответствовать
только состоянию с наибольшим I, а отнюдь не с I — 0.
178
Глава 6. Спектры атома водорода и водородоподобных ионов
соответствующими значениям (6.13) энергии, и имеют вид
Ф = фп^ = Rni(r)Ylmi (в, р),	(6.40)
где Rni(r) — радиальная функция, a <р) — угловая функция.
Квадрат волновой функции ф2 (а в случае комплексной функции квадрат ее модуля |^|2)
дает, как известно, вероятность различных значений координат электрона, отнесенную к еди-
нице объема, иначе говоря, плотность вероятности. Для наглядности можно рассматривать
заряд электрона е распределенным по всему объему атома, и тогда е|^|2 определяет плотность
электронного заряда в атоме. Величина
p = e|V>|2	(6.41)
и представляет введенную выше электронную плотность или плотность электронного облака.
Ее распределение определяется, таким образом, распределением плотности вероятности \ф\2.
Согласно (6.40), плотность вероятности
М2=Я^(г)|Г(пч(<?,9>)|2"),	(6.42)
где R2m(r) и |г;га((б>,^)|2 совпадают с точностью до постоянных множителей с функ-
циями pni(r) и	(см. (6.38)); соответственно R2j(r)r2 совпадает с функцией
Dni(r) = pni(r)r2. При нормировке f R2t(r)r2 dr = 1 произведение l?2z(r)r2 дает вероят-
о
ность нахождения электрона на данном расстоянии г от ядра, рассчитанную на единицу
расстояния, и, аналогично, при нормировке
тг	2тг
У |у(т,(0,^)|2<ю = у sin<M0 у |у;т,((9,у>)|2<^= 1
о	о
величина | Ylmi (в, <р) |2 дает вероятность нахождения электрона в данном направлении, рас-
считанную на единицу телесного угла.
Радиальные волновые функции имеют вид
Rnitr) = Nnt exp < - —— >r* (1 + c,r + ... + сПггПг),	(6.43)
п Oq J
т.е. представляют произведения показательного множителя на rz и полинома степени пТ =
п — I — 1 от г; нормировочный множитель
_ 1	2,+1	/ (п + i)! ( Z \1+2/2
~ п^(21 + 1)! V (п-1- 1)!	)
Радиальное квантовое число пг совпадает с радиальным квантовым числом в (6.36), удо-
влетворяющим условию пт = п - к. В силу наличия множителя г1, при 1 = 0 Япо(О) # 0
и при I > 0 Rni(0) = 0 (ср. выше, с. 175), что весьма существенно при рассмотрении взаи-
модействия электронных оболочек с ядром; это взаимодействие будет велико, если электрон
обладает значительной вероятностью находиться вблизи ядра, т. е. велико для «-состояний
(см. гл. 16, с. 452).
В табл. 6.3 приведены выражения для радиальных функций (в безразмерных перемен-
00
ных, согласно условию нормировки f R2nl(<y)(y2d(T = 1) при значениях п от 1 до 4 и даны
о
соответствующие графики; число узлов функции Rni(r) равно п - I - 1 = nr. С помощью этих
функций и построены графики функций Dni(a) = R2t(a)a2 (рис. 6.7).
11) Радиальная функция оказывается вещественной, а угловая функция, вообще говоря, является
комплексной, см. табл. 6.3 и 6.4.
§ 6.3. Характеристика стационарных состояний
179
Таблица 6.3
Радиальные функции атома водорода
п I
Радиальная волновая функция Rni
График
-—(орб)2
Угловые волновые функции, являющиеся собственными функциями оператора Мр ,
представляют собой сферические функции Лапласа и имеют вид (тп = тщ)
д\™\
Ytmi(0,V)=NlnP^(cos0)e,mv = Nlm-^Pt(x)(l-x2) 2 e'm\	(6.44)
где P|m'(cost?) является произведением полинома степениполучающегося |т|-кратным
дифференцированием по х = cos полинома Лежандра Pi(x) степени 112), на (1 - ж2) 2 = (1 -
cos20)¥ = (sin0)lmL Нормировочный множитель N[m — \ /------ ~—j—Множитель е'т(р
у 4тг (I 4- |ш|)!
представляет собственную функцию оператора (ср. (3.38)).
|2)Ро(г) = 1, Pdx) = х, Р2(х) = | х2 - i, Р3(х) ж3 - | ж,... .
180
Глава 6. Спектры атома водорода и водородоподобных ионов
Таблица 6.4
Угловые функции для сферически симметричного силового поля
1	mj	Угловые волновые функции (0, <р)		
0	0	1 -= 1 74тг		
	0	./I У 4тг	COS0	
1				
	±1	./I V 4тг	4= sin#e±'*’ Л	
	0	Ji	Gcos2₽-I)	
2	±1	Г£ У 4тг	4= 3 cos в sin в Vf>	
	±2	/т У 4тг	-4=3 sin2 9 et2i4> V24	
	0	Ji	(I cos29 - | cose)	
	±1	Г У 4тг		cos 29 - |) sin 9 e±uf
3	±2	.д V 47Г	1 7120	15 cose sin 29 e±2'v
	±3	/V У 4тг	1 7720	15sin3ee±3iv
В табл. 6.4 приведены выражения для угловых функций при значениях I от 0 до 3.
Функции Yim(0, у?) и Yj_w(0, у?) отличаются лишь знаком показателя в экспоненте егт<р.
Квадрат модуля угловой функции (6.44) равен N?m (p/m*(cos0)) , т.е. не зависит от <р
и одинаков для состояний с mz = т и mi = — т; его относительные значения и изображены
графически на рис. 6.8.
С помощью волновых функции (6.43) и (6.44) находится, согласно (6.41) и (6.42), общее
распределение электронной плотности, показанное на рис. 6.5.
§ 6.4. Правила отбора и вероятности переходов
для одноэлектронных атомов
Рассмотрим теперь правила отбора и вероятности переходов для одноэлектрон-
ного атома. Мы при этом не будем, как и в предыдущих параграфах, принимать
во внимание тонкую структуру уровней и ограничимся случаем дипольного излуче-
ния, как наиболее важным. Практически для атома водорода и водородоподобных
ионов наблюдается только дипольное излучение.
§ 6.4. Правила отбора и вероятности переходов
181
Для главного квантового числа п возможны любые его изменения, что приводит
к появлению серий, высокие члены которых могут соответствовать очень большим
изменениям Дп — ni — п\. Правда, с увеличением Дп вероятность переходов
постепенно уменьшается (см. ниже, с. 185).
Для азимутального квантового числа имеет место правило отбора
дг = ±1.	(6.45)
Это правило отбора вытекает из правила отбора Д/ = 0, ±1 (см. (4.156)) для кванто-
вого числа J, определяющего величину механического момента, и из правила отбо-
ра (4.153), запрещающего в дипольном излучении переходы между состояниями оди-
наковой четности. Как можно показать, все состояния с четным I (т. е.1 — 0, 2,4,...)
являются четными, а все состояния с нечетным I (т. е. I = 1, 3, 5,...) — нечетны-
ми; в частности, четными являются 5-состояния и d-состояния, а нечетными —
p-состояния и /-состояния. Поэтому переходы с Д1 = 0 запрещены, что и приводит,
в сочетании с правилом отбора (4.156), запрещающим изменения |Д/| > 1, к (6.45).
Свойства четности состояний, в зависимости от четности Z, определяются видом угловых
функций (6.44), которые являются четными при четном I и нечетными при нечетном I. В этом
легко убедиться, учитывая, что угловые координаты в и преобразуются, при отражении
всех координат вначале (х' = -х, у1 = —у, z' = -z), по закону 0' = л- - 0, <р' =	4- тг,
в силу чего cos0' = -cos0 и sin0' = sin0, е™*' = (-l)me*w. Поэтому функция YJm(0, у?)
при I = 0,1,2,... четная, а при I = 1,3,... нечетная. Данные свойства выводятся еще
проще, если представить сферические функции в максвелловской форме как потенциалы
мультиполей порядка 21 (ср. с. 97):
где г — расстояние точки с координатами ж, у, z, в которой определяется потенциал, от муль-
типоля. При отражении в начале, т. е. при изменении знака всех координат на обратный,
выражение (6.46) сохраняет свой знак при четном и меняет его при нечетном I = а 4- р 4- 7.
Функции У/т(0, у?) представляют линейные комбинации функций (6.46), относящихся к за-
данному значению Z, и обладают теми же свойствами симметрии.
Согласно правилу отбора (6.45), 5-состояния комбинируют только с р-состояни-
ями, p-состояния комбинируют как с 5-состояниями, так и с d-состояниями,
d-состояния комбинируют как с p-состояниями, так и с /-состояниями и т.д. Это
можно представить в виде схемы
(6-47)
Правило отбора для азимутального квантового числа играет очень важную роль
в атомной спектроскопии, и мы будем неоднократно встречаться с ним в дальнейшем.
Для орбитального магнитного квантового числа т/ правило отбора, соглас-
но (4.157), имеет вид
Дт/=0,±1,	(6.48)
т.е. nti может либо сохранять свое значение, либо менять его на ±1.
Доказательство правила отбора (4.157) было приведено в §4.8, причем как раз для случая
орбитального момента (см. примечание на с. 119), поскольку мы исходили из явного вида
волновых функций оператора = hlz.
182
Глава 6. Спектры атома водорода и водородоподобных ионов
Правило отбора (6.48) также является весьма важным; оно, в частности, очень
существенно при рассмотрении эффекта Зеемана в сильных полях (см. гл. 14, с. 391).
В соответствии с правилами отбора (6.45) и (6.48) для переходов между уровнями
с определенными значениями п — П\ и п = т.е. для отдельных спектральных
линий с частотами (6.14), комбинируют друг с другом лишь состояния, для которых
одновременно AZ = ±1 и Дт/ = 0, ±1. Разрешенные переходы показаны на схеме
рис. 6.9, слева указаны значения квантовых чисел п и Z, а справа — квантового
числа т/. Мы получаем по 3 возможных составляющих для переходов с уровня п — 1,
т. е. для членов серии Лаймана, и по 12 составляющих для переходов с уровня п — 2,
т. е. для членов серии Бальмера,3).
Для одноэлектронного атома для переходов n\l\ - можно вывести общие
формулы, определяющие значения сил осцилляторов и вероятностей испускания
и поглощения, что сводится, согласно (4.117) и (4.45)-(4.47), к квантовомеха-
ническому расчету дипольных моментов переходов = Pn2z2m2,niZ1m1 и сил
При учете спина вместо каждого состояния с заданными Z и пц получаются два состояния
I
С ms = ±-.
При пренебрежении спин-орбитальным взаимодействием имеет место правило отбора
Дт3 = 0 и удвоение числа состояний приводит просто к удвоению числа возможных переходов.
§ 6.4. Правила отбора и вероятности переходов
183
переходов 5^ип) =	= £ 1-Рп2г2т2,I2- Дипольные моменты переходов Р
обратно пропорциональны Z, что связано с изменением масштаба расстояний
для членов изоэлектронного ряда (6.1) (ср. (6.29) и с. 176), и соответственно силы
переходов S обратно пропорциональны Z2. Частоты переходов, согласно (6.14),
пропорциональны Z2, поэтому для сил осцилляторов /, вероятностей А спонтанных
и вероятностей В вынужденных переходов мы имеем
A~v3S~Z4, B~S~Z~2.	(6.49)
Таким образом, для аналогичных переходов в одноэлектронных атомах силы
осцилляторов одинаковы, что естественно, так как силы осцилляторов представляют
относительные вероятности переходов (см. (4.104)).
В табл. 6.5 приведены численные значения сил осцилляторов для перехо-
дов njlj - nl в одноэлектронном атоме (для значений п = 1,2,3), вычисленные
по формулам (4.117) (см. [134], §63). Эти значения положительны при п > nj
(силы осциллятора для поглощения) и отрицательны при п < nj (силы осциллятора
для испускания).
Таблица 6.5
Значения сил осцилляторов для атома водорода
Начальное состояние njlj	1s	2s	2р		3s	Зр		3d	
. Конечное состояние nl	пр	пр	ns	nd	пр	ns	nd	пр	nf
п = 1 п — 2 п — 3 п = 4 п = 5 п = 6 п — 7 п = 8 Сумма от п — 9 до оо	0,4162 0,0791 0,0290 0,0139 0,0078 0,0048 0,0032 0,0110	0,4249 0,1028 0,0419 0,0216 0,0127 0,0081 0,0269	-0,139 0,014 0,0031 0,0012 0,0006 0,0003 0,0002 0,0007	0,696 0,122 0,044 0,022 0,012 0,008 0,024	-0,041 0,484 0,121 0,052 0,027 0,016 0,048	-0,026 -0,142 0,032 0,007 0,003 0,002 0,001 0,002	0,619 0,139 0,056 0,028 0,017 0,045	-0,417 0,011 0,0022 0,0009 0,0004 0,0002 0,0007	1,016 1,156 0,053 0,025 0,015 0,037
Весь дискрет- ный спектр	0,5650	0,6489	-0,119	0,928	0,707	-0,121	0,904	-0,402	1,302
Непрерыв- ный спектр	0,4350	0,3511	0,008	0,183	0,293	0,010	0,207	0,002	0,098
Сумма	1,000	1,000	-0,111	1,111 	✓	1,000	-0,111	1,111 	V	-0,400	1,400 	J
			1,000			1,000		1,000	
Помимо сил осциллятора для переходов на дискретные уровни, в таблице
приведены силы осцилляторов для переходов на непрерывные уровни, лежащие
выше границы ионизации. Только при учете этих сил осцилляторов выполняется
правило сумм (4.118), согласно которому сумма сил осцилляторов, соответствующих
всем переходам, возможным с данного уровня, равна единице.
Как показывает рассмотрение таблицы, с увеличением п силы осциллятора
быстро убывают, составляя несколько десятых для переходов между глубокими
уровнями и сотые и тысячные доли при переходах на более высокие уровни.
184
Глава 6. Спектры атома водорода и водородоподобных ионов
В соответствии с (4.120) в таблице даны средние силы осцилляторов, связанные с веро-
ятностями спонтанного испускания и поглощения формулами,4)
8тг2е21/2 -	тге2 -	.	.
А* =	Bki =	(6.50)
т€сл	птеи
При квантовомеханическом расчете непосредственно вычисляются дипольные моменты
переходов (Р\)пг12т2,пх1хтх (А =	2/, -г), т. е. матричные элементы типа (4.53). Для составляющей
дипольного момента по оси z, Pz = -ez = -er cos0, мы, например, получаем, с учетом (6.40),
(Рх)п2^2”12>п1^гп1 = ~е	<p)l* dr d£l =
°f ,	Г	(6.51)
= -е / ЯП2Ь(г)г3Япи1(г)с/г / У^2(0,^)Г/1ТП,(0,<р) cos 0sin0 dO dtp,
о
и так как интеграл по угловым функциям легко вычисляется (он отличен от нуля лишь
при т2 = т,\ и /2 = li i 1, что и дает правила отбора (ср. 4.8)), то расчет сводится
к вычислению радиальных интегралов
эо
J R^r^R^dr.	(6.52)
о
Эти же интегралы входят в качестве множителя в матричные элементы составляющих Рх
и Ру дипольного момента. Однако в силу равноправия осей х, у, z для свободного атома,
достаточно вычислить матричные элементы (6.51) (ср. (4.57)); определив с помощью формулы
- 3 S |(^s)n2z2m2,nli1ml I силу перехода, можно, согласно (4.117) и (4.120), найти
7711 ,7712
искомые силы осцилляторов 4 15\
При помощи сил осцилляторов легко находятся и вероятности переходов.
В табл. 6.6 приведены для атома водорода вероятности спонтанных переходов с верх-
них уровней с заданными значениями где щ — 2,3,4, на нижние уровни
с различными значениями nkh < Щ, h ~ Ц ± 1). В таблице даны как вероятности
отдельных переходов, так и суммы 5Z Aik — Ai вероятностей переходов с уровня Ei
к
на все уровни Е^, для которых эти вероятности отличны от нуля. Согласно (4.16),
величина, обратная Аг, равна времени жизни т, атома, находящегося на уровне 2%;
соответствующие значения времени жизни приведены в последнем столбце таблицы.
Помимо этого, в таблице указаны средние значения вероятности спонтанного пере-
хода с уровня с заданным значением п. Они получены путем усреднения значений
вероятностей переходов с уровней, имеющих при данном п различные значения I
(эти уровни, в силу вырождения по /, имеют одинаковую энергию) по формуле
Ап = ^j|Anl = 1 52 (21 + 1)Ап1	(6.53)
X 9i
с учетом статистических весов gi отдельных уровней.
В таблице также указаны времена жизни, соответствующие средней вероят-
ности. Средние вероятности существенны, если распределение атомов по уровням
l4) В первой формуле учтено, что сила осциллятора для испускания отрицательна.
15^ Более подробное изложение расчета сил осцилляторов и вероятностей перехода можно найти
в монографии Бете и Солпитера [134].
§ 6.5. Тонкая структура уровней энергии и спектральных линий
185
Таблица 6.6
Вероятности спонтанных переходов Aik для атома водорода (в 108 с-1)
Начальное состояние	Конечное состояние nklk				Сумма вероятностей	Время жизни, 10-8с
	тип состояния	п* = 1	п» = 2	nt = 3		
2з	пр	—	—	—	0	00
2р	пз	6,25	—	—	6,25	0,16
= 2	среднее	4,69	—	—	4,69	0,21
Зз	пр	—	0,063	—	0,063	16
Зр	пз	1,64	0,22	—	1,86	0,54
3d	пр	—	0,64	—	0,64	1,56
ni = 3	среднее	0,55	0,43		0,98	1,02
4s	пр	—	0,025 0,095	0,018	0,043	23
4р	( пз [ nd	0,68		0,030 0,003	|	0,81	1,24
4d	пр	—	0,204	0,070	0,274	3,65
4/	nd	—	—	0,137	0,137	7,3
n, = 4	среднее	0,128	0,083	0,089	0,299	3,35
энергии с различными I при заданном п все время остается пропорциональным
их статистическим весам gi — 21 4- 1, что будет иметь место при большом числе
столкновений.
Вероятности переходов убывают с увеличением главного квантового числа п,
верхнего уровня, а при заданном п, — с увеличением главного квантового числа nk
нижнего уровня. При тех же значениях п, и пк они увеличиваются с увеличением
азимутального квантового числа Ц верхнего уровня. Вероятности переходов между
более глубокими уровнями получаются порядка 108 с“’; им соответствуют времена
жизни г порядка 10“8с. Самая большая вероятность перехода (Л = 6,25 • 108 с"1)
и самое малое время жизни (г = 0,16 • 10“8 с) получаются для перехода 15 - 2р,
т. е. для первого члена серии Лаймана.
Вероятности спонтанных переходов для водородоподобных ионов получаются,
согласно (6.49), умножением значений, приведенных в табл. 6.6, на Z4, времена
жизни соответственно уменьшаются в Z4 раз.
Расчет значений Aik для атома водорода производится по первой формуле (6.50) с по-
мощью значений / сил осцилляторов, приведенных в табл. 6.5. При этом надо учитывать,
что fik = -^fki (см- (4->14)).
§ 6.5. Тонкая структура уровней энергии и спектральных линий
До сих пор мы пренебрегали влиянием спина электрона на энергию атома. На-
личие спина обусловливает для одноэлектронных атомов тонкую структуру уровней
энергии и тонкую структуру спектральных линий, получающихся при переходах
между этими уровнями, согласно основной формуле (6.14).
Рассмотрение тонкой структуры уровней энергии и спектральных линий атома
водорода и водородоподобных ионов представляют особый интерес. Подобно тому
как вывод боровской формулы (6.13) для уровней энергии явился проверкой нереля-
тивистской квантовой механики, ее основного уравнения — уравнения Шредингера,
186
Глава 6. Спектры атома водорода и водородоподобных ионов
(6-55)
вывод в основном правильных формул для тонкой структуры, обусловленной реля-
тивистскими эффектами, явился проверкой релятивистской квантовой механики, ее
основного уравнения — уравнения Дирака. Вместе с тем обнаружились отступления
от теории Дирака, имеющие большое принципиальное значение и объясняемые
квантовой электродинамикой (см. §6.6, с. 193).
Мы разберем сперва вопрос о характеристике уровней энергии при учете спин-
орбитального взаимодействия.
Благодаря спин-орбитальному взаимодействию орбитальный момент электро-
на I складывается со спиновым моментом з в полный момент
j — I + з,	(6.54)
величина которого определяется внутренним квантовым числом j, принимающим
полуцелые значения (см. (2.21)-(2.24) и табл. 2.1, с. 48).
7 = i + 2> 3 = 1 “ 2	J = 5 = 2
Значение проекции jz вектора j определяется соответственно полным магнитным
квантовым числом mj, принимающим 2j 4- 1 значений от j до —j. Вместо набора
квантовых чисел (6.7) мы получаем набор квантовых чисел
п, I, j, mj,	(6.56)
причем энергия свободного атома не должна зависеть от mj, т.е. для уровня
с заданными значениями п, I и j степень вырождения равна gj = 2j + 1.
Отметим, что число независимых состояний при заданных п и I по-прежнему
равно 2(214-1). Действительно, при j — I + ’/2 получается 2j 4-1 =2/4-2 состояний,
а при j = I-’/2 получается 2j4-1 = 21 состояний, т. е. всего4/4-2 = 2(2/4-!) состояний.
Мы имеем частный случай общего соотношения (3.35) (J| = l\, J2 = ’/2, J = j).
Существенно, что в общем случае энергия одноэлектронного атома, при учете
спин-орбитального взаимодействия, должна зависеть от квантовых чисел I и j.
Зависимость энергии атома при заданных п и I от j легко понять на основе наглядных
представлений о магнитном взаимодействии спина электрона с орбитальным моментом —
о спин-орбиталъном взаимодействии типа (/, з). Электрон, вращаясь вокруг ядра, создает
орбитальный механический момент I и пропорциональный ему орбитальный магнитный
момент fa — — (см. (2.48)). С другой стороны, электрон, наряду с собственным спи-
новым механическим моментом з, обладает и собственным спиновым магнитным момен-
том дБ = -2рьЗ (см. (2.55)). Орбитальный и спиновый магнитные моменты взаимодействуют
между собой, причем это взаимодействие зависит от взаимной ориентации моментов I и з,
следовательно, от величины j полного момента количества движения j = l + з (ср. §2.6, с. 61).
Значение j = I 4- ’/2 соответствует параллельной ориентации I и з, значение j = I — */2 —
анти параллельной ориентации. Энергии при j = 14- */2 и j = I - */2 будут различны, получится
расщепление уровня с заданными п и I на два уровня. Такое расщепление на два уровня — ду-
блетное расщепление — в чистом виде наблюдается для атомов щелочных металлов, имеющих
один внешний электрон, энергия которого зависит не только от п, но и от I. Это дублетное
расщепление будет подробно рассмотрено в § 8.4. Для атома водорода положение осложняется
тем, что в нерелятивистском приближении энергия зависит только от п, но не от I. Добавка
к энергии, зависящая от I, притом того же порядка, что и величина дублетного расщепления,
получается, если учесть зависимость массы от скорости как малую поправку к решению нере-
лятивистской задачи. Именно при учете зависимости массы от скорости, в рамках боровской
теории эллиптических орбит, Зоммерфельдом была впервые получена формула для тонкой
структуры, согласно которой уровень с заданным п расщепляется на п подуровней, соответ-
ствующих различным значениям азимутального квантового числа боровской теории k = 14-1.
Поправка АЕПук к энергии (6.13) получилась равной [10]
Ra2ZA (1	3
Д^п,1 =-----5— I ~ ~ —
п5 \к 4п
(6.57)
§ 6.5. Тонкая структура уровней энергии и спектральных линий
187
где а — постоянная тонкой структуры (см. (6.31)). К этой же формуле непосредственно
приводит теория Дирака (см. ниже, с. 188), согласно которой также получается расщепление
уровня с заданным п на п подуровней. В рамках нерелятивистской квантовой механики
та же формула получается, если учесть, как зависимость энергии от из-за изменения массы
со скоростью, так и дублетное расщепление уровня с заданным I вследствие спин-орбитального
взаимодействия.
Рассмотрим подробнее возможные уровни энергии атома водорода при задан-
ном п, различающиеся значениями I и j.
Согласно (6.55), при I = 0 j = s = x/i и получается одно значение /, а при всех
других значениях I получается по два значения j, j = I + ’/2 и j = I - У2 (при I = 1
j = '/2 и j = при I = 2 j = 3/2 и j = s/i и т.д.). С точки зрения наглядных пред-
ставлений мы имеем сложение ме-
ханических моментов, изображенное
на рис. 6.10. Спиновый момент ориен-
тируется либо параллельно, либо ан-
типараллельно орбитальному момен-
ту, соответственно складываясь с ним
или вычитаясь из него.
Возможные уровни энергии с раз-
личными значениями I и j для значе-
ний п от 1 до 4 показаны схематичес-
ки на рис. 6.11. Общее число уровней
с различными парами значений I и j
равно 2п - 1. При этом j принимает
п значений, меняясь от 1/2 до п - ’/2,
7 = 1/21
7 = 1/2]
Рис. 6.10. Сложение орбитального и спинового
моментов: жирная стрелка обозначает
результирующий момент j
причем каждое значение j встречается по два раза, кроме максимального значения,
равного п — У2, которое получается один раз (I — п - 1, j = I -}- ’/2 = п — ’/2)-
Каждое значение I также встречается по два раза, кроме минимального значения,
равного нулю, которое получается один раз (j = ’/2,1 = j - У2 = 0). Таким образом,
состояния можно группировать попарно, либо по значениям j, либо по значениям I,
что на рисунке указано скобками.
На рис. 6.11 приведены также общепринятые обозначения уровней энергии
одноэлектронного атома. Цифра впереди указывает значение п. Прописными бу-
квами S, Р, D, F обозначены значения I = 0, 1,2,3 орбитального механического
момента атома. Как мы видели (см. (6.4)), состояния электрона со значениями
орбитального момента I = 0,1, 2, 3 называют а-, р-, d-, /-состояниями. Для атома
в целом значения орбитального момента принято обозначать не строчными, а про-
писными буквами 5, Р, Z>, F, ... соответственно. Для атома, имеющего лишь
один электрон, орбитальный момент атома в целом, разумеется, и есть орбитальный
момент электрона,6). При учете спина полный момент, при каждом значении I
орбитального момента, принимает два значения j = I — */2 и j — I -}- */2 и мы имеем
вместо каждого уровня два уровня — дублет. Это обозначается индексом 2, стоящим
слева сверху17*. Индекс справа снизу указывает значение квантового числа j. Этим
,6* В общем случае атома со многими электронами орбитальный момент атома в целом является суммой
орбитальных моментов отдельных электронов и его значение будет, вообще говоря, отлично от значений
орбитальных моментов отдельных электронов (ср. гл. 9, с. 246).
,7*Этот индекс дает число возможных ориентаций спина (мультиплетность), равное в общем случае
к = 2S+ 1, где S — значение спина для атома в целом (также обозначаемое прописной буквой). В данном
случае S = з = ’/2 и х = 2 • ’/2 + 1 = 2. Поэтому индекс 2 пишется и для состояния S (L = I — 0), которому
соответствует лишь одно значение j = I + */2 = ’/2-
188 Глава 6. Спектры атома водорода и водородоподобных ионов
п 1	J	H	He+
	 7/2	42F7/2		.	
3 <	5/2	42F5/2 1			[> 0,0075см’1 0,12 cm’1
	5/2	42Ds/2 J	
2		> 0,015см 1 0,24см 1
4	3/2	42DV2 1		
	3/2	42P3/2 f	
1 <		>0,046 cm’1 0,73cm’1
	‘/2	42Pl/2 1		
0	1/2	4%2 J	
	5/2	32Ds/2 		
2 <	3/2	32DJ/2 1	,	> 0,036 cm’1 0,57 cm”1
3	I	[ 3/2	32Pj/2 J	
1 J		►0,108 см1 1,72 cm
	[ 1/2	3>,/2 1			
0	Ml	325i/2 J	
	3/2	2>j/2	,	
1 <		► 0,366 cm 1 5,86 cm 1
2	• '/2	2>i/2 1		
0	1/2	225,/2 J	
1	0	1/2	125i/2 		
Рис. 6.11. Уровни энергии атома водорода
с различными значениями п, I и j
индексом принято обозначать значение полного момента атома; в данном случае
полный момент атома совпадает с полным моментом электрона18).
Например, символ 321>зд обозначает уровень с п — 3, I = 2 и j = 3/ь символ
4 2S у2 — уровень с п = 4,1 = 0 и j = ‘/2 и т.д.
Число уровней при заданном значении п, равное 2п - 1, получается, если
энергия зависит как от значения j, так и от значения I. Согласно теории Дирака
(релятивистской квантовой механике), оказывается, что при заданном п энергия
зависит от значения j, но не зависит от значения I. Каждый уровень с заданным п
должен расщепляться на п подуровней, соответствующих значениям j от '/2 до п— ’/г.
Энергии для каждой пары уровней (2 ’«л-	W- (’Ч-
и т. д. с одинаковыми значениями j в теории Дирака совпадают.
Поправка AEnj к энергии Еп, определяемой формулой (6.13), получается равной
Ra2ZA fl 3 \
пз \Г+Т72"4^Л
(6.58)
,8) В общем случае атома со многими электронами их значения, так же как и для орбитальных
моментов, не совпадают. Отметим, что речь идет о полном моменте, являющемся суммой орбитальных
и спиновых моментов электронов, но не включающем спиновый момент ядра (ср. §6.1, с. 164).
§ 6.5. Тонкая структура уровней энергии и спектральных линий
189
Эта поправка является функцией квантового числа j. В формулу (6.58) входит
безразмерная постоянная тонкой структуры а (см. §6.3, с. 172),
2тге2 е2	1
а = ~hc ~ hc = 137,0373 ± 0,0006’
(6.59)
п 1ДМ
Отношение ——~
|ЯП|
имеет порядок
|ДДП>| __ a2Z2
l^nl п
(6.60)
1
Так как а ~ —— и
137	_____
стотысячных, и в зависимости от j получается тонкая структура уровня энергии
с заданным п. Поэтому а и называют постоянной тонкой структуры.
Разность энергий fyj+i уровней с j + 1 и j равна
Ra2Z4
п3
2	1
а ~ 18 800? Т° ЭТ° отношение ПРИ % ~ 1 порядка нескольких
&Enj —
(6.61)
В частности,
(6.62)
(6.63)
1
Ra2Z4
S'/2, % = ДЯП)3Л - ДЯП11Л = ~^3~-
Для уровня атома водорода с п = 2 получается расщепление <5у2 Зд, равное
Ra2
Й1/2, 3/2 = ^Е2,3/2 ~ ^Е2,'/2 = ~ЙГ = 0,366 СМ~‘-
Эта величина очень мала по сравнению с разностями энергий уровней с различны-
ми п. Для перехода между уровнями п — 2 и п = 3, т. е. для первой линии серии
Бальмера (На), Л = 6 563 А, и — 15 234 см-1, следовательно, относительное расщеп-
ление линии за счет удвоения уровня п — 1 (j — */2, V2) составляет примерно
Весьма существенной является зависимость тонкой структуры от п и, в осо-
бенности, от Z. Как видно из формулы (6.61), абсолютная величина расщепления
с увеличением п быстро убывает (обратно пропорционально п3), а с увеличением Z,
т.е. при переходе от нейтрального атома водорода (Z = 1) к ионам Не II, Li III
и т. д. (Z = 2, 3,...), очень быстро возрастает (пропорционально Z4). По сравнению
с атомом водорода при том же значении п расщепление для Не II возрастает в 16 раз,
для Li III — в 81 раз, для Be IV — в 256 раз, составляя для уровня п = 2 соответ-
ственно 5,85 см"1, 29,6 см-1 и 94 см-1. Относительное расщепление, как показывает
формула (6.60), изменяется медленнее, но также убывает с увеличением п (обратно
пропорционально п) и возрастает с увеличением Z (пропорционально Z2).
В правой части рис. 6.11 показаны расщепления уровней п = 2, 3 и 4 (уровень
п = 1 не расщепляется) и приведены значения разностей для атома водорода
и ионизованного атома гелия, вычисленные по формуле (6.61).
Зная расщепления уровней с заданными значениями п, легко определить тонкую
структуру спектральных линий, получающихся при переходах между уровнями п — п\
нп = П2. Возможные компоненты тонкой структуры линий определяются правилами
190
Глава 6. Спектры атома водорода и водородоподобных ионов
отбора AZ = ±1, Aj = 0, ±1 (см. (6.45) и (4.156)), согласно которым разрешены
следующие переходы jx -
'h + 'h [^/г-2ру2^
'/2-V2	1Л1/2- 2Р3/2(2)	f2Pl/2- 2Рз/2(5)
3/2 — 3/2	<2Р3/2- 2Рз/2(1)
% ~ 5/2	<2Рз/2 - Ъ5/2 (9) Г2Рз/2 - 2Р5/2 (14)
5/2 — 5/2	\ 2Z>5/2 — 2Р5/2(0
5/2-7/2	12£>5/2- 2F7/2(20).
(6.64)
А = 6563 А
Рис. 6.12. Схемы переходов
и картина расщепления для линии
водорода На, Л = 6 563Л
В одной строке выписаны переходы, дающие,
в силу независимости энергии от I, совпадающие
компоненты.
Схема переходов и соответствующая карти-
на расщепления первой линии серии Бальмера,
На(п2 — 3 —► П\ — 2), ожидаемые по теории Дира-
ка, показаны на рис. 6.12. Символы совпадающих
по этой теории уровней объединены скобками.
Относительные интенсивности различных
компонент определяются, во-первых, отношени-
ем рассмотренных в предыдущем параграфе ве-
роятностей различных переходов n\l\ n2b(ni
и П2 фиксированы, 1Х ~ 0, 1,..., п\ — 1, I2 —
0, 1,..., П2 — 1) и, во-вторых, значениями стати-
стических весов как начальных, так и конечных
уровней. Статистическим весам g = 2j 4-1 началь-
ных уровней пропорциональны их заселенности.
При заданных 1Х и 12 для различных переходов
с уровней jx = I] ± ’/2 на уровни j2 = I2 ± ’Л
получаются относительные интенсивности, кото-
рые зависят от статистических весов этих уров-
ней и определяются по правилу сумм интенсив-
ностей. Согласно этому правилу, сумма интен-
сивностей линий, возникающих при переходах
с уровня jx на уровни J2 =	’/2, пропорциональ-
на gx = 2jx 4- 1, а сумма интенсивностей линий,
возникающих при переходах с уровня J2 на уров-
ни jx — lx i ’/2, пропорциональна д2 = 2j2 4- 1.
Данное правило является частным случаем более общего правила сумм интен-
сивностей для мультиплетов, которое будет рассмотрено в дальнейшем (см. § 9.6,
с. 273).
Для переходов S—P, P—D и D—F из правила сумм получаются относи-
тельные интенсивности компонент, указанные в скобках в (6.64). Интенсивность
линии 25у2~ 2Ру2 вдвое меньше интенсивности линии ^1/2““2^з/2, интенсивности
линий 2Р|д—2£>зд, 2Р3д—2£>зд и 2^3/2~2Ds/2 находятся в отношении 5:1:9,
а интенсивности линий 2^з/2“-2^5/2, 2D5^—2F5/2 и 2D5^~2Fy2 находятся в отноше-
нии 14:1: 20.
§ 6.5. Тонкая структура уровней энергии и спектральных линий
191
а
Рис. 6.13. Статистические веса уровней и интенсивности переходов:
а — переход 2S— 2Р; б — переход 2Р— 2D
Эти результаты получаются следующим образом. Для переходов 2Sy2— 2Ру2 и
с уровней 2Ру2 и 2Р3д на единственный уровень %>у2 (рис. 6.13, а, переходы 7 и 2) интенсив-
ности пропорциональны статистическим весам уровней 2Ру2 и 2Р3д, равным д^ = 2^4-1 = 2
3
и д^ = 2-4-1 = 4, т. е. относительная интенсивность компонент равна 1 : 2. Для перехо-
дов 2Р|д— 2Z)y2, 2Ру2~2Ру2 и 2Р3/2—21>5/2 (рис. 6.13,6, переходы 7, 2 и 3) интенсивность
перехода относится к сумме интенсивностей переходов 2 и 3, как веса уровней 2Ру2 и 2Рз^
т. е. как 2 : 4, а сумма интенсивностей переходов 7 и 2 относится к интенсивности перехода 3,
как веса уровней 2Р3д и 2Z)y2, т. е. как 4 : 6. Таким образом,
/1 =2=1	Ъ+h _4 = 2
724-13~4“2’	13 ~б“з’
откуда 1\ : 12 : 13 = 5 : 1 : 9. Аналогичным образом получается отношение интенсивностей
и для переходов D—F.
Следует подчеркнуть, что отношение интенсивностей двух линий, получающихся при пе-
реходах с уровня j| на два уровня j2 = 12 ± равно отношению соответствующих вероятно-
стей и что равенство отношения сумм интенсивностей при переходах с уровней j\ = ± ’/2
на уровни j2 = 12 4- ’Л отношению статистических весов 2(Z| 4- У?) 4-1 и 2(1} - }/2) 4- 1 озна-
чает равенство соответствующих вероятностей перехода. Так, при переходах 2Sy2 —> 2Ру2
и 2Sy2 -♦ 2Р3д с уровня 2Sy2 на уровни 2Ру2 и 2Р3д интенсивности и вероятности находятся
в отношении 1 : 2 (в случае рис. 6.13, а это будут переходы в поглощении). При обратных
1
переходах 2Ру2 -+ и 2Ру2 2Sy2 отношение интенсивностей -— = - ,9\ а отношение
^Уг ^3Л
вероятностей —— = —• : —— = 1, т.е. вероятности одинаковы (в случае рис.6.13,а это
Лз/2 2	4
будут переходы в испускании). При переходах с уровней 2Ру2 и 2Р3д на уровни 2Р3д и 2Ру2
,	h 6	3	23 /1+/2
(рис.6.13,б) --— = - = - и -— = — : ---------= 1, т.е. вероятности опять одинаковы.
Л 4-12	4	2 Лу2 6	4
Для спонтанного испускания одинаковым вероятностям соответствуют и одинаковые времена
жизни обоих уровней с j — I ± у2.
Если заселенности уровней пропорциональны статистическим весам.
192 Глава 6. Спектры атома водорода и водородоподобных ионов
На рис. 6.12 показаны относительные интенсивности компонент в испускании,
рассчитанные с учетом вероятностей переходов 31\ —* 2/2 и статистических весов
уровней (длина штрихов пропорциональна интенсивностям компонент).
В оптической области сначала не удавалось полностью разрешить тонкую струк-
туру спектральных линий и достаточно точно проверить выводы, к которым приводит
теория Дирака. Общий характер распределения интенсивностей соответствовал этим
выводам; для линии На, в частности, получалось два максимума, расстояние между
которыми примерно равнялось расстоянию между наиболее интенсивными компо-
нентами. Это рассматривали как подтверждение теории Дирака. Однако дальнейшие
исследования тонкой структуры уровней атома водорода и иона гелия показали на-
личие отступлений от теории Дирака и было обнаружено новое явление — сдвиг
уровней. Это явление, представляющее очень большой принципиальный интерес,
рассмотрено в следующем параграфе.
§6.6. Сдвиг уровней
Явление сдвига уровней состоит в том, что пары уровней с данным значением j,
которые по теории Дирака должны совпадать, в действительности обладают различ-
ной энергией, причем в основном это происходит для пар уровней п25у2 и п2Ру2
за счет сдвига вверх уровней п 25у2 — 5-уровней20) 21.
Действительная картина тонкой структуры, наиболее подробно исследованная
экспериментально и теоретически для уровня п = 2 атома водорода, показана
на рис. 6.14. При расстоянии между уровнями 22Р3д и 22Ру2, практически почти
совпадающем с получаемым по теории Дирака и равным 0,366 см"1 (ср. рис. 6.14),
уровень 2^у2 смещается вверх на 0,035 см"1, т.е. примерно на 0,1 расстоя-
ния 2 2Гз/2~2 2Р\/2- Для уровней со значениями п > 2 сдвиг тоже существует, однако
2 он значительно меньше, так же как и все рассто-
2 Рз/2 яния между уровнями тонкой структуры. С уве-
личением заряда ядра, т. е. при переходе от атома
водорода к водородоподобным ионам, сдвиг ра-
стет примерно пропорционально Z4, т. е. так же,
как и масштаб тонкой структуры (см. (6.61)).
Физической причиной сдвига уровней явля-
ются типичные квантовые эффекты взаимодей-
ствия электронов с излучением, так называемые
радиационные поправки, учет которых возможен
на основе квантовой теории излучения — кванто-
вой электродинамики2|). Результаты, к которым
приводит квантовая теория излучения, находят-
22^ ся, как мы видели на примере естественной ши-
2 1/2 рины спектральных линий (см. §4.6, с. 111), в со-
2 Р\/2 ответствии с результатами классической теории.
Рис. 6.14. Тонкая структура уровня
п = 2 атома водорода
Однако это относится только к первому прибли-
жению теории. В следующих приближениях по-
лучаются отличия, специфические для квантовой
20) Поэтому часто о сдвиге уровней говорят как о сдвиге 5-уровней, что не совсем точно, так как
сдвигаются и другие уровни, хотя и гораздо меньше.
21) Очень ясное изложение вопроса о радиационных поправках можно найти в монографии Гейтлера
«Квантовая теория излучения» [140], см. также [134].
§6.6. Сдвиг уровней
193
электродинамики и поэтому имеющие весьма важное значение для ее дальнейшего
развития; эти отличия и проявляются в виде радиационных поправок. При учете
радиационных поправок получаются два следствия, которые могут быть проверены
на опыте, — сдвиг уровней и аномалия магнитного момента электрона, состоящая
в небольшом отличии величины этого магнитного момента от магнетона Бора22).
Несмотря на то, что квантовая электродинамика, в современной ее форме, имеет
принципиальные недостатки, с помощью ее методов удается с большой точностью
рассчитать, в очень хорошем согласии с опытом, как сдвиг уровней, так и аномалию
магнитного момента электрона. Это свидетельствует о том, что она во многом явля-
ется правильной теорией, и позволяет надеяться на устранение имеющихся в ней
недостатков.
Трудности квантовой электродинамики связаны с использованием представления о то-
чечном электроне, что приводит к появлению в теории бесконечных величин. Для электрона
получаются бесконечная масса, обусловленная его взаимодействием с излучением, и бес-
конечный заряд, связанный с так называемой поляризацией вакуума. Для устранения этих
бесконечностей и других связанных с ними бесконечностей применяется прием перенормиров-
ки массы и заряда электрона, согласно которому рассматривается не вся бесконечная масса
и весь бесконечный заряд, а лишь их конечные части, выделяемые по определенным правилам.
Такой прием является искусственным и с чисто математической точки зрения неза-
конным, так как конечные величины получаются как разности двух бесконечных величин,
однако получающийся результат несомненно является правильным, как показывает сравнение
с опытом теоретических значений сдвига уровней и аномалии магнитного момента электрона.
Приближенное выражение для сдвига 5-уровней, к которому приводит кванто-
вая электродинамика, имеет вид
^s=Enis - Еп2Р =-------------—CnZ,	(6.65)
72	72 П
где Cnz — численная постоянная порядка единицы, зависящая от п и от Z. Отноше-
ние сдвига 5-уровня к разности энергий уровней п 2Ру2 и п 2Р\/2 (см. (6.62))
равно	’
А.	16
т-— = I6aCnZ = —CnZ,	(6.66)
6'/2, %	137
7,75
т. е. порядка 0,1. Для уровня п — 2 атома водорода С21 = ----- = 0,822, что дает
Зя-
значение
4S = 0,03505 см-1 = 1 051 МГц.	(6.67)
Учет небольших дополнительных поправок приводит к более точным значениям
сдвига, несколько различающимся для обычного водорода и для тяжелого водорода.
Получается [248а]
для атома Н As = 1 057,70 МГц, 1	,,
для атома D А, = 1 058,96 МГц J
с погрешностью менее 0,20 МГц.
Для водородоподобного атома для уровня с заданными значениями п и I дополнительная
энергия обусловленная радиационными поправками порядка а3, равна
Д47’= 4,^ + 4^.	(6.69)
22>Мы уже упоминали об аномалии магнитного момента электрона в §2.5 (с. 56). Более подробное
рассмотрение вопроса см. в гл. 14, с. 400.
7 Зак 103
194 Глава 6. Спектры атома водорода и водородоподобных ионов
Первый член в (6.69) зависит от значения волновой функции электрона в атоме в начале
координат, т. е. в месте нахождения ядра, и отличен от нуля только для 5-состояний (см. § 6.3,
с. 178), т.е. для уровня 25|д. Он составляет для этого уровня
Д"Б"01/г = £^{(1п^--|п2+^) -5}=^
где LnZ — постоянная, равная
тес2	31
|П “1П2+ 120
(6.70)
1 8$a3Z4
LnZ = т-----—	6.71
Зтг п5
В (6.70) члены в круглой скобке определяются радиационными поправками, помимо по-
1	тес2
правки на поляризацию вакуума, которая дает член	Основную роль играет член In ——,
5	KnZ
в который входит отношение собственной энергии электрона тес2 к постоянной KnZ,
представляющей некоторую среднюю энергию возбуждения электромагнитного поля и про-
порциональной Z2:
KnZ=KnlK2.	(6.72)
Для атома водорода Кц = 19,77$, $21 = 16,64$; $31 = 15,92$;	= 15,64$ для п = 1, 2, 3, 4
соответственно.
Второй член в (6.69) (обусловленный релятивистским взаимодействием спина электрона
в электрическом поле ядра) отличен от нуля как для 5-состояний (I = 0), так и для состояний
с I > 0. Он равен
г 3__________1_
”z 8(21+ 1)1+ 1
-L 3	1
nZ 8(21+ 1) I
Это дает для уровня (I = 0, j = 'Д)
А гЛрад) _
Д2Ьп0 -
(6-73)
Л Р(рад)
(6-74)
для уровня П2Р|Д (I = 1, j - '/2)
д Т7|(рад) _______ г 1
(6-75)
для j =
для j =

И ДЛЯ уровня П2Р3д (I = 1, j' = ’Л)
(6.76)
(6-77)
nl 72	16
Полное смещение уровня п25у2, согласно (6.69), (6.70) и (6.74), составляет
{|п	-,п 2 +	{,п	"|п 2 + 55
Вычитая из смещения (6.77) уровня п25|д смещение (6.75) уровня п2Р|д, мы получаем
величину сдвига 5-уровня
А	( теС2	191 I
As = Lnz In —-----In 2 4- —- > - <
t KnZ	) I
что можно также записать в виде (6.65)
1 8$a3Z4 ( т€с2	t 91 1	8$a3Z4
Аз = Ч-----— Ъп - in 2 + — > =---------------— CnZl
Зтг п3	I	KnZ	120 J п5
1	1 f пгес2	19	11	.	.
—LnZ\ =£nJln-^--ln2+-4--k (6.78)
О J	HnZ	JU О J
(6-79)
§6.6. Сдвиг уровней
195
где
1 f тес2	91
CnZ = Зтг 1 1П К 1П 2 + ПО
ЗТГ I	1<*U
Для состояния 25 атома водорода KnZ = К2[ = 16,641? и
In = 7,6876 « 7,6923’,
#21
(6.80)
(6.81)
91
а сумма членов - In 2 и составляет лишь около 0,06. В результате
7,69 + 0,06	7,75
G, =	.	= -f- = 0,822,
Зтг Зтг
т.е. мы приходим к значению С2|, приведенному выше.
Численное значение постоянной LnZ для состояния 25 атома водорода равно (см. (6.71))
Г21 = З-Яа3 = 135,6 МГц.
Зтг
Полная величина смещения уровня 225|д составляет, согласно (6.77), (6.81) и (6.82),
(6.82)
= 135,6{7,69 - 0,69 4- 0,63} = 135,6 • 7,63 = 1 034 МГц.	(6.83)
Отметим, что в эту величину входит поправка на поляризацию вакуума, равная (см. (6.70))
L2] = -0,20 • 135,6 = -27 МГц.
Смещения уровней 22Ру2 и 22Р3д малы и равны (см. (6.75) и (6.76))
ДЕ0*? =-135,6- =-17,0 МГц	(6.84)
nl 72	8
И
= 135,6	= 8,5 МГц.	(6.85)
*1 72	16	v 7
Разность значений (6.83) и (6.84) дает значение (6.67) сдвига уровня 225|д.
Уточнение значения величины сдвига уровня 225у2 можно получить, если учесть ра-
4	5	6
диационные поправки порядка а , а и а и ввести поправки на конечную массу ядра,
а для дейтерия и на конечность радиуса дейтрона [248а]. В результате и получаются значе-
ния (6.63) сдвигов уровня для Н и D, разность которых определена точнее, чем абсолютные
значения сдвигов, и составляет
A,(D) - AS(H) = 1,26 МГц	(6.86)
с погрешностью порядка нескольких сотых долей МГц.
Сдвиг уровней с очень большой точностью, позволяющей производить сравне-
ние результатов теоретических расчетов с опытом, можно определить при помощи
радиоспектроскопических методов непосредственного наблюдения переходов между
уровнями тонкой структуры. Весьма точные радиоспектроскопические измерения
тонкой структуры уровня сп = 2 атомов легкого и тяжелого водорода были выполне-
ны Лэмбом с сотрудниками [248] по методу магнитного резонанса в атомном пучке.
Именно в этих опытах было доказано существование сдвига уровней, который часто
называют лэмбовским сдвигом, и получены очень точные значения величины сдвига.
23^ Величина тес2 примерно равна 0,5 МэВ = 5 • 105 эВ, а #21 — 16,647? = 16,64 • 13,6 ~ 230 эВ. Их
отношение составляет около 2 200 ~ е7,7.
Т
196 Глава 6. Спектры атома водорода и водородоподобных ионов
Для сдвига уровня 225у2 по отношению к уровню 22Ру2 были найдены следу-
ющие значения разности:
для атома Н	= 1 057,77 4- 0,10 МГц, 1
для атома D	~ 1 059,00 ±0,10 МГц. J
(6.87)
Эти значения находятся в исключительно хорошем согласии со значения-
ми (6.68), к которым приводят наиболее точные теоретические расчеты, отличаясь
от этих значений менее чем на 0,1 МГц, т. е. на 0,01 %. Таким образом, опыт полно-
стью подтверждает выводы, полученные на основе применения методов квантовой
электродинамики.
Следует отметить, что разность значений сдвигов для Н и для D составляет 1,23 МГц,
что очень хорошо совпадает с теоретическим значением 1,26 МГц (см. (6.86)).
Наряду с разностью уровней 2 25у2 и 2 2Ру2, Для дейтерия была измерена, с наи-
большей возможной точностью, и разность уровней 22Рзд и 225у2 (см. рис. 6.14).
Она оказалась равной
(6.88)
-E2iSlJ = 9 912,58 ±0,10 МГц.
72	72
Общее расстояние уровней 2 2Рзд и 2 2Ру2 получается прибавлением к (6.88) значения
Д5 = Е225 ~E2ip = 1 059,00 ± 0,10 МГц для дейтерия:
72	72
(6.89)
ц = Е22Р — E2ip = 10 971,58 ±0,20 МГц.
/2, /2	1/2
Отметим, что высокая точность этого значения позволяет определить с большой
точностью и постоянную тонкой структуры а. При этом надо пользоваться для б у2 Зд
не формулой (6.63), а более точной формулой (при R => R& и М = Мо)
Ra2
а 0,656 2
-------— а
я я1
(6.90)


которая получается при учете членов порядка а3 и а4.
Главная поправка к единице в скобках, равная а/тг, получается за счет
смещений (6.76) и (6.75) уровней 22Р3д и 22Р|д. Действительно, если учесть (6.82),
3/2 - ДБП, |/2 - Ь21 — - I —£2| - I - -£2|
разности
(6.91)
Ra2	Ra2 а
т. е. к —— добавляется —-—.
16	16 тг
С экспериментальной точки зрения опыты Лэмба представляют большой ин-
терес. Уровень 225у2 атома водорода является метастабильным, и это позволило
в атомном пучке, в котором атомы водорода возбуждались электронным ударом,
наблюдать переходы при зеемановском расщеплении уровней 2 25у2 и 2 2Р|д, 2 2Р3д.
Более подробно эти опыты будут рассмотрены в гл. 14, посвященной явлению
Зеемана (см. с. 400).
§6.6. Сдвиг уровней
197
Со значительной точностью был намерен радиоспектроскопическим методом
и сдвиг уровня 2 у2 для иона гелия (Не II). Величина сдвига оказалась равной [249]
для иона Не As = 14 040 ± 5 МГц = 0,4684 см-1,	(6.92)
что находится в хорошем согласии с теоретическим значением 14 046 ± 3 МГц.
Сдвиг уровня 225у2 для Не II определяется по формуле (6.65), в которой надо поло-
жить п = 2 и Z = 2; при вычислении CnZ = С22 по формуле (6.80) следует подставить,
согласно (6.72), K2Z = К2\ Z2 = 4К2\, что приводит к появлению в скобке дополнительного
1,38
члена — In 4 = —1,38 и уменьшает постоянную CnZ на —— = 0,147 по сравнению с ее
Зтг
/	0,147\
значением 0,822 для атома водорода. Поэтому Д3 для Не II в 16 [ 1 - -- - I = 13,1 раза,
\	0,822 /
а не точно в Я4 = 16 раз больше, чем для Н и D.
Оптические методы также позволяют определять сдвиг уровней, но со зна-
чительно меньшей точностью. Сдвиг уровня 225у2 атома был измерен по тонкой
структуре линии На серии Бальмер^ с точностью порядка 10% [250]. С точно-
стью порядка нескольких процентов были измерены сдвиги уровней 2^>у2, 325у2
и 425у2 иона Не по тонкой структуре линий п2 = 3 п\ = 2 (Л = 1 640 А)
и п2 = 4 —> п\ = 3 (Л = 4 086 А) [251]. Особый интерес представляет определение
оптическими методами сдвига основного уровня 1^>у2 одноэлектронных атомов;
этот сдвиг не может быть измерен радиоспектроскопическими методами, посколь-
ку уровень 125у2 не имеет тонкой структуры. Герцбергу удалось определить сдвиг
уровня 125у2 для дейтерия [252] на основе очень точного измерения длины волны
первого члена La серии Лаймана (п2 — 2 —► пх = 1, Л = 1 215,3378 ± 0,00025 А24)).
Измеренное значение частоты отличается от значения, вычисленного без учета сдви-
га уровней (по формуле (6.13), принимая во внимание поправку (6.58), согласно
теории Дирака), на 0,262 см-1, что согласуется в пределах точности измерений
с теоретическим значением сдвига уровня 1 равным = 0,2726 см4.
Сдвиг уровня 1^1/2 лля D определяется по формуле (6.65), причем CnZ = Си вычисля-
ется, согласно (6.80), со значением KnZ — К\\ = 19,771?.
24) Такая точность измерений в вакуумной области спектра была достигнута сравнением длины волны
линии La с длинами волн близколежащих линий Нд, найденными с помощью комбинационного
принципа по данным для линии Нд в видимой и близкой ультрафиолетовой области (см. с. 294).
ГЛАВА 7
ЭЛЕКТРОННЫЕ ОБОЛОЧКИ АТОМОВ
И ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ
§7Л. Квантовые числа электронов в сложном атоме
и принцип Паули
В сложном атоме, содержащем два и более электронов, эти электроны взаи-
модействуют между собой, и поэтому нельзя считать, что каждый из них движется
в поле ядра независимо от всех остальных. Однако приближенно действие всех
остальных электронов на данный электрон можно заменить некоторым усреднен-
ным эффективным полем, обладающим сферической симметрией и убывающим
с увеличением расстояния т рассматриваемого электрона от ядра. Дополнительная
потенциальная энергия электрона С7ДОП в этом поле будет, согласно предположению
о сферической симметрии, функцией только от г, и полная потенциальная энергия
электрона в поле ядра и остальных электронов запишется в виде
U = U(r) =-------+ Uaa„(r).	(7.1)
Г
С точки зрения наглядных представлений все остальные электроны образуют сфе-
рически симметричное электронное облако, и на электрон, находящийся на рассто-
янии г от ядра, действует, наряду с зарядом ядра Z (выраженным в единицах е),
заряд р(г) всех электронов, расположенных внутри сферы радиуса г!), что приводит
к экранированию ядра электронами.
На рис. 7.1 показано распределение электронной плотности как функции расстояния г
в атоме со сферически симметричным электронным облаком. Для конкретности взято рас-
пределение электронной плотности в атоме Rb, вычисленное Хартри [207]. Полная площадь
кривой равна заряду всех электронов, кроме одного, т. е. для Rb 36е (Z — 37). На рас-
стоянии Г{ на электрон будет действовать поле р^г], соответствующее заряду р:, равному
площади, заключенной между ординатами г = 0 и г = п.
Пунктирные кривые соответствуют более грубым приближениям: кривая с максимума-
ми — применению водородоподобных волновых функций по Паулингу [209а], сглаженная
кривая — применению статистической теории атома Томаса—Ферми [44].
Потенциал С7дОП(г) можно представить в виде
сг(г) е2
^доп(г) =	,	(7.2)
Г
Как известно, сферически симметричный заряд действует на внешний по отношению к нему
точечный заряд так, как если бы он был весь сосредоточен в центре, а на внутренний по отношению
к нему заряд вообще не действует.
§7.1. Квантовые числа электронов в сложном атоме и принцип Паули 199
Рис. 7.1. Сферически симметричное распределение
электронной плотности [13]
где а(г) — функция расстояния, характеризующая экранирование ядра электронами.
С помощью (7.2) формула (7.1) запишется в виде
= = (73)
Т	т
где
Z(r) = Z - а(г)	(7.4)
можно рассматривать как эффективный заряд ядра (в единицах е), действующий
на электрон на расстоянии т. Это такой заряд ядра, при котором для силы, обратно
пропорциональной квадрату расстояния (кулоновской силы), потенциал на данном
расстоянии г как раз равен U(r). Функция экранирования а (г) с расстоянием возраста-
ет от а(0) = 0 при г = 0 (вблизи начала координат потенциал убывает как -Ze2/г)
до постоянного значения на бесконечности. При г —* оо на электрон будет дей-
ствовать поле ядра за вычетом поля всех электронов, кроме одного (поскольку
рассматривается действие всех остальных электронов на данный), и для нейтрально-
го атома Z(oo) = 1, а(оо) = Z - 1, а для fc-кратно ионизованного атома, у которого
не хватает к электронов, Z(oo) = к -4- 1, а(оо) = Z - к - 1.
Электрон в сферически симметричном поле можно, так же как и в атоме
водорода, характеризовать набором квантовых чисел (6.7): n, 1, тгц, ms. Кванто-
вые числа 1, тгц, ms по-прежнему определяют орбитальный момент электрона I,
проекцию этого момента lz на некоторое направление z и проекцию спинового
момента электрона sz на то же направление. Они полностью сохраняют свой смысл
в сферически симметричном поле.
Число возможных состояний электрона остается неизменным, и главное кван-
товое число п сохраняется как характеристика состояний электрона, согласно схе-
ме (6.12) (см. с. 166). Последовательные «-состояния (I = 0) будут характеризоваться
значениями п = 1,2, 3,..., последовательные р-состояния (1=1) — значениями п =
2,3,4,..., последовательные d-состояния (1 = 2) — значениями п = 3,4, 5,... и т. д.
Волновые функции электрона при потенциале (7.3) будут иметь по-прежнему вид (6.40),
т.е. представлять произведение двух множителей. При этом угловые функции Ylmi остаются,
в силу сферической симметрии, неизменными (ср. с. 175), а радиальные функции Rni(r)
будут уже иными. Однако их, так же как и раньше, можно характеризовать радиальным
квантовым числом пт, равным числу узлов этих функций (см. с. 178), а главное квантовое
число определится как п = пг 4-1 + 1. При заданном значении 1 энергия будет тем меньше,
чем меньше пг и, следовательно, чем меньше п.
200	Глава 7. Электронные оболочки и периодическая система
В дальнейшем каждый электрон в сложном атоме мы будем характеризовать
набором квантовых чисел n, Z, ш/, ms. Очень важно подчеркнуть, что подобное
рассмотрение является приближенным, так как введение усредненного сферически
симметричного поля является лишь приближенным методом учета взаимодействия
электронов. Степень приближения зависит от того, какие электроны рассматривают-
ся. Для внешнего сильно возбужденного электрона, слабо связанного с остальными,
образующими вместе с ядром атомный остаток (остов), это приближение может
быть очень хорошим. Наоборот, для внутренних, сильно взаимодействующих между
собой электронов оно будет значительно хуже. Тем не менее, и в этом случае инди-
видуальное рассмотрение электронов2) и характеристика каждого электрона своим
набором квантовых чисел является весьма плодотворным методом и представля-
ет разумное приближение, исходя из которого можно решать задачу о движении
электронов в сложном атоме более точно.
Объяснение периодической системы, вся систематика спектров и большинство
методов квантовомеханического расчета свойств атома основаны на таком одноэлек-
тронном приближении. Мы в дальнейшем будем говорить об отдельных электронах
в атоме, об их энергии и моментах количества движения, об электронных слоях
и оболочках, характеризуя каждый электрон набором квантовых чисел и определяя
свойства атома в целом, исходя из свойств отдельных электронов. Следует лишь
помнить о приближенности подобного рассмотрения.
С квантовомеханической точки зрения введение квантовых чисел отдельных электронов
соответствует тому, что полная волновая функция атома ф(х) = гр(х}, х2,..., xN), где ж, —
совокупность координат отдельного электрона (трех пространственных и одной спиновой),
строится, исходя из волновых функций ^(хд отдельных электронов. Если не принимать
во внимание тождественности электронов (см. ниже, с. 202), то полная волновая функция
берется в виде произведения
^(аг) = ipdx^ipt^Xi) ... ^)n{xn).	(7.5)
Для приближенного учета взаимодействия электронов в качестве волновых функ-
ций &(хд берутся решения уравнения Шредингера для движения одного электрона в усред-
ненном поле ядра и всех остальных электронов. Соответствующий метод расчета усредненного
поля и волновых функций — метод самосогласованного поля — был разработан Хартри [207,
136а, 1366].
При точном решении задачи атом, естественно, характеризуется волновой функцией
^(ж|, х2,..., хх), не разбивающейся на сомножители, зависящие только от координат отдель-
ных электронов. Физически это соответствует тому, что в атоме электроны образуют единую
систему, в которой уже нельзя выделить отдельные электроны. Само понятие об отдельном
электроне в атоме является лишь приближенным.
Очень важен вопрос о зависимости энергии электрона от квантовых чисел. Эта
энергия, в силу наличия сферической симметрии, не должна зависеть ни от mi,
ни от ms, определяющих проекции орбитального и спинового моментов на напра-
вление, которое может быть выбрано произвольно. Иначе говоря, вырождение по тп/
и ms сохраняется3). Однако энергия будет теперь зависеть не только от главного
квантового числа п, но и от азимутального квантового числа I. Лишь в случае
одноэлектронного атома, когда потенциал U(r) убывает обратно пропорционально
Ze2
расстоянию г электрона от ядра (кулоновское поле U —-------, ср. § 6.3, с. 171), энер-
т
гия, при заданном п, не зависит от I. Для поля типа (7.3), убывающего с расстоянием
2) При котором их взаимодействие учитывается лишь путем введения усредненного поля.
3) В рассматриваемом приближении пренебрегают спин-орбитальным взаимодействием (см. с. 186),
в силу чего и рассматривают набор (6.7) квантовых чисел п, /, mi, ms, а не набор (6.56) квантовых
чисел п, I, j, mj.
§7.1. Квантовые числа электронов в сложном атоме и принцип Паули 201
более быстро, чем кулоновское (с увеличением г одновременно уменьшается Z(r),
стоящее в числителе), энергия электрона тем меньше при заданном п, чем меньше I.
Физическая причина подобной зависимости состоит в том, что электроны с меньшим I
подходят ближе к ядру, где Z(r) больше, что увеличивает их энергию связи. Более подробно
этот вопрос рассмотрен ниже, в §7.3 (с. 206).
Энергию электрона как функцию квантовых чисел п и I можно представить
в виде, аналогичном формуле (6.13):
RZ*2	/ V
Ent =-----(7.6)
где вместо заряда ядра Z введен эффективный заряд Z*, вообще говоря, зависящий
и от п, и от I. Как правило, Z* < Z и его записывают в виде
Z* = Z-anh	(7.7)
где ani — постоянная экранирования, являющаяся функцией от п и от I.
Формулу (7.6) можно получить путем решения задачи о движении электро-
на в поле ядра и остальных электронов, если в выражении для потенциальной
энергии (7.3) заменить переменный эффективный заряд Z(r) — Z - а(г) некото-
рым постоянным значением Z* — Z - а (г) = Z — а. Экранирование а (г), зависящее
от расстояния г, при этом заменяется некоторым средним экранированием <т(г) = а,
одинаковым для всех расстояний, а некулоновское поле (7.3) сводится к кулонов-
скому полю с измененным значением Z. При потенциальной энергии
мы получаем энергию в виде (7.6). Таким образом, приравнивание энергии электрона
как функции п и I выражению, стоящему в правой части формулы (7.6), соответ-
ствует замене усредненного поля (7.3) эффективным кулоновским полем ядра (7.8),
приводящим к тому же значению энергии. Формула (7.6) позволяет в весьма нагляд-
ной форме сравнивать значения энергии электронов в сложных атомах в различных
состояниях между собой и с энергией электрона в одноэлектронном атоме, опре-
деляемой формулой (6.13), которая получается из (7.6) как частный случай, если
в (7.7) положить anj — 0.
Рассмотрим теперь сложный атом с определенным числом электронов N (N
равно Z для нейтрального атома и Z - к для fc-кратного ионизованного атома). Его
состояние будет характеризоваться в одноэлектронном приближении совокупностью
квантовых чисел
П\Цтцт8х, 712/2^2^2, щЦт^т^, ..., nNlNmiNmSN, (7.9)
Если атом содержит один электрон, этот электрон может находиться в любом
состоянии, для которого п — 1, 2, 3,...; I — 0,1, 2,..., п - 1; mi — 1,1 - 1,..., —I;
ms — У2, — V2. Для атома, содержащего два и более электронов, возможные со-
стояния отдельных электронов определяются принципом Паули [191], имеющим
фундаментальное значение для теории сложных атомов и представляющим основу
для физического объяснения периодической системы элементов Менделеева.
Согласно принципу Паули, в атоме не может быть двух электронов в одинаковых
состояниях, т. е. не может быть двух электронов, характеризуемых одинаковыми
наборами четырех квантовых чисел п, I, mi, т8, т.е. все N наборов в (7.9) должны
202
Глава 7. Электронные оболочки и периодическая система
быть разными. Любые два электрона должны отличаться значением хотя бы одного
из четырех квантовых чисел п, I, ттц, ms.
Данная формулировка принципа Паули является частным случаем его общей форму-
лировки (см. § 3.3, с. 75), согласно которой частицы, описываемые антисимметричными
волновыми функциями, не могут находиться в одинаковых состояниях. Электроны являются
частицами с полуцелым спином, и поэтому все состояния системы электронов антисимме-
тричны (см. с. 74), т. е. описываются антисимметричными волновыми функциями. Поэтому
для электронов имеет место принцип Паули. В соответствии с тем, что в атоме состояние
каждого электрона характеризуется набором четырех квантовых чисел n, /, тг, ms, мы
для случая атома получаем приведенную выше формулировку принципа Паули. Чтобы удов-
летворить принципу Паули, приближенную волновую функцию многоэлектронного атома
можно представить в виде определителя (3.25) (где = фщЦтцтя^ Фн = Фп212т12тЯ2 и т.д.),
являющегося линейной комбинацией функции (7.5) и всех функций, получающихся из нее
при перестановках электронов. Так как число возможных перестановок N объектов равно 7V1,
то (3.25) представляет линейную комбинацию NI функций типа
• • • >	(7-10)
соответствующих тому, что в состоянии I находится i-й электрон, в состоянии II — J-й,
в состоянии III — k-й и т.д. В частном случае двух электронов антисимметричная волновая
функция имеет вид (3.23), ф = Cfyi(xi)ipn(x2) - ф\(х2)фн(х1)] и является линейной комбина-
цией двух функций ф1(х1)фи(х2) и ф1(х2)^п(х1), отличающихся перестановкой электронов.
Для состояния, описываемого функцией (3.25)4), определенный электрон уже не нахо-
дится в определенном состоянии (например, i-й электрон в состоянии njt-m^m5i), каждый
электрон может находиться с некоторой вероятностью в любом из N состояний п^т^т^;
nNlNmiNmSN. Однако мы, тем не менее, будем в дальнейшем говорить о том,
что электроны определенным образом распределяются по состояниям, подразумевая под этим,
что электроны занимают рассматриваемые N состояний. «Электрон находится в заданном со-
стоянии» — означает, что соответствующее одноэлектронное состояние, при приближенном
рассмотрении системы электронов, занято. Однако при этом в принципе электроны нельзя
отличить и приписать каждому отдельное состояние. Все N тождественных электронов вместе
занимают N определенных состояний.
Введению вместо функции (7.5) функции (3.25) соответствует и приближенный метод
расчета атомов — метод самосогласованного поля с учетом антисимметрии волновых функций,
разработанный Фоком [208]5). Метод Фока является более точным, чем метод Хартри,
и представляет собой лучший метод расчета сложных атомов.
Следует отметить, что перестановка электронов означает перестановку всех координат
электронов, как пространственных, так и спиновых. В случае, когда волновую функцию
можно представить в виде произведения
V’.Uk) - ф',(гк, 0к, <Рк)ф'/(<^к)	(710
функции только от пространственных координат гк, 6к, <рк на функцию ф" только от спино-
вой координаты ак, линейные комбинации произведении одноэлектронных функций только
от пространственных координат или только от спиновых координат не обязательно должны
быть антисимметричными. Они могут быть, в частности, симметричными. Подробнее мы
рассмотрим этот вопрос в гл. 10 на примере атома гелия (см. § 10.2, с. 283).
Принцип Паули позволяет определить возможное число электронов в атоме,
обладающих заданными значениями определенных квантовых чисел.
Если задано значение главного квантового числа п и азимутального квантового
числа I, то, согласно (6.8), возможны 2(21 4- 1) состояний, отличающихся значени-
ями mi и ms. Следовательно, в атоме может быть не более 2(21 4- 1) электронов
4) И тем более для состояния, описываемого линейной комбинацией таких функций, что получается,
если учитывать взаимодействие электронов между собой.
5) Так как при расчетах по методу Фока получаются дополнительные, так называемые обменные
члены, зависящие от перестановки электронов, то этот метод называют методом самосогласованного
поля с обменом.
§ 7.2. Электронные слои и оболочки и их заполнение
203
с заданными п и I. Электроны в состояниях с I = 0,1,2, 3,..., т.е. в s-, р-, d-,
f-, ... состояниях, называют соответственно s-, р-, d-, f-, ... электронами. Та-
ким образом, при заданном п в атоме может иметься 2(2 • 0 4- 1) = 2 s-электрона
(I = 0), 2(2 • 1 4- 1) = 6 р-электронов (I = 1), 2(2 • 2 4- 1) = 10 d-электронов (I = 2),
2(2 • 3 4-1) = 14 /-электронов (I = 3) и т.д.
Если задано значение главного квантового числа п, то возможны 2п2 состояний,
отличающихся значениями I, mj и ms (см. (6.10)). Следовательно, в атоме может
быть не более 2п2 электронов с заданным п, т.е. может иметься 2,8,18,32,...
электронов с п = 1,2, 3,4,... .
Электроны с одинаковыми значениями п и I принято называть эквивалентными
электронами. Их обозначают, согласно (6.12), символами ns, пр, nd, nf, ...
для I = 0,1,2, 3,... и указывают число таких электронов в виде показателя у символа,
например, 2р3, 3d4, 5/2 и т.д. (если имеется один электрон данного рода, то
показатель 1 не указывается).
Возможные числа эквивалентных электронов с различными значениями п и I
даны в табл. 7.1.
Таблица 7.1
Эквивалентные электроны с различными п и I
п — 1	1з2	2п2 = 2
п — 2	2s1	Ip6	2п2 = 8
п = 3	Зз2	Зр6	3d10	2п2 = 18
п = 4	4з2	4р6	4d10	4/14	2п2 = 32
п = 5	5з2	5р6	5d10	5/14	5918	2п2 = 50
		
Сумма показателей в горизонтальном ряду дает полное число электронов 2п2,
т.е. 2,8,18,32,50,... для п = 1,2,3,4,5,... .
Совокупность значений п и I для всех N электронов в атоме
П|^1, П2^2? п3/3,	..., n^ltf	(7.12)
характеризует определенную электронную конфигурацию. Например, для трехэлек-
тронного атома в принципе возможны конфигурации
1s22s, ls22p, ls2s2, \s2s2p и т.д.
Вопрос о том, какие электронные конфигурации реально осуществляются,
требует рассмотрения их устойчивости, что будет сделано в следующем параграфе.
§ 7.2. Электронные слои и оболочки и их заполнение
С наглядной точки зрения электроны с разными значениями п распределяются
относительно ядра различным образом, тем дальше от ядра, чем больше п. Электро-
ны с заданным значением главного квантового числа п образуют определенный слой,
содержащий, при полном его заполнении, 2п2 электронов. Электроны с различны-
ми значениями I при заданном п отличаются своей энергией и пространственным
распределением. При данном значении азимутального квантового числа I они обра-
зуют оболочку, содержащую, при полном ее заполнении, 2(21 4- 1) эквивалентных
электронов.
В литературе встречается различная терминология. Мы в дальнейшем всегда будем
говорить о слое с определенным п и об оболочке с определенными пи/.
204
Глава 7. Электронные оболочки и периодическая система
В соответствии с табл. 7.1 мы имеем следующую картину.
Самый внутренний слой соответствует п — 1 и состоит только из одной оболочки
1s. Он заполняется двумя электронами.
Следующий, более внешний слой соответствует п = 2, состоит из двух оболочек
2$ и 2р и заполняется 8 электронами.
Последующие, еще более внешние слои, соответствуют п — 3,4, 5,... и состоят
из трех, четырех, пяти, ... оболочек, заполняясь 18, 32, 50, ... электронами.
Таким образом, табл. 7.1 приобретает наглядный смысл, определяя распреде-
ление электронов в атоме по слоям и оболочкам. Слои с п — 1,2, 3,4, 5, 6 часто
называют, применяя терминологию рентгеновской спектроскопии (см. подробнее
гл. 13, посвященную рентгеновским спектрам), К-, L-, М-, N-, О-, Р-слоями.
Заполнение электронных слоев и оболочек в атоме определяется энергией
электронов в этих слоях и оболочках. Электроны стремятся заполнить состояния
с наименьшей энергией, т. е. соответствующие наиболее прочной связи. Нормальная
электронная конфигурация любого атома соответствует заполнению электронных со-
стояний с наименьшими возможными значениями энергии. Согласно (7.6), энергия
электрона тем меньше, чем меньше п; с уменьшением п не только уменьшается
знаменатель п2, но и увеличивается Z*2, так как эффективный заряд ядра Z*,
действующий на электрон, будет больше из-за уменьшения экранирования. Сна-
чала должен заполняться слой п = 1, затем слой п — 2, затем слой п — 3 и т. д.
Иначе говоря, слои заполняются в порядке их удаления от ядра, начиная с самого
внутреннего.
Заполнение слоев с последовательными значениями п определяет общую струк-
туру периодической системы элементов (см. табл. 7.2).
Начало каждого периода соответствует началу заполнения соответствующего
электронного слоя. У Н начинается заполнение первого слоя, у Li — второго,
у Na — третьего, у К — четвертого, у Rb — пятого, у Cs — шестого, у Fr — седьмого.
В начале периодической системы происходит полное заполнение слоев и число
элементов в периоде совпадает с полным числом 2п2 электронов в слое. У Не с двумя
электронами (Z — 2) полностью заполняется слой п — 1 и в первом периоде имеются
два элемента. У Ne с десятью электронами (Z = 10) полностью заполняется вслед
за первым слоем п = 1 и второй слой п — 2; во втором периоде имеется восемь
элементов.
Дальнейшее заполнение слоев осложняется тем, что, наряду с зависимостью
энергии электрона от п, весьма существенна и ее зависимость от I при заданном п,
и поэтому нужно учитывать не только порядок заполнения слоев, но и порядок
заполнения оболочек.
В то время как в атоме водорода энергия при заданном значении п не зависит
от I, в сложных атомах, как мы уже отмечали (см. с. 201), энергия электрона
тем меньше при заданном п, чем меньше I. Эффективный заряд Z*, входящий
в формулу (7.6), при заданном п увеличивается с уменьшением I, а постоянная
экранирования ani (см. (7.7)) уменьшается; s-электроны экранируются меньше, чем
р-электроны, р-электроны — меньше, чем d-электроны, d-электроны — меньше,
чем /-электроны:
&ns < &пр < &nd <	(7.13)
Вследствие того, что энергия электронов при заданном п тем меньше, чем
меньше I, сначала заполняется оболочка ns, затем оболочка пр, затем оболочка nd
и т. д.
Таблица 7.2
Периодическая система элементов Менделеева в форме, показывающей заполнение электронных слоев и оболочек [122]
Перио-I Обо-
ды дочки
1 2
Н Не
с с2
3 4
2 2s Li Be
s s2	5	6	7	8 9 10
2p	В	C	N	О F	Ne
_________________P	P2	P3	P4 P5	P6
3	3s зр	11 12 Na Mg s s2 13 14 15 16 17 18 Al Si P S Cl Ar P p2p3p4p5p6	
4 1	4s 3d 4р	19 20 К Ca s s2	21 22 23 24 25 26 27 28 29	30 Sc Ti V Cr Mn Fe Co Ni Cu Zn 31 32 33 34 35 36 ds2 d2s2 d3s2 d5s d5s2 d6s2 d1 s2 d8s2 d10s d,0s2 Ga Ge As Se Br Kr p P2P3P4P5P6	
51	5s 4d 5р	37 38 Rb Sr s s2	39 40 41 42 43 44 45 46 47	48 Y Zr Nb Mo Tc Ru Rh Pd Ac Cd 49 50 51 52 53 54 ds2 d2s2 d^s d5s d5s2 d1 s d8s dt0 d’WV In Sn Sb Те J Xe P P2 P3 P4 P5 P6	
6 <		6s 4/ 5d 6p	55 56 Cs Ba s s2	57 58	59	60	61	62 63	64	65	66	67	68	69	70 La	Ce	Pr	Nd	Pm	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm	Yb 71	72	73	74	75	76	77	78	79	80	ds2f2s2	f3s2	f*s2	f5s2	f6s2	f s2	fds2	f*ds2 f}Qs2 f"s2	f'2s2	fl3s2 f'*s2 Lu	Hf	Ta	W	Re	Os	Ir	Pt	Au	Hg 81	82	83	84 85 86	ds2 d2s2	d3s2	d*s2 d5s2 d6s2 d7s2	d9s	d10s d10s2 Tl	Pb	Bi	Po At Rn P	P2	P3	P4 P5 P6
7 4	f	7s 5/ 6d	87 88 Fr Ra s s2	89 90	91	92	93	94 95	96	97	98	99	100 101	102 Ac Th Pa U Np Pu Am Cm Bk Cf Es Fm Md ds2 d2s2 f2ds2 f2ds2 f*ds2 f6,2 fs2 fds2 f^ds2 f'°s2 f",2 f>2s2 f,3s2
Типы спектров			1 2	T	4	5	(1)	2	6
§ 7.2. Электронные слои и оболочки и их заполнение
206
Глава 7. Электронные оболочки и периодическая система
Так, для элементов второго периода периодической системы элементов сначала
происходит заполнение оболочки 2s у Li (Z — 3) и Be (Z = 4), а затем заполнение
оболочки 2р у В, С, N, О, F и Ne (Z = 5, 6, 7, 8, 9, 10).
В силу зависимости энергии от I при п 4 электроны с большими п и меньши-
ми I оказываются связанными прочнее, чем электроны с меньшими п и большими I.
Электрон 4s оказывается связанным прочнее, чем электрон 3d, электрон 5s прочнее,
чем электроны 4d и 4/, а электрон 6s прочнее не только, чем электроны 5d, 3f и 5g,
но и чем электрон 4/.
Это приводит к тому, что действительный порядок заполнения слоев и оболочек
оказывается, если его несколько схематизировать, следующим:
12	3	4	5	6	7	8
Is2;	2s2, 2р6;	3s2,Зр6;	4s2,3d'°,4p6;	5s2,4dl0,5p6;	6s2,4/l4,5d'°,6p‘;	7s2,5/14, ...	(7.14)
2	8	8	18	18	32
Табл. 7.2 составлена в соответствии с этим порядком заполнения.
Как уже отмечалось, заполнение оболочки 1s2 заканчивается у Не (Z = 2), а за-
полнение оболочки 2р6 заканчивается у Ne (Z = 10). Заполнение оболочек Зр6, 4р6,
5р6 и бр6 заканчивается у
Аг(^=18), Kr(Z = 36), Хе (Z = 54) и Rn (Z = 86),
соответственно стоящих в конце 3, 4, 5 и 6-го периодов периодической системы.
В последовательных периодах имеется 2, 8, 8, 18, 18 и 32 элемента, в полном
соответствии с заполнением одной оболочки ns2 при п — 1, двух оболочек ns2np6
при п — 2 и п = 3, трех оболочек ns2(n - l)d10np6 при п = 4ип = 5и четырех
оболочек ns2(n-2)/14(n— l)d,0np6 при п — 6. Эти числа электронов, определяющие
число элементов в периоде, указаны в (7.14).
В длинных периодах, четвертом и пятом, мы имеем заполнение «более внутрен-
ней» (с меньшим п) оболочки d десятью электронами, а в шестом периоде, кроме
того, оболочки f четырнадцатью электронами. Заполнение оболочки nd приводит
к появлению характерных групп переходных элементов от Sc до Ni (в четвертом
периоде, п — 3), от Y до Pd (в пятом периоде, п = 4) и от Lu до Pt (в шестом
периоде, п = 5), а заполнение оболочки 4/ — к появлению группы редкоземельных
металлов — лантаноидов, состоящей из 14 элементов. В седьмом периоде проис-
ходит заполнение оболочки 5/; ей соответствует вторая редкоземельная группа —
актиноиды, в которую входят урановые и трансурановые элементы.
Мы видим, что число элементов в периодах периодической системы и на-
личие характерных групп элементов естественным образом объясняются порядком
заполнения электронных оболочек. При этом очень важно, что энергия электронов
зависит не только от главного квантового числа п, но и от азимутального кванто-
вого числа I. Благодаря тому обстоятельству, что электроны с меньшим I связаны
более прочно, чем электроны с большим I, даже если для них п больше, порядок
заполнения оказывается более сложным и число элементов в периодах не совпадает
с полным числом электронов 2п2 в последнем заполняющемся слое.
§ 7.3.	Зависимость энергии электронов
от азимутального квантового числа
Разберем подробнее зависимость энергии электрона от азимутального квантово-
го числа I при заданном п. Эта зависимость связана с различиями в распределении
§ 7.3. Зависимость энергии электронов от азимутального квантового числа 207
электронной плотности для электронов с различными I. Как мы видели в §6.3,
при уменьшении I появляются максимумы электронной плотности, лежащие ближе
к ядру (см. рис. 6.5, сравнить, например, ее распределение для электронов 3d, Зр
и 3s). В случае одноэлектронного атома это не сказывается на значении энергии,
так как поле, действующее на электрон, является везде кулоновским, его потенциал
убывает обратно пропорционально расстоянию.
Положение существенным образом меняется для сложного атома. На дан-
ный электрон будет действовать поле, потенциал которого зависит, согласно (7.3),
не только от 1 /г, но и от экранирования ядра остальными электронами, которое будет
с увеличением расстояния увеличиваться. С точки зрения наглядных представлений
на электрон, находящийся на расстоянии г от ядра, действует заряд ядра, уменьшен-
ный на заряд всех электронов, расположенных внутри сферы радиуса г (рис. 7.2),
если предположить, что электронная плотность этих электронов распределена сфе-
рически симметричным образом. Когда рассматриваемый электрон приближается
к ядру, то эффективный заряд, действующий на него, увеличивается; чем большую
долю времени он будет проводить вблизи ядра, тем прочнее он будет связан.
Рассмотрим, например, внешний электрон в атоме лития,
имеющего заполненную внутреннюю оболочку 1s2. Для внеш-
него электрона 2s мы имеем, согласно рис. 6.5, два максиму-
ма электронной плотности, причем в то время, как второй
максимум электронной плотности лежит далеко за пределами
внутренней электронной оболочки, первый максимум частично
попадает внутрь этой электронной оболочки. Согласно нагляд-
ным представлениям, мы можем сказать, что электрон 2s будет
проникать внутрь заполненной оболочки; часть времени он бу-
дет находиться вблизи ядра6). Если вне оболочки 1s2 на него
приближенно будет действовать заряд Z* — 1 (заряд ядра минус
заряд двух электронов 1s), то внутри этот заряд увеличится
до Z* — Z — 3. Для электрона 2р, когда электронная плотность
Рис. 7.2.
Экранирование
внешнего электрона
внутренними
электронами
имеет лишь один далекий максимум, проникновение вглубь внутренней оболочки
будет мало. В результате связь с ядром электрона 2s будет прочнее связи с ядром
электрона 2р.
Представление о том, что при заполнении электронами слоев с п— 1, 2,3,...
эти слои совершенно отделены друг от друга и что электроны определенного слоя
с п = п' локализованы, независимо от значения I, между слоями с п = п' - 1
и с п = п1 + 1, является слишком грубым. В действительности, локализация является
только частичной, и электроны проникают вглубь более внутренних слоев. Это
проникновение тем больше, чем меньше 1\ с увеличением проникновения связь
электрона с ядром упрочняется и его энергия уменьшается. Таким образом, энергия
электронов при заданном п тем меньше, чем меньше I.
Квантовомеханический расчет проникновения электронов более внешних обо-
лочек (с большими п) внутрь более внутренних оболочек (с меньшими п) чрез-
вычайно сложен, но уже качественные соображения, изложенные выше, выясняют
существо дела.
Впервые представление о проникновении электронов внешних оболочек внутрь
заполненных оболочек было развито в рамках боровской теории как представление
о проникающих орбитах. Чем больше вытянута эллиптическая орбита, т. е. чем
6) Согласно квантовой механике, для него будет иметься определенная вероятность находиться
на малых расстояниях от ядра.
208
Глава 7. Электронные оболочки и периодическая система
меньше k = I + 1, тем сильнее электрон проникает внутрь заполненных оболочек
и тем больше упрочняется его связь.
Рис. 7.3. Проникающие и непроникающие орбиты
На рис. 7.3, показываю-
щем взаимное расположение
орбит с п = 1,2,3 для од-
ноэлектронного атома, наг-
лядно видно проникновение
электронов 2s (п = 2, к = 1),
3s (п = 3, к = 1) и Зр
(п = 3, к — 2) внутрь ор-
бит Is (n = 1, к — 1) и 2р
(п = 2, к = 2). Следует
иметь в виду, что для слож-
ных атомов вследствие уве-
личения эффективного заря-
да, действующего на элек-
трон при приближении его
к ядру, проникновение уве-
личивается еще больше.
О «проникающих орбитах» условно можно говорить и в рамках квантовомехани-
ческих представлений, основываясь на аналогии между орбитами боровской теории
и распределением электронной плотности.
Если мы имеем внешние электроны с большими значениями Z, особенно
при больших п, то они практически движутся за пределами заполненных оболочек,
электронная плотность во внутренних областях для них мала и они не проникают за-
метным образом внутрь этих оболочек; их состояния соответствуют непроникающим
орбитам. Если имеется только один внешний непроникающий электрон, движущий-
ся под действием ядра с зарядом Z и всех остальных Z - 1 более внутренних электро-
нов, то его энергия будет определяться той же формулой, что и для атома водорода;
в этом случае Z* в формуле (7.6) равно просто 1. Состояние такого электрона явля-
ется водородоподобным. Наоборот, для внешних электронов с малыми значениями I
электронная плотность во внутренних областях достаточно велика, и они сильно
проникают внутрь заполненных оболочек; их состояния соответствуют проникающим
орбитам. Проникновение приводит к резкому уменьшению постоянной экраниро-
вания и к соответствующему увеличению эффективного заряда. Как мы увидим
в дальнейшем, на примере атомов щелочных металлов (см. гл. 8, с. 217), прочность
связи электрона может при этом увеличиваться в несколько раз. Наиболее значителен
этот эффект для s-электронов; для них электронная плотность в начале координат
отлична от нуля (см. §6.3, с. 175), что особенно способствует упрочению их связи.
§ 7.4.	Ход заполнения электронных слоев и оболочек
Рассмотрим более детально ход заполнения слоев и оболочек для последова-
тельных элементов, показанный в табл. 7.2 (с. 205). В этой таблице для каждого эле-
мента указано в сокращенной записи число электронов в последних заполняющихся
оболочках (например, для Cr (Z = 24) d5s означает наличие пяти электронов 3d и од-
ного электрона 4s), и легко выписать полную электронную конфигурацию (для Сг
ls22s22p63s23p63d54s).
Для первых трех периодов системы Менделеева заполнение идет в нормальном
порядке Is, 2s, 2р, 3s, Зр и у Ar (Z = 18) заканчивается заполнение оболочек 3s2
§7.4. Ход заполнения электронных слоев и оболочек
209
и Зр6 Af-слоя (п = 3). Аргон представляет аналог неона с заполненными внешними
оболочками 2s2 и 2р6.
У К (Z — 19) начинается заполнение четырехквантовой оболочки (п = 4). Это
указывает на то, что энергия электрона 4s меньше энергии электрона 3d. Оболоч-
ка 4s заполняется полностью, т. е. двумя электронами, у следующего элемента —
Са (Z = 20), и затем, начиная с Sc (Z = 21), происходит заполнение «более внутрен-
ней» трехквантовой оболочки 3d (п — 3) — ее «достройка». При этом энергии связи
электронов 4s и 3d близки друг к другу и между этими электронами происходит
«конкуренция», что отмечено в табл. 7.2 скобками. В частности, для Cr (Z = 24)
более выгодной конфигурацией оказывается такая, при которой в состоянии 3d
связывается лишний электрон, а в состоянии 4s остается лишь один электрон.
Здесь проявляется тенденция электрона 3d с меньшим п быть связанным прочнее
электрона 4s с большим п. При этом особенно выражено стремление электронов 3d
образовывать либо заполненную наполовину (3d5), либо полностью укомплекто-
ванную (3d10) d-оболочку. У Си (Z = 29) оболочка 3d уже полностью заполнена,
но в состоянии 4s имеется лишь один электрон. У Zn (Z = 30) добавляется второй
электрон 4s, после чего, начиная с Ga (Z — 31), заполняется оболочка 4р, заканчи-
вающаяся у Кг (Z = 36). Элементы от Ga до Кг аналогичны элементам от В до Ne
и от Al до Аг.
Четвертый, большой период системы заканчивается у Кг и, таким образом,
соответствует заполнению оболочек 4s, 3d и 4р.
С Rb (Z = 37) начинается заполнение пятиквантовой оболочки 5s; дальней-
шее заполнение происходит аналогично четвертому периоду. После оболочки 5s
достраивается оболочка 4d, причем происходит конкуренция электронов 4d и 5s.
Тенденция электрона 4d быть связанным прочнее электрона 5s проявляется весьма
сильно. Для большинства элементов, у которых заполняется оболочка 4d, в обо-
лочке 5s имеется лишь один электрон, а у Pd (Z = 46) стремление к образованию
заполненной оболочки 5d10 настолько велико, что оболочка 5s остается вообще
незаполненной. Оболочка 5s окончательно заполняется у Cd (Z — 48), после чего
у элементов от In (Z = 49) до Хе (Z — 54) заполняется оболочка 5р. Хе является
последним элементом в пятом периоде.
Пятый период аналогичен четвертому периоду и соответствует заполнению
оболочек 5s, 4d и 5р.
С Cs (Z = 55) начинается заполнение шестиквантовой оболочки 6s, однако
дальнейшее заполнение осложняется тем, что с электронами 6s конкурируют, на-
ряду с электронами 5d, и электроны 4/. У La (Z = 57) один электрон попадает
в оболочку 5d, однако у следующих элементов электроны 5d отсутствуют и достраи-
вается оболочка 4/; только у Gd (Z = 64) и, возможно, у Tb (Z = 65) в оболочку 5d
попадает опять один электрон. Заполнение «редкоземельной» оболочки заканчива-
ется у Yb (Z = 70), а начиная с Lu (Z = 71) происходит окончательное заполнение
оболочки 5d, которое заканчивается у Au (Z = 79). При этом продолжается конку-
ренция электронов 6s и 5d с выраженной тенденцией к образованию заполненной
оболочки 5d10. Так, у Pt (Z — 78) в оболочке 6s имеется один электрон.
Шестой период заканчивается элементами от Т1 (Z — 81) до Rn (Z — 86),
у которых заполняется оболочка бр6.
С искусственного элемента Fr (Z — 87) начинается заполнение семикван-
товой оболочки 7s. Затем происходит конкуренция электронов 7s, 6d и 5/,
причем, в отличие от конкуренции электронов 6s, 5d и 4/ в шестом периоде,
тенденция к заполнению /-оболочки сперва выражена менее сильно. Не только
210
Глава 7. Электронные оболочки и периодическая система
у Ac (Z = 89), но и у Th (Z = 90) еще нет 5/-электронов, один 6</-электрон оста-
ется у U (Z = 92) и Np (Z = 93). 6</-электроны уже отсутствуют у Pu (Z — 94)
и Am (Z — 95) [254а]. У далеких трансурановых элементов — эйнштейния
Es (Z = 99), фермия Fm (Z = 100) и менделевия Md (Z = 101) — несомненно
должна заполняться только оболочка 5/, а электроны 6d отсутствуют.
До сих пор мы говорили о ходе заполнения электронных слоев и оболочек ней-
тральных атомов. Спектроскопическими методами, наряду с нейтральными атомами,
широко изучаются ионы. При ионизации атом сперва теряет наиболее слабо связан-
ный электрон, превращаясь в однократно заряженный ион, затем теряет следующий
по прочности связи электрон, превращаясь в двукратно заряженный ион, и т.д. Чле-
ны изоэлектронного ряда, состоящего из нейтрального атома с числом электронов Z
и ионов с числом электронов Z-k (fc-кратность ионизации, к = 1, 2, 3,...), обладают
значительным подобием. Они обычно имеют нормальные электронные конфигура-
ции с одинаковым распределением электронов по слоям и оболочкам, аналогичным
образом расположенные уровни энергии и схожие спектры. При этом с увеличени-
ем заряда ядра при том же числе внешних электронов увеличиваются расстояния
между уровнями. Как мы видели для простейшего изоэлектронного ряда (6.1) эти
расстояния увеличиваются пропорционально Z2 (см. (6.13)). Для,сложных атомов
увеличение расстояний между уровнями определяется увеличением эффективного
заряда Z* в формуле (7.6). Если постоянные экранирования сохраняют свои значе-
ния при увеличении заряда ядра (что в ряде случаев имеет место с хорошей степенью
приближения, особенно для внутренних электронных оболочек), то при переходе
от нейтрального атома элемента с порядковым номером Z к изоэлектрон ному с ним
fc-кратно заряженному иону элемента с порядковым номером Z + к эффективный
заряд Z* = Z - ап\ заменяется зарядом Z*’ — Z + к - ani = Z* + к. Энергии уровней
будут относиться, как
Так как Z* для разных уровней может быть разным (большим для более глубоких
уровней и меньшим для более высоких), то и масштаб расстояний между уровнями
может меняться для них различным образом.
При наличии конкуренции между различными электронами, например в на-
чале достройки d- и /-оболочек, при изменении заряда ядра может меняться
относительная прочность связи этих электронов и последовательность уровней бу-
дет различной. Типичным примером является изоэлектронный ряд Cs I, Ba II,
La III и Се IV (55 электронов); для Cs I и Ba II нормальным состоянием внеш-
него электрона является состояние 6s, для La III — состояние 5d и для Се IV —
состояние 4/ (см. подробнее гл. 8, с. 237).
§ 7.5.	Свойства элементов
с заполненными и незаполненными оболочками
Физические и химические свойства элементов определяются в основном наи-
более слабо связанными электронами во внешних оболочках. Элементы с анало-
гичными конфигурациями внешних электронов, отличающимися только главными
квантовыми числами при тех же азимутальных числах, обладают схожими свойства-
ми и относятся к той же химической группе. Так, для щелочных металлов характерно
наличие одного внешнего s-электрона вне заполненных внутренних слоев: у Li —
электрона 2s (заполнен слой п = 1 электронами 1s), у Na — электрона 3s (заполнен
§ 7.5. Свойства элементов с заполненными и незаполненными оболочками 211
слой п = 2 электронами 2s и 2р), у К — электрона 4s (заполнен слой п = 3
электронами 3s и Зр) и т. д. Для элементов третьей группы характерно наличие трех
внешних электронов ns2np : 2s22p у В, 3з23р у А1, 4з24р у Ga и т.д.
Число внешних электронов определяет максимальную валентность элемента.
В приведенных примерах она равна 1 и 3 соответственно. Особой устойчивостью
обладают элементы с заполненными внутренними оболочками, у которых отсутству-
ют слабо связанные внешние электроны, — инертные газы Не, Ne, Ar, Кг, Хе, Rn
с конфигурациями электронов последней заполненной оболочки 1s2, 2р6, Зр6, 4р6,
5р6, бр6. Эти элементы химически неактивны.
С точки зрения спектроскопических свойств очень важную роль играет отличие
заполненных и незаполненных оболочек. Для заполненной оболочки (или совокупности
таких оболочек) значения орбитального, спинового и полного моментов количества
движения равны нулю, и ей соответствует один невырожденный уровень энергии.
В этом можно убедиться следующим образом. Полный механический момент J
совокупности к электронов равен
«7 = /1 4" Ъ 4- • ♦. 4- Ik 4-	4-	4- • • ♦ “h sk,	(7.16)
где lj и Sj — орбитальный и спиновый моменты г-го электрона. Его можно
представить как сумму полного орбитального момента L и полного спинового
момента S:
J = L + S,	(7.17)
к	к
где L = 52^» и S = 525»- Соответственно этому проекция полного момента
i=l	i=l
на выделенное направление z равна
Jz — hz 4- hz 4- • • • 4- hz 4- S\z 4- S2Z 4-... 4- SkZ	(7-18)
или
JZ=LZ+SZ,	(7.19)
к	k
где Lz = 52 hz И ^Z = 52 siz — проекции полного орбитального и полного спинового
»=1	1=1
моментов.
Для заполненной оболочки, содержащей 2(21 + 1) эквивалентных электронов,
квантовые числа mi и т3 принимают все возможные пары значений. Для I — 0, 1, 2, 3
эти пары значений приведены в табл. 6.1 (с. 166).
Сумма тц для отдельных электронов дает значение mL проекции Lz полного
орбитального момента L, сумма ms — значение ms проекции Sz полного спинового
момента S, а полная сумма всех тц и mSi (равная т^ + ms) — значение mj
проекции Jz результирующего момента J.
Ввиду того, что для электронов заполненной оболочки тц и mSt принимают
все возможные значения, как положительные, так и отрицательные,
У^ = mL - 0; У^ mSt = ms = 0; У^(ш^ +	~ mL + ms ~ mJ = 0,
i	i	i
(7.20)
т.е. происходит полная компенсация проекций моментов L, S и J. Это сразу видно
из табл. 6.1. Сумма значений Ш/ или ms, стоящих в одной строке, равна нулю.
Из равенства нулю проекций вытекает равенство нулю и значений соответству-
ющих моментов:
L = Q, 5 = 0, J = 0.	(7.21)
212
Глава 7. Электронные оболочки и периодическая система
Получается одно-единственное состояние, характеризующееся равными нулю значе-
ниями квантовых чисел L, S и J, определяющих орбитальный, спиновый и полный
моменты заполненной оболочки. Сделанное выше утверждение доказано.
С точки зрения наглядных представлений можно сказать, что для заполнен-
ной оболочки происходит полная компенсация орбитальных и спиновых моментов
отдельных электронов.
Состояние (7.21) обозначается как Sq. Прописное S указывает на значе-
ние L = 0; индекс 1 слева сверху дает мультиплетность х — 2S 4- 1 — число
возможных ориентаций полного спинового момента, равное в данном случае еди-
нице (получается синглетное или одиночное состояние), индекс 0 справа снизу
указывает значение J = 0.
Для неполностью заполненной оболочки (или совокупности таких оболочек) полу-
чается ряд возможных значений характеризующих ее моментов количества движения,
и ей соответствует ряд уровней энергии.
Это объясняется тем, что полной компенсации орбитальных и спиновых мо-
ментов электронов уже не происходит. Они могут складываться различным образом,
и получается ряд состояний. Вследствие взаимодействия моментов эти состояния
будут обладать различной энергией, т. е. получается ряд уровней энергии.
В случае одного электрона в оболочке при сложении, согласно (6.54), его ор-
битального и спинового моментов в полный момент атома j получается 2(21 -h 1)
различных состояний. Энергия зависит от квантового числа j ~ I ± 1Д, принимаю-
щего два значения, и получается два уровня энергии.
В случае двух или нескольких электронов определение числа и характеристик
возможных состояний и уровней энергии представляет более сложную, чем в случае
одного электрона, задачу, которая будет рассмотрена в гл. 9.
Существенно, что совокупности электронов, не образующих полностью запол-
ненных оболочек, соответствует ряд различных состояний и ряд уровней энергии.
Основными характеристиками уровней энергии при этом являются четность уровней
и значения квантового числа J, определяющего значения полного механического
момента атома.
Четность всех уровней и соответствующих им состояний определенной элек-
тронной конфигурации одинакова. Поэтому можно говорить о четных и о нечетных
конфигурациях. Четность заданной конфигурации, т. е. является ли она четной или не-
четной, определяется очень простым правилом. Если конфигурация содержит четное
число электронов с нечетным I (нечетных электронов, т. е. электронов р, /,...), то
она является четной', если конфигурация содержит нечетное число таких электронов,
то она является нечетной. Конфигурации, содержащие только электроны с четным I
(четные электроны, т. е. электроны s, d, ...), всегда четные независимо от числа
таких электронов.
Приведенное правило выводится очень просто. Если представить волновую функцию
для некоторого состояния атома в виде (7.5), то при отражении в центре сохраняют свой
знак сомножители, соответствующие четным электронам, и меняют его сомножители, со-
ответствующие нечетным электронам. Поэтому знак полной волновой функции, который
и определяет четность или нечетность данного состояния (см. §3.3, с. 73), определяется тем,
будет ли число сомножителей, меняющих знак (т. е. число нечетных электронов), четным
или нечетным. При четном числе таких сомножителей функция будет четной, при нечетном —
нечетной. Это свойство сохраняется и для любой линейной комбинации волновых функций,
так как можно комбинировать только волновые функции одной четности7\ В частности,
Только в этом случае вид линейной комбинации будет инвариантен относительно отражения
в центре, т.е. — У^ Ci'tyi будет переходить в ф1 = У^ с теми же коэффициентами Сг (ф1 = ±^).
§ 7.6. Типы спектров различных элементов
213
при переходе от функций (7.5) к антисимметризованным волновым функциям (3.25) чет-
ность сохраняется, что сразу следует из неизменности четности при перестановке электронов
(четность функции (7.20) та же, что и функции (7.5)).
Все конфигурации, состоящие только из заполненных оболочек, являются чет-
ными, как содержащие всегда четное число электронов каждого рода. Конфигурации
с незаполненными оболочками могут быть как четными, так и нечетными, причем их
четность определяется только электронами в незаполненных оболочках. Например,
нормальная конфигурация ls22s22p63s23p2 атома кремния четная, как содержащая
четное число нечетных р-электронов в незаполненной оболочке Зр, а нормальная
конфигурация атома фосфора ls22s22p63s23p3 нечетная, как содержащая нечетное
число электронов в этой же оболочке.
Отметим, что в соответствии с правилами отбора (4.153) и (4.154) при дипольном
излучении комбинируют уровни конфигураций разной четности, а при магнитном
дипольном и при квадрупольном излучениях — уровни конфигураций одной чет-
ности (в том числе и уровни данной конфигурации между собой, как имеющие все
одинаковую четность). Уровни нечетных конфигураций принято в атомной спектро-
скопии обозначать индексом «о» справа сверху от символа уровня, а уровни четных
конфигураций пишут без индекса.
Квантовое число J для уровней конфигурации с незаполненными оболочками
всегда принимает ряд значений, причем при четном числе электронов в атоме все
значения J будут целыми, а при нечетном числе электронов — полуцелыми. Этот
важный вопрос мы подробно рассмотрим в дальнейшем, в гл. 9 (см. с. 251); в ней же
будет рассмотрен в общем виде и вопрос о других характеристиках уровней энергии,
помимо их характеристики заданием четности и значений J.
§ 7.6.	Ъшы спектров различных элементов
С положением различных элементов в периодической системе связаны особен-
ности их оптических спектров.
По своему характеру оптические спектры различных элементов, обусловлен-
ные внешними электронами, можно разделить на ряд типов. Элементы, стоящие
в табл. 7.2 в одном столбце, относятся к одному типу (типы спектров указаны
в нижней строке). Эти типы спектров следующие:
1.	Одноэлектронные спектры элементов с внешней s-оболочкой. В нормальном
состоянии имеется один внешний s-электрон, переход которого на более высокие
уровни приводит к возникновению спектра с хорошо выраженными спектральными
сериями. Такие спектры имеют щелочные металлы — Li, Na, К, Rb, Cs, Fr.
Спектром с хорошо выраженными сериями обладают также Си, Ag и Au, имею-
щие один внешний электрон ns помимо последней заполненной оболочки (n- l)d10.
Однако на этот простой одноэлектронный спектр, обусловленный переходами внеш-
него электрона, налагается более сложный спектр, получающийся при возбуждении
одного из электронов оболочки (n — l)d10; соответствующий спектр следует отнести
к пятому типу спектров (см. ниже).
К первому типу спектров относят и разобранный нами в гл. 6 спектр водо-
рода, который, конечно, занимает особое место по своей простоте и значению
для понимания всех остальных спектров.
2.	Двухэлектронные спектры элементов с внешней s-оболочкой. В нормальном
состоянии имеются два внешних s-электрона, заполняющих соответствующую обо-
лочку. Эти электроны легко возбуждаются; при возбуждении одного из них возникает
214
Глава 7. Электронные оболочки и периодическая система
спектр также с хорошо выраженными сериями, но более сложный, чем в случае
атомов с одним внешним электроном.
Такие спектры имеют Be, Mg, Са, Sr, Ва и Ra, у которых оболочка ns1 сле-
дует за заполненной оболочкой (п — 1)р6, как и у щелочных металлов (у Be —
2s2 вслед за 1s2), и Zn, Cd и Hg, у которых эта оболочка следует за заполненной
оболочкой (n - l)d10. Двухэлектронный спектр имеет и Не с нормальной конфигура-
цией 1s2, занимающий особое место; хотя этот спектр в ряде отношений и является
типичным двухэлектронным спектром, но отличается от двухэлектронных спектров
других элементов тем, что электроны 1s связаны очень прочно по сравнению с элек-
тронами nl (п 2) и спектр является трудно возбудимым, подобно спектрам других
инертных газов.
3.	Спектры элементов с заполняющимися р-оболочками. Характерные черты этих
спектров определяются наличием в нормальной конфигурации внешних электронов
и существенной ролью конфигураций, содержащих два или более эквивалентных
р-электронов.
Сложные спектры этого типа имеют элементы от В до F во втором периоде,
от А1 до С1 в третьем периоде, от Ga до Вг в четвертом периоде, от In до J в пятом
периоде и от Т1 до At в шестом периоде.
При этом для спектров элементов с одним и с двумя р-электронами в нормаль-
ной конфигурации (В, Al, Sc, Y, Т1 и С, Si, Ge, Sn, Pb) характерна существенная роль
s-электронов оболочки ns2. Нормальные конфигурации ns2пр и ns2пр2 при возбу-
ждении дают, в частности, конфигурации nsnp2 и nsnp3 соответственно.
4.	Спектры элементов с заполненными р-оболочками. В нормальном состоянии
имеется последняя полностью заполненная оболочка пр6. При возбуждении воз-
никает конфигурация, состоящая из остова пр5 и одного возбужденного внешнего
электрона, что определяет своеобразные черты получающихся спектров. Спектры
такого типа имеют инертные газы — Ne, Аг, Кг, Хе, Rn.
5.	Спектры элементов с достраивающимися d-оболочками. Характерные черты
спектров элементов, у которых происходит достройка внутренней d-оболочки, опре-
деляются наличием эквивалентных электронов (n - l)d и их конкуренцией с элек-
тронами ns. Спектры этого типа, еще более сложные, чем спектры предыдущих
типов, имеют элементы от Sc до Ni в четвертом периоде (достройка оболочки 3d),
от Y до Pd в пятом периоде (достройка оболочки 4d) и от Lu до Pt в шестом периоде
(достройка оболочки 5d).
6.	Спектры элементов с достраивающимися f -оболочками. Характерные черты
спектров элементов, у которых происходит достройка внутренней /-оболочки,
определяются наличием эквивалентных электронов (п — 2)/ и их конкуренцией как
с электронами (п - 1 )d, так и с электронами ns. Спектры этого типа, отличающиеся
особой сложностью, имеют элементы от La до Yb в шестом периоде (достройка
оболочки 4/) и элементы от Ас в седьмом периоде (достройка оболочки 5/).
Следует подчеркнуть, что деление спектров на типы является до некоторой сте-
пени условным. Например, как уже указывалось, спектры Си, Ag, Аи представляют
собой наложение простого спектра первого типа и сложного спектра пятого типа.
Спектры элементов с достраивающимися оболочками могут значительно отличаться
по своему характеру в зависимости от числа эквивалентных электронов и наличия
других конкурирующих электронов. Однако такое деление весьма целесообразно
при систематическом рассмотрении спектров.
Мы в первую очередь рассмотрим, в гл. 8, одноэлектронные спектры щелоч-
ных металлов. Гл. 9 посвящена основам общей систематики сложных спектров.
§7.6. Типы спектров различных элементов	215
В следующих главах разобраны различные типы сложных спектров, обусловленные
наличием двух и более внешних электронов, в соответствии с изложенной выше
классификацией. При этом, наряду со спектрами нейтральных атомов, мы будем
параллельно рассматривать, в соответствующих главах, и спектры изоэлектронных
с ними ионизованных атомов, обладающих аналогичными нормальными конфигу-
рациями (с. 210).
ГЛАВА 8
ОДНОЭЛЕКТРОННЫЕ СПЕКТРЫ АТОМОВ
С ОДНИМ ВНЕШНИМ S-ЭЛЕКТРОНОМ
§8.1.	Основной уровень атомов щелочных металлов
Атомы щелочных металлов — лития, натрия, калия, рубидия, цезия, а также
искусственного элемента франция — имеют один внешний электрон, который
в нормальном состоянии является s-электроном. Их спектры являются типичными
одноэлектронными спектрами.
Электронные конфигурации атомов щелочных металлов в нормальном состоя-
нии приведены в табл. 8.1.
Электронные конфигурации атомов щелочных металлов
Таблица 8.1
Название элемента	Символ	Z	Электронная конфигурация
Литий	Li	3	Is2 Is
Натрий	Na	11	Is2 2s22p6 3s
Калий	К	19	Is2 2s22p6 3s23p6 4s
Рубидий	Rb	37	Is2 2s22p6 3s23p6 4s23d'°4p6 5s
Цезий	Cs	55	Is2 2s22p6 3s23p6 4s23d'°4p6 5s24d'°5p6 6s
Франций	Fr	87	fo23d'04p6' 5s24dl05p6y 6s24/l0M'°6p6j 7s
			2	8	8	18	18	32
			Число электронов в оболочках
Внешним электроном является электрон ns, причем п меняется от 2 для лития
до 7 для франция.
В отличие от атома водорода и водородоподобных ионов, в которых ядро непо-
средственно воздействует на единственный электрон, в атомах щелочных металлов
на внешний электрон воздействует не только ядро, но экранирующие его внутренние
оболочки.
Последней заполненной оболочкой для всех элементов группы, кроме лития,
является оболочка (n-1 )р6, для которой главное квантовое число на единицу меньше
главного квантового числа внешнего электрона: оболочка 2р6 для Na (с внешним
электроном 3s), оболочка Зр6 для К (с внешним электроном 4s) и т. д. Литий занимает
несколько особое место, поскольку он имеет лишь внутреннюю оболочку 1s2
и не имеет р-электронов, внутренних по отношению к электрону 2s.
Очень важен вопрос о прочности связи внешнего электрона в нормальном
s-состоянии, иначе говоря, об энергии ионизации атома.
§8.1. Основной уровень атомов щелочных металлов
217
Выражая энергию s-электрона через эффективный заряд Z* — Z — апз по фор-
муле (7.6), мы можем написать
Ens ~~
RZ*2
п2
R(Z - <тп,)2
п2
WHOH
(8-0
У всех рассматриваемых атомов во внутренних слоях имеется Z - 1 электронов.
Поэтому, если бы внутренние электроны полностью экранировали внешний элек-
трон, то постоянная экранирования имела бы значение ans = Z - 1 и формула (8.1)
свелась бы к обычной формуле (1.5) для атома водорода. Соответствующие значения
энергии связи приведены в четвертом столбце табл. 8.2. Мы видим, что если бы экра-
нирование внутренними оболочками было полным, то энергия связи резко падала бы
от Li к Cs и для К, Rb и Cs была бы меньше, чем 1 эВ. Однако действительная энергия
связи гораздо больше благодаря тому, что s-электроны «проникают» внутрь запол-
ненных оболочек и экранирование не является полным (см. § 7.3). Значения действи-
тельной энергии связи, сравнительно медленно убывающие от Li и Cs, приведены
в пятом столбце табл. 8.2. Мы видим, что если для Li энергия связи увеличивается
примерно на 60 % по сравнению с энергией связи электрона с тем же п в атоме водо-
рода (WhOh = 3,40 эВ для п = 2), то для Cs она увеличивается в десять раз. Качествен-
но это понятно: при увеличении главного квантового числа внутренний максимум
электронной плотности остается очень близким к ядру, а заряд ядра возрастает, и по-
этому все большую роль играет проникновение электрона внутрь заполненных оболо-
чек. С точки зрения боровской теории это означает движение электрона по все более
вытянутым эллипсам, с минимальным расстоянием от ядра порядка — (см. (6.34)).
lZ
Таблица 8.2
Энергетические характеристики нормального состояния атомов щелочных металлов
Название элемента	Символ	Z	Энергия связи, эВ		Z*	&пз	п	п*	Д	т	S
			при &пз = Z — \	действи- тельная							
Литий	Li	3	3,40	5,39	1,26	1,74	2	1,59	0,41	1	0,59
Натрий	Na	11	1,51	5,14	1,84	9,16	3	1,63	1,37	1	0,63
Калий	к	19	0,850	4,34	2,25	16,75	4	1,77	2,23	1	0,77
Рубидий	Rb	37	0,545	4,18	2,77	34,23	5	1,80	3,20	1	0,80
Цезий	Cs	55	0,378	3,89	3,12	51,88	6	1,87	4,13	1	0,87
В шестом и седьмом столбцах табл. 8.2 приведены значения Z* эффективного
заряда и постоянной экранирования, вычисленные по формуле (8.1), исходя
из действительных значений энергии ионизации. Эффективный заряд растет от лития
к цезию — электрон, проникая внутрь заполненных оболочек, относительно все
сильнее подвергается действию ядра.
Энергию электрона (8.1) можно представить в иной форме, считая заряд ядра,
действующий на электрон, равным единице, но вводя вместо действительного
значения главного квантового числа п его эффективное значение п*. Тогда мы
приходим к формуле
R
Е =----
п*2
(8-2)
где
72* — 72 - А.
(8-3)
218
Глава 8. Спектры атомов с одним внешним s-электроном
Величину А называют квантовым дефектом.
Значения эффективного квантового числа п* и квантового дефекта А для основ-
ного состояния атомов щелочных металлов также приведены в табл. 8.2 (столбцы 9
и 10). Квантовый дефект закономерно возрастает от лития к цезию.
§ 8.2.	Возбужденные уровни и спектральные серии
атомов щелочных металлов
Возбужденные уровни атомов щелочных металлов соответствуют возможным
состояниям внешнего электрона, в которых он связан слабее, чем в основном со-
стоянии ns. Возможными являются все з-состояния с главным квантовым числом,
превышающим п, а также и все р-, d-, /-состояния, кроме тех, которые соответству-
ют заполненным оболочкам (см. табл. 8.3). Для атома данного элемента возможны
все состояния, лежащие выше разделительной линии в табл. 8.3, причем самое ниж-
нее s-состояние является нормальным, а все остальные состояния — возбужденные.
Так, для лития заполнена оболочка 1 з, состояние 2з является нормальным, а состо-
яния Зз, 4з, ...; 2р, Зр, ...; 3d, 4d,	. возбужденными. Для натрия заполнены
оболочки 1з, 2з и 2р, состояние Зз является нормальным, а состояния 4з, 5з, ...;
Зр, 4р,...; 3d, 4d,...;... — возбужденными. Аналогично обстоит дело и для других
щелочных металлов.
Таблица 8.3
Возбужденные состояния атомов щелочных металлов
Уровни с заданным значением азимутального квантового числа I образуют
последовательность, сходящуюся к границе ионизации. Действительное располо-
жение уровней для щелочных металлов показано на рис. 8.1°. Уровни обозначены
кружками.
Горизонтальные пунктирные линии указывают положение уровней атома водо-
рода. Сильно проникающие з- и р-электроны связаны в атомах всех щелочных метал-
лов гораздо прочнее, чем в атоме водорода. Для d-электронов этот эффект проявля-
При этом пренебрегается дублетным расщеплением уровней, см. §8.3.
§ 8.2. Уровни и спектральные серии атомов щелочных металлов
219
ется лишь для калия, рубидия и цезия, /-электроны во всех случаях связаны прак-
тически так же, как и в атоме водорода, их состояния являются водородоподобными.
Следует отметить, что в то время как прочность связи s- и р-электронов
с наименьшим возможным п убывает от лития к цезию, прочность связи d-элект-
ронов с наименьшим возможным п возрастает и приближается к прочности связи
р-электронов.
Мы видим, что отличие уровней атомов щелочных металлов от уровней атома
водорода тем больше, чем меньше I при заданном п и чем меньше п при заданном I.
Это объясняется увеличением проникновения внешнего электрона во внутренние
оболочки с уменьшением I (т. е. с увеличением числа максимумов плотности элек-
тронного облака и с их приближением к ядру) и с уменьшением п (т. е. с уменьшением
размеров электронного облака).
В табл. 8.4 приведены численные данные, характеризующие прочность связи
электрона в атоме натрия в зависимости от п и I. Для сравнения приведены также
данные для атома водорода. Под каждым значением для натрия приведено отношение
этого значения к соответствующему значению для водорода2). При заданном Z, как
показывают данные табл. 8.4, для s- и р-уровней с увеличением п не только
уменьшается абсолютная разница в энергиях связи электрона в атомах натрия
и водорода, но и отношение энергий связи приближается к единице.
2) Корень квадратный из этого отношения дает значение Z*.
220
Глава 8. Спектры атомов с одним внешним s-электроном
Таблица 8.4
Прочность связи внешнего электрона в атоме натрия в зависимости от п и I (в см-1)
Квантовые числа	п = 3	п = 4	п = 5	п = 6	п = 7	п = 8	п = 9
1=0	41450 3,40	15710 2,30	8 249 1,88	5077 1,66	3438 1,54	2481 1,45	1875 1,39
1 = 1	24483 2,01	11 179 1,73	6408 1,46	4152 1,36	2909 1,30	2151 1,25	1655 1,22
1 = 2	12277 1,008	6901 1,006	4413 1,006	3062 1,005	2 249 1,004	1 721 1,004	1359 1,004
1 = 3		6861 1,001	4392 1,001	3050 1,001	2 240 1,001	1 716 1,001	1356 1,001
Атом водорода	12186	6855	4387	3047	2 238	1714	1354
Из таблицы видно, что для Na электрон в d- и /-состояниях связан практически
так же, как и в атоме водорода. Это свидетельствует о том, что в данных состояниях,
в отличие от состояний s и р, электрон является непроникающим.
Закономерное изменение энергии в зависимости от п, при заданном Z, позволяет
дать приближенные общие формулы для уровней энергии, которые были найдены
эмпирически Ридбергом [164] еще до появления теории Бора3).
Вводя, согласно (8.2) и (8.3), эффективное квантовое число п* и квантовый
дефект Д, мы можем записать энергию уровня с заданными значениями квантовых
чисел п и I в виде
R	R
(8-4)
где квантовый дефект, вообще говоря, может зависеть как от Z, так и от п. Однако
оказывается, что при заданном I квантовый дефект приближенно постоянен. Мы
получаем формулы
R	R	R
Ens “ “7 Л \2 > Епр ~ д \2 ? End — л ч2 ’	(8’5)
(п-Д5)2 F (n-Др)2	(п-Дй)2
где п пробегает целые значения, начиная от минимально возможного (см. табл. 8.3).
Значения п* и Д для s-уровней атомов лития и натрия приведены в табл. 8.5. Как
мы видим, Д5 действительно является приближенно постоянным.
Формулы (8.5) могут быть обоснованы теоретически, исходя из представления о про-
никновении внешнего электрона внутрь заполненных оболочек. Можно дать и более точные
формулы, в которых учитывается небольшая зависимость квантового дефекта от п.
Из табл. 8.5 видно, что квантовые дефекты Д5 для Na по абсолютной величине
больше единицы. Для К, Rb и Cs они еще больше, как показывают данные
табл. 8.2 (см. с. 217) для основного состояния атомов щелочных металлов. Можно,
однако, ввести вместо абсолютных значений квантового числа п его относительные
См. гл. 1, с. 37. Эти формулы были первоначально даны для выраженных в волновых числах
спектральных термов, разностям которых равны волновые числа спектральных линий. Лишь на основе
теории Бора была установлена пропорциональность значений термов значениям энергии.
§ 8.2. Уровни и спектральные серии атомов щелочных металлов
221
Таблица 8.5
Эффективные квантовые числа п* и квантовые дефекты Д5 для «-уровней лития и натрия
Элемент		Главное квантовое число					
		п = 2	п = 3	п = 4	п = 5	п = 6	п = 7
Литий	п*	1,589	2,596	3,598	4,599	5,599	6,599
		0,411	0,404	0,402	0,401	0,401	0,401
Натрий	п*	—	1,627	2,643	3,648	4,651	5,652
	А»	—	1,373	1,357	1,352	1,349	1,348
значения т, согласно следующей схеме:
5s	5p	5d	
4s	4p	4d	4
3s	3p	3d	
2s	2p		
Is			
55
(8.6)
заменяющей схему табл. 8.3 и одинаковой для атомов всех щелочных металлов.
При этом самое глубокое s-состояние обозначается как 1s, самое глубокое р-состо-
яние — как 2р и т.д. Тогда формулы (8.5) запишутся в виде
Ems —	/	। \2 ’	Етр	—	/	. \2 ’	Emd —	,	j\2 >	(&-7)
(т + s)2 F (т + р)1	(т +	а)2
где постоянные s, р, d отличаются от квантовых дефектов знаком и равны
s = -Д5 + (п - т),
р = -Ар + (п - т),	(8.8)
d = —Ad + (n — т).
Эти поправки являются положительными и для проникающих электронов оказыва-
ются одного порядка 0,5-1. Так, для основного s-уровня атомов щелочных металлов
получаются значения, приведенные в последнем столбце табл. 8.2, меняющиеся
от 0,59 для Li до 0,87 для Cs4).
Формулы (8.7) и представляют выражения, полученные Ридбергом. Более точные форму-
лы, отличающиеся от (8.7) добавлением в скобке, стоящей в знаменателе, членов типа а/т\
были получены Ритцем.
Хотя при относительной нумерации уровней энергии, согласно (8.6), наибо-
лее отчетливо выявляется сходство спектров атомов различных щелочных металлов
и поправки s и р получаются для них одного порядка, в настоящее время предпо-
читают применять нумерацию табл. 8.3, дающую действительные значения главного
квантового числа п и находящуюся в соответствии с теорией периодической системы
элементов.
4) Эти значения получаются из значений Д5 по первой из формул (8.8). Для Li, согласно табл. 8.2,
для уровня 2s Д5=0,41 и «=-0,41+ (2-1)=0,59, для Na для уровня 3« Д5 = 1,37 и « = -1,37+(3-1)=0,63
и т.д. Для всех приведенных в табл. 8.2 уровней т = 1.
222
Глава 8. Спектры атомов с одним внешним s-электроном
Общая структура спектров атомов щелочных металлов определяется возможны-
ми переходами между уровнями с различными значениями азимутального квантового
числа I. Согласно правилу отбора AZ ~ ±1, рассмотренному в §6.4 (см. (6.45) и осо-
бенно схему (6.47)), s-уровни комбинируют только с р-уровнями, р-уровни —
с «-уровнями и с d-уровнями, d-уровни — с р-уровнями и с /-уровнями. Главное
квантовое число может изменяться, так же как и для одноэлектронного атома,
на любую величину, и при комбинации нижнего уровня с заданным п\ с верхними
уровнями с различными п2 тоже получаются хорошо выраженные серии. Отличие
состоит в том, что при заданном п уровни с различными I находятся на значи-
тельном расстоянии друг от друга (см. рис. 8.1), и поэтому число возможных серий
увеличивается.
Важнейшие серии атомов щелочных металлов возникают при разрешенных
переходах между нижним уровнем — «-уровнем (основным), р-уровнем или d-уров-
нем — и верхними «-, р-, d- и /-уровнями. Данные для этих серий приведены
в табл. 8.6. Для каждой серии нижний уровень является заданным и соответствует
наименьшему возможному, при данном Z, значению п\ главного квантового числа п;
для главной серии это основной уровень 2s, 3«, 4«, 5«, 6« для Li, Na, К, Rb и Cs
соответственно (при относительной нумерации уровней энергии, согласно (8.6), это
уровень 1«). Для верхнего уровня П2 переменно и пробегает все возможные, согласно
табл. 8.3, значения; при п —► оо линии серии сходятся к границе, положение которой
определяется энергией связи электрона на нижнем уровне. В табл. 8.6 приведены
положения границ серий и соответствующие энергии связи «-, р-, d-электронов
для Li, Na, К, Rb и Cs. Мы видим, что граница главной серии для всех щелочных
металлов лежит в ультрафиолетовой части спектра, постепенно смещаясь от Li к Cs
в сторону больших длин волн. Граница резкой и диффузной серий только для Li
лежит в ультрафиолетовой области, а для остальных щелочных металлов она сме-
щается в видимую область спектра. Граница серий n\d—п2р и n\d—n2f еще дальше
перемещается в сторону больших длин волн; для Li и Na она попадает в близкую
инфракрасную область и ее положение мало отличается, в силу водородоподобности
уровня 3d, от положения границы серии Пашена (nj = 3, см. § 1.2, с. 20) для атома
водорода, лежащей при 12 187 см“’ (8 204 А).
Линии главной серии могут наблюдаться как в испускании, так и в поглоще-
нии. Последнее возможно, так как начальным уровнем при поглощении является
основной уровень П|«, на котором при низких температурах находятся практически
все атомы, а при высоких температурах находится значительная доля атомов. Первая
линия главной серии (п2 = п\, переходы 2«—2р для Li, 3«—Зр для Na и т.д.) являет-
ся резонансной линией и обладает наибольшей интенсивностью в спектре. Именно
она позволяет, как очень чувствительная (так называемая последняя) линия, об-
наруживать малые концентрации щелочных металлов при спектральном анализе5).
Остальные серии наблюдаются в испускании. Для появления их в поглощении
нужны высокие температуры, при которых заметная доля атомов будет находиться
в возбужденных состояниях щр (щ = 2, 3,4, 5,6 для Li, Na, К, Rb, Cs) и n\d (п\ = 3
для Li, Na, К, п\ — 4 для Rb и п\ — 5 для Cs).
Отметим в заключение данного параграфа, что общепринятые обозначения уровней
с I = 0, 1,2,3 буквами s, р, d, / возникли из первых букв английских названий серий —
резкой (sharp), главной (principal), диффузной (diffuse) и фундаментальной (fundamental);
верхними уровнями для этих серий являются уровни с I = 0, 1,2 и 3 соответственно.
5) Таблицу чувствительных линий см. [1211.
§8.3. Дублетная структура уровней атомов щелочных металлов
223
Спектральные серии атомов щелочных металлов
Таблица 8.6
Название серии			Главная	Резкая (вторая побочная)	Диффузная (первая побочная)		Бергмана (фундамен- тальная)
Нижний уровень			П\8	nip		n\d	
Верхние уровни			п2р	fl2«	П2</	n2p	«2/
Переходы			П\8 — П2р (Ь - тр)	flip — П23 (2р — ms)	nip — fl2<Z (2р - md)	Tl\d — fl2P (3d - mp)	n|d — nif (3d-mf)
Li	Граница серии	см 1 А	43 487 2 299	28 584 3 497		12 204 8 192	
	Энергия связи электрона, эВ		5,39 (2s)	3,54 (2р)		1,51 (3d)	
Na	Граница серии	см 1 А	41450 2412	24 493 4 082		12 277 8 143	
	Энергия связи электрона, эВ		5,14 (3s)	3,04 (Зр)		1,52 (3d)	
к	Граница серии	см 1 А	35 010 2 855	22 025 4 539		13 464 7 423	
	Энергия связи электрона, эВ		4,34 (4s)	2,73 (4р)		1,67 (3d)	
Rb	Граница серии	см 1 А	33 691 2 967	21 112 4 735		14 336 6 973	
	Энергия связи электрона, эВ		4,18 (5s)	2,62 (5р)		1,78 (4d)	
Cs	Граница серии	см 1 А	31407 3 183	20 228 4 942		16 907 5 913	
	Энергия связи электрона, эВ		3,89 (6s)	2,51 (6р)		2,09 (5d)	
Примечание. Для р- и d-электронов границы серий указаны для уровней
соответствующих дублетных термов (см. § 8.3, с. 223).
Л и Ч
§ 8.3.	Дублетная структура уровней атомов щелочных металлов
В случае атомов щелочных металлов, так же как и в случае атома водоро-
да, наличие у электрона спина обусловливает тонкую структуру уровней энергии
и спектральных линий. Орбитальный момент I и спиновый момент s складываются
в полный момент j = I + s и внутреннее квантовое число j принимает значения
j = I ±	0 > 1) и j = s = | 0 = 0) (см. (6.54) и (6.55)).
Каждый уровень с заданным значением I > 0 расщепляется на два уровня —
мы получаем дублетное расщепление. Совокупность таких двух уровней называют
дублетным термом.
Именно для атомов щелочных металлов влияние спина проявляется в наиболее
отчетливой форме. Это происходит благодаря тому, что уровни с различными
значениями Z, при заданном значении п, отстоят, как мы видели, далеко друг
от друга (см. рис. 8.1, расстояние уровней 2s и 2р у Li составляет, например, 1,85 эВ,
224
Глава 8. Спектры атомов с одним внешним s-электроном
а уровней 3s и Зр у Na — 2,10 эВ), и каждый из них расщепляется независимым
образом. Вырождение по Z, которое усложняло картину тонкой структуры уровней
энергии и линий атома водорода и водородоподобных ионов, здесь отсутствует; мы
имеем дублетное расщепление, обусловленное спином электрона, в чистом виде.
Для атомов с двумя или несколькими внешними электронами картина получается
более сложной благодаря сложению спиновых моментов этих электронов; вместо
дублетной структуры получается мультиплетная структура — происходит спиновое
расщепление уровней энергии не только на два, но и на большее число уровней.
Мультиплетная структура уровней энергии и спектров будет нами рассмотрена
в следующей главе (см. § 9.2 и § 9.5). Разбор случая дублетной структуры, как
простейшего случая мультиплетной структуры, является весьма важным.
Дублетная структура р-, d- и /-уровней показана на рис. 8.2. На нем также
изображен s-уровень, который не расщепляется. Справа приведены общепринятые
обозначения получающихся уровней (см. с. 187). Буквы 5, Р, D, F указывают
значения орбитального момента атома L = I — 0, 1,2, 3, индекс слева сверху —
мультиплетность х — 2S + 1 = 2 • ’/г + 1 = 2 (значение спинового момента атома
равно S = s = ’/г), индекс справа снизу — значение полного момента атома
J — j. В более полном обозначении перед символом *Lj указывается электронная
конфигурация; для атомов щелочных металлов это будут значения п и I для внешнего
электрона. Например, основной уровень Na будет обозначаться как 3s25y2, а самый
глубокий двойной р-уровень — как Зр2Р3^ (сокращенно Зр2Ру^ или 32Ру2 Зд).
При учете дублетной структуры мы можем построить диаграмму уровней, более
полную, чем изображенная на рис. 8.1, и показывающую важнейшие переходы между
уровнями энергии. Такие диаграммы стандартного типа (диаграммы Гротриана [16])
для атомов всех щелочных металлов изображены на рис. 8.3-8.7. Уровни показаны
короткими горизонтальными черточками, а переходы между уровнями — наклон-
ными прямыми с разрывами, в которых даны значения длин волн соответствующих
спектральных линий. Сбоку указан масштаб в эВ и в см-1; слева отсчет энергий
производится от нормального уровня, справа — от границы ионизации6*.
Возможные переходы между уровнями с различными значениями I определяют-
ся правилами отбора AZ = ±1, что дает, в соответствии с табл. 8.6 (с. 222), различные
серии.
Наряду с этим необходимо учесть правило отбора AJ = 0, ±1 (см. (4.156))
для квантового числа J = j, определяющего значения полного момента количества
движения.
Возможные переходы показаны на схеме рис. 8.2 (ср. (6.64)). Уровень 2S\/ ком-
2Р'/2 И
бинирует с обеими составляющими
двойного уровня 2Р° и получаются
две линии — дублет. При комбинациях дублетных термов 2Р° и 2Р, 2D и 2Р° и т.д.
получается по три линии7*, например, для переходов 2Р°— 2D линии
Ч-Ч- (8-9)
Хотя для подобных переходов получается не две, а три линии, все же и в этих
случаях принято говорить о группе, состоящей из трех линий, как о дублете.
6* Обычно энергии в эВ отсчитываются от нормального уровня, а в см-1 от границы ионизации (что
дает значение термов). Однако рациональнее давать в обоих направлениях масштаб и в эВ, и в см-1.
7* Более подробное рассмотрение картины, получающейся при учете величины расщепления и отно-
сительной интенсивности трех составляющих, см. ниже, §8.4 (с. 234).
§8.3. Дублетная структура уровней атомов щелочных металлов
225
/ = 0 S
/ = з f
1 = 2 d
l=\ p
i=
j=
_7
2
J.
2
2D5f2
2d3/2
2p°
*3/2
2pO
*1/2
° Г/2
Рис. 8.2. Дублетная структура уровней
Рис. 8.3. Диаграмма уровней энергии лития
a rtf
-5Ш
-10080
'-15000
-20000
3 -25W0
-soooo
* :
-35000
-5 -mo
ф-43487,2
’ CM4
8 Зак. 103
226
Глава 8. Спектры атомов с одним внешним s-электроном
Рис. 8.5. Диаграмма уровней энергии калия
§ 8.3. Дублетная структура уровней атомов щелочных металлов 227
—15000
-20000
3 -25000
-30000
-3^-32^06,7
'эб ’’ см~9
Рис. 8.7. Диаграмма уровней энергии цезия
г0
- 5000
~-юооа
8*
228
Глава 8. Спектры атомов с одним внешним s-электроном
Аналогично об уровне 25|д говорят как о дублетном терме, хотя он и не расщеп-
ляется на два уровня. Название «дублет», «дублетный» определяется наличием двух
возможных ориентаций спина
S = s = | (х = 25 + 1 = 2),
ср. §6.5, с. 189, и ниже, §9.6, с. 264.
Наиболее характерны дублеты в главной серии, получающиеся при переходах
с основного уровня П1$ на уровни п2р 2Ру2 и п2р 2Ру2 дублетного терма п2р 2Р°.
В частности, дублетом является резонансная линия ns—пр (п = 2, 3, 4, 5, 6 для Li,
Na, К, Rb, Cs), которая состоит из двух линий
ns2St/-np2Po{/2 и ns2S^-np2Po3/2.	(8.10)
Для Na мы имеем (см. рис. 8.4) дублет 5 895,9 А, 5 890,0 А — известную желтую
D-линию натрия, о которой мы неоднократно упоминали. Уже при небольшой
дисперсии эта линия наблюдается как двойная.
Важным является вопрос о величине дублетного расщепления и о зависимости
этой величины от различных факторов.
Дублетное расщепление определяется магнитным взаимодействием орбитально-
го и спинового моментов электрона. Согласно наглядным представлениям, именно
этим спин-орбитальным взаимодействием определяется различие в энергиях сосед-
них уровней j = I - V2 и j1 = j + 1 = I 4- У2, приводящее к возникновению тонкой
структуры в спектре одноэлектронного атома (см. рис. 6.11 и формулу (6.61)). Форму-
лу (6.61) можно применить и для рассматриваемого случая дублетного расщепления
уровня с заданным I атома щелочного металла, считая, что внешний электрон
движется в поле ядра с эффективным зарядом
Z* = Z-s,	(8.11)
где $ — постоянная экранирования. Заменяя в (6.61) Z через Z* и полагая j —I - х/г
и j + 1 = I + ’/2, мы получаем
Ra2Z^4 1	Z*4
= пз щ + 0 = 5’82пзг(/ + 1) CM '• <8-12)
Формулу (8.12) можно также записать в виде
=	+ 2) ’	(813)
где
Сы = ,Ra\T4-----------= 5,82	-Z-^-------см-' (8.14)
n3l(l 4- - J (Z + 1) nUh 4- -	4- 1)
— зависящий от п и I фактор дублетного расщепления, определяющий величину
этого расщепления по формуле (8.13).
Следует иметь в виду, что введенная нами постоянная экранирования s (см. (8.11)),
определяющая величину дублетного расщепления, не тождественна с постоянной экраниро-
вания а, определяющей по формулам (7.6) и (7.7) величину энергии электрона, в данном
случае внешнего. Постоянная s для тяжелых атомов оказывается значительно меньше, чем
§8.3. Дублетная структура уровней атомов щелочных металлов
229
постоянная а, т.е. эффективный заряд Z* — Z - s, вычисленный из дублетного расщепления,
оказывается значительно больше эффективного заряда Z* = Z-a, вычисленного из величины
энергии (о величине постоянных экранирования <г и s см. также конец этой главы, с. 241,
и гл. 13, с. 359).
Как показывает формула (8.12), величина дублетного расщепления убывает как
с увеличением п, так и с увеличением I. Для р-уровней расщепление больше, чем
для d-уровней, а для d-уровней больше, чем для /-уровней. У последовательных
уровней, в связи с быстрым возрастанием п3, расщепление резко убывает. Самое
большое расщепление получается для самых глубоких р-уровней. Для последова-
тельных линий главной серии величина расщепления, определяющаяся дублетной
структурой верхнего терма п2 2Р°, комбинирующего с нижним нерасщепленным
основным термом ni %, быстро убывает; наибольшее расщепление наблюдается
для первого члена главной серии — резонансного дублета щелочных металлов.
Зависимость от эффективного заряда получается очень резкой — расщепление
растет пропорционально Z*4.
В табл. 8.7 приведены данные для дублетного расщепления резонансных линий
атомов щелочных металлов и вычисленные из этого расщепления по формулам (8.12)
и (8.11) значения эффективного заряда Z* и постоянной экранирования $.
Таблица 8.7
Дублетное расщепление для резонансных линий атомов щелочных металлов
Элемент	Z	n	Составляющие дублета		Расщепление п2Р°}. -п2Р° 41	72	Z*	а
			ns2Sy2~np2P°^	пзЪ^-пр2?^			
Li	3	2	6707.95А 14903,66 см”1	6707,80А 14904,00 см-1	0,34 см-1	0,98	2,02
Na	11	3	5 895,92 А 16956,18 см"1	5 889,95 А 16973,38 см"1	17,20 см-1	3,55	7,45
К	19	4	7698,98 А 12985,17 см-1	7 664,91 А 13042,89 см-1	57,72 см"1	5,97	13,03
Rb	37	5	7 947,60 А 12578,96 см"1	7800,23 А 12 816,56 см"1	237,60 см"1	10,05	26,95
Cs	55	6	8 943,5 А 11 178,2 см"1	8521,|А 11732,3 см-'	554,1 см-1	14,2	40,8
Мы видим, что расщепление очень быстро возрастает с увеличением Z. Для Cs
расстояние между составляющими дублета составляет свыше 400 А, что соответствует
расщеплению более 500 см'1, тогда как у Li это расщепление порядка - см'1. Этот
быстрый рост происходит, несмотря на увеличение главного квантового числа п, вхо-
дящего в знаменатель формулы (8.12). Для Rb и особенно для Cs говорить о «тонкой»
структуре можно, разумеется, лишь в условном смысле. Такое положение вообще
типично для тяжелых атомов; для них спин-орбитальное взаимодействие велико.
Основная формула (8.12) может быть выведена непосредственно путем рассмотрения
спин-орбитального взаимодействия, иначе говоря магнитного взаимодействия спинового мо-
мента з и орбитального момента I электрона. Согласно (2.85), оператор этого взаимодействия
для электрона, находящегося в сферически симметричном электрическом поле, имеет вид
7 = А(г)(Й),
(8.15)
230
Глава 8. Спектры атомов с одним внешним s-электроном
где А(г) — функция расстояния электрона от ядра. Усреднение по г дает постоянную
А = А(г)^
а оператор (Is) в состоянии с определенным значением j полного механического момента
j имеет собственное значение, равное [см. (2.86), где нужно положить Jj = Z, J2 = s = ]/2,
J=j]
„ . _ Л; + 1)-Ц/ + 1)-ф+1) _ Я; + 1)-Ф + 1)--
2	2	' ’ * '
В результате дополнительная энергия в состоянии с определенными n, I и j будет иметь вид
3
j(j 4-1) - 1(1 + 1) - -
E„isi = А----------------1,	(8.18)
где необходимо вычислить постоянную А, т.е. среднее значение (8.16) функции 4(г). Эта
функция в общем случае сферически симметричного поля, вообще говоря, отличного от ку-
лоновского, имеет вид [14]
А(г) =
Л2 1 dU (г)
2тп2с2 г дг '
(8-19)
где U(г) — потенциал поля, в котором движется электрон и который можно положить
равным (7.3).
Если известны радиальные функции Rni(r) для состояния с заданными п и I, то среднее
значение (8.19) равно
2т2с2 г дг
где
--------г аг
г дг
(8.20)
(8-21)
о
— матричный элемент, взятый по радиальным функциям, т. е. усреднение производится
с учетом радиального распределения Я2,(г)г2 вероятности (ср. с. 178). Для одноэлектронного
Ze2
атома с потенциалом U(r) =---(ср. (6.39)) среднее значение вычисляется в общем виде,
г
Мы имеем
, , ft2 Ze2
ЛИ = 5^—	М
И
—-	h2Ze2 Т h2Ze2 7 1,	,
А г =	- = ——2 / -й ,(r r! dr,	8.23)
2т2с2 г5 2т2с2 Jr5
о
где интеграл представляет среднее значение обратного куба расстояния электрона от ядра,
взятое по уже известным радиальным функциям (6.43). Он равен (см. [134], с. 33):
1
г3
[ ^RlMr2 dr =
J r
0
Z}_________1_
(1 + I)(1 + 1) ao
(8.24)
§8.3. Дублетная структура уровней атомов щелочных металлов
231
Л2
Согласно (8.23) и (8.24), мы получаем, подставляя значение а0 = -г (см. (6.30)) радиуса
тпее2
первой боровской круговой орбиты,
12	/	2 \ 2	/уЗ	8	гг4
—7—	п, / тее \ п	Z	тее	Z
= 2mjc2 \~rf~) Ze 7 А~ = 2AV 7 А
4	7	пзН/+_Ь+1) п3Н1 + -)(1+1)
тее8
(8.25)
т ^8
Множитель —z— равен, как легко проверить, произведению Ra , где R — постоянная
2Л4с2
Ридберга (6.15) (расчет производится в единицах энергии), а а — постоянная тонкой
структуры (6.59). Таким образом, для одноэлектронного атома
Ra2Z4
А = А(г) =
п3/Н + |)(/ + !)
Это выражение можно применить и для атомов щелочных металлов, если ввести вместо Z
эффективный заряд Z* = Z-s, где s — постоянная экранирования. Обозначая постоянную А,
зависящую от п и Z, через Q, и подставляя ее в (8.18), мы получим
3
№ + i)-i(i+i)--
Enlsj — Ст
(8.26)
где
2
(8.27)
Ra2(Z - s)4
RcrZ'
<п' “ 7 А ( 1 \
п3111 + -Н1 + 1) n’lh + -j(l + l)
Дублетное расщепление мы найдем, беря разность энергий уровней j! = I + */2 и j = I — ’Д
(8.28)
1/2? 1 У2 Em,i+ У2 Em,i- У2
2
2
— Ст + у >
(8.29)
т.е. мы приходим к формуле (8.13).
Отметим, что выражение для оператора энергии взаимодействия, из которого мы ис-
ходили в приведенном выводе, находится в соответствии с наглядными представлениями
о магнитном взаимодействии орбитального магнитного момента Pi
и спинового магнитного момента пропорциональном их скаляр-
ному произведению pips — pips cos (ph ps) (ср. с. 61). В этом легко
убедиться на примере спин-орбитального взаимодействия для элек-
трона, движущегося по круговой орбите радиусом а вокруг ядра
с зарядом Ze (рис. 8.8). Если представить себе, наоборот, электрон
покоящимся, а ядро движущимся вокруг него по круговой орбите,
то легко вычислить энергию ориентации спинового магнитного мо-
мента электрона в магнитном поле Н, создаваемом ядром в месте
нахождения электрона. Это поле Н может быть вычислено как поле
кругового тока
+Ze
Рис. 8.8. Переход
от покоящегося ядра
к покоящемуся
электрону
2tti
(8.30)
са
сила г которого равна произведению заряда Ze на число оборотов
V
времени, т.е. (ср. аналогичное рассмотрение в §2.5, с.55), i = Ze-,
2тга
по орбите в единицу
откуда
а2 с
2Z eva
а3 2с
(8-31)
232
Глава 8. Спектры атомов с одним внешним s-электроном
Мы получаем, вводя, согласно (2.49), магнитный момент обусловленный орбитальным
движением (магнитное поле направлено противоположно магнитному моменту pi)\
2Z
К = - —мр	(8.32)
Формула (8.32) представляет частный случай пропорциональности магнитного поля соответ-
ствующему магнитному моменту, о которой мы говорили при рассмотрении прецессии одного
магнитного момента вокруг направления другого магнитного момента (см. § 2.6, с. 62).
Энергия ориентации спинового магнитного момента ps в магнитном поле Н равна,
согласно известной формуле для энергии магнита в магнитном поле,
U = -psH cos (Мз, Н) = ~(м,Я),	(8.33)
откуда
2Z
и = —(М(М,).	(8.34)
Таким образом, мы действительно получаем энергию взаимодействия, пропорциональ-
ную скалярному произведению магнитных моментов ps и рь Подставляя в (8.34) выраже-
ния (2.48) и (2.55) магнитных моментов через механические, мы найдем
2Z о
и = —2рБ(/з),	(8.35)
где — магнетон Бора. Подставляя его значение, согласно (2.46), мы можем записать (8.35)
в виде
2Z 2егП2 „ ч Л2 Ze2 „ ч
U = =
а3 <¥ГПеС£	тп?сл а3
(8.36)
где множитель при (Is) отличается от (8.22) (при г = а) лишь коэффициентом 2. Можно
показать (см. [10]), что при наглядном рассмотрении задачи о спин-орбитальном взаимо-
действии с учетом теории относительности появляется дополнительный коэффициент
1
2
В результате множитель в (8.36) при (Is) в точности совпадает с выражением (8.22) и, таким
образом, наглядные представления приводят к правильному выражению для спин-орбиталь-
ного взаимодействия. При этом можно получить, если рассматривать движение электрона
в произвольном сферически симметричном поле U(r), не только формулу (8.22) при г = а,
но и общую формулу (8.19).
В заключение данного параграфа отметим, что для одноэлектронного атома выраже-
ние (6.58) для энергии уровней тонкой структуры получается, если к смещению уровней
вследствие спин-орбитального взаимодействия
AEnisj — A(ls) —
Ra2Z4 jQ + l)-/(i+l)-a(s+l)
”34i+5 )(,+l)
2
(8.37)
прибавить поправку на их смещение вследствие зависимости массы электрона от скорости.
Эта поправка зависит только от п и I, но не от J, и имеет вид ([201], см. также [14], с. 119)
д . Ra2Z4
1
(8.38)
Если сложить (8.37) и (8.38), то как для j = I 4- у2 (т. е. I = j - у2), так и для j = I - 1/2
(т. е. I = j 4- Уг) получается выражение
дг.,„ + лв;, = -^/-!-г-2.у	(8J9)
V + i )
совпадающее с (6.58) и зависящее только от п и J, но не от I. Таким образом, из двух
уровней j = I - У2 и j = I 4- Уг, получающихся за счет спин-орбитального взаимодействия,
§ 8.4. Интенсивности в спектрах атомов щелочных металлов
233
первый совпадает с уровнем / = I' + ’/2, где I1 = I - 1, а второй с уровнем j" = I" — ’/2, где
= I + 1. Это является специфическим для одноэлектронных атомов, для которых, согласно
нерелятивистской теории, имеет место связанное с кулоновским полем вырождение по /,
отсутствующее для атомов щелочных металлов, в силу того, что в этих атомах электрон
движется в некулоновском поле ядра и остальных электронов.
§ 8.4. Интенсивности в спектрах атомов щелочных металлов
Очень существенным является вопрос об интенсивностях в спектрах атомов
щелочных металлов.
Для линий каждой серии вероятности переходов (и соответствующие им интен-
сивности испускания при термическом возбуждении атомов) закономерно убывают
при увеличении главного квантового числа, аналогично тому, как это имеет место
для атомов водорода (ср. табл. 6.6). Однако законы этого убывания не совпадают
в обоих случаях вследствие того, что в атомах щелочных металлов электрон движется
в электрическом поле ядра и других электронов, отличающемся от кулоновского.
Лишь для переходов, у которых не только верхнее, но и нижнее состояние явля-
ется водородоподобным, можно ожидать совпадения вероятностей с вероятностями
соответствующих переходов для атома водорода.
Вероятности переходов для линий серий атомов щелочных металлов, особенно
для главной серии П\3~П2Р (где п\ — 2, 3,4, 5, 6 для Li, Na, К, Rb, Cs), неоднократно
рассчитывались теоретически и измерялись на опыте. Большое количество точных
измерений сил осцилляторов было выполнено путем исследования аномальной дис-
персии по методу крюков Рождественским и его учениками. В табл. 8.8 приведены
данные для сил осцилляторов для линий главной серии лития и натрия. Приведены
абсолютные и относительные значения, определенные на опыте [198], и результаты
теоретических расчетов для первых членов этих серий. Характерно резкое убывание
сил осцилляторов для второго и последующих членов серии по сравнению с первым,
т. е. с резонансной линией. Для атома водорода хотя и имеется убывание, но далеко
Таблица 8.8
Силы осциллятора для линий главной серии лития и натрия [14]
Литий				Натрий			
	Сила осциллятора				Сила осциллятора		
п2	абсолютное значение	относительное значение	теор.	п2	абсолютное значение	относительное значение	теор.
2 3 4 5 6 7 8 9 10 11 12 13	0,750 0,00549 0,00478 0,00314 0,00192 0,00128 0,00091 0,000676 0,000520 0,000406 0,000327 0,000266	100 0,733 0,637 0,419 0,256 0,170 0,122 0,0902 0,0693 0,0542 0,0437 0,0355	0,750 0,00551 0,00471 0,00253	3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18	0,97550 0,01403 0,00205 0,000631 0,000256 0,000134 0,0000811 0,0000537 0,0000384 0,0000284 0,0000217 0,0000173 0,0000140 0,0000116 0,0000092 0,0000075	100 1,44 0,211 0,0648 0,0262 0,0138 0,00832 0,00550 0,00393 0,00291 0,00223 0,00178 0,00144 0,00119 0,00095 0,00077	0,9796 0,01426 0,00221 0,00073
234
Глава 8. Спектры атомов с одним внешним s-электроном
не такое резкое. Причиной подобной разницы является упомянутое выше отличие
электрического поля в атомах щелочных металлов от кулоновского. Эксперименталь-
ные значения хорошо согласуются с теоретическими значениями, вычисленными
с учетом самосогласованного поля, в котором движется внешний электрон.
Относительные интенсивности составляющих дублетной структуры линий ато-
мов щелочных металлов определяются статистическими весами комбинирующих
уровней, как это было рассмотрено в § 6.5. Там были приведены для случая атома
водорода значения относительных интенсивностей для переходов 2S— 2Р°, 2P°—2D
и 2D—2F° (см. (6.64)), которые применимы для линий соответствующих серий
атомов щелочных металлов, при условии, что можно считать поле, в котором
в этих атомах движется электрон, сферически симметричным. Для дублетов (8.10)
в главной серии, особенно характерных для спектров щелочных металлов, отноше-
ние интенсивностей линий дублета равно просто отношению статистических весов
уровней 2Ру2 и 2Р°]/2> т. е. 2 : 1. Это хорошо оправдывается на опыте для первых
членов главной серии, в частности для D-линий натрия, но для более высоких
членов наблюдаются весьма значительные отступления, как показывают данные
табл. 8.9 [7]. В ней приведены значения относительных интенсивностей, измерен-
ные по методу крюков. Наблюдающиеся отступления от теоретического отношения
интенсивностей 2:1, как показал впервые Ферми [210], объясняются спин-ор-
битальным взаимодействием; точные расчеты этих отступлений были выполнены
Петрашень и Яноух [217].
Таблица 8.9
Отношение интенсивностей для дублетов в главной серии атомов щелочных металлов
Натрий		Калий		Рубидий		Цезий	
п2	/2/71	п2	л//|	п2	А//.	п2	fl/fl
3	2,05	4	1,995	5	2,015	6	2,053
		5	2,046	6	2,575	7	4,07
				7	2,90	8	7,4
						9	9,1
При учете спин-орбитального взаимодействия нельзя рассматривать независимо уров-
ни п2Р°, соответствующие различным значениям главного квантового числа п. Матричные
элементы оператора энергии спин-орбитального взаимодействия (8.15), взятые по отношению
к p-состояниям с различными п и равные
(y)npj,n'pj=f	JA(r)Rnp(r)R*p(r)r2dr, (8.40)
отличны от нуля и обусловливают изменения радиальных волновых функций Rnp, зависящие
от значения квантового числа}. Это и приводит к изменению относительных интенсивностей,
которое тем больше, чем ближе друг к другу уровни пр и п'р, следовательно, увеличивается
для высоких членов серии.
Для переходов 2Р° - 2Z>, т. е. для диффузной серии, и для переходов 2D—2F°,
т. е. для фундаментальной серии, получающиеся три составляющие должны иметь,
согласно (6.64), относительные интенсивности 5 : 1 : 9 и 14 : 1 : 20, соответ-
ственно. С учетом того, что, согласно формуле (8.12), дублетное расщепление
убывает с увеличением пи/, мы получим картину расщепления, изображенную
на рис. 8.9. На рисунке также показана картина расщепления для переходов 2Р°— 2S,
т. е. для резкой серии. Благодаря слабости составляющих 2Ру — 2Рз/2 и 2#5/2“ 2F°5^
§ 8.5. Спектры ионов, изоэлектронных с атомами щелочных металлов 235
и их близости к составляющим
И 2^5/2-^/2
2PV2-2D5/2
соответственно, картины рас-
щепления для переходов 2Р°—21>и 2D—2F°
схожи между собой и с картиной расщеп-
ления для переходов 2Р— 2S и напоминают
дублеты главной серии. Особенно это отно-
сится к высоким членам серий, для кото-
рых расщепления 2Z>5/2—2£>з/2и 2Fy^—2F°5^
верхних термов становятся очень малыми,
даже для более тяжелых атомов рубидия
и цезия с весьма большими дублетными
расщеплениями более низких термов.
Отметим, что в отличие от дубле-
тов главной серии, для которых разность
П2 2Ру2 — П2 2Ру2, обусловленная расщепле-
нием верхнего дублетного терма, убывает
2P — 2S 2P-2D	2d-2f
Рис. 8.9. Картина расщепления
для дублетных переходов
с увеличением п, для резкой, диффузной и фундаментальной серий разности
п\ 2Ру2 - п\ 2Ру2 и ni 2Z>5/2 - п\ 2Z>3/2, обусловленные расщеплением нижнего ду-
блетного терма с заданным п\, остаются постоянными. Поэтому для главной серии
дублетное расщепление убывает для высоких членов серии (ср. выше, §8.3, с. 229),
а для резкой, диффузной и фундаментальной серий дублетное расщепление остается
постоянным для всех членов каждой серии8).
Отметим также, что для высоких дублетных термов 2D и 2Р° одновременно
с уменьшением величины расщепления терма иногда наблюдается обратное распо-
ложение уровней — уровень с большим значением j лежит глубже уровня с меньшим
значением j — получается обращенный дублетный терм.
Вопрос о величине дублетного расщепления термов атомов щелочных металлов был
рассмотрен теоретически Фоком [211], который показал и возможность обращения термов
при учете обмена (см. примечание на с. 202).
§ 8.5. Спектры ионов, изоэлектронных с атомами щелочных металлов
Спектры ионов, имеющих то же самое число электронов, что и атомы щелоч-
ных металлов, изоэлектронных с ними ионов, представляют весьма значительный
интерес, так как позволяют проследить изменения в одноэлектронном спектре
в зависимости от заряда ядра.
Аналогично тому как атом водорода является первым членом простейшего изо-
электронного ряда (6.1) с одним электроном, атомы Li, Na, К, Rb, Cs и Fr являются
первыми членами изоэлектронных рядов с 3, 11, 19, 37, 55 и 87 электронами:
К I, Са II, Sc III, Ti IV...
Rb I, Sr II, Y III, Zr IV...
Li 1, Be II, В III, С IV ... (Z = 3,4,5,6,...)
Na I, Mg II, Al III, Si IV... (Z= 11,12,13, 14,...)
(Z = 19, 20,21,22,...)
(Z = 37, 38, 39,40,...)
(8.41)
(8-42)
(8.43)
(8.44)
81Для диффузной и фундаментальной серий это
И ^7/2-2^/2-
^5/-^
справедливо при малых разностях
236
Глава 8. Спектры атомов с одним внешним s-электроном
Cs I, Ba II, La III, Се IV ... (Z = 55, 56, 57, 58,...)	(8.45)
Fr I, Ra II, Ac III, Th IV... (Z = 87, 88, 89, 90,...)	(8.46)
Для ряда (8.41) имеется один внешний электрон, помимо заполненной оболоч-
ки 1s2, а для всех остальных рядов — один внешний электрон, помимо последних
заполненных оболочек ns ^пр6 (п = 2, 3, 4, 5,6).
Если бы экранирование внешнего электрона внутренними электронами было
полным, то эффективный заряд, действующий на этот электрон в fc-кратно иони-
зованном атоме (т.е. для к 4- 1-го члена изоэлектронного ряда), равнялся бы просто
Z* = Z - (Zo - 1) = (Zo + к) - (Zo - 1) = к + 1,	(8.47)
где Z — заряд ядра рассматриваемого элемента, a Zo — заряд ядра атома щелочного
металла, стоящего в начале ряда. В этом случае спектры были бы водородоподоб-
ными.
По аналогии с формулами (6.13) и (6.14) энергия электрона с заданным значе-
нием п равнялась бы
а частоты возможных переходов давались бы формулой
v = R(k+ 1)2( -4 - -4 ),	(8.49)
\nf п~>/
где {к 4- I)2 = 1,4,9,16,... для последовательных членов изоэлектронного ряда.
Масштаб спектра для fc-кратно заряженного иона был бы в (к 4-1)2 раз больше,
чем для нейтрального атома, и, разделив (8.48) и (8.49) на (к 4- I)2, мы получили
бы совпадающие схемы термов и переходов. В действительности экранирование
для различных термов различное, в первую очередь в зависимости от квантового
числа I, и схемы получаются неодинаковые. Однако такой масштаб весьма удобен
для сравнения членов изоэлектронных рядов и позволяет выявить для них сходство
и различия в расположении термов и в относительных частотах переходов.
На рис. 8.10 сопоставлены схемы термов для изоэлектронного ряда (8.42),
начинающегося с Na. Горизонтальными линиями показаны, как и на схеме рис. 8.1,
положения термов одноэлектронных атомов (совпадающие при выбранном масштабе
для всех членов изоэлектронного ряда (6.1)). Мы видим, что имеется большое
сходство в расположении термов. Для водородоподобных термов nd и nf получается
практически полное совпадение. Для глубоких термов пр и особенно ns такого
совпадения нет, но их положения изменяются закономерно. По мере увеличения
кратности ионизации к происходит сближение термов с различными I при том же п;
вместе с тем они начинают больше походить на водородоподобные термы. Эти
тенденции являются характерными для изоэлектронных рядов и весьма отчетливо
проявляются для рядов, начинающихся с атомов легких элементов. Несколько
особое положение получается для изоэлектронных рядов, начинающихся с атомов
более тяжелых элементов. Для К, Rb, Cs и Fr, как мы видели в гл. 7 (см. § 7.4,
с. 209 и дальше), начинается заполнение слоев с п = 4,5,6 и 7, для которых
характерна конкуренция электронов ns с электронами (n - l)d и затем с (п - 2)/
(последнее при п = 6 и 7). Это находит свое отражение в схемах термов членов
соответствующих изоэлектронных рядов. По мере увеличения кратности ионизации
все больше и больше выявляется тенденция электронов с меньшим п находиться
глубже электронов с большим п, независимо от значения I.
§ 8.5. Спектры ионов, изоэлектронных с атомами щелочных металлов 237
Рис. 8.10. Схема термов для членов изоэлектронного ряда, начинающегося с натрия
На рис. 8.11 сопоставлены схемы термов для членов изоэлектронного ряда (8.43),
начинающегося с К. Уже для Sc III терм 3D лежит глубже терма 45. У последующих
ионов расстояние термов 3D и 45 увеличивается, а расстояние термов 45 и 4Р
уменьшается. Электрон 3d связывается все прочнее, в соответствии с меньшим
значением п9).
Еще более характерная картина получается для членов изоэлектронного ря-
да (8.45), расположение термов которых сопоставлено на рис. 8.12. У La III терм 5D
лежит глубже терма 65, а у Се IV его перегоняет терм 4F и восстанавливается нор-
мальный порядок прочности связи электронов 4/, 5d и 6s, при котором электрон 4/
связан прочнее электрона 5d, а электрон 5d — прочнее электрона 6s.
Следует отметить, что по мере перехода к более тяжелым элементам увеличи-
ваются отклонения термов от водородоподобных, благодаря тому, что постоянные
экранирования при больших Zq по абсолютной величине все больше отличаются
от Zo - 1 (ср. (8.47)).
Для сравнения прочности электронов в зависимости от заряда ядра, как для чле-
нов изоэлектронных рядов, так и для нейтральных атомов или ионов данной крат-
ности, очень наглядными являются диаграммы Мозли, впервые примененные им
при сравнении рентгеновских спектров последовательных элементов в периодичес-
кой системе Менделеева (о диаграммах Мозли для рентгеновских спектров см. гл. 13,
с. 355). Для построения этих диаграмм мы будем исходить из выражения для энергии
Абсолютная прочность связи всех электронов возрастает. Здесь существенно увеличение именно
относительной прочности связи.
238
Глава 8. Спектры атомов с одним внешним s-электроном
Рис. 8.11. Схема термов для членов изоэлектронного ряда, начинающегося с калия
электрона в форме (7.6)
RZ*2 R(Z - ап1)2
&nl =-------~
п2
п2
(8.50)
CsI
Ball
Lalll
Се IV
4f—
0,22
7s
0,41
4,0
4,7
0,40
0,47 \
Абсолютное значение энер-
гии, отсчитываемой от гра-
ницы ионизации, выражен-
ное в единицах частоты или
в волновых числах (значе-
ние терма), будет
2,09
5d —
r 2,46
bp —
0,54
0,63
73
0,73
8,9
0,51
_J39
0,54
7s
13,6
0,76
2jj0
0,81
bp
RZ*
откуда
z
R(Z - ani)2
n2 ’
(8.51)
z -(Tni
bs
W
93
10,0___
'И0И = 3,89эВ ^ион=10,0э'в<^
^ион=19,1эВ
1,00
0,93
1,00
n
\ 17,4
1,00
(1,04)
СЕ
Д9
1,00
65
303
1,17
5d
'363
^ион = 36,5эЙ
Рис.8.12. Расположение термов для Се I, Ba II, La III, Се IV
1,41
П
(8.52)
V
Отношение — пред-
R,
ставляет величину энергии
связи электрона в едини-
цах R, равных энергии ио-
низации атома водорода.
Квадратный корень из это-
го отношения, как показы-
вает формула (8.52), равен
§ 8.5. Спектры ионов, изоэлектронных с атомами щелочных металлов 239
эффективному заряду, деленному на главное квантовое число п, и является не-
П7
которой функцией от Z. Графики зависимости < / — от Z и образуют диаграммы
Мозли. Если постоянная экранирования а при заданных п и I не зависит от I, то
1
эти графики будут прямолинейными и их наклон будет равен просто —; графики
п
с различными I при том же п будут идти параллельно.
На рис. 8.13 представлена диаграмма Мозли для первых членов изоэлектронного
ряда (8.42), начинающегося с Na I и известного до Си XIX, т.е. до 19-го члена.
Z при этом меняется от 11 до 29. При заданных значениях п = 3 (для термов 3S, ЗР,
3D), п = 4 (для термов 45, 4Р, 4Z>, 4F) и п = 5 (для термов 55, 5Р, 5Z>) получаются
параллельные графики, близкие к прямолинейным, что свидетельствует о примерной
1 1 1
одинаковости постоянных экранирования. Наклоны графиков равны -, - и -
Z Z
соответственно, как показывает сравнение с наклонами пунктирных прямых —
Z	Z ПТ Z - а	„ а
и —. Отметим, что разница значений — и U— =---------, при заданном Z, дает —,
5	п у R п	п
т. е. значение постоянной экранирования, деленное на п.
Рис. 8.13. График Мозли	Рис. 8.14. График Мозли
для изоэлектронного ряда,	для изоэлектронного ряда,
начинающегося с натрия	начинающегося с калия
Иная картина, чем для ряда (8.42), получается для изоэлектронного ряда (8.43),
начинающегося с КI и известного до Fe VIII, т. е. до 8-го члена (рис. 8.14). В то время
как для термов с п = 4 получаются слегка изогнутые графики, идущие примерно
параллельно, с наклоном, близким к -, для терма 3D получается гораздо более
4
соответствующее наклону, значительно пре-
крутое возрастание значений
1
восходящему -. Этот наклон постепенно уменьшается и при больших Z дол-
3
1
жен быть равен -. Таким образом, постепенное упрочнение связи электрона 3d
240
Глава 8. Спектры атомов с одним внешним s-электроном
по сравнению с электроном 4s (а также с электронами 4р, 4d и 4/) отчетливо
выявляется и на диаграммах Мозли.
Аналогичные диаграммы получаются и для изоэлектронных рядов, начинаю-
щихся с Rb I и Cs I; для электрона 4d в первом случае и для электронов 5d и 4/
/V	Z
во втором случае наблюдается более быстрое возрастание </—, чем —.
V R	п
Рассмотрим теперь дублетное расщепление для членов изоэлектронного ря-
да. Мы можем применить формулу (8.12), в которую входит эффективный за-
ряд Z* = Z - s, в общем случае отличный от эффективного заряда в формуле (8.50).
В соответствии с формулой (8.12) дублетное расщепление запишется в виде
_Ra\Z-S^_ (Z-sf ,
61- '/2,1+ '/2 пЩ1 + !)	5’82п1Ц1 + 1) см
и будет очень быстро возрастать с увеличением Z, особенно если экранирование
внутренними электронами велико и близко к Zq - 1 (см. (8.47)).
В табл. 8.10 приведены для последовательных членов изоэлектронных ря-
дов (8.41)-(8.45) значения величины дублетного расщепления пр2Р^ — пр2Р\^
самого глубокого терма пр2Р° и вычисленные из этого расщепления по форму-
ле (8.53) значения эффективного квантового числа Z - s и постоянной экранирова-
ния s. Для сравнения в таблице приведены также значения величины терма пр 2Р°
(8.53)
Таблица 8.10
Дублетное расщепление для членов изоэлектронных рядов
Z	Атом	Дублетное расщепление n2P°3/ -n2P° 72	41 CM-1	Z — s	s	Величина терма n 2P°, cm-1	Z-cr	cr	Изоэлект- ронный ряд
3	Li I	0,338	0,98	2,02	28 582	1,021	1,979	
4	Be II	6,61	2,06	1,94	114948	2,047	1,953	
5	В III	34,1	3,12	1,88	257 550	3,064	1,936	Ряд (8.41)
6	С IV	107,1	4,14	1,86	455610	4,076	1,924	п = 2
7	N V	258,4	5,16	1,84	708900	5,084	1,916	
8	О VI	532,5	6,18	1,82	1017 280	6,091	1,909	
11	Na I	17,20	3,55	7,45	24482	1,417	9,583	
12	Mg II	91,55	5,40	6,60	85 537	2,650	9,350	
13	Al III	232,5	6,45	6,55	175616	3,795	9,205	
14	Si IV	460,3	8,09	5,91	292 500	4,898	9,102	Ряд (8.42)
15	P V	794,6	9,27	5,73	435 280	5,975	9,025	п = 3
16	S VI	1 263,0	10,4	5,6	603480	7,036	8,964	
17	Cl VII	1 890,0	11,5	5,5	797 640	8,089	8,921	
19	K I	57,7	5,97	13,03	21985	1,790	17,210	
20	Ca II	222,9	8,37	11,63	70400	3,204	16,796	Ряд (8.43)
21	Sc III	473,7	10,1	10,9	137 270	4,474	16,526	п = 4
22	Ti IV	818,4	11,6	10,4	220360	5,669	16,331	
37	Rb I	237,6	10,1	26,9	20945	2,184	34,816	
38	Sr II	801,5	13,6	24,4	64715	3,840	34,160	Ряд (8.44)
39	Y III	1 553,5	16,1	22,9	122 850	5,289	33,711	п = 5
40	Zr IV	2486,0	18,1	21,9	190400	6,588	33,412	
55	Cs I	554,1	14,2	40,8	19870	2,554	52,446	
56	Ba II	1 690,9	18,8	37,2	59 300	4,412	51,588	Ряд (8.45)
57	LaHI	3 095,7	21,9	35,1	110400	6,019	50,981	п = 6
58	Се IV	4 707,0	24,3	33,7	170700	7,484	50,516	
§ 8.5. Спектры ионов, изоэлектронных с атомами щелочных металлов 241
и вычисленные из нее по формуле (8.50) значения эффективного квантового чи-
сла Z - а и постоянной экранирования а.
Мы видим, что для сильно ионизованных атомов получаются очень большие
дублетные расщепления, составляющие многие сотни и тысячи см-1. Постоянные
экранирования s и а для изоэлектронного ряда, начинающегося с лития, близки
друг к другу и мало отличаются от 2. Иначе говоря, экранирование электрона-
ми If-слоя (т.е. слоя п — 1, заполненного двумя электронами 1s) соответствует их
числу. Наоборот, для изоэлектронных рядов, членами которых являются тяжелые
ионизованные атомы, постоянные s и а сильно различаются, причем s значительно
меньше, т. е. для дублетного расщепления эффективный заряд ядра больше. Это
понятно, так как спин-орбитальное взаимодействие сильно зависит, в силу наличия
множителя — в (8.22), от распределения электронной плотности вблизи ядра, где
гз
эффективный заряд Z(r) — Z - <т(г) (ср. (7.3)) велик; соответственно Z* — Z - з
будет велико.
Мы увидим, что аналогичное положение имеется и для электронов внутрен-
них оболочек, переходы между уровнями которых дают рентгеновские спектры:
постоянная экранирования з для них меньше, чем постоянная экранирования а,
см. гл. 13 (с. 359).
Отметим, что если учитывать при построении диаграммы Мозли отдельно две
составляющие дублета с j = 1 - !/г и j — I 4- !/г, то, благодаря сильной зависимости
дублетного расщепления от Z, получающиеся две линии будут быстро расходиться
с увеличением ZI0). С этим мы встретимся также в гл. 13 при рассмотрении вопроса
о дублетном расщеплении в рентгеновских спектрах.
|0) При построении диаграмм Мозли, приведенных выше (рис. 8.12 и 8.13), в качестве величины
дублетного терма при расчете по формуле (8.52) бралось взвешенное среднее — «центр тяжести» —
для двух составляющих j\ = I— 'Ди ji = /+ ’Д терма, с учетом их статистических весов, равных gi = 2ji 4-1,
т. е. бралась величина
[2(' - ]) +	4) + _ Ч, + « + 0-л
НЧМ4НМ = -
ГЛАВА 9
ОСНОВЫ ОБЩЕЙ СИСТЕМАТИКИ СЛОЖНЫХ СПЕКТРОВ
§9.1. Сложение орбитальных и спиновых моментов и типы связи
Типичные оптические спектры элементов определяются электронами, находя-
щимися вне заполненных оболочек. В рассмотренном простейшем случае атомов
щелочных металлов одноэлектронной конфигурации (п и I единственного внешне-
го электрона заданы) соответствует два уровня (при I > 0, j = I ± ’/2) или один
уровень (при I = 0, j = s = Когда имеется два или несколько электронов
вне замкнутых внутренних оболочек, положение значительно усложняется. Данной
электронной конфигурации
П\1\,п212,... ,пк1к,	(9.1)
где к — число внешних электронов, соответствует ряд уровней. Число их в не-
которых случаях доходит до многих тысяч, и задача определения характеристик
и расположения получающихся уровней требует специального рассмотрения, иногда
достаточно сложного.
Примером конфигураций типа (9.1) могут служить двухэлектронные конфигу-
рации атома Mg и четырехэлектронные конфигурации атома С.
Атом Mg (Z — 12) имеет нормальную конфигурацию ls22s22p63s2 с двумя
внешними электронами 3s2. При возбуждении одного из электронов 3s возникают
двухэлектронные конфигурации 3s4s, 3s5s, ... ; 3s3p, 3s4p, ...; 3s3d, 3s4d, ... ,
каждой из которых соответствует определенный набор уровней. Атом С (Z = 6) име-
ет нормальную конфигурацию ls22s22p2 с четырьмя внешними электронами 2s22p2.
При возбуждении одного из электронов 2s получаются четырехэлектронные конфи-
гурации 2s2p23s, 2s2p24s, ...; 2s2p3, 2s2p23p, ...; 2s2p23d, 2s2p24d, ..., которым
соответствует значительно более сложный набор уровней, чем двухэлектронным
конфигурациям.
Для электронной конфигурации (9.1) полный механический момент J —
h 4- h 4- • •• 4- 5] 4- s2 4- ... (см. (7.16)), в отличие от частного случая заполнен-
ных оболочек, не обязан равняться нулю; орбитальные и спиновые моменты могут
складываться различным образом. Существенно, что для определения возможных
уровней нужно учитывать лишь электроны, находящиеся вне заполненных оболочек;
орбитальные и спиновые моменты электронов, образующих заполненные оболочки,
компенсируют друг друга и нужно складывать лишь моменты к электронов, не вхо-
дящих в заполненные оболочки и характеризующихся квантовыми числами (9.1):
J — 1\ 4- ^2 4- • • • 4- Ik 4*	4- $2 4-... 4~ Sk-	(9.2)
Если бы электроны между собой не взаимодействовали, и отсутствовало также
взаимодействие спина каждого электрона с орбитальным моментом этого же электро-
на, то данной электронной конфигурации соответствовал бы один уровень энергии.
§9.1. Сложение орбитальных и спиновых моментов и типы связи
243
Благодаря взаимодействию электронов между собой и взаимодействию спинового
момента каждого электрона с его орбитальным моментом, заданной электронной
конфигурации соответствует целая совокупность уровней. При систематике слож-
ных спектров необходимо знать, какая именно совокупность уровней соответствует
данной конфигурации, т. е. сколько будет уровней, какими квантовыми числами
они будут характеризоваться и как они будут расположены.
Для определения числа уровней и их квантовых чисел можно воспользоваться
квантовым законом векторного сложения моментов (см. § 2.4, с. 50)!). За исключени-
ем случая одного электрона, когда складываются лишь два момента I и s, сложение
можно производить в различном порядке. Например, в случае двух электронов
можно сложить моменты по схеме I] + I2 = L, $i + S2 = S и L + S — J или по схе-
ме 1[ + «1 = I2 + 82 — j2 и J = Ji + j2- С возрастанием числа электронов
возрастает и число возможных схем сложения.
Если нужно получить только общее число уровней, соответствующих данной
конфигурации, и значения квантового числа J, определяющего величину полного
момента количества движения, то безразлично, в каком порядке производить сложение
моментов, результат получится тот же самый, независимо от способа сложения.
Однако расположение уровней в различных случаях может быть различным. Оно
будет определяться тем, какие взаимодействия между электронами велики и какие
малы. От величины взаимодействий будет зависеть и возможность характеристики
уровней при помощи других квантовых чисел, помимо J.
Моменты следует складывать в определенном порядке, в соответствии с тем,
каковы относительные величины различных взаимодействий в атоме. В зависимости
от выбранного порядка сложения моментов мы получаем различные типы (схемы)
связи. Необходимо при этом подчеркнуть, что для применяемой в теории слож-
ных спектров векторной схемы сложения моментов характерно именно сочетание
квантового закона сложения моментов с некоторыми предположениями о порядке
величины различных взаимодействий.
Самый важный случай сочетания моментов количества движения в атоме случай
нормальной связи или связи Расселя—Саундерса, чаще всего встречающейся и особенно
характерной для сложных спектров.
Представление об этом типе связи в общем виде было сформулировано известным
американским астрофизиком Расселем совместно с Саундерсом в 1925 г. [192], откуда и про-
исходит название «связь Расселя—Саундерса». Наиболее правильно название «нормальная
связь», которое мы и будем применять.
При нормальной связи орбитальные моменты электронов /г складываются
в полный орбитальный момент атома L, и спиновые моменты электронов S{
складываются в полный спиновый момент атома S, а затем L и S складываются
в полный момент атома в целом J. Мы имеем:
к	к
=	+	(9.3)
:=1	i=l
Соответственно, наряду с квантовым числом J вводятся квантовое число L, опреде-
ляющее значение полного орбитального момента, и квантовое число S, определяю-
щее значение полного спинового момента, согласно обычным формулам типа (2.11),
L2 = L(L+V), S2 = S(5 + 1).	(9.4)
^Для очень важного случая, когда имеются эквивалентные электроны, например р2, р3, d2, f\ f9
и т.д., этот метод непригоден и нужно применять метод сложения проекции (§2.4, с. 53), см. ниже
§9.3, с. 255.
244
Глава 9. Основы общей систематики сложных спектров
Проекции Lz — 22 hz и Sz — 22 siz моментов L и S соответственно квантуются
:	i
по формулам
Lz—mL (rnL — L,L- 1,...,-L), Sz=ms (ms = S, S - 1,..., -S).	(9.5)
Нормальная связь имеет место, когда электростатическое взаимодействие элек-
тронов между собой — их отталкивание по закону Кулона — велико по сравнению
со спин-орбитальным взаимодействием — магнитным взаимодействием спиновых
и орбитальных моментов. Электростатическое взаимодействие определяет, как мож-
но показать, зависимость энергии от квантовых чисел S и L, а малое по сравнению
с ним магнитное взаимодействие — зависимость энергии от квантового числа J
при заданных значениях L и S (мультиплетное расщепление, см. ниже §9.5).
В отличие от квантового числа J, являющегося точной характеристикой состояния
свободного атома (если пренебрегать возможным очень малым взаимодействием полного
электронного момента атома J с собственным моментом ядра Г), квантовые числа L и S
представляют приближенную характеристику, справедливую при малости мультиплетного
расщепления по сравнению с расстояниями между уровнями с различными L и S. Отметим,
что наряду с квантовым числом J точной характеристикой уровня является его характеристика
как четного или нечетного, в соответствии с поведением волновых функций по отношению
к отражению в центре атома (совпадающем с его ядром).
Нормальную связь принято обозначать как связь (L, S) в соответствии со сло-
жением моментов L и S.
Противоположный тип связи представляет так называемая связь (j, J). В этом
случае сначала для каждого электрона складываются его орбитальный и спиновый
моменты Ц и Si в полный момент данного электрона а затем полные моменты
отдельных электронов складываются в полный момент атома J; мы имеем
к
li + Si = ji,	=	(9.6)
1=1
Соответственно вводятся квантовые числа jt , определяющие значения моментов j •
по формулам
J.M.Ch + l)-	(9-7)
Проекции jiZ = liz + SiZ моментов квантуются по формулам
jiz = mit (mji - ji, ji - 1,...,-ji).	(9.8)
Связь (j,j) получается, когда магнитное спин-орбитальное взаимодействие
велико по сравнению с электростатическим взаимодействием различных электронов
между собой. Энергия в первую очередь зависит от значений ji, а затем уже
от значений J при заданных значениях J,.
В качестве примера обоих типов связи на рис. 9.1 показаны схемы уровней энер-
гии при связи (L, S) и при связи (j, j) для двухэлектронной конфигурации dp (Ц = 2,
s\ — */2; h — Г s2 — V2), дающей 12 уровней: 4 уровня с J = 2, по 3 уровня с J — 1
и J — 3 и по 1 уровню с J = 0 и J ~ 4. В первом случае уровни группируются по зна-
чениям L и S (L = 1\ +L = 3, 2, 1 и S —	+ s2, S — 1, 0), во втором случае —
по значениям jx и j2 + $i, j\ - V2, и j2 = h + s2, ji - V2, V2). На схе-
мах указаны значения квантовых чисел, а также даны общепринятые обозначения
уровней (см. ниже).
Общее расположение уровней при связи (L, S) соответствует конфигурации 3d3p для Si I,
а при связи (j,j) — конфигурации 6dlp для Th III (масштаб не выдержан). Пунктирны-
ми линиями показано сопоставление уровней для обоих типов связи, согласно правилу
непересечения (см. с. 394).
§9.1. Сложение орбитальных и спиновых моментов и типы связи
245
Связь(£,5)
Связь(/,/)
1 0 1
3 0 3
1 1 О
3 1 4
3 1 3
3 1 2
2 0 2
2 1 3
2 1 2
2 1 1
L S J
^-5/2 3/2 3 г
/5/2 3/2 2<
^'*5/2 3/2 1
/5/2 3/2 4 ‘
3/2 3/2 О
3/2 3/2 1
3/2 3/2 3
3/2 3/2 2
^5/2 1/2 Зг
'^'—5/2 1/2 2\
^^"3/2 1/2 1 Г
е''	3/2 1/2 2 V
(5/2, 3/2)3
(5/2, 3/2)2
(5/2, 3/2),
(5/2, 3/2)4
(3/2, 3/2)О
(3/2, 3/2),
(3/2, 3/2)3
(3/2, 3/2)2
(5/2, 1/2)3
(5/2, 1/2)2
(3/2, 1/2),
(3/2, 1/2)2
Рис. 9.1. Сравнение связи (£, S) и связи (j, j)
Какой именно тип связи осуществляется, зависит, как подчеркивалось выше,
от относительных величин различных взаимодействий. В большинстве случаев связь
в большей или меньшей степени близка к нормальной; в некоторых случаях нор-
мальная связь осуществляется с высокой степенью приближения, и тогда получается
особенно характерная структура спектров. Значительно реже встречаются достаточно
резко выраженные случаи связи (j, j); они могут иметь место, в частности, в случае
двух электронов, состояния которых сильно отличаются друг от друга2).
Наряду с типами связи (Z, S) и (j, j) могут осуществляться, если имеется
три и более электронов, более сложные, промежуточные типы связи. Например,
для группы электронов может иметь место нормальная связь, особенно если эти
электроны эквивалентные, и группа характеризуется значениями S', L' и J' —
спинового, орбитального и полного моментов. Затем полный момент J' складывается
с моментами I и з более внешнего электрона по схеме
= где j — l^s (связь (J,j)),	(9.9)
или по схеме
= Jn + s — J (связь (J, 0).	(9.10)
Последний случай осуществляется, например, для атомов инертных газов (см. § 11.7);
его обозначают как случай связи (J, Z) (или (j, I)).
Таким образом, возможно много разных способов сложения моментов. Реальные
случаи часто бывают промежуточными и иногда оказывается вообще невозможным
отдельные уровни характеризовать другими квантовыми числами, помимо кванто-
вого числа J, определяющего полный механический момент атома.
Следует отметить, что возможны и такие случаи, когда действительные свойства
и расположение близко лежащих уровней разных конфигураций возможно объяс-
нить, лишь учитывая взаимодействие конфигураций. Взаимодействие конфигураций
в отдельных случаях может быть так велико, что вообще нельзя отнести уровни
к одной из них.
2) Именно такой случай осуществляется для конфигурации 6dlp Th III с более внутренним электроном
6d и более внешним электроном 7р.
246
Глава 9. Основы общей систематики сложных спектров
С квантовомеханическои точки зрения сложению моментов соответствует введение вме-
сто волновых функции ^Л, характеризующих состояния (7.9) многоэлектронной системы
без учета взаимодействия электронов линейных комбинаций V’m = 22 Сда^а» характери-
А
зующих состояние системы при учете взаимодействия электронов. Различные типы связи
получаются в зависимости от того, какие взаимодействия электронов учитываются в первую
очередь; при этом образуются и различные линейные комбинации.
Если в первую очередь принимать во внимание лишь электростатические взаимодействия
(случай нормальной связи), то волновые функции будут характеризоваться, помимо значе-
ний квантовых чисел пД,, значениями квантовых чисел Z, mL и S, ms. В этом первом прибли-
жении энергия будет зависеть от квантовых чисел L и S. Лишь затем учитываются, во вторую
очередь, магнитные спин-орбитальные взаимодействия, и из функций составляются новые
линейные комбинации = 22 СуцФ^ которые соответствуют, при заданных L и S, различ-
д
ным значениям квантовых чисел J и mj. Два этапа решения задачи соответствуют схеме (9.3).
Если в первую очередь принимать во внимание лишь магнитные взаимодействия спи-
нового момента каждого электрона с орбитальным моментом этого же электрона (случай
связи (j,j)), то волновые функции ^д будут характеризоваться, помимо значений кванто-
вых чисел значениями квантовых чисел	j2,	jk, mjk. Тогда во вторую
очередь учитываются электростатические взаимодействия электронов4) и составляются новые
линейные комбинации волновых функций, соответствующие, при заданных j2, ..., j*,
различным J и тj. Два этапа решения задачи соответствуют схеме (9.6).
Промежуточные типы связи соответствуют порядку учета различных взаимодействий,
отличающемуся как от порядка в случае нормальной связи, так и от порядка в случае
связи (j, j) (ср. (9.9) или (9.10)).
При близости уровней энергии, соответствующих различным конфигурациям, нужно
также учитывать возможность того, что действительное состояние может описываться волно-
выми функциями, являющимися линейными комбинациями волновых функций, отвечающих
различным наборам квантовых чисел Это и будет «взаимодействие конфигурации», о ко-
тором упоминалось выше. «Взаимодействовать» могут лишь уровни энергии конфигураций
одной четности, имеющие одинаковые значения J, так как нельзя составлять линейные
комбинации функций различной четности или с различными значениями J5).
Подробное изложение квантовомеханической теории сложных спектров можно найти
в монографии Кондона и Шортли [14]. Волновые функции для простейшей двухэлектронной
системы — для атома гелия — будут рассмотрены нами ниже (см. § 10.2, с. 281).
§ 9.2. Общая характеристика нормальной связи
Нормальная связь, как самая важная, требует подробного рассмотрения. Это
рассмотрение естественно начать со случая двух электронов.
Сложение моментов 1\ и первого электрона с моментами 12 и «2 второго
электрона при нормальной связи происходит по схеме
Si + s2 = S, l{+l2 = L, L + S = Jy	(9.11)
представляющей собой частный случай схемы (9.3).
Проще всего произвести сложение спиновых моментов: согласно общему за-
кону векторного сложения, имеем sj = з2 = ‘/2, S = 0,1. S = 1 соответствует
3) Часть этого взаимодействия может быть учтена предварительно по методу Хартри (см. с. 200), путем
введения самосогласованного поля. Можно с самого начала исходить из антисимметризованных функций
типа (3.25) и находить самосогласованное поле с обменом по методу Фока (см. с. 202).
4) А также могут учитываться магнитные взаимодействия разных электронов.
5) Такие линейные комбинации соответствовали бы состояниям, которые не обладали бы определенной
четностью и определенными значениями J, а это противоречит тому, что четность и значения J являются
точными характеристиками состояния атома (см. с. 244).
§ 9.2. Общая характеристика нормальной связи
247
параллельной ориентации спинов, их величины складываются, S — 0 соответствует
антипараллельной ориентации спинов, их величины вычитаются, компенсируя друг
Друга.
Число возможных ориентаций вектора S по отношению к другому вектору
или внешнему полю равно 2S 4-1; это число к = 25 4-1 называют мультиплетностью.
В случае 5 = 0 имеем к = 1, и соответствующие уровни называют синглетными
или одиночными', при 5 = 1 к = 3, и соответствующие уровни называют триплетными.
При сложении орбитальных моментов получаются следующие значения орби-
тального квантового числа:
L = h+h- 1,.-. ,Ri -/2|,	(9.12)
т.е. 2^2 4- 1 значений при l\ I2 и 21 \ 4-1 значений при Ц fa.
Уровень с заданным L может быть в рассматриваемом случае синглетным (х = 1)
или триплетным (к = 3). Для различных конфигураций мы получаем, в соответствии
с (9.12), типы уровней, приведенные в табл. 9.1. Значения L = 0, 1, 2, 3,4, 5, 6
указаны буквами 5, Р, D, F, G, Н, 16\ аналогично обозначениям (6.4) для I,
а мультиплетность отмечена индексом слева сверху (см. § 8.3, с. 224).
Таблица 9.1
Термы двухэлектронных конфигураций при нормальной связи
h	h	Конфигурация	Термы	Число термов	Число уровней
0	0	S3	'5 3S	2	2
1	0	рз	Ip 3p	2	4
2	0	ds	'£> 3Z>	2	4
3	0	fs	}p 3p	2	4
1	1	рр	'SPD 3SPD	6	10
2	1	dp	'PDF 3PDF	6	12
3	1	fp	'dfg 3DFG	6	12
2	2	dd	'SPDFG 3SPDFG	10	18
3	2	fd	'PDFGH 3PDFGH	10	20
3	3	ff	'SPDFGHI 3SPDFGHI	14	26
Совокупность уровней с заданными значениями L и 5 мы будем называть
мультиплетным термом или просто термом. Таким образом, табл. 9.1 представляет
собой таблицу термов для двухэлектронных конфигураций при нормальной связи.
В таблице для сокращения места, как это принято, мультиплетность указывается
одним индексом для всех термов данной мультиплетности, например, вместо 3Р 3D 3F
пишут просто 3PDF.
Название «терм» применяют также для обозначения абсолютной величины энергии,
выраженной в см-1 и отсчитываемой от границы ионизации. Применение этого названия,
для обозначения совокупности уровней с заданными L и 5, что широко распространено
в литературе (см. книгу Кондона и Шортли [14]), не приводит к недоразумениям, тем
более, что мультиплетный терм характеризуется значениями термов (в смысле абсолютной
величины энергии) отдельных входящих в него уровней. Мы уже применяли в предыдущих
главах название «дублетный терм» для совокупности двух уровней с заданным значением L
и со значением S = ’/2 (* — 2S 4- 1 = 2), а также говорили об абсолютной величине энергии
уровня, выраженной в см-1 (или в единицах частоты), как о терме (ср. с. 21).
6)Далее, в порядке алфавита значения L — 7,8,9,10, 11, 12, 13, 14,... обозначаются буквами К, Ь,
М, N, О, Q, R,T, ... (с пропуском Р и S).
248
Глава 9. Основы общей систематики сложных спектров
Для конфигураций рр, dp и fp мы имеем, на основании (9.12), триады
термов SPD, PDF и DFG, для конфигураций dd и fd — пентады термов SPDFG
и PDFGH и для конфигурации ff — гептаду термов SPDFGHI.
Значения J при заданных L и S, т. е. значения J для отдельных уровней
мультиплетного терма, мы получаем, складывая L и S,
При S — 0 и J = L мультиплетный терм сводится к одному уровню —
синглетному. Мы имеем
J=L=°	123456
уровень 'So 'Р, 'D2 ]F3 te4 ‘Я5 'h
Согласно общепринятому обозначению, индекс справа снизу указывает значе-
ние J (см. с. 224).
При S — 1 и J = L + 1, L, L — 1 получается триплетный терм, состоящий из трех
уровней, за исключением случая L = 0, когда J — S и имеется лишь один уровень.
Мы получаем
L = 0	1	2	3	4	5	6 '	
	0	1	2	3	4	5	
J = 1	1	2	3	4	5	6	
	2 3Ро	3	4 3Р2	5	6	7 3/5	>	(9.14)
				^3	Зя4		
уровни 35|	3Р1	Зя2	3Рз	^4	Зя5	34	
	3Р2	Зв3	3Г4	^5	3Яб	% J	
Числа уровней, получающиеся для различных двухэлектронных конфигураций,
легко подсчитать; они приведены в последнем столбце табл. 9.1. Пример конфигура-
ции dp, дающей 12 уровней, уже был рассмотрен в предыдущем параграфе (см. с. 244).
При подсчете числа триплетных уровней нужно, разумеется, учитывать, что для три-
плетного терма 3S (L = 0) получается не три уровня, как при L 1, а лишь один.
Очень важен вопрос о расположении мультиплетных термов в зависимости
от значений S и L. Это расположение, как показывают теоретические расчеты
и огромный экспериментальный материал, относящийся к случаю нормальной
связи, определяется следующими общими правилами.
1. Положение термов определяется прежде всего значением спина S, т. е.
мультиплетностью к = 2S + 1, причем термы, как правило, лежат для данной
конфигурации тем глубже, чем больше 5, т. е. чем больше мульти пл етность.
2. Положение термов зависит, при заданном значении S, от L, причем термы
с большими значениями L имеют тенденцию лежать глубже термов с меньшими зна-
чениями L. Это особенно выражено для термов с наибольшей возможной для данной
конфигурации мультиплетностью.
Для рассмотренного случая двухэлектронных конфигураций, в соответствии
с этими правилами, триплетные термы лежат глубже синглетных, а из триплетных
термов глубже лежат уровни с наибольшими L. Например, для конфигурации 2р4р
углерода порядок термов, начиная с самых глубоких, следующий:
3D, 'Р, 3S, 3Р, }D, ]S.
Здесь триплетные термы лежат глубже одиночных, самым глубоким из триплетных
термов является терм 3D, термы 3D и XD лежат глубже термов 3S и lS соответственно.
§ 9.2. Общая характеристика нормальной связи
249
Первое правило очень хорошо выполняется для конфигураций, содержащих
s-электрон, ps, ds, fs. Термы ps 3Р лежат глубже термов ps ХР, термы ds 3D — глубже
термов ds XD, термы fs 3F — глубже термов fs lF.
Как уже указывалось выше (см. с. 244), зависимость энергии от S и L является
результатом электростатических взаимодействий электронов.
Таким образом, расположение термов в зависимости от значений спинового кван-
тового числа S и орбитального квантового числа L определяется электростатическими
взаимодействиями.
С первого взгляда этот результат может показаться неожиданным. С наглядной точки
зрения естественно себе представить, что положение уровней будет определяться магнитными
взаимодействиями моментов Ц между собой и моментов з: между собой, аналогичными
магнитным взаимодействиям моментов I и з отдельного электрона. Такие взаимодействия
действительно существуют, однако они очень малы. Решающую роль играет то обстоятельство,
что вид волновых функций существенно зависит от значений S и L, что связано со свойствами
симметрии, а именно с тем, что волновая функция системы электронов должна быть
антисимметричной относительно перестановки любых двух электронов (см. гл. 3, с. 75);
для случая атома гелия мы это покажем в дальнейшем, в гл. 10 (см. с. 283).
Можно произвести расчеты расположения термов для различных двухэлектронных кон-
фигураций, применяя приближенные методы учета электростатического взаимодействия элек-
тронов, которое имеет вид:
•к
(i<k)
где rik — расстояние между t-м и к-м электронами, и суммирование производится по всем
внешним электронам.
Результаты подобных расчетов для всех двухэлектронных конфигураций табл. 9.1 при-
ведены в монографии Кондона и Шортли [14] в гл. 7, где они сопоставлены с некоторыми
экспериментальными данными. В общем получается удовлетворительное согласие теории
с экспериментом. Расположение термов лишь в грубых чертах соответствует сформулиро-
ванным выше правилам. Эти правила значительно лучше выполняются для конфигураций,
состоящих из эквивалентных электронов, которые будут рассмотрены ниже (см. §9.3, с. 258).
Наборы термов для конфигураций, состоящих более чем из двух электронов,
можно определять, исходя из наборов термов для двухэлектронных конфигура-
ций (табл. 9.1), последовательно добавляя электроны — сначала третий, потом
четвертый и т. д. Получающиеся наборы при этом не зависят от порядка добавления
электронов, например, добавляется ли сначала р-электрон, а затем d-электрон,
или наоборот.
Наиболее важно знание значений мультиплетности х = 25 4- 1, как величины,
определяющей общее расположение уровней и число уровней в мультиплетном
терме. Рассмотрим поэтому в первую очередь возможные значения полного спина S
для системы, состоящей из заданного числа электронов.
При добавлении к двум электронам третьего спины складываются, согласно
схеме,
S' + s = S,	(9.16)
где S' — спиновый момент для двухэлектронной конфигурации, s — спиновый
момент добавляемого электрона, S — полный спиновый момент. Мы получаем
и
для 5 — 0, з = -	5 — -
2	2
/	1	3 1
для 5 = 1, з= 5 =	,
(9.17)
250
Глава 9. Основы общей систематики сложных спектров
т. е. значение S = 3Д встречается один раз и значение S = дважды. При S = *Д
х = 2S + 1 = 2, при S — 3/2 х = 25 + 1 = 4, поэтому мы имеем дублеты, уже
известные нам из рассмотрения одноэлектронных спектров, и квартеты. Добавление
четвертого электрона дает, по той же схеме (9.16), значения 5 — 0 (два раза), 5 = 1
(три раза) и 5 — 2 (один раз), соответствующие синглетам, триплетам и квинтетам.
1 электрон
2 электрона о
3 электрона
4 электрона
5 электронов
6 электронов
7 электронов
8 электронов
9 электронов
10 электронов 0 а 1 А 2 А 3 А 4 А 5
Синглеты | Триплеты|КвинтетыТ Септеты т Нонеты | Ундектеты
Дублеты Квартеты Секстеты Октеты Дектеты
Рис. 9.2. Схема возможных мультиплетностей
при различном числе электронов
Результат добавления электронов хорошо поясняет схема рис. 9.2. Максималь-
k
ный спин для системы, состоящей из к электронов, равен -, а максимальная
мультиплетность
к
х = - - 2+ 1 =	1.	(9.18)
Мы получаем при различных значениях числа электронов максимальные значения
полного спина и мультиплетности, приведенные в табл. 9.2.
Значению полного спина 5 = 0, не приведенному в таблице, соответствует
мультиплетность 1, т.е. синглеты (одиночники). Таблицу 9.2 можно и продолжить.
Однако максимальная мультиплетность, с которой практически приходится встре-
чаться, для наиболее сложных спектров — спектров редкоземельных элементов —
равна одиннадцати, что соответствует наличию десяти электронов с одинаково на-
правленными спинами (5 = 10 • !Д = 5; 25 4- 1 = 11)- Обычно же приходится иметь
дело с мультиплетностями, не превышающими, даже в случае спектров сложных
атомов, семи-восьми. Мультиплетность х обозначается, как мы уже указывали,
индексом у L слева сверху: 65, 4Р, 7D и т.д. Для нечетных термов (которыми явля-
ются все уровни, а следовательно, и все термы нечетных конфигураций, см. с. 212)
добавляется индекс «о» справа сверху, в то время как четные термы не отмечаются
дополнительными индексами.
Чрезвычайно важным является для спектроскопии следующая очевидная зако-
номерность, сразу бросающаяся в глаза при рассмотрении схемы рис. 9.2: при четном
§ 9.2. Общая характеристика нормальной связи
251
Таблица 9.2
Мультиплетности термов с различными S
Число электронов	Максимальное значение		Название термов
	полного спина S	мультиплетности х	
1	1 2	2	дублеты
2	1	3	триплеты
3	Э 2	4	квартеты
4	2	5	квинтеты
	5		
5	2	6	секстеты
6	3	7	септеты
	7		
7		8	октеты
8	Z 4	9	нонеты
	9		
9	2	10	дектеты
10	5	11	ундектеты
числе электронов спин принимает целочисленные значения и мультиплетностъ является
нечетной, при нечетном числе электронов спин принимает полуцелые значения и мулъти-
плетность является четной. Частный случай четной мультиплетности представляет
случай одного электрона, когда S — ]/2 и х = 2, т. е. получаются дублеты, как
для атома водорода и атомов щелочных металлов.
Система с четным и система с нечетным числом электронов, следовательно,
с целым и с полуцелым спином соответственно, в отношении некоторых спек-
троскопических свойств существенно отличаются друг от друга; это относится,
в частности, к их поведению в электрической поле (см. гл. 15, с. 408). Весьма важное
значение имеет то, что в зависимости от четности числа электронов в системе целым
или полуцелым является не только полный спин S, но и квантовое число J. Так
как L всегда целое, то при сложении полного орбитального момента L и полного
спинового момента S в полный момент атома J при целом S квантовое число J
является целым, а при полуцелом S — полуцелым. Таким образом, все уровни
атомов с четным числом электронов характеризуются целыми значениями J, а все
уровни атомов с нечетным числом электронов — полуцелыми значениями J, на что
мы уже указывали в конце §7.5 (с. 2137)).
Отметим еще одно важное обстоятельство. Так как при нечетном числе электро-
нов квантовое число J является полуцелым, то оно в этом случае не может равняться
нулю. Поэтому и магнитный момент такой системы будет отличен от нуля. В ре-
зультате, магнитным моментом, отличным от нуля, обладают все атомы с нечетным
числом электронов.
Устойчивые молекулы, как правило, имеют четное число электронов (причина этого
рассмотрена в гл. 24 и 26), и их магнитные моменты обычно равны нулю, нечетное же число
электронов встречается у разного рода радикалов; в ряде случаев радикалы можно обнаружи-
вать по их магнитным моментам методом парамагнитного резонанса (см. гл. 14, с. 404).
7) Этот результат, разумеется, не зависит от типа связи. Мы можем получить его и исходя из сложения
моментов по схеме связи (j, j) или по любой иной схеме. Квантовые числа ji для отдельных электронов
всегда полуцелые, и сложение четного числа векторов j дает целые значения J, а сложение нечетного
числа таких векторов — полуцелые значения J.
252
Глава 9. Основы общей систематики сложных спектров
Легко найти число уровней в мультиплетном терме. При заданном значении
спина S для терма с заданным значением L получаются, согласно (2.24) (где J\ = L,
J2 — 5), значения квантового числа J, определяющего полный момент J = L + S,
J = £ + 5, £ + 5- 1,...,|£-5|,	(9.19)
т. е. 25+1 значений при L S и 2L + 1 значений при L < 5. В последнем
случае мы имеем неполные мультиплетные термы с числом уровней, меньшим
чем 25 + 1; в частности, при L — 0 (для 5-термов) получается лишь один уро-
вень (см., например, (9.13)). В табл. 9.3 приведено число уровней в мультиплетных
термах при значениях 5 от х/2 до 4 и значениях L от 0 до 6. Максимальное число
уровней, равное 25+1, получается только для термов с L 5. Таким образом,
мулыпиплетностъ к = 2S + 1 определяет максимальное число уровней в мультиплетных
термах с заданным значением спина S.
Таблица 9.3
Число уровней N в мультиплетных термах
L	Дублеты ч		Триплеты S = 1		Квартеты		Квинтеты S = 2		Секстеты		Септеты S = 3		Октеты 4		Нонеты S = 4	
					S =	3 2			S =	5 2						
	терм	N	терм	N	терм	N	терм	N	терм	N	терм	N	терм	N	терм	N
0	2S	1	3S	1	fe	1	fe	1	fe	1	fe	1	fe	1	fe	1
1	2Р	2	Зр	3	fe	3	fe	3	fe	3	fe	3	fe	3	fe	3
2	2d	2	3D	3	fe	4	fe	5	fe	5	fe	5	fe	5	fe	5
3	2f	2	3F	3	fe	4	fe	5	fe	6	fe	7	fe	7	fe	7
4	fe	2	fe	3	fe	4	fe	5	fe	6	fe	7	fe	8	fe	9
5	2Н	2	3H	3	fe	4	fe	5	fe	6	fe	7	fe	8	fe	9
6	2I	2	3I	3	fe	4	fe	5	fe	6	fe	7	fe	8	fe	9
Более подробно важный вопрос о мультиплетных термах рассмотрен ниже
(см. §9.5).
Разберем теперь вопрос о значениях L полного орбитального момента £ для кон-
фигураций, содержащих более двух электронов в незаполненных оболочках. Эти
значения определяются, согласно схеме, аналогичной схеме (9.16) для сложения
спиновых моментов. Мы имеем:
L' +1 = L,	(9.20)
где L1 — орбитальный момент для исходной конфигурации, I — для добавляемого
электрона, L — полный орбитальный момент. В качестве исходной конфигурации
берется сначала двухэлектронная конфигурация, затем трехэлектронная и т.д.
Например, добавление р-электрона (неэквивалентного) к конфигурации dp
(см. табл. 9.1) дает
L' = 1,2,3;	/ = Г, £ = 0,1,2; 1,2,3; 2,3,4.	, п
(термы PDF)	(1 + 1) (2+1) (3+1)
Получаются значения L = 0 (один раз), L = 1 (два раза), L = 2 (три раза), L = 3 (два
раза), L = 4 (один раз), что обозначается как SPDFG] здесь цифры под буквами
указывают, сколько раз встречается данный терм, причем единица не указывается.
Легко проверить, что тот же набор получится, если добавить к конфигурации рр
d-электрон. Мультиплетность термов определяется сложением спиновых моментов,
§ 9.2. Общая характеристика нормальной связи
253
как было описано выше, т. е. получаются два раза дублеты и один раз квартеты
(см. (9.17)). В результате окончательно имеем для конфигурации dpp набор термов
2SPDFG 4SPDFG	(9.22)
24642	232
Мы видим, что уже при трех электронах получается сложный набор уровней,
причем термы каждого типа повторяются по несколько раз, например, дублетные
термы 2Р и 2F четыре раза, а терм 2D даже шесть раз. При этом каждый дублетный
терм является двойным (за исключением терма 2S), а каждый квартетный терм —
четверным (за исключением простого терма 4S и тройного терма 4Р; в последнем
случае S — 3/г, L — 1 и J — 5/г, 3/2, ’/г). Общее число уровней легко получить,
если просуммировать число дублетных уровней и число квартетных уровней. Мы
получаем 21 + (4 + 6 + 4 + 2)-2+11+2-3 + (3 + 2+1) -4 — 65 уровней.
Легко определить полное число состояний, соответствующих данной конфигурации.
Для электрона с заданным I мы имеем 2(2/ 4-1) состояний (см. §6.1, с. 165). Для электрон-
ной конфигурации, состоящей из к неэквивалентных электронов, можно любым образом
комбинировать состояния отдельных электронов и каждой комбинации соответствует новое
состояние системы. Общее число состояний будет равно произведению
к
П 2(21, + 1).	(9.23)
1=1
Например, для конфигурации dpp получается 10-6-6 = 360 состояний, что легко проверить
непосредственным подсчетом, учитывая, что уровень с заданным значением J имеет степень
вырождения 2/4-1; при этом возможные значения J для каждого мультиплетнопо терма
сразу получаются из формулы (9.19) по известным значениям L и S.
Подсчет общего числа состояний, соответствующего данной конфигурации, подобным
методам и сравнение полученного числа со значением, даваемым формулой (9.23), явля-
ется хорошим контролем правильности определения набора термов для рассматриваемой
конфигурации.
В заключение данного параграфа мы остановимся на правилах отбора для случая
нормальной связи.
В дополнение к общим правилам отбора для переходов между уровнями одина-
ковой и разной четности (см. (4.153) и (4.154)) и правилам отбора для квантового
числа J (см. (4.156) и (4.157)) получаются приближенные правила отбора для кван-
товых чисел L и S.
При дипольных переходах квантовое число S не меняется
Д5 - 0,	(9.24)
а квантовое число L может изменяться на 0 и на ±1:
Д£ —0, ±1.	(9.25)
Правило отбора (9.24) запрещает переходы между термами различной муль-
типлетности — интеркомбинационные переходы. Оно выполняется тем лучше, чем
легче атом. Для тяжелых атомов интеркомбинационные переходы происходят и при-
том со значительными вероятностями. Нарушение правила отбора (9.24) связано
с наличием спин-орбитального взаимодействия, которое мало для легких атомов
и становится значительным для тяжелых.
Правило отбора (9.25) нарушается тем сильнее, чем больше отступления от нор-
мальной связи.
254
Глава 9. Основы общей систематики сложных спектров
Правило отбора (9.24) справедливо (в той степени, в которой оно не нарушается
наличием спин-орбитального взаимодействия) и для магнитного дипольного и ква-
друпольного излучений (а также для излучений более высокого порядка). Правило
отбора (9.25) справедливо и для магнитного дипольного излучения, а для квадру-
польного излучения оно заменяется следующим условием:
Д£ = 0, ±1, ±2.	(9.26)
§ 9.3. Термы конфигураций, состоящих из эквивалентных электронов
Определение набора возможных термов непосредственно путем применения ме-
тода векторного сложения моментов возможно лишь в том случае, если все электроны
разные, иначе говоря, если нет эквивалентных электронов, т. е. электронов с совпада-
ющими значениями квантовых чисел пи/. Метод векторного сложения неприменим
к случаю эквивалентных электронов, не полностью заполняющих соответствующую
оболочку (случай полностью заполненных оболочек, для которых все моменты рав-
ны нулю, нас сейчас не интересует). Рассмотрение конфигураций эквивалентных
электронов чрезвычайно важно. Эквивалентные электроны имеются для нормальных
конфигураций всех элементов с заполняющимися р-, d- и /-оболочками (при запол-
нении этих оболочек не менее чем двумя электронами). Примером могут служить
конфигурации углерода, содержащие два или три электрона 2р (см. с. 242), в частно-
сти, его нормальная конфигурация ls22s22p2 и возбужденная конфигурация l«s22<s2p3.
Только случай двух эквивалентных электронов ns является тривиальным, так как
они полностью заполняют соответствующую 5-оболочку.
Неприменимость метода векторного сложения к эквивалентным электронам
является следствием принципа Паули. Не все термы, которые для эквивалентных
электронов получились бы по методу векторного сложения, удовлетворяют прин-
ципу Паули. При учете принципа Паули для незаполненных оболочек, содержащих
эквивалентные электроны, число возможных термов меньше, чем получающееся путем
векторного сложения.
Например, для конфигурации р2 из шести термов ]SPD 3SPD, получающихся
для конфигурации рр (см. табл. 9.1), оказываются возможными лишь три тер-
ма lSD 3Р, для конфигурации d2 из десяти термов *SPDFG 3SPDFG конфи-
гурации dd остается пять термов lSDG3PF и для конфигурации /2 из четыр-
надцати термов \SPDFGHI3SPDFGHI конфигурации // остаются лишь семь
термов XSDGI3PFH. Иначе говоря, остаются лишь синглетные термы с четным L
и триплетные термы с нечетным L.
Можно определить наборы термов для всех конфигураций, состоящих из экви-
валентных электронов с заданным значением I. Результаты такого определения
содержатся в табл. 9.4, 9.5, 9.6 для р-, d-, /-электронов соответственно8). При этом
оказывается, как можно показать в общем виде, что для оболочки, в которой не хва-
тает до полного заполнения некоторого числа электронов, получается тот же набор
термов, что и для оболочки, содержащей это число электронов. Таким образом, одина-
ковые наборы термов получаются для оболочек, дополнительных друг другу, в одной
из которых имеется к электронов, а в другой к свободных мест, т. е. к' — 2(21 + 1) - к
электронов. Например, для р-электронов [2(21 + 1) — 6] одинаковые наборы термов
получаются для конфигураций р2 и р4. Особенно существенно, что для оболочки,
в которой не хватает для полного заполнения только одного электрона, получается
8> Об обозначениях см. с. 247 и 252.
§ 9.3. Термы конфигураций, состоящих из эквивалентных электронов 255
Таблица 9.4
Термы конфигураций, состоящих из эквивалентных р-электронов
Конфигурации	Термы	Число	
		термов	уровней
Р и р5	2р.	1	2
Р2 и р4	'SD	3Р	3	5
р3	2PD°	45°	3	5
Таблица 9.5
Термы конфигураций, состоящих из эквивалентных d-электронов
Конфигурации	Термы	Число	
		термов	уровней
d и d9	2d	1	2
d2 и d8	'.SDG	3PF	5	9
d3 и d7	2pdfgh	4pf 2	8	19
d4 и d6	'SDFGI 3PDFGH 3D 2 2	2	2	2	16	34
d5	2spdfghi 4pdfg 6s 3 2 2	16	37
такой же терм 2Р, 2D, 2F (для р-, d-, /-электронов соответственно), как и для од-
ного электрона. В табл. 9.4, 9.5 и 9.6 каждый набор термов соответствует, кроме
случая оболочки, заполненной как раз наполовину (т.е. 21 4- 1 электронами), двум
конфигурациям, дополнительным одна к другой.
Наибольшее число термов получается для оболочек, заполненных наполовину,
т. е. 21 4- 1 электронами, и для оболочек, в которых число электронов на единицу
больше или меньше, чем 2/4-1. В таблице приведено как общее число термов, так
и полное число уровней энергии; последнее является наибольшим для оболочек,
заполненных наполовину.
Определение возможных термов конфигураций, состоящих из эквивалентных
электронов, производится по методу сложения проекций (см. § 2.4, с. 53), ко-
торый позволяет легко учесть принцип Паули. Для этого составляются проек-
k	к
ции mL = 52 mk и ms = 52 полного орбитального и полного спинового момен-
:=1	i=l
тов; набор значений mL от L до -L (2L 4-1 значений) и ms от S до -S (25 4-1 зна-
чений) соответствует терму с заданными L и S. При составлении пц и ms берутся
только те наборы значений тц, mS}', mi2, mS2, ...\ mik, mSk, которые удовлетво-
ряют принципу Паули. Кроме того, наборы, отличающиеся только перестановкой
квантовых чисел электронов, считаются за один; этим учитывается неразличимость
электронов. Как известно, в квантовой теории электроны считаются неразличимыми,
а состояния, отличающиеся лишь перестановкой электронов, тождественными.
Рассмотрим применение этого метода для определения возможных термов
в простейшем случае конфигурации р2. Мы имеем при п\ =П2,1\ = li — 1 значения
Таблица 9.6
Термы конфигураций, состоящих из эквивалентных /-электронов
Конфигурации	Термы	Число	
		термов	уровней
/И/'3		1	2
/2 и /12	}SDGI	3PFH	7	13
/’и/"	2pdfghikl°	4sdfgi° 2 2 2 2	17	41
Г и /10	'SDFGHIKLN	3PDFGHIKLM	sSDFGI 24	423	2	3243422	47	107
/5И/9	2pdfghiklmno°	4spdfghiklm°	6pfh° 457675532	2344332	73	198
/и/8	'SPDFGHIKLMNQ 3PDFGHIKLMNO	5SPDFGHIKL	2F 4	648473422	659796633	32322	119	295
г	2spdfghiklmnoq° 4spdfghiklmn°	6PDFGHI° 2 5 7 1010 997542	226575533	119	327
ю
Ln
О
Глава 9. Основы общей систематики сложных спектров
§ 9.3. Термы конфигураций, состоящих из эквивалентных электронов 257
проекций
хпц — 1,0, -1,	m/2 — 1, 0, -1,
11 11
s, 2,	2,	s2 2>	2
Возможные значения mL и ms будут (ср. табл. 2.2 и 2.3, с. 53, 54)
(9.27)
При т8] = mS2 = ’Л (т.е. ms = 1) и при mSl = mS2 = -1/? (т.е. ms = -1), со-
гласно принципу Паули, Ф mi2, т. е. в таблице для mL исключаются диагональные
значения 2, 0, -2, взятые в скобки. Кроме того, значения, симметричные отно-
сительно диагонали, отличаются только перестановкой квантовых чисел и т/2
и должны учитываться лишь один раз (например, для = 1 имеем наборы тц — О,
mi2 = 1 и тц — 1, mi2 = 0 при mS[ = mS2, l\ — l2, n} — n2, соответствующие одному
и тому же квантовому состоянию). В результате получаем набор (1) (mL = 1, О, -1),
отделенный в (9.27) пунктиром. При mSi — ’/2, mS2 = - ’/2, ms = 0 возможны все
значения mL, и мы, аналогично табл. 2.3, получаем наборы (2) (mL — 2, 1,0, -1, —2),
(1) (mj, = 1,0, -1) и (0) (mi = 0), отделенные сплошными линиями. Прк mSi = - xj2,
mS2 = ’/2, ms = 0 мы не будем иметь новых состояний, так как при этом получаются
наборы, отличающиеся лишь перестановкой электронов.
В результате находим
при ms = 1
при ms — 0
при ms = -1
набор
наборы (2)
набор
(1)
(1)
(1)
(9.28)
Набор (1) при ms = 1, 0, -1 дает терм 3P(L =1,5= 1), наборы (2) и (0) при ms = 0
дают термы ]D и ’5. Таким образом, для конфигурации р2 мы получаем термы
]SD 3Р,	(9.29)
приведенные в табл. 9.4.
Аналогичным в принципе способом можно определить возможные термы для любой
конфигурации, состоящей из эквивалентных электронов [221, 15]. Только в случае сложных
конфигураций вычисления становятся более громоздкими.
При этом для дополнительных конфигураций получаются те же наборы значений
и ms и, следовательно, те же наборы термов. Это связано с тем, что каждой паре значений
к	к	к1
mL =	= УЗ mSt для к электронов соответствует пара значений m'L = УЗ mit — ~mL,
i=i	i=i	t=i
к’
m's = УЗ mst = ~ms для к1 = 2 (21 4- 1) - к электронов. Поясним это на простейшем
j=i
примере конфигураций р и р5. Согласно табл. 6.1 (с. 166), мы имеем шесть возможных пар
9 Зак.103
258	Глава 9. Основы общей систематики сложных спектров
VI
J	(9.30)
2
значений тщ, ms для р-состояний
1 II 111 IV V
mi	1	10	0-1
1	_1 1	_1 1
т’	2	2 2	~2	2
Один р-электрон может занимать любое из этих состояний, и мы имеем набор mi = 1,0, —1
при ms = |, что дает терм 2Р°(Ь = 1,5 = |). Для пяти р-электронов будет занято пять
состояний из шести. Если свободно состояние 1, то электроны занимают состояния II, HI, IV,
5	5
V, VI, суммирование по которым дает m'L = У2 = 14-0 + 0-1-1 = — 1 и ms = УЗ mst =
t=i	t=i
+	+	значения mL = mi = 1 и ms = ms = | для состояния I, взятые
с обратным знаком и совпадающие со значениями т/, ms для состояния VI. Если свободно
состояние 11, то m'L = -1, m!s = |, что совпадает со значениями тщ, ms для состояния V, и т.д.
В итоге мы получим те же шесть пар значений проекций I, 11, Ill, IV, V, VI, только взятые
в обратном порядке, что, разумеется, несущественно. Таким образом, для конфигурации р5
будем иметь только терм 2Р°.
Для контроля правильности составления табл. 9.4-9.6 можно произвести подсчет числа
состояний, соответствующих заданной конфигурации lk. Это число состояний получится,
если для каждого терма учесть все возможные уровни (25 + 1 уровней при L S и 2L + 1
уровней при L < 5) и степень вырождения 2 J + 1 этих уровней. С другой стороны, для одного
электрона с заданным I мы имеем г — 2(21 + 1) возможных состояний, а для к эквивалентных
электронов нужно комбинировать эти состояния, что можно сделать, при учете принципа
Паули, Ск способами, где Ск — число сочетаний по к из г. Как известно,
r kl(r - fc)!‘
Например, для конфигурации р2 мы должны брать сочетания по 2 из 6 состояний (9.30), что
дает Cl = 15. Действительно, для терма 3P(L = 1,5 = 1) мы имеем значения J = 0, 1,2,
что дает 1 + 3 + 5 состояний, а для термов ’5(J = L = 0, 5 = 0) и lD(J = L = 2, 5 = 0)
1 + 5 состояний; всего получаем 15 состояний.
Рассмотрим некоторые особенности табл. 9.4-9.6.
Значение максимальной мультиплетности для оболочек, заполненных не более
чем наполовину (к 21 + 1), в соответствии с (9.18) равно к + 1 и является
таким же для дополнительных к ним оболочек, заполненных более чем наполовину.
Наибольшее возможное значение мультиплетности, равное (21 + 1) + 1 = 2(1 + 1),
получается для оболочек, заполненных как раз наполовину, а именно р3(х = 4),
d5(x — 6) и /7(х = 8).
При четном к мультиплетность нечетная, при нечетном к — четная. Более
подробно на этом вопросе мы остановимся в §9.6 (см. с. 264), а сейчас разберем
вопрос о числе возможных термов наибольшей мультиплетности.
Таблицы показывают, что для ряда конфигураций число получающихся тер-
мов весьма велико. Особенно велико оно для конфигураций, содержащих от 4
до 10 /-электронов. При этом, однако, число термов максимальной мультиплетно-
сти невелико и не превышает пяти, а для конфигураций /6, /8 и /7 имеется только
один терм максимальной мультиплетности, в последнем случае состоящий из одного
уровня 85°7/ (L = 0, 5 = J = 7/г). Наличие единственного уровня наибольшей муль-
типлетности, вообще, характерно для оболочек, заполненных как раз наполовину.
Для оболочки d5 мы имеем уровень 655д, а для оболочки р3 уровень 45у2.
Расположение термов для конфигураций, состоящих из эквивалентных электро-
нов, обычно находится в соответствии с общими правилами, сформулированными
§ 9.4. Термы смешанных конфигураций
259
выше (см. с. 248). Термы лежат тем глубже, чем больше мультиплетность. При задан-
ном S термы с большими L, имеют тенденцию лежать глубже термов с меньшими L.
Эти правила, вообще говоря, выполняются лучше, чем для конфигураций, состоящих
из неэквивалентных электронов.
Причиной лучшего выполнения правил является то, что эквивалентные электроны
взаимодействуют между собой сильнее, чем неэквивалентные электроны, и для них электро-
статические взаимодействия играют решающую роль. Связь моментов близка к нормальной.
Очень важным является более частное правило Гунда [12, 7, 13], всегда выполня-
ющееся для конфигураций, состоящих из эквивалентных электронов: самый глубокий
терм обладает наибольшей мультиплетностью и наибольшим возможным, при заданной
мультиплетности, значением L. Это эмпирическое правило подтверждается и тео-
ретическими расчетами. Самые глубокие термы, получающиеся, согласно правилу
Гунда, для конфигураций, состоящих из эквивалентных электронов, приведены
в табл. 9.7.
Таблица 9.7
Самые глубокие термы конфигураций, состоящих из эквивалентных электронов
Конфигурации	р р3	р2 РА	р3		d		d2 d8		d3 d7		d* d6		d5
Термы		Зр	4S°		2d		3F		af		5D		6S
Конфигурации	f f'3	f fn		f3 f"		fA /l0		fS		f6 f		f	
Термы	2р°	Зн		4jo		5I		6H°		if		8S°	
Особенно резко правило Гунда проявляется, когда имеется только один терм
наибольшей мультиплетности, т. е. когда при наибольшем S возможно лишь одно
значение L. Такие термы в табл. 9.7 выделены жирным шрифтом. Они лежат зна-
чительно глубже всех остальных термов данной конфигурации. Примером может
служить основной терм Fe 3d64s2 5Z>, лежащий почти на 20000 см-1 глубже следую-
щего терма 3d64s2 3Р той же конфигурации (см. рис. 12.5, с. 333). Особенно глубоко
лежат термы 4S°, и 8S° конфигураций р\ ds и f1, соответствующих оболочкам,
заполненным как раз наполовину.
Как показывают данные для основных уровней атомов, правило Гунда выпол-
няется для всех нормальных конфигураций типа pk, dk и fk (какой именно уровень
основного терма является самым глубоким, см. ниже, с. 263).
§ 9.4. Термы смешанных конфигураций,
содержащих эквивалентные электроны
Для элементов с заполняющимися р-, d- и /-оболочками, наряду с конфигу-
рациями, состоящими только из эквивалентных электронов, обычно существенную
роль играют конфигурации смешанного типа. Эти смешанные конфигурации со-
держат, помимо некоторого числа к эквивалентных электронов, другие электроны,
обычно один или два. Примером могут служить конфигурации атома углерода, полу-
чающиеся при возбуждении одного из электронов 2s (см. с. 242); они содержат, поми-
мо группы 2р2, два неэквивалентных электрона 2s и nl (п = 3,4, 5,...; I = 0,1, 2,...).
Термы смешанных конфигураций легко получаются по схеме
= Д S' + s = S,	(9.32)
9
260
Глава 9. Основы общей систематики сложных спектров
где I/ и S' относятся к исходной конфигурации, а I и s к добавляемому электрону.
Схема применяется к каждому терму исходной конфигурации с заданными L' и S'.
В случае конфигурации типа nlkn'l' за исходную берется конфигурация, состо-
ящая из к эквивалентных электронов nl.
Наиболее простым является часто встречающийся случай конфигурации ти-
па nlkn's, когда добавляется s-электрон. Из каждого терма с заданным L конфи-
гурации nlk мультиплетности х1 возникает два терма с тем же Д мультиплетно-
стей х1 4- 1 и х' — I. Примером может служить возбужденная конфигурация атома
кислорода 2p33s. Из термов 45°, 2D° и 2Р° конфигурации 2р3 (см. табл. 9.4, с. 255)
возникают термы 5S°, 35°, 3Z>°, [D° и 3P°, {P° соответственно (L не изменяется,
S = S’ ± ’/2, следовательно, x = 2S 4- 1 = 2(5' ± »/2) 4- 1 = 25' 4- 1 ± 1 = x' ± 1).
Существенно, что расположение термов получившейся конфигурации обычно
соответствует расположению термов исходной конфигурации, причем термы с х =
х' 4- 1 (5 = S' 4- ’/2) лежат ниже, чем термы с х — х' - 1 (5 = 5'- У2), возникшие
из того же исходного терма. Исходный терм указывают в скобках после символа
исходной конфигурации. Для конфигурации 2p33s имеем соответственно в полной
записи
Г 2р3 (4S°) 3s 5S° ( 2р3 (2D°) 3s 3Р° f 2p3 (2P°) 3s 3P°
t 2p3 (4S°) 3s 3S° t 2p3 (2D°) 3s lD° 1 2p3 (2P°) 3s 'P°
На рис. 9.3 положение термов конфигурации 2p33s нейтрального атома кисло-
рода (О I) сопоставлено с положениями термов конфигурации 2р3 однократно заря-
женного положительного иона кислоро-
да (О II), которые можно рассматривать
как исходные. Как видно из рисунка, со-
поставление получающихся термов О I
с исходными термами О II имеет ре-
альный физический смысл. Это связано
с тем, что взаимодействие эквивалентных
электронов 2р3 между собой, приводящее
к возникновению термов 45°, 2D° и 2Р°,
велико по сравнению с взаимодействием
этих электронов с электроном 3s, при-
водящим к возникновению термов 55°,
2Р----------
40467
2D----------
26815
(9.33)
40918 1р
----------3Р
38920
27662
26145
3d
D
1795
5
°	-1232	5
О II	0 1
Рис. 9.3. Сопоставление положения термов
конфигурации 2р33$ О I с термами исходной
конфигурации 2р3 О II
45
При добавлении к конфигурации nlk
р-, d- и /-электрона из каждого терма
с данным L' возникают соответственно
триады, пентады и гептады термов, при-
веденные в табл. 9.8. При этом из терма
мультиплетности х' возникают термы мультиплетности х = х' 4- 1 и х = х' — 1, что
удваивает число термов (кроме случая х' — 1, х — 2, когда из синглетных термов
получаются только дублетные).
Термы, получающиеся при добавлении еще одного неэквивалентного электрона nV,
легко находятся повторным применением схемы (9.32), причем исходным термом является
терм конфигурации nlknfl' и может применяться табл. 9.8. Термы получающейся конфигу-
рации пМп'Т могут быть найдены и путем добавления электронов в обратном порядке.
Рационально добавлять электроны в соответствии с их прочностью связи, чтобы получить со-
ответствие с действительным расположением термов. Обычно в таблицах уровней приводится
§ 9.5. Мультиплетное расщепление
261
Таблица 9.8
Термы, возникающие из термов исходной конфигурации с заданными значениями L'
Добавляемый электрон	Исходный терм				
	S	Р	D	F	G
Р	Р	SPD	PDF	DFG	FGH
d	D	PDF	SPDFG	PDFGH	DFGHI
f	F	DFG	PDFGH	SPDFGHI	PDFGHIK
терм, получающийся после присоединения более прочно связанного электрона, и указывается,
вслед за символом второго присоединяемого электрона, окончательный терм.
Примером присоединения двух электронов к конфигурации, состоящей из эквивалент-
ных электронов, являются возбужденные термы Мп I, имеющего нормальную конфигура-
цию 3d54s2. При возбуждении электрона 4s получается конфигурация 3d54s4p, самые глубокие
термы которой возникают из терма 3d5(6S)4s7S Мп II. Мы получаем термы 3d5 4s (7S) 4р 8Р°
и 3d54s(7S)4p6P°. Выше лежат термы 3d54s(5S)4p6P° и 3d54s(5S)4p4P°, возникающие из тер-
ма 3d5(6S)4s5S Мп И.
Если имеется смешанная конфигурация, состоящая из двух групп эквивалентных элек-
тронов, то ее термы определяются по более общей схеме:
L' + L" = L, S' + S" = S,	(9.34)
где Z', S' и Z", S" относятся к исходным термам этих групп. Примером может слу-
жить конфигурация 3d54p2 Мп I, для которой самый глубокий терм получается добавлением
к самому глубокому терму 6S (L’ = О, S' = 5Д) конфигурации 3d5 самого глубокого тер-
ма 3Р (L" = 1,S" = 1) конфигурации 4р2. Это будет терм 8Р (L = L" — 1, S = S' 4- S" = 7/2).
§ 9.5. Мультиплетное расщепление
Зависимость энергии от квантового числа J при заданных L и S определя-
ет мультиплетное расщепление, частным случаем которого является рассмотренное
в гл. 8 (см. § 8.3) дублетное расщепление. О мультиплетном расщеплении часто
говорят как о тонкой структуре, хотя она является действительно тонкой лишь
для легких атомов, а для тяжелых атомов составляет сотни и тысячи см~’. При-
чиной мультиплетного расщепления является, как и в частном случае дублетного
расщепления, магнитное взаимодействие спиновых и орбитальных моментов.
Энергия магнитного спин-орбитального взаимодействия в случае нормальной
связи пропорциональна скалярному произведению моментов L и S; она может быть
представлена, согласно общим формулам (2.79) и (2.83), в виде
Elsj = A(LS) = C(L, S)(LS) = C(L, S) J(<+ 9-~	~ 5(5 +	(9.35)
где ({L, S) = A — фактор мультиплетного расщепления, зависящий от значений L
и S и определяющий абсолютную величину мультиплетного расщепления.
Расстояние между соседними уровнями с квантовыми числами J и J 4-1 будет
равно
Elsj+i - Elsj —	S)(J + 1),	(9.36)
т. e. пропорционально большему квантовому числу. Это дает правило интервалов', рас-
стояние между соседними уровнями мультиплетного терма пропорционально большему
квантовому числу J.
262
Глава 9. Основы общей систематики сложных спектров
Примером могут служить триплетные термы 3Р и 3D (рис. 9.4). Согласно
правилу интервалов, расстояние 3Р2—3Р\ вдвое больше расстояния 3Р\ — 3Ро, а рас-
стояние 3Dy—3D2 в полтора раза больше расстояния 3D2~3D\.
3
Рис. 9.4. Правило интервалов для термов 3Р и 3D
Общая ширина мультиплетного терма, т. е.
L 4- S и с J = \L - 5|, равна
Выполнение правила интер-
валов служит одним из критери-
ев близости связи к нормальной.
Обычно оно хорошо оправдыва-
ется для глубоких термов, осо-
бенно для глубоких термов кон-
фигураций, состоящих из экви-
валентных электронов. Хотя пра-
вило интервалов и является при-
ближенным, но оказывает суще-
ственную помощь при рассмо-
трении расположения уровней и
при группировке их в мульти-
плетные термы9).
расстояние между уровнями с J =
<(L,S)[(L +S) +(£ + S- 1) + ... + (|£ — 5| 4-1)],
что дает
«L,S)(2L+l)S при
£(L, S)(2S + \)L при S. J	{ ' '
Для термов 3P и 3Z> мы получаем, согласно (9.37), общую ширину 3£(3Р)
и 5С(3Р).
Факторы мультиплетного расщепления £(£, 5) терма, возникающего из неко-
торой конфигурации	, nrlr, состоящей из г электронов, могут быть
выражены через факторы дублетного расщепления (см. (8.14)), относящиеся
к отдельным электронам, образующим данную конфигурацию [13, 15]. Это позволя-
ет, зная Q, находить £(£, 5) и, обратно, из опытных значений £(£, 5) определять £п/
для отдельных электронов.
Особенно простое соотношение имеется между £(Д5) и fa для всех тер-
мов максимальной мультиплетности конфигураций, состоящих из эквивалентных
электронов. В этом случае (для конфигураций типа nlk, где к < 21 4- 1)
<(Д5макс) = —— fa.	(9.38)
^^макс
Например, для конфигураций d2, d3 и d4 (см. табл. 9.5) получается £ =
1	/	3\	1
для термов 3PF (SMaKC = !),< = -fa Для термов 4PF \Sмакс — 2 ) И С —
для терма 5D (5макс = 2) соответственно.
Для конфигураций, состоящих из эквивалентных электронов, имеется очень
простое общее соотношение для факторов расщепления дополнительных друг к дру-
гу конфигураций nlk и nlk (k + k1 = 2(21 4-1), см. § 9.3, с. 254), для которых, как мы
Можно уточнить формулы для мультиплетного расщепления, если учесть магнитные взаимодействия
спинов различных электронов между собой [216]. Это позволяет объяснить ряд отступлений от правила
интервалов.
§ 9.6. Мультиплеты в спектрах
263
видели, получается тот же набор термов. Факторы расщепления £(£, S) для одина-
ковых термов этих конфигураций одинаковым образом выражаются через £п/, только
с противоположными знаками.
Для конфигурации nlk (k < 21 + 1, заполнение оболочки меньше, чем наполо-
вину) £(£, 5), как правило, положительно, и поэтому в мультиплетном терме уровни
лежат тем/выше, чем больше J (см. (9.36)); самым глубоким является уровень
с наименьшим J. Такие мультиплетные термы называют нормальными. Для конфигу-
рации nlk (k' = 2(214-1) - k > 214-1, заполнение оболочки больше, чем наполовину)
£(£, S) обратно по знаку, т. е., как правило, отрицательно, и поэтому в мультиплет-
ном терме уровни лежат тем выше, чем меньше J; самым глубоким является уровень
с наибольшим J. Такие мультиплетные термы называют обращенными.
Формула (9.38) относится к оболочкам, заполненным меньше, чем наполови-
ну; для оболочек, заполненных больше, чем наполовину, будет, согласно общему
правилу, стоять знак минус. Поэтому
С(Д5макс) = -——Сы	(9.39)
^макс
(конфигурация типа nlk , А/ > 2/ 4-1).
Основным уровнем для конфигураций типа nlk (k < 2/4-1) будет уровень
самого глубокого терма с наименьшим возможным J, а для конфигураций ти-
па nlk (k1 > 2/4-1) — уровень самого глубокого терма с наибольшим возможным J. Это
правило в сочетании с правилом Гунда, рассмотренным нами в §9.3 (с. 259), позво-
ляет определить основной уровень атомов всех элементов, для которых происходит
заполнение р-, d- и /-оболочек. Как показывают опытные данные, основные уровни
во всех известных случаях находятся в соответствии с этим правилом. Например,
у V (Z = 23) с нормальной конфигурацией 3d3 и самым глубоким термом 4F основ-
ным уровнем является (L = 3, S = 3/i^J = L-S= 3/г), а у Со (Z = 27) с допол-
нительной конфигурацией 3d7 и с таким же самым глубоким термом 4F основным
уровнем является (L — 3, S = 3/г, J = Ь4-5 = 9Л)« В первом случае оболочка 3d
заполнена меньше, чем наполовину, во втором — больше, чем наполовину.
Отметим, что для оболочки п1к, где k = 214-1, заполненной как раз наполовину
и являющейся дополнительной по отношению к самой себе, £(£, S) = -((L'S),
т.е. ((Д5)=0и, следовательно, термы не должны расщепляться. Этот результат
является лишь приближенным, как и все рассмотрение спин-орбитального взаи-
модействия. В действительности расщепление имеет место, но, как правило, оно
невелико, гораздо меньше, чем расщепление термов для оболочек п1к, где k 214-1.
Для термов смешанных конфигураций, рассмотренных в предыдущем параграфе, можно
одновременно с их нахождением по схеме (9.34) определять и факторы расщепления £(£, S)
через факторы расщепления ((£',5') и ((£",5") для исходных термов (в частном случае,
когда (9.34) сводится к (9.32), через ((£', S') для исходного терма и для добавляемого элек-
трона). Соответствующая формула была выведена Гаудсмитом и Хампфри [215], см. также [15].
§ 9.6. Мультиплеты в спектрах
При переходах между уровнями двух мультиплетных термов возникает совокуп-
ность линий — мультиплет. Расположение линий в мультиплете и распределение
их интенсивностей часто настолько характерно, что мультиплеты сразу выделяются
в спектре. При переходах между уровнями дублетных термов возникают дублеты.
264
Глава 9. Основы общей систематики сложных спектров
при переходах между уровнями триплетных термов — триплеты и т. д. Полное число
линий в мультиплете в общем случае не совпадает с мультиплетностью и обычно
превосходит ее; правда, в ряде случаев число наиболее интенсивных линий совпа-
дает с мультиплетностью. Само название дублет, триплет и т. д. связано, в первую
очередь, со значением х — 2S -F 1 для комбинирующих термов, а не с числом
линий в мультиплете. Наряду с мультиплетами, удовлетворяющими правилу отбо-
ра Д5 = 0 (см. (9.24)), возможны интеркомбинационные мультиплеты с нарушением
этого правила, например, комбинации дублетных термов с квартетными, триплетных
с квинтетными и т. д.
Как было показано в §9.2 (с. 251), при нечетном числе электронов получается
четная мультиплетность и полуцелые значения J, а при четном числе электронов —
нечетная мультиплетность и целые значения J. Для атомов последовательных эле-
ментов в периодической системе нечетное число электронов чередуется с четным;
поэтому для последовательных элементов чередуются четная и нечетная мульти-
плетность. Для данного элемента нечетное число электронов чередуется с четным
при последовательной ионизации атома путем отрыва первого электрона, второго
электрона и т.д.; поэтому для последовательных ионов одного элемента также че-
редуется четная и нечетная мультиплетность. Следовательно, имеется чередование
четной и нечетной мультиплетности при переходе от одного элемента к следующему,
а для данного элемента — при последовательной ионизации. Это очень важный закон
чередования мультиплетности. С чередованием мультиплетности связано и чередова-
ние целых и полуцелых значений J: при четной мультиплетности значения J всегда
полуцелые, а при нечетной — всегда целые,0).
Примером закона чередования мультиплетности могут служить значения муль-
типлетностей наблюдаемых термов атомов и ионов (однократно и двукратно заря-
женных) последовательных элементов четвертого периода, приведенные в табл. 9.9.
Для большинства атомов и ионов наблюдаются термы различной мультиплетности,
четной или нечетной. Жирным шрифтом выделена максимальная мультиплетность
для термов нормальной конфигурации; последняя указана под значениями муль-
типлетности. В скобки взяты значения мультиплетности термов, которые хотя
и являются в принципе возможными, но не были наблюдены.
Таблица наглядно показывает чередование мультиплетностей. Одновременно
хорошо выявляется изменение максимальной мультиплетности в зависимости от чи-
сла внешних электронов и сходство значений мультиплетности для изоэлектронных
атомов и ионов. Максимальная мультиплетность сперва возрастает в соответствии
с возрастанием числа внешних электронов, равняясь этому числу, увеличенному
на единицу (см. (9.18)). После заполнения оболочки 3d наполовину, т. е. пятью элек-
тронами, она начинает убывать, так как для d-оболочки, заполненной больше чем
наполовину, т.е. для конфигурации dk (k' > 21 + 1 = 5), максимальная мультиплет-
ность такая же, как для конфигурации d10”* (см. §9.3, с. 258). Наибольшая наблю-
даемая мультиплетность, равная 8, получается при добавлении к самому глубокому
терму 65 конфигурации 3d5 двух неэквивалентных электронов (например, 4s и 4р).
Октетные термы (х=8) наблюдаются для Мп I. Это термы 3d54s(7S)nd SD и 3d54s(7S)nf 8F°,
получающиеся при добавлении электрона nl к терму 3d54s7S Мп II (ср. §9.4, с. 261).
Для нейтрального атома и изоэлектронных с ним ионов получаются, по большей
части, в точности те же значения мультиплетности; лишь в некоторых случаях
для ионов не обнаружены термы наибольшей или наименьшей мультиплетности.
,0) Следует подчеркнуть, что чередование целых и полуцелых значений J имеет место и в тех случаях,
когда связь отличается от нормальной и квантовое число S теряет свой смысл.
Таблица 9.9
Чередование мультиплетностей для последовательных элементов в периодической системе
19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
К I	Са I	Sc I	Ti I	VI	CrI	Mn I	Fe I	Co I	Ni I	Си I	Zn I	Ga I	Ge I	As I	Se I	Br I
	1		1		1		1		1		1		1		1	
2		2		2		2		2		2		2		2		2
	3		3		3		3 ,		3		3		3		3	
		4		4		4		4		4		4		4		4
			5		5		5		5						5	
				6		6		6								
					7	8	7									
4s	4s2	3d4s2	3d24s2	3d34s2	3ds4s	3ds4s2	3d64s2	3d74s2	3d84s2	3d104s	3d104s2	4s24p	4s24p2	4s24p3	4s24p4	4s2 4p5
	Са II	Sc II	Till	VII	Cr II	Mn II	Fe II	Co II	Ni II	Си II	Zn II	Ga II	Ge II	As II	Se II	Вг II
		1		1		1		1		1		1		1		1
	2		2		2		2		2		2		2		2	
		3		3		3		3		3		3		3		3
			4		4		4		4		4		4		4	
				5		5		5		(5)						5
					6		6		(6)							
						7	8	(7)								
	4s	3d4s	3d24s	3d4	3d5	3d54s	3d64s	3d8	3d9	3d10	3d104s	4s2	4s24p	4s24p2	4s2 4p3	4s24p4
		Sc III	Ti III	VIII	Cr III	Mn III	Fe III	Co III	Ni III	Cu III	Zn III	Ga III	Ge III	As III	Se III	Br III
			1		1		1		1		1		1		1	
		2		2		(2)		2		2		2		2		2
			3		3		3		3		3		3		3	
				4		4		4		4		(4)		(4)		4
					5		5		5		5					
						6		6		(6)						
							7		(7)							
								(8)								
		3d	3d2	3d3	3d4	3d5	3d6	3d7	3d8	3d9	3d10	4s	4s2	4s2 4p	4s24p2	4s24p3
§ 9.6. Мультиплеты в спектрах
ю
CS
266
Глава 9. Основы общей систематики сложных спектров
Рассмотрим подробнее характеристики мультиплетов. Они определяются прежде
всего значениями L и S комбинирующих термов и правилами отбора Д/ = 0, ±1
для квантового числа J. При соблюдении правил (9.24) и (9.25) для S и для L
оказываются возможными два типа мультиплетов:
мультиплеты типа х£ —► *L, т. е. переходы между уровнями двух термов мульти-
плетности х с одинаковыми значениями L, например 2Р— 2Р, 3F— 3F и т.д.;
мультиплеты типа XL —> \L - 1), т.е. переходы между уровнями двух термов
мультиплетности х со значениями L, отличающимися на единицу, например 2D— 2Р,
5F-5D, й-3Гит.д.
Для мультиплетов типа L -> L, согласно правилам отбора для J, получаются
два рода переходов: переходы J —* J (главные линии), число которых равно 25 + 1
или 2L + 1 (для L S и для L 5), и переходы J —> J - 1 и J - 1 —> J (спутники),
число которых на единицу меньше. Общее число линий в мультиплете равно
65 4- 1 при L S, 6L 4- 1 при L 5.
(9.40)
В табл. 9.10 приведены данные для характерного мультиплета типа L —> L, получа-
ющегося для Fe I при комбинировании термов 3<r4s4p 5D° и Зс^452 SD. Значения
длин волн (курсивом) и волновых чисел (прямым шрифтом) расположены в виде
прямоугольной схемы. Разности между волновыми числами двух строк и двух столб-
цов (числа в скобках) дают интервалы между уровнями комбинирующих термов.
В квадратных скобках приведены относительные интенсивности линий (сравнение
этих данных с теоретическими будет дано ниже, см. с. 273). Общее число линий,
согласно (9.40), равно 131,). Отношение интервалов между уровнями для комбини-
рующих термов равно 1,09 : 2,15 : 3,07 : 3,67 и 0,92 : 1,88 : 2,95 : 4,25, что примерно
соответствует теоретическому отношению 1 : 2 : 3 : 4, вытекающему из (9.36), и сви-
детельствует о приближенной справедливости предположения о нормальной связи.
Для мультиплетов типа L —* L — 1, согласно правилам отбора, получается три
рода переходов: /->/-!,/—>/и/—>/4-1. Для переходов J —♦ J - 1 изменение J
такое же, как изменение L, и равно —1 (главные линии); для переходов J —> J оно
равно 0 (спутники первого порядка), и для переходов J —> J 4- 1 оно равно 4-1,
т. е. изменение J противоположно изменению L (спутники второго порядка). Число
главных линий равно 25 4- 1 при L S 4- 1, 25 при L = S 4- х/г и 2L - 1 при L S,
число спутников первого порядка равно 25 при L > 5 и 2L - 1 при L < 5, число
спутников второго порядка равно 25 - 1 при L > 5 и 2L - 1 при L < 5. Общее число
линий в мультиплете равно
65 при
65 - 1 при
6L - 3 при
L>5+1,
1
£ = 5+-, >
L^S.
(9-41)
В табл. 9.11 приведены данные характерного мультиплета типа £ —> L — 1, полу-
чающегося для Fe 1 при комбинировании термов 3d54s4p 5F° и 3d54s2 5D. Построение
таблицы такое же, как и предыдущей. Однако в отличие от случая мультиплетов типа
L —> £, дающих схему переходов, симметричную относительно диагонали, для слу-
чая мультиплетов типа L —> L — 1 получается несимметричная схема. Общее число
линий, согласно (9.41), равно 12. Правило интервалов приближенно соблюдается:
для 5F°-терма получается отношение 1,88 : 2,91 : 4,03 : 5,18 вместо 2 : 3 : 4 : 5,
данные для 5/>-терма уже приводились выше.
’0 Фактически 12, так как интенсивность линии 5DQ— 5Dq равна нулю.
Таблица 9.10
Характерный мультиплет типа L —► L
Комбинирующие уровни			
		J = 0	J= 1
3d64s4p5D° Fe I	J = 0	3895,658 25662,36 [151 (71,10) 3920,260	3906,482 25501,32	(89,94)	25 591,26 [14]	[5,4] (139,69) 3927,922 25451,57 [20]	
	J = 1		
	J = 2		
	J = 3		
	J = 4		
3d6 4«2 5Р Fe I
	J = 2	J = 3	J = 4
3878,575 (184,13)	25775,39 [25] (139,69) 3899,709	3856,373 (184,13)	25636,70	(288,08)	25923,78 [20]	[32] (199,52)	(199,52) 3930,299	3886,284	3 824,444 25436,18	(288,08)	25 724,26	(415,94)	26140,20 [22]	[46]	[25] (240,20)	(240,19) 3922,914	3859,913 25484,06	(415,95)	25900,01 [17]	[100]			
§ 9.6. Мультиплеты в спектрах
В квадратных скобках — относительные интенсивности линий по Кингу [228].
В круглых скобках — разности волновых чисел соседних линий.
Характерный мультиплет типа L —► L - 1
Таблица 9.11
Комбинирующие уровни		3d5 4s2 5D Fe I
		J = 0	1	J = 2	J = 3	J = 4
3d6 4s4p SF° Fe I	J = 1	3745,901	3 733,319	3707,824 22668,29	(89,94)	26778,23	(184,12)	26962,35 [21]	[17]	[2,5] (106,77)	(106,76) 3 748,264	3722,564	3683,054 26671,46	(184,13)	26855,59	(208,09)	27143,68 [36]	[23]	[1,7] (164,88)	(164,91) 3745,661	3705,567	3 649,304 26690,71	(288,06)	26978,77	(415,94)	27394,71 [64]	[21]	[0,5] (227,87)	(227,88) 3 737,133	3679,915 26750,90	(415,93)	27166,83 [85]	[12] (292,26) 3 719,935 26874,57 [100]
	J = 2	
	J = 3	
	J = 4	
	J = 5	
Глава 9. Основы общей систематики сложных спектров
В квадратных скобках — относительные интенсивности линий по Кингу [228].
В круглых скобках — разности волновых чисел соседних линий.
§ 9.6. Мультиплеты в спектрах
269
Схемы переходов и расположение линий для обоих случаев приведены
на рис. 9.5. Высоты линий дают их интенсивности.
Для рассмотренных двух типов мультиплетов, соответствующих выполнению
правил отбора (9.24) для S и (9.25) для L, получаются вполне определенные
относительные интенсивности линий мультиплета (соответствующих различным
переходам между уровнями комбинирующих термов), справедливые для случая
нормальной связи [14, 15]. При этом предполагается, что заселенности начальных
б
Рис. 9.5. Схемы переходов и расположение линий
для мультиплетов: а — переход 3d64s4p5D°—3d64s2 5D
для Fe I; б — переход 3d64s4p5F0— 3d*4s2 5D для Fe I
270
Глава 9. Основы общей систематики сложных спектров
уровней относятся, как их статистические веса, т. е. что для всех уровней начального
мультиплетного терма условия возбуждения одинаковы.
Формулы для относительных интенсивностей имеют вид:
переходы L <-	-+£ P(J+1)Q(J)	[ J+l •	)
переходы L <-	->Z- 1 P(J)P(J - 1)	, R(J)Q(J) J+l ’	J
где введены обозначения
Р(J) = (J 4- L 4- S 4- 1)(J 4- L - S) = [(J 4- L 4- 1)(J 4- L) - S(S 4-1)]/
Q(J) = (J - L 4- S 4- V)(L + S-J) = [5(5 4- 1) - (J - L 4- 1)(J - L)],	(9.44)
R(J) = [J(J 4-1)4- L(L 4- 1) - 5(5 4-1)].
В табл. 9.12 приведены вычисленные по этим формулам значения относительных
интенсивностей линий мультиплетов для переходов между термами со значениями
мультиплетности от 2 до 5 и значениями L от 0 до 4. Самой интенсивной всегда явля-
ется линия, соответствующая переходу между уровнями с наибольшими возможны-
ми значениями J, ее интенсивность принята за 100. Распределение интенсивностей
в мультиплетах типа L L и в мультиплетах типа L L — 1 получается различное.
В случае мультиплетов типа L L наиболее интенсивны главные линии («диа-
гональные» переходы J —» J), а спутники являются более слабыми; при этом
интенсивности симметрично расположенных (в схеме переходов) линий J -* J - 1
и J - 1 —> J одинаковы. Распределение интенсивностей получается симметричное.
В случае мультиплетов типа L —> L - 1 интенсивности убывают от главных ли-
ний к спутникам первого порядка и далее к спутникам второго порядка (переходы
J —> J - 1,J —>JhJ-*7 4-1). Распределение интенсивностей получается несим-
метричное.
Общее правило состоит в том, что линии тем интенсивнее, чем изменение А7
меньше отличается от изменения Д£; самыми интенсивными являются линии,
для которых Д7 = AL (главные линии), самыми слабыми (в случае L L - 1)
являются спутники второго порядка, для которых Д7 = 4-1 при AL — -1.
Для главных линий и для спутников зависимость интенсивности от J различ-
на. Для главных линий интенсивность убывает с уменьшением J, для спутников
она максимальна при промежуточных значениях J. При L < S у мультиплетов
типа L w L для главных линий получается минимум интенсивности при промежу-
точных значениях 7, а для мультиплетов типа L L - 1 для спутников второго
порядка наблюдается максимум интенсивностей при наименьших J.
Для рассмотренных мультиплетов Fe 1 наблюденные интенсивности в общем
соответствуют теоретическому распределению, данному в табл. 9.12, хотя и имеются
отдельные отклонения. Как соблюдение правила интервалов, так и наличие рас-
пределения интенсивностей, согласующегося с теорией, могут служить критерием
близости связи с нормальной.
Относительные интенсивности линий мультиплетов
Таблица 9.12
Дублеты (S = V2)									Триплеты (5=1)										
		'/2	3/2	J	J	'/2					0	1	2	J		J	1		
2Р-	2Р	40,0 20,0	20,0 100	'/2 3/2	'/2 3/2	50,0 100	2P-	2S	3P-	2P	0 26,7	26,7 20,0 33,3	33,3 100	0 1 2		0 1 2	20,0 60,0 100	3P-	3S
		%	S/2	J	'/2	3/2					1	2	3	J	0	1	2		
2d-	2d	64,3 7,2	7,2 100	3/2 %	55,6	11,1 100	2d-	2P	3P-	3D	36,2 12,1	12,1 55,8 12,5	12,5 100	1 2 3	23,8	17,9 53,6	1,2 17,9 100	3Z>-	3P
		5/2	’/2	J	3/2	%					2	3	4	J	1	2	3		
2f-	2f	74,1 3,7	3,7 100	3/2 %	70,0	5,0 100	2f-	2d	3P —	3F	52,6 6,6	6,6 69,6 6,7	6,7 100	1 3 4	46,7	8,8 69,1	0,2 8,8 100	3P-	3D
		’/2	’/2	J	S/2	7/2					3	4	5	J	2	3	4		
2g-	ъ	79,5 2,3	2,3 100	% %	77,1	2,9 100	2g-	2f		3G	62,1 4,1	4,1 76,9 2,9	2,9 100	3 4 5	58,4	5,1 76,7	0,1 5,1 100	3G-	3F
																			
§ 9.6. Мультиплеты в спектрах
272
Глава 9. Основы общей систематики сложных спектров
Продолжение таблицы 9.12
§9.7. Случай связи (j,j)
273
Важное значение при рассмотрении вопроса об интенсивностях мультиплетов
имеет правило сумм интенсивностей. Согласно этому правилу, сумма интенсивностей
для переходов с заданного уровня одного терма на различные уровни другого терма
пропорциональна статистическому весу этого уровня.
Например, для квартета 4Р—4Р суммы интенсивностей переходов с уровней
терма 4Z> с J = Уг, 3/г, 5/г, % равны 25, 50, 75 и 100, т. е. относятся как 2 : 4 : 6 : 8,
а суммы интенсивностей переходов с уровней терма 4Р с J — 1/г, 3/г, 5/2 равны 41,6,
83,4 и 125, т. е. относятся как 2:4: 6. Если комбинирующие термы хорошо
соответствуют случаю нормальной связи, то правило сумм для интенсивностей
применимо также и для мультиплетов, получающихся с нарушением правил отбора
для S и для £, т. е. для интеркомбинационных мультиплетов и для мультиплетов
с Д£> 1.
В простейших случаях правила сумм интенсивностей достаточно, чтобы полностью
определить относительные интенсивности отдельных линий. Это имеет место, в частно-
сти, для переходов между дублетными термами, как было рассмотрено в гл. 6 на примере
переходов 2Р - 2D и 2D - 2F (см. с. 190).
Для тривиального случая переходов *Р - XS, когда получаются три линии (при х > 2),
их интенсивности относятся как веса трех уровней Р-терма.
Правило сумм было впервые установлено эмпирически Бургером, Орнштейном и Дор-
гело [13]. Оно может быть выведено квантовомеханически. Отметим, что из формул для от-
носительных интенсивностей линий в мультиплетах типов L L и L L - 1 это правило
получается автоматически.
Правила сумм получаются и в ряде других случаев, например в случае связи (J, j).
Их важное значение определяется тем, что эти правила можно сформулировать в форме,
независимой от типа связи, если рассматривать переходы между двумя группами уровней.
Сумма интенсивностей линий, возникающих при переходах с данного уровня одной группы
на различные уровни второй группы, пропорциональна статистическому весу этого уров-
ня [14]. В случае расщепления спектральных линий в магнитном поле (ср. гл. 14, с. 375) также
справедливо соответствующее правило сумм для интенсивностей.
§9.7. Случай связи (j, j)
При связи (j, j) уровни группируются по значениям квантовых чисел от-
дельных электронов, определяющих значения моментов количества движения этих
электронов ji по формуле (9.7).
Мы рассмотрим простейший случай двух электронов. Сложение моментов
происходит, согласно (9.6), по схеме
l\+s\=ji, l2 + s2=j2i j\+j2 = J-	(9.45)
Квантовое число J принимает значения
j = j\ + 72, ji + h ~ 1, • • •, IJI - J21-	(9.46)
Соответствующие уровни обозначают символом (jj,j2), указывая значение j ин-
дексом справа снизу. Таким образом, (5/2, 3/г)4 означает уровень с j\ = %, 72 “ 72
и J — 4.
В данном примере возможными значениями J будут, помимо 4 (что соответ-
ствует, согласно наглядным представлениям, параллельности j\ и J2), также 3, 2
и 1. Мы получаем уровни
/5 3\	/5 3\	/5 3\	/5 3\
\2’2/4’	\2’2/3’	\2’2/2’	\2’2//	(947'
274
Глава 9. Основы общей систематики сложных спектров
В §9.1 (см. рис. 9.1) был уже приведен пример уровней конфигурации dp
при связи (j, j). Помимо уровней типа (5/2, 3/г)/ получаются, в соответствии со зна-
чениями ji = 5/2, 3/г Gi = 2, S| = »/2) и j2 = 3Л, ‘/г (h = L з2 = ’/г), уровни
типов (5/2, i/2)j5 (з/2, з/2)7 и (з/2) i/2)7.
Для конфигураций, состоящих из двух эквивалентных электронов, закон сло-
жения (9.46) остается справедливым при j\ j2, а при ji = j2 = j число уровней
уменьшается и остаются лишь четные значения J.
Для того чтобы убедиться в этом, достаточно составить таблицу возможных
значений mj —	4- mj2, по схеме табл. 2.2. (с. 53). Например, для j\ — j2 = 3/2 мы
получим
\77lj,	%	’/2	-'/2	-%	
	(3)	2	1	0	
'/2	2	(1)	0	-1	(9.48)
-'/2	1	0	(-1)	—2	
-%	0	-1	—2	(-3)	
наборы			(0)	(2)	
Диагональные значения mj исключаются в силу принципа Паули. Состоя-
ния, соответствующие значениям mj, симметрично расположенным относительно
диагонали, учитываются один раз (ср. §9.3, с. 255), и остаются наборы (0) и (2),
соответствующие четным значениям J.
Для случая конфигурации р2, состоящей из двух эквивалентных р-электронов,
мы получим пять уровней (^ = l2 = 1, $i — s2 = ’/2, j\ = j2 = 3/2, l/2)
/3	1\	/3	1\	/3	3\	/3	3\	/1 1\	/л Л ч
\2	2/2’	\2	2/,’	\2	2/2’	\2	2/0’	\2’ 2/0	v 7
Число уровней и их значения J те же, что и для случая нормальной связи, когда
конфигурации р2 соответствуют (см. табл. 9.4) уровни 1Sq, lD2, 3Pq, 3Р\, 3Р2.
Группы уровней (j|, j2) при связи (J, j) расположены, как правило, тем глубже,
чем меньше значения j\ и j2. Это хорошо иллюстрируется примером уровней
конфигурации 6d7p Th III (правая часть рис.9.1).
Для связи (j, j) получаются, в дополнение к общим правилам отбора для перехо-
дов между уровнями одинаковой и разной четности (см. (4.153) и (4.154)) и правилам
отбора для квантового числа J (см. (4.156) и (4.158)), приближенные правила отбора
для квантовых чисел j\ и j2. Эти правила отбора для дипольного излучения имеют
вид
Aji = 0, ±1, Aj2 — 0,	1
или	>	(9.50)
Д>! -0, Aj2 = 0,±1. J
При переходах между группой уровней с заданными j\yj2 (J' = j\ 4- j2, j\ 4-
j2 “	“ J2I) и группой уровней с заданными j", j" (J" - j" + j2,j" 4-
j2 “ 1, • • •, \j" ~ j"I) получается совокупность линий, аналогичная мультиплету
в случае нормальной связи. Расположение этих линий можно рассчитать, при-
чем величина расщеплений будет зависеть от электростатических взаимодействий
электронов [14],2). Относительные интенсивности будут определяться формулами,
,2^ Которые учитывают во втором приближении, см. выше §9.1, с. 246.
§9.7. Случай связи (j,j)	275
аналогичными (9.42)-(9.44), где L и S нужно заменить на ji и j'2 О2 не изменяется,
подобно S, a j\ подчиняется правилу отбора Aji = 0, ±1, подобно L).
Случаем, аналогичным случаю связи (j, j) для двух электронов, является случай
связи (J, j), получающийся, когда к некоторой конфигурации, состоящей из сильно
взаимодействующих электронов, присоединяется слабо связанный электрон, взаи-
модействующий с этой конфигурацией по схеме
j'+j = J	(9.51)
Если присоединяемый электрон является s-электроном, для которого j = 1/г,
то
J = J' ± '/2	(9.52)
и каждый уровень исходной конфигурации расщепляется на два.
Более подробное рассмотрение связи (j, j) и других типов связи, отличных
от нормальной, будет произведено в следующих главах при разборе конкретных
спектров.
ГЛАВА 10
СПЕКТРЫ АТОМОВ С ДВУМЯ ВНЕШНИМИ
«-ЭЛЕКТРОНАМИ
§ ЮЛ. Общая характеристика спектров атомов
с двумя внешними электронами
Простейшим типом сложных спектров являются спектры атомов с двумя внеш-
ними s-электронами в нормальном состоянии. Эти два внешних «-электрона обра-
зуют оболочку ns2, которая сама по себе, как заполненная, не дает результирующего
момента, отличного от нуля: ей соответствует единственный невырожденный уро-
вень 'Sq (S = 0, L = 0, J = 0). Однако внешние «-электроны могут возбуждаться.
При этом возможны два случая:
1. Может возбуждаться один электрон, что происходит особенно легко и при-
водит к возникновению характерных спектров рассматриваемой группы атомов. Их
разбору и будет посвящена основная часть данной главы.
2. Могут возбуждаться одновременно два электрона, что требует значительно
большей затраты энергии. Одновременное возбуждение двух электронов приводит
к возникновению так называемых смещенных термов и уровней, что сильно усложняет
спектр. Этот вопрос будет разобран отдельно в конце главы.
При возбуждении одного из «-электронов получаются различные двухэлек-
тронные конфигурации. Возбужденный электрон может переходить в «-состояния,
соответствующие большему значению главного квантового числа п, и в р-, d-,
f-, ... состояния. Получаются возбужденные конфигурации типа
nsn s nsnp nsnd nsn '/,	(10.1)
где n' принимает последовательные целые значения. Конкретным примером могут
служить возбужденные конфигурации Mg (п = 3, см. с. 242).
Для конфигураций типа nsn'l, содержащих «-электрон, получается, согласно
табл. 9.1 (с. 247, см. первые строки этой таблицы), по два терма — одиночный
и триплетный, с L = I. Для конфигураций nsn's это будут термы *5 и 3S, для кон-
фигураций nsnp — *РО и 3Р°, для конфигураций nsn'd — lD и 3D и т.д. Отличие
от случая спектров атомов щелочных металлов с одним электроном п'1 в возбужден-
ных состояниях состоит в том, что вследствие наличия электрона ns вместо одного
дублетного терма n'l2L получается два терма lL и 3L — одиночный и триплет-
ный. В результате вместо одной системы термов — системы дублетных термов —
получается две: система синглетных термов и система триплетных термов; к си-
стеме синглетных термов относится и основной терм ns2 xSq, являющийся первым
членом последовательности nsn's XS 3S, возбужденные термы которой начинаются
с п«(п -|-1)« (для Mg с 3«4«).
§10.1. Характеристика спектров атомов с двумя внешними электронами 277
Для каждой системы термов — синглетной и триплетной — при переходах меж-
ду термами данной системы, допускаемых правилами отбора (6.45) для квантового
числа I, возникают серии пвп'I9—nsn"l" (I" = f ± 1), аналогичные сериям атомов ще-
лочных металлов. В результате получаются серии, соответствующие синглетно-син-
глетным переходам, и серии, соответствующие триплетно-триплетным переходам.
Первые состоят из синглетов, вторые — из триплетов: мы имеем синглетную систему
переходов и триплетную систему переходов. Наряду с этим возможны интерком-
бинационные синглетно-триплетные переходы, связанные с нарушением правила
отбора (9.24) для спинового квантового числа S и обусловленные спин-орбиталь-
ным взаимодействием. С увеличением порядкового номера атома спин-орбитальное
взаимодействие увеличивается (ср. § 8.4) и соответственно растет как интенсивность
интеркомбинационных синглетно-триплетных переходов, так и величина триплет-
ного расщепления термов 3Р°, 3Р, 3F° (синглетные термы и триплетные 35-термы
не расщепляются). Для тяжелых атомов расщепление термов достигает тысяч см-1,
а интенсивность интеркомбинационных переходов становится сравнимой с интен-
сивностью переходов с сохранением мультиплетности и для отдельных линий может
быть даже больше (при учете заселенности верхнего уровня, см. ниже § 10.4, с. 293).
Нормальными конфигурациями типа ns1 обладают элементы, приведенные
в табл. 10.1. В скобках перед символом конфигурации ns1 внешних электронов
указана также предыдущая заполненная оболочка. В последнем столбце таблицы
даны энергии ионизации нейтрального атома. Эти энергии определены с большой
точностью по схождению к границе ионизации последовательностей термов данного
рода с возрастающими значениями главного числа п. Так как высокие термы
являются водородоподобными, то можно очень хорошо производить экстраполяцию
к значению п — оо, соответствующему границе, если известно достаточное число
последовательных термов.
Таблица 10.1
Нормальные конфигурации элементов с двумя внешними электронами
Z	Элемент	Конфигурация	Энергия ионизации, эВ
2	Не	1?	24,580
4	Be	(l?)2s2	9,320
12	Mg	(2p6)3?	7,644
20	Са	(3p6)4s2	6,111
38	Sr	(4p6)5s2	5,692
56	Ba	(5p6)6s2	5,210
88	Ra	(6p6)7?	5,277
30	Zn	(3d'°)4s2	9,391
48	Cd	(4dl0)5?	8,991
80	Hg	(5d'°)6s2	10,434
Для экстраполяции могут быть применены формулы типа формулы Ридберга (8.7) или же,
если известно небольшое число последовательных термов, типа формулы Ритца (см. с. 221),
являющейся при малых п более точной. При достаточно больших квантовых числах хорошие
результаты дает и применение формулы (1.5) для атома водорода, так как при этом поправка
Ридберга и, тем более, поправка Ритца а/т2 играют малую роль.
Рассматриваемые элементы можно разделить на три группы:
1)	Не с оболочкой 1s2.
2)	Элементы от Be до Ra с оболочкой ns2 (п — 2, 3,4, 5, 6, 7), следующей за труд-
но возбудимыми оболочками 1s2 (для Be) и (п - 1)р6 (для остальных элементов).
278
Глава 10. Спектры атомов с двумя внешними s-электронами
3)	Zn, Cd, Hg с оболочкой ns2 (п = 4, 5,6), следующей за более легко возбуди-
мой оболочкой (n - l)d10.
В следующих параграфах мы рассмотрим, в соответствии с этим разделением
на группы, спектры атомов отдельных элементов, а также изоэлектронных с ними
ионов.
§ 10.2.	Спектр атома гелия
Атом гелия отличается от всех остальных атомов с двумя внешними электронами
тем, что он не имеет внутренних электронов и поэтому является двухэлектронной
системой в чистом виде. Рассмотрение такой системы, наряду с одноэлектронной
системой в чистом виде, какой является атом водорода, имеет большое значение.
При переходе от атома водорода к атому гелия впервые приходится учитывать взаи-
модействие между двумя электронами. Рассмотрение этого взаимодействия является
очень существенным для приближенного расчета многоэлектронных атомов, в кото-
рых каждый электрон одновременно взаимодействует с двумя или более электронами.
Для атома гелия, в силу малости спин-орбитального взаимодействия, особенно
отчетливо проявляется разделение переходов на синглетные и триплетные. Рассмо-
трим схему уровней атома гелия. Она приведена на диаграмме рис. 10.1. В левой
части диаграммы показаны синглетные термы, в правой — триплетные термы;
для каждого уровня отмечено главное квантовое число п возбужденного электрона,
другой электрон является электроном 1s.
CM'1 .
198310,4 -
190000 -
зв
24-
23:
180000-
22-
170000-21
160000-®-
19-
150000 \
20000Д
10000-
Сингулеты (парагелии)
's,	'p;
1sns	Isnp
.2121 (пара)
-2O96(opmo)
'2щ51(параТ
-19,82(opmo)
0- 0
2301{орто).
‘М2(/шро^
22,Т2(ррто)
%
1$nd
3S,
Isns
11111
!
Триплеты (ортогоналей)
Зр»
Isnp
3pl,2 fyzj
Isnp lead Isnf
г0
‘10000
-20000
•3
-30000
-4
•5 '40000
V6
не I
8»
-180000
-23'
-190000
-24,
.1$.198310,4
CMJt


2
1
1
Рис. 10.1. Диаграмма уровней энергии Не I
§ 10.2. Спектр атома гелия	279
Основной одиночный терм 1s2 ’5о лежит очень глубоко по сравнению со всеми
остальными. Энергия возбуждения самого глубокого триплетного терма ls2s3Si
составляет 19,82 эВ при энергии ионизации 24,59 эВ, а энергия возбуждения
соответствующего синглетного терма ls2s *5о равна 20,61 эВ. Физически это понятно,
так как электрон 1s связан очень прочно, а электрон 2s гораздо слабее, и нужна
большая энергия порядка 20 эВ, чтобы возбудить один из электронов 1s, превратив
заполненную оболочку гелия в незаполненную.
Разность ls2s'Sg—-ls2s 35| одиночного и триплетного термов, возникающих
из одной и той же конфигурации ls2s, равна 0,80 эВ. Триплетный терм, в соответ-
ствии с общим правилом (см. с. 248), лежит глубже одиночного. Это соблюдается
и для всех остальных пар термов гелия, возникающих из одной и той же конфи-
гурации. Разность одиночных и триплетных термов уменьшается при увеличении
возбуждения. При этом для Р-термов она меньше, чем для 5-термов, а для D-термов
и F-термов становится ничтожно малой, как показывают данные, приведенные
в табл. 10.2 °.
Таблица 10.2
Разности одиночных и триплетных термов гелия (в см-1)
п	S-термы 's- }S	Р° -термы 1р° _ Зро	D -термы 'D - }D	F° -термы
2	6421,38	2047,89	—	—
3	1 627,98	644,60	3,32	—
4	642,04	275,53	1,88	0,63
5	316,45	141,68	1,06	1,48
6	178,71	81,96	0,65	0,12
7	110,56	51,69	0,31	0,11
8	73,24	34,48	0,31	0,12
9	50,76	24,27	0,14	0,06
Сингулетные термы комбинируют друг с другом, давая серии, аналогичные се-
риям атомов щелочных металлов. При этом «главная серия» 1s — пр (п — 2, 3,4,...)
лежит в очень далекой ультрафиолетовой области спектра (от 500 до 600 А), а осталь-
ные серии — в инфракрасной, видимой и близкой ультрафиолетовой областях. Серии
состоят из одиночных линий.
Триплетные термы комбинируют между собой, также давая серии, аналогичные
сериям щелочных металлов и лежащие в инфракрасной, видимой и близкой ультра-
фиолетовой областях спектра. Серии состоят из триплетов. Триплетная структура
для гелия очень узкая; наибольшее расщепление — расщепление 3Р0°— 3Р2° триплет-
ного терма \s2p 3Р° — составляет 1,07 см-1. Для терма ls3p 3Р° расщепление 3Pq — 3Р2°
равно 0,36 см"1, а для остальных триплетных термов расщепление настолько мало,
что не разрешается даже спектральными приборами высокой дисперсии. Первый
член триплетной серии 2р 3P°—nd 3D (п = 3,4,5,...) (диффузной триплетной серии)
лежит в желтой части видимого спектра — это желтая линия Dy (А — 5 876 А),
обнаружение которой в спектре протуберанцев Солнца в 1868 г. привело к открытию
Некоторая нерегулярность изменений разностей lD- 3D и особенно lF— 3F связана с возмущениями
(см. с. 299).
280
Глава 10. Спектры атомов с двумя внешними s-электронами
гелия. Она состоит из трех компонент
3Р1~ 3DW,	А = 5 875,618 А, '	
3Pl- 3Р2,!,	А = 5875,650 А,	>	(10.2)
3Ро - 3Pi,	А = 5875,989А ,	
с относительными интенсивностями 5:3:1 соответственно статистическим ве-
сам уровней 3Р2°, 3Р\, 3Р0° терма 3Р° (см. правило сумм интенсивностей, с. 273;
уровни 3£>з, 3Z>2, терма 3D практически совпадают).
Отметим, что для терма 2р3Р° не только не соблюдается правило интервалов, но он
даже является обращенным — уровень 3Р2° лежит глубже всего, затем очень близко к нему,
на 0,078 см-1 выше, лежит уровень 3Р{ и еще выше на 0,996 см-1 лежит уровень 3Р0°.
Обращенным является и терм Зр3Р°. Это объясняется теоретически, если учесть спин-
орбитальное и спин-спиновое взаимодействие двух электронов между собой, а не только
спин-орбитальное взаимодействие для каждого электрона в отдельности (см. [14]).
Интеркомбинационные переходы между синглетными и триплетными терма-
ми для такого легкого атома, как атом гелия, в соответствии с малостью спин-
орбитального взаимодействия, очень слабы, но все же удается наблюдать интерком-
бинационную линию 591,44 А, получающуюся в результате перехода 1з2р 3Pf—Is2 \Sq.
Вследствие слабости интеркомбинационных линий спектр гелия распадается на две
практически независимые системы линий — одиночную систему и триплетную си-
стему. Физически это означает сохранение значения суммарного спина S, равного 0
или 1. Гелий в состояниях со спином S — 0, дающий синглетную систему линий,
называют парагелием, а гелий в состояниях со спином 5=1, дающий триплетную
систему линий, называют ортогелием. Такое строение спектра гелия первоначально
привело к предположению о наличии двух разных химических элементов, и лишь
затем выяснилось, что оно связано с двумя типами состояний атома гелия, переходы
между которыми очень мало вероятны. С точки зрения наглядных представлений
переход парагелия в ортогелий связан с тем, что антипараллельно ориентированные
спины электронов становятся параллельными, иначе говоря, происходит переориен-
тация спинов.
Статистический вес термов ортогелия в три раза больше статистического веса
соответствующих термов парагелия:
Рорто-Не   25орто 4“ 1	2 1 4~1  (10 3)
//пара-He	25пара 4“ 1	2*04-1
То обстоятельство, что с самого глубокого Р-терма 1 з2р 3Р° триплетной системы
уровней ортогелия возможен лишь весьма мало вероятный переход Is2p 3Р\ —> Is2 ’5о,
делает соответствующее состояние атома гелия весьма устойчивым. Атом гелия
в состоянии \s2p3P° имеет время жизни т « 10~2 с. Это состояние является
типичным примером метастабильного состояния (см. гл. 4, с. 88).
Спектрами, аналогичными спектрам гелия, но еще более трудно возбудимыми,
обладают гелиоподобные ионы: Li II, Be III, В IV и т.д. Спектры членов этого
изоэлектронного ряда исследованы до F VIII, кроме того, для ионов Mg XI и Al XII
удалось наблюдать в рентгеновской области спектра от 9 до 6 А несколько первых
членов синглетной главной серии Is2 '5о— Isnp 'Pf. С возрастанием Z усиливается
интеркомбинационная линия ls2p3P|° —> Is2 ’Sq, начиная с В IV, она найдена
для всех ионов до F VIII включительно.
§ 10.2. Спектр атома гелия
281
Таблица 10.3
Энергии ионизации, эффективный заряд и постоянные экранирования
для гелики гелиоподобных ионов
Атомы	Не I	Li II	Be III	В IV	С V	N VI	О VII	F VIII	Ne IX	Na X	Mg XI	Al XII
Z	2	3	4	5	6	7	8	9	10	II	12	13
Энергия												
ионизации,												
эВ	24,59	75,6	153,8	259,3	392,0	552,0	739,0	954	—	—	1761	2 085
Z’2	1,81	5,55	11,3	19,1	28,8	40,6	54,5	70,2	—	—	129,5	153,3
Z*	1,35	2,36	3,36	4,37	5,37	6,37	7,38	8,38	—	—	11,38	12,38
а	0,65	0,64	0,64	0,63	0,63	0,63	0,62	0,62	—	—	0,62	0,62
В табл. 10.3 приведены энергии ионизации для членов изоэлектронного ряда,
начинающегося с Не I, и соответствующие значения Z*2, Z* и а, вычисленные
по формуле (7.6), которая для п = 1 принимает вид Е\ = -RZ*2 = -И^он. Значения
постоянной экранирования а, остающиеся почти постоянными для членов ряда,
характеризуют взаимодействие электронов, которое уменьшает энергию связи элек-
трона в двухэлектронной гелиоподобной системе по сравнению с одноэлектронной
водородоподобной системой.
Задача об атоме гелия может быть решена квантовомеханическими методами
с большой степенью точности. В частности, энергию основного состояния гелия уда-
лось рассчитать с точностью порядка 10~6 (т. е. 0,0001 %), что позволило подтвердить
наличие сдвига основного уровня Is2 ’So Не I, аналогичного сдвигу основного уровня
одноэлектронного атома (см. конец §6.6, с. 197). Экспериментальное значение вели-
чины сдвига, определенное Герцбергом [253] путем очень точного измерения линий
Не 1, равно 1,20 ±0,15 см-1 и находится в прекрасном согласии с теоретическим
значением 1,33 ± 0,20 см”1.
Наиболее точные квантовомеханические расчеты атома гелия выполнены вариационным
методом (Хиллераас в 1928-1930 годах [214], ссылки на ряд последних работ см. у Герцбер-
га [253]). При этом берется волновая функция с произвольными параметрами и ищется, при ва-
риации этих параметров, минимум энергии; чем больше число варьируемых параметров, тем
большей точности можно достигнуть. Для основного состояния гелия число параметров было
доведено до 200; расчеты производились с помощью электронных вычислительных машин.
Более грубый квантовомеханическии расчет энергии состояний атома гелия может быть
произведен приближенным методом, путем рассмотрения двухэлектронной задачи, исходя
из решения одноэлектронной [213]. Этот метод может быть обобщен на случай любого атома
с двумя внешними электронами и является весьма простым и наглядным (хотя и не дает
большой точности), и поэтому мы его рассмотрим.
Оператор энергии для двухэлектронного атома или иона имеет вид:
Н = Т 4- U = Т} 4- U} 4- Т2 4- U2 4-1/,2,	(Ю.4)
h2	h2
где T\ =---;—Д| и Т2 =-------—Д2 ~ операторы кинетической энергии первого и второго
8тг2т	8тг2т
Ze2	Ze2 z
электронов, U\ = U(г|) =----и U2 = U(r2) =--------(fj и r2 — расстояния электронов
Г|	г2
от ядра) — потенциальные энергии первого и второго электронов в поле ядра, a U\2 —
б2	2\
и(г\2) = — (г|2 — расстояние между электронами) — энергия отталкивания электронов '.
Г12
’ Для получения большей точности вместо потенциала-------можно взять улучшенный потенциал,
Гг
уже частично учитывающий взаимодействие электронов. В случае атома с двумя внешними электронами
282
Глава 10. Спектры атомов с двумя внешними s-электронами
В нулевом приближении, рассматривая U]2 как энергию возмущения, мы имеем волновое
уравнение
М(1,2) = Д^(1,«),	(10.5)
где
ЯО = Я1+Я2 = (Т|+Я1) + (Т2 + Я2),	(10.6)
Eq — значение энергии в нулевом приближении, а ^(1,2) — волновая функция в нулевом
приближении, зависящая от пространственных координат первого и второго электронов.
Уравнение (10.5) решается методом разделения переменных и удовлетворяется волновой
функцией
^(1,2) = ^,(1)^(2),	(10.7)
где V’aO) и ^д(2) — решения волновых уравнений
Я.О) = Eaifia(}), Н2^(2) = Е^(2)	(10.8)
для одноэлектронной задачи, а Еа и Ер — соответствующие значения энергии первого
и второго электронов (Еа Ер — Eq).
Правильными функциями нулевого приближения для системы, состоящей из двух
одинаковых частиц, удовлетворяющими условию неизменности |^(1,2)|2 при перестановке
частиц, являются симметричная и антисимметричная функции (см. §3.3, с. 75)* 1 * 3):
^.(1>2) = -^[^„(1)^(2) + 1&а(2)^(1)]
(Ю.9)
И
^(1,2) = -Jx [^(1)^(2) - ^(2)^(1)],	(10.10)
представляющие линейные комбинации функции (10.7) и функции ^а(2)^(1), получающейся
из нее перестановкой электронов.
Энергия в первом приближении равна среднему значению оператора А в состояни-
ях (10.9) и (10.10):
Е = | / [^(1)^(2) ±^(2)^(1)] Я [^„(1)^(2) ±^а(2)^(1)] dx,	(10.11)
где верхний знак относится к симметричной функции, а нижний — к антисимметричной.
Согласно (10.4) и (10.6), получаем:
[^(1)^(2)±^(2)^(1)] {^(2)(Т,+Я1)^(1)+^а(1)(Т2+Я2)^(2)+
+Я12^а(1)^(2)±^а(2)(Г1+Г|)^(1)±^(1)(Т2+Я2)^о(2)±Г12^(2)^(1)}аа:)
(10.12)
что с учетом (10.5) и (10.8) дает
Е =
2(Еа + Ер)+ / ^(1)^(2)^2^а(1)^(2)^+ / ^(2)^(1)^2^(2)^(0^±
(10.13)
± / Й(1)^(2)МЖ(1)&± / «(l)Wo(lW2)(fc
откуда 4)
Е = Еа+Ер+К±А = Е0 + К±А,
(10.14)
для этих электронов можно взять потенциал------, где Z* — эффективный заряд ядра, или же взять
ri
более точный потенциал типа (7.3).
В силу ортогональности функций ipa и коэффициенты и СА в формулах (3.22) и (3.23),
1
при нормированных функциях, равны, как легко проверить, Cs = С& = —.
v2
4) Учитывая, что перестановка аргументов 1 и 2 не меняет значения интегралов.
§ 10.2. Спектр атома гелия
283
где
к= f l^a(l)|2^2l^(2)|2 dxtdx2 = / |V>a(l)|2 —(10.15)
J	J	Г12
И
A~ f ^а(1)^(1)^12^(2)^а(2)^|^2 = j	OlM 0 ^^(2)^а(2) dxtdx2.	(10.16)
В первом интеграле |^a(l)|2 и |^(2)|2 представляют, с наглядной точки зрения, элек-
тронные плотности первого и второго электронов, и интеграл дает энергию кулоновского
отталкивания зарядов двух электронных облаков. Его называют кулоновским интегралом.
Второй интеграл содержит произведение «смешанных» (или «обменных») электронных плот-
ностей ^*(1)^(1) и ^(2)^а(2), зависящих от наложения волновых функций гра и
смешанная плотность велика в тех точках, где и велики. Этот интеграл также зависит
от кулоновского отталкивания электронов; его появление связано с тем, что электроны нераз-
личимы и их можно переставлять — обменивать местами (см. последние два члена в (10.13)).
Интеграл (10.16) называют обменным интегралом.
В рассматриваемом случае оба интеграла, кулоновский и обменный, положительны
и энергия антисимметричного состояния (10.10) меньше энергии симметричного состоя-
ния (10.9). Вместо двух первоначальных вырожденных между собой состояний с энерги-
ей Eq = Еа + Ер мы получаем, согласно (10.14), антисимметричное состояние с меньшей
энергией и симметричное состояние с большей энергией. Разность их энергий равна ТА.
Легко показать, что симметричное состояние является синглетным (S = 0), а антисим-
метричное — триплетным (S = 1).
Полная волновая функция получается, если координатную функцию (10.9) или (10.10)
умножить на функцию от спиновых координат, от которой энергия в рассматривае-
мом приближении не зависит (мы пренебрегаем спин-орбитальным взаимодействием).
В силу двукратного вырождения, связанного со спином каждого электрона, возмож-
ны четыре функции x(aha2) типа Хтяа(а\)Хтяр(Р1), являющиеся произведениями функ-
ций Хтяа(а\) (msa — ’/2, “ ’/2) °т спиновой координаты (Т| первого электрона и функций
Xmsft(^i) (тзр — ’/2, - ’/2) от спиновой координаты а2 второго электрона. Это будут функции
Xi/^iJXi//^), Xi/2(^i)X-i/2(^2), Х-|/2(<Г1)Х1/2(<т2), X-i/2(o-i)X-i/2(^2)-	(10.17)
Умножением функций (10.9) и (10.10) на функции (10.17) мы получим восемь возможных
функций, однако они не все будут удовлетворять требованию антисимметрии волновых
функций системы электронов относительно перестановки любой пары электронов (см. § 3.3,
с. 75 и §7.1, с. 202) — в данном случае относительно перестановки двух рассматриваемых
электронов.
Очевидно, полная функция ^>s(l, 2)x(ah <т2) будет антисимметричной, если х^ь^г)
будет антисимметричной, а полная функция ^a(l, 2)х(<Г|, <г2) будет антисимметричной, если,
наоборот, х(аь a?) будет симметричной. Только в этих случаях при перестановке электронов,
т. е. при одновременной перестановке пространственных и спиновых координат, полная
волновая функция будет менять знак.
Симметричными из функций (10.17) являются функции х \/2(а\)Х\/2(а2) и
у_|д(а|)у_|д(а2), две другие функции не обладают симметрией относительно перестанов-
ки электронов, однако их сумма является симметричной, а разность антисимметричной.
В результате мы получаем три симметричные спиновые функции
Xi/2(<^i>Xi/2(^2)	(ms	= msa + ms0 = 1),
^=[xi/2(*i)x-i/2(ff2) + Xi/2(^2)x-i/2(^i)]	("»s	= rnsa + msl3 = 0),	(10.18)
X-i/2(ffi)X-i/2(ff2)	(ms	= msa + ms0 = -1),
соответствующие триплетному состоянию	(ms	=	1,0,-1; S = 1), на которые умножается
функция (10.10), и одну антисимметричную функцию
^[xi/2(<^i)X-i/2(^2) - Xi/2(<72)X-!/2(*i)] (ms = т,а + т,13 = 0),	(10.19)
284
Глава 10. Спектры атомов с двумя внешними s-электронами
соответствующую синглетному состоянию (ms = 0; S = 0), на которую умножается функ-
ция (10.9). Таким образом, действительно, симметричное состояние, описываемое функци-
ей ф8, является синглетным, а антисимметричное, описываемое функцией ^а, — триплетным.
Триплетный уровень, как соответствующий антисимметричной координатной функ-
ции ^а, обладает меньшей энергией, а синглетный уровень, как соответствующий симме-
тричной координатной функции ф8, обладает большей энергией. Мы получили для рассма-
триваемого случая атома гелия обоснование правила, что для данной конфигурации уровни
с большими значениями S лежат глубже, и вместе с тем показали, каким образом зависи-
мость энергии от 5, следовательно от мультиплетности, определяется электростатическим
взаимодействием (см. §9.2, с. 249).
Для основной конфигурации 1s2 атома гелия в силу эквивалентности электронов
(^а(0 —	^(2) = ^is(2)) отлична от нуля только симметричная координатная функ-
ция (10.9), которая сведется к ips — ^u(l)^u(2)5 6\ и ей соответствует антисимметричная
спиновая функция (10.19). Мы получаем синглетный уровень 1s2 ’50, энергия которого
равна Е = 2Е1з 4- К, что легко получается прибавлением к энергии 2Е\3 в нулевом при-
е2
ближении значения U\2 — — энергии отталкивания электронов, усредненного по функ-
г
ции гр3 = ipis(\)ipis(2) (это среднее значение и равно К, см. (10.15)).
Для возбужденных конфигураций Isnl (n > 1) атома гелия вместо одного уровня
с энергией Eq = Е\3 4- Eni получаются два терма — триплетный с энергией Е3 = Ei3 4- Ent 4-
К - А, лежащий ниже и соответствующий функции ipa = ^=[^1з(1)^п/(2) - ip\3(2)ipni(V)],
и синглетный с энергией Е\ = Е\3 4- Eni 4- К 4- А, лежащий выше и соответствующий
функции^ = —^=[^|S(l)^n/(2)4-^is(2)^n/(l)]. Вычисленные значения расстояний Е\ —Е2 = 2А
между одиночным и триплетным термами примерно (с точностью до нескольких десятков
процентов) совпадают с опытными значениями, что является удовлетворительным согласием,
если учесть приближенность метода.
§ 10.3.	Спектры атомов щелочноземельных металлов
Атомы щелочноземельных металлов — бериллия, магния, кальция, стронция,
бария и радия, — в отличие от трудно возбудимого атома гелия, с большой энергией
ионизации, имеют сравнительно небольшие энергии возбуждения и ионизации, хотя
и превосходящие энергии возбуждения и ионизации соответствующих атомов ще-
лочных металлов. Их самый глубокий возбужденный терм — триплетный терм 3Р° —
возникает из конфигурации nsnp с тем же главным квантовым числом р-электрона,
что и для нормальной конфигурации (п — 2, 3, 4, 5, 6, 7 для Be, Mg, Са, Sr, Ba, Ra);
энергия возбуждения невелика, составляя 2,72 эВ для Be и убывая с увеличени-
ем порядкового номера. Из той же конфигурации nsnp возникает более высокий
одиночный терм !Р°, комбинация которого с основным термом ns2 lS дает линию
ns2 \$Q—nsnp ’pf.	(10.20)
В табл. 10.4 приведены данные для термов 3Р° и ’Р°; в ней указаны положения
уровней, триплетные расщепления, длины волн и примерные интенсивности в дуге
(в квадратных скобках) резонансных линий — линии (10.20) и интеркомбинационной
линии6)
ns2 }S(y—nsnp3P\.	(10.21)
5> Нормировочный множитель в этом случае равен, при нормированной функции V’is, единице.
6) Переход ’Sq—3Р2 запрещен для дипольного излучения правилами отбора (4.156), а переход
’Sb—3Pq запрещен для любого типа излучения (см. (4.170) и (4.171)). Эю делает уровни 3Р2° и особенно
3Pq метастабильными.
§ 10.3. Спектры атомов щелочноземельных металлов
285
Таблица 10.4
Глубокие термы атомов с двумя внешними s-электронами и переходы между ними
Эле- мент	z	n	Конфигурации, термы и уровни в см 1 и в эВ			Резонансные линии, A	
			ns2	nsnp		'50- 'p;	'So - X
			's	Зр°	lp°		
			'So	Зрс	3p°	3p°			
Be	4	2	0	21979,43	21980,11	21982,46 (2,73)	(2,73)	(2,73) 0,68	2,35	42565,3 (5,28)	2 348,61 [2000]	—
Mg	12	3	0	21 850,37	21 870,43	21 911,14 (2,71)	(2,71)	(2,72) 20,06	40,71	35051,36 (4,34)	2852,13 [300]	4571,15 [20]
Са	20	4	0	15 157,91	15210,07	15315,95 (1,88)	(1,89)	(1,90) 52,16	105,88	23652,32 (2,93)	4226,73 1500]	6572,78 [50]
Sr	38	5	0	14 317,52	14 504,35	14898,56 (1,78)	(1,80)	(1,85) 186,83	394,21	21698,48 (2,69)	4607,33 (1000]	6892,59 1100]
Ba	56	6	0	12 266,02	12 636,62	13 514,74 (1,52)	(1,57)	(1,58) 370,60	878,12	18060,26 (2,24)	5 535,48 [1000]	7911,34 [200]
Ra	88	7	0	13078,44	13999,38	16688,54 (1,52)	(1,74)	(2,07) 920,94	2 689,16	20715,71 (2,57)	4825,91 [800]	7141,21 [2000]
Zn	30	4	0	32311,31	32501,39	32890,32 (4,01)	(4,03)	(4,08) 190,08	388,93	46745,37 (5,81)	2138,56 [800]	3075,90 [150]
Cd	48	5	0	30114,02	30656,13	31827,00 (3,73)	(3,80)	(3,95) 542,11	1170,87	42692,47 (5,31)	2 288,02 [1500]	3261,05 [300]
Hg	80	6	0	37645,08	39412,30	44042,98 (4,67)	(4,89)	(5,46) 1767,22	4630,68	54068,78 (6,71)	1 849,50 1100]	2536,52 [2000]
Положения уровней даны в см-1 по отношению к основному уровню ns1 So,
принятому за нуль, в скобках указаны энергии возбуждения P-уровней в эВ, между
столбцами для триплетных уровней приведены интервалы между этими уровнями:
001 = X - >0°, *12 = >2° - Н,	(10.22)
которые, согласно правилу интервалов (см. (9.36)), должны относиться как 1 : 2.
Мы видим, что с увеличением Z энергии возбуждения постепенно уменьшаются,
одновременно уменьшается расстояние ,Р°— 3Р° между одиночным и триплетным
термами. Величина триплетного расщепления, наоборот, быстро возрастает, и очень
резко увеличивается интенсивность интеркомбинационной линии (10.21). Для Be
она не наблюдается, для Mg еще слаба, а для последующих элементов усиливается
и становится у Ra самой интенсивной линией в спектре.
На рис. 10.2 сопоставлены общие схемы спектров атомов щелочноземельных
металлов, аналогично рис. 8.1 (с. 219) для спектров атомов щелочных металлов7).
Для более тяжелых атомов, наряду с общим уменьшением масштаба, происходит
7) Для триплетных термов даны их центры тяжести (ср. примечание на с. 241).
286
Глава 10. Спектры атомов с двумя внешними s-электронамЪ
Рис. 10.2. Уровни энергии атомов щелочноземельных металлов
относительное смещение вниз термов * 3D и XD с наименьшим возможным значе-
нием п; у Ва они вообще являются самыми глубокими возбужденными термами,
а для Ra также лежат очень глубоко. Общее расположение термов у атомов ще-
лочноземельных металлов схоже с их расположением у атомов щелочных металлов.
Главное отличие от последних состоит в наличии двух систем термов — синглетной
и триплетной — и двух систем переходов, что приводит к удвоению числа серий.
Для тяжелых атомов наблюдается и ряд интеркомбинационных переходов, помимо
перехода (10.21).
На рис. 10.3-10.5 приведены в качестве примера диаграммы уровней и переходов
для Mg 1, Ca 1 и Ba I.
В спектрах Mg I и Ca 1 особенно характерны триплеты
пр 3P°-n's 3S и пр 3P°—nd 3D,	(10.23)
получающиеся при комбинациях самого глубокого триплетного Р-терма с три-
плетными S- и D-термами и аналогичные членам резкой и диффузной серий
(см. табл. 8.6, с. 222) атомов щелочных металлов. Благодаря тому, что правило
интервалов для терма 3Р° приближенно соблюдается, получаются три линии8),
Для триплета 3Р°— 3S число составляющих равно трем, для триплета 3Р°— 3D оно равно шести,
но в силу малости расщепления терма 3D при не очень большой дисперсии наблюдаются три линии
3P0o-3D,, 3Р,°—3D1?2, 3P;~3DW (ср. (10.2)).
§10.3. Спектры атомов щелочноземельных металлов
287
Рис. 10.3. Диаграмма уровней энергии магния
Ог-О
л '
чоооо
-2 :
тгоооо
-з :
А гЗОООО
Рис. 10.4. Диаграмма уровней энергии кальция
288
Глава 10. Спектры атомов с двумя внешними s-электронами
интервалы между которыми приближенно относятся как 1 : 2. В спектре Ba I также
имеются такие триплеты, но из-за большой величины триплетного расщепления они
менее выражены.
Спектрами, аналогичными спектрам атомов щелочноземельных металлов, обла-
дают изоэлектронные с ними ионы с двумя внешними электронами. Для Be I
изоэлектронный ряд известен до Р XII, для Mg I — до Со XVI, для Са I —
до Ni IX, для Sr I — до Mo V9). Для членов первых двух рядов спектры аналогичны,
для членов остальных рядов аналогия нарушается тенденцией электронов (n - \)d
связываться при увеличении Z прочнее электронов ns (п — 4 для ряда, начинаю-
щегося с Са I, и п — 5 для ряда, начинающегося со Sr I); подобную тенденцию мы
уже отмечали для членов изоэлектронных рядов, начинающихся с атомов щелочных
металлов (ср. рис. 8.11, с. 237 для ряда, начинающегося с К I).
§ 10.4.	Спектры атомов цинка, кадмия и ртути
Спектры атомов Zn, Cd и Hg очень схожи между собой. Эти атомы име-
ют энергии возбуждения и ионизации более высокие, чем энергии возбуждения
и ионизации атомов щелочноземельных металлов. Их энергии ионизации близки
к 10 эВ. В нижней части табл. 10.4 приведены данные для самых глубоких Р-термов
атомов Zn, Cd и Hg и для резонансных переходов (10.20) и (10.21) между уровнями
этих термов и основным термом ns2 }S. Триплетное расщепление и интенсивность
интеркомбинационной резонансной линии возрастает от Zn к Hg. Для ртути эта
9> Для Ba I известен лишь один изоэлектронный спектр La II, а для Ra I известны только изоэлек-
тронные спектры Ac II и Th III.
§ 10.4. Спектры атомов цинка, кадмия и ртути
2М
линия — широко известная ультрафиолетовая линия ртутного спектра — является
самой интенсивной в спектре, и ей посвящено очень большое число исследований.
Весьма большое сходство схем уровней Zn, Cd и Hg наглядно показывает
рис. 10.6, аналогичный рис. 10.2 для атомов щелочноземельных атомов. На рис. 10.7-
10.9 приведены диаграммы уровней и переходов для атомов каждого из трех элемен-
тов в отдельности. Общая структура спектров такая же, как и у атомов щелочнозе-
мельных металлов.
Особый интерес представляет спектр атома ртути как в связи с изучением физи-
ческих процессов при оптическом возбуждении паров ртути (см. § 1.3), так и, в^осо-
бенности, в связи с широким применением источников света, в которых использу-
ется свечение паров ртути. Разного рода ртутные лампы применяются для получения
мощного ультрафиолетового излучения, для возбуждения спектров комбинационно-
го рассеяния и т. д. В применяемых для целей освещения люминесцентных лампах
пары ртути, при возбуждении атомов ртути в электрическом разряде, испускают
1Г $ак 103
Рис. 10.7. Диаграмма уровней энергии цинка
Глава 10. Спектры атомов с двумя внешними s-электронами
Рис. 10.8. Диаграмма уровней энергии кадмия
§ 10.4. Спектры атомов цинка, кадмия и ртути
292 Глава 10. Спектры атомов с двумя внешними s-электронами
Рис. 10.9. Диаграмма уровней энергии ртути
§ 10.4. Спектры атомов цинка, кадмия и ртути
293
ультрафиолетовое резонансное излучение, возбуждающее, в свою очередь, флуорес-
ценцию (в видимой области спектра) люминофора, покрывающего стенки лампы.
Мы разберем спектр атома ртути несколько подробнее и начнем наше рассмо-
трение с резонансных линий 2 537 А и 1 850 А, точные Значения длин волн которых
приведены в табл. 10.4.
Очень большая интенсивность резонансной линии 2 537 А (соответствующей,
как мы видели, интеркомбинационному переходу 6s2 ^о—бзбр 3Pf, сокращен-
но 6 15о~63Р|°) связана с тем, что хотя вероятность перехода для этой линии
несколько меньше, чем при переходах без нарушения правил отбора Д5 = 0,
и составляет 0,93- 106 7 * с"1 (время жизни т = 1,08- 10-7с, т.е. примерно одна
десятимиллионная секунды), но условия возбуждения весьма благоприятны. Она
получается не только за счет непосредственного возбуждения уровня 6 3Р? с энер-
гией возбуждения 4,89 эВ, но и за счет других процессов возбуждения. Наряду
с уровнем б3Р° в разряде непосредственно возбуждаются метастабильные уров-
ни 6 3Pq и 6 3Р2 того же терма с близкими энергиями возбуждения 4,67 эВ и 5,46 эВ.
Вероятность безызлучательного перехода с этих уровней на основной уровень 6 ’So
мала в силу того, что при этом должна перейти в кинетическую очень большая
энергия, порядка 5 эВ (ср. §5.4, с. 149); при столкновениях со значительной ве-
роятностью возбуждается уровень 63Pf, переход на который с уровня 63Р2° связан
с отдачей энергии 0,57 эВ, а с уровня 6 3Р0° — с получением энергии 0,20 эВ (которая
берется за счет тепловой энергии при столкновениях).
С более высоких возбужденных уровней атома ртути происходят переходы как
на уровень 3Pf, так и на уровни 3Р0° и 3Р2°, и в конечном счете число процессов,
заканчивающихся высвечиванием линии 2 537 А, оказывается весьма большим.
Очень большой вероятностью перехода, близкой к 109 с~' (т ~ 10-9 с), обладает
резонансная линия 1 850 А. Ее интенсивность весьма велика, однако практически
в кварцевых ртутных лампах она сильно ослаблена за счет сильного поглощения со-
ответствующей области спектра в кварце. Эта линия сильно поглощается и в воздухе.
Весьма интенсивные линии получаются в видимой части спектра при переходах
между возбужденными уровнями. При переходе с уровня 6sls 3Sj на три уровня
терма бзбр 3Р° возникают линии
6 3Р2° - 7 35,
6 3Р|° - 7 35,
63Ро -73S,
5 460,73 А, '
4 358,33 А, ►
4 046,56 А. ,
(10.24)
Это три наиболее ярких линии ртутного спектра в видимой области: зеленая, синяя
и фиолетовая. Синяя линия 4 358 А особенно часто применяется для возбуждения
спектров комбинационного рассеяния.
В ультрафиолетовой области спектра лежит триплет, возникающий при пе-
реходах с уровней терма 6s6d3D на уровни терма 6s6p3P°. Он состоит из шести
линий, расположенных тремя группами 3 662,88 А, 3 654,83 А, 3 650,15 А (три ли-
нии), 3 131,55 А, 3 125,67 А (две линии) и 2 967,54 А (одна линия). Это обусловлено
малостью расщепления терма 63D по сравнению с термом 63Р°. Триплетное рас-
щепление термов и получающаяся совокупность линий показаны на рис. 10.10.
Мы имеем хороший пример выраженного триплета. Отметим, что правило ин-
тервалов соблюдается лишь приближенно, как для терма 63Р°, так и для тер-
ма 63Р: для терма б3Ро3Р^— 3Р$ : 3Р2 — 3Р\ = 0,83 : 2,17 вместо 1 : 2, а для тер-
ма 6 3D 3D2- 3D{ : 3D3—3D2 = 1,84 : 3,16 вместо 2 : 3.
294
Глава 10. Спектры атомов с двумя внешними s-электронами
Рис. 10.10. Триплетное расщепление
термов атома ртути
димой и близкой ультрафиолетовой
В видимой области спектра лежит ряд
интенсивных линий синглетной системы: ли-
нии, возникающие при переходах 6s6p ’Pf—
6snd }D2 и образующие серию, аналогичную
диффузной серии щелочных металлов, и ли-
нии, возникающие при переходах бзбр ’Pf—
6sns 1Sq и образующие серию, аналогичную
резкой серии щелочных металлов. Первая
линия второй серии, взвр 'Р^—взТз lS$, Л =
10 140,6 А попадает в инфракрасную область,
как и ряд других линий ртутного спектра.
Интенсивными являются интеркомби-
национные линии: 3 663,28 А, возникающая
при переходе 6s6p3P2°—6s6d4 077,83 А,
возникающая при переходе 6s6p3P|°— 6s7s 'So,
5 789,66 и 5 769,60 А, возникающие при пере-
ходах бзбр ‘Pf— 6s6d 3D\ и 6s6p ‘Pf—6s6d 3Z>2-
В табл. 10.5 приведены данные для наи-
более интенсивных линий, лежащих в ви-
областях ртутного спектра. Данные для ин-
тенсивностей, которые сильно зависят от условий возбуждения, являются лишь
ориентировочными.
Наиболее интенсивные линии ртутного спектра
в видимой и близкой ультрафиолетовой областях
Таблица 10.5
Обо- зна- чения	Длина волны А (в воздухе), А	Волновое ЧИСЛО I/, см-1	Интен- сив- ность	Переходы		Энер- гия воз- бужде- ния, эВ
				полная запись	сокращен- ная запись	
а {	5 790,65 5 789,66	17 264,394 17 267,376	} 20	бзбр 'р;— 6s6d 'd2 бзбр'р;—6«6d3D,	6 'pf—6 'd2 e'pf—63D|	J 8,84
ь	5 769,60	17 327,439	40	6s6p'Pf—6s6d3D2	e'p;—63p2	8,85
с	5460,73	18 307,479	100	бзбр 3Р2°— 6.ч7з 3St	6 3P°—7 3S|	7,73
d	4916,07	20 335,809	15	бзбр 'Pf—6s8s 'Sb	6 'Р,— 8 'So	9,22
е	4358,33	22938,083	100	6s6p 3P|°—6s7s 35j	63P°—73S,	7,73
f	4347,49	22995,283	12	бзбр ’P| — 6s7d 'D2	б'Р]0—7'P2	9,55
i	4077,83	24 515,877	30	6s6p 3P°—6з7з 'SQ	6 3P°—7 'So	7,93
k	4046,56	24705,376	100	6s6p 3P0°—6s7s 3St	63P0°—73S,	7,73
т	3 906,37	25 591,954	20	6s6p 'Pf—6з8</ lD2	6 'Pf—8 'D2	9,88
° 1	3 663,28 3662,88	27 290,205 27 293,187	} 40	6s6p3P2~6s6d'D2 f>sf>p3P2—f>sf>d3Dy	6 3P2°—6 'd2 63P2°—63D,	J 8,84
Р	3 654,83	27 353,243	50	6s6p3P2—6s6d3D2	63P2°—63D2	8,85
Ч	3 650,15	27 388,334	100	6s6p3P^—6s6d3D}	63P2“—63£>3	8,86
Наряду с линиями, лежащими в видимой и близкой ультрафиолетовой области
спектра, у атома ртути имеются линии, лежащие в вакуумной области спектра
и представляющие более высокие члены серий 6s2 lSQ—6snp3Pi и 6s2 ^о—бзпр 1Р|°,
первыми членами которых являются резонансные линии 2537 Аи 1 850 А. В табл. 10.6
§ 10.5. Смещенные термы
295
Таблица 10.6
Линии ртутного спектра в вакуумной области спектра
Длина волны А (в вакууме), А	Волновое ЧИСЛО 1/, см”1	Переходы	Энергия возбуждения, эВ
1435,5031	69661,990	6s2 'So - 6s7p X	8,64
1402,6190	71295,198	6з2 ‘So - 6s7p X	8,84
1 307,7509	76467,160	6з2150-6з8р }Р°	9,48
1 268,8247	78813,095	6s2 'So - 6з8р X	9,77
1259,2418	79412,863	6s2 'So - 6s9p X	9,85
1 250,5637	79963,938	6з2 'So - 6s9p 'P,°	9,91
1235,8371	80916,814	6s2 'So - 6«10p X	10,03
1 232,2293	81 153,724	6s2 'So - 6з10р X	10,06
1 222,3711	81 808,217	6? 's0-6«llpX	10,14
1 220,3672	81942,551	6s2 'So - 6«1 Ip X	10,16
1 213,9035	82 378,874	6з2 'So -6з12рХ	10,21
1212,6478	82464,176	6з2 'So - 6з12р X	10,22
1 208,2242	82766,094	6s2 'So-6313pX°	10,26
1 207,3784	82 824,075	6s2 'So - 6з13р X	10,27
1 203,6273	83082,194	6з2 'So - 6з14р X	10,30
приведены данные для этих линий, согласно Герцбергу [252]. Частоты переходов
определены с большой точностью на основе комбинационного принципа с использо-
ванием точных значений длин волн для линий в близкой ультрафиолетовой, видимой
и инфракрасной областях; например, 6 ’Sq— 12 = (б Sq—6 3Pf) + (б 3Pf—7 35i) +
(7^i-12’Pf) = 39412,464 + 22938,083 + 20028,327 = 82 378,874 см'1. Благодаря
большой точности полученных таким образом данных, Герцбергу удалось найти
сравнением с линиями ртути в области 1 200-1 230 А очень точное значение длины
волны линии La для дейтерия (см. §6.6, с. 197).
§ 10.5.	Смещенные термы
Как уже отмечалось в самом начале главы (с. 276), наряду со случаем возбу-
ждения одного из s-электронов нормальной конфигурации ns2, возможен и случай
одновременного возбуждения обоих электронов. При этом, вообще говоря, для обоих
электронов I будет отличаться от нуля и совокупности термов для соответствующей
возбужденной конфигурации будут более сложными, чем в случае конфигураций ти-
па nsn'l, дающих два терма lL и 3L. Согласно табл. 9.1 (с. 247), для конфигураций рр
и dp будут получаться триады, а для конфигураций dd и fd — пентады одиночных
и триплетных термов.
Мы разберем более подробно в качестве примера Са с нормальной конфигу-
рацией 4s2, схема уровней которого приведена на рис. 10.11. Наряду с уровнями
конфигураций типа 4snl показаны уровни конфигураций типа 3dns, 3dnp, 3dnd
и 4рпр. Из этих конфигураций наиболее глубокими являются конфигурации 3d4p
и 4р2. Первой соответствуют триады термов }PDF° и 3PDF°, второй, как состоящей
из эквивалентных электронов, — термы ]SD 3Р. Все уровни этих термов найдены.
Далее возможны лежащие выше конфигурации 3d2 и 3d5s, некоторые уровни
296
Глава 10. Спектры атомов с двумя внешними s-электронами
'sWS 3Р 3D
СМ'*,
20000 -
i-
10000 -
0 - 4S
10000 '
20000 -
30000-
40000-
Рис. 10.11. Схема уровней энергии кальция
Чети
4s4s
которых также обнаружены. Возможны и еще более высоко лежащие конфигура-
ции, получающиеся при достаточно сильном возбуждении. Их уровни оказываются
лежащими уже выше границы ионизации для одноэлектронного возбуждения. Если
один из электронов оставлять в неизменном состоянии возбуждения (отличном
от нормального), а второй электрон возбуждать все сильнее и сильнее, то получается
система термов, сходящаяся к новой границе ионизации, лежащей выше границы
ионизации для одноэлектронного возбуждения. Исходя из конфигурации 3d4p и со-
храняя один электрон в состоянии 3d, можно получить путем возбуждения второго
электрона следующие конфигурации:
3d5p	3d6p	3d7p ..	типа	3dnp,
3d2	3d4d	3d5d ..	типа	3dnd,
3d5s	3d6s	3d7s ...	типа	3dns.
(10.25)
При стремлении п к оо уровни сходятся к границе ионизации, соответствующей
иону Ca (Ca II) не в нормальном состоянии 4s25y2, а в состоянии 3d2P. Эта
граница будет лежать выше на величину энергии возбуждения 3d2D—4s 2S Ca И,
равную примерно 13 700 см-1. На схеме рис. 10.11 показано положение границы
и указаны термы, сходящиеся к ней; сплошными кружочками обозначены уровни,
которые удалось наблюдать, светлыми — примерное положение уровней, которые
не удалось обнаружить.
В частности, представляет интерес последовательность термов 3dnd (п = 3,4,5,6).
Именно для Са Расселем и Саундерсом впервые было установлено наличие уровней, лежа-
щих выше границы ионизации; для термов 3dnd (п = 3,4, 5,6) они путем экстраполяции
определили положение новой границы ионизации и получили, что она лежит на 13 960 см1
§ 10.5. Смещенные термы
297
выше границы одноэлектронного возбуждения, в хорошем согласии со значением энергии
возбуждения 3d 2D—4s 2S для Са II.
Наряду с конфигурациями, для которых при возбуждении один из электронов
остается в состоянии 3d, возможны в принципе конфигурации, для которых один
из электронов остается в состоянии 4р, как это показано на схеме рис. 10.11
справа. Однако соответствующих уровней пока не удалось обнаружить. Они должны
сходиться к еще более высокой границе 4р2Р Са II.
Для сокращения принято отмечать штрихами символ возбужденного электрона, дающего
уровни, сходящиеся к границам, лежащим выше первой границы ионизации. Схождение
ко второй границе отмечается одним штрихом, схождение к третьей границе — двумя
штрихами и т. д. Например, для Са конфигурации
3</(2Р)пв, 3d(2I>)np, 3d(2Z))nd и 4р(2Р)пр
сокращенно обозначаются, как ns', пр', nd' и пр" соответственно. Символ в скобках, как
обычно, указывает исходный терм, в данном случае терм Са II. В сокращенной записи
терм 3d(2D)5p3F° обозначается как 5р' 3F°, терм 4p(2P)np 3D как пр" 3D и т.д.
Термы, сходящиеся к границам, лежащим выше первой границы ионизации,
называют смещенными. Эти границы соответствуют последовательным уровням ио-
низованного атома, а в случае уже ионизованного атома — уровням атома, кратность
ионизации которого на единицу выше. Каждая последовательность смещенных тер-
мов сходится, таким образом, к определенной границе, положение которой опре-
деляется суммой энергии ионизации данного атома и энергии возбуждения иона,
получающегося при ионизации.
При отнесении последовательностей уровней к определенной границе следу-
ет учитывать и мультиплетное расщепление термов иона. Например, для кальция
границы ионизации 3d2D и 4р2Р, показанные на рис. 10.11, являются двойными
в соответствии с тем, что термы 2D и 2Р дублетные. В первом случае мы имеем две
границы 2&з/2 и 2&5/2 с расщеплением 60,69 см-1, во втором — две границы 2Ру2
муль-
и 2Рзд с расщеплением 222,88 см. Если учитывать значения J для уровней
типлетных термов, образующих последователь-
ность, сходящуюся к определенной границе,
можно определить, какие именно уровни будут
сходиться к какой составляющей этой границы.
Например, для Si с нормальной конфигура-
цией 3з23р2 к границе Зз2Зр2Р°3^ будут сходиться,
для двухэлектронных конфигураций 3з23рпз, даю-
щих термы 3Р° и ’Р°, одиночные уровни и уров-
ни триплетных термов с наибольшим значением J,
а к границе 3з23р 2Р°^ — остальные уровни триплет-
ных термов; таким образом, к границе 2Р°^ сходятся
уровни 3pns 3Р0° и Зрпз 3Р|°, а к границе 2Ру2 ~ Уров-
ни Зрпз 3Р2° и Зрпз ’Р|°.
В рассматриваемом случае уровни конфигурации Зрпз расположены в порядке 3Р0°, 3Р|°,
3Р2°, 'Р|°. Зависимость расстояний между ними от п может быть представлена графически,
как показано на рис. 10.12. С увеличением п расстояние уровней 3Р0° и 3Р? стремится к нулю
и они сходятся к границе расстояние уровней 3Р2° и ’Pf также стремится к нулю
Рис. 10.12. Зависимость
расположения уровней 3Р° и *Р0
кремния от главного квантового числа
298
Глава 10. Спектры атомов с двумя внешними s-электронами
и они сходятся к границе 2Р3д, а расстояние 3Р2~3Р\, наоборот, стремится к постоян-
ному значению	О™етим’ что эт0 соответствует переходу от нормальной связи
к связи (j, j) (ср. § 11.3, с. 311).
Вопрос об отнесении уровней с определенным J к определенной границе может быть
решен и в более сложных случаях, если учитывать расположение уровней для рассматриваемой
конфигурации, согласно схеме связи (j,J), и правило, что порядок уровней с одинаковым
значением J не должен изменяться при изменении п.
Рассмотрим теперь переходы для смещенных термов.
Смещенные термы могут комбинировать как с несмещенными термами, так
и между собой. При этом наиболее интенсивными будут линии, соответствующие
одноэлектронным переходам, при которых изменяется на ±1 квантовое число Ц
одного из электронов при неизменном квантовом числе 12 второго электрона:
дг1 = =ы, д/2 = о.	(Ю.26)
Примером таких переходов между смещенными и несмещенными термами
являются характерные триплеты кальция
3</4в3О|,2,з-3</4рХз,4 '
3d4s3D|i2,3-3d4p3D|i2,3 *
3d4s3D|52,3-3d4p3P0o,iI2 ,
(10.27)
первый из которых лежит в красной области спектра, а второй и третий — в зеленой.
Очень существенно, что не все смещенные уровни, лежащие выше первой гра-
ницы ионизации, удается наблюдать. Часто при переходах со смещенных уровней
получаются размытые линии. Эти факты естественным образом объясняются, если
учесть, что выше первой границы ионизации лежит непрерывный энергетический
спектр, примыкающий к этой границе. Таким образом, выше границы одновремен-
но получаются дискретный энергетический спектр и непрерывный энергетический
спектр. При таких условиях имеется, в принципе, и определенная вероятность того,
что атом, возбужденный в одно из дискретных состояний с энергией, большей, чем
энергия ионизации, перейдет из дискретного состояния в непрерывное, т. е. ио-
низуется: имеется возможность автоионизации. При наличии автоионизации, пред-
ставляющей безызлучательный переход, сокращается время жизни возбужденного
состояния; это приводит, в соответствии с общим соотношением (4.125), к уве-
личению ширины дискретного уровня энергии и к соответствующему уширению
спектральных линий, возникающих при переходах с данного уровня. Если веро-
ятность автоионизации достаточно велика по сравнению с вероятностью перехода
с излучением, то вообще дискретный уровень не будет наблюдаться.
Возможности безызлучательных переходов из дискретных состояний в непре-
рывные и вероятности этих переходов зависят от свойств и тех, и других состояний.
В некоторых случаях переходы могут быть запрещены, а в других маловероят-
ны и также не будут наблюдаться. При большой вероятности безызлучательных
переходов будут иметь место значительное уширение или полное исчезновение
соответствующих спектральных линий.
Автоионизация представляет собой частный случай «взаимодействия» уровней энер-
гии. Если для данной атомной системы возможны два типа уровней энергии, например,
две последовательности дискретных уровней, или дискретная и непрерывная последователь-
ность (рис. 10.13, а и 0, то совпадающие или близкие по энергии уровни двух типов могут
«взаимодействовать» друг с другом. Это означает, с квантовомеханической точки зрения,
§ 10.5. Смещенные термы
299
что действительное состояние системы является
наложением (суперпозицией) состояний, соот-
ветствующих этим уровням, и характеризуется
волновой функцией являющейся линейной
комбинацией волновых функций гр\ и ^2> опи-
сывающих исходные состояния двух типов
гр = C^ipt + С2гр2. (10.28)
Здесь Cj и С2 — коэффициенты, квадраты
модулей которых |CJ2 и \С2\2 дают вероятно-
сти найти систему, описываемую функцией
в состояниях гр\ и ^2 соответственно и удовле-
творяют условию
|С,|2 + |С2|2 = 1.	(10.29)
В случае наложения дискретного и непре-
рывного состояний с одинаковыми энергиями,
Рис. 10.13. Две последовательности
уровней: а — дискретные
последовательности; б — дискретная
и непрерывная последовательности
при возбуждении дискретного состояния, описываемого функцией система в действи-
тельности оказывается в состоянии, описываемом функцией гр и распадается с тем большей
вероятностью, чем больше будет наложение состояний, т. е. чем больше будет С2.
Линейные комбинации (10.28) можно образовывать для уровней, обладающих одина-
ковой симметрией; только такие уровни взаимодействуют. В частности, для атомов уровни
должны обладать одинаковой четностью (т. е. принадлежать к конфигурациям одинаковой
четности — или к четным, или к нечетным) — и одинаковыми значениями J, а в случае
нормальной связи и одинаковыми значениями L и S (в случае связи (j, j) — одинаковыми
значениями fa и j2). При этом для непрерывных уровней, лежащих выше границы ионизации,
симметрия совпадает с симметрией уровней, образующих последовательность, сходящуюся
к этой границе.
Отметим, что при взаимодействии двух дискретных уровней Е\ и Е2 (Е\	Е2) получается
два новых уровня, описываемых волновыми функциями гр' и гр" типа (10.28),
Ф' = с^+ с'2ф2, ф" = С{ф, + С{ф2,
(10.30)
Е>
Рис. 10.14. Взаимодействие двух уровней
Е2
Е’1
и имеющих энергии Е\ > Е\ и Е2 < Е2, т. е. уровни как бы «расталкиваются» (рис. 10.14).
О смещении уровня из-за взаимодействия с другим уровнем говорят как об его возмуще-
нии. Возмущать друг друга, согласно сказанному выше, могут лишь уровни одной сим-
метрии. Возмущение тем больше, чем
меньше первоначальная разность Е\ -Е2
энергии этих уровней, и максималь-
но, при прочих одинаковых условиях,
для первоначально совпадающих уров-
ней. При сильном взаимодействии, ко-
гда взаимное возмущение уровней зна-
чительно, коэффициенты С\ и С2 полу-
чаются одного порядка, наложение со-
стояний велико — эти состояния сильно
Е\
«перемешиваются».
При взаимодействии дискретного уровня с близкими к нему непрерывными уровнями —
с континуумом — смещения может и не быть, но так же как и в случае дискретных уровней,
при сильном взаимодействии наложение состояний будет велико и они сильно перемешаются;
велика будет и вероятность перехода из дискретного состояния в непрерывное.
Примером взаимодействия уровней энергии могут служить в случае Са I взаимодей-
ствия уровней конфигураций 4snd (n = 4,5,6,... ) с уровнями конфигураций 3dns (п = 5,
6,7,...) (рис. 10.15). Обе эти последовательности начинаются конфигурацией 3d4s, только
в первом случае возбуждается d-электрон, а во втором случае — s-электрон. Уровни 3D3, 3D2
и 3Р| конфигурации 3d5s, лежащие ниже границы ионизации, взаимодействуют с соответ-
ствующими уровнями 3D3, 3Z>2 и 3D| (с теми же значениями J) конфигураций 4snd, особенно
300
Глава 10. Спектры атомов с двумя внешними s-электронами
с уровнями конфигураций 4s8d и 4s9d. В результате взаимных возмущений расщепление
для триплетных термов 4snd 3£> увеличивается, а для триплетного терма 3d5s 3D уменьшается,
<fs9d 3Р 1 —41	4,
ЬзЫ 3В 4	£ 4,	10	Ь
t	' ' h
4s7d 3P $ .......
QsOd 9 3^
4s5d 9 | I " I  T-,
4s4n9	------
НеЬознуц. вознущ. Вознущ. НеОазиущ.
рг---------------------------------&
ши 9 ,	f — ----------------®
9,---------------%-----------------%
как показано на рисунке ,0\ Триплетный
терм 3d6s3D, который должен лежать
W выше границы ионизации, не наблюда-
ется. Это объясняется автоионизацией
из-за сильного взаимодействия дискрет-
3d6s ных Уровней этого терма с континуум-
ом, примыкающим к границе иониза-
ции и обладающим той же симметрией,
как и дискретные уровни конфигура-
ции 4snd, симметрия которых совпа-
дает с симметрией уровней конфигура-
ции (Те же значения 12 и L).
Для уровней четных триплетных
термов 3dnd3P, лежащих выше грани-
цы ионизации (см. рис. 10.11), автоио-
низация маловероятна, так как к этой
границе сходятся только нечетные тер-
мы 3Р° и взаимодействие дискретных
уровней 3Р2, 3Pj, 3Р0 с непрерывными
уровнями может осуществляться лишь
за счет сходящихся к границе четных
термов 3S и 3Р, с нарушением прибли-
женного правила отбора для квантового
числа L. Именно поэтому получаются
резкие линии, наблюдаемые на опы-
те. Уровень 3d4d3S\, лежащий выше
границы, взаимодействует с континуум-
ом, соответствующим последовательно-
&№ сти четных уровней 4sns3Siy и перехо-
ды с этого уровня хотя и наблюдаются,
т» 1Л г»	-	.	но дают размытые линии.
Рис. 10.15. Взаимодействия уровней конфигурации Мы кипим таким обпазом что
л j j	|	1V1Ы пИДИМ^ IcaIvxIiVa иириэи IV* у 41U
sn и ns а	автоионизация очень вероятна, когда
одинаковы значения 12, значения L
и значения S (термы 3d6s 3D, симметрия континуума ds 3Z>), менее вероятна, когда одинаковы
значения L и значения 5, но различны значения Ц и 12 (терм 3d4d35, симметрия континуу-
ма ss 35), и еще менее вероятна, когда одинаковы лишь значения 5, но различны значения
/2 и значения L (термы 3dnd 3Р, симметрия континуума ss 3S и sd 3D).
’°) Расстояния 3Dj—3D2 для термов 3dns3D должны при отсутствии возмущений стремиться к рас-
щеплению 2Psy2—2Рзу2 для границы, ср. рис. 10.12 для Р-термов Si (см. с. 297).
ГЛАВА 11
СПЕКТРЫ АТОМОВ
С ЗАПОЛНЯЮЩИМИСЯ И ЗАПОЛНЕННЫМИ
р-ОБОЛОЧКАМИ
§ 11.1. Общая характеристика спектров атомов
с заполняющимися р-оболочками
Заполнение р-оболочек происходит у элементов от В до Ne во втором периоде,
от А1 до Аг в третьем периоде, от Ga до Кт в четвертом периоде, от In до Хе в пятом
периоде и, наконец, от Те до Rn в шестом периоде.
Нормальные конфигурации этих элементов имеют вид ns2npk, где п меняется
от 2 до 6, а к — от 1 до 6; они приведены в табл. 11.1. В последнем столбце
таблицы указаны основные уровни; для атомов с дополнительными нормальными
конфигурациями основные термы те же самые, но отличаются порядком уровней:
термы 2Р и 3Р для конфигураций пр и пр2 нормальные (основные уровни 2Ру2
и 3Р0), а для конфигураций пр5 и пр4 обращенные (основные уровни 2Рз/2 и 3Р2),
ср. § 6.5, с. 263. Максимальная мультиплетность основного терма получается для кон-
фигурации пр3, когда р-оболочка заполнена как раз наполовину (ср. с. 258).
В таблице приведены также значения энергий ионизации. Энергии ионизации
и соответственно масштаб уровней энергии и спектров возрастают, при данном
значении п, с увеличением числа р-электронов. Лишь для атомов с четырьмя
р-электронами энергии ионизации мало отличаются от энергий ионизации для ато-
мов с тремя р-электронами. С увеличением п энергии ионизации и масштаб спектров
довольно сильно уменьшаются при изменении п от 2 до 3, а затем также убывают,
но гораздо медленнее, а для атомов с одним р-электроном практически постоянны.
Заполнение р-оболочки у всех рассматриваемых элементов происходит со-
вершенно регулярно и структура спектров для атомов всех элементов группы,
обладающих тем же числом р-электронов, является весьма похожей. Наличие экви-
валентных р-электронов приводит к возникновению характерных совокупностей
термов, приведенных в табл. 9.4, а именно термов }SD 3Р для конфигураций пр2
и пр4 и термов 2PD°4S0 для конфигураций пр3. Теоретический расчет приводит
к следующим выражениям для энергии термов0:
Конфигурации пр2 и пр4 Конфигурация пр3
= 4-127*2,	Я(2Р°) = +6Р2,	(Ц.1)
PfD) = +ЗР2,	Р(2Р°) = О,
Р(3Р) = -ЗР2,	Р(45°) = -9Р2,
° См. [14], с. 193; энергии указаны относительно центра тяжести всех термов конфигурации.
Таблица 11.1
Нормальные конфигурации элементов с заполняющимися р-оболочками
	п = 2				п = 3				п = 4				п = 5				п = 6				
Число р-элек-			Нор- маль-	Энер- гия			Нор- маль-	Энер- гия			Нор- маль-	Энер- гия			Нор- маль-	Энер- гия			Нор- маль-	Энер- гия	Ос- нов-
тронов	Z	Эле- мент	ная кон- фигу- рация	иони- зации в эВ	Z	Эле- мент	ная кон- фигу- рация	иони- зации в эВ	Z	Эле- мент	ная кон- фигу- рация	иони- зации в эВ	Z	Эле- мент	ная кон- фигу- рация	иони- зации в эВ	Z	Эле- мент	ная кон- фигу- рация	иони- зации в эВ	ной уро- вень
1	5	В	2?2р	8,30	13	А1	3з23р	5,98	31	Ga	4s24p	6,00	49	In	5з25р	5,78	81	Т1	6з26р	6,11	2ро */2
2	6	С	2?2р2	11,26	14	Si	Зз2 Зр2	8,15	32	Ge	4з24р2	7,88	50	Sn	5з2 5р2	7,34	82	РЬ	6з26р2	7,42	Зг>0 Л)
3	7	N	2?2р3	14,53	15	Р	3s2 Зр3	10,48	33	As	4з24р3	9,81	51	Sb	5з25р3	8,64	83	Bi	6з26р3	7,29	4г>° *'/2
4	8	О	2?2р4	13,61	16	S	3з23р4	10,36	34	Se	4з24р4	9,75	52	Те	5з2 5р4	9,01	84	Ро	6з26р4	8,43	>2
5	9	F	2?2р5	17,42	17	С1	3з23р5	13,01	35	Br	4з24р5	11,84	53	J	5з2 5р5	10,45	85	At	6з26р5	9	'So
6	10	Ne	2з22рб	21,56	18	Аг	3з23р6	15,76	36	Кг	4s24p6	14,00	54	Хе	5з25р6	12,13	86	Rn	6з26рб	10,75	
Таблица 11.2
Термы конфигураций пркпг1'
Конфигурации	Исходный терм	Добавляемый электрон							
		п' S		n'p		nfd		n’f	
пр и пр5	2Р°	1ро	3Р°	'SPD	3SPD	'pdf	3PDF	'DFG	3DFG
			2S	2po		2d		2P°	
пр2 и пр4	’о		2d	2PDF'	3	2spdfg		2pdfgh°	
	Зр	2Р	4Р	2spd°	4spd°	2pdf	4PDF	2dfg°	*DFG°
	2jpc	ljo°	3jp0	'SPD	3SPD	'PDF°	3pdf°	'dfg	3DFG
пр3	2d°	1Д°	3d°	'pdf	3PDF	'SPDFG°	3SPDFG°	'PDFGH	3PDFGH
	4S°	Зуо	5S°	3P	3P	3D<>	5D<>	3F	SF
Глава 11. Спектры атомов с р-оболочками
§11.1. Характеристика спектров атомов с заполняющимися р-оболочками 303
где F2 для данного атома или иона постоянно. F2 характеризует электростатическое
отталкивание электронов и существенно положительно, а поэтому термы 3Р и 4S°
являются самыми глубокими.
Согласно (11.1) мы имеем
E('s) -E(lD)	3	Е(2Р°) - ePd°)	2
-A-Ц------= _ = 1 50, 	'----44 = -= 0,67.	(11.2)
E(JD) - E(P) 2	E(2D°) -Е(Ъ°) 3	v '
Порядок расположения термов удовлетворяет общим правилам (см. § 9.2, с. 248): тер-
мы с большей мультиплетностью лежат глубже, из термов данной мультиплетности
глубже лежат термы с большими L. Соотношения (11.2) выполняются лишь прибли-
женно и притом тем хуже, чем больше отступления от нормальной связи, в предпо-
ложении которой выведены формулы (11.1); численные примеры см. ниже, с. 309.
При добавлении к конфигурациям пр* неэквивалентного электрона n'f возни-
кают совокупности термов, приведенные в табл. 11.2; из каждого исходного терма
конфигурации пр* получается один или несколько термов, причем при возбуждении
электрона п'1' (при увеличении п') эти термы сходятся к соответствующей грани-
це npk *L. Расположение термов для результирующей конфигурации соответствует
расположению исходных термов; при этом термы мультиплетности к' — к 4- 1 лежат
глубже термов к1 = к - 1 (см. с. 260), например в случае конфигурации np3n's
из терма 45° возникают термы 5S° и 35°, из которых первый лежит ниже и является
самым глубоким термом данной конфигурации.
Важное значение имеет четность конфигураций прк и пр*п'Г. Так как p-элект-
роны являются нечетными (см. § 7.5, с. 212), то конфигурация прк при четном к явля-
ется четной, а при нечетном — нечетной. Присоединение четных з- и d-электронов
не меняет четности, а присоединение нечетных р- и /-электронов меняет ее. Мы
имеем четные конфигурации (значения пип' опущены)
р2, Р4>	P4d, рр, р3р, р5р, pf, p3f, р5f	(11.3)
и нечетные конфигурации
р, р3, р5, ps, p3s, p5s, pd, p3d, p5d, p2p, p4p, p2/, p4/.	(11-4)
Согласно правилам отбора (4.153) уровни четных конфигураций комбини-
le Is— 1 /
руют с уровнями нечетных, поэтому разрешены переходы типа пр —пр n s,
npk—npk~}n'd и запрещены переходы типа прк— прк~хп'р, npk—npk~ln'f.
В известных таблицах атомных уровней энергии, составленных Шарлоттой Мор-Ситтер-
ли [122], значения волновых чисел четных уровней энергии напечатаны основным шрифтом,
а нечетных уровней — курсивом, что сразу позволяет находить, с учетом правила отбора
AJ = 0, ±1, комбинации уровней, которым соответствуют разрешенные переходы.
Структура спектров изменяется с увеличением числа р-электронов в нормаль-
ной конфигурации прк. Эта структура существенно зависит как от свойств нор-
мальной конфигурации ns2npk, так и от свойств возбужденных конфигураций
типа ns2npk~ln’l’ и типа nsnpknl', получающихся при возбуждении электронов пр
и ns соответственно; при этом с ростом к роль конфигураций nsnpkn'l' уменьшается.
При данном числе р-электронов с увеличением п, т. е. при переходе к более тяжелым
элементам, увеличивается величина мультиплетного расщепления и соответственно
возрастает интенсивность интеркомбинационных линий.
Ниже рассмотрены последовательно спектры атомов и ионов с различным
числом р-электронов (к = 1, к — 2, 3,4, к = 5 и к = 6).
304
Глава 11. Спектры атомов с р-оболочками
§11.2. Спектры атомов с одним внешним р-электроном
Для атомов с одним внешним р-электроном — В, Al, Ga, In и Т1 с нормаль-
ными конфигурациями 2s22p, 3s23p, 4s24p, 5s25p, 6s26p — при возбуждении этого
электрона возникает одноэлектронный спектр и характерным является наличие ду-
блетных спектральных серий. Общая схема дублетных термов этих атомов приведена
на рис. 11.1. Существенное отличие от атомов щелочных металлов состоит прежде
Рис. 11.1. Уровни энергии атомов с одним внешним р-электроном
всего в том, что основным термом является терм пр2Р°, а не терм ns 15о, как у по-
следних. С терма ns2np 2Р° начинаются серии — резкая и диффузная: п\р 2Po—n2s 2S
и п\р 2Р°— n2d 2D (ср. табл. 8.6). Именно эти серии наблюдаются в поглощении.
Первые члены серий представляют резонансные дублеты. Величина дублетного рас-
щепления основного терма 2Р° быстро возрастает от В к Т1. В табл. 11.3 приведены
данные для резонансных дублетов и для величин расщепления Al, Ga, In и Т1.
Таблица 11.3
Резонансные дублеты атомов с одним p-внешним электроном
Элемент	Z	n	Дуплет пр 2P°—(n + 1)5 2S			Дуплет np 2P°—nd 2D			
			составляющие		2po 	2po P41	72	составляющие			2d° — 2n° ^5/2	%
			ч-ч	2po „ 2q 4	S'/2		2Р1/2~2РЗ/2	2P3/2-2PV2	2P3/2"2P3/2	
А1	13	3	3944,03 A 25347,69 cm"1	3961,53 A 25235,65 cm"1	112,04 cm"1	3082,16 A 32435,45 см"1	3092,71 A 32324,75 cm"1	3092,84A 32 323,41 cm"1	1,34 cm"1
Ga	31	4	4032.98A 24788,58 cm-1	4172,06 A 23962,34 см"1	826,24 cm"1	2 874,24 A 34781,67 cm"1	2943.64A 33961,68 cm"1	2944,18 A 33955,43 cm"1	6,25 cm"1
In	49	5	4101,77 A 24372,87 cm-1	4511,32A 22160,31 cm"1	2212,56 см"1	3039,36 A 32892,12 см"1	3256,09 A 30702,86 cm"1	3258,56 A 30679,56 cm"1	23,30 cm"1
TI	81	6	3775,72 A 26477,5 cm"1	5 350,46A 18684,8 см'1	7 792,7 cm"1	2 767,87 A 36117,9 см"1	3519,24A 28407,2 cm"1	3529,43 A 28 325,2 см"1	82,0 cm"1
§11.2. Спектры атомов с одним внешним р-электроном
306
Глава 11. Спектры атомов с р-оболочками
Из таблицы видно, что для Т1 величина дублетного расщепления 2^з/2""2^у2 теР"
ма 62Р° составляет около 1 эВ. Дублетное расщепление 2^5/2~2#з/2 терма 2D также
возрастает от В к Т1, но по абсолютной величине оно гораздо меньше.
Второе отличие от спектров щелочных металлов состоит в том, что наряду
с системой дублетных термов, получающихся при возбуждении р-электрона, воз-
можны термы, квартетные и дублетные, возникающие при возбуждении одного
из s-электронов. Наблюдаются термы конфигурации nsnp2 и прежде всего наиболее
глубокий терм этой конфигурации 4Р с энергией возбуждения 3,6 эВ у В и А1,
4,7 эВ у Ga, 4,4 эВ у In и 5,6 эВ у TI; у В этот терм даже является самым глубоким
возбужденным термом (энергия возбуждения терма 2s23s 2S равна 5,0 эВ). Остальные
термы конфигурации nsnp2 лежат значительно выше, в большинстве случаев выше
первой границы ионизации ns2 \Sq.
Для рассматриваемых атомов такие термы, возникающие при возбуждении
s-электрона, не играют особенно существенной роли, благодаря тому, что s-элект-
роны связаны значительно прочнее, чем р-электрон. Однако положение меняется
при переходе от этих атомов к изоэлектронным ионам, например от В I к С II, N III,
О IV и т. д. Относительная разница между прочностью связи s- и р-электронов
уменьшается, и роль конфигураций, получающихся при возбуждении s-электронов,
возрастает. Наряду с наиболее глубокими термами конфигурации nsnp2 наблюдаются
§11.3. Спектры атомов с оболочками р\ р3 и р4
307
термы конфигурации пр3 и многочисленные термы конфигураций nsnpn'l', обра-
зующие ряд последовательностей, сходящихся к границе соответствующего иона
с конфигурацией nsnp; наблюдаются также термы конфигураций np2n'f. В резуль-
тате схема термов очень сильно усложняется, и спектр утрачивает типичные черты
одноэлектронного спектра с резко выраженной дублетной структурой.
Схемы уровней и спектры рассматриваемых атомов очень схожи не только
по общей структуре, но и по масштабу, что связано с очень близкими значениями
энергий ионизации (см. табл. 11.1 и рис. 11.1). Лишь для атома В с энергией
ионизации, большей на 30%, масштаб увеличивается и, кроме того, для самого
глубокого терма 2D главное квантовое число на единицу больше, чем для основного
терма 2Р°, тогда как для самого глубокого терма 2D и основного терма 2Р° остальных
атомов главное квантовое число одинаково (ср. табл. 11.3).
В качестве типичных для рассматриваемой группы атомов на рис. 11.2 и 11.3
приведение диаграммы спектров Al I и TI I, с которыми приходится часто встречаться
при спектроскопических исследованиях.
§ 11.3. Спектры атомов с оболочками р2, р3 и р4
Для атомов с р-оболочками, содержащими 2, 3 и 4 электрона, к числу кото-
рых относятся атомы таких важных элементов, как С, N и О (оболочки 2р2, 2р3
308
Глава 11. Спектры атомов с р-оболочками
Таблица 11.4
Уровни и термы для элементов с нормальными конфигурациями пр2, пр3 и пр4
пр2	Элемент		С	Si	Ge	Sn	РЬ
	Оболочка		2р2	Зр2	4р2	5р2	6р2
	Терм 3Р	Уровень 3Р0 Уровень 3Pi Уровень 3Р2	0 16 44	0 77 223	0 557 1410	0 1692 3428	0 7819 10650
		Среднее	29	149	969	2467	8523
	Терм lD	Уровень *Р2	10194	6299	7125	8613	21458
	Терм ]S	Уровень ’Sq	21648	15 394	16 367	17163	29467
	E(lS) - E('D) Отношение E(lD) - Е(3Р)		1,13	1,48	1,50	1,39	0,62
пр3	Элемент		N	р	As	Sb	Bi
	Оболочка		2р2	Зр3	4р3	5р3	6р3
	Терм 4S	Уровень 45зу2	0	0	0	0	0
	Терм 2D	Уровень 2Рзу2 Уровень 2Е>5/2	19 223 19231	11362 11 376	10 592 10915	8512 9854	11419 15438
		Среднее	19228	11 370	10 784	9317	13 830
	Терм 2Р	Уровень 2Р\/2 Уровень 2Рз/2	j 28 840	18 722 18 748	18186 18 648	16 396 18464	21661 33165
		Среднее	28 840	18 739	18 494	17 768	29330
	Е(гР) - E(2D) Отношение —		-г— E(2D) - E(?S)		0,50	0,65	0,71	0,91	1,12
4 пр	Элемент		О	S	Se	Те	Ро
	Оболочка		2р4	Зр4	4р4	5р4	6р4
	Терм 3Р	Уровень 3Р2 Уровень 3Р\ Уровень 3Р0	0 158 226	0 397 574	0 1989 2 534	0 4751 4 707	0 16831 7514
		Среднее	78	195	945	2107	6445
	Терм	Уровень xDi	15 868	9239	9576	10 559	21676
	Терм ’S	Уровень ’Sq	33 792	22181	22446	23 199	42 718
	E('S)-E('D) Отношение E('D) - Е(3Р)		1,13	1,44	1,50	1,50	1,38
§ 11.3. Спектры атомов с оболочками р2, р3 и р4
309
и 2р4 соответственно), характерно наличие глубоко лежащей нормальной конфигу-
рации 2рк и высоко лежащих возбужденных конфигураций 2p*~1n'f.
В табл. 11.4 приведены данные для нормальных конфигураций пр2, пр3 и пр4
элементов от С до РЬ, от N до Bi и от О до Ро соответственно. Указаны положения
уровней и термов2), а также отношения расстояний между термами; эти отношения
удовлетворительно согласуются с (11.2), особенно при п — 3 и п = 4. Общее
расстояние между нижним и верхним уровнем составляет от 15 000 до 43 000 см ’1;
оно сперва уменьшается, а затем увеличивается при увеличении п, и увеличивается
при переходе от оболочки пр2 к оболочкам пр3 и пр .
Возбужденные конфигурации типа npk~}nl' дают многочисленные термы, ко-
торые определяются, согласно табл. 11.2. Наиболее глубокими термами этого типа
являются термы, получающиеся при добавлении электрона (п-f-1)$ к самому глубо-
кому терму конфигурации прк]. Для атомов С, N и О это термы 2p(2P°)3s 3Р° ’Р°,
2p2(3P)3s4P2P и 2p3(45°)3s55° 35°, лежащие на высоте 60000-62000 см"1, 83 000-
86000 см"1 и 74000-77000 см"1 соответственно.
При переходах npk—npk~xn'l' между термами нормальной конфигурации и тер-
мами возбужденных конфигураций возникают линии, лежащие в далекой уль-
трафиолетовой области, а переходы прк~хп'1!—прк~]п"1" дают линии в видимой
и инфракрасной областях. На рис. 11.4-11.6 показаны схемы уровней и некоторые
переходы для атомов С, N и О.
Рис. 11.4. Схема уровней энергии углерода
-юоооо

2) Для термов взяты центры тяжести уровней, из которых они состоят.
Рис. 11.5. Схема уровней энергии азота
нечетп.	Чети.	Нечетн
2p3ns	2р3пр	2р3пР
Глава 11. Спектры атомов с р-оболочками
§ 11.3. Спектры атомов с оболочками р2, р3 и р4
311
Возбужденные термы образуют последовательности, сходящиеся к границам 2р2Р° С II,
2р2 3Р ’S N II и 2р3 45° 2D° 2Р° О II; при этом для N I в основном наблюдены возбужденные
уровни типа 2р2(3Р)п'Г, сходящиеся к границе 2р2 3Р, а для О I наблюдены, помимо уров-
ней, сходящихся к границе 2p34S°, многочисленные уровни, сходящиеся к границе 2р3 2Р°,
и уровни, сходящиеся к границе 2р3 2Р°.
Наряду с возбужденными конфигурациями типа npk~'n'l' (в более полной запи-
си ns2 прк~*п'1') возможны возбужденные конфигурации типа ns прк+[ и ns прк n'lf.
Особенно существенна конфигурация 2s 2р3 в случае атома С, дающая, согласно
табл. 11.2, набор термов {PD° 3SPD° 5S°, из которых наиболее глубокий квинтетный
терм 2s 2р3 5Si имеет энергию возбуждения 4,2 эВ (33 375 см-1). Эта конфигура-
ция играет важную роль в образовании атомом углерода четырехвалентных связей
при соединении с другими атомами (см. подробнее гл. 26, с. 797). Для атома N найден
самый глубокий терм 4Р конфигурации 2s 2р4, а для атома О — самый глубокий
терм 3Р° конфигурации 2s 2р5 (лежащей выше первой границы ионизации).
Для более тяжелых атомов с нормальными конфигурациями пр2, пр3 пр4 спек-
тры аналогичны спектрам Cl, N1, 01, но сдвинуты, в соответствии с уменьшением
энергии ионизации, в сторону длинных волн. Одновременно с сильным возрастани-
ем мультиплетного расцепления (для конфигураций прк см. табл. 11.4) усиливаются
интеркомбинационные линии. Связь начинает значительно отступать от нормаль-
ной, и для ряда случаев можно проследить переход от связи (L, S) к связи (У, У).
На рис. 11.7 показан такой переход для конфигураций пр2 и пр(п+ l)s (п = 2, 3,4, 5, 6
для С, Si, Ge, Sn, Pb). Группировка уровней с J = О, 1, 2 в триплетный терм в обоих
случаях становится все менее выраженной и для конфигурации пр(п + l)s Sn и Pb
получается типичная связь (У, У). Этот переход определяется тем, что постепен-
но возрастает роль магнитного спин-орбитального взаимодействия по сравнению
с электростатическими взаимодействиями.
Рис. 11.7. Переход от связи (£, S) к связи (У, У): слева — для конфигурации пр2;
справа — для конфигурации пр(п + l)s
Переход от связи (£, S) к связи (У, У) может быть рассчитан (см. [14], с. 263). Располо-
жение уровней зависит от значения параметра Qp/c, где Qp — фактор дублетного расщепления
для р-электрона, а с — постоянная, характеризующая электростатическое взаимодействие3).
3) Для конфигурации пр2 она совпадает с постоянной 7*2 в формуле (11.1).
312
Глава 11. Спектры атомов с р-оболочками
Значение ^р/с = 0 соответствует нормальной связи, значение £р/с = оо(с/£р = 0) — свя-
зи (j, j). Для случаев, иллюстрируемых рис. 11.7, получается хорошее согласие опыта с теорией;
при этом из опытных данных определяются параметры и с и с их помощью рассчитывается
полная картина расположения уровней.
Для ионов, изоэлектронных с атомами, обладающими нормальными конфигура-
циями пр2, пр3 и пр4, получаются аналогичные спектры, отличающиеся масштабом
в соответствии с ростом эффективного заряда ядра. При этом с увеличением степени
ионизации возрастает роль конфигураций типа ns npk+l и ns npkn,ll, они лежат все
глубже, и появляются также конфигурации типа прк+2, Например, для иона О III,
изоэлектронного с С I, вслед за термами конфигурации 2s2 2р2 сразу лежат все
термы конфигурации 2s 2р3, а выше наблюдены и все термы конфигурации 2р4.
Аналогично, для иона F III, изоэлектронного с N I, найден терм 2р5 2Р°.
§11.4.	Спектры атомов галоидов
Атомы галоидов обладают нормальной конфигурацией пр5, где п — 2, 3,4, 5, 6
для F, Cl, Br, J и искусственного элемента At. Основным термом является терм 2Р°,
такой же, как для случая одного электрона пр, только обращенный, вследствие
чего основным уровнем является уровень пр5 2Р
Расщепление терма 2Р° велико
о
благодаря большим значениям эффективного заряда. Оно равно
404 см-1 881см-1 3 685 см-1 7 603 см-1 <1L5'
элемент F	Cl	Br	J
2р° __21
При возбуждении одного из р-электронов образуются конфигурации ти-
па пр4пТ, которые и определяют характер спектра. Возможные термы определяются
табл. 11.2. Иа рис. 11.8 приведена общая схема уровней атомов F, С1, Вг и J; показаны
основные и наиболее типичные возбужденные уровни. Главную роль играют термы
конфигураций типа пр4(3Р)пТ, квартетные и дублетные, сходящиеся к первой грани-
це ионизации пр4 3Р иона. Величина энергии возбуждения, благодаря значительной
прочности связи р-электронов в почти заполненной оболочке, велика, и поэтому
соответствующие уровни лежат очень высоко. Для возбуждения спектра необходима
энергия 12,4 эВ для F, 8,9 эВ для С1, 7,9 эВ для Вг и 7,8 эВ для J при энергиях
ионизации, равных 17,42 эВ, 13,01 эВ, 11,84 эВ и 10,45 эВ соответственно. Поэтому
переходы с основного терма пр5 2Р° на верхние уровни дают линии, лежащие в дале-
кой ультрафиолетовой области спектра, а переходы между верхними уровнями дают
линии в видимой и близкой ультрафиолетовой областях спектра.
Расположение возбужденных термов для всех рассматриваемых атомов очень
схоже. Мультиплетное расщепление термов, квартетных и дублетных, так же как
и для основного терма 2Р°, весьма значительно, достигая у F и О сотен см -1, а у Вг и J
тысяч см'1. Термы, как правило, обращенные, в соответствии с тем, что р-оболочка
заполнена более чем наполовину, и исходный терм пр4 3Р большинства наблюденных
термов является обращенным. Однако правило интервалов соблюдается плохо,
особенно для Вг и J, что свидетельствует о значительных отступлениях от нормальной
связи при взаимодействии электронов оболочки пр4 с присоединяемым электроном.
Спектры изоэлектронных ионов схожи со спектрами соответствующих атомов,
с тем отличием, что возрастает роль термов типа np4(1Z>)n/Z' и пр4(tyn'l' и по-
является терм пр6 ]S. По мере возрастания кратности ионизации терм пр6 }S лежит
относительно все ниже а ниже, что свидетельствует об упрочнении оболочки пр6.
§ 11.5. Спектры атомов инертных газов
313
СМ''
О
V 1(2-9)
2р5 2p*3s 2p*3pZp*nd
10000-
20000-
30000-
т-
*№3-‘№3‘
гР--5/2,312
'Р 5/2.3/2.I/2
ЬП(2-35)
4р5 4p*5s4p*np4pfa
11(2-53)
5р5 5p*fc5p*np5p*nd
Ul(2-19)
Зр53p*4s Зр*'пр ЗрЫ
50000-
60000-
70000-
80000-
--1/2
л» *
3-з/г
1р-
90000-
100000
№000-
'3/2
120000
130000
3/2


Рис. 11.8. Уровни энергии атомов галоидов
§ 11.5.	Спектры атомов инертных газов
Особый случай представляют спектры атомов, у которых заканчивается за-
полнение р-оболочки. Для этих атомов — Ne, Аг, Кг, Хе, Rn с нормальными
конфигурациями типа пр6 — основным состоянием, так же как для любых ато-
мов с заполненными оболочками, является состояние ’-So- В отличие от атомов
с заполненной внешней оболочкой ns2, электроны которой сравнительно легко
возбуждаются, для возбуждения одного из р-электронов заполненной оболочки прв
требуется значительная затрата энергии — от 21,56 эВ для Ne до 10,74 эВ для Rn,
т.е. оболочка пр6 обладает особой устойчивостью, что и обусловливает химическую
неактивность рассматриваемых элементов и их газообразное состояние при обыч-
ных температурах; инертный газ при этом состоит не из двухатомных молекул (как,
например, водород или кислород), а из атомов.
При возбуждении одного из р-электронов возникают конфигурации типа пр5п11г.
Например, для Ne с заполненной оболочкой 2р6 это будут конфигурации 2р5 3s,
2р5 4s, ...; 2р5 Зр, 2р54р, ...; 2р5 3d, 2р5 4d,	.
Внешний электрон п'1' связан гораздо слабее, чем р-электроны «остова» пр5. Это
хорошо показывают данные табл. 11.5, в которой произведено сравнение энергий
связи наиболее прочно связанных внешних электронов (n + l)s с энергией связи
314
Глава 11. Спектры атомов с р-оболочками
Таблица 11.5
Энергия связи электронов для атомов инертных газов
Элемент	Энергия ионизации в эВ	Электрон (п 4- l)s			Электрон пр		Wnp
		(и 4- 1)«	энергия возбуждения в эВ	энергия СВЯЗИ ^(„+1), в эВ	оболочка иона	энергия связи Wnp в эВ	
							w{n+})a
Ne	21,56	Зз	16,51	4,95	2р5	41,07	8,30
Аг	15,76	4s	11,55	4,21	зр5	27,62	6,56
Кг	14,00	5s	9,91	4,09	4р5	24,56	6,00
Хе	12,13	6s	8,32	3,79	5р5	21,21	5,60
электронов пр в остове пр5 (энергия связи электронов (n + l)s равна разности
энергии ионизации нормального атома и энергии возбуждения, энергия связи
электрона пр в остове равна энергии ионизации иона). Даже для Хе электрон 6s
связан в 5,5 раза слабее, чем электрон 5р.
С наглядной точки зрения мы имеем расположенные во внутренней оболочке
эквивалентные р-электроны остова и находящийся на периферии атома возбужден-
ный электрон.
Спектр по своему характеру является двухэлектронным спектром, так как обо-
лочка пр5, в которой не хватает одного р-электрона до полного заполнения, дает
дублетный терм 2Р°, как и один р-электрон. Однако расположение уровней резко
отличается от расположения уровней для двухэлектронной системы при наличии
нормальной связи. Спин-орбитальное взаимодействие спинового момента S' и ор-
битального момента I/ остова настолько значительно, что их сложение в полный
момент остова J' не нарушается взаимодействием с внешним электроном. Поэтому
не имеет смысла складывать момент I/ с моментом I внешнего электрона в полный
орбитальный момент £', согласно схеме нормальной связи.
Мерой спин-орбитального взаимодействия является дублетное расщепление
2Р°д— 2Рзд терма 2Р° однократно заряженных ионов (являющегося обращенным,
ср. с. 263); оно равно
Ne II Аг II Кг II Хе II
782 см"1 1 432 см"1 5 371 см"1 10 537 см"1
(11.6)
Мы видим, что это расщепление весьма велико.
Для простейшего случая внешнего s-электрона его полный момент J совпадает
со спиновым моментом s, и мы имеем связь типа (j, j), согласно схеме J1 4- j =
J' 4- з = J. Каждый из уровней 2Ру2 и 2Ру2 дает два уровня с J = J' 4- Уг, J' - Уг.
Например, для Ar I и Кг I мы имеем для конфигураций Зр5 4s и 4р5 5s картину
расположения уровней, изображенную соответственно на рис. 11.9, а и б; особенно
типично для связи (j, j) расположение уровней для Кг 14).
Для случая внешних электронов с I 0 спин-орбитальное взаимодействие
для внешнего электрона оказывается малым и чистая схема (j, j) [Z4-s = J, J1 Л-j = J]
плохо применима. Нужно сначала учитывать взаимодействие (J', I), и сложение мо-
ментов следует производить по схеме Jr 4-1 = J", J" 4- з = J. Таким образом,
В случае связи (£, S) конфигурация р5з дает термы 3Р° и 1Р°, т. е. уровни 3Р2°, 3Р°, 3Р£
и уровень ’Р®. Если для Аг такая группировка еще имеет некоторый смысл, то для Кг она носит лишь
чисто формальный характер.
§ 11.5. Спектры атомов инертных газов
315
в первую очередь учитывается сложение моментов для остова I/ + Sl = J'9 во вто-
рую — сложение момента J1 остова с орбитальным моментом I внешнего электрона
в момент J", и в третью — сложение
момента J" со спиновым моментом з
внешнего электрона в полный момент
J. Мы имеем случай смешанной свя-
зи (J, I) (см. §9.1, с. 245). Располо-
жение уровней для атомов инертных
газов ближе всего именно к этому слу-
чаю. Отметим, что сложение моментов
для s-электрона, рассмотренное выше,
можно трактовать и как частный слу-
чай связи (J, I): (J+l)+s = J"+s = J
при I = 0 (т. е. J" = J').
Рассмотрим подробнее сложение
моментов, согласно схеме связи (J, I).
Сложение J1 и I дает значения
момента J", равные J" = J' + Z,
J' + I - 1,..., |J' - 1\9 а сложение J"
и з дает значения полного момента J
равные J = J" + У2, J" - х/1- В част-
ности, для добавляемого р-электрона
при J1 = 3/г (для исходного терма
2Руз) и при J' = (для исходного
терма 2Ру2) мы получаем следующие
схемы:
1 S2n.
ЭР Рщ


4P51Pv2
Аг II

“г-;
1423см
	846 см
	803 см
	607 см
3p(>;/2)4s
О
а
Кг II
Кг I
2
3P’('p;/2)4s
-------pl
655см
—--о
4р’('р;/2)55
5371см 1	4275см 1
------
945см
-------2
4pVP;/2)5s
б
Рис. 11.9. Расположение уровней конфигураций
пр5(п 4-1)«: а — для аргона; б — для криптона
пр5 2Pj'

’/2
//
пр5 2Pj< + п'р
5/2
3Л
'/2
3/2
'/2.
(11.7)
3 2
1 О
2 1
Аналогично для добавляемого d-электрона получаются
%
пр5 2Pj-
It
2
1 О
схемы
’/2
пр5 2Pji + n'd
7/2
%
3/2
’/2
%
3/з
(11.8)
4 3
3 2
2 1
1 О
3 2
2
значениями J" и J
[122]: сперва указывают символ внешнего электрона
= 1/2 и без штриха для J1 = 3/г (например, 4р' для Зр5(2Ру )4р
связи (J, /) применяют
Для уровней с заданными
сокращенные обозначения
со штрихом для J1
и 4р для Зр5 (2Ру2)4р в случае аргона), затем в квадратных скобках дается значение J"
и, наконец, при помощи индекса справа снизу указывается значение J, как обычно.
Таким образом, 4р[5/г]2 означает уровень со значениями J" = и J = J" - 1/2 = 2,
возникающий из уровня 2Ру2 остова при добавлении электрона 4р, a 5d'[ V2I2 означает
в случае
316
Глава 11. Спектры атомов с р-оболочками
2ро
Р'/2
уровень со значениями J" = 3/г и J = J" 4- Уз = 2, возникающий из уровня
остова при добавлении электрона 5d.
В качестве примера на рис. 11.10 приведено расположение уровней для конфигу-
рации Зр5 4р аргона. Все уровни группируются в пары по значениям J". Исключение
составляют уровни с J" = У2, для которых уровни с J = 0 и J — 1 лежат весьма
далеко друг от друга. Аналогичная картина наблюдается и для других конфигураций.
Ar II
3^5(2Р°1/2)4р
/'=1/2
Ar I
-------------J" = l/2, J = 0 '
> 4Р'И/2]>.О
-----------------------J" = 1/2, J = 1
----------------------J" = 3/2, J = 2
•/" = 3/2,
/" = 1/2,
/=1
4p'I3/2]2J
4p'[l/2]1
1432 см
J" = 3/2, /=1
Г = 3/2, / = 2
4р'[3/2]2Л
3^5(2Р°3/2)4р
/' = 3/2
/" = 5/2, J = 3 j 4/''I5/2b
/" = 1/2, / = 0	4p'[l/2|0
Рис. 11.10. Расположение уровней конфигурации Зр5 4р для аргона
Благодаря очень значительным энергиям возбуждения спектр атомов инертного
газа распадается на спектр, лежащий в далекой ультрафиолетовой области и получаю-
щийся при переходах с высоких возбужденных уровней на основной уровень пр6 [Sq,
и на спектр, лежащий в инфракрасной, видимой и близкой ультрафиолетовой обла-
стях и получающийся при переходах между возбужденными уровнями. Благодаря
большому числу таких уровней, этот спектр весьма сложен. Схемы уровней и перехо-
дов для различных инертных газов очень схожи между собой и отличаются в основном
лишь уменьшением масштаба при переходе от Ne к Аг, от Аг к Кг и от Кг к Хе.
Отметим, что в видимой области для неона характерно наличие интенсивных
линий в красной области спектра (которые у аргона лежат в инфракрасной области),
а для аргона — в синей области спектра (которые у неона лежат уже в ультра-
фиолетовой области). Это используется в неоновых и аргоновых газоразрядных
трубках, применяемых в осветительной технике, преимущественно для светящихся
рекламных надписей, красных и синих.
В соответствии с наличием у остова атомов инертных газов, т. е. у однократ-
но заряженных ионов, дублетного терма пр5 2Р°, состоящего из двух уровней 2Ру
§ 11.6. Запрещенные линии в спектрах туманностей и солнечной короны 317
и 2Ру2> граница ионизации является двойной. Часть возбужденных уровней сходится
к границе пр5 2Рзд, часть уровней — к границе пр5 2Р°д, лежащей выше на вели-
чину дублетного расщепления (11.6). Смещенные уровни, лежащие выше второй
границы, наблюдать не удается, что несомненно связано с большой вероятностью
автоионизации. Отнесение уровней к определенной границе сразу вытекает из схемы
связи (J, I) и является тривиальным. Уровни с исходными уровнями иона пр5 2Рз/2
и пр5 2Р°/2 сходятся к соответствующим границам.
Между границами ионизации наблюдаются дискретные уровни, для которых исходным
является уровень пр5 2Р°^ (J' = ’/г), что понятно, так как безызлучательные переходы с из-
менением J' маловероятны, а континуум выше границы пр5 но ниже границы пр5 2Р\^
обусловлен только первой границей с J' = 3/г (ср. § 10.5, с. 299) и поэтому автоионизация
не имеет места при J' — 'fa.
Спектрами, аналогичными спектрам атомов инертных газов, но еще более труд-
но возбудимыми, обладают изоэлектронные с ними ионы. Для изоэлектронного
ряда, начинающегося с Ne I, они известны до Со XVIII, а для ряда, начинающе-
гося с Аг I, — до Fe IX. Расположение возбужденных уровней всех этих ионов
соответствует схеме связи (J, I).
§ 11.6.	Запрещенные линии в спектрах туманностей
и солнечной короны
Для спектров атомов и ионов с заполняющимися р-оболочками значительный
интерес представляют так называемые запрещенные линии, соответствующие перехо-
дам, запрещенным для обычного дипольного излучения (см. с. 114). Значительное
число спектральных линий, наблюдаемых в спектрах астрономических объектов,
долгое время не могли приписать известным элементам; они оказались запрещен-
ными линиями, принадлежащими хорошо знакомым элементам и получающимся
при переходах между глубокими уровнями ионов с нормальными конфигурациями
типа 2рк и Зрк. Такими загадочными линиями являлись в течение десятков лет яркие
линии в спектрах газовых (планетарных) туманностей5), которые приписывались ги-
потетическому элементу «небулию», и в спектре солнечной короны, приписываемые
гипотетическому элементу «коронию».
Как мы видели выше (см. §4.7, формула (4.154)), при квадрупольном и магнит-
ном дипольном излучениях переходы происходят между уровнями одинаковой четно-
сти; таким образом, оказываются возможными переходы между уровнями одной кон-
фигурации и, в частности, между уровнями одного и того же мультиплетного терма.
Правила отбора для J в случае магнитного дипольного излучения те же, что
и для обычного электрического дипольного излучения, т. е. AJ = 0, ±1, а для квад-
рупольного излучения AJ = 0, ±1, ±2 (см. (4.156) и (4.158)). Приближенное правило
запрета Д5 = 0, запрещающее интеркомбинационные переходы, сохраняется; по ме-
ре нарушения этого запрета такие переходы становятся возможными.
Наиболее важные запрещенные переходы, оказывающиеся возможными между
уровнями конфигураций типа рк, показаны на рис. 11.11. Переходы, обозначенные
5) Туманностей, состоящих из разреженных газовых масс и дающих спектры испускания из отдельных
линий.
318
Глава 11. Спектры атомов с р-оболочками
Р
3/2-
1/2*
3
Р
d\2-
Рис. 11.11. Важнейшие запрещенные переходы для конфигураций типа рк
3/2

сплошными линиями, возможны как для магнитного дипольного, так и для квадру-
польного излучений; переходы, обозначенные пунктирными линиями, возможны
только для квадрупольного излучения.
Вероятности запрещенных переходов очень малы и имеют, согласно самой
грубой оценке, порядок 1с1, таким образом, время жизни г = — возбужденных
А
состояний порядка секунды. Для магнитного дипольного излучения эти вероятности
несколько больше, доходя до 102 с’1, для квадрупольного излучения — несколько
меньше (см. оценки в §4.4). Для интеркомбинационных переходов вероятности
соответственно еще меньше на несколько порядков.
В обычных лабораторных условиях при наблюдении атомных спектров запре-
щенные линии не появляются, так как благодаря значительному числу столкновений
(при давлении 1 мм и обычной температуре имеющему порядок 107 столкновений
в секунду) возбужденные атомы успевают отдать свою энергию за счет ударов второго
рода; при увеличении разрежения остаются столкновения со стенками сосуда. Лишь
в чрезвычайно разреженном газе при отсутствии стенок время между столкновени-
ями становится порядка времени жизни возбужденных состояний или больше этого
времени, и запрещенные переходы могут осуществляться. Такие условия имеются
в газовых туманностях и в солнечной короне, а также в очень высоких слоях земной
атмосферы.
Многие запрещенные линии удается наблюдать и в лаборатории, если создать
специальные условия, при которых метастабильные атомы длительное время сохра-
няют свою энергию возбуждения. Такие условия могут быть осуществлены в элек-
трическом разряде при малых концентрациях атомов исследуемого газа в смеси
этих атомов с атомами другого газа, обычно инертного, с высокими потенциала-
ми возбуждения (что уменьшает вероятность дезактивации метастабильных атомов
при столкновениях и увеличивает вероятность их возбуждения).
Загадка линий «небулия» была разрешена в 1928 г. Бауэном [224]. Наиболее
интенсивные линии «небулия» 5 007 А и 4 959 А, обозначаемые обычно как N\ и AS,
оказались принадлежащими дважды ионизованному кислороду О III с нормальной
конфигурацией 2s2 2р2 и возникают при переходах lD2— 3Р2 и XD2— 3Р\. Наблюдается
также и линия, соответствующая переходу ^о— }D2. В табл. 11.6 приведены данные
для наиболее интенсивных запрещенных линий туманностей.
Вероятности переходов для линий и N2, являющихся интеркомбинационны-
ми, очень малы и составляют 0,018 с-1 и 0,06 с”1, что соответствует времени жизни
2 1	1
состояния 2р D2 О 111, равному q q qq^ = с’ Однако благодаря очень малой
§ 11.6. Запрещенные линии в спектрах туманностей и солнечной короны 319
Таблица 11.6
Наиболее интенсивные запрещенные линии туманностей
Длина волны в А	Волновое число в см”1	Атом	Переход	Энергия возбуждения в эВ
6583	15184	N 11	2р2,Р2-3Р2	1,90
5007	19964	О III	2р2,Р2-3Р2	2,51
4959	20158	ОШ	2Р21р2—Зр,	2,51
4363	22912	ОШ	2р2 '50-	5,35
3 729	26808	ОН	2р3Ч“Ч	3,32
3 726	26829	О 11	2р3Ч_Ч	3,32
плотности в туманностях и малой энергии возбуждения (2,51 эВ) эти линии очень
интенсивны.
Изучение запрещенных линий в спектрах туманностей позволяет сделать ряд
конкретных заключений о физическом состоянии вещества в туманностях (см. [151],
с. 417).
Отметим, что ряд запрещенных линий кислорода, особенно нейтрального атома
кислорода О I, наблюдается в спектре полярных сияний. Появление этих линий
обусловлено возбуждением атомов кислорода в сильно разреженных верхних слоях
атмосферы (на высоте в несколько сотен километров) под действием корпуску-
лярного излучения Солнца. Самая интенсивная линия 5 577 А в спектре полярных
сияний, наблюдаемая также в спектре свечения ночного неба, соответствует пе-
реходу 1Sq— для О I. Она лежит в желто-зеленой части спектра и является
весьма характерной^. Наряду с ней в спектре полярных сияний появляются крас-
ные линии О I 6 300 А и 6 364 А, соответствующие переходам 3Р2 и XD2~3P\
и присутствующие также в спектрах туманностей, и более слабые линии О II и О III.
После разрешения в 1928 г. загадки небулия оставалась еще загадка корония.
Было ясно, что линии «корония» принадлежат ионам каких-то известных элементов,
но каким именно, не удавалось объяснить до 1939 г., когда Гротриан показал [225],
что две линии 6 375 А и 7 892 А могут быть приписаны переходу 2^у2~”2^у2 междУ
уровнями терма 2Р° конфигурации Зр5 Fe X и переходу 3Р\— 3Рг между уровнями
терма 3Р конфигурации Зр4 Fe XI; положения соответствующих уровней были най-
дены Эдленом при изучении спектров очень сильно ионизованных атомов в области
спектра короче 200 А. Основываясь на идее Гротриана о принадлежности линий
короны очень сильно ионизованным атомам и используя свои опытные данные
об уровнях таких атомов, Эдлену удалось отождествить все наиболее яркие линии
солнечной короны с запрещенными линиями [226]. Наиболее интенсивная зеле-
ная линия «корония» 5 302,86 А оказалась принадлежащей тринадцатикратно (!)
ионизованному атому железа и интерпретируется как возникающая при перехо-
де Зр2Рзд—2Ру2 Fe XIV. В табл. 11.7 приведены данные для наиболее интенсивных
линий короны.
Весьма интересны выводы о физическом состоянии короны, которые можно
сделать на основе изучения запрещенных спектральных линий [154]. Наличие очень
Поэтому ее называют линией северных сияний —• авроральной линией (от латинского aurora
borealis — северное сияние).
320
Глава 11. Спектры атомов с р-оболочками
Таблица 11.7
Наиболее интенсивные запрещенные линии солнечной короны
Длина волны в А	Волновое число в см-1	Атом	Переход	Энергия возбуждения в эВ
10 798	9258	Fe XIII	3s2 3p2 3P2— 3P|	2,30
10 747	9302	Fe XIII	3s23p23P,—3P0	1,15
7 892	12668	Fe XI	3s23p43P,—3P2	1,57
6702	14917	Ni XV	3«23p23P| —3P0	1,85
6375	15683	Fe X	з?зр52р;/2-2р;/2	1,94
5303	18 852	Fe XIV	3?3P2p»/2-2p;/2	2,34
5116	19541	Ni XIII	3s2 3p4 3P|— 3P2	2,42
4231	23626	Ni XII	3?3p52P1/2-2P3/2	2,93
3987	25075	Fe XI	3s2 3p4 'D2— 3P|	4,68
3 388	29507	Fe Xlll	3s2 Зр2 '£>2— ’ft	5,96
сильно ионизованных атомов показывает, что, несмотря на очень высокую степень
разрежения вещества в короне, ее эффективная температура очень высока, порядка
миллиона градусов.
ГЛАВА 12
СПЕКТРЫ АТОМОВ С ДОСТРАИВАЮЩИМИСЯ
d- И /-ОБОЛОЧКАМИ
§ 12.1. Особенности спектров атомов с достраивающимися оболочками
Число возможных уровней, как мы видели в гл. 9 (см. табл. 9.4-9.6), возра-
стает по мере увеличения числа эквивалентных электронов и квантового числа I.
Поэтому спектры элементов с заполняющимися /-оболочками сложнее спектров
элементов с заполняющимися d-оболочками, а эти спектры, в свою очередь,
сложнее рассмотренных в предыдущей главе спектров элементов с заполняющи-
мися р-оболочками. Возрастает и максимальная мультиплетность. В то время как
для элементов с р-оболочками она не превышает четырех и пяти, для элемен-
тов с d-оболочками мультиплетность доходит до семи и восьми, а для элементов
с /-оболочками она достигает десяти и одиннадцати.
Максимальная мультиплетность, равная пяти, при оболочке типа прк возни-
кает для случая конфигураций p3(4S°)l с одним электроном, помимо р-оболочки,
заполненной как раз наполовину и дающей наиболее глубокий квартетный терм 4S°,
см. примеры спектров углерода и кислорода в § 11.3. Максимальная мультиплетность,
равная восьми, при оболочке типа ndk возникает для случая конфигураций d5(65)«Z
с двумя электронами, помимо d-оболочки, заполненной наполовину и дающей
секстетный терм ^S, см. ниже пример спектра Мп (§ 12.4). Один из этих электронов
является s-электроном, конкурирующим с d-электронами (см. табл. 7.2, с. 203, пери-
оды 4 и 5). Наконец, максимальная мультиплетность, равная одиннадцати, при обо-
лочке типа nfk возникает для конфигураций типа /7(8S°)d2Z и f7(*S°)dsl с тремя
электронами, помимо /-оболочки, заполненной наполовину и дающей октетный
терм 85°; см. ниже случай спектра Gd (§ 12.9). Два из этих электронов являются d-
и «-электронами, конкурирующими с /-электронами (см. табл. 7.2, периоды 6 и 7).
Однако спектры элементов с d- и /-оболочками отличаются от спектров эле-
ментов с р-оболочками не только большим числом уровней и более высокой
мультиплетностью. Весьма существенно, что для этих спектров имеет место конку-
ренция электронов (n — l)d и ns (в случае d-оболочек) и электронов (n-2)/, (п- l)d
и п« (в случае /-оболочек). При начале достройки оболочек (п - l)d и (п - 2)/
энергии электронов удовлетворяют соотношениям:
E(n-\)d > Ens И ^(п-2)/ > E(n-])d > Ens-	(12.1)
По мере достройки оболочки, состоящей из эквивалентных электронов, положение
меняется и получается обратное соотношение между энергиями /-, d и «-электронов.
Расположение одноэлектронных уровней энергии стремится к нормальной после-
довательности, когда электроны с меньшим п лежат глубже и электронные слои
не перемешиваются друг с другом.
1 1 i.lK ."1
322 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
Упрочнение связи d- и /-электронов весьма выражено, как мы видели в §9.6,
в изоэлектронных рядах, начинающихся с атомов щелочных металлов, т. е. для одно-
го внешнего электрона в поле ядра и электронов внутренних заполненных оболочек.
Это имеет место при п > 3 и наглядно показывается схемами рис. 8.11 и 8.12 и диа-
граммой Мозли рис. 8.14. С увеличением заряда ядра для изоэлектронных рядов К I,
Са II, Sc III, ... и Rb I, Sr II, Y III, ... (см. (8.43) и (8.44)) электроны 3d и 4d
связываются все прочнее по сравнению с электронами 4s и 5з соответственно,
а для изоэлектронного ряда Cs I, Ba II, La III, Се IV (ряд (8.45)) подобное явление
имеет место для электронов 5d и 4/, причем последний связывается прочнее всего,
как обладающий наименьшим п. Тенденция (n - l)d- и (п - 2)/-электронов быть
связанными прочнее электронов ns проявляется весьма отчетливо также при уве-
личении кратности ионизации атомов данного элемента. Это понятно, так как
и в этом случае эффективный заряд ядра возрастает. Для нейтральных атомов
(или ионов одинаковой кратности) последовательных элементов с достраивающи-
мися d- или /-оболочками возрастание эффективного заряда происходит медленнее,
чем для изоэлектронных рядов или при последовательной ионизации атомов дан-
ного элемента, и изменение относительной прочности связи з-, d- и /-электронов
происходит постепенно. Наличие конкуренции d- и з-электронов наиболее от-
четливо проявляется для d-оболочки при заполнении ее наполовину и особенно
при окончании ее заполнения. В этих случаях более выгодным оказывается обра-
зование конфигураций d*+13, чем конфигураций dks\ и конфигураций dfc+1, чем
конфигураций dks. Конкуренция /-и d-электронов особенно существенна в нача-
ле заполнения /-оболочки и при ее заполнении наполовину. Аналогично случаю
d-оболочки упрочнение /-электронов по сравнению с з-электронами приводит
для /-оболочки, при заполнении ее наполовину и при окончании ее заполнения,
к образованию конфигураций /*+1з вместо конфигураций fks2 и конфигураций /*+1
вместо конфигураций fks.
Вследствие конкуренции близких по энергии электронов в ряде случаев нару-
шается регулярный ход изменения нормальных конфигураций от элемента к элемен-
ту (ср. нормальные конфигурации для элементов с достраивающимися d- и /-обо-
лочками, приведенные в табл. 7.2, с. 205) и усложняется совокупность глубоких
уровней. Более подробно влияние этой конкуренции будет рассмотрено в следую-
щих параграфах при разборе конкретных типов спектров.
Большое число термов и уровней различных конфигураций делает задачу интер-
претации спектров атомов и ионов с достраивающимися d- и /-оболочками часто
весьма трудной. Затруднено и определение энергий ионизации путем экстраполяции
последовательных термов одного рода, сходящихся к границе ионизации, особенно
для тяжелых атомов с большими мультиплетными расщеплениями.
Характерным является наличие ряда термов одного рода, возникающих из од-
ной и той же конфигурации (см. табл. 9.5 и 9.6, где число термов одного рода
отмечено цифрами под символом терма) или из близких по расположению конфи-
гураций одной четности. Принято последовательные глубокие термы одного рода,
начиная с самого глубокого, обозначать буквами а, Ъ, с,... для конфигураций той же
четности, что и четность нормальной конфигурации, и буквами z, г/, я,... для кон-
фигураций противоположной четности. Высокие термы той же четности, что и термы
нормальной конфигурации, обозначают как е, /,<;,... .
Например, для V I последовательные четные термы 3d34s2 4F (основной терм)
и 3d3 4s 4F обозначаются как a 4F и b 4F, более высокие четные термы 3d5 4F,
3d34s5s4F — как e4F, f4F, а последовательные нечетные термы 3d34s4p4F°,
§ 12.2. Спектры атомов с достраивающимися d-оболочками 323
ЗсГМр4/^0, 3d34«4p4F° — как г4/*10, y4F°, x4F° (см. таблицы атомных уровней
энергии [122], т. I, с. 292).
Важную роль играют смешанные конфигурации, содержащие, помимо эквива-
лентных d- или /-электронов, неэквивалентные электроны. Для термов подобных
конфигураций указывается, когда это может быть сделано, исходный терм, так же
как и в случае смешанных конфигураций, содержащих эквивалентные р-электроны
(см. предыдущую главу, например, с. 309).
Мы сперва рассмотрим спектры атомов с достраивающимися d-оболочками,
а затем спектры атомов с достраивающимися /-оболочками.
§ 12.2. Общая характеристика спектров атомов
с достраивающимися d-оболочками
Достройка оболочек (n - l)d происходит в четвертом, пятом и шестом периодах
системы Менделеева для п = 4, 5 и 6 соответственно (см. табл. 7.2). В табл. 12.1
приведены нормальные электронные конфигурации и энергии ионизации (в эВ)
атомов и ионов элементов, у которых происходит достройка оболочек (n - l)d.
В таблицу включены и элементы, у которых d-оболочка только что закончена
и окончательно заполняется s-оболочка следующего слоя. Для каждой конфигурации
указан основной уровень.
Основной уровень для конфигураций типа dk и dks2 определяется согласно
табл. 9.7, с учетом того, является ли соответствующий терм нормальным (при к < 5)
или обращенным (при к > 5) (см. с. 263). Для конфигураций типа dks получается
из исходного самого глубокого терма *L конфигурации dk основной терм с тем
же значением L, но с мультиплетностью на единицу большей (см. §9.4, с. 260).
Благодаря конкуренции d- и «-электронов нормальные конфигурации атомов
некоторых аналогичных элементов в разных периодах различны. Например, в то
время как Fe I, Со I и Ni I имеют нормальные конфигурации типа d*« , Ru I
и Rh I имеют нормальные конфигурации типа d*+1«, a Pd I — даже типа dk+2.
Таким образом, в пятом периоде тенденция к упрочнению d-электронов для обо-
лочки, приближающейся к заполнению, выражена сильнее и вместо «-электронов
присоединяются дополнительные d-электроны.
При ионизации атомов отрываются в первую очередь «-электроны. Для од-
нократно заряженных ионов получаются, при отрыве одного «-электрона, как
нормальные конфигурации типа (n - i)dkns, так и конфигурации типа (n — l)d*+1.
Дважды заряженные ионы рассматриваемых элементов имеют нормальные конфи-
гурации типа (n - l)dk (где к — номер элемента в группе), в которых отсутствуют
электроны ns. Для ионов с конфигурациями dk энергии отрыва d-электрона увели-
чиваются с увеличением числа электронов в d-оболочке, однако для оболочки d5,
заполненной наполовину, энергия ионизации больше, чем для оболочки d6 (ср. Fe III
и Мп III).
Наличие для нормальной конфигурации наряду с d-электронами «-электронов
делает аналогию между конфигурациями и между термами изоэлектронных атомов
и ионов менее полной, чем в случае элементов с заполняющимися р-оболочками.
В частности, при переходе от нейтрального атома к изоэлектронным ионам, одно-
кратно и двукратно заряженным, изменяется нормальная конфигурация. Например,
согласно табл. 12.1, Sc I имеет нормальную конфигурацию 3d4s2, Ti II — 3d24s,
V III — 3d3, Мп I имеет нормальную конфигурацию 3d54«2, Fe II — 3d64«,
Co III - 3d7. Вместе с тем обнаруживается сходство между нейтральным атомом
и ионами данного элемента.
н
Таблица 12.1
Нормальные конфигурации атомов и ионов с достраивающимися d-оболочками
Sc		Ti		V		Cr		Mn		Fe		Co		Ni		Cu		Zn
21		22		23		24		25		26		27		28		29		30
Sc I 3d 4s2 2^3/2 6,54		Ti I 3d24s2 3F2 6,82		V I 3d34s2 ^3/2 6,74		Cr I 3d54s 7S3 6,76		Mn I 3d54s2 6^5/2 7,43		Fe I 3d64s2 6Z>4 7,90		Co I 3d74s2 %/2 7,86		Ni I 3d84s2 4 7,63		Cu I 3d104s 2^l/2 7,72		Zn I 3d'%>2 'So 9,39
\		\		\		\				\				\		\		
Sc II 3d 4s 3£>i 12,80		Ti II 3d24s 4^3/2 13,57		V II 3d4 5Po 14,65		Cr II 3d5 6^5/2 16,49		Mn II 3d54s 7s3 15,64		Fe II 3d64s 6Р9/2 16,18		Co II 3d8 X 17,05		Ni II 3d9 2&5/2 18,15		Cu II 3d10 'Sb 20,29		Zn II 3d104s 2^l/2 17,96
\		\		\		\				\								
Sc III 3d 2d3/2 24,75		Ti in 3d2 3F2 27,47		V III 3d3 4^3/2 29,31		Cr III 3d4 5Po 30,95		Mn III 3d5 6^5/2 33,69		Fe III 3d6 5P4 30,64		Co III 3d7 4F9/2 33,49		Ni III 3d8 3f4 35,16		Cu III 3d9 2D5/2 36,83		Zn III 3d10 'So 39,70
k=l		2		3		4		5		6		7		8		9		10
Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
Продолжение таблицы 12.1
Y		Zr		Nb		Mo		Tc		Ru		Rh		Pd		Ag		Cd
39		40		41		42		43		44		45		46		47		48
Y I 4d5s2 ^З/З 6,38		Zr I 4d25s2 ^2 6,84		Nb I 4d45s ^1/2 6,88		Mo I 4ds5s 7S3 7,10		Тс I 4d55s2 6q ^>5/2 7,28		Ru I 4d75s ^5 7,36		Rh I 4d85s 4F9/2 7,46		Pd I 4d10 ’So 8,33		Ag I 4d105s 2^l/2 7,57		Cd I 4dl05s2 ’So 8,99
\		\		\		\		\		\		\		\		\		
Y II 5s2 '«о 12,23		Zr II 5d24s 4-^3/2 13,13		Nb II 4d4 5£>o 14,32		Mo II 4d5 6^5/2 16,15		Тс II 4d55s 753 15,26		Ru II 4d7 4F3/2 16,76		Rh II 4d8 ^4 18,07		Pd II 4d9 2#5/2 19,42		Ag II 4d10 ’So 21,48		Cd II 4dl05s 2^l/2 16,90
\		\		\		\		\		\		\		\		\		
Y III 4d 2I>3/2 20,51		Zr III 4d2 ^2 22,98		Nb III 4d3 ^3/2 25,04		Mo III 4d4 5Po 27,13		Tc III 4d5 6^5/2		Ru III 4d6 5P4 28,46		Rh III 4d7 4l7l 2*9/2 31,05		Pd III 4d8 3К» 32,92		Ag HI 4d9 2^3/2 34,82		Cd III 4d10 ’So 37,47
к=1		2		3		4		5		6		7		8		9		10
§ 12.2. Спектры атомов с достраивающимися d-оболочками
326 Глава 12. Спектры атомов с достраивающимися d- и f-оболочками
Продолжение таблицы 12.1
40
§ 12.2. Спектры атомов с достраивающимися d-оболочками
327
Одинаковые совокупности термов получаются для конфигураций (n — \)dkns2
и (n - \)dk нейтрального и дважды ионизованного атомов данного элемента. Так как
у большинства элементов с d-оболочками обе эти конфигурации являются нормаль-
ными для нейтральных и дважды ионизованных атомов соответственно (для неко-
торых нейтральных атомов (n- l)d2ns2 не является нормальной конфигурацией), то
и основные термы у них одинаковы (см. табл. 12.1, примерно для двух третей эле-
ментов основные термы нейтрального и дважды ионизованного атомов одинаковы).
Для нейтрального и однократно ионизованного атомов данного элемента имеется
значительное сходство как конфигураций dks2 и dfc+13 атома с конфигурациями dks
и dk+] иона, так и конфигураций dksl атома с конфигурациями dkl иона. Добавление
s-электрона к исходному терму *L конфигурации dk или d*+1 дает, как было
рассмотрено в § 9.4 (с. 260), два терма и х+1£, что и определяет сходство термов
перечисленных пар конфигураций.
Например, для титана получаются одинаковые совокупности термов lDG 3PF
3d2 Ti III, расположенные очень сходным образом
Ti I
3dV
и
Ti II
3</24s
2„
Ti III
3</2
‘G
‘G
2G
3P
3P
'D
2d
2
3F
3
для конфигураций 3d2432 Ti I
(рис. 12.1). Для конфигура-
ций 3d24s Ti II из термов
]DG возникают термы 2DG,
а из термов 3PF — термы
2PF и 4PF, схожие с соот-
ветствующими термами Ti I
и Ti III. Термы 4F, 2D, 4Р,
fe Ti II расположены анало-
гично термам 3F, }D, 3Р, te
Ti I и Ti III, термы 2F и 2P
Ti II, возникающие из тех
же исходных термов 3d2 3F
и 3d2 3Р, что и 4F и 4Р, ле-
жат соответственно выше.
Различие и сходство
спектров различных элемен-
тов с d-оболочками опреде-
ляется, в первую очередь, за-
висимостью числа и распо-
ложения уровней оболочки
(n - l)d* от числа электро-
нов в ней. На рис. 12.2 показаны термы оболочек 3dk последовательных ионов
от Sc III до Си III. Некоторые высокие термы не найдены, их ориентировочное
расположение указано пунктирными скобками.
Характерными чертами спектров являются:
1.	Усложнение схемы уровней при увеличении числа d-электронов от 1 до 4
и при уменьшении числа этих электронов от 9 до 6.
2.	Значительная симметрия для оболочек dk и d}0~k, как и должно быть (см. § 9.3,
с. 255).
3.	Увеличение от краев к середине расстояния основного терма до более вы-
соких. Для оболочки d5 это расстояние максимальное; для Мп III оно составляет
около 27 000 см-1, т. е. более 3 эВ.
В спектрах нейтральных и однократно ионизованных атомов данного эле-
мента главную роль играют конфигурации, содержащие (n - \)dk и (n - l)d*+1,
F
Рис. 12.1. Глубокие термы Ti I, Ti II и Ti III
328 Глава 12. Спектры атомов с достраивающимися d- и /-оболочками
-1
см
-	50 000
-	40 000
-	30 000
-	20 000
-	10 000
5
3Р
lD
1 ==^	50 000-
3F------4F------lF
F	40 000-
30 000-
x20 000-
10 000-
2D 5/2 3F ,4
Sc ^/2 Ti 2
5	0	*p 3/2 3F
6S -Ь-A
^—5/2=^ =^/2----------
Mn	Fe	\3	Co	9/2	Ni
25	26	4	27	28
d5	/	d1	d*
2D3/2
Cu V2
Рис. 12.2. Термы конфигураций dk для двухзарядных ионов элементов
третьего периода
а в спектрах двукратно ионизованных атомов — конфигурации, содержащие
(п - \)dk~] и (п - \)dk.
Например, в случае Fe (п — 4, к = 6) такими конфигурациями являются для Fe I
и Fe II конфигурации, содержащие 3d6 и 3d7, а для Fe III — содержащие 3d5 и 3d6.
Это будут:
Fe I	3d6 4s2,	3d64snZ,	3d7 4s,	3d7nZ,	(12-2)
Fe II	3d64s,	3d6nZ,	3d7,		(12.3)
Fe 1П	3d5 4s,	3d5nl,	3d6.		(12-4)
Комбинируют друг с другом, в соответствии с правилом отбора (14.153), уровни
конфигураций различной четности. Так как d-электроны являются четными, то все
конфигурации типа (п - \)dk четные, независимо от числа электронов, в отличие
от конфигураций прк, попеременно четных и нечетных (в зависимости от четности к,
см. гл. 11, с. 303). Поэтому нечетными являются конфигурации, содержащие элек-
трон п'р или электрон п1 /. Наиболее важными типами переходов являются переходы
(n- l)dkns2—(п- \)dknsn'p, (n- l)dk+]ns—(n- l)dknsn'p, (п - \)dkns-(n- V)dkn'p
и (n - \)dk—(п - \)dk~{,n!p.
Для Fe I это будут переходы
3d64s2 - 3d64sn'p, 3d74s - 3d64sn p, 3d7 4s ~ 3d7np, (12.5)
§ 12.3. Атомы с d-оболочками, заполненными менее чем наполовину 329
для Fe II —
3d64s - 3d6zi'p, 3d7 - 3d6n'p	(12.6)
и для Fe HI —
3d54s - 3d5n'p, 3d6 — 3d5n'p.	(12.7)
В соответствии с типами конфигураций и с характером расположения термов
этих конфигураций спектры элементов с достраивающимися d-оболочками могут
быть разделены на ряд групп, в зависимости от степени заполнения d-оболочки. Эти
группы будут более подробно рассмотрены в следующих параграфах, причем главное
внимание будет уделено спектрам элементов четвертого периода, которые наиболее
важны в практическом отношении. Большинство элементов четвертого периода вхо-
дит в состав важных в техническом отношении сплавов на железной основе. Особое
положение занимает спектр железа, что определяется как широким применением
спектрального анализа всевозможных сталей, основу которых составляет железо, так
и использованием спектра железа в качестве спектра сравнения при разнообразных
спектроскопических исследованиях.
§ 12.3. Спектры атомов с d-оболочками,
заполненными менее чем наполовину
Атомы Sc, Ti, V — элементов четвертого периода — и аналогичные им атомы
элементов пятого периода (Y, Zr, Nb) и шестого периода (Lu, Hf, Та) обладают
d-оболочками, заполненными меньше чем наполовину. Их схемы уровней и спектры
постепенно усложняются по мере увеличения общего числа внешних электронов
и числа d-электронов. Усложнение происходит как при переходе от Sc к Ti и от Ti
к V, так и при переходе для данного элемента от двукратно ионизованного атома
к однократно ионизованному и от однократно ионизованного к нейтральному.
При этом возрастает максимальная мультиплетность (см. табл. 9.5, с. 255), и главную
роль в спектре начинают играть термы высокой мультиплетности.
Для скандия мы имеем одноэлектронный спектр Sc III (ср. рис. 8.11, с. 237),
двухэлектронный спектр Sc II и трехэлектронный спектр Sc I. Последний является
уже довольно сложным и для него характерны квартетные и дублетные термы
конфигураций 3d4snl и 3d2nl, возникающие из триплетных и одиночных термов
конфигураций 3d4s и 3d2 Sc II. Более сложным является спектр Ti I и еще
более сложным спектр V I. Для 11 I характерны квинтетные и триплетные термы
конфигураций 3d24snl и 3d3nl, возникающие из квартетных и дублетных термов
конфигураций 3d24s и 3d3 Ti II, для V I характерны секстетные и квартетные
термы конфигураций 3d34snl и 3d4nl, возникающие из квинтетных и триплетных
термов конфигураций 3d34s и 3d4 V II. На рис. 12.3 сопоставлены схемы глубоких
уровней Sc I, Ti I и V I.
В отличие от ранее применявшихся схем, уровни термов одной мультиплетности изо-
бражены на общих вертикальных линиях для каждого значения J, независимо от значения L
и конфигурации. Уровни одного терма соединены между собой сплошными или пунктирными
линиями1^ и рядом указан символ терма. Указывается также конфигурация, причем термы
данной конфигурации подчеркнуты одинаковым образом. Расстояния вертикальных линий,
соответствующих различным значениям J, пропорциональны этим значениям. Благодаря
этому при соблюдении правила интервалов все уровни одного мультиплетного терма должны
лежать на одной прямой, наклон которой пропорционален величине мультиплетного расщеп-
ления. В данном случае, когда мультиплетные расщепления еще не очень велики (особенно
Для четных и нечетных конфигураций соответственно.
330 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
ScI(Z-21)
54000-
52000-
।
।
26000-
24000-
22000-
20000-
18000-
16000-
14000-
12000-
10000-
6000-
4000-
1/23/2 5/2 112^/2
7ТТ7»
ЗОг4$
Ti IfZ-22)
т-----ts5136 4-------- -
&64j0)
3d34s
V I(Z-23)
Рис. 12.3. Схемы уровней Sc I, Ti I и V I
для Sc I), прямые невелики и наклоны; для дальнейшего, однако, такой способ изображения
мультиплетных расщеплений весьма удобен и нагляден.
Мы видим, что схема термов усложняется от Sc к Ti и что, вместе с тем,
имеется сходство в общем расположении как глубоких четных термов конфигура-
ций 3d*4s2, 3d*+14s, так и более высоких нечетных термов конфигураций 3d*4s4p.
При этом самый глубокий терм конфигурации 3d*+14s (a4F для Sc I, a5F для Ti I
и a 6D для V I) приближается к основному терму, принадлежащему конфигурации
3d*4s2 (a2D для Sc I, a3F для Ti I и a4F для V I). В этом проявляется тенденция
к упрочнению электрона 3d.
§ 12.4. Атомы с d-оболочками, заполненными наполовину
331
Следует отметить, что для Ti II, изоэлектронного со Sc I, основным термом являет-
ся 3d24s a 4F, лежащий много глубже терма 3d4s2c 2D и лишь немного глубже терма 3d3b 4F
конфигурации, состоящей лишь из d-электронов. Уже у V II, изоэлектронного с Ti I, основным
термом является терм 3d? a 5D, тогда как у Ti I этот терм лежит весьма высоко (на 28 600 см-1
выше основного терма).
Во всех спектрах получаются хорошо выраженные мультиплеты, примером ко-
торых могут служить характерные квартеты Sc I, возникающие при переходах между
четным термом 3d2 (a3F)4sa?F и триадой нечетных термов 3d2(a3F)4pz^G°y4Foy^D°
и лежащие в желтой, зеленой и голубой областях видимого спектра. Приближенное
выполнение правила интервалов и распределение интенсивностей в наблюдаемых
мультиплетах свидетельствует о близости связи к нормальной.
Спектры атомов и ионов элементов пятого и шестого периодов схожи со спек-
трами соответствующих атомов и ионов элементов четвертого периода. Так, на-
пример, спектр Zr I схож со спектром Ti I, спектр Zr II — со спектром Ti II.
При этом, разумеется, увеличивается мультиплетное расщепление и интенсивность
интеркомбинационных мультиплетов.
§ 12.4. Спектры атомов с d-оболочками, заполненными наполовину
Для Мп и Сг и аналогичных им элементов пятого периода (Мо, Тс) и шестого
периода (W, Re) характерна существенная роль конфигурации d5 с очень глубоко
лежащим термом 65. Для Cr II этот терм 3d56S является основным, и из него
возникают и самые глубокие термы 7S и 5S нормальной конфигурации 3d54$ Cr I.
Основным термом для Mn I является терм 3d54s2a 65, для Мп II — терм 3d5(а 65)4з 7S
и для Мп III — терм 3d5a6S, который лежит особенно глубоко (см. рис. 12.2).
На рис. 12.4 сопоставлены глубокие четные термы атомов и ионов марганца и хрома.
Мы имеем схожее расположение термов конфигурации 3d5 для Cr II и Mn III,
3d54s для Cr I и Мп II и 3d54s2 для Мп 1. Одновременно имеется сходство
конфигураций 3(^45 Cr II и 3d? 4s Мп I и конфигураций 3d44$2 Cr I и 3d6 Мп И,
связанное со сходством дополнительных конфигураций 3d4 и 3d6. Число глубоких
термов, лежащих ниже 20000 см-1, во всех случаях невелико.
Нечетные термы конфигураций, содержащих электроны 4р, лежат значительно
выше основного терма. Для Cr I и Мп I они начинаются с 23 300 см"1 и 18 400 см"1,
для Cr II и Мп II — с 46800 см"1 и 38400 см"1. Число высоких термов, как четных,
так и нечетных, получается весьма значительным как для нейтральных атомов, так
и для однократно заряженных ионов, и спектры являются типичными сложными
спектрами высокой мультиплетности. Максимальная мультиплетность для Cr II
и Mn III равна шести, для Cr I и Мп II — семи и для Мп I — восьми.
Наиболее интенсивные линии в спектрах Мп и Сг возникают при переходах s—р
типа 3dk+}4s—3dk+}4p и 3dk4s2—3dk4s4p с возбуждением 5-электрона. Например,
для Mn I это будут переходы 3d?4s—3d?4p и 3d54$2—3d54s4p, для Mn II — перехо-
ды 3d?4s—3d5 4р.
Три очень ярких линии Mn I 4 034,5 А, 4033,1 А и 4030,8А соответствуют перехо-
дам 3d54s(a7S)4pz6P^ 5д 7д—3d54s2a6S5^ (на
основной уровень), а три также очень
ярких линии 2 801,1 А, 2 798,3 А и 2 794,8 А — переходам 3d54s(a 5S)4p у вР^ 5д 7д—
3d54s2a6Ss/2. Три наиболее ярких характерных линии Mn II 2 605,7 А, 2 593,7 А
и 2 576,1 А возникают при переходах 3d5 (a 6S)4p z 7Р2°Д4~3d5 (а ^>)4з a 7S3 на основ-
ной уровень. Аналогичные переходы для Cr I дают три самых ярких линии 4 289,7 А,
332 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
см i
40 000-
30 000-
20 000-
10 000-
----Ч ----------------7S -----------Ч
Л d5s2 * d* d5s d5
Сг I	Cr II
Mn I	MnII MnIIl
Рис. 12.4. Глубокие термы атомов Мп и Cr
4 274,8 А и 4 254,3 А. Три других ярких линии Cr I 5 208,4 А, 5 206,0 А и 5 204,5 А
соответствуют переходам 3d5(а 6S)4p z 5PjO2)3—3d5 (a 6S)4s a 5S2.
Интенсивные линии также возникают при переходах d-p типа 3dk4s—3d*-14s4p
и 3dk—3dk~i4p, связанных с возбуждением электрона 3d. В частности, три
очень ярких линии Cr I 3 605,3 А, 3 593,5 А и 3 578,7 А возникают при переходе
3d44s(a6P)4p^7P£3 4—3d5(a6S)4s а75з. В спектре Cr II имеется триплет 2 065,4 А,
2 061,5 А и 2 055,52 А, соответствующий переходам 3d4 ^a5D)4pz6P^ 5д 7д— 3d5a655/2.
Во всех приведенных примерах одним из комбинирующих термов является
S-терм, состоящий из одного уровня и комбинирующий с тремя уровнями Р-терма
той же мультиплетности, что и приводит к появлению трех близких линий большой
интенсивности. Мы видим, что характерные для спектров Мп и Сг «триплеты», пред-
ставляющие в действительности септеты, секстеты и квинтеты, связаны с наличием
исходной конфигурации 3d5, дающей очень глубокий терм 6S5/22).
Отметим, что для термов конфигурации 3d5 (а также для таких термов, для кото-
рых термы этой конфигурации являются исходными) мультиплетные расщепления
малы. Это находится в соответствии с тем, что для оболочек, состоящих из эквива-
лентных электронов и заполненных как раз наполовину, мультиплетное расщепление
2> Именно в спектре марганца впервые были открыты Каталаном в 1922 г. [219] мультиплеты.
Первоначально считали найденные Каталаном серии типа s—р Mn I триплетными и лишь затем было
показано, что они являются секстетными и октетными.
§ 12.5. Атомы с d-оболочками, заполненными более чем наполовину
333
должно при нормальной связи приближенно обращаться в нуль3) (см. гл. 9, с. 263).
Например, для Mn I полная ширина мультиплетных термов а V?, а 3 4Р и b 4D конфигу-
рации 3d5 6s2 составляет 22,0 см-1,81,3 см-1 и 71,5 см-1, тогда как для мультиплетных
термов a6D и a 4D конфигурации 3d6(a 5D)4s она составляет 584,9 см-1 и 522,2 см1.
Отметим также, что для конфигураций Сг, содержащих 3d4, характерны нор-
мальные мультиплетные термы, а для конфигураций Мп, содержащих 3d6, характер-
ны обращенные мультиплетные термы.
Спектры соответствующих атомов и ионов элементов пятого и шестого периода
схожи со спектрами атомов и ионов Сг и Мп. В частности, три самые яркие ли-
нии Mo I 3 903,3 А, 3 864,1 А и 3 798,2 А аналогичны трем самым ярким линиям Cr I,
обусловленным переходом z 7Р°—а 7S.
§ 12.5.	Спектры атомов с d-оболочками,
заполненными более чем наполовину
Начиная с Fe и аналогичных ему элементов пятого периода (Ru) и шестого
периода (Os), для нормальных и однократно ионизованных атомов главную роль
играют конфигурации, содержащие более пяти эквивалентных d-электронов. Это
конфигурации, содержащие 3d6 и 3d7 для Fe, 3d7 и 3d8 для Со и 3d8 и 3d9 для Ni.
Число глубоких четных термов увеличивается по сравнению с Сг и Мп. Общее
число термов весьма велико, особенно для Fe. Все термы обращенные, за редкими
исключениями. Максимальная мультиплетность равна семи для Fe I, шести для Fe II
и Со I и пяти для Со II и Ni I.
Наиболее важное значение имеет для спектроскопии и спектрального анализа
спектр железа, на что уже указывалось выше. Поэтому мы рассмотрим спектр железа
более подробно. Спектры Fe I и Fe II весьма полно интерпретированы, установлено
около 150 термов Fe I и свыше 100 термов Fe II.
На рис. 12.5 приведены самые глубокие термы Fe I и Fe II.
Для Fe I характерны (ср. (12.2)) четные термы конфигураций 3d64s2 и 3d74s, к чи-
слу которых относятся основной квинтетный терм 3d64s2 5D и глубокие термы, квин-
тетный и триплетный, 3d7 (a 4F)4s a 5Fa 3F, и нечетные термы конфигураций 3d64s4p
и 3d7 4р. Все термы, лежащие ниже 42 000 см4, относятся к этим конфигураци-
ям (кроме двух термов 3d8c3F и 3d54s24p у 7Р°), появляются и термы, обусловленные
конфигурациями, содержащими наряду с электронами 3d6 и 3d7 электроны 5s, 6s,
7s, 5р, 4d и 5d. Для всех конфигураций глубже всего лежат термы, возникающие
из самых глубоких исходных термов Fe II, 3d6(a 5Z>)4s a 6Da 4D и 3d7a 4F.
Наибольшей интенсивностью обладают квинтеты и триплеты, возникающие
при переходах между нижними четными термами a 5D конфигурации 3d64s2 (основ-
ным) и a5F, a3F конфигурации 3d74s и триадами верхних нечетных термов z5D°,
z5F° и z5P° конфигурации 3d64s(a eD)4p и y5D°, y5F°, z5G°9 y3D°, y3F°, z 3G°
конфигурации 3d74p соответственно^. Эти мультиплеты лежат в близкой ультрафи-
олетовой области и примыкающей к ней фиолетовой части видимой области.
3> При пренебрежении магнитными взаимодействиями, помимо спин-орбитального взаимодей-
ствия Si) для каждого электрона в отдельности.
4) Примером квинтетов могут служить переходы
3d64s(a6D)4pz5D°—3d64s2a5D и 3d64s(a6D)4p z5F°—3d64s2a5D,
данные для которых приведены в табл. 9.10 и 9.11 (см. с. 267).
334 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
Наряду с квинтетами и триплетами наблюдаются септеты и интеркомбинаци-
онные мультиплеты.
Для спектра Fe II характерны (ср. (12.3)) четные термы конфигураций 3d64s
и 3d7, к числу которых относятся основной терм 3d6(a 5Z))4sa 6Z>, глубокий терм a *D,
возникающий из того же исходного терма 3d6a5D Fe III, и глубокий терм 3d7a4F,
и нечетные термы конфигурации 3d64p. К этим термам относятся все термы,
лежащие ниже 54000 см-1 (кроме терма 3d54s2a 6£). Выше 54000 см-1 появляются
§ 12.5. Атомы с d-оболочками, заполненными более чем наполовину
335
термы конфигураций 3d54$4p и 3d54s2, а выше 78000 см-1 — термы конфигураций
с 3d6, содержащих электроны 5s и 4d.
Наибольшей интенсивнрстью обладают секстеты и квартеты, возникающие
при переходах между нижними четными термами a 6D (основным) и a 4D конфигу-
рации 3d6(a5Z?)4s и триадами верхних нечетных термов z6F°, z6D°, z6P° и z4F°,
z4D° и z4P° конфигурации 3d? (a 5D)4p соответственно5). Эти мультиплеты лежат
в ультрафиолетовой области спектра короче 3 000 А.
Между термами Fe I и Fe II имеется значительное сходство. Термы Fe I могут
быть получены присоединением электрона 4s или nl из термов Fe II (ср. (12.2)
и (12.3)). Мультиплетные расщепления соответствующих термов Fe I и Fe II очень
близки друг к другу.
3d7(?F)45a3F
3(?4s2aD
3d\aF)4saF
1/2
• 3(f(aD)4saD
7/2
9/2
1/2
: 3(f(aD)4saD
9/2
Рис. 12.6. Глубокие термы Fe I и Fe II
Сравнение трех самых глубоких термов Fe I с тремя самыми глубокими термами Fe II
показано на рис. 12.6. Здесь соединены пунктирными линиями соответствующие друг другу
уровни мультиплетных термов. Уровню с заданным J определенного терма соответствуют
уровни с J + и J - ’/г сравниваемых термов. Величины расщепления термов близки друг
к другу и можно по расщеплениям данного терма вычислить расщепления сравниваемых
с ним термов (подробнее см. [15], с. 72). Все расщепления могут быть выражены через фактор
расщепления £3d для электрона 3d. В частности, для терма a SD Fe I расщепление определяется
оболочкой 3d6. Так как терм SD является термом наивысшей (S = 2, х = 2S+1 = 5) возможной
5) Наиболее интенсивная пара линий в спектре Fe II, 2 599,4 А и 2 598,4 А, относится к мультиплету
a6D—z6D° и соответствует переходам 6Р9^—6Р9^ и 6Р7^—6^5/2*
336 Глава 12. Спектры атомов с достраивающимися d- и f-оболочками
мультиплетности, то для него согласно (9.39) имеем С(5Р) =	Согласно правилу
интервалов (9.36), получаем расстояния между уровнями:
5D{ - 5Dq = С(5Р). 1,	5D2 - 5Р, = С(5Р). 2,
5d3 - 5D2 = С(5Р) • 3,	5Р4 - 5Р3 = С(5Р). 4
и полное расщепление терма равно 5Р4 - 5Р0 = С(5Г>) • 10 = C3d (знак минус указы-
4
вает, что терм обращенный). Опытное значение полного расщепления равно -978 см-1,
откуда (за~ 390 см“1. Для терма 3d7a4F Fe II аналогично (S = 3/2, х = 2S + 1 = 4)
С	5	7
С(4Г) = —р расстояния между уровнями равны %/2~ %/2 = №)-, %/— *Fsk = C(4F)--,
9	21	21
4Fy2—4F?^ = C(*F) • - и полное расщепление составляет 4Р9д—4F3^ = £(4F) • — = £з<ь
Опытное значение полного расщепления равно -1 245 см-1, откуда £3d ~ 355 см-1. В том,
что для оболочки 3d7 £3(/ меньше, чем для оболочки 3d6, нет противоречия, так как для кон-
фигурации 3d7 экранирование должно быть несколько больше, что приводит к уменьшению
фактора расщепления (см. (8.28)).
Для железа именно спектры Fe I и Fe II имеют наибольшее значение, так
как спектры источников — дуги и искры, — обычно применяемых в спектральном
анализе и для получения спектра сравнения железа, состоят из линий Fe I и Fe II.
При этом в спектре дуги преобладают линии нейтрального атома железа Fe I,
а в спектре искры весьма интенсивны линии однократно ионизованного атома
железа Fe П6).
Для спектра Fe III, который получается лишь при достаточно сильном возбу-
ждении в источниках света, характерны многочисленные четные термы конфигура-
ции 3d6, к которой относится и основной терм a5D7\ и 3d54s и комбинирующие
с этими термами многочисленные нечетные термы конфигурации 3d54р.
Спектры Со и Ni проще спектра Fe в связи с приближением оболочки 3d
к заполнению. При этом все сильнее проявляется и тенденция к упрочнению связи
d-электронов. У Ni I наиболее глубокие термы a 3F и a 3D конфигураций 3d84s2
и 3d9(a2Z>)4s лежат на одной глубине: основной уровень 3Р4 расположен ниже
уровня 3£>з лишь на 205 см-1. У Ni II основным термом является терм 3d9a2D
конфигурации, не содержащей электронов 4$.
Спектры Ru, Rh и Pd в пятом периоде и Os, Ir и Pt в шестом периоде
схожи со спектрами Fe, Со и Ni. Вследствие больших мультиплетных расщеплений
мультиплетная структура является менее выраженной.
§ 12.6.	Спектры атомов с внешними з-электронами,
помимо заполненной d-оболочки
Для Си и Zn и аналогичных им элементов пятого периода (Ag, Cd) и шестого
периода (Au, Hg) нормальная конфигурация нейтрального атома содержит запол-
ненную оболочку d10 и з-электроны — один в случае Cu, Ag, Аи и два в случае
В данном случае названия «дуговой спектр» для спектра Fe I и «искровой спектр» для спектра Fe II
примерно соответствуют характеру спектра железа в дуге и в искре соответственно (ср. с. 149).
7> Полное расщепление этого терма равно 1 027 см-1, что очень близко к полному расщеплению
основного терма 3d64s2a 5D Fe I, равному 978 см-1. Небольшая разница в расщеплении возникает за счет
дополнительного экранирования двумя электронами 4s для Fe I.
§ 12.6. Атомы с внешними s-электронами и заполненной d-оболочкой 337
см-}
62317,2 -
60000'--.
50000-
40000 + 5+
30000
20000 -
10000 + z
0-0
--10000
20000
30000
40000
50000
3#
Рис. 12.7. Диаграмма уровней энергии меди
о-о+о 4
-60000
62317,2
см4
" г+
Zn, Cd, Hg. При возбуждении з-электрона возникают типичные одноэлектронные
и двухэлектронные спектры; диаграмма одноэлектронного спектра Си приведена
на рис. 12.7. Однако в принципе возможно и возбуждение электрона d-оболочки.
У группы Zn, Cd, Hg для возбуждения электрона d-оболочки требуется энергия,
превышающая энергию ионизации, которая равна энергии отрыва з-электрона,
и уровни конфигураций типа d9s2l лежат выше границы ионизации. Возбуждение
таких уровней происходит при поглощении в далекой вакуумной ультрафиолето-
вой области. Подобные спектры поглощения — спектры возбуждения внутренних
электронов — были изучены Бейтлером [221]. Обычные двухэлектронные спектры
цинка, кадмия и ртути, лежащие в видимой и в обычной ультрафиолетовой области
и возникающие при возбуждении одного из s-электронов внешней оболочки з2,
были нами уже рассмотрены в гл. 10 (см. § 10.4).
При возбуждении электрона внутренней оболочки (n — l)d10 начальным состоянием
для поглощения является состояние (n - l)d,ons2 ’So (n = 4,5,6 для Zn, Cd, Hg), и в силу
правила отбора для квантового числа I, = ±1, могут образовываться конфигурации
(n — l)d9ns2np (n — l)d9ns2nf)	(12.8)
дающие такие же термы, как и конфигурации dp и df (оболочка d9 эквивалентна одно-
му d-электрону), приведенные в табл. 9.2. Однако в силу правил отбора (4.156) и (4.160)
для квантового числа J переход из состояния (J = 0) разрешен только в состояние
с J = 1 и могут возбуждаться лишь следующие уровни триад lPDF° 3PDF° и пентад
lPDFGH° 3PDFGH°:
d9р [Р° 3Р° 3D°, d9fxPx3Px3D\.	(12.9)
Для Zn, Cd и Hg особенно хорошо наблюдаются последовательности уровней ’Pf
и 3Р|° конфигурации (n - l)d9ns2n'p (п' = п, п + 1,п + 2,...), сходящиеся соответственно
^38 Глава 12. Спектры атомов с достраивающимися d- и f-оболочками
Рис. 12.8. Уровни атома ртути,
соответствующие возбуждению внутреннего электрона
к границам (n - l)d9ns2 21)з^ и (n - l)d9ns2 2Р3д однократно заряженного иона данного
элемента. На рис. 12.8 приведена схема получающихся уровней для Hg. Самый глубокий
Pi уровень, 5d96s26p ’Pf (сокращенно обозначаемый 6р' ’Р°), лежит ниже границы иониза-
ции 84 184 см-1 (10,4 эВ) атома ртути (состояния 5d,06s 2Sy2 Hg II) на 7 321 см-1, т. е. примерно
на 0,9 эВ. Все остальные уровни лежат выше этой границы ионизации и сходятся к грани-
цам, соответствующим состояниям 5d?6s2 2Р5д и 5d96s2 2Р3д Hg II и лежащим по отношению
к нормальному уровню 5d106s2 ’So Hg I на высоте 119 692 см-1 и 134 732 см-1, т. е. около 14,9 эВ
и 16,7 эВ. Спектр поглощения Hg, связанный с возбуждением внутреннего электрона 5d,
лежит в области короче 1 300 А вплоть до 750 А.
Возбуждение внутренних электронов наблюдено и для ряда других элементов, помимо
Zn, Cd и Hg. Принято спектры нейтральных атомов и ионов, соответствующие возбуждению
электронов внутренних оболочек, обозначать как 1&, Iе, Г*,... и II*, IF, IГ*, ..., где индексы 6,
с, d, ... относятся к возбуждению последовательных внутренних оболочек, считая снаружи
внутрь. Таким образом, рассмотренные нами спектры возбуждения оболочки (п - l)d’°
нейтральных атомов Zn, Cd и Hg обозначаются как Zn l\ Cd Р и Hg Р [11].
Иначе, чем для Zn, Cd и Hg, обстоит дело с энергией возбуждения d-электрона
для Си, Ag и Au. Самому глубокому терму, возникающему при возбуждении такого
электрона, а именно терму (n - l)d9ns2 2D (n = 4, 5, 6 для Си, Ag, Аи) соответствуют
энергии возбуждения, приведенные в табл. 12.2 (энергии возбуждения даны в см-1
и в эВ).
Другие конфигурации, содержащие (n - l)d9, также возбуждаются сравнитель-
но легко, особенно у Си и Ag. Поэтому для атомов рассматриваемых элемен-
тов характерно наличие двух систем термов — дублетных термов конфигураций
типа (n - l)d’°n'Z, аналогичных термам атомов щелочных металлов, и дублет-
ных и квартетных термов конфигураций (n - \)<Pnsn'l. Соответственно имеется
§ 12.7. Спектры атомов с достраивающимися f -оболочками
339
Таблица 12.2
Энергия возбуждения уровней конфигурации (n - l)d9ns2
для меди, серебра и золота
Элемент	Конфигурация	Уровни		Энергия ионизации
		2р%	Ч	
Си	3d94s2	11202,6 см-1 1,39 эВ	13 245,4 см"1 1,64 эВ	62317,2 см"' 7,73 эВ
Ag	4d95s2	30242,3 см"1 3,75 эВ	34714,2 см-1 4,30 эВ	61 106,5 см"1 7,58 эВ
Аи	5d96s2	9161,3 см"1 1,14 эВ	21435,3 см"1 2,66 эВ	74410,0 см"1 9,23 эВ
и две системы переходов. Наиболее интенсивны для первой системы дублеты
главной серии (n - l)d10ns2S—(n - \)д™п'р2Р° и для второй системы дублеты се-
рии nd9 ns2 2D~—nd9nsn p2P°. Наблюдаются для второй системы также квартеты
и интеркомбинационные мультиплеты, получающиеся при переходах между уров-
нями дублетных и квартетных термов.
Отметим, что с легкостью возбуждения электрона d-оболочки связано то, что рассма-
триваемые элементы могут быть не только одновалентными, но и двухвалентными и трех-
валентными. Особенно это выражено у Си и Au с энергиями возбуждения лишь немного
превышающими 1 эВ; для меди весьма характерны соединения, в которых она двухва-
лентна, для золота — соединения, в которых оно трехвалентно. Хотя серебро с большей
энергией возбуждения обычно и одновалентно, оно также иногда бывает двух- и трех-
валентным.
§ 12.7.	Общая характеристика спектров атомов
с достраивающимися /-оболочками
Достройка оболочек (п - 2)/ происходит в шестом и седьмом периодах системы
элементов Менделеева для п — 6 и п = 7 соответственно. В табл. 12.3 приведены
нормальные конфигурации атомов и ионов элементов, у которых происходит до-
стройка /-оболочек. Для каждой конфигурации указан основной уровень. Данные
для трансурановых элементов весьма неполные, и взятые в скобки конфигурации
менее надежны.
Основные уровни конфигурации fks2 определяются, согласно табл. 9.7, с учетом того,
является ли соответствующий терм нормальным (при к < 7) или обращенным (при к > 7)
(см. с. 263). Для конфигурации типа fkds2 основной терм определяется в результате сложения
моментов оболочки fk с моментами d-электрона; например, для нормальной конфигурации U
оболочка 5/3 дает терм V (S1 = 3/2, L1 = 6) и добавление d-электрона (s = у2, I = 2) дает,
по правилу Гунда, самый глубокий терм 5L (S = 3/2 + ‘А = 2, L = 6 + 2 = 8) с основным
уровнем 5Ь6 (J = L - S = 6).
Для группы редкоземельных элементов, следующих за лантаном, — лантанидов
(или лантаноидов) — /-электроны оказываются связанными прочнее конкурирую-
щих с ними d-электронов, и нормальные конфигурации имеют вид 4/*6з2. Только
для Gd и, возможно, для ТЬ (для которого окончательно не установлено, является ли
340 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
нормальной конфигурация 4/85d6s2 или 4/96s2) нормальная конфигурация содержит
электрон 5d. В противоположность этому для элементов, следующих за актинием, —
актинидов (или актиноидов) — d-электроны успешно конкурируют с /-электронами,
последние связаны относительно менее прочно, чем у лантанидов, и нормальная
конфигурация не только Ас, но и Th не содержит /-электронов, а у следующих
элементов, в частности у U, вместо одного из /-электронов имеется d-электрон. Не-
сомненно, что для трансурановых элементов с к > 8, т. е. начиная с Cf, нормальная
конфигурация, подобно конфигурациям, соответствующим лантанидам, уже не со-
держит d-электронов. Это вытекает из общей тенденции к упрочнению /-электронов
по сравнению с d-электронами (см. выше, с. 321).
При ионизации в первую очередь отрываются, как правило, s-электроны, а за-
тем, в случае их наличия, d-электроны. Однако в отдельных случаях возможен
и обратный порядок отрыва. Кроме того, в силу тенденции к упрочнению свя-
зи /-электронов, при переходе к следующей ступени ионизации d-электроны могут
заменяться /-электронами. К сожалению, из-за сложности спектров и трудности
нахождения последовательностей уровней, сходящихся к границе ионизации, энер-
гии ионизации большинства атомов и ионов лантанидов и актинидов не определены
достаточно точно. Для нормальных атомов лантанидов энергии ионизации близки
к 6 эВ, для нормальных атомов актинидов — к 4 эВ.
Как показывает табл. 12.3, для трижды заряженных ионов получаются нормаль-
ные конфигурации fk~\ состоящие только из /-электронов. Для дважды заряженных
ионов возможны нормальные конфигурации как типа fk, так и типа fk~xd. Для од-
нократно заряженных ионов возможны нормальные конфигурации fks (особенно
для лантанидов), fk~xds и fk~xз2 (последняя для актинидов). Наконец, для ней-
тральных атомов нормальные конфигурации содержат по два s-электрона и иногда,
кроме того, d-электрон вместо /-электрона.
В начале периода для актинидов встречаются конфигурации (у Th), содержащие
не только один, но и два d-электрона; правда, при переходе от Th I к Th II один
из d-электронов отрывается, а при переходе от Th III к Th IV вместо d-электронов
появляется /-электрон. Мы видим, что из-за наличия трех типов конкурирующих
электронов нормальные конфигурации могут быть различными.
Так же как и для элементов с достраивающимися d-оболочками, при дострой-
ке /-оболочек спектры изоэлектронных атомов и ионов не являются вполне анало-
гичными и, наоборот, обнаруживается значительное сходство между нейтральным
атомом и ионом данного элемента. Это определяется наличием той же самой оболоч-
ки 4/* у нормального атома и его ионов и особенно проявляется в сходстве спектров
нейтрального и однократно ионизованного атомов, обладающих глубокими конфи-
гурациями fks2, fk~xds2 и /*s, fk~xds соответственно. Для нейтрального и дважды
ионизованного атомов получаются, вероятно во всех или почти во всех случаях,
нормальные конфигурации, отличающиеся только двумя лишними s-электронами
у нейтрального атома.
Термы ионов и нейтрального атома данного элемента могут быть найдены путем последо-
вательного прибавления электронов к нормальной конфигурации 4/*-1 трижды заряженного
иона. При этом обычно легко указать, особенно для глубоких термов, исходные термы.
Например, мы получаем глубокие термы Gd III, добавляя электрон 5d к основному тер-
му 4/78s;/2
Gd IV, затем добавлением еще двух электронов от исходных термов Gd III
переходим к термам Gd II и Gd I.
§12.7. Спектры атомов с достраивающимися f -оболочками
341
Нормальные конфигурации атомов и ионов с достраивающимися /-оболочками
342 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
Характерные триады термов Gd I могут быть получены следующим образом:
Gd IV
Gd I
7	,ч	=,	in	o/4/75d6s('°Do)6c"PI>F0'
4/5d(V)	\	?
д #’ / V	’n«/	x 4/ 5rf 6s( 7? ) 6p PDF
/ Pi/2)5 u \	0/4/75d6s(sD°)6p9PPF°
4/75d(9D°) 6a *D°( J 7	\ '	7
1 V	x 4f5d6s(3D°)6p1PDF°	>
7 ,7 „	. o/4/75d6s(8£>°) 6p9PDF°
7o/4/75^)6.^(4>5rf6s^;6;7ppr
(Si/,)5d D \	llp PlJP
Аналогичные D-термы получаются для Eu II и Eu I из конфигурации 4/7 857д Eu III.
Характерно при этом то, что исходный терм 9D° Gd III и Eu I является нормальным,
а терм 7D° — обращенным. Возникающие из них термы также являются нормальными
и соответственно обращенными, что позволяет установить исходные термы.
4/,s5°7/2
Gd III
Gd II
(12.10)
Спектры элементов с достраивающимися /-оболочками еще сложнее, чем спек-
тры элементов с достраивающимися d-оболочками, и являются самыми сложными
атомными спектрами. Это определяется не только тем, что из конфигураций ти-
па fk возникает больше термов, чем из конфигураций типа dk, но и наличием
конкурирующих электронов трех типов (/-, d- и s-электронов) вместо двух ти-
пов (d- и s-электронов). Существенно притом, что конфигурации /*-1s2, fk~xsd
и fks, fkd обладают разной четностью, тогда как конфигурации dk~xs2 и dks,
характерные для элементов с достраивающимися d-оболочками, обладают одина-
ковой четностью (см. с. 328). Различие четности конфигураций, содержащих fk~x
и fk, приводят к возникновению двух систем переходов: переходов fk~xsd~fk~xpd,
fk~xsd~fk~xsp и переходов fks—fkp, fkd—fkp, отличающихся четностью нижних
и четностью верхних уровней.
К наибольшему усложнению спектров приводит наличие конфигураций, со-
держащих помимо /-электронов один или два d-электрона. Наряду с переходами
типа з—~р, дающими более простой спектр, состоящий из интенсивных линий, име-
ют место переходы типов р—d и d—f, дающие более сложный спектр, состоящий
из менее интенсивных, но очень многочисленных линий. К числу таких перехо-
дов относятся переходы fkxds2—fk~xps2 и fks2—fk~xds2 для нейтральных атомов
и переходы fk~xds—fk~xps и fks—fk~xds для однократно заряженных ионов.
Для двукратно и трехкратно ионизованных атомов, у которых нормальные
конфигурации не содержат s-электронов (см. табл. 12.3), переходы типа d—/ и р—d
играют основную роль; к ним относятся переходы fk—fk~xd и fk~xd—fk~xp.
Изменения спектров рассматриваемых элементов с изменением числа /-элект-
ронов аналогичны изменениям спектров элементов с достраивающимися d-оболоч-
ками при изменении числа d-электронов (см. с. 327). Схемы уровней усложняются
при увеличении числа /-электронов от 1 до 6 и при уменьшении их числа от 13 до 8,
имеется значительная симметрия для оболочек / и /	, от краев к середине групп
лантанидов и актинидов увеличивается расстояние от основного терма до более вы-
соких; оно достигает максимума для оболочки /7 с очень глубоким основным термом
85°, составляя для Gd IV около 31 000 см"1, т. е. 4 эВ. Особенно наглядным является
изменение расположения уровней, с изменением числа /-электронов, для трижды за-
ряженных ионов лантанидов, обладающих нормальными конфигурациями типа 4fk.
см			 	 см 40000		 	 	 	 40000- -30000	_____		 	 	 	 	 30000- -20000	_____		 	 20000- 	 =====	—	9/2	 	 .		 	4 	11/2	 	 	 	5	5/2 - юооо 	 	 	 	,5/2	8		15/2		0.	п/2		13/2 	6	15/2___7	;з/2	6	s===f	11/2	7		< 	13/2	6 	W			4 	13/2 	К	5	11/2- " ~6 	9/2_22j		5 	5 	7/2	, J^l	7/2 5/2	1	9/2	*	5/2'"	" n	1/2	z-	ic/2	о	ic/*>	z* 	
Се	Рг	Pd	Pm	Sm	Ей	Cd	Tb	Dy	Ho	Er	Tu	Yb 58	59	80	61	62	63	64	65	66	67	68	69	70 4/	4/2	4/3	4/4	4/5	4/6	4/7	4/8	4/’	4/‘°	4/"	4/*2	4/‘3 2F5/2	3H4	4/9/2	5/4	H’s/2	Л)	$7/2	^6	^15/2	h	Л5/2	#6	F7/2 Рис. 12.9. Термы конфигураций fk для трехзарядных ионов редкоземельных элементов
§ 12.7. Спектры атомов с достраивающимися f -оболочками
344 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
На рис. 12.9, аналогичном рис. 12.2, показаны уровни таких ионов для конфигура-
ций 4/*, определенные на основе изучения спектров ионов лантанидов в кристаллах
и растворах.
В кристаллах и растворах, содержащих редкоземельные элементы — лантаниды, —
обычно имеются трижды заряженные ионы. Между уровнями конфигурации 4/Л наблю-
даются переходы, в поглощении и в испускании, запрещенные для дипольного излучения
свободных атомов и ионов. Это либо магнитные дипольные и квадрупольные переходы, либо
вынужденные дипольные переходы, обусловленные нарушением правил отбора под действием
электрических полей окружающих ионов. Вероятности подобных переходов могут дости-
гать 103-104 с~’ [230]. В электрических полях окружающих ионов уровни трижды заряженных
ионов лантанидов расщепляются, однако эти расщепления не превышают нескольких со-
тен см-1 и значительно меньше мультиплетных расщеплений. Поэтому изучение характерных
дискретных спектров ионов редкоземельных элементов в кристаллах и в растворах позволяет
определить расположение уровней, соответствующих конфигурациям 4/*. С наглядной точки
зрения дискретность спектров определяется тем, что размеры /-оболочки ионов малы (ра-
диус этой оболочки порядка 0,5 А) и эта оболочка поэтому хорошо защищена от внешних
воздействий, приводящих лишь к сравнительно малому расщеплению уровней.
Отметим, что аналогичные переходы возможны для дважды и трижды заряженных
ионов элементов с достраивающимися d-оболочками, в частности для Сг, Мп и Fe [229].
В этих случаях, однако, расщепления уровней иона в электрическом поле окружающих ионов
в кристалле или в растворе того же порядка или больше, чем мультиплетные расщепления.
С увеличением числа электронов в /-оболочке существенно возрастают мульти-
плетные расщепления термов соответствующих конфигураций fk. Это определяется
тем, что факторы расщепления (nf, согласно формуле (8.28), растут с увеличением
эффективного заряда Z* = Z - з, где з — постоянная экранирования, остающаяся
приближенно постоянной для достраивающейся оболочки; для оболочки 4fk з рав-
но примерно 35 и Z* меняется при переходе от Се (Z = 58) до Yb (Z = 70) от 23
до 35, что и приводит, благодаря пропорциональности факторов расщепления Z*4,
к значительному росту мультиплетных расщеплений. Для Yb IV величина дублетного
расщепления терма равна 10 300 см-1 и превосходит величину этого расщепления
для Се IV, равную 2 250 см-1, более чем в 4,5 раза (см. [15], §23).
Ниже рассмотрены подробнее спектры атомов и ионов элементов с достраива-
ющимися /-оболочками.
§ 12.8.	Спектры атомов с /-оболочками,
заполненными менее чем наполовину
Спектры элементов, у которых /-оболочки заполнены меньше чем наполо-
вину, — La, Се, Pr, Nd, Pm в шестом периоде и Ac, Th, Ра, U, Np в седьмом
периоде — усложняются как при увеличении числа /-электронов, так и при пе-
реходе от ионизованных атомов данного элемента к нейтральным. Аналогично
элементам с заполняющимися d-оболочками при этом возрастает максимальная
мультиплетность. В частности, у U I она достигает уже семи (5 = 3).
У La самые глубокие конфигурации еще не содержат s-электронов, одна-
ко для возбужденных конфигураций эти электроны уже играют существенную роль.
Спектры La III, La II и La I с нормальными конфигурациями 5d, 5d2 и 5d6s2 — типич-
ные одноэлектронный, двухэлектронный и трехэлектронный спектры, соответствен-
но усложняющиеся. Еще более сложные спектры имеют Се, Рг и Nd, причем для этих
элементов особенно характерны конфигурации, содержащие 4/2, 4/3 и 4/4, дающие
очень схоже расположенные термы, показанные на рис. 12.10 для Се II, Pr II и Nd IL
Получаются правильно расположенные мультиплетные термы, свидетельствующие
§ 12.8. Апюмы с f-оболочками, заполненными менее чем наполовину
345
Рис. 12.10. Термы конфигураций 4/* для Се И, Pr II и Nd II
о близости связи к нормальной. Однако спектр является очень сложным, так как
наряду с глубокими уровнями конфигураций 4fk5d и 4fk6s имеются еще более мно-
гочисленные глубокие уровни противоположной четности, соответствующие конфи-
гурациям 4/*-15d2 и 4fk5d6s. Это приводит к появлению второй системы переходов,
дающей, правда, менее интенсивные, но зато весьма многочисленные линии. Наи-
более интенсивные линии получаются при переходах типа 4/2 (3Я)б$—4/2 (3Я)бр
для Се II, 4/3(4Г)б$—4/3(41°)бр для Pr II и 4/4(5l)6$—4/4(5l)6p для Nd II. Эти
переходы относятся к первой из упомянутых систем.
Значительный интерес представляют спектры важных элементов группы акти-
нидов, аналогичные спектрам Се и Nd, а именно Th и U. Как уже отмечалось
в начале предыдущего параграфа, для актинидов d-электроны связаны относительно
прочнее, чем для лантанидов. У Th нормальные конфигурации Th I, Th II и Th III
не содержат /-электронов и лишь у Th IV основным состоянием является состоя-
ние 4/2Fy2, как и у Се IV; у последнего, однако, d-электрон связан значительно
менее прочно. Спектры Th IV, Th III, Th II и Th I являются одно-, двух-, трех-
и четырехэлектронными. Уже двухэлектронный спектр Th III с глубокими четны-
ми конфигурациями 6d2, 6d7s, 6s1 и глубокими нечетными конфигурациями 5/6d
и 5/6$ является достаточно сложным.
Следует отметить, что для Th III расположение уровней для большинства конфигура-
ций сильно отличается от расположения, которое должно быть в случае нормальной связи,
а для сильно возбужденных конфигураций связь близка к связи (j, j). Приведенный выше
типичный пример связи (J, j) (рис. 9.1, на с. 244, правая половина) относится как раз к Th III.
Для Th III Рака [218] произвел полуэмпирическим методом расчет расположения уровней,
на основе экспериментальных данных Клинкенберга, и получил для всех рассмотренных
конфигураций хорошее согласие с опытом; расхождение вычисленных положении уровней
с наблюденными составляет не более чем несколько сотен см-1 при расстояниях между ниж-
ним и верхним уровнями конфигурации до 35000 см-1 (для конфигурации 5/2 уровни Th III
находятся на высоте от 16000 см-1 до 51 000 см-1).
346 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
Благодаря наличию двух систем глубоких уровней, четной и нечетной, в спек-
тре Th III имеется две системы переходов. То же самое получается и для очень
сложного спектра Th II. Для уровней Th II можно указать соответствующие исход-
ные уровни Th III.
Сопоставление уровней энергии для Th II, Th III и Th IV показывает постепенное упроч-
нение электрона связи 5/ по сравнению с электроном 6d. Разность энергий D- и F-термов
составляет
Th II
5d7s2 2D - 5f7s2 2F°
-0,52 эВ
Th III
5d7s 3D - 5f7s 3F°
0,37 эВ
Th IV
6d2D — 5f2F° ►
1,22 эВ.
(12.11)
Очень сложным спектром, содержащим много тысяч линий, обладает уран.
U I имеет нормальную конфигурацию 5/36d7s2, a U II — 5/37s2. Число глубо-
ких уровней невелико, однако весьма велико число возбужденных уровней, что
и приводит к очень сложному спектру. Глубокие уровни U I и U II показаны
на рис. 12.11. Найдены лишь самые глубокие уровни термов высокой мультиплет-
ности. Для конфигураций, содержащих d-электроны, получаются очень большие
значения £, доходящие до 9 (М-термы), и соответственно весьма большие зна-
чения J. Для U II, наряду с нечетными уровнями конфигураций 5/37s2, 5/36d7s
и 5/36d2, установлены четные уровни конфигураций 5f47s и 5/46d, аналогичные
четным уровням Nd II (см. рис. 12.11)8).
UII
Четные	Нечетные
7^7^23/2 11^ 13/2 1512^Л
Рис. 12.11. Глубокие уровни U I и U II
8) Относительное положение обеих систем уровней не установлено. По-видимому, вторая система
(четная) лежит примерно на 5 000 см-1 выше первой, что не показано на рис. 12.11.
§ 12.9. Атомы с f -оболочками, заполненными наполовину и более
347
Многочисленные высокие возбужденные уровни U II и U I можно характеризовать
значениями <7, однако их классификация представляет затруднения, так как, несомненно,
связь не является нормальной и, по-видимому, имеет место взаимодействие конфигура-
ций (ср. с. 246).
Расположение глубоких уровней U I и U II легко можно сопоставить, указав для уровней
U I исходные уровни U II; для U II можно указать исходные уровни U III, подробнее
см. [15], с. 383).
По сравнению со спектрами Nd спектры U характеризуются большей ролью
конфигураций, содержащих /3, чем конфигураций, содержащих /4.
§ 12.9.	Спектры атомов с /-оболочками,
заполненными наполовину и более
Для элементов с /-оболочками, заполненными примерно наполовину, — Sm,
Ей и Gd в шестом периоде и Pu, Ат и Ст в седьмом периоде — характерно
наличие небольшого числа глубоких уровней, соответствующих термам наибольшей
мультиплетности. Для оболочки /6 (а также для оболочки /8) получается один
септетный терм 7F, состоящий из семи уровней со значениями J от 0 до 6,
а для оболочки /7 — единственный октетный уровень (см. с. 258). В последнем
случае этот уровень лежит особенно глубоко. Спектры рассматриваемых элементов
проще спектров элементов с /-оболочками, заполненными менее чем наполовину,
и содержат очень интенсивные линии.
На рис. 12.12 приведена схема глубоких уровней Sm 1 и Sm II. Для Sm II
получаются два глубоких терма и 6F конфигурации 4/6$, а для Sm I —
глубокий терм 7F конфигурации 4/66$2. Переходы между этими термами и термами
конфигураций 4/66р и 4/66$6р дают самые интенсивные характерные линии Sm II
и Sm I соответственно.
Для Ей получается еще более характерный, чем для Sm, спектр с очень ин-
тенсивными линиями. Для Eu III основным уровнем является уровень 4/7 85°д.
Прибавление электрона 6$ дает два самых глубоких уровня Eu II и a7S^ кон-
фигурации 4/7(85°)6$, и прибавление электрона 5d — два глубоких мультиплетных
терма a9D° и a7D° конфигурации 4/7(85°)5d. Эти нечетные уровни комбинируют
с более высокими четными уровнями термов z9P и z7P конфигурации 4/7(85°)6р,
давая самые интенсивные линии спектра линии 4/76$—4/76р, аналогичные линиям
первого члена главной серии одноэлектронного спектра, с тем отличием, что внеш-
ний электрон добавляется к оболочке, спин которой равен не нулю, а 1/ъ Основным
уровнем Eu I является 4/76$2а комбинации которого с уровнями термов z 10Р,
z 8Р, z вР, у 8Р конфигурации 4f7бзбр дают самые интенсивные линии спектра. Эти
линии аналогичны линиям первого члена главной серии двухэлектронного спектра.
Более сложным спектром, чем Ей, обладает Gd. Однако и для спектра Gd ха-
рактерны термы, для которых исходным является терм 4/7 85°. Такой терм в качестве
основного имеет ион Gd IV, изоэлектронный с ионом Eu III. Из этого терма воз-
никают термы 4/7(85°)б$95° 7S° Gd III, 4/7(85°)6$2 85° Gd II и 4/76$2(85°)5d9P° 7D°
Gd I, а также термы 4/7(8S°)5d9D° 7D° Gd III, из которых, в свою очередь (см. схе-
му (12.10)), получаются многочисленные другие термы Gd II и Gd I. Все интенсивные
линии в спектрах Gd II и Gd I соответствуют переходам с исходным термом 4/7 85°.
На рис. 12.13 приведена схема глубоких уровней Gd I и Gd II. Характерными явля-
ются термы высокой мультиплетности, доходящей до 10 для Gd II и до 11 для Gd I.
348 Глава 12. Спектры атомов с достраивающимися d- и f -оболочками
Рис. 12.12. Схема глубоких уровней Sm I и Sm II	Рис. 12.13. Схема глубоких уровней Gd I и Gd II
§ 12.9. Атомы с f -оболочками, заполненными наполовину и более
349
Хорошее выполнение правила интервалов показывает, что связь для глубоких конфи-
гураций близка к нормальной. Спектры Gd II и Gd I являются хорошими примерами
весьма сложных спектров, которые удалось успешно интерпретировать [231].
Из элементов группы актинидов наиболее простым спектром обладает Ат.
Основным уровнем Am I является 5/77s2 85?д, а основным уровнем Am II —
5/77s 9S4, так же как и для Eu I и Eu II. В спектре имеются весьма интенсивные линии,
делающие его, подобно спектру Ей, характерным. Для следующего за Ат элемента
Ст нейтральный атом имеет нормальную конфигурацию 5/76d7s2, аналогичную
нормальной конфигурации нейтрального атома Gd.
Элементы, стоящие за Gd в шестом периоде и за Ст в седьмом пе-
риоде, обладают /-оболочками, заполненными более чем наполовину, и име-
ют очень сложные спектры, гораз-
до менее характерные, чем спек-
тры элементов с /-оболочками, за-
полненными наполовину. По мере
приближения /-оболочки к пол-
ному заполнению спектры опять
упрощаются и их структура ста-
новится более характерной. Наи-
более сложен спектр ТЬ, спектры
Dy, Но и Ег проще и еще про-
ще спектр Тт с нормальными кон-
фигурациями 4/136$2 для нейтраль-
ного атома и 4/136$ для одно-
кратно ионизованного атома. У Yb
и Lu имеется уже заполненная обо-
лочка 4/14. Мультиплетные рас-
щепления для термов /-оболочки
получаются весьма значительными
(ср. с. 344).
В качестве примера мульти-
плетного расщепления у атомов с
/-оболочками, близкими к полно-
му заполнению, можно рассмотреть
Tm I и Тт II. Для Тт I основным
термом является обращенный ду-
блетный терм 4/136s22F°, расщеп-
Е, см
9 000-
8 800-
8600-
Tu I	Tull
______	--...(5/2,1/2)°3
м_____I...............(5/2,1/2)о2
Рис. 12.14. Глубокие уровни Tm I и Tm II
ление которого равно 8 771,2 см-1, т. е. более 1 эВ. Нормальная конфигурация Tm II,
4/136$, дает четыре уровня, расположение которых соответствует схеме связи (J, j),
как показывает сопоставление этих уровней с уровнями Tm I (см. рис. 12.14). Рас-
стояние между центрами тяжести пар уровней Tm II равно 8 775,6 см, что всего лишь
на 3,4 см-1 отличается от расщепления терма 2F° Tm I. Мы имеем весьма типичный
пример связи согласно схеме (9.51).
Спектры актинидов с оболочками 5/, заполненными более чем наполовину,
иначе говоря, далеких трансурановых элементов, начиная с Bk (Z = 97), должны
быть аналогичными спектрам лантанидов с оболочками 4/, заполненными более
чем наполовину, начиная с Tb (Z = 65). У трансуранового элемента с порядковым
номером Z = 102 должна иметься уже заполненная оболочка 5/ (см. табл. 12.3.)
ГЛАВА 13
РЕНТГЕНОВСКИЕ СПЕКТРЫ
§ 13.1. Общая характеристика рентгеновских спектров
поглощения и испускания
Рентгеновские спектры атомов естественным образом укладываются в общую
систематику атомных спектров. Они возникают при возбуждении электронов вну-
тренних оболочек атома, и их отличие от оптических спектров в видимой и уль-
трафиолетовой области определяется тем, что эти оболочки полностью заполне-
ны, а поэтому переход электрона из одной оболочки в другую невозможен, пока
в этой последней не появится свободное место. Обычный рентгеновский спектр
поглощения соответствует переходу электрона из внутренней оболочки за пре-
делы атома, т. е. с дискретного уровня внутренней оболочки на непрерывные
уровни, примыкающие к границе ионизации (рис. 13.1, а). Таким образом, при по-
глощении фотона атом ионизуется,
подобно тому, как ионизуется атом
водорода, находящийся в основном
состоянии ls25y2, при поглощении
фотона с энергией больше 13,60 эВ.
Разница состоит лишь в том, что
для вырывания электрона из вну-
тренней оболочки, где он связан
очень прочно, энергия фотона долж-
на быть весьма большой. Для ио-
низации атомов тяжелых элементов
за счет вырывания электрона (за счет
фотоэффекта) из оболочки 1s требу-
ется энергии порядка ста тысяч эВ.
Например, для U граница иониза-
ции для электрона 1s соответствует
энергии 1,164 • 105 эВ.
В рентгеновской спектроскопии обычно выражают волновые числа и частоты
в единицах, равных постоянной Ридберга Я, — в ридбергах (часто обозначаемых так-
же Ry). Эти единицы могут служить и единицами энергии (см. с. 19): 17? = 13,60 эВ.
Энергия ионизации U соответственно равна 8 555 R = 8 555 • 13,60 = 1,164 • 105 эВ.
На опыте поглощение начинается у границы ионизации резким скачком и затем
постепенно спадает, как схематически показано в нижней части рис. 13.1, а. Поэтому
обычно говорят о краях поглощения. Положение края поглощения в спектре дает
величину энергии ионизации.
а	б	в
Рис. 13.1. Возникновение рентгеновских спектров:
а, б — поглощения; в — испускания
§13.1. Общая характеристика рентгеновских спектров
351
В действительности край поглощения не является совершенно резким. Вблизи границы
ионизации имеются свободные уровни энергии (показанные на рис. 13.1 точечным пункти-
ром), на которые возможен переход электрона, и край может иметь тонкую структуру с рассто-
яниями между ее составляющими порядка нескольких эВ, т. е. порядка десятых долей Ry. Разу-
меется, эта структура будет обнаруживаться только при большой разрешающей силе применяе-
мых рентгеноспектральных приборов. Наряду со структурой, существующей с длинноволновой
стороны края поглощения, в молекулах и кристаллах наблюдается и структура с коротковол-
новой стороны, связанная с влиянием окружающих частиц на поглощающий атом [21].
Самый коротковолновый край поглощения соответствует вырыванию электрона
из оболочки 1s, т. е. из слоя с п — 1. Более длинноволновые края поглощения полу-
чаются при вырывании электрона из слоев с п = 2, п — 3 и т. д. На рис. 13.1, показана
граница поглощения, соответствующая удалению электрона из слоя 2, более внеш-
него по сравнению со слоем 1, к которому относится рис 13.1, а. Ионизованный атом
в состоянии 2?1оо, у которого имеется свободное место в более внутреннем слое 1,
обладает большей энергией, чем в состоянии 1%оо> для которого имеется свободное
место в более внешнем слое 2. Дискретные рентгеновские спектры испускания, так
называемые рентгеновские характеристические спектры, возникают при переходе
электрона из более внешней оболочки на свободное место в более внутренней обо-
лочке. При этом испускается фотон с энергией - Е2оо (рис. 13.1, в). Поэтому ча-
стоты в спектре испускания соответствуют переходам между уровнями энергии иони-
зованного атома и равны разностям положений (в шкале частот) краев поглощения.
Рассмотрим подробнее возможные состояния ионизованного атома, соответ-
ствующие удалению электрона из различных заполненных оболочек (рис. 13.2).
При вырывании электрона из слоя п = 1 возникает уровень Is 2Su (сокращен-
п п
гзЛ
К-край
К-серия
Энергия
ЧХ5Ш-----Я
Поглощения
ai
К
А
L,-Kpau
Ц-ьрай
Цг^рай
-3
,0 -ф 38
’ Зр5
АЗ/2-М9
Ф за9 гв&-
Мокрой
Мц-край
\Мискрой
\ Искрой
Испускание
L-серия
Lrnodcepun
Lff -подсерия
fe
-mis----
-355,1-----И,
-330,6— М,,
-г?9,2----МЛ
-гзз,2—М„
-228,7-----
..2>stp1T"
1 HU? 2?^-

Л|
Л
?
А
К
Л|
Л
,0
-4
.92As, fy/t------------------------------------------------------------
92- 4>s Ifa- - 	—.11. - -   L-----------------------------------
• -зр Л* &------т----------L - - -  —-------------------------
----------* -----------------------------------------------------
 иг иа vj-----ч-------------------------------------------------------
-5
..	:........ I:—
.Q ^-92-6s 5llr~ — — - - — - - - - — - - —     — ~	-	 -     -	"	'
Ч 'I ... '-==
-/ 0—1/2 7s ^Ч-|1г1111гТп1И|-пН1 I I l~Г".-.............- ‘ 	.......... L-
Основное состояние
Рис. 13.2. Схема уровней ионизованного атома и переходов между ними
9^4:
A-'i':
3,22—^р,
1,32_
352
Глава 13. Рентгеновские спектры
но	соответствующий незаполненной оболочке 1s с одним электроном.
При вырывании из слоя п = 2 электрона 2s возникает аналогичный уровень 2s ^у2,
а при вырывании электрона 2р — уровни 2р52Р°{^ и 2р52Р^ соответствующие
обращенному основному терму ‘Г (для которого уровень лежит глубже уров-
ня 2jPy2)« При вырывании электрона из слоя п = 3 возникают уровни 3s25y2,
Зр52Ру2 3/2» 3d92Dy2 5д и т.д. Мы получаем набор уровней, аналогичный набору
уровней одноэлектронного атома (см. рис. 6.11, с. 187), с тем отличием, что уровни
расположены в обратном порядке — схема уровней перевернута; выше всего лежит
уровень 12£у2- Схема рис. 13.2 представляет схему границ ионизации нейтрального
атома. Эти границы аналогичны границам ионизации, к которым сходятся смещен-
ные уровни (см. § 10.5) в случае двух или нескольких внешних электронов, с той
разницей, что здесь возбуждаются и удаляются из атома электроны не внешних,
а внутренних оболочек. Границы ионизации, соответствующие возбуждению не вну-
тренних, а внешних электронов, лежат очень близко к самому глубокому уровню,
соответствующему основному состоянию нейтрального атома.
Схема рис. 13.2 отвечает атому радия (Z = 88) и построена в масштабе, позволяющем
изобразить границы ионизации, соответствующие удалению как внутренних электронов, так
и внешних электронов нормальной конфигурации 7s2 нейтрального атрма. С правой стороны
приведены значения энергии ионизации в ридбергах для соответствующих краев поглощения,
т. е. для границ ионизации.
В рентгеновской спектроскопии принято слои с п = 1, 2, 3,4, 5, 6,... обозначать
буквами К, L, М, N, О, Р, ... и последовательные уровни отмечать римскими
цифрами в качестве индексов (см. рис. 13.2). Таким образом, мы имеем следующее
соответствие:
Is Кх	2s 2р 3s Зр 3d £i £ц,ш М\ Miijn Miv;	4s 4р 4d / -Nl ^11,111 Niv,y	4/ Nvi,vn —>
К-слыл	£-слой	М-слой	TV-слой	
	5s 5р 5d 5f	6s 6p 6d	
	> О| 011,111 6>iv,v 6>vi,vn	Pl £*11,111 Piv,v	(13.1)
О-слой	Р-слой
В поглощении получается один Tf-край, три £-края, пять М-краев и т.д., как
показано в левой половине рис. 13.2. К каждой границе примыкает континуум —
непрерывная совокупность уровней.
При испускании дипольного излучения возможны переходы, допускаемые пра-
вилами отбора (6.112) и (4.156) для квантовых чисел I и J, т. е. Д/ = ±1, Д/ = 0, ±1.
Таким образом, получаются линии испускания
К - £п, К-Ьш; К-Мц, К-Мш; К - Nu,	(13.2)
£i~Afn, - М\\\; L\ - N\\,
L\\ - M\^ L\\ -	L\\ - N\, L\\ - JViv; •..
>	(13.3)
£in - £ш ~ ^lv; bin - ^vJ bin ~ Nh £iii - 2Viv; £щ -	...
Индекс I у К обычно опускают.
§13.1. Общая характеристика рентгеновских спектров
353
и т.д. Совокупности линий, возникающих при переходах электрона в данный слой,
образуют серии — X-серию, в которую входят линии (13.2), Z-серию, в кото-
рую входят линии (13.3), и т.д. Каждая серия, за исключением If-серии, состоит
из подсерий — Z-серия из подсерий L\, Lu, Дп, М-серия — из подсерий М\,
М\\, Мщ, Miv, Му и т.д. Линии данной подсерии, вследствие уменьшения рас-
стояний уровней М, N, О, ... от нормального уровня (самого нижнего на схеме
рис. 13.2), сходятся к соответствующему краю. Отдельные линии данной серии при-
нято обозначать греческими буквами а, /3, 7 с индексами, в частности первые
две линии If-серии (переходы K—L) обозначают как а2, «ь а следующие две
линии (переходы К—М) как Д, р\. На рис. 13.3 показано расположение линий
в спектре для If-серии и Z-серии; пунктиром отмечены края поглощения.
Следует помнить, что фотон ис-
пускается при переходе электрона из
более внешнего слоя, где он обладает
большей энергией, в более внутрен-
ний слой, где он обладает меньшей
энергией; уровни на рис. 13.2 соот-
К-край
• п
о । Линии
^ll^] К-еернй
^11,111^11 ш v
ветствуют состояниям, для которых
в данном слое не хватает электро-
на. Испускание линии К\— Lu озна-
чает переход электрона из слоя п = 2
Zq-край
У3’ Линии
llji Феерий
на свободное место в слое п = 1, в ре-
зультате чего ионизованный атом ока-
МПМИ1 М^щОщц
01 Г1 ;Ьп-край
зывается в конечном состоянии Zn,
т.е. 1$22$22р52Ру2 вместо начально-
го состояния К, т.е. Is2s22p625у2;
стрелка на рис. 13.2 показывает на-
правление изменения энергии; элек-
трон при этом переходит из Z-слоя
в Tf-слой.
Помимо дипольных переходов,
MIV
02
0о\
I hi! ft
j £ш-край
^i^iv.vQQv.v
Рис. 13.3. Расположение линий
К-серии и Z-серии
возможны квадрупольные и магнит-
ные дипольные переходы между уровнями одной четности, которые дают дополни-
тельные линии в соответствующих сериях и подсериях. Для квадрупольных переходов
справедливы правила отбора AZ = 0, ±2 и AJ = 0, ±1, ±2, для магнитных дипольных
переходов — Д/ = О и ДJ = 0, ±1 (см. (4.158), (4.156) и (4.154); последнее правило
отбора запрещает переходы Д/ = ±1).
Самой важной особенностью рентгеновских спектров, связанной со свойствами
внутренних оболочек, является монотонное изменение частот переходов и длин волн
аналогичных линий испускания или краев поглощения при изменении порядкового
номера Z. Для аналогичных линий и краев поглощения с увеличением Z частоты по-
степенно увеличиваются, а длины волн уменьшаются. Это иллюстрируется рис. 13.4,
на котором показано положение краев поглощения и наиболее интенсивных линий
испускания каждой серии2) для элементов с нечетным Z. Если для легких элементов
характеристический спектр лежит в области мягких рентгеновских лучей, то для тя-
желых элементов If-серия лежит в области очень жестких рентгеновских лучей;
Наиболее интенсивными являются линии каждой серии, возникающие при переходах между сосед-
ними слоями (К—L, L—М, М—N, ...) и соответствующие уровням с максимальными возможными
значениями J, см. § 13.4, с. 365.
12 Зак. 103
354
Глава 13. Рентгеновские спектры
для U переходу K—Lm соответствует длина волны 0,1257 А, а краю поглощения —
0,1066 А (или частота 8 555 R, см. выше, с. 350).
Отметим, что линии определенной серии могут появляться, когда заполняется
слой, из которого электрон переходит в более внутренний слой. Поэтому сперва,
при заполнении L-слоя (п = 2), появляется К-серия, затем, при заполнении
Жесткий Мягкий	Очень мягкий Ультра-фиол.
Рис. 13.4. Рентгеновские линии испускания и края поглощения для элементов с нечетным Z
М-слоя (п = 3), появляется L-серия и т.д. В данной серии сначала появляются
более длинноволновые линии, а затем более коротковолновые, по мере заполнения
слоев с большими значениями п (см. рис. 13.2).
Увеличение частот с увеличением Z определяется постепенным увеличением
прочности связи электронов в заполненных оболочках, согласно основной форму-
§ 13.1. Общая характеристика рентгеновских спектров
355
ле (7.6), которую мы запишем в виде
^too - Eq — —Ei —
(13.4)
где индекс i указывает совокупность квантовых чисел n, I, j, от которых зави-
сит энергия ионизованного атома. Эта формула определяет энергию ионизации
нейтрального атома и, следовательно, частоту края поглощения. Частота перехода
из г-го состояния в k-е равна
( zf zt2 \
р — Eioo — Ekoo ~ R I 2	2~ I 5	(13.5)
\ п\ П2 I
где П] и пг — главные квантовые числа для электронов соответствующих слоев.
Рис. 13.5. Диаграмма Мозли для краев поглощения
При приближенном постоянстве а (как функции Z) на диаграмме Моз-
ли (см. с. 237) для i-го края поглощения (nj = п, п2 -* оо, и = величина
Гщ	Z-	Z-ъ	z
Л = =	‘3.6
у л	п п
12*
356
Глава 13. Рентгеновские спектры
будет линейной функцией от Z. Такая диаграмма приведена на рис. 13.5. Ближе
всего к прямой подходит график для If-края поглощения. В этом случае постоянная
экранирования очень мала, поскольку электроны 1s являются самыми внутренними
электронами, и поэтому график приближенно проходит через нуль. В соответ-
ствии с большими значениями постоянной экранирования для более внешних слоев
графики для Z-, М-,... слоев не проходят через нуль; отклонения графиков от пря-
молинейности свидетельствуют о том, что постоянные экранирования зависят от Z.
Рис. 13.6. Диаграмма Мозли линий
If-серии
(например, между L\ и Бц, т.е.
Диаграммы Мозли строят и для линий
испускания. Так как в формуле (13.5) глав-
ную роль играет первый член (п\ <П2, Z*>Zk),
то и эти графики могут быть близки к пря-
молинейным. Для линий If-серии К—Lu,
K—Lu\ (линии Ка2, Ках) и К—Мц, К—М\\\
(линии Кр3, Крх) диаграмма Мозли приведена
на рис. 13.6. Графики очень близки к прямоли-
нейным.
Закономерности в рентгеновских спектрах бы-
ли открыты в 1913 г. Мозли ([176], см. с. 35)
при изучении характеристических спектров элемен-
тов от Ca (Z = 20) до Си (Z = 29). Для линий Ка
и Кр (не разрешенных им на составляющие Ка2, Ка]
и Кр3, Крх) он установил закон квадратичной зави-
симости величины и от Z - а (закон Мозли) в виде
./=^-l)2 = K(Z-l)2(l-l). (13.7)
Формула (13.7) получается из (13.5), если положить
щ = 1, П2 = 2 и Z- = Z*k = Z - 1. Интересно отме-
тить, что Мозли впервые установил, по положению
линий Ка и Кр, что Со стоит в периодической си-
стеме раньше Ni, несмотря на несколько больший
атомный вес.
Диаграммы Мозли наглядно показывают
закономерное изменение расстояний между
уровнями, соответствующими данному слою.
При этом на диаграммах разности значений
\JvfR для соседних уровней с одинаковым J
между 22Р°д и 2^5у2) приближенно остаются
постоянными, а разности между соседними уровнями с одинаковым I (например,
между Би и Бц|, т. е. между 2 2Р°д и 2 2^зд) растут с увеличением Z. Более подробно
этот вопрос рассмотрен в следующем параграфе.
§ 13.2. Регулярные и иррегулярные дублеты
Особенно характерной для рентгеновских спектров является структура, обусло-
вленная спин-орбитальным взаимодействием. Она аналогична дублетной структуре
в спектрах щелочных металлов и, в особенности, дублетной структуре основного
терма атомов, у которых в заполняющейся оболочке не хватает до полного комплекта
одного электрона, как в случае атомов галоидов с нормальной конфигурацией пр5,
§13.2. Регулярные и иррегулярные дублеты
357
Таблица 13.1
Дублетные термы для рентгеновских спектров
Терм	2Pi/2, 2Рз/2				2Рз/2, 2d5/2							
Слой	Обо- лочка	Обозна- чение	Появление		Обо- лочка	Обозна- чение	Появление		Обо- лочка	Обозна- чение	Появление	
			элемент	Z			элемент	z			элемент	Z
£ (п = 2) М (п = 3) N (п = 4) О(п = 5) Р(п = 6)	2р5 Зр5 4р5 5р5 6р5	Ьп, £ш Мц, Miп АГп, Мп Он, Ош Рп, Pin	Li Na Cu Cd Bi	3 11 29 48 83	3d’ 4d’ 5d’ 6d’	Mjv, My Mv, JVy Oiv, Oy Piv, Pv	P Sr Tb U	15 38 65 92	4/13	JVvi, JVyii	La	57
дающей обращенный основной терм 2Р°. Дублетные термы для схемы уровней
рис. 13.2 также обращенные и соответствуют внутренним оболочкам, в которых
не хватает одного электрона до полного заполнения.
Мы имеем дублетные термы, приведенные в табл. 13.1. В таблице наряду
с обозначениями пар уровней, образующих дублетные термы, указаны элементы,
д ля которых в рентгеновских спектрах впервые появляются переходы на эти уровни.
При комбинировании уровней данного дублетного терма с другими уровнями
в спектрах появляются характерные пары линий, которые называют регулярными
дублетами или спин-дублетами3\ Разность частот соответствующих линий для дан-
ного элемента является постоянной. Так, для дублетного терма £ц, Lm одина-
ковы разности частот линий ot\, ot2 (K—L\\\, K—L\\) If-серии и пар линий ту,
I	а2(Ьц—М\у9 £|ц—Mjv), 75, ^б(Ьц—ЛГ|, Lu\—N\) и т.д.
L-серии (см. рис. 13.2).
При увеличении порядкового номера Z элемента дублетное расщепление возра-
стает и приближенно определяется основной формулой (8.12) для спин-орбитального
взаимодействия:
Ra2Z*4 _ Ra2(Z - s)4
Ар - 6i- '/2,1+ 'И - пЩ1 + 1) -	+ !)
(13.8)
где s — постоянная экранирования, отличающаяся от постоянной экранирова-
ния а в формуле (13.6). Величина расщепления для дублетного терма L\\, £1П,
т.е. для терма 2р5 2Р° (n = 2,l = 1), получается равной, в ридбергах,
= а (Z24 *- =	- з)2 = 3,32 • 10-6(Z - s)4.	(13.9)
Она быстро возрастает с увеличением Z. Для легких элементов дублетное расщеп-
ление составляет сотые и десятые доли ридберга: для Mg (Z = 12) — 0,020 R,
для Са (Z = 20) — 0,26 R. Уже для Cu (Z = 29) расщепление равно 1,5 Я,
для Ag (Z = 47) оно составляет 12,8 R, для W (Z = 74) — 98,5 R и для U (Z = 92) —
288 R. Приближенное значение постоянной экранирования з для не очень тяжелых
атомов равно 3,5. Для самых тяжелых атомов расщепление возрастает быстрее, чем
по закону (Z - 3,5)4; для U вместо 203 R получается 288 R. Это объясняется прибли-
женностью формулы (13.8), которая является первым членом разложения в ряд точ-
ной релятивистской формулы для энергии одноэлектронного атома (см. ниже, с. 360).
3) А также релятивистскими дублетами, поскольку спин является релятивистским эффектом и дублет-
ное расщепление объясняется релятивистской теорией Дирака.
358
1лава 13. Рентгеновские спектры
Для грубой оценки величины дублетного расщепления у не очень легких атомов
можно положить в (13.8) Z* ~ Z, т.е. пренебречь экранированием. Мы получим
Др ~ a2Z4
~R ~ п31(1 + 1)’
Если перейти от разности частот Др к разности длин волн ДА, то получим, что ДА
a2Z4
пропорционально, при заданных п и I, величине —:
и1
(13.10)
Z4	,
Частоту перехода, пренебрегая вторым членом в правой части формулы (13.5)
*	Z2
и заменяя Z, через Z, можно положить равной R —9 т. е. считать, что она
п2
приближенно пропорциональна Z2, Поэтому р2 ~ Z4 и окончательно получаем, что
ДА ~ const.
(13.12)
Таким образом, в шкале длин волн расщепление для регулярных дублетов при-
ближенно не зависит от частоты, что подтверждается экспериментально. Именно
в соответствии с постоянством ДА рассматриваемые дублеты и называют регуляр-
ными.
Регулярные дублеты связаны с зависимостью энергии, при заданном значении
квантового числа I, от квантового числа принимающего два значения j = I + -
и j = I — -. С зависимостью энергии от квантового числа I при заданном значении j
связаны иррегулярные дублеты или дублеты экранирования. Мы имеем пары уровней
Li, Ln Afj, М\\ Мщ, Afjv N\, N\\ ЛГ|ц, N\y Ny, TVvi
v'k’^h !S'h- 1ДУ<	ipv.-*%
n = 2	n = 3	n = 4
(13.13)
для которых, как отмечалось в конце предыдущего параграфа, разности значе-
ний y/v/R остаются приближенно постоянными, т. е. на диаграммах Мозли со-
ответствующие графики идут параллельно (см. рис. 13.5). Постоянство разностей
при том же значении j означает, согласно (13.6), постоянство разностей постоянных
экранирования а. Если для двух уровней дублета
/I=£F’	(13Л4)
то
(1315)
Для дублета L\, Ьц разность Да составляет около 1,4, что, согласно наглядным пред-
ставлениям, согласуется с дополнительным экранированием электронов 2р, которым
соответствует уровень 2р5 двумя электронами более внутренней оболочки 2з,
которым соответствует уровень 2s
§ 13.2. Регулярные и иррегулярные дублеты
359
Легко найти и выражение разности частот для дублетов экранирования. Мы
получаем
= 2R^ / г _	= 2Й д.
п2	п2 \	2 J п2 '	'
(13.16)
_ ffi + <Т2
где а = —-----среднее значение постоянной экранирования для рассматривае-
мых уровней.
Для ДА мы соответственно находим, учитывая, что и ~
(Z-a)2
п2
&v	n4(Z - а) п2
и2	n2(Z - a)4	(Z - а)3 ’
т. е. в отличие от регулярных дублетов
расщепление быстро уменьшается с уве-
личением Z.
Представляет значительный интерес
сравнение постоянных экранирования з
и а, т. е. постоянной экранирования, оп-
ределенной по формуле (13.8) из дублет-
ного расщепления, обусловленного спин-
орбитальным взаимодействием, и посто-
янной экранирования, определенной по
формуле (13.4) из величины энергии ио-
низации (по положению краев поглоще-
ния). Так же, как и для внешнего электро-
на в случае изоэлектронных рядов, начи-
нающихся с атомов щелочных металлов
(см. §8.5, с. 241), постоянная экраниро-
вания а больше постоянной экранирова-
ния з. Зависимость постоянных экрани-
рования от порядкового номера для двух-,
трех- и четырехквантовых оболочек пока-
зана на рис. 13.7. Сплошные линии дают
значения постоянной а, пунктирные —
постоянной з. Как мы видим, з остает-
(13.17)
Рис. 13.7. Зависимость постоянных
экранирования а и s от порядкового номера
ся постоянным, а а принимает значения,
превышающие значения з, и возрастает с увеличением Z. С точки зрения наглядных
представлений это объясняется тем, что для спин-орбитального расщепления (следо-
вательно, для постоянной з) существенно экранирование внутренними электронами,
а для энергии связи электрона существенно экранирование как внутренними, так
и внешними электронами. Число внешних электронов для заданной оболочки воз-
растает с увеличением Z, в то время как число внутренних остается неизменным.
Таким образом, з можно рассматривать как постоянную внутреннего экранирования,
а — как постоянную полного экранирования, а их разность а - з — как постоянную
внешнего экранирования.
Изменение постоянной экранирования а с изменением Z может быть получено из на-
глядных соображений, если считать, что энергия данного электрона при отсутствии внешних
360
Глава 13. Рентгеновские спектры
R(Z - з)2
оболочек определяется формулой---------г---, и прибавить к этой энергии потенциаль-
п2
ную энергию электрона в поле внешних электронов. Для внешней оболочки радиуса at-,
содержащей Ni электронов, потенциальная энергия электрона внутри этой оболочки рав-
е2ДГ,- /	Nie2	\
на ---- I работе против силы отталкивания ——, проинтегрированной от оо до сь |.
а*	\	г2	/
Суммирование по всем внешним оболочкам дает дополнительную потенциальную энер-
\ e2Ni
гию > -----, а полная энергия электрона составит
' а.
R(z-s)2
п2
e2Nj
Qi
R(Z - s)2
п2
(13.18)
1	1 ап
Величину — можно представить в виде---------, где ап — радиус круговой орбиты рассматри-
at	ап ai
ваемого электрона. Согласно (6.29), где Z нужно заменить через Z - з, имеем
2R(Z - з)
е2п2
1
an
(13.19)
и (13.18) принимает вид
E_ fR(Z-s)2 e2
1 n2 an
ап
di
^|(^-а)2-2(Я-а)^^^|,	(13.20)
/ \2
что при (	~ J (Z - з)2 можно записать в виде
I	' a, I nz
(13.21)
где
di
(13.22)
т. e. действительно a > s и увеличивается с увеличением числа внешних электронных
оболочек.
Следует отметить, что постоянные экранирования, значения которых использо-
ваны для построения графиков рис. 13.7, вычислены не по формулам (13.8) и (13.4),
а по уточненным формулам.
Как отмечалось выше, формула (13.8) является лишь приближенным решением одно-
. электронной релятивистской задачи. Точное решение этой задачи, т. е. уравнения Дирака,
дает для энергии значение (см. [134], с. 133)
Е = тес2
-+
(13.23)
При разложении в ряд по степеням a2Z2 получается выражение
RZ2 Ra2Z* ( \	3 \
Е = — ——— — —— ( —— — _— I _
п2 п3 I 1	4n I
V + 2 J
(13.24)
§13.3. Внутренняя конверсия рентгеновского излучения
361
где первый член в правой части дает (6.13), а второй — (6.58). Именно из формулы (6.58) и по-
лучается формула (13.8). Дальнейшие члены в (13.24) содержат множители a4Z6, a6Z8 и т.д.,
т. е. по порядку величины меньше второго члена. Однако для тяжелых атомов этими членами
68	1	2 7	1	4 4	1
уже нельзя пренебрегать; для Z = 68, aZ = —— « - следовательно, a Z « - и a Z «
137	2	4	16
При применении формулы (13.24) к многоэлектронным атомам надо Z в первом члене
заменить через Z - а, а в остальных членах, связанных со спином, через Z - з, что дает
_ R(Z-<rnlj)2 _ K(Z-<rnl)2 _ Ha2(Z — s)4 / 1	_ 3_
п'2	п2	п2	п3 I .	1 4п
V + 2
(13.25)
Учитывая, наряду со вторым членом, третий и четвертый, можно выразить Z — з через дублет-
ное расщепление по формуле более точной, чем формула (13.8) (см. [10], с. 230). Определенные
таким образом постоянные з практически не зависят от Z и равны для регулярных дублетов:
ь„, Zin Мц,Мц| M|v,Mv ЛТщЛТш iViv^v	1	П3 261
3,49	8,5	13,0	17,0	24,4	34 J * ’ '
Эти значения и даны на рис. 13.7.
Для иррегулярных дублетов правильнее сравнивать не положения уровней с заданным j
и со значениями /, отличающимися на 1, а значения первого члена в (13.25) для этих
значений Z, т.е. вместо разности Enj+ij - Eni] следует брать разность Enl+i - Enh где
_ Я(я-<7П/)2	Ra\Z-s)4 (	1	3
-Е^+ п3
V+2
(13.27)
Пользуясь «приведенными» значениями (13.27) энергии уровней с различными Z, можно вычи-
слить значения постоянных экранирования anh при помощи которых и построены сплошные
кривые на рис. 13.7. Разности значений ап /+1 - ап/ для заданного п оказываются, в отличие
от разностей, вычисленных по формуле (13.6) для пар уровней Бп^+1 j, Enij, обнаруживающих
некоторую зависимость от Z, практически постоянными; например, для дублета L\\ вместо
значения около 1,4 получается значение 1,18. Таким образом, постоянство разностей (13.15)
имеет место, если исходить из значений энергии (13.27), а не (13.25).
§ 13.3. Внутренняя конверсия рентгеновского излучения
и недиаграммные линии
Наряду с переходами с излучением в ионизованном атоме возможны переходы
без излучения, при которых энергия возбуждения этого атома расходуется на вы-
рывание еще одного электрона. Такой процесс можно формально трактовать как
«поглощение» фотона внутри самого атома; этот процесс называют внутренней кон-
версией (т. е. внутренним преобразованием) излучения или эффектом Оже. В действи-
тельности имеет место безызлучательный переход, конкурирующий со спонтанным
испусканием. Явление внутренней конверсии рентгеновского излучения представля-
ет частный случай общего явления автоионизации — перехода с дискретных уровней
на непрерывные, сопровождающегося ионизацией атома (см. гл. 10, с. 298).
Условием внутренней конверсии для рентгеновского излучения является вы-
полнение общего соотношения
Ei-Ek>E^	(13.28)
где Ei -Ек — изменение энергии ионизованного атома при переходе с уровня Ei
на уровень Ek, а 2?ион — энергия вырывания электрона из одной из оболочек данного
атома, т. е. энергия его дальнейшей ионизации. Для уровней энергии, связанных
362
Глава 13. Рентгеновские спектры
с ионизацией внутренних оболочек атома и изображенных на диаграмме рис. 13.2,
условие (13.28) всегда выполняется: всегда имеются более слабо связанные электро-
ны, энергия вырывания которых меньше энергии, освобождающейся при переходе
между возбужденными уровнями иона.
Когда происходит переход электрона из более внешнего слоя в более внутрен-
ний, т.е. переход с изменением п, освобождающаяся энергия значительно больше,
чем энергия вырывания электрона из этого более внешнего слоя (и подавно, чем
энергия его вырывания из еще более внешних слоев). Например, при переходе K—L
для Cs освобождается энергия свыше 2 000 R, в то время как энергия вырывания
электрона из Е-слоя порядка 400 R, а из М-слоя менее 100 R. Избыточная энергия
переходит при этом в кинетическую энергию вырываемого электрона4). Возмож-
на, однако, и внутренняя конверсия, связанная с переходом электрона с одного
уровня на другой внутри данного слоя; тогда основная часть освобождающейся
энергии может тратиться на ионизацию, и лишь небольшая ее доля будет переходить
в кинетическую энергию.
При этом необходимо учитывать, что Еион в (13.28) представляет энергию удаления
второго электрона из атома; для электронов более внешних оболочек можно приближенно
считать, что она равна энергии удаления электрона из соответствующей оболочки атома с за-
рядом, на единицу большим. Действительно, при однократной ионизации внутреннего слоя
эффективный заряд ядра, действующий на электроны более внешнего слоя, увеличивается,
в силу уменьшения экранирования, на единицу. Условие (13.28) можно записать в виде
Ei(Z) - Ek(Z) > Et(Z 4- 1),	(13.29)
где Ei(Z + 1) относится к 1-му уровню энергии ионизованного атома с зарядом Z 4-1.
Применяя условие (13.29), можно определить, при каких Z возможна внутрен-
няя конверсия для данных i, к и I. Например, при переходе L\—Ъц у Yb (Z = 70)
ELl (70) - EL|l(70) = 37,9 R, что достаточно для удаления электрона с уровня Ni с энергией
1^(71) = 37,0 R\ внутренняя конверсия еще возможна. При переходе к следующему элемен-
ту, Lu (Z = 71), ELi(71) - EL|I(71) = 39,0 R, a ENl(72) = 39,4 R; внутренняя конверсия уже
невозможна. Таким образом, процесс внутренней конверсии с уровня N\ за счет перехода
L[—L\\ (сокращенно обозначаемый как L\—L\\N\) возможен при Z 70. Так как связь более
внешних электронов упрочняется быстрее с увеличением Z, чем более внутренних, то граница
внутренней конверсии ограничена со стороны больших Я5).
Вероятность переходов без излучения при прочих равных условиях возрастает
при уменьшении доли энергии, переходящей в кинетическую энергию. Поэтому
вероятность внутренней конверсии, связанной с переходом электрона с одного
уровня на другой внутри данного слоя, велика.
Вероятность внутренней конверсии определенного типа мала при Ei(Z) - Ek(Z)
Et(Z 4- 1), возрастает при приближении разности Ei(Z) - Ek(Z) к Ej(Z 4- 1) и затем резко
уменьшается до нуля, в силу условия (13.29), при Ei(Z)—Ek(Z) = Ei(Z-j-l). При уменьшении Z
вероятность внутренней конверсии также убывает вследствие увеличения Ei(Z) - Ек(Z)
по сравнению с Et(Z 4- 1). В приведенном выше примере для перехода L\— она будет
велика для Yb, а для более легких элементов будет меньше в соответствии с возрастанием доли
энергии, переходящей в кинетическую; например, для Sn (Z = 50) 2?£|(50) — £?£,и (50) = 22,6 R,
(51) = 11,3 Я, а для Rb (Z = 37) Е£|(37)-Е£||(37) = 14,8 Я, а Е^(38) = 2,3 Ди вероятность
внутренней конверсии должна резко падать.
Внутренняя конверсия была открыта Оже именно по следам таких электронов в камере Вильсона.
Эти электроны называют электронами Оже или электронами внутренней конверсии.
5) Со стороны меньших Z имеется лишь естественное ограничение из-за отсутствия соответствующих
заполненных оболочек.
§13.4. Интенсивности в рентгеновских спектрах
363
Важным следствием внутренней конверсии является то, что атом оказывается
уже не однократно, а двукратно ионизованным. Может происходить и повтор-
ная внутренняя конверсия при переходе электронов на освобождающиеся места
во внутренних оболочках, что приведет к еще более высокой кратности ионизации.
Атомы, ионизованные более чем однократно, могут образовываться и под действи-
ем электронного удара. При этом в принципе могут выбиваться и два электрона
из К-слоя, в то время как при внутренней конверсии электроны могут вырываться
лишь из L-слоя или из еще более внешних слоев.
Переходы между уровнями внутренних оболочек в двукратно (или многократно)
ионизованных атомах несколько отличаются по своим частотам от соответствую-
щих переходов в однократно ионизованных атомах. Это приводит к появлению так
называемых недиаграммных линий, не укладывающихся в диаграмму переходов для од-
нократно ионизованного атома (см. рис. 13.2). Такие линии называют также сател-
литами (спутниками) основных линий рентгеновских серий. Кратной ионизацией
могут быть хорошо объяснены ряд наблюдающихся сателлитов с коротковолновой
стороны основных линий (при увеличении кратности ионизации частоты переходов
увеличиваются). Наблюдаются и длинноволновые сателлиты, связанные со взаимо-
действием, в конденсированных системах, атомов с окружающими частицами [21].
Для нахождения числа возможных сателлитов и их расположения для определенного
перехода при заданном типе ионизации следует учитывать сложение моментов количества
движения для соответствующих начальных и конечных конфигураций. При удалении двух
электронов возникают конфигурации, термы которых аналогичны термам двухэлектронных
систем, и указанный расчет легко выполнить. Например, при удалении электронов из оболо-
чек К и Z/ц возникает конфигурация 1з2р5, дающая термы, согласно схеме нормальной связи,
такие же, как конфигурация зр, т.е. !Р° и 3Р°. При переходе К—Lu, т.е. при переходе элек-
трона из оболочки 2р в оболочку 1з, из конфигурации 1з2р5 возникает конфигурация ls22p4,
дающая такие же термы, как конфигурация р2, т. е. lSD 3Р (см. табл. 9.4, с. 255). Возможные
переходы между уровнями ’Pf, 3Р2°, 3Р|° 3Р0° конфигурации ls2p5 и уровнями *50, ]D2, 3Рг,
3РН 3Р0 конфигурации 1з22р4 и определяют число сателлитов. Для определения положения
сателлитов необходимы расчеты расположения уровней соответствующих конфигураций.
Отметим в заключение данного параграфа, что на основе аналогичного рассмотрения
уровней различных возможных конфигураций может быть объяснена в ряде случаев и тонкая
структура рентгеновских линии испускания и краев поглощения элементов, для которых
основное состояние нейтрального атома не является состоянием *50, как это молчаливо
предполагалось при составлении схемы рис. 13.2. Начальный и конечный уровень для опре-
деленного перехода будут обладать тонкой структурой, получающейся в результате сложения
моментов, соответствующих внешним электронам, и моментов для рассматриваемых уровней
иона. Например, если атом обладает одним внешним электроном, то для каждого уровня
иона с заданными L', S', J' атомного остова (лишенного одного внутреннего электрона)
будет получаться тонкая структура с набором уровней, таким же, как для двухэлектронной
системы =1, з\ = з = -, ji = I ± - и l2 = Lr, з2 = S', j2 = J', и зависящим от схемы связи
моментов. Тонкая структура уровней и будет определять тонкую структуру линий испускания
и краев поглощения. Учет подобной тонкой структуры наиболее существен для элементов
с достраивающимися d- и /-оболочками (см. [20], с. 76).
§ 13.4. Интенсивности в рентгеновских спектрах
Интенсивности в рентгеновских спектрах испускания определяются заселенно-
стью уровней и вероятностями соответствующих спонтанных переходов.
Заселенность начальных уровней зависит от условий возбуждения. Возбуждение
может производиться электронным ударом, что имеет место в рентгеновских труб-
ках, в которых анод бомбардируется потоком электронов, или путем поглощения
364
Глава 13. Рентгеновские спектры
фотонов. В отличие от оптических спектров температурное возбуждение, вследствие
очень больших энергий, необходимых для возбуждения внутренних электронов,
не играет никакой роли даже при весьма высоких температурах.
Даже при температуре порядка миллиона градусов, когда кТ порядка 100 эВ
(см. (5.29)), могут возбуждаться лишь уровни с энергиями порядка 1 000 эВ, что
соответствует весьма мягкому рентгеновскому излучению. Отметим, что при этом
атомы уже многократно ионизованны и возбуждаемые уровни энергии являются
уровнями внешних электронов; переходы между такими уровнями дают спектры,
хотя и лежащие в коротковолновой области, но вполне аналогичные обычным
оптическим спектрам. Подобные спектры могут получаться в весьма конденсиро-
ванном электрическом разряде и именно их изучение позволяет получить данные
для высоких членов изоэлектронных рядов (ср. §8.5).
Характеристический спектр испускания, возникающий под действием элек-
тронного удара, называют первичным. Вероятность возбуждения определяется ви-
дом функций возбуждения (см. с. 25); возбуждение начинается, когда кинетическая
энергия Т электронов становится равной энергии, необходимой для возбуждения6)
(см. условие (1.12)). Вероятность возбуждения сперва быстро возрастает, затем
достигает максимума, когда кинетическая энергия электронов примерно в 3 раза
превышает энергию возбуждения (для К- и Z-серий), и затем постепенно спадает.
Характеристический спектр испускания, возникающий в результате поглощения
фотонов, т. е. путем оптического возбуждения, называют вторичным.
Вероятности испускания в рентгеновской области спектра для дипольного излу-
чения весьма велики, гораздо больше, чем в оптической области. Это определяется
тем, что силы осцилляторов того же порядка, а частоты переходов значительно
возрастают. Согласно формуле (4.107), вероятность перехода пропорциональна силе
осциллятора и квадрату частоты:
Aik ~ v2fik.	(13.30)
Частоту перехода, согласно (13.5), можно приближенно доложить пропорци-
ональной отношению Z*2/п2 для начального состояния (учитывая, что п\ < П2,
a Z* > Z£)7), и мы получаем
Z*4
Aik~—fik.	(13.31)
гт
Отсюда видно, что вероятности действительно сильно возрастают для тяжелых
атомов, особенно для Х-серии с наибольшим Z* и наименьшим п, равным 1.
Вероятности могут достигать значений порядка 1015—1016 с”1.
В численном виде мы имеем, подставляя в (4.109) приближенное значение
и RZ*1	,
волнового числа - = —где R выражено в см ,
с п/
iZ*4
А,к = 0,22 R2—T-fik,	(13.32)
тг
6) При возбуждении внутренних электронов тяжелых атомов для кинетической энергии электронов
\ ? f	1	12
нужно пользоваться уже релятивистским выражением (т — т$)с = I —	— 1 I т$с , где —
масса покоя электрона.	\ \/1 - v2/c2	/
7) Пренебрежение вторым членом в (13.5) соответствует замене действительной частоты перехода
частотой соответствующего края поглощения.
§13.4. Интенсивности в рентгеновских спектрах
365
что при R « 1,1 • 105 см 1 приводит для Aik к значению
Ла = 2,6 109—fikc~'.
ГГ
Для К-, L-, ЛГ-серий (n = 1, 2, 3):
(13.33)
(13.34)
А1п- = 2,6 • 10’zr4/in' с"', А2п. = 1,6 • 108Z24/2n> с’1,
Л3п. =3,2-1О7^4/ЗП'С-'.
Здесь первый индекс у Aik дает значение щ = п, а второй — значение п2 = п1.
Для переходов с Дп = 1 силы осцилляторов могут быть порядка 1, а при увеличе-
нии Дп они быстро убывают (ср. табл. 6.5 для атома водорода, с. 183, а также табл. 8.8
для лития и натрия, с. 233). Полагая для перехода К—Ьп,ш, т. е.	'/г'
/)2 = I8, мы получаем вероятность перехода
Л)2 = 2,6- 109Я*4 с-1	(13.35)
и время жизни
1 ~ 1 _4'1О~10
ЕЖ ~	~ я*4 с’
п1
(13.36)
При больших Z* вероятность переходов получается очень большой, а время жизни
очень малым. Для Z* = 45 Л12 = Ю16 с-1, а т = 10-16 с.
Для L- и М-серий вероятности получаются меньше, в соответствии с увели-
чением и4 и с уменьшением Z*4, однако они также достаточно велики, особенно
для первых членов серий. Достаточно велики и вероятности квадрупольных пере-
ходов, отношение которых к вероятностям дипольных переходов, согласно (4.83),
/а\2
пропорционально 1-1 , где а — размеры излучающей системы, а А — длина волны,
у Л J
Размеры излучающей системы, т. е. размеры области, где электронная плотность зна-
чительна, убывают обратно пропорционально Z* (ср. (6.29); электронная плотность
с
значительна в области порядка размеров боровских круговых орбит), а А = - убы-
v
.	а	.
вает обратно пропорционально квадрату Z . Следовательно, - возрастает как Z ,
(а\2	*2	(а\2
а I - I — как Z и может увеличиваться, по сравнению со значением I - 1
\л/	\л/
в оптической области, при больших Z* на три-четыре порядка. Соответствен-
но вероятности квадрупольных переходов вместо 10-7 могут составлять 10-4-10-3
по отношению к вероятностям дипольных переходов.
Относительные интенсивности линий в данной серии определяются уменьше-
нием вероятностей переходов с увеличением изменения Дп главного квантового
числа и, при заданных Дп и Д/, — статистическими весами уровней, на которые
происходит переход. Так, для К-серии интенсивности линий K—L\\, Lui (Дп = 1)
больше интенсивностей линий К—М\\, Мщ, а интенсивности последних больше ин-
тенсивности линий K—Nn, Nu\. Для переходов на уровни L\\, Тщ (2 2Р°д и 2 2Ру ),
8>Для атома водорода, согласно табл. 6.5, /12 ~ 1,2, если учесть, что в этой таблице приведены силы
осциллятора на одну степень свободы и их нужно умножать на 3 для атома с тремя степенями свободы
электрона. Разумеется, множитель 3 при оценке лишь порядка величины мало существен.
366
Глава 13. Рентгеновские спектры
на уровни Ми, М\\\ (3 2Р°д и 3 2Ру2) и т- Д-> интенсивности для каждой пары линий
должны относиться как статистические веса ру2 и рзд, т.е. как 1 : 2, аналогично
дублетам главной серии щелочных металлов. Это хорошо оправдывается на опыте.
Ширина спектральных линий при отсутствии безызлучательных переходов опре-
деляется вероятностями переходов, и так как вероятности, согласно (13.30), возра-
стают с частотой пропорционально i/2, то относительная ширина в рентгеновской
области, обусловленная естественным уширением, больше чем в оптической области.
При силе осциллятора, равной единице, согласно (4.144) естественная ширина
равна примерно 10“4 А. При длине волны 0,5 А (длина волны линий К-серии
при Z ~ 50) относительная ширина составляет 2 • 10-4, а абсолютная ширина
в единицах энергии равна 5 эВ (длине волны 0,5 А соответствует энергия фотонов
около 25 000 эВ).
При наличии внутренней конверсии, т.е. безызлучательных переходов, ширина
линий будет определяться полной вероятностью переходов, равной сумме вероят-
ностей переходов с излучением и переходов без излучения. Так как вероятность
внутренней конверсии значительна, то получается существенное увеличение шири-
ны линий характеристического спектра, особенно для L- и М-серий, для которых
весьма вероятны безызлучательные переходы между уровнями L-оболочки и между
уровнями М-оболочки соответственно (см. выше, с. 362). Ширина линий может
увеличиваться при этом на один-два порядка. Параллельно увеличению вероятно-
сти безызлучательных переходов уменьшается выход испускания при оптическом
возбуждении (см. (4.26)), падая при большой вероятности внутренней конверсии
до сотых долей. Интенсивность сателлитов, получающихся за счет кратной иониза-
ции при внутренней конверсии, соответственно возрастает.
Мы рассмотрели интенсивности в спектрах испускания. Интенсивности в спек-
трах поглощения, определяемые коэффициентами поглощения, пропорциональны
числу поглощающих атомов и вероятностям поглощения. Вероятности поглоще-
ния обнаруживают характерный ход, резко возрастая у границы ионизации от нуля
до значительных величин и затем монотонно убывая с увеличением энергии фотонов,
что и дает характерную картину краев поглощения. Вероятность поглощения, сопро-
вождающегося ионизацией, т.е. вероятность фотоэффекта или фотоэлектрического
поглощения может быть рассчитана квантовомеханическими методами. При энергиях
фотонов, значительно превосходящих энергию ионизации, вероятность поглощения
убывает обратно пропорционально и1^2. Коэффициенты поглощения для фотоэлек-
трического поглощения электронами более внешних оболочек весьма велики и по-
этому более длинноволновое излучение очень сильно поглощается и обладает малой
проникающей способностью. Наоборот, коротковолновое излучение поглощается
гораздо слабее и обладает большой проникающей способностью, с увеличением
частоты быстро возрастающей (вдали от краев поглощения, в соответствии с умень-
шением поглощения, убывающего обратно пропорционально i/7^2). Отсюда, как
известно, и происходит разделение рентгеновского излучения на мягкое и жесткое.
ГЛАВА 14
ЯВЛЕНИЕ ЗЕЕМАНА И МАГНИТНЫЙ РЕЗОНАНС
§ 14.1. Расщепление уровней энергии в магнитном поле
В магнитном поле происходит расщепление вырожденных уровней энергии
атома на невырожденные подуровни. Это приводит к магнитному расщеплению
спектральных линий, соответствующих переходам между различными уровнями
энергии, на ряд составляющих и к появлению вынужденных переходов между
подуровнями данного уровня энергии.
Явление расщепления спектральных линий и уровней энергии в магнитном поле
называют явлением Зеемана. Зееман первоначально обнаружил (в 1896 г., см. § 1.6,
с. 37) расширение линий дублета Na 5 890—5 896 А (первого члена главной серии,
см., например, с. 228) в магнитном поле; затем ему удалось наблюдать не только
расширение, но и расщепление спектральных линий. На основе классической элек-
тронной теории это расшепление было объяснено Лоренцом как результат расщепле-
ния частоты колебаний в атоме упруго связанного электрона, и лишь впоследствии,
на основе теории Бора, оно было истолковано естественным образом как результат
расщепления уровней энергии. Термин «явление Зеемана» теперь применяют к рас-
щеплению в магнитном поле как спектральных линий, так и уровней энергии (что
уже отмечалось в § 1.5, с. 35). Изучение явления Зеемана на спектральных линиях
атомов в видимой и ультрафиолетовой областях сыграло большую роль в развитии
учения о строении атома, в особенности в период, последовавший за созданием
теории Бора. В настоящее время исследование явления Зеемана на спектральных
линиях атомов представляет один из важных методов определения характеристик
уровней энергии атомов и сильно облегчает интерпретацию сложных атомных спек-
тров (см. ниже, с. 387); изучение зеемановского расщепления спектральных линий
позволяет также получать ценные сведения о магнитных полях в источниках света,
в частности при исследовании Солнца — о магнитных полях в солнечных пятнах.
Вынужденные переходы между зеемановскими подуровнями данного уровня
энергии происходят под действием излучения частоты, равной частоте возможных
переходов, т.е. при наличии резонанса, и это явление называют магнитным резонан-
сом. Частоты переходов между зеемановскими подуровнями лежат в радиочастотной
области спектра и изучаются радиоспектроскопическими методами [40, 41]. Впервые
магнитный резонанс наблюдали в 1938 г. Раби и его сотрудники [243] в молекуляр-
ных пучках’\ Им удалось обнаружить сперва резонансные переходы для молекул
водорода между подуровнями зеемановского расщепления, обусловленного ядерны-
ми магнитными моментами протона и дейтрона, а затем, в 1940 г. [244], резонансные
’) Направленные пучки нейтральных частиц принято называть молекулярными. Их подразделяют
на собственно молекулярные пучки, состоящие из молекул, и на атомные пучки, состоящие из атомов.
368
Глава 14. Явление Зеемана и магнитный резонанс
переходы для атомов между подуровнями зеемановского расщепления, обусловлен-
ного электронными магнитными моментами атомов. Изучение магнитного резонан-
са, как электронного, так и ядерного, в пучках, атомных и молекулярных, является
сложным по своей экспериментальной методике, и исследования этого явления
стали широко развиваться лишь после открытия в 1944 г. Завойским в Казани [245]
электронного парамагнитного резонанса — поглощения микроволнового излучения
веществом за счет переходов между подуровнями зеемановского расщепления, свя-
занного с электронными магнитными моментами частиц вещества (определяющими
парамагнитные свойства вещества, откуда и название «парамагнитный» резонанс);
в ферромагнитных веществах наблюдается аналогичное явление ферромагнитного
резонанса2). В 1945 г. американскими исследователями [246] был наблюден ядерный
парамагнитный резонанс — поглощение излучения веществом в области коротких
радиоволн при зеемановском расщеплении, обусловленном ядерными магнитными
моментами; парамагнетизм, связанный с ядерными магнитными моментами, был от-
крыт Лазаревым и Шубниковым в 1937 г. [242] при исследовании магнитных свойств
твердого водорода при температурах 2-4° К. В настоящее время большинство весьма
многочисленных радиоспектроскопических исследований производится различными
методами магнитного резонанса. Существенно, что эти методы позволяют с очень
большой точностью определять магнитные моменты атомов и ядер (см. с. 399 и с. 426).
Ниже мы детально рассмотрим зеемановское расщепление спектральных ли-
ний (§ 14.2-14.5) и магнитный резонанс (§ 14.6-14.8); в данном параграфе мы
разберем зеемановское расщепление уровней энергии как основу дальнейшего рас-
смотрения.
Причиной зеемановского расщепления уровней энергии является, согласно
наглядным представлениям, то, что магнитные моменты могут ориентироваться
различными способами по отношению к магнитному полю.
Дополнительная энергия в магнитном поле любой атомной системы, обла-
дающей магнитным моментом, зависит от ориентации рассматриваемого момента
по отношению к полю, а именно от величины проекции этого момента на на-
правление поля. Проекция pz магнитного момента д пропорциональна проек-
ции Jz механического момента J и квантуется вместе с ней (см. § 2.5, с. 55).
В результате каждому значению проекции момента количества движения соот-
ветствует определенное значение проекции магнитного момента и свое значение
дополнительной энергии в магнитном поле. В соответствии с 2J 4- 1 возможными
значениями mj — т — J, J —1,..., — J проекции Jz механического момента J крат-
ность вырождения равна gj — 2J 4- 1 и определяет число подуровней в магнитном
поле (см. (2.12) и (2.15)). Квантовое число т, как характеризующее подуровни зеема-
новского расщепления, получило название магнитного квантового числа (ср. с. 54).
Рассмотрим подробнее расщепление в постоянном внешнем магнитном поле на-
пряженности Н уровня энергии атома, обладающего в соответствующем состоянии
электронным магнитным моментом р.
Дополнительная энергия атома, согласно известной формуле для энергии маг-
нита, находящегося в магнитном поле, равна
=	= -pHcos(p,H) = -pzH,	(14.1)
где pz — р cos (/z, Н) — проекция магнитного момента на направление поля, при-
нятое за направление оси z и являющееся в рассматриваемом случае тем выделенным
2) Первые опыты по ферромагнитному резонансу были произведены еще Аркадьевым в 1926 г. [36],
а общая теория разработана в 1935 г. Ландау и Лифшицем [241]. Многочисленные экспериментальные
исследования ферромагнитного резонанса были выполнены, начиная с 1946 г.
§ 14.1. Расщепление уровней энергии в магнитном поле
369
направлением, которое мы и рань-
ше выбирали за ось z. В отли-
чие от случая свободной системы,
для которой могло быть выбрано
любое направление оси квантова-
ния, сейчас мы имеем физически
выделенное направление магнит-
ного поля.
Проекция pz магнитного мо-
мента на направление поля име-
ет определенное значение (2.43),
и мы получаем
&Ет = -yhrnH, (14.2)
где 7 — гиромагнитное (магнето-
механическое) отношение и т =
mj принимает 2J + 1 значений.
Формула (14.2) дает расщепление
исходного уровня на 2 J 4-1 равно-
отстоящих подуровней, как пока-
зано на рис. 14.1, для наименьших
целых и полуцелых значений J.
Пунктиром показано первоначаль-
ное положение уровня до его рас-
щепления. Расщепление симмет-
рично относительно этого положе-
ния, с которым при целом J совпа-
дает положение подуровня т = 0.
Расстояние между соседними под-
уровнями равно yhH, т. е. пропор-
ционально гиромагнитному отно-
шению и напряженности магнит-
Рис. 14.1. Расщепление уровней с различными
значениями J в магнитном поле:
а — при J = !/2; б — при J — 1; в — при J — 3/2;
г — при J = 2; д — при J = 5/2; е — при J = 3
ного поля.
Для чисто орбитального момента гиромагнитное отношение определяется фор-
мулой (2.45) и (14.2) принимает вид
eh
АЕт = -^ihHm = ------Нт — р^Нт,
2тп^ с
(14.3)
где /4б — магнетон Бора (2.46). Подуровни с последовательными значениями т
расположены на расстояниях Подобно тому как магнетон Бора представляет
естественную единицу для измерения электронных магнитных моментов, величи-
на рьН представляет естественную единицу для измерения расщепления уровней
энергии атомов в магнитном поле. Она дает величину расщепления для чисто
орбитального момента и ее часто называют величиной нормального расщепления.
Для чисто спинового момента, согласно (2.55), мы получаем
АЕт = -yfiHm =-------Нт = 2/1бЯтп.	(14.4)
тес
Расстояние между соседними подуровнями равно 2рьН, т. е. удвоенной величине
нормального расщепления. Для очень важного случая одного электрона с некомпен-
сированным спином, при I = 0, т = ms = ± !/г (см. (6.6)), и первоначальный уровень
370
Глава 14. Явление Зеемана и магнитный резонанс
со значением j = s = ’/2 расщепляется на два подуровня (см. рис. 14.1, а), находя-
щихся на расстоянии 2дБЯ. Отметим, что как для орбитального, так и для спинового
момента в силу отрицательности 7 (из-за отрицательности заряда электрона) глубже
всего лежит подуровень с наименьшим т (см. (14.3) и (14.4)).
Оценим теперь порядок величины нормального расщепления р^Н. Численное
значение магнетона Бора, согласно (2.47), равно
ДБ = 0,92731 • Ю-20	« 1,400 • 106	» 4,67 • 10-5	(14.5)
В магнитном поле напряженностью
равно 4,67 • 10“5 см-1, т. е. примерно
мы получим
Дб = 0,934 см'1 ~
в 1 Гс
1
20000
1 см-1
зеемановское расщепление р^Н будет
см'1. В магнитном поле Н = 20000 Гс
(Я = 20 000 гаусс).	(14.6)
Таким образом, величина нормального расщепления в поле 20 000 Гс поряд-
ка 1 см"1. В наиболее сильных постоянных магнитных полях порядка 100000 Гс,
которые практически применяются для изучения явления Зеемана, дБЯ составляет
примерно 5 см-13). Поэтому даже в очень сильных магнитных полях относительное
расщепление спектральных линий в видимой и в ультрафиолетовой областях спектра
(волновые числа порядка нескольких десятков тысяч см-1) невелико.
При изучении электронного магнитного резонанса применяют магнитные поля,
не превышающие 5 000-10000 Гс. В поле Я = 5 000 Гс р^Н = 0,233 см“’/Гс, что
соответствует длине волны Л резонансного перехода между соседними подуровнями,
равной приблизительно 4,3 см и относящейся к микроволновой области спектра.
Для произвольного электронного момента атома мы имеем, согласно (14.2)
и (14.3):
ЬЕт = -—yfiHm = -иъНт.	(14.7)
71
У
Вводя множитель д = —, можно записать (14.7) в виде
11
ЛЕт=дрьНт (m = J, J- !,...,-/).	(14.8)
Множитель д (множитель Ланде) определяет отношение величины расщеп-
ления дрьН для произвольного электронного магнитного момента к величине
нормального расщепления р^Н. Для чисто орбитального момента д = 1 и для чи-
сто спинового момента д = 2. Для электронного момента, являющегося суммой
орбитальных и спиновых моментов, д может принимать различные значения, от до-
лей единицы до нескольких единиц, что зависит от числа слагаемых моментов
и от типа связи. Значения множителя д являются важной характеристикой уровней
энергии (подробнее см. ниже, § 14.3, с. 378).
Формула (14.8) приводит к линейной зависимости зеемановского расщеп-
ления от напряженности магнитного поля Я. Это иллюстрируется диаграммой
рис. 14.2, на которой энергии подуровней представлены как функции Я для зна-
чений J — ’/г, 1, 3/2 и 2. Такого рода диаграммы очень удобны во всех тех случаях,
когда изучается расщепление уровней энергии при различных значениях магнитного
поля и особенно, когда имеются отступления от линейной зависимости.
3) Такие поля применяли Гаррисон и Биттер [240]; еще более сильные пола получили Капица, Стрелков
и Лаурман [239].
§ 14.1. Расщепление уровней энергии в магнитном поле
371
Линейная зависимость, определяемая основной формулой (14.8) для зеема-
новского расщепления, справедлива лишь для отдельного уровня энергии Ei,
далеко отстоящего от других
уровней Ej. «Далеко» озна-
чает (считая, что д поряд-
ка единицы), что расстояния
до соседних уровней много
больше величины р^Н
рБН<\Е{-Е^\.	(14.9)
Поле, удовлетворяющее ус-
ловию (14.9), называют сла-
бым, и, таким образом, фор-
мула (14.8) определяет зеема-
новское расщепление в сла-
бом поле. В отличие от (14.9)
поле, для которого выполня-
ется обратное условие
рБН>\Е{-^\, (14.10)
Рис. 14.2. Зависимость расщепления от напряженности
магнитного поля:
а — при J = Уз; б — при 7=1;
в — при J — 3/з; г — при 7 = 2
называют сильным. Случай сильных полей и полей, промежуточных между сильными
и слабыми, когда рБН ~ \Ei - Ej\, будет разобран ниже (см. § 14.5, с. 389).
Очевидно, что понятие слабого и сильного поля являются относительными
понятиями, поскольку они зависят от величины расстояний между соседними
уровнями энергии в отсутствии магнитного поля.
Исходная формула (14.2) для дополнительной энергии в магнитном поле получается
квантовомеханически, если от классического выражения для дополнительной энергии ДЕ =
V = -pzH атома с магнитным моментом р (см. 14.1)) перейти к оператору
V = -Hpz
(14.11)
и рассматривать V как возмущение.
Дополнительная энергия в первом приближении теории возмущений равна среднему
значению оператора V:
A\Eajm — V — VaJm,aJm — I "ФаЗтУ tyaJm	— Н I ^paJmPz^PaJm 6>Х — Hpz,
(14.12)
взятому по функциям нулевого приближения ^ajm (где а включает характеристики состояния
помимо 7 и т). Среднее значение оператора проекции магнитного момента пропорционально
среднему значению оператора Mpz = hJz проекции механического момента и может быть
представлено в виде
Pz
tyaJmPztyaJm 6>Х — I ^PaJm^z^PaJm бх — 9РБ I ^PaJm^z^PaJm бх,
(14.13)
где 7 — отношение магнитного момента к механическому, введенное в гл. 2, которое
для электронных моментов может быть выражено через магнетон Бора рБ и множи-
I	У
тель д 1 yh = — yfi = -дрь, см. (14.7)
\	7/
Учитывая, что, согласно (2.19) и (2.10),
JztyaJm — WtyaJm (гП — Wlj — J, J 1, . . . , 7)
(14.14)
372
Глава 14. Явление Зеемана и магнитный резонанс
и, следовательно, J*	dx — т, мы находим
= 7йт = -дрьт,
(14.15)
откуда получаем
= АЕт =-'уЬНт = дрьНтп,	(14.16)
т.е. формулы (14.2) и (14.8).
Мы, разумеется, и раньше в неявной форме использовали квантовую механику, когда
в классическую формулу (14.1) подставили квантованное значение д2, согласно (2.43).
Из приведенного вывода следует, что результат (14.2) справедлив только в первом
приближении теории возмущении. Во втором приближении теории возмущений поправка
к энергии определяется недиагональными матричными элементами Vajmiaij>m энергии возму-
щения, связывающими состояния с тем же значением т и со значениями J, отличающимися
не более чем на единицу (J' — J = ±1, 0). Эта поправка равна
ДзБ = У2	(а' # J’ = Jt J ± 1)(	(14.17)
где суммирование производится по всем уровням a'J7, для которых J’ отличается от J
не более чем на единицу. Так как матричные элементы Vajm>a>j>m пропорциональны, подобно
матричным элементам (14.12), напряженности поля Н, то А2Е будет пропорционально Я2,
что приводит к квадратичному явлению Зеемана. Отношение величины квадратичного явления
Зеемана к величине линейного явления по порядку величины равно
е ~
\VaJm , a'J'ml
|Ej - Eji | ’
(14.18)
т. e. отношению матричных элементов энергии возмущения к разности энергий соседних
уровней. Так как для электронных моментов матричные элементы имеют порядок рьН, то
отношение (14.18) будет порядка
ДбЯ
\Ej - Eji |
(14.19)
Если данное отношение перестает быть малым, то это означает, что магнитное поле уже
не является слабым и нельзя рассматривать расщепление данного уровня энергии независимо
от расщепления других уровней. Мы получаем обоснование критерия (14.9) применимости
формулы (14.2).
Отметим в заключение данного параграфа, что формулы (14.1) и (14.2) являют-
ся общими и применимы не только к атомам, но и к любым частицам, как более
сложным, какими являются молекулы, так и к более простым, какими являют-
ся элементарные частицы, в частности, электрон, протон и нейтрон. Для любых
электронных магнитных моментов справедливы формулы (14.8)—(14.10), а для ядер-
ных и вращательных моментов применимы аналогичные формулы, отличающиеся
лишь заменой магнетона Бора Дб через ядерный магнетон дЯд (ср. §2.5, с. 57), что
Дб тР
приводит к уменьшению всех масштабов в — = — раз.
Дяд
§ 14.2. Общая картина зеемановского расщепления
спектральных линий в слабом поле
Картина зеемановского расщепления заданной спектральной линии определяет-
ся расщеплением комбинирующих уровней и правилами отбора для магнитного кван-
тового числа. Эти правила, согласно (4.157), для дипольного излучения имеют вид
Дт — тп\ - m2 — 0, ±1,	(14.20)
§ 14.2. Общая картина зеемановского расщепления в слабом поле 373
где и m2 — магнитные квантовые числа комбинирующих уровней. Таким
образом, при переходе проекция Jz = тп механического момента ^выраженная
h \
в единицах h = — либо остается неизменной, либо изменяется на ±1.
2тг 7
В соответствии с правила-
ми отбора (14.20), при переходах
между подуровнями двух ком-
бинирующих уровней получает-
ся два типа составляющих —
7г-составляющие, для которых
Дттг — ТП\ - 7712 — 0, И СГ-СО-
ставляющие, для которых Дттг =
тп\ -7712 — ±1. Возможные пере-
ходы между подуровнями уров-
ней J] = 3 и J2 = 2 показаны
на рис. 14.3. Группа тг-состав-
ляющих соответствует перехо-
дам ттг -+ ттг (ттг] = 7712), ле-
вая группа а-составляющих —
переходам тп — 1 —* ттг (ттг] —
ттг2 = -1) и правая группа
а-составляющих — переходам
т + 1 —> ттг (ттг] - m2 — 1).
Группа тг-составляющих
(Дттг = 0) и две груп-
пы a-составляющих (Дттг = -1,
Дт = -1-1) отличаются поля-
ризацией, тг-составляющие (па-
раллельные составляющие) со-
ответствуют линейным колеба-
ниям излучающего диполя, па-
раллельным направлению по-
ля z, ст-составляющие (пер-
пендикулярные составляющие)
соответствуют круговым коле-
баниям излучающего диполя
Рис. 14.3. Переходы между подуровнями уровней
7 = 3и J = 2
в плоскости ху, перпендикуляр-
ной направлению поля, как это показано в нижней части рис. 14.2. При этом
для Дттг = +1 направление вращения связано с направлением магнитного поля как
для правого винта, а для Дттг = -1 — как для левого винта.
Поляризация зеемановских составляющих следует из соотношений (4.172) для соста-
вляющих вектора, которые были выведены в §4.8 (см. с. 120). Правилу отбора Дт = 0
соответствует линейный осциллятор, ориентированный вдоль оси z, а правилу отбора
Дт = ±1 — два линейных осциллятора, ориентированных по осям х и у и колеблю-
7Г
щихся с разностью фаз ±~,
что дает круговые колебания. Для дипольного излучения мы
имеем обычные электрические осцилляторы, — с классической точки зрения электроны,
совершающие гармонические колебания с ускорением а = -ш2г, где г — rQei(t}t (классическое
рассмотрение вопроса см. в конце данного параграфа, с. 376). В модели, соответствую-
314
Глава 14. Явление Зеемана и магнитный резонанс
щей квантовомеханическим представлениям, дипольный момент перехода, т.е. матричный
элемент составляющей дипольного момента, периодически изменяется с частотой перехода.
При наблюдении вдоль направления поля, т. е. по оси z, тг-составляющие
будут отсутствовать и будут наблюдаться только a-составляющие двух типов, по-
ляризованные по кругу противоположным образом (продольное явление Зеемана).
При наблюдении перпендикулярно направлению поля (например, вдоль оси х
или вдоль оси у) будут наблюдаться и тг- и a-составляющие, и те и другие поляризо-
ванные линейно, но во взаимно перпендикулярных плоскостях (поперечное явление
Зеемана). Для тг-составляющих направление колебаний (электрического вектора ис-
пускаемой или поглощаемой электромагнитной волны) совпадает с направлением
поля z, для a-составляющих оно перпендикулярно этому направлению.
Число составляющих каждого типа легко определить. Для случая, изображенного
на рис. 14.3, оно равно 5. тг-составляющие соответствуют переходам 2—2, 1—1, 0—0,
(-!)—(-!), (-2)—(-2), две группы a-составляющих — переходам 3—2, 2—1, 1—0,
0-(-1), (-1)-(-2) и 1-2, 0-1, (-1)-0, (-2)—(-1), (-3)-(-2). Общее число
составляющих равно 15.
Расположение составляющих в картине расщепления зависит от соотношения
между множителями g комбинирующих уровней. Чем меньше разница между этими
множителями, тем теснее расположены составляющие каждой группы. Согласно
формуле (14.8) и правилам отбора, мы имеем:
переходы т —> т (Дт = 0)	АЕт,т = (g} - д^р^Нт,
переходы т 4- 1 —> гл (Дт = 4-1) ДЕ^+i т —
= [5i(ra + 1) -дгт\цъН = [(<п - дг)т +дх]ръН, >
переходы т - 1 —> т (Дт = -1)	Д^т-1 т —
- [51 (га- 0-52га]дБЯ = [(</1 - д2)т- дх]цьН. л
(14.21)
. тг-составляющие расположены симметрично относительно первоначаль-
Расположение составляющих показано в нижней части рис. 14.3 ( для случая
6
9\ — у 92
ного положения нерасщепленной линии, a-составляющие каждой группы распо-
ложены симметрично относительно смещенных положений ±gipsH. Расстояния
соседних составляющих внутри каждой группы одинаковы и равны (д\ - д2)р>ьН,
т. е. действительно тем меньше, чем меньше разность д^ - дг- Вся картина в це-
лом симметрична. Одинаково расположены относительно центра тг-составляющие
+т —> 4-т, — т —> — т и а-составляющие тп 4- 1 —> m и — т— 1 —> — т, например,
2 —> 2, —2 —> —2 и 3 —> 2, —3 —> —2.
Если множители д комбинирующих уровней одинаковы, то все составляющие
каждой группы совпадают и получается особенно простая картина — простое явление
Зеемана: первоначальная спектральная линия расщепляется на три линии — зее-
мановский триплет. Этот триплет образуется несмещенной тг-составляющей и дву-
мя a-составляющими, симметрично расположенными на расстояниях ±др,ъН от нее.
Возникающая в этом случае картина для поперечного и продольного наблюдения
изображена на рис. 14.4. В последнем случае центральная несмещенная составляю-
щая, соответствующая колебаниям осциллятора вдоль направления поля, отсутствует
и триплет сводится к дублету с расщеплением Igp^H.
§ 14.2. Общая картина зеемановского расщепления в слабом поле
375
Формула (14.21) в случае простого явления Зеемана дает
переходы
переходы т 4-1 —* т
переходы т - 1 —► т
A^m,m —
А#т+1,т =0ДБЯ, >
ЛЕт_^т = -дрьН.,
(14.22)
т —* т
s *-	**	-*
Продольное
наблюдение
2<тиБЯ-
Рис. 14.4. Зеемановский триплет
Простое явление Зеемана, если не считать случаев, когда случайно совпада-
ют множители д для комбинирующих уровней, получается в слабом поле лишь
в некоторых вполне определенных частных случаях, а именно:
1.	При переходах между оди-
ночными уровнями. В этом случае
S = 0, полный момент являет-
ся чисто орбитальным (J = L),
и для всех одиночных уровней
<7=1. Получаются зеемановские
триплеты с нормальным расщеп-
лением рьН.
2.	При переходах между уров-
нями, для которых полный ор-
битальный момент равен нулю
(L = 0). В этом случае L = 0, полный момент является чисто спиновым (J = S),
и для всех таких уровней д = 2. Получаются зеемановские триплеты с расщеплени-
ем 2дрьН, вдвое больше нормального.
3.	При переходах между уровнем J = 1 и уровнем J = 0. Второй уровень
не расщепляется (т = 0), а первый расщепляется на три подуровня с т = 0, ±1.
Спектральная линия расщепляется на три составляющих, давая зеемановский три-
плет с расщеплением др^Н, где множитель д относится к уровню J = 1.
В общем случае, когда д\ дг, в слабом поле наблюдается более сложная
картина — сложное явление Зеемана.
В зависимости от значения разности д\ - дг и значений J\ и Зг получаются
весьма разнообразные картины расщепления, которые будут рассмотрены более
подробно ниже, в § 14.4 (с. 382), посвященном типам зеемановских расщеплений.
Наряду с числом составляющих и их расположением, для сложного явления
Зеемана весьма характерно вполне определенное распределение относительных ин-
тенсивностей a-составляющих и тг-составляющих с различными т при заданных
значениях квантовых чисел 3 комбинирующих уровней. Это распределение не зави-
сит от типа связи.
Общие формулы для относительных интенсивностей приведены в табл. 14.1.
Эти формулы были впервые получены на основе опытных данных в сочетании с клас-
сическими представлениями Орнштейном и Бюргером в 1924 г., а затем выведены на основе
принципа соответствия Кронигом и Гаудсмитом и независимо Хенлем в 1925 г. [236]. Они
легко получаются из основных квантовомеханических формул для матричных элементов
вектора [14] и могут также быть выведены методами теории групп [138].
Интенсивности даны для поперечного наблюдения. При продольном наблюде-
нии интенсивность a-составляющих вдвое больше, чем при поперечном. Это связано
с тем, что при продольном наблюдении получается круговая поляризация, и нужно
учитывать поперечные колебания вдоль обеих осей х и у, а при поперечном наблю-
дении получается линейная поляризация, соответствующая колебанию вдоль оси,
перпендикулярной направлению наблюдения, и нужно учитывать лишь это колеба-
ние (например, при наблюдении вдоль оси х колебание вдоль оси у, см. рис. 14.3).
376
Глава 14. Явление Зеемана и магнитный резонанс
Таблица 14.1
Общие формулы для относительных интенсивностей
составляющих зеемановской картины расщепления
(для поперечного наблюдения)
Переходы	J -*J-\	J
а-составляющие т + 1 -> т	~(J + т+ 1)(J + т) 4	+ т+ 1)(J - т) 4
тг-составляющие т —> т	(J + m)(J - т)	т2
сг-составля ющие т - 1 —> т	j(J -т + 1)(J — т)	~(J -т + 1)(J + т)
Иначе говоря, в первом случае наблюдаются два осциллятора, колеблющиеся вдоль
осей х и у, а во втором случае — лишь один из этих осцилляторов.
Интенсивности симметрично расположенных в картине расщепления соста-
вляющих +т и — т (ср. с. 374) одинаковы, что сразу вытекает из формул
табл. 14.1: при замене т на -т формулы строки т —* т переходят сами в се-
бя (тг-составляющие), а формулы строки т + 1 —> т переходят в формулы строки
т-1 —* т и наоборот (a-составляющие). Поэтому картина расщепления симметрич-
на не только в отношении расположения составляющих, но и в отношении распреде-
ления интенсивностей. Значения относительных интенсивностей для случая, изобра-
женного на рис. 14 .3, указаны цифрами, расположенными над соответствующими
составляющими. Вопрос о распределении интенсивностей в различных случаях будет
разобран в § 14.4 при подробном рассмотрении типов зеемановских расщеплений.
Отметим, что полная интенсивность всех тг-составляющих равна полной интен-
сивности всех а-составляющих (обеих групп), что можно проверить, просуммировав
формулы табл. 14.1 по всем аначениям т от +J до -J. В частном случае про-
стого явления Зеемана интенсивность центральной тг-составляющей равна сумме
интенсивностей обеих а-составляющих (имеющих одинаковые интенсивности).
Мы рассмотрели картину зеемановского расщепления в слабом поле и выяс-
нили, что в общем случае получается сложное явление Зеемана, лишь в отдельных
частных случаях сводящееся к простому явлению Зеемана, при котором наблю-
даются триплеты. Первоначально считали нормальным случаем, в соответствии
с классической теорией явления Зеемана, данной Лоренцем, именно случай три-
плета, и говорили в этом случае о нормальном явлении Зеемана, а в случае более
сложной картины расщепления — об аномальном явлении Зеемана. Эта терминоло-
гия, которую иногда еще применяют, является устаревшей, и рационально называть
явление Зеемана в общем случае дх ф д2 сложным, а в частном случае д} = д2
простым, как и было сделано.
Классическая теория не дает объяснения сложного явления Зеемана, одна-
ко позволяет дать очень элементарное и весьма наглядное объяснение простого
явления Зеемана, с которым квантовая теория находится в соответствии. Это
объяснение особенно просто, если воспользоваться представлением о ларморовой
прецессии электронных орбит и связанных с ними орбитальных моментов в маг-
нитном поле (см. с. 59), и основывается на рассмотрении колебаний квазиупруго
связанного электрона41.
В классической электронной теории такие колебания получаются для точечного электрона в атоме,
положительный заряд которого равномерно заполняет некоторую сферу (модель атома Томсона); сила,
действующая на электрон, в этом случае пропорциональна его расстоянию от центра сферы.
§ 14.2. Общая картина зеемановского расщепления в слабом поле
377
Рис. 14.5. Разложение
колебаний электрона
Пусть имеется электрон, под действием квазиупругой силы колеблющийся
с частотой Fo в направлении, составляющем некоторый угол 0 с направлением маг-
нитного поля (рис. 14.5). Это линейное колебание можно
разложить на колебание вдоль направления поля и коле-
бание в плоскости, перпендикулярной направлению поля.
На колебание вдоль направления магнитного поля
это поле не действует, и частота колебаний vq остается
неизменной. Мы имеем линейный осциллятор, ориенти-
рованный по направлению поля и дающий максимальное
излучение в плоскости, перпендикулярной полю; излу-
чение в направлении поля отсутствует. Этому осцилля-
тору и соответствует, с квантовой точки зрения, переход
с Дт — 0 — тг-составляющая зеемановского триплета
с линейной поляризацией вдоль направления поля.
Линейное колебание, перпендикулярное полю (см. рис. 14.5), можно разложить
на два круговых колебания половинной амплитуды с противоположными направле-
ниями вращения5). Относительно координатной системы, вращающейся с лармо-
ровой частотой vl = ---- (см. (2.70)), они будут обладать прежней частотой i/n.
47гтес
Следовательно, для кругового колебания с направлением вращения, совпадающем
с направлением прецессии, получится (относительно неподвижной координатной
системы) частота vq 4- vl, а для колебания с противоположным направлением вра-
щения получится частота vq — v^. В результате получаются две частоты колебаний,
смещенные относительно первоначальной частоты i/0 на
= ±
еН
4тгтес
(14.23)
Круговым осцилляторам в плоскости ху с частотами vq ± соответствуют, с кван-
товой точки зрения, переходы Дт = ±1: a-составляющие зеемановского триплета,
поляризованные по кругу.
Энергии испускаемых или поглощаемых квантов получаются умножением со-
ответствующих частот и uq ± &L на постоянную h. Мы находим, учитывая, что
------= Дб (см. (2.46)), для этих энергий:
4тгтес
Eq = hVQ)
линейное колебание
по оси z
круговые колебания
в плоскости ху
Eq 4- ДЕ — hi/Q 4- -----— hvQ 4-
4тгтес
л	ehH
Eq — ДЕ — hvQ —---------— hi/Q —
4irmec
(14.24)
Получается в точности та же картина расщепления, что и, согласно (14.22),
при д = I. При этом поляризации определяются характером колебаний соответ-
ствующих осцилляторов, а интенсивности одинаковы для колебаний вдоль осей ж, у
5) Колебание х = a cos 2тгро^ У = 0 можно представить в виде
а	а	а	а
х = - cos 2iu/qI - cos 27п/о£, у = - sin 2тгро* - - sin
а	а
т. е. как наложение кругового колебания х — - cos у = - sin 2тгро1 (вращение от оси х к оси у)
а	а
и кругового колебания х = - cos 2тгро£, У = - - sin 2тгро* (вращение от оси у к оси х).
378
Глава 14. Явление Зеемана и магнитный резонанс
и z, что при поперечном наблюдении дает интенсивность тг-составляющей, равную
сумме интенсивностей a-составляющих, а при продольном наблюдении удвоенную
интенсивность a-составляющих (ср. с. 375).
Таким образом, на основе классических представлений полностью объясняется
простое явление Зеемана с нормальным расщеплением ДбЯ.
Отметим, что мы имеем совпадение частоты перехода между соседними подуров-
ня 1	w ръН
нями при нормальном расщеплении —— = —Мб# с частотой vL =--------прецессии
h h	h
орбитального магнитного момента д, = -Дб^ вокруг направления магнитного поля.
Соответствие получается и для расщеплений, отличных от нормального. Для произ-
7
вольного магнитного момента д = yhJ = — yfiJ = -gpbJ частота перехода между
7/
ДБ	дрьН
соседними подуровнями в магнитном поле •— = —-—, равная с учетом (2.46)
h h
урБН	уН	и	уН
—-— = — —— совпадает с частотой и = — = — —— прецессии этого момен-
7/Л	2тг	2тг	2тг
та, определяемой формулой (2.59). Это соответствие существенно при наглядной
трактовке магнитного резонанса (см. ниже, § 14.6, с. 396).
Сложное явление Зеемана для спектральных линий, получающееся при пере-
ходах между двумя уровнями с различными значениями ду т. е. уровнями, которым
соответствуют различные магнитные моменты (и, следовательно, согласно нагляд-
ным представлениям, различные угловые скорости прецессии), в принципе не может
быть объяснено классической теорией.
Все изложенное в данном параграфе относилось к явлению Зеемана для дипольных пере-
ходов. Для спектральных линий, получающихся при магнитных дипольных переходах, правила
отбора те же, что и для обычных электрических дипольных переходов (см. (4.157)), и картина
расщепления получается совершенно такая же. Единственная разница состоит в том, что
электрический и магнитный векторы излучаемой волны меняются местами; это при попе-
речном наблюдении приводит к тому, что плоскости поляризации для тг- и а-составляющих
меняются местами. Для спектральных линий, получающихся при квадрупольных переходах,
для т имеют место правила отбора (4.159), т.е. т может изменяться не только на 0 и ±1,
но и на ±2. Картина расщепления усложняется; при этом более сложны и свойства поляриза-
ции составляющих. Явление Зеемана такого типа наблюдается для ряда запрещенных линий,
в частности, для линии 5 577 А в спектре полярных сияний, соответствующей квадрупольному
переходу ‘So— *D2 для О I (см. с. 319).
§ 14.3.	Множители д в случае слабого поля
Как мы видели, величина зеемановского расщепления зависит от значения
множителя д, а разность множителей д для комбинирующих уровней определяет
расстояние составляющих при зеемановском расщеплении спектральных линий.
Значение д для заданного уровня существенным образом зависит от типа связи.
В наиболее важном случае нормальной связи значение множителя д для уровня
с заданным значением квантовых чисел J, S, L определяется известной формулой
Ланде6* [17]
, J(J+1) + S(S + 1)-L(Z+1)
3~ +	2J(J+1)
Эта формула в частном случае чисто орбитального момента (S = О, J = L) дает
д = 1, а в частном случае чисто спинового момента (L = О, J = S) — д = 2,
Откуда и часто применяемое название множителя д — множитель Ландё.
§ 14.3. Множители д в случае слабого поля
379
в соответствии с основными формулами (14.3) и (14.4), представляющими частный
случай общей формулы (14.8). В общем случае, когда и L и S отличны от нуля,
формула (14.25) приводит к различным значениям которые, однако, обнаруживают
вполне определенные закономерности. При заданных L и S, т. е. для мультиплетного
терма, разным значениям J соответствуют, как правило, и разные значения д,
В табл. 14.2 приведены значения множителя д для мультиплетностей от 2
до 7 (S от Уг до 3) и для значений L от 0 до 4 (т. е. для S-, Р-, D-, F- и (7-термов).
Как обычно, значения д даны для каждой мультиплетности в отдельности. В табли-
це приведены значения д в виде обыкновенных и в виде десятичных дробей. Мы
видим, что д принимает как значения между 1 и 2, так и значения, меньшие 1 и даже
отрицательные, и значения, большие 2. При L > S д возрастает с увеличением J,
при L < S — убывает с увеличением J, а при L — S (что возможно при целом J)
остается постоянным и равно 3/г. При заданных L и S при максимальном возмож-
ном J всегда д > 1; для S-терма оно равно 2, а затем убывает с увеличением £,
Таблица 14.2
Множители д при нормальной схеме связи
L	Терм	J='h		Уг		Уг		Уг		Уг
0 1 2 3 4	S Р D F G	2 2,000 2/з 0,667		Уз 1,333 Уз 0,800		Уз 1,200 У? 0,857		Уг 1,143 ’А 0,889		Дублеты s= '/г
										ю/9 1,111
L	Терм	J = 1		2		3		4		5
0 1 2 3 4	S Р D F G	2 2,000 3/2 1,500 ‘/2 0,500		Уг 1,500 ’А 1,167 Уз 0,667		Уз 1,333 |3/|2 1,083 3/4 0,750		Триплеты 5 = 1		
								¥4 1,250 2’/20 1,050		Уз 1,200
L	Терм	}=Уг	%		¥2		Уг	’/2	"/2	
0 1 2 3 4	S Р D F G	8/з 2,667 0 0,000	2 2,000 26/15 1,733 ,8/15 1,200 2/5 0,400		% 1,600 48/35 1,371 36/з5 1,029 4/7 0,571		юд 1,429 »/« 1,238 62/бЗ 0,984	Квартеты 5=¥г		
								12/, 1,333 "«А» 1,172	'Ун 1,273	
380
Глава 14. Явление Зеемана и магнитный резонанс
Продолжение таблицы 14.2
L	Терм	J = 1	2		3		4		5		6	
0 1 2 3 4	S Р D F G	% 2,500 % 1,500 0 0,000	• 2 2,000 п/б 1,833 9/б 1,500 % 1,000 ‘/з 0,333		5/з 1,667 18/|2 1,500 15/|2 1,250 "/12 0,917		6/4 1,500 27го 1,350 23/20 1,150		Квинтеты S = 2			
									75 1,400 38/зо 1,267		8/6 1,333	
L	Терм	J='l2	3/2	5/2		72		’/2		п/2		13/2
0 1 2 3 4	S Р D F G	ю/з 3,333 -2/з -0,667	,2/5 2,400 28/|5 1,867 16/l5 1,067 0 0,000	2 2,000 66/35 1,886 5%5 1,657 ^35 1,314 30/з5 0,857		12/7 1,714 10%з 1,587 88/бЗ 1,397 72/бЗ 1,143		14/, 1,556 '42/99 1,434 126/,, 1,278		Секстеты		
										|6/11 1,455 ’7143 1,343		|8/|3 1,385
L	Терм	J = 1	2	3		4		5		6		7
0 1 2 3 4	S Р D F G	6/2 3,000 3Л 1,500 -'/2 -0,500	7з 2,333 ,2/б 2,000 % 1,500 % 0,833	2 2,000 23/12 1,917 21/12 1,750 18/12 1,500 14/12 1,167		% 1,750 33/20 1,650 ЗО/2О 1,500 26/2О 1,300		% 1,600 45/зо 1,500 4|/зо 1,367		Септеты S = 3		
										1,500 5’/42 1,405		ю/7 1,429
стремясь к значению g = 1. При минимальном возможном J для L> S всегда g < 1
и растет с увеличением L. также стремясь к значению g = 1, а для L < S оно боль-
ше 2 и возрастает с увеличением L (достигая наибольшего значения при L = S - 1
или при L = S - 1/г).
Для дублетов, в частности для случая одного электрона, формула (14.25) при-
нимает очень простой вид. В этом случае S = 72, J = L± и мы имеем
1
1	Ь+1	J+7
при/ = Ь+- д=---г = ——,
1 Ь	J+ 2
при/ = £--	.
L+2
(14.26)
§ 14.3. Множители д в случае слабого поля
381
Отметим, что сумма этих значений равна 2. Для терма 2Р расщепление уров-
ня 2Рз/2 вдвое больше расщепления уровня 2Р\/2, затем разница значений д, рав-
1
ная-----р убывает с увеличением £, стремясь к нулю при L —* оо.
Ь + -
Формулу (14.25) для множителя д можно вывести из наглядных соображе-
ний о прецессии магнитных моментов. Полный магнитный момент //, получа-
ющийся в результате сложения магнитных моментов и р,2 (см. (2.78)), где
Д! = 71Л71 =	И р2 = 72^2 = -^2Дб^2 (ср. с. 378), будет прецесси-
ровать вокруг направления полного механического момента J = J\ 4- J2, давая
проекцию (см. рис. 2.7, с. 61)
Hj = Н\ cos(Ji, J)+/i2cos(J2, J) = -g\p>bJ\ cos(Ji,/)-^2/£бЛсо8(72, J). (14.27)
Согласно соотношениям J2 = (J - J\)2 и j\ = (J - J2)2, мы имеем
(т П j2 + ji J2	n J2 + J22-J2
cos (J1, J) =---—------, cos (J2, J) =-----—------.
ZJ[J	Z.J2J
Подстановка (14.28) в (14.27) дает
= -fiKJ
’ J2 + J2i-J22
9'	2J2
(14.29)

Множитель g равен, если заменить J2, J2 и J2 через J(J 4-1), J\(J\ -I-1), /2(Л 4- 1)
(см. c. 46)
7(/+1) + ад + 1)-72(Л + 1)	/(J+O + J^ + lJ-J^ + l)
9=51--------2ЛТЙ)-----------+®----------S(7Tij--------- (I4M)
Вектор
fij = -gp-bJ,	(14.31)
представляющий усредненное значение магнитного момента атома, ориентируется
во внешнем магнитном поле, давая проекцию Hz = (hj)z = -gp>bJz — ~9Нь^>
при подстановке которой в (14.1) мы получаем (14.8) со значением определяемым
общей формулой (14.31). В частном случае J\ = L, J2 = S и соответственно д\ = 1,
д2 = 2 формула (14.31) сводится к формуле (14.25).
Можно получить формулу (14.25) (так же, как и общую формулу (14.30)) чисто кван-
товомеханически. Для этого надо исходить из оператора проекции pz полного момента
Д = hl +	= -Дб-Б - 2gbS [ср. (2.48) и (2.55)]
Hz = Hlz + Hsz —	4- 25г) = ~Мб(Л + Sz}	(14.32)
и вычислить среднее значение этого оператора в состоянии с заданными L,S,Jnm (см. (14.13)
и (14.14)):
Hz = ~НБ tyaJm(jz 4" Sz^tyaJm	~ ~~НБ^ ~ НБ tyaJmSztyaJm dx.	(14.33)
Среднее значение оператора Sz пропорционально т и равно, как показывает вычисле-
ние (см., например, [131], с. 538),
? - ^1Л</+1) + 5(5+1)-£(£+1)	.а _
Sz 2	’	<14’34)
382
Глава 14. Явление Зеемана и магнитный резонанс
Подставляя этот результат в (14.33) и записывая рг = рг, согласно (14.15), в виде
мы получаем
J(J + 1) + S(S + 1) - L(L +1)
Мг = -Цьт - цъ----------2J(J+1)-----------т = ~9(*ьт’	(14.35)
откуда и следует (14.25). Мы имеем конкретный пример определения д (и, следовательно,
гиромагнитного отношения 7) в формуле (14.15).
Для других типов связи получаются иные формулы для множителей д, выра-
жающиеся через значения множителей д для складываемых моментов и зависящие
от порядка их сложения. В частности, при связи (j, j) для случая двух электронов,
полагая в (14.30) J\ = j\ и Ji — ji получаем формулу
J(J + 1)+JiO'i + 1) — J2V2 + 1)	+ O+J2O2+ 1)_У10’1 + 0 /1Л
»=9'---------------------------+S!-----------upTi)------------’ (l4 36)
симметричную относительно квантовых чисел j\ и j2, определяющих моменты
Jj и j2 (сумма которых дает момент J =	+ j2). Множители д\ и gi харак-
теризуют исходные состояния электронов и зависят от квантовых чисел l\9 j\
и I2, ji = 82 = для этих состояний. Значения и gi даются формула-
ми (14.26) (в которых надо положить L = l\, J = j\ и L = li, J = ji соответственно)
и могут быть взяты из табл. 14.2 (для дублетов). В табл. 14.3 приведены значе-
ния д для связи (jjj) для двухэлектронных конфигураций, образованных з-, р-
и d-электронами. Для данной конфигурации в строке, соответствующей определен-
ным значениям ji (ji = l\ ± 1/2» ji =	± У2), даны значения g при различных
возможных значениях J (как в табл. 14.2 в виде обыкновенных и десятичных дробей).
При переходе от одного типа связи к другому множители д отдельных уровней
постепенно изменяются, однако можно установить определенное правило сумм.
Согласно этому правилу, независимо от типа связи сохраняется сумма значений д
для всех уровней рассматриваемой конфигурации с заданным значением J [237, 13]:
У^^а(7) = const (J задано).	(14.37)
а
Например, для конфигурации dp (см. §9.1, с. 244), дающей четыре уровня
с J = 2, по три уровня с/ = 3и7=1ипо одному уровню с J = 4 и J — 0,
для каждого из этих типов уровней выполняется правило (14.37), как для нормальной
связи и для связи так и для всех промежуточных случаев. В частности,
для единственного уровня с J = 4, который в случае нормальной связи является
уровнем 3Р4, а в случае связи (j,j) — уровнем (5/г, 3/г)4, значение д сохраняется
и равно 1,250.
В случае конфигурации р2 сохраняется значение д для единственного уровня
с J = 1 и сумма значений д для двух уровней с J — 2. Для уровня с J = 1 (3Р\ в случае
нормальной связи и (3/2> 1/г)| в случае связи (j, j)) д = 1,500. Для уровней с J = 2
имеем в случае нормальной связи g^Pi) = 1,500, g([Pi) = 1,000 и в случае связи (j, j)
<?[(3/2, ’/2)2] = 1,167, <?[(3/2, 3/2)г] = 1,333, т.е. в обоих случаях сумма равна 2,500.
Для наиболее простых случаев, например для случая конфигурации р2, можно
полностью рассчитать изменение множителей д отдельных уровней при переходе
от одного типа связи к другому. Наблюденные значения множителей д могут служить
критерием (наряду с расположением уровней) близости связи к предельным случаям.
§ 14.4. Типы зеемановских расщеплений спектральных линий
383
Таблица 14.3
Множители д при связи (j,j) для двухэлектронных конфигураций
Конфигурация	(j\,h)	J = 1	2	3	4	5
S3	('Л,'/2)	2 2,000				
Р»	(‘/2, ’/2) (3/2, 41)	Уз 1,333 7А 1,167	41 1,500			
ds	(%, '/2) (5/2, 4i)	4i 0,500	»/10 1,100 |6/|5 1,067	Уз 1,333		
РР	(4i,4i) (%, 4i) (4i, 4i)	2/з 0,667 3/2 1,500 4/з 1,333	7/б 1,167 Уз 1,333	Уз 1,333		
dp	(4i, 4i) (4i,4i) (4i, 4i) (4i,4i)	% 0,833 'У15 1,067 "/ю 1,100	23/зо 0,767 |6/|5 1,067 Я/45 1,289 "»/90 1,211	'У|5 1,067 10/, 1,111 223/180 1,239	% 1,250	
dd	(4i,4i) (4i, 4i) (4i,4i)	Уз 0,800 41 1,500 Уз 1,200	Уз 0,800 Уб 1,167 Уз 1,200	Уз 0,800 13/|2 1,088 Уз 1,200	21/2О 1,050 Уз 1,200	Уз 1,200
При интерпретации сложных спектров можно применять правило сумм (14.37)
для проверки правильности этой интерпретации. Если отдельным уровням правиль-
но приписаны определенные квантовые числа, то для уровней данной конфигурации
с заданным значением J правило сумм должно выполняться.
§ 14.4. Ъшы зеемановских расщеплений спектральных линий
Рассмотрим теперь более подробно типы зеемановских расщеплений. Как мы
уже указывали, вид картины расщепления сильно зависит от разности д\ - дг
и от значений J\ и Л- Значения J\ и J2 при этом определяют число составляющих
и распределение интенсивностей, а разность д\ - д2 определяет расстояния между
составляющими в каждой группе.
Положение отдельных составляющих в картине расщепления может быть
найдено по формулам (14.21); при этом удобно для нахождения картины рас-
щепления пользоваться следующей схемой, которую мы приводим для частно-
го случая комбинации уровней 7Рз и 7С?2 при нормальной связи. Для первого
384
Глава 14. Явление Зеемана и магнитный резонанс
из этих уровней д\ = д(^з) = 1,500, для второго — gi =	= % = 0,833
(значения д см. в табл. 14.2, с. 379).
т -	3	2 t 0 -I -2	-3
Т/Гз(я°$) ух ,<Г\	гТ (14.38)
Ч'Л4А!-А4Л4/
Здесь даны для обоих уровней расщепления в единицах нормального рас-
щепления рьН, равные тп\д\ и тг^2 (см. 14.8)). Сплошными линиями указаны
переходы с Дт = 0, т. е. тг-составляющие, пунктирными — переходы с Дт = ±1,
т. е. a-составляющие. Положения отдельных составляющих относительно первона-
чальной линии определяются разностями т\д\ -т2^2- Для тг-составляющих (Дт = 0)
6	10	8 3	5	4
имеем - —т ~ > т-- = 7,0-0 = 0ит.д. В результате получаем: 8/б» 76, 0,
2	6	6 2	6	6
-4/б, -8/б. Для a-составляющих аналогично находим 17/б, 13/б, 9/б, 5/б, ’/б (при Дт =
mj — т2 — +1) и -	-5/б, -9/б, -13/б, ~,7/б (при Дт = mj - т2 = -1). Картина
получается, как подчеркивалось в § 14.2 (с. 374), симметричной относительно по-
ложения первоначальной линии. Постоянное расстояние д\ - д2 между соседними
3	5	4	2
составляющими в каждой группе в данном случае равно-- — - — -.
2	6	6	3
Полученный результат записывают следующим образом, указывая лишь поло-
вину составляющих
(°) И) (8) I S 9 13 Я	(1439)
6
где в скобки взяты тг-составляющие, отсутствующие при продольном наблюдении.
Знаменатель в подобной формуле (иногда называемый знаменателем Рунге) есть наи-
меньшее общее кратное знаменателей множителей д\ и д2 (в данном случае равное 6).
В десятичных дробях тот же результат может быть записан в виде
(0) (0,667) (1,333) 0,167 0,833 1,500 2,167 2,833.	(14.40)
Относительные интенсивности составляющих могут быть определены по фор-
мулам табл. 14.1 (с. 375). Численные данные для относительных интенсивностей
тг-составляющих и сг-составляющих (при поперечном наблюдении) для перехо-
дов J—>7и7->7-1с целыми значениями J от 1 до 4 и с полуцелыми значениями J
от ’/г до 7/г приведены в табл. 14.4. Для удобства значения интенсивностей, даваемые
формулами табл. 14.1, умножены на 2. Для переходов J —> J и J —> J - 1 получа-
ется различная зависимость интенсивности от т. Для переходов J —> J наиболее
интенсивны тг-составляющие с наибольшими, а а-составляющие — с наименьшими
значениями |т|. Для переходов J J - 1 наиболее интенсивны тг-составляющие
с наименьшими значениями |т|, а для a-составляющих в группе т 4- 1 —> m
интенсивность возрастает при росте т, и в группе т - 1 —► т — при убыли т.
Согласно табл. 14.4, относительные интенсивности в рассматриваемом случае
7Гз - 7(72 (переход J J - 1, где J целое; J — 3, J - 1 = 2) для тг-составляющих
равны 10, 16, 18, 16, 10, а для ^-составляющих 1, 3, 6, 10, 15. Наиболее интенсивна
тг-составляющая 0—0, для которой смещение равно 0, и а-составляющие 3—2
17
и (-3)—(-2), для которых смещение равно ±— = ±2,833. Эти составляющие
6
отмечены в (14.39) и (14.40), как принято, жирным шрифтом.
§ 14.4. Типы зеемановских расщеплений спектральных линий
385
Таблица 14.4
Относительные интенсивности составляющих зеемановской картины расщепления
для конкретных случаев (поперечное наблюдение)
Переходы J —> J (целые значения J и т)
J J	Переходы т —> т (тг-составляющие)								
	т =	4	3	2	1	0	-1	—2	-3	—4
0-0					0				
1-1				2	0	2			
2—2			8	2	0	2	8		
3-3		18	8	2	0	2	8	18	
4-4	32	18	8	2	0	2	8	18	32
		Переходы т -ь 1 			-> т (а-составляющие)				
J —> J	т + 1 =	4	3	2		1	0	-1	—2	-3
	т =	3	2	1		0	-1	-2	-3	—4
1-1					1	1			
2-2			2		3	3	2		
3-3		3	5		6	6	5	6	
4-4	4	7	9		10	10	9	7	4
Переходы J —► J (полуцелые значения J и т)
J J	Переходы т —> т (тг-составляющие)							
	m =	7/2	5/2	3/2	‘/2	-'/2	-3/2	-’/2	-72
Чг-'h				0,5	0,5			
3/2-3/2			4,5	0,5	0,5	4,5		
5/2-5/2		12,5	4,5	0,5	0,5	4,5	12,5	
’/2-’/2	24,5	12,5	4,5	0,5	0,5	4,5	12,5	24,5
		Переходы т + 1 —► т			(а -составляющие)			
J —> J	т + 1 =	7/2	%	3/2		'/2	-'/2	-3/2	-5/2
	т =	%	3/2	‘/2		-'/2	-3/2	-5/2	-7г
'/2-'/2					0,5			
3/2-3/2			1,5		2	1,5		
5/2—5/2		2,5	4		4,5	4	2,5	
72-72	3,5	6	7,5		8	7,5	6	3,5
Переходы J —> J — 1 (целые значения J и т)
J -+ J - 1	Переходы т —> т (тг-составляющие)							
	т —	3	2	1	0	-1	—2	-3
1-0					2			
2-1				6	8	6		
3-2			10	16	18	16	10	
4-3		14	24	30	32	30	24	14
			Переходы т -ь 1 —>		т (^-составляющие)			
J-»J-1	т + 1 =	4	3	2	1	0	-1	—2
	т —	3	2	1	0	-1	—2	-3
1-0					1			
2-1				6	3	1		
3-2			15	10	6	3	1	
4-3		28	21	15	10	6	3	1
13 Зак. 103
386
Глава 14. Явление Зеемана и магнитный резонанс
Продолжение таблицы 14.4
Переходы J —> J - 1 (полуцелые значения J и т)
J —► J - 1	Переходы т —> т (тг-составляющие)						
	т =	72	72	'/2	-72	-72	-72
%-’/2				4	4		
5/2-%			8	12	12	8	
7/2-5/2		12	20	24	24	20	12
		Переходы т + 1		—> т	(а-составляющие)		
J —► J - 1	т 4- 1 =	72	72	72	72	-72	-72
	т —	72	72	72	-72	-72	-72
72-’/2				3	1		
72-72			10	6	3	1	
72-72		21	15	10	6	3	1
Картина расщепления для линии 7F3— 7(?2 изображена на рис. 14.6. В данном
случае Дд = #(7^з) ~ ^(7^г) = 1 >500 - 0,833 = 0,667. Длины черточек пропорци-
ональны интенсивностям, причем для тг-составляющих черточки отложены вверх,
а для а-составляющих — вниз. Как видно из рисунка, наибольшей интенсивностью
обладают крайние a-составляющие и центральная тг-составляющая.
По распределению интен- ,р_,с,	Д9=0667	<,=<>,» = 1.500 ,=(’с2>=одо
сивностей картины расщепле-
ния можно разделить на три	i	।
типа, которые иллюстрируют-	.    .......J--J-----------Ц----L____j_____
ся рис. 14.7.	I ’	’I
Первый тип распределе-
ния интенсивностей получает- Рис. 14.6. Картина зеемановского расщепления
ся для переходов J —> J — 1	для линии 7F3— 7G2
при gj < gj-i (рис. 14.7, а).
Из тг-составляющих наиболее интенсивны центральные, соответствующие мини-
мальным |тп|, а из а-составляющих — внутренние, соответствующие наиболь-
шим \т\ (см. табл. 14.1). Таким образом, интенсивность тг-составляющих спадает
от середины группы к краям и интенсивность а-составляющих также спадает к краям
картины расщепления — получается оттенение наружу.
7G5-7f4 Ьд--0,133
Ft-Gs a?=0,133
5FS-SG5 Д? = о,133
f7(’Gs) = 1,367 g(7F4) = 1,500
g('F6) = 1,500 p(Gs) = 1,367
. I I gfa) = 1,400 gCG,) = 1,267
I I L.l L... 	„ ..
Рис. 14.7. Три типа зеемановского расщепления:
a — J J - gj < б — J-*J-\tgj> gj-X\в — J -> J
Второй тип рас-
пределения интенсив-
ностей получается так-
же для переходов J —>
J - 1, но при gj >
gj-i (рис. 14.7, а так-
же рИС. 14.6). ИЗ 7Г-СО-
ставляющих по-преж-
нему наиболее интен-
сивны центральные,
однако из а-составля-
ющих наиболее интен-
сивны внешние, так
как они теперь со-
ответствуют наиболь-
6
в
§ 14.4. Типы зеемановских расщеплений спектральных линий
387
шим |т|. Таким образом, интенсивность яг-составляющих спадает от середины
группы к краям, а интенсивность a-составляющих спадает от краев картины рас-
щепления к ее середине — получается оттенение внутрь.
Третий тип распределения интенсивностей получается для переходов J —* J
(рис. 14.7, в). Из яг-составляющих наиболее интенсивны крайние, а из a-составляю-
щих — составляющие, расположенные в середине каждой группы и соответствующие
наименьшим |т|. Таким образом, интенсивность тг-составляющих возрастает от се-
редины к краям, а интенсивность а-составляющих спадает для каждой группы от ее
середины в обе стороны.
Приведенные на рис. 14.7 характерные примеры трех типов расщепления со-
ответствуют переходам 7Gs~ 7Рд, 7F6—7G5 и 5F5— Ъ5, для которых |Д<?| = 0,133.
При возрастании разности |Дд| = |gi - ^2| увеличиваются интервалы между соста-
вляющими в каждой группе и внутренние составляющие двух групп а-составляющих
постепенно сближаются. Начинают перекрываться внутренние а-составляющие
и внешние тг-составляющие;
примером является пере-
ход 7Fy— 7G2, рассмотренный
выше (см. рис. 14.6) и от-
носящийся ко второму ти-
пу распределения интенсив-
ностей. При очень больших
разностях |<?1 перекрыва-
ются и a-составляющие двух
групп (рис. 14.8, а); при этом
возможен случай точного
совпадения а-составляющих
обеих групп (рис. 14.8,0.
а <	<
5Н3 - 5D2 Д<7 = -1,000	9( Н3) = 0,500 д( Ъ2) = 1,500
Рис. 14.8. Картина зеемановского расщепления
при больших разностях |#i -
а — перекрывание a-составляющих обеих групп;
б — точное совпадение a-составляющих обеих групп
В основу классификации типов расщепления обычно кладется наличие трех описанных
типов распределения интенсивностей. По Баку [17] эти типы расщепления обозначаются как
типы I, II и III.
тип I	тип II	тип III
J —> J — 1, gj<gj-\ /—►/—!, gj>gj-\	J —> J
К типу IV Бак относит предельные случаи зеемановских триплетов.
Несколько более подробную классификацию применяет Гаррисон [240]; он обозначает
типы I, II, III как типы 1, 2, 3 для случая четных мультиплетностей (J полуцелое) и как ти-
пы 4, 5, 6 для случая нечетных мультиплетностей (J целое). Предельные случаи зеемановского
триплета обозначаются как тип 7a при J - 1 = 0 (переход 1 -* 0) и как тип 76 при д{ = д2.
По экспериментально наблюденной картине расщепления можно сделать вы-
воды о значениях J и д для комбинирующих уровней. Необходимо различать
два случая: случай полностью разрешенной картины расщепления, когда сосед-
ние составляющие отделены друг от друга, и случай неполного разрешения, когда
соседние составляющие сливаются, что часто наблюдается при малых значениях раз-
ности |Д^| — |^1 —д21. В обоих случаях по общему характеру распределения интенсив-
ностей обычно можно сразу определить, имеют ли комбинирующие уровни одинако-
вые J или разные, и в случае разных J установить, какой из уровней имеет большее д.
При полностью разрешенной картине расщепления легко находятся значения J и д.
Возможность нахождения, на основе анализа картины расщепления, значений J
и д для отдельных уровней энергии определяет очень важное значение изучения
явления Зеемана для интерпретации сложных атомных спектров. Если из теорети-
ческих соображений или из сравнения с аналогичными спектрами известно, уровни
13*
388
Глава 14. Явление Зеемана и магнитный резонанс
каких конфигураций следует ожидать для спектра исследуемого атома или иона, то
по набору значений J и д можно решить, какой тип связи имеет место, и найти,
если связь близка к нормальной, квантовые числа L и S.
Отметим, что при нахождении значений L и S обычно применяют не таблицы типа
табл. 14.2, а таблицы, в которых значения множителей д расположены в порядке их возра-
стания и указан уровень, дающий это значение д. Подобные таблицы составлены отдельно
для уровней термов четных и нечетных мультиплетностей, вплоть до значений мультиплет-
ности и = 10 и 11 (см. [15], с. 205).
Определение значений Jug при полностью разрешенной картине расщепления произ-
водится следующим образом.
Число составляющих сразу дает значение J. Дяя переходов J —> J число а-составляющих
в каждой группе равно 2J, а число тг-составляющих равно 2J + 1 для полуцелых J и 2J
для целых J (с учетом запрета перехода т = 0 -* т = 0, см. табл. 14.2 и 14.4). Для пере-
ходов J —* J — 1 как число a-составляющих в каждой группе, так и число тг-составляющих
равно 2J - 1 (ср. схему (14.38), соответствующую J = 3, 2J - 1 = 5).
Значения множителей и д2 определяются на основе измерений расстояния соседних
составляющих е = |gi — ^2| и расстояния 2/ между наиболее интенсивными ^-составляющими
обеих групп. Для этих величин мы имеем соотношения:
переход типа J —* J — 1
переход типа J —* J — 1
9\ <92
9i >92
переход типа J —* J
gt=f + (J- 1)е,
9i =f-(J-l)e,
е
9i = f + j
9i = f + Je, '
g2 = f-Je, ,
е
92 ~~ f ~ 2" ,
(14.41)
Действительно, для переходов J —» J — 1 наиболее интенсивные а-составляющие соот-
ветствуют |т|, равному J - 1. Их положение, согласно (14.21), будет (в единицах рьН):
при т = J — 1
при т = -J -I- 1
(переход m + 1 = J —>m = J- 1)
(переход т — 1 = — J —> т = —J + 1)
(9\ -92)(J~ 1) Ч-5П, 1
~(9\ ~92)(J - 1) ~9\, J
(14.42)
а разность этих положений равна
2[<7i+Gi-^)(J-1)] = 2/.	(14.43)
Отсюда f = gt -e(J- 1) при < д2, когда д2 -	= е и f = gt + e(J - 1) при д{ > д2, когда
д{ - д2 = е и мы получаем окончательный результат (14.41) для переходов J —> J - 1.
Для переходов J —> J наиболее интенсивные a-составляющие соответствуют переходам
с минимальным |т|, а именно (см. табл. 14.4):
переходам ]/2 —> - у2 и - у2 —» ’/2	при полуцелых J,
переходам 1—>0,0—>—1 и — 1—> 0,0—>1 при целых J.
В первом случае мы, согласно (14.21), находим положения составляющих:
1 / 1 1\ 1 ч 1
при т = - - I переход 1 = --> m =	1	~(9\+92),
1 Г , 1 п >, >	"444)
при ш — — I переход m - 1 = ---* m =- 1 --(91+92)- I
Разность этих положений равна
£П+32 = 2/.	(14.45)
Отсюда, считая д\ > д2 находим
9\ + 92 = (9\ -92) + 2^ = е + 2д2 = 2f, 9\ + д2 = 2д{ - (д} - д2) = 2g}-e = 2f (14.46)
и получаем результат (14.41) для переходов J —> J. Тот же результат получается и во втором
случае, если брать расстояние между составляющими 1 —> 0 (положение д^) и 0 —> 1
(положение -д2) или расстояние между составляющими 0 —> -1 (положение д2) и -1 -> 0
(положение -д}) или же, наконец, расстояние между центрами пар 1—>0, 0—>-1и0-*1,
-1 —► 0 (см. рис. 14.9).
§ 14.5. Явление Зеемана в сильных и в промежуточных полях
389
Примером может служить картина расщепления, изображенная на рис. 14.6. Предполо-
жим, что значения J и д нам неизвестны. Мы имеем распределение интенсивностей, при
котором наиболее интенсивны цен-
тральная 7Г-составляющая и крайние
a-составляющие обеих групп, т. е. слу-
чай J —> J - 1,	> д2. Число со-
ставляющих в каждой группе равно
5 = 2 J - 1, откуда = 3, J2 — J - 1 = 2.
Расстояние соседних составляющих
равно е = 0,667, а расстояние наи-
более интенсивных а-составляющих
2/ = 5,666. Отсюда, согласно (14.41)
(строка вторая),
д{ = 2,833- 2-0,667 = 1,500,
Рис. 14.9. Расстояние между составляющими
картины расщепления для переходов J —> J
при целом J
д2 = 2,833 - 3 • 0,667 = 0,833.
При неполностью разрешенной картине расщепления уже не удается однозначно опре-
делить все величины J(, J2, д{, д2. Однако и в этом случае можно сделать ряд заключений
о свойствах комбинирующих уровней. Помимо отнесения перехода по характеру распреде-
ления интенсивностей к одному из трех основных типов, можно измерить расстояние 2f'a
между центрами тяжести двух неразрешенных максимумов, которые образуют две группы
а-составляющих. Для перехода типа J —> J группа яг-составляющих дает два неразрешенных
максимума вследствие того, что при минимальных значениях |тп| интенсивность минимальна
и образуется провал; расстояние 2Д между центрами тяжести этих максимумов дает второй
параметр, характеризующий данный переход, что позволяет при известном J определить
значения д{ и д2 [238].
§ 14.5. Явление Зеемана в сильных и в промежуточных полях
В предыдущих параграфах мы подробно рассмотрели явление Зеемана в сла-
бых полях, когда величина зеемановского расщепления много меньше расстояния
между соседними уровнями энергии (см. (14.9)). Разберем теперь случай сильного
поля, когда, наоборот, величина зеемановского расщепления много больше этого
расстояния (см. (14.10)).
Для интересующих нас в данной главе электронных магнитных моментов ато-
ма, имеющих порядок величины /хБ, для которых и были выписаны условия (14.9)
и (14.10), наиболее важен случай, когда расстояние соседних уровней определяет-
ся мультиплетной структурой. Иначе говоря, наиболее важен случай нормальной
связи, когда имеются близкие уровни, образующие мультиплетные термы с муль-
типлетным расщеплением порядка <(L, 5), где C(L, 5) — фактор мультиплетного
расщепления (см. § 9.5, особенно с. 262). При расстоянии между соседними уровнями
порядка ((£, S) условия (14.9) и (14.10) принимают вид:
слабое поле	/гБЯ <С <(£, 5),	(14.47)
сильное поле	/хБЯ > £(L, 5).	(14.48)
В последнем случае уже нельзя говорить о независимом расщеплении каждого
уровня данного мультиплетного терма — получается картина расщепления, общая
для всех уровней. В результате в очень сильном поле наблюдается вместо сложного
явления Зеемана для каждой линии мультиплета зеемановский триплет для всего
мультиплета в целом с нормальным расщеплением /хБЯ. Это явление, впервые
обнаруженное Пашеном и Баком в 1912 г. [174, 16], получило название явления
Пашена—Бака. Оно имеет место в достаточно сильных магнитных полях для легких
390
Глава 14. Явление Зеемана и магнитный резонанс
атомов, у которых фактор мультиплетного расщепления £ мал и может выполняться
условие (14.48).
Явление Пашена—Бака легко объясняется на основе наглядных представлений
о прецессии магнитных моментов; получаемые результаты совпадают с результатами
строгой квантовомеханической теории.
Физически условие (14.48) означает, что дополнительные энергии -pLH
и ~p>sH орбитального и спинового магнитных моментов в магнитном поле, имею-
щие порядок р^Н, много больше энергии спин-орбитального взаимодействия
A(LS) = S)(LS) (см. (9.35)).
Согласно наглядным представлениям, угловые скорости прецессии
=	=	(14-49)
Мр	Мр '
(см. (2.59), (2.45) и (2.54)) орбитального и спинового моментов L и S вокруг
направления поля становятся гораздо больше угловой скорости их совместной
прецессии вокруг направления полного момента J (ср. рис. 2.8, в, с. 62, Jj = L,
J2 — S). В результате магнитное поле разрывает связь (L, S) и каждый из век-
торов L и S прецессирует вокруг направления магнитного поля независимым
образом, давая квантованные про-
екции ть и ms на это напра-
вление. Таким образом, в то вре-
мя как в слабом поле вокруг его
направления прецессирует полный
момент J (рис. 14.10, а; угловая
скорость прецессии Wj = уН =
Pj
--------vH много меньше угло-
м*пол">
вой скорости прецессии Z и S
вокруг J), в сильном поле во-
круг этого направления прецесси-
руют моменты L и S в отдельности
(рис. 14.10, б). В последнем случае
квантовое число J вообще теряет
свой смысл —- полный момент ато-
ма J не сохраняется, состояние си-
стемы характеризуется квантовыми
числами L, mL и S, ms.
Для дополнительной энергии в магнитном поле для L и для S в отдельности
справедливы формулы (14.3) и (14.4), которые можно записать в виде
для L ^EmL=fibHmL1	(14.50)
для S AEms = 2рьНт3.	(14.51)
Полная дополнительная энергия в магнитном поле равна
4- AEms = рьН(ть 4- 2ms).	(14.52)
Так как mL всегда целое и 2ms также целое (даже при полуцелом ms), то получаются
подуровни, расстояния между которыми являются целыми кратными нормального
расщепления р^Н.
§ 14.5. Явление Зеемана в сильных и в промежуточных полях
391
Формула (14.52) непосредственно получается квантовомеханически, если исходить из ви-
да оператора дополнительной энергии в магнитном поле (см. (14.11) и (14.32)). Когда
спин-орбитальное взаимодействие A(ZS) можно считать малым по сравнению с опера-
тором V = ръН(Ь2 4- 2S2) то проекции L и S на направление поля нужно квантовать
в отдельности, собственное значение оператора Lz равно mL, собственное значение операто-
ра Sz равно т$, а среднее значение оператора V в состоянии с заданными L, mL и 5, ms
совпадает с его собственным значением и равно (ср. (14.12)-(14.15))
V ~ ^aLmiSrnsPbH faz 4" ^aLmiSmg ~
= рБН J iplLmLSms(mL^2ms)ipaLmLsmsdx^ pBH(mL + 2ms).
(14.53)
Для квантовых чисел и ms для обычного дипольного излучения справедливы
правила отбора
Дть = 0,±1	(14.54)
и
Ams=0.	(14.55)
Эти правила отбора являются частным случаем общих правил отбора (4.157), при-
чем для спинового магнитного квантового числа ms дополнительно запрещены
переходы Дт$ = ±1, возможные в общем случае.
Это связано с тем, что электрический дипольный момент атома Р зависит только
от пространственных координат (см. (4.33)). Представляя волновую функцию в виде
“Фт^тз (у, <?) = Фпц (y)ipms (<?),	(14.56)
где — функция от пространственных координат у,	— функция от спиновых
координат а, мы получим для матричного элемента дипольного момента выражение
Фть т$(.У> ^Р^У^Фт^ т'5(У, ^)
\	(И.57)
= J	ЛУ^Ф>ms
а
которое обращается в нуль, в силу ортогональности функций ^ms(a) и ^m's(a), если m$ # m's,
что и дает правило отбора (14.55). Отметим, что данный вывод справедлив в случае достаточно
сильного поля, когда можно, пренебрегая спин-орбитальным взаимодействием, представить
волновую функцию в виде (14.56).
В силу правил отбора (14.54) и (14.55) в сильном поле при переходе меж-
ду совокупностями уровней двух мультиплетных термов получаются несмещенная
тг-составляющая (при — kms — 0) и две симметрично расположенные сме-
щенные a-составляющие (при £±mL = ±1, Дт$ — 0), т. е. получается зеемановский
триплет с нормальным расщеплением Таким образом, в сильном поле должно
наблюдаться простое явление Зеемана с нормальным расщеплением.
В правой части рис. 14.11 для частного случая перехода между подуровнями
терма 2Р (L = 1, S — ’/г) и подуровнями терма 2S (L — 0, S = ’/г) показана
схема переходов и получающаяся картина расщепления. Для каждого подуровня
указаны значения mL, ms, а также значения их суммы т — mL 4- ms. При заданных
значениях т^ и ms дополнительная энергия в магнитном поле определяется фор-
мулой (14.52). Отметим, что для терма 2Р &EmLms как при mL — 1, ms = - ’/2, так
и при mL = -1, ms = ’/2.
392
Глава 14. Явление Зеемана и магнитный резонанс
Сильное поле
Рис. 14.11. Сопоставление расщеплений в слабом поле и в сильном поле
для перехода 2Р— 25
(14.59)
Рассмотренная картина расщепления получается, когда можно полностью пре-
небречь спин-орбитальным взаимодействием. Если это взаимодействие учитывать
в качестве поправки при условии (14.48), то ее величина легко может быть определена
и равна	.	,
(14.58)
Складывая (14.58) с (14.52), получаем полную дополнительную энергию в силь-
ном магнитном поле
^Emims = цьН(ть + 2ms) + C(L, S)mLms.
Формулу (14.58) можно легко получить, исходя из выражения для энергии спин-
орбитального взаимодействия
A(LS) = S)(LS) = <(Z, S)LS cos (Z, S).	(14.60)
В то время как в слабом поле (LS) имеет вполне определенное значение }/i[J(J 4-1)-
S(S + 1) - L(L 4- 1)] (см. (2.86) и (9.35)), в сильном поле, когда L и S прецессируют
независимым образом, нужно брать среднее значение (LS) = LS cos (Z, S). Косинус угла
между векторами L и S можно представить в виде (см. рис. 14.10, б)
cos (JD.S) = cos (ж, Z) cos (ж, S) 4- cos (у, L) cos (у, S) 4- cos (z, L) cos (z, S).
При усреднении этого выражения среднее значение первых двух членов в правой части равно
нули ! углы L и S с осью х и осью у меняются независимо), а в третьем члене cos (z, L) =
L
ms
cos(z, S) = —- и, следовательно,
ij
C(L, S)(JLS) = <(L, S)LS cos(£,S) - C(L, S)LS^^- = <(L, S)mLms,
L S
т. e. мы получаем выражение (14.58).
§ 14.5. Явление Зеемана в сильных и в промежуточных полях
393
Учет второго члена в (14.59), обусловленного спин-орбитальным взаимодей-
ствием, приводит к тому, что подуровни с различными значениями тп^ ms не будут
равноотстоящими и картина расщепления при переходе между подуровнями двух
термов будет лишь приближаться к зеемановскому триплету, отличаясь от него
наличием структуры отдельных составляющих триплета.
Например, в рассмотренном случае перехода 2Р—2S (рис. 14.11) для терма 2Р
член C(2P)mLms дает для подуровней mL = -1, ms = - ’/? и mL = 1, ms — '/2 поправ-
ку 1ДС(2Р) и для совпадающих подуровней mL = — 1, ms = !/2 и mL = 1, ms = — !/2
поправку -’ДС^Р); подуровни mL = 0, ms — -’/г и mL = 0, ms = */г сохраня-
ют свое положение, тг-составляющая в картине расщепления сохранит свое положение,
а a-составляющие будут двойными, с расщеплением, равным С(2Р). Смещение подуровней
и расщепление а-составляющих показано в правой части рис. 14.11. Подобная картина на-
блюдается для первого члена главной серии Li, представляющего в отсутствие магнитного
поля дублет 2s 25]д—2р2Ру2 Зд с расщеплением 0,34 см-1 (см. табл. 8.7, с. 229), равным,
согласно (8.29), fyCip — 3ЛС(2Р), откуда £(2Р) = 0,23 см-1. В магнитном поле 20000 Гс, соглас-
но (14.6), расстояние 2дБЯ между a-составляющими составляет 2-0,934 см-1 = 1,87 см-1;
расщепление этих составляющих равно С(2Р) = 0,23 см-1.
До сих пор мы рассматривали независимо явление Зеемана в слабых и в сильных
полях. При постепенном росте магнитного поля происходит и постепенное изме-
нение картины расщепления уровней и спектральных линий — переход от явления
Зеемана в слабых полях к явлению Зеемана в сильных полях. Величина зеема-
новского расщепления в промежуточных или средних полях, переходных от слабых
к сильному, того же порядка, что и мультиплетное расщепление,
^бЯ-С(Д5),	(14.61)
и это сильно усложняет картину расщепления. Расстояния между составляющими
уже не изменяются пропорционально магнитному полю, и различные составляющие
ведут себя по-разному. Полный расчет расщепления термов сложен и приводит
к громоздким формулам, однако качественную картину в промежуточных полях
можно получить и без расчета, путем сопоставления зеемановских подуровней
в предельных случаях слабого поля и сильного поля.
При переходе от слабого поля к сильному, как мы видели, полный механи-
ческий момент J не сохраняется (см. с. 390); однако полная проекция механиче-
ских моментов атома на направление поля остается постоянной и сохраняет свое
значение т. В слабом поле эта проекция т — mj, где mj принимает 2J 4- 1 зна-
чений (mj — J,J— 1,..., — J) для уровня с заданным J. В сильном поле полная
проекция равна сумме проекций mL и ms моментов L и S:
m = mL-\-ms,	(14.62)
где mL ~ L, L - 1,..., -L и ms = S,S - 1,..., ~S. Для заданного терма число
подуровней в слабом поле и в сильном поле, равное числу (2L4- 1)(2S 4-1) независи-
мых состояний (см. с. 51), одинаково. При этом для каждого подуровня сохраняется
значение т.
Сохранение значения полной проекции связано с аксиальной симметрией однородного
магнитного поля (см. с. 64). При наличии аксиальной симметрии эта проекция квантуется
независимо от напряженности магнитного поля. Оператор Jz = Lz 4- Sz полной проекции
механических моментов при этом совпадает с оператором бесконечно малого поворота вокруг
направления поля.
394
Глава 14. Явление Зеемана и магнитный резонанс
Для сопоставления подуровней в слабом и в сильных полях знания значений т
еще недостаточно. Однозначное сопоставление получается, если учесть, наряду
с сохранением ш, правило, что различные подуровни с тем же значением т
не должны пересекаться при переходе от слабого поля к сильному. Данное правило
является частным случаем общего правила непересечения уровней. Согласно этому
правилу, установленному Вигнером и Нейманом [203], если при переходе от одного
предельного случая к другому сохраняются некоторые квантовые числа, то уровни
с одинаковыми наборами таких квантовых чисел не могут пересекаться.
Принимая во внимание сохранение т и правило непересечения, легко произ-
вести сопоставление подуровней в слабом поле с подуровнями в сильном поле.
Такое сопоставление показано на рис. 14.11 для случая терма 2Р. В слабом поле
уровень 2Ру2 расщепляется на два подуровня cm — mj— ’Д, - ’Л, а уровень 2Рзд —
на четыре подуровня с т — mj —	’/2, — ’/2, ~3Л; всего получается (2L-|-1)(2S4-1) =
3-2 = 6 подуровней. В сильном поле получается тоже 6 подуровней, которые мы
уже рассмотрели выше, из которых два (mL = 1, ms = — 1/г и mfj = — 1, ms = 1/г)
совпадают. Нижний подуровень с mj — — ’/2 переходит в подуровень с т/7 = 0,
ms = - ’/2, а верхний подуровень с mj = - ’/2 — в подуровень с т^ = -1, ms = 4- ’/2,
так как не должно иметь место пересечение этих подуровней при промежуточных
полях. Аналогично нижний подуровень mj = ’/2 переходит в подуровень mL = 1,
ms = - ’/2, а верхний подуровень mj = ’/2 — в подуровень mL = Q, = x/i.
Наконец, подуровни mj = -3/2 и mj = 3Д переходят в подуровни mL — -1,
ms — —’/2 и тпь = 1, ms = ’/2 соответственно. Расположение подуровней
на рис. 14.11 показано с учетом фактора мультиплетного расщепления соглас-
но (14.59).
В других случаях сопоставление производится аналогичным образом. Можно
проследить и изменение картины расщепления спектральных линий при переходе
от слабого поля к сильному, на чем мы не будем здесь останавливаться.
Наше рассмотрение относилось к случаю нормальной связи. Совершенно так же
может быть разобран разрыв связи (J, j) в сильном магнитном поле или вообще связи
любых двух векторов Jj и J2, образующих результирующий вектор J — J\ +J2.
Дополнительная энергия в сильном магнитном поле, разрывающая связь (Jb J2),
будет иметь вид, аналогичный (14.52) (ср. (14.8)):
&Ет, mi = fibH(giml + д2т2).	(14.63)
В отличие от (14.52), однако, расстояния между получающимися подуровнями не бу-
дут, вообще говоря, целыми кратными нормального расщепления и при пере-
ходах не будут получаться зеемановские триплеты с нормальным расщеплением.
Разрыв связи различных моментов может происходить в несколько этапов.
Например, для триплетных термов двухэлектронных конфигураций сначала будет
разрываться связь между L и S, как было описано выше, а затем, в достаточно
сильных полях, связь между 1\ и 12 и между sj и s2 (полное явление Пашена—Бака).
Практически явление Зеемана в сильных и в промежуточных полях наблюдается
для легких атомов, а также для высоких термов тяжелых атомов, т. е. в тех случаях,
когда расщепления, обусловленные спин-орбитальным взаимодействием, не очень
велики и не превышают нескольких см1.
В заключение данного параграфа отметим, что при сопоставлении расщеплений
уровней энергии в магнитных полях различной напряженности могут быть устано-
влены весьма полезные правила сумм для групп подуровней с заданным значением
квантового числа т, сохраняющего свой смысл в магнитном поле, а именно правила
сумм для множителей д и правила сумм для величин расщепления (см. [13], с. 241).
§ 14.6. Общая характеристика магнитного резонанса
395
^(квадр)	^(квадр)
Е — ---------- — ----------
^(магн)	2?(магн)
(14.64)
2 '
§ 14.6. Общая характеристика магнитного резонанса
Рассмотрим теперь магнитный резонанс, т. е. вынужденные переходы между
подуровнями зеемановского расщепления (см. с. 367). В данном параграфе мы дадим
общую характеристику магнитного резонанса, справедливую как для электронного
магнитного резонанса, обусловленного электронными магнитными моментами, так
и для ядерного магнитного резонанса, обусловленного ядерными моментами, и вра-
щательного магнитного резонанса, обусловленного вращательными магнитными
моментами7).
Переход между имеющими одинаковую четность двумя зеемановскими подуров-
нями уровня с заданным значением J возможен, согласно правилу отбора (4.154),
лишь в магнитном дипольном и в квадрупольном излучениях. Однако в радио-
частотной области спектра вероятность квадрупольных переходов по сравнению
с магнитными дипольными очень мала (вероятность квадрупольных переходов го-
раздо быстрее, на множитель и2, убывает с частотой) и нужно учитывать лишь
магнитные дипольные переходы, вероятность которых определяется магнитными
моментами этих переходов (см. (4.73)). Действительно, согласно (4.85), отноше-
ние вероятности квадрупольных переходов к вероятности магнитных дипольных
переходов по порядку величины равно
и
с
Для длины волны Л — 1 см ( - = 1 см ) мы находим, полагая Q & еа «
\ с	/
5 • 10-,° • 10-16 = 5 • 10-26, р я ~ Ю-20, что отношение е по порядку величины
равно 10“10, т.е. очень мало.
Таким образом, переходы между подуровнями зеемановского расщепления обу-
словливаются магнитным дипольным излучением.
Весьма существенно, что вероятности спонтанных переходов между зееманов-
скими подуровнями ничтожно малы и спонтанное испускание отсутствует. Это
вообще характерно для переходов с излучением в радиочастотной области спектра;
спонтанное испускание в обычных условиях отсутствует и может наблюдаться лишь
в исключительных условиях8). В радиочастотной области, как правило, наблюда-
ются вынужденные переходы — поглощение и вынужденное испускание; частный
случай вынужденных переходов в радиочастотной области спектра и представляет
магнитный резонанс.
Легко произвести оценку вероятностей спонтанных переходов между под-
уровнями зеемановского расщепления, исходя из формулы для магнитного ди-
Z \ з
польного излучения (см. (4.85)), А^магн^ = 3- 1029(- 1 |д|2. Для расщепления,
\ с /
обусловленного электронными магнитными моментами, имеющими порядок маг-
нетона Бора рь « 1О~20 эрг/Гс (см. (2.47)), мы получаем, полагая Л = 4 см,
1/	1
- = 0,25 см (что соответствует магнитному полю Н « 5 000 Гс, см. с. 370),
^(магн) ~ . ю29 • 0,253 • Ю"40 с-1 ~ 5 • 10"13 с"1, т.е значение А<магн> мало. Еще * * 8
^Магнитный резонанс, обусловленный ядерными моментами, будет рассмотрен в гл. 16 (с.426),
а обусловленный вращательными моментами — в гл. 19 (с. 564).
8) Такие условия осуществляются для космического радиоизлучения, см. ниже, гл. 16, с. 435.
396
Глава 14. Явление Зеемана и магнитный резонанс
меньше А^магн^ будет для переходов, обусловленных ядерными и вращательными
моментами, имеющими порядок ядерного магнетона.
Для магнитного дипольного излучения, согласно правилу отбора (4.157), так
же как и для обычного электрического дипольного излучения, возможны переходы
с изменением магнитного квантового числа т не более чем на единицу, т. е. | Am| <С 1.
т
1
О
1
Рис. 14.12. Переходы между соседними
подуровнями зеемановского расщепления
В силу этого правила отбора
разрешены переходы лишь между
соседними подуровнями зееманов-
ского расщепления, как показа-
но на рис. 14.12 для значений J
от ’/г до 2. Переходы снизу вверх
представляют поглощение, пере-
ходы сверху вниз — вынужден-
ное испускание. Переходам с из-
менением т на единицу, Дт =
±1, соответствуют круговые коле-
бания в плоскости ху, перпендику-
лярной направлению постоянно-
го магнитного поля, обусловлива-
ющего зеемановское расщепление
(ср. с. 372). Такие переходы могут
вызываться переменным магнит-
ным полем резонансной частоты
и = -\Ет-Ет^, перпендикуляр-
гь
ным постоянному магнитному полю. Таким образом, магнитный резонанс происходит
под действием переменного магнитного поля частоты
v=^\Em-Em±i\,	(14.65)
п,
перпендикулярного постоянному магнитному полю.
Согласно общим формулам (4.172), при переходах Дт — т\ - т2 = ±1 отличны от нуля
только матричные элементы Ах ± iAy составляющих вектора. Для магнитного дипольного
излучения нужно рассматривать матричные элементы магнитного момента. Отличие от нуля
матричных элементов (см. (4.175) и далее)
(mi |/их ± г>9|т2) = У Vm, (у>)(Рг ±	(14.66)
при ГП| = т2 ± 1 означает, с точки зрения наглядных представлений, что этим переходам
соответствуют магнитные круговые осцилляторы в плоскости ху, имеющие частоту (14.65).
Колебания таких осцилляторов могут возбуждаться магнитным полем той же частоты, распо-
ложенным в плоскости ху.
Следует специально отметить, что рассматриваемые переходы, являясь магнитными
дипольными переходами, происходят под действием переменного магнитного поля, в то время
как обычные электрические дипольные переходы происходят под действием переменного
электрического поля.
Так как частота перехода между соседними подуровнями зеемановского расщепления
совпадает с частотой прецессии магнитного момента вокруг направления постоянного маг-
нитного поля Н, что уже подчеркивалось выше (см. с. 378), то условием магнитного резонанса
является совпадение частоты переменного магнитного поля, перпендикулярного постоянному
магнитному полю, с частотой прецессии.
С чисто классической точки зрения с вращением составляющей магнитного момен-
та д±, перпендикулярной оси прецессии, т.е. направлению Н, связано излучение частоты,
§ 14.6. Общая характеристика магнитного резонанса
397
равной частоте прецессии. Можно, со-
гласно наглядным представлениям, по-
нять, пользуясь принципом соответствия,
и изменение при вынужденном перехо-
де величины проекции магнитного мо-
мента на направление Н. Для этого мы
рассмотрим действие перпендикулярно-
го магнитного поля Hv на магнитный
момент в подвижной координатной си-
стеме, прецессирующей вокруг направле-
ния Н с угловой скоростью
(рис. 14.13, д). Как мы видели в гл. 2
/ dMp\
(с. 59), изменение ( I механи-
\ at /
X / вращ
ческого момента в такой системе при от-
сутствии других воздействий, кроме по-
ля Н, равняется нулю. При наличии пер-
пендикулярного поля Hv, создающего до-
полнительный момент силы [//,	=
[yMp)Hvl мы получим
Рис. 14.13. Действие перпендикулярного
магнитного поля на прецессирующий
магнитный момент:
а — прецессия вокруг поля Я;
б — дополнительная прецессия вокруг поля Я'
в противоположных направлениях с угловыми
dM,, \
/ вращ
(14.67)
(л)
Переменное поле Ни частоты и = — мы
2тг
можем разложить на два магнитных по-
ля Ну и той же частоты, вращающиеся
скоростями ш и —о>9\ Поле Ну, вращающееся с угловой скоростью ш, будет постоянно от-
носительно подвижной системы, а магнитный момент должен прецессировать вокруг напра-
вления Ну (см. рис. 14.13, б) и, следовательно, будет менять свою ориентацию относительно
поля Н, т.е. будет изменяться pz. Постепенному изменению ориентации магнитного момен-
та в классической теории будет соответствовать скачкообразное изменение этой ориентации
и проекции pz в квантовой теории. В частности, при первоначальной ориентации, параллель-
ной Н, магнитный момент будет постепенно менять ее на антипараллельную. Для спинового
момента электрона (з = Уг) этому соответствует квантовый переход с подуровня ms =
на подуровень ms = — ’Д.
Существует два различных способа наблюдения магнитного резонанса — из-
мерение воздействия излучения на молекулярный пучок и измерение поглощения
излучения веществом.
Первый способ состоит в том, что пучок исследуемых частиц (обладающих
магнитным моментом), отклоняющийся определенным образом в постоянных маг-
нитных полях (которые для этой цели делаются неоднородными) и попадающий
в приемник, регистрирующий частицы, подвергается воздействию радиочастотного
излучения. Если под действием магнитного поля излучения происходят переходы
9) Например, колебание по оси х, Нх = H^cosut, можно, добавив равное нулю поле по оси у,
разложить следующим образом:
/Яо Яо \ /Яо Яо
Нх + iHy = Нх + i О = ( — cos wt + — cos wt) + 11 — sin ivt--------— sin wi
Hq л	Я0/	4 . .	. Яо iwt , Яо -iut
— — (cosort +1 smart) + — (cosort — i smart) = — e	+ —e
Первый член представляет магнитное поле, вращающееся от оси х к оси у с угловой скоростью о/,
а второй член — магнитное поле, вращающееся от оси у к оси х с угловой скоростью -а>.
398	Глава 14. Явление Зеемана и магнитный резонанс
между подуровнями зеемановского расщепления, что имеет место при наличии резо-
нанса, т. е. при совпадении частоты поля излучения с частотой перехода, то частицы
с измененной вследствие перехода проекцией магнитного момента отклоняются уже
иначе и не попадают больше в приемник. Таким образом, измеряется наблюдающее-
ся при резонансных частотах ослабление интенсивности пучка исследуемых частиц.
На рис. 14.14 приведена типичная схема прибора для исследования магнитного
резонанса в молекулярных пучках [42]. Пучок частиц из источника И проходит
Рис. 14.14. Схема прибора для исследования магнитного резонанса в молекулярных пучках:
И — источник, П — приемник, Д — диффузионные насосы
через неоднородные постоянные поля магнитов А и В, отклоняющие частицы в про-
тивоположные стороны и осуществляющие фокусировку пучка, и попадает в прием-
ник П. Между магнитами А и В магнитом С создается однородное постоянное поле
и одновременно создается перпендикулярное ему переменное радиочастотное маг-
нитное поле (поле излучения), вызывающее переходы. Когда частота переменного
поля не совпадает с частотой переходов, в приемник попадает вполне определенный
поток частиц, при совпадении частот все частицы, для которых проекция магнит-
ного момента изменилась вследствие переходов между подуровнями зеемановского
расщепления, будут иначе отклоняться вторым неоднородным полем В и не попадут
в приемник.
Существенно, что изменение интенсивности пучка пропорционально общему
числу процессов перехода с первоначальных подуровней, равному сумме числа всех
процессов поглощения и всех процессов вынужденного испускания. Например,
в случае расщепления в магнитном поле уровня с J — 1 (см. рис. 14.12) изменение
интенсивности пучка будет происходить как за счет переходов — 1 —> 0 и 0 —> 1
(поглощение), так и за счет переходов 0	-1 и 1 —> 0 (испускание). В данном
случае вероятности всех этих переходов будут одинаковы.
Относительные вероятности переходов даются формулами табл. 14.1 (с. 375) для слу-
чая J —► J и m ± 1 -> т, которые справедливы и для переходов между подуровнями одного
и того же уровня. Поэтому можно пользоваться в конкретных случаях табл. 14.4.
Метод магнитного резонанса в молекулярных пучках является чрезвычайно
чувствительным и позволяет достигать очень высокой степени точности. Важным
§ 14.7. Исследование магнитного резонанса методом атомных пучков 399
его достоинством является то, что изучается воздействие радиочастотного поля
на свободные частицы. Однако с экспериментальной точки зрения метод весьма
труден, так как работа с молекулярными пучками, особенно в магнитных полях,
является сложной, в частности требует специальной вакуумной техники.
Второй способ наблюдения магнитного резонанса состоит в измерении поглоще-
ния радиочастотного излучения веществом, помещенным в постоянное однородное
магнитное поле. Радиочастотное магнитное поле вызывает переходы между подуров-
нями зеемановского расщепления, причем происходят как переходы т —> т 4- 1,
так и переходы т 4- 1 —> т, т. е. имеют место как поглощение, так и вынужденное
испускание. Например, в простейшем случае зеемановского расщепления уровня
с J — ’Д (см. рис. 14.12) это будут переходы -’Д —> х/1 и !Д —► -!Д. Наблюдаемое
поглощение является разностью поглощения и вынужденного испускания, и коэф-
фициент поглощения, измеряемый на опыте, определяется формулой (5.98), содер-
hy
жащей множитель а — —, где в данном случае hy — Ет. - Ет^ — разность энергий
кТ
подуровней зеемановского расщепления. Магнитный резонанс удается наблюдать
благодаря высокой чувствительности современных радиотехнических методов, даже
для очень близких подуровней зеемановского расщепления. Несмотря на отличие
экспериментальной методики, в принципе, изучение поглощения в радиочастотной
области не отличается от изучения поглощения в оптической области, в то время
как метод магнитного резонанса в молекулярных пучках обладает той существен-
ной особенностью, что измеряется не излучение, а изменение состояния частиц,
подвергшихся действию излучения.
По своей методике изучение магнитного резонанса методом поглощения зна-
чительно проще, чем методом молекулярных пучков, и вместе с тем также позволяет
достигать высокой разрешающей силы и весьма большой точности измерений. Этим
методом обычно исследуется вещество в твердом и в жидком состоянии, что, с одной
стороны, позволяет сделать разнообразные выводы о конденсированном состоянии
вещества, но, с другой стороны, требует введения ряда поправок при определении
свойств отдельных частиц. Значения магнитных моментов, определенные для ча-
стиц, взаимодействующих с окружающими частицами, могут отличаться от значений
этих моментов для свободных частиц.
Отметим, что обычно при наблюдении магнитного резонанса изменяют не ча-
стоты излучения, вызывающего переходы, а напряженность постоянного магнит-
ного поля, в котором эти переходы наблюдаются (по методу молекулярных пуч-
ков или по методу поглощения). Таким образом, чтобы удовлетворить соотно-
шению hy — АЕт - АЕт_] = дрьН, оставляют у постоянным и изменяют Н.
Спектры соответственно получаются не в шкале частот (или длин волн), а в шкале
напряженностей магнитного поля.
§ 14.7. Исследование электронного магнитного резонанса
методом атомных пучков
Измерения магнитного резонанса в атомных пучках, являющихся частным
случаем молекулярных пучков|0), позволяют с очень большой точностью, порядка
одной стотысячной, определять электронные магнитные моменты атомов в основ-
ном состоянии. Особенно простой случай представляют атомы с одним внешним
s-электроном, для которых основным уровнем является уровень ns2S\/ (атомы
|0) Относительно терминологии см. примечание на с. 367.
400
Глава 14. Явление Зеемана и магнитный резонанс
водорода, щелочных металлов, а также Си, Ag и Au, см. табл. 7.2). Для таких атомов
наблюдаются переходы — х/г х/г и */г —► — Уг (см. рис. 14.12, с. 396), связанные с из-
менением ориентации в магнитном поле спинового момента электрона. Важнейшим
результатом опытов с этими атомами (а также с атомами в других основных состоя-
ниях, в частности, в состоянии пр 2Р\/^ является то, что множитель д для спинового
магнитного момента электрона оказывается отличным от значения 2, к которому
приводит теория Дирака, т. е. величина магнитного момента оказывается неравной
магнетону Бора рБ (см. (2.56)). Эта аномалия магнитного момента электрона, как
уже указывалось в гл. 6 (см. с. 192), обусловлена радиационными поправками, кото-
рые можно найти, пользуясь методами квантовой электродинамики. Теоретическое
1
значение магнитного момента рзл = электрона при учете поправок порядка а
и а2, где а — постоянная тонкой структуры (6.48), равно [2546]
q (а	а \
Дэл = ^б = 1 + — — 0,328— дБ = 1,0011596 дБ.
2	\ Z7F	ТГ /
(14.68)
Точные измерения зеемановского расщепления для основного состояния ls25y2
атома водорода по методу магнитного резонанса в атомном пучке приводят к значе-
нию [254, 42, 43]
|	= 1,001146 ±0,000012,	(14.69)
близкому к теоретическому значению (14.68). Еще лучше согласуется с (14.68) зна-
чение д/2, непосредственно измеренное для свободных электронов (см. (14.81),
с. 406). Такое согласие наряду с совпадением теоретического и эксперименталь-
ного значений сдвига 5-уровня для состояния п = 2 атома водорода (см. с. 195)
является основной проверкой правильности выводов квантовой электродинамики,
полученных на основе учета радиационных поправок.
Экспериментальное значение множителя д/2 для Н1 равно 1,001128 ± 0,000012, для D2 —
1,001128±0,000030, для Не4 - 1,001117±0,000020, для Li6 и Li7 - 1,00114±0,00012, т.е. во всех
а
случаях поправка получается примерно равной — = 0,00116. Нужно учесть релятивистское
2тг
изменение массы электрона, связанного в атоме водорода, по сравнению со свободным
электроном. Это изменение массы составляет 1,8 • 10~5 и дает поправку ±0,000018, что
приводит к значению (14.69) для свободного электрона.
Теоретический расчет значения д/2 для Не4 в основном состоянии 35| приводит к зна-
чению 1,0011044, что также хорошо совпадает с приведенным выше экспериментальным
значением 1,001117 ± 0,000020.
По методу магнитного резонанса в атомных пучках можно исследовать картину
зеемановского расщепления уровней энергии не только в слабых, но и в промежуточ-
ных и в сильных полях. Наряду с изучением зеемановского расщепления основных
уровней атомов можно в принципе исследовать и картину расщепления возбужден-
ных уровней, если создать в пучке достаточную концентрацию таких атомов. Такое
исследование и было выполнено Лэмбом и его сотрудниками при изучении сдвига
5-уровней ([248], см. §6.8); именно изучение зеемановского расщепления уровней
с п — 2 позволило определить с большой точностью значение этого сдвига.
Особенность зеемановского расщепления возбужденных уровней атома водорода
состоит в том, что существуют близко лежащие уровни с различными значениями I.
Для п = 2 мы имеем уровни 2s25y2, 22Ру2 и 22Ру2 (см. рис. 6.14, с. 192). При этом
§ 14.7. Исследование магнитного резонанса методом атомных пучков	401
величина расщепления в маг-
нитных полях величиной в
несколько тысяч гаусс того
же порядка, что и рассто-
яния между уровнями
и 2Рзд. Картина расщепле-
ния уровней с п = 2 приве-
дена на рис. 14.15. При этом
четный уровень iд расщеп-
ляется независимо от нечет-
ных уровней 2Ру2 и 2Ру2,
для которых имеет место слу-
чай расщепления в промежу-
точных полях, соответствую-
щий средней части рис. 14.11.
В данном случае это расщеп-
ление можно легко рассчи-
тать, учитывая взаимодей-
ствия между собой двух уров-
ней с m = Уг и двух уровней
с т = - Уг. Всего мы имеем
два четных уровня ст = У2 и m = — Уг, обозначенные через а и /3, и шесть нечетных
уровней с m = 3/г, У2, -Уг, -3/г (от 2-Ру2) И т — ’/2, “Уг (от 2Ру2), обозначенных
через a, b, с, d, е, f. В отличие от случая переходов между подуровнями одного
и того же уровня, возможными только при магнитном дипольном излучении, меж-
ду подуровнями уровней 2S и 2Р°, обладающих различной четностью, возможны
обычные электрические дипольные переходы с правилом отбора Ат = 0, ±1, такие
же, как и при расщеплении спектральных линий в оптической области спектра.
При этом вынужденные переходы с Ат — 0 будут вызываться радиочастотным
электрическим полем, параллельным постоянному магнитному полю, а переходы
с Ат = ±1 — полем, перпендикулярным постоянному магнитному полю. Согласно
правилам отбора, возможны переходы:
а—е, а—Ь\
a-—f, а—с, а—а,
Р-с,
Р - е, (З—d, /3—Ь.
Am = 0
Am = ±1
(14.70)
В опытах Лэмба атомы водорода в пучке возбуждались, как уже указывалось в § 6.8,
электронным ударом. Атомы в возбужденных состояниях 22Ру2 и 22Р|д сразу
высвечиваются благодаря оптическим переходам на основной уровень 12Sy2, а ато-
мы в возбужденном состоянии 22Sy2 являются метастабильными и сохраняются
в пучке, попадающем в магнитное поле, в достаточном числе. При этом атомы,
находящиеся на подуровне (3 (т = - ’/г), оказываются менее стабильными, чем
на подуровне а (т = 1/г), из-за возможности переходов без излучения под дей-
ствием перпендикулярного электрического поля10 на подуровень е, с которым
подуровень /3 пересекается примерно при Н = 540 Гс. В результате атомный пучок
10 Такое поле действует, в силу закона индукции, на быстродвижущуюся частицу, пролетающую через
магнитное поле. О переходах без излучения под действием электрического поля см. гл. 15 (с. 417).
402
Глава 14. Явление Зеемана и магнитный резонанс
оказывается поляризованным — он содержит практически только атомы в состо-
янии a (2%д/, т = Уг). Тщательное измерение частот переходов а—е и a—f
(вынужденное испускание) в поле Н = 1 160 Гс для водорода (частота перехода
2 195 МГц) и в поле 704 Гс для дейтерия (частота перехода 2 395 МГц) позволило
найти точные значения (6.87) сдвига 5-уровня. По измерениям частоты перехо-
да а~~а (поглощение) в поле 630 Гс (частота перехода 10 795 МГц) было найдено
для дейтерия значение (6.88) разности энергий 22P^—22S\^. Отметим, что наряду
с электрическими дипольными переходами наблюдался и магнитный дипольный
переход а — р в виде очень резкого резонансного максимума, который использо-
вался для калибровки магнитного поля; частота этого перехода с хорошей степенью
приближения равна, согласно формулам (14.4) и (14.68),
ДЯ1/2 - АЕ_ 1/2 - дрБН = 2^1 + “ j ДбЯ.	(14.71)
Переходы между подуровнем а уровня и подуровнями е, f, а уровней 2Ру2
и 2Р3/2 являются гораздо менее резкими из-за большой естественной ширины
P-уровней, связанной с разрешенными оптическими переходами
2гр;/Г1%|/г„2гр;/-2!5|/г,
которые происходят со значительными вероятностями. Согласно табл. 6.6 (с. 184),
эта вероятность равна 6,25 • 108 с-1, что, согласно формуле (4.128), дает ширину
уровней, равную
Л 6,25 108	.	,
Дг/ = — = -- -......с-1 « 100 МГц.	(14.72)
2тг 6,28
Ширина еще увеличивается за счет сверхтонкой структуры. Однако в силу сим-
метрии контура линии удается со значительной точностью определить значение
максимальной интенсивности (при введении малых поправок на имеющуюся не-
большую асимметрию), что и дает возможность найти точные значения частот
переходов.
§ 14.8. Исследование электронного магнитного резонанса
методом поглощения
Весьма важным методом поглощения является метод электронного парамаг-
нитного резонанса (ЭПР), часто называемого просто парамагнитным резонансом.
Электронный парамагнитный резонанс, открытый Завойским (см. выше с. 368),
наблюдается в микроволновой области радиочастотного спектра в соответствии
с тем, что расстояния между соседними уровнями зеемановского расщепления
порядка рБН и в полях порядка тысяч гаусс составляют доли см-1 (см. (14.6)).
Причиной, обусловливающей одновременно поглощение и парамагнетизм веще-
ства, является ориентация электронных магнитных моментов внешним магнитным
полем. При тепловом равновесии заселенность подуровней зеемановского расщеп-
ления определяется формулой Больцмана (5.10)12)
_ АЕт	УгН	_ gilbHm
— п0Ае = nGAe k? = п0Ае kT ,	(14.73)
12) При этом учитываем, что статистический вес всех подуровней одинаков и равен 1 (вырождение
в магнитном поле снимается). Отсчет энергии в (14.73) мы производим относительно нерасщепленного
уровня АЕт = 0.
§ 14.8. Исследование магнитного резонанса методом поглощения
403
где £±Ет — дополнительная энергия в магнитном поле (см. (14.1) и (14.8)), п$ —
число частиц, а А — постоянная (определяемая из условия, что общее число частиц
на всех уровнях равно по). Вследствие несколько большей заселенности уровней
с меньшими значениями т вещество в магнитном поле обладает, при р / 0,
результирующим магнитным моментом, т. е. намагничивается. Благодаря той же
причине число переходов m —> тп + 1, т. е. число процессов поглощения, будет
больше числа переходов т + 1 —> ш, т. е. числа процессов вынужденного испуска-
ния; это и приводит к отличному от нуля приведенному коэффициенту поглощения
(см. формулу (5.68) и вытекающие из нее формулы (5.84), (5.91) и (5.98)), который
и определяет поглощение, наблюдающееся на опыте и представляющее разность
поглощения и вынужденного испускания. Коэффициент поглощения для перехо-
да т —> т 4-1, согласно (5.98), равен
1	hy
ни = - hynm—Bm^m+x(y),	(14.74)
С	KJ.
где ВГПуГП+](и) — вероятность поглощения для магнитного дипольного излучения.
В микроволновой области коэффициенты поглощения оказываются достаточно
большими для их измерения даже при сравнительно малых концентрациях парамаг-
нитных частиц.
Легко оценить порядок величины вероятности Bm m+i(i/) перехода с подуров-
ня т на подуровень тп + 1 и, исходя из этой оценки, найти порядок величины
коэффициента поглощения.
В формулу (14.74) входит спектральная вероятность поглощения, отнесенная
к единице интервала частот и равная, согласно (5.126),
Bm,m+l(v) = ??^-,	(14.75)
где — интегральная вероятность поглощения, a Др — ширина спектральной
линии при переходе т —> т+ 1. Выражая Вт,т+\ через магнитный момент перехода
по формулам (4.8) и (4.73), мы получим (gm = gm+i = 1)
1 с2	1с2 64тг4 з 2	1 8тг3	2
Bm,m+i(p) -	т =	= АГ 3^lMm’m+li ’
(14.76)
Магнитный момент перехода по порядку величины равен магнетону Бора
т. е. |//т}ГП+1|2 « 1О~40 эрг/Гс (см. (2.47)). При ширине линии порядка 108 Гц
/	Др 1	)п
т.е. — = — при у — 10 0 Гц
\ у	100
8-ЗО1О-40	6
Вт,т+\(У) ~ 1о8 3 6,б2. 10_54 - 2-10	(14.77)
и для коэффициента поглощения (14.74), полагая
— ~ 1/3 см ~	3 Т =	(5.31)),
кТ 200 см-' ’	v v
v _ Ю10 _ 1
с ~ 3 • Ю10 “ 3’
найдем
kv « | • 6,6 • 10-27nm • 1,6 • 10'3  2 • 106 « 10~23nm.
(14.78)
404
Глава 14. Явление Зеемана и магнитный резонанс
Считая пт равным числу частиц в единице объема для конденсированной среды,
имеющему порядок 1022см~3, мы получим хи « 10-1, т.е. коэффициент поглоще-
ния имеет достаточно большую величину. С уменьшением ширины линии этот
коэффициент будет соответственно возрастать.
Вводя поперечное сечение а для поглощения по формуле к = ап0, где п0 —
число поглощающих частиц (см. (5.86))|3), мы получаем, что а по порядку величины
равно 10-23 см2.
На наиболее чувствительных современных установках для изучения парамаг-
нитного резонанса в благоприятных условиях удается обнаруживать поглощение
в образцах, содержащих 1011 поглощающих частиц [262].
Наиболее простой случай парамагнитного поглощения мы получаем, когда по-
глощающие атомы обладают орбитальным моментом, равным нулю, и одним элек-
троном с некомпенсированным спином, дающим спиновый момент S = s = Уг. Этот
случай имеет место для атомов или ионов с одним внешним s-электроном (основ-
ное состояние см. рис. 6.1 и 8.3-8.7). Так же как и при магнитном резонансе
в атомных пучках, в магнитном поле имеют место переходы - Уг —> Уг и Уг —> - Уг
(поглощение и вынужденное испускание, см. рис. 14.12). В отличие от магнитного
резонанса в атомных пучках интенсивность единственной получающейся линии
определяется разностью поглощения и вынужденного испускания (а не их суммой).
Аналогичный случай имеет место в случае более сложных атомных систем
для свободных (химически неустойчивых) радикалов, образующихся в качестве про-
межуточных продуктов при химических реакциях и обладающих одним электроном
с некомпенсированным спином. Обычные химически устойчивые молекулы, как
правило, обладают четным числом электронов, образующих заполненные молеку-
лярные оболочки, и имеют полный механический и магнитный моменты, равные
нулю (см. с. 793). В отличие от них свободные радикалы имеют полный элек-
тронный механический момент J = s = Уг и соответственно полный магнитный
момент ps — Мб (см. (2.56)), и эти радикалы можно легко обнаруживать, если их
концентрации не очень малы, методом парамагнитного резонанса [101].
Для случая атомов, имеющих в основном состоянии отличный от нуля электрон-
ный момент, не являющийся чисто спиновым, получается существенная разница
при исследовании магнитного резонанса в атомных пучках и при исследовании
парамагнитного резонанса. Так как парамагнитный резонанс изучается обычно
для вещества в конденсированном состоянии, то поглощающие атомы нельзя счи-
тать свободными, как в случае магнитного резонанса в атомных пучках. Даже когда
атом не входит в состав молекулы (что, в частности, имеет место для парамагнитных
ионов в кристаллах), его основной уровень расщепляется в электрическом поле,
создаваемом окружающими частицами, и зеемановское расщепление будет иным,
чем для свободного атома,4). Разбор вопроса о парамагнитном резонансе в подобных
случаях требует предварительного рассмотрения взаимодействия поглощающей ча-
стицы с окружающими частицами. Взаимодействия между частицами существенным
образом сказываются и на контуре линий парамагнитного резонанса. В настоящее
время парамагнитный резонанс является одним из эффективных методов изучения
13)	Если для поглощающих частиц имеется один основной уровень кратности gj = 2J 1, то
ДЕ	1	по по
при --1 постоянная А в (14.73) равна — и пт ~ — = ——-, т.е. пт и По одного порядка.
kT	gj	gj 2J +\
14)	Для рассмотренного рыше случая атомов или ионов в основном состоянии 2Sy2 такого расцепления
не происходит, в силу теоремы Крамерса, см. подробнее ниже, § 15.1, с. 408.
§14.8. Исследование магнитного резонанса методом поглощения
405
взаимодействия между частицами в конденсированных системах, и вообще строения
таких систем как в твердом, так и в жидком состояниях.
Особый случай парамагнитного резонанса представляет наблюдаемое для метал-
лов магнитное резонансное поглощение электронами проводимости («свободными
электронами»), обусловленное их спином [259]. Величина расщепления, как и в слу-
чае состояния ns атомов, равна 2рьН. Так как проникновение магнитного поля
в металл определяется скин-эффектом, то существенную роль играет диффузия элек-
тронов в область скин-эффекта и из нее; эту диффузию можно учесть теоретически.
Наблюдаемый в ферромагнитных телах ферромагнитный резонанс (см. с. 368)
представляет частный случай электронного спинового магнитного резонанса. Он свя-
зан со спиновым взаимодействием частиц в ферромагнитных
телах и представляет интерес с точки зрения изучения этих
взаимодействий.
До сих пор мы рассматривали магнитный резонанс,
обусловленный наличием у частиц постоянного магнитно-
го момента, который ориентируется в магнитном поле, что
и обусловливает наблюдаемое расщепление уровней. Для сво-
бодных электронов возможен магнитный резонанс, обусло-
вленный их движением в магнитном поле по круговым тра-
екториям — орбитальным движением. Этот тип резонанса,
связанный с диамагнетизмом свободных электронов, назы-
Рис. 14.16. Движение
электрона по круговой
траектории
вают циклотронным резонансом.
В магнитном поле электрон, движущийся со скоростью v, описывает, как
известно, подобно любой заряженной частице,5), круговую траекторию в плоско-
сти, перпендикулярной магнитному полю. Радиус г такой траектории (рис. 14.16)
V2
определяется из условия равенства величины те— центростремительной силы ве-
evH	е	r v2 е
личине-----силы Лоренца --|гЯ|, т.е. из условия те— = -vH. Отсюда угловая
с	с	г с
v еН
скорость движения по круговой траектории равна ш — — =--и соответствующая
частота составляет (см. (2.46))	г ШеС
и) еН	2рьН
2тг	2тгтес h
(14.79)
Круговое движение в плоскости ху, перпендикулярной магнитному полю, мы можем
разложить на два линейных гармонических колебательных движения по осям х и у,
квантование которых дает возможные значения энергии (см. [145, 146]):
Еп = hv
ehH
2ятес
= 2рБН\п+ |
(п = 0, 1,2,...). (14.80)
Таким образом, вместо непрерывных уровней свободных электронов получаются
дискретные уровни, расстояние между которыми равно 2рьН (рис. 14.17). Наличие
подобного квантования приводит к диамагнетизму свободных электронов.
Этот тип диамагнетизма обычно называют диамагнетизмом Ландау; Ландау в 1930 г.
теоретически доказал [204], что, согласно квантовой теории, свободные электроны обусловли-
вают диамагнетизм, в отличие от классической теории, в которой диамагнетизм свободных
электронов отсутствует.
15)	В частности, как заряженные тяжелые частицы в циклотроне, откуда и название — циклотронный
резонанс.
406
Глава 14. Явление Зеемана и магнитный резонанс
-------------т-т—	Между уровнями свободных электронов в магнит-
ном поле возможны переходы с изменением квантово-
 р [	го числа п осциллятора на ± 1. Это будут обычные элек-
м	трические дипольные переходы, соответствующие со-
ставляющей дипольного момента, перпендикулярной
------------------ полю, и, следовательно, происходящие под действи-
ем переменного электрического поля частоты и, пер-
v-----------------пендикулярного постоянному магнитному полю. Вы-
||	нужденные переходы подобного типа (циклотронный
резонанс) получаются, когда частота радиочастотного
. .1 -------------- электрического поля, перпендикулярного постоянно-
I2 Н МУ магнитномУ полю, совпадает с частотой перехода.
ч	Г Б	С классической точки зрения мы имеем излуче-
ние частоты и, определяемой формулой (14.79) и рав-
Рис. 14.17. Уровни энергии	eff
для свободных электронов ной -----. В координатной системе, вращающейся
в магнитном поле	2тгтес
еН
с угловой скоростью и) — 2тги — --, равной удво-
тес
енной угловой скорости (2.69) ларморовской прецессии, электрон будет покоиться
и на него не будет действовать магнитное поле Н. Таким образом, для свободных
электронов в магнитном поле возникает прецессия, частота которой равна удвоенной
частоте ларморовской прецессии.
Циклотронный резонанс удается наблюдать для медленных электронов в ми-
кроволновой области спектра. Его измерение позволяет определить циклотронную
частоту (14.79). Можно в заданном магнитном поле измерить отношение частоты
магнитного резонанса для исследуемого магнитного момента, пропорциональной
величине р этого момента (см. (2.59)), к циклотронной частоте, которая выражается
через магнетон Бора //&, иначе говоря, с точки зрения наглядных представлений,
можно измерить отношение частоты прецессии исследуемого магнитного момента
к частоте прецессии свободных электронов. При этом непосредственно получает-
ся значение магнитного момента в магнетонах Бора р^. Подобным методом был
измерен с большой точностью магнитный момент протона [268].
Для свободных электронов удалось очень точно измерить аномалию магнитного
момента электрона по разности частоты прецессии спина электрона и частоты
циклотронного резонанса (при д — 2 эти частоты совпадают и равны (14.79)).
Измерения производились при двойном рассеянии (на золотой фольге) электронного
пучка в магнитном поле и дали значение [268а]
- = — = (1,0011609 ±0,0000024),	(14.81)
2	Дб
в полном согласии с (14.68).
Циклотронный резонанс можно, согласно идее Дорфмана [260], получить
для электронов проводимости в металлах и полупроводниках. При этом в фор-
мулу (14.79) будет входить вместо действительной массы электрона те эффективная
*
масса тпе, расстояние между уровнями в магнитном поле уменьшится в — раз
те
и по частоте резонанса можно определить значение эффективной массы. Цикло-
тронный резонанс удается наблюдать для полупроводников (в кристаллах кремния
и германия), причем не только для электронов, но и для дырок [261].
ГЛАВА 15
ЯВЛЕНИЕ ШТАРКА
§15.1. Общая характеристика явления Штарка
Наряду с изучением расщепления уровней энергии и спектральных линий в маг-
нитном поле важное значение имеет и изучение их расщепления в электрическом
поле — явление Штарка. При этом большой интерес представляет исследование
как явления Штарка для атомов и молекул, находящихся во внешнем электричес-
ком поле, так и штарковского расщепления уровней энергии частиц, находящихся
в электрическом поле окружающих частиц. Такое расщепление получается, в част-
ности, для иона в твердом теле или в жидкости. Штарковское расщепление является
и одной из причин уширения линий атомов и молекул в газе, о чем уже упоминалось
в гл. 5 (см. с. 160).
Расщепление спектральных линий водорода во внешнем электрическом поле
было открыто Штарком в 1913 г. [179]. На основе теории Бора эффект Штар-
ка для атомов водорода был объяснен Эпштейном и Шварцшильдом [181, 180].
Основные результаты этих расчетов были впоследствии подтверждены квантовоме-
ханической теорией, на основании которой удается полностью рассчитать явление
Штарка. Штарковское расщепление уровней энергии ионов в кристаллах было
теоретически рассмотрено в работе Бете [202] и в ряде последующих работ (ссыл-
ки см. в [15]); задача сводится к расчету расщепления уровней в электрических
полях определенной симметрии, создаваемых окружающими ион частицами; сим-
метрия этих полей связана с симметрией кристалла. В большом числе работ, по-
священных теории уширения спектральных линий при столкновениях, разбирается
штарковское расширение, обусловленное электростатическими взаимодействиями
частиц (см., например, [183, 24, 24а]).
В данном параграфе мы рассмотрим основные особенности явления Штарка,
в следующих параграфах будет разобрано штарковское расщепление уровней энергии
и спектральных линий атомов в однородном электрическом поле; последний пара-
граф данной главы посвящен уширению спектральных линий вследствие явления
Штарка.
Вопросы расщепления уровней энергии ионов в электрических полях определенной
симметрии мы рассматривать не будем, как относящиеся к спектроскопии конденсированных
систем. Мы также не будем в данной главе специально разбирать переходы в радиоча-
стотной области спектра между подуровнями штарковского расщепления — электрический
резонанс, который удается наблюдать для молекул, обладающих постоянным дипольным
моментом; эти вопросы будут рассмотрены в главе, посвященной вращательным спектрам
молекул (см. гл. 19, с. 563).
В однородном электрическом поле, обладающем аксиальной симметрией, со-
храняется квантование проекции момента количества движения, и поэтому, так же
408
Глава 15. Явление Штарка
как и в магнитном поле, сохраняет свой смысл магнитное квантовое число т, опре-
деляющее значение этой проекции. Однако существенная разница состоит в том, что
в однородном электрическом поле дополнительная энергия зависит только от аб-
солютного значения \т\ квантового числа т. Поэтому состояния с одним и тем
же \т\ вырождены. В результате происходит расщепление уровня с заданным целым
значением J на подуровни со значениями
\т\ = 0, 1, 2,..., J (J целое),
(15-1)
т. е. на J + 1 подуровней, и уровня с заданным полуцелым значением J на подуровни
со значениями
II 135
W =2’2'2'
. ,J (J полуцелое),
(15.2)
1
2
1 z ч 1
т. е. на - (2J + 1) = J + - подуровней.
Таким образом, расщепление не является полным. Все подуровни являются два-
жды вырожденными, кроме подуровня с т = 0 при целых значениях J, и относятся
к дважды вырожденным типам симметрии группы (см. с. 77).
Как указывалось в гл. 3 (см. с. 66), отличие однородного электрического поля от од-
нородного магнитного поля состоит в том, что они обладают различной дополнительней
симметрией. Электрическое поле не изменяется при отражении в плоскости проходящей
через направление поля, и это приводит, как было показано на примере атома водоро-
да (см. с. 78), к двукратному вырождению. Волновые функции фт и оказываются
связанными между собой неразрывным образом, образуя, с точки зрения теории групп,
неприводимое представление группы С^.
С точки зрения наглядных представлений наличие двукратного вырождения
легко объясняется тем, что электрическое поле одинаковым образом изменяет тра-
ектории движения заряженных частиц независимо от направления их вращения
вокруг направления поля, т. е. от знака проекции момента количества движения.
В частности, для орбитального движения электронов в атоме безразлично, будет
ли проекция тп/ орбитального момента положительна или отрицательна. В этом
отношении существует отличие от случая магнитного поля, в котором система элек-
трических зарядов прецессирует вокруг направления поля и два противоположных
направления вращения являются неравноценными.
В неоднородном электрическом поле может происходит расщепление уровня
с заданным J на число составляющих, отличное от числа составляющих в однород-
ном электрическом поле. Это число зависит от симметрии поля и может быть как
больше, так и меньше, чем в случае однородного поля. В случае целых значений J
при низкой симметрии неоднородного электрического поля возможно полное рас-
щепление уровней, как и в однородном магнитном поле. Однако при полуцелом J,
в частности для всех атомов с нечетным числом электронов (см. с. 251), в про-
извольном электрическом поле сохраняется, как установил Крамере, двукратное
вырождение.
Доказанную им теорему о наличии двукратного вырождения уровней системы
с нечетным числом электронов, находящейся в произвольном электрическом поле,
называют теоремой Крамерса, а само вырождение — крамерсовым вырождением.
Крамере показал наличие такого вырождения для системы, содержащей нечетное чи-
сло электронов, путем рассмотрения свойств спиновых функций для систем с нечетным
и с четным числом электронов [205]. Тот же результат был затем получен Вигнером из рассмо-
трения симметрии атомных систем по отношению к изменению знака времени (временной
симметрии, о которой упоминалось в гл. 3, см. с. 64).
§15.1. Общая характеристика явления Штарка
409
Из наличия крамерсова вырождения вытекает, что число подуровней в одно-
родном электрическом поле для уровней с полуцелым J, равное J + 'Д, является
максимально возможным и в случае любого электрического поля. В частном случае
J z= i/2 (например, для уровней у2) расщепления вообще не происходит. Наоборот,
для уровней с целым J в произвольном электрическом поле возможно расщепление
не на J 4-1, а на 2J + 1 невырожденных подуровней.
Разберем вопрос о зависимости штарковского расщепления от напряженности
электрического поля и о величине этого расщепления. Мы здесь ограничимся
случаем однородного электрического поля.
Дополнительная энергия системы, обладающей дипольным моментом Р, в элек-
трическом поле напряженности 8 равна
У = -(Р/).	(15.3)
Выражение (15.3) для дополнительной энергии в электрическом поле анало-
гично выражению (14.1) для дополнительной энергии в магнитном поле. Однако
в отличие от магнитного момента (магнитного дипольного момента) дипольный
момент (дипольный электрический момент) не квантуется и заданное состояние
атомной системы характеризуется средним значением этого момента. Для атом-
ных систем, имеющих центр симметрии, среднее значение дипольного момента
в любом состоянии равно нулю. К числу подобных систем относятся все атомы,
а также молекулы, имеющие центр симметрии. Поэтому атомы не имеют диполь-
ного момента. Только для таких молекул, которые не обладают центром симметрии
и имеют достаточно низкую симметрию, дипольный момент может быть отличен
от нуля (см. § 18.6, с. 527).
При Р = 0 дополнительная энергия (15.3) в электрическом поле обращает-
ся в нуль. При Р 0 получается дополнительная энергия, пропорциональная
напряженности электрического поля — линейное явление Штарка; для молекул,
обладающих дипольным моментом, это явление будет рассмотрено в гл. 19°.
Мы говорили о постоянном дипольном моменте, которым атомная система
обладает в отсутствие электрического поля. Однако следует иметь в виду, что любая
система электрических зарядов в электрическом поле будет обладать и дипольным
моментом, обусловленным электрической поляризацией системы. Такой индуциро-
ванный дипольный момент будет (при не очень сильных полях) пропорционален
напряженности поля:
Ринд-^,	(15.4)
где а — поляризуемость2).
С учетом (15.4) мы получаем дополнительную энергию3)
Г = -^2,	(15.5)
^Там же будет рассмотрен и электрический резонанс для этих молекул, о котором упоминалось
в начале параграфа (см. с. 407).
^Выражение (15.4) справедливо для атомов. Для молекул в общем случае направление Ринд не со-
впадает с направлением /, и поляризуемость будет тензором (см. гл. 17, с. 495).
3) Работа поляризации, определяющая дополнительную энергию, равна

о
о
о
410
Глава 15. Явление Штарка
пропорциональную квадрату напряженности поля. Для состояний с различными
значениями |тп| дополнительная энергия будет различна и получается квадратичное
явление Штарка, типичное для атомов. Величина расщепления мала, составляя
в полях порядка 100000 В/см десятые доли см-1.
Квадратичное явление Штарка имеет место для атомов в слабом электрическом
поле, т. е. в таком поле, в котором дополнительная энергия мала по сравнению
с расстояниями между соседними уровнями. В сильных и в промежуточных полях,
где дополнительная энергия либо больше, чем расстояние между соседними уровня-
ми, либо того же порядка величины, может наблюдаться линейное явление Штарка,
Рис. 15.1. Сдвиг
орбиты электрона
в электрическом поле
при котором расщепление пропорционально напряженно-
сти поля. Такое линейное явление Штарка наблюдается
для атома водорода и для водородоподобных возбужденных
уровней сложных атомов. При этом существенно наличие
близких уровней энергии различной четности; такими уров-
нями являются уровни атома водорода с тем же значением п,
но со значениями I, различающимися на единицу — уров-
ни I = 0 и I = 1 при п — 2, уровни I — 0, 2 и I = 1 при п = 3
и т. д. Вследствие того, что в электрическом поле сим-
метрия атома относительно центра нарушается, состояния
со значениями I различной четности (четные и нечетные со-
ответственно), независимые друг от друга в отсутствие поля,
оказываются между собой связанными, что и приводит, как
можно показать, к линейному явлению Штарка. Расщеп-
ление при линейном явлении Штарка значительно больше,
чем при квадратичном явлении (см. ниже, § 15.3, с. 415).
Для атома нарушение симметрии относительно центра, которым является ядро,
объясняется, согласно наглядным представлениям, тем, что орбиты электронов
под действием электрического поля сдвигаются относительно ядра, как показано
на рис. 15.1 для случая одного электрона. Это смещение не зависит от направления
движения электрона по орбите, в соответствии с рассмотренным выше сохранением
в электрическом поле двукратного вырождения состояний с одинаковым |тп/|.
В квантовомеханической теории штарковского расщепления исходят из дополнительной
энергии (15.3) в электрическом поле и применяют теорию возмущений. Для атома дипольный
момент Р можно представить в виде (см. (4.33)) Р = -е УЗ где г, — радиусы-векторы
t
электронов относительно ядра, считаемого неподвижным, и суммирование производится
по всем электронам. Тогда для энергий возмущения в электрическом поле, направленном
по оси г, найдем:
Среднее значение этой энергии в состоянии с определенной четностью равно нулю. Дей-
ствительно, оно равно
dx =
гр* Ziip dx.
(15.7)
При отражении в центре координаты меняют знак, а произведение гр*гр остается неизмен-
ным, матричный элемент изменяет знак, т. е. не инвариантен и, следовательно, равен нулю.
Однако матричные элементы энергии возмущения по отношению к функциям и
различной четности будут отличны от нуля
Vaf) = / ^„V^dxjto.
(15.8)
§15.2. Явление Штарка для атомов в общем случае
411
При достаточно близких уровнях разной четности эти матричные элементы могут
не удовлетворять условию, выполняющемуся для слабого поля,
|Кд| « |Еа - Е?\.	(15.9)
При обратном условии
\Vafi\>\Ea-E^	(15.10)
соответствующем сильному полю, или при условии
\Vap\~\Ea-Ep\	(15.11)
(случай промежуточного поля) состояния атома в электрическом поле будут описываться
не функциями гра и а их линейными комбинациями
*1>'а = Саа<ра + Caf)il>f>, = С^а + Cppti).	(15.12)
Среднее значение энергии возмущения V в соответствующих состояниях будет отлично
от нуля, что и приводит к линейному явлению Штарка.
Отметим, что волновые функции (15.12), составленные из функций гра и разной
четности, не обладают уже симметрией относительно центра. Однако именно они будут
правильными приближенными функциями при учете возмущения (15.6), нарушающего сим-
метрию атома относительно центра. Для атома водорода при отсутствии поля можно с самого
начала решать задачу в параболических, а не в сферических координатах, при этом уже
в нулевом приближении получаются волновые функции, обладающие только аксиальной,
но не сферической симметрией (см. ниже § 15.3, с. 414).
§ 15.2. Явление Штарка для атомов в общем случае
Как мы видели в предыдущем параграфе, в общем случае для атомов полу-
чается квадратичное явление Штарка — величина расщепления уровней энергии,
а следовательно, и спектральных линий, пропорциональна квадрату напряженности
электрического поля.
Поляризуемость атома а, характеризующая способность электронов смещаться
относительно ядра под действием поля и определяющая по формулам (15.4) и (15.5)
индуцированный дипольный момент и дополнительную энергию в поле, зависит
только от абсолютного значения |тп| квантового числа т. Согласно квантовомеха-
ническому расчету, она выражается приближенной формулой (см. [131], с. 290)
а = А + Вт2.	(15.13)
Дополнительная энергия в электрическом поле равна
АЕт =	= -^(А + Вт2)#2,	(15.14)
и, таким образом, при заданном значении S смещение подуровней с |тп| / 0 отно-
сительно подуровня тп — 0 пропорционально т2 = |тп|2. Число подуровней равно
числу возможных значений (тп|, даваемых формулами (15.1) и (15.2). При отсутствии
вырождения (J = 0 и т — 0) формула (15.14) определяет смещение невырожденного
уровня.
Так как поляризуемость атома тем больше, чем слабее электроны связаны
с ядром, т. е. чем сильнее они возбуждены, то штарковское расщепление для более
высоких уровней больше. Однако даже для высоких уровней абсолютная величина
расщепления мала, составляя, как уже указывалось выше (см. с. 410), даже в весьма
сильных внешних электрических полях всего лишь доли см-1.
Картина штарковского расщепления спектральной линии определяется вели-
чиной расщепления комбинирующих уровней и правилами отбора. Так же, как
412
Глава 15. Явление Штарка
и в явлении Зеемана, имеют место правила отбора (4.157) для дипольного излуче-
ния, Дт = 0, ±1, и при Дт = 0 получаются тг-составляющие (иногда называемые
p-составляющими), соответствующие дипольному моменту перехода, параллельному
полю, а при Дт = ±1 — a-составляющие (иногда называемые ^-составляющими),
соответствующие дипольному моменту перехода, перпендикулярному полю. Вслед-
ствие того, что уровни расщепляются несимметричным образом (см. (15.14)), кар-
тина штарковского расщепления также получается несимметричной; это характерно
для квадратичного явления Штарка.
Для тг- и а-составляющих получаются определенные относительные интенсив-
ности, имеющие разную величину для переходов J —> J nJ —> J-1. Эти интенсивно-
сти можно найти по применимым и к этому случаю формулам табл. 14.1 (см. с. 375),
если учесть совпадение тг-составляющих т —> т, —т —> —т и а-составляющих
т + 1 —> т, —т - 1 —> -т и т - 1 —> т, -т + 1 —> -т.
При квантовомеханическом рассмотрении квадратичное явление Штарка получается
во втором приближении теории возмущении. В первом приближении теории возмущений
среднее значение энергии возмущения (15.3), т.е. матричный элемент f ip'Vipdr, как мы
видели, обращается в нуль (см. с. 410) и А{Е = V = 0.
Во втором приближении мы имеем
д^=Ера7п1,Т|2'	<15-15)
‘ ^a'J'
сс J'
где матричные элементы энергии возмущения (15.6) равны
VaJm, a' J'm $ I ^aJm^ 2 J'mdT.	(15.16)
Так как они пропорциональны то дополнительная энергия (15.15) пропорциональна <^2.
Матричные элементы (15.16) отличны от нуля только для состояний различной четности
и при Д/ = 0, ±1. Из общих выражений для матричных элементов составляющей вектора
по оси z вытекает (см. [14], с. 70), что квадраты модулей матричных элементов
^aJm,a' Jmt VaJm,a' J+lmi VaJm,a’ J—\m
пропорциональны m2, (J 4-1)2 - m2 и J1 - m2 соответственно. При подстановке в (15.15) это
дает член, зависящий от J и для всех подуровней одинаковый, и член, пропорциональный т2,
что и приводит к формулам (15.13) и (15.14).
По мере увеличения энергии атома расстояния между уровнями уменьшаются, сле-
довательно, уменьшаются разности EaJ — Еа<j<, а величина расщепления увеличивается.
При этом нужно учитывать лишь влияние уровней противоположной четности со значения-
ми J' = J, J ± 1.
Из выражения (15.15) получается и критерий, позволяющий определить, является ли
поле слабым или сильным. Поле будет слабым, если |2\2J*7[ < \EaJ - Eaij<\, т.е. когда
отношение
1<1.	(15.17)
Это отношение, согласно (15.15), порядка
VaJm, a' J'm
EaJ ~ Eatjr
(15.18)
и при выполнении условия (15.9) будет мало. Наоборот, если имеет место (15.11), рассматри-
ваемое отношение будет порядка 1, а при условии (15.10) — много больше 1. Таким образом,
мы получаем обоснование критериев (15.9)-(15.11). Существенно, что штарковское расщеп-
ление в слабых полях, т.е. когда выполняется условие (15.9), пропорционально квадрату
напряженности поля.
§15.3. Явление Штарка для атома водорода
413
Явление Штарка, получающееся при условии (15.9), представляет аналогию явления
Зеемана в слабых полях. Отличие, однако, состоит в том, что явление Штарка в слабых полях
квадратично, тогда как явление Зеемана в слабых полях линейно.
§ 15.3. Явление Штарка для атома водорода
Для атома водорода во внешнем электрическом поле $ порядка десятков ты-
сяч В/см наблюдается линейное явление Штарка, представляющее аналогию явления
Зеемана в сильных полях (рассмотренного в гл. 14, с. 389). Теорию штарковского рас-
щепления уровней энергии и спектральных линий в таких полях можно построить,
если пренебречь спин-орбитальным взаимодействием по сравнению с дополнитель-
ной энергией атома в электрическом поле, иначе говоря, если не учитывать тонкой
структуры уровней энергии с заданным значением п, т. е. считать, что для свобод-
ного атома существует вырождение не только по гщ и по ш5, но и по I. Именно
вырождение по Z, вследствие которого совпадают уровни с четными и с нечетны-
ми Z, и является причиной линейного явления Штарка. Расщепляются все уровни
атома водорода, кроме основного уровня 1$25у2 с п = 1, для которого I — О,
mi = 0 (и который лишь смещается), и в любом электрическом поле, даже неод-
нородном, сохраняется двукратное вырождение по ms, в соответствии с теоремой
Крамерса (см. выше, § 15.1, с. 408).
Рассмотрим расщепление уровня
энергии атома водорода с заданным зна-
чением п > 1 в однородном электриче-
ском поле, считая этот уровень перво-
начально вырожденным, в отсутствие
поля, по I, mi и ms. Дополнительная
энергия в электрическом поле не бу-
дет зависеть от ms, так как такое поле
непосредственно не действует на спин
электрона и может оказывать влияние
на него только через спин-орбитальное
взаимодействие; двукратное вырожде-
ние по ms будет сохраняться для всех
подуровней штарковского расщепления
и это расщепление можно рассчиты-
вать, учитывая лишь орбитальное дви-
жение электрона.
Квантовое число т/, определяю-
щее проекцию орбитального механиче-
Рис. 15.2. Параболические координаты
ского момента в однородном электри-
ческом поле (как обладающим аксиаль-
ной симметрией, ср. с. 407), сохраняет
свой смысл. Однако квантовое число I теряет свой смысл и можно вообще его
не вводить, если решать квантовомеханическую задачу об атоме водорода (без учета
спина) не в сферических координатах г, 0 и р (см. рис. 6.6, с. 175), как обычно,
а в так называемых параболических координатах.
Параболические координаты £, ту, р (см. рис. 15.2) являются естественными координа-
тами для решения задач с аксиальной симметрией. Если в качестве выделенной оси взять
ось z, то параболические координаты легко связать со сферическими координатами г, 0 и ср
414
Глава 15. Явление Штарка
по формулам
£ = r(l + cos0) = г + z, tj = r(l - cos 0) = г - z, <р — (р.	(15.19)
Таким образом, угол <р не изменяется, а вместо координат г и 0 вводятся координаты £ и tj.
Поверхности £ = const и tj = const представляют собой параболоиды вращения с осью сим-
метрии z, сечение которых плоскостью, проходящей через ось z, дает два семейства парабол.
В результате квантовомеханического решения задачи об одноэлектронном атоме
в параболических координатах получается (см., например, [131], с. 155) обычное
7 X	RZ2
выражение для энергии (6.13), Е —---где главное квантовое число п выражается
п2
через параболические квантовые числа п\ и п2 и магнитное орбитальное квантовое
число mi по формуле
п = П\ + п2 + \mi\ + 1.	(15.20)
Квантовое число mi определяет, как обычно, значение проекции орбитального
механического момента Mp^=hlz и принимает значения ш/=0,±1,±2,.. ,,±(n-1),
т. е.
\mi\ = 0, 1, 2,..., п - 1,
(15.21)
что находится в согласии с тем, что наибольшее возможное значение I при заданном п
равно п - 1.
Квантовые числа п\ и п2 являются характерными для решения задачи в пара-
болических координатах и принимают значения:
п\ — 0, 1, 2,..., п - 1,
п2 = 0,1, 2,..., п - 1.
(15.22)
При заданном п получается, как легко проверить, п2 состояний, отличающих-
ся значениями гщ, п\ и п2, а при учете двух возможных при этом значе-
/ 1 1\
ний ms, ( ms —	— 2п состояний, в согласии с (6.10), т. е. получается
правильная степень вырождения уровня энергии с заданным значением п.
Действительно, при заданном значении |mj сумма П]+п2 равна п—|тп/|—1, т. е. получается
n-|mj разных состояний (ni = n-|m/|-l, п2 = 0; П] = n-|mJ-2, n2 = 1 и т.д.). При 0
это число нужно еще умножить, учитывая вырождение, на 2. Общее число состояний находим,
суммируя по \mi| = 0, 1, 2,..., п - 1, что дает
п-1
п +	2(п - \mi\) = п + 2п(п - 1) - п(п - 1) = п.
|тп/|=1
Следует подчеркнуть, что эти п2 состояний иные, чем п2 состояний с заданными значе-
ниями п, I и т/, которые мы рассматривали в §6.3 и которым соответствуют волновые
функции (6.40), зависящие от координат г, 0 и Состояниям с заданными п2 и I
соответствуют функции
Ъ <?) = /nI|m/|(0/n2|m/|(v)^m/(^),	(15.23)
являющиеся линейными комбинациями функций (6.40), относящихся к тому же значению mf,
но к разным значениям I. Существенно, что функции (15.23), в отличие от функций (6.40), уже
не являются четными или нечетными. Поэтому среднее значение энергии возмущения (15.3),
взятое по этим функциям, не обязано равняться нулю, как это получается при усреднении
по функциям (6.40), обладающим определенной четностью.
В однородном электрическом поле квантовые числа п\ и п2, так же как и кванто-
вое число гщ, сохраняются, причем энергия оказывается уже зависящей от значений
§15.3. Явление Штарка для атома водорода
415
этих чисел, что и приводит к расщеплению уровня с заданным п на подуровни с раз-
личными значениями п\, П2 и |mj. Дополнительная энергия в электрическом поле,
согласно квантовомеханическому расчету, выражается приближенной формулой
ДЕ = А# + В<£2 +С<?3 + ...,	(15.24)
где коэффициент при линейном члене отличен от нуля и равен
37г2	.	. Aon .	z .
4 =	- ”!) = “Г<”' - ”г)-	<15-25)
Именно этот член играет основную роль при полях, не превышающих нескольких
сотен тысяч В/см, и определяет линейное расщепление уровней энергии и спек-
тральных линий в зависимости от напряженности
ЗЛ2 /
Численное значение постоянной До —	----в (15.25) равно
8тг2тпее
Ао = 1,28 • КГ20-^- = 6,42 • 10-6^—,	(15.26)
В/см	В/см
т.е. в поле напряженности $ — 2 • 104 В/см Aq$ = 1,28 см-1 и штарковское
расщепление для уровней водорода значительно превосходит (даже для уровня
с п = 2) расщепление, связанное с тонкой структурой (см. рис. 6.11, с. 168). Это
и позволяет в полях порядка десятков тысяч В/см не учитывать спин-орбитального
взаимодействия при расчете явления Штарка.
Согласно формуле (15.25), расщепление не зависит непосредственно от значе-
ния mi и определяется только разностью параболических квантовых чисел, п\ — П2,
являясь целым кратным величины AqS'ti (при Z = 1). Разность п\ — П2 принимает,
согласно (15.22), все целые значения от (п - 1) - 0 — п - 1 до 0 - (п - 1) = -п 4-1,
т.е. всего 2(п — 1) 4- 1 = 2п — 1 значений. Соответственно получаются 2п — 1 рав-
ностоящих и симметрично расположенных подуровней. Для п = 2 и п = 3 эти
подуровни показаны на схеме рис. 15.3. В левой части рисунка приведены значения
квантовых чисел mi, п\ и П2- Они принимают значения, определяемые формула-
ми (15.20)—(15.22). Кратность д' вырождения подуровней без учета спина равна 1 и 2
для п = 2 и 1, 2 и 3 для п — 3, а с учетом спина удваивается и равна д = 2д'. Сумма
кратностей вырождения всех подуровней равна, разумеется, 2п2.
Картина расщепления спектральных линий определяется, как и в случае
явления Зеемана, расщеплением комбинирующих уровней и правилами отбо-
ра (4.157) для mi (ms не изменяется, т.е. = 0). При Дт/ — 0 получаются
тг-составляющие, которым соответствует дипольный момент перехода, параллель-
ный полю, а при Дт/ — ±1 получаются a-составляющие, которым соответствует
дипольный момент перехода, перпендикулярный полю. С точки зрения наглядных
представлений тг-составляющие характеризуются линейным осциллятором, ориен-
тированным по полю, а а-составляющие — круговым осциллятором в перпендику-
лярной плоскости.
Поляризация составляющих при поперечном наблюдении такая же, как и при
явлении Зеемана, а при продольном наблюдении, когда имеются лишь а-состав-
ляющие, поляризация отсутствует. Это объясняется совпадением право- и лево-
поляризованных составляющих с Дт/ = 1 и Дтп/ = -1 (а именно составляющих
mi 4-1 mi и -mi - 1 -mi) из-за независимости энергии от знака т/.
На схеме рис. 15.3 показаны возможные переходы, а в нижней части рисунка по-
лучающаяся картина расщепления линии п = 3 —> п = 2, т. е. первого члена На серии
416
Глава 15. Явление Штарка
Г° 2
±1 1
±2 О
О 1
±1 О
1-0 О
2
4
6
4
2
л а ал л л а а ал л л а а л
Рис. 15.3. Подуровни штарковского расщепления для п = 2
и п = 3 и возможные переходы между ними
Бальмера. Картина расщепления линий симметрична как в отношении расположения
составляющих, так и в отношении распределения интенсивностей. Последние мож-
но рассчитать, причем внешние а- и тг-составляющие оказываются весьма слабыми.
Аналогичная картина расщепления получается и для других линий атома водорода.
В очень сильных полях наблюдаются отступления расщепления от линейно-
го закона, обусловленные следующими членами в разложении (15.24), в первую
очередь, квадратичным членом В<^2, который существенным образом сказывается
при напряженности поля /, превосходящей 105 В/см. Коэффициент В определяется
формулой
h6 / п\ 4
S =	tl7»’ - 3<"I - - 9»? + 1’] =
(15.27)
-3(п! -п2)2-9тп? + 19],
h6
где численное значение постоянной Вп —--------?—=—7 равно
1 024тг6т2е6
Во = -1,04- 10~31
эрг	_|А см
----— - -5 22 • 10		.
(В/см)2	’	(В/см)2
(15.28)
Квадратичный член, в отличие от линейного, дает несимметричную картину расщеп-
„	2
ления, а именно смещение подуровней вниз; при этом наличие зависимости от т,
приводит к дальнейшему расщеплению всех подуровней, для которых кратность
вырождения (с учетом спина) больше двух. В полях, превышающих 4 • 105 В/см,
сказывается и кубический член С&3 в разложении (15.24), который также вычислен.
§15.4. Штарковское уширение спектральных линий
417
Исследование явления Штарка для линий водорода в очень сильных полях, вплоть
до полей порядка 106 В/см, показывает хорошее совпадение теории с опытом.
Расщепления при таких полях достигают сотен см-1.
Расчет явления Штарка производится, согласно квантовомеханической теории возму-
щений, исходя из выражения (15.3) для энергии возмущения. В первом приближении теории
возмущений получается линейный член, во втором — квадратичный, в третьем — кубический.
Отметим, что иногда о линейном члене говорят как об явлении Штарка первого порядка,
о квадратичном члене — как об явлении Штарка второго порядка и т.д.
До сих пор мы рассматривали для водорода явление Штарка в сильных полях, когда
можно не учитывать тонкой структуры. Можно рассчитать расщепление в слабых полях,
когда выполняется условие (15.9), и в промежуточных полях, когда имеет место соотноше-
ние (15.11) (см. [134], с. 375). Расстояния между первоначальными уровнями тонкой структуры
определяются при этом величиной спин-орбитального взаимодействия; нужно также учиты-
вать, что для атома водорода совпадают (с точностью до сдвига уровней, см. §6.6, с. 191)
уровни со значениями I = j - !Д и I = j 4- ’Д при заданном значении j. Вследствие этого
совпадения в слабых полях, так же как и в сильных, наблюдается линейное явление Штарка.
В промежуточных полях, наряду с линейным членом, появляется и квадратичный член.
При переходе к сильным полям спин-орбитальное взаимодействие можно учесть в качестве
поправки, которая обусловливает тонкую структуру подуровней штарковского расщепления.
Эта поправка имеет, подобно аналогичной поправке в случае явления Зеемана в сильных
полях (см. (14.58)), вид £mim3, где £ — постоянная4 5\ и приводит к тому, что подуров-
ни с |mj 0 расщепляются на два подуровня, каждый со смещениями £mim3 = ,Д^|т/|
(при mt = |mz|, т3 = !Д и при mt = -|mz|, т3 = -’Д), Cmzm5 - -’Д^т/! (при mz = |mj,
т3 = -’Д и при mi = -|m/|, ms = ’Д). Разумеется, двукратное вырождение подуровней
в электрическом поле, вытекающее из теоремы Крамерса, сохраняется. Например, для уровня
с п = 2 (см. рис. 15.3) четырехкратно вырожденный подуровень ст/ = ±1, т3 = ±’Д рас-
щепляется на два двукратно вырожденных подуровня, а двукратно вырожденные подуровни
с mi = 0, т3 = ± ’Д вообще не расщепляются.
Переход от явления Штарка в слабых полях к явлению Штарка в сильных полях
наблюдается не только для атома водорода, но и для уровней атома гелия и для высоких
возбужденных уровней других атомов, когда при возрастании поля перестает выполняться
условие (15.9). В достаточно сильных полях получается, аналогично случаю атома водорода,
линейное явление Штарка.
В заключение данного параграфа отметим, что благодаря отличию от нуля матрич-
ных элементов дополнительной энергии (15.3), по отношению к двум близким по энергии
состояниям различной четности, возможен переход без излучения между этими состояни-
ями, вероятность которого будет тем больше, чем ближе эти уровни. Именно благодаря
таким переходам в опытах Лэмба при расщеплении в магнитном поле уровня 2 2Si / на два
подуровня а (т = ’Д) и р (т = — ’Д) последний оказывается менее устойчивым (см. с. 401).
Состояние р при наличии электрического поля взаимодействует с состоянием е, со-
ответствующим подуровню т = ’Д уровня 22Р
о
’Д
5)
а так как уровень
22р-/г
не является
метастабильным, то уменьшается и стабильность состояния р. Возможно и взаимодействие
состояния а с состоянием f (m = — ’Д), однако соответствующие подуровни с увеличением
магнитного поля расходятся (тогда как подуровни р и е пересекаются при Н ~ 540 Гс)
и вероятность безызлучательного перехода будет мала.
§ 15.4. Штарковское уширение спектральных линий
Уширение спектральных линий частицы в газе вследствие столкновений этой
частицы с другими частицами газа, согласно статистической теории (см. с. 160),
4) Эта постоянная для разных подуровней будет различной в силу различия первоначальных значений I.
5) Взаимодействие подуровней р и е (Дт = 1) имеет место для электрического поля, перпенди-
кулярного магнитному полю; именно так направлено электрическое поле, возникающее вследствие
электромагнитной индукции, см. примечание на с. 401.
14 1.1К. кв
418
Глава 15. Явление Штарка
получается в результате изменения положений уровней энергии при взаимодействии
данной частицы с окружающими. Изменение положений уровней энергии — их
смещение и расщепление — представляет, как мы указывали, явление Штарка
под действием электрических полей окружающих частиц. Такая точка зрения име-
ет физический смысл, когда продолжительность столкновений достаточно велика
и электрические поля можно считать медленно меняющимися — квазистатическими,
что является основным предположением статистической теории.
Определенный контур рассматриваемой спектральной линии, обусловленный
уширением при столкновениях, является, согласно этим представлениям, результа-
том того, что изменение положения уровней в момент перехода для отдельных частиц
данного рода различно, вследствие различия мгновенных расстояний этих частиц
от частиц, с которыми они сталкиваются. Соответственно для отдельной испускаю-
щей или поглощающей частицы частота перехода и будет отличаться от частоты пе-
рехода Ро Для изолированной частицы, и при усреднении по всем возможным распо-
ложениям частиц, окружающих данную частицу, вместо частоты и получается сово-
купность частот, образующая контур линии. Вид этого контура зависит от характера
электрических полей, создаваемых окружающими частицами и вызывающих штар-
ковское расщепление уровней энергии, и от свойств рассматриваемых частиц, что
определяет величину расщепления и его зависимость от напряженности полей (ква-
дратичную, линейную или иную). При этом величина напряженности поля частицы,
вызывающей расщепление, зависит от ее расстояния R до рассматриваемой частицы.
1
Поле ионов убывает, как —г, поле молекул, обладающих постоянным дипольным
1 R
моментом, — как —, поле атомов и молекул, не обладающих дипольным момен-
том, — еще быстрее. В случае линейного явления Штарка расщепление будет убывать
1
также, как —т, где к — показатель степени, характеризующий быстроту убывания по-
Нг
ля (к = 2 дли ионов, к = 3 для дипольных молекул), в случае квадратичного явления
1
Штарка — как —тг, т.е. значительно быстрее. Чем быстрее будет убывать расщеп-
ление с расстоянием, тем меньше будет уширение спектральных линий, так как тем
меньшее число столкнтовений будет вызывать значительное расщепление. При уве-
личении плотности р газа средние расстояния между частицами будут убывать как
1	-1/3	1 fc/3
—— = р ' и соответственно расщепление будет возрастать как —г~р в случае
3/Р	1	R
линейного явления Штарка и как —тг- ~ р2к^3 случае квадратичного явления Штарка.
RZK
Отметим, что при рассмотрении действия полей окружающих частиц на данную
частицу следует учитывать, что эти поля являются неоднородными [24, 235]. В не-
однородном поле наряду с обычным дипольным взаимодействием между частицами,
которое в случае действия на атом иона, рассматриваемого как точечный заряд,
1
пропорционально —, появляются взаимодействия более высоких порядков, про-
1 1 1
порциональные —г, —,... . Квадрупольное взаимодействие, пропорциональное —г,
Л U К V	л и
может играть особенно существенную роль в тех случаях, когда в однородном по-
ле получается квадратичное явление Штарка. В случае действия точечного заряда
на атом это квадрупольное взаимодействие будет обусловливать расщепление, про-
1
порциональное в то время как учет квадратичного явления Штарка в однородном
§15.4. Штарковское уширение спектральных линий
419
1	11
поле даст убывание расщепления как — (к = 2, —= —т, см. выше), т.е. более
лЪ	л V	Л V
быстрое.
Энергия взаимодействия атома, заряд ядра которого равен Ze, с ионом, обладающим
зарядом еь равна
~ z
у — ^е61 _ V" —
~ R	г' ’
t=i *
где R — расстояние иона от ядра, a г' — от г-го электрона до иона (см. рис. 15.4).
Представляя rj в виде
(15.29)
2
r'i = y/R2 yrl-lRncosPi = у/r2 + г? - 2Rzt = R
2zt- / Ti
~R + \ R
(15.30)
и разлагая это выражение в ряд по степеням г,, мы получим
„ z
у _ %eei _ V”4 gei
~ R R
2z,	( гг
1 “ ~R +
ei 52 е2-
R2
R3
2 -| -
Рис. 15.4.
Взаимодействие атома
с ионом
(15.31)
где первый член дает энергию дипольного взаимодействия атома в электрическом поле
иона» пропорциональную составляющей Pz = - ezi вектора дипольного момента,
а второй член — энергию его квадрупольного взаимодействия,
пропорциональную составляющей Qzz = - ^2 e(zi “ тен’
зора квадрупольного момента (см. (4.76)).
В случае, когда усреднение дипольного члена в (15.31) да-
ет нуль (отсутствие линейного явления Штарка), дополнитель-
ная энергия в первом приближении теории возмущений будет
определяться квадрупольным членом и может быть значительно
больше, чем дополнительная энергия во втором приближении,
обусловленная первым членом (и соответствующая квадратично-
му явлению Штарка).
Если рассматривать взаимодействие атома не с ионом,
а с дипольной молекулой, то дипольное взаимодействие будет
1 1
пропорционально —, а квадрупольное — —, в то время как
квадратичное явление Штарка в данном случае пропорциональ-
1 Л . 1	1 \ „
но I к = 3,	= дб I' ^ак в этом, так и в других
случаях квадрупольное взаимодействие, получающееся при учете
неоднородности поля, может являться, как показывают оценки,
основной причиной уширения спектральных линий [24, 233].
Контур линии, обусловленный штарковским расщеплением, можно, согласно
статистической теории, приближенно рассчитать. Конкретный вид контура зависит
от закона убывания расщепления с расстоянием.
Для простейшего случая, когда возмущающее действие на частицу произ-
водит лишь одна, ближе всего расположенная частица6), контур линии дается
® Это соответствует учету только двойных столкновений, что допустимо при не очень большой
плотности газа.
14-
420
Глава 15. Явление Штарка
формулой [24]
\ л n^/S	/ ( Vs
J(u) = А—-----------777—7 ехР S “ ----------- )
а|р - 1/O|3/S+1	I
(15.32)
где п0 — число частиц в единице объема, а А — коэффициент пропорциональности.
Здесь Ли — среднее изменение частоты, выражающееся через среднее расстояние R
_______________________________________________ Cs
возмущающей частицы от данной по формуле Ли — где s = к в случае
R
линейного и s = 2к в случае квадратичного явления Штарка, a Cs — постоянная,
определяющая абсолютную величину изменения частоты и зависящая от абсолютной
величины штарковского расщепления. Так как среднее расстояние между частицами
1	-1/3
пропорционально —= = п0
то Ли ~ nJ3, т.е. пропорционально ps^3,
где р —
плотность газа, в согласии со сказанным выше (см. с. 418).
Контур (15.32) отличается от контура типа (5.136), характерного для ударной
теории (см. с. 159). Лишь при s = к = 3 для больших \и - i/0| > Ли эти контуры
совпадают.
ГЛАВА 16
МОМЕНТЫ ЯДЕР
И ИХ СПЕКТРОСКОПИЧЕСКОЕ ИССЛЕДОВАНИЕ
§ 16.1. Общая характеристика моментов ядер
Очень важную характеристику атомных ядер представляют их механические
моменты и связанные с ними магнитные и электрические моменты, обусловлива-
ющие сверхтонкую структуру уровней энергии атомов и молекул (см. гл. 1, с. 34).
Основными методами исследования моментов ядер являются весьма разнообразные
спектроскопические методы; к их числу относятся оптические методы изучения
сверхтонкой структуры спектральных линий при помощи приборов высокой раз-
решающей силы, методы магнитного резонанса в молекулярных пучках, методы
поглощения в радиочастотной области спектра. В результате спектроскопических
исследований моментов ядер накоплен, особенно за последние годы при помощи
радиоспектроскопических методов, очень большой материал, на основе которого
можно сделать ряд заключений о строении атомного ядра.
Идея, что сверхтонкая структура спектральных линий обусловлена моментами
ядер, была впервые высказана в 1924 г. Паули [189]. Первые определения моментов
ядер были сделаны в 1927-1928 гг. на основе изучения этой структуры оптическими
методами, затем в 1938-1940 гг. были применены методы магнитного резонанса
в молекулярных пучках и, наконец, с 1946-1948 гг. широко используются методы
поглощения в радиочастотной области спектра, в первую очередь метод ядерного
парамагнитного резонанса. Интерпретация полученных результатов связана, пре-
жде всего, с моделями ядерных оболочек, особенно с моделью сильного спин-
орбитального взаимодействия в ядре, предложенной в 1949 г. Гепперт-Майер [277]
и Йенсеном, Хакселем и Сюсом [278], и с динамической моделью деформируемого
ядра, развитой О. Бором [279].
В данной главе мы изложим основные положения теории моментов ядер и не-
которые применения этих положений для интерпретации результатов спектроскопи-
ческих исследований, не останавливаясь на деталях теории и не разбирая подробно
модели ядра (вкратце они рассмотрены в последнем параграфе главы). Мы начнем
с общих характеристик моментов ядер.
Квадрат спинового механического момента ядра определяется формулой
1г = 1(1 + 1) (см. табл. 2.1, с. 48), где квантовое число I — спин ядра — при-
нимает целые значения I = 0, 1, 2,... для ядер с четным А и полуцелые значения
для ядер с нечетным А; массовое число А равно при этом числу нуклонов (протонов
и нейтронов), образующих данное ядро. Проекция Iz механического момента ядра I
на произвольно выбранное направление z принимает II4-1 значений mj = I, I - 1,
Для протона и нейтрона значение спина полуцелое и равно ’Д’
1Р = 1п= Чг-	(16.1)
422
Глава 16. Моменты ядер и их спектроскопическое исследование
Согласно закону сложения моментов количества движения (см. § 2.4, особенно
с. 51), отсюда следует, что спин ядер, состоящих из четного числа нуклонов, целый,
а спин ядер, состоящих из нечетного числа нуклонов, полуцелый. В частности,
для дейтрона — ядра тяжелого водорода (дейтерия), состоящего из протона и ней-
трона, I = 1. В данном случае при сложении двух моментов, равных [/г, из двух
возможных взаимных ориентаций, параллельной и антипараллельной (/ = 1 и I = О
соответственно), осуществляется первая.
Следует иметь в виду, что полный спин ядра будет, в общем случае, определяться
не просто суммой Г = спинов отдельных нуклонов, а полной суммой как
i
спиновых, так и орбитальных моментов нуклонов:
1=5>+5>’	(16.2)
i	i
где Ц — орбитальный момент г-го нуклона в ядре (подробнее см. ниже, § 16.6, с. 454).
Однако так как значения орбитальных моментов определяются, подобно случаю
электронов в атоме (ср. (6.3)), целыми квантовыми числами, последнее обстоятель-
ство не отражается на зависимости значений I, целых и полуцелых, от четности А.
В соответствии с общей квантовомеханической связью между спином и типом квантовой
статистики (см. с. 74), согласно которой при полуцелом спине имеет место статистика Ферми-
Дирака (волновые функции системы антисимметричны), а при целом спине — статистика
Бозе—Эйнштейна (волновые функции системы симметричны), ядра с нечетным А (I по-
луцелое) подчиняются статистике Ферми—Дирака, а ядра с четным А (I целое) — стати-
стике Бозе—Эйнштейна. Их состояния соответственно описываются антисимметричными
и симметричными волновыми функциями. Наличие у нуклонов целочисленных орбитальных
моментов не изменяет статистики.
Существенное значение для ядерных моментов имеет не только четность общего
числа А частиц в ядре, но четность числа протонов и числа нейтронов. Число
протонов в ядре равно его заряду Z, а число нейтронов равно A- Z. Все ядра можно
разделить на четыре типа:
1) четно-четные ядра:	Z	— четное,	A-Z	— четное	(А	— четное),
2) четно-нечетные ядра:	Z	— четное,	A-Z	— нечетное	(А	— нечетное),
3) нечетно-четные ядра:	Z	— нечетное,	A-Z	— четное	(А	— нечетное),
4) нечетно-нечетные ядра:	Z	— нечетное,	A-Z	— нечетное	(А	— четное).
В первом и в последнем случаях массовое число А четное и, следовательно,
спин 1 целый, во втором и в третьем случаях А нечетное, и следовательно, спин I
полуцелый.
Для четно-четных ядер, как показывает опыт и как вытекает из представлений
о ядерных оболочках (см. ниже, с. 458), спин всегда равен нулю. В противополож-
ность этому нечетно-нечетные ядра имеют, вообще говоря, спин, отличный от нуля.
В частности, для ядра азота №4(Z = 7, A - Z = 1) I = 1.
Для четно-нечетных ядер и нечетно-четных ядер (А — нечетное) спин всегда
отличен от нуля и его минимальное значение равно !/2.
Следует отметить, что больше половины (162 из 273) всех устойчивых ядер —
стабильных изотопов — являются четно-четными ядрами и имеют спин I = 0.
Почти все остальные устойчивые ядра являются четно-нечетными или нечетно-
четными (тех и других имеется примерно поровну, 56 и 50соответственно) и имеют,
следовательно, полуцелый спин. К нечетно-нечетным устойчивым ядрам относятся
Не считая нейтрона (Z = 0, А - Z = 1), и протона (Z — 1, А — Z = 0).
§ 16.1. Общая характеристика моментов ядер
423
лишь пять ядер D2, Li6, В10, N14 и V50; все они имеют целый спин, отличный
от нуля (равный 6 для V50, 3 для Li6 и 1 для остальных ядер).
До сих пор мы говорили о механических моментах ядер. Ядра со спином I ’Д
обладают магнитными моментами, а ядра со спином / > 1 — электрическими мо-
ментами. Как известно, электрические и магнитные моменты могут быть различных
порядков (ср. с. 97), а именно порядка
п = 2, 22, 23,..., 2Z,..., где 1 = 1,2,3,....	(16.3)
Таким образом, возможны мультиполи порядка 2l (I — целое).
В случае электрических моментов мы имеем: момент второго порядка — момент
обычного электрического диполя, образованного двумя равными по величине и про-
тивоположными по знаку зарядами, расположенными на некотором расстоянии,
момент четвертого порядка — момент электрического квадруполя, образованного
двумя противоположно ориентированными и равными по абсолютной величине
диполями (ср. с. 99 и рис. 4.4), момент восьмого порядка — момент электрического
октуполя, образованного двумя квадруполями противоположного знака, и т. д. Пол-
ное число зарядов, положительных и отрицательных, равно 21, откуда и название
диполь, квадруполь и т.д. (в общем случае мультиполь). В случае магнитных момен-
тов мы, аналогично, имеем момент второго порядка — момент магнитного диполя,
т. е. обычный магнитный момент, момент четвертого порядка — момент магнитного
квадруполя, образованного двумя противоположно ориентированными магнитными
моментами, момент восьмого порядка — момент магнитного октуполя, и т.д.
Поле (электрическое или, соответственно, магнитное) убывает с расстоянием г
1
от места нахождения зарядов или магнитных моментов: для диполя — как —,
1	,	у	1	2>
для квадрулоля — как и, вообще, для 2 -поля — как .
Поле произвольной системы движущихся частиц, обладающих зарядами и маг-
нитными моментами, можно характеризовать заданием значений электрических
и магнитных моментов различных порядков. Можно показать в общем виде ([30],
ср. § 19.8, с. 562), что для ядер возможны магнитные мультипольные моменты с не-
четными I, т. е. дипольный момент (I = 1), октупольный момент (I = 3) и т.д.,
и электрические мультипольные моменты с четными I, т. е. квадрупольный мо-
мент (1 = 2), гексадекапольный момент (I = 4) и т.д. При этом ядро со спином I
может обладать моментом с I С 21, т. е. с I = 1 при I = с I = 1, 2 при I = 1,
с I = 1, 2, 3 при I = 3/г и т.д. Таким образом, мы имеем:
1 = 0	1=1/2 1=1 1= 3/2 1 = 2 1=У2			
1 = 0	/А Ь—А /А /А /А /А СП		
МО-	магнитный диполь	(п = 2)
менты	| электрический квадруполь	(п = 4)
отсут-	| магнитный октуполь	(п = 8)
ствуют	| электрический гексадекаполь	(п = 16)
Отдельный заряд можно рассматривать как обладающий моментом первого порядка (в (16.3) ему
соответствует I = 0; поле в этом случае убывает как Уг2).
424 Глава 16. Моменты ядер и их спектроскопическое исследование
Наиболее существенно наличие у ядер с I !/г магнитного дипольного мо-
мента (т. е. обычного магнитного момента) и у ядер с J 1 электрического ква-
друпольного момента, сокращенно называемого просто квадрупольным моментом
ядра3). Лишь в последнее время исследованы отдельные случаи, когда сказывается
наличие у ядер октупольного магнитного и гексадекапольного электрического мо-
ментов [33]. Мы в дальнейшем ограничимся рассмотрением магнитных (магнитных
дипольных) и квадрупольных (электрических квадрупольных) моментов ядер.
§ 16.2. Магнитные и электростатические
взаимодействия ядерных моментов
Спектроскопические проявления моментов ядер и возможность определения их
спектроскопическими методами связаны с тем, что на эти моменты действуют маг-
нитные и электрические поля, внешние и внутренние. Соответствующие магнитные
и электростатические взаимодействия определяют структуру уровней энергии, зави-
сящую как от самих моментов ядер, так и от характера действующих на них полей.
На магнитные моменты ядер действуют магнитные поля, причем энергия маг-
нитного момента в поле пропорциональна величине момента и напряженности поля,
согласно общей формуле (14.1), &Е = —(jtH), для энергии магнита в магнитном
поле Н, Это может быть внешнее магнитное поле, обусловливающее зеемановское
расщепление, и может быть магнитное поле, связанное с электронными моментами
атомов и молекул и обусловливающее взаимодействие магнитных моментов ядер
с электронными оболочками и соответствующую магнитную сверхтонкую структуру
уровней. Возможны также малые взаимодействия магнитных моментов ядер с враща-
тельными магнитными моментами молекул и, наконец, взаимодействия магнитных
моментов ядер между собой; такие взаимодействия приводят к еще более тонкой
структуре.
На квадрупольные моменты ядер действуют электрические поля, причем энергия
квадрупольного момента в электрическом поле пропорциональна величине момента
и градиенту напряженности поля. Так как для однородного поля градиент равен
нулю, то такое поле не влияет на квадрупольный момент. Не влияют на него и не-
однородные внешние электрические поля, вследствие малости значений градиента,
которые могут быть получены на опыте. Достаточно неоднородные электростатиче-
ские поля создаются в атомах, молекулах и кристаллах электронами, обусловливая
взаимодействие квадрупольных моментов ядер с электронными оболочками и соот-
ветствующую электрическую сверхтонкую структуру уровней энергии.
Энергия взаимодействия ядерного момента, магнитного или электрического, поряд-
ка 2*, в соответствующем поле пропорциональна величине момента и I - 1 производной
напряженности поля, т.е. l-й производной потенциала поля. Таким образом, для дипольного
момента это взаимодействие пропорционально самой напряженности поля, для квадруполь-
ного момента — первой производной напряженности, т. е. градиенту поля, для октупольного
момента — второй производной напряженности поля и для гексадекапольного момента —
третьей производной напряженности поля. Так же как и для квадрупольных моментов, доста-
точно большие значения производных напряженности имеют место лишь для внутриатомных
полей, поэтому на моменты высших порядков (I 3) не влияют внешние поля. Эти моменты
проявляются в сверхтонкой структуре, давая дополнительные смещения уровней, помимо
обусловленных дипольными и квадрупольными моментами.
Рассмотрим сначала взаимодействия магнитных моментов ядер; такими момен-
тами обладают (см. с. 424) ядра с J Уз. Мы будем исходить из уже упомянутой
3) Что не может привести к недоразумениям, так как ядра не могут обладать магнитным квадрупольным
моментом.
§ 16.2. Магнитные и электростатические взаимодействия
425
формулы &Е = -(pH) и запишем ее в виде
- -(Ц/Н) = -fJ-iH cos = -Ц/гН,
(16-4)
где pj и piz — магнитный момент ядра и его проекция на выделенное направление z.
Момент рр мы представим, аналогично (14.31), в форме (см. (2.44) и (2.57))
7
Hi =	= 5/Дяд.Г,	(16.5)
7яд
где дЯд = 7ядй
----h — ядерный магнетон, a gj =-------ядерный множитель д.
2трс	'Уяд
За меру величины магнитного момента ядра мы возьмем максимальное значение его
проекции piz, равное
(ДГг)макс — /7/Дяд(/г)макс — 9l Дяд-^ — Д/*
(16.6)
Формулу (16.5) можно также записать, вводя магнетон Бора дб = — Дяд (см. (2.46)
и (2.57)), следующим образом:
те	,
Pi=9i— Дб/ = 9iPtI,	(16.7)
тр
где множитель
9i=9i—	(16.8)
тр
/	те 1 \
и очень мал (gi порядка единицы, а — ~	• I.
\	тр 1 836/
Простейшим случаем является случай, когда магнитный момент ядра может
свободно ориентироваться в однородном внешнем магнитном поле Н. В этом случае
направление магнитного поля является выделенным направлением, соответствующая
проекция piz момента квантуется, принимая значения
THj
Hiz= mcos(fiI,H) = щ— = giH«ami (mj = I, I - I,...,-I),	(16.9)
и мы получаем 21 + 1 равноотстоящих уровней (см. (16.4) и (16.6))
AEmi =	= -у Нт.! (mj = I, I-I).	(16.10)
Аналогично формуле (14.8), определяющей зеемановское расщепление, обусло-
вленное электронными магнитными моментами и имеющее порядок рьН, форму-
ла (16.10) определяет зеемановское расщепление, обусловленное ядерными магнит-
ными моментами и имеющее порядок р^Н. Величина р^Н является естественной
единицей для измерения этого расщепления, по порядку величины в тысячу раз
меньшего, чем нормальное зеемановское расщепление р^Н (см. с. 372). Для ядерного
магнетона, беря его численное значение (2.58), мы получим (ср. (14.5))
Дяд = 0,5050 • 10"23 эрг/Гс = 0,762 • 103 с~'/Гс = 2,54 • 108 см"'/Гс. (16.11)
При изучении ядерного магнитного резонанса в полях порядка 5000-10000 Гс вели-
чины расщеплений будут порядка десятитысячных долей см-1. В поле Н = 5 000 Гс
рЯЛН = 1,27- 10-4см-1, что соответствует частоте резонансного перехода между
соседними подуровнями, равной 3,8 МГц, или длине волны А — 8 • 103 см = 80 м,
относящейся к области коротких радиоволн.
426
Глава 16. Моменты ядер и их спектроскопическое исследование
Отметим, что в магнитном поле Земли порядка #=0,5Гс рЯЛН будет равно 1,27-10 8см 1 =
3,8-102с-1, что соответствует длине волны Л = 800 км; были наблюдены резонансные
переходы при частотах порядка килогерц — ядерный магнитный резонанс в земном магнитном
поле [263]. Удалось получить ядерный резонанс в еще более слабых полях вплоть до Н « 0,01 Гс
при минимальной частоте 40 Гц [263а].
Наблюдение по методу магнитного резонанса вынужденных переходов между
соседними уровнями (16.10) позволяет с большой точностью определять значе-
Д/
ния giPwH — а следовательно, находить, при известной напряженности Н
магнитного поля, величины (16.6) магнитных моментов ядер с данными значениями
спина. Магнитный резонанс, связанный с магнитными моментами ядер, можно
исследовать как в молекулярных пучках, так и методом поглощения; в последнем
случае говорят об ядерном парамагнитном резонансе или просто об ядерном маг-
нитном резонансе (ЯМР) (см. с. 368). Так же, как и в случае магнитного резонанса,
связанного с электронными магнитными моментами, при переходах имеет место
магнитное дипольное излучение с правилами отбора Дтп/ = ±1, и эти переходы
происходят под действием радиочастотного магнитного поля, перпендикулярного
однородному внешнему полю Н.
Вероятности вынужденных переходов могут быть оценены по формуле (14.76),
а коэффициенты поглощения, в случае ядерного парамагнитного резонанса, —
по формуле (14.74). При этом в формуле (14.76) надо брать магнитный момент
перехода, по порядку величины равный ядерному магнетону дЯд-
В настоящее время особенно широко применяются методы ядерного парамаг-
нитного резонанса как для измерений магнитных моментов ядер, так и, в особен-
ности, для изучения строения вещества в конденсированном состоянии, жидком
и твердом4*.
Следует подчеркнуть, что условием применимости основной формулы (16.10)
и возможности расчета pj по этой формуле, исходя из наблюденных значений
частот магнитного резонанса, является наличие свободной ориентации магнитного
момента ядра во внешнем магнитном поле независимо от других взаимодействий.
С наглядной точки зрения это означает, что момент свободно прецессирует
вокруг направления поля.
Свободная прецессия магнитных моментов ядер может приближенно иметь место как
в молекулярных пучках, так и в веществе, в случае равенства нулю электронных магнитных
моментов, что для атомов и ионов осуществляется при J = 0. В подобном случае наличие
электронных оболочек сказывается лишь в некотором экранировании магнитного момента;
это экранирование, обусловленное диамагнитным эффектом, пропорционально напряженно-
сти магнитного поля и приводит к смещению частоты магнитного резонанса. В частности,
при изучении ядерного парамагнитного резонанса в различных веществах наблюдаются сме-
щения — химические сдвиги, зависящие от состава и строения молекул вещества, содержащих
ядра с р! 0. Эти сдвиги могут достигать десятых долей процента, и их исследование в на-
стоящее время является одним из эффективных радиоспектроскопических методов изучения
молекул (см., например, [73, 72]).
В наиболее чистом виде магнитный резонанс ядер и элементарных частиц может на-
блюдаться в пучках этих частиц; в магнитном поле, через которое пропускается такой пучок,
происходит свободная прецессия магнитных моментов. В частости, такой метод был применен
4) Изложение применения ядерного парамагнитного резонанса для исследования строения вещества
можно найти в монографиях Эндрью [37] и Лёше [38]. Здесь же и в монографии Гриве [39] можно
найти описание разнообразных применяемых экспериментальных методов (метода поглощения, метода
индукции, импульсных методов и других, в различных их вариантах).
§ 16.2. Магнитные и электростатические взаимодействия
427
для измерения магнитного момента нейтронов по схеме, аналогичной схеме измерения маг-
нитного резонанса в молекулярных пучках (см. рис. 14.14, с. 398, подробнее см. [42], с. 172) 5\
Очень важным является случай взаимодействия магнитного момента ядра с элек-
тронным магнитным моментом этого атома: именно это взаимодействие в первую
очередь определяет сверхтонкую структуру уровней энергии и спектральных линий
атомов.
Магнитный момент ядра ориентируется в магнитном поле 1Г(0), создаваемом
электронной оболочкой в точке, где находится ядро, и энергию взаимодействия,
согласно общей формуле (16.4), можно записать в виде
ДЯ = -(/z7K(0)).	(16.12)
Магнитное поле Н(0) пропорционально электронному магнитному момен-
ту p>j атома, следовательно, согласно (14.31), и электронному механическому
моменту J(pj = -gpbf)- Так как пропорционально механическому моменту
ядра (д7 = <7/дЯдТ, см. (16.5)), то формулу (16.12) можно записать в виде
&Е = A(IJ) = AIJ cos (I, J),	(16.13)
где А — постоянная магнитного взаимодействия, характеризующая величину вза-
имодействия ядерного и электронного моментов и пропорциональная величине
магнитного момента ядра (о значении постоянной А см. § 16.3, с. 435).
Здесь мы имеем частный случай взаимодействия двух моментов (см. общую
формулу (2.79)). Вводя полный механический момент атома
Г = 1 + 7,	(16.14)
включающий в себя как электронный, так и ядерный моменты, мы можем применить
формулу (2.83), положив в ней J\ — I, J2 = J, J = F, E = &E = Д^агн\
В результате получаем основную формулу для сверхтонкой структуры, обусловленной
магнитным моментом ядра,
, = Z(r+1)-/(/ + |)-J(J + 1)|	(1б15)
где, согласно закону сложения моментов количества движения (2.21)-(2.24), кван-
товое число, определяющее полный механический момент, равно
F = I + J, I + J-1, ...,	(16.16)
т. е. принимает 2J +1 значений при I J и 21+1 значений при I < J. Первоначаль-
ный уровень энергии атома с заданным J расщепляется на соответствующее число
уровней сверхтонкой структуры, причем расстояние между соседними уровнями
этой структуры равно
с _ДР AF - J(F+1)(F + 2) F(F+V>\
4F,F+i — AEf+i — /ХЕр —	------------------------> = A(F + 1).	(16.17)
Расстояние пропорционально, таким образом, F + 1. Мы получили пра-
вило интервалов для сверхтонкой структуры, аналогичное правилу интервалов (9.36)
для мультиплетного расщепления5 6).
5) Удалось измерить подобным способом и магнитный момент д-мезона [271].
6) Связь между векторами, образующими I (см. (16.2)), и векторами, образующими J (см. (9.2)),
не нарушается малым взаимодействием (16.13).
428 Глава 16. Моменты ядер и их спектроскопическое исследование
Абсолютная величина постоянной магнитного взаимодействия А очень мала
по сравнению с постоянной спин-орбитального взаимодействия входящей в фор-
мулы (9.35) и (9.36), которая даже для легких атомов порядка см-1, а для тяжелых
атомов достигает сотен и тысяч см-1. Постоянная А в формулах (16.15) и (16.17)
порядка тысячных и сотых долей см-1; наибольшие ее значения достигают десятых
долей см-1.
В молекулах, наряду с взаимодействиями магнитных моментов ядер с электронными
магнитными моментами, имеют место взаимодействия магнитных моментов ядер с вращатель-
ными магнитными моментами. Формулы (16.13) и (16.17) применимы и в этом случае, если
под J подразумевать вращательный механический момент молекулы. Постоянная магнитного
взаимодействия А вследствие малости магнитных вращательных моментов молекул, которые
по порядку величины равны ядерному магнетону (см. с. 57), чрезвычайно мала и составляет
миллионные доли см-1.
В молекулах и в конденсированных системах возможны и взаимодействия магнитных
моментов ядер между собой. Эти взаимодействия также чрезвычайно малы.
Рассмотрим теперь взаимодействия квадрупольных моментов ядер, которыми
обладают ядра с I 1 (см. с. 423).
Наличие у ядер квадрупольных моментов вызывается тем, что распределение
заряда в ядре не является сферически симметричным. Если бы положительный
заряд ядра Ze был бы распределен сферически симметричным образом, то ядро
не обладало бы электрическими моментами — квадрупольным и более высоких по-
рядков (моментами порядка 2*, где I = 2,4,..., см. выше, с. 423). Если считать, что
ядро не является сферой, а имеет вытянутую или сплюснутую форму с центром сим-
метрии и осью симметрии (см. рис. 16.1, а и б), что находится в согласии с теоретиче-
скими представлениями о ядре, способном деформироваться, то оно будет обладать
электрическими моментами. Электрическое поле вытянутого или сплюснутого ядра
можно представить как наложение поля заряженной сферы, эквивалентного полю
точечного заряда, сосредоточенного в ее центре, и поля положительных и отрица-
тельных зарядов, расположенных на поверхности сферы, приближенно являющегося
полем квадруполя. Квадрупольный момент такого ядра определяется формулой
J (3(2 - r2)p dr = eQ,	(16.18)
V
где р — плотность электрического заряда в точке с координатами £, ту, ( (ось симме-
трии ядра выбрана за ось (), находящейся на расстоянии г от центра ядра, и интегри-
рование производится по всему объему ядра. Полный заряд ядра равен / р dr = Ze
и квадрупольный момент имеет размерность заряда, умноженного на квадрат длины,
т. е. величина Q имеет размерность квадрата длины. Соответственно квадрупольный
момент обычно выражают в см2 и приводят значения Q, а не eQ. Квадрупольные
моменты ядер имеют порядок величины 10-26-10“24см2, т.е. порядок поперечного
сечения ядра. Как известно, радиус г ядра составляет 10-13-10-12 см, и соот-
ветственно г2 порядка 10“26-10“24 см2. Часто применяют специальную единицу
для измерения поперечного сечения ядер, барн. 1 барн = 10-24см2. Соответственно
квадрупольные моменты ядер можно выражать в барнах.
Для сферического ядра квадрупольный момент (16.18) автоматически обраща-
ется в нуль7). Для вытянутого ядра он положителен, а для сплюснутого отрицателен;
71 В этом случае среднее значение г2 = J* r2p dr равно утроенному среднему значению £2, J (?р dr =
С2 = 42 = ч2 = | г2-
§16.2. Магнитные и электростатические взаимодействия
429
Рис. 16.1. Несферическая форма ядра:
а — вытянутая форма; б — сплюснутая форма
это легко видеть из рис. 16.1, если учесть, что квадрупольный момент определяется
лишь избыточными положительными и отрицательными зарядами, расположенными
у поверхности сферы.
Энергия ядра, обладающего квадрупольным моментом (16.18), в неоднородном
электрическом поле, направленном по оси z под углом д к оси симметрии (
ядра (рис. 16.2), как можно показать [32], имеет вид
1 2 1\ ,
&E = ~2eQ~^ ?cos(1619>
4 OZ \ 2.	L J
где — — градиент электрического поля8). Механический момент ядра, в силу
oz
аксиальной симметрии ядра, направлен по оси (. Для атома электрическое поле,
создаваемое электронным облаком, обладает осевой симметрией относительно на-
правления электронного механического момента J и, таким образом, $ есть угол
между направлениями векторов I nJ. Мы получаем энергию взаимодействия (16.19)
8) Так как f =
dtp
dz ’
где <р — потенциал поля,
то
df _ o1 2tp
dz dz2
1 d2tp / 3	2
и AE = -eQ-—-r I - cos ti -
4 dz2 \ 2
1
2
430
Глава 16. Моменты ядер и их спектроскопическое исследование
в виде
Рис. 16.2. Взаимная
ориентация момента
ядря и неоднородного
электрического поля
(16.20)
(16.21)
(16.22)
(16.23)
1 2/ ч	1\
ЛЕ = -~eQ— ( - cos 2(I, J) - - .
4	dz \2 v ’ 7	2/
Вводя постоянную квадрупольного взаимодействия
d<$	d2<p
B = -eQ— = eQ-^
dz	dzz
и подставляя вычисленное Казимиром [265] значение выра-
жения, стоящего в скобках, мы получаем
^С(С + 1) -1(1+1)1(1 + 1)
д р(квадр) _ л4___________
F	21(21 - 1)1(21 - 1)
где введено обозначение С для выражения
С = F(F + 1) - 1(14-1) - J(J + 1),
входящего также в формулу (16.15).
Формула (16.22) определяет, при заданных значениях I и J, дополнительную
энергию состояний с различными значениями F, обусловленную квадрупольным
взаимодействием.
д2<р
Величина — =-------- представляет, с квантовомеханической точки зрения, значе-
dz dzz
ние второй производной потенциала, создаваемого электронами в месте нахождения ядра,
усредненной по электронной
вычислена.
3	2	1
Выражение - cos & — -,
(ср. (14.28)), равно
плотности, т.е. по |^|2, и в простейших случаях может быть
F2 - I2 - J2
входящее в (16.20), если подставить cos (Г, J) = ---------
-J2)2
1 _ 3(F2 - I2 - J2)2 - 4I2 J2
2 ~
I COS 2 (I, J) -	--------- — --------------------.
2 V 7 2	4I2J2	2	8I2J2
Квантовомеханическое выражение, входящее в (16.22), отличается от этого выражения лишь
заменой в числителе, как обычно, F2, I2 и J2 через F(F 4- 1), /(/ 4- 1), J(J 4- 1) и затем С2
через С (С 4- 1), а в знаменателе 2I2 и 2J2 через 1(21 - 1) и J(2J - 1).
Постоянная квадрупольного взаимодействия В для атомов имеет порядок де-
сятитысячных, тысячных и сотых долей см-1. Обычно она значительно меньше А,
но не настолько мала, чтобы ею можно было пренебречь. Имеются случаи, когда
постоянные Л и В по порядку одинаковы.
Для ядер с J 1 сверхтонкая структура определяется как магнитным взаи-
модействием (16.15), так и квадрупольным взаимодействием (16.22) и положение
уровней с различными F при заданных Л и В дается формулой
3
г -С(С + 1) - 1(1 + 1)J(J +1)
= д4магн> + д4ккшр) = А— +	——————------------------,	(16.24)
£	1 1с/ I ^с/	1 }
где, согласно обозначению, введенному выше, С = F(F 4- 1) - 1(14- 1) - J(J 4- 1).
Формула (16.24) является основной формулой, согласно которой из наблюден-
ных расстояний между уровнями сверхтонкой структуры могут быть определены
§ 16.2. Магнитные и электростатические взаимодействия
431
постоянные А и В, связанные с величиной ядерного магнитного момента
и с величиной ядерного квадрупольного момента Q соответственно.
Наблюдаемая в видимой и ультрафиолетовой областях спектра сверхтонкая
структура линий атомов соответствует электрическим дипольным переходам между
уровнями сверхтонкой структуры комбинирующих электронных уровней; линии,
наблюдаемые при исследовании сверхтонкой структуры атомов в радиочастотной
области спектра, соответствуют магнитным дипольным переходам между уровнями
сверхтонкой структуры данного электронного уровня. В обоих случаях имеет место
правило отбора
ДГ = 0,±1	(16.25)
для квантового числа F, являющееся частным случаем общего правила отбора (4.156).
В заключение данного параграфа мы разберем влияние магнитного поля
на сверхтонкую структуру. При сложении моментов I и J магнитный момент
атома можно представить в виде
Др = -9FHf,F,	(16.26)
и так как магнитный момент ядра рТ очень мал по сравнению с электронным
магнитным моментом то множитель др практически определяется множителем gj
для pj. др выражается через gj по формуле
F(F+l)+J(J+l)-/(/+l)
9f-9j	2F(F+1)
(16.27)
Эта формула получается из общей формулы (14.30). Полагая в последней J — F, J\ = J,
J2 — I, д\ = gj, gi — g'j (см. (16.8)), мы находим9)
F(F+1) + J(J + 1)-I(/+1)	,F(F+1)+J(I+1)-J(J + 1)
9F = 9j-------2F(FHj-------------91--------wTIj-------------•	(16-28)
Так как gj очень мало, то, пренебрегая вторым членом в (16.28), мы получим (16.27).
Так как др порядка единицы, то расщепление в магнитном поле, определяемое
магнитным моментом (16.26), порядка р^Н.
В слабом магнитном поле, т. е. в поле, для которого
ДбЖЛ	(16.29)
где А — постоянная магнитного взаимодействия, входящая в (16.15) и (16.24), мы
получаем расщепление каждого уровня сверхтонкой структуры на 2F+1 подуровней.
Однако ввиду малости А условие (16.29) будет выполняться только в очень
малых по абсолютной величине напряженности полях. В обычных полях будет
выполняться противоположное условие
дБЯ> А,	(16.30)
т. е. поле будет сильным и связь моментов I будет нарушаться. Эти моменты будут
независимо ориентироваться во внешнем магнитном поле Н, и полная магнитная
энергия будет равна сумме энергий моментов pj и pj9 определяемых формула-
ми (14.8) и (16.10), и среднего значения энергии их взаимодействия (16.13), которая
при независимой ориентации моментов равна Amjmj. В результате мы имеем
= 9зР-ъНт]-д1р,Я11Нт1+Ат]т1 =	(16.31)
У g'j надо брать знак минус в связи с различием знака в (14.31) и (16.7).
432
Глава 16. Моменты ядер и их спектроскопическое исследование
Обычно малым членом, содержащим дЯд, можно пренебречь, и получается формула
= gjpbHmj + Агг^т^	(16.32)
Это дает большое расщепление порядка р^Н для подуровней с различными mj и ма-
лое расщепление порядка А при заданном mj для подуровней с различными т/.
Среднее значение энергии взаимодействия Л(Г, J) получается по методу, описанному
в § 14.5 (с. 392), исходя из наглядного представления о независимой прецессии моментов J
и I вокруг направления магнитного поля. В отсутствие поля моменты J и I прецессируют
вокруг момента J1, в слабом поле продолжают прецессировать вокруг этого момента, который
более медленно прецессирует вокруг JET, и, наконец, в сильном поле моменты J ni, каждый
в отдельности, прецессируют вокруг Н.
При постепенном увеличении напряженности поля происходит переход от слу-
чая слабого поля к сильному, описанный для электронных моментов в § 14.5
(см. с. 393). При этом сохраняется значение т полной проекции механического
момента, равное
т = mF = mj + mj.	(16.33)
Рис. 16.3. Зависимость расщепления от напряженности магнитного поля
при J = »/2 и / = 3/г-
По оси ординат отложено Е/А, по оси абсцисс — х = gjpbH/2A\ расчет
произведен по формуле Е/А = -
1
21 + 1
4т	-у
ж + ж (см. [142],
формула (3.120) при ДРИ =	= 2А и pt - 0)
§ 16.3. Сверхтонкая структура уровней атома водорода	433
Сопоставление подуровней в слабом и в сильном магнитных полях легко
произвести, если, как было рассмотрено, учесть, помимо сохранения значений т,
правило непересечения подуровней.
Для случая J = х/г (например, для уровней 25у2 и 2Ру2), I = 3/г и зависимость
положения уровней от напряженности магнитного поля Н показана на рис. 16.3.
Для переходов между подуровнями зеемановского расщепления получаются
разные правила отбора в слабых и в сильных полях [32]. Приведем эти правила
для случая магнитного резонанса (магнитные дипольные переходы, для которых
поляризация при поперечном наблюдении противоположна поляризации при элек-
трических дипольных переходах, ср. рис. 4.3, с. 99).
В слабом магнитном поле имеют место правила отбора
= 0	(a-составляющие) при ДР = ±1,
Amf = ±1	(тг-составляющие) при ДР = ±1,0. J	(16.34)
В сильном магнитном поле получаются правила отбора (тг-составляющие)
Дтп/= 0, Amz = ±l	(16.35)
и
Дт7 = ±1, Amz = 0.	(16.36)
В силу правил отбора (16.36) и (16.35) при магнитном резонансе в сильном поле
могут наблюдаться как переходы между уровнями с различными тп/, с частотами
порядка дб#, так и переходы между уровнями с различными mz, с частотами
порядка А. Соответствующие переходы показаны на рис. 16.3.
§ 16.3. Моменты протона, нейтрона и дейтрона
и сверхтонкая структура уровней атома водорода
Особое место при изучении моментов ядер занимает вопрос о моментах про-
тона и нейтрона — частиц, из которых образованы все ядра. Простейшим ядром,
составленным из одного протона и одного нейтрона, является дейтрон — ядро
дейтерия D. Наличие у протона и у дейтрона ядерных моментов непосредственно
определяет и сверхтонкую структуру уровней простейшего атома — атома водорода,
легкого и тяжелого.
Перечисленные вопросы, тесно связанные между собой, мы рассмотрим в дан-
ном параграфе, а в следующем параграфе разберем вопрос о моментах более сложных
ядер и о сверхтонкой структуре уровней энергии и спектральных линий соответству-
ющих элементов.
Сверхтонкую структуру уровней энергии в молекулах и в конденсированных системах
(например, уровней ионов в кристаллах), мы рассматривать в этой главе не будем. Однако,
приводя значения моментов конкретных ядер, мы будем также пользоваться данными, полу-
ченными при спектроскопических исследованиях свободных молекул и вещества в твердом
и в жидком состояниях.
Важнейшей характеристикой протона как элементарной частицы являются,
наряду с его массой тр и зарядом е, механический момент Ip — }/i и соответствующий
магнитный момент рр. Этот магнитный момент положителен, однако не равен
ядерному магнетону, как можно было бы ожидать по аналогии с электроном10).
,0) Что имело бы место, если протон, подобно электрону, точно описывался бы уравнением Дирака.
434
Глава 16. Моменты ядер и их спектроскопическое исследование
Значение магнитного момента протона было определено с очень большой
точностью и оказалось равным
цр = (2,79275 ± 0,00003)/гяд = 1,41044 ± 0,00004 • 1023 эрг/Гс, (16.37)
что соответствует, согласно формуле (16.6) при I — */2, значению множителя gi —
= 5,58550 ± 0,00006.
Дяд
Гиромагнитное отношение для протона имеет значение	=
Ур = (2,67530 ± 0,00004) • 104
(16.38)
Значение ур определено с наибольшей точностью методом ядерного парамагнитного
резонанса [266]. рр получено непосредственно в ядерных магнетонах путем измерения маг-
нитного резонанса в протонном пучке [267]. Окончательные значения были найдены после
внесения небольших поправок.
Нейтрон, не обладая зарядом, имеет, однако, отличный от нуля магнитный
момент рп [269]. Значение магнитного момента нейтрона, согласно наиболее точным
измерениям, равно (см. [42], с. 178)
цп = -(1,91314 ± 0,00005)/хяд = -(0,96620 ±0,00006) • 1023 эрг/Гс, (16.39)
2дп
что соответствует значению множителя gi =-------— —3,82628 ± 0,00010.
Мяд
Таким образом, момент нейтрона отрицателен и по абсолютной величине
меньше магнитного момента протона.
Значение магнитного момента нейтрона определялось в ряде работ [42] по методу маг-
нитного резонанса в нейтронном пучке, как уже отмечалось выше (с. 426). Специальными
опытами было показано, что нейтрон не может обладать дипольным моментом, превышаю-
щим ег0, где г0 — 5 • 1О“20 см.
Дейтрон имеет механический момент, равный сумме механических моментов
протона и нейтрона, т. е. Id = 1. Его магнитный момент равен
Hi = (0,85740 ± 0,00004)дяд = (0,43301 ± 0,00004)  10~23 эрг/Гс,	(16.40)
V>d /Т
что соответствует значению множителя gj, равному — (I — 1), т. е.
Дяд
дт = 0,85740 ± 0,00004.
Значение pd определялось в целом ряде работ; наиболее точные данные получены мето-
дом магнитного резонанса в молекулярных пучках [270]. Сравнение значения (16.40) со зна-
чениями (16.37) и (16.39) показывает, что магнитный момент дейтрона приближенно равен
сумме магнитных моментов протона и нейтрона (0,87961 ^яд). Разница значений pd и рр 4- рп
составляет 0,0222 ^яд, т. е. 2,6 %. Эта разница представляет значительный интерес с точки
зрения теории дейтрона, как простейшего ядра, составленного только из двух нуклонов.
Наряду с магнитным моментом дейтрон, как ядро с I > ’/г, обладает квадру-
польным моментом Q (см. с. 423). Значение этого квадрупольного момента равно
Q = 2,73 • 10“27 см2 = 0,00273 • 10“24 см2.	(16.41)
§16.3. Сверхтонкая структура уровней атома водорода
435
Значение (16.41) вычислено из величины постоянной
квадрупольного взаимодействия, определенной по методу
магнитного резонанса в молекулярных пучках, состоящих
из молекул HD и D2 (наряду с молекулами Н2) [243, 274].
Рассмотрим теперь сверхтонкую структуру уров-
ней энергии атома водорода.
Наличие у протона спина I = приводит к рас-
щеплению каждого уровня атома обычного водорода
с заданным значением J на два уровня со значения-
ми F = J - У2 и F = J + У2. В частности, основной
уровень атома водорода 15 25у2 расщепляется на уров-
ни с jF = 0 и F = 1 (рис. 16.4, а). Уровни атома
тяжелого водорода, дейтерия, расщепляются на три
уровня при J 3/г (F = J + 1, J, J - 1) и на два
уровня при J — V2 (F — 3Д, V2). Расщепление на два
уровня имеет место и для основного уровня 12Sy2
атома дейтерия (рис. 16.4, 6).
Величины расщепления для основных уровней
атомов Н и D были определены с исключительно
высокой точностью при исследовании магнитного ре-
зонанса в атомных пучках [272].
F=1----------
1420МГц
Г=0----------
р= —
' 2
1=1
р=—
р 2
| 327 МГц
б
Рис. 16.4. Сверхтонкое
расщепление:
а — основного уровня атома Н;
б — основного уровня атома D
Измеряя частоты переходов AF — 1, Дт = =Ы между зеемановскими подуров-
нями в зависимости от напряженности поля, легко определить и разность dj_ J+
уровней F — J + 1/2 и F = J - */2 в отсутствие поля.
Для атома водорода
Is 2S|/2 <5о,1 = 1 420,40573 ± 0,00005 МГц » 0,04771 см-1.	(16.42)
Для атома дейтерия
15 ^'/2 д'/г, 3Л = 327>38430± 0,00003 МГц И 0,01092 см-1.	(16.43)
Переходу F — 1 —> F = 0 между уровнями сверхтонкой структуры основно-
го уровня атома водорода соответствует, согласно (16.42), частота 1 420 МГц, что
дает длину волны Л = 21,1 см. Соответствующая линия испускания наблюдается
на опыте — это линия космического радиоизлучения. В данном случае мы имеем
спонтанное испускание, которое оказывается возможным, несмотря на очень ма-
лую вероятность А перехода (составляющую 2,85 • 10~15с-1 [153], что соответствует
времени жизни т ~ 3,5 • 1014 с), благодаря чрезвычайно малой плотности вещества;
испускают эту линию атомы водорода, самого распространенного элемента во все-
ленной, который заполняет, с очень малой плотностью, межзвездное пространство.
Линия водорода Л = 21,1 см в спектре космического радиоизлучения является пока
единственной линией в радиочастотной области спектра, которую удалось наблюдать
в спонтанном испускании.
Величина (16.42), согласно (16.17), равна постоянной магнитного взаимо-
действия А. Для водородоподобного атома можно вычислить значение А. Оно
оказывается, согласно квантовомеханическому расчету, равным [32]
Ra2Z3 тпе
А	—7-----Г\-----------
«Н + -Ьо +1)
436 Глава 16. Моменты ядер и их спектроскопическое исследование
т. е. пропорционально квадрату постоянной тонкой структуры а и множителю gj.
Зная значение этого множителя, можно по найденному из опыта значению А
определить постоянную а. Данный способ позволяет получить значение а с очень
большой точностью.
Формула (16.44) получается при расчете энергии взаимодействия ядерного магнитного
момента pi =	= 9iPbI в магнитном поле, создаваемом в водородоподобном атоме
электроном в состоянии, характеризуемом квантовыми числами n, I и j (ср. (16.12) и ниже).
Постоянная А пропорциональна pj и, следовательно, gh
Для атома водорода в основном состоянии Is 2Sy2 (п = 1, I = О, J = j = ]/2, F = 0, 1),
согласно (16.17) и (16.44),
йо,1 = А = | Ra2 — gi.	(16.45)
3 Hip
Для наиболее точного определения а с помощью значения (16.42) сверхтонкого расщеп-
ления и значения множителя g для протона следует в формулу (16.45) ввести ряд поправок,
в частности, поправку, учитывающую аномалию магнитного момента электрона (см. с. 400)
и значение приведенной массы тп атома (что дает множитель	в формулах (16.44)
и (16.45)). В результате для а получается значение
1
а~ 137,0387 ±0,0010’
очень хорошо согласующееся со значением
1
“ “ 137,0390 ±0,0012’
(16.46)
(16.47)
соглас-
получающимся из измерений тонкой структуры уровня п = 2 атома водорода (см. с. 195).
3
Величина (16.43), согласно (16.17), равна ~А. Отметим, что при этом можно
по-прежнему применять, несмотря на I > ’/г, формулу (16.17), зависящую только
от постоянной Л, но не от постоянной В, учитывающей квадрупольное взаимодей-
ствие. В самом деле, при J = Уг квадрупольный член в (16.24) не зависит от F
и при образовании разности	~ ^EF этот член сокращается10.
Численное значение А для состояния ls25y2 атома дейтерия равно,
но (16.43),
(16.48)
А = |(5у2? зд = 218,25620 ± 0,00002 МГц.
Отношение постоянных А для Н и D должно равняться, согласно
Лн 1 240,40
отношению множителей д/. Действительно, — =-----------— = 6,508 близко
ссосс	218,26
6,515.
0,8574
Лн дн
Некоторое расхождение значений — и — связано с различием приведен-
ных масс атомов водорода и дейтерия и с другими эффектами, обусловленными
свойствами дейтрона. При учете различия приведенных масс введением множите-
/т\3
ля ( — ) (см. выше, с. 436) относительное расхождение составляет 1,7 • 10 4 [42].
\те/
(16.44),
5н
к — =
3d
10 Как при F = Z+ Уг, так и при F = I— Уг величина С(С+ 1) в (16.24) равна /(/+1), см. ниже, с. 442.
§16.3. Сверхтонкая структура уровней атома водорода
437
Согласно формуле (16.44), для заданного водородоподобного атома величина А
и, следовательно, расстояние между уровнями сверхтонкой структуры убывают
с увеличением квантовых чисел п, I и j. В частности, для уровней 2з25|д, 2р2Р\^
и 2р2Рзд атома водорода эти расстояния меньше, чем для уровня Is^S^, в 8, 24
и 60 раз соответственно12).
Уменьшая значение расщепления для атома водорода (16.42) в 8, 24 и 60 раз, мы получим
расщепления для двухквантовых состояний:
2*ч	(п = 2, 1 = 0, J = j =	р р = °,1)	<50,1 = 177,551 МГц,	
2Р^	(п = 2, 1 = 1, J =j =	1	\ -, F = 0,1 ) 2	)	<50 j = 59,184 МГц,	►	(16.49)
2р2Рз/2	(п = 2, 1 = 1, J =j =	з	\ 2’	’ J	<5|>2 = 23,673 МГц. j	
Непосредственное измерение сверхтонкой структуры метастабильного уровня 2s 2Sy2
атома водорода, выполненное по методу магнитного резонанса в атомном пучке [273], дало
значение
2s 2Sy2 $o,i = 177,5566 ± 0,0003 МГц « 0,00591 см'1	(16.50)
в хорошем согласии с соответствующим значением (16.49).
Мы рассмотрели сверхтонкую структуру уровней атома водорода. При переходах
между двумя уровнями, имеющими сверхтонкую структуру, должна получаться сверх-
тонкая структура соответствующих спектральных линий, которую легко рассчитать,
исходя из величины расщеплений (см. (16.17) и (16.44)) и правила отбора (16.25). Од-
нако эту структуру не удается разрешить ввиду малости относительных расщеплений
для линий, лежащих в видимой и ультрафиолетовой областях спектра.
В частности, для линий серии Лаймана (см. рис. 1.2, с. 19) с I/ » 100 000 см-1 и рас-
щеплением нижнего уровня 1$25у2, равным, согласно (16.42), 0,048 см-1, относительная
величина расщепления составляет около 5 • 10-7. Аналогично для линий серии Бальме-
ра с I/ ~ 20 000 см-1 и расщеплением нижнего уровня 2$25у2, равным, согласно (16.50),
0,0059 см-1, соответствующая величина равна примерно 3 • 10-7. Эти значения лежат на пре-
деле разрешения оптических приборов с высокой разрешающей силой, в частности обычно
применяемого для исследования сверхтонкой структуры эталона Фабри и Перо. К тому же
для атома водорода относительная допплеровская ширина даже при очень низких температу-
-6	Az/	-6
рах порядка 10 (см. (5.149)); при Т = 4 К и р = 1 — = 1,42 • 10 —, и лишь при работе
с	с
с атомными пучками можно получить достаточно тонкие спектральные линии.
На примере атома водорода хорошо видны достоинства радиоспектроскопических мето-
дов (в частности, метода магнитного резонанса в атомных пучках), позволяющих измерять
очень малые расстояния между уровнями энергии и притом с очень большой точностью.
Следует, однако, отметить, что эти методы применимы, в первую очередь, для исследования
нормальных состояний атомов. Лишь с трудом их удается применять для изучения мета-
стабильных возбужденных состояний, а для исследований короткоживущих возбужденных
состоянии они практически неприменимы. Такие исследования, однако, возможны при ком-
бинации оптического и радиоспектроскопического методов (см. ниже о методе двойного
резонанса, с. 448).
12^ При этом учтено, что для уровня 2р2Рз^, согласно (16.17), ^1,2 = 2Л.
438 Глава 16. Моменты ядер и их спектроскопическое исследование
§ 16.4. Моменты ядер и сверхтонкая структура уровней
и спектральных линий сложных атомов
В настоящее время накоплен большой материал по моментам ядер. Почти
для всех устойчивых ядер, имеющих отличные от нуля механические моменты,
определены значения этих моментов и, с большей или меньшей точностью, значения
соответствующих магнитных моментов. Для многих устойчивых ядер со спином I
’Д найдены значения квадрупольных моментов. Имеются некоторые данные, хотя
и гораздо менее полные, о моментах неустойчивых ядер.
В табл. 16.1 приведены основные данные о моментах устойчивых ядер, а также
некоторых неустойчивых ядер [30, 42],3). Данные в левой части таблицы относятся
к нечетно-четным и нечетно-нечетным ядрам (последние выделены курсивом),
а в правой части — к четно-нечетным ядрам.
Как показывает таблица, большое число ядер имеет спины I = ’Д и I = 3/г,
однако существует достаточное количество ядер, особенно тяжелых, со значения-
ми I > 3/г. Например, для Bi209 I = 9/2,4).
Магнитные моменты ядер составляют от нескольких десятых дяд до 5-6дяд.
Они являются как положительными, так и отрицательными; при этом для не-
четно-четных ядер значения магнитных моментов, как правило, положительны,
а для большинства четно-нечетных ядер эти значения отрицательны. Различие знака
естественным образом объясняется на основе представлений об ядерных оболочках,
согласно которым моменты нечетно-четных ядер определяются протонами (маг-
нитный момент протона рр > 0), а моменты четно-нечетных ядер определяются
нейтронами (магнитный момент нейтрона рп < 0), см. ниже § 16.6, с. 458.
Наиболее точные значения магнитных моментов получены радиоспектроскопическими
методами магнитного резонанса в молекулярных и атомных пучках и ядерного магнитного
резонанса. Точность этих данных составляет 10“4 и выше. Менее точны данные, получен-
ные при изучении сверхтонкой структуры спектральных линий. Погрешности приведенных
в таблице численных значений магнитных моментов составляют одну или несколько единиц
последнего знака.
Квадрупольные моменты ядер возрастают с увеличением массы ядра. Для легких
ядер они порядка 10“26см2, а для тяжелых ядер — порядка 10“24см2. Значения
квадрупольных моментов как положительны, что соответствует вытянутым ядрам,
так и отрицательны, что соответствует сплюснутым ядрам (см. с. 428).
Точность определения квадрупольных моментов невелика и обычно составляет процен-
ты или даже десятки процентов. Это связано, прежде всего, с тем, что непосредственно
из опыта определяется постоянная квадрупольного взаимодействия (16.21), представляющая
произведение квадрупольного момента eQ и градиента — электрического поля, создавае-
dz
мого электронами в месте нахождения ядра. Градиент — получается путем приближенных
О Z
расчетов, точность которых, как правило, невелика. Со значительной точностью может быть
получено лишь отношение квадрупольных моментов ядер изотопов одного и того же элемента
путем определения постоянной квадрупольного взаимодействия для этих изотопов в одина-
д$
, т. е. при том же значении —,
dz
В\	~	Q\
тогда отношение — постоянных квадрупольного взаимодействия дает отношение — квад-
#2	Q1
рупольных моментов.
ковых условиях (например, для того же атома или молекулы)
13) В таблицу не включены данные для протона, нейтрона и дейтрона, рассмотренные в § 16.3.
,4) Для неустойчивых ядер найдены также и значения I > % (например, I = 8 для Cs134).
Таблица 16.1
Моменты устойчивых ядер
Нечетно-четные и нечетно-нечетные ядра							Четно-нечетные ядра						
ядро	z	A-Z	I	P (В Ряд)	Q (в 10 24 cm2)	конфигурация	ядро	z	A-Z	I	P (в Ряд)	Q (в 10“24 cm2)	конфигурация
уЗ *)	1	2	1/2	2,9788		1-51/2	Не3	2	1	1/2	-2,1274		151/2
Li6	3	3	1	0,82193		(2Рз/2)р(2Рз/2)п	Be9	4	5	3/2	-1,1773	0,02	2^3/2
Li7	3	4	3/2	3,2560		2^3/2							
В10	5	5	3	1,8006		(2Рз/2)р(21?з/2)п	С13	6	7	1/2	0,70216		2^1/2
в"	5	6	3/2	2,6880	0,0355	(M/2)							
N14	7	7	1	0,40357	0,02	(2Pl/2)p(2pi/2)n	О17	8	9	5/2	-1,8930	-0,004	3^5/2
N'5	7	8	1/2	-0,2830		2pi/2							3d35/2
F19	9	10	1/2	2,6285		2s 1/2	Ne21	10	11	3/2	<0		
Na23	11	12	3/2	2,2161	0,11	3d5/2	Mg25	12	13	5/2	-0,85471		3rf5/2
Al27	13	14	5/2	3,6385	0,149	34/2	Si29	14	15	1/2	-0,55476		2s 1/2
рЗ!	15	16	1/2	1,1316		2S]/2	S33	16	17	3/2	0,64274	-0,064	3d3/i
Cl35	17	18	3/2	0,82088	-0,0789	3d3/2							
Cl37	17	20	3/2	0,6833	-0,0621	3d3/2							
К39	19	20	3/2	0,3909	0,14	3d3/2	Са43	20	23	7/2	-1,3172		4Лт/2
j^40 *)	19	21	4	— 1,2981		(3d3/2)p(4/7/2)n							
к41	19	22	3/2	0,2151		3d3/2							
Sc45	21	24	7/2	4,7490		4A/2	Ti47	22	25	5/2	-0,7881		
							Ti49	22	27	7/2	-1,1038		4Л/2
V5O	23	27	6	3,3413		(4/73/4)p (4/7/2 )n	Cr53	24	29	3/2	-0,4744		Зрз/2
V51	23	28	7/2	5,139									
Mn55	25	30	5/2	3,4614	-0,5		Fe57	26	31		-0		
Co59	27	32	7/2	4,6488	>0	4Л/2	Ne61	28	33		-0		
Cu63	29	34	3/2	2,2266	-0,16	3P3/2	Zn67	30	37	5/2	0,8735		4/5/2
Cu65	29	36	3/2	2,3847	-0,15	Зрз/2							
Ga69	31	38	3/2	2,0160	0,178	3^3/2	Ge73	32	41	9/2	-0,8791	-0,21	509/2
§ 16.4. Моменты ядер и сверхтонкая структура уровней сложных атомов 439
Продолжение таблицы 16.1
Нечетно-четные и нечетно-нечетные ядра							Четно-нечетные ядра						
ядро	z	A-Z	I	Д (в Дяд)	Q (в 10 24 cm2)	конфигурация	ядро	z	A-Z	I	Д (в Дяд)	Q (в 10 24 cm2)	конфигурация
Ga71	31	40	3/2	2,5616	0,112								
As75	33	42	3/2	1,4349	0,3	4/,/2	Se77	34	43	1/2	0,5341		3P1/2
Br79	35	44	3/2	2,0992	0,355	3Рз/2	Кг83	36	47	9/2	-0,9671	0,15	59,/2
В г81	35	46	3/2	2,2625	0,280	3^3/2							
Rb85	37	48	5/2	1,3482	0,30	Щг	Sr87	38	49	9/2	-1,0829		55,/2
Rb87 **	37	50	3/2	2,7414	0,14	3^3/2							
у89	39	50	1/2	-0,1368		Ipip	Zr91	40	51	5/2	-1Д		4d5/2
Nb93	41	52	9/2	6,1437		509/2	Mo95	42	53	5/2	-0,9290		4<2
							Mo97	42	55	5/2	-0,9485		44
Тс99’»	43	56	9/2	5,6572		509/2	Ru99	44	55	5/2			4d5/2
							Ru101	44	57	5/2			Ц2
Rh103	45	58	1/2	-0,11		3Р1/2	pdIO5	46	59	5/2	-0,6		
Ag'07	47	60	1/2	-0,1130		3Р1/2	Cd"1	48	63	1/2	-0,59216		3sl/2
Ag109	47	62	1/2	-0,1299		3Р1/2	Cd"3	48	65	1/2	-0,61947		351/2
In"3	49	64	9/2	5,5232	0,750	50^2	Sn"5	50	65	1/2	-0,91319		351/2
Ln"5	49	66	9/2	5,5344	0,761	509/2	Sn"7	50	67	1/2	-0,99489		351/2
Sb121	51	70	5/2	3,3418	-0,5	4^5/2	Те123	52	71	1/2	-0,7359		351/2
Sb123	51	72	7/2	2,5333	-0,7	507/2	Те125	52	73	1/2	-0,8872		3sl/2
J127	53	74	5/2	2,7935	-0,59	4^5/2	Хе129	54	75	1/2	-0,77255		351/2
jl29 .)	53	76	7/2	2,6030	-0,43	50у2	Хе13'	54	77	3/2	+0,68680	-0,12	3d3/2
Cs133	55	78	7/2	2,5789	-0,003	507/2	Ba135	56	79	3/2	0,8306		3d3/2
La139	57	82	7/2	2,761	0,9	50у2	Ba137	56	81	3/2	0,9290		3d3/2
Pr141	59	82	5/2	3,9	-0,05	ц2	Nd143	60	83	7/2	-1,0		5/7/2
							Nd145	60	85	7/2	-0,65		5/y2
							Sm147	62	85	7/2	-0,7		5Л/3
							Sm149	62	87	7/2	-0,6		5/7/2
Глава 16. Моменты ядер и их спектроскопическое исследование
Продолжение таблицы 16.1
Нечетно-четные и нечетно-нечетные ядра							Четно-нечетные ядра						
ядро	z	A-Z	I	(в Дяд)	Q (в 10 24 cm2)	конфигурация	ядро	z	A-Z	I	(в Мяд)	Q (в 10 24 cm2)	конфигурация
Ей151	63	88	s/l	3,4	1,2	42	Gd155	64	91	5s5/2	-0,2		
Ей153	63	90		1,5	2,5	507/2	Gd157	64	93	J: 5/2	-0,3		
ТЬ159	65	94	3/2	1,5		4d3/2	Dy161	66	95				
							Dy163	66	97				
Но165	67	98	7/2			507/2	Er167	68	99	7/2	0,5	-10	
Тт169	69	100	1/2	-0,20			Yb171	70	101	1/2	0,45		
							Yb173	70	103	5/2	-0,66	3,9	5^7/2
Lu175	71	104	7/2	2,9	5,9	507/2	Hf177	72	105	^1/2			
							Hfi”	72	107	>1/2			
Та181	73	108	7/2	2,1	6,0	50p	W183	74	109	1/2	0,1185		
Re185	75	110	5/2	3,1437	2,8		Os'87	76	111				
Rel87.)	75	112	5/2	3,1760	2,6	^5/2	Os189	76	113	3/2	0,6559		
Ir191	77	114	3/2	0,17	1,5	4	Pt195	78	117	1/2	0,6060		4P1/2
Ir193	77	116	3/2	0,17	1,5								
Au197	79	118	3/2	0,14	0,6	4d3 ^“3/2	Hg199	80	119	1/2	0,5041		4P1/2
							Hg201	80	121	3/2	-0,5590	0,65	4H/2
урОЗ	81	122	1/2	1,5960		3s 1/2	Pb207	82	125	1/2	0,5894		4Pi/2
-р|205	81	124	1/2	1,6115		3s 1/2							
Bi209	83	126	9/2	4,080	-0,4	6Л9/2							
Ac227 ‘>	89	138	3/2										
Pa231 ♦>	91	140	3/2				u233 ‘>	92	141	5/2			
							u235 *>	92	143	7/2	-0,8		
Np237 *)	93	144	5/2	6,0	-15		pu239*)	94	145	1/2	0,4		
Np239 *>	93	146	1/2				Pu24l*>	94	147	5/2	1,4		
Am243 *»	95	148	5/2										
*) Неустойчивое ядро
§ 16.4. Моменты ядер и сверхтонкая структура уровней сложных атомов 44
442
Глава 16. Моменты ядер и их спектроскопическое исследование
Рассмотрим сверхтонкую структуру уровней энергии и спектральных линий
атома, обусловленную наличием момента I у ядра. Как мы видели в § 16.2, каждый
уровень атома с полным электронным моментом J расщепляется на 21-]-1 (при I J)
или 2J + 1 (при I J), уровней, характеризуемых значениями (16.6) квантового
числа F, F = J +1, J +1 - 1,..., \J - 1\, и дополнительной энергией (16.24).
Разность энергий двух уровней с F = Fi и F = Fj соответственно равна
= —(Сг ~ Сх) + -В
L	О
c2(£2 + i)-Ci(Ci + i)
1(21- 1)J(2J- 1)
(16.51)
т. е. зависит от постоянной А магнитного взаимодействия и от постоянной В
квадрупольного взаимодействия.
Простейшими являются случаи, когда второй член в (16.51) обращается в нуль;
тогда расщепление уровня с данным J зависит только от Л, т. е. полностью обу-
словлено магнитными взаимодействиями. Формула (16.51) сводится при Fi = F\ +1
к формуле (16.17).
1	d<$	z
Такие случаи осуществляются, когда В = ~^О— = 0 или £2(6*2 + 1) -
4 dz
С\(С\ + 1) = 0. Это будет иметь место:
1.	Для всех ядер с I = х/г> В этом случае квадрупольный момент Q — 0
(см. с. 423), В = 0. Каждый уровень с J Уг расщепляется на два уровня с F = J+ >/2
и F = J - У, и, применяя формулу (16.17), мы получаем величину сверхтонкого
расщепления
^-'/2,j+'/2 = a(j + 0-	<16-52)
Конкретным примером является рассмотренная в предыдущем параграфе сверхтон-
кая структура уровней атомов Н и D.
2.	Независимо от значения I для всех уровней с J — х/г. Для двух возможных
значений F2 = I + ’/2 и F\ = I - х/г разность £2(6’2 + 1) - С\ (С\ + 1) обращается
в нуль (ср. с. 436).
Действительно, согласно (16.23), мы получаем при J = у2 и F2 — I + у2
/	1\ /	3\	3
C2 = F2(F2 + 1)-1(1+1)- J(J+1)= (l+- ) (/+2 )	J;
т. e. C2(C2 + 1) = 1(1 + 1), и при J - i/2, Fj = I - >/2,
Ct + !)-/(!+ 1) - J(J+ 1) = (1-0 (/+ 0 - J -/(/+ ’) = -J~ *>
t. e. Ci (Ci + 1) = 1(1 + 1), откуда и следует, что
C2(C2 + l)-Ci(C1 + l) = 0.
В данном случае для сверхтонкого расщепления имеем, аналогично (16.52),
61-'/2, !+'/! = Л(/+0-	(16‘53)
Примером может служить расщепление уровня пр 2Р\/2 при любом I.
dS
3.	Независимо от значений I и J для всех уровней, для которых — = 0,
dz
т. е. градиент электрического поля, создаваемого электронами, обращается в нуль.
§ 16.4. Моменты ядер и сверхтонкая структура уровней сложных атомов 443
Этот градиент равен нулю для электронов замкнутых оболочек и для s-электронов;
он отличен от нуля при наличии во внешних оболочках атома электронов с I > О,
в частности р-электронов. Соответственно В = 0 для уровней ns %у2, nsn's 3Sj и т.д.
и В / О (при I x/i) для уровней пр 2Рз/^ пР2 3^2°» пР2 3Р\> пР2 ^3, nd 2Ds/2 и т. д.
Равенство нулю градиента поля для замкнутых оболочек и для s-электронов является
следствием сферически симметричного распределения электронной плотности относительно
ядра атома: действительно, отличный от нуля градиент поля, как и любой вектор, ха-
рактеризуется выделенным направлением, а при сферически симметричном распределении
электронной плотности все направления в пространстве, проходящие через ядро, равноправ-
ны. При аксиально симметричном распределении электронной плотности (которое имеет
место, в частности, для р-электронов) ось симметрии является выделенным направлением
и градиент поля ориентирован вдоль этой оси; выбирая ее за ось z, имеем
— — — — 0,	— 7^ О
дх ду dz
(см.(16.19); электронный механический момент также ориентирован вдоль оси симметрии
электронной плотности).
При I > !/з и J > !/з квантовое число F принимает не менее трех значений
и для рассматриваемого случая | — = 0 и, следовательно, Q = О I характерно
у dz	/
выполнение правила интервалов (16.17)
• #F+1, F+2 • • • ♦ = (F+l):(F + 2):... .	(16.55)
В отличие от правила интервалов для тонкой структуры (для мультиплетных
термов с заданными L и S, см. (9.36)), которое является лишь грубо приближенным,
д<£
правило интервалов для сверхтонкой структуры оправдывается, в случае — = О,
dz
с большой точностью. Отступления от него свидетельствуют о наличии квадруполь-
ного взаимодействия15).
Мы рассмотрели ряд частных случаев. В общем случае, когда при I > Уз
для уровней с J > У? градиент поля — / 0, нужно применять полную форму-
az
лу (16.51). Зная не менее двух разностей между соседними уровнями, можно,
согласно этой формуле, найти две постоянные А и В.
При двух известных разностях для определения А и В имеются два уравнения. При трех
или более известных разностях мы получаем соответствующее число уравнений для нахо-
ждения тех же двух постоянных, что делает их определение более надежным. Если соот-
ветствующие уравнения не согласуются друг с другом, то это указывает на отступления
от формулы (16.51), что может иметь место за счет моментов высших порядков, в пер-
вую очередь за счет октупольного момента. При учете октупольного момента надо добавить
в правой части формулы (16.51) член типа C/(F, Z, J), где С — постоянная октупольного
взаимодействия, a /(F, I, J) — определенная функция от квантовых чисел [275].
Наиболее точные данные для сверхтонкой структуры основных уровней ряда
сложных атомов, ядра которых обладают спином I У 0, были найдены по методу
магнитного резонанса в атомных пучках. Так же как и для атома водорода, измерялись
частоты переходов между подуровнями в магнитном поле и из них вычислялись
на основе теории явления Зеемана для сверхтонкой структуры (см. с. 431 и дальше,
подробнее в [32] и [42]) величины расщеплений.
15^ Или взаимодействий высших порядков, в частности октупольных.
444 Глава 16. Моменты ядер и их спектроскопическое исследование
В качестве типичных примеров можно привести данные, полученные для Na,
Т1 и С1.
Для Na23 с I — 3/2 основное состояние 3s 25у2 расщепляется на уровни с F = 2, 1,
расстояние между которыми равно
$1}2 = 2А = 1 771,631 ± 0,002 МГц я 0,059 см-1.
(16.56)
Отметим, что при этом одновременно имеют место перечисленные выше случаи
д&
2(J = i/2, С2(С2 + 1) - СХ(СХ + 1) = 0) и 3 (s-электрон, — = 0).
д z
Для Т1203 и Т1205 с I = ’/г основное состояние 6р 2Ру^ расщепляется на уровни
с F = 1,0, расстояния между которыми равны:
TI203 5lj0 = А = 21 106,1 ± 0,5 МГц я 0,704 см-1,
Т1205 £1>0 = А = 21 311,5 ± 0,2 МГц « 0,711 см"1.
(16.57)
Здесь одновременно осуществляются случаи 1 (/ = !/2, Q = 0) и 2 (J = ’/г).
Мы имеем для атомов Na и Т1 расщепления, обусловленные только магнит-
ными взаимодействиями, аналогично случаю атома водорода. Абсолютная величина
расщеплений может быть представлена формулой, аналогичной формуле (16.44)
для водородоподобного атома, с заменой Z3 и п3 некоторыми эффективными зна-
чениями [32]. Для тяжелых атомов, примером которых является Т1, наблюдаются
значительные расщепления, порядка десятых долей см4, что обусловлено большими
эффективными зарядами ядра.
Для С135
и С137
с I — 3/2 основное состояние Зр5 2Рз/2
расщепляется на четыре
уровня с F = 3,2, 1,0. Здесь мы имеем общий случай, когда нужно учитывать
квадрупольное взаимодействие, и формула (16.51) дает
— А ±- 23, $|,2 — 2А — 23, 52 з — ЗА — В.
(16.58)
Из найденных на опыте значений расстояний $0,ь ^1,2 и 52 3, согласно (16.58),
получаются значения А и В:
,с ( А = 205,050 ± 0,005 МГц» 0,00685 см-1, '
С135 <!
[ В = 54,873 ± 0,005 МГц » 0,00185 см”1,
„ ( А = 170,681 ± 0,010 МГц » 0,00569 см”1,
С137 <!
(В= 43,253 ±0,001 МГц и 0,00144 см”1. J
(16.59)
Мы видим, что в данном случае расщепление обусловлено как магнитными,
так и электростатическими взаимодействиями, причем последние в несколько раз
меньше первых (ср. с. 430).
Имеются и случаи, когда В > А. Такой случай осуществляется для I127 с I = 5/2. Основной
уровень атома 5р5 2Р°3^ расщепляется на 4 уровня с F — 4, 3, 2, 1 и для А и В получаются
значения:
1Г7 ( А = 827,265 ±0,003 МГц « 0,0276 см"1,
I127 <
I В = 1 146,356 ± 0,010 МГц « 0,0382 см”1.
(16.60)
§ 16.4. Моменты ядер и сверхтонкая структура уровней сложных атомов 445
Отметим, что здесь имеются отступления от формулы (16.51), которые объясняются
наличием октупольного взаимодействия с постоянной С — 0,0023 ± 0,0004 МГц. Из величины
этой постоянной можно вычислить значение Q октупольного момента, равное Q — (0,17 ±
0,003) • 10"24ряд. Данное значение имеет правильный порядок величины рядй2, где R —
размеры ядра!6) (см. [42], с. 243 и [70], с. 129 и 137).
Сверхтонкая структура уровней энергий атомов может быть определена пу-
тем изучения оптическими методами сверхтонкой структуры спектральных линий
в видимой и ультрафиолетовой областях спектра. Точность оптических методов
значительно ниже, чем точность метода магнитного резонанса в атомных пучках;
расщепления определяются в лучших случаях с точностью до десятых долей про-
цента, а обычно с точностью порядка процентов. Однако эти методы позволяют
находить расщепления не только нормальных, но и возбужденных уровней атомов,
и обладают более широкой областью применимости, с экспериментальной точки
зрения, по сравнению с методом магнитного резонанса в атомных пучках. Они
особенно эффективны для определения значений спина ядра и для приближенной
оценки величины магнитных моментов ядер.
Спектральная линия, обладающая сверхтонкой структурой, представляет сово-
купность составляющих, соответствующих переходам между двумя расщепленными
уровнями, верхним и нижним, со значениями F\ = J\ 4-1, J\ 4-1 - 1,..., | Jj - I\
и F2 = J2 + I, Jz +1 - 1,..., IJ2 - I\- Согласно правилам отбора, разрешены пере-
ходы F2 = F\, F\ ± 1 и получающаяся картина сверхтонкой структуры аналогична
картине тонкой структуры при нормальной связи. Квантовым числам L, S и J
соответствуют квантовые числа J, I и F, мультиплетам типа L —> L — ли-
нии J —> J (J2 — J\), мультиплетам типа L L- 1 — линии J —> J - 1 (J2 = J\ - 1),
сохранению значения S (т. е. мультиплетности х = 2S 4- 1) — неизменность I.
При этом, при значении спина, равном I, мы имеем картину, аналогичную муль-
типлету с к — 21 4- 1, т.е. сверхтонкая структура линий при I = ’Д аналогична
дублетам, при 1=1— триплетам и т.д. Общие формулы (9.42)-(9.44) для отно-
сительных интенсивностей остаются справедливыми при замене J на F, L на J
и S на Т. Соответственно применима, при целых значениях J для комбинирующих
уровней (т. е. для сверхтонкой структуры спектральных линий атомов с нечетным
числом электронов), и табл. 9.12 (с. 270). Для линий J-*JhJ->J-1 получаются
характерные распределения интенсивностей, описанные в §9.6.
Примером может служить сверхтонкое строение резонансного дублета Na
5 895,9 А и 5 890,0 А (D-линий), связанное с наличием у Na23 спина I = 3/г-
На рис. 16.5 показаны схемы соответствующих переходов и получающиеся картины
расщепления.
Сверхтонкая структура D-линий была впервые обнаружена Терениным и Добрецовым
в 1928 г. [197]. Каждая линия оказалась состоящей из двух компонент, соответствующих
переходам на два нижних уровня с F — 2 и F = 1 (расщепление верхних уровней 2р2Р°^
и 2р 2Ру2 много меньше расщепления нижнего уровня 2s 2S у2 и не было обнаружено вследствие
недостаточного разрешения).
В данном случае величина спина не может быть определена из числа компонент
(равного двум, так как J = У2), но может быть найдена из отношения интенсивностей
16) Порядок величины электрических моментов с заданным I (см. с. 423) равен eRl, а магнитных
моментов с заданным I равен pRl~l, где д — дипольный магнитный момент (I — 1). Для октуполя I = 3.
446
Глава 16. Моменты ядер и их спектроскопическое исследование
2
F — 2
F=1
F = 2
F= 1
2
F = 3
F = 2
F=1
F = 0
F = 2
F=1
Л = 5896 A
Л = 5896 A
Рис. 16.5. Сверхтонкая структура D-линий.
A(2Sy2) = 0,02955 см"1. Расщепления уровней 2Р^ и 2Р^ малы
и показаны в преувеличенном масштабе
двух компонент, равного
21 4- 2 _ I 4- 1
21 ~ I
(16.61)
На опыте получилось отношение 1,7, согласующееся лишь с теоретическим отно-
шением 5/з = 1,67 статистических весов для I = (е = 3 при I — и е С 1,4
при I 5/2).
Другой пример представляет сверхтонкая структура линии 4 324 А Со I, для ко-
торой схема переходов и получающаяся картина расщепления показаны на рис. 16.6.
В данном случае на опыте наблюдаются восемь компонент, соответствующих наи-
более интенсивным переходам типа AF —	= 1. По числу компонент сразу
определяется значение I = 7/2 (21 + 1=8).
Ценную информацию об ядерных моментах может дать изучение явления
Зеемана на сверхтонкой структуре спектральных линий. Характерным для явления
Зеемана в данном случае является то, что, в силу малости сверхтонкого расщепления,
уже сравнительно небольшие по абсолютной величине внешние поля являются
сильными (выполняется условие (16.30)) и легко может наблюдаться независимая
ориентация моментов I и J, каждый из которых будет прецессировать независимо
вокруг направления поля. В соответствии с формулой (16.32), при переходе между
двумя уровнями с множителями д, равными д\ и д2, и с постоянными магнитного
взаимодействия Aj и А2, частоты переходов	—► mj2 будут равны
6mjs,mj2 = (д2Тп]г - дхгпз^ЦъН + (Агт]г - А^т^Упц.	(16.62)
Аналогично (14.54) и (14.55) правила отбора будут Amj = 0, ±1 и Amj = 0.
В результате каждая составляющая mj, —> mj2, получающаяся при отсутствии сверх-
тонкой структуры (тг-составляющая при Amj =	— mj2 = 0 и a-составляющая
§ 16.4. Моменты ядер и сверхтонкая структура уровней сложных атомов 447
9
8
7
6
5
4
3
2
8
7
6
5
12
И,Н	,1. , .1 ... I,	см-
-100 0	100 200 300 400 500 600 700
Рис. 16.6. Сверхтонкая структура линии
Л =
4234 А Со I, 3d74s24F9/;!—3d74s(a5F)4p6^y2(a4ry2-26FJ1/j).
А! = A(4F9/2) = 0,014 см"1, Л2 = AfiF^) = 0,028 см"';
сплошные линии — переходы AF = F2—F = 4-1,
крупный пунктир — переходы ДГ = F2—F\ — 0,
мелкий пунктир — переходы &F = F2—F\ — -1
(очень слабы и в нижней части рисунка не показаны)
при Дтп/ = тпjj - mj2 = ±1, см. начало § 14.2), будет расщепляться на 214-1 соста-
вляющих mj = /, I - 1,..., -I, находящихся на равных расстояниях ^2mj2 - A\mJr
По числу этих составляющих сразу определяется значение I.
Подобная картина наблюдается, в частности, у висмута, для которого бы-
ла подробно изучена сверхтонкая структура большого числа спектральных линий
и впервые проверены теоретические схемы расщепления. В достаточно сильном
магнитном поле получается обычная картина зеемановского расщепления, согласно
схеме типа (14.38), но каждая составляющая расщеплена на 10 равноотстоящих
составляющих в соответствии со значением I = ЭД для ядра Bi209. На рис. 16.7
показана картина расщепления линии 4 722 A Bi I, для которой описанное явление
наблюдается очень отчетливо.
448
Глава 16. Моменты ядер и их спектроскопическое исследование
D„-'P
-3
1/2 -*-1/2
3/2 —1/2
1/2-1/2
I	<л = <А>3/2) = 1,225, g2 = g(*Py2)j= 2,088
1	2	3 см 1
Г IГТ1ТП------------“мпт-
-1/2-1/2
-3/2--1/2
Рис. 16.7. Сверхтонкая структура линии Л = 4 722,55 A Bi I,
6s26p3 2Л°3д—6s26p2(3Po)7s4Py2 в магнитном поле. Картина расщепления
рассчитана по формуле (16.62) для поля Я = 42 800 Гс (рьН = 2 см !)
при 4, = A(2D^) = -0,040 см-1 и А2 = А(4Р^) = 0,166 см“';
Jl = 3/2, J2='/2, I=9/2
Для линий со сверхтонкой структурой зеемановское расщепление существенным обра-
зом влияет на поляризацию резонансного испускания (см. с. 24). Как можно показать,
получающаяся при возбуждении линейно-поляризованным светом частичная поляризация
резонансного испускания атомов, находящихся в магнитном поле, зависит от значения I
спина ядра. Это явление используется в одном из вариантов метода двойного резонанса,
разработанном Кастлером с сотрудниками [255] ,7\ Поляризация резонансного испускания
атомов, находящихся в постоянном магнитном поле Яо, уменьшается, если одновременно
приложить радиочастотное поле Н\, вызывающее резонансные переходы между подуровнями
зеемановского расщепления возбужденного уровня атомов, являющегося начальным для это-
го испускания. По этому методу можно определять сверхтонкую структуру возбужденных
уровней атомов и притом как при больших, так и при малых расщеплениях.
В заключение этого параграфа следует отметить, что наблюдение сверхтонкой
структуры спектральных линий осложняется при наличии изотопов тем, что разные
изотопы данного элемента дают различную сверхтонкую линий, которые имеют
место также для изотопов со спином ядра I — 0 и различны для разных изотопов.
В следующем параграфе мы рассмотрим более подробно изотопическое смещение
уровней энергии и спектральных линий.
§ 16.5. Изотопическое смещение уровней энергии
и спектральных линий
В спектроскопии важную роль играют изотопические эффекты, связанные с изо-
топическим замещением, т. е. с заменой в изучаемой атомной системе данных ядер
ядрами изотопов, имеющими другую массу при том же заряде ядра. Особенно су-
щественны эти эффекты в молекулярной спектроскопии: относительные положения
как колебательных, так и вращательных уровней энергии и частоты соответствую-
щих переходов могут при изотопическом замещении изменяться весьма значительно,
в частности, при замене легкого водорода тяжелым на десятки процентов. Здесь
изменение массы ядер непосредственно сказывается на скорости их колебательного
и вращательного движений. Соответствующие молекулярные изотопические эффек-
ты, вращательный и колебательный, будут рассмотрены в части III (см. с. 558 и с. 597).
Изотопические эффекты в атомной спектроскопии проявляются в гораздо меньшей
степени, так как изменение массы ядра при том же его заряде лишь незначитель-
но сказывается на движении электронов атома (см. § 6.2). Только при изучении
|7) Методом двойного резонанса принято называть метод, в котором одновременно осуществляется
для данной атомной системы резонанс на двух частотах.
§ 16.5. Изотопическое смещение уровней энергии и спектральных линий 449
сверхтонкой структуры электронных уровней энергии атомов изотопические эф-
фекты становятся весьма существенными. По сути дела изотопическим эффектом
является изменение сверхтонкой структуры, вызванное изменением моментов ядра,
различных для разных изотопов данного элемента.
Так как большинство химических элементов, встречающихся в природе, имеют
несколько изотопов, то наблюдаемая для этих элементов картина расщепления
представляет наложение картин расщепления для разных изотопов.
При переходе от четного изотопа к нечетному, вместо целого спина (для четных
изотопов чаще всего равного нулю), получается полуцелый спин. При переходе от одного
изотопа к другому, обладающему той же четностью, спин может не изменяться, однако
и в таких случаях всегда в большей или меньшей степени изменяются магнитные (при I ’Д)
и электрические (при 1^1) моменты ядра. В табл. 16.1 можно найти ряд таких примеров:
Ga69 и Ga71, Мо95 и Mo97, Cd111 и Cd113 и т.д.
Изотопическим смещением называют не связанное со сверхтонким расщеплени-
ем смещение электронных уровней энергии и изменение частот переходов между
ними (выражающиеся в смещении линий в спектре) при изотопическом замещении.
Величина изотопических смещений обычно того же порядка, что и величина сверх-
тонкого расщепления, и составляет десятые и сотые доли см'1. При наблюдении
в видимой или ультрафиолетовой областях спектра смеси изотопов (естественной
или искусственной) при помощи оптических приборов с большой дисперсией по-
лучающаяся картина очень часто определяется как сверхтонким расщеплением, так
и изотопическим смещением. Каждый изотоп дает свою линию, соответствующую
данному электронному переходу, простую при I = 0 и расщепленную при I 1/г.
При этом величина сверхтонкого расщепления может быть в конкретных случаях
как больше, так и меньше величины изотопического смещения.
Наиболее сложная картина получается, когда сверхтонкое расщепление при-
мерно такой же величины, что и изотопическое смещение.
Подобный случай имеет место для линий ртути, в частности для резонансной
линии 2 537 А, структуру которой мы рассмотрим подробнее. У ртути существует
семь устойчивых изотопов со следующим процентным содержанием:
196	198	199	200	201	202	204 1	,	.
0,146	10,02	16,84	23,13	13,22	29,80	6,85 /	(10.63)
За исключением изотопа Hg196, процентное содержание всех других изотопов до-
статочно велико и поэтому их линии достаточно интенсивны. Четыре четно-четных
изотопа Hg198, Hg200, Hg , Hg204 имеют спин I — 0 и дают четыре нерасщеп-
ленные линии, расположенные примерно на равных расстояниях. Изотопы Hg199
с I = ’Д и Hg201 с I = % дают линии, расщепленные соответственно на 2
и на 3 компоненты (рис. 16.8, а). В результате получается сверхтонкая структура
линии 2 537 А, изображенная на рис. 16.8, d; пунктиром показаны положения линий
изотопов Hg199 и Hg201, которые получились бы при отсутствии расщепления18). Все-
го получается пять компонент, интенсивность которых определяется содержанием
соответствующих изотопов и отношениями интенсивностей компонент сверхтонкого
расщепления для Hg199 и Hg201.
В наиболее чистом виде изотопическое смещение можно изучать, когда сверх-
тонкое расщепление отсутствует или достаточно мало по сравнению с этим смеще-
нием. Следует подчеркнуть, что если для изучения сверхтонкого расщепления лучше
всего работать с разделенными изотопами, то изотопическое смещение в принципе
18)Эти положения соответствуют центрам тяжести уровня бзбрЗр*, отмеченным на рис. 16.8, о
пунктиром.
15 Зак. 103
450
Глава 16. Моменты ядер и их спектроскопическое исследование
(201)
199А
204:201 а
Hg 1
(/-{)
202
0,246	2
6s6p3PjF=4
0,493
6s%F=y
200
),444
0,190
201 с°
I____2
199 В
(199)
5 ;i98
20lli
-0,354-0,329 -0,179 -0,0540
-0,350
0,136 0,168
0,143
0,389 0,390 СМ




Рис. 16.8. Сверхтонкая и изотопическая структура
линии Л — 2 537 A Hg I:
а — сверхтонкая структура для изотопов 199 и 201;
б — картина расщепления линии
необходимо изучать в смеси изотопов; притом желательно работать с примерно
одинаковыми содержаниями исследуемых изотопов.
Для легких элементов изотопические смещения убывают с увеличением массы,
для средних элементов они малы, а затем, для тяжелых элементов, возрастают
с увеличением массы. Это связано с тем, что для легких элементов изотопические
смещения определяются конечной массой ядра (массу ядра дЯд = М нельзя считать
бесконечно большой по сравнению с массой те электрона), а для тяжелых элемен-
тов — конечным объемом ядра (нельзя считать ядро точечным и пренебрегать его
размерами). Таким образом, изотопическое смещение обусловлено двумя разными
факторами. Мы рассмотрим их в отдельности и начнем с массового эффекта.
Как отмечалось в §6.2, для одноэлектронного атома постоянная Ридберга,
при учете движения ядра, определяется формулой (6.17):
р -	Д°°	~ р (1 _ 7716 А
М
Соответственно абсолютное значение Т энергии атома, отсчитываемое от границы
ионизации (величина терма), выражается, согласно (6.13), формулой
Z2	Z1 /	те \	(	те\
Т--^-Я-у=Л0О— 1--^ =Тоо 1“ ,	(16.64)
п2	п2 \	М J	\	М )
где через Тж обозначено абсолютное значение энергии при бесконечно большой
массе ядра. Уровень энергии лежит тем глубже, чем больше масса ядра, и величина
смещения при переходе от ядра с меньшей массой М] к ядру с большей массой М2
равна
ДТ — Т2 - Т| — Too (
у Mj
тЛ _т те(М2-М})
М2) ~ 00 MiM2
(16.65)
§ 16.5. Изотопическое смещение уровней энергии и спектральных линий 451
Изотопические смещения принято считать положительными, когда уровень
энергии сдвигается вниз и когда частота перехода увеличивается при увеличении
массы ядра. Формула (16.65) дает положительные изотопические смещения. При этом
для получения смещения Др спектральной линии нужно вычесть из смещения ДТ"
нижнего уровня смещение ДТ; верхнего уровня. В данном случае
. // А , и	тпе(М2-М\)
&V = ДТ" - ДТ' = (Т" -		(16.66)
М}М2	М\М2
Для атома дейтерия по сравнению с атомом водорода получается относительное
1 тпе 1	_4	,
смещение ----- « -  „ ~ 2,7 • 10 , что дает при и — 20 000 см абсолютное
2 7ПН 3 670
смещение порядка 5 см-1 (ср. табл. 6.2, с. 169).
С увеличением массы ядра изотопическое смещение быстро убывает, при М2 «
1
М1 = М как —г, т.е. обратно пропорционально квадрату массы. При М — 10
М* 1
и ДМ — 1 мы получим относительное смещение -^тнс, а ПРИ М = 40 и ДМ —
1 - - Jnn^e19)> В последнем случае, соответствующем Ca (Z = 20), изотопические
1 600
смещения для видимой области спектра будут порядка тысячных долей см-1.
Формула (16.66) относится к одноэлектронным атомам. Для многоэлектронных
атомов учет движения ядра сложнее, однако порядок величины изотопического
смещения, обусловленного конечной массой ядра, по-прежнему определяется этой
формулой и отличие получается лишь в численных значениях смещения, которые
могут расходиться на несколько десятков процентов. При этом относительные
смещения Д^м,м+1 и Д^м+1,м+2 Для изотопов с массами М, М + 1 иМ + 1, М + 2
обычно близки друг к другу, в согласии с формулой (16.66); расхождения по большей
части не превышают 10%.
Особенно малы изотопические смещения для элементов периодической системы
с Z от 30 до 40. Они обычно не превышают тысячных долей см-1 и в ряде
случаев не могут быть обнаружены. Для более тяжелых элементов изотопические
смещения возрастают вследствие влияния конечного объема ядра — объемного
эффекта, к рассмотрению которого мы и перейдем.
Следует отметить, что этот эффект представляет значительный интерес для изу-
чения строения атомных ядер (в частности, четно-четных, для которых I = 0).
Физическое объяснение объемного эффекта состоит в том, что в атоме элек-
тростатическое взаимодействие электронов с ядром зависит, для ядра конечных
размеров, от распределения заряда по объему ядра. Для точечного ядра с заря-
дом Ze потенциальная энергия электрона на малом расстоянии г от ядра рав-
Ze^
на------(ср. (7.1)) и неограниченно убывает с уменьшением г (см. рис. 16.9,
г
кривая а). Для ядра с объемно распределенным зарядом потенциальная энергия
при расстояниях г < R, где R — радиус ядра, будет убывать медленнее и остается
конечной (кривые б и в для двух значений R{ и R2 радиуса ядра при том же его
заряде). Если электрон все время движется вне ядра, то его энергия не зависит
от радиуса ядра; если же он временами проникает внутрь ядра, то его энергия
зависит от радиуса ядра и будет тем больше, чем больше этот радиус. Для такого
Где М к тпе выражены в единицах атомной массы, т.е. те =. ——.
1 835
15*
452
Глава 16. Моменты ядер и их спектроскопическое исследование
Рис. 16.9. Зависимость потенциальной
энергии электрона от размеров ядра
проникающего электрона должен наблюдать-
ся сдвиг уровня энергии вверх, который бу-
дет возрастать с увеличением радиуса ядра.
На рис. 16.9 схематически показаны положе-
ния А, В нВ одного и того же уровня энергии,
соответствующие кривым а, б и в.
Как известно, радиус ядра R растет с уве-
личением его массового числа А (объем ядра
пропорционален А и радиус соответственно
пропорционален Л1/3), поэтому для более тя-
желых изотопов данного элемента R больше,
чем для более легких. Соответственно изото-
пическое смещение должно быть отрицатель-
ным при переходе от изотопа с массой М\
к изотопу с массой М2 > М\, уровень смеща-
ется вверх (от В к В в случае рис. 16.9).
Согласно описанной картине, изотопи-
ческое смещение для состояния электрона, характеризуемого определенным рас-
пределением электрической плотности, должно быть велико, если эта плотность
велика вблизи ядра. Действительно, изотопическое смещение для тяжелых ядер
в основном определяется наличием s-электронов, для которых максимум электрон-
ной плотности достигается в начале координат (см. с. 175); изотопическое смещение,
обусловленное электронами I Ф 0, очень мало.
На опыте наблюдается изотопическое смещение Дг/ спектральных линий,
равное разности № — ДТ' изотопических смещений комбинирующих уров-
ней (ср. с. 451). Отметим, что при этом существенно то смещение, которое опре-
деляется внешними электронами, участвующими в переходах, смещение же, обу-
словленное электронами внутренних оболочек, состояния которых не изменяются
при оптических переходах, одинаково для начального и конечного состояний. По-
этому под ДТ" и ДТ; можно подразумевать изотопические смещения уровней,
обусловленные только внешними электронами. При этом обычно для конфигу-
раций, не содержащих внешних s-электронов, смещение ДТ полагается равным
нулю. Опыт показывает, что смещение уровней для конфигураций, содержащих два
электрона ns, примерно вдвое больше смещения для конфигураций, содержащих
один такой электрон, как этого и следует ожидать.
Знак смещения линии зависит от того, какой уровень смещается сильнее,
верхний или нижний. Для часто наблюдаемых переходов ns -> пр между ниж-
ним 5-уровнем и верхним P-уровнем, например, для резонансных линий атомов
с одним и с двумя s-электронами в нормальном состоянии, нижний уровень сдвига-
ется вверх сильнее, чем верхний, и смещение линии отрицательно, т. е. происходит,
при увеличении массы изотопа, в сторону меньших частот, т. е. больших длин волн.
Для одного внешнего s-электрона (случай атомов щелочных металлов) ДТ" = ДТ < О
для уровня ns
2s'h
и ДТ'
О для уровней пр
2ро
Ч, V/
Для двух внешних электронов (слу-
чай атомов щелочно-земельных металлов и атомов Zn, Cd и Hg) ДТ" « 2ДТ для уров-
ня ns2 г5о, ДТ' ~ ДТ для уровня nsnp3P{. В обоих случаях получается отрицательное
смещение резонансных линий порядка ДТ, где ДТ — смещение, обусловленное одним
электроном ns. Примером может служить изотопическое смещение для резонансной ли-
нии Hg2537A (см. рис. 16.8).
§ 16.6. Модели ядра и теории моментов ядер
453
Существенной является зависимость изотопического смещения от массы при на-
личии трех или более изотопов. Наибольшее число данных имеется для элементов
с четным Z, у которых существует по нескольку стабильных изотопов. Расстояния
линий для последовательных четно-четных изотопов (Z четное, А четное) по боль-
шей части примерно одинаковы, обычно совпадая в пределах 10%. Однако центры
тяжести20) линий четно-нечетных изотопов того же элемента располагаются не посре-
дине между линиями четных изотопов, а дополнительно сдвинуты в сторону изотопов
с меньшей массой. Например, для линии Hg 2537 А (аналогичная картина получается
и для других линий) расстояния для пар четных изотопов 198-200, 200-202, 202-204
относятся как 0,94 : 1 : 0,98; для нечетных изотопов 199 и 201 центры тяжести линий
близки к линиям изотопов 198 и 200 соответственно (см. рис. 16.8).
Абсолютная величина изотопического смещения для тяжелых ядер возрастает,
как отмечалось выше (с. 451). Для U, Ри и Ат изотопические смещения (для изо-
топов с массовыми числами, отличающимися на 2 единицы) достигают величины
около 1 см-1.
Считая ядра сферически симметричными с радиусом R, пропорциональным А1/3
и выбирая определенным образом распределение заряда (например, полагая плот-
ность заряда внутри ядра постоянной2’)) можно вывести формулу для изотопического
смещения, обусловленного объемным эффектом [276]. Согласно этой формуле, изо-
топическое смещение возрастает с ростом заряда и радиуса ядра и получается
правильный порядок величины смещения.
Однако численные значения для большинства элементов оказываются меньше
теоретических, за исключением элементов с Z около 60, для которых наблюденные
значения смещений значительно больше теоретических. Расхождение опыта с тео-
рией можно объяснить приближенностью теории, не учитывающей ряда факторов,
в частности, несферичности ядра и возможности его деформации при взаимодей-
ствии с электронами. Учет этих факторов позволяет объяснить, по крайней мере
качественно, большие значения изотопического смещения [276, 35, 32]. Существен-
но, что при этом в изотопическом эффекте проявляются свойства не только ядер
с I > 0, но и ядер I — 0, т. е. не обладающих спином.
§ 16.6. Модели ядра и теории моментов ядер
Теоретическая интерпретация большого экспериментального материала по мо-
ментам ядер, а также данных по изотопическим смещениям для тяжелых ядер
возможна на основе современных моделей ядра. Для объяснения свойств атомных
ядер был предложен ряд моделей ядра, начиная от капельной модели и кончая оболо-
чечными моделями. Для капельной модели характерно рассмотрение коллективного
движения нуклонов, подобного движению в капле жидкости, для оболочечных
моделей, наоборот, в основу кладется рассмотрение ядра как системы, состоя-
щей из частиц в определенных индивидуальных квантовых состояниях, подобно
2°) Четно-нечетные изотопы (/ > 0) имеют, в отличие от четно-четных изотопов (/ = 0), сверхтонкую
структуру.
21) В этом случае потенциальная энергия при г < R имеет вид
3 1 / г \21 Ze1
U~ ~2 + 2\R)	1Г'
Ze2	3 Ze1
что дает U = ——- при г = R и U =------при г = 0. Именно так построены кривые на рис. 16.8.
R	2 R
454
Глава 16. Моменты ядер и их спектроскопическое исследование
электронам в атоме22). Эти модели представляют разные подходы к решению задачи
о строении атомного ядра и каждая из них позволяет истолковать значительное
число фактов, но является лишь определенным приближением, не позволяющим
объяснить всю их совокупность.
Основой теории ядерных моментов является оболочечная модель ядра в пред-
положении сильного спин-орбитального взаимодействия (см. с. 421), которая весьма
успешно объясняет значения спинов ядер и периодические закономерности стро-
ения ядер, так называемые «магические числа» нуклонов, равные 2, 8, 20, 28, 50,
82, 126; ядра, содержащие такое число протонов или нейтронов, являются особенно
устойчивыми и имеют свойства, характерные для заполненных оболочек.
Для ряда ядер эта модель позволяет приближенно рассчитать и значения маг-
нитных и квадрупольных моментов, однако во многих других случаях она приводит
к неудовлетворительным результатам. В частности, это относится к аномально боль-
шим значениям квадрупольных моментов для некоторых тяжелых ядер. Объяснение
значений магнитных и особенно квадрупольных моментов тяжелых ядер, а также
аномально больших изотопических смещений (см. с. 453) возможно на основе дина-
мической модели деформируемого ядра О. Бора. Эта «обобщенная» модель удачно
дополняет оболочечную модель сильного спин-орбитального взаимодействия там,
где последняя не дает удовлетворительных результатов.
Мы вкратце рассмотрим принципы современной теории ядерных моментов23).
Согласно модели ядерных оболочек, движение каждого нуклона в ядре проис-
ходит в усредненном поле, создаваемом всеми остальными нуклонами. Важнейшей
характеристикой движения нуклона является значение его орбитального момента I.
Также как и для электронов в атоме, для последовательных значений I применяются
обозначения:
/=0123456
з р d f g h i
(16.67)
Получается ряд 8-состояний нуклона в ядре, обозначаемых в порядке возрастания
энергий нуклона как 18, 28, 38,..., ns (где п 1), ряд p-состояний, обозначаемых
как 2р, Зр,..., пр (где п 2) и т.д., и мы приходим к схеме состояний
18	"
28	2р
38	Зр	3d
48	4р	4d	4f	►
58	5р	5d	5f	5g
6s	6p	6d	6f	6g	6h
7s	7p	Id	7/	7g	7h 7г, >
(16.68)
аналогичной схеме (6.12).
Расположение соответствующих уровней
может быть легко получено в двух
предельных случаях: для потенциала, соответствующего гармоническому осциллято-
ру (рис. 16.10, а), и для сферической потенциальной ямы радиуса R, равного радиусу
ядра (рис. 16.10,0.
22) Частицы (протоны или нейтроны) при этом, так же как и электроны в атоме, рассматриваются как
неразличимые, и речь идет об «одночастичных» квантовых состояниях, описываемых антисимметричными
волновыми функциями (см. с. 202).
23) Более подробное изложение этих вопросов можно найти в монографиях Майер и Йенсена [27],
Блин-Стойля [33] и Финберга [28]. Работы по обобщенной модели ядра собраны в двух выпусках «Проблем
современной физики» [29].
§16.6. Модели ядра и теории моментов ядер
455
Рис. 16.10. Потенциал для нуклонов:
а — модель гармонического осциллятора; б — модель ящика
В первом случае получаются равноотстоящие уровни, причем самым глубоким
является s-уровень, далее следуют — р-уровень, совпадающие з- и d-уровни, р-
и /-уровни и т.д., как указано на рис. 16.10,а.
Этот результат вытекает из решения квантовомеханической задачи для трехмерного
гармонического осциллятора с потенциальной энергией
U(г) = ~ кг2 = ~ к(х2 + у2 + z2),	(16.69)
соответствующей квазиупругой силе / — —кг. Возможные значения энергии равны сумме
энергий трех линейных гармонических осцилляторов, колеблющихся вдоль осей ж, у, z:
(	1 \	/	1 \	/	3\
Е = hv\vx +	+ hvlvy + - j +hvlvy + - I = hvlv+-j.
(16.70)
где v — классическая частота колебаний, v
Vx, Vy, Vz
квантовые числа,
принимающие целые значения 0,1,2,..., v = vx + vy + vz — полное колебательное квантовое
число, также принимающее любые целые значения. Нулевая энергия, в соответствии с тремя
1	3
степенями свободы, равна 3 • - hv — -hv. В отличие от одномерного случая, все уровни,
кроме уровня v = 0 (ух — vy — vz = 0), являются вырожденными, в соответствии с числом
возможных комбинаций квантовых чисел vx, vy, vz при заданном v. При v = 1 получаются 3
комбинации 1 +0 + 0 = 1, 0+1 +0 = 1, 0 + 0+1 — 1, при v = 2—6 комбинаций: 1 + 1 +0 = 2,
14-0+1 = 2, 0+1 + 1 = 2, и2 + 0 + 0 = 2, 0 + 2 + 0 = 2, 0 + 0 + 2 = 2 и т. д. Общее число
комбинаций, т. е. степень вырождения, равно сумме целых чисел от 1 до v + 1
1 + 2 + 3 +... + (v + I) =	+	+ 2\	(16.71)
что дает при v = 0,1,2, 3,4,5,6 степени вырождения 1, 3, 6, 10, 15, 21, 28. Как можно
показать, это будут состояния с / = 0, с I = 1, с I = 0 и 2, с I = 1 иЗ, с I = 0,2
и 4 и т.д., т. е. последовательные состояния с четными I при четном v и с нечетными I
при нечетном v, в согласии с тем, что состояния с четными v и I четные, а состояния
с нечетными v и I — нечетные (меняют знак при отражении в начале). Полная степень
вырождения 52 21+1 равна (16.71) как при суммировании по четным I от 0 до v при четном v,
так и при суммировании по нечетным I от 1 до v при нечетном v, что легко проверить24\
24> Мы имеем при четных v 1 + (2 + 3) + (4 + 5) + ... + [v + (v + !)] = 1 + 5 + 9 + ... + (2v + 1) =
v(v + 1)
(2 • 0 + 1) + (2 • 2 + 1) + ... + (2v + 1) =--—- и при нечетных v (1 + 2) + (3 + 4) + ... + [v + (v + 1)] =
3 + 7+11 + ... + (2v + 1) = (2 • 1 + 1) + (2 • 3 + 1) + ... + (2v + 1) =	—-.
456
Глава 16. Моменты ядер и их спектроскопическое исследование
Во втором случае, т. е. для постоянного потенциала, получаются уровни, распо-
ложенные более сложным образом, причем уже нет совпадения уровней с различ-
ными значениями /, как в первом случае.
Расположение уровней при постоянном потенциале получается решением соответству-
ющей квантовомеханической задачи, причем аналогично случаю кулоновского потенциа-
ла (задача об атоме водорода) в силу сферической симметрии переменные разделяются
в сферических координатах, и волновые функции ищутся в виде произведения типа (6.40) ра-
диальной функции на угловую функцию. Угловые функции получаются те же, что и для атома
водорода (ср. замечание на с. 199), а радиальные функции, так как здесь U(r) = 0 при г R
и U(г) — оо при г R, имеют уже иной вид (получаются бесселевы функции порядка 14- ’Д).
При нумерации состояний, согласно схеме (16.68), при помощи целого числа п уровни
при заданном п лежат тем глубже, чем больше I.
Легко произвести сопоставление уровней в обоих случаях. При постепенном
изменении потенциала от параболической формы к прямоугольной расположение
уровней будет меняться, однако будут сохраняться значения I и уровни с одинако-
выми I не должны пересекаться, в соответствии с общим правилом непересечения
уровней с одинаковыми сохраняющимися квантовыми числами (см. §14.5, с. 394).
Такое сопоставление произведено на рис. 16.11, причем учтено расщепление уровней
гармонического осциллятора с О 2.
Можно ожидать, что для легких ядер потенциал будет ближе к параболическому потен-
циалу, а для тяжелых ядер — к прямоугольному. Это может дать разницу в расположении
более высоких уровней. Для более глубоких уровней, как показывает рис. 16.11, их порядок
при переходе от одного предельного случая к другому сохраняется.
Для полной характеристики состояний нуклонов в ядре нужно, наряду с кван-
товыми числами пи/, задать, так же как и для электронов в атоме, значения
проекций орбитального и спинового моментов количества движения. При задан-
ном I mi — I, I - 1,..., -I, т. е. принимает 21 + 1 значений. Спин нуклонов I =
(спин для протона и для нейтрона одинаков, 1р — 1п = ’Д, см. (6.1)) и mj — 1/г, - ’/2-
Подобно уровням электронов в атоме, для уровней нуклонов в ядре заданным
значениям п и I соответствует gi — 2(2/ + 1) состояний с различными mi и тп/,
и числа gi определяют степени вырождения этих уровней. Для нуклонов в ядре
также имеет место принцип Паули25): не может быть двух нуклонов с одинаковыми
наборами квантовых чисел, т. е. в данном случае с одинаковыми наборами п, /, mi
и mj. Соответственно получаются нуклонные оболочки, заполняющиеся 2(2/+ 1)
нуклонами каждая.
При этом необходимо учесть весьма существенное обстоятельство, что в отли-
чие от электронной оболочки атома, в ядре имеются два сорта частиц — прото-
ны и нейтроны. Принцип Паули следует применять для каждого сорта нуклонов
в отдельности25 26*, т.е. рассматривать независимо последовательное заполнение про-
тонных и нейтронных оболочек. Отметим, что при том же наборе уровней для про-
тонов и нейтронов само расположение уровней может несколько отличаться, так
как силы, действующие в ядре на протоны и на нейтроны, не совсем одинаковы27).
25) Так как спин нуклонов полуцелый и, следовательно, они описываются антисимметричными вол-
новыми функциями (см. с. 74 и 202).
26) Свойства волновых функций по отношению к перестановкам частиц (из свойства антисимметрии
волновых функций и вытекает принцип Паули) относятся к одинаковым частицам.
27) Наряду с ядерными силами, которые предполагаются одинаковыми для протонов и нейтронов
и играют основную роль, для протонов, особенно в тяжелых рядах, необходимо, как известно, учитывать
кулоновские силы отталкивания.
§ 16.6. Модели ядра и теории моментов ядер
457
hv
6—56-С168;
4s/5,d> t
5—42—(112
•Ц/2-П -С^38) S
1V2-14-(F2'6)^'
-1/2- 2—.,'(112)
"i37z—уг- б-ч(Юб),,'-
Л'\____7/2_ 8 _У(100)
г—VI-10^(82)
K/timR'
--5p-6-(038)-~55
 _7г—26—(132)-__ sn
-5/--14-(106)-
-7г—26-(132)-
-45
4 —30—(70)
j /—3/2“ 4 —_ _ _
a--4—V2— 6 -^'(64)
8 “\(50)
g-/ к
--3s—2—(92)-“ 40
--6Л—22-(90)~
-4<Z-10-(68)- зз
1 3—2О-(4О)4;)--
^-9/2-10^(50)
-30
-5р-18-(58)-
— Зр-6—(40)- 25
'И*- 8 -'(28)
— 20
--4/"—14—(34)-
.,/2-2 —
у2-4-(18)
•У2- 6 “^(14)
--2s-2—(20)—15
—3d-10-(18)-
- 10
1/2-2-<*>
3/2-4-('6)
~--2р —6 —(8)— 5
2—12-(20)-$—
Р
S .
d
Р
Е
(2)
0-L2-(2)4jH-------S-------1/2- 2—--
-L-1 № 2 -(2)0
Рис. 16.11. Схема уровней нуклонов в ядре
Согласно принципу Паули для схемы рис. 16.11, числа нуклонов в последова-
тельно заполняющихся оболочках равны 2, 6, 10, 2, 14, ... . Полное число нуклонов
данного сорта, указанное на рис. 16.11 в скобках и соответствующее заполнению всех
глубоких уровней, кончая данным, равно 2, 8, 18, 20, 34, 40, 58, 68, 90, 92, ... . Та-
ким образом, можно ожидать особой стабильности ядер с соответствующим числом
протонов или нейтронов.
В описанной схеме объясняются магические числа 2, 8, 20, соответствующие
особенно стабильным ядрам Не4 (7=2, А - Z = 2), О16(7 = 8, А - Z = 8)
и Са40 (Z = 20, А - Z = 20) с заполненными как протонными, так и нейтронными
оболочками, однако магические числа 28, 50, 82 и 126 остаются необъясненными.
Требуется также дополнить схему, для объяснения наблюдаемых значений спинов
ядер, предположениями о сложении орбитальных и спиновых моментов. Характери-
зуя каждый нуклон орбитальным моментом Ц и спиновым моментом Г:, мы можем
458
Глава 16. Моменты ядер и их спектроскопическое исследование
складывать эти моменты в полный момент I (см. (16.2) и ср. (9.2)) в различной
последовательности.
Конкретизацией модели ядерных оболочек является предположение о сильном
спин-орбитальном взаимодействии, которое и привело к успешному объяснению
магических чисел и значений спинов ядер, о чем уже упоминалось в начале пара-
графа (с. 454). Согласно этому предположению, для каждого нуклона его спиновый
момент и орбитальный момент I,- складываются в полный момент
j, =1,4-1,,	(16.72)
и соответственно при каждом значении Ц > 0 получаются два уровня со значения-
1
2
ми ji = Z, ± Только при Ц = 0 ji = li
получается один дважды вырожденный
уровень. Спин-орбитальное расщепление <Vi/2,z+i/2 уровня нуклона с заданным I
будет зависеть от I и предполагается, что оно возрастает с увеличением I и что глубже
лежит уровень с большим j. Тогда расположение уровней получается таким, как
показано в центральной части схемы рис. 16.11. В результате оболочки, характеризу-
ющиеся значениями n, I и j, заполняются 2j + 1 частицами. Последовательные обо-
лочки будут содержать 2,4, 2, 6,4, 2, 8,... нуклонов и их общее число составляет 2, 6,
8, 14, 18, 20, 28, 32, 40, 50, ... , причем в этом ряду будут встречаться и магические
числа 28, 50, 82, 126. Именно эти числа будут соответствовать наибольшим рассто-
яниям между уровнями, т. е. наибольшей устойчивости соответствующих оболочек.
Для каждого ядра, состоящего из Z протонов и А - Z нейтронов, легко опреде-
лить, согласно схеме рис. 16.11, протонную и нейтронную конфигурации. Например,
для Al27 (Z = 13, A-Z — 14) мы получим конфигурацию протонов
и конфигурацию нейтронов Ьу^ру^р^дЗс^д. Нуклоны с заданными значения-
ми n, I и j обозначены символом nlj, а их число указано, как и для электронных
оболочек, индексом справа сверху. В данном случае последняя нейтронная оболочка
заполнена полностью, а в последней протонной оболочке не хватает одного протона.
Теперь рассмотрим, на основе представления об ядерных оболочках при сильном
спин-орбитальном взаимодействии, интересующий нас вопрос о моментах ядер.
Для заполненных оболочек результирующий механический момент равен нулю
и для ядер, у которых заполнены как протонные, так и нейтронные оболочки, 1 = 0.
Эти ядра содержат четное число протонов и четное число нейтронов, а поэтому
являются четно-четными. Для объяснения равенства нулю спина четно-четных ядер
с незаполненными оболочками и для нахождения значений спина четно-нечетных,
нечетно-четных и нечетно-нечетных ядер делается дополнительное предположение.
Оно состоит в том, что при четном числе протонов или нейтронов в незаполненных
оболочках их моменты, складываясь, дают I = 0, и что значения I > 0 получаются
благодаря сложению моментов нуклонов в оболочках, содержащих нечетное число
частиц. Равенство нулю момента при четном числе частиц в оболочке легко понять
на основе наглядного представления о том, что происходит попарная компенсация
моментов.
В результате данного предположения для всех четно-четных ядер как с запол-
ненными оболочками (например, О16, Z — 8), А - Z = 8, так и с незаполненными
оболочками (например, Ne22, Z = 10, А - Z = 12) спин 1 = 0.
Для четно-нечетных ядер, содержащих нейтронные оболочки с нечетным числом
нейтронов (например, Ca43, Z = 20, А - Z — 23), и для нечетно-четных ядер, содер-
жащих протонные оболочки с нечетным числом протонов (например, V51, Z = 23,
А - Z = 28), спин определяется моментами частиц в такой оболочке. Как правило,
§ 16.6. Модели ядра и теории моментов ядер
459
он просто равен моменту одного неспаренного нейтрона или протона, что находится
в соответствии с представлением о попарной компенсации моментов. Например,
для Са43 с нейтронными оболочками 15у22р4д2ру23^д3^4/2252у24/3/2 и для V51
с такими же протонными оболочками / = 7/г, т. е. равно значению полного момента
нуклона 4/7Д. В обоих случаях три внешних нуклона с заданным j дают такой же
спин, как и отдельный нуклон; можно представить себе, что моменты пары нуклонов
компенсируют друг друга и остается неспаренный нуклон. Имеются, однако, случаи,
когда момент ядра определяется всеми нуклонами в незаполненной оболочке. На-
пример, для Na23 (Z = 11, A-Z ~ 12) с протонными оболочками Uy22py22py23dy2
спин имеет значение I = 3/г (а не 5/г) и, таким образом, определяется всеми тремя
протонами 3^5д. Следует подчеркнуть, что число таких случаев невелико.
Для нечетно-нечетных ядер во всех известных случаях спин определяется сло-
жением моментов неспаренного протона и неспаренного нейтрона, \jp - jn| I <
Эр + in. где jp и jn — моменты протона и нейтрона в незаполненных оболочках.
Например, для В10 (Z = 5, А - Z — 5) с одинаковыми протонными и нейтронными
оболочками ls2y22py21 = 3, т. е. равно сумме jp + jn (jp = jn = 3/г).
Мы видим, что описанная модель очень хорошо объясняет наблюденные зна-
чения спинов ядер. Можно с ее помощью вычислить значения магнитных и квадру-
польных моментов.
В простейшем случае, когда спин ядра определяется моментом неспаренного
нуклона, для магнитного момента получаются формулы [32, 33]28)

для неспаренного
протона
для неспаренного _
нейтрона /**ч-1/2 — /*я
1
Д1-1/2 — I IG “Ь 1)Дяд Рр\ч
1 + 2
Ч
Д/-1/2 =----уДп,
/+2
► (16.73)
ДИ 1/2 — ^Дяд Рр
где рр w — магнитные моменты протона и нейтрона.
/	1	7\
Например, для приведенных выше примеров V51 и Са43 H = 3,j = /+ - = -!
моменты должны равняться Здяд + 2,79дяд = 5,79дяд и -1,91дяд соответствен-
но (см. (16.37) и (16.39)). Действительные значения равны 5,14дяд и -1,3дяд,
т.е. по абсолютному значению меньше теоретических. Расхождения имеют место
и в других случаях. При этом разница между значениями pi+]/2 и pi-\/2 получает-
ся меньше теоретической. Частично это расхождение можно объяснить, учитывая
взаимодействия моментов нуклонов, однако для тяжелых ядер в ряде случаев расхо-
ждения все же остаются значительными.
28>Они выводятся, применяя формулы, аналогичные (14.30) и (14.31) (с дяд вместо дб), и учитывая,
что для орбитального момента протона g = 1, а для орбитального момента нейтрона g = 0 (нейтрон, как
незаряженная частица, не имеет орбитального магнитного момента).
460 Глава 16. Моменты ядер и их спектроскопическое исследование
Особенно большие расхождения с результатами опытов получаются для значе-
ний квадрупольных моментов. Для тяжелых ядер в некоторых случаях эксперимент
дает значения, превосходящие теоретические (рассчитанные, согласно модели ядер-
ных оболочек) в 10-20 раз. Перечисленные расхождения могут быть объяснены,
исходя из представлений о деформациях ядра, играющих особенно большую роль
для ядер с конфигурациями нуклонов, далекими от соответствующих заполненным
оболочкам. Форма ядра перестает быть сферической и возможны коллективные ко-
лебания нуклонов по отношению к их равновесному распределению по объему ядра.
Наряду с коллективным колебательным движением, возможны и особого рода кол-
лективные вращения, подобные поверхностным волнам, обегающим жидкую сферу.
Такая динамическая модель деформируемого ядра — «обобщенная» модель О. Бора,
о которой упоминалось в начале параграфа, — дает хорошие результаты для тяжелых
ядер, позволяя, в частности, объяснить аномально большие квадрупольные моменты
и аномально большие изотопические смещения.
Мы не имеем возможности подробно останавливаться на этих вопросах, свя-
занных с современной теорией ядра.
ЧАСТЬ III
МОЛЕКУЛЯРНАЯ
СПЕКТРОСКОПИЯ

ГЛАВА 17
ВИДЫ ДВИЖЕНИЯ В МОЛЕКУЛЕ
И ТИПЫ МОЛЕКУЛЯРНЫХ СПЕКТРОВ
§17.1. Разделение энергии молекулы на части
и основные типы спектров
Характерные особенности молекулярных спектров и их отличия от атомных
определяются тем, что во всех молекулах, как двухатомных, состоящих из двух ато-
мов, так и, в особенности, многоатомных, состоящих не менее чем из трех атомов,
движение является более сложным, чем в атомах. Наряду с движением электронов
существенную роль играют периодические изменения относительного расположения
ядер — колебательное движение молекулы — и периодические изменения ориентации
молекулы как целого в пространстве — вращательное движение молекулы (ср. § 1.5).
Таким образом, в молекуле существуют три вида движений — электронное, коле-
бательное и вращательное. Это приводит к тому, что спектры молекул значительно
сложнее спектров атомов и обычно имеют очень характерный вид. В видимой
и ультрафиолетовой областях вместо линейчатых спектров получаются полосатые
спектры, состоящие из отдельных более или менее широких полос, которые при до-
статочной дисперсии могут быть разрешены на отдельные близко расположенные
линии — это электронные спектры молекул. В близкой инфракрасной области мо-
лекулы обладают характерными колебательными спектрами, которые также состоят
из отдельных полос и могут быть разрешены при большой дисперсии на близко рас-
положенные линии. В далекой инфракрасной области и в микроволновой области
лежат состоящие из отдельных линий вращательные спектры.
В соответствии со сказанным энергия молекулы может быть представлена как
сумма энергий электронного, колебательного и вращательного движений: Еэл, Екол,
#вращ. Мы имеем
— Ял + Яол + Яращ-	(17-0
Следует сразу подчеркнуть, что такое разделение энергии молекулы являет-
ся приближенным. При более точном рассмотрении необходимо учитывать взаи-
модействия различных видов движения, и к энергии (17.1) добавляются члены,
соответствующие энергиям взаимодействия различных видов движения
Е ~ Ял “Ь Яол “Ь -Яращ ^эл. кол “Ь ^Ял. вращ + *Яол. вращ?	(17-2)
где РИэл.кол — энергия взаимодействия электронного движения с колебательным,
Иэл.вращ — электронного с вращательным и РИКОл.вращ — колебательного с враща-
тельным. Вопрос о взаимодействиях различных видов движения требует правильного
выбора исходных приближений и будет более подробно рассмотрен в дальнейшем.
Существенно, что при определенных условиях РИэл.кол можно включить в Яол,
464 Глава 17. Виды движения в молекуле и типы молекулярных спектров
а Вращ и lFK(WI.Bpam — в 2?вращ, и тогда разделение энергии на части, согласно
формуле (17.1), остается справедливым и при учете взаимодействий.
Наиболее важным обстоятельством при разделении энергии на части, со-
гласно (17.1), является различный порядок величин электронной, колебательной
и вращательной энергий. Электронная энергия молекулы, имеющая тот же порядок
величины, что и в атоме, много больше колебательной энергии, а колебательная
энергия, в свою очередь, много больше вращательной энергии:
-Г^враш •	(17-3)
Если выражать энергию в эВ, то электронная энергия имеет порядок нескольких
эВ, колебательная энергия — десятых и сотых долей эВ, а вращательная энергия —
тысячных и десятитысячных долей эВ (ср. § 1.5). Именно различие в порядке
величины электронной, колебательной и вращательной энергий приводит к тому,
что электронные, колебательные и вращательные спектры отличаются по диапазонам
длин волн и частот.
Энергия молекулы, так же как и энергия атома, квантуется. При этом с хорошей
степенью приближения можно квантовать сперва электронную энергию, затем ко-
лебательную энергию при заданной электронной энергии и, наконец, вращательную
энергию при заданных электронной и колебательной энергиях. В формуле (17.1)
каждый член принимает определенные значения. При заданных значениях Еэл, Екол
и Евраш полная энергия Е молекулы имеет определенное значение, соответству-
ющее определенному электронно-колебательно-вращательному состоянию, и мы
получаем совокупность далеко расположенных электронных уровней (различные
значения Еэл,) более близко расположенных колебательных уровней (различные
значения Екол) и еще более близко расположенных вращательных уровней (раз-
личные значения #вращ). Соответствующая схема уровней (для простейшего случая
двухатомной молекулы) изображена на рис. 17.1. Схема иллюстрирует лишь общий
характер расположения уровней без полного соблюдения действительных масштабов.
При переходе молекулы из одного состояния в другое могут изменяться все три
части полной энергии — электронная, колебательная и вращательная. Для переходов
с излучением, согласно условию частот (1.2), имеем
hy = Е' - Е" = (Хл " X) + (Хол ~ Хол) + (Хращ - Хращ). (П.4)
Здесь, как обычно принято в молекулярной спектроскопии, величины, отно-
сящиеся к верхнему электронно-колебательно-вращательному уровню, обозначены
одним штрихом, а величины, относящиеся к нижнему, — двумя штрихами.
Согласно (17.4), полное изменение энергии при переходе слагается из изменений
электронной энергии Д^ = Е'эл — Е”л, колебательной энергии Д#кол = Е'кол — Е"ол
и вращательной энергии Д^вращ = Хращ ~ Храш- В соответствии с (17.3), как
правило,
Д^эл Д^кол Д-^вращ-	(И.5)
Изменение электронной энергии обычно сопровождается одновременными из-
менениями колебательной и вращательной энергий. При этом получаются спектры,
которые было бы правильно называть электронно-колебательно-вращательными
и которые сокращенно называют просто электронными спектрами (а иногда элек-
тронно-колебательными спектрами). Отдельные полосы в этих спектрах соответ-
ствуют различным Д#кол при заданном ДД>л, а отдельные линии в полосах —
различным AjE7Bpaw при заданных Д$эл и Д^кол. Подобные спектры расположены
в видимой и ультрафиолетовой областях. Электронным спектрам молекул посвящено
очень большое число исследований.
§17.1. Разделение энергии молекулы на частии основные типы спектров 465
— ....-5
--------------------------------- О
а
Рис. 17.1. Схема уровней двухатомной молекулы:
а и б — электронные уровни, г/ и v" — квантовые числа колебательных уровней,
J' и J" — квантовые числа вращательных уровней
Если ДЯЭЛ = 0, т. е. электронное состояние не изменяется, то при изменении
колебательной энергии возникают спектры, лежащие в близкой инфракрасной
области. Изменение колебательной энергии в этом случае обычно сопровождается
изменением вращательной энергии, и мы имеем
hv = Е1 - Е" = (Хол - <ол) + (Храш - Хращ)-	(17-6)
Получающиеся спектры, состоящие из отдельных полос (Д£7К0Л задано), рас-
падающихся на отдельные линии (соответствующие различным Д2?вращ при задан-
ном Д£7К0Л), правильно было бы называть колебательно-вращательными спектрами;
их чаще сокращенно называют колебательными спектрами. Переходы типа (17.6)
можно наблюдать не только в близкой инфракрасной области спектра в поглощении
или (гораздо реже) в испускании, но и в комбинационном рассеянии. В последнем
случае формула (17.6) определяет изменение энергии фотона hunajl - hupacc при рассе-
янии и соответственно изменение ипад - ирасс частоты света (см. § 1.3, с. 25). Обычно
466 Глава 17. Виды движения в молекуле и типы молекулярных спектров
название «колебательные спектры» применяют как объединяющее инфракрасные
колебательно-вращательные спектры и колебательно-вращательные спектры комби-
национного рассеяния (рамановские колебательные спектры); колебательные спек-
тры обоих типов весьма широко изучаются методами инфракрасной спектроскопии
и методом комбинационного рассеяния света соответственно; этим спектрам, так же
как и электронным, посвящено очень большое число исследований. Расположение
полос в колебательных спектрах определяется величиной изменения колебательной
энергии Д#кол, а положение отдельных линий в полосе — величиной изменения
вращательной энергии Д^вращ.
При изучении спектров комбинационного рассеяния, как правило, наблюдаются колеба-
тельные полосы, вращательная структура которых не разрешена, и обычно говорят о линиях
комбинационного рассеяния, подразумевая эти неразрешенные и часто достаточно узкие
полосы. Иногда говорят о колебательных линиях и применительно к колебательным полосам
в инфракрасных спектрах.
Если ДЯЭЛ = 0 и Д1?кол = 0 и изменяется только вращательная энергия,
то возникают чисто вращательные спектры, лежащие в далекой инфракрасной
и микроволновой областях. В данном случае
hv - Е’ - Е" = Хращ - Х'ращ.	(17.7)
Эти спектры состоят из отдельных линий, соответствующих различным возмож-
ным значениям Д#вращ. Можно наблюдать и чисто вращательные спектры комбина-
ционного рассеяния (рамановские вращательные спектры); однако в большинстве
случаев исследуются вращательные спектры поглощения в далекой инфракрасной
и особенно в микроволновой областях.
Таким образом, на основе разделения энергии молекулы на электронную, коле-
бательную и вращательную (формулы (17.1) и (17.4)) с учетом порядка их величин
(формулы (17.3) и (17.5)) можно в принципе объяснить характер молекулярных
спектров в различных диапазонах длин волн и частот, описанный в начале парагра-
фа (с. 463).
Так как число различных колебательных переходов, сопровождающих элек-
тронный переход (различные Д#кол при заданном Д^эл), и число различных вра-
щательных переходов, сопровождающих колебательный переход (различные Д#вращ
при заданном Д^кол), может быть очень большим, получается весьма сложная струк-
тура наблюдаемых молекулярных спектров. Наиболее сложна структура электронных
спектров, особенно многоатомных молекул. Необходимо отметить, что для много-
атомных молекул, состоящих из значительного числа атомов, число возможных
уровней и переходов между ними становится настолько большим, что меняется
и сам характер электронных спектров: вместо спектров, состоящих из отдельных
сравнительно узких полос, получаются спектры, состоящие из очень широких по-
лос, в которых не удается обнаружить не только вращательную, но и колебательную
структуру, и спектры становятся сплошными (см. гл. 27, с. 825).
Рассмотренное деление молекулярных спектров на электронные, колебательные
и вращательные находится в соответствии с делением энергии молекулы на элек-
тронную, колебательную и вращательную, следовательно, в соответствии с класси-
фикацией уровней энергии (ср. § 1.5, с. 33 и далее). С экспериментальной точки
зрения очень важно деление молекулярных спектров на спектры поглощения и ис-
пускания, с одной стороны, и на спектры комбинационного рассеяния, с другой
стороны. Как указывалось выше, колебательно-вращательные и вращательные пе-
реходы можно наблюдать как в поглощении и испускании, так и в комбинационном
§ 17.2. Порядок величин различных видов энергий
467
рассеянииПри этом обычно изучаемые колебательные и вращательные спектры
поглощения лежат в инфракрасной и в микроволновой областях, а колебатель-
ные и вращательные спектры комбинационного рассеяния исследуют, как правило,
в видимой области спектра.
Почти всегда спектры комбинационного рассеяния получают путем облучения исследуе-
мого вещества наиболее интенсивными линиями ртутного спектра, чаще всего линией 4 358 А,
иногда линиями 4 047 А и 5 461А (см. (10.24)). При этом наблюденные разности 1/пад -
непосредственно дают частоты колебательных или вращательных переходов. Для определения
этих частот практически пользуются только стоксовыми линиями (см. § 1.3, с. 24), для кото-
рых 1/расс < ^пад и которые соответствуют переходам в молекуле с более низких уровней (чаще
всего с основного уровня) на более высокие.
Отметим, что для колебательных и вращательных спектров комбинационно-
го рассеяния правила отбора отличаются от правил отбора для соответствующих
спектров поглощения и испускания (см. ниже, § 17.7, с. 497).
§ 17.2. Порядок величин электронной, колебательной
и вращательной энергий
Основное соотношение (17.3) порядков величин электронной, колебательной
и вращательной энергий связано с общими свойствами соответствующих типов
движений и, прежде всего, с различием масс ядер и массы электрона.
Рассмотрим подробнее относительные порядки величин энергии для различных
видов движений. Это можно сделать на основе классических и полуклассичес-
ких представлений; получаемые оценки остаются справедливыми и при переходе
к квантовой теории.
Сравним сперва колебательную энергию с электронной.
С классической точки зрения электронные спектры соответствуют собственным
колебаниям упруго связанного электрона, частоты которых равны
1
1'эЛ = тГ\	<17-8)
2% у те	'	'
где &эл — силовая постоянная (постоянная упругой связи), а те — масса электрона.
Колебательные спектры соответствуют колебательному движению ядер друг
относительно друга с частотой, определяемой, по порядку величины, аналогичной
формулой
где М — величина порядка массы ядер, а ккол — силовые постоянные, харак-
теризующие колебательное движение. В частности, для двухатомной молекулы
формула (17.9) дает частоту, с которой изменяется расстояние р между ядрами
МХМ2
двух образующих ее атомов; в этом случае М = —-----—, где и М2 ~ массы
М\ -h М2
ядер, и представляет приведенную массу молекулы, а &кол — силовая постоянная,
характеризующая квазиупругую силу, возникающую при изменении р, если считать
колебание чисто гармоническим.
Для изучения электронных спектров молекул и атомов метод комбинационного рассеяния практи-
чески совсем не применим.
468 Глава 17. Виды движения в молекуле и типы молекулярных спектров
Так как движение электронов в молекуле и колебательное движение ядер про-
исходит под действием электростатических (кулоновских) сил, то порядок величины
постоянных кэл и &кол одинаков:
&эл &КОЛ-	(17.10)
Отсюда вытекает, что порядок отношения 1/кол к 1/эл, а следовательно, и отно-
шения энергии Еэл = Кизл к энергии Екол = huKQn будет равен
(17.11)
^кол __ ^кол _	/
^эл Еэл у М
т. е. корню квадратному из отношения массы электрона к массе ядра.
Для простейшей молекулы водорода Н2 можно положить Еэл равной 10 эВ
(энергии, соответствующей первому члену лаймановской серии, обусловленному
переходом атома водорода из состояния п — 1 в состояние п — 2; такой же поря-
док величины имеет энергия электронного возбуждения молекулы водорода). Раз-
ность энергий соседних колебательных уровней (величина соответствующего кванта,
см. рис. 17.1) для молекулы водорода составляет примерно 0,5 эВ (около 4000 см"1).
Таким образом, отношение
^КОЛ 1
#7 ~ 20
Мн
Приведенная масса молекулы водорода М —
тельно,
(17.12)
1 836тпе
-------— 918те, следова-
2
1
30’
(17.13)
т€ __ 1 Г
М ~ 918’ V
что по порядку величины совпадает с (17.12).
Мы видим, что, действительно, отношение величины колебательной энергии
к электронной приближенно равно корню квадратному из отношения масс электрона
и ядра.
Сравним теперь вращательную энергию с электронной.
Электронная энергия по порядку величины равна кинетической энергии вра-
щения электрона вокруг ядра:
д4орб)г
2тпеа2 ’
(17-14)
где А1рОр6) — момент количества движения электрона, а а — его расстояние от ядра.
jjfap6)2
Для боровских круговых орбит формула (17.14) является точной. \Е\ = Т =
2теа2
где а — радиус круговой орбиты (см. §6.3, с. 171). В квантовой теории оператор кинетической
-—-(орб)2
Мр	-—-(орб)2	2
энергии вращения Т =	—г, где Мр = hl — оператор квадрата орбитального
2тег2	*
момента количества движения, а г — расстояние электрона от ядра. Усредняя это выражение
по электронному состоянию, получим для Твращ формулу, аналогичную (17.14), в которой
я>г(орб)2 *2,/, .	5Гг(орб)2 1
Мр = h 1(1 + 1) — собственное значение оператора Мр , а — представляет среднее
а2
значение —. Подставляя в (17.14) значение МрОрб> при 1 = 1, равное 2h2 и полагая
§ 17.2. Порядок величин различных видов энергий
469
-8	„	2Л2 * *	(1,05 • 10-27)2
а = 10 см , мы получаем Т = --------- — „ „	 .
2теа2 0,9 • IO’27 • 10-’
порядок величины электронной энергии.
~ 10!! эрг ~ 6 эВ, т. е. правильный
Вращательная энергия молекулы по порядку величины определяется формулой,
аналогичной формуле (17.14):
„(вращ)2 „(вращ)2
=	(17.15)
где Мр — вращательный момент количества движения молекулы, а I — момент
инерции, т. е. величина порядка Мр2, где р — размеры молекулы; М, как и раньше,
величина порядка массы ядер2).
Величина квадрата момента количества движения, согласно общему закону (2.5)
его квантования, имеет одинаковый порядок (Л/)2 для всех моментов количества
движения; при малых квантовых числах J ее порядок равен просто h2.
Если положить
М<о₽б)2 « М'вращ,!	(17.16)
и учесть, что размеры электронных орбит по порядку величины равны размерам
молекулы, т. е.
акр,	(17.17)
мы, согласно (17.14) и (17.15), получим отношение
^вращ ^71 е
#эл ~ М'
Таким образом, отношение вращательной энергии к электронной равно по по-
рядку величины отношению массы электрона к массе ядра.
Для молекулы водорода расстояние между первым (J — 0) и вторым (J = 1)
вращательными уровнями равно примерно 120 см-1, т. е. 0,015 эВ. Мы имеем
Явоащ 0,015	1	z
« -----«------,	(17.19)
Еэл 10	700’	V 7
в согласии с соотношением масс (17.13).
Сопоставляя (17.11) и (17.18) и принимая порядок величины электронной
энергии за единицу, мы получаем

1
(17.20)
что представляет конкретизацию соотношения (17.3). 7 является малым параметром
и соответственно Екол — малая первого порядка, а 2?Вращ — малая второго порядка
по сравнению с Еэл.
Результат (17.20) может быть получен и при последовательном квантовомеханическом
рассмотрении.
2) Формула (17.15) представляет классическое выражение для энергии вращения двухатомной моле-
кулы с моментом инерции I — Мр2, где М — приведенная масса молекулы, ар — расстояние между
ядрами. Для многоатомных молекул эта формула правильна по порядку величины.
470 Глава 17. Виды движения в молекуле и типы молекулярных спектров
Квантовомеханическая оценка порядков величин электронной, колебательной и враща-
тельной энергий была впервые произведена Борном и Оппенгеймером в 1927 г. [280]. Они
разложили оператор энергии по параметру р =
H = H0 + pilf + р2Н2+р3Н3+р4Н4 + ... ,	(17.21)
и нашли, что энергия молекулы имеет вид
Е = Ео + р2Е2 + р4Е4 + ... .	(17.22)
В этом разложении члены, содержащие нечетные степени параметра /3, обращаются
в нуль. Член нулевого порядка дает электронную энергию, член второго порядка — ко-
лебательную и член четвертого порядка — вращательную. Члены более высоких порядков
соответствуют взаимодействиям движений различного рода.
Порядок величины членов в (17.22), если принять порядок первого за единицу, будет
что совпадает с (17.20) при 7 = р2 =
Из (17.20) вытекает не только малость колебательной энергии по сравнению
с электронной и вращательной энергии по сравнению с колебательной, но и умень-
шение колебательной и вращательной энергий с увеличением массы атомов в моле-
куле. Порядок величины электронной энергии не изменяется существенным образом
при переходе к более тяжелым атомам (для внешних электронных оболочек), частоты
же колебаний, а следовательно, и энергия колебаний уменьшаются с увеличением
массы колеблющихся атомов. При этом уменьшается и энергия вращения. Уве-
личение размеров молекулы р по сравнению с размерами электронных орбит а
при переходе к более сложным молекулам еще уменьшает вращательную энергию
(ср. (17.15)).
Следует иметь в виду, что речь идет об уменьшении минимальной величины колеба-
тельной и вращательной энергий, определяемой расстояниями между основным и наиболее
глубокими возбужденными уровнями энергии, соответственно колебательными или враща-
тельными. Средний запас колебательной или вращательной энергии молекулы на одну степень
свободы при достаточно высоких температурах (ДЕ кТ см. (5.20)) не зависит от массы
атомов, а при низких температурах (ДЕ > кТ) даже будет меньше для молекул, содержащих
более легкие атомы (из-за того, что ДЕ при данном кТ будет больше, и при условии ДЕ > кТ
заселенность возбужденных уровней, пропорциональная е~^Е^кТ, будет резко уменьшаться
с увеличением ДЕ).
§ 17.3. Зависимость электронной энергии молекулы
от расстояний между ядрами
Важнейшим следствием малости массы электронов по сравнению с массой ядер
является то, что электроны движутся в молекуле гораздо быстрее, чем ядра. Именно
этим определяется малость колебательной и вращательной энергий по сравнению
с электронной.
В силу медленности движения ядер по сравнению с движением электронов
физически разумным приближением является рассмотрение движения электронов
в молекуле при заданном расположении ядер, считая их неподвижными. Соот-
ветственно имеет смысл говорить об энергии молекулы в каждый данный момент
при определенном расположении ядер в этот момент — об электронной энер-
гии для мгновенной конфигурации ядер — и рассматривать изменение электронной
§ 17.3. Зависимость электронной энергии от расстояний между ядрами 471
энергии с изменением расстояний между ядрами. Мы приходим к представлению
об элекгроннцй энергии молекулы как функции относительных координат ядер.
При таком рассмотрении в электронную энергию молекулы включается кинети-
ческая энергия быстро движущихся электронов, энергия взаимодействия электронов
с неподвижными ядрами и между собой, а также энергия взаимодействия ядер друг
с другом. В электронную энергию молекулы не входит, и это является существен-
ным, кинетическая энергия ядер. Само название «электронная» энергия указывает
на то, что учитывается только движение электронов, но не движение ядер.
Электронную энергию молекулы как функцию от координат ядер рьр2, • ••,Pk
(где к — число независимых координат, см. ниже § 17.4) мы запишем в виде
£эл — £эл(рь Р2> • • • ? Рк)-	(17.24)
Мы применяем здесь обозначение вместо Еэл в формулах §§ 17.1 и 17.2, так как
в эти формулы входят вполне определенные, не зависящие от мгновенных расстояний
между ядрами, значения электронной энергии, которые не следует смешивать со значениями
электронной энергии как функции расстояния между ядрами. Несколько ниже будет показано,
что Ёэл представляет минимальное значение еэл(р1? р2> • • • > Рк), получающееся для вполне
определенной конфигурации ядер — для равновесной конфигурации (см. (17.49)).
Выясним общий характер зависимости электронной энергии (17.24) от коорди-
нат ядер. Прежде всего, электронная энергия при неподвижных ядрах не зависит
от положения в пространстве заданной конфигурации ядер как целого — от ее по-
ворота или перемещения в некотором направлении £эл является функцией только
относительных координат ядер. Таким образом, под р в (17.28) следует понимать
независимые относительные координаты ядер. Для простейшего случая двухатом-
ной молекулы имеется только одна такая относительная координата — расстояние р
между двумя ядрами — и
£эл ~ £эл(р)«	(17.25)
Рассмотрим данный случай подробнее, так как в нем наиболее отчетливо
выявляется ряд характерных свойств электронной энергии молекулы как функции
относительных координат ядер.
При стремлении р к бесконечности мы получаем два атома (считая, что молекула
разделяется на нейтральные атомы, а не на ионы), сумма электронных энергий
которых и дает £Эл(°о)
Еэл + 4л = еЭл(оо).	(17.26)
При стремлении р к нулю бэл будет стремиться к бесконечности вследствие
.	Z|Z2e2
отталкивания между ядрами (энергия отталкивания ядер равна -----------, где Z\e
Р
и Z2e — заряды ядер).
Устойчивая молекула будет существовать лишь в том случае, если имеется такое
значение р, 0 < р < оо, при котором еэл(р) имеет минимум (рис. 17.2, кривая I).
Если минимум отсутствует (рис. 17.2, кривая II), то это означает, что при сближении
атомов не образуется устойчивой молекулы. Первый случай соответствует притяже-
нию атомов при их сближении, второй случай — отталкиванию. Расстояние ре ядер,
при котором (в случае I) электронная энергия £эл имеет минимум, представляет
равновесное расстояние. Разность
— £эл(°°) ~ ^эл(Ре)	(17.27)
Т. е. от вращения и от поступательного движения молекулы.
472 Глава 17. Виды движения в молекуле и типы молекулярных спектров
Рис. 17.2. Кривые потенциальной энергии
есть энергия диссоциации молекулы, т. е. энергия, которую нужно затратить на раз-
рыв связи между атомами. Индекс е указывает, что величины ре и De относятся
к равновесной конфигурации молекулы.
Определение энергии диссоциации (17.27) для реальных молекул является не совсем
точным, так как нужно учитывать так называемую нулевую колебательную энергию молекулы
и отсчитывать энергию диссоциации не от бэл(р), а от нулевого уровня энергии Eq, лежащего
несколько выше, чем еэл(ре) (Е^л > ^эл(ре)), см. ниже, §20.4, с. 590.
По отношению к движению ядер энергия еэл(р), зависящая от расстояния между
ядрами и имеющая определенное значение при каждом значении р, играет роль
потенциальной энергии. Легко видеть, что движение ядер при малых отклонениях
расстояния р от его равновесного значения ре будет гармоническим колебательным
движением.
Действительно, вблизи минимума функцию £эл(р) можно разложить в ряд
по степеням отклонения р - ре расстояния между ядрами р от его равновесного
значения ре:
£эл(р) = гэл(ре) +	(р-Ре) +	(Р~Ре)2 +
\dP/P=Pe	2\ dp2 J р=Ре
(17.28)
При р — ре в силу условия равновесия (минимума функции еэл(р)) первая произ-
водная обращается в нуль. Для малых по абсолютной величине отклонений р - ре
можно в разложении (17.28) пренебречь всеми членами, начиная с кубического:
^эл(р) — ^эл(Ре) ~ k(j) ~ ре) ,	(17.29)
где
к —
<г2еэ.,(р) \
dp2 )
(17.30)
§ 17.3. Зависимость электронной энергии от расстояний между ядрами 473
Таким образом, электронная энергия вблизи минимума является квадратичной
функцией от q = р - ре.
Согласно (17.29), имеем
(17.31)
(17.32)
1	2
£эл(р) ~~ ^эл(Ре) =	*
Это выражение и играет роль потенциальной энергии U(q) для движения ядер:
1	9
U(q) = ~ kq1 2.
Кинетическая энергия относительного движения ядер, связанного с изменением
расстояния между ними, равна
, ч 1	(dp\2	1	( dq\2	1	,
=эМ(^) = эМ*>
2	у dt j	2	К dt 1	2
(17.33)
где
м =-----------
М\ -f~
— приведенная масса молекулы (М\ и М2 — массы ядер).
Полная кинетическая энергия движения ядер равна
1	( dRx\2	\	(dR2\2
1	\ at /	2	\ at /
где R\ и R2 — радиусы-векторы ядер. Вводя радиус-вектор центра тяжести
_ М] 1?! + m2r2
с~ м}+м2
и относительный радиус-вектор ядер (рис. 17.3)
R — R2 — R\j
(17.34)
(17.35)
(17.36)
(17.37)
мы получаем
1	/dRc\2 1 М}М2
Т — — (М j + ЛГ2) (—) ч— -----
2V 27 \ dt J 2 М} +М2
(17.38)
где первый член представляет кинетическую энергию движения центра тяжести ядер, а вто-
рой — кинетическую энергию движения ядер относительно их центра тяжести. Записывая
v2 = I — I в виде (ср. рис. 17.3; |R| = р)
\ dt /
V2
(17.39)
dp	dq	dip
где — = — = q — скорость движения ядер вдоль линии, их соединяющей, а — = <р —
dt	dt	dt
угловая скорость поворота оси молекулы, мы получаем
1 МХМ2 /dR\2	1 fdR\2 1	2	1	22
2	=2МЬ) =2^^-2МР2р2,
(17.40)
т. е. сумму кинетической энергии колебания (17.33) и кинетической энергии вращения ^М2<р2.
Формулы (17.33) и (17.32) представляют обычные выражения для кинетической
энергии и потенциальной энергии гармонического колебания с частотой
У =
(17.41)
474 Глава 17. Виды движения в молекуле и типы молекулярных спектров
Рис. 17.3. Радиусы-векторы ядер
Соответственно колебательная коорди-
ната
Ч = Р~Ре (V1A2)
изменяется по закону
q = qo cos 2n(vt + a),
где qo — амплитуда малых колебаний,
a a - начальная фаза.
Кривую
U(q) = U(p-pe) =
— ^эл(р) — ^эл(Ре)
(17.44)
зависимости электронной энергии
двухатомной молекулы от расстояния р
между ядрами принято называть кривой
потенциальной энергии.
Следует, однако, помнить, что е^(р) можно рассматривать как потенциальную
энергию лишь по отношению к движению ядер. Как мы уже указывали, вэДр)
представляет в действительности полную электронную энергию молекулы при не-
подвижных ядрах. Она включает в себя как кинетическую, так и потенциальную
энергию электронов, а также потенциальную энергию взаимодействия ядер друг
с другом.
Рассматривая е^р) как потенциальную энергию, мы получаем для силы взаи-
модействия между атомами, образующими молекулу, выражение
.. ч <кэл(р) dU(p)
м = -~dT =
(17.45)
Кривой I рис. 17.2 при р > ре соответствует сила притяжения (/(р) < 0),
а при р < ре — сила отталкивания (/(р) > 0). На больших расстояниях друг от друга
атомы притягиваются и при сближении могут образовать молекулу. Соответствую-
щую кривую принято называть кривой притяжения. Вблизи минимума кривой U(q),
согласно (17.32) и (17.45),
f(p) = f(Pe + q) = -kq,
(17.46)
т. e. сила пропорциональна отклонению q = p — pe от положения равновесия и на-
правлена к положению равновесия, иначе говоря, является квазиупругой.
(^эл(р)
—----- < о,
ар
f(p) > 0^. При этом атомы отталкиваются тем сильнее, чем больше они сближаются,
и молекула не может образоваться. Соответствующую кривую называют кривой
отталкивания.
К вопросу о кривых притяжения и кривых отталкивания мы вернемся в даль-
нейшем при рассмотрении электронных состояний двухатомных молекул (см. гл. 24,
с. 727).
На основе изложенного для случая двухатомной молекулы легко выяснить физи-
ческий смысл выделения электронной и колебательной энергий в выражении (17.1).
§ 17.3. Зависимость электронной энергии от расстояний между ядрами 475
Для равновесного расстояния ре между ядрами q = 0 и колебания отсутствуют,
и энергия молекулы определяется электронной энергией
ЕЭЛ ~ ^эл(Ре)	(17.47)
— получается электронный уровень энергии. К этой энергии добавляется коле-
бательная энергия Екол, соответствующая определенному колебательному уровню,
лежащему выше, чем (см. рис. 17.2), и получающемуся при квантовании полной
колебательной энергии, равной сумме кинетической энергии (17.33) движения ядер
(вдоль оси молекулы) и «потенциальной» энергии еэл(р) -еэл(ре) = U(p- ре) = U(q).
При заданном расстоянии р между ядрами полная колебательная энергия Екол
слагается, таким образом, из потенциальной энергии U(q) = еэл(р) - еэл(ре) =
£эл(р) - Езл и кинетической энергии T(q) = Екол - U(q).
Подобное разделение, разумеется, возможно только в рамках классического рассмотре-
ния. При квантовомеханическом рассмотрении, приводящем к квантованию колебательной
энергии (см. гл. 20, с. 580), ее оператор состоит из оператора кинетической энергии и опе-
ратора потенциальной энергии, но определенное значение (равное Екол) имеет лишь полная
колебательная энергия, а не кинетическая или потенциальная энергия в отдельности.
В случае многоатомных молекул электронная энергия зависит от нескольких
или многих относительных координат. В этом общем случае образование устой-
чивой молекулы возможно лишь при условии, что при некоторых конечных зна-
чениях всех к независимых относительных координат ядер электронная энергия
£эл(Р1, Р2) • • •, рк) имеет минимум, т. е. при условии существования некоторой рав-
новесной конфигурации ядер
Р\=Р\е, Р2 = Р2е, , Pk = Рке-	(17.48)
Значение
£эл(Р1е> Р2еч • • • > Рке) —	(17.49)
так же как и значение еэл(ре) в случае двухатомной молекулы, определяет поло-
жение электронного уровня энергии. Функция еэл(р1,Ръ ... ,рк) ~ Еэл играет роль
потенциальной энергии для колебательного движения ядер, и колебательная энергия
молекулы является суммой этой «потенциальной» энергии и кинетической энергии
относительного движения ядер. Около равновесных положений ядер (17.48) будут
происходить малые колебания, более сложные, чем в случае двухатомной молекулы4).
С геометрической точки зрения функция £эл(рь Р2> • •• >Рк) представляет по-
верхность к измерений в пространстве к 4- 1 измерений, обладающую в случае
существования устойчивой молекулы минимумом (17.48). Наглядной картиной та-
ких потенциальных поверхностей мы будем пользоваться в дальнейшем.
Отметим, что разобранный нами метод решения задачи о движениях в молекулах, соглас-
но которому рассматривается движение электронов при неподвижных ядрах и не учитывается
обратное влияние движения ядер на движение электронов, можно назвать квазистатическим.
Часто при подобном рассмотрении говорят об адиабатическом изменении расстояний между
ядрами — изменении, медленном по сравнению с движением электронов.
Квазистатическое (адиабатическое) рассмотрение является, разумеется, приближенным.
В действительности движение ядер в какой-то степени сказывается и на движении электро-
нов. Это влияние можно учесть как взаимодействие электронного движения с колебательным
путем введения соответствующих членов в выражение для полной энергии молекулы. Од-
нако неадиабатическое взаимодействие электронного движения с колебательным невелико
и на электронном движении сказывается мало, что и делает квазистатическое рассмотрение
законным.
4) Это будут малые колебания системы не с одной, ас fc степенями свободы. Колебания многоатомных
молекул будут подробно рассмотрены в гл. 21.
476 Глава 17. Виды движения в молекуле и типы молекулярных спектров
§ 17.4. Колебательные и вращательные степени свободы
и отделение колебаний от вращения
Электронная энергия еэл для молекулы является, как мы видели в предыдущем
параграфе, функцией относительных положений ядер. Для TV-атомной молекулы,
т. е. молекулы, содержащей N ядер, общее число независимых координат, характери-
зующих положение ядер, равно 32V., При выделении трех координат центра тяжести
молекулы, изменение которых характеризует поступательное движение молекулы
как целого, остается 3N - 3 внутренних координат, характеризующих как изменения
относительного расположения ядер, происходящие при колебаниях молекулы, так
и поворот молекулы как целого, т. е. ее вращение.
Из общего числа 3N-3 независимых переменных, характеризующих колебатель-
ное и вращательное движения, в общем случае нелинейной многоатомной молекулы,
т. е. молекулы, ядра которой для равновесной конфигурации не лежат на одной
прямой, вращение определяется тремя независимыми переменными и, следователь-
но, колебательное движение характеризуется 3N - 6 независимыми переменными.
Нелинейная многоатомная молекула имеет 3N - 6 колебательных и 3 вращательные
степени свободы.
В случае двухатомной молекулы и линейной многоатомной молекулы, все ядра
которых для равновесной конфигурации лежат на одной прямой, вращение опреде-
ляется двумя независимыми переменными и, следовательно, колебательное движе-
ние характеризуется 3N - 5 независимыми переменными. Линейная молекула имеет
3N - 5 колебательных и 2 вращательные степени свободы. В частности, для двухатом-
ной молекулы (N — 2), представляющей простейший случай линейной молекулы,
имеется 1 колебательная степень свободы, а для линейной трехатомной молекулы
(примером которой может служить молекула СО2, см. ниже рис. 17.6, с. 487) —
4 колебательные степени свободы.
Рис. 17.4. Подвижная координатная система:
а — для нелинейной молекулы С2Н4; б — для линейной молекулы С2Н2
Число степеней свободы, приходящихся на вращательное движение, сразу опре-
деляется, если приближенно рассматривать молекулу как твердое тело. Для нели-
нейной молекулы ее ориентация в пространстве определяется тремя независимыми
угловыми переменными. За такие переменные обычно выбирают эйлеровы углы $
и tp, которые связанная с молекулой подвижная система координатных осей х, у, z
образует с неподвижной системой координатных осей £,?/,£ фиксированной в про-
странстве, как это показано на рис. 17.4, а. В качестве примера нелинейной молекулы
§ 17.4. Колебательные и вращательные степени свободы	477
приведена плоская молекула этилена С2Н4, ядра которой образуют симметричную
равновесную конфигурацию; за ось z выбрана ось молекулы (проходящая через
ядра С), ось у лежит в плоскости молекулы, а ось х направлена перпендику-
лярно этой плоскости. Для линейной молекулы ее ориентация в пространстве —
ориентация прямой, на которой лежат ядра, — определяется двумя независимыми
переменными. За такие переменные всегда выбирают углы 3 и <р, характеризующие
направление этой прямой — оси линейной молекулы — в сферической системе
координат, как показано на рис. 17.4, б. В качестве примера линейной молекулы
взята молекула ацетилена С2Н2, ядра которой лежат на одной прямой и также
образуют симметричную равновесную конфигурацию. Отметим, что если выбрать,
как и для молекулы этилена, ось молекулы за подвижную ось z, то направления
подвижных осей х и у, в отличие от этого случая, остаются неопределенными.
Независимые угловые координаты <ф, 0, <р для нелинейной молекулы и 3, <р
для линейной молекулы представляют вращательные координаты, изменения кото-
рых характеризуют вращательное движение молекулы. Аналогично для колебатель-
ного движения молекулы можно ввести 3N - 6 (для нелинейной молекулы; в случае
С2Н4 N = 6, 3N -6=12) или 3N - 5 (для линейной молекулы; в случае С2Н2
N = 4, 3N -5 = 7) колебательных координат q, характеризующих смещения ядер
из положений равновесия и обращающихся в нуль для равновесной конфигурации.
В частном случае двухатомной молекулы имеется одна такая вполне определенная
колебательная координата q — p — pe (см. предущий параграф). В отличие отданного
простейшего случая для трехатомных и более сложных молекул, с числом колебатель-
ных степеней свободы не менее трех (при N 3 3N — 6	3, a 3N — 5^4), введение
колебательных координат может быть произведено различными способами, которые
будут подробно рассмотрены в гл. 21. Существенным является то, что колебатель-
ные координаты определяют смещения ядер из равновесных положений в связанной
с молекулой подвижной системе координатных осей; периодические изменения этих
координат и представляют колебательное движение. В свою очередь, положение
подвижной системы определяется угловыми вращательными координатами; перио-
дические изменения этих координат и представляют вращательное движение. Мы
получаем, таким образом, разделение движения на вращательное и колебательное —
на движение молекулы как целого и на относительное движение ядер. Для двухатом-
ной молекулы, в частности, движением молекулы как целого является вращение
оси молекулы, которое происходит вокруг оси, перпендикулярной к оси молекулы
(см. гл. 19, с. 536), а относительное движение ядер состоит в изменении расстояния
между ними — в колебаниях ядер вдоль оси молекулы.
Мы получаем разделение движения молекулы на вращательное и колебательное, рас-
сматривая вращение подвижной системы координат, связанной с конфигурацией молекулы,
и относя колебания к подвижной системе.
Однако здесь имеются трудности из-за того, что моле-
кула не является твердым телом, — ее конфигурация изме-
няется при колебаниях. Возникает вопрос, как именно свя-
зать с непрерывно изменяющейся конфигурацией молекулы
подвижную систему координат. Только для двухатомной мо-
лекулы, где можно провести подвижную ось через оба ее
ядра, этот вопрос решается однозначно. Уже для линейной
трехатомной молекулы при произвольных смещениях ядер
(рис. 17.5) они не будут лежать на одной прямой и подвиж-
ные оси можно ввести различным образом.
Рис. 17.5. Произвольные
смещения для линейной
трехатомной молекулы
Для твердого тела подвижные оси выбирают обычно так, чтобы они являлись главными
осями инерции. С первого взгляда представляется естественным и для колеблющейся моле-
кулы выбирать в каждый момент времени в качестве подвижных осей главные оси инерции
478 Глава 17. Виды движения в молекуле и типы молекулярных спектров
(этот выбор в общем случае однозначен) и рассматривать поворот введенных таким образом
мгновенных главных осей как вращение, а периодические изменения положения ядер относи-
тельно этих осей — как колебания. Оказывается, однако, что подобный способ, примененный
в первых работах, посвященных разделению колебаний и вращения, приводит к неверным
результатам: энергия движения ядер распадается на энергию колебаний, энергию вращения
и энергию «взаимодействия колебаний и вращения», причем последняя не является малой,
т. е. не получается действительного отделения колебаний от вращения (см. подробнее [281]
и [282], с. 43). Причиной этого является наличие у многоатомных молекул дополнительного
момента количества движения (кроме чисто вращательного момента), связанного с колебани-
ями, — колебательного момента количества движения. При различных выборах подвижной
системы колебательный момент количества движения будет различным. Можно выбрать
подвижные оси так, чтобы колебательный момент был мал при малых отклонениях ядер
от положений равновесия (при малых колебаниях) и обращался в нуль при прохождении ядер
через положение равновесия, т. е. при равенстве нулю колебательных координат. Оказывает-
ся, что именно при таком выборе получается правильное отделение колебаний от вращения;
энергия взаимодействия колебаний и вращения является малой величиной. Подвижные оси
для этого случая вводятся однозначно, как и мгновенные главные оси инерции, однако не со-
впадают с ними. Таким образом, задача об отделении колебаний от вращения решается путем
введения подвижной системы, удовлетворяющей условию равенства нулю колебательного мо-
мента количества движения при нулевых значениях колебательных координат. Отметим, что
решение данной задачи еще усложняется, когда отдельные части молекулы могут вращаться
друг относительно друга (случай «свободного вращения», см. ниже, с. 504); подобный случай
был подробно рассмотрен Зайцевым [283].
Когда колебательное и вращательное движения ядер разделены, можно произ-
вести квантование каждого из них в отдельности и получить возможные (для за-
данного электронного состояния) значения колебательной (^кол) и вращательной
(#Вращ) энергий. Складывая Екол и ^вращ с электронной энергией Еэл, мы получаем
в соответствии с (17.1) полную энергию молекулы Е.
Рассмотрение, выполненное в предыдущем и в этом параграфах, является, как
мы видели, приближенным. При более точном рассмотрении должно учитываться
взаимодействие различных видов движений, что и приводит к формуле (17.2).
В дальнейших главах книги будет дано подробное изложение систематики уров-
ней энергии и спектров молекул, которому предшествует рассмотрение (в гл. 18)
важного вопроса о равновесной конфигурации молекулы и о симметрии этой конфи-
гурации. Изложение систематики начинается с разбора вращения молекул и враща-
тельных спектров (гл. 19), затем рассматриваются колебания молекул и колебатель-
ные спектры (гл. 20-23). Последние главы книги (гл. 24-27) посвящены электронным
состояниям молекул и электронным спектрам; при этом разбирается также и тесно
связанный с электронными состояниями молекул вопрос о химической связи.
Для каждого вида уровней энергии и спектров — вращательных, колебательных
и электронных — рассматриваются как двухатомные молекулы (N = 2), так и много-
атомные (N 2), причем изложение начинается с простейшего случая двухатомных
молекул.
Мы будем применять наряду с результатами, получаемыми более наглядными
классическими и полуклассическими методами, и результаты, полученные более
строгими квантовомеханическими методами, особенно при рассмотрении электрон-
ных состояний молекул. Поэтому в следующем параграфе данной главы (§ 17.5)
мы разберем основные положения квантовомеханической теории молекул. Краткое
изложение данного вопроса рассчитано на читателя, достаточно хорошо знакомого
с квантовой механикой, и этот параграф может быть опущен лицами, интере-
сующимися только результатами квантовомеханической теории, а не методами
их получения. На подготовленного читателя рассчитано и изложение решения
квантовомеханическими методами ряда конкретных задач в последующих главах,
§ 17.5. Основные положения квантовомеханической теории молекул 479
в частности, некоторых вопросов, касающихся химической связи в двухатомных
и многоатомных молекулах.
В последних параграфах данной главы мы разберем ряд общих вопросов, связан-
ных с характеристиками переходов и интенсивностями как в случае молекулярных
спектров поглощения и испускания (§ 17.6), так и в случае молекулярных спектров
комбинационного рассеяния (§ 17.7). При разборе этих очень важных для моле-
кулярной спектроскопии вопросов особенно существенно применение результатов
квантовомеханической теории молекул, рассматриваемой в § 17.5.
§ 17.5. Основные положения квантовомеханической теории молекул
При квантовомеханическом рассмотрении для нахождения полной энергии молекулы
нужно определить собственные значения Е оператора энергии молекулы Я, зависящего как
от координат электронов, так и от координат ядер. Это может быть выполнено прибли-
женным образом [280, 47, 51] в соответствии с наглядными представлениями о разделении
движения в молекуле на электронное, колебательное и вращательное, как было рассмотрено
в предыдущих параграфах.
В неподвижной системе координат С» *7, С оператор энергии молекулы как системы,
состоящей из п электронов с зарядом —е и N ядер с зарядами +ZQe (а = 1,2,..., N)5\ может
быть записан в виде
Я = Тэл + Тяд + У.	(17.50)
Здесь
п
1=1
2т‘ ~ 2т' ~?\д$ + + )
(17.51)
— оператор кинетической энергии электронов (&, ту,-, & — координаты электронов, те —
масса электрона),
N	N 1	N 1	/ Я2	Я2 \
а=1	а=1	а=1	4	z
— оператор кинетической энергии ядер (xQ, yQ, zQ — координаты ядер, Ма — массы ядер),
— оператор взаимодействия электронов и ядер.
В операторе (17.53) первый член представляет энергию притяжения электронов ядрами
и зависит от расстояний га:- электронов от ядер, второй член представляет энергию отталкива-
ния электронов и зависит от расстояний г,, между ними, и третий член представляет энергию
отталкивания ядер и зависит от расстояний рар между ядрами. Помимо этих членов, учитыва-
ющих основные электростатические взаимодействия электронов и ядер, в (17.53) входят малые
члены, включенные в W и учитывающие все прочие взаимодействия, как магнитные, так
и электростатические. Среди них наиболее существенными являются магнитные взаимодей-
ствия, связанные со спином электрона, в первую очередь, спин-орбитальные взаимодействия
для отдельных электронов, пропорциональные (см., например, с. 62 и с. 230). В W входят
и очень малые взаимодействия моментов ядер, электрических и магнитных, с электронными
оболочками и также очень малые магнитные взаимодействия, связанные с вращательными
магнитными моментами. Мы не выписываем все эти члены в явном виде. Достаточно указать,
5) Для общности мы не считаем, что п = ZQ, т.е. включаем и случай ионизованных молекул.
480 Глава 17. Виды движения в молекуле и типы молекулярных спектров
что они обусловливают тонкую и сверхтонкую структуры уровней энергии молекул и могут
быть учтены по методам квантовомеханической теории возмущений 6\
Оператор Н зависит от Зп координат электронов и от 3N координат ядер. В квантовой
механике, как и в классической механике, можно точно отделить движение центра тяжести
системы от относительного движения. При этом оператор взаимодействия V не изменяется,
а оператор кинетической энергии Т =	+ Тяд распадается на оператор Тц. тяж кинетической
энергии движения центра тяжести и оператор Т' кинетической энергии движения относитель-
но центра тяжести, по-прежнему представляющий сумму кинетической энергии электронов
и кинетической энергии ядер. В результате полный оператор энергии движения относительно
центра тяжести будет равен
H^i^+^ + V,	(17.54)
где операторы и 7^д будут иметь прежний вид (17.51) и (17.52) с заменой координат ту,, &
иха, уа и za относительными координатами	и х'а, у'а и z'a. Однако число независимых
координат уменьшится на три. Так как положение центра тяжести практически определяется
положениями тяжелых ядер, но не легких электронов (Ма те), то 3N координат х'а, у'а
и z'a будут связаны тремя дополнительными соотношениями
N	N	N
22^=0, ^Maz'a=Q	(17.55)
а=1	а=1	а=1
и можно вместо этих координат ввести 3N — 3 независимых координат, от которых и будет
зависеть Тяд, а также V. В частности, в случае двухатомной молекулы (а = 1,2) это будут
координаты х' = х'2 - х\, у' = у2 - у\, z' = z2 - z\, и легко показать, что
1 f	\	f.2
= <17-56>
м}м2
где М =	—----приведенная масса молекулы (см. с. 467).
Отметим, что если не пренебрегать массами электронов по сравнению с массами ядер, то
в операторе массы те электронов заменятся несколько отличными приведенными масса-
ми т' и появятся малые дополнительные члены; это обусловливает массовый изотопический
эффект электронных уровней, имеющий тот же порядок величины, что и в случае атомов
(см. §16.5, с. 450).
В (17.54) оператор кинетической энергии ядер учитывает как кинетическую энергию
колебаний, так и кинетическую энергию вращения, а сумма операторов и V хотя
и представляет оператор электронной энергии, но еще не в окончательном виде, так как
электронное движение отнесено к координатной системе, оси которой сохраняют неизменные
направления в пространстве, а не к координатной системе, полностью связанной с молекулой.
Мы преобразуем оператор (17.54) так, чтобы отделить колебание от вращения и отнести
электронное движение к координатной системе, связанной с молекулой. С этой целью
мы перейдем от координатной системы т]1, £ с началом в центре тяжести, оси которой
сохраняют неизменные направления в пространстве (от неподвижной координатной системы),
к подвижной координатной системе х, у, z с началом также в центре тяжести, но с осями,
ориентация которых может изменяться. При классическом рассмотрении это означает, что
углы, определяющие ориентацию подвижных координатных осей, меняются со временем;
при квантовомеханическом рассмотрении это означает, что операторы, соответствующие
механическим величинам, будут содержать дифференцирование по угловым переменным 7\
При этом спин-орбитальное взаимодействие в зависимости от его относительной величины учиты-
вается либо сразу при рассмотрении электронных уровней, либо позже при рассмотрении вращательных
уровней (для двухатомных молекул это так называемые случаи Гунда а и б, см. §25.4).
7) В частном случае вращения вокруг неподвижной оси на угол (р, согласно классической механике,
do?
отличны от нуля угловая скорость — = ф и соответствующий ей обобщенный импульс (равный
Т
-*яд
§17.5. Основные положения квантовомеханической теории молекул 481
При переходе к подвижной системе 3 (для нелинейной молекулы) или 2 (для ли-
нейной молекулы) угловые координаты будут определять положение подвижной системы,
а остальные (37V - 3) - 3 = 3N - 6 или (3N - 3) - 2 = 3N - 5 координат будут определять
относительное расположение ядер. Они будут характеризовать вращательное и колебательное
движения соответственно, и оператор Тяд кинетической энергии ядер распадется на оператор
Твраш кинетической энергии вращения, содержащий дифференцирование по угловым коор-
динатам, и оператор Ткол кинетической энергии колебания, содержащий дифференцирование
по координатам, определяющим относительное расположение ядер.
В случае двухатомной молекулы разделение оператора Тяа на две части будет точным.
Действительно, если координаты х, у, z в (17.56) выразить через сферические координаты,
согласно формулам (см. рис. 6.6, с. 175), х' = psin0cosy>, yf = р sin в sin <р, zf — pcos0,
где р — расстояние между ядрами, то оператор Т^д примет вид
Л2 1 д
п2 Г 1 д /. дх
2Мр2 sin0<?0\ П дд)
— ^кол “Ь ^вращ —
Т
1 д2 I .
"7-57>
где первый член Ткол соответствует кинетической энергии колебаний, а второй Твращ — кине-
тической энергии вращения. Мы имеем две вращательных угловых координаты в и <р и одну
относительную координату р — расстояние между ядрами, изменяющуюся при колебаниях8*.
Оператор
—2	, Г 1 д / д \	1 д2 '
Mv = -h2	— (sin0— ) +	т-7	(17.58)
р [sin0 д0\ дО / sin20 ду>2\	V 7
представляет оператор квадрата момента количества движения ядер, а выражение I = Мр2 —
момент инерции ядер относительно прямой, проходящей через центр тяжести молекулы
перпендикулярно к ее оси (см. с. 537). Отсюда следует, что
(17-59)
в согласии с классическим выражением (17.14). Необходимо подчеркнуть, что момент инерции
является функцией расстояния между ядрами, что уже приводит к зависимости вращательной
энергии от колебаний, так как при колебаниях момент инерции изменяется. Лишь если счи-
тать момент инерции постоянным9*, то оператор Твращ будет зависеть только от вращательных
координат, но не от относительной координаты р.
В случае многоатомной молекулы разделение оператора Тяд на два оператора Ткол и Твращ
может быть произведено только приближенно, пренебрегая получающимися при переходе
к подвижной системе членами, соответствующими связи колебания и вращения. В результате
такого приближенного разделения, как можно показать [281, 282], получается оператор
Тад — Т’кол + Твращ >
(17.60)
где оператор Ткол кинетической энергии колебания зависит от 3N - 6 или 3N - 5 координат,
определяющих относительное расположение ядер (вместо одной координаты р в случае двух-
атомной молекулы), а оператор Твраш кинетической энергии вращения является квадратичной
функцией от операторов Мрх, Мру, Mpz проекций момента количества движения, содержащих
дифференцирование по 3 или 2 угловым координатам. Он имеет вид
Твращ — 2 Д*д(р)^рА^Црд>
Ад
(17.61)
проекции момента количества движения на ось вращения); в квантовой механике это вращение соот-
h д z
ветственно характеризуется оператором = - — (оператором проекции момента количества движения
на выделенную ось), содержащим дифференцирование по угловой переменной (р.
8* Колебательной координатой является q = р — ре, см. (17.42).
9* Положив, например, р = ре н I = Мр%, гце ре — равновесное расстояние, что при малой амплитуде
колебаний (q < ре) представляет хорошее приближение.
16 L
482 Глава 17. Виды движения в молекуле и типы молекулярных спектров
где индексы Л и р пробегают значения х, у, z, а коэффициенты представляют функции
от относительных координат. Если оси х, у, z являются главными осями инерции некоторой
конфигурации ядер,0\ то (17.61) для этой конфигурации принимает более простую форму
представляют обратные моменты инерции. Операторы (17.61) и (17.62)
—	1 /	— э — э —) \	1 /	М2.	ML \
Т^т = -(ВхМгрх + ВуМгп + ВгМггг) = -[^ + -^- + ^],	(17.62)
\	-Ly	J-Z /
1
где 1Х, 1у, 1г — главные моменты инерции относительно осей ж, у, z, т. е. величины Вх = у,
совершенно аналогичны классическим выражениям для вращательной энергии системы,
состоящей из N взаимодействующих частиц.
Наряду с разделением оператора на части нужно преобразовать оператор Тзл кинети-
ческой энергии электронов от координат ?/', в неподвижной системе к координатам xit
yi, Zi (i = 1,2, 3,..., п) в подвижной. Оператор ТэЛ инвариантен к соответствующему ортого-
нальному преобразованию поворота (ср. (3.16)) и будет иметь в координатах ж,-, &•, zt- прежний
вид (17.51):
2тпе у дх2г ду2 dz?)
(17.63)
Наконец, оператор V энергии взаимодействия, зависящий от относительных координат
электронов и ядер, при переходе к подвижной системе не изменяется и сохраняет вид (17.53).
Таким образом, в подвижной системе оператор энергии может быть записан в форме
Я(ж, р, 0) = Тэл(х) 4- Г(ж, р) + ?кол(р) 4- Твращ(0, р).
(17.64)
Оператор Тзл(х) является функцией Зп координат х электронов и определяется форму-
лой (17.63) (штрихи мы опускаем). Оператор взаимодействия (в основном электростатиче-
ского) V(x, р) зависит от координат х электронов и от 3N - 6 или 3N - 5 относительных
координат р ядер и определяется формулой (17.53). Оператор Ткол(р) кинетической энергии
колебаний зависит только от 3N - 6 или 3N - 5 координат р. Наконец, оператор ТВраш(^> р)
кинетической энергии вращения зависит от 3 или 2 угловых координат $, а также через
посредство постоянных ВдДр) (см- (17.61)) от координат рн). Существенно, что ТК01(р)
содержит дифференцирование по координатам р (ср. (17.57)), а в V(x,p) и в Твращ($, р) эти
координаты входят как параметры.
Выражение (17.64) является основным при квантовомеханическом рассмотрении элек-
тронного, колебательного и вращательного движений в молекуле.
Можно получить приближенное решение уравнения
Hip(x, р, 0) = Etf^x, р, 0)	(17.65)
и, следовательно, найти возможные значения Е энергии молекулы, представляя 1/>(х, р, 0)
в виде
р, -д) = ^(х, р)^кал(р)^»ращ(’7),	(17.66)
|0* Например, главными осями инерции равновесной конфигурации ядер. Однако нельзя выбрать
оси х, у, z подвижной системы так, чтобы они при любой конфигурации ядер были главными
осями инерции, потому что тогда не получается правильного разделения энергии на колебательную
и вращательную, см. предыдущий параграф (с. 478). При правильном выборе подвижной системы,
удовлетворяющем условию равенства нулю колебательного момента количества движения, оператор
Твращ имеет для произвольной конфигурации ядер общий вид (17.61), а не частную форму (17.62).
11) Следует отметить, что при переходе к подвижной системе производные по угловым координатам
должны браться не при постоянных ?/', а при постоянных ж,, од, zx-, что приводит к добавлению
в (17.61) к Мру, MpZ членов, зависящих от электронных угловых моментов (см., например, [47]).
Мы этого, однако, для простоты здесь учитывать не будем. Такое пренебрежение законно для молекул
с электронным моментом количества движения, равным нулю.
§ 17.5. Основные положения квантовомеханической теории молекул 483
т.е. в виде произведения электронной волновой функции ^ЭЛ(ж, р), колебательной волновой
функции ^кол(р) и вращательной волновой функции ^вращ($). В соответствии с порядками
величин электронной, колебательной и вращательной энергий (см. (17.3)) сначала решается
задача об электронном движении, затем задача о колебательном движении и, наконец, задача
о вращательном движении. При этом последовательно находятся ^эл(х,р), ^кол(р) и ^враш(^)-
Для получения решений сперва рассматривается оператор
Нэл =Гэл(х) + У(х,р),	(17.67)
который в силу того, что те Ма, много больше оператора Тяд(р, — Ткол(р) + Твра1Ц($, р)
(ср. (17.51) или (17.63) с (17.52)), затем принимается во внимание также и оператор Ткол(р)
и в последнюю очередь учитывается оператор Твраш($, р).
Электронная функция ^Эл(^?р) естественном образом определяется как решение волно-
вого уравнения
(I)	=еэл(р)^>м(х,р),	(17.68)
где £эл(р) представляет электронную энергию как функцию отнсительных координат р ядер.
Решение уравнения (17.68) с оператором Нэл(х, р), в который координаты р входят только
как параметры, соответствует рассмотрению электронного движения при неподвижных ядрах
(см. § 17.3). Для устойчивых молекул, рассмотрением которых мы здесь ограничиваемся,
функция еэл(р) может быть представлена в виде
^эл(р) ^эл(Ре) “Ь [^эл(р) ^эл(Ре)] — -®эл “Ь [^эл(р) ^эл(Ре)] ?	(17.69)
где Еэл = езл(ре) — значение электронной энергии для равновесной конфигурации,
а £эл(р) — ^эл(Ре) = 17(g) — функция от колебательных координат д, обращающаяся в нуль
для равновесной конфигурации (ср. (17.28) и (17.44)).
Уравнение (17.68) представляет первое основное уравнение квантово-механической тео-
рии молекул — уравнение для электронной энергии молекулы. Из его решения находятся
равновесные значения р = ре относительных координат ядер (для двухатомной молекулы
значения равновесного расстояния р — ре между ядрами) и соответствующие значения
электронной энергии Езл = гэл(Ре), т.е. электронные уровни энергии.
Для нахождения волновых уравнений для колебаний и вращений мы усредним оператор
энергии (17.64) Н(х, р, б) по координатам х, т.е. по электронному движению, что физически
соответствует предположению о медленности движения ядер по сравнению с движением
электронов. Мы имеем
У tt»(x,P)H^(x,p)dx = У ф*„(х, р)Нэл(х, p)^(x, р) dx +
+ У фЦх, p)TK01,(p)^M(x, р) dx + У фЦх, р)Твраш(0, р) dx. (17.70)
Первый интеграл в правой части, согласно (17.68), равен еэл(р), последний интеграл
в силу независимости ^(ж, р) от угловых координат б (дифференцирование по которым
содержится в Твраш($, р)) равен Твращр, р). Во втором интеграле оператор Ткол(р), содержащий
дифференцирование по р (ср. (17.57)), действует на электронную функцию, также зависящую
от координат р; однако считая эту зависимость слабой, можно приближенно положить, что
Ткол(р) коммутирует ^(ж, р),2) и тогда
^’эл(а'? р)7кол(р)^’эл(а?? р) dp — I $эл(х, р)1рэл(Х) р) dx • Ткол(р) — Ткол(р). (17.71)
,2) Электронная волновая функция медленно изменяется в зависимости от координат р и такое
приближение является разумным. При более точном рассмотрении для членов типа
мы получим
в результате дифференцирования [282а]:
д2
др2
а2 ,	э дг
= тт- + 2 “о- Т" + V7
dpz	др1 др др др1
* д2,	_ д2,фэл di/>3Ji д
др2	др2 др др
д2
др2
16*
484 Глава 17. Виды движения в молекуле и типы молекулярных спектров
В результате мы получаем усредненный по электронному движению оператор
Н — £эл(р) “Ь ^кол + Твращ — Еэл “Ь { [^эл(р) — ^эл(Ре)] “Ь ^кол(р)} + ТВращ(19, />),	(17.72)
равный сумме значения Еэл = ^эл(Ре) электронной энергии для равновесной конфигурации
оператора
Нкол(р) = [^эл(р) — ^эл(Ре)] + Ткол(р)	(17.73)
колебательной энергии, в котором разность еэл(р)-еэл(ре) играет роль потенциальной энергии,
и оператора Твращ($, р) вращательной энергии.
Колебательная волновая функция ^кол(р) естественным образом определяется как реше-
ние волнового уравнения
00	ГГКОЛ (р)^кол(р) — ^кол^кол{р)у	(17.74)
которое представляет второе основное уравнение квантовомеханической теории молекул —
уравнение для колебательной энергии молекулы. Из его решения находятся колебательные
уровни энергии.
Остается учесть вращательное движение. Усредняя оператор энергии (17.72), зависящий
от координат р и $, по координатам р, что соответствует предположению о медленности
вращения молекул по сравнению с их колебаниями, мы получим
J	J	dp +
4" J" ^,(рИк<и1(рЖол(р) dp + ^кол(р)Твраш(^» р)^кол(р) (17.75)
Первый интеграл в правой части равен £?эл, второй в силу (17.74) равен Екол, третий дает
среднее значение оператора кинетической энергии вращения, имеющего в общем случае
вид (17.61). Это среднее значение равно
Явраш(^) — Т’враш ~ ВхрМр\Мрр,	(17.76)
А/*
где
Влд = J ^w{p)Bx„(p)^Km(p) dp.	(17.77)
В результате мы получаем усредненный как по электронному, так и по колебательному
движению оператор
f = ^+£KO,+HBpaui(t?).	(17.78)
Вращательная волновая функция естественным образом определяется как решение вол-
нового уравнения
(Ш)	^враш($)^враш($) ~ -^вращ^враш^)?	(17.79)
которое представляет третье основное уравнение квантовомеханической теории молекул —
уравнение для вращательной энергии. Путем его решения находятся вращательные уровни
молекул.
Отметим, что оператор (17.76), входящий в уравнение (17.79), можно всегда привести
ортогональным преобразованием координат х, у, z к сумме квадратов:
= '-(вхм}х + вум2ру + ВгмД) =	,	(17.80)
\	-Ly	J-Z /
где введены эффективные главные моменты инерции Ix = Iy = Iy*^\ Iz = /<эфф)
(ср. (17.62)). Они, вообще говоря, отличаются (хотя обычно и не слишком сильно) от главных
моментов инерции нормальной конфигурации.
Этот оператор отличается от оператора —г первыми двумя членами, являющимися малыми.
др1
§ 17.6. Характеристики спектров поглощения и испускания 485
В соответствии с (17.79) усреднение оператора (17.78) по координатам 0, т.е. по враща-
тельному движению, дает
^’вращ(^)^^’вращ(^)	— / ^вращ(^)(ЕЭл Екол)^враш(1?) Н~
“Ь / ^вращ(^)7^вращ(^)^вращ(^)	— Екол 4“ Еэл “Ь Евра1ц.
(17.81)
Таким образом, в результате последовательного тройного усреднения полного опера-
тора (17.64) по электронному, колебательному и вращательному движениям мы получаем
значение полной энергии молекулы
Е — н — Еэл Екол “Ь Евращ
(17.82)
как сумму значений электронной, колебательной и вращательной энергий. Значения энер-
гии Ёэл = еэл(Ре), Екол и Евраш и соответствующие волновые функции ^эл(х,р), ^кол(р)
и ^враш(^) удовлетворяют основным уравнениям (17.68), (17.74) и (17.79) (I, II и III). Значение
энергии (17.82) и произведение (17.66) этих волновых функций являются приближенным
решением общего уравнения (17.65), соответствующим физическим представлениям о разде-
лении движения в молекуле на электронное, колебательное и вращательное.
§ 17.6. Характеристики переходов и интенсивности
в случае спектров поглощения и испускания
Переходы между уровнями молекул — электронные (электронно-колебатель-
но-вращательные), колебательные (колебательно-вращательные) и вращательные
(чисто вращательные), изучаемые при наблюдении соответствующих электронных,
колебательных и вращательных спектров испускания и поглощения, связаны с из-
менениями электрических или магнитных моментов молекулы. Вероятность этих
переходов выражается через соответствующие моменты переходов, как было рассмо-
трено в гл. 4 для случая электрического дипольного излучения (§ 4.3) и для случаев
магнитного дипольного и электрического квадрупольного излучений (§4.4). Там
же, в §4.7 и §4.8, был разобран вопрос о правилах отбора, а в гл. 5 — вопросы
интенсивностей в спектрах. Полученные в гл. 4 и 5 результаты являются общи-
ми и применимы к молекулам, однако требуют конкретизации, особенно в связи
с разделением энергии молекулы на электронную, колебательную и вращательную.
Так же как и для атомов, для молекул наиболее важен случай дипольного излу-
чения (электрического). При этом существенно, обладает ли молекула дипольным
моментом или нет.
Для атомов дипольный момент в любом стационарном состоянии равен нулю
в силу сферической симметрии атома в целом: все направления, проходящие через
центр атома — через его ядро, — равноправны, а дипольный момент является век-
тором и характеризует некоторое выделенное направление, отсутствующее в атоме.
Однако для перехода из одного электронного состояния атома в другое дипольный
момент перехода Pjk (см. с. 91), определяющий его вероятность, может быть отличен
от нуля.
Дипольный момент атома в определенном стационарном состоянии представляет среднее
значение вектора дипольного момента (4.33), взятое по волновым функциям этого состояния:
Р— I ipiPipidx = -е I	(17.83)
486 Глава 17. Виды движения в молекуле и типы молекулярных спектров
Это среднее значение обращается в нуль, так как il>i(xyil>i(x) не изменяется при операции
инверсии, а дипольный момент меняет знак (ср. вывод правил отбора на с. 115). В противо-
положность этому дипольный момент перехода (4.40)
Рц, = У il>*(x)Pipk(x)dx =-е У	(17.84)
i
может быть отличен от нуля, если комбинирующие состояния отличаются четностью и следо-
вательно, ф*(х)фк(х) меняет знак при инверсии. Именно так были выведены правила отбора
в §4.7.
Молекула в отличие от атома может обладать дипольным моментом в ста-
ционарных состояниях, если ее симметрия не слишком высока (см. подробнее
§18.6, с. 527).
Для электронных переходов в молекулах наличие дипольного момента в ста-
ционарных состояниях не существенно. Так же как и в случае атомов, вероятность
электронного перехода определяется дипольным моментом перехода Рц., который
может быть отличен от нуля, независимо от того, имеет ли молекула дипольный
момент в стационарных состояниях или нет. При этом величина дипольного мо-
мента электронного перехода зависит от движения электронов при неподвижных
ядрах, а колебательное и вращательное движения молекулы не оказывают на нее
существенного влияния.
Иначе обстоит дело для колебательных и вращательных переходов. Для них
существенно наличие у молекулы дипольного момента Р в заданном электронном
состоянии, которое при таких переходах не изменяется (ср. (17.6) и (17.7) с (17.4)).
Если для молекулы Р / 0, то как при колебательном, так и при вращательном движе-
нии этот момент изменяется и соответствующие переходы являются возможными.
Согласно наглядным представлениям, при колебаниях изменяется относительное
расположение ядер, — конфигурация ядер в молекуле, что и приводит к измене-
нию дипольного момента; дипольный момент является функцией колебательных
координат р:
Р = Р(р).	(17.85)
При вращении молекулы как целого меняются составляющие Р^, Pv, ди-
польного момента, связанного с молекулой (т. е. сохраняющего свою ориентацию
в подвижной системе), относительно неподвижной системы £,?/,£; эти составляю-
щие являются функциями угловых вращательных координат г?:
Р(=Р&), РЧ = РЧЮ, P( = P(W-	(17-86)
Если обозначить неизменные составляющие дипольного момента Р в подвижной системе
через Рх, Ру, Pz и ввести эйлеровы углы 0 и у? (рис. 17.4, а, с. 476), то Р^, Рп и Р^ выразятся
через Рг, Ру и Pz по хорошо известным формулам:
Р^ = Px(cos <р cos ф - sin cos 0 sin ф) 4-
4- Ру(~ sin 9? cos ф — cos у? cos 0 sin V>) + Рг sin 0 sin Vs
Р^ zz Px(cosy> sin + sin у? cos $ cos V>) 4-	►
4- Py(- sin y? sin V> 4- cos tp cos 0 cos ф) - Pz sin 0 cos Vs
Pc = Px sin sin 0 4- Py cos tp sin 0 4- Pz cos i?,
(17.87)
которые легко получаются из наглядных соображений и представляют собой формулы (17.86)
в раскрытом виде для общего случая нелинейной молекулы. Для линейной молекулы диполь-
ный момент в силу ее симметрии направлен по оси молекулы, и если ввести углы 0 и
§ 17.6. Характеристики спектров поглощения и испускания
487
в сферической системе координат (рис. 17.4,6), то
Р^—Р sin в cos у?, ”
Ру = Р sin 0 sin у?,
Pq = Р cos 0,	4
(17.88)
ОС	О
о-х х о------о-*»
в
г
Рис Л 7.6. Колебания
линейных молекул,
имеющих центр
симметрии:
а — колебания
молекулы Н2;
б — симметричное
колебание молекулы СО2;
в — антисимметричное
колебание молекулу СО2;
г — деформационное
колебание молекулы СОз
Эти формулы получаются как непосредственно из чертежа, так и из формул (17.87), если
положить Рх — Ру — О, Рг — Р, в 0 и р — чр — 90°.
Если дипольный момент молекулы в силу ее сим-
метрии равен нулю, то при колебаниях, не нарушающих
симметрию молекулы, он остается равным нулю и со-
ответствующие переходы невозможны. Это имеет место
для колебаний двухатомной молекулы, состоящей из двух
одинаковых атомов (например, Оз, Н2): такая молекула
имеет центр симметрии и ее дипольный момент равен
нулю (см. ниже, §18.6, с. 527). При колебаниях центр
симметрии сохраняется (рис. 17.6, а), и молекула не может
иметь инфракрасного спектра поглощения или испуска-
ния, обусловленного колебательными переходами. Однако
при колебаниях, нарушающих симметрию молекулы, мо-
жет появляться дипольный момент, отличный от нуля,
и колебательные переходы в поглощении и испускании
становятся возможными. Примером может служить моле-
кула СОз, не имеющая, так же как и молекула Н2, диполь-
ного момента из-за наличия центра симметрии. В отличие
от последней наряду с колебанием, не нарушающим сим-
метрию (рис. 17.6, б, симметричное колебание) молекулы,
для СОз возможны колебания, не удовлетворяющие этому
условию (рис. 17.6, в, г, антисимметричное колебание и де-
формационное колебание) и создающие отличный от нуля
дипольный момент. Поэтому молекула СОз обладает ин-
фракрасным спектром поглощения и испускания. Вообще
все многоатомные молекулы могут иметь колебательные
спектры поглощения и испускания даже при равном нулю
дипольном моменте благодаря появлению дипольного мо-
мента при колебаниях, нарушающих симметрию молекулы; подобные колебания воз-
можны для всех многоатомных молекул, обладающих симметрией (см. § 20.1 и гл. 22).
Таким образом, двухатомные молекулы с Р = 0 не имеют колебательных
спектров поглощения и испускания, а многоатомные молекулы с Р = 0 имеют такие
спектры вследствие возможности колебаний, нарушающих симметрию молекулы.
При вращении молекул, для которых дипольный момент равен нулю, он
не изменяется и остается равным нулю ((в 17.86)	= 0). Поэтому все
молекулы с Р = 0 не имеют чисто вращательных спектров поглощения и испускания
как в инфракрасной области, так и в микроволновой области.
Мы разобрали дипольное излучение молекул, исходя из наглядных представлений. Мож-
но этот вопрос рассмотреть более строго на основе квантовомеханической теории молекул,
изложенной в предыдущем параграфе.
Вероятности дипольных переходов определяются, согласно формулам (4.45) для спон-
танного испускания, (4.46) для поглощения и (4.47) для вынужденного испускания, квадратом
модуля матричного элемента дипольного момента (через дипольный момент перехода),
488 Глава 17. Виды движения в молекуле и типы молекулярных спектров
который может быть представлен в форме (ср. (4.51))
|Р.*Г = |Шх-Г + |(Л).*Г+ |<Рс)*Г = £ 1<РД‘-Г (М>»7,0,	(17.89)
А
где Р^, Р^, Р^ — составляющие дипольного момента в неподвижной системе координат £, tj,
Для молекул эти матричные элементы в соответствии с (17.66) будут иметь вид
(Рд)й = (Px)n'v'j',n"v"j" = У ф'/'РхФк dxdpdti =
= J	(17.90)
Здесь интегрирование производится по электронным координатам х, колебательным коорди-
натам р и вращательным координатам д. n'v'j' и n"v"j" — совокупность квантовых чисел,
характеризующих верхний и нижний комбинирующие уровни (обозначенные соответственно
одним и двумя штрихами); для краткости у волновых функций ^эл, ^кол и ^вРаш не указаны
соответствующие индексы п, v и j ,3\ Следует отметить, что, вообще говоря, волновые функ-
ции ^Кол(р) различны для различных электронных состояний, а волновые функции ^Враш($)
различны для различных колебательных состояний, т. е. даже при одинаковых квантовых
ЧИСЛаХ £,(/>) # Ф"оАР) (V' = V"’ Н0 «' 7* П") И V,Bpaw(’7) / ’/’"pamW 0" = j", НО v' £ V").
Как и в § 17.5, мы будем в соответствии с предположением о медленности колебательного
движения по сравнению с электронным и вращательного по сравнению с колебательным
сначала интегрировать по электронным координатам, затем по колебательным и, наконец,
по вращательным. При этом интегрирование по электронным и колебательным координатам
относится к подвижной системе координат, поэтому составляющие Рх дипольного момента
в неподвижной системе надо выразить через его составляющие Ра в подвижной системе
(Л — 4, rjj а = ж, у, z). Представляя (17.87) (или (17.88) с Р — Pz) в виде
Рх^^С^)Ра(х,р),	(17.91)
где Ра(Х) р) являются функциями электронных координат х и колебательных координат р,
а САа($) функциями вращательных координат д, мы получим
(Px)n’v'j',n"v"jn — I ^,вращ(^)^,вращ(^)
2 C*c№)(Pa)n,v,,n"vl
(17.92)
где
(Pa)n'v',n"v" = У ФэАх, р)ф'^л(р)Ра(х, р)ф"л(х, р)-ф"т(р) dx dp	(17.93)
— матричный элемент составляющей дипольного момента в подвижной системе, взятый
по электронным и колебательным волновым функциям.
Матричный элемент вектора дипольного момента Р(х,р) с составляющими Ра(х, р)
будет равен
Pn'»',n"v" = У ф'*л(х, р)ф'*а1(р)Р(.х, р)ф"я(х, р)ФтЛр) dx dp	(17.94)
и его можно представить, выполняя сперва интегрирование по электронным координатам,
в форме
Pn’t1, n'!v" — Фкол (р)Рп'п" (p)V’kOj(p)	(17.95)
где
Рп'п"(р)= I ^эАх) р)Р(т,р)^Рэа(х, р) dx	(17.96)
Эти уровни могут быть вырожденными; в nvj тогда включаются квантовые числа для вырожденных
между собой состояний, например, под j могут подразумеваться квантовые числа j, mj.
§17.6. Характеристики спектров поглощения и испускания
489
— матричный элемент дипольного момента, взятый по электронным волновым функциям.
Он является функцией колебательных координат р. Векторы Рп/п„(р) и	определен-
ным образом ориентированы относительно подвижной системы. При этом вектор Рп'п"(р)
зависит от мгновенной конфигурации ядер, а вектор Pnv,n%" является постоянным вектором,
связанным с подвижной системой.
Рассмотрим теперь последовательно электронные (электронно-колебательно-вращатель-
ные), колебательные (колебательно-вращательные) и вращательные (чисто вращательные)
переходы.
Для электронного перехода (Е'зл - Е":Л Ф О, ^41(Ж,Р) Ф Ф"л(х,р)) матричный эле-
мент (17.96) можно представить, учитывая (4.33), в виде
Рп’п"(р) = У	+	(17.97)
где Рзл(х) — дипольный момент электронов, а Ряд(р) — дипольный момент ядер. В силу
ортогональности электронных волновых функций член, содержащий Ряд(р), обращается
в нуль и мы получаем
Рп'п"(р) = [ Р)Ры^)Фэл(я:> р) dx.	(17.98)
Через этот дипольный момент чисто электронного перехода выражается, согласно (17.95),
дипольный момент электронно-колебательного перехода, определяющий вероятность соответ-
ствующего электронно-колебательного перехода и представляющий вектор, определенным
образом ориентированный относительно молекулы. Согласно наглядным представлениям,
мы имеем осциллятор, связанный с молекулой (ср. §4.3, с. 94). Для данного электронно-ко-
лебательного перехода в соответствии с (17.92) возможны различные вращательные переходы,
ДЛЯ которых (РА)гЛ = (Px)nlvtj',nllvl,j,t # О-
Если в (17.98) пренебречь зависимостью Рп<п'1 от р и считать его постоянным (что
является разумным приближением, когда амплитуды колебаний не очень велики и поэтому
значения Рп’п" (ft) мало отличаются от его значений для равновесной конфигурации), то
дипольный момент электронного колебательного перехода (17.95) равен
Pn'v’,n"v" = Рп’п" 'ФкОЛ (р)^КОЛ (р) dp,	(17.99)
т. е. просто произведению дипольного момента Рп'п" электронного перехода и интеграла
наложения
Iv'v" = J Koh(p)^'Hp) dp	(17.100)
колебательных функций комбинирующих электронных состояний. Значение этого интеграла
будет определять относительные вероятности различных колебательных переходов при за-
данном электронном переходе. Существенно, что колебательные функции — ^кол(р),
И - Лл (р) относятся к разным электронным состояниям для колебательных функций,
относящихся к тому же электронному состоянию, интеграл наложения (17.100) обратился бы
в нуль в силу их ортогональности. Рассмотрение свойств интеграла наложения существенно
при разборе вопроса об относительных интенсивностях колебательных полос в электронных
спектрах (см. гл. 25, с. 758 и гл. 27, с. 833).
Когда электронное состояние не изменяется, т. е. для колебательно-вращательных
и для чисто вращательных переходов, усреднение дипольного момента Р(ж, р) по элек-
тронной функции ф3л(хур), согласно (17.96), дает
р = Рпп(р) = У |чМ®,р)|2-Р(я, р) dx.	(17.101)
Это есть дипольный момент молекулы в данном электронном состоянии как функция
колебательных координат р.
490 Тлава 17. Виды движения в молекуле и типы молекулярных спектров
Для колебательного перехода (Е'кол -Е"ол # 0, ^кол(р) 'ФкоАр)) дипольный момент этого
перехода (17.95) будет равен
(Р U-. = Рп< nv„ = J tMtMPnntp) dp.	(17.102)
В данном случае существенной является зависимость дипольного момента Рпп(р) элек-
тронного состояния от колебательных координат (которой мы пренебрегали при переходе
от (17.95) к (17.99)). При Рпп(р) — const интеграл (17.102) в силу ортогональности коле-
бательных функций одного и того же электронного состояния обращается в нуль. Однако
при учете зависимости Рпп(р) от р этот интеграл будет отличен от нуля и колебательные
переходы являются возможными. Согласно (17.92), для данного колебательного перехода
будут возможными и вращательные переходы, для которых (PA)tfc = (Px)nv'j',nv"j" £ 0- Более
подробно зависимость Рпп(р) будет рассмотрена в гл. 20 и 25 (см. с. 578 и с. 760). Для молекул
с равновесной конфигурацией, обладающей достаточно высокой симметрией, дипольный
момент РпАре) обращается в нуль. Он будет оставаться равным нулю и для любой конфигу-
рации с той же симметрией. Если колебания не нарушают симметрии (если ^кол(р) и ^кол(р)
обладают необходимой симметрией), то интеграл (17.102) обращается в нуль и колебательные
переходы запрещены. В частности, для двухатомных молекул, состоящих из двух одинаковых
атомов, РПп{р) — $ при любом расстоянии между ядрами в силу наличия центра симме-
трии (в (17.101) при инверсии |^эл(ж, р)|2 не изменяется, а Р(х,р) меняет знак, ср. (17.83))
интеграл (17.102) равен нулю, и такие молекулы не могут иметь колебательных спектров
поглощения и испускания. Мы доказали утверждение, сделанное ранее на основе наглядных
соображений (см. с. 486).
Для чисто вращательного перехода матричный элемент (17.102) (P)v'v« — Pnv',nv" сво-
дится к среднему значению момента Рпп(р) в заданном колебательном состоянии v, т. е. мы
получаем дипольный момент, усредненный как по электронным, так и по колебательным
волновым функциям. Мы имеем
Р — Рпщпг — J | V’kOJi(p) | Р dp — I | ^кол(р) | Р пп(р} dp =
f if Г J 2	1	(17Л03)
= /	S / |чЫ*,/’)| P(x,p)dx> dp.
В частности, для основного электронно-колебательного состояния молекулы мы по-
лучаем определенное среднее значение дипольного момента Роо,оо, которое и представляет
постоянный дипольный момент, определяющий ее поведение как диполя в электрическом
поле. Значение (17.103) дипольного момента в заданном электронно-колебательном состоянии
будет определять, согласно (17.92), возможные чисто вращательные переходы. При # 0
будут возможны те переходы, для которых (Px)ik = (Pxjnvf.nef 0. Если для молекулы в силу
ее симметрии дипольный момент (17.103) обращается в нуль, то для всех чисто вращательных
ПереХОДОВ Наряду С (Px)nB,nv, (Р0П»,пО И (Р2)пг,,пр будут раВНЫ НУЛЮ И (PfJnv^nvj*. (P4)nVjf,nvj"
и (P<)nv/,n»;w; следовательно, такая молекула не может иметь чисто вращательного спектра
поглощения и испускания в соответствии с наглядными соображениями (см. с.487).
Наряду с дипольным излучением для молекул возможны магнитное дипольное
и квадрупольное излучения. Соответствующие переходы гораздо менее вероятны,
чем дипольные переходы; их учет может быть осуществлен при исследовании элек-
тронных спектров молекул, находящихся в условиях, способствующих наблюдению
переходов, запрещенных в дипольном излучении и возможных в квадрупольном
и в магнитном излучениях.
Для молекул справедливы правила отбора для квантовых чисел, определяющих
значения момента количества движения и его проекции (см. §4.8, с. 117). Эти
правила отбора особенно существенны при рассмотрении вращательных переходов
как в случае чисто вращательных, так и в случаях колебательно-вращательных
и электронно-колебательно-вращательных спектров.
§ 17.7. Характеристики спектров комбинационного рассеяния 491
Для колебательных и электронных переходов очень важны правила отбора, опре-
деляемые симметрией равновесной конфигурации молекулы. Эти правила отбора
для простейших случаев (центр симметрии, плоскость симметрии, ось симметрии
второго порядка) были рассмотрены в §4.7. Правила отбора для более сложных
случаев будут подробно рассмотрены в дальнейшем (см. гл. 23, с.678 и гл. 27, с. 827).
Для вывода правил отбора для дипольного излучения необходимо исследовать свойства
соответствующих матричных элементов (17.98) для электронных переходов, (17.102) для ко-
лебательных переходов и (17.92) для вращательных переходов. При этом для электронных
и для колебательных переходов рассматриваются значения дипольного момента перехода
в связанной с молекулой подвижной системе х, у, z\ для разных составляющих Рх, Ру, Pz век-
тора дипольного момента могут получаться различные правила отбора. Обычно определяют
правила отбора для каждой составляющей в отдельности или для их линейных комбинаций.
Для магнитного и для квадрупольного излучений правила отбора получаются путем рассмо-
трения свойств матричных элементов составляющих аксиального вектора магнитного момента
и тензора квадрупольного момента.
Мы не будем здесь подробно останавливаться на вопросах интенсивностей
в молекулярных спектрах, связанных с зависимостью интенсивностей от заселенно-
сти уровней. Отметим только, что для молекулярной спектроскопии важную роль
играет учет заселенности колебательных и вращательных уровней в связи с тем,
что расстояния между этими уровнями, особенно вращательными, малы и наряду
со случаем &Е > кТ очень важны случаи &Е ~ кТ и ДЕ <С кТ (см. §5.2). В этих
случаях является существенным и учет вынужденного испускания.
§ 17.7. Характеристики переходов и интенсивности
в случае спектров комбинационного рассеяния
Колебательные (колебательно-вращательные) и вращательные (чисто враща-
тельные) переходы, наблюдаемые путем изучения соответствующих спектров ком-
бинационного рассеяния, связаны с изменениями поляризуемости молекул. Поля-
ризуемость молекулы определяет ее способность поляризоваться — приобретать
под действием электрического поля индуцированный (наведенный) дипольный
электрический момент — и является важной характеристикой молекулы. В слу-
чае рассеяния этот индуцированный момент создается под действием падающего
света: с классической точки зрения — под действием переменного электрического
поля падающей электромагнитной волны.
Рассмотрим подробнее действие на атомную систему переменного электричес-
кого поля
S = <А) cos 2ти/0£,	(17.104)
имеющего амплитуду/о и изменяющегося с частотой Uq. В простейшем случае атомов
и высокосимметричных молекул (обладающих кубической симметрией, см. ниже,
§ 18.6, с. 528) индуцированный дипольный момент Р совпадает по направлению
с направлением поля S и пропорционален ему по величине:
(17.105)
где а — поляризуемость атомной системы, в данном случае не зависящая от напра-
вления вектора
Если поляризуемость постоянна, а = ао, где «о не зависит от времени, то,
согласно (17.105) и (17.104), мы получаем
Р — Qo<^o cos 2тгро^	(17.106)
492 Глава 17. Виды движения в молекуле и типы молекулярных спектров
Таким образом, индуцированный дипольный момент периодически изменяется, по-
добно переменному электрическому полю падающей световой волны, с частотой vq.
Мы имеем гармонически колеблющийся диполь и, согласно основной формуле (4.29)
для излучения диполя, энергия, испускаемая во всех направлениях в единицу вре-
мени, будет равна

2 d2P
"° ~ 3? IF
г 32ir4d , , 2	,
=	, , ° «о cos227ri/0L
3cJ
(17.107)
Мы получаем рассеяние света с неизменной частотой и фазой — когерентное
рассеяние (см. с. 25). Усреднение энергии WUo во времени дает (ср. (4.30))
W„o = FF' |а°|2^ cos 227rz/o/ =	(17.108)
Эта формула определяет интенсивность рассеяния отдельной частицей, которое,
таким образом, пропорционально квадрату амплитуды падающего света, четвертой
степени частоты и квадрату поляризуемости.
Так как плотность р(у) энергии излучения частоты v для электромагнитной волны равна
P(-V}=F
то
— 128тг5Ра , 12 , ч
= Зе3 '““I Р‘')'
Число рассеянных атомом или молекулой за единицу времени фотонов равно
(17.109)
(17.110)
(17.111)
^(расе) =	= 12^1 М2рм^
и можно ввести понятие о вероятности рассеяния как о числе фотонов, рассеянных одной
частицей за единицу времени (ср. определение вероятностей поглощения Bki, согласно (4.4)).
Вероятность рассеяния равна Cp(vq), где коэффициент
1	_ 128тг5^	2
p(uQ) hvQ 3hc3 |ао1
(17.112)
и пропорциональна кубу частоты и квадрату поляризуемости. Коэффициент С аналогичен
коэффициентам Эйнштейна А и В и представляет вероятность рассеяния, рассчитанную
на единицу плотности излучения частоты. Следует, однако, иметь в виду, что для рэлеевского
рассеяния нельзя определять число квантов, рассеянных N частицами за единицу времени,
формулой Z = Cp(vv)N, аналогичной (4.3), так как это рассеяние является когерентным.
При совершенно равномерном распределении частиц рассеяние отсутствует вследствие ин-
терференции света, рассеянного отдельными частицами. Рэлеевское рассеяние происходит
только за счет нарушений равномерного распределения частиц по объему рассеивающего ве-
щества, в случае газа — за счет флуктуаций плотности. В частности, флуктуациями плотности
объясняется рассеяние солнечного света воздухом; при этом более коротковолновый свет
рассеивается, согласно (17.108), сильнее, что и определяет спектральный состав рассеянного
атмосферой света, приводящий к голубому цвету неба.
Сложнее обстоит дело, если поляризуемость рассеивающей частицы не является
постоянной. Именно такой случай имеет место для колеблющейся молекулы: с клас-
сической точки зрения при колебаниях молекулы ее поляризуемость периодически
меняется с частотой колебания р,4).
14) Для вращающейся молекулы с поляризуемостью а, не зависящей от ориентации молекулы по отно-
шению к направлению электрического поля, вращение не может привести к изменению поляризуемости.
§ 17.7. Характеристики спектров комбинационного рассеяния
493
Пусть
а — «о + «1/ cos2xi4,	(17.113)
где наряду с постоянным членом поляризуемость содержит член, периодически
изменяющийся с частотой Тогда вместо (17.106) мы получаем, согласно (17.105)
и (17.104),
Р = сио^о cos I'kuqI + cos liryt cos 2iri/0^	(17.114)
Второй член соответствует колебанию с частотой у$, амплитуда которого меняется
с частотой у (амплитудная модуляция). При этом мы считаем у < yQ; для интере-
сующих нас случаев колебаний дипольного момента под действием видимого света
частоты yQl модулированных колебаниями молекул, происходящими с частотой
всегда
(17.115)
так как частоты колебаний молекул соответствуют инфракрасной области спек-
тра. Представляя произведение cos Inyt cos l^y^t в виде суммы - cos 2тг(г^> — y)t +
| cos 2тг(ц) + ^)£, находим
Р — cos2ttz/()£ + |Oi/^o cos 2тг(ц) - v)t + cos 2tt(i/q + v)t, (17.116)
т. e. индуцированный дипольный момент наряду с членом РРв, изменяющимся
с частотой Уо и обусловливающим когерентное рассеяние, содержит члены Р^-у
и Р|/о+|/, изменяющиеся с частотами Ув — у и у^ Ч- у. Эти члены обусловливают
некогерентное комбинационное рассеяние с частотой yf — yQ — у < yQ (стоксова линия
со смещением у = yQ-у1, где у§ > у1, см. с. 25) и с частотой у" — uq+у (антистоксова
линия со смещением — у — у$ — у'\ где у$ < у").
Интенсивность комбинационного рассеяния отдельной молекулой получается
равной аналогично (17.108)
—	_ 4тг4(г'О - I/)4	2 2
uq-u —	2^3	(17.117)
для частоты у1 = у^ — у и
--	47Г4(ро + f)4	2 2
WVn+v =------Д *0	(17.118)
для частоты у" ~ у$ + у. т. е. в обоих случаях пропорциональна квадрату ампли-
туды падающего света, четвертой степени частоты рассеянного света и квадрату
амплитуды, с которой изменяется поляризуемость.
Выражения (17.117) и (17.118) получаются при подстановке (17,116) в (4.29) и усред-
нении. При этом, наряду с членами, содержащими квадраты IPJ2, IP^.^I2 и (P^+J2
(что дает (17.108), (17.117) и (17.118) соответственно), получаются члены, содержащие про-
изведения P^Ppo-j,, P^P^+j, и PV^VPV^V9 которые при усреднении обращаются в нуль
(так как cos27ri/0^ cos2tt(i/0 - y)t = 0 и т.д.).
,5) Выражение (17.113) соответствует случаю высокосимметричной молекулы, колеблющейся с часто-
той 1/0 так, что ее симметрия не нарушается (случай полносимметричных колебаний, см. §20.1, с. 571).
Для других случаев нельзя считать поляризуемость в (17.105) не зависящей от направления вектора £
по отношению к молекуле, см. ниже, с. 495.
494 Глава 17. Виды движения в молекуле и типы молекулярных спектров
С квантовой точки зрения комбинационное рассеяние с частотой vq — v соответ-
ствует переходу молекулы с уровня Ek на уровень Ei, а комбинационное рассеяние
с частотой vq + и — с уровня Ei на уровень Ek, где
hv = hvik = Ei - Ек (Е{ > Ek).	(17.119)
Переход от классических формул к квантовым формулам, производится, как
и для спонтанного испускания (см. § 4.3 и § 4.4, например, переход от (4.34) к (4.35)),
заменой классической амплитуды в заданном состоянии молекулы аналогичной
величиной для соответствующего квантового перехода. Заменяя в (17.117) и (17.118)
классические амплитуды поляризуемости величинами и lotik, где otki и —
поляризуемости перехода, мы получим
---	16тг4(1/о — ^)4 ,	.2^2	-- 167T4(lZ0 + I/)4	2 2	/ ч
Wv,_v = .....\°3....|аь|2^о, WVo+v = —--------------4<*ik№0.	(17.120
3cJ	3cJ
Поляризуемости перехода &ki и определяют интенсивности линий комби-
национного рассеяния, аналогично тому как моменты перехода (Pki и Р^ в случае
дипольных переходов) определяют интенсивности линий поглощения и испуска-
ния. Формула (17.120) справедлива для невырожденных состояний и, как можно
показать, |«ь|2 = |«ц:|2. Легко перейти аналогично (4.45)-(4.47) к общему случаю
вырожденных состояний; в этом случае (\otk€,i6 I2 = \oti6, ke |2)l
wva_v =
+ =
16tt4(i/q - г/)4 2 J_ V
Зс3 ° 9к\
167F4(i/q + I/)4	2	1 y^
0 ^4-
б£
(17.121)
где величина 53 1°Ч*J2 аналогична величине Sik (см. (4.44)).
б£
Вводя плотность р(и) энергии падающего излучения, согласно (17.109), мы получим
—	_ 1287T5(l/0 - и)4 1 у 2 / ч
1аг<5, fcj р(^о)->
к бе
—	_ 1287Г5(1/ + 1/0)4 1у.	,2 ( ч
^3	*	fcel р(^о)'
(17.122)
Числа рассеянных молекулой за единицу времени фотонов, т. е. вероятности комбинационного
рассеяния, равны
W
Vq-V
h(vn - р)
h(vn + Iх)
I28ir5(i/n - v)3	1	. i2 , x ^(fo) / \
-----------------— Z .	P("o) = Q>("o),
6e
128тг5(1/0 + v)3 1 y-'।	|2 , >	^(ro) . ,
-----ЗдР---------Z Z > кс I pM = C^'p(un).
9‘ ie
Здесь введены коэффициенты
4"o) _
ki ~
1287Г5(ро - v)3 1	। i2
—^3— - —	,
-4^o) _
'ik ~
1287T5(l/0 + v) 1 y-A 2
(17.123)
(17.124)
§ 17.7. Характеристики спектров комбинационного рассеяния
495
дающие вероятности комбинационного рассеяния, рассчитанные на единицу плотности
энергии излучения.
Вероятности рассеяния находятся в соотношении
С<?>	O'o-I')3 ft O'o + i')3	( ‘	)
В силу некогерентности комбинационного рассеяния число фотонов, рассеянных в еди-
нице объема за единицу времени п частицами, будет пропорционально этому числу частиц,
и мы получаем
4Г’ - пкС^р(и0), Zir’ = п.Ф>о)>	(17.126)
где пк и п: — заселенности уровней Ек и Ei молекулы. Величины
= h(ua - vik)C^p(v0)nk и и‘Гс) = Л(ц> + МФ’рО'о)’».	(17.127)
представляют мощности комбинационного рассеяния, стоксового и антистоксового, — энергии,
рассеиваемые в единице объема в единицу времени (ср. (5.2)). Именно эти величины
являются мерой интенсивности комбинационного рассеяния и определяют относительные
интенсивности смещенных линий в спектре комбинационного рассеяния.
Так как при термодинамическом равновесии вещества, согласно (5.15),
П,	Qi _ E*~Ek Qi _ hvtk
— — — e = — e tT
nk	дь	9k
(17.128)
то отношение интенсивностей антистоксовых линий к интенсивностям стоксовых, соглас-
но (17.127) и (17.125), равно
Антист = Ц,(ГС> = (И) + «/.*) .
Тст	("0 - Vik) с£0>
9.
— ехр
9k
hvik 1
kT )
{hvik 1
"ТТГ (,7129)
KJ J
(t'o + i/it)4
("о -«',*)“
В силу vik C Ц) (cm. (17.115)) при hvik кТ отношение интенсивностей определяется
показательным множителем и является малым, а при hvik <£. кТ это отношение равно
(Уо + ^ik)4
-------— и близко к 1.
(уо - Vik)4
Как отмечалось в начале параграфа, основное соотношение между индуцирован-
ным дипольным моментом Р и напряженностью электрического поля $ справедливо
лишь в простейшем случае атомов и высокосимметричных молекул,6). В общем слу-
чае для молекул составляющие дипольного момента Рх, Ру, Pz в подвижной системе
являются линейными функциями составляющих Sx, <£у, Sz напряженности поля:
Рх — СХ-хх&х “Ь ®-ху&у “Ь ®-xz&zi
Ру — Otyx(f>x + OlyySy -f- Olyz^z,
Pz — otzx(£x -h otzySy -|- azzcz.
(17.130)
Совокупность величин (Д 7 = ж, 1/, z) образует тензор поляризуемости,
характеризующий способность молекулы поляризоваться в различных направлениях
под действием различным образом направленного электрического поля. Например,
ахх характеризует поляризуемость в направлении оси х под действием поля, также
направленного по оси х, а аху — под действием поля, направленного по оси у.
ахх, ауу> azz являются диагональными составляющими тензора, а аху, axz, аух,
ayz, azx, azy — недиагональными. Можно показать, что этот тензор симметричный,
т. е. аху = аух, ayz = azy, azx — axz, и, следовательно, определяется шестью
составляющими: ахх, ауу, azz, аху, ayz, azx. Всегда можно выбрать подвижные оси,
,6)Для последних при колебаниях, не нарушающих симметрию молекулы, см. примечание на с. 493.
496 Глава 17. Виды движения в молекуле и типы молекулярных спектров
связанные с молекулой, таким образом, чтобы три недиагональные составляющие
аху = аух, ayz — ctzy и otzx = axz обратились в нуль|7). Тогда соотношения (17.130)
приобретают более простой вид
=	Ру = <*у<?у, Pz = otz^z.	(17.131)
Вдоль этих осей — главных осей поляризуемости —
молекула поляризуется по-разному, но в направле-
нии поля. Если поле направлено по оси ж, инду-
цированный момент Р тоже направлен по оси х
и поляризуемость равна ах, и т.д. Однако главные
поляризуемости ах, ау, az, вообще говоря, различ-
ны — молекула в разных направлениях поляризу-
ется по-разному и притом в направлениях, не со-
впадающих с главными осями, дипольный момент
Р не совпадает с направлением поля (см. рис. 17.7,
— £у, но Рх Ф Ру, так как ах Ф ау). Лишь в слу-
► чае ах — ау = az = а поляризуемость не зависит
х от направления и (17.131) сводится к (17.105). В этом
случае диагональные составляющие равны друг другу,
а недиагональные равны нулю в любой повернутой
системе координат. В случае ах = ау az тензор со-
налравлений векторов Р и £ храняет свою форму при любом повороте подвижной
системы вокруг оси z.
Симметричный тензор можно наглядно представить при помощи эллипсоида, в данном
случае эллипсоида поляризуемости. Уравнение эллипсоида получается сразу, если представить
энергию молекулы в электрическом поле в виде (ср. (15.5))
= - j ^dP = -X-	<W/A'8)-	(17-132)
о
Уравнение
У7 = ~2и	(17.133)
07
и есть уравнение эллипсоида, которое при приведении к главным осям принимает вид
&Х(”х 4- <*у<”у ~Ь az^z ~ ~2U
или
б2	<2	«2
&у_	<”z_	=	.
а2	Ь2	с2	’
главные оси эллипсоида равны
/—2*7 I-2U I-2U
V (*г Ь У «у С У az
В случае ах = ау = az эллипсоид поляризуемости превращается в сферу, а в случае
ах = ау Ф az — в эллипсоид вращения вокруг оси z.
,7) Это возможно, так как поворот подвижной системы относительно молекулы определяется как раз
тремя независимыми параметрами, которые можно выбрать произвольно.
18) В силу (17.130) J* 3dP = f
0	07 0
(17.135)
(17.136)
§17.7. Характеристики спектров комбинационного рассеяния
497
В общем случае, когда тензор поляризуемости определяется шестью составля-
ющими (где = а7^, а, /3 = ж, y,z), каждую составляющую тензора можно
представить в виде, аналогичном (17.113)
«д7 = (а>у)о + («/з7)р cos 2тгИ,	(17.137)
где (а/з7)о — составляющие постоянного тензора, характеризующего неколеблющу-
юся молекулу, а (ад7)Р cos 2^14 — составляющие переменного тензора, характеризу-
ющего изменения поляризуемости при колебаниях молекулы.
Составляющие cos 2тп4 изменяются с частотой колебаний р, их амплиту-
ды (а^7)1/ определяют интенсивность комбинационного рассеяния, связанного с ко-
лебаниями частоты р, а соотношения этих амплитуд определяют его поляризацию.
При переходе к квантовым формулам классические амплитуды составляющих тензо-
ра поляризуемости заменяются соответствующими составляющими тензора поляри-
зуемости колебательного перехода	ИЛИ 2(Q£7)ifc (где |(c^7)fci|2 = |(<^7)i&|2) l9),
через которые и определяются интенсивность и поляризация комбинационного
рассеяния с частотой i/0 _ pik или vq -h уц.. Таким образом, при комбинационном
рассеянии каждый колебательный переход Ek -* Ei характеризуется совокупностью
шести величин:
(&xx)kii (&yy)kij (pLzz)kii (&xy)ki> (S^yz)kii {^zx)ki*	(17.138)
Для возможности перехода необходимо, чтобы хотя бы одна из составляющих
тензора поляризуемости перехода была отлична от нуля. Получающиеся правила
отбора для колебательных спектров комбинационного рассеяния отличаются от пра-
вил отбора для инфракрасных колебательных спектров. Эти правила отбора будут
рассмотрены в гл. 23 (см. с. 678).
С квантовомеханической точки зрения величины (17.138), определяющие комбинацион-
ное рассеяние, по своим свойствам симметрии подобны матричным элементам симметричного
тензора, т. е. величинам типа
(ai>y)ki = / ф*к(х)а^(х)ф{(х) dx,	(17.139)
где а^(х) — симметричный тензор, аналогично тому, как величины (Px)ik, (Py)ik, (Pz)ik> опре-
деляющие дипольное излучение (см. с. 94), представляют матричные элементы составляющих
полярного вектора. При выводе правил отбора в случае комбинационного рассеяния можно
для величин (17.138) исходить из выражений (17.139); отличие этих правил отбора от правил
отбора для дипольных переходов при поглощении и испускании в инфракрасной области
будет определяться отличием матричных элементов симметричного тензора поляризуемости
от матричных элементов полярного вектора дипольного момента. Однако действительный
вид величин (17.138) более сложен, чем (17.139); в квантовой механике нельзя определять
поляризуемость просто как среднее значение классической функции от координат, подобно
тому как дипольный момент определяется как среднее значение функции (4.33). К вопросу
о тензоре поляризуемости для колебательных переходов мы вернемся в гл. 23 (см. с. 695).
Составляющие (17.137) тензора поляризуемости берутся в подвижной коор-
динатной системе, связанной с молекулой. Так как колебание происходит быстро
по сравнению с вращением, то комбинационное рассеяние, связанное с колеба-
ниями, можно рассматривать при заданной ориентации молекулы и лишь затем
производить усреднение по различным возможным ориентациям.
19) В случае вырожденных состояний вместо величин |(ад7)д;г|2 и |(ад7)г&|2 будут входить величины
|(<Wi<,k£ |2 И	|(а/)7)й,л-£|2 (ср. (17.121)).
б£
498 Глава 17. Виды движения в молекуле и типы молекулярных спектров
При вращении молекулы поляризуемость в заданном в пространстве напра-
влении будет определяться составляющей индуцированного дипольного момента
по этому направлению, и в неподвижной системе координат мы будем иметь
аналогично (17.130):
pi =	'
Рс =	j
(17.140)
В отличие от составляющих (/3, у = х,у, z) тензора поляризуемости в по-
движной системе, которые не зависят от поворота молекулы, его составляющие адд
(Л, д = С, 1/, <) в неподвижной системе будут периодически изменяться при вра-
щении молекулы. Например, если сначала с осью £ совпадает ось х молекулы,
а затем ось у, то поляризуемость будет сначала равна ахх, а затем ауу. Имен-
но подобные изменения составляющих тензора поляризуемости со временем будут
определять комбинационное рассеяние, связанное с вращением. Только если тензор
поляризуемости сводится к скаляру а = ахх — ауу = azz (аху — ayz = azx — 0),
то при переходе к неподвижной системе	— а,	= 0;
поляризуемость в заданном направлении не изменяется при вращении молекулы
и вращательный спектр комбинационного рассеяния отсутствует.
В остальных случаях молекула будет иметь такой спектр, причем интенсивность
комбинационного рассеяния с частотой у - иц- или у + будет определяться со-
ставляющими (А, Р — С Ъ 0 тензора поляризуемости, согласно классической
теории, и соответствующими составляющими (oix^ki или («аД** тензора поля-
ризуемости вращательного перехода, согласно квантовой теории. Таким образом,
при комбинационном рассеянии каждый вращательный переход Ek Ei характе-
ризуется совокупностью шести величин:
(а«)ь,	(ап<)н, (а«)н-
(17.141)
Отличие от нуля этих величин определяет правила отбора.
С квантовомеханической точки зрения величины (17.141), так же как и величины (17.138),
по своим свойствам симметрии подобны матричным элементам симметричного тензора,
что позволяет найти соответствующие правила отбора. Эти правила отбора для момента
количества движения и его проекции будут совпадать с правилами отбора (4.158), (4.159)
и (4.161) (см. также (4.173)), справедливыми для любого симметричного тензора.
ГЛАВА 18
РАВНОВЕСНАЯ КОНФИГУРАЦИЯ МОЛЕКУЛЫ
И ЕЕ СВОЙСТВА СИММЕТРИИ
§ 18.1.	Форма и размеры молекул
Каждое устойчивое электронное состояние молекулы характеризуется, как мы
видели в предыдущей главе (см. с. 475), определенной равновесной конфигурацией ядер.
Эта равновесная конфигурация соответствует минимуму электронной энергии £эл(р)
молекулы в рассматриваемом состоянии как функции относительных координат
ядер1* и определенному электронному уровню Еэл = £эл(ре) молекулы.
Значения параметров равновесной конфигурации — равновесных значений
относительных координат — являются важнейшей характеристикой как самого
электронного уровня, так и соответствующих ему колебательных и вращательных
уровней. При заданном относительном расположении ядер в молекуле электро-
ны движутся определенным образом и получается соответствующее распределение
электронной плотности. Колебания ядер в молекуле совершаются около равно-
весных положений, поэтому от равновесной конфигурации существенным образом
зависят колебательные уровни и колебательные спектры. Кроме того, от равновес-
ной конфигурации ядер непосредственно зависят моменты инерции молекулы и,
следовательно, вращательные уровни и вращательные спектры.
Среди всех возможных для данной молекулы равновесных конфигураций, ка-
ждая из которых соответствует определенному электронному уровню молекулы, осо-
бенно важную роль играют свойства равновесной конфигурации молекулы в основ-
ном электронном состоянии. Значение Еэ^ = ^эл(ре°СН^) для такой конфигурации
представляет наименьшее возможное значение энергии молекулы* 2) и соответствует
основному электронному уровню. В дальнейшем мы будем называть равновесную
конфигурацию в основном электронном состоянии молекулы просто равновесной
конфигурацией молекулы и при рассмотрении равновесных конфигураций для воз-
бужденных электронных состояний будем специально отмечать это.
Заметим, что параметры равновесных конфигураций для возбужденных элек-
тронных состояний могут сильно отличаться от соответствующих параметров для ос-
новного состояния. Когда говорят о равновесных значениях параметров, характе-
ризующих молекулу, не указывая особо, к каким электронным состояниям эти
параметры относятся, то всегда подразумевают их значения для основного элек-
тронного состояния (для нормальной конфигурации).
Под р мы подразумеваем совокупность рз? • • •, Pk всех независимых относительных координат.
2) Если пренебречь нулевой энергией колебаний (подробнее см. с. 639). Действительное наименьшее
возможное значение получается добавлением к этой нулевой энергии.
500
Глава 18. Равновесная конфигурация молекулы
Форма и размеры молекулы определяются ее равновесной конфигурацией.
Как известно, теория химического строения приводит к представлениям об опре-
деленном расположении атомов в молекуле, которое выражается структурными
формулами. Эти представления конкретизируются в физической теории строения
молекул, и современная стереохимия — учение о пространственной структуре хи-
мических соединений — исходит из модели молекулы, состоящей из определенным
образом расположенных ядер и движущихся вокруг них электронов, образующих
химические связи различных типов. Равновесная конфигурация и является тем
расположением ядер, которое определяет пространственную структуру химических
соединений. Направления химических связей между атомами — это направления от-
резков, соединяющих ядра соответствующих атомов, а длины химических связей —
это значения равновесных расстояний между ядрами. Для характеристики формы
молекулы очень удобно, в соответствии с представлениями о направленных химиче-
ских связях (с представлениями теории направленной валентности, см. гл. 26, с. 794),
задавать наряду со значениями равновесных расстояний между атомами3) значения
равновесных углов между связями. Например, для молекулы метана СН4, имеющей
тетраэдрическую форму (см. ниже, рис. 18.3, б, с. 502), можно задать значение рСн
четырех одинаковых длин связей С—Н и значение «нсн шести одинаковых углов
Н—С—Н между связями.
Говоря о размерах молекулы, необходимо уточнить, что следует понимать
под размерами. Для заданной равновесной конфигурации электроны движутся опре-
деленным образом вокруг ядер, образуя электронную оболочку молекулы, и полные
размеры молекулы определяются размерами внешних электронных оболочек. Однако
эти оболочки не имеют резких границ, их можно характеризовать лишь распределе-
нием электронной плотности, и при изучении различных явлений могут получаться
различные значения для размеров молекул. В газе столкновения молекул зависят
от их размеров, и из опытных данных можно найти по формулам кинетической
теории поперечные сечения молекул. Поперечные сечения молекул можно также
определить, изучая рассеяние этими молекулами потока частиц, например электро-
нов. Значения поперечных сечений (и вычисленные из них при предположении, что
молекулы имеют сферическую форму, радиусы молекул) оказываются различными
при расчете их на основе различных данных. В противоположность этому значения
равновесных расстояний между ядрами дают вполне определенную характеристику
размеров молекул, не зависящую от метода определения этих расстояний и, кро-
ме того, позволяющую говорить о размерах молекулы в различных направлениях.
Учитывая распределение электронной плотности вокруг определенным образом рас-
положенных ядер, можно оценить полные размеры молекул и в принципе рассчитать
поперечные сечения молекул для различных процессов столкновений и процессов
рассеяния. В дальнейшем под размерами молекулы мы будем подразумевать размеры
равновесной конфигурации, определяемые значениями ее параметров — равновес-
ных расстояний и углов.
Форма и размеры молекул могут быть весьма разнообразны в соответствии
с разнообразием состава и строения химических соединений. Молекулы могут быть
линейными, плоскими, неплоскими; они могут состоять из цепей атомов, не-
разветвленных и разветвленных, из кольцевых структур и т. д. При этом скелет
молекулы — ее равновесная конфигурация — может обладать различной степенью
гибкости, и возможны молекулы, для которых одни ее части легко вращаются отно-
сительно других частей. Размеры молекулы, вообще говоря, тем больше, чем больше
В дальнейшем мы будем часто говорить о положении атомов и о расстояниях между атомами
в молекуле, подразумевая при этом положения ядер и расстояния между ними.
§18.1. Форма и размеры молекул
501
число атомов, из которых она состоит. Расстояния соседних атомов, химически свя-
занных друг с другом, обычно составляют 1—2 А, т. е. порядка 10-8 см. Чем прочнее
связь между атомами, тем, как правило, меньше равновесная длина этой связи.
Простейшим случаем является частный случай линейных молекул, к числу
которых относятся все двухатомные молекулы, многие трехатомные молекулы,
например СО2, CS2, HCN, N2O и некоторые молекулы, состоящие из большого числа
атомов, например, С2Н2, C2N2, С4Н2 (рис. 18.1). Для этих молекул ядра расположены
на одной прямой, и равновесная конфигурация полностью определяется заданием
равновесных длин связей между соседними атомами; в случае двухатомной молекулы
этим расстоянием является единственное равновесное расстояние ре (см. с. 471).
Более сложным является частный случай нелинейных плоских молекул, ядра кото-
рых расположены в одной плоскости. К таким молекулам относятся все нелинейные
трехатомные молекулы (для них положение трех ядер определяет положение соот-
ветствующей плоскости), например, Н2О, H2S, NO2, Оз и ряд молекул, состоящих
из четырех, пяти, шести и более атомов, например, Н2СО, С2Н4, СбНб (рис. 18.2).
Отметим, что молекула бензола СбНб представляет пример плоской кольцевой
структуры; подобного рода шестичленное плоское углеродное кольцо называют
бензольным кольцом.
Равновесную конфигурацию можно характеризовать заданием равновесных
длин связей между соседними атомами и равновесных углов между связями или же
только расстояний между атомами. Например, для молекулы воды Н2О можно задать
значение рон двух одинаковых длин связей О—Н и значение «нон угла Н—О—Н
между связями или то же значение рон длин связей О—Н и значение расстояния
рнн между атомами водорода. Для молекулы этилена С2Н4 можно задать, например,
значение рсс длины связи С—С, значение рсн четырех одинаковых длин связей
ОСО
1,16	1,16
S С S
1,54	1,54
HCN
в
1,06	1,15
N J4 О
1	* 1,12 * 1,19 *
НС с н
’1,06 е 1,20 *1,06*
N	С	С	N
е	•....>.
1,16	1,38	1,16
н С	С	с	с н
Ж • '	 »---—-
1,06 1,19	1,36	1,19 1,06
Рис. 18.1. Линейные молекулы:
а — двуокись углерода;
б — сероуглерод;
в — синильная кислота;
Рис. 18.2. Плоские молекулы:
а — вода; б — сероводород; в — двуокись азота; г — озон;
д — формальдегид; е — этилен; ж — бензол
г — закись азота;
д — ацетилен; е — циан;
ж — диацетилен
502
Глава 18. Равновесная конфигурация молекулы
С—Н и значение «нсн Двух одинаковых углов Н—С—Н ( углы С—С—Н одинаковы
2тг - «нсн
и равны --------
Рис. 18.3. Пирамидальные
и тетраэдрические молекулы:
а — аммиак; б — метан
Самым общим является случай неплос-
ких молекул, ядра которых образуют про-
странственную структуру. Большинство мо-
лекул, состоящих не менее чем из четы-
рех атомов, обладают неплоскими равно-
весными конфигурациями. В простейших
четырех- и пятиатомных молекулах один
центральный атом связан с тремя или че-
тырьмя другими одинаковыми атомами, как
в молекулах NH3 и СН4, имеющих соот-
ветственно форму правильной трехгранной
пирамиды и тетраэдра (рис. 18.3). В послед-
нем случае четырехвалентный атом углерода
образует четыре простые связи, составляющие между собой одинаковые углы, что
является типичным для огромного числа предельных органических соединений. При-
мером является равновесная конфигурация нормальных предельных углеводородов
(нормальных парафинов) типа СпН2П+2, в которых атомы углерода, соединенные
простыми связями, образуют плоскую зигзагообразную цепочку, а соединенные
с ними атомы водорода лежат вне плоскости этой цепочки, за исключением двух
крайних атомов (рис. 18.4, а, б, в, г); каждый атом С, кроме крайних в цепочке,
связан с двумя атомами С и с двумя атомами Н, а крайние атомы С связаны с одним
атомом С и с тремя атомами Н. Наряду с такими неразветвленными цепочками ато-
мов углерода возможны и разветвленные цепи, например, для изомеров предельных
углеводородов типа СпН2п+2 (рис. 18.4, д). Возможны не только такие «открытые»
цепи, но и замкнутые цепи — кольцевые структуры, примером которых является
молекула циклогексана СбН|2 (рис. 18.4,е). Так же как и в случае бензола СбНб, мы
имеем шестичленное кольцо; отличие состоит в том, что это кольцо неплоское.
Особой сложностью состава и особым разнообразием формы и размеров облада-
ют органические молекулы, ряд примеров пространственной структуры которых мы
привели, рассматривая линейные, плоские и неплоские молекулы. Форма органи-
ческих молекул существенным образом зависит от того, какими связями соединены
атомы углерода, — простыми связями (С—С), двойными связями (С=С), тройными
связями (ОС) или связями промежуточного типа. Примерами последних являют-
ся связи в молекуле бензола (см. рис. 18.2, ж), которые можно рассматривать как
полуторные связи (см. гл. 26, с. 810). От кратности связей между атомами углерода
зависят значения равновесных расстояний и равновесных углов. Равновесное рас-
стояние рсс между атомами углерода уменьшается с увеличением кратности связи.
Оно равно около 1,54 А для простой связи С—С, около 1,34 А для двойной связи
С=С и около 1,20 А для тройной связи С=С; для связи бензольного типа получается
Рсс ~ 1,40 А. Для атома углерода, образующего четыре простые связи (как с атомами
углерода, так и с другими атомами), эти связи точно или приближенно направлены
по осям тетраэдра с атомом углерода в центре (ср. рис. 18.3, б для метана); значение
«тетраэдрического» угла равно 109°28'. Для четырех совершенно одинаковых свя-
зей, как в метане, углы будут точно тетраэдрические, для случая различных связей
они будут в большей или меньшей степени приближаться к тетраэдрическим. Атом
углерода, соединенный двойной связью С=С с другими атомами углерода, может
§18.1. Форма и размеры молекул
503
Рис. 18.4. Молекулы предельных углеводородов:
а — пропан; б — бутан; в — пентан; г — гексан; д — изобутан; е — циклогексан
одновременно образовывать две простые связи, причем все три связи лежат в одной
плоскости, составляя одинаковые углы, приближенно равные 120°; в этом случае мо-
лекула может быть плоской. Примером является молекула этилена (см. рис. 18.2, е).
Атомы углерода, соединенные тройной связью С=С с другим атомом углерода, могут
одновременно образовывать одну простую связь, лежащую на одной прямой с трой-
ной связью. В этом случае молекула может быть линейной. Примером являются
молекулы ацетилена С2Н2 и диацетилена С4Н2 (см. рис. 18.1, д,ж). Для бензольного
кольца атомы углерода, соединяясь двумя «полуторными» связями с соседними ато-
мами углерода, образуют простую третью связь (с атомом водорода в случае бензола
и с другими атомами в случае производных бензола). Все три связи лежат в одной
плоскости, составляя одинаковые углы, равные 120°.
Важной особенностью простых связей С—С является то, что части молеку-
лы, соединенные простой связью, например, группы СН3 в простейшем случае
молекулы этана С2Н6 (рис. 18.5), могут сравнительно легко поворачиваться вокруг
направления этой связи. Электронная энергия молекулы является функцией от угла
взаимного поворота % частей молекулы вокруг направления связи С—С и играет
роль потенциальной энергии для внутреннего вращения вокруг этого направления:
еМ = и(Х\	(18.1)
504
Глава 18. Равновесная конфигурация молекулы
Рис. 18.5.
Молекула этана
Рис. 18.6. Потенциальная энергия молекулы
для внутреннего вращения
Предельным случаем является случай свободного вращения, когда U(x) — const.
При наличии сил, препятствующих такому свободному внутреннему вращению,
оно будет заторможенным. Функция U(x) будет зависеть от х и иметь максиму-
мы и минимумы (рис. 18.6). Каждому возможному минимуму будет соответствовать
определенный поворотный изомер. Когда энергия внутреннего вращения меньше
высот потенциальных барьеров, отделяющих минимумы потенциальной энергии, то
около этих минимумов будут происходить повороты то в одну, то в другую сторону —
крутильные колебания вокруг положений равновесия (7(Хмин), где Хмин — значения х,
соответствующие минимумам. Когда энергия внутреннего вращения больше высоты
потенциальных барьеров, вращение будет происходить в одну сторону, но с перемен-
ной угловой скоростью. В предельном случае очень больших энергий внутреннего
вращения его можно считать свободным4).
Каждый поворотный изомер характеризуется своей равновесной конфигураци-
ей. Возникает вопрос о том, каковы будут эти конфигурации. Для случая тетраэдриче-
ских групп, соединенных простой связью С—С, можно ожидать, исходя из общих со-
ображений симметрии, что будет осуществляться либо цисконфигурация (рис. 18.7, а),
либо трансконфигурация (рис. 18.7, б). Для первой из них тетраэдры расположены
друг под другом, для второй они взаимно повернуты на 60°. В обоих случаях мы име-
ем по две связи С—Н, образованные атомами углерода и лежащие в одной плоскости;
однако в первом случае они расположены с одной стороны связи (в цисположении,
рис. 18.7, в), во втором случае — с разных сторон (в трансположении, рис. 18.7, г).
Рис. 18.7. Взаимное положение тетраэдрических групп:
а — цисконфигурация; б — трансконфигурация; в — цисположение; г — трансположение
Подробнее о внутреннем вращении см. гл. 21, с. 640.
§ 18.2. Свойства симметрии равновесной конфигурации
505
Для этана и для более сложных предельных углеводородов (а также для многих
их замещенных) осуществляются трансконфигурации. Это соответствует тому, что
атомы, с которыми связаны атомы углерода, отталкиваются и стремятся располо-
житься на наибольшем возможном расстоянии (ср. рис. 18.7, б, г с рис. 18.7, а, в).
Трансположение связей и приводит к образованию плоской зигзагообразной цепоч-
ки для предельных углеводородов.
Численные значения параметров, характеризующих равновесную конфигура-
цию молекулы, — равновесных расстояний и равновесных углов — могут быть
найдены экспериментально методами дифракции рентгеновских лучей, электронов
и нейтронов (на этих методах мы останавливаться не будем (см. [77])), и спек-
троскопическими методами, которые будут описаны ниже (см., в особенности,
гл. 19, с. 556). На рис. 18.1-18.5 приведены значения равновесных расстояний (вА)
и равновесных углов для соответствующих молекул.
§ 18.2.	Свойства симметрии равновесной конфигурации
и точечные группы симметрии
Во всех примерах конкретных молекул, рассмотренных в предыдущем парагра-
фе, равновесные конфигурации обладают той или иной симметрией (см. рис. 18.1-
18.5). Так, ось любой линейной молекулы является осью симметрии бесконечного
порядка, все плоские молекулы имеют плоскость симметрии а — плоскость молеку-
лы, неплоская молекула NH3 имеет ось симметрии Сз третьего порядка и обладает
высокой симметрией правильной трехгранной пирамиды, а неплоская молекула
СН4 имеет четыре оси симметрии третьего порядка (проходящие через четыре связи
С—Н) и обладает еще более высокой симметрией тетраэдра. Даже когда равно-
весная конфигурация молекулы в целом не обладает симметрией, отдельные части
молекулы могут являться приближенно симметричными — обладать приближенной
симметрией. Примером служат группы СН2 и СН3, входящие в состав органичес-
ких молекул; радикал СН2 имеет форму равнобедренного треугольника, а радикал
СНз — правильной трехгранной пирамиды (рис. 18.8); эти группы будут приближен-
но сохранять свою форму и в сложной молекуле, при отсутствии точной симметрии
молекулы в целом.
Наличие определенной симметрии равновесной конфигу-
рации молекулы существенным образом определяет свойства
симметрии состояний этой молекулы, в частности, симметрию
колебаний молекул и симметрию в распределении электронной
плотности. Классификация по типам симметрии, вырожден-
ным и невырожденным (см. с. 65), колебательных и элек-
тронных уровней молекул при этом получается совершенно
аналогичная и целиком определяется симметрией равновесной
конфигурации. Принято под симметрией молекулы понимать
именно симметрию ее равновесной конфигурации в основном
состоянии, поэтому в дальнейшем мы будем говорить о симме-
трии молекулы в этом смысле.
Следует отметить, что, как правило, симметрия равно-
весной конфигурации для различных электронных состояний
данной молекулы одинакова, т. е. при возбуждении меняются
только численные значения параметров, определяющих равно-
весную конфигурацию.
Рис. 18.8.
Симметрия групп
СН2 (а) и СН3 (б)
506
Глава 18. Равновесная конфигурация молекулы
Симметрия молекулы характеризуется принадлежностью к определенной то-
чечной группе симметрии (см. с. 71). При операциях симметрии данной точечной
группы — поворотах и отражениях — равновесная конфигурация рассматриваемой
молекулы переходит сама в себя; примерами могут служить молекулы, изображен-
ные на рис. 18.1-18.5 и обладающие осями и плоскостями симметрии. Существенно,
что многие молекулы одновременно имеют ряд осей симметрии и ряд плоскостей
симметрии в определенных сочетаниях; в подобных случаях мы имеем сложные
свойства симметрии. Рассмотрим более подробно в качестве типичных случаев
молекулы воды Н2О, аммиака NH3 и бензола СбНб.
Рис. 18.9. Симметрия молекулы
воды
Для Н2О (рис. 18.9) равновесная конфигурация
переходит сама в себя при отражении в плоскости
молекулы = а„х\ при повороте на 180° вокруг
оси второго порядка С2 = и при отражении
в плоскости а^ = а^. Ось С2 и взаимно-пер-
(1)	(2)
пендикулярные плоскости и av , проходящие
через нее, представляют элементы симметрии. Им
соответствуют операции симметрии С2 — поворот
на 180° вокруг оси С2, сг^ и — отражения
(О (2) о
в плоскостях ai и ai . В данном случае повторе-
ние каждой операции два раза дает тождественную
операцию С\ (единичный элемент группы, см. с. 67)
Г2 _ (I)2 _ (2)2 _ г
^2 —	— <?v	— О|.
(18.2)
Точечная группа состоит
из четырех операций симметрии
с„ с2,	«!!|.
(18.3)
Эту группу четвертого порядка обозначают символом C2V (индекс v указывает
наличие плоскостей симметрии, проходящих через ось, — вертикальных плоскостей).
Легко проверить, что произведение двух операций, отличных от тождественной, дает
третью:
С2а<" = а<'>С2 = а<2\ С2<7<2) = а<2>С2 = а<’>, <№> = <,<№> = С2.	(18.4)
Этот результат легко получить по методу, примененному в §3.2 (с. 71), рассматривая
преобразование трех взаимно-перпендикулярных векторов 1, 2, 3 (рис. 18.10). При отражении
в плоскости dj’) меняет направление вектор 1, при последующем повороте С2 меняют
направление векторы 1 и 2, в результате мы получаем отражение в плоскости <т£2). Таким
Л-	(0	(2)
образом, C2av = av , аналогично выводятся и все остальные соотношения.
Рис. 18.10. Преобразование трех взаимно-перпендикулярных векторов:
а — первоначальная ориентация; б — действие отражения
в — последующее действие поворота С2
§ 18.2. Свойства симметрии равновесной конфигурации
507
Отметим, что правила умножения (18.2), (18.4) операций симметрии, т.е. элементов
группы, совершенно аналогичны правилам умножения (3.29) группы поворотов вокруг трех
взаимно-перпендикулярных осей (группы D2). В обоих случаях эти правила могут быть
записаны в виде групповой таблицы (а = С2, b = с = е = С\ и а = С^\ b =
с = с = С\ соответственно)
	е	а	Ь	с	(18-5)
е	е	а	Ь	с	
а	а	е	с	Ь	
Ь	Ь	с	е	а	
с	с	Ь	а	е	
С точки зрения абстрактной теории групп (см. примечание на с. 73) обе группы тожде-
ственны.
Рассматриваемая группа Civ абелева — произведение операций не зависит
от порядка перемножения этих операций.
Существенно, что поведение равновесной конфигурации при различных опера-
гт	(О
циях группы различно. При отражении в плоскости молекулы все атомы остаются
на месте и каждое из двух расстояний О—Н переходит само в себя. При повороте С2
и отражении (ffl в плоскости, перпендикулярной к плоскости молекулы, атомы
и Н<2) меняются местами, а атом О остается на месте; соответственно расстояния
О—и О—переходят друг в друга, а угол Н^—О—и расстояние Н^—
переходят сами в себя. Атомы, меняющиеся местами при отражениях и поворотах,
называются эквивалентными', аналогичную терминологию применяют к расстояниям
и углам. В данном случае мы имеем два эквивалентных атома водорода, и Н^2\
два эквивалентных расстояния О—Н : О—и О—Н<2> (две эквивалентные связи).
Понятие об эквивалентных атомах и об эквивалентных расстояниях и углах весьма
полезно при рассмотрении свойств состояний молекул.
Наряду с симметрией молекулы можно говорить о собственной симметрии атомов
и о собственной симметрии определенных расстояний (или связей) и углов. Под собственной
симметрией понимают совокупность операций симметрии, переводящих данный атом, данное
расстояние или данный угол самих в себя (а не друг в друга). Для молекулы воды атом О и угол
Н—О—Н переходят в себя при всех операциях С2,	\ и С\ обладают той же симметрией,
что и молекула в целом — собственная симметрия совпадает с симметрией молекулы. Ато-
мы и Н<2) и расстояния (связи) О—и О—Н<2) переходят сами в себя при операциях
и С|, образующих точечную группу отражений в плоскости, состоящую всего лишь из двух
операций (группу Cs) и являющуюся подгруппой группы (18.3) (группы С2г).
Число эквивалентных величин данного рода равно отношению порядка h точечной
группы молекулы к порядку Лсо6ств точечной группы, определяющей собственную симметрию:
h
г=-------.	(18.6)
Лсобств
h 4
Для атомов Н и для связей О—Н в молекуле Н2О г =----= - = 2.
^собств 2
Для NH3 (рис. 18.11) равновесная конфигурация переходит сама в себя при по-
воротах С3 (на 120°) и С2 = С71 (на 240°, т.е. на -120°) вокруг оси симметрии
третьего порядка Сз и при отражениях в трех плоскостях	и проходящих
через ось С3. Элементами симметрии являются ось Сз, которой соответствуют две
508
Глава 18. Равновесная конфигурация молекулы
Рис. 18.11. Симметрия
молекулы NH3
операции симметрии Сз и С}, и три плоскости симметрии
(1)	(2)	(3) ~
Ov и сг У, сг у. Точечная группа состоит из шести операции
симметрии
Сь Сз, С}=С3\	а*1*, <т<2), 43).	(18.7)
Эту группу шестого порядка обозначают символом С^.
Правила умножения операций симметрии сложнее, чем
в случае группы (см. (18.4)). Мы имеем наряду с со-
отношениями
Сз-Сз’1 =С3_|-Сз = С|, а*'*2 =	= <т<3)2 = Cj (18.8)
правила умножения операций поворота и операций отра-
жения
а<3>-Сз<7<'\	<7<')	=	Сз<т<2>,	а<2»	= Сза<3),
а<2> = Cj-'a^,	<т<3)	=	С^'^2»,	</’>	=
а<2> = а(|)С3,	<7(3)	=	<т<2>Сз,	а<’>	= а^С3,
а^=а^С3',	а^	= а^С3',	а^=а^С3'	,
(18.9)
и правила умножения двух разных операций отражения
Сз = а( V2) = А(3> = <W>, 1
С3-' = а<2>а(|) = <т<3)</2> = а(|)а<3>. J
(18.10)
Как показывают (18.9) и (18.10), результат умножения зависит от порядка
применения операций симметрии, следовательно, группа Сз« в отличие от группы C2V
является неабелевой.
Правила умножения операций группы легко получаются путем рассмотрения поведения
молекулы NH3 при двух последовательных операциях симметрии. Например, при отражении
в плоскости а!,1) атом Н(2^ становится на место атома Н<3\ а при последующем отражении
в плоскости <у^ атом Н<2) становится на место атома и получается вместо прежнего
расположения атомов Н(|), Н(2), Н(3> новое их расположение Н<2), Н(3), Н(|), соответствующее
повороту молекулы С] = (рис. 18.12). Групповая таблица для группы C3v имеет вид
(а = Сз, ъ = С3~', с = 4°, d = 42), / = 43), е = С{):
	е	а	Ъ	с	d	f
е	е	а	Ь	с	d	f
а	а	Ь	е	f	с	d
b	Ь	е	а	d	f	с
с	с	d	f	е	а	Ь
d	d	f	с	b	е	а
f	f	с	d	а	Ь	е
(18.11)
При различных операциях, так же как в случае молекулы Н2О, равновесная
конфигурация NH3 ведет себя различным образом. При поворотах С3 и C3d все три
атома Н переставляются циклическим образом, например, при повороте С3 ста-
новится на место Н<2>, н<2> — на место Н(3) и Н(3) — на место Н^; аналогично ведут
§ 18.2. Свойства симметрии равновесной конфигурации
509
н(з>
Рис. 18.12. Поведение молекулы NH3 при операциях симметрии: а — первоначальная
.	(1) •	(2)
конфигурация; б — действие отражения av ; в — действие последующего отражения av
себя три расстояния N—Н и три угла Н—N—Н. При отражениях один из атомов Н
остается на месте, а два других меняются местами. Мы имеем три эквивалентных
атома Н, три эквивалентных расстояния (связи) N—Н и три эквивалентных угла
Н—N—Н. Атом N остается на месте при всех операциях симметрии группы.
Для атома N собственная симметрия совпадает с симметрией молекулы, для атомов Н,
переходящих сами в себя при отражениях в одной из плоскостей симметрии, собственная
симметрия есть симметрия группы Cs отражения в плоскости. Согласно (18.6), число экви-
h 6
валентных величин в этих случаях равно г —-------— - = 3 (порядок h группы С31) равен 6,
^собств
а порядок Лсобств группы Cs равен 2).
Для СбН6 (рис. 18.13) рав-
новесная конфигурация облада-
ет гораздо более высокой симме-
трией, чем для Н2О и NH3. На-
ряду с осью симметрии шес-
того порядка молекула обладает
центром симметрии г; при опе-
рации отражения в этом цен-
тре (при инверсии) симметрич-
но расположенные на одинако-
вых расстояниях от центра атомы
меняются попарно местами (ато-
мы С(|) и С(4), С<2) и С(5) и т.д.).
Молекула имеет целый ряд дру-
гих элементов симметрии — го-
ризонтальную плоскость симме-
трии Oh (плоскость молекулы), перпендикулярную к оси Сб, шесть вертикальных
плоскостей симметрии, проходящих через эту ось, шесть горизонтальных осей сим-
метрии второго порядка, лежащих на пересечении вертикальных плоскостей с го-
ризонтальной плоскостью (на рисунке показана лишь часть элементов симметрии).
Общее число операций симметрии, как можно показать, равно 24 (см. ниже, с. 519).
Соответствующую точечную группу обозначают символом Х>6Л5)- Рассмотренные
выше группы C2v и являются подгруппами этой группы.
Для молекулы СбНб эквивалентными являются все шесть атомов С и все
шесть атомов Н. Соответственно мы имеем шесть эквивалентных связей С—С
и шесть эквивалентных связей С—Н. Эквивалентными углами являются шесть
углов С—С—С (углы правильного шестиугольника, образованного атомами С) и две-
надцать углов С—С—Н.
5) Об обозначении D см. с. 512.
510
Глава 18. Равновесная конфигурация молекулы
24
— — 6. Для углов
Собственная симметрия атомов С и атомов Н, связей С—С и С—Н и углов С—С—С,
как легко видеть, есть С2г. Например, связь С—Н переходит сама в себя при повороте вокруг
проходящей через нее оси С2 и при отражениях в горизонтальной и вертикальной плоскостях,
проходящих через эту ось, т. е. при операциях, образующих вместе с тождественной операцией
группу С2„ (ср. (18.3); то, что ось С2 расположена горизонтально, а не вертикально, разумеется,
ч	h
несущественно). Число эквивалентных величин равно г — --------------
*^собств
С—С—Н собственная симметрия есть Cs (они остаются неизменными лишь при отражении
ч h 24
в плоскости молекулы ah) и г —--------— — — 12.
^собств
Во всех рассмотренных примерах мы имели равновесные конфигурации моле-
кул, обладающие рядом элементов симметрии — осями симметрии, плоскостями
симметрии и центром симметрии. Совокупность операций симметрии, соответству-
ющих этим элементам симметрии в определенном их сочетании, и образует точеч-
ную группу, к которой принадлежит рассматриваемая молекула. Для определенной
точечной группы получаются вполне определенные типы симметрии состояний
соответствующей молекулы. С точки зрения возможных типов симметрии, невы-
рожденных и вырожденных, целесообразно разделить все точечные группы на три
рода групп:
группы низшей симметрии, соответствующие молекулам с осями симметрии
порядка не выше 2;
группы средней симметрии, соответствующие молекулам с выделенной осью
симметрии порядка п 3;
группы высшей симметрии, соответствующие молекулам с несколькими осями
симметрии порядка п 3.
Для групп низшей симметрии получаются только невырожденные типы сим-
метрии, для групп средней симметрии возможны также дважды вырожденные типы
симметрии, а для групп высшей симметрии возможны и типы симметрии с кратно-
стью вырождения выше двух.
Это деление групп, находящееся в соответствии с классификацией состояний молекул
по типам симметрии, вырожденным и невырожденным, очень важно при рассмотрении коле-
бательных и электронных уровней молекул. Вместе с тем молекулы, принадлежащие к группам
различного рода, существенно различаются и по своим вращательным уровням (молекулы
типа сферического, типа симметричного и типа асимметричного волчка, см. гл. 19, с. 533).
Они различаются также по виду тензора поляризуемости (см. § 18.6, с. 528).
В § 18.3, 18.4 и 18.5 последовательно разобраны группы низшей, средней и выс-
шей симметрии, а в § 18.6 сделаны некоторые общие выводы. Следует отметить,
что кристаллы по своей симметрии принадлежат к тем же точечным группам, что
и молекулы. Мы также имеем систему точек, переходящую саму в себя при опе-
рациях точечной группы. Разница состоит в том, что кристаллы обладают не толь-
ко симметрией относительно операций точечных групп-поворотов и отражений,
но и трансляционной, или переносной, симметрией, связанной с тем, что кристалл
(рассматриваемый как бесконечная решетка) переходит сам в себя при операциях
переноса на расстояния, кратные постоянным решетки. При операциях перено-
са отсутствуют точки, сохраняющие свое положение в пространстве. При учете
трансляционной симметрии для кристаллов оказываются возможными не все то-
чечные группы, а лишь точечные группы, не содержащие осей симметрии порядка
п — 5 и п 7. Таким образом, остаются группы, содержащие оси симметрии
порядка п — 2, 3, 4 и 6 (а также не содержащие осей симметрии). Всего для кри-
сталлов получаются 32 точечные группы симметрии (32 кристаллических класса),
§ 18.3. Точечные группы низшей симметрии
511
разбивающиеся на шесть кристаллических систем — триклинную, моноклинную,
ромбическую, тетрагональную, гексагональную и кубическую.
По собственной симметрии узлов пространственной решетки кристаллы разделяют
на семь сингоний, однозначно соответствующих кристаллическим системам, за исключе-
нием гексагональной и тригональной сингоний, соответствующих одной кристаллической
системе — гексагональной [I48J. Деление сингоний на низшие — триклинную, моноклинную
и ромбическую, средние — тригональную, тетрагональную и гексагональную, и высшую —
кубическую — совпадает с делением точечных групп на группы низшей симметрии, средней
симметрии и высшей симметрии.
§ 18.3.	Точечные группы низшей симметрии
Точечными группами низшей симметрии являются группы, не содержащие
операций поворота вокруг осей порядка п 3; к ним принадлежат молекулы,
не имеющие таких осей симметрии. Возможные элементы симметрии в рассма-
триваемых случаях — это оси симметрии второго порядка, плоскости симметрии
и центр симметрии. Все соответствующие операции симметрии ~ повороты Сг
вокруг осей второго порядка, отражения а в плоскостях симметрии и инверсия i —
при их повторении дают тождественную операцию Ci:
с\ = a2 = i2 = Cj.	(18.12)
Когда имеется лишь один элемент симметрии, мы получаем группы второго порядка,
состоящие из двух операций (см. с. 73):
группу Сг поворотов на 180° вокруг оси симметрии второго порядка, состоящую
из операций С\ и Сг;
группу Cs отражений в плоскости симметрии, состоящую из операций С\ и а;
группу Ci отражений в центре симметрии, состоящую из операций С\ и г.
Сочетание двух элементов симметрии приводит к появлению третьего и полу-
чаются группы четвертого порядка, состоящие из трех соответствующих операций
симметрии и тождественной операции. Эти группы можно образовать наиболее ра-
циональным образом, исходя из одной оси симметрии Сг второго порядка и добавляя
другой элемент симметрии.
При добавлении к Сг плоскости av, проходящей через ось, возникает вторая
плоскость, перпендикулярная к первой и также проходящая через ось; мы полу-
чаем рассмотренную в предыдущем параграфе группу C2v, состоящую из операций
симметрии (18.3), сочетания которых определяются формулами (18.4) (рис. 18.14, а).
При добавлении к Сг плоскости перпендикулярной к этой оси (рис. 18.14, б),
возникает центр симметрии i; мы получаем группу Сги, состоящую из тождественной
операции С\ и операций симметрии Сг, и г, две из которых определяют третью
аналогично соотношениям (18.4).
Действительно, при повороте С2 вокруг оси z меняют знаки оси х и у, а при отражении ah
в плоскости ху, перпендикулярной к оси z, меняет знак ось z, в результате меняют знаки все
три оси х, у и z, т.е. получается инверсия i, i = (?hC2 = Сг&к и т.д.
Та же группа получается, если добавить к оси Сг центр симметрии г (а также
сочетанием отражений а и г).
При добавлении к Сг перпендикулярной к ней оси также второго порядка
появляется и третья ось второго порядка, перпендикулярная к первым двум осям.
Получается совокупность трех взаимно-перпендикулярных осей второго порядка
(рис. 18.14,в), которые можно обозначить как оси С^\ С^\ С^. Соответствующая
512
Глава 18. Равновесная конфигурация молекулы
Рис. 18.14. Группы с осями симметрии второго порядка:
а — группа C2v; б — группа C2h-, в — группа D2\ г — группа D2h
группа состоит из операций С|,	\ и была уже рассмотрена в гл. 3 (с.70
и с. 76). Эту группу обозначают как группу D2 или группу V.
Она является представителем групп диэдра, которые будут в общем случае рассмотрены
ниже (см. с. 518) и образуются присоединением к оси Сп перпендикулярной к ней оси второго
порядка; отсюда обозначение D. Обозначение V происходит от немецкого названия этой
группы — Vierergruppe (четверная группа).
Характерно для группы Z>2, что она содержит три операции симметрии одного
рода, в то время как группа C2v содержит лишь две операции симметрии одного
рода (два отражения в плоскости), а для группы C2h все операции симметрии
(С2, <Jh и г) различного рода. Для групп C2v и C2h ось С2 является выделенной осью,
для группы D2 выделенной оси нет и при сравнении этой группы с группами C2v
и C2h можно любую из трех осей взять за исходную6).
Рассмотренными группами четвертого порядка исчерпываются группы, полу-
чающиеся попарным сочетанием двух операций симметрии типов С2, а и г. Таким
образом, мы имеем наряду с тремя группами второго порядка С2, Cs и Ci три группы
четвертого порядка C2v, C2h и D2. При добавлении к сочетанию двух независимых
элементов симметрии еще одного независимого элемента симметрии появляются
и другие возможные элементы симметрии, которыми являются три взаимно-пер-
пендикулярные оси второго порядка, три проходящие через них и также взаимно-
перпендикулярные плоскости и центр симметрии (рис. 18.14, г). Этому соответствует
группа восьмого порядка, представляющая совокупность операций7)
Cl, С^\ С^,	ст(у), а(г), i.	(18.13)
Данную группу обозначают как группу D2h или Vh, так как она может быть
получена присоединением к поворотам вокруг трех взаимно-перпендикулярных осей
второго порядка отражения в плоскости, перпендикулярной к одной из этих осей
и проходящей через две другие оси (в горизонтальной плоскости сгЛ, если исходную
ось выбрать вертикальной). Группа Р2л включает в себя в качестве подгруппы все
рассмотренные в этом параграфе группы и является самой общей точечной группой,
не содержащей операций поворота вокруг осей порядка п 3.
Все три группы четвертого порядка, C2v, С2ь и D2, имеют одинаковую структуру, определяемую
групповой таблицей (18.5) (для группы C2h можно положить а = С^\ Ъ = с — i, е = С], см. с.507).
<у^х\ <у^у\ <№ — операции отражения в плоскостях, перпендикулярных к осям х, у, z.
§ 18.3. Точечные группы низшей симметрии
513
Для всех операций группы £>2Л справедливы соотношения (18.12) — результатом
повторения любой операции является тождественная операция. Произведение двух
разных операций (не равных С\) дает третью операцию (также не равную Ct) и может
быть легко найдено из наглядных соображений. При этом произведение любых двух
операций не зависит от их порядка и группа D2h является абелевой, так же как
и все ее подгруппы. Это и приводит к тому, что для молекул, не содержащих
осей симметрии порядка п 3 и принадлежащих к рассматриваемым простейшим
группам, возможны только невырожденные типы симметрии (см. с. 73).
Групповая таблица для группы Р2Л имеет вид
	Сх			c’2’	a(x)		a(z)	i
с.	С,	cd		С<г>	a(x}			i
cd	cd	Cx	c<2)	c*y)	i			<T{x)
cd	cd	cd	Cx	C(2X>	a<2>	i	<T(X)	
cd	с*г)	cd	cd	Cx		<?(*)	i	a*2’
		i		a®	Cx	cd	cd	cd
			i		cd	С,	cd	cd
<т(2>				i	cd	C(2X)	Cx	cd
i	i	<7(I)			cd		cd	Cx
Как частные случаи из этой таблицы могут быть получены групповые таблицы для групп
четвертого и второго порядков, являющихся подгруппами группы Р2Л.
Всего мы имеем, если считать и группу первого порядка С\, состоящую из тожде-
ственной операции и соответствующую отсутствию симметрии, восемь простейших
групп:
C\	С2, Cs? G	c2v, c2h, d2 = v	D2h = Vh
первого	второго	четвертого	восьмого
порядка	порядка	порядка	порядка
(18.15)
Отметим, что из этих групп инверсию содержат группы Ci, C2h и Дгл-
Можно привести много примеров молекул, не имеющих осей симметрии по-
рядка п 3 и относящихся к одной из точечных групп (18.15). К группе D2h
принадлежит молекула этилена С2Н4 (см. рис. 18.2, е) и ее замещенные типа С2Х4,
например, тетрахлорэтилен С2С14. К группе C2W, помимо молекулы Н2О и всех
других нелинейных трехатомных симметричных молекул (см. рис. 18.2, б, в, г), от-
носится, например, молекула Н2СО (см. рис. 18.2, д) и двузамещенные этилена
с осью симметрии С2, лежащей в плоскости молекулы (рис. 18.15, а, б). Двузаме-
щенные этилена с осью симметрии С2, перпендикулярной к плоскости молекулы
(рис. 18.15, в), будут относиться к группе C2h. Из неплоских молекул к группе C2v
принадлежат двузамешенные метана типа С2Н2Х2 (рис. 18.15, д). Молекулы нор-
мальных предельных углеводородов типа СпН2п+2 при п = 3,5,7,... относятся
к группе C2v, а при п = 4, 6, 8 — группе С2л; примером могут служить пропан
17 Зак ЮЗ
514
Глава 18. Равновесная конфигурация молекулы
(п = 3) и пентан (п = 5) — группа C2V и бутан (п = 4) и гексан (п = 6) — группа С2д
(рис. 18.4, а, в и б, г). К группе Cs относятся все плоские молекулы, не имеющие
осей симметрии, например, однозамещенные этилена типа С2Н3Х (рис. 18.15, г);
симметрией Cs обладают, в частности, все нелинейные трехатомные молекулы,
состоящие из трех разных атомов, например NOC1 (рис. 18.15, е). Симметрию Cs
могут иметь также и неплоские молекулы; примером являются двузамещенные эта-
на типа С2Н4Х¥ с трансположением атомов X и Y (рис. 18.15, ж). К группе С2
относятся некоторые неплоские молекулы, например, молекула перекиси водорода
Н2О2, для которой связи О—Н не лежат в одной плоскости (рис. 18.15,з). Возмож-
на для неплоских молекул и симметрия С,; такую симметрию имеет трансформа
четырехзамещенных этана типа C2H2X2Y2 (рис. 18.15, и). В принципе, возможны
и молекулы с симметрией Z>2, однако практически такие молекулы не встречаются,
так как при наличии трех взаимно-перпендикулярных осей С2 молекула имеет, как
правило, также и плоскости симметрии и относится к группе Z>2h- Все молекулы,
вообще не обладающие симметрией, принадлежат к группе С] (рис. 18.15, к).
Рис. 18.15. Молекулы низшей симметрии: а, б, в — двузамещенные этилена;
г — однозамещенные этилена; д — двузамещенные метана; е — NOC1;
ж — двузамещенные этана (трансформа); з — перекись водорода; и — смешанные
четырехзамещенные этана (трансформа); к — смешанные двузамещенные этана
Число эквивалентных атомов и эквивалентных расстояний и углов для молекул,
принадлежащих к рассмотренным группам, может равняться 1 и 2 для групп второго
§ 18.4. Точечные группы средней симметрии
515
порядка, т. е. С2, Cs и Сг ; 1, 2 и 4 — для групп четвертого порядка, т. е. C2v, С2^ и Z>2;
1, 2, 4 и 8 — для группы восьмого порядка
Для этилена, например, эквивалентными являются четыре связи С—Н, четыре
угла С—С—Н и два угла Н—С—Н; легко привести и другие примеры. Особенно ча-
сто встречаются пары эквивалентных величин. Существенно, что в данной молекуле
не обязательно все одинаковые атомы эквивалентны. Так, для молекулы QH4XY
(рис. 18.15, ж) мы имеем два эквивалентных атома Н в группе СН2Х и два других
эквивалентных атома Н в группе СН2У. Для молекулы пропана (рис. 18.4, а) из вось-
ми атомов Н эквивалентными являются четыре атома Н в крайних группах СН3,
лежащие вне плоскости молекулы, два атома Н в этих же группах, лежащие в плос-
кости молекулы, и два атома Н, соединенные со средним атомом С; из трех атомов С
два крайних образуют эквивалентную пару, а для среднего атома не имеется эквива-
лентных атомов, и он переходит сам в себя при любых операциях симметрии группы.
То, что число эквивалентных величин для молекул, принадлежащих к простейшим
группам симметрии, равно 1, 2, 4 и 8, вытекает из формулы (18.6), если учесть, что как
порядок h группы для молекулы в целом, так и порядок Лсобств группы, определяющей
собственную симметрию, принимают значения 1, 2, 4 и 8 (при этом 7гсобств С Л). Для группы
Р2л Л — 8 и Лсобств может равняться 1, 2, 4 и 8, что дает г — 8,4, 2, 1; для группы C2h h = 4
и Лсобств = Ь2,4, что дает г — 4, 2, 1 и т.д. Максимальное число эквивалентных координат
равно порядку группы h и получается при Лсобств = 1 (т. е. когда атомы или расстояния
ч	h
и углы не обладают собственной симметрией), тогда г = у = h. Примером являются четыре
рассмотренных выше эквивалентных атома Н (и соответственно четыре связи С—Н) в крайних
группах СН3 молекулы пропана, лежащие вне плоскости молекулы (симметрия пропана C2h,
h = 4).
В заключение данного параграфа отметим, что все восемь групп (18.15) являются
возможными для кристаллов.
Это группы, возможные для триклинной системы (Ci и Cs), для моноклинной системы
(Cs, С2 и C2h) и для ромбической системы (C2v, D2 и D2h), см., например, [148], с. 83; мы
применяем, как это принято в молекулярной спектроскопии, обозначения точечных групп
по Шенфлису.
§ 18.4. Точечные группы средней симметрии
Исходным элементом симметрии при рассмотрении групп средней симметрии,
к которым принадлежат молекулы с выделенной осью симметрии Сп порядка п 3
(п = 3, 4, 5, 6,...), является эта ось симметрии.
Оси симметрии Сп соответствует п операций симметрии Сп, С„, С„,... ,
СГ' =СП-’, С” = С (см. (3.8)).
Особенно важное значение имеют случаи осей третьего, четвертого и шестого
порядков, часто встречающихся для молекул и возможных также и для кристаллов.
Мы имеем:
ось Сз; операции Сз,	С^С^1,	cj = С\\	(18.16)
ось С4; операцииС4,	С4=С2,	<4=0;	(18.17)
ось С6; операции С6,	€%=С3,	Cl=C2,	С^=С3=С3',	с£=С6-1,	С%=С}.	(18.18)
При отсутствии	других элементов симметрии	имеем	циклическую	группу Сп
порядка п. Эта группа является абелевой (С^С^ = С„С^’ = С*н). Она обладает той
важной особенностью, что операции симметрии встречаются попарно — каждому
17*
516
Глава 18. Равновесная конфигурация молекулы
повороту Сп
соответствует отличный от него обратный поворот С™ k
(Cn})k. Например, повороту Сз на 120° соответствует поворот С3 = С3 1 на 240°,
т.е. на -120°; повороту С6 на 60° — поворот С% = Св] на 300°, т.е. на -60°, и т.д.
Можно показать, что это приводит, несмотря на то, что группа абелева, к возможности
двукратно вырожденных уровней, так же как и для неабелевых групп. Это вырождение,
однако, особого рода. Получаются пары раздельно-вырожденных комплексно-сопряженных
волновых функций, не переходящих друг в друга при операциях симметрии в отличие от пар
совместно-вырожденных волновых функций, переходящих друг в друга при операциях симме-
трии (см. с. 79), волновые функции (3.38) при заданном |ш| образуют пары, преобразующиеся
неприводимым образом, т.е. совместно, при операциях симметрии группы Сх„. Подробнее
о раздельном вырождении см. гл. 22, с. 657.
Наряду с обычными поворотными осями симметрии Сп возможны и так называ-
емые зеркально-поворотные оси симметрии Sn, для которых основная операция, Sn,
2тг
представляет поворот на угол — вокруг оси с одновременным отражением сг^ в nep-
тг
пендикулярной к оси плоскости. Примером можег служить молекула этана, имеющая
равновесную конфигурацию с трансположением связей (рис. 18.16). При повороте
2тг о
молекулы на угол — = 60 вокруг вертикальной оси и отражении в горизонтальной
6
плоскости Oh она переходит сама в себя; мы имеем зеркально-поворотную ось
шестого порядка и соответствующую ей операцию S& поворота на 60° с отраже-
нием. Применяя операцию последовательно и учитывая, что при четном числе
операций отражения компенсируются, мы получаем:
Sb	— поворот на 60° с отражением;
Si = С3 — поворот на 120°;
Si—i	— поворот на 180° с отражением8);
Si = С] = С3Х — поворот на 240°;
Si = S6 1	— поворот на 300°, т. е. на - 60°, с отражением;
Si = Ci	— поворот на 360°, т. е. на 0°.
Рис. 18.16. Зеркально-поворотная ось 56 для молекулы этана:
а — исходная конфигурация; б — действие поворота С6;
в — последующее действие отражения ah
Поворот С2 на 180° с отражением представляет инверсию, см. с. 511.
§ 18.4. Точечные группы средней симметрии
517
Таким образом, зеркально-поворотной оси шестого порядка соответствует шесть
операций; эта ось одновременно является обычной (поворотной) осью третьего
порядка. Вообще при четном п ось Sn является одновременно осью С±. Для четного п
мы получаем п операций:
q q2 ____ х-»2 q3	qTl~2 _ л-чП — 2 qTl~ 1 _ q~ 1 qTl _	/in 1 Q\
образующих группу Sn порядка n.
В частном случае п = 4 имеем ось S4; операции
54, S4=C2, S4=54"', S4=Ct.	(18.20)
При п = 2 мы получаем операцию S2 поворота на угол 180° с отражением, т. е. инверсию г;
следовательно, группа S2, состоящая из операций С\ и S2 = г, совпадает с группой Сг. Вообще
п /	п	\
при четном п и нечетном -	— 2,6, 10,...; — = 1, 3, 5, 7,... J группа Sn содержит инверсию
(при п — 6	= г, при п = 10 S5[Q = i и т.д.). В этом случае группу Sn можно обозначить
как С«г, рассматривая ее как группу С± с присоединением инверсии. В частном случае
п — 6 56 = С3г. При п четном и — четном (п = 4, 8, 12,...) группа Sn инверсии не содержит
(ср. (18.20)).
При нечетном п = аЛ, зеркально-поворотная ось представляет просто сочетание оси
симметрии Сп и плоскости симметрии ah и не является независимым элементом симметрии.
При четных п, наоборот, ось Sn является независимым элементом симметрии, содержащим
п
в себе ось С» порядка — (С3 в случае оси 56 и С2 в случае оси 54).
Группа Sn, так же как и группа Сп, является абелевой. Для нее операции
симметрии тоже встречаются попарно (при четном n и S„~k =
Группы Сп (п = 3, 4, 5,...) и Sn (п = 4, 6,...) представляют группы, к ко-
торым могут в принципе относиться молекулы, однако практически для молекул
соответствующие оси Сп и Sn, как правило, сочетаются с другими элементами
симметрии. К выделенной оси симметрии могут добавляться плоскости симметрии,
центр симметрии и оси симметрии второго порядка. Мы рассмотрим сначала груп-
пы, получающиеся, если исходить из поворотной оси симметрии Сп порядка п
(п 3) и добавлять к ней, как и в случае оси С2 (см. выше, с. 511), плоскость av,
перпендикулярную ось С2 и плоскость а/г.
При добавлении к Сп плоскости av, проходящей через ось, возникает еще п — 1
плоскость; общее число плоскостей av равно п, друг с другом они составляют углы
2 7Г 7Г	/1) (7)
— = —. В частности, при п = 3 это будут три плоскости симметрии: ст (г '
2п п	я
и </3), составляющие между собой углы — = 60°, которыми обладает молекула NH3
(см. с. 508, особенно рис. 18.11). При п = 4 получается четыре плоскости симметрии,
показанные на рис. 18.17, а. Соответствующая группа порядка 2п состоит из п
операций (18.16) и п отражений в плоскостях	..., и обозначается как
группа Cnv. При п = 3 это будет группа шестого порядка (18.7). Группа Сп (п 3)
является уже неабелевой (ср. (18.9)).
При добавлении к Сп перпендикулярной оси второго порядка С2 возникает
еще п — 1 ось. Общее число таких осей равно п и они составляют друг с другом углы
2тг
2п
ТС .	ТГ	о
— - (см. рис. 18.17, б для случая т = 4, — = 45 ).
п	4
Соответствующая группа по-
рядка 2п состоит из п операций (18.16) и п поворотов вокруг осей С^\ С^\ ...,
518
Глава 18. Равновесная конфигурация молекулы
Ряс. 18.17. Группы с осью симметрии четвертого порядка:
а — группа С4„; б — группа 1>4; в — группа С4Л; г — группа S4v = D2d; д — группа D4h
и обозначается как группа Dn3\ Она является неабелевой и по своей структуре
совершенно подобна труппе Cnv.
С точки зрения абстрактной теории групп группы Cnv и Dn тождественны. Их эле-
менты находятся в однозначном соответствии — эти группы изоморфны. Для изоморфных
групп C3v и D3 групповая таблица имеет вид (18.11). Легко составить аналогичные таблицы
и для изоморфных групп Cnv и Dn при п > 3.
При добавлении к Сп перпендикулярной плоскости сг/г (см. рис. 18.17, в для слу-
чая п = 4) наряду с п операциями (к = 1,2, ...,п) становятся возможными
п операций (ТкСп — поворотов с отражениями. Получается группа порядка 2п,
которую обозначают как группу CTlh. При четном п она содержит операцию инвер-
сии, так как поворот на 180° с отражением в плоскости представляет инверсию
(см. примечание на с. 516); сочетание оси Сп с плоскостью сг^ при четном п дает
центр симметрии. В отличие от групп Cnv и Dn группа Спд, подобно группам Сп
и Sn, абелева.
При четных п имеется еще группа порядка 2п, которая получается добавлением
к зеркально-поворотной оси Sn плоскости или перпендикулярной оси С^, что
п
приводит к тому же самому результату. Всего появляется — плоскостей симметрии,
27Г	п	2
проходящих через ось и составляющих углы —, и — перпендикулярных осей С2,
п	2
делящих углы между плоскостями симметрии пополам, как показано на рис. 18.17, г
для случая оси S4. Соответствующая группа содержит, наряду с операциями S*
(к = 1, 2,... , п), — отражений в плоскостях av и - поворотов на 180° вокруг
осей С2. Эту группу обозначают как Snv (или Di а, см. ниже). При п = 4 получается
группа S4V-'(1>2</), и при п = 6 группа S^^hd)- Группа Snv — неабелева.
Она изоморфна с группами Cnv и Dn, от которых отличается тем, что вместо оси Сп
п	п
имеется ось 5П, а вместо п плоскостей av или п осей С2 имеется — плоскостей <тг и — осей С2
(ср. рис. 18.17, а, б и г для п — 4).
Наибольшей симметрией при заданном п обладает группа порядка 4п, которая
получается проще всего, если исходить из группы Dn порядка 2п и добавить к оси
^Труппа диэдра, см. с.512.
§18.4. Точечные группы средней симметрии
519
симметрии Сп и к перпендикулярным осям С2 плоскость перпендикулярную
к выделенной оси Сп. При этом появляется п плоскостей симметрии проходящих
через ось Сп (см. рис. 18.17,д для п — 4), которым соответствует п отражений, и ста-
новятся возможными п операций поворотов с отражениями (аЛС*). Данную группу
обозначают как Dnh- Она содержит в качестве подгрупп все ранее рассмотренные
группы порядка п и 2п. Таким образом, при заданном п мы получаем группы:
четное п	Cr^Sn	бчт Dn, Cnh, Snv	Dnhy	(18.21)
	порядка п	порядка 2п	порядка 4п	
нечетное п	сп	^ПУу Dn, Cnh	Dnh.	(18.22)
	порядка п	порядка 2п	порядка 4п	
Следует отметить, что группу Snv можно получить из группы Dz порядка 2 — — п, если
к оси Ci и к осям С2 добавить плоскости, проходящие через ось Cz и делящие углы
между осями С2 пополам (диагональные плоскости аД В соответствии с этим данную группу
п
обозначают как Dzd = Dn>d, где п = —. Таким образом, S4v = D2d и	В частности,
группа D2d получается из группы D2 при добавлении плоскостей, делящих прямые углы между
осями и пополам (ср. рис. 18.14, & и 18.17,г); поэтому ее называют также Vd (D2 — V).
Целесообразнее, однако, рассматривать группу Snvr исходя из оси Sn порядка п.
Всего мы получаем, согласно (18.21), по семи групп с п — 4,6, 8У... иу соглас-
но (18.22), по пяти групп с п = 3, 5, 7,... При п — 3,4 и 6 мы имеем группы:
п = 3			Dt,	СзЛт	D^y 1
п — 4	с4,		d4,	C4h,	S4v = D2d, D4hA	(18.23)
п = 6	Сб,	8в — Сзь £*6v>	А,		8^v = Dm,	J
Это девятнадцать групп, возможных для кристаллов наряду с группами (18J5),0).
Предельными случаями групп (18.21) и (18.22), получающимися при п —> сю,
являются группы бесконечного порядка, соответствующие выделенной оси симмет-
рии бесконечного порядка, допускающей поворот на любой угол вокруг этой оси
(см. с. 69). Это группы:
Соо (предельный случай группы Сн) — совокупность любых поворотов вокруг
оси бесконечного порядка;
Схв (предельный случай группы Cnv) — с добавлением отражений av
в бесконечном числе плоскостей, проходящих через ось;
£>оо (предельный случай группы Dn) — с добавлением поворотов С2 вокруг
бесконечного числа осей С2, перпендикулярных к оси;
Cooh (предельный случай группы Сп^) — с добавлением отражения
в плоскости, перпендикулярной к оси;
Dooh (предельный случай групп Snv и Dnh) — с добавлением отражений av,
поворотов С2 и отражения
Отметим, что среди рассмотренных групп содержат инверсию группы Cnfl и Dnh
при четном п (а также группы Sn и Snv при п = 6, 10, 14,...). Из бесконечных групп
содержат инверсию группы C^h и ДхЛ-
1 °) Группы (18.23) с п = 4 относятся к тетрагональной системе, а группы с п = 3 и с п = 6 —
к гексагональной системе 1148|.
520
Глава 18. Равновесная конфигурация молекулы
Имеется значительное число молекул, обладающих выделенной осью симметрии
порядка п 3, и, следовательно, принадлежащих к соответствующим группам. Все
линейные молекулы имеют ось симметрии бесконечного порядка, на которой
расположены атомы. При наличии центра симметрии они принадлежат к группе
такими молекулами являются все двухатомные молекулы, состоящие из одинако-
вых атомов (точнее, из одинаковых ядер — это так называемые гомонуклеарные
молекулы), — Н2, О2, N2 и т. д., симметричные линейные трехатомные молекулы,
например СО2, и симметричные линейные молекулы, состоящие из четырех и более
атомов, например, С2Н2, C2N2, С4Н2 (см. рис. 18.1, с. 501). При отсутствии центра
симметрии линейные молекулы принадлежат к группе к таким молекулам
относятся все двухатомные молекулы, состоящие из двух разных атомов, — НС1,
NaH, HgH, СО, NO и т.д., несимметричные линейные трехатомные молекулы, как
HCN, OCS, несимметричные линейные молекулы, состоящие из четырех и более
атомов, например, замещенные ацетилена типа С2НХ и C2XY. Группы С^,
и Cooh для молекул не реализуются.
Отметим, что симметрией обладает однородное магнитное поле, переходящее само
в себя при отражении в перпендикулярной к нему плоскости; электрическое однородное поле
обладает симметрией C^v и переходит само в себя при отражении в плоскости, параллельной
полю (см. гл. 3, с. 66 и примечание на с. 71).
Плоские молекулы, обладающие осью симметрии порядка п 3, перпенди-
кулярной к плоскости молекулы10, принадлежат практически всегда к группе Dnh
(хотя в принципе они могут относиться и к группе Cnh более низкой симметрии).
Важнейшим примером является рассмотренная в § 18.2 молекула бензола СбНб
(см. рис. 18.13), имеющая симметрию D^. Другой пример представляет молекула
BCI3, имеющая симметрию все три связи В—О лежат в одной плоскости
и атомы С1 образуют равносторонний треугольник с атомом В в центре (рис. 18.18).
Примерами неплоских молекул, обладающих выделенной осью симметрии Сп
порядка п 3, являются уже рассмотренные молекулы аммиака NH3 (см. рис. 18.11,
с. 508) с симметрией C^v и этана С2Н6 (рис. 18.16), с симметрией	(наряду
с осью S6 имеются три вертикальные плоскости симметрии av и три горизонтальные
оси С2, делящие углы между ними пополам). Другие примеры представляют молекула
аллена С3Н4 (рис. 18.19, симметрия S^, — Du), циклические молекулы С3Нб, С4Н8,
С5Н ю и с5н 12 (рис. 18.20,а,б,в и рис. 18.14,г, симметрия	D^, Д/г и S^v =
Рис. 18.18. Молекула треххлористого бора
Рис. 18.19. Молекула аллена
Во всех рассмотренных молекулах с выделенной осью симметрии конечно-
го порядка п 3 встречаются эквивалентные атомы и эквивалентные расстояния
(связи) и углы. Наиболее типичны для оси Сп порядка п совокупности п экви-
валентных величин, например, для NH3 трех атомов N, трех связей N—Н и трех
углов Н—N—Н (см. с. 508) и для С6Н6 шести атомов С, шести атомов Н, шести
связей С—С и шести связей С—Н (см. с. 509). Для групп Cnv и Snv порядка 2п
10 Осью Сп порядка п 3, лежащей в плоскости молекулы, они обладать не могут.
§ 18.4. Точечные группы средней симметрии
521
Рис. 18.20. Циклические молекулы: а — циклопропан; б — циклобутан; в — циклопентан
а
Рис. 18.21. Эквивалентные повороты:
а — поворот С^, б — поворот С-^>
одного рода, которые можно пре-
возможны совокупности 2п эквивалентных величин, а для группы Dnh порядка
4п — совокупности 2п и 4п величин. Например, для циклопентана (группа D^h,
4п = 20) имеется 10 эквивалентных атомов Н, 10 эквивалентных связей С—Н и 20
эквивалентных углов С—С—Н (рис. 18.20, в).
Важное значение для молекул с вы-
деленной осью симметрии порядка п 3,
принадлежащих к неабелевым группам Cnv,
Dn, Snv и Dnh (группы Сп, Sn и Cnh абеле-
вы), имеет наличие эквивалентных элемен-
тов симметрии — плоскостей симметрии av
и осей симметрии Сз, переходящих друг
в друга при поворотах вокруг выделенной
оси Сп. Например, в случае молекулы NH3
при поворотах переходят друг в друга три
плоскости а® и а^ (см. рис. 18.11).
С наличием эквивалентных элементов сим-
метрии связано деление операций симме-
трии на классы эквивалентных операций.
К одному классу относятся эквивалентные
операции симметрии — операции симметрии
вратить друг в друга путем поворотов и отражений. Такими эквивалентными опе-
рациями являются операции отражения в эквивалентных плоскостях и операции
поворота на 180° вокруг эквивалентных осей. К операциям одного класса принадле-
жат для рассматриваемых групп пары поворотов вокруг выделенной оси на углы
и -<р (например, повороты Сз на 120° и С3 — С^1 на -120° для группы С3у).
Действительно, при отражении в плоскости av поворот на угол превращается
в поворот на угол — <р (рис. 18.21); такое же действие оказывает поворот на 180°
вокруг оси Сз, перпендикулярной к оси Сп. Операция отражения в плоскости ah,
отражение в центре симметрии г, поворот на 180° вокруг выделенной оси Сп четного
п
порядка (операция С„) и, наконец, тождественная операция образуют отдельные
классы. Действительно, любая из этих операций представляет операцию особого
рода и группа может содержать только одну такую операцию.
Для группы C3v мы имеем три класса операций — класс поворотов Сз
^2	-	(1)	(2)	(3)	„
и С3 — С3 , класс отражении av ai , ai и класс тождественной операции С|.
Сокращенно это записывается в виде (цифра указывает число операций в классе)
группа C3v 2Сз, 3<ту, С|.	(18.24)
Число классов операций является важной характеристикой группы. Для абе-
левых групп каждая операция группы образует отдельный класс, и поэтому число
522
Глава 18. Равновесная конфигурация молекулы
классов равно просто порядку группы. Примером может служить рассмотренная
в предыдущем параграфе группа Z>2h, где мы имеем восемь операций (18.13),
каждая из которых соответствует элементу симметрии, остающемуся неизменным
при операциях группы (тождественная операция соответствует оси первого порядка),
и не может превратиться в другую операцию.
Отметим, что для групп Cn, Cnh и Sn, для которых отсутствуют отражения av
в вертикальных плоскостях и повороты Ci вокруг горизонтальных осей, операции
поворота на угол (р и на угол -<р не переходят друг в друга, и поэтому образуют
отдельные классы. В результате число классов для этих групп равно порядку группы,
как для всех абелевых групп.
Понятие класса элементов является одним из важных понятий теории групп, которое
формулируется математически следующим образом: элементы а и b группы относятся к одному
классу, если существует такой элемент группы с, что
6 = сас~'.	(18.25)
Элементы а и b называют при этом сопряженными. Для абелевых групп са = ас и, сле-
довательно, b = сас~[ = асс~] = а, откуда вытекает, что каждый элемент сопряжен только
сам с собой и, следовательно, образует отдельный класс. Для неабелевых групп, наоборот,
имеются элементы а и с, для которых са / ас, и, следовательно, сас~1 Ф а, т. е. равно
другому элементу группы. Поэтому для неабелевых групп имеются классы, состоящие более
чем из одного элемента. В результате для них число классов всегда меньше порядка группы.
Для группы C3v легко получить деление операций симметрии на классы, исхо-
дя из соотношений (18.8)—(18.10). Умножая = С3а^ справа на Cf’, мы полу-
чим	= С3а^С3[ = а умножая = С3а<2> справа на С31, мы получим
<т^С31 — С3а^С3* = а(3); следовательно, а(1), и а(3) принадлежат к одному классу. Ана-
логично, умножая а(2) = а(,)С3 на	мы получаем </2)о-(1> = <r(,)C3(^,))-1 = С31,
т.е. С3 и С3-1 принадлежат также к одному классу. Тождественная операция образует класс
сама по себе (для единичного элемента при любом а аеа~' = еаа~1 = е). Мы пришли
к результату, совпадающему с полученным выше (см. (18.24)).
§ 18.5. Точечные группы высшей симметрии
Точечные группы высшей симметрии, к которым принадлежат молекулы с не-
сколькими осями симметрии порядка п 3, соответствуют симметрии трех типов
правильных многогранников — симметрии тетраэдра (правильного четырехгранни-
ка), симметрии октаэдра (правильного восьмигранника) и симметрии икосаэдра
(правильного двадцатигранника). Эти многогранники показаны на рис. 18.22. Тетра-
эдр и октаэдр обладают осями симметрии второго, третьего и четвертого порядков,
Рис. 18.22. Правильные многогранники: а — тетраэдр; б — октаэдр; в — икосаэдр
§ 18.5. Точечные группы высшей симметрии
523
октаэдра и лишь в общих чертах
и
а	б
Рис. 18.23. Правильные многогранники,
вписанные в куб:
а — тетраэдр; б — октаэдр
а икосаэдр — осями симметрии второго, третьего и пятого порядков. Известны лишь
молекулы, обладающие тетраэдрической и октаэдрической симметрией, поэтому мы
более подробно разберем группы тетраэдра
рассмотрим группы икосаэдра.
Симметрия октаэдра совпадает с сим-
метрией куба, а симметрия тетраэдра лег-
ко получается из симметрии куба отбрасы-
ванием части элементов симметрии, по-
этому мы рассмотрим группы тетраэдра
и октаэдра — кубические группы — ис-
ходя из симметрии куба. Тетраэдр полу-
чается, если расположить четыре точки
в вершинах куба, не имеющих общих ребер
(рис. 18.23, а), а октаэдр — если располо-
жить шесть точек посредине граней куба
(рис. 18.23,6).
Куб обладает тремя эквивалентными
осями симметрии: С^\ С^\ четверто-
го порядка, проходящими через центры его граней, четырьмя эквивалентными осями
^(1) ^(2) ЛЗ) х4*)
симметрии:	, С'3', Q , С3 , проходящими через противоположные вершины,
^(1) г^(2) ^(3) ^»(4)
и шестью эквивалентными осями симметрии второго порядка: CJ , С2 , С} , С2 ,
С^5\ С^\ проходящими через середины противоположных ребер (рис. 18.24, а, б, в).
Группу, состоящую из совокупности соответствующих поворотов вокруг трех
осей С4 (шесть эквивалентных поворотов С4 и С4 — C4d и три эквивалентных пово-
рота С2), вокруг четырех осей Сз (восемь эквивалентных поворотов Сз и С} — С^1)
и вокруг шести осей С2 (шесть эквивалентных поворотов С2) обозначают как груп-
пу О. Порядок этой группы равен 24. Все операции симметрии разбиваются на пять
классов:
группа О C|, 6С4, ЗС2, 8С3, 6С2.
(18.26)
Наряду с осями симметрии куб обладает тремя эквивалентными плоскостя-
ми симметрии, перпендикулярными к осям С4, шестью плоскостями симметрии,
проходящими через противоположные ребра, и центром симметрии. Присоедине-
ние к операциям поворота операций отражения, а также получающихся при этом
операций поворота с отражением (поворотные оси Сз третьего порядка становят-
а	б	в
Рис. 18.24. Оси симметрии куба: а — три оси С4; б — четыре оси С3; в — шесть осей С2
524
Глава 18. Равновесная конфигурация молекулы
ся зеркально-поворотными осями шестого порядка) приводит к образованию
группы Oh, имеющей порядок, равный 48, и содержащей инверсию. Эта группа
соответствует полной симметрии куба. Группы О и Oh представляют возможные
октаэдрические группы.
Симметрия тетраэдра является более низкой, чем симметрия октаэдра. Для те-
траэдра сохраняются четыре оси Сз третьего порядка, проходящие через противопо-
ложные вершины куба (ср. рис. 18.23, а и 18.24,0, а три оси С$ четвертого порядка
превращаются в оси второго порядка. Совокупность соответствующих поворотов
вокруг осей Сз и Сз образуют группу Т, состоящую из С|, четырех эквивалентных
поворотов Сз, четырех эквивалентных поворотов С3 — Cf1 и трех эквивалентных
поворотов Сз. Порядок группы равен 12 и образующие ее операции симметрии
разбиваются на четыре класса:
группа Т Сн 4С3, 4С3~', ЗС2.	(18.27)
К этой группе Т, состоящей из поворотов, можно добавить отражения в трех
плоскостях, перпендикулярных к осям Сз; при этом становятся возможными
инверсия и повороты с отражениями вокруг осей Сз, превращающихся в оси S^.
Получается группа Th, состоящая из 24 операций.
Добавление к группе Т шести отражений в плоскостях, проходящих через
противоположные ребра куба, приводит к образованию группы Та, также состоя-
щей из 24 операций. Группа Та содержит, кроме поворотов и отражений, шесть
эквивалентных поворотов с отражениями вокруг трех осей Сз, становящихся зер-
кально-поворотными осями S4 четвертого порядка. Именно такой симметрией
обладает тетраэдр. Он переходит сам в себя как при поворотах и отражени-
ях, так и при операциях S4 и S4 = поворота с отражением (число таких
эквивалентных операций равно шести). Действительно, тетраэдр, изображенный
на рис. 18.23, а, при повороте вокруг вертикальной оси на 90° (повернутое поло-
жение тетраэдра показано пунктиром) с отражением в горизонтальной плоскости
переходит сам в себя.
24 операции группы Та разбиваются на пять классов (все 8 поворотов Сз
и Сз = С3‘ вокруг четырех осей Сз являются эквивалентными, так же как и для груп-
пы О,2)):
группа Та С|,	8С3, ЗС3, 6S4,	6а.	(18.28)
Группы Т, Th и Та представляют возможные тетраэдрические группы. Всего мы
получаем пять групп кубической симметрии:
Г, Th, Та, О, Oh.	(18.29)
Симметрия икосаэдра характеризуется шестью осями С5 пятого порядка, де-
сятью осями Сз третьего порядка и пятнадцатью осями Сз второго порядка. Соот-
ветствующая группа состоит из 60 операций поворота и обозначается как группа I.
Присоединение плоскостей симметрии приводит к образованию группы Ih, сос-
тоящей из 120 операций и включающей инверсию. Таким образом, возможны две
икосаэдрические группы:
I, Ih.	(18.30)
Для кристаллов возможны кубические группы (18.29), но не могут осуществляться
икосаэдрические группы (18.30).
|2^ Группы Td и О изоморфны.
§ 18.6. Общие выводы о симметрии молекул
525
Рис. 18.26. Молекула
тетраметил метана
Рис. 18.25. Молекулы октаэдрической симметрии:
а — шестифтористая сера; б — шестифтористый уран
Группы (18.29) относятся к кубической кристаллической системе, поэтому их и называют
кубическими. Они возможны для кристаллов, так как содержат оси лишь второго, третьего
и четвертого порядков; невозможность групп (18.30) для кристаллов связана с наличием в этих
группах осей пятого порядка (см. конец § 18.12, с. 510).
Для молекул наиболее существенны группы Oh и Tj. К группе Oh принадлежат
такие молекулы как SFs и LIFg (рис. 18.25, а, б), в которых атомы фтора располагают-
ся вдоль трех взаимно-перпендикулярных осей симметрии. Особенно важны случаи
симметрии Та. Симметрией Td (тетраэдрической симметрией) обладают молекула
метана СН4 и его замещенные типа СХ4. К группе Td принадлежат и более сложные
молекулы тетраэдрической структуры, примером которых является молекула тетра-
метилметана С(СНз)4 (рис. 18.26), в которой центральный атом углерода соединен
с четырьмя симметрично расположенными группами СН3. Симметрию Td имеют
и такие неорганические молекулы, как, например, SiCU, GeH4, T1CI4.
Во всех молекулах, принадлежащих к группам кубической симметрии, имеются
эквивалентные атомы и эквивалентные связи и углы. Типичными являются сово-
купности 4, 6 и 12 эквивалентных величин, например, четырех связей С—Н и шести
углов Н—С—Н для метана и четырех связей С—С и двенадцати связей С—Н для те-
траметил метана. Особенно важную роль играет эквивалентность четырех простых
связей атома углерода с другими атомами, представляющая результат тетраэдричес-
кого распределения электронной плотности вокруг этого атома (см. гл. 26, с. 797).
§ 18.6. Общие выводы о симметрии молекул
В результате рассмотрения точечных групп мы получаем их классификацию,
приведенную в табл. 18.1. В таблицу включены и точечные группы наивысшей воз-
можной симметрии, соответствующие сферической симметрии (симметрии шара).
Шар имеет бесконечное число осей симметрии бесконечного порядка, проходящих
через его центр, и совокупность всех возможных поворотов вокруг этих осей образует
группу трехмерных вращений (см. с. 71), обозначенную через П^. Добавление к этой
группе плоскостей симметрии, проходящих через центр, дает группу трехмерных
вращений с отражениями (полную ортогональную группу), обозначенную через
и содержащую инверсию. Симметрией обладают атомы.
Для каждой точечной группы в скобках указан ее порядок. Расположение табли-
цы позволяет легко сопоставлять группы различной сложности. Первые два столбца
Таблица 18.1
Классификация точечных групп
Род групп	Оси симметрии	Точечные группы							Примечание	Тензор поляризуемости
группы низшей симметрии	порядка п 2	С1(1)		С,„ = С, (2)					кристалличе- ские группы то же _гг _	7^	7^
		С2(2)	S1 = С; (2)	С2,(4)	Р2(4)		С2Л(4)	Х>2л(8)		
группы средней симметрии	одна ось порядка п 3	С3(3)	•	Сз„(6)	Рз(6)		Сзл(6)	Рз*(12)		аХ — ау 7^ &Z
		С4(4)	S4(4)	С4„(8)	Р4(8)	Sav = £>2d(8)	С4Л(8)	В4Л(16)		
		С5(5)		С5„(10)	Р5(10)		С5Л(Ю)	£>5л(20)		
		С6(6)	5б(6)	С6„(12)	2>б(12)	S6„=r>3d(12)	С6Л(12)	Рб»(24)		
		[Сх]		^Х1'	i£i		[Соей]	^осЛ		
группы высшей симметрии	несколько осей порядка п 3				Т(12) 0(24) /(60)	Td(24)		П(24) Ол(48) А(120)		ах = ау = аг
	бесконечное число осей	[Их]						[Hoch]		
дипольный момент		Р#0 Р = 0	Р#0	Р = 0	Р = 0	Р = 0 Р = о								
Взятые в квадратные скобки группы не могут осуществляться для молекул.
Глава 18. Равновесная конфигурация молекулы
§ 18.6. Общие выводы о симметрии молекул
527
соответствуют группам Сп и Sn, следующий — группам Cnv. В столбец для групп
диэдра, содержащих только повороты, включены и группы Т, О, I и Поо, также
содержащие только повороты. Далее идут группы, для которых имеются плоскости,
делящие пополам углы между осями второго порядка. Наконец, последние два
столбца соответствуют группам Cnh и Dnh. В таблице указаны группы, возможные
для кристаллов. Их общее число равно 32 (см. с. 510).
Группы низшей симметрии и группы Сп, Sn, Cnh при п 3 являются абелевыми,
все остальные группы неабелевы и для соответствующих молекул возможны выро-
жденные типы симметрии (ср. с. 73 и с. 510). Из абелевых групп для групп низшей
симметрии получаются только невырожденные типы симметрии, а для групп Cn, Sn
и Cnh при п 3 возможны и дважды вырожденные типы симметрии особого рода
(раздельно-вырожденные типы симметрии, ср. с. 516 и см. подробнее гл. 22, с. 657).
Важное значение для молекул и кристаллов имеет наличие центра симметрии.
Для атомных систем с центром симметрии, т. е. принадлежащим к точечным группам,
содержащим инверсию, как мы видели, состояния делятся на четные и нечетные
(см. с. 74) и имеет место альтернативный запрет (см. с. 116)13). Группы, содержащие
инверсию, к которым принадлежат системы с центром симметрии, в табл. 18.1
выделены жирным шрифтом. Это группы Cnh и Dnh (при четном n), Sn и Snv
(при четном п и нечетном —), Th, Oh, Ih, C^h, ПооЛ- Среди групп, возможных
для кристаллов, подобных групп 11. Существенно, что центр симметрии отсутствует
для молекул, принадлежащих к группам Cnh, Dnh (при нечетном n), Td и ряд
примеров таких молекул был приведен в предыдущих параграфах.
Весьма существенной характеристикой молекулы является ее дипольный мо-
мент. Молекулы, для которых дипольный момент равен нулю, не могут иметь чисто
вращательных спектров поглощения и испускания (см. § 17.6, с. 487). Двухатомные
молекулы при отсутствии дипольного момента не могут иметь и колебательных
спектров поглощения и испускания (см. там же, с. 486). Наличие или отсутствие ди-
польного момента непосредственно связано с симметрией молекулы. Для молекул,
обладающих симметрией и имеющих дипольный момент, его направление частично
или полностью определяется этой симметрией.
Дипольный момент молекулы не должен изменяться при операциях симметрии,
переводящих молекулу саму в себя. При отсутствии симметрии (группа С]) он
может быть направлен произвольным образом. При наличии только плоскости
симметрии (группа Cs) он должен лежать в этой плоскости. При наличии одной
поворотной оси симметрии (группы Сп и Cnv, включая группу С^) он должен быть
направлен вдоль этой оси симметрии. Только для этих групп дипольный момент
не изменяется при всех операциях симметрии группы и может отличаться от нуля.
Для всех остальных групп дипольный момент должен равняться нулю, так как эти
группы содержат операции симметрии, которые изменяют направление дипольного
момента.
Действительно, при наличии двух или нескольких осей симметрии дипольный момент,
направленный вдоль одной из осей, изменяет свое направление при повороте вокруг другой
оси. Это обусловливает равенство нулю дипольного момента для групп Dn, Snv, Т, О, I и Пх.
При наличии одной выделенной оси, при операциях ah и Sn = (ThCn дипольный момент,
направленный в силу симметрии вдоль этой оси, будет менять свой знак на обратный.
Следовательно, он должен равняться нулю для групп Cnh и Sn. Наконец, дипольный момент,
|3) Согласно этому запрету, переходы, разрешенные для дипольного излучения, запрещены для маг-
нитного и квадрупольного из пучений, и наоборот. Для комбинационного рассеяния правила отбора такие
же, как и для квадрупольного излучения. Это приводит к альтернативному запрету для колебательных
спектров, инфракрасных и комбинационного рассеяния (см. гл. 23, с. 679).
528
Тлава 18. Равновесная конфигурация молекулы
любым образом направленный, меняет свой знак при инверсии, следовательно, равен нулю
при наличии центра симметрии, в частности, для группы Сг. Равенство нулю дипольного
момента для групп наивысшей симметрии Dnh, Th, Oh, Ih и ПхЛ вытекает из того, что они
включают в себя в качестве подгрупп группы, для которых дипольный момент равен нулю
уже при более низкой симметрии.
Внизу табл. 18.1 отмечено, для каких групп дипольный момент Р / 0 и для каких
групп Р = 0.
Другой существенной характеристикой молекулы является ее поляризуемость,
определяемая симметричным тензором поляризуемости (0, у = ж, у, z) с соста-
вляющими
<*ХХ)	^-ху — ttyx, &yz ~ ^zyt &ZX = &XZ	(18.31)
(см. § 17.7). Наличие симметрии накладывает определенные условия на тензор
поляризуемости.
При наличии у молекулы нескольких осей симметрии порядка п 3 диагональ-
ные составляющие тензора одинаковы, а недиагональные равны нулю. Оси ж, у, z
при любой их ориентации являются главными осями поляризуемости. Обозначая
главные поляризуемости через ах, ау и az, мы имеем
ах = ау = az = а (несколько осей симметрии порядка п 3).	(18.32)
При наличии одной выделенной оси симметрии порядка п 3 равны друг другу,
при выборе этой оси в качестве оси z, составляющие ахх и ауу, а недиагональные
составляющие обращаются в нуль, т. е. оси ж, у, z являются главными осями поля-
ризуемости, а ахх = ах, ауу — ау и azz = az представляют главные поляризуемости.
Имеем
ах — ау az (одна ось симметрии порядка п 3).	(18.33)
Наконец, при наличии только осей симметрии порядка п 2 диагональные
составляющие, вообще говоря, не равны друг другу. Выбирая оси х, у, z в качестве
главных осей поляризуемости, мы имеем
ах ф ау Ф az (оси симметрии порядка п 2).	(18.34)
Мы видим, что в соответствии с тремя родами точечных групп тензор поляри-
зуемости может быть также трех родов.
Представляя тензор поляризуемости при помощи эллипсоида поляризуемости (см. § 17.7,
с. 496), мы получаем в случае (18.32) сферу, в случае (18.33) эллипсоид вращения и в слу-
чае (18.34) эллипсоид с тремя разными полуосями.
Приведенные результаты получаются из условия инвариантности тензора поляризуе-
мости, т. е. из условия, что при операциях симметрии тензор поляризуемости не должен
изменяться. При кубической симметрии имеются три эквивалентные взаимно-перпендику-
лярные оси, что и приводит к (18.32) (тот же результат получается и для группы икосаэдра).
При наличии выделенной оси симметрии порядка п 3 при поворотах вокруг этой оси
координаты хну преобразуются между собой, что и приводит к ахх — ауу, т. е. к (18.33).
При отсутствии осей симметрии порядка п 3 нет причин, вызывающих равенство двух
или всех трех главных поляризуемостей, поэтому, вообще говоря, имеет место (18.34). От-
метим, что в силу симметрии для всех групп с осью симметрии С2 второго порядка одна
из главных осей тензора поляризуемости будет совпадать с этой осью, а для групп С2г,, D2
и D2h, кроме того, и две другие главные оси будут ориентированы вполне определенным
образом; в случае группы C2v они лежат в плоскостях а в случае групп D2 и D2fl они
совпадают с двумя осями С2, перпендикулярными к исходной оси С2.
§ 18.6. Общие выводы о симметрии молекул	529
В дальнейшем мы будем неоднократно пользоваться классификацией молекул
по их принадлежности к точечным группам, приведенным в табл. 18.114). В част-
ности, в следующей главе, при рассмотрении вращения молекул будет применена
общая классификация молекул по наличию осей симметрии порядка п < 2, одной
выделенной оси симметрии порядка п 3 или нескольких выделенных осей сим-
метрии порядка п 3, т.е. по принадлежности молекул к группам низшей, средней
и высшей симметрии.
14) К группам, символы которых взяты в квадратные скобки, молекулы не могут относиться.
ГЛАВА 19
ВРАЩЕНИЕ МОЛЕКУЛ И ВРАЩАТЕЛЬНЫЕ СПЕКТРЫ
§ 19.1. Общая характеристика вращения молекул
Основной характеристикой вращающейся молекулы, приближенно рассматри-
ваемой как твердое тело (см. § 17.4, с. 476), являются ее моменты инерции относи-
тельно связанной с молекулой подвижной системы координатных осей (рис. 17.4, а
и б). Оси х, у, z этой системы мы выбираем так, чтобы они были главными осями
инерции. Тогда три момента инерции Ix, Iy, Iz TV-атомной молекулы относительно
главных осей (главные моменты инерции °) будут равны
N
4 = £ М,(У2 + 4),
г—1
N
1у — ТИДг, -Т Xi), >
г=1
N
4 =	+ у2),
(191)
где Mi — массы ядер, a Xi, уг, Zi — их координаты в подвижной системе, начало
которой совпадает с центром тяжести молекулы.
Таким образом, момент инерции относительно заданной главной оси равен сум-
ме произведений масс ядер на квадраты их расстояний до этой оси. Расположение
ядер принимается неизменным, соответствующим равновесной конфигурации моле-
кулы. в согласии с рассмотрением молекулы как твердого тела. Такое рассмотрение
явля лся физически правильным приближением, когда амплитуды колебаний ядер
относ ительно положений равновесия достаточно малы.
Например, идя молекулы воды Н2О, принадлежащей к точечной группе С2б.
и имеющей форму равнобедренного треугольника (см. гл. 18, с. 506) с расстоянием
Лэн ' 0,0534А — 0,9584- 10-8см между ядрами атомов водорода (з.е. протонами)
и с ртом «нон “ 104°27' между связями (см. рис. 19.1).
1Х = Мцу] +Мну1 +Моу1 = 1,024 - 1О“40 г- см2,
1у = . /нх2 + Мцх1 = 1,921 • КГ4" г см2,	>
Iz = Мн(Д + У2) 4 М„(х] + уЬ М()у1 = 2,947 • КГ40 г • см2. ,
(19.2)
В дальнейшем мы будем всегда говорить ) моментах инерции молекулы, подразумевая главные
моменты инерции.
§19.1. Общая характеристика вращения молекул
531
В данном частном случае главные оси
инерции выбраны так, что ось у явля-
ется осью симметрии (осью Ci) молеку-
лы, ось х лежит в плоскости молекулы
(плоскость </’)), а ось z перпендикулярна
к этой плоскости. При подобном выборе
осей жз = 0 и z\ — zi — Z3 = 0; индексы 1
и 2 относятся к атомам водорода с мас-
сой Мн, индекс 3 — к атому кислорода
с массой Mq. В силу симметрии равно-
весной конфигурации Х\ = —я?2 и у\ — у2.
Координаты х и у связаны соотношения-
ми, очевидными из рис. 19.1:
Рис. 19.1. Расстояния атомов О и Н
в молекуле Н2О от главных осей инерции
Гон = У(2/3 - 2/1)2 + =
= У(г/з - 2Л>)2 +	О9-3)
анон a?i	^2
tg —— =------------=------------.
2	2/3 - 2/1	2/3 - 2/2
Положение центра тяжести удовлетворяет условиям:
Ml 2/1 + М22/2 + М3у3 = Мн(2/1 + 2/2) + Мо2/з = 0,
Mi + М2Х2 = Мн(«| + Х2) = 0.
(19-4)
В силу того, что молекула плоская, = 1Х + 1у (подробнее об этом см. ниже,
§19.4, с. 545).
Возможность сделанного выбора осей определяется симметрией молекулы. В общем
случае ядра не будут расположены симметричным образом относительно главных осей и про-
извольно выбранные оси не будут главными осями инерции. Как известно, при произвольной
ориентации подвижных осей х', у1, z' динамические свойства твердого тела характеризуются
тензором момента инерции — симметричным тензором второго ранга с составляющими
4 = £ м(2/.'2 + *?), 4 = £
i=l	i=l	»=|
N	N	N
4 = 4 = -М'Хм, 4 = 4 = _У2
i=l	:=1	:=1	,
который получается из линейной связи между составляющими момента количества движе-
ния Мр и составляющими угловой скорости о/.
Действительно, для системы частиц
N
Mp = '^/[RiMivi],	(19.6)
1=1
где Л, — радиус-вектор и г, — скорость г-й частицы, и при неизменных расстояниях между
частицами
Vi = [cvJRj.	(19.7)
Подстановка (19.7) в (19.6) дает
N	N
Мр =	М,- [fl,4-R.I] =У^ Mj{u  Rj - RijRiw)},	(19.8)
i=l	г=1
532
Глава 19. Вращение молекул и вращательные спектры
что в раскрытом виде приводит к соотношениям
Совокупность коэффициентов (19.9), связывающих линейным образом^составляющие Мрх>,
Мру<, Mpz> момента количества движения с составляющими шх>, шу>, wz' угловой скоро-
сти, и образует тензор момента инерции. Этот тензор симметричен и может быть наглядно
представлен как любой симметричный тензор эллипсоидом инерции, совершенно аналогич-
но тому, как симметричный тензор поляризуемости может быть представлен эллипсоидом
поляризуемости (см. § 17.7, с. 496).
Наряду с диагональными составляющими Ixx, l'yy, l'zz — моментами инерции относитель-
но соответствующих осей ж', у', z' — получаются недиагональные составляющие 1ху = 1ух,
I'yz = I'zy, I'zx — I'xz — так называемые произведения инерции или центробежные моменты
инерции. Путем поворота координатных осей можно всегда перейти от произвольно ориенти-
рованных осей х', у', z' к осям х, у, z, относительно которых произведения инерции равны
нулю, и тогда (19.5) сводится к (19.1). Это и будут главные оси инерции. Легко видеть, что
в рассматриваемом частном случае молекулы воды произведения инерции обращаются в нуль
в силу того, что ж, - -х2, у\ — У1, жз = О, Z\ — z2 — з3 = 0 и М\ = М2 = Мн, т. е. оси х, у, z
действительно главные оси инерции.
Когда говорят о моментах инерции молекулы, то, как правило, подразумевают моменты
инерции (19.1) относительно главных осей, т. е. главные моменты инерции (см. примечание
на с. 530).
Для наиболее легких молекул, содержащих атомы водорода, моменты инерции,
как и для молекулы воды, имеют порядок величины Ю40 г • см2. Для более тяжелых
молекул они увеличиваются с числом и массой атомов и с размерами молекулы
и могут быть на один или несколько порядков больше. Задача о вращении молекулы
приближенно сводится к задаче о вращении твердого тела с заданными моментами
инерции. При вращении свободной молекулы, рассматриваемой как твердое тело,
постоянными движения, т. е. величинами, сохраняющими постоянные значения,
являются вращательный момент количества движения и энергия вращения. В соот-
ветствии с законами квантовой теории вращательный момент количества движения
и вращательная энергия квантуются, принимая определенные дискретные значения.
Квантование квадрата вращательного момента количества движения определя-
ется общей формулой (2.5),
Mp = h2J(J+ I),	(19.10)
где квантовое число J, в данном случае вращательное квантовое число, принимает
целые значения
7 = 0, 1,2,3,... .	(19.11)
Одновременно квантуется, согласно (2.9), проекция вращательного момента количе-
ства движения на выделенное направление, которое мы примем за ось ( неподвижной
координатной системы £, у, £2). Мы имеем
MpC=hmj,	(19.12)
2) Мы обозначаем оси закрепленной в пространстве координатной системы — неподвижной систе-
мы — через т/, ( в отличие от осей х, у, z подвижной системы (см. § 17.4, с. 476).
§19.1. Общая характеристика вращения молекул
533
где
mj = J, J - 1,... ,-J,	(19.13)
т. е. принимает 2J + 1 значений.
Квантование вращательной энергии молекулы связано с квантованием момента
количества движения и зависит от числа вращательных степеней свободы, от ве-
личины моментов инерции и от соотношений между ними. При этом энергия
молекулы зависит от величины момента количества движения и является функци-
ей вращательного квантового числа, но не зависит от величины проекции этого
момента, т. е. от квантового числа mj. Поэтому вращательные уровни свободной
молекулы всегда вырождены (кроме уровня J — 0, для которого кратность вырожде-
ния 2J -f- 1 = 1), что связано с произвольностью ориентации момента количества
движения по отношению к неподвижной системе координат.
Для линейных молекул вращательному движению соответствуют две степени
свободы (см. § 17.4, с. 476). Для характеристики состояния вращательного движения
достаточно двух квантовых чисел J и rrij. Вращение в этом случае происходит, со-
гласно наглядным представлениям, вокруг оси, перпендикулярной к оси молекулы,
на которой расположены ядра. Момент инерции относительно оси молекулы, кото-
рую мы выбираем за ось z, равен, очевидно, нулю, а моменты инерции относительно
любой перпендикулярной к ней оси одинаковы. Мы имеем
1Х=1У = /, Iz=0-	(19.14)
Ориентация осей х и у в плоскости, перпендикулярной к оси z, произвольна.
Квантование энергии в этом случае производится очень просто (см. § 19.2).
Энергия вращения зависит только от значений момента инерции I и вращательного
квантового числа J.
Для нелинейных молекул вращательному движению соответствуют три степе-
ни свободы (см. § 17.4, с. 476), поэтому для его характеристики необходимы три
квантовых числа. Вращение нелинейной молекулы может происходить, согласно
наглядным представлениям, вокруг любой оси, проходящей через центр тяжести.
Все три момента инерции отличны от нуля и возможны три случая квантования
вращательной энергии в зависимости от соотношения между величинами моментов
инерции 1Х, 1у и Iz.
1.	Случай молекул типа сферического (шарового) волчка, имеющий место, когда
все три момента инерции равны друг другу
Ix = Iy = Iz.	(19.15)
2.	Случай молекул типа симметричного волчка, имеющий место, когда два
из трех моментов инерции равны друг другу:
Ix = Iy^Iz.	(19.16)
Отметим, что в соответствии с (19.14) линейные молекулы могут рассматриваться как
молекулы типа симметричного волчка с моментом инерции Iz = 0 (см. ниже, с. 543).
3.	Случай молекул типа асимметричного волчка, имеющий место, когда все три
момента инерции разные:
Ix^Iy^Iz.	(19.17)
Квантование вращательной энергии усложняется при переходе от первого случая
ко второму и от второго к третьему.
Соотношение моментов инерции для заданной молекулы зависит от ее симме-
трии и определяется принадлежностью молекулы к определенной точечной группе
(см. табл. 18.1, с. 526).
534
Глава 19. Вращение молекул и вращательные спектры
Для молекул с высокой симметрией, имеющих несколько осей симметрии
порядка п 3 (в частности, для молекул, относящихся к группам Td и Оь), моменты
инерции вокруг трех взаимно-перпендикулярных осей одинаковы. Поэтому молекулы
с несколькими осями симметрии порядка п > 3 являются сферическими волчками.
Действительно, молекулы с кубической симметрией (относящиеся к группам тетра-
эдра и октаэдра) имеют три эквивалентные взаимно-перпендикулярные оси симметрии
(С2 для групп тетраэдра и С4 для групп октаэдра, см. § 18.5) и моменты инерции вокруг этих
осей должны быть одинаковы; моменты инерции будут одинаковы в силу свойств эллипсоида
инерции, представляющего в этом случае сферу, и в любой повернутой системе координатных
осей. Тот же результат получается и для групп икосаэдра.
Рис. 19.2. Определение моментов
инерции для трех атомов, образующих
равносторонний треугольник
Для молекул, имеющих выделенную ось
симметрии порядка п 3, эта ось является
главной осью инерции. Относительно всех
перпендикулярных к ней осей (проходящих
через центр тяжести, обязательно лежащий
на оси симметрии Сп) моменты инерции
одинаковы. Таким образом, молекулы с вы-
деленной осью симметрии порядка п являются
симметричными волчками с моментом инер-
ции Iz относительно оси симметрии и с мо-
ментами инерции 1Х = 1у относительно осей,
перпендикулярных к оси симметрии; выбор
направлений осей х и у при этом остается
произвольным.
На первый взгляд, равенство моментов инер-
ции молекулы относительно любых осей, перпен-
дикулярных к оси симметрии конечного поряд-
ка п (п 3), кажется неожиданным. Например,
для трех одинаковых атомов, образующих равносторонний треугольник (рис. 19.2), не оче-
видно равенство моментов относительно осей х и у и относительно произвольной оси, со-
ставляющей с осью х угол у?. Однако легко проверить, что эти моменты инерции одинаковы.
Обозначая через а расстояние атомов от центра треугольника, лежащего на оси симметрии Сз
z	3 ч
третьего порядка, мы получим (высота равностороннего треугольника равна - а)
Ix = Mty2 + Мгу2 + Mwl = М Q)2 + М (^)1 + Ma2 = 1 а2,
/ УЗ \2	(\2 3
1у = М]Х2! + М2х\ = М ( — а ]	al = - а2.
(19.18)
Из равенства двух моментов инерции 1Х и 1у относительно двух взаимно-перпенди-
кулярных осей х и у вытекает, что момент инерции относительно любой оси, лежащей
в плоскости ху, имеет то же самое значение. Действительно,
I = Ma2 sin 2(ЗО° - <р) + Ma2 sin 2(30° + у>) + Ma2 cos V = “2-	(19-19)
Аналогичный результат может быть получен для любого правильного многоугольника
с п > 3. Эллипсоид инерции в случае выделенной оси симметрии порядка п 3 является
эллипсоидом вращения.
Для линейных молекул, которые, как молекулы с выделенной осью симмет-
рии, должны быть симметричными волчками, обращается в нуль момент инерции
§19.1. Общая характеристика вращения молекул
535
относительно этой оси (оси молекулы Соо) и условие (19.16) превращается в усло-
вие (19.14).
Для молекул, не имеющих осей симметрии порядка п 3, все три момента
инерции, как правило, будут различны. Таким образом, молекулы с осями симметрии
порядка п 2 являются асимметричными волчками.
Следует отметить, что деление молекул на типы (19.15), (19.16) и (19.17) в зави-
симости от соотношения между моментами инерции Ix, Iy, Iz совпадает с их делением
на типы (18.32), (18.33) и (18.34) в зависимости от соотношений между главными поляризуе-
мостями. Это естественно, так как в обоих случаях молекула характеризуется симметричным
тензором, который должен быть инвариантен по отношению к операциям симметрии соот-
ветствующих точечных групп.
Примером молекулы типа сферического волчка является СН4 (симметрия Tj),
примером молекулы типа симметричного волчка — NH3 (симметрия С^), приме-
ром молекулы типа асимметричного волчка — Н2О (симметрия Cyv). Следует иметь
в виду, что для молекулы более низкой симметрии моменты инерции могут иногда
совпадать точно или приближенно в силу причин, не зависящих от симметрии мо-
лекулы («случайное» совпадение). Например, для молекулы С2Н4, принадлежащей
к группе симметрии которой соответствуют асимметричные волчки, момент
инерции относительно оси молекулы С—С (оси z, см. рис. 19.3), определяемый
только легкими атомами Н, очень мал, а другие два момента инерции (относи-
тельно осей х и у) почти одинаковы; их разница определяется только различием
расстояний рх и ру атомов Н от осей х и у.
Рис. 19.3. Расстояния томов С и Н в молекуле С2Н4 от главных осей инерции
Изложенное деление молекул на сферические, симметричные и асимметричные в j г
ки пригодно только для молекул, которые можно приближенно рассматривать как тверды;:
тела — для квазитвердых молекул. Для молекул, в которых возможны внутренние вращения
одних ее частей относительно других (см. § 18.1, с. 502), а также внутренние перегруппирс хи
необходима специальная классификация, учитывающая, что с остовом молекулы могут ;ьг ь
связаны волчки различных типов, симметричные и асимметричные. Такая классификация
была дана Годневым [ПО]. В тайной главе мы ограничиваемся рассмотрением квазитвердых
молекул. В гл. 21, посвященной колебаниям многоатомных молекул, мы рассмотрим и не-
которые вопросы, связанные с внутренним вращением и с внутренними перегруппировками
(см. §21.8, с. 640).
Основные характеристики вращательных уровней молекулы и расположение
этих уровней существенным образом зависят от типа, к которому принадлежит мо-
лекула. Общими характеристиками вращательных уровней молекул всех типов явлч
ются значения квантовых чисел J и mj, определяющих, согласно (19.10)—(19.13),
536
Глава 19. Вращение молекул и вращательные спектры
квантование квадрата вращательного механического момента и его проекции и свя-
занных со сферической симметрией свободной системы. При этом вращательные
уровни с последовательными значениями J обладают противоположной симметрией
относительно инверсии координат всех ядер и делятся на положительные и отри-
цательные по отношению к соответствующей операции симметрии. Таким образом,
либо уровни с четными J (J = 0, 2, 4,...) являются положительными, а уровни с не-
четными J (J — 1, 3, 5,...) отрицательными, либо, наоборот, уровни с четными J
являются отрицательными, а уровни с нечетными J — положительными.
Деление вращательных уровней на положительные и отрицательные связано с тем,
сохраняет ли или меняет знак полная волновая функция молекулы (17.66) при отражении
всех координат в начале. Наиболее существенно это деление для линейных молекул, так как
отражение в начале означает изменение направления оси линейной молекулы на противопо-
ложное. Мы вернемся к данному вопросу в дальнейшем (см. § 19.9, с. 569, и §25.4, с. 770).
В следующих параграфах мы рассмотрим для молекул различного типа вра-
щательные уровни и переходы между ними (§ 19.2-19.6). Последние параграфы
главы посвящены некоторым результатам изучения вращательных спектров (§ 19.7)
и вопросам влияния на вращательные уровни и на вращательные спектры внешних
полей (§ 19.8) и моментов ядер (§ 19.9).
В данной главе мы ограничимся рассмотрением молекул, для которых полный
электронный момент количества движения равен нулю и поэтому полный момент
количества движения (без учета спинов ядер) является чисто вращательным. К таким
молекулам относится подавляющее число устойчивых в химическом отношении мо-
лекул, находящихся в основном электронном состоянии (см. с. 793, ср. также с. 404).
§ 19.2. Вращательные уровни и вращательные переходы
в случае линейных молекул
Вращательные уровни энергии линейной молекулы можно очень просто найти
на основе наглядных представлений.
Линейная молекула вращается вокруг оси, перпендикулярной к оси молекулы
и проходящей через центр тяжести. При этом ее момент количества движения Мр
направлен по оси вращения, а энергия вращения равна
М2
Е=-^--	(19.20)
Здесь I — момент инерции относительно оси вращения, равный
N
I =	(19.21)
i=l
где Ri — расстояния ядер от центра тяжести молекулы.
Действительно, энергия вращения молекулы представляет кинетическую энергию вра-
щения ядер и равна (v, ± Ri)
E =	=	= |( S	|	(19.22)
i=l	i=l	г=1
dip
где ш = — =	— угловая скорость, а величина момента количества движения Мр =
N	/ N \	/ М \2 М2
УЗ RiMiVi = УЗ	— Iw, т.е. 1ш2 —	и мы получаем (19.20).
§ 19.2. Вращательные уровни и переходы для линейных молекул
537
Зависимость (19.20) между энергией и квадратом механического момента со-
храняется и в квантовой теории. Подставляя значение Мр, согласно (19.10), мы
получаем для квантованной энергии вращения выражение
=	=	(19.23)
где
Л2	Л2	h	h	z
В = — =	——	эрг =	——	с =	—-Z—	см	(19.24)
21	8тг27	8тг27	8тг27с	v 7
— вращательная постоянная, определяющая абсолютные значения вращательной
энергии линейной молекулы. При изучении оптических спектров, в частности
инфракрасных спектров, постоянную В выражают в волновых числах, а при изучении
спектров в области радиочастот, в частности микроволновых спектров, — в единицах
частоты (обычно в МГц; 1 МГц = 106 Гц — 106 с"1). В численном виде
2,80 • 10~39
В —-------------см
0,83  10~28	0,83 - 10~34
-----------с —------------- МГц.
(19.25)
Формула
(рис. 19.4):
(19.23) определяет совокупность вращательных уровней энергии
7 = 0	1	2	3	4	5	6	7	8	9	10	(19.26)
Е = 0	2В	6В	12В	20В	ЗОВ	42В	56В	72В	90В	НОВ	
Расстояния между последовательными
уровнями энергии возрастают пропорцио-
нально квантовому числу 7:
= + +	(|9.27)
-BJ(J +\) = 2B(J +1).	7
10В
18В
Абсолютная величина расстояний между вра-
щательными уровнями энергии, определяе-
мая величиной постоянной В, обратно про-
порциональна моменту инерции I молекулы.
Она поэтому тем меньше, чем тяжелее моле-
кула и чем больше ее размеры. Для важней-
шего случая двухатомной молекулы момент
инерции равен
7 = 5
7 = 4
7 = 3
7 = 2
7=1
7 = 0
8В
14В
6В
10В	
6В
4В
~]2В
ЗОВ
20В
12В
6В
2В
о
I = Мр2,
(19.28)
М}М2
где М = ---------- — приведенная масса
TVfj Л/2
молекулы и р — расстояние между ядрами
(ср. (19.22) и второй член в (17.40)).
Для молекулы водорода Н2 приведенная
Л7ц	-24
масса М = -у- = 0,84 10 г, а расстоя-
ние между ядрами (в основном электронном
состоянии) равно 0,74 А = 0,74 • 10~8 см, сле-
довательно, I = 0,84 ♦ 10~24 • 0,742 • 10~16 =
7' 1234	2345
7" 0 1 2 3	0 1	2 3
Рис. 19.4. Вращательные уровни
энергии и переходы между ними
для линейной молекулы
538
Глава 19. Вращение молекул и вращательные спектры
0,46- 10 40 г см2. Вращательная постоянная, выраженная в см ’, согласно (19.25),
равна
2,80 • 10~39	,
В = ----------- « 60 см"’,	(19.29)
0,46 10"40	’	V 7
что дает расстояние между уровнями J — 0 и J = 1, равное 120 см-1, значение
которого было использовано в гл. 17 при оценке порядка отношения вращательной
энергии к электронной (см. с. 469).
Для более тяжелых двухатомных молекул В убывает в основном благодаря
увеличению массы. Расстояния между ядрами возрастают с массой, хотя и сравни-
тельно медленно, что также уменьшает В. Например, для молекулы 12 (в основном
электронном состоянии) имеем
р = 2,667 А = 2,667-10-8 см, М =	= 63,5-1,67-10’24 г = 1,06-10~22 г,
следовательно, I — 1,06 • 10~22 • 2,6672 • 10~16 — 0,75 • 10~37 г • см2. Отсюда
в = ---° '10 „ = 0,037 см-1 = 1,12 • 109 Гц = 1 120 МГц. (19.30)
0,75 - 10~37
Таким образом, по сравнению с молекулой водорода момент инерции на три порядка
больше, а вращательная постоянная на три порядка меньше.
Для линейных многоатомных молекул моменты инерции вычисляются по общей
формуле (19.21). Например, для молекулы СО2, в которой атомы кислорода рас-
положены симметрично относительно центрального атома углерода (см. рис. 18.1, а,
с. 501), находящегося в центре тяжести молекулы I — 2МоРсо> гДе ^о — масса
атома кислорода, а рсо — длина связи С—О,
Мо= 16- 1,67 - 10—24 г = 2,68 - 1О-23 г, Рсо = 1,16 А = 1,16- 1(Г8см,
откуда 1 = 2- 2,68 • 1(Г23 • 1,162 • 10-16 г • см2 = 7,1 • 10~39 г • см2 и
В= jq0 39 — 0,394 см ' = 1,18- 1010 Гц = 11 800 МГц.	(19.31)
Энергия свободной молекулы, как уже подчеркивалось в предыдущем параграфе
(см. с. 532), не зависит от значения квантового числа mj. Вместе с тем совокупность
квантовых чисел J и mj полностью определяет вращательное состояние линейной
молекулы, имеющей две степени свободы, и степень вырождения gj уровней
энергии равна числу возможных значений mj при заданном I, т. е. 2J + 1. Мы
имеем для последовательных вращательных уровней статистические веса gj — 2J + 1
(J = 0, 1,2,...).
При тепловом равновесии число молекул во вращательных состояниях с задан-
ным значением J будет определяться формулой (см. 5.17)3)
f	Ej}	(	BJ(J+1)1
nj = (2J + 1 )n0 exp < - — > = (2J + l)n0 exp <!------—----->,	(19.32)
L J	L	)
где через пц обозначена заселенность основного вращательного уровня (J — 0),
для которого статистический вес до = 1 и энергия Eq — 0. 3 * *
3) Формула несправедлива для молекул, обладающих центром симметрии. Такие молекулы содержат
эквивалентные ядра, статистические веса зависят от значения спина этих ядер и необходимо специальное
рассмотрение, учитывающее свойства симметрии (см. подробнее ниже, с. 567).
§ 19.2. Вращательные уровни и переходы для линейных молекул
539
Чисто вращательными спектрами поглощения и испускания могут обладать
все линейные молекулы с постоянным дипольным моментом, отличным от нуля.
Такими молекулами являются линейные молекулы, не имеющие центра симметрии,
т.е. обладающие симметрией (см. выше, § 18.6, с.527).
Возможные чисто вращательные переходы для дипольного излучения опреде-
ляются правилом отбора (см. (4.156))
Д7 = ±1,	(19.33)
т. е. комбинируют только соседние вращательные уровни. В соответствии с форму-
лой (19.27) частоты возможных переходов равны
j" -J'	0- 1	1 - 2	2 - 3	3 - 4	4 - 5	5 - 6	... 1	,	.
AfyJ+1 2В 4В 6В SB 10В	12В	... J
Это дает спектр, состоящий из ряда равноотстоящих (в шкале частот) линий,
схематически изображенный в нижней части рис. 19.4 (слева). Для спектров комби-
национного рассеяния правило отбора иное, а именно (см. (4.158), дополнительно
запрещены переходы Д7 — ±14)),
Д<7 = ±2,	(19.35)
т.е. переходы происходят не между соседними уровнями, а между уровнями, вра-
щательные квантовые числа которых отличаются на две единицы. Мы имеем,
согласно (19.23),
/	3\
BJ+2 -Ej = B(J + 2)(J 4- 3) - BJ(J 4- 1) = 4B(J 4- - J .	(19.36)
Частоты возможных переходов равны
J"-J1	0 - 2	1 - 3	2 - 4	3 - 5	4 - 6	...	1	,
ДВЛ7+2 6B	10В	14В	18В	22В	...	J
что дает спектр, также состоящий из равноотстоящих линий, но с интервалами
(в шкале частот) 4В. Этот спектр изображен в нижней части рис. 19.4 (справа).
Чисто вращательным спектром комбинационного рассеяния могут обладать все
линейные молекулы, как имеющие центр симметрии, так и не имеющие его,
т.е. принадлежащие как к группе D^h, так и к группе С^.
Как указывалось выше, рассмотрение вращающейся молекулы как твердого
тела является лишь приближенным. В действительности расстояния между ядрами
не являются неизменными. При вращении молекулы они увеличиваются вследствие
центробежного растяжения. Очевидно, что этот эффект будет тем больше, чем боль-
ше с классической точки зрения угловая скорость вращения, т. е. чем больше враща-
тельное квантовое число J. Так как расстояния между ядрами вследствие вращения
увеличиваются, то вращательная постоянная В уменьшается с увеличением J. При-
ближенный расчет центробежного растяжения, которое является небольшим, может
быть произведен, согласно квантовомеханической теории возмущений, и приводит
к формуле для вращательной энергии
Ej=BJ(J +1)-D[J(J +1)]2.	(19.38)
4) Между положительными и отрицательными уровнями (см. с. 536, а также [46], с. 67).
540	Глава 19. Вращение молекул и вращательные спектры
Формула (19.38) содержит, таким образом, наряду с квадратичным членом,
член четвертой степени относительно вращательного квантового числа J. Ее можно
переписать в виде
Ej= [В - DJ(J + 1)]J(J + 1) = BjJ(J + 1),	(19.39)
где величина
Bj = B-DJ(J + 1)	(19.40)
не строго постоянна, а уменьшается с увеличением J. Энергия вращения, согласно
формуле (19.38) или (19.39), растет с увеличением J медленнее, чем это дает
формула (19.23).
Частоты переходов при больших J уменьшаются и поэтому линии враща-
тельного спектра уже не будут равноотстоящими, а будут постепенно сходиться.
Постоянная D всегда очень мала и не превышает 10~4В, поэтому ее учет необходим
лишь при больших значениях J.
§ 19.3. Вращательные уровни молекул типа сферического волчка
Простейшим случаем вращения нелинейных многоатомных молекул является
вращение молекул типа сферического волчка, т. е. молекул, для которых все три
момента инерции равны друг другу (см. (19.15)). Этот случай осуществляется, как
мы указывали (с. 533), для молекул с несколькими осями симметрии порядка п 3,
например, для молекулы метана СН4 (симметрия Т^). Другим примером является
молекула шестифтористого урана UF6 (симметрия Oh).
Вращательные уровни молекулы типа сферического волчка легко находятся,
если исходить из классического выражения для энергии вращения молекулы с тремя
моментами инерции, отличными от нуля. Это выражение имеет вид
I / М2	М2	М2 \
( 11рх 1 ру _1_ pz ]
2 V 1Х	1У	Iz J
где Мрх, Мру, Mpz — составляющие механического момента по подвижным осям,
за которые выбираются главные оси инерции, a Ix, Iy, Iz — соответствующие
моменты инерции вокруг этих осей.
Энергия вращения молекулы, рассматриваемой как твердое тело, равна кинетической
энергии (ср. (19.5)—(19.9)):
v	N
Е = Т = - ^2	= 2 12 М< ^Я.]2 =
!	"1	! " , (19Л2)
= т 52	= -шмр = - 52
Z z	Z	Z
Г-1	аД
где а, /3 = х', у', z'. При введении главных осей инерции
Е = т= ^52J“w“ = I ^+'2	+	(19.43)
и при подстановке значений ша = —— (формула (19.9) в системе главных осей сводится
J-a
к Мрх = I£wx, Мру = lyUy, Mpz = Izwz) мы получаем (19.41).
В квантовомеханической теории классическому выражению (19.41) для энергии враще-
ния соответствует оператор (17.62). При более точном рассмотрении коэффициенты в (17.62)
§ 19.3. Вращательные уровни молекул типа сферического волчка
541
представляют эффективные значения моментов инерции, получаемые в результате усред-
нения оператора энергии по колебательным координатам (см. (17.76) и (17.80)), и зависят
от колебательного состояния.
Для сферического волчка Ix = Iy = Iz = I и, следовательно,
1	М
Е = -(М2Х + Мр2у + мД) =	(19.44)
Так же как в случае линейной молекулы, зависимость (19.44) между Е и Мр
сохраняется и в квантовой теории, и подстановка (19.10) в (19.44) дает квантованные
значения энергии
Ej = J-J(J+1) = BJ(J+1) (J = 0,1,2,...),	(19.45)
Л2 _ й2
21 ~ №l’
где В =
что совпадает с (19.23).
Таким образом, вращательные уровни молекулы типа сферического волчка
определяются совершенно такой же формулой, как и вращательные уровни линейной
молекулы. Однако имеется весьма существенное различие в свойствах вращательных
уровней в обоих случаях, а именно, в их степени вырождения. Это различие связано
с числом степеней свободы.
Линейная молекула имеет две вращательные степени свободы, и для полной
характеристики ее вращательного движения достаточно, как уже указывалось выше
(см. с. 538), двух квантовых чисел J и mj, определяющих значения квадрата
момента количества движения и проекции момента количества движения на одну
из неподвижных в пространстве осей.
Молекула типа симметричного волчка, как и любая нелинейная молекула, имеет
три вращательные степени свободы, и для полной характеристики ее вращательного
движения необходимо задание трех квантовых чисел. Третьим квантовым числом,
характеризующим вращательное движение (наряду с квантовыми числами J и mj,
которые сохраняют свой смысл), для сферического волчка является квантовое
число К, определяющее значение проекции момента количества движения на одну
из подвижных осей. Направление этой оси в рассматриваемом случае молекулы типа
сферического волчка может быть выбрано произвольно; существенно лишь, что эта
ось закреплена в молекуле, т. е. вращается вместе с молекулой. Проекция момента
количества движения на подвижную ось, которую мы выберем за ось г, квантуется
совершенно так же, как и проекция на неподвижную ось (например, на ось (),
а именно,
Mpz =hK,	(19.46)
где
K =	(19.47)
т.е. принимает 2J + 1 значений, соответствующих 2J + 1 независимым состояниям.
Так как энергия от квантового числа К не зависит, то получается дополнитель-
ное вырождение уровней кратности 2J + 1. Это вырождение имеет место наряду
с вырождением по mj кратности 2J 4- 1. Общая степень вырождения по mj и по К
равна
gj = (2J + 1)(2J + 1) = (2J + I)2.	(19.48)
Для каждого значения J возможны 2J + 1 ориентации относительно непо-
движных осей и 2J + 1 ориентации относительно подвижных осей, что и приводит
к (2J + I)2 возможным состояниям, т.е. к общей степени вырождения (2J + I)2.
542
Глава 19. Вращение молекул и вращательные спектры
В соответствии с формулой (5.17) при степени вырождения (т. е. при статисти-
ческом весе) gj = (2J 4- I)2 вращательных уровней, число молекул во вращательных
состояниях с заданным значением J будет определяться формулой
2	( Ej}	\2	(	BJ(J+1)1
nj = (2J + 1) По ехр < - — > = (2J + 1)4 ехр -----—----->.	(19.49)
KI J	Ki J
Сравнение с формулой (19.32) показывает, что для молекул типа сферического
волчка большая доля молекул будет находиться на высоких вращательных уровнях,
чем для линейных молекул (при тех же значениях вращательной постоянной В
и температуры Т).
В табл. 19.1 сопоставлены значения с 1тистических весов вращательных уровней
для линейных молекул и для молекул тии сферического волчка. Различие этих
статистических весов существенно при термодинамических расчетах (см. [НО]).
Таблица 19.1
Статистические веса вращательных уровней для линейных молекул
и для молекул типа сферического волчка
J	0	1	2		3	4	5	6	7	8	9	10
wj = 2J + 1	1	3	5	7	9	11	13	15	17	19	21
wj = (2J+V)2	1	9	25	49	81	121	169	225	289	361	441
Возможность характеристики молекулы рассматриваемого типа при помощи трех кван-
товых чисел J, mj и К связана со свойствами момента количества движения по отношению
к неподвижным и по отношению к подвижным осям. Как можно показать (см. [284] и [131]),
-----------------------------2	—
одновременно с операторами и Мр^ (£ — выделенная неподвижная ось) определенное
значение может иметь одна из составляющих Мрх, Мру, Mpz момента количества движения
относительно подвижных осей5). Выбирая составляющую Mpz (z — выделенная подвижная
----------------------------------------------------------2 —	—
ось), мы получаем три коммутирующих друг с другом оператора Мр, МР( и Mpz, собственные
значения которых h2J(J + 1), hmj и hK определяются тремя квантовыми числами J, mj и К.
Для молекулы типа сферического волчка все три оператора коммутируют и с оператором
- м2
энергии Н — И поэтому вырожденные между собой состояния, принадлежащие к уров-
ню энергии (19.45) с определенным значением J, можно характеризовать тремя квантовыми
числами J, mj и К. Степень вырождения этого уровня (2J + I)2.
Молекулы типа сферического волчка в силу своей высокой симметрии не имеют
дипольного момента (см. § 18.6, в частности, табл. 18.1) и поэтому не могут обладать
чисто вращательными спектрами поглощения и испускания. Благодаря высокой
симметрии они не могут обладать и чисто вращательным спектром комбинационного
рассеяния.
Отсутствие спектра комбинационного рассеяния объясняется тем, что для молекулы
с несколькими осями симметрии порядка п 3 эллипсоид поляризуемости превращается
в сферу (подобно тому, как эллипсоид инерции превращается в сферу, см. с. 533). При вра-
щении молекулы ее поляризуемость в заданном направлени не меняется, и комбинационное
рассеяние невозможно (см. § 17.7, с. 497).
5) Операторы Мрх, Мру, Mpz удовлетворяют перестановочным соотношениям, отличающимся только
знаком от перестановочных соотношений для Мр^, Мрт}, Мр^ и коммутируют как с Мр, так и с Мр^,
МрУ, МрС
§ 19.4. Классификация симметричных и асимметричных волчков 543
Чисто вращательные спектры могут иметься лишь у молекул, которые только случайно
(а не в силу симметрии) являются сферическими волчками и поэтому для них дипольный
момент не обращается в нуль, а эллипсоид поляризуемости не обязательно должен быть
сферой.
В заключение данного параграфа отметим, что при учете центробежного ра-
стяжения вращательные уровни молекулы типа сферического волчка будут опреде-
ляться формулой того же типа, как и для линейных молекул, т.е. формулой (19.38)
или (19.39).
§ 19.4. Моменты инерции и вращательные постоянные молекул
типа симметричных и асимметричных волчков
Наиболее важные типы молекул — симметричные
волчки и асимметричные волчки — характеризуются со-
ответственно двумя или тремя различными моментами
инерции (см. (19.16) и (19.17)). Для этих типов молекул,
подробно рассматриваемых в § 19.5 и § 19.6, мы ввели об-
щепринятые обозначения моментов инерции вращатель-
ных постоянных, учитывая их относительные величины.
Будем обозначать через а и с оси, которым соответству-
ют наименьший и наибольший моменты инерции молеку-
лы, а через Ь ось, которой соответствует промежуточный
или средний момент инерции. Таким образом, мы получим
(19.50)
Для асимметричного волчка:
Ia<Ib<Ic^	(19.51)
Для симметричного волчка возможны два случая — случай
вытянутого волчка с выделен но осью а и случай сплюсну-
того волчка с выделенной осью с. Для вытянутого волчка
(рис. 19.5, а)
1а<1ь = 1с,	(19.52)
для сплюснутого волчка (рис. 19.5, б)
Ia-=Ib<Ic-	(19.53)
Рис. 19.5. Симметричный
волчок: а — вытянутый;
б — сплюснутый
Таким образом, выделенной осью (осью z) является ось а наименьшего момента
инерции для вытянутого волчка и ось с наибольшего момента инерции для сплюс-
нутого волчка.
Трем моментам инерции 1а, 1ъ и 1С соответствуют три вращательные постоянные,
обозначаемые через А, В и С:
h2 h2	h2	h2	h2 h2
^4 —____—________ p —_______—________ Q —_______—________
2Ia	Ък21а'	2Ib	8ir2Ib’	2Ie	8tt24’
Для вращательных постоянных, согласно (19.50),
А В С.
В случае асимметричного волчка
А > В > С.
(19.54)
(19.55)
(19.56)
544
Глава 19. Вращение молекул и вращательные спектры
В случае симметричного волчка либо
А > В — С (вытянутый волчок),	(19.57)
либо
А — В > С (сплюснутый волчок).	(19.58)
В соответствии с этими формулами случай асимметричного волчка можно рассма-
тривать как промежуточный между крайними случаями вытянутого и сплюснутого
симметричных волчков. Увеличивая, при заданных Аи С, В от значения С до зна-
чения А (т. е., уменьшая при заданных 1а и 1С, 1Ь от Д = 1С до 1ь — 1а), мы совершим
переход от (19.57) к (19.58) через промежуточный случай (19.56), т. е. переход от вы-
тянутого волчка с осью симметрии а к сплюснутому волчку с осью симметрии с.
Чем меньше отличается В от С или А, тем ближе асимметричный волчок к симме-
тричному, вытянутому или сплюснутому. В качестве параметра, характеризующего
асимметрию волчка, принято вводить отношение
Для вытянутого волчка (В — С) к — — 1, для сплюснутого волчка к — 1, для наиболее
„ Л + С
асимметричного волчка, получающегося при В — —-—, это отношение обращается
в нуль, к — 0.
Например, для случая молекулы воды с моментами инерции (19.2), соглас-
но (19.50) и (19.54), получим6)
А =
В =
С —
h2	h2
8тг27о	~ 8ъ21х
h2	h2
^21ь	~ 8тг2/у
h2	h2
8тг21с	~ 8я21г
= 27,33 см*1,
= 14,57 см’1, >
= 9,50 см’1,
_ 29,14- 27,33 - 9,50
Я ~	27,33 - 9,50
7,69
— = -0,430.
17,83
(19.60)
(19.61)
При значениях х, близких к -1, получается слегка асимметричный волчок, близ-
кий к вытянутому симметричному, а при значениях х, близких к 4-1, — слегка
асимметричный волчок, близкий к сплюснутому симметричному.
Существенным является не только значение параметра х, но и значение от-
А — С
ношения —-—, определяющего относительное различие постоянных А и С. Это
А
отношение
А-С
А=-^-	(19.62)
может изменяться от 0 до 1. Предельное значение 0 получается при А — С (сле-
довательно, в силу (19.55) при В — А = С) и соответствует сферическому волчку.
Значения А, В, С в (19.60) и 1а, 1ь, 1С в (19.2) экстраполированы для равновесной конфигурации
(для минимума потенциальной поверхности) и несколько отличаются от соответствующих значений
для нулевого колебательного уровня (0,0,0) (см. с. 552).
§ 19.4. Классификация симметричных и асимметричных волчков 545
Предельное значение 1 получается при А — оо, т. е. при 1а = 0 (случай С — 0 невоз-
можен, так как соответствует 1С — оо), что осуществляется для линейных молекул.
Таким образом, линейную молекулу можно рассматривать как предельный случай
вытянутого симметричного волчка (1а —* 0 в (19.52) и А —* оо в (19.57)).
Специальное соотношение между моментами инерции получается для плоских
молекул. Момент инерции 1С относительно оси, перпендикулярной к плоскости
молекулы (эта ось всегда является одной из главных осей), равен сумме моментов
инерции 1а и 1Ь относительно двух других главных осей, лежащих в плоскости
молекулы.
Мы имеем
Ic=Ia+Ib-	(19.63)
Момент инерции относительно оси, перпендикулярной к плоскости молекулы,
является, разумеется, наибольшим моментом инерции, поэтому он и обозначается
как 1С.
В случае симметричного волчка 1а — Д формула (19.63) приобретает особенно
простой вид
1С = 2/6,	(19.64)
т. е. момент инерции относительно оси симметрии сплюснутого волчка равен удво-
енному моменту инерции относительно любой перпендикулярной к ней оси.
Из (19.63) вытекает, согласно (19.54), соотношение для вращательных постоян-
ных
111	АВ
— = —|-, С —-.
С А В	А + В'
которое для частного случая симметричного волчка приобретает вид
1	2	В
- = —, С=—.
СВ'	2
(19.65)
(19.66)
Соотношение (19.63) легко получается из общих формул (19.5), если выбрать плоскость
молекулы за плоскость х’у'. Тогда для всех ядер z\ — 0, и (19.5) сводится к равенствам
1'хх = 52	М(х'\ l'zz =	М(Ж'2 + у?) = 1'хх + 4, j
i=l N i=’	i=‘	>	(19.67)
^xy lyx ~ MiXiyi, Iyz IZy 0, Izx Ixz 0.
»=1 ,
Путем поворота осей x' у1 в плоскости молекулы можно обратить в нуль 1ху, и мы
получаем
1а = 4 = 52 1ь = 1у = ^М^, 1с = 1г = ^2м^ + у^ = Та + 1ь (19.68)
2=1	1=1	2=1
(что и дает (17.63)). При этом ось х выбрана так, что 1Х 1у.
Примером выполнения соотношения (19.63) является молекула воды. Со-
гласно (19.2), 1Х + 1У = 2,945- Ю~40г -см2, что практически совпадает с Iz —
2,947- 1О“40 г- см27).
^Соотношение (19.63) выполняется для равновесной конфигурации, но уже для нулевого колеба-
тельного уровня имеются заметные расхождения (см. примечание на с. 544).
18 Зак. ЮЗ
546
Глава 19. Вращение молекул и вращательные спектры
Случай (19.64) реализуется для плоских молекул с выделенной осью симметрии
порядка п 3. К числу таких молекул относится молекула бензола; для нее должно
иметь место Ia — Ib,Ic — 2I&.
Для плоских молекул параметр х, определяющий асимметрию, согласно (19.59) и (19.65),
равен
2В-А-С _2В А А +в _2В2- А2
К~ А-С ~	' АВ “ А?
А~А^ё
(19.69)
Его можно представить в виде
X =	1 = 2р2- 1,
(19.70)
В
где р = — — отношение меньшей из постоянных В и А к большей (В < А, см.
Для плоских молекул удобно вместо параметра к вводить параметр р. Для предельного случая
симметричного волчка (являющегося сплюснутым, см. (19.64) и (19.53)) В = А, р = 1.
14,57
Для молекулы воды р =	= 0,534.
[. (19.56)).
§ 19.5. Вращательные уровни и вращательные переходы
в случае молекул типа симметричного волчка
Уровни энергии симметричного волчка можно найти, исходя из общего выра-
жения (19.41) для энергии вращения, которое при Ix = Iy / Iz принимает вид
Е = ц- (МД + М2„) + M2pz.	(19.71)
Эту формулу можно переписать так:
1 z 1	2	2x1/1	1 \	2	1	2	1 ( 1	1 \ 2 Z
Е = — (м2х+м2т+м2рг) + -	- - j m2pz = — м2 + -^--TJM2pz. О9-72)
Она справедлива и в квантовой теории. При этом в первый член входит квадрат
полного момента количества движения Мр, который квантуется, согласно (19.10),
а во второй член входит проекция Mpz момента количества движения на выделенную
подвижную ось z, являющуюся осью симметрии волчка; эта проекция квантуется, со-
гласно (19.46). Таким образом, квантованное выражение для энергии будет иметь вид
t2	/ «-2	«-2 \
^K = ^-J(J+1)+( — -—V2.	(19.73)
Zlj,	\ Zlz	Zly /
Для случая вытянутого волчка ось z является осью а наименьшего момента
инерции 1а и, согласно (19.54) и (19.57), мы получаем
Ejk = BJ(J + 1) + (4 - В)К2 (А > В) 1
(J = 0,1,2,..., К = 0,±1,±2,...). J	' ’ 7
Для случая сплюснутого волчка ось z является осью с наибольшего момента
инерции 1С и, согласно (19.54) и (19.58), мы получаем
EjK=BJ(J+V) + (C-B)K2 (С<В)1
(J = 0, 1,2,..., К = 0, ±1, ±2,...). J	 7
§ 19.5. Вращательные уровни для молекул типа симметричного волчка 547
В этих формулах В — вращательная постоянная, соответствующая момен-
ту инерции относительно осей, перпендикулярных к оси симметрии (т. е. оси а
для вытянутого волчка и оси с для сплюснутого волчка).
Первый член в формулах (19.74) и (19.75) зависит от вращательного квантового
числа J и по своему виду совпадает с выражением (19.23) для энергии линейной
молекулы и с выражением (19.45) для энергии молекулы типа сферического волчка.
В него входит только вращательная постоянная В, но не вращательная постоянная
(Л или С), соответствующая моменту инерции относительно оси симметрии волчка.
Второй член зависит от квантового числа К, определяющего проекцию момента
количества движения на ось симметрии волчка, и притом только от абсолютного
значения К. Каждый уровень с заданным J (с кратностью вырождения 2J + 1
относительно К в случае сферического волчка) расщепляется на J +1 составляющих
со значениями |1Г|, равными 0, 1,2,...,/. Поэтому обычно для К не указывают
знака, а приводят его абсолютное значение, изменяющееся при заданном J от О
до К. В дальнейшем через К мы будем обозначать абсолютное значение проекции
механического момента на ось волчка.
Степень вырождения уровней с заданными значениями J и К равна 2(2/ +1),
а уровней с заданным значением J и с К = 0 равна 2/+1. Для уровней с К = 0, таким
образом, сохраняется только вырождение, связанное с независимостью энергии
от квантового числа mj, принимающего 2/ +1 значений. Остальные уровни (К ф 0)
остаются дважды вырожденными по отношению к К.
Расстояние уровней с различными К (при заданном /) зависит для вытянутого
волчка от величины А - В, а для сплюснутого волчка от величины С — В, т. е. оно
тем больше, чем сильнее отличаются соответствующие моменты инерции. При этом
для вытянутого волчка уровни расположены тем выше, чем больше К (А — В > 0),
а для сплюснутого волчка уровни расположены тем ниже, чем больше К (С — В < 0).
На рис. 19.6 показано расположение уровней с If от 0 до 3 для вытянутого волчка
(В — С = 1,0, А = 1,5, левая часть рисунка) и для сплюснутого волчка В = А — 1,5,
С — 1,0, правая часть рисунка).
В данном примере моменты инерции и, следовательно, вращательные по-
стоянные не очень сильно отличаются друг от друга (в полтора раза); поэтому
при заданном / уровни с различными К близки друг к другу и образуют отдельные
группы. При большом различии моментов инерции, что часто имеет место для ре-
альных молекул, такая группировка будет менее выражена и нормальный порядок
уровней с различными / может нарушаться; например, для вытянутого волчка
уровень с J — 3, К — 0 будет лежать ниже уровня с J — 2, К — 2 и т.д.
Чисто вращательный спектр молекулы типа симметричного волчка определяется
правилами отбора. Наряду с обычными правилами отбора для квантового числа /,
А/ = ±1, имеет место правило отбора для квантового числа К,
ЛК = 0,	(19.76)
т. е. при переходах проекция момента количества движения на ось волчка не долж-
на изменяться. Это правило отбора справедливо как для спектров поглощения,
и испускания, так и для спектров комбинационного рассеяния.
Правило отбора (19.76) аналогично правилу отбора Лт = 0 для тг-составляющих в явле-
нии Зеемана (см. с. 373). Дипольный момент молекулы типа симметричного волчка направлен
вдоль оси симметрии (Р — Pz) и не зависит от угла поворота у> вокруг этой оси. Волновые
функции, соответствующие заданному значению К, имеют вид
фк = фое^,	(19.77)
18*
548
Глава 19. Вращение молекул и вращательные спектры
Рис. 19Л>. Уровни энергии волчков: слева — вытянутого симметричного (В = С = 1,0, А = 1,5);
посередине — асимметричного (А = 1,5, В = 1,25, С — 1,0);
справа — сплюснутого симметричного (В = А = 1,5, С = 1,0)
и матричный элемент дипольного момента, определяющий вероятность перехода,
Ркк'
^KPz1p'Kd<p= / e-iKvPzeiK'^ dp = Рг /	dp
(19.78)
обращается в нуль, если К1 / К (ср. (4.165)). Отсюда следует правило отбора (19.76)
при дипольных переходах для спектров поглощения и испускания. Тензор поляризуемости
молекулы типа симметричного волчка обладает осевой симметрией и подобно дипольному
моменту не зависит от угла у?, в результате и матричные элементы составляющих этого
тензора, определяющие вероятность комбинационного рассеяния, отличны от нуля лишь
при К1 / К (ср. (4.173); при осевой симметрии ахх — ауу, azx = ayz = аху = 0). Поэтому
правило отбора (19.76) справедливо и для спектров комбинационного рассеяния.
Так как, согласно (19.76), квантовое число К не изменяется, то для комбиниру-
ющих уровней второй член в формулах (19.74) и (19.75) при образовании разности
ДЕ = Ej<k ~ Ej"K сократится. Мы получаем
ДЕ = Ехк - Егк = В [J\J' + 1) - j"(j" + 1)].	(19.79)
§ 19.5. Вращательные уровни для молекул типа симметричного волчка 549
Для дипольного излучения возможные переходы определяются правилом от-
бора (19.33), AJ ± 1, и, так же как для линейных молекул, AJ? определяется
формулой (19.27) (J' = J" + 1 > J", J" = J):
&E = EJ+lyK-EJK = 2B(J + 1) при AJ=1.	(19.80)
Таким образом, в поглощении и испускании получается серия равноотстоящих
линий, как и для линейных молекул (рис. 19.4, слева).
Для комбинационного рассеяния возможные переходы определяются правилом
отбора (4.158), AJ = ±1, ±2, что дает (J' = J" + 1, J" + 2 > J", J" = J)
(	3\
&E = Ej+2,k-Ejk =4B( J + - j при A J = 2 (J = 0, 1,2,...)	(19.81)
и
&E = Ej+hK-EJK = 2B(J+l) при A J = 1 (J = 1,2,3,...)	(19.82)
(переход 1 —0 запрещен, ср. (4.161)). Мы получаем две серии линий, одна из которых
совпадает с (19.80). Линии второй серии (АВ = 4В, 6В, SB, 10В, 12В,...) располо-
жены вдвое чаще, чем линии первой серии (АВ = 6В, 10В, 14В,...), и совпадают
с ними через одну, что приводит к чередованию интенсивностей^.
Весьма существенной особенностью формул (19.79)—(19.82) является то, что они
содержат только одну вращательную постоянную В. Поэтому по расстояниям между
вращательными линиями молекул типа симметричного волчка нельзя определять
момент инерции относительно оси волчка, через который выражается постоянная А
(в случае вытянутого волчка) или постоянная С (в случае сплюснутого волчка).
По найденному из опыта значению В можно определить лишь момент инерции
относительно осей, перпендикулярных к оси симметрии волчка.
Вращательные спектры поглощения и испускания могут иметь не все молекулы
типа симметричного волчка, а лишь обладающие отличным от нуля дипольным
моментом. Как мы видели, молекулами типа симметричного волчка являются мо-
лекулы с выделенной осью симметрии порядка п 3 (см. § 19.1, с. 534). Из них
имеют неравный нулю дипольный момент только молекулы с симметрией Сп и Cnv
(см. табл. 18.1, с. 526). К числу последних относятся пирамидальные молекулы
типа XY3 (NH3, РН3 и другие) с симметрией С3и, имеющие характерные вращатель-
ные спектры поглощения. Примером молекулы, не имеющей дипольного момента
и соответственно не обладающей вращательным спектром поглощения, является
молекула бензола СбНб (симметрия D^).
Все молекулы типа симметричного волчка могут иметь вращательные спектры комби-
национного рассеяния, так как для них имеется выделенная ось симметрии порядка п 3
и тензор поляризуемости не сводится к скаляру (см. § 17.7, с. 495, и § 18.6, с. 528).
Полученные нами формулы (19.74) и (19.75) для вращательных уровней энергии
молекул типа симметричного волчка и вытекающие из них формулы (19.79)—(19.82)
для частот переходов являются приближенными. Существенное значение имеет
учет центробежного растяжения; это связано с тем, что центробежное растяжение
зависит не только от квантового числа J, но также, в отличие от случая молекул
типа сферического волчка, и от квантового числа К. При учете центробежного
растяжения в формулах (19.74) и (19.75) добавляются члены четвертого порядка
относительно J и К, а именно, члены, зависящие от [J(J 4- I)]2, от КА и, что
Которое нужно отличать от чередования интенсивностей, обусловленного ядерным спином и име-
ющего гораздо более важное значение.
550
Глава 19. Вращение молекул и вращательные спектры
наиболее важно, от J(J 4- 1)1Г2. С учетом этих членов для вращательной энергии
получается формула
EJK = Е® - DjJ2(J + I)2 - D}KJ(J + \)К2 - DKK4, (19.83)
где дается выражениями (19.74) или (19.75). Здесь постоянные Dj, Dr и Djr
очень малы по сравнению с В, А и С.
В соответствии с правилами отбора A J = 1 и Д1Г = 0 для возможных переходов
мы имеем формулу
ДЕ = Ej+^k - Ejk = 2BJ(J + 1) - 4Dj(J + I)3 - 2DJK(J + I)#2.	(19.84)
В то время как второй член приводит лишь к небольшому изменению расстояний
между последовательными уровнями, последний член, зависящий от К2, вызывает
расщепление линии J J 4- 1 на J 4- 1 составляющих, соответствующих значени-
ям К от 0 до J. Такое расщепление удается наблюдать для высоких вращательных
уровней, несмотря на малость постоянной DJK (имеющей порядок 10“4-10“6В),
при исследовании вращательных спектров в микроволновой области, благодаря
большой разрешающей силе применяемых микроволновых спектрографов.
§ 19.6. Вращательные уровни и вращательные переходы
в случае молекул типа асимметричного волчка
Для молекул типа асимметричного волчка полностью снимается вырождение,
связанное с ориентацией полного момента количества движения J относительно
подвижной системы координат. Уровень с заданным J расщепляется на 2J 4- 1
уровней. Каждый из этих уровней остается вырожденным — сохраняется вырождение
кратности 2J 4- 1, связанное с независимостью энергии от квантового числа mj,
определяющего ориентацию J относительно неподвижной системы координат.
В противоположность случаю симметричного волчка, для которого квантуется
проекция момента количества движения на ось волчка, в случае асимметричного
волчка не существует такой оси, связанной с молекулой, относительно которой
в состоянии с определенной энергией квантовалась бы одна из проекций момента
количества движения. Расположение уровней с заданным J не может быть выражено
общей формулой; оно зависит от значений вращательных постоянных А, В и С
(А > В > С, см. (19.56)) и находится путем решения систем алгебраических урав-
нений, получающихся при квантовомеханическом рассмотрении задачи о вращении
асимметричного волчка. Для уровней с J = 0, 1, 2, и 3 значения энергии приведены
в табл. 19.2. Для каждого значения J уровни расположены в порядке возрастания их
энергии. Их принято нумеровать индексом т, принимающим 2J 4-1 значений
r — —J\-J +1,..., 4- J.	(19.85)
Таким образом, самый нижний уровень будет J_j, а самый верхний J+j.
Для частного случая, когда А — 1,5, В = 1,25, С — 1,0 (параметр к в этом слу-
чае, согласно (19.59), равен 0), значения энергии, получающиеся из общих формул,
даны в последнем столбце таблицы. Соответствующее расположение уровней пока-
зано на рис. 19.6 (в центре). Характерной является близость двух нижних уровней
(J_j, J-j+i) и двух верхних уровней (J+j, J+j_|), которая тем более выражена, чем
больше J.
Выражения для энергии уровней с J = 2 и с J - 3. содержащие квадратные
корни, получаются путем решения квадратных уравнений. Для нахождения зна-
чений энергии уровней с J > 3 приходится решать уравнения третьей, четвертой
§ 19.6. Вращательные уровни для молекул типа асимметричного волчка 551
Та&шцз 19.2
Глубокие уровни энергии асимметричного ветка
Зна- че- ния J	Число уров- ней	Обозначение		Сим- метрия ас	Энергия уровня	
		Л	Тас		общая формула	значение пр и Л = 1,5; В = 1,25; С = 1,0
0	1	оь		оо	0	0
		1-1	loi	ео	в + с	2,25
1	3	1о	1ц	00	А +С	2,50
		h	110	ое	А + В	2,75
		2-2	2о2	ее	2А + 2Я + 2С - 2у/(В-С)2 + (Л - С)(Л - В)	6,63
		2-!	212	ое	Л + В + 4С	6,75
2	5	2о	2ц	оо	Л + 4В+С	7,50
		21	2ц	ео	4 А + В + С	8U5
		22	2го	ее	2А + 2В + 2С + 2^/f.B - С)? + (А - С)(А - В)	8,37
		З-з	Зоз	еа	2 А + 5В + 5€ - 2у/4(В - С)2 + (А - В)(А - С)	13,02
		2-2	Зв	оо	5 А + 2В + 5С - 2	А - С)? - (А - В)(В- С)	13,06
		3-1	312	ое	5А + 5В + 2С-2 у/4(А - В)2 + (А-С)(В- С)	14,52
3	7	Зо	322	ее	4А + 4В + 4С	15,00
		3,	321	ео	2А + 5В + 5С + 2у/ЦВ - С)2 + (А - В)(А - С>	15,48
		З2	3з1	оо	5А + 2В + 5С + 2 у/4(А - С)2 — (А - В)(В - С)	16,94
		Зз	Ззо	ое	5А + 5В + 2С+ 2у/ЦА - В)? + (А - С)^В- С)	16,98'
и более высоких степеней, что выполнено для значений J вплоть до 40 [70]. Однако
общий характер расположения уровней и некоторые их свойства можно устано-
вить путем сопоставления уровней асимметричного волчка с уровнями вытянутого
и сплюснутого симметричных волчков, рассматриваемых как предельные случаи
асимметричного волчка, получающиеся при значениях параметра х, равных -1 и +1
(см § 19.4, с. 543).
Можно построить диаграмму, дающую расположение уровней энергии как функ-
цию параметра х. Такая диаграмма приведена на рис. 19.7. По оси абсциссотложены
значения параметра х, по оси ординат значения энергии уровней. При переходе
от вытянутого симметричного волчка к близкому к нему слегка асимметричному
волчку с В ~ С все уровни с К / 0, являющиеся дважды вырожденными, будут
расщепляться на два, как показано в левой части диаграммы. То же самое будет
происходить при переходе от сплюснутого симметричного волчка к близкому к нему
слегка асимметричному волчку (Л ~ В), что видно на правой части диаграммы. Пра-
вило сопоставления получающихся в обоих случаях 2J + 1 уровней очень простое.
Вырождение имеет место лишь в предельных случаях вытянутого и сплюснутого
симметричных волчков, а для промежуточных значений х все 2J + 1 значений энер-
гии при данном J должны быть разными, т. е. уровни как функции х не должны
пересекаться. Таким образом, более глубокие уровни слева переходят в глубокие
уровни справа, как показано на диаграмме.
Как указывалось выше, нельзя ввести квантовое число, определяющее проекцию
момента количества движения на одну из подвижных осей и характеризующее
уровни энергии. Однако можно указать, каким уровням в предельных случаях
соответствует данный уровень. Каждый уровень с данным J асимметричного волчка
однозначно определяется заданием двух квантовых чисел: квантового числа К_\
552
Глава 19. Вращение молекул и вращательные спектры
для вытянутого волчка и квантового числа К\ для сплюснутого волчка (индекс
указывает значение х). Поэтому каждый уровень можно характеризовать символом
^С|,К| или’ сокращенно, Jac (где а указывает на квантовое число для вытянутого
волчка с осью симметрии а, а с — на квантовое число К\ для сплюснутого волчка
с осью симметрии с). Эти символы приведены в табл. 19.2 (четвертый столбец),
и их правильность может быть легко проверена при помощи диаграммы рис. 19.7.
Например, для J = 2 нижний уровень соответствует уровню с к = 0 для вытянутого
волчка и уровню с К = 2 для сплюснутого волчка, т.е. обозначается как 2q2-
Рис. 19.7. Уровни энергии асимметричного волчка как функции параметра х
Легко видеть, что введенный выше индекс г просто равен разности К_\ и К
т = К-.1-К1.	(19.86)
Так, для уровней с J = 2 мы имеем символы 202 — 2-2, 2^ = 2_j, 2ц = 2о, 221 — 2+i
и 220 — 2+2В 9)-
Примером действительного расположения уровней асимметричного ротатора
могут служить вращательные уровни молекулы воды. В табл. 19.3 приведены энергии
вращательных уровней со значениями J от 0 до 4 для молекулы воды в нулевом
колебательном состоянии. Значения вращательных постоянных равны10):
А = 27,79 см-1, В =14,51 см-1, Л = 9,29 см-',	(19.87)
в согласии с положением уровней lot, 1ц и 1ю, для которых энергия равна В + С,
А + С и А + В соответственно (см. табл. 19.2).
В литературе применяются как обозначения с одним индексом (</т), так и обозначения с двумя
индексами (Jac —	связь между которыми дается формулой (19.86).
10) Некоторое отличие этих значений от значений (19.60) связано с тем, что последние относятся
не к нулевому колебательному уровню, а к уровню ЕГ1, лежащему ниже на величину нулевой колеба-
тельной энергии (см. с. 639) и соответствующему равновесной конфигурации молекулы.
§ 19.6. Вращательные уровни для молекул типа асимметричного волчка 553
Таблица 19.3
Энергии вращательных уровней молекулы воды (в см ’)
J = 0	J = 1	J = 2	J = 3	J = 4
Оо 0	l_i 23,78 1о 37,09 11 42,31	2_2 70,09 2_| 79,43 20 95,15 2| 134,98 22 136,24	З-з 136,76 3-2 142,23 3_| 173,31 30 206,35 3| 212,24 32 286,80 З3 286,93	4_4 222,07 4-з 224,81 4-2 275,50 4_i 300,44 40 315,83 4| 384,03 42 385,44 43 490,64 44 490,79
Для молекулы воды, как содержащей легкие атомы водорода, моменты инерции сравни-
тельно малы, а вращательные постоянные, наоборот, велики, и частоты переходов попадают
в далекую инфракрасную область. Соответствующий спектр был подробно изучен в основ-
ном американскими исследователями [291]. Что касается значений энергии вращательных
уровней, то их впервые определил в 1933 г. Мекке [319] на основе изучения колебательно-
вращательного спектра молекулы воды, лежащего в близкой инфракрасной области спектра;
это был первый случай интерпретации вращательной структуры в спектре молекулы типа
асимметричного волчка.
В противоположность спектру симметричного волчка спектр асимметричного
волчка весьма сложен. Наблюдаемые чисто вращательные линии определяются как
расположением вращательных уровней, так и правилами отбора. Наряду с общими
правилами отбора для J при дипольном излучении, AJ = 0, ±1, имеются правила
отбора, связанные с симметрией уровней асимметричного волчка.
Вопрос о симметрии уровней асимметричного волчка имеет существенное зна-
чение для классификации уровней энергии и для вывода правил отбора и требует
более подробного рассмотрения. Этот вопрос может быть проще всего разобран, если
исходить из предельных случаев вытянутого и сплюснутого симметричных волчков.
Энергия вращения (19.41), которую мы с учетом (19.50) запишем в виде
1а
МрЬ М2Л
+ lb + 1с /’
(19.88)
не изменяется при операциях поворота С2 на 180° вокруг осей а, b и с, т. е. при опе-
рациях, для которых одна из осей сохраняет свое направление, а две другие оси
меняют его на обратное (рис. 19.8) и соответственно сохраняют или изменяют зна-
ки Мра, МрЬ и Мрс. Это
приводит к делению состояний на четные и нечетные
г
1

2
а	б
Рис. 19.8. Действие операций поворота: а — исходная ориентация осей;
б — действие поворота С^; в — действие поворота С^\ г — действие поворота
554
Глава 19. Вращение молекул и вращательные спектры
относительно каждой из операций симметрий	\ которые вместе с то-
ждественной операцией С\ образуют абелеву группу Z>2 четвертого порядка. Для нее
получается четыре возможных невырожденных типа симметрии А, Ва, Въ, ВС9
которые при поворотах ведут себя следующим образом (см. (3.30)):
Типы симметрии	Е		с®	cf	Обозначение
А	е	е	е	е	ее
Ва	е	е	о	о	ео
Вь	е	о	е	о	оо
вс	е	о	о	е	ое
Здесь е и о указывают, что состояние является четным (-h) и нечетным (—) соответ-
ственно.
Для характеристики симметрии состояния достаточно задать его поведение
при двух операциях поворота; мы выберем повороты вокруг осей а и с, и соответ-
ственно уровни четырех типов симметрии будем обозначать как ее, ео, оо и оеп).
Первый индекс указывает на симметрию относительно оси наименьшего момента
инерции а, второй — относительно оси наибольшего момента с.
Для симметричного волчка последовательные вращательные уровни являются
четными или нечетными относительно оси волчка, в зависимости от того, является К
четным или нечетным.
Это непосредственно вытекает из того, что волновые функции симметричного волчка
как функции угла поворота вокруг оси волчка имеют вид (19.77). При повороте на 180°
вокруг оси волчка, т.е. при увеличении угла на тг, мы имеем
+ Z) =	(19.90)
т. е. волновые функции не меняют знака (являются четными) при четном К и меняют знак
(являются нечетными) при нечетном К.
Для вытянутого волчка с осью симметрии а получается симметрия е и о
при четном и нечетном К_\9 а для сплюснутого волчка с осью симметрии с —
симметрия е и о при четном и нечетном К\ соответственно. Эти свойства симметрии
сохраняются и для промежуточных случаев асимметричного волчка, уровни которого
характеризуются, как мы видели, значениями 1Г_| и К\. Четность или нечетность К_i
и К\ определяет однозначным образом симметрию соответствующих состояний,
указанную для уровней с J — 0, 1, 2, 3 в пятом столбце табл. 19.2.
Мы видим, что четыре последовательных уровня имеют различную симметрию,
причем затем все повторяется сначала. По отношению к оси а самый глубокий
уровень с данным J (К_\ = 0) является четным, а следующие являются попарно
нечетными и четными; по отношению к оси с получается та же картина, если
начинать с самого высокого уровня (К\ — 0).
Свойства симметрии вращательных уровней асимметричного волчка весьма существенны
при расчете положения этих уровней. Как указывалось выше, для определения значений
энергии асимметричного волчка приходится решать алгебраические уравнения. При этом
для уровней данной симметрии с заданным значением J получается отдельное алгебраическое
Симметрия относительно оси b определяется симметрией относительно осей а и с, так как
(см. с. 70); если симметрия относительно осей а и с одинакова, то состояние четное
относительно оси Ъ и наоборот.
§ 19.6. Вращательные уровни для молекул типа асимметричного волчка 555
Таблица 19.4
Правила отбора при вращательных переходах для молекулы типа асимметричного волчка
Дипольное излучение			Комбинационное рассеяние					
составляющие дипольного момента			составляющие тензора поляризуемости					
Ра	Ръ	Рс	ааа		Осс	ааЬ	аЬс	Оса
ее-ео ое-оо	ее-оо ео-ое	ее-ое ео-оо	ее-ее оо-оо ео-ео ое-ое			ее-ое ео-оо	ее-ео ое-оо	ее-оо ео-ое
уравнение, степень которого равна числу таких уровней. Например, при J — 3 мы имеем,
согласно табл. 19.2, по два уровня симметрии ео, оо и ое и один уровень симметрии ее. Энергия
последнего находится сразу, а энергии уровней остальных типов симметрии находятся путем
решения трех квадратных уравнений, что и приводит к выражениям с квадратными корнями.
Для больших J соответственно повышается и степень уравнений; так, для J = 7 получается
2J + 1 = 15 уровней, значения энергий которых находятся путем решения одного уравнения
третьей степени для симметрии ее и трех уравнений четвертой степени для других типов
симметрии.
Исходя из свойств симметрии вращательных уровней, можно легко найти
правила отбора для дипольного излучения. Эти правила различны для различных
составляющих дипольного момента. Они приведены в табл. 19.4.
Как показывает таблица, для каждой составляющей комбинируют попарно уров-
ни различной симметрии. Это будут уровни, для которых т отличается на нечетное
число, если составляющая дипольного момента направлена по оси а или по оси с,
и уровни, для которых т отличается на четное число, если составляющая дипольного
момента направлена по оси Ъ.
Для вывода правил отбора нужно рассмотреть матричные элементы составляющих
дипольного момента
(Р/0« = J tfP/rtk dr (0 = а,Ь,с)	(19.91)
для комбинирующих уровней i и к. Они должны быть инвариантны при поворотах С2.
Составляющая Ра сохраняет свой знак при операции и меняет его при операциях
и следовательно, произведение • ij)k должно вести себя таким же образом; это имеет
место для произведений функций типов симметрии ее и ео и типов симметрии оо и ое,
что дает первое правило отбора табл. 19.3. Аналогичным образом получаются и остальные
правила.
При исследовании вращательных спектров поглощения на основании того,
какие правила отбора имеют место, можно установить, какие составляющие диполь-
ного момента отличны от нуля.
В частности, для молекулы воды наблюдаются переходы ее—со и ео—ое; отсюда
вытекает, что дипольный момент направлен по оси среднего момента инерции. Так
как дипольный момент направлен по оси симметрии (см. § 18,6, с. 527), то эта ось
(ось у на рис. 19.1) является осью среднего момента инерции. Перпендикулярная
к ней ось ж, тоже лежащая в плоскости молекулы, является осью наименьшего
момента инерции, а ось z, перпендикулярная к плоскости молекулы — осью
наибольшего момента инерции (для молекулы воды, как плоской, Iz = Ix 4- 1у,
см. (19.63) и (19.2)).
В таблице 19.4 также приведены правила отбора для комбинационного рассея-
ния.
556	Глава 19. Вращение молекул и вращательные спектры
Для диагональных составляющих тензора поляризуемости комбинируют уровни оди-
наковой симметрии, а для недиагональных составляющих — уровни различной симметрии
попарно, причем правила отбора для составляющих оа6, аЬс и аса те же, что и для Рс, Ра и Рь
соответственно при дипольном излучении.
Эти результаты сразу получаются, если рассмотреть элементы составляющих симметрич-
ного тензора (см. (17.139)),
= У dT (а,Р = а,Ъ,с),	(19.92)
учесть, что при поворотах , С2 и С2 диагональные составляющие оаа, аьь, асс не изме-
няются (они преобразуются как а2, Ь2 и с2), а недиагональные составляющие ааЬ, аЬс и аса
преобразуются как Рс, Ра и Рь (например, при повороте вокруг оси а сохраняет знак аЬс,
преобразующееся как 6с, и меняют знак ааЬ и &са, преобразующиеся как ab и са).
Если главные оси инерции а, 6, с молекулы одновременно являются и главными осями
поляризуемости, что имеет место при достаточно высокой симметрии молекулы (для групп
симметрии C2r, D2 и D2h), то ааЬ = аЬс = аса = 0 и в комбинационном рассеянии комбинируют
только вращательные уровни одной симметрии.
Как и в ранее рассмотренных случаях, вращательные спектры поглощения
и испускания могут иметь лишь молекулы с отличным от нуля дипольным моментом.
Такими молекулами являются молекулы, обладающие симметрией С\, С^, Cs и Civ-
Типичным и уже неоднократно приводившимся в качестве примера является случай
молекулы воды Н2О. Молекулы с симметрией Сг, D2, C^h и для которых
дипольный момент равен нулю (см. табл. 18.1, с. 526), не имеют вращательных
спектров поглощения и испускания, примером является молекула этилена С2Н4
(симметрия 7?2л).
Все молекулы типа асимметричного волчка могут иметь чисто вращательные спектры
комбинационного рассеяния, так как для них, подобно молекулам типа симметричного
волчка, тензор поляризуемости не сводится к скаляру (ср. § 19.5, с. 549). Можно рассчитать
для молекул типа асимметричного волчка, имеющих отличный от нуля дипольный момент,
относительные интенсивности вращательных линий [286].
Для высоких вращательных уровней молекул типа асимметричного волчка
следует учитывать центробежное растяжение молекулы. Однако в отличие от случая
молекул типа симметричного волчка оно приводит лишь к смещениям вращательных
линий, а не к их расщеплению.
§ 19.7. Вращательные спектры и структура молекул
В настоящее время накоплен очень большой экспериментальный материал
по чисто вращательным спектрам. Изучены вращательные спектры поглощения
ряда самых легких молекул, лежащие в далекой инфракрасной области, в частности,
вращательный спектр молекулы воды, являющийся типичным спектром молекулы
типа асимметричного волчка. За последние годы исследованы вращательные спектры
поглощения очень большого числа молекул, лежащие в микроволновой области
спектра; метод микроволнового поглощения стал теперь основным методом изучения
чисто вращательных спектров и позволил получить большое число данных о строении
молекул, обладающих дипольным моментом. Этот метод обладает очень большой
чувствительностью и чрезвычайно высокой точностью.
Микроволновое поглощение обычно изучается при помощи микроволновых
спектрографов, состоящих из источника микроволнового излучения — клистрона,
волновода, в который вводится исследуемое вещество в газообразном состоянии,
и приемника излучения (кристаллического или теплового). Волновод является,
§ 19.7. Вращательные спектры и структура молекул
557
таким образом, поглощающим сосудом. Наиболее чувствительные микроволновые
спектрографы позволяют обнаруживать коэффициенты поглощения (см. (5.98))
порядка 10“9. В микроволновых спектрографах можно достигнуть разрешающей
I/	6
силы — порядка 10 и измерять частоты вращательных линий с относительной
Ai/
точностью до 10~7.
Точность метода поглощения в далекой инфракрасной области значительно
ниже. Современные спектрографы для этой области все же позволяют измерять
частоты линий с относительной точностью порядка 10~4 [117].
Ограничением методов поглощения как в микроволновой области, так и в ин-
фракрасной области является то, что эти методы применимы лишь к молекулам,
обладающим дипольным моментом. Правда, для многоатомных молекул, не обла-
дающих дипольным моментом в основном электронно-колебательном состоянии,
такой момент может появляться в возбужденных колебательных состояниях (при ко-
лебаниях, нарушающих симметрию молекулы) [289]. Получающийся при колебани-
ях дипольный момент мал, но благодаря чувствительности методов микроволновой
спектроскопии может быть обнаружен этими методами.
Для некоторых молекул исследованы и вращательные спектры комбинационного рассе-
яния, которыми, как мы видели, могут обладать все молекулы типа симметричного и асим-
метричного волчков (см. с. 549 и 556). Следует отметить такие исследования, выполненные
за последнее время канадскими учеными [290].
Важное значение изучения вращательных спектров состоит
в том, что по полученным из опыта значениям вращательных посто-
янных можно определять размеры и форму молекул. Для простейших
молекул можно найти все параметры нормальной конфигурации ис-
следуемой молекулы. Для двухатомных молекул по значению посто-
янной В с большой точностью определяется расстояние между ядра-
ми. Для нелинейных симметричных трехатомных молекул типа XY2,
подобных молекуле воды и являющихся асимметричными волчка-
ми, из значений трех постоянных Д, В и С находятся два момента
инерции 1а и 1Ь (1С — 1а + Д) и из них вычисляется расстояние X—Y
и угол Y—X—Y. Например, для молекулы SO2 (рис. 19.9, а) из изу-
чения микроволнового спектра поглощения получаются значения
вращательных постоянных (в нулевом колебательном состоянии):
До = 60 778,79 МГц, Во = 10 318,10 МГц,
С = 8 799,96 МГц.	(19.93)
Рис. 19.9.
Нелинейные
молекулы
типа XY2:
а — двуокись
серы;
б — озон
Отсюда вычисляются значения моментов инерции и из них — зна-
чения равновесных расстояний S—О и равновесного угла О—S—О, равные
pso=l,432A, aOso= И9°32'.
(19.94)
Для молекулы озона О3 (рис. 19.9, б), также из изучения микроволнового спектра
поглощения, получаются значения
До = 106 530,0 МГц, В = 13 349,1 МГц, Со = 11 834,3 МГц, (19.95)
откуда находятся значения равновесных расстояний 0—0 между центральным
и крайними атомами О и равновесного угла О—О—О, равные
роо = 1,278 ±0,003 А, аооо = 116°50'± 30'.	(19.96)
558
Глава 19. Вращение молекул и вращательные спектры
Отметим, что для молекулы типа XY2 при тех же значениях вращательных постоянных
и моментов инерции возможны два значения угла а, одно соответствующее острому углу,
а другое — тупому. Выбор между ними определяется тем, что для молекул SO2 и О3 (так же
как и для молекулы Н2О, см. с. 555) ось симметрии является осью среднего момента инерции,
что возможно лишь при тупом угле.
Для нелинейных несимметричных трехатомных молекул типа XYZ и для моле-
кул, состоящих более чем из трех атомов, трех постоянных Л, В и С недостаточно
для определения всех параметров равновесной конфигурации, однако число вели-
чин, находимых из опыта, можно увеличить, исследуя изотопические молекулы.
Изотопические молекулы обладают той же равновесной конфигурацией, но другим
распределением масс и другими моментами инерции. При этом в случае несим-
метричного изотопического замещения Меняются не только значения моментов
инерции, но и ориентация главных осей инерции молекулы по отношению к ее
равновесной конфигурации.
Рис. 19.10. Изотопические хлорзамещенные метана: а — СН2С125, б — CD2C135; в — CD2C137;
г — CHDC125; д — СН2С135С137; е — CD2C135C137, ж — CHDC135C137
Примером могут служить тетраэдрические молекулы СН2С125, CD2C125, CD2CI27,
CHDCl^5, СН2С135С137, CD2C135C137, CHDC135C137 (рис. 19.10). Равновесная конфи-
гурация обладает симметрией С2и, и для первых трех молекул, обладающих той же
симметрией распределения масс, одна из главных осей инерции совпадает с осью С2,
а две другие лежат в плоскостях av\ для остальных молекул главные оси направлены
иначе. При этом в молекулах CHDCl^5, СН2С135С137, CD2C135C137 для распределения
масс сохраняется плоскость симметрии (плоскость CDH для CHDCh и плоскость
СС135С137 для остальных двух молекул) и две главные оси лежат в этой плоскости,
а третья к ней перпендикулярна; для самой несимметричной (по распределению
масс) молекулы CHDC135C137 все три главные оси лежат вне плоскостей av.
Изучение вращательного спектра этих молекул в микроволновой области позво-
лило определить с большой точностью по 21 найденной из опыта вращательной
постоянной (по три постоянные Ло, Со для каждой из семи изученных молекул)
четыре параметра равновесной конфигурации: два расстояния С—Н и С—С1 и два
угла Н—С—Н и Cl—С—С1. Численные значения оказались равными:
рсн = 1,068 ±0,005 А,
ансн = 112°0'± 20”,
peci = 1,7724 ±0,0005 А,
ас1сс1 = И1°47'±1'.
(19.97)
§ 19.8. Действие внешних полей на вращательные уровни и линии
559
В данном случае углы Н—С—Н и Cl—С—С1 несколько больше тетраэдрического угла
109°28', следовательно, углы Н—С—С1 несколько меньше тетраэдрического угла. Это
можно понять как результат некоторого притяжения электроположительного атома Н
электроотрицательным атомом С1.
Для многоатомных молекул точность определения расстояний между атома-
ми из микроволновых вращательных спектров обычно составляет тысячные доли
или одну-две сотые доли ангстрема, точность определения углов от одной-двух
минут до нескольких десятков минут. С еще большей точностью, достигающей де-
сятитысячных долей ангстрема, могут быть определены расстояния между атомами
в случае двухатомных молекул.
Методы микроволновой спектроскопии не только дают возможность с боль-
шой точностью определять параметры равновесных конфигураций молекул и делать
определенные заключения о расположении атомов в молекулах, но и позволя-
ют, благодаря очень высокой разрешающей силе микроволновых спектрографов,
исследовать расщепления вращательных линий и вращательных уровней. Эти рас-
щепления могут быть связаны как с действием внешних электрических и магнитных
полей (явление Штарка и явление Зеемана), так и с влиянием ядерных моментов
(сверхтонкая структура). Расщепления вращательных уровней в электрических и маг-
нитных полях могут изучаться также непосредственно по методам электрического
резонанса и магнитного резонанса в молекулярных пучках. Вопросы расщепления
вращательных уровней мы рассмотрим в следующих параграфах.
Следует отметить, что возможны также расщепления вращательных уровней, связанные
с взаимодействиями вращения с колебаниями и с электронным движением. Эти расщеп-
ления мы сейчас рассматривать не будем и разберем их позже, — в главах, посвященных
колебательным и электронным спектрам молекул.
§ 19.8. Действие внешних полей на вращательные уровни
и вращательные линии
Как мы видели, чисто вращательными спектрами поглощения обладают моле-
кулы, имеющие отличный от нуля дипольный момент. Для таких молекул суще-
ственную роль играет расщепление вращательных уровней молекулы во внешнем
электрическом поле, т. е. явление Штарка на вращательных уровнях.
В зависимости от типа молекулы имеет место линейное явление Штарка,
пропорциональное напряженности электрического поля $ или квадратичное явле-
ние Штарка, пропорциональное квадрату этой напряженности (см. §15.1, с. 409).
Для молекул типа симметричного волчка, обладающих дипольным моментом, и,
следовательно, принадлежащих к точечным группам Cnv или Сп(п 3), получается
линейное расщепление вращательных уровней. Для уровня с заданными значениями
квантовых чисел J и К получаются в соответствии со значениями mj проек-
ции вращательного момента J на направление электрического поля $ подуровни
с энергиями
Р(^К
&EJKmj = - ^	(mj = J, J - 1,... ,-J),
(19.98)
где P — величина дипольного момента молекулы.
Формула (19.98) легко получается из наглядных соображений, если учесть, что
дипольный момент направлен по оси молекулы и, следовательно, параллелен соста-
вляющей вектора J по оси молекулы (рис. 19.11, а). При вращении молекулы вокруг
560
Глава 19. Вращение молекул и вращательные спектры
Рис. 19.11. Проекция дипольного момента молекулы:
а — для молекулы типа симметричного волчка; б — для линейной молекулы
направления вектора J дипольный момент дает проекцию Pj = Р cos а — Р— на это
направление. Энергия диполя с моментом Pj, направленным вдоль вектора J,
в электрическом поле будет равна (см. (15.3))
ДЕ = -(Р/Л = -PjS cos 0 = -Pj^ — = -Р£ —mj (19.99)
J J
и при замене J2 на J(J 4- 1) мы получаем (19.98),2).
Для дипольных переходов J —► J 4- 1 и К —> К (см. (19.76)); мы получаем
при Дт/ = 0 (тг-составляющие, дипольный момент перехода параллелен полю Л
= &Ej^Km] - &EJKmj = 2Р<£	a.	<19-,0°)
J\J 4- l/yV 4~
и при Дт/ — ±1 (^-составляющие, дипольный момент перехода перпендикуля-
рен к Л
(19.101)
^т.7,т7±1 —	~	— Р$
K(2mj ± J)
J(J 4-1)(J 4-2)
Расстояния соседних подуровней (Дт/ — 1) при К — J равны, согласно (19.98),
PS
——j-, наибольшие смещения линий при К = J и mj = J составляют, соглас-
z ч z ч 2PSJ	3PSJ
но (19.100) и (19.101), --—-------- и --—-------таким образом, расщепления
'	7	''(J+V)(J + 2)	(J4- 1)(J 4-2)
PS	1	-18	z	х
имеют порядок величины -у- и убывают как При Р = 10 СГСЕ (1 дебаю)
и S — I 000 В/см мы получаем
Р$ 10~|8Ю00 1	3,3-10'18	0,017	500
----7эрг=---------т--эрг =— см = —— МГц, (19.102)
т. е. расщепления весьма значительны даже при больших J. В микроволновой
-1	-э -з
области, при частоте v — 1 см = 30 000 МГц, — имеет порядок 10 -10 .
v
,2^ Формула (19.98) легко получается квантовомеханически как среднее значение энергии возмущения
в состоянии с заданными значениями J, К и mj.
§ 19.8. Действие внешних полей на вращательные уровни и линии
561
Для линейных молекул и для молекул типа асимметричного волчка (обладающих
дипольным моментом и, следовательно, принадлежащих к точечным группам C^v
и Ci, С2 и C2V соответственно) получается только квадратичное явление Штарка.
Это связано с тем, что среднее значение дипольного момента в неподвижной
системе координат может быть отлично от нуля, как можно показать (см. ниже),
только при наличии вырождения уровней энергии (помимо вырождения по mj).
Для молекул типа симметричного волчка имеется вырождение по К, благодаря чему
среднее значение дипольного момента оказывается при К ф 0 отличным от нуля.
Для линейных молекул и молекул типа асимметричного волчка вырождение по К
отсутствует, так как в первом случае К = 0, а во втором — вырождение снимается
при переходе от предельных случаев вытянутого и сплюснутого симметричных
волчков к асимметричному волчку (см. § 19.6, с. 551).
Согласно наглядным представлениям, средняя проекция дипольного момента
вращающейся молекулы на любое направление в пространстве в обоих этих случаях
равна нулю. Это сразу видно в случае линейной молекулы: при ее вращении,
происходящем вокруг оси, перпендикулярной к оси молекулы (рис. 19.11, б), среднее
значение направленного по оси молекулы дипольного момента равно нулю.
Равенство нулю среднего значения дипольного момента для невырожденных состояний
вытекает из того, что для атомной системы при отражении всех координат в начале (£' = -£,
rf = —rf, £'- = —() энергия Е, механический момент J и его проекция не изменяются
(причем механический момент с точки зрения наглядных представлений сохраняет свое
направление, оператор Мр = hJ не меняет знака), а дипольный момент меняет знак.
Получается, при тех же Е, J и mj, дипольный момент обратного знака, что невозможно,
если состояние невырожденное, но может иметь место для вырожденных между собой
состояний, отличающихся противоположными направлениями дипольного момента. Следует
при этом учитывать, что дипольный момент системы представляет среднее значение оператора
дипольного момента Р = etrt (см. (4.33)), которое для невырожденного состояния должно
иметь вполне определенное значение.
Отметим, что из приведенного вывода, имеющего общий характер (см. [70], с. 128),
вытекает, в применении к ядру с невырожденными (при заданных Е, J и rnf) состояни-
ями, равенство нулю электрического дипольного момента ядра. То же самое имеет место
для электрических моментов порядка 23, 25,..., 2l (I — нечетные) и для магнитных моментов
порядка 22, 24,..., 2l (I — четное), так как соответствующие моменты меняют знак при отра-
жении в начале координат, аналогично дипольному моменту [30]. Таким образом, для ядер
возможны электрические моменты порядка 2l (I — четное) и магнитные моменты порядка 21
(I — нечетное). Мы получаем один из результатов, приведенный без доказательства в § 16.1
(см. с. 423).
Для линейной молекулы квадратичное расщепление вращательных уровней
энергии определяется формулой
Р2/2	J(J+V)-3m2j	_ P2S2
Ejm’ ~ BJ(J+\) 2(2J- 1)(2J —3)’ A£o° ~	6B~
(J >0)	(J = °)
Эта формула получается квантовомеханически во втором приближении теории возму-
щений путем вычисления поправки к энергии (см. [70], с. 231)
AEjmj —
J'mj
\РI &
Ej — Ej'
(19.104)
562	Глава 19. Вращение молекул и вращательные спектры
где	— матричные элементы энергии дипольного момента, взятые по функциям
состояний J’mj и Jmjt, причем в рассматриваемом случае J’ = J ± 1 и mj< = mj, т.е. сумма
сводится к двум членам.
Рис. 19.12. Вращение линейной
молекулы вокруг оси,
перпендикулярной к полю:
а — ориентация диполя в сторону поля;
б — ориентация диполя
в противоположную сторону
Формулу (19.103) можно приближенно полу-
чить и из наглядных соображений, рассматривая
влияние электрического поля на вращающуюся мо-
лекулу (см. [70], с. 229 и [42], с. 252), которое про-
PS
порционально малому отношению 7 =	-----
BJ(</ 4~ 1)
энергии молекулы в поле к энергии вращения
Евращ = BJ(J 4-1). Дополнительная энергия ока-
зывается отличной от нуля и по порядку величины
(Р^)2
равна PSy = ----------. В частности, для случая
В J (J 4- 1)
вращения молекулы вокруг оси, перпендикулярной
к полю $ (рис. 19.12), что соответствует т = 0,
дополнительная энергия получается за счет боль-
шей скорости вращения диполя при его ориента-
ции в сторону поля, чем при противоположной
ориентации (ср. рис. 19.12, а и б). Изменение меха-
нического момента Мр = равно моменту силы
PScos 9? (о/ — угловая скорость молекулы с мо-
ментом инерции 7, а — угол поворота диполя,
являющийся функцией времени). Мы имеем
dM„ dw
----= I — = PS cos <p.
dt dt	Y
(19.105)
Приближенно заменяя 9? через w$t,
и интегрируя (19.105), мы получаем
где о>о — угловая скорость в момент времени t — 0,
PS
Ш = О>0 4- ---- sin W$t — (aJq
IWq
PS
откуда видно, что при малом --------
-7ш02
1	2	1	2	0
энергии вращения - 1ш к - добавляется энергия, равная
PS
—----- (а)
-^враш
ЛЕ = - PS
8
(19.106)
мало отличается от При усреднении
PS
2^
(19.107)
что при замене - 1ш^ через BJ(J + 1) дает выражение, отличающееся от (19.103) при mj = 0
2 J(J+V
лишь множителем —---т------z— « 1.
Расстояние соседних подуровней, согласно (19.103), составляет
S'2 6ш I J
^EJm, - ДЯ,.т,+1 =	2(27-1X27-3)’	(19’°8)
что при mj — J дает величину порядка PS'----------- т.е. на множитель
J BJ(J 4- 1)
§ 19.8. Действие внешних полей на вращательные уровни и линии 563
Р£
7 ~ BJ(J 4- 1) меньшую’ чем при линей«ом расщеплении уровней (см. выше,
с. 560). При Р = 10”18 СГСЕ и = 1 000 В/см, Р$ = 0,017 см"’ = 500 МГц
и при энергиях вращения порядка 1-10 см”1, т. е. порядка 30 000-300 000 МГц,
отношение 7 порядка 10“2-10”3.
Существенно, что благодаря пропорциональности расщепления вращательных
уровней и соответствующего расщепления спектральных линий квадрату напряжен-
ности поля эти расщепления быстро возрастают с увеличением поля.
Можно получить формулы для квадратичного штарковского расщепления в слу-
чае молекул типа асимметричного волчка, причем величина расщепления является
функцией параметра х (см. (19.59)), характеризующего асимметрию волчка [288].
Формула для дополнительной энергии в электрическом поле имеет вид
&EjTmi =	+ BjT(K)m2j)P2^,	(19.109)
где AjT и BjT — постоянные, убывающие с увеличением J и зависящие от т —
К.\ - К\ (см. (19.86)). Аналогично (19.103) AEjTTnj зависит от m2j. Для слегка
асимметричных волчков и в общем случае для близких уровней, когда расстояние
между соседними уровнями волчка порядка Р£, квадратичное расщепление уровней
в электрическом поле переходит в линейное.
Явление Штарка на вращательных линиях поглощения легко наблюдать в ми-
кроволновой области как расщепление этих линий. Наряду с этим можно непосред-
ственно наблюдать переходы между подуровнями при штарковском расщеплении
по методу электрического резонанса в молекулярных пучках: под действием пере-
менного электрического поля частоты р, перпендикулярного к постоянному элек-
трическому полю, происходят резонансные переходы между подуровнями с Am = 1
при частоте поля, совпадающей с частотой перехода.
Важное значение изучения явления Штарка состоит в том, что по найденной
из опыта величине штарковского расщепления можно определять значения диполь-
ных моментов молекул. По методу микроволнового поглощения получено большое
число данных о дипольных моментах молекул.
В микроволновой спектроскопии явление Штарка играет важную роль и с методической
точки зрения. Под действием переменного электрического поля получается расщепление
линий, периодически меняющееся со временем, что можно использовать для модуляции
частоты в микроволновых спектрографах. Такие микроволновые спектрографы со штарковской
модуляцией широко применяются в настоящее время [70]; частоты модуляции при этом могут
быть различными, чаще всего выбирают частоту модуляции порядка 100 кГц.
Для ряда молекул значения дипольных моментов найдены по методу электри-
ческого резонанса в молекулярных пучках, позволяющему получать весьма точные
данные. Этот важный метод аналогичен методу магнитного резонанса в молекуляр-
ных пучках, только в соответствующих установках (см. схему рис. 14.14, с. 398) все
магнитные поля заменяются электрическими. Фокусировка пучка осуществляется
неоднородными постоянными полями А и В, отклоняющими частицы в пучке
в противоположные стороны, а переходы происходят под действием переменного
радиочастотного поля, которое накладывают на однородное постоянное поле С,
расположенное между полями А и В. Отклонение частиц в молекулярном пуч-
ке в неоднородном электрическом поле из-за наличия у них дипольного момента
может быть использовано для сортировки вращающихся молекул по состояниям
с отличающимися значениями J. В частности, можно выделить молекулы в опре-
деленном состоянии и получить вынужденное испускание в чистом виде. Это
564	Глава 19. Вращение молекул и вращательные спектры
осуществлено Прохоровым и Басовым в молекулярном генераторе [256] (см. с. 150);
аналогичная установка разработана американскими исследователями [257]13). В мо-
лекулярном пучке, проходящем через неоднородное электрическое поле, молекулы
в разных состояниях отклоняются по-разному; молекулы в возбужденном состоя-
нии Ei, отклонившиеся определенным образом, попадают в резонатор, настроенный
на частоту перехода и — —(Ei — Ek) в микроволновой области из возбужденного
h
состояния Ei в не возбужден ное (или более низкое возбужденное) состояние Ек. Мо-
лекулы под действием радиочастотного поля испускают излучение, которое, в свою
очередь, стимулирует испускание излучения другими молекулами. Если мощность
потерь в резонаторе меньше, чем мощность вынужденного испускания, то наступает
самовозбуждение — генерация колебаний резонансной частоты и. Стационарное
состояние генератора определяется эффектом насыщения, когда дальнейшее возра-
стание мощности испускания становится невозможным из-за возрастания мощности
потерь. Так как вероятность переходов с возбужденного уровня в микроволновой
области очень мала и, следовательно, ширины этого уровня и испускаемой линии
малы, то получается очень большая разрешающая сила и возможна стабилизация
частоты с исключительно большой точностью, порядка 10-11.
Рассмотрим теперь явление Зеемана на вращательных уровнях молекул. Для мо-
лекул, имеющих электронный механический момент, а следовательно, и электрон-
ный магнитный момент, — для парамагнитных молекул — расщепление уровней
имеет тот же порядок р^Н, что и для атомов (см. § 14.1, с. 370). Нас будет инте-
ресовать, однако, обычный случай устойчивых молекул с электронным моментом,
равным нулю (см. конец §19.1, с. 536)14), когда зеемановское расщепление вра-
щательных уровней определяется очень малыми магнитными моментами, порядка
ядерного магнетона, связанными с вращением молекул (см. §2.4, с. 57). Представляя
вращательный магнитный момент аналогично (16.5) в виде
(19.110)
получаем дополнительную энергию в магнитном поле, равную
Е =	= -9j^hJzH =	(mj = J, J - 1,..., -J),	(19.111)
т. e. каждый вращательный уровень расщепляется на 2J -h 1 подуровней. Соот-
ветственно происходит расщепление вращательных линий, аналогичное явлению
Зеемана в слабом поле на электронных уровнях энергии атомов. Вращательные мо-
менты ядер очень малы; величины gjp^ обычно составляют десятые или даже сотые
доли ядерного магнетона. Поэтому мала и величина зеемановского расщепления.
В магнитных полях порядка 10 000 Гс она обычно не превышает нескольких МГц
(10~4 см-1, см. (16.11)).
Величины вращательных магнитных моментов могут быть найдены при изу-
чении явления Зеемана на вращательных линиях поглощения в микроволновой
области и по методу магнитного резонанса в молекулярных пучках. Последним
методом были с большой точностью определены значения вращательных магнитных
моментов ((/о2)макс, ср. (16.6)) молекул водорода и дейтерия.
13) Она названа ими «мазером» — «maser», что означает «microwave amplification by stimulated emission
of radiation» (микроволновое усиление при помощи вынужденного испускания излучения). Название
«мазер» широко применяется для парамагнитных усилителей в микроволновой области, а аналогичное
название «лазер» («laser» — light amplification, т. е. усиление света) — для квантовых усилителей света
в оптической области (см. конец §5.4, с. 150).
14) Об явлении Зеемана в случае парамагнитных молекул см. [70|, с. 259.
§ 19.9. Влияние ядерных моментов на вращательные уровни и на линии 565
Для Н2
^ = *Т= 9 jP-ял = (0,8829 ± 0,0007)дяд	при J = 1, '
У = у = gjpm = (0,882265 ± 0,000035)дяд	при J = 2
И ДЛЯ Z>2
Uj Uj
у = у- = д]ряа = (0,442884 ± 0,000052)дяд при J = 1.
(19.112)
(19.113)
Как показывают экспериментальные данные, имеются небольшие отступления
Дн
от пропорциональности /Zj значению J. Отношение — также несколько отли-
м0
чается от отношения масс---.
Мн
Значения вращательных магнитных моментов могут быть оценены теоретически;
при этом оказывается, что электронная оболочка отстает от ядер при вращении молеку-
лы. Отметим, что в общем случае для многоатомных молекул вместо одного множителя, gj,
связывающего векторы /z = p.j и J (ср. (14.31)), нужно вводить тензор второго ранга д^,
линейно связывающий в подвижной системе составляющие g.Jf3 магнитного момента p,j
с составляющими J7 механического момента J (0,у = x^y^z). Таким образом, согласно
наглядным представлениям, связанный с молекулой магнитный момент не совпадает по на-
правлению с ее механическим моментом. Согласно квантовой механике, магнитный момент
в определенном состоянии вообще представляет некоторую усредненную величину Д —
подобно дипольному моменту и поляризуемости.
§ 19.9. Влияние ядерных моментов на вращательные уровни
и на вращательные линии
Наличие у ядер моментов существенным образом сказывается на вращатель-
ных уровнях молекул, обусловливая сверхтонкую структуру этих уровней. При этом
в противоположность атомам, для которых главную роль играет магнитная струк-
тура, связанная с магнитными моментами ядер, для молекул, электронный момент
которых равен нулю, главную роль играет электрическая структура, связанная с ква-
друпольными моментами ядер.
Дополнительная энергия ядра, имеющего спин I и обладающего квадруполь-
ным моментом Q, в неоднородном электрическом поле, направленном по оси (
и составляющем угол $ с направлением вектора J, определяется формулами (16.19)-
z ч	а/
(16.23), в которых надо заменить — через —— и под моментом J следует понимать
dz dQ
вращательный момент молекулы. Мы имеем
д4квадр)
3
д2 -C(C+1)-I(I+1)J(J+1)
еО__— л---------------------
с?(2	21(21 ~ V)J(2J - 1)
(19.114)
где С = F(F = 1) -1(1+ 1) - J(J + 1); F определяет значение полного механического
момента молекулы F = J + J. Разница со случаем атома состоит в том, что градиент
dS
электрического поля — =
а2^
= -q^, взятый по фиксированному в пространстве
направлению (, зависит от вращения молекулы и необходимо перейти к градиенту
поля в подвижной системе, связанной с молекулой. Градиент поля, создаваемого
566
Глава 19. Вращение молекул и вращательные спектры
электронной оболочкой молекулы в подвижной системе, не зависит от вращения
молекулы и является характеристикой этого поля.
При переходе от неподвижной системы £, ?/,£(£ — направление вектора J
совпадающее с направлением неоднородного электрического поля, обусловленного
электронной оболочкой вращающейся молекулы, ср. с. 429; там направление поля
было обозначено z) к подвижной системе для молекулы типа симметричного волчка
с осью симметрии z имеем [70]
д2у _ Г ЗК2 1 J д2$
д<? ~ [j(j + 1) ~ j2J + 3 'dz2'
Для линейной молекулы (К = 0) (19.115) сводится к
д2(р J д2(р
4- 3 ₽
Дополнительная энергия (19.114) принимает вид
/ К2 \
231 з__________1 j
иквадр) =	----------------------- Г-С(С + 1) - 1(1 + 1)J(J + 1) ,
F 21(21 — 1)(2J — l)(2J + 3) [_4 V	V ’
(19.115)
(19.116)
(19.117)
где
d2ip
B = eQdz> =eQqz
— постоянная квадрупольного взаимодействия, равная произведению квадруполь-
д£ д2<р
ного момента на градиент поля qz — — — — —7, взятый по оси симметрии
az azz
молекулы.
(19.118)
Для молекул типа асимметричного волчка получается более сложное выражение
d2w	д2ср	д2ср	д2<р
<’9-119)
д2<р	д(п	д2<р	д(%	д2(р	д$
где —г —-------, —- =-------, —- =---------составляющие градиента электрического поля
да2	да	дЬ2	дЬ	дс2	дс
по главным осям инерции, a х), ^&(J, х) и ^C(J, х) — функции от квантового числа J
и от параметра х, характеризующего асимметрию волчка.
Постоянные квадрупольного взаимодействия в различных случаях имеют зна-
чения, лежащие в широких пределах от нескольких МГц до нескольких тысяч МГц,
т.е. от 10“4 до 10-1см“1. Соответственно расщепления вращательных линий по-
глощения в микроволновой области могут быть весьма значительны. Наблюдаемая
в спектре картина, которая определяется величиной этих расщеплений (для случая
симметричного волчка, согласно формуле (19.117)) и правилами отбора AF = 0, ±1,
AJ — 0, ±1 и AI — 0 (такими же, как и в случае сверхтонкой структуры в атомных
спектрах, см. с. 445), может быть очень сложной.
Мы рассмотрели случай сверхтонкого расщепления, определяемого одним ядром
со спином I # 0. Если в молекуле имеется несколько таких ядер, то картина
расщепления еще более усложняется.
Важное значение имеет определение из опытных данных постоянных квадру-
польного взаимодействия. Эти постоянные могут быть найдены при исследовании
§ 19.9. Влияние ядерных моментов на вращательные уровни и на линии 567
в микроволновой области электрической сверхтонкой структуры вращательных ли-
ний поглощения, а также по методу электрического резонанса в молекулярных
пучках, состоящих из молекул, вращательные уровни которых имеют электрическую
сверхтонкую структуру.
Мы не будем здесь разбирать явление Штарка для таких молекул, лежащее в основе
определения постоянных квадрупольного взаимодействия по методу электрического резонанса
в молекулярных пучках (рассмотрение этого вопроса см. [70], [42] и [43]).
Зная постоянную квадрупольного взаимодействия, можно, рассчитав теорети-
чески значение градиента электрического поля, найти квадрупольный момент ядра,
и обратно, зная значение квадрупольного момента, найти градиент поля. Опре-
деление градиентов электрических полей, действующих внутри молекул на ядра,
представляет значительный интерес с точки зрения изучения свойств электронных
оболочек молекул и, в частности, изучения распределения электронной плотности
при различных типах химической связи.
Магнитная сверхтонкая структура для молекул, электронный момент которых
равен нулю, обусловлена взаимодействием магнитных моментов ядер с враща-
тельными магнитными моментами молекулы. Энергия взаимодействия имеет вид
(см. (2.79) и (2.83), J = F, Jx = I, J2 = J)
z x F(F 4-1) - 1(1 + 1) - J(J 4- 1)
E = A(IJ) = A —-------------—----------------,	(19.120)
где постоянная А, пропорциональная магнитному моменту ядра и вращательному
моменту, очень мала, порядка 1-100 кГц. Поэтому очень мало и магнитное сверх-
тонкое расщепление. Это расщепление можно наблюдать на вращательных линиях
поглощения в микроволновой области. Такие исследования требуют применения
микроволновых спектрографов высокой разрешающей силы (см. с. 557).
Влияние ядерных моментов на вращательные уровни и вращательные линии
проявляется, однако, не только в их сверхтонком расщеплении. Для молекул, обла-
дающих симметрией и содержащих эквивалентные ядра, различные вращательные
уровни обладают различными статистическими весами, зависящими от значения
спина ядра I. Это приводит к явлению чередования интенсивностей вращательных
линий в молекулярных спектрах (как чисто вращательных, так и колебательно-
вращательных и электронно-колебательно-вращательных). Различные статистиче-
ские веса вращательных уровней должны учитываться и при термодинамических
расчетах [110].
Мы рассмотрим статистические веса вращательных уровней на примере двух-
атомных молекул, содержащих одинаковые ядра со спином I — - К числу таких
2	1
молекул относится молекула водорода Н2, содержащая два протона (1р — Спины
двух ядер, складываясь, дают суммарный спин
1—1,0.	(19.121)
Состояния с результирующими спинами I = 1 и / = 0, как можно показать,
обладают противоположными свойствами симметрии. Состояние с I — 1 является
симметричным (s), а состояние с I — 0 — антисимметричным (а) относитель-
но перестановки одинаковых ядер. По отношению к перестановке одинаковых
ядер различаются, однако, также и вращательные состояния, а именно, состояния
с четным J (J — 0, 2, 4,...) являются симметричными, а состояния с нечетны-
ми J (J — 1, 3, 5,...) — антисимметричными. Симметрия состояния молекулы
568
Глава 19. Вращение молекул и вращательные спектры
с заданными значениями I и J будет определяться симметрией по отношению к ре-
зультирующему спину ядер и симметрией по отношению к вращению. Мы получаем
в результате свойства симметрии, приведенные в табл. 19.5.
Таблица 19.5
1
Симметрия состояний молекулы, состоящей из двух одинаковых ядер с I — -
Значения I	Симметрия ядерного состояния	Значения J	Симметрия вращательного состояния	Симметрия состояния молекулы
1	S	0, 2, 4, 6, ...	8	8
0	а	0, 2, 4, 6, ...	S	а
1	S	1, 3, 5,	а	а
0	а	1, 3, 5, ..., ...	а	3
Как было разобрано в гл. 3 (см. с. 74), все состояния атомной системы, содер-
жащей одинаковые частицы с полуцелым спином, антисимметричны по отношению
z 1 ч
к перестановке таких частиц; следовательно, в рассматриваемом случае (I — - )
полные состояния молекулы антисимметричны15). Поэтому возможными являются
при четном J лишь состояния с I — 0, а при нечетном J — состояния с I = 1.
Статистический вес состояний с I — 0 равен (214- 1)(2J 4-1) = (2J4-1), а состояний
с I — 1 — (21 4- 1)(2J 4- 1) = 3(2J 4-1). Таким образом, существуют два рода мо-
лекул — молекулы с I — 0, которые могут находиться во вращательных состояниях
с четными J (J = 0, 2, 4,...), и молекулы с I — 1, которые могут находиться
в состояниях с нечетными J (J — 1, 3, 5,...), причем для последних статистические
веса будут втрое больше, чем для первых.
Молекулы в пара-состояниях с I = 0 очень медленно превращаются в молекулы
в орто-состояниях с I ~ 1* 16), и поэтому смесь таких молекул можно рассматривать
как смесь двух газов. В частности, для водорода мы получаем пара-водород, состоя-
щий из молекул с I — 0, т. е. молекул в состояниях с J — 0, 2, 4,... и орто-водород,
состоящий из молекул с I — 1, т. е. молекул в состояниях с J — 1, 3, 5, 7,... При вы-
соких температурах (kT > 2В) молекул орто-водорода будет в три раза больше, чем
молекул пара-водорода. Наоборот, при очень низких температурах (кТ 2В) все
молекулы будут, согласно (19.32), находиться в состоянии с I — 0. Если такой охла-
жденный в течение длительного времени (многих недель или месяцев) газ быстро
нагреть, то он будет состоять только из пара-водорода и в нем будут отсутствовать
молекулы во вращательных состояниях с нечетными J [292].
Существование двух модификаций водорода — пара-водорода и орто-водоро-
да — было установлено опытами Бонгеффера и Хартека [293] и других ученых [79];
оно является наглядным доказательством роли ядерного спина и подтверждением
правильности классификации состояний молекул по их симметрии.
Различие в статистических весах вращательных уровней с четными и нечет-
ными J проявляется и в чередовании интенсивностей вращательных линий в мо-
15) Это справедливо, если колебательное состояние и электронное состояние молекулы симметричны.
Для двухатомной молекулы колебательное состояние всегда симметрично относительно перестановки
одинаковых ядер, а электронное состояние симметрично для подавляющего большинства гомонуклеарных
молекул (исключение составляет молекула О2).
16) Из-за запрета переходов между состояниями, симметричными и антисимметричными по отношению
к спину ядра. Этот запрет является почти строгим.
§ 19.9. Влияние ядерных моментов на вращательные уровни и на линии 569
лекулярных спектрах водорода. В частности, в чисто вращательных спектрах ком-
бинационного рассеяния (возможных для всех двухатомных молекул, в том числе
для молекул, состоящих из одинаковых атомов, см. § 19.2, с. 539) с правилом отбора
AJ — ±2 (см. (19.35)) линии, соответствующие переходам между четными уров-
нями 0—2, 2—4, 4—6,..., будут менее интенсивны, чем линии, соответствующие
переходам 1—3, 3—5, 5—7,..., в согласии с заселенностью уровней
и
П] = (2J + l)noe w
_Е±
nj — 3(2J 4- l)noe w
при J — 0, 2,4,...
>
при J — 1,3, 5,... . ,
(19.122)
В случае, если одинаковые ядра в двухатомной молекуле имеют произвольный
спин 4, отношение весов антисимметричных и симметричных состояний оказыва-
z	х Л	1	1
ется равным (без учета множителя 2J 4-1)	. При li — - это дает отношение -,
полученное выше для состояний, антисимметричных и симметричных по отно-
li 1
шению к результирующему спину ядер I. При I, — 1 отношение ~
при этом полные состояния молекулы симметричны и статистический вес симмет-
ричных вращательных состояний (J — 0, 2, 4,...) вдвое больше статистического
веса антисимметричных (J = 1, 3, 5 ...). Такой случай имеет место для дейтерия D2
и азота N24; для молекул азота, в частности, наблюдаются чередующиеся интенсив-
ности в чисто вращательном спектре комбинационного рассеяния: линии 0—2, 2—4,
4—6, ..., вдвое интенсивнее линий 1—3, 3—5, 5—7, ...
Ii
Особым является случай It = 0, тогда ------ — 0 и возможны лишь сим-
| 1
метричные ядерные состояния. Так как при 1г — 0 полные состояния молекулы
по отношению к перестановке одинаковых ядер симметричны, то осуществляются
лишь симметричные вращательные состояния с J — 0, 2, 4,...,7). Для многоатомных
молекул, обладающих симметрией и содержащих эквивалентные ядра, также можно
определить статистические веса различных вращательных состояний (см. моногра-
фию Годнева [ПО], с. 212).
Свойства симметрии вращательных волновых функций и статистические веса соответ-
ствующих вращательных уровней могут быть найдены при рассмотрении свойств полной
волновой функции молекулы по отношению к перестановке эквивалентных одинаковых ядер.
Полную волновую функцию мы представим в виде
V’no/iH ф(х, ру “&, О’) — ^эл (*^)^,кол(р)^,враш(^)^,яд(^)?	(19.123)
отличающемся от (17.66) добавлением множителя фпа((у), который зависит от спиновых
координат (У ядер. Функция ф(х, р, $, а) симметрична относительно перестановки любых двух
одинаковых ядер в случае ядер с целым I (I = 0,1,2,3,...) и антисимметрична в случае
ядер с полуцелым I ^7 =	...^. При симметричных функциях ^эл(ж) и Фкол(р) это
определяет симметрию или антисимметрию произведения ^вра1и(^)^яд(^)- При этом, если
^полн симметрична, то ^вращ(^) И ^яд(о-) обладают одинаковой симметрией (обе симметричны
или обе антисимметричны), а если ^полн антисимметрична — противоположной симметрией.
Для любой линейной молекулы, как мы отмечали в конце § 19.1 (см. с. 536), отражение
в начале координат, с которым связано деление состояний молекулы на положительные
и отрицательные, означает изменение направления оси молекулы на обратное. При этом
,7)Для молекулы кислорода Oj6 основное электронное состояние антисимметрично относительно
перестановки одинаковых ядер и поэтому, наоборот, возможны лишь антисимметричные вращательные
состояния (см. с. 778).
570
Глава 19. Вращение молекул и вращательные спектры
Рис. 19.13. Отражение в начале координат:
а — исходные положения ядер;
б — действие отражения в начале
углы в и у?, определяющие ориента-
цию оси молекулы (см. рис. 19.13),
переходят в углы 01 = ir — 0 и <р‘ =
(р + тг; мы получаем cos 0' = — cos 0,
sin 0' = sin 0,	и в резуль-
тате вращательные волновые функ-
ции ^враш(0), совпадающие с угло-
выми волновыми функциями Yimi
(0,<р) (см. (6.44) и табл. 6.3, с. 180),
сохраняют знак при четном J = I
и меняют его при нечетном J = I,
т. е. являются соответственно по-
ложительными и отрицательными.
В рассматриваемом случае двух-
атомной молекулы с одинаковы-
ми ядрами перестановка одинако-
вых ядер приводит к изменению на-
правления оси молекулы на обратное, и положительные волновые функции симметричны
относительно перестановки ядер, а отрицательные — антисимметричны. Таким образом,
при четном J волновые функции ^враш (0, (р) симметричны, а при нечетном J — антисимме-
тричны, как это указано в табл. 19.5. Ядерные волновые функции при спине ядра 1' можно
представить в виде
’М*) = ХГт'(^1)ХГт'(^2),	(19.124)
где т\ и m2 — значения проекции спина, меняющиеся от I' до -1'. Мы имеем (21' + I)2
функций; ИЗ НИХ 21' + 1 функций Хт’т’ =	(m' = Г, Г - 1, . . . , -Г) ЯВЛЯЮТСЯ
симметричными, а из остальных функций можно составить (21'+ 1)1' симметричных функций
(хГт', (^l)Xrm'(^) + ХГт', (^Xl'm'^i)) (я»'| / ш'2)
и (21' + 1)1' антисимметричных функций
Хт-та- =	(ХГ'т', (<71 )ХГт'2 (<ъ) - Xl'm\ (^ХЩ (<П)) (™'|	т'2).
Всего имеем (21' + 1)1' антисимметричных функций и (21' + 1) + (21' + 1)1' = (21' + 1)(1' + 1)
(21' + 1)Г Г
симметричных, что дает отношение статистических весов --—------ =----. В частном
(2Г + 1)(Г + 1)	Г+1
случае I' — 0 имеем лишь одну симметричную функцию хо,о> а в частном случае 1' = - —
одну антисимметричную х7д (1 = 1{ - 12 = 0, mj = 0) и три симметричных ху2 у2>
(1 = 1[ +12 = 1, 771/ = 1, 0, -1), ср. случай атома гелия, с. 284. В общем
х+'/1,

случае значениям I = 21', 21' - 2,... полного спина соответствуют симметричные функции,
а значениям 1 = 21' - 1, 21' - 3,... — антисимметричные функции, в чем легко убедиться,
выбирая из (21' + I)2 функций (симметричных и антисимметричных) наборы 21 + 1 функций
с заданным 1 и со значениями mi — т\ + 77i'2, меняющимися от I до —1, начиная с набора
1 = 21', например, при Г = 1 мы имеем девять функций Х1,ь Хо,о, Х-1,-ь Х^о» Х7,о» х7,-р
Х7,-р х£-р Хо,-р что дает наб°Р из пяти симметричных функций Xi,i, х£о* Хо,о, Хо^-р
Х-1,-ь U = 2, 771/ = 2, 1,0, -1, -2), набор из трех антисимметричных функций Xi,o> Xi,-i
Хо (1 — 1, 771/ — 1,0, -1) и, наконец, симметричную функцию х^_| (1 — 0, тТ — 0).
ГЛАВА 20
КОЛЕБАНИЯ ДВУХАТОМНЫХ МОЛЕКУЛ
§20.1. Колебания двухатомных молекул
как частный случай колебаний любых молекул
Рассмотрение колебаний двухатомной молекулы, наряду с его значением
для спектроскопии двухатомных молекул, очень важно для теории как простейший
частный случай колебаний любых молекул. Колебания многоатомных молекул мож-
но приближенно рассматривать как совокупность отдельных нормальных колебаний
с различными частотами, каждое из которых состоит в периодическом изменении
расположения ядер по отношению к их равновесной конфигурации и по своим ха-
рактеристикам в большей или меньшей степени аналогично колебанию двухатомной
молекулы, сводящемуся к периодическому изменению расстояния между ее ядрами.
При этом с точки зрения симметрии все колебания многоатомной молекулы можно
разделить на два основных класса — полносимметричные и неполносимметричные.
Полносимметричными колебаниями называют такие колебания, при которых
симметрия молекулы не нарушается, т. е. смещенные мгновенные конфигурации
ядер обладают той же симметрией, что и равновесная конфигурация.
Неполносимметричными колебаниями называют такие колебания, при которых
симметрия смещенных мгновенных конфигураций ниже, чем симметрия равновес-
ной конфигурации, т.е. такие колебания, при которых нарушается симметрия рав-
новесной конфигурации. Симметричные многоатомные молекулы всегда обладают
такими колебаниями.
Легко привести конкретные примеры. Для молекулы воды Н2О полносимме-
тричными являются симметричные колебания, при которых одинаковым образом из-
меняются длины связей О—Н, а также может изменяться угол Н—О—Н (рис. 20.1, а}.
Рис. 20.1. Полносимметричные и неполносимметричные колебания: а — симметричные
колебания Н2О; б — антисимметричные колебания Н2О; в — симметричные колебания СО2;
г — деформационные колебания СО2; д — колебания О2; е — колебания NO
572
Глава 20. Колебания двухатомных молекул
Неполносимметричными являются антисимметричные колебания, при которых дли-
ны связей О—Н изменяются противоположным образом: в то время как одна связь
удлиняется, другая укорачивается (рис. 20.1, б). В первом случае смещенная кон-
фигурация остается равнобедренным треугольником и сохраняет симметрию С^,
во втором — она уже имеет иную форму и обладает лишь симметрией Cs. Для мо-
лекулы углекислого газа СО2 полносимметричными колебаниями являются симме-
тричные колебания атомов кислорода по отношению к атому углерода (рис. 20.1, в),
а неполносимметричными — деформационные колебания, перпендикулярные к оси
молекулы (рис. 20.1, г). В первом случае молекула при колебаниях остается ли-
нейной, сохраняя симметрию D^, а во втором — изгибается и обладает лишь
симметрией Civ.
Колебания двухатомной молекулы не нарушают ее симметрии, как в слу-
чае молекулы, состоящей из двух одинаковых атомов и колеблющейся симметрично
относительно центра, например, молекулы кислорода О2 (рис. 20.1, Э), — так и в слу-
чае молекулы, состоящей из двух разных атомов и колеблющейся несимметричным
образом, например, молекулы окиси азота NO (рис. 20.1, е). В первом случае со-
храняется симметрия во втором — симметрия Колебания двухатомной
молекулы являются, таким образом, полносимметричными колебаниями. Колеба-
ниям двухатомных молекул наиболее аналогичны полносимметричные колебания
многоатомных молекул.
Следует отметить, что у двухатомных молекул, состоящих из атомов двух изотопов одного
и того же элемента (например О16О18 или N,4N15), колебания происходят несимметрично
относительно их центра. В этом случае, строго говоря, центр симметрии вообще отсутствует
и молекула в целом имеет симметрию СХ1,. Однако электронная оболочка молекулы с высокой
степенью точности обладает симметрией D^h (с центром симметрии). При колебаниях
симметрия электронной оболочки нарушается, и поэтому такие колебания в известной
степени аналогичны неполносимметричным колебаниям многоатомных молекул.
Колебания как двухатомных, так и многоатомных молекул при малых ампли-
тудах с хорошей степенью приближения можно считать гармоническими. Такое
приближение имеет широкую область применимости и играет при изучении ко-
лебаний молекул важную роль. Поэтому рассмотрение колебаний, естественно,
начинают со случая гармонических колебаний и лишь затем учитывают отступления
от гармоничности — ангармоничность.
§ 20.2. Гармонические колебания двухатомной молекулы
Как было показано в гл. 17, электронная энергия двухатомной молекулы, рас-
сматриваемая как функция расстояния между ядрами р и играющая роль потенци-
альной энергии для движения ядер, при расстояниях р, близких к равновесному ре,
имеет вид (17.32), U(q) — ГДе ~	~ колебательная координата, a к —
силовая постоянная, характеризующая квазиупругие силы, возникающие в молекуле
при отклонениях ядер от их равновесных положений °.
Кривая потенциальной энергии U(q) представляет параболу (рис. 20.2, а), кру-
тизна ветвей которой будет тем больше, чем больше силовая постоянная к.
Кинетическая энергия колебаний молекулы имеет вид (17.33):
1	/ dq\z 1	7
Г=	= ,Mq2=T(q),
2	\at j	2
В дальнейшем мы, как это обычно принято, будем часто говорить не о движении ядер, а о движении
атомов, подразумевая, что речь идет о ядрах этих атомов (ср. примечание на с. 500).
§ 20.2. Гармонические колебания двухатомной молекулы
573
где М = —-------— — приведенная масса молекулы. Таким образом, мы прихо-
М\ + М2
дим к классической механической задаче о гармоническом осцилляторе. Ее хорошо
известное решение представляет гармоническое колебание
q — qo sin (wt + p)	(20.1)
с амплитудой qo, начальной фазой p и круговой частотой
2?Г /Т	z
= 2тгр = - =	(20.2)
где и — обычная частота, а Т — - — период.
и
Согласно (17.32) и (20.1), потенциальная энергия равна
U = -kq = - kql sin 2(wt + p),	(20.3)
а для кинетической энергии получим, подставляя в (17.33) значение скорости
dq
№ cos № + p) и учитывая (20.2), выражение
Т = 2^^ ~ | cos 2(wt + р) = | kql cos 2(wt + p).	(20.4)
Полная энергия E, равная сумме кинетической и потенциальной энергии, остается
при колебаниях постоянной:
Е = Т + U = | kq^ cos 2(wt + р) + | kcfc sin 2(wt + p) = - kq%. (20.5)
При q — qo и q — —qQ полная энергия E равна потенциальной, а скорость
q = q^w cos (wt + p) и кинетическая энергия обращаются в нуль [ sin (wt + р) = ±1,
cos (wt + р) = О]; мы получаем поворотные точка классического движения
(см. рис. 20.2, а, точки А и С), ограничивающие область, в которой оно проис-
ходит. При q — 0, т. е. при прохождении через положение равновесия, абсолютная
величина скорости максимальна [sin (y)t + р) = 0, cos (ut + р) — ±1, q —
полная энергия равна кинетической, а потенциальная энергия обращается в нуль
Рис. 20.2. Гармонические колебания двухатомной молекулы:
а — кривая потенциальной энергии; б — уровни энергии
574
Глава 20. Колебания двухатомных молекул
(рис. 20.2, а, точка В). На рис. 20.2, а изображающая точка D колеблется вдоль
1
отрезка АС с частотой и — причем ордината точки D в каждый момент времени
представляет сумму отрезков, равных по величине потенциальной и кинетической
энергиям в этот момент времени.
Для сравнения с результатами, получающимися, согласно квантовой механике (см. ниже,
с. 580), существенно знать вероятность различных значений координаты д, т.е. различных
положений изображающей точки. Время т прохождения единицы длины равно величине,
обратной величине скорости:
1 1 1 1
Н |g0^cos(o;f+ <р)| q№ | ^/1 - sin 2(оЛ + <р) |
q№
= .	(20.6)
£ \
qoj
Доля времени, которое изображающая точка находится на участке от q до q + dq, равна
2т dq 2dq 1	dq 1
Т qQa>T I CT 7rg0 /	/ y2
1/1 - ( - )	1/1 - ( - 1
V \ ^0 /	V	\ Яо /
(20.7)
Это выражение и дает вероятность w(q)dq различных значений координаты q. Вероят-
ность q(w) имеет минимум, равный — д0 при q — 0, и стремится к бесконечности при при-
7Г
ближении к поворотным точкам q — qQ и q — -qQ классического движения. Соответствующая
2т
кривая w(q) = — изображена на графике рис. 20.2, а пунктиром.
Основной характеристикой гармонического колебания с классической точки
зрения является его частота, не зависящая от его амплитуды. Согласно (20.2),
w2 = D,	(20.8)
где
(20.9)
— постоянная, являющаяся произведением двух постоянных, характеризующих
1
молекулу, — обратной массы — и силовой постоянной к. Такое представление,
М
тривиальное в случае одной степени свободы, допускает весьма рациональное
обобщение на случай колебаний многоатомных молекул с числом колебательных
степеней свободы не менее трех.
Для обобщения на случай колебаний многоатомных молекул полезно привести вы-
вод (20.8), исходя из уравнений движения в форме Лагранжа. Эти уравнения, как известно,
имеют вид
d dL 8L	z
Tt7T-7r = 0’	(20.10)
dt dqt dqi
где Q2j • • ♦, qr — обобщенные координаты системы с г степенями свободы, а
L = T-U	(20.11)
— функция Лагранжа.
2> Точка D проходит путь от А до С за время —.
§ 20.2. Гармонические колебания двухатомной молекулы	575
Если кинетическая энергия зависит только от обобщенных скоростей gt , а потенциальная
энергия только от обобщенных координат qi9 то
8L
dU „
---- = Fi,
dqt
dL _ 9Т
dqi дф ’ dqi
где Fi — обобщенные силы, и система уравнений (20.10) принимает вид
dqi dqi
(20.12)
d
dt
>•)•
(20.13)
Для рассматриваемого случая
мы получаем
1	2	1	2
одной степени свободы Т = -Mq , U = -kq
, т. е. обычное уравнение для гармонического колебания,
Mq = —kq, которое, согласно (20.9), можно переписать в виде
9 = -^kq = -Dq.	(20.14)
м
Записывая периодическое решение уравнения (20.14) в тригонометрической форме (20.1)
или в показательной форме
q = q^t+V>	(20.15)
и подставляя его в (20.14), получим
-a)2qQ = ~DqQ,	(20.16)
т. е. линейное однородное уравнение
(D-w2)qQ = Q	(20.17)
относительно q0, которое имеет отличное от нуля решение при D = и>2, что и приводит
к (20.8).
При решении задачи о гармоническом осцилляторе в квантовой механике
получается известное выражение для энергии
Ev = hv(v + ^\	(20.18)
где v — классическая частота колебаний, определяемая формулой (см. (20.2))
<20.19)
2тг V М
av~ колебательное квантовое число, принимающее целые значения
v = 0, 1,2,... .	(20.20)
Формула (20.18) дает равноотстоящие невырожденные уровни энергии (рис. 20.2,б),
причем разность энергий последовательных уровней равна
Ev+\ - Ev- hv,
а частота перехода между этими уровнями
Ev^\ - Ev
V~ h
в точности равна классической частоте колебаний.
(20.21)
(20.22)
576
Глава 20. Колебания двухатомных молекул
Как известно, гармонический осциллятор явился той системой, лля которой Планк
впервые ввел квантование. Первоначальная формула Планка имела вид
E = hi/n, (п = 0,1,2,...),	(20.23)
отличающийся от квантовомеханической формулы (20.18) отсутствием постоянного слага-
емого - hi/. Формула (20.18), содержащая член - 7ц/, была впервые предложена Планком
в 1911 г. (см. [10], с. 76), однако только квантовая механика позволила сделать выбор между
формулами (20.18) и (20.23).
Таким образом, имеется очень важное соответствие между результатами клас-
сической и квантовой теорий: для гармонического осциллятора частота квантового
перехода между соседними колебательными уровнями совпадает с классической часто-
той колебаний.
В отличие от классической теории минимальная энергия гармонического коле-
бания равна не нулю, а
/ip
Яо=у,	(20.24)
т. е. молекула в основном колебательном состоянии v = 0 обладает определенной
нулевой энергией. Так как частоты колебаний молекул составляют от нескольких
сотен до нескольких тысяч см-1, то того же порядка будет и нулевая энергия.
В частности, для молекулы водорода Н2 в основном электронном состоянии, име-
ющей частоту колебаний, равную 4400 см-1 (точнее, 4405,3 см-1), нулевая энергия
составляет 2 200 см-1, т. е. примерно - эВ. При частоте колебаний 1 000 см-1 ну-
4
левая энергия составляет 500 см-1, т. е. около 0,06 эВ. Наличие нулевой энергии
колебаний необходимо учитывать при рассмотрении ряда вопросов, в частности,
при термодинамических расчетах на основе молекулярных данных [НО].
Энергии (20.18) соответствует, согласно (20.5), амплитуда классических колеба-
ний, определяемая соотношением
Ev = | kqo„ = hv (v + |),	(20.25)
откуда, учитывая, что к = Мш2 — 4ir2Mv2, находим
т. е. при заданном значении v амплитуда колебаний обратно пропорциональна
корню четвертой степени из приведенной массы М и из силовой постоянной к.
В численном виде мы получаем для амплитуды qov, выраженной в ангстремах:
Qov —
А,
(20.28)
§ 20.2. Гармонические колебания двухатомной молекулы
577
где приведенная масса выражена в единицах атомной массы (т. е. 1,66- 10 24 г),
а частота и
(«->Т
в см
1
“ 2’
. Для молекулы водорода в основном состоянии мы получаем
и = 4400 см"1) дь — 0,12 А, что составляет примерно 0,16
равновесного расстояния ре — 0,74 А.
Ввиду того, что в формулу (20.26) входит отношение энергии колебаний Ev
к силовой постоянной к, которая не очень сильно различается для разных молекул
(как правило, не более чем в 2-3 раза), то при заданной энергии колебаний их
амплитуда имеет вполне определенный порядок величины. Беря Лг = 5 - 105 дин/см,
мы получаем при Ev = 1 эВ,
Z* 1,0* ш	i-------—	о	о
---— = л/6,4 • 10~18 = 0,25 • 10"8 см = 0,25 А.
Величина дает максимально возможное по классической теории значение ко-
лебательной координаты при данной энергии. Среднее значение координаты можно
характеризовать средним квадратичным отклонением от положения равновесия
(20.29)
которое с учетом (20.26) равно ^sin 2(<*й 4- ip) —
где
/ 1
ьЬ + -
(20.30)
4tt2Mf
(20.31)
= Q0V2tr4r I,
представляет значение Qv при v = 0. Обычно эту величину, дающую среднее квадра-
тичное значение колебательной координаты в нулевом колебательном состоянии,
называют нулевой амплитудой колебаний. Она представляет удобную единицу дайны
при рассмотрении колебаний определенной молекулы.
Для колебательных переходов между уровнями энергии гармонического осцил-
лятора имеет место правило отбора
Дг; = ±1,
(2032)
т. е. возможны лишь переходы между соседними уровнями, частоты которых опреде-
ляются формулой (20.19) и равны классической частоте гармонических колебаний.
При этом совпадают частоты переходов 0—1, 1—2, 2—3 и т.д. (рис. 20.2,0). Сле-
довательно, классическому колебанию гармонического осциллятора с частотой и
соответствует совокупность квантовых переходов той же частоты f между соседними
равноотстоящими уровнями бесконечной последовательности (20.
Правило отбора (20.32) справедливо как для дипольных переходов в поглощении
и испускании, возможных для двухатомных молекул, имеющих дипольный момент
(см. с. 527), так и для переходов при комбинационном рассеянии, возможных
Часто проводимое сопоставление классических колебаний с одним только квантовым переходом
0—1 между двумя уровнями имеет ограниченный характер, см. ниже, с. 50
19 kiic. W3
578
Глава 20. Колебания двухатомных молекул
для всех двухатомных молекул. Этим правилом запрещены переходы с измене-
нием колебательного квантового числа более чем на единицу, |Av| = 2, 3,4,...,
т. е. переходы, для которых частоты соответственно равнялись бы 2р, Зр, 4р, ... —
обертонам основной частоты. Таким образом, для молекулы, которая строго является
гармоническим осциллятором, в колебательных спектрах может проявляться только
одна частота, а именно, основная частота гармонических колебаний, определяемая
формулой (20.19).
Следует иметь в виду, что при этом существен не только гармонический закон (20.1)
изменения со временем колебательной координаты — механическая гармоничность, но и гар-
монический закон изменения со временем дипольного момента (для переходов в поглощении
и испускании) или поляризуемости (для переходов в комбинационном рассеянии) — элек-
трооптическая гармоничность.
Рассмотрим подробнее испускание и поглощение для молекулы, дипольный
момент которой изменяется по гармоническому закону. Такой закон получится
для молекулы с постоянным дипольным моментом
Ро = ере,	(20.33)
где е* — эффективный заряд атомов, а ре — расстояние между ними4), если считать,
что при колебаниях эффективный заряд не изменяется. Тогда
Р - ер = е* [р€ + (р - ре)] = е* ре + е* q = Ро + Р9,	(20.34)
где
Pq = е*Q ~ е*qo sin (wt 4- <р)	(20.35)
— переменный дипольный момент молекулы, обусловливающий ее излучение.
С классической точки зрения мы получаем испускание, рассматривая затухание
осциллятора с зарядом е*, массой М и амплитудой а, убывающей по закону
(20.36)
где а0 — Qo (см. (4.89)). Коэффициент затухания 7о определяется формулой (4.91)
и ему соответствует вероятность (4.103) спонтанного испускания 4q:
8тг2е*2р2
л" = 4 * * 7” = ^Г-	<20'37)
Вероятности спонтанного испускания (20.37), согласно (4.8) (при дг = дь), соответ-
ствует вероятность поглощения
с3	тге*2
8tt/ip3
откуда мощность поглощения (см. (5.2)) равна
у^погл) _ hup^nBo _ ^_пр^^	(20.39)
где р(и) — плотность излучения частоты и, а п — число поглощающих частиц
в единице объема.
4) Эффективный заряд соответствует определенному распределению электронной плотности вокруг
ядер. При симметричном распределении электронной плотности вокруг двух одинаковых ядер для моле-
кулы симметрии D^h мы имеем е* = 0 и Ро = 0- Для молекул симметрии Cxw, состоящих из двух разных
атомов, в общем случае эффективный заряд не равен нулю, е* / 0, и в предельном случае чисто ионной
молекулы типа А+В~ (см. с. 720) совпадает с зарядом электрона е* = е.
§ 20.2. Гармонические колебания двухатомной молекулы
579
Отметим существенное обстоятельство, что формула (20.39) для мощности по-
глощения может быть выведена чисто классически при рассмотрении поглощения
излучения п диполями в единице объема, совершающими вынужденные гармониче-
ские колебания с затуханием под действием электрического поля соответствующей
электромагнитной волны, напряженность которого считается не зависящей от ча-
стоты в пределах ширины линии поглощения (см., например, [106], с. 14).
Отметим также, что формула (20.39) относится к поглощению излучения с объемной
плотностью р(у), равномерного во всех направлениях. Для направленного излучения той же
плотности с вектором напряженности электрического поля, совпадающим с направлением
колебаний диполей, мощность поглощения увеличивается втрое, т. е.

(20.40)
Коэффициент - при переходе от (20.40) к (20.39) возникает при усреднении cos 2д, где & — угол
между направлениями напряженности поля и колебаний диполя. Этот угол при равномерном
во всех направлениях излучении может принимать любые значения от 0 до тг.
Необходимо подчеркнуть, что с классической точки зрения п есть полное число гармони-
ческих осцилляторов в единице объема, а с квантовой точки зрения это есть число осциллято-
ров, находящихся в определенном начальном квантовом состоянии. Подробнее о соответствии
классической и квантовой теорий для гармонического осциллятора см. ниже, с. 582.
Разберем теперь комбинационное рассеяние. Для двухатомной молекулы, как
обладающей выделенной осью симметрии, тензор поляризуемости характеризуется
двумя поляризуемостями: а\ — а2 вдоль оси молекулы и «2 — ах = ау вдоль
перпендикулярной оси. Представим «1 и аг, предполагая, что они изменяются
по гармоническому закону с частотой колебаний и — — (ср. (17.137))5) в виде,
2тг
аналогичном (20.34) и (20.35):
«1 — «10 + «1^ — «10 + «1д>	«2 — «20 “F «2*7 = «20 “F «2д>	(20.41)
где
«Ig = «iQ = «1^0 sin (wt + <р), a2q = a2q = a2qQ sin (wt + <p).	(20.42)
«iq и a2q представляют переменные составляющие тензора поляризуемости молекул,
обусловливающие комбинационное рассеяние с частотами г/0 — и ^о +	(^о —
. da\	da2
частота падающего света). Величины а1 = --- и а2 = ---- будут, вообще говоря,
dq	dq
отличны от нуля, что и обусловливает, с классической точки зрения, отличную
от нуля интенсивность комбинационного рассеяния. Из наглядных соображений
можно ожидать, что поскольку колебания ядер происходят вдоль оси z, то они будут
сильнее сказываться на поляризуемости вдоль оси z, чем на поляризуемости вдоль
перпендикулярных осей, т.е. можно ожидать, что продольная поляризуемость (а'|)
будет больше поперечной поляризуемости (а'2), а\ > а2.
Реальные молекулы являются ангармоническими (т. е. негармоническими) ос-
цилляторами. При наличии ангармоничности колебательные уровни энергии уже
не будут равноотстоящими и частоты переходов 0—1, 1—2, 2—3, ... не совпада-
ют; нарушается также и правило отбора (20.32) и становятся возможными, наряду
5) Чтобы получить (20.41) и (20.42) как частный случай формул (17.137), надо в последних положить:
nzz = <*1, (azz)o = <*10, (&zz)i/ = ахх ~ ауу ~ tt2> (^arx^O ~ (ttyy)o = tt20, (axx)v ~ (ayy)v =
^ху ~ <%yz = &zx = 9.
19;
580
Глава 20. Колебания двухатомных молекул
с переходами с At? — ±1, переходы с |Av| > 1 (|At?| = 2,3,4,...), частоты кото-
рых приближенно равны |Av| • и (2г/, 3i/,4i/,...), т. е. наряду с основной частотой
появляются обертоны. Учету ангармоничности колебаний посвящен §20.4. В §20.3
мы рассмотрим квантовомеханические характеристики гармонического осциллятора;
изложение рассчитано на читателя, интересующегося обоснованием приведенных
выше результатов и более детальным сопоставлением классической и квантовой
теорий для гармонического осциллятора.
§ 20.3. Квантовомеханическая характеристика
гармонического осциллятора
Для получения квантовомеханической характеристики состояния гармонического ос-
циллятора необходимо, как обычно, найти собственные значения и собственные функции
оператора энергии Я, соответствующего классическому выражению Н(р, q) функции Га-
мильтона от обобщенных импульсов и обобщенных координат. Вводя обобщенный импульс
1 1
р = — = Mq, мы имеем, согласно (20.4) и (20.3), H(p,q) — Т(р) +U(q) = ттт:р2 + - kq2.
dq	2М 2
h d h d
Заменяя классический импульс р через оператор импульса р = — — =-------, получаем
2тп dq i dq
оператор энергии гармонического осциллятора:
1^1, Л2 d2 1	,
я =	= -УТ7 ^7 + 7 kq2,
2М 2 2М dqz 2
(20.43)
собственные значения и собственные функции которого находятся путем решения уравнения
Шредингера	*
ЩЦ«) = { ~ 777 V5 + |	= Evil>„(q).	(20.44)
k 2М aq 2 j
Это уравнение имеет решения при значениях Ev полной энергии, определяемых формула-
ми (20.18) и (20.19). Соответствующие волновые функции tyv(q) имеют вид
= 2- Н,(/М	е-^-,
iNv	iyv
(20.45)
аде N„ — иормяроючный множитель, £ = ftq — безразмерная переменная, a ft равно
(см. (30.2) и (30.31))
<Гмк 41м2ш2
2 /4тг21Иг/ 1 I
V h	V2Qq	^оо
(20.46)
т.е. представляет величину, обратную классической амплитуде колебаний для состояния v = 0
(равной половине ширины нижней ступеньки на рис. 20.2,6, с. 573).
Функции Hv(/lf) = Hv(— ) = Hv(£) представляют полиномы Эрмита — полиномы
Моо/
степени г, для ® = О,1,2, 3,4 имеющие вид:
яо(4) = 1, Н,® = 2$,	Н&) = 4{2 - 2,
ЯзШ = «С3 - 124,	Н«(0 = 1664 - 48f2 + 12.
(20.47)
Наличие множителя е“г* в (20.45) приводит к быстрому спаданию волновых функ-
ций за пределами области классического движения (для v = 0 при |£| > 1). Число узлов
функций (20.45) равно числу нулей полиномов Эрмита, равному v. Вид волновых функций
для малых v изображен графически на рис. 20.3, *7; каждый график построен на прямой,
изображающей соответствующий уровень энергии. На рис. 20.3,6 показана зависимость от £
квадрата волновой функции, определяющего вероятность различных значений коор-
динаты. Мы видим, что для основного состояния имеется один максимум вероятности
§ 20.3. Характеристика гармонического осциллятора
581
при £ = pq = 0, а для возбужденных состояний получается ряд максимумов, причем наиболь-
шая вероятность получается вблизи поворотных точек классического движения. Чем больше и,
тем ближе общий характер квантовомеханического распределения вероятности как функции
колебательной координаты к соответствующему распределению, получающемуся на основе
классической теории и приведенному на рис. 20.2, а. Отличие состоит в том, что, согласно
квантовой механике, вероятность отлична от нуля за пределами классического движения
(хотя и быстро убывает), всегда остается конечной и при некоторых значениях координаты,
определяемых положением узлов полиномов Эрмита, обращается в нуль.
Важным свойством волновых функций гармонического осциллятора является их поведе-
ние по отношению к изменению знака колебательной координаты q. При изменении знака q
на обратный функции с четным v не изменяются, а функции с нечетным v изменяют знак
на обратный:
при v = 0,2,4,... ipv(q) = tpv(-q),
при v= 1,3,5,... $v(q) = -$v(-q).
Это непосредственно вытекает из того,
(20.48)
что множитель ехр
ется при замене q через -д, а полиномы
Эрмита при четном v содержат лишь
четные степени координаты и не ме-
няют знака, а при нечетном v содер-
жат лишь нечетные степени координаты
и меняют знак.
Из графиков волновых функций
на рис. 20.3, а наглядно видно, что
функции ipQ и fa являются четными,
а функции ipi и -ф3 — нечетными. Сле-
дует подчеркнуть, что деление волновых
функций гармонического осциллятора
на четные и нечетные по отношению
к операции изменения знака колебательной координаты связано с инвариантностью опера-
тора энергии (20.43) (ср. § 3.2, с. 72) по отношению к этой операции, образующей вместе
с тождественной операцией группу второго порядка.
Важное значение при квантовомеханическом рассмотрении колебаний молекул имеют
свойства матричных элементов координаты и ее степеней. Матричные элементы координаты
а	б
Рис. 20.3. Волновые функции
гармонического осциллятора:
а — вид волновых функций;
б — распределение вероятности различных
значений координаты
(v|g|t/) = / V„(.q)qiM<l) dq
отличны от нуля только при v' = v ± 1. При v' = v 4- 1 вычисление дает
(v|g|v +!) = («+ 1 |g|v) = yj = QoaATT,
(20.49)
(20.50)
где Qq — нулевая амплитуда колебаний (20.31). Существенно, что среднее значение коорди-
наты
(v|g|t>) = У ipl(q)qdq = 0.	(20.51)
Этот результат, разумеется, получается сразу, без вычислений, из инвариантности ttf,(q)
при изменении знака координаты q. Среднее значение квадрата координаты равно, если
учесть (20.50),
(v|g2|v) = 5<(t>|g|v') (i>'|g|i>) = (v|g|i> + l)2 + (v|g|v - l)2 = 2Qo(v +	7).	(20.52)
6) Мы пользуемся дираковским обозначением для матричных элементов.
Это находится в согласии с (20.30); (v|^2|v) = Q%, в частности, (о|^2|о) = Qq.
582
Глава 20. Колебания двухатомных молекул
Легко найти матричные элементы qk, где к — любое целое число. При четных к отличны
от нуля матричные элементы
(tr|/|v),	(v|g*|v ± 2),	(v|g>±4),	(t;|g*|v±fc);
при нечетном к — матричные элементы
1),	(v|g*|v ± 3), (t4g*|v±5),	(v|g*|v±fc).
Все остальные матричные элементы равны нулю8).
Отметим., что с помощью матричных элементов типа |г/) легко вычисляется доба-
вочная энергия при рассмотрении ангармонических колебаний по методу теории возмущений
(см. ниже, с. 587). Свойства матричных элементов координаты особенно существенны при раз-
боре вопроса о правилах отбора и вероятностях переходов для гармонического осциллятора.
Рассмотрим этот вопрос подробнее.
Согласно (4.35) и (4.40), вероятность дипольных переходов между колебательными
уровнями Ev> и Ev„ равна
64я-4
Av = ЧГз	(20.53)
3hc3
где
- (v'|P(g)|v") = J ^'(g)P(g)^»(g)<ig
— матричный элемент дипольного момента Р как функции от колебательной координаты q.
Беря дипольный момент в виде (20.35), мы получим
Av = -yV (v'|?|v")2.	(20.54)
Так как матричный элемент координаты отличен от нуля только при v' = и" 4-1 (Ev> > Ev„), то
в испускании возможны лишь переходы 1 —► 0, 2 —> 1, 3 —> 2,... Вероятности этих переходов,
согласно (20.50) и (20.31), равны
64тг4р3е*2 ,	64тг41/3е*2
Л+’’’ = 3ftc3 + ° = ЗЛс3
h .	8тг21/2е*2
(20.55)
Для перехода 1 —> 0 мы получаем значение, совпадающее со значением До, соответствующим
затуханию классического осциллятора (см. (20.37)). Для переходов v 4- 1 —> v вероятности
растут пропорционально v 4-1. Таким образом,
Л+1,, = Aq(v 4-1),	(20.56)
и вероятности переходов 1 -* 0, 2 —> 1, 3 —> 2, ... относятся как 1 :2:3 : ... .
Вероятности поглощения и вынужденного испускания при переходах v —> «4-1 и v4-1 —> v,
согласно (4.8), соответственно равны (колебательные состояния невырождены)
с3 8z2i/2e*2	тге*2
Bv,v+I = в,+ ц. = —} (v + 1) = (v + 1) = Bo(v + 1),	(20.57)
где величина Во, определяемая формулой (20.38), представляет вероятность вынужденных
переходов между уровнями v = 0 и v = 1. Зная вероятности вынужденных переходов
и мы можем определить мощности поглощения и вынужденного испускания
и сравнить результаты квантовой теории с результатами классической теории, которая, как
мы подчеркивали в предыдущем параграфе, приводит к формуле (20.39), где п — общее число
поглощающих диполей.
Согласно (5.2), мощности поглощения и вынужденного испускания равны
ip(v)nv = hvB9p(v)n,(y + 1) = nvp(v){y + 1)
(20.58)
8^ О матричных элементах тида	и	где у — оператор импульса, см. |55], том 1,
с.555.
§ 20.3. Характеристика гармонического осциллятора
583
и
тге*2
= huBv+itVp(u)nv+i = hvBQp(ify*v+i(v + 1) = b+ifiMv + 1).	(20.59)
Мощность поглощения (20.58) даже при v = 0, т. е. для перехода О —> 1, отлмается класси-
ческого выражения (20.39) тем, что в последнее вместо п$ — числа молекул в состоянии Eq —
входит их полное число п.
Однако фактическая мощность поглощения, обусловленная молекулами, находящимися
в состоянии Ev, число которых равно nv (и может быть различным, в зависимости от условий
возбуждения), будет равна
7ге*2
= hvBop(v)n„(v + 1) - lwBop(v)nvv = buBop(v)a„ = — p(v}n„,	(20.60)
т. e. энергия, поглощенная молекулами в состоянии Д, при переходах и —> г 4- 1, будет
частично компенсироваться вынужденным испусканием молекул в том же состоянии Ev
при переходах v —> v - 19\ Иначе говоря, приведенная вероятность поглощения Д>,»+1 - Д^-i
молекулами в состоянии Д. для всех колебательных состояний одинакова и равна Bq. Полная
приведенная мощность поглощения
=	=	= Ы^р^ = аМп, (20.61)
и=0	в=0
ос
что совпадает с классическим выражением (20.39). Существенно, что nv =- к, независимо
от заселенностей nv отдельных уровней.	v=o
Мы видим, что результаты квантовой теории для мощности поглощения полностью
совпадают с результатами классической теории, если классическому осциллятору сопоста-
влять не два уровня, Eq и Д, а весь набор квантовых уровней гармонического осциллятора.
Такое же совпадение, как показали Грибковский, Апанасевмч и Степанов, которым принад-
лежит данный выше вывод формулы (20.61), имеет Место и для мощности люминесценции
при стационарном режиме и для закона затухания люминесценции |300|. Следовательно,
для гармонического осциллятора имеется не только соответствие результатов классической
и квантовой теории, но и полное совпадение этих результатов.
Для случая комбинационного рассеяния правила отбора, определяемые неравенством
нулю матричных элементов типа (17.139), будут в предположении, что переменные составляю-
щие тензора поляризуемости имеют вид (20.42), те же, что и для случая дипольных переходов
в испускании и поглощении. Действительно, матричные элементы этих составляющих равны
(v|alt|»') = a'f ),	= а2 (»|v|t)')	(20.62)
и отличны от нуля лишь при Av = v - vr = ±1. Для комбинационного рассеяния с частотой
так же как для дипольного поглощения, возможны переходы О —> 1, I -* 2, 2 —► Зу. ..,
а для комбинационного рассеяния с частотой 4- f, так же как для дипольного испускания,
возможны переходы 1 —► 0, 2 —> 1, 3 —> 2, .... Вероятности соответствующих переходов
v —> v 4- 1 и v 4-1 —> v будут пропорциональны (v|f|v 4-1) , т.е. v 4- 1 (см. (20.50)).
Мы до сих пор считали дипольный момент и поляризуемость в соответствии с (20.34)
и (20.41) линейными функциями колебательной координаты. В общем случае надо доложить
Р(д) = Ро +
(20.63)
Qi(?) —	+
<*г(?) — в20 +
(2&64)
9* При v = 0 вынужденное испускание отсутствует (I/o,-t = 0).
584
Глава 20. Колебания двухатомных молекул
fdP\ fdai\ (da2\
где коэффициенты при линейных членах I — I , I ---) и I------) дают эффективный
X dq / g=o \ dq / 9=о	\ dq / 9=о
р
заряд е* (который уже не обязательно будет совпадать с эффективным зарядом е* = — )
Ре
и постоянные а\9 а'2. При учете нелинейности дипольного момента и поляризуемости
(электрооптической ангармоничности) становятся возможными переходы с Av = 2,3,...
(за счет членов с q\ q\ ...). Электрооптическую ангармоничность, приводящую к появлению
в колебательных спектрах обертонов основных частот колебаний, естественно рассматривать
вместе с вопросом об ангармоничности вообще, что и будет сделано в дальнейшем. Укажем
лишь, что, с точки зрения разделения движения в молекуле на электронное и колебательное,
выражение (20.63) представляет результат усреднения дипольного момента по электронной
волновой функции (ср. (17.98)) и последующего разложения в ряд по степеням колебательной
координаты, а выражения (20.64) образуются более сложным образом (что уже отмечалось
на с. 497, см. подробнее гл. 23, с. 695).
§ 20.4. Ангармоничность колебаний
и схождение колебательных уровней к границе диссоциации
Ангармоничность колебаний, т. е. отличие колебательного движения от гар-
монического, определяется расхождением между реальной кривой потенциальной
энергии U(q) и параболой U^(q) =
- kq2. Реальная кривая, близкая в своей нижней
части, вблизи минимума, к параболе, затем расширяется более быстро, чем парабо-
ла, и одна из ее ветвей, как мы видели в гл. 17 (см. рис. 17.2, с. 471), приближается
к конечному пределу. Это приводит к тому, что расстояния между последовательны-
ми колебательными уровнями не остаются постоянными, как для гармонического
осциллятора, а постепенно уменьшаются, и получается картина, изображенная
на рис. 20.4. Колебательные уровни постепенно сближаются — сходятся — по мере
приближения к границе диссоциации. Рис. 20.4 относится к молекуле водорода Н2;
аналогичная картина получается и для других молекул.
Явление схождения колебательных уровней при увеличении величины колеба-
тельной энергии и при приближении этих уровней к границе диссоциации играет
весьма важную роль в спектроскопии молекул, и мы его рассмотрим сначала каче-
ственно.
Сближение колебательных уровней при приближении к границе диссоциации
связано с тем общим свойством уровней энергии, что они располагаются тем теснее,
чем в более широкой области происходит классическое движение, т. е. чем шире
потенциальная кривая. Для кривой, имеющей форму параболы, как мы видели
в § 20.2, получаются равноотстоящие уровни, расположенные тем реже, чем уже
эта парабола (рис. 20.5, а и б). Для кривой, близкой к параболе вблизи положения
равновесия, но расширяющейся кверху быстрее, чем парабола, уровни будут посте-
пенно сближаться. Если одна из ветвей кривой приближается к конечному пределу,
т. е. ее ширина стремится к бесконечности при конечном значении энергии, как это
имеет место для молекулы, то выше предела — за границей диссоциации — получа-
ется непрерывная совокупность уровней энергии, а вблизи границы диссоциации,
с нижней ее стороны, происходит сгущение уровней (рис. 20.5, в).
Весьма существен при этом закон приближения кривой к пределу, так как
от характера этого закона зависит, получается ли вблизи границы бесконечное
или конечное число уровней. Для одноэлектронного атома потенциальная энер-
гия электрона убывает обратно пропорционально расстоянию г электрона от ядра
§ 20.4. Ангармоничность колебаний
585
Рис. 20.4. Кривая потенциальной энергии и колебательные уровни для молекулы водорода
а	бег
Рис. 20.5. Расположение колебательных уровней энергии:
а, б — для гармонических колебаний; в — сгущение уровней к границе диссоциации;
г — сгущение уровней для атома водорода к границе ионизации
и вблизи границы ионизации получается бесконечное число уровней (рис. 20.5, г),
энергии которых определяются формулой (6.13), Еп = -
RZ2
п2
В противоположность этому для молекул число колебательных уровней конечно;
в частности, для молекулы водорода (рис. 20.4) получается всего лишь 15 уровней
(v = 0,1, 2,..., 13,14). За последним уровнем (v = 14) следует граница диссоциации,
выше которой находится непрерывная совокупность уровней.
Как можно показать (см. [131], с. 69), для одномерного движения при потенци-
альной энергии, изменяющейся на бесконечности по закону
В
U = А--
(20.65)
586
Стажа 20. Колебания двухатомных молекул
и имеющей предел А, бесконечное число уровней получается при а < 2. Если
а > 2, т.е. потенциальная энергия достаточно быстро стремится к пределу, то
число уровней конечно; дискретный спектр обрывается на некотором уровне,
расположенном на конечном расстоянии от предела, в то время как при а < 2
имеются дискретные уровни, сколь угодно близкие к пределу,0).
Для двухатомной молекулы, диссоциирующей обычно на нейтральные атомы,
при больших расстояниях между ядрами этих атомов будет иметь место взаимодей-
ствие двух нейтральных систем за счет их взаи мной поляризации (ван-дер-ваальсовы
силы), которое убывает гораздо быстрее, чем по закону (20.65) с а = 2 (см., напри-
мер, [87а], с. 184). Поэтому число колебательных уровней и получается конечным.
Таким образом, конечность числа колебательных уровней двухатомной молекулы
связана с быстрым приближением кривой потенциальной энергии к конечному
пределу при стремлении р = /?е 4- q к бесконечности.
Рассмотрим теперь расположение колебательных уровней, принимая во вни-
мание аналитическое выражение для ангармоничности. Приближенная формула
для колебательной энергии, учитывающая ангармоничность, имеет вид!,)
/ 1
= i/l v-h -
- УХ
(20.66)
Она содержит наряду с основным членом, пропорциональным (^4- - J и соответству-
ющим квадратичному члену в выражении для потенциальной энергии, поправочный
/	1\2
член, пропорциональный 4- -J и обусловленный ангармоничностью.
Постоянная х характеризует ангармоничность и не превышает нескольких
сотых, т. е. не очень велика. Больше всего она для молекулы водорода Н2 и некоторых
гидридов. Для Н2 она равна 0,0285.
Формула (20.66) может быть выведена, если исходить из разложения потен-
циальной энергии U{q) — £эл{р) в ряд, согласно формуле (17.28). Для не очень
больших амплитуд, когда имеет смысл это разложение, ангармоничность можно
приближенно учесть, вводя в качестве поправочных членов к
СГ<°>(9) = X-kq2
(20.67)
кубический член и член четвертой степени относительно q, которые можно записать
в виде
где
и
U\q) = ag3 + &</,
1 / d3U\
&\dp3 ) р=Р' 6\dq3)q=Q
1 (с[*и\ - 1 (d4U\
M\d^)p=p~ 24U7/,=o'
(20.68)
(20.69)
(20.70)
Кубический член aq3 является нечетным относительно q — он меняет знак при из-
менении знака q — и определяет асимметрию кривой потенциальной энергии.
На рис. 20.6 показано влияние этого члена; при отрицательном а в (20.68) кривая
|0) Если пренебрегать шириной уровней.
!|) Множитель h мы в дальнейшем опускаем.
§ 20.4. Ангармоничность колебаний
587
Рис. 20.6. Влияние
кубического члена
на форму кривой
потенциальной энергии
будет идти справа более полого, а слева более круто, чем парабола, что и должно
иметь место для реальных потенциальных кривых (ср. рис. 20.4). Действительно, а,
как правило, отрицательно. Член четвертой степени является четным относительно q
и не меняет симметрии кривой. При b > 0 кривая будет идти в обе стороны круче,
при b < 0 — в обе стороны более полого.
Может показаться, что член четвертой степени
не нужно учитывать, поскольку в разложении он будет
мал по сравнению с кубическим членом. Если отноше-
ние
» X,	(20.71)
где
Л«1,
ТО
» Л2.	(20.72)
I 7
Однако в окончательном выражении для энергии оба
эти члена дают, как можно показать квантовомехани-
ческим расчетом, поправки одинакового порядка А2,
пропорциональные (у + 1 /2)2.
Поправка порядка Л могла бы получиться от усреднения члена aq3. В первом при-
ближении нужно брать его среднее значение, считая движение гармоническим. Однако уже
с классической точки зрения, при усреднении по гармоническому колебательному движению,
член aq3 = aql sin3(cut + как нечетный обращается в нуль. Этот же результат получает-
ся при применении квантовомеханического метода теории возмущений; поправка первого
приближения к энергии, обусловленная членом ад3, равна в силу его нечетности нулю:
= ^|ag3[v) = o(v|g3|v) = 0.	(20.73)
Таким образом, поправка к энергии порядка А отсутствует. Во втором приближении член aq3
приводит к поправке, равной
(v|«g3K)(v'lag3|t>) =	a2(v|gV)2
2-» Ev — E^ 2-^ E„-E,t '	* ’ '
V1
Поправка (20.74) пропорциональна а2 и всегда отрицательна. Такую же по порядку величины
поправку дает и член bg4 в первом приближении теории возмущений:
bg4 = (v|bg4|v) = b(v|g4|v).	(20.75)
Знак поправки (20.75) определяется знаком постоянной Ь, так как g4 = (v|g4|v) положительно.
Следовательно, полная поправка к энергии ДЕ^ порядка А2 слагается из (20.74) и (20.75)
и вычисление ее дает (см., например, [135], с. 94 и [55], т. I, с. 558):
где
(20.76)
С=-Г 2 V~b2QoJ-
(20.77)
588
Глава 20. Колебания двухатомных молекул
Пренебрегая малой аддитивной постоянной с, которая дает лишь небольшое смещение всех
колебательных уровней энергии (малое по сравнению с нулевой энергией | i/0), получим
поправку к энергии вида
—vx
(20.78)
где
1/2зо$	Л
ж — 1о	— о оС/п I.
I/ \ I/	/
(20.79)
которая совпадает со вторым членом в формуле (20.66), причем постоянная х выражена через
коэффициенты а и Ъ в (20.68). х > 0 даже при положительном 6, если только оно не очень
велико; последнее за редкими исключениями и имеет место в действительности.
При учете членов более высоких степеней (q5 и q6) в разложении (17.28), а также
поправок в следующих приближениях теории возмущений от членов aq3 и 6g4, получится
поправка к энергии ЛК(4> порядка Л4 (поправка порядка Л3 обращается в нуль, подобно
поправке порядка Л, как нечетная относительно д), которая имеет вид
i/г/
(20.80)
где у <С х <С 1. В некоторых случаях эту поправку необходимо учитывать и пользоваться
для определения положения колебательных уровней трехчленной формулой вместо двух-
членной формулы (20.66). Следует при этом подчеркнуть, однако, что двухчленная формула
типа (20.66) может получиться не только при приближенном учете членов ад3 и 6д4 в разложе-
нии (17.88), но и если исходить из полной кривой потенциальной энергии типа, изображенного
на рис. 17.2, при определенных предположениях о ее виде (см. ниже, §20.5, с. 593).
Рассмотрим зависимость от v расстояний между последовательными уровнями
энергии, вытекающую из двухчленной формулы (20.66). Мы имеем
AEVjV+] = Ev+] — Ev = и — 2i/x(v 4- 1) — и[ 1 — 2х(у 4- 1)].	(20.81)
Разности энергий и частоты переходов v —► v 4- 1 будут убывать линейно с увеличе-
нием v и для переходов 0—1, 1—2, 2—3 и т.д. Мы получаем ряд частот
1/(1—2ж), i/(l - 4ж),	i/(l— 6ж),	...,	(20.82)
не совпадающих друг с другом и убывающих по величине. При этом частота перехода
0—1 — основная частота колебаний молекулы, получаемая из опыта, — не будет
совпадать с частотой гармонического осциллятора и, определяемой формулой (20.19).
Обозначая постоянные и и х, входящие в формулу (20.66), в которой энергия
отсчитывается от ее значения при р — ре (от минимума кривой потенциальной
энергии), индексом е (от латинского слова equilibrium — равновесие), мы запишем
в виде
Ev = l'e\V+ 2) ~ "еХе + 2/ ’	(20.83)
4,£ = =i/e[l -2®е(г»+1)].	(20.84)
Частота перехода 0— 1 равна
"0,1 = "е(1 - 2же) = ve - 2vexe,	(20.85)
т. е. меньше ve на удвоенную величину коэффициента при квадратичном члене
в (20.83).
§ 20.4. Ангармоничность колебаний
589
Разности частот (20.82) последовательных переходов
(вторые разности) равны
Д2Я = 2i/c«c	(20.86)
и остаются постоянными при условии справедливости исходной двухчленной фор-
мулы (20.83). Для ряда молекул действительно с хорошей степенью приближения
первые разности (20.84) линейно убывают с увеличением v, а вторые разности (20.86)
остаются постоянными.
Примером могут служить данные для мо-
лекулы НС1. Расположение уровней и = 0,2,3,4
приведено на рис. 20.712). Справа указаны
опытные данные для значений колебательных
энергий (в см-1), первые и вторые разно-
сти. Вторые разности практически постоянны
и дают для 2xeve значение 103 см”1. Соглас-
но (20.85), мы получаем v€ = i/0,i 4- 2хеие =
2 886 см"1 -F 103 см"1 = 2 989 см"1. хе в этом
случае получается равным 0,0172.
Большой интерес представляет экстрапо-
ляция формулы (20.83) к границе диссоциа-
ции, соответствующей схождению колебатель-
ных уровней, т. е. обращению в нуль первой
разности (20.84). При справедливости (20.83),
т. е. при строго линейном законе убывания пер-
вых разностей, для энергии диссоциации De
экстраполяция дает значение
i/e uj
De = — = ——
4хе 4хеие
Таким образом, De выражается через отно-
шение квадрата ve к хеи€, т.е. через величины,
определяемые непосредственно из опыта.
(20.87)
Формулу (20.87) легко получить следующим образом13). Границе диссоциации будет,
вообще говоря, соответствовать дробное значение v: имеется последний возможный дискрет-
ный уровень с v — vMaKC, а следующий уровень с v = vMaKC -Ь 1 будет отсутствовать. Граница
получается при таком значения v, при котором Ev как функция v достигает максимума
(рис. 20.8; сплошными кружками показаны дискретные уровни, лежащие ниже границы,
светлыми кружками — уровни с v vMaKC -Ь 1, даваемые формулой (20.83), но не суще-
ствующие в действительности, так как они соответствуют убыванию Ev с увеличением v).
Максимум Ev находится из условия
dEv ,	( Л
— 2иехе I VppaH 4-	|,
dv	у 2 J
откуда получается значение v — для границы диссоциации
1 - "е - 1
^гран “Ь Т	~	~
2	2иехе	2хе
(20.88)
(20.89)
|2^Оно определено по нулевым линиям полос инфракрасного поглощения 0—1, 0—2, 0—3 и 0—4,
см. ниже, с. 596.
13) В литературе имеются утверждения о приближенном характере формулы (20.87). При строго
квадратичном законе (20.83) для энергии эта формула является точной, в частности, при потенциальной
энергии, выражающейся формулой Морза, см. ниже, с. 592.
590
Глава 20. Колебания двухатомных молекул
Подстановка vrpaH в (20.83) дает
Z)c — (^К^гран
Уе _ УеХе _ Уе_
2хе 4х* 4хе ’
(20.90)
т. е. формулу (20.87).
Рис. 20.8. Колебательная энергия	Рис. 20.9. Графическое определение
как функция v	энергии диссоциации
Энергию диссоциации можно найти графически, построив зависимость
от v + 1 (рис. 20.9). Площадь, ограниченная получающейся линией, дает энергию
диссоциации. При справедливости формулы (20.83) график является прямой ли-
нией и соответствующая площадь выражается формулой (20.87); при отступлениях
от линейной зависимости (20.84) получаются иные значения энергии диссоциации.
При линейной зависимости (20.84) ордината в нулевой точке v + 1 = 0, т. е. при v = -1
равна ve. В точке, для которой ордината обращается в нуль, значение абсциссы v + 1 = -—.
1	1	i/e	z	2х<
Площадь равна - ve-— =--------= De в согласии с (20.87).
2	2хе	4хе
В формулу (20.87) входит энергия диссоциации De, отсчитываемая от энергии
Ev = 0, т. е. от минимума кривой потенциальной энергии. Реальную энергию
диссоциации Dq следует отсчитывать от уровня v = 0, для которого нулевая энергия
равна
1 1 1
Eq — —Уе — — УеХе — — Уе
(20.91)
значения (20.24) для строго гар-
- реже. Отсчитывая энергию
4
Значение нулевой энергии (20.91) отличается от ее
1 1
монических колебаний на малую величину - уе- хе =
диссоциации от уровня v = 0, мы получаем
1?о — Ее Eq — De 2 Ре \	2 Хе
(20.92)
На рис. 20.4 показаны значения Dq и De. Для молекулы Н2 их разница составляет
2 180 см-1 = 0,270 эВ; для большинства других молекул эта разница много меньше,
однако при точных определениях энергии диссоциации ее следует обязательно
учитывать. Непосредственно из опыта определяется Dq, а значение De находится,
согласно формуле (20.92), если известны уе и хе.
§ 20.4. Ангармоничность колебаний
591
Если отсчитывать энергию от уровня v = 0 (а не от минимума кривой потенци-
альной энергии), то формулу (20.83) можно записать в виде
(	1\	(	1\2	1	1	2
Е„ - Ео = ve I v +	- 1 - vexe I v	+ - I -	- ve	+ - vexe	= i/e( 1 - xe)v - vexev
ИЛИ
E„ - Eo - vov ~ W2>	(20.93)
где
i/0 = i/e(l - xe) = ve- vexe	(20.94)
и
voXo — Vexe.	(20.95)
Частоты переходов между соседними уровнями получаются равными
1 - 2ж0

(20.96)
Формулам (20.93) и (20.96) соответствует выражение для энергии диссоциации Dq,
аналогичное (20.87):
„ "о "о
JJq = --- — ------.
4ж0 4жО1/о
(20.97)
Формула (20.97) выводится совершенно
максимума выражения (20.93) как функции и.
так же, как и (20.87), — путем нахождения
Рис. 20.10. Определение энергии диссоциации
молекулы водорода
При графическом определении
энергии диссоциации нужно отклады-
вать, согласно (20.96), AEvv+\ как фун-
1
кцию от v + -. Площадь дает значе-
ние Dq. Мы получаем прежний график
рис. 20.9, но только с отсчетом абсцис-
1
сы, смещенным вправо на разница
значений De и Dq выражается площа-
дью, заштрихованной на графике,4).
Для молекулы водорода график для
определения энергии диссоциации при-
веден на рис. 20.10. Действительный вид
кривой AjE^+| показан на графике
сплошной линией, а линейная экстраполяция — пунктиром. Заметное различие
получается лишь вблизи границы диссоциации, у которой сплошная кривая за-
гибается. Расчет по формуле (20.97) дает для энергии диссоциации молекулы Н2
(vq — 4 280 см~!, vqXq — 125 см~’)
Uq 4 2802	.
Dq = —=--------------= 36 640 см"1 = 4,5 эВ,
4xqVq 500
14) Легко убедиться, что эта площадь действительно равна (20.91). При v +• 1 = 0, согласно (20.84),
1	i/e + 1/Q	1
АЕ = i/e, а при v + - —0, согласно (20.96), АЕ = i/q. Заштрихованная площадь равна —-— • - ~
2ve - i/exe
----------, что и дает (20.91).
592
Глава 20. Колебания двухатомных молекул
в то время как действительная энергия диссоциации равна 4,48 эВ, т. е. получается
очень хорошее согласие. Однако в большинстве случаев расхождения значительно
большие, и вычисленные значения обычно намного превышают действительные.
Например, для молекулы НС1 (f0 = 2 937 см-1, x$vq = 51,6 см-1) получается
Dq — 5,20 эВ, тогда как действительная энергия диссоциации равна 4,43 эВ, т. е. рас-
хождение этих значений составляет почти 20%.
§ 20.5. Построение кривых потенциальной энергии
по опытным данным
Вид кривых потенциальной энергии для определенных электронных состоя-
ний является важнейшей характеристикой этих состояний. Знание вида кривых
существенно как для решения вопроса об интенсивностях колебательных полос
в электронно-колебательных спектрах, так и в ряде других случаев.
Теоретический расчет кривых потенциальной энергии является очень трудным,
и поэтому весьма необходимы методы построения кривых потенциальной энергии
по экспериментальным данным. С этой целью был предложен ряд аналитических
формул с определяемыми из опыта постоянными (сравнение различных формул
см. [298]). Практически наиболее удобной формулой, обладающей притом рядом
достоинств с теоретической точки зрения, является формула, предложенная Морзом
(Morse) [294].
Формула Морза содержит три постоянные и позволяет построить кривую потен-
циальной энергии по данным для энергии диссоциации D€, частоты колебаний и€
и равновесного расстояния Она имеет следующий простой вид:
U(p) = De [1 - е“№“А)]2.	(20.98)
В формулу явно входят постоянные De и ре, а постоянная
Гм~
(»*»
т. е. пропорциональна частоте колебаний i/e, а также зависит от De и приведенной
массы молекулы М.
Легко видеть, что кривая (20.98) правильно передает общий ход кривых потен-
циальной энергии (см. рис. 17.2, с. 471). Действительно, при р = ре U(pe) принимает
минимальное значение, равное нулю; при всех других значениях, р / ре, U(pe)
существенно положительно. Далее, при р —► оо е~^р~ре^ —> 0 и, следовательно,
и U(p) —► De. Наконец, при р = 0 17(0) = De(\ - е^ре)2. При достаточно боль-
ших Дре, что всегда имеет место, е@ре 1 и £7(0) De, т. е. левая ветвь кривой
достигает таких значений, которые практически можно считать бесконечными.
Около точки р — ре кривая приближенно имеет форму параболы, соответствующей
при значении (20.99) постоянной Д частоте колебаний ve.
В самом деле, когда |Д(р - ре)\ = \/3q\ < 1, 17(р) « [1 - (1 - /3q)]2 = De/32q2 =
-M4ir2vlq2, т. е. является квадратичной функцией от q — р — ре, совпадающей,
согласно (20.2), с (20.3). Именно из условия, что
U = Х- kq2 = M4ir2v2q2 = Dep2q\	(20.100)
и выбирается значение (20.99) постоянной /3.
§ 20.5. Построение кривых потенциальной энергии по опытным данным 593
Замечательным свойством формулы Морза является то, что при строгом ре-
шении квантовомеханической задачи с потенциальной энергией (20.98) в точности
получается двухчленная формула (20.83) для энергии колебаний, где ие определяется
i/g
формулой (20.99), а иехе = -— в согласии с (20.87).
Давая правильный результат вблизи р = ре и на бесконечности, в промежу-
точной области формула Морза представляет интерполяционную формулу, притом
такую, которая точно приводит к двухчленному выражению для энергии колебаний.
Если двухчленная формула является хорошим приближением к действительности,
то формула Морза дает и правильное значение постоянной хе, связанной с ангар-
моничностью колебаний.
На рис. 20.4 полная кривая потенциальной энергии для молекулы водорода
построена по формуле Морза (пунктир).
Следует иметь в виду, что
из того факта, что при заданном
виде потенциальной кривой полу-
чаются правильные значения энер-
гии колебательных уровней, еще
не следует правильность исходной
кривой U(p). Как показали Пешль
и Теллер [295], те же уровни энер-
гии получаются для кривых, в оди-
наковой степени расширяющихся
при увеличении энергии, но дефор-
Рис. 20.11. Деформация кривой потенциальной
энергии: а — первоначальная кривая;
б — деформированная кривая
мированных в горизонтальном на-
правлении (рис. 20.11, а и б). Для та-
ких кривых разность рмакс—рмин рас-
стояний между ядрами для поворот-
ных точек классического движения
Рмакс и Рмин одинакова. Если заданы положения уровней энергии, то кривая потенциальной
энергии определяется лишь с точностью до сдвига в горизонтальном направлении. Для одно-
значного определения вида кривой потенциальной энергии нужны дополнительные данные.
Такими данными могут служить сведения о среднем расстоянии между ядрами, получаемые
из значений вращательных постоянных для соответствующих колебательных уровней.
Согласно (19.24) и (19.28), вращательная постоянная двухатомной молекулы равна
® = Siw'	™
где р — расстояние между ядрами. Для колеблющейся молекулы значение вращательной
постоянной нужно усреднить по колебательному движению
BV=B =
h2
8тг2М
(20.102)
В (20.102) входит среднее значение -г для уровня с заданным v, которое, очевидно, находится
Р
в пределах
< 7 <	(20 103)
гмакс г Кмин
Это среднее значение может быть вычислено как на основе классических представлений, так
и квантовомеханически (ср. (17.77)).
Чем сильней сдвинута кривая потенциальной энергии вправо при том же р = р€ и той
же разности рмакс - рмин, тем, очевидно, меньше будет среднее значение — и значение
Р2
постоянной Bv.
594
Глава 20. Колебания двухатомных молекул
Ридберг и Клейн дали конкретный метод построения кривых потенциальной энергии
по экспериментальным значениям колебательных уровней энергии Ev и вращательных посто-
янных Bv [296]. В этом методе, являющемся полуклассическим, для колебательного движения
применяется условие квантования (6.35), причем целое число п заменяется полуцелым числом
v + - (v = 0, 1, 2,...). Для изменения расстояния р между ядрами получаем условие
<j> Ppdp=
Выражая импульс рр = тр при помощи соотношения
1 Рп
Е = Т(рр) + и(р)=-^+и(р)
через полную энергию и функцию Щр), найдем
(20.104)
(20.105)
У"	dp = (v + 0 h.
(20.106)
В (20.106) для полной энергии берутся значения Ev. Соотношению (20.106) должна удов-
летворять искомая функция Щр). Другое соотношение для функции U(p) получается из усло-
вия (20.102), если выразить I
представляя это среднее в виде
8тг2М	/------—
v = —-z—Bv через х/Ev - Щр), что можно сделать,
п/
1_1/df_1/d'9_l/ MdP _ 1 1 MdP
где т — период колебаний, равный,
.________
J J Р J Рр J y/2M[Ev - Щр)]
(20.107)
(20.108)
С помощью рационального введения вспомогательных функций можно дать удобную схему
последовательного нахождения значений Щр), соответствующих v ~ 0, 1, 2,... и удовлетво-
ряющих условиям (20.106) и (20.107), что и было сделано Клейном (см. также [297]).
Метод Ридберга—Клейна позволяет построить действительный вид кривой потенци-
альной энергии для области значений квантового числа v, для которой известны из опыта
как величины Ev, так и величины Bv. Результаты применения этого метода к молекуле
водорода показаны на рис. 20.4: сплошная кривая построена по методу Ридберга—Клейна.
Значительные отклонения кривой Морза от кривой Ридберга—Клейна получаются лишь
вблизи границы диссоциации, когда двухчленная формула, как показывает рис. 20.10, уже
становится неприменимой. Достоинством метода Ридберга—Клейна является возможность
определения хода кривой на отдельных участках независимо от каких-либо предположений
о кривой в целом.
§ 20.6. Колебательно-вращательные спектры
двухатомных молекул
Рассмотрим теперь колебательно-вращательные спектры двухатомных молекул.
Этими спектрами в инфракрасной области обладают молекулы симметрии С™,
состоящие из неодинаковых атомов и имеющие дипольный момент (см. § 18.6,
табл. 18.1), и при комбинационном рассеянии все двухатомные молекулы (как
симметрии CooV, так и симметрии D^h).
§ 20.6. Колебательно-вращательные спектры двухатомных молекул 595
Переходы между колебательными уровнями сопровождаются, как правило,
одновременными изменениями вращательной энергии (ср. § 17.1, с. 466). Это и при-
водит к возникновению колебательно-вращательных спектров. Так как изменения
вращательной энергии, как правило, малы по сравнению с изменениями коле-
бательной энергии, то в спектрах получаются полосы, соответствующие опреде-
ленному колебательному переходу, структура которых обусловлена вращательными
переходами, — колебательно-вращательные полосы. При исследованиях с малой
дисперсией каждая полоса наблюдается в виде широкой линии, которая при увели-
чении дисперсии распадается на ряд отдельных линий, соответствующих отдельным
вращательным переходам.
Изменение энергии при отдельном переходе можно представить, как обычно,
в виде = Е' - Е", где Е' — энергия верхнего уровня, а Е" — энергия нижнего
уровня. Каждая из них является суммой колебательной и вращательной энергий,
и мы можем записать:
Е" = Е" +	+ О (нижний уровень),	(20.109)
Е' — Е[ Л- -I- 1) (верхний уровень).	(20.110)
При этом Е" и E'v будут определяться формулами типа (20.83), которые мы не будем
выписывать в явном виде. Для вращательной энергии мы ограничиваемся первым
членом типа BJ(J -F 1) в общей формуле (19.38). Связь вращения и колебания
учитывается в формулах (20.109) и (20.110) тем, что вращательная постоянная Bv
является функцией колебательного квантового числа v. С хорошей степенью при-
ближения
Bv = Ве - ae(v + 0,	(20.111)
где ае — постоянная, отношение которой к Ве, как показывает опыт, порядка
их
постоянной х = — (см. § 20.4, с. 586) и не превышает нескольких сотых. На-
р
пример, для молекулы НС1 значения вращательных постоянных уровней v = 0
и v — 1 равны Во = 10,440 см-1 и В\ = 10,137 см-1, что соответствует величине
-1	а
а = 0,303 см ; отношение — равно 0,030. Постоянная х для НС1 равна 0,0172
(см. с. 589).
В силу (20.111) вращательная постоянная убывает по линейному закону с уве-
личением v. С физической точки зрения это связано с тем, что для колеблющейся
молекулы должен увеличиваться момент инерции вследствие ослабления связи меж-
ду атомами и увеличения среднего расстояния между ними, и соответственно должна
уменьшаться, согласно (19.24), вращательная постоянная.
С увеличением колебательной энергии и ослаблением связи между атомами увеличива-
ется асимметрия кривой потенциальной энергии, определяемая в первую очередь кубическим
членом aq3 (см. текст на с. 587 и рис. 20.6). При усреднении величины — по колебательному
Р
движению (см. (20.102)) с увеличением v все большую роль будут играть большие значения р,
1
что приводит к уменьшению среднего значения — и, следовательно, к уменьшению В.
Р
Формула (20.111) подтверждается и приближенным квантовомеханическим расчетом [49].
Постоянная а€ тем больше, чем больше постоянная а, определяющая асимметрию кривой
потенциальной энергии.
596
Глава 20. Колебания двухатомных молекул
Следует отметить, что для чисто гармонических колебаний постоянная ае отрицательна.
Действительно, при усреднении величины Д-, согласно наглядным представлениям, равной
р1
1 1
р2 (ре + 9о sin 2тгр«)2
(20.112)
и меняющейся от —— = --------— до —— = ---------— большую роль будут играть члены
Рмин (Ре-go)2 рмакс (ре + ?о)2
с р < ре, чем члены с р > ре, и в результате В будет возрастать с увеличением амплитуды
колебаний д0, т. е. с увеличением v. Однако в силу асимметрии кривой потенциальной энергии
(Рмакс ~ Ре > Ре ~ Рмин) роль членов с р > ре настолько возрастает, что в конечном результате,
как правило, В уменьшается с увеличением v, т.е. постоянная а положительна.
Согласно (20.109) и (20.110),
E,-E,,^E,v-E” + B,vJt(Jt+	1).	(20.113)
Разность E'v-E" определяет частоту i/Oo чисто колебательного перехода, который по-
лучился бы при J1 = J" — 0, т. е. частоту «нулевой линии». В силу запрета переходов
0—0 (даже при правиле отбора AJ = 0, см. (4.160), а также (4.161)) нулевая линия
не может наблюдаться, и ее положение определяют расчетом. Вследствие того, что
X - X > B'J'U' + 0 -	+ 1)	(20.114)
(ср. (17.5)), положение полосы в спектре определяется положением нулевой линии.
Для чисто гармонических колебаний, как мы видели выше (см. (20.32)), имеет
место правило отбора Av = ±1, следовательно, v' — v" = 1. В силу ангармоничности
оказываются возможными переходы, для которых v'-v" = к. Частота колебательного
перехода (нулевой линии), для которого v' - v" = к, равна, согласно (20.83),
Е' - X' =	= Ev«+k ~ Е„" = ve \v" + к + -J - vexe (j" + к + -J -
/ ] \ / 1 \2
- v" + -] + УеХе\у" + -} = к[уе - yexe(2v" + к + 1)],	(20.115)
что при к = 1 дает прежнюю формулу (20.84).
Наиболее важны обычно наблюдаемые в поглощении и при комбинационном
рассеянии переходы между нулевым колебательным уровнем (v" = 0) и возбужден-
ными колебательными уровнями (v1 = 1, 2, 3,...). Для них
i/Oy = Aj&oy = к[уе - уехе(к + 1)].	(20.116)
Наряду с переходом 0— 1 с основной частотой
1/0,1 = AjE?oj = уе - 21/еже,	(20.117)
при ангармонических колебаниях будут появляться первый обертон (к = 2) с частотой
I/O,2 = Д#о,2 = 2(уе - ^УеХе),	(20.118)
второй обертон (к = 3) с частотой
1/0,2 = AjE?0,2 = 3(i/e - 4уехе)	(20.119)
и т.д.
Благодаря отличию, в общем случае, хе от нуля, частоты обертонов не явля-
ются точно целыми кратными основной частоты 0—1 и, как правило (в обычном
§ 20.6. Колебательно-вращательные спектры двухатомных молекул	597
случае хе > 0), будут несколько меньше, чем Интенсивность обертонов быстро
убывает с увеличением v' = к, т. е. первый обертон значительно слабее основной
частоты, второй обертон значительно слабее первого обертона и т. д. Чем меньше
ангармоничность, тем быстрее происходит это убывание интенсивности и, наоборот,
при большой ангармоничности убывание становится более медленным и наблюда-
ется большее число обертонов.
В инфракрасных спектрах поглощения удается наблюдать несколько обертонов
основной частоты. Например, для молекулы НС1 наблюдаются полосы 0—1, 0—2,
0—3, 0—4 с быстро убывающими интенсивностями. Приведенная в предыдущем
параграфе диаграмма рис. 20.7 построена по данным для нулевых линий этих полос.
В спектрах комбинационного рассеяния обычно удается наблюдать для двухатомных
молекул лишь переходы 0—1, а обертоны вследствие их малой интенсивности
отсутствуют.
При рассмотрении вопроса об интенсивности обертонов следует учитывать как меха-
ническую ангармоничность, связанную с отличием колебания молекулы от гармонического
и определяющую отличие постоянной хе от нуля, так и электрооптическую ангармонич-
ность, связанную с нелинейной зависимостью дипольного момента и составляющих тензора
поляризуемости от колебательной координаты, т. е. с наличием членов с g2, д3,... в разложе-
ниях (20.63) и (20.64). За счет электрооптической ангармоничности обертоны могут появляться
и в случае, когда механическая ангармоничность не играет роли и глубокие колебательные
уровни являются равноотстоящими.
Важную роль при изучении колебаний и колебательных спектров двухатомных
молекул (как и при изучении колебаний и колебательных спектров любых молекул)
играет изотопический эффект. Частота колебаний и положения в спектре нулевых
линий i/qo колебательных полос (см. выше, с. 596) изменяются, при замещении
в данной молекуле одного или обоих атомов, вследствие изменения приведенной
массы молекулы. Для молекул, состоящих из различных изотопов тех же атомов,
частоты колебаний и положения нулевых линий будут различны. Особенно важный
случай представляет изотопическое замещение в случае водорода — дейтерирование,
т. е. замена атома Н атомом D, имеющим вдвое большую массу, что приводит к очень
значительному изменению частот колебаний.
Частота ve чисто гармонических колебаний, согласно (20.19), равна ve —
1 Гк
— \ — и обратно пропорциональна корню квадратному из приведенной мас-
2тг V М
сы, т. е. при увеличении массы вдвое уменьшается в л/2 = 1,41 раз. Формулу (20.115)
для нулевых линий можно записать в виде
1/00 = Е»' - Е„» - ve(y' - v") - vexe
1\2
2/
(20.120)
и так как второй член мал по сравнению с первым, то относительное изменение г/оо
при изотопическом замещении приблизительно такое же, как и относительное
изменение частоты уе.
Отношение р частот ие для двух изотопических молекул будет равно
I/' Гм
'-Чг	<2о12|>
Обозначив массы атомов в первой молекуле через М\ и М2, а во второй молекуле
,	,	М\М2 , M'iM'2
через М, и Мг, мы получим, учитывая, что М =-------и М = —---------, общую
М] + М2 М{ + М2
598
Глава 20. Колебания двухатомных молекул
формулу
IM,М2 М\ + М'2
р~ у М\М2 М\ + м2
которая в случае изотопического замещения лишь одного из атомов (М\ = М\)
сводится к формуле
(20.122)
М2М1+М1>
Р~ \~M~2 М\+М2
Для молекул HD и D2 мы, согласно (20.123) и (20.122), получим (полагая М2 = 2
для HD и = М2 = 2 для Z>2 при М] = М2 = 1 для Н2)
^(ио) Д	u(d2)
Phd =	= V 4= °’865, PD2 =
Для молекул гидридов типа ХН замещение атома Н атомом D, согласно (20.123),
дает (М, = Мх, М2 = 1, М2 = 2)
(20.123)
(20.124)
/1Мх + 2
Р ~ V 2 Мх + 1 ’
(20.125)
где Мх — масса атома X. Например, для молекул НО35 и DC135 мы получаем
ГГзТ	/Т
^~V2 36 = °’717 “ величинУ» близкую к предельному значению р = U - = 0,707,
к которому стремится р при увеличении Мх. Этот результат понятен, так как
при большой массе атомаХ по сравнению с атомом водорода практически колеблется
лишь последний,5).
Для случая, когда массы изотопов в противоположность случаю водорода мало
отличаются друг от друга, изменение частот колебаний будет невелико, т. е. р будет
мало отличаться от 1. В этом случае, полагая М{ — М\ + Дь М2 — М2 + А2, мы
приближенно получим, согласно (20.122),
М\ Mj
_________ _ Ml +м2 +Д1 + д2 _
Р~ Ц (М\ +Д,)(М2 + Д2)	М|+М2	~
Д1 Д2 Aj + А 2
“ ~ 2М} ~ 2М2 + 2(М, + М2) ’
Д
т. е. относительное изменение частот порядка —. Например, для молекул
М
и С137С137 отношения частот их колебаний к частоте колебаний молекулы
2	2	1	:	:
будут равны 1----Ч-----= 1-----и 1------+----- = 1-----, т. е. эти
У У И	70	140	70	70	140	35’
отличаются друг от друга на — = 1,4 %. При более точных расчетах изотопического
эффекта нужно пользоваться точными значениями атомных весов (в частности,
70	140
35’
(20.126)
С135С137
С135С135
частоты
4	4
’^Действительно, для двух частиц, движущихся вокруг общего центра тяжести (задача двух тел), их
„	R\ М2
расстояния /С| и R2 от него находятся в отношении — = — и в том же отношении находятся их
Т?2 М\
скорости V| и v2, т. е. при М2 М j v2 > v}.
§ 20.6. Колебательно-вращательные спектры двухатомных молекул 599
Мн — 1,008 и Md = 2,014) и учитывать зависимость от массы второго члена в фор-
муле (20.120), которая будет иной, чем зависимость первого члена. Постоянная хе
1 1
пропорциональна —=, а vexe пропорционально —:
VM	М
Хе
М'
(20.127)

Этот результат может быть получен из формулы (20.79), если учесть, что нулевая амплиту-
да колебаний Qo, согласно (20.31), обратно пропорциональна \/М; оба члена в скобках (20.79)
обратно пропорциональны массе. Тот же результат получается и из формулы (20.87): и] ~ —,
М
a J9 от массы не зависит.
Учет зависимости (20.127) величин хе и 1/еже от массы наиболее существен
при сравнении колебаний молекул, содержащих водород и дейтерий, так как ангар-
моничность сказывается больше всего для колебаний таких молекул.
Для основной частоты колебаний молекулы (частоты перехода 0—1), определяемой
формулой (20.117), мы получаем при учете зависимости постоянных ие и хе от массы
(20.128)
где в соответствии с (20.127) введена постоянная А = хе\/М. Так как 2хе = —= мало,
то (20.128) можно приближенно представить в виде
(20.129)
где
/ 4Л \
М’ = М[ 1 + -=	(20.130)
у vM /
— эффективная масса. Иначе говоря, можно по-прежнему считать колебания гармонически-
ми, приближенно учитывая ангармоничность путем введения эффективной массы или, как
ее называют, спектроскопической массы (20.130). Метод спектроскопических масс [311] ока-
зывается полезным при рассмотрении колебаний многоатомных молекул, содержащих связи
С—Н и С—D или связи других тяжелых атомов с атомами Н и D (см. ниже, § 21.7, с. 639).
Необходимо отметить, что в случае моле-
кул, состоящих из двух одинаковых атомов, изо-
топическое замещение может приводить к по-
явлению инфракрасных спектров поглощения
и испускания у молекул, имеющих симметрию
D^h и не обладающих дипольным моментом
(см. § 18.6. с. 527, а также начало параграфа).
М2
=5^
Рис. 20.12. Несимметричное
колебание для изотопической
молекулы
Если молекула состоит из изотопических атомов с разной массой, как, например,
молекулы HD, С135С137 и т.д., то колебание происходит несимметричным образом
(см. рис. 20.12|6)) и возникает переменный дипольный момент, обусловливающий
16) Этот рисунок соответствует случаю молекулы HD, для которой М2 = 2М\ и q2 = —~q\, где qi
и — смещения атомов Н и D.
600
Глава 20. Колебания двухатомных молекул
отличную от нуля вероятность дипольных переходов. При этом симметрия моле-
кулы нарушается колебаниями, которые уже не являются полносимметричными.
Только при одинаковых ядрах двухатомная молекула сохраняет при колебаниях
симметрию D^h- При разных ядрах колеблющаяся молекула обладает симметрией
Сооу. Интенсивность инфракрасных спектров подобной молекулы будет тем больше,
чем больше асимметрия колебаний и, следовательно, увеличивается с увеличением
относительной разницы в массах изотопических атомов.
§20.7. Вращательная структура
колебательно-вращательных полос
Вращательная структура колебательно-вращательных полос определяется двумя
последними членами в формуле (20.113). Эту формулу мы запишем в виде
Е' - Е" = Роо +	4- 1) —	4- 1),	(20.131)
где Роо — частота нулевой линии, т. е. частота чисто колебательного перехода.
Существенная разница по сравнению со случаем чисто вращательных спектров,
когда возможные переходы определяются также разностями типа B'J’^J1 4- 1) -
B"J"(J" 4- 1) (см. (19.27) и (19.36)), состоит в том, что В1 и В” в формуле (20.131)
относятся к различным колебательным состояниям, в то время как для чисто враща-
тельных спектров они принадлежат одному и тому же колебательному состоянию.
В последнем случае разница В' и В” определяется лишь наличием центробежного
растяжения и для не слишком высоких вращательных уровней очень мала. Отли-
чие В1 и В" в формуле (20.131), определяемое зависимостью (20.111) вращательной
постоянной от колебательного квантового числа, более существенно|7).
Для колебательно-вращательных переходов, определяемых формулой (20.131),
необходимо рассматривать, в отличие от чисто вращательных переходов, не только
положительные значения AJ = Jf -J", но и отрицательные значения этой разности,
а также значения, равные нулю (последние, однако, не во всех случаях). Для чисто
вращательных переходов уровень, лежащий выше, всегда обладает и большим зна-
чением J (причем J1 - J" — 1 для спектров поглощения и испускания и J' - J" — 2
для спектров комбинационного рассеяния). Для колебательно-вращательных пере-
ходов вращательные уровни верхнего колебательного состояния лежат выше вра-
щательных уровней нижнего колебательного состояния, даже когда J' значительно
меньше J".
Заданному значению A J разности J' — J" соответствует ряд переходов, отлича-
ющихся значениями J1' (следовательно, и значениями J' = J" 4- A J). Совокупность
линий, получающихся при таких переходах, принято называть ветвью соответству-
ющей полосы. Эти ветви обозначают следующим образом:
переходы	AJ = J'	- J" = +2	5-ветвь, '		
переходы	&J = J'	- J" = +1	Я-ветвь,		
переходы	kJ = J'	- J" = 0	Q- ветвь,	►	(20.132)
переходы	kJ = j'	- J" = -1	Р-ветвь,		
переходы	= J'	- J" = —2	О-ветвь. ,		
17^Оно еще более существенно для вращательной структуры электронно-колебательных полос
(см. с. 760), когда также применима формула (20.131), но только iz00 дает частоту электронно-коле-
бательного перехода, а В' и В" относятся к разным электронным состояниям. Приводимые в данном
параграфе формулы применимы и для этого случая, что будет использовано при его рассмотрении.
§ 20.7. Вращательная структура колебательно-вращательных полос 601
Для обычных колебательно-вращательных полос поглощения и испускания в ин-
фракрасной области, соответствующих дипольному излучению молекул с дипольным
моментом, отличным от нуля, имеет место правило отбора для вращательного кван-
тового числа
AJ = j'-j" = ±l.	(20.133)
Это правило отбора относится к молекулам, не обладающим в нормальном элек-
тронном состоянии электронным механическим моментом. Большинство устойчи-
вых двухатомных молекул удовлетворяет данному условию18*. Для таких молекул
колебательно-вращательные полосы состоят из Р-ветви, т.е. совокупности линий,
для которых AJ = Jf- J" = 4-1, и из Р-ветви, т. е. совокупности линий, для которых
&J = J' - J" = -1.
Схема переходов, дающих колебательно-вращательную полосу, показана
на рис. 20.13. Переходы Р-ветви AJ = 4-1 дают частоты v > vqq, переходы Р-ветви
с Д/ = -1 дают частоты v < z/qq.
7
6
5
4
Г
7
6
5
4
./"=10 98765432 1/=1 2 3 4 5 6 7 8 910
Р-ветвь (т = —J”)	Р-ветвь (m=J')
Рис. 20.13. Схема переходов для колебательно-вращательной полосы
Соответствующие формулы для частот переходов легко получаются из (20.131).
Для Р-ветви (J' - J" = 4-1) мы имеем
Vj< = l/оо +	+ 1) - В"О' - 1) J' = l/оо + (В' + B")J' + (В' -	(20.134)
,8* Подробнее о том, какие молекулы не имеют в нормальном электронном состоянии электронного
момента, см. § 24.8 и 24.9.
602
Глава 20. Колебания двухатомных молекул
если выразить J" через J', и
Кг = Vw + B'(J" + l)(j" + 2) - В"J"(J" + 1) =
= 1,00 + (В' +	+ 1) - (В' - B")(J" + I)2 =	(20.135)
= voo + 2B' + (ЗВ' - В") J" + (В' - B")J"2,
если выразить J1 через J".
Формула (20.134) или (20.135) дает ряд линий с и > рОо, которые при В1 = В"
были бы равноотстоящими, а в силу наличия квадратичного члена с В1 < В",
что, как правило, имеет место для колебательно-вращательных полос (см. (20.111),
v > v"), будут сходиться (при В1 > В” они бы расходились).
Для Р-ветви (J' - J" = -1) мы имеем
V]„ = 1/00 + B'(J" - 1)J" - B"j"(j" + 1) = i/oo - (в' + в")J" + (В' - B")j"2, (20.136)
если выразить J' через J", и
vj' = Ию + B'J'(J' + 1) - B"(J' + 1)(J' + 2) =
= 1,00 - (B' + B")(J' + 1) + (B' - B")(J' + I)2 =	(20.137)
= Poo - 2B" - (3B" - B')J' + (B' - B")J'2,
если выразить J" через J1,
Формула (20.136) или (20.137) дает ряд линий с р < Роо, которые также
при В1 = В" были бы равноотстоящими, а в силу наличия квадратичного члена
с В1 < В" будут расходиться (при В' > В" они бы сходились).
Следует обратить внимание на сходство формул (20.134), в которой J' принимает
значения 1,2, 3,... , и (20.136), в которой J" принимает те же значения. Разница этих
формул состоит только в знаке линейного члена. Если положить в (20.134) Jf = т,
где т = 1,2, 3,... , а в (20.136) положить JH = -т, где т = -1, -2, -3,... , то обе
формулы становятся одинаковыми и их можно будет записать в виде
Ип = Ию + (В' + В")т + (В' - В")т2,	(20.138)
где
т= 1, 2, 3,...	для Р-ветви, 1	.
т= -1, —2, -3,...	для Р-ветви. J
В соответствии со знаком т часто называют Р-ветвь положительной ветвью,
а Р-ветвь отрицательной ветвью.
Нулевая линия (отсутствующая в спектре) соответствует т = 0. При В’ = В11 =
В формула (20.138) еще более упрощается и принимает вид
vm = ^оо + 2Вт.	(20.140)
Выражение (20.140) дает равноотстоящие линии, симметрично расположенные от-
носительно нулевой линии Роо-
Применяя формулу (20.138), нужно, разумеется, помнить, что т > 0 соот-
ветствует значению квантового числа J — Jf для верхнего колебательного уровня,
а т < 0 — значению квантового числа J = J" для нижнего, так что симметрия
формулы (20.138) не является полной.
В случае, если наряду с переходами AJ — ±1 разрешены переходы AJ — 0,
что имеет место для спектров поглощения и испускания двухатомных молекул,
§ 20.7. Вращательная структура колебательно-вращательных полос	603
(20.143)
(20.144)
с интервалами около 4 В
наблюдается лишь Q-ветвь
интенсивной линии, a S-
для которых электронный момент количества движения не равен нулю, то наряду
с Р-ветвью и Р-ветвью будет появляться Q-ветвь — нулевая ветвь (AJ = 0).
Для Q-ветви, согласно (20.133), получаем (/' = J" = J)
VJ = t'oo + (в' -	+ 1).	(20.141)
В силу малости В' - В" по сравнению с В' + В" линии Q-ветви расположены
весьма тесно и при малой дисперсии сливаются в одну узкую полосу.
Для спектров комбинационного рассеяния имеет место правило отбора
Д J = 0, ±2.	(20.142)
Наряду с Q-ветвью (20.141), состоящей из близко расположенных линий, будут
получаться 5-ветвь и О-ветвь. Аналогично формулам (20.134)-(20.137) для 5-ветви
(Д/ = J' - J” = 4-2) имеем
v = I/оо - 2В" + (В' + ЗВ") J' + (В' - В") J'* 2 =
= i/oo + 6В' + (5В' - В") J" + (В' - В") J"2,
и для О-ветви (AJ - J' — J" = — 2)
Е = i/oo + 2В' - (ЗВ' + В") J" + (В' - В") J"2
= l/оо - 6В - (5В" - В') J' + (В'
Получаются совокупности далеко отстоящих линий
( в' + в"|9> \
1гдеВ =--------— I.
Обычно в спектрах комбинационного рассеяния
в виде одной неразрешенной и поэтому достаточно
и О-ветви отсутствуют из-за недостаточной интенсивности отдельных линий этих
ветвей.
Для инфракрасных колебательных полос поглощения существенную роль играет
распределение интенсивности внутри полос между вращательными линиями. Ин-
тенсивности приближенно пропорциональны заселенностям вращательных уровней
для нижнего колебательного уровня, являющегося начальным при поглощении,
которые даются формулой (19.32). Мы имеем
/погл = C(2J" + 1) exp |= c(2j" + 1) exp | - —L2.+91	(20.145)
L h*-*- J	L A/х J
где с — постоянная. При малых	4- 1) <C kT) заселенность возра-
стает за счет множителя 2J" 4- 1, определяющего статистический вес вращательных
уровней, а затем при больших	4- 1) > kT) быстро убывает за счет
показательного множителя. При промежуточных значениях заселенность достигает
максимума и в обоих ветвях полосы поглощения (Я-ветви и в Р-ветви) наиболее
интенсивны линии, соответствующие этим значениям J". Получается не вполне
симметричная, из-за асимметрии в схеме переходов (см. рис. 20.11), картина распре-
деления интенсивностей в полосе, изображенная на рис. 2О.142о), причем расстояние
,9) При В' « В" В1 + ЗВ" я ЗВ' + в" « 2В' + 2В" = 4В.
2°) Интенсивности вычислены по более точной формуле, получающейся из (20.145) заменой множителя
2.J" 4- 1 множителем f + Ju + 1 (см. [46], с. 93).
604
Глава 20. Колебания двухатомных молекул
между максимумами растет пропорционально корню квадратному из абсолютной
температуры
Др~\<Г.	(20.146)
При малой дисперсии вращательные линии сливаются и образуют дублет (дублет
Бьерума [301]). Из расстояния Др между максимумами для неразрешенной полосы
можно найти приближенное значение вращательной постоянной В.

т=зоо°к

+20+10 0-10-20 m
Т=1000°К
+ 10	+5
0	—5 m ^mnilllllllllllllllMlllilillllll^
+40	+20	0 -20	-40 m
Рис. 20.14. Распределение интенсивностей во вращательно-колебательной полосе:
а — при В = 10,44 см~‘(НС1); б — при В = 2 см-1
R
Положение максимума интенсивности как функции от J" легко находится дифферен-
цированием выражения (20.145), которое мы запишем приближенно в виде (опуская штрихи)
f BJ2
Лют — 2cJ ехр \ —
I кТ
(20.147)
Имеем
«Ц™	.	(	В J2\	BJ2	(	BJ2
——- = 2с ехр < ——- > - 4с —— ехр < ——-
dJ	[	кТ J	кТ	[	кТ
Приравнивая это выражение нулю, находим соотношение
•^Лакс = -^^макс = 2
(20.148)
(20.149)
т. е. максимумы интенсивностей соответствуют значению энергии вращения, равному - кТ.
Расстояние — максимумов от нулевой линии (см. рис. 20.14), согласно (20.140), равно
Д1/
— 2-В«7макс«
Подставляя значение JMaKC из (20.149), находим
[кТ
^2В
= 2V2BkT,
(20.150)
(20.151)
т.е. мы получаем формулу (20.146).
§ 20.7. Вращательная структура колебательно-вращательных полос 605
Обратно, значение В равно
(Ai/)2	1 А Ai/
-—— = - Ai/—
8ЛТ	8 kT’
(20.152)
что и позволяет определить В по расстоянию между максимумами для неразрешенной полосы.
ГЛАВА 21
КОЛЕБАНИЯ МНОГОАТОМНЫХ МОЛЕКУЛ
§21.1. Общая характеристика нормальных колебаний
многоатомных молекул
В отличие от двухатомных молекул, имеющих только одну колебательную
степень свободы, многоатомные молекулы, как состоящие более чем из двух атомов,
имеют не менее трех колебательных степеней свободы. Уже одно это определяет
сложность колебательного движения таких молекул. С увеличением числа атомов
в молекуле N увеличивается и число колебательных степеней свободы, равное г =
3N - 6 в общем случае нелинейных молекул и г = 3N - 5 в частном случае линейных
молекул (см. гл. 17, с. 476); соответственно усложняются колебания молекул и их
колебательные спектры.
Подобно колебаниям двухатомной молекулы, колебания многоатомной моле-
кулы при малых амплитудах будут гармоническими. Как известно, для системы
с г степенями свободы, совершающей малые колебания около положений равнове-
сия, получается г нормальных колебаний. Каждое нормальное колебание происходит
с определенной частотой i/t (г == 1,2, 3,..., г). Колебательное состояние системы
частиц, какой является молекула, характеризуется в соответствии с числом коле-
бательных степеней свободы г независимыми колебательными координатами жд,
определяющими смещения частиц из положений равновесия: при определенном
нормальном колебании с частотой i/t эти
Жд) — Жд^ sin Zirvit (Л = 1,
а
ОСО
о----о---о
Ро Ро
б
-----------------------Ч/-------- (S) _	(S)
Р1=Ро+£?1 Рг-Ро+Яг Ч\~Чг
'----V----*-------'	(а) _ _ (д)
Р1=Р0 + <71	P2=PQ+(l2
Рис. 21.1. Линейные колебания молекулы СО2:
а — равновесная конфигурация;
б — симметричное колебание;
в — антисимметричное колебание
координаты будут изменяться по закону
2,3..., г; i = 1,2,... , г).	(21.1)
э (О
Здесь ж\о — амплитуда, с которой изме-
няется при г-м нормальном колебании
координата жд, ив каждом нормаль-
ном колебании будут, вообще говоря,
участвовать все частицы. Соотношение
амплитуд для данного нормального ко-
лебания определяет его форму.
Простейшим примером нормаль-
ных колебаний могут служить симме-
тричные и антисимметричные линейные
колебания молекулы СО2 — симметрич-
ной линейной трехатомной молекулы,
в которой атомы кислорода для рав-
новесной конфигурации расположены
на одинаковых расстояниях ро от ато-
ма углерода (рис. 21.1, а).
§21.1. Характеристика нормальных колебаний многоатомных молекул 607
Полагая
Р\ = Ро + «ь Р2 = Ро+?2,	(21.2)
где gi и д2 — изменения длин связей С—О, имеем для симметричного колебания,
происходящего с определенной частотой (vs — 1 337 см-1)^
91S) = «10 sin 27Г"Л «2S) = «20 sin 27гг/Л («1 о* = «от = «о° )•	(21 -3)
При этом колебании	и pt = pi, т.е. обе связи одновременно удлиняются
и одновременно укорачиваются. Форма колебаний определяется тем, что амплиту-
ды gj0 и ^20 , с которыми изменяются обе связи, и фазы колебании одинаковы.
Для антисимметричного колебания, происходящего с другой частотой (z/e —
2 350 см-1), имеем
«!О) = «ю sin 27ГМ,	= «м sin 27T2/af (9ш =-9м =«0О))-	(21-4)
При этом колебании = -<$ и р\ # р2; в то время как одна связь удлиня-
ется, другая укорачивается, и наоборот. Форма колебаний определяется тем, что
(а)	(а)	с
амплитуды 9j0 и q2Q , с которыми изменяются обе связи, по-прежнему одинаковы
по величине, но фазы колебаний этих связей противоположны.
Симметричные и антисимметричные нормальные колебания молекулы СО2
аналогичны нормальным колебаниям системы, состоящей из двух одинаковых свя-
занных между собой маятников, часто рассматриваемой в качестве простейшего
примера связанных колебаний системы с двумя степенями свободы2).
Связь между маятниками может осуществляться, например, как показано на рис. 21.2, а, б,
через нить АВ, к точкам С и D которой подвешены эти маятники, или, как показано
на рис. 21.2, в, г, при помощи пружины.
Уравнения движения системы таких маятников, при малых углах ai и а2 их отклонения
от положения равновесия, могут быть записаны в виде
d2aii
«I =	= ~Р<*\ +7«2,
? <21-
ст а2
«2 =
где р определяет угловое ускорение данного маятника при его отклонении от положения
равновесия, а 7 — коэффициент связи — определяет угловое ускорение одного из маятников
при отклонении другого
Уравнения (21.5) надо решать совместно. Решение ищем в виде
ai=aiosinart, а2 — а2о sin wt.	(21.6)
Подстановка (21.6) в (21.5) приводит к системе линейных однородных уравнений
(0 - w2)a10 - 7«2о = о, |	)
-7«ю + (0 - w2)«20 = 0, J
Среднее значение двух частот vs\ = 1 286 см 1 и vs2 = 1 388 см 1, наблюдаемых в действительности,
см. ниже, с. 696.
2) Линейным колебаниям молекулы СО2 соответствуют две степени свободы из т — 3N -5 = 4 коле-
бательных степеней свободы. Две другие степени свободы соответствуют деформационным колебаниям,
перпендикулярным к оси молекулы (см. §21.2, с. 610).
Для примера рис. 21.2, в, г /3 = До 4- 7, где До определяет ускорение данного маятника при отсут
ствии пружины (см., например, [127], с. 441).
608
Глава 21. Колебания многоатомных молекул
условием разрешимости которой является равенство нулю ее определителя
(Р - и2)2-у2 = (р-Ш2-^(р-Ш2+^ = 0.
Отсюда находим две частоты нормальных колебаний
4тг2р2 = ш2 = р - 7, 4tt2i/2 = ш2 = р + 7.
(21-8)
(21-9)
(21.10)
Получающееся при подстановке в (21.7) симметричное (а^ = нормальное колебание
с частотой и9 = —	- 7
2тг
= а/ю sin 2irt/sty = а^о sin 2irvst (= а2о = ао) )	(21.11)
аналогично симметричному колебанию (21.3) молекулы СО2 (ср. рис. 21.2, а, в и рис. 21.1,6).
Получающееся при подстановке в (21.7) антисимметричное (а,^ = -а2а>) нормальное
колебание с частотой иа — — у/p + у
2тт
= &\q sin 2лч/а$, а2а) = о$ sin 2irvat (о$ = -о$ =	)	(21.12)
аналогично антисимметричному колебанию молекулы СО2 (ср. рис. 21.2,6, г и рис. 21.1, в).
Отметим, что для системы связанных маятников нормальные колебания (21.11)
и (21.12) получаются лишь при вполне определенных начальных условиях, в частности,
если при t = 0 оба маятника отклоне-
ны одинаково (О| = а2 = что дает
колебание (21.11)) или противополож-
ным образом («! = —а2 = а^, что дает
колебание (21.12)). При произвольных
начальных условиях получается слож-
ное движение, являющееся наложением
обоих нормальных колебаний, при ко-
тором амплитуды колебаний маятников
периодически изменяются и происхо-
дит обмен энергией между маятника-
ми. Отдельному нормальному колеба-
нию системы маятников соответствует
возбуждение одного определенного нор-
мального колебания молекулы. Сложно-
му движению системы маятников, по-
лучающемуся при наложении ряда нор-
мальных колебаний этой системы, со-
ответствует одновременное возбуждение
ряда нормальных колебаний молекулы.
Рис. 21.2. Колебания связанных маятников:
а и б — симметричное и антисимметричное
колебания маятников, связанных нитью;
в \л г — симметричное и антисимметричное
колебания маятников, связанных пружиной
Для полной характеристики г
нормальных колебаний молекулы
нужно знать частоты этих колеба-
ний и соответствующие этим частотам формы колебаний. В рассматриваемом при-
ближении малых колебаний, имеющем широкую область применимости, энергия
квантуется независимо для каждого нормального колебания и равна
1
2
E«i =
(21.13)
§21.2. Классификация нормальных колебаний молекул по их форме 609
где Ui — частота данного нормального колебания, a — соответствующее коле-
бательное квантовое число, в полной аналогии с квантованием малых колебаний
двухатомной молекулы, определяемым формулой (20.18)4). Полная колебательная
энергия равна
— 52 (Vi	2/
i=i	'	'
а соответствующая нулевая энергия колебаний
r j
= ^о,о,...,о = 52 2	(21.15)
i=i z
Простейшие возбужденные колебательные состояния молекулы получаются,
когда Vj — 1, a \ — 0 (г j). Энергия такого состояния равна
r j
Eq = ^0,0,О = 52 2 Рг +	=	4- Vj.	(21.16)
г=1
В этом случае часто говорят, что возбужден один квант j-го нормального колебания.
При переходе между уровнями энергии (21.16) и (21.15) испускается или поглощается
фотон частоты Vj (если не учитывать возможного одновременного малого изменения
вращательной энергии).
Совокупность частот колебательных переходов = 0 —*• Vj\ 1 (г = 1,2,..., г)
и является основной характеристикой нормальных колебаний многоатомной моле-
кулы.
Мы сначала разберем качественные вопросы классификации нормальных ко-
лебаний молекул по их форме (§21.2) и рационального’ выбора колебательных
координат (§21.3), а затем уже рассмотрим количественную теорий колебаний
многоатомных молекул.
§21.2. Классификация нормальных колебаний молекул по их форме
Форма заданного г-го нормального колебания определяется, согласно (21.1),
соотношениями амплитуд ar10 , x2q, ..., с которыми изменяются колебательные
координаты при этом колебании. Если выбрать в качестве колебательных координат
изменения qx длин связей между атомами и изменения углов между связями,
то форма каждого колебания будет характеризоваться соотношениями амплитуд q\Q
и адо, с которыми изменяются различные связи и углы.
Например, для нелинейной трехатомной молекулы Н2О (рис. 21.3) форма ко-
лебаний будет характеризоваться соотношением амплитуд, с которыми будут изме-
няться две связи О—Н и угол Н—О—Н. Если положить
Р1=Ро + ?1, Р2 = Ро+Я2, <Р = <Ро + <*,	(21.17)
где <?|, <?2 и а — колебательные координаты, равные изменениям длин связей
О—Н и угла Н—О—Н (ро и — равновесные значения длин связей О—Н и угла
Н—О~Н), то форма колебаний определяется соотношением амплитуд (/ю, <720 и «о
при данном нормальном колебании. Одно такое колебание показано на рис. 21.3,6;
оно состоит в одновременном изменении длин обоих связей О—Н и угла Н—О—Н
и характеризуется амплитудами <7ю, <720 (причем = <720) и а0, с которыми
изменяются координаты q\, q% и а.
4) Множитель h мы опускаем, как и в (20.66).
20 За. *03
610
Глава 21. Колебания многоатомных молекул
Рис. 21.3. Форма колебаний молекулы Н2О: а — равновесная конфигурация;
б — полносимметричное колебание с одновременным изменением длин связей и угла
В случае более сложной молекулы дело обстоит аналогично. Когда молекула
совершает колебания с определенной частотой, в движении участвуют в принципе
все атомы и одновременно изменяются все связи и углы. Однако это не означает,
что при всех колебаниях все атомы принимают существенное участие в общем дви-
жении и что одновременно значительно изменяются все колебательные координаты.
Наоборот, очень часто колебание практически происходит в определенной части
молекулы, а в некоторых предельных случаях сводится вообще к изменению лишь
длины одной связи или величины лишь одного угла. Могут существовать колебания,
в которые вовлечены все атомы, но при этом изменяются только длины связей
(при неизменных углах) или же только величины углов (при неизменных длинах
связей).
Рассмотрение формы колебаний позволяет произвести классификацию колебаний
по их форме. Прежде всего колебания можно разделить на валентные и деформаци-
онные.
Валентными колебаниями называют колебания, при которых в основном изме-
няются длины связей, а углы между связями приближенно остаются неизменными.
Таким образом, для валентных колебаний
* 0,
га 0.
(21.18)
Для молекулы воды валентным будет колебание, для которого # 0,	# 0, а « 0.
Предельным является случай чисто валентных колебаний, для которых из-
менения углов между связями точно равны нулю. Такие случаи осуществляют-
Рис. 21.4. Полносимметричное
колебание молекулы СН4
ся для некоторых колебаний молекул, обладающих
определенной симметрией. Например, для линей-
ных молекул существуют линейные нормальные ко-
лебания, при которых атомы двигаются вдоль оси
молекулы. Такие колебания (симметричные и ан-
тисимметричные) осуществляются у молекулы СО2
(см. рис. 21.1). Другим примером чисто валентных
колебаний являются полностью симметричные коле-
бания молекулы метана СН4 (симметрия Tj), при ко-
торых все атомы одновременно колеблются отно-
сительно центрального атома вдоль тетраэдрических
осей третьего порядка (рис. 21.4); все четыре свя-
зи изменяются одинаковым образом, а углы между
связями остаются постоянными (равными 109°28/,
см. с. 503).
Деформационными колебаниями называют колебания, при которых в основном
изменяются углы между связями, а длины связей приближенно остаются неизмен-
ными. Таким образом, для деформационных колебаний
7а* ~ °> <4° °-
(21.19)
§21.2. Классификация нормальных колебаний молекул по их форме 611
Рис. 21.5. Деформационное
колебание молекулы СО2
Для молекулы воды деформационным будет колебание, для которого q\ ~ 0, <72 ~ О,
а Ф 0.
Предельным является случай чисто деформаци-
онных колебаний, для которых изменения длин свя-
зей точно равны нулю. Эти колебания, так же как
и чисто валентные, осуществляются для молекул,
обладающих определенной симметрией. В случае
линейных молекул наряду с линейными колеба-
ниями существуют колебания, при которых атомы
движутся перпендикулярно к оси молекулы. При-
мером может служить колебание молекулы СО2,
при котором атом С и атомы О колеблются с про-
тивоположными фазами перпендикулярно к оси молекулы (рис. 21.5). При этом
изменяется угол между связями СО, а длины связей при малых колебаниях остаются
неизменными5).
Действительное колебание молекулы может быть близко как к валентному,
так и к деформационному. Может также осуществляться промежуточный случай,
когда одновременно велики и амплитуды q\$ изменения длин связей и амплитуды
изменений углов. Обычно все же удается приближенно разделить колебания
молекулы на валентные и деформационные.
Кроме классификации колебаний молекулы на валентные и деформационные,
очень важное значение имеет разделение колебаний по степени их локализации.
Наряду с колебаниями всей молекулы как целого, могут иметь место колебания
отдельных частей молекулы и колебания, локализованные на определенных связях
или углах.
Типичным примером нелокализованных колебаний всей молекулы как целого
являются колебания углеродной цепи в молекулах углеводородов, в частности, ко-
лебания углеродного кольца, представляющего замкнутую цепь, в молекуле бензола.
Примером колебаний, локализованных в определенной части молекулы, могут
служить колебания атомов, в основном атомов водорода, в группах СН2 и СН3
молекул углеводородов. Пример колебаний, локализованных на определенной свя-
зи, мы встречаем у органических молекул, содержащих одну двойную связь С=С.
Изменения длины этой связи происходят в значительной степени независимо от из-
менений других связей и углов. Локализация колебаний в определенных частях
молекулы или на определенной связи непосредственно зависит от соотношения
между массами колеблющихся атомов.
Когда между собой связаны два атома различной массы, то в колебаниях отно-
сительно общего центра тяжести участвует в основном легкий атом. Это имеет место
в очень важном случае связей С—Н в органических молекулах: масса атома водорода
в 12 раз меньше массы атома углерода. Атом углерода практически остается в покое,
а колеблется связанный с ним атом водорода. В группах СН, СН2 и СН3 валентные
колебания атомов водорода относительно атома углерода являются внутренними
колебаниями этих групп и мало влияют на связи атома углерода с другими, более
тяжелыми атомами. Изменения последних связей будут происходить в значительной
степени независимо от изменений связей С—Н внутри групп, содержащих атомы
водорода. Например, в молекуле этана (см. рис. 18.5, с. 504) приближенно являются
5) Если обозначить смещения атомов О относительно атома С, перпендикулярные к оси молекулы,
/ У2 \
через у, то длина связи С—О равна р — у/ р^ + у2 я р0 ( 1 4-т I, т. е. изменение длины связи второго
X 2р0 /
порядка малости относительно у, и можно считать колебания чисто деформационными.
612
Глава 21. Колебания многоатомных молекул
независимыми колебания внутри групп СНз и колебание групп СНз, соединенных
связью С—С, друг относительно друга.
Если между собой связаны атомы одинаковой массы, например, атомы углерода
в углеродной цепи, то в изменении длины каждой связи участвуют оба образующих
ее атома. Возникают колебания, охватывающие все атомы цепи.
Существенную роль для классификации колебаний, наряду с соотношени-
ями между массами колеблющихся атомов, играют и относительные величины
сил, возникающих при изменениях длин различных связей и углов между ними;
величина этих сил приближенно определяется соответствующими квазиупругими
постоянными.
Для самой грубой оценки частот различных колебаний можно пользоваться
формулами, аналогичными формуле (20.19) для частоты гармонических колебаний
двухатомной молекулы,
= 2тг
(21.20)
где кх — квазиупругая (силовая) постоянная, а Мх — приведенная масса атомов,
образующих данную связь (или аналогичная величина для атомов, образующих
данный угол)6) 7.
Как следует из (21.20), соотношение частот, соответствующих различным связям
и углам, будет зависеть от соотношения силовых постоянных и от соотношения
приведенных масс:
(21.21)
l/д _ кх Mf,
i/р у кц Мх
Изменение углов между связями происходит гораздо легче, чем изменение длин этих
связей; силовая постоянная &деф для изменения углов мала по сравнению с силовой
постоянной &вад для изменения длин связей
^деф &вал-	(21.22)
Обычно &деф примерно в десять раз меньше, чем &вад. Например, в метане постоянная
ка — ^деф Для изменения углов Н—С—Н почти в 12 раз меньше постоянной kq = къал
для изменения длин связей С—Н. В молекуле воды постоянная &деф для изменения
угла Н—О—Н в 11 раз меньше постоянной &вад для изменения длины связи О—Н.
Для углеродной цепи отношение &деф и &вад (для угла С—С—С и связи С—С)
1 7>
равно — .
В силу соотношения (21.21) частоты деформационных колебаний оказываются
значительно меньше частот валентных колебаний связей, образующих эти углы.
6) Для угла Y—X—Y между связями X—Y, образованными атомом X с атомами Y, при равновесном
Мх
значении этого угла, равном 90°, в (21.20) будет входить просто приведенная масса —— двух атомов X;
в других случаях (при (р / 90°, а также для угла типа Y—X—Z, где Y и Z — различные атомы) Мд
будет выражаться более сложным образом через массы атомов. При этом при сравнении Рд для связей
и для углов, исходя из соответствующих значений кх и Мд, следует брать вместо угловых координат а
линейные координаты р$а (ро — равновесная длина связи), имеющие размерность длины.
7) Если брать значение постоянной £деф с учетом того, что обычно приводимое значение (см. ни^се,
с. 712) рассчитано не для произведения рсс7, а Для произведения рсн7> и поэтому £дсф = к^ (	) =
/1,09\2	/1	7	7	1	2	2	\РСС/
Ц I j = 0,5fc7 I - &7pCH7 = - &дефРсс7 , см- примечание на с. 710; 7 — изменение угла С—С—С).
§21.2. Классификация нормальных колебаний молекул по их форме
613
При &деф — 0,1&вал и том же значении приведенной массы8) отношение частот
|	^вал
равно примерно -. Действительно, частоты деформационных колебаний в два-три
раза меньше частот соответствующих валентных колебаний.
Для молекулы Н2О « 0,43 (рдеф = 1 600 см-1, среднее значение рвал для симметрии-
3 650+ 3 750	_1Ч
ных и антисимметричных колебаний---------= 3 700 см ), для молекулы СО2 это отно-
шение равно 0,50, если брать частоту валентных симметричных колебаний 1 335 см-1, и 0,28,
если брать частоту валентных антисимметричных колебаний 2 350 см-1 (рдеф = 667 см-1).
В важном случае молекул углеводородов частоты деформационных колеба-
ний углов Н—С—Н, образованных двумя связями С—Н, примерно вдвое меньше,
а частоты деформационных колебаний углов С—С—Н, образованных связью С—Н
со связью С—С, примерно втрое меньше частот валентных колебаний С—Н. В этом
случае целесообразно различать два типа деформационных колебаний С—Н —
внутренние и внешние.
При внутренних деформационных колебаниях С—Н изменяются углы Н—С—Н
внутри группы СНз (углерод этой группы соединен еще одной простой связью
с другим атомом С, см. рис. 21.6, а) или внутри группы СН2 (углерод этой группы
соединен еще двумя простыми связями с двумя атомами С или двойной связью
с одним атомом С, см. рис. 21.6,6, в).
Рис. 21.6. Деформационные колебания: а, б, в — внутренние деформационные колебания;
г, д, е, ж, з, и — внешние деформационные колебания
При внешних деформационных колебаниях С—Н изменяются углы С—С—Н
или С=С—Н, определяющие ориентацию всей группы СНз или СН2 в целом
8) Что не совсем правильно, так как для деформационных колебаний входит в общем случае величина,
которая может несколько отличаться от приведенной массы связи, ср. табл. 21.1, с. 630.
614
Глава 21. Колебания многоатомных молекул
относительно связей С—С или С=С (рис. 21.6, г, д, е). К внешним деформационным
колебаниям следует отнести и изменения углов С—С—Н, С=С—Н или С=С—Н,
определяющих ориентацию связи С—Н в случае группы СН, углерод которой со-
единен еще с одним, двумя или тремя атомами С (см. рис. 21.6, ж,з, и).
Деление деформационных колебаний на внутренние и внешние может быть
произведено и в других группах, содержащих атомы водорода, например в груп-
пах NH2.
При сравнении частот различных валентных или различных деформационных
колебаний главную роль играет различие масс атомов и меньшую роль — различие
силовых постоянных.
Малая масса атомов водорода приводит к тому, что частоты валентных коле-
баний связей С—Н, О—Н, N—Н составляют 3 000-3 500 см”* 1. Частоты колебаний
простых связей С—С составляют около 1 000 см-1. Это находится в соответствии
с тем, что приведенная масса связей С—С значительно больше приведенной мас-
сы связей С—Н. Для связей, содержащих тяжелые атомы, частоты колебаний еще
меньше. Например, для связи С—С1 частота колебаний составляет около 700 см-1,
а для связи С—I — около 500 см-1.
Аналогичные соотношений получаются и для деформационных колебаний.
В то время как частоты изменения углов Н—С—Н составляют около 1 400 см-1,
частоты изменения углов С—С—С порядка 300-400 см-1, т.е. примерно втрое
меньше. Последнее хорошо согласуется с тем, что масса атомов, присоединенных
к центральному атому углерода, увеличивается в 12 раз. Частоты изменения углов
С—С—Н, соответствующие внешним деформационным колебаниям, составляют
около 1000 см~* и примерно в 1,4 раза меньше частот изменения углов Н—С—Н,
соответствующих внутренним деформационным колебаниям; это связано с тем, что
в последнем случае приведенная масса, входящая в (21.20), примерно вдвое меньше
При одинаковых массах атомов различие частот валентных колебаний может
определяться различием силовых постоянных для связей различной кратности.
Наиболее важным случаем является случай простых, двойных и тройных связей
между атомами углерода — связей С—С, С=С и С=С. Частота колебаний возрастает
при переходе от простой связи к двойной от 1 000 см-1 до 1 600 см-1 и при переходе
от двойной связи к тройной от 1 600 см-1 до 2 000 см-1, что соответствует общему
/2000 \2
увеличению силовой постоянной в ----- | = 4 раза.
\ 1000У
На основе классификации колебаний по их форме для рассматриваемой мо-
лекулы получается ряд типов колебаний. Например, для молекул углеводородов
основными типами колебаний будут: валентные колебания С—Н, валентные ко-
лебания С—С, внутренние и внешние деформационные колебания углов Н—С—Н
и С—С—Н, деформационные колебания углов С—С—С.
Очень существенным результатом классификации колебаний молекулы по их
форме является то, что определенные частоты колебаний соответствуют определен-
ным связям и определенным группам связей в молекуле, определенной простран-
ственной структуре молекулы. Наличие таких характерных частот колебаний —
характеристических частот — позволяет делать выводы о строении изучаемых мо-
лекул и имеет большое значение для молекулярного спектрального анализа вещества
по колебательным спектрам. Весьма важный вопрос о характеристических частотах
9) См. табл. 21.1, с. 630. Очень грубо можно положить приведенную массу для углов Н—С—Н равной
1
- а для углов С—С—Н — просто Мц.
§21.3. Вид потенциальной энергии и выбор колебательных координат 615
и о характеристичности колебаний молекул вообще (включая и вопрос о характе-
ристичности интенсивностей) будет специально рассмотрен в дальнейшем, в гл. 23,
посвященной колебательным спектрам (см. § 23.6).
Следует подчеркнуть, что в большинстве случаев классификация колебаний
по их форме является лишь приближенной. Встречаются и колебания промежуточ-
ного типа, например, колебания, промежуточные между валентными и деформа-
ционными, о чем уже упоминалось выше (см. с. 611). Отнесение таких колебаний
к определенному типу вообще теряет смысл. Однако и приближенная классифи-
кация, основанная на рассмотрении предельных случаев, имеет большое значение
при изучении колебательных спектров, особенно в связи с возможностью нахо-
ждения характеристических частот, являющихся признаками определенного состава
и определенной структуры молекулы.
В дальнейшем мы будем широко пользоваться классификацией колебаний мо-
лекул по их форме. В соответствии с этой классификацией может быть решен
и вопрос о рациональном выборе колебательных координат, который рассматрива-
ется в следующем параграфе.
§21.3. Вид потенциальной энергии и выбор колебательных координат
Вопрос о правильном выборе колебательных координат имеет существенное
значение для решения задачи о колебаниях многоатомных молекул, так как ввиду
сложности этой задачи, обусловленной большим числом степеней свободы, особенно
важно решать ее наиболее рациональными и возможно менее громоздкими методами.
Здесь идет речь об исходных колебательных координатах, в которых выражают
потенциальную и кинетическую энергию молекулы, и амплитуды изменения ко-
торых определяют наглядным образом форму колебаний. Окончательными колеба-
тельными координатами являются нормальные координаты, т. е. координаты, каждая
из которых изменяется с определенной частотой vi соответствующего нормального
колебания по закону
6 — 6о sin 2Tri/tL	(21.23)
Нормальные координаты линейно связаны с исходными колебательными коор-
динатами. Эта связь будет подробно рассмотрена ниже, в §21.4.
Для случая колебаний связанных маятников (§21.1) нормальными координатами будут
& =	= Oq ) sin 2тг^, £а =	sin 2лту.	(2Г.24)
Для отдельных нормальных колебаний исходные колебательные координаты аг и а2 находятся
по формулам (21.11) и (21.12), которые примут вид
a\s) =	= а(а) = £>.	(21.25)
Полные выражения исходных колебательных координат через нормальные будут следу-
ющими:
О] =	+ а,а) = & +	1
«2 = «2Л) +	= 6 -	)
т.е. координаты «| иа2 линейно связаны с координатами £3 и £а. Это соответствует тому, что
действительные колебания являются наложением нормальных.
Так как колебательное движение состоит в периодическом изменении отно-
сительного расположения атомов, то в качестве колебательных координат следует
выбирать изменения величин, характеризующих это расположение. Подобными
616
Глава 21. Колебания многоатомных молекул
величинами служат расстояния между атомами рх и углы между связями Изме-
нения qx и dp расстояний и углов (по отношению к их равновесным значениям рдо
и см. (21.2) и (21.17)) и представляют естественные колебательные координаты.
Следует отметить, что при введении естественных координат как относительных отпадает
необходимость в учете вращательного и поступательного движений и сразу получается чисто
колебательная задача. В ряде работ в качестве колебательных координат вводились смещения
атомов из положений равновесия в прямоугольной системе координат и приходилось учиты-
вать дополнительные условия равенства нулю количества движения молекулы и ее момента
количества движения, чтобы отделить колебание от поступательного движения и вращения.
В естественных колебательных координатах полное количество движения и полный момент
количества движения молекулы автоматически обращаются в нуль [305].
Изменения длин связей и углов между связями, введенные нами в качестве
колебательных координат в предыдущих параграфах, представляют частные слу-
чаи естественных колебательных координат; можно вводить изменения расстояний
и между атомами, не образующими друг с другом химических связей, и изменения
углов, не являющихся углами между соседними связями, имеющими общий атом.
В выборе независимых естественных колебательных координат всегда имеется
определенный произвол10). Например, для молекулы воды вместо координаты а
(см. (21.17)) можно выбрать изменение q расстояния pi2 между атомами водорода
(ср. с. 501).
Выбор колебательных координат (под которыми мы в дальнейшем будем все-
гда понимать естественные колебательные координаты) следует производить в со-
ответствии с силами взаимодействия между атомами в молекуле, определяющими
колебательное движение. Эти силы характеризуются постоянными, входящими в вы-
ражение для потенциальной энергии. Таким образом, вопрос о выборе колебательных
координат оказывается тесно связанным с вопросом о виде потенциальной энергии.
Рассмотрим подробнее выражение для потенциальной энергии многоатомной
молекулы.
Потенциальная энергия молекулы, т. е. ее электронная энергия при непо-
движных ядрах (см. § 17.3, с. 475), является функцией естественных колебательных
координат:
U = U(xhx2,...,xr).	(21.27)
Для малых колебаний около положений равновесия, ограничиваясь квадратичными
членами в разложении потенциальной энергии по колебательным координатам,
аналогично (17.32), мы получаем
U = ^2k^x*xr (k^ = k^)-	(21.28)
A/i
Разложение функции (21.27) от г переменных Z|, х2у..., хТ около точки Xi = х2 = ... =
хг = 0 имеет вид
U = UQ +
1 V-Л / d2U \
. 1 о ) хХхц “Ь
2!	' \дххдхп / о
Ад
1 у-л / д3и \
3! 2^
Хци
(21.29)
,0) Только в случае двухатомной молекулы имеется лишь одна возможная естественная колебательная
координата — изменение q расстояния р между атомами.
§21.3. Вид потенциальной энергии и выбор колебательных координат 617
Линейный член обращается в нуль в силу условий равновесия —j = 0J, которые
должны выполняться для всех координат; кубическим и высшими членами разложения мы
пренебрегаем, считая их малыми, a Uq = (^эл)о полагаем равным нулю, т. е. отсчитываем
потенциальную энергию от ее минимума. Обозначая
д2Ц \
Ад
мы получаем (21.28).
Выражение (21.28) существенным образом от-
личается от выражения (17.32) для потенциальной
энергии двухатомной молекулы тем, что оно со-
держит не только квадраты х\ каждой координа-
ты, но и произведения разных координат хх
и Хр. Для того чтобы выяснить смысл членов обоих
типов, мы выпишем потенциальную энергию в яв-
ном виде для нелинейной трехатомной молекулы
общего типа XYZ (рис. 21.7) в координатах q\, q2
и а, где gi и дг - изменения длин связей X—Y
и X—Z, а а — изменение угла Y—X—Z. Мы имеем,
(21.30)
Рис. 21.7. Естественные
колебательные координаты
для молекулы типа XYZ
полагая хх — qx,x2 = qi, ху — а и учитывая, что kXfJl = kfiX
U — - k\\ql + - k22ql + ^зз®2 + &12<71<72 + &i3<7iа + &23<72а>	(21.31)
т.е. получаются три диагональных члена, аналогичных (17.32) и содержащих ква-
драты колебательных координат, й три недиагональных члена, содержащих произ-
ведения разных колебательных координат.
Рассмотрим действующие в этом случае силы.
Сила, изменяющая длину первой связи, равна
0U
/| =-т—= -fcn9i-fci2g2-fci3a.	(21.32)
oqi
Первый член в (21.32) представляет обычную квазиупругую силу, зависящую от зна-
чения рассматриваемой координаты, второй и третий члены дают квазиупругие
силы, изменяющие данную координату, но зависящие от изменения второй связи
и от изменения угла. Коэффициент к^ представляет силовую постоянную первой
связи, а коэффициенты к^ и &1з характеризуют действие на первую связь изменений
второй связи и угла.
Аналогично сила, изменяющая длину второй связи, равна
017
А — ~~тг~ — ~км\ - ^iiqi - ^2з«-	(21.зз)
oq2
Сравнение (21.33) с (21.32) показывает, что действие изменения первой связи на вто-
рую определяется тем же коэффициентом к\ 2, что и действие изменения второй связи
на первую. Таким образом, коэффициент &|2 определяет взаимодействие связей; со-
кращенно часто говорят о «взаимодействии» соответствующих координат. Вообще,
недиагональные коэффициенты в (21.28) кх^ (р # Л) определяют взаимодействие
координат хх и а диагональные коэффициенты кхх — «действие координаты хх
на саму себя».
618
Глава 21. Колебания многоатомных молекул
Наконец, для угловой координаты имеем”*
dU
/з =	= —&13#1 - k23q2 - k33a.	(21.34)
оа
В дальнейшем мы будем обозначать диагональные постоянные к\\ — силовые
постоянные для соответствующих расстояний и углов — через кХх, а недиагональные
постоянные другими буквами. Полагая
— kq{,	к22 — kq2,	к33 — ка,
А?|2 — h,	feu = Ai,	к23 = Л2, J
мы запишем (21.31) и (21.32)-(21.34) в виде
1	2	1	2 ~ 2	+ 2	+ 0L7	1	2 - k„a + hq,q2 +A\qya +A2q2a,		(21.36)
Л ~~Oqi f =_™ h dq2	= ~k4iq\ ~ hq2 - Ata, = -hqt - kq2q2 - A2a,	►	(21.37)
h	dq,	= -Aiqi — A2q2 — kaa.		
Последние три члена в (21.36) можно рассматривать как энергию взаимодействий
координат qi, q2 и а друг с другом. При h =	= А2 = 0 эта энергия обращается
в нуль и остаются лишь члены, содержащие квадраты координат. Силы (21.37)
при этом сводятся к обычным квазиупругим силам, зависящим только от свойств
данной связи или данного угла. Однако пренебрежение недиагональными силовыми
постоянными возможно лишь для самых грубых оценок, и при всех расчетах коле-
баний их необходимо учитывать. Это является одной из причин, обусловливающих
сложность расчетов колебаний молекул.
В общем случае многоатомных молекул потенциальную энергию можно пред-
ставить в виде, аналогичном (21.31):
U ~ 2	> &аажа кх^хххр (&А/х — 1^/ха)-	(21.38)
А
В (21.38) выделены члены, зависящие от квадрата одной координаты, и члены,
зависящие от произведений двух координат и характеризующие их взаимодействие.
Сила, изменяющая координату жд, равна12*
у—'
fx — ~	~ / j кхц^ц — —кхх^х ~ кх^ц)	(21.39)
А	р
т. е. слагается из обычной квазиупругой силы, зависящей от значения данной
координаты, и суммы квазиупругих сил, зависящих от значений всех остальных
координат.
1 **Это есть обобщенная сила, представляющая в данном случае момент силы относительно оси,
перпендикулярной к плоскости угла.
,2) В общем случае это есть обобщенная сила, соответствующая обобщенной координате жд, в частно-
сти, для угловых координат — момент силы.
§21.3. Вид потенциальной энергии и выбор колебательных координат 619
В принципе, все / 0, однако практически в сложных молекулах для коор-
динат х\ и соответствующих связям или углам, далеко отстоящим друг от друга,
их можно полагать равными нулю.
Исходя из выражения (21.38) для потенциальной энергии, можно решить
и вопрос о наиболее рациональном выборе колебательных координат. Так как
решение задачи о колебаниях сильно усложняется наличием недиагональных членов,
то целесообразно эти координаты выбирать так, чтобы недиагональные члены
были по возможности малыми. Подобными координатами обычно и являются,
в соответствии с наглядными представлениями о строении молекул, изменения длин
связей и изменения углов между связями.
Мы рассмотрим данный вопрос опять на примере нелинейной трехатомной
молекулы. Потенциальная энергия такой молекулы при выборе в качестве коордйнат
изменений и q2 длин связей и изменения а угла между связями выражается, как
мы видели, формулой (21.36), при пренебрежении недиагональными постоянными
сводящейся к
1 2 1 ? 1 7 z
- k(hq2 + - kaa .	(21.40)
Соответствующую силовую модель молекулы называют моделью валентных сил; в ней
учитываются квазиупругие силы, характеризующие изменения длин связей, т. е. рас-
стояний между атомами, связанными химическими (валентными) силами, и изме-
нения углов между связями (валентных углов), но пренебрегается взаимодействиями
связей и углов.
Однако можно выразить потенциальную энергию, вводя в качестве координат
(см. с. 616) £1, и <7з, где q^ — изменение расстояния между атомами, не связанными
химически (рис. 21.7). Таким образом, координата а заменяется координатой <73,
при тех же координатах q\ и <72- В координатах q\, <72 и q2 потенциальная энергия
будет иметь вид
— 2	+ 2	+ 2 Чз^з +	13^1^3 + /г-2з^2^з>	(21.41)
где силовые постоянные будут иными даже в членах, содержащих, как и прежде, д*,
<72 и Иной будет и энергия взаимодействия, определяемая тремя последними
членами в (21.41). Если положить в (21.41) h! — h" — h'" = 0, то получается модель
молекулы, которую называют моделью центральных сил; в ней учитываются только
квазиупругие силы, действующие вдоль линий, соединяющих атомы, т. е. централь-
ные силы.
Как показывают конкретные расчеты (см., например, [55], т. 1, гл. 15), обычно
модель валентных сил ближе к действительности, чем модель центральных сил, — не-
диагональные члены для модели валентных сил значительно меньше, чем для модели
центральных сил. Иначе говоря, модель валентных сил является лучшим нулевым
приближением. Поэтому при решении задач о колебаниях молекул следует, как пра-
вило, вводить в качестве координат изменения длин связей и величин углов между
связями. Эту систему колебательных координат принято называть валентно-силовой
системой координат. Систему колебательных координат, при которой вводятся толь-
ко изменения расстояний между атомами, как связанными, так и не связанными
химическими (валентными) силами, принято называть центрально-силовой системой
координат.
|3) Переход от (21.36) к (21.41) можно произвести, выразив а через q\, q2 и qj и подставив в (21.41).
Мы имеем (см. рис. 21.7) р]2 = р\ + р\ - ^P\pi cosy? и, дифференцируя это выражение, легко найти а,
если учесть малость колебательных координат (см. [55], т. 1, с. 536).
620
Глава 21. Колебания многоатомных молекул
В дальнейшем мы будем пользоваться валентно-силовыми координатами. Сле-
дует иметь в виду, что применение этой системы координат отнюдь не означает, что
берется потенциальная энергия типа (21.40) для модели валентных сил14), без учета
взаимодействий. Нужно исходить из полного выражения типа (21.36) для потенци-
альной энергии (в общем случае из выражения (21.38)).
Разумеется, если исходить из полного выражения (21.41), то конечный результат по-
лучится тот же, что и при применении выражения (21.36), однако расчеты будут сложнее.
В валентно-силовых координатах уже в нулевом приближении получится разделение колеба-
ний на валентные и деформационные, рассмотренное нами в предыдущем параграфе.
При использовании валентно-силовых координат необходимо иметь в виду, что
для полной характеристики колебательного движения молекул не всегда достаточно
введения изменения длин связей и величин углов между связями, имеющими общий
атом. Очень важным для многих сложных молекул является случай, когда одна часть
молекулы может поворачиваться относительно другой (см. § 18.1, с. 503). В этом
случае внутреннего вращения для характеристики поворотов одной части молекулы
относительно другой вводят углы взаимного поворота от значения которых
зависит потенциальная энергия. Пренебрегая взаимодействиями координат Xv между
собой, а также с изменениями q\ длин связей и с изменениями углов между
связями, что является разумным приближением, можно представить дополнительную
потенциальную энергию молекулы, зависящую от углов в виде
и' = 52
V
(21.42)
где U(xv) ~ функции вида, изображенного на рис. 18.6 (с. 504). Возможные при этом
крутильные колебания рассмотрены более подробно в §21.8. Там же разобран
и вопрос о внутренних перегруппировках атомов, возможных для некоторых молекул,
имеющих не одну, а две равновесные конфигурации, соответствующие различным
взаимным расположениям ядер.
Рис. 21.8. Выход связи
из плоскости
В случае плоских молекул, содержащих не менее че-
тырех атомов, существуют колебания, сопровождающиеся
выходом рассматриваемой связи из плоскости молекулы.
В этом случае можно ввести угол </?, характеризующий вы-
ход данной связи из плоскости (рис. 21.8). Для неплоских
колебаний иногда бывает рационально ввести смещения
атомов, перпендикулярные к плоскости молекулы, хотя
при этом и приходится в явном виде учитывать условия ра-
венства нулю полного количества движения и полного мо-
мента количества движения молекулы (см. выше, с. 616).
§21.4. Общий метод решения задачи
о нормальных колебаниях молекул
Задача о нормальных колебаниях многоатомной молекулы решается на осно-
ве общей теории малых колебаний с учетом специфических особенностей моле-
кул [305, 55].
,4) Иногда моделью валентных сил называют модель, в которой учитываются, при применении
валентно-силовых координат, и некоторые взаимодействия.
§21.4. Общий метод решения задачи о нормальных колебаниях молекул	621
В теории малых колебаний исходят из квадратичных выражений для кинетиче-
ской энергии Т и потенциальной энергии U, которые можно записать в виде
1 г 1 т
Т — — ^A/i^A^/iy U 2 ^АдЗ'А^'д?	(21.43)
А, /1=1	А, /1=1
dxx
где Т зависит только от скоростей х\ = &U — только от координат жд.
dt
Выделяя в выражениях для Т и U члены с квадратами х\ и х\ (см. (21.38)),
получим (МА/1 = МРЛ, kXfl = k^x)
Т =	+	U^kxx^^xxx,. (21.44)
AV	А	V
(/х>А)	(ц>Х)
Мы видели, что вторая сумма в правой части формулы для потенциальной энер-
гии соответствует взаимодействию координат. Это взаимодействие можно назвать
динамическим, так как оно определяется квазиупругими силами и выражается через
силовые постоянные. Аналогично можно считать, что вторая сумма в правой части
формулы для кинетической энергии также характеризует взаимодействие; это взаи-
модействие следует назвать кинематическим, так как оно не зависит от квазиупругих
сил и связано с характером движения.
Если недиагональные коэффициенты и (р # А) обращаются в нуль,
т. е. отсутствует как кинематическое, так и динамическое взаимодействие, то мы
получаем
U=[-^k^L	(21-45)
А	А
а полная энергия
H = T + U = ^~ (Mxxx2x+kxxx2x) =^НХ	(21.46)
А	А
равна сумме энергий Яд гармонических осцилляторов, колеблющихся по закону
жА = ж до sin оад£ = ж до sin liruxt	(21.47)
с частотами
(21.48)
Таким образом, при отсутствии кинематического и динамического взаимодействий
каждая координата изменялась бы независимо от других с частотой о»д.
В общем случае, когда взаимодействия координат не равны нулю, можно всегда
привести Т и U к виду, аналогичному (21.45), если перейти от исходных координат х\
к их линейным комбинациям:
6 = 52 Са^л.	(21.49)
А
В этих нормальных координатах Т и U имеют вид
CZ=|l2fc^2>	(21-50)
622
Глава 21. Колебания многоатомных молекул
где Mi и ki — новые постоянные, зависящие от прежних постоянных МХ[к и кх^
и коэффициентов С,д преобразования (20.49). Полная энергия
Н = Т + и = ^-(м£ + к£)=^Н,,	(21.51)
t	i
т. е. опять равна сумме энергий гармонических осцилляторов, колеблющихся по за-
кону (см. (21.23))
6 = 6о s^n &it — 6о sin 2тгц^,	(21.52)
где
Ui = 2ТГ1/,- = 4	(21.53)
У Mi
— частоты нормальных колебаний.
Исходные координаты будут выражаться через нормальные координаты при помощи
линейных соотношений, обратных (21.49):
=	(21.54)
к
Для определенного г-го нормального колебания (£, # 0, & = 0 при к / г) мы получим
(см. (21.52))
= dA.<.0 Sin lirvil.	(21.55)
z(i)
Сравнение c (21.1) показывает, что коэффициенты dxi = —— определяют форму г-го нор-
6о
мального колебания. Пример подобной связи исходных координат с нормальними был уже
рассмотрен выше в начале §21.3 (см. (21.26)). В этом простейшем случае колебаний двух
связанных маятников, аналогичном случаю линейных колебаний молекулы СО2, d]s = 1,
— 1 И d|a — 1,	— 1.
Отметим, что Т и U часто записывают в несколько ином виде, вводя в качестве
нормальных координат = \/Жб- Учитывая, что ki = получаем вместо (21.50)
г=|52<-'2’ и =	<21-56)
i	i
При этом, однако, £, имеют иную размерность, чем хх. Можно ввести в Т и U постоянный
множитель Мо, имеющий размерность массы. Тогда
Т=^М0УЧ"2, U=l-M0 УЖ	(21-57)
i	i
„ 1 /
где А- =	& = \ — & имеют размерность длины, что очень удобно.
VMq V Мо
Задача о малых колебаниях всегда по существу сводится к приведению Т и U
к виду (21.50) и разбивается на два этапа. Первый состоит в составлении алге-
браических уравнений для определения частот и формы колебаний, а второй —
в решении полученных уравнений. На втором этапе задача является чисто матема-
тической и сложность ее решения зависит от степени получающихся алгебраических
уравнений, которая для системы с г степенями свободы в общем случае равна г.
При составлении алгебраических уравнений возникают специфические трудности,
зависящие от характера рассматриваемой системы и возрастающие с увеличением
числа степеней свободы; для решения задачи могут быть применены различные
конкретные способы.
§21.4. Общий метод решения задачи о нормальных колебаниях молекул 623
Потенциальная энергия молекулы может быть представлена как функция есте-
ственных колебательных координат, являющихся относительными координатами,
и задачу следует решать именно в этих координатах. Если кинетическая энергия
также явно выражена через естественные колебательные координаты, что легко
сделать лишь в самых простейших случаях, то при решении задачи можно исходить
из выражений Т и U, выписанных в явном виде.
Рассмотрим подобное решение для случая валентных колебаний линейной трех-
атомной молекулы типа АВС, состоящей из трех атомов А, В и С разной массы
(рис. 21.9). На данном примере мы сможем
одновременно показать, каким методом наи-
более рационально решать задачу о колебани-
ях многоатомной молекулы в общем случае.
Потенциальная энергия имеет вид
МА гАВ Мв гвс мс
хА	хв	хс
Рис. 21.9. Линейная молекула типа АВС
1	2	1	2
и = - k\\q\ + - &22<?2 +
(21.58)
где
qi=xQ-xM q2 = xc-xB	(21.59)
— естественные колебательные координаты, выражающиеся через смещения жА,
жв и хс атомов вдоль оси молекулы и представляющие изменения длин связей
А—В и В—С соответственно. Последний член в правой части формулы (21.58)
характеризует динамическое взаимодействие связей А—В и В—С.
Кинетическая энергия, выраженная через производные координат q\ nqi, имеет
вид
1 Э 1	9
т = -Mi\q} + -м22<?2 + ^\2q\q2i	(21.60)
, где
Мд(Мв + Мс)	(МА + Мв)Мс	. МАМс
, М22 = -------------, М12 = -------------. (21.61)
Мд + Мв + Мс7	МА + Мв + Мс’	Мд+Мв + Мс V 7
Действительно, кинетическая энергия движения относительно центра тяжести, выра-
женная через смещения атомов из первоначальных положений, равна
Т=Х-Мкх\+Х- Мвхв + | Мсх2с	(21.62)
при условии, что
МАхА + Мвхв + Мсхс = 0.	(21.63)
Согласно (21.59), q\ = хв — хЛ и q2 = хс - жв> откуда с учетом (21.63) находим
• —	МсИ1 + Mcq2 . _ МА ji — Mcq2 _ AfA*Zi + (МА + MB)q2
М/± + Мв + Мс	М& + Мв + Mq	М^ -j- Мв + Mq
Подстановка (21.64) в (21.62) после соответствующих выкладок и дает (21.61). Мы видим,
что даже в этом самом простом случае преобразование кинетической энергии к естественным
колебательным координатам связано с громоздкими выкладками.
Последний член в выражении кинетической энергии (21.60) характеризует
кинематическое взаимодействие связей А—В и В—С, которое осуществляется через
атом В, участвующий в изменении длин обеих связей. При возрастании массы
атома В коэффициент Мп будет стремиться к нулю, и взаимодействие будет
исчезать. Коэффициенты М\\ и М22 при этом станут равными Мд и Мс, так как
будут двигаться лишь атомы А и С, а атом В будет неподвижен.
624
Глава 21. Колебания многоатомных молекул
Для системы с кинетической энергией (21.60) и с потенциальной энерги-
ей (21.58) уравнения движения имеют вид (для симметрии мы вводим М2\ = М\2
И *21 = *12)
Л/ц9| + Mi2q2 = -*n9i - *1292, )	... ...
?	(21.65)
М2\Ц\ + M22q2 —	~ &22<?2- J
Они получаются сразу из уравнений Лагранжа (20.13). Мы имеем
d	ЭТ	dU			
di d	—- = Muq] +Mnq2 = ^q\ от	dqi dU	= Ft =	-*ii9i -*1292, I	(21.66)
di	—- — M22q2 4- Mi2qi — oq2	dq2	= f2 =	—*2292 — *129l> J	
что и дает систему (21.65), если для симметрии ввести М21 = Мп и fc2i = &12-
Можно сразу решать систему дифференциальных уравнений (21.65), что часто
и делают. Однако более рационально сначала разрешить ее относительно ускоре-
ний q\ и q2. При этом непосредственно выявляется связь задачи для двух степеней
свободы с соответствующими задачами для одной степени свободы каждая, полу-
чающимися при отсутствии взаимодействия (к\2 — М\2 = 0), когда M\\q\ = —k\\q\,
M22q2 = -k22q2, т. e.
..&11 '
q\ = -77- — -D^q^
(21-67)
n?22
<?2 = “77“ <72 = -D22q2-
Л^22	j
Отсюда определяются частоты колебаний в «нулевом приближении»
О), = 27ГР1 = 4,	<*> = 2хи2 = \	= \/^22,	(21.68)
у М\\	у М22
£ц	^22
где введены обозначения (см. (20.9)) D\\ —- и D22 —
М{\	М22
Для разрешения системы (21.65) относительно q\ и q2 нужно умножить ее
уравнения на Ли и Д|2 и сложить их, а затем умножить на Д21 и А22 и опять
сложить, подобрав Дц, Д12, А2\, А22 так, чтобы,5)
А\\М\\ + Д12М21 = 1, А\\М\2 + Д12М22 — 0, 1
Д21 М\ 1 + А22М2\ — 0, ^21^12 + А22М22 = 1. f
В результате получаем
(ДцМп + Ai2M2\)q\ + (ДцМ12 + A\2M22)q2 — q\ —
— ^!l(—&11<7| ~ ^12^2) + ^!2(“&21<71 “ ^2292)?
(Д21 Afj 1 + A22M2\)q\ + (Д21 ^fi2 + A22M22)q2 = q2 =
— ^21(“~ k|2<Z2) + ^22(~^2191 ~ ^22^2)? >
откуда
q\ =	+ ^12^21)^1 “ (^11^12 -h ^12^22)92, 1
q2 — —(^21^1! + ^22^21 )q\ ” (^21^12 + ^22^22)?!- J
(21.69)
(21.70)
(21.71)
,5) Это можно сделать, так как мы имеем четыре уравнения для четырех неизвестных. При этом в силу
М\2 = М2] оказывается, что и = ^12, т.е. фактически число разных коэффициентов А равно трем.
§21.4. Общий метод решения задачи о нормальных колебаниях молекул 625
(21.72)
Систему (21.71) можно записать в виде, аналогичном (21.67):
Ц\ — ~D\\q\ - Z>i2^2, 1
q2 — -D^qi - D22q2- )
Коэффициенты Dn и D2i характеризуют взаимодействие связей А—В и В—С
и зависят как от динамических постоянных к, так и от кинематических постоянных А.
Коэффициенты D называют поэтому коэффициентами полного взаимодействия.
Соответственно коэффициенты к называют коэффициентами динамического взаимо-
действия и коэффициенты А — коэффициентами кинематического взаимодействия.
Коэффициенты с двумя одинаковыми индексами — диагональные коэффициенты —
будут определять при этом действие данной координаты на саму себя.
Рассмотрим подробнее все три типа коэффициентов и соотношения между
ними.
Динамические коэффициенты к\^ характеризуют, как мы знаем, силовые свой-
ства молекулы, рассматриваемой как совокупность атомов, связанных квазиупругими
силами.
Кинематические коэффициенты Адд, так же как и коэффициенты в выра-
жении (21.60) для кинетической энергии, характеризуют кинематические свойства
молекулы. По отношению к коэффициентам М\ц они являются обратными и име-
ют размерность —, где М — масса. Для рассматриваемого случая вычисление
М
коэффициентов А, согласно (21.69) и (21.61), дает
МА + Мц	М& + Мс ла	1
Ан = “ТГТГ—>	=	—» Л12 - Л21 - ~ —,
Л/д Л/в	МцМс	Mq
т. е. они имеют более простой вид, чем коэффициенты Л/ц, ЛГ22 и ЛГ12 = М21.
Коэффициенты Ац и А22 равны обратным величинам приведенных масс
МдМв	МВМС
— -------- Л12 = -----------
Л/д + ЛГв	Л/в + ЛГс
связей А—В и В—С, а коэффициент А|2 — обратной величине массы атома В,
общего для связей А—В и В—С. Это не является случайностью, а вытекает из общих
свойств коэффициентов А, которые будут нами подробно рассмотрены в даль-
нейшем. Оказывается, что коэффициенты А можно заранее вычислить для все-
возможных комбинаций связей и углов, имеющих общие атомы (при отсутствии
общих атомов эти коэффициенты равны нулю), не рассматривая явного выражения
для кинетической энергии.
Если записать коэффициенты кинетической энергии Л/дд в виде симметричной
(ЛГ!2 — М2\) матрицы
(21.73)
1й £!	(2|-74)
то соотношения (21.69) будут представлять систему уравнений для определения обратной
матрицы
Л|2
Л 22
Ли	А\2 |
	А22 1
Мп	М12
м21	ЛГ22
(21.75)
удовлетворяющей условию
I Ап
I A2i
Таким образом, совокупность кинематических коэффициентов образует матрицу, обрат-
ную матрице коэффициентов кинетической энергии. В символическом виде АТ = 1.
(21.76)
626
Глава 21. Колебания многоатомных молекул
Коэффициенты полного взаимодействия D\u, введенные в (21.72), определятся
через коэффициенты ЛА/1 и к^и по формулам (ср. (21.71) и (21.72)):
£>12 = ^11^12 -h ^12^22)
£>22 = ^21^12 + ^22^22?
£>11 = ^1!&11 + ^12^21,
£>21 = ^21^11 + -422&2Ь
которые можно записать в общем виде
А\^к^у.
р
Суммирование происходит по второму значку коэффициента 4 и по первому значку
коэффициента к.
Если коэффициенты ЛАр и к^и известны, то по формулам (21.78) легко находятся
и коэффициенты D\v.
Формула (21.78) выражает закон умножения матрицы кинематических коэффициентов
на матрицу динамических коэффициентов
I -411 -4-12 I I
I -421 А22 I I &21
(21.77)
(21.78)
ki2 I _ I £>н
к 22 I I £>21 £>22 I
Здесь каждую строку первой матрицы нужно умножать на каждый столбец второй матрицы.
Умножение первой строки на первый столбец дает £>н, умножение первой строки на второй
столбец дает D]2 и т.д. В символическом виде AU = D.
Существенно отметить, что коэффициенты D\v в отличие от коффициентов ЛАр
и кри не являются симметричными
£>др £>рА)
что сразу видно из сравнения D\2 и D2\.
Перейдем теперь к решению системы уравнений (21.72), которое будем искать
в виде гармонических колебаний:
qi — q\Q sin q2 = q2o sin wt.
Подстановка (21.81) в (21.72) приводит к системе уравнений
(£>11 - (Д2)^ю + £>12<?20 = О, 1
£>21 <710 + (£>22 - <^2)<72О = 0- J
В этой системе неизвестными являются частота колебаний сд и амплитуды коле-
баний «/io, <720, определяющие, согласно (21.81), форму колебаний. Относительно
неизвестных q\$ и д2о система (21.82) является линейной и однородной. Для суще-
ствования отличного от нуля решения такой системы нужно, чтобы определитель,
составленный из ее коэффициентов, равнялся нулю:
Ви - шг
D2i
£>12
Z?22 ~
D[2
= 0
(21.79)
(21.80)
(21.81)
(21.82)
(21.83)
или в раскрытом виде
(Z)|| — (Д2)(£>22 — W2) — Di2^2l — W4 — (Z>n + D22)(^2 + £>ц£>22 ~ £>12£>21 = 0- (21.84)
Квадратное уравнение (21.84) относительно Л = сд2 имеет два решения:
(21.85)
§21.4. Общий метод решения задачи о нормальных колебаниях молекул 627
которые в данном простейшем случае можно выписать в явном виде
2 _ Р, 1 + £>22 , /(-Dll +-Е>22)2	_
— -----Z---- ± \ ---------------Ь'цЬ'22 + Ь'12Ь'21 —
2 V 4
V 	(21.86)
Dl}+D22 (Dn - D22)2
— -----~± V ------------------- + b'12b'21 •
2 у 4
При отсутствии взаимодействия (D\2 — D2\ — 0)
u;<1)2=Z?u, (л(2)2 = D22,	(21.87)
что, разумеется, непосредственно получается из (21.83). Подставив решения (21.85)
в (21.82), получаем значения амплитуд колебаний		_ о/1*2 - р22 ' d2] <Х-Р22 D2[	’	►	(21.88)
ДЛЯ (Д = (У1) ДЛЯ (Д =	910 _			
	1°’	Ра			
				
определяющих форму обоих колебаний. Тем самым		задача полностью решена.		
Описанный метод решения задачи о валентных колебаниях линейной трех-
атомной молекулы, основанный на введении коэффициентов полного взаимодей-
ствия Dxy, может быть обобщен и на общий случай любых малых колебаний
молекулы с г колебательными степенями свободы. В естественных координатах х\
дифференциальные уравнения движения записываются в виде
хх = -^Рх,х„ (у = 1,2,..., г)	(21.89)
р
и их решениями являются гармонические колебания с частотой сд,
9а = 5ао sin wf,	(21.90)
что приводит к системе линейных однородных уравнений для амплитуд колебаний
- <5Л^2)др0 = 0 (А,р= 1,2,3,..., г)	(21.91)
— 1 при и — Л и дХи — 0 при и Ф Л). Условие разрешимости этой системы состоит
в равенстве нулю определителя г-го порядка, составленного из ее коэффициентов:
£>и - ш2 D2\	7712 £>22 ~	-	D\r d2t	= 0.	(21.92)
Он	Dr2	Drr — ел		
Определитель (21.92) представляет уравнение r-й степени относительно сд2 — ве-
ковое, или секулярное, уравнение16), корни которого дают г частот нормальных
колебаний
а/1*, а>(2), ..., и(г\	(21.93)
|6) Уравнения аналогичного типа встречаются в небесной механике при решении задач о вековых
(секулярных) возмущениях движений планет.
628
Глава 21. Колебания многоатомных молекул
Подстановка частот в систему уравнений (21.91) приводит к соответствующим
значениям амплитуд
<$, <$, , <$,	(21.94)
определяющим форму данного нормального колебания.
Таким образом, второй этап решения механической задачи о нормальных ко-
лебаниях молекулы состоит в решении векового уравнения r-й степени (21.92)
для нахождения частот колебаний и в решении системы г линейных однородных
уравнений (21.91) для нахождения формы колебаний. Для решения первого этапа за-
дачи — составления векового уравнения (21.92) — необходимо найти коэффициенты
полного взаимодействия Dxu по формуле
г
Dxv = ^Axltkltv	(21.95)
Входящие в формулу (21.95) кинематические коэффициенты Лдр определяются
по общим формулам, рассматриваемым более подробно в следующем параграфе,
и могут быть найдены в численном виде для молекулы с известными массами
атомов и с известными параметрами (значениями расстояний и углов) равновесной
конфигурации.
Входящие в формулу (21.95) динамические коэффициенты kfll, — силовые
постоянные — в принципе могут быть найдены путем квантовомеханического
расчета. Однако даже для самых простых молекул квантовомеханический метод
приводит к весьма сложным вычислениям и для определения силовых постоянных
приходится пользоваться полуэмпирическими методами, основанными на опытных
значениях частот колебаний.
Задача численного расчета колебаний некоторой молекулы может быть решена
только в случае, если значения силовых постоянных уже найдены из данных
для других молекул похожей структуры.
Если значения силовых постоянных для молекулы неизвестны, то нахождение
коэффициентов полного взаимодействия сводится к умножению заданных в числен-
ном виде кинематических коэффициентов на силовые постоянные, рассматриваемые
как неизвестные, подлежащие определению. Их значения должны быть подобраны
так, чтобы вековое уравнение (21.92) давало при его решении частоты, совпадающие
с найденными на опыте. К вопросу об определении значений силовых постоянных
мы вернемся в дальнейшем (см. гл. 23, с. 707).
§21.5. Коэффициенты кинематического взаимодействия
и составление вековых уравнений
Рассмотрим более подробно коэффициенты кинематического взаимодейст-
вия A\fl и составление с их помощью вековых уравнений. Каждый коэффициент Лдр
определяет взаимное влияние координат и т.е. различных связей и углов, ко-
торое зависит в общем случае как от масс атомов, так и от взаимного расположения
этих связей и углов17). Коэффициенты 4др обладают двумя основными свойствами18).
1. Значение заданного коэффициента Лдр зависит только от характеристик
связей и углов, изменения которых определяются координатами х\ и ж/х, но не за-
висит от характеристик всех других связей и углов (изменение которых определяется
17^ Мы будем говорить для определенности о связях, однако все дальнейшее относится и к расстояниям
между атомами, не связанными между собой валентными (химическими) силами.
18) См. [551, т. 1, гл. 5 и 6.
§21.5. Коэффициенты кинематического взаимодействия
629
з, но и от жА;.
Рис. 21.10. Молекула типа ABCD
координатами где и # Л и /г). Этим коэффициенты Адр отличаются от коэффи-
циентов Мдр в выражении для кинетической энергии (см. (21.43)), не обладающих
таким свойством инвариантности. В частности, в рассмотренном выше случае ко-
лебаний линейной трехатомной молекулы диагональные коэффициенты Ан и Ац
для связей А—В и В—С зависят, согласно (21.73), только от масс двух атомов,
образующих эту связь (Ап от МА и Мв, А^ от Мв и Мс), а коэффициенты Мп
и М22, согласно (21.61), — от масс всех трех атомов (Мц зависит не только от МА
и Мв, но и от Me, а М22 зависит не только от Мв и *'	’' 4
2. Отличны от нуля только коэффициен-
ты Адр, характеризующие кинематическое взаи-
модействие связей или углов, имеющих по край-
ней мере один общий атом, и в выражения
для этих коэффициентов входят массы лишь об-
щих атомов. Например, для молекулы ABCD,
изображенной на рис. 21.10, отличен от нуля ко-
эффициент взаимодействия (дВА, «ас) связи В—А
с углом А—В—С, одну сторону которого образует
эта связь, и в его выражение входят массы общих
атомов А и В; также отличен от нуля коэффи-
циент взаимодействия (<Jcd, «ас) связи С—D с углом А—В—С, содержащий массу
общего атома С. Коэффициент взаимодействия (^ва? 9ср) связей В—А и С—D,
не имеющих ни одного общего атома, равен нулю. Сами значения коэффициентов,
отличных от нуля, совершенно не зависят в силу их инвариантности от наличия
в молекуле других связей и углов; например, наличие или отсутствие связи С—D
не влияет на значение коэффициента взаимодействия (двл, «ас)-
Можно найти явный вид коэффициентов Ад^ для различных комбинаций связей
и углов. Для нециклических молекул получается одиннадцать комбинаций связей
и углов (образованных соседними связями), для которых коэффициенты Ад^ отлич-
ны от нуля. Формулы для этих коэффициентов приведены в табл. 21.1. В таблице
даны также пояснительные чертежи для каждого случая; атомы, общие для взаи-
модействующих связей и углов, показаны сплошными кружками, остальные атомы
светлыми кружками.
Формулы даны в векторном виде, а в про-
стейших случаях также и в развернутой форме.
При этом введены следующие векторы, характе-
ризующие нормальную конфигурацию и пока-
занные на пояснительных чертежах стрелками.
1.	Единичный вектор ег, направленный
вдоль г-й связи.
2.	Единичный вектор /t--, перпендикуляр-
ный к г-й связи, лежащий в плоскости угла ij
и направленный от г-й связи к j-й (рис. 21.11).
3.	Вектор
f — til 1 Zzi
-c ij — i
POi POj
Рис. 21.11. Введение векторов f
(21.96)
где pQi и poj — равновесные длины г-й и j-й связей. Он лежит в плоскости угла ij
и при poi = poj направлен по биссектрисе этого угла (см., например, пояснительный
чертеж для взаимодействия угла с самим собой).
Коэффициенты кинематического взаимодействия
Таблица 21.1
Вид взаимодействия	Номера по порядку	Взаимодействую- щие координаты	Пояснительный чертеж	Значение коэффициента взаимодействия
Взаимодействие связи с самой собой	1	(9,9)	е мх я м2	1 1 mJ + mJ
Взаимодействие двух связей	2	(9i,92)	бу/" м0	1 1 ТГ6162 = ТГ cos^12 Мо	Мо
Взаимодействие связи с углом, образованным этой связью	3	(gi,<xi2>	о. е Мо	-77—61/21 = -77— Sin ^>12 М0Р2	MqP2
Взаимодействие связи с углом, имеющим один общий атом со связью	4	(91, «23)	е, Г2тг^А/2з о	~—e]F 23 Мо
	5	(91,«12)	>^1	
Глава 21. Колебания многоатомных молекул
Продолжение таблицы 21.1
Взаимодействие угла с самим собой	6	(а 12, «12)	f124. м' м0		'м~^П + Юг" 2	+ ЮГ 2 ^21 “ Mq	М\р\	М2Р2 1/112	\	1	1 = — s + -у	cos ^12	4	у 4	г ^0 ур2 р\ Р\р2	J	М\р\	М1р*
Взаимодействие углов, имеющих два общих атома	7	(«12, «1з)	а /12М,	мй	~jTTF 12F13 + --3/1/13 Мо	М{р\
	8	(«12, «13)	а «12 Ч.Л, “13 мр/13		~ v; "п F12/ 1з ~ п F13/12 M2pi	М3Р1
Взаимодействие углов, имеющих один общий атом	9	(«12, «34)	еК\ «12 f17^^,F34 а34 <<7з	е4\		—F12F 34 Мо
	10	(«12, «34)	°X«i., /	V an\Fn^C^— 6X34 С<^е2	Z34		~~юг—& 12/34 Морз
	11	(«12, «34)	° ап 6X34 ° /ц* 7м		
Обозначения-. ех — единичный вектор вдоль связи А; /Ад — единичный вектор в плоскости (Хр), перепендикулярный
к связи A; = —fx 4--------f А; М — массы атомов; рх — длина связи; <р\„ — угол между связями А и р.
Рх Ри
§21.5. Коэффициенты кинематического взаимодействия
632
Глава 21. Колебания многоатомных молекул
В формулы входят значения Мг масс атомов, равновесные значения р0« длин
связей и произведения векторов е:, и Fij, которые могут быть выражены через
равновесные значения углов между связями и равновесные значения длин связей.
Вектор выражается через единичные векторы et и е;- по формуле
fa =	~ е'cos	(21 -97>
Sin Vjj
Действительно, прибавляя к вектору е7 вектор — et costf:j (рис. 21.11), мы получаем вектор
длины sin Оф перпендикулярный к et и лежащий в плоскости угла ij, т.е.
fij sin Oij = ej - costftJ,	(21.98)
откуда и получается (21.97).
С помощью формул (21.97) и (21.96) легко вычислить все произведения, в которые
входят векторы и учитывая углы между векторами et, т.е. между направлениями
связей, для равновесной конфигурации молекулы.
Таблица 21.1 позволяет без труда находить значения коэффициентов Адм
для конкретных случаев. Так, для линейной трехатомной молекулы значения ко-
эффициентов Ап и Л22 (см. (21.73)) для взаимодействий (gj,gi) и (<?2, <?2) сразу
находятся из таблицы, а значение коэффициента Л12 для взаимодействия (q^ q2) по-
лучается, если положить cos $j2 = -1 (ei и е2 в этом случае имеют противоположные
направления).
Вывод выражений для коэффициентов кинематического взаимодействия основан на не-
посредственном составлении уравнений движения, связывающих ускорения х\ с обобщен-
dU
ными силами Fx = - -— в естественных колебательных координатах.
дхх
В случае линейной трехатомной молекулы коэффициенты определяются по этому методу
следующим образом. Уравнение движения атомов А, В и С (см. рис. 21.9, с. 623) имеют вид
dU	dU	dU
=	=	M^q = Fq = - — , Mcxc = Fc = - — .	(21.99)
дхА	dx^	Oxq
Потенциальная энергия является функцией координат q{ = жв — жА и q2 = хс- жв (см. (21.58)
и (21.59)), т.е. U(q\yq2) = U(xQ -х^хс - жв), причем для дальнейшего нет необходимости
выписывать явное выражение (21.58).
Рассматривая U как сложную функцию, имеем
dU _ дхЛ du _ дхй du _ dxc	dU dqi dqi дхА dU dqi dqi дхв _dU_ dq^ dq2 dxc	- dU dqC dU dq2 _ dq2 дхц - dq2	du du ~ у—ь у—> dqi dq2		>	(21.100)
что дает систему уравнений - ди	, MqXq =	dU dU - “t; F t 5 oq\ dq2	Mcxc = ~	dU dq2		(21.101)
Деля эти уравнения на МА, 7ИВ и Мс соответственно и вычитая из второго уравнения первое,
а из третьего второе, получим
/1	1 \ dU 1 dU Л
Q\ —	—	— I + ТУ I У I" ТТ У >
уМА Mq J dqi Mq dq2
(21.102)
1 dU / 1	1 \ dU
\Mb+	,
§21.5. Коэффициенты кинематического взаимодействия
633
Коэффициенты, связывающие ускорение qx и обобщенную силу — -—, представляют
dU
искомые коэффициенты AXtl (ср. (21.70), где, согласно (21.58), — k{\q\ — k\2q2 =---
, . ди , 9q>
и -«21 <71 “ «22<?2 —-), и мы получаем
dq?
А	1 ^Мд+Мв = J_ 1 = Мв + Мс =	=___1_
Л/д Л/в ЛГдЛГв	Л<7В	ЛГв-Л^с	Л<7В
т.е. снова приходим к выражениям (21.73), однако несравнимо более простым способом.
Из приведенного вывода видно, что недиагональный коэффициент Л|2 = 42i не равен
нулю потому, что от хв зависят как дь так и q2 в аргументе функции U(q\, q2)\ взаимодействие
осуществляется через атом В, участвующий одновременно в изменениях обеих связей А—В
и В—С.
В случае произвольной многоатомной молекулы коэффициенты AXll определяются проще
всего векторным методом, если представить для малых колебаний естественные координаты
в виде
«л =	(21.103)
где rt — смещение из положения равновесия г-го атома, a EXi — векторы, определяемые
заданием равновесной конфигурации.
В частности, изменение длины связи двух атомов А и В равно
Qx = вл(гв - rA) = eAB(rB - гл)	(21.104)
(см. рис. 21.12; проекция малого смещения гв ~ г а считается совпадающей, ввиду малости
угла поворота связи, с величиной этого смещения), а изменение угла В—А—С между
двумя связями А—В и А—С равно
(га-Гв)Увс , (га-ГсЦсв
-----------------1	 (21.105)
Рав--------------Рас
(см. рис. 21.13;	= -<рв ~^с, где малые углы <рв и <рс равны отношениям (гв -га)/вс к Рав
и (гс - гА)/св к рдс соответственно, а /вс и /св — векторы, определенные выше, см. с. 629,
и рдв и рАС — равновесные длины связей).
Рис. 21.12. Изменение длины связи
Рис. 21.13. Изменение угла между двумя связями
Уравнения движения в векторной форме имеют вид
= -^iU(x^x2i..., хГ) = -^iU(xx),	(21.106)
где U — функция естественных координат. Градиент от потенциальной энергии по г, равен,
с учетом (21.103),
ЕЭ(7	Y—dU	.qx
= 22 —19>.	(21.107)
дХц	дХу
ц	д
,9) Как известно, Vt/(y>) — a V(Ao,r), где Aq — постоянный вектор, равен просто Ао-
о<р
634
Глава 21. Колебания многоатомных молекул
Согласно (21.106) и (21.107),
1 V—г 9U
(2LIW)
д
Переходя и в левой части уравнения к относительным координатам, получаем
EY—ExiEui dU	v—г	6U	y—
^А.г. = - 22 М. д^ = ~^2Ах1‘д^ = ~^2	(21.109)
1	IД	Д	ДР
где
i
Суммирование в (21.110) происходит по всем атомам, для которых Exi и Е^ одновременно
отличны от нуля, т. е. по атомам, общим для координат хх и хц. Формула (21.110) представляет
общее выражение для коэффициентов кинематического взаимодействия, позволяющее легко
находить их значения, если известны Exi и Е^. Например, для взаимодействия связи с самой
собой, согласно (21.104), ЕХЛ = -еАВ, Ехв — -еАВ и
-^АА ~^АВ _ еАВ	еАВ _ _J  
МА	мв ~ МА	мв - МА мв’
(21.111)
для взаимодействия связи А—В с углом В—А—С (общие атомы А и В), согласно (21.105),
-®да =	-Едв = и так как еАВ/вс = 0 (см. рис. 21.11 и рис. 21.13), то
Рав Рас	Рав
.	_ -^АА-^дА ^АВ^дв _ _ еАв/сВ
д МА Мв Мдрдс '
(21.112)
что дает выражение, приведенное в табл. 21.1, если обозначить
сав — /св /гм МА — Мо и Рас — Pi-
Помимо коэффициентов взаимодействия связей и углов между соседними связями,
можно, найдя выражения типа (21.103) для изменений х углов между связями, не имею-
щими общих атомов, и для углов определяющих выход связей из некоторых плоскостей
(см. рис. 21.8, с. 620), вычислить коэффициенты взаимодействия и для координат х и
При составлении вековых уравнений коэффициенты кинематического взаи-
модействия обычно выписывают в виде таблицы. Так же поступают и с коэф-
фициентами динамического взаимодействия — силовыми постоянными (таблицу
силовых постоянных записывают либо в численном виде, если их значения из-
вестны, либо в буквенном виде, если их значения требуется найти). По форму-
лам (21.95) определяются коэффициенты полного взаимодействия, причем, если
расположить их в виде таблицы, то для получения векового уравнения достаточно
добавить к диагональным членам -щ2 и приравнять соответствующий определитель
нулю.
В качестве примера можно рассмотреть случай нелинейной трехатомной мо-
лекулы XYZ (рис. 21.7, с. 617), равновесная конфигурация которой характеризуется
равновесными длинами связей рю = Pxy, Р20 — pxz и равновесным углом
При введении естественных координат fl, ?2 и а таблица кинематических
коэффициентов АХр (согласно табл. 21.1) имеет вид
§21.6. Свойства векового уравнения и методы его решения
635
Я2
111 1
---1-- 	 	COS <Pq
Мх Му Мх-------------------Мхр\
111 1
---	---1_	 	cos (pQ
Мх Мх Mz------------------MxPi Y
1	1	1/112	\	1	1
----COS - —- COS ^0 — ~2 + “2-COS ^0 + w-2 + ‘ТТЛ
МхР\	Мхр2 Мх \Р\ р2 Р\р2 / MYpf MZp\
(21.113)
Согласно (21.35), таблица динамических коэффициентов будет
Ч\ 42 ol
q\ kq{ h Ai
42 h ^2
a Ai A2 ka
(21.114)
Перемножая кинематические и динамические коэффициенты, согласно (21.95)20) 21,
находим коэффициенты полного взаимодействия и соответствующее вековое урав-
нение
jfc9l-hAi2?&-l-А|зЛ1 — о;2 Ацк + Ai2kq2 4-А13А2 Ан А| 4- А12А24- Ацка
A2\kqx-\-A22h-\-A22)Ai Л21/1 + A22kq2+ Л23А2—й?2 Л21 Ai 4- A22A2 4- A^k^
АцкЯ1 4-4з2^4- А33Л1	Л31Л4-Аз2&£2 4-А33Л2	A31A1	4-	A32A24-	A^ka	—	u>2
= 0,
(21.115)
в котором численные значения кинематических коэффициентов (21.113) обозначены
через Ац, Л22, А33, А13 = А31 и А23 = А32.
§21.6. Свойства векового уравнения и методы его решения
Рассмотрим некоторые свойства векового уравнения. Вековое уравнение в фор-
ме (21.92) обладает тем важным свойством, что если все недиагональные элемен-
ты Ъдр (и А) равны нулю, то частоты колебаний равны просто
W<1)2=_DI1; <42)2=D22, 4Г)2 =Drr.	(21.116)
Мы получаем определенное приближение для частот колебаний — нулевое прибли-
жение2,).
Если недиагональные элементы малы по абсолютной величине по сравнению
с разностью значений диагональных элементов
|PaJ < \DXX - Dvv\,	(21.117)
то нулевое приближение будет давать хорошие результаты и эти результаты легко
можно еще уточнить.
Для простоты мы рассмотрим случай векового уравнения второго порядка,
для которого было получено точное решение (21.86). Мы будем считать Е>ц — D22 > 0,
20) Каждая строка матрицы (21.113) умножается на каждый столбец матрицы (21.117) (ср. (21.78)).
21) Если исходить из уравнений движения типа (21.65) и сразу искать решение системы в виде (21.81),
то получается определитель, содержащий ш2 также и в недиагональных членах, и подобное нулевое
приближение не получается естественным образом, как для определителя (21.92).
636
Глава 21. Колебания многоатомных молекул
Решение (21.86) можно представить в виде
2 _	+ D22 D\i - Z>22 A 4Z>i2Z>21
(jJ —	zb	A / 1	.
2	2 V (Ли-£>22)2
(21.118)
При выполнении условия (21.117) второй член в подкоренном выражении мал
по сравнению с единицей и приближенно мы имеем
(/T+S.1+I)
2	D\\ + D22	Г£>ц - D22	D\2D2\
ш —---------±----------р--------
2	L	2 Du-D22
(21.119)
что дает решения
J')2	_ (i)2	Г>127?21
“ -П|| + п11-в2!		 Ul)r\ “р £>и - d22
J2)2 _	- 27112721	_ (2)2	D^D2\
UJ	— -*-^22 du-d22	— D\ 1 - £>22
(21.120)
и
Если £>12 и Z>2i порядка А по сравнению с Dn, £>22 и £>ц - £>22, то член -
D\ 1 - £>22
имеет, очевидно, порядок А2 по сравнению с ними, и поэтому дает поправку
«второго приближения» (поправку первого приближения представляли бы члены
порядка А). При £>12^21 > 0 (что по большей части, хотя и отнюдь не всегда,
имеет место22)) большая частота вследствие взаимодействия еще увеличивается,
а меньшая частота — уменьшается; разность этих частот увеличивается. Про-
исходит как бы «отталкивание» частот. При £>^£>21 < 0, наоборот, разность частот
уменьшается, они как бы «притягиваются». Этот качественный результат остается
справедливым и когда взаимодействия не являются малыми, т.е. не удовлетворяется
условие (21.117).
Можно показать, что и в общем случае при выполнении условия (21.117)
применимы формулы, аналогичные (21.120), и приближенные значения частот
равны
(21.121)
В случае, когда одна из частот сильно отличается от всех других, формула (21.121)
будет справедлива и для нее, даже если для других пар частот соотношение (21.117)
не выполняется. Для такой частоты форма колебаний будет характеризоваться
тем, что23)
*ао>^о О'/А),	(21.122)
т.е. в основном будет изменяться лишь координата жд.
Подобный случай может иметь место, когда в молекуле существует одна связь,
содержащая атом водорода, что приводит к большому значению £>дд, I £>ЛЛ «--).
V Мн 7
На частоту колебаний такой связи мало влияют взаимодействия с другими связями
и углами, а само колебание будет в основном сосредоточено на этой связи.
22) Как отмечалось выше (см. с. 626), Р12 # Di\.
23)Для случая г = 2 это видно из формулы (21.88); аналогичный результат получается и в общем
случае.
§21.6. Свойства векового уравнения и методы его решения
637
При малости коэффициентов полного взаимодействия одной группы коорди-
нат с другой группой координат колебания этих групп приближенно разделяются.
В частности, при наличии ряда связей С—Н в молекулах углеводородов колебания
этих связей можно приближенно отделить от остальных колебаний.
Когда разности £>ЛЛ - Duu не удовлетворяют условию (21.117), даже если их
абсолютные величины и не очень велики, роль взаимодействий становится весь-
ма существенной и действительные частоты колебаний будут сильно отличаться
от частот колебаний в нулевом приближении.
Важным является случай, когда в нулевом приближении частоты совпадают,
т. е. Dxx — Dvim что имеет место при наличии в молекуле одинаковых связей
или углов. Этот случай также можно разобрать на примере векового уравнения вто-
рого порядка. Положим Рц = D22 = D и D\2 = D2\24). Решение (21.86) принимает
очень простой вид
ш2 = Р0±£>12,	(21.123)
т. е. вместо одной частоты нулевого приближения получаются две — одна большая,
а другая меньшая — происходит расщепление частот. Примером могут служить
валентные колебания молекулы СО2, аналогичные колебаниям двух одинаковых
связанных маятников (ср. (21.10); р = Dq, у = —D\2).
Аналогичный результат получается и при совпадении п коэффициентов Dxx
(п 3). Вместо п одинаковых частот нулевого приближения получается п отличных
друг от друга частот, причем порядок величины расщепления определяется порядком
величины коэффициентов взаимодействия Dxu между одинаковыми координатами.
При нахождении действительных частот колебаний, обычно сильно отличаю-
щихся от частот нулевого приближения, приходится решать вековые уравнения вы-
соких степеней. Для численного решения таких уравнений разработаны специальные
методы и в настоящее время успешно применяются электронные вычислительные
машины, позволяющие быстро определять корни вековых уравнений очень высокой
степени вплоть до нескольких десятков. Одновременно могут быть получены и ре-
шения системы уравнений (21.91) для определения отношений амплитуд колебаний,
т. е. формы колебаний.
Решение в численном виде вековых уравнений высоких степеней может производиться
различными способами. В частности, рациональным методом в ряде случаев является метод
последовательной диагонализации [307], согласно которому в вековом уравнении при по-
мощи последовательных линейных преобразований для пар координат жЛ, xv постепенно
уничтожаются недиагональные элементы, начиная от самых больших. Для одновременного
определения корней векового уравнения и формы колебаний могут применяться методы ите-
рации, позволяющие путем повторения определенной операции переходить от приближенных
значений искомых величин к более точным, например, методы итерации Гопштейна [308]
и особенно Маянца [309] (обзор различных методов см. [55], т. 1, гл. 8). В соответствии
с различными методами решения вековых уравнений ведется программирование при расчетах
на электронных вычислительных машинах.
В алгебраическом виде решение вековых уравнений высоких степеней практи-
чески невыполнимо (такие уравнения получаются тогда, когда надо определять неиз-
вестные силовые постоянные, см. конец §21.4, с. 627). Поэтому очень существенно
понижение степени вековых уравнений, подлежащих решению. Если молекула
обладает симметрией, то понижение степени уравнений происходит автоматически.
24^ При одинаковых связях или углах Лц = Л22 и £ц = &22, поэтому, согласно (21.77), одновременно
Рц = Лц&ц + Л 12^21 = Л22&22 +^21&12 = ^22 И = Л11 fc|2 + Л I2&22 = Л22АГ21 + Л21^ц = D2\ \ При ЭТОМ
учтено, что fc|2 = &2i и Л|2 = Л21 (см. (21.65) и примечание на с.624).
638
Глава 21. Колебания многоатомных молекул
Колебания молекулы при этом разделяются на колебания различных типов сим-
метрии, и для каждого типа симметрии задача решается отдельно. Классификация
колебаний по типам симметрии имеет большое значение и для интерпретации спек-
тров; от типов симметрии колебаний зависят правила отбора при колебательных
переходах как в поглощении и испускании, так и в комбинационном рассеянии. Вви-
ду важности вопроса о симметрии колебаний молекул он будет подробно рассмотрен
в следующей главе.
§21.7. Ангармоничность колебаний многоатомных молекул
Для колебаний многоатомных молекул, так же как и для колебаний двухатом-
ных, нужно учитывать ангармоничность, проявляющуюся тем сильнее, чем больше
колебательная энергия, приходящаяся на отдельные нормальные колебания. Эта
ангармоничность обусловлена отличием реальных сил в молекуле от квазиупругих.
Соответственно и потенциальная энергия не является чисто квадратичной функцией
вида (21.28).
Если принять во внимание ангармоничность, то в общем случае колебательная
энергия молекулы будет определяться не формулой (21.14), содержащей лишь члены,
линейные относительно колебательных квантовых чисел, а формулой
Яызд,- =	+ |) + 53 d'k\Vl + (Vk + 0>	(21.124)
I	'	/	lk	X	' X	'
(*»
содержащей наряду с линейными членами и квадратичные.
Формула (21.124) существенно отличается от формулы (20.83) для энергии
колебаний двухатомной молекулы: во второй сумме в (21.124) (заменяющей член
/	1\2	/ Ц2
vexe\v + -J в (20.83)) имеются не только диагональные члены типа da\Vi + -) ,
но и недиагональные члены типа du-	(к > г), характеризую-
щие взаимное влияние нормальных колебаний. В этом проявляется то важное
обстоятельство, что при наличии ангармоничности не только изменяется каждое
нормальное колебание, но они перестают быть независимыми друг от друга. Само
понятие о нормальных колебаниях становится приближенным и при очень боль-
ших амплитудах колебаний вообще теряет смысл. Следует подчеркнуть, однако, что
при не очень больших амплитудах колебаний выделение нормальных колебаний
является разумным нулевым приближением.
В рассматриваемом приближении, в котором справедлива формула (21.124),
dik
коэффициенты dik малы по сравнению с коэффициентами ц- и отношения —
не превышают нескольких сотых, подобно отношению хе = -------- для двухатомных
Ve
молекул.
Формула (21.124) получается, подобно формуле (20.83), при учете членов третьей и че-
твертой степени в разложении потенциальной энергии по колебательным координатам. Если
исходить из вида потенциальной энергии, уже выраженной в нормальных координатах
(см. (21.50)), то при учете этих членов ее можно записать в виде
=	+	+	+ - •	(21.125)
г	i]k	ijkl
Наряду с членами типа аги^ и Ъпг1^ появляются и смешанные члены третьей и четвертой
степени, что указывает на невозможность точного разделения энергии на части, зависящие
§21.7. Ангармоничность колебаний многоатомных молекул
639
только от одной координаты каждая. Энергия Н = Т 4- U уже не является суммой энергий
независимых осцилляторов, даже ангармонических.
Кубические члены (первого порядка малости) и члены четвертой степени (второго
порядка малости) дают при применении квантовомеханической теории возмущении поправки
второго порядка малости к энергии, что и приводит ко второй сумме в формуле (21.124).
Усложнение формулы (21.124) по сравнению с формулой (20.83) делает учет ан-
гармоничности для многоатомных молекул практически весьма трудным; такой учет
может быть выполнен лишь для простейших многоатомных молекул. Учет ангармо-
ничности наиболее существен для молекул, содержащих атомы водорода, например,
для молекулы воды Н2О. Для органических молекул, в частности молекул углеводо-
родов, ангармоничность в первую очередь необходимо учитывать при рассмотрении
валентных колебаний связей С—Н, особенно при их сравнении со связями С—D
в дейтерозамещенных соединениях.
Приближенный учет ангармоничности для связей С—Н и С—D может быть выполнен
путем введения спектроскопических масс (см. §20.7, с. 599). Рассматривая колебания С—Н
и С—D как колебания атомов Н и D и беря эмпирическое значение постоянной 4А
в формуле (20.130), равное 0,080, мы получаем спектроскопические массы
Мн = 1,088, Мр = 2,128
(21.126)
вместо обычных масс М'п = 1,088 и = 2,014 (в единицах
Значения (21.126) спектроскопических масс часто применяются
Мо.б ч
атомной массы —— ).
16
при расчетах колебаний
органических молекул.
Вследствие ангармоничности частоты переходов Vi = 0 —* Vi = 1, соответству-
ющих отдельным нормальным колебаниям, не совпадают с нулевыми частотами
соответствующих гармонических колебаний.
Нулевая энергия колебаний равна
= ^о,о,...,о = У^ - 4- У2 4	(21.127)
i	ik
и частота перехода Vi — 0 —> Vi = 1 составляет
v'i — (^o,i)i = 1Sd,o,...,i,...,o - Eq = Ui + 2da + ~ У^ dij. (21.128)
Здесь коэффициент da характеризует ангармоничность данного нормального ко-
лебания, а коэффициенты dij (j г) — связь различных нормальных колебаний,
обусловленную ангармоничностью.
Для случая нелинейной трехатомной молекулы частоты переходов будут
, 1 i/j —	4- 2d\। 4- ~ d\2 4-	1 \ 2 ^13’ 1
, 1 i/2 - ^2 + 2d22 + ~ d\2 4-	|<*23, >	(21.129)
, 1 Щ — рз 4- 2d33 4- - ^13 4-	1 2 23 >
Для молекулы воды, в частности, разница наблюдаемых частот и нулевых частот ц
оказывается весьма заметной. Мы имеем
= 3 650,0 см-1,	= 1 595,0 см“’,	= 3 755,4 см-1,
= 3 825,3 см”1,	i/2 = 1 653,9 см-1,	i/3 = 3 965,6 см-1.
(21.130)
640
Глава 21. Колебания многоатомных молекул
Важная роль ангармоничности определяется тем, что наряду с переходами
с Av, — 1 оказываются возможными переходы с |AvJ > 1 — обертоны, подобные
обертонам двухатомных молекул, и составные частоты, получающиеся при одно-
временном изменении квантовых чисел для двух или нескольких колебаний.
Наиболее существенную роль играют обычно переходы между основным состо-
янием (0,0,...) и возбужденными состояниями (v\,v2,...). Для таких переходов
мы получаем следующую классификацию (указано, как это принято, только возбу-
жденное состояние):
основные частоты (1, 0, 0,...) (0, 1,0,...) (0, 0, 1,...)...
первый (2, 0,0,...) (0, 2, 0,...) (0, 0, 2,...)...
второй (3,0, 0,...) (0, 3, 0,...) (0,0, 3,...)...
обертоны <
(1, 1,0,...) (1,0, 1,...) (0, 1, 1,...)...
(21.131)
составные частоты
(2,1,0,...) (1,2, 0,...) (2,0, 1,...)...
(1, 1, 1,0,...) (1, 1,0, 1,...)........
Таким образом, получается большое число возможных переходов. К вопросу
об обертонах и составных тонах мы вернемся при рассмотрении колебательных
спектров многоатомных молекул (см. гл. 23, с. 676).
Рассмотрение ангармоничности в данном параграфе относилось к случаю, когда
все частоты колебаний различны. Для молекул, обладающих достаточной симме-
трией, имеются совпадающие частоты, соответствующие вырожденым колебаниям,
которые подробно будут разобраны в гл. 22. Для выроженных колебаний основная
формула для энергии колебаний с учетом ангармоничности несколько отличается
от формулы (21.124) (см. ниже, с. 674). В частности, это имеет место для линейных
молекул, у которых деформационные колебания, перпендикулярные к оси молекулы,
являются вырожденными.
§21.8. Внутренние движения с большими амплитудами
в многоатомных молекулах
До сих пор мы подробно рассматривали колебания квазитвердых молекул, харак-
теризующихся одним вполне определенным (в заданном электронном состоянии)
равновесным расположением ядер, т. е. обладающих одним минимумом потенци-
альной энергии, вокруг которого происходят колебания малыми амплитудами.
Выше уже отмечалась (см. § 18.1, с. 503 и § 21.3, с. 620) возможность внутреннего
вращения; при этом одна часть молекулы может поворачиться относительно другой
на значительные углы и в предельном случае получается свободное вращение. В § 21.3
также упоминалось о внутренних перегруппировках атомов в молекулах, для которых
имеется не одно, а два равновесных расположения ядер; такие перегруппировки
представляют особого рода колебания большой амплитуды и малой частоты. Как
в случае внутреннего вращения, так и в случае внутренних перегруппировок молекулу
нельзя уже считать квазитвердой — имеется два или более минимумов потенциальной
энергии и становятся возможными периодические внутренние движения с большими
амплитудами; молекулу же приближенно нельзя рассматривать как твердое тело.
Мы сперва разберем случай внутреннего вращения на примере молекулы эта-
на С2Н6, затем случай внутренней перегруппировки примере молекулы аммиака NH3.
§21.8. Внутренние движения с большими амплитудами
641
Равновесная конфигурация этана, изобра-
женная на рис. 21.14, я, соответствует транспо-
ложению связей С—Н (см. с. 504). Если рас-
сматривать молекулу вдоль связи С—С, то ато-
мы в группах С—Н образуют два равносторон-
них треугольника, повернутых друг относительно
друга на 60° (рис. 21.14,6). Потенциальная энер-
гия как функция угла поворота % одной группы
СНз относительно другой будет иметь вид, при-
веденный на рис. 21.15. Три одинаковых мини-
мума получающейся кривой соответствуют трем
взаимным расположениям групп СНз, X — 60°,
180°, 300°; эти расположения отличаются лишь
перестановкой атомов Н. Минимумы отделены
максимумами, сответствующими цисположению
связей, X — 0°, 120°, 240°25); разность высот
максимумов и минимумов определяет высоту Uq
Рис. 21.14. Равновесная
конфигурация молекулы этана:
а — вид сбоку; б — вид вдоль связи
потенциальных барьеров, отделяющих минимумы друг от друга. Возможны два пре-
дельных случая внутреннего вращения. Когда энергия внутреннего вращения много
меньше Uq, оно будет сильно заторможенным, и вокруг каждого из трех миниму-
мов возможны крутильные колебания, состоящие в периодических изменениях угла
X ~ Xoi (i = 1, 2, 3) с амплитудой, меньшей 60°. Соответствующие уровни энергии
показаны на рис. 21.15; переходы между двумя самыми глубокими уровнями v = О
и v = 1 определяют основную частоту крутильного колебания.
Рис. 21.15. Потенциальная энергия этана как функция угла взаимного поворота х группы СН3
Когда энергия внутреннего вращения много больше Uq, оно близко к свобод-
ному, при котором будет иметься лишь небольшое торможение при значениях х
вблизи точек %Oi ±60°, соответствующих максимумам потенциальной энергии. Уров-
ни энергии будут близки к уровням энергии для свободного вращения. Расположение
25) В принципе, возможны минимумы и при цисположениях связей, как показано рис. 21.14, а
пунктиром, однако имеющиеся данные указывают на отсутствие таких минимумов.
21 Зак. 103
642
Глава 21. Колебания многоатомных молекул
уровней для внутреннего вращения как для энергий Е <С Uq и Е Uq, так и для про-
межуточных энергий порядка Uq может быть рассчитано квантовомеханически, если
сделать определенные предположения о конкретном виде потенциала U(x}-
Следует подчеркнуть, что задача решается совместно для всех областей значений х,
О х 2тг, и даже при Е <С Uq получаются уровни энергии, общие для трех потенци-
альных ям. Вместо трех отдельных одинаковых уровней энергии для каждой ямы имеются
три общих уровня энергии, приближенно совпадающие при малых энергиях (трехкратное
вырождение) и постепенно расходящиеся при увеличении энергии (снятие вырождения)26) 27.
С квантовомеханической точки зрения волновые функции отличны от нуля как в классиче-
ских областях, для которых Е > U(x)> так и Для областей барьеров, где Е < U(x)- Однако
при Е <£ Uq значения волновых функций в областях барьеров будут малы, что и делает
возможным приближенное рассмотрение крутильных колебаний как происходящих вблизи
одного из максимумов.
Для расчетов обычно выбирается потенциал простейшего вида
Uq
Щх) = у (1+cos3X).	(21.132)
Мы не будем останавливаться на решении задачи о внутреннем вращении при по-
тенциале (21.132) (см., например, [55], т. 2, с. 315); отметим только, что определенные
из опытных данных (см. ниже), при предположении (21.132) о виде потенциала, значения
высоты потенциального барьера являются до некоторой степени условными.
Высота Uq потенциального барьера может быть приближенно определена, если
известны уровни энергии при заторможенном вращении. Однако для большинства
молекул, в которых возможно внутреннее вращение, эти уровни не удается опреде-
лить спектроскопическими методами, и основным методом нахождения Uq служит
метод, основанный на определении термодинамических функций соответствую-
щих соединений [110]. Термодинамические функции существенным образом зависят
от расположения уровней энергии для внутреннего вращения, так как расстояния
между этими уровнями обычно порядка кТ.2Г) Можно вывести выражения для тер-
модинамических функций, в которые Uq входит как параметр, и из опытных данных
определить его. Порядок величины Uq в молекулах с внутренним вращением вокруг
простых связей обычно составляет от нескольких сотен до нескольких тысяч см-1; на-
пример, для этана Uq — (I 000±50) см-1. Частоты крутильных колебаний не превыша-
ют нескольких сотен см-1. Для ряда молекул, у которых возможно внутреннее враще-
ние и которые имеют микроволновой спектр поглощения, удалось определить часто-
ты крутильных колебаний и вычислить Uq по интенсивностям вращательных линий.
Частоты вращательных линий молекулы, у которой возбуждены крутильные колебания,
отличаются от частот этих линий для молекулы в нулевом колебательном состоянии; отно-
шение интенсивностей аналогичных вращательных линий возбужденной и невозбужденной
молекул равно отношению заселенностей начальных уровней (см. (5.16))
/] П1 Д1-Др _ъе
— — -- — С кт — 6
Iq по
(21.133)
Измерив —, можно определить частоты крутильных колебаний и — &Е — Е} - Ео.
Л)
В микроволновой области удалось обнаружить также переходы между очень близкими
подуровнями, на которые расщепляются вырожденные уровни (см. выше, с. 642), соответству-
ющие крутильным колебаниям [304]; это расщепление аналогично рассматриваемому ниже
инверсионному удвоению.
26) В рассматриваемом случае вырождение снимается не полностью и расщепление происходит на два
уровня — один невырожденный и один дважды вырожденный.
27) Изменения в расположении уровней энергии сильнее всего сказываются на термодинамических
функциях, когда ЛЬ1 « кТ (АЕ — расстояния соседних уровней).
§21.8. Внутренние движения с большими амплитудами
643
Характерная внутренняя перегруппировка в молекуле
с двумя равновесными расположениями ядер осуществля-
ется у молекулы аммиака, имеющей форму трехгранной
пирамиды (см. рис. 18.3, а, с. 502 и рис. 18.11, с. 508).
Для этой молекулы возможны две равновесные конфигура-
ции, получающиеся друг из друга инверсией — отражением
координат ядер вначале (рис. 21.16, а). Эти две конфигу-
рации можно перевести друг в друга, если отразить коор-
динаты атома N в плоскости, проходящей через атомы Н
(рис. 21.16,0. Потенциальная энергия является функцией
расстояния I атома N от данной плоскости и имеет вид,
изображенный на рис. 21.17; два минимума, соответствую-
щие значениям I = ±Iq, где Zo — равновесное расстояние
атома N от плоскости атомов Н, отделены барьером, кото-
рый препятствует колебаниям атома N относительно ато-
мов Н происходить по обе стороны от плоскости28) 29. Около
двух положений равновесия будут происходить колебания,
которым соответствуют при бесконечно высоком барьере
одинаковые уровни энергии в каждой потенциальной яме.
Однако при конечной высоте и ширине барьера движения
в этих ямах не будут независимыми и вместо двух совпада-
ющих уровней получатся два общих для обоих ям уровня, расстояние АЕ = и между
которыми будет тем больше, чем уже и чем ниже барьер, разделяющий ямы. Меньше
всего будет расщеплен нулевой колебательный уровень v = 0. Уровни, для которых
энергия Е близка к высоте барьера Uq, будут уже далеко отстоять друг от друга,
а при Е uq расположение уровней соответствует уровням одного осциллятора.
Согласно наглядным представлениям, частота и = АЕ есть частота колебатель-
ного движения большой амплитуды (порядка Zo), с которой молекула будет пере-
ходить из одной потенциальной ямы в другую, — частота инверсии. Само явление
расщепления колебательных уровней при наличии двух минимумов потенциальной
энергии, обусловленных инверсией, называют инверсионным удвоением1^.
Переход между уровнями, на которые расщепляется основной колебательный
уровень молекулы NH3, соответствует частоте
а
Рис. 21.16. Внутренняя
перегруппировка
в молекуле NH3:
а — две равновесные
конфигурации;
б — отражение атома N
в плоскости, проходящей
через атомы Н
ро = 23 786 МГц = 0,7935 см-1,
(21.134)
и его наблюдению при поглощении в микроволновой области посвящено очень
большое число исследований, начиная с исследований Клитона и Вильямса [302]
в 1934 г., положивших начало развитию микроволновой спектроскопии. При этом
получается не одна линия, а целая совокупность линий — инверсионный спектр —
вследствие того, что частота наблюдаемого перехода зависит от вращательных кван-
товых чисел J и К, притом весьма значительно. Всего наблюдено 66 линий в области
от 17 000 до 40000 МГц, отвечающих значениям J от 1 до 17 и различным значени-
ям К. Частота (21.134) соответствует состоянию с J — 0 и К = 0.
Для колебательного уровня v = 1 расщепление составляет, по данным измере-
ний в инфракрасной области спектра, 35,84 см-1.
28) В действительности, разумеется, атомы Н и атом N движутся относительно общего центра тяжести.
29) С квантовомеханической точки зрения описанное явление обусловлено туннельным эффектом,
вероятность которого резко возрастает, по экспоненциальному закону, с уменьшением высоты барьера
^(0) - Е и его ширины 2Zz, где I' — граница области классического движения.
21
644
Глава 21. Колебания многоатомных молекул
Рис. 21.17. Потенциальная энергия
молекулы NH3 как функция расстояния
атома N от плоскости атомов Н:
вверху — общий вид кривой;
внизу — нижняя часть кривой
и глубокие уровни энергии
Инверсионные спектры удалось наблю-
дать в микроволновой области спектра и
для дейтерозамещенных аммиака — как для
молекулы ND3, обладающей той же симме-
трией, что и молекула NH3, так и для менее
симметричных молекул NH2D и NHD2. Ве-
личина расщепления быстро убывает с уве-
личением числа атомов D и составляет
12 182 МГц у NH2D, 5 111 МГц у NHD2
и 1 600 МГц у ND3.
Частота инверсии определяется приближен-
ной формулой [303]
"е
v = — ехр
7Г
о
(21.135)
где ve — частота колебаний около положений рав-
новесия I — ±l0, М — приведенная масса, Е —
энергия рассматриваемого колебательного уровня,
а интегрирование производится от I — 0 до зна-
чения I = I’, при котором потенциальная энергия
U(l) = Е. С увеличением ширины барьера 21'
и его высоты (7(0) - Е по отношению к уровню Е
интеграл, стоящий в показателе, увеличивается,
а вероятность прохождения через барьер и частота
инверсии при этом уменьшаются по экспоненци-
альному закону.
При переходе от NH3 к дейтерозамещенным
увеличивается приведенная масса М и умень-
шается колебательная энергия Е (как -/==,
ср. (20.121)), что приводит к увеличению инте-
грала и к резкому уменьшению частоты.
В соответствии с показательным законом (21.135) инверсионную частоту как функцию
квантовых чисел J и К, характеризующих вращение молекулы NH3 типа симметричного
волчка, можно представить при помощи формулы типа
и = р0 exp {-A'J(J + 1) + В'К2 + С' [J(J + I)]2 + D'J(J + 1)К2 + 0К4},	(21.136)
где vQ, А1, В', С', D1 и Е1 — постоянные, определяемые из опыта. С помощью этой формулы
все 66 наблюденных частот находятся со средней ошибкой 1,3 МГц, а значение vQ, которому v
равно при J — 0 и К = 0, оказывается равным (21.134).
ГЛАВА 22
СИММЕТРИЯ КОЛЕБАНИЙ МНОГОАТОМНЫХ МОЛЕКУЛ
§22.1. Общие принципы классификации колебаний по их симметрии
и координаты симметрии
Симметрия колебания молекул связана с симметрией их равновесных конфигу-
раций, рассмотренной в гл. 18. Для молекулы, равновесная конфигурация которой
относится к определенной точечной группе симметрии, получается вполне опре-
деленная классификация нормальных колебаний по типам симметрии, возможным
для данной группы. С математической точки зрения эта классификация та же, что
и электронных состояний молекул. Поэтому ряд результатов, которые получаются
при рассмотрении симметрии колебаний молекул, применим и при рассмотрении
симметрии электронных состояний молекул.
С симметрией равновесной конфигурации связано наличие таких типов сим-
метрии, которым соответствуют вырожденные колебания, т. е. нормальные колебания
различной формы, происходящие с одинаковой частотой. При этом возможны три
случая.
Для молекул, равновесные конфигурации которых относятся к группам низ-
шей симметрии и которые не обладают осями симметрии порядка выше второго,
возможны только невырожденные колебания. Число различных частот нормальных
колебаний равно числу колебательных степеней свободы. Правда, практически не-
которые частоты могут совпадать, однако это будет лишь приближенное совпадение.
Для молекул, равновесные конфигурации которых относятся к группам сред-
ней симметрии и которые обладают выделенной осью симметрии порядка не ниже
третьего, наряду с невырожденными колебаниями имеются дважды вырожденные,
т. е. пары колебаний различной формы с одинаковыми частотами. Число различ-
ных частот нормальных колебаний будет меньше числа колебательных степеней
свободы. К таким молекулам принадлежат и линейные многоатомные молекулы,
деформационные колебания которых дважды вырождены.
Для молекул, равновесные конфигурации которых относятся к группам высшей
симметрии — к группам тетраэдра и октаэдра — и которые обладают несколькими
осями порядка не ниже третьего, имеются, наряду с невырожденными и два-
жды вырожденными колебаниями, и трижды вырожденные, т. е. тройки колебаний
различной формы с одинаковыми частотами. Число различных частот колебаний
в этом случае уменьшается еще больше по сравнению с числом колебательных сте-
пеней свободы. В частности, у метана, с равновесной конфигурацией симметрии Та
и с девятью колебательными степенями свободы, имеется только четыре различные
частоты, соответствующие одному невырожденному, одному дважды вырожденному
и двум трижды вырожденным колебаниям.
Для выяснения принципов классификации колебаний по их симметрии разбе-
рем простейший пример колебаний молекулы типа Н2О (нелинейной симметричной
646	Глава 22. Симметрия колебаний многоатомных молекул
трехатомной молекулы), равновесная конфигурация которой обладает симметри-
ей Civ (см. § 18.2, с. 506). В качестве естественных колебательных координат мы
введем валентно-силовые координаты qz и а — изменения длин связей О—Н
и изменение угла Н—О—Н (рис. 22.1, а). В молекуле имеется два эквивалентных
положения равновесия атомов Н, 1 и 2; в соответствии с симметрией молекулы ее
равновесная конфигурация переходит сама в себя при повороте Cz и при отраже-
нии а®. Для определенности будем говорить о повороте и рассмотрим поведение
смещений атомов из положений равновесия. После поворота Cz (рис. 21.1,d) смеще-
ние из второго положения равновесия равно прежнему смещению q\ из первого
положения равновесия, а смещение q\ из первого положения равновесия — преж-
нему смещению qz из второго положения равновесия
9i=92, 92 = 91-	(22.1)
Угол Н—О—Н при повороте не меняется и координата а переходит сама в себя.
а
Можно себе представить, что обе связи отклонились на угол —, так что полное
а а 2
изменение угла есть а. Оно остается прежним, а = —I— = а, т. е.
а = as
(22.2)
представляет симметричную координату as, не изменяющуюся при операции Cz.
Иначе обстоит дело с координатами q} и qz, которые переходят друг в друга
и сами по себе никакой симметрией не обладают. Однако очень легко найти также
смещения, которые будут либо сохраняться, либо менять знак. В самом деле,
если q\ = qz (рис. 22.1, в, слева), то при повороте они останутся неизменными
Рис. 22.1. Симметрия смещений из положений равновесия для молекулы Н2О:
а — первоначальные смещения; б — результат поворота на 180°;
в — симметричные и антисимметричные смещения; г — результат поворота на 180°
§ 22.1. Общие принципы классификации колебаний по симметрии 647
(рис. 22.1,г, слева): q\ — q2 = q\, q2 = q\ — q2. Это будут симметричные смещения.
Если, наоборот, q\ — —q2, (рис. 22.1, в, справа), то при повороте они переменят знак:
q\ = q2 = — q}, q2 — q} = -q2. Это будут антисимметричные смещения. В первом
случае мы можем положить q\ = q2 = qs, где q3 — симметричная координата,
во втором — q\ — — q2 = qa, где qa — антисимметричная координата.
Произвольные смещения /71 и q2 (рис. 22.2, а) всегда мож-
но разложит^ {^симметричные смещения (оба атома сме-
щаются на —-— — qs, рис. 22.2, б) и на антисимметрич-
z	Ч\~ 42
ные (один атом смещается на —-—' = qa, другой атом —
Ч2 — Ч\
на —х— — — Ча, рис. 22.2, в). Мы имеем
2
Ч\ 4- 42	Ч\ ~ 42
Чз —	2	’ Ча —	2
координаты q\ и выразятся через симметричную
(22.3)
Исходные
и антисимметричную координаты по формулам
— 4s 4" Чач 42 ~ 4s ~ Ча*
(22.4)
Отметим, что координаты (22.3) являются ортогональными,
qj 4- Qa = - (qi 4- q})- Их можно также выбрать и нормированными,
т.е. так, чтобы q} 4- q2a = q2 + q2- Для этого нужно положить
1	/	х	1	/
qs = -f= (qi + g2), qa = (gi - qi);
Рис. 22.2.
Разложение
произвольных
смещений
на симметричные
и антисимметричные:
а — первоначальные
смещения;
б — симметричные
смещения; в —
антисимметричные
смещения
(22.5)
тогда, обратно,
01 =	+ ««>’ 92 = 75	- ч^'
В теории колебаний молекул обычно применяют именно такие ор-
тонормированные координаты.
Согласно (22.2) и (22.3), мы получаем для молекулы типа
Н2О вместо трех координат q\, q2 и а три новые координаты —
две симметричные, не меняющие знака при повороте,
(22.6)
& = 4s, as = о
и одну антисимметричную, меняющую знак
(22.7)
Ча = -<7«.	(22.8)
Можно показать (см. § 22.6, где этот вопрос специально рассмотрен), что
задача о колебаниях решается отдельно для координат каждого типа симметрии
и координаты определенной симметрии изменяются независимо от координат других
типов симметрии.
В данном случае мы имеем две симметричные координаты q3 и as; для них
получается задача с двумя степенями свободы, решение которой определяет две
частоты симметричных колебаний. Этим колебаниям будут соответствовать нор-
мальные координаты и £2> выражающиеся через координаты q3 и ots:
Ci ~	4" b\OtSl
£2 — агЧз 4- b2a3.
(22.9)
648	Глава 22. Симметрия колебаний многоатомных молекул
В общем случае Ь\ Ф 0 и а2 Ф 0, и эти колебания не будут представлять изме-
нения только координаты qs или только координаты as, что имело бы место, если
бы одно из колебаний было чисто валентным, а другое чисто деформационным.
В действительности, два получающихся симметричных колебания не будут ни чисто
валентными, ни чисто деформационными. Обычно приближенно все же можно одно
колебание считать валентным, а другое деформационным. Вследствие значитель-
ной разности частот в нулевом приближении взаимодействия будут сравнительно
невелики (Z>i2 и D2\ <	- Z>22 =	см. (21.117) и (21.116)) и в (22.9)
получится а\ , а а2 <С &2-
Наряду с двумя симметричными координатами мы имеем одну антисимметрич-
ную qa, которая будет изменяться независимо от этих координат qs и as; для нее полу-
чится задача с одной степенью свободы, решение которой определяет частоту иа анти-
симметричного колебания. Координата q2 уже представляет нормальную координату,
6 = 9а,	(22.10)
а само колебание является чисто валентным.
Мы видим на этом примере, что, исходя из соображений симметрии, действи-
тельно можно разделить колебания молекулы на колебания различных типов симме-
трии. При этом мы ввели колебательные координаты различных типов симметрии,
являющиеся линейными комбинациями исходных естественных колебательных ко-
ординат. Подобные координаты, обладающие определенными свойствами симме-
трии, обусловленными симметрией равновесной конфигурации молекулы, называют
координатами симметрии. Их можно ввести для любых молекул с симметричной
равновесной конфигурацией, что позволяет классифицировать колебания по типам
симметрии и сильно облегчает решение задачи о колебаниях. Само решение задачи
о колебаниях разбивается на два этапа: сначала учитывают свойства симметрии
путем перехода от исходных естественных колебательных координат к координатам
симметрии, а затем в координатах симметрии для каждого типа симметрии в отдель-
ности решается механическая задача!) и находятся частоты нормальных колебаний
и нормальные координаты данной симметрии. Соответственно координаты симме-
трии можно рассматривать как промежуточные между исходными естественными
колебательными координатами и окончательными нормальными координатами.
В рассмотренном примере молекулы типа Н2О от исходных координат q\, q2, а
мы перешли к координатам симметрии (см. (22.3) и (22.2))
91 + 92	91 ~ 92
9s = —~, qa = —~, ots = а,
(22.11)
а затем от координат симметрии к нормальным координатам (см. (22.9) и (22.10))
6 = a\qs + Ms, 6 = «29s + ^2«s, 6 = 9а-	(22.12)
Подстановка (22.11) в (22.12) дает
6 — ~а191 + ~а192 + &1«, 6 = ~а291 + ~а292 + Ъ2а, — -q\ — -q2,	(22.13)
что представляет частный случай общей связи (21.49) между нормальными и есте-
ственными колебательными координатами.
В следующих параграфах мы рассмотрим типы симметрии колебаний и введение
координат симметрии для молекул с равновесными конфигурациями, относящими-
ся к различным точечным группам симметрии, а затем применим полученные
результаты к упрощению решения механической задачи о колебаниях молекулы.
В свою очередь разбивающаяся на два этапа, см. с. 628.
§ 22.2. Типы симметрии для молекул низшей симметрии
649
в заключение данного парагра-
фа следует отметить, что операции
симметрии, переставляющие эквива-
лентные смещения (см. (22.1)), от-
личаются от операций симметрии,
переводящих равновесную конфигу-
рацию молекулы саму в себя и пе-
реставляющих эквивалентные атомы.
В (22.1) мы имеем новые смещения gj
и q'2 из прежних положении равнове-
сия 7 и 2, что может рассматривать-
ся как результат поворота молекулы
Рис. 22.3. Операция поворота с перестановкой
эквивалентных атомов: а — первоначальные
смещения; б — действие поворота на 180°;
в — действие последующей перестановки
эквивалентных атомов
с последующей перестановкой эквивалентных атомов (см. рис. 22.3; при повороте равновесные
положения атомов и их смещения меняются местами, а последующая перестановка атомов
приводит к новым смещениям из прежних положений равновесия). При этом каждой опера-
ции симметрии, переводящей равновесную конфигурацию молекулы саму в себя, однозначно
соответствует операция симметрии с перестановкой, преобразующая колебательные координа-
ты. Поэтому при рассмотрении симметрии колебаний молекулы получаются те же точечные
группы, что и при рассмотрении симметрии равновесной конфигурации, и указанное отличие
для нас несущественно (см. [55], т. 1, с. 113).
§ 22.2. Тйпы симметрии для молекул, относящихся
к точечным группам низшей симметрии
Наиболее простая классификация колебаний
по типам симметрии получается для молекул, рав-
новесные конфигурации которых не имеют осей по-
рядка п > 2 и относятся к точечным группам низшей
симметрии, т.е. к группам С\, Ci, Cs, С2, C2h, C2v,
D2 = V, D2h = Vh. Для этих групп, согласно (18.12),
всем элементам симметрии соответствуют операции
Рис. 22.4. Типы смещений
и координаты симметрии
для нелинейной молекулы
типа XY2: а — симметричная
симметрии второго порядка, т. е. такие операции,
при повторении которых система переходит сама в се-
бя. В силу (18.12) смещения и соответствующие им
координаты симметрии относительно каждой опера-
ции могут быть симметричными или антисимметрич-
ными, т. е. не менять или менять анак при данной
операции симметрии. При повторении любой опера-
координата;
б — антисимметричная
координата
ции два раза знак всегда сохраняется. В рассмотрен-
ном в предыдущем параграфе случае молекулы типа Н2О (рис. 22.1) симметричные
смещения q\ и q2 = q\ и координата qs ~ q\ ~ q2 не меняют знака ни при каких опе-
рациях группы C2v (Ci, С2, а$\ а®, см. (18.3)), а антисимметричные смещения q\
и qi ~ и координата	м от знак при повороте С2 и при от-
(2)	(I)
ражении al , сохраняя его при отражении al и при тождественной операции С\
(рис. 22.4, ср. рис. 18.9, с. 506).
Это можно записать для координат симметрии в виде
Qs	— C\qs — qSl
Qs	C2qs	Qsj
ш	(0
qs = fqs = qs,
ни	(2)
q$ — <?» Qs — qs.
q<i — C\qa — qa,
qa c2qa	qai	I
qa =	’qa	=
uh	(2)
Qa =	4a	=	“Qa-	/
(22.14)
650	Глава 22. Симметрия колебаний многоатомных молекул
Таким образом, координата qs является симметричной по отношению ко всем
операциям группы, а координата qa — симметричной по отношению к операциям С|
(2)	-	„	(1)
и al и антисимметричной по отношению к операциям С2 и а„ , что можно записать
в виде таблицы (табл. 22.1).
Таблица 22.1
Типы для группы C2v
Обозначения	Операция симметрии				
	с.	с2 = с{2}	JO - (Ту 	 (Ту	J2) -	
Л| А Si в2	1 1 1 1	1 1 -1 -1	1 -1 -1 1	1 -1 1 -1	РZ1	ayyt azz l^z-t <*xy Pflyi ®-xz Py, 1^X1 <*yz
В таблице приведены множители, на которые умножается координата сим-
метрии при соответствующей операции и которые равняются либо 1, либо — 1.
Координаты, симметричные и антисимметричные относительно оси, обозначают
буквами А и В, а координаты, симметричные и антисимметричные относительно
плоскости (в данном случае относительно плоскости а^) — индексами 1 и 2 (справа
снизу) соответственно. Координаты qs и а — as обладают в этих обозначениях сим-
метрией А], а координата qa — симметрией В2. Отметим, что свойства симметрии
(О	-
относительно плоскости al определяются свойствами симметрии относительно С2
и а^ в силу	(см. (18.4) и ср. с. 76).
Для группы C2v У возможны еще два типа симметрии, А2 и В\, характеризу-
ющиеся антисимметрией относительно плоскости а*\ Для плоской молекулы Н2О
такие смещения невозможны^. Однако они возможны для более сложных молекул,
обладающих симметрией C2V, например, для молекулы пропана СзНя (рис. 22.5,
ср. рис. 18.4, а. с. 502), у которой атомы С и два атома Н расположены в одной
плоскости (плоскость а^), а остальные атомы Н расположены вне этой плоскости,
симметрично относительно нее. Смещения, получающиеся при изменении длин
четырех эквивалентных связей С—Н, показанные на рис. 22.5, б и 22.5, в, относят-
ся к типам симметрии А2 и В\ соответственно и выражаются через координаты
симметрии дл2 и Яв^ для которых
q\ = ~Я2 = ~Яз = Я4 = Яа2,
Я\ = ~Я2 = Яз = ~Я4 = Явг
Для молекулы пропана, разумеется, возможны и смещения типов симметрии А\
и В2; в частности, к ним относятся смещения
Я\ = Я2 = Яз = Я4 = Я а. ,
Я\ = Яг = ~Яз = ~Я4 = Яв2
выражающиеся через координаты симметрии и q$2 (рис. 22.5, а, г).
2) Они невозможны при колебаниях. Вращательное и поступательное движения могут характеризо-
ваться такими смещениями.
(22.16)
§ 22.2. Типы симметрии для молекул низшей симметрии
651
Рис. 22.5. Типы смещений и координаты симметрии для молекулы пропана С3Н8:
а — координаты симметрии А\\б — координаты симметрии А2;
в — координаты симметрии Вх\ г — координаты симметрии В2
Легко видеть, что координаты симметрии будут выражаться через произвольные смеще-
ния gb g2, (ft, по формулам:
1 /
QAi —	+ qi + дз + Яа)у
1 .
Qa2 — TW1 “ Ql - <13 + <14h
j	(22.17)
9 b, = 4(91-92 + 93- 9t),
1,
9b2 = 4 W + 92 - 9з - 94),
а произвольные смещения qi9 q2, g3, q^ можно представить в виде
Q\ —	+ qA2 +	+ qB2y
1,-1.,(221g)
Q3 = Qa{ ~ Qa2 + qBi ~ Яв2у
<14 - <1a} + qA2 ~ Qb} ~ <1b2
как суммы смещений разной симметрии.
Если ввести нормированные координаты симметрии (ср. (22.5)), то как в форму-
лах (22.17), так и в формулах (22.18) будет стоять коэффициент - и тогда q\x + q1A1 +д|2 =
д? Ч- q2 4- q] + q}.
В последнем столбце табл. 22.1 указаны составляющие Рд дипольного момента,
рх магнитного момента и тензора поляризуемости, которые при операциях
симметрии преобразуются, согласно данному типу симметрии. Поведение этих
составляющих необходимо знать при выводе соответствующих правил отбора.
Принадлежность рассматриваемых составляющих к определенному типу симметрии лег-
ко определяется из наглядных соображений. Составляющие дипольного момента ведут себя
как координаты ж, у, z (дипольный момент — полярный вектор); например, составляю-
щая Рх ведет себя подобно координате ж, т. е. меняет знак при операциях С2 и
и принадлежит к типу симметрии Bt. Составляющая магнитного момента по некоторой оси
не меняет знака при отражении в плоскости, перпендикулярной к оси, и меняет его при от-
ражении в плоскости, проходящей через ось (магнитный момент — аксиальный вектор),
а при повороте С2 преобразуется как и соответствующая составляющая дипольного момента.
Составляющие тензора поляризуемости (а также квадрупольного момента и любого другого
симметричного тензора) преобразуются как произведения координат как х2, аху как ху
и т. д.). Отметим, что смещения при вращении и при поступательном движении ведут себя
как составляющие аксиального вектора и полярного вектора, т. е. как рх и Р\ соответственно.
Для группы C^v мы имеем четыре типа симметрии; число типов симметрии
равно числу элементов группы, т. е. ее порядку. Это всегда имеет место для групп
низшей симметрии, соответствующих молекулам, не содержащим осей симметрии
652
Глава 22. Симметрия колебаний многоатомных молекул
порядка выше второго. Для таких групп число типов симметрии равно порядку группы.
Следовательно, оно равно 2 для групп второго порядка Сг, Cs и С2, 4 для групп
четвертого порядка С2л, С2у и D = V и 8 для группы восьмого порядка D2h = Vh-
Мы приводим таблицу симметрии (табл. 22.2) для группы наивысшего поряд-
ка D2h, так как из этой таблицы как частные случаи могут быть получены все
результаты и для остальных групп (являющихся ее подгруппами, см. § 18.3, с. 512).
В таблице указано поведение смещений и координат симметрии при всех операциях
симметрии (18.13). При этом достаточно указать поведение по отношению к трем
независимым операциям симметрии, так как поведение по отношению к остальным
операциям симметрии однозначно определяется соотношениями между ними3).
Таблица 22.2
Типы симметрии для группы £>2л
Обозначения	Операция				симметрии				
	с.	i	С2	г(у) С2	г(г) С2				
Ад	1	1	1	1	1	1	1	1	^ХХ1	®-zz
Аи	1	-1	1	1	1	-1	-1	-1	
В\д	1	1	1	-1	-1	1	-1	-1	Р-х, Ct-yz
В]и	1	-1	1	-1	-1	-1	1	1	Рх
Big	1	1	-1	1	-1	-1	1	-1	Руу axz
В2и	1	-1	-1	1	-1	1	-1	1	Ру
В1>д	1	1	-1	-1	1	-1	-1	1	ftzi С*ху
Взи	1	-1	-1	-1	1	1	1	-1	Pz
Обозначения выбраны по отношению к операции инверсии и к операциям
поворотов, g и и обозначают четные и нечетные типы симметрии, для которых
при инверсии соответственно сохраняется и меняется знак. А означает сохранение
знака по отношению ко всем поворотам, В — изменение знака при двух поворотах
и сохранение знака при третьем повороте; последнее отмечается индексами 1, 2, 3
для осей х, у и z соответственно, т. е. Bj, В2, В3 означают сохранение знака
при поворотах С^, С^\ соответственно.
В последнем столбце табл. 22.2, как и в последнем столбце табл. 22.1, указа-
ны составляющие Рх дипольного момента, ^д магнитного момента и а\/л тензора
поляризуемости, которые при операциях симметрии преобразуются, согласно дан-
ному типу симметрии. Отметим то существенное обстоятельство, что составляющие
дипольного момента меняют знак при инверсии и принадлежат к нечетным типам
симметрии (и), а составляющие магнитного момента и тензора поляризуемости
(а также квадрупольного момента) не меняют знака при инверсии и принадлежат
к четным типам симметрии (</)* 4).
Примером молекулы симметрии D2h является молекула этилена QH4 (ср. § 18.3,
с. 513), все атомы которой лежат в одной плоскости (рис. 22.6); центр симметрии
молекулы совпадает с серединой двойной связи С=С. Все колебания молекулы раз-
деляются на колебания, происходящие в плоскости молекулы, — плоские колебания —
и на колебания, происходящие перпендикулярно к плоскости молекулы, — неплоские
колебания. При выборе плоскости молекулы за плоскость плоские колебания
Эти соотношения легко выводятся из наглядных соображений и даются групповой таблицей (18.14).
4) Это связано с тем, что дипольный момент является полярным вектором, меняющим знак при ин-
версии, магнитный момент — аксиальным вектором, не меняющим знака, и тензор поляризуемости
(и квадрупольный момент) — тензором второго ранга, также не меняющим знака.
§ 22.2. Типы симметрии для молекул низшей симметрии
653
как симметричные относительно этой плоскости
должны принадлежать к типам симметрии Ад,
В\ду В2и и Взи, а неплоские колебания как ан-
тисимметричные относительно нее — к типам
симметрии Аи, В\и, В2д, В2д.
Можно определить симметрию всех возмож-
ных независимых видов смещений и найти соот-
ветствующие координаты симметрии. При этом
определяются также числа колебаний, относя-
щихся к каждому из типов симметрии. Молекула
Рис. 22.6. Естественные координаты
для молекулы этилена
этилена имеет 3N — 6=36-6= 12 колебательных степеней свободы, из которых 9
соответствуют плоским колебаниям, а 3 — неплоским; смещения 12 возможных ви-
дов показаны на рис. 22.7, причем для неплоских колебаний знаками + и - показаны
положительные и отрицательные смещения атомов вдоль оси х. При действительных
нормальных колебаниях одновременно будут происходить различные смещения дан-
ного типа симметрии, аналогично тому, как для молекулы типа Н2О одновременно
изменяются координаты q\ и q2 (#1 = qi — qs) и a (a — as) (ср. выше с. 647).
Д1=-Д2=-Дз=Д4=^
01 = ~02=03= "Л =0В2и	01 = 02 = ~03= -0, =0Biu
Рис. 22.7. Типы смещений и координаты симметрии для молекулы этилена
Всего двенадцати возможным видам смещений соответствуют три колебания Ад,
по два колебания В\д, В2и и B^u и по одному колебанию Аи, В\и и В2д.
В качестве естественных координат для плоских колебаний мы вводим изменение Q
двойной связи С~С, изменения q\, q2, qz, qt связей С—Н, изменения СГ|2 и а34 углов
Н—С—Н и изменения р}, р2, Рз, fit углов С—С—Н. Число этих координат равно 11,
но из них независимыми являются 9, так как имеются два дополнительных условия, очевидные
из чертежа (рис. 22.6),
(22.19)
а12 + Р\ + Р2 — 0, &34 + Рз + 04 — 0.
654	Глава 22. Симметрия колебаний многоатомных молекул
Изменение связи С=С, обладающей собственной симметрией (см. § 18.2, с. 507) Р2Л, относит-
ся к типу симметрии А\д, соответствующему полносимметричным колебаниям. Изменения
двух углов Н—С—Н, обладающих собственной симметрией C2v (с осью симметрии z),
т.е. не изменяющихся при операциях С2, сг^ и <т(у\ относится к типам симметрии Ад и В3и
(см. в табл. 22.2 строки, для которых при операциях С^, и стоят множители 4-1).
Изменения четырех связей С—Н, обладающих собственной симметрией Cs (по отношению
к плоскости <t(i)), т. е. не изменяющихся при операции а{х\ относятся к типам симметрии Ад,
В[д, В2и и В3и (см. в табл. 22.2 строки, для которых при операции стоит множитель 4-1).
Для изменений четырех углов С—С—Н (собственная симметрия Cs) получаются те же типы
симметрии Ад, Big, В2и и В3и, но в силу условий (22.19) для типов симметрии Ад и В3и
— Pi — ~~ <*12 и /З3 = /34 — — - а34 и соответствующие смещения совпадают со смещениями
<*12 = <*34 (лля Ад) и а|2 — -а34 (для В3и). Таким образом, остаются независимые смещения
типов В\д и В2и.
В результате мы получили все 9 видов смещений для плоских колебаний.
Для неплоских колебания достаточно рассмотреть углы р выхода связей С—Н из плос-
кости молекулы (что и показано знаками 4- и - в зависимости от знака смещений б атомов Н
по оси х и, следовательно, от знака углов р = -----, где рсн — длина связи С—Н). Та-
Pc н
кие колебания могут относиться к четырем типам симметрии: В[и (/9| = р2 = р3 — р$),
А» (Pi = -р2 = ~Рз = Ра), В2д (р, = рг = —Рз = ~Ра) И В}д (Р( = -р2 = Рз = -Ра), однако
смещения последнего типа (В3д) соответствуют не колебанию, а вращению вокруг оси z
(вокруг связи С=С), и поэтому их учитывать не надо. В результате мы получаем три вида
смещений для неплоских колебаний.
Соотношения между естественными координатами и координатами симметрии для всех
видов смещений указаны на рис. 22.7.
В соответствии с числом колебаний каждого типа симметрии при решении задачи
о плоских колебаниях получается одно кубическое уравнение и три квадратных. Для неплоских
колебаний получаются три уравнения первой степени, т. е. для соответствующих степеней
свободы задача решается сразу.
§ 22.3. Дважды и трижды вырожденные колебания
Для молекул, равновесная конфигурация которых имеет оси симметрии порядка
п 3 и относится к точечным группам средней и высшей симметрии, классифика-
ция колебаний по типам симметрии более сложна, чем в случае отсутствия таких
осей. В этих случаях, как уже указывалось в начале главы (см. с. 645), имеются
типы симметрии, которым соответствуют вырожденные колебания, а именно, два-
жды вырожденные колебания при наличии выделенной оси симметрии порядка
и дважды и трижды вырожденные колебания при наличии нескольких осей
симметрии порядка п 3. В этом параграфе мы рассмотрим примеры дважды
и трижды вырожденных колебаний, с тем чтобы в дальнейшем произвести полную
классификацию колебаний по типам симметрии.
Простейшим примером дважды вырожденных колебаний являются деформа-
ционные колебания молекулы СО2. Мы уже разобрали выше валентные колебания
(симметричное и антисимметричное) этой молекулы, происходящие вдоль оси мо-
лекулы и являющиеся невырожденными (см. с. 606 и рис. 21.1). Соответствующие
смещения и координаты симметрии q\ —	— qs и q\ = -qi = qa не изменяются
при повороте вокруг оси на любой угол <р, в частности, на угол 180° (т.е. при опе-
рации симметрии С2); при отражении в центре координата qs сохраняет знак,
т.е. является четной, а координата qa меняет знак, т. е. является нечетной. Согласно
§ 22.3. Дважды и трижды вырожденные колебания
655
обозначениям предыдущего параграфа, данные колебания принадлежат к типам сим-
метрии Ад и Аи. В противоположность этому при деформационном колебании атомы
движутся перпендикулярно к оси молекулы (рис. 22.8,0, что и приводит к изгибу
молекулы. Легко видеть, что смещения меняют знак при повороте С2 на 180° вокруг
оси молекулы (оси z), а также при отражении в центре симметрии i и в плоскости,
проходящей через ось молекулы и перпендикулярной к плоскости колебаний.
Наиболее существенной особенностью деформационных колебаний молеку-
лы СО2 является то, что они могут происходить в любой плоскости, проходящей
через ось молекулы (см. рис. 22.8,0. Рассматривая для простоты смещение атома С
относительно атомов О, разложим его на смещения по двум взаимно перпендику-
лярным осям х и у. Колебание в произвольной плоскости, проходящей через ось
молекулы, таким образом разлагается на два независимых колебания в плоскостях xz
и yz, что соответствует двум степеням свободы. Именно поэтому молекула СО2 имеет
четыре, а не три колебательных степени свободы — две степени свободы валентных
колебаний и две степени свободы деформационных колебаний. Так как частота
колебаний в силу осевой симметрии не может зависеть от плоскости, в которой они
происходят, то деформационные колебания будут дважды вырожденными; незави-
симые колебания в двух взаимно перпендикулярных плоскостях будут происходить
с одной и той же частотой.
Рассмотрим, как преобразуются колебательные координаты при операциях сим-
метрии. В качестве независимых колебательных координат мы введем смещения х
и у атома С вдоль соответствующих осей (см. рис. 22.8,6 и рис. 22.9).
Рис. 22.8. Дважды вырожденные колебания молекулы:
а — колебание в плоскости yz\
б — колебание в произвольной плоскости
Рис. 22.9. Преобразование
смещений атома при повороте
вокруг оси молекулы
При повороте вокруг оси молекулы на угол <р координаты х и у преобразуются
по хорошо известному закону
х — Сц>х — х cos ip + у sin ip,
,	г У	(22.20)
у — Cpy — -x sin ip + у cos ip.
Обратно,
x — x cos ip - у sin ip.
, .	",	(22.21)
у ~ x sin ip + у COS ip.
656
Глава 22. Симметрия колебаний многоатомных молекул
Таким образом, колебательные координаты при повороте на некоторый угол
ТГ о
преобразуются друг через друга, в частности, при повороте С4 на угол р = — — 90
х1 — С^х — у, у' — С4У = -х, т.е. х иу переходят друг в друга.
Вырождение связано именно с тем обстоятельством, что нельзя выделить ко-
лебательные координаты, соответствующие отдельным степеням свободы, которые
при операциях симметрии преобразовывались бы независимо друг от друга. Крат-
ность вырождения равна числу существенным образом связанных друг с другом
координат. В рассматриваемом случае мы имеем две существенным образом связан-
ные между собой координаты и получается двукратное вырождение.
Для абелевых групп, все элементы которых коммутируют друг с другом, координаты
всегда можно выбрать так, чтобы они при любых операциях симметрии переходили с точно-
стью до постоянного множителя, равного по модулю единице, сами в себя, и вырождение
отсутствует. Для неабелевых групп этого сделать нельзя и всегда будут существовать совокуп-
ности связанных между собой координат, что приводит к вырождению. Для рассмотренных
в предыдущем параграфе групп низшей симметрии, являющихся абелевыми, колебания всех
типов симметрии невырождены (см., например, для случая группы C2v преобразования (22.14);
координаты qs и qa переходят сами в себя с точностью до знака).
С точки зрения теории групп линейные преобразования колебательных координат
при операциях симметрии образуют представление точечной группы, к которой принад-
лежит молекула. Как было указано в гл. 3 (см. с. 79), представлением группы называют
совокупность линейных преобразований, соответствующих элементам этой группы, а число
преобразующихся между собой величин определяет размерность представления 5\ В разбира-
емом случае преобразования координат х и у мы имеем двухмерное представление, которое
можно записать в виде, аналогичном (3.51):
операции
группы
С.
crv С2


I
матрицы
преобразования
| 1	Oil cos tp	sin р I	I - cos <р	sin ip I	I -1 О I I 1 О I I 1	01
I 0	1 j j — sin <р	cos <£> |	I — sin ip	cos <р |	| 0	— 1 | | 0	— 1 | | 0	— 1 |
(22.22)
Здесь введены матрицы преобразований, причем учтено, что для молекулы СО2 мы имеем
группу симметрии D^h, включающую инверсию г, отражения в вертикальных плоскостях
повороты с отражениями Sv = и повороты С2 — ahav вокруг горизонтальных осей
второго порядка; для двух последних операций получаются такие же матрицы, как для
и av соответственно, в силу того, что операция не изменяет координат х и у.
Матрицы (22.22) образуют двухмерное представление группы D^h, которое является
неприводимым (см. с. 79): его нельзя свести путем иного выбора колебательных координат
к совокупности двух одномерных представлений так, чтобы каждая координата преобразо-
вывалась сама в себя. Неприводимость представления (22.22) и обусловливает двукратное
вырождение колебаний — неразрывно связанным между собой равноправным координатам х
и у соответствуют одинаковые частоты колебаний. Представление (22.22) определяет дважды
вырожденный тип симметрии.
В неприводимости представления (22.22) можно убедиться, если ввести вместо колеба-
тельных координат х и у их линейные комбинации х + гу и x-iy, имеющие в этом случае про-
стой смысл, а именно, х ± iy дает наложение колебания вдоль оси х и колебания вдоль оси у,
5) В гл. 3 линейно преобразовывались волновые функции, здесь мы рассматриваем линейные пре-
образования координат, однако с точки зрения теории групп это безразлично.
6) к < I 1	0 I	(у)
' Матрица I _j относится к отражению av в плоскости xz, для которого
х — х = 1 • х + 0 • т/,
У = -у = 0- X - 1 -у.
§ 22.3. Дважды и трижды вырожденные колебания
657
7Г
смещенного по фазе на ±— (при х — х^егшЬ
и у = у$егш1 имеем ±iy = Уое±г г
eiut =
ср. примечание на с. 120). Согласно (22.20), х' + iy' = (х cos <р + у sin ^>)-Н(—х sin <р + у cos <р) =
a;(cos <р - i sin р) 4- t/(sin <р 4- г cos р) = a;(cos 92 - i sin р) 4- ii/(cos р - i sin 92), откуда в силу соот-
ношения cos р — i sin р = е~г{р получим х* + iy' — e~i(p(x-{-iy)\ аналогично, х' -iy' — et<p(x-iy).
Таким образом, координаты х 4- iy и х — iy переходят при операции сами в себя с точ-
ностью до множителей е~г* и равных по модулю едиенице, и матрица коэффициентов
о
о
преобразования имеет вид
. Для операций С\ и i получаются прежние матрицы,
однако для операции отражения av результат будет иной: при отражении в плоскости xz
(х' — х, у1 = -у) и при повороте вокруг оси х на 180°
х 4- iy = av(x 4- iy) = х- iy = 0(я 4- iy) 4- 1(ж - iy),
x - iy = crv(x - iy) = x + iy = \(x 4- iy) 4- 0(x - iy),
(22.23)
т. e. координаты x 4- iy и x - iy переходят друг в друга и матрица преобразования имеет вид
к 0 . Вместо представления (22.22) мы получаем новое представление:
операции
группы
С,
матрицы
преобразования
*5^	i	av С*2
e’tV	0	1-1	0 1	10	11	10	11
0	ei<p	I 0	-1 I	I 1	0|	I 1	0I
I 1 0 I
I 0 1 I
0
0
(22.24)
Таким образом, координаты х 4- iy и х - iy преобразуются друг через друга, а не только
сами в себя, т. е. колебательные координаты действительно не удается разделить; это значит,
что представление неприводимо.
Отметим, что для группы Сх, в которой отсутствуют операции crv и С2, x+iy и x — iy будут
преобразовываться независимо друг от друга. Мы получаем два одномерных представления
операции группы С\
преобразование
для х 4- iy 1	е~1<р	(22.25)
преобразование
для х - iy 1	е1*
Однако эти представления хотя и независимы, но являются комплексно-сопряженными.
Частоты изменения комплексно-сопряженных координат х 4- iy и х - iy будут по-прежнему
одинаковы. Координаты х 4- iy и х - iy для абелевой группы являются примером раздель-
ного вырождения координат (в отличие от совместного вырождения координат), о котором
уже говорилось в § 18.4 (с. 516). Для линейных молекул, всегда обладающих плоскостями сим-
метрии crv, обусловливающими совместное вырождение, раздельное вырождение колебаний
не имеет места, однако оно получается для молекул, равновесные конфигурации которых
обладают симметрией Сп или Cnh (п^ 3).
Важнейшей характеристикой преобразований координат при операциях симметрии
и представлений соответствующей группы являются характеры (см. конец §3.4, с. 81) —
суммы диагональных элементов матриц преобразования.
Для матриц представления (22.22) характеры равны:
X(G) = 2, x(^) = x(^) = 2cos^, х(0 = -2, Х(<М = х(С2) = 0.	(22.26)
Характеры не зависят от выбора исходных координат7\ В частности, при переходе от коорди-
нат х, у к координатам х 4- iy, х - iy характеры не изменяются, что видно из (22.22) и (22.24).
Другим важным свойством характеров является то, что они одинаковы для операций симме-
трии, принадлежащих к одному классу (см. § 18.4, с. 521), в частности, для принадлежащих
7) В случае преобразований волновых функций (см. с. 79) — от выбора системы этих функций.
658	Глава 22. Симметрия колебаний многоатомных молекул
к одному классу (в случае наличия плоскостей av) операций С? и (см. (22.26)). Поэтому
обычно указывают характер сразу для всех операций, относящихся к данному классу. В случае
группы Dx/l для дважды вырожденных типов симметрии имеем следующую совокупность
характеров:
класс операций	Ct	i	av	С2	(	.
характер	2	2cos^ 2cos^> -2	0	0.	'	’ '
Такая таблица характеров определяет соответствующее неприводимое представление и,
следовательно, тип симметрии. Таблицы 22.1 и 22.2 типов симметрии для групп C2v и D2h
представляют таблицы характеров одномерных представлений, по которым для групп низшей
симметрии преобразуются колебательные координаты; в этих простейших случаях коэф-
фициенты, на которые умножаются колебательные координаты при операциях симметрии,
являются одномерными матрицами, характеры которых совпадают с соответствующими ко-
эффициентами. Одномерные матрицы мы имеем и в примере (22.25), когда характеры двух
представлений, образованных преобразованиями комплексно сопряженных координат х + iy
и х - iy, также комплексно сопряжены.
Различным неприводимым представлениям соответствуют и различные совокупности
характеров.
Характеры обладают и рядом других важных свойств, на которых мы не имеем возмож-
ности здесь останавливаться (см., например, [137], §20).
Рис. 22.10. Валентные плоские
колебания молекулы типа XY4:
а — равновесная конфигурация
молекулы; б — симметричные
смещения; в — антисимметричные
смещения; г, д — дважды
вырожденные смещения
Другим примером дважды вырожденных ко-
лебаний служат валентные плоские колебания
молекулы типа XY4 (рис. 22.10, я)8), имеющей
симметрию D^.
Для изменений длин четырех связей X—Y
мы можем ввести координаты симметрии
(рис. 22.10,d, в, г, д)
q\ =	q2=	яз =	^4	~ дд,
q\ —	-qi —	q3 —	-q^	—
q\ =	-qi =	-q3 =	q*	= qi,
q\ —	qi~	~q3 —	~q$	~ 7n-
(22.28)
Координата qA не изменяется при любых опе-
рациях симметрии, координата qB меняет знак
при повороте С4 на 90°, координаты q\ и дп, как
легко видеть, при этой операции переходят друг
в друга, а именно (см. рис. 22.10, г и д):
q\ — C$q\ — q\\,
q'u —	= ~q\-
(22.29)
но очевидно, что смещениям,
одинаковые частоты колебаний
При повороте Ci на 180° они меняют знак, что
легко получить, повторяя операцию С4 дважды
(С4 = Ci), и сразу видно на рисунке. Совершен-
изображенным на рис. 22.10, г и д, соответствуют
в полном согласии с тем, что координаты симме-
трии qi и qn преобразуются совместно. Таким образом, в данном случае четырем
координатам qA, qB, q\ и q\\ соответствует одно колебание невырожденного типа
симметрии А (полносимметричное колебание), одно колебание невырожденного
К данному типу должен относиться ион (PtCl4)“; хотя этот случай встречается практически редко,
его разбор представляет интерес с методической точки зрения ввиду его простоты.
§ 22.3. Дважды и трижды вырожденные колебания
659
типа симметрии В (антисимметричное относительно оси С4) и одно колебание
дважды вырожденного типа симметрии, который обозначают как Е.
Более сложный случай представляют колебания молекул типа XY3, плоской
(группа D3h, рис. 22.11, а) или пирамидальной (группа C3v, рис. 22.11, б), важным
примером которой служит молекула аммиака NH3.
Для изменений длин трех эквивалентных связей q\, q2, q3 можно ввести коор-
динаты симметрии (см. рис. 22.11, в, г, д)
4i — Ч2 — Чз — 4а,
4\ —	42 — ~4з — 41, >
4\
у = —42 = ~Чз ~ Чп-
Координата q^ не изменяется при
любых операциях симметрии и соот-
ветствует полносимметричным колеба-
ниям; координаты q\ и дн преобразуются
при операциях симметрии по двухмерно-
му неприводимому представлению, и им
соответствуют, как можно показать [55],
одинаковые частоты колебаний. Таким
образом, мы имеем дважды вырожден-
ные колебания, отличающиеся по своей
форме; для одного из них изменяют-
ся противоположным образом (q2 = -q3)
только две связи, а для другого все три,
причем с различными амплитудами. Во-
прос о типах симметрии для группы C3v
мы рассмотрим подробнее в следующем
параграфе (см. с. 661 и табл. 22.3).
До сих пор мы рассматривали при-
меры дважды вырожденных колебаний.
Примером трижды вырожденных коле-
1	,1	о1
в	г	д
Рис. 22.11. Валентные колебания молекулы
типа XY3: а — равновесная конфигурация
плоской молекулы; б — равновесная
конфигурация пирамидальной молекулы;
в — полносимметричные смещения;
г, д — дважды вырожденные смещения
баний могут служить валентные колебания молекулы метана СН4, обладающей
симметрией Td (см. § 18.5, с. 524). Для изменения длин четырех связей С—Н можно
ввести координаты симметрии (рис. 22.12, а, б, в, г).
41	— 42	—	Чз	—	44	— Ча,
41	— 42	=	~Чз	=	~Ч4	= 41,
41	- ~Ч2	—	Чз	—	~Ч4	- Qu,
4\	— ~Ч2	~	~Чз	—	44	— Qin- ,
(22.30)
(22.31)
Координата q^ не изменяется при любых операциях симметрии и соответствует,
как и в случае плоской молекулы типа XY4 (см. (22.28)), полносимметричным
колебаниям. Координаты q\, qu, gm при операциях симметрии, как легко видеть,
преобразуются друг в друга или сами в себя. Например, при повороте на 120°
вокруг оси третьего порядка, проходящей через атом /, атом 2 становится на место
атома 3, атом 3 на место атома 4 атом 4, на место атома 2, и мы имеем
41 — Чи, Ч\\ — <7пь <7ш — 41'
(22.32)
660
Глава 22. Симметрия колебаний многоатомных молекул
При повороте на 180° вокруг оси х переставляются местами атомы 1 и 2
и атомы 3 и 4:
Q\ — Q\> Qu — ~Qu> tfin =	(22.33)
Рис. 22.12. Валентные колебания молекулы
метана: а — полносимметричные смещения;
б, в, г — трижды вырожденные смещения
„(х)
а при повороте С2
х = У, У = ~У,
в согласии с (22.32) и (22.33).
Смещения для координат симмет-
рии q\, #ц, gm расположены одина-
ковым образом относительно осей х,
у, z соответственно — вдоль данной
оси две связи спереди удлиняются,
в то время как две связи сзади уко-
рачиваются (рис. 22.12,5, в, г).
Совершенно очевидно, что трем
видам смещения соответствуют оди-
наковые частоты колебаний, т.е. мы
имеем трижды вырожденные коле-
бания.
Отметим, что закон преобразо-
вания координат симметрии #|, #ц,
#1П совпадает с законом преобразо-
вания координат ж, у, z. Например,
^0)
при повороте Сз ось х становится
на место оси у, ось у — на место
оси z и ось z — на место оси ж, т. е.
х — у, у = z, z — ху (22.34)
? = -z,	(22.35)
Легко определить характеры трижды вырожденных колебаний рассматриваеюго типа
для всех пяти возможных классов операций симметрии группы Td (см. (18.28)).
При поворотах С3 все координаты меняются местами и х(С^) — 0. При поворотах
вокруг осей х, у, z координаты переходят сами в себя, причем одна коорината сохраняет знак,
а две координаты его меняют (см. (22.33)), следовательно, х(^) = ~ 1- При поворотах
вокруг осей х, у, z с отражением одна из координат изменяет знак, а две другие переходят
друг в друга, поэтому также х(^) = -1. При отражениях ad в диагональных плоскостях,
проходящих через противоположные грани, одна из координат переходит сама в себя,
сохраняя знак, а две другие переходят друг в друга и x(ad) — 1. Наконец, для тождественной
операции С\ х(С\) — 3.
Таким образом, имеем следующую совокупность характеров для трижды вырожденных
колебаний и для самих координат х, у, z\
операции симметрии...	С}	8С3	ЗС2	6ad	6S4
характеры........... 3	0	—1	1	—1	( • /
(22.36) служит еще одним примером характеристики типа симметрии при помощи
задания совокупности характеров, определяющих закон преобразования координат симметрии
при различных операциях симметрии.
Рассмотренные примеры показывают, как связано появление вырожденных колебаний
со свойствами симметрии молекулы, с принадлежностью ее равновесной конфигурации
к группе симметрии определенного рода.
§ 22.4. Типы симметрии для молекул средней и высшей симметрии
661
§ 22.4. Ъшы симметрии для молекул, относящихся
к точечным группам средней и высшей симметрии
Теперь мы можем рассмотреть, какие именно типы симметрии колебаний,
невырожденные и вырожденные, возможны для различных групп с осями симметрии
порядка п 3.
Прежде всего можно определить для заданной группы общее число различных
типов симметрии и число типов симметрии каждой степени вырождения.
Общее число типов симметрии для любой группы, как можно показать [59, 137],
равно числу г классов операций симметрии. Как мы видели в гл. 18 (с. 521), для абелевых
групп число классов т равно порядку группы h и отсюда вытекает результат,
сформулированный нами в §22.2 (с. 651) для групп низшей симметрии, что число
типов симметрии равно порядку группы h. Для неабелевых групп число классов
меньше порядка группы и поэтому число типов симметрии всегда меньше порядка
группы.
Существует общая формула, позволяющая определить для заданной группы чис-
ло типов симметрии с различной степенью вырождения. Пусть степень вырождения
г-го типа симметрии равна ki (г = 1, 2,..., г, где г — число классов). Тогда порядок
группы
h = k\ + k$ + ... +к2г=^к-,	(22.37)
г=1
т. e. порядок группы равен сумме квадратов степеней вырождения всех возможных
типов симметрии. При этом разложение (22.37) порядка группы на сумму г квадратов
является всегда единственным. Для абелевых групп все ki равны единице и h просто
равно сумме h единиц.
Проиллюстрируем формулу (22.37) на конкретных примерах.
Для группы Су» порядка h = 6 операции симметрии, согласно (18.24), разбива-
ются на три класса. Следовательно, 6 надо разложить на сумму трех квадратов, что
дает
6 = 12 + 12 + 22 = 1 + 1 +4,	(22.38)
т. е. получаются два типа симметрии невырожденных колебаний и один тип симме-
трии вырожденных колебаний.
Для более сложной группы Tj порядка h = 24 операции симметрии, соглас-
но (18.28), разбиваются на пять классов. Следовательно, 24 надо разложить на сумму
пяти квадратов, что дает
24 = I2 + I2 + 22 + З2 + З2 = 1 + 1 + 4 + 9 + 9,	(22.39)
т. е. получаются два типа симметрии невырожденных колебаний, один тип симме-
трии дважды вырожденных колебаний и два типа симметрии трижды вырожденных
колебаний.
Принято обозначать невырожденные типы симметрии так же, как и в случае
групп низшей симметрии, буквами А и В, дважды вырожденные типы симме-
трии буквой Е и трижды вырожденные типы симметрии буквой F. Для групп
средней симметрии, содержащих операции поворота вокруг выделенной оси сим-
метрии Сп порядка п 3, А означает невырожденные типы симметрии, для ко-
торых колебательная координата не изменяется при поворотах вокруг этой оси,
а В — невырожденные типы симметрии, для которых эта координата изменяет
662
Глава 22. Симметрия колебаний многоатомных молекул
знак при операции Сп9). Различные типы симметрии данного рода (Л, В, В, В),
когда их имеется несколько, отмечаются дополнительными индексами: буквами д, и
(для четных и нечетных типов симметрии), штрихами (один штрих ' и два штриха "
для указания поведения по отношению к отражению в плоскости сг^, перпендику-
лярной к выделенной оси) или цифрами (например, 1, 2 для отличия двух типов
симметрии по отношению к определенному повороту вокруг оси С2, перпендику-
лярной к выделенной оси, или к отражению в плоскости crv, проходящей через
выделенную ось).
Возможные типы симметрии для группы C3v, два невырожденных и один
дважды вырожденный, обозначаются как А2 и Е. Типы Л] и Л2 отличаются
поведением при отражении в плоскостях симметрии av: для полносимметричного
типа Л] при этом сохраняется знак, а для типа Л2 знак изменяется. Таким образом,
разложению (22.38) соответствуют типы симметрии:
C3v Л1, Л2, Е.	(22.40)
Координата симметрии qA в (22.30) относится к типу Ль а пара координат q\ и —
к типу Е.
Возможные типы симметрии для группы 2^, два невырожденных, один дважды
вырожденный и два трижды вырожденных обозначаются как Л], Л2, Е, F] и F2.
Типы Л| и Л2, подобно случаю группы C3v, отличаются поведением при отражении:
для полносимметричного типа Л] сохраняется знак, а для типа Л2 знак изменяется
при отражении в плоскостях пд, проходящих через противоположные ребра куба.
Типы F\ и F2 также отличаются поведением при отражении в этих плоскостях,
но только более сложным образом. В соответствии с разложением (22.39) мы имеем,
таким образом, типы симметрии
Td Л|, Л2, F, Fh F2.	(22.41)
Координата симметрии qA в (22.31) относится к типу Ль а тройка координат q\,
Ч\\, Яш — к типу F2.
Отметим, что полносимметричные колебания всегда относятся к невырожден-
ному типу симметрии Л (для групп C3v и Td — к типу Л|).
В приведенных ниже таблицах (табл. 22.3-22.11) даны типы симметрии для то-
чечных групп средней и высшей симметрии, наиболее важных при рассмотрении
колебательных и электронных спектров молекул|0). В первом столбце таблицы даны
обозначения типов симметрии, а в последнем столбце указаны составляющие РА, рх
и &хц принадлежащие к соответствующим типам симметрии, как и в случае табл. 22.1
и 22.2. Для каждого типа симметрии содержатся данные, характеризующие его
поведение при операциях симметрии различных классов. Невырожденные типы
симметрии сохраняют или изменяют знак при каждой из операций симметрии
(1 или -1). Поведение вырожденных типов симметрии более сложно. Ниже даны
объяснения к таблицам для читателя, интересующегося детальной характеристикой
типов симметрии.
В таблицах приведены совокупности характеров для всех возможных у данной группы
1ипов симметрии, подобно том} как это было сделано в предыдущем параграфе для дважды
вырожденного типа симметрии группы D^h и для трижды вырожденного типа симметрии
группы Td (см. (22.27) и (22.36)). * 10
Это возможно лишь при четном п, так как при нечетных п операция давала бы (-1)п = — 1,
аСл"=С|.
10> Таблицы для других точечных групп имеются в монографии Герцберга 153].
§ 22.4. Типы симметрии для молекул средней и высшей симметрии
663
Таблица 22.3
Типы симметрии для группы C3v
	Сх	2С3	ЗбТг,	
	1	1	1	Pz \ &ZZ1 &хх ауу
а2	1	1	-1	Mz
Е	2	-1	0	[Рх, Ру\ I^Xl Цу\ &хг, Otxx — Otyyi Otxy
Таблица 22.4
Типы симметрии для группы D3h
D3h	C,	2C3	3(TV	<?h	2S3	3C2	
A'l	1	1	1	I	1	1	&ZZ ? &XX "b rtyy
A"	1	1	-1	-1	1	1	
A'i	1	1	-1	1	1	-1	Mz
4'	1	1	1	-I	-1	-1	Pz
JS'	2	-1	0	2	-1	0	fT’r, Py; ^ууч &xy
E"	2	-1	0	-2	1	0	&XZ1 &yz'i P’XI Р’У
Таблица 22.5
Типы симметрии для группы D3d
D3d	Cx	2C3	3(rd	i	2S6	3C2	
	1	1	1	1	I	1	&ZZ, &XX + Otyy
	1	1	-1	-1	1	1	
Л2д	1	1	-1	1	1	-1	Vz
^2u	1	1	1	-1	-1	-1	Pz
	2	-1	0	2	-1	0	1 &XX ~ <-*yy'’ &xy> &-XZ-) ayz ‘t Vy
Eu	2	-1	0	-2	1	0	Pxi Py
Таблица 22.6
Типы симметрии для группы Л4Л
Dth	Cx	2C4	c42 = c2	2C2	2C2	(Th	2(rv	2ffd	2S4	i	
	I	1	1	I	1	1	1	1	1	1	&ZZ •) &XX + Otyy
^Iw	1	1	1	1	1	-1	-1	-1	-1	-1	
A2g	1	1	1	-1	-1	1	-1	-1	1	1	f^z
A2u	1	1	1	-1	-1	-1	1	1	-1	-1	Pz
B\g	1	-1	1	1	-1	1	1	-1	-1	1	CH-xx &yy
B\u	1	-1	1	1	-1	-1	-1	1	1	-1	
Big	1	-1	1	-1	1	1	-1	1	-1	1	O^xy
Blu	1	-1	1	-1	1	-1	1	-1	1	!	
E9	2	0	-2	0	0	-2	0	0	0	2	P'Xf P'yy ^xzi ^yz
Eu	2	0	-2	0	0	2	0	0	0	—2	Pxi Py
664
Глава 22. Симметрия колебаний многоатомных молекул
Таблица 22.7
Типы симметрии для группы D5h
Dsh	С|	2С5	2Cj	5trv	°h	2S5	2S52	5C2	
A'l	1	1	1	1	1	1	1	1	^zz, (%-xx &yy
А1;	1	1	1	-1	-1	-1	-1	1	
А'2	I	1	1	-1	1	1	1	-1	Pz
	1	1	1	1	-1	-1	-1	-1	Pz
В',	2	2 cos 72°	2 cos 144°	0	I	2 cos 72°	2 cos 144°	0	Pxi Py
е"	2	2 cos 72°	2 cos 144°	0	-1	-2 cos 72°	-2 cos 144°	0	axz > ayz» Px, Py
е'2	2	2 cos 144°	2 cos 72°	0	1	2 cos 144°	2 cos 72°	0	(*XZ ~ (T-yy-) &xy
Е2	2	2 cos 144°	2 cos 72°	0	-1	-2 cos 144°	-2 cos 72°	0	
Таблица 22.8
Типы симметрии для группы Л6Л
Deh	Ci	2C6	2C62	c3 G6	3C2	3C'	<?h	3(TV	3(Td	256	2S3	6 “ г	
	1	1	1	1	1	1	1	1	1	1	1	1	&ZZ ) &XX + rtyy
	1	1	1	1	I	I	— i	-1	-1	-I	-1	-1	
Alg	1	1	1	1	-1	-1	1	-1	-1	1	1	1	Pz
Alu	1	1	1	1	-1	-1	— 1	1	1	-1	-1	-1	Pz
D\g	1	-1	1	-1	I	-1	— i	-1	1	1	-1	1	
D\u	1	-1	1	-1	1	-1	1	1	-1	-1	1	-1	
Big	1	-1	1	-1	-1	1	— i	I	-1	1	-1	1	
Blu	1	-1	1	-1	-1	1	1	-1	1	-1	1	-1	
Elg	2	1	-1	—2	0	0	—2	0	0	-1	1	2	aXZl ayz‘i Pxi Py
E\u	2	1	-1	—2	0	0	2	0	0	1	-1	-2	Px, Py
Elg	2	-1	-1	2	0	0	2	0	0	-1	-1	2	СИ-ХХ ^-yyi &xy
E?u	2	-1	-1	2	0	0	—2	0	0	1	1	—2	
Типы симметрии для групп Cxv и Dxh
Таблица 22.9
Cxv	Dxh	С|	2С^	(Гу	<?h	Si — i	25^	Ci	
{	)	1 I	1 1	1 1	1 -1	1 -1	1 -1	1 -1	azz у axx + ауу Pz
Л2(Я“) |	A2g(^g ) ^2и(^и )	1 1	1 1	-1 -I	1 -1	1 -1	1 -1	-1 1	Pz
Е,(П) |	Е^Пд)	2	2 cos р	0	-2	2	-2 cos р	0	Рхч Py 't (Txz-) &yz
	Е\и (Пи)	2	2 cos р	0	2	-2	2 cos р	0	Px, Py
В2(Д) {	Е2д^д)	2	2 cos 2р	0	2	2	2 cos 2р	0	(^XX ~~ (Ttyy, Otxy
	Elui^u}	2	2 cos 2р	0	-2	—2	-2 cos 2р	0	
В2(Ф) {	Е3д(Фд)	2	2 cos Зр	0	—2	2	—2 cos Зр	0	
	Ези(Фи)	2	2 cos Зр	0	2	—2	2 cos Зр	0	
									
§ 22.4. Типы симметрии для молекул средней и высшей симметрии
665
Таблица 22.10
Типы симметрии для групп Td
Td	Cj	8С3	6(?d	654	зс2	
	1	1	1	1	1	&ХХ ^уу ®-zz
42	1	1	-1	-1	1	
Е	2	-1	0	0	2	&ХХ — &ууч 2otZZ &ХХ Otyy
Fl	3	0	-1	1	-1	P'Xi №уч llz
F2	3	0	1	-1	-1	Рхч Руч Pz’i ayz4 агхч axy
Таблица 22.11
Типы симметрии для групп Oh
Oh	I	8C3	6C2	6C4	3C42	Si ~~ i	6S4	856		6(Td	
A]g	1	1	1	1	1	1	1	1	1	1	@ix Oyy + Otzz
	1	1	1	1	1	-1	-1	-1	-1	-1	
42g	1	1	-1	-1	1	1	-1	1	1	-1	
^2u	1	1	-1	-1	1	-1	1	-1	-1	1	
Fg	2	-1	0	0	2	1	0	-1	2	0	<*Х1 ayyi 2(XZZ Ot-xx ayy
Eu	2	-1	0	0	2	-1	0	1	—2	0	
Fig	3	0	-1	1	-1	1	1	0	-1	-1	Р'Хч Р'уч P'Z
Flu	3	0	-1	1	-1	-1	-1	0	1	1	
Fig	3	0	1	-1	-1	1	-1	0	-1	1	ayz4 azx4 axy
Flu	3	0	1	-1	-1	-1	1	0	1	-1	Рхч Руч Pz
Данные для групп C3v, D3h и D3d с выделенной осью третьего порядка содержатся
в табл. 22.3-22.5. Характеры даны для каждого класса операций симметрии, причем число
операций в классе указано рядом с символом операции (ср. (18.26)). Группы D3h и D3d = S6r,
имеющие одинаковый порядок (h — 12) и одинаковое число типов симметрии с теми же
совокупностями характеров, отличаются поведением составляющих РА, и аАд. Число типов
симметрии для групп D3h и D3d по сравнению с группой C3v просто удваивается; это связано
с тем, что группы D3h и D3d могут быть получены из группы C3v добавлением соответственно
операции симметрии ah и г, коммутирующих со всеми операциями исходной группы. Поэтому
можно было бы не приводить отдельной таблицы для группы C3v, а пользоваться табл. 22.4
или 22.5, вычеркнув из них три последних столбца и оставив первую, третью и пятую строчки.
В дальнейшем мы приводим таблицы лишь для групп наибольшей симметрии при данном
порядке п выделенной оси. В табл. 22.6-22.8 приведены данные для групп Dnh, п = 4,5,6.
Они составлены так же, как и предыдущие таблицы.
Отметим, что для групп D3h и D6h с осями порядка п = 5 и п = 6 получаются два
дважды вырожденных типа симметрии Е} и Е2, отличающихся характерами по отношению
к поворотам Сп. По мере увеличения п увеличивается и число дважды вырожденных типов
симметрии. Для групп Cxv и Dxh с осью симметрии бесконечного порядка получается
и бесконечное число таких типов симметрии (табл. 22.9; для труппы Cxv нужно брать лишь
столбцы С], 2С^ и av).
Для нормальных колебаний линейных молекул могут осуществляться только типы сим-
метрии Ai и Е\11 \ Остальные типы симметрии возможны для обертонов деформационных
колебаний. В таблице приведены обозначения, аналогичные обозначениям для конечных
групп, и обозначения (в скобках), применяемые для электронных состояний линейных
молекул, которые будут рассмотрены ниже (см. §24.2).
Рассмотренные в предыдущем параграфе дважды вырожденные колебания СО2 относятся к типу
симметрии Е1м(Пи) [ср. (22.26)].
666	Глава 22. Симметрия колебаний многоатомных молекул
Для групп с осью симметрии C^v бесконечного порядка дважды вырожденные типы
симметрии получаются, если рассмотреть закон преобразования пар величин типа (х 4- iy)1
и (х - iy)112). При повороте на угол ip (х + iy)1 умножается на е~г1<р, а (х - iy)1 умножается
на (см. с. 657) и характер равен
1(Q) = e~il* + ё1* = 2 cos (I = 1, 2, 3,...).	(22.42)
Для произвольного ip различным значениям I будут соответствовать, вообще говоря,
и различные значения 2cos/</?, т. е. различные характеры. При переходе к группам с осью
2тг
симметрии Сп конечного порядка п нужно рассматривать повороты только на угол —
п	п
и на кратные ему углы; различные значения 2cos/9? получаются лишь при I < —, т.е. I = 1
п
при п = 3ип = 4, I = 1,2 при п = 5 и п = 6 и т.д. Что касается значения I = —, возможного
27Г	2
при наличии оси четного порядка п, то при этом 2 cos / — = 2 costt = —2 и вместо дважды
п
вырожденного типа симметрии получается невырожденный тип симметрии (обозначаемый
через В).
Мы рассмотрели важнейшие группы средней симметрии. В табл. 22.10 и 22.11 приведены
данные для наиболее важных групп высшей симметрии, а именно, групп Td и Для них
характерно появление трижды вырожденных типов симметрии F. Отметим, что трижды
вырожденные координаты q}, дщ для молекулы метана (см. (22.31)) имеют, согласно (22.36),
характер х(а<1) — 1, следовательно, принадлежат к типу симметрии F2, как было уже указано
выше без доказательства (см. с. 662).
Знание характеров, приведенных в таблицах 22.1-22.11 для важнейших точечных групп,
позволяет решать ряд вопросов, связанных с симметрией колебательных и электронных
состояний молекул. С помощью этих характеров можно находить правила отбора как для ко-
лебательных, так и для электронных переходов. При этом для колебательных переходов
при поглощении и испускании нужно учитывать свойства симметрии составляющих РЛ ди-
польного момента и при комбинационном рассеянии — составляющих aXfl тензора поляризу-
емости. Для электронных переходов при поглощении и испускании нужно учитывать свойства
составляющих дипольного момента, а также свойства составляющих рх и Q\p. магнитного
и квадрупольного моментов, что существенно при рассмотрении переходов, запрещенных
при дипольном излучении.
§ 22.5. Подсчет числа колебаний различных типов симметрии
и нахождение коэффициентов симметрии
При рассмотрении нормальных колебаний молекулы, имеющей заданное число
колебательных степеней свободы и обладающей заданной симметрией, возникает
вопрос о том к каким типам симметрии относятся ее колебания и чему равно число
колебаний каждого типа симметрии.
Для молекул, относящихся к группам низшей симметрии, подобный подсчет
не представляет трудности, как было уже показано на примере молекулы этилена
(см. §22.2, с. 652). При этом следует исходить из рассмотрения естественных коле-
бательных координат различного вида. Наряду с координатами, не изменяющимися
при любых операциях симметрии группы (например, Q для молекулы С2Н4), могут
быть пары, четверки и восьмерки эквивалентных координат. Совокупность эквива-
лентных координат (например, двух координат «34 и четырех координат q\, q2,
qj, q$ для C2H4) дает к колебаний, относящихся к к различным типам симметрии.
Перебрав все виды эквивалентных координат, мы определяем полное число коле-
баний каждого типа симметрии и одновременно находим координаты симметрии,
в которых следует решать механическую задачу о малых колебаниях.
12^Так преобразуются колебательные волновые функции для обертонов вырожденных колебаний
линейных молекул, ср. §22.6, формула (22.72).
§ 22.5. Подсчет числа колебаний различных типов симметрии

Ча, Ч\, q\\, что дает
N
Н<2>
Для молекул, относящихся к группам средней и высшей симметрии, подсчет
числа колебаний каждого типа симметрии также может быть произведен на основе
рассмотрения естественных колебательных координат различного вида. При этом,
вообще говоря, для заданной совокупности эквивалентных координат получаются
как невырожденные, так и вырожденные типы симметрии.
Простейшим примером может служить подсчет колебаний различных типов
симметрии для молекулы аммиака NH3, имеющей симметрию C$v (см. .§ 18.2, с. 507).
В качестве независимых колебательных координат мы введем валентно-силовые
координаты: три изменения q\, q2, q^ длин связей N—Н и три изменения «12,
«23, «31 углов Н—N—Н (рис. 22.13,а). Для трех эквивалентных координат q\, q2,
qi можно ввести, согласно (22.30), координаты симметрии
одно невырожденное колебание типа А], и одно дважды
вырожденное колебание типа Е (см. с. 662). Эквивалентные
координаты «23, «зь «12 по свойствам преобразования со-
вершенно подобны координатам q\, q^ и qi и также дают
одно невырожденное колебание типа А\ (координата сим-
метрии аА = «23 — «31 = «12) и одно дважды вырожденное
колебание типа Е (координаты симметрии «| = «31 = «!2,
при «2з = 0, и «и =	— ~«3i — “«12)- Таким образом,
получается два невырожденных колебания типа А\ (пол-
носимметричных) и два вырожденных колебания типа Е,
которым соответствуют координаты qA, аА и q\, «1; q\\, «ц.
Несколько сложнее подсчет числа колебаний различ-
ных типов для молекулы метана СН4, имеющей симме-
трию В качестве колебательных координат мы также
введем валентно-силовые координаты: четыре изменения q\,
#2, <7з, ^4 длин связей С—Н и шесть изменений «12, «13, «14,
«23, «24, «34 углов Н—С—Н (рис. 22.13, б). 6 координат «г&
не являются при этом независимыми и удовлетворяют до-
полнительному условию,3):
У2 aik = «12 + «13 + «14 + «23 + «24 + «34 = 0-	(22.43)
Исключение одной из координат «^ нарушило бы сим-
метрию, и его производить нерационально, а учет усло-
вия (22.43) при решении задачи о колебаниях может быть произведен по определен-
ным правилам и в простейших случаях не представляет затруднений. Для четырех
эквивалентных координат qi мы получаем, согласно (22.32), одно невырожденное
колебание типа А\ (координата симметрии qA) и одно трижды невырожденное ко-
лебание типа F2 (координаты симметрии qy7\ = q\, qp2\\ —	^2ш = <7ш, см. с. 659).
Для шести эквивалентных координат как можно показать, получается одна ко-
ордината симметрии типа At, одна пара координат симметрии типа Е и одна тройка
координат симметрии типа F2. При этом, однако, надо учесть условие (22.43);
для координаты симметрии «л, мы имеем
Рис. 22.13.
Колебательные
координаты:
а — для молекулы NH3;
б — для молекулы СН4
«12 — «13 — «14 = «23 = «24 = «34 = «Л,,
«Л, — т(«12 + «13 + «14 + «23 + «24 + «34),
О
(22.44)
Справедливость этого условия легко проверить, если воспользоваться формулой (21.105) (см. [551,
т. 1,с. 101).
668
Глава 22. Симметрия колебаний многоатомных молекул
и, согласно (22.43), она обращается в нуль. Поэтому для координат получается
одно колебание типа Е и одно колебание типа F2. Всего мы имеем одно невыро-
жденное полносимметричное колебание типа А\ (координаты симметрии qA), одно
дважды вырожденное колебание типа Е (координата симметрии а#ц) и два
трижды вырожденных колебания типа F2 (координаты симметрии qF1\, qF2\\, tfFjib
Аналогичным образом можно произвести подсчет числа колебаний различных
типов симметрии и для других молекул, относящихся к группам средней и высшей
симметрии. При этом можно заранее подсчитать числа координат симметрии раз-
личных типов для совокупностей эквивалентных координат, возможных для данной
группы, подобно тому, как мы это сделали на примере молекулы СН4 для четверок
эквивалентных координат q\, q2, q^, q$ для группы Т(/.
Наряду с определением числа нормальных колебаний каждого типа симметрии
важное значение имеет нахождение коэффициентов, связывающих смещения с ко-
ординатами симметрии — коэффициентов симметрии. Знание этих коэффициентов
необходимо при решении механической задачи о нормальных колебаниях с учетом
свойств симметрии, которое будет рассмотрено в следующем параграфе.
Для частных случаев, рассмотренных нами в данной главе, эти коэффициенты
получаются из формул, связывающих смещения с соответствующими координатами
симметрии. Например, для изменений четырех эквивалентных длин связей С—Н
в молекуле метана мы имеем формулы (22.31). Из этих формул следует, что|4)
Qi — Qa + Q\ + qw + <?ni, '
Q2 = Qa + Q\ ~ (Zn ~ tfni,
Q3 = Qa ~ Q\ + Qw ~ <7iih
Q^ — Qa ~ Q\ ~ Qw + <7iii >
и обратно,
Qa = ~(9i +?2 + ?з+94),
9i = |(9i + 92 - 93 -94),
9n = |(9i - 92 + 93 -94),
9111 = ^(9i - 92 - 93 + 94)-
(22.45)
(22.46)
Коэффициенты этих преобразований и представляют коэффициенты симме-
трии. В общем виде мы можем написать
к
Xi
i— 1
(22.47)
где Xi — эквивалентные естественные координаты, a Zj — координаты симметрии.
’^Формулы (22.31) можно получить из (22.45), полагая одну из координат qA, q\, 7ц, дщ не равной
нулю, а остальные равными нулю.
§ 22.5. Подсчет числа колебаний различных типов симметрии
669
Для данного частного случая мы имеем совокупность коэффициентов
^1А —	1,	С|1 = 1,	C1II = 1,	С1Ш = 1,
С2А =	1,	C2I = 1,	с21! = “I,	С2Ш = -1,
^ЗА	1,	C31 = -1,	сзп — 1,	сзш := -1,
С4А —	1,	с4| = -1,	с41! ~	с41!1 = 1,
(22.48)
которую можно выписать сразу, исходя из формул (22.31). Коэффициенты, состо-
ящие в одном столбце, определяют относительные смещения qi при изменении
заданной координаты симметрии.
Для изменений эквивалентных длин связей N—Н (или изменений эквивалент-
ных углов Н—N—Н) в молекуле NH3, согласно (22.30), получаем коэффициенты
симметрии
С\а =	1,	си	=	0,	с1П	=	2,
С2А —	I,	С21	—	1,	С2П	=	>
СЗЛ —	1,	С31	=	-1,	Сзц	==	-1.
(22.49)
Можно определить коэффициенты симметрии для других различных случаев
и представить их в виде таблиц.
Подобные таблицы коэффициентов симметрии составлены для важнейших групп сим-
метрии (см. [55], т. 1, гл. 4) и применяются для получения вековых уравнений с учетом
симметрии по методу, вкратце описанному в следующем параграфе. Этим и таблицами можно
пользоваться также и для определения числа колебаний различных типов симметрии.
Следует отметить, что коэффициенты симметрии удовлетворяют условиям ортогональ-
ности
52 сис<‘ = 0 0V 0	(22.50)
i
и могут быть выбраны нормированными так, что
= <22-51)
Тогда преобразование, обратное преобразованию (22.47), имеет вид
k
Zj —	(22.52)
»=1
и выполняется соотношение
52*> = 52a:i2	<22-53)
i	1
(частный случай которого мы имели в §22.1, см. с. 647), а также соотношение
52 cucji = ° {) / *)•	(22.54)
Однако для составления вековых уравнений важны только относительные значения ко-
эффициентов симметрии для данной координаты симметрии (т. е. коэффициентов, состоящих
в одном столбце в (22.48) и (22.49)), и нормировка не является обязательной.
670
Глава 22. Симметрия колебаний многоатомных молекул
§ 22.6. Решение задачи о колебаниях молекулы
при учете свойств симметрии
При введении координат симметрии задача о нормальных колебаниях решается
отдельно для колебаний каждого типа симметрии, как уже указывалось выше
(см. с. 638 и с. 647). Именно этим определяется необходимость введения координат
симметрии как промежуточных между исходными естественными колебательными
координатами и окончательными нормальными координатами.
Разделение общей задачи о всех нормальных колебаниях молекулы на ряд задач
для колебаний отдельных типов симметрии определяется тем, что кинетическая
и потенциальная энергии, выраженные в координатах симметрии, разбиваются
на части, каждая из которых зависит только от координат симметрии определенного
типа. Иначе говоря, кинетическая и потенциальная энергии не содержат членов
с произведениями координат симметрии различных типов, т. е. членов вида k'apzazp,
M'apZazp, где za и zp — координаты симметрии различных типов.
Для невырожденных координат симметрии это доказывается очень просто. Действи-
тельно, кинетическая и потенциальная энергия как функции, характеризующие физическое
состояние, инвариантны по отношению к операциям симметрии, т.е. не должны изменяться
при операциях симметрии. Однако для координат симметрии zn и zp различных типов обяза-
тельно найдется такая операция симметрии, при которой одна из координат сохраняет свой
знак, а другая его изменяет; например, при наличии центра симметрии четная координата
при инверсии сохранит знак, а нечетная его изменит. Поэтому произведения zQzp и zazp
должны изменять знак, а так как потенциальная и кинетическая энергии инвариантны, то
k'af3 = 0 и — 0, что и требовалось доказать. Доказательство для вырожденных координат
несколько сложнее (см., например, [59] или [55], т. 1, с. 201). При этом оказывается, что
для вырожденных колебаний каждого типа обращаются в нуль и члены с произведениями
вырожденных между собой координат симметрии, а коэффициенты при членах, содержащих
квадраты этих координат, одинаковы.
Чтобы проиллюстрировать разделение задачи о колебаниях при учете свойств
симметрии, рассмотрим конкретный пример нелинейной симметричной трехатом-
ной молекулы (типа молекулы Н2О) и непосредственно выразим потенциальную
и кинетическую энергию в координатах симметрии. Будем исходить из общего ви-
да (21.36) потенциальной энергии для нелинейной трехатомной молекулы, причем
в силу одинаковости связей О—Н будут равны друг другу коэффициенты при q2 и q2
(kq{ = kq2 = kq) и при q^a и q2a (At = A2):
U — 2	+ #2) H" 2 kaa2 4- hq\q2 4- A(q\ 4- qi)®-	(22.55)
Введем теперь координаты симметрии qs, qa и as, согласно (22.4) и (22.2). Мы
получим
и = kqq2s + kqq\ + kaas + h{q} - q2) + 2AqsaSy	(22.56)
откуда
Z7 = ^(A^ + h)qs +	4- - kaa2 4- (kq — h)q^	(22.57)
т. e. потенциальная энергия разделяется на две части — часть, зависящую только
от симметричных координат qs и ots и часть, зависящую только от антисимметричной
координаты qa.
§22.6. Решение задачи о колебаниях при учете свойств симметрии
671
Кинетическая энергия преобразуется совершенно аналогичным образом. Если
ее записать в виде
Т — 2	+ 2	+ ^qqQ\Q2 + ^a(<7l 4- «h)6*,	(22.58)
то в координатах симметрии
Т = / {Mq + Mqq)q2 + 2Mqaqsas + | Маа} | + {Mq - Mqq)q2a. (22.59)
В результате полная энергия разделилась на две части и задача для трех степеней
свободы сводится к решению двух задач: к задаче для двух степеней свободы
(координаты qs и а5) и к задаче для одной степени свободы (координата qa).
Последняя задача решается сразу и дает частоту антисимметричного колебания
1 / Е - h
и = — л —---------------
2тг V Mq - Mqq
(22.60)
Еще большие упрощения получаются для молекулы СН4, обладающей тетраэдрической
симметрией. Для простоты мы ограничимся лишь валентными колебаниями и с учетом
одинаковости связей С—Н запишем потенциальную энергию в виде,5>
U = - кя(^ + 72 + Оз + 74) + h(o\O2 + 717з + 7i74 + 7?7з + 7274 + 7374)-	(22.61)
Вводя координаты симметрии согласно (22.45), получим
U = - kg (4q\ + 47? + 47ц + 47hj) 4- Л (67^ - 27? — 27^ — 27^1),	(22.62)
откуда
и ={- (4kq + 6h)q2A + 1 (4fc, - 2h)q2 + (4kq - 2ft)g?, + | (4fc, - 2h)g?„.	(22.63)
Аналогичным образом преобразуется и кинетическая энергия. Таким образом, задача для че-
тырех степеней свободы сводится к четырем задачам, для одной степени свободы каждая
(для координат qA и 71 = qF^, 7ц = 7f2h, 7ш = 7f2iii)> причем для вырожденных между собой
координат 7F2i, 7^11, 7f2hi коэффициенты в (22.63) одинаковы, что приводит к совпадающим
частотам колебаний.
Если учесть зависимость энергии от угловых координат и ввести координаты симме-
трии аЕ\, аЕц типа Е и координаты симметрии a^j, ар2ц, а/?21п типа F2 (см. выше, с. 668),
то потенциальная энергия примет в координатах симметрии вид
1	2	1	2	1	2	( 1	2	1	2	1
17 — - kAqA + - kEaEi + - kEaEn + < - kqFqF2i + - kaFotF2i 4- aFqF2iaF2i > +
f 1	2	1	2	1	/ X
+ s ~ ^qfQf2u + 2 ^aFaF2\\ + aF7F2iiQF2n г +	(22.64)
J 1	2	1	2	1
+ I 2	+ 2 ^а^2П1 + aF7r2lll«F2lll p
для двух вырожденных между собой координат аЕ\ и аЕц и для трех вырожденных пар
координат (7f2haF2|), (7f2ii, «f2ii) и (7г2нн лг2ш) получаются одинаковые коэффициенты.
Аналогичный вид примет и кинетическая энергия. Получается одна задача для одной степени
Сохранение коэффициента h при отбрасывании членов, зависящих от угловых координат, разуме-
ется, не имеет физического смысла, однако для нас это сейчас несущественно.
672
Глава 22. Симметрия колебаний многоатомных молекул
свободы для невырожденного типа симметрии Л, две одинаковые задачи, для одной степени
свободы каждая, для дважды вырожденного типа симметрии Е и три одинаковые задачи,
для двух степеней свободы каждая, для трижды вырожденного типа симметрии F2. Решение
этих задач дает одну частоту полносимметричных колебаний типа Л|, одну частоту дважды
вырожденных колебаний типа Е и две частоты трижды вырожденных колебаний типа F2.
Вообще, для вырожденных колебаний определенного типа приходится решать задачу для числа
степеней свободы, равного числу различных видов вырожденных координат того типа. В данном
случае мы имеем два вида (qF1 и а^2) трижды вырожденных координат типа F2, и хотя им
соответствует шесть степеней свободы (шесть коорданат qF1\, qF2\\, 7f2iii и «г2ь <*r2ib аг2ш),
получается задача для двух степеней свободы.
Для конкретного решения задачи о колебаниях необходимо составить веко-
вые уравнения. Это проще всего сделать, как мы видели в §21.4 и 21.5, если
исходить из коэффициентов кинематического взаимодействия, а не из выражения
для кинетической энергии, определение коэффициентов в которой практически
очень затруднительно. В соответствии с разделением энергии колебаний, при уче-
те симметрии молекулы, на независимые части, вековое уравнение r-й степени
(г — число колебательных степеней свободы) также распадается на вековые уравне-
ния более низких степеней. Именно эти уравнения и требуется составить. Можно
показать16), что в окончательные вековые уравнения для колебаний определенного
типа симметрии входят «приведенные» коэффициенты полного взаимодействия Da@
для координат симмерии za и zp данного типа. Например, для нелинейной симме-
тричной молекулы типа Н2О получаются вековые уравнения
D™' - и2 D4,^	=0, Dq q - w2 = 0,	(22.65)
Da„q, Da„a,-<v2	ЧЛ	’
в соответствии с выражениями (22.57) и (22.59) для потенциальной и кинетической
энергий.
Для тетраэдрической молекулы типа СН4 получаются вековые уравнения
о„.„-» = «,	=	(22.66)
соответствующие выражению (22.64) потенциальной энергии и аналогичному выражению
для кинетической энергии. При этом второе уравнение определяет частоту vF дважды выро-
жденного колебания, при котором изменяются координаты aFi и «яп, а третье уравнение —
две частоты, v'F2 и р^2, трижды вырожденных колебаний, при которых изменяются тройки
нормальных координат
04*2Ki1) ~ aiQF2\ + Ь|Лг2ь = «i<7f2ii + Ь|«г21ь Ci > = «i7f2iii + &1аг2пь [	.	.
>	(ZZ.b/)
(I/F2)d,) = а2<?Г21 +^2qF2I,	(2П) — al^2ll + &2«F2lb	(2	~ а2<7г2П1 + &2aF2lll- )
г.	«	ДО ЛЮ Л111)
Вырожденные между собой нормальные координаты	одинаковым образом
выражаются через пары координат симметрии (<7F2i,aF2i), (<Zr2ib qf2ii), (<7г2пь аг2ш) соот-
ветственно. Аналогично выражаются также координаты q2 ,	, Q2 . Каждая пара фор-
мул (22.67), стоящих друг под другом, аналогична формулам (22.9). При отсутствии взаимо-
действия валентных колебании с деформационными Ъ\ = а2 = 0, колебания	, <]
будут чисто валентными, а колебания £2^,	~ чисто деформационными.
Приведенные коэффициенты полного взаимодействия могут быть легко най-
дены, если исходить из коэффициентов кинематического и динамического взаимо-
действий и коэффициентов симметрии. Оказывается, что достаточно знать коэф-
фициенты кинематического и динамического взаимодействий одной эквивалентной
|6) См. [55|, т. 1, гл. 7.
§ 22.6. Решение задачи о колебаниях при учете свойств симметрии 673
естественной координаты каждого вида со всеми естественными координатами. Эти
коэффициенты умножаются на коэффициенты симметрии и складываются, давая
приведенные коэффициенты кинематического и динамического взаимодействий Аар
и кр^, через которые приведенные коэффициенты полного взаимодействия Dai
определяются по формуле
2 ^а/3^7»	(22.68)
р
аналогичной формуле (21.95).
Конкретные примеры составления вековых уравнений при учете свойств сим-
метрии мы не будем рассматривать17>.
До сих пор при решении задачи о малых колебаниях мы принимали во внимание
симметрию, не учитывая их ангармоничности. Как было указано в §21.7 (с. 638),
при учете ангармоничности нормальные колебания перестают быть независимыми.
Взаимодействие различных нормальных колебаний, обусловленное ангармонично-
стью, зависит от их симметрии. Для вырожденных колебаний наличие ангармо-
ничности приводит к расщеплению уровней энергии, которые при гармонических
колебаниях совпадают.
Потенциальная и кинетическая энергии должны быть инвариантны при операциях
симметрии. Выраженные через координаты симметрии или нормальнее координаты U и Т
не должны содержать членов, изменяющихся при операциях симметрии. В частности, для слу-
чая невырожденных колебаний будут отсутствовать члены, содержащие нечетные степени
координат, меняющих знак при операциях симметрии. Это можно видеть на простейшем
примере нелинейной молекулы типа Н2О, для которой квадратичные члены в U и Т имеют
вид (22.57) и (22.59), где отсутствуют члены с qsqa, asqa и qsqa, asqa, так как qa и qa меняют
знаки при операциях С2 и Кубические члены в U должны соответственно иметь вид
3“ ^а^з 3“ QqaQs&s 3“ ^aq^l^s 3“ ^qqQsqa 3“ ^qa^Qai	(22.69)
где антисимметрическая координата qa входит лишь в квадрате, но не в первой и третьей
степенях. В (22.69) в силу симметрии отсутствуют, таким образом, члены с q%, qaq2s, qaa2s
и qaqs<*s’ Однако наличие в U членов с qsq2 и asql приводит к взаимодействию симметричных
и антисимметричных колебаний. Энергия колебаний при учете ангармоничности для моле-
кулы Н2О и вообще для любых молекул, относящихся к группам низшей симметрии, будет
иметь вид (21.124) и содержать квадратичные члены, отвечающие взаимодействию любых пар
нормальных колебаний как одной симметрии, так и разной симметрии. Упрощение задачи
состоит лишь в том, что коэффициенты dik в формуле (21.124) будут зависеть от меньшего
числа постоянных, характеризующих ангармоничность.
При наличии вырожденных колебаний, т. е. для молекул, относящихся к группам средней
и высшей симметрии, в выражении для потенциальной энергии также будет отсутствовать
ряд членов, содержащих как нечетные степени вырожденных координат, так и произведения
вырожденных между собой координат (ср. выражение (22.63), в котором нет членов с £|7п,
£|<7пь 9пфи)« При учете ангармоничности в потенциальной энергии все же остаются члены,
определяющие взаимодействие вырожденных колебаний одной симметрии. В силу наличия
вырождения энергия колебаний получается отличной от (21.124).
Для дважды и трижды вырожденных частот в сумме линейных членов в выраже-
нии (21.124) будет иметься по два и по три одинаковых члена, и ее можно записать в виде
(ср- (21.14))
4,™,.+у).	(22.70)
i
где «,- = 1,2, 3 для невырожденных, дважды вырожденных и трижды вырожденных колебаний
соответственно, а суммирование происходит по разным частотам нормальных колебаний.
|7) Такие примеры можно найти в [55], т. 1, гл. 7, и в [56].
22 Зак. 10'
674
Глава 22. Симметрия колебаний многоатомных молекул
Для молекулы типа СН4 получим, в частности,
/	1 \	ill 3 \ и ( и
~ Уа ( иА + 2 ) + Ue(Ve + 0 + u'f2 ( v'f2 + 2 ) + I иf2 + 2 ) •
(22.71)
Вместо квадратичных членов типа 4- - J [vk 4- -J в (21.124), появляется, как
можно показать [318], два рода членов, обусловленных ангармоничностью, — члены типа
/ sa\ /	sk \	1	1	Si	sk
dik 4- — J \ vk 4-	— J, отличающиеся лишь заменой	vt, + -	и vk 4- - через	vt< + —	и vk 4- —,
и дополнительные члены того же порядка, зависящие от квантовых чисел колебательных
уровней, вырожденных при отсутствии ангармоничности. Наличие дополнительных членов
приводит к расщеплению этих уровней.
Для простейшего случая симметричной линейной молекулы типа СО2, для дважды
вырожденного деформационного колебания (см. §22.3, с. 654) наряду с квантовым числом v
вводится квантовое число /, принимающее значения
I = и, v - 2,..., 0 при v четном,
I = v, v - 2,..., 1 при v нечетном
(22.72)
и имеющее очень простой физический смысл. Оно определяет значение момента количества
движения = hl, связанного с колебаниями и направленного вдоль оси молекулы.
Отметим, что для дважды вырожденных колебаний степень вырождения уровня с заданным v
равна v + 1,8). Уровни с I = 0 являются невырожденными, а уровни с I > 0 — дважды
вырожденными; при v = 1 имеем дважды вырожденный уровень с I = 1, который не может
расщепляться, а при v > 1 — вырожденные уровни, которые при наличии ангармоничности
могут расщепляться на две (при v = 2nv = 3)n более составляющих. Выражение для энергии
колебаний будет иметь вид [318, 53]
/ А	/ А / А2
+ 2 ) + u2\v2 4“ 1) 4-	[ из 4- 2 ) +	4- - )
4- <*22(^2 4- I)2 4- d33 f v3 4- - j 4- ^12 f t>i 4- - j (i>2 4- 1) 4-
(22.73)
+ <*13
+ <*2з(и2 + 0 ( и3 + ~ ) + 922^ ч
где через V\, v2 и v3 обозначены частоты симметричного, деформационного и антисимметрич-
ного нормальных колебаний19). Наличие последнего члена, в котором постоянная д22 зависит
от ангармоничности, вызывает расщепление всех уровней с v2 > 1 на число составляющих,
v2	v2 1
равное числу значений I в (22.72), т. е. на — 4- 1 составляющих при четном v2 и на — 4- ~
составляющих при нечетном v2; следовательно, первый обертон (v2 = 2) и второй обертон
(г>2 = 3) расщепляются на две составляющих, третий (v3 = 4) и четвертый (v3 = 5) — на три
составляющих и т. д. * 20)
Двойное вырождение для составляющих с I > 0 снимается, если учесть взаимодей-
ствие колебаний с вращением, что приводит к так называемому Z-удвоению. Подобное
удвоение имеет место для линейных молекул как типа СО2, так и типа молекул синиль-
ной кислоты HCN; формула (22.73) применима и для несимметричных линейных молекул
|8) Мы имеем, аналогично случаю трехмерного осциллятора (16.70), энергию деформационных коле-
баний по осям х и у, равную и (vx 4- -4- у (vy 4- -	= v(v 4-1), где v = vx 4- vy и vx = 0, 1,2,...;
vy = 0, 1, 2,..., т. е. при заданном v возможны v 4- 1 комбинаций vx и vy.
,9)Эти нормальные колебания относятся к типам симметрии 4[ff(S^), 7?1и(Пи) и	соответ-
ственно, см. табл. 22.9, с. 664.
20) Симметрия этих составляющих при I = 0, 1,2, 3,... будет 4)g(S^), Е\и (Пщ), Е2д(Дд), Е3и(Фи) и т.д.
§22.6. Решение задачи о колебаниях при учете свойств симметрии
675
типа HCN, только в этом случае исчезает деление невырожденных колебаний на симме-
тричные и антисимметричные21^. Величина Z-удвоения для I = 1 выражается приближенной
формулой [70, 71]
|(v2 +1)J(J+1),	(22.74)
где J — вращательное квантовое число. Переходы между получающимися подуровнями
удается наблюдать для молекул типа HCN при поглощении в микроволновой области,
в частности, для состояния v2 — 1 молекулы HCN наблюдаются переходы, данные для которых
приведены в табл. 22.12.
Таблица 22.12
/-удвоение для молекулы HCN
Значения J	Частоты переходов в МГц	ДЕ
		9 - J{ J +1)
6	9423,3	224,365
8	16147,8	224,274
9	20181,4	224,238
10	24660,4	224,185
11	29585,1	224,129
12	34953,5	224,061
Как показывает таблица, q почти постоянно и составляет около 224 МГц = 0,075 см ’.
Небольшое убывание q с увеличением J объясняется членами, содержащими [j(J + I)]2
и отброшенными при выводе формулы (22.74).
2|) Невырожденные колебания i/| и щ будут типа Л], дважды вырожденное и2 будет типа Е\.
ГЛАВА 23
КОЛЕБАТЕЛЬНЫЕ СПЕКТРЫ МНОГОАТОМНЫХ МОЛЕКУЛ
§23.1. Правила отбора в колебательных спектрах
Мы уже подчеркивали в гл. 17 (с. 466), что колебательные спектры весьма
широко изучаются методами инфракрасной спектроскопии и комбинационного
рассеяния. В инфракрасной области спектра, как правило, наблюдают спектры по-
глощения, соответствующие переходам с нижних колебательных уровней на верхние.
В комбинационном рассеянии наблюдают стоксовы линии, также соответствующие
переходам с нижних колебательных уровней на верхние.
Весьма важное значение имеют правила отбора. Аналогично случаю двухатом-
ных молекул существует правило отбора для гармонических колебаний, наруша-
ющееся при наличии ангармоничности. Кроме того, что особенно существенно,
существуют правила отбора, связанные с симметрией колебаний.
При чисто гармонических колебаниях для каждого нормального колебания
справедливо правило отбора (20.32), Av — ±1, и возможны переходы, для которых
Avj = 0 0VO,	(23.1)
т. е. энергия данного (i-ro) нормального колебания изменяется на величину одного
колебательного кванта, при неизменной энергии всех других нормальных колебаний.
В инфракрасном поглощении и при стоксовом комбинационном рассеянии мы
получаем переходы
(vh v2,..., vt-,..., vfc) —> (vH v2,..., Vi 4- 1,..., vfe),	(23.2)
соответствующие частотам ц- нормальных колебаний — основным или фундаменталь-
ным частотам.
При наличии ангармоничности правило отбора (23.1) нарушается, и становятся
возможными переходы, для которых либо одно из колебательных квантовых чисел
изменяется больше, чем на 1, либо одновременно изменяются несколько квантовых
чисел (на 1 или более). В результате получаются обертоны (Av, > 1) и составные
частоты (Avi 0, Avy 0) (см. §21.7, с. 640); аналогично (23.2) имеем переходы:
(г»,, v2,... ,vit... ,vk) (vb v2,... Vi + 2,..., vk) = 2),
(vb vb..., Vi,..., Vj,..., vk) -+ (vb v2,..., V, +1,..., Vj± 1,..., vk) (Avj +|Av,| = 2),
(vb v2,..., Vi,..., vk) -+ (vb v2,..., Vi + 3,..., vk) (Av,- = 3),
(23.3)
для которых сумма абсолютных изменений колебательных квантовых чисел рав-
на 2, 3, 4, ...:
к
6 = ^2 |Av,-| = 2, 3,4,... .	(23.4)
г=1
§23.1. Правила отбора в колебательных спектрах
677
Частоты получающихся переходов приближенно равны 2ц, ц ± Vj, 2vi ± i/j,
ц ± Vj ±vi ит. д. Соответственно такие переходы и обозначают обычно как 2ц,
ц +ць ц-ц, 3i/6, ц +ц —ц и т.д. Вероятности переходов убывают с увеличением б
и будут тем меньше по сравнению с вероятностями переходов (23.2), для которых
б = 1, чем меньше ангармоничность.
Правило отбора (23.1) справедливо, когда одновременно имеет место механическая
гармоничность, т.е. потенциальная энергия является квадратичной функцией (21.28), и элек-
трооптическая гармоничность, т. е. дипольный момент и поляризуемость, являются линей-
ными функциями колебательных координат (ср. §20.2, с. 578 и с. 579). Нарушение правила
отбора (23.1) и появление переходов (23.3) может происходить как вследствие механичес-
кой ангармоничности, так и вследствие электрооптической ангармоничности. Механическая
ангармоничность определяется, в первую очередь, членами третьей и четвертой степеней
в потенциальной энергии (см. (21.125)). Оптическая ангармоничность определяется нели-
нейной зависимостью дипольного момента и поляризуемости от колебательных координат;
аналогично (20.63) и (20.64) составляющие дипольного момента и тензора поляризуемости
в общем случае имеют вид1)
л(б,е2,...,б) = (А)о+$2(^) * +	<•< + ••	<23-5)
и
Ад (Соб, ♦••,&) ~ (^Ад)о + f 6 + ~	‘	(23.6)
“ X / о 2 ~ х^г / О
Члены второй и более высоких степеней в этих разложениях определяют возможность
переходов с 6	2 даже при отсутствии механической ангармоничности.
Действительно, матричные элементы типа (vjl^lv-') и	) будут отличны
от нуля для колебаний, не обладающих механической ангармоничностью, при |Диг| = 2
и при |Дц| = 1, |Дц| = 1 соответственно (см. §20.3, с. 581), т.е. при <5 = 2, что приводит
к появлению первого обертона 2ц г-го колебания и составных частот, равных сумме и разности
основных частот г-го и j-ro колебаний, ц + ц и ц - ц (ц > ц). За счет членов третьей
степени в (23.5) и (23.6) становятся возможными переходы с б = 3 и т.д.
Наличие механической ангармоничности приводит к тому, что могут быть отличными
от нуля и матричные элементы типа (vj, t^,..., ц',...	v",..., v",...) при |Дц| > 1
и |Дц| 0 (г J), которые берутся теперь по волновым функциям связанных между собой
ангармонических осцилляторов; таким образом, даже при отсутствии электрооптической ан-
гармоничности (т. е. при наличии в (23.5) и (23.6) лишь линейных членов относительно &)
возможно появление обертонов и составных тонов. В общем случае появление оберто-
нов и составных тонов будет определяться одновременно механической ангармоничностью
и электрооптической ангармоничностью; с их увеличением будет возрастать вероятность
соответствующих переходов.
При исследовании инфракрасного поглощения и стоксового комбинационного
рассеяния при обычных температурах, как правило, значительная часть молекул
(а часто и подавляющее большинство) находится в нулевом колебательном состоя-
нии. В результате наблюдаются преимущественно или даже исключительно переходы
с нулевого колебательного уровня,
(0, 0, 0,..., 0) -* (v}, v2, v3,..., vk).	(23.7)
Мы получаем схему (21.131), которая в сокращенной записи имеет вид:
основные частоты ц, ц, Ц, • Vk,
обертоны	2ц, Зц, ..., 2ц, Зц, ..., ... ;	(23.8)
составные частоты v\ + ц, i/| + ц +ц, 2ц 4-ц, ... .
*) Об обосновании общих формул (23.5) и (23.6) см. конец §23.2, с. 694.
678
Глава 23. Колебательные спектры многоатомных молекул
При этом в отличие от (23.3) отсутствуют разностные частоты типа v\ —1/2,
2v\ — Р2 и т. д.
Для многоатомной молекулы, равновесная конфигурация которой обладает
определенной симметрией, получаются и определенные правила отбора для ко-
лебательных переходов, различные для инфракрасных спектров и для спектров
комбинационного рассеяния. Эти правила отбора обусловливаются симметрией
комбинирующих колебательных состояний и симметрией составляющих Р\ диполь-
ного момента Р или составляющих тензора поляризуемости а соответственно.
Симметрия колебательных состояний, в свою очередь, определяется симметрией
отдельных нормальных колебаний и квантовыми числами vt, характеризующими
их возбуждение. Простейшими являются случаи, когда одно из комбинирующих
состояний полносимметрично; в таких случаях переход разрешен, если симметрия
составляющих Р\ или адд совпадает с симметрией другого колебательного состо-
яния. Отсюда сразу же вытекает правило отбора при инфракрасном поглощении
или комбинационном рассеянии для важнейшего случая основных частот, получа-
ющихся при переходах (0,0,..., 0) —* (0,0,..., 1,..., 0) из нулевого колебательного
состояния, являющегося всегда полносимметричным, в состояния, в которых воз-
бужден квант одного из нормальных колебаний (vt — 1, > — 0, (г j)). Разрешены
такие переходы, для которых симметрия рассматриваемой составляющей дипольного
момента или тензора поляризуемости совпадает с симметрией данного нормального
колебания. Применяя табл. 22.1-22.11 предыдущей главы, мы сразу получаем прави-
ла отбора как для инфракрасных спектров, так и для спектров комбинационного
рассеяния. При этом колебания, которым соответствуют разрешенные переходы, на-
зывают активными, а колебания, которым соответствуют запрещенные переходы —
неактивными. В инфракрасных спектрах (или спектрах комбинационного рассея-
ния) активны те колебания, для которых в соответствующих строках таблицы стоят
составляющие дипольного момента (или составляющие тензора поляризуемости).
Например, для молекулы с симметрией C^v (см. табл. 22.1, с. 650) в инфракрасных
спектрах активны колебания типов симметрии At, В\ и Bi, а в спектрах комби-
национного рассеяния — колебания всех типов симметрии. Для молекулы Н2О,
обладающей симметрией Civ, возможны колебания типов А\ и В^ (колебания
в плоскости молекулы), поэтому для нее все три частоты колебаний активны как
в инфракрасных спектрах, так и в спектрах комбинационного рассеяния. Для моле-
кулы с симметрией Cyv (см. табл. 22.3, с. 663) в инфракрасных спектрах и в спектрах
комбинационного рассеяния активны колебания типов А\ и Е (возможные для мо-
лекулы NH3) и неактивны колебания типа А2 (возможные лишь для более сложных
молекул этой симметрии2).
Полносимметричные колебания, при которых симметрия молекулы не изменя-
ется, всегда активны в комбинационном рассеянии, так как тензор поляризуемости
всегда имеет составляющие, не изменяющиеся при любых операциях симметрии
и относящиеся к полносимметричному типу. Для групп C2V и Сз„ это тип сим-
метрии А|, для группы £>2л — Ад. В инфракрасном спектре полносимметричные
колебания активны только для молекул, обладающих дипольным моментом. Дей-
ствительно, для молекул, не обладающих в силу симметрии дипольным моментом
(Ро = 0), он равен нулю не только для равновесной конфигурации, но и для любой
конфигурации, получающейся при полносимметричных колебаниях. Для молекул,
обладающих дипольным моментом (Ро 0), он изменяется при полносимме-
тричных колебаниях, одновременно изменяется и тензор поляризуемости, поэтому
2) Например, для молекулы изобутана СН(СНз)з.
§23.1. Правила отбора в колебательных спектрах
679
полносимметричные колебания являются активными как в инфракрасных спектрах,
так и в комбинационном рассеянии (например, для молекул симметрии C2v и C3v).
Для молекул, имеющих центр симметрии, составляющие дипольного момента
всегда принадлежат к нечетным типам симметрии, а составляющие тензора поляри-
зуемости — к четным типам симметрии (см. § 22.2, с. 652). В результате нечетные ко-
лебания, активные в инфракрасном спектре, неактивны в спектре комбинационного
рассеяния, и, наоборот, четные колебания, активные в спектре комбинационного
рассеяния, неактивны в инфракрасном спектре. Таким образом, имеет место альтер-
нативный запрет, аналогичный альтернативному запрету (4.153), (4.154) (см. с. 116).
Необходимо подчеркнуть, что альтернативный запрет исключает одновременное
появление одной и той же основной частоты в инфракрасном спектре и в спектре
комбинационного рассеяния, но из него не следует, что колебания, неактивные
в инфракрасном спектре, обязательно должны проявляться в спектре комбинаци-
онного рассеяния, и наоборот. Могут быть колебания, неактивные в обоих случаях.
Примером правил отбора для молекул, обладающих центром симметрии, являются
молекулы симметрии Из восьми возможных типов колебаний Ад, Аи, Big, В\и,
В2д, В2и, В3д, В3и, согласно табл. 22.2 (с. 652), колебания В\и, В2и и В3и активны
в инфракрасном спектре и неактивны в комбинационном рассеянии, колебания Ад,
В\д, В2д и В3д активны в комбинационном рассеянии и неактивны в инфракрасном
спектре, а колебания Аи неактивны и в инфракрасном спектре, и в комбинацион-
ном рассеянии. Для молекулы этилена С2Н4, имеющей 12 возможных колебаний
(колебания всех типов симметрии, кроме В3д, см. рис. 22.7, с. 653), в инфракрасном
спектре активны 1 колебание В1и, 2 колебания В2и и 2 колебания В3и, т. е. 5 коле-
баний, а в комбинационном рассеянии активны 3 колебания Ад, 2 колебания В\д
и 1 колебание В2д, всего 6 колебаний; двенадцатое колебание, Аи, вообще неактивно.
Для обертонов, получающихся при переходах (0, 0,..., 0) —* (0, 0,... , г>г ,..., 0)
(vi > 1), правила отбора очень просты для невырожденных колебаний. В этом
случае при четных Vi возбужденное колебательное состояние полносимметрично
и переходы разрешены в комбинационном рассеянии для полносимметричных со-
ставляющих тензора поляризуемости, а при нечетных Vi возбужденное колебательное
состояние обладает симметрией данного нормального колебания и разрешены пе-
реходы для составляющих Рх или aXfi той же симметрии. Например, для молекулы
С2Н4 обертоны колебаний симметрии В2и, В3и при vt- = 2,4,... являются
полносимметричными (симметрия А\д) и активны в комбинационном рассеянии,
а при Vi — 3,5,... обладают симметрией В\и, В2и, В3и и соответственно активны
в инфракрасном поглощении.
Для составных частот, получающихся при переходах типа (23.7), если не менее
двух квантовых чисел отличны от нуля (v, Ф 0, Vj 0), правила отбора в слу-
чае невырожденных колебаний можно легко найти, определяя симметрию полного
колебательного состояния с помощью таблиц типов симметрии. Например, для мо-
лекулы С2Н4 при одновременном возбуждении основных частот у' симметрии В\д
и и" симметрии В3и симметрия полного колебательного состояния находится, со-
гласно табл. 22.2 (с. 652), сочетанием типов симметрии В\д и В3и, что дает тип
симметрии В2и (при операции i 1 • (-1) — -1, при операции 1 • (-1) — —1,
при операции (-1) • (-1) = 1) и переход разрешен в инфракрасном поглощении
для составляющей Ру; в спектре получается составная частота и' 4- и".
В общем случае, когда оба комбинирующих колебательных состояния являются
неполносимметричными, их сочетание характеризуется определенной симметрией
и переход разрешен, если симметрия составляющих Рх или aXti совпадает с этой
результирующей симметрией.
680
Глава 23. Колебательные спектры многоатомных молекул
(23.9)
В частности, для колебательных состояний одинаковой четности (двух чет-
ных или двух нечетных)3) результирующий тип симметрии будет четным, переход
разрешен в комбинационном рассеянии (адд четное) и запрещен в инфракрасном
поглощении (Рд нечетное); обратное имеет место для состояний противоположной
четности, дающих нечетный результирующий тип симметрии. Мы получаем правила
отбора:
инфракрасное поглощение д - и,
комбинационное рассеяние q - 7, и - и,
приводящие к альтернативному запрету, который, таким образом, справедлив
не только для основных частот, но и для любых переходов между колебательными
уровнями молекул, обладающих центром симметрии. Отметим, что альтернативный
запрет будет нарушаться при отступлениях симметрии от центральной. Для молекул
в газовой фазе он соблюдается строго, для молекул в жидкостях и растворах на-
блюдаются его нарушения — частоты, интенсивные в инфракрасных спектрах, дают
в спектрах комбинационного рассеяния слабые линии, и наоборот. Это обусловле-
но тем, что при взаимодействиях данной молекулы с окружающими центральная
симметрия будет лишь приближенной, а не точной, как для свободной молекулы.
Для невырожденных состояний результирующая симметрия определяется при
помощи таблиц типов симметрии совершенно так же, как и симметрия полного
колебательного состояния при одновременном возбуждении двух частот нормальных
колебаний (см. выше).
Для вырожденных состояний можно найти, при помощи методов теории групп,
результирующую симметрию для любых сочетаний состояний различной симметрии.
Для важнейших групп соответствующие данные приведены в табл. 23.1, позволяю-
щей определять по симметрии обоих комбинирующих состояний результирующую
симметрию. Эта таблица может также применяться для нахождения симметрии пол-
ных колебательных состояний при одновременном возбуждении двух нормальных
колебаний. В последних столбцах таблицы указана симметрия обертонов (v > 1)
для нормальных колебаний соответствующих вырожденных типов симметрии.
Например, для молекулы СН4 составная частота 1/3-1/4 соответствует переходу
(0, 0, 1, 0)—(0, 0, 0, 1) между колебательными уровнями симметрии 2*24) - Результирую-
щая симметрия, согласно таблице, будет F2 х F2 = А1 4- E+F\ +F2 и переход разрешен
как в инфракрасном поглощении, так и в комбинационном рассеянии. Составная
частота и2 4-2д/4 соответствует переходу (0, 0, 0, 0)—(0, 1, 0, 2) из основного состояния
в состояние, в котором возбуждена основная частота и2 симметрии Е и первый обер-
тон 2i/4 частоты 1/4 симметрии F2. Согласно таблице, симметрия обертона Д] 4- E+F2,
а симметрия полного колебательного состояния будет (Д| 4- Е 4- F2) хЕ, что дает
Д| + А2 4~ 2Е 4~ F\ -f- 2*2(Д| х Е — Е, Е х Е — Д| 4- А2 4- Е, F2 х Е — jF1] 4~ F2}, и пе-
реход также разрешен как в инфракрасном поглощении, так и в комбинационном
рассеянии.
Для вывода правил отбора3 * 5\ связанных с симметрией равновесной конфигурации мо-
лекулы, необходимо рассмотреть поведение при операциях симметрии соответствующих
3) Легко показать, что колебательное состояние является четным, если для всех нечетных
i
колебаний четная, и нечетным, если эта сумма нечетная.
О нумерации частот для молекулы СН4 см. ниже, с. 702.
5) Вывод правил отбора для обертонов и составных частот был дан Тиссой [315], см. также статью
Компанейца [316].
Таблица 23.1
Результирующая симметрия для сочетаний вырожденных состояний
Суп		А|				а2				E						v = 2		v = 3			v = 4		v = 5		V = 6	
Е		Е				Е				A\ + A2 + E						A\ +E		A] 4- A2 4- E			Ai +2E		Ai 4- A2 4- 2E		2A| 4* A2 4* 2E	
£>3h		А		А'[		4		4'		E'				E"		v = 2		v = 3			v = 4		v = 5		v = 6	
Е' Е"		Е’ Е"		Е" Е'		Е' Е"		E" E'		a!^ 4- a2 + E’ A" + A,{+E"				A'{ + A^+E" A\ 4- Ai 4- E1		A\ + E' A\ +E'		A\ +A'2+E' A'[ + A^ + E"			A j + 2E' A\ + 2E'		A\ + A'j + 2E' A'l + A'j' + 2E"		24'j + 4'2 + 2E' 24' + 4'2 + 2E1	
D^d		^10				А2д		A2u		Eg				Eu		v — 2		v = 3			v — 4		v = 5		V = 6	
Ед Ей		Ед Еи		Еи Ед		Ед Ей		Eu Jg		A\g + A2g + Eg Aju 4- Azu 4- Eu				А|й 4- A2u + Eu Alg 4- A2g 4- Eg		A10 4- Eg A \g 4- Eg		A\g 4" A2g 4- Eg Aju 4- ^2u + Eu			A I g 4- 2 Eg A Ig 4- 2Eg		A10 4- A20 4- 2Eg Aju 4- A2u + 2.EU		2A10 4- A2g 4- 2.Eg 2A[g 4- A20 4- 2Eg	
D4h			А]и		А2д		А2и			В lu	B2g	B2u	Eg				Eu			v = 2			v = 3	v = 4		v = 5
Ед Еи	Ед Еи		Еи Ед		Ед Еи		я о» Eq bq	f9 !		Eu Eg	Eg Eu	Eu Eg	A|0 + A2g 4" B\g + B2g А|й 4- A2u 4- J5]u 4- B2u				A|u 4- A2U 4- B}u + B2u + A2g 4- B[g 4- B2g			+ Big 4- B2g A\g 4- Big 4- B2g			2Eg 2EU	2A10 4- A20 4- Big 4- B20 2A|0 4- A20 4- В|0 4- B20		3Eg 3EU
D$h		л',			а';		А2		A'l		E't				E\'		E'2		E'l			v = 2		v = 3	v = 4	
Е\ Е" е'2 Е'{		Е\ Е" е'2 е2			Е',' Е\ Е" е'2		bq bq bq Eq	1 7 2 7 >	e'; E't E'J e'2		A j + A2 + E2 A'l + A'^ + E'^ E'i+E'2 E" + E'i				A” + A”+E^ A j 4- A2 + B2 E" + E'[ E\ +Е'г		E\ + E'i E”+E” A\ 4- Ai 4- E^ A” + A'2' 4- E’{		E'l + E'{ Е\+Е’г A" + A" + E'J a\+a’2 + e\			4' +B' 4'+^ 4'1+e; 4'i+b;		E\ +E’2 E'l + E'-^ E'i+E'2 e'; + e'{	4', + E\ + 2EI2 4' + E\ + E’2 4' +B', +E'2 4| 4- E\ + E’2	
§23.1. Правила отбора в колебательных спектрах
682
Глава 23. Колебательные спектры многоатомных молекул

II &	CO to to	to qq q q CM CM CM CM 4* 4- 4- 4- to to to	to ’Ч* <Ч< "Ч* "Ч}	II	Г to ^_to 4- 4- to to <1 <1 4- 4- + to + to M M	II	tq 4-	4* й cq ~ cq m cq m Cq t + tx -7 + „Г + CM	II	_	4“Д?4-дл4-«л4-,5> кГй ++++++++++ e-	to	to	to	to to <»> to	to	to r.— to _— ГМ~СМ~СМ'СМ~
II &	to	ss	to	a q q q q 4- 4- 4- 4- to	S3	to	S3 cq cq q cq 4- 4- 4- 4- to	S3	to	S3 q cq q cq						
						II Sa	to	=3 cq cq 4-	+	.	+ 4- 4-	* X to ss Eq	to q	= [\	rsi gj.	гм ^^4424 + ^+ ^ + + t+ =+ - + 5 + э =	ч ч: ч; cq
		II	4- 4- to S3 к к				
				мп II	<4	+	£	+ +	t	&7	t	в;; •	’Ч!	4-	tx;	cm ^	4-	4-		
СМ II &	Oi	Oi	O) ГЧ ГЧ ГМ ГЧ q q q q 4- 4- 4- 4- to	to	to to "Ч*	II	to to <1 <1 4- 4- + to + to M M				
						CM II Ss	to	to	to	to ГМ	ГЧ	ГЧ	rs| cq	q	q	q q* q*	4-	4-	4-	4- + +	в?	йГ	cf	q" J1 J1	4-	4-	4-	4- 44» 44* to	to	to	to 43	444	444	444
				II	4- ггм 4- К) Й 6q ft. CM	CM	, +	+	t	+	t м	X	4	+ CM	'	CM	’		
	S3 to S3 to cq Eq Eq Eq 4- 4- 4- 4- S3 to S3 O> cq cq 4- 4- 4- + S3 _to a _to cq q	<1^ S3 q	^3 ^to 4- 4- S3 to к к				
						S3 £	S3 । to 4. S3 1 to S3 to • ггч 1 _гч 1 _<-4	гч + + +1 +1 +1 +1 ь7 Л q <^q - cq 2>q q^^4-^4-^4-^4-
				II	cq	Eq	Eq* +	+	7 ГЧ	r—	1 Й	ft? t	+	+ x	?		
		"”to to C§‘	4- 4- to S3 к к				
to fef	to J-3 to S3 cq cq cq cq 4- 4- 4- 4- to S3 to ss ГМ ГМ ГМ ГМ cq cq 4- 4- 4- 4- J&j	S3	J31 S3 cq cq						
						to t4	1	to 1	=4-	®»4-	53 r<N	Ггч	to	Eq*	S3	Eq to	Cq*	ss	Eq* +	+	4-	14-	t	4-	14-	t ^q	*	cq ^q	*	q q	q	4,4	+	4_	4,3	4.	^4.
		£ S3 cq	S3 to <1 <1 4- 4- 1 S3 1 to M M 4- 4- t? И*				
				II	t£	cC 4	+	+ 4-	cq	cq 4~	4-		
						S3 Cq	S3 to 4"	4- r<~? 4*	4- r? +	=4- o, 4- a 4- * q ^q	cq J?q q	4-	4-	4-	4-
а К]	to s ел Eq Eq Eq cq 4- 4- 4- 4- s3 to ss to cq cq 4- 4- 4- 4~ S3 to =! to cq cq						
		''"to £ to cq	to S3 <1 <1 4- 4- 1 to 1 S3 M м 4- 4- + to + S3 M M				
				с£	Eq	Eq 4-	4- cC	iq	cq +	4-	+ q	bq	cq 4-	4-		
						to cq	to	S3	"Г	гч	।	гч	1	rsi	’	rsi +	+	+	t	+	t	+	t	+	t .?q * q ^q * e< q	q	4-	4-	+
to q	to	to s cq cq cq cq + 4- + + to S3 to ss cq cq 4- + + 4- _to ss _to s3 cq cq						
		1 S3 S3	S3 to К к			bq	S3 to q q 1	1	S3	to	S3	to 11	£	£	£	£ 4? ч£ 4-	4-	4-	4- ।	।	S3	to	S3	to + + Й7	ь,	ь;	ь. ч; ч;
				q	C£	E? 4-	4- <£*	q	cq +	4-	4- Cq 4-	4-		
а q	S3 to a to q q q q	1 to to	to S3 К к				
						в?	q"q3 1	1	to	ss	to	ss "Г 1	ГГЧ	гм	,гм	гм to	q	q	q	q 4^* ч^*	+	4-	4-	4~ ।	।	to	S3	to	S3 ь. ч; -ч;
о» cq	to sa to S3 Eq cq cq cq						
а cq	S3 to S3 to q q q q	M S3	S3 to С к				
				cq	cq t 4-	4- + Eq"	Cq		
to q	to ss to S3 Eq Eq cq cq						
s	S3 to S3 to cq cq Eq cq						
						S3	S3 to Д’	Д?	3s q q q q q q
		4 to M to	to ss К к				
to	to ss to S3 cq Eq Eq Eq						to sa 3?	д!	j5>	3 q q q q q q
					cq cqj q		
a	S3 to з to Exi q q q						
							я rto ?	»	ДР	1 q q q q q* q 
	to S3 & s3 Eq cq Eq cq	to p	'"to S3 к к to S3 cq Eq		cq cq cq		to S3 2'	±	<4	43 q q q q q q
q	to S3 to S3 q q q q			Е*?	<£'	о	to ss	3	Д?	r?, q q q q q q
§ 23.1. Правила отбора в колебательных спектрах
683
матричных элементов
(МА)Ы = f	(23.10)
где Мх — составляющая дипольного момента или тензора поляризуемости, t/>k и —
колебательные волновые функции комбинирующих состояний. Интегрирование в (23.10)
производится по нормальным колебательным координатам.
Если функции и ipi преобразуются по представлениям Г* и Гь а составляющие Мх
по представлению Гм, то матричные элементы (23.10) будут преобразовываться по пред-
ставлению, являющемуся прямым произведением Г* х Гм х Г/, и будут отличны от нуля
(т. е. переход будет разрешен), если Г* х Гм х Г/ содержит тождественное представление
(см. §4.8, с. 120).
Неприводимые представления находятся по табл. 22.1-22.11; принадлежность со-
ставляющих Рх и aXfi к определенному типу симметрии и означает, что они преобразуются
по соответствующим неприводимым представлениям. Если эти представления одномерные,
то каждая составляющая Мх при операциях симметрии переходит сама в себя, если они двух-
или трехмерны, то две или три составляющие преобразуются друг через друга (например, Рх
и Ру или axz и аХу для типа симметрии Е при выделенной оси z в случае групп средней
симметрии и Рх, Ру, Pz или ayz, azx, аху для типа симметрии F в случае групп высшей
симметрии).
Представления Г* или Гг для колебательных состояний определяются законом преобра-
зования соответствующих колебательных функций, для нахождения которого можно исходить
из приближенного вида этих функций, как произведений волновых функций к гармонических
осцилляторов (см. с. 580; £ в (20.45) — безразмерная координата):
Ш	   Vsfe) = с exp (- 52 |
(23.11)
Показательный множитель при операциях симметрии не изменяется6 7\ полином Эрмита Hv(£)
преобразуется как и поэтому волновые функции ^(£) преобразуются как £р£р
В частности, для основного состояния, Vi — v2 = ... = vk = 0, волновая функция ^од...,о(С)
инвариантна относительно всех операций симметрии (Hq(£})Hq(£2) ... HQ(£k) = const) и, сле-
довательно, принадлежит к полносимметричному типу (представление Го), а для состояния
Vi = Vj = 0 (j Ф г) функция ^o,o,...,i,...,o(£) преобразуется просто как нормальная координа-
та & единственного возбужденного колебания по неприводимому представлению Г,-, которое
находится при помощи табл.22.1-22.11. В общем случае произведения £р£р ---£kk (следова-
тельно, и волновые функции) преобразуются по прямому произведению Гр х Гр х ... Г£ ,
где Гр — представления для волновых функций соответствующих обертонов. Для невы-
рожденных колебаний инвариантно при четном г,, (представление Го) и преобразуется
как & при нечетном г, (представление Г;); для вырожденных колебаний представления Гр8>
приведены в последних столбцах табл. 23.1 (для значений от 2 до 4-6). Основная часть этой
таблицы дает прямые произведения Г, х Г7 , и с ее помощью можно находить произведения
Гр х Гр х... х Гр. Вычисление табл. 23.1 выполнено методами теории представлений с учетом
свойств характеров (см. [137] и [139]).
6) Для невырожденных колебаний	для вырожденных колебаний Ч- + ... ) =
(jn + •••); в результате | ^2	= j
i	i	v v"
7) Для дважды и трижды вырожденных колебаний нужно заменить через f (vj + v" = Vj)
v' v" v"'
(<+< + <' = ”,)•
8) Представления Гр (v: = 2, 3,...) являются так называемой симметричной частью прямых произ-
ведении х Г», Г, х Г; х (см., например, [315] и [55], т. 2, с. 179), определяющей для вырожденных
нормальных колебаний преобразования совокупностей произведений &ц,	(v, = 2);	&ц,
6т £,?п>	(» = 3) и Т.д.
684
Глава 23. Колебательные спектры многоатомных молекул
Когда известны представления Гм для составляющих Рх и и представления Г*
и Гг для комбинирующих состояний, то, составляя Г* х Гм х ... х Гг, мы легко находим
правила отбора. Если Г* = Го (в частности, для случая переходов из основного колеба-
тельного состояния), то Го х Гм х Гг = Гм х Гг. Представление Гм х Гг содержит Го,
только если Гг содержит неприводимое представление Гм или совпадает с ним (тожде-
ственное представление Го получается только при перемножении одинаковых представлений,
ср. с. 120); отсюда вытекают правила отбора, сформулированные выше (с. 678). Например,
для молекулы симметрии Td по неприводимому представлению Гм = F2 преобразуются,
кроме координат ж, у, z, составляющие Рх, Ру, Pz дипольного момента и составляю-
щие ayz, axz, аху тензора поляризуемости; также преобразуются тройки координат $р2|,
£f2ii> £f2iii> и переход А} - F2 (возбуждение основной частоты типа F2, ГЛ = Го = А,
Г/ = F2) разрешен как в инфракрасном поглощении, так и в комбинационном рассея-
нии (Г* х Гм х Гг = Го х Гм х Tf = Гм х Г/ = F2 х F2 = А} + Е + F} + F2, т. е. содержит
Го = А}, которому соответствуют инвариантные суммы произведений Px£f2i+7^£f2ii+7)z£f2iii +
и «у2Сг21 + а2а;£г211 + axy^F2iib преобразующиеся как ж2 + у2 + z2). В общем случае (Г* / Го,
Ф Го) ГЛ х Гм х Г1 = (Г* х Г^) х Гм 9) и достаточно найти Г^хГгс помощью табл. 22.1-22.11
для невырожденных состояний (как, например, для С2Н4, см. с. 679) и с помощью табл. 23.1
для вырожденных состояний (как, например, для СН4, см. с. 680); переход разрешен, если
ГЛ х Г/ содержит Гм (а в случае невырожденных состояний совпадает с Гм).
§ 23.2. Интенсивности и поляризации в колебательных спектрах
Переходы между колебательными уровнями v”, v",,.. (сокращенно v”)
и vj, • •• , vk (сокращенно v) при дипольном поглощении характеризуются со-
ставляющими дипольного момента перехода (см. (4.51)).
(-fz)v"v')	(Py)v"v1') ^Pz}v"v'l
(23.12)
а при стоксовом комбинационном рассеянии составляющими тензора поляризуемо-
сти перехода (см. (17.138))
^xx)v"v' , (s^yy)v"v'•)	is^zz}v"v' 1	(&-Xy)v"v'•) (<Xyz)v"v'') is*zx)v"v' ’	(23.13)
Интенсивности колебательных полос в спектре инфракрасного поглощения и ко-
лебательных линий в спектре комбинационного рассеяния определяются значени-
ями отличных от нуля, в соответствии с правилами отбора, составляющих (23.12)
и (23.13); поляризации полос и линий зависят от соотношений значений различных
составляющих.
С физической точки зрения отличие от нуля составляющих дипольного момента
и тензора поляризуемости перехода является следствием того, что в рассматриваемом
электронном состоянии дипольный момент и тензор поляризуемости представляют
функции колебательных координат и изменяются при колебаниях (см. § 17.6, с. 486
и §17.7, с. 493). Чем больше эти изменения, тем более вероятны колебательные
переходы и тем больше интенсивности соответствующих колебательных полос. Ин-
тенсивности для основной частоты колебаний щ (см. (23.2); для молекул в нулевом
колебательном состоянии переход v" —	— 0 —> v- — Vi 4- 1 = 1, v" = Vj — Vj — 0
при j i или в сокращенной записи переход 0 —> 1) при этом определяются пер-
выми производными составляющих дипольного момента и тензора поляризуемости
по нормальной координате 1-го колебания
(2^.} т е ((А
\OtJo
(23.14)
9) Прямое произведение не зависит от порядка сомножителей и от последовательности их перемно-
жения, т. е. для него выполняются коммутативный и ассоциативный законы.
§ 23.2. Интенсивности и поляризации в колебательных спектрах 685
и
dotzx \
^ёГ/о’
dazz
Z даху
дауг
т. е.
(А,д=|,2,3).
X ) 0
(23.15)
о
) о
) о
Наряду со значениями составляющих (Рд)о и (аА/х)0 для равновесной конфигура-
ции, значения (23.14) и (23.15) первых производных являются характеристикой
электрических свойств молекул.
Для двухатомных молекул, у которых имеется одна-единственная нормальная
колебательная координата £ — q = р — ре (изменение длины связи между атомами),
производные (23.14) и (23.15) сводятся к производным (—и (	; в силу
X dq Jo X dq / о
аксиальной симметрии молекулы отличны от нуля лишь производные (при выборе
оси молекулы за ось z)
(23.16)
/ dPz\ /	/ dazz\ / da^\
\^/о \^/о’	\ /о \ д(1 /о’
/ 6otxx \ _ / dotyy \ _ / da2 \
\ /о \	/ о \	/о’
которые и характеризуют электрические свойства связи между атомами наряду
с величинами
(-fz)o — -Rb (^zz)o — ^10? (^жя)о — (^2/)о — ^20-	(23.17)
Отметим, что для двухатомных молекул с симметрией Dxh, т.е. имеющих центр симме-
/	X	[6Р\
трии, притом сохраняющийся при колебаниях (см. с. 572), Ро ~ 0 и I — ) = 0. Действитель-
х dq Jo
но, для таких молекул, в силу сохранения центра симметрии, P(q) = 0 и, согласно (20.63),
отсюда вытекает равенство нулю всех членов в разложении, что возможно лишь при равенстве
fdnP\	/8Р\
нулю не только Ро, но и всех производных I —— ) . Ро и ( —— ) отличны от нуля для мо-
X dqn Jo	\ dq J о
( da\\	/ da2\
лекул симметрии Cxv, а а!0, «20 и I —— I , I —- ) — как для молекул симметрии Cxv,
X dq J о X dq Jo
так и для молекул симметрии Dxh, т.е. для всех двухатомных молекул. В силу	0
двухатомные молекулы симметрии Cxv имеют инфракрасные колебательные спектры погло-
( da\\	/ da2\
щения и испускания, а в силу I —- )	0 и —- 1	0 все двухатомные молекулы имеют
X dq Jo	х dq J о
колебательные спектры комбинационного рассеяния (см. с. 594).
Для многоатомных молекул разумным приближением является применение схе-
мы аддитивности, широко используемой в молекулярной оптике [4]. Согласно этой
схеме, физическая величина, характеризующая молекулу в целом, полагается равной
сумме соответствующих величин, характеризующих отдельные связи. В частности,
дипольный момент молекулы и тензор поляризуемости полагаются равными
Р = ^Р(п), а =	(23.18)
п	п
где Р^ и — дипольный момент и тензор поляризуемости n-й связи, и сумми-
рование производится по всем связям. Соответственно для составляющих вектора Р
и тензора а мы имеем
686
Глава 23. Колебательные спектры многоатомных молекул
Рх = ^рх} (х=:Х>У>2)> ах/‘ = '52°$ (\/* = х,У,2)-	(23.19)
п
Если считать выражение (23.19) справедливым для колеблющейся молекулы, то
аддитивность будет иметь место как для равновесных значений (РА)0 и (аА/1)о ве-
о	(дРх\
личин Рх и ахи, так и для производных I —— ) и I —-) данных величин
' \ ' 0	' #6 ' о
е	п	(дРх\	(да^\
по нормальным координатам	При	этом производные	I---)	и	(---- )	могут
\	/	о	\ д£г) °
/ дР^ \	/ да^ \	/ до№ \	/ dotf* \
быть выражены через производные	и (—
характеризующие зависимость дипольного момента и тензора поляризуемости
данной связи от изменения ее длины. Здесь Р^ — дипольный момент, напра-
вленный вдоль рассматриваемой связи, а «з — главные поляризуемости связи
(ср. с. 496) вдоль ее направления10) и двух перпендикулярных к нему направлений.
Из экспериментальных данных по интенсивностям основных частот в колебатель-
ных спектрах инфракрасного поглощения и комбинационного рассеяния можно
определить значения производных (23.14) и (23.15) и по ним найти значения про-
/#Р(п)\ /да^х
изводных ( —tv ) и ( —tv ) (i = 1, 2, 3) для отдельных связей, дающих вместе
X dq(n) J о X dq(n> /о
с равновесными значениями Рц и а-0' характеристику электрооптических свойств
этих связей.
Мы не будем подробно разбирать теорию интенсивностей в колебательных спектрах,
основанную на схеме аддитивности (подробное изложение этой теории см. [55], т. 2, гл. 20-22,
дальнейшее ее развитие см. [324] и [325]), и рассмотрим лишь общий вид получающихся
формул, применив их к частному случаю молекулы типа Н2О. На этом примере можно
уяснить характерные особенности применения схемы аддитивности, с учетом определенных
свойств симметрии равновесной конфигурации и нормальных колебаний.
Первую формулу (23.19) можно представить в виде
рЛ = 22 p<n> cos А>’	<23-20>
где cos (п, Л) — косинус угла между направлением п-й связи и осью Л. Для молекулы Н2О
(рис. 23.1)
(23.21)
Рх = Р^ cos (1, х) + Р^ cos (2, ж),
Ру = Р(,) cos (1, у) + Р(2) cos (2, г/), Р2 = 0.
Дипольный момент молекулы лежит в ее плоскости. Для равновесной конфигурации (Р^)о =
(Р(2))о — р0; в силу симметрии этой конфигурации cos(l,z) = - cos(2,ж) = -sin—,
cos (1, у) = cos (2, у) — - cos —, следовательно,
(PJo = O, (P,)o = -2PoCOs^, (Р2)о = О,
т. е. дипольный момент направлен по оси симметрии молекулы.
(23.22)
10) При естественном предположении, что направление связи является одной из главных осей
поляризуемости.
§ 23.2. Интенсивности и поляризации в колебательных спектрах 687
Вторую формулу (23.19) можно аналогично представить в виде
«лм = cos (nj, Л) cos (nj, ц) (j = 1, 2, 3),	(23.23)
nj
где cos (nj, Л) и cos (nj, р) — косинусы углов
между направлениями 1, 2, 3 главных по-
ляризуемостей n-й связи и осями Аир.
Выражение (23.23) является следствием то-
го, что при переходе от системы координат
с осями 1, 2, 3 к системе координат ж, г/, z
составляющие тензора преобразуются как
произведения координат п>. Направление 1
совпадает с направлением связи (см. при-
мечание на с. 686), т.е. cos(nl,A) совпада-
ет с cos(n, Л) в (23.20), а направления 2
и 3 к нему перпендикулярны. Для молеку-
лы Н2О в силу симметрии эти направления
будут лежать в плоскости молекулы и в пер-
пендикулярной к ней плоскости (рис. 23.1),
и формулы (22.23) дают, учитывая, что на-
правление 3 совпадает с осью z и перпенди-
кулярно к осям х и у, а направления / и 2
перпендикулярны к оси z\
поляризуемости связей молекулы XY2.
Оси z и 3, перпендикулярные к плоскости
чертежа, показаны кружками
ахх = а^ cos 2(11, х) + а^ cos ?(12, ж) + а,2) cos2(21, ж) +	cos (22, ж), '
ауу -	cos 2(11, у) +	cos2(12, у) + а(]2) cos2(21, у) +	cos (22, г/),
а — аН) (1) 4-а(2)
+ 3 ’	,	>	(23.24)
Otxy = COS (1 1, ж) COS (11, у) -f- «2^ COS (12, ж) COS (12, у) +
+ «]2) cos (21, ж) cos (21, у) + cos (22, ж) cos (22, ?/),
— Qyz — 0.
Для равновесной конфигурации (а^^о = (а^о = «ю, («2^)0 = (а^о = а20, («3^)0 =
(а32))0 — а30 и, далее, cos (11, ж) = - cos (21, ж) = - sin	cos (11, у) — cos (21, у) = - cos —,
cos (12, ж) — - cos (22, ж) = - cos cos (12, у) = cos (22, у) = sin .
Поэтому (23.24) сводится к
2 ^0	2 ^0	2 ^0	2 Фо
(<*хх)о = 2a10sin — + 2а2О cos —, (а^)0 = 2аю sin —- + 2a2Osin —,
z	z	Z	L	(23.25)
(a^zz)o 2a3O, (aJ.J/)o — (aX2)o —
t. e. (axa.)0 — olxq, (ayy)$ = ayQ, (a22)0 = a20 представляют главные поляризуемости неколе-
блющейся молекулы.
Для колеблющейся молекулы составляющие (23 20) и (23.23) дипольного момента и по-
ляризуемости будут изменяться как вследствие изменения и для отдельных связей,
так и вследствие изменения косинусов углов. Для производных (23.14) и (23.15) мы получим
[cos (п, А)]о + £(P<n))0 [£(_, А)
У / о	У	/ Л
и	П	U
(23.26)
Н)В общем случае для тензора второго ранга tX(l = ^2	cos (j, A) cos (А:,/1). В данном случае
tjk = ctjdjk (6jk = 1 при k = j и S}k = 0 при k j) и остается суммирование по j, далее t}j =
суммируются по п.
688
Глава 23. Колебательные спектры многоатомных молекул
и
д&Х»
)/	\	_Л г
=Уд ) [cos(nj,A)]n [cos(nj»]f|+y^(a*'1))o —- (cos(nj,A)cos(n;») .
О nJ \	/ о	„) L Si	Jo
(23.27)
В нулевом приближении можно считать, что величины Р^ и (j — 1, 2, 3), характе-
ризующие данную связь, зависят только от изменения длины данной связи, т. е. от координа-
ты q^. Тогда, учитывая линейную связь нормальных и естественных координат (см. (21.54)),
мы получим
(23.28)
где dvi — коэффициенты, определяющие форму г-го нормального колебания, a dni — ко-
связи. В результате производные (23.26) и (23.27) будут зависеть от
эффициент, определяющий амплитуду изменения при этом колебании рассматриваемой п-й
ЭР(п)\ /да*п)\
------------------------------------------------------------ТТ ) И I —— ]
dq^ /о V dq^ / о
(j = 1,2,3), как указывалось выше (см. с. 686). Из формул видно, что производные за-
висят и от значений (Р^)9 и (а^)0, причем эта зависимость определяется изменением
cos (п, А) и cos (nj, A) cos (nj, р) при колебаниях. В простейших случаях соответствующие
косинусы являются функциями только углов между связями и будут зависеть от их изме-
нений, т.е. от угловых естественных координат|2). Тогда при чисто валентных колебаниях
дР^ \	/	\
) и ( —— ) , а при чисто
dq^Jo \dqWJv
деформационных колебаниях — только от (Р<п))0 и (ajn))0; действительно, в первом случае
производные (23.26) и (23.27) будут зависеть только от
— cos(n, А) = — [cos (nj, A) cos (nj, д)] = 0 и в (23.26) и (23.27) обращаются в нуль члены
%	#6
. .	(&р(п) \	/ да^ \
с (Рм)о и (а,п )о, а во втором случае dni = 0, т. е. ( —— ~ ) = ( —I = 0, и в этих
3	\ /о х /о
формулах обращаются в нуль соответствующие члены.
Для молекулы Н2О (23.26) сводится к выражениям (см. (23.21))
sin ~ +
cos (2, х)
Ро ,
COSy +
(23.30)
i2^ В общем случае, при учете условия равенства нулю колебательного момента количества движения
(см. с. 478), они будут зависеть и от изменений длин связей.
§23.2. Интенсивности и поляризации в колебательных спектрах 689
эр(|)
т. е. производные составляющих дипольного момента зависят от Ро и-
дР(2}
-----. Аналогии-
ные выражения для
мы не будем выписывать в явном виде; они будут содержать
как «ю, «20, «зо, так и
Рассмотрим для примера случай полносимметрич-
ных колебаний, для которых (ср. §22.1, с. 646 и §22.6,
с. 671)
g(0 = g<2> = q, = а£„ a = b&.	(23.31)
Для них, согласно (23.28),
дРт \
9Р{'} \
v>A"
дРт \
(23.32)
причем в силу эквивалентности связей
ар(,)\	/др(2)\
Рис. 23.2. Углы, образуемые
связями с осями для молекулы
типа ХУ2
дР(д)
Эд
(23.33)
о
Углы (1,ж), (1,?/), (2, ж), (2, у) входящие в (23.30), равны (рис. 23.2):
, ч 7Г V()	«
О.’) = 1 + Т+2'
(2,«/) = тг - у
а
2’
а
2*
(23.34)
Г д 1
На основании (23.34) можно вычислять производные в (23.30). Имеем —• cos(l,ar)
Г д t .1 да	/тг (р0\ 1	Г д ,	.1	/ /тг <£>о\°
— С05(1,ж)1	= -bi
L да	7 J о д£3
= bsin (-
Ldfs	Jo	х
находим
(дРД = 0 I =-2
X / о	X / 0
sin ( — 4- — ) • - и аналогично I — cos (2, ж) = b sin (-I • - ,
\2	2 7 2	L56 Jo \2	2/2
¥>о\	1 Г д	1	/	<р0\	1
тг —— ) • - и — cos (2,?/)	= Ь sin I тг —— ) • -. В результате
2/2 L d^s	Jo \	2/2
Vo (дРг \
acos^ +Pobsin (—	= 0.	(23.35)
о 2	2	\^/о
Отметим, что в данном случае полносимметричных колебаний, при которых симметрия
(9Р\
молекулы сохраняется, изменение I —- ]£s дипольного момента имеет то же направле-
\ д£3 /
ние, что и сам дипольный момент Р, совпадающее с осью симметрии молекулы, в со-
ответствии с правилами отбора (см. табл. 22.1, с. 650); за ось у принята теперь ось
симметрии молекулы С2). Для антисимметричных колебаний, наоборот, изменение ——£а
д^а
дипольного момента перпендикулярно к этой оси; действительно, легко проверить, что
/5Р«\	/дРх\	m
I —- ) = 0,	а	I -I	Ф 0, в частности, для изменений длин связей	'	= —q{ > = с£а
V д£,а /о	х д£а / о
/дР(|>\	/эр(2>\	/ар(|)\	/эр(2)\	/дР(д)\
и(----) +(--------) = 0, а (----) - ------) =2с(——] #0.
к Э£а h к А к д£а /о к д£а Jo к дд )ь
и	-	(дач\	(да)(д}\
Не представляет труда наити явные выражения для I ——- I через а;0 и I —-— ) ,
аналогичные (23.35).	6 о	х 5g /о
690	Глава 23. Колебательные спектры многоатомных молекул
Рассмотрим теперь вопросы поляризации в колебательных спектрах. Как отме-
чалось в начале параграфа, поляризация зависит от соотношений значений различ-
ных составляющих дипольного момента или тензора поляризуемости (см. с. 684),
в частности, если в силу правил отбора лишь одна из составляющих отлична от нуля,
то сразу находится поляризация излучения, поглощенного или рассеянного молеку-
лой при данном переходе. Следует, однако, иметь в виду, что на опыте определяется
поглощение или рассеяние не отдельной молекулой, а совокупностью молекул,
которые могут различным образом ориентироваться в пространстве. Особенно важ-
ным является обычный случай, осуществляющийся в газе или в жидкости, когда
все ориентации молекул равновероятны (свободно ориентирующиеся молекулы);
в дальнейшем мы будем рассматривать именно этот случай.
При пропускании через вещество, состоящее из свободно ориентирующихся
молекул, различным образом поляризованного излучения поглощение не будет
зависеть от поляризации этого излучения. Неодинаково ориентированные молекулы
будут поглощать по-разному, но среднее поглощение одной молекулой получается,
благодаря усреднению по всем возможным ориентациям, то же самое.
Например, если колебания в падающей электромагнитной волне происходят в на-
правлении оси С (рис. 23.3), а молекула поглощает колебания, направленные по оси z
((Px)v"v' = (Py)v"v' — 0, (Pz)v"v' 0), то интенсивность поглощения будет пропорциональна
cos2(£,z). Усреднение по всем возможным равновероятным ориентациям оси z, связанной
I(cos2«,z) =
с молекулой, дает
независимо от выбора направления оси
Поляризация в инфракрасных спектрах поглощения может наблюдаться толь-
ориентации молекул в каких-то направлени-
ко при наличии преимущественной
Рис. 23.3. Поглощение и рассеяние
падающего излучения
ях. В противоположность этому рассеянное
излучение в общем случае является поляри-
зованным и для свободно ориентирующих-
ся молекул благодаря тому, что молекулы
в разных направлениях поляризуются пада-
ющим излучением по-разному. Для интере-
сующего нас случая комбинационного рас-
сеяния по поляризации рассеянного излуче-
ния можно делать важные выводы о колеба-
ниях молекул, поэтому мы разберем более
подробно поляризацию излучения при его
рассеянии молекулами.
Пусть падающее излучение распростра-
няется в направлении оси ту, а наблюдение
ведется в перпендикулярном к нему направлении оси £ (рис. 23.3). Дипольный мо-
мент, индуцированный световыми колебаниями </Кпад), будет, вообще говоря, иметь
иное направление и обладать наряду с составляющей составляющими и РР).
В рассеянном излучении наряду с колебаниями ^j|Pacc^ в направлении ( (обусло-
вленными составляющей Р^) будут существовать колебания ^расс^ в направлении ту
(обусловленные составляющей Рг/; составляющая Р^ не дает излучения в направле-
нии £). Только если молекула под воздействием составляющей <^пад> поляризуется
в том же направлении (что будет иметь место лишь для молекул, поляризующих-
ся одинаково во всех направлениях1^), отлична от нуля лишь составляющая Р(
13/Для которых = ау = о., т.е. эллипсоид поляризуемости сводится к сфере, см. с.496 и 528.
§ 23.2. Интенсивности и поляризации в колебательных спектрах
691
и для рассеянного излучения <£|расс) 0, <^расс^ ф 0, т. е. это излучение будет
(расе)
полностью поляризовано. При Prj Ф 0	# 0 и мы получим деполяризацию рас-
сеянного света. Отношение интенсивности 1± для перпендикулярной составляющей
(1± ~ (<^расс^)2) к интенсивности для параллельной составляющей (1ц ~ (^уРасс^)2)
называют степенью деполяризации рассеянного излучения:
(23.36)
Jll
Световые колебания <^пад^ происходящие по оси £, в общем случае будут
индуцировать дипольный момент, для которого не только 0, но и О,
р^ 0, и поэтому рассеяние будет происходить и в направлении £ с ^расс^ ф О
и <£||Расс) Ф 0 (при Рл — Р{ — О, Р^ 0 рассеяния в направлении £ не происходит).
Если связать с молекулой подвижные оси х', у', z', ориентированные определен-
ным образом относительно неподвижных осей £, rj, (, то получится и определенное
соотношение интенсивностей 1± и 1ц, зависящее от составляющих тензора поля-
ризуемости молекулы и от углов между осями х‘, у', z' и £, ту, £. Для свободно
ориентирующихся молекул можно произвести усреднение по всем возможным зна-
чениям этих углов, считая все ориентации осей х', у', z' равновероятными (см. [55],
т. 2, с. 48). В результате такого усреднения значение р степени деполяризации вы-
разится через составляющие тензора поляризуемости. При этом р зависит от этих
составляющих не в отдельности, а от их вполне определенных комбинаций, а имен-
но, от следа Ь и анизотропии g тензора поляризуемости. След тензора равен сумме
его диагональных элементов
Ь — ах>х> + ау>у> + az>z',	(23.37)
а анизотропия имеет вид
9 =	| [(«I’»' ~ ау'у'У + (аУ'у' - azizi)2 + (azV - ах'х>)2] + За2,у, + 3a2y,z, + 3a2z,x,.
(23.38)
В системе главных осей получаем
b = ax + ay+az, 9=	[(«х - аУУ + («» - «г)2 + (аг - "х)2] •	(23.39)
След тензора а характеризует среднюю поляризуемость молекулы вдоль главных
4-\
осей (6 — 3------------ I, а анизотропия — разности поляризуемости в различных
направлениях. Если поляризуемость молекулы во всех направлениях одинакова,
ах — ау — az — т. е. молекула изотропна, то 6 — За, a g — 0.
Величины Ъ и g представляют инварианты тензора, не зависящие от выбора подвижных
осей. В произвольной системе осей х', у', z' инвариантами любого тензора являются его
след ^2 qaa и сумма квадратов его элементов (Л, р = х', yf, zf). Поэтому инвариантом
А	Ар
является и выражение - [з “ (УЗ Qaa) ] ’ котоРое для симметричного тензора
Ад	А
сводится, как легко проверить, к д2. Таким образом, степень деполяризации выражается
через инварианты тензора, как и должно быть, так как она не должна зависеть от выбора
ориентации осей координатной системы, связанной с молекулой.
692
Глава 23. Колебательные спектры многоатомных молекул
Для неполяризованного падающего излучения степень деполяризации рассея-
ния, наблюдаемого в перпендикулярном направлении, оказывается равной
= —6g2
Р 5Ь2+7д2'
(23.40)
Она, естественно, обращается в нуль при д = 0 (в этом случае = а^пал\
= а^пал\ Р^ = 0, индуцированный момент лежит в плоскости и /Jpacc) = 0)
и тем больше по величине, чем больше анизотропия по сравнению со следом;
6
при b = 0 р = Выражение (23.40) является основной формулой, определяющей
деполяризацию рассеянного света.
Для случая линейно поляризованного падающего излучения (^пад^ ф 0,
^пад) _ q) вместо (23.40) получается выражение
= 3^2 = р
Рр 5Ъ2 + 4д2	2 - р
(23.41)
Формула (23.40) справедлива как для рэлеевского, так и для комбинационного
рассеяния. Для рэлеевского рассеяния нужно брать след и анизотропию тензора
поляризуемости молекулы в данном состоянии, для комбинационного рассеяния —
тензора поляризуемости перехода (23.13). В случае основных частот в спектре
комбинационного рассеяния след и анизотропия тензора поляризуемости перехо-
да (23.13) пропорциональны следу и анизотропии тензора (23.15) и применимы
формулы (23.37), (23.38) и (23.40), если в последних для основной частоты
заменить ot\u через I--- ) .
\	/о
Этот результат легко получается из разложения (23.6). Составляющие тензора по-
ляризуемости перехода, определяющие комбинационное рассеяние для переходов 0—1
(v, = 0 —> = 1, v3; = 0 при j г), представляют матричные элементы
(0,0,..., 0,..., 0|аАм|0,0,..., 1,...,0) =
0,0,..., 0,.
£,+... 0,0,..., 1,...,0 );
о	/
для гармонических колебаний отличен от нуля лишь матричный элемент (0|&| 1), одинако-
вый для всех составляющих тензора поляризуемости и равный, согласно (20.50), нулевой
амплитуде QQi г-го нормального колебания. Следовательно,
(aAM)oi = (	) Qoi =	(23.42)
у	/
а след и анизотропия тензора (23.13) будут иметь вид14)
bv'v" =(a'xx + ayy + a'Zz)Qo,=b'Qoi,	(23.43)
g,'v'’=Qoid ^[(а'хх.-ау!1)2 + (а'п-ахг)2 + (а'г.-а'хх)2] + Заху + З'Д + З'Д = s'Qoi, (23.44)
|4) В качестве главных осей можно взять оси х, у, z, для которых (ом)о = «г, (ага)о = (“zz)o = ал
(azji)o = («jiz)o = (azz)o- При этом, вообще говоря, а'д = (	не равно нулю как при А = д, так
М X / о
и при
§ 23.2. Интенсивности и поляризации в колебательных спектрах
693
где штрих указывает на производную по & и через Ъ' и д' обозначены след и анизотропия
тензора (23.15). Степень деполяризации
6g2	Gg'Qli	6д'2
Р = 562 + 7g2 = 5d'2Q20 + lg'2Q20i = 5Н2 + 7д'2'	(23’45)
Для степени деполяризации основных частот имеют место важные правила,
установленные Плачеком [60]:
1.	Для неполносимметричных колебаний
Р = у-	(23.46)
2.	Для полносимметричных колебаний молекул, принадлежащих к группам
высшей симметрии (к кубическим группам),
р = 0.	(23.47)
3.	Для полносимметричных колебаний молекул, принадлежащих к группам
средней и низшей симметрии,
6
0 </><-•	(23.48)
Эти правила являются следствием того, что для неполносимметричных колебаний
след b тензора поляризуемости обращается в нуль, а для полносимметричных ко-
лебаний он отличен от нуля, и, кроме того, для молекул, обладающих кубической
симметрией, для полносимметричных колебаний анизотропия тензора поляризу-
6
емости равна нулю. При Ь = 0 р = при д = 0 р = 0, при Ъ 0 и д 0
6	7
Q< р< -.
F 7
Равенство нулю следа для неполносимметричных колебаний легко доказывается, если
исходить из выражений (17.139). Для тензора поляризуемости перехода, avw, след будет
равен:
Ь - bv> v'l - (pXX)vl,Vt -|-	4“ (^zz)v"v/
/(23.49)
‘$v"(pxx Olyy -f- Otzz'Wv'
След тензора а инвариантен относительно всех операций симметрии, и Ь будет отлично
от нуля, если функции и обладают одинаковой симметрией (преобразуются согласно
одному и тому же неприводимому представлению); так как для основных частот =
V>o,o,...,o принадлежит к полносимметричному типу, то к тому же типу должна принадлежать
и волновая функция = V’o,о,о- Для неполносимметричных колебаний след Ь будет
преобразовываться как V’o,о,о, т.е. как 6', и> следовательно, должен равняться нулю.
У молекул, обладающих кубической симметрией, для равновесной конфигурации
ах = ау = az (см. табл. 18.1, с. 526); при полносимметричных колебаниях симметрия бу-
дет сохраняться, и это условие будет по-прежнему соблюдаться, следовательно, д = 0.
Для степени деполяризации наряду с правилами (23.46)-(23.48) имеется при-
ближенное правило, выполняющееся при справедливости схемы аддитивности
(см. [55], т. 2, с. 101). Для чисто деформационных полносимметричных колебаний,
как и для неполносимметричных колебаний,
6
р=-.	(23.50)
694
Глава 23. Колебательные спектры многоатомных молекул
Действительно, для чисто деформационных колебаний след Ь' тензора
деляемый выражениями (23.43) и (23.27), сводится к
, опре-
о
\ и$г / о	. •
А	и	Xnj
nj
^cos\nj, А)
= 0.
(23.51)
д
% .
Помимо правила (23.50), можно получить приближенные правила для степеней депо-
ляризации валентных полносимметричных колебаний, в которых участвует лишь одна связь
или несколько эквивалентных связей (см. [55], т. 2, с. 103 и 111); верхний предел р для таких
колебаний равен 1/2.
Применение схемы аддитивности позволяет рассчитать для конкретных случаев
степени деполяризации полносимметричных колебаний. Обратно, данные для де-
поляризации линий комбинационного рассеяния могут быть использованы наряду
с данными об интенсивностях для определения значений производных
для отдельных связей.
В заключение данного параграфа мы остановимся на вопросе квантовомеханического
обоснования разложений (23.5) и (23.6), которыми мы пользовались при рассмотрении
вопросов правил отбора, интенсивностей и поляризаций в колебательных спектрах.
Для инфракрасных колебательных спектров, обусловленных дипольными переходами,
данный вопрос решается на основе формулы (17.101). Согласно этой формуле, при усреднении
дипольного момента молекулы (зависящего от электронных и колебательных координат)
по электронным координатам получается дипольный момент молекулы в данном электронном
состоянии как функция только колебательных координат. Вводя в качестве колебательных
координат р нормальные координаты £, мы получаем для составляющей дипольного момента
по оси Л (Л = ж, ?/, z)
Рх = (Рпп^= / \^Л)\2Рх^Л)Лх = Рх(^,^...^г).	(23.52)
Величину РА(£|,	• • •, 6-) можно разлагать по нормальным координатам, согласно (23.5).
Дальнейшее усреднение (23.5) по колебательным координатам, согласно (17.102), дает, учи-
тывая, что (г/'|(РА)о|г/) = 0 (при v' # v"),
(Рх)м = («"1Л1«) = / ММШМ =

(23.53)
Согласно этой формуле, и определяются матричные элементы дипольного момента для коле-
бательных переходов в инфракрасной области спектра.
Сложнее обстоит дело для колебательных спектров комбинационного рассеяния. Как уже
подчеркивалось в § 17.7 (с. 497), в квантовой механике нельзя определить поляризуемость аАд
просто как среднее значение классической функции от координат. Согласно квантовомехани-
ческой теории рассеяния (строгое обоснование которой дается квантовой электродинамикой),
для рэлеевского рассеяния компоненты тензора поляризуемости aXfi (определяющие связь
п(пад)	л
составляющих Рх индуцированного дипольного момента с составляющими напряжен-
ности поля падающей электромагнитной волны, см. (17.130)) для определенного квантового
§ 23.2. Интенсивности и поляризации в колебательных спектрах
695
состояния Ек рассеивающей системы имеют вид (см. [130] и [55], т. 2, с. 28)
(а^)кк = г / А--------------и------:--- >1	(23.54)
л ; I р uik + v J
где суммирование производится по промежуточным квантовым состояниям Д- (Ei ?= Ек).
Здесь v — частота падающей и рассеиваемой волн, а
(Л).1 = У	(23.55)
— матричные элементы дипольного момента рассеивающей системы, соответствующие пе-
Ei — Ек
реходам с частотами = ----------- между состояниями Ек и Eit Виртуальные переходы
h
из состояния Ек в промежуточные состояния Ei и обратно (рис. 23.4,а) определяют (аддКл
и, следовательно, интенсивность рассеяния. Рассеяние обусловливается взаимодействием
падающей электромагнитной волны с электронами рассеивающей системы, и виртуальные
переходы представляют электронные переходы между рассматриваемым электронно-колеба-
тельным состоянием n"v” и возбужденными электронно-колебательными состояниями n'v'
(п' / п"). Для рассеяния света молекулой в нулевом колебательном состоянии (у” = 0) (23.54)
можно записать в виде
(«Ар)
(Р^Р^п' (Р^'Ж)пХ ]
"n'n"+V Г
(23.56)
где суммирование производится по всем промежуточным электронно-колебательным состо-
яниям riv (п' / п"). Нижние индексы дают электронные квантовые числа, верхние —
колебательные квантовые числа.
Для комбинационного рассеяния, соответ-
ствующего переходу из начального состояния Ек
в конечное состояние Ej, составляющие тензора
поляризуемости перехода будут иметь вид
M kj h	Vik~ У + Ц; + V )
(23.57)
где также суммирование производится по проме-
жуточным состояниям, а виртуальные переходы
происходят из состояния Ек в состояние Ei и,
обратно, в состояние Ej (рис. 23.4, б). Для ко-
лебательного перехода из состояния nv” в со-
стояние n”v2 будем иметь виртуальные переходы
n”v” —► n'v' и n'v' —> n”v”. Соответствующие выра-
жения для составляющих тензора поляризуемости
перехода, получающиеся из (23.57), будут
Рис. 23.4. Виртуальные переходы
в промежуточные состояния:
а — при рэлеевском рассеянии;
б — при комбинационном рассеянии
Z_—/ I v'v"
n'v' 1	^п" - V
(23.58)
Vn'n'
Для частного случая основных частот («" = 0, v" = 1, переход 0—1) это дает
(аЛд)п"п" — V
n'v'
’'n'Z'-V	vn'n''+v )
(23.59)
Выражение (23.59) аналогично (23.56).
Формула (23.58) не может быть точно представлена в виде, аналогичном (23.53). Однако
это может быть сделано приближенно при определенных разумных предположениях, как было
696
Глава 23. Колебательные спектры многоатомных молекул
показано для простейшего случая переходов 0—1 в двухатомной молекуле (см. [321] и [55],
т. 2, с. 38). При этом величина	определяемая формулой (23.56), представляется
в виде среднего значения, в колебательном состоянии v" = 0, величины (ахц)п"п" =
в заданном электронном состоянии. Величина («аД^!^, определяемая формулой (23.59),
выражается также через (ахр)п"п" — «аД^),
(«Ад)л-=	(0|€|1),	(23.60)
что соответствует разложению
(аЛ/,)„»я» =	= адДО) + (	£ + ....	(23.61)
\ Jo
Обобщением (23.61) является разложение (23.6), что и обосновывает приближенную
справедливость последнего.
§ 23.3. Колебательные спектры простейших многоатомных молекул
Простейшие многоатомные молекулы, состоящие из небольшого числа атомов,
обладают в соответствии с малым числом колебательных степеней свободы и сравни-
тельно простыми колебательными спектрами. Наиболее интенсивными в спектрах
как в инфракрасных, так и комбинационного рассеяния являются основные частоы
колебаний (см. выше, § 23.1, с. 676), число которых для менее симметричных молекул
равно числу степеней свободы, а для более симметричных молекул меньше его.
Мы рассмотрим в данном параграфе некоторые примеры колебательных спек-
тров простейших многоатомных молекул.
Типичным для трехатомных молекул является наличие трех основных частот
колебаний — двух валентных и одного деформационного. Последнее для линей-
ных молекул дважды вырождено. Наряду с основными колебаниями возможны,
разумеется, обертоны и составные частоты.
Для линейной симметричной трехатомной молекулы XY2 (рис. 23.5, а) симме-
трии Dooh все три основные колебания обладают разной симметрией: мы имеем
симметричное валентное колебание типа А\д, антисимметричное валентное колеба-
ние типа А\и и деформационное колебание типа Е\и. Согласно табл. 22.9, (с. 664)
и в соответствии с альтернативным запретом (с. 679) первое из них активно в спек-
тре комбинационного рассеяния, а второе и третье — в инфракрасном спектре.
В качестве примера мы разберем спектр молекулы СО2.
В инфракрасном спектре СО2 наблюдаются две очень интенсивные полосы
2 349,3 см-1 и 667,3 см"115), соответствующие нечетным основным колебаниям А\и
и ЕХи и обычно обозначаемые как (0, 0, 1) и (0, 1, 0),6). В спектре комбинацион-
ного рассеяния наблюдается интенсивная двойная линия 1 285,5 см"1, 1 388,3 см"1,
соответствующая четным колебаниям А\д. Наличие двух линий вместо одной явля-
ется результатом весьма характерного для колебательных уровней резонанса Ферми,
получающегося, когда два разных колебательных уровня имеют, если не учитывать
взаимное влияние соответствующих колебаний, одинаковую или почти одинако-
вую энергию, т. е. когда имеет место случайное вырождение. Благодаря взаимному
|5) Мы приводим значения нулевых линий, полученные в результате анализа вращательной структуры
полос.
16) Принято колебательные квантовые числа для колебаний А\д, Е\и и А\и обозначать в последова-
тельности Vi, V2 и V3.
§23.3. Колебательные спектры простейших многоатомных молекул 697
молекулы типа ХУ2; в — нелинейной молекулы типа ХУ2; г — нелинейной молекулы типа XYZ
влиянию колебаний — «возмущению» колебательных уровней — вырождение сни-
мается и происходит расщепление вырожденного уровня, тем большее, чем сильнее
взаимодействие. В данном случае основная частота V\ симметричного валентного
колебания (1, 0, 0) почти точно равна частоте 2у2 первого обертона деформацион-
ного колебания (0, 2, 0). Согласно расчету Деннисона [318], нулевые частоты равны
Pi — 1 351,2 см-1 и у2 = 672,2 см-1 (т. е. 2у2 — 1 344,4 см-1 « i/j) и вычисленные
из них, с учетом ангармоничности колебаний, положения уровней (1,0, 0) и (0, 2, 0)
разнятся всего лишь на 16,7 см-117). Вследствие взаимодействия колебаний щ и 2у2
расстояние уровней увеличивается до 1 388,3 - 1 285,5 = 102,8 см-1 и вместо интен-
сивной основной частоты У\ и слабого обертона 2у2 получается две интенсивные
частоты, каждая из которых соответствует наложению обоих колебаний. Хотя ре-
зонанс Ферми и является результатом случайного вырождения, однако встречается
довольно часто, особенно у сложных молекул; из-за большого числа различных
обертонов и составных частот вероятность случайных совпадений колебательных
уровней достаточно велика. Следует отметить, что резонанс Ферми может иметь
место лишь для колебательных уровней одной симметрии; в рассмотренном случае
колебания щ и 2у2 имеют симметрию Д|/8).
Объяснение расщепления симметричной частоты для молекулы СО2 было дано Ферми
в 1931 г. [317], впервые рассмотревшим взаимные возмущения колебательных уровней данного
типа. Здесь мы имеем частный случай общего явления возмущения уровней (ср. с. 299). Легко
вывести общую квантовомеханическую формулу для взаимного возмущения двух близких * 18
|7)Это вычисление производится по формуле (22.73), где нужно положить = 1, v2 = 0, «з = 0
и Г| = 0, v2 = 2, vy = 0. При v2 — 0 I = 0 и при v2 — 0 I = 0,2 (см. (22.72)), но колебания с разными I
не взаимодействуют и нужно брать I = 0 для обоих уровней. Значение I отмечают индексом у v2; в данном
случае мы имеем уровни (1, 0°, 0) и (0, 2°, 0), (0, 22, 0).
18) Эта симметрия получается для уровня (0, 2°, 0) с I = 0. Для уровня (0, 22, 0) с I = 2 получается
симметрия Eig(Ag).
698	Глава 23. Колебательные спектры многоатомных молекул
уровней, если пренебречь их взаимодействиями со всеми другими уровнями. Если в нулевом
С	, (0)	, (0)
приближении существуют два решения гр\ и г/>2 , удовлетворяющие уравнениям
= в‘°^!0). Яо^О) =	(23.62)
и соответствующие уровням Е^1' и Е^'1 с разностью энергий <5 = Е^ — Е^'	0, то при учете
оператора энергии возмущения V решение уравнения
Нф = Н^гр + Угр = Егр	(23.63)
должно иметь вид
гр = c,^j0) + с2^2О).	(23.64)
Подставляя (23.64) в (23.63) и умножая получившееся уравнение последовательно на
/ (о)*
и гр2 , получим
(23.66)
Рис. 23.6. Зависимость положения
уровней от отношения
их первоначального расстояния
к энергии возмущения
Для случая молекулы СО2 б =
V-!O>‘(ffo + П(м!0) + c2^)dr = С|(Я<0) + Ун) + С2У|2 = CtE,
V (23.65)
^(Яо + У)(М<0) + c2^)dr = С|У21 + с2(Е{Р + У22) = с2Е. J
Таким образом, для определения коэффициентов С\ и с2 имеем систему двух однородных
уравнений
(В*о> + Ун - E)ct + У12с2 = 0,
У21С| + (<’ + У22 - Я)с2 = 0,
условием разрешимости которой является равен-
ство нулю определителя
+ УН-Е У|2
У2| Е{Р + У22 - Е
Раскрывая (23.67) и решая получившееся ква-
дратное уравнение (ср. (21.83)-(21.86)), найдем
(при Гц — V22 = 0)
ip(®) I	1
Е = ----- ± | л/й2 + 4|У2||2,	(23.68)
где учтено, что V12 = J* гр]Угрг dr = V2*i — J tyiVty* dr
и поэтому V|2V2i — |Г)2|2.
На рис. 23.6 показана зависимость положе-
б
ний уровней от отношения ттг-?. В частности,
1ч2|
при <5 — 0 (точный резонанс) расстояние уровней
равно 2|Г121.
16,7 см-1; полагая расстояние между уровнями,
у/16,72 + 4|Vi2|2, равным экспериментально наблюденному значению 102,8 см-1, мы находим
постоянную взаимодействия )Vj2| = 50,5 см-1, т. е. она примерно втрое больше расстояния
между уровнями.
Наряду с рассмотренными очень интенсивными полосами для молекулы СО2
наблюдается значительное число более слабых полос в комбинационном рассеянии
и особенно в инфракрасном поглощении. Эти полосы соответствуют возбуждению
обертонов и составных частот. Частоты всех наблюденных полос очень хорошо,
с точностью до нескольких см-1, определяются формулой типа (21.124), согласно
§23.3. Колебательные спектры простейших многоатомных молекул 699
которой колебательная энергия содержит линейные и квадратичные члены относи-
тельно квантовых чисел v\, v2 и V3.
Для СО2 в соответствии с наличием дважды вырожденного колебания нужно применять
формулу (22.73), отличающуюся от (21.124) добавочным членом д2212, зависящим от колеба-
тельного момента количества движения, и тем, что вместо
входит (v2 + 1). Согласно
Деннисону, эта формула в численном виде имеет вид (в см ’)
EViWl = 1 351,2	+ IJ + 672,2(v2 + 1) + 2 394,4(v3 4- 1) -	0,3	|
/ ] \2 / 1 \
-	1,3(«2 +	I)2 - 12,5 Ь3 + - 1 + 5,7 Ь, + - I («2 + 1) -
-	21,9 ( vi	+ |)(г'з + |)- Ч,0(«2 4- 1) (t)3 + ij	+ l,7g22l2.
(23.69)
По формуле (23.69) и вычислено приведенное выше значение 6 — 16,7 см 1 для полос (1, 0, 0)
и (0, 2°, 0).
Интересно отметить, что очень слабые колебательные полосы молекулы, лежащие
в близкой инфракрасной области, обнаружены в спектре поглощения атмосферы Венеры.
Они соответствуют переходам с нулевого уровня на уровни (0, 0, 5), (0, 2°, 5) и (1, 0°, 5).
Отметим также, что помимо полос с нулевым начальным уровнем обнаружены полосы
с начальными уровнями (0, I1, 0), (0, 2°, 0), (0, 22, 0) и (1, 0, 0).
Как и должно было быть, согласно альтернативному запрету, в инфракрасном спектре
наблюдаются переходы между уровнями разной четности (Av2 4- Av3 — нечетное), а в спектре
комбинационного рассеяния — между уровнями одной четности (Av2 4- Av3 — четное);
четными являются уровни с четной суммой v2 4- v3, нечетными — уровни с нечетной суммой
v2 4- v3 (см. примечание на с. 680 и ср. с. 683).
Для линейной несимметричной трехатомной молекулы типа XYZ (рис. 23.5, б)
симметрии Coot, оба валентные колебания щ и 1/3 принадлежат к полносимметрич-
ному типу Ai, а деформационное v2 — к типу Е. Все колебания активны в ин-
фракрасном поглощении, а в комбинационном рассеянии активны лишь колебания
типа Ai (vi и р3),9). Примером может служить несимметричная линейная молеку-
ла N2O, имеющая структуру N—N—О; для этой молекулы в инфракрасном спектре
и спектре комбинационного рассеяния наблюдаются частоты их — 1 285,5 см-1
и 1/3 = 2 223,5 см-1 и только в инфракрасном спектре частота v2 — 588,8 см-1.
В данном случае, как и в ряде других, отсутствие альтернативного запре-
та для наиболее интенсивных линий в колебательных спектрах является одним
из доказательств того, что молекула N2O не имеет центра симметрии (линейность
молекулы доказывается вращательной структурой инфракрасных полос поглощения,
см. ниже, §23.4, с. 703).
Для нелинейной симметричной трехатомной молекулы типа ХУ2 (рис. 23.5, в)
симметрии C2t> оба полносимметричные колебания типа Ai, валентное и деформа-
ционное (i/j и i/2), и антисимметричное валентное колебание типа В2(уз) активны
и в инфракрасном спектре, и в спектре комбинационного рассеяния, как уже
отмечалось выше (с. 678). Для наиболее важного случая молекулы этого типа —
молекулы Н2О — в инфракрасном поглощении и в комбинационном рассеянии
19) В комбинационном рассеянии для колебаний типа Е могут быть отличны от нуля, согласно
табл. 22.9, лишь составляющие axz и ayz тензора поляризуемости, а они обращаются в нуль в силу осевой
симметрии (ахх ~ ауу / azz, аху - ayz = azx - 0, см. (18.33)).
700
Глава 23. Колебательные спектры многоатомных молекул
для паров воды, действительно, со значительной интенсивностью наблюдается ча-
стота = 3 652 см”1. Частоты и2 — 1 595 см-1 и и = 3 756 см1 получаются только
в инфракрасном поглощении.
Отсутствие этих частот в комбинационном рассеянии естественным образом объясняется
малой зависимостью тензора поляризуемости от изменения нормальных координат, соответ-
ствующих антисимметричному валентному и деформационному колебаниям. Для первого
из них след тензора поляризуемости, в первую очередь определяющий интенсивность ком-
бинационного рассеяния, равен нулю в силу антисимметрии этого колебания (см. с. 693); он
равен нулю и для чисто деформационных колебаний, если исходить из схемы аддитивности
(см. (23.51)).
Для молекулы Н2О подробно изучен инфракрасный спектр поглощения. Наряду
с основными частотами i/2 и 1/3 наблюдается ряд обертонов и составных частот,
причем не только в инфракрасной, но и в видимой области. В табл. 23.2 приведены
данные для положения колебательных полос поглощения Н2О. Особенно суще-
ственными являются полосы поглощения 6,27 мкм, 3,17 мкм, 2,66 мкм, 1,87 мкм,
1,38 мкм, 1,13 мкм, 0,94 мкм и 0,91 мкм. Именно благодаря наличию этих полос
пары воды, содержащиеся в атмосфере, поглощают значительную долю проходя-
щего через нее инфракрасного излучения, в частности, инфракрасного излучения
Солнца [282]. Между этими полосами имеются участки спектра, в которых атмо-
сфера сравнительно прозрачна для инфракрасного излучения — окна прозрачности:
0,95-1,05 мкм, 1,2-1,3 мкм, 1,5-1,8 мкм, 2,1-2,4 мкм, 3,5-5 мкм [155а].
Таблица 23.2
Колебательно-вращательные полосы поглощения молекулы воды
Z/j, Vly V3	Тип полосы	Длина волны, мкм	Частота, см-1	0|, Vi, V3	Тип полосы	Длина волны, А	Частота, см-1
0, 0, 0	—	—	0	1, 2, 1	±	9670	10 328,85
0, 1, 0	II	6,27	1 594,78	0, 2, 2	II	9510	10 523
0, 2, 0	II	3,17	3 151,53	3, 0, 0	II	9440	10 599,7
1, 0, 0	II	2,73	3656,65	2, 0, 1	±	9420	10613,12
0, 0, 1	-L	2,66	3 755,79	1, 0, 2	II	9 190	10 868,3
0, 3, 0	II	2,14	4666,65	0, 0, 3	±	9 060	11 032,36
1, 1, о	II	1,91	5 235,0	0, 5, 1	±	8 880	11 248,4
0, 1, 1	-L	1,87	5331,19	1, 3, 1	±	8460	11813,44
0, 4, 0	II	1,63	6136,4	0, 3, 2	II	8 330	12012
1, 2, 0	II	1,48	6 775,0	2, 1, 1	±	8 230	12 151,22
0, 2, 1	-L	1,45	6871,65	1, 1, 2	II	8 070	12 407,65
2, 0, 0	II	1,39	7201,4	0, 1, 3	1	7 960	12 565,01
1, 0, 1	±	1,38	7 249,8	2, 2, 1	1	7 330	13652,65
0, 0, 2	II	1,34	7445,0	3, 0, 1	±	7 230	13 830,92
1, 3, 0	II	1,21	8 273,98	1, 0, 3	±	6 990	14318,77
0, 3, 1	±	1,19	8 373,6	3, 1, 1	±	6 520	15 347,91
2, 1, 0	II	1,14	8761,5	1, 1, з	1	6 320	15 832,47
1, 1, 1	±	1,13	8 807,65	3, 2, 1	1	5 950	16821,61
0, 1, 2	II	1,11	9000,10	4, 0, 1	±	5 920	16899,01
0, 4, 1	X	1,02	9 833,5	2, 0, 3	1	5 770	17 495,49
Частоты полос поглощения молекулы Н2О могут быть представлены, так же
как в случае молекулы СО2, с хорошей точностью порядка см”1 при помощи
формулы (21.124).
§23.3. Колебательные спектры простейших многоатомных молекул 701
Более точное представление экспериментальных данных для большинства частот с точ-
ностью порядка десятых долей см-1 может быть получено с помощью формулы для энергии
колебательных уровней, в которой учитываются, наряду с членам, линейными и квадратич-
ными относительно vb v2, v3, также и кубические члены [320].
Для нелинейной несимметричной трехатомной молекулы XYZ (рис. 23.5, г)
симметрии Cs все три колебания принадлежат к типу А\ и являются активными как
в инфракрасном спектре, так и в спектре комбинационного рассеяния.
Для четырехатомных молекул в общем случае число основных частот может
равняться шести, причем три частоты будут валентными и три деформационными.
При наличии симметрии число частот соответственно уменьшается. Важными част-
ными случаями являются линейная симметричная молекула X2Y2 симметрии
и пирамидальная симметричная молекула XY3 симметрии Сз„.
Рис. 23.7. Колебания четырехатомных молекул: а — линейной молекулы X2Y2;
б — пирамидальной молекулы типа ХУ3
Для линейной симметричной четырехатомной молекулы X2Y2 (рис. 23.7, а) с се-
мью степенями свободы получается три невырожденных валентных колебания
1/2, уз и Два вырожденных деформационных колебания 1/4, 1/5. Колебания v\ и V2
обладают симметрией А\д, колебание — симметрией 4ju, колебания щ и 1/5 —
симметрией Е\д и Е\и соответственно. Поэтому v\, V2 и 1/4 активны в спектре
комбинационного рассеяния, а р3 и 1/5 - в инфракрасном спектре. Для молеку-
лы ацетилена С2Н2 в инфракрасном спектре наблюдаются интенсивные частоты
1/3 = 3 287 см-1 и 1/5 — 729,1 см-1, а в спектре комбинационного рассеяния —
интенсивные частоты v\ = 3 373,7 см-1 и — 1 973,8 см-1 и очень слабая частота
щ = 611,8 см-1. При этом у\ и 1/3 представляют колебания связей С—Н, симметрич-
ное и антисимметричное, а ^2 — колебание тройной связи ОС. В инфракрасном
спектре наряду с основными частотами имеется большое число обертонов и состав-
ных частот. Отметим, что для молекулы C2HD, отличающейся от молекулы С2Н2
заменой атома Н атомом D, частоты У\ и г/2 являются активными не только в спект-
ре комбинационного рассеяния, но и в инфракрасном спектре (у\ = 3 334,8 см~1,
702	Глава 23. Колебательные спектры многоатомных молекул
i/2 = 1 851,2 см ’), что связано с исчезновением центра симметрии при переходе
от С2Н2 к C2HD.
Для пирамидальной симметричной четырехатомной молекулы XY3 (рис. 23.7, б)
существует по одному полносимметричному колебанию типа А] и по одному два-
жды вырожденному колебанию типа Е, как валентному, так и деформационному
(см. § 22.5, с. 667). Таким образом, мы имеем два валентных колебания vx (Л1) и из(Е)
и два деформационных колебания ^(Aj) и ^(Е). Все они активны и в инфракрасном
спектре, и в спектре комбинационного рассеяния. Для молекулы аммиака NH3 все
четыре колебания появляются в инфракрасном поглощении и из них полносимме-
тричные колебания наблюдаются и в комбинационном рассеянии; соответствующие
линии комбинационного рассеяния полностью поляризованы.
Отсутствие в спектре комбинационного рассеяния дважды вырожденных колебаний,
для которых след тензора поляризуемости равен нулю, естественным образом объясняется,
как и в случае Н2О, их малой интенсивностью.
Частоты основных колебаний равны: их — 3 336,7 см-1, i/2 = 949,8 см-1, 1/3 —
3 414 см-1 и 1/4 = 1 627,5 см-1; валентные частоты i/j и гх3, как обычно, значительно
больше деформационных частот i/2 и щ. Для частот vx и i/2 наблюдается инверсионное
удвоение (см. с. 643).
Для пятиатомных молекул в общем случае число основных частот может рав-
няться девяти. Однако в случае наиболее симметричной пятиатомной молекулы
XY4 симметрии Та число частот равно всего четырем (см. §22.5, с. 668). При этом
получается два валентных колебания нх и 1/3 симметрии Ах и F2 и два деформаци-
онных колебания симметрии i/2 и 1/4 симметрии Е и F2. Согласно табл. 22.9, все эти
колебания активны в спектре комбинационного рассеяния, а в инфракрасном спек-
тре активны лишь трижды вырожденные колебания F2. Для молекулы метана СН4
в инфракрасном спектре наблюдаются частоты 1/3 = 3 022 см-1 и 1/4 = 1 304 см-1,
а в спектре комбинационного рассеяния наряду с трижды вырожденной частотой 1/3
наблюдается лишь симметричная валентная частота vx — 2 914 см-1. Таким образом,
в спектре комбинационного рассеяния отсутствуют деформационные частоты i/2 и г/4.
Вычисленное значение частоты i/2 равно 1 528 см-1. Для метана наблюдается ряд
обертонов и составных частот в инфракрасном спектре и в спектре комбинационного
рассеяния. К вопросу о колебательном спектре метана, как простейшей органической
молекулы, мы вернемся в § 23.5, посвященном колебательным спектрам органичес-
ких молекул. В следующем параграфе мы разберем вопрос о вращательной структуре
колебательных полос простейших молекул.
§ 23.4. Вращательная структура колебательных полос
Для простейших многоатомных молекул, так же как и для двухатомных молекул,
удается разрешить при достаточной дисперсии вращательную структуру колебатель-
ных полос поглощения в инфракрасном спектре. Изучение этой структуры позволяет
получить значения вращательных постоянных комбинирующих колебательных со-
стояний. Вместе с тем, по правилам отбора и интенсивностям при вращательных
переходах, сопровождающих колебательный переход, можно судить об ориента-
ции дипольного момента перехода; для молекул, обладающих выделенной осью
симметрии, можно определить, направлен ли этот момент вдоль оси молекулы
(параллельно ей) или перпендикулярно к ней. Соответственно инфракрасные по-
лосы поглощения разделяют на параллельные полосы (обозначаемые значком ||)
и перпендикулярные полосы (обозначаемые значком ±).
§ 23.4. Вращательная структура колебательных полос
703
В противоположность этому вращательную структуру колебательных полос
в спектре комбинационного рассеяния многоатомных молекул обычно не удается
разрешить и полоса наблюдается в виде одной неразрешенной линии, как и в случае
двухатомных молекул (ср. §20.7, с. 603).
Мы ограничимся рассмотрением вращательной структуры инфракрасных полос
поглощения.
Вращательная структура колебательных полос зависит от того, является ли моле-
кула линейной или нелинейной, и в случае нелинейных молекул от того, к какому ти-
пу волчков она принадлежит — к сферическим, симметричным или асимметричным.
Для линейных многоатомных молекул, так же как и для двухатомных, энергия
вращения определяется формулой (19.23), Рвращ = BJ(J 4-1), и поэтому положения
вращательных линий находятся по формуле, совпадающей по виду с (20.131),
Е’ - Е" = 1/00 + Мращ - М'ращ = ^оо + W + 1) - B"j"(j" + 1),	(23.70)
где i/qo — частота нулевой линии, которая получилась бы при J1 = J" — 0, т. е. для чи-
сто колебательного перехода. Отличие состоит, однако, в том, что вращательные
постоянные являются функциями уже не одного квантового числа (см. (20.111)),
а всех колебательных квантовых чисел Vj, V2,..., vk, характеризующих колебатель-
ные состояния. Аналогично (20.111) соответствующая зависимость приближенно
является линейной.
В согласии с (22.70) эту зависимость можно представить в виде
Bv\,V2,- ..,Vk ~ Ве ~	2 f 4” j >	(23.71)
i х 7
где В€ — значение вращательной постоянной для равновесной конфигурации, a — кратность
вырождения i-ro колебания. В частном случае трехатомной линейной молекулы
= Ве - ае| (1>! + 0 - ае2(г>2 + 1) - аез («з + 0 •	(23.72)
Определив на опыте значения вращательной постоянной для ряда колебательных уров-
ней, с помощью формулы типа (23.71) можно найти равновесное значение Ве вращательной
постоянной.
Как мы видели в (20.7), при AJ = J' -J" — 2, 1,0, -1, -2, согласно (20.131), по-
лучаются совокупности вращательных линий, образующие 5-, R- и Q-, Р- и О-ветви
соответственно. Для дипольного поглощения в инфракрасной области справедливо
общее правило отбора (4.156) для дипольных переходов, AJ = 0, ±1, соответствен-
но которому получаются как положительная Р-ветвь и отрицательная Р-ветвь, так
и нулевая Q-ветвь. Можно показать [53], что это действительно имеет место для пер-
пендикулярных полос с дипольным моментом перехода, перпендикулярным к оси
молекулы, т. е. для полос с (Pz)v»v> = 0 (z — направление оси молекулы). Для парал-
лельных полос с дипольным моментом перехода, направленным по оси молекулы,
т.е. для полос с (Px)v"v< — (Py^'v' — 0, получается дополнительный запрет переходов
с A J — 0 и Q-ветвь отсутствует; полосы в этом случае имеют структуру, аналогичную
полосам двухатомных молекул, не обладающих электронным моментом количества
движения.
Для основных полос линейных молекул, соответствующих валентным коле-
баниям, дипольный момент направлен по оси молекулы; для них получаются
параллельные полосы. В случае деформационных колебаний, наоборот, для основ-
ных полос дипольный момент перпендикулярен к оси молекулы и получаются
704
Глава 23. Колебательные спектры многоатомных молекул
перпендикулярные полосы. Например, для СО2 полоса (0, 0, 1) (колебание симме-
трии Л1и) с частотой 1/3 = 2 349,3 см-1 является параллельной, а полоса (0, 1, 0)
(колебание симметрии Е\и) с частотой и2 — 667,3 см-1 — перпендикулярной; среди
обертонов и составных частот часть относится к параллельным полосам и часть
к перпендикулярным.
Деление полос на параллельные и перпендикулярные связано для линейных много-
атомных молекул с колебательным моментом количества движения. Для квантового числа Z,
определяющего значение этого момента, при дипольных переходах имеет место правило
отбора AZ = 0, ±1. Параллельные полосы получаются при AZ = 0 и перпендикулярные
при AZ = ±1. Это сразу вытекает из того, что колебательный момент количества движе-
ния направлен по оси молекулы и квантовое число I аналогично квантовому числу т,
определяющему проекцию Jz момента количества движения J на выделенное направле-
ние (см. с. 120, формула (4.172)). (Pz)v«v< отлично от нуля лишь при А/ = I' - I" — 0,
а (Рх ± iPy)v"v> — лишь при AZ = I* - I" = ±1. Состояния с I = 0, 1, 2,... относятся к типам
симметрии Л,Ei,E2, ... (см. §22.4, табл. 22.9), поэтому параллельные полосы получаются
при переходах А—Л, Е\—Ех, Е2—Е2 и т.д., а перпендикулярные — при переходах Л—Ех,
Е[ Е2,....
Для основных частот молекулы СО2 мы получаем соответственно для перехода Aiff—Л1и
(частота i/3) параллельную полосу и для перехода А1д—Eiu (частота v2) перпендикулярную.
Перпендикулярные полосы получаются лишь при изменении квантового числа v2 дефор-
мационного колебания на нечетное число, так как, согласно (22.72), четность I совпадает
с четностью v2 и при четном Ди2 = и'2 - v", AZ = I' - Z" также четное.
Для параллельных полос в случае I' — I" = 0, который и имеет место при перехо-
дах с нулевого колебательного уровня (когда, разумеется, Z" = 0), запрещены переходы
AJ = 0. Это является результатом деления уровней энергии на положительные (+) и от-
рицательные (-) по отношению к отражению всех координат в начале (см. § 19.1, с. 536).
Для невырожденных колебательных состояний с Z = 0 последовательные вращательные уров-
ни будут положительными (при четном J) и отрицательными (при нечетном J), т. е. полная
волновая функция молекулы будет сохранять или менять свой знак при отражении. Так
как дипольный момгнт при таком отражении меняет знак, то будут разрешены переходы
-I--► - и запрещены переходы -|—> + и---> в частности, будут разрешены переходы
J J ± 1 и запрещены переходы J —> J. Для дважды вырожденных колебательных со-
стояний (Z 0) каждый вращательный уровень дважды вырожден и, как можно показать
(ср. ниже, § 24.2, с. 725), представляет совокупность положительного и отрицательного со-
стояний, поэтому запрет A j = 0 уже не имеет места. Следовательно, для перпендикулярных
и параллельных полос с Z' = Z" / 0 разрешены как переходы AJ = ±1, так и перехо-
ды AJ = 0; однако появляющаяся в параллельных полосах с Г = Г ф 0 ветвь Q слабая
(см. [53], с. 409).
Для ряда линейных трех- и четырехатомных молекул удалось разрешить враща-
тельную структуру инфракрасных полос поглощения и определить со значительной
точностью вращательные постоянные. Следует отметить, что заключение о том,
является полоса параллельной или перпендикулярной, можно сделать из общего ви-
да полосы, в первом случае около нулевой линии имеется минимум интенсивности,
а во втором — максимум.
Для молекул типа сферического волчка, так же как и для линейных молекул,
справедлива формула (23.70). Для дипольного излучения имеет место обычное пра-
вило отбора AJ = 0, ±1, и полосы состоят из трех ветвей R, Р и Q. При этом
для трижды вырожденных колебаний получается расщепление, связанное со взаи-
модействием колебания и вращения. Структуру инфракрасных колебательных полос
удалось разрешить для метана и некоторых других молекул типа XY4.
Для молекул типа симметричного волчка энергия вращения определяется фор-
мулой (19.74) или (19.75) и соответственно положение вращательных линий дается
§ 23.4. Вращательная структура колебательных полос
705
формулой
или
Е' - Е" = 1/оо +	+ 1) - В" J“(J" + 1) +
+ (Л' - В')#'2 - (Л" - В")К'2 (Л > В)
Е' - Е" = 1/00 + B'J\J' +1) - B"J"(J" + 1) +
+ (С' - В')А-'2 - (С" - В")к"2 (С < В).
(23.73)
(23.74)
Так же как и в случае линейных молекул, мы получаем параллельные и пер-
пендикулярные полосы в соответствии с тем, параллелен или перпендикулярен
к оси молекулы момент перехода. Для них существуют различные правила отбора,
а именно:
для параллельных полос
дк=о,
дк=о,
Д7 = ±1
при К Ф 0,
при К — О,
для перпендикулярных полос
(23.75)
[(-Рr)v"v' Ф	(Рy)v,,vr Ф О]
ДК = ±1,
AJ = 0,±l.

Правило отбора для К при дипольном излучении представляет частный случай общих
правил отбора (4.172) для составляющих вектора (на эти правила мы уже ссылались при рас-
смотрении правил отбора для квантового числа /, определяющего значение колебательного
момента количества движения линейных молекул, см. с. 704).
В отличие от случая чисто вращательных спектров, когда дипольный момент
направлен по оси молекулы, что и приводило к правилу отбора ДЙГ — 0, для коле-
бательно-вращательных спектров дипольный момент перехода может не совпадать
с направлением оси молекулы.
Вращательные постоянные комбинирующих состояний, как и для линейных
молекул, зависят от колебательных квантовых чисел. Эта зависимость невелика,
и поэтому для параллельных полос член в (23.73) или (23.74), содержащий К2
и имеющий вид [(4' - В1) - (А“ - В")]К2 или [(С' - В') — (С" - В*)] К2, будет
мал. Полоса состоит из ветвей Р, R и Q, и ее структура сходна со структурой
перпендикулярной полосы линейных молекул. В противоположность этому для пер-
пендикулярных полос члены, содержащие Kf и К", будут играть существенную роль.
Выражение (23.73) можно представить в виде
Е1 - Е" = (i/oo)±x + B'J'(J' + 1) -	+ 1),
(23.76)
где
(»оо)±к = Уьо + (Т - В') ± 2(А' - В')К" + [(Т - В1) - (Аи - В")] К2 (23.77)
и знаки + и - соответствуют К1 = К" 1 и К1 = К" - I; в аналогичном виде
запишется и формула (23.74). Каждая полоса будет состоять из ряда подполос с раз-
личными значениями нулевых линий (i/oo)±x, что сильно усложняет ее структуру.
Однако в отличие от случая параллельных полос из анализа перпендикулярных полос
можно определить не только постоянную В, но и постоянную А (или (7). К дальней-
шему усложнению структуры колебательных полос молекулы типа симметричного
волчка приводит взаимодействие колебаний и вращения.
Структура колебательных полос поглощения исследована для молекулы NHj
и для целого ряда других молекул типа симметричного волчка.
23 Зак. 103
706
Глава 23. Колебательные спектры многоатомных молекул
Для молекул типа асимметричного волчка вследствие сложного расположения
вращательных уровней вращательная структура колебательных полос является так-
же весьма сложной. При этом необходимо учитывать зависимость вращательных
постоянных А, В и С от колебательных квантовых чисел.
Указанная зависимость приближенно будет иметь вид, аналогичный (23.71). В частности,
для трехатомной нелинейной молекулы получим:
А = А,
“ «41 Щ
1\	( И (	1
2 I - «42 I ^2 4- - I - «43 I Щ 4- -
В — Bt
- Qb\ I Vi
1\ ( 1\ ( 1
2 I ~ «В21	4- - ) - «вз I Уз 4- -
(23.78)
С = Се
- «С1
1\
+ v
“ «С2
( И
- «сз Из 4- - ) •
Постоянные а можно выразить через постоянные ангармоничности а, входящие в кубические
члены разложения (21.125), а определив а из опыта, можно найти и постоянные а. Это
оказалось возможным сделать для молекулы Н2О [54, 282].
Вращательная структура полос зависит от правил отбора, которые различны
в зависимости от того, по какой оси направлен дипольный момент перехода: по оси а
наименьшего момента инерции, по оси среднего момента b инерции или по оси с
наибольшего момента инерции (см. табл. 19.4, с. 555). В общем случае мы получаем
три типа полос: полосы типа а, полосы типа b и полосы типа с. В частном случае
нелинейной симметричной трехатомной молекулы XY2 дипольный момент может
быть направлен либо по оси симметрии молекулы, либо вдоль перпендикулярной
к ней оси, лежащей в плоскости молекулы, и будут иметься два типа полос —
параллельные и перпендикулярные полосы. Для молекулы Н2О ось молекулы служит
осью среднего момента инерции (см. (19.2)) и параллельные полосы будут относиться
к типу Ъ, а перпендикулярные полосы — к типу а; отсутствие в этом случае полос
типа с является следствием того, что для плоской трехатомной молекулы дипольный
момент не может быть перпендикулярен к плоскости молекулы, т. е. не может
быть направлен вдоль оси с наибольшего момента инерции (см. § 19.4, с. 545).
Большинство полос поглощения молекулы воды, данные для которых приведены
в табл. 23.2 (с. 700), являются перпендикулярными полосами.
Детальный анализ колебательных полос поглощения молекулы воды в инфракрасной,
а также в видимой области спектра был выполнен Мекке; как уже отмечалось (см. с. 553),
ему удалось впервые интерпретировать вращательную структуру в спектре молекулы типа
асимметричного волчка. В дальнейшем в ряде других работ были продолжены исследования
инфракрасных полос поглощения молекулы воды (ссылки на эти работы см. в статьях
Хачкурузова [320]).
§ 23.5. Колебательные спектры органических молекул
Особенно широко исследованы колебательные спектры, как инфракрасные, так
и комбинационного рассеяния, органических молекул, начиная с самых простых —
таких как метан СНд, этан С2Нб, этилен С2Щ, ацетилен С2Н2 и их галоидозамещен-
ные — и кончая весьма сложными молекулами органических соединений всевоз-
можных классов и самого разнообразного строения. По мере усложнения молекулы
увеличивается число наблюдаемых частот, причем по-прежнему с наибольшей ин-
тенсивностью проявляются основные частоты. При этом обычно некоторые частоты
являются характеристическими (см. §21.2, с. 614) и связаны с наличием в молекулах
§23.5. Колебательные спектры органических молекул
707
определенных связей и групп связей, определенных типов пространственных струк-
тур. Особенно важно проявление в спектрах частот, соответствующих различным
валентным колебаниям углеродных цепей, валентным и деформационным колеба-
ниям групп CH, СН2, СНз, частот, характерных для двойных связей и связей С—X,
где X — разного рода атомы, замещающие атомы водорода. Весьма существенным
является сходство спектров молекул, принадлежащих к определенному классу соеди-
нений, например спектров молекул нормальных предельных углеводородов СпН2п+2-
Если для простой молекулы ее спектр может быть интерпретирован на основе ис-
следования только этой молекулы, то для более сложных молекул такая интерпре-
тация оказывается возможной лишь при систематическом сопоставлении спектров
ряда молекул данного класса соединений. Исходными должны, естественно, слу-
жить спектры наиболее простых молекул данного класса. В частности, исходными
при интерпретации спектров являются спектры метана и этана — для предельных
углеводородов, спектр этилена — для непредельных углеводородов с открытыми
цепями, спектр бензола — для ароматических углеводородов.
Наиболее полная и уверенная интерпретация колебательных спектров слож-
ных молекул возможна лишь на основе расчета частот колебаний, который может
быть выполнен по методам, описанным в гл. 21 и 22. При этом силовые постоян-
ные (динамические коэффициенты), через которые выражаются частоты колебаний,
приходится определять, как уже отмечалось в конце §21.4 (с. 628), полуэмпири-
ческими методами из опытных значений частот колебаний. Самым рациональным
путем решения задачи о расчете колебаний молекул является использование зна-
чения силовых постоянных, найденных для более простых молекул, для расчета
колебаний более сложных молекул рассматриваемого класса соединений. Именно
таким путем удалось рассчитать и интерпретировать колебательные спектры ряда
сложных молекул углеводородов и их производных.
Основой для интерпретации колебательных спектров сложных молекул явля-
ются надежные экспериментальные данные, причем большую помощь оказывает
сопоставление инфракрасных спектров поглощения и спектров комбинационного
рассеяния. Наряду с точными значениями частот колебаний важно иметь и данные
об интенсивностях, а в случае комбинационного рассеяния — также и данные
о поляризациях. Последние данные оказывают, в частности, существенную помощь
при решении вопроса о том, какие частоты соответствуют полносимметричным
колебаниям и какие неполносимметричным (см. правила (23.46)-(23.48)). Следует
отметить, что для спектров комбинационного рассеяния большого числа углеводоро-
дов имеются прекрасные данные, полученные в результате цикла работ, проведенных
Ландсбергом и его сотрудниками.
Итоги этих работ изложены в монографии Ландсберга, Бажулина и Сущинского [63].
В ней приведены данные для частот, интенсивностей, ширины линий и степеней деполяриза-
ции линий комбинационного рассеяния 140 углеводородов различных классов, исследованных
авторами, а также обработанные литературные данные еще для 138 углеводородов.
Интерпретация колебательных спектров значительно облегчается, а иногда толь-
ко и становится возможной, при применении метода изотопического замещения.
Изотопические молекулы обладают той же потенциальной энергией, но в силу
различия масс атомов частоты их колебаний различаются, и, таким образом, увели-
чивается число данных, получаемых из опыта. Для органических молекул особенно
большое значение имеет исследование дейтерированных молекул, в которых атомы
легкого водорода Н замещаются атомами тяжелого водорода D. При этом значи-
тельно уменьшаются частоты валентных и деформационных колебаний С—Н, в то
время как частоты остальных колебаний изменяются значительно меньше.
708
Глава 23. Колебательные спектры многоатомных молекул
При изотопическом замещении всех эквивалентных атомов данного рода сим-
метрия колебаний сохраняется, а при изотопическом замещении части таких атомов
она уменьшается, и в спектре могут сильно изменяться не только значения частот
колебаний, но и правила отбора, в частности, если при изотопическом замещении
исчезает центр симметрии (например, при переходе от молекулы этилена С2Н4
к молекуле монодейтероэтилена C2H3D), то перестает быть справедливым альтерна-
тивный запрет.
Мы рассмотрим некоторые конкретные примеры интерпретации колебательных
спектров органических молекул, иллюстрирующие применение теории колебатель-
ных спектров. Простейшим насыщенным углеводородом является первый член ряда
СгНзя+г — метан СН4, общая характеристика колебательного спектра которого была
дана в конце § 23.3 (см. с. 702). Как мы видели, на опыте наблюдаются три часто-
ты колебаний V\(A\), v^Fi) и 1/4(^2); их значений недостаточно для определения
силовых постоянных молекулы, число которых равно пяти. Этими постоянными
являются следующие: kq — постоянная связи С—Н, ка — постоянная угла Н—С—Н
и три постоянные взаимодействия, а именно: h — двух связей С—Н, а — связи С—Н
с прилежащим углом Н—С—Н и I — двух смежных углов Н—С—Н (рис. 23.8, а).
Потенциальная энергия молекулы записывается в общем виде как
и=529,?+52 ;+h 52qi<11+а' 52 +
’	°	°	°	(23.79)
+ Ь'	j,а,* +1' У aijaik + o' 52 ву-Лы (« / j # I # к),
ijk	ijk	ijkl
причем, кроме перечисленных пяти постоянных, в (23.79) входят постоянная взаимодей-
ствия Ъ1 связи С—Н с несмежным углом (например, qi9 а2з) и постоянная взаимодействия о'
двух несмежных углов (например, а12, «34)- Однако при учете условия (22.43) формулу (23.79),
полагая а = а1 — У и I = I' - о', можно переписать следующим образом (см. [55], т. 1, с. 230):
и=у» 52+5ка 52 i+h 52 +«У 9,а,>+152 аиа*- (23.80)
i	ij	ij	ij	ijk
8 (23.80) входит пять независимых постоянных, как и должно быть (см. формулу (22.64),
с. 671, в которую входит пять постоянных, являющихся линейными комбинациями постоян-
ных kq, ка, й,« = а' —	1 = Г - о').
Отметим, что так как взаимодействия связи с несмежным углом и двух несмежных углов
малы, то, пренебрегая постоянными Ь* и о' в (23.79), можно было бы сразу получить (23.80).
Однако можно уверенно определить все пять постоянных, если использовать
данные для дейтерозамещенных метана CH3D, CH2D2, CHD3 и CD4 (рис. 23.8, б,
в, г, д), для которых исследованы как инфракрасные спектры поглощения, так и спек-
тры комбинационного рассеяния. При этом молекула CD4 имеет, подобно СН4,
Рис. 23.8. Молекула метана и ее дейтерозамещенные:
а — СН4; б — CH3D; в — СН2О2; г — CHD3; д — CD4
§ 23.5. Колебательные спектры органических молекул
709
симметрию Та и 4 основные частоты, молекулы CH3D, CHD3 — симметрию
и по 6 основных частот (3 частоты типа и 3 частоты типа Е) и, наконец, молекула
C2H2D2 имеет симметрию и 9 основных частот (4 частоты А\, 1 частоту
и по 2 частоты В\ и В2). Общее число частот равно 27, и они почти все наблюдены.
Таблица 23.3
Частоты колебаний молекул метана и его дейтеропроизводных
Тип симметрии	Род колебаний	СН4		cd4	
		наблюдено	рассчитано	наблюдено	рассчитано
А	Я	2914	2914	2085	2085
Е	а	—	1528	—	1096
F2	а	1304	1304	988	995
Fi	Я	3022	3022	2 258	2 255
Тип	Род	CH3D		CHD3	
симметрии	колебаний	наблюдено	рассчитано	наблюдено	рассчитано
Ai	а	1307	1303	988	100
	Я	2 205	2 209	2141	2143
	Я	2950	2 950	3000	2988
Е	а	1 156	1149	—	1025
Е	а	1474	1473	1292	1288
Е	Я	3031	3012	2 860	2 278
Тип	Род	ch2d2			
симметрии	колебаний	наблюдено		рассчитано	
Л-1	а	1035		1020	
Л|	а	1450		1435	
Л]	Я	2139		2161	
Л]	Я	2974		2973	
Л2	а			1330	
	а	1091		1086	
Bl	Я	3020		3020	
Bl	а	1286		1276	
Bl	Я	2 255		2 254	
В табл. 23.3 приведены данные для частот колебаний метана и всех его дейте-
ропроизводных, экспериментальные и рассчитанные Степановым [310] с помощью
пяти постоянных. Для большинства частот расхождения наблюденных и вычислен-
ных значений не превышают 5-10 см”1. Для каждого колебания указано, какие
координаты в основном изменяются.
Следует отметить, что для надежного нахождения системы силовых постоянных необхо-
димо, учитывая ошибки как в теоретических расчетах, из-за приближенности применяемых
моделей, так и в экспериментальных данных, иметь число опытных значений частот, значи-
тельно превышающее число определяемых постоянных, как в данном случае. Следует также
подчеркнуть, что только при учете недиагональных силовых постоянных может быть полу-
чено удовлетворительное согласие с опытом; модель валентных сил (см. §21.3, с. 619) дает
неудовлетворительные результаты, а результаты, получаемые на основе модели центральных
сил, еще хуже. Это относится не только к рассматриваемому случаю, но и к подавляющему
большинству других. Только принимая во внимание важнейшие динамические взаимодей-
ствия, можно правильно рассчитывать колебания молекул. В данном случае значения силовых
710
Глава 23. Колебательные спектры многоатомных молекул
постоянных, если выразить их в см 22О\ равны
к, = (8,34 ± 0,03) • 10б 7 см’2, ка = (0,71 ± 0,03) • 106 см’2,
Л = (0,05 ± 0,01) • 106 см”2, а = (0,35 ± 0,05) • 106 см’2,	(23.81)
I = (-0,035 ± 0,005) • 106 см’2.
Мы видим, что постоянная а взаимодействия связи С—Н с прилегающим углом Н—С—Н
весьма значительна и составляет 50% постоянной ка.
Следующий член ряда С2Н2п+2 ~ молекула этана СгЩ — является простейшей
молекулой, содержащей связь С—С. Молекула этана обладает 18 колебательными
степенями свободы (число атомов N = 8, 3N — 6 = 18), в том числе одной степенью
свободы крутильных колебаний. Две группы повернуты друг относительно друга
на 60° (трансконфигурация, см. рис. 21.14, а, с. 641), и молекула обладает симметрией
Дм(Зби). Помимо неактивной частоты крутильных колебаний типа Агд молекула
обладает 11 частотами колебаний, а именно, 3 частотами типа А\д и 3 частотами
типа Ед, активными в спектре комбинационного рассеяния, 2 частотами типа АХи
и 3 частотами типа Еи, активными в инфракрасном спектре. В сокращенной записи
имеем
ЗЛ^ 4- ЗЕд 4- 2Л1и 4~ ЗЕи.
Подсчет числа колебаний производится легко. Мы имеем одну
координату Q (изменение связи С—С) и по шести эквивалентных
координат qi, аг], Д (изменения связей и углов а1; и Д , рис. 23.9).
Связи С—С соответствует валентное колебание типа А]д. Трем связям
С—Н, трем углам Н—С—Н и трем углам С—С—Н в каждой группе
соответствуют, как и в молекуле NH3, по одному колебанию типа Л1
и по одному колебанию типа Е, причем колебания в группах могут
быть симметричны и антисимметричны относительно центра; в ре-
зультате получается по одному валентному колебанию типов АХд, А1и,
Ед, Еи для 6 связей С—Н и по одному деформационному колебанию
тех же типов для 6 углов Н—С—Н и для 6 углов С—С—Н. Однако в си-
лу дополнительных условий для углов (аналогично условию (22.43)),
ai2 4-«1з 4-«23 4-/3| 4-/Зг4-/З3 = 0 и с*45 4-«46 «56 4-/З4 -Ь/З5 4-/36 = 0, число
деформационных колебаний типов АХд и уменьшается на единицу.
В результате имеем следующие колебания:
координата Q
координаты q
координаты а
координаты р
А}и
А[и
Ед Еи
Ед Еи
Ед Еи
(23.83)
^15 |
откуда и вытекает разделение 11 частот по типам симметрии, соглас-
но (23.82).
Потенциальная энергия этана содержит 21 постоянную, однако некоторыми
из них можно пренебречь, кроме того, часть постоянных можно положить равными
2°)Для этого силовые постоянные в соответствии с формулой (20.2) представляют в виде
7	э 9Г-СМ2
к = 4тг Me I - I и делят к, выраженное в дин/см, на 4тг Мс ------т-. Приводимые нами значения
\ с /	сек2
постоянных вычислены со значением т, равным «спектроскопической» массе атома водорода (см. §20.6,
с. 599), приближенно учитывающей ангармоничность колебаний связей С—Н. Эта масса равна (принимая
за единицу — массы атома кислорода О16) 1,088, а спектроскопическая масса атома дейтерия равна
16
2,126 (см. с. 536 и [55], т. 1, с. 562). Вместо угловых переменных а взяты линейные переменные рсн«» где
Рен = 1,09 к = 1,09 • IO’8 * * * * * см — равновесная длина связи СН (см. там же, с. 328).
§23.5. Колебательные спектры органических молекул
711
аналогичным постоянным для метана. В результате при некоторых естественных
дополнительных предположениях число неизвестных постоянных уменьшается до 7;
их можно надежно определить из данных для 22 наблюденных частот этана С2Н6
и дейтероэтана C2D6. Результаты расчета и интерпретации колебательного спектра
этана приведены в табл. 23.4 [310].
Таблица 23.4
Частоты колебаний молекул этана и дейтероэтана (в см4)
Тип симметрии	Род колебаний	с2н6		c2d6	
		наблюдено	рассчитано	наблюдено	рассчитано
Afg	Q	993	997	852	847
А1д	ар	1375	1376	1 158	1 152
Л i0	Я	2925	2901	2115	2 105
	Р	I 170	1 167	970	971
	а	1460	1467	1055	1055
	Я	2960	2970	2225	2221
А1и	ар	1380	1380	1 072-1 100	1070
Aiu	Я	2895	2 897	2100	2 097
Еи	Р	827	827	601	601
Еи	а	1465	1472	1 072-1 100	1080
	Я	2980	2984	2 237	2231
Число силовых постоянных можно найти из (23.83); для г координат симметрии одного
г(г + 1)
типа получается-------постоянных, что и дает 64-3 + 6 + 6 = 21. Постоянными взаимодей-
ствия удаленных друг от друга углов и связей, например, связей q\, q2, q$ со связями q4, q5, q6,
можно пренебречь. Постоянные взаимодействия углов (^на12) и (t/i, А) приравниваются друг
другу и постоянной а для метана, постоянные типов (а12, «13), («12, А) и (А, А) приравнива-
ются постоянной I для метана и постоянная типа (qh q2) — постоянной h для метана. Следует
отметить, что постоянная ка угла Н—С—Н считается отличной от постоянной ка для метана,
однако в результате расчета оказывается ей равной. Постоянная kq связи С—Н для этана
отлична от постоянной kq для метана. Значения постоянных kq, kq и кр связей С—Н, С—С
и угла С—С—Н и постоянных А, т и п взаимодействия типов (Q, /3), (А, А) и (А, А) равны
fcg(CH3) = (8,08 ± 0,05) • 106 см"2,
kfi = (0,92 ± 0,05) • 106 см"2,
m = (0,12 ± 0,01) Ю6 см"2,
кд = (7,02 ± 0,05)- 106 см"2,
Л = (0,43 ± 0,05) • 106 см"2,
п = (-0,02 ± 0,01) 106 см"2
(23.84)
Удалось рассчитать частоты колебаний более сложных молекул насыщенных
углеводородов, в частности пропана СзНю, бутана С4Н]2 и пентана СзН^, и удо-
влетворительно интерпретировать их колебательные спектры, исходя из результатов
расчета колебаний СН4 и С2Н6. При этом применялась система силовых постоянных,
полученных для СН4 и С2Нб, с добавлением лишь небольшого числа дополнитель-
ных постоянных. Обычно получается удовлетворительное согласие рассчитанных
значений частот с наблюденными; расхождения по большей части не превышают
10-20 см"1.
Подобные расчеты для пропана, бутана и некоторых других молекул предельных угле-
водородов были выполнены Степановым (см. [55], т. 1, гл. 14), а затем другими советскими
учеными, в частности Сущинским и Подловченко, применившими для решения вековых урав-
нений высоких степеней электронные вычислительные машины [314]. К постоянным (23.81)
712
Глава 23. Колебательные спектры многоатомных молекул
и (23.84) при этом добавляются постоянная угла С—С—С, fc7 = 1,1 • 106 см-2, постоянная
взаимодействия Л7 связей С—С со смежными углами С—С—С и постоянные взаимодей-
ствия /77 и /7д углов С—С—С со смежными углами С—С—С и С—С—Н; в расчетах
принимается, что А7 = Ар — А и Z77 = l7j9 = I. Были рассчитаны частоты колебаний и ин-
терпретированы спектры ряда галоидозамещенных предельных углеводородов, в частности
галоидозамещенных метана. Для простых галоидозамещенных метана были также рассчита-
ны интенсивности и поляризации в колебательных спектрах на основе схемы аддитивности
(см. §23.2, с. 686) [322].
Наряду с предельными углеводородами удалось успешно рассчитать частоты
колебаний и интерпретировать спектры и других классов органических соедине-
ний. Мы остановимся еще на колебательных спектрах простейшего ароматического
углеводорода — бензола СбНб.
Наиболее полно расчет и интерпретация колебательных спектров бензола и целого ряда
его производных были выполнены Ковнером и его сотрудниками [312].
Молекула бензола имеет 30 колебательных степеней свободы (число атомов
N = 12, 3N -6 = 30). Из них 21 степень свободы соответствует плоским колебаниям
и 9 степеней свободы соответствуют неплоским. Молекула обладает симметрией Г>6Л
и для нее получается 14 частот плоских колебаний и 6 частот неплоских, а именно
плоские колебания 2Аiа 4- А2а 4- 4£\ 4- 2Biu 4- 2В2и 4- 3Е\и.
*	(23.85)
неплоские колебания 2В2д 4- Е2д 4- А2и 4- 2Е2и.
Четные колебания активны в комбинационном рассеянии, нечетные — в ин-
фракрасном поглощении.
В табл. 23.5 приведены результаты расчета и интерпретации колебательных
спектров бензола СбНб и дейтеробензола СбВб.
Таблица 23.5
Частоты колебаний молекул бензола и дейтеробензола (в см-1)
Тип симметрии	Род колебаний	C6H6		C6D6	
		наблюдено	рассчитано	наблюдено	рассчитано
Л	Q	992	990	943	947
4|д	q	3 062	3 062	2 293	2292
Л 2g	P	1326	1319	1037	1041
		606	600	577	571
	P	1 178	1 170	867	854
#2g	Q	1596	1589	1552	1566
B2g	q	3047	3049	2265	2 265
B\u	7	1010	1008	963	965
B\u	q	3 060	3059	2 290	2 289
B2u	P	1 110	1099	825	831
b2u	Q	1648	1655	1577	1568
E\u	Q	1037	1024	813	817
E\u	P	1485	1480	1333	1320
B\u	q	3 080	3 074	2 290	2 306
B2g		703	705	601	599
B2g	<u s	985	983	827	829
B2g		849	844	662	665
	О 5	671	669	496	497
В2Ц	c <u	405	405	352	354
e2u		970	970	793	792
§ 23.6. Характеристичность в колебательных спектрах
713
Одновременно Ковнером были рассчитаны и интерпретированы также и колебатель-
ные спектры ряда неполностью дейтерированных молекул: C6H5D симметрии C2v, C6H2D4
и C6H4D2 симметрии Р2Л и C6H3D3 симметрии РЗЛ (рис. 23.10). Была найдена система си-
ловых постоянных бензола, причем для связей С—Н и С—С постоянны оказались равными
kq — 8,63-106 см-2 и kq ~ 11,36-106 см-2. Последнее значение больше значения kq для простой
связи С—С, равного примерно 7 (см. (23.84)), и меньше значения kq для двойной связи,
равного примерно 14, как это и должно быть для «полуторной» связи (см. §26.4, с. 810).
Рис. 23.10. Молекула бензола и ее дейтерозамещенные:
д — CgHgj б — CeH5D; в — СбН4О2; г — СбН2О4; д — C6H3D3
§ 23.6. Характеристичность в колебательных спектрах
Важнейшее значение изучения колебательных спектров состоит в установлении
связи между этими спектрами и строением молекулы, что прежде всего проявляете?
в наличии характеристических частот колебаний (см. §21.2, с. 614, а также §23 е
с. 706) для определенных связей и углов и их различных комбинаций, для различи
групп в молекуле и для различных пространственных структур. Именно н^ю
характеристических частот служит основой применения колебательны#04-3 010
для структурного анализа, т.е. для определения структуры молекулы, 8404-790
трального анализа в узком смысле этого слова, т. е. для определения с
Характерными признаками могут являться как сами частоты ко"
инфракрасных полос поглощения и частоты линий комбинации
так и значения интенсивностей инфракрасных полос поглощу
тенсивностей и поляризаций линий комбинационного рассе
ширин полос или линий. Таким образом, помимо основн'
колебаний — могут иметься и другие характеристически
всего говорить о характеристических полосах и линиях
характеристических параметров.	да
Следует иметь в виду, что часто под частотами в кои
ют не значения частот, а определенные колебательные в
о частоте данного типа симметрии. Соответственно под
подразумеваться полоса или линия со всеми присущи*'
стическая полоса или линия.
3 300
~ 3 030
7704-730
7104-690
7704- 735
8104- 750
8604-800
9004-860
3 5004-3 300
1 6504-1 550
3 5004-3400
3 4004-3 300
16504-1590
Данному структурному элементу в молет
или определенным типам разветвления угг
не одна определенная полоса или линия, ?‘я вод°р°днои связью
НОСТЬ ЛИНИЙ И ПОЛОС, И МОЖНО ввести 'е соединения
элементах молекулы [313], проявЛЯЮЩИИнения, содержащие серу
точки зрения выделение таких струк^ие соединения
соответствуют определенные совокуп "	“
3 6504-3590
3 5704-2 500
24404-2350
2 6004-2550
2 3004-2100
бательных спектрах по наличию хара
714
Глава 23. Колебательные спектры многоатомных молекул
Характеристичность инфракрасных полос и линий комбинационного рассеяния
и их совокупностей связана с характеристичностью самих нормальных колеба-
ний молекулы. Колебание может быть характеристично для данной координаты
или группы координат (т. е. соответствовать определенной связи или углу или их
совокупности) по частоте, т. е. частота сохраняет свое значение в разных молекулах
при наличии этих координат, и по форме, т. е. при рассматриваемом колебании могут
меняться лишь соответствующие координаты. Следует подчеркнуть, что даже если
по форме колебание не является характеристическим и при изменении некоторой
координаты меняются и другие, оно может приближенно быть характеристичес-
ким по частоте. Например, при изменении связей обычно значительно изменяются
и прилежащие углы, однако частота может при этом мало зависеть от изменения
этих углов, т. е. взаимодействие связи с прилежащим углом может мало влиять
на значение частоты колебания связи, и мы имеем характеристическое по частоте
валентное колебание. Полосы инфракрасного поглощения и линии комбинацион-
ного рассеяния могут быть характеристичны по интенсивности, т. е. интенсивности
могут сохранять свои значения в разных молекулах. Вообще говоря, значения интен-
сивностей гораздо более чувствительны, чем значения частот, к форме колебаний,
и при отсутствии характеристичности колебаний по форме может отсутствовать ха-
рактеристичность по интенсивности при сохранении характеристичности по частоте.
Например, колебание двойной связи С=О (карбонильной связи) в органических
молекулах является приближенно характеристичным по частоте, меняющейся в раз-
ных соединениях примерно в пределах от 1 550 до 1 800 см-1, и нехарактеристичным
по интенсивностям, которые для линий комбинационного рассеяния изменяются
з десятки раз; в частности, при переходе от молекулы ацетона СН3СОСН3 к мо-
Ф?куле ацетофенона СбНзСОСбНз частота связи С=О изменяется лишь на 50 см”1
1 708 до 1 653 см”1), а интенсивность соответствующей линии комбинационного
спектра ия возрастает почти в 20 раз [323].
?т иметь в виду то существенное обстоятельство, что выводы о струк-
ч можно делать не только на основе характеристичности колебаний,
Че/тениям от характеристичности, которые, вообще говоря, различны
Тип
симметрии
го, с какими другими структурными элементами взаимодействует
и элемент. Приведенный пример ацетона и ацетофенона хорошо
ксим образом, если по присутствию характеристических полос
Л
Е2д
Е2д
Е2д
Е2д
В\ц
В1и
В2и
Е\и
Е\и
s выводы о наличии в молекуле определенных структурных
q чиям параметров этих полос или линий можно делать
Р чх структурных элементов.
7
р
Q
Q
Q
Р
Q
Q
Р
q
>актеристические признаки наблюдаются, когда имеет
'баний по форме, и в особенности при колебаниях,
дна определенная связь или один определенный угол,
?ультатом малости взаимодействия соответствующей
баний и критерии характеристичности были подробно
ретим, что за меру характеристичности колебания
0 п^т быть взято отношение
Big
Big
Big
^2u
Elu
E2u
703
985
849
671
405
970
(23,86)
со взаимодействия, который в предельном
'одинаг (DXfl -- 0 при А # /1. см. (21.126))
ния (подробнее см. [55], т. 2. с. 360).
§ 23.6. Характеристичность в колебательных спектрах
715
Характеристические частоты колебаний
Таблица 23.6
№ п/п	Связи	Молекулы и группы	Частоты, см1
1	С—Н	Связи с водородом Алифатические соединения R1R2R3CH	2 890± 10
2	/Н с\	Алифатические соединения R1R2CH2	2 926 ± 10
3	хн /н с—н	Алифатические соединения RCH3	2853 ± 10 1 465 ± 20 2 962 ± 10
4	с—н	Алкены —СН=СН— (транс)	2 872 ± 10 1 450 ± 20 1 375 ± 5 3 0404-3010
5	с—н	Алкены —СН=СН— (цис)	9704-960 1 310—1 295 3 0404-3010
6	с—н	Алкены —СН=СН2 (винил)	-690 3 0404-3010
7	с—н	Алкены CR1R2=CH2	3 0954-3075 9954-985 9154-905 1 4204-1410 1 3004-1290 3 0954-3 075
8	с—н	Алкены CRi R2=CHR3	8954-885 14204-1410 3 0404-3 010
9	с—н	^с-н	8404-790 3 300
10	с—н	С2Н2, HCN Ароматические соединения	- 3 030
11	N—Н	а)	пять соседних незамещенных атомов водорода б)	четыре незамещенных атома водорода в)	три незамещенных атома водорода г)	два незамещенных атома водорода д)	один незамещенный атом водорода Вторичные амины R1R2NH	7704-730 7104-690 7704- 735 8104- 750 8604-800 9004-860 3 5004-3 300
12	,н N\	Первичные амины R.NH2	1 6504-1550 3 5004-3400
13	хн о—н	Спирты	3 4004-3 300 16504-1590
14	Р—н	1. Свободная группа ОН 2. Группа ОН, связанная водородной связью Фосфорорганические соединения	36504-3590 3 5704-2500 24404-2 350
15	S—н	Органические соединения, содержащие серу	2 6004-2550
16	Si—Н	Кремнеорганические соединения	2 3004-2100
716
Глава 23. Колебательные спектры многоатомных молекул
Продолжение таблицы 23.6
№ п/п	Связи	Молекулы и группы	Частоты, см1
17	С—F	Простые связи Фторпроизводные органических соединений	1 4004-1 000
18	С—С1	Хлорпроизводные органических соединений	8004-600
19	С—Вг	Бромпроизводные органических соединений	6004-500
20	С—J	Иодопроизводные органических соединений	~ 500
21	С—S	Органические соединения, содержащие серу	7004-570
22	С—N	Первичные ароматические амины	1 3404-1250
23	С—N	Вторичные ароматические амины	1 3504-1280
24	С—N	Третичные ароматические амины	1 3604-1310
25	С—0	СНзОН	1034
26	0—0	Н2О2	877
27	N—N	h2nnh2	876
28	С—С	СНз 1 СНз—с—сн2—	1 250 ± 5
29	с—с	сн3 СНзХ ) сн—сн2	12504-1200 1 170 ± 5
30	с—с	CH3Z н 1 —сн2—с—сн2—	1 1704-1 140 - 950
31	с—с	СНз СНз 1 —сн2—с— сн2—	- 1 140 - 1 170 - 925
32	с=с	СНз Двойные связи /Н ; с=с<	12504-1200 16484-1638
33	с=с	«ас зс и II и \ ~ Qi	16584-1648
34	с=с	£ и II и & X	16784-1668
35	с=с	всас и и о: х	16624-1652
36	с=с	то я п II п	16754-1665
37	с=с	r2z	xr R\	ZR2 >c=c(	16754-1665
38	с=с	Rr	XR3 Связь, сопряженная с фенилом	- 1 625
39	с=с	Связь, сопряженная с С=0 или С=С	- 1600
§ 23.6. Характеристичность в колебательных спектрах
717
Продолжение таблицы 23.6
№п/п	Связи	Молекулы и группы	Частоты, см1
40	с=с	Насыщенные алифатические альдегиды Н\ ;о=о RZ	1 74041 720
41	с=о	Ненасыщенные альдегиды	1 7054-1 660
42	с=о	Замещенные кетоны с открытой цепью R\ )с=о RZ	172541705
43	С=О	Ненасыщенные кетоны	168541663
44	с=о	Арилкетоны с6н5—с=о	1 7004 1 680
45	с=о	^R о-дикетоны	173041 710
46	0=0	—С—С— И II о о /Здикетоны (фенольные)	1 64041 540
47	с=о	—С—СН2—С— II	II о	о Насыщенные алифатические кислоты НО\ )С=О RZ	17254 1 700
48	0=0	Ароматические карбоновые кислоты	1 7004 1 680
49	с=о	Нормальные насыщенные сложные эфиры RO\ ;о=о Rz	1 75041 735
50	C=N	Соединения с открытой цепью	169041640
51	C=N	о, /3-ненасыщенные соединения с открытой цепью	16804 1 630
52	C=N	Сопряженные циклические соединения	16604 1 480
53	N=N	—N=N—	163041575
54	N=O	Нитриты —О—N=O	
		а) трансформа б) цисформа	168141655 162541613
55	-O-N<q	Нитраты R—0—NO2	16504 1 610 1 30041 250
56	N<0	R—NO2	1 5604 1 500 137041300
57	s=o	Сульфооксиды —S=O	10604 1 020
58	s=o	Сульфоны —SO2—	1 16041 140 135041300
718
Глава 23. Колебательные спектры многоатомных молекул
Продолжение таблицы 23.6
№ п/п	Связи	Молекулы и группы	Частоты, см1
		Тройные связи	
59	с=с	R-C=C-H	2 1404-2 100
60	с=с	R-C^C-R	2 2604-2190
61	C^N	Нитрилы —C=N	23004-2210
62	N^N	Азиды	2 1604-2120
		Циклические системы	
63		Производные циклопропана	865
		СН2	10204-1000
		сн2 —сн2	
64		Производные циклобутана	1 0004-866
65		Производные циклогексана	1 0054-925 10554-1000
В настоящее время накоплен весьма боль-
шой материал по характеристичности колеба-
ний и найдены характеристические частоты раз-
личных типов связей и различных структурных
элементов, содержащих две или более связей.
В большом числе случаев установлены и изме-
нения этих характеристических частот в зависи-
мости от того, в состав каких молекул входит
соответствующий структурный элемент.
В табл. 23.6 приведены характеристические
частоты для ряда связей и более сложных струк-
турных элементов. Данные о характеристиче-
ских полосах и линиях могут быть применены
для структурного анализа различных классов со-
единений.
Для предельных углеводородов парафинового
Рис. 23.11. Поворотные изомеры
бутана: а — трансформа;
б — повернутая форма
ряда основные признаки, необходимые для струк-
турного анализа, были найдены Степановым [55]. Сущинский разработал схему структурного
анализа по спектрам комбинационного рассеяния как для парафинов, так и для нафтенов
и для непредельных углеводородов, основываясь на выделении характеристических структур-
ных элементов [313, 64, 65].
Отметим, что для парафинов удается легко различать разные изомеры по ха-
рактерным признакам различных разветвлений углеродных цепей. Имеются ха-
рактерные особенности при наличии четвертичных атомов углерода (разветвление
С	С	С
I	I	I
типа С— С —смежных третичных атомов (разветвления типа С— С — С -С)
।	9
с	।
и несмежных третичных атомов (разветвления типа С— С — С).
Наряду с изомерами разного строения по колебательным спектрам можно раз-
личать и разные поворотные изомеры (см. § 18.1, с. 504), отличающиеся взаимным
поворотом групп вокруг простых связей. Примером могут служить поворотные
изомеры нормального бутана С4Н10 (рис. 23.11). Колебательные спектры различ-
ных поворотных изомеров отличаются тем, что для некоторых колебаний частоты
получаются разными; это и позволяет различать такие изомеры [55, 62].
ГЛАВА 24
ЭЛЕКТРОННЫЕ СОСТОЯНИЯ И ХИМИЧЕСКАЯ СВЯЗЬ
В ДВУХАТОМНЫХ МОЛЕКУЛАХ
§24.1. Свойства электронных состояний молекул и химическая связь
Рассмотрение наиболее сложных вопросов молекулярной спектроскопии —
электронных состояний и электронных спектров молекул — естественно начать, так
же как и рассмотрение колебаний молекул и колебательных спектров, со случая
двухатомных молекул.
Двухатомная молекула представляет систему, состоящую из двух ядер и опре-
деленного числа электронов, взаимодействующих с ядрами и между собой, что
и определяет свойства электронных состояний молекулы. Для характеристики элек-
тронных состояний важны, с одной стороны, свойства симметрии, позволяющие
классифицировать эти состояния, и, с другой стороны, зависимость электронной
энергии молекулы от расстояния между ядрами, т. е. вид кривых потенциальной
энергии. Если при рассмотрении колебаний молекулы мы исходили из наличия
устойчивого электронного состояния, т. е. кривой притяжения с минимумом, со-
ответствующим равновесному расстоянию между ядрами, то при разборе свойств
электронных состояний необходимо наряду с устойчивыми состояниями рассматри-
вать и неустойчивые, т. е. кривые отталкивания (см. § 17.3, с. 474).
При сближении двух взаимодействующих атомов могут возникнуть как устой-
чивые, так и неустойчивые состояния: в первом случае образуется химическая связь,
во втором — такой связи не возникает; тем не менее в момент сближения ато-
мов их можно рассматривать как неустойчивую молекулу и определенным образом
характеризовать ее электронное состояние, например, свойствами симметрии.
Весьма существенно, что вопрос об устойчивости электронных состояний моле-
кулы есть вопрос о химической связи. Поэтому исследование электронных состояний
молекул спектроскопическими методами имеет важное значение для теории хими-
ческой связи и, обратно, свойства электронных состояний молекул нельзя изучать
обособленно от теории химической связи.
При характеристике электронных состояний молекул (как двухатомных, так
и многоатомных) возможны два подхода. Можно рассматривать состояние молекулы
в целом и можно, исходя из свойств отдельных электронов в молекуле, рассматривать
электронную конфигурацию молекулы, ее электронные оболочки. Эти два подхода
аналогичны соответствующим подходам в теории атомных спектров, где можно
сразу характеризовать состояние атома в целом и можно рассматривать электрон-
ную конфигурацию атома, исходя из свойств отдельных электронов. Мы видели,
какое важное значение при изучении атомных спектров имеет второй подход. Вся
теория атомных спектров основана на приближенной характеристике состояний
электронов при помощи определенных наборов квантовых чисел и на рассмотрении
720
Глава 24. Электронные состояния в двухатомных молекулах
для каждой электронной конфигурации сложения орбитальных и спиновых момен-
тов, согласно векторной модели. Представление об электронных оболочках атомов
является хорошим приближением к действительности. Для молекул наряду со вто-
рым подходом, весьма плодотворным при рассмотрении устойчивости электронных
состояний и химической связи, важную роль играет и первый подход, при котором
электронное состояние молекулы характеризуют в целом, не вдаваясь в детальный
анализ электронных конфигураций. Само представление об электронных оболочках
молекул является обычно более грубым приближением, чем в случае атомов; это
приближение дает в первую очередь качественную картину. В значительной степени
качественный характер имеет и теория химической связи. Достаточно точное ре-
шение задачи о химической связи практически выполнимо не слишком сложными
методами лишь для самых простых случаев молекулы водорода Н2 и ее иона Н^.
При этом уже для молекулы водорода взаимодействие между электронами играет су-
щественную роль при образовании химической связи. Для более сложных двухатом-
ных и многоатомных молекул, содержащих большое число электронов, приходится
ограничиваться лишь грубыми приближениями. Эти приближения позволяют понять
ряд свойств электронных состояний молекулы, определить, устойчивы или неустой-
чивы эти состояния, выявить существенные особенности химической связи, но они
совершенно непригодны для достаточно точных расчетов.
При изучении электронных состояний молекул важную роль играет возмож-
ность приближенного разделения электронов в молекуле на электроны, принадле-
жащие отдельным атомам, и на электроны, принадлежащие всей молекуле в целом
и образующие молекулярные электронные оболочки. Это разделение существен-
но при рассмотрении двух основных типов химической связи — гетерополярной,
или ионной, связи и гомеополярной, или атомной, связи. В случае ионной связи
электроотрицательные атомы отдают лишние электроны вне заполненных оболо-
чек электроположительным атомам. В результате образуются ионы с заполненными
оболочками, которые удерживаются электростатическими силами притяжения. Вза-
имодействие ионов можно при этом приближенно рассматривать как взаимодействие
точечных зарядов. Каждый электрон в такой ионной молекуле принадлежит одному
из ионов. Хорошо известным примером ионной молекулы является молекула NaCl,
которую приближенно можно считать состоящей из иона Na+ и иона СГ с запол-
ненными электронными оболочками 2р6 и Зр6 соответственно; электрон 3s атома Na
с нормальной конфигурацией 2p63s переходит к атому С1 с нормальной конфигу-
рацией Зр5, образуя оболочку Зр6. В наиболее важном случае гомеополярной связи
внешние электроны атомов, образующих молекулу, принадлежат уже всей молекуле
в целом1) — становятся молекулярными электронами. Для рассмотрения гомеопо-
лярной связи необходимо вводить квантовые представления. Типичным примером
гомеополярной связи является химическая связь в молекулах, состоящих из двух
одинаковых атомов. Поэтому в основу теории гомеополярной связи кладется рас-
смотрение иона молекулы водорода и особенно нейтральной молекулы водорода,
в которой в образовании химической связи участвуют два электрона, по одному
от каждого из атомов, но принадлежащие уже всей молекуле в целом. Следует
подчеркнуть, что ионная и гомеополярная связи представляют предельные слу-
чаи, которые могут осуществляться с большей или меньшей степенью точности;
возможны промежуточные случаи, достаточно далекие от этих предельных случаев.
Наряду с образованием молекул с достаточно прочными химическими связя-
ми — ионными, гомеополярными и промежуточными — возможно образование
’)Для многоатомных молекул — отдельным связям или совокупностям связей, подробнее см. гл. 26,
с. 808.
§ 24.2. Классификация электронных состояний молекулы как целого 721
гораздо менее прочных молекул за счет поляризационных межмолекулярных сил,
часто называемых силами Ван-дер-Ваальса, поскольку они учитываются в уравнении
состояния Ван-дер-Ваальса. Рассмотрение этого типа связи представляет некото-
рый интерес в связи со спектроскопическими исследованиями некоторых очень
непрочных молекул, в частности, двухатомных молекул ртути, кадмия и цинка.
Силы Ван-дер-Ваальса малы по сравнению с химическими силами, приводящими
к образованию прочных молекул, электронными состояниями которых мы и будем
заниматься в дальнейшем. При этом главное внимание будет обращено на электрон-
ные состояния молекул с гомеополярной связью.
Наше рассмотрение начнем с характеристик электронных состояний двухатом-
ной молекулы как целого и разберем вопросы о классификации этих состояний
и об их соответствии электронным состояниям атомов, из которых образовалась
молекула (§24.2 и 24.3). Далее перейдем к приближенной характеристике отдельных
электронов в молекуле и применим к ним принцип Паули, что позволит установить
число электронов в молекулярных электронных оболочках и определить возможные
состояния молекулы с различными электронными конфигурациями (§24.4 и 24.5).
В последних параграфах гл. 24 (§ 24.6-24.9) будут разобраны вопросы устойчивости
электронных состояний молекулы и теория химической связи, сначала для про-
стейших систем — иона молекулы водорода Hj и молекулы водорода Н2, а затем
и для более сложных двухатомных молекул. Рассмотрение этих вопросов имеет
большое значение и для теории многоатомных молекул (см. гл. 26). Свойства от-
дельных химических связей между соседними атомами в многоатомной молекуле
в значительной степени схожи со свойствами химической связи в двухатомной
молекуле; с проявлением такого сходства мы уже встречались при изучении ха-
рактеристичности колебаний отдельных связей в сложных молекулах. Электронным
спектрам двухатомных молекул, их колебательной и вращательной структуре по-
священа гл. 25. Там же разбирается взаимодействие электронного и вращательного
движений в этих молекулах. Последний вопрос хотя и относится к характеристи-
ке электронных состояний двухатомных молекул, но является более частным, чем
остальные вопросы, разбираемые в гл. 24; с ним непосредственно связан вопрос
о вращательной структуре электронно-колебательных полос.
§ 24.2. Классификация электронных состояний
двухатомной молекулы как целого
Классификация электронных состояний двухатомных молекул определяется,
прежде всего, наличием аксиальной симметрии — оси симметрии бесконечного
порядка Соо, проходящей через ядра молекулы. Такой осью, как мы знаем, обладает
не только двухатомная молекула, но и любая линейная многоатомная молекула,
поэтому результаты, вытекающие из наличия аксиальной симметрии, справедливы
для любых линейных молекул.
Линейные молекулы с точки зрения общей классификации равновесных кон-
фигураций по их симметрии могут относиться к двум точечным группам (см. § 18.4,
с. 520) — к группе C^v и к группе D^. В первом более общем случае молекула
обладает осью симметрии С^, при повороте Ср вокруг которой на произвольный
угол р она переходит сама в себя, и бесконечным числом плоскостей симметрии av,
проходящих через эту ось2). Эти элементы симметрии, и av, имеются для любых
2) Вертикальных плоскостей симметрии (v) при вертикальном расположении оси симметрии. На ри-
сунках, однако, часто ось линейной молекулы изображают горизонтальной прямой, как на рис. 18.1
(с. 501).
722 Глава 24. Электронные состояния в двухатомных молекулах
линейных молекул. Примером могут служить все двухатомные гидриды (НС1, LiH,
NaH, СаН, HgH и т.д.), СО, NO, радикалы CH, NH из многоатомных молекул
HCN, OCS. Во втором случае молекула дополнительно обладает центром симметрии i
и плоскостью симметрии проходящей через центр симметрии, перпендикулярно
к оси молекулы (а также зеркально-поворотной осью симметрии и бесконечным
числом перпендикулярных к оси Соо осей симметрии второго порядка С2). Симме-
трию D^oh имеют все двухатомные молекулы, состоящие из двух одинаковых ядер
(гомонуклеарные молекулы), например Н2, О2, N2, и линейные многоатомные моле-
кулы, содержащие пары симметрично расположенных одинаковых ядер, например,
со2, с2н2, c2n2, С4Н2.
Наличие оси симметрии бесконечного порядка Соо приводит к тому, что проек-
ция момента количества движения на эту ось сохраняется. Эта проекция квантуется,
согласно общему закону (2.12), и принимает определенные значения. Подобно тому
как классификация электронных состояний атомов, в соответствии со сферической
симметрией, основана на квантовании момента количества движения, классифика-
ция электронных состояний линейных молекул основана на квантовании проекции
момента количества движения.
Для атома типичным является случай нормальной связи, когда квантуется
полный орбитальный момент количества движения L и полный спиновый момент
количества движения S. Отметим существенное для нас сейчас обстоятельство, что
на полный спиновый момент S непосредственно действуют только магнитные поля,
а на полный орбитальный момент L — и электрические поля, причем обычно
действие электрических полей более существенно, чем действие магнитных.
В молекуле, как и в атоме, существуют электростатические и магнитные вза-
имодействия между электронами, приводящие к векторному сложению моментов
количества движения. Однако в отличие от атома в линейной молекуле имеется
не сферически симметричное, как в атоме, а аксиально симметричное электри-
ческое поле. Это поле действует, и притом обычно весьма сильно, на полный
орбитальный момент, вызывая, с наглядной точки зрения, его прецессию вокруг
оси поля, т. е. оси молекулы. В результате полный орбитальный момент перестает
квантоваться и сохраняется лишь квантование его проекции Lz на ось молекулы
Lz = mL, mL = 0, ±1, ±2,... .	(24.1)
Энергия состояния будет существенным образом зависеть от mL, причем толь-
ко от абсолютного значения Это соответствует наглядным представлениям
о том, что в электрическом поле оба направления вращения электронов вокруг
оси равноправны3). Абсолютную величину проекции полного орбитального момента
по оси молекулы принято обозначать через Л Квантовое число Л принимает целые
значения
Л = \mL\ =0, 1,2...	(24.2)
и играет для классификации электронных состояний линейных молекул ту же
роль, что и квантовое число L для классификации электронных состояний атомов.
По аналогии с обозначениями S, Р, D, ... состояний с L = 0, 1, 2,... , состояния
с последовательными значениями Л принято обозначать прописными греческими
буквами:
Л = 0 1 2 3 4 ...
Е II А Ф Г ...
(24.3)
У) Равноправность противоположных направлений вращения нарушается вращением молекулы, что
приводит к расщеплению уровней (Л-удвоение, см. ниже, §25.4, с. 768).
§ 24.2. Классификация электронных состояний молекулы как целого 723
Практически для двухатомных молекул приходится иметь дело со значениями Л,
не превышающими 2. Чаще всего встречаются нормальные состояния с Л = О,
т. е. ^-состояния, и возбужденные состояния с Л = 0 и Л = 1, т. е. Е- и П-состояния.
Это можно понять на основе рассмотрения молекулярных электронных оболочек,
которое будет произведено ниже (см. §24.4, с. 728).
В соответствии с тем, что при Л 0 возможны два значения проекции,
положительное и отрицательное, mL — Л и mL = -Л, уровни энергии с Л О
дважды вырождены. В противоположность этому Е-уровни (Л = 0) невырождены.
В отличие от полного орбитального момента полный спиновый момент, на ко-
торый аксиально-симметричное электрическое поле не действует, обычно при-
ближенно сохраняется и квантуется обычным образом. Молекула, подобно атому,
характеризуется определенным значением спинового квантового числа S. При за-
данном значении S полный спиновой момент может ориентироваться х = 2S 4- 1
способами, что определяет для молекулы, как и для атома, мультиплетность к
электронных состояний. В соответствии с этим могут быть синглетные состояния
’Е, *П, ’А, ..., дублетные состояния 2Е, 2П, 2А, ..., триплетные состояния 3Е,
3П, 3 А, ... и т.д. Мультиплетность состояний при этом указывается, как и в слу-
чае атомов, индексом слева сверху. Что касается тонкой структуры электронных
уровней молекулы и роли спин-орбитального взаимодействия, то рассмотрение этих
вопросов требует учета вращения молекулы и будет произведено в следующей главе
(см. § 25.4, с. 763). В данной главе мы будем указывать мультиплетность электронных
состояний, но не будем принимать во внимание мультиплетного расщепления.
Наряду с квантовым числом Л при классификации электронных состояний
линейных молекул важную роль играют характеристики, связанные с наличием
плоскостей симметрии <jv и, в случае молекул, содержащих одинаковые ядра, центра
симметрии i. По отношению к отражению в плоскости симметрии проходя-
щей через ось молекулы, электронные состояния разделяются на положительные
и отрицательные, обозначаемые знаками 4- и —.
Для положительных состояний электронная волновая функция не меняет знака при от-
ражении в плоскости для отрицательных состояний — меняет:
о'Ж. = V’m, = -фзя-	(24.4)
При рассмотрении свойств полной волновой функции молекулы также подразделяют
состояния на положительные и отрицательные, однако при этом нужно учитывать свойства
симметрии не только электронной, но и вращательной волновой функции, см. ниже, с. 770.
Состояния с Л = 0 — Е-состояния — как невырожденные являются либо
положительными (Е+), либо отрицательными (Е“).
Дважды вырожденные состояния с Л 0 представляют, как можно показать
(см. с. 725), совокупность положительного и отрицательного состояний. Если вы-
рождение снимается (что происходит под действием вращения, см. примечание
на с. 722) и уровень расщепляется на два, то один из подуровней будет положитель-
ным, а другой отрицательным.
Для линейных молекул, принадлежащих к точечной группе D^h и обладающих
центром симметрии, электронные состояния делятся по отношению к отражению
в центре на четные и нечетные, аналогично тому, как это имеет место для элек-
тронных состояний атомов по отношению к отражению в точке, где находится ядро.
Для электронных состояний молекул, так же как и для колебательных состояний,
четность и нечетность обозначаются символами д и и. Каждое электронное состояние
724 Глава 24. Электронные состояния в двухатомных молекулах
является либо четным, либо нечетным,
Получается четыре типа £-состояний и
и мы имеем соответственно состояния
Д^, ...
* ।
П«, Д«, ...
по два типа П-, Д-, ... состояний.
(24.5)
2
Рис. 24.1. Связь свойств симметрии по отношению
к операциям av, i и С2
х = -х, у = -у,
а при отражении av — преобразование
х" = х, у" = -у,
Для четных состояний электрон-
ная волновая функция не меняет зна-
ка при отражении в центре симме-
трии, а для нечетных меняет:
=	(24.6)
Наряду со свойствами + и — и свой-
ствами g и и электронной функции
молекул с центром симметрии можно
рассматривать и третье свойство, свя-
занное с этими двумя. Если ввести ко-
ординатную систему ж, у, z с началом
в центре симметрии и осью z, совпа-
дающей с осью молекулы, и считать
плоскость а совпадающей с плоско-
стью ху (рис. 24.1), то для координат
всех электронов при инверсии i име-
ем преобразование
z = -z,	(24.7)
z = z,	(24.8)
В результате инверсии и отражения мы получаем преобразование координат всех элект-
ронов
х = -ж, у = у, z = -z,	(24.9)
т.е. поворот С2 на 180° вокруг оси у, эквивалентный для электронной функции перестановке
одинаковых ядер4\ По отношению к операции перестановки одинаковых ядер электронные
состояния разделяют на симметричные (з) и антисимметричные (а). Для первых при опера-
ции Р электронная функция не меняет знака, для вторых — меняет знак:
Р^=С2^ = Ф^\	= С21$ = -№.	(24.10)
В силу связи (24.7)-(24.9) между операциями i, crv и С2 четные положительные и нечетные
отрицательные состояния симметричны, четные отрицательные и нечетные положительные
состояния антисимметричны:
9,
и,
9->
и.
а.
(24.11)
+
Классификация (24.5) электронных состояний линейных молекул полностью
совпадает с общей классификацией типов симметрии для группы приведенной
в табл. 22.9 (с. 664), справедливой как для колебательных, так и для электронных
состояний. В этой таблице в скобках приведены обозначения, принятые для элек-
тронных состояний линейных молекул.
Волновые функции оператора Lz проекции орбитального момента количества движения
в соответствии с формулой (3.38) имеют вид
=	(24.12)
Электронная функция зависит от координат электронов относительно ядер. Поворот на 180° всех
электронов относительно центра симметрии эквивалентен обратному повороту ядер, который сводится
к их перестановке.
§ 24.3. Соответствие молекулярных и атомных электронных состояний 725
что дает одну функцию	при Л = 0 и две функции	и ^-л = ifoe~tAv>
при Л > 0. Закон преобразования функции tfc = tfo дает в соответствии с (24.4), (24.6) и (24.10)
характеры, приведенные в табл. 22.9 для невырожденных состояний X), а закон совместного
преобразования функций и ifoe~tAv> — характеры, приведенные в табл. 22.9 для выро-
жденных состояний П, Д, Ф, ... (для Л = 1 получаются матрицы преобразования (22.22)).
Легко видеть, что хотя волновые функции и фое~'А* не обладают в отдельности свой-
ством положительности или отрицательности по отношению к операции av, их линейные
комбинации
-^V’o(eiA*’ +	= д/2^о cos Л.<р, -^=^0{ё^ - е”^) = sin	(24.13)
обладают этим свойством. При операции отражения Ср = (р) первая из них не меняет
знака (cos (-Л92) = cosA^), т. е. является положительной, а вторая меняет знак (sin (-Л92) =
-sinAv?), т. е. является отрицательной. При расщеплении уровня с заданным значением Л
под действием возмущения, вызванного вращением молекулы (при Л-удвоении, см. § 25.4,
с. 768), правильными функциями нулевого приближения являются именно функции (24.13);
из двух получающихся подуровней один будет положительным (подуровень, описываемый
волновой функцией cosA^), а другой отрицательным (подуровень, описываемый волновой
функцией sin Л9?).
§ 24.3. Соответствие между электронными состояниями молекулы
как целого и образующих ее атомов
2(3)
1-1=0
0 + 0 = 0
-1 О +1
-1 0+1	-10 +1
-1 + 1=0
—1+0 = —Г
0-1 = -1
0+1 = 1
1+0=1 .
1 + 1=2
-1- 1=-2
0 + 0 = 0
0- 1=-1
0+1 = +1
0 + 0 = 0
П(2)

S + P
о

Каждое заданное электронное состояние двухатомной молекулы, устойчивое
или неустойчивое, возникает из некоторых состояний образующих ее атомов, причем
в принципе это могут быть основные и возбужденные состояния как нейтральных
атомов, так и их ионов. Чаще всего основное электронное состояние молекулы
возникает из основных состояний нейтральных атомов.
Очень существенно, что из
определенных электронных сос-
тояний исходных атомов возни-
кает вполне определенный набор
электронных состояний молеку-
лы, причем на основе рассмо-
трения свойств симметрии можно
установить характеристики этих
состояний — значения кванто-
вых ч исел Л и 5, положитель-
ность или отрицательность S-сос-
тояний, четность и нечетность
состояний в случае молекулы,
состоящей из одинаковых ато-
мов [326, 46].
Прежде всего легко определить значения Л состояний молекулы, возникающих
из состояний атомов с заданными значениями L\ и Li полных орбитальных момен-
тов. Два взаимодействующих атома можно рассматривать как молекулу (рис. 24.2),
на ось которой проектируются моменты L] и Li,
mLi =Lh Lx - 1, ..., -L\, 3
mL2 — -^2, 772—1, • • • , —L2. J
Полная проекция равна mLx 4- mL1 и ее абсолютное значение равно Л, т. е.
Л - |тЬ1	(24.15)
0	0
Рис. 24.2. Значение Л для молекулы, образованной
из атомов в S- и Р-состояниях
(24.14)
726
Глава 24. Электронные состояния в двухатомных молекулах
Таблица 24.1
Электронные состояния молекулы, получающиеся из заданных состояний атомов
Состояния атомов	Состояния молекулы
S + S S + P S + D Р + Р P + D D + D	Е* Е’, П Е*. п, Д Е+, Е*, Е", П, П, Д Е+, Ет, Е', П, П, П, Д, Д, Ф Е\ Е+, Е*. Е", Е-, П, П, П, П, Д, Д, Д, Ф, Ф, Г
Примечание. При одинаковой четности состояний атомов для S-состояний
берется верхний знак, при разной — нижний.
Таким образом, Л принимает значения от 0 до L\ 4- L2. При этом S-состояния
получаются столько раз, сколько раз сумма 4- оказывается равной нулю,
П-состояния — столько раз, сколько эта сумма равна 4-1 и -1 и т.д. Например,
комбинация двух атомных 5-состояний дает только одно S-состояние, комбинация
состояний S и Р дает по одному S- и П-состоянию, комбинация двух атомных
P-состояний дает три S-состояния, два П-состояния и одно Д-состояние (рис. 24.2).
Возможные значения L для разных случаев приведены в табл. 24.1.
Для S-состояний требуется еще знать их положительность или отрицательность.
Как можно показать [326], в зависимости от одинаковой или разной четности
состояний атомов получаются результаты, приведенные в табл. 24.1.
При каждом значении Л состояния могут быть различной мульти пл етности.
Спиновые моменты S\ и S2 атомов при образовании молекулы векторно склады-
ваются в полный спин молекулы S = S\ 4- S2, и возможные значения спинового
квантового числа молекулы равны
S = S}+S2, 5! 4-52-1,	|51-52|.	(24.16)
Соответственно мультиплетность к состояния молекулы при заданных мультиплет-
ностях X] и х2 состояний атомов будет принимать значения
x = Xi 4-х2- 1, xi4-x2-3, ..., |xi -х2| 4-1,	(24.17)
например, при = х2 = 2 имеем х = 3,1; при Xj = 3, х2 = 2 имеем к = 4, 2;
при X] = х2 = 3 имеем х — 5, 3, 1.
С помощью табл. 24.1 и формулы (24.17) легко определить все состояния
молекулы, образованной из разных атомов, находящихся в заданных состояниях.
Например, из атомов в состояниях и 2Р, что мы имеем при образовании гидрида
А1Н из нормальных атомов водорода (основной терм 25) и алюминия (основной
терм 2Р°), получаются состояния 1 S+, *Пи 3S+, 3 П; нормальным состоянием
молекулы оказывается состояние 1 S+.
Табл. 24.1 и формула (24.17) могут применяться также для молекул, состоящих
из двух одинаковых атомов, но тогда нужно еще знать четность состояний. Здесь
возможны два случая.
Если атомы находятся в разных состояниях, то общее число получающихся
состояний молекулы удваивается5) и каждое состояние может быть четным или не-
четным.
5) При этом безразлично, в каком из двух состояний находится какой атом, что и приводит к удвоению
числа состояний.
§ 24.4. Характеристики отдельных электронов в молекуле	727
Если атомы находятся в одинаковых состояниях (5 или Р), то состояния
молекулы, получающиеся, согласно табл. 24.1, будут:
S + S Е^ при х= 1,5, Е^ при х = 3,7,	(24.18)
р + р е9 , s9, sj, п9, п„, д9 е;,п9,пи>ди (24.19)
при х = 1,5,	при х = 3, 7.
Например, согласно (24.18) и (24.17), два атома водорода в основном состоянии 2S
образуют молекулу водорода в состояниях (к = 1, 3)1Е*, 3Е„,а из двух атомов азота
в основном состоянии 4S (х = 1, 3, 5, 7) возникают состояния молекулы азота 1 Е*,
3Е*, 5 Е*, 7 Е*. Согласно (24.19) и (24.17), из двух атомов углерода или кисло-
рода в основном состоянии 3Р (х = 1,3, 5) получаются состояния соответствующей
молекулы 1 Е+,	%, 1 Пм, 1 Д^; 3 Ej, 3Е*, 3Е;, 3 П„ 3Пм, 3Дм;
5Е+, 5^д, 5Е~, 5Щ, 5Пи, 5 А,. Как мы видим, число получающихся состояний
может быть весьма большим. Однако лишь те из этих состояний, которым соот-
ветствуют кривые притяжения, являются устойчивыми, остальные — неустойчивы.
На основе приведенного сопоставления атомных и молекулярных состояний нельзя
решить, какие состояния устойчивы. Для этого необходимо произвести анализ,
основанный на рассмотрении взаимодействий электронов в молекуле, приводящих
или к притяжению атомов с образованием химической связи или к отталкиванию
атомов. Такой анализ может быть произведен приближенными методами, которые
будут разобраны ниже. В простейших случаях он позволяет однозначно установить,
каким из состояний системы, состоящей из двух взаимодействующих атомов, со-
ответствуют кривые отталкивания и каким — кривые притяжения. Для молекулы
водорода, в частности, из двух возможных состояний 1 Е* и 3 Е„, возникающих
при взаимодействии атомов водорода в основном состоянии 25, первое устойчиво
и является основным состоянием молекулы, а второе неустойчиво (см. рис. 24.11,
с. 740). Состоянию 1 Е* соответствует типичная кривая притяжения с глубоким
максимумом, состоянию 3 Е„ — типичная кривая отталкивания. В более сложных
случаях также получаются как устойчивые, так и неустойчивые состояния, причем
число тех и других, как правило, одинаково, точно или приближенно.
§ 24.4.	Характеристики отдельных электронов в молекуле
и молекулярные электронные оболочки
Рассмотрим теперь характеристики состояний отдельных электронов в двухатом-
ной молекуле (одноэлектронных состояний) и молекулярные электронные оболочки,
в которые группируются отдельные электроны.
Такое рассмотрение представляет, как мы уже подчеркивали, более грубое при-
ближение, чем в случае атомов. Взаимодействие между электронами в молекуле,
осуществляющими химическую связь, весьма велико, и для различных предельных
случаев приходится пользоваться различными приближениями, сопоставляя их меж-
ду собой, чтобы получить правильную качественную картину электронной структуры
молекулы.
Разберем сначала характеристики одноэлектронных состояний в молекуле вне
зависимости от свойств образующих ее атомов.
Важнейшей приближенной характеристикой состояния отдельного электрона
в атоме (см. § 7.1) является азимутальное квантовое число Z, определяющее значения
728
Глава 24. Электронные состояния в двухатомных молекулах
орбитального момента I этого электрона. В зависимости от значений I мы различа-
ли s-, р-, J-, /-, ... электроны и получили оболочки, которые заполняются 2, 6,
10, 14, ... электронами. Сама возможность введения квантового числа I была
связана с приближенным представлением о том, что каждый электрон движется
в сферически симметричном поле ядра и остальных электронов.
В двухатомной или линейной многоатомной молекуле можно аналогично при-
ближенно считать, что отдельный электрон движется в аксиально симметричном
поле ядер, образующих ось молекулы, и остальных электронов. В соответствии
с этим, основной приближенной характеристикой одноэлектронных состояний слу-
жит квантовое число Л, определяющее абсолютную величину проекции орбитального
момента электрона на ось молекулы. Так как величина этой проекции равна
lz = тщ, где mi = 0, ±1, ±2,... ,	(24.20)
то Л принимает значения
А = \mi\ = 0, 1,2,3,... .	(24.21)
Энергия электрона в молекуле зависит только от абсолютной величины проекции,
так как на электрон в молекуле действует электрическое поле (ср. выше аналогичное
рассмотрение для квантового числа Л).
Состояния с Л = 0,1,2, 3,... по аналогии с I — 1, 2, 3,... для атомов (см. с. 164)
обозначают строчными греческими буквами:
А = 0, 1, 2, 3, ...
сг, тг, <5, 9?, ...
(24.22)
и говорят о сг-, тг-, б-, ... состояниях и сг-, тг-, б-, ... электронах.
Легко определить число эквивалентных электронов данного рода, т. е. электро-
нов с определенным А, обладающих одинаковыми свойствами, если не учитывать
спина и знака проекции lz6\ Согласно принципу Паули, в молекуле не может быть
двух электронов в одинаковых квантовых состояниях, следовательно, и с одинако-
выми совокупностями квантовых чисел. Эквивалентные сг-электроны (А = 0) могут
отличаться лишь величиной ms проекции спина на ось молекулы, принимающей
/ 1 1\ 2
два значения \ms = - и ms = --J; мы получаем молекулярную оболочку а ,
заполняющуюся двумя электронами. Эквивалентные тг-, б-, ... электроны могут
отличаться знаком проекции орбитального момента и знаком проекции спина на ось
( 1
молекулы, т. е. существуют четыре различных состояния \mi = X, ms — mi = А,
1 1 1\
ms = mi = —X, ms — тг = —X, ms = и получаются молекулярные обо-
лочки тг4, б4, ... , заполняющиеся четырьмя электронами каждая. Итак, в линейных
молекулах не может быть более четырех эквивалентных электронов, т. е. не суще-
ствует молекулярных электронных оболочек, заполняющихся более, чем четырьмя
электронами. При этом сг-оболочки (А = 0) заполняются двумя электронами, а тг-,
б-, ... оболочки (А > 0) — четырьмя электронами.
6)Для молекулы электроны нельзя однозначно характеризовать квантовым числом, аналогичным
главному квантовому числу, но при заданном значении Л электроны могут описываться разными
волновыми функциями, зависящими от координат электрона, помимо координаты определяющей
азимут электрона относительно оси молекулы. От зависит собственная функция оператора lz проекции
орбитального момента количества движения на ось молекулы, имеющая вид е±гХ<р, см. ниже, с. 729.
§ 24.4. Характеристики отдельных электронов в молекуле
729
При прочих одинаковых условиях энергия а-электронов меньше, чем тг-электро-
нов, а энергия тг-электронов меньше, чем 5-электронов. Поэтому сначала происходит
заполнение а-оболочек, затем тг-оболочек, а потом 5-оболочек.
В нормальных и не очень сильно возбужденных состояниях молекул главным
образом приходится иметь дело с а-электронами и с тг-электронами, поэтому разбор
их свойств представляет особый интерес.
Аналогично тому как 5-электроны в атомах {I = 0) обладают сферической
симметрией, а-электроны в молекулах (Л = 0) обладают аксиальной симметрией.
Согласно наглядным представлениям, электронное облако а-электронов распреде-
лено симметричным образом вокруг оси молекулы — плотность заряда не зависит
от угла р — азимута относительно этой оси (рис. 24.3, а). В силу аксиальной
симметрии а-состояние является положительным.
Рис. 24.3. Распределение электронной плотности как функция угла 9?:
а — для а-электрона; 5, в — для тг-электрона (5 — вертикальная узловая плоскость,
в — горизонтальная узловая плоскость)
В противоположность а-электронам тг-электроны не обладают аксиальной
симметрией, подобно тому как в атомах не обладают сферической симметрией
р-электроны. Согласно наглядным представлениям, электронное облако тг-электро-
нов распределено вокруг оси таким образом, что в некоторой плоскости, проходящей
через ось, его плотность обращается в нуль (рис. 24.3,5, в). При этом тг-состояние,
дважды вырожденное относительно знака ml {mi = ±Л = ±1), представляет сово-
купность положительного и отрицательного состояний (ср. §24.2, с. 725).
Описанные свойства а- и тг-электронов весьма существенны при изучении элек-
тронных состояний не только двухатомных и линейных многоатомных, но и любых
многоатомных молекул. В частности, с ними оказываются связанными такие свой-
ства молекул, как способность к свободному вращению частей молекулы вокруг
отдельных связей.
Согласно квантовомеханическому рассмотрению движения отдельного электрона в ак-
сиально симметричном поле, в его волновую функцию входит множитель е±гА9?, являющийся
собственной функцией оператора lz проекции орбитального момента количества движения:
= V’oe±,A*’
(24.23)
где не зависит от <р.
Для a-состояния Л = 0 и ^д(у?) = т. е. не зависит от азимута Отсюда следует,
в частности, что волновая функция не изменяется при отражении в плоскости, проходящей
через ось молекулы (при котором меняет знак), т. е. положительна7\ Квадрат волновой
функции определяющий, согласно наглядным представлениям, плотность электронного
7) В случае многоэлектронной задачи это рассуждение неприменимо к S-состояниям, так как в вы-
ражении 'ф =	может зависеть от разности <pi — <рь азимутов отдельных электронов, которая
меняет знак при отражении. Именно по этой причине S-состояния молекулы в целом (Л = 0) могут быть
как положительными (S+), так и отрицательными (S~).
730
Глава 24. Электронные состояния в двухатомных молекулах
облака для a-состояния, разумеется, также не зависит от угла у?, что и приводит к картине,
изображенной на рис. 24.3, а.
Состояния с Л > 0 дважды вырождены, и волновые функции — ipoeiXtp и — грое~гХ>/>
комплексно сопряжены. Аналогично (24.13) вместо них мы можем ввести вещественные
волновые функции
гр+ =	4- е-,А<р) = VltpQ cos Ay?,
1	(24.24)
= —— гр0(ех<р - е iX<p) = \/2^о sin Ay?,
iV2
которые соответствуют определенному значению Л (но не mi = ±Л). Именно эти веществен-
ные волновые функции являются правильными функциями нулевого приближения при кван-
товомеханических расчетах химической связи с учетом электростатического взаимодействия
электронов, для которого энергия возмущения вещественна.
Квадрат гр2+ пропорционален cos2Ay?, что дает распределение электронной плотности,
изображенное на рис. 24.3,6. Аналогичное распределение, повернутое на 90° и изображенное
на рис. 24.3, в, получается для ^1. Мы получаем плоскости, в которых и обращаются
тг
в нуль; для гр+ это будет плоскость — —, для — плоскость у? = 0.
Угловая зависимость самих волновых функций (24.24) изображена на рис. 24.4. Для ка-
ждого угла отложено абсолютное значение гр, причем область положительных значений
отмечена знаком 4-, а область отрицательных значений — знаком -. При отражении в плос-
Л	тг
кости у? = 0 гр+ сохраняет знак, а гр_ меняет его, при отражении в плоскости у? = —,
наоборот, гр+ меняет знак, а гр_ сохраняет его. Таким образом, гр+ и гр_ обладают противопо-
ложными свойствами симметрии по отношению к отражению в этих плоскостях. Мы видим,
что тг-состояние действительно представляет совокупность положительного и отрицательного
состояний. То же самое имеет место и для состояний с А > 1.
Рис. 24.4. Угловая зависимость волновых функций для тг-электрона:
а — вертикальная узловая плоскость; б — горизонтальная узловая плоскость
Для линейных молекул, обладающих центром симметрии, одноэлектронные
состояния можно, так же как и состояние всей молекулы в целом, разделить
на четные (д) и нечетные (и). Таким образом, мы получаем состояния
ад> 'кд-> $д-> Уд, •••
фи, • ♦ •
(24.25)
и соответственно можем говорить о четных и нечетных электронах.
Для двухатомных молекул, состоящих из двух одинаковых атомов, четные
и нечетные электроны с заданным значением А существенно отличаются по своим
свойствам. Для ои-электрона плотность электронного облака обращается в нуль
в средней плоскости, проходящей через центр молекулы и перпендикулярной к ее
оси, для од-электронов она не равна нулю в этой плоскости (рис. 24.5, а, б). Это озна-
чает, согласно наглядным представлениям, что во втором случае электрон при своем
§ 24.5. Возможные состояния молекулы в целом
731
движении чаще находится между ядрами, чем в первом. Часто находясь между
ядрами, электроны их притягивают и способствуют образованию химической связи.
Подобные электроны называют связывающими. Если, наоборот, электроны редко на-
ходятся между ядрами, будет проявляться отталкивание ядер. Подобные электроны
мешают образованию химической связи; их называют разрыхляющими или раз-
вязывающими или, наконец, антисвязывающими. Мы будем применять последний
термин. Таким образом, сг^-электроны являются связывающими, сги-электроны —
антисвязывающими. В противоположность этому тг5-электроны являются антисвя-
зывающими, а тги-электоны — связывающими. Для первых плотность электоронного
облака обращается в нуль в средней плоскости, для вторых она отлична от нуля
в этой плоскости (рис. 24.5, в, г). Для «5-электронов, так же как и для сг-электронов,
^-электроны являются связывающими, а ^-электроны — антисвязывающими.
Наличие средней узловой плоскости меж-
ду ядрами, в которой электронная плотность,
т. е. вероятность нахождения электрона, обра-
щается в нуль, легко установить из рассмо-
трения симметрии волновой функции. Для
а-состояний в точках, симметрично располо-
женных относительно оси (А и В на рис. 24.5),
волновая функция имеет одинаковые значения;
в случае аи-состояний в точках D и С, располо-
женных по другую сторону центра симметрии
на равных расстояниях, она будет иметь значе-
ния, равные по абсолютной величине, но обрат-
Рис. 24.5. Свойства симметрии
для молекулярных электронов относительно
центра: а — для электрона ад;
б — для электрона аи‘,
в — для электрона тгэ; г — для электрона яи
ные по знаку, что возможно лишь при условии,
что функция обращается в нуль в средней плос-
кости. В случае ^-состояний волновая функ-
ция в точках D и С будет иметь те же значения,
что в точках А и В, и в средней плоскости
не обязана обращаться в нуль. Для тг-состояний
в точках А и В, симметрично расположенных
относительно узловой плоскости, проходящей через ядра (см. рис. 24.4; на рис. 24.5, в, г эта
плоскость выбрана горизонтальной), волновая функция имеет различные знаки. В случае
тгд-состояний она будет иметь в точке D то же значение, что и в точке А, а в точке С то же
значение, что и в точке В; следовательно, в точках А и С и в точках В и D знаки волновой
функции будут противоположные и она должна обращаться в нуль в средней плоскости.
В случае 7ги-состояний, наоборот, в точках А и С и в точках В и D знаки волновой функции
будут одинаковы и она не обязана обращаться в нуль в средней плоскости.
Для двухатомных молекул, состоящих из одинаковых атомов и, следователь-
но, имеющих центр симметрии, возможны, в соответствии с делением электронов
на четные и нечетные, электронные оболочки типов сг^ и сг^ для сг-электронов,
типов тг* и тг* для тг-электронов, типов бд и б* для ^-электронов и т.д. При прочих
равных условиях энергия связывающих электронов будет меньше энергии анти-
связывающих, и поэтому оболочки Од должны заполняться раньше оболочек сг^,
а оболочки тг* — раньше оболочек тг*. Более подробно вопрос о порядке запол-
нения таких электронных оболочек будет рассмотрен в § 24.8 вместе с вопросом
о химической связи в молекулах, состоящих из двух одинаковых атомов.
§ 24.5.	Возможные состояния молекулы
с заданной электронной конфигурацией
Электронная конфигурация молекулы, аналогично электронной конфигурации
атома, определяется заданием для каждого вида эквивалентных электронов их
732
Глава 24. Электронные состояния в двухатомных молекулах
числа ki и значения Л:
(aa)k'(ba)k2(cx)k}... ,	(24.26)
где а, Ь, с, ... — символы, характеризующие различные виды эквивалентных
электронов и заменяющие для молекулы главные квантовые числа электронов
в атоме. Как мы увидим ниже (см. §24.6, с. 735), характеристики различных видов
эквивалентных электронов в молекуле можно определенным образом сопоставить
с квантовыми числами электронов в атомах.
В данном параграфе мы будем, опуская символы а, Ь, с, ... , записывать
электронную конфигурацию в виде (/'а^тг*3... Например, а2ах3 означает кон-
фигурацию, состоящую из двух эквивалентных а-электронов одного вида, одного
а-электрона другого вида и трех эквивалентных тг-электронов.
Подобно тому как для заданной электронной конфигурации атома можно найти
в случае нормальной связи возможные мультиплетные термы, т. е. возможные зна-
чения L и S, для заданной конфигурации молекулы можно найти значения Л и S —
определить мультиплетные термы молекулы. При этом алгебраически складываются
все Xi для отдельных электронов
Л = | ± Aj ±Л2±Л3±... |.	(24.27)
Векторное сложение заменяется алгебраическим в связи с тем, что все проекции
направлены вдоль оси молекулы; при этом надо лишь учитывать два возможных
направления вдоль оси. Сложение спиновых моментов з, отдельных электронов
производится обычным образом и дает целый или полуцелый результирующий
спин, в зависимости от того, является ли число электронов четным или нечетным
(ср. §9.2, с. 251).
Определение возможных термов не представляет затруднений ни в случае
неэквивалентных электронов, когда принцип Паули удовлетворяется автоматически,
ни в случае эквивалентных электронов, когда нужно его учитывать. Для случаев,
в которых получаются S-термы, необходимо дополнительно определить, являются
ли они термами S+ или S“.
Для двух эквивалентных электронов сложение Ai и А2 дает Л = А] 4- Л2
и Л = |А] — А2|.
При Aj = А2 = А получается состояние сЛ = А;+А2 = 2Аи два состояния
с Л — 0, т. е. S-состояния; одно из этих S-состояний будет состоянием S+,
другое — состоянием S~. Действительно, возможные значения полной проекции
mL —	+ ttii2 равны (тц = ±А|,	= ±А2)
т^ — Ai + Аг, А] — А2, — Ai 4- А2, — Aj — А2.	(24.28)
Первое и последнее соответствуют дважды вырожденному состоянию с Л = Ai 4- А2,
второе и третье — дважды вырожденному состоянию с Л = | A i — А2| (см. рис. 24.6,а
для случая Ai — 2, А2 = 1). При Aj = А2 значение Л = 0 получается дважды (-A-J-A = О
и А 4- (-А) = 0, см. рис. 24.6, б для случая Ai = А2 = 1). S-состояния невырождены,
и одно из них будет положительным (S+), а другое отрицательным (S~).
Так как спин для двух электронов может равняться 0 и 1, то получаются
одиночные или триплетные термы. Для заполненной оболочки, состоящей из двух
эквивалентных электронов (оболочка сг2) или из четырех эквивалентных электро-
нов (оболочки тг4, £4, у?4, ...) в силу принципа Паули получается результирующее
состояние 1 S (Л = О, S = 0), которое является состоянием 1 S+. Действительно,
при Aj = А2 = 0 имеем для двух электронов тц = 0, mSi = - и т/2 = 0, mS2 =
следовательно, = тц 4- ттц2 = 0, ms = mSi 4- mS2 — 0, т- е- Л = 0, 5 = 0.
§ 24.5. Возможные состояния молекулы в целом
733
При Л1 = Л2 = А / 0 имеем для четырех электронов гпц — A,
1
1
2; mh =
mS2 = этц, = -A, т„2 =	т<4 = -A, ms„
mi, + mh + mtj + тц = 0 и ms = ms, + mS2 4- ms, + mS4
2’
следовательно mL =
= 0, т. e. опять Л = 0 и S = 0.
Положительность терма S для оболочки а2 вытекает из положительности волновых
функций для a-электронов. Можно показать, что он будет положительным и для оболо-
4 с4
чек тг , о , ... .
Для неполностью заполненных обо-
лочек случай одного электрона тривиа-
лен, мы получаем термы a2S+, тг2П, #2Д
и т.д. Для оболочек тг3, б3, ..., в которых
не хватает одного электрона, получается
тот же результат, что и для одного элек-
трона. Наконец, для оболочки тг2 легко
находятся на основе принципа Паули тер-
мы ]S, 3S, причем терм lS будет
положительным, а терм 3S — отрица-
Рис. 24.6. Сложение проекций орбитальных
моментов двух электронов:
а — при А! А2 (Ai = 2, А2 = 1);
б — при А! = Л2 (Aj = Л2 = 1)
тельным. Аналогичные результаты полу-
чаются и для оболочки б2.
Действительно, для двух эквивалент-
ных тг-электронов при гпц = mi2 — 1
— 2 и при тц — mi2 — mL = -2,
т. е. для Д-терма (Л = 2) проекции спинов электронов в силу принципа Паули
должны быть противоположны, mSl = — mS2, т. е. S = 0 х = 2S -h 1 = 1 (одиночный
терм *A). При тц = 1, mi2 = -1, т.е. для S-терма (Л = 0) проекции спинов могут
быть любые, т. е. имеет место векторное сложение спинов (ср. § 9.3, с. 255): S = 0, 1,
следовательно, х = 1, 3 и получаются термы ’Ей 3S. Можно показать, что первый
положителен, а второй отрицателен.
Доказательство того, что для трех эквивалентных тг-электронов получается тот же
результат, что и для одного тг-электрона, аналогично доказательству одинаковости термов
для конфигурацийр5	(с.257).
Таблица 24.2
Термы простейших молекулярных электронных конфигураций
Электронная конфигурация	Термы	Электронная конфигурация	Термы
а	2Е+	(Т(У	'£+, 3£+
(У2	1 £+	ааа	+ ^я г? + я гч
7Г	2П	ап	'п, Зп
7Г2	1Е+, 3£", 'Д	аап	2П, 2П, 4П
7Г3	2 ПО)	пп	м + м ^ + м 1 и" с>
7Г4	'£+	ап2	2г+, 2е~, 2д, 4s~
б	2Д	аб	д, Зд
б2	'£+, 3£+, 'Г	пб	р р ф
б3	2Д0)	бб	я м + я 4- " я
б4	'е+	ааб	2Д, 2Д, 4Д
Буквой i отмечены обращенные П-термы.
734
Глава 24. Электронные состояния в двухатомных молекулах
Получающиеся термы для простейших конфигураций, состоящих как из экви-
валентных, так и неэквивалентных электронов, приведены в табл. 24.2.
Не представляет труда определить возможные термы и для более сложных
конфигураций, складывая для исходных конфигураций проекции Aj и Л2 и спины S\
И $2 в полную проекцию Л и полный спин S.
Для молекул, обладающих центром симметрии, все термы данной конфигурации
будут четными или нечетными, в зависимости от того, является ли число нечетных
электронов (аи, ки, би) четным или нечетным.
§ 24.6.	Электронные состояния
и химическая связь в ионе молекулы водорода
До сих пор мы рассматривали состояния отдельных электронов в молекуле, неза-
висимо от того, из каких атомов образуется молекула и каковы состояния электронов
в этих атомах. Однако состояния электронов в молекуле находятся в определенном
соответствии с состояниями электронов в исходных атомах. При увеличении до бес-
конечности расстояния между ядрами в молекуле, т. е. при разъединении молекулы
на атомы, состояния электронов в молекуле должны переходить в их состояния
в атоме. С другой стороны, можно сопоставить состояния электронов в молекуле
с их состояниями в объединенном атоме, получающемся при стремлении расстоя-
ния р между ядрами к нулю. Если заряды ядер равны Z\ и Z2, то такой объединенный
атом будет обладать зарядом Z — Z\+Zi. Разумеется, что последний случай не может
иметь место в действительности и подобное сопоставление состояний электронов
в молекуле с их состояниями в объединенном атоме носит формальный характер,
однако и такой подход при решении ряда вопросов весьма полезен.
Состояния электрона в отдельных атомах и в объединенном атоме можно
рассматривать как предельные случаи состояний электрона в двухатомной молекуле,
соответствующие значениям расстояния между ядрами р = оо и р — 0.
В простейшей молекуле — ионе молекулы водорода — состояния единственного
электрона можно сопоставить с состояниями электрона в атоме водорода, получаю-
щимся при расщеплении иона Hj на Н и Н+, и с состояниями водородоподобного
иона (с зарядом ядра Z — 2, равным заряду ядра гелия), получающегося при мыс-
ленном объединении протонов. Подобное сопоставление может быть произведено
строго, так как задача об уровнях энергии иона решается точно. Решение этой
задачи особенно существенно с точки зрения теории химической связи — в ионе Н^
химическая связь осуществляется единственным электроном, взаимодействующим
с обоими ядрами, и получаемые результаты можно сравнить с результатами в случаях,
когда связь осуществляется двумя или несколькими электронами, взаимодейству-
ющими как с ядрами, так и между собой. Подобное сравнение позволяет выявить
роль взаимодействия электронов при образовании химической связи, в частности,
в важнейшем случае ее образования парами электронов, как в молекуле водорода
и в более сложных химически устойчивых молекулах8).
Рассмотрим подробнее электронные состояния и химическую связь для иона
молекулы водорода [46, 87]. Для объединенного атома имеем уровни
Is; 2s, 2р; 3s, Зр, 3d; ... .	(24.29)
В аксиально симметричном поле, получающемся при разделении объединенного
ядра на два, будет квантоваться проекция орбитального момента количества движе-
ния на ось молекулы, причем уровень с заданными п и I (при I Ф 0) расщепляется,
8) Ион молекулы водорода в химическом отношении неустойчив, так как легко может присоединять
электрон, в отличие от нейтральной молекулы водорода, являющейся химически устойчивой.
§ 24.6. Электронные состояния в ионе молекулы водорода
735
так как энергия будет зависеть от абсолютной величины проекции орбитального
момента, т. е. от квантового числа Л.
Для s-электронов расщепления происходить не будет, и из уровня ns, mi = X = 0,
возникает один сг-уровень, остающийся дважды вырожденным (ms =	). Этот
уровень обозначают как nsa, т. е. Isa, 2sa, 3sa, ..., для n = 1, 2, 3,... .
Для тг-электронов проекция орбитального момента mi = 0, ±1 и возникают
уровни сг (mi — Л — 0) и тг (|mj = Л = 1), являющиеся дважды и четырежды
вырожденными соответственно. Эти уровни обозначают как пра и пртг, т. е. 2ра,
2ртг; Зра, Зртг; ... Аналогичным образом для электронов nd возникают уровни nda,
nd'K и nd6, а для электронов nf — уровни nfa, nfir, п/би nfip. Сумма кратностей
вырождения 2 + 4 + 4 + ... получающихся уровней равна кратности вырождения
2(21 + 1) первоначального уровня nl объединенного атома. Мы получаем следующую
схему:
Is—User 2s —>2scr	3s —>3scr
2р—*2ра, 2ртг Зр—^Зра, Зря
3d-+3da, 3dir,
4s —> 4scr
4p—>4рсг, 4ртг
3d6 4d—>4d<r, 4</тг, Ш
4f—>4fa, 4 fir, 4f6, 4ftp ,
(24.30)
При этом, как показывает расчет, при расщеплении уровня nl Получающиеся уровни
лежат тем глубже, чем меньше Л, т. е. уровень nla лежит глубже, чем уровень п1тг,
а уровень n/тг глубже, чем уровень п1б.
Отметим, что в случае разделения объединенного ядра на два одинаковых
ядра сохраняется центр симметрии, поэтому сохраняется четность или нечетность
уровней, т.е. уровни, возникающие из s- и d-уровней, будут четными, а уровни,
возникающие из р- и /-уровней, нечетными.
Для малого расстояния между ядрами различные квантовые состояния сг-, тг-,
б-, ... электронов в молекуле могут быть приближенно охарактеризованы заданием
квантовых чисел п и I для объединенного атома. Этот метод может быть применен
и для молекулы, состоящей из двух неодинаковых атомов, если расстояние между
ядрами сравнительно мало или одно из ядер обладает зарядом, значительно меньшим,
чем другое.
Такой случай имеет место для двухатомных молекул ги-
дридов. Гидрид, состоящий из атома с ядром заряда Z и атома
водорода, можно приближенно рассматривать как атом с элек-
тронной оболочкой, содержащей Z + 1 электрон, и с ядром
заряда Z + 1, разделенным на ядро с зарядом Z и про-
тон, внедренный в эту электронную оболочку. В дальнейшем
(см. § 24.9, с. 751) мы рассмотрим случай гидридов более
подробно.
При разделении иона Hj на нейтральный атом Н
и на протон, для атома Н также получаем набор состоя-
ний (24.29): Is; 2s, 2р\ 3s, ... В поле второго протона
(рис. 24.7, а) будет квантоваться, вследствие наличия аксиаль-
ной симметрии, проекция орбитального момента электрона,
которая принимает значения А = 0,1, 2,..., Z. Мы получим
состояния, обозначаемые через Xnl, например, crls, а2р, я2р, ... и т.д. Сумма
кратностей вырождения всех состояний Xnl, А = 0, 1, 2,..., при заданных п и I будет
равна, как и в случае объединенного атома, кратности состояния nl, т.е. 2(21 + 1).
Однако в этом случае положение осложняется тем, что получающиеся состояния
П
Н
Рис. 24.7.
Образование иона
молекулы водорода:
а — из Н + Н+;
б — из Н+ + Н
736 Глава 24. Электронные состояния в двухатомных молекулах
не являются единственно возможными и, вместе с тем, не удовлетворяют условиям
симметрии относительно центра молекулы, т. е. точки, расположенной на половине
расстояния между протонами. Необходимо принять во внимание возможность раз-
деления иона на Н+ и Н, при котором электрон будет не у первого протона,
а у второго (рис. 24.7,6). Если обозначить первый и второй протоны через А и В, то
мы будем иметь два набора состояний:
<т2с>^4 сг2рл х2рл о'Ззд ггЗрл 'к^Ра o~3d^ хЗдд 63d^ ... 'I (24 31)
(?\sb v2sb &2рв я2рв ^Звв сгЗрв лЗрв (гЗ<1в хЗдв 63йв • )
Таким образом, мы получаем пары состояний с одинаковой энергией, от-
личающиеся расположением электрона, который может находиться у протона А
или у протона В. Из каждой пары состояний с одинаковыми п, I и Л, как можно
показать, возникнет два состояния — одно четное, а другое нечетное, которые мы
обозначили как Xgnl и Хип1. Мы получим состояния9)
Og\.s Og2s ag2p тгg2p ag3s (Tg3p тГдЗр ag3d Trg3d 6g3d ...
Cyls au2s au2p тг^2р (Xy3s а^Зр тГцЗр a^3d 7Tn3d fiy3d ...
(24.32)
В соответствии с общими свойствами электронов (Уд, аи, тгд, тги,..., рассмотренными
в §24.4 (см. с. 730), следует ожидать, что электроны в состояниях ад, тги, бд, ...
будут связывающими, а в состояниях аи, тгд, 6и, ... — антисвязывающими.
В согласии с этим при сближении протонов энергия электрона должна в первом
случае убывать по сравнению с его энергией в атоме водорода, а во втором случае
возрастать. Из каждого состояния nl атома водорода получается, согласно (24.32),
два состояния. Можно ожидать, что одно из них будет характеризоваться кривой
притяжения, а другое — кривой отталкивания.
Рис. 24.8. Кривая притяжения и кривая
отталкивания для иона HJ
Действительно, из основного со-
стояния атома водорода Is 2Si возни-
2
кают, как показывает точный расчет,
устойчивое состояние ag\s2^g, являю-
щееся основным состоянием Hj с энер-
гией диссоциации 2,65 эВ, и неустойчи-
вое состояние cruls2XJ^. Соответствую-
щие кривые потенциальной энергии —
кривая притяжения для первого состоя-
ния и кривая отталкивания для второго
состояния — изображены на рис. 24.8.
Теоретическое значение энергии диссо-
циации (2,65 эВ) совпадает со значени-
ем, определенным из опыта по энергии
диссоциации молекулы Н2 и по потен-
циалам ионизации Н и Н2. Из двух-
квантовых состояний атома водорода также возникают устойчивые и неустойчивые
состояния иона Hj, однако энергия диссоциации для устойчивых состояний получа-
ется значительно меньше энергии диссоциации основного состояния, и их не удается
наблюдать спектроскопическими методами.
9) В противоположность случаю сопоставления с объединенным атомом здесь четность и нечетность
электронов з, р, d, ... не играет роли, так как положение протонов в молекуле не совпадает с центром
симметрии.
§ 24.6. Электронные состояния в ионе молекулы водорода	737
Существование устойчивой молекулы наглядно показывает, что возможна
одноэлектронная химическая связь гомеополярного типа, осуществляемая молеку-
лярным электроном, движущимся между ядрами и притягивающим эти ядра. Весьма
важной является при этом зависимость между плотнстью электронного облака
молекулярного электрона и свойствами электронного облака атомного электрона.
Атомный электрон может находиться у ядра Л и у ядра В. Плотность электронного
облака между ядрами, определяющая прочность связи (см. § 24.4, с. 731), оказывается
тем большей, чем сильнее перекрываются электронные облака электрона, соответ-
ствующие его нахождению у ядра Л и у ядра В. Таким образом, наиболее прочная
связь получается тогда, когда имеется наибольшее перекрывание электронных обла-
ков, соответствующих нахождению электрона у обоих атомов, образующих связь.
Если перекрывание, наоборот, мало, то связь между атомами не может образовать-
ся. Мы получаем качественный критерий, характеризующий прочность химической
связи. Этот критерий играет существенную роль в теории направленной валентности
в многоатомных молекулах, которая будет рассмотрена в гл. 26 (см. с. 796).
Изложенные результаты вытекают из зависимости между волновыми функциями мо-
лекулярных состояний Х9п1 и Х*п1 и волновыми функциями соответствующих атомных
состояний nlA и nlв. Приближенные выражения для молекулярных волновых функций, чет-
ной $\gni и нечетной через атомные волновые функции ^niA и -фП1в получаются, если
взять сумму и разность этих функций:
= c(V>nU ± falB),
fa.nl = c(falB Т falB)-
Верхний знак берется для а- и 6-состояний, ниж-
ний — для 7Г-СОСТОЯНИЙ; с — нормировочный множитель.
В силу симметрии задачи значения атомных волно-
вых функций ipniA и ipniB в средней плоскости будут оди-
наковы с точностью до знака; так как волновая функция
вообще определена с точностью до множителя, равного
по модулю единице, то знак всегда можно выбрать так,
чтобы значения волновых функций в средней плоскости
совпадали и по знаку. Например, для «-состояния вол-
новая функция зависит только от расстояния электрона
от ядра и на сферах радиуса г имеет постоянное зна-
чение (рис. 24.9, а); в средней плоскости для всех точек
гА — гв (га м гв — расстояния электрона от ядер А к В
соответственно) значения ^niA(rA) и фп1д(гв) одинаковы.
Можно проверить, что при наложении волновых
функций получаются знаки, указанные в (2433). Когда
волновые функции налагаются со знаком +, то в слу-
чае а- и 6-состояний получаются четные состояния,
а в случае тг-состояний — нечетные; наоборот, когда
волновые функции налагаются со знаком —, то в первом
случае получаются нечетные состояния, а во втором —
четные. Для пар состояний (а^1«, <тш1«), (<г^2р, аи2р),
и (тг^2р, 7гм2р) наложение волновых функций иллюстри-
руется рис. 24.9,а,б и в, г. При этом наложение волновых
функций «-состояний дает аксиально-симметричные
волновые функции и наложение волновых
функций ip2pt p-состояний, ориентированных вдоль оси
молекулы z, дает также аксиально-симметричные волно-
вые функции фад2р и а наложение волновых функций ^2Рх p-состояний, ориенти-
рованных вдоль оси х, перпендикулярной к оси молекулы, дает волновые функции ф^2Р
и обладающие узловой плоскостью, проходящей через ось молекулы (плоскостью yz
а
в
г
Рис. 24.9. Перекрывание
волновых функций атомных
электронов:
а — для s/r-электронаа;
б — для /яг-электронов;
в, г — для ртг-электршов
(2433)
6
24 Зак. 103
738 Глава 24. Электронные состояния в двухатомных молекулах
на рис. 24.9, в). Сравнение с рис. 24.5 (с. 731) показывает, что при наложении функции со зна-
ком плюс мы имеем состояния ад и тги, а при наложении со знаком минус — аи и пд. Отметим,
что тг-функции могуг получаться как при наложении волновых функций ориентирован-
ных вдоль оси ж, так и при наложении аналогичных волновых функций ф1Ру, ориентированных
вдоль оси у; эти функции будут обладать узловой плоскостью xz (рис. 24.9, г). В результате
получаем по две функции фЖд и вместо одной функции фад и одной что и приводит
к двукратному вырождению тг-состояний, если не учитывать спина, и к четырехкратному их
вырождению при учете спина.
Волновые функции (24.33) обладают тем важным свойством, что одна из них сохраняет
знак, а другая меняет его при перестановке одинаковых ядер, т. е. одна является симме-
тричной, а другая антисимметричной (см. § 24.2, с. 724). Перестановка одинаковых ядер
(эквивалентная повороту Сг на 180° вокруг оси, перпендикулярной к оси молекулы) приводит
к замене в (24.33) ipniA на ipniB и обратно; в результате волновая функция при знаке плюс
не изменяется, а при знаке минус меняет знак. В первом случае волновая функция ф и элек-
тронная плотность \ф\2 отлична от нуля в средней плоскости, а во втором случае они равны
нулю; мы соответственно имеем связывающие и антисвязывающие электроны. Чем больше
перекрывание в средней плоскости атомных волновых функций, тем больше при знаке плюс
будут значения волновой функции и электронной плотности в средней плоскости, тем сильнее
будет связывающее действие электронов ад и тги. Точные волновые функции молекулярного
электрона отличаются от приближенных волновых функций (24.33), однако они обладают
той же симметрией10) и сохраняется основное свойство функции (24.33) — электронная
плотность в средней плоскости отлична от нуля для симметричных функций и равна нулю
для антисимметричных. Поэтому качественные соображения о наложении волновых функций
и о перекрывании соответствующих электронных облаков, полученные для приближенных
функций, должны быть справедивы и для точных.
Можно получить зависимость энергии симметричного и антисимметричного (следова-
тельно, четного и нечетного) состояний от расстояния между ядрами, т.е. найти соответству-
ющие кривые потенциальной энергии. Оператор энергии имеет вид
н = т^и = -—г-
ътгт
h2 е2 е2
Д +--------
Р гА
(24.34)
А	Р	В
Рис. 24.10. Расстояния
между частицами в ионе
молекулы водорода
где — — энергия отталкивания ядер,--------— энергия при-
Р	е2 Га
тяжения электрона ядром А,------— энергия его притяжения
гв
ядром В, зависящие соответственно от расстояния между ядра-
ми р и от расстояний гА и гв электрона до ядер АиВ (рис. 24.10).
Из вида оператора энергии, зависящего только от расстояний,
лежащих в одной плоскости, но не от азимута <р этой плоско-
сти относительно оси молекулы, сразу следует, что переменные
разделяются, и при решении волнового уравнения
H^(rA, rBj <р- р) = Е(рУф(гА, гв, <р; р),
(24.35)
где расстояние р между ядрами входит как параметр (ср. (17.68)), волновая функция имеет
вид
^(гл, rB, <р; R) = ^>о(гл, ГВ-р)ф(<р),	(24.36)
т. е. представляет произведение волновой функции фо(гАу гв; р), зависящей только от коорди-
нат гАигв и от параметра р, на волновую функцию Ф(у>), зависящую только от координаты <р.
Функция Ф(у?) = е±,А<р является собственной функцией оператора lz проекции орбитального
момента электрона на ось молекулы (см. (24.23)).
,0) Наряду с четностью и нечетностью (д и и), симметрией и антисимметрией (з и а) волновые
функции (24.33) будут в согласии с (24.11) положительными и отрицательными (+ или -), причем либо
обе положительными, лцбо обе отрицательными, в частности, в случае a-состояний обе положительны,
см. рис. 24.9,о и б\ в этом случае четная функция является симметричной, а нечетная антисимметричной.
§ 24.6. Электронные состояния в ионе молекулы водорода
739
Как уже указывалось выше (с. 734), для иона квантовомеханическая задача решается
точно, однако мы ограничимся приближенным решением уравнения (24.35), которое может
быть обобщено и на более сложные молекулы, состоящие из двух одинаковых атомов.
При бесконечно большом расстоянии между ядрами, когда электрон находится у ядра А
(р —> оо, гв -* оо), мы получаем уравнение
(	h2	е2 1
НйЛфл = S	----fV’A = Еофл	(24.37)
[ 8тг2пг	rA J
для волновой функции = фпгА. Аналогично в случае нахождения электрона у ядра В
(р —> оо, гл —> оо) мы получаем уравнение
— f h2 е2 1
НовФв = | А “ ~ рв — Еофв	(24.38)
для волновой функции фв = Фп1в- Выбирая в качестве ф(гА, гв, р) в нулевом приближении
линейные комбинации функций фА = фП1А и фв — Фп1в в виде (24.33), мы можем найти энер-
гию в первом приближении, усредняя оператор энергии по функциям нулевого приближения.
Получаем
Et = J фНф dr = с2 J(фл ± Ув)Н(фл ± фв) dr,	(24.39)
где dr — элемент объема интегрирования.
Постоянная с в (24.33) определяется из условия нормировки (мы берем вещественные
функции)
J ip2dr = c2^J ipAdr + J ip2Bdr±2 j	= 2c2(l ± 5) = 1,	(24.40)
где
8 = f ФаФв dr	(24.41)
— интеграл наложения, не равный нулю в силу неортогональности функций фА ифв, соответ-
ствующих нахождению электрона у разных атомов (см. рис. 24.7), и зависящий от наложения
этих функций. Из (24.40) следует, что
1
\/2(1±5)’
(24.42)
Вычисление энергии Е[ по формуле (24.39) с учетом (24.34), (24.37), (24.38), (24.42) и (24.41)
дает
1 f	( е2 е2\ е2
Ei = 37ГТ 7.7 / (У’л ±	( Т +--) Фа---Фл±
IA р г Л) Гв
е2 е2 \ е2 1	1 Г / е2 \
± I Т +----feT - фв>Лт=	21 Ео + — ) (1 ± S) -
\ Р гв) та )	2(1±S)[ \ pj
f е2 г f е2	f е2 2 Ге2
- I —Фл^г^ I — ФаФв dr- / — фв dT Т / — ФвФл dr ,
J Гв	J гА	j Га	J гв
откуда
где
и
24*
е
Е\ = Eq ------h
р
К±С
е 9
— 'Фв
(24.43)
(24.44)
(24.45)
(24.46)
— ФаФв dT = -
Га
— фвфА dr.
Гв
740 Глава 24. Электронные состояния в двухатомных молекулах
Здесь К — кулоновский интеграл, определяющий среднее значение энергии притяжения
электрона другим ядром, а С — так называемый резонансный интеграл. Резонансный интеграл
отрицателен и по абсолютной величине будет тем больше, чем больше наложение волновых
функций и $в. Для симметричного состояния энергия равна
EXs - Eq 4- — 4- ——- 4- Т—(24.47)
р 14-5	14-5
а для антисимметричного —
= Ео + — + --~ ~ -j-(24.48)
1 О 1 О
С уменьшением расстояния между ядрами увеличивается наложение волновых функ-
ций и Фво резонансный интеграл по абсолютной величине возрастает и обусловливает
уменьшение энергии симметричного состояния и увеличение энергии антисимметричного
состояния, что и приводит к возникновению кривой притяжения в первом случае и кривой
отталкивания во втором случае. Кривые, рассчитанные по описанному методу для состоя-
ний иона HJ, получающихся из основного состояния атома водорода, показаны пунктиром
на рис. 24.8 (с. 736); для устойчивого состояния 2£+, являющегося основным состоянием
иона Н^, энергия диссоциации оказывается равной 1,7 эВ вместо 2,65 эВ, а равновесное
расстояние составляет 1,30 А вместо 1,06 А, что связано с приближенностью расчета. Хотя ко-
личественного согласия и не получается, качественная картина оказывается совершенно пра-
вильной и свидетельствует о применимости метода для выяснения природы химической связи.
§ 24.7. Электронные состояния и химическая связь
в молекуле водорода
Ряс. 24.11. Кривая притяжения
и кривая отталкивания
для молекулы водорода
изображенные на рис. 24.11, и
Молекула водорода, спектр которой предста-
вляет большой интерес и сам по себен), является
простейшей молекулой, в которой связь осуще-
ствляется двумя электронами. Наряду со взаимо-
действиями электронов с протонами, существен-
ную роль играет и взаимодействие электронов меж-
ду собой — их взаимное отталкивание. Именно
наличие взаимодействия электронов между собой
и составляет характерное отличие молекулы Н2
и всех более сложных молекул от молекулы Н^,
рассмотренной в предыдущем параграфе.
Задача о молекуле водорода может быть ре-
шена квантовомеханически с высокой степенью
точности и при этом решении все взаимодействия
в молекуле учитываются полностью. Для состо-
яний '1^ и 3S„, возникающих из двух атомов
водорода в основном состоянии (см. § 24.3, осо-
бенно его конец), могут быть рассчитаны соот-
ветствующие кривые притяжения и отталкивания,
теоретически определено значение энергии дис-
социации; оно совпадает с экспериментально найденным. Однако с точки зрения
изучения устойчивости электронных состояний и химической связи в более сложных
молекулах для нас наибольший интерес представляет применение приближенных
11) Спектру этой молекулы посвящена даже специальная монография Ричардсона [52].
§ 24.7. Электронные состояния и химическая связь в молекуле водорода 741
квантовомеханических методов рассмотрения вопроса о химической связи. Эти
методы применимы как к молекуле водорода, так и к более сложным молеку-
лам, двухатомным и многоатомным, и позволяют объяснить на основе квантовых
представлений природу гомеополярной химической связи.
К вопросу о химической связи возможны два подхода и соответственно приме-
няются два основных приближенных метода расчета химической связи.
Один подход основан на рассмотрении молекулярных электронов и обра-
зованных ими молекулярных электронных оболочек. При этом подходе сначала
характеризуется состояние каждого электрона в отдельности и затем уже учитыва-
ется взаимодействие электронов12) * 4. Соответствующий метод, впервые примененный
Мелликеном и Гундом и развитый Герцбергом и Леннард—Джонсом, обычно на-
зывают методом молекулярных орбит или молекулярных орбиталей (orbitals) и часто
обозначают сокращенно как метод МО,3).
Термин «орбиталь» применяют, если не хотят пользоваться термином «орбита» для элек-
трона, при этом под орбиталью подразумевают волновую функцию молекулярного электрона
в определенном состоянии. Молекулярные одноэлектронные волновые функции в мето-
де молекулярных орбит могут определяться непосредственно для молекулы или строиться
из атомных волновых функций электронов атомов, образующих молекулу, ср. (24.33); в по-
следнем случае широко пользуются обозначением LCAO (Linear Combinations of Atomic
Orbitals — линейные комбинации атомных орбиталей).
Второй подход основан на рассмотрении взаимодействий двух электронов,
принадлежащих образующим химическую связь атомам и осуществляющих дан-
ную связь. Для этих электронов, принадлежащих к разным атомам, одновременно
учитываются взаимодействия каждого из электронов с другим ядром и взаимодей-
ствия электронов между собой. Два рассматриваемых электрона с противоположно
направленными спинами образуют электронную пару, осуществляющую простую
(или единичную) связь. Данный метод, впервые примененный Гейтлером и Лон-
доном к молекуле водорода и развитый для многоатомных молекул Слейтером
и Паулингом, обычно называют методом электронных пар или методом валентных
связей и часто сокращенно обозначают как метод VB,4).
В методе валентных связей из волновых функций электронов атомов, образующих связь,
сразу строится полная приближенная волновая функция для пары электронов.
Метод молекулярных орбит и метод электронных пар представляют два раз-
личных приближения в теории химической связи, приводящие в ряде случаев
к одинаковым конечным результатам. В других случаях один из методов позволяет
легко получить результаты, которые другой метод не дает или которые требуют
его усложнения. В методе электронных пар образование химической связи двумя
электронами заложено в самой его основе, в методе молекулярных орбит тот же
результат получается благодаря наличию двух эквивалентных молекулярных элек-
тронов, например, а2 или тг2. При этом в случае оболочки а2 автоматически
происходит, в силу принципа Паули, компенсация спинов (оболочка а2 дает состо-
яние см. табл. 24.2, с. 733), как и для метода электронных пар,5), в случае же
,2) Частичный учет этого взаимодействия может быть в принципе произведен по методу самосогласо-
ванного поля, рассматривая движение молекулярного электрона в поле остальных электронов, аналогично
тому, как это производится при расчете атомов (см. §7.1, с. 200).
,3) «МО method» — метод молекулярных орбиталей (Molecular Orbitals).
l4) «VB method» — метод валентных связей (Valence Bonds).
,5) Компенсация спинов для электронной пары в методе валентных связей также происходит в силу
принципа Паули.
742
Глава 24. Электронные состояния в двухатомных молекулах
2 с2
двух электронов тг или о такая компенсация не обязательна, что отличает метод
электронных орбит от метода электронных пар. Существенное отличие этих методов
состоит в том, что метод электронных пар вообще неприменим к простейшему
случаю одноэлектронной связи (а также к случаям связи, осуществляемой любым
нечетным числом электронов), естественным образом объясняемой на основе ме-
тода молекулярных орбит (см. расчет химической связи в ионе в предыдущем
параграфе). Однако метод электронных пар имеет преимущество, состоящее в том,
что он с самого начала учитывает взаимодействие электронов.
Следует подчеркнуть, что это взаимодействие учитывается не только непосредственно
при вычислении энергии молекулы, но и благодаря тому, что автоматически исключается
возможность одновременного нахождения обоих электронов у одного атома. При примене-
нии метода молекулярных орбит оба электрона могут находиться у одного атома (см. ниже
формулу (24.50)), однако отталкивание между электронами должно сильно уменьшать веро-
ятность этого (согласно методу Гейтлера—Лондона, вероятность одновременного нахождения
электронов у одного атома равна нулю).
Рассмотрим применение обоих методов к молекуле водорода, причем мы будем
считать, что исходные атомы водорода находятся в состоянии 1s.
По методу молекулярных орбит основное состояние молекулы получается, когда
двумя электронами заполняется молекулярная оболочка crgls, в которой у иона
в основном состоянии имеется один электрон. Конфигурации (ag\s)2 соответствует
состояние , которое и является основным состоянием молекулы водорода. Энер-
гия диссоциации молекулы в состоянии 1 Яд определяется связывающим действием
обоих электронов agls. То, что эта энергия, составляющая 4,75 эВ16), меньше чем
вдвое превосходит энергию диссоциации иона Н^, равную 2,65 эВ, качественно
объясняется взаимным отталкиванием электронов, уменьшающим прочность свя-
зи. Причиной образования химической связи в молекуле Н2, как и в ионе Н2,
является притяжение ядер электронами, движущимися между ними. Неправильно
считать, как иногда делают, что для образования связи существенно взаимодействие
электронов между собой; это взаимодействие уменьшает прочность связи. Участие
в образовании связи двух равноправных электронов есть результат действия прин-
ципа Паули, допускающего наличие двух, и в случае а-электронов только двух
эквивалентных электронов.
Приближенная волновая функция для состояния (сгд 1s)2 1 молекулы Н2, представля-
ющая произведение волновых функций отдельных электронов, согласно (24.33), будет иметь
вид
V = ^,1,(1) ^,н(2) = с2(^(1) + <Ы0) (^л(2) + Vb(2)),	(24.49)
где аргументы 1 и 2 в скобках относятся к координатам первого и второго элетронов,
и V’aO) — ^1за(0» ^в(1) — ^1зв(1)- Волновую функцию (24.49) можно записать в виде
<1> = с2 [^(№(2) + ^(1)^л(2) + ^(1)^л(2) + ^в(1)^в(2)].	(24.50)
Первые два члена соответствуют нахождению электронов у разных ядер — либо первого
у ядра А и второго у ядра В, либо наоборот, — первого у ядра В и второго у ядра А. Последние
два члена соответствуют нахождению обоих электронов у одного ядра — у ядра А или у ядра В;
эти члены поэтому можно назвать ионными. Вероятность нахождения электронов у одного
ядра оказывается такой же, как и у разных ядер,7). Отталкивание между электронами должно
,6) Энергия диссоциации Dq равна 4,48 эВ, а энергия De = Dq +	^1 -	= 4,75 эВ (см. (20.92)).
,7) Как известно, если состояние является наложением состояний ^t,	c^i, то вероятность
найти систему в состоянии ifa пропорциональна |с,|2. В данном случае все сг одинаковы.
§ 24.7. Электронные состояния и химическая связь в молекуле водорода 743
уменьшать эту вероятность (см. выше, с. 741), т. е. коэффициенты у ионных членов в (24.50)
завышены.
По методу электронных пар, впервые примененному, как уже указывалось выше,
Гейтлером и Лондоном именно к молекуле водорода, в качестве исходного состоя-
ния рассматривается состояние системы, когда у каждого ядра находится по одному
электрону. Такому состоянию при стремлении к бесконечности расстояния между
атомами соответствует энергия 2Eq, где Eq — энергия атома водорода в состоянии 15.
При этом подобное состояние может быть осуществлено двумя способами. Либо
первый электрон находится у ядра А, а второй — у ядра В (первый способ), либо, на-
оборот, второй электрон находится у ядра А, а первый — у ядра В (второй способ).
Однако эти два состояния не удовлетворяют условиям симметрии относительно
перестановки электронов. Состояние системы в целом должно быть симметрич-
ным или антисимметричным относительно перестановки электронов (см. с. 74)|8),
а при перестановке электронов первое состояние переходит во второе, а второе —
в первое. Таким образом, мы имеем два состояния с одинаковой энергией, отли-
чающиеся расположением электронов у ядер А и В, аналогично случаю иона Н2Ь
(см. с. 735). Здесь также возникают два новых состояния. Одно будет симметрично,
другое антисимметрично относительно перестановки электронов. Приближенный
расчет показывает, что при учете взаимодействий ядер между собой, электронов
с чужими ядрами и электронов между собой энергия Es симметричного состояния
будет уменьшаться при уменьшении расстояния между ядрами, а энергия Еа ан-
тисимметричного состояния будет при этом увеличиваться. Мы получаем в первом
случае кривую притяжения, во втором случае кривую отталкивания, в соответствии
с рис. 24.11, показывающим результаты точного расчета. Можно также показать, что
первое состояние будет синглетным, 1 S*, а второе — триплетным, 3 S*. Таким
образом, метод Гейтлера—Лондона приводит к правильным результатам, сразу давая
как кривую притяжения, так и кривую отталкивания.
В методе молекулярных орбит исходными являются одноэлектронные состояния agls
и auls и, кроме рассмотренного состояния (ag 1 s)2 возможны состояния (ag\s)(au Is) 3Sj,
(адls)(<ruIs) 1 и (auls)2 1 Ед. Специальное исследование показывает, что последние два
состояния возникают из ионных состояний Н’ + Н+иН+ + Н“. Состояние (a5Is)(attls)
не будет устойчивым, и получается согласие с выводами метода Гейтлера—Лондона, который
сразу приводит к этому результату.
Одним из важных следствий решения задачи по методу электронных пар
является то, что прочность связи будет тем больше, чем сильнее перекрываются
электронные облака атомных электронов. Этот результат совпадает с результатом,
получающимся по методу молекулярных орбит, несмотря на то, что зависимость
энергии электронных состояний от расстояния между ядрами здесь несколько иная.
Критерий перекрывания электронных облаков, характеризующий прочность связи,
оказывается общим для обоих приближенных методов.
Рассмотрим подробнее решение задачи о молекуле водорода по методу Гейтлера—
Лондона [327].
Оператор энергии имеет вид, аналогичный (24.34):
тг — гг — л а е2 е2 е2 е2 е2 е2
+ 8тг2т 1 8тг2т р г]А г]В г2А г22? + г,2’
,8^Ср. также § 10.2, с. 282. Здесь идет речь о перестановке пространственных координат электронов,
и поэтому волновая функция может быть как антисимметричной, так и симметричной. Только при учете
спина она обязана быть антисимметричной (см. с. 283 и ниже, с. 745).
744
Глава 24. Электронные состояния в двухатомных молекулах
।	где г1Л, г]В, г2Аз Г2В ~ расстояния первого и второго
2	электронов до соответствующих ядер, а г12 — расстоя-
r /	ние межДУ электронами (рис. 24.12). Основное отличие
/	\г1в	от (2^.34) состоит в том, что добавляется энергия оттал-
—----------------------->4	кивания электронов —. Мы ищем решение уравнения
А	Р	В	гп
Рис. 24.12. Расстояния между	Я^(1,2) = J57(p)^( 1,2),	(24.52)
частицами в молекуле водорода
где волновая функция </>(1,2) зависит от координат пер-
вого и второго электронов и от расстояния между ядрами
как параметра. При стремлении к бесконечности расстояния между ядрами мы получаем,
если первый электрон находится у ядра Л, а второй электрон — у ядра В (р -* оо,
г12_оо) уравнение
(Яол + ЯОвШ1,2) =
IV Л2 е2 \	/ h2 е2 \ 1	(24.53)
= {	- -J + ТГ, ) )*"<'• 2> =
в котором перемещенные разделяются. Решением (24.53) является функция
^о(1,2) = ^(1)^в(2),	(24.54)
где V'aO) и ^в(2) — решения уравнений (24.37) и (24.38), причем ipA зависит от координат
первого электрона, a грв — от координат второго; Е(оо) = 2 Eq. Если второй электрон
находится у ядра Л, а первый — у ядра В, то при р оо получается аналогичное уравнение,
решением которого является функция
V>0(2,1) = ^(2)^(0-
(24.55)
Условиям симметрии относительно перестановки электронов удовлетворяют сумма и разность
функций (24.54) и (24.55):
= с(фА(1) фв(2) + i/>a(2) V’b(O),
V’a = с(^л(1) ^в(2) - ^л(2) V’b(O)-
(24.56)
При перестановке электронов функция ips не меняет знака, т. е. является симметричной,
а функция i/ja меняет знак, т. е. является антисимметричной. Эти функции являются правиль-
ными функциями нулевого приближения. Энергия в первом приближении получается, как
и в случае иона Н^, усреднением оператора Н по функциям нулевого приближения
Е,= т dr = c2 (^(1) <М2) ± ^(2) V-b(1))5(v>a(1) Vb(2) ± Vu(2) ^(l))dr, (24.57)
где dr — элемент объема интегрирования, производимого теперь по координатам обоих
электронов (dr = dr} dr2, где dr} и dr2 относятся к первому и ко второму электронам).
Постоянная с в (24.56) определяется из условия нормировки
>2dr = C2
dT} ±
(24.58)
±2
= 2с2[1 ±S2] = 1,
где S — интеграл наложения (24,41), тот же, что и для иона Н^, и, следовательно, равна
1
С~ -^/2(1 ±52)
(24.59)
§ 24.7. Электронные состояния и химическая связь в молекуле водорода 745
Вычисление энергии Е\ по формуле (24.57) с учетом (24.51), (24.37), (24.38), (24.59) и (24.41)
дает
,2 1
1
Е' “ 2(1 ±$2)
/ е2 е2
Л е2 "I	_
Т|---Ы0+Ы0 Т2-------<М2)+
Г1А J
е2 1
Г2В
Л 1
Г\В
(е2
е2 е2
----+ — )^(1)^в(2)±^(2) Ti-— <М0±Ы0 Т2~— фА(2)±
г2А 1
е2
Т\В
Г2А
Т\А
?\2)
е2 е2 \	I	11
-----+ — ^л(2) V-b(I) Нт, dr2 =	Ъ  2Б0(1 ± S2) +
г2В г12/	J	2(1 ±S2)V
е2 \
— ) drj dr2 ±
Г|2 /
е2 \	1
+ — dr2 >,
Г|2 7	J
е2
е2 е2
J	\Р
±2 У 1Сл(1)^(1)^л(2)^(2)^
г\в
е2
Г2А
е2
г\в
Г2А
(24.60)
Р
Р
+ 2
е
е
1
откуда
К±А
Б|-2Бо + ТТ^’
(24.61)
где
Г 9	7	/е2	е2
К= vd(i)^(2)--------------
J	\Р	Т\в
е2
?2А
е2 \
— I drj dr2
г«2 /
(24.62)
е2 е2 \
----1----I di\ dr2.
Г\В Г2А Г\2 /
Здесь К — кулоновский интеграл, дающий среднее значение электростатического взаимо-
действия атомов, а А — так называемый обменный интеграл, который подобно резонансному
интегралу (24.46) будет тем больше по абсолютной величине, чем больше наложение волновых
функций 1рА и фв. Обменный интеграл, как показывает расчет, отрицателен. Поэтому энергия
симметричного состояния
А = У V’x(l) ^в(0^а(2)
е2
(24.63)
И
Е,’-2Ео + ТТ&+ТТ&
оказывается меньше энергии антисимметричного состояния
(24.64)
К А
(24.65)
Как функция от расстояния между ядрами, (24.64) дает кривую притяжения, а (24.65) — кри-
вую отталкивания. Соответствующие кривые, полученные на основе расчета интегралов К, А
и 8 по формулам (24.62), (24.63) и (24.41), показаны пунктиром на рис. 24.11. Энергия диссо-
циации получается равной 3,1 эВ вместо 4,75 эВ, а равновесное расстояние — равным 0,87 А
вместо 0,74 А. Таким образом, метод Гейтлера—Лондона дает качественно правильную карти-
ну. Как и вообще, при применении приближенных методов рассматриваемого типа, исходящих
из атомных волновых функций, хорошего количественного согласия и нельзя ожидать.
Рассмотрим теперь свойства симметрии состояний с волновыми функциями (24.56),
чтобы выяснить их характеристики. Из аксиальной симметрии атомных s-функций грА и фв
относительно оси молекулы вытекает аксиальная симметрия и положительность относительно
отражения в плоскости, проходящей через ось молекулы, функций и гра, т. е. эти функции
соответствуют состояниям S+. При отражении в центре, что эквивалентно для S-состояний
перестановке ядер, первая функция сохраняет знак, т.е. является четной (состояние Е*),
а вторая функция меняет знак, т.е. является нечетной (состояние S„). Состояние Е*, опи-
сываемое функцией tp8f симметричной относительно перестановки координат электронов,
будет антисимметрично относительно перестановки спинов электронов и, следовательно,
одиночным, а состояние S„, описываемое антисимметричной функцией ^а, будет сим-
метрично относительно перестановки спинов электронов, и, следовательно, триплетным
746
Глава 24. Электронные состояния в двухатомных молекулах
(см. § 10.2, доказательство для функции (24.56) молекул водорода тождественно с доказатель-
ством для функций (10.9), (10.10) атома гелия). Таким образом, окончательно для молекулы
водорода мы получаем устойчивое основное состояние с энергией (24.64) и неустойчивое
состояние с энергией (24.65).
Для основного состояния молекулы водорода можно сравнить вид волновой функции,
получаемой по методу молекулярных орбит, с ее видом, получаемым по методу электронных
пар. В первом случае, согласно (24.50) и (24.42),
Vm.o =	{ [¥>л(1) ^(2) + Va(2) «М»)] + [^л(1)^(2) + ^(1)^(2)]},	(24.66)
-I- Ь)
во втором — согласно (24.56) и (24.59),
Vb.n. =	. 1	{^(1)^в(2) + ^(2)^в(1)}.	(24.67)
у 2(1 4- 5 )
Как мы уже указывали (см. с. 742), два последних члена в (24.66) — ионные члены —
соответствуют нахождению обоих электронов у одного атома. Мы видим, что в (24.67)
эти члены отсутствуют, тогда как первые два члена совпадают. Функции (24.66) и (24.67)
представляют два крайних случая — в первом роль ионных членов преувеличивается, так как
отталкивание электронов уменьшает вероятность их одновременного нахождения у одного
ядра, во втором же эти члены совсем отсутствуют. Можно было бы ввести приближенную
функцию промежуточного типа
ф = С| [Va(1> ^в(2) + ^л(2) V’b(I)] + с2[фА(])фА(2) + V’b(I) ^в(2)]	(24.68)
и подобрать в ней коэффициенты С| и с2 так, чтобы получить наилучшее согласие с опытом.
В этом случае значение с2 будет меньше, чем сь но больше нуля. Конкретный расчет для мо-
лекулы водорода показывает, что с2 < с, и составляет 0,06сг Формулу типа (24.68) можно
применять не только для основного состояния молекулы водорода, но и для возбужденных
состояний более сложных молекул. Можно при этом обобщить ее на случай неодинаковых
электронных состояний фА и фв взаимодействующих атомов; тогда коэффициенты при двух
членах во второй скобке будут различны и мы получим
Ф = С| [^1(0 Фв(1) + ^л(2) Vb(2)] +сгфА(\)фА(Т) + С)фв(\) фв(2).	(24.69)
В предельном случае ионной связи, когда оба электрона находятся у одного атома, будем
иметь с2 с, и с3 или с3 С| и с2, в зависимости оттого, какой из атомов электроотрицателен.
При Ci с2 и с3 связь, как в случае молекулы водорода, является типично гомеополярной.
Основной вывод, который можно сделать при сравнении методов молекулярных
орбит и метода электронных пар, состоит в том, что оба метода приводят к обра-
зованию связей, осуществляемых парами электронов. Паре электронов в методе
валентных связей соответствует пара связывающих эквивалентных молекулярных
электронов в методе молекулярных орбит.
§ 24.8. Электронные оболочки и химическая связь в молекулах,
состоящих из двух одинаковых атомов
Рассмотрим электронные оболочки и химическую связь в молекулах, состоящих
из двух одинаковых атомов, на основе представлений о связывающих и антисвязы-
вающих электронах.
Мы видели, что ион H-t и молекула Н2 имеют в основном состоянии один
бг^-электрон (ag\s) и два (Тд-электрона ((a^ls)2) соответственно. Следующие элек-
троны будут заполнять оболочку on\s. Это происходит у иона Не2 и у молекулы Не2.
-Ион Не2 помимо двух связывающих электронов (c^ls)2 в нормальном состоянии
§ 24.8. Электронные оболочки в гомонуклеарных молекулах
747
имеет один антисвязывающий электрон аи\з, т.е. его электронная конфигурация
будетI9) (a^Is)2a*ls 1 Е+.
Электрон a* 1s как антисвязывающий уменьшает прочность связи по сравне-
нию с молекулой водорода. Нейтральная молекула Не2 должна иметь нормаль-
ную конфигурацию, содержащую уже два электрона a* 1s, т. е. конфигурацию
(apls)2(a*ls)21	. Действие двух антисвязывающих электронов компенсирует дей-
ствие двух связывающих, поэтому связь не образуется, т. е. не существует устой-
чивой молекулы гелия в нормальном состоянии. Образуются только молекулы Не2
в возбужденных состояниях, притом весьма непрочные. Сопоставление энергий
диссоциации Hj, Н2, Не^ и Не2 дано в табл. 24.3.
Таблица 24.3
Энергии диссоциации молекул водорода и гелия и их ионов
Молекула	Конфигурация	Основное состояние	Энергия диссоциации, эВ
Н2 Не+ Не2	13 (<7ffls)2 (affls)2ajls ((Tg\s)2((rl 1з)2	+ &>+ »>+ s + &> м м м м	2,65 4,48 ~ 3
Для молекул, состоящих из атомов элементов второго периода системы элемен-
тов Менделеева (к ним относятся такие важные молекулы, как N2 и О2), формально
можно для всех электронов ввести молекулярные квантовые числа. Однако практи-
чески одноквантовые оболочки атомов остаются неизменными, и считать, что мы
имеем два электрона ад\з и два электрона a* 1s, образовавшихся из двух электро-
нов 1s одного атома и двух таких же электронов другого атома, не имеет смысла.
Молекулярными электронами становятся электроны двухквантовых оболочек ато-
мов, т. е. оболочек 2s и 2р. При этом, согласно (24.32), получаются оболочки
(<T92s)2(<T;2s)2(<T92p)2(<T*2p)2(7r*2p)4(5r‘2p)4.	(24.70)
Связывающими являются электроны ag2s, ад2р и тги2р, остальные антисвязыва-
ющие. Прочность химической связи, грубо говоря, будет определяться числом
связывающих электронов, уменьшенным на число антисвязывающих.
Приближенные волновые функции рассматриваемых молекулярных электронов могут
быть получены, согласно (24.33), как линейные комбинации — суммы и разности — атомных
волновых функций. Например, для электронов ag2s и a*2s мы получим
tfffgls = Cs($lsA + ^hs в),
(24.71)
'Фа^з — са\ФъА ~ Ф2зв)’
Для молекулы U2 мы получим нормальное состояние (ap2s)2 со сравнитель-
но малой энергией диссоциации D — 1,14 эВ. Для молекулы Ве2 добавляются еще
два антисвязывающих электрона (T*2s, т. е. получается состояние (ад2s)2(a*2s)21S*,
являющееся неустойчивым.
Особый интерес представляют молекулы, для которых образующие их атомы
имеют внешние электроны 2р. Связывающее действие электронов (ap2s)2 будет
примерно компенсироваться антисвязывающим действием электронов (a*2s)2, так
,9) Антисвязывающие электроны мы в дальнейшем будем обозначать звездочкой (а*, тг* и т.д.).
748
Глава 24. Электронные состояния в двухатомных молекулах
же как у молекулы Ве2, и химическая связь определяется наличием связывающих
электронов (Уд^р и тги2р. Максимальное число электронов в этих оболочках равно
шести. Если будут добавляться антисвязывающие электроны а£2р и тгрр, то связь
ослабляется. В табл. 24.4 приведены электронные конфигурации для ряда молекул,
состоящих из атомов с внешними электронами 2р, и их ионов. Эти электронное
конфигурации определены на основе теоретических соображений и опытных данных
для основного терма и энергии диссоциации.
Таблица 24.4
Электронные конфигурации и энергии диссоциации молекул, состоящих из атомов
с заполняющимися оболочками 2р, и их ионов
Молекулы и ионы	Конфигурация	Основной терм	Энергия диссоциации, эВ
с2	(тга2р)3<гд2р	Зп„	(3,6)
N+	(тг„2р)4<тд2р	2s;	8,73
n2	(тг.2р)4(<гд2р)2		9,76
	(тг„2р)4(о'д2р)2тг*2р	2ng	6,48
О2	(тг„2р)4(<г92р)2(?г’2р)2	Ч	5,08
f2	(7г„2р)4(<7д2р)2(?г’2р)4	%+	(2,8)
Наиболее прочная связь получается для молекулы азота. Она осуществляется
шестью связывающими электродами, т. е. тремя парами электронов, и является
тройной связью в согласии с обычными представлениями химии. Удаление одного
электрона приводит к некоторому ослаблению связи у иона Nt; связь в этом ионе
1
осуществляется пятью электронами. Ее можно назвать 2--й связью. У молекулы
кислорода имеется шесть связывающих электронов и два антисвязывающих, что
примерно эквивалентно четырем связывающим электронам, и можно рассматривать
связь как двойную, также в согласии с представлениями химии. Наличие для нор-
мальной конфигурации молекулы О2 двух электронов тг *, т.е. незаполненной обо-
лочки, подтверждается тем, что основным термом является триплетный терм 3S”.
Наличие основного триплетного состояния, т. е. состояния со спином 5=1, обусло-
вливает парамагнетизм молекулы кислорода. Антисвязывающее действие последних
двух электронов, заполняющих молекулярные электронные оболочки молекулы О2,
убедительно подтверждается данными для иона 0^", имеющего энергию диссоциации
большую, чем у молекулы О2, — удаление антисвязывающего электрона упрочняет
молекулу. Основной терм 2Пр этой молекулы свидетельствует о наличии молекуляр-
ного электрона 7г7, который может быть только электроном тг*2з. Связь в ионе
1
можно рассматривать как 2--ю.
Отметим, что значение D^2 энергии диссоциации молекулы азота было долгое время
предметом дискуссии и лишь в 1954 г. было окончательно установлено, что D^2 = 9,76 эВ,
а не 7,38 эВ, как одно время считалось наиболее вероятным. Самое убедительное доказа-
тельство правильности значения 9,76 эВ, а не значения 7,38 эВ (только эти два значения
являлись совместимыми со спектроскопическими данными) было получено при изучении
термической диссоциации молекулы N2 [341]. Азот нагревался до температуры 3 500°, а затем
продукты диссоциации сортировались путем отклонения ионов в магнитном поле. Степень
диссоциации молекул оказалась меньше 2 %; согласно расчетам химического равновесия,
при DN2 = 7,38 эВ должно было диссоциировать более 30%, а при D^2 = 9,76 эВ — лишь
0,5 % молекул. Только последнее значение согласуется с результатами опыта.
§ 24.8. Электронные оболочки в гомонуклеарных молекулах
749
Аналогичным образом может быть рассмотрена химическая связь и в более
тяжелых молекулах, состоящих из двух одинаковых атомов.
Существенно, что представление о связывающих и антисвязывающих электро-
нах может быть применено не только к молекулам, состоящим из двух одинаковых
атомов, но и к молекулам, состоящим из двух атомов, мало различающихся по за-
ряду ядер. В подобных случаях для молекул с одинаковым числом электронов —
изоэлектронных молекул — получаются схожие электронные оболочки и химиче-
ская связь приблизительно той же прочности. Примером таких молекул являются
молекула СО, изоэлектронная с молекулой N2 и имеющая энергию диссоциации
11,11 эВ, молекула NO, изоэлектронная с ионом О2Ь и имеющая энергию диссоци-
ации 6,49 эВ, молекула CN и ион СО+, изоэлектронные с ионом N2 и имеющие
энергии диссоциации, примерно равные 6 эВ и 6,5 эВ соответственно. Связь в мо-
лекуле СО можно считать тройной, как и в молекуле N2, а связь в молекулах NO,
CN и в ионе СО+ 2—й как в ионах Ot и Nt.
2	2	2
Приближенные волновые функции молекул, состоящих из атомов, мало отличающихся
по заряду ядер, можно составлять аналогично (24.33) как линейные комбинации — сумму
и разность — волновых функций соответствующих атомных электронов:
^Л+п1 = С(^Я|Л + ^<в),
^Л_п1 = Ф1>п1А - Фп1в),
где теперь tpniA и <фП1в не совсем одинаковые волновые функции, соответствующие внешним
электронам обоих атомов с теми же квантовыми числами nl. Распределение электронной
плотности будет уже не вполне симметричное относительно средней плоскости, однако
по-прежнему электроны будут разделяться на связывающие (а, тг,... ) и антисвязывающие
(а*,тг*,...); для последних электронная плотность обращается в нуль между ядрами, хотя
и не точно в средней плоскости.
В рассмотренных случаях связи между одинаковыми или мало различающи-
мися по заряду ядра атомами мы имеем два основных типа связей. Это связи,
образованные а-электронами, — а-связи, и связи, образованные тг-электронами, —
к-связи. Как уже подчеркивалось ранее (см. § 24.4, с. 729), а-электроны облада-
ют аксиальной симметрией, ось молекулы является осью симметрии электронного
облака, а тг-электроны не обладают аксиальной симметрией; для них плотность элек-
тронного облака обращается в нуль в плоскости, проходящей через ось молекулы,
и распределена симметрично относительно этой плоскости.
Если исходить из распределения электронных облаков отдельных электронов
и рассматривать их перекрывание, от которого зависит прочность химической связи,
то для s- и для р-электронов получается различная картина.
Для s-электронов атомов, образующих молекулу, например, в случае молекул Н2
или Li2, мы имеем картину, изображенную на рис. 24.13, л; при этом образуется
а-связь.
Для р-электронов атомов, образующих молекулу, картина получается более
сложная. Рассмотрим ее на примере молекулы азота, образованной из двух атомов
с электронными оболочками р3.
Если р-электроны каждого атома являются неспаренными (основное состояние
3	1
атома азота 4S со спином S = - = 3- - ), то они будут находиться в состояниях, в ко-
2	2
торых их электронные облака направлены вдоль трех осей — оси молекулы z и двух
перпендикулярных к ней осей х и у, как изображено на рис. 24.13,62Q\ При этом
20) Подробнее о распределении электронной плотности для р-электронов см. § 26.2.
750
Глава 24. Электронные состояния в двухатомных молекулах
д
Рис. 24.13. Образование связи s- и р-электронами: а — образование сг-связи s-электронами;
б — распределение электронной плотности для р-электронов; в — образование сг-связи
р-электронами; г, д — образование тг-связи р-электронами
состояния pz соответствуют проекции тщ — Q и обладают аксиальной симметрией
относительно оси z\ из них возникают молекулярные a-состояния. Состояния рх
и ру соответствуют проекции = 1, не являются аксиально-симметричными
относительно оси z и из них возникают молекулярные тг-состояния. К каждой паре
состояний (p2, рг), (рж, рх), (ру, ру) можно применить метод электронных пар. Пере-
крывание электронных облаков для этих пар показано на рис. 24,13, в, г, д. В первом
случае мы получаем a-связь, во втором и в третьем случаях — тг-связи. Таким обра-
зом, получается одна a-связь и две тг-связи, что и дает тройную связь в молекуле N2,
осуществляемую тремя парами электронов в согласии с результатами, к которым при-
водит рассмотрение молекулярных оболочек (см. табл. 24.4, оболочки (тги2р)4(а^2р)2).
Для молекулы кислорода можно исходить из атомов в состояниях с двумя
неспаренными электронами (основное состояние атома кислорода 3Р со спином
5=1=2-1).
По методу электронных пар мы получаем одну a-связь и одну
тг-связь, т. е. двойную связь, осуществляемую двумя парами электронов. Это на-
ходится в согласии с представлениями о молекулярных оболочках, если учесть
компенсацию двух антисвязывающих электронов тг*2р двумя связывающими элек-
тронами оболочки тги2р2,).
Наглядные представления об образовании электронных пар, соответствующих
ст- и 7Г-связям, могут быть применены при рассмотрении химической связи в мно-
гоатомных молекулах (см. гл. 26, с. 803).
§ 24.9. Электронные оболочки и химическая связь в молекулах,
состоящих из двух разных атомов
В молекулах, состоящих из двух разных атомов, связь может сильно отличаться
от гомеополярной. Уже для разобранного в предыдущем параграфе случая, когда
21) Недостатком метода электронных пар в этом случае является то, что он приводит к молекулярному
состоянию с полным спином S — 0, так как для каждой пары спины электронов компенсируются.
§ 24.9. Электронные оболочки в молекулах, состоящих из разных атомов 751
эти атомы мало отличаются по заряду ядра, распределение плотности электронного
облака не будет вполне симметрично относительно центра и у молекулы будет
возникать дипольный момент. В случае, когда один из атомов электроположителен,
а другой электроотрицателен и происходит переход электрона от одного атома
к другому, как в случае NaCl (см. §24.1, с. 720), молекула будет обладать большим
дипольным моментом, а химическая связь будет ионного типа. В этом случае
все электроны принадлежат отдельным атомам, либо одному, либо другому, и нет
смысла формально рассматривать эти электроны как молекулярные, характеризуя их
квантовым числом Л, так же как нецелесообразно рассматривать подобным образом
электроны внутренних оболочек атомов.
Возможны различные промежуточные случаи, переходные между гомеополяр-
ной и ионной связями. Особым предельным случаем молекул, состоящих из атомов
с различными зарядами ядер, является случай двухатомных гидридов, когда заряд
ядра одного из атомов, атома водорода, равен единице. В этом случае разумное при-
ближение представляет подход, основанный на рассмотрении объединенного атома
с зарядом Z + 1, где Z — заряд ядра атома, образующего гидрид (см. § 24.6, с. 735).
Электроны молекулы характеризуются, согласно схеме (24.30), их соответстви-
ем с электронами объединенного атома. Оболочки nla будут заполняться двумя
электронами, оболочки п/тг, п/<5, ... — четырьмя электронами. Таким образом, мы
получаем молекулярные оболочки
(25а)2, (2ра)2, (2ртг)4,	1
(35а)2, (Зра)2, (Зртг)4, (3da)2, (Зйтг)4, (3d<5)4, ।	(24.73)
Внутренние электронные оболочки атома, образующего гидрид, можно считать
неизменными и характеризовать при помощи (24.73) лишь электроны внешней
электронной оболочки, участвующие в образовании связи.
Для простейшего случая молекулы LiH мы получаем оболочку (25а)2, запол-
ненную двумя электронами. Этот гидрид напоминает атом с двумя внешними элек-
тронами 2$2. Электронная конфигурация (2sa)“ дает основной терм Первой
возбужденной электронной конфигурацией будет конфигурация 2sa 2ра, дающая
термы и 3Е+.
В табл. 24.5 приведены основная и первая возбужденная электронные конфи-
гурации с указанием возможных термов для молекул гидридов элементов второго
периода системы Менделеева.
Связь в гидридах является связью промежуточного типа. При этом для молекул,
стоящих в начале таблицы, электроны имеют тенденцию переходить к атому И:
в LiH атом Li является донором, а атом Н — акцептором, поэтому и дипольный
момент направлен от Н к Li (от Н~ к Li+). Наоборот, для молекул, стоящих в конце
таблицы, электрон имеет тенденцию переходить от атома Н; в HF атом Н является
донором, а атом F — акцептором, поэтому дипольный момент в HF направлен от F
к Н (от F~ к Н+).
Молекулы CH, NH и ОН обладают неспаренными электронами во внешней
электронной оболочке. С точки зрения химии атомы С, N и О в CH, NH и ОН
имеют свободные валентности. Поэтому эти молекулы химически неустойчивы
и встречаются как радикалы. С физической точки зрения они представляют типичные
устойчивые молекулы с энергиями диссоциации в основном электронном состоянии
порядка нескольких электроновольт; они обладают спектрами, наблюдающимися
при весьма разнообразных условиях — в электрическом разряде, при химических
реакциях, при исследовании Солнца и т.д.; эти спектры особенно характерны
для пламен [95].
752 Глава 24. Электронные состояния в двухатомных молекулах
Таблица 24.5
Электронные конфигурации и возможные термы двухатомных гидридов
элементов второго периода
Молекула	Основная электронная конфигурация	Первая возбужденная электронная конфигурация	Энергия диссоциации в основном состоянии, эВ
UH	(2ва)2,Е+	2*e-2pa’E+, 3S+	(2,5)
ВеН	(2жг)22р<г 2Е+	(2мг)2 2ртг 2П	(2,2)
ВН ;	(2лг)2 (2ра)2 'Е+	(2мг)2 2р<г 2рг ' П, 3П	(3,5)
сн	(2«а)2 (2р<г)22рт 2П	(2мг)22ро (2pit)12	2Е+, 2Е", 4S“	3,47
NH	(2мг)2 (2/мг)2(2рт)23Е-, ’А, 'Е+	(2мг)2 2ра (2рк)3 ’ П 3П	3,4
ОН	(2мг)2 (2рг)2 (2рх)”П	(2мг)2 2р<г (2ря)4 2 Е+	4,33
HF	(2мг)2 (2р<г)2 (2рх)4 'Е	(2мг)2 (2paj2 (2рг)} Змг 1П, 3П	6,4
Наблюденные термы выделены жирным шрифтом.
Элементы последующих периодов системы Менделеева образуют гидриды с мо-
лекулярными электронными конфигурациями, аналогичными конфигурациям, при-
веденным в табл. 24.5.
ГЛАВА 25
ЭЛЕКТРОННЫЕ СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
§25.1. Колебательная структура электронных переходов
При переходе между двумя электронными состояниями, как правило, од-
новременно изменяются и колебательная и вращательная энергии (см. гл. 17,
с. 464). Согласно (17.4) и (17.5), полное изменение энергии молекулы при пере-
ходе ДЯ = А#Эл + А^кол + Д^вращ, причем Д^эл > Д^кол » Д^вращ- КАЖДЫЙ
электронный переход между двумя электронными термами характеризуется опре-
деленной колебательной структурой, состоящей из совокупности полос, а каждая
полоса характеризуется определенной вращательной структурой, представляя сово-
купность отдельных линий.
Разберем сначала колебательную структуру, которая в противоположность вра-
щательной, рассматриваемой ниже, не зависит непосредственно от свойств сим-
метрии комбинирующих электронных состояний и определяется видом кривых
потенциальной энергии для этих состояний.
Положение полос колебательной структуры определяется разностью Д#кол =
Мол ~ Мол энергии колебаний Мол Для верхнего электронного уровня и энергии
колебаний Мол Для нижнего электронного уровня, которые, если ограничиться
двухчленной формулой (20.83), равны
/	1 \ /	1 \2
nl	f	I	1 i	1 I / f i t	.	1 1
Екол = Ц, I v +	z I	- xeve I v	+	- I ,
/	/	j\2
nft	,f I 11 I 1	///////.	1 \
= Ve I V +?]- XeVe ( V + - I .
Значения постоянных ve и xe, т.е. частот колебаний и коэффициентов, опре-
деляемых ангармоничностью, для разных электронных состояний в общем случае
различны. Как правило, для возбужденных состояний прочность связи меньше,
а равновесное расстояние ре между ядрами больше, чем для основного состояния,
и кривая потенциальной энергии идет более полого. В результате частота коле-
баний ve в возбужденных состояниях меньше, чем в нормальном; с увеличением
возбуждения она, вообще говоря, убывает. Поэтому обычно и" > у'е, следовательно,
и расстояния между колебательными уровнями для верхних электронных состояний
меньше, чем для нижних. Например, для основного электронного состояния
молекулы СО у" = 2 169 см-1, а для ее возбужденного электронного состояния ’11
р' = 1 515 см~’, т.е. частота колебаний в возбужденном состоянии на 30% меньше,
чем в нормальном.
Частота уе, согласно (20.2), непосредственно связана с силовой постоянной к
молекулы в рассматриваемом электронном состоянии. Уменьшение уе при возбужде-
нии молекулы означает уменьшение силовой постоянной, которое происходит, как
правило, одновременно с уменьшением прочности связи, т. е. энергии диссоциации.
754
Глава 25. Электронные спектры двухатомных молекул
Характерное отличие колебательной структуры электронных переходов от струк-
туры чисто колебательных переходов состоит в том, что правило отбора (20.32)
для гармонического осциллятора, Av = v' - v" = 1, не имеет места даже прибли-
женно. В принципе могут комбинировать колебательные уровни с любой разностью
колебательных квантовых чисел; относительные вероятности различных колебатель-
ных переходов (v', v") определяются, как будет подробно рассмотрено в следующем
параграфе, видом и взаимным расположением кривых потенциальной энергии ком-
бинирующих состояний.
Полная система колебательных полос для заданного электронного состояния
получается, если менять как v', так и v". Поэтому обычно записывают волновые
числа соответствующих полос в виде прямоугольной схемы, столбцы которой соот-
ветствуют различным v", а строки — различным v'. Такую схему обычно называют
схемой Деландра °.
В табл. 25.1 приведена часть схемы Деландра для системы полос СО, полу-
чающейся при переходе ’П— ’Е+ (для так называемой четвертой положительной
системы полос, см. рис. 25.22, с. 778). Разности частот в двух соседних столбцах дают
разности энергий колебательных уровней основного электронного состояния, раз-
ности частот в двух соседних строках дают разности энергий колебательных уровней
возбужденного электронного состояния. Соответствующие разности являются, как
показывает таблица, постоянными для данной пары строк или столбцов и убывают
с увеличением v' и v", что связано со схождением колебательных уровней к границам
диссоциации возбужденного и нормального электронных состояний. На рис. 25.1
соответствующая схема переходов показана графически.
При переходе между определенным нижним уровнем v" и различными верхни-
ми уровнями v' получится серия линий, частоты которых стоят в табл. 25.1 в одном
столбце. Это так называемая поперечная серия Деландра. Такую серию, начинаю-
щуюся с уровня v" = 0, можно хорошо наблюдать в поглощении с основного уровня
при достаточно низких температурах, когда остальные колебательные уровни либо
совсем не возбуждены, либо возбуждены слабо.
При переходах между определенным верхним уровнем v' и различными нижни-
ми уровнями v" получится серия линий, частоты которых стоят в табл. 25.1 в одной
строке. Это так называемая продольная серия Деландра. Такую серию можно по-
лучить в испускании, если возбуждать молекулы в узкой области частот, так чтобы
мог возбудиться только один верхний колебательный уровень.
Подобные резонансные серии хорошо наблюдаются для 12, Вг2 и для других
молекул.
На рис. 25.1, б, в отдельно показаны переходы для поперечных и продольных
серий Деландра, причем в нижней части рисунка приведен получающийся спектр.
С увеличением v' при заданном v" частоты полос увеличиваются, с увеличением v"
при заданном vf они уменьшаются, причем в обоих случаях полосы обнаруживают
схождение.
В общем случае, когда отсутствуют специальные условия возбуждения, карти-
на расположения полос часто получается весьма сложная, особенно когда часто-
ты I/' и и" сильно различаются и происходит наложение полос (см. нижнюю часть
рис. 25.1, а). Если разность v'e и v" невелика, то полосы группируются по величине
разности квантовых чисел Av -- v' - v"; получается ряд близких полос, соответству-
ющих Av = 0, ряд близких полос, соответствующих Av = 1 и т.д. (см. рис. 25.2).
Французский ученый Деландр впервые установил в 1886 г. [162], на основе анализа большого
эмпирического материала, определенные закономерности в расположении полос, о чем уже упоминалось
на с. 37.
Таблица 25.1
Схема колебательных переходов для четвертой положительной системы полос СО
V	0	1	2	3	4	5	6	7	8
0	62606 (2117) 60485 (2092) 58 393 (2064) 56329 (2037) 54292 (1486)	(1489)	(1489)	(1489) 66231	(2 143)	64088	59882	(2064) 57818 (2037)	55781	(2013)	53768	(1986)	51 782	(1959)	49823 (1444)	(1445)	(1443)	(1443)	(1445)	(1446)	(1445) 67675	(2142)	65533	(2117) 63416 (2091)	61325	57224	(2011)	55213	(1985)	53228	(1960)	51268 (1413)	(1411)	(1412)	(1412)	(1412)	(1413) 69088 (2144) 66944 (2116) 64828	60674 (2038) 58636	54640 (1959) 52681 (1 382)	(1379)	(1381) 70470 (2 147) 68323	64116 (2061) 62055	58003 (1 337)	(1343)	(1 342) 71801 (2 141) 69666	65458	61357	57360 (1959) 55401 (1 307)	(1 308)	(1307) 70973 (2 117) 68 856	62665	58667								
1									
2									
3									
4									
5									
6									
§25.1. Колебательная структура электронных переходов
756
Глава 25. Электронные спектры двухатомных молекул
Рис. 25.1. Система электронно-колебательных полос:
а — общий случай; б — поперечная серия; в — продольная серия
Дг> = 0 Дг> = 1	= 2
Рис. 25.2. Система электронно-колебательных полос
при р" - р' < г/"
На основе опытных данных
для положений полос могут быть
определены постоянные ve и хег/е
для комбинирующих уровней. Ес-
ли установлено достаточное чис-
ло последовательных уровней, то
можно произвести грубую экстра-
поляцию их схождения, чтобы по методу, изложенному в § 20.4, найти энергии
диссоциации комбинирующих состояний.
Говоря о положении полос, мы не уточнили, что именно подразумевается
под этим. В табл. 25.1 приведены положения нулевых линий, которые не всегда
удается определить. Часто на опыте измеряются резкие границы полос — их канты
(см. ниже, §25.3, с. 761).
§ 25.2. Принцип Франка—Кондона
и относительные интенсивности электронно-колебательных полос
Общий характер распределения интенсивностей в системе электронно-колеба-
тельных полос можно получить, исходя из принципа Франка—Кондона, основанного
на рассмотрении кривых потенциальной энергии комбинирующих электронных со-
стояний. Идея принципа принадлежит Франку [193], который сформулировал ее
на основе классических представлений. Квантовомеханическое рассмотрение во-
проса было дано Кондоном [328].
Сущность принципа Франка—Кондона заключается в следующем. Электрон-
ный переход состоит в перестройке электронных оболочек и происходит очень
быстро по сравнению с движением ядер. Поэтому относительное положение ядер,
т. е. расстояние р между ними, и их скорости не успевают измениться за вре-
мя перехода. Данному условию удовлетворяют поворотные точки потенциальных
§ 25.2. Принцип Франка—Кондона
757
Рис. 25.3. Наиболее вероятные переходы,
согласно принципу Франка—Кондона
Рис. 25.4. Переходы при подобных
потенциальных кривых, расположенных
одна под другой
кривых комбинирующих электронных состояний, соответствующие тому же значе-
нию р, т. е. лежащие на графике кривых потенциальной энергии на одной вертикали
(рис. 25.3); скорость в этих точках равна нулю. Квантовомеханическое рассмотрение
приводит к выводу, что возможны и переходы, соответствующие изменениям рас-
стояния между ядрами и их скоростей, однако вероятность подобных переходов тем
меньше, чем больше эти изменения. Таким образом, наиболее вероятные переходы
соответствуют сохранению расстояния между ядрами при их скорости, равной нулю,
т. е. вертикальным линиям на графике потенциальных кривых. В этом и состоит
содержание принципа Франка—Кондона.
Рассмотрим, к какому распределению интенсивностей полос колебательной
структуры приводит принцип Франка—Кондона.
Если потенциальные кривые комбинирующих состояний подобны друг другу
и соответствуют одинаковому равновесному расстоянию (рис. 25.4), то наиболее
вероятны переходы между колебательными уровнями с одинаковыми значениями v"
и v'. Действительно, в этом случае поворотные точки классического движения
при v1 = v" расположены друг над другом. По мере увеличения Av = v' — v"
вероятность переходов будет убывать; в случае, показанном на рис. 25.4, наиболее
интенсивна будет группа полос Av = 0, слабее будут группы полос Av = +1
и Av = -1, еще слабее группы полос Av = +2 и Av = -2.
Однако для двухатомных молекул подобный случай не типичен. Как мы уже
отмечали, обычно потенциальные кривые возбужденных состояний имеют минимум
при больших р и являются более пологими. Для расположения кривых, изобра-
женных на рис. 25.5, а, с нулевого колебательного уровня основного электронного
состояния (v" = 0) наиболее вероятен будет переход на колебательный уровень
возбужденного электронного состояния с некоторым значением v' = v\. Переходы
на уровни с меньшими и с большими значениями v' будут менее вероятны. Когда
поглощают молекулы, находящиеся на нулевом колебательном уровне, распреде-
ление интенсивностей в спектре поглощения (представляющем поперечную серию
Деландра с v" = 0, см. выше, с. 754) будет иметь максимум при соответствующем
значении v' = v\. В обе стороны от этого максимума интенсивность спадает.
758	Глава 25. Электронные спектры двухатомных молекул
Рис. 25.5. Переходы при потенциальных кривых с различными значениями равновесного
расстояния ре: а — поглощение с основного электронно-колебательного уровня;
б — испускание с колебательных уровней верхнего электронного состояния;
в — поглощение с высоких колебательных уровней основного электронного состояния
При испускании с колебательных уровней vl верхнего электронного состояния
(рис. 25.5,6) или при поглощении с достаточно высокого колебательного уровня v’
нижнего электронного состояния (рис. 25.5, в), как правило основного2), наиболее
вероятны будут переходы с уровня с заданным v' или v" на два уровня с опре-
деленными Vй — v" И Vй = v2 или V1 — v\
из рисунков.
и v’ = v2 соответственно, как следует
Легко видеть, что значения v"
и v” отличаются тем сильнее, чем
больше v' и, аналогично, значе-
ния v\ и v2 отличаются тем силь-
нее, чем больше v". Если предста-
вить распределение вероятностей пе-
реходов в схеме типа схемы Деландра
(рис. 25.6), то наибольшие вероятно-
сти переходов будут получаться для
полос, лежащих на этой схеме на па-
раболе. Эту параболу называют пара-
болой Кондона. При заданном зна-
чении v получается два значения v”,
а при заданном значении v" получа-
ется два значения г/, соответствую-
щие максимальной вероятности пе-
реходов.
Распределение интенсивностей, соответствующее параболе Кондона, в испуска-
нии будет наблюдаться, если возбуждено достаточное число колебательных уровней
верхнего электронного состояния с примерно одинаковой заселенностью. В погло-
щении подобное распределение интенсивностей может наблюдаться при возбужде-
нии большого числа колебательных уровней нижнего электронного состояния, что
возможно при достаточно высокой температуре.
2) Поглощение с колебательных уровней возбужденных электронных состояний возможно лишь
при высоких температурах, при которых обычно молекула будет уже диссоциировать.
§25.2. Принцип Франка—Кондона
759
Парабола Кондона будет тем уже, чем меньше сдвинуты друг относительно дру-
га потенциальные кривые комбинирующих электронных состояний. В предельном
случае, когда они лежат одна над другой, парабола вырождается в прямую и при оди-
наковой форме кривых эта прямая будет соответствовать v' = v", т.е. Av = 0. Мы
приходим к случаю, с разбора которого мы начали данное рассмотрение (рис. 25.4).
Следует иметь в виду, что принцип Франка—Кондона определяет только общий
характер распределения интенсивностей в системе полос. Интенсивности отдельных
полос при изменении v' и v” могут изменяться достаточно неравномерным образом.
Некоторые полосы могут быть аномально слабы, а другие аномально интенсивны.
Принцип Франка—Кондона может
быть обоснован квантовомеханически, ес-
ли исходить из выражения (17.99) для ма-
тричного элемента электронно-колеба-
тельного перехода. Так как вероятности
переходов пропорциональны квадрату мо-
дуля соответствующих матричных элемен-
тов, то относительные вероятности
различных колебательных переходов для
заданного электронного перехода будут
пропорциональны квадрату интеграла на-
ложения (17.100):
WvV, = С|У i/>',(p) ^„(р) dp\\ (25.2)
где с — постоянная3^. Таким образом, ве-
роятности колебательных переходов опре-
деляются наложением колебательных вол-
новых функций комбинирующих уровней.
Если мы изобразим для каждого
уровня колебательную волновую функцию
на соответствующей ступеньке (ср. § 20.3,
с. 581), то получим картину, представлен-
ную на рис. 25.7. Интеграл наложения
будет велик, если максимумы волновых
функций для комбинирующих состояний
лежат в тех же областях значений р. Так
как наибольшие максимумы расположены
вблизи поворотных точек классического
движения, то мы приходим к результату,
что наибольшая вероятность получается
при переходах, для которых поворотные
Рис. 25.7. Колебательные волновые функции
для комбинирующих электронно-колебательных
уровней
точки классического движения соответствуют одинаковому расстоянию между ядрами, т. е. ле-
жат на одной вертикальной линии (см. рис. 25.3 и 25.4).
Совершенно ясно, что условие равенства расстояний между ядрами для поворотных
точек является лишь приближенным. Оно должно оправдываться тем лучше, чем больше
колебательные квантовые числа комбинирующих уровней. Для низких колебательных уровней
это будет выполняться хуже, а для нулевого колебательного уровня, когда максимум лежит
при р = ре, нужно проводить вертикальную прямую для р — ре. Чем круче идут потенциальные
кривые, тем резче будут максимумы волновых функций и тем лучше будет соблюдаться
принцип Франка—Кондона.
Так как для больших колебательных квантовых чисел волновые функции быстро осцил-
лируют, то в среднем их произведение будет мало. Однако возможны случаи, когда функции
налагаются так, что интеграл случайно окажется достаточно велик. В других случаях он может
3) Если пренебречь зависимостью вероятностей перехода от четвертой степени частоты, которая мало
меняется, в силу Д£’КОл < Д/£Эт
760
Глава 25. Электронные спектры двухатомных молекул
быть, наоборот, особенно мал. Это объясняет возможность появления аномально интенсив-
ных и аномально слабых полос. Можно для конкретных случаев произвести расчеты значений
интеграла наложения. Однако подобные вычисления затрудняются тем, что действительные
колебательные функции отличаются от собственных функций гармонического осциллятора
и обычно известны с недостаточной точностью. Необходимо отметить, что сама формула (25.2)
является лишь приближенной, поскольку в (17.98) пренебрегается зависимостью Рпп(р) от р.
§ 25.3. Общая характеристика вращательной структуры
электронно-колебательных полос
Перейдем теперь к рассмотрению вращательной структуры электронно-колеба-
тельных полос и начнем с общей характеристики этой структуры [46]. Вращательная
структура электронно-колебательных полос определяется изменением вращательной
энергии при соответствующем переходе ДЕ'вращ = Хращ~Хращ, где, согласно (19.23),
для вращательных уровней верхнего электронно-колебательного состояния имеем
Хращ —	4- 1) и для вращательных уровней нижнего электронно-колеба-
тельного состояния имеем аналогично Хращ — B"hJ"(J" 4- 1). Мы ограничиваемся
основным членом в выражении для вращательной энергии, не учитывая малой
поправки на центробежное растяжение (см. (19.38)). Таким образом,
АЯвраш = B’v, j'(j' + 1) -	j"(j" + 1).	(25.3)
Вращательные постоянные для верхнего и нижнего состояний, как правило, раз-
личны и лишь в некоторых случаях приближенно совпадают. При этом их основное
различие определяется различием электронных состояний, а именно, изменением
равновесного расстояния ре между ядрами при переходе молекулы из одного элек-
тронного состояния в другое. Как уже отмечалось, при электронном возбуждении
молекулы ре обычно увеличивается; это приводит к увеличению момента инерции
и уменьшению вращательной постоянной. Поэтому обычно В' < В1'. Возможен, од-
нако, особенно при переходе не между нормальным и возбужденным состояниями,
а между двумя возбужденными состояниями, и противоположный случай: В1 > В".
Наряду с зависимостью значения В от электронного состояния имеется и неко-
торая зависимость от колебательного состояния, определяемая формулой (20.111)
(в которой будет различным для нижнего и для верхнего электронных состояний).
В качестве примера можно привести значения вращательных постоянных В",
и B'v, для перехода между электронными состояниями А 1и С 1в молекуле ВеО,
равные (в см’1) В% = 1,6422, В'( = 1,6232, В" = 1,6052 и В$ = 1,5691, В\ = 1,5536
и В'2 — 1,5363 соответственно.
При электронных переходах в общем случае для вращательного квантового
числа J имеет место обычное правило отбора (4.156) для моментов количества
движения:
AJ — j'- J,z — ±1,0.	(25.4)
Для изменения вращательной энергии при электронно-колебательных переходах
применимы все формулы, выведенные для изменения вращательной энергии при чи-
сто колебательных переходах (см. §20.7, формулы (20.134)—20.141)). Мы имеем
для R-, Р- и Q-ветвей:
Л-ветвь ДВ = р0 + (В' + В") J' + (В' - В") J'2
(ДВ = J'-J" = +1)	= р0 + 2В' + (ЗВ' - В") J" + (В1 - В") J "2, (25.5)
Р-ветвь ДР = р0 - 2В' - (ЗВ" - В') J' + (В' - В") J2 =
§25.3. Вращательная структура электронно-колебательных полос 761
(ДБ = J' - J" = -1)
Q-ветвь
(Д£ = J' - J" = 0)
= i/0 - (В' + В") J" + (В1 - В") J"2,
ДЕ = р0 + (В' - B")J'(J' + 1) =
= р0 + (В' - B")j"(j" + 1).
(25.6)
(25.7)
Если ввести целое число т, где
m — J1	для	Я-ветви,	т = 1,2,3,... ,	
т — -J"	для	Р-ветви,	т = —1,—2,—3,..	• 5	>
m = j' = j"	для	Q-ветви,	1,2,3,... ,	>
(25.8)
то формулы (25.5)-(25.7) принимают вид:
R- и Р-ветви ДЕ =р0 + (В1 + В")т + (В1 - В")т\	(25.9)
Q-ветвь ДР =Ро + (В' - В")т(т + 1).	(25.10)
Здесь Ро — частота электронно-колебательного перехода, соответствующая т = 0
(частота нулевой линии).
Существенное отличие вращательной структуры электронно-колебательных
спектров от вращательной структуры колебательных спектров в инфракрасной обла-
сти состоит в том, что величина В1 — В" может быть значительной; отличие В1
и В" достигает в некоторых случаях десятков процентов. Поэтому при увеличе-
нии т квадратичный член (В1 — В")т2 в формуле (25.9) может достаточно скоро
по абсолютной величине стать больше линейного члена (В1 -Ь В")т; это приводит
к сгущению линий для одной из ветвей и ее повороту, что лучше всего иллю-
стрируется графически при помощи так называемой диаграммы Фортра (рис. 25.8).
По оси абсцисс откладывается частота переходов, а по оси ординат — абсолют-
ное значение т. Каждая ветвь, согласно формулам (25.9) и (25.10), дает параболу.
При этом, если В' < В", то в Я-ветви знаки линейного и квадратичного членов
противоположны и при некотором т значение частоты достигает максимума и затем
начинает уменьшаться (рис. 25.8, а). Получается коротковолновая граница полосы
в виде резкого края, у которого происходит сгущение линий, — кант полосы. Поло-
са, как говорят, оттенена в сторону больших длин волн — в красную сторону. Если
В1 > В", то кант образуется в Р-ветви и соответствует длинноволновой границе
полосы (рис. 25.8,6); в этом случае получается оттенение в сторону меньших длин
волн — в фиолетовую сторону. Положение канта можно получить из (25.9), полагая
Рис. 25.8. Диаграмма Фортра: а — случай В' < В"; б — случай В' > В1
762
Глава 25. Электронные спектры двухатомных молекул
du
— = 0, что дает
dm
В' + В"	z
ГПклт~~2(в>-в11У	(2511)
При подстановке этого выражения обратно в (25.9) получается расстояние канта
от нулевой линии:
(В' + В")2
г^кант ~	_-д„) (Я-и Р-ветви).	(25.12)
На опыте частоту нулевой линии, если полоса не разрешена или разрешена
неполностью, не удается определить и приходится измерять положение канта.
Даже когда не удается разрешить полосы и измерить вращательную структуру,
по оттенению полос в красную или фиолетовую сторону можно решить, имеет ли
место случай В1 < В" или В1 > В". Как отмечалось выше (с. 760), первый случай
является обычным и поэтому оттенение в красную сторону (в В-ветви) встречается
чаще.
Как показывают диаграммы рис. 25.8, в полосе вблизи канта происходит наложе-
ние линий ветви, образующей кант. Около нулевой линии образуется, при наличии
Q-ветви (что имеет место для всех переходов, кроме переходов Е—Е, см. ниже,
с. 772) и при не очень сильно отличающихся вращательных постоянных В1 и В"
сгущение линий этой ветви, дающее второй кант. Из формулы (25.10) и диаграмм
рис. 25.8 следует, что оттенение второго канта такое же, как и первого — при В' < В"
в красную сторону (канты в ветвях R и Q) и при В1 > В" в фиолетовую сторону
(канты в ветвях Р и Q).
По канту в Q-ветви можно со значительной точностью, даже для неразрешенных
полос (в которых, однако, наряду с кантом в R- или Р-ветви виден и кант в Q-ветви),
определять положение нулевой линии. Первая линия в Q-ветви соответствует,
согласно (25.10), частоте и — у$ 4- 2(В' — В"); значение этой частоты и определяет
положение канта. Его расстояние от нулевой линии равно
^кант -	= 2(В' - В”) (Q-ьеыъ).	(25.13)
За нулевой линией (на стороне, противоположной канту в R- или Р-ветви, —
в «хвосте» полосы) происходит наложение линий всех трех ветвей. Это приводит
к сложной структуре полосы.
Вид полосы может еще усложняться при наличии нескольких ветвей каждого
рода, что может иметь место из-за тонкой структуры электронных уровней; на-
ряду с этим вращательные линии могут расщепляться за счет снятия двукратного
вырождения электронных уровней сЛ/0 (см. ниже, §25.4).
Вид электронно-колебательных полос очень сильно зависит от дисперсии при-
меняемых спектральных приборов. При малой дисперсии полоса представляется
сплошной и лишь обнаруживается один или два канта с оттенением в ту или дру-
гую сторону. С увеличением дисперсии сперва разрешается хвост полосы, а затем
и ее остальные части. При очень большой дисперсии вообще утрачивается вид
полосы и получается линейчатый спектр. При этом существенна не только аб-
солютная величина дисперсии, но и соотношение между величиной дисперсии
и величиной вращательной постоянной. В случае малых вращательных постоянных
для разрешения полосы необходима большая дисперсия, чем в случае значительных
вращательных постоянных.
§ 25.4. Взаимодействие электронного движения с вращательным
763
§ 25.4. Взаимодействие электронного движения с вращательным
Вращательная структура электронно-колебательных полос существенным обра-
зом зависит от свойств комбинирующих электронных состояний. При этом
необходимо учитывать взаимодействие электронного движения с вращатель-
ным [50].
Классификация возможных случаев взаимодействия электронного движения
с вращательным была дана Гундом [329]. Они отличаются типом связи момен-
тов — различным порядком сложения электронных и вращательных моментов —
и их обычно называют случаями Гунда. Основными двумя случаями являются слу-
чаи Гунда а и Ъ, которые получаются в зависимости от того, велико или мало
мультиплетное расщепление, обусловленное спин-орбитальным взаимодействием,
по сравнению с расстояниями между вращательными уровнями.
Случай а имеет место, когда спин-орбитальное взаимодействие достаточно вели-
ко и его нужно учитывать раньше, чем вращение. Как мы подчеркивали, электриче-
ское поле внутри молекулы не действует непосредственно на спин. При достаточно
большом спин-орбитальном взаимодействии при А 0 спин будет ориентироваться
относительно оси молекулы. Его проекция на ось молекулы будет определяться
квантовым числом ms, принимающим значения 5, 5—1, ..., -5, т.е. 2S 4- 1
значений. По аналогии с L и А проекцию вектора S обозначают через Е, т. е.
£ = т5 = 5, 5-1, ..., -5,	(25.14)
причем S в отличие от А может быть как положительной, так и отрицательной.
Полная проекция электронных моментов на ось молекулы равна сумме проекций
орбитального и спинового моментов. Ее обозначают через Q:
Q = A + £ = A + 5, А 4-5-1, ..., А-5.	(25.15)
Значение Q указывают индексом справа снизу у А и одновременно индексом
слева сверху указывают мультиплетность х = 25 4- 1, аналогично обозначению *Lj
для атомных уровней при нормальной связи. Например, при А = 1 и 5 = 1 (х = 3),
Е = 1,0, -1,Q = A4~S = 2, 1,0и получаются состояния 3П2, 3П|, 3По.
Спин-орбитальное взаимодействие приводит к расщеплению уровня с задан-
ным А на 25 4- 1 уровней с различными значениями Q, в приведенном примере
на три уровня. Получается мультиплетный терм, для которого дополнительная
энергия уровней определяется формулой (см. [46], с. 159)
A Eq = АЛЕ,	(25.16)
аналогичной формуле (9.35) для спин-орбитального взаимодействия в атомах. Вме-
сто скалярного произведения векторов L и S в (25.16) входит произведение их
проекций А и Е. Величина расщепления определяется величиной постоянной А,
характеризующей спин-орбитальное взаимодействие, — молекулярным фактором
мультиплетного расщепления. В отличие от правила интервалов (9.36) для муль-
типлетов в атомных спектрах, уровни с различными значениями Q получаются
равноотстоящими
AEq,q+i = АА.	(25.17)
764
Глава 25. Электронные спектры двухатомных молекул
Для П-состояний (Л — 1) возможные значения Q и соответствующие уровни будут
2Пз/2, 2П1/2,
5=1, Е= 1, 0, -1,	Q = 2, 1, О,
3П2, 2П(, 3П0,
3	3	1	1	3	5	3	1	1
S =	2 = -,	—, —, Q =	,
2	2	2	2	2	2	2	2’	2’
4п5/2, 4п3/2, 4п1/2, >1/2,
5 = 2, 2 = 2, 1,0, -1, —2, Q = 3, 2, 1, 0, -1,
5П3, 5П2, 5П1, 5По, 5П_1.
(25.18)
Для Д-состояний (Л = 2) аналогично
1	1	1
S =	2 =	,
2’	2	2
(25.19)
5 = 2, 2 = 2, 1,0, -1, —2,
Все уровни дважды вырождены, в том числе и уровни с Q = 0.
Возможные значения полной проекции т3 вектора L 4- 5 мы получим, учитывая, что
mL = ±Л, и рассматривая суммы Л 4- 2 и -Л — 2 (2 = 5, S — 1,..., —5); всего mj принимает
2(25 4-1) значений. Однако значениям Л 4- 2 и -Л - 2 при заданном 2 будет соответствовать
та же энергия, поскольку направление проекции орбитального момента не существенно
и если одновременно меняют знаки mL и 2, то это не может сказаться на величине энергии.
В формулу (25.16) входит абсолютное значение Л проекции орбитального момента, а не mL.
С точки зрения наглядных представлений мы имеем картину, изображенную на рис. 25.9
3
для случаев Л = 1, 5 — 1 и Л = 1,5 = -.
Для каждого уровня с заданным значением Q нужно учесть сложение полного
электронного момента количества движения, направленного по оси молекулы,
с вращательным моментом количества движения в полный момент количества
движения молекулы. Согласно наглядным представлениям, мы имеем картину,
изображенную на рис. 25.10, а\ электронные орбитальный и спиновый моменты
прецессируют вокруг оси молекулы, давая вектор Q = Л 4- X, направленный по оси
молекулы. Этот вектор, складываясь с вращательным моментом R, направленным
§ 25.4. Взаимодействие электронного движения с вращательным
765
перпендикулярно к оси, образует полный момент количества движения J, вокруг
направления которого прецессируют Q и R.
Квантовое число J может принимать значения, начиная с минимального зна-
чения Q, соответствующего случаю, когда вращательный момент равен нулю и,
следовательно, J — 12. Таким образом,
J = Q, Q+ 1, Q + 2, ... .
(25.20)
В случае, когда Q < 0 (например, для уровня 4П_у2), в (25.20) нужно брать абсо-
лютное значение |Q| квантового числа Q. Согласно общему закону квантования, J
будет целым при целом Q и полуцелым при полуцелом Q.
1г 1г
Q
-1 -1
-Q -2
а
-1/2
13/2	1 1/2	1 +-
П	5/2	3/2 Г	1/2
-1 л-3/2	-1 -1/2 1/2 ^-1
“П	-5/2	-3/2	-1/2
б
-3/2
1
-1/2
3/2
™L = 1
mL = -1
Рис. 25.9. Сложение проекций орбитального и спинового моментов в случае Гунда а:
3
а — при Л = 1, S = 1; б — при Л = 1, S = -
Можно показать, что вращательная энергия определяется приближенной фор-
мулой [47, 46]
^BPam=B[j(J+l)-Q2].	(25.21)
Данная формула может быть получена как частный случай формулы (19.74) для энергии
вращения вытянутого волчка. Действительно, Q представляет проекцию вектора J на ось
молекулы, т. е. совпадает с К, а вращательная постоянная А соответствует моменту инер-
ции 1А электронов относительно оси молекулы, весьма малому, и член АК2 = AQ2 следует
рассматривать как электронную энергию. Включая во вращательную энергию члены BJ(J+1)
и -ВК2 = -BQ2, мы получаем (25.21).
Описанный случай сложения моментов количества движения и представляет
случай а Гунда. В результате для каждой составляющей мультиплетного терма
получается своя последовательность вращательных уровней. На рис. 25.11 показано
расположение вращательных уровней для электронного терма 3П.
Случай Ъ получается, если можно пренебречь связью спина с осью, что имеет
место при очень слабом спин-орбитальном взаимодействии. В этом случае сначала
учитывается вращение, а потом спин: проекция орбитального момента склады-
вается с вращательным моментом в результирующий момент R, который затем
складывается со спиновым моментом S в полный момент молекулы J.
766
Глава 25. Электронные спектры двухатомных молекул
Рис. 25.10. Схема сложения
моментов для случая Гунда а
4------ 2--------3П2
5------ J
3------
4------ 2--------
1 — ч
3------ J
2------
•------3
о------ По
J
Рис. 25.11. Схема вращательных уровней
для терма 3П в случае Гунда а
С наглядной точки зрения мы имеем картину, изображенную на рис. 25.12:
электронный орбитальный момент прецессирует вокруг оси молекулы, давая век-
тор Л, направленный по оси молекулы; этот вектор складывается с вращательным
моментом R', направленным перпендикулярно к оси молекулы, образуя момент R,
вокруг которого прецессируют Л и R1. В свою очередь момент R складывается
с моментом S, образуя полный момент J, вокруг которого прецессируют R и S.
Сложение Л и R' в момент R происходит аналогично сложению Q и R
в момент J. Момент R квантуется, и квантовое число R принимает значения
R = Л, Л+ 1, Л+ 2, ... ,	(25.22)
т. е. все целые значения, начиная с Л. Это будут для П-уровней значения 1, 2, 3, ...
и для Д-уровней значения 2, 3, 4, ... Очевидно, что именно случай b имеет место
для S-уровней; для них спин не может давать проекции на ось молекулы, так как его
взаимодействие с орбитальным моментом равно нулю вследствие равенства нулю
проекции орбитального момента. Для S-уровней R представляет чисто вращатель-
ный момент и квантовое число R принимает значения 0, 1, 2, ... , начинающиеся
с нуля.
Энергия вращения определяется формулой
Явраш = B[R(R + 1) - Л2],	(25.23)
аналогичной формуле (25.21).
При сложении моментов R и S в момент J для каждого значения R получается
2S + 1 значений J:
J = R + S, R + S - 1, ..., |Я - 5|.	(25.24)
Вследствие взаимодействия вращательного момента со спиновым энергия при за-
данном значении R будет зависеть от J и каждый уровень расщепляется на 2S + 1
составляющих. Таким образом, получается мультиплетное расщепление вращатель-
ных уровней.
Величина мультиплетного расщепления вращательных уровней линейно растет
с увеличением Я, что физически понятно, так как с увеличением вращательного
момента R должно увеличиваться и его взаимодействие со спиновым моментом,
§ 25.4. Взаимодействие электронного движения с вращательным

Рис. 25.12. Схема сложения моментов
для случая Гунда Ь
Рис. 25.13. Дублетное расщепление
в случае Гунда Ь для терма 2£
пропорциональное скалярному произведению RS. На рис. 25.13 изображена зави-
симость вращательной энергии от квантового числа R для дублетных состояний 2Е.
Каждому значению R соответствуют два значения J =
1	1
R — ~ и J — 72 4- -,
2	2
и полу-
чаются два уровня, расстояние между которыми пропорционально R.
Случаи а и b Гунда являются предельными, и возможны промежуточные случаи.
При не очень большом мультиплетном расщеплении по мере увеличения вращатель-
ного квантового числа, т. е. с увеличением скорости вращения, будет нарушаться
связь между S и А и, наконец, станет преобладать связь между S и Л, т. е. про-
изойдет разрыв связи (5, Л). С точки зрения наглядных представлений скорость
вращения становится больше скорости прецессии. Можно сопоставить уровни энер-
гии в случаях а и b и произвести расчет перехода от одного случая к другому [330].
На рис. 25.14 показано сопоставление вращательных уровней в обоих случаях для тер-
ма 2П. Согласно общему правилу, при переходе от одного предельного случая к другому
не должны пересекаться уровни с одинаковым значением квантового числа J, сохраняющего
свой смысл (см. с. 394). При приближении к случаю Ъ уровни с одинаковыми значениями R
будут с увеличением J сближаться, в то же время уровни с одинаковыми J будут удаляться
друг от друга, так как они принадлежат разным значениям Л, а расстояния между соседними
вращательными уровнями растут с увеличением R.
При спине, равном нулю, т. е. для синглетных уровней, различие случаев а
и Ь, разумеется, пропадает. Электронный момент А складывается с вращательным
моментом R1 в полный момент R — J; квантовое число J принимает целые
значения
7 = А, А 4- 1, А 4- 2, ... ,	(25.25)
а вращательная энергия равна
EBpaul=B[j(J+l)-A2].
(25.26)
Формулы (25.25) и (25.26) могут быть получены из формул (25.20) и (25.21) для слу-
чая а при Q = Л (так как S в (25.15) равно нулю) и из формул (25.22) и (25.23)
для случая b при R — J (так как S в (25.24) равно нулю).
768
Глава 25. Электронные спектры двухатомных молекул
Рис. 25.14. Сопоставление случаев Гунда а и b для терма 2П
Помимо случаев а и b и переходных между ними, в принципе, возможны и другие случаи
связи, которые обозначают как случаи Гунда с, d и е. В случае с при сильной связи (Z, S)
L+S = и вектор Jz» дает проекцию Q, а затем Q+Я = J. В случае d момент Z сильнее свя-
зан с вращением, чем с осью молекулы; он складывается с вращательным моментом R': R14-
JD = Я, а затем R+S = J. В случае е вращательный момент Я, при сильной связи (Z, S) и от-
сутствии связи Z с осью молекулы, складывается с L+S = давая J = R+J3Jt. Случаи с и d
встречаются значительно реже, чем случаи а и Ь, а случай е практически совсем не встречается.
Для уровней с Л # О, являющихся дважды вырожденными, наблюдается наряду
с усложнением структуры, обусловленным наличием спина (при S # 0), явление Л-
удвоения. Оно состоит в расщеплении дважды вырожденных уровней под действием
вращения. При отсутствии вращения энергии положительного и отрицательного
электронных состояний при заданном Л совпадают, при наличии вращения их
энергии будут отличаться и притом тем больше, чем сильнее молекула вращается.
Благодаря этому каждый вращательный уровень оказывается расщепленным на два
и притом тем сильнее, чем больше квантовое число J; в отличие от спинового
расщепления в случае Ь, Л-расщепление растет пропорционально квадрату кванто-
вого числа. Абсолютная величина расщепления невелика, составляя доли см"1, даже
при значительных вращениях не превышает нескольких см"1.
Важную роль при рассмотрении структуры уровней энергии, обусловлен-
ной взаимодействием электронного движения с вращательным, играют свойства
симметрии.
§ 25.4. Взаимодействие электронного движения с вращательным 769
Мы видели, что Е-уровни (Л = 0) могут быть положительными и отрица-
тельными, а уровни с Л # 0 (П, Д и т.д.) дважды вырождены и соответствуют
одному положительному и одному отрицательному состоянию. При Л-удвоении
один из уровней становится положительным, а другой отрицательным. При этом
свойство положительности и отрицательности для электронного состояния опреде-
лено по отношению к отражению в плоскости, проходящей через ось молекулы.
Вращательные уровни также могут быть разделены на положительные и от-
рицательные по отношению к отражению в начале координат (см. § 19.1, с. 536).
Последовательные вращательные уровни обладают противоположной симметрией,
т. е. происходит чередование положительных и отрицательных уровней. Если рас-
сматривать чистое вращение, то при четном вращательном квантовом числе уровни
положительны, а при нечетном — отрицательны.
Положительность или отрицательность получающихся уровней вращательной
структуры электронного состояния определяется положительностью или отрицатель-
ностью электронного состояния и чередованием положительных и отрицательных
вращательных уровней.
Для состояний нулевой вращательный уровень (R = 0) положителен, следу-
ющий уровень (R = 1) отрицателен и т.д., т.е. уровни с четным R положительны,
а уровни с нечетным R отрицательны; для состояний наоборот, при четном R
вращательные уровни отрицательны, а при нечетном R положительны (рис. 25.15, а).
При мультиплетном расщеплении вращательных уровней (для Е-состояний имеет
место случай 6, см. выше, с. 765) все составляющие обладают одинаковой сим-
метрией.
3/2
5/2
6 -
5 +
4 -
3 +
2 -
1 +
0 -
J
6
5
4
3
2
1
0
J
+
7/2
7/2
3/2
5/2
3/2
+------- 1/2
Пц2 Пз/2
Случай а
б
Случай б
3/2 J
Рис. 25.15. Симметрия вращательных уровней:
а — для состояний и б — для состояний ’П и 2П
25 Зак. 1U5
770	Глава 25. Электронные спектры двухатомных молекул
Сложнее обстоит дело при Л Ф 0, т. е. для П-, Д-, ... состояний. Каждый
вращательный уровень вследствие Л-удвоения становится двойным и состоит из по-
ложительного и отрицательного подуровней, но для последовательных вращательных
уровней нижний подуровень попеременно является положительным и отрицатель-
ным, как показано на рис. 25.15, б для состояний !П и 2П, в последнем случае
отдельно для случая а и для случая Ъ [47].
в
Рис. 25.16. Связь отражения в начале
и отражения в плоскости:
а — первоначальное расположение
электрона 2 и ядер А \л В\
б — результат поворота вокруг оси С2;
в — результат последующего отражения
в плоскости av
Связь свойств положительности и от-
рицательности для электронных и вра-
щательных состояний получается следу-
ющим образом. Положительность и от-
рицательность определяются поведением
полной волновой функции при отражении
всех координат в начале, т. е. координат
ядер и электронов. Вращательная волновая
функция ^врат зависит от координат ядер
и сохраняет или меняет знак в зависимости
от того, является ли вращательное кванто-
вое число четным или нечетным 4\ Элек-
тронная волновая функция зависит от ко-
ординат электронов относительно ядер.
Отражение всех координат как ядер, так
и электронов в начале эквивалентно по-
вороту молекулы на 180° вокруг оси С2,
перпендикулярной к оси молекулы, и по-
следующему отражению в плоскости, про-
ходящей через ось молекулы и перпенди-
кулярной к оси С2 (рис. 25.16). При по-
вороте на 180° вокруг оси С2 координа-
ты электронов относительно ядер не из-
меняются и ^эл также остается неизмен-
ной. Таким образом, операция отражения
всех координат в начале для электронной
функции эквивалентна операции отраже-
ния в плоскости crv, проходящей через ось
молекулы; эту операцию мы и рассматри-
вали (ср. §24.2, формулы (24.4) и (24.8)).
Колебательная волновая функция, завися-
щая только от расстояния между ядрами,
при отражении в начале не изменяется.
Следовательно, поведение полной волно-
вой функции молекулы, гр = ^эл^кол^вращ,
при отражении всех координат в начале
определяется положительностью и отри-
цательностью V’epam по отношению к отра-
жению координат ядер в начале и поло-
жительностью или отрицательностью грэл
по отношению к отражению относитель-
ных координат электронов в плоскости,
проходящей через ось молекулы.
В случае молекул, состоящих из одинаковых атомов, четность и нечетность
уровней определяются четностью или нечетностью электронного состояния. Все
вращательные уровни данного электронного состояния имеют одинаковую четность.
Отражение координат ядер в начале означает изменение направления оси молекулы на обратное
и при четном вращательном квантовом числе ^вращ сохраняет знак, а при нечетном меняет его, см. § 19.9,
с. 569.
§25.5. Правила отбора и типы электронных переходов
771
Так как свойство (</, и) и свойство (+, -) определяют, согласно (24.11), свойство (s, а) —
симметричность и антисимметричность состояний, то будет иметься чередование симме-
тричных и антисимметричных уровней: для четных электронных состояний положительные
уровни будут симметричны, а отрицательные — антисимметричны; наоборот, для нечетных
электронных состояний положительные уровни будут антисимметричны, а отрицательные —
симметричны.
§25.5.	Правила отбора и типы электронных переходов
Основные типы электронных переходов в двухатомных молекулах определяются
правилами отбора для дипольного излучения, как общими, так и более частными,
имеющими место для случаев связи а и Ъ, рассмотренных в предыдущем параграфе.
Прежде всего для полного момента количества движения молекулы J справед-
ливо общее правило отбора (4.156), AJ = 0, ±1 (с дополнительным запретом (4.160)
перехода J' = 0 —* J" — 0).
Аналогичное правило отбора AJ? = 0, ± 1 имеет место в случае Ь Гунда для мо-
мента количества движения R = A+R1 (см. с. 766 и рис. 25.12). В результате в случае Ъ
одновременно выполняются правила отбора AJ = 0, ±1 и AR = 0, ±1. Отметим,
что когда для характеристики уровней нужны оба квантовых числа R и J, название
ветвей — R, Q, Р — относят к переходам, для которых AR — R! - R" = 1, 0, -1.
В соответствии с делением состояний молекулы на положительные и отри-
цательные имеется правило отбора, разрешающее переходы между состояниями
противоположной симметрии и запрещающее переходы между состояниями одина-
ковой симметрии:
+ <—► -.	(25.27)
Для молекул, обладающих центром симметрии, т.е. молекул симметрии
четные электронные состояния комбинируют с нечетными:
g <—> и.	(25.28)
Правило отбора (25.27) получается сразу, если учесть, что дипольный момент меняет
знак при отражении всех координат в начале, и поэтому полные волновые функции молекулы
для начального и конечного состояний должны обладать противоположной симметрией
по отношению к этой операции (ср. конец § 19.1, с. 569). Существенно, что это правило
отбора относится именно к полной волновой функции молекулы.
Правило отбора (25.28) вытекает из того, что дипольный момент электронов Рс, вхо-
дящий в матричный элемент (17.98), меняет знак при отражении электронных координат
в центре симметрии молекулы, и поэтому электронные волновые функции должны обладать
противоположной симметрией по отношению к инверсии. Это правило отбора справедливо
и для молекул, состоящих из двух изотопических атомов, поскольку в случае гомонуклеарных
молекул при изотопическом замещении сохраняется по отношению к электронному движе-
нию центр симметрии, и волновые функции будут делиться на четные и нечетные. В данном
случае симметрия молекулы по отношению к движению электронов есть D^h, а симметрия
молекулы в целом — C^v.
Для гомонуклеарных молекул имеет место также правило отбора
s <—► s, а <—> а,	(25.29)
определяемое свойствами симметрии полной волновой функции молекулы по отношению
к перестановке одинаковых ядер, приводящей к делению состояний молекул на симме-
тричные ($) и антисимметричные (а). Правило отбора (25.29) непосредственно вытекает
из инвариантности дипольного момента по отношению к перестановке одинаковых ядер
и находится в согласии с соотношением (24.11) между свойствами (</, и), (+, -) и (s, а).
25*
772	Глава 25. Электронные спектры двухатомных молекул
Важнейшей характеристикой электронных состояний молекулы, как мы видели
в §24.2, является квантовое число Л, определяющее величину проекции орбитально-
го момента количества движения на ось молекулы и равное абсолютному значению
этой проекции. Для Л имеет место правило отбора
ДА = О, ±1.	(25.30)
Таким образом, возможны переходы Е—Е, Е—П, П—II, П—Д, Д—Д и т.д. Эти
переходы можно разделить на три типа:
тип I — переходы Е—Е, для которых ДА — 0 и Л — 0,
тип 11 — переходы Е—П, П—Д, ..., для которых |ДА] = 1,
тип III — переходы П—П, Д—Д, ..., для которых ДА = 0 и Л # 0.
Правило отбора (25.30) является частным случаем общих правил отбора (4.172) для про-
екции момента количества движения. В данном случае надо положить т' = Л.', т” = Л.".
При этом переходы ДА = Л' - Л" = 0 связаны с составляющей Pz = Рц дипольного момента
по оси молекулы, а переходы ДА = Л' - Л" = ±1 с составляющими Рх и Ру дипольного
момента, перпендикулярными коси молекулы, — с Р±. Таким образом, правило отбора (25.30)
аналогично правилу отбора для явления Зеемана (см. § 14.2, с. 374).
Отметим, что обычно при обозначении электронных переходов сначала пишут
символ верхнего состояния, а затем нижнего, и соответственно переходы записыва-
ются как А'—Ля. Например, S—П обозначает переход между верхним Е-состоянием
и нижним П-состоянием, а П—Е, наоборот, обозначает переход между верхним
П-состоянием и нижним Е-состоянием. При этом испускание записывают как
А1 —► Ада, а поглощение как Л' Л” [342].
Для переходов первого типа, Е—Е, имеется дополнительное ограничение,
связанное с тем, что Е-состояния могут быть положительными (Е+) и отрицатель-
ными (Е“). Разрешены переходы лишь между Е-состояниями одной симметрии:
Е+~Е+, Е~-Е".	(25.31)
Переходы между состояниями Е+ и Е~ запрещены.
Правило отбора (25.31) получается, если учесть, что при переходах с ДА = 0 в силу
аксиальной симметрии отличен от нуля матричный элемент составляющей Pz = Рц дипольного
момента
= J	Рг(х)фп'А’(х)(1х,	(25.32)
взятый по электронным функциям VW'aw(*0 — $п"о(х) и V’n'A'(z) = ^п'о(^) комбинирующих
состояний. Для электронных состояний положительность и отрицательность определяются
по отношению к отражению в плоскости, проходящей через ось молекулы (см. (24.8)).
При таком отражении Pz не изменяется и, следовательно, функции ^п"о(ж) и ^п'о(ж) должны
иметь одинаковые свойства симметрии, т. е. обе быть положительными или обе отрицатель-
ными. Это не противоречит правилу отбора (25.27), которое относится к полным волновым
функциям, учитывающим и вращение; при переходе (25.31) будет изменяться симметрия
вращательных состояний и положительные вращательные состояния будут комбинировать
с отрицательными.
Переходы трех типов существенно отличаются своей вращательной структурой.
Для переходов первого типа, Е—Е, имеется дополнительное правило отбора, за-
прещающее Q-ветвь, и появляются только R- и Р-ветви. Для переходов второго
типа, в частности для переходов Е—П (и П—Е), появляются все три ветви, R, Р
и Q, причем в центральной ф-ветви распределение интенсивностей того же типа,
что и в ветвях R и Р, с максимумом при некотором значении J (рис. 25.17, п.
§ 25.5. Правила отбора и типы электронных переходов
тп
ср. рис. 20.14, с. 604). Для пере-
ходов третьего типа, в частно-
сти для переходов П—П, также
возможны все три ветви, однако
в Q-ветви интенсивность быстро
спадает с увеличением квантово-
го числа, не достигая максимума
(рис. 25.17,6), и эта ветвь слаба.
Запрет Q- ветви для переходов
£—£ является следствием правил
отбора (25.27) и (25.31). Последова-
тельные вращательные уровни при
электронном состоянии £ являются
попеременно положительными и от-
рицательными (см. предыдущий па-
раграф, с. 768, рис. 25.15), перехо-
ды типа R—R между уровнями оди-
Рис. 25.17. Распределение интенсивностей
в ветвях R, Р и Q: а — для переходов ДА = ±1;
б — для переходов ДА — 0 (Л # 0)
наковой симметрии с одинаковыми
значениями вращательного кванто-
вого числа R (рис. 25.18, AR = 0)
запрещены и возможны лишь пере-
ходы типа R± 1 —► R между уровнями
разной симметрии со значениями R, отличающимися на единицу (ДТ? = ±1); эти переходы
дают R- и Р-ветви, а Q-ветвь отсутствует.
При учете спина получается дальнейшая классификация типов электронных
переходов. Как и для атомов, имеет место приближенное правило отбора для полного
спинового механического момента S (см. (9.24)), Д5 = 0. Согласно этому правилу
отбора, получаются с учетом (25.30) и (25.31) следующие возможные переходы:
2Е+—2S+,
2xr-2s~,
3£+-3£+,
3S“-3S“,
(тип 1)
(25.33)
's-'n, 'п-'s, 2s-2n, 2n-2s, 3s-3n, 3n-3s,
'П-'Д, 'д-'п, 2П-2Д, 2Д-2П, 3П-3Д, 3Д-3П, ... (тип II) (25.34)
'п-'п, 2П-2П, 3П-3П,
'Д—*Д, 2Д—2Д, 3Д—3Д, ... ► (тип III)
(25.35)
Разнообразие возможных переходов увеличивается еще тем, что уровни П и Д
при S ф 0, т. е. уровни 2П, 3П, ... и 2Д, 3Д, ... могут относиться к случаю а
или к случаю b Гунда.
Наиболее проста вращательная структура переходов 1£±—,£±. Для них получа-
ются две ветви R и Р (ветвь Q отсутствует, см. выше), состоящие из простых линий.
Для переходов 2£±—2£± и 3£±—3£± также получаются только ветви R и Р, но ли-
нии будут иметь структуру, так как вращательный уровень с заданным квантовым
774
Глава 25. Электронные спектры двухатомных молекул
числом R расщепляется на две и три составляющих
соответственно (J — R ± | при S = - и J = R,
R± 1 при S = 1, см. (25.24)).
Для переходов типов II и 111 получаются все
три ветви, R, Р и Q, структура которых усложня-
ется с увеличением мультиплетности. Мы не будем
подробно разбирать возможные случаи5) и отметим
лишь, что для переходов между двумя уровнями,
относящимися к случаю а Гунда, для квантового
числа Е, определяющего проекцию спинового мо-
мента на ось молекулы (см. (25.14)), имеет место
приближенное правило отбора
ДЕ = 0,	(25.36)
Рис. 25.18. Переходы между
вращательными уровнями:
а — для электронных переходов
Е+—Е+; б — для электронных
переходов Е"—Е“
с правилами отбора
ограничивающее число возможных переходов.
В частности, для наиболее важных случаев — пере-
ходов 2П—2П и 3П—3П — мы получаем разрешенные
комбинации
2П./2-2П1/2, 2П3/2-2Пз/2 и (25 37)
3П0-3П0, 3П1—3П|, 3П2-3П2,
и отдельные полосы состоят из двух и трех под-
полос соответственно, каждая из которых име-
ет интенсивные R- и Р-ветви и слабую Q-ветвь
{см. рис. 25.17,6). Вместо одного канта у каждой
полосы будут два или три канта.
Помимо рассмотренных переходов возможны пере-
ходы, связанные с нарушением отдельных правил отбора.
При увеличении массы образующих молекулу ато-
мов увеличивается роль спин-орбитального взаимодей-
ствия электронов и появляются интеркомбинационные
переходы — нарушается правило отбора AS = 0. В част-
ности, для обычного случая молекул, обладающих чет-
ным числом электронов, будут появляться синглетно-
триплетные переходы. Для вращающихся молекул может
нарушаться правило, запрещающее переходы Е+—Е+; при нарушении вследствие вращения
аксиальной симметрии, с которой связано это правило (см. выше, с. 772), подобные пере-
ходы становятся возможными, причем в силу правила отбора (25.27) и свойств симметрии
вращательных уровней (см. рис.25.18), AR = 0, т.е. будет появляться Q-ветвь.
Наряду с дипольным излучением возможны также магнитное и квадрупольное излучения
+
(25.38)
и, в случае молекул симметрии D^h,
9 <—► g, и <—> и	(25.39)
(см. (4.154)). Для квадрупольного излучения, кроме того, согласно (4.158) и (4.159), имеем
(полагая |т| = А):
AJ = 0, ±1, ±2 и АА = 0, ±1, ±2.	(25.40)
5) Подобный разбор имеется в монографии Герцберга (см. [46|, с. 182).
§ 25.6. Примеры электронных спектров двухатомных молекул
775
Интенсивность «запрещенных» магнитных и квадрупольных переходов, как и для ато-
мов, по порядку величины в 106 раз меньше, чем интенсивность дипольных переходов,
в соответствии с общими оценками, произведенными в §4.4.
§ 25.6.	Примеры электронных спектров двухатомных молекул
Мы разберем некоторые примеры электронных спектров двухатомных молекул
и, прежде всего, спектр молекулы водорода.
Основное состояние молекулы Н2,	, было подробно рассмотрено в пре-
дыдущей главе (§ 24.7). Оно является единственным состоянием, возникающим
для молекулярной оболочки а2, состоящей из двух невозбужденных сг-электронов
(табл. 24.2, с. 733). Наряду с этим состоянием молекула водорода обладает высоко
лежащими возбужденными состояниями, получающимися при возбуждении одно-
го из а-электронов. На рис. 25.19, а показана соответствующая схема наблюденных
электронных уровней данной молекулы, одиночных и триплетных [52J; они сходятся
к границе ионизации, лежащей при 15,38 эВ, т. е. энергия ионизации молекулы Н2
близка к энергии ионизации атома Н (равной 13,60 эВ, см. (1.7)).
Помимо этих уровней, получающихся при возбуждении одного сг-электрона, найдено
некоторое число уровней, получающихся при возбуждении обоих а-электронов и аналогичных
смещенным уровням атомов с двумя внешними электронами (см. § 10.5, с. 295).
В силу правила отбора Д5 = 0, выполняющегося для молекулы водорода как
очень легкой, с высокой степенью приближения, мы имеем две системы электронных
переходов — синглетную и триплетную. Для синглетной системы получается спектр,
лежащий в далекой ультрафиолетовой области и соответствующий комбинациям
основного уровня ’S* с высокими возбужденными уровнями, и спектр, лежащий
в основном в видимой области и соответствующий комбинациям возбужденных
уровней между собой. Для триплетной системы получается спектр последнего ти-
па, т. е. лежащий в основном в видимой области. Особенностью наблюдающихся
спектров является то, что из-за значительной величины вращательной постоян-
ной В (для основного состояния она равна 60 см-1, для возбужденных состояний
еще больше), при наличии большого числа различных электронно-колебательных
переходов, отсутствует характерная для молекулярных спектров полосатая структу-
ра. Получается многолинейчатый спектр, состоящий из огромного числа отдельных
линий и напоминающий по виду сложные атомные спектры.
Интерпретация таких многолинейчатых спектров, наблюдающихся, помимо
молекулы водорода, для наиболее легких гидридов, представляет значительные труд-
ности и несколько облегчается лишь наличием серий линий, сходящихся к границам
ионизации. Для водорода интерпретацию спектра удалось произвести (см. уже упо-
минавшуюся в начале § 24.7 монографию Ричардсона [52]).
На диаграмме рис. 25.19, а, кроме устойчивых электронных состояний, пока-
зано неустойчивое триплетное состояние 3S„, получающееся из двух нормальных
атомов водорода одновременно с состоянием 1Переход в это неустойчивое
состояние из наиболее глубокого триплетного состояния приводит к возникно-
вению сплошного спектра испускания, который будет подробнее рассмотрен ниже,
в §25.7 (с. 783).
Общая схема электронных переходов для двухэлектронной молекулы Н? напоминает
схему электронных переходов для двухэлектронного атома Не. Это особенна выявляется, если
произвести классификацию электронных состояний молекулы водорода, исходя из состояний
объединенного атома, которым для молекулы водорода и является атом Не: при мысленном
776
Глава 25. Электронные спектры двухатомных молекул
Рис. 25.19. Схема электронных уровней: а — для молекулы водорода, согласно опытным
данным; б — для электрона в поле двух центров
объединении двух протонов мы получаем ядро с Z = 2. Рассматривая нормальную элек-
тронную конфигурацию молекулы водорода а2 как конфигурацию (Iscr)2 и возбуждая один
из электронов, получаем конфигурации типа IsanlX, которые даются схемой (24.30) с до-
бавлением к электрону п1Х электрона Isa в невозбужденном состоянии. Соответствующая
схема уровней для электрона в поле двух одинаковых ядер, находящихся на небольшом
расстоянии друг от друга, показана на рис. 25.19, Наличие второго электрона в состоянии
Isa приводит к образованию из каждого возбужденного уровня п1Х двух уровней, синглетного
и триплетного, причем последний, как и для атомов, лежит ниже. Сравнение рис. 25.19, a
и б показывает общее соответствие в расположении уровней, наблюдающихся на опыте,
с расположением уровней, получаемым, исходя из представления об объединенном атоме.
Это понятно, так как для сильно возбужденного электрона в молекуле водорода размеры
орбиты велики по сравнению с расстояниями между ядрами и приближение объединенного
атома является разумным. Более глубокое расположение для молекулы Н2 уровней пра и пртг
по сравнению с уровнем nsa естественным образом объясняется тем, что электрон nsa силь-
ней отталкивается электроном Isa, чем электроны в состояниях пра и пртг с более отличным
распределением электронной плотности.
Типичным примером электронного спектра молекулы, состоящей из двух одина-
ковых атомов, служит спектр молекулы азота N2. Этот спектр представляет большой
интерес, наряду со спектром молекулы кислорода О2, с точки зрения изучения про-
цессов в верхних слоях атмосферы, при которых большую роль играют возбужденные
и ионизованные молекулы Н2 и О2 [155].
На рис. 25.20 показана диаграмма важнейших наблюденных уровней и перехо-
дов для молекулы N2. Наряду с синглетными уровнями, к которым принадлежит
и основной уровень , имеются триплетные уровни, играющие существенную
роль. Буквы X, а, Ь, с, ..., А, В, С, ... служат для характеристики последователь-
ных уровней молекулы, синглетных и триплетных, согласно принятым условным
обозначениям.
Наиболее важными системами полос являются синглетная система полос
Лаймана—Берджа—Гопфильда (переход X’S*), триплетные первая, вторая
и четвертая положительные системы полос (переходы В3Пд—Л3£„, С3Пи—В3П9
§ 25.6. Примеры электронных спектров двухатомных молекул
111
Рис. 25.20. Схема уровней молекулы N2
и D3Yju—В3Пд соответственно) и интеркомбинационная система полос Вегарда—
Каплана (переход Х1^). Хотя некоторые из систем полос N2 являются
запрещенными (переходы д—д и интеркомбинационные переходы), но их удает-
ся наблюдать в соответствующих условиях — при толстых слоях в поглощении
и при большом разрежении в испускании.
Наряду с уровнями молекулы N2 на диаграмме показан основной и первый
возбужденный уровень молекулы Nj. Основной уровень этой молекулы, X2S*,
соответствует первой границе ионизации молекулы N2 (15,58 эВ), первый возбу-
жденный уровень, — второй границе ионизации этой молекулы (18,75 эВ).
778	Глава 25. Электронные спектры двухатомных молекул
Переход B2S« — Х2Е* дает так называемую первую отрицательную систему полос
азота6*.
Распределение интенсивностей в наблюдаемых системах полос соответствует
принципу Франка—Кондона (см. §25.2, с. 756).
Отметим, что первая и вторая положительные системы полос N2 и первая
отрицательная система полос наблюдаются в спектре полярных сияний. Первая
положительная и первая отрицательная системы наблюдаются и в спектрах соб-
ственного свечения верхних слоев атмосферы; в этом свечении также наблюдается
система полос N2 Вегарда—Каплана.
Другим важным примером
электронного спектра молеку-
лы, состоящей из двух одинако-
вых атомов, является электрон-
ный спектр молекулы кислоро-
да О2, для которой на рис. 25.21
приведены кривые потенциаль-
ной энергии для важнейших
электронных состояний. В от-
личие от большинства других
устойчивых двухатомных моле-
кул с четным числом электро-
нов, основным состоянием мо-
лекулы является не синглетное
состояние, а триплетное, 3Е“;
это обусловливает парамагне-
тизм газообразного кислорода,
связанный со спиновым мо-
ментом 5=1.
Наряду с запрещенными
Рис. 25.21. Кривые потенциальной энергии молекулы О2
системами атмосферных полос
(’Д^—3Е~,	3Е~), обусловливающими слабое поглощение спектра Солнца
в земной атмосфере, и системой полос Герцберга (3£+—3Е~), имеется система
полос Шумана—Рунге (3Еа—3Е^), обусловливающая сильное поглощение кисло-
рода в области 1 925-1 760 А; этим поглощением объясняется граница пропускания
воздуха для ультрафиолетовых лучей, лежащая около 1 850 А; отметим, что дальше
1 760 А находится сплошное поглощение (см. ниже, с. 782).
Для молекулы характерны первая и вторая отрицательные системы полос
(4Пи—4П^ и 2Пи—2Пр соответственно).
Вращательная структура полос молекул азота и кислорода находится в согласии
с классификацией типов электронных переходов, изложенной в §25.5.
Например, хорошим примером полос 3Е—3Е являются полосы Шумана—Рунге молеку-
лы O2(3S^—3Е~), состоящие из ветвей R и Р, каждая линия которых является тройной (5=1,
J — R, 1). При этом вследствие равенства нулю момента ядра кислорода отсутствуют
все линии с четными вращательными квантовыми числами R” (см. § 19.9, с. 569; основное
состояние 3Е~ антисимметрично, согласно (24.11), относительно перестановки ядер, полная
Название систем полос «положительная система» и «отрицательная система» возникло исторически
и связано с их наблюдением в разряде в положительном столбе и вблизи катода соответственно.
§ 25.6. Примеры электронных спектров двухатомных молекул
779
Рис. 25.22. Схема уровней молекулы СО
функция ip = 'фяд'Фкрат'Фкол'Фэл должна быть симметричной, следовательно, при антисимме-
тричности 1рэп также и ^вращ антисимметрична, В” = I, 3,5,...).
Схемы уровней и переходов, сходные с соответствующими схемами для молекул
N2 и С>2 , имеют изоэлектронные с ними молекулы СО и NO (см. с. 749). На рис. 25.22
и 25.23 показаны важнейшие уровни и переходы для молекул СО и NO.
Типичным примером электронного спектра молекулы, состоящей из двух сильно
различающихся по массам атомов, является спектр молекулы гидрида кальция, СаН.
На рис. 25.24 приведены кривые потенциальной энергии для основного дублетного
состояния Z2E+ и для ряда возбужденных дублетных состояний этой молекулы.
Характерные электронные спектры имеют радикалы CH, NH и ОН (см. конец
§24.9, с. 752). В частности, для радикала ОН имеется система полос в ультрафиоле-
товой области спектра, соответствующая переходу 2S+—2П и являющаяся типичным
примером переходов 2S—2П.
780
Глава 25. Электронные спектры двухатомных молекул
Рис. 25.24. Кривые потенциальной
энергии для молекулы СаН
Рис. 25.23. Схема уровней молекулы NO
§ 25.7.	Сплошные спектры поглощения
и испускания двухатомных молекул
До сих пор мы рассматривали дискретные спектры двухатомных молекул.
Наряду с дискретными спектрами у них наблюдаются и сплошные спектры как
в поглощении, так и в испускании. Они возникают при переходах между двумя
состояниями, по крайней мере одно из которых соответствует непрерывной после-
довательности значений энергии, т. е. непрерывному энергетическому спектру —
континууму. В отличие от атомов, для которых непрерывный энергетический спектр
примыкает только к границам ионизации (см., например, рис. 10.11, с. 295), для мо-
лекул континуумы примыкают не только к границам ионизации, но и, что особенно
существенно, к границам диссоциации. При этом они могут быть связаны как
с кривыми притяжения, так и с кривыми отталкивания. В последнем случае данной
кривой соответствует лишь непрерывный энергетический спектр, в то время как
кривой притяжения соответствует дискретный энергетический спектр ниже границы
диссоциации и непрерывный энергетический спектр выше границы диссоциации.
Это иллюстрируется рис. 25.25, а. Выше обеих границ диссоциации — нижнего
и верхнего электронных состояний — имеются континуумы, примыкающие к ним
и соответствующие кривым притяжения и кривым отталкивания; для каждого элек-
тронного состояния приведено по две кривые и соответственно по два континуума.
На рис. 25.25, б то же самое показано на схеме уровней.
Сплошные спектры, связанные с рассматриваемыми континуумами, могут по-
лучаться при переходах между дискретными нижними уровнями и непрерывными
§25.7. Сплошные спектры поглощения и испускания двухатомных молекул 781
Рис. 25.25. Континуумы для устойчивых и неустойчивых состояний:
а — на диаграмме потенциальных кривых; б — на диаграмме уровней энергии
верхними, между непрерывными нижними и дискретными верхними — оба эти слу-
чая соответствуют свободно-связанным переходам. Сплошные спектры возникают
также при переходах между непрерывными нижними и непрерывными верхними
уровнями — этот последний случай соответствует свободно-свободным перехо-
дам. Существенно, что распределение интенсивностей в сплошных спектрах, как
и в дискретных, будет определяться принципом Франка—Кондона (см. выше, § 25.2,
с. 756), т. е. наиболее вероятны будут переходы, которые изображаются вертикальны-
ми линиями, соединяющими потенциальные кривые комбинирующих состояний;
отметим также, что правила отбора для переходов между различными электронными
состояниями остаются справедливыми и в рассматриваемых случаях.
Мы не будем разбирать всех разнообразных возможностей возникновения
сплошных спектров и ограничимся характеристикой наиболее важных случаев7).
При поглощении с основного электронно-колебательного уровня будет полу-
чаться серия полос (поперечная серия Деландра, см. §25.1, с. 754), сходящаяся
к границе диссоциации верхнего электронного состояния, со сплошным спектром,
примыкающим к этой границе (см. схему рис. 25.26) и соответствующим фотодис-
социации. При этом обычно по крайней мере один из получающихся при фотодис-
социации атомов является возбужденным.
Сплошные спектры поглощения, связанные с фотодиссоциацией, хорошо наблюдаются,
в частности, для молекул галоидов; на примере молекулы J2 такие спектры были впервые
интерпретированы Франком в 1925 г. [193]. Диссоциация молекул галоидов типа Х2 происходит
на нормальный атом в состоянии пр5 2Р3д и на возбужденный атом в состоянии пр5 2Р\/2
(см. гл. 11, с. 312).
Определение из опыта положения i/rp границы схождения полосы, т. е. границы
диссоциации, имеет существенное значение. По положению этой границы можно
7) Подробному рассмотрению сплошных спектров как атомных, так и молекулярных посвящены
специальная монография и обзор Финкельбурга [93], см. также монографию Герцберга [46].
782
Глава 25. Электронные спектры двухатомных молекул
определять со значительной точностью энергии диссоциации. Если обозначить
через i/0 энергию электронного возбуждения и через D' — энергию диссоциации
возбужденного электронного состояния, то (см. рис. 25.26)
(25.41)
/////////////////////////,
Рис. 25.26. Схождение полос
к границе диссоциации
^гр = Щ + D1
и, зная i/o, можно найти D1. С другой стороны, i/rp
можно представить в виде
i/rp - D" + W,	(25.42)
где D" — энергия диссоциации основного элек-
тронного состояния, a W — энергия возбуждения
продуктов диссоциации. Таким образом, если W
известно, то, зная можно определить энергию
диссоциации молекулы в основном электронном
состоянии, что особенно важно.
Примером может служить схождение систе-
мы полос Шумана—Рунге, 3£~—3£~ (см. с. 778),
в случае молекулы О2 к границе диссоциации
1 759 А, что соответствует 7,05 эВ. При этом мо-
лекула в возбужденном состоянии 3SJ диссоции-
рует на атом О в невозбужденном состоянии 3Р
и на атом О в возбужденном состоянии }D, тогда
как молекула в основном триплетном состоянии
диссоциирует на два невозбужденных атома
в состояниях 3Р. Таким образом, энергия возбу-
ждения W = E(]D) - Р(3Р) = 15 868 см"1 = 1,97 эВ
(см. табл. 11.4, с. 308). Согласно (25.42), энергия
диссоциации молекулы О2 равна
D" = i/rp - W = 7,05 эВ - 1,97 эВ = 5,08 эВ.	(25.43)
Следует отметить, что в данном случае состояния атомов, возникающих в резуль-
тате диссоциации молекулы в возбужденном состоянии 3SJ, определяются вполне
однозначно: состояние 3SJ может возникать лишь из состояний 3Р и ]D или из со-
стояний 3Р и ]S (из двух атомов в состояниях 3Р оно не возникает, см. §24.3,
с. 726), а в последнем случае W = 4,19 эВ и энергия диссоциации получалась бы
меньше энергии самого высокого наблюдаемого колебательного уровня в основном
состоянии, что невозможно.
В силу принципа Франка—Койдона границу схождения полос не удается на-
блюдать, если потенциальная кривая верхнего электронного состояния сдвинута
относительно кривой нижнего электронного состояния так, что переходы, соответ-
ствующие границе диссоциации, маловероятны, как показано на рис. 25.27. В данном
случае будет наблюдаться сплошной спектр с максимумом поглощения, лежащим
при частотах и > i/rp.
На рис. 25.27 показан вид колебательных волновых функций для нижнего дискретного
состояния и для верхних непрерывных состояний. В последнем случае волновые функции
непрерывного энергетического спектра могут быть приближенно представлены при помощи
функций Эйри, подробно исследованных Фоком (см. [299], а также [55], т. 1, с. 571).
Квадрат интеграла наложения (см. (25.2)) будет наибольшим для переходов, соответствующих
неизменному расстоянию между ядрами. Рис. 25.27 соответствует случаю молекулы С12 [332].
§ 25.7. Сплошные спектры поглощения и испускания двухатомных молекул 783
Рис. 25.27. Сплошное поглощение при сдвиге потенциальных кривых
Возможны и сплошные спектры погло-
щения, возникающие при переходе с основ-
ного электронного уровня на непрерывные
уровни, соответствующие кривой отталкива-
ния для неустойчивого верхнего электронного
состояния (рис. 25.28). Распределение интен-
сивностей в сплошном спектре и в этом слу-
чае будет соответствовать принципу Франка-
Кондона.
Процессами, обратными поглощению при
переходах с нижних дискретных на верхние не-
прерывные уровни, являются процессы испус-
кания при переходах с верхних непрерывных
уровней на нижние дискретные уровни. Это
будут процессы образования устойчивой моле-
кулы при двойном столкновении с испусканием
фотона — рекомбинация с излучением. Такие
Рис. 25.28. Переход при поглощении
процессы, хотя и возможны, но весьма малове-	на кривую отталкивания
роятны, так как испускание должно произойти во время столкновения (например,
в случае рис. 25.28, при сближении сталкивающихся атомов на расстояние р « ре),
длительность которого в обычных условиях порядка 10“13 с и очень мала при срав-
нении со временем жизни возбужденных состояний, имеющем порядок 10~8 с.
784
Глава 25. Электронные спектры двухатомных молекул
Гораздо более вероятна, особенно при значительных давлениях, рекомбинация ато-
мов без излучения при тройных столкновениях8*.
Интенсивные сплошные спектры
испускания могут получаться при пе-
реходах с дискретных верхних уров-
ней на непрерывные нижние уров-
ни. Важнейшим случаем сплошного
спектра испускания такого типа явля-
ется спектр испускания молекулы во-
дорода, возникающий при триплет-
ном переходе из верхнего устойчивого
электронного состояния в ниж-
нее неустойчивое электронное состо-
яние , как показано на рис. 25.29.
В данном случае кривая оттал-
кивания нижнего электронного со-
стояния идет весьма круто, и в со-
ответствии с принципом Франка-
Кондона оказываются интенсивными,
при возбуждении ряда колебатель-
ных уровней верхнего электронно-
Рис.25.29. Схема возникновения сплошного состояния, переходы в значитель-
спектра молекулы водорода	ном диапазоне частот, соответствую-
щем длинам волн примерно от 5 000
до 1600 А. При испускании фотона в этом диапазоне частот возбужденная молекула
водорода диссоциирует и получающиеся невозбужденные атомы водорода разлетают-
ся с кинетической энергией, примерно равной U{р) (для перехода при расстоянии р
между ядрами).
Сплошной спектр, получаемый в водородных трубках специальной конструкции, широко
применяется при исследованиях спектров поглощения в ультрафиолетовой области. Однако
его интенсивность в водородной трубке все же недостаточно велика дня быстрой съемки
спектров поглощения. Поэтому в настоящее время актуальной задачей является создание
более мощных источников сплошного спектра в ультрафиолетовой области. Таким источником
может служить конденсированный разряд через капилляр [333] или узкое отверстие [334].
§ 25.8.	Возмущения и предиссоциация в спектрах двухатомных молекул
Для молекул является характерным наличие ряда независимых последователь-
ностей уровней, расположенных в тех же диапазонах энергий. Эю могут быть
юследовательности близко расположенных дискретных электронною? г юательно-
фащательных уровней или последовательности непрерывных уровней о косящихся
к разным континуумам. Например, на рис. 25.30 показаны две дискретные по-
следовательности молекулярных уровней и одна непрерывная последов . юность.
При выполнении определенных условий в некоторых интервалах уровни различных
последовательностей нельзя считать независимыми — они влияют друг на друга —
возмущают друг друга, что проявляется в спектрах различным образом. Могут на-
блюдаться смещения уровней энергии, изменения интенсивностей спектральных
линий и даже их исчезновение. Взаимодействия уровней — их возмущения, на-
блюдаются и в атомных спектрах, однако именно в молекулярных спектрах их учет
8* Для случая йода сплошной спектр, получающийся при рекомбинации атомов J, удалось наблюдать
в 1929 г. Кондратьеву и Лейпунскому [331|.
§ 25.8. Возмущения и предиссоциация в спектрах двухатомных молекул 785
особенно существен, ввиду разнообразия последовательно-
стей уровней и близкого расположения соседних уровней
в отдельных последовательностях.
Мы уже рассматривали примеры возмущений в спектрах ато-
мов для случая смещенных уровней в двухэлектронных атомных
спектрах (см. § 10.5, с. 299) и в колебательных спектрах сложных
молекул (резонанс Ферми, §23.3, с. 696). Существенным является
наличие точного или приближенного случайного вырождения со-
стояний, могущих взаимодействовать между собой. С квантовоме-
ханической точки зрения возмущения являются результатом того,
что практически всегда исходят не из точного, а из приближенного
решения задачи об уровнях энергии атомной системы и пренебре-
гают определенными взаимодействиями (например, электронного
и вращательного движений в молекулах); это дает независимые
последовательности уровней. При учете первоначально отброшен-
ных взаимодействий действительные состояния оказываются уже
иными, что приближенно учитывается по методу возмущений, как
это было сделано при рассмотрении резонанса Ферми для простей-
шего случая двух дискретных уровней. Выведенные там формулы
справедливы и для любого случая взаимодействия двух дискрет-
ных уровней; от рода взаимодействия зависит лишь вид энергии
возмущения V.
Рис. 25.30. Попарные
возмущения
вращательных уровней
Взаимодействия уровней, принадлежащих к определенным электронным и вра-
щательным состояниям, подчиняются и определенным правилам отбора, которые
были впервые установлены Кронигом [335, 47]. Эти правила отбора следующие:
1.	Взаимодействуют уровни с одинаковыми значениями J:
J\ = J2.	(25.44)
2.	Симметрия уровней по отношению к операциям отражения должна быть
одинакова, т. е. положительные уровни взаимодействуют с положительными и от-
рицательные — с отрицательными, а в случае одинаковых ядер четные с четными
и нечетные с нечетными:
+ <—> +, - <—*	g<—► g,	U <—> и9\	(25.45)
3.	Для взаимодействующих уровней квантовые числа Л не должны различаться
более чем на 1:
Ai = Л2, Л2± 1.	(25.46)
4.	Мультиплетность взаимодействующих уровней должна быть одинакова:
S}=S2.	(25.47)
Это последнее правило справедливо лишь при пренебрежении спин-орбитальным
взаимодействием и для тяжелых молекул нарушается.
Если имеются две дискретные последовательности вращательных уровней, при-
надлежащие к электронно-колебательным состояниям, взаимодействие которых
допускается правилами отбора (25.45)-(25.47), то при близости уровней с одина-
ковыми J будут наблюдаться попарные возмущения. На рис. 25.31 схематически
показан пример такого расположения уровней. В результате взаимодействия каждой
пары уровней один из уровней будет сдвинут вверх, а другой вниз — мы получаем
9) Отсюда, согласно (24.11), следует, что симметричные уровни взаимодействуют с симметричными,
и антисимметричные с антисимметричными, т. е. взаимодействуют уровни, обладающие одинаковой
симметрией относительно перестановки ядер.
786
Глава 25. Электронные спектры двухатомных молекул
Рис. 25.31. Разные последо-
вательности уровней энергии
как бы отталкивание близких уровней, тем большее,
чем ближе были бы расположены эти уровни при от-
сутствии взаимодействия. Первоначальное располо-
жение уровней показано пунктиром, окончатель-
ное — сплошными линиями. В спектрах двухатом-
ных молекул наблюдаются многочисленные приме-
ры таких возмущений, проявляющихся на опыте
в виде нарушения правильности расположения вра-
щательных линий в отдельных ветвях|0).
Наиболее важным типом возмущений в спектрах
молекул являются возмущения, возникающие вслед-
ствие взаимодействия дискретных уровней с не-
прерывными, образующими континуумы, примы-
кающие к границам диссоциации. Результатом та-
ких возмущений является безызлучательный пере-
ход из дискретного состояния в непрерывное, со-
провождающийся диссоциацией (показанный стрел-
кой на рис. 25.30). Это явление получило название
предиссоциации', его изучение весьма существенно
для определения схем электронных уровней моле-
кул и позволяет в ряде случаев определить значения
энергии диссоциации. Так как при предиссоциации
сокращается время жизни возбужденного дискретно-
го уровня, совпадающего по энергии с непрерывным
уровнем, то этот дискретный уровень расширяется.
В спектрах поглощения наблюдается соответственно
расширение вращательных линий и получаются диф-
фузные полосы, в которых вращательная структура
полностью или частично исчезает. В спектрах испус-
кания соответствующие полосы сильно ослабляются
или совсем исчезают.
Для предиссоциации, связанной с переходом
молекулы из устойчивого электронного состояния
в неустойчивое, наряду с общими правилами отбо-
ра (25.44)-(25.47) для возмущений необходимо учи-
тывать принцип Франка—Кондона. Так как пре-
диссоциация является переходом без излучения, то
для потенциальных кривых соответствующих элек-
тронных состояний при той же энергии расстояния
между ядрами должны быть одинаковы, что имеет
место при наличии пересечения этих кривых, как показано для типичного случая
на рис. 25.32,,). Предиссоциация будет наблюдаться для уровней, близких к точке
пересечения, и наибольшая вероятность переходов, а следовательно, и наиболь-
шее расширение будут получаться для уровней энергии, лежащих на высоте точки
пересечения. Высота А этой точки над границей диссоциации будет тем больше,
чем круче идет кривая отталкивания. При достаточно пологом ходе кривой оттал-
10)	Ряд случаев возмущений в спектрах двухатомных молекул был подробно рассмотрен Степано-
вым [336].
1 Возможен также случай, когда кривые, не пересекаясь, близко подходят друг к другу, как это имеет
место для кривой отталкивания, изображенной на рис. 25.32 пунктиром.
§ 25.8. Возмущения и предиссоциация в спектрах двухатомных молекул 787
кивания Д может быть мало и то-
гда граница предиссоциации будет
близка к границе диссоциации.
Такой случай имеет место, в част-
ности, для молекулы азота. В элек-
тронном состоянии В3П3 (рис. 25.20)
наблюдается граница предиссоциации,
лежащая на высоте 9,88 эВ по отноше-
нию к основному состоянию, что всего
на 0,12 эВ больше энергии диссоциа-
ции Z>n2 — 9,76 эВ (см. с. 748).
Наряду с предиссоциацией опи-
санного типа возможна предиссо-
циация вращением, получающаяся
благодаря безызлучательному пе-
реходу с высоких вращательных
уровней данного электронно-ко-
лебательного состояния на непре-
рывные уровни, соответствующие
тому же электронному состоянию.
На рис. 25.33 показана схема уров-
Рис. 25.32. Схема предиссоциации
ней для подобного случая. С дискретных вращательных уровней, лежащих выше
границы диссоциации, возможен безызлучательный переход на непрерывные уров-
ни, который и представляет диссоциацию вращением. Рис. 25.33 относится к очень
непрочной молекуле гидрида ртути HgH в основном электронном состоянии, с энер-
гией диссоциации £>нён = 3 050 см"1 = 0,378 эВ [340].
Более подробное рассмотрение предиссоциации вращением, а также вообще различных
случаев предиссоциации можно найти в монографии Герцберга [46] (см. также [339]). Теория
предиссоциации была рассмотрена Райсом [337] и Степановым [338].
Е, см
4000
3000
К
23
К
^-^v = 4
----v = 3
-------20	Ш=-----------------------------v = 2
ZZZZZZ	—— io
ZZZZZZZZ “r~	----------------------------------v= 1
...	10
2000
1000
Рис. 25.33. Предиссоциация вращением
ГЛАВА 26
ЭЛЕКТРОННЫЕ СОСТОЯНИЯ И ХИМИЧЕСКАЯ СВЯЗЬ
В МНОГОАТОМНЫХ МОЛЕКУЛАХ
§26.1. Общая характеристика электронных состояний
многоатомных молекул
Как мы видели в гл. 24 и 25, задача об электронных состояниях и электрон-
ных спектрах молекул является весьма сложной даже для простейших молекул —
двухатомных. Она еще усложняется при переходе от двухатомных молекул к много-
атомным, и при этом возникают новые закономерности, наиболее резко проявляю-
щиеся для нелинейных многоатомных молекул. Линейные многоатомные молекулы
обладают рядом свойств, аналогичных свойствам двухатомных молекул и связан-
ных с наличием оси симметрии бесконечного порядка. Поэтому они во многих
отношениях представляют особый случай, схожий со случаем двухатомных молекул,
но более сложный.
В соответствии с разнообразием строения многоатомных молекул (см. гл. 18,
особенно § 18.1) их электронные состояния также весьма разнообразны. Наблюда-
ются электронные спектры самых различных типов, начиная от спектров с типичной
дискретной структурой, в случае простейших и наиболее симметричных молекул,
и кончая сплошными спектрами, особенно характерными для сложных многоатом-
ных молекул
Многоатомная молекула состоит не менее чем из трех ядер и из значительного
числа электронов. Устойчивость ее электронных состояний определяется свойства-
ми этих состояний по отношению к взаимному расположению ядер. Для решения
вопроса об устойчивости электронных состояний многоатомных молекул — вопроса
о химической связи — применяют приближенные методы, представляющие обобще-
ние и дальнейшее развитие методов рассмотрения химической связи для двухатомных
молекул (см. гл. 24). В отличие от двухатомных молекул, в которых существует толь-
ко одна химическая связь, в устойчивой трехатомной молекуле типа XYZ имеются
уже две связи X—Y и X—Z, и число связей возрастает с увеличением числа атомов.
Важнейшее значение имеет вопрос о взаимном расположении связей, качественное
решение которого дается в теории направленной валентности. Краткому изложению
этой теории, играющей весьма существенную роль при более детальном рассмотре-
нии электронных состояний многоатомных молекул, посвящен следующий пара-
граф (§26.2). В данном параграфе мы разберем общие характеристики электронных
состояний многоатомных молекул, рассматривая сначала многоатомную молекулу
как целое, а затем учитывая заполнение ее электронных оболочек, т. е. применяя два
возможных подхода к изучению электронных состояний молекулы, как это делалось
выше для двухатомной молекулы (ср. с. 719).
Электронные состояния молекулы в целом могут быть классифицированы по их
свойствам симметрии. Для молекулы, обладающей определенной пространственной
§ 26.1. Характеристика электронных состояний многоатомных молекул 789
симметрией, т. е. для молекулы, равновесная конфигурация которой принадле-
жит к определенной точечной группе, электронные состояния относятся к типам
симметрии, возможным для данной группы. Классификация по типам симметрии
для электронных состояний та же, что и классификация по типам симметрии
для колебательных состояний, рассмотренная нами в гл. 22. Приведенные там
таблицы (табл. 22.1-22.11) полностью применимы для электронных состояний мно-
гоатомных молекул, относящихся к соответствующим точечным группам.
В случае групп низшей симметрии получаются только невырожденные элек-
тронные состояния (А и В), в случае групп средней симметрии — невырожденные
и дважды вырожденные состояния (Л, В и Е) и в случае групп высшей симметрии —
невырожденные, дважды вырожденные и трижды вырожденные состояния (А, В,
Е и F). По отношению к заданной оси симметрии второго порядка, к заданной
плоскости симметрии и к центру симметрии каждое электронное состояние, как
и каждое колебательное, обладает свойством + или —. В частности, для молекулы,
имеющей центр симметрии, все электронные состояния распадаются на четные (д)
и нечетные (и). Для молекул, относящихся к группам Dnh, Dn, Cnv и т.д. с выде-
ленной осью симметрии, по отношению к горизонтальным осям С*2, вертикальным
плоскостям av и горизонтальной плоскости ah электронные состояния распадаются
на симметричные и антисимметричные (что указывается индексами 1, 2 и 1, 2, 3
для осей С2 и плоскостей av и штрихами для плоскости ад, см. с. 661).
Для электронных состояний, принадлежащих к различным типам симметрии, электрон-
ные волновые функции обладают различной симметрией и преобразуются различным образом
при операциях симметрии (согласно различным неприводимым
представлениям соответствующей точечной группы, к которой
принадлежит молекула, см. с. 665). Это можно иллюстрировать
на примере одноэлектронной волновой функции молекулы, обла-
дающей плоскостью симметрии. Волновая функция либо имеет
одинаковую величину и одинаковый знак в точках, симметрично
расположенных относительно плоскости (рис. 26.1, а), — тогда
она не изменяется при отражении в этой плоскости и является
симметричной, либо имеет одинаковую величину, но противо-
положный знак в таких точках (рис. 26.1,6) — тогда она меняет
знак при отражении и является антисимметричной. В последнем
случае волновая функция обращается в нуль в плоскости симме-
трии, т. е. плоскость симметрии представляет узловую плоскость.
Мы уже рассматривали подобный случай для двухатомной моле-
кулы симметрии Dxh (см. с. 731, рис. 24.5): волновые функции
состояний и 1гд являются антисимметричными относительно
средней плоскости и обращаются в ней в нуль.
Для невырожденных электронных состояний волновая фун-
кция при всех операциях симметрии переходит сама в себя с точ-
ностью до знака (если она вещественная) и с точностью до мно-
жителя, равного по модулю единице (если она комплексная), и ее
квадрат (для комплексной функции квадрат модуля), определяю-
щий электронную плотность, не изменяется при этих операциях.
Для вырожденных электронных состояний волновые функ-
ции преобразуются между собой неприводимым образом. Это
значит, что их нельзя выбрать так, чтобы они преобразовывались
с точностью до множителя сами в себя. Примером могут служить
волновые функции дважды вырожденного типа симметрии Е
для квадратной молекулы симметрии D^h, состоящей из четырех
атомов, расположенных в вершинах квадрата (рис. 26.2). Волно-
вые функции, антисимметричные относительно плоскостей
(у)
и av , являющихся для них узловыми плоскостями, переходят
б
Рис. 26.1. Волновые
функции молекулы,
обладающей плоскостью
симметрии:
а — симметричная
волновая функция;
б — антисимметричная
волновая функция
790 Глава 26. Электронные состояния в многоатомных молекулах
друг в друга при повороте С4 на 90° вокруг оси четвертого порядка (перпендикулярной
к плоскости чертежа)
Рис. 26.2. Волновые функции дважды
вырожденных состояний для квадратной
молекулы симметрии D4h
Для линейных многоатомных молекул классификация электронных состояний
та же, что и классификация для двухатомных молекул, подробно рассмотрен-
ная в гл. 24. Наиболее существенно, что для этих молекул электронные состо-
яния характеризуются квантовым чи-
слом Л, определяющим значение про-
екции полного орбитального механиче-
ского момента, и соответственно раз-
деляются на невырожденные состояния
с Л = 0 (S-состояния, которые могут
быть S+ и S') и на дважды выро-
жденные состояния с Л = 1,2,... (П-,
Д-, ... состояния). При наличии цен-
тра симметрии, т. е. для молекул сим-
метрии Х>ооЛ, например молекулы СО2,
все состояния делятся на четные и не-
четные, и мы получаем набор возмож-
ных состояний (24.5).
Следует подчеркнуть, что для нелинейных многоатомных молекул не имеет
определенного значения не только полный орбитальный момент L, но и его
проекция на какое-либо направление, связанное с молекулой. Среднее значение
такой проекции равно нулю, и классификация состояний по значениям Л уже
невозможна* 2).
Для нелинейных многоатомных молекул, обладающих одной или нескольки-
ми осями симметрии конечного порядка, п 3, так же как и для линейных
многоатомных молекул, согласно общей классификации, наряду с невырожденны-
ми, в принципе, возможны вырожденные электронные состояния. Однако можно
показать, что подобные состояния неустойчивы. Таким образом, для нелинейных
многоатомных молекул возможны только невырожденные устойчивые состояния, а вы-
рожденные состояния для них неустойчивы. Это положение было доказано Яном
и Теллером [344] и его часто называют теоремой Яна—Теллера. Оно связано с тем,
что для нелинейных многоатомных молекул симметричная конфигурация ядер,
являющаяся при вырожденном электронном состоянии устойчивой относительно
полносимметричных колебаний, оказывается, вообще говоря, неустойчивой по от-
ношению к некоторым неполносимметричным колебаниям. В противоположность
этому вырожденные состояния линейных молекул могут быть устойчивыми. Линей-
ная конфигурация ядер, устойчивая относительно полносимметричных колебаний,
происходящих вдоль оси молекулы, вообще говоря, устойчива и относительно непол-
носимметричных колебаний, перпендикулярных к оси молекулы. Таким образом,
неустойчивость вырожденных электронных состояний представляет особенность,
характерную для нелинейных молекул.
Эти функции будут типа Ед, т.е. четными, если они антисимметричны и относительно плоскости
молекулы, и типа Еи, т.е. нечетными, если они симметричны относительно этой плоскости. Однако
с точки зрения вырождения несущественно, являются ли они четными или нечетными.
2) Можно лишь ввести, при наличии выделенной оси конечного порядка Сп, понятие о квазимоменте
относительно этой оси (ср. [15], с. 127).
§ 26.1. Характеристика электронных состояний многоатомных молекул 791
Рис. 26.3. Устойчивость
вырожденных колебаний
для линейной молекулы:
а — дважды вырожденное
колебание; б — угловая
зависимость волновых функций;
в — зависимость потенциальной
энергии от смещения б
Мы не будем приводить доказательства сформулированного положения 3\ Это дока-
зательство основано на применении теории групп при расчете зависимости электронной
энергии от смещений ядер (по отношению к заданной симметричной конфигурации).
Мы ограничимся рассмотрением двух примеров, показывающих, в чем причина различ-
ных свойств вырожденных электронных состояний по отношению к колебаниям в случае
линейных и в случае нелинейных молекул.
Предположим, что для равновесной конфигурации молекулы электронное состояние
вырождено и рассмотрим влияние смещений ядер, которые нарушают симметрию этой кон-
фигурации и приводят к расщеплению первоначального вырожденного электронного уровня.
Разберем сначала случай линейной молекулы СО2 симметрии Dxh в дважды выро-
жденном электронном П-состоянии с А = 1. При деформационном колебании, происходя-
щем в плоскости xz (рис. 26.3, а), симметрия молекулы
уменьшается и будет соответствовать группе Czv с осью
симметрии С2 второго порядка, совпадающей с осью х.
Мы имеем две электронные функции для П-состояния,
V’o cosy? и V’o sin у? (см. (21.13), А = 1), зависимость ко-
торых от угла у? изображена на рис. 26.3, б, причем
первая функция симметрична относительно плоско-
сти ОСО (положительна), а вторая антисимметрич-
на. При смещении б, отличном от нуля, для соот-
ветствующих состояний энергия будет различна, т. е.
первоначально вырожденный П-уровень расщепляет-
ся на два подуровня, положительный и отрицатель-
ный, и функции cos у?, sin у? будут правильными
функциями нулевого приближения. Получится зави-
симость энергии подуровней от смещения бу изобра-
женная на рис. 26.3, в, при этом из симметрии распре-
деления электронной плотности относительно плоско-
сти yz следует, что при изменении знака смещения б
на обратный энергии обоих подуровней будут те же
самые, и поэтому значение б = 0 отвечает для обоих
подуровней минимуму электронной энергии как функ-
ции б, т. е. электронное состояние при расщеплении
остается устойчивым 4\
Рассмотрим теперь случай дважды вырожденного
электронного состояния типа Е нелинейной квадрат-
ной молекулы симметрии Р4Л (см. выше, рис. 26.2).
Симметрия молекулы нарушается при колебаниях ти-
па В\, антисимметричных относительно оси С4, кото-
рые изображены на рис. 26.4; при этом рис. 26.4, ау б
отличаются от рис. 26.4, в, г изменением фазы ко-
лебаний на 180°, т. е. изменением знака смещений.
Для первого электронного состояния с узловой плос-
костью	(рис. 26.4, а и в) смещениям б и -б будут
соответствовать, вообще говоря, различные энергии
и притом отличные от значения при б = 0 мы полу-
чим какую-то зависимость энергии от б (рис. 26.4, д
кривая Е\)у причем нет причин, обусловленных сим-
метрией, по которым значению б = 0 соответствовал
бы минимум. Для второго электронного состояния
с узловой плоскостью <№ (рис. 26.4, б и г) как легко
видеть, энергия при смещении б будет такая же, как
Полное доказательство имеется в работе Яна и Теллера [344], а его идея изложена в книге Ландау
и Лифшица ([131], с. 423).
4) В принципе может быть и максимум, однако, как правило, наиболее симметричной конфигура-
ции (<5 = 0) будет соответствовать именно минимум.
792
Глава 26. Электронные состояния в многоатомных молекулах
Рис. 26.4. Неустойчивость вырожденных
состояний для нелинейной молекулы:
а — первое состояние при смещении б\
б — второе состояние при смещении б\
в —- первое состояние при смещении -б\
г — второе состояние при смещении -д;
д — зависимость потенциальной энергии
от смещения при отсутствии минимума;
е — зависимость потенциальной энергии
от смещения при наличии сдвинутого
минимума
для первого электронного состояния при смеще-
нии —б и наоборот; действительно, рис. 26.4,6 от-
личается от рис. 26.4, <?, а рис. 26.4, г от рис. 26.4, а
лишь поворотом на 90°. Мы получаем на рис. 26.4, д
кривую Е2, причем кривые Е\ и Е2 пересекаются
при б = 0, в согласии с тем, что для конфи-
гурации симметрии D4h электронные состояния
вырождены и их энергии совпадают. Может ока-
заться, что между значениями смещения б и — б
энергия имеет минимум (рис. 26.4, е); для обоих
электронных состояний этот минимум имеет оди-
наковую форму, однако соответствует не б = 0,
а другому значению, т. е. устойчивой будет кон-
фигурация более низкой симметрии, для которой
электронные состояния уже невырождены.
Разобранный пример молекулы симметрии
D4h является типичным для нелинейных много-
атомных молекул, принадлежащих к точечным
группам средней и высшей симметрии конечно-
го порядка. Только в случае линейных молекул
симметрия равновесной конфигурации такова, что
вырожденные электронные состояния могут быть
устойчивыми.
До сих пор мы рассматривали свойства
электронных состояний многоатомных мо-
лекул, которые определяются их простран-
ственной симметрией. Вырождение, о кото-
ром шла речь, являлось орбитальным выро-
ждением. Большое значение имеет характе-
ристика электронных состояний многоатом-
ных молекул их мультиплетностью х — 25-1-1,
где 5 — значение спинового квантового чи-
сла, определяющего полный спиновый мо-
мент. Подобно случаю двухатомных молекул
этот момент, как правило, приближенно со-
храняется и квантовое число 5 имеет физический смысл. В принципе, так же
как и для атомов (см. с. 251), для молекул с четным числом электронов 5 может
принимать значения 5 = 0,1,..., а для молекул с нечетным числом электронов —
1 3
значения 5	. Однако фактически в первом случае обычно 5 = 0 или 5=1,
а во втором	jto можно понять, исходя из представления о молекулярных
электронных оболочках многоатомных молекул, подобно тому, как это было сделано
в Li. 24 для двухатомных молекул (ср. с. 733).
Отдельные молекулярные электроны по своей симметрии относятся к типам
симметрии, определяемым симметрией равновесной конфигурации, т. е. к невыро-
жденным, к дважды вырожденным и к трижды вырожденным типам. При учете двух
возможных ориентаций спина дня электрона в заданном молекулярном состоянии,
характеризуемом определенным распределением электронной плотности, мы полу-
чаем оболочки, заполняемые соответственно двумя, четырьмя и шестью эквивалент-
ными молекулярными электронами, причем наиболее типичными являются оболоч-
ки, получающиеся для невырожденных типов симметрии и заполняемые двумя экви-
валентными электронами. Только такие электронные оболочки возможны для много-
§26.1. Характеристика электронных состояний многоатомных молекул 793
атомных молекул, относящихся к группам низшей симметрии, т. е. для значительного
большинства молекул; число молекул, относящихся к группам средней (в частности,
линейных) и высшей симметрии, сравнительно невелико. Уже среди трехатомных
молекул нелинейные (т. е. симметрии Cs или C2V) встречаются чаще линейных.
Из четырехатомных молекул только молекулы типа XY3 (симметрии C^v или
и немногочисленные линейные молекулы не относятся к группам низшей симме-
трии. С увеличением числа атомов все большая доля молекул обладает низшей сим-
метрией и все реже встречаются молекулы средней и особенно высшей симметрии.
Рассмотрим подробнее важнейший случай молекул, имеющих лишь молеку-
лярные оболочки, заполняемые двумя электронами. Для химически устойчивых
молекул, обладающих, как правило, четным числом электронов.			, в основном элек- _________ 1
		 А	__________			 А	
	и __ А		и ___ 1	1 .	1
иметься лишь заполнен-	и 		 9	_________	I 	 1	1 __________ 1
ные оболочки и полный 5 = 0		; 5=0,1		1 	э	5 = 0, 1,2 	
спин 5 = 0 (рис. 26.5, а).			2 	э	..	2 	э	1
	2	2	
	— Э			э	
	2	2	
кулы один из электро-	а	6		в
нов переходит в незапол-			
	__ А	____	— А	__________ А
ненную оболочку и воз-	и 	А					и 	 1	и ,	л, ___________ 1
никают два неэквивалент-			и	1 	А	С —_1, 3	*
ных электрона, что при- S=*j		-|сч II 1 7Г	и -2 	э	3 2 2		1 	1
ВОДИ! К ЗНйЧСНИЯМ D —	2	2	2
		Э		__ А	____________ э
0,1 (рис. 26.5, б). Таким	2	2	2
образом, основное состоя-	г	д		е
ние молекулы будет син-
глетным, а возбужден-
ные состояния будут син-
глетными и триплетными.
Для молекул с нечетным
Рис. 26.5. Заполнение молекулярных электронных оболочек:
а, б, в — при четном числе электронов;
г, д, е — при нечетном числе электронов.
Справа указаны числа заполнения молекулярных оболочек
числом электронов, обычно неустойчивых, например, для разного рода радикалов,
в основном состоянии будет иметься один неспаренный электрон (рис. 26.5,г) и пол-
ный спин равен спину этого электрона, т. е. S — -. Именно этот электрон будет легче
всего возбуждаться, переходя в свободные оболочки (рис. 26.5, д), и опять возникают
состояния с S = -. Таким образом, как основное состояние, так и возбужденные
состояния будут дублетными.
В принципе, возможно при нечетном числе электронов возбуждение электрона запол-
ненной оболочки, приводящее к состояниям с S =
£ 3
2’2
(рис. 26.5, е), однако это будет
редким случаем. Еще более редким будет случай возбуждения при четном числе электронов
двух электронов из двух разных оболочек, приводящего к состояниям с S = О, 1, 2 (рис. 26.5, в).
Для молекул средней и высшей симметрии, имеющих также и молекуляр-
ные оболочки, заполняемые четырьмя и шестью электронами, при четном числе
электронов в основном состоянии могут быть незаполненные оболочки с двумя
и с четырьмя электронами (последнее для оболочек, заполняемых шестью элек-
тронами), что приводит к возможному значению 5=1, как в случае двухатомной
молекулы кислорода О2 с основным состоянием 3S~. Однако такие случаи редки.
Редко будет встречаться и спин S > 1 для возбужденных состояний. При нечетном
числе электронов по-прежнему, как правило, и для основного, и для возбужденных
794
Глава 26. Электронные состояния в многоатомных молекулах
1
состояний получается S = Разбор различных конкретных возможностей пока-
зывает, что вообще в подавляющем большинстве случаев сформулированные выше
правила сохраняются и для молекул средней и высшей симметрии. Таким образом,
для всех многоатомных молекул S обычно принимает следующие значения:
четное число	S	=	О
электронов:	S	=	0,1
нечетное число	_	1
электронов:	~	2
для основного состояния,
для возбужденных состояний,
для всех состояний.
(26.1)
Благодаря наличию спина, молекулы с нечетным числом электронов можно
обнаруживать по методу парамагнитного резонанса (см. § 14.8, с. 404). В настоя-
щее время этот метод широко применяется для исследования свободных радика-
лов [101, 73].
Рассмотрим теперь влияние вырождения, связанного со спином, на устойчи-
I
вость электронных состояний многоатомных молекул. При S = - имеется двукрат-
ное вырождение и при 5=1— трехкратное. Двукратное спиновое вырождение
для молекул с нечетным числом электронов, сохраняющееся, согласно теореме
Крамерса, в любом электрическом поле (см. с. 408), не нарушает и устойчиво-
сти электронных состояний. При трехкратном спиновом вырождении ^а также
электронные состоя-
ния молекул средней и высшей симметрии оказываются неустойчивыми [345], как
и при орбитальном вырождении, рассмотренном выше. Однако, как можно пока-
зать, при отсутствии орбитального вырождения наличие спина 5	1 приводит лишь
к весьма незначительному нарушению симметрии равновесной конфигурации.
3
вырождении более высокой кратности при 5 = -,2,...
Мы имеем случай, соответствующий рис. 26.4, е, когда минимум энергии получается
при небольших смещениях из первоначального положения равновесия.
При наличии орбитального вырождения спин-орбитальное взаимодействие может при-
вести к расщеплению, при котором нижний подуровень будет невырожденным и соответству-
ющая симметричная конфигурация ядер устойчива [345, 96].
Следует отметить, что неустойчивость вырожденных электронных состояний
нелинейных многоатомных молекул имеет место для электронных состояний моле-
кулы в целом. Электронные состояния отдельных молекулярных электронов могут
быть вырожденными без того, чтобы это приводило к неустойчивости молекулы.
В частности, при наличии двух электронов в молекулярной оболочке, заполняе-
мой четырьмя электронами, результирующее электронное состояние может быть
невырожденным и, следовательно, устойчивым5).
§ 26.2. Основы теории направленной валентности
Существенная особенность химической связи в многоатомных молекулах, от-
личающая ее от химической связи в двухатомных молекулах, состоит в том, что
в многоатомной молекуле всегда имеются атомы, соединенные с двумя другими
атомами или с большим их числом. Так, уже в трехатомной молекуле типа ХУз,
5) Вопрос о возможных электронных состояниях для заданной молекулярной электронной конфигу-
рации будет рассмотрен в § 26.5.
§ 26.2. Основы теории направленной валентности
795
как линейной (например, СО2), так и нелинейной (например, Н2О), центральный
атом X образует две химические связи X—Y^ и X—Y<2^ с двумя атомами Y В более
сложных молекулах атомы могут образовывать по три (как атом N в NH3 или атомы С
в С2Н4), четыре (как атом С в СН4 или СгНб) и более связей (как атом U в UFe).
Весьма важны вопросы о числе химических связей, которые может образовать
данный атом, и о взаимном расположении этих связей.
В случае гомеополярных (ковалентных) связей, осуществляемых парами мо-
лекулярных электронов, в каждой паре участвует по одному внешнему электрону
рассматриваемого атома и полное число связей этого атома с соседними определяет-
ся его максимальной валентностью, равной числу внешних (валентных) электронов.
При этом, как и у двухатомных молекул, двойные связи осуществляются двумя
парами электронов, а тройные —- тремя. Для определенной связи — простой, двой-
ной или тройной — приближенно сохраняется и в многоатомной молекуле деление
электронов по типам в соответствии со значением проекции орбитального момента
электрона А на направление связи, в частности, сохраняет смысл понятие о а-
и тг-электронах (А = 0 и А = 1). Особое значение понятие о тг-электронах имеет
для молекул, в которых ряд связей лежит в одной плоскости.
В частности, многие молекулы красителей, обладающие поглощением в видимой области
спектра, имеют тг-электроны. Эти электроны обусловливают появление сравнительно близких
уровней, переходы между которыми приводят к подобному поглощению. В дальнейшем мы
рассмотрим качественную теорию таких тг-электронных уровней (см. § 26.4, с. 812).
Состояние атома (обладающего валентными электронами), в котором он может
образовывать химические связи, называют валентным состоянием. Для валентного
состояния характерно наличие неспаренных электронов, т. е. электронов, спины
которых взаимно не компенсируются. В каждом одноэлектронном орбитальном
состоянии может находиться, согласно принципу Паули, два электрона с противо-
/ 1 1 \
положными спинами I ms = ms = ср. с. 201 1. Такие спаренные электроны
не участвуют в образовании химической связи. Наоборот, каждый неспаренный
внешний электрон данного атома может участвовать в образовании связи, составляя
вместе с внешним, также неспаренным, электроном другого атома электронную
пару эквивалентных молекулярных электронов, которые и образуют связь.
При образовании молекулы азота N2 с тройной связью (см. § 24.8, с. 750) валент-
ным состоянием для каждого из атомов азота является основное состояние 2р3 4S,
и мы имеем три одноэлектронных орбитальных состояния рх, Ру, Pz с одним элек-
троном в каждом из них; именно эти электроны участвуют в образовании трех элек-
тронных пар, дающих одну a-связь и две тг-связи (см. рис. 24.13 и табл. 24.4 в § 24.8).
Следует подчеркнуть, что компенсация спинов для каждой пары электронов обяза-
тельна лишь для молекулярных оболочек, содержащих два эквивалентных электрона (случай
а-оболочек), и является в этом случае следствием принципа Паули, как и компенсация спинов
в одноэлектронных орбитальных состояниях атома. Для молекулярных оболочек, содержащих
четыре эквивалентных электрона (случаи тг- и 6-оболочек), у двух эквивалентных электронов
спины могут не компенсироваться, что, например, имеет место в молекуле О2 с основным
состоянием 3S” (см. табл. 24.4).
Вопрос о взаимном расположении гомеополярных связей, образуемых данным
атомом, может быть решен, исходя из представлений о распределении электронной
плотности для валентного состояния атома, если учесть, что прочность образующихся
связей тем больше, чем сильнее перекрываются электронные облака соответствующих
атомных электронов (см. § 24.6, с. 737, и § 24.7, с. 743). Энергетически наиболее
796
Глава 26. Электронные состояния в многоатомных молекулах
выгодно взаимное расположение атомов, при котором перекрывание электрон-
ных облаков для неспаренных электронов данного атома и электронных облаков
для неспаренных электронов присоединяемых атомов будет наибольшим. Подобное
расположение атомов, соответствующее минимуму энергии всей системы в целом,
и будет осуществляться в действительности. Таким образом, наглядное представле-
ние о перекрывании электронных облаков или, как часто говорят, о перекрывании
электронных орбит позволяет качественно понять взаимное расположение связей,
образуемых атомами в валентных состояниях, и является основой теории напра-
вленной валентности.
Теория направленной валентности была разработана Паулинго” (Полингом) в 1931 г.
[347] и изложена в ряде монографий, в частности, в монографии лмого Паулинга [88],
посвященной природе химической связи, и в монографиях по кванк й химии (см., на-
пример, [86-87а]). Хорошее изложение теории направленной валенгности, как и ряда других
вопросов квантовой теории молекул, имеется в книге Веселова [82].
Для атома с одним внешним неспаренным 5-электроном, имеющим сферически
симметричное распределение электронной плотности (рис. 26, а, ср. рис. 24.13, а,
с. 749), образование связи может происходить в любом направлении. Такой случай
мы имеем для образования связей атомом водорода с одним электроном Is и атомом
лития с одним внешним электроном 2s. Валентным состоянием в обоих случаях
является состояние 2S.
Рис. 26.6. Образование связей:
а — атомом с неспаренным «-электроном;
б — атомом с тремя неспаренными р-электронами;
в, г — атомами с двумя неспаренными р-электронами
Для атома с тремя внешними неспаренными р-электронами, имеющими ак-
сиально симметричное распределение электронной плотности вдоль трех взаимно-
перпендикулярных осей (рис. 26.6, ср. рис. 24.13,6), наибольшее наложение элек-
тронных облаков получается вдоль этих осей, т. е. такой атом может образовать
три взаимно-перпендикулярные связи. Примером может служить атом азота с тремя
внешними электронами 2р и с квартетным валентным состоянием 4S (см. выше,
с. 795). Он может образовать три связи с атомами водорода, которые, согласно
изложенным представлениям, должны быть расположены под прямыми углами.
Мы приходим к пирамидальной форме молекулы аммиака NH3, т. е. получаем
качественно правильный результат.
Действительные углы в молекуле NH3 больше, они равны 106°47' вместо 90°. Это
естественным образом объясняется отталкиванием атомов водорода. Такое увеличение углов
между связями, образованными атомами с внешними р-электронами, имеет место и в ряде
лругих случаев.
§ 26.2. Основы теории направленной валентности
797
Другой случай образования связей атомом с внешними р-электронами осу-
ществляется при наличии четырех внешних р-электронов. При этом одна из трех
возможных р-орбит будет заполнена двумя электронами и для образования связей
остается две орбиты (например рх и ру, как изображено на рис. 26.6, в) с двумя не-
спаренными электронами. Примером подобного случая служит атом кислорода с че-
тырьмя внешними электронами 2р, дающими триплетное валентное состояние 3Р.
Атом кислорода может образовать две связи с атомами водорода, составляющие
прямой угол. Мы приходим к треугольной форме молекулы воды Н2О, т. е. опять
получаем качественно правильный результат6).
Мы рассмотрели образование связей атомом либо с неспаренным 5-электроном,
либо с неспаренными р-электронами. При этом существенно, что для р-электронов
имеется вырождение — трем возможным р-орбитам (рж, ру, pz) соответствует оди-
наковая энергия и они равноправны в образовании связей. 5-электроны с тем же
главным квантовым числом п, что и р-электроны (например, электроны 25), свя-
заны более прочно в оболочке ns2; именно поэтому их можно было не учитывать
в разобранных случаях образования связей электронами 2р. Однако в большом числе
случаев и, в частности, в чрезвычайно важном случае атома углерода с нормальной
конфигурацией 2s22p2 было бы неправильно считать, что в образовании связей
участвуют только электроны одного типа. Если для атома углерода в двухвалентном
основном состоянии 2s22p2 3Р можно объяснить образование радикала СН2, имею-
щего нелинейную форму, за счет двух неспаренных р-электронов (см. рис. 26.6, г),
то для объяснения четырехвалентности атома углерода необходимо учитывать все
четыре внешних электрона в двухквантовом слое. С физической точки зрения это
объясняется тем, что энергии электронов 25 и 2р сравнительно мало отличаются
друг от друга. Разность их энергий значительно меньше энергии, выделяющейся
при образовании атомом углерода химических связей.
Энергия, необходимая для перевода атома углерода из двухвалентного состояния 2s22p2 3Р
в четырехвалентное 2s2p3 55, в котором все четыре электрона являются неспаренными,
составляет 4,2 эВ (см. § 11.3, с. 311), а энергия образования молекулы метана СН4 из атома С
и четырех атомов Н равна 43,5 эВ, т.е. примерно в 10 раз больше.
Считая, что электроны в состояниях ns и пр имеют одинаковую энергию, т. е.
рассматривая эти состояния как вырожденные между собой, мы приходим к новым
состояниям, в которых распределение электронной плотности может быть уже иным,
отличающимся от распределения электронной плотности для 5- и р-электронов
в отдельности. Это распределение, соответствующее смеси s- и p-состояний, или,
как говорят, их гибридизации, следует выбирать таким образом, чтобы оно давало
наибольшую концентрацию электронной плотности в определенных направлениях,
способствующую образованию наиболее прочных химических связей (в соответствии
с критерием перекрывания электронных орбит).
Исходя из распределений электронной плотности для 5-состояния и трех
p-состояний, изображенных на рис. 26.7, а, можно получить новые распределения
электронной плотности, наиболее выгодные для образования связей и соответ-
ствующие гибридным (смешанным) состояниям; эти распределения изображены
на рис. 26.7, б, в, г. Комбинируя 5-состояние и все три p-состояния (гибриди-
зация 5р3), мы приходим к четырем состояниям с концентрацией электронной
плотности вдоль четырех осей тетраэдра (рис. 26.7,0. Это приводит к тетраэдриче-
скому расположению связей, образуемых атомом углерода. Комбинируя 5-состояние
В этом случае также действительный угол между связями больше теоретического и равен 104° 27'
(см. с. 530).
798
Глава 26. Электронные состояния в многоатомных молекулах
Рис. 26.7. Распределение электронной
плотности для гибридных состояний:
а — исходные состояния;
б — гибридизация sp\
в — гибридизация sp2\
г — гибридизация sp
и два p-состояния (гибридизация sp2), полу-
чаем три состояния с концентрацией элек-
тронной плотности вдоль трех направле-
ний, лежащих в одной плоскости и соста-
вляющих между собой углы в 120°; вдоль
перпендикулярного направления мы имеем
прежнюю р-орбиту (рис. 26.7, в, гибридиза-
ция происходит в плоскости ху). Наконец,
комбинируя s-состояние и одно р-состояние
(гибридизация sp), мы приходим к двум
состояниям с концентрацией электронной
плотности в противоположных направлени-
ях вдоль одной из осей; в перпендикуляр-
ных направлениях мы имеем две прежние
р-орбиты (рис. 26.7, г, гибридизация sp про-
исходит вдоль оси у).
В первом случае sp3 имеется про-
странственное расположение четырех связей,
во втором (sp2) — плоское расположение трех
связей и в третьем (sp) — линейное распо-
ложение двух связей. Соответственно с этим
получается пространственное, плоское и ли-
нейное расположение атомов, присоединяе-
мых рассматриваемым атомом.
Отметим, что гибридизация sp2 позво-
ляет объяснить образование двойных свя-
зей С=С, а гибридизация sp — тройных связей CSC, как это будет рассмотрено
ниже (см. §26.3).
С квантовомеханической точки зрения для r-кратно вырожденного состояния мы имеем г
независимых волновых функций (см. с. 42), которые можно выбирать различными способами,
образуя линейные комбинации первоначально взятых функций. Однако при наличии возму-
щения имеющийся произвол в выборе волновых функций устраняется. В рассматриваемом
случае возмущением является взаимодействие атома в валентном состоянии с окружающи-
ми атомами. Нужно найти такие линейные комбинации независимых волновых функций
вырожденных состояний, которые давали бы правильные функции нулевого приближения;
подобными функциями являются одноэлектронные волновые функции данного атома, силь-
нее всего перекрывающиеся с одноэлектронными волновыми функциями присоединяемых
атомов. Мы рассмотрим эти функции на примере s и р-электронов.
Если учитывать только трехкратное орбитальное вырождение для р-электронов, то
для значений mt — 0, ±1 проекции орбитального момента при I = 1 волновые функции будут
иметь следующий вид (см. (6.40) и табл. 6.4):
V’r.I.O =	COS0,
V’ni.i = ^>/б/„|(г) sin 0 e'v,
V’ni-i = ^v/6/ni(r)sin(9e'**’.
(26.2)
Угловое распределение электронной плотности для функций (26.2) определяется множителя-
ми cos2# и sin2# и обладает осевой симметрией относительно оси z (рис.26.8,а). При этом
распределение электронной плотности для состояний с = 1 и = -1 одинаково.
§ 26.2. Основы теории направленной валентности
799
Правильными функциями нулевого приближения, дающими наибольшую концентрацию
электронной плотности в определенных направлениях, будут наряду с функцией
линейные комбинации функций фпХ,х и ^ni-ь
]	e»V e-»V
y=(^ni,i + Фп\ -|) = fni(r) sine--------------Vi = Vifnl(r) sinflcosy?,
1	ei<f> —
—7=(^ni,i “ Фп1 -i) = fn\(r) sinO-------------Vi = Vifnl(r) sinesinp.
iV2	2г
(26.3)
Для них мы получаем угловые распределения электронной плотности, обладающие осевой
симметрией относительно осей х и у соответственно и совершенно подобные распределению
электронной плотности для функции ^п10 относительно оси z (рис. 26.8,6). В результате мы
приходим к функциям ^Ру, фРг
Рис. 26.8. Распределение электронной
плотности:
а — для состояний фп1$, фпХА и фп\_х\
б — для состояний фРг — фпХуо,
и =	“ V’m-t)
tv2
= ^fn\(r) sin е cos
ФРу = -^=(^„1,1 -^ni,-i) = V3fn}(r) sin е sin <р,
г\/2
ФР, = Фп\$ = VijnX (г) cos е,
которым соответствуют распределения элек-
тронной плотности, положенные в основу
рассмотрения связей, образуемых р-электро-
нами.
Таким образом, мы обосновали вид
распределения электронной плотности для
р-электронов, которым пользовались ранее
при рассмотрении образования а- и тг-связей
в двухатомных молекулах (§ 24.8, с. 749)
и в данном параграфе при разборе образова-
ния двух или трех связей (являющихся в си-
лу аксиальной симметрии a-связями) атомом
с валентными р-электронами. Мы видим, что
выбор в качестве независимых функций ну-
левого приближения функций фРг, фРу, фРг
соответствует принципу образования волно-
вых функций, дающих наибольшую возмож-
ную концентрацию электронной плотности
в некоторых направлениях.
Рассмотрим теперь случай, когда мож-
но приближенно считать «-состояние выро-
жденным совместно с p-состояниями. Тогда
орбитальное вырождение будет четырехкрат-
ным и наряду с тремя функциями (26.4) мы
будем иметь четвертую функцию
& = V’no.o = fno(r)Yoo(0, <р) = f„o(r), (26.5)
не зависящую от угловых переменных
(Y00(e,p) = 1, см. табл. 6.4, с. 180). Теперь
нужно образовывать правильные функции
нулевого приближения как линейные комбинации функций (26.4) и функции (26.5), да-
ющие наибольшую возможную концентрацию электронной плотности в некоторых напра-
влениях. Если брать линейные комбинации всех четырех функций (гибридизация sp3), что
соответствует случаю взаимодействия рассматриваемого атома с четырьмя другими атомами
800 Глава 26. Электронные состояния в многоатомных молекулах
(одновалентными), то правильные линейные комбинации будут иметь вид [347, 88|
1,	ч з
= '~(Ф, + Фр, - Фр, - Фр,),
>
Фз = 2^5 - фр, + Фр, - Фр,),
ф4 = ^(Ф, - фр, - фр, + Фр.)- ,
(26.6)
Они и соответствуют четырем состояниям с распределением электронной плотности, изобра-
женным на рис. 26.7,6. Если брать линейные комбинации s-функции и двух p-функций (гиб-
ридизация зр2), что соответствует случаю взаимодействия рассматриваемого атома с тремя
другими атомами (двумя одновалентными и одним двухва-
лентным), то правильные линейные комбинации будут иметь
вид
(26.7)
Рис. 26.9. Расположение
связей при гибридизации:
а — типа зр3; б — типа зр2;
в — типа зр
Они соответствуют рис. 26.7, в. Наконец, если брать линей-
ные комбинации «-функции и одной p-функции (гибриди-
зация «р), что соответствует случаю взаимодействия рассма-
триваемого атома с двумя другими атомами (двухвалентными
или одним трехвалентным и одним одновалентным), то пра-
вильные линейные комбинации будут представлять просто
сумму и разность функций ij)s и $Px;
ф\ = 75 + ь,),
1 /
= 75 ~	'
(26.8)
Они соответствуют рис. 26.7, г.
Мы получили объяснение трех случаев образования свя-
зей четырехвалентным атомом, имеющим «- и р-электроны,
в частности, атомом углерода. Легко найти те значения вол-
новых функций, которым соответствуют наибольшие кон-
центрации электронной плотности в определенных напра-
влениях. Для функций (26.6), если воспользоваться изобра-
жением тетраэдрического расположения связей при помощи
куба (ср. рис. 18.23, с. 523), эти максимальные значения по-
лучаются для направлений, проходящих через вершины ку-
ба (рис. 26.9, а). Считая приближенно радиальные функции
/п1(г) и /по(^) в (26.4) и (26.5) при значениях расстояния г,
для которых существенно перекрывание электронных функций, одинаковыми и равны-
ми /(г), мы можем записать функции (26.4) и (26.5), переходя от сферических координат
§ 26.2. Основы теории направленной валентности
801
(26.9)
, р, z). Так как
к прямоугольным, в виде
]>,=№) К '
Ь: =
Ь. =
Первая из функций (26.6) максимальна в направлении 1 (лежащем в октанте х
х	у	z	1 7)
для этого направления — = - = - =	, то ее значение равно
г	г	г	УЗ
V’l = if (?) (1 + л/3- + >/3- + Л- ) = 2/(г)	(26.10)
2	\ г г г J
и такими же будут значения функций Ф2, Фз и V4 в направлениях 2, 3 и 4, в то время как
значения функций фРх, фРуУ фРг в направлениях г, у* z равны Уз/(г), а значение функции ф3
в любом направлении равно просто /(г).
Аналогичным образом находятся максимальные значения 1,991 /(г) для функций (26.7)
в направлениях 1, 2 и 5, лежащих в плоскости ху и образующих друг с другом
углы 120° (рис. 26.9, б), а также максимальные значения 1,930 /(г) для функций (26.8)
в направлениях I и 2 вдоль оси х (рис. 26.9, в) 8\
В результате, если принять за единицу значение для функции фЛЧ наибольшие возможные
значения функций типов sp3, sp2, sp, р и s будут равны
вр’	5р-’	5Р р	Ц
2	1,991	1,930	1,732	1 J	'	'
Если считать, что энергия связи пропорциональна произведению угловых частей одноэлек-
тронных волновых функций для атомов, образующих связь (что подтверждается приближен-
ным квантовомеханическим расчетом {348]), то прочности связей будут равный (если принять,
прочность связи s—s за 1):
3	3	2	2
sp — sp sp —sp sp—sp p—p s—p s—s
4	3,982	3,725	3	1,732	1
Таким образом, образование связей с участием гибридных орбит энергетически выгодно.
Отметим, что значение 2/(г) является максимальным значением функции, получающей-
ся путем наложения функции ф3 и одной из функций фр. Действительно, если мы составим
линейную комбинацию ф = аф3 4 ЬфРх, где коэффициенты а и Ъ удовлетворяют условию
нормировки а2 4- b2 = 1, откуда & = л/1 - а2, то функция
(26.12)
Ф = аф, + ЪфРг = f(r)
а + v^3(l - а2) |
(26.13)
будет наибольшей при х = г (т. е. в направлении оси х) и при а, удовлетворяющем условию
максимума —= 0. Дифференцируя выражение а + 4*0 ~ а2) по а и приравнивая его нулю,
7) Эти отношения равны cos у, где а — 109°28' — тетраэдрический угол, см. рис.26.9,а.
^Действительно, при — = I для функции в (26.7) имеем = —/(?)( 1 + ^) = 1У991 /(г)
и для функции в (26.7) —	= ~=/(г)(1 4 V3) — 1,930/(г).
При том же значении расстояний между атомами.
26 Зак. 103
802
Глава 26. Электронные состояния в многоатомных молекулах
1
мы получим а = откУДа

1	3 х
2	2 г
(26.14)
и ее максимально возможное значение равно
/(г)
= 2/(г).
До сих пор мы рассматривали атом с внешними s- и р-электронами. Если атом
обладает, помимо этих электронов, также внешними d-электронами, что имеет место
для более тяжелых атомов, начиная со стоящих в третьем периоде системы элементов,
то в образовании связей будут участвовать и d-электроны. При этом обычно нужно
учитывать одновременно s-, р- и d-орбиты, и так как число возможных d-орбит равно
пяти (I — 2, степень вырождения 2Z+1 = 5), то имеется большое число возможностей
для образования гибридных состояний и получаются разнообразные случаи взаимно-
го расположения связей. В частности, для конфигурации внешних электронов d2sp\
дающей септетное валентное состояние (5 = 3, 2S+ 1 = 7), это расположение связей
оказывается октаэдрическим. В принципе возможны случаи, когда в образовании
связей участвуют и /-электроны. Критерием того, какие орбиты нужно принимать
во внимание, служит близость энергий связи рассматриваемых внешних электронов.
Состояния электронов, мало отличающиеся по энергии по сравнению с энерги-
ями образующихся связей, следует рассматривать как вырожденные между собой
и соответственно следует находить гибридные состояния с наибольшей возможной
концентрацией электронной плотности в некоторых направлениях.
Мы не будем подробнее разбирать образование связей с участием d-
и /-электронов и приведем только данные о расположении связей (табл. 26.1)
для некоторых конфигураций внешних электронов [86, 85].
Таблица 26.1
Расположение связей для различных конфигураций
внешних электронов
Число электронов	Тип гибридизации	Расположение связей
2	sp dp р2 ds d2	линейное угловое
3	— R, S*	плоский треугольник треугольная пирамида
4	d3s rf4 d2p2 dsp2	тетраэдраическое тетрагональная пирамида плоский четырехугольник
6	dr sp3	октаэдр
§ 26.3. Химические связи четырехвалентных атомов углерода
803
В следующем параграфе мы рассмотрим более подробно, на основе представле-
ний о направленной валентности, вопрос об образовании связей четырехвалентными
атомами углерода, имеющий важное значение для органической химии и весьма су-
щественный для спектроскопии органических молекул.
В заключение данного параграфа следует подчеркнуть, что хотя в применениях
теории направленной валентности существенную роль играет рассмотрение обра-
зования валентных связей двумя электронами (по одному от каждого вступающего
в соединение атома), тем не менее исходные положения теории позволяют применять
ее с таким же успехом при рассмотрении химической связи по методу молекулярных
орбит. Как мы отмечали (см. с. 743), критерий перекрывания электронных облаков,
характеризующий прочность связи, является общим для метода молекулярных орбит
и для метода электронных пар. Исходя из гибридных орбит атомов, можно строить
молекулярные орбиты для многоатомных молекул. Физически это связано с тем, что
распределение электронной плотности для молекулярного электрона, связывающего
два атома, вблизи этих атомов будет качественно такое же, как для соответствующих
атомных электронов в гибридных состояниях.
Если найдены волновые функции грА и фв электрона у атомов А и В, между которыми
образуется связь, то по методу молекулярных орбит берется волновая функция (ср. (24.33))
V> = c(^a±V>b)	(26.15)
и для двух эквивалентных молекулярных электронов мы имеем функцию с2[^л(1) ± if)B( 1)] х
[^>л(2) ± ^в(2)] (ср. (24.49)). По методу валентных связей берется функция с[^л(1)^в(2) ±
фА (2)Фв( 1)] (ср. (24.56)) сразу для электронной пары. В соответствии с теорией напра-
вленной валентности в качестве фА и 'Фв следует выбирать функции, дающие наибольшее
перекрывание, в частности, для атомов углерода — гибридные функции типа sp3, sp2
или sp (см. (26.6)-(26.8)), в зависимости от того, имеем ли мы дело с образованием одиноч-
ных, двойных или тройных связей.
Отметим, что приближенная молекулярная волновая функция (26.15) около атомов А
и В будет мало отличаться от функция фА и фв, а между атомами Аи В будет по абсолютной
величине тем больше (для случая связывающих электронов, т. е. при одинаковом знаке
функций грА и грв при знаке -F в (26.15)), чем больше в этой области по абсолютной
величине фА и Фв> т.е. чем больше они перекрываются.
§ 26.3. Образование химических связей
четырехвалентными атомами углерода
Распределение электронного облака, соответствующее трем основным типам
гибридизации для s- и р-электронов, позволяет объяснить различные возможности
образования связей четырехвалентным атомом углерода с соседними атомами.
Первому типу гибридизации, sp3, соответствует тетраэдрическое расположение
простых связей в насыщенных органических соединениях. В простейшем случае
молекулы типа СН4 атом углерода образует четыре простые равноценные связи,
соответствующие наложению орбит sp3 атома углерода и орбит 1s атомов водоро-
да (рис. 26.10, а). Эти связи обладают аксиальной симметрией по отношению к напра-
влениям С—Н и являются a-связями. По отношению к распределению электронной
плотности для электронных пар направления связей приближенно служат осями
точная симметрия есть Сз. Углы между связями строго равны тетраэдрическим.
Аналогичным образом четыре эквивалентные простые a-связи получаются в мо-
лекулах тетразамещенных метана типа СХд, например, в молекуле четыреххлористого
углерода СС14. Для галоидных тетразамещенных мы при этом имеем наложение орбит
sp3 атома углерода и орбит р атомов галоида (рис. 26.10,6), поскольку для атомов
26*
804
Глава 26. Электронные состояния в многоатомных молекулах
Рис. 26.10. Образование тетраэдрических
связей:
а — типа зр3 - s; б — типа зр3 — р
галоидов с внешней электронной обо-
лочкой р5 из трех р-орбит две заня-
ты парами электронов, а третья содер-
жит неспаренный электрон и участвует
в образовании связи (валентное состо-
яние 2Р°).
Когда атомы, замещающие атомы
водорода в метане, различны (заме-
щенные типа СН3Х, СН2Х2, СН2ХУ,
СНХ3, CHX2Y, CHXYZ, CX3Y, CX2Y2,
CX2YZ, CXYZU), to четыре одиноч-
ных связи, оставаясь a-связями, уже
не равноценны. Однако обычно рас-
положение связей не очень сильно от-
личается от тетраэдрического, лишь несколько искажаясь за счет взаимного влияния
этих связей, и углы остаются близкими к тетраэдрическому углу 109°28'. Это
объясняется тем, что главную роль играет распределение электронной плотности
по отношению к атому углерода, энергетически наиболее выгодное при одинаковых
углах между четырьмя связями.
С данным атомом углерода может быть связан одиночной связью не отдельный
атом, а радикал R. Как известно, возможно огромное разнообразие комбинаций
атома углерода с различными атомами и радикалами, связанными с ним четырьмя
простыми связями. Углы при этом остаются приближенно тетраэдрическими и,
разумеется, точно равны тетраэдрическим для молекул типа CR4, когда атом углерода
связан с четырьмя одинаковыми радикалами.
Особенно важны случаи связи атома углерода с одним, двумя, тремя и четырьмя
другими атомами углерода, т. е. когда атом углерода является первичным, вторич-
ным, третичным и четвертичным. Простейшими примерами молекул углеводородов
с такими атомами углерода служат молекулы этана СН3СН3, пропана СН2(СНз)2
изобутана СН(СНз)з и тетраметилметана С(СНз)4, структура которых показана
на рис. 26.11. Во всех случаях мы имеем а -связи С—С и С—Н, причем возможное
расположение связей, образованных соседними атомами углерода, является распо-
ложением транс, что приводит к симметрии для этана, С2» для пропана, Cjv
для изобутана и Та для тетраметилметана.
Вокруг простых а-связей С—С возможно внутреннее вращение, которое есте-
ственным образом объясняется аксиальной симметрией этих связей.
При точной аксиальной симметрии с осью бесконечного порядка было
бы возможно свободное вращение. Отступления от такой симметрии приво-
дят к заторможенному вращению, соответствующему определенному потенциа-
лу U(x) Ф const (см. с. 504). Наличие точной симметрии Сз, как в молекуле этана,
приводит к появлению трех одинаковых минимумов этого потенциала.
Второму типу гибридизации, sp2, соответствует плоское расположение связей
(одной двойной и двух простых) в ненасыщенных органических соединениях, содер-
жащих двойные связи. В простейшем для этого типа гибридизации случае молекулы
этилена С2Н4 (рис. 26.12) двойная связь образуется путем наложения орбит зр2 обоих
атомов углерода, что дает а-связь, и наложения орбит рх этих же атомов, что дает
%-связь; в результате получается связь, осуществляемая двумя парами электронов.
В плоскости молекулы (плоскость pz) атомами углерода образуются еще по две
а-связи С—Н в результате наложения орбит зр2 атомов углерода и орбит 1s атомов
§ 26.3. Химические связи четырехвалентных атомов углерода
805
Рис. 26.11. Связи атома углерода с другими атомами углерода:
а — первичный атом углерода в этане;
б — вторичный атом углерода в пропане;
в — третичный атом углерода в изобутане;
г — четвертичный атом углерода в тетраметилметане
водорода. Углы С—С—Н приближенно равны 120°,
в соответствии с гибридизацией типа sp2.
Поскольку a-связи С—Н отличаются от a-связи меж-
ду атомами углерода, участвующей в образовании двойной
связи (вместе с тг-связью) и лежащей также в плоско-
сти молекулы, то углы отличаются, правда незначитель-
но, от 120°, а именно, для этилена угол Н—С—Н равен
119°54', а углы С—С—Н равны 120°3' (сумма трех углов,
разумеется, равна 360°).
При замещении в молекуле этилена атомов Н
другими атомами или же радикалами получаются
Рис. 26.12. Образование связи
в молекуле этилена
плоские структуры для совокупности связей /С=С\; угол между связями, образо-
ванными атомами С, по-прежнему, как правило, близок к 120°, что определяется
распределением электронной плотности для плоской структуры, наиболее выгодным
при одинаковых углах между тремя связями.
Важными, как и для связей атома углерода при гибридизации типа sp3, являются
случаи, когда атом углерода, образующий двойную связь, соединен еще с одним
806
Глава 26. Электронные состояния в многоатомных молекулах
или с двумя атомами углерода простыми связями, давая структуру типа
С\	С\
)с=с (Х/С) или )с=с.
X	С
Простые связи С—С, как и в случае насыщенных соединений, представля-
ют а-связи и допускают внутреннее вращение, в то время как для двойных
связей, не имеющих даже приближенной аксиальной симметрии (из-за наличия
тг-электронов), внутреннее вращение невозможно,()).
Третьему типу гибридизации, sp, соответствует линейное расположение связей,
образованных с участием двух противоположно направленных орбит sp. При этом
возможны два случая. В первом из них атом углерода образует тройную связь с одним
атомом и простую с другим, во втором — две двойных связи.
Рис. 26.13. Образование связи
при гибридизации типа зр:
а — в молекуле ацетилена;
б — в молекуле аллена
Простейшим примером первого
случая является молекула ацетилена
С2Н2 (рис. 26.13, а), в которой трой-
ная связь представляет результат нало-
жения орбит sp обоих атомов угле-
рода, что дает а-связь, и орбит рх
и pz этих атомов, что дает две 7Г-связи
со взаимно-перпендикулярными узло-
выми плоскостями, проходящими че-
рез ось молекулы. По оси молекулы
атомы углерода образуют еще по од-
ной a-связи С—Н путем наложения
орбит sp и орбит 1s атомов водорода.
Молекула имеет линейную структуру
и обладает симметрией D^h. Возмож-
ны замещения атомов Н другими ато-
мами, а также радикалами. Линейная
структура — С=С- при этом сохраня-
ется. В частных случаях могут быть
структуры типа С—С=С—X (X / С)
и С-С=С-С.
Простейшим примером второго случая является молекула аллена С3Н4
(рис. 26.13, б), в которой центральный атом углерода образует две двойные свя-
зи вдоль одной оси путем наложения орбит sp этого атома и орбит sp2 двух других
атомов углерода, что дает а-связи, и наложения его орбит рх и pz с орбитами рх
одного и р2 другого крайних атомов углерода, что дает 7Г-связи. При этом узловые
плоскости двух тг-связей, С<’)-С<2> и С(2)-С<3> (С(|> и С<3> — крайние атомы, —
центральный атом), взаимно-перпендикулярны. В соответствии с этим связи С—Н,
образованные путем наложения орбит sp2 атомов и и орбит 1s атомов водо-
рода, будут лежать во взаимно перпендикулярных плоскостях, и поэтому молекула
аллена обладает симметрией — $4v (см. с. 520). В принципе возможно замещение
в аллене атомов Н другими атомами или же радикалами.
Наряду с образованием атомом углерода двойных и тройных связей с другими
атомами углерода при гибридизациях типа sp2 и sp, возможно образование им
двойных и тройных связей с другими атомами, в частности, двойной связи /С=О
10) Вместо него мы имеем обычные неплоские колебания.
§26.3. Химические связи четырехвалентных атомов углерода
807
б
Рис. 26.14. Образование связей С=О
и C=N: а — связи С—О в молекуле
формальдегида; б — связи ON
в молекуле синильной кислоты
(карбонильной связи) и тройной связи —С=Н
(циановой связи). Структура простейших мо-
лекул, содержащих такие связи — молекулы
формальдегида Н2СО и молекулы синильной
кислоты HCN — показана на рис. 26.14. Двой-
ная связь С=О образуется за счет наложения
орбиты sp2 атома углерода и орбиты ру атома
кислорода, дающих a-связь, и орбит рх атомов
углерода и кислорода, дающих 7Г-связь. Трой-
ная связь С-N образуется за счет наложения
орбиты sp атома углерода и орбиты ру атома
азота, дающих a-связь, и орбит рх и pz атомов
углерода и азота, дающих две %-связи со вза-
имно-перпендикулярными узловыми плоско-
стями. Особенность связей /С=О и — C=N,
отличающая их от связей ^С=С^ и —CsC—,
состоит в том, что атомы О и N не связаны
с другими атомами, помимо атома С.
Возможность образования атомами угле-
рода связей с соседними атомами углерода
приводит к образованию углеродных цепей,
неразветвленных и разветвленных, открытых
и замкнутых (кольцевых систем), содержащих
простые, двойные и тройные связи (ср. § 18.1).
При большом разнообразии возможных структур органических молекул надо разли-
чать, с точки зрения представлений об электронной природе химической связи, два
различных случая.
Для простейших и многих более сложных устойчивых молекул, в том числе
для молекул, содержащих только простые a-связи, разумным физическим прибли-
жением служит представление о связях, осуществляемых парами локализованных
электронов, сосредоточенных на этих связях. Основному состоянию устойчивой
молекулы соответствует одно вполне определенное распределение электронных пар
по связям. Такое состояние может быть описано как по методу молекулярных орбит,
так и по методу электронных пар. В первом случае мы рассматриваем для соседних
атомов, связанных друг с другом, электронные оболочки а2, %2, %4, состоящие
из эквивалентных о- или %-электронов, во втором — электронные пары, соот-
ветствующие а- или 7Г-связям. В обоих случаях электроны рассматриваются как
локализованные на соответствующих связях.
Можно дать общую схему расчета основных состояний подобных молекул по ме-
тоду электронных пар, находящуюся в соответствии с обычной валентной схемой
химии; именно поэтому метод электронных пар и называют методом валентных свя-
зей. Существенно, что в этом методе с самого начала учитывается взаимодействие
электронов (см. с. 741).
В общей схеме приближенного расчета гомеополярной связи в многоатомных молекулах
по методу электронных пар [84-88], наряду со взаимодействием электронов, образующих
пару, учитывается и взаимодействие электронов различных пар. Для энергии молекулы
в «приближении полного спаривания» получается формула, являющаяся обобщением
**) «Approximation of perfect pairing», см. например, [85], с. 170.
808
Глава 26. Электронные состояния в многоатомных молекулах
формулы (24.64) для основного состояния молекулы водорода (в которой полагается S = 0,
т. е. пренебрегается неортогональностью волновых функций электронов в разных атомах,
см. (24.41)). Обобщенная формула имеет вид
Е=12 Е>+12 +12' A'i - |12"ло -	(2б-1б)
3	ij
где Ej — энергия одноэлектронных атомных состояний, Kjj — кулоновский интеграл ти-
па (24.62), a Aij — обменный интеграл типа (24.63) для данных двух одноэлектронных атомных
состояний i и J, описываемых функциями и При этом суммирование производится
по всем состояниям валентных электронов каждого из атомов, например, в случае моле-
кулы СН4 по четырем состояниям sp3 атома С (i = 1,2,3,4) и по четырем «-состояниям
атомов Н (г = 5, 6,7,8). Для обменных интегралов сумма берется по всем парам электронов
с компенсированными спинами, образующими связи (для СН4 пары 1—5, 2—6, 3—7, 4—8),
сумма — по парам электронов, участвующих в образовании различных связей, и сумма
5?" — по парам электронов с параллельными спинами,2). Так как обменные интегралы
отрицательны, то взаимодействия спаренных электронов (У^ АД играющие основную роль,
уменьшают энергию, а остальные взаимодействия и (УТ'Дт) увеличивают ее.
Следует отметить, что расчеты по формуле (26.16), несмотря на ряд пренебрежений
при ее выводе, приводят к удовлетворительным результатам для молекул, в которых связи
осуществляются локализованными парами электронов.
Для целого ряда более сложных устойчивых молекул и многоатомных ради-
калов, в частности для молекул, в которых, согласно валентной схеме химии,
имеются сопряженные двойные связи (двойные связи, разделенные простыми свя-
зями) предположение о локализации электронов на отдельных связях уже недо-
статочно. Для подобных молекул, согласно этой схеме, оказываются возможными
валентные структуры, отвечающие различным распределениям электронных пар
по связям, и действительное состояние молекулы не соответствует одной-единствен-
ной электронной структуре с электронами, локализованными на отдельных связях.
Физически правильным является представление о нелокализованных электронах, со-
гласно которому отдельные электроны участвуют в образовании не одной связи,
а совокупности связей. Это противоречит представлению об электронных парах,
локализованных на определенных связях, но является обобщением представления
о молекулярных орбитах. Наряду с молекулярными орбитами, локализованными
на отдельных связях, естественно рассматривать нелокализованные молекулярные ор-
биты, охватывающие совокупность связей.
§ 26.4. Нелокализованные электроны и методы их рассмотрения
Типичным примером молекулы с нел окал изованн ым и электронами служит
молекула бензола с плоской кольцевой структурой симметрии (см. гл. 18, с. 509),
свидетельствующей об эквивалентности всех шести связей С—С. На этом примере
можно выяснить основные особенности случая нелокализованных молекулярных
орбит. Отметим, что правильность плоской модели молекулы бензола с шестью
равноценными связями подтверждается всей совокупностью экспериментальных
фактов и, в частности, с полной убедительностью, исследованием колебательных
спектров бензола (см. §23.5, с. 712).
Рассмотрим молекулу бензола с точки зрения теории направленной валент-
ности, исходя из кольцевого расположения атомов углерода в виде правильного
,2) В случае, если у атомов остаются внешние неспаренные электроны.
§ 26.4. Нелокализованные электроны и методы их рассмотрения
809
Рис. 26.15. Образование связей в молекуле бензола:
а — образование a-связей; б — образование тг-связей (вид сбоку);
в — образование тг-связей (вид сверху)
шестиугольника. В плоскости кольца (рис. 26.15, а) для каждого четырехвалентного
атома углерода получается гибридизация типа sp2, и он образует две a-связи с со-
седними атомами углерода путем наложения орбит sp2 и одну a-связь с атомом
водорода путем наложения орбит sp2 и 1s. Для каждого атома углерода остает-
ся по одной орбите pz, ориентированной по оси, перпендикулярной к плоскости
молекулы (рис. 26.15,6); этой орбите соответствует один неспаренный р-электрон,
так как остальные три внешних электрона атома углерода участвуют в образовании
только что рассмотренных а-связей. Всего для шести атомов углерода имеется шесть
неспаренных электронов, причем для них распределение электронной плоскости ха-
рактеризуется наличием узловой плоскости, совпадающей с плоскостью молекулы.
Теория направленной валентности сама по себе не может объяснить, каким образом
эти шесть электронов участвуют в образовании связи в бензольном кольце, так как
электронные орбиты pz каждого атома углерода перекрываются одинаковым образом
с электронными орбитами двух соседних атомов углерода (рис. 26.15, в, вид сверху).
Наиболее естественный ответ на данный вопрос можно дать с точки зрения
представления о молекулярных орбитах. Благодаря перекрыванию соседних орбит
все шесть атомных орбит pz образуют единую систему с кольцевым распределением
электронной плоскости — нелокализованную молекулярную орбиту, охватываю-
щую все бензольное кольцо. В силу того, что плоскость кольца является узловой
плоскостью, наибольшая электронная плотность будет получаться сверху и снизу
от плоскости, и электрон должен сравнительно легко передвигаться по кольцу, осу-
ществляя «подвижные» химические связи13); именно данное обстоятельство и делает
представление о нелокализованных молекулярных орбитах физически правильным.
Убедительным доказательством подвижности электронов служит сильный диамагне-
тизм бензола. Во внешнем магнитном поле, перпендикулярном к плоскости кольца,
электроны рассматриваемого типа будут двигаться по кольцу, образуя замкнутый
ток и создавая дополнительный магнитный момент — диамагнитный момент, про-
порциональный напряженности поля и обусловливающий диамагнетизм бензола.
С данной точки зрения в бензоле имеется шесть электронов, занимающих
нелокализованные орбиты, причем все эти электроны принадлежат кольцу в це-
лом. Находясь между атомами углерода, они будут их связывать, и в результате
получится химическая связь, определяемая шестью электронами, т. е. на каждую
13) «Mobile bonds» по английской терминологии.
810 Глава 26. Электронные состояния в многоатомных молекулах
эквивалентную связь С—С будет приходиться по одному электрону, что соответ-
ствует «половинной» связи. Таким образом, вместе с парой электронов, образующих
простую a-связь между соседними атомами углерода, на каждую связь С—С в бен-
золе будет приходиться по три связывающих электрона и, следовательно, эту связь
можно рассматривать как трехэлектронную или «полуторную».
Аналогичным образом рассматриваются нелокализованные 7Г-электроны в более
сложных ароматических молекулах, содержащих ряд бензольных колец (нафталин
антрацен и т.д.), и в непредельных соединениях с открытыми цепями при нали
чии сопряженных двойных связей (напри
CH ' СН *4 сн
СН СН I сн
Рис. 26.16. Цепочка с чередующимися
двойными и одиночными
связями в полиенах
(пол и мети новая цепочка)
Имеется два основных способа
мер, бутадиен СН2=СН—СН=СН2). Нело-
кализованные молекулярные орбиты охва-
тывают систему бензольных колец или от-
крытую цепь с сопряженными связями;
вследствие подвижности электронов осу-
ществляется передача влияний из одной
части молекулы в другую, в частности,
вдоль полиметиновой цепи в случае поли-
енов (рис. 26.16; звеньями цепи являются
группы —(СН=СН)—).
расчета ненасыщенных органических молекул,
базирующихся на методе молекулярных орбит.
Можно исходить из атомных электронных орбит, рассматривая их перекры-
вание и находя нелокализованные молекулярные орбиты. Соответствующие кван-
товомеханические методы расчета были применены Хюккелем к бензолу [357]
и успешно развивались за последнее время в различных вариантах (см. обзор
Лонге—Хиггинса [89]), позволив получить ряд результатов не только для основных,
но и для возбужденных состояний разных ненасыщенных органических молекул,
в частности, молекулы бензола.
Можно, учитывая значительную подвижность нелокализованных тг-электронов,
применить к ним хотя и грубую, но весьма наглядную металлическую модель мо-
лекулы. Эта модель аналогична модели свободных электронов в металле, согласно
которой их движение в металле считается происходящим в поле с постоянным
Рис. 26.17. Потенциальный
ящик с бесконечно высокими
стенками
потенциалом, ограниченном поверхностью металла —
в потенциальном ящике. Для нелокализованных элек-
тронов в молекуле можно также приближенно считать,
что они находятся в потенциальном ящике, размеры
которого совпадают с размерами молекулы; предпола-
гается, что электроны могут свободно передвигаться
вдоль углеродной цепи, но не могут передвигаться по-
перек цепи, т. е. что потенциальный ящик в отличие
от случая металла является одномерным. Для моле-
кулы бензола это будет передвижение по замкнутому
кольцу (см. выше, с. 809), для открытой цепи в по-
лиенах — передвижение с одного конца цепи до дру-
гого. Для модели потенциального ящика с бесконеч-
но высокими стенками, согласно простому квантово-
механическому расчету, получаются уровни энергии,
показанные на рис. 26.17 и соответствующие определенным молекулярным орбитам;
уровни будут расположены тем ближе друг к другу, чем больше размеры ящика; по-
этому для открытых цепей с увеличением их длины уровни сближаются. Для молекул
§ 26.4. Нелокализованные электроны и методы их рассмотрения
811
не очень больших размеров расстояния между соседними уровнями имеют порядок
нескольких эВ. Основное электронное состояние молекулы с нелокализованными
электронами будет соответствовать заполнению наиболее глубоких уровней. Так как
каждый уровень заполняется двумя электронами с противоположно направленны-
ми спинами, то при четном числе электронов N будет заполнено N/2 уровней,
при нечетном (N — 1 )/2 уровней и один электрон с некомпенсированным спином
будет находиться на первом свободном уровне (ср. рис. 26.5, г). Возбужденные со-
стояния будут соответствовать переходу одного или нескольких электронов на более
высокие уровни. Несмотря на свою схематичность, металлическая модель молекулы
с нелокализованными электронами, правильно отражая характерные особенности
этих электронов, приводит к удовлетворительным результатам и позволяет наглядно
понять ряд свойств молекул, а некоторые из них даже приближенно рассчитывать,
в частности, диамагнетизм и поляризуемость.
Весьма существенно, что несмотря на различие способов расчета, исходящих
из атомных электронных орбит и из металлической модели, основные результаты
получаются весьма близкими, как было показано Хемом и Руденбергом [356],
произведшими детальное сравнение обоих способов.
Наряду с методом молекулярных орбит в его различных формах, для расчета со-
стояний молекул с нелокализованными электронами может быть применен и метод
валентных связей, усложненный рассмотрением так называемого резонанса валент-
ных структур. Этот способ расчета был предложен Паулингом [348, 88] и основан
на определенном квантовомеха-
ническом приближении, находя-
щемся в соответствии с валент-
ной схемой химии. Упрощен-
ная и совершенно неправильная
интерпретация резонанса валент-
ных структур подверглась обо-
снованной критике [83а, 80], что
не затрагивает, однако, законно-
сти данного способа расчета, ко-
торый мы рассмотрим на примере
молекулы бензола.
Согласно представлению об
электронных парах, шесть неспа-
ренных р-электронов могут обра-
Рис. 26.18. Картина двойных связей в бензоле:
а — наложение орбит р-электронов атомов углерода;
б — структуры Кекуле; в — структуры Дьюара
зовать три тг-связи, причем двумя
способами, как показано на рис. 26.18, а. Таким образом, получаются две возможные
структуры, где двойные связи, каждая из которых образована парой а-электронов
и парой тг-электронов, чередуются с простыми связями, образованными лишь парой
а-электронов. Эти структуры полностью соответствуют обычной валентной схеме
и были впервые предложены для бензола Кекуле (рис. 26.18,6).
Следует отметить, что Кекуле еще в 1865 г. дал формулу бензола как симметричного
шестичленного кольца и лишь впоследствии, чтобы удовлетворить валентной схеме химии
с четырехвалентным атомом углерода, предложил структуру с чередующимися двойными
и простыми связями [81].
Структуры Кекуле соответствуют симметрии (выделенная ось симметрии
третьего порядка), более низкой, чем действительная симметрия бензола (вы-
деленная ось симметрии шестого порядка). Если бы в молекуле бензола имелись
812 Глава 26. Электронные состояния в многоатомных молекулах
чередующиеся двойные и простые связи, то она была бы значительно менее устой-
чивой, чем в действительности. Можно, однако, прийти к симметрии с шестью
эквивалентными связями С—С, если представить структуру бензола не одной струк-
турой Кекуле, а их наложением. При этом действительная структура молекулы
бензола рассматривается как содержащая в себе в одинаковой степени обе структу-
ры Кекуле. Реально структуры Кекуле в отдельности не существуют, однако такой
метод рассмотрения является полезным, так как позволяет сопоставлять действи-
тельную структуру молекулы с валентной схемой химии, правильно отражающей
структуру соединений с локализованными электронными парами. Отсутствие лока-
лизации электронов в бензоле получается как результат наложения двух структур
Кекуле со связями, осуществляемыми локализованными парами электронов.
С квантовой точки зрения двум структурам Кекуле с локализованными элек-
тронными парами соответствуют два электронных состояния с одинаковой энер-
гией Eq, т. е. в соответствующем приближении, когда рассматриваются три неза-
висимых тг-связи, получается двукратное вырождение. При учете взаимодействия
между связями вырождение снимается, и вместо этих двух состояний возникают два
новых с энергиями Е\ < Eq и Е2 > Eq. В этих состояниях электроны уже не будут
локализованными. Первое из них более устойчиво и является основным состоянием
бензола. По формальной аналогии с резонансом двух маятников с одинаковыми
частотами колебаний говорят о резонансе двух структур с локализованными элек-
тронными парами и отрицательную энергию Е\ — Eq называют энергией резонанса.
Это соответствует принятой в квантовой теории терминологии, согласно которой
при совпадении энергии двух состояний говорят о резонансе между уровнями энер-
гии. Следует иметь в виду, что наложение валентных структур нельзя рассматривать
как реальный резонанс, при котором в системе происходит обмен энергиями между
ее частями14), и нельзя считать, что молекулы действительно существуют в состо-
яниях, соответствующих отдельным валентным структурам — в случае бензола —
структурам Кекуле. Именно такое ложное понимание резонанса валентных структур
и резонансных энергий является ошибочным.
Результаты, получающиеся при рассмотрении резонанса валентных структур,
оказываются в основном совпадающими, несмотря на различие способов расчета,
с результатами метода молекулярных орбит; анализ имеющегося соответствия был
дан в работах Лонге-Хиггинса, Дьюара и Хема [354].
Следует подчеркнуть, что в спектроскопии молекул большое значение при-
ближенных методов рассмотрения нелокализованных тг-электронов определяется
тем, что эти электроны, являющиеся относительно слабо связанными и дающие
сравнительно тесно расположенные уровни энергии, обусловливают поглощение
и испускание в видимой и близкой ультрафиолетовой областях спектра; в частности,
цветность органических соединений связана именно с наличием нелокализованных
тг-электронов (см. §27.1, с. 827).
Рассмотрим теперь квантовомеханическую формулировку различных способов расчета
молекул с нелокализованными электронами.
При расчете по методу молекулярных орбит, исходя из атомных одноэлектронных состо-
яний, приближенная волновая функция $ для нелокализованного молекулярного электрона
составляется как линейная комбинация атомных волновых функций (ср. (24.33); метод
LCAO МО, см. с. 741):
=	(26.17)
|4* Подобно случаю системы, состоящей из двух резонирующих маятников с одинаковой частотой
колебаний, см. §21.1, с. 607.
§ 26.4. Нелокализованные электроны и методы их рассмотрения
813
где — постоянные коэффициенты. С помощью функций гр решается приближенная
квантовомеханическая задача.
В частности, для бензола функции гр выбирают в виде
6
t=l
(26.18)
где гр£ — волновые функции атомов углерода, обладающие осевой симметрией относительно
оси z, перпендикулярной к плоскости бензольного кольца (см. (26.4) и рис. 26.15,6). Шес-
ти независимым функциям грр* соответствуют шесть независимых линейных комбинаций
типа (26.18), характеризующих шесть нелокализованных состояний тг-электронов. Решение
соответствующей задачи при учете взаимодействия лишь электронов соседних атомов углерода
и при пренебрежении интегралами наложения (24.41) дает шесть уровней энергии |349j:
Е\ — Eq + 2С, Е2 — Eq 4~ Е3 — Eq — Су Е4 — Eq — 2Су
(симметрия Л2и) (двойной, (двойной, (симметрия В2$),	(26.19)
симметрия Е}д) симметрия Е2и)
где Eq — полная энергия шести р-электронов атомов углерода, а С — резонансный интеграл
типа (24.46) для электронов соседних атомов. Согласно (26.19), мы получаем самый глубо-
кий уровень Ei (С < 0), заполняемый двумя электронами, и более высокие уровни Е2, Е3
и Е4, заполняемые четырьмя, четырьмя и двумя электронами соответственно. Для основно-
го состояния бензола заполнены уровни Е{ и Е2 шестью связывающими электронами (тг),
для возбужденных состояний один или несколько электронов являются антисвязывающи-
ми (я*) и находятся на более высоких уровнях. Уровню Et соответствует волновая функция
1
симметрии А2и, для которой Cj = с2 = с3 = с4 = с5 — с& = т.е.
V 6
V-.=4 w?++о-
Vu
(26.20)
Согласно (26.20), электронная плотность между атомами одинакова и определяется перекры-
ванием функций грРг для соседних атомов. Уровню Е2, как дважды вырожденному (симме-
трии Eig), соответствуют две функции с Cj = с4 = 0,
1 1 1
с2 — с3 — с5 — С(у — — и Cj — с4 —	^6
т.е.
и
Я =	+ rf? - « -	+ rf).
для которых электронная плотность между некоторыми атомами обращается в нуль.
Были предложены различные варианты способов расчета по описанному методу как чисто
теоретических, так и полуэмпирических. Следует отметить хорошие результаты, полученные
на основе полуэмпирического способа Паризером и Парром [353].
При расчетах по методу молекулярных орбит, исходя из металлической модели молекулы
(модель свободных электронов, сокращенно модель FE15^), решается квантовомеханическая
задача для движения электрона в потенциальных ящиках различной формы, соответствующих
структуре молекулы.
Самой простой металлической моделью молекулы является модель одномерного ящика
с бесконечно высокими стенками. Уже эта простейшая модель дает приближенно правильные
15) От английского «free electrons» (свободные электроны); более полное обозначение FE МО.
814 Глава 26. Электронные состояния в многоатомных молекулах
результаты для полиметиновых цепей, звеньями которых служат группы -(СН=СН)-.
Для такого ящика мы имеем одномерное уравнение Шредингера
h2 d2'0
+	=	26.21
8тг2те dx2
где потенциал
U — 0 при 0 < х < L.
U = оо при х < 0 и х > L
(L — ширина ящика). Решением этого уравнения, обращающимся в силу условий (26.22)
в нуль при х = 0 и х = L, являются волновые функции
X
гр = гро sin П7Г-,
Lt
(26.23)
где п — квантовое число, принимающее целые значения, п = 1,2,3,..., и определяющее
энергию по формуле
Л2п2
Еп~ 8теЬ2'
Расположение уровней энергии (26.24) аналогично расположению вращательных уровней
энергии линейной молекулы и изображено на рис. 26.17; на этом же рисунке показаны
волновые функции — для последовательных уровней в ящике укладываются 1, 2, 3, 4, ...
/	АЛЛА	2L\
полуволны I L =	2—, 3 —, 4—, ..., т.е. А = — ).
\	2 2	2	2	nJ
При L = 10 А 10~7 см мы получаем
(26.24)
(6,56 • Ю’27)2	,	,	2	2
Еп = ~8~-о^9 - ю~27~" Го-|Ч~” эрг = 6 ‘10 ” эрг ~ °’4п эВ’
что дает последовательные уровни с энергиями 0,4 эВ, 1,6 эВ, 3,6 эВ, 6,4 эВ, ... (п = 1,2,
3,4,...), т.е. действительно расстояние между глубокими уровнями (только для которых
и справедлива модель ящика с бесконечно высокими стенками) не превышает нескольких эВ.
Для полиенов, в которых цепь состоит из к звеньев длины Z, мы имеем L = kl
и по формуле (26.24) получаем
h2n2
8тек212
С увеличением числа звеньев расстояния между уровнями, равные
h2 In ч- 1
АЕпп+\ = Еп+] — Еп - — — ,
ът€12 к2
(26.25)
уменьшаются. Так как каждое звено дает два нелокализованных тг-электрона, то общее
число тг-электронов равно N = 2к и они заполняют к уровней от уровня п — 1 с энерги-
h2	h2
ей Е\ =-----— до уровня п = к с энергией Ек = -—-г. Полная энергия всех электронов
%mek2l2	8те12
равна
чД	h2 1=1	X 2 _ Л2 fc(fc+l)(2fc+l) П 4тек212	6 П=1	(26.27)
На одно звено цепи приходится энергия		
Е h2
~к ~ 24те12
(	3	1 \
\2+k + k'2)'
(26.28)
которая уменьшается с увеличением числа звеньев, т. е. связи, образованные нелокализован-
ными электронами, при этом упрочняются — электронам энергетически выгоднее двигаться
в большей области.
§ 26.4. Нелокализованные электроны и методы их рассмотрения
815
Расстояние между первым незаполненным уровнем Ек+\ и последним заполненным
уровнем Ек, согласно (26.26), равно (n = k)
h2 2k + 1	,
АЕи,^Е.,.-Е. = ~г —,	.	(26.29)
т. е. убывает с увеличением числа звеньев. Оно определяет положение первой полосы погло-
щения молекулы.
Общая схема расчета молекул с нелокализованными тг-электронами, согласно модели
свободных электронов с учетом разветвления цепей и кольцевых структур, была дана Руден-
бергом и Шером [355]. Они получили удовлетворительные результаты для частот электронных
переходов ряда молекул с сопряженными двойными связями.
Можно уточнить металлическую модель, заменяя постоянный потенциал периодическим,
вводя конечный потенциал на границах ящика и т.д.; однако такие уточнения мало целесо-
образны ввиду грубости металлической модели. Ценность этой модели заключается в том, что
при самых простых предположениях она приводит к качественно правильным результатам.
Квантовомеханический расчет по методу валентных связей с учетом резонанса валентных
структур основан на нулевом приближении, в котором берутся волновые функции многоэлек-
тронных состояний, соответствующих валентным структурам и обладающих одинаковыми
или близкими энергиями (т. е. волновые функции точно или приближенно вырожденных со-
стояний), V'io, ^20» • • • > “Фго (г — степень вырождения). При учете взаимодействия электронные
состояния молекулы будут описываться г волновыми функциями
c.jV’jo-	(26.30)
»=1
Энергии Е2, • • •, Ег этих состояний отличны от первоначальной энергии Eq. Применяя
теоргю возмущений, можно найти волновые функции (26.30) и энергии Е{ Е2	Ег,
причем состояние с наименьшей энергией Е} будет основным, а остальные состояния —
возбужденными. Разность энергии Ei - Eq будет выражаться через обменные интегралы,
которые можно приближенно рассчитать или определить из опытных данных. Энергия Е} — Eq
есть энергия резонанса, а разности энергий Е2- Е\, Е3 - Е}, ..., Ег - Е{ определяют частоты
электронных переходов из основного состояния в возбужденные.
Расчет для бензола, основанный на двух структурах Кекуле, при учете взаимодействия
только р-электронов соседних атомов, приводит к следующим значениям энергий [349]:
Е\ — Eq + 0,90 А, Е2 = Eq — 1,50 А,	(26.31)
где Ег) — энергия для структур Кекуле, А — отрицательный обменный интеграл для
р-электронов соседних атомов, зависящий от перекрывания атомных электронных волно-
вых функций грРг. При этом волновая функция для основного состояния с энергией Е},
отличающейся от Ео на величину энергии резонанса 0,90 А, имеет вид
= cQfa + Vh),	(26.32)
где и — шестиэлектронные волновые функции для структур Кекуле. Эта функция со-
ответстгует равномерному распределению электронов по шести эквивалентным связям. Если
наряду сдвумя структурами Кекуле учитывать три структуры Дьюара (рис. 26.18, в), то в резуль-
тате решения задачи для пяти структур энергия резонанса оказывается равной 1,11 А, что пред-
ставляет 1ишь несущественное уточнение, принимая во внимание приближенность метода.
Следует отметить, что когда для бензола берутся волновые функции электронных со-
стояний, соответствующие структурам Кекуле (или другим структурам, например, структурам
Дьюара), го подразумеваются структуры, которые хотя и характеризуются распределением
электронов, обладающих симметрией более низкой, чем симметрия Р6Л 16\ но отвечают распо-
ложению ядер в виде правильного шестиугольника симметрии Dbh. Если бы структуры Кекуле
реально суцествовали (чего в действительности нет), то равновесная конфигурация не была
бы правилыым шестиугольником из-за различия длин связей С—С и С=С (см. с. 502).
,6) Структуры Кекуле соответствуют, как мы видели, симметрии а структуры Дьюара соответствуют
симметрии Dy.
816
Глава 26. Электронные состояния в многоатомных молекулах
С усложнением молекул увеличивается и число валентных структур, которые нужно
учитывать при применении данного способа расчета, и он становится менее эффективным.
Вообще, для расчета возбужденных состояний молекул с нелокал изованны ми тг-электронами
метод молекулярных орбит более эффективен и в настоящее время ему уделяется наибольшее
внимание (см. уже цитированный обзор Лонге-Хиггинса [89], а также обзоры по методам
квантовомехацрческого расчета молекул в ежегодниках «Annual Review of Physical Chemistry»).
§ 26.5. Электронные конфигурации и электронные состояния
простейших многоатомных молекул
В гл. 24 мы разобрали систематику состояний отдельных электронов для двух-
атомных молекул, соответствующую представлению о молекулярных орбитах, рас-
смотрели электронные оболочки двухатомной молекулы и возможные состояния
такой молекулы в целом, как основное, так и возбужденные. Аналогичным, толь-
ко более сложным образом можно систематизировать одноэлектронные состояния
для простейших многоатомных молекул, рассмотреть их электронные оболочки и по-
лучающиеся основные и возбужденные состояния. Существенно, что при помощи
качественных соображений можно получить выводы об электронных состояниях
молекул и о переходах между этими состояниями. Наиболее полно систематика
электронных состояний простейших молекул разобрана в серии работ Уолша [358],
где дан метод сопоставления одноэлектронных состояний молекул различной фор-
мы, линейных с нелинейными и плоских с неплоскими; пример получающихся
при этом корреляционных диаграмм приведен ниже.
Одноэлектронные состояния многоатомной молекулы, обладающей симметри-
ей, классифицируются по типам симметрии, так же как и состояния всей молекулы
в целом, для важнейших точечных групп в соответствии с табл. 22.1-22.11. Для того,
чтобы отличать одноэлектронные состояния от состояния молекулы в целом, мы бу-
дем обозначать их строчными буквами вместо прописных. Например, для молекулы
симметрии C2v (табл. 22.1) возможные типы симметрии одноэлектронных состояний
будут а\, а2, Ъ], Ь2 аналогично типам симметрии At, А2, В\, В2 для молекулы в целом.
Рассматривая одноэлектронные молекулярные состояния, мы будем говорить
о соответствующих орбитах, например, об орбитах ст, тг, ... для линейных молекул,
орбитах а}, а2, ... для нелинейных молекул симметрии C2v и т. д. Аналогично случаю
двухатомных молекул молекулярные орбиты могут быть связывающими и антисвя-
зывающими: последние, как и раньше (см. с. 747), будем обозначать звездочкой.
Наряду с этим могут быть орбиты, локализованные у отдельных атомов и не участ-
вующие в образовании связей — несвязывающие орбиты; примером таких орбит
служит орбита pz атома кислорода при образовании связи С—О (рис. 26.14,а), за-
полненная двумя электронами. Подобные орбиты мы будем отмечать индексом нуль
справа сверху. Таким образом, а, , fl! соответственно обозначают свя мшаощую,
несвязывающую и антисвязывающую орбиты в случае типа симметрии
Электронная конфигурация многоатомной молекулы определяем- .данием
чисел электронов в различных молекулярных оболочках, соответствующих различ-
ным молекулярным орбитам. Когда орбитальное вырождение отсутствует, сболочки
заполняются двумя электронами, при двухкратном и трехкратном орбитальном вы-
рождении — четырьмя и шестью электронами соответственно (см. §26.., с. 792).
Электронные состояния молекулы для данной электронной конфигурации можно
легко определить. Разберем важнейшие встречающиеся случаи.
Для линейных многоатомных молекул, так же как для двухатомных, голучаются
а-, тг-, 6-оболочки при симметрии Cqqv и ад-ч сгп~, яд~, бд-, ft-оболочки
§ 26.5. Электронные состояния простейших многоатомных молекул	817
при симметрии Джл, причем а-оболочки заполняются двумя электронами, а тг-
и <5-оболочки — четырьмя. Электронные состояния молекулы в целом находятся,
как это было рассмотрено в § 24.5 (с. 731).
Аналогичным образом получаются электронные состояния нелинейных много-
атомных молекул. Для случая полностью заполненных оболочек, что обычно имеет
место для основных состояний молекул с четным числом электронов (ср. выше
§26.1, особенно рис. 26.5, с. 793), электронное состояние обладает симметрией
равновесной конфигурации и не изменяется при любых операциях симметрии —
является полносимметричным17). Мы имеем состояния ’Aj (для групп Cnv и ТД
’А1р (для групп Z)2h и Oh) и т. д., причем индекс 1 слева сверху указывает, как
обычно, мультиплетность; в данном случае все эти состояния синглетные.
Для случая одного неспаренного электрона, помимо заполненных оболочек, что
имеет место (см. с. 793) для основных и возбужденных состояний молекул с нечет-
ным числом электронов, электронные состояния молекулы в целом будут относиться
к тому же типу симметрии, как и состояние этого электрона, и будут дублетны-
ми (например, 2Ai или b2 2В2 для молекулы симметрии C2V)> Такие же состояния
будут получаться при наличии трех электронов в оболочке, заполняемой четырь-
мя электронами (в оболочке е4 дважды вырожденного типа симметрии Е, состоя-
ние е3 2Е), и при наличии пяти электронов в оболочке, заполняемой шестью электро-
нами (в оболочке /6 трижды вырожденного типа симметрии F, состояние /5 2F). Это
вытекает из дополнительности оболочек е3 и е и оболочек f5 и f,8), аналогичной до-
полнительности оболочек атомов (р5 и р, d? и d, /13 и /) и линейных молекул (тг3 и тг,
б3 и б, что является частным случаем дополнительности оболочек е3 и е).
При наличии двух электронов в двух различных незаполненных оболочках (по-
мимо заполненных оболочек), что типично для возбужденных состояний молекул
с четным числом электронов, симметрия электронного состояния молекулы мо-
жет быть найдена по общим правилам теории групп. Мультиплетность при этом
будет равна 1 и 3 (полный спин S — О, I). Если один из электронов находится
в полносимметричном состоянии, то симметрия электронного состояния молеку-
лы будет просто совпадать с симметрией состояния другого электрона. Например,
при симметрии С2т, для конфигурации получаются состояния !В2 и 3В2,
а при симметрии для конфигурации а^е - 1Е и 3Е. Когда оба электрона находят-
ся в неполносимметричных орбитальных состояниях, то симметрия электронного
состояния молекулы находится аналогично тому, как это делается для колебатель-
ных состояний при возбуждении двух неполносимметричных колебаний (см. §25.1).
Для невырожденных орбитальных состояний применяются таблицы типов симме-
трии, приведенные в гл. 22. Например, для симметрии C2v (см. табл. 22.1) для кон
фигурации а2д2 состояние меняет знак при операм и С2 (А2 не меняе, _ ика, В2
меняет знак) и не меняет знака при операции и (А2 и В2 оба меняют знак),
следовательно, относится к типу симметрии Вь с учетом сложения спинов мы
получаем состояния а2Ь2 JBi и а2Ь23В]. Для вырожденных орбитальных состояний
применяется табл. 23.1 результирующей симметрии. Например, при симметрии СзУ
для конфигурации ее, т. е. для двух электронов в дважды вырожденных состояниях
типа симметрии Е, согласно этой таблице, получаются состояния Аь А2 и Е, что
дает ее1 ’А^ ее13А\, ее1 !А2, ее13А2, ее1 \Е и ее' 3Е, если электроны неэквивалентны; * 18
|7) Применяя ту же терминологию, что и для колебательных состояний.
18) Не смешивать с обозначениями f и F для атомных электронов.
818 Глава 26. Электронные состояния в многоатомных молекулах
для эквивалентных электронов (конфигурация е2), как можно показать, в силу
принципа Паули возможны лишь состояния е2 ’Л1? е2 3Д2 и е2 1Е.
Симметрия электронного состояния, для которого отдельные электроны характеризуются
волновыми функциями ^4, ^2,..., преобразующимися, согласно неприводимым предста-
влениям Г|, Г2,..., Г*, определяется прямым произведением Г|ХГ2х... х Гь согласно
которому преобразуются полные волновые функции ф — ^1^2.. .tpk. Применение таблиц
типов симметрии и таблицы результирующей симметрии сводится к нахождению прямых
произведений Г( х Г2 для пар электронов. Для нахождения прямых произведений трех и более
неприводимых представлений надо повторно применять эти таблицы.
Учет принципа Паули для эквивалентных электронов производится по аналогии со слу-
чаем атомов. Требование антисимметрии полной волновой функции относительно переста-
новки электронов позволяет определить возможные значения мультиплетности. В частности,
в рассмотренном примере конфигурации е2 симметрии C3v состояния Л| и Е оказываются
симметричными при перестановке пространственных координат электронов и, следовательно,
антисимметричны относительно перестановки спиновых координат, т. е. являются синглет-
ными (5 = 0), а состояние А2 оказывается антисимметричным и триплетным (ср. § 10.2).
Действительно, одноэлектронному состоянию симметрии Е соответствуют две волновые
функции и которые при повороте С3 умножаются соответственно на е = е з
и на el<fi — ег~ (см. (22.24) и (22.42)). Для двух электронов симметрии Е мы получаем
четыре функции = ^+(0^+(2), 4>+- = ^+(1)^-(2), V-+ = ^-0Ж(2) и = ^_(1)^_(2).
Функции tp++ и t/>_при повороте С3 умножаются на е * = е з = е з и е * — е з = е з
г—	—t'-
ii образуют двухмерное представление Е с характером х(Г'з) = е * + е з
2тг
= 2 cos —;
3
функции и инвариантны при повороте С3 и их линейные комбинации 4-^-+
и	обладают симметрией А| и Л2 соответственно, так как отражение av превращает гр+
в и обратно, т.е. в Ф-+ и </>-+ в ^+_. Относительно перестановки пространственных
координат электронов ________(состояние Е) и 4- (состояние симметричны,
а	(состояние А2) антисимметрично, и мы получаем ’А|, ]Е и 3Д2-
Для систематики состояний простейших молекул рассмотрение молекулярных
орбит имеет то большое преимущество по сравнению с рассмотрением электрон-
ных пар, что оно позволяет одинаково хорошо исследовать как свойства основных,
так и возбужденных состояний. При возбуждении одного из пары связывающих
электронов изменяется прочность соответствующей связи, и метод электронных пар
становится к ней неприменимым, тогда как с точки зрения метода молекулярных
орбит мы просто получаем вместо двух эквивалентных электронов, заполняющих
данную молекулярную оболочку, два неэквивалентных электрона, находящихся
в разных оболочках.
Наряду с этим, существенным достоинством метода молекулярных орбит явля-
ется простота учета возбуждения электронов при наличии в случае симметричных
молекул эквивалентных связей. Нельзя рассматривать независимо электронное воз-
буждение одной из эквивалентных связей, так как такие связи тождественны.
Для того, чтобы принять во внимание тождественность связей и удовлетворить
условиям симметрии, достаточно ввести в рассмотрение нелокализованные моле-
кулярные орбиты, как это было сделано в предыдущем параграфе для основных
состояний молекул, имеющих, согласно валентной схеме, сопряженные двойные
связи. Если для основных состояний молекул с простыми связями и с несопряжен-
ными двойными связями можно приближенно считать электроны локализованными
на этих связях и рассчитывать энергию молекулы, исходя из такого представления
(например, по методу электронных пар), то для возбужденных состояний подобный
подход неприменим. Для молекулы с эквивалентными простыми связями уже при-
ходится при рассмотрении электронных уровней энергии и переходов между ними
§ 26.5. Электронные состояния простейших многоатомных молекул	819
считать электроны нелокализованными и вводить молекулярные орбиты, общие
для эквивалентных связей. Например, для молекулы воды Н2О из молекулярных
орбит для двух связей О—Н в отдельности следует составить две новые молеку-
лярные орбиты — симметричную (Л)) и антисимметричную (В2) относительно оси
молекулы и плоскости (№ = как это схематически показано на рис. 26.19.
Рис. 26.19. Нелокализованные орбиты для молекулы Н2О:
а, б — исходные локализованные орбиты;
в, г — нелокализованные орбиты, симметричная и антисимметричная
Если — волновая функция молекулярного электрона, локализованного на свя-
зи О—а ^2 — волновая функция молекулярного электрона, локализованного на свя-
зи О—Н(2), то условиям симметрии будут удовлетворять волновые функции
+ *’!'	(26.33)
Фв2 = с(^1 - ^2),
обладающие симметрией Л| иВ2; они и будут характеризовать одноэлектронные состояния —
«орбиты» — типов симметрии Q] иЬ2, согласно принятым выше обозначениям.
Рассмотрение нелокализованных связывающих и антисвязывающих молеку-
лярных орбит в сочетании с количественными соображениями о прочности связи
электронов на этих орбитах, а также на несвязывающих орбитах, позволяет дать
систематику электронных уровней энергии и объяснить наблюдаемые электронные
переходы для простейших многоатомных молекул. Вместе с тем оказывается возмож-
ным учесть прочность связи электронов для молекул различной формы — линейных
и нелинейных, плоских и неплоских — и сделать выводы о том, какие именно
формы при каком общем числе электронов в молекуле данного типа являются
энергетически более выгодными [358].
Мы рассмотрим классификацию молекулярных электронов, получающиеся
электронные конфигурации и электронные состояния, а также одновременно выяс-
ним роль формы молекулы, на типичном примере молекулы ХН2.
В молекуле такого типа центральный атом X, обладающий s- и р- электронами,
соединяется с двумя атомами водорода. К подобным молекулам относятся моле-
кула Н2О, радикалы СН2 и NH2. Предельными формами молекулы ХН2 являются
нелинейная прямоугольная форма с углом 90° между связями X—Н и линейная
форма с углом 180° между этими связями. Атомные орбиты и их наложение, приво-
дящие к образованию связей, согласно теории направленной валентности, показаны
для обеих форм на рис. 26.20.
Для нелинейной формы атом X имеет четыре орбиты — две орбиты р\ и
накладывающиеся на орбиты 1s атомов водорода и образующие две связывающие
молекулярные орбиты а (ср. рис. 26.6) и две несвязывающие орбиты s и рх. По-
следние две имеют симметрию Л| и В| соответственно и обозначаются как
и (ср. с. 816). Две локализованные связывающие молекулярные орбиты при уче-
те симметрии дают две нелокализованные связывающие орбиты симметрии Л|
820
Глава 26. Электронные состояния в многоатомных молекулах
Рис. 26.20. Образование связей
в молекуле типа ХН2:
а — для нелинейной формы;
б — для линейной формы
и В2 (ср. рис. 26.19), которые мы обозначим
просто как а\ и Ь2. Энергия электрона в симме-
тричном состоянии в] будет меньше, чем в ан-
тисимметричном Ь2. В состоянии энергия
ДО)
электрона будет меньше, чем в состоянии о, ,
причем можно предполагать, что примерно та-
кая же, как и энергия в состояниях Д] и 6219)-
Мы получаем расположение одноэлектронных
уровней энергии, показанное на рис. 26.21 сле-
ва для угла 90° между связями X—Н. Эти уровни
являются четырьмя самыми глубокими уровня-
ми, так как другие молекулярные орбиты будут
либо антисвязывающими, либо вообще образо-
ваны из сильно возбужденных атомных орбит,
и могут давать лишь высоколежащие уровни.
Для линейной формы атом X имеет две ги-
бридные орбиты sp, накладывающиеся на ор-
биты 15 атомов водорода и образующие две
связывающие молекулярные орбиты а и две
несвязывающие орбиты рх и pz. Последние две
орбиты вырождены между собой и принадле-
жат к типу симметрии Пи (Б1и, см. табл. 22.9,
с. 664); мы обозначим их через тг£°\ Две лока-
лизованные связывающие молекулярные орби-
ты а при учете симметрии дают, как и в случае
нелинейной молекулы, две нелокализованные связывающие орбиты симметрии
и которые мы обозначим как ад и аи. Электрон в четном состоянии ад будет
Рис. 26.21. Расположение
уровней энергии
молекулярных электронов
для молекулы типа ХН2
обладать меньшей энергией, чем в нечетном аи, при-
чем энергии электронов будут меньше, чем в состо-
яниях и Ь2 для нелинейной молекулы, так как
в последней связи образуются с участием атомных
орбит р, а в рассматриваемом случае линейной мо-
лекулы — с участием гибридных орбит sp, что энер-
гетически выгоднее. Энергия электрона в состоянии
тгу должна быть такой же, как и энергия электрона
6® в нелинейной молекуле; в обоих случаях мы име-
ем несвязывающие р-электроны центрального атома.
В результате получается расположение одноэлектрон-
ных уровней энергии, показанное на рис. 26.21 справа
для угла 180° между связями X—Н.
При увеличении угла между связями от 90 до 180°
полносимметричная связывающая орбита а\ будет
превращаться в полносимметричную орбиту ад, ан-
тисимметричная связывающая орбита Ь2 — в анти-
симметричную орбиту аи (обе они антисимметричны
|9) Атомный ??.$-электрон должен, разумеется, быть связан прочнее, чем пр-электрон. Соотношение
(°)	к
энергии несвязывающего электрона а\ и связывающих электронов О| и Ь2 подтверждается получающи-
мися результатами.
§ 26.5. Электронные состояния простейших многоатомных молекул 821
относительно оси С2 и плоскости а^ = а^у\ перпендикулярной к оси у)\ несвязы-
вающие орбиты а) и Ъ\ превратятся в вырожденные между собой орбиты тги (как
с	(°)	t(°)	с	(2)
орбиты а; и о, , так и орбиты тгм симметричны относительно плоскости ак } — а™’).
В результате мы получаем корреляционную диаграмму рис. 26.21, наиболее харак-
„	(0) о С
тернои чертой которой является увеличение энергии электрона а, - тг”, орбита
которого превращается из атомной 5-орбиты в атомную р-орбиту.
Сопоставление состояний молекул симметрии C2v и Dxh легко может быть получено
при помощи табл. 22.1 и 22.9. Характеры для типов симметрии и В2 группы С2ъ совпадают
с характерами для типов симметрии Aig(Eg ) и Л1и(£+) группы Dxh (сГуУ\ и С2 для группы
C2v соответствуют crh, av и С2 для группы Dxfl, так как в рассматриваемом случае осью Сх
является ось у), а суммы характеров для невырожденных типов симметрии Л] и Вх равны
характерам для дважды вырожденного типа симметрии £71и(Пи). При понижении симметрии
от Dxh до C2v двухмерное представление распадается на два одномерных, чему и соответствует
(0)	(0)	,(0)
расщепление уровня тг; на два уровня а, ио,.
Из корреляционной диаграммы можно сразу сделать выводы о форме молекул
типа ХН2 в зависимости от числа внешних электронов. При четырех электронах,
что имеет место для ВеНз и HgH2 (два внешних электрона атомов Ве или Hg
и два электрона атомов Н), будут заполнены оболочки - ад и 62 — &и, и так
как энергия принимает наименьшее значение при угле Н—X—Н, равном 180°, то
эти молекулы в основном состоянии должны быть линейными. Основное состояние
будет a] al 1 St. При увеличении числа электронов более выгодными благодаря
zr	(0)	(0)
заполнению оболочки а] - станут меньшие значения угла между связями,
что, в частности, будет иметь место для восьмиэлектронной нелинейной молекулы
воды Н2О. Основная конфигурация этой молекулы будет
(а})2(а?У(Ь2)2(Ь^2 %,	(26.34)
и так как все нижние уровни заполнены, то для электронного возбуждения молекулы
требуется значительная энергия.
Нелинейными молекулами должны быть и радикалы — шестиэлектронная
молекула СН2 и семиэлектронная молекула NH2 с основными состояниями
СН2 (а|)2(Ь2)2(а<0>)2 'Л,	(26.35)
NH2 (ai)2(b2)2(a{^2b^ 2В[.	(26.36)
В отличие от молекулы Н2О для них возможны сравнительно глубоко лежащие
возбужденные состояния
СН2 (а,)2(Ь2)2(а^0))(&^0)) *В| и 3В|	(26.37)
И
NH fwWW)2 1
2	2bJ
Мы рассмотрели пример трехатомной молекулы типа ХН2. Для трехатомных
симметричных молекул типа XY2, не являющихся гидридами, можно построить
корреляционную диаграмму, аналогичную диаграмме рис. 26.21, но более сложную,
потому что в этом случае для атомов Y нужно учитывать s- и р-орбиты, так же как
и для атома X. Такая диаграмма, построенная с учетом s- и р-орбит атома X и обоих
822
Глава 26. Электронные состояния в многоатомных молекулах
атомов Y, позволяет объяснить линейную форму молекул с числом внешних электро-
нов, не превышающим 16, в частности, линейную форму молекулы СО2, имеющей
16 внешних электронов (электроны 2s и 2р атома С и двух атомов О). Для молекул
с 17-20 электронами получается в согласии с опытом нелинейная структура (при-
мером могут служить молекулы SO2 и Оз с 18 электронами). При 22 электронах
должна опять получиться линейная структура.
Для четырехатомных молекул хорошие результаты дает рассмотрение молекул
типа ХН3 и XY3 в зависимости от угла между связями X—Н или X—У, составляюще-
го 90° для предельного случая пирамидальной молекулы симметрии Cjv со связями,
образованными тремя р-электронами, и 120° для предельного случая плоской моле-
кулы симметрии Х>зд со связями, образованными в результате гибридизации типа sp2.
Аналогичным образом могут быть рассмотрены и менее симметричные мо-
лекулы. Существенным является то, что с помощью корреляционных диаграмм,
аналогичных диаграмме рис. 26.21, можно сделать ряд выводов о свойствах возбу-
жденных электронных уровней, в частности, возможны случаи, когда возбужденная
молекула будет иметь другую симметрию и по своей форме сильно отличаться
от невозбужденной20).
Для молекул с нелокализованными тг-электронами можно классифицировать
их по молекулярным оболочкам, основываясь на рассмотрении нелокализованных
электронов по методу молекулярных орбит (см. выше, §26.4). Получаются нелока-
лизованные молекулярные оболочки, заполняемые связывающими и антисвязыва-
ющими тг-электронами (тг и тг* соответственно). Наряду с такими оболочками надо
учитывать и другие оболочки молекулы, из которых может происходить возбужде-
ние электронов, в частности, оболочки, заполняемые несвязывающими электрона-
ми (что обозначается буквой п2,)). Для заданной электронной конфигурации можно
определить возможные термы, как это было описано выше (см. с. 817).
Для молекулы бензола, согласно методу молекулярных орбит, для нелока-
лизованных тг-электронов получаются последовательные одноэлектронные уровни
энергии симметрии Е\д, Eiu, Вгд, которым соответствуют оболочки (а2м)2,
(elff)4, W, (b2y.
Этот результат получается, согласно (26.19), если исходить из атомных волновых функ-
ций ,фРг (метод LCAO МО), или применять модель свободных электронов (метод FE МО,
см. [355]). Таким образом, оба варианта метода молекулярных орбит приводят к согласую-
щимся результатам.
Первые две оболочки соответствуют связывающим электронам (тг), последние
две — антисвязывающим (тг*). Когда шесть нелокализованных электронов бен-
зольного кольца заполняют оболочки Д2« и е\д, получается основное состояние
молекулы СбНб, (a2u)2(^i^)4 При возбуждении одного электрона е]д и переходе
его в следующую оболочку е2и возникает конфигурация (a2u)2(ei5)3C2U. Термы этой
конфигурации можно найти с помощью табл. 23.2, учитывая, что (е^)3 дает ту же
симметрию Е\дч что и один электрон е^. Мы имеем Eig х Ezu = В\и 4-
и так как возможные значения спина равны 0 и 1, то мы получаем синглетные тер-
мы ’В|М, lB2u, (обозначаемые часто буквой S) и триплетные термы 3B|U, 3B2u,
3Biu (обозначаемые соответственно буквой Т). Расположение термов, получающе-
еся в результате расчета по методу молекулярных орбит, исходя из атомных орбит
20> Подробный разбор электронных конфигураций, результирующих электронных состояний и элек-
тронных спектров ряда простых многоатомных молекул содержится в уже цитированных работах Уол-
ша |358|.
2|) От английского «non-bonding» — несвязывающий.
§ 26.5. Электронные состояния простейших многоатомных молекул 823
при учете взаимодействия электронов [350],
показано на рис. 26.22. Триплетные термы рас-
положены глубже синглетных; однако пере-
ходы между ними и основным термом А\д
должны быть как интеркомбинационные ма-
ловероятны.
Аналогичным образом можно рассмотреть
электронные конфигурации и электронные со-
стояния других молекул с нелокализованны-
ми тг-электронами с учетом симметрии рав-
новесной конфигурации. При этом для бен-
зола и более сложных ароматических моле-
кул оказывается весьма плодотворным упро-
щенное рассмотрение, основанное на класси-
фикации состояний кольцевых систем по их
моменту количества движения, предложенное
Платтом [351] и развитое Моффитом [352].
Для бензола, в частности, состояния а2«, е\д
и е2и соответствуют значениям механического
момента, равным 0, 1 и 2 соответственно. Мы
не будем разбирать данную классификацию,
отметим только, что такой подход позволяет
построить для кольцевых систем молекуляр-
ные орбиты, соответствующие различным зна-
чениям момента количества движения.
Рис. 26.22. Схема уровней
молекулы бензола.
В скобках даны длины волн полос,
согласно расчету,
без скобок — опытные данные
Волновые функции, получаемые, согласно этой «модели периметра» (perimeter model),
можно связать с волновыми функциями, получаемыми по методу линейных комбинаций
атомных функций (LCAO).
ГЛАВА 27
ЭЛЕКТРОННЫЕ СПЕКТРЫ МНОГОАТОМНЫХ МОЛЕКУЛ
§27.1.	Общая характеристика электронно-колебательных переходов
и типы электронных спектров
Так же как и для двухатомных молекул, при переходе между двумя электронны-
ми состояниями многоатомных молекул одновременно изменяются и колебательная,
и вращательная энергии (см. начало гл. 25, с. 753). Число различных возможных ко-
лебательных и вращательных переходов для заданного электронного перехода будет
гораздо большим, чем у двухатомных молекул, и сильно возрастает с увеличением
числа атомов в молекуле. Особенно существенно при этом возрастание количе-
ства колебательных уровней вместе с числом 3N колебательных степеней свободы.
Вместо одной последовательности колебательных уровней двухатомной молекулы,
для многоатомной возникает сложная совокупность таких уровней. Эта совокупность
приближенно определяется формулой типа (21.124), приводящей к числу уровней,
быстро возрастающему с увеличением полного запаса колебательной энергии, благо-
даря увеличению возможных комбинаций квантовых чисел Д|,	^з, ... , vr, где г —
число различных частот нормальных колебаний.
Уже для трехатомной молекулы, имеющей три различные частоты колебаний,
число сильно возбужденных уровней становится весьма большим. На рис. 27.1 сопо-
ставлено расположение колебательных уровней для двухатомной молекулы с частотой
колебаний 1/ и для трехатомной молекулы с частотами колебаний Р|, р2 и
Рис. 27.1 соответствует г/ — 800 см”'1 и V\ — 580 см-1; р2 = у = 800 см~!, причем
для простоты учитывалась лишь первая сумма в формуле (21.124), т.е. колебания считались
гармоническими. Учет второй суммы, обусловленной ангармоничностью, привел бы к нару-
шению правильности расположения уровней и к некоторому дополнительному их сгущению
при больших энергиях. Показаны все уровни, для которых -Ь ^2^2 4- ЩУз < 5 000 см-1.
Для молекул с большим числом атомов колебательны* уровни будут распо-
лагаться чрезвычайно гесно. При электронном переходе комбинируют две подоб-
ные совокупности колебательных уровней. Необходимо, разумеется, учитывать,
что не все изменения колебательной энергии одинаково вероятны, многие из них
маловероятны или вообще не происходят, однако и при этом фактическое число раз-
личных колебательных переходов Д75КОЛ = Е'ол ~Мол ПРИ заданном изменении &ЕЗЛ
электронной энергии может быть весьма большим.
Если учесть вращательные уровни энергии, то плотность расположения уровней
еще возрастет; происходит сильнее наложение последовательностей вращательных
уровней, соответствующих различным колебательным уровням. В результате дис-
кретная вращательная структура, которую удается разрешить при сильной диспе-
рсии, наблюдается лишь для самых простых молекул. Такая структура для линейных
многоатомных молекул аналогична вращательной структуре двухатомных молекул,
§27.1. Электронно-колебательные переходы и электронные спектры 825
а для нелинейных молекул, особенно
являющихся асимметричными волч-
ками, более сложна. Следует иметь
в виду, что для многоатомных мо-
лекул возможны разнообразные вза-
имодействия колебаний и вращения
(см., например, [53], гл. IV), что еще
усложняет вращательную структуру
и может приводить к невозможно-
сти раздельного рассмотрения коле-
бательной и вращательной структур.
Мы в дальнейшем не будем разби-
рать вращательную структуру элек-
тронно-колебательных полос много-
атомных молекул, детально исследо-
ванную лишь для некоторых наибо-
лее простых многоатомных молекул,
трех- и четырехатомных.
В соответствии с быстрым
увеличением плотности располо-
жения колебательно-вращательных
уровней энергии — их густоты —
с возрастанием числа атомов в мо-
лекуле, электронный спектр (точ-
нее, электронно-колебательно-вра-
щательный спектр) молекулы услож-
няется, и в нем постепенно исчеза-
ет полосатая структура, соответству-
ющая отдельным электронно-коле-
бательным переходам. Для простых
молекул эта структура напоминает
полосатую структуру для двухатом-
ных молекул. Для более сложных
молекул она сливается, и для опре-
деленного электронного перехода
в пределах широкой полосы погло-
щения или испускания наблюдается
ряд отдельных максимумов; для еще
более сложных молекул такие мак-
Е, см i
5000-
4000-
3000-
2000-
1000 -
6
5
симумы исчезают и получается общий
201 -------------------
3	озо ------------------
400 -------------------
120 ------------------
101 ———
210 ___________________
101 ------------------
300 -------
020 ———————
НО ----------------
001 ---------------
0J --------------------------0	ооо -----------------
Рис. 27.1. Сгущение колебательных уровней
энергии при увеличении общего запаса
колебательной энергии
контур полос с одним максимумом. Ин-
дивидуальность молекулы при этом в значительной степени или даже полностью
утрачивается — при различном положении полосы в спектре для разных молекул их
форма становится примерно одинаковой. Для полос поглощения и полос испускания
наблюдается зеркальная симметрия (подробнее см. ниже, §27.4, с. 843).
Можно естественно разделить спектры многоатомных молекул на спектры
простых молекул с полосатой электронно-колебательной структурой и на спектры
сложных молекул со сплошными полосами; промежуточное место занимают спектры
полусложных молекул, для которых в полосах имеется ряд максимумов. С физической
точки зрения это деление отвечает увеличению числа колебательных степеней сво-
боды и соответствующему усложнению колебательного движения, что проявляется.
826
Глава 27. Электронные спектры многоатомных молекул
в частности, в описанном выше увеличении густоты уровней энергии и в пере-
ходе от совокупности дискретных к совокупности непрерывных уровней. Так как
сгущение уровней энергии имеет место при достаточно большом общем запасе коле-
бательной энергии молекул, то при заданной сложности молекулы оно проявляется
тем сильнее, чем выше температура. В связи с этим деление молекул по сложности
их спектров зависит от температуры; при низких температурах даже для молекул, со-
стоящих из большого числа атомов, могут наблюдаться дискретные спектры вместо
широких сплошных полос, получающихся при более высоких температурах. Весьма
характерные дискретные спектры получаются при низких температурах для молекул
ароматических соединений в кристаллах и замороженных растворах. Обширные ис-
следования спектров поглощения и испускания молекулярных кристаллов аромати-
ческих углеводородов выполнены Обреимовым, Прихотько и их сотрудниками [366];
важные исследования спектров испускания и поглощения ароматических углеводо-
родов в замороженных растворах принадлежат Шпольскому и его сотрудникам [365].
В молекулярных кристаллах бензола, нафталина, антрацена и других ароматических
углеводородов при низких температурах наблюдается весьма сложная дискретная структу-
ра спектров поглощения и люминесценции. При этом, наряду со слабо поляризованными
линиями, связанными с внутримолекулярными колебаниями, имеются сильно поляризован-
ные линии, которые удается объяснить, учитывая взаимодействия правильно расположенных
молекул в кристалле на основе теории, разработанной Давыдовым [367].
В замороженных растворах коронена, пирена и других ароматических углеводородов
в нормальных парафиновых углеводородах при низких температурах в спектрах флуоресцен-
ции и фосфоресценции наблюдается открытая Шпольским очень резкая линейчатая структура
с характерными последовательностями линий (эффект Шполъского). Эти последовательности
несомненно принадлежат молекулам ароматических углеводородов и обусловлены их ко-
лебаниями; вместе с тем на них сказывается влияние растворителя, однако без нарушения
дискретности спектров; при этом из каждой последовательности получается две или несколько
поел едовател ьносте й.
Более детальное рассмотрение исследований спектров молекул в кристаллах и заморо-
женных растворах выходит за рамки данной монографии.
Для объяснения спектров простых и сложных молекул следует применять раз-
личные методы. В первом случае можно ограничиться методами, изложенными
в гл. 21-23 и относящимися к колебаниям, близким к гармоническим; здесь необхо-
димо учитывать индивидуальность колебаний в различных молекулах, приводящую
к характерной для каждой данной молекулы или для данного типа молекул колеба-
тельной структуре электронных спектров. Во втором случае естественными являются
статистические методы, позволяющие выявить закономерности, которым подчиня-
ется молекула как система с большим числом колебательных степеней свободы.
Колебания сложной молекулы нельзя рассматривать как гармонические даже при-
ближенно; взаимодействие между нормальными колебаниями играет решающую
роль и приводит к сложному колебательному движению, при котором, согласно на-
глядным представлениям, происходит постоянное перераспределение энергии между
различными связями. Статистический характер колебательных процессов в сложных
молекулах и приводит к общим закономерностям в спектрах таких молекул. Не-
которые вопросы спектроскопии сложных молекул будут рассмотрены в последних
параграфах данной главы (§27.4 и 27.5).
Деление молекул на простые, сложные и полусложные, исходя из сравнения времени пе-
рераспределения колебательной энергии с длительностью жизни возбужденных электронных
состояний, было предложено Непорентом [375], который произвел ряд важных экспери-
ментальных исследований флуоресценции сложных органических молекул в парах [377|.
Фундаментальные теоретические исследования по спектроскопии сложных молекул были
§ 27.1. Электронно-колебательные переходы и электронные спектры 827
выполнены Степановым. Ряд результатов этих исследований, лишь частично затрагиваемых
в дальнейшем, подробно изложен в его монографии «Люминесценция сложных молекул» [106].
Положение системы узких электронно-колебательных полос для простых мо-
лекул и широкой сплошной полосы для сложных молекул определяется частотой
чисто электронного перехода. Эти частоты различны для разных молекул; в случае
молекулы сложной структуры они могут быть характерными для определенных ее
частей, подобно характеристическим частотам колебаний. В частности, очень важ-
ным является наличие для целого ряда органических молекул электронных переходов
между основным и глубоким возбужденным уровнем, характерных для определенных
групп атомов и обусловливающих избирательное поглощение молекулы в различных
участках видимой области спектра. Такое поглощение приводит к окраске соответ-
ствующих соединений. Группы, обусловливающие появление окраски — цветность —
органического соединения, называются хромофорами. Обычно этот термин приме-
няют и к группам, обусловливающим избирательное поглощение в близкой инфра-
красной (до 10 000 А) и в обычной ультрафиолетовой областях спектра (до 2 000 А).
Таким образом, поглощение хромофорных групп соответствует электронным пе-
реходам с основного электронного уровня на более высокие, для возбуждения
которых требуется энергия примерно от 1 до 6 эВ. Подобные уровни получаются
при наличии легко возбуждаемых тг-электронов, и хромофорными являются группы
с двойными и тройными связями. Примером простейшей хромофорной группы
является этиленовая группа /С=С^ с максимумом поглощения около 2 000 А
и карбонильная группа )с=О с максимумом поглощения около 2 700 А. Особенно
важное значение имеет цветность молекул с нелокализованными тг-электронами, со-
ответствующими наличию, согласно валентной схеме химии, сопряженных двойных
связей. Для сопряженных тг-электронных систем может получаться, благодаря бли-
зости основного и возбужденного электронных уровней, окраска в видимой области
спектра. При увеличении размеров сопряженной системы (например, длины цепи
в молекулах полиенов) происходит сближение уровней и смещение поглощения
в длинноволновую область1*. Вообще, на положение полос поглощения хромофоров
оказывает влияние строение молекулы, и, в частности, присутствие в ней групп,
взаимодействующих с хромофорными группами. Группы, которые в результате вза-
имодействия с хромофорами приводят к усилению поглощения и его смещению
в длинноволновую область (к усилению окраски), называют ауксохромами1^.
Различные электронные переходы в многоатомных молекулах имеют неодинако-
вую вероятность. При наличии симметрии имеют место правила отбора. Эти правила
отбора для дипольных переходов (разрешенных переходов, см. с. 114 и 491) между
полносимметричным уровнем (в частности, полносимметричным основным уров-
нем) и уровнями различной симметрии те же, что для основных частот колебаний,
и даются табл. 22.1-22.11. Разрешены такие переходы, для которых симметрия рассма-
триваемой составляющей дипольного момента совпадает с симметрией возбужденного
электронного уровня энергии (ср. с. 678). Для переходов между двумя неполносимме-
тричными уровнями разрешены переходы, для которых симметрия рассматриваемой
составляющей дипольного момента совпадает с результирующей симметрией ком-
бинирующих электронных уровней; результирующая симметрия для вырожденных
*) См. приближенную формулу (26.29) (с. 815), применимую для перехода с основного уровня на пер-
вый возбужденный.
2) В этой книге мы не имеем возможности останавливаться подробнее на теории цветности, которой
посвящено значительное число исследований. Ссылки на эти исследования можно найти в монографиях
Теренина |99| и Ферстера [98].
828
Глава 27. Электронные спектры многоатомных молекул
состояний при этом определяется, согласно табл. 23.1. Для магнитных дипольных
и для квадрупольных переходов правила отбора аналогичны, только нужно вместо
составляющих Р\ дипольного момента брать составляющие р\ магнитного момента
и составляющие квадрупольного момента (обладающие теми же свойствами,
как и составляющие тензора поляризуемости).
Это доказывается совершенно так же, как и для колебательных переходов (см. с. 680
и дальше), с той разницей, что нет надобности переходить от свойств симметрии колеба-
тельных координат к свойствам симметрии волновых функций, так как сразу рассматрива-
ются свойства симметрии функций и для комбинирующих электронных состояний.
Для полносимметричного состояния tpn" инвариантно, и составляющие дипольного момен-
та Р\ должны преобразовываться так же, как функции грпг для возбужденного состояния,
т. е. согласно тому же неприводимому представлению (Гп„ = Го, Гп« х Гр = Го х Гр = Гр
и лишь при Гп, = Гр произведение Гр х Гп, содержит Го). Для переходов между электронными
состояниями, принадлежащими к полносимметричным типам симметрии, прямое произве-
дение Гп„ х Гп, представлений Гп„ и Гга, для комбинирующих состояний должно содержать
представление Гр, согласно которому преобразуются составляющие дипольного момента.
Для магнитных дипольных и квадрупольных переходов нужно заменить Гр на Гд или Гд,
т. е. вместо преобразования составляющих полярного вектора рассматривать преобразования
составляющих аксиального вектора (псевдовектора) и симметричного тензора соответственно.
Примером применения сформулированных правил отбора служит молекула XY2
симметрии C2V. Согласно табл. 22.1 (см. с. 650), основное состояние типа симме-
трии А] может комбинировать с возбужденными состояниями типов симметрии
В\ и В2, а переход 42~^i запрещен. Состояния В\ и В2 не могут комбинировать, так
как для них результирующая симметрия будет А2 (при операции С2(-1) • (-1) = 1
и при операции а<24 • (-1) = -1, что дает А2), тогда как составляющие Рг, Рх
и Ру дипольного момента обладают симметрией А\, В\ и В2. Отсюда следует, что
для радикала NH2 (см. (26.36) и (26.38)) переход 2В2— 2В} запрещен и разрешен
лишь переход 2Л| — 2В\.
Наряду с правилами отбора, определяемыми принадлежностью электронных
уровней к определенным типам симметрии, возможным для рассматриваемой то-
чечной группы, существенную роль играет приближенное правило отбора Д5 = 0,
запрещающее переходы между уровнями различной мультиплетности, т. е. интерком-
бинационные переходы. Запрещенными будут, в частности, переходы для молекул
с четным числом электронов между синглетным основным состоянием и возбужден-
ными триплетными состояниями. Наиболее низкое из этих состояний будет поэтому
метастабильным; наличие такого метастабильного триплетного состояния позволяет
объяснить большое число фактов, относящихся к сложным органическим молекулам.
В 1943 г. Терениным было впервые сделано предположение о том, что метастабильные
состояния для возбужденных молекул красителей являются триплетными [368]; в 1945 г.
к такому же выводу пришел независимо Льюис [369]. Теренину удалось убедительно объяснить
ряд оптических свойств красителей на основе представления о метастабильных триплетных
состояниях (бирадиальных состояниях3^). Результаты исследований Теренина изложены в его
монографии «Фотохимия красителей» [99].
Существенную роль при изучении электронных спектров многоатомных мо-
лекул играют процессы диссоциации молекул. Здесь также возможна диссоциация
молекулы при поглощении фотона, энергия которого достаточно велика и превышает
сумму энергии электронного возбуждения и энергии диссоциации соответствующего
Названных так в соответствии со спином 5=1, вдвое большим, чем для состояний радикалов
со спином S — */2 (два неспаренных электрона вместо одного).
§ 27.2. Принцип Франка—Кондона для многоатомных молекул
829
возбужденного электронного состояния (ср. (25.41)). При этом возникает сплошное
поглощение, аналогичное континуумам в спектрах двухатомных молекул, примыка-
ющим к границам диссоциации. Сплошное поглощение такого типа следует отличать
от сплошного поглощения, связанного с непрерывной последовательностью враща-
тельно-колебательных уровней для устойчивых электронных состояний сложных
молекул (см. выше). Однако не всегда на опыте удается различить эти два различных
типа сплошного поглощения.
Для многоатомных молекул, так же как и для двухатомных, возможна, по-
мимо диссоциации, и предиссоциация (см. [361]). Наблюдение предиссоциации
затрудняется сложностью структуры электронных спектров многоатомных молекул,
а для сплошных спектров поглощения и испускания ее вообще не удается наблю-
дать. Однако с увеличением числа колебательных степеней свободы в молекуле роль
предиссоциации должна возрастать, так как увеличивается число способов, кото-
рыми она может быть осуществлена. Процессы предиссоциации могут оказаться
существенными (наряду с процессами непосредственной диссоциации при погло-
щении фотона) при фотохимических процессах, первым этапом которых является
фотодиссоциация.
Мы кратко разобрали некоторые общие вопросы, касающиеся электронных
спектров многоатомных молекул. Следует подчеркнуть, что изложение в данном
и в последующих параграфах этого очень актуального и быстро развивающего-
ся раздела спектроскопии по необходимости весьма беглое и схематичное. Более
обстоятельное рассмотрение основных теоретических и экспериментальных иссле-
дований электронных спектров многоатомных молекул потребовало бы написания
специальной монографии.
§ 27.2.	Принцип Франка—Кондона для многоатомных молекул
Для многоатомных молекул справедлив и играет важную роль принцип
Франка—Кондона, рассмотренный нами в § 25.2 (с. 756) для случая двухатомных мо-
лекул, для которого он и был впервые сформулирован. Принцип Франка—Кондона
позволяет понять ряд особенностей спектров многоатомных молекул, как простых,
так и сложных4).
Согласно этому принципу, для многоатомных молекул наиболее вероятны элек-
тронно-колебательные переходы, соответствующие неизменной мгновенной конфи-
гурации ядер, при их скорости, равной нулю. Применимость принципа Франка-
Кондона к многоатомным молекулам является следствием того, что для них, подобно
двухатомным молекулам, электронный переход происходит очень быстро и относи-
тельное положение и скорость ядер при таком переходе не успевают измениться.
При этом наиболее вероятны переходы при малых скоростях ядер, соответству-
ющих их положениям, близким к поворотным точкам классического движения;
колеблющаяся молекула дольше всего задерживается именно в подобных положе-
ниях (ср. §20.2, с. 573).
Графическую иллюстрацию принципа Франка—Кондона можно дать для случая
валентных колебаний линейной трехатомной молекулы XYZ, откладывая по осям х
и у переменные расстояния р\ и между атомами X и Y и атомами X и Z (X —
центральный атом, р\ ~ рх\, р2 — Pxz, см. рис. 23.5, б, с. 697), а по оси Z —
потенциальную энергию молекулы (т. е. электронную энергию при неподвижных
4) Обобщение принципа Франка—Кондона на случай многоатомных молекул и подробный анализ воз-
можных случаев были произведены в 1933 г. Герцбергом и Теллером |359] (см. также [96]); дополнительные
соображения были высказаны Душинским [359а].
830
Глава 27. Электронные спектры многоатомных молекул
ядрах) U(p\, Р2). Для каждого электронного состояния мы получаем потенциальную
поверхность, имеющую минимум при определенных значениях р\ = рю и = Р2о-
Изображение двух таких поверхностей сверху дано на рис. 27.2, причем показа-
ны линии одинаковой высоты. Для одной поверхности, соответствующей нижнему
электронному состоянию с минимумом р" = р'|'о, р" — Р2О, проведены сплошные ли-
нии, для другой поверхности, соответствующей верхнему электронному состоянию
с минимумом р\ = Р|0, р'2 = р'20 ~ пунктирные линии. Мы имеем две потенциальные
ямы. Разность
U (Рю, Р20) “ U (p10j Р20) — £эл(РЮ) Р2о) ~ ^эл(рю> Pio) ~ Мл ~ Мл “	(27.1)
Рис. 27.2. Потенциальные
поверхности для валентных
колебаний линейной трехатомной
молекулы типа XYZ
определяет частоту чисто электронного перехода.
С классической точки зрения при определенной
колебательной энергии мы имеем движение в обла-
сти, ограниченной линией одинаковой высоты, со-
ответствующей величине этой энергии. Наиболее
вероятные переходы будут соответствовать верти-
кальным линиям, соединяющим точки рассматри-
ваемых потенциальных поверхностей, расположен-
ные друг под другом аналогично тому, как это
имеет место для двух потенциальных кривых, ле-
жащих друг под другом в случае двухатомных мо-
лекул (см. рис. 25.3, с. 757).
Для молекулы с г колебательными степенями
свободы с геометрической точки зрения потенци-
альная энергия представляет поверхность г изме-
рений в пространстве г + 1 измерений (см. § 17.3, с. 475), поэтому при г 3 уже
невозможно ее наглядное изображение. К счастью, наиболее существенные новые
результаты применения принципа Франка—Кондона к многоатомным молекулам,
отличные от результатов его применения к двухатомным, можно иллюстрировать
при помощи двухмерной диаграммы типа рис. 27.2, а при рассмотрении зависимости
потенциальной энергии от одной из нормальных координат & можно применять
диаграммы U — Ufa), аналогичные диаграммам U — U(q) = U(p - ре), для двух-
атомных молекул.
Разберем теперь, какие именно новые результаты вытекают для многоатомных
молекул из принципа Франка—Кондона. Эти результаты связаны с делением ко-
лебаний молекулы на полносимметричные и неполносимметричные. Сохранение
при переходе мгновенной конфигурации ядер означает и сохранение ее симметрии.
Особенно важен случай, когда начальная конфигурация при переходе является пол-
носимметричной — обладает симметрией нормальной конфигурации. Это имеет
место при переходах из нулевого колебательного состояния, в частности, при по-
глощении молекулами в основном электронно-колебательном состоянии, в котором
находится значительная или даже подавляющая часть молекул при не слишком вы-
соких температурах. Начальная конфигурация является полносимметричной и в том
случае, когда в начальном состоянии возбуждены только полносимметричные коле-
бания. При полносимметричной начальной конфигурации и конечная конфигурация
полносимметрична, и поэтому при переходе, согласно принципу Франка—Кондона,
будут возбуждаться полносимметричные колебания. Наиболее вероятными при этом
будут переходы, которые по отношению к полносимметричным колебаниям со-
ответствуют неизменности расстояний между ядрами. Если возможно лишь одно
полносимметричное колебание, как, например, для молекулы СО2 (симметрии D^h)
§ 27.2. Принцип Франка—Кондона для многоатомных молекул
831
или молекулы СН4 (симметрии Tj), то потенциальная энергия будет функцией
от ро + где ро — равновесное расстояние С—О или С—Н, а £4 — полносимме-
тричная координата (с — коэффициент пропорциональности). Действительно, по-
тенциальная энергия является функцией от эквивалентных расстояний pt = ро 4- ф,
где qi — изменения эквивалентных связей С=О или С—Н (г = 1,2 и г = 1,2, 3,4
соответственно). Для полносимметричного колебания q\ =	.. — qk — Ча — ^a,
следовательно, pt- — ро 4- c£a-
Для полносимметричных электронных состояний функции t7(p) — t/^Po + cgA)
и U(p) — Un(pQ + с&) будут изображаться кривыми, подобными кривым потенци-
альной энергии двухатомных молекул, с минимумами, вообще говоря, сдвинутыми
друг относительно друга (р{> Ф р"^) (см. рис. 25.5, с. 757). Наиболее вероятные пере-
ходы будут соответствовать неизменному значению р, т.е. вертикальным линиям,
соединяющим две кривые. Таким образом, существует полная аналогия полносим-
метричных колебаний многоатомных молекул и колебаний двухатомных молекул.
При наличии к полносимметричных колебаний нужно рассматривать переходы при не-
изменных значениях к переменных, определяющих возможные значения U и зависящих
от нормальных координат полносимметричного типа, например, для молекулы Н2О (к = 2)
переходы при неизменных значениях длины р связей О—Н (pi = р2 = р) и угла <р между этими
связями. В этом частном случае р = pQ 4- cqs = ро +	+ с2£2 и <р = <ро 4- &s = <Ро 4- Ф£| 4-
где £i и £2 — полносимметричные нормальные координаты (см. (22.13)). Минимумы обеих
потенциальных поверхностей будут сдвинуты относительно друг друга, вообще говоря, вдоль
всех к осей, и аналогия со случаем двухатомных молекул сохраняется, хотя рассмотрение
возможных переходов усложняется из-за увеличения числа переменных.
Наряду с переходами между электронными состояниями, в которых (в одном
или в обоих) возбуждены полносимметричные колебания, возможны также и пере-
ходы между состояниями, в которых возбуждены неполносимметричные колебания.
При неполносимметричных колебаниях в момент прохождения атомов через
положения равновесия конфигурация является полносимметричной и потенциаль-
ные поверхности для комбинирующих электронных состояний отличаются только
по отношению к полносимметричным колебаниям. По отношению к неполносимме-
тричным колебаниям потенциальные поверхности этих состояний имеют минимумы,
расположенные один под другим, подобно тому, как это имеет место в случае двух-
атомных молекул, когда pQ = р§ (см. рис. 25.4, с. 757). При одинаковой или близкой
форме потенциальных поверхностей вблизи минимума поэтому будут наиболее веро-
ятны переходы типа 0—0, 1 — 1, 2—2,..., для которых колебательные квантовые чи-
сла v антисимметричных колебаний одинаковы; по мере увеличения |Av| = \v' — v"\
вероятность переходов убывает. Если подобный случай для двухатомных моле-
кул (см. с. 757) не типичен, то для многоатомных молекул, в которых существуют
неполносимметричные колебания (а такими являются все молекулы, обладающие
симметрией, т.е. не относящиеся к точечной группе Cj), он является основным
наряду со случаем сдвинутых минимумов потенциальной энергии. Первый случай
(отсутствие сдвига минимумов) имеет место для неполносимметричных колебаний,
второй случай (сдвиг минимумов) — для полносимметричных колебаний.
Мы рассмотрим изложенные соображения на примере валентных колебаний
линейной симметричной трехатомной молекулы XY2. В отличие от случая, когда
центральный атом X связан с разными атомами Y и Z и потенциальная энергия
зависит несимметричным образом от р\ и р2 (т. е. от расстояний Х-Y и X-Z),
здесь зависимость потенциальной энергии от обоих расстояний X-Y^ и X-Y^,
которые мы также обозначим через pi и р2, будет одинакова. Вместо графика
рис. 27.2 мы получим график, изображенный на рис. 27.3. Этот график симметричен
832
Глава 27. Электронные спектры многоатомных молекул
Ц
ЪикЛТЗ. Потенциальные поверхности
для валентных колебаний
линейной трехатомной молекулы типа ХУ2
относительно прямой р\ = р2, и
равновесные расстояния рю и рго
равны друг другу (в чем и состоит
симметрия равновесной конфи-
гурации молекулы XY2), отлича-
ясь, вообще говоря, для разных
электронных состояний (ро / pj),
где ро = Pio — Р20 и Ро — Pio —
Р20). Прямая Pi = р2 соответству-
ет, в силу равенств р\ — рщ 4- q\
и р2 = Р20 + симметричным
колебаниям q\ = перпендику-
лярная к ней прямая соответству-
ет gj — -q2, т. е. антисимметрич-
ным колебаниям5). Можно полу-
чить графики зависимости потен-
циальной энергии от симметрич-
Q\ 4- д2
нои qs — —-— и антисимме-
тричной qa — —-— координат (ср. (22.3)), если повернуть оси х = р\, у = р2
графика рис. 27.3 на 45°, как показано на нем пунктиром. Полагая
t
х
1
У
1 1
— х cos <р 4- у sin <р =
1 1
(27.2)
и подставляя х = pt = р0 + q\, у — р2 = ро + <72, мы получим
х — (Ро 4- <Zi)^= + (Ро +	— ^(р0 4-	“ ^(Ро + Qs),
У — ~(Ро 4- <Zi)^ + (Ро + Ф)^ =	“'“2 ~2' ~ -'/iQa.
(27.3)
Вводя нормальные координаты, полносимметричную & = qs (симметрии А\д
для линейной молекулы типа XY2) и неполносимметричную £2 — ~qa (симме-
ч	1	/	1	,
трии aiu), и обозначая —ж = и и -^=У = V, мы окончательно получим
^ = Ро+€1» ^ = 6-
(27.4)
Множитель V2 отсутствовал бы при применении нормированных координат симме-
трии (22.5) (в данном случае совпадающих с нормальными координатами) qs = -^(gi 4- qi)
и qa — — (gi ~ Qi) и замене постоянной р0 через постоянную х/2ро- Знак координаты qa
5) Чтобы получить q\ — -^2, нужно положить р\ = -pz + ZpQ, тогда pQ + q\ ~ -po~q2 + 2po и q\ = -72-
Прямая АА на рис. 27.3 соответствует р\ — -pi + 2^q, т.е. q" — -q”, прямая ВВ - р\ — -р? +
т.е. q\ -72-
§ 27.2. Принцип Франка—Кондона для многоатомных молекул	833
в (27.3), разумеется, не существен, так как его изменение на обратный означает только выбор
фазы колебаний, измененной на тг.
От координат и = ро 4- £ и v — £2 потенциальная энергия U в соответствии
с диаграммой рис. 27.3 зависит различным образом. При v — £2 — § для потен-
циальной энергии как функции
от и для нижнего и верхнего элек-
тронных состояний мы получаем
несимметричные кривые с раз-
личными положениями равнове-
сия и и = Pq и и = pq (рис. 27.4, а,
аналогичный рис. 25.5). При за-
данном и — const для v получа-
ются симметричные кривые с по-
ложением равновесия при v =
£2 = 0 (рис. 27.4, б, аналогичный
рис. 25.4). Таким образом, дей-
ствительно, имеется существенное
различие для полносимметричных
и неполносимметричных колеба-
ний.
Рис. 27.4. Кривые потенциальной энергии:
а — для симметричного колебания;
б — для антисимметричного колебания
Следует подчеркнуть, что потенциальные поверхности обладают симметрией только
относительно неполносимметричных нормальных координат. В случае диаграммы рис. 27.2
для каждой из двух потенциальных ям можно найти нормальные координаты, соответ-
ствующие определенным линейным комбинациям колебательных координат = Р\ ~ Рю
и <72 = Pi - Р20 (притом в общем случае разным для этих ям6)). Это будут полносимметричные
координаты, и потенциальная энергия зависит от них несимметричным образом. Число неза-
висимых параметров, определяющих равновесную конфигурацию молекулы, равно в данном
случае двум. Отметим, что число полносимметричных координат всегда совпадает с числом к
таких независимых параметров. Действительно, если выбрать некоторую полносимметричную
конфигурацию, не совпадающую с равновесной, то изменяя к независимых координат симме-
трии, возможных для данной молекулы и соответствующих полносимметричным колебаниям,
можно получить равновесную конфигурацию. В случае молекулы Н2О такими координатами
симметрии являются координаты
<71 + <72	(р\ - Рю) 4- (р2 ~ P2q)
qs = —-— =--------------- и as = а = <р -
(27.5)
2
Изменением этих координат можно получить (полагая их равными нулю) из любой сим-
метричной конфигурации равновесную, и, наоборот, из равновесной конфигурации, беря
различные значения qs и а5, можно получить любую другую симметричную конфигура-
цию.
До сих пор мы рассматривали переходы между электронными состояниями
для которых симметрия равновесной конфигурации одинакова. Однако возможны
случаи, когда при возбуждении молекулы меняется симметрия ее равновесной кон-
фигурации (ср. с. 822). Это приводит к увеличению числа возможных, согласно
принципу Франка—Кондона, электронно-колебательных переходов. Возможны те
переходы, при которых колебания в обоих комбинирующих состояниях обладают
свойствами симметрии, общими для этих состояний. Например, если для обоих
Геометрически они будут соответствовать главным нормальным сечениям потенциальных ям в точках
минимума.
27 Зак 103
834
Глава 27. Электронные спектры многоатомных молекул
состояний равновесная конфигурация имеет плоскость симметрии, то из электрон-
но-колебательного состояния, в котором возбуждены колебания, симметричные
относительно плоскости, возможны переходы в электрон но-колебательное состоя-
ние, в котором возбуждены колебания такой же симметрии.
Увеличение числа возможных переходов вследствие понижения симметрии од-
ного из комбинирующих электронных состояний будет иметь место для вырожден-
ных состояний нелинейных симметричных молекул, когда эти состояния в силу
их неустойчивости (см. §26.1, с. 790) расщепляются и получаются равновесные
конфигурации более низкой симметрии. При этом происходит соответствующее
усложнение спектра (см. [96], с. 92).
Все рассмотренные в данном параграфе следствия принципа Франка—Кондона могут
быть обоснованы путем квантовомеханического рассмотрения, согласно которому волновая
функция молекулы приближенно представляется в виде произведения ^эл(^)^кол(р) и веро-
ятности электронно-колебательных переходов определяются значениями интеграла наложе-
ния J Ф*оАр)Ф"ы(р) dp (см. § 17.6, с. 489, и ср. §25.2, с. 759).
Переписывая интеграл наложения в форме
/ VwAp\i Ръ  •  Pr^KoApt, Ръ - , Pr)dp\dpt... dpr,	(27.6)
где интегрирование производится по всем г = 3N - 6 (или 3N - 5 для линейных молекул)
степеням свободы, мы видим, что он будет велик, если при одинаковых значениях всей
совокупности колебательных координат р2, • • • > Рг, в достаточно большой области их
изменений, произведение ^кол^кол велико. Иначе говоря, существенно наложение волновых
функций в пространстве г измерений. Колебательные волновые функции можно приближенно
представить как произведения колебательных волновых функций для отдельных степеней
свободы:
ФкоАр) = Vv,(й)^Ц(й) • • • 'К'М'г), <ол(р) = ^;'(й')^''(й') • • • ^“(Й')>	(27.7)
где введены нормальные координаты
J.H J.H	J.H
Тогда интеграл (27.6) можно записать в виде
f К,(Й)(Й) • • • <'г (Й)^ (ЙН; (Й) • • • и (Й')<*Й'<*Й' • • • <•	(27.8)
Здесь интегрирование производится по нормальным колебательным координатам нижнего
электронного состояния, через которые выражаются нормальные колебательные координаты
верхнего электронного состояния. Например, для случая валентных колебаний молекулы XY2,
рассмотренного выше (см. с. 831), интегрирование надо производить по различным значениям
координат и и v и, согласно (27.4), для комбинирующих состояний имеем
“ = Ро + й, «=й и « = Ро'+й'1 «=й',	(27.9)
откуда
Й = Й' - (ро - Ро), Й=Й-	(27.10)
Если деформационные колебания не возбуждены, то (27.8) сводится к
У ^(й - (Ро - Ро))^(й)<*й /	(27.11)
где интегрирование выполняется по координатам = £" и £2 = Из этого примера вид-
но, что интеграл (27.8) разбивается на множители, относящиеся к колебаниям различной
§ 27.2. Принцип Франка—Кондона для многоатомных молекул
835
симметрии7^, и что существенно наложение волновых функций в каждом из интегралов
в отдельности. Отметим, что наложение волновых функций в первом интеграле соответствует
рис. 27.4,а (полносимметричные колебания), во втором интеграле — рис. 27.4, б (неполно-
симметричные колебания). При v" = 0 второй интеграл будет велик (и близок к единице),
когда v'2 — 0, и наиболее вероятными будут такие переходы v" —► vj (в частности, пере-
ход v" = 0 -* vj), для которых велико наложение функций и
Интеграл наложения (27.6), а следовательно, и интеграл (27.8) отличен от нуля, лишь
когда волновые функции ^ол и ^"ол обладают одинаковой симметрией. Это приводит к опре-
деленным правилам отбора. В частности, для антисимметричных колебаний могут комбини-
ровать лишь состояния, для которых разность Av, = v' — v" является четной (ср. с. 680)7 8).
Отметим, что правила отбора, выведенные из рассмотрения свойств интеграла (27.6),
могут нарушаться, если предположение о независимости интеграла (17.98) (см. § 17.6, с. 489)
от колебательных координат, сделанное при переходе от (17.95) к (17.99), не оправдывается.
Разложение дипольного момента (17.96), Р„'п», выраженного через нормальные координа-
ты, по этим координатам (см. (23.5)) и рассмотрение интеграла типа J* ^кол(С)С»^кол(С)^
позволяет найти переходы, которые становятся возможными за счет зависимости Рп'п«(£)
от соответствующей нормальной координаты & [96].
В заключение данного параграфа следует вообще подчеркнуть, что при рассмо-
трении возможных переходов следует тщательно учитывать допустимость сделанных
приближений. Прежде всего делается предположение о малости взаимодействия
электронного движения с колебательным, что позволяет представить волновую
функцию	в виде р)^кол(р)- Это предположение основано на том, что
движение ядер происходит значительно медленнее, чем движение электронов (от-
сюда вытекает возможность рассматривать движение электронов при неподвижных
ядрах). Поэтому следует ожидать, что оно будет справедливым как для простых,
так и для сложных молекул, и в конкретных случаях нужно лишь оценивать ве-
личину малых поправок. Предположение о независимости дипольного момента
электронного перехода Рп>п»{р) от колебательных координат р является лишь грубо
приближенным, и учет зависимости Рп>п„(р) от р может быть весьма существен-
ным, особенно при больших запасах колебательной энергии. Далее, предположение
о возможности разделения полной колебательной функции ^кол(р) на сомножители,
зависящие от отдельных нормальных координат или их совокупностей, приближен-
но справедливо лишь при малых запасах колебательной энергии, когда отступления
от гармоничности малы. При больших запасах колебательной энергии взаимодей-
ствие различных колебаний может быть настолько велико, что введение нормальных
координат вообще теряет физический смысл. Однако даже при значительной ко-
лебательной энергии, распределенной по большому числу колебательных степеней
свободы, взаимодействие в заданном электронном состоянии электронного движе-
ния с колебательным будет оставаться малым вследствие малой скорости движения
ядер [360]. Иначе обстоит дело со взаимодействием разных электронных состояний.
При больших колебательных энергиях может сильно возрастать вероятность безыз-
лучательных переходов между разными электронными состояниями, и в предельном
случае вообще теряет смысл рассмотрение этих состояний как независимых, даже
в нулевом приближении (ср. [106], гл. 5, §3).
7) При наличии к колебаний одной симметрии соответствующий сомножитель будет содержать
интегрирование по к координатам, причем
8) Для случая одного колебания данного типа симметрии. В общем случае Диг- по всем антисим-
i
метричным колебаниям данного типа симметрии должна быть четной.
27*
836
Глава 27. Электронные спектры многоатомных молекул
§ 27.3.	Примеры электронных спектров
простейших многоатомных молекул
Мы разберем некоторые примеры электронных спектров простейших много-
атомных молекул, начиная с трехатомных.
Примерами спектров линейных трехатомных молекул являются спектры моле-
кул HgX2, где X — атом галоида. Они обладают электронным спектром поглоще-
ния в далекой ультрафиолетовой области, характерные системы полос получаются
для HgCl2 от 1 670 до 1 730 А, для HgBr2 — от 1813 до 1861А и для HgJ2 — от 2 066
до 2 108 А. Структура этих систем полос находится в соответствии с правилами отбо-
ра для неполносимметричных колебаний, Av — 0, 2,4,... (см. с. 835). Наблюдаются
переходы из нижних электронно-колебательных состояний, для которых изменения
квантового числа V\ полносимметричного колебания могут быть как четными, так
и нечетными, а изменения квантового числа v2 неполносимметричного деформаци-
онного колебания только четными. На рис. 27.5 приведена схема наблюдающихся
переходов у молекулы HgCl2 [362]. Значения колебательных частот для нижнего
электронного состояния равны у" = 365 см-1, у" = 70 см-1 и для верхнего элек-
тронного состояния — i/{ = 289 см”1, р2 = 65 см”1; разности |Avi| заключены
для различных полос в пределах от 0 до 5, |Дv2| принимает только значения 0 и 2.
Для HgBr2 и HgJ2 спектры аналогичны, только частоты колебаний уменьшаются
в соответствии с увеличением массы атомов галоида; они равны у" = 229 см”1,
р* — 41 см”1,	= 194 см”1, р2 = 36 см”1 для HgBr2 и у" = 156 см”1, у" = 33 см”1,
у\ — 126 см”1, у'2 = 30 см”1 для HgJ2. В верхнем электронном состоянии, как
обычно, частоты колебаний меньше, чем в нижнем.
Для изоэлектронных линейных молекул СО2 и N2O полосы поглощения явля-
ются сплошными и лежат при длинах волн короче 1 700 и 3 000 А соответственно;
при этом молекула уже может диссоциировать (на СО + О и N2 + О соответственно).
Различие областей поглощения для изоэлектронных молекул естественным образом
объясняется на основе рассмотрения молекулярных орбит этих молекул (ср. вы-
ше, §26.5, с. 821). В испускании для СО2 получается также и система дискретных
полос в области 6 000-3 000 А; они наблюдаются в пламени окиси углерода СО.
Эти полосы можно объяснить как соответствующие переходу между возбужденными
электронными уровнями [363]. Системы дискретных полос в испускании получают-
ся и для иона СО^; они наблюдаются в разрядах через СО2. Наряду с основными
полосами при 2 982 и 2 896 А, соответствующими переходу 2S„ —► 2П5 (где 2П5 —
основное электронное состояние), имеется более слабая система полос, простираю-
щаяся от 5000 до 2900 А [363, 96, 358] и соответствующая переходу 2Пи—2Пр.
Для ряда нелинейных трехатомных молекул наблюдены наряду со сплошными
областями поглощения системы дискретныхо полос. Для молекулы Н2О найдены
две системы полос в области короче 1 240 А, что находится в согласии с элек-
тронной структурой молекулы (см. §26.5, с. 821). Среди трехатомных нелинейных
молекул, поглощающих в видимой области спектра, следует отметить молекулу NO2,
имеющую систему полос поглощения, которая простирается, уменьшаясь по интен-
сивности, от 4000 до 7 000 А. Систему полос поглощения в видимой области имеет
также молекула озона Оз.
Из спектров четырехатомных молекул значительный интерес представля-
ет спектр молекулы формальдегида, Н2СО, содержащей простую хромофорную
группу /С=О. Для нее наблюдаются дискретные системы полос как в поглоще-
§ 27.3. Электронные спектры простейших многоатомных молекул
837
-1
см
1200
- 1000
800
600
- 400
200
- 0
н см 1
- 1800
1600
1400
1200
- 1000
800
600
4оо
200
t О
Рис. 27.5. Схема электронно-колебательных переходов
для молекулы НдС12
нии, в области короче 3 570 А, так и во флуоресценции; полосы флуоресценции,
исследованные Брандом [364], простираются и в видимую область спектра.
Подробное обсуждение спектра молекулы Н2СО имеется у Уолша. Наряду с электронны-
ми состояниями, в которых молекула является плоской, необходимо учитывать электронные
состояния, в которых молекула имеет уже не плоскую, а пирамидальную форму. При этом
существенной становится корреляция состояний плоской и неплоской форм молекулы, ха-
рактеризуемая диаграммой типа рис. 26.21 (см. с. 820).
Спектры дискретных полос поглощения и испускания наблюдаются для це-
лого ряда молекул, содержащих пять и больше атомов. Однако для тетраэдриче-
ских пятиатомных молекул типа XY4 характерны сплошные области поглощения
838	Глава 27. Электронные спектры многоатомных молекул
и испускания, что естественным образом объясняется неустойчивостью вырожден-
ных состояний этих молекул (см. §26.1, с. 790). Основным электронным состоя-
нием этих молекул должно являться полносимметричное состояние Согласно
табл. 22.10 (с. 665), в дипольном излучении разрешены только переходы в трижды
вырожденные электронные состояния типа F2. В силу неустойчивости этих состо-
яний (для симметричной конфигурации ядер) будут получаться либо устойчивые
состояния с несимметричными конфигурациями ядер, либо вообще неустойчивые
состояния. В первом случае, согласно принципу Франка—Кондона, при погло-
щении будет происходить возбуждение неполносимметричных колебаний верхне-
го электронного состояния и может получиться сплошной спектр, характерный
для сложных молекул (см. §27.1, с. 825); если структура и будет наблюдаться, то
весьма сложная и трудно разрешимая. Во втором случае при поглощении будет про-
исходить диссоциация молекулы. Фотодиссоциация молекулы метана действительно
наблюдается под действием коротковолнового ультрафиолетового излучения.
Сплошное поглощение в далекой ультрафиолетовой области для молекул эта-
на С2Н6, диборана В2Н6 и дисилана Si2H6, обладающих симметрией D^, также
может быть объяснено как результат переходов из основного электронного состоя-
ния симметрии А\д в неустойчивое возбужденное электронное состояние, которое
для симметричной конфигурации ядер соответствовало бы дважды вырожденному
типу симметрии Е (см. табл. 22.5).
Весьма характерными дискретными системами электронно-колебательных по-
лос в ультрафиолетовой области спектра обладают молекулы бензола и ряда его
производных. Для молекулы бензола наблюдаются полосы типа тг—тг*, соответ-
ствующие переходам между основным состоянием (а2«)2(е^)4 хАд и возбужденными
состояниями конфигурации (а2иУ(^\д)3^2и, дающей одиночные и триплетные тер-
мы (см. рис. 26.22, с. 823). Согласно правилам отбора для молекул симметрии,
Бы (см. табл. 22.8) состояние А{д комбинирует с состояниями Е\и и получаются
весьма интенсивные полосы хЕ\и— хА\д в области 1 800 А и очень слабые интерком-
бинационные полосы 3Е\и— хА\д в области 3 500 А. Наряду с этим наблюдаются по-
лосы хВ2и— xAig в области 2 500 А и *В1М— хА1д в области 2 000 А; переходы становятся
возможными за счет колебаний, нарушающих симметрию молекулы (см. с. 835).
В частности, для перехода 'B2u— ’4^ такими колебаниями могут быть колебания типов
симметрии В]д или Е2д, для которых полная симметрия электронно-колебательного состояния
будет В]д х В2и — А2и (см. табл. 22.8) и Е2д х В2и = Е]и (см. табл. 23.1 и 22.8). У молекулы
бензола отсутствуют колебания типа Big, но имеются четыре колебания типа Е2д (см. (23.85)),
которые и обусловливают возможность переходов.
Для молекул производных бензола наряду с переходами типа тг—тг*, получаю-
щимися при возбуждении тг-электрона (который при этом становится антисвязыва-
ющим), возможны переходы типа п—тг*, при которых возбуждается несвязывающий
электрон (который также становится антисвязывающим). Исследованию электрон-
но-колебательных полос бензола и его производных посвящено большое число
исследований, на которых мы не будем останавливаться, так же как и на мно-
гочисленных исследованиях электронно-колебательных спектров других молекул
с нелокализованными тг-электронами; это потребовало бы слишком много места9).
Ссылки на работы по дискретным электронно-колебательным спектрам молекул, выполненные
за последнее время, можно найти в обзорах, посвященных молекулярным электронным спектрам,
в ежегодниках «Annual Review of Physical Chemistry».
§ 27.4. Полосы поглощения и испускания сложных молекул
839
§ 27.4.	Полосы поглощения и испускания сложных молекул
В настоящее время накоплен очень большой экспериментальный материал
по сплошным полосам поглощения и испускания сложных органических молекул,
прежде всего в конденсированном состоянии.
Систематизация экспериментальных данных по спектрам поглощения органических
соединении дана в монографии Гиллема и Штерна [97]. Флуоресценции органических со-
единений посвящена монография Форстера [98], см. также монографии Левшина [102]
и Прингсхейма [103].
Из опыта получаются данные о положении сплошных полос в спектре и о рас-
пределении интенсивностей в этих полосах. Однако в противоположность случаю
дискретных спектров, только одних этих данных недостаточно для получения глу-
боких выводов о строении молекул и об их взаимодействиях в конденсированном
состоянии, в частности, в растворах, поглощению и люминесценции которых
посвящено очень много исследований. Поэтому весьма важно изучение наряду
с обычными характеристиками спектров поглощения и испускания — частотами
и интенсивностями, специфических характеристик фотолюминесценции — кван-
тового выхода, длительности и поляризации [385]. Особенно существенно иссле-
дование спектральной зависимости квантового выхода и поляризации — спектров
выхода и спектров поляризации, согласно терминологии, предложенной Вавиловым,
которому принадлежат фундаментальные работы по люминесценции.
Мы сначала в данном параграфе рассмотрим вопрос о природе сплошных полос
поглощения и испускания сложных молекул и о связи между полосами поглощения
и испускания, а затем, в следующем параграфе (§27.5), вкратце разберем вопрос
о квантовом выходе и поляризации фотолюминесценции сложных молекул.
Для сложных молекул, как мы видели в §27.1 (см. с. 824), характерно очень
большое число колебательных уровней энергии, образующих при не очень малых
запасах колебательной энергии непрерывную последовательность. Такая последо-
вательность получается как для основного, так и для возбужденных электронных
состояний. Для основного и первого возбужденного электронных состояний мы
будем иметь картину, схематически изображенную на рис. 27.6. Запас колебательной
энергии в нижнем состоянии обозначен через Е^ол, в верхнем — через Е'кол. При этом
распределение колебательных уровней по энергиям можно характеризовать их гу-
стотой — числом уровней д(Екол) на единицу интервала энергий. Соответственно
в интервалах энергии dE"on и dE'KOJl числа уровней равны
dg" = /«ол)^"ол, dg' = д'(Е'кол)4Е[ол.	(27.12)
Они представляют кратности приближенного вырождения колебательных уровней
в рассматриваемых интервалах энергии. Числа д” и д' при большом числе колеба-
тельных степеней свободы весьма велики (что и делает последовательность уровней
непрерывной) и возрастают с увеличением запаса колебательной энергии,0).
При переходе с основного электронного уровня на возбужденный получается
широкая полоса поглощения, причем самая длинноволновая полоса поглощения
соответствует переходу на первый, наиболее глубокий возбужденный уровень. Такие
полосы наблюдаются для огромного числа молекул при разнообразных условиях как
в газовой фазе, так и, в особенности, в конденсированной фазе. Для значительного
10) Для независимых гармонических колебаний д(Екол) ~ Е*ол, где г — число степеней свободы. Однако
эта формула совершенно неприменима из-за наличия сильного взаимодействия между колебаниями,
характерного для сложных молекул |106|.
840
Глава 27. Электронные спектры многоатомных молекул
числа молекул наряду с широкими полосами поглощения наблюдаются и широкие
полосы испускания, обычно одна полоса, соответствующая переходу с первого воз-
бужденного электронного уровня на основной, т. е. процессу, обратному процессу
поглощения с основного уровня на первый возбужденный. При оптическом возбу-
ждении эти полосы появляются в виде полос флуоресценции. Связь между длин-
новолновой полосой поглощения и соответствующей полосой испускания сложной
молекулы существенным образом определяется свойствами такой молекулы как
системы, подчиняющейся определенным статистическим закономерностям (ср. вы-
ше, с. 826). Сначала мы разберем свойства полос поглощения, а затем испускания
и произведем их сравнение10.
Рис. 27.6. Схема возникновения полос поглощения и испускания сложных молекул
Длинноволновая полоса поглощения соответствует переходам с колебательных
уровней нижнего (основного) электронного состояния, возбужденных при заданной
температуре, на различные колебательные уровни верхнего электронного состоя-
ния (см. рис. 27.6). При низкой температуре, когда практически все молекулы на-
ходятся в нулевом колебательном состоянии и возможны переходы только из этого
колебательного состояния, полоса будет иметь длинноволновую границу при ча-
стоте рэл, соответствующей изменению Л#эл — Езл — Е"л электронной энергии.
При повышении температуры эта граница должна сдвигаться, за счет поглощения
с термически возбужденных колебательных уровней, на величину, определяющую-
ся запасом колебательной энергии, возрастающим с температурой. Это смещение
невелико при обычной ширине полос поглощения, порядка сотен или тысяч см-1,
относительное смещение длинноволнового края полосы поглощения мало. Основная
часть полосы соответствует частотам и > иэл; с увеличением частоты поглощение
возрастает, достигает максимума и затем убывает, как схематически изображено
на рис. 27.7, дающем зависимость коэффициента поглощения от частоты; пунктиром
показана кривая, соответствующая низкой температуре и начинающаяся от и — иэл.
’° Более подробное рассмотрение данных вопросов см. в монографии Степанова [106]; ниже частично
изложен материал, содержащийся в гл. II и III этой монографии.
§ 27.4. Полосы поглощения и испускания сложных молекул
841
Рис. 27.7. Форма полосы поглощения
Участок сплошной кривой, ле-
жащий влево от и = иэл (у < рэл),
возникает за счет поглощения с воз-
бужденных колебательных уровней.
Форму полосы поглощения —
ее контур — можно качественно
объяснить, если учесть, во-первых,
что при не очень сильно отличаю-
щихся равновесных конфигурациях
основного и возбужденного состоя-
ний наиболее вероятными будут, со-
гласно принципу Франка—Кондона, переходы, при которых запас колебательной
энергии изменяется не очень сильно, и, во-вторых, что густота колебательных
уровней верхнего состояния	возрастает с увеличением -Е?'ол. При задан-
ном Е"ол вероятность В(Е"ал, Е'ко:1) отдельных переходов будет при увеличении раз-
ности |^кол - Мол I убывать, а число таких переходов будет возрастать пропорциональ-
но ^'(Мол)- В результате произведение В(Е"ОЛ, Е^д^Е^) имеет максимум при не-
котором положительном значении Мол “ Мол, т.е. при частотах и > иэл. На рис. 27.6
переходы, для которых достигается этот максимум, показаны жирными стрелками.
Зависимость от частоты вероятности перехода с определенного нижнего уровня с энер-
гией Е"ол на верхние уровни с энергией Е'кол при отнесении этой вероятности к единице
интервала энергий верхних уровней (что отмечено индексом Е), будет иметь вид
Ве^,») = В(Е^, £Uj'(C),	(27.13)
где
v = им + Е'к(а - Е1^	(27.14)
(см. рис. 27.6). Эта зависимость определяет форму полосы, возникающей при поглощении
с колебательного уровня с энергией Е"ол. Общую вероятность поглощения фотонов частоты 1/
и ее зависимость от этой частоты можно определить, зная (27.13) и функцию распреде-
ления /"(Мол) молекул по непрерывным колебательным уровням основного электронного
состояния. При больцмановском распределении молекул по уровням (см. (5.10)) доля мо-
лекул, приходящаяся на интервал dE"QA, будет (беря в (5.10) в качестве д, g'^E^dE"™,
см. (27.12), и полагая Ej = Е"ол)
df = /"(E^dE^ = fcV«,)e-^dC»,	(27.15)
где коэффициент пропорциональности к" определяется из условия нормировки
f df = J /"(X'M)d<M = 1.	(27.16)
Функция
/"(Х'ол) -	е”®1	(27.17)
имеет максимум при некотором значении Е"ол = (#кол)м> показанный графически на рис. 27.6
слева (значения f"(E"OJl) отложены по горизонтали как функция от значений Е"ол). Мак-
симум полной кривой поглощения лежит примерно при значении г/, для которого функ-
ция Ве((Е"ол)М1 и) достигнет максимума, т.е. когда сильнее всего поглощает наибольшее
число молекул. Сама полная кривая поглощения, согласно (27.13) и (27.17), будет иметь вид
оо	оо
/Г	е"
f"(E"oa)BE(E'^u,,i>)dE"o„=k" J g"(E‘^)e-^LBB(E^0J,,V)dE'^. (27.18)
о	о
К вопросу о форме полосы поглощения мы еще вернемся несколько ниже (с. 845).
842
Глава 27. Электронные спектры многоатомных молекул
При возбуждении колебательных уровней верхнего электронного состояния
с этих уровней возможны переходы с излучением на колебательные уровни ниж-
него электронного состояния и будет возникать полоса испускания, в случае
оптического возбуждения в виде полосы флуоресценции. При переходах с опре-
деленного верхнего электронно-колебательного уровня с энергией Е'кол испуска-
ется широкая полоса, соответствующая переходам на различные колебательные
уровни нижнего электронного состояния, коротковолновая граница которой ле-
жит при частоте узл + Хол (а при Е'кол = 0 — при частоте узл, см. рис. 27.6).
Наиболее вероятными будут переходы, для которых достигает максимума произве-
дение Л(Хол,Хол)/(Хол), где Л(Хол,Хол) — вероятность отдельного перехода,
а /(Хол) — число конечных уровней (на единицу интервала энергий, см. (27.12)).
Соответственно вероятность испускания, рассчитанную на единицу интервала энергий
нижних уровней, можно записать аналогично вероятности поглощения в виде
-МХол, У) = Жол, Х™)/(Хол),	(27.19)
где и выражается той же формулой (27.14), что и при поглощении.
Так как при заданном Хол вероятность 4 (Хол, Хол) будет, вообще говоря, убы-
вать с увеличением |Хол ~Хол1 (см- выше, с. 841), a gn(E^Qn) возрастает с увеличени-
ем Хол (и, следовательно, Хол ~ Хол), то максимум вероятности будет получаться
при некотором положительном значении Хол ~ Хол, т. е- при частотах и < узл.
Соответствующая форма полосы ис-
пускания показана на рис. 27.8.
Весьма существенной и харак-
терной чертой флуоресценции слож-
ных молекул, особенно хорошо про-
являющейся при их флуоресценции
в растворах, является независимость
спектра флуоресценции от длины
волны возбуждающего света. Даже
при возбуждении светом частоты у,
много большей, чем частота узл элек-
Рис. 27.8. Форма полосы испускания
тронного перехода, спектр флуоресценции практически остается неизменным. Это
естественным образом объясняется тем, что возбужденная молекула за короткое
время, много меньшее времени жизни возбужденного состояния, успевает отдать
избыточную энерппоокружающей среде, в результате чего подобная молекула будет
обладать запасом Хол колебательной энергии (в возбужденном электронном состо-
янии Хл)> соответствующим температуре окружающей среды. Поэтому испускание
происходит аналогично поглощению из состояний с относительно малым (на одну
степень свободы колебательного движения) запасом колебательной энергии, таким
же, как для основного электронного состояния. Получается кривая интенсивности
испускания, которая в основном соответствует частотам у < уэл, а при достаточ-
но низких температурах вообще целиком лежит при частотах у < узл с границей
при у = узл. На рис. 27.8 эта кривая показана пунктиром.
После установления теплового равновесия молекул, находящихся в возбужденном элек-
тронном состоянии, с окружающей средой, их распределение по колебательным уровням будет
определяться больцмановским законом (5J0), и аналогично (27Л7) мы получаем функцию
распределения
/'(Хол) -	е .	(27.20)
§27.4. Полосы поглощения и испускания сложных молекул	843
Это распределение показано графически на рис. 27.6. Для полной кривой испускания
усреднение выражения (27.19) дает формулу, аналогичную (27.18):
00	00
Л(1/) = ЛЙЖ^) = У/(Мол)Ля(^ол,р)</Мол = *'Уgl(E,m„)e^AE(E’MI,u)dE'mi. (27.21)
О	о
Следует подчеркнуть, что для сложных молекул наиболее характерно испускание
с первого возбужденного электронного уровня. Переход молекул на этот уровень про-
исходит благодаря безызлучательным переходам и при возбуждении более высоких
электронных уровней. Существенно, что возбуждение не обязательно должно быть
оптическим, и поэтому правильнее говорить о полосе испускания как о полосе лю-
минесценции (а не как о полосе флуоресценции), если идет речь об общих свойствах
этой полосы, не зависящих от способа возбуждения. Разумеется, при рассмотрении
вопроса о квантовом выходе существенно исследование именно флуоресценции.
Отметим, что в случае флуоресценции паров, даже достаточно разреженных, наблюдается
приближенная ее независимость от длины волны возбуждающего излучения, хотя при этом
и не всегда успевает установиться равновесное распределение молекул по колебательным
уровням возбужденного электронного состояния. Приближенную независимость от длины
волны в данном случае можно объяснить, если предположить, что вероятность испуска-
ния (27.19) при данном и мало зависит от запаса Е'кол колебательной энергии возбужденного
электронного состояния (подробнее см. [106], с. 156).
На основе рассмотрен-
ного механизма возникно-
вения полосы поглощения
и соответствующей ей по-
лосы испускания естествен-
ным образом объясняется
закон зеркальной симмет-
рии полос поглощения и ис-
пускания, впервые устано-
вленный эмпирически Лев-
шиным в 1931 г. [378] и
подтвержденный качествен-
но исследованиями большо-
го числа флуоресцирующих
молекул. Согласно этому за-
Рис.27.9. Закон зеркальной симметрии для полос
поглощения и испускания
кону, в шкале частот полоса
поглощения и полоса испускания имеют одинаковую форму и расположены сим-
метрично относительно частоты иэл, лежащей посредине между максимумами обеих
полос (рис. 27.9).
Соответствующие кривые могут быть получены друг из друга отражением в плоско-
сти симметрии («зеркальной» плоскости), перпендикулярной к плоскости чертежа, откуда
и происходит название закона.
Для объяснения закона зеркальной симметрии достаточно предположения, что
свойства последовательности колебательных уровней для различных электронных
состояний одинаковы (рис. 27.10). Тогда каждому переходу в поглощении с уров-
ня Хол — на уровень Хол = X, имеющему частоту и — г/погл = г/эл + (X ~ X),
будет соответствовать в испускании переход с уровня Хол ~ на уровень Хол — X,
844
Тлава 27. Электронные спектры многоатомных молекул
Рис. 27.10. Схема переходов для двух одинаковых
последовательностей колебательных уровней
имеющий частоту и 1/исп = и3л +
(Е\ — Ег). Частоты этих перехо-
дов будут расположены в спектре
симметрично относительно часто-
ты 1/эл. Дипольные моменты и их
зависимость от разности \v -	|
для обоих переходов одинаковы
(так как в обоих случаях ком-
бинируют одинаковые колебатель-
ные состояния — одно состояние
с энергией Е\ и одно с энерги-
ей ^2)- Далее, одинаковой будет
густота конечных колебательных
уровней при поглощении (верх-
них) и густота конечных колеба-
тельных уровней при испускании
(нижних). Наконец, одинаковыми
будут и относительные заселенно-
сти начальных уровней при по-
глощении (нижних) и начальных
уровней при испускании (верхних);
для последних существенно устано-
вление теплового равновесия возбужденных молекул с окружающей средой. В ре-
зультате распределение интенсивности (в зависимости от \и — //эл|) в поглощении
и в испускании, определяемое заселенностью начальных уровней, квадратом ди-
польного момента перехода и густотой конечных уровней, будет то же самое.
Закон зеркальной симметрии, хотя и имеет для сложных молекул широкую
область применения, но все-таки не является универсальным. В ряде случаев
наблюдаются значительные отступления от него. Это и понятно, поскольку пред-
положение об одинаковости свойств колебательных состояний комбинирующих
уровней не обязательно должно быть справедливым для всех сложных молекул даже
приближенно.
Рассмотрим подробнее обоснование закона зеркальной симметрии с квантовомеханиче-
ской точки зрения [379] (см. также [106], с. 169).
Вероятность переходов в поглощении с нижних уровней Е"ол на верхние Хол определяет-
ся формулой (27.13) и аналогично вероятность переходов в испускании с верхних уровней Хол
на нижние Хол определяется формулой (27.19).
Согласно предположению об одинаковости последовательностей колебательных уровней
Хол и Хол, мы имеем д"(Е^л) = д\Екол) — д(Екол). Подставляя для поглощения в (27.13)
Хол = El, Хол = Е2 и для испускания В (27.19) Хол — El, Хол = Е2 (см. рис. 27.10), получим
вероятности
ВЕ(Х,^поГл) = B(Ei,E2)g(E2), АЕ(Х,Ц<сп) - A(Eh Е2)д(Е2),	(27.22)
отличающиеся только множителями B(Ei,E2) и A(Ei,E2), относящимися к отдельным
переходам. Согласно (4.45) и (4.46)|2), для невырожденных состояний
В(ЕЬ Ег) = |^|Р2| |2, 4(Р„Р2) = ^i4,|Pi2|2,	(27.23)
3/г	Зпс5
где Ргк — дипольный момент перехода из определенного верхнего состояния в определенное
нижнее.
,2) В дальнейших формулах этого параграфа мы пишем постоянную h.
§ 27.4. Полосы поглощения и испускания сложных молекул
845
Электронно-колебательные волновые функции комбинирующих состояний можно пред-
ставить в виде (ср. (17.66))
Ф, = р) = V’U®, р)^кол(р), Фк = ф"(х, р) = ^м(®, р)ф"ол(р)- (27.24)
Учитывая, что при той же колебательной энергии Vk<m(p) — Ф"ол(р) — Ф(р) и обозначая эту
функцию через для состояния с энергией Е} и через ^г(р) ДЛЯ состояния с энергией Е2,
мы получим (см. (17.94)-( 17.98))
•Р21 = J ФэАх, р)Ф'^л(р)р3"Ф"Ах, р)Ф'^(р)аР =
= [ Ф^(х,р)ф2(р)РМф'^(.Х^Р)Ф^.Р)аР= [ ф*г(р)Р(р}ф\(р)Лр,
J	J	(27.25)
Pl2 = J Фэл(х,р)Ф'^Р)РЭ1,ф"Ах,р)^1,(р)(1р =
= У ФэАх,Р)Ф*(р)рЭ“Ф^(х,р)Ф2(р)^р= У 11>'(р)Р(р)Ф1(р)(1р,
где Р(р) = J Фм(х-> Р)Р^Ф'^(х, р) dx — дипольный момент электронного перехода. Соглас-
но (27.25), Р2\ = Pl2, |Р2| I2 = |Р|2|2 и, учитывая (27.22) и (27.23),
С? 1
— — Л(РИ Е2) = B(Et, Е2)	(27.26)
оТГП, 1/исп
И
1
— — Ае(Е,
? ^исп ) = BE(EhvnoTn).	(27.27)
8тгп 1^сп
Для усредненных вероятностей B(z/noM) и А(иКСП) (см. (27.18) и (27.21)) имеем аналогично
1
7 Т —з -4(^исп) — ^(^погл),	(27.28)
о7ГП 1/исп
в силу 7"(®кол) = f'(EK0I,) = f(EK0JI), где Екол = Е,.
Следовательно, вероятность испускания кванта частоты hvucn = hv3n -F (Е\ — Е2), де-
ленная на z/„cn, пропорциональна вероятности поглощения кванта зеркально-симметричной
частоты 7и/погл = ЬЩл + (^2 — -2ч), и при соответствующем выборе масштаба мы получаем
закон зеркальной симметрии.
Вместо вероятности поглощения можно ввести, как обычно делают, коэффициент погло-
щения хр, пропорциональный ЦЮГл^(^пог.1) (см. (5.67)), а вместо вероятности испускания —
его мощность Г7”сп, пропорциональную z/MCnA(z/MCn) (см. (5.2)) и определяющую интенсивность
испускания. Тогда
1 гт(исп) гг(исп)
=	-----—•	(27.29)
^ИСП ^исп ^исп ^погл
Отметим, что первоначально Левшин и другие авторы сравнивали коэффициент погло-
щения с интенсивностью, т.е. с мощностью испускания. При таком сравнении для от-
Az/
носительной ширины полос — порядка нескольких процентов, как это обычно имеет
^эл
место, получается заметная ошибка [106], и правильно сравнивать, как впервые было указано
, , к, Е^ИСП)
Блохинцевым [379], ----с —-—. Соответствующие шкалы и изображены на рис. 27.9.
Цюгл ^исп
Закон зеркальной симметрии связывает контур длинноволновой полосы погло-
щения и контур соответствующей полосы испускания, однако из него не вытекает,
каким именно должен быть этот контур. Как установил Вавилов [376] и как впослед-
ствии было подтверждено обширным экспериментальным материалом, для весьма
846
Глава 27. Электронные спектры многоатомных молекул
значительного числа молекул контур полосы является практически одинаковым,
т. е. обладает в значительной степени универсальным характером. Причина по-
добной универсальности заключается в статистическом характере закономерностей
для сложных молекул, на что и было указано Вавиловым. Важному вопросу о кон-
туре полос поглощения и испускания сложных молекул посвящено много работ,
тем не менее данный вопрос еще нельзя считать окончательно решенным (краткий
обзор работ см. [106], с. 272; см. также [376а]).
До сих пор мы сравнивали контур полосы поглощения и контур полосы ис-
пускания и нашли связь между ними. Наряду с этим имеется соотношение между
поглощением и испусканием для каждой данной частоты, установленное Степано-
вым [380] и имеющее гораздо более универсальный характер, чем закон зеркальной
симметрии. Согласно этой универсальной связи, для данной частоты отношение
мощности испускания U^cn^ к коэффициенту поглощения определяется формулой
^ИСП) п з I Мг'эл - ^)
-----= Си ехр < ----—----
[ кТ
(27.30)
где С — постоянная, зависящая от условий возбуждения спектра испускания. Дан-
ное отношение резко убывает с увеличением частоты и вблизи значения и — 1/эл,
что и приводит к очень быстрому изменению (около этой точки) отношения ор-
динат двух кривых на рис. 27.9. Применяя соотношение (27.30), можно по контуру
полосы поглощения находить для значений и, близких к г/Эл, контур полосы ис-
пускания, и наоборот, по контуру полосы испускания находить контур полосы
поглощения (см. [381]).
Формулу (27.30) можно записать в форме
с^исп> 3	( hv 1
— = d(T>3exp|-—	(27.31)
С ~1
где функция d(T) = С ехр < —— > зависит по показательному закону от темпе-
I кТ J
ратуры, но не зависит от частоты. В таком виде особенно отчетливо проявляется
универсальный характер соотношения между испусканием и поглощением.
Условием справедливости соотношения (27.30) является наличие для моле-
кул в возбужденном электронном состоянии теплового равновесия с окружающей
средой,3). Следует подчеркнуть, что это соотношение весьма общее, в отличие
от приближенного закона зеркальной симметрии, благодаря тому, что при его
выводе не делается никаких предположений о свойствах колебательных уровней
основного и возбужденного электронных состояний,4).
Формула (27.30) легко выводится, если воспользоваться выражениями (27.13) и (27.19)
для вероятностей поглощения и испускания при переходах между верхними уровнями с энер-
гиями Хол и нижними с энергиями Е"ол.
Согласно (5.2) и (27.13), мощность поглощения молекулами с энергией Хол равна15)
Г(.юга) = n"f"(E^huB(E^ E'KO!!)g(E'KOJl)p(v),	(27.32)
А также отсутствие других видов поглощения помимо обычного поглощения, связанного с переходом
молекулы в возбужденное электронное состояние ([106, 385], см. также ниже, с. 848).
,4) См. приведенный ниже вывод.
,51 Полагая в (5.2) щ = п” f"(Е"ол), где J* nkdE"Ojl = п", см. (27.16).
§ 27.4. Полосы поглощения и испускания сложных молекул
847
где п" ~ число молекул в основном электронном состоянии, р(и) — плотность излучения,
а мощность испускания молекулами с энергией .Е7'ол, согласно (5.2) и (27.19), равна16)
^исп) = п'/(Хол)/!1/Л(М<м,	(27.33)
где п' — число молекул в возбужденном электронном состоянии (зависящее от способа
возбуждения).
^-(исп)
Для отношения £7рИСп) к объемной поглощательной способности av —	.- (см. (5.60))
Р\у)
получим
=	А(Е'КОЛ, Е'^д'^Е"^)
а, п" В{Е'^,Е'колМЕ'тяУ	' ’ '
Согласно основной формуле (4.8) (где невырожденным состояниям с энергиями _E^OJ1
и Е*ол соответствуют значки i и fe),
AjE'^E^) _ 8тг/н/3
В(Е^,Е'КОЛ) с3
Учитывая (27.17) и (27.20), имеем
7/‘ис">
Др
ех ^кол 1
п' к' Р {	кТ	j 8тгки3
(	е:ол	\	сз
ехР >----FFF	f
I	кТ	(
Так как
•Е'кол Т* hi/ — Ь,иэл 4- Екол
(см. рис. 27.6 и формулу (27.14)), то
ЭЛ
( Е’ }
I -‘-'кол I
ехри IFJ ГЛ(,Э1-
Г E'L\=exp[-W
I кТ I
(27.35)
(27.36)
(27.37)
(27.38)
Заменяя а„, согласно (5.67), через коэффициент поглощения = —, окончательно находим
с
1/<исп>
пк 8тг/г з г hii/ы - и) 1 з f Ъ,(узл -
————у ехр <-----—---- > = Си ехр < --—
Хр п"к" с2 1 кТ I	| кТ
(27.39)
т.е. формулу (27.30), где
n'kf 8тг7г
C=^~ •	(27.40)
Существенно, что хотя мы рассматривали переход между уровнями с определенными значени-
ями энергии, .Е7'ол и Е*ол, тем не соотношение (27.40) не зависит от Е'кол и Е'^ол в отдельности,
а только от
Е' - Е”
х-/кол -LJKO,I
h '
V = иэл +
Формулу (27.39) можно записать в виде
иУсп)	п'к'
Ку	II К
hvM 1 Sirhv3 ( hv)	8тг/ц/3 f hv
IF Г — exH - Г P(T) ~exp I ~ fc?
(27.41)
,6) Полагая в (5.2) п: = п'/'(Е'К0Л), где аналогично f njdE^ — п'.
Глава 27. Электронные спектры многоатомных молекул
где
(27.42)
&	f 1 17)
D(T) =------ехр < ---- > '
v 7 n”k"	[ кТ )
и сравнить ее с законом Кирхгофа. Согласно (5.62), закон Кирхгофа для объемных величин
имеет вид,8)
^у(равн)
—------=	(27.43)
av
где — мощность равновесного спонтанного испускания, — объемная плотность
равновесного излучения, определяемая формулой Планка (5.42). Так как hv Э» кТ, то для ри
можно взять приближенное выражение (5.44) (закон Вина), и, учитывая, что av — схи) мы
получим
Ww3 ( Лм
__ = __ ехр; __
(27.44)
Из (27.41) и (27.44) вытекает, что
^исп) = D(T)U^‘H\	(27.45)
т.е. мощность люминесценции — неравновесного испускания (см. с. 148) — пропорциональна
мощности равновесного теплового испускания. Множитель пропорциональности D(T) зави-
сит, согласно (27.42), от температуры и от условий возбуждения, но не зависит от частоты.
§27.5. Квантовый выход и поляризация
фотолюминесценции сложных молекул
Важнейшей характеристикой сложной молекулы и ее взаимодействия со средой,
в которой она находится, служит квантовый выход флуоресценции, т. е. отноше-
N
ние (4.26), (3 — -"исп, числа ?7ИСП испущенных фотонов к числу 7УПогл поглощенных
™асгл
фотонов (мы обозначаем в (4.26) N-Q = Nucn и = ЛГпогл). За время между моментом
поглощения и моментом испускания, т.е. за время жизни возбужденного состояния,
в молекуле могут происходить разнообразные процессы перераспределения погло-
щенной энергии (включая и распад молекулы) и обмена энергией с окружающей
средой. Квантовый выход зависит от этих процессов.
На основе изучения для растворов зависимости выхода флуоресценции от ча-
стоты возбуждающего света (спектров выхода, см. выше, с. 839), Вавилов установил
закон, который получил название закона Вавилова: квантовый выход флуоресценции
не зависит от частоты возбуждающего света в стоксовой области спектра возбужде-
ния (i/возб > ^исп) и начинает при уменьшении частоты быстро падать в области частот
возбуждения, близких к максимуму полосы флуоресценции (цЮ1б « ^исп)- Наряду
с этим Вавилов установил (для флуоресценции растворов) независимость длитель-
ности возбужденного состояния от частоты возбуждающего света, причем в отличие
от падения выхода при переходе в антистоксову область возбуждения (г/воз6 < ^исп)
длительность и в антистоксовой области остается постоянной.
Работы Вавилова, посвященные выходу и длительности люминесценции, были им
выполнены, начиная с 1922 г. Ссылки на эти работы, собранные в тт. I и II избранных
17) функция D(T) отличается от функции d(T) в (27.31) только постоянным множителем. Соглас-
. 8тгЛ.
но (27.41) и (27.31), d(T) = D(T) —.
с2
|8) Разницей между а'и и аи, т.е. вынужденным испусканием, мы пренебрегаем.
§ 27.5. Квантовый выход и поляризация фотолюминесценции
849
сочинений Вавилова, и на ряд других работ по данному вопросу, подтверждающих выводы
Вавилова, можно найти в обзоре Степанова «Закон Вавилова» [107].
Из закона Вавилова вытекает, что, независимо от величины избытка ДЕ? —
^(^возб “ ^исп) энергии в возбужденном состоянии, в результате процессов перерас-
пределения и отдачи энергии совокупность молекул, первоначально поглотивших
фотоны, оказывается в последующие моменты времени, перед актами испускания,
в одинаковых исходных состояниях. Это подтверждается независимостью длительно-
сти флуоресценции от цюзб и, следовательно, от ДЕ7. Для более глубокого понимания
следствий закона Вавилова и для объяснения падения выхода в антистоксовой обла-
сти существенна возможность двух типов тушения — тушений первого и второго ро-
да, согласно Вавилову. Если при поглощении фотона его энергия идет на ионизацию
или диссоциацию молекулы или на возбуждение только колебательно-вращательных
уровней энергии, т. е. если не происходит электронного возбуждения молекулы (и,
следовательно, последующего испускания фотонов частоты 1/исп), — имеет место
тушение первого рода. Если энергия поглощенного фотона идет на электронное
возбуждение и происходит дезактивация возбужденного электронного состояния
при безызлучательных переходах, то имеет место тушение второго рода. Тушение
первого рода происходит очень быстро, за время, не превышающее 10”12-10”13 с,
и приводит к тому, что число молекул, для которых возбуждается электронный уро-
вень, равно не ^огл, а 7УПогл(1 - «1)» где аь — доля молекул, испытавших тушение
первого рода. Тушение первого рода не сказывается на законе затухания и дли-
тельности флуоресценции, которые будут определяться вероятностью А испускания
и вероятностью С тушения второго рода, т. е. безызлучательных переходов (см. § 4.2).
Можно ввести, следуя Вавилову, понятие о чистом выходе тушения второго рода
fl __ ^исп _ ^исп _ &	/27 46)
0 — #1)^погл л2^погл #2
где «2 — 1 ~	— доля молекул, для которых произошло электронное возбуждение.
Применяя для р' формулы (4.26) и (4.24), учитывающие безызлучательные переходы,
мы получаем
А 1	г'
Р = а2р' = а2-—— = а2- = а2 —,	(27.47)
А + С у	т
, 1
где т = ——— — время жизни возбужденных молекул, т. е. длительность флуо-
А 4- С
1
ресценции, при наличии тушения второго рода, а т = — — при его отсутствии.
А
Соотношение (27.47) можно записать в виде
р а2	z
— = — = const.	(27.48)
т' т
Если известно т, то, измеряя р и т',9), можно определить а2 и, следовательно,
долю а\ = 1 - а2 поглотивших молекул, испытавших тушение первого рода. Для ту-
шения второго рода, согласно (27.47), выход р и длительность флуоресценции т'
должны изменяться параллельно. Таким образом, формулы (27.47) и (27.48) могут
быть применены для определения того, какой род тушения имеет место. Необходимо,
однако, помнить, что эти формулы справедливы лишь в случае, если вероятность А
19  Об измерении длительности см. [374].
850	Глава 27. Электронные спектры многоатомных молекул
спонтанного испускания остается неизменной. Последнее при наличии сильного
взаимодействия молекул с окружающей средой не всегда соблюдается.
Из неизменности длительности при антистоксовом возбуждении (рвозб < ^исп)>
следует, согласно (27.46), что падение выхода происходит за счет уменьшения «2» сле-
довательно, за счет увеличения , т. е. тушения первого рода. Это физически можно
понять, учитывая, что возбуждение антистоксовой флуоресценции происходит с вы-
соких колебательных уровней основного электронного состояния. При большом
запасе колебательной энергии может существенно возрастать тушение второго рода.
Отметим, что вопрос о причинах падения выхода при антистоксовом возбуждении
еще далеко неясен и является предметом дискуссии.
Следует подчеркнуть, что закон Вавилова справедлив для флуоресценции мо-
лекул в конденсированных системах. В разреженных парах, когда за время жизни
возбужденных состояний молекулы не успевают отдать избыточную колебатель-
ную энергию другим молекулам, квантовый выход флуоресценции с уменьшением
частоты сначала возрастает и лишь затем начинает падать. Возрастание выхода
было объяснено Непорентом, установившим и исследовавшим данную закономер-
ность [377, 386], уменьшением вероятности безызлучательного перехода электронной
энергии возбуждения в колебательную при уменьшении 1/возб, т. е. запаса колеба-
тельной энергии возбужденного электронного состояния.
Рассмотрим теперь другую важнейшую характеристику сложной молекулы —
поляризацию флуоресценции, так же как и выход, зависящую от свойств молекулы
и ее взаимодействия со средой.
Поляризация в электронных спектрах молекул связана с тем, что в них каждому
переходу соответствуют вполне определенные значения составляющих дипольного,
магнитного или квадрупольного моментов (см. §4.3 и 4.4):
дипольный	магнитный	квадрупольный
момент	момент	момент
перехода Pik	перехода plk	перехода Qik
(Px)ik	Mik	(Qx)ik	(27.49)
(Т'жХ'А:) (Py)iki (Pz)ik	(j4y)ik> (P>z)ik (Qxx)iki (Qyy)ik^ (Qzz)ik
(Qyz)iky (Qzx)iky (Qxy)ik
При этом для молекул данные составляющие берутся в координатной системе, свя-
занной с молекулой. Согласно наглядным представлениям, каждому электронному
переходу соответствуют определенным образом ориентированные осцилляторы —
электрический для дипольных переходов (см. с. 93) и магнитный — для магнит-
ных переходов (см. с. 98), или пары осцилляторов — для квадрупольных перехо-
дов (см. с. 102). Такие элементарные излучатели характеризуют электронный переход.
Свойства элементарных излучателей с подробным анализом пространственного
распределения излучения и получающейся для него интерференционной картины
были изучены Вавиловым (см., в частности, его книгу о микроструктуре света [2]).
Для молекул, обладающих симметрией, при переходах между электронными
уровнями заданных типов симметрии ориентация соответствующих осцилляторов
относительно молекулы частично или полностью определяется правилами отбора
и может быть найдена с помощью табл. 22.1-22.11. Если, например, для молекулы
с выделенной осью симметрии при данном типе перехода отлична от нуля составля-
ющая Pz дипольного момента, то это означает, что такие переходы характеризуются
электрическим диполем, ориентированным по оси z.
В принципе, поляризацию можно исследовать как для электронных спектров
испускания, так и для электронных спектров поглощения. Однако в последнем
§ 27.5. Квантовый выход и поляризация фотолюминесценции 851
случае, подобно колебательным спектрам поглощения в инфракрасной области,
при пропускании через исследуемое вещество, состоящее из свободно ориенти-
рующихся молекул, различным образом поляризованного излучения поглощение
не будет зависеть от поляризации этого излучения (см. с. 690).
Если молекулы ориентированы определенным образом, то можно обнаружить и ис-
следовать дихроизм — зависимость поглощения излучения, пропускаемого через вещество,
от поляризации этого излучения. Такие исследования для молекул красителей, адсорбиро-
ванных на прозрачных полимерных пленках, подвергнутых значительному растяжению, были
выполнены Смирновым [384].
Для спектров испускания, возбуждаемых оптическим путем, т. е. для спектров
фотолюминесценции, излучение будет поляризованным также и в важнейшем слу-
чае свободно ориентирующихся молекул, аналогично тому, как это имеет место
для комбинационного рассеяния. В направлении, составляющем определенный угол
с направлением возбуждающего излучения, получается определенная поляризация
люминесценции. Именно исследования поляризации люминесценции (поляризо-
ванной люминесценции) позволяют получить наиболее существенные данные о ди-
польных, магнитных и квадрупольных моментах электронных переходов в сложных
молекулах и связать свойства этих моментов со структурой изучаемых молекул.
Значение изучения поляризованной люминесценции сложных молекул было показа-
но Вавиловым. Фундаментальные исследования поляризованной люминесценции молекул
и кристаллов принадлежат Феофилову [108], в работах которого можно найти подробное
изложение вопросов, лишь бегло рассматриваемых ниже.
Мы разберем только некоторые вопросы, касающиеся поляризации люминес-
ценции молекул.
Поляризацию люминесценции обычно характеризуют степенью поляризации.
Пусть возбуждающее излучение распространяется вдоль оси г] (рис. 27.11), а наблю-
дение люминесценции ведется по направлению, лежащему в плоскости £г] и соста-
вляющему угол х с направлением т]. Степенью поляризации называют отношение
Рис. 27.12. Поляризация
люминесцении при поперечном
наблюдении (х = тг/2)
Рис. 27.11. Поляризация
люминесценции в общем случае
852
Глава 27. Электронные спектры многоатомных молекул
где 1ц — интенсивность составляющей световых колебаний, параллельной оси
a Ij_ — интенсивность составляющей, перпендикулярной к оси Степень поляри-
зации зависит от угла х и от угла /3 между направлением колебаний возбуждающего
света (в случае линейно поляризованных колебаний) и осью Для случая /3 = О
7Г
и х — у, т. е. когда Для возбуждающего света колебания происходят вдоль оси £, а на-
блюдение люминесценции ведется в перпендикулярном направлении, т. е. по оси £,
мы получаем картину, изображенную на рис. 27.1220).
Тогда
1--^
P=kzA =_____к.
ТС +	1 . h
Ic
(27.51)
Поляризация люминесценции при заданных углах х и Р будет зависеть от того,
какой элементарный излучатель поглощает и какой элементарный излучатель ис-
пускает свет, а также от того, какова взаимная ориентация в молекуле излучателя,
поглощающего возбуждающий свет, и излучателя, испускающего люминесценцию.
Для дипольного излучения эта взаимная ориентация определяется углом между по-
глощающим и испускающим осцилляторами. Если непосредственно возбуждается
электронный уровень, являющийся начальным для перехода в испускании, то эле-
ментарный излучатель будет тем же самым для поглощения и испускания. В этом
случае для дипольного излучения испускающий и поглощающий осцилляторы тожде-
ственны, и степень поляризации люминесценции для свободно ориентирующихся
молекул равна ( при = 0 и %	~ I
Ро=1 = 5О%.
(27.52)
Данный результат получается следующим образом. Если амплитуда колебаний задающего
света а^, то амплитуда Ъ возбуждаемых этим светом колебаний осциллятора, ориентирован-
ного под углом 0 к оси £ (см. рис. 27.12), будет пропорциональна cos0. Разлагая колебания
осциллятора по осям £ и //, мы получим амплитуды = b cos (Z, £) и bv = Ь cos (Z, т?), где I —
направление осциллятора. Так как cos (Z, () = cos 0, a cos (/, tj) = sin 0 sin p, то эти амплитуды
будут пропорциональны cos20 и cos 0 sin 0 sin p. Для люминесценции интенсивности 1ц =
и I± = составляющих световых колебаний будут пропорциональны Ь* 1^ и &2, следова-
тельно, пропорциональны cos40 и cos 20 sin 20 sin 2р соответственно. Усреднение по всем
равновероятным ориентациям осциллятора, связанного с молекулой, даст средние значения,
пропорциональные f cos 40 sin 0 d0 dp и J cos 20 sin 20 sin 2p sin 0 d0 dp, в результате
A "T-L f cos20sin20sin2(/?sin0d0<fy?
Ту	f cos 40 sin 0 d0 dp
20) Рис. 27.12 аналогичен рис. 23.3 (с. 690). Степень поляризации легко связать с введенной там степенью
Л
деполяризации р — — — —:
7Н Ч
1 - —
Р == Lzp.
i-Л 1+/
'и
(27.53)
Очевидно, что при р = 0 Р = 1.
§ 27.5. Квантовый выход и поляризация фотолюминесценции
853
Элементарное интегрирование для отношения I^/Ц дает значение, равное */з, откуда и выте-
кает равенство (27.52) для Ро-
Исследование поляризованной флуоресценции позволяет решать три рода задач.
Во-первых, находя поляризационные диаграммы, дающие пространственное рас-
пределение поляризации люминесценции, можно определять природу элементарных
излучателей — устанавливать, являются ли они электрическими или магнитными
диполями или квадруполями. Такие поляризационные диаграммы для зависимости
тг
степени поляризации от угла х при заданном угле /3, обычно при /3 = 0 и (3 — —,
и для зависимости степени поляризации от угла /3 при заданном угле х, обычно
тг
при х — б и х — j (см- Рис* 27.11), могут быть рассчитаны для различных комбина-
ций поглощающих и испускающих элементарных излучателей с разными взаимными
ориентациями. Поляризационные диаграммы получаются весьма разнообразными.
Для ряда случаев, рассчитанных Вавиловым [382], они показаны на рис. 27.13 (угол rj
на этом рисунке соответствует углу р в нашем обозначении).
Во-вторых, изучая поляризационные спектры (см. выше, с. 839) — кривые,
дающие зависимость значений степени поляризации люминесценции от частоты
возбуждающего света, — можно находить взаимную ориентацию элементарных
Диполь -►
—► Диполь
Квадруполь-*
-► Квадруполь
Диполь-*
-* Квадруполь
Квадруполь-*
—► Диполь
Рис. 27.13. Поляризационные диаграммы
854	Глава 27. Электронные спектры многоатомных молекул
излучателей для поглощения и испускания. При возбуждении в области различ-
ных полос поглощения могут получаться и различные значения степени поляри-
зации, в том числе и отрицательные. Последний случай имеет место, в частно-
сти, для дипольного излучения, когда испускающий осциллятор перпендикулярен
к поглощающему.
В-третьих, измеряя предельные значения степени поляризации, наблюдаемые
в максимуме поляризационного спектра (при устранении деполяризации, обусло-
вленной разного рода факторами, не связанными непосредственно со строением
молекулы), можно делать определенные выводы о симметрии молекулы. Можно
показать, например, что для плоской молекулы с перпендикулярной осью симме-
трии порядка п 3 предельная степень поляризации не превышает ’/?, в то время
как для плоских молекул низшей симметрии, не имеющих такой оси, предель-
ная степень поляризации может равняться [383]. Малые степени поляризации,
меньше У?, действительно наблюдаются для бензола, обладающего симметрией
и для ряда его производных, у которых поглощение и люминесценция, как и у самого
бензола, определяются переходами, связанными с возбуждением нелокализованных
электронов бензольного кольца. Для бензола СбЩ Ро = 7,7 %, для толуола СбН5СН3
Ро = 5,8 %, для мезителена СбН3(СН3)3 Ро = 8,75 %.
Большое значение имеют исследования поляризации флуоренсценции раство-
ров. Степень поляризации зависит, помимо частоты возбуждающего света, от дли-
тельности жизни возбужденного состояния т, от вязкости среды г], от абсолютной
температуры Т, от концетрации молекул, и можно установить ряд закономерностей,
связывающих эти величины. Мы ограничимся приведением формулы Перрена [387],
связывающей степень поляризации Р с т, т] и Т. Она имеет вид
1 _ 1 /1 1\ RT
Р Ро + \Ро з/ vr) ’
(27.54)
где R — газовая постоянная, v — молекулярный объем испускающих молекул,
а Ро — предельное значение поляризации, соответствующее ту = оо.
ПРИЛОЖЕНИЯ

ЛИТЕРАТУРА
1.	МОНОГРАФИИ, УЧЕБНИКИ И ОБЗОРЫ
а)	Общие вопросы оптики
1.	Ньютон И. Лекции по оптике. Изд-во АН СССР, 1946; Оптика. Гостехиздат, 1954.
2.	Вавилов С. И. Микроструктура света. Изд-во АН СССР, 1950; см. также Собр. соч. Т. II.
3.	Вуд Р. Физическая оптика. ОНТИ, 1936; Ландсберг Г. С. Оптика. Гостехиздат, 1957.
4.	Волькенштейн М. В. Молекулярная оптика. Гостехиздат, 1951.
5.	Фабри Ш. Общее введение в фотометрию. ГТТИ, 1934.
б)	Атомная спектроскопия и смежные вопросы
6.	Bohr N. Atom. Enzyclop. Britt. Vol. 2 (издание 1928 г. и последующие).
7.	Фриш С.Э. Атомные спектры. ГТТИ, 1933.
8.	Теренин А. И. Введение в спектроскопию. Кубуч, 1933.
9.	Кондратьев В. Н. Структура атомов и молекул. Физматгиз, 1959.
10.	Зоммерфельд А. Строение атома и спектры. Т. 1. Гостехиздат, 1956 (первое немецкое
издание: Sommerfeld A. Atombau und Spektrallinien. 1919).
11.	Герцберг Г. Атомные спектры и строение атомов. ИЛ, 1948 (имеется второе английское
издание: Herzberg G. Spectra of Diatomic Molecules. 1950).
12.	Hund F. Linienspektren und Periodisches System der Elemente. 1927.
13.	White H. Introduction to Atomic Spectra. 1984.
14.	Кондон E., Шортли Г. Теория атомных спектров. ИЛ, 1949.
15.	Ельяшевич М.А. Спектры редких земель. Гостехиздат, 1953.
16.	Grotrian W. Graphische Darstellung der Spektren von Atomen mit ein, zwei und drei Valen-
zelektronen. 1928.
17.	Back E., Lande A. Zeeman-Effekt und Multiplettstruktur der Spektrallinien. 1925; Back E.
Zeeman-Effekt // Handb. d. Exper. Phys. 22, 1. 1929; Van der Bosch J. Zeeman-Effekt 11
Handb. d. Phys. 28, 296, 1957.
18.	Колесников В. H, Лесков Л. В. Вероятность оптических переходов для атомов и двухатом-
ных молекул // УФН. 65, 3, 1958.
19.	Борисоглебский Л. А. Запрещенные линии в атомных спектрах // УФН. 66, 603, 1958.
20.	Боровский И. Б. Физические основы рентгеноспектральных исследовании. Изд-во МГУ,
1956.
21.	Вайнштейн Э. Е. Рентгеновские спектры атомов в молекулах химических соединений
и в сплавах. Изд-во АН СССР, 1956.
22.	Митчелл А., Земанский М. Резонансное излучение и возбужденные атомы. ОНТИ, 1937.
23.	Фриш С. Э. Роль эффективных сечений атомов при возбуждении спектров // УФН. 61,
461, 1957.
24.	Собельман И. И. О теории ширины атомных спектральных линий // УФН. 54, 551, 1954.
24а. Traving G. Uber die Theorie der Druckverbreihung von Spektrallinien. 1960.
858
Приложения
246.	Margenau Н., Lewis М. Structure of Spectral Lines from Plasma // Rev. Mod. Phys. 31, 569,
1959.
25.	Чей ILL, Такео M. Уширение и сдвиг спектральных линий, создаваемые посторонними
газами Ц УФН. 66, 391, 1958.
26.	Breene R. Line Shape // Rev. Mod. Phys. 29, 94, 1957.
27.	Гепперт-Майер M., Йенсен И. Элементарная теория ядерных оболочек. ИЛ, 1958.
28.	Feenberg Е. Shell Theory of the Nucleus. 1955.
29.	Обобщенная модель ядра // Современные проблемы физики. ИЛ. №9, 1955; №2, 1956.
30.	Рамзей Н. Моменты и статистика ядер // Экспериментальная ядерная физика / Под ред.
Э. Сегре. Т. 1, с. 299. ИЛ, 1955.
31.	Дорфман Я. Г. Магнитные свойства атомного ядра. Гостехиздат, 1948.
32.	Копферман Г. Ядерные моменты. ИЛ, 1960.
33.	Blin-Stoyle В. Theories of Nuclear Moments. 1957 (монография); Theories of Nuclear
Moments // Rev. Mod. Phys. 28, 75, 1956 (обзор).
34.	Фриш С. Э. Спектроскопическое определение ядерных моментов. Гостехиздат, 1948.
35.	Стриганов А. Р., Донцов Ю. П. Изотопический эффект в атомных спектрах // УФН. 65,
315, 1955.
36.	Аркадьев В. Е. О магнитной спектроскопии и радиоспектроскопии атомного ядра // УФН.
44, 80, 1951.
37.	Эндрью Э. Ядерный магнитный резонанс. ИЛ, 1957.
38.	Леше А. Ядерная индукция. ИЛ, 1961.
39.	Grivet Р. La resonance paramagnetique nucleaire. 1955.
40.	Инграм Д. Спектроскопия на высоких и сверхвысоких частотах. ИЛ, 1959.
41.	Ельяшевич М.А. Современное состояние радиоспектроскопии // УФН. 54, 513, 1954.
42.	Рамзей Н. Молекулярные пучки. ИЛ, 1960.
43.	Kusch Р. Atomic and Molecular Beam Spectroscopy // Handb. d. Phys. 37/1, 1, 1959.
44.	Гомбаш П. Статистическая теория атома и ее применения. ИЛ, 1951.
45.	Подгорецкий М. И. Мезоатомы // УФН. 51, 253, 1953; Иваненко Д. Д., Пустовалов ЕЕ.
Мезоатомы // УФН. 61, 27, 1957; West D. Mesonic Atoms // Rep. Progr. Phys. 21, 271, 1958.
в)	Молекулярная спектроскопия и смежные вопросы
46.	Герцберг Г. Спектры и строение двухатомных молекул. ИЛ, 1949 (второе английское
издание: Herzberg G. Spectra of Diatomic Molecules. 1950).
47.	Крониг P. Полосатые спектры и строение молекул. ГНТИУ, 1935.
48.	Sponer Н. Molekulspektren und ihre Anwendung auf Chemische Probleme. 1. 1985; 2. 1936.
48a. Penner S. Quantitative Molecular Spectrescopy and Gas Emissivities. 1959.
49.	Teller E. Theorie der langwelligen Molekulspektren // Handb. u. Jahrb. d. Chem. Phys. 9/II,
43, 1934.
50.	Mulliken R. Interpretation of Band Spectra // Rev. of Mod. Phys. 2, 60, 1930 (part I); 3, 69,
1931 (part 11); 4, 1, 1932 (part III).
51.	Никольский К. В. Квантовая механика молекулы. ГТТИ, 1934.
52.	Richardson О. Ж. Molecular Hydrogen and its Spectrum. 1934.
53.	Герцберг Г. Колебательные и вращательные спектры многоатомных молекул. ИЛ, 1949.
54.	Nielsen Н. Vibration-Rotation Energies of Molecules // Rev. Mod. Phys. 23, 90, 1951; The
Vibration-Rotation Energies of Molecules and their Spectra in the Infrared // Handb. d. Phys.
37/1, 173, 1959.
55.	Волькенштейн M. В., Ельяшевич M.A., Степанов Б. И. Колебания молекул. Т. 1 и 2.
Гостехиздат, 1949.
55а. Маянц Л. С. Теория и расчет колебаний молекул. Изд-во АН СССР, 1960.
56.	Ельяшевич М.А. Механика колебаний молекул // УФН. 28, 482, 1946.
Литература
859
57.	Вильсон Е., Дешиус Д., Кросс П. Теория колебательных спектров молекул. ИЛ, 1960.
58.	Ta-You-Wu. Vibrational Spectra and Structure of Polyatomic Molecules. 1939.
59.	Rosenthal G., Murphy G. Group Theory and the Vibrations of Polyatomic Molecules // Rev.
Mod. Phys. 8, 317, 1936.
60.	Плачек Г. Рэлеевское рассеяние и раман-эффект. ОНТИ, 1935.
61.	Кольрауш К. Спектры комбинационного рассеяния. ИЛ, 1952.
62.	Mizuschima S. Raman-Effect // Handb. d. Phys. 26, 171, 1958.
63.	Ландсберг Г. С., Бажулин П.А., Сущинский М.М. Основные параметры спектров комби-
национного рассеяния углеводородов. Изд-во АН СССР, 1956.
64.	Сущинский М. М. Применение комбинационного рассеяния света к исследованию состава
и строения вещества // УФН. 63, 301, 1957.
65.	Сущинский М. М. Применение вращательных спектров комбинационного рассеяния
для определения структурных параметров молекул // УФН. 65, 441, 1958.
66.	Шефер К., Матосси Ф. Инфракрасные спектры. ОНТИ, 1935.
67.	Леконт Ж. Инфракрасные спектры. ИЛ, 1958; Lecompte J. Spectroscopic dans 1’infrarouge //
Handb. d. Phys. 26, 244, 1958.
68.	Беллами Л. Инфракрасные спектры молекул. ИЛ, 1957.
69.	Стренберг М. Радиоспектроскопия. ИЛ, 1956.
70.	Таунс С., Шавлов А. Радиоспектроскопия. ИЛ, 1959.
71.	Горди В., Смит В., Трамборуло Р. Радиоспектроскопия. ИЛ, 1955.
72.	Brownstein S. High Resolution Nuclear Magnetic Resonance and Molecular Structure // Chem.
Rev. 59, 463, 1959.
73.	Wertz J. Nuclear and Electronic Spin Magnetic Resonance // Chem. Rev. 55, 829, 1955.
74.	Орвилл-Томас У. Ядерное квадрупольное взаимодействие и химическая связь // Успехи
химии. 27, 731, 1958.
75.	Альтшулер С. А., Козырев Б.М. Электронный парамагнитный резонанс. Физматгиз, 1960.
76.	Волькенштейн М. В. Строение и физические свойства молекул. Изд-во АН СССР, 1955.
77.	Стюарт Г. Структура молекул. ГНТИУ, 1937.
78.	Мидзусима С. Строение молекул и внутреннее вращение. ИЛ, 1957.
79.	Фаркас А. Орто-водород, пара-водород и тяжелый водород. ОНТИ, 1936.
80.	Реутов О. А. Теоретические проблемы органической химии. Изд-во МГУ, 1956.
81.	Хюккель В. Теоретические основы органической химии. Т. 1. ИЛ, 1955; Темникова Т.Н.
Курс теоретических основ органической химии. Госхимиздат, 1959.
82.	Веселов М. Г. Элементарная квантовая механика атомов и молекул. Гостехиздат, 1955.
83.	Состояние теории химического строения в органической химии. Доклад комиссии ОХН
АН СССР. Изд-во АН СССР, 1954.
83а. Хюккель В, Химическая связь. ИЛ, 1960.
84.	Гайтлер В. Квантовая теория и гомеополярная химическая связь. ГНТИУ, 1934; Борн М.
Химическая связь и квантовая механика. ГНТИУ, 1932.
85.	Coulson С. Valence. 1952.
86.	Эйринг Г., Уолтер Д., Кимбалл Д. Квантовая химия. ИЛ, 1948.
87.	Гельман Г. Квантовая химия. ОНТИ, 1937.
87а. Козман У. Введение в квантовую химию. ИЛ, 1960.
88.	Паулинг Л. Природа химической связи. Госхимиздат, 1947.
89.	Longuet-Higgins Н. Recent Development in Molecular Orbitals Theory // Adv. Chem. Phys. 1,
239, 1958.
90.	Ван-Аркель, de-Бур. Химическая связь с электростатической точки зрения. ОНТИ, 1935.
91.	Райс О. Электронное строение и химическая связь в неорганической химии. ИЛ, 1949.
92.	Гейдон А. Энергия диссоциации и спектры двухатомных молекул. ИЛ, 1949 (имеется
второе английское издание: Gaydon A. Dissociation Energies and Spectra of Diatomic
Molecules. 1953).
860
Приложения
92а. Сошников В. Н. Абсолютные интенсивности электронных переходов в двухатомных мо-
лекулах // УФН. 74, 61, 1961.
93.	Finketburg ИС Kontinuirliche Spektren. 1938; Kontinuirliche Spektren Ц Handb. d. Phys. 28,
79, 1957.
94.	Пирс P, Гейдон А. Отождествление молекулярных спектров. ИЛ, 1949 (имеется второе
английское издание: Pearse R., Gaydon A. Indentification of Molecular Spectra. 1950).
95.	Гейдон А. Спектроскопия пламен. ИЛ, 1959.
96.	Sponer И., Teller Е. Electronic Spectra of Polyatomic Molecules // Rev. Mod. Phys. 13, 76,
1941.
97.	Гиллем А., Штерн E. Электронные спектры поглощения органических соединений. ИЛ,
1957.
98.	Forster Т. Fluoreszenz organischer Verbindungen. 1951.
99.	Теренин А. Н. Фотохимия красителей и родственных органических соединений. Изд-во
АН СССР, 1947.
99а. Sandorphy С. Les spectres electroniques en chimie theorique. 1959.
100.	Рид С. Возбужденные электронные состояния в химии и биологии. ИЛ, 1960.
101.	Инграм Д. Парамагнитный резонанс и его применения к изучению свободных радикалов.
ИЛ, 1961.
102.	Д Левшин В. Фотолюминесценция жидких и твердых веществ. Гостехиздат, 1951.
103.	Прингсгейм П. Флуоресценция и фосфоресценция. ИЛ, 1951.
104.	Garlick G. Luminescence // Handb. d. Phys. 26, 1, 1958.
105.	Пайпер В., Вильямс Ф. Электролюминесценция // УФН. 70, 621, 1960.
106.	Степанов Б. И. Люминесценция сложных молекул. Изд-во АН БССР, 1956.
107.	Степанов Б. И. Закон Вавилова // УФН. 58, 3, 1956.
108.	Феофилов П. П. Поляризованная люминесценция // УФН. 36, 417, 1948; Поляризованная
люминесценция атомов, молекул и кристаллов. Физматгиз, 1959.
109.	Кондратьев В. И., Ельяшевич М.А. Элементарные процессы обмена энергии в газах.
ГТТИ, 1933.
110.	Годнее И. Н. Вычисление термодинамических функций по молекулярным данным. Госте-
хиздат, 1956.
г)	Прикладная спектроскопия
111.	Мандельштам С. Л. Введение в спектральный анализ. Гостехиздат, 1946.
112.	Прокофьев В. К. Фотографические методы спектрального анализа. Ч. 1 и 2. Гостехиздат,
1951.
113.	Чулановский В. М. Введение в молекулярный спектральный анализ. 2-е изд. Гостехиздат,
1951.
114.	Применение спектроскопии в химии / Под ред. В. Веста. ИЛ, 1959.
115.	Фриш С. Э. Техника спектроскопии. Изд-во ЛГУ, 1936.
116.	Королев Ф.А. Спектроскопия высокой разрешающей силы. Гостехиздат, 1953.
117.	Ярославский Н. Г Методика и аппаратура длинноволновой инфракрасной спектроско-
пии И УФН. 62, 159, 1957.
118.	Бобович Я., Пивоваров В. Аппаратура и методы исследования спектров комбинационного
рассеяния в газах // УФН. 60, 689, 1956.
119.	Гаррисон Д., Лорд Р., Луфбуров Д. Практическая спектроскопия. ИЛ, 1950; Сойер Р.
Экспериментальная спектроскопия. ИЛ, 1953.
120.	Гуревич М. М. О спектральном распределении мощности излучения // УФН. 62, 159, 1969
(см. также: Сапожников В. А. // УФН. 70, 387, 1960).
121.	Зайдель А. Н., Прокофьев В. К, Райский С. М. Таблицы спектральных линий. Гостехиздат,
1952.
Литература
861
122.	Moore С. Atomic Energy Levels. Vol. 1 (IH-23V). 1949; Vol. II (24Cr-41Nb). 1952; Vol. Ill
(42Mo-57La, 72Hf-89Ac). 1958.
123.	Kayser H. Tabelle der Schwingungszahlen. 1925.
123a. Edlen B. The Dispersion of Standard Air // J. Opt. Soc. 43, 339, 1953.
д) Теоретическая физика, астрофизика и другие вопросы
124.	Cohen Е., Crawe К, du Mond J. The Fundamental Constants of Physics. 1957 (монография);
Cohen E., du Mond J. The Fundamental Constants of Atomic Physics // Handb. d. Phys. 35.
1957; Cohen E., du Mond J., Layton T., Rollet J. Analysis of Variance of the 1952 Data on the
Atomic Constants and a New Adjustment. 1955; Rev. Mod. Phys. 27, 363, 1955 (см. также:
Новые значения мировых постоянных // УФН. 65, 727, 1958; du Mond J. // Ann. of Phys.
7, 365, 1959).
125.	Компанеец А. С. Теоретическая физика. Гостехиздат, 1957.
126.	Голъдстейн Г. Классическая механика. Гостехиздат, 1957.
127.	Булгаков Б. В. Колебания. Гостехиздат, 1954.
128.	Ландау Л. Д., Лифшиц Е. М, Теория поля. 3-е изд. Физматгиз, 1960.
129.	Шпольский Э. В. Атомная физика. Гостехиздат. Т. 1, 1951 (4-е изд.); Т. 2, 1952 (3-е изд.).
130.	Блохинцев Д. И. Основы квантовой механики. 2-е изд. Гостехиздат, 1949.
131.	Ландау Л. Д., Лифшиц Е. М. Квантовая механика. Гостехиздат, 1948.
132.	Шифф Л. Квантовая механика. 2-е изд. ИЛ, 1959.
133.	Hund F. Allgemeine Quantenrftechanik des Atom und Molekulbaues // Handb. d. Phys. 24/1,
561, 1933; Quantenmechanik der Atome // Handb. d. Phys. 36. 1, 1966.
134.	Бете Г., Солпитер E. Квантовая механика атомов с одним и двумя электронами.
Физматгиз, 1960.
135.	Фок В. А. Начала квантовой механики. Кубуч, 1932.
136.	Зоммерфельд А. Строение атома и спектры. Т. 2. Гостехиздат, 1956.
136а. Хартри Д. Расчет атомных структур. ИЛ, 1960.
1366. Гомбаш П. Проблема многих тел в квантовой механике (теория и методы решения).
2-е изд. ИЛ, 1959.
137.	Любарский Г. С. Теория групп и ее применение в физике. Физматгиз, 1958.
138.	Wigner Е. Gruppentheorie und ihre Anwendungen auf die Quantenmechanik und Atomspektren.
1931.
139.	Багавантам С., Венкатарайуду T. Теория групп и ее применения к физическим пробле-
мам. ИЛ, 1959.
140.	Гайтлер В. Квантовая теория излучения. ИЛ, 1956.
141.	Роуз М. Теория мультиполей. ИЛ, 1955.
142.	Паули В. Релятивистская теория элементарных частиц. ИЛ, 1947.
143.	Грошев Л. В., Шапиро И. С. Спектроскопия атомных ядер. Гостехиздат, 1952.
143а. Бета- и гамма-спектроскопия / Под ред. К. Зигбана. Физматгиз, 1959.
144.	Месси Г., Бархоп Е. Электронные и ионные столкновения. ИЛ, 1958.
145.	Вонсовский С. В. Современное учение о магнетизме. Гостехиздат, 1952.
146.	Дорфман Я. Г. Магнитные свойства и строение вещества. Гостехиздат, 1955.
147.	van Vleck J. The Theory of Electric and Magnetic Susceptibilities. 1932.
148.	Шубников А., Флинт E., Бокий Г. Основы кристаллографии. Изд-во АН СССР, 1940.
149.	Соболев В. В. Перенос лучистой энергии в атмосферах звезд и планет. Гостехиздат, 1956;
Чандрасекар С. Перенос лучистой энергии. ИЛ, 1953; Мустель Э. Р. Звездные атмосферы.
Физматгиз, 1960.
149а. Франк-Каменецкий Д. А. Физические процессы внутри звезд. Физматгиз, 1959.
150.	Milne Е. Thermodynamics of Stars // Handb. d. Astrophys. 3/1. 1930.
862
Приложения
151.	Амбарцумян В. А., Мустель Э. Р, Северный А. Б., Соболев В. В. Теоретическая астрофизика.
Гостехиздат, 1952.
152.	Унзольд А. Физика звездных атмосфер. ИЛ, 1949 (имеется новое немецкое издание:
Unsold A. Physik der Stemenatmospharen. Zweite Auflage, 1955).
153.	Шкловский И. С. Космическое радиоизлучение. Гостехиздат, 1956.
154.	Шкловский И. С. Солнечная корона. Гостехиздат, 1961.
155.	Митра С. Верхняя атмосфера. ИЛ, 1955.
155а. Кондратьев К. Я. Лучистая энергия Солнца. Гидрометеоиздат, 1954; Кондратьев К. Я.,
Филипович О. П. Тепловой режим верхних слоев атмосферы. Гидрометеоиздат, 1960.
2.	ОРИГИНАЛЬНЫЕ РАБОТЫ
а) Работы, характеризующие развитие спектроскопии
до создания квантовой механики (в хронологическом порядке)
156.	Wollaston W. Phil. Trans. Roy. Soc. II, 265, 1802 (обнаружение темных линий в спектре
Солнца).
157.	Frauenhofer J. Gilberts Ann. 56, 264, 1817 (подробное изучение темных линий в спектре
Солнца).
158.	Stokes G. Phil. Trans. Roy. Soc. 143, 463, 1852 (смещение спектра испускания по отношению
к спектру поглощения).
159.	Kirchhoff G. Monatsber. Akad. d. Wiss. 662, 783, 1859; Pogg. Ann. 109, 148, 275, 1860 (связь
испускательной и поглощательной способности тел).
160.	Bunsen R., Kirchhoff G. Pogg. Ann. 110, 160, 1860; 113, 337, 1861 (открытие спектрального
анализа).
161.	Balmer J. Ann. d. Phys, und Chemie. 25, 80, 1885 (закономерности в спектре водорода).
162.	Deslandres Н. С. R. 103, 375, 1886 (сериальные закономерности в полосатых спектрах).
163.	Wiedeman Е. Wied. Ann. 34, 446, 1888; 37, 117, 1889 (определение люминесценции).
164.	Rydberg R. С. R. 110, 394, 1890; Wied. Ann. 50, 625, 1893; Astrophys. J. 4, 91, 1896
(сериальные закономерности в спектрах щелочных металлов).
165.	Kayser Н., Runge С. Wied. Ann. 41, 302, 1890; 43, 385, 1891; 46, 225, 1892; 48, 126, 1893;
Runge С, Paschen F. Berl. Ber. 139. 1895; Astrophys. J. 3, 4, 1895; Wied. Ann. 61, 641, 1897
(сериальные формулы).
166.	Larmor J. Phil. Mag. 44, 503, 1897 (прецессия электронных орбит в магнитном поле).
167.	Zeeman Р. Phil. Mag. 5, 43, 226, 1897 (открытие расщепления спектральных линий
в магнитном поле).
168.	Pickering Е. Astrophys. J. 4, 369, 1896; 5, 94, 1897 (серия ионизованного гелия).
169.	Wood R. Phil. Mag. 10, 513, 1905 (резонансное испускание паров натрия).
170.	Ritz W. Phys. Zs. 9, 521, 1908; Gesammelte Werke. 1911 (сериальные закономерности
в спектрах атомов, комбинационный принцип).
171.	Рождественский Д. С. ЖРФХО. 42, 87, 1910; Работы по аномальной дисперсии в парах
металлов. Изд-во АН СССР, 1955 (аномальная дисперсия в парах натрия и других
металлов).
172.	Кравец Т. П. Абсорбция света в растворах окрашенных веществ. Диссертация. Изд-во
Имп. Московского инженерного училища. Ч. 2, вып. 6, 1912; Труды по физике. Изд-во
АН СССР, 1959 (связь силы осциллятора и коэффициента поглощения для полос
поглощения).
173.	Fowler A. Monthly Notices. 73. 1912 (серия ионизованного гелия).
174.	Paschen Е, Back Е. Ann. d. Phys. 39, 897, 1912; 40, 960, 1913 (расщепление спектральных
линий в сильных магнитных полях).
175.	Bohr N. Phil. Mag. 26, 1, 476, 857, 1913 (теория атома и атомных спектров).
Литература
863
176.	Moseley Н. Phil. Mag. 26, 1024, 1913; 27, 703, 1914 (закономерности в рентгеновских
спектрах и их истолкование).
177.	Frank J., Hertz Н. Verh. d. Deutsch. Phys. Ges. 15, 34, 373, 613, 929, 1914; 16, 12, 457, 512,
1914; 18, 213, 1916 (возбуждение атомов электронным ударом).
178.	Sommerfeld A. Ann. d. Phys. 51, 1, 1916 (эллиптические орбиты электронов в атоме
и истолкование атомных спектров).
179.	Stark J. Sitzungsber. Beri. Akad. d. Wiss. 40, 932 1913; Ann. d. Phys. 43, 965, 983, 1914
(открытие расщепления спектральных линий в электрическом поле).
180.	Schwarzschild К. Sitzungsber. Beri. Akad. d. Wiss. 548, 1916 (теория явления Штарка;
истолкование молекулярных спектров).
181.	Epstein Р. Ann. d. Phys. 50, 489, 1916; Phys. Zs. 17, 148, 1916 (теория явления Штарка).
182.	Einstein A. Mitt. Phys. Ges. Zurich. 18. 1916; Phys. Zs. 18, 121, 1917 (квантовое рассмотрение
равновесия излучения с веществом).
183.	Holtsmark J. Phys. Zs. 20, 162, 1919; 25, 73, 1924; Debye P. Phys. Zs. 20, 160, 1919
(штарковское уширение спектральных линий при столкновениях).
184.	Рождественский Д.С. Спектральный анализ и строение атомов // Труды ГОИ. Т. 1,
вып. 6, 1920 (закономерности в атомных спектрах).
185.	Бор Н. Три статьи о спектрах и строении атомов. Госиздат, 1923 / Пер. с нем. изд. 1922 г.
(спектры атомов; теория периодической системы элементов Менделеева).
186.	Klein О., Rosseland S. Zs. f. Phys. 4, 46, 1921 (удары второго рода).
187.	Cario G., Frank J. Zs. f. Phys. 11, 161, 1922 (сенсибилизированная флуоресценция).
188.	Kratzer A. Ann. d. Phys. 67, 127, 1923; Zs. f. Phys. 3, 289, 1920; 16, 353, 1923; 23, 198, 1924
(теория молекулярных спектров).
189.	Pauli И< Naturwiss. 12, 741, 1924 (моменты ядер как причина сверхтонкой структуры).
190.	Goudsmit S., Uhlenbeck G. Naturwiss. 13, 953, 1925; Nature. 117, 264, 1924 (открытие спина
электрона).
191.	Pauli Ж Zs. f. Phys. 31, 765, 1925 (принцип запрета).
192.	Russel H., Saunders F. Astrophys. J. 61, 98, 1925 (схема нормальной связи для сложных
спектров).
193.	Frank J. Trans. Far. Soc. 21, 536, 1925 (фотодиссоциация молекул; неизменность расстоя-
нии между ядрами и их скоростей при электронных переходах).
194.	Теренин А. Н. Zs. f, Phys. 31, 26, 1925; 37, 98, 1926 (оптическое возбуждение паров
металлов).
195.	Raman И Nature. 121, 501, 619, 711, 1928 (открытие комбинационного рассеяния света
в жидкостях.
196.	Мандельштам Л. И., Ландсберг Г. С. ЖРФХО. 60, 335, 1928; Naturwiss. 16, 557, 1928; С. R.
189, 109, 1928 (открытие комбинационного рассеяния света в кристаллах).
197.	Добрецов Л.Н., Теренин А. И. Naturwiss. 16, 656, 1928 (сверхтонкая структура D-линий
натрия).
198.	Филиппов А. Н. Zs. f. Phys. 69, 526, 1931; Филиппов А. Н., Прокофьев В. К. Zs. f. Phys.
69, 526, 1931 (определение сил осцилляторов для атомов щелочных металлов методом
аномальной дисперсии).
199.	Birge R., Menzel D. Phys. Rev. 37, 1669, 1931 (возможность обнаружения тяжелого изотопа
водорода спектральным методом).
200.	Urey И., Brickwedde Е, Murphy G. Phys. Rev. 39, 164, 564, 1932; 40, 1, 1933 (открытие
тяжелого изотопа водорода спектральным методом).
б)	Теоретические работы по атомным спектрам и смежным вопросам
201.	Heienberg ИС, Jordan Р. Zs. f. Phys. 37, 263, 1926 (релятивистские поправки в уравнении
Шредингера).
202.	Bethe Н. Ann. d. Phys. 3, 133, 1929 (теория расщепления уровней атомов в поле кристал-
лической решетки).
864
Приложения
203.	Neumann J., Wigner E. Phys. Zs, 39, 467, 1929 (правило непересечения).
204.	Ландау JI. Zs. f. Phys. 64, 629, 1930 (диамагнетизм свободных электронов).
205.	Kramers Н. Proc. Akad. Sci. Amst. 33, 959, 1930 (двукратное вырождение в электрическом
поле при нечетном числе электронов).
206.	Wigner Е. Gott. Nachr. 546, 1932 (связь двукратного вырождения при нечетном числе
электронов с обратимостью времени).
207.	Hartree D. Proc. Cambr. Phil. Soc. 24, 189, 1928 (метод самосогласованного поля).
208.	Фок В. А. Труды ГОИ. Т. 5, вып. 51, 1931; Zs. f. Phys. 61, 126, 1930 (метод самосогласо-
ванного поля с обменом).
209.	Slater J. Phys. Rev. 34, 1293, 1930 (метод расчета многоэлектронных атомов).
209а. Pauling L. Proc. Roy. Soc. 114, 181, 1927 (водородоподобные волновые функции).
210.	Fermi Е. Zs. f. Phys. 59, 680, 1930 (теория относительных интенсивностей дублетов
в спектрах атомов щелочных металлов).
211.	Фок В. А. ЖЭТФ. 4, 5. 1934; 5, 891, 1935 (теория дублетного расщепления в спектрах
атомов щелочных металлов).
212.	Фок В. А. Изв. АН СССР, сер. физ. 2, 169, 1935 (четырехмерная симметрия для атома
водорода).
213.	Heisenberg W. Zs. f. Phys. 39, 499, 1927 (приближенный расчет атома гелия).
214.	Hylierass Е. Zs. f. Phys. 48, 469, 1928; 54, 347, 1929; 65, 209, 1930 (точный расчет атома
гелия по вариационному методу).
215.	Goudsmit S. Phys. Rev. 31, 946, 1928; Goudsmit S., Humphreys C. Phys. Rev. 31, 960, 1938
(теория факторов мультиплетного расщепления).
216.	Araki G. Progr. Theor. Phys. 3, 152, 262, 1948; Trees R. Phys. Rev. 82, 683, 1951 (теория
отступлений от правила интервалов).
217.	Петрашень М.И., Яноух А. И. Вестник ЛГУ. №2, 135, 1955 (уточненная теория относи-
тельных интенсивностей дублетов в спектрах атомов щелочных металлов).
218.	Racah G. Physica. 16, 651, 1950 (теория спектра Th III).
219.	Друкарев Г.Ф. ЖЭТФ. 25, 139, 1953; 31, 287, 1956 (теория столкновений медленных
электронов с атомами).
в) Работы по атомной спектроскопии и смежным вопросам
220.	Catalan М. Phil. Trans. Roy. Soc. Lond. 223, 127, 1922 (мультиплеты в спектре марганца).
221.	Russel Н. Phys. Rev. 29, 781, 1927; Gibbs R., Wilber D., White H. Phys. Rev. 29, 790,
1927; Shudemann G., Frankl J. Inst. 224, 501, 1937 (термы для конфигураций, состоящих
из эквивалентных электронов).
222.	Beutler Н. Zs. f. Phys. 86, 710, 1933; 87, 29, 1934; Beut/er H, Guggenheim К Zs. f. Phys. 87,
176, 1934 (возбуждение электронов внутренних оболочек).
223.	Humphreys С. J. Res. Nat. Bur. Stand. 50, 1, 1953 (шестая спектральная серия атома
водорода).
224.	Bowen I. Astrophys. J. 61, 1, 1928 (отождествление запрещенных линий в спектрах
туманностей).
225.	Grotrian W. Naturwiss. 27, 214, 1939 (отождествление линий железа в спектре солнечной
короны).
226.	Edlen В. Zs. f. Astrophys. 22, 47, 1942 (отождествление основных линий солнечной
короны).
227.	King A. Astrophys. J, 56, 318, 1922 (исследования спектров атомов при возбуждении
в высокотемпературной электрической печи).
228.	King A. Astrophys. J. 87, 24, 1938 (интенсивности в спектре железа).
229.	Hartmann Н. Zs. f. Phys. Chem. 4, 376, 1955; Orgel L., Chem J. Phys. 23, 1004, 1819,
1824, 1955 (расщепление уровней ионов переходных элементов в полях, обладающих
кристаллической симметрией).
Литература
865
230.	Broer L., GorterC., Hoogschagen J. Physica. 11, 231, 1945 (вероятности переходов для ионов
в кристаллах и растворах).
231.	Russel Н. Astrophys. J. 96, 11, 1942; J. Opt. Soc. 40, 550, 1950 (интерпретация спектра
гадолиния).
232.	van Week J. Phys. Rev. 74, 1168, 1948 (резонансное сужение спектральных линий).
233.	Собелъман И. И., Вайнштейн Л. А. ДАН СССР. 90, 757, 1953 (учет неоднородности поля
при штарковском расширении спектральных линий).
234.	Собелъман И. И. ДАН СССР. 87, 653, 1953; Изв. АН СССР, сер. физ. 17, 554, 1953 (теория
некоторых эффектов уширения спектральных линии).
235.	Милианчук В. С. ДАН СССР. 59, 671, 1948; 67, 1001, 1949; 68, 41, 1949; Материалы
X Всесоюзного совещ. по спектроскопии. Т. 2, с. 5, 1958 (действие неоднородного
электрического поля на атомные спектры).
г) Работы по явлению Зеемана, магнитному резонансу,
сверхтонкой структуре и смежным вопросам
236.	Omstein L., Burger Н. Zs. f. Phys. 28 135, 1924; 29, 241, 1924; KronigR., Goudsmit S. Naturwiss.
13, 90, 1925; Zs. f. Phys. 31, 885, 1925; Honl H. Zs. f. Phys. 31, 340, 1925 (интенсивности
составляющих в явлении Зеемана).
237.	Pauli ИС Zs. f. Phys. 16, 155, 1923 (правило сумм для множителей g).
238.	Shenstone A., Blair Н Phil. Mag. 8, 765, 1925; Герасимов Ф. М. ЖЭТФ. 9, 1036, 1939 (анализ
неполностью разрешенной картины расщепления в явлении Зеемана).
239.	Капица П.Л., Стрелков П. Г, Лаурман Э. Я. ЖЭТФ. 8, 276, 1938 (явление Зеемана
в сверхсильных полях).
240.	Harrison G., Bitter F. Phys. Rev. 57, 15, 1940 (явление Зеемана в очень сильных магнитных
полях).
241.	Ландау Л.Д., Лифшиц Е. М. Phys. Zs. d. Sow. 8, 153, 1935 (теория ферромагнитного
резонанса).
242.	Лазарев Б. Г, Шубников Л. В. Phys. Zs. d. Sow. 11, 445, 1937 (открытие ядерного
парамагнетизма).
243.	Rabi L, Zacharias L., Milman S., Kusch P. Phys. Rev. 53, 318, 1938; 55, 526, 1939; Rabi
Zacharias J., Milman S., Kellog J. Phys. Rev. 55, 728, 1939; 56, 728, 1939 (магнитный
резонанс в молекулярных пучках).
244.	Kusch Р, Milman S., Rabi I. Phys. Rev. 57, 765, 1940 (магнитный резонанс в атомных
пучках).
245.	Завойский Е. К. J. Phys. USSR. 9, 245, 1945; 10, 170, 1946 (открытие парамагнитного
резонанса).
246.	Purcell Е, Torrey Н., Pound R. Phys. Rev. 69, 37, 1946; Bloch F. Phys. Rev. 69, 127, 1946; 70,
460, 474, 1946 (открытие ядерного магнитного резонанса).
247.	Townes С. Phys. Rev. 70, 109, 665, 1946; Bleaney В., Penrose R. Proc. Phys. Soc. Lond.
60, 83, 1948; Carplus R. Phys. Rev. 73, 1120, 1948; 74, 223, 1948 (явление насыщения
в радиочастотной области спектра).
248.	Lamb ИС, Retherfbrd R., Triebwasser S., Dayhoff Е. Phys. Rev. 79, 549, 1950. См. перевод:
УФН. 45, 553, 1951 (ч. I); 81, 222, 1953 (ч. II); 85, 259, 1952 (ч. Ill); 86, 1014, 1952 (ч.1У);
89, 98, 1953 (ч. V); 89, 106, 1953 (ч. VI) (сдвиг 5-уровня для атома водорода).
248а. Lauzer A. Phys. Rev. Lett. 4, 580, 1960 (расчет сдвига 5-уровня для атома водорода).
249.	Lamb ИС, Skinner М. Phys. Rev. 78, 539, 1950; Novick R.r Lipworth E., Yergin P. Phys.
Rev. 100, 1153, 1955; Lipworth E., Novick R. Phys. Rev. 108, 1434, 1957 (сдвиг 5-уровня
для ионизованного гелия).
250.	Series G., Kuhn H. Proc. Roy. Soc. 202, 127, 1956; 208, 277, 1951 (оптические измерения
тонкой структуры для атома водорода).
251.	Herzberg G. Zs. f. Phys. 146, 269, 1956 (оптические измерения тонкой структуры для Не И).
252.	Herzberg G. Proc. Roy. Soc. 234, 516, 1956 (сдвиг основного 5-уровня для дейтерия).
28 Зак. 103
866
Приложения
253.	Herzberg G. Proc. Roy. Soc. 248, 309, 1958 (сдвиг основного 5-уровня для гелия).
254.	KoenigS., Prodell A., Kusch Р. Phys. Rev. 83, 687, 1951; 88, 191, 1952 (измерение аномалии
магнитного момента электрона).
254а. Nierenberg Proc. Nat. Acad. Sci. 45, 429, 1959 (определение в атомных пучках основных
состояний радиоактивных атомов).
2546. Sommerfield С. Phys. Rev. 107, 328, 1957 (расчет аномалии магнитного момента электрона).
255. Brossel Е, Kasller А. С. R. 229, 1213, 1949; Brossel L., Sagalin R., Bitter F Phys. Rev. 79, 225,
1950 (метод двойного резонанса).
256.	Басов Н.Г., Прохоров А. М. ЖЭТФ. 27, 431, 1957; УФН. 57, 485, 1955 (молекулярный
генератор).
257.	Gordon J., Zeiger И, Townes С. Phys. Rev. 95, 285, 1954; 99, 1264, 1955 (молекулярный
генератор).
258.	Bloemberger N. Phys. Rev. 104. 324, 1956; Weber J. Rev. Mod. Phys. 31, 681, 1959 (парамаг-
нитное усиление в микроволновой области).
258а. Maiman Т Phys. Rev. Lett. 4, 564, 1960; Nature. 187, 493, 1960; Electr. 33, 43, 1960;
см. также Хазов Л.Д. Опт. мех. пром. № 1, 48, 1961.
259.	Dyson F. Phys. Rev. 98, 349, 1955 (электронное спиновое резонансное поглощение
в металлах).
260.	Дорфман Я. Г. ДАН СССР. 81, 765, 1951 (циклотронный резонанс электронов проводи-
мости).
261.	Dresselhaus G., Kip A., Kittel С. Phys. Rev. 98, 368, 1955 (циклотронный резонанс для полу-
проводников).
262.	Buckmaster Н., Scovil Н. Can. J. of Phys. 34, 711, 1956 (установка высокой чувствительности
для исследования парамагнитного резонанса).
263.	Скрипов Ф. И. ДАН СССР. 121, 998, 1958 (ядерный резонанс в магнитном поле Земли).
263а. Wilking S. Zs. f. Phys. 157, 384, 1959 (ядерный магнитный резонанс при очень малых
частотах).
264.	Rabi /., Ramsey N., Schwinger J. Rev. Mod. Phys. 26, 167, 1954 (вращающаяся координатная
система при решении задач о магнитном резонансе).
265.	Casimir Н. On the Interaction between Atomic Nuclei and Electrons. 1936 (теория взаимо-
действия ядерных моментов с электронными оболочками).
266.	Thomas Н, Driscoll R., Hippie J. Phys. Rev. 75, 902, 1949; 78, 787, 1949; J. Res. Nat. Bur.
Stand. 44, 569, 1950; Thomas H. Phys. Rev. 80, 901, 1950 (измерение магнитного момента
протона методом ядерного магнитного резонанса).
267.	Hippie J., Sommer Н, Thomas Н Phys. Rev. 76, 1877, 1949; 80, 487, 1950; 82, 697, 1951;
Bloch F., Jeffries C. Phys. Rev. 80, 305, 1940; 81, 1040, 1951 (измерение магнитного момента
протона в ядерных магнетонах).
268.	Gardner J., Purcell Е. Phys. Rev. 76, 1262, 1949; Gardner J. Phys. Rev. 83, 996, 1951; Franken P,
Liebes S. Phys. Rev. 104, 1197, 1956 (и шерение магнитного момента протона в магнетонах
Бора).
268а. Schupp A., Pidd R., Crane Н. Phys. Rev. 121, 1, 1961 (измерение для свободного электрона
аномалии магнитного момента).
269.	Alvarez L., Bloch F. Phys. Rev. 57, 111, 352, 1940 (определение магнитного момента
нейтрона резонансным методом).
270.	Bray Р, Barnes R., Harrik N., Ramsey N. Phys. Rev. 87, 220, 1952; Kolsky H, Phipps T,
Ramsey N., Silsbey H Phys. Rev. 87, 395, 1952 (определение магнитного момента дейтрона
по методу магнитного резонанса в пучках).
271.	Garwin К, Hutchinson D., Penman 5., Shapiro J. Phys. Rev. Lett. 2, 213, 1959 (определение
магнитного момента (р-мезона резонансным методом).
272.	Prodell A., Kusch Р. Phys. Rev. 79, 1009, 1950; 88, 184, 1952; Kusch Р. Phys. Rev. 100,
1188, 1955 (измерение сверхтонкой структуры для атомов водорода и дейтерия по методу
магнитного резонанса в атомных пучках).
273.	Heberle J., Reich И, Kusch Р Phys. Rev. 98, 1194, 1955 (сверхтонкое расщепление
метастабильного уровня атома водорода).
Литература
867
274.	Kellog J., Rabi L, Ramsey N., Zacharias J. Phys. Rev. 57, 677, 1940; Harrik N., Barnes R.,
Bray P., Ramsey N. Phys. Rev. 90, 260, 1953 (определение квадрупольного взаимодействия
и квадрупольного момента дейтрона).
275.	Schwarz С. Phys. Rev. 97, 380, 1955; 105, 173, 1967 (теория сверхтонкой структуры).
276.	Brix Р., Kopfermann Н. Cott. Nachr. 31. 1947; Zs. f. Phys. 126, 344, 1949 (объяснение
аномально больших квадрупольных моментов деформацией ядер).
277.	Goppert-Mayer М. Phys. Rev. 75, 1959, 1949 (модель ядра с сильной спин-орбитальной
связью).
278.	Haxel О., Jensen Н., Suess Н. Phys. Rev. 75, 1766, 1949; Zs. f. Phys. 128, 295, 1950 (модель
ядра с сильной спин-орбитальной связью).
279.	Bohr A., Mollelson В. Dan. Mat. Fys. Medd. 26, № 16, 1952 (обобщенная модель ядра).
д) Работы по вращательным и колебательным спектрам молекул
280.	Вот М., Oppenheimer R. Ann. d. Phys. 84, 457, 1927 (разделение энергии молекулы
на электронную, колебательную и вращательную как результат приближенного решения
квантовомеханической задачи).
281.	Eckart С. Phys. Rev. 47, 552, 1985 (отделение колебательного движения от вращательного).
282.	Ельяшевич М.А. Труды ГОИ. Т. 12, вып. 106, 1938 (вращательно-колебательная энергия
многоатомных молекул).
283.	Зайцев Г. А. Оптика и спектроскопия. 1, 729, 1956; 4, 309, 1958 (отделение колебательного
движения от вращательного для молекул с внутренним вращением).
284.	Casimir Н. Rotation of a Rigid Body in Quantum Mechanics. 1931 (теория вращательных
уровней энергии молекул типа асимметричного волчка).
285.	King G., Cross Р, Hainer R. J. Chem. Phys. 11, 27, 1943; 17, 826, 1949 (уровни энергии
асимметричного волчка).
286.	Cross Р., Hainer R., King G. J. Chem. Phys. 12, 210, 1944; King G. J. Chem. Phys. 15, 280,
1947 (интенсивность вращательных линий молекул типа асимметричного волчка).
287.	Slawsky Z., Dennison D. J. Chem. Phys. 7, 509, 522, 1939 (учет центробежного растяжения).
288.	Golden S., Witson E. J. Chem. Phys. 16, 669, 1948 (явление Штарка для молекулы типа
асимметричного волчка).
289.	Muzischima М., Venkateswarlu Р. J. Chem. Phys. 21, 705, 1953; Phys. Rev. 89, 896, 1953
(возможность наблюдения вращательных спектров для недипольных молекул).
290.	Stoicheff В. Can. J. Phys. 32, 330, 339, 1954; 33, 81, 1955; Langeth A., Stoicheff В. Сап.
J. Phys. 34, 350, 1956; Callomen J., Stoicheff В. Can. J. Phys. 35, 373, 1957; Suryanarayana
Rao K, Stoicheff B., Turner R. Can. J. Phys. 38, 1516, 1960 (чисто вращательные спектры
комбинационного рассеяния).
291.	Randall Н, Dennison D., Ginsburg N., Weber P. Phys. Rev. 52, 160, 1937; Fuson H., Randali H.,
Dennison D. Phys. Rev. 56, 982, 1939; Me. Cabbin T., Sinton W. J. Opt Soc. Am. 42, 113, 1952;
Genzel L., Eckhardt W. Zs. f. Phys. 139, 578. 592, 1954; Genzet L. Zs. f. Phys. 144, 311, 1956
(чисто вращательные спектры поглощения воды в далекой инфракрасной области).
292.	Dennison D. Proc. Roy. Soc. 115, 483, 1927 (теория орто- и пара-водорода).
293.	Bonhoefer К, Harteck Р. Zs. f. Phys. Chem. 4, 113, 1929 (опыт с модификациями водорода
при низких температурах).
294.	Morse Р Phys. Rev. 34, 57, 1929 (формула для кривой потенциальной энергии двухатомных
молекул).
295.	PoschlG., Teller Е. Zs. f. Phys. 83, 143, 1933 (свойства кривых потенциальной энергии).
296.	Rydberg R. Zs. f. Phys. 73, 376, 1932; 80, 564, 1933; Klein О. Zs. f. Phys. 76, 226, 1932 (метод
построения кривых потенциальной энергии по экспериментальным данным).
297.	Ельяшевич М.А., Кричагина А. Р. Изв. АН СССР, сер. физ. 4, 69, 1940 (построение кривых
потенциальной энергии по методу Ридберга—Клейна).
298.	Yatendra Pot Verschi. Rev. Mod. Phys. 29, 664, 1957 (сравнение различных кривых потен-
циальной энергии для двухатомных молекул).
868
Приложения
299.	Фок В. А. Таблица функций Эйри. 1946 (таблицы, применимые для построения колеба-
тельных функций для непрерывных состояний).
300.	Грибковский В. П., Апанасевич П.А., Степанов Б. И. Труды Ин-та физ. и матем. АН
БССР. Вып. 3, 131, 1959 (соответствие результатов классической и квантовой теорий
для гармонического осциллятора).
301.	BJerrum N. Nemstfestschrift. 60, 1912 (колебательно-вращательные полосы в инфракрасной
области в виде дублетов).
302.	Cleeton С., Williams N. Phys. Rev. 45, 234, 1934 (микроволновое поглощение молекулы
аммиака, обусловленное инверсионным расщеплением).
303.	Dennison D., Uhlenbeck G. Phys. Rev. 41, 313, 1932 (формула для инверсионного расщеп-
ления).
304.	Burkhard Р., Dennison D. Phys. Rev. 84, 408, 1951; Ivash E., Dennison D. J. Chem. Phys. 21,
1804, 1953; Phys. Rev. 91, 222, 1953 (переходы в микроволновой области, обусловленные
расщеплением уровней для крутильных колебаний).
305.	Ельяшевич М.А. ДАН СССР. 28, 605, 1940; ЖФХ. 14, 1381, 1940 (общий метод составления
вековых уравнений для расчета колебаний многоатомных молекул).
306.	Маянц Л. С. Труды Физ. ин-та АН СССР. 5, 63, 1950 (теория характеристических частот
колебаний молекул).
307.	Ельяшевич М.А., Степанов Б. И. ЖФХ. 17, 145, 1943 (метод последовательной диагона-
лизации при решении вековых уравнений).
308.	Гопштейн Н. М. ДАН СССР. 43, 372, 1944 (метод итерации при решении вековых
уравнений).
309.	Маянц Л.С. ДАН СССР. 48, 334, 1945; 50, 121, 1946 (усовершенствованные методы
итерации при решении вековых уравнений).
310.	Степанов Б. И. ЖФХ. 15, 865, 1941 (расчет колебаний молекул метана и этана).
311.	Hemptinne М., MannenbackG. Proc. Ind. Acad. Sci. 9, 286, 1939 (метод спектроскопических
масс для приближенного учета ангармоничности колебаний).
312.	Ковнер М.А. ЖЭТФ. 26, 598, 1954; 26, 704, 1954; Оптика и спектроскопия. 1, 348,
742, 1956; Ковнер М.А., Богомолов А. М. Оптика и спектроскопия. 1, 364, 1956 (расчет
колебаний бензола и его производных).
313.	Сущинский М. М. Изв. АН СССР, сер. физ. 17, 608, 1958 (характеристические структурные
элементы при изучении колебательных спектров).
314.	Подловченко Р. И., Сущинская М. М. Оптика и спектроскопия. 2, 49, 1957 (расчет колеба-
ний молекул с помощью электронных вычислительных машин).
315.	Tisza L. Zs. f. Phys. 82, 48, 1933 (правила отбора для колебательных обертонов и составных
частот).
316.	Компанеец А. С. ЖЭТФ. 10, 1175, 1940 (симметрия колебательных обертонов).
317.	Fermi Е. Zs. f. Phys. 71. 250, 1931 (резонанс при наличии случайного вырождения
колебательных уровней энергии).
318.	Dennison D. Rev. Mod. Phys. 3, 280, 1931 (ч. I); 12, 175, 1940 (ч. II) (инфракрасные спектры
простейших многоатомных молекул).
319.	Mecke R., Baumann W., Freudenberg К. Zs. f. Phys. 81, 313, 445, 1933 (интерпретация
вращательной структуры колебательных полос поглощения молекулы воды).
320.	Хачкурузов Г. А. Труды ГИПХ. Вып. 42, 51, 1959; Оптика и спектроскопия. 6, 463, 1959
(уточненный расчет положений колебательных полос молекулы воды).
321.	Волькенштейн М.В., Ельяшевич М.А. Изв. АН СССР, сер. физ. 12, 548, 1948 (теорети-
ческое обоснование формулы Плачека для колебательных спектров комбинационного
рассеяния).
322.	Волькенштейн М.В., Ельяшевич М.А. ДАН СССР. 43, 56, 1944 (расчет интенсивностей
в колебательных спектрах галоидометанов).
323.	Волькенштейн М. В. ЖФХ. 17, 62, 1943 (изменения интенсивности комбинационного
рассеяния в различных молекулах).
Литература
869
324.	Ferigle 5., Weber A. Can. J. Phys. 32, 799, 1954; Malhiot R., Ferigle S. J. Chem. Phys. 22, 717,
1954; Long D.A. Proc. Roy. Soc. 217, 203, 1953 (теория интенсивностей в колебательных
спектрах).
325.	Грибов Л. А. Оптика и спектроскопия. 8, 769, 1960; 9, 658, 1960 (теория интенсивностей
в колебательных спектрах),
е) Работы по электронным спектрам молекул,
химической связи и смежным вопросам
326.	Wigner Е., Witmer Е. Zs. f. Phys. 51, 859, 1928 (корреляция атомных и молекулярных
состояний).
327.	Heiller W., London F. Zs. f. Phys. 44, 455, 1927 (приближенная теория химической связи
в молекуле водорода).
328.	Condon Е. Phys. Rev. 32, 858, 1928 (квантовомеханическое обоснование неизменности
расстояний и скоростей ядер при электронных переходах).
329.	Hund Е Zs. f. Phys. 36, 657, 1926 (различные случаи связи моментов в двухатомных
молекулах).
330.	Hill Е., van Week J. Phys. Rev. 32, 250, 1928 (переход от случая а к случаю б).
331.	Кондратьев В.Н., Лейпу некий А. И. Trans. Far. Soc. 25, 736, 1929 (наблюдение сплошного
спектра, обусловленного рекомбинацией атомов).
332.	Gibson G., Rice О., Bayliss N. Phys. Rev. 44, 183, 1933 (расчет сплошного спектра при дис-
социации молекулы хлора).
333.	Овечкин Г. В. Материалы X Всесоюзн. совещ. по спектроскопии. Т. 1, с. 365. Изд-во
Львовского гос. ун-та, 1957; Уч. зап. БГУ. Вып. 32, 219, 1957; Вып. 41, 105, 1958
(изучение конденсированного разряда через капилляр).
334.	Подмошенский И. В., Огурцова Н. Н. Оптика и спектроскопия 4, 439, 1958 (изучение
конденсированного разряда через отверстие в текстолите).
335.	Kronig R. Zs. f. Phys. 50, 347, 1928 (правила отбора для возмущении в молекулярных
спектрах).
336.	Степанов Б. И. J. Phys. USSR. 2, 81, 89, 197, 205, 317, 381, 1940; 4, 411, 1941 (возмущения
в спектрах двухатомных молекул).
337.	Rice О. Phys. Rev. 33, 748, 1929; 35, 1551, 1930; J. Chem. Phys. 1, 375, 1933 (теория
предиссоциации).
338.	Степанов Б. И. ЖЭТФ. 15, 435, 1945 (теория предиссоциации для системы дискретных
уровней).
339.	Ельяшевич М.А., Степанов Б. И. Труды ГОИ. Т. 12, вып. 105, с. 20, 1937 (различные случаи
предиссоциации).
340.	Hulten Е. Zs. f. Phys. 32, 32, 1925 (предиссоциация вращением для гидрида ртути).
341.	Hendrie J. J. Chem. Phys. 22, 1503, 1954 (исследование термической диссоциации молекул
азота).
342.	Jenkins F. J. Opt. Soc. 43, 425, 1953 (обозначения для спектров двухатомных молекул).
343.	Mullikan R. J. Chem. Phys. 23, 1997, 1955 (обозначения для спектров многоатомных
молекул).
344.	Jahn Н, Teller Е. Proc. Roy. Soc. 161, 220, 1937 (неустойчивость вырожденных электронных
состояний многоатомных молекул).
345.	Jahn Н Proc, Roy. Soc. 164, 117, 1938 (учет спина при рассмотрении устойчивости
электронных состояний многоатомных молекул).
346.	Opik U., Pryce М. Proc. Roy. Soc. 238, 425, 1957; Longuet-Higgins H., Opik U., Pryce M. Proc.
Roy. Soc. 224, 1, 1958 (исследования по эффекту Яна—Теллера).
347.	Pauling L. J. Am. Chem. Soc. 53, 1367, 1931 (теория направленной валентности).
348.	Pauling L., Schermann J. J. Am. Chem. Soc. 59, 1450, 1937 (приближенный расчет энергии
связи соседних атомов).
870
Приложения
349.	Pauling L., Wheland G. J. Chem. Phys. 1, 362, 1933 (приближенный расчет энергии связи
в молекуле бензола).
350.	Sciar A. Rev. Mod. Phys. 14, 232, 1942 (теория спектра бензола и его производных).
351.	Platt J. J. Chem. Phys. 17, 484, 1949; 18, 1168, 1950 (приближенный расчет кольцевых
систем).
352.	Mofflt W. J. Chem. Phys. 22, 320, 1520, 1954 (усовершенствование метода приближенного
расчета кольцевых систем).
353.	Pariser R., Parr R. J. Chem. Phys. 21, 466, 767, 1953; Pariser R. J. Chem. Phys. 24, 250, 1956;
25, 112, 1956 (приближенные способы расчета молекул по методу молекулярных орбит).
354.	Longuet-Higgins Н. J. Chem. Phys. 18, 265, 1950; Dewar M., Longuet-Higgins H. Proc. Roy.
Soc. 214, 482, 1952; Ham N. J. Chem. Phys. 29, 355, 1958 (сравнение метода молекулярных
орбит и метода валентных связей).
355.	Ruedenberg К., Scherr С. J. Chem. Phys. 21, 1565, 1581, 1953 (приближенные расчеты
молекул на основе металлической модели).
356.	Ruedenberg К. J. Chem. Phys. 22, 1878, 1954; Ham N., Ruedenberg К. J. Chem. Phys. 29, 1199,
1958 (анализ методов металлической модели и метода молекулярных орбит).
357.	Hiickel Е. Zs. f. Phys. 60, 423, 1930; 70, 240, 1931 (электронные состояния многоатомных
молекул).
358.	Walsh A. J. Chem. Soc. 2260, 1953 (ч. I-Х) (молекулярные электронные орбиты, форма
простейших многоатомных молекул и их спектры).
359.	Herzberg G., Teller Е. Zs. f. Phys. Chem. 21, 410, 1933 (принцип Франка—Кондона
для многоатомных молекул).
359а. Duschinsky F. Acta phys. chim. USSR. 7, 551, 1937 (применение принципа Франка-
Кондона для многоатомных молекул).
360.	Ельяшевич М.А. УФН. 71, 156, 1960 (взаимодействие электронного движения с колеба-
тельным в сложных молекулах).
361.	Frank J., Sponer Н, Teller Е. Zs. f. Phys. Chem. 18, 88, 1932 (предиссоциация для много-
атомных молекул).
362.	Wherli М. Helv. Phys. Acta. 11, 339, 1938; 13, 153, 1940 (электронные спектры молекул
хлорида, бромида, иодида ртути).
363.	Mrosowski S. Phys. Rev. 60, 730, 1941; 60, 270, 1942; Rev. Mod. Phys. 14, 216, 1942
(электронный спектр иона двуокиси углерода).
364.	Brand R. J. Chem. Phys. 19, 377, 1951 (флуоресценция молекулы формальдегида).
365.	Шпольский Э. В. УФН. 71, 215, 1960 (спектры испускания ароматических углеводородов
при низких температурах).
366.	Обреимов И. В., Прихотько А. Ф. Phys. Zs. d. Sow. 1, 203, 1932; 9, 34, 48, 1936; Обреимов И. В.,
Прихотько А.Ф., Шабалдас К. Г. ЖЭТФ. 6, 1082, 1936; Обреимов И. В., Шабалдас К. Г.
ЖЭТФ. 6, 1662, 1936; Прихотько А. Ф. Оптика и спектроскопия. 3, 434, 1957; Брауде В.Л.,
Прихотько А. Ф., Рашба Э. И. УФН. 67, 99, 1959 (спектры молекулярных кристаллов
органических соединений при низких температурах).
367.	Давыдов А. С. Труды Ин-та физ. АН УССР. Вып. 1, 1951 (теория поглощения света
в молекулярных кристаллах).
368.	Теренин А. Н. Acta phys. chim. USSR. 18, 210, 1943; ЖФХ. 18, 1, 1944; Изв. АН СССР,
сер. физ. 9, 305, 1945 (метастабильное триплетное состояние).
369.	Lewis G., Kasha М. J. Am. Chem. Soc. 66, 2100, 1944; Lewis A., Kalwin M. J. Am. Chem. Soc.
67, 1232, 1945 (метастабильное триплетное состояние).
370.	Вавилов С. И. Изв. АН СССР, сер. физ. 9, 277, 1945; Собр. соч. Т. II, ст. 20 (определение
люминесценции).
371.	Апанасевич П.А., Степанов Б. И. ДАН СССР. 116, 772, 1957; Апанасевич П.А. Оптика
и спектроскопия. 5, 97, 1958; Труды Ин-та физ. и матем. АН БССР. Вып. 3, 72, 1959
(классификация процессов рассеяния и люминесценции).
372.	Антонов-Романовский В. В., Степанов Б. И., Фок М. В., Хапалюк А. П. ДАН СССР. 105, 50,
1955 (отрицательная люминесценция).
Литература
871
373.	Степанов Б. И. Оптика и спектроскопия. 1, 225, 1956; 3, 3, 1957; Основы спектроскопии
отрицательных световых потоков. Изд-во БГУ, 1961 (общее теоретическое исследование
отрицательных процессов излучения).
374.	Толстой Н. А., Феофилов П. П. УФН. 41, 44, 1950 (тауметр для измерения времен
до 10-5-10-7 сек); Галанин М.Д. ДАН СССР. 40, 925, 1950; Бонч-Бруевич М.А. УФН. 58,
85, 1956 (флуорометр для измерения времен до 1О-8-1О-10 сек).
375.	Непорент Б. С. ЖФХ. 24, 1219, 1950 (классификация сложных молекул).
376.	Вавилов С. И. Phil. Mag. 43, 307, 1922; Собр. соч. Т. I, ст. 8 (универсальный контур полос).
376а. Ребане К. К., Пурга А. П., Силъд О. И., Хижняков В. В. Труды Ин-та физ. и астрон. АН Эст.
ССР. № 14, 31, 48, 1961 (теория контуров полос сложных молекул).
377.	Непорент Б.С. ЖФХ. 13, 965, 1939; 21, 4, 1947; ЖЭТФ. 21, 172, 1951; Труды ГОИ. Т.25,
вып. 150, 1957 (люминесценция сложных молекул).
378.	Левшин В. Л. Zs. f. Phys. 72, 368, 382, 1931; ЖФХ. 2, 641, 1931 (закон зеркальной
симметрии).
379.	Блохинцев Д. И. ЖЭТФ. 9, 459, 1939; J. of Phys. USSR. 1, 117, 1939 (квантовомеханическое
обоснование закона зеркальной симметрии).
380.	Степанов Б. И. ДАН СССР. 112, 839, 1957 (универсальное соотношение между поглоще-
нием и испусканием сложных молекул).
381.	Аленцев М. Н., Пахомычева А. А. Изв. АН СССР, сер. физ. 22, 1377, 1958 (проверка
универсального соотношения между поглощением и испусканием в спектрах молекул).
382.	Вавилов С. И. ЖЭТФ. 10, 1363, 1940; Собр. соч. Т. II, ст. 8 (поляризационные диаграммы).
383.	Феофилов П. П. ДАН СССР. 57, 343, 1947 (предельная поляризация люминесценции).
384.	Смирнов Л. В. ДАН СССР. 82, 237, 1952 (анизотропное поглощение молекул).
385.	Вавилов С. И. Изв. АН СССР, сер. физ. 9, 300, 1945; Собр. соч. Т.П. ст. 21 (фотолюми-
несценция растворов).
386.	Непорент Б. С., Борисевич Н.А. ДАН СССР. 94, 447, 1954; Оптика и спектроскопия. 1,
143, 536, 1956 (фотолюминесценция паров ароматических соединений).
387.	Perrin F. С. R. 180, 581, 1925; 182, 219, 1926; J. de Phys. 7, 390, 1926 (поляризация
фотолюминесценции растворов).
3. ДОПОЛНЕНИЯ К БИБЛИОГРАФИИ
После выхода настоящей книги М. А. Ельяшевича были опубликованы сотни моногра-
фий по теории атомных и молекулярных спектров. Нет никакой возможности привести
достаточно полный список их. Поэтому ограничиваемся лишь небольшим числом до-
статочно крупных работ, по своему содержанию охватывающих весьма широкий круг
вопросов и доступных русскоязычным читателям. Основное внимание уделено при этом
теории молекулярных спектров, где был достигнут наибольший прогресс.
388.	Степанов Б. И., Грибковский В. П. Введение в теорию люминесценции. Минск: Изд-во
Академии наук БССР, 1963. 443 с.
389.	Lev A. Gribov. Intensity Theory for Infrared Spectra of Polyatomic Molecules. Consultants
bureau. New York, 1964. 113 p.
390.	Слэтер Дж. Электронная структура молекул. М.: Мир, 1965. 586 с.
391.	Методы расчета оптических квантовых генераторов. Ред. Степанов Б. И. Т. 1. Минск:
Наука и техника, 1966. 483 с.
392.	Теренин А. Н. Фотоника молекулярных красителей и родственных органических соеди-
нений. Л.: Наука, 1967. 616 с.
393.	Typo Н. Молекулярная фотохимия М.: Мир, 1967. 328 с.
394.	Ребане К. К. Элементарная теория колебательной структуры спектров примесных центров
кристаллов. М.: Наука, 1968. 232 с.
872
Приложения
395.	Методы расчета оптических квантовых генераторов. Т. 2. Ред. Степанов Б. И. Минск:
Наука и техника, 1968. 466 с.
396.	Герцберг Г. Электронные спектры и строение многоатомных молекул. М.: Мир, 1969.
772 с.
397.	Каплан И. Г. Симметрия многоэлектронных систем. М.: Наука, 1969. 407 с.
398.	Сущинский М. М. Спектры комбинационного рассеяния молекул и кристаллов. М.: Нау-
ка, 1969. 576 с.
399.	Борн М., Вольф Э. Основы оптики. М.: Наука, 1970. 856 с.
400.	Свердлов Л. М., Ковнер М.А., Крайнов Е. П. Колебательные спектры многоатомных
молекул. М.: Наука, 1970. 559.
401.	Нурмухаметов Р. Н. Поглощение и люминесценция ароматических соединений. М.: Хи-
мия, 1971. 216 с.
402.	Сивин С. Колебания молекул и средне-квадратичные амплитуды. М.: Мир, 1971. 487 с.
403.	Волькенштейн М. В., Грибов Л. А., Ельяшевич М.А., Степанов Б. И. Колебания молекул.
Изд. 2. М.: Наука, 1972. 699 с.
404.	Мак-Вини Р., Сатклиф Б. Квантовая механика молекул. М.: Мир, 1972. 380 с.
405.	Мак-Глинн С., Адзуми Т., Киносита М. Молекулярная спектроскопия триплетного состо-
яния. М.: Мир, 1972. 448 с.
406.	Грибов Л. А. Введение в молекулярную спектроскопию. М.: Наука, 1976. 400 с.
407.	Введение в фотохимию органических соединений. Под ред. Г. О. Беккер. Л.: Химия, 1976.
378 с.
408.	Califano S. Vibrational States. London, New York: John Wiley & Sons, 1976, 333 p.
409.	Грибов Л. А. Теория инфракрасных спектров полимеров. М.: Наука, 1977. 240 с.
410.	Собельман И. И. Введение в теорию атомных спектров. М.: Наука, 1977. 320 с.
411.	Свиридов Д. Т., Смирнов Ю. Ф. Теория оптических спектров ионов переходных металлов.
М.: Наука, 1977. 328 с.
412.	Слэтер Дж. Методы самосогласованного поля для молекул и твердых тел. М.: Мир, 1978.
660 с.
413.	Макомбер Дж. В. Динамика спектроскопических переходов (пер. с англ, под ред.
М. А. Ельяшевича) М.: Мир, 1979. 347 с.
414.	Эляшберг М. Е., Грибов Л. А., Серов В. В. Молекулярный спектральный анализ и ЭВМ.
М.: Наука, 1980. 307 с.
415.	Степанов Б. И. Введение в современную оптику. Квантовая теория взаимодействия света
и вещества. Минск.: Наука и техника, 1980. 318 с.
416.	Полуэмпирические методы расчета электронной структуры. Ред. Дж. Сигал.
М.: Мир, 1980 Т. 1. 323 с., Т. 2. 368 с.
417.	Грибов Л. А., Дементьев В. А. Методы и алгоритмы вычислений в теории колебательных
спектров молекул. М.: Наука, 1981. 356 с.
418.	Колебательная спектроскопия. Современные тенденции. Ред. А. Барнс, У. Орвил-Томас.
М.: Мир, 1981. 479 с.
419.	Флайгер У. Строение и динамика молекул. М.: Мир, 1982. Т. 1, 2. 870 с.
420.	Person И< В., Zerbi G. Vibrational Intensities in Infrared and Raman Spectroscopy. Elsevier.
1982. 466 c.
421.	Спектроскопия комбинационного рассеяния света в газах и жидкостях. Под ред. А. Ве-
бера. М.: Мир, 1982. 373 с.
422.	Браун П. А., Киселев А. А. Введение в теорию молекулярных спектров. Л.: Из-во Лен ун-та,
1983. 232 с.
423.	Берсукер И. Б., Полингер В. 3. Вибронные взаимодействия в молекулах и кристаллах.
М.: Наука, 1983. 333 с.
424.	Грибов Л. А. Баранов В. И., Новосадов Б. К. Методы расчета электронно-колебательных
спектров многоатомных молекул. М.: Наука, 1984. 325 с.
425.	Лисица М. И., Яремко А. М. Резонанс Ферми. Киев: Наукова думка, 1984. 260 с.
Литература
873
426.	Майер Г. В., Данилова В. И. Квантовая химия, строение и фотоника молекул. Томск: Том-
ский ун-т., 1984. 218 с.
427.	Бенуэлл К. Основы молекулярной спектроскопии. М.: Мир, 1985. 384 с.
428.	Соловьев К. И, Гладков Л. Л., Старухин А. С., Шкирман С. Ф. Спектроскопия порфиринов:
колебательные состояния. Минск: Наука и техника, 1985. 425 с.
429.	Steinfeld J. I. Molecules and Radiation: An Introduction to Modern Molecular Spectroscopy.
Mit Pr, 1985. 388 p.
430.	Берсукер И. Б. Электронное строение и свойства координационных соединений. Л.: Хи-
мия, 1986. 281 с.
431.	Берсукер И. Б. Эффект Яна-Теллера и вибронные взаимодействия в современной химии.
М.: Наука, 1987. 344 с.
432.	Летохов В. С., Матвиц Ю.А., Шарков А. В. и др. Лазерная пикосекундная спектроскопия
и фотохимия биомолекул. М. Наука, 1987. 252 с.
433.	Gribov L.A., Orville-Thomas W.J. Theory and Methods of Calculation of Molecular Spectra.
Chichester, New York: John Wiley & Sons, 1988. 636 p.
434.	Степанов Б. И. Введение в современную оптику: Основные представления оптической
науки на пороге XX века. Минск: Наука и техника, 1989. 359 с.
435.	Struve И< S. Fundamentals of Molecular Spectroscopy. John Wiley & Sons, 1989. 379 p.
436.	Herzberg G. The Spectra and Structures of Simple Free Radicals: Introduction to Molecular
Spectroscopy. Dover Pubns. 1989. 226 p.
437.	Летохов B.C., Рябов E.A., Макаров А. А. и др. Лазерная спектроскопия колебательно-
возбужденных молекул. М.: Наука, 1990. 278 с.
438.	Шувалов В. А. Первичное преобразование световой энергии при фотосинтезе. М.: Нау-
ка, 1990. 208 с.
439.	Степанов Б. И. Введение в современную оптику. Поглощение и испускание света кван-
товыми системами. Минск: Наука и техника, 1991. 480 с.
440.	Kroto Н. W. Molecular Rotation Spectra. Dover Pubns, 1992. 311 p.
441.	Шигорин Д. H., Валькова Г. А., Гастилович E. А. и др. Электронно-возбужденные состояния
многоатомных молекул и процессы их дезактивации. М.: Наука, 1993. 496 с.
442.	Harter W.G. Principles of Symmetry, Dynamics, and Spectroscopy. John Wiley & Sons, 1993.
880 p.
443.	Computing Application in Molecular Spectroscopy / Ed. by George W. O. London: The Royal
Soc. of Chemistry, 1995. 248 p.
444.	Dynamics During Spectroscopic Transitions / Ed. by Lippert E., Macomber J. D. Berlin:
Springer, 1995. 680 p.
445.	High Resolution Laser Photonization and Photoelectron Studies / Ed. by Powis L, Baer T.
Nd C.-Y: Wiley, 1995. 509 p.
446.	Galabov B. 5., T. Dudev. Vibrational Intensities. Elsevier, 1996. 316 p.
447.	Грибов Л.А., Баранов В. И., Зеленцов Д. Ю. Электронно-колебательные спектры много-
атомных молекул. Теория и методы расчета. М.: Наука, 1997. 475 с.
448.	Грибов Л. А., Павлючко А. И. Вариационные методы решения ангармонических задач
в теории колебательных спектров молекул. М.: Наука. 1998. 334 с.
449.	McHall J. L. Molecular Spectroscopy. Prentice Hall, 1998. 463 p.
450.	Bunker P. R., Jensen P. Molecular Symmetry and Spectroscopy. NCR Research Press, 1998.
747 p.
ТАБЛИЦА ВОЛНОВЫХ ЧИСЕЛ, СООТВЕТСТВУЮЩИХ
ЭНЕРГИЯМ, ВЫРАЖЕННЫМ В ЭЛЕКТРОНВОЛЬТАХ
эВ	0	1	2	3	4	5	6	7	8	9
0,0	0	81	161	242	323	403	484	565	645	726
0,1	807	887	968	1049	1 129	1210	1291	1371	1452	1533
0,2	1613	1694	1775	1855	1936	2017	2097	2178	2258	2339
0,3	2420	2500	2581	2662	2742	2823	2904	2984	3065	3146
0,4	3226	3 307	3388	3468	3 549	3630	3710	3791	3 872	3952
0,5	4033	4114	4194	4275	4356	4436	4517	4598	4678	4759
0,6	4840	4920	5001	5082	5162	5243	5 324	5404	5485	5 566
0,7	5646	5727	5808	5888	5969	6050	6130	6211	6291	6372
0,8	6453	6533	6614	6695	6775	6856	6937	7017	7098	7179
0,9	7259	7340	7421	7 501	7582	7663	7 743	7824	7905	7985
1,0	8066	8147	8227	8308	8389	8469	8 550	8631	8711	8 792
U	8873	8953	9034	9115	9195	9276	9357	9437	9518	9599
1,2	9679	9760	9841	9921	10002	10083	10163	10244	10324	10405
1,3	10486	10566	10647	10728	10808	10889	10970	11050	11 131	11212
1,4	11292	11373	11454	11534	11615	11696	11776	11857	11938	12018
1,5	12099	12180	12260	12 341	12422	12 502	12583	12664	12 744	12825
1,6	12906	12986	13067	13 148	13 228	13 309	13 390	13 470	13551	13632
1,7	13712	13 793	13874	13954	14035	14116	14196	14277	14357	14438
1,8	14519	14599	14680	14 761	14841	14922	15003	15 083	15164	15245
1,9	15 325	15406	15487	15 567	15648	15 729	15819	15 890	15971	16051
2,0	16132	16213	16293	16374	16455	16 535	16616	16697	16777	16858
2,1	16939	17019	17100	17181	17 261	17 342	17423	17503	17 584	17665
2,2	17 745	17 826	17907	17987	18068	18149	18 229	18310	18 390	18471
2,3	18 552	18 632	18713	18 794	18 874	18955	19036	19116	19 197	19278
2,4	19358	19439	19520	19600	19681	19762	19842	19923	20004	20084
2,5	20165	20246	20 326	20407	20488	20568	20649	20 730	20810	20891
2,6	20972	21052	21 138	21214	21294	21375	21456	21536	21617	21698
2,7	21778	21859	21940	22020	22 101	22182	22262	22343	22423	22504
2,8	22585	22665	22 746	22827	22907	22988	23069	23 149	23230	23 311
2,9	23 391	23 472	23 553	23633	23 714	23 795	23875	23 956	24037	24117
3,0	24198	24279	24359	24440	24521	24601	24682	24 763	24843	24924
3,1	25005	25085	25166	25247	25 327	25408	25489	25569	25650	25 731
3,2	25811	25 892	25973	26053	26134	26 215	26295	26 376	26456	26537
3,3	26618	26698	26779	26860	26940	27021	27102	27182	27 263	27 344
3,4	27424	27 505	27 586	27666	27 747	27 828	27908	27989	28070	28150
3,5	28 231	28312	28 392	28473	28 554	28 634	28 715	28 796	28 876	28957
3,6	29038	29118	29199	29280	29360	29441	29522	29602	29683	29764
3,7	29844	29925	30006	30086	30167	30248	30328	30409	30489	30570
3,8	30651	30 731	30812	30893	30973	31054	31 135	31215	31296	31377
3,9	31457	31538	31619	31699	31780	31861	31941	32022	32103	32183
4,0	32 264	32 345	32425	32 506	32 587	32 667	32 748	32 829	32 909	32990
4,1	33 071	33 151	33 232	33313	33 393	33 474	33 555	33 635	33716	33 797
4,2	33 877	33958	34039	34119	34 200	34 281	34 361	34442	34 522	34604
4,3	34684	34 764	34 845	34926	35 006	35 087	35 168	35 248	35 329	35410
4,4	35490	35 571	35 652	35 732	35 813	35 894	35974	36С	36 136	36216
Таблица волновых чисел
875
Продолжение таблицы волновых чисел
эВ	0	1	2	3	4	5	6	7	8	9
4,5	36297	36378	36458	36539	36620	36700	36781	36862	36942	37023
4,6	37104	37184	37 265	37 346	37426	37 507	87588	37 668	37749	37 830
4,7	37910	37991	38072	38152	38 233	38 314	38 394	38 475	38555	38636
4,8	38717	38797	38 878	38959	39039	39120	39201	39281	39362	39443
4,9	39523	39604	39685	39765	39846	39927	40007	40088	40169	40249
5,0	40330	40411	40491	40572	40653	40733	40814	40894	40975	41056
5,1	41 137	41217	41298	41379	41459	41540	41 621	41701	41782	41863
5,2	41943	42024	42105	42185	42266	42 347	42427	42508	42588	42669
5,3	42750	42830	42911	42992	43072	43 153	43234	43 314	43395	43476
5,4	43556	43637	43 718	43 798	43 879	43960	44040	44121	44202	44282
5,5	44363	44444	44524	44605	44686	44766	44847	44928	45008	45089
5,6	45170	45250	45 331	45412	45492	45573	45654	45 734	45 815	45896
5,7	45976	46057	46138	46218	46299	46380	46460	46541	46621	46702
5,8	46783	46863	46944	47025	47 105	47186	47267	47 347	47428	47509
5,9	47 589	47670	47 751	47831	47912	47993	48073	48154	48235	48315
6,0	48396	48477	48 557	48638	48 719	48 799	48 880	48961	49041	49122
6,1	49203	49 283	49364	49445	49525	49606	49687	49767	49848	49929
6,2	50009	50090	50171	50251	50332	50413	50493	50574	50654	50735
6,3	50816	50896	50977	51058	51 138	51219	51300	51380	51461	51542
6,4	51622	51703	51784	51864	51945	52026	52106	52187	52268	52 348
6,5	52429	52510	52 590	52671	52752	52 832	52913	52994	53074	53155
6,6	53 236	53316	53397	53478	53558	53 639	53720	53800	53 881	53962
6,7	54042	54123	54204	54284	54365	54446	54526	54607	54687	54768
6,8	54849	54929	55010	55091	55171	55 252	55333	55413	55494	55575
6,9	55655	55 736	55 817	55 897	55978	56059	56139	56220	56301	56381
7,0	56462	56543	56623	56704	56785	56865	56946	57027	57107	57188
7,1	57 269	57349	57430	57511	57 591	57672	57 753	57 833	57914	57995
7,2	58075	58156	58 237	58317	58 398	58 479	58 559	58640	58 720	58801
7,3	58 882	58962	59043	59124	59204	59285	59366	59446	59527	59608
7,4	59688	59769	59850	59930	60011	60092	60172	60253	60334	60414
7,5	60495	60576	60656	60737	60818	60898	60979	61060	61 140	61221
7,6	61302	61382	61463	61544	61624	61705	61786	61866	61947	62028
7,7	62 108	62189	62270	62 350	62431	62 512	62 592	62673	62753	62 834
7,8	62915	62995	63 076	63157	63237	63318	63 399	63479	63560	63641
7,9	63 721	63 802	63 883	63963	64044	64125	64205	64286	64367	64447
8,0	64528	64609	64689	64770	64851	64931	65012	65093	65173	65254
8,1	65335	65415	65496	65577	65 657	65 738	65 819	65899	65980	66061
8,2	66141	66222	66303	66383	66464	66545	66625	66706	66786	66867
8,3	66948	67028	67 109	67 190	67 270	67 351	67432	67512	67 593	67 674
8,4	67754	67835	67916	67996	68077	68158	68 238	68319	68400	68480
8,5	68561	68642	68 722	68803	68 884	68964	69045	69126	69206	69287
8,6	69368	69448	69529	69610	69690	69771	69852	69932	70013	70094
8,7	70174	70255	70 336	70416	70497	70578	70658	70 739	70819	70900
8,8	70981	71061	71 142	71223	71303	71384	71465	71545	71626	71707
8,9	71787	71868	71949	72029	72110	72191	72271	72352	72433	72513
9,0	72594	72675	72 755	72836	72917	72997	73078	73159	73239	73 320
9,1	73401	73481	73 562	73 643	73 723	73 804	73885	73 965	74046	74127
9,2	74207	74288	74369	74449	74530	74611	74691	74772	74852	74933
9,3	75014	75094	75 175	75 256	75336	75417	75498	75 578	75659	75 740
9,4	75820	75901	75982	76062	76143	76224	76304	76385	76466	76546
9,5	76627	76708	76788	76869	76950	77030	77111	77192	77272	77 353
9,6	77434	77514	77 595	77676	77 756	77 837	77918	77998	78079	78160
9,7	78240	78 321	78402	78482	78 563	78 644	78724	78805	78885	78966
9,8	79047	79127	79208	79289	79369	79450	79531	79611	79692	79773
9,9 10,0	79853 80660	79934	80015	80095	80176	80257	80337	80418	80499	80579
Примечание. Таблица вычислена с переводным множителем 1 эВ = 8 066,0 см“\ т.е. 1см-1 =
1,23977 • 10-4эВ (см. табл. 1.1, с. 17); в таблицах уровней энергии [122] принят переводной множитель
1 см-1 = 1,23950 • 10-4 эВ, что дает значения энергии (в эВ) на 0,02% меньшие.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Авогадро число 127, 144, 157
Автоионизация 298, 300, 361
Адиабатическое приближение 475
Азимутальное квантовое число к в теории
Бора 174
-------I 48, 164
Азота атом N I 311, 312, 319
— ион N II 311
----N III 306
----N V 240
----N VI 281
—	молекула N2 520
----N2 699, 722, 747, 748, 778, 787
—	молекулярный ион Nj 748, 777, 778
Аксиальная симметрия 64, 65, 69, 117, 177,
393, 407, 413, 685, 721, 729, 735, 772, 804
Аксиальный вектор 66, 651
Актиния атом Ac I 210, 214, 340, 341, 344
—	ионы Ac II, Ac III 341
Аллена молекула С3Я4 520, 806
Альтернативный запрет 116, 527, 679, 680,
696
Альфа-спектроскопия 32
Алюминия атом Al I 209, 211, 214, 301, 302,
304,305,307
-	ион Al III 236, 240
----Al XII 280, 281
Америция атом Am I 210, 341, 347, 349, 453
—	ион Am II 341, 349
----Am III 341
----Am IV 341
Аммиака молекула NH3 502, 506, 508, 509,
517, 520, 535, 549, 640, 643, 644, 659, 667,
669, 678, 702, 795, 796
Амплитуда колебаний 576
—	— нулевая 577
Ангармоничность колебаний 572, 579, 584,
586, 593, 596, 597, 599, 638-640, 673, 674
—	— механическая 597, 677
----электрооптическая 584, 677
Аномалия магнитного момента электрона
39, 56, 193, 400, 406, 436
Аномальная дисперсия 37
Антисвязывающие электроны 731, 736,747-
749, 813, 819, 822, 838
Антисимметрия волновых функций 202
Антистоксово испускание 24, 25
Антистоксовы линии 24, 25
Аргона атом Аг I 206, 208, 209, 211, 214, 301,
302, 314, 316, 317
Асимметричный волчок 544
Ассоциативный закон 68, 80
Астатина атом At I 214, 302, 312
Атомная спектроскопия 12, 32, 96, 163, 181,
213, 448
Атомный остаток 200
Ауксохромы 827
Ацетилена молекула С2Н2 477, 501, 520, 701,
706, 722, 806
Ацетона молекула СО(СН3)2 714
Ацетофенона молекула СО(С6Н5)2 714
Бальмера серия 20, 37, 142, 167-169, 189,
415, 437
— —, первая линия (Яа) 189, 190, 192, 222
—	формула 36, 37
Бария атом Ba I 214, 277, 284-286, 288
-	ион Ba II 210, 236, 238, 240
Барн 428
Беера закон 141
Безызлучательные переходы 16, 23, 88, 89,
293, 298, 317, 361, 366,417, 786, 787, 835,
849
Бензола молекула С6Н6 69, 501, 502, 506,
509, 520, 549, 712, 713, 808-812, 815,
822, 823, 838, 854
Бериллия атом Be I 206, 214, 277, 284, 285,
288, 821
-	ион Be II 236, 240
---Be III 280, 281
---Be IV 163
—	молекула Be2 747, 748
Берклия атом Bk I 341, 349
-	ионы Bk II, Bk III, Bk IV 341
Бета-спектроскопия 32
Бирадикальные состояния 828
Бозе—Эйнштейна статистика 64, 74, 422
Больцмана постоянная 17
Больцмана—Гиббса статистика 64
Бора атом В I 206, 211, 214, 304, 306, 307
-	ион В III 236, 240
---В IV 280, 281
—	магнетон 55, 57, 98, 193, 232, 369, 371,
395
Предметный указатель
877
— постулат 15, 16, 32, 38
-	теория 38, 39,45, 169-173, 175, 220, 367,
407
—	условие частот 16
—	формула 19, 38, 164-166
Брекета серия 20
Брома атом Br I 214, 302, 312
—	ион Вг И, Вг III 265
Бромной ртути молекула HgBr2 836
Бутана молекула С4Ню 503, 514, 711
—	—, поворотные изомеры 718
Бьерума дублет 604
Вавилова закон 848
—	определение люминесценции 27
Валентное состояние атома 795
---— азота 795, 796
—	— — кислорода 797
Валентные колебания 610, 611, 613, 614,
623, 658-660, 688, 700
— — молекулы аммиака NH3 702
-------ацетилена С2Н2 701
-------бензола С6Н6 712
-------воды Н2О 648, 687, 699, 700
---— двуокиси углерода СО2 696
—------метана СН4 659, 672
-------этана С2Н6 710, 711
—	— плоской молекулы типа XY4 658
Валентных связей метод 741
Ванадия атом V I 265, 322, 324, 329, 330
-	ион VII 265, 324, 329, 331
---V III 265, 324
---VV 238, 239
Ван-дер-Ваальса силы 721
Вегарда—Каплана система полос N2 776,
778
Вековое уравнение для колебаний молекул
628, 672
Вероятность внутренней конверсии 362
—	возбуждения электронным ударом 26
—	вынужденного испускания 85, 93, 122,
582
—	дипольного излучения 100
—	испускания 83, 364
—	квадрупольного излучения 101
—	магнитного излучения 98, 155
—	переходов 22, 83, 85, 86, 88, 89, 91, 93,
95, 102, 105, 107, 108, ПО, 113, 115, 122,
141, 147, 185, 318, 344, 362, 426,485, 582,
583, 677, 844
—	— для атомов одноэлектронных 183
—------— щелочных металлов 233
— поглощения 21, 83, 84, 89, 93, 139, 141,
143, 151, 153, 154, 366,403,492, 578, 582,
583, 844
— рассеяния 492, 494, 495
— спонтанного испускания 83-87, 89, 92,
108, 151, 184, 578
Ветви вращательной структуры 600
Взаимодейстие движений в молекуле 475
— — — — колебательного с вращатель-
ным 478
—-------— электронного колебательным
475, 835
—	— — — — с вращательным 763
—	конфигураций 245, 347
—	уровней энергии 124, 298, 299, 785
Вигнера и Неймана правило непересечения
394
Видемана определение люминесценции 27
Виды движений в молекуле 463
Вина закон смещения 131
—	формула 131
Влияние ядерных моментов на вращатель-
ные уровни и линии 565, 567
Внутреннее вращение 503, 504, 535, 620,
640-642
Внутренние перегруппировки в молекуле
535, 620, 640, 643
Внутренняя конверсия рентгеновского из-
лучения 361
Водорода атом Н 15, 19-22, 36, 38, 44, 72,
78, 163, 165, 168, 169, 171, 174, 180, 184,
189, 192, 193, 196,217-220,400,401,408,
410, 413,435, 639, 735, 736, 743, 751, 796,
803, 804, 806, 819
—	молекула Н2 468, 469, 487, 537, 564, 584,
591, 593, 720, 740, 741, 743, 746, 775, 784
Водородоподобные ионы 163
—	состояния 208, 219, 233
Воды молекула Н2О 501, 506, 507, 513, 530,
545, 552, 553, 556, 571, 611, 616, 639,
648-650, 673, 678, 687, 699, 702, 706,
797, 819, 821, 833, 837
Возбуждение оптическое 143, 144
—	термическое 144, 146
—	электрическое 144
—	электронным ударом 16, 26, 148, 363
—	электронов внутренних оболочек 338,
350
Возбужденные уровни 22
Возмущения уровней 299, 697, 784-786
Волновое уравнение 42, 79
—	число 18, 19, 21
Вольфрама атом W I 326, 357
-	ионы W II, W III 326
Вращательная волновая функция 483, 484,
770
—	постоянная 537, 538, 595, 705, 760
—	структура полос колебательных 466, 600,
702-704, 706, 760, 763
—	температура 147
— электронно-колебательных 721
— энергия молекулы 464,466,469, 536, 537,
540
--------, порядок величины 464
878
Предметный указатель
Вращательное квантовое число 48, 532
Вращательные магнитные моменты 55, 57,
395, 564, 565
— переходы 466, 486, 489, 537
— — в молекулах линейных 536
— — — — типа асимметричного волчка
550, 554
_ _ _ _ _ симметричного волчка 546
— постоянные в молекулах типа асимме-
тричного волчка 557
_ _ _ _ _ симметричного волчка 549
— — для волчков 543
— — электронных состояний 705, 760
— спектры 34, 463, 536, 539, 542, 543, 547,
549, 555, 556
— степени свободы 476, 533, 538, 541
—	уровни энергии 33, 35
—	— — молекул линейных 536, 542
—	— — — типа асимметричного волчка
510, 550
—	— — — — симметричного волчка 510,
546, 549
—	— — — — сферического волчка 510,
540
Вращательный момент молекулы 35, 47, 533
Временная симметрия 64, 408
Время жизни 85, 86, 88, 89, 113, 185, 365
—	полураспада 87
Выделенная ось волчка 543
Выделенное направление 42, 46, 368, 425
Вынужденное испускание 85, 122, 134, 135,
137, 142, 143, 150, 395, 396, 398, 399, 403,
404, 582, 583
Вырождение случайное 65
—	уровней энергии 42, 43
—	—	—	вращательных 541
—	—	—	колебательных 839
—	—	—	одноэлектронного атома	165
Вырожденные колебания молекул	640, 654,
658, 660, 665
Вытянутый волчок 544
Гадолиния атом Gd I 209, 321, 339-342,
347, 348
---Gd II 348
-	ион Gd II 340-342, 347
---Gd III 340, 342, 347
---Gd IV 340-342, 347
Галлия атом Ga I 209, 211, 214, 265, 302,
304-306
—	ионы Ga II, Ga III 265
Гамма-спектроскопия 30, 32
Гармонические колебания двухатомной мо-
лекулы 572, 573, 606
Гармонический осциллятор 15, 41, 44, 454-
456, 573, 575-577, 579-583
Гармоничность механическая и электрооп-
тическая 578
Гафния атом Hf I 326, 329
-	ионы Hf II, Hf III 326
Гексадекапольный момент ядра 424
Гексана молекула С4Н14 503, 514
Гелия атом Не I 206, 211, 277, 281, 400, 775
-	ион Не II 39, 163, 167, 169, 189, 197
—	молекула Не2 746
—	молекулярный ион HeJ 746
Гептады термов 248, 260
Германия атом Ge I 214, 265, 302, 308, 311
—	ионы Ge II, Ge II 265
Германоводорода молекула GeH4 525
Герцберга система полос О2 778
Гибридизация состояний 797
—	типа sp 798, 800, 806
---sp2 798, 800, 804, 806
---sp3 797-800, 803
Гидрида алюминия молекула А1Н 726
—	бериллия молекула ВеН 752
-------ВеН2 821
— бора молекула ВН 752
— кальция молекула СаН 722, 779, 780
— лития молекула LiH 722, 751
— натрия молекула NaH 520, 722
— ртути молекула HgH 520, 722, 787
-------HgH2 821
Гидриды 586, 722, 735, 751, 752
Гиромагнитное отношение 54, 58, 369
—	— для протона 434
Главная серия атомов щелочных металлов
222, 229, 234
—	— гелия 279
Главное квантовое число п 19, 45, 164, 165,
202, 217
—	— — п, относительная нумерация 222
Главные линии в мультиплете 266, 270
— моменты инерции 484, 530, 532
—	оси инерции 477, 530, 540
—	— поляризуемости 496
—	поляризуемости 496
—	связи 686
Гольмия атом Но I 341, 349
-	ион Но II 341
---Но III 341
---Но IV 341, 343
Гомеополярная связь 720
Градиент электрического поля в месте на-
хождения ядра 438
—	— — — — нахождения ядра 429, 565
Граница диссоциации 584, 589, 591, 594
—	ионизации 19, 352
—	поглощения 350, 351
—	предиссоциации 787
Границы ионизации для внутренних элек-
тронов 352
—	— — смещенных уровней 297
Гротриана диаграмма 224
Групп теория 53
Предметный указатель
879
Группа 67
— абелева 73, 75
- атомов СН 611, 614, 707
---СН2 505,611, 613, 707, 713
---СН3 505, 612, 613, 641, 707, 713
---NH2 614
—	бесконечная 68
—	вращений вокруг оси 69
—	второго порядка 69, 71, 73
—	конечная 68
—	неабелева 70, 73, 77
—	непрерывная 69
—	отражения в плоскости 68
—	— — центре 68
—	перестановок 68, 72, 73
—	поворотов 68-70
—	пространственная 71, 73
—	точечная 71, 512
—	циклическая 75
Групповая таблица 507, 508, 512, 513
Гунда правило 259, 263, 339
—	случаи связи 768
—	случай связи а 768
-------Ъ 768
Густота d-оболочки 214
—	уровней энергии сложных молекул 825,
826, 839
Дважды вырожденные колебания 645, 654,
655, 659
—	— уровни 42, 65
Движение центра тяжести 44
Двойного резонанса метод 437, 448
Двойные связи 502, 716
Двумерные представления группы 79
Двуокиси азота молекула NO2 501, 836
—	серы молекула SO2 557, 822
— углерода молекула СО2 476, 487, 501,
520, 538, 571, 572, 606, 608, 610, 611,
613, 622, 654, 656, 665, 674, 696-699,
704, 790, 791, 795, 822, 836
—	— молекулярный ион COJ 836
Двухатомные молекулы 464, 465, 467, 469,
471, 474, 501, 520, 527, 537, 557, 570, 719,
721, 723, 728, 729, 731, 757, 771, 775
Дейтерирование 597
Дейтерия атом D 168, 169, 193, 195, 197,
400, 639, 710
—	молекула D2 564, 565, 569, 598
Дектеты 251
Деландра продольная и поперечная серии
754
—	схема 754, 758
Детальное равновесие 134, 145, 148
Деформационные колебания 572, 607, 610,
645, 665, 674
—	— внешние 613
—	— внутренние 613
— — молекулы ацетилена С2Н2 701
— — — бензола С6Н6 712
-------воды Н2О 648, 687, 700
— — — двуокиси углерода СО2 654, 656,
696
-------метана СН4 672, 674, 702, 709
— — — этана С2Н6 710, 711
Диаграмма уровней энергии 17
Диаграммы поляризационные 853
Диамагнетизм бензола 809
— свободных электронов 405
Диацетилена молекула С4Н2 501, 520, 722
Диборана молекула В2Н6 838
Динамическая модель деформируемого ядра
421, 454, 460
Динамическое взаимодействие колебаний
621
Диполь электрический 97, 99, 423
Дипольное взаимодействие 418, 419
— излучение 89, 90, 96
— — молекул 485, 487, 490, 578, 601
Дипольный момент 89, 91, 93, 183, 485, 651,
652, 666, 677, 751, 844
— — индуцированный 409, 491, 493, 495,
498, 690
---молекулы 409, 418, 485, 486, 527, 542,
547, 686
— — —, определение из штарковского
расщепления 563
— — перехода 91, 183, 844, 850
— — — для молекулы 489
Дирака теория 186-188, 190, 192, 197, 357,
400
— уравнение 56, 186, 360
Диспрозия атом Dy I 341, 349
—	ион Dy II 341
---Dy III 341
---Dy IV 341, 343
Дифракционная решетка 30, 169
Дихроизм 851
Диэдра группа 512, 518, 527
Длительность люминесценции 27, 848
—	послесвечения 23
Донор 751
Дополнительная энергия атома в магнитном
поле 368
—	— молекулы в магнитном поле 564
—	—-----электрическом поле 562
Дополнительные условия для колебатель-
ных координат 616
Допплера явление 156
Допплеровское уширение спектральных ли-
ний 158
Достраивающиеся оболочки 209, 214, 321
Дублетное расщепление 186, 218, 223, 224,
228, 231, 234, 240, 306
— — атома иттербия 344
880
Предметный указатель
----тзлаов щелочных металлов 186, 229,
214,235
----в рентгеновских спектрах 241, 357
----для членов изоэлектронных рядов
240, 241
Дублетные состояния молекул с нечетным
числом электронов 793
— термы 223, 224, 357
Дублеты 187, 224, 228, 250, 251, 253, 264,
379
Дуга 30, 146, 284, 336
Дуговой спектр 145, 150
— — железа 336
Европия атом Eu I 341, 342, 347, 349
- ион Ей 11 341, 342, 347, 349
----Eu III 341, 342, 347
----Eu IV 343
Единичный элемент группы 68
Естественная ширина спектральных линии
102, 108, НО, 156, 192
Естественные колебательные координаты
616, 617
Железа атом Fe I 36,265-268,323, 324,328,
333-336
- ион Fe II 265, 323, 324, 328, 333-336
----Fe III265, 323, 324, 328, 329, 334, 336,
344
----Fe VIII 239
----Fe IX 317
----Fe X 319, 320
----Fe XI 319, 320
----Fe XIII 320
----Fe XIV 320
Закиси азота молекула N2O 501, 699, 836
Запаздывание электромагнитных волн 96
Запас колебательной энергии 470, 824, 839
Заполнение электронных оболочек атома
204, 206, 210, 793
Заполненные оболочки атома 207
Запрещенные линии в спектрах туманно-
стей и солнечной короны 317
— переходы 88, 114, 317, 828
Заселенность уровней 22, 42, 122, 124-126,
135, 141-144, 269, 363, 491, 569
Затухание осциллятора 102, 104, 578
Зеемана явление 34, 35, 196, 367, 370, 376,
378, 387, 389,415,417,446, 547, 559, 564,
772
— — аномальное 376
— — в сильных и в промежуточных полях
389, 394
— — — слабых полях 393, 413
— — для сверхтонкой структуры 443, 446
—	— квадратичное 372
---линейное 372, 413
---нормальное 376
—	— поперечное 374
---продольное 374
---простое 374, 375, 391
—	, классическая теория 376
Зеемановские подуровни 367
Зеемановский триплет 374, 375
Зеемановское расщепление спектральных
линий 367, 368, 372, 374, 375, 378, 389
— — уровней энергии 368, 371, 389, 400
Зеркальная симметрия 825, 843, 845, 846
Золота атом Au 1209, 213, 214,326, 336, 338,
339,400
—	ионы Au II, Au III 326
Излучение электромагнитное 15, 21
Изменение длины связи 607, 612, 616, 633
—	расстояния 616
—	углов 609, 610, 612, 616, 619, 654
Изобутана молекула СН(СН3)3 503,678, 804
Изотопический эффект вращательный 448
---колебательный 448, 597
---массовый 453, 480
—	— объемный 451, 453
Изотопическое смещение уровней энергии
и спектральных линий 448
Изоэлектронный ряд 163, 167,210,235-237,
240, 317, 322, 359
Инвариантность оператора энергии 72, 79
— потенциальной и кинетической энергий
673
Инверсионное удвоение 642, 643
Инверсия 67
Индия атом In I 209, 214, 301, 302, 304-306
Индуцированный дипольный момент 409,
491-493, 495, 498
Инертные газы 211, 214, 245, 313-316
Интеграл наложения 489, 739, 744, 759, 760,
782, 813, 834, 835
Интегральная вероятность 153
—	мощность 153
Интенсивности в спектрах 22, 122, 148
—	— — атомов щелочных металлов 233
—	— — вращательных 556, 603
—	— — для мультиплетов 270, 273
—	— — колебательно-вращательных 604
—	— — колебательных 684
—	— — комбинационного рассеяния 493,
495
—	— — поглощения и испускания моле-
кул 22, 122, 494
—	— — при явлении Штарка 416
—	— — рентгеновских 363
Интеркомбинационные мультиплеты 264,
273
—	переходы 253
—	— триплетно-сингулетные 280, 286
Предметный указатель
881
Инфинитное движение 44
Инфракрасная спектроскопия 28
Инфракрасное поглощение 677
Инфракрасные спектры 279, 316, 466
Иода атом J I 214, 302, 312, 781, 784
—	молекула J2 781
Иодной ртути молекула HgJ2 836
Ионизованные атомы 215, 236, 241, 297, 351
Ионная связь 720
Ионные члены 742, 746
Иридия атом 1г I 326, 336
-	ионы 1г II, Ir III 326
Иррегулярные дублеты 356, 358, 361
Искра 30, 31, 336
Искровой спектр 149
—	— железа 336
Испускание 21
—	спонтанное и вынужденное 83
—	стоксово и антистоксово 25
Испускательная способность 130, 133, 136
Источники излучения 22, 30
—	света 289, 336
Исходная конфигурация 260
Иттербия атом Yb I 209, 214, 341, 349, 362
—	ион Yb II 341
---Yb III 341
---Yb IV 341, 344
Иттрия атом Y I 206, 214, 325, 329
-	ион YII 325
---Y IH 236, 240, 322, 325
Кадмия атом Cd I 209, 214, 277, 278, 285,
289, 291, 325, 336, 337, 357, 452
-	ион Cd II 325
---Cd III 325
Кайзер 18, 37
Калифорния атом Cf I 340, 341
-	ионы Cf П, Cf III, Cf IV 341
Калия атом К I 204, 209, 211, 213, 216, 217,
220, 222,223,226, 229,233, 234, 239, 240,
265, 322
Кальция атом Са I 36, 209, 214, 265, 277,
284-286, 288, 295, 299, 300, 356, 357
-	ион Са II 236, 238-240, 265, 296, 297, 322
Кант полосы 756, 761, 762
Карбонильная связь 807
Картина зеемановского расщепления 376,
387
— штарковского расщепления 411
Катодолюминесценция 27
Квадруполь 97, 99, 423
Квадрупольного взаимодействия постоян-
ная 430, 438, 566
Квадрупольное взаимодействие электрон-
ное 418
— — ядер 424, 428
— излучение 96, 99-101, 105, 254
---молекулы 490
Квадрупольные моменты ядер 424, 428,438,
460, 565
—	переходы рентгеновские 353
Квадрупольный момент 99, 419, 428, 651,
652
—	— перехода 100, 101, 828, 851
—	резонанс 143
Квазиклассическое приближение 174
Квазистатический метод рассмотрения мо-
лекул 475
Квазитвердые молекулы 535, 640
Квантование вращательной энергии 533
—	колебательной энергии 475
—	магнитных моментов 54
—	момента количества движения 42, 45,47,
65, 77
Квантовая механика 39, 50, 56, 91
—	— релятивистская 56
—	электродинамика 38, 192
Квантовое число J 45, 65, 213
—	— J, правило отбора 117
Квантовомеханическая теория молекул 478,
479
Квантовомеханический расчет атома галия
Не I 281
—	— гармонического осциллятора 580
—	— молекулы водорода Н2 743
—	— молекулярного иона водорода 739
Квантовые законы основные 15
—	числа 45, 166, 199
—	— электрона в линейной молекуле 728
— — — — одноэлектронном атоме 164
---— — сложном атоме 199
Квантовый выход 89, 839, 848, 850
— дефект 218, 220
---для атомов лития и натрия 218, 220
Кванты излучения 16, 37, 128
Квартеты 250-253, 331, 335, 379
Квинтеты 250-252, 332, 333
Кекуле структуры 811, 812, 815
Кинга печь 146
Кинематическое взаимодействие 621
Кинетическая энергия вращения 473, 480,
481
---колебания 473, 481, 572, 621, 623, 670
— — относительного движения ядер 473,
480
— — электронного движения в молекуле
479
Кирхгофа закон 36, 136, 848
Кислорода атом О I 36, 206, 260, 302, 307-
309, 311, 319, 378, 750, 751, 782, 797, 807,
822
- ион О II 260,311,319
---О III 312, 318, 319
---О IV 306
---О VI 240
---О VII 281
882
Предметный указатель
- молекула О2 487, 520, 568, 569, 572, 747,
748, 750, 776, 778, 782, 793, 795
— молекулярный ион 748, 778, 779
Классы операции симметрии 521, 522
Клебша—Горлана коэффициенты 81
Клистрон 30, 31, 556
Кобальта атом Со I 265, 323, 324, 333, 336,
446, 447
— ион Со II 265, 324, 333
---Со III 265, 323, 324, 328
---Со XVI 288
---Со XVIII 317
Когерентное рассеяние 25, 492
Колебания двухатомных молекул 571, 572,
638
— многоатомных молекул 475, 535, 574,
599, 609, 615, 638
— — — активные и неактивные 678
— — — валентные и деформационные
610, 611
— — — неполносимметричные 571, 572,
693, 790, 830, 831, 833, 838
— — — нормальные 33, 65, 571, 606, 608,
610, 645
— — — полносимметричные 493, 571,
572, 654, 658, 659, 662, 672,678,689,693,
790, 830
Колебательная волновая функция 483, 484,
488, 683
—	структура электронных переходов 753,
754
—	температура 147
—	энергия молекулы 33, 65, 149, 463, 464,
466, 470
Колебательное движение 448, 460, 463
Колебательно-вращательные спектры двух-
атомных молекул 594
Колебательные координаты 474, 477, 478,
488, 541, 577, 578, 583, 597
—	переходы 466
—	спектры молекул 33, 463, 606, 676
—	уровни энергии 33, 65, 448, 468, 478,484,
577, 579, 584, 588, 696, 701, 754, 825, 839
Кольцевые структуры 500, 501
—	—, классификация состояний по значе-
ниям момента количества движения 722
Комбинационного рассеяния спектры 466
Комбинационное рассеяние 25, 27, 33, 34,
39
—	— антистоксово 25
—	—, открытие 38
—	—, стоксово 25
Комбинационный принцип 18, 19, 37, 38,
197, 295
Конденсированные системы 15, 32, 33, 83,
124
Кондона парабола 758
Конкуренция электронов 209, 236, 321, 322
Контур полос сложных молекул 825, 846
— спектральной линии 108, НО, 150,418
Координаты симметрии 646-654, 658, 659
Кориолиса сила 60
Короний 317, 319
Корреляционные диаграммы Уолша 816
Коэффициент затухания осциллятора 104,
152
— испускания 138, 152, 153
— поглощения 122, 137
—	— в области радиочастот 30, 143
—	— отрицательный 150
—	— приведенный 137, 403
—	рассеяния 138
—	Эйнштейна А 84
	-В 84
Коэффициенты динамического взаимодей-
ствия 625, 634, 672
— кинематического взаимодействия 625,
628, 632, 634, 672
— полного взаимодействия 625, 626, 628,
634, 635, 637, 672
— симметрии 658, 668, 669, 673
Кравца формула 144
Край поглощения 350-353, 355, 359, 364,
366
Крамерса теорема 404, 408, 413, 417, 794
Крамерсово вырождение 408, 409
Кратность вырождения 41, 368, 416, 656
Кремния атом Si I 214, 244, 302, 308, 311
- ион Si IV 236, 237, 239, 240
Кривые потенциальной энергии 474, 584,
586, 588, 590, 592-594, 719
— — —, притяжения и отталкивания 736
Кристаллические системы 510, 511
Кристаллофосфоры 23, 27
Крон ига правила отбора для возмущений
уровней 785
Круговые орбиты 16, 38, 55, 98, 171
Крутильные колебания 504, 620, 641, 642,
710
Кулоновский интеграл 283
Кюрия атом Cm I 341, 347
— ионы Cm II, Cm III, Cm IV 341
Лагранжа уравнения 574, 624
Лазеры 150, 564
Лаймана серия 20, 22, 167, 170, 182, 185,
197, 437
Лаймана—Берджа—Гонфильда система по-
лос N2 776
Ландау диамагнетизм свободных электро-
нов 405
Ланде множитель g 370, 378
— формула 378
Лантана атом La I 209, 214, 322, 341, 344,
357
— ион La II 341, 344
Предметный указатель
883
----La III 210, 236-238, 240, 341, 344
Лантаниды 339, 340, 342, 345, 349
Лапласа сферические функции 179
Лармора теорема 59
Ларморова прецессия 59, 376
Лежандра полиномы 179
Линейные молекулы 64, 71, 476, 477, 500-
503,	505,	520,	533,	534,	536-539,	541,
542,	545,	547,	549,	561,	569,	572,	610,
611,	629,	640,	645,	657,	665,	674,	696,
703,	705,	721-724,	728,	730,	788,	790,
792, 814, 816, 819, 821, 832, 836
Лития атом Li I 204, 206, 210, 213, 216, 217,
221-223, 225, 228, 229, 233, 236, 240, 751
— ион Li II 280, 281, 393, 400
----Li III 163, 167, 189
— молекула Li2 747, 749
Локализованные электроны 807
Лошмидта число 127
Лучистая теплопроводность 148
Лэмба опыт 196, 401, 417
Люминесценция 27
—	отрицательная 28
—	сложных молекул 851
Лютеция атом Lu I 206, 209, 214, 326, 349,
362
—	ионы Lu I, Lu II 326
Магические числа 454, 457
Магнетомеханическое отношение 55, 58,
369
Магнитного взаимодействия постоянные
427, 428, 431,435
Магнитное излучение 96-99
—	— молекул 490
—	квантовое число т 368
--------т 46, 49, 54, 79, 118, 164, 174, 396,
408
—	— — орбитальное 164
—	полное 186
— — — ядерное 425
--------, правило отбора 114, 116, 117, 120,
181
— — —, спиновое 48, 164, 391
Магнитные взаимодействия ядра 424
- моменты 34, 39, 174, 186, 193, 231, 232,
251, 367, 423
----вращательные 55, 57, 395, 424, 428,
564, 565
----перехода 60, 89, 98
----ядер 423, 424, 426, 428, 438, 445, 479
Магнитный момент р-мезона 427
----дейтрона 434
----нейтрона 427, 434, 459
----протона 57, 367, 406, 433, 434, 459
— — электрона 39, 55, 56
- резонанс 30, 367, 368, 378, 395, 396, 398,
399, 404, 405
— — в молекулярных пучках 39, 368, 398,
399, 421,427, 438
— — электронный 143, 368, 370, 395, 405,
426
—	— ядерный 34
—	—, изучение методом поглощения 368,
397, 399
Магния атом Mg I 36, 214, 276, 277, 284-286,
288
-	ион Mg II 236, 237, 239, 240
-------XI 280, 281
Мазеры 150, 564
Максвелла электромагнитная теория света
37
Максвелла—Больцмана закон 22, 124, 143,
145
Максвелловское распределение 147, 148,
157
Малых колебаний задача 622
Марганца атом Mn I 261, 264, 265, 321, 323,
324, 331-333
- ион Мп II 261, 264, 265, 324, 331
---Мп III 265, 323, 324, 327, 331, 344
---Мп VII 238
Матричные элементы для гармонического
осциллятора 582
Матричный элемент дипольного момента
91, 92, 94
Мгновенная конфигурация ядер 470, 489
Меди атом Cu I 209, 213, 214, 265, 324, 336,
338, 339, 356, 357, 400
— ион Cu II 265, 324
---Си III 265, 324, 327, 328
---Си XIX 239
Мезитилена молекула С6Н3(СН3)3 854
Мезоатомы 163, 170
Менделевия атом Md I 210, 341
-	ионы Md I, Md II, Md III, Md IV 341
Менделеева периодическая система элемен-
тов 39, 166, 201, 205, 237
Металлическая модель молекулы 810, 811,
813
Метана молекула	СН4	500,	502,	525,	535,
540, 610, 659,	667,	668,	671,	672,	674,
680, 684, 702,	706,	708,	709,	711,	795,
797, 803, 804, 808
Метастабильные состояния 88, 89, 280
—	— атома ртути 293
Метод векторного сложения моментов 53,
254
—	сложения проекции 53, 243, 255
Механический момент 45, 46
Микроволновая спектроскопия 28, 557, 643
Микроволновое поглощение 556
Многолинейчатый спектр 775
Множитель g (множитель Ланде) 370
—	g в слабом поле 378
—	g ядерный 425
884
Предметный указатель
Модель периметра 823
Мозли диаграммы 237, 239-241, 322, 355,
356, 358
—	закономерности 39, 356
Молекулярная спектроскопия 12, 15, 32, 35,
39, 71, 96, 448, 464, 479, 491, 515, 719
Молекулярные кристаллы 826
-	орбиты 741-743, 803, 807, 808, 810
—	электроны 404
Молекулярный генератор 150, 564
Молекулярных орбит метод 741-743, 746,
803, 807, 810-813, 816, 818, 822
Молибдена атом Mo I 325, 333
—	ион Mo II 325
---Mo III 325
---Mo V 288
Момент количества движения 38, 43
—	— — излучения 118
—	молекулы 469, 478
—	— —, квантование 45, 47
—	перехода 92, 93, 113-115, 118
—	— дипольный 91, 92, 94
—	— квадрупольный 100, 115
—	— магнитный 60, 89, 98
Моменты инерции 33, 499, 530, 532
—	— молекулы линейной 538
—	— — типа сферического волчка 540
—	— наибольший, наименьший и проме-
жуточный 543
—	—, таблица 438
—	—, теория 453
- ядер 34, 421, 423, 424, 426, 428, 433, 438,
445, 446, 453, 454, 458, 459
Морза формула 589, 592-594
Мощность вынужденного испускания 122,
564, 582
— люминесценции 583, 848
— поглощения 122, 123, 134-136, 143
— — приведенная 123, 134, 583
— спонтанного испускания 122, 134, 135,
138, 848
Мультиплетная структура 224
Мультиплетное расщепление 244, 261, 262,
297
Мультиплетность 187, 212, 224, 247, 248,
250-253, 258, 259
— максимальная 250, 258, 262, 264, 301, 321
Мультиплетный терм 247
—	— неполный 252
Мультиплеты 263
—	в спектре железа 266
—	, открытие 332
Мультиполи 423
Мышьяка атом As I 265, 302, 308
—	ионы As II 265
---As III 265
Наложение волновых функций 283, 737,
738, 740, 745, 759, 834, 835
— состояний 742
Направленная валентность 177, 500, 737,
788, 796, 803, 808, 809, 819
Насыщение в радиочастотной области 143
Натрия атом Na I 24, 36, 157, 204, 210, 213,
216, 217, 220, 222, 224, 226, 228, 229, 233,
235, 236, 239, 240, 357, 367, 444
Небулий 317-319
Невырожденные колебания молекул 645
Недиаграммные линии 363
Незаполненные оболочки атома 213
Нейтронная конфигурация 458
Нелинейные молекулы 824, 834, 836
Нелокализованные орбиты 808, 809
— электроны 808-812, 814
Неодима атом Nd I 341, 344, 345
- ион Nd II 341, 344, 345
----Nd III 341
----Nd IV 341, 343
Неона атом Ne I 204, 206, 209, 211, 214, 301,
302, 313, 314, 316, 317
Неоптические переходы 16
Неплоские колебания 620, 652-654
— молекулы 500, 502
Неполносимметричные колебания молекул
571, 790, 830
Неполные мультиплетные термы 252
Неприводимые представления 67, 73, 79,
656, 658, 683
Непроникающие орбиты 208
Нептуния атом Np I 210, 341, 344
—	ионы Np I, Np II 341
Неравновесные спектры испускания 144,
147
Неразличимость одинаковых частиц 64
Нерезонансное испускание 24, 27
Несвязывающие орбиты 816, 819
—	электроны 749
Неупругие столкновения 148, 158
Неустойчивость вырожденных состояний
многоатомных молекул 790, 794, 838
Нечетно-нечетные ядра 422, 438, 458
Нечетно-четные ядра 422, 438, 440, 458
Никеля атом Ni I 206, 214, 265, 323, 324, 336
-	ион Ni II 265, 324, 336
----Ni III 265, 324, 328
----Ni IX 288
Ниобия атом Nb I 325, 329
-	ионы Nb II, Nb III 325
Нитрозила молекула NOCI 514
Нонеты 251, 252
Нормальная связь 243-248, 253, 261, 266,
273, 382, 722
Нормальное расщепление 369, 370, 389, 391
Нормальные колебания 33, 65,606-609,615,
620, 622, 627
Предметный указатель
885
—	конфигурации атомов 204
—	— — с двумя внешними з-электронами
277
—	— — — достраивающимися d-оболоч-
ками 323
—	— — — — /-оболочками 339
—	— — — заполняющимися р-оболочка-
ми 302
—	— — щелочных металлов 216
—	координаты 615, 621, 622
—	термы 263, 301
—	— при достройке d-оболочки 323
Нормировочные множители 75, 580
Нулевая амплитуда колебаний 577
—	ветвь (Q) 603, 703
-	линия 596, 597, 602, 703, 762
—	энергия колебаний 499, 576, 609, 639
Нулевые частоты колебаний 639
Ньютона открытие спектров 35
Обертоны 578, 580, 584, 596, 597, 640
Обмен энергией 16
Обменные члены 202
Обменный интеграл 283
Обобщенная модель ядра 454, 460
Оболочечная модель ядра 453, 454
Обратный элемент группы 68
Обращенные термы 263
—	— для атомов галоидов 356
—	— при достройке d-оболочки 323
Обращенный дублетный терм 235
Объединенный атом 734-736, 751, 775, 776
Объемная поглощательная способность 136
—	— — приведенная 136
Одномерное представление группы 80
Одноэлектронные спектры 163
—	— атомов с одним внешним з-электро-
ном 216
Оже эффект 361
Озона молекула Оз 501, 557, 558, 822
Окиси азота молекула NO 520, 571, 572, 779,
780
—	— молекулярный ион NO+ 749
—	бериллия молекула ВеО 760
—	углерода молекула СО 520, 749, 753, 754,
779, 836
—	— молекулярный ион СО+ 749
Октаэдр 522-524
Октеты 251, 252
Октуполь 97, 423
Окгупольный момент ядра 443, 445
Оператор энергии 42, 43
—	— атома водорода 72, 78
— — гармонического осциллятора 580, 581
—	— молекулы 479
Операция симметрии 66, 67
Оптическая глубина 140
—	спектроскопия 28, 30
—	толщина 140
Оптические переходы 16
Оптическое возбуждение 23, 24, 27
Орбитали 741
Орбитальный момент 42, 44, 47, 55, 242
—	— магнитный 44
—	— нуклона 422
—	— полный 186, 188, 211, 212
Ориентация спина 42, 49
Ортоводород 568
Ортогелий 280
Оси симметрии 67-69, 71, 74
Осмия атом Os I 326, 333, 336
—	ионы Os II, Os III 326
Основная частота 596, 676, 678
Основной уровень 22
Осциллятор гармонический 15, 41, 44, 454-
456, 573, 575-577, 579-583
Осцилляторы для переходов дипольных 105,
850
—	— — квадрупольных 105, 850
—	— — магнитных 105
Отражения операция 66, 68, 71, 79, 118
Отрицательная ветвь (Р) 602, 703
—	люминесценция 28
Отрицательное поглощение 85
Оттенение полос 761, 762
Палладия атом Pd I 206, 209, 214, 325
-	ионы Pd II, Pd III 325
Параболические квантовые числа 414
—	координаты 411, 413
Параводород 568
Парагелий 280
Параллельные полосы 702-706
Парамагнетизм вещества 368, 402
Парамагнитные молекулы 564
Парамагнитный резонанс 39, 251, 368, 402,
404
—	—, открытие 402
Параметры асимметрии волчка 544, 566
—	равновесной конфигурации 499, 500,
558, 628
Паули принцип 39, 53, 75, 198, 201, 202,
254, 255, 257, 258, 274, 456, 457, 721,
728, 732, 733, 741, 742, 795, 818
Пашена серия 20, 222
Пашена—Бака явление 389, 394
Пентады термов 248, 260, 295
Пентана молекула C5Hi2 514
---С5Н12 503, 711
Первая отрицательная система полос N2 778
—	положительная система полос С6Н12 502
Переводные множители 17
Передача энергии возбуждения 16, 149
Перекиси водорода молекула Н2О2 514
Перекрывание электронных облаков 737,
738, 743, 750, 796
886
Предметный указатель
Перенормировка массы и заряда электрона
193
Перенос излучения 138, 140
Переносная симметрия 510
Переориентация спинов у гелия 280
Перестановка частиц 64, 66, 68
Перестановочная симметрия 64, 67, 71
Переход от вытянутого волчка к сплюсну-
тому 548, 551
—	— связи (£, S) к связи (j,j) 311
—	— слабого поля к сильному в явлении
Зеемана 393, 432
—	— — — — сильному в явлении Штар-
ка 417
Переходные элементы 206
Переходы безызлучательные 16, 23, 88
—	квантовые 16
—	с излучением 15-17, 21
Периодическая система элементов Менде-
леева 39, 166, 201, 205, 237
Перпендикулярные полосы 702-706
Перрена формула 854
Пикеринга серия 38, 168, 169
Плазма электрического разряда 147
Планка постоянная 16, 38, 45
-	формула 23, 83, 129, 131, 134, 135, 145,
151, 153, 576, 848
Платины атом Pt I 206, 209, 214, 326, 336
-	ионы Pt II, Pt III 326
Плачека правила 693
Плоские колебания 652
—	молекулы 501, 503, 514, 520, 546, 620
Плоскость симметрии 66-68, 491
Плотность излучения 84, 128, 129
—	— спектральная 128, 129
Плутония атом Pu I 210, 341, 347
-	ионы Pu II, Pu III, Pu IV 341
Поворотные изомеры 504, 718
—	точки классического движения 573, 757,
759, 829
Повороты вокруг оси 49, 67-69, 114, 115
Подвижные координатные оси 58, 476, 477,
480, 530
—	химические связи 809
Подгруппа 69
Позитроний 163, 170
Полиены 810, 814, 827
Полиметиновая цепочка 810
Полносимметричные колебания 493, 571,
572, 654, 659, 678, 790
Положительные и отрицательные состоя-
ния 74, 569, 704, 723, 738, 768, 769,
771
Полония ионы Ро I 302, 308, 309
Полусложные молекулы 825, 826
Полуторные связи 502, 503, 713
Полуцелые квантовые числа 39, 45, 47-49,
51, 169, 174, 251,421
Поляризационные диаграммы 853
— спектры 853, 854
Поляризация в колебательных спектрах 690,
694, 712
—	вакуума 193-195
—	излучения 85, 118, 193, 690
—	— при явлении Зеемана 415
— — — — Штарка 412
— люминесценции 839, 851-853
Поляризованный атомный пучок 401
Поляризуемость атома 411
— молекулы 409, 491, 492, 497, 498, 528
Полярные сияния 319, 778
Полярный вектор 66, 98
Поперечная серия 754, 756, 757
Поперечные сечения для поглощения фо-
тона 141
—	— молекул 500
Порядок группы 68, 69, 509, 515, 524, 661
Послесвечение 23, 27, 85, 88
Потенциалы возбуждения, диссоциации и
ионизации 26
Потенциальная поверхность 475, 544, 830,
831, 833
—	энергия колебаний 473, 504, 592, 615,
621, 640, 670, 673
—	— молекулы 474, 475, 504, 707, 708
—	— нуклонов в ядре 455
Потенциальные кривые 451, 472, 474, 572
Потенциальный барьер для внутреннего
вращения 504
Поток излучения 130, 136
Правила квантования 16, 38, 174
—	отбора 114
—	— для взаимодействия уровней 114, 121,
372, 411, 785
—	— — двухатомных молекул 771
— — — квантового числа F 431
--------------  J	117
---------------К	547,	705
-------------L 253
-------------I 181, 704
---------------т	117,	372,	396
-------------S 253
-------------v 577
—	— — колебаний двухатомных молекул
578
—	— — — многоатомных молекул 676
—	— — магнитного резонанса 395
—	— — нормальной связи 253
—	— — одноэлектронного атома 180
—	— — отражения в плоскости 115
—	— — — — центре 116
—	— — поворота вокруг оси С2 115
—	— — сверхтонкой струтуры 431
—	— — электронных спектров много-
атомных молекул 827
—	— — явления Зеемана 396
Предметный указатель
887
— — — — Штарка 415
Правило интервалов для мультиплетного
расщепления 262, 329
— — — сверхтонкой структуры 427, 443
— непересечения Вигнера и Неймана 394
— сумм для множителей g 394
— — интенсивностей 190, 273
— — сил осцилляторов 107, 108
Празеодима атом Рг I 341, 344
- ион Рг II 341, 344, 345
----Рг III 341
----Рг IV 341, 343
Предельные углеводороды 502, 503, 505,
707, 711, 718
Предиссоциация 786, 787, 829
—	вращением 787
Представления группы 73, 79
Прецессия магнитных моментов 57, 59, 60,
381, 390, 426
—	— — ларморова 59, 376
—	— — ядер 426
Приближенная симметрия 505, 680
Приведенная масса 19, 163, 167, 436, 468,
537, 612
Приемники излучения 30, 31
Призмы 30, 31, 36
Принцип соответствия 38, 39, 89, 375
Пробег излучения 139
Продольная серия 754
Проекция момента количества движения
43, 65, 368
Произведения инерции 532
Промежуточные поля 371, 393, 394, 400,
401,410
Прометия атом Pm I 341, 344
—	ион Pm II 341
----Pm III 341
----Pm IV 341, 343
Проникающие орбиты 207, 208
Пропана молекула С3Н8 513
----С3Н8 503, 650, 711, 805
Пропускание 140
Пространственная симметрия 64, 67, 71
Пространственное квантование 47, 173
Простые молекулы 628, 707, 813, 824, 825,
827
Протактиния атом Ра I 341, 344
—	ионы Ра II, Ра III, Ра IV 341
Протонная конфигурация 458
Прямое произведение представлений 81,
121, 683, 818
Псевдовектор 66, 828
Пфунда серия 20
Равновесная конфигурация молекулы 71,
77, 472, 478, 490, 491, 499, 500, 505, 510,
516, 530, 552, 558, 559
Равновесное излучение 23, 128, 129, 131,
136, 138
— расстояние 471, 500, 557, 719
Радиальное квантовое число 174, 178, 199
Радиальные функции 178, 179, 230, 800
Радиационные поправки 192-195
Радикал СН 722, 752, 779
-	CN 749
-	NH 722, 752, 779
-	ОН 752
Радиоизлучение космического водорода 435
Радиоспектроскопия 28, 30, 34
Радиус первой борове кой орбиты 171
Радия атом Ra I 214, 277, 284, 285
Радона атом Rn I 206, 209, 211, 214, 302, 313
Развязывающие электроны 731
Разделение колебаний и вращения 477, 478
Размерность представления группы 81, 656
Размеры молекул 469, 470, 500, 502
— —, определение из микроволновых
спектров поглощения 557
Разрешающая сила 31, 351, 399, 421, 550
Разрыхляющие электроны 731
Расположение термов при нормальной свя-
зи 248, 249
Рассел я—Саундерса связь 243
Расщепление уровней в магнитных и элек-
трических полях 559
— — сверхтонкое 34, 165, 424, 448, 449
Регулярные дублеты 357, 358
Редкоземельные элементы 206, 339, 343, 344
Резерфорда модель атома 38
Резкая серия атомов щелочных металлов 222
Резонанс валентных структур 811, 812
Резонансное испускание 23, 24, 152
Резонансные линии 24
---атома ртути 24, 293, 294
—	— атомов с одним внешним р-электро-
ном 306
—	— — щелочноземельных металлов 285
—	— — щелочных металлов 229
Резонансный интеграл 740
Рения атом Re I 326
—	ионы Re II, Re III 326
Рентгеновская спектроскопия 30
Рентгеновские спектры 33, 39, 204, 241, 350,
353, 356, 357
—	— характеристические 351
Ридберг 350, 352, 357
Ридберга постоянная 19, 167-170, 231, 350,
450
—	формулы 37, 220, 277
Ридберга—Клейна метод 593, 594
Ритца комбинационный принцип 18
—	формулы 277
Родия атом Rh I 323, 325, 336
—	ионы Rh I, Rh II 325
Рождественского метод крюков 108
888
Предметный указатель
Ртути атом Hg I 24, 88, 149, 158, 214, 277,
278, 285, 288, 289, 292, 294, 326, 336-338,
449, 452, 821
- ионы Hg II, Hg III 326, 338
Рубидия атом Rb I 198, 204, 209, 213, 217,
220, 222, 228, 229, 233, 235, 236, 240, 322,
362
Рунге знаменатель 384
Рутения атом Ru I 323, 325, 333, 336
— ионы Ru II, Ru III 325
Рэлеевское рассеяние 25, 27, 492, 692, 694
Рэлея-Джинса формула 131, 135
Самария атом Sm I 341, 347, 348
- ион Sm II 341, 347, 348
---Sm III 341
---Sm IV 341, 343
Самосогласованного поля метод 200, 202
Сателлиты рентгеновские 363
Сверхтонкая структура 34
— — спектральных линий 421, 437, 438,
445, 447, 448
---уровней энергии 424, 427, 433, 442,
445, 449
— — — — атома водорода 433, 435, 437
— — — — молекул 421, 433, 480, 565
Свечение ночного неба 319
Свинца атом Pb I 214, 302, 308, 309, 311
Свободное вращение 478, 504, 640, 641, 729,
804
Свободно-свободные и свободно-связан-
ные переходы 21, 781
Свободные радикалы 404, 794
— состояния электрона 19, 171
Свойства симметрии 43, 64-67, 72, 73, 75,
76, 78
—	— равновесной конфигурации 505
Связанные состояния электрона 19
Связывающие электроны 731,738,742,746-
748, 803, 813, 818
Связь (j, J) 244, 245, 251, 273-275, 314, 315,
317
-	О’, 0 245
Сдвиг уровней 39, 192, 193, 195, 197, 417
Секстеты 321, 332, 335, 380
Секулярное уравнение 627
Селена атом Se I 265, 302, 308
—	ионы Se II 265
Сенсибилизированная флуоресценция 149
Серебра атом Ag I 213, 214, 325, 336, 338,
357, 400
—	ионы Ag I, Ag II 325
Серии рентгеновские 353
—	спектральные 20
—	— атома водорода 20, 37, 38
—	— — гелия 279
—	— — ртути 294
— — атомов с двумя внешними «-электро-
нами 277
— — — щелочных металлов 36, 164, 222
Сероводорода молекула H2S 501
Сероокиси углерода молекула OCS 520, 722
Сероуглерода молекула CS2 501
Серы атом S I 302, 308
-	ион S VI 237, 239, 240
Сила осциллятора 92, 102, 103, 105-108
—	— атомов лития и натрия 233
—	— для испускания 106
—	— — одноэлектронного атома 182
—	— — поглощения 106, 143
—	— — рентгеновских переходов 364
—	перехода 93-95
Силовая постоянная 467, 572, 577, 612
Силовые постоянные валентных и дефор-
мационных колебаний 614
—	— молекулы бензола 713
—	— — метана 710
— — — этана 710
Сильное поле 370, 371, 389, 391, 393, 394,
409, 410, 417
Симметричные и антисимметричные вол-
новые функции 74, 422, 570, 743
— — — состояния 66, 74, 75, 724, 738, 740,
743
______ правила отбора 117
Симметричный волчок 543, 544
Симметрия колебаний многоатомных моле-
кул 645, 654, 659
- куба 523, 524
— равновесной конфигурации молекулы
71, 491, 505, 791
— смещений 571, 646, 649, 650
— уровней энергии асимметричного волчка
553
Сингонии 511
Сингулетная система термов 277
Сингулетные состояния молекул 793
Сингулеты 250
Синильной кислоты молекула HCN 501,
520, 674, 675, 722, 807
Скандия атом Sc I 206, 209, 214, 265, 323,
324, 329-331
- ион Sc II 265, 324, 329
---Sc III 236, 237, 240, 265, 324, 327
Скин-эффект 405
Слабое поле 371, 372, 376, 390, 392, 393,
410, 426
Сложение магнитных моментов 61
— моментов количества движения 50, 54,
78, 81, 243, 363, 422, 427, 722, 765
Сложные молекулы 785, 825-829, 835, 839,
840, 842-844, 846, 848, 850, 851
Случайное вырождение 65, 696
Смещенные термы 276, 295, 297, 298
Снятие вырождения 42, 642
Предметный указатель
889
Собственная симметрия 507, 509, 510, 515,
654
Солнечная корона 317-320
Соответствие классической и квантовой те-
ории для гармонического осциллятора
576, 579, 583
Соотношение моментов инерции для моле-
кул 533
—	неопределенности для времени и энер-
гии 109
Составные частоты 640, 676, 679, 696
Спаренные электроны 795
Спектр возбуждения внутренних электро-
нов 337
—	выхода 839
—	дискретный 16, 19, 36
—	комбинационного рассеяния 25
—	линейчатый 21
—	многолинейчатый 775
—	непрерывный 16, 123, 134, 298, 780
—	полосатый 21
—	поляризации 839
—	сплошной 19, 31, 35
—	электромагнитного излучения 15, 16, 28
—	энергетический 16
Спектральная вероятность 151
—	интенсивность излучения 137
—	линия 18, 31
—	мощность 151, 152
—	плотность излучения 128, 129
Спектральный анализ 32, 36
—	— молекулярный 27, 614
—	— эмиссионный 147
Спектры поглощения, испускания и рассе-
яния 16, 21, 26, 30
Спин нейтрона 421
—	протона 421
—	электрона 34, 39, 42, 44, 48
—	ядра 44, 48, 421
—	— полный 422
Спиновое квантовое число s 48
Спиновые волновые функции для системы
двух частиц 283
Спиновый момент электронный 57
—	— — магнитный 55
-------полный 211, 242, 243, 249
— — ядерный 48, 421
Спин-дублет 357
Спин-орбитальное взаимодействие 62, 164,
170, 182, 186, 187, 200, 228, 229, 231, 232,
234, 244, 246, 253, 261, 277, 280, 311, 314,
333, 356, 359, 390, 392, 394, 413, 417, 479,
723, 763, 774, 785, 794
— — сильное (в ядре) 241, 417, 421, 454,
458
Спин-спиновое взаимодействие 280
Сплошной спектр молекулы водорода 784
Сплошные спектры двухатомных молекул
780
— — сложных молекул 788, 825, 838
Спонтанное испускание 83-85, 395, 435
Статистическая сумма 125
— теория уширения спектральных линий
159, 417
Статистический вес 42, 47, 85
— — вращательных уровней 538, 542
— — — — в зависимости от спина ядер
569
Стационарные состояния 15, 16, 22, 26, 41,
43
Степанова универсальное соотношение 846
Степени свободы 41, 43, 147
— — колебательные и вращательные 470,
476
Степень вырождения 41, 42, 52, 65, 66, 77,
78, 93, 123, 165
—	— вращательных уровней энергии 541
—	— колебательных уровней энергии 673
—	— при сложении моментов 51
—	деполяризации 691, 852
—	поляризации 851-854
—	—, предельные значения 854
Стефана—Больцмана закон 129, 130, 132
Стокса правило 24
Стронция атом Sr I 214, 240, 277, 284, 285,
288, 322, 357
—	ион Sr II 236
Сурьмы атом Sb I 24, 25, 302, 308
Сферическая симметрия 64-66, 71, 72, 77,
95, 722
Сферически симметричное поле 175, 199,
200, 229, 232
Сферические функции 179
Сферический волчок 33, 533-535, 540-543
Схождение колебательных уровней 584, 589,
754
Таллия атом TI I 24, 25, 149, 209, 214, 302,
304-307, 444
Тантала атом Та I 326, 329
—	ионы Та II, Та III 326
Теллура атом Те I 302, 308
Тензор квадрупольного момента 491
—	момента инерции 531
—	поляризуемости 409, 495, 497, 510, 528,
651, 652, 677, 678
—	— колебательного перехода 497
Теория групп 67
—	— абстрактная 73, 507
—	представлений групп 73
Тепловая энергия 125, 126
Тепловое испускание 22, 145, 146
Тербия атом Tb I 209, 339, 341, 349, 357
— ион Tb II 341
---Tb III 341
890
Предметный указатель
----Tb IV 341, 343
Терм дублетный 223, 228, 235, 241, 247
— мультиплетный 247
— спектральный 21, 37, 220
— триплетный 248, 263
Термическая диссоциация N2 748
Термодинамическое равновесие 22, 23, 124,
125, 128, 143
Термы конфигураций смешанных 259
— — типа dk 328
-------fk 343
— —, состоящих из эквивалентных элек-
тронов 254
Тетраметилметана молекула С(СН3)4 525,
805
Тетрахлорэтилена молекула С2С1| 513
Тетраэдр 502, 522, 524
Технеция атом Тс I 325, 331
- ионы Тс II, Тс III 325
Тиндаля эффект 25
Типы атомных спектров 213
— зеемановских расщеплений 375, 376, 383
— молекулярных спектров 464
— мультиплетов 266
— связи 243
----промежуточные 245, 246
— симметрии 64-67, 72, 73, 76, 114, 115,
638, 645
— — вырожденные 65, 77, 505
— — для точечных групп низшей симме-
трии 649
_____ средней и высшей симме-
трии 511
— — невырожденные 65, 73, 505
— — электронных состояний многоатом-
ных молекул 789
----, число 651, 661
— электронных переходов в двухатомных
молекулах 824
Титана атом Ti I 265, 324, 327, 329-331
- ион Ti II 265, 323, 324, 327, 329, 331
----Ti III 265, 324, 327
----Ti IV 236, 238-240
Тождественная операция 68
Тождественное представление 120
Томсона модель атома 376
Тонкая структура 34
----атома водорода 185, 192
— — атомов щелочных металлов 223
----для молекул 480
----краев поглощения рентгеновских 363
— — учет при явлении Штарка 417
— труктура атома гелия 279
Тонкой структуры постоянная 172, 187, 189,
196
Тория атом Th I 210, 340, 341, 345
- ион Th II 340, 341, 345, 346
----Th III 244, 340, 341, 345, 346
-----Th IV 340, 341, 345, 346
Точечная группа 525, 527
-----Поел 525, 528
-----Сх 513, 525, 527, 831
-----С2 73, 511, 513, 525,652
-----С3 519, 525, 803
-----С4 525
-----С5 525
-----С6 519, 525
-----Сх 519, 525, 657
-----Ci(S2) 73, 116, 511-513, 525, 652
-----G(CIt?) 73, 116, 511-513, 525
-----C2h 512, 515,652
-----C2v 506-508, 511,	526,	658,	678,	709,
791, 816, 817, 821, 828
-----C3h 519, 526
-----C3v 508, 509, 518,	519,	521,	522,	526,
659, 661-663, 665,678, 679,709, 793, 804,
817, 822
-----C4h 518, 519
-----C4v 518, 519, 526
-----C5h 526
-----C5v 526
-----Cbh 519, 526
-----C6r 519, 526
-----Cxh 71, 519, 527
-----Cxv 66, 71, 77, 79, 516, 519, 520, 526,
539, 664, 665, 699, 721, 771, 816
-----D2(V) 70, 76, 80, 512, 519, 528, 649
-----D3 518, 519, 526
-----D4 518, 519
-----D5 526
-----Db 519, 526
-----Dx 526
-----Dx 519
-----D2d(S4vVd) 518-520, 526, 806
-----D2h(Vh) 512, 513, 515, 522, 528, 535,
556, 649, 652, 658, 678, 713, 815, 817
-----P3d(S60 518-520, 665, 681, 804, 838
-----D3h 519, 520, 526, 659, 663, 665, 681,
713, 793, 811, 815, 822
-----D4h 519, 520, 658, 663, 681, 789-791
-----D5h 518, 520, 526, 664, 665, 681
-----Dbh 509, 519, 520, 549, 664, 665, 712,
808, 811, 815, 838, 854
-----Dxh 519, 527, 539, 572, 656, 658, 662,
664, 665, 682, 696, 701, 721, 724, 771, 774,
789, 806, 817, 821, 830
-----I 524, 525, 527
-----Ih 524, 525, 527
-----О 524, 527
-----Oh 525, 527, 665, 666, 682, 817
-----S4 519, 526
-----56(C3t) 516, 519, 524
-----T 524, 527
-----Td 524-527, 534, 610, 659-662, 666,
668, 682, 702, 709, 804, 817, 831
-----Th 527
Предметный указатель
891
Точечные группы высшей симметрии 510,
522
— — низшей симметрии 510, 511
— — средней симметрии 510, 515
---типа Сп 68, 517, 520, 527, 657
-------Cnh 518, 519, 527, 657
-------Cnv 517-519, 527, 789, 817
-------Dn 518, 519, 527, 789
-------Dnh 519, 521, 527, 789
-------Sn 516-518, 527
—	—, таблица 525
Трансконфигурация 504
Трансляционная симметрия 510
Трансурановые элементы 206, 210, 339
Триады термов 248, 260, 295, 331
Трижды вырожденные колебания 645, 654,
659, 660
Триплет зеемановский 374
Триплетная система термов 276
Триплетные состояния молекул 778, 782,
793, 828
Триплеты 250, 252, 264, 379
—	в спектрах марганца и хрома 331
—	— спектре гелия Не I 280
—	железа Fe I 333
—	кальция Ca I 298
-------ртути Hg I 293
Тройные связи 502
Тулия атом Tm I 341, 349
—	ион Tm II 341, 349
---Tm III 341
---Tm IV 341, 343
Туннельный эффект в молекуле аммиака
NH3 643
Тушение 27, 88
—	первого и второго родов 849
Углерода атом С I 206, 214, 242, 302, 307,
309, 751, 797, 808, 813
-	ион С II 306, 311
---С IV 236, 239
---С V281
—	молекула С2 748
Угловая скорость вращения молекулы 531
—	— прецессии 58, 59, 62
Угловое распределение излучения для ди-
поля 102
— — — — — магнитного 99
----------- квадруполя 102
Угловые функции для сферически симме-
тричного поля 178
Ударная теория уширения спектральных ли-
ний 158, 159
Удары первого и второго родов 148
Узловая плоскость 729, 731, 737
Ультрафиолетовая спектроскопия 28
Ундектеты 251
Уолша корреляционные диаграммы 816
Упругие столкновения 148, 158
Урана атом U I 210, 340, 341, 344, 346, 347,
350, 354, 357, 453
- ион U II 341, 346, 347
---U III 341, 347
---U IV 341
Уровни энергии 16
— — вырожденные и невырожденные 41,
42
— — двухатомной молекулы 475, 586
—	— ионизованного атома 351
—	— нуклонов в ядре 456
—	—, основные типы 33, 35
—	—, — характеристики 35, 41
—	—, схема для атома азота N I 310
—	—,— — — алюминия Al I 306
—	—,— — — бария Ba I 288
—	—,— — — водорода Н I 20
—	—,— — — гелия Не I 278
—	—,— — — кадмия Cd I 291
—	— калия К I 226
—	—,— — — кальция Ca I 287, 296
—	—,— — — кислорода О I 310
—	—,— — — лития Li I 225
______ магния Mg I 287
— меди Си I 337
—	— натрия Na I 226
— ртути Hg I 292
— —,— — — рубидия Rb I 227
_ таллия TI I 307
—	—,—	—	—	цезия Cs I 227
---1 _	_	_	цинка Zn I 290
—	—, —	—	молекулы азота N2	777
_	—f _	_	_	окиси азота NO	780
—	—,—	—	—	— углерода СО	779
— —, — сравнительная для атома и иона
гадолиния (Gd I и Gd II) 348
атома и иона самария (Sm I
и Sm II) 348
---,-----------------урана (U I и U II)
346
—	— атомов галоидов (F I, Cl II,
Вг I, J I) 313
—	— с одним внешним элек-
троном (В I, Al I, Cd I, In I, TI I) 304
—	— скандия, титана и вана-
дия (Sc I, Ti I, V I) 330
______ цинка, кадмия и ртути
(Zn I, Cd I, Hg I) 289
—	— щелочноземельных ме-
таллов (Be I, Mg I, Ca I, Sc I, Ba I)
286
_	_ ------щелочных металлов
(Li I, Na I, К I, Rb I, Cs I) 219
—	— членов изоэлектронного
ряда калия (К I—Мп VII) 238
—	—, —	натрия
(Na I-Cl VII) 237
892
Предметный указатель
—	—,— — — — — — цезия
(Cs I—Се IV) 238
Условие частот излучения 16
Условия возбуждения 23, 146-148, 363
Устойчивость электронных состояний мо-
лекулы 719, 740, 788, 794
Устойчивые молекулы 251, 471, 475, 601,
734, 737, 808
—	ядра 422
Уширение спектральных линий 113, 150,
154-156, 158, 160, 407, 417, 419
Фактор дублетного расщепления 228, 311
— мультиплетного расщепления 261, 262
— — — молекулярный 763
Фаулера серия 38, 169
Ферми резонанс 696, 697, 785
Ферми—Дирака статистика 64, 74, 422
Фермия атом Fm I 210, 341
—	ионы Fm II, Fm III, Fm IV 341
Ферромагнитный резонанс 368, 405
Финитное движение 44
Флуктуации излучения 129
Флуоресценция 23
—	сенсибилизированная 149
—	сложных молекул 826, 842
Фока метод 202, 246
Форма колебаний 606, 609, 610, 614
—	молекул 714
— —, определение по микроволновым
спектрам поглощения 557
— полос поглощения и испускания слож-
ных молекул 843
Формальдегида молекула Н2СО 501, 513,
807, 836
Фортра диаграмма 761
Фосфора атом Р I 213, 302
- ион Р V 237, 239, 240
-------XII 288
Фосфоресценция 23
Фосфористого водорода молекула РН3 549
Фотодиссоциация молекул 781, 838
Фотолюминесценция 23, 27, 148, 839, 851
Фотоны 16, 37, 83, 84
Фотоэлектрическое поглощение 366
Франка—Герца опыт 26
Франка—Кондона принцип 756, 757, 759,
778, 781, 783, 784, 786, 829, 830, 833,
834, 838, 841
Франция атом Fr I 204, 209, 213, 216
Фраунгоферовы линии 36
Фтора атом F I 206, 214, 302, 312, 751
---F VIII 280, 281
—	ион F III 312
—	молекула F2 748
Фундаментальная серия атомов щелочных
металлов 222, 234
Функция возбуждения 26
—	распределения 123, 124
—	экранирования 199
Хампфри серия 20
Характеристики переходов 26
—	уровней энергии 26, 42, 45
Характеристические спектры рентгеновские
351, 353
—	частоты колебаний 614, 713
—	— —, таблица 714, 718
Характеристичность в колебательных спек-
трах 713
Характеры представлений 81, 82, 657
—	— для точечных групп 657
Хартри метод 200, 246
Химическая связь 719
—	— в ионе 734
—	молекуле Н2 740
—	— гомеополярная 720
—	— ионная 720
Химические сдвиги 426
—	силы 721
Хлора атом Cl I 214, 302, 312, 444
- ион Cl VII 237, 240
— молекула С12 598, 782
Хлористого бора молекула ВС13 520
— водорода молекула НС1 520, 589, 592,
595, 597, 598, 722
— натрия молекула NaCl 720
Холодное свечение 23
Холодной ртути молекула HgCl2 836, 837
Хрома атом Cr I 209, 265, 324, 331-333
- ион Cr II 265, 324, 331, 332
---Cr III 265, 324, 328, 344
---Сг VI 238
Хромофоры 827
Цветность 827
Цезия атом Cs I 204, 209, 210, 213, 216, 217,
220, 222, 227-229, 233, 235, 236, 240,
322, 362
Центр симметрии 66, 67, 71
— тяжести линий при сверхтонком расщеп-
лении 449, 453
— — мультиплетных термов 241, 301, 309
Центробежное растяжение 539, 543, 549,
556, 600
Центробежные моменты инерции 532
Церия атом Се I 341, 344
- ион Се II 341, 344, 345
---Се III 341
---Се IV 210, 238, 240, 322, 341, 343, 344
Циана молекула C2N2 501, 520, 722
Циановая связь 807
Циклическая группа 75
Циклобутана молекула С4Н8 69, 520
Циклогексана молекула С6Н12 502
Предметный указатель
893
Циклопентана молекула С5Ню 69, 520
Циклопропана молекула С3Н6 69, 521
Циклотронная частота 406
Циклотронный резонанс 405, 406
Цинка атом Zn I 209, 214, 277, 278, 285,
288-290, 324, 336, 338, 452
— ионы Zn I, Zn III 265, 324
Циркона атом Zr I 325, 329, 331
—	ион Zr II 325
---Zr III 325
---Zr IV 236, 240
Цисконфигурация 504
Частицы с целым и с полуцелым спином
78
Частота инверсии 643, 644
—	колебаний 574 х
—	перехода 17, 18; 28, 33
Чередование интенсивностей вращательных
линий 567, 568
—	мультиплетностей 264
Черенкова свечение 27
Черное излучение см. Равновесное излуче-
ние
Четно-нечетные ядра 422, 438, 440, 453, 458
Четно-четные ядра 422, 449, 458
Четность электронных конфигураций для
атомов с d-оболочками 328
—	— — — — — /-оболочками 342
______ р-оболочками 303
Четыреххлористого кремния молекула SiC^
525
—	титана молекула T1CI4 525
—	углерода молекула ССЦ 803
Четыреххлористой платины молекулярный
ион (PtCh)" 658
Число дисперсионных электронов 108
—	колебаний различных типов симметрии
653, 666-669
—	типов симметрии 651, 652
Чисто валентные и чисто деформационные
колебания 648
—	вращательные переходы 489, 539
—	— —, отсутствие для сферического
волчка 542
Чувствительные линии 222
Шестифтористого урана молекула UF6 525,
540, 795
Шестифтористой серы молекула UF6 525
Ширина спектральной допплеровская 157,
158
—	— — естественная 157
— — — — в рентгеновской области 366
---линии 108, 111, 112
Шкала электромагнитных волн 29
Шкалы частот, волновых чисел и длин волн
17, 129
Шпольского эффект 826
Шредингера уравнение 177, 185, 200, 580,
814
Штарка явление 35, 160, 407, 409
— — квадратичное 410, 412, 417-419, 559,
561
— — линейное 409-411, 413, 417-419
— —, открытие 407
Штарковская модуляция 563
Штарковское расщепление спектральных
линий атома водорода 415
— — уровней энергии 407, 410, 413, 418
— уширение спектральных линий 407, 417
Шумана—Рунге система полос О2 778
Щелочноземельные металлы 284-286, 288,
289
Щелочные металлы 208, 210, 214, 216, 218-
224, 228, 229, 233-235
Эйнштейна коэффициенты 83, 84
— —, соотношение 85, 151
Эйнштейния атом Es I 210, 341
— ионы Es II, Es III, Es IV 341
Эйри функции 782
Эквивалентные атомы, связи и углы 509,
515, 520, 525
- электроны 203, 245, 249, 254, 728, 732
— элементы симметрии и операции сим-
метрии 521
Экранирование внутреннее и внешнее 359,
362
— ядра в сложном атоме 198, 201, 207, 236
Экранирования дублеты 358
— постоянная 201, 208, 217, 241
—	— для атомов щелочных металлов 231
—	— — рентгеновских спектров 359
—	— — членов изоэлектронных рядов 241
Электрические источники света 26
— моменты ядер 424
Электрический резонанс 407, 409, 563
Электрическое возбуждение 23, 25
Электролюминесценция 27
Электронная волновая функция молекулы
483
- пара 741-743, 746
— плотность 174, 177, 178
—	—, распределение радиальное 176
---, — угловое 177
—	температура 147
—	энергия молекулы 463, 464, 466, 503
—	— — как функция координат ядер 471,
483
—	— —, порядок величины 464
Электронные конфигурации 203, 242
—	— атома магния 242
894
Предметный указатель
—	— — углерода 242
—	— атомов щелочных металлов 216
—	— двухатомных молекул 731
— — простейших многоатомных молекул
816
— — четные и нечетные 212, 303
— оболочки атома 200
— — двухатомных молекул 731, 816
— — многоатомных молекул 792
— переходы в молекулах 486, 827
— слои атома 200, 210
— состояния молекул двухатомных 719,
721, 729
— — — многоатомных 719, 788, 790, 792,
794, 816, 817
— спектры атомов 163, 213
----молекул 463, 464
----— двухатомных 719, 721, 753, 775,
788
----— многоатомных 155, 824, 828, 829,
836
— уровни энергии 32, 33
Электронный парамагнитный резонанс 34,
143, 368, 402
Электронных пар метод 741
Электроновольт 751
Электростатические взаимодействия элек-
тронов 244, 246, 249
— — ядер 444
Элементы группы 67
Эллипсоид инерции 532, 534, 542
— поляризуемости 496, 528, 532
Эллиптические орбиты 172, 173
Энергия взаимодействия движений в моле-
куле 463
— возбуждения 26
— диссоциации 18, 26, 472, 584, 589-592,
736, 740, 742, 745, 748, 749, 756, 782, 786
— излучения осциллятора 90, 102
— ионизации 16, 18, 19, 26, 167, 216, 217,
277, 281, 284, 288, 297, 301, 307, 311, 322,
340, 350, 359
— молекулы, разделение на части 463, 464,
482
Эрбия атом Er I 341, 349
— ион Er II 341
-----Er III 341
-----Er IV 341, 343
Эрмита полиномы 580
Этана молекула С2Н6 504, 505, 516, 640-642,
706, 710, 711, 795, 805, 838
Этилена молекула С2Н4 477, 501, 503, 513,
515, 535, 556, 652, 653, 666, 679, 684, 706,
708, 795, 805
Эффективное квантовое число 217, 218, 220,
240, 241
Эффективный заряд диполя 578
-----ядра 199, 201, 204, 207, 217
Ядерная спектроскопия 32
Ядерный магнетон 57, 425, 426, 428, 433
— магнитный резонанс 34, 143, 367, 368,
425, 426
— множитель g 425
0-оболочки 728, 729
0-состояния 728
0-электроны 729
А-удвоение 725, 768
тг—тг-переходы 838
тг-оболочки 729
7г-связи 749
тг-составляющие 373, 412, 433
7г-состояния 728
тг-электроны 728
а-связи 749
^-составляющие 373, 412
сг-состояния 728
сг-электроны 728
jD-линии 23, 36, 157, 224, 445, 446
d-состояния 166
d-электроны 203
/-оболочки 214
/-состояния 166
/-электроны 203
I-удвоение 674
п—тг-переходы 838
р-оболочки 214
s-оболочки 208, 213, 729
s-состояния 166, 199
s-электроны 203