Author: Айвазян С.А. Мхитарян В.С.
Tags: теория статистики статистические методы учебники и учебные пособия по статистике задачи по математике математическая статистика учебник для вузов
ISBN: 5-238-00303-Х
Year: 2001
Text
1
С. А. Айвазян
В. С. Мхитарян
f
I
I
X>Tacis
юнити
с
к
Прикладная
СТАТИСТИКА
В ЗАДАЧАХ
И УПРАЖНЕНИЯХ
С. А. Айвазян
В. С. Мхитарян
S. A. Aivazian
V. S. Mkhitarian
APPLIED STATISTICS
In the PROBLEMS and EXERCISES
Textbook
Ж
ЮНИТИ
UNITY
Moscow
2001
Книга подготовлена
при поддержке
Tacis-проекта Delphi
‘Развитие образовательных
связей и инициатив в области
высшего ипрофессионального
образования* - EDRUS 9706
С. А. Айвазян
В. С. Мхитарян
Прикладная
статистика
В ЗАДАЧАХ И УПРАЖНЕНИЯХ
Рекомендовано Министерством общего
и профессионального образования Российской
Федерации в качестве учебника для студентов
экономических специальностей высших
учебных заведений
юнити
UNITY
Москва
2001
УДК 311(076.1)
ББК 60.6я73
А36
Рецензенты:
кафедра статистики Московского государственного университета
коммерции (зав. кафедрой д-р экон, наук, проф. О.Э. Башина);
д-р экон, наук, проф. Г.Л. Громыко
Главный редактор издательства Н.Д. Эриашвили
Айвазян С.А., Мхитарян В.С.
А36 Прикладная статистика в задачах и упражнениях: Учебник для вузов. —
М.: ЮНИТИ-ДАНА, 2001. - 270 с.
ISBN 5-238-00303-Х
Учебник содержит необходимый теоретико-методический материал, а также задачи и упражне-
ния по математической статистике и прикладному многомерному статистическому анализу.
Математический аппарат, необходимый для решения предложенных в книге задач и
упражнений, не выходит за рамки современных курсов по данным дисциплинам, соответст-
вующих принятым в российском высшем экономическом образовании стандартам. Особое
внимание, уделенное в учебнике разделам А («Краткие сведения из теории») и Б («Примеры
решения типовых задач и упражнений»), позволяет использовать его для самостоятельного
освоения методов прикладной статистики в режиме экстерна. По своему содержанию, струк-
туре, логике исследования, основным понятиям и обозначениям книга ориентирована на
базовый учебник Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконо-
метрики (Москва, ЮНИТИ, 1998 г.) — главы 6—13 и 1-й том второго издания этого учеб-
ника, рекомендованные Министерством образования РФ для студентов экономических спе-
циальностей вузов.
ББК 60.6я73
ISBN 5-238-00303-Х
© С.А. Айвазян, В.С. Мхитарян, 2001
© «ИЗДАТЕЛЬСТВО ЮНИТИ-ДАНА», 2001
Воспроизведение всей книги или любой ее
части запрещается без письменного
разрешения издательства
ОГЛАВЛЕНИЕ
Предисловие 6
Раздел I. Математической статистика 8
Глава 1. Статистическое оценивание неизвестных значений па-
раметров модели 8
1.А. Краткие сведения из теории 8
1.Б. Примеры решения типовых задач и упражнений 21
1.В. Задачи и упражнения 48
Глава 2. Статистическая проверка гипотез 64
2.А. Краткие сведения из теории 64
2.Б. Примеры решения типовых задач и упражнений 77
2.В. Задачи и упражнения 92
Раздел II. Прикладной многомерный статистический анализ 101
Глава 3. Корреляционный анализ 101
З.А. Краткие сведения из теории 101
З.Б. Примеры решения типовых задач и упражнений 118
З.В. Задачи и упражнения 132
Глава 4. Снижение размерности анализируемых многомерных
признаков и построение интегральных показателей... 140
4.А. Краткие сведения из теории 140
4.Б. Примеры решения типовых задач и упражнений 156
4.В. Задачи и упражнения 163
Глава 5. Классификация: распознавание образов и типологиза-
ция (дискриминантный и кластерный анализы) 172
5.А. Краткие сведения из теории 172
5.Б. Примеры решения типовых задач и упражнений 182
5.В. Задачи и упражнения 198
Литература 206
Приложение 1. Таблицы математической статистики 207
Приложение 2. Исходные статистические данные 225
Ответы и решения:
Упражнения: 229
Задачи: 247
ПРЕДИСЛОВИЕ
В предисловии к учебнику «Прикладная статистика и основы эконо-
метрики» (издательство «Юнити», Москва, 1998 г.) мы писали, что
«несмотря на наличие ряда иллюстративных примеров и упражнений,
предлагаемый учебник не решает проблемы задачника по эконометри-
ке. Поэтому для проведения полноценного учебного процесса он должен
быть дополнен набором эконометрических задач и упражнений ...». Про-
анализировав известные нам по отечественной и мировой специальной
литературе учебники и задачники1^ мы, к сожалению, не смогли най-
ти такого издания, которое отвечало бы нашему взгляду на содержание
математико-статистического инструментария эконометрики, причисляю-
щего к последнему, в частности, основной спектр методов прикладного
многомерного статистического анализа (включающего, помимо тради-
ционных для эконометрики регрессионного анализа и анализа временных
рядов, также методы классификации многомерных наблюдений и сниже-
ния размерности). Это и явилось для нас главным побудительным моти-
вом к тому, чтобы попытаться профильтровать и просистематизировать
весьма большое количество задач и упражнений, которое накопилось за
несколько десятков лет нашей преподавательской деятельности в Москов-
ском государственном университете им. М.В. Ломоносова, Московском го-
сударственном университете экономики, статистики и информатики, Рос-
сийской экономической школе, Государственном университете — Высшей
школе экономики, и представить результаты этой работы в форме учеб-
ника.
Среди проанализированных изданий: W.H. Green. Econometric Analysis. — Maxwell
Macmillan Int. Publ. Group, 1993; R.S. Pindyck, D.L. Rubinfeld. Econometric
Models and Economic Forecasts. — MeG raw-Hill Kogakusha Ltd, 1976; П.К. Каты-
шее, А.А. Пересецкий. Сборник задач к начальному курсу эконометрики. — Дело,
Москва, 1999; Г.В. Емельянов, В.П. Скитович. Задачник по теории вероятностей
и математической статистике. — Изд-во Ленинградского университета, 1967; Сбор-
ник задач по теории вероятностей, математической статистике и теории случайных
функций (под ред. А.А. Свешникова). — «Наука», М.: 1970; E.R. Berndt. The
Practice of Econometrics. Classic and Contemporary. — Addison-Wesley Publ. Comp.,
1990 и многие другие.
7
Предлагаемое издание лишь частично решает поставленную задачу.
Оно содержит задачи и упражнения только по математической стати-
стике и прикладному многомерному статистическому анализу. Авторы
планируют дополнить это издание вторым томом, содержащим задачи и
упражнения по методам и моделям регрессионного анализа, по анализу
временных рядов, по системам одновременных уравнений.
Математический аппарат, используемый при решении предложенных
задач и упражнений, не выходит за пределы современных курсов по ма-
тематической статистике и прикладному многомерному статистическому
анализу, читаемых, в частности, в упомянутых выше вузах. Каждая из
пяти глав задачника состоит из трех частей (А, Б и В): в первой приводят-
ся краткие сведения о понятиях и результатах соответствующего раздела;
во второй части (Б) подробно разбираются решения набора типовых за-
дач; наконец, в третьей части главы (В) приводятся формулировки задач
и упражнений для самостоятельного решения. Следует подчеркнуть, что
повышенное (по сравнению с другими аналогичными изданиями) внима-
ние, уделенное авторами первым двум частям каждой из глав, позволяет
нам высказать мнение, что данное издание может быть использовано
читателем и как самостоятельный учебник по освоению методов при-
кладной статистики в режиме «экстерна». Именно этим объясняется
и наш выбор заглавия данного издания: не «Задачник», а «Прикладная
статистика в задачах и упражнениях».
Авторы признательны Европейскому фонду подготовки кадров (про-
ект Делфи, TACIS), признавшему наш учебник, вышедший в свет в 1998
г., победителем «Конкурса на лучший учебный материал, разработанный
в рамках проектов TACIS» и поддержавшему издание этого задачни-
ка. Мы благодарны, конечно, и главным потребителям и рецензентам
представленной в задачнике продукции — многим поколениям студентов
упомянутых вузов, без которых появление этого учебника-задачника было
бы невозможным.
Раздел I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Глава 1. Статистическое оценивание
неизвестных значений
параметров модели
1.А. Краткие сведения из теории
Одна из центральных задач эконометрического анализа реальной си-
стемы (формализуемой в математической статистике с помощью понятия
«исследуемая генеральная совокупность») заключается в вычислении
на основании имеющихся в распоряжении исследователя исходных ста-
тистических данных (или выборки) как можно более точных прибли-
женных значений (статистических оценок) для одного или нескольких
параметров, участвующих в модельном описании этой системы, или для
анализируемого закона распределения вероятностей (з.р.в.), представлен-
ного в виде некоторой функции. При этом статистику приходится опери-
ровать такими понятиями как выборочная (эмпирическая) функция
распределения, относительная частота, выборочная (эмпириче-
ская) функция плотности вероятности, состоятельность, несме-
щенность и эффективность статистической оценки, функция прав-
доподобия имеющихся наблюдений, знать основные методы точечного и
интервального оценивания неизвестных параметров (метод макси-
мального правдоподобия, метод моментов) и способ измерения эф-
фективности оценки (неравенство информации), иметь представление
о байесовском подходе к статистическому оцениванию. Напомним спра-
вочно выделенные понятия.
Генеральная совокупность — удобный в статистических приложе-
ниях синоним понятий «вероятностное пространство», «случайная вели-
чина», «закон распределения вероятностей», «исследуемая реальная сто-
хастическая система», — определяется как совокупность всех мыслимых
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
9
наблюдений анализируемой случайной величины, которые могли бы быть
сделаны в данном неизменном реальном комплексе условий.
Выборка ж15 ж2,..., хп — это имеющиеся в распоряжении статисти-
ка результаты наблюдений анализируемой случайной величины £, или —
статистически обследованная часть генеральной совокупности, по которой
мы хотим судить об интересующих нас свойствах генеральной совокупно-
сти в целом.
Если условия наблюдений анализируемой случайной величины £ не
меняются от одного наблюдения к другому и если п-кратный процесс на-
блюдения £ организован таким образом, что результаты наблюдения на
каждом (г-м) шаге никак не зависят от предыдущих и не влияют на бу-
дущие результаты наблюдений, то, очевидно, вероятностные закономер-
ности, определяющие результат г-го наблюдения ж, выборки, остаются
одними и теми же для всех i = 1,2,..., п и полностью определяются зако-
ном распределения вероятностей наблюдаемой случайной величины, т. е.
P{xi < х} = Р{£ < х} = Г^(ж). В подобных случаях выборка называется
случайной. В дальнейшем, если специально не оговорено противное, мы
будем иметь дело только со случайными выборками.
Выборочная (эмпирическая) функция распределения F^n\x)
является непараметрической статистической оценкой теоретической функ-
ции распределения F(x) = Р{£ < ж} и определяется по случайной выборке
ж^, ж2,..., жп соотношением
(1.1)
где р(ж) — число элементов в выборке, меньших заданной величины ж.
Выборочные данные могут быть представлены в группированном виде,
когда весь статистически обследованный диапазон [жт;п, жтах] значений
анализируемой случайной величины £ разбивается на s » log2 п+1 равных
интервалов группирования
Д, ✓ . , \ Я'тах ~ •J'min , . *^max “ *^min \ /i л\
j = *min + (j “ I)-----------; Emin + J---------- I , (1.2)
3 3 J
j = 15 2,..., s,
и вместо наблюденных выборочных значений ж, (г = 1,2,..., п) исследова-
тель располагает лишь знанием количеств Vj выборочных данных, попав-
ших в j-й интервал группирования Aj (очевидно, щ + i/2 + • • • + va = n).
Тогда выборочная функция распределения определяется соотношением
г<»>(1) = (1,3)
10
1. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
где ix — номер самого правого из интервалов группирования, правый
конец которых не превосходит заданного значения х.
Выборочная (эмпирическая) относительная частота р\п^ вво-
дится при анализе дискретной случайной величины £, принимающей воз-
можные значения с вероятностями р< = (» = 1,2,...). Она
является статистической оценкой вероятности р< и определяется соотно-
шением
р<“’ = (1.4)
п
где — число наблюдении в выборке Xi, , яп, равных заданному
о
возможному значению х,.
Выборочная (эмпирическая) функция плотности f^n\x) в за-
данной точке х является непараметрической статистической оценкой те-
оретической функции плотности /(ж) и определяется по группированным
выборочным данным для непрерывной случайной величины с помощью
соотношения
/П)(®) = (1-5)
в котором А(х) — порядковый номер интервала группирования, накрыва-
ющего заданную точку х, a Vk(x) — число выборочных данных, попавших
в этот интервал.
Гистограмма — это график эмпирической функции плотности
/'“’(*)
Статистическая оценка 9 неизвестного параметра 9 — это не-
которая функция от результатов наблюдения ж1,Ж2,... ,жп (т.е. 9 =
0(Ж1,Ж2,... ,жп)), используемая в качестве приближенного значения неиз-
вестного параметра 9. Поскольку при повторении выборки того же объема
п из той же самой генеральной совокупности и при подстановке получен-
ных новых выборочных значений x'i,x'2,... ,х'п в ту же самую функцию-
оценку 9(х\, а?2,..., х'п) мы, вообще говоря, получаем другое число в каче-
стве приближенного значения для интересующего нас параметра 9 (т. е.
имеем некоторый неконтролируемый разброс в значениях оценки 9 при
повторениях выборки), то сама оценка 9 по своей природе является вели-
чиной случайной.
Оценка 9(х^, • • •, хп) неизвестного параметра 9 называется состо-
ятельной, если по мере неограниченного роста объема выборки п (т. е.
при п —> оо) ее значение стремится (по вероятности) к истинному значе-
нию оцениваемого параметра 9.
Оценка 9(xi,ж2,...,хп) неизвестного параметра 9 называется несме-
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
11
щенной, если при любом объеме выборки п результат ее осреднения по
всем возможным выборкам данного объема приводит к точному истинно-
му значению оцениваемого параметра, т. е. Е0 = 0.
Эффективность оценки 0 измеряется средним квадратом ее откло-
нения от истинного значения параметра 0 (усреднение — по всем возмож-
ным выборкам данного объема из анализируемой генеральной совокупно-
сти): чем меньше Е(0 - О')2, тем эффективнее оценка 0.
Неравенство информации устанавливает для широкого класса ге-
неральных совокупностей то пороговое значение Amin среднего квадрата
ошибки Е(0 — 0)2 оценок 0, уменьшить которое невозможно, а именно:
Е(« - в)’ >
(1 + У/
(1-6)
где /(я | 0) = Р{£ = х | в}, если анализируемая случайная величина
дискретная, f(x | О') — функция плотности вероятности анализируемой
случайной величины £, если она непрерывна, а b(0) = [E0(zi,..., жп)-в] —
величина смещения оценки 0.
Неравенство (1.6) позволяет измерять эффективность оценок 0(х\,...
... ,хп) в единой шкале, а именно, если обозначить правую часть (1.6) с
помощью Amin, то эффективность е(0) оценки 0 определяется как отноше-
ние
- А2 •
'(») = 57^7?
Из определения эффективности следует, что ее значения могут
варьироваться от нуля (самые неточные оценки) до единицы (эффектив-
ные, или предельно точные оценки).
Средний квадрат ошибки оценивания Е(0 — в) и связанное с ним
понятие эффективности оценки частично проясняют вопрос, как силь-
но может отклоняться оценка 0 от оцениваемого истинного значения
9. Еще более точный ответ на этот вопрос получают с помощью
интервальной оценки, задаваемой в виде определяемого по резуль-
татам выборки ж1,ж2,... ,жп числового интервала [0т|п(я1,Ж2, • • •,sn),
0max(sbS2,...,zn)], который обладает тем свойством, что с некоторой,
близкой к единице, вероятностью Pq накрывает истинное значение 0 оце-
ниваемого параметра, т.е.
< 0 < ^m&x} ~ ^0-
12
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Вероятность Pq называют уровнем доверия или доверительной веро-
ятностью.
Существуют два подхода к построению интервальных оценок: точ-
ный^ конструктивная реализация которого удается лишь в сравнитель-
но узком классе модельных ситуаций, и асимптотически приближенный,
наиболее распространенный в практике эконометрического анализа.
Точный подход удается реализовать лишь в случаях, когда существу-
ет принципиальная возможность подбора такой функции от результатов
наблюдения xi,x2,.. .хп (т. е. такой статистики), закон распределения
вероятностей которой обладал бы одновременно следующими свойствами:
(i) не зависит от оцениваемого параметра 0;
(ii) описывается одним из стандартных затабулированных распределений
(стандартным нормальным, х2-> t- или /"-распределением);
(iii) из того факта, что значения данной статистики заключены в опре-
деленных пределах с заданной вероятностью, можно сделать вывод,
что значение оцениваемого параметра 0 тоже должно лежать между
соответствующими границами с той же вероятностью.
Как правило, такая статистика подбирается с помощью подходящей
нормировки точечной оценки параметра (см. пример 1.3).
Приближенный подход основан на асимптотической нормальности то-
чечных оценок максимального правдоподобия 0МП, из которой следует при-
ближенное выполнение (с заданной вероятностью Pq = 1 —2g) следующего
неравенства:
|0МП — 0| < wq • ^0(0), (1.8)
или, что то же
#мп - W, • as(0) < е < 0МП + wq • (1.8')
где wq — lOOg-процентная точка стандартного нормального распределе-
ния, а а|(0) = D0Mn — дисперсия оценки 0МП, при вычислении которой,
в случае ее зависимости от неизвестного значения параметра 0, вместо
этого неизвестного значения подставляется значение ее оценки 0МП. При
этом предполагается, что оценка 0МП — несмещенная (если это не так, то
ее предварительно «подправляют» соответствующим образом на несме-
щенность).
Функция правдоподобия L наблюдений , хз,... , жп для дискрет-
ной случайной величины ( определяется как вероятность получить в ка-
честве первого элемента выборки число в качестве второго элемента
выборки — число Х2 и т. д., т. е.
Z(x1,x2,... ,хп) = Р{1-е набл.= х\, 2-е набл. = ж2,..., n-е набл.= жп}.
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
13
Для непрерывной случайной величины функция правдоподобия Цх^, ж2,...
. ..,жп) определяется как совместная n-мерная плотность вероятности,
описывающая закон распределения вероятностей (з.р.в.) для п наблю-
дений анализируемой случайной величины. Соответственно, если /(ж |
0) — зависящая от параметра 0 функция, описывающая з.р.в. анали-
зируемой случайной величины £ (т.е. /(ж | 0) = Р{£ = ж} для дис-
кретной случайной величины £ и /(ж | 0) — плотность распределения
вероятностей для непрерывной случайной величины £), а наша выборка
Ж1,ж2,...,®п состоит из статистически независимых наблюдений, то
п
L(xux2,.. .,хп | 0) = [р(ач | 0). (1.9)
1=1
Во многих ситуациях при статистическом анализе выборки ж1}ж2,.. . ,жп
удобнее пользоваться так называемой логарифмической функцией
правдоподобия /(ж1? ж2,..., хп | 0) = 1п1(ж1,ж2,... ,жп | 0), которая,
соответственно, определится соотношением
l(xi,x2,...,xn I 0) = ^2In f<Zi I 0). (1-10)
«=1
Метод максимального правдоподобия определяет оценки макси-
мального правдоподобия 0МП = (0мп Лм«> • • • ,^мп )Т неизвестных параме-
тров 0 = по наблюдениям хг,х2,...,хп анализируе-
мой случайной величины £ из условия
L(xi,x2,...,xn | 0МП) = max£(®i,®2, • • • ,®„ I 0). (1.11)
е
Если функция f(x | 0) удовлетворяет некоторым условиям регуляр-
ности (дифференцируемость по 0 и т.п., см. условия в п. 7.3 [1]) и экс-
тремум в (1.11) достигается во внутренней точке допустимых значений
параметров 0 = (0(1),0(2),...,0(/t))T, то оценки 0М„ = ЙМ2!, • • •,^мп)Г
определяются как решения системы уравнений
,=1>2 (112)
Метод моментов определяет оценки 0ММ = (0мм > • • •, 0^м) неиз-
вестных параметров 0 = (0^\ ..., 0^)Т по наблюдениям Жх, ж2,..., жп
анализируемой непрерывной случайной величины £ как решения системы
14
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
уравнений
/1 п
x}f(x |0)d®= -Va:', j = 1,2,..., к. (1.13)
В случае дискретной переменной £ интеграл в левой части (1.13) заменя-
ется на соответствующую сумму, т. е.
N 1 п
I ©) = J = i,2, ...,Л, (1.13')
1=1 «=1
где г? — 1-ое возможное значение дискретной переменной £, a N — общее
число всех возможных значений £ (JV может быть равно и +оо).
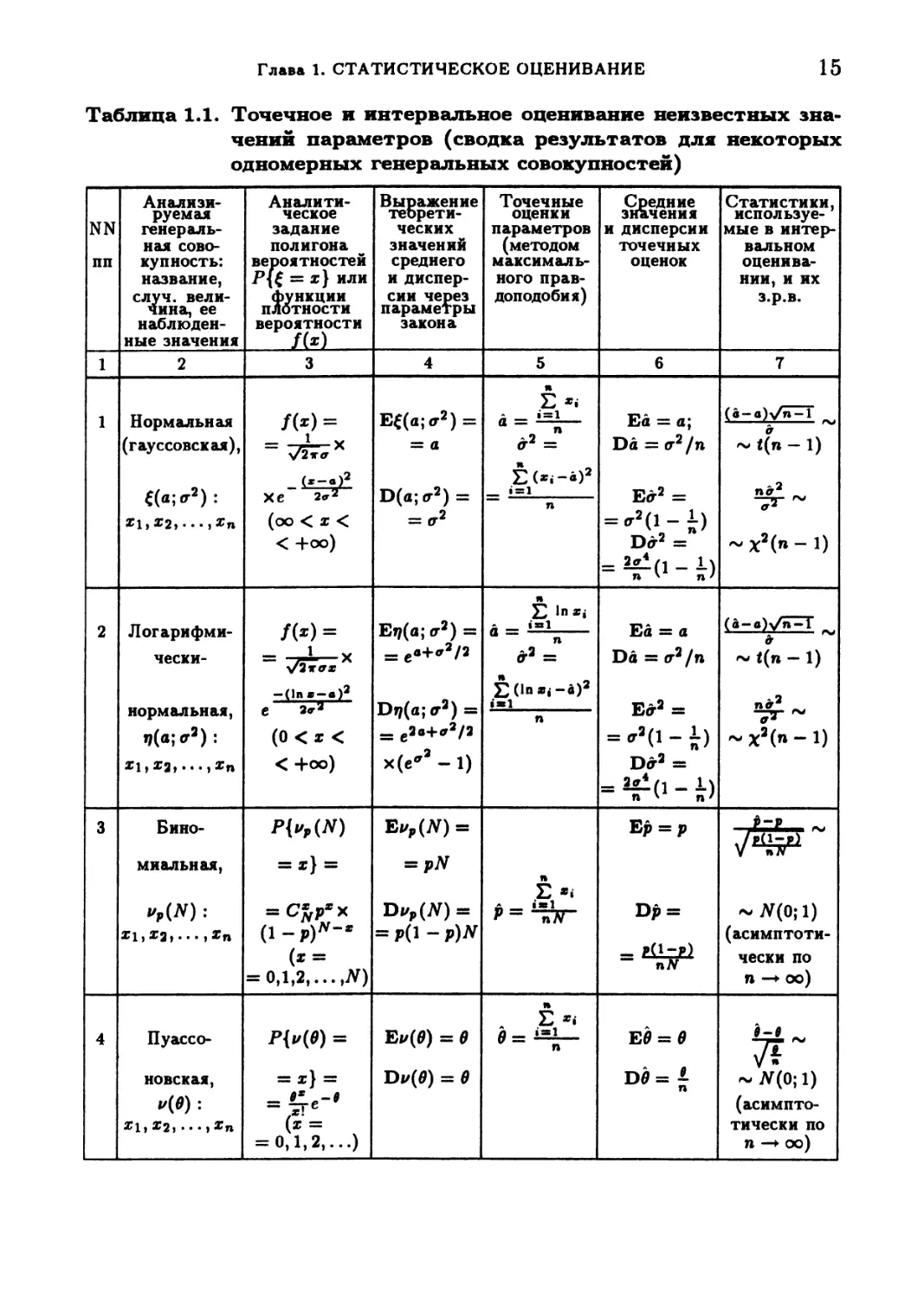
В таблице 1.1 приведена сводка результатов о наиболее распростра-
ненных в статистической практике одномерных законах распределения ве-
роятностей. В ней описаны точечные оценки максимального правдоподо-
бия для неизвестных значений параметров и статистики, используемые
при построении интервальных оценок.
При достаточно общих условиях регулярности, относящихся^ изу-
чаемому з.р.в. /(®|0), и оценки максимального правдоподобия 0МП, и
оценки метода моментов 0ММ являются состоятельными, асимптотиче-
ски (по п —► оо) несмещенными и асимптотически нормальными. К до-
стоинствам метода моментов следует отнести его сравнительно простую
вычислительную реализацию. Однако асимптотическая эффектив-
ность оценок, полученных методом моментов, оказывается, как прави-
ло, меньше единицы, ив этом отношении они уступают оценкам
максимального правдоподобия. Последние, как известно (см., например
[1], п. 7.5), являются асимптотически эффективными,
т.е. их ковариационная матрица S(0Mn) асимптотически (по п —► оо)
имеет вид
s(e„.) = 1г*(0),
п
где 1(6) — так называемая информационная матрица Фишера (ее элемен-
ты определены соотношениями (7.7) из п. 7.2 [1]).
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
15
Таблица 1.1. Точечное и интервальное оценивание неизвестных зна-
чений параметров (сводка результатов для некоторых
одномерных генеральных совокупностей)
NN пп Анализи- руем ая генераль- ная сово- купность: название, случ. вели- чина, ее наблюден- ные значения Аналити- ческое задание полигона вероятностей Р{( = х} или функции ПЛОТНОСТИ вероятности fM Выражение теорети- ческих значений среднего и диспер- сии через параметры закона Точечные оценки параметров (методом максималь- ного прав- доподобия) Средние значения и дисперсии точечных оценок Статистики, используе- мые в интер- вальном оценива- нии, и их з.р.в.
1 2 3 4 5 6 7
1 Нормальная (гауссовская), е(а;а2): Xi, Х2, • • • , Хп /(»)= — "7?—х хе 2<г2 (оо < х < < +оо) I II СЧ Z'“'4CN Ь « % ь .2, И у II Н Q Н «М.н е " S е II ”ь «Мн ,e II „Л -Тс «« II 1 II 1 п % Хт » g н % ° $1в и и и (а-д)у^Т ~ t(n — 1) ~ №(»» ~ 1)
2 Логарифми- чески- нормальная, ij(a;<ra): • • • > *п л*)= = 757^х е а*3 (0 < х < < +оо) Ет/(а; гт2) = = ев+*2/2 Dq(a; a2) = = c2a+<72/2 х(е’’ - 1) Е In Xi a’ = 2 (in х, -а)2 »Ж1 n Ей = а Dd = о-2/п Ед-2 = ='а(1-*) Da’ = = 2zi(i _ 1) n ' п 1 (а-а)уп-! ~
3 Бино- миальная, РЫЮ = х} = = Wx (!-₽)"- (х = = 0,1,2,... Л) Ei/,(AT) = = pN Dv,(N) = = Р(1 - P)N R L> «Мир II «а. Ер = р Dp = _ Hi-p) ПЛ -Х-g,,- ~ ^4^ ~ЛГ(0;1) (асимптоти- чески по п —► 00)
4 Пуассо- новская, 1/(0): Ж1, Х2> • • • » хп ** II КЗ II л Ъ : -"и Ei/(0) = 0 D</(0) = в II 3|им» н *ь|е II II и Q “7^ ~лГ(0;1) (асимпто- тически по п —► оо)
16
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 1.1 Продолжение
1 2 3 4 5 6 7
5 Экспонен- циальная (показатель- ная) с пара- метром масштаба в\ г 7 Xl, Х2, .. .,хп II X о 'ы' '« VI II Е6(0) = 0; D6(0) = 02; «Ни В II О И » II 2п$ ~Х2(2п)
6 Экспонен- циальная (показа- тельная) с парамет- ром сдвига о, 6(0): Z1,Z2, ...,Хп /(*) = = е-(«-О, я > 0; Е6(0) = = 1 +0 D6(0) = l 9 = min {х,} 1<»<п (нерегуляр- ный случай) Е0 = 0 + 1 D0=^" Статистика 6(0) = = п(0 - 0) распреде- лена по экспонен- циальному закону (без сдвига) с парамет- ром масш- таба. рав- ным еди- нице
7 Экпонен- циальная (показа- тельная) с парамет- ром масш- таба 01 и параметром сдвига 02, 61 (0а): 11 I <£ А\ 1 R -к* E6,(02) = = 01+^2 D6i(o2) = II £ || 1 <<£ н I Ей »И.»| ЕО2 = О2 + DOj = 02/п2 EOi = = 0!-1б D01SSb- (с точностью до о(п-1)) 62-62-^- 1 О— ли fll/n ~ АГ(0;1) (асимпто- тически по п —► оо); ^1/хА ~ N(0; 1) (асимпто- тически по п —► оо)
8 Парето, о(0): Xl,2?2,---,^n /(х) = = £W+1. Z > СО (значение со известно) En(0) = ~ Нтс° (сущест- вует при о> 1); D»/(0) = е (»-1)а(»-2)С° (существу- ет при 0 > 2) 0 = + „и 3 << II тЧ" i|-.+ il + +11- 3ng ~ ~№(2п)
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
17
Продолжение
Таблица 1.1
1 2 3 4 5 6 7
9 Равномер- но распре- деленная, 6(а;6) : Х\, 12)••• , хп /(*) _ 1 Ь— a ’ а х 1 Е6(а; 6) = а 4-6 ~ 2 D«(a;6) = “ 12 а = min {г,} 1 < i С п Ь = тал {z,} 1 Ed = “+£t Da = n(6—a)2 (n+l)*(n+2) E6 = k b—a Di> = n(6—a)2 (n + l)'2(n+2) b-& -Л , "t,1 / n(*~A)2 V (n + l)2(n+2) ~ 7V(0; 1) I n(b-a)2 V (n + l)2(n+2) ~ 7V(0; 1) (асимпто- тически no n —> oo)
10 Случай независимых выборок из двух генеральных совокупностей: 1) ^11,^12) • • • , Zlni из (ai;tr2)- норм. ген. сов-сти; 2) Х2Ь 2^22, • • • , х2п2 из (a2;tr2)- норм. ген. сов-ти См. п. 1 таблицы при а = ai См. п.1 таблицы при а = а2 Статистика (51-52)-(ai ~д2) подчинена t(ni 4- n2 - 2)- распределению; *1 = xii) /ni; / п2 \ £2 = 1 52 x2i) /пг; \1 = 1 / -2 _ *1«i + ”2*2 ni+n2—2 ’ где = J 1 = 1 Используется для интервальной оценки разности ai — аз
11 Случай независимых выборок из двух генеральных совокупностей: 1) Zll|Z12,---,Zlni их (ai; )- норм. ген. сов-сти; 2) 2?31,^32,---.®2n2 из (дг;^2)’ норм. ген. сов-сти. См. п. 1 таблицы при а = а\ и <г2 = <г2 См. п. 1 таблицы при а = аз и а2 = ст2 Статистика (n2-l)ni<? t <г| (ni-l)n24j 0^ подчинена F(ni — 1; пз — 1) - распределению (обозначения предыдущего пункта). Используется для интерваль- ной оценки отцрш^ния
Комментарий к использованию табл. 1.1. Приведенные в ше-
стом столбце таблицы точечные оценки для неизвестных значений па-
раметров получены с помощью описанного выше метода максимального
18
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
правдоподобия. Вывод всех этих оценок содержится в помещенном ниже
разборе примеров типовых задач либо предусмотрен в самостоятельных
решениях задач и упражнений, имеющихся в данном учебнике. Для по-
строения интервальных оценок следует воспользоваться информацией, со-
держащейся в последнем (седьмом) столбце таблицы. А именно: по задан-
ному уровню доверия Pq определяют с помощью таблиц (или с помощью
непосредственных вычислений, как это следует сделать в п. 6 таблицы)
100^^-%-ную и 100 lr2Pfl %-ную точки wi+p0 и wi-pa соответствующего
(указанного в том же седьмом столбце) распределения, которые гаранти-
руют выполнение неравенств
Wl + Pg < < Wl-Pn (1.14)
с вероятностью Pq (здесь 7(0; 0) — указанная в столбце 7 статистика);
после этого разрешают данные неравенства относительно неизвестного
параметра в. Поясним это на примере, скажем, п. 8 таблицы. Пусть
Ро = 0,95 и п = 20. В данном примере статистика 7(0; 0), используемая
для построения интервальной оценки, имеет вид 7(0; 0) = 2п0/0 и рас-
пределена по закону %2 с 2п степенями свободы. В соответствии с (1.14)
имеем:
Хо,97в(40) < -у < Хо,о2в(40) (1.14*)
с вероятностью Ро — 0,95. Определяя по таблицам процентные точки
Х2(40)-распределения (xo,97s(40) = 24,43 и Xo,O2s(40) = 59,34) и разрешая
неравенства (1.14') относительно 0, имеем:
24,430 л 59,3340
40 40
или
0,610 < 0 < 1,480 с вероятностью Ро = 0,95.
Байесовский подход к оцениванию предполагает наличие априор-
ных (т.е. имеющихся до получения выборочных данных Х\,Х2,... ,®п)
сведений об оцениваемом параметре 0 в виде априорного з.р.в. р(0)
(плотности вероятности, если 0 — непрерывен по своей природе, и веро-
ятности того, что неизвестный параметр равен значению 0, если этот па-
раметр дискретен). В этом случае байесовские оценки 0^ определяются
как среднее значение апостериорного з.р.в. <p(Q | x^,X2t... ,®п) параме-
тра 0, вычисляемого после получения выборочных данных хъх2,..., хп
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
19
по формуле
</>(0 | 1^X2,
ч _ p(Q)L(xi,x2,...,xn I 0)
f p(Q)L(x1,x2,...,xn I 0) dQ'
(1-15)
Однако именно трудоемкость вычисления по формуле (1.15) апосте-
риорного распределения оцениваемого параметра является одним из двух
главных «узких мест» в практической реализации байесовского подхода.
Определенное упрощение этой задачи достигается с помощью выделения
в множестве всех возможных априорных распределений так называемых
сопряженных (по отношению к анализируемой генеральной совокупности)
распределений. А именно: параметрическое семейство априорных рас-
пределений {р(0)} называется сопряженным по отношению к анализи-
руемой генеральной совокупности (характеризуемой функцией правдо-
подобия А(я1, ^2,..., яп | О)), если соответствующее (вычисленное по
формуле (1.15)) апостериорное распределение <р(0 | хг,х2^... ,жп) будет
относиться к тому же самому параметрическому семейству, что
и р(0). Очевидно, для сопряженных априорных распределений вычисле-
ние апостериорного распределения ^(0 | ®i, х2,... ,хп) сводится лишь к
пересчету значений его основных числовых характеристик, т. к. общий
параметрический вид функции <р нам задан видом априорного распреде-
ления р(0). В табл. 1.2 приведены примеры сопряженных априорных рас-
пределений для некоторых случаев оценки единственного неизвестного
параметра.
Таблица 1.2. Сводка сопряженных семейств априорных распределе-
ний р(0) для ряда з.р.в., зависящих от единственного па-
раметра 0
NN пп Анализируемый з.р.в. плотность f(x | 0) или Р{£ = х | 0} Априорный з.р.в.: плотность р(0), Е0, D0 Апостериорный з.р.в.: | Xi,...,®п). Байесовская оценка 0<Б) параметра 0
1 2 3 4 5
1 (9; а2 )-нормальный, /(*1*) = , 1 = , с 2а2 УЗга (значение дисперсии <г2 известно) (во; а2)- нормальный; Е0 = 0о; D0 = a2 (во и а2 - заданы) (<М2)- нормальный, где ej = ^H 'о’= £(!+ ?)-’, а 7 = a2 /nag $(Б) _ *+7»0 14-7 ’ где x = (Ezf)/n i=i a2 и 7 =
20
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 1.2 Продолжение
1 2 3 4 5
2 (а; |)-нормальный /(*!') = (значение среднего а известно) Н*) = (0 > о), гамма-распре- деление; Е0= п»4 (а и р заданы) Г амма-распреде- ление с параметрами а' = а+|, Р' = Р+^, где ^ = (Е(х.-«)2)/п 1=1 и х = (Е х,)/п 1=1 " 11 Sl-fef; -«1* «ф>|« ± + " : + « * -г. и и
3 Экспоненциальный ,/ , (9е~1х,х^0 1 0, х < 0 = Ца)х (0 > 0), гамма- распределение; Е0 = а/0; D0 = а/р2 (а и р заданы) Г амма-расп реде- ление с параметрами а1 = а 4- п; /?' = Р + £ х,- 1=1 0(Б) = 4 = = а-Ьп 0+Е i=i
4 [0; ^-равномерный: /(х I 0) = ( j для 0 < х < 0; 1 0 для х & [0; 0] в₽ю = J при 6 60; ( 0 при 0 < 0о; (00 > 0; а > 2), распределение Парето: Е0 = (a—l)a(or—2) (а и 0о заданы) Распределение Парето с параметрами а1 = а + п, max{0o; Xi, хз> • • • > хп} № = а' — 1 ’ где а' и определены в предыду- щем столбце
5 Распределение Пуассона: P{i = х} = х = 0,1,2,.*.. ,(«) = (0 > 0), гамма- распределение; (а и /9-эаданы) Гамма-распределе- ние с параметрами а1 = а + 52 i=i Р’ = Р + п = ^ = i=l 0+п
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
21
Таблица 1.2 Продолжение
1 2 3 4 5
6 Биномиальное распределение: РК = г} = CxN0x(l - 0)N~X (значение параметра N известно) ₽(<?) = Г(а+6) до —1/1 _ Д\6-1 г(.)г(»)(' и (0 < 0 < 1), бета-распределение; Е0 = -fr; о-г о т\д ab w ~ (а+6)2(в+Ь+1) (а и Ь заданы) Бета-распределение с параметрами а1 = а 4- £ X,-; i=i 6' = b 4- nN - £ xi i=i 0(Б) = у = л* 4- п Е ч ,~*т1~+'Ат
Комментарий к использованию табл. 1.2. Приведенные в столб-
це 4 плотности апостериорных з.р.в. неизвестного параметра 0 получены
по формуле Байеса (1.15). Вывод этих конкретных выражений для апо-
стериорной плотности <р(0 | х\, х2,..., хп) содержится в разборе примеров
типовых задач (см. следующий п.Б) либо предусмотрен в самостоятель-
ных решениях задач и упражнений, помещенных в данном учебнике (см.
п.В в данном разделе). Для построения байесовских интервальных оце-
нок следует воспользоваться знанием апостериорного з.р.в. параметра О
(см. столбец 4), а именно: по заданному уровню доверия Ро необходимо
найти ЮО1"^0 %-ную и НЮ1"/’0 %-ную точки wi+p0 и wi-p0 указанного в
4-м столбце распределения <р(0 | х^, х2,. • •, хп), которые и гарантируют
нам выполнение неравенств
Wi-bP0 < 0 < W1-PO
2 2
с вероятностью Ро (см. ниже пример 1.8).
Приведенные в столбце 5 байесовские точечные оценки являются
средними значениями соответствующих апостериорных распределений. С
помощью х2,..., хп в таблице обозначены, как обычно, п независимых
наблюдений анализируемой случайной величины.
1.Б. Примеры решения типовых задач и упражнений
Пример 1.1 (упражнение). В табл. 1.3 представлены ре-
зультаты выборочного обследования малых предприятий по величине £-
соотношению заемных и собственных средств. Было обследовано 100 пред-
приятий (результаты обследования выстроены в таблице 10 X 10 в порядке
регистрации по строкам, так что 2-я строка начинается с 11-го наблюде-
ния, 3-я — с 21-го и т. д.). Таким образом, объем нашей выборки п = 100,
22
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
a Xi — значение анализируемого признака на »-м обследованном предпри-
ятии (i = 1,2,..., 100).
Таблица 1.3 Коэффициенты соотношения заемных и собственных
средств предприятии
5,56 5,45 5,48 5,45 5,39 5,37 5,46 5,59 5,61 5,31
5,46 5,61 5,11 5,41 5,31 5,57 5,33 5,11 5,54 5,43
5,34 5,53 5,46 5,41 5,48 5,39 5,11 5,42 5,48 5,49
5,36 5,40 5,45 5,49 5,68 5,51 5,50 5,68 5,21 5,38
5,58 5,47 5,46 5,19 5,60 5,63 5,48 5,27 5,22 5,37
5,33 5,49 5,50 5,54 5,40 5,58 5,42 5,29 5,05 5,79
5,79 5,65 5,70 5,71 5,85 5,44 5,47 5,48 5,47 5,55
5,67 5,71 5,73 4,97 5,35 5,72 5,49 5,61 5,57 5,69
5,54 5,39 5,32 5,21 5,73 5,59 5,38 5,25 5,26 5,81
5,27 5,64 5,20 5,23 5,33 5,37 5,24 5,55 5,60 5,51
Требуется:
построить выборочные (эмпирические) функции распределения (F^n\x))
и плотности вероятности (f^n\x)), а также представить их гео-
метрическое изображение (графики).
Решение
Эмпирическая плотность вероятности f^n\x) строится по груп-
пированным выборочным данным, поэтому сгруппируем выборку, пред-
ставленную в табл. 1.1, в соответствии с рекомендациями (1.2). В
нашем случае: zmin = 4,97 (минимальный элемент выборки); хтлх =
5,85 (максимальный элемент выборки); число интервалов группирова-
ния s = log2 100 + 1 = 7,62 » 8; ширина интервала группирования
Д — (®т»х — xmin)/s = (5,85 — 4,97)/8 = 0,11; левый (су-i) и правый (cj)
концы j-го интервала группирования вычисляются, в соответствии с
(1.2), по формулам:
су-1 =4,97 + 0 -1) -0,11;
Су = 4,97 + j • 0,11, j = l,2,...,s;
середины интервалов группирования вычисляются по фор-
муле
x°j = (с>-1 + ci)/2-
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
23
После подсчета числа выборочных данных Vj, попавших в каждый
(j-й) интервал группирования (j = 1,2,...,$), и использования формул
(1.3) и (1.5) для подсчета значений, соответственно, F^n\x) и f^n\x)
получаем результаты, представленные в табл. 1.4:
Таблица 1.4. Группированные выборочные данные и значения функ-
ций р(п'(х) И /<П\х)
3- номер интервала группиро- вания Значения х: 9-1 < ® < 9 Середины интервалов (*?) 9 9 + • • • + F(n)(x) /п)(х)
1 4,97 < х < 5,08 5,03 2 0 0,00 0,18
2 5,08 < х < 5,19 5,14 3 2 0,02 0,27
3 5,19 < х < 5,30 5,25 12 5 0,05 1,09
4 5,30 < х < 5,41 5,36 19 17 0,17 1,73
5 5,41 < х < 5,52 5,47 29 36 0,36 2,64
6 5,52 < х < 5,63 5,58 18 65 0,65 1,64
7 5,63 < х < 5,74 5,69 13 83 0,83 1,18
8 5,74 < х < 5,85 5,80 4 96 0,96 0,36
х > 5,85 — 100 1,00 —
Заметим, что если выборочное значение лежит на границе j-го
и (j + 1)-го интервалов группирования, то оно относится к право-
му, (j + \)-му интервалу (так, например, лежащие на границе 4~г° и
5-го интервалов группирования наблюдения = ®24 = 5,41 отнесе-
ны к 5-му интервалу). Исключение составляет наибольшее наблюдение
Х65 = жтах = 5,85.* при подсчете значения f^n\x) для величин х, принад-
лежащих последнему интервалу группирования, это наблюдение включа-
ется в данный (8-й) интервал.
Для построения гистограммы (графика функции f^n\x)) на ось аб-
сцисс наносятся граничные точки со,с>,... ,с#, а по оси ординат —
приведенные в последнем столбце табл. 1.4 значения функции f^n\x).
При этом j-му интервалу группирования будет соответствовать пря-
моугольник, основанием которого является замкнутый слева интервал
[cj-i,Cj), а высота этого прямоугольника равна значению f^n\x) (по-
скольку это значение остается постоянным для всех , cj)). Резуль-
24
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
mam построения графика функции (гистограммы) представлен
на рис. 1.1.
Рис. 1.1. Гистограмма, построенная по данным примера 1.1
Для построения графика эмпирической функции распределения
х(ж) на ось абсцисс наносятся граничные точки с0, с15..., са, а по оси ор-
динат — так называемые «накопленные относительные частоты», при-
веденные в предпоследнем столбце табл. 1.4. Значения функции F^n\x)^
так же как и функции меняются скачкообразно при переходе х
через граничные точки интервалов, поскольку ее значения остаются, по
определению (см. (1.3)), постоянными для всех ж, принадлежащих одно-
му и тому же интервалу группирования. Результат построения графика
функции F^n\x) представлен на рис. 1.2.
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
25
Пример 1.2 (упражнение). Имеется случайная выборка
9 Ж2? * * • 5 Хп
из нормальной генеральной совокупности с неизвестными значениями
среднего (а = Е£) и дисперсии (а2 3 = DQ.
Требуется:
1) построить оценки максимального правдоподобия амп и для па-
2
раметров, соответственно, а и а ;
2) доказать состоятельность оценок амп иа2п, несмещенность оценки
^2
амп и вычислить величину смещения оценки амп;
3) предложить несмещенную оценку 6q для а2. Найти наиболее эффек-
тивную оценку <тЭфф. параметра а в классе оценок вида а (с) = са0.;
вычислить средние квадраты ошибок для оценок до и (7эфф. и срав-
нить их между собой.
26
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Решение
1) Выпишем логарифмическую функцию правдоподобия (1.10) для
(а; о2) -нормально распределенных наблюдений х\, а^,..., хп:
(1 \ n I
-т==-) “ г-? -а)2 =
vJ 20 jsi
= - ? 1п(2тг) - In а2 - ~~2 S(®‘‘ “ °)’'
2 2 2ст “7
2
Для составления системы уравнений относительно параметров а и о
возьмем частные производные от функции I по в и по а и приравняем
полученные таким образом выражения к нулю:
1д1 2 А. . п
в“ ” 2^ S ° ~ °'
А " J_ + —' У(х, - «)’ = 0.
да2 2 а2 2(о2)2 ££ '
Решение этой системы относительно а и а2 дает оценки максималь-
2
ного правдоподобия, соответственно, амп и амп для этих параметров:
1 п 1 п 2
®мп ~ ^мп = ~~ ^(*Ei — ®мп) •
1=1 «=1
2) Докажем состоятельность оценок амп и а^п. То, что оценка
п
амп = п 52 xi стремится по вероятности к а, непосредственно следует
t=i
из закона больших чисел, т. к. наблюдения х\,х2,...,хп по условию неза-
висимы, одинаково распределены со средним значением а (т. е. EaSj = а) и
с конечной дисперсией <г2 (т. е. Da:, = а2).
Непосредственно применить закон больших чисел к центрированным
наблюдениям У\ = хх - аип, у2 = х2 - амп, .уп = - амп для то-
го, чтобы доказать сходимость по вероятности оценки <7„п = у2/п
1 -
к а , нельзя, т.к. после центрирования наблюдения уг,у2,...,уп стано-
вятся зависимыми. Поэтому доказательство состоятельности оценки
а„п основано на трех фактах:
(а) из закона больших чисел непосредственно следует, что при наличии
конечных четвертых моментов анализируемой случайной величины f
выборочные начальные моменты первых двух порядков сходятся по
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
27
вероятности к соответствующим теоретическим начальным момен-
там, т.е.
1 n 1 п
по веР- ~ „ 1 по веР- рс2.
“2^ —* Е^ = а и Xi ~* Е^ ;
t=i i=i
(б) первые два начальные и центральные момента (как выборочные, так
и теоретические) связаны между собой соотношениями:
’мп = = “12 х* ~(ймп)2; (*)
(72 = Е(е - а)2 = Е£2 - (Е£)2 = Е£2 - а2
(в справедливости этих соотношений убеждаемся, применив формулу
квадрата разности двух чисел к выражениям (ж< — амп)2 и (£ — а)2 и
произведя затем необходимые операции суммирования и осреднения);
(в) из сходимости по вероятности уменьшаемого правой части (*) к Е£2,
а вычитаемого — к (Ff)2 = а2, следует сходимость по вероятности
^мп к а2 = D£ (следствие теоремы Е.Е. Слуцкого, см. п. 6.2.6 в [1]).
тт а2
Проверим оценки амп и амп на несмещенность:
28
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
1_
п
£
п
Отсюда следует, что оценка амп является несмещенной, а оценка ст„п
имеет смещение, равное — а /п.
3) Очевидно, что если мы разделим оценку на 1 - 1/п = (п- 1)/п,
т. е. воспользуемся оценкой
а 2 а 2 п — 1 1 А ч2
°мп — °‘мп: — 1 °мп) 5
п п — 1
1=1
то полученная таким образом оценка будет уже несмещенной (будем
называть ее «подправленной на несмещенность оценкой максимального
правдоподобия»).
Однако в ряде ситуаций стремление к несмещенности оценки может
вредить ее точности, т.е. уменьшать ее эффективность. В частности,
а /2
зададимся вопросом: является ли несмещенная оценка амп наилучшеи с
точки зрения эффективности в классе оценок {самп}?
Другими словами, мы попытаемся определить такое положительное
с0, при котором Е(с0<Тмп — а2)2 = min.
Рассмотрим средний квадрат ошибки для оценок определенного выше
класса:
п/ а/2 2x2 /-'2 2\ 2/. 2
Е(самп - а ) = Е[с(бтмп — ст) — сг(1 — c)J =
= с Е(стмп - ст ) - 2сст (1 - с)Е(стмп - ст ) + (1 - с) ст =
= с2Е(д<2п - ст2)2 + (1 - с)2ст4,
(**)
ТР /2 2 А/2
т. к. Еамп = а в силу несмещенности оценки сгмп.
Для вычисления дисперсии оценки стмп(т. е. — выражения Е(стмп —ст )
в правой части (**)) воспользуемся теоремой Фишера (см. п. 6.2.8 в [1]), в
п 2 2
соответствии с которой случайная величина 53 (хг^мп) /и > построенная
i=i
по выборке из (а; а ) — нормальной генеральной совокупности, подчиня-
ется %2-распределению с (п- 1)-й степенью свободы. Известно (см. п. 3.2.1
в [1]), что дисперсия ^-распределенной случайной величины равна удво-
енному значению числа степеней ее свободы. Используя эти два факта,
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
29
имеем:
2(п — 1) =
2ст4
п — 1
Подставляя этот результат в (**), имеем:
./2 2\2 2 2<Т4 \2 4
Е(сстмп - ст ) = с --- + (1 - с) ст =
п — 1
л/2 \ 2
= ° -----г + 1 С - 2с + 1 .
\п - 1 /
Таким образом, задача свелась к определению такого значения с0,
которое минимизирует величину квадратного трехчлена
/ 2 \ 9
¥>(с) = (---7 + 1 ) с - 2с + 1.
\п - 1 /
Приравнивая производную функции <р(с) по с к нулю, имеем:
Подставляя это значение, имеем наиболее эффективную в классе
Г А /2 Ч
{сстмп} оценку
.2 п ~ 1 «/2 1 - \2
<Мф. - п + 1 амп - п +1 ZJXi •
1=1
Ее средний квадрат ошибки вычислим, опираясь на (**):
(1 \ 2 п 4 / 1 \ 2 о 4
п - 1 \ 2а ( п - 1X 4 2а
1 1 / 1 ' 11 ; г ) — i г*
п+1/ п — 1 \ п + 1/ п+1
w а2 2
Мы видим, что смещенная оценка аэфф. параметра а оказалась точ-
нее (эффективнее) несмещенной оценки (7^2п!
30
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Пример 1.3 (упражнение). Дана случайная выборка хА,
х2,...,хп из генеральной совокупности, подчиняющейся экспоненциаль-
ному закону распределения вероятностей с функцией плотности
/(«!»)= (К'’ (1.16)
I 0 при х < 0,
где 0 — неизвестный параметр модели.
Требуется:
1) вывести оценку максимального правдоподобия 0МП для параметра 0,
вычислить ее среднее значение, средний квадрат ошибки и эффек-
тивность;
2) построить точную и приближенную интервальные оценки для па-
раметра 0 с уровнем доверия Pq = 0,95.
Решение
1) Выпишем логарифмическую функцию правдоподобия (1.10):
1 Л
i(x1,x2,...,xn | е) = -nine -
«=1
Для составления уравнения относительно 0 продифференцируем функцию
I по 0 и приравняем полученную производную к нулю:
31 п 1
эе~ е + д2 2>-°-
Решая это уравнение относительно в, получаем оценку максимально-
го правдоподобия 0МП параметра 0:
L =
n i=l
При подсчете среднего значения (Е0МП) и дисперсии (D0Mn) оценки
0МП воспользуемся правилом вычисления среднего и дисперсии линейной
функции от статистически независимых случайных величин (см. пп. 2.6.2
и 2.6.2 в [1]):
xi
D0Mn
Xi
1 1 1 л л
= n^EXi=n^e=n'ne = e'
1=1 t=l
1 A.. i .2 e2
n2 n2 n
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
31
При этом мы воспользовались тем, что среднее значение и дисперсия
случайной величины, распределенной по закону (1.16), равны, соответ-
ственно, 6 и в2, а также тем, что каждый элемент Xi случайной выборки
распределен так же, как наблюдаемая случайная величина.
Из того, что Е0МП = в, следует несмещенность оценки 0МП, а следова-
тельно, ее дисперсия совпадает со средним квадратом ее ошибки.
Эффективность оценки 0МП определяется по формулам (1.6)-(1.7), так
что нам остается подсчитать правую часть неравенства информации (1.7):
2
/ain/(x|e)V (в / F( i
г(Х~вХ 1 Ft, 1 «2-±
\ ~ o' ( } ~e4 "o2
Следовательно, правая часть неравенства информации (1.6), опреде-
А 2
ляющая нижнюю грань Дт|п среднего квадрата ошибки по всем возмож-
ным оценкам анализируемого параметра, равна в нашем случае (с учетом
несмещенности оценки 0МП, т. е. того, что смещение Ь(0) = 0):
Отсюда получаем значение эффективности оценки 0МП:
т. е. оценка 0МП является эффективной.
2) Для построения точной интервальной оценки параметра 6 необ-
А П
ходимо так пронормировать точечную оценку 0МП = 52 xdn> чтобы полу-
1=1
ченная в результате этой нормировки статистика подчинялась бы одному
из стандартных затабулированных законов распределения вероятностей.
Обычно это достигается с помощью вычитания из оценки значения пара-
метра в либо деления или умножения точечной оценки на в. Решение в
нашем случае основано на следующих соображениях:
(а) распределение (1.16) является частным случаем гамма-распределе-
ния^ а именно, мы наблюдаем гамма-распределенную случайную ве-
личину с параметрами а = 1 и b = | (см. п.е. 3.2.4 в [1]);
32
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
(б) сумма любого числа независимых гамма-распределенных случайных
величин i = 1,2, — с одинаковым «параметром мас-
штаба Ь» снова подчиняется гамма-распределению с параметрами
п
а = ai и Ь'
г=1
(в) умножение гамма-распределенной случайной величины 7(а;Ь) на кон-
станту с приводит снова к гамма-распределенной случайной величине,
но с измененным параметром масштаба, а именно: С7(а;6) = 7(а; |);
(г) если параметры а и b гамма-распределенной случайной величины по-
ложить равными, соответственно, п (положительное целое число) и
1/2, то мы получим стандартное х2(2п)-распределение, т. е. 7(72; |) =
%2(2п).
Таким образом, мы будем стараться подобрать такой нормирующий
л п
множитель с к оценке 0МП = £ xiln4 чтобы полученная в результате ста-
г=1
тистика с 0МП подчинялась бы %2(2п) распределению. Ниже приведен ряд
последовательных домножений оценки 0МП, приводящих к цели:
• Xi -»7(1;|),см. (а);
• П0мп = 7 (п; }), см. (б);
• | • п0мп = j 1X1 z, 7 (n; 1) = %2(2п), см. (в) и (г).
Таким образом, статистика 0МП подчиняется закону %2(2п)-распре-
деления. Следовательно, задавшись уровнем доверия Ро = 0,95 и опреде-
лив из таблиц 97,5%-ную и 2,5%-ную точки х2(2^)-распределения (соот-
ветственно, Хо,97б(2п) и Хо,О2б(2п)), мы можем выписать неравенство
Хо,97б(2п) < —-— < Хо,о2б(2п),
которое выполняется с вероятностью Pq = 0,95. Разрешая это неравенство
относительно 0, получаем:
2т70мп л 2п0мп
2 ✓ < < 2 ’
Х0,025 (2п) Хо,975 (2п)
Это и есть точная интервальная оценка для параметра 0, справедливая
с уровнем доверия Pq = 0,95.
Приближенный подход к построению интервальной оценки основан на
асимптотической нормальности точечной оценки 0МП, используя которую
можно выписать неравенство (1.8*). В нашем случае а|(0) = D0Mn —
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
33
02/пт Owning q = 0,025 и wq = 1,96, так что приближенная интервальная
оценка для 0 задается неравенством:
в в
0МП - 1,96-^ < 0 < 0МП + 1,96-^,
х/п у/п
которое должно выполняться с вероятностью, приблизительно равной
Ро = 0,95.
Пример 1.4 (упражнение). Имеются независимые наблюде-
ния ж1? ж2,..., хп случайной величины подчиняющейся экспоненциаль-
ному (со сдвигом) распределению с функцией плотности вероятности
(х—0) Л
е при xjft (1Д7)
0 при х < 0,
где в — неизвестный параметр модели.
Требуется:
1) вывести оценку максимального правдоподобия 0мп для параметра 9,
вычислить ее среднее значение, дисперсию и средний квадрат ошиб-
ки;
2) рассмотреть подправленную на несмещенность оценку максималь-
ного правдоподобия 0'иа и вычислить ее средний квадрат ошибки;
3) вывести оценку по методу моментов для параметра в, доказать
ее несмещенность и вычислить ее средний квадрат ошибки;
4) сравнить средние квадраты ошибок оценок vMn и 0ММ, взяв их отно-
шение.
Решение
1) В данном упражнении мы имеем дело с так называемым «нере-
гулярным случаем», поскольку область возможных значений исследуемой
случайной величины £, в которых функция плотности (1.17) положитель-
на, зависит от оцениваемого параметра 0. Это значит, в частности, что
мы не имеем возможности составить уравнение максимального правдо-
подобия с помощью дифференцирования функции правдоподобия (или ее
логарифма) по в и приравнивания к нулю полученного выражения. По-
этому придется непосредственно решать экстремальную задачу вида
{-
max L(xx, ж2,..., хп | 0) = max е 1=1
0 0 (*)
0 < min {®f} = xmin
1<1<п
2 Прикладная статистика
в задачах и упражнениях
31
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Докажем, что 0МП = ®т-,п является решением этой задачи. Действи-
тельно, при любом другом 9, удовлетворяющем условию (*), т.е. при
0 = ®min ~ £, гДе £ > О, имеем:
п п п п
[®i ~ (®min — £)] = ~ ®min) 4" ~ ^мп)?
t=l t=l t=l i=l
а, следовательно,
• • • ? | ^мп) > ®2,•••> | ^)«
Для вычисления среднего значения и дисперсии оценки 0МП = хт1П
определим сначала закон распределения вероятностей, которому она под-
чиняется:
= ^{^min < у} — 1 ~ > У} =
= 1 - P{xi >у\ х2>у\ ...; Хп > у} =
= i-np{«i>ri = i-(i-W))".
i=l
У
где F^(y\e) = f e^^dx = 1 - — функция распределения анали-
в
зируемой случайной величины. Дифференцируя функцию распределения
^min(2/) по У» получаем функцию плотности вероятности Amin(y) случай-
ной ВеЛИЧИНЫ Zrnin*
_ Г пе~<‘п~1^у~6)е~(у~в) при у > 9;
I 0 при у <9,
или
"р" у1в.-
I 0 при у < в.
Мы килим, что оценка 0МП = xmin распределена по экспоненциально-
му (со сдвигом в) закону с параметром масштаба, равным 1/п. Теперь
мы можем полечи гать среднее значение и дисперсию случайной величины
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
35
^мп ~ ^min •
е(0мп-0)2 = е (®min - е - i) + i
оо
Е0МП = Exmin = [ yne~n(v~e}dy = 6+
J п
е
(1 \ 2 лоо / | \ j
2!min-^---) =/ {У-0---------) ne-n(v-9)dy =-у;
п/ Je \ п) п
+J--A
— ^“мп Т j — 2 '
П П
Отсюда следует, в частности, что оценка ®мп является смещенной со
смещением, равным
2) Рассмотрим подправленную на несмещенность оценку О'мп = 0МП —
п = Imin — п и вычислим ее средний квадрат ошибки, который в силу ее
несмещенности совпадает с ее дисперсией:
Е(^п - f)2 = Е fxmin - - - = D0Mn =-у.
\ п / п
3) Следуя (1.13), составляем уравнение для определения оценки 0ММ
по методу моментов:
или
1 + 0 = ®(п).
Л п
Отсюда 0ММ = х(п) — 1, где х(п) = £ ж,/п.
t=i
Для подсчета среднего значения и дисперсии оценки вмм воспользу-
емся следующими фактами:
(а) заданную функцией плотности (1.17) случайную величину £ и каждое
из ее независимых наблюдений Х{ можно интерпретировать как част-
ный случай гамма-распределенной случайной величины 7(0; 6) с па-
раметрами а - b = 1 и с параметром сдвига в (см. п. 3.2.5 в [1]);
(б) грел нее значение и дисперсия гамма-распределенной случайной вели-
чины •(</:/>) выражаемся через ее параметры по формулам (см. п. 3.2.5
в Hi):
E-Z(o: А)-- у; D7(a;6)=^.
° ь
2 А-
36
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Опираясь на (а) и (б), имеем:
£(!+«)-!= ^-1 = 0;
\ г=1 / г=1
(1 1 7Z 1
-У>-1 -—£1 = 4 = --
J п п п
4) Учитывая ранее полученные выражения для Е(0„п — 0)2 и Е(0ММ —
О)2, имеем:
E(gLn - е)2 _ 1/n2 _ I
Е(0мм-0)2 1/п «’
т. е. в данном случае асимптотическая (по п —► оо) эффективность оценки
по методу моментов стремится к нулю по сравнению с эффективностью
оценки максимального правдоподобия.
Пример 1.5 (упражнение). Имеются независимые наблюде-
ния Ж1,ж2> • • дискретной случайной величины £, подчиняющейся за-
кону распределения вероятностей Пуассона, а именно:
f(x\0) = Р{£ = z|0} = е~е~в (х = 0,1,2,...),
XI
где 9 > 0 — неизвестный параметр модели.
Требуется:
1) вывести оценку максимального правдоподобия 0МП для параметра О
и вычислить ее среднее значение и средний квадрат ошибки;
2) вычислить эффективность оценки 0МП;
3) построить приближенную интервальную оценку для параметра 0 с
уровнем доверия Ро = 0,95.
Решение
1) Логарифмическая функция правдоподобия (1.10) в данном случае
имеет вид
/(а^, ж2,... ,яп|0) = (х; In 0 - 1п(а^!) - 0) =
г=1
п п
= (1П0)
Xi -
zj) — П0.
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
37
Отсюда после дифференцирования функции I по 0 получаем уравнение
метода максимального правдоподобия, из которого и определяем оценку
0ЦП •
п
- п = О,
откуда
1 п
0Мп “ = 2,5.
n f-'
1=1
Вычислим среднее значение и средний квадрат ошибки оценки 0МП:
2) Чтобы определить эффективность оценки 0МП, необходимо подсчи-
тать правую часть неравенства информации (1.6), т.е. то минимальное
значение Дт,п, меньше которого не может быть средний квадрат ошибки
любой оценки:
(1 + ь'Ю?
•££«
1 вг _ е
ей
В данной выкладке мы воспользовались несмещенностью оценки 0МП (так
что = 0) и тем обстоятельством, что
°° /, \ 2 и оо 1
Е (»-1) /(‘i’)=?D‘-*)2да»)=
k=0 ' ' fc=0 *
где D£ — есть дисперсия анализируемой пуассоновской случайной величи-
ны, а она, как известно (см. п. 3.1.3 в [1]) равна 9. Сравнивая полученное
выше выражение для Е(0МП — 0)2 со значением Дтш> убеждаемся в том,
что оценка 6МП является эффективной.
38
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
3) Приближенный подход к построению интервальной оценки для не-
известного параметра 9 основан на (9; о%(9)) -нормальном характере рас-
пределения точечной оценки 0МП. В нашем случае <т$(0) = D0Mn = £ ~
q = 0,025 и Wq = 1,96, так что неравенство (1.8*), задающее интервальную
оценку для параметра 9 с уровнем доверия Ро = 0,95, будет иметь вид:
0МП
. V ^МП Л Л < ЛЛ V ^МП
- 1,96-*-=- < 9 < 9мп + 1,96-54=-,
к/П \/П
или:
1,52 < 0 <3,48.
Пример 1.6 (задача). Из многочисленного коллектива сотруд-
ников фирмы случайным образом отобрано п = 25 работников. Средняя
месячная заработная плата этих работников составила х(п) — 700 де-
нежных единиц при среднеквадратическом отклонении з(п) = 100 ден.ед.
Предполагается, что распределение работников фирмы по размерам зара-
ботной платы с достаточной точностью может быть описано нормальным
законом и что мы можем интерпретировать результаты статистического
обследования заработной платы 25-ти сотрудников как случайную выбор-
ку из бесконечной генеральной совокупности.
Требуется:
1) построить интервальную оценку (с уровнем доверия Pq = 0,95) для
средней месячной заработной платы на фирме;
2) определить сумму денег, которой хватило бы с вероятностью Pq =
0,95 для расчета с персоналом отделения фирмы, состоящего из 520
человек, (вычисления провести с учетом необходимости отчисле-
ния государству 40%-ного федерального налога от общей суммы вы-
плачиваемой персоналу заработной платы и в предположении, что
распределение сотрудников отделения по заработной плате то же
самое, что и во всей фирме).
Решение
1) В данном пункте речь идет об интервальной оценке неизвестного
теоретического среднего значения а нормальной генеральной совокупно-
сти в ситуации, когда мы располагаем подсчитанными по выборке из этой
генеральной совокупности средним значением х(п) = 700 и среднеквадра-
тическим отклонением з(п) = 100. Воспользуемся одним из следствий
теоремы Фишера (см. (6.30) в [1] или столбец 7 в п. 1 табл. 1.1), в со-
ответствии с которым статистика (®(п) - а)\/п — 1 /з(п) распределена по
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
39
закону Стьюдента с п — 1 степенями свободы. А это значит, что
-1.(п-1)<№)~°)У^Т<Мп-1) (*)
а\п)
с вероятностью Pq = 1 — 2а (в неравенствах (*) ta(n — 1) это 100а%-ная
точка распределения Стьюдента с п-1 степенями свободы). Подставляя в
(♦) числовые данные условия задачи (®(п) = 700, л(п) = 100, п = 25, 2а =
0,05) и определяя из таблиц 2,5%-ную точку io,O2s(24) = 2,064, имеем
2,064.
Разрешая эти неравенства относительно а, имеем неравенства
657,88ден. ед. < а < 742,12ден. ед.,
которые выполняются с вероятностью Pq = 0,95.
2) Ответ на второй вопрос задачи должен быть, очевидно, предста-
влен в форме неравенства
520а -1,4 < М,
справедливого с вероятностью Pq = 0,95.
Для этого достаточно построить верхний односторонний доверитель-
ный интервал (с уровнем доверия Pq = 0,95) для а вида
а<т= 520Пц4' (”>
С этой целью снова воспользуемся i(n — 1 )-распределенностью ста-
тистики (г(п) — а)х/п — и, соответственно, односторонней версией
неравенств (*), по которой:
(а - х(п))у/п -1 л .
з(п) <«а(п-1) (***)
с вероятностью Pq = 1 - а. В нашем случае Ро = 0,95, следовательно
а = 0,05, соответственно, <о,ов(24) = 1,711, так что из (* * *) имеем (с
вероятностью Pq = 0,95):
а < х(п) + ta(n — 1) = 734,92ден. ед.
40
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Возвращаясь к соотношению (**), определяющему связь между най-
денной нами величиной т = 734,92 и искомой суммой Л/, получаем:
М = 520 • 1,4 • т = 530021,76ден. ед.
Именно такая сумма на счету фирмы в банке гарантирует осуще-
ствление полного ежемесячного расчета с ее персоналом с вероятностью
Ро = 0,95.
Пример 1.7 (задача). При анализе точности фасовочного ав-
томата было проведено п = 24 независимых контрольных взвешива-
ния пятисотграммовых пачек кофе. Известно, что фасовочный автомат
отрегулирован без смещения, так что его ошибка подчиняется ((^би-
нормальному закону распределения вероятностей, однако значение пара-
метра а неизвестно. По результатам контрольных взвешиваний была
рассчитана выборочная дисперсия з2 = 0,64(г2).
Требуется:
1) оценить точность работы фасовочного автомата, т.е. постро-
ить интервальную оценку для его среднеквадратической ошибки а
с уровнем доверия Pq = 0,95;
2) дать интервальную оценку для доли расфасованных автоматом па-
чек кофе, вес которых отличался бы от номинала (равного 500 г.)
не более, чем на 2 г. с вероятностью Pq = 0,95.
Решение
1) По теореме Фишера (см. (6.27) в п. 6.2.8 [1]) статистика ns2/а2 под-
чиняется %2-распределению с (п— 1)-й степенью свободы. Следовательно,
с вероятностью 0,95 выполняется неравенство
2
2 / 1 \ 2 7 \
ХО,975(П - I) < — < %О,О25(П - I),
а
где Xg(n — I) это Ю0д%-я точка %2-распределения с (п — 1)-й степенью
свободы. Отсюда получаем
2 2
ns 2
“2--------- <° < ~2--------•
Х0,025(и - 1) Xo,97s(n ” 1)
Производим необходимые вычисления при п = 24; s2 = 0,64, Xo,97s(23) =
11,6885; Xo,O2s(23) = 38,0757. В результате получаем:
0,403(г2) < а2 < 1,314(г2)
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
41
и, соответственно,
0,635(г.) < а < 1,146(г.) (*)
с вероятностью 0,95.
2) Как известно, для (0; 1)-нормально распределенной случайной ве-
личины f(0; 1) доля наблюдений, отклоняющихся от нуля не более чем на
заданное число х, определяется вероятностью
X
/1
-=е Дг</г = 2Ф(г)- 1,
у2тг
—х
х kL
где Ф(ж) = J dz — функция распределения стандартного нор-
— оо
мального закона.
Анализируемая нами случайная величина (отклонение веса в расфа-
совочной пачке от номинала) £(0;<т2) отличается от стандартной £(0; 1)
только отличной от единицы дисперсией а2. Так что в нашем случае мы
должны построить интервальную оценку для вероятности
9 / 9\
= Р{|£(0; 1)| < —} = 2Ф (-J-1.
Поскольку мы не знаем точного значения среднеквадратического откло-
нения а, а знаем лишь его наименьшее (0,635) и наибольшее (1,146) зна-
чения, то эта вероятность будет, очевидно, заключена в пределах
2ф (пУ - 1 < < 2> < 2Ф(о^) - 1
ИЛИ
2Ф(1,75) - 1 < Р{К(0;<т2)| < 2} < 2Ф(3,15) - 1.
Определяя из таблиц значения Ф(1,75) и Ф(3,15), имеем неравенство:
0,920 < Р{|£(0; а2)| < 2} < 0,998,
которое выполняется с вероятностью 0,95, т. к. именно с этой вероятно-
стью нам гарантировано выполнение неравенства (*).
Пример 1.8 (задача). По результатам опроса 25 клиентов
банка были вычислены средняя величина их вклада х = 4880ден.ед. и
12
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
срсдпсквадратическое отклонение з = 454ден.ед. В предположении, что
величина вклада подчиняется (а,а2)-нормальному з.р.в., требуется:
1) определить вероятность того, что генеральная средняя вели-
чина а вкладов будет заключена в пределах от 0,975® до 1,025®;
2) определить вероятность того, что генеральное значение сред-
неквадратического отклонения о будет заключено в пределах от 0,795з
до 1,340з.
Решение
1) В соответствии с п. 7.5.4 [1] (см. соотношение (7.29)) довери-
тельный интервал 6ap(xi,.. .,®п) для генеральной средней а по выборке
®1,®2,...,®п из нормальной генеральной совокупности имеет вид
daF(®!,...,®n) = [®т«1-р(п- 1) * ,
I 2 уп— 1J
где ta(y) —100а%-ная точка распределения Стъюдента с и степенями сво-
боды. Из того, что в нашем случае этот доверительный интервал имеет
вид
6ap(xi,...,xn) = [0,975®; 1,025®]
следует, что
454
<4₽(24) • ~^= = 0,025 • 4880.
Отсюда h-e (24) = 1,318.
Из таблиц процентных точек ^-распределения (см., например,
табл. П 1.6 в [1]) в строке, соответствующей числу степеней свободы и =
24, находим значение (1 - Р)/2, соответствующее имеющейся у нас ве-
личине процентной точки ti-e(24) = 1,318. Это значение оказывается
равным 0,1, т. е. (1 — Р)/2 = 0,1. Отсюда определяем вероятность Р= 0,8,
гарантирующую выполнение неравенств
0,975® < а < 1,0£5®.
2) Одним из результатов теоремы Фишера является утверждение о
х(п — 1)-распределенности статистики ns2/а1 (см. (6.27) в [1]). Отсюда,
в частности, следует выполнение неравенств
2
^(n- 1) < Ц- < X?a(n- 1) (*)
СТ
с вероятностью Р = 1 —(1—ft)—ft = ft —ft (здесь xi(v) -100а%-ная точка
X (^-распределения, a ft < ft). Решая неравенства (*) относительно а2,
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
43
жмеем
2 2
ПЗ 2 ПЗ , .
—я------- < <7 < -я------- С вероятностью 92 - 91- (**)
Из заданного в условии задачи вида доверительного интервала для ст3
следуют равенства: (0,795)3 = хз (1,340л)2 = хд "п-1) • Отс1°Да
Х?,(24) = = 39,56 и xgi(24) = j^g56 = 13,92. Из таблиц П1.4 про-
центных точек %2 (^-распределения находим значения q2 ид], соответ-
ствующие полученным величинам процентных точек Хда(24) и хд1(24) :
92 » 0,025, gi и 0,950, — так что Р = qx - д2 = 0,925.
Пример 1.9 (задача). Анализируется закон распределения ве-
роятностей (з.р.в.) семей определенной социально-экономической страты
по величине среднедушевого дохода.
Мы располагаем следующей информацией об анализируемой гене-
ральной совокупности
1) Логарифм (натуральный) от величины среднедушевого дохода
(g = In () распределен нормально с неизвестным средним значением 9
известной дисперсией <72, т. е.
Д(ж; 0) = -i- е" ; <т3 = 0,28.
V 27Г(Т
2) Из предыстории и опыта обследований семей той же самой стра-
ты в других регионах известно, что величина 9 ведет себя как (90-,а9)-
нормальная случайная величина, где значения 9q и <т2 известны, т. е.
1 <»-*я>а ,
р{9) = -=— е 2’t ; 0О = 0,60; (т0 = 0,03.
V27T<70
3) Имеются результаты обследования п (п = 10) случайно отобранных
от анализируемой страты семей по среднедушевому доходу, т. е. случай-
ная выборка значений х4,х2,.. .,хп, где х, = In у,, а у,- — среднедушевой
доход i-й обследованной семьи. Ниже приводятся конкретные значения Х(:
xi = 0,54; х2 = 1,20; х3 = 0,36; х4 = 0,80; xs = 0,42
х6 = 2,10; = 0,70; х9 — 0,25; х9 = 0,90; ж10 = 0,48
Требуется:
1) вывести оценку максимального правдоподобия 9ЫП для параметра
9, определить ее численное значение и доверительный интервал с
уровнем доверия Р9 = 0,95;
44
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
2) вывести байесовскую оценку для параметра 0, определить ее
численное значение и доверительный интервал с уровнем доверия
Ро = 0,95.
Решение
1) Функция правдоподобия (1.9) в данном случае имеет вид
Ь(Х1,Х2,...,Хп\0)=-^—е (*)
(у2я-<т)
Переходя к логарифмической функции правдоподобия
/(®1,
и приравнивая ее производную по 6 к нулю, получаем уравнение для опре-
деления оценки 0МП:
-Л(-2)£>,-в) = 0,
2(7
Л п
откуда имеем 0МП = £ 53 =
1=1
Известно (см. (6.26) в п. 6.2.8 [1]), что статистика (ж - подчи-
няется стандартному нормальному закону распределения, следовательно
с вероятностью Pq = 1 — 2q выполняются неравенства:
<
(ж — 0)у/п
< Wq,
где wq — 100д%-ная точка (0;1)-нормального распределения. Решая эти
неравенства относительно 0, имеем
^мп “ Wq ““/F < 9 < 0МП + Wg—7=
у п уП
с вероятностью Pq = 1 - 2q.
Подставляя в это неравенство и в выражение для 0МП исходные ста-
тистические данные и учитывая, что п = 10, а2 = 0,28 и Ро = 0,95 и,
соответственно, q = 0,025, w0,025 = 1,96 (из табл. П1.3), имеем:
*мп = 0,775
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
45
и
0,447 < 9 < 1,103 (с вероятностью 0,95).
2) Для вывода байесовской оценки 9' ' мы должны вычислить по фор-
муле (1.14) апостериорное распределение ср(9 | а?!, ж2, • • •,х ~ п) оценивае-
мого параметра в. Поскольку знаменатель правой части (1.15) не зависит
от то вид распределения ср(0 | . ,жп) определяется (с точностью
до нормирующего множителя) числителем этого выражения.
Анализ произведения p(0)L(a:1, х2,..., хп | 0), стоящего в числите-
ле правой части (1.15), приводит нас к выводу, что в данном приме-
ре это произведение является «гауссообразным», т. к. оно распадается
на два множителя, один из которых не зависит от в (так называемый
нормирующий множитель), а другой определяется экспонентой, возве-
денной в отрицательную степень, представленную некоторым квадрат-
ным трехчленом относительно в. Для того чтобы определить сред-
нее значение и дисперсию получающегося при этом нормального рас-
пределения | X], х2,..., ^п), проанализируем подробнее произведение
p(0)Z/(zi, ж2,..., хп | 0). Преобразования в этом анализе будем произво-
дить иногда лишь с точностью до нормирующих множителей, поэтому
вместо знаков равенства между такими преобразованными выражениями
будем указывать знак «~» эквивалентности:
| хг,х2,.
,хп)~ ехр <
(*-*о)2
2
<70
= ехр
= ехр <
lie2 #о n<s2 п 20пх пх2\
9 I ~2 2~ 2 Г 2 2 I 2~ I *
\0о сг0 п0 ст о (у о /
(**)
где а = А2 = 7 = s2 = 1 £ fa - х)2 и х = 0МП = 1 £ ц
1=1 1=1
(при переходе от первой строки выкладок ко второй мы воспользовались
46
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
2 2
тождественным преобразованием ^(а:, — 0) = [(х« — х) - (0 - х)] =
>=1 t=i
$3 (®, - ®)2 + »(^ - ®)2 = ”[з2 + (0 - *)2].
1=1
Мы видим, что выражение (**) определяет (с точностью до норми-
рующего множителя) функцию плотности нормального распределения со
м м А 2
средним значением, равным а, и дисперсией, равной Д .
Поэтому байесовская оценка параметра О определится выражени-
ем
j(B) = „ =
1 + 7
2
(У
где 7 = —,,
пао
а байесовская интервальная оценка (с уровнем доверия Pq = 0,95) — не-
равенствами
0(Б) - 1,96Д <0< 0(Б) + 1,96Д.
Подстановка в эти выражения численных данных условия задачи да-
ет:
7 = = 0,933; = °.775 + 0 033 ^,6°0 =
' 10 • 0,03 1 + 0,933
а2 0,28/10 ЛЛ,₽ А
Д = = 0,015; Д = 0,122,
1 + 0,933
0,451 < 0 < 0,929 (с вероятностью 0,95).
Мы видим, что использование априорной информации о неизвестном
параметре и применение, соответственно, байесовского подхода в данной
задаче позволили уточнить оценку и, в частности, сузить интервальную
оценку по сравнению с классическим подходом почти в полтора раза.
Пример 1.10 (упражнение). Условия примера 1.5 дополне-
ны следующей априорной информацией о значении оцениваемого параме-
тра 0: априорное среднее значение этого параметра известно и равно 0q,
а случайный разброс значений этого парметра характеризуется средне-
квадратическим отклонением До (значение До известно) и подчиняется
гамма-распределению.
Требуется:
основываясь на исходных данных примера 1.5, дополненных приведен-
ной выше априорной информацией, вывести точечную и интерваль-
ную (с уровнем доверия, равным Ро) байесовские оценки, соответ-
ственно, 0^Б) и [0^п(Ро)< дтмС^о)] парметра 0 пуассоновского
распределения.
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
47
Указание. При определении lOOc-процентных точек 7е(а/,0')
гамма-распределения с парметрами (а*, 0') воспользоваться соот-
ношением, связывающим (при а кратных 0,5) 7г(о/,//) с соот-
ветствующими процентными точками хе(2а') хи-квадрат распре-
деления с 2а степенями свободы:
7е(<О')= 2^-Хв(2«).
Подберем параметры а и 0 в гамма-распределении, описывающем
априорное распределение оцениваемого параметра в, опираясь на соот-
ношения:
' е/? = । = е0
' ъе = $ = ь20.
Решение этой системы относительно а и 0 дает:
Поскольку априорное гамма-распределение является сопряженным по
отношению к анализируемой пуассоновской генеральной совокупности,
то апостериорное распределение оцениваемого параметра 9 снова будет
гамма-распределением, а его параметры а' и 01 вычисляются по формулам
(см. п. 5 в табл. 1.2):
a'=a+±Ii=*+±,i;
1-1 (=1
0' = 0 + п = ^ + п.
До
Байесовская точечная оценка 9^ параметра 9 определяется как сред-
нее значение апостериорного распределения этого параметра, т. е.
I &0 / До + 12
) = Е(0 I ®1, Х2, .. . , хп) = = 2 /Л “ •
0 9$/ До + п
Левый и правый концы (соответственно, и ^тах) байесовской
интервальной оценки параметра 9 определяются (при уровне доверия
Ро) как, соответственно, ^^^%-ная и -^^у^%-ная точки апостериорного
48
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
гамма-распределения. Воспользовавшись указанием, имеем:
^nii(po) = 7h£l(«',0') = т^Х1^(2а'),
2 zp 2
ffix(^o) = 7цеа(а У) =
zp
где величина доверительной вероятности Pq задана в условии упражнения,
значения а и /З' параметров апостериорного распределения определены
выше, а значения процентных точек %2 (2а/^распределения определяются
из табл. П1.4.
1.В. Задачи и упражнения
Упражнение 1.1
По данным I выборок объемов n15n2,... , п/ получены I средних
^1,^2,.. Найти общую среднюю х, определяемую как среднюю объ-
/
единенной выборки объемом п = £ nj-
>1
Упражнение 1.2
На основе данных двух выборок объемов щ и п2 рассчитаны соответ-
ственно две средние арифметические Ё] и Ё2 и две выборочные дисперсии
s2 и s2. Требуется выразить характеристики суммарной выборки х и з2
через характеристики двух выборок.
Упражнение 1.3
По данным I выборок объемов П!,п2,...,п/ получены соответствен-
но средние ж2,..., ж/ и выборочные дисперсии s2, s2,..., s2. Доказать
справедливость формулы разложения общей дисперсии:
2 2.2
50 — 5М + 5В,
2 _ _ _
где so — общая дисперсия, полученная на основе суммарной выборки объ-
I
емом п = $3 nj-
i=i
j=i «=1
2
Xji — результат г-го наблюдения в j-й выборке; $м — межгрупповая дис-
персия:
*М = - - х)2 njt
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
49
Xj — средняя арифметическая, вычисленная по элементам j-й выборки;
х — общая средняя арифметическая, полученная по суммарной выборке;
2 2 1 V—s 2
$в — средняя внутригрупповая дисперсия: $в = „ * nj-
j=i
Упражнение 1.4
По данным выборки объема п найдены начальные моменты
1 п
1 к
тк = ~>xi
п
и центральные моменты
1 п
Л о 1 V^z _хк
тк = ~ ~ •
i=l
Вывести формулы, устанавливающие связь между центральными (тп^) и
начальными (тд.) выборочными моментами для к — 2,3,4.
Упражнение 1.5
Вывести соотношения между следующими выборочными характери-
стиками случайных величин т? и £, если известно, что независимые наблю-
дения (zi,2/i),(z2,2/2),- • • Лхп^Уп) этих величин связаны соотношениями
yi = axi + Ь,- i = 1,2,..., п,- где а и Ь — постоянные, причем а 0:
а) средними арифметическими у и х\
б) выборочными дисперсиями зу и зх;
в) выборочными центральными моментами т^у) и = 1? 2,3,4).
г) выборочными коэффициентами асимметрии и 31(х) и эксцесса
02(у) И Д?(х)-
Упражнение 1.6
Из нормальной генеральной совокупности с математическим ожида-
нием а и дисперсией а2 извлечена случайная выборка , х2,..., хп объема
п. Вывести формулы для дисперсий выборочной средней х и выборочной
2
дисперсии з .
Упражнение 1.7
Пусть F^n\x) — эмпирическая функция распределения, построенная
по выборке x1,x25 • • • ?жп из генеральной совокупности с функцией рас-
пределения F{(x). Доказать, что Е(/^п\ж)) = Г^(ж) и D(F<n\a:)) =
50
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
**(*№ воспользовавшись представлением F^n\x) ~ £ £ ’/•С®)» где
1=1
/ к ( 1 при Xi < X
T)i(x) = < п
7 [0 при Xi х.
У п^ражнение 1.8
Оценка зх(к) дисперсии а генеральной совокупности, найденная по
2 П“1 2
выборке х^хг,...^ определяется формулой зх(к} = к 5Z (ж«+1 ~ xi) •
i=i
Каким должно быть Л, чтобы з2х(к) была несмещенной оценкой дисперсии
2
а .
Упражнение 1.9*
В условиях упражнения 1.8, дополненных информацией о том, что вы-
борка Ж1,Х2,...,хп извлечена из нормальной генеральной совокупности:
2 2
1) подобрать в классе оценок sx(k) — к (®i+i “ ®i) такое значение
1=1
свободного параметра к, которое минимизирует средний квадрат ошиб-
2 w
ки в оценивании дисперсии а анализируемой генеральной совокупности;
2) вычислить этот средний квадрат ошибки и сравнить его со средним
квадратом ошибки несмещенной оценки з2(Л), найденной в упражнении
1.8.
Упражнение 1.10
На основании п независимых наблюдений , ®j,..., хп из нормальной
генеральной совокупности получены две оценки дисперсии генеральной
совокупности по следующим формулам:
2 _ 1 _ч2 2 _ 1 х2
1 " п - 1 ’ 32 " 2(п - 1) S(®<+1 •
Требуется:
сравнить эффективность оценок з2 и з2 при конечных пив асим-
птотике п —► оо, а также доказать состоятельность этих оценок.
Упражнение 1.11
По выборке ху,Х2,...,хп из (а;<т2)-нормальной генеральной совокуп-
ности наити эффективную оценку дисперсии а в предположении, что ма-
тематическое ожидание а известно.
Главе 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
51
Упражнение 1.12
Доказать, что средняя арифметическая х, полученная по выборке
объема п из пуассоновской генеральной совокупности, есть
эффективная оценка параметра А в распределении Пуассона
а:!
Упражнение 1.13
В результате реализации к серий испытаний Бернулли объемов, со-
ответственно: nj, п2,..., Пк интересующее нас событие А наблюдалось
соответственно xi, ®2,..., Хк Р33- Определить оценку р метода максималь-
ного правдоподобия параметра р — вероятности появления события А в
отдельном испытании.
Упражнение 1.14
Из (а; О’2) -нормальной генеральной совокупности взята выборка
Z],z2,.. .,хп. Вывести закон распределения для средней арифметической
X = ( £ ®i)/n.
'|=1 '
Упражнение 1.15
Имеется к независимых случайных выборок Xji,Xj2,... ,xjn (j =
1,2,..., к), извлеченных, соответственно, из к (а7;<т2)- нормальных ге-
неральных совокупностей, в которых средние значения aj неизвестны, а
величина дисперсии <т2 известна.
Требуется:
^22
доказать, что статистика n{xj-xy /а будет подчиняться х -
7=1
распределению с к — 1 степенями свободы в случае, если а^ = аз =
... = ajt (здесь Xj — выборочное среднее значение, оцененное по j-й
выборке, аж — среднее арифметическое, подсчитанное по всем кп
имеющимся наблюдениям)
Упражнение 1.16*
Доказать, что если случайная выборка х\, Ж3,..., хп взята из (а; суб-
нормальной генеральной совокупности, то средняя х и выборочная диспе-
рсия s взаимно независимы, а статистика ns /о распределена по закону
X с п — 1 степенями свободы (лемма Фишера).
Упражнение 1.17
Из (а; а2)-нормальной генеральной совокупности взята выборка
Ж!,ж2,... ,хп, на основании которой определены средняя х и среднеква-
дратическое отклонение з. Доказать, что статистика - 1 имеет
52
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
распределение Стьюдента (^-распределение) с числом степеней свободы
и = п — 1.
Упражнение 1.18
Из двух нормальных генеральных совокупностей с параметрами соот-
ветственно (ai,ai) и (fl2>a2) взяты взаимно независимые случайные вы-
борки • • • )хп! и 2/1,2/2, • • • , Уп2 объемов щ и п2- По ним построе-
ны выборочные дисперсии, соответственно, з2 и з2. В предположении
а? = а? = О’2 доказать, что:
\ /2 2\/ 2 2
а) статистика (П1$1 + п2з2)/^ имеет % -распределение с числом сте-
пеней свободы и = Hi + п2 — 2;
б) статистика
имеет F-распределение с числами степеней свободы числителя и знамена-
теля, соответственно, щ = п\ — 1 и i/2 = п2 - 1-
Упражнение 1.19
В условиях упражнения 1.18 доказать, что статистика
(» - у) - (Д1 - Дг)
f{x I е) =
подчиняется распределению Стьюдента с + п2 — 2 степенями свободы
(ж и у — арифметические средние, построенные по наблюдениям, соот-
ветственно, первой и второй выборок, as = ^fn^2 (nisi + n2s2))-
Упражнение 1.20
По случайной выборке хА, х2,..., яп, извлеченной из генеральной со-
вокупности, подчиняющейся з.р.в. с функцией плотности
при я > О
при х < О,
п
подсчитано (при п = 12) среднее выборочное значение х = ± ^2 xi = 36.
n i=i
Требуется:
1) доказать, что случайная величина & = 20Х{ подчиняется %2-
распределению с двумя степенями свободы]
2) определить (в общем виде и численно) точечную оценку максималь-
ного правдоподобия параметра в, ее среднее значение, дисперсию, а
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
53
также — средний квадрат ошибки оценки максимального правдопо-
добия^ подправленной на несмещенность]
3) построить в общем виде и численно точную и приближенную ин-
тервальные оценки для параметра 0 с уровнем доверия Pq = 0,95.
Упражнение 1.21
Условия упражнения 1.20 дополнены следующей априорной информа-
цией о поведении параметра 0 в других аналогичных генеральных сово-
купностях: среднее значение параметра 0 равно 0,04, а его случайный раз-
брос характеризуется среднеквадратическим отклонением, равным 0,01, и
подчиняется гамма-распределению.
Требуется:
использовать эту дополнительную информацию (наряду с условия-
ми упражнения 1.20) для вывода и численного подсчета точечной
и интервальной (с уровнем доверия Pq = 0,95) байесовских оценок
параметра 0] сравнить полученный результат с ответом, получен-
ным в упражнении 1.20.
Указание. Для определения ЮОе-процентных точек 7с(с/; ft)
гамма-распределения воспользоваться соотношением, связываю-
щим их (при а , кратных 0,5) с соответствующими процентными
точками Хе(^а') хи-квадрат распределения с 2а степенями сво-
боды: 7е(а';^') = ^Хе(2а).
Упражнение 1.22
Имеются независимые наблюдения , х2,..., хп случайной величины
£ = подчиненной з.р.в. с функцией плотности вероятности
ЛИ -Р"
I 0 при X < 02
(соответственно, функция распределения F^(x) = Р{£ < ж} = 1 —
е“*г(г“*2), а е^(02) = 01 + 02 и D^/02) = 0J, см. п. 7 в табл. 1.1).
Требуется:
1) дать вывод оценок максимального правдоподобия 01МП и 02мп для па-
раметров, соответственно, 0± и 02;
2) вычислить средние значения и дисперсии этих оценок и предложить
вариант «подправленной на несмещенность» оценки максимального
правдоподобия 0^мп для параметра 0г (дисперсию оценки 0гмп вычи-
слить с точностью до величин порядка о(^))]
3) выписать и обосновать общий вид интервальных оценок параме-
тров 01 и 02 с уровнем доверия Pq = 0,95.
54
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Упражнение 1.23
Имеются независимые наблюдения xi,x2,...,xn случайной величи-
ны &(0), подчиняющейся экспоненциальному со сдвигом 0 распределению,
имеющему функцию плотности вероятности
A(«l<?) = {j
при х > 0;
при х < 0.
Требуется:
построить (вывести) точную и приближенную интервальные оцен-
ки параметра 0 с заданным уровнем доверия Pq.
Упражнение 1.24
Условия примера 1.5 дополнены следующей априорной информацией о
значении оцениваемого параметра 0: априорное среднее значение этого паг
раметра равно 0о, случайный разброс его значений характеризуется сред-
неквадратическим отклонением До и подчиняется гамма-распределению.
Требуется:
основываясь на исходных данных примера 1.5, дополненных приве-
денной выше априорной информацией, вывести точечную и интер-
вальную (с уровнем доверия, равным Ро) байесовские оценки 0<Б) и
[0^п,0твх] для параметра 9 пуассоновского распределения.
У казаки е. См. «У казание к упражнению 1.21.»
Упражнение 1.25
Вычислить среднее значение и дисперсию построенной по случайной
выборке объема п оценки 0МП максимального правдоподобия параметра 0
в распределении Парето вида
F(x) = P{f = ПРИ ® > *о5
I 0 при х < х0
Указание. Воспользоваться результатами решения помещенной
ниже задачи 1.21 (видом оценки 0МП и соотношением, связывающим ее
со случайной величиной х3(2п)), а также приемом, использованным в
решении упражнения 1.20 для подсчета моментов случайных величин,
обратных к х .
Упражнение 1.2в
Имеются независимые наблюдения х^, х2,..., хп случайной величины
6(а;Ь), равномерно распределенной на отрезке [а; 6].
Главе 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
55
Требуется:
1) вывести оценки максимального правдоподобия амп и 6М„ неизвест-
ных параметров, соответственно, а и 6;
2) вычислить средние значения и дисперсии оценок ам„ и 6МП;
3) построить приближенные интервальные оценки (с уровнем доверия
Ро) для параметров а и Ь;
4) вывести точечные оценки для параметров а ub с помощью метода
моментов.
Задача 1.1
У вошедших в выборку 50 матерей, рожавших пять раз, число сыно-
вей составило:
4; 1; 4; 2; 1; 2; 2; 3; 3; 3; 3; 4; 3; 3; 3; 3; 2; 3; 1; 3; 3; 0; 1; 1; 2; 2; 2; 2; 1; 3; 1;
2; 2; 2; 3; 3; 2; 5; 4; 4; 2; 4; 1; 2; 2; 3; 3; 3; 3; 4
Предполагая, что число сыновей у матерей, рожавших пять раз, есть дис-
кретная случайная величина t/p(5), подчиняющаяся биномиальному рас-
пределению, найти точечные оценки вероятности р, математического ожи-
дания Еир(5) и дисперсии Di/p(5). Построить полигон относительных ча-
стот для распределения случайной величины t/p(5).
Задача 1.2
Из продукции работающей в стационарном режиме автоматической
линии извлекались для контроля партии по 20 изделий. Предполагается,
что число дефектных изделий в партии t/p(20) подчинено биномиальному
закону. Числа дефектных изделий, обнаруженные в 50 проконтролирован-
ных партиях, следующие:
1; 2; 1; 1; 1; 1; 2; 2; 3; 3; 2; 1; 0; 2; 2; 2; 2; 2; 2; 1; 4; 2; 4; 1; 1; 5; 2; 2; 2; 1; 3;
3; 0; 2; 3; 1; 3; 3; 1; 3; 2; 4; 4; 3; 1; 3; 2; 1; 2; 1.
Найти точечные оценки вероятности р появления дефектного изделия, ма-
тематического ожидания числа дефектных изделий в партии Е1/р(20) и
дисперсии Dizp(20). Построить полигон относительных частот распреде-
ления случайной величины izp(20).
Задача 1.3
В течение часа на АТС регистрировалось число неправильных соеди-
нений в минуту:
1; 2;.l; 1; 0; 2; 1; 1; 1; 3; 1; 1; 1; 4; 2; 2; 2; 2; 0; 1; 4; 3; 3; 1; 1; 0; 0; 1; 2; 2; 4;
5; 3; 3; 3; 2; 2; 2; 1; 1; 2; 1; 0; 2; 2; 2; 1; 1; 3; 3; 4; 0; 2; 2; 2; 1; 3; 1; 3; 2.
Предполагая, что число неправильных соединений в минуту есть дискрет-
ная случайная величина 1/(9), подчиняющаяся распределению Пуассона,
найти точечную оценку параметра 9 этого распределения и построить по-
лигон относительных частот.
56
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Задача 1.4
Темп роста курса акций 50 фирм относительно предыдущего месяца
составил (в %):
104; 103; 102; 98; 99; 94; 119; 115; 110; 103
92; 97; 95; 92; 104; 105; 93; 96; 105; 78
93; 95; 99; 100; 103; 109; 122; 102; 96; 92
ill; 83; 87; 80; 84; 89; 85; 90; 95; 90
96; 100; 103; 105; 107; ill; 116; 94; 98; 102
В предположении, что темп роста курса акций есть (а; ст2) — нормаль-
ная случайная величина, построить «группированный» ряд наблюдений,
выборочные функции плотности и распределения для анализируемой слу-
чайной величины. По «группированному» ряду наблюдений найти оцен-
2 2
ки х и з параметров распределения, соответственно, а и а .
Задача 1.5
Хронометраж затрат времени на сборку узла машины у 50 слесарей
дал следующие результаты (мин):
Hl; 106; 109; 76; 88; 89; 82; 88; 102; 98
87; 99; 80; 75; 89; 55; 68; 80; 86; 95
56; 61; 61; 58; 59; 92; 123; 71; 81; 72
82; 93; 65; 72; 81; 94; 94; 83; 75; 66
79; 65; 78; 85; 79; 85; 85; 95; 92; 95
В предположении, что время сборки узла машины есть (а; а2) — нормаль-
ная случайная величина, построить «группированный» ряд наблюдений,
а также выборочные функции плотности и распределения. По «группиро-
- w _ 2
ванному» ряду наблюдении наити оценки х и з параметров распределе-
ния, соответственно, а и а2.
Задача 1.6
При разработке нормы времени на изготовление изделия проведен
хронометраж работы четырех рабочих. Было измерено время (в секун-
дах) изготовления щ = 10 изделий первым рабочим, п2 = 15 — вторым,
п3 = 11 — третьим и п4 = 20 — четвертым рабочим. По результатам
этих четырех порций наблюдений найдены следующие выборочные сред-
ние и дисперсии для каждой порции: хг = 28 и з2 = 4; х2 = 25 и з2 = 3;
х3 = 20 и з3 = 5; ±4 = 23 и з4 = 2. Определить для суммарной выборки
4
объемом 52 nj = 56 среднее время изготовления изделия х и дисперсию
i=i
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
57
Задача 1.7
Из 300 сотрудников фирмы взята случайная выборка из 25 работни-
ков. Средний заработок этих работников равен 1885 рублей, а средне-
квадратическое отклонение — 250 рублей. Предположив, что заработная
плата работника фирмы есть нормальная случайная величина, опреде-
лить, какая минимальная сумма должна быть на счету фирмы в конце
месяца, чтобы с вероятностью 0,95 обеспечить выплату зарплаты всем
сотрудникам фирмы (учесть необходимое налоговое отчисление в размере
40,0% от суммы, выплачиваемой сотрудникам).
Задача 1.8
Годовой удой 10 коров племенного стада представлен в таблице.
коровы 1 2 3 4 5 6 7 8 9 10
удой Xi (тыс. л.) 4,6 5,5 4,5 5,6 4,1 3,8 4,6 5,2 4,4 4,7
Предположив, что годовой удой коровы есть (а; ст2) — нормальная
случайная величина, определить вероятность того, что: а) абсолютное
значение ошибки в определении математического ожидания а не превысит
6% от я; б) абсолютное значение ошибки в определении ст будет меньше
30% от 5.
Задача 1.9
По результатам контрольных проверок 18 однородных (в профиль-
ном и объемном смыслах) торговых точек получены средняя величина
их дневной выручки х = 5100ден.ед. и среднеквадратичное отклонение
з = 630 ден.ед.
Предположим, что сумма дневной выручки торговой точки есть
(а, а2)-нормальная случайная велиина, определить вероятность того, что
параметры исследуемой генеральной совокупности а и сг попадут соответ-
ственно в интервалы (0,95я; 1,05±) и (0,6s; 1,4s).
Задача 1.10
Из 80000 человек, проживающих в городе, было опрошено 200 жи-
телей, из которых 60% высказались в пользу определенной федеральной
программы. В предположении, что проведенный опрос может быть опи-
сан в рамках схемы испытаний Бернулли, определить с вероятностью 0,88
интервальную оценку для доли жителей города, поддерживающих данную
программу. Опираясь на построенную интервальную оценку, определить
максимально возможное число жителей города, на поддержку которых мо-
гут рассчитывать авторы программы.
58
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Задача 1.11
Из 300 опрошенных будущих избирателей 32% поддержало кандида-
та партии на пост мэра города. В предположении, что проведенный опрос
может быть описан в рамках схемы испытаний Бернулли, определить с
вероятностью 0,95 интервальную оценку доли жителей города, поддержи-
вающих этого кандидата.
Задача 1.12
Условия примера 1.7 дополнены результатами п = 16 взаимно
независимых контрольных взвешиваний фасовочного автомата конкури-
рующей марки, который также отрегулирован без смещения, так что его
ошибка подчиняется (0;о,,2)-нормальному з.р.в. (однако, величина о'2 не-
известна). По этим 16-ти контрольным взвешиваниям была подсчитана
выборочная дисперсия »2 = 0,49(г2). Требуется с доверительной веро-
ятностью Ро = 0,90 построить и обосновать интервальную оценку для
отношения о /а .
Задача 1.13
Условия примера 1.9 дополнены независимой от уже имеющих-
ся наблюдений случайной выборкой значений логарифмов среднедуше-
вых доходов 8 представителей другой социально-экономической страты:
х\ = 1,00; х2 = 0,60; х'3 = 0,28; х4 = 0,70; Ц = 0,05; х6 = 0,50; 2:7 = 0,22;
х6 = 1,7. Полагая, что это выборка из (0 ; сг ) — нормальной генеральной
совокупности, построить с доверительной вероятностью Ро = 0,90 интер-
вальную оценку для разности д' — 9.
Задача 1.14
Отдел маркетинга некоторой фирмы разослал почтой 30 направлен-
ных рекламных предложений по поводу покупки определенного вида своей
продукции.
Требуется:
используя одну из моделей з.р.в., оценить вероятность того, что
число «.откликнувшихся» (т. е. изъявивших готовность купить
продукт) клиентов будет равно 4, если известно, что в пяти пре-
дыдущих таких же рассылках числа откликнувшихся респондентов
были, соответственно, равны = 3, х2 = 2, 2:3 = 1, х4 = 4, 2:5 = 2.
Задача 1.15
За последний отрезок времени (например, за месяц) продано N = 1000
единиц товара.
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
59
Требуется:
используя одну из моделей з.р.в., оценить вероятность того, что
число рекламаций, которые поступят на зти продажи, не будет
превосходить к = 3, если числа рекламаций на четыре проданные
ранее такие же партии товара составляли, соответственно, хг =
7, =2, х3 = 6, х4 = 5.
Задача 1.16
Используя одну из моделей з.р.в., оценить вероятность того, что чи-
сло заявок на товар, которые поступят в следующую неделю, окажется
больше б, если из предыстории известно, что числа полученных в преды-
дущие 5 недель заявок равнялись, соответственно, ajj = 4, — 2, z3 = 5,
Х4 -“ 3, —- 2.
Задача 1.17
Для массового производства некоторых изделий компания приобрела
автоматическую линию. Кондиционность произведенного этой автома-
тической линией изделия определяется соответствием его веса номиналу
(номинал равен 400 г.). Допуски, в пределах которых изделие считается
кондиционным, заданы интервалом [380 г.; 415 г.].
Специальные испытания показали, что веса производимых работаю-
щей в стационарном режиме автоматической линией изделий подвержены
некоторому неконтролируемому разбросу, подчиняющемуся нормальному
закону распределения вероятностей.
Требуется:
предсказать долю брака, которая будет характеризовать работу
этой автоматической линии (или другими словами, определить ве-
роятность того, что вес случайно отобранного от продукции этой
автоматической линии изделия окажется меньше 380 г. или боль-
ше 415 г.), если известны результаты взвешиваний 64 изделий, слу-
чайно отобранных из контрольной партии, произведенной на этой
автоматической линии (см. таблицу).
60
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
№ изделия Вес (в г.) № изделия Вес (в Г.) № изделия Вес (в г.) № изделия Вес (в Г.)
1 404,6 17 398,1 33 407,8 49 397,3
2 400,6 18 407,0 34 401,9 50 399,6
3 414,9 19 435,2 35 397,4 51 409,1
4 410,2 20 403,2 36 413,0 52 411,8
5 413,9 21 399,3 37 388,1 53 385,0
6 401,4 22 405,4 38 390,4 54 393,1
7 396,5 23 409,3 39 411,9 55 413,7
8 374,3 24 405,7 40 404,2 56 394,9
9 395,3 25 429,4 41 402,4 57 389,5
10 394,4 26 403,0 42 400,2 58 395,1
11 424,5 27 384,4 43 391,5 59 407,6
12 394,7 28 413,7 44 395,0 60 402,3
13 393,7 29 381,5 45 404,4 61 394,8
14 412,8 30 419,7 46 390,4 62 400,1
15 400,4 31 397,1 47 405,3 63 398,4
16 396,7 32 401,9 48 381,4 64 383,8
Задача 1.18
Предприятие приобрело новую автоматическую линию (АЛ). Для
оценки так называемой «необходимой доли брака» р (величина р — это
вероятность того, что произведенное этой АЛ в режиме стационарного
функционирования изделие окажется некондиционным) было проконтро-
лировано п = 5 партий по N = 80 изделий в каждой партии. Результаты
контроля следующие: хг = 2, х2 = 0, х3 = 3, х4 = 1, х5 = 2, где х^ —
это число дефектных изделий, обнаруженных в i-й проконтролированной
партии.
Полагая, что число дефектных изделий в партии объема N изделий,
произведенных АЛ в режиме стационарного функционирования, это (р, N)-
биномиальная случайная величина,
требуется:
1) вывести и численно оценить оценку максимального правдоподобия
«необходимой доли брака» р, характеризующей данную АЛ]
2) построить приближенную интервальную оценку для р (с уровнем
доверия Pq = 0,90) и обосновать способ ее построения.
Задача 1.19
Условия задачи 1.18 дополнены информацией, содержащейся в техни-
ческом паспорте приобретенной АЛ. В соответствии с этой информацией
проведенный анализ работы аналогичных АЛ, установленных на других
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
61
предприятиях, показал, что необходимая доля брака р в среднем равна
0.01, имеет разброс, характеризуемый среднеквадратическим отклонени-
ем 0,003, и ведет себя как бета-распределенная случайная величина.
Требуется:
использовать эту дополнительную информацию (наряду с условиями
задачи 1.18) для вывода и численного подсчета точечной и интер-
вальной (с уровнем доверия Pq = 0,90) байесовских оценок параме-
тра р\ сравнить результат с ответом, полученным в задаче 1.18
Указание. При отсутствии таблиц квантилей или процент-
ных точек бета-распределения (см., например, [Л. Н. Болыпев,
НВ. Смирнов], табл. 3.4) подробно описать способ получения ле-
вого и правого концов байесовского доверительного интервала,
реализуемый на основе знания значений соответствующих про-
центных точек при заданных Вами значениях а и bf. При а и bf,
кратных 0,5, воспользуйтесь соотношением, связывающим ЮОе-
процентные точки бета- и /"-распределений:
/□ / f, Lf\ a1 Feffa1 fib1)
0Л<1-,Ь)= +
Задача 1.20
Условия примера 1.7 дополнены информацией, содержащейся в техни-
ческом паспорте фасовочного автомата. В соответствии с этой априорной
информацией, основанной на анализе работы контрольной партии анало-
гичных фасовочных автоматов, известно, что среднее значение параметра
точности расфасовки в = 1/сг2 равно 2, случайный разброс параметра точ-
ности характеризуется среднеквадратическим отклонением, равным 0,5,
ж подчиняется гамма-распределению.
Требуется:
1) вывести и численно определить точечную и интервальную (с уров-
нем доверия Pq = 0,95) байесовские оценки для среднеквадратиче-
ской ошибки в работе фасовочного ^автомата]
2) дать байесовскую интервальную оценку (с уровнем доверия Pq =
0,95) для доли расфасованных автоматом пачек кофе, вес которых
отличался бы от номинала (равного 500 г.) не более, чем на 2 г.
У Казани е. См. указание к примеру 1.10.
Задача 1.21
С целью оценки доли «очень богатого» населения Российской Феде-
рации (а именно, населения со среднедушевым месячным доходом, превы-
шающим 5 тыс. условных денежных единиц) используются следующие
модельные допущения и исходные статистические данные:
62
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
(i) доля населения со среднедушевым месячным доходом, превышающим
2 тыс. у.д.е., составляет 2,5%;
(И) эта категория населения распределена по величине среднедушевого
месячного дохода £ (тыс. у.д.е.) в соответствии с так называемым
законом Парето, т. е.
Fe(x) = PR < т} = ( 1 " (1)' при х > 2 тыс- У-Д-е-
I 0 при х < 2 тыс. у.д.е.
(iii) По случайной выборке а?!, а:2, • • • э а?40 из генеральной совокупности,
объединяющей только эту категорию населения, подсчитано числен-
ное значение среднего геометрического, а именно:
(40 \ &
Пх*) = 3,7795 (у.д.е.).
1=1 /
Требуется:
1) найти общее выражение и численное значение, вычисленное по дан-
ным выборки, оценки максимального правдоподобия 0МП неизвестно-
го параметра 0;
2) получить численное значение оценки доли «очень богатого» насе-
ления России среди всего населения РФ;
3) с доверительной вероятностью, равной 0,95, построить точную
интервальную оценку для параметра 6 (выписать в общем виде
и подсчитать конкретные значения для концов доверительного
интервала).
Указание. При ответе на последний вопрос доказать, что
случайные величины
(X' \
v), * = 1,2,...,40,
распределены по закону %2(2), и воспользоваться этим фактом.
Для справки: функция распределения %2(2) случайной величины
имеет вид:
Р{%(2) < У} = 1 ~ (для у > 0).
Задача 1.22
Приходящий в случайные моменты времени на остановку пассажир
в течение 5 своих поездок фиксировал время ожидания авзобуса (в ми
нутах): Zj = 1,2; х2 = 2,5; х3 = 0,5; х4 = 3,2; xs - 2,9. Известно, чк>
Глава 1. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
63
автобус ходит строго по расписанию с интервалом в 6 минут, так что вре-
мя ожидания автобуса пассажиром можно считать случайной величиной
£(О;0), подчиненной (0; 0)-равномерному закону распределения вероятно-
стей (з.р.в.), т. е. ее функция плотности Л(о:в)(®) определяется соотноше-
нием
) |0 при £(0; 0) ff. [0; 0],
а, соответственно, функция распределения
FW)(*) = P{W)<®} =
о
X
0
1
при х < 0;
при 0 < х < 0\
при х > 0.
Пытаясь оценить интервал движения автобуса, пассажир сумел полу-
чить дополнительную априорную информацию о параметре 0: из анализа
опыта работы различных автобусных маршрутов города, функционирую-
щих в едином регламентном режиме, следовало, что априорное среднее
значение этого параметра равно 5,38 мин., а случайный разброс в его зна-
чениях характеризуется средним квадратическим отклонением, равным
1,39 мин., и подчинен з.р.в. Парето. Функция плотности вероятности
распределения Парето определена соотношением
р(«) = при 9>в„;
I 0 при 0 < 0Q,
а функция распределения, соответственно:
F(0) = { 1 “ (^) при 6 - ^°’
I 0 при 0 < 0О,
где а и 0о — некоторые числовые параметры, значения которых могут
быть восстановлены по имеющейся априорной информации. Наблюдения
z15 ж2,..., х$ образуют случайную выборку.
Требуется:
1) вывести общий вид и подсчитать численно оценку максимального
правдоподобия 0МП, определить «подправленный на несмещенность»
вариант этой оценки 0МП и основанную на нем оценку среднего вре-
мени ожидания автобуса;
2) вывести и вычислить точную интервальную оценку параметра 0 с
уровнем доверия Pq = 0,95;
3) дополняя исходные статистические данные ж2,...,имеющейся
априорной информацией о параметре 0, вывести и вычислить то-
чечную и интервальную (с тем же уровнем доверия) байесовские
64
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
оценки параметра 0, сравнить их с оценками, полученными с помо-
щью метода максимального правдоподобия.
Задача 1.23
При выборочном обследовании малых и средних фирм, нацеленном на
оценку доли фирм, так или иначе уклоняющихся от налогов, был использо-
ван «метод рандомизированных ответов», который помогает преодолеть
нежелание людей давать честные ответы на «деликатные» вопросы.
Руководителю фирмы предлагается анкета, содержащая два вопроса:
Вопрос 1: Является ли нечетной последняя цифра года Вашего рождения?
Вопрос 2: Все ли доходы фирмы, подлежащие налогооблажению, Вы заяви-
ли в налоговой декларации в прошлом году?
Для того чтобы решить, на какой из двух вопросов отвечать, респон-
дент должен бросить игральную кость: если выпало 5 или 6 очков, он
отвечает на вопрос 1, в противном случае — на вопрос 2 (результат бро-
сания игральной кости он не сообщает).
С помощью случайной выборки было обследовано таким образом 120
налогоплательщиков и получено 44 утвердительных ответа.
Требуется:
(полагая всю анализируемую генеральную совокупность малых и
средних фирм бесконечной) построить точечную оценку максималь-
ного правдоподобия, а также приближенную интервальную (с до-
верительной вероятностью, равной 0,95) оценку для доли честных
налогоплательщиков.
Глава 2. Статистическая проверка гипотез
2.А. Краткие сведения из теории
На разных стадиях статистического исследования и эконометриче-
ского моделирования возникает необходимость в формулировке и экспери-
ментальной проверке некоторых предположительных утверждений (гипо-
тез) относительно природы или величины неизвестных параметров ана-
лизируемой стохастической системы. Например, исследователь высказы-
вает предположение: «исследуемые наблюдения извлечены из нормаль-
ной генеральной совокупности» или «среднее значение анализируемой
генеральной совокупности равно нулю». Будем обозначать в дальнейшем
высказанное нами предположение (гипотезу) с помощью буквы Н. На-
ша цель — проверить, не противоречит ли высказанная нами гипотеза Н
имеющимся выборочным данным.
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
65
Приведем здесь кратко основные понятия и результаты теории ста-
тистической проверки гипотез.
Статистический критерий — это процедура обоснованного сопо-
ставления высказанной (проверяемой) гипотезы Н с имеющимися в рас-
поряжении статистика выборочными данными Xi, я2,..., жп, сопровожда-
емая количественной оценкой степени достоверности получаемого вывода.
Критическая статистика 7(a?i, х2, • • • >хп) — функция от резуль-
татов имеющихся выборочных данных, на основании численного значения
которой принимается решение об отклонении или принятии проверяемой
гипотезы.
Основная («нулевая») гипотеза Hq — выдвинутое исследователем
предположительное утверждение, подлежащее статистической проверке.
Конкурирующая гипотеза Н\ — форма конкретизации утвержде-
ния, альтернативного к основной гипотезе Hq.
Простая гипотеза — гипотеза, сводящаяся к предположительному
утверждению, что значение некоторого (возможно — векторного) пара-
метра 0 анализируемой стохастической модели в точности равно задан-
ной величине (вектору) 0О (например, утверждения типа: «теоретическое
среднее значение анализируемой случайной величины в точности равно
0О> т. е. Ef = 0О», или «закон распределения вероятностей анализируе-
мой случайной величины является нормальным с заданными конкретны-
ми значениями среднего и дисперсии»). В остальных случаях гипотеза
называется сложной.
Критическая область Г^1 — область «малоправдоподобных», в
условиях справедливости проверяемой гипотезы Hq (при альтернати-
ве Н^), значений критической статистики 7(^1, х2,..., хп). Если значе-
ние критической статистики попадает в критическую область (т. е. если
7(ж1, ж2,..., хп) Е Гп1)» то гипотеза Hq отвергается (соответственно, при-
нимается гипотеза Hi).
Уровень значимости критерия (ошибка 1-го рода) а — веро-
ятность отвергнуть проверяемую гипотезу Hq в ситуации, когда в дей-
ствительности она верна (т. е. а = Р{у 6 Г^1 | Hq}).
Ошибка 2-го рода (3 рассматривается в схеме проверки простой
основной гипотезы Hq при простой альтернативе Н\, и она равна вероят-
ности отвергнуть альтернативу Н^ (т. е. принять основную гипотезу Hq)
в ситуации, когда альтернатива верна (т. е. /3 = Р{^ Г^1 | Я1}).
Мощность критерия р = \—[3 — это вероятность принять правиль-
ное решение в условиях справедливости конкурирующей гипотезы (т. е.
д = Р{7 6 Г^1 | Hi}). Если проверяется гипотеза о числовых значениях
параметра 0, а конкурирующая гипотеза Hi является сложной и сформу-
i Прикладная статистика
в задачах и упражнениях
66
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
лирована в виде утверждения {0 € А,}, где А] — некоторое множество
значений параметра, то вероятность /х(0) = Р{7 € Г^1 | 0 Е А]} подсчи-
тывается как функция от значений 0 и называется функцией мощно-
сти.
Сравнение статистических критериев по их качеству произ-
водится, как правило, с помощью сравнения их мощности: из двух кри-
териев, характеризующихся одной и той же ошибкой 1-го рода а, пред-
почтение отдается тому, который сопровождается меньшей ошибкой 2-го
рода /3 (или большей мощностью д). Если же при сложной альтернатив-
ной гипотезе Нг вида {0 Е Ai} функция мощности некоторого критерия
мажорирует функцию мощности любого другого критерия при всех зна-
чениях 0 Е 41, то такой критерий называется равномерно наиболее
мощным.
Критерий называется состоятельным, если вероятность откло-
нить основную гипотезу Hq в условиях справедливости конкурирующей
(Я1) стремится к единице при неограниченном росте объема выборки (т.е.
при п -+ оо).
Критерий называется несмещенным, если при проверке пара-
метрических гипотез вида «Яо:0 6 Aq и Е Аг» (где множества
значений параметра Ао и Аг не пересекаются) с заданным уровнем зна-
чимости а0 вероятность неправильно отклонить основную гипотезу Яо не
превосходит величины а0, в то время как вероятность правильно откло-
нить эту гипотезу всегда превосходит тот же уровень ао-
Критерии согласия предназначены для статистической провер-
ки гипотез об аналитическом виде закона распределения вероятностей
(з.р.в.) анализируемой генеральной совокупности. При этом проверяемая
гипотеза может вполне определенно (однозначно) задавать гипотетиче-
ский з.р.в. (например, «з.р.в. анализируемой генеральной совокупности
является равномерным на отрезке [0; 1]»), а может определять лишь общий
вид (тип) з.р.в. (например, «з.р.в. анализируемой генеральной совокуп-
ности относится к классу нормальных распределений»).
К тому же классу критериев относятся критерии, предназначенные для провер-
ки гипотез об общем виде моделей, описывающих статистическую зависимость между
компонентами наблюдаемой многомерной случайной величины (эти модели могут быть
линейными, степенными, полиномиальными и т. д.). Однако задачи для этих критери-
ев размещены в разделах II и III данного издания.
Критерии однородности двух или нескольких анализируемых вы-
борок предназначены для статистической проверки равенства соответ-
ствующих теоретических числовых характеристик в генеральных сово-
купностях, из которых извлечены имеющиеся выборки (например, для
проверки равенства теоретических средних значений или теоретических
Глав* 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
67
дисперсий), а также для проверки полной эквивалентности анализируе-
мых генеральных совокупностей, т. е. для проверки совпадения их законов
распределения вероятностей.
Критермм проверка гипотез о числовых значениях параме-
тров наблюдаемой генеральной совокупности предназначены для стати-
стической проверки гипотез вида «Яо: ® = ®о> или «Яо: ® € ^о» Мо —
некоторое параметрическое множество), где параметр в (числовой или
векторный) в различных задачах интерпретируется и как среднее значе-
ние анализируемой случайной величины, и как ее дисперсия, и как коэф-
фициенты корреляции или регрессии и т. п.
Результат статистической проверки гипотезы Яо может быть
либо отрицательным (данные наблюдений противоречат высказанной ги-
потезе, а потому от этой гипотезы следует отказаться), либо неотрица-
тельным (данные наблюдений не противоречат высказанной гипотезе, а
потому ее можно принять в качестве одного из естественных и допусти-
мых решений). При этом неотрицательный результат статистиче-
ской проверки гипотезы не означает, что высказанное нами предпо-
ложительное утверждение является наилучшим, единственно подходя-
щим: просто она не противоречит имеющимся у нас выборочным дан-
ным, однако таким же свойством могут наряду с Но обладать и дру-
гие гипотезы. Так что даже статистически проверенное предположение
Яо следует расценивать не как раз и навсегда установленный, абсолютно
верный факт, а лишь как достаточно правдоподобное, не противоречащее
опыту утверждение.
В табл. 2.1 приводится сводка результатов по наиболее распростра-
ненным в практике статистических и экономических исследований ста-
тистическим критериям. Отправляясь от конкретного содержания своей
задачи, исследователь может найти в данной таблице нужный ему тип
подлежащей проверке гипотезы Но (столбец 3), а также правила вычи-
сления критической статистики и определения критического множества
(столбцы 4 и 5).
68
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 2.1. Наиболее распространенные статистические критерии
и их критические статистики
NN пп Исходные статистические данные Проверяемая («нулевая») гипотеза Hq Критическая статистика 7n = и название критерия З.р.в. Д(у) или F7 (у) критич. статистики 7 в условиях спра- ведливости гипотезы Hq
1 2 3 4 5
1 Случайная выборка , ®2, • • •, и построенная по ней выборочная функция распределе- ния Г<п)(х) = где |/(х)-число выборочных данных, меньших z F(z) = F0(x), где гипотети- ческий вид функции рас- пределения Fq(x) задан однозначно 7п = sup |F<n)(х) — Fq(х)|, X критерий согласия Колмогорова- Смирнова Асимптотический (по п —► оо) з.р.в. статистики у/пуп задается функцией распределения ^<1/п7п < у} = = К {у) (см. п. 8.6.1 [1], с. 304)
2 Группированные данные, построен- ные на основании независимых наблюдений > ®2»•••» хп непрерывной слу- чайной величины: s-количество интервалов группирования, F(x) = F0(x), где гипотети- ческий вид функции распределения Fq(x) задан однозначно Уп = A (pj-npj)2 1=1 n₽> ’ где pj = Fo(cj) - Fo(c,-i), > = 1,2 s. Критерий сог- ласия x2 Пирсона При больших п (т. е. асим- птотически ПО 71 —► оо) статистика 7П распределена по закону х2 С (s - 1) степенями свободы
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
69
Табл. 2.1. Продолжение
1 2 3 4 5
1 Cj-правый конец j-ro интервала группирования Uj-число выбо- рочных данных, попавших в j-й полузамк- нутый (слева) интервал [с;- _ i, Cj), > = 1,2 5
3 i i Те же, что и в п. 2. F(x)6 е {F(x 1 ®)}, где семейство функций задан- ного общего вида {?(«!©)} зависит от Л-мерно го неизвестного параметра 7п = __ у^ (^j -WPjCQmh))2 j = l ЛР(®мп) где Pj = F(c; рЭмп)- -Г(с;_! | ©мп), а* ©мп-оценка максимального правдоподобия параметра 0, построенная по группированным данным (> = 1,2,..., з). Кри- терий согласия Пирсона х2 При больших п (т. е. асимпто- тически ПО П -4 00) статистика 7п распре- делена по закону х2 с (з - к - 1) степенями свободы
4 Группированные данные, постро- енные на основа- нии независи- мых наблюдений 11, Ж2, • • •, хп дискретной слу- чайной величины ( (возможные значения которой /(х)е е {/(* 1 ©)}, где вероятности 7(х | ©) = = Р{£ = X I 0} заданы с точностью до неизвестного ^-мерного па- раметра 0 = 7п = у^ (pj ~пР_Д®мп))2 У = 1 пР>(®мп) где Р>(®мп) = = 7(х9|©мп), а* ©мп-оценка максимального правдоподобия неизвестного па- раметра 0. При больших п (т.е. асимпто- тически по п —► оо) статистика 7п распре- делена по закону х2 с (ЛГ -Л-1) степенями свободы
70
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 2.1. Продолжение
1 2 3 4 5
суть -0 -0 -0 z1,z2,...,zArj. Vj -число вы- борочных данных, равных j-му возможному значению zj Критерий сог- ласия Пирсона ха
5 Случайные и взаимно независимые выборки из /(/ > 2) генераль- ных совокупностей ®11» • • •» ®lni» ®21» ®22> •••» *3n2; ®Н » ®/2» • • •» и построенные по ним группирован- ные данные с одним и тем же разбие- нием на интервалы группирования: з-количество интервалов груп- пирования, су-правый конец j-ro интервала группирования, Vij-число элементов i-й выборки, попавших в j-й интервал группи- рования (• = 1,2,...,/; > = 1,2 «) Fi(z) = Fa(z) = ... ... = F/(z), где Fi (х)-функция распределе- ния i-й гене- ральной со- вокупности (« = 1»2 /) 7п = J=ll=l где: t "i. = Е Vij = П{ - /=1 число элементов в i-й выборке; / v i = Е щ - 1=1 общее (по всем выбор- кам) число вы- борочных данных, попавших в j-й интервал группирования; « = Е »»<• 1=1 Критерий одно- родности 1 вы- борок (Смирнова) При больших п(* (т.е. асимпто- тически по min {П{} —► оо) ККГ 7 статистика 7п подчиня- ется з.р.в. Х3(т) с чис- лом степеней свободы т = = (1-!)(»-!)
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
71
Таблица 2.1. Продолжение
'1 2 3 4 5
6 i i Наблюденные значения ViW) = («*<1 полиномиально распределенной многомерной слу- чайной величины ••»₽!•)» статистически не- зависимые (по •) между собой; 1 = 1,2,...,/. Fi(x) = = Г2(х) = ... ... = Л(х), т. е. Plj = P2J = • • • • • = PU для всех j = 1,2,..., а 7п = = у* у> )а J=1 is I где Pij = $*•, Е Nitij Pi = • E Nt ial Критерий однород- ности / выборок Смирнова (част- ный случай для полино- миальных рас- пределений). При больших Ni (т.е. асимптоти- чески по статистика уп подчиняется з.р.в. ха с числом степе- ней свободы
7 i i Независимые наб- людения случай- ной величины и независимые наблюдения случай- ной величины (а *21,^22, ...» Х2па (выборки упорядо- чены так, чтобы П1 п2) Efi = Е(2 *y — V* где in — 2^ Л} , где л^ ранг i-го члена вариационного ряда 1-й выборки в общем вариа- ционном ряду, построенном по двум объединен- ным выборкам. Критерий од- нородности средних значений двух выборок (Вилкоксона- Манна- Уитни) При больших Л1 и п2 (т.е. асим- птотически по ni —► оо) статис- тика 7п под- чиняется (лог- нормальному распределению, в котором, а = |П1(П1 + П2 + 1), (Г2 = yjnin2(ni +п2)
72
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 2.1. Продолжение
2 3 4 5
8 Две случайные выборки и Z21,X22,«. представлены ые независимыми наблюдениями, соответственно, (аца2)- и (a2;a3)- нормальных слу- чайных величин и (2 (значения пара- метров а 1,аг и <г2 неизвестны) Е(1 = Е^2 (т.е. ai = аг) 7п = гНпр-ЗгСпг)., где nj Mn>) = Е 1=1 в?(пу) = lni (j = 1, 2) и З3 = П1+П2-2 Критерий однород- ности средних значений Стьюдента (t-критерий) Статистика уп распределена по закону Стьюдента с ni 4- пг — 2 сте- пенями свободы. Примечание: Критерий может применяться как приближенный и к выборкам из негауссов- ских генераль- ных совокуп- ностей
9 Имеется 1 случайных выборок хj 1 > xj 2 > • • • » хj nj 0=1.2 /), где каждая (j-я) из этих выборок представлена неза- висимыми наб лю де- ден ия ми (ay; (г2 ^нор- мальной случайной величины (у (значе- ние параметров а11 а2> * * * и/; <г2 неизвестны) Е6 = = Е6 = ... ... = Е6 (т.е. ai = аг = ... • •• = <ч) 7п = г-г Е п>(Мп>)“г)2 j=i " г2 > где i Е nj®>(nj) % _ J=i "1 +п2 + ... + п( ’ Ё », «?(•»,) 52 _ 1Z2 3 — П1 + ...+п,_р а в?(п,) = (Й(хл-х,(п;-))3)/п,-. \j=l / Критерий диспер- сионного анализа Статистика уп распределена по закону 1; Е »»; - А. ;=1 / Примечание: Критерий может применяться как приближенный и к выборкам из негауссовских генеральных совокупностей
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
73
Таблица 2.1. Продолжение
Г— 1 2 3 4 5
10 1 i ! । I Независимые наблюдения ХЦ 9 Х12 > • • • j Я1ГЧ (ai; af )-нормальной случайной величи- ны и независи- мые наблюдения 9 х22, • • • , ®2п2 (аг; (т|)-нормальной случайной величи- ны (2 (значения параметров ai,az, ет2 и trj неизвестны) D6 = D6 (т.е. <т? =<ф 7п = (®ii -®i(*i))2 1 i=i Статистика 7П распределена по закону F(ni - 1;п2 - 1). Примечание: Критерий может применяться как прибли- женный и к выборкам из негауссоеских генеральных совокупностей
w * j 5? (®21-*2(*з))2 2 i = l где i ny xj(nj) = 52 xii J 1=1 0 = 1,2). F - критерий одно- родности дисперсий
i I и i Имеется 1 случай- ных выборок х j 1) х j 2) • • • ) xj nj 0 = 1.2 0. где каждая (j-я) выборка представ- лена независимыми наблюдениями (а/; ст?)-норм альной случайной величи- ны (у (значения параметров ay, Оу неизвестны). min{ni,n2,...,n/} > 3 11 : Q „ Q W - II j II II 7n = где 5? (nJ = = «J (»»j )/(»»/ “ 1). «?(nj) = Z2 (xji - xj(nj ))2. J 1=1 / nJ \ xj(nj) = ( 53 xj» Ilni t \i=i / S3 "/‘/("j) «2 _ П1 + ... + П/-1 ’ ? - [1 + 3(1-1) x x (k \j=i > ni + ...+пн)] Критерий Бартлетта одно- родности ряда дисперсий Статистика 7П подчиняется (приблизительно) закону распре- деления вероят- ностей х2 с (/ — 1) степе- нями свободы Примечание: Критерий может применяться как приблц^ женный и к выбор- кам из негауссов^ ских генераль- ных совокуп- ностей
74
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 3.1. Продолжение
1 2 3 4 5
12 Независимые наблюдения (TV, Pi)-биномиаль- ной случайной величины и независимые наблюдения Z31>X33>”*>£3n3 (ЛГ, Рз)-биномиаль- ной случайной величины (з (пара- метры pi и рз неиз- вестны, N- известно). E(i « E(j (или: pi = рз) 7п = где PiM - ^niN 0 = 1,2,), а й = П1Р1(г»1)+п3ра(па) г *1+^3 Критерий одно- родности двух биномиальных выборок Статистика 7П асимптоти- чески (по min(ni, пэ) —* оо) подчиняется (0; 1 ^нормаль- ному распреде- лению
13 Независимые наблюдения х j 1» xj 2 > • • •» xj n j (Nj>Pj )-биномиальных случайных величин (у 0 = 1,2 1; 2). Е6 = ... ... = Е6 (или: pi = ... • • • = Pl = р) 7п = v4 n-> А, Ki-р) ’ г —* где Р; = 1 Е «у, I !n>Nj, \«=1 / j = 1,2,...,!; Е njNjfj Р=" i Статистика 7П асимптотически по подчиняется X2-распределе- нию с / — 1 степе- нями свободы.
Гл»в* 3. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
76
Таблица 3.1. Продолжение
1 2 3 4 5
14 Независимые наблюдения , Х2,•. • , Хц (N, р)-биномиальный случайной величины ( (значение пара- метра N известно, значение параметра р неизвестно) Р~Р0, где значение ро вероятности «успеха» в единичном испытании задано п 7п » £ С< Критерий проверки гипотезы о число- вом значении параметра р биномиального распределения а) С л у ч а й 0,1 < ро < 0,9: статистика уп асимптотически (по nN —* оо) подчиняется (nJVpo;n7Vpo(l -ро))- нормальному рас- пределению. б) С л у ч а и ро < 0,1 или ро > 0,9: статистика уп асимптотически (по nN —► оо) под- чиняется распре- делению Пуассона с параметром, равным nWpo
15 Независимые наблюдения » хп (а; а2)-нормальной случайной величины ( (значения пара- метров а и а2 неизвестны) Е£ = ао, где значение ао теорети- ческого сред- него задано ~ _ (*(п)-а0)Уп-1 Гл ~~~ _ , где х(п) = ( 52 ) /п» \|=1 / s2 = = (е(®< -х(п))2} /п. \i=l / Критерий Стьюдента (или: t-критерий) Статистика уп подчиняется распре- делению Стьюдента с (п — 1) степенями свободы. Примечание: Критерий может применяться как приближенный и к выборкам из нега- уссовских генераль- ных совокупностей
76
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 2.1. Окончание
1 2 3 4 5
16 Те же, что и в п. 12 De = a’, где значение сг$ теорети- ческой дис- персии задано „ — w<a(n) 7п- 4 1 где в2(п) = \»=1 / / п \ a i(n) = ( 22 xi ) /”• \| = 1 / Критерий проверки гипотезы о чис- ленном значении дисперсии Статистика уп подчиняется X2-распреде- лению с числом степеней свободы, равным п — 1. Примечание: Критерий может применяться как приближенный и к выборкам из нега- уссовских гене- ральных совокупностей
Комментарий к использованию табл. 2.1.. Общая логика стати-
стической процедуры проверки гипотез, на которой основан всякий ста-
тистический критерий, состоит в следующей цепочке рассуждений:
1) если верна проверяемая гипотеза Но, то критическая статисти-
ка должна вести себя в соответствии с законом распределения
вероятностей (з.р.в.), указанным в последнем (5-л) столбце табли-
цы;
2) это значит, что ее конкретное числовое значение должно при-
надлежать области естественных (наиболее вероятных)
для данного з. р. в. значений случайной величины, т. е. оно не
должно быть «неправдоподобно маленьким», или оно не должно
быть «неправдоподобно большим», или (в случае двусто-
ронней альтернативы) оно не должно быть «ни не-
правдоподобно маленьким, ни неправдоподобно большим».
3) «неправдоподобно маленькие» значения критической стати-
стики уп при уровне значимости критерия, равном а, и при
односторонней альтернативе определяются отрезком (-оо,
7л1 г^е 7п1-а) это 100(1 — а)-%-ная точка распределения, ука-
занного в последнем столбце; «неправдоподобно большие» зна-
чения критической статистики ~fn при том же уровне значимо-
сти критерия и при односторонней альтернативе опреде-
ляются отрезком (7^,00), где это 100а-%-ная точка того
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
77
же распределения', и, наконец, область «неправдоподобно ма-
леньких и неправдоподобно больших» значений критической
статистики уп при уровне значимости критерия, равном а, и при
двусторонней альтернативе состоит из объединения двух
отрезков (-оо, 7^~а^) и (7я“/2), +оо);
4) попадание численного значения критической статистики в область
«неправдоподобных» (в условиях справедливости проверяемой ги-
потезы Hq) значений говорит о противоречии имеющихся исходных
статистических данных и этой гипотезы, а потому в этом случае
проверяемая гипотеза Hq отклоняется (с вероятностью ошибить-
ся, равной а, т. к. по построению при справедливости гипотезы
Hq это событие возможно, хотя и маловероятно, а именно, оно
может произойти с вероятностью, равной а).
Таким образом, табл. 2.1 содержит всю необходимую информацию для
построения статистического критерия, позволяющего проверить любую из
16-ти гипотез Но, обозначенных в ее третьем столбце, а именно: она да-
ет правило подсчета численного значения критической статистики 7Я и
определяет ее закон распределения вероятностей. Для определения обла-
сти значений уп, в которой гипотезу Но следует отклонить (т.е. для
определения критической области критерия), остается воспользоваться
таблицами процентных точек этого з.р.в. и приведенными выше рекомен-
дациями (см. пп. 3) и 4) «Комментария»).
2.Б. Примеры решения типовых задач и упражнений
Пример 2.1 (упражнение). В нашем распоряжении — ре-
зультаты выборочного обследования малых предприятий по соотношению
заемных и собственных средств (см. исходные статистические данные
примера 1.1, представленные в табл. 1.3 и 1.4).
Требуется:
с помощью одного из критериев согласия статистически проверить
(с уровнем значимости критерия а = 0,05) гипотезу о том, что
имеющаяся в нашем распоряжении выборка извлечена из нормаль-
ной генеральной совокупности.
Решение
Речь идет о статистической проверке гипотезы о типе з.р.в. имею-
щихся наблюдений в ситуации, когда неизвестные значения параметров
гипотетичного закона должны быть оценены по этим наблюдениям. Сле-
довательно, целесообразно воспользоваться критерием согласия %2 (см.
78
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
п. 3 табл. 2.1). Эта процедура предусматривает в качестве первых шагов
предварительную группировку исходных статистических данных в соот-
ветствии с рекомендациями (1.2) (см. также п. 6.1 в [1]), а также оценку
по этим данным с помощью метода максимального правдоподобия неиз-
вестных параметров гипотетического распределения (в нашем случае —
среднего значения а и дисперсии а ). Поэтому мы воспользуемся уже
сгруппированными данными, представленными в табл. 1.4 (так что в
нашем случае число интервалов группирования л равно восьми). Оцен-
ки амп и 7мп по этим данным вычисляются по формулам (в дальнейшем
сохранены обозначения примера 1.1):
®МП —
2-5,03+3-5,14+12-5,25+19-5,36+29-5,47+18-5,58+13-5,69+4-5,80
100
= 5,466
;=1
Для подсчета значения критической статистики
у' ~ п?Я®мп))а
J=1 пРд(®мп)
(*)
необходимо^ предварительно вычислить «модельные» значения вероят-
ностей ру(0) попадания в j-й интервал группирования. В нашем случае
2
®мп = (^мп! ^мп)) а
Pj(®Mn) — I ®мп! ^мп) 1 | ®мп! ^мп)1 j' — 1,2, (**)
где
♦(« | а; <?) = [
J —оо
О-a)3
е dz
— функция распределения (а; <т2)-нормального з.р.в. и cj-i,Cj, — соот-
ветственно, левая и правая граничные точки j-го интервала группирова-
ния. Значения функций в правой части (**) находим из таблиц значений
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
79
стандартной нормальной функции распределения Ф(х | 0; 1), используя
известное соотношение
। 2х А / z-a
Ф(г I а; а ) = Ф I -
0;1
Проведенные расчеты представлены в табл. 2.2.
Таблица 2.2. Значения Ф(с, | амп;^мП) и р,(0Мп)
У 0 1 2 3 4 5 6 7 8
4,97 5,08 5,19 5,30 5,41 5,52 5,63 5,74 5,85
(CJ -*мп) -2,970 -2,311 -1,653 -0,994 -0,335 0,323 0,982 1,641 2,299
♦(с/|ймп> ^мп) = = ф/££^1 0;1) 0,0015 0,0100 0,0490 0,1600 0,3800 0,6250 0,8370 0,9500 0,9891
р/(§мп) - 0,0085 0,0390 0,1110 0,2200 0,2450 0,2120 0,1130 0,0391
прДвмп) - 0,85 3,90 11,10 22,00 24,50 21,20 11,30 3,91
ч - 2 3 12 19 29 18 13 4
(Vj -прДвмп))’ - 1,323 0,81 0,81 9,00 20,25 10,24 2,89 0,008
npj (в мп) - 1,56 0,21 0,07 0,41 0,83 0,48 0,26 0,00
Суммирование чисел, стоящих в последней строке, дает нам, в соот-
ветствии с (*), значение критической статистики:
7п = 3,82.
В случае, если проверяемая гипотеза о нормальности генеральной со-
вокупности, из которой извлечена наша выборка, не противоречит имею-
щимся наблюдениям, критическая статистика 7П должна вести себя как
- к - 1) (в нашем случае, как % (5)) случайная величина, т.е. ее
значение не должно превысить 5%-ной точки этого распределения Хо,О5-
Определив из таблиц величину %о,оз(5) = 11,07, делаем вывод о непроти-
воречивости проверяемой гипотезы имеющимся в нашем распоряжении
исходным статистическим данным, поскольку уп < Xo,os(5).
Пример 2.2 (упражнение). Имеется случайная выборка
Х1,Ж2,... ,хп (достаточно большого объема, п > 100) из (АГ,/^-биномиаль-
ной генеральной совокупности. Значение вероятности «успеха» р неиз-
вестно, а общая длина серии испытаний Бернулли N известна.
80
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Требуется:
1) предложить и обосновать основанную на теореме Муавра-Лапласа
критическую статистику уп для проверки гипотезы Hq о числен-
ном значении неизвестного параметра р (Н$:р = Pq, где р0 — за-
данное число);
2) подробно описать критерий проверки гипотезы Hq при альтерна-
тиве:
(a) Hi.pypo-,
(б) Н1:р<р0-,
(в) Hi:p/pQ.
Решение
1) Из теоремы Муавра-Лапласа (см. п. 4.3.3 в [1], с. 159) следует, что
если случайная выборка xi,x2,...,xn извлечена из (Я,ро)-биномиальной
генеральной совокупности (т.е. если справедлива гипотеза Яо), то стати-
стика
п
22 Xi - nNpo
7n = - (*)
y/nNp0(l -р0)
асимптотически (по п —* оо) подчиняется стандартному нормальному
з.р.в., т.е. должна вести себя (в условиях справедливости гипотезы Яо)
как (0;1)-нормальная случайная величина.
Какие именно отклонения значения 7п от нуля (отрицательные или
положительные) следует признать «неправдоподобно большими» в усло-
виях гипотезы Яо (т.е. как именно строить критическое множество кри-
терия), зависит от способа конкретизации альтернативной гипотезы Яг.
2) Рассмотрим три варианта конкретизации альтернативы И,,
п
(а) Нр р > р0. Очевидно в этом случае сумма 52 xi в условиях спра-
1=1
ведливости конкурирующей гипотезы (т.е. гипотезы должна стати-
стически значимо превышать свое среднее значение, подсчитанное в рам-
ках условий основной гипотезы Яо, т.е. — величину nNpQ. Следователь-
но, большие положительные значения статистики (*) будут сигнализиро-
вать о большей правдоподобности конкурирующей гипотезы (а). Поэтому
правило «принятия-отклонения» гипотезы Hq строится следующим обра-
зом: по заданному уровню значимости критерия а из таблиц стандартно-
го нормального распределения определяем его 100а%-ную точку wa (или,
что то же — (1 — а)-квантиль если определенное соотношением
(*) значение уп > wa, то гипотеза Яо отклоняется (и принимается, если
7n < wo).
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
81
(б) Hi: р < ро- В этом случае в условиях справедливости гипоте-
п
зы Hi сумма 52 xi будет статистически значимо меньше, чем nNpQ.
г=1
Следовательно, именно большие по абсолютной величине отрицательные
значения статистики (*) будут сигнализировать о малой правдоподобно-
сти основной гипотезы Но- Поэтому если окажется, что -уп < — wa, то
гипотезу Но следует отклонить (и принять, если уп — wa).
(в) Н]:р / р0. В этом случае и отрицательные, и положитель-
ные большие по абсолютной величине отклонения статистики уп от ну-
ля будут сигнализировать о большей правдоподобности конкурирующей
гипотезы Яр Поэтому для проведения процедуры статистической про-
верки гипотезы Но с заданным уровнем значимости критерия а следует
определить из таблиц 100у%-ную точку wa/2 стандартного нормального
распределения, после чего:
гипотезу Но отклонить, если |7n| > wa/2;
гипотезу Но принять, если |7n| С ша/2.
Заметим в заключение, что все описанные здесь статистические кри-
терии являются приближенными (в том смысле, что сопровождаются ве-
личиной ошибки 1-го рода лишь приближенно равной заданному значению
а), т. к. распределение критической статистики (*) в условиях справедли-
вости гипотезы Но является лишь приближенно (асимптотически точно
поп —► оо) (0;1)-нормальным.
Пример 2.3 (упражнение). Имеется к независимых слу-
чайных выборок ...,xjn (j = 1,2,...,&), извлеченных, соответ-
ственно, из к (af, сг2)-нормальных генеральных совокупностей (значения
2 х
параметров аг, а2,..., и о неизвестны).
По этим выборкам подсчитаны:
кп - к Д' ’
j=i
82
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Требуется:
1) доказать, что если а\ = а% = ... — Oky т° статистика
2 2
52 n(xj — x)/s подчиняется F-распределению с числами степе-
j=i
ней свободы числителя и знаменателя, равными, соответственно,
к - 1 и кп — к-,
2) построить и обосновать критерий статистической проверки ги-
потезы Hq: oi = аг ... = а/с при уровне значимости, равном а.
Решение
1) Из результата решения упражнения 1.15 следует, что статистика
k
$2 n(ij — ®)2/ст2 распределена по закону - 1). Опираясь на теорему
j=i
Фишера (см. п. 6..2.8 в [1]), можем заключить, что статистики n^j/o?
распределены по закону х2(п-1) и не зависят от числителя анализируемой
статистики. Из взаимной независимости к выборок следует, что сумма
2 2 2
(£ пз^/а подчиняется х (кп - к). Таким образом, получаем:
i=i
/с
3=1
>1
что и требовалось доказать, поскольку правая часть данного выраже-
ния и есть, по определению, случайная величина, подчиняющаяся з.р.в.
F(k - 1‘,кп-к).
2) Используем доказанный факт для построения критерия проверки
гипотезы Но: ai = a2 = ... = a^. Поскольку нам известно, что величина
дисперсии О’2 одна и та же для всех к генеральных совокупностей, то в
этих условиях (т. е. в условиях справедливости гипотезы Яо) статистика
_ 52j=i n(®i —
^п~ 1 2
кп—к n3s3
должна вести себя как F(k - 1; кп - /^-распределенная случайная ве-
личина. Поскольку именно большие значения (ij - ®)2 будут сигнали-
зировать о нарушении гипотезы Яо, то в качестве неправдоподобных (в
условиях справедливости гипотезы Яо) значений статистики уп класси-
фицируются «слишком большие» значения этой статистики. А именно,
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
83
гипотеза Но будет отвергаться (с вероятностью ошибиться, равной а),
если 7П > Fa(k — 1; кп — к), где Fa(k — 1; кп — к) это 100а%-ная точка
F(k — 1; кп — ^-распределения.
Пример 2.4 (упражнение). По наблюдениям Xi, х2,..., хп
(а;ст2)-нормальной случайной величины £(а;ст2) (значения параметров
а и а2 неизвестны) построена критическая статистика 7П = (ж(п) —
ao)Vn - 1/в, где ®(п) = ($2 xi)/n> 3 = _ х(п)) /п н а0 — заданное
1=1 1=1
(гипотетичное) значение теоретического среднего Е£(а;ст2). Решение об
отклонении гипотезы
Hq’ Е£(а;ст2) = ао
принимается в ситуации, когда |7n| > f*(n-1), где t|(n-l) — 100?%-ная
точка распределения Стьюдента с п - 1 степенями свободы (в противном
случае гипотеза Но не отклоняется).
Требуется:
1) ответить на вопрос, является ли гипотеза Но простой;
2) доказать, что описанная выше процедура проверки гипотезы Но со-
провождается вероятностью ошибки 1-го рода, равной а;
3) доказать несмещенность данного критерия.
Решение
1) Распределение анализируемой случайной величины £(а; о2) зависит
от двумерного параметра 0 = (а; ст2), так что проверяемая гипотеза Но
должна быть сформулирована в виде
Н0‘. 0 6 До = {(а;<г2): а = «о; <?2 > 0}.
Поскольку множество До — это положительная полупрямая на плос-
кости аОа2, параллельная оси Ост2 и проходящая через точку а = а0 на
оси Оа, то гипотеза Но является сложной.
2) Известно, что статистика 7П = (ж(п) —ao)\/n - 1/s, построенная по
выборке из (а; ст2)-нормальной генеральной совокупности, в предположе-
нии справедливости гипотезы Но подчиняется з.р.в. Стьюдента с п — 1
степенями свободы (см. (6.30) на с. 221 [1], а также п. 15 в табл. 2.1).
Поэтому
А это и значит, что ошибка 1-го рода в данном критерии равна а.
84
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
3) Для доказательства несмещенности данного критерия необходимо
показать, что при любом значении («г; ст2) параметра 0, не принадлежа-
щем прямой До (т.е. при / во)>
„ f |ят(п) — ап\\/п — 1 . г!
р J ------------о|Д--------> (п _ л I >
I 5 2 J
или, что то же:
^{|7п| < Ц(«- 1) I < ^{|7п| < t$(n- 1) | а0;cr2} = 1 - а.
Чтобы доказать последнее неравенство, преставим 7П в виде
х(п) — ао !---т ( х(п) — ai
7п = ----Vn -1=1 ----
3 \ 3
_ (®(n) — ai)Vn - 1 ( е
" ii + S'
Д1 - a0\ /-—-
+-------I уп — 1 =
5 J
rno c (01 " “о)\/П(П - 1)
где £ =-----------------
Тогда
p{|7n| < ^(n - 1) | ai;erf} =
< Ц(п- 1) | at,-a? * .
Зафиксируем значение x\n — 1) = w и подсчитаем условную вероят-
ность
т. к. площадь фигуры (Ц(п - 1) - ^,Д,В,Ц(п - 1)) очевидно больше
площади фигуры (-Ц(п - 1) - ^,Д', В',-Ц(п - 1)) как при положи-
тельных, так и при отрицательных значениях £ (см. рис. 2.1, соответ-
ствующий положительным £; при отрицательных значениях £ отрезок
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
85
[-Ц(п - 1),£^.(п — 1)] сдвигается вправо на £ и все рассуждения доказа-
тельства производятся аналогично).
Рис. 2.1. Пояснение к доказательству несмещенности критерия, основан-
ного на t(n — 1)-статистике (пример 1.13).
Действительно, обозначив с помощью Л(п-1)(я) функцию плотности
распределения стьюдентовской случайной величины t(n— 1) с п— 1 степе-
нями свободы, имеем:
р |-ч(п -
= / dx < / Л(П-1)(®Н® = 1 -а,
что и требовалось доказать.
П р и м е р 2.5 (з а д а ч а). В табл. 2.3 приведены данные о зара-
ботной плате сотрудников двух фирм.
Требуется:
проверить (при уровне знаимости критерия а = 0,05) гипотезу о
том, что распределения работников двух анализируемых фирм по
размерам заработной платы не отличаются друг от друга.
86
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Табл. 2.3 Группированные данные о заработной плате работников
двух фирм
Номер интервала группи- рования О) Границы интервала группи- рования (усл.ден.ед.) Кол-во работников фирмы, попавших в j-й интервал + "ЗУ
(*у) из выборки 1-й фирмы ("31) из выборки 2-й фтрмы
1 130 ~ 150 4 1 5 3
2 150 ~ 170 4 1 5 3
3 170 ~200 15 8 23 7
4 200 ~250 51 43 94 8
5 250 ~ 300 22 34 56 -12
6 300 ~ 350 3 7 10 -4
7 350 ~400 1 3 4 -2
8 400 ~ 500 - 3 3 -3
Решение
Речь идет о статистической проверке гипотезы Hq: Fi(ar) = ^(т), где
Fj(x) — функция распределения работников j-й фирмы по размерам за-
работной платы (j = 1,2), причем, не делается никаких предположений
об общем параметрическом виде распределений Fj(x). В подобных ситуа-
циях используют непараметрический критерий однородности I выборок
Смирнова (см. п.5 табл. 2.1). В нашем случае I = 2, п\ = п2 = 100, так
что критическая статистика тп имеет вид (см. [1], формулу (8.20*)):
8
7п =
J=1
= 14,58.
+ v2j
По критерию Смирнова статистика уп в предположении справедли-
вости проверяемой гипотезы Но должна вести себя приблизительно как
%2((/ — 1)(з - 1))-распределенная случайная величина (соответственно, в
нашем случае — как х2(7)-распределенная случайная величина, поскольку
в данном примере I = 2 и з = 8).
Однако 5%-ная точка х2(7)-распределения равна Xo,os(7) = 14,07 (см.
табл. П 1.4) и , следовательно, величина уп = 14,58 относится к области
практически неправдоподобных (в условиях справедливости гипотезы Яо)
значений случайной величины х2(7). Значит, гипотеза Но о статистиче-
ски незначимом расхождении распределений сотрудников двух фирм по
заработной плате противоречит имеющимся в нашем распоряжении ста-
тистическим данным, и мы эту гипотезу должны отвергнуть (с вероят-
ностью ошибиться, равной 0,05).
Пример 2.6 (задача). Реклама утверждает, что из двух ти-
пов пластиковых карт «American Exspress» и «Visa» богатые люди
Глав* 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
87
предпочитают первый. Другими словами, среднемесячные платежи одно-
го среднестатистического обладателя «American Express» существенно
(статистически значимо) превышают среднемесячные платежи одного
среднестатистического обладателя карты «Visa» . С целью статистиче-
ской проверки этого утверждения были обследованы среднемесячные пла-
тежи 32 обладателей «American» (nj = 32) и 30 обладателей «Visa»
(п2 = 30). В результате первичной статистической обработки этих двух
выборок были получены следующие значения выборочных характеристик:
®i(ni) = $563
4(nt) = 31684
®2(п2) = $485
э1(п2) = 38416.
При этом предварительный анализ законов распределения месячных
расходов как среди обладателей «American Express» , так и среди обла-
дателей «Visa», показал, что и тот и другой з.р.в. достаточно хорошо
описываются нормальной моделью.
Требуется:
проверить справедливость утверждения рекламы, т. е. проверить
(с уровнем значимости критерия а = 0,025) гипотезу Hq: — Efa
при альтернативе Н\: Е^у > E&i где и £2 это месячные кре-
дитные расходы случайно выбранных обладателей кредитных карт,
соответственно, «American Express» и «Visa».
Решение
Мы находимся в ситуации, описанной в п. 8 табл. 2.1 при условии, что
выборочные дисперсии двух анализируемых совокупностей (s2 = 31684
и s2 = 38416) различаются статистически незначимо (т.е. при условии
D6 = D& = о2). Поэтому начнем с того, что проверим (при стандарт-
ном значении уровня значимости критерия, т.е. при а = 0,05) гипотезу
Н: D& = D£2. В соответствии с рекомендациями п. 10 табл. 2.1 вычислим
значение критической статистики F-критерия однородности дисперсий
Тп
^j-n2s2(n2)
Поскольку 1,22 < FotQs(29;31) ~ 1,84 (см. табл. П1.5), то мы имеем
основания принять допущение о равенстве теоретических дисперсий D&
и D£2 в анализируемых совокупностях в качестве статистически прове-
ренной рабочей гипотезы.
88
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Теперь мы можем воспользоваться критерием Стьюдента (/-критерием,
см. п. 8 табл. 2.1) для проверки гипотезы Hq: E£j = Е£2. Вычисление кри-
тической статистики
Дг(пг) - Ж2(пг)
где s2 = ^j^T2(nisi(ni) + пг4(п2)), Дает 7П = 1,61.
Поскольку гипотеза Hq проверяется при односторонней альтернативе
(Я1? E£i > Е£2)5 то значение 7П = 1,61 следует сравнивать с 2,5%-ной
точкой <о,025(30 + 32 — 2) /-распределения с 60-ю степенями свободы.
Из таблиц П1.6 находим <o,02s(60) = 2,00. Поскольку 7П < 2,00, то у
нас нет основанийк отклонению гипотезы HQ: E£i = Е£2, а следовательно,
по тем данным, которыми мы располагали, мы не можем подтвердить
справедливость утверждения рекламы.
Пример 2.7 (задача). Поставщик аттестует свою продукцию
так называемой «необходимой долей брака» р0 = 0,05 (изделия продукции
контролируются по альтернативному признаку, т. е. признаются в резуль-
тате контроля либо «кондиционными» либо «дефектными»). Заказчик,
учитывая имеющийся у него опыт предыдущих поставок, утверждает, что
в действительности продукция этого поставщика характеризуется долей
брака pi = 0,10. Для разрешения спора из массового стационарно функци-
онирующего производства поставщика извлекается контрольная случай-
ная выборка изделий объема п = 100 единиц.
Требуется:
1) построить наиболее мощный критерий (с уровнем значимости а =
0,01) проверки гипотезы Hq: р = р + 0 = 0,05 при альтернативе
Н\‘. р = Pi = 0,10, т.е. определить такое пороговое значение Xq
(«браковочное число») дефектных изделий в данной выборке, начи-
ная с которого гипотеза Hq должна быть отвергнута (с вероят-
ностью ошибки, равной а = 0,01) и, соответственно, принимается
решение об истинности альтернативного утверждения Н^,
2) определить численное значение мощности построенного критерия.
Решение
1) Рассматриваемая задача относится к анализу результатов серии
п независимых испытаний Бернулли (см. [1], п. 3.1.1). При этом в име-
ющейся у нас выборке объема п интересующее нас событие произошло
х раз. Можно интерпретировать эту серию (выборку) как единственное
наблюдение (п,р)-биномиальной случайной величины в ситуации, когда
параметр п известен, а параметр р нет. Далее речь пойдет о проверке
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
89
гипотез о численном значении параметра р биномиального распределения
при различных альтернативах.
Принимая во внимание утверждение леммы Неймана-Пирсона о том,
что критерии отношения правдоподобия являются наиболее мощными
среди всех других возможных критериев (см. п. 8.3.1 в [1]), попробуем
вывести критическую статистику критерия, руководствуясь именно этим
принципом. При этом нам удобнее будет, как это часто бывает при ра-
боте с функциями правдоподобия, не само отношение правдоподобия, а
его логарифм (монотонность этого преобразования обеспечивает нужный
результат).
Функция правдоподобия биномиального закона с параметрами п и
р при единственном наблюдении ж, как известно (см. п. 3.1.1 в [1]), имеет
вид:
£(х|р;п) = С:/(1-р)я-*.
Так что критическая статистика критерия ^п\ определяемая лога-
рифмом отношения правдоподобия при произвольном значении параметра
р по отношению к основному гипотетическому р0, будет иметь вид:
(п) = , Да: |р;п)
Т(х | ро?«)
= х In ( —-—
\1 -Р
i-PoA , i-р
-----I + п In ---
Ро J 1 ~ Ро
(*)
Из смысла статистики 7П ясно, что «достаточно большие» ее значе-
ния сигнализируют о большей правдоподобности конкурирующей гипоте-
зы «Я: р ро» , т.е. о необходимости отвергнуть основную гипотезу
<Я0: Р = Ро» •
Для того чтобы построить критерий при заданном значении уровня
значимости а, нужно уметь назначить такое пороговое значение са, при
котором
Р{7(Л) > са | Но} = а. (**)
А для того, чтобы вычислить ошибку второго рода /3 или мощность кри-
терия 1 — X?, нужно уметь вычислять вероятность
l-/3=P{7(n)>Ca|^}.
(* * *)
Из (*) следует, что обе эти задачи решаются, если мы будем знать
распределение случайной величины х как при условии справедливости
«нулевой» гипотезы Hq (т.е. при значении параметра, равном задан-
ной величине р0)> так и ПРИ условии справедливости любой альтернативы
(т.е. при любом другом значении р анализируемого параметра). Но при-
знак х, по построению, есть (п^р)-биномиально распределенная случай-
90
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ная величина со значением параметра р, определяемым в зависимости от
того, в условиях справедливости какой из гипотез мы ее рассматриваем.
Поэтому в дальнейшем мы в качестве критической статистики
будем рассматривать (п,р)-биномиально распределенную случайную ве-
личину или любую удобную для нас ее линейную комбинацию. Правда,
при переходе от непосредственно вычисленной критической статистики
уп\ задаваемой соотношением (*), к ее линейным комбинациям смысл
неравенств в фигурных скобках (**) и (* * *) может меняться на противо-
положный.
Итак, мы проверяем простую гипотезу Hq: р = Ро при простой аль-
тернативе Н\‘.р = pi, причем pi > ро- Тогда смысл неравенств в (*)
и (**) сохраняется при замене 7П на х, а именно, по заданному уровню
значимости а требуется найти такое са, что
Р{х > св|р = ро} = а. (* * **)
Т. е. мы должны решить уравнение (****) относительно са с учетом того,
что случайная величина х подчиняется (п,ро)-биномиальному з.р.в.
Воспользуемся теоремой Муавра-Лапласа (см. [1], п. 4.3.1) о при-
ближенной (асимптотической) (0,1)-нормальности случайной величины
Тогда при р = ро имеем:
Р{х>са|р = р0} = Р( ;~Ро > f I
I /Ро(1~Ро) /Ро(1~Ро) I
\ у п у п )
» 1 - Ф I I = а.
\ /Ро(1-Ро) /
\ V п /
Следовательно, аргумент функции Ф стандартного нормального рас-
пределения является ни чем иным, как квантилем «1-а уровня 1 - а этого
распределения (или, что то же, —100а%-ной точкой этого распределения
wa), т.е.
Ро(1-Ро)
п
1) Как известно (см., например, [1], п. 8.6.3, или п. 14 в нашей табл. 2.1), при малых
значениях параметра р и достаточно больших п возможна также аппроксимация
з.р.в. случайной величины г с помощью пуассоновского закона с парметром А = пр,
т.е. Р{х = *} » i2^e-n₽.
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
91
По условию задачи Ро = 0,05, п = 100, а = 0,01. Из табл. П1.3 находим
квантиль уровня 0,99 — значение «о,99 = 2,34, так что в нашем случае
имеем: ________
са ^/0,05 • 0,95
УД-0’05- 10 2’34’
откуда
са = 10,1.
Таким образом, если в контрольной выборке объема п = 100 будет об-
наружено более 10 дефектных изделий, то признается правота заказчика,
т.е. подтверждается гипотеза Hi', р = 0,10 (при риске ошибиться лишь в
одном случае из ста!).
2) Для определения численного значения мощности предложенного
критерия необходимо вычислить вероятность
Р{х > св|р = pi} « 1 - Ф
(1211 л ю\
юо u,iu I
/0,10-0,90 /
V 100 /
= 1 - Ф(0,033) « 0,49.
Мы видим, что мощность критерия невысока. Соответственно, ошиб-
ка 2-го рода 0 (т.е. вероятность ошибочно отвергнуть гипотезу Hi) весь-
ма велика (0=1 — 0,49 = 0,51). Повысить мощность можно двумя спо-
собами: либо существенно увеличить объем контрольной выборки, либо
договориться об увеличении уровня значимости критерия, т.е. ошибки
1-го рода (например, до 0,05).
Пример 2.8 (задача). Независимому статистику поручено про-
верить информацию маркетинговой службы некоторого туристического
бюро о том, что 70% клиентов выбирают в качестве формы обслуживания
полупансион. Статистик провел опрос 150 случайно выбранных туристов,
мз них полупансион предпочли 84 человека.
Требуется:
определить, к какому выводу пришел статистик при проверке ги-
потезы (с уровнем значимости критерия а = 0,05) Но: р = 0,70 при
альтернативе Hi', р / 0,70, где p-доля клиентов туристического
бюро, предпочитающих полупансион.
92
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Решение
Речь идет о проверке гипотезы о численном значении параметра р
биномиального распределения (см. п. 14 табл. 2.1).
В данном случае мы располагаем единственным наблюдением х = 84
(т.е. n = 1), причем длина серии испытаний Бернулли N = 150.
Воспользовавшись приближенной (асимптотической) (Npo,Npo(l - Ро))-
нормальностью числа клиентов, предпочитающих полупансион, из общего
числа N — 150 случайно опрошенных клиентов туристического бюро, и
рассчитав численное значение приблизительно (0;1)-нормально распреде-
ленной критической статистики
7„ = 4^2= = = -3,74,
. /Ро(1 ~Ро) . /Qi^*Qi3
у N V 150
приходим к отклонению гипотезы Яо, т. е. — к выводу о недостоверности
информации маркетинговой службы упомянутого туристического бюро
(поскольку значение критической статистики по абсолютной величи-
не существенно превосходит 2,5%-ную точку стандартного нормального
распределения w0|025 = 1,96).
2.В. Задачи и упражнения
Упражнение 2.1
Имеются независимые наблюдения , ж2,..., хп (а, а2)-нормально
распределенной случайной величины. Значения обоих параметров (сред-
2\
него а и дисперсии а ) неизвестны.
Требуется:
1) предложить и обосновать (с помощью критерия логарифма отно-
шения правдоподобия, см. п. 8.3.2 в [1]) критическую статистику
для проверки гипотезы Но о численном значении неизвестного па-
раметра a (Hq: а = ао, где ао — заданное число);
2) подробно описать критерий проверки гипотезы Но при альтерна-
тиве:
(а) Нг: а > aQ;
(б) Яр а < а0;
(в) Яр aQ;
3) ответить на вопрос, является ли гипотеза Но простой.
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
93
Упражнение 2.2
Имеются независимые случайные выборки: я?ц,®12,... ,г1П1 из
(в1;ст2)-нормальной генеральной совокупности и ®2i,®22, • • • >®2па из
(аг; ст2)-нормальной генеральной совокупности (значения параметров , а2
и ст2 неизвестны).
Требуется:
построить и обосновать критерий статистической проверки ги-
потезы Hq'. в] = а2 при уровне значимости, равном а.
Упражнение 2.3
Имеется к независимых случайных выборок xji,ij2,... ,ijnj (j =
1,2, ...,&), извлеченных, соответственно, из к (aj;a )-нормальных гене-
ральных совокупностей, в которых значения средних а,- неизвестны, а об-
2
щая величина дисперсии ст задана.
Требуется:
построить статистический критерий проверки гипотезы Hq. а\ =
а2 = ... = при уровне значимости, равном а.
Упражнение 2.4
Имеются две независимые случайные выборки х, хj2,..., хjn. (j =
1,2), извлеченные, соответственно, из двух (aj; ctj )-нормальных генераль-
„ , 2 2 х
ных совокупностей (значения параметров а^, а2, Ст], ст2 неизвестны).
Требуется:
1) предложить и обосновать критическую статистику для проверки
гипотезы Яо: = а2 пРи уровне значимости^ равном а;
2) подробно описать критерий проверки гипотезы Hq при альтерна-
тиве:
(а) Нх: а? > ст2;
(б) Нг : < а%;
(в) Нг: af ст2.
Задача 2.1
По данным и результатам решения задачи 1.1 рассчитать теоретиче-
ские частоты для значений я, равных 0,1,2,3,4,5, и проверить на уровне
значимости 0,01 гипотезу о биномиальном законе распределения с помо-
щью критерия согласия % Пирсона.
Задача 2.2
По данным и результатам решения задачи 1.3 рассчитать теорети-
ческие частоты для значений я, равных 0,1,2,3,4,5,6,7, и проверить при
a = 0,05 гипотезу о законе распределения Пуассона с помощью критерия
согласия %2 Пирсона.
94
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Задача 2.3
По данным и результатам решения задачи 1.4 рассчитать теоретиче-
ские частоты и проверить на 5% уровне значимости с помощью критерия
согласия х2 Пирсона гипотезу о нормальном законе распределения.
Задача 2.4
Рассчитать теоретические частоты и проверить при а = 0,01 с по-
мощью критерия согласия %2 Пирсона гипотезу о нормальном законе рас-
пределения по данным и результатам решения задачи 1.5.
Задача 2.Б
Во время вступительного экзамена в институт двухстам абитуриен-
там было предложено 7 задач, соответственно, из семи разделов школьно-
го курса математики. Результаты экзамена приведены в таблице:
Номер раздела курса (j) 1 2 3 4 5 6 7
Число абитуриентов, решавших задачи 200 200 200 200 200 200 200
Число правильных решений задач 140 134 130 177 162 174 163
Предполагается, что число решенных абитуриентами задач j-ro раз-
дела (j = 1,2,...,7) есть случайная величина v(n,pj), имеющая биноми-
альное распределение с параметрами (n,pj). Сравните уровень подготов-
ки абитуриентов по разделам школьного курса, для чего проверьте при
уровне значимости критерия а = 0,1 гипотезу о том, что вероятность ре-
шения задачи не зависит от того раздела, к которому она относится, т. е.
необходимо проверить гипотезу Но: рг = ... = рj = ... = рг = р, где
Pj-вероятность решения абитуриентом задачи j-ro раздела.
Задача 2.6
Одну и ту же контрольную работу из 7 задач по математической ста-
тистике писали студенты пяти групп. Результаты контрольной работы
представлены в таблице:
Номер группы (j) 1 2 3 4 5
Число предложенных задач Nj 133 175 189 196 154
Число решенных задач Uj 71 109 99 106 95
Предполагается, что число решенных студентами j-й группы (j =
1,2,..., 5) задач есть случайная величина u(Nj,pj), имеющая биномиаль-
ное распределение. Сравните уровень подготовки студентов этих групп к
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
95
контрольной работе для чего проверьте при уровне значимости критерия
а = 0,05 гипотезу о том, что вероятность решения задачи не зависит от
того из какой группы студент, т.е. нулевую гипотезу Яо* Pi = • • • = Pj =
... = р5 = р, где pj (вероятность решения задачи студентом j-й группы)
характеризует уровень подготовки к контрольной работе студентов этой
группы.
Задача 2.7
В целях изучения потребительского спроса автомобильная фирма про-
вела опрос вошедших в случайную выборку 50 мужчин и 50 женщин, ко-
торые в предыдущем году купили автомобили этой фирмы. В таблице
представлены частоты ответов Vij опрошенных на вопрос о том, какое из
установленных дополнительных устройств (J) является наиболее важным
для повышения безопасности движения. Здесь ^-число покупателей г-го
рода (i = 1,2), выбравших устройство j-ro вида.
Покупатели (•) Дополнительные устройства (J)
Дисковые тормоза Складывающееся рулевое колесо Автоматические дверные замки Сигнал превыше- ния скорости
Мужчины 15 25 5 5
Женщины 5 15 20 10
Предполагается, что частоты </<4) есть наблюдения слу-
чайной величины Vi(Ni,Pn,Pi2,Pi3,Pi4), имеющей полиномиальное распре-
деление и наблюдаемые значения i/y (j = 1,2,3,4). Проверить при уров-
не значимости критерия а = 0,05, имеются ли расхождения во взгля-
дах мужчин и женщин — владельцев автомобилей на дополнительные
устройства безопасности движения, т.е. требуется проверить гипотезу
Яо: рц = p2j = Pj для всех j = 1,2,3,4.
Задача 2.8
Фирма, торгующая бытовыми пылесосами, провела маркетинговое ис-
следование, опросив 100 покупателей. Полученные частоты i/jj ответов.о
месте покупки изделия и источнике сведений о нем приведены в табли-
це. Здесь — число покупателей, узнавших о пылесосе в j-м источнике
информации и купившем его в г-м месте.
96
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Место покупки (1) Источник сведений (j)
Друзья Газеты Журналы
Универмаг 10 15 5
Магазин с низкими ценами 15 20 5
Специализированный магазин 5 10 15
Предполагается, что частоты (^ь^г^з) (г = 1)2,3) есть наблю-
дение случайной величины i/(pti,Pt2)Pt3)> имеющей полиномиальное рас-
пределение с парметрами (-Л^;Рй)Р»2,Р»з)‘ Руководство фирмы предпо-
лагает, что структура источников информации о пылесосах для покупа-
телей магазинов трех анализируемых типов одинакова. Проверьте это
предположение при 5%-м уровне значимости, т.е. проверьте гипотезу
Но: Pij = P2j = P3j = Pj для всех j = 1,2,3.
Задача 2.9
Средний съем ткани с 16 станков, работавших в первую смену, со-
ставил Xi = 5,6 тыс.м. при SJ = 0,6 тыс.м., а с 10 станков, работавших
во вторую смену — х2 — 4,9 тыс.м. при зз = 0,5 тыс.м. Проверьте при
а = 0,05 гипотезу об одинаковой производительности станков, работав-
ших в первую и вторую смены (предполагается, что производительность
станков 1-й и 2-й смен подчиняется нормальному з.р.в. с одинаковой дис-
персией).
Задача 2.10
Сравнивается точность обработки деталей на четырех станках. По-
грешность обработки выражается отклонением размера от номинала (в
мм) и описывается (0,о\ )-нормальным распределением (г = 1,2,3,4). Наи-
большую точность имеет тот станок, дисперсия контролируемого парме-
тра которого меньше. С этой целью анализируется 8 деталей, обработан-
ных на первом станке, 12 — на втором и по 16 деталей — на третьем и
четвертом. По выборкам найдены несмещенные оценки з?(г = 1,2,3,4)
дисперсий, которые, соответственно, равны: 0,0051; 0,0038; 0,0064 и
0,0028. Проверить (при уровне значимости критерия а = 0,05) гипо-
тезу о том. что все станки имеют одинаковую точность, т.е. гипотезу
Я 2 2 2 2
о* Oj _ а2 — — 04.
Задача 2.11
С целью изучения влияния количества осадков за год на урожайность
пшеницы (ц/га) исследуются данные за 13 лет, представленные в следу-
ющей таблице:
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
97
i — номер наблюдений Уровень осадков (j)
j = 1: 260-270 мм j = 2: 270-280 мм j = 3: 280-290 мм
Урожай- 1 27 35 33
ность 2 29 34 37
3 28 34 36
4 30 36 34
5 35
Предполагается, что урожайность пшеницы при j-m уровне осадков
(j = 1,2,3) есть (aj, а2)-нормальная случайная величина. Требуется: а)
при уровне значимости критерия а = 0,05 сравнить урожайность пшени-
цы при годовом количестве осадков, варьируемом в диапазоне от 260 мм.
до 290 мм.; б) проверить при уровне значимости критерия а = 0,05 вли-
яет ли на урожайность пшеницы изменение годовых осадков в диапазоне
270-290 мм.
Задача 2.12
В паспорте купленного автомобиля утверждается, что расход бензи-
на на 100 км. пробега равен 10 литрам при скорости 90 км/ч. С целью
оценки соответствия реальности этой записи в паспорте было проведено
п = 10 наблюдений, по результатам которых установлена средняя вели-
чина расхода бензина на 100 км., равная х = 11 л. и среднеквадратиче-
ское отклонение s — 2 л. Предполагается, что расход бензина на 100 км.
пробега есть случайная величина, имеющая (а, а )-нормальное распреде-
ление. Проверьте при уровне значимости критерия а = 0,01 гипотезу
HQ: а = Юл. при конкурирующей гипотезе Нг: а ф Юл. Сделайте за-
ключение о соответствии автомобиля параметру, указанному в паспорте.
Задача 2.13
По данным 12 рейсов установлено, что в среднем рейсовый автобус
проходит свой маршрут за х = 43 мин. при среднеквадратическом от-
клонении з = 4 мин. Предполагается, что время поездки есть случай-
ная величина, имеющая (а, а )-нормальное распределение. Проверьте, не
устарел ли норматив, который равен 45 мин., с помощью подходящего
статистического критерия при уровне значимости критерия а = 0,05.
Задача 2.14
Реклама утверждает, что употребление данной пищевой добавки, раз-
рушающей жировой слой, позволяет человеку за месяц ее применения сни-
зить свой вес на 7 кг. В результате обследования 20 человек, употребляю-
щих данную добавку, установлено, что они похудели в среднем на х = 6кг
при s = 1,5кг. Предполагается, что эффект от применения пищевой доба-
вик есть случайная величина, имеющая (а, а )-нормальное распределение.
4 Прикладная статистика
в задачах и упражнениях
98
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Проверьте (при уровне значимости критерия а = 0,05) справедли-
вость утверждения рекламы.
Задача 2.15
Фасовочный автомат для мелкооптовой торговли должен обеспечи-
вать точность, которая характеризуется среднеквадратическим отклоне-
нием, не превосходящем 2 грамма. С целью оценки точности фасовки на
контрольных весах было взвешено п = 15 пакетов муки и найдено, что
среднеквадратическое отклонение з = 2,3г. Предполагается, что ошибка
измерения есть случайная величина, имеющая (0, а )-нормальное распре-
деление.
При уровне значимости критерия а = 0,05 проверьте, отвечает ли
фасовочный автомат требуемой точности (т.е. требуется проверить ги-
потезу Hq: ст2 = 4 при альтернативе Н^: а1 > 4).
Задача 2.16
Работа конвейера, осуществляющего сборку коробок передач для лег-
ковых автомобилей, считается стабильной, если вариация времени сборки
одной коробки передач храктеризуется (при отлаженной фиксированной
средней продолжительности) среднеквадратическим отклонением, не пре-
вышающим 2,5 мин. С целью оценки стабильности был проведен хрономе-
траж времени изготовления 22 случайно отобранных в течение смены ко-
робок передач и по выборке рассчитано среднеквадратическое отклонение
з = 3,2мин. Предполагается, что отклонение времени сборки от номинала
есть случайная величина, имеющая (0,ст2)-нормальное распределение.
Проверьте (при уровне значимости критерия а = 0,01) предположе-
ние о стабильной работе конвейера (т.е. требуется проверить гипотезу
Яо: ст2 = 6,25 при альтернативе Нг: ст2 > 6,25). Сделайте содержатель-
ный вывод по результатам хронометража.
Задача 2.17
Маркетинговая служба компании рассматривает возможность разме-
щения рекламы в сетке телепередач, режиссер которой утверждает, что
его передачу смотрят 30% телезрителей. С целью проверки правильности
утверждения режиссера было опрошено 400 телезрителей, из которых, как
оказалось, эту передачу смотрят 100 человек.
Проверьте (при 5%-м уровне значимости критерия) справедливость
утверждения режиссера (т.е. необходимо проверить гипотезу Hq: р = 0,3
при Н\: р < 0,3 где р — это доля телезрителей, смотрящих рекламную
передачу компании).
Задача 2.18
Поставщик семенного зерна в рекламе гарантирует его 90%-ную всхо-
жесть. При испытании из 200 посаженных зерен взошло! 70.
Глава 2. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
99
Проверьте (при уровне значимости критерия а = 0,05) справедли-
вость утверждения рекламы (т. е. необходимо проверить гипотезу Но : р =
0,9 при альтернативе Н\: р < 0,9, где p-доля взошедших семян).
Задача 2.19
Статистик располагает результатами взвешиваний 64 изделий, слу-
чайно отобранных из контрольной партии, произведенной работающей в
стационарном режиме автоматической линией (см. исходные статистиче-
ские данные в таблице задачи 1.16).
Требуется:
убедиться в справедливости рабочего допущения задачи 1.16, а
2
именно: произвести с помощью критерия согласия х статистиче-
скую проверку гипотезы (при уровне значимости критерия а — 0,05)
о том, что имеющиеся статистические данные действительно из-
влечены из нормальной генеральной совокупности.
Задача 2.20
Используя условия задачи 1.6, проверить гипотезу (при уровне зна-
чимости а = 0,05) о том, что выборочные средние времена изготовления
одного изделия четырьмя обследованными рабочими различаются ста-
тистически незначимо, т.е. что E£j = Е£2 = Е& = Е&, где (у(сек.) —
время изготовления одного изделия, случайно отобранного из продукции
j-ro рабочего.
Задача 2.21
Используя исходные данные примера 1.7 и задачи 1.12, проверить ги-
потезу (при уровне значимости критерия, равном 0,01) о том, что точность
расфасовки кофе автоматом конкурирующей марки (о котором речь идет
в задаче 1.12) статистически незначимо выше точности расфасовки ко-
фе автоматом, о котором речь идет в примере 1.7 (несмотря на то, что
s2 = 0,64, а / = 0,49).
Задача 2.22
В качестве исходных данных задачи используются сведения о сред-
недушевых доходах 10-ти семей одной социально-экономической страты
населения (см. пример 1.9) и 8-ми семей другой социально-экономической
страты (см. задачу 1.13).
Требуется:
проверить гипотезу (с уровнем значимости критерия а = 0,05) о
том, что доходы двух обследованных страт различаются стати-
стически незначимо, т. е. что E£j = Е£2, г де £j — логарифм средне-
душевого дохода семьи, случайно извлеченной из населения j-й стра-
ты (j = 1,2).
4*
100
I. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Задача 2.23
Население региона разбито по социально-демографическим и экономи-
ческим характеристикам на три страты, причем известно, что удельный
вес 1-ой страты в два раза превышает удельный вес 2-ой страты. При
статистическом обследовании населения региона из общего числа жите-
лей региона извлечена случайная выборка объема п = 800 чел., среди
которых оказалось 480 представителей 1-ой страты и 220 представите-
лей 2-ой страты. Проверить (при уровне значимости критерия а = 0,05)
статистическую гипотезу о том, что при повторениях выборок такого же
объема из общего числа жителей данного региона распределение вероят-
ностей многомерной случайной величины может быть
описано полиномиальным (мультиномиальным) законом, где Vj(n) — чи-
сло представителей J-ой страты (j = 1,2,3) в выборке объема п (в нашем
случае п = 800).
Указание.
При реализации критерия согласия воспользоваться оценкой макси-
мального правдоподобия неизвестного значения параметра полиноми-
ального распределения.
Раздел II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ
СТАТИСТИЧЕСКИЙ АНАЛИЗ
Глава 3. Корреляционный анализ
З.А. Краткие сведения из теории
Место корреляционного анализа в статистическом исследо-
вании. При исследовании реальных социально-экономических явлений
и систем статистику, экономисту приходится сталкиваться, как прави-
ло, с необходимостью статистического анализа многомерной генеральной
совокупности, т. е. с ситуациями, когда на каждом из статистически об-
следуемых объектов этой совокупности регистрируются значения целого
набора признаков х^\х^2\...,х^. В дальнейшем мы будем обозначать,
как и прежде, этот набор признаков с помощью X = (®^\а/2\... ,а/р))Т,
а результат регистрации значений этих признаков на i-м статистиче-
ски обследованном объекте — i-е многомерное наблюдение — с помощью
Xi = (а;^,х<?\ ...,а;(р))Т. Таким образом, «стартовая позиция» при ста-
тистическом анализе многомерной генеральной совокупности аналогична
одномерному случаю: исследователь по имеющейся у него случайной вы-
борке
ХъХ2>...,Хп (3.1)
значений анализируемой многомерной случайной величины £ =
• ..,f(p))T должен сделать те или иные статистические выводы о ее
«поведении».
Как мы знаем, исчерпывающие сведения о поведении анализируемой
случайной величины £ содержатся в ее законе распределения вероятностей
(з.р.в.) f{(X), где под f((X) понимается значение функции плотности ве-
роятности в точке X, если случайная величина £ непрерывна, и вероят-
ность Р{£ = X} того, что случайная величина примет значение, равное X,
102 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
если £ дискретна. Однако з.р.в. анализируемой случайной величины ис-
следователю, как правило, не известен. И если при описании поведения од-
номерных случайных величин исследователь еще имеет практически ре-
ализуемые возможности подбора и использования подходящих модельных
законов распределения (см. [1], гл. 3) с последующей статистической оцен-
кой участвующих в их записи параметров (см. гл. 1), то при исследовании
признаков размерности р > 2 ему чаще всего приходится ограничиваться
информацией, которую доставляют оценки моментов первых двух поряд-
ков, а именно оценками сектора средних значений а = (а^\..., а^)Т и
ковариационной матрицы Е = (ау), — i,j = 1,2,...,р (см. [1], п.2.6.6).
Другими словами, можно сказать, что за редким исключением1, все вы-
водымногомерного статистического анализа строятся на базе оценок
а и Е.
Оценка а вектора средних значений дает представление о центре
группирования наблюдений анализируемого многомерного признака. От-
личие от одномерного случая, когда мы располагаем оценкой а = х сред-
него значения анализируемой случайной величины, заключается лишь в
том, что а определяет точку в р-мерном пространстве, в то время как
выборочное среднее а = х определяет точку на числовой прямой. По су-
ществу вся специфика многомерного случая сосредоточена в ковариа-
ционной матрице Е, а при статистическом анализе — в ее оценке S.
Именно знание ковариационной матрицы позволяет исследователю стро-
ить и анализировать характеристики случайного рассеивания и статисти-
ческой взаимосвязи (коррелированности) компонент анализируемого мно-
гомерного признака. Данный раздел как раз и посвящен так называемо-
му корреляционному анализу многомерной генеральной совокупности,
назначение которого — получить (на основе имеющейся выборки (3.1))
ответы на следующие основные вопросы:
• как выбрать (с учетом специфики и природы анализируемых пере-
менны^ подходящий измеритель статистической связи (коэффици-
ент корреляции, корреляционное отношение, какую-либо информацион-
ную характеристику связи, ранговый коэффициент корреляции и т. п.)?
• как оценить (с помощью точечной и интервальной оценок) его
числовое значение по имеющимся выборочным <?анныл<?
• как проверить гипотезу о том, что полученное числовое значе-
ние анализируемого измерителя связи действительно свидетельствует
1 Исключения относятся в основном к генеральным совокупностям, описываемым либо
многомерным нормальным, либо полиномиальным з.р.в. (см. соответственно (3.9')
и (3.7) в [1].)
Глав* 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
103
о наличии статистической связи (или, как говорят, проверить иссле-
дуемую корреляционную характеристику на статистически значимое
ее отлнчне от нуля?
• как определить структуру связей между компонентами исследу-
емого многомерного признака, сопоставив каждой паре компонент дво-
ичный ответ («связь есть» или «связи нет»)?
Какое место занимает корреляционный анализ в общем прикладном
статистическом исследовании? В гл. 9 [1] обозначены три центральные
проблемы прикладной статистики. Начнем с первой и наиболее значимой
из них — с проблемы статистического исследования зависимостей. В
соответствии с предложенным в гл. 10 [1] разбиением процесса решения
этой проблемы на этапы корреляционный анализ составляет содержание,
по существу, первого (после постановки задачи и сбора необходимых ста-
тистических данных) этапа статистического исследования зависимостей.
Действительно, при исследовании зависимостей между анализируемыми
переменными мы должны дать в первую очередь ответ на вопрос: а суще-
ствует ли такая зависимость или анализируемые признаки статистиче-
ски независимы? И только после утвердительного ответа на этот вопрос
заняться выявлением вида и математической формы этой зависимости.
Корреляционный анализ как раз и предоставляет средства, позволяющие
ответить на первый вопрос. Выявление же вида и математической формы
искомой зависимости производится с помощью разнообразных методов и
моделей регрессионного анализа и анализа временных рядов, составляю-
щих основные разделы эконометрики. В то же время рассматриваемые
в рамках корреляционного анализа характеристики статистической связи
(ковариации, различные коэффициенты корреляции и т.п.) используют-
ся в качестве «входной» (базовой) информации при решении задач дру-
гих двух центральных проблем прикладной статистики — классификации
объектов и признаков и снижения размерности анализируемого призна-
кового пространства (методы и модели, предназначенные для решения
этих двух проблем, описываются ниже в главах 4 и 5). Поэтому именно
с раздела, посвященного корреляционному анализу, по существу, начина-
ется изложение методов и моделей прикладной статистики.
Ниже приводятся краткие сведения по основным измерителям степе-
ни тесноты статистической связи (и.с.т.с.с.). Определения и интерпре-
тация и.с.т.с.с. между количественными переменными даются в рамках
распространенной общей аддитивной модели регрессии вида
у = /(Х) + е(Х), (3.2)
где е(Х) - остаточная случайная компонента, з.р.в. которой, вообще го-
104 П. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
воря, может зависеть от X, но при этом предполагается, что Ее(Х) = 0
и D£(X) = а2(Х) < оо при всех возможных значениях X. Соответствен-
но, функция f(X) = Е(у|Х) описывает поведение условного значения пе-
ременной у в зависимости от «значения» (вообще говоря, - векторного)
объясняющей переменной X и называется функцией регрессии у по X.
Пояснения некоторых фактов будут даваться с апелляцией к много-
мерному нормальному распределению анализируемой случайной величины
£ = функция плотности у>(Х|а; Е) которого в точке
X определяется формулой
V(X|«; S) = ! , (3.3)
(2х)>|Б|*
где X — (а/1), х^2\ ..., а/р))т — текущее значение анализируемой случай-
ной величины £, а = (а^\а^2\...,а^)т — вектор средних значений ее
компонент, Е — ковариационная матрица случайного вектора £ (см. ни-
же), а |£| — определитель этой ковариационной матрицы.
Если р-мерная случайная величина £ подчинена з.р.в. с функцией
плотности вида (3.3), то по аналогии с одномерным случаем она будет
определяться как (а, £)-нормальная р-мерная случайная величина, или
как случайная величина, имеющая з.р.в. Np(a; S).
Ковариационной матрицей Е многомерной случайной величины
£ = • • • Л(₽))Т называется (р х р)-матрица, составленная из ко-
вариаций ajk = Е[(£^ - - </**)], - j, k = 1,2,... ,р. В статисти-
ческом анализе используется ее статистическая оценка, или выборочная
ковариационная матрица Е = (а^), где
1 я
= <3-4)
1=1
(х(,} = 23 — выборочные средние значения случайных величин ,
i=i
—/ = 1,2,...,р). Ковариационная матрица содержит сведения о степени
случайного разброса анализируемых переменных, а также — о характере
и структуре статистических взаимосвязей между ними. Из определения
следует, что она является симметричной и неотрицательно-определенной.
Парный коэффициент корреляции между случайными пере-
t(i) М - -
менными f ' я f ' измеряет степень тесноты линеинои связи между
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
105
этими переменными и определяется через ковариации по формуле
_ _ °ik
rjk = ~'---*
* &кк
(3-5)
В статистическом анализе используют статистические оценки, или
выборочные парные коэффициенты корреляции, подсчитываемые, соот-
ветственно, по формуле
Е^-^Х^-^)
fjk = , ,=1 (3.5')
у t=l t=l
Парный коэффициент корреляции (п.к.к.) может принимать значения
в диапазоне от -1 до +1, причем для статистически независимых перемен-
ных и п.к.к. равен нулю, но из равенства нулю значения г^,
вообще говоря, не следует взаимной независимости и ^к^ (а следует
лишь тот факт, что если связь между и ^к^ и существует, то она
нелинейна)1 2^. С другой стороны, из факта |rjfc| = 1 следует, что перемен-
ные и связаны чисто функциональным линейным соотношением,
т.е. = 0о + ^1^к\ где #о и #1 — некоторые постоянные коэффициенты.
Для проверки факта статистически значимого отличия от нуля
величины выборочного п.к.к., т. е. для проверки гипотезы
Но' Т]к — О,
(3.6)
используется критическая статистика
fjfcVn - 2
/i ’
yl “ rjk
7п =
(3-7)
которая в предположении справедливости гипотезы (3.6) должна «вести
себя» приблизительно^ как стьюдентовская случайная величина t(n — 2)
1) Правда, в частном случае двумерной нормальной распределенности переменных
из rjk = ° следует взаимная статистическая независимость этих
переменных.
2) Этот факт доказывается как точный для случая, когда выборочный п.к.к. гуд стро-
ится по выборке, извлеченной из двумерной нормальной генеральной совокупности.
106 11. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
с п — 2 степенями свободы. Соответственно, если окажется, что
> ^(«-2),
(3-7')
то гипотеза Яо отвергается (с вероятностью ошибки, т. е. с уровнем зна-
чимости критерия, равным a; i^.(n — 2) — это 100у%-ная точка t(n — 2)-
распределения, см. табл. П1.6).
Интервальная оценка (при уровне доверия Pq = 1 — 2а)
для истинного значения строится по формуле
thz\ < rjk < thz^, (3.8)
где th z — это тангенс гиперболический от аргумента г, соответственно,
z = arctg = | In — так называемое z-преобразование Фишера
(см. табл.П1.7), так что
1 + Гй wtt
1 - fy* 0» - 3
xi,a = |1п
-
2(п-1)’
(3.9)
где we — это 100а%-ная точка стандартного нормального распределения
(см. табл. П1.3).
Корреляционная матрица R. многомерной случайной величины
( = (f . ,^)т — это (р х р)-матрица, составленная из п.к.к. г^,
- j, к = 1,2,...,р. В статистическом анализе используется выборочная
корреляционная матрица R. = (г,>), где элементы Гу* определяются по
формуле (3.5). Так же, как и ковариационная матрица Е, корреляционная
матрица R, является симметричной и неотрицательно-определенной.
Пйрное корреляционное отношение (п.к.о.) р,* является изме-
рителем степени тесноты нелинейной связи, существующей между ко-
личественной переменной (интерпретируемой как результирующий
признак у в соотношении (3.2)) и количественной переменной (интер-
претируемой как единственный объясняющий признак X в соотношении
(3.2)). Оно определяется формулой
(3.10)
где £j(^*^) — остаточная случайная компонента в соотношении
€0) = /(^(М) + ^(М),
(3.2')
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
107
a Ex[D(£j(^fc))|f(/') = ж)] — усредненная по всем возможным значениям
условная дисперсия остатков вычисленная при условии, что
= X.
Статистическая оценка (выборочный аналог) Pjk п.к.о. подсчиты-
вается по группированным (по оси Оа/^) данным (см. выше,
п. 1.А и формулу (1.2)) по формуле
EErf’-^’)2
.2 , 1=1 «=1
A/* — 1 в i/i ,,.. „
Е Е(4?)-’(”)
(з.и)
В этой формуле s — число интервалов группирования по оси —
число наблюдений двумерной случайной величины попавших в
1-й интервал группирования; х\р — »-е наблюденное значение переменной
в 1-м интервале группирования (i = 1,2,х\^ = (£ xn)lvi —
t=l
условное среднее подсчитанное по наблюдениям, попавшим в l-й ин-
тервал группирования, и х^ = (ЕЙ ®н)/п — общее среднее значение
<И1 1 = 1
подсчитанное по всем наблюденным значениям.
П.к.о. pjit может принимать значения в диапазоне от 0 до 1; значение
Pjit = 0 свидетельствует об отсутствии какой бы то ни было связи между
и ^(*). если же р _ j, то меЖду £<Л и существует чисто функ-
циональная связь = /($(*)), т.е. отсутствует остаточная случайная
компонента в соотношении (3.2*).
В отличие от ковариаций ffjk и корреляций Tj^ корреляционные от-
ношения pjk несимметричны, т.е. pjk / Pkj- Другими словами, значение
этой парной характеристики степени тесноты связи зависит от того, ка-
кую из двух переменных или х^ интерпретируют как результирую-
щий показатель.
Для проверки факта статистически значимого отличия от нуля
величины выборочного п.к.о., т. е. для проверки гипотезы
Н0'. pjk = 0, (3.12)
используется критическая статистика
а2
71 S Pjk
7п ~ ‘ -2 »
3 1 1 “ Pjk
(3.13)
108 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
которая в предположении справедливости гипотезы (3.12) должна «вести
себя» как F(s — 1; п — ^-распределенная случайная величина. Соответ-
ственно, если окажется, что
_ "2
^-4--^2->FQ(s-l;n-s), (3.13')
5 - 1 1 - Pjk
то гипотеза (3.12) отвергается (с вероятностью ошибки, т.е. с уровнем
значимости критерия, равным а). Здесь Fa(s — 1; п —л) — это 100а%-ная
точка F(s — 1; п — ^-распределения (см. табл. П1.5).
Приближенная интервальная оценка (при уровне доверия Pq = 1 — 2а)
2
для истинного значения строится по формуле
(n - s)p2jk_____S - 1 < 2 < _________(n - S)Pjk_______S- 1
n(l - Pjk)Fa{m\n- s) п Р}к n(l - pjk)F^a(m\n - s) п
(3-14)
где т = [(л — 1 4- npjk)2/(з — 1 + 2np,-fc)], символ [z] означает целую часть
числа ®, a Fq(m\ п- s) — это 100д%-ная точка F(m; п - ^-распределения.
Следующие два типа и.с.т.с.с., — частные и множественные коэф-
фициенты корреляции, — используются при анализе множественных
корреляционных связей (так называют статистические связи между более
чем двумя переменными в отличие от парных связей, рассмотренных вы-
ше). Множественные корреляционные связи имеют свою специфику, при
их анализе возникают принципиально новые проблемы. Эта специфика
связана в первую очередь с необходимостью уметь измерять степень тес-
ноты связи между результирующей переменной у и множеством объясня-
ющих переменных х^ ,х^2\..., х^ в соотношении (3.2), а также с возни-
кающими трудностями в интерпретации парных коэффициентов корреля-
ции между у и х^\ обусловленными возможным опосредованным влияни-
ем на эту парную связь других (явно не учтенных в вычислении г(у; х^))
объясняющих переменных / j). Последнее обстоятельство, в част-
ности, делает необходимым введение таких измерителей статистической
связи, которые были бы «очищены» от опосредованного влияния других
переменных, давали бы оценку степени тесноты интересующей нас связи
между переменными у и х^ (или х^ и х^) при условии, что значения
остальных переменных зафиксированы на некотором постоянном уровне.
В этом случае говорят о статистическом анализе частных (или «очищен-
ных») связей и используют соответственно частные («очищенные» ) ко-
эффициенты корреляции.
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
109
Частные коэффициенты корреляции г/к.Ма—im измеряют сте-
пень тесноты линейной связи между переменными и при анали-
зе множественных статистических связей компонент случайного вектора
(а/0) = у, а/1),... ,а/₽))Т в общей схеме (3.2) в ситуации, когда значе-
ния переменных яг а\..., х^1т^ зафиксированы на их средних уровнях
(т. е. в ситуации, когда исключено опосредованное влияние этих перемен-
ных на взаимосвязь между х^ и х^). В общем случае эти частные харак-
теристики статистической связи зависят от заданных (фиксированных)
уровней «мешающих» переменных х^'\..., x^m\ а для подсчета выбо-
рочных значений необходимо было бы иметь выборку специаль-
ной структуры, обеспечивающей наличие хотя бы нескольких наблюдений
при фиксированном значении каждой из «мешающих» переменных
q = 1,2,...,m. Однако, если исследуемые переменные (а/°\... ,а/р))Т
подчиняются (р+ 1)-мерному нормальному закону, то для подсчета значе-
ний может быть использована следующая формула:
R •
rjk.N(j,k) = ГО > D • (3.15)
V КН Ккк
В этой формуле N(j,k) обозначает набор номеров всех анализируемых
переменных за исключением номеров j и к, a Rqt — это алгебраическое
дополнение элемента rqa в корреляционной матрице R, соответствующей
ряду исследуемых переменных (т.е. Rqa = (-l),+s|R.gs|, где 114в-матрица,
получающаяся из матрицы R. вычеркиванием из нее g-й строки и з-го
столбца). Так, например, если мы хотим вычислить значение частного
коэффициента корреляции г12.з между а/1) и х^ при исключенном опосре-
дованном влиянии переменной я/3\ то следует рассмотреть (ЗхЗ)-матрицу
(1 Г12 г13 \
Г21 1 Г23 1 ,
Г31 г32 1 /
и формула (3.15) нам даст
_ Я12__________П2 - г13г23 /0 , ,/ч
Г12.3 — ГК-----тч— — !----------------- (3.15 )
Л1-Я22 у(1-П3)(1-Т23)
Последовательно присоединяя к «мешающим» переменным все но-
вые признаки из рассматриваемого набора, можно получить рекур-
рентные соотношения для подсчета частных коэффициентов корреляции
110 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
порядка т+ 1 по частным коэффициентам корреляции по-
рядка т:
rjk.llla...lm+1 = -r=---------- 2 • (З-16)
V I1 ~ X1 ” r*U+r<l...U)
Выборочные значения частных коэффициентов корреляции Tjk.N(j,k)>
^12.з> 6'fc-hb...im+i вычисляются по тем же формулам (3.15)~(3.16) с заме-
ной теоретических значений парных коэффициентов корреляции rj* их
выборочными аналогами г,-*.
При проверке гипотез Яо: rjk.hia...im = 0 и ПРИ построении интерваль-
ных оценок для следует пользоваться теми же правилами, что и
для обычных (п&рных) коэффициентов корреляции с одной поправкой:
в формулах (3.7), (3.7') и (3.9) объем выборки п надо заменить на п - т,
где т — порядок частного коэффициента корреляции.
Коэффициент детерминации К^у\Х) результирующей перемен-
ной у по X = определяет долю общей вариации ре-
зультирующего признака у в соотношении (3.2), объясненную изменени-
ем функции регрессии /(X), или, что то же, — изменением аргументов
а/1),х^\ ...,х{р} этой функции. Он определяется формулой
= (3.17)
где е(Х) — остаточная случайная компонента в соотношении (3.2), Dy —
дисперсия результирующего признака у (измеряющая его общую вариа-
цию), a Ejf[D(e(X)|X = X)] — усредненная по всем возможным значениям
X объясняющих переменных X условная дисперсия остатков е(Х) (вычи-
сленная при условии, что X = X).
В общем случае вычисление выборочного значения (статистической
оценки) К^(у;Х) коэффициента детерминации Х^(у;Х) требует предва-
рительной оценки функции регрессии f(X) или, по аналогии с вычисле-
нием выборочного парного корреляционного отношения — перехода
к группированным (в пространстве .. ,,®^) данным. Предва-
рительное оценивание функции регрессии /(X) относится к компетенции
регрессионного анализа и выходит за рамки данной главы, а переход к
группированным данным в пространстве размерности р > 2 требует очень
больших объемов п выборочных данных. Поэтому мы ограничимся при-
ближенными рекомендациями, имеющими обоснование и точный смысл в
рамках (р+1)-мерной нормальной распределенности исследуемого набора
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ 111
переменных (а/°) = у; х^\х^,...,х^)Г, но позволяющими вычислять
Kd(y,X) и проводить его статистический анализ до оценивания функции
/т-
Множественный коэффициент корреляции Rv,x используется
в качестве измерителя с.т.с.с. между результирующим показателем у
и набором объясняющих переменных х^\х^2\...,х^ в соотношениях
вида (3.2) при линейной форме регрессионной зависимости f(X) (т.е.
при f(X) = 0о + 01®^ 4- ... + 6рх^). Как было упомянуто, ниже-
следующие формулы и утверждения по поводу интерпретации Ry.x и
его связи с коэффициентом детерминации Kd(y,X) имеют точный смысл
лишь в рамках (р + 1)-мерной нормальной распределенности переменных
(х"=> = #! ....
Множественный коэффициент корреляции (м.к.к.) Ry,x может быть
вычислен по (р+ 1) х (р +1)-матрице парных коэффициентов корреляции
Я = (г Jfc)j,/s=0,l,2,...,p:
R2v.x = 1 - тгк (3-18)
Лоо
где ЯОо> как и прежде, алгебраическое дополнение элемента г00 = 1 в
матрице R.
М.к.к. Ry.x может быть также подсчитан по частным коэффициен-
там корреляции с помощью формулы
R2y.X = 1 - (1 - Г01 )(1 - Г02.1 )(1 - г03.1г) • • -(1 - ГорД2...(р-1)). (3.19)
В рамках упомянутой выше схемы вычисленный по формуле (3.18)
или (3.19) м.к.к. связан с коэффициентом детерминации простым соотно-
шением:
Kd(y,X) = R2y.x, (3.20)
и поэтому имеет ту же интерпретацию, что и коэффициент детерми-
нации, а именно: квадрат множественного коэффициента корреляции
определяет долю общей вариации результирующего признака у в ли-
нейном варианте соотношения (3.2), объясненную изменением функции
регрессии^.
1) В статистической практике, и в частности, в большинстве статистических пакетов,
величина R2 подсчитывается после статистического оценивания функции регрессии
по выборочному аналогу формулы (3.17), а потому просто совпадает, по определе-
нию, с коэффициентом детерминации.
112 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Выборочное значение Ry.x (т. е. статистическая оценка коэффи-
циента Ry.x) подсчитывается по формулам (3.18), (3.19) с заменой коэф-
фициентов корреляции, участвующих в правых частях этих выражений,
их выборочными аналогами.
Проверка гипотезы
Яо: Ry.x = 0, (3.21)
(т. е. проверка гипотезы об отсутствии линейной связи между у, с од-
ной стороны, и совокупностью переменных . ,а/р\ — с другой)
осуществляется с помощью критической статистики
_ п - р - 1 R2y.x
р
которая в условиях справедливости гипотезы (3.21) должна «вести себя»
как F(p; п - р — ^-распределенная случайная величина. Поэтому, если
окажется, что
п~р~- • -%- > Л(р; п - р - 1), (3.22')
Р 1 - Ry.x
то гипотеза (3.21) отвергается с вероятностью ошибки (т.е. с уровнем
значимости критерия), равной а. В неравенстве (3.227) величина Fa(p; п-
р— 1) — это 100а%-ная точка F(p; п—р— ^-распределения (см. табл. П1.5).
Ранговая корреляция предназначена для изучения статистической
связи между различными упорядочениями (ранжировками) объектов по
степени проявления в них того или иного свойства (качества). Обозна-
чим Х^ = (®i*\ х¥\ • • •»хпрезультат ранжировки п объектов по j-
му свойству (результат j-й ранжировки). Компонента х\^ определяет
то порядковое место (тот ранг), которое присвоено г-му объекту в об-
щем ряду п анализируемых объектов, упорядоченных по убыванию рас-
сматриваемого свойства. При этом другая ранжировка тех же объектов
/ (/с) (^) (/с)\ с.
X ' = (a?i , а?2 j • • • чхп ) может интерпретироваться либо как их упоря-
дочение по некоторому другому (А>му) свойству, либо как их упорядочение
по тому же свойству, но, например, другим экспертом.
Ранговый коэффициент корреляции (р.к.к.) Спирмэна Tjk
является измерителем степени согласованности двух различных ранжи-
ровок Х^ = (&iJ\ ..., Яд)) и Х^ = (ж^, Хук\ ..., х^) одного и того
же множества, состоящего из п объектов. Его выборочное значение Tjk
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
113
определяется формулой
= (3.23)
п -П.=1
Р.к.к. Спирмэна может принимать значения в диапазоне от -1 до 4-1,
причем значение -1 достигается при противоположных ранжировках (т. е.
при = п-х^ + 1), а значение +1 при совпадающих ранжировках (т.е.
при Нулевые значения коэффициента fj* (или статистиче-
ски незначимо отличающиеся от нуля) свидетельствуют об отсутствии
какой бы то ни было статистической связи между ранжировками Х^ и
Х(*)П
Связные (объединенные) ранги возникают в ситуациях, когда в
той или иной ранжировке наблюдаются факты «дележки мест», напри-
мер, в j-и ранжировке три объекта разделили места с 3-го по 5-е, а еще
два объекта — места 9-е и 10-е. В этом случае объектам, разделившим
места, приписывается ранг, равный среднему арифметическому соответ-
ствующих разделенных мест. Это значит, что в нашем примере трем
первым объектам будет присвоен одинаковый ранг 4 = (3 4- 4 4- 5)/3, а
двум последним объектам ранг 9,5 = (9 4- 10)/2. В подобных ситуаци-
ях формула для подсчета должна быть скорректирована следующим
образом:
1 (п3 - п) - £ (z^ - а:^)2 - Т(;) - Т{к)
rjk = I i=L . - (3.23')
01(n3 _ n) _ 2T{j)][l(rt3 - n) - 2T(fc)]
где
m(/)
E K»!'1)3 - "!'>], (3.23")
1 t=l
m(/) — число групп, ранги внутри каждой из которых неразличимы в 1-н
ранжировке, а — число элементов (рангов), входящих в t-ю группу
неразличимых рангов (Z = J, &). В частном случае отсутствия связных
рангов общее число групп т(Г) = п, соответственно, = ... =
= 1 и, следовательно, = 0.
1) Определение теоретических значений Tjk требует введения вероятностного про-
странства в пространстве пар ранжировок и не является необходимым в контексте
целей данного задачника (см. п. 11.3.7 в [1]).
114
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Проверка гипотезы
Яо: rj!t = О
(3.24)
о полном отсутствии статистической связи в двух анализируемых ранжи-
ровках (т.е. о статистически незначимом отличии от нуля выборочного
р.к.к. Спирмэна fjic) при п > 10 проводится с использованием критиче-
ской статистики
7п =
Tjky/n - 2
(3.25)
которая в предположении справедливости гипотезы (3.24) должна «вести
себя» приблизительно как стьюдентовская случайная величина t(n — 2) с
п - 2 степенями свободы. Поэтому, если окажется, что
V1 - tjk
(3.25')
то гипотеза (3.24) отвергается (с вероятностью ошибки, т.е. с уровнем
значимости критерия, равным а).
При п^10 проверка гипотезы (3.24) осуществляется с помощью
табл.П1.9. В частности, по заданному уровню значимости критерия а
и числу ранжируемых объектов п из табл. П 1.9 определяем значения Sc
(при Q = у) и вспомогательной константы Кп = (п — п)/3 (из последней
строки таблицы). После этого вычисляется пороговое значение
max 2S'c(h;Q)
----------------*
Если оказывается, что > т™х, то гипотезу (3.24) следует от-
вергнуть. т. е. признается наличие статистически значимой связи между
ранжировками и Х^ (с вероятностью ошибки, равной а).
Коэффициент конкордации (согласованности) Кендалла
W(m) является измерителем степени тесноты статистической связи (со-
гласованности), существующей между m > 2 различными ранжировками
v(0 t (0 (0 (0\ ; 1 п
X = (х\ , х2 ,..., ®п ), -< = 1,2,..., т, — одного и того же множества,
состоящего из п объектов. Его выборочное значение IV(m) определяется
формулой
Ж(т) =
(\ 2
(0 + 1) ।
> , х\-5—
2 7
(3.26)
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
115
Коэффициент конкордации W(m) может принимать значения в диа-
пазоне от 0 (что соответствует полному отсутствию статистической связи
между анализируемыми ранжировками) до 1 (что сигнализирует о полном
совпадении всех т анализируемых ранжировок).
При наличии связных (объединенных) рангов в анализируемых
ранжировках формула (3.26) должна быть откорректирована:
fy(m) =
W(n3 - n) - т £ Т(0 ’
1=1
(3.26')
где поправочные коэффициенты подсчитываются по формуле (3.23z).
Проверка гипотезы
Яо= W(m) = 0 (3.27)
о полном отсутствии статистической связи между т анализируемыми
ранжировками (т.е. о статистически незначимом отличии от нуля вы-
борочного значения W(m)) при п > 7 проводится с использованием кри-
тической статистики
7„ = тп(п - 1)1У(т), (3.28)
которая в условиях справедливости гипотезы (3.27) должна «вести себя»
приблизительно как х(п — ^-распределенная случайная величина. По-
этому, если оказалось, что
тп(п - l)W(ni) > Ха(» - 1), (3.28')
то гипотеза (3.27) отвергается, т.е. признается, что между т анализи-
руемыми ранжировками существует статистически значимая связь (с ве-
роятностью ошибиться, равной а). Величина %2(п — 1) — это 100а%-ная
точка х2(п — ^-распределения (определяется из табл. П1.4).
При п < 7 проверка гипотезы (3.27) осуществляется с использовани-
ем табл. П1.11* и Ш.1 Iе. «Входами» в табл. П1.11* является тройка чисел
т,п и S = 22(22 «Р ~ «выходом» — вероятность «о того, что
«=1 /=1
величина S в условиях справедливости гипотезы (3.27) может быть такой,
какой она оказалась в нашей выборке, или большей. Если окажется, что
эта табличная вероятность «о меньше принятой нами величины а уровня
значимости критерия, то гипотезу (3.27) об отсутствии связи между ран-
жировками следует отвергнуть. Табл. П1.116 построена несколько иначе.
116
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
В ней при уровне значимости критерия а = 0,05 и в соответствии с «вхо-
дами» т и п даны пороговые значения Sq.os величины 5, при превышении
которых гипотеза (3.27) должна быть отвергнута.
Корреляция категоризованных переменных. Признак называ-
ют категоризованным, если его возможные «значения»1^ описываются
конечным числом состояний (категорий, градаций).
Статистический анализ парных связей между категоризованными пе-
ременными и производится на базе исходных данных, предста-
вленных в виде так называемых двухвходовых таблиц сопряженно-
сти следующего типа:
Таблица 3.1 Результаты п наблюдений категоризованных
переменных х^ и х^
Градации признака Градации признака х^ Пу.
1 2 1 m/c
1 пи П12 П1/ . . . nim* ni.
2 П21 П22 . . . «2/ П2тп* n2.
I • . . . • •
i П£1 742 nil nimjk П».
mj nrrij 1 Птпу 2 nmj I mk Пщу •
П.ц n.i П.2 n./ n.mk n
В табл 3.1 представлены результаты статистического обследования п
объектов по категоризованным признакам и . В ней пц означает
число объектов (из общего числа п обследованных), у которых «значение»
(5)
признака х' ' зафиксировано на уровне г-й градации, а значение призна-
ем 1 - vA _ _
ка — на уровне /-и градации; пи. = >, пр/х — общее число объек-
Д=1
тов, «значение» признака у которых осталось зарегистрированным
mj
на уровне р-й градации (р = 1,2,..., mj)- п.^ = £ — общее число
Р=1
1) Слово «значения» взято в кавычки, т. к. речь идет часто не о числовых значениях,
а лишь об определенных условных метках возможных состояний (качество жилья:
плохое, удовлетворительное, хорошее, отличное; пол: мужской, женский и т. д.)
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
117
zr (*)
объектов, «значение» признака х ’ у которых оказалось зарегистриро-
ванным на уровне /z-й градации (ji = 1,2,..., т^).
Коэффициент квадратической сопряженности Xjk категоризо-
(j) W
ванных признаков яг ' и х ' является измерителем степени их статисти-
ческой взаимозависимости. Его выборочное значение Xjk определяется на
базе исходных данных n^(i = 1,2,...,тп^; I = 1,2,..., см. табл. 3.1)
соотношением:
Его значение может меняться от нуля ( при статистической независимости
переменных ху ' и х' ') до +оо.
Проверка гипотезы
Яо: Х-к = 0 (3.30)
о статистической независимости переменных и осуществляет-
ся с использованием критической статистики Xjk, которая в условиях
справедливости гипотезы (3.30) должна «вести себя» приблизительно как
X2((mj-1) X(mfc — 1)^распределенная случайная величина. Поэтому, если
оказалось, что
^i>X2«((mj-l)x(mfc-l)), (3.31)
то гипотеза (3.30) отвергается, т. е. делается вывод (с вероятностью ошиб-
ки, равной а), что категоризованные признаки х^ и х^ не являются
статистически независимыми.
Информационная мера связи УД между категоризованными пе-
ременными х^ и х^к\ так же как и коэффициент Xjk, является изме-
рителем степени их статистической взаимозависимости. Его выборочное
значение УД определяется на базе исходных данных пц (г = 1,2, ...,тп^;
I = 1,2,..., тк, см. табл. 3.1) соотношением:
^А = 2ЕЕп‘'1п
1=1 1=1
Ее значение может меняться от нуля (при статистической независимости
переменных х^ и х^) до +оо.
Проверка гипотезы
Яо: УД = 0 (3.33)
пц \
(3.32)
118 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
о статистической независимости переменных х^ и х^ осуществляется
с помощью критической статистики УД, которая в условиях справедли-
вости гипотезы (3.33) должна «вести себя» как x2((mj — 1) X (m* — 1))-
распределенная случайная величина. Поэтому, если оказалось, что
УД > xl((™j - 1) х (тк - 1)), (3.34)
то гипотеза (3.33) отвергается с вероятностью ошибки (т.е. с уровнем
значимости критерия), равной а. Или, другими словами, делается вывод,
что категоризованные переменные х^ и х^ не являются статистически
независимыми.
З.Б. Примеры решения типовых задач и упражнений
Пример 3.1 (упражнение). Пусть Е = (ajfc)j)fc_ii2......... —
ковариационная матрица случайного вектора f т.е.
ajk = Е[(£0) - а^к} - а(*>)], где а<° = Ее(0, -/ = 1,2..
Требуется доказать:
1) матрица Е всегда симметрична и неотрицательно определена;
2) если компоненты вектора { не связаны между собой ли-
нейным соотношением, то матрица Е — положительно определена.
Решение
1) Возьмем произвольный вектор С = (с^\с^\...,с^)т, компонен-
ты которого — любые действительные, не все равные нулю числа, и рас-
смотрим выражение
Г 13 Г
£сО)({(Л-0й) =Е ££eU’e<‘>({<«
_=! J [;=! *=1
= £ Е е<Ле'%л = CTSC.
j=l Ь=1
(3.35)
Но левая часть этого выражения очевидно неотрицательна, следовательно,
и произведение С ЕС > 0, что и означает неотрицательную определен-
ность матрицы £.
2) Левая часть выражения (3.35) обращается в нуль тогда и толь-
р
ко тогда, когда с^\^ — а^) = 0, т.е. когда компоненты вектора
i=i
£ связаны между собой линейным соотношением. Следовательно, если
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
119
не связаны линейным соотношением, то СТЕС > 0, что и
означает положительную определенность матрицы Е.
Замечание. При проведении многомерного статистическо-
го анализа линейная взаимозависимость компонент анализируе-
мой случайной величины, по существу, означает избыточность
ее размерности, поскольку в этом случае по меньшей мере одна
из компонент £ может быть выражена в виде линейной комби-
нации остальных. Поэтому в прикладных задачах многомерного
анализа, как правило, полагается, что компоненты анализируе-
мой случайной величины £ не связаны линейной зависимостью и,
следовательно, ее ковариационная матрица положительно опре-
делена.
Пример 3.2 (у п р а ж н е н и е). Пусть £ = — двумер-
ная случайная величина и Гц = ^/(^цО’зз)1^2 — парный коэффициент
корреляции между ее компонентами.
Требуется доказать:
1) -1 <г12 < 1;
2) для того, чтобы |ru| = 1, необходимо и достаточно, чтобы между
и fW существовала чисто функциональная линейная связь.
Решение
1) Воспользуемся очевидным неравенством
Е
(3.36)
в котором а№ = Е£^ и оц = Е(£^ - а^)2. Беря поочередно неравен-
ство (3.36) со знаком «+» и «-» и возводя в квадрат сумму (разность) в
круглых скобках, получаем (с учетом того, что г13 = Е[(^ - в^)(^ -
в^)]/(аи<*м)^ по определению):
(3.37)
что и требовалось доказать.
2) Необходимым и достаточным условием достижения точного знака
равенства в соотношении (3.36) (а следовательно, — точного знака ра-
венства в соотношениях (3.37)) является равенство нулю содержимого в
круглых скобках левой части (3.36). А это и означает существование чи-
сто функциональной линейной связи между компонентами и
120 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Пример 3.3 (упражнение). При статистическом анализе
двумерной случайной величины ( = (£^,£^) удается наблюдать лишь
ее «зашумленные» значения, т.е. в действительности мы имеем дело со
- - ё Zt(l) г(2)\ - t(l) И1) । r(i) c(2)
случайной величиной f = (£ '), в которой f ' = £ + o' ' и £ =
^(2) _|_ ^(2), где СЛучайные ошибки 6^ и 6^ имеют нулевые средние зна-
чения (Е6^ = Е6^ = 0), конечные дисперсии (Dt№ = <т%, = о?),
f(i) t(2)
взаимно независимы и статистически не зависят от £ и £' .
Требуется доказать,
что |г(^(1),^(2)|) > |г(ё(1),ё(2))|, т.е. что теснота парной корреля-
ционной связи между случайными величинами ослабевает при адди-
тивном наложении на них случайных ошибок.
Решение
В соответствии с формулой (3.5) парный коэффициент корреляции
г(^1\^2^) между случайными переменными и определяется соот-
ношением
Из условия следует для j = 1,2,:
a(J) = E£(i} = E^{j) + £(j)) = E£(j) = a(j);
D£(j) = + 6(J)) = D£(j} + a2
(в последней выкладке мы воспользовались статистической независимо-
стью и №);
Е[(?" - amXf(!l - aW)] = Е[({'” + Sm - a(I)X«(2) + - aW)]
= £[(«<” -a(”)(em -a'21)]
(здесь мы воспользовались взаимной независимостью и их незави-
симостью с и а также тем обстоятельством, что Е6^ = Е6^ =
0).
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
121
Таким образом, имеем:
= ^(1)-а(1))(^-а(2))]_
У(Т»е(1) + а?)(Т»е(2) + <т22)
г(е(1),^(2))
У(! + ^hy)(! + о^гу)
д[(е(1)-а(1))(е(2)-а(2))]
Dfb))
откуда непосредственно и следует, что |г(^1\^2^)| < |г(^1\^2^)|.
Пример 3.4 (задача). Деятельность п = 8 карьеров характе-
рируется себестоимостью 1 т. песка (я^), сменной добычей песка (а/2)) и
фондоотдачей (ж^3^). Значения показателей представлены в табл. 3.2.
Таблица 3.2. Показатели деятельности песчаных карьеров
i — номер карьера 1 2 3 4 5 6 7 8
Zj1) (тыс. руб.) 32 21 39 36 44 27 51 31
(т.) 63 80 32 50 27 56 23 57
*Ч3) (%) 21 25 19 17 10 29 9 22
Значения х\2\ ж^), — i = 1,2,... ,8, — образуют выборку из
трехмерной нормальной генеральной совокупности.
Требуется:
1) оценить средние значения а^ = среднеквадратические от-
клонения Gj = (j = 1,2,3) и корреляционную матрицу R =
(га*)м=1,2,з анализируемого трехмерного признака
2) вычислить матрицу выборочных частных коэффициентов корре-
ляции 1-го порядка, т. е. оценить значения коэффициентов
(j> Л, / = 1,2,3; j т£ k, I / j, I / к);
3) проверить гипотезы (при уровне значимости критерия а = 0,05) о
статистически незначимом отличии от нуля выборочных парного
и частного коэффициентов корреляции, соответственно, г13 и г13в2
и построить их интервальные оценки с уровнем доверия Pq = 0,95;
4) найти точечную оценку Л1.23 множественного коэффициента кор-
реляции Яг(1).г(2)я.(з) = Лиз и проверить гипотезу (при уровне зна-
чимости критерия а = 0,05) о его статистически незначимом от-
личии от нуля.
122
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Решение
1) Выборочные значения (оценки) и *,* (j,fc « 1,,2,3) пара-
метров, соответственно, и подсчитываются по формулам:
t=l
t=l
£(«!’> -*»>)(»<*’
£ _ ____t=l__________________________
у t=l t=l
Подставляя в эти формулы значения из табл. 3.2 и п = 8, получа-
ем:
а = Х = (z(1),z(2),z(3))T = (35,12; 48,50; 19,00)Т;
* = (*1;*2;*з)Т = (8,94; 18,43; 6,46)Т;
(1 *12 *13 \ / 1 -0,944 -0,920 \
Гл 1 Г23 I = I ~0,944 1 0,802 1 .
*31 *32 1 / \-0,920 0,802 1 /
2) Для вычисления выборочных частных коэффициентов корреляции
т,кА воспользуемся формулой (3.15), т.е.
rjk.l ~--->
У Rjj • Л/с/с
где Ryq — алгебраическое дополнение элемента ryq в матрице R. В нашем
случае
Я12 = (-1)3 -0,944 -0,920 0,802 1 = 0,206;
Л13 = (-1)4 -0,944 -0,920 1 0,802 = 0,163;
Ягз = (-1)5 1 -0,920 -0,944 0,802 = 0,066;
Глав* 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
123
An = (-!)’ 1 0,802 0,802 1 = 0,357;
«22 = (-1)4 1 -0,920 -0,920 1 = 0,154;
Язз = (-1)6 1 -0,944 -0,944 1 = 0,109.
Подставляя эти значения Rvq в формулу для для различных
j,k,l = 1,2,3 (при условиях j / к, I / j, I / к), получаем:
1
Г12.3
Йз.2
Г12.3
1
^23.1
1
-0,879
-0,826
-0,879
1
-0,513
-0,826
-0,513
1
3) Для проверки статистически незначимого отличия от нуля коэф-
фициентов Г1з = —0,920 и гхз.2 = —0,826 (т.е. для проверки гипоте-
зы Яо:г13 = 0 и гипотезы Яо:г1з,2 = 0) определим по табл. П1.8 при
Q = а/2 — 0,025 и числе степеней свободы и = п — 2 = 6 (для Г13) или
v = п — 2-1 = 5 (для Г13.2) верхние границы г*зИТ’ и r*3"2T доверительных
интервалов для истинных значений, соответственно, Г13 и Г13.2, построен-
ных в предположении отсутствия линейной корреляционной связи между
а/1) и х^: г*з"т’ = 0,707; г?здт' = 0,754. А поскольку |г13| > г^з"т' = 0,707
и |Пз.2| > Г1з.2Т' = 0>754, то гипотезы Яо и Яо должны быть отвергнуты
(с вероятностью ошибки а = 0,05). Другими словами, между себестоимо-
стью одной тонны песка а:^ и фондоотдачей х^ существует статистиче-
ски значимая отрицательная линейная корреляционная связь.
Представляет интерес сравнить парный коэффициент корреляции
г13 = —0,920, который характеризует степень тесноты линейной связи
между х^ и х^ на фоне влияния х^ и частный Г13.2 = -0,826, который
характеризует степень тесноты линейной связи между а/1) и а/3^ при
исключенном влиянии переменной х^. Так как |fi3| > |г13.гЬ мож-
но утверждать, что исключение влияния х^ ослабляет тесноту связи
между а/1) и х^.
Определим теперь интервальные оценки для коэффициентов корре-
ляции Г1з и Г13.2 при Pq = 0,95. Для этого воспользуемся правилами
(3.8)~(3.9), а именно: по табл. П1.7 найдем значение z, соответствую-
щее величине выборочного п.к.к. г13 = —0,92 (z = arcth (-0,92) =
-arcth 0,92 = —1,589); определяем значения z\ и z2 по формуле (3.9) (zli2 =
= -1,589 ±^ + так что zy = -2,400, z2 = -0,646);
124
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
затем по формуле (3.8) с помощью табл. П 1.7 определяем нижнюю и верх-
нюю границы, соотвественно, thz\ и thz2, интервальной оценки для ис-
тинного значения Г12 (thz\ = th (—2,400) = —th 2,400 = —0,983; th Z2 =
th(-0,646) = -th0,646 = -0,568). Итак: -0,983<г13<-0,5в8, при-
чем, данные неравенства выполняются с доверительной веро-
ятностью Ро=1 — 2-0,025= 0,95.
Полученная интервальная оценка подтверждает вывод о статистиче-
ски значимом отличии от нуля парного коэффициента корреляции г^з, т. к.
нуль не находится внутри доверительного интервала.
Доверительный интервал для Г13.2 строится аналогично тому, как
это делалось для п.к.к. ri3 с уменьшением числа степеней свободы на
порядок частного коэффициента корреляции (в нашем случае — на едини-
цу). Так что по значению Г13.2 = —0,826 находим из табл. П 1.7 величину
z = -1,175, затем значения гг и z2 по формуле z1<2 = z^ — 2(n-i2-l) >
где wq — 100<?%-ная точка стандартного нормального распределения (на-
ходится из табл. П 1.3), а I — порядок частного коэффициента корреля-
ции (в нашем случае п = 8, I = 1). Вычисления дают: z^ = —2,086,
z2 = -0,264.
Воспользовавшись табл. П1.7 находим соответствующие границы ин-
тервальной оценки 7*13.2: —0,969<Г13.2<—0,258, причем данные не-
равенства выполняются с доверительной вероятностью Ро=
1 - 2-0,025= 0,95.
Полученная интервальная оценка подтверждает вывод о статистиче-
ски значимом отличии от нуля выборочного ч.к.к. T13.2 (нуль не попадает
в пределы интервальной оценки).
4) Наконец, определим точечную оценку Я1.23 Для м.к.к. Я1.23 и про-
верим гипотезу (при уровне значимости а = 0,05) Но: Я] .23 = 0.
Точечная оценка Лиз определяется по формуле (3.18), т.е. в нашем
случае
Л1.23 = 1/1-^,
у ли
где |R| — определитель выборочной корреляционной матрицы R, а Ац —
алгебраическое дополнение элемента Гц = 1 в матрице R.
|R| = 1 + (-0,944) • 0,802 • (-0,920) + (-0,944)0,802(-0,920)
- (—0,920)2 - (0,802)2 - (—0,944)2 = 0,012;
Яп =(-1)2
1
0,802
0,802
1
= 1 - (0,802)2 = 0,357;
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
125
- /1 - 0,012 п поп
#1.23 = \ —р-дду — 0,983.
у U,oo7
Критическая статистика (3.22) для проверки гипотезы Но: A1-23 = 0
в нашем примере равна
п — р — 1
7п =---------
Р
#1,23 _ 5 0,966 _
1 ~ #1.23 ~ 2 °’034 ”
Найденная из табл. П1.5 5%-ная точка Fqi05(р; п — р— 1) = /*Ь,05(2; 5) =
5,79. Поскольку уп > Fo,os(2;5), то гипотеза HQ: Pi,23 = 0 должна быть
- (1)
отвергнута, т.е. между переменной я , с одной стороны, и совокупно-
(2) (з)
стью переменных г 7 их^,с другой, существует статистически значи-
мая линейная корреляционная связь.
Пример 3.5 (задача). По данным п = 39 предприятий полу-
чен коэффициент корреляции г = -0,654, характеризующий тесноту свя-
зи между себестоимостью продукции (р) и производительностью труда
(ж). Исходные статистические данные {(яьуОК^гзэ, по которым была
получена оценка г, можно интепретировать как случайную выборку из
нормальной генеральной совокупности.
Требуется:
построить интервальную оценку для истинного значения парного
коэффициента корреляции г с уровнем доверия Р = 0,95.
Решение
По табл. П1.7 для г = —0,654 найдем z — | In — —0,7823. Тогда в
соответствии с (3.9)
1,96 -0,654
zx = -0,7823 -~^=- = -1,10;
л/36 2-38
1,96 -0,654
z2 = -0,7823 + 4= " -тгЧ-п = -0,45.
л/36 2-38
Теперь по табл. П1.7 по найденным значениям zx и z2 найдем соответству-
ющие значения гх = —0,80 и г2 = —0,42.
Таким образом, можно утверждать, что с доверительной вероятно-
стью Ро = 0,95 истинное значение коэффициента корреляции г между се-
бестоимостью продукции у и производительностью труда х будет лежать
в интервале от —0,80 до —0,42, т.е. —0,80 г -0,42.
Пример 3.6 (задача). По итогам года тридцати семи одно-
родных предприятий легкой промышленности были зарегистрированы
126 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
следующие показатели их работы: = у — среднемесячная характе-
ристика качества ткани (в баллах); — среднемесячное количество
профилактических наладок автоматической линии; х^ — среднемесяч-
ное число обрывов нити.
По матрице исходных данных были подсчи-
таны (с помощью (3.5*)) выборочные парные коэффициенты корреляции
= 0,1,2): г01 = 0,105; г02 = 0,024; г12 = 0,996.
Предполагается, что данные можно рассматри-
вать как случайную выборку из нормальной генеральной совокупности.
Требуется:
1) проверить, можно ли полученные значения foi u ^02 считать ста-
тистически значимо отличающимися от нуля (с уровнем значимо-
сти критерия а = 0,05);
2) вычислить точечные и интервальные (с уровнем доверия Pq = 0,95)
оценки для ч.к.к. г01.2 и ’’02.17
3) определить точечную оценку Rxw.xwxw = Я0.12 для м.к.к.
Решение
1) Проверка гипотез Н\: roi = 0 и Я2: го2 = 0 производится с помо-
щью критических статистик (3.7). В нашем случае:
7(.) = = 0.105У>55 = 0625.
\71-fSi у1-(0,105)’
7<’> = Й>МГ~2 = 0,024,/М = 0142.
^l-foa У1 -(0,024)2
Сравнения значений 7^ и 7^ с 2,5%-й точкой 1(35)-распределения
fo,025(35) = 2,03, найденной по табл. П1.6, свидетельствуют о статистиче-
ски незначимом отклонении от нуля выборочных п.к.к. fOi и fo2. Други-
ми словами этот результат свидетельствует об отсутствии статистически
значимой парной линейной корреляционной связи между качеством ткани,
с одной стороны, и числом профилактических наладок и обрывов нити —
с другой, что не согласуется с профессиональными представлениями тех-
нолога.
2) Однако расчет частных коэффициентов корреляции по формуле
(3.15) дает значения foi,2 = 0,907; го2д = —0,906, которые вполне соот-
ветствуют нашим представлениям о естественном характере связей между
изучаемыми показателями.
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
127
Доверительные интервалы для истинных значений roi(2) и г02(1) (в
соответствии с рекомендациями (3.7)~(3.9)) найдем с использованием
«-преобразования Фишера для доверительной вероятности Р = 1 - 2а.
Тогда
1 1 + г wa г
Z1’2 " 2 1П 1 - г Т 7(п-1)-3 2[(п - 1) - 1] ’
где w4 — 100д%-ная точка стандартного нормального распределения (см.
табл. П1.3).
В нашем примере п = 37, 2а = 0,05. Подставляя поочередно в эту
формулу значения roi(2) = 0,907 и гог(1) = —0,906 и пользуясь табл. П1.7
значений z = |1п найдем:
1,16 < 201(2) < 1,83
и
1,83 < 202.1 < 1,16,
откуда, вновь воспользовавшись табл. П1.7, окончательно получим:
0,820 < г01(2) < 0,950;
—0,950 < 2*02(1) < —0,820.
3) Оценка коэффициента детерминации ^.(®<i)x(3)) между
характеристикой качества ткани у и совокупностью двух факторов: ко-
личеством профилактических наладок а/1) и числом обрывов нити х^2\
подсчитанная с помощью формулы (3.19), дает:
Ry.(xWxW) = 1 “ (1 “ ^01) (1 — 2*02(1))
= 1 - [1 - (0,105)2] [1 - (0,906)2]
= 1 - 0,989 • 0,179 = 1 - 0,177 = 0,823.
Отсюда = \/0,823 = 0,9072.
Пример 3.7 (задача). С целью исследования влияния погод-
ных условий на урожайность кормовых трав Хукер (Journ. Roy. Stat. Soc.,
1907, v.65, p. 1) рассмотрел данные Министерства земледелия Англии за
20 лет, характеризующие урожайность х^ (в ц/акр), весеннее количе-
ство осадков а/1) (в дюймах) и накопленную за весну сумму «активных»
(т.е. выше +5,5°(7) температур х^ (в градусах по Фаренгейту) одно-
родной в метеорологическом отношении области Англии, включающей в
себя группу восточных графств. По выборке были
128 и. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
подсчитаны выборочные значения средних (а^), дисперсий (sj) и парных
коэффициентов корреляции (г^) изучаемой трехмерной величины:
а(0) = 28,02; а(1) = 4,91; а(2) = 594,0;
so = 19,54; s? = 1,21; 4 = 7225;
rOi = 0,80; Гог = “0,40; Г12 = —0,56.
Требуется:
1) определить у действительно ли высокая температура в период со-
зревания трав отрицательно влияет на их урожайность (ведь Гог =
-о,4о;;
2) построить интервальные оценки для гои и г02.1 с уровнем доверия
Ро = 0,95;
3) вычислить значение выборочного множественного коэффициента
корреляции = Т?0.12-
Решение
1) Вычисление частных коэффициентов корреляции по рекуррентной
формуле (3.15х) дает:
Ли(2) = 0,759; ro2(i) = -0,097; ri2(o) = -0,436.
Как видим, если исключить одновременное влияние количества осад-
ков а/1) на урожайность (с ростом а/1) она повышается) и на сумму ак-
тивных температур (с ростом а/1) она понижается), то мы уже не обна-
ружим отрицательной корреляции между температурой и урожайностью
(^02(1) = 0,097, в то время как г02 = -0,40).
2) Построение доверительных интервалов для г01(2) и г02(1) (с уровнем
доверия Ро = 0,95) с использованием z-преобразования Фишера дает (см.
выше рекомендации (3.7)~(3.9)) в данном случае:
0,448 < 7*01(2) < 0,890; —0,419 < т*02(1) < 0,525.
Последнее неравенство свидетельствует о том, что у нас нет осно-
ваний считать положительную очищенную корреляционную связь между
урожайностью и температурой (г02(1) = 0,097) статистически значимой,
т. к. нуль находится внутри доверительного интервала.
3) Оценка коэффициента множественной корреляции меж-
ду урожайностью кормовых трав (у = ж^0^) и природными факторами —
весенним количеством осадков (а/1)) и накопленной суммой «активных»
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
129
температур (я^), подсчитанная по формуле (3.19), дает:
= 1-(1-Г01)(1- 7*02(1))
= 1 - [1 - (0,80)2] [1 - (1.097)2]
= 1 - 0,36 • 0,99 = 0,6436.
Отсюда Ry.(x(A)xW) = \/0,6436 = 0,802.
Пример 3.8 (задача). Два эксперта проранжировали 10 пред-
ложенных им проектов реорганизации научно-производственного объ-
единения (НПО) с точки зрения их эффективности (при заданных ре-
сурсных ограничениях). Пронумеровав проекты в порядке ранжиров-
ки 1-го эксперта, получаем в качестве исходных данных: Х^ =
(1;2;3;4;5;6;7;8;9; 10)Т; XW = (2;3; 1;4;6;5;9;7;8; 10)Т.
Требуется:
оценить степень согласованности мнений двух экспертов, исполь-
зуя в качестве измерителя ранговый коэффициент корреляции
(р.к.к.) Спирмэна.
Решение
Вычисления по формуле (3.23) дают:
# = 1 - ихиГ—И)fI+1+2'J+0+12+P+2a +1+1+0> = ‘-Йо44 = °’915’
что свидетельствует о существенной положительной ранговой связи меж-
ду исследуемыми переменными.
Пример 3.9 (задача). Десять однородных предприятий по-
дотрасли были проранжированы вначале по степени прогрессивности их
оргструктур (признак а/1 ), а затем — по эффективности их функциони-
рования в отчетном году (признак а/2)). В результате были получены
следующие две ранжировки: Х^1^ = (1; 2,5; 2,5; 4,5; 4,5; 6,5; 6,5; 8; 9,5; 9,5)Т;
Х(2) = (1;2;4,5; 4,5; 4,5; 4,5; 8; 8; 8; 10)Т.
Требуется:
с помощью р.к.к. Спирмэна оценить степень согласованности ран-
жировок десяти анализируемых предприятий по качеству их орг-
структуры и по эффективности их функционирования.
Решение
В первой ранжировке имеем четыре группы неразличимых рангов,
число элементов в которых больше единицы, а во второй ранжировке —
5 Прикладная статистика
в задачах и упражнениях
130 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
две такие группы. В соответствии с формулой (3.23”) получаем:
Т(1) = [(23 - 2) + (23 - 2) + (23 - 2) 4- (23 - 2)] = ^ = 2,00;
1а 1а
т(2) = А К4" "4)+ (33-3)] = 7,00.
1 А
Точная формула (3.23') дает = 0,917. Вычисление этого же ко-
эффициента корреляции по приближенной формуле (3.23) дает значение
0,921. Эти результаты оказываются совпадающими при округлении до
второго десятичного знака и свидетельствуют о высокой согласованности
двух анализируемых ранжировок.
Пример 3.10 (задача). Рассмотрим три порядковые пере-
/ (1) (2) (3)х я
менные (а: , а: , аг ') и соответствующие им упорядочения десяти объ-
ектов:
Таблица 3.3 Значения рангов десяти объектов по трем переменным
%(!)Т 1 4,5 2 4,5 3 7,5 6 9 7,5 10
%<2>Т 2,5 1 2,5 4,5 4,5 8 9 6,5 10 6,5
Х(3)Т 2 1 4,5 4,5 4,5 4,5 8 8 8 10
Сумма 5,5 6,5 9 13,5 12 20 23 23,5 23,5 26,5
Требуется:
с помощью коэффициента конкордации Кендалла оценить степень
согласованности в ранжировании десяти объектов по трем анали-
зируемым переменным.
Решение
Для оценки коэффициента конкордации Кендалла по формуле (3.26*)
подсчитаем:
s = Е (Е - 4й) = (-»)’+(-s * * * * 10)1 + (-w)2
i=l \j=l /
+ (-3)2 4- (-4,5)2 + (3,5)2 4- (6,5)2 4- 72 4- 92 4- Ю2 = 591;
Т(1) = ^(23 - 2)2 = 1;
Т(2) = ^(23-2)2=1,5;
Т(3) = jTj(43 - 4 4- З3 - 3) = 7.
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
131
Следовательно, в соответствии с (3.2б') имеем:
5Р(3)=_ 10)-з(7Т1у;п==°’828’
что свидетельствует о высоской степени согласованности трех разных
ранжировок.
Пример 3.11. (задача). В табл.3.4 (из [Gilby W.Н.,
Biometrika, 8, 94]) дано распределение 1725 школьников (т. е. п = 1725) по
значениям двух анализируемых категоризованных признаков: по качеству
одежды (а/1)) и по их умственным способностям (я^). Были определе-
ны 4 градации (т.е. тп\ = 4) по первому признаку (1: «очень хорошо»;
2: «хорошо»; 3: «удовлетворительно»; 4: «плохо») и 6 градаций (т.е.
та = 6) по второму признаку (1: «плохие»; 2: «ниже средних»; 3: «сред-
ние»; 4: «выше средних»; 5: «высокие»; 6: «превосходные»).
Таблица 3.4 Распределение 1725 школьников по значениям двух ка-
тегоризованных переменных
Градации признака _(1) Л Градации признака х^ Е
1 2 3 4 5 6
1 33 48 113 209 194 39 636
2 41 100 202 255 138 15 751
3 39 58 70 61 33 4 265
4 17 13 22 10 10 1 73
Е 130 219 407 535 375 59 1725
Нас интересует, существует ли связь между манерой одеваться и спо-
собностями, и если «да», то какова степень тесноты этой связи. С целью
ответа на эти вопросы
требуется:
1) используя данные табл. 3.4 , вычислить выборочное значение X2 ко-
эффициента квадратической сопряженности X2 между категори-
зованными признаками х^ и х^;
2) проверить гипотезу об отсутствии статистической связи между
манерой одеваться (переменной х^) и умственными способностями
школьников (переменной х^) с уровнем значимости критерия а =
0,005.
5*
132
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Решение
1) Содержащиеся в табл.3.4 исходные данные задачи пред-
ставлены в виде таблицы сопряженности вида табл. 3.1, в ко-
торой число градаций mi по признаку х^ равно четырем (mi = 4), а
число градаций т2 по признаку х^ равно шести (т2 = 6). Подсчет зна-
чения Хи по формуле (3.29) дает: Х12 — 174,92, что свидетельствует о
(1) (2)
весьма высокой степени тесноты связи между х' и х'
2) Чтобы убедиться в этом, проверим гипотезу Яо; Х22 = О, т.е. ста-
_ (1) (2) т,
тистически проверим гипотезу об отсутствии связи между х' и х' '. Ру-
ководствуясь рекомендациями (3.31), из табл. П1.4 находим 0,5%-ную точ-
ку Хо,005(15) «хи-квадрат»-распределения с (mi — 1) • (m2 — 1) = 3 • 5 = 15
степенями свободы: Xo,oos(15) = 32,80. Мы видим, что Х12 = 174,92 на-
много превосходит Хо,оо5(15) = 32,80, что подтверждает наше заключение
о наличии статистической связи между манерой одеваться и умственными
способностями школьников (при значении вероятности ошибиться в этом
заключении, равном всего 0,005).
Поскольку даже при уровне значимости а = 0,001 соответствующее
пороговое значение Xo,ooi(15) = 37,697 оказывается намного меньшим ста-
тистики X2, то связь есть и, по-видимому, характеризуется достаточно
высокой степенью тесноты.
З.В. Задачи и упражнения
Упражнение 3.1
Доказать, что для статистически независимых случайных величин
и ^(2) парНЫй коэффициент корреляции между ними (Г12) равен нулю.
Упражнение 3.2
Пусть случайная величина £ = подчиняется двумерному
нормальному распределению. Доказать, что если парный коэффициент
корреляции Г12 = = 0, то случайные компоненты и
являются статистически независимыми.
Упражнение 3.3
Пусть многомерная случайная величина подчи-
няется (р+ 1)-мерному нормальному з.р.в. Доказать, что Д2.^!)^»).^(₽>)
не может быть меньше парного или частного коэффициента корреляции
между TJ и любой из объясняющих переменных (j = 1,2,... ,р)
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
133
Упражнение 3.4
Рассматриваются т упорядочений ..., п объектов и
соответствующая матрица ранговых коэффициентов корреляции Спирмэ-
на (Tjk)j,k=i,2v..,m> построенная по этим упорядочениям.
По этим же упорядочениям вычислен коэффициент конкордации Кен-
далла W(m). Доказать, что между W(m) и средней величиной г =
т т
53 53 к рангового коэффициента корреляции Спирмэна существует
m j=l /с=1
(з<*)
соотношение
mW(m) - 1
т — 1
или, что то же:
W(m) = г + -—
т
Упражнение 3.5
Доказать, что если все т рассматриваемых ранжировок п объектов
одинаковы, то построенный по ним коэффициент конкордации Кендалла
Ж(7п) будет равен единице.
Упражнение 3.6
Доказать, что область значений рангового коэффициента корреляции
Спирмэна г определяется отрезком [—1; +1], причем, в случае совпадаю-
щих ранжировок т = 1, а в случае противоположных т = — 1.
Упражнение 3.7
Рассматривается табл. 3.1 сопряженности, представляющая резуль-
таты наблюдения категоризованных признаков х^ и х^. Введем меру
отклонения от статистической независимости признаков х^ и х^ в виде
D
jk~ П
t=l /=1
(А< - Pi-P-i)2
PiP-i
2 1
где рц = pi. = ^j=- и р.{ = (как известно, по определению, признаки
и х1'^ называются статистически независимыми, если соответствую-
щие теоретические частоты рц, рц и рц связаны тождеством рц —р,.рц = О
при всех г = 1,2,m,j и I = 1,2,..., т^). Доказать, что = Xjk,
где X2 — коэффициент квадратической сопряженности признаков х^ и
х^, определяемый формулой (3.29).
134 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Упражнение 3.8
Пусть из двумерной генеральной совокупности взята вы-
борка объема п и пусть — »-й элемент этой выборки (г =
1,2,...,п).
Требуется:
1) доказать тождественность выражений:
1 - S(”)(^!l - S<2>) _
Г12 —--------------------------->
7^ = j £ «<-Ч2). *(Л = 1Ё»!” и А = J -
«=1 1=1 »=1
xW)2 (у = 1,2);
2) доказать справедливость равенства
где
J1) - аш(1) + Ь и zW - сх(-2) + d
(а, Ь, с и d — некоторые постоянные числа, причем, а / 0 и с / 0).
Упражнение 3.9
Пусть из трехмерной нормальной генеральной совокупности (х^\ а/2\
а/3>) взята выборка объема п, на основании которой получена корреляци-
онная матрица
л /1 Пг Пз\
R= I г21 1 ^23 I
\ Ли Гзг 1 /
Требуется доказать тождественность формул для определения:
1) частного коэффициента корреляции
А Я]2 Й2 “ Й3^23
г12(3) =---------Г = z
(Ян Ям Г ^/(1 -г?з)(1 -41)
где Ri2,Rn,R22 — алгебраические дополнения соответствующих
элементов матрицы R,;
2) множественного коэффициента корреляции
d а А I®*! /4г + 4з “ Зги • Из • ^23
Л1-(2,3) = V 1 “ дГ- = \ --------л----------»
V "и у 1 — г2з
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
135
где |R| — определитель корреляционной матрицы R.
Задача 3.1
В табл, представлены цены (в руб.) на следующие виды продоволь-
ственных товаров: говядина (а/1)), растительное масло (а/2^), сахар-песок
(а/3)) и хлеб белый в/с (а/4)) в п = 12 городах Центрального района Рос-
сии на июнь 1996 г.
i Город X™ _(2) т(3) Л*)
1 Брянск 12500 7726 3410 4875
2 Владимир 13857 7880 3183 7125
3 Иваново 14150 6182 3209 4998
4 Калуга 12697 8237 3400 5170
5 Кострома 13000 8750 3600 5476
6 Москва 14120 11024 4418 6466
7 Орел 10678 8456 3634 4200
8 Рязань 12163 9172 4033 4720
9 Смоленск 12833 8320 3909 4354
10 Тверь 14400 7083 3416 5440
11 Тула 12083 8259 3486 5140
12 Ярославль 14379 7991 3938 5283
Требуется:
1) найти точечную оценку г14 парного коэффициента корреляции г14
между ценами на говядину (а/1)) и хлеб белый в/с (а/4)), при уровне
значимости критерия а = 0,01 проверить гипотезу Hq: г14 = 0;
найти интервальную оценку для г14 с уровнем доверия Ро = 0,875;
2) с помощью п.к.к. оценить тесноту связи между и а/3\ при
уровне значимости критерия а = 0,05 проверить гипотезу Hq: г2з =
0; найти интервальную оценку для т2з с уровнем доверия Pq = 0,90;
3) определить долю (в %) дисперсии х^\ обусловленную изменением
ч ч (2)
значений переменной х' , проверить статистическую значимость
отличия от нуля выборочного коэффициента корреляции г24 при
уровне значимости критерия а = 0,1.
Провести неформальный анализ и предложить интерпретацию по-
лученных решений.
136 П. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Задача 3.2
В таблице представлены темпы прироста (%) следующих макроэконо-
мических показателей десяти развитых стран мира за 1992 г.: ВНП (а/1)),
промышленного производства (а:^2^), индекса цен (аг^3^) и доли безработ-
ных (а:^4^).
Страны _(1) «[/ х(2) т(з) а£/ _(4) al/
Япония 3,5 4,3 2,1 2,3
США 3,1 4,6 3,9 6,3
Германия 2,2 2,0 3,4 5,1
Франция 2,7 3,1 2,9 9,7
Италия 2,7 3,0 5,6 11,1
Великобритания 1,6 1,4 4,0 9,5
Канада 3,1 3,4 3,0 10,0
Австралия 1,8 2,6 4,0 2,6
Бельгия 2,3 2,6 3,4 8,9
Нидерланды 2,3 2,4 3,5 6,4
Требуется:
1) найти оценку парного коэффициента корреляции между темпами
прироста ВНП и промышленного производства (х^); при
уровне значимости критерия а = 0,05 проверить гипотезу Hq: =
0; найти интервальную оценку для Т\2 с уровнем доверия Pq = 0,95;
2) с помощью п.к.к. оценить тесноту связи между а/1) и а/3\ про-
верить гипотезу Hq: rj3 — 0 при уровне значимости критерия
а = 0,05; найти интервальную оценку для Г]3 с уровнем доверия
Ро = 0,90;
3) найти точечную и интервальную оценки парного коэффициента
корреляции между и а/3\ приняв в качестве уровня доверия
Ро = 0,95;
4) определить долю дисперсии х^2\ обусловленную изменением перемен-
ной х^;
5) найти точечную и интервальную оценки парного коэффициента
корреляции между х^ и х^\ приняв в качестве уровня доверия
Pq = 0,90; при уровне значимости критерия а = 0,05 проверить
гипотезу Hq: т34=0.
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
137
Провести неформальный анализ и предложить интепретацию полу-
ченных решений.
Задача 3.3
При исследовании взаимосвязи цен на следующие виды продоволь-
ственных товаров: говядина (а:^1^), растительное масло (а/2)), сахар-песок
(а/3)) и хлеб белый в/с (а/4)) в п = 22 городах Центрального района Рос-
сии получена матрица оценок парных коэффициентов корреляции:
/ 1,00 -0,18 0,01 0,61 \
р _ "°»18 Ь00 0,82 0,24 |
0,01 0,82 1,00 -0,05 I
\ 0,61 0,24 -0,05 1,00 /
гг « (1) (2) (4)
Для трехмерной совокупности z' , г' ' и г '
требуется:
1) построить матрицу выборочных частных коэффициентов корреля-
ции’,
2) построить интервальную оценку для т^а с уровнем доверия Ро =
0,90; проверить гипотезу Hq: г^а = 0 пРи уровне значимости кри-
терия а = 0,1; как влияет показатель х^ на тесноту связи между
XW и а:(2)?
3) вычислить выборочное значение R^,\2 множественного коэффици-
ента корреляции Rx(4).^(1)^(2); проверить гипотезу Hq: Я4Л2 = 0 пРи
уровне значимости критерия а = 0,05.
Провести неформальный анализ и предложить интепретацию полу-
ченных решений.
Задача 3.4
По данным задачи 3.3 для трехмерной совокупности а/4)
требуется:
1) построить матрицу выборочных частных коэффициентов корреля-
ции;
2) построить интервальную оценку для Г23.4 с уровнем доверия Pq =
0,90; проверить гипотезу HQ: г2за = 0 при уровне значимости кри-
терия а = 0,05; как влияет показатель на тесноту связи между
х(3) и я(2)?
3) вычислить выборочное значение Л2.34 множественного коэффици-
ента корреляции Ят(2),а?(з)а[?(4); проверить гипотезу HQ: Я2.34 = 0 пРи
уровне значимости критерия а = 0,05.
Провести неформальный анализ и предложить интепретацию полу-
ченных решений.
138
П. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Задача З.Б
При исследовании взаимосвязи темпов прироста (%) следующих ма-
кроэкономических показателей десяти развитых стран мира за 1992 г.:
ВНП объема промышленного производства (®^), индекса цен (®^)
и доли безработных рассчитана матрица R выборочных парных
коэффициентов корреляции, а также векторы средних арифметических
значений ~Х = и среднеквадратических отклонений
& ~ (^1««а»«з»«<) •
/ 1,00 0,90 й _ ( 0,90 1,00 “ 1 -0,39 -0,28 \-0,05 -0,23 -0,39 -0,28 1,00 0,41 -0,05 \ /2,53\ -0,23 | у _ 2,94 0,41 1 ’ Л ~ 1 3,58 1 ' 1,00 / \7,19/ /0,57\ , с _ I 0,93 ’ 1 0,87 ’ \2,98/
Предполагается, что исходные данные, по которым рассчитаны эти
характеритсики, представляли собой случайную выборку из соответству-
ющей четырехмерной нормальной генеральной совокупности.
Требуется:
1) вычислить значение выборочного частного коэффициента корреля-
ции Г12.з и найти интервальную оценку для т*12.з с уровнем доверия
Ро = 0,95;
2) вычислить значение выборочного множественного коэффициента
корреляции Лиз = Ла.(1).;с(а)г(з) и проверить его (при уровне значи-
мости а = 0,05^ на статистически значимое отличие от нуля.
Провести неформальный анализ и предложить интепретацию полу-
ченных решений.
Задача З.в
По данным задачи 3.5
требуется:
1) вычислить значение выборочного частного коэффициента корреля-
ции fi2.4, найти интервальную оценку для с уровнем доверия
Ро = 0,90; проверить гипотезу Но'. 7*12.4 = 0 при уровне значимости
критерия а = 0,05;
2) вычислить значение выборочного коэффициента детерминации Л1.24
и проверить его на статистически значимое отличие от нуля (при
уровне значимости а = 0,05).
Провести неформальный анализ и предложить интерпретацию по-
лученных решений.
Глава 3. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
139
Задача 3.7
По данным задачи 3.5 провести корреляционный анализ трехмерной
совокупности и приняв аг1* за результативный признак, и
дать экономическую интерпретацию полученным результатам.
Задача 3.8
По данным задачи 3.5 провести корреляционный анализ трехмерной
генеральной совокупности и приняв за результативный
признак, и дать экономическую интерпретацию полученным результатам.
Тест 3.1. Известно, что при фиксированном значении х$ между ве-
личинами Х\ и хз существует положительная связь. Какое значение имеет
частный коэффициент корреляции г1а.з?
а) -0,8;
б) 0;
в) 0,4;
г) 1.3.
Тест 3.2. По результатам п = 20 наблюдений получен частный коэф-
фициент корреляции Г12,з = 0,8. Определите, чему равна разность между
оцененным значением ч.к.к. т = 0,8 и верхней границей интервальной
оценки для Г12.з:
а) *0,513;
б) 0,344;
в) 0,700;
г) -0,133.
Тест 3.3. Известно, что хз усиливает степень тесноты связи между
величинами Xi и х2. По результатам наблюдений получена оценка для
частного коэффициента корреляции Гц.з = —0,45. Какое значение может
принять парный коэффициент корреляции
а) 0,4;
б) 0,2;
в) -0,8;
г) 1,2.
Тест 3.4. По результатам п = 10 наблюдений рассчитан частный
коэффициент корреляции Г12.3 — 0,83 и с доверительной вероятностью
Ро = 0,95 найдена интервальная оценка 0,37 < г 12.3 < 0,96. Какое значе-
ние принимает верхняя граница доверительного интервала для 7*12.3 ПРИ
Ро = 0,9:
а) 0,94;
б) 0,98;
в) 0,82;
г) 0,27.
140
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Тест 3.5. По результатам п = 20 наблюдений рассчитан йз.г = 0,62
и найден доверительный интервал 0,23 < Г13.2 < 0,83, при доверительной
вероятности Pq = 0,95.
Какое значение примет нижняя граница доверительного интервала
для Г13.2 при п = 10, если Ро и Г13.2 остались неизменными:
а) 0,45;
б) 0,20;
в) 0,32;
г) 0,59.
Тест 3.6. Множественный коэффициент корреляции Л1.23 = 0,8.
Определите, какой процент дисперсии величины хг объясняется варьи-
рованием значений Х2 и ху.
а) 28%;
б) 32%;
в) 64%;
г) 80%.
Тест 3.7. По результатам 20 наблюдений найдено выборочное зна-
чение множественного коэффициента корреляции Я1.23 = 0,8. Определи-
те, какое из нижеприведенных чисел дает разность между наблюдаемым
Рнабл и Ркр в задаче проверки статистической гипотезы Но: Pi.23 = 0 при
уровне значимости критерия а = 0,05:
а) 2,8;
б) -13,6;
в) 9,4;
г) 11,5.
Глава 4. Снижение размерности анализируемых
многомерных признаков и построение
интегральных показателей
4.А. Краткие сведения из теории
О сущности задач снижения размерности. В исследовательской
и практической статистической работе приходится сталкиваться с ситуа-
циями, когда общее число р признаков х^2\ ..., х^р\ регистрируемых
на каждом из множества обследуемых объектов (стран, регионов, городов,
предприятий, семей, фирм, банков и т. п.), очень велико — порядка ста и
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
141
более. Тем не менее имеющиеся многомерные наблюдения
i — 1,2,..., я.
(4.1)
\x^J
следует подвергнуть статистической обработке, осмыслить либо ввести в
базу данных для того, чтобы иметь возможность их использовать в нуж-
ный момент.
Желание статистика представить каждое из наблюдений (4.1) в ви-
Г7 - (1) (2) (₽')
де вектора Z некоторых вспомогательных показателей '..., 7 с
существенно меньшим (чем р) числом компонент р бывает обусловлено в
первую очередь следующими причинами:
• необходимостью наглядного представления (визуализации) исход-
ных данных (4.1), что достигается их проецированием на специально по-
добранное трехмерное пространство (pz = 3), плоскость (р = 2) или чи-
словую прямую;
• стремлением к лаконизму исследуемых моделей, обусловленному не-
обходимостью упрощения счета и интерпретации полученных статисти-
ческих выводов;
• ограниченными возможностями человека в одновременном анали-
зе («охвате») большого числа частных критериев какого-либо свойства
системы (например, в анализе ряда разноаспектных характеристик каче-
ства жизни населения) и вытекающим отсюда стремлением к определен-
ного вида «сверткам» этих частных критериев, к их агрегированию, а в
отдельных случаях — к переходу к единств енному интегральному инди-
катору анализируемого синтетического свойства системы;
• необходимостью существенного сжатия объемов хранимой стати-
стической информации (без видимых потерь в ее информативности), если
речь идет о записи и хранении массивов типа (4.1) в специальной базе дан-
ных.
При этом новые (вспомогательные) признаки z^2\ . ..,z^p^ могут
выбираться из числа исходных или определяться по какому-либо правилу
по совокупности исходных признаков, например как их линейные комбина-
ции. При формировании новой системы признаков к последним предъявля-
ются разного рода требования, такие, как наибольшая информативность
(в определенном смысле), взаимная некоррелированность, наименьшее ис-
кажение геометрической структуры множества исходных данных и т.п.
В зависимости от варианта формальной конкретизации этих требований
142
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
приходим к тому или иному алгоритму снижения размерности. Имеет-
ся, по крайней мере, три основных типа принципиальных предпосылок,
обусловливающих возможность перехода от большого числа р исходных
показателей состояния (поведения, качества, эффективности функциони-
рования) анализируемой системы к существенно меньшему числу р наи-
более информативных переменных. Это, во-первых, дублирование инфор-
мации, доставляемой сильно взаимосвязанными признаками', во-вторых,
неинформативностъ признаков, мало меняющихся при переходе от одно-
го объекта к другому (малая «вариабельность» признаков); в-третьих,
возможность агрегирования, т.е. простого или «взвешенного» суммиро-
вания, по некоторым признакам.
Формально задача перехода (с наименьшими потерями в информатив-
ности) к новому набору признаков г 1 аг' может быть описана
следующим образом. Пусть Z — Z(X) ~ (^1\z^2\...,^p^)T — некото-
t ж (1) (2) (р)
рая р-мерная вектор-функция от исходных переменных аг ' ,х' х^ '
(Р < Р) и пусть Ipi(Z(X)) — определенным образом заданная мера инфор-
мативности р'-мерной системы признаков Z(X) = (z^(X),..., z^p \х))Т.
Конкретный выбор функционала Zp<(£) зависит от специфики решаемой
реальной задачи и опирается на один из возможных критериев: критерий
автоинформативности, нацеленный на максимальное сохранение инфор-
мации, содержащейся в исходном массиве относительно самих
исходных признаков; и критерий внешней информативности, нацеленный
на максимальное «выжимание» из информации, содержащейся
в этом массиве относительно некоторых других (внешних) показателей.
Задача заключается в определении такого набора признаков Z, най-
денного в классе F(X) допустимых преобразований исходных показателей
а/1),... ,х^р\ что
7,.(Z(X)) =
(4-2)
Тот или иной вариант конкретизации этой постановки (определяю-
щий конкретный выбор меры информативности Zp/(Z) и класса допусти-
мых преобразований) приводит к конкретному методу снижения размерно-
сти: к методу главных компонент, факторному анализу, экстремальной
1 Речь идет о нахождении (в виде функции от X) такого вектора Z(X) =
..., >(Х))Т, который обращает в максимум или минимум (в зависимо-
сти от конкретного содержательного смысла оптимизируемого критерия информа-
тивности) значение Ip>(Z). Поэтому справа в данном соотношении записано extr
(экстремум).
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
143
группировке параметров и т. д. (см. гл. 13 в [1]). При решении помещен-
ных ниже задач предполагается использование только метода главных
компонент (МГК).
Метод главных компонент. Во многих задачах обработки много-
мерных наблюдений и, в частности, в задачах классификации исследова-
теля интересуют в первую очередь лишь те признаки, которые обнаружи-
вают наибольшую изменчивость (наибольший разброс) при переходе от
одного объекта к другому.
С другой стороны, не обязательно для описания состояния объек-
та использовать какие-то из исходных, непосредственно замеренных на
нем признаков. Так, например, для определения специфики фигуры че-
ловека при покупке одежды достаточно назвать значения двух признаков
(размер-рост), являющихся производными от измерений ряда параметров
фигуры. При этом, конечно, теряется какая-то доля информации (портной
измеряет до одиннадцати параметров на клиенте), как бы огрубляются
(при агрегировании) получающиеся при этом классы. Однако, как пока-
зали исследования, к вполне удовлетворительной классификации людей с
точки зрения специфики их фигуры приводит система, использующая три
признака, каждый из которых является некоторой комбинацией от боль-
шего числа непосредственно замеряемых на объекте параметров.
Именно эти принципиальные установки заложены в сущность того
лилейного преобразования исходной системы признаков, которое приводит
к главным компонентам. Формализуются же эти установки следующим
образом.
Следуя общей оптимизационной постановке задачи снижения размер-
ности (4.2) и полагая анализируемый признак X р-мерной случайной ве-
личиной с вектором средних значений а = (а^\...,в^) и ковариацион-
ной матрицей Е = (<7у) (i,j = 1,2,...,р), вообще говоря, неизвестными,
определим в качестве класса F(X) допустимых преобразований исследуе-
мых признаков ..,х^ их всевозможные линейные ортогональ-
ные нормированные комбинации, т.е.
F= 1 Z: z0) = ^civ(x(v)-а^), j = l,2,...,pl,
Р=1 '
где
р р
= 1 и CjyCkv = 0 (4.3)
р=1 р=1
для j = 1,2,...,р и к = 1,2,...,р, но j / k, а в качестве крите-
рия (меры) информативности р'-мерной системы показателей Z(X) =
144
П. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
(z^\%), z^2\X), ...,z{p \х)) выражение
Т - D*(1) + --- + D*(P,) ,,,ч
D/1> + ... + DI(>’>’ ( ’
Тогда при любом фиксированном р = 1,2,..., р вектор искомых вспо-
могательных переменных Z(X) = (z^1\A’),... ,z^p \х))Т определяется
как такая линейная комбинация
Z = LX
(4-5)
(где X — вектор-столбец центрированных исходных переменных, а
(hi ••• hp \
............................................ —
/р>1 ... Ip/р )
матрица, строки которой удовлетворяют условию ортогональности), что
I,. (5°>(Х),.... 5<’'>(Х)) = max Ip. (Z(X)).
Jtr
Полученные таким образом переменные ^^(Х),... ,^р\х) и назы-
вают главными компонентами вектора X. Отсюда вытекает следующее
определение главных компонент.
Первой главной компонентой z^^(X) исследуемой системы
Ч V /(1) (р)\Т~
показателей X = (а? , ...,агг') называется такая нормированное
центрированная линейная комбинация этих показателей, которая среди
всех прочих нормированно-центрированных линейных комбинаций пере-
менных ., х^ обладает наибольшей дисперсией.
k-й главной компонентой 2^к\х) (к = 2,3, ...,р) исследуе-
мой системы показателей X = называется такая
нормированно-центрированная линейная комбинация этих показателей,
которая не коррелирована с к — 1 предыдущими главными компонентами
и среди всех прочих нормированно-центрированных и некоррелированных
с предыдущими к — 1 главными компонентами линейных комбинаций пе-
ременных х^\...,х^ обладает наибольшей дисперсией.
Замечание 1 (переход к центрированным переменным). По-
скольку, как увидим ниже, решение задачи (а именно вид матрицы ли-
нейного преобразования L) зависит только от элементов ковариационной
матрицы Е, которые в свою очередь не изменяются при замене исходных
переменных х^ переменными х^ -с^ (с^ — произвольные постоянные
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
145
числа), то в дальнейшем будем считать, что исходная система показателей
уже центрирована, т.е. что Ear ' = 0, j = 1,2,... ,р. В статистической
практике этого добиваются, переходя к наблюдениям = х^ — х^\ где
х^ = 52Р=1 х^/п (для упрощения обозначений волнистую черту над цен-
трированной переменной и над главной компонентой в дальнейшем ста-
вить не будем).
Замечание 2 (переход к выборочному варианту). Поскольку в
реальных статистических задачах располагаем лишь оценками а и Е со-
ответственно вектора средних а и ковариационной матрицы Е, то во всех
—(?)
дальнейших рассуждениях под а' ' понимается аг", а под — выбороч-
ная ковариация = 53?=1(ж:^ -х^)(х\^ -х^)/п (j,k = 1,2,...,р).
Замечание 3. Использование главных компонент оказывается
наиболее естественным и плодотворным в ситуациях, в которых все ком-
поненты я/1), х^2\ ..., х(р) исследуемого вектора X имеют общую физиче-
скую природу и соответственно измерены в одних и тех же единицах. К
таким примерам можно отнести исследование структуры бюджета време-
ни индивидуумов (все х^ измеряются в единицах времени), исследование
структуры потребления семей (все х^ измеряются в денежных единицах),
исследование общего развития и умственных способностей индивидуумов
с помощью специальных тестов (все измеряются в баллах), разного ро-
да антропологические исследования (все х^ измеряются в единицах меры
длины) и т. д. Если же признаки х^2\ ..., х^ измеряются в различ-
ных единицах, то результаты исследования с помощью главных компонент
будут существенно зависеть от выбора масштаба и природы единиц из-
мерения. Поэтому в подобных ситуациях исследователь предварительно
переходит к вспомогательным безразмерным признакам х 4", например,
с помощью нормирующего преобразования
j — 15 2,..., р\
i ~ 1,2,...,п,
где &jj соответствует ранее введенным обозначениям, азатем строит глав-
ные компоненты относительно этих вспомогательных признаков X* и их
ковариационной матрицы £%•, которая, как легко видеть, является одно-
временно выборочной корреляционной матрицей R исходных наблюдений
Xi.
(4.6')
146 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Вычисление главных компонент. Из определения главных компо-
нент следует, что для вычисления первой главной компоненты необходимо
решить оптимизационную задачу вида (4.2), т.е. в данном случае:
' D (1лХ) -* max;
т '* (4-6)
где — первая строка матрицы L (см. (4.5)). Учитывая центрирован-
ность переменной X (т.е. ЕХ = 0)и то, что Е(ХХТ) = Е, имеем
D(/iX) = Е (/i X )2 = E(/iXXT/iT) = Л
Следовательно, задача (4.6) может быть записана
{ЛЕ/Т —* max;
h
ШТ = 1,
Вводя функцию Лагранжа <p(Ji, А) = li^li - А(/г/^ - 1) и дифференцируя
ее по компонентам вектор-столбца /]", имеем:
™ = 2E/iT - 2А/Л
что дает систему уравнений для определения Ц:
(Е - AI)/iT = 0 (4.7)
(здесь 0 = (0,0,..., 0)Т — р-мерный вектор-столбец из нулей).
Для того чтобы существовало ненулевое решение системы (4.7) (а оно
должно быть ненулевым, так как = 1), матрица Е - AI должна быть
вырожденной, т.е.
|Е - А1| = 0. (4.8)
Этого добиваются подбором соответствующего значения А. Уравне-
ние (4.8) (относительно А) называется характеристическим для матрицы
Е. Известно (см. [1], Приложение 2), что при симметричности и неотри-
цательной определенности матрицы S (каковой она и является как всякая
ковариационная или корреляционная матрица) это уравнение имеет р ве-
щественных неотрицательных корней Ai Аг > > Ар > 0, называемых
характеристическими (или собственными) значениями матрицы Е.
Учитывая, что Dz^ = D(GX) = hEl^ и Wil — Ь (последнее
соотношение следует из соотношения (4.7) после его умножения слева на
11, с учетом М7 = 1), получаем Dz^(.X) = А.
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
147
Поэтому для обеспечения максимальной величины дисперсии пере-
менной 2^ нужно выбрать из р собственных значений матрицы Е наи-
большее, т. е.
D2(1)(X) = Av
Подставляем Ai в систему уравнений (4.7) и, решая ее относительно
1г1,..., /1р, определяем компоненты вектора Ц.
Таким образом, первая главная компонента получается как линей-
ная комбинация = 1\Х, где Ц — собственный вектор матрицы
Е, соответствующий наибольшему собственному числу этой матрицы.
Далее аналогично можно показать, что ^*\х) = l^X, где — соб-
ственный вектор матрицы Е, соответствующий Л-му по величине соб-
ственному значению А*. этой матрицы.
Таким образом, соотношения для определения всех р главных ком-
понент вектора X могут быть представлены в виде (4.5), где Z =
... ,^₽^)Т, X = (а/1\...,®^)Т, а матрица L состоит из строк
/,• = (Ijx,..., ljp), j = ТТр, являющихся собственными векторами матрицы
Е, соответствующими собственным числам Xj. При этом сама матрица L
в соответствии с условиями (4.3) является ортогональной, т. е.
LLT = LTL = I. (4.9)
В дальнейшем в целях упрощения обозначений мы будем опускать
«тильду» над переменными главных компонент, т. е. обозначать главные
компоненты просто Z = ...,z^p ^).
Основные числовые характеристики главных компонент.
Определим основные числовые характеристики (средние значения, дис-
персии, ковариации) главных компонент в терминах основных числовых
характеристик исходных переменных и собственных значений матрицы
Е:
a) EZ = E(LX) = L • EX = 0;
б) ковариационная матрица вектора главных компонент:
Ez = E(ZZT) = E((LX)(LX)T) = E(LXXTLT)
= L • Е(ХХТ) • LT = L • Е • LT.
Умножая слева соотношения
(Е - Afel)/fc = О, А = Т^,
148
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
на lj (j = 1,р), получаем, что
Из (4.10), в частности, следует подтверждение взаимной некоррелиро-
ванности главных компонент, а также тот факт, что D = Хк (к = 1,р);
в) сумма дисперсий исходных признаков равна сумме дисперсий всех
главных компонент. Действительно,
р
]TD.z(fc) = tr = tr(LELT) = tr ((LE)LT)
fc=l
p
= tr(LT(LS)) = tr((LTL)E) = trS = 52D®(fe);
/c=l
г) обобщенная дисперсия исходных признаков X (det Е) равна обоб-
щенной дисперсии главных компонент. Действительно, обобщенная дис-
персия вектора Z равна
det = det (LELT) = det ((LE)LT) = det (LT(LE)) ,
= det ((LLT)S) = det (E). 440
Следствие 1. Из б) и в), в частности, следует, что критерий
информативности метода главных компонент (4.4) может быть пред-
ставлен в виде
= + + (4.4')
+ ---г
где Ai,A2,...,Ap — собственные числа ковариационной матрицы Е век-
тора X, расположенные в порядке убывания.
Кстати, представление Zp/(Z(X)) в виде (4.4х) дает исследователю не-
которую основу, опорную точку зрения, при вынесении решения о том,
сколько последних главных компонент можно без особого ущерба изъ-
ять из рассмотрения, сократив тем самым размерность исследуемого про-
странства.
Действительно, анализируя с помощью (4.4Z) изменение относитель-
но доли дисперсии, вносимой первыми р главными компонентами, в за-
висимости от числа этих компонент, можно разумно определить число
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
149
компонент, которое целесообразно оставить в рассмотрении. Так, при из-
менении 1р1, изображенном на рис. 4.1, очевидно, целесообразно было бы
сократить размерность пространства ср=10дор* = 3, так как добавле-
ние всех остальных семи главных компонент может повысить суммарную
характеристику рассеяния не более чем на 10%.
Рис. 4.1. Изменение относительной доли суммарной дисперсии исследуе-
мых признаков, обусловленной первыми р1 главными компонен-
тами, в зависимости от р' (случай р = 10)
Следствие 2. Если X* — вектор нормированных признаков
..,s*(p), т.е. = 0 и = 1 для j = 1,р, то соглас-
но замечанию 3 ковариационная и корреляционные матрицы совпадают
(т. е. = R) и из б) и в) следует
trEz = trEx- = trR = р
или
р
= р.
/с=1
Тогда критерий информативности (4.4х) может быть представлен в
виде
= (4.4")
150 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Матрица «нагрузок» А = (a,;), i,j = 1,2, ...,р, главных
компонент на исходные признаки также является важной характери-
стикой главных компонент. Если анализируемые переменные X =
(х^,®^,...,®^)7 предварительно процентрированы и пронормирова-
ны (см. выше замечания 1 и 3), т.е. если главные компоненты стро-
ятся для признаков X* = (®*^\®*^а\...,®*^^)7, Е®*^ = 0, D®*^ = 1,
1 = 1,2,... ,р, то элементы матрицы нагрузок ац определяют одновре-
менно степень тесноты парной линейной связи (т. е. парный коэффициент
корреляции) между ®*<’) и и удельный вес влияния пронормированной
У’й главной компоненты на признак ®*^'\
Матрица нагрузок А определяется соотношением
A = LTA*, (4.11)
где
Она связывает исходные процентрированные и пронормированные пе-
ременные X* с пронормированными главными компонентами z^ =
/у/Х] соотношениями:
X* = LTA*A-iZ = AZH, (4.12)
®*(,) = aixz^ + ai2z^ + • • • + aipz(Hp). (4.12')
Таким образом, коэффициент действительно определяет удельный вес
влияния j-й нормированной главной компоненты z^ на i-й исходный при-
знак. Это подтверждается, в частности-, и следующим фактом:
_ Е[(х*(0 - Е®*(0)(®0) - Ez(i))]
_E(Z<V>) / (i)S<>’\
' д/Ai/
= E (®*(,)4J)) = E [(a.141) + • • • + aip4P))4J)]
~ aij^ ^(гн')) — aij> (4.13)
r(x*(i),z0))
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
151
т. е. коэффициент ац действительно определяет величину парного коэф-
фициента корреляции между и х^ (при выводе соотношения (4.13)
использовались нормированность и центрированность переменных х*^ и
zj/\ а также тот факт, что х^ =
Отметим еще два свойства элементов матрицы нагрузок А.
Из определения матрицы А (4.11) следует:
АТА = (A*L)(LTA*) = А*(ААТ)А* = А*А* = А,
а это означает, что сумма квадратов элементов любого j-го столбца
матрицы А равна дисперсии (j-й) главной компоненты Xj, т. е.
a3j + a3j + • ’ • + ejj = Xj. (4-14)
Возводя в квадрат обе части соотношения (4.12') и беря математиче-
ское ожидание от результата, непосредственно имеем:
D ®*(<) = Е (anz*1* + • • • + ajpz<p))3 = £ a?j Е (z<j))3 = £ a3ijt (4.15)
j=i j=i
т.е. с учетом Dz*^ = 1 получаем, что сумма квадратов элементов
любой (i-й) строки матрицы нагрузок А равна единице.
Приведенные здесь свойства используются, в частности, при содержа-
тельной интерпретации главных компонент. Так, соотношение (4.13) дает
основание придавать главной компоненте х^ содержательный смысл, со-
ответствующий исходному признаку для которого коэффициент а;о;-
достигает максимального значения (при условии, что |a,oj| > 0,6).
Геометрическая интерпретация главных компонент. Всякий
переход к меньшему числу (р') переменных z^\...,z^p\ осуществля-
емый с помощью ортогонального линейного преобразования (матрицы)
С = (с<у), i = 1,2,...,р', j = 1,2,...,р, можно рассматривать как про-
екцию исследуемых р-мерных наблюдений Xi, Х2,..., Хп в пространство
размерности р', натянутое на оси Oz^\ Ох^,..., Ох^р , где
р
z(,) = i= 1,2, ...,р'. (4.16)
i=i
При этом проекциями р-мерных исходных наблюдений X, (i = 1,2,..., п)
будут р'-мерные точки
Zi = CXi, i=l,2,...,n. (4.17)
152
И. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Для пояснения сущности того линейного преобразования исходной си-
стемы признаков, которое приводит к главным компонентам, рассмотрим
его геометрическую интерпретацию на примере двумерной системы на-
блюдений ), i = 1,2,...,п, извлеченной из нормальной генераль-
ной совокупности со средним значением а = и ковариационной
матрицей
(2 \
Г<Г122 ) , И < 1, <Т1 >0, <Т2 > 0.
Т(Т\О"2 О"2 /
Здесь <т2 и ст2 — дисперсии компонент соответственно х^ и я/2\ аг —
коэффициент корреляции между ними. Геометрически это означает, что
точки (х; , х; ') будут располагаться примерно в очертаниях эллипсоидов
рассеивания вида (см. рис. 4.2а)
В этом случае для изучения (х^\х^2^) удобно перейти к новым координа-
там (xv ,z' ') с помощью преобразования:
z(i) _ _ а(П\ cosa . f_(2) _ (2)ч -
— I U I LUo LX I Jb ------ U J bill (X,
(2) / (1) (1)\ • , I (2) (2)\
х — — \х — <г ’) sin а + (я — а ) cos а,
где
„ 2г(71(72
tg2a — —j 2 •
°-! - °2
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
153
б
Рис. 4.2. Эллипс рассеяния исследуемых наблюдений и направление коор-
динатных осей главных компонент и/2^: а) умеренный раз-
брос точек; б) отсутствие разброса точек в направлении второй
главной компоненты (вырожденный случай)
154 И. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
После этого преобразования точки (zp\z^) также будут распреде-
лены нормально, но компонента уже не будет зависеть от z^. Кроме
того, если выбрать направления так, что Dz^ > Dz^2\ то геометриче-
ски это будет означать следующее: сначала производится перенос начала
координат в точку а затем оси поворачиваются на угол а так,
чтобы ось z^ шла вдоль главной оси эллипсоида рассеивания (рис. 4.2а).
Чем ближе | г| к единице, тем теснее группируются наблюдения около глав-
ной оси эллипсоида рассеивания (т.е. около новой оси z^) и тем менее
значащим для исследователя является разброс точек в направлении оси
z^2\ а следовательно, и сама эта координата. В предельном случае |r| = 1,
исследуемые наблюдения в координатах (z^\z^) вообще не отличаются
по координате z^ (см. рис. 4.26).
Оптимальные свойства главных компонент. Описываемые ни-
же свойства первых р главных компонент во многом объясняют их широ-
кую распространенность в практике статистических, в том числе эконо-
метрических, исследований. Оказывается, к главным компонентам можно
прийти, решая оптимизационные задачи, на первый взгляд не имеющие
ничего общего с оптимизационной задачей типа (4.2).
Свойство наименьшей ошибки «автопрогноза» или наилуч-
шей самовоспроизводимости. Можно показать, что с помощью пер-
вых р' главных компонент z^\z^\ ...,z^p^ (р < р) исходных признаков
(1) (2) (Р)
аг , аг ,...,аг ' достигается наилучшии прогноз этих признаков среди
всех прогнозов, которые можно построить с помощью р линейных комби-
наций набора из р' произвольных («вспомогательных») признаков.
Поясним и уточним сказанное. Пусть требуется заменить ис-
ходный исследуемый р-мерный вектор наблюдений X на вектор Z =
/ (1) (2) (р’КТ » I
(z' ',z' ,...,z' ') меньшей размерности р, теряя при этом не слиш-
ком много информации. Информативность нового вектора Z определим
таким образом, чтобы она зависела от того, в какой степени р* введенных
вспомогательных переменных дают возможность «реконструировать» р
исходных (измеряемых на объектах) признаков с помощью подходящих
линейных комбинаций z^\z^2\ ...,z^p\ Естественно полагать, что ошиб-
ка прогноза X по Z (обозначим ее а) будет определяться так называемой
остаточной дисперсионной матрицей вектора X при вычитании из него
наилучшего прогноза по Z, т.е. матрицей Д = (Д^), где
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
155
Здесь 23Г=1 — наилучший, в смысле метода наименьших квадратов,
прогноз по компонентам ..., (см. [1] гл. 15). Ошибка ст
прогноза X по Z задается как функция от элементов матрицы А, т. е. ст =
/(А), где /(А) определяет некоторый критерий качества предсказания.
Рассмотрим следующие естественные меры ошибки прогноза:
/(А) = \/tr(A) = ^/Дц + Д22 4-----F (4-18)
/₽ я v
/(А) = II А|| = • (4Л9)
\i=l ,=1 /
Здесь tr(A) и ||А|| — соответственно след и евклидова норма матрицы А.
Доказано, что функции (4.18) и (4.19) одновременно достигают минимума
тогда и только тогда, когда в качестве z^2\..., z^p выбраны первые
р' главных компонент вектора X, причем величина ошибки прогноза ст
явным образом выражается через последние р-р' собственных чисел ис-
ходной ковариационной матрицы £ или приближенно — через последние
р-р' собственных чисел Ap>+i,..., Ар выборочной ковариационной матри-
цы Е, построенной по наблюдениям Xi,X2,...,Xn. В частности,
при /(А) = tr(A): ст » \/Ар»+1 + Ар<+2 + • • • + Ар; (4.18 )
при /(А) = ||Д||: f * ^Ар»+1 + Ар>+2 + • • • + Ар. (4.19*)
Свойства наименьшего искажения геометрической структу-
ры множества исходных р-мерных наблюдений при их проекти-
ровании в пространство р первых главных компонент. Речь идет
о следующих трех оптимальных свойствах главных компонент (формули-
руются без доказательства).
Свойство 1. Сумма квадратов расстояний от исходных точек-
наблюдений Xi,X2,...,Xn до пространства, натянутого на первые
р' главных компонент, наименьшая относительно всех других подпро-
странств размерности р , полученных с помощью произвольного линей-
ного преобразования исходных координат.
Наглядным пояснением этого свойства может служить рис. 4.2а, на
котором ось z^ соответствует подпространству, натянутому на первую
главную компоненту (т.е. р = 2 и р = 1), а сумма квадратов расстоя-
ний до этого подпространства есть сумма перпендикуляров, опущенных
из точек, изображающих наблюдения Xi = на эту ось.
Свойство 2. Среди всех подпространств заданной размерности
Р (.Р < p)i полученных из исследуемого признакового пространства с
156
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
помощью произвольного линейного преобразования исходных координат
х^\х^2\ ..., х^р\ в подпространстве, натянутом на первые р главных
компонент, наименее искажается сумма квадратов расстояний между
всевозможными парами рассматриваемых точек-наблюдений.
В данном свойстве за критерий наименьшего искажения геометриче-
ской структуры совокупности исходных наблюдений Х^, Х2,•••, Хп при-
нимается величина
п п
м„(х) = 52 5? х‘ -
t=l J = 1
т. е. сумма квадратов евклидовых расстояний между всевозможными па-
рами имеющихся наблюдений.
После проектирования точек Xi в р -мерное пространство, определя-
емое матрицей преобразования С, мы получим точки-проекции Z, = СХ,
(г = 1,2,..., п) и соответствующую им сумму квадратов евклидовых рас-
стояний
«„(Z(C)) = 5252(2. - Zi)T(Zl - Z,).
1=1 j=l
Можно показать, что при р < р Мр(Х) Mpf(Z(C\).
Так вот, на преобразовании L, с помощью которого получают первые
р главных компонент, достигается минимум разности Afp(X)—Mp»(Z(C)),
т. е.
МР(Х) - мр1 (Z(L)) = nun [л/р(Х) - Мр, (Z(C))].
Свойство 3. Среди всех подпространств заданной размерности
Р (j? < р), полученных из исследуемого факторного пространства с
помощью произвольного линейного преобразования исходных координат
(1) (р) '
хк хк, в пространстве, натянутом на первые р главных компо-
нент, наименее искажаются расстояния от рассматриваемых точек-
наблюдений до их общего «центра тяжести», а также углы между пря-
мыми, соединяющими всевозможные пары точек-наблюдений с их общим
«центром тяжести».
4.Б. Примеры решения типовых задач и упражнений
Пример 4.1 (задача). При формировании типообразующих
признаков предприятий отрасли были обследованы 24 предприятия (п =
24) по трем технико-экономическим показателям: объему выпускае-
мой продукции (тыс.условных денежных единиц), основным фон-
Главе 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
157
дам а/2) (тыс.у.д.е.) и фонду оплаты труда х^ (тыс.у.д.е.). По по-
лученным в результате обследования исходным статистическим данным
х^\ я,-3)), — i = 1,2,..., 24, — были получены оценки вектора сред-
них значений а = сР\ а^3^)Т = (420; 240; 85)Т и ковариационной
матрицы
/451,39 271,17 168,70 \
S = 271,17 171,73 103,29
\ 168,70 103,29 66,65 )
Требуется:
1) вывести уравнения для вычисления главных компонент z^\z^ и
z™ по заданным значениям исходных технико-экономических пока-
„ (1) (2) (3)
зателеи х ,х' ' и х' ,
2) определить относительные доли суммарной дисперсии, обусловлен-
ные одной и двумя главными компонентами;
3) используя первую главную компоненту z^ как прогнозирующую
(объясняющую) переменную в задаче автопрогноза исходных пока-
« (1) (2) (з)
зателеи я , яг ' и я , вычислить значение оценки суммарной от-
носительной ошибки асум.отн. прогноза этих показателей по z^\ где
под ^сум отн- понимается величина
у—
E(i(j) -6jz(1))2
^сум.ОТН. = I == ‘ 100%,
Je Di(j)
V j=i
— это центрированная переменная (т. е. х^ = х^ —
a bj — это коэффициент регрессии х^ по z^.
Решение
1) Для определения коэффициентов линейного преобразования (4.5), с
помощью которого осуществляется переход к главным компонентам, не-
обходимо решить вначале характеристическое уравнение (4.8), а затем
использовать найденные собственные значения А1,Аз,...,Ар для подста-
новки в системы уравнений (4.7), решения которых и дают коэффициенты
/у = (^ч, Zj2,..., /jp). В данной задаче
|Е - А/| =
451,39 - А
271,17
168,70
217,17
171,73- А
101,29
168,70
103,29
66,65 - А
= 0,
158
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
откуда находим Ai = 680,40, А3 = 6,50, Аз = 2,86.
Последовательно подставляя эти значения в систему (4.7) и решая
эти системы относительно /,• = (l/i, /ja, Оз), ~3 = 1,2,3,— получаем: /1 =
(0,813; 0,496; 0,307); 12 = (-0,545; 0,832; 0,101), 13 = (-0,205;-0,249; 0,947),
так что уравнения для вычисления главных компонент z^ (j = 1,2,3)
будут иметь вид:
z(1) = 0,81(х(1) - 420) + 0,50(хг(2) - 240) + 0,31(х(3) - 85),
z(2) = -0,55(ж(1) - 420) + 0,83(®(2) - 240) + 0,10(х(3) - 85), (4.20)
z(3) = -0,21 (а;(1) - 420) - 0,25(г(2) - 240) + 0,95(х(3) - 85).
2) В соответствии с равенствами (4.10) и (4.10*) и вытекающим из них
представлением Ip>(Z) в виде (4.4') имеем:
A(Z(.Y)) = = 0,9864;
Al + Аг Т Аз
A(Z(X)) = . = 0,9958;
Ai + Л2 + A3
что свидетельствует о том, что почти вся информация (а именно, 98,64%)
о специфике предприятия данного типа, описанной с помощью переменных
а/1),а/2) и а/3\ содержится в одной лишь первой главной компоненте
Z™.
3) Располагая исходными статистическими данными ®j3\ —
i = 1,2,..., 24, — и используя уравнение (4.20), можно подсчитать значе-
ния первой главной компоненты z^ для каждого из анализируемых пред-
приятий. Затем, последовательно рассматривая наблюдения пар перемен-
ных — i = 1,2,...,24, х\^ = - а<, — и интерпретируя
как прогнозирующую (объясняющую) переменную в модели парной ре-
грессии по можно вычислить (с помощью метода наименьших
квадратов, см. [1], п. 15.3.1) оценки коэффициентов регрессии bj в прогно-
стических моделях вида z^ = bjZ^ +ej, где £,• — ошибка прогноза по
значениям z^. Далее, воспользовавшись результатами и обозначениями
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
159
(4.18)~(4.18/), получаем:
JEE(i(i)-6;z(1))2
V о/
^сум.отн. = Г“— ’ 100% =
Е 4-
------100%
Е
j=i
Аг + Аз
Ai + Аг + Аз
О QR
• 100% = 11,65%
ОоУ) (и
(точный знак равенства заменен на приближенный в силу того, что тео-
ретические значения Ajj и Dij заменены на их выборочные аналоги).
Пример 4.2 (упражнение). Компонентный анализ прове-
ден по данным двадцати сельскохозяйственных районов (п = 20) области,
которые содержат результаты измерений следующих показателей: а/1) —
(2)
число колесных тракторов на 100 га; ху — число зерноуборочных ком-
(3)
байнов на 100 га; х' ’ — число орудий поверхностной обработки почвы
на 100 га; х^ — количество удобрений, расходуемых на гектар; х^ —
количество средств защиты растений, расходуемых на гектар (исходные
(1) (2) (3) (4) (5) • 1 п пл
статистические данные я} ,х\ 'х\ ,х] ,— г = 1,2,...,20, — приве-
дены в табл. П2,1 Приложения 2).
Расчеты проводились по нормированным данным вида (4.17) и пред-
ставлены в следующей таблице:
Главные компоненты г(2) ?3> z™ z™
Собственные значения 3,04 1,41 0,43 0,10 0,02
Вклад i-й главной компоненты (%) в суммарную дисперсию 60,8 28,2 8,6 2,0 0,4
Суммарный вклад первых главных компонент (%) 60,8 89,0 97,6 99,6 100,0
При расчете относительного вклада главных компонент учитывалось,
что Aj = р = 5. Для анализа были оставлены две первые главные
компоненты (р = 2), на которые приходится 89% суммарной вариации.
Для интерпретации главных компонент построена матрица фактор-
ных нагрузок
( 0,95* 0,97* 0,94* 0,24 0,56 \Т
0,19 -0,17 -0,28 0,88* 0,67*/
160
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Звездочкой (*) отмечены элементы, удовлетворяющие условию |а^| > 0,6,
т. е. те, которые следует учитывать при интерпретации главных компо-
(1) (2)
нент г ' иг .
Требуется:
дать содержательную интерпретацию первых двух главных компо-
нент.
Решение
Из вида матрицы А следует, что первая главная компонента наи-
U)
более тесно связана с показателями: х — число колесных тракто-
ров (ап = r{x^\z^) = 0,95); х^ — число зерноуборочных комбайнов
(а21 — r(x^,2^) — 0,97); х^ — число орудий поверхностей обработ-
ки почвы на 100га (а31 — г(а/3\лР)) — 0,94). Поэтому первая главная
компонента интерпретирована как уровень механизации работ.
Вторая главная компонента z^ тесно связана с количествами удо-
брения (а/4)) и средств защиты растений (я^), расходуемых на гектар
(а42 = г(ж^4\^2^) = 0,88; а52 = г(ж^5\^2^) = 0,67). Соответственно z^
интерпретируется как уровень химизации растениеводства.
Пример 4.3 (задача). В табл. П2.2 Приложения 2 приведены
(1) (10)
значения десяти характеристик х\ ~ z- 7 качества жизни населения по
15-ти странам мира (г = 1,2,..., 15).
Требуется:
1) предложить и обосновать метод вычисления интегрального ин-
дикатора качества жизни {ИИКЖ), основанного на знании зна-
чений х^ этих десяти частных {статистически регистрируемых)
критериев;
2) численно реализовать этот метод (с помощью подходящей компью-
терной программы) и оценить степень информативности ИИКЖ]
3) проранжироватъ заданные характеристики {частные критерии) в
порядке убывания удельного веса их влияния на ИИКЖ.
Решение
1) Определим в качестве ИИКЖ такую переменную, зная значения
которой можно с наибольшей точностью восстановить значения всех де-
сяти анализируемых частных критериев в виде линейной аппроксимации
от этой переменной. Именно этим свойством (см. в п.4.А «Свойство наи-
меньшей ошибки автопрогноза» , соотношения (4.18х) и (4.19х)) обладает
1-я главная компонента.
Таким образом, в качестве интегрального индикатора качества жиз-
ни населения предлагается использовать линейную комбинацию десяти
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
161
„ (1) (2) (Ю)
анализируемых показателей х' , х ,..., х' вида
/> = („(г'1’ - <.<») + /12(х<2’ - «'”) + +- «<10)), (4.21)
где = jy 52 — средние значения этих показателей, а коэффици-
«=1
енты определяются как компоненты собственного вектора ковариаци-
онной матрицы S многомерного признака X = (х^\х^2\. . ,,х^10^)Т при
наибольшем собственном значении Ар
2) Численная реализация метода построения 1-й главной компоненты
в данной задаче сводится к реализации следующих вычислений:
х . /~(1) *(2) -(Ю)\Т / (1) (2)
а) оценка а = (а' ',<г ',..., а' ’) вектора средних а = (а' ',<г
а(10))Т по формуле а№ = 52
t=l
б) оценка S = (ajt) ковариационной матрицы Е = (ау{) по формуле =
в) решение характеристического уравнения |Е — А1| = 0 и определение
наибольшего корня А) из 15-ти корней этого уравнения;
г) определение коэффициентов (у = 1,2,...,10) искомого линейного
преобразования (4.21) из системы уравнений
/
I ^12
(S-Ail)
G.io
/О
О
\0
3) Сравнительную оценку удельного веса влияния заданных харак-
теристик а/1) ~ а/10) на ИИКЖ будем производить, основываясь на
абсолютных величинах коэффициентов корреляции r(z^,z^1^). С этой
целью вычислим матрицу нагрузок А с помощью формулы (4.11), по-
скольку r(x^\z^) = r(x*^\z^^) = aji (см. формулу (4.13)). Тогда
х^ будет обладать наибольшим удельным весом влияния на z^\ если
|r(®Oo),z(1))| = imaxo|r(®0),/1))|, и т.д.
Пример 4.4 (упражнение). Переход от исходных перемен-
ных а;^ и х^ (Еа/‘) = = of и г(а:^\ х^) = г) к новым пере-
6 Прикладная статистика
в задачах и упражнениях
162 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
менным и осуществлен с помощью линейного преобразования
= (а/1) — a^Jcosa + - а^)вша;
= — (а/1) — a^Jsina + (х^ — a^)cosa,
где а — некоторый угол поворота исходных осей.
Требуется:
1) доказать, что данное линейное преобразование ортогонально-,
2) определить (в терминах а^, и г) такой угол а, при котором новые
переменные будут взаимнонекоррелированными.
Решение
1) Матрица С коэффициентов линейного преобразования в данном
случае имеет вид
Q _ | С11 с12 j _ | COS а sin 0 j
\ С21 с22 / \ — S*n а COS а /
Ортогональность этой матрицы следует непосредственно из тождеств:
С11 + с12 = с°82 <* + sin2 а=1,
С21 + с22 = (— sin а)2 + cos2 а=1,
ciic2i + с12с22 = — sin а • cos а 4- sin а cos а = 0.
2) Поскольку, очевидно, Ez^ = Ez^ = 0, то
cov(z^\z^2^) = E(z^^z^2^) = Е (a/1) — а^)2 cos а sin а + (a^1) — а^) х
X (a/2) - а^) cos2 а - (х^ - а^)(х^ — а^2^) sin2 а+
, / (2) (2)ч2 . 12.
+(аг — д' ') sin a cos а = — sin a cos а+
+ cov(a:^1\a:^2^)co32a — cov(a:^1\ a/2)) sin2 а + aj sin а cos а =
2 1 . 2 1
= —• - sin 2а + <т2 • „ s*n + <71<Т2Г • cos 2а.
Приравнивая это выражение к нулю и решая полученное уравнение
относительно а, имеем:
1 2а1а2г
а = - arctg ----j
* ^1-^2
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
163
4.В. Задачи и упражнения
Упражнение 4.1
В условиях примера 4.4 определить дисперсии Dz^ и Dz^ и дать
содержательную интерпретацию частных случаев г = 1 и г = 0.
У пражнение 4.2
Пусть из р-мерной генеральной совокупности х^2 3 4\..., х^) взята
выборка объема п, на основании которой получена корреляционная матри-
ца Я с элементами гц (j,l = 1,2,..., р).
Требуется доказать:
1) справедливость равенства
R = -Х*ТХ*,
п
где X* — матрица значений нормированных признаков размерности
(n х р) с элементами я/ ’ = , х\ ' — значения у-го показателя
(у = 1,2,..., р) у t-го элемента выборки (» = 1,2,..., п),
2) след матрицы собственных значений Л., полученной по корреляци-
онной матрице R, равен числу р исходных признаков, т.е. trh. =
р
Е Ai = р;
1=1
3) справедливость равенства
р
|й.| = П А<-
»=1
где A; (i = 1,2,...,р) — собственные значения корреляционной ма-
трицы R;
4) если матрица факторных нагрузок А получена по корреляционной
матрице R, то справедливы равенства:
164
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
где aji — элемент матрицы факторных нагрузок A (j,i = 1,2,..., р).
У пражнение 4.3
Доказать, что для матрицы факторных нагрузок А размерности (рхр)
справедливо равенство (А-1)Т = (А1) \
У пражнение 4.4
Пусть i-й объект характеризуется р значениями главных компонент
и известна ортогональная матрица собственных векторов L с
элементами где v,j = 1,2,.. . ,р. Найти выражение для значения j-ro
исходного признака у t-ro объекта
Упражнение 4.5
Доказать, что
-ZZ =
f I
[А
п
при X* = (х,*0)),
при X =
где X* — матрица размерности (п хр) нормированных значений исходных
признаков x*(j} (t = l,n; j = l,p);
X — матрица (n x p) центрированных значений исходных признаков
Z — матрица (n х р) значений главных компонент;
I — единичная матрица (р X р).
Задача 4.1
В таблице представлены общие затраты на рубль товарной продукции
и фондоотдача (а/2^) по п = 10 предприятиям приборостроения
Номер предприятия (0 J1) •4/ х™
1 0,92 0,51
2 0,93 0,59
3 0,83 1,03
4 0,81 1,21
5 0,95 0,63
6 0,88 0,68
7 0,89 0,57
8 0,80 1,52
9 0,72 1,04
10 0,82 0,99
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
165
Требуется:
1) найти точечную оценку г12 парного коэффициента корреляции г12 и
построить матрицу парных коэффициентов корреляции R;
2) рассчитать матрицы собственных значений Л и факторных нагру-
зок А;
3) графически представить п = 10 предприятий в пространстве двух
главных компонент и ранжировку предприятий по 1-й главной ком-
(1)
поненте z .
Провести неформальный анализ и предложить интерпретацию по-
лученных решений.
Задача 4.2
Условия жизни населения п = 10 стран характеризуются тремя пока-
зателями: о/1) — оценка ВВП по паритету покупательской способности в
1994 г. на душу населения (в % к США); — расходы на здравоохра-
нение (в % от ВВП); х^ — численность врачей на 10000 населения. Их
значения приводятся в следующей таблице:
i Страна _(1) •4/ (2) х' 7 х™
1 Россия 20,4 3,2 44,5
2 Австралия 71,4 8,5 32,5
3 Австрия 78,7 9,2 33,9
4 Азербайджан 12,1 3,3 38,8
5 Армения 10,9 3,2 34,4
6 Белоруссия 20,4 5,4 43,6
7 Бельгия 79,7 8,9 41,0
8 Болгария 17,3 5,4 36,4
9 Великобритания 69,7 7,1 17,9
10 Венгрия 24,5 6,0 32,1
Т ребуется:
по исходным статистическим данным (®Р,х^), — i = 1,2, ...,10:
1) определить дисперсии главных компонент и их относительный
вклад в суммарную вариацию признаков',
2) определить матрицу факторных нагрузок А и матрицу значений
главных компонент Z;
3) графически представить страны в пространстве двух главных ком-
ч ч (1)
понент и ранжировку стран по первой главной компоненте z '.
Провести интерпретацию полученных решений.
166
И. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Задача 4.3
Деятельность предприятий, попавших в выборку, оценивалась по
двум показателям (® аг2)). По данным выборки найдены значения глав-
ных компонент для »-го предприятия z^ = 0,661, я,-2) = -2,151, матрица
факторных нагрузок
. /-0,756 0,654 \
0,756 0,654 J ’
а также вектора средних х = (10; 15)Т и среднеквадратических отклоне-
ний S = (0,072; 0,333).
Требуется:
1) определить значения исходных показателей для i-го предприятия]
2) вычислить дисперсии первой и второй главных компонент и их от-
носительный вклад в суммарную дисперсию]
3) найти значение коэффициента корреляции fi2 между исходными по-
казателями х^ и х^.
Задача 4.4
По данным выборки объемом п = 10 из двумерной генеральной со-
вокупности (a/1),:)/2)) проведен компонентный анализ и найдена матрица
значений главных компонент Z, в которой оказалось пропущенным послед-
нее (десятое) наблюдение,
/—0,484
1,227
0,773
0,606
0,799
0,136
-0,671
0,720
-0,921
\ ?
1,053 \
-1,572
0,527
-0,175
0,314
2,097
-1,109
-0,507
-0,231
? /
а также матрица факторных нагрузок
/-0,791 0,611 \
\ 0,791 0,611)
Требуется:
1) определить значения главных компонент для десятого наблюдения
(М я(2)У
к *10 > *10 h
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
167
2) для десятого наблюдения рассчитать соответствующие нормиро-
ванные значения (ж^1),®*^);
3) определить относительный вклад 1-й главной компоненты в сум-
марную дисперсию;
4) найти точечную оценку коэффициента корреляции между исходны-
ми показателями Гц = г(ж^\ж^^).
Задача 4.6
Задачу 4.2 решить для показателей ж^ — расходы на здравоохране-
ние (в % от ВВП) и а/3) — численность врачей на 10000 населения.
Задача 4.6
На основании данных задачи 4.2 провести компонентный анализ по
всем трем показателям С этой целью
требуется:
1) рассчитать матрицу собственных значений Л и относительный
вклад 1-й и двух первых главных компонент в суммарную дисперсию;
2) определить матрицу факторных нагрузок А и содержательно ин-
терпретировать две первые главные компоненты (z^ и z^);
3) графически представить страны в плоскости двух первых главных
компонент (z^\z^) и ранжировку стран по первой главной ком-
поненте.
Задача 4.7
Уровень цен в п = 12 городах Центрального района России в июне
1996 г. сравнивался по следующим видам продовольственных товаров:
говядина - ж^; растительное масло - х^; сахар-песок - х^ и хлеб белый
в/с - х^. Статистические данные по ценам (в руб.) представлены в
следующей таблице:
168
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
i Город _(1) Л _(2) Л ,(3) Л _(4) Л
1 Брянск 12500 7726 3410 4875
2 Владимир 13857 7880 3183 7125
3 Иваново 14150 6128 3209 4998
4 Калуга 12697 8237 3400 5170
5 Кострома 13000 8750 3600 5476
6 Москва 14120 11024 4418 6466
7 Орел 10678 8456 3634 4200
8 Рязань 12163 9172 4033 4720
9 Смоленск 12833 8320 3909 4354
10 Тверь 14400 7083 3416 5440
11 Тула 12083 8259 3486 5140
12 Ярославль 14379 7991 3938 5283
Требуется:
1) рассчитать матрицу выборочных парных коэффициентов корреля-
ции R.;
2) определить дисперсии главных компонент и их относительный
вклад в суммарную вариацию;
3) по матрице факторных нагрузок А дать интерпретацию первым
двум главным компонентам;
4) графически представить города в плоскости двух первых главных
компонент (z^\z^) и содержательно проинтерпретировать ре-
зультаты.
Задача 4.8
Уровень жизни в п = 20 странах оценивался по среднедушевому по-
треблению мяса (а/1)) и фруктов По данным этих стран рассчитан
выборочный коэффициент корреляции Гц = 0,63.
Требуется:
1) определить относительный вклад первой главной компоненты z^
в суммарную дисперсию;
2) оценить степень тесноты линейной статистической связи между
1-й главной компонентой z^ и вторым исходным показателям х^2\
т.е. найти оценку г(х^2\ z^).
Задача 4.9
По данным выборки из трехмерной генеральной совокупности (х^\
(2) (3)\
х' аг ) для нормированных признаков рассчитана матрица факторных
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
169
нагрузок А:
(ац 0,68 —0,14\
0,88 aj2 0,18 I ,
0,95 0,14 а33 /
в которой оказались пропущены диагональные элементы ап,а22 и а33.
Известно только, что ац < 0, а32 > 0 и а33 < 0.
Требуется:
1) определить относительный вклад первой компоненты z^ в диспе-
рсию нормированного первого признака (в %);
2) определить относительный вклад двух первых главных компонент
в суммарную дисперсию (в %);
3) найти оценку выборочного парного коэффициента корреляции fi2 =
Задача 4.10
Деятельность п = 5 строительных организаций характеризуется чи-
сленностью рабочих и фондом зарплаты (я/2)). Значения показате-
лей, полученных по данным годовых отчетов, представлены в следующей
таблице:
г-номер предприятия 1 2 3 4 5
(тыс. чел.) 3 6 8 2 7
х^ (млн. руб.) 4 5 9 3 6
Значения —i = 1,2,...,5 — образуют выборку из двумер-
ной генеральной совокупности.
Требуется:
1) оценить средние значения среднеквадратические от-
клонения aj = (j = 1,2) и корреляционную матрицу R =
анализируемого двумерного признака (а/1), а/2));
2) вычислить оценки дисперсий главных компонент и их относитель-
ный вклад (в %) в суммарную вариацию анализируемых показателей]
3) рассчитать ортогональную матрицу собственных векторов L и ма-
трицу факторных нагрузок А;
4) ранжировать строительные организации по значениям первой глав-
ной компоненты и графически представить результаты ранжи-
рования.
Расчеты произвести по нормированным данным.
170
И. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Тест 4.1. Финансовая устойчивость предприятия характеризуется
р = 8 показателями. В результате расчетов получены собственные значе-
ния трех первых главных компонент пронормированных исходных пока-
зателей: Ai = 4,0; А3 = 1,6 и A3 = 0,8. Чему равен относительный вклад
2-х первых компонент (в %):
а) 30;
б) 70;
в) 60;
г) 80.
Тест 4.2. Матрица А факторных нагрузок для главных компонент,
построенных по трем нормированным показателям, равна
(-0,72 0,69 -0,08 \
0,88 0,44 0,19 .
0,96 0,12 —0,24/
Чему равен относительный вклад второй главной компоненты х^ в сум-
марную дисперсию (в %):
а) 74;
б) 37;
в) 4;
г) 23.
Тест 4.3. В матрице факторных нагрузок А оказались пропущенны-
ми элементы а13, а22, аз1:
(-0,90
-0,54
а31
-0,30
а22
0,20
“13 \
0,03 .
0,33/
Чему равно собственное значение Аз, соответствующее третьей глав-
ной компоненте
а) 1,95;
б) 0,63;
в) 0,21;
г) 0,84.
Тест 4.4. В каких пределах меняются элементы матрицы факторных
нагрузок А:
а) (-1;0);
б) (0,1);
в) (-1,1);
г) (0;2).
Глава 4. СНИЖЕНИЕ РАЗМЕРНОСТИ
171
Тест4.5. Дана матрица факторных нагрузок А:
(-0,72
0,88
0,96
0,69
0,44
0,12
-0,08
0,19
-0,24
Чему равен парный коэффициент корреляции между переменной
и второй главной компонентой z^'.
а) 0,12;
б) 0,96;
в) -0,24;
г) (0,19).
Тест 4.6. Дана матрица факторных нагрузок А:
/-0,79 0,61 \
0,79 0,61) ’
Чему равен коэффициент корреляции между переменными а/1) и х^:
а) 0,75;
б) 1,25;
в) 0,25;
г) -0,25.
Тест 4.7. По данным наблюдений (п = 5) получена матрица значе-
ний главных компонент Z, в которой пропущено пятое значение первого
столбца:
/ -0,84 0,08 0,6 \ — 1,26
z = 1,52 -1,30 =? 1,26 0,50 -1,1 ) •
Чему равно пропущенное значение z$
а) -0,58;
б) 0,65;
в) 0,54;
г) 1,08.
Тест 4.8. По матрице Z теста 7 определить, чему равен парный ко-
эффициент корреляции между 1-й и 2-й главными компонентами z^ и
z™:
а) 0;
б) 1;
172
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
в) -1;
г) 0,6.
Тест 4.9. При исследовании взаимосвязи двух показателей и
получен коэффициент корреляции Гц = 0,9. Чему равно собственное зна-
чение Ai, соответствующее первой главной компоненте, построенной по
(О (2)
нормированным показателям аг и х'
а) 0,1;
б) 1,9;
в) 1,8;
г) 0,2.
Тест 4.10. Деятельность п предприятий региона характеризуется
четырьмя показателями. При проведении компонентного анализа по ма-
трице R получены собственные значения, одно из которых оказалось про-
пущенным: 1,2; 1,4 и 0,6. Чему равно собственное значение А3, соответ-
ствующее третьей главной компоненте:
а) 2,5;
б) 1,2;
в) 0,4;
г) 0,8.
Глава 5. Классификация: распознавание образов
и типологизация (дискриминантный
и кластерный анализы)
5.А. Краткие сведения из теории
О сущности задач классификации. В процессе решения широкого
круга социально-экономических исследовательских и управленческих за-
дач возникает необходимость анализа и формализации задач, связанных
со сравнением и классификацией объектов, явлений, систем.
В самой общей формулировке под классификацией мы будем пони-
мать разделение рассматриваемой совокупности объектов или явлений
на однородные, в определенном смысле, группы либо отнесение каждого
объекта (из заданного множества классифицируемых объектов) к одно-
му из заранее известных классов (при этом классифицируемое «заданное
множество» может состоять из единственного объекта). Заметим, что
термин «классификация» используется, в зависимости от контекста, для
обозначения как самого процесса «разделения-отнесения», так и его ре-
зультата.
Глава 5. КЛАССИФИКАЦИЯ
173
Как и ранее (см. выше, гл. 3 и 4), будем полагать, что каждый (i-й) из
анализируемых объектов (процессов, явлений) характеризуется значения-
ми определенного набора признаков (свойств) т.е. речь
идет о классификации многомерных наблюдений
ХъХ2,...,Хп, (5.1)
где Xi = (ж^,®^,...,®^)1*. Возможна другая форма задания
исходной статистической информации, когда каждому (i-му) объекту ста-
вится в соответствие набор значений 7й?7»2, • • • >7in, характеризующих
попарные отношения этого объекта со всеми остальными классифициру-
емыми объектами1^. Тогда вместо (п х р)-матрицы исходных данных,
образуемой векторами-столбцами (5.1), исследователь располагает в ка-
честве исходных данных (n х п)-матрицей попарных отношений
Г = (7ij)i J=l,2,...,n • (5.2)
Таким образом, на «входе» задачи классификации исследователь
имеет:
(i) априорные сведения о классах: о числе классов, об общем виде или
некоторых свойствах законов распределения наблюдений X внутри каждо-
го из классов, о диапазонах изменения анализируемых показателей; основ-
ные источники априорных сведений о классах — результаты предыдущих
аналогичных исследований, теоретические, предметно-профессиональные
соображения, экспертные оценки;
(п) обучающие выборки
> Xj2,..., Xjnj, (5»3)
j = 1,2,...,/?,
где k — общее число (априори заданное) классов, а о наблюдениях (5.3) из-
вестно, что все они характеризуют объекты, принадлежащие j-му классу;
обучающие выборки получают обычно с помощью специальным образом
организованных дополнительных статистических выборочных обследова-
ний анализируемой совокупности объектов.
В частном случае щ = п2 = • • • = пк = 0, т. е. в ситуации, когда
исследователь не имеет в своем распоряжении обучающих выборок (5.3),
Конкретный смысл попарных отношений определяется содержательной сущно-
стью задачи: они могут измерять в определенной шкале как степень различия i-ro
и j-ro объектов, так и степень их сходства.
174 П. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
говорят о задаче классификации без обучения и пользуются, соот-
ветственно, методами кластер-анализа; если же обучающие выборки
имеются в распоряжении исследователя, то решается задача классифи-
кации при наличии обучения (или задача распознавания образов)
и используются для ее решения методы дискриминантного анализа.
«На выходе» задачи классификации должны быть: 1) набор наи-
более информативных объясняющих переменных (так называемых типо-
образующих признаков) z^(X),z^2\x), ...,z^p \х), которые либо отби-
раются по определенному правилу из числа исходных описательных при-
знаков а/2\..., либо строятся в качестве некоторых их комби-
наций (р* < р); 2) правило отнесения (дискриминантная функция, клас-
сификатор) каждого классифицируемого объекта О,-, заданного значени-
ями своих описательных признаков Xi, к одному из априори описанных
(или выявленных в процессе предварительной типологизации) классов или
образов. При этом типообразующие признаки Z = (z^\x),..., z^p \x))T
и искомое правило классификации должны быть подобраны таким обра-
зом, чтобы обеспечивать наивысшую (в определенном смысле) точность
решения задачи отнесения объекта к одному из анализируемых классов
по заданным значениям его описательных признаков X.
Дискриминантный анализ (ДА) и распознавание образов.
Итак, если исследователь (статистик, эконометрист) располагает наря-
ду с классифицируемыми данными (5.1), так называемыми обучающими
выборками (5.3), то для решения задачи классификации он должен обра-
титься к методам дискриминантного анализа (см. [1], п. 12.2). При
этом каждый класс (или «образ») интерпретируется как одномодальная
генеральная совокупность, закон распределения вероятностей (з.р.в.) ко-
торой оценивается по соответствующей обучающей выборке. Если апри-
орные сведения позволяют сделать вывод об общем параметрическом ви-
де з.р.в. каждого класса, то используют методы параметрического ДА.
Если общий вид закона распределения внутри классов неизвестен, то обу-
чающие выборки используются для получения непараметрических оценок
внутриклассовых з.р.в., а сами процедуры классификации называют ме-
тодами непараметрического ДА. В специальной литературе (особенно,
в литературе физико-технического профиля) методы решения задач клас-
сификации при наличии обучающих выборок называют также методами
распознавания образов.
Байесовское оптимальное правило (БОП) классификации осно-
вано на следующей идее наибольшего правдоподобия', классифициру-
емое наблюдение Xi следует отнести к тому классу (к той одномо-
дальной совокупности), в рамках которого (которой) оно выглядит
Глава 5. КЛАССИФИКАЦИЯ
175
наиболее правдоподобным. Формальная реализация этой
идеи может быть описана следующим образом:
«наблюдение Xi следует отнести к классу jo,
если irjofjo(Xi) = max (5.4)
1
где к — общее число классов, itj — удельный вес элементов класса j (или
априорная вероятность принадлежности случайно извлеченного элемен-
та к классу j), fj(X) — функция, описывающая з.р.в. анализируемого
многомерного признака внутри класса j (т.е. fj(X) — это вероятность
того, что анализируемый многомерный признак примет значение, равное
X, если этот признак дискретен по своей природе, или это функ-
ция плотности вероятности в точке X, если анализируемый многомерный
признак непрерывен).
Оптимальность описанного классификационного правила заключа-
ется в том, что если потери c(j|г), которыми сопровождается отнесение
одного объекта i-го класса к классу j, постоянны при всех i / j (т.е.
не зависят от i и j при i / j), то процедура (5.4) характеризуется ми-
нимальной величиной вероятности ошибочной классификации объектов
(или минимальной долей ошибочно расклассифицированных объектов).
Параметрический дискриминантный анализ заключается в
статистической реализации правила (5.4) в ситуации, когда известно,
что fj(X) е {/(X | 0)}, где задан общий вид функций f(X | 0) пара-
метрического семейства {/(X | 0)}, а 0 — некоторый, вообще говоря
векторный, параметр, значения компоненты которого внутри каждого из
классов неизвестны. Тогда /,(Х) = f(X | 0(j)), а неизвестное «значе-
ние» параметра 0(j)> характеризующего з.р.в. в классе j, заменяется
в (5.4) его статистической оценкой 0(у), построенной по обучающей
выборке (5.3). Участвующие в (5.4) априорные вероятности irj либо счи-
таются заданными, либо (если это возможно) также заменяются их ста-
тистическими оценками 5гл-.
Так, например, при различении нормальных (гауссовских) клас-
сов имеем:
(5-5)
где 0(j) = (a(j),E(j)), а оценки a(j) и S(j) параметров a(j) и E(j) по
наблюдениям обучающей выборки (5.3) имеют вид:
ад=^-Ел-ад)л<-«(л). (в.в>
<=1 i=l
176
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Соответственно, при различении двух нормальных классов (т. е. при
к = 2) классифицирующая процедура (5.4) с учетом (5.5) и (5.6) может
быть описана в виде:
(а) п р и Е (1) = Е (2) = Е:
наблюдение X, следует отнести к классу 1,
где оценка общей ковариационной матрицы Е вычисляется по форму-
ле: 1
Е = ---о (n^(l) + n2S(2)), (5.8)
а оценки Е(1) и Е(2) вычислены в соответствии с (15.6); функция
D(X) = [X — |(d(l) + а(2))]ТЕ-1(а(1) — d(2)), по значениям которой
принимается решение об отнесении наблюдения X к 1-му или 2-му
классу, называется линейной дискриминантной функцией Фи-
шера;
(б) при Е(1) / Е(2):
наблюдение Х{ следует отнести к классу 1,
если [(Xf - a(l))TE-1(l)(Xi - а(1)) - (Х< - d(2))TE-1(2)x
х(Х,-.а(2))] > In (а) (5.9)
Непараметрический дискриминантный анализ объединяет в
себе методы статистической реализации байесовского оптимального
правила (5.4) в ситуации, когда общий параметрический вид функций
fj(X) неизвестен. В этом случае участвующие в (5.4) функции /ДХ) заме-
няются их непараметрическими оценками fj(X), построенными по соот-
ветствующим обучающим выборкам (5.3) (гистограммные оценки, ядер-
ные оценки Порзена и т.п.). Существуют специальные методы непара-
метрического ДА, не использующие прямых непараметрических оценок
плотностей. К таким методам относится, например, метод N ближай-
ших соседей: вокруг классифицируемой точки Х{ описывается сфера
минимального радиуса, содержащая N элементов из обучающих выборок;
точку X,- относят к тому классу, представителей которого в этой сфере
оказалось больше, чем представителей любого другого класса.
Кластер-анализ (автоматическая классификация) объединяет
методы решения задачи классификации объектов в условиях отсутствия
обучающих выборок. Если подобно тому, как это было принято в рамках
параметрического ДА, каждый (у-й) класс интерпретируется как пара-
метрически заданная одномодальная генеральная совокупность /(X|0(j))
Глава 5. КЛАССИФИКАЦИЯ
177
при неизвестном значении определяющего ее векторного значения параме-
тра 0(j), то кластер-процедура строится на базе модели смеси вероят-
ностных распределений. Если же исследователь не имеет оснований для
интерпретации классифицируемых наблюдений (5.1) в качестве выборки
из смеси к одномодальных генеральных совокупностей или не располагает
априорными сведениями, достаточными для параметрического предста-
вления искомых классов, то используются методы кластер-анализа, апел-
лирующие к характеристикам геометрической структуры множества
классифицируемых наблюдений и к понятию критерия качества класси-
фикации.
Модель смеси распределений описывает закон распределения ве-
роятностей в смеси из к одномодальных генеральных совокупностей, име-
ющих в общей генеральной совокупности удельные веса, соответственно,
7Г1, тг2, • • • > я к и функции плотности (полигоны вероятностей —
при дискретном характере наблюдаемой случайной величины) /1(Х |
0(1)), f2(X | 0(2)),.. .,fk(X | 0(2)). Соответственно, функция плотности
(полигон вероятностей) /(X | А; 0(1),..., 0(A)) модели смеси распределе-
ний имеет вид:
к
f(X | fc; 74,... тгк; 0(1),..., 0(fc)) = £ | 0(j)). (5.10)
j=i
Многомерный параметр A = (Ar; ttj ,..., тг^.; 0(1),..., 0(A)), от кото-
рого зависит функция f(X | А), содержит в себе число классов к (если
оно априори не известно исследователю), удельные веса (априорные ве-
роятности) классов 7Г1,... и многомерные (вообще говоря) параметры
0(1),.. .0(A), определяющие з.р.в. внутри каждого из классов.
Кластер-процедура, основанная на модели смеси распределений, ре-
ализуется по следующей общей схеме. На 1-м этапе решается зада-
ча статистического оценивания параметров А по случайной выборке (5.1),
извлеченной из генеральной совокупности, являющейся смесью к одномо-
дальной генеральных совокупностей (однородных классов) и подчиняю-
щейся з.р.в. (5.10). При известных общих видах функций fj(X | 0(j)) и
числе классов к этот этап может быть реализован, например, с помощью
метода максимального правдоподобия (см. выше, n.l.A, соотношения
(1.9)~(1.12)), т.е. — решением оптимизационной задачи вида
п / к \
П > max (5.11)
178 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
На 2-м этапе, располагая полученными из (5.11) оценками iq,..., л>,
0(1),..., 0(Л) параметров, соответственно, <1,..., 0(1),..., 0(Л), ис-
следователь осуществляет классификацию наблюдений (5.1), используя
для этого байесовское оптимальное правило (см. выше, (5.4)), а имен-
но: наблюдение Xi относится к классу jo (i = 1,2,..., п), если
I §0»)) = I §«))• (5-4')
Метод ^-средних предназначен для разбиения многомерных наблю-
дений (5.1) на заданное число к (к < п) классов, однородных в смысле
геометрической взаимной близости элементов, принадлежащих к одному
классу. Понятие однородности классов формализуется в данном методе с
помощью критерия качества разбиения вида
«($) = £ Е Л*.; XW). (512)
j=i x(es<>)
где S = (5^\5<2\ ...,5^) определяет конкретное разбиение наблю-
дений (5.1) на к классов (т.е. — это подмножество наблюдений
(5.1), содержащие только наблюдения, отнесенные к j-му классу), X(j) =
— это «центр тяжести» j-ro класса (здесь nj — это число
’ XiGS(j) _
элементов в j- классе), а </2(Х<; X(j)) — это квадрат евклидова рассто-
яния от наблюдения Xi до центра тяжести X(j). Таким образом, (5.12)
определяет усредненную меру внутриклассового разброса наблюдений, ха-
рактеризующую разбиение S.
Метод средних обычно используется при достаточно больших
объемах п классифицируемых данных (его «хорошие свойства» доказы-
ваются в асимптотике поп -♦ оо)и реализуется по следующей
общей схеме. На 1-м этапе производится последовательное (ите-
рационное) уточнение местоположения центров тяжести классов X =
(Х^(1),... ,J^v\kj) (v — номер итерации, v = 0,1,2,...) с соответству-
ющим пересчетом приписываемых им «весов»
При этом нулевое приближение строится, например, с помощью слу-
Глава 6. КЛАССИФИКАЦИЯ
179
чайно выбранных первых k точек исследуемой совокупности, т.е.1)
х<0)(0 = ^
ч(0) = 1, » = 1,2,...,А.
Затем на 1-й итерации «извлекается» точка Л\+1 и выясняется, к какому
из эталонов Х^°\») она оказалась ближе всего. Именно этот,самый близ-
кий к Xfc+i, эталон заменяется эталоном, определяемым как центр тяже-
сти старого эталона и присоединенной к нему точки (с увеличением
на единицу соответствующего ему веса), а все другие эталоны остаются
неизменными (с прежними весами) и т. д. Таким образом, пересчет эта-
лонов и весов на v-ы шаге, т.е. при извлечении очередной точки
происходит по следующему правилу:
если ”(()) =
= min
1 J к
в противном случае,
(v) f + 1. если d(Xfc+v,X<‘'-1)(0) = min d(Xfc+v,X<*,-,)(»),
or' = <
1 1 (v-l)
(в противном случае,
i = 1,2,/, k.
При этом если обнаруживается несколько (по i) одинаковых мини-
мальных значений d(Xl\i)), то можно условиться относить точ-
ку Хь+v к эталону с минимальным порядковым номером.
При достаточно большом числе итераций или при достаточно боль-
ших объемах классифицируемых совокупностей п и при весьма широких
ограничениях на природу исследуемых наблюдений дальнейший пересчет
эталонных точек практически не приводит к их изменению, т. е. имеет ме-
сто сходимость (в определенном смысле) к некоторому пределу при
v —► оо.
Нулевое приближение местоположения центров тяжести классов может опре-
деляться и более осмысленно, например, из соображений их наибольшей взаимной
разнесенности в анализируемом признаковом пространстве , х^) или
с использованием имеющейся априорной информации о классах. Приведенный здесь
способ выбора E(q) реализуется в большинстве типовых статистических пакетов
(например, в SPSS) <по умолчанию» пользователя.
180
И. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Если же в какой-то конкретной задаче исследователь не успел до-
браться до стадии практически устойчивых (по v) значений эталонных
точек, то пользуются одним из двух вспомогательных приемов. Либо «за-
цикливают» алгоритм, «прогоняя» его после рассмотрения последней точ-
ки Хп = A\+(n_fc) снова через точку Xi, затем Х2? и т. д., либо произво-
дят многократное повторение алгоритма, используя в качестве начального
эталона различные комбинации из к точек исследуемой совокупности
и выбирая для дальнейшего наиболее повторяющийся (в некотором смы-
сле) финальный эталон ~Х^п к\ На этом заканчивается 1-й этап процеду-
ры.
Второй (заключительный) этап метода A-средних по-
священ собственно процедуре классификации. Окончательное разбиение S
исследуемой совокупности многомерных наблюдений на к классов произво-
дится в соответствии с правилом «минимального дистанционного разбие-
ния» относительно центров тяжести (эталонов) X = Х^п~к\ а именно: на-
блюдение Xi относится к классу jo, если </(Xj,X(jo)) = min d(Xj,X(J)).
Доказано, что в весьма широком классе исходных геометрических
структур классов метод fc-средних является асимптотически (по п —► оо)
оптимальным в смысле минимизации среднего внутриклассового разброса
(5.12).
Иерархические процедуры классификации позволяют получить
представление о стратификационной структуре классифицируемой сово-
купности наблюдений (5.1) в форме так называемой дендограммы. Иерар-
хические процедуры классификации могут быть агломеративны-
м и (последовательно объединяющими элементы и группы элементов) и
дивизимными (последовательно разъединяющими группы элемен-
тов).
Так, например, агломеративные иерархические процедуры классифи-
кации на первом шаге рассматривают каждое из классифицируемых на-
блюдений Xi (г = 1,2,...,п) как отдельный кластер. Далее на каждом
шаге алгоритма происходит объединение двух самых близких наблюде-
ний, а затем — двух самых близких групп наблюдений (кластеров). Ра-
бота алгоритма заканчивается, когда все исходные наблюдения (5.1) ока-
зались объединенными в один класс. Очевидно, один агломеративный
иерархический алгоритм отличается от другого выбором способа вычи-
сления расстояния между кластерами. Наиболее распространенные спо-
собы вычисления этого расстояния: «расстояние ближайшего
сосед а», «расстояние средней связ и», «расстояние
дальнегососеда». Все они являются частными случаями обоб-
Глава 5. КЛАССИФИКАЦИЯ
181
щенного расстояния dT(S^\ S^), основанного на понятии обобщенного
степенного среднего, а именно:
1
П\ П2
</т(5(1),5(2)) =
x,es<'» x^sw
(5.13)
где и — группы наблюдений (кластеры), nj — число наблюдений
в кластере S^\ d(X,,Xj) — расстояние между наблюдениями X, и Xj, а
т — свободный параметр процедуры (—оо < т < +оо).
Действительно:
d_00(SW,SW) = lim dT(5(1),5(2)) = min </(ХьХ.) (5.13')
т—►—оо XjgsU)
Xj €$(*)
расстояние, вычисленное по правилу «ближайшего соседа»;
1 2 Xtes(»» Xjesw
расстояние «средней связи»]
d+oo(5(1), 5(2)) = dT(5(1), 5(2)) = max, d(X,-, Xj) (5.13w)
Xj €S<2)
расстояние, вычисленное по правилу «дальнего соседа».
Наряду с приведенными выше способами вычисления расстояния меж-
ду двумя классами в качестве последнего часто используют расстояние
между центрами тяжести этих классов, т. е.
d(5(1),5(2)) = d(X(l),X(2)), (5.14)
rneX(j) = i Е Xi, 3 = 1,2.
Xtest’»
Наконец, если расброс наблюдений внутри у-го класса (j = 1,2,..., к)
может быть описан (afj),!^))-нормальным распределением, то расстоя-
ние между j-м и / м классами измеряют в так называемой метрике Кал-
лбэка (S. Kullback), а именно:
<l2(S«>,Sll))=i(aO)-a(0)T (s~*0)+=“*(О) («0)- <•(»))+
2 4 ' (5.15)
+ itr[(S(;)-S(l))(s'’O)-S_,(O)],
182
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
где а(д) и 2(g), соответственно, вектор средних значений и ковариацион-
ная матрица g-го нормального класса (<? = j, I).
В частном случае, когда анализируемые нормальные классы (нор-
мальные генеральные совокупности) различаются только своими сред-
ними значениями и а(/) (но 2(1) = 2(2) = 2) формула (5.15) упро-
щается и дает так называемое расстояние Махаланобиса:
d,(SMS‘)= (а(;)-а(|))ТЕ-1 («(;•)-«(<)). (5.15')
5.Б. Примеры решения типовых задач и упражнений
Пример 5.1 (задача). Специальное исследование показало,
что склонность фирм к утаиванию части своих доходов (и, соответствен-
но, — к уклонению от уплаты части налогов) в существенной мере опре-
деляется двумя показателями:
— соотношением «быстрых активов» и текущих пассивов;
— соотношением прибыли и процентных ставок (оба показателя
оцениваются по определенной методике в шкале от 300 до 900 баллов).
В таблице представлены значения этих показателей (данные налого-
вой инспекции) по 10 фирмам, уличенным в тех или иных формах укло-
нения от уплаты налогов, и по 13 фирмам, не имеющим замечаний по
уплате налогов. Кроме того, имеющаяся статистика и специальные об-
следования свидетельствуют о том, что доля фирм, в той или иной форме
уклоняющихся от уплаты налогов, достигает 50%. Наконец, статистиче-
ская проверка гипотез о нормальном характере распределения двумерного
признака X = внутри каждой из анализируемых совокупно-
стей фирм, уклоняющихся от уплаты налогов (совокупности 1) и платя-
щих налоги (совокупности 2), и о равенстве их ковариационных матриц
(2(1) = 2(2) = 2) дала неотрицательный результат, т.е. можно счи-
тать, что имеющиеся у нас обучающие выборки извлечены из нормальных
генеральных совокупностей с одинаковыми ковариационными матрицами.
Глава 5. КЛАССИФИКАЦИЯ
183
N* пп (0 Обучающая выборка (1) (фирмы, уклоняющиеся от налогов) Обучающая выборка (2) (фирмы, не уклоняю- щиеся от налогов)
,(П х(2) *1» J1) *2i х(2) ®2«
1 740 680 750 590
2 670 600 360 600
3 560 550 720 750
4 540 520 540 710
5 590 540 570 700
6 590 700 520 670
7 470 600 590 790
8 560 540 670 700
9 540 630 620 730
10 500 600 690 840
11 - - 610 680
12 - - 550 730
13 - - 590 750
На фирме, не прошедшей проверку налоговой инспекции, зарегистри-
рованы значения переменных X = х^ = 740, х^ = 590.
Требуется:
1) предложить (с обоснованием) и реализовать метод, с помощью ко-
торого можно определить, к какой совокупности (7 или 2) следует
отнести фирму с показателями = 740 и = 590;
2) предложить (с обоснованием) и вычислить расстояние, измеряющее
степень различия двух анализируемых совокупностей фирм.
Решение
1) Из условия задачи следует, что число анализируемых классов
к = 2, мы располагаем двумя обучающими выборками объемов ni = 10 и
П2 = 13, классы нормальны и различаются только средними значениями,
а их удельные веса 7Г] и я? одинаковы (т.е. 7Г] = тг2 = |). Следова-
тельно, мы находимся в условиях применимости параметрического дис-
криминантного анализа и, в частности, можем воспользоваться линейной
дискриминантной функцией Фишера вида (5.7).
Воспользовавшись формулами (5.6) и (5.8), мы на основании исходных
184
И. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
данных («iV»и получаем:
d(l) = (576,0; 596,0)Т; d(2) = (598,5; 710,8)Т;
Е(1) =
Е =
5624
1724
8467
2041
1724\
3324 J ’
2041 \ .
4273 ) ’
Е(2) =
9351 1970 X
1970 4345J
Е-1 = 10-4
1,335
-0,637
-0,637 X
2,645 J '
Для определения значения левой части (5.7) вычисляем:
Е-1 (d(l) - d(2)) = Е"1
-22,5 \ _ ( 0,0043 X
— 114,8/ “ -0,0289 J
|(d(l) + d)(2)) = (587,25; 653,40)Т;
587,25
653,40
152,75
-63,40
Наконец:
Хо-
|(d(l) + d(2))
Е-1 (d(l) - d(2))
152,75 V С 0,0043 X
-63,40 ) \ -0,0289 J
Следовательно, наблюдение Xq должно быть отнесено к совокупности
1, а это значит, что есть основания к тому, чтобы диагностировать
анализируемую фирму как фирму в той или иной форме уклоняющуюся
от налогов.
2) Поскольку мы имеем дело с нормальными классами, различающи-
мися только своими средними значениями (d(l) и а(2)), то в качестве
расстояния между классами мы должны использовать расстояние Ма-
ханобиса (5.15;). Используя подсчитанные выше значения
Е-1 (d(l)-d(2)) = (0,0043; -0,0289)Т и (d(l)-d(2))T = (-22,5; -114,8),
d\SW, SW) = (d(l) - d(2))TE-1 (d(l) - d(2))
= (-22,5;-114,8)(_^24839)= 3,22.
Пример 5.2 (упражнение - тест). В качестве исходных
статистических данных Вы располагаете результатами обследования
Глава 5. КЛАССИФИКАЦИЯ
185
п = 2500 потребительских бюджетов московских семей по 8-ми статьям
расхода, т.е. данными вида Yi = (yjl\yj2\..., у-8^)Т, i = 1,2,...,2500,
где — удельные расходы i-й семьи по j-й расходной статье — рас-
(2) (3)
ходы на одежду и обувь, у' ’ — на питание, у' ’ — на товары культурно-
му
бытового назначения и длительного пользования, у ' — на алкоголь и
табак, у^ — на культуру и отдых, у^ — на лечение, санитарию и гиги-
ену, у™ —на услуги, у^ — сбережения).
Основная цель статистического анализа этих данных — выявление
основных типов потребительского поведения семей. При этом ранее про-
веденные исследования показали, что разброс в потребительском поведе-
нии семей каждого (j-ro) из имеющихся типов (J = 1,2,...,&, где к —
известное нам общее число типов потребительского поведения) описы-
вается 8-мимерным нормальным законом с вектором средних значений
a(j) = (a^\j), a^2\j),..., </8\j))T и одной и той же (для всех типов
потребительского поведения) ковариационной матрицей Е (a(j) и Е —
неизвестные параметры).
Требуется ответить на следующие вопросы:
1) Какой из нижеуказанных методов Вы используете для достижения
этой цели?
(&)Метод параметрического дискриминантного анализа.
(б) Одну из иерархических процедур классификации.
(в) Кластер-процедуру «к-средних» с известным числом классов.
(г) Метод расщепления смеси многомерных нормальных распределе-
ний с известным числом классов.
(д) Метод непараметрического дискриминантного анализа.
Кратко поясните свой выбор и схему реализации выбранного метода,
а именно:
2) на какие содержательные исходные допущения опирается Ваш вы-
бор модели?
3) дайте содержательную интерпретацию участвующим в модели па-
раметрам;
4) назовите метод и опишите алгоритм статистического оценивания
неизвестных параметров модели, а также опишите саму процедуру
классификации семей;
5) как измерить (с помощью какого расстояния) разницу в структурах
потребления семей разных типов потребительского поведения?
Решение
1) Речь идет о задаче классификации в условиях отсутствия обуча-
ющих выборок, известного числа классов к и известного общего параме-
186
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
трического вида з.р.в. анализируемого восьмимерного признака. Следо-
вательно, целесообразно использовать кластер-процедуру, основанную на
модели смеси нормальных распределений (п. (г)).
2) Каждый (a(j), S) — нормальный класс интерпретируется как j-й
тип потребительского поведения семей (домашних хозяйств), т. е. случай-
ный разброс в показателях потребительских бюджетов различных семей
одного и того же типа потребительского поведения описывается восьми-
мерным нормальным з.р.в.
3) Вектор средних значений a(j) задает усредненную (по всем семьям
j-ro типа потребительского поведения) структуру бюджета домашних хо-
зяйств этого типа, а ковариационная матрица S (общая для всех типов
потребительского поведения) содержит характеристики степени случай-
ного разброса одноименных расходных статей внутри данного типа (диа-
гональные элементы) и характеристики степени попарной взаимозависи-
мости различных расходных статей (внедиагональные элементы). Кроме
того, в модели смеси участвуют удельные веса тгьтгг,... ,тг* (априорные
вероятности) различных типов потребительского поведения во всей ана-
лизируемой совокупности домашних хозяйств.
4) Для оценки параметров iq, в(1),..., а(Л) и S в модели смеси
вида
f(Y | а(1),... ,a(fc); Е) =
_ V» 1 -Их-аЬ-))тД“1(х-а(Л) (*)
используется метод максимального правдоподобия, т. е. оценки ТГ],...,
а(1),... ,а(к) и S этих параметров получаются как решения оптимизаци-
онной задачи вида
п
I’1’!»«(1),•••,<»(*);s)-* ,тах. >
i=i a(i),.'...a(*)lx
где функция f имеет вид (*).
После получения оценок #i,...,£*; a(l),...,a(fc); S производит-
ся классификация наблюдений (семей) У< в соответствии с байесовским
оптимальным правилом (5.4), раелизованным с учетом нормальности
классов и равенства их ковариационных матриц (т.е. в форме (5.7)), а
именно: наблюдение относится к классу jQ, если
-5(^0) +ЭД)
S"1 (a(j0) - a(j)) > In
Глава S. КЛАССИФИКАЦИЯ
187
при всех j = 1,2,..., г.
5) Поскольку измеряется расстояние между нормальными классами с
одинаковыми ковариационными матрицами, то следует использовать рас-
стояние Махаланобиса (5.15').
Пример 5.3 (задача). Потребительское поведение пяти се-
мей характеризуется удельными (на душу) расходами за летние месяцы
на: культуру, спорт, отдых тыс. руб.) и питание (®^ тыс. руб.).
Значения показателей представлены в следующей таблице:
Номер семьи (i) 1 2 3 4 5
(тыс.руб.) 2 74 8 12 13
а:;' (тыс.руб.) 10 7 6 И 9
Требуется:
с помощью агломеративного иерархического алгоритма провести
классификацию семей и построить дендограмму:
1) при использовании обычной евклидовой метрики методом а) бли-
жайшего соседа", б) дальнего соседа; в) центров тяжести; г) сред-
ней связи;
2) при использовании взвешенной евклидовой метрики (с весами w\ =
0,05 u wj = 0,95) методом ближайшего соседа.
Решение
1а) Проведем классификацию, выбрав при обычном евклидовом рас-
стоянии принцип «.ближайшего соседа».
В обычной евклидовой метрике расстояние между наблюдениями 1 и
2 равно
52(4Л - ®5Л)2 = ^(2 — 4)2 + (10 - 7)2 = 3,61.
;=1
Аналогично находим расстояния между всеми пятью наблюдениями и
строим матрицу расстояний
/ 0 3,61 7,21 10,05 11,05\
3,61 0 4,12 8,94 9,22
D = 7,21 4,12 0 6,40 5,83
10,05 8,94 6,40 0 2,24
\ 11,05 9,22 5,83 2,24 0 /
188
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Из матрицы расстояний следует, что объекты 4 и 5 наиболее близки
(</4.5 = 2,24), поэтому объединим их в один кластер. После объединения
объектов имеем четыре кластера: 82,82,83,84^.
Расстояния между кластерами будем находить по принципу «ближай-
шего соседа». Так, расстояние между кластером S\ и кластером 54,5 рав-
но:
d(l, (4,5)) = min(di.4, di.5) = min(10,05; 11,05) = 10,05.
Проводя аналогичные расчеты
для d(2,(4,5)) и d(3, (4,5)), получим ма-
трицу расстояний
/ 0 3,61 -7,21 10,05
D2 = 3,61 7,21 0 4,12 4,12 0 8,94 5,83
\ 10,05 8,94 5,83 0
Объединим наблюдения 1 и 2, имеющие наименьшее расстояние di,2 =
3,61. После объединения имеем три кластера 5(1,2), 53 и •5(4,5)•
Вновь строим матрицу расстояний. Для этого необходимо рассчитать
расстояния d(3; (1,2)) и d((l,2); (4,5)):
d(3; (1,2)) = min(d3>1, d3>2) = 4,12;
d((l,2); (4,5)) = min(di.4,d1.5,d2.4,d2.5) = 8,94.
Получаем матрицу расстояний
( 0 4,12 8,94 \
4,12 0 5,83 .
8,94 5,83 0 )
Далее объединяем кластеры 5(i,2)) и 5(3), расстояние между которы-
ми, как это видно из матрицы D3, минимально: d(i,2),3 = 4,12. В резуль-
тате этого получим два кластера: 5(1,2,3) и 5(4,5). Матрица расстояний
будет иметь вид:
п _ ( 0 5,83 \
4 ~ \ 5,83 0 ) •
Из матрицы D4 следует, что на расстоянии d(it2,3).(4,5) = 5,83 все
пять наблюдений объединяются в один кластер. Результаты кластерного
анализа представим графически в виде дендрограммы (см. рис. 5.1).
Глава 5. КЛАССИФИКАЦИЯ
189
Рис. 5.1. Дендограмма (обычное евклидово расстояние, ближайший сосед)
На основании анализа результатов применения кластерной процедуры
можно сделать вывод, что наилучшим является разбиение пяти семей на
два кластера: 5(1,2,з) и 5(4,5).
16) Проведем классификацию, выбрав при обычном евклидовом рас-
стоянии принцип «дальнего соседа».
Как и в случае (1а), мы используем обычное евклидово расстояние,
поэтому матрица Di остается без изменения. Согласно агломеративному
алгоритму объединяются в один кластер объекты 4 и 5, как наиболее близ-
кие d4.5 = 2,24. После объединения имеем четыре кластера: 51, 52, 5з и
5(4,5)-
Вычисляя расстояние между кластерами по принципу «дальнего со-
седа», имеем:
di.(4,5) = max(d1.4,d1.5) = 11,05;
</2.(4,5) = max(d2.4,^2.s) = 9,22;
<^3.(4,5) = тах(^з.4> ^3.5) = 6,40.
Соответственно, имеем новую матрицу попарных расстояний:
D2 =
0 3,61 7,21 11,05\
3,61 0 4,12 9,22
7,21 4,12 0 6,40
11,05 9,22 6,40 0 /
Объединим объекты 1 и 2 в один кластер, как наиболее близкие (di 2 =
3,61).
После объединения имеем три кластера: 5(1.2),5з и 5(4,5).
190
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Строим матрицу расстояний D3, воспользовавшись принципом «даль-
него соседа».
( 0 7,21 11,05\
7,21 0 6,40 .
11,05 6,40 0 /
Объединим кластеры S3 и S^^y, расстояние между которыми ^з.(4,5) —
6,40 минимально, и получим два кластера: 5(1,2) и 5(з,4,5), расстояние
между которыми определяется по матрице
D4 =
11,05 \
0 J
и равно d(i,2).(3,4,s) = 11,05.
Графические результаты классификации представлены в виде дендо-
граммы на рис. 5.2.
Рис. Б.2. Дендограмма (обычное евклидово расстояние, дальний сосед)
Как и в предыдущем случае, наилучшим является разбиение семей
на два кластера (рис. 5.2): 5(1,2) и 5(з,4,5).
Таким образом, используя принцип «дальнего соседа» мы получили
разбиение семей на два кластера 5(112) и 5(з,4,5), которое отличается от
разбиения по принципу «ближайшего соседа»: 5( 1,2,3) и 5(4,5).
1в) Классификация на основе обычного евклидова расстояния и прин-
ципа «центра тяжести».
Так как мы используем обычное евклидово расстояние, то матрица
остается без изменения. Согласно алгомеративному алгоритму объединя-
ются в кластер 5(4,5) объекты 4 и 5 как наиболее близкие d4.5 = 2,24.
Глава б. КЛАССИФИКАЦИЯ
191
Кластер *S'(4,5) характеризуется в дальнейшем его центром тяжести,
V /12,5\ D
определяемым вектором средних Л(4(5) = I I. Расстояние от этого
кластера до первого наблюдения равно:
d(4,5).i = У(12,5-2)2 + (Ю- 10)2 = 10,50.
Аналогично пересчитываются расстояния t*(4,5).2 и <*(4,5).з- В результате
получаем матрицу расстояний
( 0 3,61 7,21 10,50 \
3,61 0 4,12 9,01 |
7,21 4,12 0 6,02 I ‘
10,50 9,01 6,02 0 /
Объединим объекты 1 и 2, расстояние между которыми d1>2 = 3,61
________________________________________________________________ / 3 \
минимальное. Кластер характеризуется центром тяжести = ( ),
’ к о,0 J
расстояние от которого до кластера равно:
</(1,2).(4,б) = У(3 - 12,5)2 + (8,5 - 10)2 = 9,62;
<*(1,2).з = У(3 - 8)2 + (8,5 - 6)2 = 5,59.
Тогда матрица расстояний примет вид:
(О 5,59 9,62 \
5,59 0 6,02 .
9,62 6,02 0 /
В матрице D3 минимальное расстояние <*(1,2).з = 5,59, поэтому обра-
зуем кластер 5(1>2>з) и определим его вектор средних
-^(1,2,3) =
2+4+8
10-Л+6
3
4,67 \
7,67) •
Найдем расстояние между З'р.г.з) и 5(4,5)
<*(1,2,3),(4,б) = ^(4.67 - 12,5)2 + (7,67 - 10)2 = 8,17,
на котором все пять объектов объединяются в один кластер. Графически
результаты классификации представлены дендограммой на рис. 5.3.
192
П. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Рис. Б.З. Дендограмма (обычное евклидово расстояние, принцип «центр
тяжести»)
Из рис. 5.3 видно, что наибольший скачок в расстояниях при объеди-
нении имеет место на последнем шаге, поэтому целесообразно выбрать
разбиение на два кластера £(1,2,3) и что совпадает со случаем 1а).
1г) Классификация на основе обычного евклидова расстояния и прин-
ципа «средней связи».
Используя матрицу Di, согласно агломеративному алгоритму объ-
единим кластеры и S5 в один 5(4,5), так как расстояние между ними
^4.5 = 2,24 — минимально.
Расстояние от кластера 5(4,5) Д° остальных кластеров определим по
принципу «средней связи»на основе матрицы Di. Например:
d(4,5).i = |(</4.1 + <*5.1) = ^(10,05+ 11,05) = 10,55.
Тогда матрица расстояний имеет вид:
D2 =
( 0 3,61 7,21 10,55
3,61 0 4,12 9,08
7,21 4,12 0 6,12
\ 10,55 9,08 6,12 0
Объединим, как наиболее близкие (di,2 = 3,61) кластеры Si и 52-
Тог да расстояния от 5(1,2) ДО остальных кластеров 5<4э5) и 5з равны:
^(1,2).(4,5) = т(^1.4 + ^1.5 +^2л + ^2.5) = 9,82; d(i,2).3 = «(7,21 + 4,12) = 5,67,
* £
Глава 5. КЛАССИФИКАЦИЯ
193
а матрица расстояний имеет вид:
/ 0 5,67 9,82 \
D3 = 5,67 0 6,12 .
\9,82 6,120 0 /
Объединим как наиболее близкие (d(i,2).з — 5,67) кластеры 5(1,2) и 53
и определим расстояния от 5(1,2,з) Д° 5(4,5)
^(1,2,3).(4,5) — g(^1.4 + ^*-5
+ ^2.4 + ^2.5 + ^3.4 + ^З.б) — 8,58,
на котором все пять объектов объединились в один кластер. Графически
результаты классификации представлены дендограммой на рис. 5.4.
Рис. 5.4. Дендограмма (обычное евклидово расстояние, принцип средней
связи)
Из рис. 5.4 следует, что наиболее целесообразным является разбиение
на два кластера 5(1,2,з) и 54,5.
Таким образом, сравнивая результаты 4-х разбиений пяти семей на
однородные группы, можно отметить, что наиболее устойчивым является
разбиение на два кластера 5(1,2,з) и 5(4,5)- Только в одном случае из четы-
рех при использовании принципа «дальнего соседа» получено разбиение
5(1,2) И 5(з,4,5).
2) Классификация на основе «взвешенного евклидова расстояния» и
принципа «ближайшего соседа».
Взвешенное евклидово расстояние между г-м и l-м наблюдениями
7 Прикладная статистика
в задачах и упражнениях
194
И. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
определяется по формуле:
(*)
i=i
По условию задачи = 0,05 и w2 = 0,95. Это означает, что расходам
на питание (я/2)) придается существенно больший вес в задаче класси-
фикации семей по потребительскому поведению. Применяя формулу (*) к
вычислению расстояний получаем матрицу расстояний:
f ° 2,96 2,96 0 4,12 1,32 2,44 4,29 2,65 \ 2,80
D1 = 4,12 1,32 0 4,95 3,13
2,44 4,29 4,95 0 1,96
\2,65 2,80 3,13 1,96 0 /
Объединив 52 и 5з, имеющих минимальное расстояние </2.з = 1,32,
в кластер 5(2,з) и применив принцип «ближайшего соседа», получим ма-
трицу расстояний:
D2 =
0 2,96 2,44 2,65
2,96 0 4,29 2,80
2,44 4,29 0 1,96
2,65 2,80 1,96 0
Образовав на расстоянии d(4.5) = 1,96 кластер 5(415), вновь построим ма-
трицу расстояний:
( 0 2,96 2,44 \
2,96 0 2,80 .
2,44 2,80 0 /
Объединим 51 и 5(4,5), имеющих минимальное расстояние d(4,5).i =
2,13, в кластер 5(13,5) и получим матрицу расстояний
( 0 2,80 \
\2,80 0
При объединении кластеров 5(ii4>5) и 5(2,з) все пять объектов образу-
ют один кластер.
Результаты классификации представлены графически в виде дендо-
граммы на рис. 5.5
Глава 5. КЛАССИФИКАЦИЯ
195
Рис. 5.5. Дендограмма (взвешенное евклидово расстояние, принцип бли-
жайшего соседа)
Как и прежде, отдадим предпочтение разбиению на два кластера; мы
получаем третий вариант разбиения, а именно 5(2,з) и 5ц 4,5).
Таким образом, используя пять иерархических алгоритмов кластер-
ного анализа, мы получили три варианта разбиения пяти семей на две
статистически однородные группы. С одной стороны, это свидетельству-
ет о гибкости (возможностях) методов кластерного анализа, с другой —
о необходимости экономических (содержательных) и статистических кри-
териев для выбора наилучшего варианта классификации. При этом часто
бывает полезной априорная информация об исследуемом явлении. В на-
шем примере окончательно следует остановиться на разбиении 5(1,2,з) и
5(4,5)> как наиболее устойчивом. Это разбиение получено по трем алго-
ритмам из пяти. Кроме того, оно согласуется с данными априорного,
качественного анализа.
Пример 5.4. (задача) Уровень жизни населения двадцати
стран за 1994 г. характеризуется следующими шестью (р = 6) показа-
телями:
а/1) потребление мяса и мясопродуктов на душу населения (кг);
хУ^ смертность населения по причине болезни органов кровообращения
на 100000 населения;
(з)
' оценка валового внутреннего продукта по паритету покупательной
способности в 1994 г. на душу населения (в % к США);
х^ рас ходы на здравоохранение (в % от ВВП);
ши ргблгние фруктов и ягод на душу населения (кг);
х^^ по । ргблгпие хлебопродуктов на душу населения (кг).
196
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Значения показателей представлены в следующей таблице:
N п/п Страны Показатели
_(1) Л» _(2) Jb ,(3) Jb z(4> _(S) «I/ Л6) Jb
1 Россия 55 84,98 20,4 3,2 28 124
2 Австралия 100 30,58 71,4 8,5 121 87
3 Австралия 93 38,42 78,7 9,2 146 74
4 Азербайджан 20 60,34 12,1 3,3 52 141
5 Армения 20 60,22 10,9 3,2 72 134
6 Белоруссия 72 60,70 20,4 5,4 38 120
7 Бельгия 85 29,82 79,7 8,3 83 72
8 Болгария 65 70,57 17,3 5,4 92 156
9 Великобритания 67 34,51 69,7 7,1 91 91
10 Венгрия 73 64,73 24,5 6,0 73 106
11 Германия 88 36,63 76,2 8,6 138 73
12 Греция 83 32,84 44,44 5,7 99 108
13 Грузия 21 62,64 11,3 3,5 55 140
14 Дания 98 34,07 79,2 6,7 89 77
15 Ирландия 99 39,27 57,0 6,7 87 102
16 Испания 89 28,46 54,8 7,3 103 72
17 Италия 84 30,27 72,1 8,5 169 118
18 Казахстан 61 69,04 13,4 3,3 10 191
19 Канада 98 25,42 79,9 10,2 123 77
20 Киргизия 46 53,13 11,2 3,4 20 134
Требуется:
используя при различных значениях к (числе классов) метод k-
средних, провести классификацию стран, т. е. разбить их на одно-
родные группы по уровню жизни населения и дать содержательную
интерпретацию полученным результатам.
Решение
Из условия задачи видно, что в рассматриваемую совокупность вхо-
дят страны бывшего СССР, бывшей «Восточной Европы» и промышлен-
но развитые страны Запада. Поэтому можно предположить, что искомое
разбиение стран по уровню жизни населения будет состоять из трех или
четырех кластеров.
Классификация проводилась на ЭВМ с помощью ППП «Statistica»
по различным вариантам метода Л-средних, но наилучшими в содержа-
тельном плане оказались результаты, полученные методом Л-средних при
разбиении на четыре класса.
В первый кластер вошли одиннадцать (ni = 11) стран: Австра-
лия, Австрия, Бельгия, Великобритания, Германия, Греция, Дания, Ир-
ландия, Испания, Италия, Канада. Наиболее удалена от центра этого
кластера Италия, которая характеризуется самым высоким для кластера
уровнем потребления фруктов (а/5)) и хлебопродуктов (а/6)).
Глава 5. КЛАССИФИКАЦИЯ
197
Во второй кластер вошли четыре (п2 = 4) страны: Россия, Бе-
лоруссия, Казахстан и Киргизия.
В третий кластер вошли две (п3 = 2) страны: Болгария и Вен-
грия.
В четвертый кластер вошли три (п4 = 3) страны: Азербайджан,
Армения и Грузия.
Средние значения показателей для четырех кластеров представлены
в следующей таблице:
Показатели Кластеры
5(П 5(2) 5(з) 5(4)
я*1* 89.45 58.50 69.00 20.33
х™ 32.75 66.99 67.65 61.07
а:(3) 69.37 16.35 20.90 11.43
х(4) 7.89 3.82 5.70 3.33
х(5) 113.55 24.00 82.50 59.67
г(6) 86.45 142.25 131.00 138.33
Кластер куда входят промышленно развитые страны запада, ха-
рактеризуется самыми высокими средними значениями: ВВП по паритету
покупательной способности (я/3)), расходов на здравоохранение (а/4)), по-
требления мяса (я/1)) и фруктов (ж^), а также самым низким значением
смертности (я/2)).
Самое высокое потребление хлебопродуктов на душу населения (я/6))
с(2) с(4)
у стран, входящих в кластеры 5' ' и 5 .
В кластер 544^ вошли: Азербайджан, Армения и Грузия, на террито-
рии которых происходили в рассматриваемый период времени вооружен-
ные конфликты.
Этот кластер характеризуется самыми низкими средними значениями
показателей и я/4\ а также — среднедушевым потреблением мяса.
Заслуживает внимания матрица расстояний между центрами четы-
рех кластеров:
( 0 126,8 83,3 120,6 \
D = 126,8 0 60,7 53,0 |
83,3 60,7 0 55,6 1 •
\ 120,6 53,0 55,5 0 /
Из матрицы следует, что кластеры , с(3) г.(4) 5 и 5 примерно оди-
наково удалены друг от друга. Евклидово расстояние между ними соот-
ветственно равно 60,7; 53,0 и 55,5. Наиболее выделяется по уровню жизни
198 II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
населения кластер S^\ куда входят промышленно развитые страны Запа-
да. Расстояния от Si до кластеров S^2\ и соответственно равны
126,8; 83,3 и 120,6.
5.В. Задачи и упражнения
Упражнение-тест 5.1
В результате решения задачи, сформулированной в примере 5.2, ис-
ходные статистические данные У1(» = 1,2,...,2500) были разбиты на 10
подвыборок
Ги Г12 ... К1П1 (1)
У21 *22 ... У2п2 (2)
*10.1 *10.2 ... *10.nJ0 (10)
каждая из которых представляет свой тип потребительского поведения.
Дополнительное исследование показало, что каждую (j-ую) из этих под-
выборок можно интерпретировать как выборку из 8-мимерной нормаль-
ной генеральной совокупности jV(a(j); S), где a(j) = (a^\j),a^2\j),...,
</8\j))— вектор средних значений, а Е— соответствующая 8 X 8— кова-
риационная матрица (> = 1,2,...,10), причем удалось оценить удельные
веса 7Г1, тг2,... ,7Г10 каждого из типов потребительского поведения.
У новой семьи, наугад извлеченной из общей совокупности российских
семей, зарегистрированы показатели семейного бюджета
Требуется ответить на следующие вопросы:
1) Какой из нижеуказанных методов Вы используете в задаче отнесе-
ния этой новой семьи к одному из ранее выявленных типов потре-
бительского поведения'!
(а) Метод иерархической классификации.
(б) Метод параметрического дискриминантного анализа.
(в) Метод непараметрического дискриминантного анализа.
(г) Метод /г-средних с известным числом классов.
(д) Кластер-анализ, основанный на модели распределений.
Кратко поясните свой выбор и схему реализации выбранного метода,
а именно:
2) представьте в математической форме правило отнесения «наблю-
дения» (семьи) Y* к одному из 10-ти типов потребительского по-
ведения;
Глава 5. КЛАССИФИКАЦИЯ
199
3) выпишите явные выражения для оценок всех (кроме уже известных
удельных весов • • • j^io) параметров, участвующих в матема-
тической записи правила классификации;
4) выпишите явный вид дискриминантной функции (ДФ) в задаче от-
несения наблюдения У* к одному из двух нормальных классов (т. .е
в предположении, что общее число классов к = 2), отличающихся
только векторами средних значений и представленных своими обу-
чающими выборками (1) и (2); объясните происхождение этой ДФ.
Задача 5.1
Деятельность двенадцати машиностроительных предприятий харак-
теризуется показателями рентабельности (а/1) %) и производительности
труда (х^ тыс. руб./чел.). Значения показателей приводятся в следую-
щей табл.:
N п/п Группы предприятий Рентабельность Производительность труда (*<2))
1 Высокий уровень 23,4 9,1
2 (X) 19,1 6,6
3 17,5 5,2
4 17,2 10,0
1 Низкий уровень 5,4 4,3
2 (Y) 6,6 5,5
3 8,0 5,7
4 9,7 5,5
5 9,1 6,6
1 Подлежат классификации 9,9 7,4
2 (Z) 14,2 9,4
3 12,9 6,7
Из предварительного анализа известно, что первые 4 предприятия
имеют высокий уровень организации управления, а следующие 5 пред-
приятий — низкий, причем случайный разброс в значениях показателей
(1) (2)
г ' и г ' описывается внутри совокупности предприятии фиксированно-
го (j-ro) уровня организации управления двумерным нормальным з.р.в.
*(«(>). S).
Требуется:
выбрать, обосновать и реализовать подходящий метод классифика-
ции трех последних предприятий.
200
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Задача 5.2
Эффективность использования земельных угодий двенадцатью сель-
скохозяйственными районами области оценивалась по объемам реализо-
ванной продукции растениеводства тыс.руб./га) и животноводства
(г/2) тыс.руб./га). Значения показателей приводятся в таблице:
N п/п Группы районов Объем продукции
Растениеводство (l(1)) Ж ивотноводство (Х(2))
1 Группа А 25 21
2 (Х1) 31 37
3 27 22
4 33 36
1 Группа В 47 38
2 (х2) 50 67
3 52 45
4 39 49
5 66 33
1 Подлежат классификации 32 42
2 (Z) 67 33
3 46 56
Предварительно известно, что в первых четырех районах земля ис-
пользуется неэффективно, а в следующих пяти районах — эффективно,
(1) (2)
причем случайный разброс в показателях г ' и г 7 описывается внутри
каждой (j-ой) группы районов двумерным нормальным з.р.в. 7V(a(j),E).
Требуется:
выбрать, обосновать и реализовать подходящий метод классифика-
ции трех последних районов области.
Задача 5.3
Условия задачи 5.2 дополнены значениями показателя производитель-
ности труда (а;^ тыс. руб./чел.) для тех же двенадцати предприятий:
i 12 3 4 5 6 7 8 9 10 11 12
31 40 42 39 82 64 58 71 79 49 56 38
Требуется:
основываясь на объединенных данных задач 5.2 и 5.3, выбрать, обо-
сновать т реализовать подходящий метод классификации трех по-
следних районов области.
Задача 5.4
Эффективность работы предприятий характеризуется производи-
тельностью труда (а/1) тыс. руб./чел.) и долей продукции, на которую
Глава 5. КЛАССИФИКАЦИЯ
201
поступили рекламации (а/2) в долях от целого). На основании предва-
рительного анализа выделены две группы предприятий, различающихся
по эффективности работы, а также установлено, что разброс в значени-
ях показателей внутри каждой (j-й) из этих групп описывает-
ся (a(j),E(j)) — нормальным з.р.в. Для выделенных двух групп пред-
приятий получены оценки векторов средних и ковариационных матриц:
а(1) = (6,72; 0,14)Т, а(2) = (4,05; 0,20)Т,
ад=
3,07
-0,05
-0,05
0,01
ад =
1,80
-0,15
-0,15\
0,04 J '
причем предприятия первой (эффективной) группы составляют 60% от
общей совокупности предприятий, а проверка гипотезы о равенстве кова-
риационных матриц (E(l) = S(2) = S) дала отрицательный результат.
Требуется:
вычислить значения дискриминантной функции для предприятий,
характеризующихся показателями = 4,92; х^ = 0,18j и =
7,05; х^ = 0,16/ и определить, к какой из групп предприятий сле-
дует отнести каждые из них.
Задача 5.5
Имеются 12 предприятий, каждое из которых характеризуется тре-
мя экономическими показателями: производительностью труда (млн.
руб./чел.), удельным весом потерь от брака (%) и фондоотдачей активной
части основных производственных фондов (руб./руб.). Данные по этим
предприятиям представлены в таблице. Из этих предприятий выделены
две обучающие выборки, первая из которых включает пг = 4 предприятий
группы А, а вторая — п2 = 5 предприятий группы В. Предполагается, что
обучающие выборки извлечены из нормальных генеральных совокупно-
стей, различающихся только векторами средних значений, причем пред-
приятия более высокого уровня эффективности (предприятия группы А)
составляют 60% от всей генеральной совокупности.
Требуется:
найти оценки векторов средних и Х2 и общей ковариационной
матрицы S;
построить дискриминантную функцию и расклассифицировать с ее
помощью два последних предприятия.
202
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Группы предприятий Производительность труда Удельный вес потерь от брака Фондоотдача
Группа А 9,4 0,15 1,91
(эффективные) 9,9 0,34 1,68
9,1 0,09 1,89
9,4 0,21 2,30
Группа В 6,6 0,48 0,88
(низкоэффективные) 4,3 0,41 0,62
7,4 0,62 1,09
6,6 0,50 1,32
5,5 1,20 0,68
Подлежат 5,5 0,05 1,02
классификации 10,0 0,32 2,62
Задача 5.6
Деятельность шести предприятий машиностроения характеризуется
показателями: я/1) — рентабельность (%) и х^ — производительность
труда. Значения показателей представлены в таблице:
Номер предприятия 1 2 3 4 5 6
23,4 17,5 9,7 18,2 6,6 8,0
9,1 5,2 5,5 9,4 7,5 5,7
Требуется: с помощью иерархического агломеративного алго-
ритма провести классификацию этих предприятий и построить дендо-
грамму:
1) при использовании обычной евклидовой метрики — методом: а) «бли-
жайшего соседа»; Ь) «дальнего соседа»; с) «центра тяжести»;
d) «средней связи»;
2) при использовании взвешенной евклидовой метрики (с весами Wi =
0,1, и W2 = 0,9) — методом «ближайшего соседа»;
3) при использовании обычной евклидовой метрики и предварительной
нормализации исходных данных — методом «ближайшего соседа».
Задача 5.7.
Уровень медицинского обслуживания населения шести регионов ха-
рактеризуется показателями: я/1) — число врачей на 10 тыс. жителей и
(2)
х — число больничных коек на 10 тыс. жителей. Значения показателей
представлены в таблице:
Глава 5. КЛАССИФИКАЦИЯ
203
№ хозяйства (г) 1 2 3 4 5 6
‘Г 34,8 31,2 32,1 35,7 30,2 34,2
4” 126,0 112,0 123,0 128,0 115,0 123,0
Требуется: с помощью иерархического агломеративного алго-
ритма провести классификацию этих регионов и построить дендограмму:
1) при использовании обычной евклидовой метрики — методом: а) «бли-
жайшего соседа»] Ь) «дальнего соседа»] с) «центра тяжести»]
d) «средней связи»]
2) при использовании взвешенной евклидовой метрики (с весами =
0,8 и W2 = 0,2) — методом «ближайшего соседа»]
3) при использовании обычной евклидовой метрики и предварительной
нормализации исходных данных — методом «дальнего соседа»]
4) провести сравнительный анализ полученных решений.
Задача 5.8
Деятельность пяти сельскохозяйственных предприятий характеризу-
ется показателями объема реализованной продукции: а/1) — растение-
водства и х^ — животноводства с одного гектара пашни (тыс.руб./га).
Значения показателей представлены в таблице:
Номер хозяйства (») 1 2 3 4 5
»'*’ 24,9 15,1 11,7 16,7 27,3
9,8 И,1 8,8 8,9 9,4
Требуется: с помощью иерархического агломеративного алго-
ритма провести классификацию сельскохозяйственных предприятий и по-
строить дендограмму:
1) при использовании обычной евклидовой метрики — методом: а) «бли-
жайшего соседа»] Ь) «дальнего соседа»] с) «центра тяжести»]
d) «средней связи»]
2) при использовании взвешенной евклидовой метрики — методом
«ближайшего соседа»,
3) при использовании обычной евклидовой метрики и предварительной
нормализации исходных данных — методом «ближайшего соседа».
Задача 5.9
Деятельность пяти сельскохозяйственных предприятий района ха-
рактеризуется показателями: х' ' — производительность труда (тыс.
руб./чел.); объем реализованной продукции: х^ — растениеводства и
— животноводства с одного гектара посевной площади (тыс.руб./га.).
Значения показателей представлены в таблице:
204
II. ПРИКЛАДНОЙ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Номер хозяйства (г) 1 2 3 4 5
8,2 4,3 6,4 6,3 4,9
2,5 4,9 5,1 2,7 3,2
4,1 3,8 5,2 4,2 5,5
Требуется: с помощью иерархического агломеративного алго-
ритма провести классификацию этих предприятий и построить дендо-
грамму:
1) при использовании обычной евклидовой метрики — методом: а) «бли-
жайшего соседа»; Ь) «дальнего соседа»; с) «центра тяжести»;
d) «средней связи»;
2) при использовании взвешенной евклидовой метрики (с весами Wi =
0,1, W2 = 0,4, w3 = 0,5) — методом «ближайшего соседа»;
3) при использовании обычной евклидовой метрики и предварительной
нормализации исходных данных — методом «дальнего соседа»;
4) провести сравнительный анализ полученных решений.
Задача 5.10
Деятельность шести машиностроительных предприятий характери-
зуется показателями: а/1) — производительность труда (млн.руб./чел.);
— удельный вес потерь от брака (%) и — фондоотдача активной
части основных производственных фондов (руб./руб.). Значения показа-
телей представлены в таблице:
Номер предприятия (г) 1 2 3 4 5 6
0,94 0,66 0,74 1,00 0,67 0,91
0,15 0,48 0,62 0,32 0,50 0,90
43’ 1,91 0,88 1,09 2,62 1,32 1,89
Требуется: с помощью иерархического агломеративного алго-
ритма провести классификацию этих предприятий и построить дендо-
грамму:
1) при использовании обычной евклидовой метрики — методом: а) «бли-
жайшего соседа»; Ь) «дальнего соседа»; с) «центра тяжести»;
d) «средней связи»;
2) при использовании взвешенной евклидовой метрики (с весами Wj =
0,5, W2 = 0,1, w3 = 0,4) — методом «ближайшего соседа»;
3) при использовании обычной евклидовой метрики и предварительной
нормализации исходных данных — методом «дальнего соседа»;
4) провести сравнительный анализ полученных решений.
Глава 5. КЛАССИФИКАЦИЯ
205
Тест 5.1. В кластер Si входят 4 объекта, расстояние от которых до
объекта X* 5 составляет соответственно: 2, 5, 6, 7. Чему равно расстояние
от объекта Х« 5 до кластера Si, если исходить из принципа «ближайшего
соседа»:
а) 2;
б) 5;
в) 6;
г) 7.
Тест 5.2. Определить по данным теста 1 расстояние от объекта 5 до
кластера Si, исходя из принципа «дальнего соседа»:
а) 2;
б) 5;
в) 6;
г) 7.
Тест 5.3. Чему равно по данным теста 1 расстояние от объекта Si,
исходя из принципа «среднией связи»:
а) 2;
б) 5;
в) 6;
г) 7.
Тест 5.4. Расстояния между пятью объектами (п = 5) характеризу-
ется матрицей расстояний:
/ 0 2,2 3,0 5,1 5,8\
2,2 0 1,4 5,0 6,4
D= 3,0 1,4 0 6,4 7,8
5,1 5,0 6,4 0 2,0
\5,8 6,4 7,8 2,0 0 /
Чему равно расстояние между кластерами Sit2 и S3i4i5, в которые вхо-
дят соответственно объекты (1, 2) и (3, 4, 5), если исходить из принципа
«ближайшего соседа»:
а) 2,2;
б) 3,0;
в) 1,4;
г) 2,0.
Тест 5.5. По данным теста 4 определите, чему равно расстояние меж-
ду кластерами 51,2 и Зз,4,5> если ИСХ°ДИТЬ из принципа «дальнего соседа»:
а) 5,8;
206
ЛИТЕРАТУРА
б) 5,1;
в) 7,8;
г) 6,4.
Тест 5.6. Чему равно по данным теста 4 расстояние между класте-
рами Sij и <§3,4,5, если исходить из принципа средней связи:
а) 4,45;
б) 3,37;
в) 4,89;
г) 2,86.
Тест 5.7. Данные о четырех фирмах, деятельность которых харак-
теризуется показателями а/1) и х^2\ представлены в таблице.
i 1 2 3 4
1 7 1 9
5 9 3 7
Чему равно расстояние между 1-м и 2-м объектами, если в качестве
метрики принять обычное евклидово расстояние:
а) 3,78;
б) 9,34;
в) 7,21;
г) 5,19.
ЛИТЕРАТУРА
[I] Айвазян ('. АМхитарян В.С. Прикладная <гагис1ика и основы эконометри-
ки. М.: ЮНИТИ, 1988. С. 1012.
ПРИЛОЖЕНИЕ!. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
Таблица П 1.1. Значения функции плотности ф(х) = ф(®;0;1) стандартного
нормального закона распределения. ф(х) = -у=е * •
X £(®) X £(«) X £(*) X £(*) X £(*) X £(®)
0,00 0,3989 0,50 0,3521 1,00 0,2420 1,50 0,1295 2,00 0,0540 2,50 0,0175
0,05 0,3984 0,55 0,3429 1,05 0,2299 1,55 0,1200 2,05 0,0488 2,55 0,0154
0,10 0,3970 0,60 0,3332 1,10 0,2179 1,60 0,1109 2,10 0,0440 2,60 0,0136
0,15 0,3945 0,65 0,3230 1,15 0,2059 1,65 0,1023 2,15 0,0396 2,65 0,0119
0,20 0,3910 0,70 0,3123 1,20 0,1942 1,70 0,0940 2,20 0,0355 2,70 0,0104
0,25 0,3867 0,75 0,3011 1,25 0,1826 1,75 0,0863 2,25 0,0317 0,0283 2,75 0,0091
0,30 0,3814 0,80 0,2897 1,30 0,1714 1,80 0,0790 2,30 2,80 0,0079
0,35 0,3752 0,85 0,2780 1,35 0,1604 1,85 0,0721 2,35 0,0252 2,85 0,0069
0,40 0,3683 0,90 0,2661 1,40 0,1497 1,90 0,0656 2,40 0,0224 2,90 0,0060
0,45 0,3605 0,95 0,2541 1,45 0,1394 1,95 0,0596 2,45 0,0198 2,95 3,00 0,0051 0,0044
Замечание 1. Значения функции плотности ф(хо\ а; аг2) нормального
закона со средним а и дисперсией а2 подсчитывается по формуле
ф(х0;а;а2) = р-Л;0; 1) = ±ф (П1.1)
(если величина аргумента (®о — а)/(Г попадает между табличными значениями
я, то для определения ф{XQ-~- ) пользуются линейной интерполяцией функции
0(®))-
Замечание 2. При определении значений функции ф(х) для отрица-
тельных величин аргумента х следует использовать тождество (выражающее
свойство четности функции ф(х))
ф(-х)= ф(х).
(П1.2)
Пример П1.1. Требуется определить значение ф(хо;а;<т2) при хо =
3,36, а = 1 и а2 = 4.
Решение: х = д°~а- = 3,3|~- = 1,18. Два окаймляющих х соседних та-
бличных значения аргумента — это X] = 1,15 и Х2 = 1,20, поэтому, используя
линейную интерполяцию, получаем:
£(1,18) = £(1,15)- Г^(1,15) - ^(1,20)1 =0,199.
1 — 1,10 1- J
Значение </>(3,36; 1; 4) получаем по формуле (П1.1):
ф(хо = 3,36; 1; 4) = | <£(1,18) = 10,199 = 0,0995.
208
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.2. Значения функции Ф(х) = Ф(я; 0; 1) стандартного нормального
X 2 /
распределения. Ф(я) = J е~ dt.
— оо
X Ф(я) X Ф(х) X Ф(х)
0,00 0,500000 1,00 0,841345 2,00 0,977250
0,05 0,519939 1,05 0,853141 2,05 0,979818
0,10 0,539828 1,10 0,864334 2,10 2,15 0,982136
0,15 0,559618 1,15 0,874928 0,984222
0,20 0,579260 1,20 0,884930 2,20 0,986097
0,25 0,589706 1,25 0,894350 2,25 0,987776
0,30 0,617911 1,30 0,903200 2,30 0,989276
0,35 0,636831 1,35 0,911492 2,35 0,990613
0,40 0,655422 1,40 0,919243 2,40 0,991802
0,45 0,673645 1,45 0,926471 2,45 0,992857
0,50 0,691463 1,50 0,933193 2,50 0,993790
0,55 0,708840 1,55 0,939429 2,55 0,994614
0,60 0,725747 1,60 0,945201 2,60 0,995339
0,65 0,742154 1,65 0,950528 2,65 0,995975
0,70 0,758036 1,70 0,955434 2,70 0,996533
0,75 0,773373 1,75 0,959941 2,75 0,997020
0,80 0,788145 1,80 0,964070 2,80 0,997445
0,85 0,802338 1,85 0,967843 2,85 0,997814
0,90 0,815940 1,90 0,971283 2,90 0,998134
0,95 0,828944 1,95 0,974412 2,95 0,998411
3,00 0,998650
Замечание 1. Значение функции распределения Ф(а?о; а; <т2) нормаль-
ного закона при среднем значении а и дисперсии аг2 в заданной точке xq подсчи-
тывается по значениям функции Ф(х) = Ф(х; 0; 1) с помощью формулы
(П1.3)
(если величина аргумента (а?о —попадает между табличными значениями ж,
то для определения Ф((хо — а)/<т) пользуются линейной интерполяцией функции
Ф(х)).
Замечание 2. При определении значений функции Ф(х) для отрица-
тельных величин аргумента х следует использовать тождество
Ф(я) = 1 — Ф(—х).
(П1.4)
Пример П1.2. В условиях примера П1.1 имеем:
ф(хо = 3,36; а = 1; ст2 = 4) = Ф(1,18)
=ф(1,15>+14!—и! Н1-20) - >15>1 = °-881-
1.ZU — 1,10 L J
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
209
Таблица П1.3. Значения g-квантилей uq стандартного нормального распреде-
ления.
Q “9 Q Q Ug Q Ug
0,50 0,000000 0,70 0,524401 0,90 1,281552 0,988 120072
51 025069 71 553385 91 340755 984 144411
52 050154 72 582842 92 405072 0,985 2,170090
53 075270 73 612813 93 475791 986 197286
54 0,55 100434 0,125661 74 0,75 643345 0,674490 94 0,95 да СОСО оооо OO<J 226212 257129
56 150969 76 706303 96 750686 989 290368
57 176374 77 738847 97 880794 0,990 2,326348
58 201893 78 772193 971 895698 991 365618
59 227545 79 806421 972 911036 992 408916
0,60 0,253347 0,80 0,841621 973 926837 993 457263
61 279319 81 877896 974 943134 994 512144
62 305481 82 915365 0,975 1,959964 0,995 2,575829
63 331853 83 954165 976 977368 996 652070
64 358459 84 994458 977 995393 997 747781
0,65 0,385320 0,85 1,036433 978 2,014091 998 878162
66 412463 86 080319 979 033520 999 3,090232
67 439913 87 126391 0,980 2,053749
68 467699 88 174987 981 074855
69 495850 89 226528 982 096927
Пример П1.3. Найти 0,9-квантиль ио,9- Величину ио,9 находим из та-
блицы в графе, расположенной справа от соответствующего значения q = 0,9,
т.е. ио,9 = 1,281552.
Замечание 1. Если заданная величина q попадает между двумя со-
седними табличными значениями gi и дз (<71 < Q2] это может случиться при
графической проверке нормальности распределения), то следует воспользовать-
ся линейной интерполяцией, а именно формулой
= “91 + (U?1 " U’^'
Замечание 2. При нахождении g-квантилей для значений g < 0,5 сле-
дует воспользоваться соотношением uq = Например, ио,4 = — ui-o,4 =
—ио,6 = —0,25335.
Замечание 3. При отыскании 100ф%-ных точек Wq следует восполь-
зоваться соотношением Wq = u^_q. Например, wo,05 = но,95 = 1,64485.
8 Прикладная статистика
в задачах и упражнениях
Таблица 111.4. Значения 10()Q%hijx точек Xq(u) X? распределения с v степс
ням и свободы.
V Q
0.995 0.990 0.975 0.950 0.900 0.100 0.050 0.025 0.010 0.005
1 392704-10'10 157088-10-' 982069-10** 393214-10"' 0.0157908 2,70554 3.84146 5,02389 6,63490 7,87944
2 0,0100251 0,0201007 0,0506356 0,102587 0,210720 4,60517 5,99147 7,37776 9,21034 10,5966
3 0,0717212 0,114832 0,215795 0,351846 0,584375 6,25139 7,81473 9,34840 11,3449 12,8381
4 0,206990 0.297110 0,484419 0,710721 1,063623 7,77944 9,48773 11,1433 13,2767 14,8602
5 0,411740 0,554300 0,831211 1,145476 1,61031 9,23635 11,0705 12,8325 15,0863 16,7496
6 0,675727 0,872085 1,237347 1,63539 2,20413 10,6446 12,5916 14,4494 16,8119 18,5476
7 0,989265 1,239043 1,68987 2,16735 2,83311 12,0170 14,0671 16,0128 18,4753 20,2777
8 1,344419 1,646482 2,17973 2,73264 3,48954 13,3616 15,5073 17,5346 20,0902 21,9550
9 1,734926 2,087912 2,70039 3,32511 4,16816 14,6837 16,9190 19,0228 21,6660 23,5893
10 2,15585 2.55821 3,24697 3,94030 4,86518 15,9871 18,3070 20,4831 23,2093 25,1882
11 2,60321 3,05347 3,81575 4,57481 5,57779 17,2750 19.6751 21,9200 24.7250 26,7569
12 3,07382 3,57056 4,40379 5.22603 6,30380 18,5494 21,0261 23,3367 26,2170 28,2995
13 3.56503 4,10691 5,00874 5,89186 7.04150 19,8119 22,3621 24.7356 27.6883 29,8194
14 4,07468 4,66043 5,62872 6,57063 7,78953 21,0642 23,6848 26,1190 29,1413 31,3193
15 4,60094 5,22935 6,26214 7,26094 8,54675 22,3072 24,9958 27,4884 30,5779 32,8013
16 5,14224 5,81221 6,90766 7.96164 9,31223 23,5418 26,2962 28,8454 31.9999 34,2672
17 5,69724 6,40776 7,56418 8,67176 10,0852 24,7690 27.5871 30.1910 33,4087 35,7185
18 6.26481 7,01491 8,23075 9.39046 10,8649 25,9894 28,8693 31.5264 34,8053 37.1564
19 6.84 398 7,63273 8.90655 10,1170 11,6509 27,2036 30.1435 32.8523 36.1908 38.5822
- 1 U П I. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
20 7,43386 8,26040 9,59083 10,8508 12.4426 28,4120 31.4104 1 34,1696 1 37,5662 39,9968
21 8,03366 8,89720 10,28293 11,5913 13.2396 29,6151 32,6705 35.4789 38.9321 41,4010
22 8,64272 9,54249 10,9823 12,3380 14,0415 30,8133 33,9244 36,7807 40,2894 42.7956
23 9,26042 10,19567 11,6885 13,0905 14,8479 32,0069 35,1725 38.0757 41,6384 44,1813
24 9,88623 10,8564 12.4011 13,8484 15,6587 33,1963 36,4151 39,3641 42,9798 45,5585
25 10,5197 11,5240 13,1197 14.6114 16,4734 34,3816 37,6525 40,6465 44,3141 46,9278
26 11,1603 12,1981 13,8439 15,3791 17,2919 35,5631 38,8852 41.9232 45,6417 48,2899
27 11.8076 12,8786 14,5733 16,1513 18,1138 36,7412 40,1133 43,1944 46,9630 49,-6449
28 12,4613 13,5648 15,3079 16.9279 18,9392 37,9159 41,3372 44,4607 48,2782 50,9933
29 13,1211 14,2565 16,0471 17,7083 19,7677 39,0875 42,5569 45,7222 49,5879 52,3356
30 13,7867 14,9535 16,7908 18,4926 20,5992 40,2560 43,7729 46,9792 50,8922 53,6720
40 2о,7065 22,1643 24,4331 26,5093 29,0505 51,8050 55,7585 59,3417 63,6907 66,7659
50 27,9907 29,7067 32,3574 34,7642 37,6886 63,1671 67,5048 71,4202 76,1539 79,4900
60 35,5346 37,4848 40,4817 43,1879 46,4589 74,3970 79,0819 83,2976 88,3794 91,9517
70 43,2752 45,4418 48,7576 51,7393 55,3290 85.5271 90,5312 95,0231 100,425 104,215
80 51,1720 53,5400 57,1532 60,3915 64,2778 96,5782 101.879 106,629 112,329 116,321
90 59,1963 61,7541 65,6466 69,1260 73,2912 107,565 113.145 118.136 124,116 128,299
100 67,3276 70,0648 74,2219 77,9295 82,3581 118,498 124,342 129.561 135,807 140,169
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.5. Значения 100Q%-hux точек ^-распределения с чи-
слом степеней свободы числителя и знаменателя 1/7.
Vi
V, 1 1 2 1 1 3 1 1 < 1 5 6 1 1 7 1 1 8 1 1 9 1 10 1 12 1 1 15 1 1 20 i 1 2« 1 1 30 1 1 <° 1 60 | 120 м
Q = 0,1
1 39,86 49,50 53,59 55,83 57,24 58,20 58,91 59,44 59,86 60,19 60,71 61,22 61,74 62,00 62,26 62,53 62.79 63,06 63,33
2 8,53 9,00 9,16 9,24 9,29 9,33 9,35 9,37 9,38 9,39 9,41 9.42 9,44 9,45 9,46 9,47 9,47 9,48 9,49
3 5,54 5,46 5,39 5,34 5,31 5,28 5,27 5,25 5,24 5,23 5,22 5,20 5,18 5,18 5,17 5,16 5,15 5,14 5,13
4 4,54 4,32 4,19 4,11 4,05 4,01 3,98 3,95 3,94 3,92 3,90 3,87 3,84 3,83 3,82 3,80 3.79 3.78 3,76
5 4,06 3,78 3,62 3,52 3,45 3,40 3,37 3,34 3.32 3,30 3,27 3,24 3,21 3,19 3,17 3.16 3.14 3,12 3,10
6 3,78 3,46 3,29 3,18 з,н 3,05 3,01 2,98 2,96 2,94 2,90 2,87 2,84 2,82 2,80 2,78 2,76 2,74 2,72
7 3,59 3,26 3,07 2,96 2,88 2,83 2,78 2,75 2,72 2,70 2,67 2,63 2,59 2,58 2,56 2,54 2,51 2,49 2,47
8 3,46 з.н 2,92 2,81 2,73 2,67 2,62 2,59 2,56 2,54 2,50 2,46 2,42 2,40 2,38 2.36 2,34 2,32 2,29
9 3,36 3,01 2,81 2,69 2,61 2,55 2.51 2,47 2,44 2,42 2,38 2,34 2,30 2,28 2,25 2,23 2,21 2,18 2,16
10 3,29 2,92 2,73 2,61 2,52 2,46 2,41 2,38 2,35 2.32 2,28 2,24 2.20 2,18 2,16 2,13 2.11 2,08 2,06
11 3,23 2,86 2,66 2,54 2,45 2,39 2,34 2,30 2,27 2,25 2,21 2,17 2,12 2,10 2,08 2,05 2,03 2,00 1,97
12 3,18 2,81 2,61 2,48 2,39 2,33 2,28 2,24 2,21 2,19 2,15 2,10 2,06 2,04 2,01 1.99 1,96 1,93 1,90
13 3,14 2,76 2,56 2,43 2,35 2,28 2,23 2,20 2,16 2.14 2,10 2,05 2,01 1,98 1,96 1.93 1,90 1,88 1,85
14 3,10 2,73 2,52 2,39 2,31 2,24 2,19 2.15 2,12 2,10 2,05 2,01 1,96 1,94 1.91 1.89 1,86 1,83 1,80
15 3,07 2,70 2,49 2,36 2,27 2,21 2,16 2,12 2,09 2.06 2,02 1,97 1.92 1,90 1,87 1,85 1,82 1,79 1.76
16 3,05 2,67 2,46 2,33 2,24 2,18 2,13 2,09 2,06 2,03 1,99 1,94 1,89 1.87 1,84 1,81 1,78 1,75 1,72
17 3.03 2,64 2 44 2,31 2,22 2,15 2,10 2,06 2,03 2,00 1,96 1.91 1.86 1.84 1.81 1,78 1,75 1,72 1,69
18 3.01 2,62 2,42 2,29 2,20 2,13 2,08 2,04 2 00 1,98 1,93 1,89 1,84 1.81 1,78 1,75 1,72 1,69 1,66
19 2,99 2,61 2,40 2,27 2,18 2,11 2,06 2,02 1,98 1,96 1.91 1,86 1.81 1,79 1.76 1,73 1,70 1,67 1,63
20 2,97 2,59 2,38 2,25 2.16 2,09 2,04 2,00 1.96 1,94 1,89 1.84 1.79 1,77 1.74 1.71 1,68 1.64 1.61
21 2,96 2,57 2,36 2,23 2.14 2.08 2,02 1.98 1,95 1,92 1,87 1,83 1,78 1,75 1.72 1,69 1,66 1,62 1,59
22 2,95 2,56 2,35 2,22 2,13 2,06 2,01 1,97 1,93 1,90 1,86 1,81 1 .76 1,73 1.70 1.67 1,64 1,60 1,57
23 2,94 2,55 2,34 2,21 2.Н 2,05 1,99 1,95 1,92 1,89 1.84 1,80 1 74 1.72 1.69 1.66 1.62 1,59 1,55
24 2,93 2,54 2,33 2,19 2,10 2,04 1,98 1,94 1.91 1,88 1,83 1.78 1.73 1.70 1.67 1.64 1.61 1.57 1,53
212 П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
25 2,92 2,53 2,32 2,18 2,09 2,02 1 .97 1 ,93 1,89 1,87 1.82 1 77 1 .72 1.69 1.66 1 .63 1.59 1.56 1.52
26 2,91 2,52 2,31 2,17 2.08 2.01 1 .96 1,92 1,88 1 .86 1.81 1 .76 1 .71 1.68 1.65 1.61 1 .58 1,54 1 ^50
27 2,90 2,51 2,30 2,17 2,07 2,00 1 ,95 1 .91 1,87 1.85 1.80 1 .75 1.70 1.67 1 .64 1 .60 1 .57 1,53 1,49
28 2,89 2,50 2,29 2,16 2.06 2.00 1 .94 1.90 1,87 1,84 1.79 1 .74 1.69 1.6G 1 .63 1 .59 1.56 1 ,52 1 ,48
29 2,89 2,50 2,28 2,15 2,06 1 .99 1,93 1.89 1,86 1.83 1 .78 1,73 1,68 1.65 1 .62 1,58 1 .55 1,51 1,47
30 2,88 2,49 2,28 2,14 2,05 1 ,98 1.93 1,88 1,85 1,82 1,77 1 .72 1,67 1.64 1 .61 1,57 1,54 1,50 1,46 1,38 1,29 1,19
40 2,84 2,44 2,23 2,09 2,00 1.93 1,87 1,83 1,79 1.76 1.71 1.66 1,61 1.57 1.54 1,51 1,47 1,42
60 2,79 2,39 2,18 2,04 1.95 1,87 1,82 1.77 1.74 1.71 1 .66 1.60 1.54 1.51 1,48 1,44 1,40 1,35
120 2,75 2,35 2,13 1,99 1.90 1,82 1.77 1.72 1.68 1,65 1.60 1,55 1,48 1,45 1.41 1,37 1,32 1,26
оо 2,71 2,30 2.08 1,94 1 .85 1 .77 1.72 1,67 1,63 1.60 1,55 1,49 1.42 1,38 1,34 1,30 1.24 1.17 1*00
Q=0,05
1 161,4 199,5 215.7 224,6 230,2 234,0 236,8 238,9 240,5 241.9 243,9 245.9 248,0 249,1 250,1 251,1 252,2 253,3 254 3
2 18,51 19,00 19,16 19,25 19.30 19,33 19,35 19,37 19,38 19.40 19,41 19.43 19,45 19,45 19,46 19,47 19,48 19,49 19.50
3 10,13 9,55 9,28 9,12 9.01 8,94 8,89 8,85 8,81 8,79 8,74 8,70 8,66 8,64 8,62 8,59 8,57 8,55 8*53
4 7.71 6,94 6,59 6,39 6.26 6,16 6,09 6,04 6,00 5.96 5,91 5,86 5,80 5,77 5.75 5,72 5,69 5,66 5,*63
5 6,61 5,79 5,41 5,19 5,05 4.95 4,88 4.82 4.77 4.74 4,68 4,62 4,56 4,53 4.50 4,46 4,43 4,40 4.36
6 5,99 5,14 4,76 4,53 4,39 4,28 4,21 4,15 4,10 4,06 4,00 3.94 3,87 3,84 3.81 3,77 3,74 3,70 3*67
7 5,59 4,74 4,35 4.12 3.97 3,87 3,79 3.73 3,68 3,64 3,57 3,51 3,44 3.41 3,38 3,34 3.30 3,27 3 23
8 5,32 4,46 4,07 3,84 3,69 3,58 3,50 3,44 3,39 3.35 3,28 3,22 3,15 3,12 3,08 3,04 3.01 2,97 2 93
9 5.12 4,26 3,86 3,63 3.48 3,37 3,29 3,23 3,18 3.14 3,07 3.01 2,94 2,90 2,86 2,83 2,79 2,75 2,71
10 4,96 4,10 3,71 3,48 3,33 3,22 3.14 3,07 3,02 2.98 2.91 2.85 2,77 2,74 2.70 2,66 2.62 2,58 2,54
11 4,84 3.98 3,59 3,36 3,20 3,09 3,01 2,95 2,90 2.85 2.79 2.72 2,65 2.61 2,57 2,53 2,49 2,45 2,40
12 4.75 3,89 3,49 3,26 3.11 3,00 2,91 2,85 2,80 2,75 2,69 2,62 2.54 2,51 2,47 2,43 2,38 2,34 2.30
13 4,67 3,81 3.41 3,18 3,03 2,92 2,83 2.77 2,71 2,67 2,60 2.53 2,46 2.42 2,38 2,34 2.30 2,25 2*21
14 4.60 3,74 1 3,34 з.н 2,96 2,85 2,76 2,70 2,65 2,60 2,53 2.46 2,39 2.35 2.31 2,27 2,22 2,18 2*13
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 213
Продолжение таблицы П 1.5
V|
VI 2 3 5 6 1 7 I ’ 1 9 1 10 | 1 12 1 1 151 1 20 1 1 2< 1 1 30 i 1 1 60 | 120 1 -
15 4,54 3,68 3,29 3,06 2.90 2,79 2.71 2,64 2,59 2,54 2.48 2,40 2,33 2,29 2,25 2,20 2,16 2,11 2,07
16 4,49 3,63 3,24 3,01 2.85 2,74 2,66 2.59 2,54 2,49 2,42 2.35 2,28 2,24 2,19 2,15 2,11 2,06 2,01
17 4,45 3,59 3,20 2,96 2,81 2.70 2,61 2,55 2,49 2,45 2,38 2,31 2,23 2,19 2,15 2,10 2,06 2,01 1,96
18 4.41 3,55 3,16 2.93 2,77 2,66 2.58 2,51 2,46 2,41 2.34 2 27 2,19 2,15 2.11 2,06 2,02 1,97 1,92
19 4,38 3,52 3,13 2,90 2,74 2.63 2,54 2,48 2,42 2,38 2,31 2.23 2,16 2,11 2,07 2,03 1,98 1,93 1,88
20 4,35 $.49 3,10 2,87 2.71 2.60 2,51 2.45 2,39 2,35 2,28 2.20 2,12 2,08 2,04 1,99 1,95 1.90 1,84
21 4,32 3,47 3,07 2,84 2,68 2,57 2,49 2,42 2,37 2,32 2,25 2,18 2,10 2,05 2,01 1,96 1,92 1,87 1.81
22 4,30 3,44 3,05 2,82 2,66 2,55 2.46 2,40 2,34 2,30 2,23 2.15 2,07 2.03 1,98 1,94 1,89 1,84 1.78
23 4,28 3,42 3,03 2,80 2,64 2,53 2,44 2,37 2,32 2,27 2.20 2,13 2.05 2,01 1,96 1,91 1,86 1,81 1,76
24 4,26 3,40 3,01 2.7Й 2,62 2,51 2,42 2,36 2,30 2,25 2.18 2,11 2,03 1,98 1,94 1,89 1,84 1,79 1,73
25 4,24 3,39 2,99 2,76 2,60 2,49 2,40 2,34 2,28 2,24 2.16 2,09 2,01 1,96 1,92 1,87 1,82 1.77 1,71
26 4,23 3,37 2,98 2.74 2,59 2,47 2,39 2,32 2,27 2,22 2,15 2.07 1,99 1,95 1,90 1,85 1,80 1,75 1,69
27 4,21 3,35 2,96 2,73 2,57 2,46 2.37 2,31 2.25 2,20 2.13 2.06 1.97 1.93 1,88 1,84 1,79 1,73 1.67
28 4,20 3,34 2,95 2,71 2,56 2,45 2.36 2.29 2,24 2,19 2.12 2,04 1,96 1,91 1,87 1,82 1.77 1.71 1,65
29 4,18 3,33 2,93 2,70 2,55 2,43 2,35 2,28 2,22 2.18 2.10 2.03 1,94 1.90 1,85 1,81 1,75 1,70 1,64
30 4,17 3,32 2,92 2,69 2,53 2,42 2,33 2,27 2,21 2,16 2.09 2.01 1,93 1,89 1,84 1.79 1,74 1.68 1,62
40 4,08 3,23 2,84 2,61 2,45 2.34 2,25 2,18 2,12 2,08 2,00 1,92 1,84 1.79 1,74 1,69 1,64 1,58 1,51
60 4,00 3,15 2,76 2,53 2,37 2,25 2,17 2,10 2,04 1,99 1.92 1,84 1,75 1,70 1,65 1,59 1,53 1,47 1,39
120 3,92 3,07 2,68 2,45 2,29 2,17 2,09 2,02 1,96 1.91 1 ,83 1,75 1,66 1,61 1,55 1,50 1,43 1,35 1,25
со 3,84 3,00 2,60 2,37 2,21 2,10 2,01 1,94 1,88 Q = 1,83 = 0,01 1,75 1,67 1.57 1,52 1,46 1,39 1,32 1,22 1,00
1 4052 <999.5 5403 5625 5764 5859 5928 5982 6022 6056 6106 6157 6209 6235 6261 6287 6313 6339 6366
2 98,50 99,00 99,17 99,25 99,30 99,33 99.36 99,37 99,39 99,40 99.42 99.43 99,45 99,46 99,47 99,47 99.48 99,49 99,50
3 34,12 30,82 29,46 28.71 28.24 27,91 27,67 27.49 27.35 27,23 27,05 26.87 26.69 26.60 26,50 26,41 26,32 26,22 26,13
4 21,20 18,00 16,69 15,98 15,52 15,21 14,98 14,80 14,66 14.55 14,37 14,20 14,02 13,93 13,84 13,75 Г3.65 13,56 13,46
214 П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
5 16.26 13,27 12,06 11,39 10.97 10.67 10.46 10.29 10.16 10,05 9.89 9.72 9.55 9.47 9,38 9,29 9.20 9.Н 9.02
6 13,75 10,92 9.78 9.15 8.75 8,47 8.26 8.10 7,98 7.87 7,72 7.56 7.40 7.31 7.23 7.14 7.06 6,97 6,88
7 12,25 9.55 8.45 7.85 7,46 7.19 6.99 6.84 6.72 6.62 6,47 6.31 6.16 6,07 5,99 5.91 5,82 5.74 5,65
8 11.26 8.65 7.59 7.01 6.63 6.37 6,18 6,03 5.91 5.81 5,67 5.52 5.36 5.28 5,20 5,12 5,03 4.95 4.86
9 10,56 8,02 6.99 6.42 6,06 5,80 5.61 5,47 5,35 5.26 5,11 4,96 4,81 4.73 4,65 4,57 4.48 4,40 4.31
10 10,04 7.56 6.55 5,99 5,64 5,39 5.20 5,06 4,94 4.85 4.71 4,56 4.41 4,33 4.25 4.17 4.08 4.00 3.91
Н 9.65 7,21 6,22 5,67 5.32 5.07 4.89 4,74 4,63 4,54 4.40 4.25 4.10 4,02 3.94 3.86 3,78 3.69 3.60
12 9.33 6.93 5,95 5,41 5.06 4,82 4,64 4,50 4.39 4.30 4.16 4,01 3,86 3,78 3.70 3.62 3,54 3,45 3,36
13 9.07 6.70 5.74 5.21 4.86 4,62 4,44 4,30 4,19 4,10 3.96 3,82 3,66 3,59 3,51 3,43 3.34 3,25 3,17
14 8,86 6,51 5.56 5,04 4.69 4,46 4,28 4,14 4.03 3.94 3,80 3,66 3,51 3,43 3,35 3,27 3,18 3.09 3,00
15 8.68 6,36 5,42 4,89 4,56 4.32 4,14 4,00 3,89 3.80 3,67 3,52 3,37 3,29 3.21 3,13 3,05 2.96 2,87
16 8,53 6,23 5,29 4.77 4.44 4,20 4,03 3,89 3,78 3.69 3,55 3,41 3,26 3,18 3,10 3,02 2,93 2,84 2,75
17 8,40 6.11 5,18 4,67 4.34 4,Ю 3,93 3,79 3,68 3,59 3,46 3,31 3.16 3,08 3,00 2,92 2.83 2.75 2,65
18 8,29 6,01 5,09 4.58 4.25 4,01 3.84 3.71 3,60 3.51 3,37 3,23 3,08 3,00 2,92 2,84 2,75 2.66 2,57
19 8,18 5,93 5,01 4,50 4.17 3,94 3,77 3.63 3,52 3.43 3,30 3,15 3,00 2,92 2,84 2,76 2,67 2.58 2,49
20 8,10 5,85 4,94 4,43 4,10 3,87 3,70 3,56 3,46 3.37 3,23 3.09 2,94 2,86 2,78 2,69 2.61 2,52 2,42
21 8,02 5,78 4,87 4,37 4,04 3,81 3,64 3,51 3,40 3.31 3,17 3,03 2,88 2,80 2,72 2,64 2,55 2,46 2,36
22 7,95 5,72 4,82 4,31 3,99 3,76 3,59 3,45 3,35 3.26 3,12 2,98 2,83 2.75 2,67 2,58 2,50 2,40 2,31
23 7,88 5,66 4.76 4,26 3,94 3,71 3,54 3,41 3,30 3.21 3,07 2,93 2.78 2.70 2,62 2,54 2.45 2,35 2,26
24 7,82 5,61 4,72 4,22 3,90 3,67 3,50 3,36 3,26 3.17 3,03 2,89 2.74 2,66 2,58 2.49 2,40 2.31 2,21
25 7.77 5,57 4,68 4.18 3,85 3,63 3,46 3,32 3,22 3.13 2.99 2,85 2,70 2,62 2,54 2,45 2,36 2,27 2,17
26 7,72 5,53 4.64 4.14 3,82 3.59 3.42 3,29 3,18 3.09 2,96 2,81 2.66 2.58 2.50 2.42 2,33 2.23 2,13
27 7,68 5,49 4,60 4,11 3,78 3.56 3,39 3,26 3,15 3.06 2,93 2,78 2,63 2.55 2,47 2,38 2,29 2,20 2,10
28 7.64 5,45 4,57 4,07 3,75 3,53 3,36 3,23 3,12 3.03 2,90 2,75 2,60 2,52 2,44 2,35 2.26 2.17 2.06
29 7,60 5,42 4.54 4,04 3.73 3,50 3,33 3,20 3,09 3,00 2,87 2,73 2.57 2,49 2,41 2,33 2,23 2.14 2,03
30 7,56 5,39 4.51 4,02 3,70 3.47 3,30 3.17 3.07 2.98 2,84 2.70 2,55 2.47 2.39 2.30 2,21 2.11 2,01
40 7,31 5,18 4.31 3,83 3,51 3,29 3,12 2,99 2,89 2.80 2.66 2.52 2.37 2,29 2,20 2.11 2.02 1,92 1,80
60 7,08 4.98 4.13 3.65 3,34 3,12 2,95 2,82 2,72 2.63 2,50 2,35 2,20 2.12 2,03 1.94 1.84 1,73 1.60
120 6,85 4,79 3.95 3.48 3,17 2,96 2,79 2,66 2.56 2.47 2,34 2.19 2,03 1.95 1,86 1.76 1,66 1.53 1.38
ОО 6.63 4,61 3,78 3.32 3,02 2,80 2,64 2,51 2.41 2.32 2,18 2.04 1.88 1.79 1.70 1.59 1.47 1.32 1.00
Примечание.
При вычислении 100%-ных точек для Q 0,9 следует
воспользоваться тождеством v^(a/ba/3) = (v’_Q(*/a, и ))“ 1 •
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 215
216
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.6. Значения 1000%-ных точек распределения Стьюдента с
4/ степенями свободы.
V Q-О.ч 2Q—0.3 0.25 0,5 0 , 1 0, 2 0.05 0. 1 0.025 0,05 0.01 0, 02 0. 005 0.01 0.00?5 0,005
1 0,325 1 ,000 3,078 6,314 12,700 31,821 63,657 127.32
2 289 0,816 1,886 2,920 4,303 6,965 9,925 14.089
3 277 765 1 ,638 2,353 3,182 4,541 5,841 7.453
4 271 741 1,533 2,132 2,776 3,747 4,604 5,598
5 0,207 0,727 1,476 2,015 2,571 3,365 4,032 4 ,773
6 205 718 1 ,440 1 ,943 2,447 3,143 3,707 4,317
7 203 71 1 1.415 1 ,895 2,365 2,998 3,499 4.029
8 202 706 1 ,397 1 ,860 2,306 2,896 3,355 3,833
9 201 703 1 ,383 1 ,833 2,262 2,821 3,250 3.690
10 0,260 0,700 1 ,372 1,812 2,228 2,764 3, 169 3,58 1
1 1 260 697 1 ,363 1 ,796 2,201 2,718 3, 106 3 ,497
12 259 695 1 ,356 1 ,782 2,179 2,681 3,055 3 .428
13 259 694 1 ,350 1 ,771 2,160 2,650 3,012 3.372
14 258 692 1,345 1,761 2,145 2,624 2 ,977 3.326
15 0,258 0.691 1,341 1 ,753 2,131 2,602 2 ,947 3.286
16 258 690 1,337 1 ,746 2,120 2,583 2.921 3 .252
17 257 689 1,333 1,740 2,110 2,567 2 ,898 3 .222
18 257 688 1 ,330 1 ,734 2,101 2,552 2,878 3 . 197
19 257 688 1,328 1,729 2,093 2,539 2,861 3.174
20 0,257 0,687 1,325 1 ,725 2,086 2,528 2,845 3. 153
21 257 686 1,323 1,721 2,080 2,518 2,831 3. 135
22 256 686 1,321 1,717 2,074 2,508 2,819 3. 119
23 256 685 1,319 1,714 2,069 2,500 2,807 3,104
24 256 685 1,318 1,711 2,064 2,492 2,797 3.091
25 0,256 0,684 1 ,316 1,708 2,060 2,485 2,787 3.078
25 256 684 1 ,315 1.706 2,056 2,479 2,779 3.067
27 256 684 1,314 1,703 2,052 2,473 2,771 3.057
28 256 683 1,313 1,701 2,048 2,467 2,763 3 .047
29 256 683 1 ,311 1,699 2,045 2,462 2,756 3.038
30 0,256 0,683 1 ,310 1,697 2,042 2,457 2,750 3.030
40 255 681 1,303 1,684 2,021 2,423 2 ,704 2.971
60 254 679 1,296 1,671 2,000 2,390 2,660 2,915
120 254 677 1,289 1,658 1,980 2,358 2,617 2.860
оо 253 674 1 ,282 1,645 1 ,960 2,326 2.576 2,807
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
217
Таблица П1.7. Преобразование Фишера (^-преобразование) выборочного коэф-
фициента корреляции г (л = arcthr).
г , 000 , 002 . 004 , 006 .008 Г . 000 , 002 , 004 , 006 , 008
0,00 0000 0020 0040 0060 0080 0,50 5493 5520 5547 5573 5600
1 0100 0120 0140 0160 0180 1 5627 5654 5682 5709 5736
2 0200 0220 0240 0260 0280 2 5763 5791 5818 5846 5874
3 0300 0320 0340 0360 0380 3 5901 5929 5957 5985 6013
4 0400 0420 0440 0460 0480 4 6042 6070 6098 6127 6155
0.05 0500 0520 0541 0561 0581 0,55 6184 6213 6241 6270 6299
6 0601 0621 0641 0661 0681 6 6328 6358 6387 6416 6446
7 0701 0721 0741 0761 0782 7 6475 6505 6535 6565 6595
8 0802 0822 0842 0862 0882 8 6625 6655 6685 6716 6746
9 0902 0923 0943 0963 0983 9 6777 6807 6838 6869 6900
0,10 1003 1024 1044 1064 1084 0,60 6931 6963 6994 7026 7057
1 1104 1125 1145 1165 1186 1 7089 7121 7153 7185 7218
2 1206 1226 1246 1267 1287 2 7250 7283 7315 7348 7381
3 1307 1328 1348 1368 1389 3 7414 7447 7481 7514 7548
4 1 409 1430 1450 1471 1491 4 7582 7616 7650 7684 7718
0, 15 1511 1532 1552 1573 1593 0,65 7753 7788 7823 7858 7893
6 1614 1634 1655 1676 1696 6 7928 7964 7999 8035 8071
7 1717 1737 1758 1779 1799 7 8107 8144 8180 8217 8254
8 1820 1841 1861 1882 1903 8 8291 8328 8366 8404 8441
9 1923 1944 1965 1986 2007 9 8480 8518 8556 8595 8634
0,20 2027 2048 2069 2090 2111 0.70 8673 8712 8752 8792 8832
1 2132 2153 2174 2195 2216 1 8872 8912 8953 8994 9035
2 2237 2258 2279 2300 2321 2 9076 9118 9160 9202 9245
3 2342 2363 2384 2405 2427 3 9287 9330 9373 9417 9461
4 2448 2469 2490 2512 2533 4 9505 9549 9594 9639 9684
0,25 2554 2575 2597 2618 2640 0,75 0,973 0,978 0,982 0,987 0,991
6 2661 2683 2704 2726 2747 6 0,996 1,001 1,006 1,011 1 ,015
7 2769 2790 2812 2833 2855 7 1 ,020 1,025 1,030 1,035 1 ,040
8 2877 2899 2920 2942 2964 8 1 ,045 1 ,050 1 ,056 1 ,061 1 ,066
9 2986 3008 3029 3051 3073 9 1,071 1,077 1,082 1,088 1 ,093
0,30 3095 3117 3139 3161 3183 0,80 1,099 1,104 1,110 1,116 1 . 121
1 3205 3228 3250 3272 3294 1 1,127 1,133 1,139 1,145 1,151
2 3316 3339 3361 3383 3406 2 1,157 1,163 1 ,169 1,175 1,182
3 3428 3451 3473 3496 3518 3 1,188 1,195 1,201 1,208 1,214
4 3541 3564 3586 3609 3632 4 1 ,221 1,228 1,235 1,242 1 ,249
0,35 3654 3677 3700 3723 3746 0,85 1 ,256 1,263 1 ,271 1,278 1,286
6 3769 3792 3815 3838 3861 6 1 ,293 1,301 1 ,309 1 ,317 1 ,325
7 3884 3907 3931 3954 3977 7 1,333 1,341 1,350 1,358 1 ,367
8 4001 4024 4047 4071 4094 8 1 ,376 1 .385 1 ,394 1,403 1 ,412
9 4118 4142 4165 4189 4213 9 1,422 1,432 1,442 1 ,452 1,462
218
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Продолжение табл. П1.7.
т ,000 ,002 ,004 ,006 ,008 Г ,000 ,002 ,004 ,006 ,008
0,40 4236 4260 4284 4308 4332 0,90 1,472 1,483 1,494 1,505 1,516
1 4356 4380 4404 4428 4453 1 1,528 1,539 1,551 1,564 1,576
2 4477 4501 4526 4550 4574 2 1,589 1,602 1,616 1,630 1,644
3 4599 4624 4648 4673 4698 3 1,658 1,673 1,689 1,705 1,721
4 4722 4747 4772 4797 4822 4 1,738 1,756 1,774 1,792 1,812
0,45 4847 4872 4897 4922 4948 0,95 1,832 1,853 1,874 1,897 1,921
6 4973 4999 5024 5049 5075 6 1,946 1,972 2,000 2,029 2,060
7 5101 5126 5152 5178 5204 7 2,092 2,127 2,165 2,205 2,249
8 5230 5256 5282 5308 5334 8 2,298 2,351 2,410 2,477 2,555
9 5361 5387 5413 5440 5466 9 2,647 2,759 2,903 3,106 3,453
Г ,000 ,002 ,004 ,006 ,008 т ,000 ,002 ,004 ,006 ,008
Указание. При работе с отрицательными значениями г и z исполь-
зуйте свойство нечетности функций th z и arcth г, т.е. arcth (-г) =
-arcth г.
Примеры.
1. Дано f — 0,206. Определить z = arcth 0,206.
Находим (в левом столбце таблицы) строку, соответствующую г =
0,20. Чтобы получить заданное значение г, к 0,20 надо прибавить 0,006, а
потому искомое число находится (в этой строке) в столбце, расположенном
под 0,006. Итак, z = arcth 0,2090.
2. Дано г = -0,515. Определить z = arcth (-0,515).
Находим (в левом столбце таблицы) строку, соответствующую г =
0,51. Чтобы получить значение г = 0,515, к 0,51 надо прибавить 0,005,
а потому arcth 0,515 находится как среднее арифметическое двух чисел
данной строки, расположенных в столбцах, соответствующих верхним ин-
дексам 0,006 и 0,004, т. е.
.t л мг 0,5709 + 0,5682 п
arcth 0,515 =------—2---= 0,56955.
Соответственно, z = arcth (-0,515) = -arcth 0,515 = -0,56955.
3. Дано z = 0,8752. Определить г = th z.
Находим в таблице число, равное 0,8752, и определяем, какому значе-
нию г оно соответствует. В нашем случае г = 0,704.
Примечание. В тех случаях, когда в таблице не найдется в
точности заданного, берут два приближенных (ближайших к нему) зна-
чения — с недостатком и с избытком. Искомое значение г будет лежать
между двумя значениями fi и г?, соответствующими этим приближенным
величинам z.
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
219
Таблица П1.8. Верхняя граница доверительного интервала для истинного зна-
чения коэффициента корреляции при условии отсутствия ли-
нейной корреляционной связи (при доверительной вероятности
Р = 1 - 2Q).
Q
л — 2 0,05 0,025 0,01 0, 005 0,0025 0,0005
1 0,9877 0,9*692 0,9*507 0,9’877 0,9*692 0,9*877
2 9000 9500 9800 9’000 9’500 9*000
3 805 878 9343 9587 9740 9’114
4 729 811 882 9172 9417 9741
5 669 754 833 875 9056 9509
6 0,621 0,707 0,789 0,834 0,870 0,9249
7 582 666 750 798 836 898
8 549 632 715 765 805 872
9 521 602 685 735 776 847
10 497 576 658 708 750 823
1 1 0,476 0,553 0,634 0,684 0,726 0,801
12 457 532 612 661 703 780
13 441 514 592 641 683 760
14 426 497 574 623 664 742
15 412 482 558 606 647 725
16 0,400 0,468 0,543 0,590 0,631 0,708
17 389 456 529 575 616 693
18 378 444 516 561 602 679
19 369 433 503 549 589 665
20 360 423 492 537 576 652
25 0,323 0,381 0,445 0,487 0,524 0,597
30 296 349 409 449 484 554
35 275 325 381 418 452 519
40 257 304 358 393 425 490
45 243 288 338 372 403 465
50 0,231 0,273 0,322 0,354 0,384 0,443
60 211 250 295 325 352 408
70 195 232 274 302 327 380
80 183 217 257 283 307 357
90 173 205 242 267 290 338
100 164 195 230 254 276 321
Примечание. Верхний индекс (2,3 и т. д.) над цифрой 9 оз’
начает, что эта цифра занимает первые 2*3 и т. д. разряда десятичной
дроби. Например, 0,9*692 в 0,9999692.
Пример. Если мы оцениваем корреляционную связь по п » 20
наблюдениям, то при доверительной вероятности Р ® 0,95 (т. е. при
2Q = 0,05) значение коэффициента корреляции, не превосходящее по
абсолютной величине 0,444, еще не говорит о статистической значимости
этой корреляционной связи (т. е. о том, что истинное значение
коэффициента корреляции г отлично от нуля).
220
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.9.
Проверка статистической значимости корреляционной связи
с помощью рангового коэффициента корреляции Спирмэна т(5)
д » 4 л=5 Лаб л«7 л = 8 л = 9 Л = 1 0
5с Q 5с <? sc Q 5с Q sc Q sc Q sc Q
12 0,458 22 0,475 50 0,210 74 0,249 108 0,250 156 0,218 208 0,233
14 375 24 392 52 178 78 198 114 195 164 168 218 184
16 208 26 342 54 149 82 151 120 150 172 125 228 139
18 167 28 258 56 121 86 118 126 108 180 089 238 102
20 042 30 225 58 088 90 083 132 076 188 060 248 072
32 0,175 60 0,068 94 0,055 138 0,048 196 0,038 258 0.048
34 117 62 051 98 033 144 029 204 022 268 030
36 067 64 029 102 017 150 014 212 ОН 278 017
38 042 66 017 106 0062 156 0054 220 0041 288 0087
40 0083 68 0083 ПО 0014 162 ООН 228 0010 298 0036
70 0,0014 308 0,001
20 40 70 112 168 240 330
Таблица П1.10.
Проверка статистической значимости корреляционной связи
с помощью рангового коэффициента корреляции Кендалла
п SK п
4 5 8 9 6 7 10
0 0,625 0,592 0,548 0,540 1 0,500 0,500 0,500
2 375 408 452 460 3 360 386 431
4 167 242 360 381 5 235 281 364
6 042 117 274 306 7 136 191 300
8 042 199 238 9 068 119 242
10 0,0083 0,138 0,179 11 0,028 0,068 0, 190
12 089 130 13 0083 035 146
14 054 090 15 0014 015 108
16 031 060 17 0054 078
18 016 038 19 0014 054
20 0,0071 0,022 21 0,0002 0,036
22 0028 012 23 023
24 0009 0063 25 014
26 0002 0029 27 0083
28 0012 29 0046
30 0,0004 31 0,0023
33 001 1
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
221
Таблица П1.11*. Вероятности того, что критическая статистика проверки
статистической значимости выборочной величины коэффи-
циента конкордации И'(т) достигнет или превзойдет та-
бличное значение S (при п = 3 сравниваемых объектах).
$ т ™ 2 т а 3 тп— 4 ГЛяи 6 /п«в7 т=» 8 т «в 9 т- 10
0 1 ,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1 ,000
2 0,833 0,944 0,931 0,954 0,956 0,964 0,967 0,971 0,974
6 0,500 0,528 0,653 0,691 0,740 0,768 0,794 0,814 0,830
8 0,167 0,361 0,431 0,522 0,570 0,620 0,654 0,685 0,710
14 0,194 0,273 0,367 0,430 0,486 0,531 0,569 0,601
18 0,028 0,125 0,182 0,252 0,305 0,355 0,398 0,436
24 0,069 0,124 0,184 0,237 0,285 0,328 0,368
26 0,042 0,093 0,142 0,192 0,236 0,278 0,316
32 0,0046 0,039 0,072 0,112 0,149 0,187 0,222
38 0,024 0,052 0,085 0,120 0,154 0,187
42 0,0085 0,029 0,051 0,079 0,107 0,135
50 0,0*77 0,012 0,027 0,047 0,069 0,092
54 0,0081 0,021 0,038 0,057 0,078
56 0,0055 0,016 0,030 0,048 0,066
62 0,0017 0,0084 0,018 0,031 0,046
72 0,0313 0,0036 0,0099 0,019 0,030
74 0,0027 0,0080 0,016 0,026
78 0,0012 0,0048 0,010 0,018
86 0,0*32 0,0024 0,0060 0,012
96 0,0*32 0,0011 0,0035 0,0075
98 0,0*21 0,0*86 0,0029 0,0063
104 0,0*26 0,0013 0,0034
1 14 0,0*61 0,0*66 0,0020
122 0,0*61 0,0*35 0,0013
0,0*61 0,0*20 0,0*83
126 128 0,0*36 0,0*97 0,0*51
134 0,0*54 0,0*37
146 0,0*11 0,0*18
150 0,0*11 0,0*11
152 0,0*11 0,0*85
158 0,0*11 0,0*44
162 0,0*60 0,0*20
168 0,0*11
182 0,0*21
200 0,0’99
222
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Продолжение
Вероятность того, что данное значение S будет достигнуто
или превзойдено, для я«4, ffiej к т-5
/ПавЗ /71 «л 5
1 1,000 1,000 61 0,055
3 0,958 0,975 65 0,044
5 0,910 0,944 67 0,034
9 0,727 0,857 69 0,031
И 0,608 0,771 73 0,023
13 0,524 0,709 75 0,020
17 0,446 0,652 77 0,017
19 0,342 0,561 81 0,012
21 0,300 0,521 83 0,0087
25 0,207 0,445 85 0.0067
27 0,175 0,408 89 0,0055
29 0,148 0,372 91 0,003!
33 0,075 0,298 93 0,0023
35 0,054 0,260 97 0.0013
37 0,033 0,226 99 0.0015
41 0,017 0,210 101 0,0014
43 0,0017 0,162 105 О.СЯ&Ч
45 0,0017 0,141 107 О,(УЗЗ
49 0,123 109 0,0’21
51 0,107 113 0.0» 14
53 0,093 117 0,0*48
57 0,075 125 0.0^30
59 0,067
П родолжен'-е
Вероятность того, что данное значение $ будет достигнуто
или превзойдено, для Л"4 н /п»2, пх“4 и
т—2 т»4 /Павб $ ,71 жб
0 1,000 1,000 1,000 82 0,035
2 0,958 0,992 0,996 84 0,032
4 0,833 0,928 0,957 86 0,029
6 0,792 0,900 0,940 88 0,023
8 0,625 0,800 0,874 90 0,022
10 0,542 0,754 0,844 94 0,017
12 0,458 0,677 0,789 96 0,014
14 0,375 0,649 0,772 98 0,013
16 0,208 0,524 0,679 100 0,010
18 0,167 0,508 0,668 102 0,0096
20 0,042 0,432 0,609 104 0,0085
22 0,389 0,574 106 0,0073
24 0,355 0,541 108 0,0061
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
223
Продолжение Таблицы П1.11*
/л» 2 /л «а 4 /Лав 6 /И ав 6
26 0,324 0,512 но 0,0057
30 0,242 0,431 114 0,0040
32 0,200 0,386 116 0,0033
34 0,190 0,375 118 0,0028
36 0,158 0,338 120 0,0023
38 0,141 0,317 122 0,0020
40 0,105 0,270 126 0,0015
42 0,094 0,256 128 0,0*90
44 0,077 0,230 130 0,0*87
46 0,068 0,218 132 0,0*73
48 0,054 0,197 134 0,0*65
50 0,052 0,194 136 0,0*40
52 0,036 0,163 138 0,0*36
54 0,033 0,155 140 0,0*28
56 0,019 0,127 144 0,0*24
58 0,014 0,114 146 0,0*22
62 0,012 0,108 148 0,0*12
64 0,0069 0,089 150 0,0*95
66 0,0062 0,088 152 0,0*62
68 0,0027 0,073 154 0,0*46
70 0,0027 0,066 158 0,0*24
72 0,0016 0,060 160 0,0*16
74 0,0*94 0,056 162 0,0*12
76 0,0*94 0,043 164 0,0*80
78 0,0*94 0,041 170 0,0*24
80 0.0*72 0,037 180 0,0*13
Продолжение
Вероятность того, что данное значение S будет достигнуто
или превзойдено, для л — 5 и /п—3
5 /л = 3 /Лав 3 Л' /Л авЗ 5 т «в 3
0 1,000 22 0,649 44 0,236 66 0,038
2 1,000 24 0,595 46 0,213 68 0,028
4 0,988 26 0,559 48 0,172 70 0,026
6 0,972 28 0,493 50 0,163 72 0,017
8 0,941 30 0.475 52 0,127 74 0,015
10 0,914 32 0,432 54 0,117 76 0,0078
12 0,845 34 0,406 56 0,096 78 0,0053
14 0,831 36 0.347 58 0,080 80 0,0040
16 0,768 38 0,326 60 0,063 82 0,0028
18 0,720 40 0,291 62 0,056 86 0,0*90
20 0.682 42 0.253 64 0,045 90 0,0*69
224
П 1. ТАБЛИЦЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Таблица П1.116. Критические значения статистики S при уровне значимости
а = 0,05 для проверки статистической значимости выбороч-
ного значения коэффициента конкордации W(m).
т п Дополнительные значения для п = 3
3 4 5 6 7 тп S
3 64,4 103,9 157,3 9 54,0
4 49,5 88,4 143,3 217,0 12 71,9
5 62,6 112,3 182,4 276,2 14 83,8
6 75,7 136,1 221,4 335,2 16 95,8
8 48,1 101,7 183,7 299,0 453,1 18 107,7
10 60,0 127,8 231,2 376,7 571,0
15 89,8 192,9 349,8 570,5 864,9
20 119,7 258,0 468,5 764,4 1158,7
ПРИЛОЖЕНИЕ 2. ИСХОДНЫЕ СТАТИСТИЧЕСКИЕ
ДАННЫЕ
Таблица П2.1. Характеристики с/х производства по 20-ти районам области
г (номер района) 41’ 4!) 43) х(4} J5) •I/ •
1 1,59 0,26 2,05 0,32 0,14
2 0,34 0,28 0,46 0,59 0,66
3 2,53 0,31 2,46 0,30 0,31
4 4,63 0,40 6,44 0,43 0,59
5 2,16 0,26 2,16 0,39 0,16
6 2,16 0,30 2,69 0,32 0,17
7 0,68 0,29 0,73 0,42 0,23
8 0,35 0,26 0,42 0,21 0,08
9 0,52 0,24 0,49 0,20 0,08
10 3,42 0,31 3,02 1,37 0,73
11 1,78 0,30 3,19 0,73 0,17
12 2,40 0,32 3,30 0,25 0,14
13 9,36 0,40 11,51 0,39 0,38
14 1,72 0,28 2,26 0,82 0,17
15 0,59 0,29 0,60 0,13 0,35
16 0,28 0,26 0,30 0,09 0,15
17 1,64 0,29 1,44 0,20 0,08
18 0,09 0,22 0,05 0,43 0,20
19 0,08 0,25 0,03 0,73 0,20
20 1,36 0,26 0,17 0,99 0,42
Таблица П2.2. Характеристики качества жизни по 15-ти странам мира
(/) N-/N- ПН Страны <|) (iNC.S) ВВП на душу <*> реальный рост ВВП Пыс J) личи, конечн потребл. на душу г,'1' (%) уровень инфляции (тыс.$) произво- дит. труда (на 1 раб.) (лег) ср продолж жизни (. долях от 1) индекс чел. разв. доля доходов у 20% бога- тых т (го) уровень безрабо- тицы iiei рамотнык (баллы) качество жизни
1 Австрия 6/20.46 5/1,14 6/15,99 5/2.30 5/62.98 9-10/76.2 8-9/0.925 5/38.00 4/4.50 8-9-10-11/2.0 2/9,17
2 Англия 11/17,92 3/1,62 9/11,98 Ю/3,30 10/43.25 9-10/76.2 11/0,916 12/44.30 9/8.10 5-6-7/1,0 10/6.85
3 Бразилия 13/5,74 13/2.15 14/73.80 12/7/34 15/66,3 14/0.804 15/67.50 5/4.60 14/16.7 13/4,30
4 Германия 8/19,94 8/0,97 4/16.71 4-5/2.00 5/67,42 11-12/76.0 10/0,921 7/40.30 10-11/8.20 5-6-7/I.0 5/8.64
5 Голландия 10/18.07 7/0,99 8/15.17 4-5/2,00 8/49.96 5-6/77.4 4/0.936 3/36.90 8/7.20 8-9-10-11/2.0 6/8.37
6 Испания 12/14.29 10/0.84 12/8.73 11/4.70 9/46.40 3/77.6 6-7/0.930 1/36.60 15/22,60 13/5.0 9/7.82
7 Италия 9/18,90 9/0,87 10/11.57 12/5,40 7/55.41 4/77.5 12/0.912 8/41.00 13-14/11.50 12/3.0 11/6,80
8 Канада 3/22,32 6/1.05 11/11.51 7/2.40 11/42,10 5-6/77,4 1/0,950 6/40.20 12/9.50 8-9-10-11/2.0 3/9.06
9 Китай 15/2,52 1/10,99 15/0.22 13/17.10 15/1.11 13/68.5 15/0.594 9/41.80 1/2.90 15/26.7 14/2,51
10 Норвегия 5/21,61 2/3.03 5/16.44 8/2.50 3/71,17 7-9/76.9 5/0.932 2/36.70 6/4.90 I-2-3/0.0 1/9.28
11 Россия 14/5,26 15/10,00 14/1.03 15/231.00 14/5.44 14/67.6 13/0,849 14/65.30 10-11/8.20 8-9-10-11/2.0 15/0.82
12 США 1/26.65 4/1,56 3/18.79 9/2.90 6/58,03 11-12/76,0 3/0,937 10-11/41.90 7/5.50 4/0.5 8/7.89
13 Франция 7/19.98 11/0,74 7/15,74 3/1.90 4/70.63 7-8/76.9 6-7/0,930 10-11/41.90 13-14/11.50 5-6-7/I.0 7/8.00
14 Швейцария 2/23.48 I4/-O.73 1/25.20 2/1.80 1/80.30 2/78,0 8-9/0.925 13/44,80 3/4.20 1-2-3/0.0 4/9,00
15 Япония 4/21.6? 13/0,29 2/24.70 1/0.00 2/79.15 1/79,5 2/0.937 4/37.50 2/3.10 1-2-3/0,00 12/5.43
226 п 2. ИСХОДНЫЕ СТАТИСТИЧЕСКИЕ ДАННЫЕ
П 2. ИСХОДНЫЕ СТАТИСТИЧЕСКИЕ ДАННЫЕ
227
Таблица П2.3 Экспорт товаров (млн. долл. США)
Все- го за год Кварталы Ян- варь Фев- раль Март Ап- рель Май Июнь Июль Ав- густ Сен- тябрь Ок- тябрь Но- ябрь Де- кабрь
I II III IV
1994 67,5 13,3 16,9 18,4 18,9 4,0 4,5 4,8 4,7 5,8 6,3 5,8 6,1 6,6 6,0 6,3 6,6
1995 81,1 18,6 20,6 19,4 22,5 5,6 6,2 6,8 6,7 6,9 7,0 6,3 6,3 6,7 7,1 7,7 7,8
1996 88,6 20,4 21,4 21,4 25,4 5,8 6,8 7,8 7,0 7,5 6,9 7,3 7,0 7,1 8,6 8,1 8,7
1997 88,4 21,2 20,5 21,5 25,2 7,0 6,8 7,4 6,9 6,7 6,9 7,5 6,9 7,1 8,0 8,2 9,0
1998 1999 73,9 18,5 18,7 17,7 19,0 5,9 4,8 5,8 6,8 6,1 6,1 6,5 6,2 5,6 5,9 6,0 5,9 7,1
Таблица П2.4 Импорт товаров (млн. долл. США)
Все- го за год Кварталы Ян- варь Фев- раль Март Ап- рель Май Июнь Июль Ав- густ Сен- тябрь Ок- тябрь Но- ябрь Де- кабрь
I II III IV
1994 50,6 11,6 12,1 12,3 14,6 3,6 3,9 4,1 3,6 4,1 4,4 3,8 4,1 4,5 5,3 4,8 5,5
1995 60,9 12,9 14,2 15,3 18,5 3,7 4,4 4,9 4,3 4,7 5,2 5,2 5,0 5,1 5,5 6,3 6,6
1996 68,8 16,6 17,3 17,2 17,7 4,8 5,8 6,0 6,1 5,7 5,5 6,1 5,8 5,3 5,7 5,6 6,4
1997 73,6 15,6 17,6 18,7 21,7 4,8 5,1 5,7 6,2 5,5 5,9 6,0 6,5 6,2 6,9 6,5 8,3
1998 1999 59,5 18,1 17,9 13,9 9,6 5,6 2,9 6,0 6,5 6,3 5,8 5,8 5,7 5,2 3,0 3,0 3,0 3,6
ТаблицаП2.5 Перевозки грузов железнодорожным транспортом (млн. тонн)
Все- го за год Кварталы Ян- варь Фев- раль Март Ап- рель Май Июнь Июль Ав- густ Сен- тябрь Ок- тябрь Но- ябрь Де- кабрь
I II III IV
1993 1346 345 356 334 311 114,0 107,9 122,6 121,5 119,6 115,1 114,4 111,2 108,1 110,8 100,0 100,4
1994 1054 267 267 258 262 91,5 83,1 92,8 91,7 88,7 86,8 84,8 87,9 85,3 89,6 85,6 86,3
1995 1024 253 257 263 251 84,2 79,7 89,1 85,8 87,6 83,8 88,7 89,0 85,8 88,1 82,4 80,1
1996 909 226 229 227 227 75,8 71,0 79,1 78,9 77,2 73,0 74,4 76,4 76,2 79,8 74,4 72,4
1997 887 213 218 227 229 69,1 67,8 76,5 73,7 72,6 71,5 74,4 76,5 75,9 79,5 75,1 74,2
1998 1999 834 207 209 204 214 69,3 70,4 64,3 67,3 73,2 71,7 70,2 67,4 68,5 69,5 66,2 73,4 68,1 72,4
ТаблицаП2.6 Официальный курс доллара на конец периода (рублей за 1 дол-
лар США)
Всего за год Ян- варь Фев- раль Март Апрель Май Июнь Июль Ав- густ Сен- тябрь Ок- тябрь Ноябрь Де- кабрь
1993 1247 572 593 684 823 994 1060 990 85 1201 1186 1214 1247
1994 3550 1542 1657 1753 1820 1901 1985 2052 2153 2596 3055 3232 3550
1995 4640 4004 4407 4897 5100 4995 4538 4415 4435 4508 4504 4578 4640
1996 5560 4732 4815 4854 4932 5014 5108 5191 5345 5396 5455 5511 5560
1997 5960 5629 5676 5726 5762 5773 5782 5798 5830 5860 5887 5919 5960
19981) 1999 20,65 6,026 22,60 6,072 22,86 6,1060 6,133 6,1643 6,198 6,238 7,905 16,0645 16,01 17,88 20,65
228
П 2. ИСХОДНЫЕ СТАТИСТИЧЕСКИЕ ДАННЫЕ
Индекс потребительских цен (в процентах к предыдущему месяцу)
ТаблицаП2.7а Продукты питания
Январь Фев- раль Март Апрель Май Июнь Июль Август Сен- тябрь Октябрь Ноябрь Декабрь
1993 131 166 201 236 276 340 416 503 600 709 825 938
1994 119 133 142 152 164 174 181 186 199 231 272 333
1995 123 136 147 158 170 183 192 196 200 207 215 223
1996 104 106 108 110 111 112 112 109 109 109 111 113
1997 103,1 104,5 105,7 106,4 107,2 108,8 109,6 108,4 106,6 105,9 106,4 107,8
1998 19991) 102,3 110,5 103,7 115,4 104,3 104,6 105,2 105,1 104,9 107,3 152,6 158,3 171,1 202,5
Таблица П2.76 Непродовольственные товары
Январь Фев- раль Март Апрель Май Июнь Июль Август Сен- тябрь Октябрь Ноябрь Декабрь
1993 116 143 172 203 234 273 325 394 482 575 665 742
1994 111 121 130 139 147 154 162 171 184 214 240 269
1995 112 123 134 146 154 161 170 180 191 201 210 216
1996 102,7 105 107 108 ПО 111 112 113 114 116 117 118
1997 101,0 101,6 102,4 103,0 103,6 104,0 104,4 105,0 105,8 106,7 107,5 108,1
1998 19991) 100,5 106,4 100,8 110,5 101,0 101,2 101,3 101,3 101,3 108,6 167,5 180,0 187,7 199,5
Таблица П2.7В Алкогольные напитки
Январь Фев- раль Март Апрель Май Июнь Июль Август Сен- тябрь Октябрь Ноябрь Декабрь
1993 122 142 156 172 193 234 287 372 521 625 714 755
1994 130 139 138 140 143 145 149 153 162 179 206 231
1995 111 121 133 146 164 176 184 195 203 212 221 227
1996 103,5 107 120 127 132 135 138,5 141 142 143 150 153
1997 102,7 104,7 107,7 111,0 112,5 114,3 115,1 115,7 116,5 117,0 117,4 118,5
1998 19991) 100,5 110,3 100,9 114,8 102,2 102,8 103,8 104,1 104,5 107,8 130,5 136,8 142,1 150,8
ТаблицаП2.7г Платные услуги
Январь Фев- раль Март Апрель Май Июнь Июль Август Сен- тябрь Октябрь Ноябрь Декабрь
1993 150 198 255 357 481 564 730 10,9р 13,6р 17,0р' 20,9р 24,1р
1994 138 167 196 258 291 324 367 403 457 505 558 622
1995 123 147 162 182 202 219 241 260 278 303 323 332
1996 108,1 114 119 125 128 129 132 136 138 143 147 148
1997 102,3 106,0 108,7 110,4 112,5 113,7 116,2 117,5 118,9 120,3 121,6 122,5
1998 19991) 1999 101,7 104,1 197,0 102,7 107,3 203,3 104,0 105,0 106,1 106,7 108,0 109,3 113,0 114,8 116,2 118,3
ОТВЕТЫ И РЕШЕНИЯ
Упражнения:
/
У.1.1. х = ± 52 njXj. У.1.2. х = + п2х2);
j=l
2
/ = ni+n2 52 nAsj + (®д ~ ®) ]• У-1-3. Указание: проанали-
/
2 2 1 / _ _ —\2
зировать представление з0 в виде з0 = - >, ~ xj + xj ~ х) •
j=l t=l
У.1.4. т2 = т2 — гп\\ m3 = т3 - Зтхт2 + 2т]; т4 = т4 - 4т^т3 +
6mlm2 - 3mf. У.1.5. у = ах 4- 6; sy = a sr; тцу) - тцх) = 0; ™2(у) —
2~0 3^0 4^0 J а а 2
& ^2(a7)i ^3(2/) — ^3(а;)» ^4(у) ® ^4(а;)7 А^1(2/) — Л^1(з7)) Р1(у) — Р2(з7)*
У.1.6. Dz = Ds2 = ^“(1 - ~) (для вывода последнего соот-
ношения воспользоваться результатом теоремы Фишера о х(п — 1)-
распределенности статистики пз2/ст2). У.1.7. Результат основан на уме-
нии вычислить средние значения и дисперсии случайных величин
У.1.8. Решение. Представим статистику s2x(k) в виде
п—1
4(&) = к [G»i+i - а) - (х> ~ а)]2
1=1
где а — это теоретическое среднее значение наблюдаемой случайной ве-
личины.
п —1
е4 (Л) = н £ Б(ж<+» -а)2 + £ Б(®< -а)2
п—1 '
“ 2 52 Б[(а:‘+1 ~ a^Xi ~ а)] * •
1=1
В силу одинаковой распределенности и взаимной независимости на-
блюдений случайной выборки Ж], х2,..., хп имеем:
Е(жр - а)2 = а2 при всех и = 1,2,..., п;
Е[(жр+1 - а)(жр - а)] = 0 при всех и = 1,2,... ,п - 1.
230
ОТВЕТЫ И РЕШЕНИЯ
Поэтому, возвращаясь к (**), получаем
Ез2(Л) = к • 2(п — 1)а2. (* * *)
Следовательно, для несмещенности оценки з2 (Л) необходимо потребо-
вать
к= 2(п-1)’
так что
1 п—1
У. 1.9*. Решение. Представим средний квадрат ошибки в оценивании
дисперсии <т2 с помощью статистики з2(Л) в виде
Е (4(Л) - а2)2 = Е[(4(А) - Ез2(Л)) + (Ез2(Л) - а2)]2
= Е(4(Л) - Ез2(Л))2 + (Ез2(Л) - <г2)2
= Е(з2(Л))2 - [е4(*0]2 + (Ез2(*) - а2)2
= E(4(fc))2-2a2Es2(A) + <A (i)
Вычисление значения Еа2(Л) приведено в решении предыдущего
упражнения (см. (* * *) в решении упражнения 1.1.8). Остается вычи-
слить значение Е(з^(Л)) .
Воспользуемся разложением (*) из решения упражнения 1.1.8 с тем,
чтобы представить величину (52(Л))2/А2 в виде:
n—1 п—1
- 4 - “)• (“)
1=1 1=1
Отметим, что операция теоретического осреднения (Е), примененная
к двум последним слагаемым правой части (И), даст нулевой результат в
ОТВЕТЫ И РЕШЕНИЯ
231
силу взаимной независимости сомножителей (х<+1 - а) и (а:^-а). Остается
вычислить средние значения первых четырех слагаемых правой части (П):
П —1
1=1
/п —1 \ 2 /п —1 п —1 п —1
= Е ЕЙ + ЕЕ
\t=l / yt=l t=l J=1
= (n - l)3a4 + (n - l)(n - 2)a2 • a2
4/ 2
= a (n - 1)
(при получении этого результата было использовано, что случайные вели-
чины fi,(г, • • • >£п-1 являются взаимно независимыми и (0; а2) - нормально
распределенными по построению и, следовательно, Е£2 = а2 и Е£4 = За4).
п-1 п-1
+ 4^2 £ Е “ а)(®« - а)(®л+1 - “)(®д - а)]
i=i j=i
(W)
= 4(п — 1)с2 • а2 = 4(п — 1)а4
(iv)
(при получении этого результата учтено, что каждое из слагаемых двой-
ной суммы во 2-й строке (iv) равно нулю в силу независимости сомножи-
телей (xt — а) и (xj — а) при i j).
Далее
232
ОТВЕТЫ И РЕШЕНИЯ
= 2(п - 2)3<т4 + 2(п - 2)(п - 3)<72 • ст2 + 2(п - 1 )<т2 • ст2 + 2(п - 1 )<т2 • ст2
= 2а4(п - 2). (v)
Подставляя в (П) полученные в (iii), (iv) и (v) результаты, получаем:
Е (s2(*))2 = к2а4(2п - 2 + 4п - 4 + 2п2 - 4) = А:2ст4(4п2 + 4п - 10). (vi)
Возвращаясь к (i) и подставляя значения Е$2(Л) (см. (***) в решении
упражнения 1.1.8) и Е(«2(Л))2 (из (vi)), получаем:
Е (s2(A) — ст2)2 = к2а4(4п + 4п — 10) - 2сг2 • к 2(п - 1)сг2 + о4
= <т4[к2(4п2 + 4п — 10) — 4к(п — 1) + 1]. (vii)
Дифференцируя правую часть выражения (vii) по А: и приравнивая
полученное выражение к нулю, получаем уравнение, определяющее опти-
мальное значение параметра к:
9^3х^ ~ а * = а4 [2к(4п +4п- 10) - 4(п - 1)] = 0.
С/ К
Отсюда
2(п—1) 1
4п2 4- 4п - 10 2(п - 1) + р
Таким образом,
i п-1
2 / ч 1
Sx (ОПТ.) = —;---х—=- > (Zj+l ~ xi) •
’ 2(n-l)+^^k ,+1
Подстановка к = l/2(n — 1) и к = l/[2(n — 1) + в (vii) позволяет
вычислить Е(з2 (несм.) - а2)2 и Е(з2 (опт.) - а2)2 и сравнить их между
собой:
Г./Г.2/ ч 2ч2 4 6п — 7 Е(5Я (несм.) а ) = 2п — 4п + 2 о _ 7 4*^ 2п / • • • \ = а п 9 2 1 ; (vin,a) п-2 + -
-,/ 2 , ч 2ч2 4 6п - 7 Е(^(опт.) <т)=ст 2п + 2п — 5 Е(з2 (опт.) — ст2)2 _ 2п2 — 4п + 2 Е(з2 (несм.) — а2)2 2п + 2п — 5 о 7 (viii.b) 1 6п"7 < - ч 1 5 . ( V111.C) 2п + 2п - 5
Из этих выражений видно, что обе оценки имеют одинаковую асим-
птотическую эффективность (их средние квадраты ошибок ведут себя
ОТВЕТЫ И РЕШЕНИЯ
233
как З/n при п —> оо). Однако при конечных объемах выборок 5^(опт.)
является более точной оценкой, чем 5^(несм.), т. к. правая 4acTb(viii.b)
меньше правой части (viii.a) при всех п 2. У.1.10. Решение.
E(s2-cr2)2 =——— а4 (см. п. 7.1.5 в [1]);
71—1
3 - —
Е(б2 - а2)2 =-----а4 (см. (viii.a) в решении упр. 1.9).
п-2+ -
Сравнение сомножителей при а4 показывает, что:
а) оценка з2 эффективнее оценки з2 при всех п 4;
б) относительная асимптотическая эффективность оценки 32 (по отно-
шению к оценке з2) равна 2/3.
Обе оценки состоятельны, т.к. среднее значение з2 равно а2, а
2 2
среднее значение з2 стремится к а при п —> оо, и в то же время дис-
персии обеих оценок стремятся к нулю при п —> оо. УД.11. д2 =
п 52 (хг “ а) • УД *12. Указание: воспользоваться неравенством ин-
г=1
k k 2
формации. У.1.13. р = 52 хз/ 52 nj- У-1-14. х G 7V(a;^-) (восполь-
j=i j=i
зоваться формулой композиции и индукцией). УЛ.15. Указание:
воспользоваться теоремой (леммой) Фишера применительно к случайным
величинам ж,, х2,..., Xk- У.1.16. Указание: общую схему доказа-
тельства см. в [1], с. 219-220. У.1.17. Указание: воспользо-
ваться результатами теоремы (леммы) Фишера. У.1.18. См. указа-
ние к упражнению 1.17. УЛ.19. См. указание к упражнению 1.17.
УЛ.20. Решение. 1) Функция распределения случайной величины
F^(x) = P{20Xi < i} = Р{х, < = 1 — е~9™ = 1 — е~7, так
, , v f 1 Р~ix Т > л.
что функция плотности /«. (ж) = < 2 с а это и есть функция
I 0, х < О,
плотности %2-распределения с двумя степенями свободы (см. (3.18*) в [1]).
2) Функция правдоподобия наблюдений Xi, х2,..., хп:
— 0 Xi
Цхх,х2,...,хп\0') = 0пе <=i .
Логарифмическая функция правдоподобия:
п
1(хих2,...,хп I 0) = п1п0-0
г=1
234
ОТВЕТЫ И РЕШЕНИЯ
д1
де
1 V’'
= П--^=0.
1=1
Отсюда 0МП = = i = ^ = 0,028.
Е xi
i = l
При вычислении среднего значения и дисперсии оценки 0МП восполь-
зуемся доказанным выше фактом х2(2)-распределенности случайных ве-
личин & = 20х^ (г = 1,2,а также их взаимной независимостью
(выборка хг, Х2,..., хп по условию случайна). Поэтому случайная вели-
чина £ & = 20 £ Zj подчинена % (2п)-распределению и, соответственно,
i=l г=1
Л гг 2
оценка 0МП может быть выражена в терминах х -распределенной случай-
ной величины:
20п
^мп — 2/« \
X (2п)
Итак:
1
(/ \ 00
-4^- | = 20пЕ ( -Д—| = 20п / - -тД—
X2(2n)J \№(2n)/ р2"Г(п)
ОО
= 20п—.-Д----— /»- 2 *-®n-2-1e~^d2;
4(п - 1)(п - 2) J 2 2Г(п —2)
_ 2вп Гу2ГдГп - 9П - 2gn2<n ~2) _ Р п
~ 4(п - 1)(п - 2)Е* (2( 2" - 4(п - 1)(п - 2) “ 9п - Г
Следовательно, оценка 0МП является смещенной и чтобы ее «подправить»
на несмещенность, ее надо домножить на (п - 1 )/п:
n- U 1
^МП — ^МП — п ~ 0,026.
Дт Е
1=1
ОТВЕТЫ И РЕШЕНИЯ
235
Чтобы вычислить дисперсию оценки 0МП подсчитаем
(\ 2 / \ 2
=4п!02В|-5^—-|
х\2п)) кх(2")/
ОО
= 4п02 f 2пГ(п\хП~'е~*аХ
О
оо
/ 1 (п—3)—1 ,
/ х - ,---------х ’ е 1 ах
2 3Г(п - 3)
пв2 • 2(п - 3)
1
— 4 2 Я2
“ 8(n — l)(n-2)(n-3) J
о
п2е2 2
= 2(п-1)(п-2)(п-3)ЕХ ~ = 2(п^1)(п - 2)(п - 3)
2д2
п 0
(п - 1)(п - 2)’
2Л2 2а2
\2 п V Пи
~ Е0МП — (Е0МП) — 7-----ТТ7--— ----------5"
мп м v ' (n—1)(п —2) (п-1)2
2л2
П в
(п — 1)2(п — 2)
Е(&п - 6)2 = В?мп = В#.,, - (Е?мп)2 = ---тг - 02
- 02
п - 2"
3) Точная интервальная оценка основана на факте %2(2п)-распреде-
ленности выражения 2пв/0ип. Следовательно:
2пЗ
Хо,97б(2п) < -хг— < Хо,О2б(2п) с вероятностью Ро = 0,95;
^мп
(где Ха(т) -Ю0а%-ная точка х2-распределение с т степенями свободы).
Или:
£мп . < е < 0мп • Хо’°^2п^ с вероятностью Ро = 0,95.
2п 2.П
Подставляя числовые данные упражнения, имеем:
0,015 < 0 < 0,046 с вероятностью Pq = 0,95.
236
ОТВЕТЫ И РЕШЕНИЯ
Приближенная интервальная оценка основана на факте асимптотиче-
о2
ской (0,1)-нормальной распределенности выражения (0МП — Следо-
вательно:
дмп - 1,96-^ < о < емп +1,96-^
у/П у/П
с вероятностью, приблизительно равной 0,95.
Подставляя числовые данные упражнения, имеем:
0,012 < в < 0,044 с вероятностью, приблизительно равной 0,95.
У. 1.21. Решение. Подберем параметры а и /3 в априорном гамма-
распределении вида р(0) = е~0в (0 > 0) из условия:
' Е0 = % = 0,04;
< D0= ^ = (0,01)2.
Решение этой системы относительно параметров а и /3 дает:
а = 16; /3 = 400.
Поскольку гамма-распределение является естественно-сопряженным
по отношению к экспоненциально распределенной случайной величине,
то апостериорное распределение параметра 0 снова будет описываться
гамма-законом. Его параметры вычисляются по формулам (см. п. 3 та-
блицы 1.2):
а = а + п = 16 + 12 = 28;
= /3 + 22 xi = 400 4- 12-36 = 832.
1=1
Байесовская точечная оценка определяется как среднее значение
апостериорного распределения, т.е.
= це\х1,х2,...,хп) = ^ = ^- = 0,034.
р ooZ
Для вычисления байесовской интервальной оценки (с уровнем дове-
рия Pq = 0,95) по таблицам неполной гамма-функции Г(ж | а/;/?7) =
/ ~1е~(3 6dG находим такое значение 0О,975 аргумента ж, при кото-
о k '
ром Г(ж | а у(3 ) = 0,025, и такое значение 0О,О25 аргумента ж, при котором
ОТВЕТЫ И РЕШЕНИЯ
237
Г(х I а,0') = 0,975. Тогда 0О ,975 < 0 < ^о,о25 с вероятностью р0 = 0,95
(здесь, по построению, величины 0а это 100а%-ные точки апостериорного
распределения параметра О'). У.1.22. Решение. 1) Функция правдо-
подобия наблюдений Xi, Х2, •.., хп:
1 1 п
Т(®1,2-2, • • • > | 01,0г) = 7п ® '(*Е« 02 )•
Логарифмическая функция правдоподобия:
1 п
/(2ГЬа:2,---,®п I 01,0г) = -nln^ - — V(xf - 0).
Наша задача найти такие значения 01мп и 02 мп, которые обращают
функцию I в максимум.
Если бы параметр 02 был известен, от относительно 0j можно было
бы решить обычное уравнение метода максимального правдоподобия (т. к.
по параметру функция I регулярна):
01
д6х
1 п
71 1 V—л ч
~ё;+ -"г) = °’
откуда в, = 1 - 02)-
1=1
С другой стороны, если бы параметр был известен, то, как известно
(см. пример 1.4), функция I достигает максимума при значении
@1 — ^min = niin{xi, а?2, . . . , #п}’
Однако то, что I как функция двух переменных достигает своего мак-
п
симума при значениях 02 = zmin и 01 = (£(®« — imin))/^, нуждается в
г=1
доказательстве.
При варьировании значений в2 мы можем лишь уменьшать оценку
#2 = Zrninj т. к. при 02 > ^min нарушается базовое модельное условие
62 < min{xi,X2, • • • А}- Поэтому в качестве альтернативы оценкам (*) и
(**) мы можем рассмотреть лишь класс оценок вида
02(e) = ®min -£ (е > о)
и, соответственно,
- 1 п 1 п
^l(^) = (^min — £)] = — Я'т’т) “I" £ — ^1(0) + €.
71 77
238
ОТВЕТЫ И РЕШЕНИЯ
Докажем, что при любых е > О
/(а?1, а?2,..., хп | $i(0),$2(0)) > ,®2> • • • j хп I (^)>
Действительно,
5 > • • • 5 ХП | 0] (0), 62(0)) /(®1 , $2> • • • > ХП I 01 (в), 02(e))
- 1 п
= -nln^(0) - 3^7—53(^1 - Zmin) + nln[^(o) + e]
и (°) «=1
1 n
+ *1(0)+ £§
0i(0)+ в
= nln
L *1(0) J
01(0)+ £
+ М2)±£ = п1„ _
«1(0) «1(0) + е «1(0)
Итак, оценки ^(0) и #1(0) действительно являются оценками макси-
мального правдоподобия параметров, соответственно, и 02, т.е.
О2 мп — Ящ’ш — min{&i, Х2,..., хп}
и
- 1 п
01 мп “ ~ /3(^1 — ^min)*
П
1=1
2) При вычислении средних значений и дисперсий этих оценок вос-
пользуемся тем фактом, что статистика 02мп = ^min снова распределена
по экспоненциальному закону со сдвигом только параметр масштаба
этого распределения в п раз меньше параметра масштаба исходной (ана-
лизируемой) случайной величины Действительно:
^Pmin('r) = ^{^min < ж} = 1 —
= 1 - Р{хг > Ж,Ж2 Ж,...,ЖП ж}
= 1 - П р(х< > г} = 1 - (1 - -f«(®))n = 1 - е~^(х~в2)
1=1
= 1 — е~т^х~в2\ где X = 0i/n.
Используя правило вычисления среднего и дисперсии для таких рас-
ОТВЕТЫ И РЕШЕНИЯ
239
пределений (см. условие задачи), имеем:
Е Zmin = Е02 мп — Л + 02 = 02 + ~;
п
О ^min — D$2 мп — — 2 '
П
Далее:
= (01 + 02) - (02 + = 01 - - = 01—.
\ п ) п п
Соответственно, «подправленная на
мального правдоподобия имеет вид
смещенность» оценка макси-
1 п
^1 мп = “ 7^1 мп ~ “ 7 / ” ®min)*
71—1 71 — i ;
К сожалению, мы не можем вычислить дисперсию оценки 01Мп как
п
сумму дисперсий (2 xi)ln и ®min> т. е- эти статистики не являются
t=l
независимыми. Но мы можем воспользоваться очевидным соотношением
D(£ -1?) = Df + Dr? - 2E[(f - Ef)(»?- Ei?)], а затем оценить сверху последнее
слагаемое с помощью неравенства Коши-Буняковского:
Е [(£ - Е^)(т? - Ет?)] [Е(е - ЕО2 • Е(1? - Ет?)2]
Итак, в нашем случае:
240
ОТВЕТЫ И РЕШЕНИЯ
Но (nDxj)/n2 = (nD£)/h2 - пв{/п = а вычитаемое в разло-
жении D#i мп оценивается сверху в соответствии с неравенством Коши-
Буняковского выражением
Теперь мы вправе заключить, что:
02 /1 \
901 мп — И о ( — ) ,
п \п J
где о(£) это величина более высокого порядка малости, чем 1/п.
3) Приближенные интервальные оценки для параметров и 02 осно-
ваны на асимптотической (0;1)-нормальности статистик, соответственно,
01МП-01 02 мп - 02 -
— -----— и ----------------—.
01 / ^1 мп
Поэтому с уровнем доверия Pq будут выполняться неравенства
01 мп - 1,96-^- < 01 < 01мп + 1,96-Г
п у/п
И
д ^1 МП п/?^1мп . Л . л ®1мп . . ЛР^1мп
02 мп---------1,96---- < 02 < 02 мп-----+ 1,96----.
п п п п
У.1.23. Решение. Как известно (см. пример 1.4), оценка максималь-
ного правдоподобия 0МП параметра в определяется в виде 0МП = a?min =
minfz], • • • •> хп}> а закон распределения статистики 0МП = ^min снова
является экспоненциальным со сдвигом, равным 0, но с параметром мас-
штаба, равным 1, т.е.
Fx . (г) = P{a:miI1 < я} = Р - е при х > 0;
( 0 при я < 0,
так что Е0МП = 0 + £ и D0Mn =
Для построения точной интервальной оценки для 0 (при заданном
уровне доверия Pq) рассмотрим функцию распределения жт-1п — 0:
- 0 < ж} = P{a:inin < х + 0} = 1 - €_n(x+l’_<’) = 1 _ е~пх
ОТВЕТЫ И РЕШЕНИЯ
241
при х > 0.
Далее найдем (1 + РО)%-НУЮ и (1 - РО)%"НУЮ точки (соответственно,
х(1+р0)/2 и ж(1-р0)/2) этого распределения, т.е. решим уравнения
- « > ^(, + Р.)/!} =
- 9 > 1(1_ро)/2} = = ЦЙ
относительно Z(i+p0)/2 и ®(i-p0)/2:
Я(1 + Ро)/2
*(1-Р0)/2
-In
п
Из построения следует, что с вероятностью Pq
•^min
ИЛИ
Построение приближенного доверительного интервала для в основа-
но, как обычно, на асимптотической (0;1)-нормальности статистики
0мп ~~ Е0МП
\Ммп
В нашем случае имеем с вероятностью Pq
0мп # п
-Wi-Pq < -------=---— < Wi-P(
2 — 2
П
где wQ — 100а%-ная точка (0;1)-нормального распределения. Раскрывая
эти неравенства относительно 0, имеем (с вероятностью Ро):
0МП
1
— W1-P,
Г 1 1
'мп-----F -W1-PQ .
п п
£
п
9 Прикладная статистика
в задачах и упражнениях
242
ОТВЕТЫ И РЕШЕНИЯ
У.1.24. Решение. Параметры а,р априорного гамма-распределения
определяем из системы
Е0 = 0О = f
D0 = До =
в е2
Решая эту систему относительно а и имеем: /3 = = д$г- Как
известно (см. п.5 в табл. 1.2), параметры о ,/? апостериорного
гамма-распределения оцениваемого параметра 0 определяются соотноше-
ниями:
<* = (3' = 0 + п = Л-4-П. (*)
4=1 Д0 ,=1 Ао
Соответственно, имеем выражения для точечной и интервальной (с
уровнем доверия Ро = 1 — 2е) байесовских оценок параметра 0:
0(Б) =Е(0|х1,х2,
< 9 < с вероятностью Ро = 1 - 2е, где 7д(а',/?') —
lOOg-процентная точка 7(0/,/^-распределения. С учетом «Указания к
упражнению 1.21» байесовская интервальная оценка для 0 может быть
представлена в виде:
wx'-’(2a')<e<wxl(2a,)
с вероятностью
Ро = 1 - 2е,
где значения а и /3' определены соотношениями (*), a %2(2а;) — это 100g-
процентные точки «хи-квадрат»-распределения с 2а степенями свободы
(определяются из таблиц П1.4). У.1.25. Решение. Из решения зада-
чи 1.21 (см. ниже) следует, что оценка 0МП максимального правдоподобия
параметра 0 в распределении Парето может быть представлена в виде
2п0
М" = №(2п)
Поэтому задача сводится к вычислению первых двух моментов слу-
чайной величины £ = 1/%2(2п). Напоминаем, что функция плотности
ОТВЕТЫ И РЕШЕНИЯ
243
вероятности случайной величины %2(2п), как известно (см. [1], п. 3.2.1),
имеет вид:
и что Е%2(т) = т.
С учетом этого имеем:
✓ \ 00
Ef_J_К j
V Хг(2» J I
-х----------------—2------------ [ х • dx
22(п - 1)(п - 2) • 2 2Г(п - 2) J
ОО
1
“ о2/ 1\/ О\ /
2 (n- l)(n-2) J
= Е[Х2(п-2)] = 2(n-2) = 1
4(п - 1)(п - 2) 4(п - 1)(п - 2) 2(п - 1) ’
Следовательно
Ев„„ = Е| I = 2и«е(—| =«—2-,
k/(W \x(2n)J п-1’
т.е. оценка 0МП является смещенной (смешение равно ;£г).
Далее:
(\ 2 оо
=Ffw/?a:
е 2 dx
____________________1__________________
” 23(п - 1)(п - 2)(п - 3) • 2п-3Г(п - 3)
X J х • a.(n~3)-1e_7 dx
О
23(п - 1)(п- 2)(» - 3) / ^х'121"-3» W d
2(п - 3) _ 1
23(п - 1)(п - 2)(п - 3) ~ 4(п - 1)(п - 2)’
9*
244
ОТВЕТЫ И РЕШЕНИЯ
D0Mn = D
= 4пв2
4(п - 1)(п - 2) 4(n _ 1)2 ] (п - 1)2(п - 2)
о2 з^2
п-2 + 2(n- I)2 + (п - 1)2(п — 2)
У.1.26. Решение. 1) В данном упражнении имеем дело с нерегуляр-
ным случаем, т. к. область положительных значений функции плотности
равномерного распределения
/б(а,Ь)(х) —
1
Ь—а
О
при а х 6;
при х $ [а; Ь]
зависит от оцениваемых параметров. Следовательно, обычная техника
метода максимального правдоподобия, основанная на дифференцировании
по неизвестным параметрам функции правдоподобия и приравнивании по-
лученных выражений к нулю, здесь непригодна. Поэтому попытаемся не-
посредственно максимизировать функцию правдоподобия
Z/(^i, ^2,..., хп | а\ 6) — . п ► шах
(о — а) а,Ь
(*)
при ограничении области допустимых значений параметров а и b соотно-
шениями
(**)
Ь Шах{#1,5^2, . . . , Хп] = ^тах-
Решение экстремальной задачи (*) при ограничениях (**) очевидно
дается соотношениями
°мп — ^min, чип — ^rnaxi
т. к. взяв любые другие решения, удовлетворяющие условиям (**) (а
такими конкурирующими решениями могут быть только решения вида
a = Zmin ~ £1 и Ь = ятах + £2? где Ei > 0 и с2 > 0)5 могут только умень-
шить значение функции правдоподобия.
2) Для вычисления средних значений и дисперсий оценок aMn = zmin
И frMn = жтах необходимо знать их закон распределения вероятностей. От-
метим, что функция распределения анализируемой случайной величины
ОТВЕТЫ И РЕШЕНИЯ
245
^б(а;б)(ж) выражается соотношением
при
при
при
х < а;
а х 6;
х > Ь,
Определим функции распределения и функции плотности статистик
^min и жтах, их средние значения и дисперсии.
^min(a') “ ^{^min < — 1 ^{Srnin
= 1 - P{xi х; х2 х;..., хп х}
= 1 - П > *} = 1 - П(1 - W)) = 1 -
-i -1 \ 0 ® J
1=1 1=1 4 '
9FXm^ _ * (Ь~ХУ~1
дх b — a \b — aJ
E^min —
1
dx = n [[b-y(b- a)]yn-1 dy = a +
J n + 1
0
dx
i
= П ][b~y(b~ °)]2УП-1 dy
о
= a +
2(6 - a)(na + b + a)
(n + l)(n + 2)
(при подсчете интегралов использовалась замена переменных у = (6 -
*)/(*-*))•
г» vt 2 \ /г \2 2 . 2(6 - a)(na + 6 + а) ( Ь-а\2
D®min — E(®min) (Elmin) — а Н / . , xz . «\ I а + '' . . )
(n+I)(n + 2) \ П + 1 /
П /А \2
=-------я-------(6 — а) .
(п + 1) (п + 2)
^®т.х(®) — ^{З'тах < ®} — -Р{®1 < X, ®2 < ®, •.., ®п <
= ПР{«, < х} = П[Г,(а1Ц(х)Г = (1^1)".
1=1 1=1 \ '
f (х\ = ^^гт.х(з;) п (д - а\ п
/хтлЛ ’ дх ь-а\ь-а)
246
ОТВЕТЫ И РЕШЕНИЯ
Подсчет значений Ezmax и проводится совершенно аналогично вы-
числениям интервалов, определяющих Eimjn и Езт;п. В результате полу-
чаем:
Е т“ - 6 п + 1 ’
D^max = ~ 1\2/ ТТГ“ а) *
(п+ 1) (п + 2)
3) Построение приближенных интервальных оценок основано на фак-
те асимптотической (0;1)-нормальности статистик вида
#мп ~ 0
yj^Omp
В нашем случае статистики
•Emin а
У (n+l)»(n+2)(fr “ “)
_________жтах ~ Ь_____________
у](n+l)”(n+5J“ а)
распределены асимптотически (0;1)-нормально. Так что, заменяя в вы-
ражениях дисперсий неизвестные параметры а и b их оценками, соответ-
ственно, амп = xmin и 6МП = жтах, получаем следующие односторонние
интервальные оценки для а и b (неравенства, ограничивающие значения
параметров с другой стороны, следует из построения):
b — а I п
®min ~ Wl-Po _ I 1 V „ I О < а < ®min
71 + 1 у П + Z
я max < b < ® max 4" Wl-Po । Г \ i о ’
П + 1 У П + 2
где wa — это 100а%-ная точка (0;1)-нормального распределения, а нера-
венства выполняются с вероятностью, приблизительно равной заданной
величине Pq.
4) В соответствии с (1.13) составляем уравнения метода моментов:
Е«(<.;6)=ф = 1Ё=ад;
1=1
П<(а;|.)=^=1£(1(-4)! = а!(п).
ОТВЕТЫ И РЕШЕНИЯ
247
Решая эту систему относительно а и Ь, определяем оценки амм и Ьмм
параметров, соответственно, а и Ь по методу моментов:
«мм = *(п) - у/Зз(п\,
Ьим = ж(п) + s/3s(n).
Задачи:
3.1.1. р = 0,5; Ерр(5) = 2,5; Di/p(5) = 1,25.
zj-значения i/p(5) 0 1 2 3 4 5
*(в) zr рг- -выборочные относительные 3 0 частоты появления Xj 0,02 0,16 0,30 0,36 0,14 0,02
3.1.2. р = 0,102; Ei/p(20) = 2,04; Di/p(20) = 1,83.
zj-значения i/p(20) 0 1 2 3 4 5 6 . .. 20
Л(в) ~ Pl -выборочные относительные 3 0 частоты появления Xj 0,04 0,30 0,36 0,20 0,08 0,02 0 ... 0
3.1.3. 0= i £ Xi = -109= 1,817.
i=l
zj-значения i/(0) 0 1 2 3 4 5 6 7 8 . .. 00
-выборочные относительные 0 частоты появления Xj 0,10 0,33 0,31 0,17 0,07 0,02 0 0 0 ... 0
3.1.4. При числе интервалов группирования т — log2 50 +1 ~ 7 и ширине
интервала группирования Д = - ®m|n) « 6,3 имеем: X = 98,54 и
82 = 92,97. 3.1.5. При числе интервалов группирования т = log2 50 + 1 ~
7 и ширине интервала группирования Д = ^(®msx - ®min) « 9,8 име-
ем: Я = 83,48 и I2 = 199,77. 3.1.6. х = = 23,84 (сек.)
Е п» »=1
»!
з2 = V— Е W* + -Г- Е ^(Xi - х)2 = 9,87 (сек.2). 3.1.7. Сум-
Е п» *=1 Е п» *=1
|В1 »В1
ма, обеспечивающая (с вероятностью 0,95) выплату зарплаты, равна
828372 руб. 3.1.8. а) 0,80; б) 0,88. 3.1.9. Р{0,955 < а < 1,055} = 0,88;
Р{0,б5 < о < 1,4з} = 0,89. 3.1.10. Р{0,546 < р < 0,654} = 0,88; 52320
жителей. 3.1.11. [0,267; 0,373]. 3.1.12. С вероятностью 0,90 можно
248
ОТВЕТЫ И РЕШЕНИЯ
утверждать, что: 0,37 < < 1,79. 3.1.13. С вероятностью 0,90 мож-
но утверждать, что: —0,209 < О' — 0 < 0,557. 3.1.14. Число отклик-
нувшихся клиентов является биномиальной случайной величиной vp(N),
где N = 30, а параметр р оценивается по имеющейся выборке величиной
Р — *1+5’.зГ6 = 0,08. Соответственно, искомая вероятность оценивается с
помощью формулы
P{vp(N) = 4} = С^р4(1 - p)N~4 = С34о(0,08)4(1 - 0,08)26 и 0,13.
3.1.15. Число рекламаций является биномиальной случайной величиной
i/p(7V), где N = 1000, а параметр р оценивается по имеющейся выборке
величиной р = = 0,005. Соответственно, искомая
вероятность оценивается с помощью формулы
з
P{^(N) < 3} = CfoooAl - P)W°°'k « 0,27.
k=o
3.1.16. Число заявок на товар, поступающих за неделю, является пуассо-
новской случайной величиной где параметр 6 оценивается величиной
9 _ =3,2. Соответственно, искомая вероятность оценивается с
6 а* _й
помощью формулы Р{и(9) > 6} = 1 — Р{«/(0) 6} = 1 — 52 1Ге ~ 0,045.
*=о
3.1.17.Вес изделия, случайно отобранного из продукции автоматической
линии, есть нормальная случайная величина £(а; а2), где параметры а
и а2 оцениваются по имеющимся исходным данным х, (г = 1,2,...,64,
64
см. табл, в условиях задачи) по формулам: а = £ 52 и 401,3 (г.) и
1=1
а2 = 4 52(®i - о)2 « 125,44 (г.2). Соответственно, доля брака оценива-
i=l
ется величиной Р{£((г,а2) < 380 г} 4- P{f(a;a2) > 415 г} = Ф (38^~а) 4-
[1 - Ф (^=^)] = Ф(-1,90) 4- 1 - Ф( 1,22) = 0,029 4- 1 - 0,890 = 0,139 (в
данных выкладках выражение Ф(х) обозначает значение функции распре-
деления (0;1)-нормального закона в точке ®). 3.1.18. Решение.
1) Функция правдоподобия наблюдений ®], ®2, • • •, гп:
п п п п
....».1р) = IJcS/Xi-?)"" = п« Пр1' -Пи-р)"’".
1=1 1=1 1=1 1=1
Логарифмическая функция правдоподобия
*(®1,®2,---,®п|р) = 1п£ = + lnPJ>+ln(l -р)
«=1 t=i \«=1 /
ОТВЕТЫ И РЕШЕНИЯ
249
91 1 А 1 „ 1 А
9р Р 1 - Р 1 ~ Р
п
Отсюда рмп = 52 xi = 400 =
1=1
1 П'^Р
Ермп “ жг Z v ~ дг — Р\
nN nN
г=1
DpMn = —1—2 VDii = ———^Nnp^l—p) =
(nN)2 £? (nN)2 PJ nN
2) Поскольку статистика
Рмп -Р
Jp^-p)
V nN
распределена асимптотически (по п —► оо) по стандартному нормальному
закону, то можно утверждать, что приблизительно с вероятностью Ро =
0,90 будут выполняться неравенства
Рмп ”* Р
-«о,95 < Л " f ч < «0,95,
4 / Рмп(1 ~~Рмп)
V nN
где «о,95 — 0,95-квантиль стандартного нормального распределения. От-
сюда с учетом «о,95 = 1,645 (см. табл. П 1.3), имеем следующую интер-
вальную оценку для р:
л 1 RA К. /?мп(1 Рмп) . ~ - ±1 «МК. /Рмп (1 Рмп)
рмп - 1,645у-----—------< Р < Рмп + 1,645у-----—------
или, с учетом числовых данных задачи:
0,02- 1,645
0,02 • 0,98
400
< р < 0,02+ 1,645
0,02 • 0,98
400
0,0085 < р < 0,0315 с вероятностью Ро ~ 0,90.
3.1.19. Решение. Подберем параметры а и Ь априорного бета-
распределения, исходя из системы уравнений:
Г Ер = А = О-01
DP = = (0,003)2.
250
ОТВЕТЫ И РЕШЕНИЯ
Из первого уравнения имеем: Ъ = 99а. Подставляя это во 2-е уравне-
ние и решая его относительно а, получаем: а = 10; Ь = 990.
Поскольку бета-распределение является сопряженным по отношению
к биномиальной случайной величине, то апостериорное распределение па-
раметра р снова будет бета-распределением. Его параметры вычисляются
по формулам (см. п. 6 табл. 1.2): а = а + £ xi = 18; Ь = 6 + nN — £ if =
t=i «=1
990 + 400 - 8 = 1382. Байесовская точечная оценка определяется как
среднее значение апостериорного распределения, т. е.
Й(Б) = fl = 18
а + Ъ' 18 + 1382
= 0,01286.
Байесовская интервальная оценка (при уровне доверия Ро = 0,90) опре-
деляется неравенствами ^о,95(д/; ь') < 9 < Pofista'ib), где 0q(а,Ь) —
100^%-ная точка бета-распределения с параметрами а и b'. Воспользо-
вавшись известными равенствами 0q(a;b>') = (см- Указа'
ние к задаче 1.19) и = f ’ а также табл- П 1.5, име-
ем: Fo,05(18; 1382) = 1,92; F0)95( 18; 1382) = 0,625, так что с вероятностью
Ро = 0,90 : 0,0081 < в < 0,0244. 3.1.20. Решение.
1) Определим параметры а и 0 априорного гамма-распределения р(0)
оцениваемого параметра в из условий:
/ЕЙ = f = 2;
1 ОЙ = £ = (0,5)2.
Решение этой системы относительно а и 0 дает: а = 16; 0 = 8.
Поскольку априорное гамма-распределение параметра й = 1/а2 явля-
ется сопряженным по отношению к (а; а2)-нормальному распределению с
известным значением а (в нашем случае а = 0 по условию), то апостериор-
ное распределение й снова будет гамма-распределением, а его параметры
а и 0' определяются соотношениями (см. п. 2 в табл. 1.2):
а' = а + = 16 + 12 = 28;
^ = ^+“=8+2£Л64 = 15,68.
£
Точечная байесовская оценка параметра й определяется как среднее
значение апостериорного распределения, т. е.
F> ...1 = 1,79.
Р 10,00
ОТВЕТЫ И РЕШЕНИЯ
251
„ 2
Отсюда имеем в качестве байесовских оценок для <т и <т, соответственно,
числа = 0,56 и = 0,75.
Левый и правый концы байесовского доверительного интервала для
параметра 0 при уровне доверия Ро = 0,95 определяются, соответственно,
как 97,5%-ная и 2,5%-ная точки 7о,975(«',^') и 70,025(0 ,/}') апостериорно-
го гамма-распределения. Определяем эти точки, воспользовавшись^равен-
ством 7e(ai',//) = 2^iXe(2aj (см. указание к примеру 1.10), где Хе(^) —
100е%-ная точка «хи-квадрат»-распределения с числом свободы, равным
и. В нашем случае имеем: 7o,97s(28; 15,68) = 31^0X0,975(66) = |р|| = 1,19;
70,025(28; 15,68) = 31^0X0,025(66) = = 2,50. Так что с вероятно-
стью Ро = 0,95: 1,19 < 0 < 2,50 и, следовательно, для <т2 = 1/0 имеем:
0,40 < ст2 < 0,84. Отсюда следует, что 0,63 <а< 0,92 с вероятностью
Ро= 0,95.
2) В точности повторяя рассуждения п. 2) решения примера 1.7, заме-
нив только неравенства (*) примера 1.7 байесовской интервальной оцен-
кой 0,63 < <т < 0,92, имеем (с вероятностью Ро = 0,95):
2Ф (2^70,975(0',^')) - 1 < Р {|€(0;<т2)| < 2} < 2Ф (2^70,025(0',^')) - 1,
где Ф(х) — значение функции распределения (0;1)-нормального закона в
точке х, а £(0; ст2) — случайная ошибка расфасовки. Подставляя значе-
ния 7о,975(28; 15,68) = 1,19 и 70,025(28; 15,68) = 2,50 и воспользовавшись
табл. П1.2, получаем: (с вероятностью Ро = 0,95):
0,986 < P{|f(0; а2)| < 2} < 0,998.
3.1.21. Решение.
1) Найдем функцию плотности вероятности распределения Парето:
/е(х|«) _ "&) _ J } (J)'+1 при и » 2;
дх (о при х < 2.
Выпишем функцию правдоподобия наблюдений ац, х2,..., хп:
/ п \ -(•+»)
Цхих2,...,хп\0) = 0п2пв Дх,
\«=1 /
Логарифмическая функция правдоподобия:
/(xi,x2,...,xn|fl) = П1п0 + п01п2- (0 + 1)У>Xj.
«=1
252
ОТВЕТЫ И РЕШЕНИЯ
Уравнение метода максимального правдоподобия:
ai(z„z2 x.w п 2 _ £ = 0
до о
1=1
Отсюда
* П 1 f \
^мп = “п = / / I т \\ ’ ' /
Е In (?) In (а111Д2.....'>)
1=1
где д{х\ьХ2^---^хп) — среднее геометрическое имеющихся наблюдений
(оно по условию равно 3,7795).
Следовательно, численное значение оценки равно
6 — 1 1 — 15712
"мп - ln (3J795) - 1п 1?88975 - 0,6364 -
2) Доля «очень богатого» населения q среди всего населения (а не
только среди населения с душевым доходом, превышающим 2 тыс. у.д.е),
очевидно, подсчитывается по формуле:
/2\ 1,5712
q = 0,025 • Р{£ > 5} = 0,025 • (1 - Fc(5)) = 0,025 • • ( - j = 0,0059,
т. е. доля населения России со среднедушевыми месячными доходами, пре-
вышающими 5 тыс. у.д.е., составляет 0,59%.
3) Для построения точной интервальной оценки параметра в необхо-
димо найти такую комбинацию 0МП и 0, которая была бы распределена по
одному из затабулированных з.р.в. и одновременно позволяла бы исполь-
зовать процентные точки этого распределения в наших целях (см. раздел
А в п. 1.1 данного издания).
Следуя указанию, приведенному в условии задачи, докажем, что слу-
чайные величины rji = 201n(xi/2) распределены по закону %2(2). Действи-
тельно:
FM = Р{Ъ < У} = Р (20In < у} = Р { < е* } =
\ ^ / J J
= р{х<<2е*} = р{е<2е^} = 1- (-^) = 1 - е’2,
2
а это и есть функция распределения закона х с двумя степенями свободы
(чтобы убедиться в этом, вычислим плотность /Ч((у) = |е“2 и сравним
ее с плотностью х2(тп)-распределения при m = 2, см. [1], п. 3.2.1).
ОТВЕТЫ И РЕШЕНИЯ
253
Если теперь взять обратную величину от оценки (*) и домножить ее
на 2п0, то получим:
Но 52 = №(2п) как сумма п независимых х2(2)-распределенных слу-
i=i
чайных величин. Определяя из таблиц 97,5%-ную и 2,5%-ную точ-
ки х2(2п)-распределения, соответственно, Хо,978 ( 2п) и Хо,О2в(2п), можем
утверждать, что с вероятностью 0,95 справедливы неравенства:
2 /« \ 2п0 2 . .
Xo,97s(2n) < — < Х0,02б(2п).
"мп
Решая эти неравенства относительно 0 и подставляя в них числен-
ные данные задачи: п = 40; Хо,97в(8О) = 57,15; Хо,о2б(80) = 106,63 (см.
табл. П1.4); 0МП = 1,5712, имеем:
1,12 < 0 < 2,09 с вероятностью 0,95.
3.1.22. Решение.
1) Функция правдоподобия наблюдений ii, Х2,..., х5
,Х2,• • • , Х$\0) =
В данном случае функция L нерегулярна относительно оцениваемо-
го параметра 0, т. к. область положительных значений функции плотно-
сти /;(о;в)(®) зависит от оцениваемого параметра 0. Следовательно, мы
не можем дифференцировать L (или In L) по параметру и приравнивать
полученное выражение к нулю с целью получения уравнения относитель-
но 0. Вместо этого мы должны непосредственно подобрать такую оцен-
ку ^мп1 которая среди всех прочих оценок 0, удовлетворяющих условию
0 max{a:i,2:2> • •давала бы максимум функции L. Очевидно, что
таким свойством обладает оценка
0МП = max{®i,a:2,...,®s} = 3,2 (мин).
Действительно, любая другая оценка 0 по своему численному значе-
нию не может быть меньше хтлх (иначе будет нарушено указанное выше
условие). Но если 0 > 0МП, то соответствующее ей значение функции прав-
доподобия (*) окажется меньшим, чем значение функции правдоподобия,
соответствующее оценке 0МП = гтах.
254
ОТВЕТЫ И РЕШЕНИЯ
Чтобы определить смещение оценки 0МП (или доказать ее несмещен-
ность) необходимо вычислить ее среднее значение Е0МП, а для этого надо
знать з.р.в. статистики хтлх.
*kn.x(®) = = Р{®1 < ®2 < х; ..., хп < ®} =
п п
= П = П ^5(0;«)(®) =
i=l «=1
{О при х < 0;
(f)n при 0 < х < 0-,
1 при X > 0 .
Вычислим функцию плотности /®тм(®) статистики ®тах:
f (х} = = | при 0 < х < в;
Хгам'' ' дх (0 при х £[О;0].
Соответственно:
в 1
— 5 — [ П (X \ 1 Л f Л J Л П
Е0МП = Е®тах = / х- I -г) dy = v I пу ау = 0——-
J ft X.V/ J n + 1
о о
(при вычислении интеграла использована замена переменных у = х/9}.
Мы видим, что оценка 0МП = ®тах оказалась смещенной.
Ее можно подправить на несмещенность домножением на (п + 1)/п,
т.е.
0мп = * 0Мп = 7 • 3,20 = 3,84 (мин.).
71 О
Основанная на оценка среднего времени ожидания автобуса, в со-
ответствии с правилом вычисления среднего значения равномерного з.р.в.,
будет равна 3,84/2=1,92 (мин).
2) Для построения точной интервальной оценки параметра 0 необхо-
димо найти такую комбинацию 0МП и 0, распределение которой относилось
бы к одному из стандартных (затабулированных) законов, либо позволя-
ло бы подсчитать свои процентные точки и использовать их в решении
нашей задачи. Обычно используют некоторым образом нормированные
разности или отношения 0МП и 0. В нашем случае рассмотрим отношение
Л = ®тах/^:
= < к} = < М =
ОТВЕТЫ И РЕШЕНИЯ
255
Воспользовавшись ранее выведенным видом (см. (*)) и учитывая,
что г) и у могут меняться только от 0 до 1, имеем
О
уп
1
при
при
при
F^V) =
У < 0;
0< у < 1;
у > 1.
Теперь найдем 97,5%-ную и 2,5%-ную точки распределения F4(y),
соответственно, 3/0,975 и 2/о,О2б- Величина j/o,975 определяется из усло-
вия Р{т] > 1/0,975} = 0,975, или Р{т} < 1/0,975} = 0,025. Аналогично:
Р{г) > 1/0,025} = 0,025, или Р{т] < 1/о,о25} = 0,975. Соответственно, имеем:
1/0,975 = 0,025
1/0,025 = 0,975
Решая эти уравнения относительно 1/0,975 и Уо,025 при п = 5, имеем:
1/0,975 = 0,438; 1/0,025 = 0,995.
Итак, по построению
р{о,438 <
Д-тах
9
< 0,995} = 0,95.
Отсюда, подставляя хтах = 3,2 и решая неравенства относительно 9, име-
ем:
Р{3,22 < 9 < 8,89} = 0,95.
Этим соотношением и определяется интервальная оценка параметра 9 (с
уровнем доверия Ро = 0,95), основанная на точечной оценке максимального
правдоподобия 0МП = ®тах.
3) Прежде всего подберем численные значения параметров а и 0О
априорного распределения. Для этого приравняем выраженные в терми-
нах этих параметров среднее значение и дисперсию распределения Паре-
то (см. табл. 1.2, п.4) к соответствующим заданным в условии задачи
численным значениям и решим полученную таким образом систему урав-
нений относительно а и 9q\
а90
а - 1
= 5,38;
(Е0)‘
D0
= а(а — 2) =
28,9444
1,9321
= 14,981
-------------= 1,39
(»-!)“(« -2)
а - 2а - 14,981 = 0
cq = 5,00; а2 = —3,00.
256
ОТВЕТЫ И РЕШЕНИЯ
Поскольку, по определению, параметр а в распределении Парето дол-
жен быть больше 2, то выбираем корень а = б. Подставляя это значение
а в 1-е уравнение системы, имеем 0о = 4,30.
Распределение Парето является сопряженным по отношению к пара-
метру 9 равномерного распределения (см. табл. 1.2, п. 4), поэтому апосте-
риорное распределение параметра 0 снова будет подчиняться з.р.в. Паре-
то, а его параметры а и 0о вычисляются по формулам:
а = а + п = 5 + 5 = 10;
0о = max{0o; , ®2,..., ®п} = 4,30.
Байесовская точечная оценка параметра 0 определяется как сред-
нее значение апостериорного распределения. Поэтому
в(Б) = Е(0 | хих2,
а0'о 10 • 4,30 л„о,
-Г-2- = —= 4,78 (мин. .
а - 1 У
Левый и правый концы 21 и 0т*х байесовской интервальной оценки
при уровне доверия Ро = 0,95 определяются как, соответственно, 97,5%-
ная и 2,5%-ная точка апостериорного распределения. Это значит, что они
вычисляются в качестве решений уравнений.
^{*>21 = 0,975;
0,025.
Вероятности в левых частях уравнений определяются в соответствии с
паретовским з.р.в., т.е.:
А] - 0 975-
-(Б) I — и,у<о,
i ^min /
I \ а>
и \
= 0,025.
’'max /
Несложные подсчеты дают при 0о — 4,30 и а = 10:
21 = 4,31; 22х = 6,22,
так что с вероятностью Ро = 0,95 выполняется неравенство
4,31(мин.) < 0 < 6,22(мин.).
ОТВЕТЫ И РЕШЕНИЯ
257
Точность байесовской интервальной оценки, как и следовало ожидать,
оказалась существенно выше точности интервальной оценки, полученной
с помощью метода максимального правдоподобия. 3.1.23. Решение.
Пусть А — событие, соответствующее ответу «да», а В — событие, соот-
ветствующее выпадению пяти или шести очков при бросании игральной
кости. Тогда в соответствии с формулой полной вероятности (см. [1], с.
67, формула (1.14))
Р(4) = Р(А | В)Р(В) + Р(А | В)Р(В). (*)
Очевидно Р(В) = j, Р(А | В) = j, Р(В) = |, величина В = Р(А | В)
и есть искомый (оцениваемый) параметр, а р = Р(Л) — безусловная ве-
роятность ответа «да», которую мы можем интерпретировать как веро-
ятность «успеха» в серии из 120 испытаний Бернулли ... ,®12о»
где
_ _ / 1,
(о
если г-й опрошенный налогоплательщик ответил «да»;
в противном случае.
Из (*) следует, что оцениваемый параметр 6 и вероятность «успеха»
р связаны соотношением:
1 2Л
Р = 7 +
о о
так что логарифмическая функция Z(x|0) правдоподобия наблюдения х =
44 соответствующей биномиальной случайной величины в терминах па-
раметра 6 будет:
l(x I 0) = In [c^V4(l-p)120‘44]
— In С^2о + 44 In f- + -0^ + 76 In (- — -6
\O о / \O о
dl ЛА i 2 , 1 / 2\ ft
00-44l +|0,3+76|-3/ ~ °
4800 = 144, 0мп = 0,3.
Для построения приближенной интервальной оценки для 0 построим
сначала такую оценку для р. По теореме Муавра-Лапласа статистика
асимптотически распределена в соответствии с (0; 1) — нормаль-
ным з.р.в., так что с вероятностью 0,95
Рмп Р f \
-^0,025 < , -' . == < «>0,025, (**)
А / Рмд(1~Рмп)
258
ОТВЕТЫ И РЕШЕНИЯ
где рмп = ^ = 0,367 — оценка максимального правдоподобия параметра
р, a wq,025 — 2,5%-ная точка стандартного нормального распределения.
Подставляя в (*♦) вместо р выражение + |0 и раскрывая полученные
неравенства относительно 0, имеем
0,171 < 0 < 0,427
с вероятностью 0,95. У.2.1. 1) Критическая статистика 7П =
(т(п)-ао^>/п--1 в предложении справедливости гипотезы «Hq: Е£ = ао»
распределена как стьюдентовская случайная величина с числом степеней
свободы п - 1 (г(п)-выборочное среднее, з2(п)-выборочная дисперсия).
2) Гипотеза Hq отвергается с уровнем значимости критерия, равном а,
если: a) 7n > ui_a (при альтернативе а > а0); б) 7П < иа (при альтер-
нативе а < ао); в) |7n| > «1-$ (ПРИ альтернативе а / ао). 3) Гипотеза
Hq не является простой. У.2.2. См. п. 8 в табл. 2.1. У.2.3. См. п. 9
в табл. 2.1. У.2.4. См. п. 10 в табл. 2.1. 3.2.1. Теоретические часто-
ты (j = 1,2,...,5) подсчитываются по формуле = Npj, где
N = 50, pj = P{i^(5) = j} = C3sp3(l - р)5~3, а р = 0,5. Критиче-
5 (р-^Т))
ская статистика критерия согласия 7П = £2 ’’ (?)— — 0,88, что мно-
j=0
го меньше значения однопроцентной точки «хи-квадрат»-распределения
с четырьмя степенями свободы (xo,oi(4) = 13,28). Так что гипотеза
о биномиальном з.р.в. случайной величины ^(5) не противо-
речит имеющимся наблюдениям. 3.2.2. Теоретические частоты
i/jr) С? — 0,1,2,...,6) подсчитываются по формуле Npj, где N = 60,
Pj = Р{х/(0) = j} = jre~e, а 0 = 1,817. Критическая статистика кри-
6 (4/ _2
терия согласия 7п = 52 '|™(Т> = 3,2, в то время как Xoos(5) = 11,1.
j=o Ч
Так что гипотеза о пуассоновском характере распределения числа
направленных соединений на АТС в течение часа не противоре-
чит имеющимся наблюдениям. 3.2.3. Используя результаты реше-
ния задачи 1.4 (группировку исходных данных и вычисленные значения
х = 98,54 и .s2 = 92,97), подсчитываем модельные значения вероятностей
Pi = по формуле pj -Ф - Ф , где Cj (j = 0,1,2,..., 7)-
грапицы интервалов группирования. Теоретические (модельные) часто-
ты npj равны: npi = 2,725; пр2 = 6,835; пр3 = 11,315; пр4 = 12,665;
nps = 9,320; пр6 = 4,550; пр7 = 1,475. Вычисление значения критической
статистики 7П критерия согласия %2 (см. п. 3 табл. 2.1) дает: 7П = 4,04.
В то же время пятипроцентная точка у2(4)-распределения Xo,os(4) = 9,49.
ОТВЕТЫ И РЕШЕНИЯ
259
Поэтому нет основания отвергать гипотезу о нормальном харак-
тере анализируемого распределения. 3.2.4. Используя группировку
исходных данных и вычисленные значения х = 83,48 и з = 199,77 (см.
решение задачи 1.5), подсчитываем теоретические (подельные) значения
частот npj = npj(0) по формуле npj = 50 Ф - Ф > 3 =
1,2,...,7: npi = 3,565; np2 = 8,620; np3 = 14,005; np4 = 11,495;
npj = 7,540; np3 = 2,875; nps = 0,685. Критическая статистика крите-
рия согласия Пирсона (см. п.З табл. 2.1) fn = 3,05. Однопроцентная точ-
ка 4^распределения Xo,oi(4) = 13,28. Следовательно, нет оснований
отвергать гипотезу о нормальности анализируемого распределе-
ния. 3.2.5. Критическая статистика уп критерия в данном случае имеет
у 2
вид (см. п. 13 табл. 2.1): 7П = 12 , где = п2 = ... = n? = 1
?
Е
= N2 = ... = N7 = 200, р = ^5оо = 0,7714, Ру = ^ = ^, а
Vj — число правильных решений задач j-ro раздела. Вычисления дают:
7П = 63,68; Хо,1(6) = 10,64. Следовательно, гипотезу о равной труд-
ности предложенных задач отвергаем. 3.2.6. См. схему решения
5 5
предыдущей задачи. В данном случае р = £ и,/ £ Nj, Pj = nj = 1,
j=i j=i J
так что 7n = 6,39 и Xo,os(4) = 9,49. Поэтому гипотеза о равной степе-
ни подготовки студентов пяти групп к выполнению контрольной
работы не противоречит имеющимся исходным данным. 3.2.7.
I 8 /___vi.v.j
Используется критическая статистика 7п = « 12 12 '^2 * ' (см. п-5
t=i j=i '
в табл. 2.1). В данном случае I = 2, з = 4, а частоты предста-
влены в табл, на пересечении :-й строки и 7-го столбца. Вычисления
дают: 7П = 19,28; Xo,os(G ~ l)(s “ 1)) = Xo,os(3) = 7,81. Гипотеза
отвергается. 3.2.8. Воспользуемся критерием однородности I выбо-
рок применительно к анализу наблюдений дискретных случайных
величин Vi = ^(Рй,Р<2,Р<з)> i = 1,2,3 (см. п.5 табл.2.1). В данной
задаче vu = 30, v2, = 40, i/3. = 30, i/д = 3-, v,2 - 45, v3 = 25,
3 3 , vi.p.j \2
n = 100 и, соответственно, 7n = «12 12 •'*2 2* ' = 16,38, что при
j=l J=1 *• •’
Xo,os(4) = 9,49 свидетельствует о противоречивости проверяемой гипо-
тезы и имеющихся исходных статистических данных. Следовательно,
структура информации о пылесосах различна для покупателей
трех рассматриваемых магазинов. 3.2.9. Воспользуемся критерием
260
ОТВЕТЫ И РЕШЕНИЯ
Стьюдента однородности средних значений в двух нормальных генераль-
ных совокупностях с одинаковой дисперсией (см. п. 7 табл. 2.1). В дан-
ной задаче з2 = ni+n3-2 (ni3i + п23г) = ^(16 ‘ ~ 0»3442,
уп _ gi(ni)-ga(na) _ 2,960, так что при *о,ов(24) = 2,064 приходим к выво-
*У"Г+"» , -
ду о том, что разница между производительностью станков 1-и и
2-й смен является статистически значимой. 3.2.10. Воспользуемся
критерием Бартлетта однородности ряда дисперсий (см. п. 10 табл. 2.1).
В данной задаче I = 4, q = [1 4- зцгц(Е Ч'ту “ щ+Дп,-!)]"1 = °>963’
S2 = n1+...+n,-T E(nJ ~ !)«? = °>0049> " 1)Н£) = 6,65,
;=1 1
так что при Xo.oeG “ 0 = Xo,os(2) = 7,81 приходим к выводу о том,
что гипотеза об одинаковой точности анализируемых станков
не противоречит имеющимся исходным статистическим дан-
ным. 3.2.11. а) Воспользуемся критерием дисперсионного анализа
4
(см. п. 8 табл. 2.1). В данной задаче I = 3; £ Х«1 = 28,5;
1 1=1
5 4
«2 = Ё ж»2 = 34,8; х3 = ± Ё xi3 = 35,0; х = ^(4 • 28,5 + 5 • 34,8 + 4 •
i=l t=l
35,0) = 32,92;4 = £ £(яй - х^2 = 1,25; s22 = ± £(zi2 - х2)2 = 0,56;
t=l t=l
*3 = ^(Zi3 - х3)2 = 2,50; з2 = П1+П21+Пз_3(п131 + п2з22 + п3з23) = 1,78;
1=1
1_ У' п (х —х}2
7п = ---- = 31,78, так что при /o,os(2; 10) = 4,1 приходим
к выводу о том, что годовое количество осадков, варьируемое в
диапазоне от 260 до 290 мм, статистически значимо влияет на
урожайность, б) Воспользуемся критерием Стьюдента однородности
средних значений в двух нормальных генеральных совокупностях с оди-
наковой дисперсией (см. п. 7 табл. 2.1). В данной задаче х2 = 34,8;
х3 = 35,0; з2 = п$+п*3_$ = 1,8286; 7п = . = -0,22, что при
S V Л2 + п3
*0,025(^2 + п3 - 2) = *0,025(7) = 2,365 свидетельствует об отсутствии
влияния годового количества осадков, варьируемого в диапазоне
от 270 до 290 мм, на урожайность. 3.2.12. Воспользуемся критерием
Стьюдента (см. п. 13 табл. 2.1). В данной задаче уп = = 1,5;
*0,05(9) = 3,25, так что имеющиеся экспериментальные данные
не противоречат записи в паспорте автомобиля. 3.2.13. Вос-
пользуемся критерием Стьюдента (см. п. 13 табл. 2.1). В данной зада-
ОТВЕТЫ И РЕШЕНИЯ
261
че 7n = = —1,653; io,025(H) = 2,201, так что имеющи-
еся сведения о движении рейсового автобуса не противоречат
принятому нормативу. 3.2.14. Воспользуемся критерием Стьюден-
та (см. п.13 табл. 2.1). В данной задаче 7П = = -2,906;
to 02б(1Э) = 2,093, так что имеющиеся результаты обследования рас-
ходятся с утверждениями рекламы. 3.2.15. Воспользуемся крите-
рием х проверки гипотезы о численном значении дисперсии (см. п. 14
табл. 2.1). В данной задаче 7П = = 15’(2»3) — 19,84; Xo,os(14) = 23,68,
так что результаты контрольных взвешиваний не противоречат
требуемой точности фасовочного автомата. 3.2.16. Воспользу-
емся критерием %2 проверки гипотезы о численном значении дисперсии
(см. п. 14 табл. 2.1). В данной задаче 7n = = 2^|,2j = 36,045;
Xo,oi(21) = 38,932, так что результаты контрольного хронометра-
жа времени не противоречат принятым нормативам производ-
ства. 3.2.17. Воспользуемся критерием проверки гипотезы о числовом
значении параметра биномиального распределения (см. п. 12 табл. 2.1).
В данной задаче п = 1, N = 400, 7П = = “2,182;
0,05-квантиль стандартного распределения и0,05 = —1,645. Поскольку
7n < ио,о5, то результаты опроса телезрителей находятся в проти-
воречии с утверждением режиссера телепередачи. 3.2.18. Вос-
пользуемся критерием гипотезы о числовом значении параметра бино-
миального распределения (см. п. 12 табл. 2.1). В данной задаче п = 1,
N = 200, 7П = = ^,м’1 = -2,358; 0,05-квантиль стандарт-
ного нормального распределения и0)05 = -1,645. Поскольку 7n < u00s,
то результаты проведенных испытаний находятся в противоре-
чии с утверждением рекламы. 3.2.19. Число наблюдений п = 64;
число интервалов группирования т = log2 п + 1 = 7; ширина интервала
группирования Д = 8,8; критическая статистика критерия согласия %2
771 z * vj
Пирсона (см. п.З табл. 2.1) 7n = S = 5,54; пятипроцентная точ-
;=1 Рз
ка %2(^-распределения Xo,os(4) = 9,49. Поскольку уп < %о,О5(4), то до-
пущение о нормальном характере распределения веса изделий,
произведенные автоматической линией, не противоречит имею-
щимся результатам контрольных взвешиваний. 3.2.20. Восполь-
зуемся критерием дисперсионного анализа (см. п. 8 табл. 2.1). В данной
задаче I = 4, пг = 10, п2 = 15, п3 = И, п4 = 20; = 28; х2 = 25;
262
ОТВЕТЫ И РЕШЕНИЯ
х3 = 20; 2!4 = 23; х = — £ njXj = 23,84; s2 = 4; si = 3; si = 5;
E n, j=i
J=1
I
I / -< 71J ( ~
si = 2; s2 = -j-1-£ n7s2 = 3,46; 7n = J~- -p------= 35,87. Посколь-
.E n;-O=i
I
ку Fq 05(^1 = I - l;i/2 = 53 nj " 0 = /*0,05(3; 52) = 2,80 и, следовательно,
J=i
7n > /*0,05(3; 52), то гипотезу о статистически незначимом разли-
чии производительности четырех рабочих отвергнуть. 3.2.21.
Воспользуемся F-критерием однородности дисперсий (см. п. 9 табл. 2.1).
В данной задаче s2 = 0,64, п = 24; s'2 = 0,49, п = 16. Соответственно,
-А-з2
критическая статистика ;г1 — = 1,28. Из таблиц П 1.5 находим
— 1 ®
однопроцентную точку F(23; 15)-распределения Fo>oi(23; 15) = 3,29. По-
скольку 7n < Fotoi(23;15) (речь идет о проверке гипотезы Hq: <т2 = а2
при односторонней альтернативе о-2 > </2), то предположение об оди-
наковой точности двух фасовочных автоматов не противоречит
имеющимся статистическим данным. 3.2.22. Воспользуемся крите-
рием однородности средних значений Стьюдента (см. п. 7 табл. 2.1), пред-
варительно проверив гипотезу (с уровнем значимости критерия, равным
0,05) Dfj = Dfo (при односторонней альтернативе Dfi > Dfo) с помощью
F-критерия однородности дисперсий (см. п. 9 табл. 2.1). 1) Критическая
статистика, с помощью которой проверяется однородность дисперсий, в
данной задаче имеет вид 7n = = Yo° 2417 = = М77; пя'
типроцентная точка F (9;7)-распределения FOiOs(9; 7) = 3,68. Поскольку
7n < Fo,os(9; 7), то гипотеза об однородности дисперсий не отклоняется.
2) Критическая статистика критерия Стьюдента 7П = —= 0,565
V Я1 *2
(здесь 5 = П1+*2_2(п131 + n2sl) = 0,2878). Поскольку f0,025(^1 + п2 - 2) =
^о,025(6) = 2,12, и, следовательно, |7П| < <0,025(16), то можно утверждать,
что доходы двух обследованных страт населения различаются
статистически незначимо. 3.2.23. Решение. Полиномиальный
з.р.в. задается функцией
Р{р,(П) = х,; = х,; р3(п) = хз} = (1> ,+р?р?р?, (.)
Х1!ж2!жз!
где Xi + х2 + 2?з = п — общий объем выборки, Xj — количество элемен-
тов выборки, обладающих j-m свойством, a pj — вероятность того, что
при случайном извлечении элемента из этой генеральной совокупности он
ОТВЕТЫ И РЕШЕНИЯ
263
окажется принадлежащим к категории элементов, обладающих j-ы свой-
ством (j = 1,2,3). Поскольку pi +р2 +рз = 1 и по условию pi = 2р2, то
в нашем случае функция правдоподобия L имеющихся у нас наблюдений
xi = 480, х2 = 220, хз = 100 может быть записана в виде
Дх.,/2,«з|й)=48|)!220!100,(2и) П (1-Зй) .
Переходя к логарифмической функции правдоподобия l(xi, х2, х3 |
р2) = Ы//(®1,Х2,хз | р2), дифференцируя I по р2 и приравнивая полу-
ченную производную к нулю, получаем уравнение относительно р2:
480 220 „ 100
----1------3 - - — 0,
Р2 Р2 1 - Зр2
откуда р2 = 0,292; pi = 2 р2 = 0,584; р3 = 1 — 3 р2 = 0,124.
Теперь воспользуемся критерием согласия х для проверки гипоте-
зы (с уровнем значимости а = 0,05) о том, что при повторениях выборок
объема п = 800 из населения города распределение состава попавших в
выборку жителей города по трем социально-демографическим и экономи-
ческим стратам может быть описано полиномиальным з.р.в. вида (♦).
Как известно, критическая статистика критерия согласия Пирсона имеет
вид
k
7n = S
j=i
(»/,- - пр,)2
пр,-
В нашем случае </,- = х,-, п = 800, Л = 3, а р,- — определенные вы-
ше оценки максимального правдоподобия параметров pj (j = 1,2,3). Ре-
зультаты необходимых для вычисления значения статистики 7П расчетов
приведены в таблице, аналогичной таблице 1.6 из примера 1.9:
Номер страты j —> 1 2 3 3 E >1
Pj 0,584 0,292 0,124
npj 467 234 99
vi 480 220 100
- nprf 169 196 1
npj 0,362 0,838 0,010 1,210
264
ОТВЕТЫ И РЕШЕНИЯ
Статистика -уп должна вести себя как №(3 - 1 - 1) = №(1) — рас-
пределенная случайная величина, т. е. — не должна превышать значение
Хо,об(1) = 3,84 5%-ной точки ^-распределения с одной степенью свободы.
В нашем случае это требование не нарушается (1,210 < 3,84), так что
нет оснований отклонять проверяемую гипотезу. 3.3.1. 1) тц =
0,608; критическая статистика уп критерия Стьюдента, рассчитанная по
формуле (3.7) равна 7П = 2,422, a 100f %-ная точка t(n - 2)-распределения
(по табл. П1.6) равна io,oos(lO) = 3,169. Т.к. 7n < <o,oos(10), то ги-
потеза Яо: г14 = 0 об отсутствии линейной корреляционной связи меж-
ду а/1) — ценой говядины и а/4^ — ценой хлеба белого в/с не противо-
речит наблюдениям; интервальную оценку для г14 при уровне доверия
Ро = 1 — 2а = 0,88 определим по (3.8) и (3.9). Значение ша = щ_а = ц0,94
найдем (по табл.Ш.З) адо,об = Uo,94 = 1,555. По табл. 1.7 для Г]4 = 0,608
найдем z = 0,706. Тогда окончательно получим 0,159 г14 0,832.
Так как ноль не попал в доверительный интервал, то коэффициент кор-
реляции г14 статистически значим. Таким образом, результаты проверки
значимости и интервального оценивания г14 не совпадают, т. к. в первом
случае использовалась доверительная вероятность Ро — 1 — 2а = 0,98, а
во втором -Ро = 1 — 2а = 0,88. 2) т23 = 0,820; критическая статистика
критерия Стьюдента, полученная по (3.7), равна 7П = 4,530, а найденная
по табл.П1.6 процентная точка <о,о2в(Ю) = 2,228. Т.к. ~/п > <o,o2s(10),
то гипотеза Яо: г23 = 0 отвергается с вероятностью ошибки а = 0,05.
Между ценами на растительное масло - и сахар-песок - х^ линей-
ная корреляционная связь существует. Интервальную оценку для г23 при
уровне доверия Ро = 0,90 определим по (3.8) и (3.9). По табл.Ш.З най-
дем ид = = u0,95 = 1,645, где q = —j?2 = 0,95. По табл. П1.7 по
f23 = 0,820 найдем z = 1,157. Тогда 0,517 г23 0,931. Между ценами
(2) (4)
на растительное масло - х ' и сахар-песок - а: ' корреляционная связь
достаточно тесная. 3) т24 = 0,056, т. е. 5,6% вариации цены на хлеб белый
в/с обусловлено влиянием х ' — цены растительного масла; критическая
статистика критерия, полученная по (3.7), равна 7П = 0,794, a 100f %-ная
точка t(n — 2) распределения (табл.П1.6) равна <o,os(10) = 1,812. Т.к.
7n < A),os(10), то не отвергается гипотеза Но'- г24 = 0, т.е. предполо-
жение об отсутствии линейной корреляционной связи между ценами на
растительное масло - а/^и хлеб белый в/с - а/14) не противоречит на-
блюдениям. 3.3.2. 1) г12 = 0,897; критическое значение для величины |г|,
найденное по табл. П1.8 для Q = | = 0,025 и v = 8 равно г*2ит = 0,632.
Т.к. |т12| > Г|2ИТ, то гипотеза Яо: г12 = 0 отвергается с вероятностью
ошибки а = 0,05. Между а/1) и х^ линейная связь существует; интер-
вальную оценку для т12 определим для Pq = 1 - 2а = 0,95. Отсюда для
ОТВЕТЫ И РЕШЕНИЯ
265
а = 0,025 по табл. П.1.3 находим ша — = «о,975 = 1,96. По табл. П1.7
определим z — 1,457 и с учетом (3.8) и (3.9) найдем 0,582 rJ2 < 0,817.
2) г13 — -0,389; критическое значение для г, найденное по табл. П1.8 для
Q = f = 0,025 и v = 8, равно г^ит = 0,632. Т.к. |г^ит| < г^ит,
то гипотеза Hq: = 0 не отвергается, т.е. предположение об отсут-
« - (1) (з)
ствии линеинои связи между г ' и г 7 не противоречит наблюдениям;
интервальную оценку для г13 найдем при Pq = 1 — 2а = 0,9. Отсю-
да для а = 0,05 по табл. П1.3 определим = щ_а = п0,95 = 1,645.
По табл.П1.7 определим z — —0,410 и с учетом (3.8) и (3.9) найдем
—0,766 Из 0,230. Интервальная оценка подтверждает вывод, что
CZ U) (4)
предположение об отсутствии связи между ' и г ' не противоречит
наблюдениям. 3) г23 = -0,278; интервальную оценку для г23 найдем
при Pq = 1 - 2а = 0,95. Отсюда для а = 0,025 по табл. П1.3 опреде-
лим = щ_а = По,975 — 1,96. По табл. П1.7 для г2з = —0,278 найдем
z = —0,286, а с учетом (3.8) и (3.9) найдем —0,766 г23 0<438. Отсю-
- (2) (3)
да следует, что предположение об отсутствии связи между аг ' и аг ' не
противоречит наблюдениям. 4) т24 = 0,053, т.е. 5,3% дисперсии обу-
(4)
словлено влиянием величины аг'. 5) г 34 = 0,418; интервальную оценку
для Г34 найдем при Pq = 1 — 2а = 0,9. Отсюда для а = 0,05 по табл. П1.3
найдем wa = щ_а = Uo,95 = 1,645. По табл.П1.7 для Г34 = 0,418 найдем
z = 0,4453, а с учетом (3.8) и (3.9) определим -0,198 Г34 0,780.
По табл.П1.8 для Q = у = 0,025 и v = 8 найдем т$4ИТ = 0,632.
Т.к. Г34 = 0,418 < т34ИТ, то гипотеза Яо; г34 = 0 не отвергается, т.е.
, - - (3)
предположение об отсутствии линеинои связи между величинами х ’ и
аг4) не противоречит наблюдениям. 3.3.3. 1)
1
И 2 4
’*14-2
П2-4
1
f*24-l
г14.2
’’241
1
1
-0,424
0,684
-0,424
1
0,449
0,684 \
0,449 ;
1 /
2) По табл.П1.3 ша = 1,645, по табл. Ш.7 z = -0,453, значения Z\ и z2
определяем по формуле zi<2 = z± - ffifPi’L]) 1 интервальная оценка
определяется неравенствами -0,680 < ги.4 -0,054, которые выполня-
ются с доверительной вероятностью Ро = 0,9.
По табл. П1.8 для Q = у = 0,05 и1/ = п- 2-1 = 19 найдем =
0,369. Т. к. Г12.4 = -0,424 по модулю больше rJ2."T, то гипотеза Но: г12.4 =
0 отвергается с вероятностью ошибки а = 0,1, т. е. ri2.4 0 и между а/1)
и х' ’ линейная зависимость существует. Т. к. по модулю г12 = —0,18
меньше г12.4 = -0,424, то а/4) снижает степень зависимости между а/1)
и х^. 3) Я4.12 = 0,706; критическая статистика критерия для проверки
266
ОТВЕТЫ И РЕШЕНИЯ
гипотезы Hq'. R4.12 = 0 равна 7П = 9,432. По табл.П1.5 находим точку
Fa(p;n - р - 1) = Го,ов(2; 19) = 3,52. Т.к. 7П > Го,о5(2; 19), то гипотеза
Яо: Г4 .12 = 0 отвергается с вероятностью ошибки а = 0,05. Между х^ и
х^\ х^ линейная зависимость существует. 3.3.4. 1)
/ 1 ^23-4 Г24-3 \ / 1 0,858
I ^23-4 1 г34-2 I = I 0,858 1
\Г24-з ^34-2 1 / \ 0,492 —0,444
0,492
-0,444
1
2) По табл. П1.3 находим №0,05 = 1,645, а по табл. П1.7 найдем z = 1,399, а
затем zi = 0,990 и z2 = 1,766. Интервальная оценка г2з-4 определяется не-
равенствами 0,758 Г23.4 С 0,943, которые выполняются с доверительной
вероятностью Ро = 0*9.
Т. к. г2з = 0,82 меньше г2з<4 = 0,858, то х^ несколько снижа-
ет степень зависимости между и х^3\ 3) Л2 34 = 0,867; критиче-
ская статистика критерия для проверки гипотезы Яо: Яг. 23 = 0 равна
7П = 28,758. По табл. П1.5 находим Fa(p; п — р - 1) = Fotos(2; 19) = 3,52.
Т.к. 7П > F0)05(2; 19), то гипотеза Яо: Я2.34 = 0 отвергается с вероят-
ностью ошибки а = 0,05. Между и (х^3\ х^) линейная связь су-
ществует. Из #2-34 = 0,752 следует, что 75,2% дисперсии х^ (цены на
растительное масло) определяется вариацией х^ — цены на сахар-песок
и х^ — цены на хлеб белый в/с. 3.3.5. 1) Г12.3 = 0,895; по табл. П1.3
находим о>о,о25 — Ъ96, а по табл. П1.7 найдем z = 1,447, а затем z\ = 0,591
и z2 = 2,191. Интервальная оценка для Г12.3 определяется неравенствами
0,531 С Г12-3 0,975, которые выполняются с доверительной вероятно-
стью Ро = 0,95; 2) Я1.23 = 0,912; критическая статистика критерия равна
7П = 17,21. По табл.П1.5 находим Fa(p;n-p- 1) = Fo,os(2;7) = 4,74.
Т.к. 7n > Fo,o5(2;7), то гипотеза Яо: Я1.23 = 0 отвергается с вероятно-
стью ошибки а = 0,05. Таким образом, линейная зависимость существует
между х^1) — темпом прироста ВНП, — с одной стороны, и темпами при-
роста промышленного производства — х^ и индекса цен — х^3\ — с
другой.
Множественный коэффициент детерминации Я2.23 = 0,831 показыва-
ет, что 83,1% дисперсии х^ объясняется вариацией величин х^2\
Из интервальной оценки 0,531 С П2 3 < 0,975 следует, что меж-
(1) (2) г
ду величинами х и х линейная корреляционная зависимость суще-
ствует (нуль не попадает в пределы интервальной оценки) и при этом
достаточно тесная. 3.3.6. 1) fi2.4 = 0,915; по табл. П1.3 находим
wo,oe = 1,645, а по табл. П1.7 значение z = 1,557, а затем Zi = 0,828 и
z2 — 2,172. Интервальная оценка для Г12-4 определяется неравенствами
ОТВЕТЫ И РЕШЕНИЯ
267
0,680 < Г12.4 0,974, которые выполняются с доверительной вероятно-
стью Ро = 0,90; 2) #1.24 — 0,836; критическая статистика критерия равна
7П = 17,841. По табл.П1.5 находим Fa(p,n - р - 1) = Fo,os(2;7) = 4,74.
Т.к. 7n > Fo,os(2;7), то гипотеза Но: #1.24 = 0 отвергается с вероятно-
стью ошибки а = 0,05. Таким образом, существует линейная зависимость
между я/1) — темпом прироста ВНП, — с одной стороны, и темпами при-
роста промышленного производства (а/2)) и доли безработных (а/4)), — с
другой.
Множественный коэффициент детерминации #1.24 = 0,836 показыва-
ет, что 83,6% дисперсии а/1) объясняется вариацией величин х^2\
Из интервальной оценки 0,680 г12-4 0,974 следует, что между ве-
личинами а/1) и х^ линейная корреляционная зависимость существует и
/ 1 _q 77 \
при этом достаточно тесная. 3.4.1. 1) Г12 = —0,77; R = I * j;
2) А = ( 0 0,23 ) ’ А = (-6,94 0'34)’ 3) 5; 1; 2; 7; 6; 3; 10; 4; 9; 8'
3.4.2. 1) Da/1) = А] = 1,93; Dz^ = А2 = 0,07; соответственно, 96,5% и
3 5%' А— (9,93 —9,49\ ZT—
0,0/0, а — ( п Qc n 1Q J,Zi —
_ / -1
“ \ —1,44
/0,98 -0,19
\0,98 0,19
1,12 1,41 -1,13 -1,17 -0,50 1,36 -0,56 0,77 -0,29\
0,07 0,21 -0,57 -0,58 1,11 -0,23 1,39 -1,40 1,43 )'
3.4.3. 1) аг*1* = 9,86; zj2) = 14,70; 2) Dz(,) = Aj = 1,14; Dz(2) = 0,86;
-0,144.3.4.4. 1) zjj> = -2,185; z($ = -0,397; 2) a^1* = 1,486;
,; 3) 63,5%; 4) f(z(1),ar(2)) = -0,252. 3.4.6. 1) Dz(1) = 1,325;
0,581 \
0,581 /
-0,68 -0,86 0,33 -0,25 1,79 0,28 \
-1,22 0,72 1,76 -0,13 -1,68 -0,41/
3) Великобритания, Австрия, Бельгия, Венгрия, Болгария, Армения, Бе-
3) Иг = '
*(2)
х10=-1,970>
Dz(2) = 0,675; 2)А= (_°’38144
ZT=f-1,54 0,94 1,01 -1,03
\-0,02 0,60 1,03 -0,66
лоруссия, Азербайджан, Россия. 3.4.6. 1) Aj = 2,15(71,7%); А2 =
/ 0,96* 0,21 - 0,19\
0,78(97,7%); 2) А = I 0,94* 0,30 0,18 I, z^ характеризует уровень
\-0,60 0,80 -0,02/
жизни населения, a — обеспеченность населения врачами (медицин-
ским обслуживанием); 3) Великобритания, Австрия, Бельгия, Венгрия,
Белоруссия, Армения, Азербайджан, Россия. 3.4.7. 1) г12 = -0,18;
Г14 = 0,61; Г2з = 0,82; г24 = 0,24; г34 = -0,05; 2) Aj = 1,84(46,0%);
А2 = 1,61(86,3%); A3 = 0,53(99,5%); 3) z^ определяет уровень цен на масло
и сахар, a z^ — на мясо и хлеб. 3.4.8. 1) 81,5%; 2) r(z^2\z^^) = 0,903.
268
ОТВЕТЫ И РЕШЕНИЯ
3.4.9. 1) 51,8%; 2) 95,67%; 3) г12 = -0,36. 3.4.10. 1) а(1) = 5,2;
а(2) = 5,4; = 2,315; а2 = 2,059; г12 = 0,906; 2) Dz(1) = At =
1,906(95,3%); Dz(2) = А2 = 0,094(4,7%); 3) Ц = (^; ; /2 = (-^5 ^);
А = (о 976 ~0022177); 4) 3; 5; 2; 1; 4- УпР-тест5Л* 0 <б);
2) У“ е типу jo, если (У - У1 х (а(у„) - А(») > 1„
при всех j = 1,2,..., 10; 3) a(j) = £ Yjif E = -jo-1---(ni^(l) + • • • +
3 i=l £ nj-10
>=1
nloS(10)), где E(j) = ^(Yji - а^))(Уц - a(j))T; 4) Y* e типу 1, если
3 t=l
(у* - E-1(a(l) - a(2)) > In %. Задачи 5.1~5.5 решаются no
схеме примера 5. 1 и упражнения теста 5.1. 3.5.6. Ответы сведены в
следующую таблицу:
Задание Расстояние объединения Объединяемые кластеры Задание Расстояние объединения Объединяемые кластеры
1а 1,71 2,28 4,26 5,21 7,81 5(3),5(6) 5(з,б), 5(5) 5(2),5(4) Sp), «$(2,4) *S,(i,2,4)> •S'o.e.s) Id 1,7 2,99 4,26 6,14 11,91 5(3), 5(6) 5(з,б), 5(5) 5(2), 5(4) 5(1), 5(2,4) 5(1,2,4), 5(3,6,5)
1b 1,71 3,69 4,26 7,07 16,88 5(з),5(6) 5(з,б), 5(5) 5(2),5(4) 5(1), 5(2.4) 5(1,2,4), 5(3.6,5) 2 0,57 1,67 1,76 2,48 3,99 5(3),5(6) 5(1), 5(4) 5(5), 5(3,6) 5(2), 5(3,6,5) 5(1,4), 5(2,3,6,5)
1с 1,71 2,56 4,26 5,08 9,22 5(3), 5(6) 55(з,6),5(5) 5(2), 5(4) 5(1), 5(2,4) 5(1.2.4),5(з.6,5) 3 0,27 0,79 0,98 1,17 2,00 5(3) ,5(6) 5(1), 5(4) 5(з,б), 5(5) 5(2), 5(з,6,5) 5(1,4), 5(2,3,6,5)
ОТВЕТЫ И РЕШЕНИЯ
269
3.5.7. Ответы сведены в следующую таблицу:
Задание Расстояние объединения Объединяемые кластеры Задание Расстояние объединения Объединяемые кластеры
2,10 5(3),5(6) 2,10 5(з),5(6)
2,19 5(1), 5(4) 2,19 5(1), 5(4)
1а 3,06 5(3,6), 5(1>4) Id 3,16 5(2),5(5)
3,16 5(2),5(5) 3,55 5(1,4), 5(з,б)
8,22 5(2,5), 5(1,4,3,6) 9,88 5(2,5), 5(1,4,3,6)
2,10 5(3),5(6) 1,2 5(1),5(4)
2,19 5(1), 5(4) 1,44 5(1,4), 5(6)
1b 3,16 5(2),5(5) 2 1,61 5(2),5(5)
6,16 5(3,6), 5(1,4) 1,88 5(з), 5(1,4,в)
16,62 5(2,5), 5(3,6,1,4) 3,96 5(2,5), 5(3,1,4,6)
2,10 5(3),5(6) 0,52 5(1),5(4)
2,19 5(1),5(4) 0,55 5(1,4), 5(6)
1с 3,16 5(2),5(5) 3 0,66 5(2),5(5)
4,62 5(з,б), 5(1,4) 0,96 5(1,4,6), 5(з)
12,09 5(2,5), 5(3,6,1,4) 1,54 5(2,5), 5(1,4,6,3)
3.5.8. Ответы сведены в следующую таблицу:
Задание Расстояние объединения Объединяемые кластеры Задание Расстояние объединения Объединяемые кластеры
2,43 5(1),5(5) 2,43 5(1),5(5)
2,72 5(2), 5(4) 2,2 5(2), 5(4)
1а 4,10 5(2,4), 5(3) Id 4,55 5(2,4), 5(3)
8,25 5(1,5), 5(2,4,3) 11,65 5(1,5), 5(2,4,3)
2,43 5(1),5(5) 0,85 5(1),5(5)
2,72 5(2), 5(4) 1,58 5(3), 5(4)
1b 5,00 5(2,4), 5(3) 2 2,15 5(3,4), 5(2)
15,61 5(1,5), 5(2,4,3) 2,73 5(1,5), 5(3,4,2)
2,43 5(1),5(5) 0,56 5(1),5(5)
2,72 55(2), 5(4) 0,76 5(3), 5(4)
1с 3,87 5(2,4), 5(3) 3 1,57 5(1,5), 5(3,4)
9,73 5(1,5), 5(2,4,3) 2,03 5(2), 5(1,5,3,4)
270
ОТВЕТЫ И РЕШЕНИЯ
3.5.9. Ответы сведены в следующую таблицу:
Задание Расстояние объединения Объединяемые кластеры Задание Расстояние объединения Объединяемые кластеры
1,91 5(1)>5(4) 1,91 3(1),3(4)
1,97 3(1,4), 3(5) 2,44 3(3),3(5)
1а 2,44 3(1,4,5) ,3(3) Id 2,50 3(3,5), 3(2)
2,48 3(1,4,5,3), 3(2) 3,19 3(3,5,2), 3(1,4)
1,91 3(1), 3(4) 0,62 3(1), 3(4)
2,44 3(3),3(5) 1,07 3(1,4), 3(5)
1b 2,53 3(3.5), 3(2) 2 1,20 3(2), З(3)
4,59 3(3,5,2), 3(1,4) 1,31 3(1,4,5), 3(2,3)
0,19 3(1),3(4) 1,27 3(1),3(4)
2,44 33(з),5(5) 1,87 3(3),3(5)
1с 2,19 3(2), 3(3,5) 3 2,70 3(2), 3(з,5)
2,59 3(1,4), 3(2,3,5) 3,25 3(1,4), 3(2,3,5)
3.5.10 Ответы сведены в следующую таблицу:
Задание Расстояние объединения Объединяемые кластеры Задание Расстояние объединения Объединяемые кластеры
0,26 3(2),3(3) 0,26 3(2), З(3)
0,27 3(2,3),3(5) 0,35 3(2,3), 3(5)
1а 0,73 3(1), 3(4) Id 0,73 3(1),3(4)
0,74 3(6), 3(2,3,5) 0,84 3(1,4), 3(6)
0,75 3(1,4), 3(2,3,5,6) 1,14 3(1,4,6), 3(2,3,5)
0,26 3(2), З(3) 0,15 3(2), З(3)
0,44 3(2,3), 3(5) 0,16 3(2,3),3(5)
1b 0,73 3(1),3(4) 2 0,24 3(1), 3(6)
0,94 3(1,4), 3(6) 0,43 3(1,6), 3(2,3,5)
1,78 3(1,4,6), 3(2,3,5) 0,45 3(4), 3(1,6,2,3,5)
0,26 3(2), З(3) 0,68 3(2), 3(6)
0,34 3(2,3), 3(5) 0,75 3(3),3(5)
1с 0,50 3(2,3,5), 3(6) 3 1,34 3(1), 3(4)
0,73 3(1),3(4) 2,47 3(2,6), 3(3,5)
1,07 3(1,4), 3(2,3,5,6) 3,57 3(1,4), 3(2,6,3,5)
Учебник
Айвазян Сергей Артемьевич,
Мхитарян Владимир Сергеевич
ПРИКЛАДНАЯ СТАТИСТИКА
В ЗАДАЧАХ И УПРАЖНЕНИЯХ
Корректор Л. И. Ганина
Оформление художника А. В. Лебедева
Лицензия серия ИД № 03562 от 19.12.2000 г.
Подписано в печать 10.08.2001. Формат 70x100 1/16
Усл. печ. л. 22. Уч.-изд. л. 16
Тираж 20 000 экз. (1-й завод - 5 000). Заказ № 1663
ООО «ИЗДАТЕЛЬСТВО ЮНИТИ-ДАНА»
Генеральный директор В.Н. Закаидзе
123298, Москва, ул. Ирины Левченко, 1-9
Тел. (095) 194-00-15. Тел/факс (095) 194-00-14
www.unity-dana.ru E-mail: unity@msm.ru
Отпечатано во ФГУП И ПК «Ульяновский
Дом печати». 432980, г. Ульяновск, ул. Гончарова, 14
Качество печати соответствует предоставленным оригиналам
ю н и т V\
ю н и т и __________________
UNITY
Учебная литература для вузов
♦ Экономика
♦ Финансы. Деньги. Банки
♦ Внешнеэкономическая
деятельность
♦ Учет. Анализ. Аудит
♦ Менеджмент
♦ Маркетинг. Гостеприимство
♦ Страхование
♦ Юридическая литература
♦ Психология. Социология
♦ История. Культура
♦ Философия
♦ Математика. Статистика.
Эконометрика. Информатика
♦ Экология
ИЗДАТЕЛЬСТВО ЮНИТИ-ДАНА
123298, Москва, ул. Ирины Левченко, 1—9
Тел.-(095) 194-00-15. Тел./Факс. (095) 194-00-14
E.mail. unity@msm.ru
АЙВАЗЯН Сергей Артемьевич - доктор
физико-математических наук, профессор, академик
Международной академии наук Высшей школы, замес-
титель директора по научной работе Центрального
экономико-математического института Российской
академии наук. Один из ведущих отечественных спе-
циалистов по эконометрике и прикладному статисти-
ческому анализу в экономике. Его работы в области
эконометрического моделирования распределитель-
ных отношений и потребительского поведения населе-
ния имеют мировую известность. Около 40 лет ведет
активную педагогическую деятельность, читая курсы
лекций по всему блоку эконометрических дисциплин
на экономическом факультете Московского государствен-
ного университета им. М.В. Ломоносова, в Российской
экономической школе, Московском государственном
университете экономики, статистики и информатики (МЭСИ),
Государственном университете - Высшей школе экономики,
Московском отделении Калифорнийского государственного
университета (г.Хейвард), в ряда зарубежных университетов
в качестве приглашенного профессора. Имеет более 150
опублизданных научных работ, в том числе 8 монографий,
среда которых - трехтомник «Прикладная статистика»
(издательство «Финансы и статистика», 19$ - 1989 г г)
МХИТАРЯН Владимир Сергеевич - доктор
экономических наук, профессор, академик Междуна-
родной академии наук Высшей школы, директор Ин-
ститута статистики и эконометрики Московского госу-
дарственного университета экономики, статистики и
информатики (МЭСИ). Автор более 150 научных и
учебно-методических работ, включая монографию,
14 учебных пособий и более 30 учебно-методических
разработок. На кафедре математической статистики
МЭСИ с 1973 г. читает курсы по теории вероятностей
и математической статистике, с 1982 г. - по много-
мерному статистическому анализу, а с 1993 г. - курс
эконометрики. Возглавляет научно-методический со-
вет по специальности «Статистика».
9 785238 003030 >