Author: Буренин А.Н.
Tags: финансы государственные финансы финансы государственного сектора банковское дело деньги экономика экономические науки биржевая торговля бизнес
ISBN: 5-90218-906-3
Year: 2005
51780
ззче
БУРЕНИН
631
8945
9352
7673
4734
’094665'> 8065751S 9 5'695106ц
634
658
>•98
95 06
6543465564456 23153’3236*85 KKEr3G9167936 45671965556
551
344
06575139518951964
’>4 'i 5 l 11 • i *
v ♦ £ ?
1 Д l Г 7
ФОРВАРДЫ
ФЬЮЧЕРСЫ
|||»'йв «I
СЕРИЯ
ISSN 1683-0393
32364854665 498478662069 9385’86238'3 415637136753
6565 6523 37 6
9655 34:6 4564
847
7862
65546634551633465
H6253446523I56253 1й$8769<66519636721
1 >89516S430 733488И
I ’65784671 3641 465Г
ОПЦИОНЫ, ш JH .
551633465456 523156253145 93367210667й
ЭКЗОТИЧЕСКИЕ И ПОГОДНЫЕ ПРОИЗВОДНЫЕ
646554363455 54-625344652 687394665190 898945786061
МОСКВА 2005
1 3466544657-53'45
64
:36t В
Серия «Теория и практика финансового рынка»
А.Н. Буренин
ФОРВАРДЫ, ФЬЮЧЕРСЫ, ОПЦИОНЫ, ЭКЗОТИЧЕСКИЕ И ПОГОДНЫЕ ПРОИЗВОДНЫЕ
Издание 1-е
Москва
Научно-техническое общество имени академика С.И. Вавилова 2005
УДК 336 763 01
ББК 65 262 2
Б 91
Буренин А.Н.
Форварды, фьючерсы, опционы, экзотические и погодные производные
М , Научно-техническое общество имени академика С.И. Вавилова, 2005, - 534 + 6 с
В книге рассматриваются вопросы организации и функционирования срочного рынка, в том числе на Фондовой бирже РТС раскрываются основные понятия, теоретические концепции инструментарии и стратегии, используемые участниками современного финансового рынка
Рекомендуется для студентов аспирантов преподавателей высших учебных заведений бизнес-школ и работников финансовой сферы
Научно-техническое общество имени академика С И Вавилова. Почтовый и юридический адрес
119019, город Москва, улица Моховая, дом 10. строение 2
E-mail: NTO@NTOvavilov ru, innashentseva@mail ru www.NTOvavilov ru
Телефон. (095)364-44-90, 203-35-03
Факс:(095)203-34-65.
© Буренин A H
ISBN 5-90218-906-3
ISSN 1683-0393
СОДЕРЖАНИЕ
ЧАСТЬ L ФОРВАРДНЫЙ И ФЬЮЧЕРСНЫЙ РЫНКИ..................3
ГЛАВА 1. ОБЩАЯ ХАРАКТЕРИСТИКА РЫНКА ПРОИЗВОДНЫХ ФИНАНСОВЫХ ИНСТРУМЕНТОВ................................3
КРАТКИЕ ВЫВОДЫ........................................14
ГЛАВА 2. ФОРВАРДНЫЕ КОНТРАКТЫ.........................15
2.1. ОБЩАЯ ХАРАКТЕРИСТИКА ФОРВАРДНОГО КОНТРАКТА.............................................15
2.2. ФОРВАРДНАЯ ЦЕНА И ЦЕНА ПОСТАВКИ .................19
2.3. ОПРЕДЕЛЕНИЕ ФОРВАРДНОЙ ЦЕНЫ И ЦЕНЫ ФОРВАРДНОГО КОНТРАКТА...............................20
2.3.1. Форвардная цена и цена форвардного контракта
на актив, по которому не выплачиваются доходы.20
2.3.1.1. Форвардная цена акции...................20
2.3.1.2. Цена форвардного контракта..............27
2.3.2. Форвардная цена и цена форвардного контракта на актив, по которому выплачиваются доходы.......36
2.3.2.1. Форвардная цена акции с учетом абсолютной величины дивиденда...............................36
2.3.2.2. Форвардная цена акции с учетом ставки дивиденда........................................41
2.3.2.3. Цена форвардного контракта..............49
2.3.3. Форвардная цена и цена форвардного контракта на валюту.......................................50
2.3.3.1. Форвардная цена.........................50
2.3.3.2. Форвардный валютный курс и инфляция.....56
2.3.3.3. Цена форвардного контракта..............57
2.3.3.4. Котировка валюты на спотовом и форвардном рынках...........................................57
2.3.4. Форвардная цена товара......................58
2.3,5. Форвардная цена при различии ставок по кредитам и депозитам.
Внутренняя ставка доходности..................62
2.4. СИНТЕТИЧЕСКИЙ ФОРВАРДНЫЙ КОНТРАКТ................70
КРАТКИЕ ВЫВОДЫ........................................72
Организация и функционирование фьючерс ного рынка...................................
3.1. ОБЩА*) характеристика фьючерсного рынка.........
3.2. ФЬЮЧЕ:рСНДЯ цЕНд БАЗИС ЦЕНА ДОСТАВКИ............
□ о о фьючерсная цена.............................
^00 г аЗИС- Мена А°с™.............................
3-2 3. Чоотношение форвардной и фьючерсной цен....
^ 2 5 КУДУЩЭЯ ЦеНЭ СП°Т...........................
vrnw отиРовка фьючерсных контрактов...............
^Ц|||Р0ВАНИЕ ФЬЮЧЕРСНЫМИ КОНТРАКТАМИ .............
3.4. ФУНКЦ^оинровдинЕ МЕХАНИЗМА EFP..................
КРАТКИЕ В<Ь|В0ДЫ.....................................
ПРИЛОЖЕН м
irKuiv/ixun^E 1 форвардная и фьючерсная цены для случая, когда ставку ^ез рИСКа постоянна и одинакова для любых периодов BR)eMeHM....................................
ПРИЛОЖЕНИЕ 2. Определение коэффициента хеджирования с помощью гПроГраМмы Excel ..........................
ФЬЮЧЕРСНЫЕ КОНТРАКТЫ НА АКЦИЮ, ИНДЕКС И ВАЛЮТУ........................
4.1. ФЬЮЧЕ(рСНЫЙ КОНТРАКТ НА АКЦИЮ ..................
4-Н1- Цианизация торговли фьючерсными контрактами
На^ акции. Фьючерсная торговля акциями на^ Фондовой бирже РТС.......................
4.1.2. ^дЖИрОвание фьючерсным контрактом на акции.
4.2. ФЬЮЧЕ^СНЬ|Й КОНТРАКТ НА ФОНДОВЫЙ ИНДЕКС.........
4-2-1 Фьючерсная цена фондового индекса.........
1 о’п' Индексный арбитраж.........................
Хеджирование фьючерсным контрактом на индекс..., 4.3. ФЫОЧЕЬСНЫй КОНТРАКТ ФОНДОВОЙ БИРЖИ РТС
НАКУРИ БЕЗНАЛИЧНОГО ДОЛЛАРА К РУБЛЮ ..............
1^'1’ Определение фьючерсной цены и арбитраж......
4.3.2. Сп^|екуЛЯТИВНЬ1е СТраТегии.................
КРАТКИЕ fej".........................................
и виды.....................................
.74 .74 .83 .83 .85 .87
.89 .89 .90 107 109
110
112
115
115
115
118
127
128
130
133
137
137
138
139
143
ГЛАВА 5. ФЬЮЧЕРСНЫЕ КОНТРАКТЫ НА ПРОЦЕНТНЫЕ СТАВКИ...........................................145
5.1. ФЬЮЧЕРСНЫЙ КОНТРАКТ НА КАЗНАЧЕЙСКУЮ ОБЛИГАЦИЮ США......................................145
5.2. ОПРЕДЕЛЕНИЕ ФЬЮЧЕРСНОЙ ЦЕНЫ ОБЛИГАЦИИ И АРБИТРАЖ.........................................147
5.2.1. Определение фьючерсной цены облигации, по которой не выплачиваются купоны в течение действия контракта............................148
5.2.2. Определение фьючерсной цены облигации, по которой выплачиваются купоны в течение действия контракта............................155
5.2.3. Расчет коэффициента конверсии казначейской облигации.....................................161
5.3. ХЕДЖИРОВАНИЕ ФЬЮЧЕРСНЫМ КОНТРАКТОМ НА ОБЛИГАЦИЮ......................................162
5.4. ХЕДЖИРОВАНИЕ ПОРТФЕЛЯ ОБЛИГАЦИЙ ............164
5.5. ДЮРАЦИЯ ФЬЮЧЕРСНОГО КОНТРАКТА.............164
5.6. УПРАВЛЕНИЕ ПОРТФЕЛЕМ ОБЛИГАЦИЙ С ПОМОЩЬЮ ФЬЮЧЕРСНОГО КОНТРАКТА.............................166
5.7. ФЬЮЧЕРСНЫЙ КОНТРАКТ НА ТРЕХМЕСЯЧНЫЙ ЕВРОДОЛЛАРОВЫЙ ДЕПОЗИТ ...........................167
5.7.1 Общая характеристика контракта на трехмесячный
евродолларовый депозит...................167
5.7.2. Определение фьючерсной цены контракта и арбитраж....................................171
5.7.3. Использование контракта для увеличения доходности инвестиций.........................181
5.7.4. Хеджирование фьючерсным контрактом на трехмесячный евродолларовый депозит........182
5.7.5. Хеджирование соглашений о форвардной ставке и процентных свопов...........................191
5.8. ФЬЮЧЕРСНЫЙ КОНТРАКТ НА КАЗНАЧЕЙСКИЙ ВЕКСЕЛЬ США.......................................193
5.8.1. Общая характеристика контракта на казначейский вексель США...................................193
5.8.2. Определение фьючерсной цены и арбитраж..196
5.8.3. Хеджирование фьючерсным контрактом на казначейский вексель.......................199
5.9. ФЬЮЧЕРСНЫЙ КОНТРАКТ ФОНДОВОЙ БИРЖИ РТС
НА РУБЛЕВЫЕ ОБЛИГАЦИИ ГОРОДСКОГО ВНУТРЕННЕГО ОБЛИГАЦИОННОГО ЗАЙМА г. МОСКВЫ......201
КРАТКИЕ ВЫВОДЫ.....................................206
ЧАСТЬ II. ОПЦИОННЫЕ РЫНКИ..........................208
ГЛАВА 6. ОРГАНИЗАЦИЯ И ФУНКЦИОНИРОВАНИЕ ОПЦИОННОГО РЫНКА...................................208
6.1. ОБЩАЯ ХАРАКТЕРИСТИКА ОПЦИОННЫХ КОНТРАКТОВ.....208
6.1.1. Опцион колл..............................209
6.1.2. Опцион пут...............................213
6.1.3. Категории опционов.......................215
6.1.4. Премия...................................216
6.2. ОРГАНИЗАЦИЯ ОПЦИОННОЙ ТОРГОВЛИ.
ОПЦИОНЫ НА ФЬЮЧЕРСЫ ФОНДОВОЙ БИРЖИ РТС..........220
6.3. ХЕДЖИРОВАНИЕ ОПЦИОНАМИ .......................224
6.4. КОТИРОВКА ОПЦИОННЫХ КОНТРАКТОВ................226
КРАТКИЕ ВЫВОДЫ.....................................227
ГЛАВА 7. ОПРЕДЕЛЕНИЕ ГРАНИЦ ПРЕМИИ ОПЦИОНОВ НА АКЦИИ...........................................228
7.1. ГРАНИЦЫ ПРЕМИИ ОПЦИОНОВ НА АКЦИИ, ПО КОТОРЫМ НЕ ВЫПЛАЧИВАЮТСЯ ДИВИДЕНДЫ ..............228
7.1.1. Стоимость американского и европейского опционов
колл к моменту истечения срока действия контрактов... 228
7.1.2. Стоимость американского и европейского опционов пут к моменту истечения срока действия контрактов.230
7.1.3. Верхняя граница премии американского и европейского опционов колл.....................231
7.1.4. Верхняя граница премии американского и европейского опционов пут......................232
7.1.4.1. Верхняя граница премии американского опциона пут...................................232
7.1.4.2. Верхняя граница премии европейского опциона пут..................................232
7.1.5. Нижняя граница премии европейского опциона колл...................................233
7.1.6. Нижняя граница премии европейского опциона пут........................................236
7.1.7. Нижняя граница премии американского опциона колл.
Раннее исполнение американского опциона колл...239
7.1,8. Нижняя граница премии американского опциона пут.
Раннее исполнение американского опциона пут....240
7.2. ГРАНИЦЫ ПРЕМИИ ОПЦИОНОВ НА АКЦИИ, ПО КОТОРЫМ ВЫПЛАЧИВАЮТСЯ ДИВИДЕНДЫ ....................240
7.2,1. Верхняя граница премии европейских
и американских опционов.......................240
7.2.2. Нижняя граница премии европейского и американского опционов колл...................241
7.2.3. Нижняя граница премии европейского и американского опционов пут....................244
7.2.4. Раннее исполнение американского опциона колл.247
КРАТКИЕ ВЫВОДЫ..........................................249
ГЛАВА 8. ОПРЕДЕЛЕНИЕ ГРАНИЦ ПРЕМИИ ОПЦИОНОВ
8.1. СТОИМОСТЬ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ КОЛЛ К МОМЕНТУ ИСТЕЧЕНИЯ СРОКА ДЕЙСТВИЯ КОНТРАКТОВ............................251
8.2. СТОИМОСТЬ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ ПУТ К МОМЕНТУ ИСТЕЧЕНИЯ СРОКА ДЕЙСТВИЯ КОНТРАКТОВ............................252
8.3. ВЕРХНЯЯ ГРАНИЦА ПРЕМИИ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ КОЛЛ....................252
8.4. ВЕРХНЯЯ ГРАНИЦА ПРЕМИИ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ ПУТ.....................254
8.4.1. Верхняя граница премии американского опциона пут.... 254
8.4.2. Верхняя граница премии европейского опциона пут.254
8.5. НИЖНЯЯ ГРАНИЦА ПРЕМИИ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ КОЛЛ...................255
8.6. НИЖНЯЯ ГРАНИЦА ПРЕМИИ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ ПУТ....................259
КРАТКИЕ ВЫВОДЫ.................................262
ГЛАВА 9. СООТНОШЕНИЯ МЕЖДУ ПРЕМИЯМИ ОПЦИОНОВ .... 264
9.1. СООТНОШЕНИЯ МЕЖДУ ПРЕМИЯМИ ОПЦИОНОВ
С РАЗНЫМИ ЦЕНАМИ ИСПОЛНЕНИЯ, СРОКАМИ
ИСТЕЧЕНИЯ И СТАНДАРТНЫМИ ОТКЛОНЕНИЯМИ ........ 264
9.1.1. Соотношения между премиями опционов с разными ценами исполнения................... 264
9.1.2. Соотношения между премиями опционов с разными сроками истечения.....................266
9.1.3. Соотношения между премиями опционов с разными стандартными отклонениями.............268
9.2. РАЗНОСТЬ МЕЖДУ ПРЕМИЯМИ ОПЦИОНОВ КОЛЛ НА
ОДИН БАЗИСНЫЙ АКТИВ С ОДНОЙ ДАТОЙ ИСТЕЧЕНИЯ.... 268
9.2.1. Разность между премиями европейских опционов..268
9.2.2. Разность между премиями американских опционов.269
9.3. РАЗНОСТЬ МЕЖДУ ПРЕМИЯМИ ОПЦИОНОВ ПУТ НА
ОДИН БАЗИСНЫЙ АКТИВ С ОДНОЙ ДАТОЙ ИСТЕЧЕНИЯ ... 270
9.3.1. Разность между премиями европейских опционов..270
9.3.2. Разность между премиями американских опционов.271
9.4. ПАРИТЕТ ЕВРОПЕЙСКИХ ОПЦИОНОВ КОЛЛ И ПУТ ......272
9.4.1. Паритет европейских опционов на акции,
по которым не выплачиваются дивиденды......272
9.4.2. Паритет европейских опционов на акции, по которым выплачиваются дивиденды. Взаимосвязь между премиями американских опционов............275
9.4.3. Паритет европейских опционов на фьючерсные контракты.......................................275
9.4.4. Паритет европейских опционов на валюту...277
КРАТКИЕ ВЫВОДЫ.....................................278
ГЛАВА 10. МОДЕЛИ ОПРЕДЕЛЕНИЯ ЦЕНЫ ОПЦИОНОВ.........279
10.1. БИНОМИАЛЬНАЯ МОДЕЛЬ..........................279
10.1.1. Простая биномиальная модель............279
10.1.1.1. Портфель из акций и заемных средств эквивалентный опционному контракту..........279
10.1.1.2. Формирование портфеля без риска .284
10.1.1.3. Риск-нейтральная вероятность.....287
10.1.2. Двухпериодная биномиальная модель......290
10.1.3. Многопериодная биномиальная модель.....291
10,1.4. Биномиальная модель оценки премии американских опционов на акции, по которым не выплачиваются дивиденды......................................297
10,1.5. Вычисление стандартного отклонения доходности акции...............................300
10.1.6. Биномиальная модель для акций, по которым выплачиваются дивиденды........................302
10.2. МОДЕЛЬ БЛЭКА-ШОУЛЗА...........................306
10.2.1. Дифференциальное уравнение Блэка-Шоулза..306
10.2.2. Формула Блэка-Шоулза для опционов на акции, по которым не выплачиваются дивиденды..........308
10.2.3. Оценка премии европейских опционов на акции, по которым выплачиваются дивиденды.............310
10.3. ОЦЕНКА ПРЕМИИ ЕВРОПЕЙСКИХ ОПЦИОНОВ
НА ИНДЕКСЫ, ФЬЮЧЕРСНЫЕ КОНТРАКТЫ И ВАЛЮТУ........311
10.3.1. Оценка премии опциона на индекс.........311
10.3.2. Формулы Блэка оценки премии опциона на фьючерсный контракт.........................313
10.3.3. Биномиальная модель оценки премии опциона на фьючерсный контракт.........................314
10.3.4. Оценка премии опциона на валюту.........319
КРАТКИЕ ВЫВОДЫ......................................320
ПРИЛОЖЕНИЕ 1. Лемма Ито.............................321
ПРИЛОЖЕНИЕ 2........................................323
2.1. Дифференциальное уравнение для производного актива
на акцию, по которой выплачивается непрерывно начисляемый дивиденд............................323
2.2. Дифференциальное уравнение для производного актива на валюту....................................324
2.3. Дифференциальное уравнение для производного актива на товар.....................................325
2.4. Дифференциальное уравнение для производного актива на фьючерсный контракт.......................325
ПРИЛОЖЕНИЕ 3. Вывод формулы Блэка-Шоулза............326
ПРИЛОЖЕНИЕ 4. Определение премии европейского опциона колл на акции, по которым не выплачиваются дивиденды, с помощью программы Excel................330
ПРИЛОЖЕНИЕ 5. Определение значений вероятности нормально распределенной стандартной случайной величины с помощью программы Excel...........................331
ГЛАВА 11. КОЭФФИЦИЕНТЫ ЧУВСТВИТЕЛЬНОСТИ ПРЕМИИ
ОПЦИОНА...........................................333
11.1. ДЕЛЬТА......................................333
11.1.1. Общая характеристика дельты...........333
11.1.2. Дельта-хеджирование...................337
11.2. ГАММА.......................................341
11.3. ВЕГА........................................345
11.4. ТЕТА........................................348
11.5. РО..........................................350
11.6. ЗАВИСИМОСТЬ МЕЖДУ ДЕЛЬТОЙ, ГАММОЙ И ТЕТОЙ....350
11.7. ФОРМИРОВАНИЕ ПОЗИЦИИ С ЗАДАННОЙ ДЕЛЬТОЙ И ВЕГОЙ...........................................351
11.8. ДЕЛЬТА-ГАММА-НЕЙТРАЛЬНАЯ ПОЗИЦИЯ............352
КРАТКИЕ ВЫВОДЫ....................................353
ГЛАВА 12. ВНУТРЕННЯЯ ВОЛАТИЛЬНОСТЬ................355
12.1. ОПРЕДЕЛЕНИЕ ВНУТРЕННЕЙ ВОЛАТИЛЬНОСТИ ОПЦИОНА...........................................355
12.1.1. Метод бисекций........................355
12.1.2. Метод Ньютона.........................358
12.2. УЛЫБКА ВОЛАТИЛЬНОСТИ........................360
КРАТКИЕ ВЫВОДЫ....................................364
ГЛАВА 13. СИНТЕТИЧЕСКИЕ АКТИВЫ....................365
13.1. СИНТЕТИЧЕСКИЕ ОПЦИОНЫ.......................365
13.2. СИНТЕТИЧЕСКАЯ АКЦИЯ.........................371
13.3. СИНТЕТИЧЕСКАЯ ФЬЮЧЕРСНАЯ ПОЗИЦИЯ............374
КРАТКИЕ ВЫВОДЫ....................................382
ГЛАВА 14. ОПЦИОННЫЕ СТРАТЕГИИ.....................384
14.1. ПОКУПКА И ПРОДАЖА ОТДЕЛЬНЫХ ОПЦИОНОВ........384
14.2. ПОКРЫТЫЙ КОЛЛ И ПОКРЫТЫЙ ПУТ................386
14.3. КОМБИНАЦИИ И СПРЭДЫ.........................388
14.3.1. Комбинации............................389
14.3.1.1. Стеллажная сделка (стрэддл)......389
14.3.1.2. Стрэнгл..........................396
14.3.1.3. Стрэп............................402
14.3.1.4. Стрип............................405
14.3.2. Спрэд.................................408
14.3.2.1. Вертикальный спрэд........................408
14.3.2.1.1. Спрэд быка..........................408
14.3.2.1.2. Спрэд медведя.......................414
14.3.2.1.3. Обратный спрэд быка.................418
14.3.2.1.4. Обратный спрэд медведя..............419
14.3.2.1.5. Бэкспрэд............................419
14.3.2.1.6. Рейтио спрэд........................425
14.3.2.1.7. Спрэд бабочка (сэндвич).............431
14.3.2.1.8. Спрэд кондор........................435
14.3.3. Временной спрэд.................................437
14.3,3.1. Длинный временной спрэд...................437
14.3.3.2. Короткий временной спрэд..................441
14.4. ТОРГОВЛЯ ВОЛАТИЛЬНОСТЬЮ................................444
14.4.1. Покупка волатильности...........................445
14.4.2. Продажа волатильности...........................453
14.5. БОКС-АРБИТРАЖ..........................................454
14.6. ВЗГЛЯД НА ОПЦИОННЫЕ СТРАТЕГИИ..........................459
КРАТКИЕ ВЫВОДЫ...............................................459
ЧАСТЬ III. ЭКЗОТИЧЕСКИЕ И ПОГОДНЫЕ ПРОИЗВОДНЫЕ...............461
ГЛАВА 15. ЭКЗОТИЧЕСКИЕ ОПЦИОНЫ...............................461
15.1. ОПЦИОНЫ, ЗАВИСЯЩИЕ ОТ ДИНАМИКИ ЦЕНЫ БАЗИСНОГО АКТИВА.............................................461
15.1.1. Опционы со средней ценой........................461
15.1.1.1. Азиатские опционы.........................461
15.1.1.2. Опционы со средним значением цены исполнения (average-strike option)..............462
15.1.2. Опционы, зависящие от одного или нескольких значений цены базисного актива .........................463
15.1.2.1. Барьерные опционы ........................463
15.1.2.2. Опцион лукбэк (lookback option)...........464
15.1.2.3. Опцион лестница (ladder option)...........465
15.1.2.4. Опцион клике (clique option)............ 466
15.1.2.5. Опцион выкрик (shout option)..............466
15.2. МНОГОФАКТОРНЫЕ ОПЦИОНЫ ................................467
15.2.1. Опцион радуга ..................................467
15.2.2. Опцион кванто...................................468
15.2.3. Опцион корзина..................................468
15.3. ДРУГИЕ РАЗНОВИДНОСТИ ОПЦИОНОВ......................468
КРАТКИЕ ВЫВОДЫ...........................................471
ГЛАВА 16. ОЦЕНКА ПРЕМИИ НЕ СТАНДАРТНЫХ ЕВРОПЕЙСКИХ ОПЦИОНОВ.....................................472
16.1. ДЕКОМПОЗИЦИЯ ФОРМУЛЫ БЛЭКА-ШОУЛЗА НА СОСТАВЛЯЮЩИЕ КОМПОНЕНТЫ.......................472
16.2. ОЦЕНКА СТОИМОСТИ БИРНАРНОГО ОПЦИОНА................473
16.2.1. Оценка стоимости европейского бинарного опциона с выплатой денег...................473
16.2.2. Оценка стоимости европейского бинарного опциона с поставкой акции..................474
16.3. ОЦЕНКА СТОИМОСТИ ДРУГИХ РАЗНОВИДНОСТЕЙ НЕ СТАНДАРТНЫХ ОПЦИОНОВ..........................475
16.3.1. Оценка стоимости опциона суперакция..........475
16.3.2. Оценка стоимости европейского опциона кэп....478
16.3.3. Оценка стоимости европейского опциона фло....480
16.3.4. Оценка стоимости европейского опциона коллар.482
КРАТКИЕ ВЫВОДЫ...........................................485
ГЛАВА 17. ПОГОДНЫЕ ПРОИЗВОДНЫЕ...........................487
17.1. ОБЩАЯ ХАРАКТЕРИСТИКА ПОГОДНЫХ ПРОИЗВОДНЫХ......................................487
17.2. ПОГОДНЫЙ СВОП......................................492
17.3. ОПЦИОН ПУТ.........................................493
17.4. КОЛЛАР ............................................494
17.5. БИРЖЕВАЯ ТОРГОВЛЯ ПОГОДНЫМИ ПРОИЗВОДНЫМИ.............................................495
КРАТКИЕ ВЫВОДЫ...........................................498
ПРИЛОЖЕНИЕ. Материалы фондовой биржи РТС «ИНСТРУМЕНТЫ
И ТЕХНОЛОГИИ СРОЧНОГО РЫНКА РТС».................499
Список основной литературы.......................523
ФОНДОВАЯ БИРЖА РТС
Во всем мире срочный рынок является важной составной частью финансового рынка. Рынок фьючерсных и опционных контрактов снискал популярность среди большого круга инвесторов благодаря широким возможностям эффективно управлять капиталом при минимальных затратах. Оборот срочного рынка в развитых странах превышает объем торгов на рынках базовых активов.
Развитие рынка срочных инструментов в России в значительной степени определили события августа 1998 года, когда деятельность участников в этом сегменте была практически парализована. Непрерывное функционирование в такой ситуации срочной секции Фондовой биржи «Санкт-Петербург» доказало надежность используемых биржей технологий и системы гарантий, что стало определяющим фактором в выборе РТС при создании рынка фьючерсов и опционов. В сентябре 2001 года две ведущие торговые площадки России - Фондовая биржа РТС и Фондовая биржа «Санкт-Петербург» - объединили свои усилия для построения качественно нового более надежного и ликвидного срочного рынка FORTS (Futures&Options on RTS). На текущий момент Фондовая биржа РТС является лидером срочного рынка России.
Фондовая биржа РТС считает, что срочный рынок в России является неотъемлемой частью отечественного финансового рынка. Развитие торговли стандартными инструментами способствует снижению общего системного риска на финансо
вом рынке На срочном рынке присутствуют различные категории участников, и рынок, уравновешивая различные интересы, распределяет риски между хеджерами и арбитражерами с одной стороны и спекулянтами с другой Все ведущие игроки финансового рынка работают на срочном рынке PTC-FORTS, и в ближайшее время их круг расширится за счет управляющих компаний и иностранных инвесторов
Сегодня срочный рынок - динамично развивающийся сегмент финансового рынка России Наибольшее развитие получили производные финансовые инструменты на ликвидные российские акции Все большую популярность среди инвесторов завоевывает фьючерс на основной индикатор российского фондового рынка - Индекс РТС Активно развивается торговля еще одним новым инструментом, появившемся в 2005 году, -фьючерсами на процентные ставки.
Фьючерсы и опционы являются достаточно сложными финансовыми инструментами, требующими высокой квалификации трейдеров и управляющих. Мы надеемся, что книга Алексея Буренина «Форварды, фьючерсы, опционы, экзотические и погодные производные» поможет раскрыть безграничные возможности срочного рынка и станет Вашей настольной книгой
Успешной работы на срочном рынке!
Управление срочного рынка Фон9№М9иржи РТС
Межрегиональная Общественная Организация
Научно-Техническое Общество
имени академика С.И. Вавилова
ОТ ИЗДАТЕЛЯ
Межрегиональная общественная организация «Научно-техническое общество имени академика С.И.Вавилова», основанное в 1947 году по инициативе академика Сергея Ивановича Вавилова, в настоящее время осуществляет деятельность по следующим направлениям:
• НАУЧНО-ТЕХНИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ
о приборостроение
о программные комплексы, компьютерные системы и сети
• ОБЩЕСТВЕННАЯ ДЕЯТЕЛЬНОСТЬ
о участие в мероприятиях Союза Научных и инженерных обществ
о программа «Бизнес-клуб»
• ИЗДАТЕЛЬСКАЯ ДЕЯТЕЛЬНОСТЬ
о серия книг «Теория и практика финансового рынка»
о электронная библиотека
• КОНСАЛТИНГ
о юридические консультации
о бухгалтерское обслуживание
о маркетинг
о финансовая инженерия и риск-менеджмент
о программы обучающего консультирования
В НТО им. академика С.И. Вавилова с 2005 года развивается программа «Финансовая инженерия и риск-менеджмент». В работе программы принимают участие лучшие профессионалы данной области.
Цель программы - оказание консультационных, образовательных услуг и разработка программных продуктов для осуществления технической поддержки финансового бизнеса.
Услуги включают консалтинг по направлениям:
1. Количественные финансы и финансовая инженерия
• Рыночные и кредитные деривативы
• Структурные продукты
• Финансовые продукты со встроенными деривативами
2. Риск-менеджмент
* Организация системы управления рисками
• Количественные методы оценки финансовых рисков Портфельные риски Хеджирование рисков
3. Управление активами/пассивами
4. Управление портфелем и оценка эффективности с учетом риска
5. Торговые стратегии и системы
Образовательные услуги представлены обучающим консультированием по тематикам:
• Рынок финансовых деривативов
• Математика финансовых деривативов
• Количественные методы в финансах
* Организация системы риск-менеджмента
• Количественные методы оценки рисков
• Практика управления рисками на Российском рынке
• Практика торговли деривативами на фондовой бирже РТС
Более подробную информацию о наших услугах можно получить на сайте
www.ntovavilov.ru
Будем рады сотрудничеству со всеми заинтересованными лицами!
IV
С 2002 года Издательство НТО имени академика С.И. Вавилова издает серию книг «Теория и практика финансового рынка». Международным центром в Париже настоящей серии был присвоен номер ISSN.
Автор серии Буренин Алексей Николаевич - доктор экономических наук, профессор, один из ведущих специалистов в области рынка ценных бумаг и производных финансовых инструментов, заведующий кафедрой «Фондового рынка» МГИМО(У) МИД РФ.
В 2004 году Институтом международных отношений МИД РФ автору серии было присвоено звание лауреата премии имени И.Д. Удальцова.
Книги серии рекомендованы Федеральной комиссией по рынку ценных бумаг России (ФСФР) для подготовки к специализированному экзамену серии 7.0 и экзамену по «Базовому курсу по рынку ценных бумаг». Книги также включают материал для подготовки к специализированным экзаменам серии 1.0 и 5.0.
Первая книга серии «Рынок ценных бумаг и производных финансовых инструментов» вышла в 2002 году. В ней рассматриваются вопросы организации и функционирования рынка ценных бумаг и производных финансовых инструментов, раскрываются основные понятия, теоретические концепции и инструментарий современного финансового рынка.
Вторая книга серии «Фьючерсные, форвардные и опционные рынки» вышла в 2003 году. В ней рассматриваются вопросы организации и функционирования срочного рынка, раскрываются основные понятия, теоретические концепции, инструментарий и стратегии, используемые участниками современного финансового рынка.
Третья книга серии «Управление портфелем ценных бумаг» вышла в 2005 году. В ней рассматриваются вопросы управления портфелем ценных бумаг, основные концепции и финансовые стратегии, используемые в этой области деятельности. В книге широко представлен материал по использованию программы Excel для финансовых расчетов и построения моделей.
Настоящее издание - четвертая книга серии.
В 2006 году издательство планирует выпустить «Сборник задач с решениями по рынку ценных бумаг». На 2006 год запланировано издание книги «Процентные финансовые инструменты и кривая доходности».
Вице-президент НТО
Шенцева Ирина
ЧАСТЬ I. ФОРВАРДНЫЙ И ФЬЮЧЕРСНЫЙ РЫНКИ
ГЛАВА 1. ОБЩАЯ ХАРАКТЕРИСТИКА РЫНКА ПРОИЗВОДНЫХ ФИНАНСОВЫХ ИНСТРУМЕНТОВ
В данной главе дается общее представление о функциях, структуре, современном состоянии и участниках рынка производных финансовых инструментов.
Временной срез рыночной экономики представлен двумя сегментами: спотовым и срочным рынками. Спотовый рынок - это рынок, на котором сделка заключается и сразу же исполняется. Законодательство разных стран обычно отводит контрагентам несколько дней с момента заключения сделки для осуществления взаиморасчетов. Цену, возникающую в сделках на спотовом рынке, называют спотовой.
Срочный рынок - это рынок, на котором заключаются и обращаются срочные контракты. Срочный контракт представляет собой соглашение о будущей поставке предмета контракта. В момент его заключения оговариваются все условия, на которых он будет исполняться, в том числе и цена.
В основе контракта лежит некоторый актив. Его называют базисным активом. В качестве базисного актива обычно выступают ценные бумаги, фондовые индексы, банковские депозиты, валюта, собственно товары, сами срочные контракты. Однако в практике встречаются и более экзотические базисные активы. Например, на западных рынках базисным активом является погода, или точнее, индексы на погоду. В отечественной практике в период выборной президентской кампании 1996 г. торговался так называемый 'президентский фьючерс", в котором базисными активами выступали кандидаты на пост президента.
В основе срочного контракта могут лежать финансовые или товарные активы. В первом случае говорят о финансовых, во втором о товарных срочных контрактах.
Срочный контракт возникает на основе базисного актива. Поэтому его также называют производным активом, т. е. инструментом, производным от базисного. Следует, однако, подчеркнуть, что понятие “производный актив” шире понятия “срочный контракт”. Произ
водный актив-это актив, цена которого зависит от базисного. Поэтому производным активом является и АДР. АДР - это производный актив спотового рынка. В качестве другого примера можно назвать сертификаты ETF.1
В отечественной литературе в качестве синонима понятия производный инструмент используется также термин дериватив. Он является прямой калькой с английского языка. На английском слово производный - это derivative.
Срочный рынок выполняет в экономике важные функции. Во-первых, позволяет согласовывать планы предпринимателей на будущее. Заключив срочный контракт, предприниматели обеспечивают себе гарантированный сбыт или покупку товара в будущем. Это дает возможность планировать производственный процесс. Во-вторых, позволяет страховать ценовые риски. В контракте контрагенты устанавливают цену будущих взаиморасчетов. Поэтому, они не зависят от конъюнктуры рынка, которая сложится к моменту истечения его срока. В-третьих, он позволяет прогнозировать будущую конъюнктуру. На срочном рынке формируются срочные цены. Они в определенной степени отражают ожидания участников рынка относительно будущего состояния экономики. Поэтому уже сегодня общество может составить представление о векторе развития будущей хозяйственной конъюнктуры.
Срочный рынок является высокодоходным, но и очень рискованным полем инвестирования. Доходность спекулятивных операций с производными инструментами потенциально может достигать нескольких тысяч процентов годовых. Однако большими могут оказаться и потери. Например, 25 февраля 1995 г. был объявлен банкротом английский инвестиционный банк “Бэрингс”, история которого насчитывала 233 года. Причина заключалась в том, что трейдер сингапурского отделения банка Ник Писон потерял за очень короткое время на фьючерсных и опционных контрактах на индекс Никкей 225 1,3 млрд. долл.
Похожая история произошла с инвестиционным фондом “Long Term Capital Management". Фонд был основан в 1994 г., и в основном осуществлял операции с такими производными активами как процентные свопы2, играя на изменении доходностей активов между различ-
1 Подробно о ETF (Exchange Traded Fund) см в книге А.Н.Буренина "Управление портфелем ценных бумаг", Научно-техническое общество им. академика С.И Вавилова, М , 2005, глава 6
2 Своп представляет собой соглашение между контрагентами об обмене в будущем платежами в соответствии с условиями контракта. Наиболее распространены процентные и валютные свопы. Характеристику свопов см. в книге А.Н.Буренина "Рынок ценных бумаг и производных финансовых инструментов", Научно-техническое общество им академика С.И.Вавилова, М., 2002, глава 15
Глава 1. Общая характеристика рынка производных финансовых инструментов ными рынками. В состав управляющих фонда вошли лауреаты нобелевской премии по экономике Р.Мертон и М.Шоулз, бывший руководитель Федеральной резервной системы США Д.Муллин и известный специалист в области международных финансов Дж. Меривеза. Капитал фонда составлял 4 млрд. долл. Фонд заключил срочные контракты более чем на 1,25 трлн, долл. В 1995 и 1996 годах доходность по его операциям превосходила 40%. Однако в 1998 г. в результате кризиса на финансовых рынках он проиграл 90% своего капитала.
Структурно на срочном рынке выделяют первичный и вторичный, биржевой и внебиржевой сегменты. По виду торгуемых инструментов его можно подразделить на форвардный, фьючерсный, опционный рынки и рынки свопов и ФРА3.
Участниками рынка являются хеджеры, спекулянты и арбитражеры. Спекулянт - это лицо, стремящееся получить прибыль за счет разницы в курсовой стоимости финансовых активов, которая может возникнуть во времени. Если спекулянт прогнозирует рост цены актива, он играет на повышение, т.е. покупает актив в надежде продать его позже по более высокой цене. Таких спекулянтов часто называют быками. Если спекулянт прогнозирует падение цены актива, он играет на понижение, т.е. продает актив в надежде выкупить его в последующем по более низкой цене. Таких спекулянтов именуют медведями. Спекулянт обычно осуществляет краткосрочные операции. Когда он начинает операцию, то говорят, что он открывает позицию, когда завершает - закрывает позицию. Спекулянт, открывающий позицию на очень короткое время, называется скальпером. Скальпер держит позицию открытой от нескольких секунд до нескольких минут. Его риск и, соответственно, прибыль по каждой операции обычно невелики, так как за небольшой промежуток времени курс актива, как правило, изменяется не сильно.
Арбитражер - это лицо, извлекающее прибыль без риска за счет одновременной покупки и продажи одного и того же актива на разных рынках, если на этих рынках наблюдаются разные цены. В результате действий арбитражеров цена одного и того же актива на разных рынках выравнивается. Синонимом понятия 'арбитражная операция ' является понятие “операция без риска”.4
' ФРА (Forward Rate Agreement) - соглашение между контрагентами об обмене в будущем платежами на основе краткосрочных процентных ставок. Подробно о ФРА см. в книге А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов", М., “Научно-техническое общество им. академика С.И. Вавилова”, 2002, параграф 15.9.
4 Более подробные определения спекулянта, арбитражера и арбитражной операции см. п книге А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов”,
Хеджер - это лицо, страхующее ценовой риск или риск изменения объемов производства или потребления некоторого актива. Операция по страхованию называется хеджированием. В качестве хеджеров выступают главным образом лица, занимающиеся бизнесом и желающие обеспечить стабильность своих доходов и расходов в условиях неустойчивой конъюнктуры рыночной экономики. Понятие ценового риска включает в себя не только риск изменения собственно товарных цен, но и процентных ставок, курсов валют, ценных бумаг. Компания, занимающаяся экспортно-импортными операциями, будет использовать срочные контракты на валюту для хеджирования валютных рисков. Если предприятие прибегает к кредитам для финансирования своей деятельности, оно воспользуется срочными контрактами на процентные инструменты для страхования от роста процентных ставок. Если компания размещает средства на депозитах, например, страховая компания, или банк, выдающий кредиты, она будет заключать срочные контракты для страхования от падения процентных ставок. Лицо, управляющее портфелем ценных бумаг, воспользуется срочными контрактами для страхования от роста или падения курсовой стоимости финансовых активов.
С появлением срочных контрактов на погоду участники рынка получили возможность хеджировать риск изменения объемов производства и потребления базисных активов в связи с изменением погоды.
На срочном рынке пользуются следующей терминологией. Если лицо заключает срочный контракт для покупки базисного актива, то говорят, что оно покупает контракт или открывает длинную позицию. Если лицо заключает срочный контракт для продажи базисного актива, то говорят, что оно продает контракт или открывает короткую позицию. Соответственно возникают понятия “длинный контракт"' и “короткий контракт"". В первом случае это означает покупку контракта, во втором - продажу.
Исторически срочный рынок возник давно. Его истоки уходят в историческое прошлое предпринимательства. Например, в средние века в Японии заключались срочные контракты на рис. Зарождение организованной срочной торговли можно отнести к появлению в 1751 г. Нью-Йоркской продовольственной биржи. Первая срочная биржа - Чикагская торговая палата (СВТ) была образована в 1848 г. для торговли фьючерсными контрактами на сельскохозяйственную продукцию. Однако действительно бурное развитие срочный рынок получил только в 70-80-е годы прошлого века. В это время
М., "Научно-техническое общество им. академика С.И.Вавилова", 2002. параграф 2.8, и »
Гпава 1 Общая характеристика рынка производных финансовых инструментов стали активно формироваться срочные биржи. В 1972 г. был образован Международный валютный рынок (IMM), являющийся подразделением Чикагской товарной биржи (СМЕ). В 1973 г. начала работу Чикагская биржа опционов (СВОЕ), где впервые открылась торговля биржевыми опционами. Лондонский рынок торгуемых опционов (LTOM) образован в 1978 г. при Лондонской фондовой бирже. В 1979 г. возникла Нью-Йоркская фьючерсная биржа (NYFE). В 1982 г. образована Лондонская международная биржа финансовых фьючерсов (LIFFE). В этом же году открылась торговля срочными контрактами на Филадельфийской фондовой бирже (PHLX). Во Франции в 1985 г. образована Биржа финансовых фьючерсов (MATIF), и т. д.
В 1998 г. произошло объединение Немецкой срочной биржи (DTB) и Швейцарской биржи опционов и финансовых фьючерсов (SOFFEX), в результате чего образовалась срочная биржа Eurex.
В 2000 г. произошло слияние Французской биржи (Societe des Bourses Francaises), Бельгийской биржи (Combined Belgian Stock Exchange and Belgian Futures and Options Exchange) и Амстердамской биржи (Combined Amsterdam Stock Exchange and Amsterdam Options Exchange) и образовалась биржа Euronext-рап European Exchange. В 2001 г. к Euronext присоединилась LIFFE, а в 2002 г. Португальская биржа. Euronext действует как самостоятельные подразделения Euronext Paris, Euronext Brussels, Euronext Amsterdam Lisbon, Euronext UK.
Активное развитие срочного рынка в конце прошлого столетия было стимулировано такими факторами как либерализацией финансового сектора экономики западных стран, быстрым ростом активов институциональных инвесторов, прогрессом в области информационных технологий. Важным фактором явилось также опубликование в 1973 г. Ф.Блэком и М.Шоулзом работы, посвященной оценке стоимости опционов. Она позволила поставить теорию оценки стоимости производных инструментов на объективную математическую основу.
К настоящему моменту срочный рынок достиг больших масштабов. Данные по общему объему биржевой торговли фьючерсными и опционными контрактами в 2003 и 2004 годах и в разбивке по базисным активам представлены в таблицах 1.1 и 1.2. В целом в 2003 г. на биржах было заключено 7920,27 млн. контрактов, в 2004 г. - 8665,38 млн. контрактов. По сравнению с 2003 г. в 2004 г. прирост составил 9,4%. В 2002 г. было заключено порядка 6 млрд, контрактов. По сравнению с 2002 г. в 2003 г. прирост соста-
вил 31%. Практически аналогичный прирост (28%) наблюдался в 2002 г. по сравнению с 2001 г.5 За последние 20 лет - с 1984 г. по 2004 г среднегодовой темп прироста количества торгуемых контрактов равнялся 21% Данная цифра соответствует удвоению объемов торговли каждые 3,5 года.6 7 8
Из общего объема торговли в 2003 г. 34,5% пришлось на фьючерсы и 64,5% на опционы. В 2004 эти цифры соответственно составили 37,1% и 62,9%. Наиболее популярными контрактами в 2003 и 2004 годах были опционы на фондовые индексы. Их уд. вес в общей биржевой торговле составил соответственно 42,4% и 36,2% Второе место занимали опционы на акции - 18,5% и 21,7%, третье - фьючерсы на долгосрочную процентную ставку -10,9% и 11,3%.
Таблица 1.1. Объем фьючерсной торговли е 2003-2004 годах
(млн, контрактов)7______[________'_______________
Год Фьючерсные контракты на Всего
акции фондовые индексы краткосрочную процентную ставку долгосрочную процентную ставку валюту товары
2003 84,96 695,99 707,75 863,42 55,65 321,22 2728,99
2004 126.06 754,47 917,23 976,83 82,59 359,00 3216,18
Таблица 1.2. Объем биржевой опционной торговли в 2003-2004
годах (млн, контрактов)8__________________________________
Год Опционные контракты на Всего
акции фондовые индексы краткосрочную процентную ставку долгосрочную процентную ставку валюту товары
2003 1468,34 3357,35 182,99 118,91 13,94 49,95 5191,48
2004 1876,89 3137,48 216,87 143,50 12,94 61,52 5449,20
5 World Federation of Exchanges Annual Report and Statistics 2004, p 16
6 G Burghard FIA Annual Volume Survey The Invigorating Effects of Electronic Trading, http //www futuresindustry org/fimagazi-1929 asp9a=1026
7 Составлено по источнику World Federation of Exchanges Annual Report and Statistics 2004, pp 85-92
8 Составлено по источнику World Federation of Exchanges Annual Report and Statistics
2004, pp 85-92
Наиболее активно на биржах торгуются финансовые срочные контракты. Уд. вес товарных контрактов составлял в 2003 и 2004 годах соответственно только 4,69% и 4,85%.9
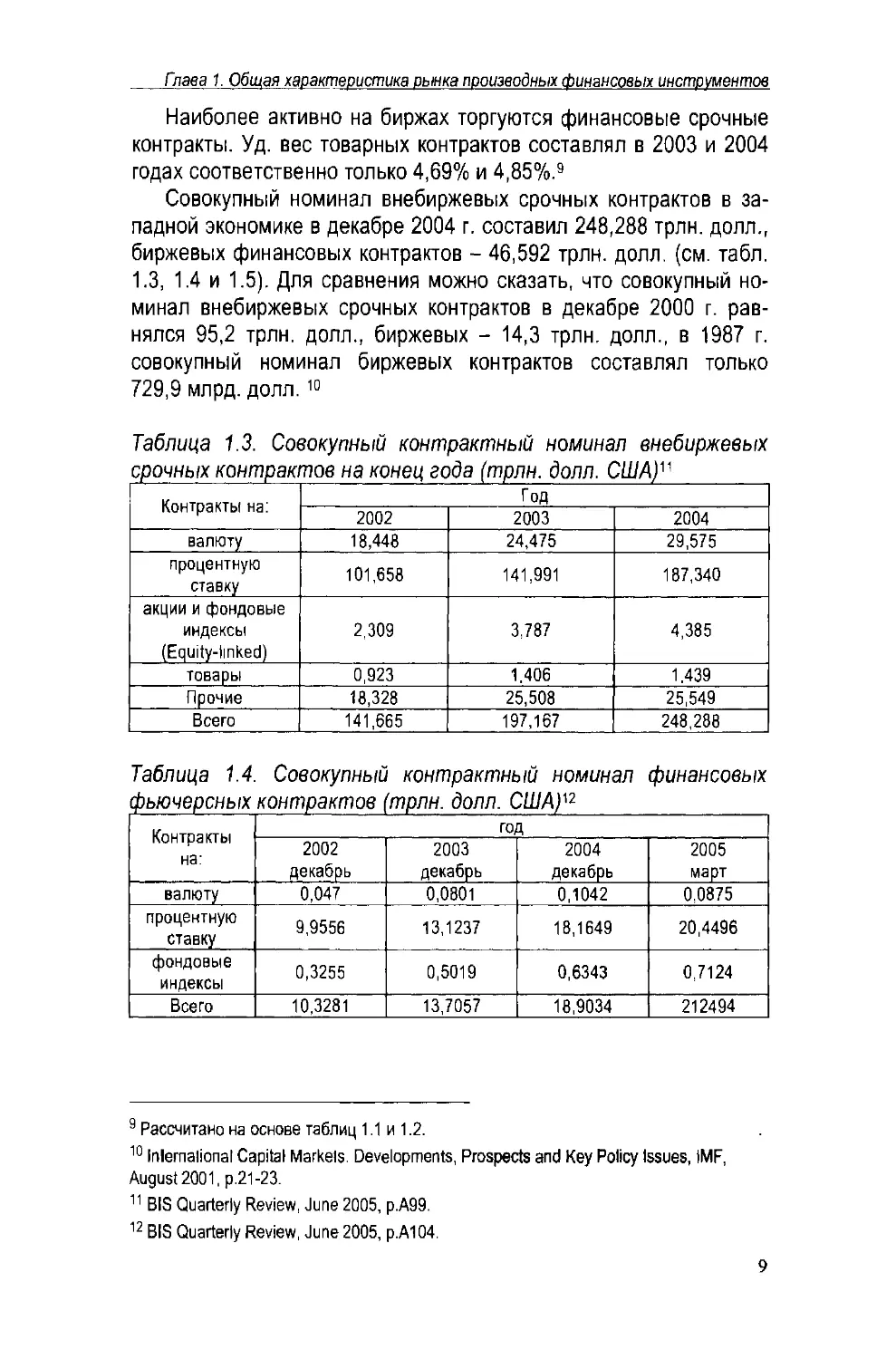
Совокупный номинал внебиржевых срочных контрактов в западной экономике в декабре 2004 г. составил 248,288 трлн, долл., биржевых финансовых контрактов - 46,592 трлн. долл. (см. табл. 1.3, 1.4 и 1.5). Для сравнения можно сказать, что совокупный номинал внебиржевых срочных контрактов в декабре 2000 г. равнялся 95,2 трлн, долл., биржевых - 14,3 трлн, долл., в 1987 г. совокупный номинал биржевых контрактов составлял только 729,9 млрд. долл. 10 11 12
Таблица 1.3. Совокупный контрактный номинал внебиржевых
срочных контрактов на конец года (трлн. долл. США)"
Контракты на: Год
2002 2003 2004
валюту 18,448 24,475 29,575
процентную ставку 101,658 141,991 187,340
акции и фондовые индексы (Equity-linked) 2,309 3,787 4,385
товары 0,923 1.406 1.439
Прочие 18,328 25,508 25,549
Всего 141,665 197,167 248,288
Таблица 1.4. Совокупный контрактный номинал финансовых фьючерсных контрактов (трлн, долл. США)'2
Контракты на: год
2002 декабрь 2003 декабрь 2004 декабрь 2005 март
валюту 0,047 0,0801 0,1042 0,0875
процентную ставку 9,9556 13,1237 18,1649 20,4496
фондовые индексы 0,3255 0,5019 0,6343 0,7124
Всего 10,3281 13,7057 18,9034 212494
9 Рассчитано на основе таблиц 1.1 и 1.2.
10 Inlernaiional Capital Markels. Developments, Prospects and Key Policy Issues, IMF, August 2001, p.21-23.
11 BIS Quarterly Review, June 2005, p.A99.
12 BIS Quarterly Review, June 2005, p.A104.
Часть i. Фореарс Таблица 1.5 биржевых on )ный и фьючерсный рынки Совокупный контрактный номинал финансовых 4ионных контрактов (трлн. долл. США)]3
Контракты на: ГОД
2002 декабрь 2003 декабрь 2004 декабрь 2005 март
валюту 0,0274 0,0379 0,0607 0,060
процентную ставку 11,7595 20,7938 24,6041 34,3286
фондовые индексы 1,7008 2,2023 3,0239 3,7689
Всего 13,4876 23,034 27,6887 38,1574
Если судить по совокупному контрактному номиналу, то наиболее популярными контрактами в мировой практике как на внебиржевом, так и биржевом рынках являются срочные контракты на процентные ставки. Их уд. вес на внебиржевом рынке составляет более 70%, а на биржевом - более 90% (см. табл. 1.6). На внебиржевом рынке наибольший уд. вес в целом и среди процентных инструментов, занимают процентные свопы. Их доля в общем объеме внебиржевого рынка за последние годы превышает 55%, а среди процентных инструментов более 77% (см. табл. 1.7).
Таблица 1.6. Уд.вес срочных контрактов на процентные ставки
на внебиржевом и биржевом рынках на конец года (%)14
год
2002 2003 2004
Внебиржевой рынок 71,76 72,02 75,49
Биржевой рынок (финансовые контракты) 91,18 92,32 91,79
Таблица 1.7. Доля процентных свопов на конец года, считая по контрактному номиналу, на внебиржевом рынке и среди кон-трактов на процентные ставки (%)15_____________
ГОД
2002 2003 2004
Внебиржевой рынок в целом 55,85 56,40 59,35
Контракты на процентные ставки 77,83 78,32 78,66
13 BIS Quarterly Review, June 2005, p.A104.
14 Рассчитано на основе BIS Quarterly Review, June 2005. рр.АЭЭ, A104, таблицы 19, 23A.
15 Рассчитано на основе BIS Quarterly Review, June 2005, p A99, таблица 19.
На внебиржевом рынке преимущественно заключаются финансовые срочные контракты. Доля товарных контрактов на нем, считая по совокупному контрактному номиналу, составила только 0,71% в 2003 г. и 0,58% в 2004 М6
В настоящее время наиболее динамично на внебиржевом рынке развиваются кредитные срочные контракты. На конец 2004 г. их совокупный контрактный номинал равнялся 6,4 трлн. долл. США. По состоянию на конец июня 2004 г. за последние три года данный сегмент рынка вырос на 568%. По сравнению с ним весь внебиржевой рынок вырос только на 121 %,17
На биржевом рынке финансовых производных инструментов лидирующая роль принадлежит Североамериканскому континенту. По итогам 2004 г. его доля на фьючерсном рынке составляла 55,4%, на опционном - 61,9%, доля Европы соответственно - 31,6% и 37,3% (см. табл. 1.8,1.9).
Таблица 1.8. Торговля финансовыми фьючерсными контрактами по регионам мира, считая по контрактному номиналу и е процентах.'*
год
2002 декабрь 2003 декабрь 2004 декабрь 2005 март
Все рынки (млрд.долл.США) 10328,1 13705.7 18903,4 21249,4
Доля (%) 100 100 100 100
Северная Америка (млрд.долл.) 5870,5 7700,0 10466,5 12445,0
Доля (%) 56,84 56,18 55,37 58,57
Европа (млрд.долл.) 3274,3 4362,8 5971,5 6340,9
Доля (%) 31,7 31,83 31,59 29,84
Азия и регион Тихого океана (млрд.долл.) 1084,5 1484,4 2293,8 2195,0
Доля (%) 10,5 10,83 12,13 10,33
Другие рынки (млрд.долл.) 98,8 158,5 171,6 268,6
Доля (%) 0,96 1,16 0,91 1,26
111 Рассчитано на основе таблицы 1.3.
17 BIS Quarterly Review, June 2005, p.50.
,н Составлено и рассчитано на основе BIS Quarterly Review, June 2005, p.A104, таблица 23A.
Часть / Форвардный и фьючерсный рынки
Таблица 1.9. Торговля биржевыми опционными контрактами по ре-
гионам мира, считая по контрактному номиналу и в процентах.™
ГОД
2002 декабрь 2003 декабрь 2004 декабрь 2005 март
Все рынки (млрд.долл.США) 13487,6 23034,0 27688.7 38157,4
Доля (%) 100 100 100 100
Северная Америка (млрд.долп.) 7823,3 11803,9 17142,5 23406,5
Доля (%) 58,0 51,25 61,91 61,34
Европа (млрд.долл.) 5526,1 11043,3 10335,5 14477,4
Доля (%) 40,97 47,94 37,33 37,94
Азия и регион Тихого океана (млрд.долл.) 107,9 128,7 133,1 207,0
Доля (%) 0,8 0,56 0,48 0,54
Другие рынки (млрд.долл.) 30,3 58,0 77,6 66,5
Доля (%) 0,23 0,25 0,28 0,18
Наиболее популярными в 2004 г. срочными контрактами были: опцион на индекс Kospi 200 Корейской фьючерсной биржи (Kofex, 2586,8 млн. контрактов), фьючерс на трехмесячный евродолларовый депозит Чикагской товарной биржи (СМЕ, 297,58 млн. контрактов) и фьючерс на Euro-Bund, представленный на Еигех (239,79 млн. контрактов).19 20
По объемам торговли в 2004 г. первое место среди срочных бирж заняла Корейская фьючерсная биржа (2586,82 млн. контрактов), второе - Еигех (1065,64 млн. контрактов), третье - Чикагская товарная биржа (805,34 млн. контрактов), четвертое - Euronext.Liffe (790,38 млн. контрактов), пятое - Чикагская торговая палата (599,99 млн. контрактов). Если рассматривать торговлю только фьючерсными контрактами, то тогда первое место приходится на Еигех (684,63 млн. контрактов), второе - на Чикагскую товарную биржу (664,88 млн. контрактов), третье - Чикагскую торговую палату (489,23 млн. контрактов), четвертое - Euronext.Liffe (310,67 млн, контрактов) и пятое -Мексиканскую биржу производных инструментов (Mexican Derivatives Exchange, 210,36 млн. контрактов).21
19 Составлено и рассчитано на основе BIS Quarterly Review, June 2005, р.А104, таблица 23A.
20 G.Burghard. Global Futures and Options Volume 2004, http://www.futuresindustry.org/ fim agazi-1929.asp?a=1032
21 Там же.
Одним из существенных моментов развития срочного рынка в 2004 г. стало развитие фьючерсной торговли в Китае. Так, по количеству фьючерсных контрактов, заключенных в 2004 г. на биржах мира китайская биржа Dalian Commodity Exchange (DCE) занимает десятое место (88,03 млн. контрактов). Для сравнения можно отметить, что девятое место приходится на Нью-Йоркскую товарную биржу (133,28 млн. контрактов). С учетом опционной торговли DCE занимает 16-е место в мире. Ее контракт на соевые бобы (No.1 Soybeans) входит в двадцатку наиболее торгуемых контрактов в мировой практике. В 2004 г. он занял 18-е место (57,34 млн. контрактов). Объем торговли другим контрактом на DCE - на сою (Soy Meal) составил 24,75 млн. контрактов. Для сравнения можно отметить, что контракт на сою-бобы (Soybeans) на Чикагской торговой палате составил только 18,85 млн. контрактов. Следует подчеркнуть, что пока DCE обслуживает только внутренний рынок Китая,22
С переходом к рыночной экономике в начале 90-х годов прошлого века срочный рынок стал развиваться и в России. Возник ряд срочных бирж. Однако в результате финансового кризиса 1998 г. срочный рынок в нашей стране практически прекратил свое существование. В настоящее время идет процесс его развития. В 2001 г. произошло объединение Фондовой биржи ‘'Санкт-Петербург" и Фондовой биржи РТС. РТС выполняет функцию организатора торгов, а СП техническую поддержку торгов. На Фондовой бирже РТС сейчас сосредоточена подавляющая часть срочной торговли в России. Кроме того, она занимает второе место в мире по торговле фьючерсными контрактами на акции. Первое место занимает Национальная фондовая биржа Индии, третье - Euronext (см. табл. 1.10).
Таблица 1.10. Ведущие мировые биржи по фьючерсам на акции23
Биржа Объем торговли (млн. контрактов) Совокупный контрактный номинал (мпн. долл. США) Количество открытых позиций (кол-во контрактов)
2004 2003 2004 2003 2004 2003
Национальная фондовая биржа Индии 44,021 25,573 344811 194659 38732 143512
РТС 39,062 31.782 10630 6414 318904 131255
Euronext 13,492 7,004 57850 20586 250838 444996
' Там же.
’ Источник: World Federation OF Exchanges. Annual Report and Statistics 2004, p.86.
Таблица 1.11. Объем торговли фьючерсами и опционами на Фондовой бирже РТС (тыс, долл. США)24__________________
Год Фьючерсы Опционы
2005 январь-апрель 3319350 518273
2004 10794123 940304
2003 6615700 397379
2002 2976857 43941
Объем торговли производными инструментами на РТС представлен в таблице 1.11. Как из нее следует, темп прироста объемов торговли фьючерсными контрактами в 2003 г. по сравнению с 2002 г. составил 122%, в 2004 г, по сравнению с 2003 г. - 63%. Аналогичные цифры по опционным контрактам составили соответственно 800% и 137%,
КРАТКИЕ ВЫВОДЫ
Срочный рынок - это рынок, на котором заключаются и обращаются срочные контракты. Срочный контракт представляет собой соглашение о будущей поставке предмета контракта.
Актив, который лежит в основе срочного контракта, называют базисным.
Срочный рынок позволяет участникам экономических отношений страховать ценовые риски, риски изменения объемов потребления продукции и согласовывать планы хозяйственной деятельности на будущее.
В структуре срочного рынка можно выделить первичный и вторичный, биржевой и внебиржевой сегменты. По виду торгуемых инструментов его можно подразделить на форвардный, фьючерсный, опционный рынки и рынки свопов и ФРА.
Участниками срочного рынка являются спекулянты, хеджеры и арбитражеры. Хеджер - это лицо, страхующее ценовой риск или риск изменения объемов производства или потребления некоторого актива. Операция по страхованию называется хеджированием. Арбитражер - это лицо, извлекающее прибыль без риска за счет одновременной покупки и продажи одного и того же актива на разных рынках, если на этих рынках наблюдаются разные цены.
Если лицо заключает срочный контракт для покупки базисного актив, то говорят, что оно покупает контракт или открывает длинную позицию. Если лицо заключает срочный контракт для продажи базисного актива, то говорят, что оно продает контракт или открывает короткую позицию.
24 Интернет сайт http //www rts ru/index cfrrPid=2403
ГЛАВА 2. ФОРВАРДНЫЕ КОНТРАКТЫ
В настоящей главе рассматриваются форвардные контракты. Вначале мы остановимся на общей характеристике контракта, определим понятия форвардной цены и цены поставки. Затем приведем формулы определения форвардной цены и цены форвардного контракта для разных базисных активов, остановимся на понятии внутренней ставки доходности форвардного контракта, В заключение рассмотрим синтетические форвардные позиции.
2.1. ОБЩАЯ ХАРАКТЕРИСТИКА ФОРВАРДНОГО КОНТРАКТА
Форвардный контракт - это срочный контракт, который заключается, как правило, вне биржи. Это индивидуальный контракт, соответствующий потребностям контрагентов. Он заключается для осуществления реальной продажи или покупки базисного актива и страхования продавца или покупателя от возможного неблагоприятного изменения цены. Заключение контракта не требует от контрагентов каких-либо расходов (здесь мы не принимаем в расчет возможные накладные расходы, связанные с оформлением сделки, и комиссионные, если она заключается с помощью посредника). Исполнение контракта происходит в соответствии с условиями, которые были согласованы участниками в момент его заключения.
Пример 1.
30 апреля лицо X заключило с лицом Y форвардный контракт на поставку 1 сентября 100 акций компании А по цене 100 руб. за одну акцию. В соответствии с условиями контракта лицо X 1 сентября передаст лицу F100 акций компании А, а лицо Yзаплатит за данные бумаги 10000 руб.
Форвардный контракт - это твердая сделка, т. е. сделка, обязательная для исполнения. Лицо, которое обязуется купить базисный актив по контракту, открывает длинную позицию, т.е. покупает контракт. Лицо, продающее базисный актив по контракту, открывает короткую позицию, т.е. продает контракт.
Предметом форвардного контакта могут выступать разные активы. Однако в мировой практике наиболее широкое развитие получил форвардный валютный рынок, и форвардные контракты активно
используются для хеджирования валютного риска. Приведем примеры страхования валютного риска с помощью валютного форварда.
Пример 2.
Импортер планирует через три месяца купить за границей товары, Ему нужна валюта. Чтобы не рисковать, он решает хеджировать покупку валюты трехмесячным форвардом на доллар США. Банки предлагают трехмесячные контракты по цене 1долл =30 руб. Импортер покупает контракт по данной котировке, т. е. заключает с банком контракт, в рамках которого обязуется купить доллары. Проходит три месяца, импортер уплачивает по контракту 30 руб. за один доллар и получает контрактную сумму.
В этот момент конъюнктура на спотовом рынке может оказаться любой. Допустим, курс доллара составил 31 руб. Однако по контракту импортер получает доллар по 30 руб.
Пусть курс доллара равен через три месяца 29 руб., но импортер обязан выполнить условия сделки и купить доллар за 30 руб.
Таким образом, заключение форвардного контракта застраховало импортера от неблагоприятной конъюнктуры, но не позволило воспользоваться благоприятной ситуацией,
В данном примере возникает общая закономерность для срочных контрактов, а именно: если страхуются от роста цены базисного актива, то покупают контракт, т.е. гарантируют себе на будущее цену покупки.
Пример 3.
Пусть в условиях примера 2 вместо импортера фигурирует экспортер, Через три месяца он должен получить валютную выручку, которую планирует конвертировать в рубли. Чтобы не рисковать, экспортер хеджирует будущую продажу долларов форвардным контрактом. Он продает форвард на доллары банку, т. е. заключает с банком контракт, в рамках которого обязуется продать доллары банку по цене 30 руб. за доллар.
Проходит три месяца, экспортер поставляет по контракту доллары по цене 30 руб. за один доллар и получает контрактную сумму.
Конъюнктура на спотовом рынке в этот момент может оказаться любой. Допустим, курс доллара составил 29 руб. Однако по контракту экспортер продает доллар по 30 руб.
Пусть курс доллара равен через три месяца 31 руб., но экспортер обязан выполнить условия сделки и продать доллар за 30 руб.
Таким образом, заключение форвардного контракта застраховало экспортера от неблагоприятной конъюнктуры, но не позволило воспользоваться благоприятной ситуацией.
В данном примере возникает общая закономерность для срочных контрактов, а именно: если страхуются от падения цены базисного актива, то продают контракт, т.е. гарантируют себе на будущее цену продажи.
Несмотря на то что форвардный контракт предполагает обязательность исполнения, контрагенты не застрахованы от его неисполнения в силу, например, банкротства или недобросовестности одного из участников сделки. Таким образом, для форвардного контракта характерен кредитный риск.
Форвардный контракт может заключаться с целью игры на разнице курсовой стоимости активов. Лицо, открывающее длинную позицию, рассчитывает на рост цены базисного актива, лицо, открывающее короткую позицию - на понижение его цены. Поясним сказанное на примерах.
Пример 4. Игра на повышение.
Пусть в примере 2 вместо импортера фигурирует спекулянт. Он ожидает, что курс доллара через три месяца составит 31 руб. Поэтому спекулянт покупает контракте котировкой 1 долл =30 руб.
Через три месяца курс доллара на спотовом рынке равен 31 руб. Спекулянт покупает доллар по контракту за 30 руб. и сразу продает его на спотовом рынке по 31 руб., выигрывая на одном долларе один рубль.
Если курс доллара к этому моменту упал до 29 руб., спекулянт проигрывает 1 руб. Он обязан исполнить форвардный контракт, т.е. купить доллар за 30 руб., а продать его может сейчас только за 29 руб.
выигрыши
30 31
проигрыши
Рис. 2.1. Игра на повышение
Графически выигрыши-проигрыши спекулянта в расчете на один доллар показаны на рис. 2.1. По горизонтальной оси представлен курс доллара в рублях, по вертикальной - выигрыши-проигрыши спекулянта. Покупка контракта, как и любого другого актива, изображена восходящей линией под углом 45 градусов, чтобы в пропорции один к одному перенести на вертикальную ось результат изменения курса доллара.
В данном примере возникает общая закономерность для срочных контрактов, а именно: если играют на повышение, то покупают контракт, выигрывают от роста цены и проигрывают от ее падения.
Пример 5. Игра на понижение.
Пусть в предыдущем примере спекулянт ожидает падения курса доллара через три месяца до 29 руб. Он играет на понижение, т.е. продает контракт за 30 руб.
Через три месяца доллар стоит 29 руб. Спекулянт покупает его на спотовом рынке за 29 руб. и поставляет по форвардному контракту за 30 руб., выигрывая рубль.
Пусть доллар стоит 31 руб. Чтобы исполнить контракт, спекулянт вынужден купить доллар на спотовом рынке за 31 руб. и поставить его по контракту за 30 руб. Его проигрыш равен 1 руб.
Графически выигрыши-проигрыши спекулянта в расчете на один доллар показаны на рис. 2.2, Продажа контракта, как и любого другого актива, изображена нисходящей линией под углом 45 градусов.
Рис. 2.2. Игра на понижение
В данном примере возникает общая закономерность для срочных контрактов, а именно: если играют на понижение, то продают контракт, выигрывают от снижения цены и проигрывают от ее роста.
Валютные форвардные контракты как правило имеют стандартные сроки обращения. Обычно это 1,2,3,6,9 и 12 месяцев.
По своим характеристикам форвардный контракт - это контракт индивидуальный. Поэтому вторичный рынок форвардных контрактов на большую часть активов но развит или развит слабо, Исключение составляет форвардный валютный рынок.
2.2. ФОРВАРДНАЯ ЦЕНА И ЦЕНА ПОСТАВКИ
При заключении форвардного контракта согласовывается цена, по которой будет исполнена сделка. Ее называют ценой поставки. Она остается неизменной в течение всего времени действия контракта.
Существует также понятие форвардной цены базисного актива. Это цена актива для определенного времени в будущем, например, трехмесячнвя форвардная цена, шестимесячная форвардная цена и г,д. Это более общее понятие по сравнению с понятием цены поставки. Оно характеризует конъюнктуру данного актива относительно определенного момента времени в будущем. Когда участники контракта согласовывают цену поставки, они учитывают конъюнктуру рынка относительно этого момента и записывают данную цену как цену поставки по контракту. Поскольку в этой цене учтены все уело-ия конъюнктуры, то a этот момент она является и форвардной ценой актива для определенного момента времени в будущем. В следующие моменты времени конъюнктура рынка будет изменятся, поэтому в новых контрактах на данный актив, которые истекают одновременно с нашим первым контрактом, будет возникать и новая цена поставки и, соответственно, новая форвардная цена базисного актива. Поэтому можно сказать, что для каждом момента времени форвардная цена базисною актива - это цена поставки форвардном контракта, который был заключен в этот момент, Таким образом, на рынке в каждый момент времени для определенной даты в будущем существует форвардная цена базисного актива и она равна цене поставки форвардных контрактов, заключаемых в этот момент.
Пример.
1 марта заключается форвардный контракт на поставку акции компании А 1 июля по цене 100 руб. В момент заключения контракта
форвардная цена акции с поставкой 1 июля равна цене поставки, т. е. 100 руб. 1 апреля заключается еще один контракт на поставку акции компании А 1 июля по цене 120 руб. В новом контракте появилась новая цена поставки, так как изменилась конъюнктура рынка. Таким образом, форвардная цена акции 1 апреля (с поставкой 1 июля) равна цене поставки второго контракта, т. е. 120 руб. В этом случае цена поставки для первого контракта остается равной 100 руб., но форвардная цена акции с поставкой 1 июля в этот момент составляет 120 руб.
2.3. ОПРЕДЕЛЕНИЕ ФОРВАРДНОЙ ЦЕНЫ И ЦЕНЫ ФОРВАРДНОГО КОНТРАКТА
Форвардная цена актива строится на безарбитражном подходе. В его рамках форвардная цена актива должна быть такой, чтобы невозможно было заработать арбитражную прибыль. Рассмотрим арбитражный подход применительно к разным активам. Чтобы показать существо вопроса, допустим, что ставки по кредитам и депозитам равны, и инвестор имеет возможность занимать базисный актив на время без уплаты процентов. В последующем данные ограничения можно будет опустить.
2.3.1. Форвардная цена и цена форвардного контракта на актив, по которому не выплачиваются доходы
2.3ЛЛ. Форвардная цена акции
Рассмотрим вопрос определения форвардной цены актива, по которому не выплачиваются доходы, на примере акции. На акцию в течение периода действия контракта дивиденды не выплачиваются.
Инвестор хотел бы владеть через шесть месяцев акцией компании А. Он может получить ее двумя способами: купить сегодня на спотовом рынке и держать полгода, или купить шестимесячный форвардный контракт. Тогда через полгода ему будет поставлена акция. Возникает вопрос, какой должна быть форвардная цена? Она должна быть такой, чтобы с финансовой точки зрения оба варианта действий для инвестора были одинаковыми, т.е. он должен быть безразличен в выборе первого или второго варианта. Как создать такое безразличие? Если инвестор купит акцию по форвардному контракту, то сегодня он может разместить под ставку без риска на шестимесячном депозите сумму денег равную спотовой цене акции. Через полгода по депозиту он получит сумму денег равную спот-цене акции
плюс начисленные на нее проценты. Поэтому, если в качестве форвардной цены акции в контракте записать данную сумму, то инвестор будет безразличен в выборе первого или второго вариантов действий. С финансовой точки зрения они для него одинаковые, поскольку и в первом и во втором случае в начальный момент времени от него требуется сумма денег равная спотовой цене акции. На основе приведенных рассуждений можно записать общий алгоритм определения форвардной цены. Она равна цене спот базисного актива плюс безрисковый процент на цену спот за период действия контракта. Представим формулу определения форвардной цены в общем виде:
F = S 1 + г--
\ базаj
(2.1)
где F- форвардная цена акции;
5 - спотовая цена акции;
г-ставка без риска;
Г- период времени до истечения форвардного контракта;
база - финансовый год.
Пример.
В момент заключения форвардного контракта цена спот акции равна 100 руб., ставка без риска 10%. Определить шестимесячную форвардную цену.
Решение.
Л = 100| 1 + 0,1 —
I 12 J
Рассчитанная в примере цена называется теоретической форвардной ценой. Она должна быть именно такой, иначе откроется возможность совершить арбитражную операцию и заработать прибыль без риска. Покажем это на цифрах.
Допустим, фактическая форвардная цена на рынке ниже теоре-1ической и равна 103 руб. Тогда арбитражер сегодня покупает форвардный контракт по цене 103 руб., так как он стоит дешевле, чем должен стоить. Купив контракт, он обязуется купить акцию через шесть месяцев, поэтому сейчас акцию надо продать по спотовой । делке. В связи с этим он занимает акцию у брокера и продает ее на i потовом рынке за 100 руб., и размещает их на шестимесячном безрисковом депозите под 10%.
Через полгода он получает от инвестирования 100 руб. сумму в 105 руб., уплачивает по контракту за акцию 103 руб. и возвращает ее брокеру. Прибыль арбитражера равна:
105-103 = 2руб.
Таким образом, если фактическая форвардная цена окажется ниже теоретической, то арбитражеры своими действиями сразу же вернут ее к 105 руб., так как начнут активно покупать форвардные контракты.
Выше мы упростили ситуацию, допустив возможность занять акцию без процентов. Это условие можно опустить, если на рынке имеется достаточное количество лиц, владеющих акциями данной компании. В этом случае при возникновении на рынке шестимесячной форвардной цены в 103 руб. владелец акции сразу же: а) купит форвардный контракт; б) продаст акцию на спотовом рынке за 100 руб.; б) разместит полученные средства на безрисковом депозите на полгода под 10%.
Через шесть месяцев он: а) получит по депозиту 105 руб.; б) уплатит по контракту 103 руб. и вернет себе акцию.
Таким образом, он по-прежнему будет владеть акцией, но дополнительно получит еще доход в размере 2 руб. за счет совершенной операции. В результате таких действий фактическая форвардная цена быстро вернется к ее теоретическому уровню.
Пусть владельцы акций не оказывают своими действиями влияния на формирование форвардной цены, и для совершения арбитражной операции арбитражеру необходимо уплатить брокеру за акцию проценты. В такой ситуации характер и последовательность действий арбитражера останутся прежними. Единственное, что может измениться, - это уровень форвардной цены. Она должна быть такой, чтобы за счет разницы между теоретической и фактической ценами арбитражер смог покрыть проценты за кредит и получить прибыль. Допустим, в нашем примере процент брокера за кредит по акции составляет 2 руб. Тогда арбитражная операция будет возможна, если фактическая форвардная цена окажется ниже 103 руб. Если же процент брокера за кредит меньше 2 руб., например, равен 1,5 руб., то инвестор совершит операцию, уплатив брокеру данную сумму за кредит по акции. В этом случае его прибыль составит 0,5 руб.
Допустим теперь, что фактическая форвардная цена выше теоретической и равна 107 руб. Тогда арбитражер сегодня продает форвардный контракт по цене 107 руб., занимает 100 руб. под 10% на полгода, покупает на них акцию и хранит ее.
Через шесть месяцев он поставляет по контракту акцию за 107 руб., возвращает кредит в сумме 105 руб. Его прибыль равна:
107 -105 = 2руб.
Таким образом, если фактическая цена окажется выше теоретической, то арбитражеры быстро восстановят их равенство своими операциями, активно продавая форвардные контракты.
В рассмотренном примере в первом случае арбитражер покупал контракт по 103 руб., осуществлял короткую продажу акции на спото-hom рынке и размещал 100 руб. на шестимесячном депозите. Финансовый результат он получал к моменту истечения контракта. Может пи арбитражер воспользоваться будущей прибылью сразу же, т.е. в момент начала осуществления арбитражной операции, и в каком объеме? Ответ на этот вопрос является утвердительным. Сумма денег, которую можно использовать сразу, равна дисконтированной сюимости будущей арбитражной прибыли. В примере арбитражная прибыль составила 2 руб. Поэтому в момент заключения контракта можно воспользоваться суммой:
--------7—--Г = 1$РУ6 1 + 0,1(6/12)
Таким образом, из 100 руб, которые арбитражер получит от пролижи акции на спотовом рынке, он может сразу израсходовать 1,9 руб. Оставшуюся сумму:
100-1,9 = 98,1^6.
ст разместит на депозите. К моменту окончания действия контракта получит по депозиту:
Г 6^
98,1 1 + 0,1 —
I 12 )
Купит акцию по контракту и вернет его брокеру.
Чтобы определить сумму арбитражной прибыли на момент начали операции, можно рассуждать следующим образом. К моменту пкончания контракта арбитражер должен располагать суммой в 103 руб чтобы уплатить их по контракту. Следовательно, в начале операции надо разместить на депозите сумму равную дисконтированной । юимости данной величины:
103
-----7----г = 98,1руб.
1+0,1(6/12) Л
От короткой продажи акции арбитражер получает 100 руб. Поэтому из этой суммы он 98,1 руб. разместит на депозите, а:
100-98,1 = 1,9 руб.
может использовать сразу в качестве арбитражной прибыли,
В рассмотренном примере во втором случае арбитражер продавал контракт по 107 руб,, занимал 100 руб, на шесть месяцев и покупал акцию на спотовом рынке. Финансовый результат он получал к моменту истечения контракта. Может ли арбитражер воспользоваться будущей прибылью сразу же, т.е. в момент начала осуществления арбитражной операции, и в каком объеме? Ответ также является утвердительным. Сумма денег, которую можно использовать сразу, равна дисконтированной стоимости будущей арбитражной прибыли, т.е. вновь:
1 + 0,1(6/12) " 1,9РУб'
Чтобы получить данную сумму в момент заключения контракта, арбитражер должен действовать следующим образом. Через полгода за акцию контрагент уплатит ему 107 руб. по контракту. Поэтому сегодня он может взять шестимесячный кредит в размере:
——7—г = 101,9 руб.
1 + 0,1(6/12)
(107 руб, составят сумму долга с процентами.)
Из этой суммы за 100 руб. он покупает на спотовом рынке акцию. Оставшиеся:
101,9-100 = 1,9руб.
составляют его прибыль. Через полгода арбитражер поставляет по контракту акцию за 107 руб. и возвращает данные средства в погашение кредита.
Формулу (2,1) можно использовать для определения форвардной цены бескупонных облигаций.
Пример.
Цена спот краткосрочной облигации равна 85%, ставка без риска - 10%. Определить форвардную цену облигации с поставкой через месяц. Она равна: 1/1
( 1
F-85 1 + 0,1— = 85,71%.
I 12J
Форвардную цену бескупонной облигации можно также определить дисконтированием номинала под форвардную процентную ставку1, а именно:
100
1 + гф(Т / база)
। де гф - форвардная ставка для периода Т.
Пример.
Государственная краткосрочная облигация погашается через 90 дней. 30-дневная форвардная ставка без риска через 60 дней равна 10% годовых, финансовый год составляет 365 дней. Определить 60-дневную форвардную цену бескупонной облигации. Она равна:
На рынке производных инструментов в формулах активно используется непрерывно начисляемый процент.2 Это в первую очередь связано с определением вероятностной модели доходности актива. Оказывается, что более приближенной к реальности вероятностной моделью доходности актива является модель, использующая в качестве случайной переменной не простую доходность, а непрерывно начисляемую доходность.3 Запишем формулу (2.1) с использованием непрерывно начисляемого процента:
F = SerT
(2.2)
где г - непрерывно начисляемая ставка без риска;
Т - время действия контракта в годах.
На практике доходность обычно задается как простой процент в расчете на год. Для пересчета его в эквивалентный непрерывно начисляемый процент служит следующая формула:
1 Определение форвардной процентной ставки см. в книге А.Н.Буренина "Рынок ценных бумаг и производных финансовых инструментов”, М., 2002, глава 6.
2 О непрерывно начисляемом проценте см. в книге А.Н. Буренина "Рынок ценных бумаг и производных финансовых инструментов". М., 2002, параграф 3,1.2,3,
3 Более подробно об этом вопросе см. в книге А.Н, Буренина "Рынок ценных бумаг и производных финансовых инструментов”, М., 2002, параграф 9.3.
i t г ru = т In 1ч—
I т
(2.3)
где гн - непрерывно начисляемый процент;
г - простой процент;
т - частота начисления простого процента в рамках года.
Соответственно, определить простой процент на основе непрерывно начисляемого можно по формуле:
г — т ет-1
(2.4)
Приведем пример на использование формулы (2.2).
Пример.
Цена спот акции 100 руб,, трехмесячная ставка без риска на основе простого процента равна 10% годовых. Определить трехмесячную форвардную цену с помощью формулы (2,2).
Решение,
Определяем эквивалентный непрерывно начисляемый процент;
Г on гл=41п 1 + — = 0,09877 или 9,877%.
4 )
Трехмесячный период, представленный в годах, составляет:
3/12 = 0,25 года.
Форвардная цена равна:
F = lOOe(),()%770,25 = 102,5дуб.
Докажем формулы (2.1) и (2.2) на основе подхода, не допускающего получения арбитражной прибыли. Доказательство проведем для случая непрерывно начисляемого процента.
Имеется два портфеля Л и В. Портфель А состоит из одного длинного форвардного контракта на акцию, который стоит f , и суммы денег равной приведенной стоимости цены поставки Ke~rl, где К - цена поставки акции, г непрерывно начисляемая ставка без риска, Т время действия контракта. Сумма денег Ке~гТ инвестируется под процент г на время Т . В портфель В входит одна акция, цена спот которой равна 5 .
По прошествии времени Т портфель В состоит из одной акции. II портфель А также входит одна акция, поскольку величина Ке~гТ hi время Т выросла до суммы К . Она была уплачена за акцию по форвардному контракту. Таким образом, стоимости портфелей Ли В равны в конце периода Т. Следовательно, в начале периода Т их стоимости также должны быть равны, чтобы исключить возможность совершения арбитражной операции. Поэтому можно записать:
f + Ке~'т = S. (2.5)
Поскольку в момент заключения контракта его стоимость (/) равна нулю, а цена поставки равна форвардной цене (К = F), то
FerT = S
ИЛИ
F = SerT.
2.3.1.2. Цена форвардного контракта
Когда заключается форвардный контракт, его цена равна нулю, так как форвардная цена равна цене поставки. Однако по прошествии времени контракт получит некоторую цену. Прошло время, возможно изменилась и процентная ставка, поэтому на рынке возникла новая форвардная цена. Однако наш форвардный контракт дает инвестору возможность получить базисный актив по цене поставки, которая отличается от цены поставки контрактов, заключаемых в данный момент времени. Рассмотрим вопрос определения цены форвардного контракта на примере.
Пример 1.
В момент заключения шестимесячного форвардного контракта цена спот акции была равна 100 руб., ставка без риска 10%. Как мы определили выше, цена поставки по данному контракту составила 105 руб. Прошло три месяца. Цена спот акции к этому моменту выросла до 120 руб. Необходимо определить цену контракта,
В соответствии с условием контракта его владелец через три месяца должен будет заплатить 105 руб. за акцию. Дисконтированная стоимость данной суммы сейчас равна:
------т----г - 102,44руб.
1 + 0,1(3/12)
Инвестор может разместить данную сумму на безрисковый депозит на три месяца и купить по некоторой цене форвардный контракт. Тогда через три месяца он получит акцию. В то же время, он может купить сегодня акцию за 120 руб. на спотовом рынке. Тогда через три месяца он также будет располагать акцией. На акцию не выплачиваются дивиденды, поэтому сегодня оба варианта действий должны быть одинаковыми для него с финансовой точки зрения, поскольку в конце периода они приносят ему одинаковый результат. Поэтому можно записать равенство:
/4102,44 = 120^6.
Отсюда:
/ = 120-102,44 = 17,56руб.
Таким образом, цена форвардного контакта равна разности между ценой акции в момент продажи форвардного контракта и приведенной стоимостью цены поставки к моменту его перепродажи. Запишем сказанное в виде формулы:
14- г(г ! база}
или для непрерывно начисляемого процента: / = 5-^г.
Умножим обе части формулы (2.6) на
база )
база)
база )
(2-6)
(27)
где Т - время, остающееся до истечения контракта.
( т \
В формуле (2.8) величина 5 1 + г---
базаJ
является новой форвард-
ной ценой акции для момента перепродажи контракта. Поэтому:
или
F-K
1 + г(Г / база)
(2.9)
Дня непрерывно начисляемого процента эквивалентом формулы (2 9) является формула:
f = (F-K)e-'T.
(2.Ю)
1аким образом, формулы (2.9) и (2.10) показывают, что цену форвардного контракта можно найти дисконтированием разности между новой форвардной ценой, т.е. форвардной ценой в момент продажи контракта, и ценой поставки контракта.
Мы рассмотрели цену форвардного контракта для участника, занимающего длинную позицию. Чтобы получить стоимость контракта для участника с короткой позицией, необходимо формулы (2.6), (2,7) и (2,9), (2.10) умножить на минус один. В частности для случая непрерывно начисляемого процента получим:
~f = Ke~rT-S
-f = (K-FYrT
где -f - цена контракта для лица с короткой позицией.
Поскольку цена спот акции в последующем может как вырасти, так и упасть, то цена форвардного контракта может иметь как положительную, так и отрицательную цену. Причем, если для участника с длинной позицией цена положительная, то для участника с короткой позицией она отрицательная, и наоборот. Отрицательная цена для участника контракта означает: для того, чтобы освободиться от обязательств по форварду, ему необходимо уплатить данную сумму новому лицу, которое займет его позицию в контракте. Так в рассмотренном примере, если контракт перепродает лицо с короткой позицией, то ему придется уплатить покупателю, который возьмет на себя его обязательства, 17,56 руб. Этого требует принцип получения одинакового результата при разных вариантах действий. В нашем случае лицо, желающее открыть короткую позицию по акции с поставкой через три месяца, может не покупать уже действующий контракт, а продать новый форвардный контракт. Тогда в нем будет записана цена поставки:
( 3
F = 120 1 + 0,1 —
I 12
Купив старый контракт, оно сможет продать акцию только по 105 руб. Естественно, такой вариант является для него не выгодным. Однако, если продавец контракта уплатит ему 17,56, то, разместив их на трехмесячном депозите, новый владелец контракта получит:
( 3 А
17,561 1 + 0,1 — 1 = 18/?уб.
В сумме с поставкой акции по контракту за 105 руб. данный вариант действий также обеспечит ему получение через три месяца 123 руб.
Если в примере 1 цена форвардного контракта будет отлична от 17,56 руб, то можно совершить арбитражную операцию. Проиллюстрируем это на цифрах.
Пример 2. (Сохраняются условия примера 1).
Алгоритм действий арбитражера можно получить на основе формулы (2.6).
Пусть форвардный контракт для участника с длинной позицией стоит 17 руб. Тогда равенство (2.6), не допускающее арбитражной ситуации, превращается в неравенство:
1 + г(Т / база)
(2-11)
Представим левую часть неравенства как портфель А правую - как портфель В. Поскольку портфель А стоит дешевле, его необходимо купить. Портфель В стоит дороже, его следует продать. Покупка актива обозначается знаком плюс. Знак плюс стоит перед знаком f. Продажа актива обозначается знаком минус. Поэтому для определения действий, которые означают продажу портфеля В, умножим правую часть неравенства (2.11) на минус один и раскроем скобки:
S------------т
1+ \Г/база) j
1 + (Гбаза)
(2.12)
Знак минус перед 5 говорит о том, что акцию надо продать. Поскольку арбитражер акцией не располагает, ее следует занять. Знак плюс перед вторым слагаемым выражения (2.12) означает: деньги, полученные от короткой продажи акции, надо разместить на депози
те. В целом в рамках арбитражной стратегии инвестор осуществляет короткую продажу акции, покупает на часть полученных средств форвардный контракт, оставшуюся часть денег размещает на депозите до момента истечения контракта.
Таким образом, арбитражер занимает акцию у брокера и продает ее на спотовом рынке за 120 руб. За 17 руб. покупает форвардный контракт. Сумму денег:
120-17 = 103^6.
размещает на депозите и получает через три месяца:
( 3 1
103 14-од— =105,
I 12 J
Из них уплачивает по контракту 105 руб. за акцию и возвращает ее брокеру. Арбитражная прибыль равна:
105,575 -105 = 0,515 руб.
Прибыль можно получить и непосредственно в начале операции. К моменту истечения контракта арбитражер должен располагать 105 руб. для покупки акции. Поэтому он разместит на трехмесячном депозите:
которые и принесут ему 105 руб. В результате, из полученных от короткой продажи акции 120 руб. он может сразу использовать прибыль в размере:
120 -17 -102,439 = 0,561/туб.
Она равна дисконтированной стоимости прибыли, рассчитанной на момент истечения контракта:
Рассмотрим другой вариант арбитража. Предположим, инвестор не имеет возможности занять акцию для короткой продажи. Тогда он займет 17 руб,, купит старый контракт и продаст новый форвардный контракт по цене 123 руб., истекающий одновременно со старым.
Через три месяца по старому контракту он покупает акцию за 105 руб. и продает ее по новому за 123 руб, выиграв на разнице цен:
123-105 = 18руб.
По кредиту возвращает сумму:
17 1 + 0,1— = 17,425руб.
Арбитражная прибыль равна:
18-17,425 = 0.575 руб.
Если инвестор желает использовать прибыль в момент заключения контрактов, то ему следует занять сумму:
77од(5/17) ‘ 7,56'
т.е. дисконтированную стоимость дохода, который будет получен через три месяца. Из них за 17 руб. он покупает контракт. Арбитражная прибыль, как и раньше, равна:
17,561-17= 0,561руб.
Если форвардный контракт стоит больше 17,56 руб., например, 18 руб., то можно совершить следующую арбитражную операцию. Для владельца короткой позиции контракт стоит минус 18 руб. Арбитражер покупает контракт с короткой позицией, т.е. его прежний владелец уплачивает ему 18 руб. Арбитражер занимает:
120-18 = 102 руб.
и покупает акцию на спотовом рынке за 120 руб.
Через три месяца он поставляет акцию по контракту за 105 руб., и отдает по кредиту:
102 1 + 0,1— =104,55руб.
Прибыль равна:
105 -104,55 = 0,45 руб.
Пусть инвестор желает использовать арбитражную прибыль сразу. Через три месяца по контракту он получит за акцию 105 руб. Поэтому сегодня он занимает:
тт^Ьг102'439^
и покупает акцию. Сумма:
18 + 102,439 -120 = 0,439 руб,
составляет его прибыль. Она равна дисконтированной стоимости величины прибыли на момент истечения контракта:
О 45
Рассмотрим другой вариант арбитража. Инвестор покупает контракт с короткой позицией, т.е. прежний владелец уплачивает ему 18 руб., и заключает новый длинный форвардный контракт по цене 123 руб., истекающий одновременно со старым, чтобы к моменту истечения первого контракта (с короткой позицией) располагать акцией. Тогда полученные 18 руб. от владельца короткой позиции по первому контракту он инвестирует на три месяца. В конце периода получает сумму:
18,45 руб.
По старому контракту арбитражер продает акцию за 105 руб., а по новому должен купить ее за 123 руб. Чтобы купить акцию по этой цене, к 105 руб. он прибавляет 18 руб. от средств, полученных по депозиту. Арбитражная прибыль равна:
105-123+ 18,45 = 0,45 руб.
Пусть инвестор желает использовать прибыль в начале периода. Тогда на трехмесячном депозите он разместит:
------г-—г = 17,561 руб.
1 + 0,1(3/12)
Разница между суммой, полученной от владельца короткой позиции и размещаемой на депозите суммой составит его прибыль. Она равна:
18-17,561=0,439руб.
Мы рассмотрели случаи, когда контракт имел положительную цену для владельца длинной позиции. Остановимся теперь на действиях арбитражера, если цена для него отрицательная, т.е. курс спот акции меньше 102,44 руб.4
4 Курс спот акции для случая, когда цена контракта будет нулевой, найдем из равенст-
Пример 3.
В момент заключения шестимесячного форвардного контракта цена спот акции была равна 100 руб., ставка без риска 10%. Как мы определили выше, цена поставки по данному контракту составила 105 руб. Прошло три месяца. Цена спот акции к этому моменту упала до 95 руб. В соответствии с формулой (2.6) цена контракта для лица с длинной позицией должна быть равна:
/ = 95-------------г = -7,439руб.
1 + 0,1(3/12)
Соответственно для лица с короткой позицией она составляет 7,439 руб.
Пусть фактическая цена равна 7 руб. (для лица с короткой позицией). Контракт стоит дешевле чем должен стоить. Поэтому арбитражер покупает короткий контракт, заняв для этого 7 руб. Одновременно он заключает новый длинный форвардный контракт с ценой поставки:
95 1 + 0,1— = 97,375руб.
Через три месяца по второму контракту он покупает акцию за 97,375 руб., по первому - продает за 105 руб. По кредиту уплачивает:
-7,175^6.
Арбитражная прибыль равна:
105 - 97,375 - 7,175 = 0,45руб.
Арбитражной прибылью можно воспользоваться и в начале операции. Чтобы определить ее величину будем рассуждать следующим образом. К моменту истечения контрактов на разности цен акций будет получена сумма:
105 -97,375 = 7,625руб.
Ее дисконтированная стоимость равна:
sa f =S----------------г, приравняв f к нулю. Отсюда следует, что в нашем при-
{ + г\Т; база)
мере при курсе спот акции меньше 102,44 руб, цена контракта для лица с длинной позицией будет отрицательной.
7,625 _
1 + 0,1(3/12) ’ РУ '
Из этой суммы на 7 руб. арбитражер покупает контракт. Соответственно сумму:
7,439-7 - 0,439 дуб.
можно использовать в качестве арбитражной прибыли.
Пусть для лица с длинной позицией контракт стоит минус 8 руб. Тогда арбитражер покупает контракт с длинной позицией, т.е. бывший владелец уплачивает ему 8 руб. Он размещает их на депозит и заключает трехмесячный контракт с короткой позицией по цене 97,375 руб.
Через три месяца по первому контракту арбитражер покупает акцию за 105 руб. и поставляет ее по второму за 97,375 руб., по депозиту получает сумму:
Арбитражная прибыль равна:
97,375 + 8,2 -105 -0,575 дуб.
Арбитражной прибылью можно воспользоваться и в начале операции. Чтобы определить ее величину будем рассуждать следующим образом. К моменту истечения контрактов по первому контракту инвестор должен уплатить 105 руб., а по второму получит 97,375 руб. Отрицательное сальдо на разности цен составит:
97,375-105 =-7,625дуб.
Следовательно, к моменту окончания срока действия контрактов он должен располагать дополнительной суммой в 7,625 руб. Ее дисконтированная стоимость равна:
7,625 п , ------т г- - 7,43 9ру о. 1+0,1(3/12)
Поэтому из полученной по первому контракту суммы 8 руб. он размещает на депозите 7,439 руб., чтобы через три месяца получить 7,625 руб. Вместе с 97,375 руб. они дадут 105 руб. для покупки акции по первому контракту. Соответственно прибыль равна:
8-7,439 = 0,561дуб.
2.3.2. Форвардная цена и цена форвардного контракта на актив, по которому выплачиваются доходы
2.3.2.1 Форвардная цена акции с учетом абсолютной величины дивиденда
Рассмотрим вопрос определения форвардной цены актива, по которому выплачиваются доходы, на примере акции. На акцию в течение периода действия контракта выплачивается дивиденд. Предполагается, что участникам рынка известна величина дивиденда.
Приобретая контракт, инвестор не получит дивиденд, а также тот процент, который можно начислить на дивиденд до момента окончания срока действия контракта. Эти условия необходимо учесть при определении форвардной цены.
Рассмотрим вначале простой случай: дивиденд выплачивается перед самым моментом истечения контракта. Тогда инвестор не получает только дивиденд. Форвардная цена равна:
г Т '
F-5 1+г--------div ,
< база)
(2.13)
где Т- период действия контракта; div- дивиденд.
Пример 1.
Цена спот акции 100 руб., ставка без риска - 10%, дивиденд - 2 руб., выплачивается через полгода. Определить шестимесячную форвардную цену. Она равна:
- 2 = 103 руб.
Следующий случай предполагает, что дивиденд выплачивается в некоторый момент времени (/,) в период действия контракта (см. рис. 2.3). Тогда покупатель контракта не получит не только дивиденд,
/ 2
г
h
Рис 2.3. Срок действия контракта-t2) день выплаты дивиденда-и
но и проценты от его реинвестирования до момента истечения срока действия контракта (/2), т. е. за период времени /2 . В этом слу-
чае формула (2.13) принимает вид:
база
- div 1 + г
база
(2.14)
где г2 - ставка без риска для периода времени
r2.i - форвардная ставка без риска для периода
t2 - период действия контракта.
В формуле (2.14) вместо абсолютной величины дивиденда можно воспользоваться значением его приведенной стоимости к моменту заключения форвардного контракта. Она равна:
(2.15)
база
где D - приведенная стоимость дивиденда;
- ставка без риска для периода .
Тогда можно сказать, что покупатель контракта не получает доход от инвестирования приведенной стоимости дивиденда на весь период действия контракта, и формула (2.14) примет вид:
база )
(2.16)
где л - период действия контракта;
г2 - ставка без риска для периода z2.
Формула (2.16) получается из формулы (2.14), подстановкой в нее значения дивиденда из формулы (2.15), а именно:
2 база
В выражении (2.17)
5 Объяснение формулы (2.18) см в книге АН. Буренина “Управление портфелем ценных бумаг", Научно-техническое общество им академика С.И.Вавилова, М., 2005, параграф 5.1.1.6.
( t Y / -Л l + n-L 1 + г21-^А ч база ' база ;
- _ь_
2 база
(2.18)
Поэтому:
F = S 1 + г2
t (
—г-----D 1 + г2
база)
/ А / J t 1
—=(S-ZH 1 + г2 — база J база)
(2-19)
Пример 2.
Цена акции 100 руб., через четыре месяца на акцию выплачивается дивиденд в размере 10 руб. Определить шестимесячную форвардную цену акции, если ставка без риска на шесть месяцев равна 20% годовых, на четыре месяца - 19,8% годовых.
Решение,
Приведенная стоимость дивиденда к моменту заключения контракта равна:
10
1 + 0,198(4/12)
= 9,38р>б.
Шестимесячная форвардная цена акции составляет:
(100 - 9,3 к/1 + 0,2 -у I = 99,68руб.
Если фактическая форвардная цена в примере не равна полученному теоретическому значению, то арбитражеры заработают прибыль без риска и восстановят единство цен. Проиллюстрируем это на цифрах.
I. Фактическая шестимесячная форвардная цена составляет 99 руб. Тогда арбитражер: а) покупает форвардный контракт, так как он стоит дешевле, чем должен стоить; б) занимает акцию и продает ее на спотовом рынке за 100 руб.; в) из 100 руб. сумму равную дисконтированной стоимости дивиденда, т. е. 9,38 руб., размещает на депозит под 19,8% на четыре месяца; г) оставшуюся сумму в 90,62 руб. размещает на шестимесячном депозите под 20%.
Через четыре месяца по депозиту он получит 10 руб. и отдаст их в качестве дивиденда кредитору (поскольку на акцию выплачивается дивиденд в 10 руб., то арбитражер должен отдать данную сумму кредитору):
Через полгода арбитражер: а) получает по депозиту:
(z. i
1 + 0,2— =99,68руб.;
б) уплачивает за акцию по контракту 99 руб. и возвращает ее кредитору. Его прибыль равна:
99,68-99 = 0,68руб.
68 копеек арбитражер получит к моменту истечения действия контракта. Если он заинтересован в использовании прибыли в момент начала операции, то он может сразу же воспользоваться суммой в размере дисконтированной стоимости 68 копеек:
0,68 П ЛП -
Тогда на шестимесячном депозите он разместит сумму:
90,62-0,62 = 90руб.
Через шесть месяцев получит:
90 1 + 0,2—
I 12
= 99 руб.
и уплатит их за акцию по контракту.
Определить величину арбитражной прибыли на начало операции можно еще следующим образом, Через полгода арбитражер должен располагать 99 руб. Их дисконтированная стоимость равна:
99
------Г—т-90 руб.
1+0,2(6/12)
Поэтому из оставшейся суммы в 90,62 руб. он 90 руб. размещает на депозите, а 0,62 руб. оставляет в качестве прибыли.
П. Фактическая форвардная цена акции составляет 100 руб. Тогда арбитражер: а) продает контракт, так как он стоит дороже, чем должен стоить; б) занимает 100 руб. и покупает акцию; (из 100 руб. он занял 9,38 руб. на четыре месяца под 19,8%; оставшуюся сумму в 90,62 руб. занял на шесть месяцев под 20%.)
Через четыре месяца арбитражер получает по акции дивиденд и возвращает первую часть кредита.
Через полгода он: а) поставляет акцию по контракту и получает 100 руб.; б) из данной суммы возвращает кредит в размере:
90,62 1 + 0,2 —
I 12
= 99,68/грб.
Его прибыль равна:
100-99,68 = 0,32руб.
Инвестор может воспользоваться арбитражной прибылью и в начале действия контракта. Она равна дисконтированной стоимости рассчитанной прибыли к моменту его окончания:
0,32 пэо л
-——-г—-Т = 0,29руб.
Чтобы рассчитать данную сумму, можно рассуждать следующим образом. По истечении контракта инвестору будет уплачено за акцию 100 руб. Поэтому в момент его заключения по второй сумме на шесть месяцев надо занять не 90,62 руб., а:
-----—г = 90,91 руб, 1+0,2(6/12)
Из них вместе с первой суммой он использует для покупки акции 90,62 руб. Разница:
90,91-90,62 = 0,29руб.
составляет его арбитражную прибыль.
На акцию в течение действия контракта дивиденды могут выплачиваться несколько раз. В этом случае формула (2.14) примет вад
( Т
F = S 1 + гт-----
\ база
« / T-t \
- V div 1 + rT. --
у база J
(2.20)
где Т - период действия контракта;
п - количество выплачиваемых дивидендов в течение действия контракта;
divf ~ i -й дивиденд, выплачиваемый в течение действия контракта;
гт - ставка без риска для периода Т;
rT,tt “ форвардная ставка для периода времени с момента выплаты
i -го дивиденда до момента окончания действия контракта.
Формула (2.16) соответственно примет вид:
(2.21)
где D( - приведенная стоимость i -го дивиденда к началу действия контракта.
Рассмотренные выше формулы применимы и для процентных инструментов, В таком случае вместо дивиденда учитывается купон, выплачиваемый на базисный актив,
С учетом непрерывно начисляемого процента формулы (2.16) и (2.21) примут вид:
и
гТ
где г - непрерывно начисляемый процент без риска для периода Т; Т - время действия форвардного контракта.
2.3.2.2. Форвардная цена акции с учетом ставки дивиденда
Форвардную цену акции можно определить, воспользовавшись вместо абсолютной величины дивиденда ставкой дивиденда. Получим соответствующую формулу. В рассуждениях используем простой процент, сделаем допущение о делимости акции на части.
Имеется два портфеля Ан В. Портфель А состоит из одного длинного форвардного контракта на акцию, который стоит f , и суммы денег равной приведенной стоимости цены поставки g
----7---------, где К - цена поставки акции, г - ставка без риска, 1 + гуТ/база)
К
Т - время действия контракта. Сумма денег -----------_ инве-
1 + г(Т/база)
стируется под процент г на время Т. В портфель В входит акция в количестве —— где 5- цена спот акции, q - ставка \ +q\T i база}
дивиденда. Дивиденд выплачивается на акцию непосредственно
перед истечением времени действия контракта и реинвестируется в акцию.
По прошествии времени Т портфель А состоит из одной акции, поскольку величина -----—------- за время Т выросла до суммы
1 + г(Т/ база)
К . Она была уплачена за акцию по форвардному контракту.
В портфель В также входит одна акция, поскольку на акцию был выплачен дивиденд по ставке q и реинвестирован в акцию. Таким образом, стоимости портфелей А и В равны в конце периода Т. Следовательно, в начале периода Т их стоимости также должны быть равны, чтобы исключить возможность совершения арбитражной операции. Поэтому можно записать:
1 + г(Г /база) 1 + /база)
Поскольку в момент заключения контракта f = 0 и К = F, то:
_ 1 + г(Т /база)
(223)
В приведенном доказательстве у читателя может возникнуть вопрос. почему в портфель В в конце периода Т обязательно будет входить одна акция, поскольку за период действия контракта ее цена изменялась не только в результате накопления дивидендной составляющей, но также и в связи со спекулятивным изменением курса? Для ответа на этот вопрос важно не забывать, что в каждый данный момент времени ставка дивиденда рассчитывается относительно текущей цены акции. Поэтому не важно, как будет изменяться ее цена в силу спекулятивной динамики рынка. На основе ставки дивиденда дивиденд будет рассчитан относительно текущей цены акции в момент его выплаты. Инвестировав данную сумму в акцию, мы получим в портфеле В одну единицу акции. В общем виде отмеченный результат можно показать следующем образом. В начальный момент акция входит в портфель В в количестве:
1 акция
1 + ц(Т/база)
Начисление дивиденда в конце периода Т на текущую цену акции и реинвестирование его в акцию дает результат:
1 акция
1 + ц(Т/база)
( Т \
1 + q---- ~ 1 акция.
ч база)
Другими словами, в результате спекулятивного изменения курса акции ее пропорция в портфеле В остается неизменной. Выплата дивиденда по ставке q от текущей цены акции позволяет докупить ее в количестве, дополняющем ее в портфеле до одной целой акции. Проиллюстрируем данный результат на цифровом примере.
Пример 3.
Курс акции равен 100 руб., ставка дивиденда 20% годовых, дивиденд выплачивается через шесть месяцев. Акция входит в портфель на сумму:
1 А^/^Г90’9091^-
1 + 0,2(6/12)
Соответственно в пропорции от одной акции это составляет 0,909091 единиц. Пусть за полгода цена акции спекулятивно выросла на 20%, т.е. до 120 руб. Тогда стоимость портфеля увеличилась до:
90,9091 1,2 = 109,091руб.
Стоимость портфеля увеличилась только благодаря росту курса акции, поэтому ее уд. вес в портфеле остался неизменным, т.е. он по-прежнему соответствует 0,909091 единицам.
На сумму акции в портфеле был выплачен дивиденд в размере:
109,091 • 0,2 — = 10,9091руб.
12
Эта сумма реинвестируется в акцию:
109,091ч-10,9091 = 120/^6.
Стоимость акции в данный момент равна 120 руб., стоимость портфеля также составляет 120 руб. Следовательно, в портфель входит одна единица акции.
В формуле (2.23) дивиденд выплачивался в конце действия контракта. Если он выплачивается в некоторый момент времени t в ходе действия контракта, то формула (2.23) примет вид:
Г = с1 + Г(Г/ба3а)
1 + q(t/6a3a)
(2.24)
Получим данную формулу, сравнивая как и выше портфели А и в. Портфель А состоит из одного длинного форвардного контракта на акцию, который стоит f, и суммы денег равной приведенной стоимости цены поставки ------------Д-------. Сумма денег
1 + г\Т/база)
------—------- инвестируется под процент г на время Т. В порт-1 + г(Г/6йзй)
s
фель В входит акция в количестве------------. Дивиденд выпла-
1 + q(t/база)
чивается на акцию в момент i.
По прошествии времени Т портфель А состоит из одной акции, Д'
поскольку величина-----:.-------за время Т выросла до суммы
1 + г{Т/ база)
К . Она была уплачена за акцию по форвардному контракту.
В портфель В также входит одна акция, поскольку в момент t от текущей цены на акцию был выплачен дивиденд по ставке q и реинвестирован в акцию. (В дальнейшем в течение времени Т -1 в портфеле В находилась одна акция.) Таким образом, стоимости портфелей Ли В равны в конце периода Т. Следовательно, в начале периода Т их стоимости также должны быть равны, чтобы исключить возможность совершения арбитражной операции. Отсюда следует формула (2.24).
Каким образом корректно определить ставку дивиденда, чтобы использовать ее в формулах (2.23) и (2.24). Для этого можно приравнять формулы (2.23) и (2.24) к формуле (2.16) и выразить из полученного равенства q . Приравняем формулы (2.24) и (2.16):
( Т л
(S-Щ 1 + г--
база)
\ + г{Т/база) \ + q{tj6a3a)
Отсюда:
S-D =
S
1 + qfy/база)
или
ИЛИ
база
t
D база
S-D t
(2.25)
Поскольку D =-------------г, то окончательно можем записать:
1 + r(tj база)
_ di v/[l + г(?/база)] база
S - {dzv/[l + г(//базя)]} t
Рассчитаем ставку дивиденда для примера 2 на основе формулы (2-25):
= —9’38 .11 = о з 10527 или 31,05%.
100-9,38 4
Рассчитаем шестимесячную форвардную цену из примера 2 с помощью формулы (2.24):
F = 100 1 + 0’2(6/12) = 99 68 6
1 + 0,3105(4/12)
Для случая непрерывного процента аналогом формулы (2.23) является формула:
F = 8е(г~ч}т , (2.26)
где q - непрерывно начисляемая ставка дивиденда.
С теоретической точки зрения непрерывно начисляемая ставка дивиденда означает, что дивиденд начисляется и постоянно реинвестируется. Если инвестор знает величину ставки дивиденда в расчете на год, то по формуле (2.3) он сможет пересчитать ее в непрерывно начисляемую ставку дивиденда. Докажем формулу (2.26) в общем виде.
Имеются два портфеля А и В В портфель А входит длинный форвардный контракт на покупку акции и сумма денег равная дисконтированной стоимости цены поставки Ке гТ. Данная сумма денег инвестируется под непрерывно начисляемый процент на период Т . В портфель В входит акция в количестве Se~qT, где S - цена спот акции, е 4 - количество единиц акции в портфеле. Мы предполагаем, что акцию можно дробить. В конце периода Т в
портфель А входит одна акция, так как величина Ке гТ выросла до суммы К, и она была уплачена по контракту. В портфель В также входит одна акция. На акцию за время Т непрерывно начислялся дивиденд и реинвестировался в бумагу. Стоимости портфелей равны в конце периода Т. Следовательно, они должны быть равны и в начале периода, чтобы арбитраж был невозможен. Поэтому можно записать:
f + Ke~rT =Se~qT. (2.27)
Поскольку в момент заключения контракта f = 0, а К = F , то
Fe~rT = Se~gT или
F = Se^7'.
В приведенном доказательстве у читателя также может возникнуть вопрос, почему в портфель В в конце периода Т обязательно будет входить одна акция? Вновь следует помнить, что в каждый данный момент времени на основе ставки дивиденда величина дивиденда рассчитывается от текущей цены акции, и на эту сумму она докупается по текущей цене. Поэтому не важно, как будет изменяться ее цена в силу спекулятивной динамики рынка. В общем виде отмеченный результат можно показать следующем образом, В начальный момент акция входит в портфель В в количестве:
1 акция • ечТ.
За период действия контракта начисление и реинвестирование дивиденда на текущую цену дает результат:
1 акция е t/7 -ечТ =1 акция.
Проиллюстрируем сказанное также на цифровом дискретном примере.
Пример 4.
В начальный момент времени цена спот акции равна 100 руб., непрерывно начисляемая ставка дивиденда составляет 20% годовых. Рассматриваемый период времени равен полгода, т.е. 0,5. Акция входит в портфель на сумму:
ЮОе02 05 = 90,48374руб.
Соответственно в пропорции от одной акции это составляет 0,9048374 единиц.
Пусть прошел период времени равный 0,1 года и цена акции спекулятивно выросла на 10%. Тогда стоимость портфеля составила: 9O,48374e0,1 0,1 = 91,39312руб.
Стоимость портфеля выросла только за счет роста курсовой стоимости акции, поэтому пропорция акции в портфеле, считая от единицы, осталась прежней, т.е. новой стоимости портфеля 91,39312 руб. соответствует по-прежнему 0,9048374 единицы акции.
В этот момент на акцию выплачивается дивиденд за время 0,1 года и реинвестируется в акцию по текущей цене. С учетом этого новая стоимость портфеля равна:
91,39312<?°’2 = 93,23938/>уб.
Так как акцию докупили на сумму выплаченных дивидендов, то ее УД-вес в портфеле вырос. Найдем его на основе следующей пропорции:
91,39312 - 0,9048374
93,23938 - х
Отсюда:
93,23938’0,9048374
91,39312
-0,923116.
Таким образом, стоимость портфеля в сумме 93,23938 руб. соответствует 0,923116 единицам акции.
Прошло еще время 0,2 года, и курс акции спекулятивно вырос на 20%. Стоимость портфеля составила:
93,23938е0’20,2 = 97,04455^6.
Так как стоимость портфеля выросла только за счет роста курсовой стоимости акции, то ее уд. вес в портфеле остался прежним, т.е. новой стоимости портфеля 97,04455 руб. соответствует по-прежнему 0,923116 единицы акции. В этот момент на акцию выплачивается дивиденд за время 0,2 года и реинвестируется в нее по текущей цене. С учетом этого новая стоимость портфеля равна:
97,О4455е0,20,2 = 101,055/^6.
Акцию докупили на сумму выплаченных дивидендов, поэтому ее УД. вес в портфеле вырос. Найдем его на основе следующей пропорции:
97,04455 - 0,923116
101,005 - л
Отсюда:
101,005-0,923116
97,04455
= 0,960789.
Таким образом, стоимость портфеля в сумме 101,005 руб. соответствует 0,960789 единицам акции.
Прошло еще время 0,2 года, и курс акции спекулятивно упал на 10%. Стоимость портфеля составила:
101,055с' ° ’°2 = 99,00498руб.
Стоимость портфеля уменьшилась только за счет снижения курсовой стоимости акции, поэтому ее уд. вес в портфеле остался прежним, т.е. стоимости портфеля 99,00498 руб. соответствует по-прежнему 0,960789 единицы акции. В этот момент на акцию выплачивается дивиденд за время 0,2 года и реинвестируется в нее по текущей цене. С учетом этого стоимость портфеля равна:
99,00498е (М *‘2 = 103,0455руб.
Так как акцию докупили на сумму выплаченных дивидендов, то ее уд. вес в портфеле вырос. Найдем его на основе следующей пропорции:
99,00498 - 0,960789
103,0455 - х
Отсюда:
103,0455 0,960789
99,00498
Таким образом, по завершении периода времени Т ~ 0,5 года в портфель входит одна акция. Данный результат не зависит от того, как спекулятивно изменялся ее курс за прошедшее время.
Для того, чтобы корректно определить ставку дивиденда для формулы (2.26), приравняем ее к формуле (2.22):
(s - D)erT = Se(r-q}T
ИЛИ
(5 - D)err
ИЛИ
1 , S a = — In--
Г S~D
Для расчета форвардной цены акции можно использовать формулы на основе приведенной стоимости дивиденда и ставки дивиденда. Какую из них применять в каком случае? Если рассматривается небольшой период времени, в рамках которого можно относительно точно прогнозировать абсолютную величину будущего дивиденда, то целесообразнее остановиться на формуле с приведенной стоимостью дивиденда. Для долгосрочного периода лучше использовать формулу на основе ставки дивиденда, поскольку обычно она является величиной постоянной или изменяется не сильно для многих компаний. Поэтому она может точнее поддаваться прогнозу чем величина дивиденда.
2.3.2.3. Цена форвардного контракта
Для определения цены форвардного контракта через некоторое время после его заключения воспользуемся формулой (2.9):
F-K
1 + г(Т / база)
Подставим в нее значение форвардной цены из формулы (2.16):
(5 - £>)[1 + г(Т/база)\-К
1 + г(Т/база)
После преобразования получим:
Для случая непрерывно начисляемого процента формула (2.28) принимает вид:
f = S-D-KerT ,
где 5 - цена спот актива в момент определения стоимости контракта. Таким образом, цена форвардного контракта равна цене спот актива минус приведенная стоимость выплачиваемого на него дохода и минус приведенная стоимость цены поставки.
При использовании в расчетах непрерывно начисляемой ставки дивиденда цену форвардного контракта получаем из формулы (2.27): f = Se <iT -KerT. (2.29)
2.3.3. Форвардная цена и цена форвардного контракта на валюту
2.3.3.1. Форвардная цена
Форвардная цена валюты основана на так называемом паритете процентных ставок, который говорит о том, что инвестор должен получать одинаковый доход от размещения средств под процент без риска как в национальной, так и иностранной валюте. В противном случае возникнет возможность получить арбитражную прибыль.
Допустим, что курс спот рубля к доллару (прямая котировка) равен 1 долл = 5 руб., ставка без риска по рублевому депозиту составляет г, по долларовому - rf. Инвестор планирует разместить средства на депозите на время Т, Перед ним два варианта. Во-первых, разместить сумму S на рублевом депозите и получить по завершении периода Т средства в размере:
( Т
5 । + г----\руб.
I база J
Во-вторых, конвертировать сумму 5 в 1 долл., разместить его под ставку rf (на период Г и по его завершении конвертировать получен-
ные средства в сумме: / р \ 1 + Г! долл. ч база>
в рубли по некоторому форвардному курсу F.
Оба варианта должны принести инвестору одинаковый результат. В противном случае возникнет возможность совершить арбитражную операцию. Поэтому можно записать, что:
база )
Т база )
Отсюда:
F --S ^ + г(т16аза)
1 +(Г / база)
(2.30)
Пример.
Курс доллара равен 30 руб., трехмесячная ставка без риска по рублям - 10%, по долларам - 5%. Определить трехмесячный форвардный курс.
Он составляет:
г=м 1*040^12)
1 + 0,05(3/12)
= 30,37/трб.
Если фактический форвардный курс в примере отличен от рассчитанной величины, можно получить арбитражную прибыль. Рассмотрим действия арбитражера.
I. Фактический форвардный курс равен 30,20 руб. Тогда арбитражер покупает контракт, так как доллар стоит дешевле, чем должен стоить. Купив контракт, он обязался купить доллар через три месяца, поэтому сейчас его необходимо продать. Для этого арбитражер занимает один доллар под 5% на три месяца и продает его, т.е. конвертирует по спот курсу в 30 руб., размещает 30 руб. на трехмесячном депозите под 10%.
Через три месяца по рублевому депозиту арбитражер получает:
30 1 + 0,1 —
30,7 5руб.
По форвардному контракту конвертирует 30,75 руб. в 30,75:30,20 = 1,0182d<wz.
По кредиту отдает сумму:
1- 1 + 0,05— = 1,0125долл.
Его прибыль равна:
1,0182 -1,0125 = 0,0057Эао.
II. Фактический форвардный курс составляет 30,60 руб. Тогда арбитражер продает контракт, так как доллар стоит дороже, чем должен стоить. Продажа контракта означает, что ему придется через три месяца продать доллар, поэтому сейчас его надо купить. Для этого он занимает 30 руб. на три месяца под 10% и конвертирует их по спот курсу в 1 долл., размещает 1 долл, на трехмесячном депозите под 5%.
Через три месяца арбитражер по долларовому депозиту получает:
1,0125болл.
По форвардному контракту конвертирует 1,0125 долл, в 1,0125-30,60 = 30,98руб.
По рублевому кредиту отдает:
30 1 + 0,1 —
= 30,75руб.
Его прибыль равна:
30,98-30,75 = 0,23 руб.
Выше мы привели примеры совершения арбитражных операций. Однако для осуществления их на практике необходимо точно рассчитать количество рублей или долларов, которые следует занимать, чтобы не выйти за рамки контрактной суммы, поскольку она представляет собой некоторую фиксированную величину, например, 100 тыс. долл., 500 тыс. долл, и т.д.
Рассмотрим первый вариант, когда арбитражер покупал контракт и занимал доллар, чтобы его продать. Расчет сделаем для контракта номиналом в один доллар. На практике необходимо занять не один доллар, а меньшую сумму. Ее можно найти на основе следующих рассуждений. Арбитражер купил контракт с ценой поставки 30,20 руб. Таким образом, к моменту истечения контракта он должен располагать ровно данной суммой. Он получит к этому моменту 30,20 руб. за счет того, что в начале арбитражной операции займет некоторую сумму в долларах, конвертирует ее в рубли по спот курсу и разместит на рублевом депозите до момента истечения контракта. Поэтому сумму, которую арбитражеру необходимо занять в долларах, можно получить, рассуждая в обратной последовательности действий от момента истечения контракта. Таким образом, необходимо дисконтировать 30,20 руб. под ставку 10% на три месяца и конвертировать полученную сумму в доллары по спот курсу, а именно:
30 20 - = 0,982114 долл.
| 1 + 0,1- 30
I 12J
0,982114 долл, является той суммой, которую необходимо занять арбитражеру. Далее он конвертирует ее в рубли по спот курсу:
0,982114-30 = 29,46341^6.
Размещает рубли на депозите под 10%:
29,463411 1 + 0,1—1 = 30, I 12 J
Через три месяца арбитражер уплачивает по контракту 30,20 руб. и получает 1 долл. По долларовому кредиту возвращает сумму:
( 3 1
0,982114 1 + 0,05 — = 0,99439долл.
12J
Арбитражная прибыль равна:
I- 0,99439 = 0,0056\долл.
Она получается к моменту истечения контракта. Однако арбитражер может воспользоваться прибылью и при его заключении. По контракту через три месяца ему поставят 1 долл. Дисконтированная стоимость 1 долл, сегодня равна:
Поэтому арбитражер занимает на три месяца данную сумму. В то же время, чтобы получить к моменту истечения контракта 30,2 руб., ему сегодня необходимо располагать:
3
1 + 0,1— 30
12 )
= 0,982114 долл.
Поэтому разницу:
0,987654-0,982114 = 0,00554датл.
он сразу получает в качестве прибыли.
Рассмотрим второй вариант, когда арбитражер продавал контракт и занимал 30 руб., чтобы купить доллар. На практике необходимо занять не 30 руб., а меньшую сумму. Ее можно найти на основе следующих рассуждений, К моменту истечения контракта арбитражер должен располагать 1 долл. Он получается за счет того, что в начале операции арбитражер занимает некоторую сумму в рублях, конвертирует ее по спот курсу в доллары и размещает их на долларовом депозите. Поэтому сумму, которую арбитражеру необходимо занять в рублях, можно получить, рассуждая в обратной
последовательности действий от момента истечения контракта. Таким образом, необходимо дисконтировать 1 долл, под ставку 5% на три месяца и конвертировать полученную сумму в рубли по спот курсу, а именно:
—зо руб. - 29,62963руб.
1 + 0,05 —
12
29,62963 руб. является той суммой, которую необходимо занять арбитражеру. Далее он конвертирует ее в доллары по спот курсу:
29,62963 —--------= 0,987654болл.
30
Размещает доллары на депозите под 5%:
0,987654 1 +0,05 — = 1болл.
Через три месяца поставляет по контракту 1 дол. и получает 30,60 руб. По рублевому кредиту должен вернуть:
29,62963 1 + 0,1— = 30,37руб.
Его прибыль равна:
30,60-30,37-0,23руб.
Она получается к моменту истечения контракта. Однако арбитражер может воспользоваться прибылью и при его заключении. По контракту через три месяца ему заплатят 30,60 руб. Дисконтированная стоимость этой величины сегодня равна:
30,60 _.. о _ -
------7——г - 29,85366руб.
Поэтому арбитражер занимает на три месяца данную сумму. В то же время, чтобы получить к моменту истечения контракта 1 долл., ему сегодня необходимо располагать:
1 д0ЛЛ' 30 руб. = 29,62963руб.
1 + 0,05 —
12
Поэтому разницу:
29,85366руб. - 29,62963 = 0,22403руб. он сразу получает в качестве прибыли.
Как следует из формулы (2.30), если ставка без риска для иностранной валюты больше ставки без риска для национальной валюты, то для более отдаленных периодов времени форвардная цена будет понижаться. Если же г > rf, она будет возрастать.
Форвардный контракт на валюту можно рассматривать как контракт на акцию, для которой известна ставка непрерывно начисляемого дивиденда. Ставкой дивиденда является ставка без риска для иностранной валюты. Поэтому форвардную цену с использованием непрерывно начисляемых процентов можно определить на основе формулы (2.26), заменив величину q на rf\
F = Se r"' ]7 , (2.31)
где г - непрерывно начисляемая ставка без риска по национальной валюте;
rf- непрерывно начисляемая ставка без риска по иностранной валюте.
Докажем формулу (2.31). Имеется два портфеля - Л и В. В портфель А входит один длинный форвардный контракт на покупку единицы иностранной валюты и сумма денег равная дисконтированной стоимости цены поставки Ке~гТ. Она инвестируется на период Т под ставку г. Портфель В содержит дисконтированную стоимость единицы иностранной валюты Se> fT (т.е. по текущему спотовому курсу S покупается иностранная валюта в количестве дисконтированной стоимости ее одной единицы). Она инвестируется под ставку г( на период Т.
По завершении периода Т портфель А состоит из единицы иностранной валюты, так как сумма К была обменена по контракту на иностранную валюту. В портфель В также входит единица иностранной валюты. Поскольку стоимости портфелей равны в конце периода Т, они должны быть одинаковы и в начале этого периода, чтобы невозможно было получить арбитражную прибыль. Поэтому можно записать:
f + Ke-rT = Ser/T. (2.32)
В момент заключения контракта f ~ 0 и К - F . Тогда из формулы
(2.32) следует:
Fe~fT = Se f'fT
или
2.3.12. Форвардный валютный курс и инфляция
В рыночной экономике обменный курс двух валют должен отвечать соотношению уровней цен товаров в этих странах. В этом состоит содержание так называемой теоремы о паритете покупательной способности. Несоблюдение данной пропорции открывает возможность совершить операцию подобную арбитражной. Поясним сказанное на примере. В расчетах абстрагируемся от транспортных и иных накладных расходов.
Пример.
Цена некоторого товара в США 1 долл., в России - 32 руб., обменный курс - 30 руб. за 1 долл. Тогда арбитражер купит 1 долл за 30 руб., приобретет на него в США единицу товара и продаст его в России за 32 руб. Прибыль составит 2 руб. Такая ситуация будет способствовать повышению курса доллара в результате спроса на него со стороны импортеров. Чтобы арбитраж был невозможен, доллар должен стоить не 30, а 32 руб.
Теорема о паритете покупательной способности утверждает, что курсы валют должны изменяться в соответствии с изменением цен на товары внутри стран. Изменение цен главным образом говорит о развитии инфляции. Поэтому форвардный курс зависит от прогнозов развития инфляции в странах рассматриваемых валют.
Обозначим через So обменный курс в начале некоторого периода, 5, - в конце этого периода, Р^9 РА^ и р^ - соответственно уровни цен в странах А и В в начале и конце периода. Тогда обменный курс в начале периода равен:
(2.33)
В конце периода он составит:
Р=~^- (2.34)
Й1
Разделим формулу (2.34) на (2.33):
jL=-p.</P< =J±k (2 35)
50 ря!Ря 1+'д v О| Dq о
где i - уровень инфляции.
Если iA и iB ожидаемая инфляция за некоторый период, то форвардный обменный курс валют А и В из формулы (2.35) можно определить следующим образом:
F = ^Sa. (2.36)
l + zg
В формуле (2.36) валютный курс представлен в прямой котировке.
Пусть страна А - это Россия, В - США. Тогда формула (2.36) говорит о том, что при опережающем росте инфляции в России форвардный курс доллара больше спотового. Напротив, если инфляция в США больше, то форвардный курс доллара меньше спотового.
2.3.3.3. Цена форвардного контракта
Если форвардный контракт продается на вторичном рынке, то его цену можно определить на основе формулы (2.32):
f = Se~r/T - Ке~г'' ,
где К - цена поставки форвардного контракта;
S - спотовый валютный курс в момент продажи контракта на вторичном рынке.
2.3.3.4. Котировка валюты на спотовом и форвардном рынках
В большинстве стран мира на спотовом и форвардном валютных рынках принята прямая котировка национальной валюты, т.е. единица иностранной валюты представляется в единицах национальной валюты. Например, 1 долл, равен 30 руб. В некоторых странах используется обратная (косвенная) котировка, т.е. единица национальной валюты приводится в единицах иностранной валюты. Примером является котировка фунта стерлингов в Великобритании. В мировой практике форвардные цены даются вместе с курсами спот параллельно на основе прямой и обратной котировок (см. табл. 1.1). На
пример, для фунта стерлингов в первых двух колонках для двух дней указан курс спот и форвардные курсы для одного, трех и шести месяцев относительно доллара США на основе прямой, а в третьей и четвертых колонках - обратной котировки.
Таблица 1.1. Котировка спотовой и форвардной цен на валютном
рынке (Wall Street Journal)
Country CURRENCY
U.S, $ EQI JIVALENT per U .S.$
Mon F" Mon Fri
Argentina (Peso) .3125 .3361 3.2000 2.9750
Australia (Dollar) .5305 .5308 1.8852 1.8841
Bahrain (Dinar) 2.6523 2.6525 .3770 .3770
Brazil (Real) ,4229 .4235 2.3645 2.3615
Bnlain (Pound) 1.4262 1.4256 .7012 .7015
1-month forward 1.4234 1.4229 .7025 .7028
3-month forward 1.4186 1.4180 .7049 .7052
6-month forward 1.4121 1,4114 .7082 .7085
2.3.4. Форвардная цена товара
Лицо, которое заинтересовано в будущем располагать некоторым товаром имеет альтернативы: купить его сегодня на спотовом рынке или по форвардному контракту. Купив товар сегодня, чтобы потребить в будущем, инвестор несет расходы по его хранению и страхованию, а также не получает процент на сумму стоимости товара, которую он мог бы разместить на счете на период действия контракта. Если форвардная цена товара равна цене спот плюс расходы по хранению и страхованию и упущенный процент, то покупатель безразличен к приобретению товара на спотовом рынке или по форвардному контракту по данной цене. Если форвардная цена не соответствует данной сумме, то возникнет возможность совершения арбитражной операции. В результате действий арбитражеров указанное равенство восстановится. Поэтому форвардную цену товара можно представить следующей формулой:
(2.37)
где F - форвардная цена товара;
S - спотовая цена товара;
Т - период действия форвардного контракта;
г - ставка без риска для периода Т ;
Z - расходы по хранению и страхованию товара за период Т.
Пример.
Цена спот пшеницы равна 4000 руб. за тонну, ставка без риска на 90 дней - 8% годовых, расходы по хранению и страхованию за этот период составляют 6,5 руб. Определить 90-дневную форвардную цену пшеницы . Финансовый год равен 360 дням.
Она равна:
4000 1 + 0,08
90
360;
+ 6,5 = 4086,5^6.
Если стоимость хранения и страхования товара пропорциональна цене спот, то формула форвардной цены примет следующий вид:
(2.38)
где 2 - процент (в расчете на год) от стоимости товара, уплачиваемый за хранение и страхование.
Пример.
Допустим, что в приведенном выше примере расходы по хранению и страхованию составляют 0,65% годовых от стоимости товара. Определить форвардную цену пшеницы.
Она равна:
90
4000 1 +(0,08+0,0065)-—
= 4086,5/7^6.
При использовании непрерывно начисляемого процента формула (2.38) принимает вид:
F = Se[r+z}T, (2.39)
где Т - период действия форвардного контракта;
г - непрерывно начисляемая ставка без риска для периода Т;
z~ непрерывно начисляемый процент (в расчете на год) от стоимости товара, уплачиваемый за хранение и страхование.
Все форвардные контракты на товары можно разделить на две группы: товары, которые приобретаются в основном для инвестиционных целей, например, золото, серебро; и 2) товары, которые в первую очередь предназначены для целей потребления. В отношении товаров первой группы арбитражеры широко прибегают к арбитражным операциям при расхождении теоретических и фактических форвардных цен.
Для второй группы арбитражные стратегии используются в более редких случаях, так как данные товары в первую очередь предназначены для целей потребления. Если Рф> FT , где Рф - фактическая форвардная цена, FT - теоретическая форвардная цена, то инвесторы будут совершать арбитражные операции. Они займут деньги, купят на спотовом рынке товар и продадут форвард. Если то лица, владеющие товаром для потребительских целей, вряд ли начнут продавать его на спотовом рынке, чтобы разместить деньги на депозите, и покупать форварды или предоставлять товар в кредит арбитражерам для осуществления коротких продаж, так как они заинтересованы в наличии товара, например, для поддержания непрерывности производственного процесса. В результате для потребительских товаров можно установить только верхнюю границу форвардной цены, которая не должна нарушаться в силу арбитражной зависимости. Поэтому можно записать:
F <S l + (r + z)~—
база
(2-40)
Неравенство (2.40) говорит о том, что фактическая форвардная цена не должна превышать цену спот на величину цены доставки, но в то же время она может быть и ниже, поскольку разница в ценах вряд ли будет стимулировать совершение арбитражных операций. Если у владельцев существует большая потребность в товарах, то фактическая форвардная цена должна упасть довольно низко, чтобы побудить участников рынка к совершению арбитражных операций.
С учетом непрерывно начисляемого процента формула (2.40) принимает вид:
F < &(г+г'7
Фактическая форвардная цена товара может оказаться ниже теоретической. Это говорит о том, что владельцы товара получают полезность от владения им. Данную полезность можно оценить с по-
мощью ставки полезности (convenience yield). В этом случае уравнение (2.38) можно представить как:
а уравнение (2.39) как:
Fe'1 = Se(r+z}T.
Из уравнений (2.41) и (2.42) соответственно получаем:
г. _ 1 + (^ + ZX^/^a3a)
1 + у(Т/база)
и
F = 5е(,+
(2.41)
(2.42)
(2.43)
(2.44)
где у - ставка полезности, получаемая от владения товаром.
Уравнения (2.43) и (2.44) показывают, что форвардная цена будет меньше при росте ставки полезности, и наоборот. Ставка полезности отражает ожидания участников рынка в отношении будущего наличия товара. Небольшое значение у говорит о том, что участники рынка не ожидают дефицитности товара в будущем. Наличие большого количества товара уменьшает степень полезности его единицы для потребителя. Большое значение у свидетельствует о дефицитности товара. Соответственно полезность единицы товара для потребителя возрастает. Таким образом, небольшое значение у прежде всего говорит о наличии значительных запасов товара у потребителей.
Формулы (2.37), (2.38) и (2.39) показывают, что форвардная цена товара должна быть больше текущей цены спот. Однако на практике форвардная цена часто оказывается ниже спотовой. Это можно объяснить рядом факторов. Как было отмечено выше, при падении фактической форвардной цены ниже теоретической арбитраж затруднен. Арбитражеры вряд ли смогут занять товар для продажи его на спотовом рынке, так как он необходим владельцам для текущего потребления. Поэтому теоретически форвардная цена может упасть довольно низко, особенно, если на рынке наблюдается дефицит товара в настоящий момент времени. Кроме того, значительный рост цены товара в настоящий момент скорее всего вызовет увеличение его выпуска в будущем. В свою очередь, при такой конъюнктуре часть потребителей данного товара может пересмотреть свои планы
по его будущим закупкам в сторону уменьшения. В совокупности оба эффекта в тенденции могут вызвать понижение форвардной цены. Производство ряда товаров имеет сезонные циклы, что также изменяет баланс спроса и предложения в разное время года.
Еще одно объяснение предложил Дж.М.Кейнс. Согласно Кейнсу на товарных рынках количество хеджеров и спекулянтов не одинаково с каждой стороны рынка. Хеджеры являются по преимуществу продавцами товаров, а спекулянты - покупателями. Спекулянт будет участвовать в сделке, если будущая цена спот окажется выше текущей форвардной цены, поскольку именно в этом случае он получит прибыль. Поэтому хеджеры соглашаются на более низкие форвардные цены в качестве платы за стабильность своего финансового положения. Таким образом, хеджеры уплачивают спекулянтам своеобразную премию за риск за счет заключения контрактов по более низким форвардным ценам.
Обычно форвардная цена бывает ниже спотовой на рынках товаров, которые сразу потребляются по мере их производства и являются дорогостоящими в хранении.
2.3.5. Форвардная цена при различии ставок по кредитам и депозитам.
Внутренняя ставка доходности
При рассмотрении вопроса определения форвардной цены мы исходили из предположения о том, что ставки по кредитам и депозитам одинаковы. Данный прием позволил представить технику расчета форвардной цены на основе безарбитражного подхода. Были получены формулы для определения теоретической форвардной цены. На примерах было показано, что при расхождении между фактической и теоретической форвардными ценами можно заработать арбитражную прибыль. Поскольку ставки по кредитам и депозитам были равны, то возникала единственная теоретическая форвардная цена, относительно которой рассматривались возможности совершения арбитражной операции. На практике ставки по кредитам выше чем по депозитам. Поэтому для определения возможности совершить арбитражную операцию необходимо рассчитать две форвардные цены -верхнюю ) на основе ставки по кредиту и нижнюю (FH) - на основе ставки по депозиту. Если фактическая форвардная цена выше верхней теоретической цены или ниже нижней теоретической цены, то существует арбитражная ситуация. Когда фактическая цена
находится в диапазоне между теоретическим ценами, то арбитраж невозможен. Поясним сказанное на примере.
Пример 1.
Курс акции 100 руб. Ставка без риска по депозиту равна 10%, по кредиту - 15%. Дивиденды по акции не выплачиваются. Определить верхнюю и нижнюю теоретические шестимесячные форвардные цены.
Решение.
Форвардная цена акции, по которой не выплачиваются дивиденды, для простого процента рассчитывается по формуле (2.1). Определяем верхнюю теоретическую границу на основе ставки по кредиту:
6
F -100 1+0,15 — -107,5/зуб.
I 12;
Определяем нижнюю теоретическую границу на основе ставки по депозиту:
( 6
/7 =100 1 + 0,1— =105/?уб.
Если форвардная цена акции в примере 105руб. < Еф <\07,5 руб,> арбитраж невозможен. Фактический уровень цены в рамках этого диапазона будет определяться соотношением спроса и предложения на рынке. Если спрос больше предложения, цена приблизится к верхней границе. Если предложение больше, - то к нижней границе. При F < 105 руб. последует арбитраж. Инвестор: а) купит более дешевый форвард; б) займет акцию, продаст ее и разместит полученные средства на безрисковом депозите на шесть месяцев под 10%.
При F(f) > 110руб. инвестор: а) продаст более дорогой форвард; б) займет 100 руб. под 15% годовых на полгода и купит акцию.
Более удобно сделать вывод о возможности арбитражной операции на основе внутренней ставки доходности форвардного контракта. Она определяется из формулы форвардной цены. Из формулы (2.1) получим:
<5 ) Т
(2.45)
где г - внутренняя ставка доходности форвардного контракта для актива, по которому не выплачиваются доходы.
Если она выше ставки по кредитам или ниже ставки по депозитам, то существует возможность получить арбитражную прибыль.
Пример 2.
Курс акции 100 руб. Ставка без риска по депозиту равна 10%, по кредиту - 15%. Дивиденды по акции не выплачиваются. Определить возможность совершить арбитражную операцию, если шестимесячная форвардная цена равна: а) 110 руб.; б) 104 руб.
Решение.
а) На основе формулы (2.45) внутренняя ставка доходности форвардного контракта составляет:
<100
-1 — = 0,2
или 20%.
Внутренняя ставка доходности выше ставки по кредиту, поэтому инвестор сейчас: продает форвард по цене 110 руб., занимает 100 руб. под 15% годовых на полгода и покупает акцию на спотовом рынке, хранит ее полгода. Через шесть месяцев: поставляет акцию по контракту и получает за нее 110 руб., по кредиту отдает сумму:
100 1 + 0,15 —
107,5/туб.
Прибыль равна:
110 -107,5 = 2,5 руб.
Арбитражной прибылью можно воспользоваться и в момент заключения форвардного контракта. По контракту за акцию инвестору заплатят 110 руб. Дисконтированная стоимость данной величины при заключении контракта составляет:
-----И?-----г = 102,3256руб.
1 + 0,15(6/12)
Инвестор занимает данную сумму на полгода и за 100 руб. покупает акцию. Сумма:
102,3256-100 = 2,3256/М7.
составляет арбитражную прибыль. (Она равна дисконтированная стоимости 2,5 руб. прибыли к моменту истечения контракта:
------------г = 2,3256руб.) 1 + 0,15(6/12)
б) Внутренняя ставка доходности форвардного контракта составляет:
<104 ^12
г = — -1 _-о,О8 или8%.
Ц00 ) 6
Она ниже ставки по депозиту, поэтому инвестор сейчас: покупает форвард по цене 104 руб., занимает акцию на полгода и продает ее на спотовом рынке за 100 руб., размещает их на шестимесячном депозите под 10% годовых. Через шесть месяцев: получает по депозиту сумму:
loofl + 0,1 — | = 105^6., V 12/
платит за акцию по контракту 104 руб. и возвращает ее кредитору. Прибыль равна:
105 -104 = \руб.
Арбитражной прибылью инвестор может воспользоваться и при заключении форвардного контракта, К моменту его истечения он должен располагать 104 руб. Дисконтированная стоимость этой величины сегодня составляет:
104 ----- z , ч = 99,0476руб. 1 + 0,1(6/12)
Поэтому именно данную сумму он будет размещать на шестимесячном депозите. От продажи акции он получает 100 руб. В результате, можно сразу воспользоваться суммой:
100-99,0476 = 0,9524руб.
(Она равна дисконтированной стоимости одного рубля прибыли к моменту истечения контракта:
-----—— = 0,9524руб.) 1 + 0,1(6/12)
На основе величины внутренней ставки доходности инвестор может принять решение об инвестировании средств.
Пример 3.
Пусть в примере 2 в ситуации (а) вкладчик не имеет доступа к кредиту, но располагает 100 руб., которые хотел бы инвестировать на полгода. Его устраивает доходность 20% годовых. Тогда он купит сейчас акцию на спотовом рынке за 100 руб. и продаст форвардный контракт. Через попгода поставит акцию по контракту за 110 руб. Доходность его операции составит:
110-100
----------2 = 0,2 или 20% годовых.
100
Следует подчеркнуть, что в рамках такой операции эта доходность является для инвестора доходностью без риска.
Пусть в ситуации (б) инвестор не может занять базисный актив, но владеет акцией. Тогда он продаст ее на спотовом рынке, разместит 100 руб. на депозит под 10% на полгода и купит форвард по цене 104 руб. Через полгода он заплатит по контракту 104 руб., получит назад акцию и дополнительно заработает 1 руб.
Для определения возможностей совершения арбитражных операций при расчете форвардных цен необходимо использовать разные ставки по кредитам и депозитам как было показано выше. Для получения еще более точной картины следует также учесть, что спотовая цена актива в каждый данный момент не является единой, а представлена котировками с ценой продавца и ценой покупателя, между которыми имеется некоторый спред. Инвестор может купить актив только по более высокой цене продавца и продать его по более низкой цене покупателя. Поэтому при расчете верхней теоретической границы форвардной цены надо использовать спотовую цену продавца, а нижней границы - цену покупателя.
Пример 4.
Котировка акции на спотовом рынке составляет: 100 руб. - цена покупателя, 101 - цена продавца. Ставка без риска по депозиту равна 10%, по кредиту - 15%. Дивиденды по акции не выплачиваются. Определить верхнюю и нижнюю теоретические шестимесячные форвардные цены.
Решение.
Форвардная цена акции, по которой не выплачиваются дивиденды, для простого процента рассчитывается по формуле (2.1). Определяем верхнюю теоретическую границу на основе ставки по кредиту и цены продавца:
F = 101| 1 + 0,15 —
I 12;
= 108,58/?уб.
Определяем нижнюю теоретическую границу на основе ставки по депозиту и цены покупателя:
FH =100 1 + 0,1— rf J -| Л
= 105 руб.
При совершении арбитражных операций с валютными форвардными контрактами одновременно одна валюта занимается, а другая размещается на депозите. Поэтому при расчете форвардных цен необходимо учитывать как котировки продавца и покупателя, так и разные ставки по кредитам и депозитам. Верхняя и нижняя теоретические границы соответственно равны:
\ + гь(Т1база) мк \ + г^(Т/база)
Р Х + г^/база) bid 1 + гбаза)
где Sask - цена продавца;
Shid ~ Мена покупателя;
гь - ставка по кредиту;
rz - ставка по депозиту;
буква f означает иностранную валюту ( или более точно, валюту, курс которой представляется в единицах другой валюты.)
Рассмотрим пример.
Пример 5.
Спотовая котировка доллара равна: 27,5 руб.(цена покупателя) - 28 руб. (цена продавца). Трехмесячная рублевая ставка по депозиту - 4%, по кредиту - 10%, по доллару - 2% по депозиту, 6% - по кредиту. Определить теоретические верхнюю и нижнюю форвардные цены.
Решение.
Верхняя теоретическая граница равна:
2g 1 + 0,1(3/12)
1 +0,02(3/12)
= 28,5572^6.
Если фактическая форвардная цена выше, например, 28,8 руб., то арбитражер продаст доллар по форварду за 28,8 руб,, возьмет рублевый кредит в размере:
----—с 28 руб. = 27,8607руб.,
1 + 0,02(3/12)
конвертирует его в доллары по спот курсу:
27,8607 :28 = 0,9950долл.,
разместит данную сумму на долларовом депозите:
0,9950 1+0,02—
- 16олл.
Арбитражер уплачивается по контракту 1 долл, и получает 28,8 руб. По рублевому кредиту он отдает:
27,8607 1 + 0,1— =28,5572руб.
I 12 7
Его прибыль равна:
28,8 - 28,5572 = 0,2428руб.
Если инвестор желает воспользоваться прибылью при заключении контракта, то он возьмет рублевый кредит в размере:
----—г = 28,0976руб.
1+0,1(3/12)
Из них:
\долл.
1 + 0,02(3/12)
28руб. = 27,8607руб.
использует на покупку долларов:
27,8607: 28 = 0,9950боо.
Его прибыль равна:
28,0976 - 27,8607 = 0,2369руб.
Нижняя теоретическая граница равна:
1 + 0,04(3/12) ’ 1 + 0,06(3/12)
= 27,ЗМ5 руб.
Если фактическая форвардная цена ниже, например, 27 руб., то арбитражер купит доллар по форварду за 27 руб., возьмет долларовый кредита размере:
27
1 + 0,04(3/12)27,5
= 0,972 \долл.
Конвертирует его в рубли по спот курсу:
0,9721-27,5 = 26,7327 руб.
Разместит данную сумму на рублевом депозите:
26,7327 1 + 0,04—
= 27 руб.
Уплачивает ее по контракту и получает 1 долл. По долларовому кредиту возвращает:
0,9721 1 + 0,06—
= 0,9867долл.
Прибыль равна:
1 -0,9867 = 0,0133доял.
Если инвестор желает воспользоваться прибылью при заключении контракта, то он возьмет долларовый кредит в размере:
1долл.
1 + 0,06(3/12)
= 0,9852долл.
Для того, чтобы располагать к моменту истечения контракта 27 руб. он конвертирует в рубли сумму:
------------------= 0,9721долл.
1 + 0,04(3/12)27,5
Прибыль составит:
0,9852 - 0,9721 = 0,0131долл.
2.4. СИНТЕТИЧЕСКИЙ ФОРВАРДНЫЙ КОНТРАКТ
На финансовом рынке существует понятие синтетического актива. Синтетический актив можно определить как портфель, состоящий из разных активов. Такой портфель обладает определенными характеристиками риска и доходности. Характеристики синтетического актива могут копировать характеристики какого-либо существующего финансового инструмента, например, акции или облигации. Тогда такой синтетический актив назовут соответственно синтетической акцией или облигацией. Вопрос формирования синтетической акции и облигации мы рассмотрим в главе 13. В настоящем параграфе остановимся на вопросе формировании синтетического форвардного контракта.
Алгоритм создания синтетической форвардной позиции можно полу* чить на основе алгоритма определения форвардной цены. Рассмотрим длинный форвардный контракт на акцию по которой не выплачиваются дивиденды. В его рамках покупатель обязуется в конце периода времени Т уплатить продавцу акции сумму денег равную форвардной цене! которая определяется по формуле (2.1), в обмен на акцию. Инвестор может получить результат аналогичный покупке форвардного контракта и иным образом. Для этого сегодня ему необходимо занять сумму денег равную спотовой цене акции 5* на время Т под процент г, купить акцию и держать ее в течение отмеченного времени. В конце данного периода он уплатит по кредиту (как и по форвардному контракту) сумму F . Таким образом, в результате отмеченных действий в конце периода Т инвестор фактически уплачивает сумму денег равную форвардной цене. В этот момент в его распоряжении находится акция. Представленный алгоритм действий связан для инвестора с такими же финансовыми издержками и фактическим результатом как и заключение форвардного контракта. Поэтому формирование длинной синтетической форвардной позиции по акции заключается в заимствовании суммы денег и покупке акции на спотовом рынке в начальный момент времени.
Короткий синтетический форвардный контракт состоит в продаже сегодня акции по стоповой цене 5 и размещении денег на время Т под процент г. В конце периода Т продавец имеет такой же результат как и по форвардному контракту, т.е. получает от инвестирования денег сумму F.
Рассмотрим формирование синтетического валютного форвардного контракта на примере.
Пример.
Курс доллара равен 30 руб., трехмесячная ставка без риска по рублям - 10%, по долларам - 5%. Трехмесячный форвардный курс составляет:
301 + 0,10(3/12)
1 + 0,05(3/12)
= 30,37 руб.
Для формирования синтетической длинной форвардной позиции инвестору следует занять на три месяца под 10% сумму в рублях:
----—ЗО/туб. = 29,6296руб.,
1 + 0,05(3/12)
конвертировать их в доллары по спотовому курсу:
29,6296:30- 0,9877долл.,
разместить доллары на трехмесячном долларовом депозите:
0,9877 1 + 0,05—
7 7 - Л
Idrwz.
По кредиту через три месяца инвестор должен вернуть:
29,
6296 1 + 0,1 —
= 30,37р^б.
Таким образом, через три месяца инвестор получит по депозиту 1 долл, и уплатит по кредиту 30,37 руб. Поскольку трехмесячный форвардный курс равен 30,37 руб., то осуществленные действия по своему результату эквивалентны покупке форвардного контракта на доллар.
Для получения синтетической короткой форвардной позиции следует занять в долларах под 5% сумму:
30,37
1 + 0,1(3/12)30
= 0,987600+.+,
конвертировать их в рубли по спотовому курсу:
0,9876-30 = 29,628^.,
разместить рубли на трехмесячном депозите:
29,628 1 + 0,1 —
30,37/туб.
По долларовому кредиту необходимо вернуть:
( ЗА
0,9876 1 + 0,05— = 1долл.
I П)
Таким образом, инвестор через три месяца получает по депозиту 30,37 руб. и отдает по кредиту 1 долл. Данная операция эквивалентна продаже доллара по трехмесячному форварду по цене 30,37 руб.
В предыдущих параграфах было показано, что инвестор может заработать арбитражную прибыль при расхождении фактической и теоретической форвардных цен. Его действия заключаются именно в том, что в случае недооценки форвардного контракта (Еф < Fr) он его покупает и продает синтетически, поскольку синтетическая форвардная позиция стоит дороже. Когда форвард переоценен (F0 > Fr), арбитражер продает контракт и формирует длинную форвардную синтетическую позицию, поскольку она стоит дешевле.
КРАТКИЕ ВЫВОДЫ
Форвардный контракт - это соглашение о будущей поставке базисного актива. Он заключается, как правило, вне биржи для реальной покупки или продажи актива и не является стандартным. С помощью форвардной сделки участник контракта получает возможность застраховаться от неблагоприятного изменения цен. Для форвардных контрактов характерен кредитный риск.
Форвардный контракт можно заключать с целью игры на разнице курсов активов. Лицо, играющее на повышение, покупает контракт. Лицо, играющее на понижение, продает контракт.
Цена поставки - это цена, по которой поставляется базисный актив по форвардному контракту. Она устанавливается в момент его заключения. Для каждого момента времени форвардная цена - это цена поставки форвардного контракта, который заключается в этот момент.
В момент заключения форвардного контракта его цена равна нулю. Если в дальнейшем контракт продается на вторичном рынке, то он получает некоторую цену, поскольку возникает разница между ценой поставки и текущей форвардной ценой.
При оценке форвардной цены исходят из посылки, что вкладчик с финансовой точки зрения должен быть безразличен в вопросе покупки базисного актива по спотовой цене сейчас или по форвардной в будущем. Данное условие предполагает невозможность получить
арбитражную прибыль на разнице между спотовой и форвардной ценами.
С теоретической точки зрения непрерывно начисляемая ставка дивиденда означает, что дивиденд начисляется и постоянно реинвестируется в акцию.
Если ставка без риска для иностранной валюты больше ставки без риска для национальной валюты, то для более отдаленных периодов времени форвардная цена будет понижаться. Если же г > rs , она будет возрастать.
Формирование длинной синтетической форвардной позиции по акции заключается в заимствовании суммы денег и покупке акции на спотовом рынке в начальный момент времени.
Формирование короткой синтетической форвардной позиции по акции заключается в продаже сегодня акции по стоповой цене и размещении денег на депозите.
ГЛАВА 3. ОРГАНИЗАЦИЯ И ФУНКЦИОНИРОВАНИЕ ФЬЮЧЕРСНОГО РЫНКА
В настоящей главе рассматриваются вопросы организации и функционирования фьючерсного рынка. Раскрывая данную тему, вначале мы остановимся на общей характеристике фьючерсного контракта, расскажем о механизме фьючерсной торговли, определим понятия фьючерсной цены, контанго, бэквардейшн, базиса и базисного риска, цены доставки, В заключение рассмотрим технику хеджирования фьючерсными контрактами и охарактеризуем коэффициент хеджирования.
3.1. ОБЩАЯ ХАРАКТЕРИСТИКА ФЬЮЧЕРСНОГО КОНТРАКТА
Фьючерсный контракт - это соглашение о будущей поставке базисного актива, которое заключается на бирже. Биржа (расчетная палата)1 сама разрабатывает его условия, и они являются стандартными для каждого базисного актива. Поэтому, по сравнению с форвардными контрактами, фьючерсные контракты высоко ликвидны, поскольку их условия одинаковы для всех инвесторов. В то же время, стандартный характер условий контракта может оказаться неудобным для контрагентов. Например, им требуется поставка некоторого товара в ином количестве, в ином месте и в другое время, чем это предусматривается спецификацией контракта на данный базисный актив. Кроме того, на бирже может вообще отсутствовать фьючерсный контракт на актив, в котором заинтересованы контрагенты. Исполнение фьючерсного контракта гарантируется расчетной палатой. Именуются контракты по месяцу их истечения. Например, мартовский фьючерс. Это означает, что контракт истекает в марте.
Фьючерсные контракты обычно являются краткосрочными. С момента, когда биржа открывает торговлю контрактом, и до момента его истечения, как правило, проходит девять месяцев. Однако существуют и долгосрочные фьючерсы, срок действия которых насчитывает несколько лет. В мировой практике котировка фьючерсного контракта дается в расчете на единицу базисного актива.
1 В большинстве случаев биржевая торговля ведется с помощью двух организаций: биржи и расчетной палаты. На бирже происходят торги срочными контрактами. Расчетная палата осуществляет финансовое сопровождение торгов.
В основе контракта могут лежать как товары, так и финансовые инструменты. Контракты, базисными активами которых являются финансовые инструменты, а именно, ценные бумаги, фондовые индексы, валюта, банковские депозиты, драгоценные металлы, называются финансовыми фьючерсными контрактами. Контракты, базисными активами которых выступают собственно товары, называются товарными фьючерсными контрактами. Современный фьючерсный рынок развивается в первую очередь за счет роста торговли финансовыми фьючерсными контрактами.
Фьючерсный контракт можно заключить только при посредничестве брокерской компании, которая является членом биржи. Поэтому первый шаг к началу фьючерсной торговли состоит в заключении контракта с брокером на брокерское обслуживание.
При открытии позиции по контракту его участник должен внести гарантийный взнос (залог). Он называется начальной или депозитной маржой. По величине маржа составляет обычно от 2% до 10% стоимости контракта. Данные средства вносятся на клиентский счет, который открывается в расчетной палате каждому участнику торгов.
Чтобы определить величину начальной маржи, инвестор должен знать текущую стоимость фьючерсного контракта. Она определяется как произведение фьючерсной цены на количество базисных активов в контракте. Например, фьючерсный контракт на акцию компании А включает 100 акций. Фьючерсная цена февральского фьючерса равна 100 долл, за акцию. Тогда текущая стоимость контракта составляет:
1 ООакций • 1 ООдолл. = 1 ООООда?,?.
Таким образом, контракт сейчас стоит 10000 долл. Пусть начальная маржа равна 10% от стоимости контракта. Это значит, что гарантийный залог составляет 1000 долл.
Размер маржи устанавливается расчетной палатой, исходя из величины наблюдавшихся дневных колебаний фьючерсной цены. Величина маржи должна быть такой, чтобы она покрывала возможный дневной проигрыш по контракту в условиях текущей конъюнктуры. При изменении конъюнктуры рынка расчетная палата будет изменять величину гарантийного взноса. Брокер может потребовать от клиента внести маржу в большей сумме. Условия контрактов могут допускать внесение начальной маржи как деньгами, так и ценными бумагами.
Рассмотрим функционирование элементарного фьючерсного рынка на примерах.
Пример 1.
Имеется фьючерсный контракт на акции компании At который насчитывает 1 акцию. Сейчас 1 декабря, контракт истекает 15 марта. Котировка мартовского фьючерса равна 100 руб. за акцию. Это означает, что акция с поставкой в середине марта стоит сейчас 100 руб. Пусть на рынке присутствуют только четыре участника. Два из них (1 и 2) хотели бы купить по одной акции компании А в марте по текущей фьючерсной цене, а два других (3 и 4) - продать по одной акции этой компании. Поэтому 1 и 2 участники отдают приказы своим брокерам купить по одному мартовскому контракту по текущей цене, а 3 и 4 - продать по одному контракту.
Так как условия контрактов стандартны, то единственное, что согласовывается на рынке - это фьючерсная цена. В нашем примере участники заявили одинаковые цены, поэтому были заключены два фьючерсных контракта. Заключив контракты, 1 и 2 участники взяли на себя обязательства купить по одной акции компании А в марте, а 3 и 4 - продать по одной акции.
Контракты заключались через брокеров. Поэтому участники торгов не знали контрагентов по сделке. Но в этом нет никакой необходимости, так как все контракты стандартны. После заключения фьючерса стороной сделки для каждого из участников становится расчетная палата, т.е. для покупателей она выступает продавцом, для продавцов - покупателем.
Наши участники хотят купить и продать акции в марте. Поэтому они открыли позиции и держат их открытыми до момента истечения контрактов. Незадолго до окончания срока действия контрактов они информируют расчетную палату о том, что собираются исполнять контракты. Хотя формально расчетная палата выступает стороной сделки, сама она не будет ни покупать, ни продавать акции. Поэтому расчетная палата начинает сводить участников контрактов парами. Поскольку контракты стандартны, то все равно, какие пары она сформирует, например, 1 и 3; 2 и 4 или 1 и 4; 2 и 3.
Контракт истек 15 марта. Согласно его условиям, покупатели уплатили деньги, а продавцы поставили им по одной акции компании^.
Остановимся теперь на действиях спекулянта одного дня. Утром он “приходит” на рынок, а вечером “уходит” с рынка, чтобы сильно не рисковать.
Пример 2. Игра на повышение.
Утром котировка мартовского фьючерса составляет 100 руб. Спекулянт полагает, что к вечеру она вырастет до 110 руб. Поэтому он играет на повышение, т.е. покупает мартовский фьючерс по 100 руб. К вечеру фьючерсная цена поднялась до 110 руб. Тогда спекулянт продает мартовский фьючерс по 110 руб.
После окончания торговой сессии расчетная палата проводит клиринг по счету спекулянта, т.е. зачитывает его противоположные обязательства. Первой сделкой спекулянт взял на себя обязательство купить одну акцию компанию А в марте, второй сделкой - продать одну акцию компании А в марте же. Таким образом, вторая сделка погасила его обязательство по первой: он уже не должен ни покупать, ни продавать акцию. Однако учитывается, что он купил первый контракт по 100 руб., а второй продал по 110 руб., т.е. дороже. Разница в 10 руб. составляет выигрыш спекулянта. 10 руб. вечером переводятся расчетной палатой на его счет. Данная сумма списывается со счета участника торгов, который имел короткую позицию по контракту.
Допустим теперь, что спекулянт ошибся в прогнозе, и к вечеру фьючерсная цена упала до 90 руб. Чтобы не рисковать еще больше, он продает контракт по 90 руб. Вновь вторая сделка погасила его обязательство по первой сделке. Однако финансовый результат для него отрицательный: он купил контракт по 100 руб., а продал только по 90 руб. Поэтому уже с его счета расчетная палата списывает сумму в 10 руб. и переводит на счет лица, которое имело короткую позицию по контракту.
Пример 3. Игра на понижение.
Утром котировка мартовского фьючерса составляет 100 руб. Спекулянт полагает, что к вечеру она упадет до 90 руб. Поэтому он играет на понижение, т.е. продает мартовский фьючерс по 100 руб. К вечеру фьючерсная цена снизилась до 90 руб. Тогда спекулянт покупает мартовский фьючерс по 90 руб.
После окончания торговой сессии расчетная палата проводит клиринг по его счету. Первой сделкой спекулянт взял на себя обязательство продать акцию компании А в марте, второй сделкой - купить акцию компании А в марте. Таким образом, вторая сделка погасила его обязательство по первой: он уже не должен ни продавать, ни покупать акцию. Однако учитывается, что он продал первый контракт по 100 руб., а купил второй по 90 руб., т.е. дешевле. Разница в 10 руб. составляет его выигрыш, который вечером переводится на его счет. Данная сумма списывается со счета участника торгов с длинной позицией по контракту.
Допустим теперь, что спекулянт ошибся в прогнозе, и к вечеру фьючерсная цена выросла до 110 руб. Чтобы не рисковать еще больше, он покупает контракт по 110 руб. Вновь вторая сделка погасила его обязательство по первой. Однако финансовый результат для него отрицательный: он продал контракт по 100 руб., а купил по 110 руб. Поэтому с его счета списывают маржу в размере 10 руб.
В первом примере спекулянт играл на повышение, поэтому открыл длинную позицию, т.е. взял на себя обязательство купить акции. Второй сделкой он снял с себя это обязательство. В этом случае скажут, что второй сделкой он закрыл позицию.
Во втором примере спекулянт играл на понижение, поэтому открыл короткую позицию, т.е. обязался продать акции. Второй сделкой он снял с себя это обязательство или закрыл позицию. Сделка, закрывающая открытую позицию по срочному контракту, называется офсетной. Она противоположна первоначальной. Если первая сделка была покупкой контракта, то офсетная будет продажей. Если первая была продажей, то офсетная будет покупкой.
Участник контракта может держать позицию открытой в течение длительного времени, например, несколько дней. Однако все равно ежедневно по его счету будет происходить движение средств: расчетная палата будет начислять ему текущий выигрыш или списывать текущий проигрыш. Текущие выигрыши (проигрыши) она определяет по итогам каждой торговой сессии на основе так называемой котировочной или расчетной цены. Котировочная цена - это цена, которая определяется по итогам торговой сессии на основе котировок или сделок, заключенных в ходе данной сессии. В мировой практике котировочная цена обычно рассчитывается на основе сделок, заключенных перед закрытием биржи. Рассмотрим механизм клиринга для данного случая на примере.
Пример 4.
Спекулянт полагает, что фьючерсная цена будет расти несколько дней подряд. Поэтому покупает утром мартовский фьючерс на акцию компании А по цене 100 руб. Котировочная цена по итогам торговой сессии в первый день составила 105 руб. Расчетная палата осуществляет клиринг по счету спекулянта. Она сравнивает цену открытия позиции - 100 руб. с котировочной ценой - 105 руб. Так как спекулянт открыл длинную позицию, то он выигрывает от роста цены. Поэтому расчетная палата вечером переводит на его счет разницу между
ценами - 5 руб. - в качестве выигрыша спекулянта за сегодняшний день.
На второй день спекулянт не предпринимает никаких действий. Мартовский фьючерс торгуется, и вечером котировочная цена определена на уровне 115 руб. Расчетная палата проводит клиринг по счету спекулянта. Она сравнивает вчерашнюю котировочную цену (105 руб.) с сегодняшней котировочной ценой (115 руб,). Цена выросла на 10 руб. Это означает, что спекулянт выиграл 10 руб. Вечером данная сумма переводится на счет спекулянта в качестве текущего выигрыша.
На третий день котировочная цена равна 110 руб. Расчетная палата проводит клиринг по позиции спекулянта. Она сравнивает вчерашнюю котировочную цену (115 руб.) с сегодняшней (110 руб.). Котировочная цена мартовского фьючерса упала на 5 руб. Поскольку у спекулянта длинная позиция, а цена понизилась, то он проигрывает в этой ситуации. Его проигрыш равен 5 руб. Данная сумма вечером списывается с его счета.
На четвертый день спекулянт продает контракт по 111 руб., т.е. закрывает свою позицию. Расчетная палата проводит клиринг по его счету. Она сравнивает вчерашнюю котировочную цену (110 руб.) с ценой закрытия позиции (111 руб.). Так как цена выросла, то спекулянт выиграл 1 руб. Данная сумма переводится на его счет.
Если нас интересует общий результат по операции спекулянта, то необходимо сравнить цены открытия и закрытия позиции. Контракт был открыт по 100 руб., а закрыт по 111 руб. Таким образом, спекулянт выиграл 11 руб.
Как было показано в примере, по результатам торгов расчетная палата ежедневно определяет выигрыши-проигрыши участников, списывает деньги со счета проигравшей стороны и зачисляет их на счет выигравшей. Сумма выигрыша или проигрыша, начисляемая по итогам торгов, называется вариационной или переменной маржой. Положительная вариационная маржа означает выигрыш, отрицательная - проигрыш.
Мы рассмотрели механизм клиринга на примере спекулянта. Следует однако подчеркнуть, что расчетная палата ежедневно проводит клиринг по всем открытым позициям, т.е. как спекулянтов, так и хеджеров и арбитражеров.
Расчетная палата устанавливает минимальную сумму средств, которая должна находится на счете участника торгов, имеющего открытую позицию. Она называется поддерживающая маржа. Она
может равняться или быть ниже начальной маржи. Если в результате проигрыша по фьючерсному контракту на клиентском счете окажется сумма меньше поддерживающей маржи, клиент обязан восстановить ее величину до уровня начальной. В противном случае брокер самостоятельно закроет его позицию офсетной сделкой. Такое условие включается в договор с брокером.
Участники торгов, которые не закрыли свои позиции до момента истечения контрактов, обязаны их исполнить. По общему правилу фьючерсные контракты исполняются по цене равной котировочной цене последнего торгового дня. Поясним это на примере.
Пример 5.
Имеется фьючерсный контракт на акции компании Л, который насчитывает одну акцию. Сейчас 1 декабря, контракт истекает 15 марта. Котировка мартовского фьючерса равна 100 руб. Инвестор хотел бы купить акцию компании А в феврале по 100 руб. Поэтому он сейчас покупает мартовский фьючерс по цене 100 руб. и держит позицию открытой до момента истечения контракта. Допустим, фьючерсная цена росла, и в последний день торгов котировочная цена составила 150 руб. Это означает, что инвестор должен исполнить контракт по цене 150 руб. Биржа назначает ему контрагента по контракту. Он уплачивает ему 150 руб. и получает акцию.
Когда инвестор покупал контракт 1 декабря, он хотел получить акцию по цене 100 руб. Несмотря на то, что он заплатил 150 руб., его фактические расходы составили 100 руб. Он открыл позицию по 100 руб. В последующем фьючерсная цена выросла до 150 руб. Это означает, что за период действия контракта в качестве выигрыша на его счет была перечислена вариационная маржа на сумму 50 руб. Таким образом, 100 руб., которые он готов был заплатить плюс 50 руб. выигрыша по фьючерсу и дают общий итог в 150 руб.
Допустим, что котировочная цена в последний день торгов составила 50 руб. за акцию. Поэтому инвестор уплачивает контрагенту 50 руб. и получает акцию. Однако его фактические расходы вновь равны 100 руб. Он открыл длинную позицию по 100 руб., а фьючерсная цена упала до 50 руб. Это означает, что с его счета за период действия контракта списали отрицательную вариационной маржу на сумму 50 руб. Таким образом, 50 руб., уплаченные контрагенту за акцию, плюс 50 руб. проигрыша на акцию по контракту дают в сумме 100 руб. Как видно из примера, инвестор в обоих случаях уплачивает за акцию ту цену, по какой он открыл позицию.
Фьючерсные контракты могут быть поставочными и беспо-ставочными или расчетными. По поставочному фьючерсу предусматривается физическая поставка базисного актива, Беспоставоч-ный фьючерс предполагает расчеты между участниками только в денежной форме, а поставка базисного актива отсутствует. Поясним сказанное на примере.
Пример 6.
! Пусть в примере 5 фьючерсный контракт на акцию является бес-поставочным. В предпоследний торговый день котировочная цена равна 145 руб. На следующий день (последний торговый день) котировочная цена составила 150 руб. В конце дня расчетная палата осуществляет последний клиринг по счетам участников, которые имели на этот день открытые позиции по контракту. Участники с длинной позицией получили положительную вариационную маржу в размере 5 руб. на один контракт, а со счетов участников с короткой позицией данная сумма была списана. Таким образом, контракт истек, взаиморасчеты между контрагентами завершены.
Как правило, фьючерсный контракт делают расчетным, если неудобно осуществлять поставку базисного актива. В мировой практике, например, беспоставочными являются контракты на фондовые индексы.
Чтобы не допустить чрезмерной спекуляции фьючерсными контрактами и усилить систему гарантий их исполнения, биржа устанавливает по каждому виду контракта лимит отклонения фьючерсной цены текущего дня от котировочной цены предыдущего дня Например, котировочная цена предыдущего дня равна 100 руб. Лимитное отклонение вверх и вниз составляет 10%. Это значит, что в ходе текущей торговой сессии фьючерсная цена может колебаться в границах от 90 руб. до 110 руб. Если фьючерсная цена выходит за рамки данного интервала, биржа останавливает торговлю контрактом. Иногда она может изменить ценовые границы. Торговля прекращается с целью ограничить спекуляцию и позволить инвесторам реально оценить конъюнктуру рынка. Торговлю могут останавливать на короткий период или до конца торгового дня.
Если фьючерсная цена отклонилась от предшествующей котировочной цены на величину, равную нескольким лимитным интервалам, то торговля контрактом в течение последующих дней будет открываться и сразу же закрываться без осуществления каких-либо сделок. Такая ситуация продлится до тех пор, пока фьючерсная цена
не установится в границах лимитного интервала. В описанной ситуации новая котировочная цена будет фиксироваться на уровне лимитной цены. Проиллюстрируем сказанное на примере.
Пример.
Котировочная цена предыдущего дня равна 100 руб. Лимитное отклонение - 10%. Резкое изменение конъюнктуры на спотовом рынке базисного актива привело к тому, что на следующий день (день 1) инвесторы готовы продавать фьючерсы по 130 руб. Биржа открыла торговлю и сразу же закрыла. Сделки по данной цене не заключались, а новая котировочная цена была установлена на уровне 110 руб., т. е. на уровне верхнего лимита. На следующий день (день 2) фьючерсная цена, по которой участники рынка готовы были продавать контракты, оставалась на прежнем уровне (130 руб.), поэтому торговля контрактом вновь не велась, а котировочную цену установили на уровне 121 руб. На третий день фьючерсная цена оказалась в рамках лимитных границ, и торговля контрактом возобновилась.
Ограничение ценовых колебаний играет важную роль с точки зрения снижения риска потерь и предотвращения банкротств участников торгов и биржи, однако такой механизм делает фьючерсные контракты неликвидными в течение периода времени, пока биржа закрыта. Система лимитов приводит к тому, что в течение некоторого времени существует разница между официально зарегистрированной фьючерсной ценой и равновесной фьючерсной ценой Следует отметить, что не всегда фьючерсная цена испытывает резкие изменения только в силу спекулятивных настроений, поскольку она является зеркалом ситуации на спотовом рынке базисного актива. Биржа, как правило, снимает лимитные ограничения для месяца поставки по фьючерсному контракту.
Для ограничения спекулятивной активности биржа устанавливает позиционный лимит, т. е. ограничивает общее число контрактов, которые может держать открытым один инвестор, и в разбивке по времени их истечения.
Фьючерсные контракты, как правило, заключаются не с целью осуществления реальной поставки, а для хеджирования и спекуляции. В мировой практике только небольшое число всех заключаемых контрактов оканчиваются поставкой, остальные закрываются офсетными сделками. Когда заключается новый контракт, число существующих на бирже контрактов возрастает на одну единицу. При совер-
число
Рис. 3.1. Число открытых позиций в течение действия фьючерсного контракта
шении офсетной сделки только одним инвестором число заключенных контрактов остается прежним. Если два лица, которые имеют противоположные позиции, заключают офсетные сделки, число контрактов уменьшается на единицу.
Общую динамику торговли фьючерсными контрактами можно охарактеризовать с помощью рис. 3.1. Как видно из графика, максимальный объем открытых позиций, т. е. действующих контрактов, приходится на момент времени После этого количество существующих контрактов начинает резко падать, поскольку хеджеры и спекулянты, как правило, не заинтересованы в осуществлении поставки. Поэтому при приближении срока истечения контрактов они начинают активно закрывать свои позиции. На дату поставки остается лишь небольшое число контрактов.
3.2. ФЬЮЧЕРСНАЯ ЦЕНА. БАЗИС. ЦЕНА ДОСТАВКИ
3.2.1. Фьючерсная цена
При заключении фьючерсного контракта участники согласовывают цену базисного актива с поставкой в определенный момент в будущем. Она называется фьючерсной ценой. Важно подчеркнуть, что согласованная фьючерсная цена не фиксируется во фьючерсном контракте. Она фиксируется только по счету каждого из участников сделки как цена открытия позиции. Фьючерсная цена может
быть выше или ниже текущей цены спот базисного актива. Ситуация, когда фьючерсная цена выше цены спот, называется кон-танго (премия к цене спот). Ситуация, когда фьючерсная цена ниже цены спот, называется бэквардейшн (скидка относительно цены спот). Графически оба случая показаны на рис. 3.2. Если для нескольких фьючерсных контрактов (ситуация контанго) с разными датами истечения фьючерсная цена ближайшего контракта ниже фьючерсной цены более отдаленного контракта, то такая ситуация называется нормальным контанго. Если фьючерсная цена ближайшего контракта (ситуация бэквардейшн) выше фьючерсной цены более отдаленного контракта, то это нормальное бэквардейшн.
На рис. 3.2 показано, что в день истечения срока действия контракта фьючерсная цена равняется цене спот. Такая закономерность для поставочных фьючерсов должна обязательно выдерживаться, иначе возникнет возможность совершить арбитражную операцию. Поясним это на примере.
фьючерсная
Рис. 3.2. Контанго и бэквардейшн; z, - дата заключения контракта, t2 - дата истечения срока действия контракта
Пример.
В последний день торгов фьючерсным контрактом на акцию в какой-то момент времени фьючерсная цена оказалась выше цены спот (цена спот акции равна 100 руб.) и составила 110 руб. Тогда арбитражер продает фьючерсный контракт за 110 руб. Одновременно он
занимает деньги и покупает акцию на спотовом рынке за 100 руб. Во исполнение фьючерсного контракта арбитражер поставляет акцию контрагенту. Его прибыль составляет 10 руб. за минусом процента по кредиту. При возникновении такой ситуации арбитражеры начнут активно продавать фьючерсные контракты, что понизит фьючерсную цену. Одновременно они начнут покупать акции на спотовом рынке, что вызовет рост спотовой цены. В результате их действий фьючерсная и спотовая цены быстро сойдутся и окажутся одинаковыми или почти одинаковыми. Некоторая разница может возникнуть в силу комиссионных расходов, которые несут арбитражеры при совершении операций.
Допустим, что фьючерсная цена в последний день торговли контрактом составила 90 руб. Тогда арбитражер купит фьючерсный контракт за 90 руб. и одновременно осуществит короткую продажу акции на спотовом рынке за 100 руб. Получив базисный актив по фьючерсному контракту, он вернет его кредитору. Его прибыль составит 10 руб. за минусом суммы кредита по заимствованию акции. В такой ситуации арбитражеры активно начнут покупать контракты, что повысит фьючерсную цену, и продавать базисный актив на спотовом рынке, что понизит спотовую цену. В результате действий арбитражеров спотовая и фьючерсная цены сойдутся.
Чтобы распространить правило единства спотовой и фьючерсной цен в последний день обращения контракта и на расчетные фьючерсы, на биржах принимается следующее правило: котировочная цена расчетного контракта в последний день торгов устанавливается равной цене базисного актива в этот день на спотовом рынке.
3.2.2. Базис. Цена доставки
Разница между ценой спот базисного актива и фьючерсной ценой называется базисом. В зависимости от того, выше фьючерсная цена или ниже спотовой, базис может быть отрицательным или положительным, К моменту окончания периода действия контракта базис будет равен нулю, так как фьючерсная и спотовая цены сойдутся. Для финансовых фьючерсных контрактов базис может также определяться и как разность между фьючерсной ценой и ценой спот. Такой порядок расчета возникает в связи с тем, чтобы сделать базис величиной положительной, так как фьючерсная цена финансовых фьючерсных контрактов часто выше спотовой. Для товарных фью-
мереных контрактов более характерна ситуация бэквардейшн. По своей величине базис представляет собой не что иное, как цену доставки базисного актива.
Понятие “цены доставки” является одним из центральных моментов определения фьючерсной цены. Цена доставки - это все затраты, связанные с владением базисным активом в течение действия контракта и упущенная прибыль. Она включает в себя следующие элементы:
а) расходы по хранению и страхованию актива;
б) процент, который получил бы инвестор на сумму, затраченную на приобретение базисного актива; процент, который инвестор уплачивает по займу. В соответствии с концепцией “цены доставки” фьючерсная цена равняется следующему соотношению:
фьючерсна цена расходы по хранению
цена спот и страхованию ' к '
При нарушении данного равенства возникает возможность совершить арбитражную операцию. Если
F>S + fk+Z , (3.2)
где /А. -процент по кредиту;
S - цена спот базисного актива;
Z - расходы по хранению и страхованию;
то арбитражер:
а) продаст контракт;
б) займет средства под процент Ik, купит на них базисный актив, уплатит сумму за хранение и страхование актива и будет хранить его до момента поставки,
в) по истечении срока контракта поставит актив и получит прибыль в размере [f - (S + lk + z)]. В случае ценных бумаг величина Z равна нулю, и неравенство (3.2) принимает вид:
F>5 + A.
Если
где 1д - процент по депозиту, то арбитражер:
а) купит контракт;
б) займет актив под процент 1к;
в) продаст актив и разместит полученную сумму под процент 1д;
г) по истечении срока контракта получит проценты по депозиту, заплатит за актив по контракту, вернет его с процентами кредитору. Его прибыль составит сумму (s +1() - Ik - F).
Как следует из формулы (3.1), цена доставки равна разности между фьючерсной ценой и ценой спот и представляет собой не что иное, как базис.
Разность между двумя фьючерсными ценами для разных месяцев поставки называется спрэд. Он равен:
спрэд - F2- F{,
где F, - фьючерсная цена контракта с более близкой датой истечения;
F2 - фьючерсная цена контракта с более отдаленной датой истечения.
Разница между двумя фьючерсными ценами представляет собой также не что иное, как цену доставки. Если цена доставки положительна (F2 > FJ , то это ситуация контанго, если цена доставки отрицательна (F2<F]), - ситуация бэквардейшн. Когда величина спрэда меньше или превышает цену доставки, возникает возможность совершить арбитражную операцию.
Одной из разновидностей фьючерсных стратегий является так называемая торговля базисом. Она предполагает покупку (продажу) фьючерсного контракта с одновременной продажей (покупкой) базисного актива. Инвестор покупает базис, если он приобретает фьючерсный контракт и продает базисный актив. Продажа базиса предусматривает противоположные действия. В первом случае инвестор надеется на расширение величины базиса, во втором - на ее сужение2. Рост величины базиса может произойти за счет роста фьючерсной цены или/и падения цены актива. Сужение величины базиса возможно за счет падения фьючерсной цены или/и роста цены актива. Инвестор использует данные стратегии, когда величина базиса не равна цене доставки.
3.2.3. Соотношение форвардной и фьючерсной цен
В главе 2 мы вывели формулы определения форвардных цен на основе безарбитражного подхода. Как следует из равенства (3.1), расчет фьючерсных цен основан на том же принципе. Поэтому для определения фьючерсных цен используют формулы расче-
' Ситуация контанго.
та форвардных цен. Однако на практике фьючерсные цены могут несколько отличаться от форвардных. Это объясняется разными факторами, например, уровнем комиссионных на форвардных и фьючерсных рынках, степенью ликвидности контрактов, необходимостью внесения начальной маржи и т.п., которые не учтены в рассмотренных выше моделях определения форвардной цены, а также особенностью арбитражного подхода на фьючерсном рынке. Здесь необходимо учитывать тот факт, что позиции участников фьючерсной торговли переоцениваются расчетной палатой ежедневно. В результате арбитражер может потерять всю теоретически рассчитанную прибыль за счет отрицательной вариационной маржи, если динамика фьючерсной цены будет не в его пользу. Поэтому арбитраж на фьючерсном рынке не является чистым, а содержит в себе долю риска.
По ряду контрактов определение точной фьючерсной цены усложнятся тем фактом, что лицо с короткой позицией имеет право поставить базисный актив в любой день в рамках отведенного для этого периода поставки. Так, инвестор может поставить актив в начале, середине или конце месяца поставки. Каждому случаю будет соответствовать своя фьючерсная цена. Момент поставки зависит от того, когда инвестору выгодно поставить базисный актив. Для такой ситуации можно сформулировать следующее правило. Если значение фьючерсной цены является возрастающей функцией от значения Т , инвестору выгодно поставить актив в начале периода поставки, поскольку он сможет инвестировать полученные по контракту средства под более высокий процент, чем он получает от владения базисным активом. Если фьючерсная цена является убывающей функцией от Т, инвестору выгоднее поставить актив в последний день периода поставки, поскольку владение активом приносит ему более высокий доход, чем тот, который он сможет получить от реинвестирования выплаченных по контракту средств. В связи с этим расчет фьючерсной цены в первом случае следует делать на начало периода поставки, во втором - на конец периода. Поясним приведенное правило на примере формулы для акции с известной ставкой непрерывно начисляемого дивиденда:
F = Se—,!.
Как из нее следует, фьючерсная цена является возрастающей функцией времени, если г > q , т.е. в этом случае инвестор может получить более высокую доходность (ставку без риска) от инвестирова
ния денег, уплаченных за акцию, по сравнению с размером дивиденда, который приносит ему владение акцией. Функция является убывающей от времени при г <q. Это значит, что вкладчик получает более высокую доходность от владения бумагой по сравнению с инвестированием полученных по контракту средств под ставку без риска.
Отметим еще следующую зависимость между форвардной и фьючерсной ценами. Дж. Кокс, Дж. Ингерсол и С.Росс доказали, что если форвардный и фьючерсный контракты имеют одинаковую дату истечения, а ставка без риска постоянна и одинакова для любых периодов времени, то форвардная и фьючерсная цены будут равны. Доказательство данного положения приводится в приложении 1 к настоящей главе.
3.2.4. Будущая цена спот
Если фьючерсный контракт заключается в спекулятивных целях, то особую важность приобретает вопрос предвидения будущей цены спот, Дж.М.Кейнс и Дж.Хикс сделали следующие замечания в этом отношении. На фьючерсном рынке присутствуют как хеджеры, так и спекулянты. Спекулянты открывают позиции для получения прибыли за счет курсовой разницы. За риск, который они берут на себя, они ‘требуют" соответствующего вознаграждения. При отсутствии ожиданий потенциального вознаграждения они не будут заключать контракты. Поэтому, если большая часть спекулянтов открыла длинную позицию по контракту, это говорит о том, что фьючерсная цена должна быть ниже будущей цены спот (ситуация бэквардешн), поскольку именно повышение в дальнейшем фьючерсной цены принесет спекулянту прибыль. Если большая часть из них открыла короткую позицию, то это свидетельствует о том, что фьючерсная цена пыше будущей цены спот (ситуация контанго), поскольку именно понижение в дальнейшем фьючерсной цены принесет спекулянтам прибыль.
3.2.5. Котировка фьючерсных контрактов
В западной финансовой прессе регулярно публикуются котировки фьючерсных контрактов. Котировки строятся по единой схеме. В качестве примера в таблице 3.1 представлена котировка контракта на пшеницу, который торгуется на Чикагской торговой палате (СВТ).
В котировке сообщаются итоги торговли зерном за 25 марта 2002 г.
Таблица 3.1. Котировка фьючерсного контракта на пшеницу
(Wall Street Journal, March 26, 2002 г., p.M9)
-------г—.---------------------------------—
Monda if March 25, 2002 LIFETIME
OPEN HIGH LOW SETTLE OHG HIGH | LOW _ OPEN INT
Corn (CBT)-5,000 bu.; cents per bu.
Мау 204 75 205 00 203 50 I 203 75 I -1 00 266 50 j 203 50 191 032
July 211 50 211 75 210 25 [ 210 50 -1 00 279 50 j 210.00 117 662
Est vol па, vol Fri 30 606 open tnt 438 880, -*-5,249
В ней указан размер контракта (5000 бушелей), цена в центах за один бушель. В первой колонке дается месяц истечения фьючерсного контракта (май, июль). Вторая колонка - это фьючерсная цена при открытии торговли (204.75 для майского контракта), третья колонка - наивысшая за день цена (205.00), четвертая колонка - самая низкая за день цена (203.50). В пятой колонке указана котировочная цена (203.75), шестая колонка - это изменение котировочной цены по сравнению с котировочной ценой предыдущего торгового дня (-1.00). Седьмая и восьмая колонки - соответственно самая высокая и самая низкая цены за время действия контракта. Девятая колонка - общее число существующих контрактов (открытых позиций). В ней приводится информация за торговый день, предшествующий дню, за который указывается котировка. В нашем примере 191.032 - это число открытых позиций, существовавших в пятницу 22 марта. Последней строчкой в таблице приводится оценка объема торговли (Est vol) за рассматриваемый торговый день для всех контрактов на пшеницу, независимо от срока их истечения - в котировке данная цифра отсутствует (па), - и точный объем торговли за предшествующий торговый день (30.606). Далее - общее число открытых позиций на предыдущий торговый день и разница в количестве контрактов по сравнению с 21 марта.
3.3. ХЕДЖИРОВАНИЕ ФЬЮЧЕРСНЫМИ КОНТРАКТАМИ
Страхование или хеджирование состоит в нейтрализации неблагоприятных изменений цены актива. Хеджирование может быть полным или неполным (частичным). Полное хеджирование целиком исключает риск потерь, частичное хеджирование осуществляет страхование только в определенных пределах. Существует хеджирование продажей и хеджирование покупкой фьючерсного контракта.
Хеджирование продажей контракта, или короткое хеджирование. используется для страхования от будущего падения цены базисного актива на спотовом рынке; хеджирование покупкой, или длинное хеджирование, - от ее повышения. Рассмотрим технику короткого и длинного хеджирования на примерах.
Пример 1. Хеджирование продажей контракта.
Фермер планирует через три месяца продать одну тонну пшеницы. Существует риск снижения к этому моменту цены на зерно. Поэтому он решает застраховаться от ее падения с помощью фьючерсного контракта. Один фьючерсный контракт включает одну тонну пшеницы. Фьючерсная котировка с поставкой пшеницы через три месяца равна 4500 руб. за тонну. Фермера устраивает цена, так как позволяет окупить затраты и получить прибыль. Он продает фьючерсный контракт по этой цене. Фермера устраивают все условия контракта, поэтому он просто исполнит его через три месяца.
Пусть через три месяца цена спот пшеницы равна 4000 руб. Поскольку спотовая и фьючерсная цены в последний день торговли контрактом одинаковы (см. рис. 3.2), то котировочная фьючерсная цена также равна 4000 руб. Биржа назначила фермеру контрагента. Он поставил ему пшеницу и получил за нее 4000 руб. По фьючерсному контракту он также выиграл 500 руб., поскольку продал фьючерс три месяца назад по 4500 руб., а в последующем фьючерсная цена упала до 4000 руб. Таким образом, в сумме по операции он получил 4500 руб.
Пусть через три месяца пшеница на спотовом рынке стоит 5000 руб. Тогда котировочная фьючерсная цена также равна 5000 руб. Фермер поставляет пшеницу контрагенту за 5000 руб. Однако по фьючерсу он проиграл 500 руб., так как продавал контракт, а цена в последующем выросла. Вновь в сумме по операции он получает 4500 руб.
Рассмотренный пример представляет собой идеальный случай хеджирования, когда фьючерсный контракт полностью соответствовал потребностям хеджера, и он просто исполнил его. В реальной практике условия ведения бизнеса достаточно разнообразны. Поэтому обычно фьючерс будет использоваться только для хеджирования, а реальная продажа пшеницы будет осуществляться на спотовом рынке. В день продажи пшеницы на спотовом рынке фермер закроет свою фьючерсную позицию офсетной сделкой. Рассмотрим сказанное на примере.
Пример 2. Хеджирование продажей контракта.
Допустим, что в примере 1 биржа требует осуществление поставки пшеницы в строго обозначенном месте, а фермеру удобнее продать ее у себя на спотовом рынке. Поэтому он использует фьючерс только для хеджирования, а пшеницу будет продавать через три месяца по спотовой сделке. Фермер сейчас продает трехмесячный фьючерс по цене 4500 руб. Через три месяца пшеница на спотовом рынке стоит 4000 руб. Фермер продает ее по этой цене на спотовом рынке. В этот же день он закрывает фьючерс офсетной сделкой. Поскольку это последний день обращения фьючерсного контракта, то фьючерсная цена равна спотовой. Поэтому фермер закрывает фьючерс по 4000 руб., выигрывая 500 руб. В сумме по операции он получает 4500 руб.
Если цена пшеницы выросла до 5000 руб., то фермер продал ее на рынке по этой цене, однако по фьючерсу проиграл 500 руб., так как закрыл его также по 5000 руб. Вновь в сумме по операции он получил 4500 руб.
Таким образом, заключение фьючерсного контракта позволило фермеру застраховаться от падения цены пшеницы. В то же время, следует подчеркнуть, что хеджирование фьючерсным контрактом не позволяет воспользоваться благоприятной конъюнктурой.
Пример 3. Хеджирование покупкой контракта.
Производителю хлеба через три месяца понадобится новая партия пшеницы. Чтобы застраховаться от возможного роста ее цены, он решает купить фьючерсный контракт с котировкой 4500 руб. за тонну. Производителя хлеба устраивают все условия контракта, поэтому он просто будет его исполнять через три месяца.
Через три месяца цена пшеницы на спотовом рынке выросла до 5000 руб. Это означает, что котировочная фьючерсная цена также равна 5000 руб. Производитель уплачивает данную сумму контрагенту и получает пшеницу. Однако по фьючерсу он выиграл 500 руб., так как купил контракт по цене 4500 руб., а в последующем она выросла до 5000 руб. Поэтому в сумме его расходы по покупке пшеницы составили 4500 руб.
Пусть через три месяца пшеница стоит 4000 руб. Тогда он покупает ее у контрагента по этой цене, однако по фьючерсу теряет 500 руб. Вновь его расходы равны 4500 руб.
Пример 4. Хеджирование покупкой контракта.
Производителю хлеба через три месяца понадобится новая партия пшеницы. Чтобы застраховаться от возможного роста ее цены,
он решает купить фьючерсный контракт с котировкой 4500 руб. за тонну. Производителя хлеба устраивают все условия контракта, кроме места покупки. Допустим, биржа требует осуществления поставки пшеницы в строго обозначенном месте, а производителю хлеба удобнее купить ее у себя на спотовом рынке. Поэтому он использует фьючерс только для хеджирования, а пшеницу будет покупать на своем рынке в день истечения фьючерсного контракта.
Через три месяца цена пшеницы на спотовом рынке выросла до 5000 руб. Производитель покупает ее по этой цене на спотовом рынке. Одновременно он закрывает фьючерс офсетной сделкой также по 5000 руб,, поскольку спотовая и фьючерсная цены в последний день действия контракта равны Таким образом, по фьючерсу он выигрывает 500 руб. В сумме его расходы по покупке пшеницы составляют 4500 руб.
Пусть через три месяца пшеница стоит 4000 руб. Тогда он покупает ее на спотовом рынке по этой цене, однако фьючерс также закрывает по 4000 руб., проигрывая 500 руб. Вновь его расходы равны 4500 руб.
Таким образом, заключение фьючерсного контракта позволило производителю хлеба застраховаться от роста цены пшеницы, однако во втором случае он не смог воспользоваться благоприятной конъюнктурой,
В приведенных примерах мы рассмотрели идеальный случай хеджирования, когда потери (выигрыши) на спотовом рынке полностью компенсировались выигрышами (потерями) по фьючерсному контракту, На практике подобная ситуация случается редко. Фьючерсные контракты истекают только в определенные моменты времени. Однако хеджер может быть заинтересован в продаже или покупке базисного актива в иные сроки. Если завершение операции хеджирования не совпадает с моментом истечения периода действия фьючерса, то не будет совпадения фьючерсной и спотовой цен, В результате хеджер может получить как некоторый выигрыш, так и понести убытки. Другими словами, для хеджера возникает риск того, что к моменту окончания хеджа спотовая цена не будет равна фьючерсной, и базис не будет равен нулю. Данный риск называют риском базиса или базисным риском. Поясним сказанное на условиях примера 2.
Пример 5.
Фермер продает пшеницу на спотовом рынке не в момент истечения фьючерсного контракта, а на две недели раньше. Пусть в это
время спотовая цена пшеницы составляет 4000 руб., а фьючерсная -4100 руб. Фермер продает пшеницу на спотовом рынке за 4000 руб. и одновременно закрывает офсетной сделкой фьючерс по 4100 руб. По фьючерсу он выигрывает 400 руб. Общая сумма, полученная фермером за пшеницу, равна 4400 руб. Таким образом, в сравнении с полным хеджированием он недополучил 100 руб.
Возможен и другой результат. Спотовая цена пшеницы 4000 руб., а фьючерсная цена в момент закрытия позиции - 3900 руб. В результате по фьючерсу фермер выиграл 600 руб. Общая сумма, полученная за пшеницу, равна 4600 руб. Таким образом, в сравнении с полным хеджированием фермер получил дополнительно 100 руб.
Когда сроки окончания хеджа и фьючерсного контракта не совпадают, надо ответить на вопрос, каким по времени истечения фьючерсным контрактом хеджировать. Для хеджирования надо остановиться на контракте, который истекает после осуществления спотовой сделки. Если выбрать контракт, истекающий раньше нее, то после его окончания спотовая позиция хеджера будет не застрахована от изменений цены базисного актива.
Как видно из рис.3.2, чем больше времени между завершением хеджа и окончанием фьючерсного контракта, тем больше базисный риск. Поэтому хеджер должен минимизировать время между окончанием хеджа и истечением срока фьючерсного контракта. В результате следует выбрать ближайший фьючерсный контракт. Хеджирование с помощью ближайшего фьючерсного контракта называют спот-хеджированием
Пусть спотовая цена пшеницы в начале операции хеджирования равна 50, фьючерсная цена - /т , в момент окончания хеджа цена пшеницы составляет 5,, а фьючерса - F}, Тогда общая сумма, которую получит фермер в результате страхования в момент завершения хеджа, равна:3
сумма, полученная хеджером = Sr+(j\t- F() 3)
или
сумма, полученная хеджером = Fo + (5, — F,), (3.4)
3 Когда рассчитываются суммы денег по позиции хеджера, то продажу актива обозначаем знаком плюс, так как это его доходы, покупку актива со знаком минус, так как это его расходы. Поэтому в формуле (3 3) £ и Fo берем со знаком плюс, a Ft - со знаком минус.
где (5, - Ff) ' базис в момент завершения хеджа.
Подставим в формулу (3.4) цифры из примера 5. Получим для первого случая результат:
4500 + (4000 - 4100) - 4400руб.;
для второго:
4500 + (4000 - 3900) - 4600руб.
Контрагентом фермера выступает производитель хлеба. Соответственно, он уплатит сумму:
сумма, уплаченная хеджером — —St + (- + Ft)
или
сумма, уплаченная хеджером = -Fo - (S, - Ft), или
сумма, уплаченная хеджером ~ + (5,-Л)1 (3.5)
Знак минус в формуле (3.5) говорит о том, что хеджер уплачивает данную сумму денег.
Как вытекает из формул (3.4) и (3.5), в результате страхования хеджер заменяет непосредственный риск изменения цены базисного актива на риск изменения базиса. Риск базиса существенно меньше прямого риска по базисному активу.
Сумму, которую получит или уплатит хеджер в результате страхования в момент завершения хеджа, можно представить еще следующим образом:
сумма, полученная или уплаченная хеджером
= 50-50 + Fu+(5(-F,)
или
сумма, полученная или уплаченная хеджером
= SO~(SO—FO)+(SI—F,),
(3.6)
где (So - Fo) - базис в момент начала хеджа.
Таким образом, результат хеджера равен начальной цене спот базисного актива плюс разница в величине конечного и начального базисов. Проиллюстрируем формулу (3.6) цифрами из примера 5 для первого случая. Пусть цена пшеницы в начальный момент равна 4600 руб. Фермер получает за пшеницу сумму:
4600 - (4600 - 4500)+ (4000 - 4100) = 4400руб.
Мы рассмотрели ситуацию применительно к товарному фьючерсу. Как было сказано выше, для финансового фьючерса базис может определяться как разность между фьючерсной и спотовой ценами. Поэтому в таком случае для финансового фьючерса формулы (3.4) и (3.6) соответственно примут вид:
сумма, полученная хеджером = Fo - - St) (
и
сумма, полученная или , , t .
= 5(1+ F0-50 -{F-S, . уплаченная хеджером
Период хеджирования может оказаться больше срока действия фьючерсного контракта. Тогда хеджер может страховать свою позицию по базисному актива за счет последовательного заключения нескольких фьючерсных контрактов. Перед истечением срока действия первого контракта он закроет его офсетной сделкой и откроет позицию по второму контракту и т.д. до момента завершения хеджа. В такой ситуации для хеджера возникает дополнительный риск, связанный со спрэдом между ценами закрываемого и открываемого контрактов при продлении хеджа, так как в начале операции точно неизвестна величина будущих спрэдов.
На бирже может отсутствовать контракт на требуемый базисный актив. В таком случае для страхования выбирается контракт на родственный актив. Данная техника называется кросс-хеджированием. Страхование контрактом с тем же активом именуют прямым хеджированием. При кросс-хеджировании возникает дополнительный риск, который состоит в том, что спотовая цена базисного актива фьючерсного контракта имеет корреляцию с ценой хеджируемого актива меньше чем плюс один.
Для страхования своей позиции хеджер должен определить необходимое количество фьючерсных контрактов, которые требуется открыть. Если время окончания хеджа и истечения фьючерса совпадает (полное хеджирование), то количество контрактов определяется по формуле:
количество
, количество единиц хеджируемого актива /п
фьючерсных =---------------:-------------------------
количество единиц актива в одном контрактов ,
фьючерсном контракте
Пример 6.
Фермер хеджирует будущую продажу 100 тонн пшеницы продажей фьючерсных контрактов. Один фьючерс включает 1 тонну пшеницы. В случае полного хеджирования ему следует продать:
\ 00 тонн
I тонна
= ХООконтрактов.
Формула (3.7) не учитывает того факта, что по фьючерсному контракту в течение периода его действия будет начисляться или списываться вариационная маржа. На положительную вариационную маржу фермер сможет получать проценты, отрицательную маржу ему придется финансировать за счет процентов на положительную маржу, или занимая средства под проценты. Поэтому в первом случае в результате хеджирования фермер получит лучший результат, чем в примере 1, а во втором случае худший результат, чем в примере 1. Аналогичная ситуация будет и с результатами производителя хлеба в примере 3. Чтобы скорректировать погрешность, возникающую при полном хеджировании, следует уменьшить количество открываемых позиций.4 Корректировку количества контрактов можно осуществить дисконтированием формулы (3.7) на величину:
2 база
где г - процентная ставка, которая начисляется или уплачивается по вариационной марже;
Т - период действия фьючерсного контракта.5
В то же время, следует подчеркнуть, что корректировку целесообразно осуществлять по расчетным фьючерсам, так как реальную продажу пшеницы фермер осуществит по спотовой сделке. Если же фьючерс поставочный, и фермер будет его исполнять, то он заинтересован в определенном количестве контрактов, поскольку планирует продать определенное количество пшеницы.
4 На сленге срочного рынка данную технику корректировки количества фьючерсных контрактов именуют словом “tailing”.
5 В литературе также можно встретить рекомендации осуществлять корректировку количества фьючерсных контрактов дисконтированием на величину । + г- ,
см., например, Ch.Smilhson. Managing Financial Risk. A Guide to Derivative Products, Financial Engineering, and Value Maximization, - McGraw-Hill, 1998, p.134.
Пример 7.
. Пусть в примере 6 г = 10% годовых, Т - 90 дней, база - 360 дней. Тогда количество контрактов, которые следует открыть хеджеру, равно:
100 контрактов __ __ --------------- = 98,77 контрактов.
1 + _1---
2 360
В примере 7 получилось дробное количество фьючерсных контрактов. Поскольку контракты не делимы, то результат следует округлить до целого значения. Поэтому количество контрактов, которые следует открыть хеджеру, равно 99. Получаемая в результате округления погрешность составляет элемент риска хеджера.
Если время окончания хеджа и истечения фьючерса не совпадает, то формулу (3.7) следует дополнить коэффициентом хеджирования, чтобы свести к минимуму риск базиса. С учетом коэффициента хеджирования она принимает вид:
количество
фьючерсных ~ КОЛцчество единиц хеджируемого актива
количество единиц актива в одном , (3.8) контрактов
фьючерсном контракте
где h - коэффициент хеджирования.
Суть коэффициента хеджирования можно понять на основе следующих рассуждений. Степень реакции фьючерсной цены на изменение спотовой цены может быть отличной от единицы. Поэтому, чтобы компенсировать изменение спотовой цены с помощью фьючерсных контрактов, необходимо открыть фьючерсные позиции в ином количестве, чем при полном хеджировании. Для расчета коэффициента хеджирования надо определить зависимость между изменением спотовой и фьючерсной цен. Поясним сказанное на примере.
Пример 8.
Допустим, хеджер заметил, что при изменении спотовой цены на 1 руб. фьючерсная цена изменяется на 2 руб. Пусть фьючерсные контракты делимы. Тогда для страхования от падения спотовой цены базисного актива на 1 руб. необходимо продать половину фьючерса. Если спот цена базисного актива упадет на 1 руб., цена фьючерса упадет на 2 руб. Соответственно цена половины фьючерса понизит
ся только на 1 руб. В результате хеджер выиграет на фьючерсе 1 руб., что компенсирует снижение цены базисного актива. Обратная ситуация наблюдается при росте цены базисного актива; хеджер выиграет 1 руб. на спот цене, но проиграет 1 руб. на фьючерсе.
Величину h в данном примере можно определить с помощью следующей формулы:
h =---- ,
&F
где Л51 - изменение цены базисного актива;
АГ - изменение фьючерсной цены.
Соответственно коэффициент хеджирования равен:
(3.9)
---~—- = 0,5 контракта. &F 2 руб.
Пример 9.
Пусть в примере (6) хеджер продает пшеницу на спотовом рынке раньше времени истечения фьючерсного контракта. Он определил, что при изменении спотовой цены пшеницы на 1 руб. цена фьючерсного контракта изменяется на 1,11 руб. Тогда коэффициент хеджирования составляет:
h = —— - —- о 9 контракта.
AF Щруб.
Количество контрактов, которые необходимо продать, равно:
lOOmoww
--------0,9 = 90 контрактов.
{тонна
Рассмотрим вопрос определения коэффициента хеджирования в общей форме. Представим позицию инвестора как портфель, состоящий из единицы базисного актива и h единиц фьючерсного контракта. Стоимость портфеля равна:
И = 5 + (3.10)
где К-стоимость портфеля;
5-стоимость единицы базисного актива;
F- стоимость фьючерсного контракта;
h - коэффициент хеджирования.
Чтобы исключить риск потерь при небольшом изменении цены базисного актива, должно выполняться условие:
АГ = AS + AAF = 0 ,
где А - изменение значения соответствующей переменной. Отсюда коэффициент хеджирования равен:
h = -~- (3'11)
Мы получили формулу аналогичную формуле (3.9). Знак минус в формуле (3.11) говорит о том, что по фьючерсному контракту позиция должна быть противоположна позиции по спотовому инструменту, В последующем мы иногда будем опускать знак минус, поскольку из существа примеров будет следовать, какую позицию необходимо открыть хеджеру по фьючерсному контракту.
Таким образом, за счет продажи фьючерсных контрактов в коли-AS
честве — инвестор исключает риск изменения стоимости порт-AF
феля.
В приведенном рассуждении мы хеджировали портфель относительно единицы базисного актива. Реальный портфель может содержать большее количество единиц спотового инструмента. Для такого случая количество фьючерсных контрактов определяют по формуле (3.8).
Для практических целей алгоритм для расчета величины h можно получить на основе минимизации дисперсии портфеля, представленного следующей формулой:
AK-AS + MF. (3.12)
Возьмем дисперсию от левой и правой частей уравнения (3.12):
Гаг(ДК) = Иаг(Д5 + h^F), (3.13)
где Var означает дисперсию.6
Формула (3.13) раскрывается как дисперсия суммы двух зависимых переменных - AS и AF:
Иаг(дГ) = + h2a2^ + Iha^a^corr^ , (3.14)
где сг^у - дисперсия переменной AS;
6 Объяснение понятий дисперсии, стандартного отклонения, корреляции и использования их в финансах см, в книге А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов", М„ 2002, параграфы 9.1 и 16.2.1.
&lF -дисперсия переменной АЛ;
соккАЗЛ/. - коэффициент корреляции между AS и АЛ.
Чтобы минимизировать величину Иаг(АИ), продифференцируем уравнение (3.14) по А и приравняем полученный результат к нулю:
Жгг(АИ) 2
----L = 2АсгЛЛ + 2&M&^corr^F = 0 .
ah
Отсюда:
= • (3.15)
<ТА, Аг
Знак минус в формуле (3.15) вновь говорит о том, что по фьючерсному контракту позиция должна быть противоположна позиции по спотовому инструменту.
Поскольку вторая производная Иаг(дк) по h величина положительная, то найденное значение коэффициента хеджирования является минимумом функции. Длину временного периода для определения переменных AS и АЛ выбирают равным сроку хеджирования.
Если осуществляется прямое хеджирование, то коэффициент корреляции между AS и АЛ скорее всего близок к единице, и поэтому его можно принять равным плюс один. Тогда коэффициент хеджирования принимает вид:
1 гг
Если осуществляется кросс-хеджирование, то коэффициент корреляции может значимо отличаться от единицы, и его следует принять но внимание. Поэтому при кросс-хеджировании коэффициент хеджирования определяют по формуле (3.15),
Пример 10.
Фермер планирует продать через два месяца 100 тонн мягкой пшеницы. На бирже торгуется фьючерсный контракт только на твердую пшеницу. Один контракт насчитывает одну тонну пшеницы. Фермер использует кросс-хеджирование. Двухмесячное стандартное отклонение изменения спотовой цены мягкой пшеницы равно 30 руб,, двухмесячное стандартное отклонение изменения фьючерсной цены тш’рдой пшеницы - 35 руб. Коэффициент корреляции между изменением спотовой цены мягкой пшеницы и изменением фьючерсной
цены твердой пшеницы за двухмесячный период равен 0,9. Определить количество контрактов, которые необходимо открыть фермеру.
Решение.
В соответствии с формулой (3.15) коэффициент хеджирования равен:
30 h = —0 9 = 0 7714.
35
Фермеру следует продать:
1 WmoHH п л __
---------0,7714 = 77,14 контрактов или 77 контрактов.
Пример 11.
Продолжим пример 10 и предположим, что через два месяца спотовая цена мягкой пшеницы упала на 15,43 руб. На основе формулы (3.15) можно записать следующие соотношения между AF и Л5:
30
= — 0,9ДГ (3.16)
и
&F = —1.111Д5. (3.17)
30
Тогда, согласно формуле (3.17), фьючерсная цена твердой пшеницы понизилась на:
AF = 22 1,111 15,43 руб. = 20 руб.
По спотовой позиции фермер проиграл сумму:
ЮОто//// 15,43pWT = 1543/трб.
Однако по фьючерсным контрактам он выиграл:
11 контрактов • 20/л б. = 1540 руб.
Таким образом, потери по спотовой сделке компенсировались выигрышем на фьючерсном рынке.
На практике разница между выигрышем и проигрышем может быть несколько больше, чем получилась в примере, поскольку взаимосвязь между изменением спотовой и фьючерсной цен определяется формулой (3.16) не жестко, а лишь в среднем.
основе рег-
(3-18)
AS и AF
Коэффициент хеджирования можно определить на рессионного анализа. Зависимость между значениями можно представить в виде:
AS = a + + е ,
где а и р - некоторые константы;
€ - остаточный член (ошибка).
На основе статистических данных прошлых значений
можно построить линию регрессии AS на AF как показано на рис.3.3. Уравнение данной линии можно представить как:
AS-^ + ftAF, (3.19)
где a - ордината точки, в которой линия регрессии пересекает ось AS;
b - коэффициент регрессии, равный тангенсу угла наклона линии регрессии к оси AF;
Уравнение (3.19) показывает, как в среднем значение AS зависит от
Рис. 3.3. Линия регрессии AS на AF
Из уравнения (3.19) и рис. 3.3 видно, что коэффициент хеджирования равен коэффициенту b , взятому с обратным знаком, т.е.:
АЛ
Коэффициент регрессии b можно определить по формулам:
ь - согг^
&\F
ИЛИ
1 COV.-AF L _ ДЛАг
<
Коэффициент регрессии легко определить с помощью программы Excel. Техника его расчета представлена в приложении 2 к настоящей главе.
Наиболее просто построить регрессию на основе данных о ежедневных изменениях спотовой и фьючерсной цен, поскольку они являются наиболее доступными. Однако следует помнить, что в этом случае можно получить некоторую ошибку оценки, так как коэффициент не учтет факта схождения фьючерсной и спотовой цен по мере приближения срока истечения контракта.
При кросс-хеджировании необходимо выбрать фьючерсный контракт, для которого изменение фьючерсной цены имеет наиболее тесную корреляцию с изменением спотовой цены страхуемого актива. Вследствие не полной корреляции позиция по фьючерсным контрактом вряд ли полностью компенсирует риск по спотовому инструменту. Поэтому целесообразно оценить величину уменьшения риска с помощью фьючерсных контрактов Это можно сделать на основе коэффициента детерминации или R2. Он говорит том, какой процент дисперсии одной переменной определяется другой переменной. Его значение изменяется от нуля до единицы и равно квадрату коэффициента корреляции между этими переменными. В качестве переменных рассматриваются - изменение фьючерсной цены (Д/7) и изменение спотовой цены хеджируемого актива (Л5). Для нашей цели мы полагаем, что независимой переменной является AF , и ее изменение определяет значение Д5 . На основе уравнения регрессии (3.18) найдем дисперсию величины AS:
= h'&l +&< (3.20)
Отсюда:
Эта величина показывает долю дисперсии изменения цены хеджируемого актива определяемую фьючерсной позицией. Таким обра
зом, значение коэффициента детерминации можно интерпретировать как величину, на которую в среднем можно уменьшить риск страхуемой позиции с помощью фьючерсного контракта.
Поскольку корреляция переменных AS и AF не полная, то дисперсия изменения цены хеджируемого актива определяется и величиной . Доля ее дисперсии в дисперсии переменной AS рав-э
(J~ п
на —Поэтому доля риска, остающаяся после открытия хеджи-
рующих позиций в среднем составляет:
средний не хеж -жируемый риск
I-/?2.
Оценить эффективность хеджирования можно с помощью коэффициента эффективности хеджа. Он равен:
коэффициент выигрыиДрроигрыш) по фьючерсной позиции эффективности хеджа проигры ш{рыигрыш) по спотовой позиции
100%
В примере (11) эффективность хеджа составила:
—И 00% = 99,8%.
1543
В задачу хеджера может входить не полное страхование, а ограничение колебания стоимости спотовой позиции в определенных границах. Для такого случая также необходимо определить значение коэффициента хеджирования, которое бы соответствовало желаемому изменению стоимости спотовой позиции. Назовем его частичным коэффициентом хеджирования и обозначим через А*. Рас-смотрим данную задачу на основе следующего уравнения:
АИ =AS + FAF, (3.21)
где ЛИ - желаемое изменение стоимости позиции инвестора.
Из уравнения (3.21) А* составит:
,, ДИ-AS
h =---------.
AF
Пушь хеджер хотел бы ограничить изменение стоимости своей позиции к процентами изменения спотовой цены актива. Тогда ДИ можно представить как:
Л7 = Ш.
(3.22)
Подставим значение ДИ из (3.22) в формулу (3.21): ASV А
(3.23)
Из формулы (3.11)
= -h. Подставим вместо — значение -h
в формулу (3.23):
ИЛИ
(3-24)
Пример 12.
Допустим, в примере 10 фермер ожидает роста цены пшеницы, и не хотел бы полностью исключать спекулятивный потенциал спотовой позиции. Поэтому он осуществляет частичное хеджирование и решает ограничить возможное колебание стоимости своей спотовой позиции 40% изменения спотовой цены. Согласно формуле (3.24) частичный коэффициент хеджирования равен:
/?*= (1 -0,4) 0,7714 = 0,463.
Количество контрактов, которые фермеру следует продать, составляет:
---------0,463 46.3 контракта или 46 контрактов.
{тонна
Допустим, через два месяца спотовая цена мягкой пшеницы выросла на 15,43 руб. Тогда фьючерсная цена твердой пшеницы увеличилась на:
35 AF = —1,111-15,43 руб, = 20 руб.
30
По спотовой позиции фермер выиграл сумму:
1 ООтонн ’ 15,43руб. = 1543руб.
Однако по фьючерсным контрактам он проиграл: ^контрактов 20руб. = 920руб.
Таким образом, за счет меньшего количества фьючерсных контрактов он получил положительное сальдо на разнице изменения цен спотовой и фьючерсной позиций в размере:
1543 -920 - ЫЗруб.
Это составляет:
= 0,4038
1543
или 40% от изменения стоимости спотовой позиции или спотовой цены. Спекулятивный прогноз фермера оправдался, и он фактически продал пшеницу на:
623pv6. п
------— = 6,23руб. за тонну дороже, чем в примере 10.
1 ООтонн
Аналогично, если спотовая цена через два месяца упала на 15,43 руб., соответственно фьючерсная цена на 20 руб., то по сумме спотовой и фьючерсной позиций фермер проиграл 623 руб., что вновь составило 40% от изменения спотовой цены:
^=L = 0,4038 или 40%.
15,43
3.4. ФУНКЦИОНИРОВАНИЕ МЕХАНИЗМА EFP
Фьючерсные контракты бывают поставочными и беспоставочны-ми. Каждый из вариантов их исполнения может отвечать интересам одних участников рынка и не подходить другим. Например, беспоста-вочные контракты более удобны для спекулянтов и при кроссхеджировании. В то же время, у части покупателей или продавцов товаров может существовать потребность в физическом исполнении контрактов. Для расчетных фьючерсов отмеченная проблема решается с помощью использования механизма, который называется ‘'exchange futures for physicals'' (EFP), На русский язык это можно перевести как обмен фьючерсных контрактов на физический актив.
EFP представляет собой договоренность между двумя участниками фьючерсной торговли одновременно исполнить две сделки, одну - на фьючерсном рынке, другую - на спотовом. Механизм EFP функционирует следующим образом. Два участника с противоположными позициями по фьючерсному контракту договариваются об осуществлении EFP. Это означает, что после завершения фьючерсной торговли один участник поставляет другому
товар, который является базисным активом фьючерсного контракта. Количество товара должно соответствовать условиям контракта. Поставка происходит по согласованной между ними цене. Одновременно на бирже по этой же цене закрываются их фьючерсные позиции. Они ликвидируются до проведения биржей общего клиринга по всем открытым контрактам. В качестве поставляемого актива также может выступать родственный актив. Например, по фьючерсам на электричество физическая поставка может включать электричество или мазут, или уголь, или природный газ. В отличие от поставочного фьючерса биржа не гарантирует исполнение физической поставки между контрагентами, поскольку EFP является их частной двусторонней договоренностью.
Рассмотренный механизм EFP является наиболее распространенным. Однако он может включать и некоторые модификации. В момент согласования EFP одна сторона может иметь, а другая не иметь фьючерсной позиции. Тогда физическая поставка товара будет сопровождаться одновременным закрытием фьючерсного контракта для первого участника и открытием его у второго. Следующий случай включает отсутствие фьючерсных позиций у обоих участников EFP. Согласовав физическую поставку товара, участники декларируют EFP на бирже для открытия соответствующих фьючерсных позиций.
EFP имеет еще одно интересное применение. Он позволяет контрагентам в их двусторонней сделке одному купить, а другому продать товар фактически по разным ценам. Каждый может рассчитывать получить более выгодную цену. Суть операции сводится к следующему. Продавец и покупатель договариваются о том, что товар будет поставлен на определенную дату в будущем по котировочной цене фьючерсного контракта. В последующем продавец и покупатель самостоятельно открывают свои фьючерсные позиции в те моменты, которые представляются им наиболее выгодными с точки зрения цен. Если продавец полагает, что существующая цена слишком низкая и она вырастет, он может дождаться ее повышения и открыть фьючерс по более высокой цене. Аналогично, покупателю существующая цена может казаться завышенной. Тогда он будет ждать ее понижения и откроет фьючерс по более низкой цене. На согласованную дату они осуществляют на бирже EFP, т.е. происходит физическая поставка товара и одновременная ликвидация фьючерсных позиций. Таким образом, с помощью EFP участники рынка могут заключать сделки с физической поставкой товара и обеспечи
вать каждому из них наиболее выгодные финансовые условия. Поясним сказанное на примере.
Пример.
Имеются покупатель и продавец нефти. Они планируют осуществить сделку через три месяца. В настоящий момент трехмесячная фьючерсная цена равна 55 долл, за баррель. Продавец полагает, что в следующем месяце цена может еще вырасти, а покупатель считает, что она может несколько упасть. Они договариваются осуществить через три месяца на бирже EFP по котировочной цене, которая будет зафиксирована в этот день. Пусть через две недели цена нефти опустилась до 50 долл, за баррель, и покупатель полагает, что дальше она будет вновь расти. Поэтому он покупает фьючерсный контракт по этой цене. Прошел еще месяц, и цена нефти выросла до 60 долл, за баррель. Продавца нефти устраивает данная цена, поэтому он продает фьючерс по этой котировке. Трехмесячный период истек, и котировочная цена нефти составила 56 долл. Участники сделки осуществляют взаиморасчеты по данной цене. В итоге, реальная цена, уплаченная покупателем за баррель нефти с учетом выигрыша по фьючерсному контракту составила 50 долл., цена, получена продавцом - 60 долл. При отсутствии механизма I I P три месяца назад наши участники могли бы заключить фьючерсную сделку по цене 55 долл, за баррель,
В рассмотренном механизме EFP реальная поставка товара может нн обязательно осуществляться в месте, который оговаривается в Пиржевом контракте, а в ином месте. В этом случае цена физической поставки актива соответствующим образом корректируется относи-шпьно котировочной цены. Кроме того, дата физической поставки может несколько отличаться от даты, на которую согласован EFP.
В качестве примера биржи, использующей механизм EFP, можно назвать Международную нефтяную биржу (IPE).
КРАТКИЕ ВЫВОДЫ
Фьючерсный контракт - это срочный контракт, который заключатся на бирже. Условия контракта для каждого базисного актива раз-1'.||>атываются биржей и являются стандартными. Контракты заклю- ишся главным образом в целях хеджирования и игры на курсовой с । шице Фьючерсных цен. Открывая позиции, участники торгов обя-- и и,| внести в расчетную палату биржи гарантийные платежи.
К моменту истечения периода действия контракта фьючерсная цена должна равняться цене спот, иначе возникнет возможность совершить арбитражную операцию.
Ситуация, когда фьючерсная цена выше цены спот, называется контанго. Ситуация, когда фьючерсная цена ниже цены спот, называется бэквардейшн.
Цена доставки - это все затраты, связанные с владением базисным активом в течение времени действия контракта и упущенная прибыль.
Базис определяется как разность между ценой спот и фьючерсной ценой.
Хеджирование - это страхование от неблагоприятного изменения рыночной конъюнктуры. Хеджирование продажей фьючерсного контракта, или короткое хеджирование, используют для страхования от падения цены базисного актива, хеджирование покупкой, или длинное хеджирование, - от ее повышения.
При неполном хеджировании используют коэффициент хеджирования для определения оптимального количества контрактов, которые необходимо открыть хеджеру. Коэффициент хеджирования можно использовать для ограничения колебания стоимости спотовой позиции в определенных границах.
EFP представляет собой договоренность между двумя участниками одновременно исполнить две сделки, одну - на фьючерсном, другую - на спотовом рынке.
ПРИЛОЖЕНИЕ!.
Форвардная и фьючерсная цены для случая, когда ставка без риска постоянна и одинакова для любых периодов времени
Докажем положение о том, что форвардная и фьючерсная цены должны быть одинаковыми, если ставка без риска постоянна и одинакова для любых периодов времени7. Для краткости доказательства рассмотрим временной отрезок длиной Т, состоящий из трех периодов: (/t - о), (t2 - Z,), (т -12) В случае более длительного промежутка времени рассуждения будут аналогичными. Для любого отрезка времени непрерывно начисляемая ставка без риска равна
7 При доказательстве данного положения мы следуем рассуждениям как они представлены в M.Capinski, T.Zastawniak, Mathematics for Finance. An Introduction to Financial Engineering, Springer, N.Y,, 2005, p, 136-138.
г. Сделаем допущение о том, что фьючерсный контракт можно дробить. Клиринг по контракту происходит в конце каждого периода.
Инвестор заключает форвардный контракт на покупку акции, истекающий в момент Т, по форвардной цене FT и размещает на депозите сумму FTe tT. В конце периода Т она вырастает до суммы F}, и уплачивается по контракту в обмен на акцию. Таким образом, по завершении периода Т инвестор располагает акцией, цена спот которой равна .
Получим аналогичный финансовый результат с помощью фьючерсного контракта. В конце нулевого дня котировка фьючерса, истекающего в момент Т, равна F’. Инвестор покупает его по котировочной цене в количестве \ В качестве начальной маржи он вносит сумму F{'e , т.е. она инвестируется под ставку г на время Т. В конце данного периода по депозиту он получит сумму:
V F^e1 =F{<.
В момент /, фьючерсная котировка равна F*. В результате клиринга по счету инвестора происходит перечисление вариационной маржи в размере:
В зависимости от конъюнктуры данная величина может быть отрицательной или положительной. Если она отрицательная, инвестор финансирует ее, заняв средства под ставку г на период Т -tA, если положительная, размещает эти средства под данный процент на этот период. Соответственно по окончании действия контракта в первом случае инвестор выплатит, а во втором получит сумму:
е г(7' ''’(f;' = F^ - F„ .
По котировочной цене в момент он докупает фьючерсный кон-тракт до величины е <
В момент /2 по контракту перечисляется вариационная маржа в размере:
е r(r -F,t)
Если она отрицательная, инвестор финансирует ее, заняв средства на период Т -t2, положительная - размещает под данный процент на этот период. Соответственно по окончании действия контракта в первом случае он выплатит, а во втором получит сумму:
б НТ -2)^Т _ pl ,2) = pl _ pl _
По котировочной цене в момент t2 инвестор докупает фьючерс до одного целого контракта.
По истечении контракта по нему перечисляется вариационная маржа в размере S, - Е,7 , поскольку котировочная фьючерсная цена равна спотовой. Если она отрицательная, эта сумма списывается, если положительная, начисляется на счет инвестора. В этот момент он погашает заимствованные средства и получает деньги по размещенным депозитам. Финансовый итог операции равен:
FJ + F’ -F' +F] =S,.
Таким образом, стоимость позиции инвестора в конце периода Т по фьючерсному контракту равна позиции по форвардному. Следовательно они должны быть одинаковыми и в начале периода:
FTerT=FjerT. (П.3.1)
(Напомним, именно эти средства были инвестированы в начале периода по каждой операции). Поскольку процентная ставка и период времени одинаковые, то в равенстве (П.3.1) Ff = Fj , т.е. форвардная цена равна фьючерсной. Если для разных периодов времени процентные ставки не одинаковые, но известны заранее, то равенство цен также сохранится.
ПРИЛОЖЕНИЕ 2.
Определение коэффициента хеджирования с помощью программы Excel
Рассмотрим определение коэффициента хеджирования на примере.
Пример.
Имеется выборка наблюдений спотовой цены (S) актива А и фьючерсной цены (F) (Для примера ограничимся одиннадцатью зна
чениями). Печатаем значения спотовой цены актива в ячейках от А2 до А12, фьючерсной цены - в ячейках от С2 до С12, как показано на рис. П.3.1. На основе значений спотовой цены необходимо получить значения ее разностей (Д5). Для этого в ячейке В2 печатаем формулу:
= АЗ-А2,
наводим курсор на квадратик в правом нижнем углу рамки ячейки В2, нажимаем левую клавишу мыши, и, удерживая ее в нажатом положении, доводим курсор до ячейки В11, отпускаем клавишу мыши В ячейках диапазона В2:В11 получили значения А5 для десяти периодов Значения AF получим аналогичным образом в диапазоне D2:D11 Для этого в ячейке D2 печатаем формулу:
-СЗ-С2,
наводим курсор на квадратик в нижнем правом углу рамки ячейки D2, нажимаем левую клавишу мыши, и, удерживая ее в нажатом положении, доводим курсор до ячейки D11, отпускаем клавишу мыши. В ячейках диапазона D2:D11 получили значения AF для десяти периодов.
Рис П.З 1. Определение коэффициента хеджирования
На основе полученных данных AS и AF определяем коэффициент хеджирования h. Решение получим в ячейке Е2, поэтому выделяем ее, т.е. наводим на нее курсор и щелкаем мышью. Открыва
ем окно “Мастер функций”, т.е. наводим курсор на значок на панели инструментов и щелкаем мышью. В поле “Категория" выбираем курсором строку “Статистические” и щелкаем мышью. Строка высветилась синим цветом. В поле окна “Функция" выбираем курсором строку “НАКЛОН” и щелкаем мышью. Строка высветилась синим цветом. Наводим курсор на кнопку ОК и щелкаем мышью. Появилось окно “НАКЛОН”. В окне две строки: “Изв_знач_у" и '‘Изв_знач_х”. В первую строку заносим значения AS . Для этого наводим курсор на знак 5J с правой стороны первой строки и щелкаем мышью. Окно “НАКЛОН” свернулось в поле первой строки. Наводим курсор на ячейку В2, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, проводим курсор вниз до ячейки В11, отпускаем клавишу. Вновь наводим курсор на знак Ч и щелкаем мышью. Появилось развернутое окно “НАКЛОН”. Заносим значения А/7 во вторую строку. Для этого наводим курсор на знак во второй строке и щелкаем мышью. Наводим курсор на ячейку D2, нажимаем левую клавишу мыши и, удерживая ее в нажатом положении, проводим курсор вниз до ячейки D11, отпускаем клавишу. Наводим курсор на кнопку 5J и щелкаем мышью. Появилось развернутое окно “НАКЛОН". Наводим курсор на кнопку ОК и щелкаем мышью. В ячейке Е2 появилась цифра 0,60396. Таким образом, коэффициент хеджирования, который соответствует использованным статистическим данным, равен 0,6.
(Получить значение коэффициента хеджирования можно другим способом: выбираем курсором ячейку Е2 и печатаем в ней формулу:
= НАКЛОНОВ!: В\ 1; D2: Di 1)
и нажимаем клавишу Enter.)
Программа Excel позволяет определить коэффициент хеджирования и другими способами. Заинтересованный читатель сможет найти их описание в книге А.Н. Буренина “Управление портфелем ценных бумаг”, М.: 2005, параграф 3.5.
ГЛАВА 4. ФЬЮЧЕРСНЫЕ КОНТРАКТЫ НА АКЦИЮ, ФОНДОВЫЙ ИНДЕКС И ВАЛЮТУ
В настоящей главе рассматриваются фьючерсные контракты на акцию, фондовый индекс и валюту. В отличие от товарных фьючерсов данные фьючерсные контракты получили распространение относительно недавно. Например, торговля контрактами на валюту началась в 1972 г.( фондовые индексы - в 1982 г.
4.1. ФЬЮЧЕРСНЫЙ КОНТРАКТ НА АКЦИЮ
4.1.1. Организация торговли фьючерсными контрактами на акции. Фьючерсная торговля акциями на Фондовой бирже РТС
Фьючерсные контракты на акции появились еще в Амстердаме в 17 веке. Однако до недавнего времени они не пользовались большой популярностью и были представлены в 80-е и 90-е годы на ряде периферийных бирж. В конце 90-х годов контракты на акции появились и в России. Например, торговля ими велась на Московской центральной фондовой бирже. В мире интерес к ним проснулся в январе 2001 г., когда торговлю фьючерсными контрактами на акции открыла UFFE (Universal Stock Futures). В частности это вызвало интерес в США, так как на LIFFE стали торговаться фьючерсы на акции американских компаний Майкрософт, Сиско, Интел, АТТ и ряда других. В ноябре 2002 г. фьючерсы на акции появились и в США. До этого на биржах Соединенных Штатов были представлены только опционы на акции.
В США торговлю фьючерсами на акции совместно регулируют Комиссия по товарным фьючерсам (Commodity Futures Trading Commission - CFTC) и Комиссия по ценным бумагам и биржам (Securities and Exchange Commission - SEC). Торговля контактами происходит на четырех основных биржах - One Chicago Exchange1, NASDAQ LIFFE (NQLX), ISLAND Electronic Communication Network (ISLAND ECN) и AMEX2. Торговля на первых трех биржах ведется в элек-
One Chicago Exchange является совместным предприятием Чикагской товарной биржи (СМЕ), Чикагской торговой палаты (СВОТ) и Чикагской биржи опционов (< НОЕ)
; В ноябре 2002 г торговля фьючерсами на акции первоначально открылась на One < Chicago Exchange и NQLX
тронной форме через компьютерную систему. На АМЕХ сохраняется традиционная торговля открытого аукциона с участием маркет мейкеров. One Chicago Exchange использует систему Lead Market Maker (LMM), т.е. систему ведущих маркет мейкеров. В рамках данного механизма биржа выделяет группу маркет мейкеров. Каждый из них котирует определенное количество контрактов на определенные акции с определенным максимальным спредом. Торговля на NQLX построена на базе системы LIFFE CONNECT, разработанной LIFFE. Она основана на технологии, называемой Central Limit Order Book (CLOB). В ее рамках приоритетность исполнения приказов определяется по цене и времени их поступления на биржу. Также имеются маркет мейкеры. Однако их меньше чем на One Chicago Exchange, и в целом ликвидность торговли зависит от самих участников рынка. Контракты на акции насчитывают в США по 100 акций и являются поставочными.
Фьючерсы на акции составляют альтернативу коротким продажам акций на спотовом рынке и по сравнению с ними обладают рядом преимуществ. Для осуществления короткой продажи инвестор должен занять акции у брокера и уплатить ему за это процент. Объем торговли ограничивается возможностями заимствования бумаг. Короткую продажу можно осуществлять только в рамках правила uptick, т.е. предшествующая короткой продаже котировка акции должна идти вверх. При торговле фьючерсом на акции правило uptick не действует. Теоретически инвестор не ограничен в объемах своих операций. Ему необходимо внести только начальную маржу. Чем больше средств перевел на свой счет инвестор, тем больше позиций он может открыть. Начальная маржа по фьючерсу составляет 20% от его стоимости. Ограничения изменения фьючерсной цены не применяются и отсутствует позиционный лимит. Поставка по фьючерсу в США осуществляется в течение трех рабочих дней со дня истечения срока действия контракта3. Последний торговый день по контракту - третья пятница месяца поставки. Контракты торгуются с поставкой в конце каждого квартала плюс два текущих месяца.
В России в настоящее время фьючерсные контракты на акции составляют основу функционирования фьючерсного рынка. Торговля главным образом представлена на бирже РТС в системе FORTS. Она организована в электронной форме. Поэтому любой инвестор,
3 На спотовом рынке США взаиморасчеты по акциям также осуществляются по правилу “T+3”, т.е. в течение трех рабочих днвй с момента заключения сделки.
как юридическое, так и физическое лицо, заключив договор с брокерской компанией, получает возможность самостоятельно заключать сделки по интернету. Контракты существуют на акции ведущих российских компаний. В момент написания данной книги на бирже торговались контракты на акции компаний РАО ЕЭС, Газпрома, Лукойла, Ростелекома, Сургутнефтегаза и Норильского Никеля. Количество бумаг в контрактах различается по эмитентам. Контракты по РАО ЕЭС и Сургутнефтегазу насчитывают 1000, Ростелекому и Газпрому - 100, Лукойлу, Норильскому Никелю - 10 акций.
Торговля новыми контрактами открывается 15 марта, июня, сентября и декабря. Последним днем обращения контракта является рабочий день, предшествующий 15 числу месяца его истечения. В каждый данный момент на акции каждой из перечисленных компаний в момент написания данной книги на бирже торговались контракты с несколькими сроками истечения. Например, на 12.06.05 на бирже обращались контракты на РАО ЕЭС с истечением в сентябре, декабре 2005 г. и марте, июне 2006 г.
Котировка контракта дается в расчете на общее количество акций в нем, т.е. как его текущая стоимость. Например, на момент завершения торгов 12.01.05 цена мартовского контракта на акции РАО ЕЭС была равна 7692 руб. Цена самой акции на спотовом рынке ММВБ в этот момент составляла порядка 7,62 руб. Минимальное изменение цены контракта равно 1 руб.
По окончании торгового дня расчетная цена контракта принимается равной цене последней сделки. Однако, если на момент окончания торговой сессии цена заявки на покупку оказалась выше или цена заявки на продажу ниже цены последней сделки, то значение цены этой заявки принимается в качестве расчетной.
Начальная маржа по контрактам определяется от их текущей стоимости. В момент написания данной книги она составляла: для РАО ЕЭС, Газпрома и Лукойла - 15%, Ростелекома, Сургутнефтегаза и Норильского Никеля - 20%.
Контракты являются поставочными. Исполнение проводится в первый торговый день после последнего дня обращения контракта. Исполнение осуществляется путем поставки-приемки акций через Фондовую биржу “Санкт-Петербург”, которая является организатором торговли на рынке акций, и Фондовую биржу РТС, которая яв-няется Клиринговой организацией по сделкам с акциями. Для исполнения контракта инвестор должен зарегистрироваться на рынке ценных бумаг Фондовой биржи “Санкт-Петербург’' в качестве участника торгов акциями или клиента участника торгов. От продавца
требуется задепонировать в расчетном депозитарии (“Депозитарно-клиринговая компания") необходимое количество акций, а от покупателя - задепонировать в расчетной организации (“Расчетная палата РТС”) соответствующее количество денежных средств, в том числе для оплаты сборов, предусмотренных на рынке акций. В случае неисполнения контракта участником на него налагается штраф в размере гарантийного обеспечения контракта, установленного на начало последнего дня его обращения. Штраф списывается с его маржевого счета в безакцептном порядке. Данная сумма в качестве неустойки зачисляется на счет лица, выполнившего свои обязательства по контракту, но не получившего исполнения от своего контрагента.4
4.1.2. Хеджирование фьючерсным контрактом на акции
В главе 3 общую характеристику фьючерсного контракта мы представили на основе примера контракта на акцию. Поэтому сейчас остановимся на вопросе хеджирования спотовой позиции по акциям с помощью фьючерсного контракта на акцию.
Пример 1.
Инвестор владеет портфелем из 10000 акций компании А и хотел бы застраховаться от падения их цены через три месяца. Он хеджирует портфель с помощью фьючерса на данную акцию. Контракт насчитывает 100 акций и истекает через три месяца. Цена спот акции равна 100 руб. На акцию в течение следующих трех месяцев дивиденды не выплачиваются. Ставка без риска составляет 10% годовых. Инвестор продает:
1ООООакиий
------------- 1ОО контрактов.
Ю^акций
В данном примере хеджер сформировал безрисковый портфель, так как проигрыш за счет падения цены акции через три месяца полностью компенсируется выигрышем по фьючерсным контрактам, и наоборот. Согласно принципам функционирования финансового рынка такой портфель должен приносить инвестору доходность равную ставке без риска. Иначе возникнет возможность получить арбит
4 Более подробную информацию о спецификации фьючерсных контрактах можно получить на сайте Фондовой Биржи РТС www.rts.ru
ражную прибыль. Покажем, что в условиях эффективного рынка5 доходность портфеля в примере действительно равна 10% годовых.
Согласно формуле (2.1), в момент начала хеджа трехмесячная фьючерсная цена акции должна была составить:
F3=100 1 + 0,1 —
102,5 руб.
Пусть через три месяца цена акции упала до 90 руб. Тогда по спотовой позиции инвестор проиграл:
1 ООООакций АО руб. = 100000/л+л
В последний день действия контракта фьючерсная цена и спотовая равны. Поэтому по фьючерсной позиции он выиграл:
1 ООконтрактов • 1 00 акций 12,5руб. ~ 125000руб.
Доходность портфеля в расчете на три месяца составила:
|250оо^-'0000»/>г6. = ад25или2Л
1000000/грб.
В расчете на год она равна:
2,5%-4 = 10%.
Таким образом, полностью хеджированный портфель должен приносить инвестору доходность равную ставке без риска. Докажем данный результат в общей форме. Проведем рассуждения для портфеля из одной акции и одного фьючерсного контракта, включающего одну акцию.
Инвестор покупает одну акцию и продает один фьючерсный контракт. Контракт истекает в момент времени Т, ставка без риска равна г (в процентах годовых), цена акции - 50, фьючерсная цена составляет:
( Т '
К=$(1 1 + г — . база)
Доходность портфеля инвестора за период времени Т равна:
т
5 Понятие эффективного рынка подробно раскрывается в книге А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов", М.,2002, глава 8.
где AF = Fr-F0;
Д5 = 5г-50;
5Г - цена спот акции в момент окончания периода Т;
Fy. - фьючерсная цена акции в момент окончания периода Т, она равна ST;
гт - ставка без риска для периода Т.
Тогда из формулы (4.1):
или
Т
гт - г—— база
Откуда:
база
В примере 1 для хеджирования спотовой позиции по акциям инвестору надо продать 100 контрактов. Однако, как отмечалось выше (пример 7 глава 3), на положительную вариационную маржу инвестор может получать дополнительный процент, отрицательную вариационную маржу ему скорее всего придется финансировать под процент. Поэтому в таких условиях количество контрактов следует
г Т
скорректировать на величину 1 +-----. Как уже отмечалось в гла-
2 база
ве 3, корректировку целесообразно осуществлять по расчетным фьючерсам, так как покупка-продажа определенного количества акций по контракту потребует открыть соответствующее, а не меньшее число контрактов.
Выше было показано, если инвестор полностью хеджирует свою позицию по акциям, то, согласно законам финансового рынка, он обеспечивает доходность на инвестиции равную ставке без риска. Поэтому хеджировать позицию по акциям на длительный период времени не имеет смысла. В этом случае целесообразно вообще не покупать акции, а приобрести безрисковую бумагу. Таким образом, если возникает необходимость хеджировать позицию по акциям, то период хеджирования является краткосрочным Например, по мнению инвестора ситуация на рынке становится очень неопределен-
но
ной, и разумно застраховаться от возможного изменения конъюнктуры на следующий день или несколько дней. Альтернативой хеджированию является просто продажа акции. Однако это связано с большими трансакционными издержками В то же время комиссионные на срочном рынке существенно ниже чем на спотовом.
Поскольку позиция по акции хеджируется с помощью фьючерсного контракта, до истечения которого остается еще какое-то время, то необходимо использовать коэффициент хеджирования. Его можно определить на основе подходов, изложенных в главе 3, однако для контракта на акции его удобно рассчитать на основе формулы определения теоретической фьючерсной цены (4.2), которая связывает фьючерсную и спотовую цену акции:
база )
(4.2)
В соответствии с формулой (4.2) зависимость между изменением фьючерсной и спотовой цен за короткий промежуток времени можно представить как:
база j
Откуда:
(4.3)
база
Пример 2.
Инвестор владеет портфелем из 10000 акций компании А и хотел бы застраховаться от падения их цены в течение следующего дня. Он хеджирует портфель с помощью фьючерса на данную акцию. Контракт насчитывает 100 акций и истекает через 90 дней. Цена спот акции равна 100 руб., в течение действия контракта дивиденды на акцию не выплачиваются. Ставка без риска равна 8% годовых. Определить количество контрактов, которые необходимо продать. База равна 360 дням.
Решение.
Согласно формуле (4.3) коэффициент хеджирования равен:
h =--------J------г = 0,9804.
1 + 0,08(90/360)
Поэтому необходимо продать:
1 ООООакгшй п п л л п л п л ----------— 0,9804 = 98,04 контракта.
1 OOdfKZ/ww
или 98 контрактов.
Допустим, через день цена акции упала до 90 руб. Тогда по спотовой позиции инвестор потерял:
10000 акций - 10руб. = 100000руб.
В момент начала хеджирования трехмесячная фьючерсная цена, согласно формуле (4.2), составляла:
( 90
=1001 + 0,08 — =102 руб.
< 360 J
Через день она равна:
( 89
К9 =90 1 + 0,08---
I 360 J
= 91,78 руб.
т.е. упала на 10,22 руб. Поэтому по фьючерсной позиции хеджер выиграл:
^контрактов Л^акций -10,22руб. = 100156руб.
Возможен другой вариант. Пусть через день спотовая цена выросла на 10 руб. По спотовой позиции инвестор выиграл 100000 руб. Новая фьючерсная цена составила:
89 >
360>
НО 1 + 0,08
= 112,18руб.,
т.е. выросла на 10,18 руб. Проигрыш по фьючерсной позиции равен: ^контракта \{^}акций 10,18руб. = 99764руб.
Таким образом, изменения стоимости спотовой и фьючерсной позиций с небольшой разницей компенсируют друг друга, и в целом стоимость портфеля остается практически неизменной.
В рассмотренном примере мы не получили полного соответствия между финансовыми результатами по фьючерсной и спотовой позициям. Дело в том, что формула (4.3) представляет собой не что иное как производную фьючерсной цены по спотовой. Как известно, значение производной учитывает лишь главное, а не полное, приращение функции при изменении аргумента. Чем существеннее измене-
Гпава 4 Фьючерсные контракты на акцию, фондовый индекс и валюту ние аргумента, тем зависимость становится все менее точной, что и находит отражение в фактических результатах хеджирования. Однако, как было показано в примере, использование коэффициента хеджирования на основе формулы (4.3) дает приемлемый результат. Если инвестор не учтет коэффициент хеджирования при страховании фьючерсным контрактом, то он может понести потери по своей позиции. Покажем это на примере.
Пример. 3.
Пусть в примере 2 инвестор открыл 100 контрактов как при полном хеджировании. Если цена акции упала до 90 руб. то по спотовой позиции инвестор потерял 100000 руб., а по фьючерсной выиграл: \00контрактов- \00акций* \0,22 руб. = 102200/птл
Таким образом, он получил прибыль в 2200 руб. Однако, в случае роста цены акции до 110 руб. по фьючерсной позиции он проиграл:
1 ^контракта -1 ООакций 10,18 руб. = 101800/туб., и его общий проигрыш составил 1800 руб.
В примере 2 наблюдается некоторое расхождение между выигрышами и проигрышами по спотовой и фьючерсной позициям. Однако, если определить доходность, которую получил инвестор по своей операции, то она будет близка к ставке без риска. Так, в первом случае вкладчик получил в рамках хеджа доходность на свои инвестиции в размере:
100156-100000 n
----------------360 = 0,05616 или 5,616% годовых.
1000000
Во втором случае:
100000-99764 36О = 0 % или 8 496% Г0Д0ВЬ|Х
1000000
Как следует из примера 1, “идеально” хеджированные инвестиции должны были бы принести доходность равную 8% годовых. Разница в фактической доходности, полученной инвестором, и ставкой без риска возникла как за счет округления цифры количества контрактов, которые необходимо было открыть, так и в связи с тем, что, формула (4 3) является производной и не учитывает полное приращение функции при изменении аргумента.
В качестве иллюстрации хеджирования на российском рынке рассмотрим пример страхования с помощью фьючерсного контракта на акции РАО ЕЭС.
Пример 4.
Сегодня 12.01.05. Акция РАО ЕЭС на ММВБ стоит 7,62 руб., котировка мартовского фьючерса на акции РАО ЕЭС на РТС равна 7692 руб. До истечения контракта остается 62 дня. Двухмесячная ставка без риска на базе 365 дней составляет 5,56% годовых. Инвестор, владеющий портфелем акций РАО ЕЭС в количестве 10 млн штук, полагает, что на следующий день возможно существенное падение курса, и поэтому принимает решение застраховать свою позицию с помощью фьючерса на РАО ЕЭС.
В соответствии с формулой (4.3), коэффициент хеджирования составляет:
h =
= 0,9906.
база
Необходимо продать контракты в количестве:
1 0000000
---------------0,9906=9906 контрактов.
1 000<7/ар/б
Пусть на следующий день курс акции упал до 7 руб., т.е. на 62 копейки, соответственно новая фьючерсная цена составила:
Г 61
1000-7 1 + 0,0556—
I 365)
= 7065руб.,
т.е. упала на:
7692-7065 = 627 руб.
Тогда по спотовой позиции инвестор потерял:
10000000 • 0,62 руб. = 6200000руб., однако по фьючерсам он выиграл:
99Q6koi [трактов • 627руб. - 6211062руб.
Если он ошибся в прогнозах, и на следующий день курс акции вырос до 8,24 руб., т.е. на 62 копейки, то цена фьючерса увеличилась до:
г 61
8240 1+0,0556-----
I 365
= 8317руб.,
т.е. на 625 руб. В результате по акциям он выиграл 6,2 млн. руб., а по фьючерсам проиграл:
9906контрактов 625руб, = 6191250руб.
Таким образом, возможные выигрыши и проигрыши по спотовой и фьючерсной позициям хорошо сбалансировали друг друга.
Фьючерсный контракт можно использовать для частичного хеджирования спотовой позиции по акциям, если инвестор желает сохранить в определенной степени их спекулятивный потенциал. Для этого служит частичный коэффициент хеджирования, определяемый по формуле (3.24). Поясним сказанное на примере:
Пример 5. (Сохраняются условия примера 4).
Пусть в примере 4 инвестор желает ограничить колебания стоимости своего портфеля на уровне 20% изменения цены акции, т.е. изменения спотовой позиции, поскольку не исключает вероятности роста курса бумаги на следующий день. Он определил, что полный коэффициент хеджирования равен 0,9906. Частичный коэффициент согласно формуле (3.24) составляет:
h’ =(1-0,2)0,9906 = 0,7925.
Инвестор должен продать:
10000000лкг/мй
-----------;—0,7925 = 7925 контрактов.
\000акций
Если на следующий день цена акции выросла до 8,24 руб., и фьючерсная цена до 8317 руб., то по акциям он выиграл 6,2 млн. руб, а по фьючерсам потерял:
7925контрактов' 625руб. = 4953125/туб.
Изменение стоимости его портфеля составило:
6200000руб. - 4953125руб.
= 0,2011
620QQ00py6.
или 20,11% от изменения стоимости спотовой позиции.
Если же курс акции упал до 7 руб, и фьючерсная цена соответственно до 7065 руб, то по спотовой позиции было проиграно 6,2 млн. руб, а по фьючерсной выиграно:
7925контрактов • 627руб. = 4968975руб.
Изменение стоимости портфеля составило:
6200000руб. - 4968975руб. _ 0 19g6 6200000руб. ” ’
или 19,86% от изменения стоимости спотовой позиции
Фьючерсный контракт на акцию можно использовать для получения арбитражной прибыли, если базис не равен цене доставки. Однако следует не забывать, что в связи с ежедневным клирингом позиций арбитражера и перечислением вариационной маржи арбитраж не будет строго безрисковым. Как и для форвардного контракта на акцию возможность совершения арбитражной операции удобно определить на основе расчета внутренней ставки доходности фьючерсного контракта. Техника расчета представлена в примере 2, приведенном в главе 2, параграф 2.3.5, Фьючерсный контракт можно также использовать для получения более высокой доходности от инвестирования средств.
Пример 6.
Курс акции 100 руб., ставка без риска 8% годовых. Двухмесячная фьючерсная цена акции равна 102 руб., контракт включает 100 акций. Контракт беспоставочный.
Внутренняя ставка доходности контракта составляет:
-----1 — = 0,12 или 12% годовых.
U00 J2
Инвестора устраивает такой уровень доходности, поэтому он покупает 100 акций и продает один фьючерсный контракт. Через два месяца фьючерсная и спотовая цены сойдутся, и инвестор получит по операции доходность на уровне 12% годовых.
Пусть через два месяца спотовая цена акции равна 90 руб. Поскольку фьючерсная и спотовая цена в последний день действия контракта одинаковы, то котировочная фьючерсная цена также равна 90 руб. В этот день инвестор продает акции на споте. Убыток от владения акциями составил.
1 ООакций -10 руб. -1 000 руб.
Выигрыш по контракту равен:
100акций 12 руб. — 1200руб.
Доходность, полученная инвестором по операции, составляет:
1200-1000
10000
6 = 0,12 или 12% годовых.
В данном примере фьючерсная цена падала, поэтому инвестор получал положительную вариационную маржу по контракту. Данные средства также можно инвестировать под процент. Поэтому при такой конъюнктуре инвестор может получить доходность и выше 12%.
Возможен и другой вариант: спотовая цена росла, поэтому инвестору приходилось финансировать отрицательную вариационную маржу. Это потребовало дополнительных средств. Поэтому при такой конъюнктуре фактическая доходность по операции будет ниже 12%.
4.2. ФЬЮЧЕРСНЫЙ КОНТРАКТ НА ФОНДОВЫЙ ИНДЕКС
В мировой практике фьючерсные контракты на фондовые индексы появились в 1982 г., когда биржа Торговая Палата Канзаса (Kansas City Board of Trade) открыла торговлю контрактом на индекс Вэлью Лайн. В этом же году на Чикагской Торговой Палате стал торговаться контракт на индекс S&P500, который является наиболее популярным фьючерсом на индекс. Сейчас на мировых биржах представлено большое разнообразие фьючерсных контрактов на индексы.
На российском рынке на Фондовой Бирже РТС также торгуется фьючерсный контракт на индекс. Базисным активом контракта является рассчитываемый агенством “РТС-Интерфакс" индекс “S&P/RUIX”. Контракт является расчетным.
Как известно, в каждый данный момент времени фондовый индекс представляет собой некоторое число. В рамках фьючерсного контракта данное число умножают на определенный множитель, представленный в денежных единицах. В результате получают стоимость контракта. Например, на Чикагской Торговой Палате (СВОТ) торгуется контракт на индекс Доу-Джонса промышленных компаний. Его множитель равен 10 долл. Поэтому, если фьючерсная цена индекса равна 10000 пунктов, то стоимость фьючерсного контракта составляет:
[Q000пунктов • 1 Одолл. ~ 1 ОООООдолл.
Контракты на индексы являются расчетными. Расчетная цена последнего торгового дня принимается равной значению базисного индекса при закрытии в этот день. В то же время, существует и дру
гой порядок определения котировочной цены. Она может рассчитываться на основе цен открытия акций на следующий день после истечения срока действия фьючерсного контракта. Примером служит контракт на индекс S&P500. Данный порядок расчета котировочной цены в США возник в ответ на так называемый час “triple-witching-hour”, наступающий в третьи пятницы марта, июня, сентября и декабря, когда одновременно истекают фьючерсные контракты, опционы на фьючерсы и опционы на индексы.
Для индексов, включающих большое количество бумаг, может случиться так, что по какой-либо акции на следующий день не будет заключено ни одной сделки. Тогда для расчета котировочной цены фьючерса берут цену данной акции при закрытии за предыдущий день.
Фьючерсные контракты на индекс используются для хеджирования портфелей ценных бумаг и изменения их состава, а также извлечения спекулятивной прибыли.
4.2.1. Фьючерсная цена фондового индекса
Фондовый индекс можно рассматривать как акцию, по которой выплачиваются дивиденды. Поэтому его фьючерсную цену можно определить по формулам форвардной цены для акции, по которой выплачиваются дивиденды в течение действия контракта.
Индексы рассчитываются по разным методикам. При строгом подходе к определению фьючерсной цены индекса следует учитывать его структуру. Фьючерсную цену индекса, который определяется как среднее арифметическое, можно определить по формуле (4.4):
г-д
база /
(4.4)
где F - фьючерсная цена индекса;
I - спотовое значение индекса в момент заключения контракта;
Т - период действия контракта;
гт - ставка без риска для периода времени Т;
rTu - форвардная ставка без риска для периода Т -t{;
п - количество акций, входящих в индекс.
divt - дивиденд на i -ю акцию, выплачиваемый в течение действия контракта;
Формула (4.4) учитывает, что дивиденд выплачивается на z-ю
, div,
акцию в момент t, и часть этого дивиденда в размере —- инве-
' < п
^тируется до истечения контракта на период Т -tt.
Вместо формулы (4.4) можно воспользоваться формулой (4.5):
где D, - приведенная стоимость величины —- на момент заключу
чения контракта.
Пример 1.
Индекс состоит из четырех акций - А, В, С и D Акция А стоит 40 руб., Я - 30 руб., С -20 руб. и D - 30 руб. Индекс рассчитывается как среднеарифметическая величина, и его спотовое значение равно 30 пунктам. Контракт истекает через 90 дней, ставка без риска 10% годовых. По акции А выплачивается дивиденд в размере 2 руб. через 60 дней, по акции В дивиденд в 1 руб. через 30 дней. Форвардные процентные ставки равны спотовой, база составляет 360 дней. Определить фьючерсную цену индекса.
Фьючерсная цена индекса равна:
30 1+0,1----
I 360 J
-0,25-2 1 + 0,1
90-60^
360 )
-0,25’1 1 + 0,1
90-30
360 )
- 29,99 пункта.
Как правило, невозможно точно знать величину будущих дивидендов, а также будут ли они выплачены. Поэтому и фьючерсная цена индекса не является точной и имеет большую дисперсию, чем дисперсия спотового значения базисного индекса.
Если фондовый индекс включает большое количество акций, то дивиденды по ним будут выплачиваться в разное время. Поэтому с достаточной степенью допустимости индекс можно рассматривать как актив, по которому выплачивается непрерывно начисляемая ставка дивиденда. В результате фьючерсную цену индекса можно определить по формуле с использованием непрерывно начисляемого дивиденда:
F = 1ег^т , где q - непрерывно начисляемая ставка дивиденда в расчете на год. Ставку q надо взять как среднюю ставок акций. входящих в индекс.
4.2.2. Индексный арбитраж
Фактическая фьючерсная цена индекса может не соответствовать ее теоретическому значению. Тогда открывается возможность совершить арбитражную операцию. Если фактическая цена [F(/)) выше теоретической (Fr), следует продать более дорогой фьючерсный контракт и купить акции, входящие в индекс. Поскольку контракт на индекс является расчетным, арбитражер не может поставить по нему акции. Поэтому в день истечения контракта он продаст их на спотовом рынке. Если F(// < F{ , арбитражер купит более дешевый фьючерс и осуществит короткую продажу акций, входящих в индекс. В день истечения контракта он купит акции на спотовом рынке. Поскольку фьючерсная цена индекса рассчитывается на основе прогнозов выплаты дивидендов, которые могут и не осуществиться, то индексный арбитраж несет в себе риск. Кроме того, риск возникает и в связи с возможным финансированием отрицательной вариационной маржи.
Принять решение о возможности арбитражной операции можно на основе внутренней ставки доходности фьючерсного контракта. Если она больше ставки по кредиту, то необходимо продать фьючерс и купить акции. Если она ниже ставки по депозиту, то надо купить фьючерс и осуществить короткую продажу акций. На основе внутренней ставки доходности инвестор также может принять решение об инвестировании собственных средств. В этом случае его действия напоминают арбитражную операцию, только с той разницей, что он использует не заемные, а собственные средства. Рассмотрим пример арбитражной операции.
Пример 2. (На основе условий примера 1).
Множитель фьючерсного контракта равен 100 руб. Как было показано в примере 1, теоретическая фьючерсная цена индекса равна 29,99 пункта. Пусть фактическая фьючерсная цена составляет 31 пункт. Поэтому возможен арбитраж. Следует продать фьючерс по цене 31 руб. и купить акции, входящие в портфель.
Текущая стоимость индекса с учетом множителя фьючерсного контракта равна:
30 100руб. = 3000руб.
Копируем индекс с помощью покупки акций, входящих в него. Для этого количество акций каждой компании, которое следует купить, рассчитаем по формуле:
количество ()-Is
акций i-й компании S-t 1
где @i - уд. вес акций i -й компании в стоимости индекса;
- текущая стоимость индекса;
S{ -текущий курс акции / -й компании.
Покупаем акции в количестве:
1) акции А :
0,25-3000 1Оле
----—-----= 18,75 или 19 акции;
2)акции В\
0,25-3000
----= 25 акции;
3)акции С
0,25-3000
———-------= 37,5 или 38 акции;
4)акции D\
0,25-3000 ---------= 25 акции.
30
Для покупки акций занимаем под 10% годовых на 90 дней сумму:
19-40+25-30 + 38-20 +25-30 = 3020руб.
Через три месяца возвращаем сумму:
= 3095,5 руб.
3020 14-0,1---
360 J
Через 30 дней получаем дивиденды по акциям В в размере:
1 руб. 25акций = 25 руб.,
инвестируем их на 60 дней под 10% годовых и получаем сумму:
25| 1 + 0,1—
I 360
= 25,42руб.
Через 60 дней получаем дивиденды по акциям А в размере: 2руб, акций = 38/ж5..
инвестируем их на 30 дней под 10% годовых и получаем сумму:
( 30
38 1+0,1----
I 360)
= 3^32 руб.
Пусть через 90 дней акция А стоит 35 руб., В - 35 руб., С - 22 руб., D - 24 руб. Новое значение индекса равно 29 пунктов. Продаем акции и получаем сумму 2976 руб. С учетом выплаченных дивидендов сумма по акциям составила 3039,74 руб.
По фьючерсному контракту получен выигрыш:
(3129 )100 руб. = 200руб.
Общий результат составил:
3039,74 + 200 = 3239,74/^6.
По кредиту отдаем 3095,5 руб. Арбитражная прибыль равна 144,24 руб.
Арбитражную операцию можно было строить и несколько иным образом, а именно, как представлено в примере 2 параграфа 2.3.2.1, т.е. занимать средства для покупки акций с учетом того, что часть их можно будет вернуть за счет будущих дивидендов.
Мы рассмотрели арбитраж с индексом, рассчитываемым как среднее арифметическое. Для средневзвешенного индекса действия будут аналогичными с той только разницей, что в формуле (4.4) дивиденды учитываются в соответствии с уд. весами бумаг в индексе.
Если индекс насчитывает большое количество акций, то полное копирование его состава в арбитражной или инвестиционной стратегиях при покупке или продаже акций может оказаться дорогостоящим делом. В этом случае можно сделать выборку из акций, входящих в индекс, динамика которых наиболее близко повторяет динамику индекса, и оперировать только этим портфелем6. Однако, следует учитывать, что возрастает риск отклонения его динамики от динамики индекса.
6 Технику копирования индекса на основе выборки из входящих в него акций см. в книге А.Н Буренина “Управление портфелем ценных бумаг’”1, Научно-техническое общество им академика С.И.Вавилова, М ,2005. параграфы 5 1.1 1 и 5.1.1.2.
4.2.3. Хеджирование фьючерсным контрактом на индекс
При использовании фьючерса на индекс для хеджирования портфеля необходимо рассчитать коэффициент хеджирования, который бы связывал портфель инвестора с фьючерсным контрактом. Это можно сделать, например, на основе уравнения регрессии. Однако приведем здесь еще один прием определения коэффициента хеджирования.
Имеется фондовый индекс (его спотовое значение равно /), на который заключаются фьючерсные контракты. Бета портфеля инвестора относительного данного индекса равна Д,. Тогда изменение единицы стоимости портфеля (АР) при изменении значения индекса (А/) составит:
АР = Д,А/.
Цена фьючерсного контракта на индекс акций равна: / Т1 \ 1 « / т- Л
(4.6)
база ) п ~ ' база)
На основе формулы (4.6) изменение фьючерсной цены при изменении значения индекса составит:
ч 7 база
Отсюда, согласно формуле (3.11):
Л, й=—=_______
(47)
Т
(4-8)
Пример.
Имеется фьючерсный контракт на индекс S&P500. Множитель контракта равен 250 долл. Контракт истекает через 90 дней. Фьючерсная цена индекса равна 1000. Ставка без риска 5% годовых. Инвестор владеет широко диверсифицированным портфелем акций на сумму 10 млн. долл. Бета портфеля равна 1,2. Он принимает решение застраховаться на следующий день от возможного падения курса акций. Какое количество контрактов необходимо открыть.
Решение.
Коэффициент хеджирования равен:
h =----------------= 1,185185.
1 + 0,05(90/360)
Стоимость контракта составляет:
XQQQ пунктов 250долл. = 250000долл.
Количество контрактов, которые необходимо открыть, определяется по формуле:
количество стоимость портфеля gj
контрактов стоимость фьючерсного контракта
Следует продать:
10000000 jд g5 j g5 _ 47 4 или 47 контрактов_
250000 н
Количество фьючерсных контрактов, которые следует открыть для хеджирования спотовой позиции, можно определить и на основе уравнения регрессии, связывающего доходность хеджируемого портфеля с доходность индекса. Как следует из главы 3, коэффициент хеджирования при таком подходе равен значению беты портфеля. Таким образом, в формуле (4,9) в качестве коэффициента хеджирования учитывается только бета портфеля. Обоснование такого подхода заключается в зависимости изменения стоимости между рыночным индексом и портфелем. Если портфель характеризуется бетой рр относительно данного индекса, то это означает, что в среднем при изменении стоимости индекса стоимость портфеля должна измениться в рр раз,
В формуле (4.9) в знаменателе мы рассчитывали стоимость фьючерсного контракта на основе фьючерсной цены индекса. Возможен и другой подход: определить стоимость контракта на основе спотового значения индекса. В частности такой метод расчета приводится в книге Hull J. Options, Futures and Other Derivatives, 4-th ed., L: Prentice-Hall, 2000, страница 66 пример 3.8.
Фьючерсные контракты на индекс можно использовать для изменения беты портфеля. Получим для этих целей соответствующую формулу.
Пусть инвестор располагает портфелем акций с бетой Рр относительно фондового индекса /. Он желал бы изменить состав портфеля таким образом, чтобы его бета составила величину /Г.
Для изменения состава портфеля инвестор использует фьючерсный контракт на индекс /,
Изменение единицы стоимости портфеля с бетой (}р при изменении значения индекса составляет Д, А/, а портфеля с бетой Д,* -fjР*Д1. Отсюда формулу (3.12) можно представить следующим образом:
/?;д/ = pp\i + h
Т 1
+ г----- А/.
база )
Тогда h равно:
/Г-В
h =__Рр .
1 + г (Г / база)
(4.10)
(4.11)
Пример.
Стоимость портфеля инвестора составляет 10 млн. долл. Его бета относительно индекса S&P500 равна 0,8. Инвестор ожидает подъема на рынке и решает перестроить портфель таким образом, чтобы его бета выросла до величины 1,2. Фьючерсный контракт на S&P500 истекает через два месяца, его цена равна 1000 пунктов, ставка без риска для этого периода равна 6% годовых. Для данных условий величина h составляет:
h =
1,2-0,8
1 + 0,06(2/12)
= 0,396.
(4-12)
Стоимость контракта равна:
250 1000- 250000^7.
Количество фьючерсных контрактов, по которым необходимо открыть позиции определяется по формуле (4.9):
10000000
250000
0,396 = 15,84.
Таким образом, чтобы получить портфель акций с бетой 1,2 необходимо купить 16 фьючерсных контракта на индекс S&P500. В данном примере следует купить фьючерсные контракты, поскольку в формуле (4.12) мы получили положительную величину. Ответ со знаком минус говорил бы о том, что необходимо продать фьючерсные контракты. Например, бета портфеля инвестора равна 1,2, а он желает получить бету 0,8, поскольку ожидает
ухудшения конъюнктуры рынка. Тогда инвестору следует продать 16 фьючерсных контрактов.
В качестве альтернативного способа определения величины h при изменении беты портфеля можно просто взять разность между новым и старым значениями бет:
h = p'-В .
Гр
В этом случае в примере величина h равна:
h = 1,2 -0,8 = 0,4.
Поэтому для увеличения беты портфеля со значения 0,8 до 1,2 инвестору необходимо купить:
10000000Л л
---------0,4 = 1 ^контрактов.
250000
Выше мы говорили о портфеле из акций. Однако они могут составлять только его часть. Поэтому возникает задача изменения удельного веса акций в портфеле. Она решается аналогичным образом с помощью фьючерсных контрактов, только в формулах (4.10) и (4.11) необходимо учесть удельный вес акций в текущем и создаваемом портфелях. Тогда формулы принимают следующий вид:
е-ар-аы = еараы+и\ 1+г-Д|д/ (4.13)
V база)
и
; в*аРа~ваРа .....
h = , (4.14)
1 + г(Г /база)
где 6»; - уд. вес акций с Д;
Д - уд. вес акций с Д.
Продолжая предыдущий пример, предположим, что уд. вес акций с Д в текущем портфеле составляет 30%, а инвестор желал бы получить портфель с пропорций акций с Д равной 70%, Стоимость портфеля равна 10 млн. долл. Найдем коэффициент h для данных условий:
^0,7-1,2-0,3-08
1 + 0,06(2/12)
Количество контрактов, которые необходимо купить, определяется по формуле7:
количество 0* > стоимость портфеля (415)
контрактов стоимость фьючерсного контракта
Оно равно:
^“•0,5941 = 16,63.
250000
Таким образом, инвестору следует купить 17 фьючерсных контрактов.
4.3. ФЬЮЧЕРСНЫЙ КОНТРАКТ ФОНДОВОЙ БИРЖИ РТС НА КУРС БЕЗНАЛИЧНОГО ДОЛЛАРА К РУБЛЮ
На фондовой бирже РТС обращается фьючерсный контракт на доллар США. Базисным активом является курс безналичного доллара к рублю на день исполнения контракта. Контракт включает 1000 долл. США, и является расчетным. В качестве расчетного курса в день исполнения контракта принимается опубликованный агенством Интерфакс средневзвешенный курс доллара к рублю по итогам единой торговой сессии межбанковских валютных бирж. Если в день исполнения контракта торги не проводились, то в качестве расчетного принимается курс, объявленный Банком России. Шаг цены контракта равен 1 рублю. Котировка контракта приводится в расчете на 1000 долл, В системе РТС код контракта обозначается буквами Si. Далее в обозначении следует месяц и год исполнения, например, Si-03.06. Это означает, что контракт истекает в марте 2006 года8.
4.3.1. Определение фьючерсной цены и арбитраж
Фьючерсная цена контракта рассчитывается на основе формулы (4.16) определения форвардной цены валюты:
1 + г, (Т / база)
1 + rd (Г / база)
(4-16)
где X - спот курс доллара к рублю в прямой котировке;
! В формуле (4.15) стоимость портфеля умножается на величину 0', так как коэффици-
ентом /Г должна характеризоваться только часть портфеля в указанной пропорции. и Подробную спецификацию контракта см. на сайте биржи PTC www,rts,ru
г - ставка без риска по рублю;
rt) - ставка без риска по доллару.
Поскольку котировка дается в расчете на 1000 долл. США, то формулу (4.18) следует записать как:
1 + гдТ /база)
(4.17)
Рассмотрим определение фьючерсной цены на примере.
Пример 1.
Курс спот доллара равен 29 руб., трехмесячная ставка без риска по рублю - 6%, по доллару - 3%. Определить цену трехмесячного фьючерсного контракта. В соответствии с формулой (4.17) цена равна:
F = 1 000 291 + 0’06(3/|2) = 29215,88руб.
1 + 0,03(3/12) к
Если фактическая фьючерсная цена отличается от полученного теоретического значения, то можно совершить арбитражную операцию. Действия арбитражера аналогичны тем, которые были рассмотрены в параграфе 2.3.3.1. Поскольку речь идет о фьючерсном контракте, то при осуществлении арбитража по контракту будет возникать вариационная маржа. За время действия контракта на положительную маржу можно получить процент, отрицательную маржу придется финансировать. Во втором случае возникает риск того, что отрицательная маржа может превысить расчетную прибыль.
Решение о возможности совершить арбитраж удобно принять на основе внутренней ставки доходности фьючерсного контракта, которую можно рассчитать на основе формулы (4.17)9:
4.3.2. Спекулятивные стратегии
Спекулятивные стратегии с использованием фьючерсного контракта на доллар принципиально не отличаются от стратегий по уже рассмотренным контрактам. Если ожидается рост курса доллара, следует играть на повышение, т.е. купить контракт. Если ожидается падение курса - играть на понижение, т.е. продать контракт. Поясним сказанное на примерах.
9 См. параграф 2,3.5,
Пример 1.
Цена фьючерсного контракта, до истечения которого остается 62 дня, равна 28734 руб. Инвестор ожидает падения курса, поэтому продает контракт по этой цене. Через три дня цена контракта упала до 28705 руб., и инвестор закрыл позицию. Выигрыш составил:
28734-28705 = 29^6.
Начальная маржа по контракту в момент его заключения была равна 864 руб. Эффективность операции инвестора в расчете на год составила:
= 4 0837 или 408,37% годовых.
864 3
Пример 2.
Цена фьючерсного контракта, до истечения которого остается 62 дня, равна 28715 руб. Инвестор ожидает роста курса в течение данной торговой сессии, поэтому покупает контракт по этой цене. Вечером он продает его по 28720 руб. Выигрыш составил:
28720-28715 = 5 руб.
Начальная маржа по контракту в момент его заключения была равна 864 руб. Эффективность операции инвестора в расчете на год составила:
-^-365 = 2,1123 или 211,123% годовых.
^864
4.3.3. Хеджирование
Контракт на доллар США является беспоставочным, поэтому в его рамках хеджер не может купить или продать доллары. В связи с этим контракт будет использоваться только для хеджирования, а сама валюта будет покупаться или продаваться на спотовом рынке в момент завершения хеджа.
При совпадении срока хеджа с моментом истечения фьючерсного контракта возникает случай полного хеджирования. Если инвестора устраивает фьючерсная цена, то он просто покупает или продает контракт. Страхуясь от возможного роста курса доллара, следует купить контракт. Страхуясь от падения курса доллара - продать контакт. Контракт насчитывает 1000 долл. Хеджер может продавать (покупать) большие суммы валюты. Поэтому необходимо рассчитать
количество контрактов, которые следует открыть. Оно определяется по следующей формуле:
количество _ хеджируемая сумма (долл} контрактов 1 ОООдялл.
Пример 3.
Инвестор планирует купить 500000 долл, через три месяца. Будущую покупку хеджирует на фьючерсном рынке. Он приобретает:
500000долл. _
------------= Ъоо контрактов.
1 ОООдолл.
Если инвестор в будущем собирается продать 500000 долл., то он продает 500 контрактов.
Для фьючерсного контракта на валюту коэффициент хеджирования можно определить на основе регрессионного анализа, используя прошлые данные статистики или с помощью формулы (4.16). Из нее следует:
1 + г (Т/база) AF = AS--------------Ь
1 + ГД71 /база)
Отсюда коэффициент хеджирования равен:
AS' _ 1 + r/Г/база) AF 1 + гр (Г / база)
Пример 4.
Экспортер получит через 30 дней 10 млн. долл. США и будет конвертировать их в рубли. Он опасается падения курса доллара и страхуется 65-дневным контрактом на доллар США. Ставка без риска по рублю составляет 6%, по доллару - 3%. Курс спот доллара равен 28 руб. Определить количество контрактов, которое необходимо продать. Финансовый год равен 365 дням.
Решение.
Экспортер будет конвертировать доллары через 30 дней. Поэтому, чтобы учесть схождение фьючерсной цены к спотовой, рассчитаем коэффициент на момент завершения хеджа, т.е., когда до истечения контракта останется 35 дней. Коэффициент равен.
h = 1 + 0,03(35/365) = 7 j 39?
1 + 0,06(35/365)
Хеджеру следует продать:
1 ОООООООдолл. q _ 9971397 или 9971 контрактов.
ЮООЭатг
В момент начала хеджа 65-дневная фьючерсная цена равна:
™ । + 0,06(65/365) _О1 г
= I 000 • 28 руб.---т—------4 “28149 руб.
6 1 + 0,03(65/365)
Пусть через месяц курс доллара на споте упал до 27 руб. Экспортер обменял 10 млн, долл, по спотовому курсу и получил сумму:
10000(К)0()ол7. • 27 руб. = 270000000 руб.
35-дневная фьючерсная цена составила:
+ ^000 27P+'|^'g;gp7077P+.
Разность между фьючерсными ценами в конце и начале хеджа равна: 28149-27077 = 1072руб.
Поэтому по фьючерсной позиции он выиграл:
991 {контрактов АГГИ руб. = 10688912 руб.
Фактический обменный курс для экспортера с учетом хеджа составил:
270000000 руб. +10688912руб.
ЮООООООболл.
-28,06889руб.
Если через месяц курс доллара вырос до 29 руб,, то по спотовой позиции от продажи валюты экспортер получил:
1 ОООООООбаял. • 29 руб. = 290000000 руб.
35-дневная фьючерсная цена составила:
г 1ЛЛЛ ™ < I + 0,06(35/365)
Гs =1000 29руб.-----{ - 29083руб.
35 1 + 0,03(35/365)
Разность между фьючерсными ценами в конце и начале хеджа равна: 28149-29083--934руб.
Поэтому по фьючерсной позиции он проиграл:
997 {контрактов • (-934)руб. = -9312914руб.
Фактический обменный курс для экспортера с учетом хеджа составил:
290000000руб,-9312914руб. = ЮООООООдолл.
Пример 5.
Импортер через 30 дней собирается конвертировать 10 млн. руб. в долл. США. Он опасается роста курса доллара и страхуется 65-дневным контрактом на доллар США. Ставка без риска по рублю составляет 6%, по доллару - 3%. Курс спот доллара равен 28 руб. Фьючерсная цена равна 28149 руб. Определить количество контрактов, которое необходимо купить.
Решение.
Коэффициент хеджирования, как и в предыдущей задаче, составляет 0,9971397. Поскольку фьючерсный контракт представлен в долларах, то, в отличие от задачи 4, количество контрактов определяется по следующей формуле:
количество стоимость хеджируемой позиции (418)
контрактов спотовая номинал фьючерсного
цена контракта
В знаменателе формулы (4.18) присутствует множитель ‘’слотовая цена”. Он необходим, чтобы определить текущую стоимость хеджируемой позиции в рублях, так как номинал фьючерсного контракта представлен в долларах10. Количество контрактов, которое необходимо купить импортеру, равно:
. q 9971397 = 35^42 или 356 контрактов.
2% руб, -ЮООЭатл.
Допустим, через месяц курс спот равен 29 руб. Импортер на спотовом рынке конвертировал 10 млн. руб. в:
10 В формуле (4,18) вместо спотовой цены можно взять фьючерсную цену. Разница между спотовой и фьючерсной ценами доллара является незначительной вследствие незначительной разности в процентных ставках. Поэтому расчетный результат и для первого и второго вариантов будет практически одинаковым. Если расчет сделать на основе курса спот, то хеджер получит более низкий курс при дальнейшем росте курса доллара. Если расчет сделать на основе фьючерсной цены, то хеджер получит более низкий курс при дальнейшем падении курса доллара.
10000000руб. ^AAQ^^ ---------—— = 344827, бдолл.
29 руб.
По фьючерсной позиции он выиграл:
ЗЬбконтрактов 934руб. = 332504руб.
Обменял их по спот курсу на:
332504руб.
------------11465,666олл.
29 руб.
Фактический обменный курс для импортера с учетом хеджа составил:
10000000руб.
= 28,06677 руб.
344827,бдолл. +11465,66д<мл.
Допустим, теперь, что через месяц курс спот упал до 27 руб.
По фьючерсной позиции он проиграл:
35бкошпрактов (-1072)руб. = —381632руб.
Поэтому на доллары он обменивает сумму:
10000000 - 381632 = 9618368руб.
После обмена получает:
9618368руб.
-----------— 356235,9долл.
27 руб.
Фактический обменный курс для импортера с учетом хеджа составил:
10000000^.^
356235,96^7/7.
КРАТКИЕ ВЫВОДЫ
Фьючерсы на акции составляют альтернативу коротким продажам акций на спотовом рынке.
Котировка контракта на акции на Фондовой бирже РТС дается в расчете на общее количество акций в нем, т.е. как его текущая стоимость.
Полностью хеджированный портфель должен приносить инвестору доходность равную ставке без риска.
Если фондовый индекс включает большое количество акций, то дивиденды по ним будут выплачиваться в разное время. Поэтому с достаточной степенью допустимости индекс можно рассматривать
как актив, по которому выплачивается непрерывно начисляемая ставка дивиденда.
Если фактическая фьючерсная цена индекса не соответствует ее теоретическому значению, можно совершить индексный арбитраж. При Еф > F} следует продать более дорогой фьючерсный контракт и купить акции, входящие в индекс. При Гф < FT надо купить более дешевый фьючерс и осуществить короткую продажу акций, входящих в индекс. Принять решение о возможности арбитражной операции удобно на основе внутренней ставки доходности фьючерсного контракта. Если она больше ставки по кредиту, необходимо продать фьючерс и купить акции. Если она ниже ставки по депозиту, надо купить фьючерс и осуществить короткую продажу акций. На основе внутренней ставки доходности также можно принять решение об инвестировании собственных средств.
Фьючерсные контракты на индекс можно использовать для изменения беты портфеля инвестора.
Базисным активом фьючерсного контракта на доллар США Фондовой биржи РТС является курс безналичного доллара к рублю на день исполнения контракта. Контракт включает 1000 долл. США и является расчетным. В качестве расчетного курса в день исполнения контракта принимается опубликованный агенством Интерфакс средневзвешенный курс доллара к рублю по итогам единой торговой сессии межбанковских валютных бирж. Котировка контракта приводится в расчете на 1000 долл. США.
ГЛАВА 5. ФЬЮЧЕРСНЫЕ КОНТРАКТЫ НА ПРОЦЕНТНЫЕ СТАВКИ
5.1. ФЬЮЧЕРСНЫЙ КОНТРАКТ НА КАЗНАЧЕЙСКУЮ ОБЛИГАЦИЮ США
Рассмотрим долгосрочный процентный фьючерс на примере фьючерсного контракта на казначейскую облигацию США, который торгуется на Чикагской Торговой Палате (СВОТ), Базисным активом контракта служит государственная облигация с доходностью до погашения 6% и номиналом 100 тыс. долл., купон выплачивается два раза в год. Котировка облигации на спотовом и фьючерсном рынках приводится для номинала в 100 долл., дробные значения даются в 32 долях доллара. Например, облигация имеет котировку 96-12. Это означает 96 долл, и 12/32 доллара или 96,375 долл. Для облигации номиналом 100 тыс. долл, ее цена равна 96375 долл. В котировке указывается чистая цена бумаги, т.е. без накопленных процентов, которые причитаются продавцу облигации, если он продает ее в ходе купонного периода. Полная цена облигации равна чистой цене плюс накопленная сумма купонного процента за время, прошедшее после выплаты последнего купона до дня продажи бумаги на спотовом рынке или поставки ее по фьючерсному контракту.
По контракту можно поставить разные казначейские облигации, до погашения которых на первый день месяца поставки остается больше 15 лет. Если поставляется облигация с правом отзыва, то она должна быть безотзывной в течение остающихся 15 лет. Разные облигации имеют разные доходности до погашения. Однако доходность поставляемой облигации в соответствии с условиями контракта должна составлять 6% годовых. Приведение фактической доходности поставляемой облигации к уровню в 6% достигается за счет использования так называемого коэффициента конверсии. Он рассчитывается биржей до начала торговли контрактом для каждой облигации, которую можно поставить по контракту? Коэффициент конверсии приводит цену поставляемой облигации на первый день месяца поставки к такому уровню, чтобы ее доходность до погаше-
Коэффициент конверсии рассчитывается следующим образом. Находят цену облигации, которая соответствует доходности до дня погашения или дня первого отзыва равной 6%, и делят ее на 100 Полученная цифра и является коэффициентом конверсии. Примеры расчета коэффициента конверсии приводятся в параграфе 5.2.3.
ния составляла 6%. Цена, получаемая продавцом фьючерса при исполнении контракта, определяется по формуле:
цена поставки котировочная коэффициент ~ • + облигации фьючерсная цена конверсии
(5.1)
сумма начисленных
процентов
По фьючерсу продавец имеет право поставить разные облигации. Поэтому он выберет ту из них, которая обойдется ему дешевле остальных, т.е. так называемую "самую дешевую облигацию”. Покупая облигацию на спотовом рынке, продавец фьючерса уплачивает за нее цену равную чистой цене плюс сумма накопленных процентов по купону. Поставляя облигацию по контракту, он получает от покупателя цену равную котировочной фьючерсной цене, умноженную на коэффициент конверсии, плюс сумма накопленных процентов по купону. Поэтому продавец выберет для поставки такую облигацию, для которой разность:
цена котировочная коэффициент спот фьючерсная цена конверсии
(5-2)
будет наименьшей. Данная облигация является для него “самой дешевой". Она принесет ему наибольший доход, так как за облигацию по контракту он получит сумму:
котировочная коэффициент
фьючерсная цена конверсии
а уплатит за нее на спотовом рынке только спотовую цену. Таким образом, “самой дешевой” будет облигация, которая дает минимум в выражении (5.2):
цена котировочная коэффициент _ _
- = минимальное значение (5.3)
енот фьючерсная цена конверсии
Разделим выражение (5.3) на коэффициент конверсии:
цена енот котировочная _ .
------------------- - ~ минимальное значение (5.4) коэффициент конверсии фьючерсная цена
Котировочная фьючерсная цена является фиксированной величиной, поэтому прибавим ее клевой и правой частям выражения (5.4):
цена спот
----------------------= минимальное значение, (э.о) коэффициент конверсии
Таким образом, "самой дешевой” облигацией для поставки по фьючерсному контракту будет бумага с наименьшим значением отношения:
цена спот коэффициент конверсии
Продавец имеет право поставить облигацию в любой день в течение периода поставки. Естественно, что конъюнктура на спотовом рынке за это время может меняться, и соответственно может меняться выбор самой дешевой облигации. Поэтому покупатель контракта до последнего момента не знает, какая облигация и в какой день будет ему поставлена.
5.2. ОПРЕДЕЛЕНИЕ ФЬЮЧЕРСНОЙ ЦЕНЫ ОБЛИГАЦИИ И АРБИТРАЖ
Фьючерсная цена рассчитывается на основе формул определения форвардной цены актива, по которому выплачиваются и не выплачиваются доходы, которые мы вывели в главе 2. Как и в случае с акцией, здесь возможны два варианта. При первом по облигации в течение периода действия контракта купон не выплачивается, при втором - выплачивается. В отличие от акции величина выплачиваемого дохода, представленного купонным процентом, известна. Однако некоторая сложность возникает в связи с тем, что, как правило, нет полной ясности по вопросу о том, в какой день периода поставки, и какая облигация будет поставлена по контракту. При изменении конъюнктуры будет изменяться и выбор "самой дешевой” облигации. Если уровень процентных ставок на рынке ниже 6%, то самой дешевой скорее всего окажется облигация с наименьшей дюрацией.2 Такую дюрацию имеют наиболее краткосрочные бумаги с наибольшим купоном. Если уровень процентных ставок на рынке больше 6%, то самой дешевой скорее всего будет облигация с наибольшей дюрацией. Дюрация является наибольшей для более долгосрочных облигаций с наименьшим купоном. Для облигаций с одинаковой дюрацией бумага с наибольшей доходностью до погашения, как правило, окажется самой дешевой.
2 Понятие дюрации подробно рассматривается в книге А.Н Буренина "Рынок ценных бумаг и производных финансовых инструментов", М., 2002, параграф 5.1.4.
Рассмотрим определение фьючерсной цены облигации на примерах, предполагая, что мы знаем, в какой день и какую облигацию поставят по контракту.
5.2.1. Определение фьючерсной цены облигации, по которой не выплачиваются купоны в течение действия контракта
Пример 1.
Фьючерсный контракт на облигацию истекает через 60 дней (т.е. через 60 дней будет поставлена облигация). Ставка без риска равна 5% годовых. По контракту поставляется облигация, котировка которой сейчас равна 134-04, купон 8%, выплачивается два раза в год. Предыдущий купон был выплачен 20 дней назад (см. рис. 5.1). Продолжительность текущего купонного периода 182 дня.3 Коэффициент конверсии равен 1,23. Определить фьючерсную цену облигации.
выплата
купона
р----20 дней--►«--------------60 дней ------------•
момеш момент
заключения окончания
контракта контракта
Рис. 5,1. В течение действия контракта купон не выплачивается
Чистая цена облигации равна 134-4/32 или 134,125 долл, в расчете на номинал в 100 долл. За 20 дней по купону накопилась сумма:
1 ООдолл. • 0,04------= 0,44долл.
182<)нем
Полная цена облигации на момент расчета фьючерсной цены равна: 134,125 + 0,44 - 134,565Эолл.
Поскольку по облигации купон в период действия контракта не выплачивается, то для расчета фьючерсной цены используем формулу для актива, по которому не выплачиваются доходы:
3 В США для казначейских облигаций определение суммы накопленных процентов осуществляется на основе учета фактического количества дней, за которые накопился процент, и фактического количества дней в текущем купонном периоде.
134,565 1 + 0,05
60
360 j
- 135,686<)а+7.4
Котировка дается на основе чистой цены. Поэтому из полученной Цифры надо вычесть сумму купонных процентов, которая накопится По облигации к моменту истечения контракта. С момента выплаты Последнего купона пройдет:
20 + 60 = 80 дней.
Соответственно сумма купонных процентов равна:
1 ООдодл. 0,04------= 1,75 Ъдолл.
182d//ew
С учетом корректировки на сумму процентов получим фьючерсную цену:
135,686-1,758 = 133,92Ядолл,
Мы рассчитали фьючерсную цену облигации с купоном 8%, а нам надо определить цену облигации с доходностью до погашения 6%. Для этого используется коэффициент конверсии. Он говорит о том, что одной облигации с купоном 8% соответствует 1,23 облигации с доходностью до погашения 6%. Поэтому искомая фьючерсная цена равна:
133,928 :1,23 = 108,8846<Ьлл.
На основе представленных рассуждений можно в общем виде записать формулу определения фьючерсной цены облигации:
(5.6)
где F - фьючерсная цена;
N - номинал облигации (100 долл.);
С - купонный процент в расчете на год;
Р - полная цена "самой дешевой облигации”, т.е. с учетом суммы накопленного купонного процента за период t;
t - количество дней, которые прошли с даты выплаты последнего купона до момента определения фьючерсной цены;
4 В данной формуле в качестве базы мы использовали 360 дней, так как в США для краткосрочных финансовых инструментов, таких как казначейские векселя и другие инструменты денежного рынка используется 360 дней в году для расчета процентных платежей.
Т - период действия фьючерсного контракта, или более точно, количество дней до даты поставки облигации по контракту;
база * - 360 дней;
база - фактическое количество дней в текущем купонном периоде;
г - ставка без риска для базы 360 дней;
К - коэффициент конверсии.
Формула (5.6) непосредственно вытекает из формулы (5.1). Чтобы это увидеть, выразим из нее котировочную фьючерсную цену:
котировочная цена поставки облигации — сумма начисленных процентов (5.7 фьючерсная цена коэффициент конверсии
В формуле (5.7) "цена поставки облигации" есть не что иное как фьючерсная цена для актива, по которому не выплачивается доход в течение действия контракта. Соответственно она равна цене спот плюс процент без риска, начисленный на цену спот за период действия контракта. При расчете фьючерсной цены облигации надо вычесть из данной цифры "сумму начисленных процентов" ПО купону, так как котировка дается на основе чистой цены. Поскольку необходимо найти фьючерсную цену облигации с доходностью до погашения 6%, то полученный результат делим на ”коэффициент конверсии", рассчитанный биржей для нашей облигации.
Фактическая фьючерсная цена облигации в какие-то моменты времени может отличаться от теоретической. Тогда открывается возможность совершить арбитражную операцию. Рассмотрим технику арбитражной операции на основе условий примера 1 для случаев недооценки и переоценки фьючерсного контракта.
I. Как было определено, теоретическая фьючерсная цена облигации равна 108,8846 долл. Пусть фактическая фьючерсная цена составляет 108,5 долл,, т.е. фьючерс недооценен. В этом случае арбитражер покупает фьючерс, занимает облигацию и продает ее на спотовом рынке за 134,565 долл. Это чистая цена облигации плюс накопленный процент по купону за 20 дней. Инвестирует данную сумму под безрисковую ставку до момента окончания контракта. Через 60 дней получает:
( 60 1
134,565 1 + 0,05---
L 360)
= 135,686далл.
Рассмотрим три варианта конъюнктуры на рынке к моменту истечения контракта.
а) Котировочная фьючерсная цена равна 108,5 долл. В соответствии с формулой (5.1) арбитражер уплачивает по контракту цену:
108ч5Эсъ7л. -1,23 + 1,758Эолл. = 135,213долл.,
получает облигацию и возвращает ее кредитору. Его прибыль в расчете на 100 долл, номинала облигации равна разности между суммой по депозиту и уплаченной за облигацию по контракту:
135,686 -135,213 = 0,473долл.
Общая прибыль по контракту составляет:
0,473бклад. 1000 = 473долл.
б) Котировочная фьючерсная цена равна 109 долл. Арбитражер уплачивает по контракту цену:
109Эа7л,-1,23 + 1,758дот,7. = 135,828долл.,
получает облигацию и возвращает ее кредитору.
Он покупал контракт по цене 108,5 долл. Котировочная цена составила 109 долл. Поэтому за период действия контракта была получена положительная маржа в сумме:
109-108,5 = 0,5Эолл.
Прибыль в расчете на 100 долл, номинала облигации равна:
135,686 -135,828 + 0,5 - 0,358дао.
Общая сумма прибыли по контракту составляет:
0,35 Ъдолл.-1000 = 358долл,
в) Котировочная фьючерсная цена равна 108 долл. Арбитражер уплачивает по контракту цену:
108с)шл. 1,23 + l,758do^7. - 134,598датл.,
получает облигацию и возвращает ее кредитору.
Он покупал контракт по цене 108,5 долл. Котировочная составила
108 долл. Поэтому за период действия контракта была получена отрицательная маржа в сумме:
108 -108,5 =-0,5Эолл.
Прибыль в расчете на 100 долл, номинала облигации равна:
135,686 -134,598 - 0,5 = 0,588^7.
Общая сумма прибыли по контракту составляет:
0,588(Ьлх4000 = 588<Ълл.
II, Пусть фактическая фьючерсная цена составляет 109 долл., т.е. фьючерс переоценен. Тогда арбитражер продает фьючерс, занимает 134,565 долл, на 60 дней под 5% годовых, покупает облигацию на спотовом рынке и хранит ее до момента истечения контракта. По кредиту он должен будет вернуть сумму:
134,565| 1 + 0,05 — | = 135,6860олл.
360
Рассмотрим три варианта конъюнктуры на рынке к моменту истечения контракта.
а) Котировочная фьючерсная цена равна 109 долл. Арбитражер поставляет по контракту облигацию, получает от контрагента в соответствии с формулой (5.1) сумму:
109дш./. 1,23 +1,758долл, = 135,828б>шл.,
возвращает кредит. Его прибыль в расчете на 100 долл, номинала облигации равна:
135,828-135,686 = 0,142долл.
Общая прибыль по контракту составляет:
0,142долл.1000 = 142долл.
б) Котировочная фьючерсная цена равна 108,5 долл. Арбитражер получает по контракту за облигацию:
108,5 долл. • 1,23 + 1,758долл. = 135,21 Здолл.
Он продавал контракт по цене 109 долл. Котировочная цена составила 108,5 долл. Поэтому за период действия контракта была получена положительная маржа в сумме:
109 -108,5 = 0,5долл.
Прибыль в расчете на 100 долл, номинала облигации равна:
135,213 -13 5,686 + 0,5 = 0,027долл.
Общая сумма прибыли по контракту составляет:
0,02 7долл. 1000 = 27долл.
в) Котировочная фьючерсная цена равна 109,5 долл. Арбитражер получает по контракту за облигацию:
109,5долл. 1,23 + 1,758долл. = 136,443долл.
Он продавал контракт по цене 109 долл. Котировочная цена составила 109,5 долл. Поэтому за период действия контракта была получена отрицательная маржа в сумме:
109-109,5 = -0,5долл.
Прибыль в расчете на 100 долл, номинала облигации равна:
136,443 -135,686-0,5 - 0,257долл.
Общая сумма прибыли по контракту составляет:
0,257долл. • 1000 = 257долл.
Мы рассмотрели арбитраж без учета возможного финансирования позиции вследствие возникновения отрицательной вариационной маржи в ходе действия контракта и получения дополнительных процентов на положительную маржу. Данные суммы составляют элемент риска при совершении арбитража на фьючерсном рынке. Как было отмечено выше, арбитраж на фьючерсном рынке не является абсолютно безрисковым.
В качестве элемента риска в рассмотренных арбитражных операциях следует выделить еще один принципиальный момент. При расчете цены поставки используется коэффициент конверсии, который приводит к тому, что изменение вариационной маржи и цены поставки, уплачиваемой по контракту за облигацию, не происходит в пропорции один к одному. Это может вызвать потери арбитражера в случае существенного изменения цены облигации, если коэффициент конверсии значительно отличается от единицы. Проиллюстрируем сказанное на примерах.
Пример 2.
Рассматриваем случай 1. Фактическая фьючерсная цена равна 108,5 долл., поэтому арбитражер покупает фьючерс, занимает облигацию, продает ее на спотовом рынке за 134,565 долл., инвестирует данную сумму под безрисковую ставку до момента окончания контракта. Через 60 дней получает сумму 135,686 долл.
а) Пусть котировочная цена выросла до 111 долл. Арбитражер уплачивает по контракту цену:
111дЛ'7л. 1,23 + 1,758Эолл. - 138,288Эолл., получает облигацию и возвращает ее кредитору.
Он покупал контракт по цене 108,5 долл. Котировочная цена составила 111 долл. Поэтому за период действия контракта была получена положительная маржа в сумме:
111-108,5 = 2,5долл.
Прибыль в расчете на 100 долл, номинала облигации равна:
135,686-138,288 + 2,5 = -0,1020олл.
Общая сумма прибыли по контракту составляет:
-0,102долл.' 1000 = -102Эо_7.7.
Таким образом, был получен убыток в 102 долл. Он возник потому, что при росте котировочной цены, цена поставки, уплачиваемая арбитражером, увеличивается с коэффициентом 1,23. В то же время, положительная вариационная маржа, призванная компенсировать этот эффект, возрастает только с коэффициентом единица.5
Отмеченный риск совершения арбитражной операции в данном примере наблюдается только в случае роста котировочной цены облигации. В случае ее падения он отсутствует. Чем больше опустится цена, тем большая прибыль будет получена. Поскольку риск связан с ростом цены, то, начиная арбитражную операцию, целесообразно оценить вероятность последующего падения процентных ставок на рынке и, соответственно, роста цен и масштабов их роста.
Пример 3.
Рассматриваем случай П. Фактическая фьючерсная цена равна 109 долл. Арбитражер продает фьючерс, занимает 134,565 долл, на 60 дней под 5% годовых, покупает облигацию на спотовом рынке и хранит ее до момента истечения контракта. По кредиту он должен будет вернуть сумму 135,686 долл.
Пусть котировочная фьючерсная цена упала 108 долл. Арбитражер получает по контракту за облигацию:
108<)шл. -1,23 + 1,758ск?лл. = 134,598сЫл.
Он продавал контракт по цене 109 долл. Котировочная цена составила 108 долл. Поэтому за период действия контракта была получена положительная маржа в сумме:
109-108 = 1долл.
Прибыль в расчете на 100 долл, номинала облигации равна:
134,598 -135,686 +1 = -0,088долл.
Общая сумма прибыли по контракту составляет:
-0,088Эолл. 1000- -Шолл.
Таким образом, был получен убыток в 88 долл.
5 Если бы в примере коэффициент конверсии был меньше единицы, то при росте цены арбитражер получал бы большую прибыль, так как цена поставки увеличивалась бы в меньшей пропорции чем размер вариационной маржи
Отмеченный риск совершения арбитражной операции в данном примере наблюдается только в случае падения котировочной цены облигации. В случае ее роста он отсутствует. Чем больше вырастет цена, тем большая прибыль будет получена. Поскольку риск связан с падением цены облигации, то, начиная арбитражную операцию, целесообразно оценить вероятность последующего роста процентных ставок на рынке и, соответственно, падения цен и масштабов их снижения.
5.2.2. Определение фьючерсной цены облигации, по которой выплачиваются купоны в течение действия контракта
Пример 4.
фьючерсный контракт на облигацию истекает через 210 дней (т.е. через 210 дней будет поставлена облигация). По контракту поставляется облигация, котировка которой сейчас равна 134-04, купон 8%, выплачивается два раза в год. Предыдущий купон был выплачен 20 дней назад, следующий купон будет выплачен через 162 дня (см. рис. 5.2). Продолжительность текущего купонного периода 182 дня, следующего купонного периода - 184 дня. Коэффициент конверсии равен 1,23. Ставка без риска для 210 дней равна 5% годовых, для 162 дней 4,85% годовых. Определить фьючерсную цену облигации.
выплата купона
выплата
4—20 дней-
162 дня
купона
---**— 48 дня
210 дней
момент момент
заключения окончания
контракта контракта
Рис. 5.2. В течение действия контракта купон выплачивается
В данном примере по облигации выплачивается купон в течение периода действия контракта. Поэтому воспользуемся формулой определения форвардной цены актива, по которому выплачиваются доходы.
Как было определено в примере 1, чистая цена облигации равна 134,125 долл. За 20 дней, прошедших после выплаты последнего купона, накопилась сумма купонного процента в 0,44 долл. Полная
цена облигации составляет 134,565 долл. За период действия контракта данная сумма на безрисковом депозите вырастет до:
134,565 1 + 0,05
210>
360;
138,49долл.
Через 162 дня будет выплачен купон, величина которого равна: ЮОдолл. 0,04 = 4долл.
После выплаты купона до истечения контракта остается еще:
210-162 - 48^w.
Форвардная ставка для периода в 48 дней через 162 дня равна:
1 + 0,05(210/360) _ Л 360
1 + 0,0485(162/360) J 48
За 48 дней на 4 долл, по форвардной ставке можно получить сумму:
4 1 + 0,0539
48
360
= 4,029долл.
Полная фьючерсная цена облигации с купоном 8% равна:
138,49-4,029 = 134,461да?л.
За 48 дней, остающихся до истечения контракта с момента выплаты следующего купона, по облигации будет начислена сумма купонного процента:
48 100долл.0,04------ 1,043долл.
184
Чистая фьючерсная цена 8%-й облигации равна:
134,461-1,043= 133,418долл.
Поскольку коэффициент конверсии для 8%-й облигации составляет 1,23, то фьючерсная цена облигации с доходностью до погашения 6% равна:
133,418:1,23 = 108,47долл.
В общем виде формулу определения фьючерсной цены можно записать как:
Р
F = —
, Т-'Л .Vе
ф база* ) 2 V база J ,
--------------------, Э.В
т
\база
2
где Р - полная цена “самой дешевой облигации” на день заключения контракта;
Т - период действия контракта;
ti - количество дней с момента расчета фьючерсной цены до момента выплаты купона в рамках действия контракта;
rf - ставка спот для периода Т.
гф - форвардная ставка для периода Т - г(.
Вместо формулы (5.8) для расчета фьючерсной цены можно воспользоваться аналогом формулы (2.16):
F =
Т } ус[т->Г база* ) 2 база j
(5-9)
где D - приведенная к моменту расчета фьючерсной цены стоимость купона, который выплачивается в ходе действия контракта; в качестве ставки дисконтирования используется ставка спот для периода .
В нашем примере величина D равна:
Лдолл.
D =---------т—:------г = 3,9146 дай.
1 + 0,0485(162/360)
Фьючерсная цена облигации согласно формуле (5.9) составляет:
(134,565-3,914б/ 1 + 0,05--Х100°-—^21° 162 *
_____________\ 360 J 2
1,23
184
= 108,47да7л
Если фактическая цена контракта отличается от рассчитанного уровня, то можно совершить арбитражную операцию. Рассмотрим технику арбитражной операции на основе условий примера 4 для случаев недооценки и переоценки фьючерсного контракта.
I. Пусть фактическая фьючерсная цена равна 108 долл. Тогда инвестор покупает контракт, занимает облигацию и продает. Поскольку на облигацию выплачивается купон, то арбитражер должен будет выплатить его владельцу бумаги. Поэтому сумму 134,565, полученную от продажи бумаги, он делит на две части: 3,9146 долл, (это дисконтированная стоимость будущего купона) и:
134,565 - 3,9146 = 130,6504долл.
Первую сумму он размещает под 4,85% на 162 дня, получает в конце этого периода 4 долл, и за счет них выплачивает владельцу облигации купон. Вторую сумму размещает под 5% до момента истечения контракта. Через 210 дней получает сумму:
( 210
130,6504 1 + 0,05 —
360)
= 134,46 Id олл.
Рассмотрим три варианта конъюнктуры на рынке к моменту истечения контракта.
а) Котировочная фьючерсная цена равна 108 долл. Тогда в соответствии с формулой (5.1) арбитражер уплачивает по контракту цену:
108дши. 1,23 +1,0433олл. = 133,8833олл.,
получает облигацию и возвращает ее кредитору. Его прибыль в расчете на 100 долл, номинала облигации равна разности между суммой по депозиту и уплаченной за облигацию по контракту:
134,461 -133,883 - 0,578долл.
Общая прибыль по контракту составляет:
0,578долл. • 1000 = 5783аял.
б) Котировочная фьючерсная цена равна 108,5 долл. Арбитражер уплачивает по контракту цену:
108,5долл. 1,23 + 1,043Эолл. = 134,4983олл
получает облигацию и возвращает ее кредитору.
Он покупал контракт по цене 108 долл. Котировочная цена составила 108,5 долл. Поэтому за период действия контракта была получена положительная маржа в сумме:
108,5-108 = 0,53олл.
Прибыль в расчете на 100 долл, номинала облигации равна:
134,461 -134,498 + 0,5 - 0,463долл.
Общая сумма прибыли по контракту составляет:
0,463долл. ’ 1000 = 463долл.
в) Котировочная фьючерсная цена равна 107,5 долл. Арбитражер уплачивает по контракту цену:
107,5долл.-1,23 + 1,043долл. - 133,268долл,, получает облигацию и возвращает ее кредитору.
Он покупал контракт по цене 108 долл. Котировочная составила 107,5 долл. Поэтому за период действия контракта была получена отрицательная маржа в сумме:
107,5-108 =-0,5долл.
Прибыль в расчете на 100 долл, номинала облигации равна:
134,461 -133,268 - 0,5 = 0,693долл.
Общая сумма прибыли по контракту составляет:
0,69 Здолл. 1 000 = 693да7,7.
II. Пусть фактическая фьючерсная цена равна 109 долл. Тогда инвестор продает контракт, занимает сумму 134,565 долл, и покупает облигацию. Поскольку на облигацию выплачивается купон, то арбитражер занимает данную сумму двумя частями: 3,9146 долл, (дисконтированная стоимость будущего купона) на 162 дня и 130,6504 долл, на 210 дней. Через 162 дня получает платеж по купону и возвращает первую часть кредита. По второму кредиту он должен вернуть на момент окончания контракта сумму:
130,6504| 1 + 0,05 — I = 134,461долл.
I 360 )
Рассмотрим три варианта конъюнктуры на рынке к моменту истечения контракта.
а) Котировочная фьючерсная цена равна 109 долл. Арбитражер поставляет по контракту облигацию, в соответствии с формулой (5.1) получает сумму:
109<Ълл. -1,23 + 1,04 Здолл. = 135,11 Здолл.
и возвращает кредит. Прибыль в расчете на 100 долл, номинала облигации равна:
135,113 -134,461 - 0,652долл.
Общая прибыль по контракту составляет:
0,652долл. -1000 = 652долл.
б) Котировочная фьючерсная цена равна 109,5 долл. Арбитражер поставляет по контракту облигацию, получает сумму:
109б)олл. 1,23 + 1,043долл. = 135,728долл.
и отдает кредит.
Он продавал контракт по цене 109 долл. Котировочная цена составила 109,5 долл. Поэтому за период действия контракта была получена отрицательная маржа в размере:
109 -109,5- -0,5долл.
Прибыль в расчете на 100 долл, номинала облигации равна:
135,728 -134,461 - 0,5 = 6,767долл.
Общая сумма прибыли по контракту составляет:
OJ 67 долл. 1000 = 767долл.
в) Котировочная фьючерсная цена равна 108,5 долл. Арбитражер поставляет по контракту облигацию, получает сумму:
108,5е)шл. 1,23 + 1,043долл. = 134,498Эолл.
и отдает кредит.
Он продавал контракт по цене 109 долл. Котировочная цена составила 108,5 долл. Поэтому за период действия контракта была получена положительная маржа в размере:
109 -108,5 = 0,5долл.
Прибыль в расчете на 100 долл, номинала облигации равна:
134,498 -134,461 + 0,5 - 0,537долл.
Общая сумма прибыли по контракту составляет:
0,537долл.-1000 = 537долл.
Планируя арбитражную операцию, как и в примере 1 следует не забывать, что в случае недооценки стоимости фьючерсного контракта можно получить убыток при дальнейшем росте котировочной цены (падении ставок). В то же время при ее падении (росте ставок) прибыль будет возрастать.
В случае переоцененности фьючерсного контракта можно получить убыток при дальнейшем падении котировочной цены (росте ставок). В то же время при ее росте (падении ставок) прибыль будет возрастать.6
Для фьючерсного контракта на облигацию существует понятие базиса. Для каждой облигации, которая может быть поставлена по контракту, существует коэффициент конверсии. Он связывает спотовую цену (р) данной облигации с соответствующей ей фьючерсной ценой (pj по формуле:
6 Противоположная тенденция будет наблюдаться, если коэффициент конверсии облигации меньше единицы
Базис можно определить как:
базис - Р - Fp.
Спотовую цену \ соответствующую данной теоретической фьючерсной цене (f) можно рассчитать по формуле:
R - FK. г
Поэтому базис также можно определить как:
базис = Pr- F.
5.2.3. Расчет коэффициента конверсии казначейской облигации
При определении коэффициента конверсии казначейской облигации остающийся период до погашения облигации округляется в меньшую сторону до целых трех месяцев. Например, до погашения бумаги 15 лет и два месяца. В этом случае для расчетных целей время до погашения принимается равным 15 годам. Если до погашения 15 лет и 4 месяца, время погашения считается равным 15 годам и 3 месяцам. По облигации доход по купону выплачивается два раза в год. Однако, если после округления время до погашения облигации не разбивается на целые 6-месячные периоды, а остается еще три месяца, то считается, что первый купон такой облигации выплачивается через три месяца. Приведем расчет коэффициента конверсии на примерах.
Пример 1.
Номинал облигации 100 тыс. долл,, купон 10%, выплачивается два раза в год, бумага погашается через 15 лет и 2 месяца. После округления период до погашения облигации принимается равным 15 годам.
Чтобы облигация приносила инвестору доходность равную 6% она должна стоить:
!«“ J, „0000 - . > 39200.90,™.
0,06 0,06 ) (1 + 0,03)
Делим данную цену на номинал облигации и получаем коэффициент конверсии 1,392.
Пример 2.
Номинал облигации 100 тыс. долл., купон 10%, выплачивается два раза в год, бумага погашается через 15 лет и 4 месяца. После
округления период до погашения облигации принимается равным 15 годам и трем месяцам. Вначале определяют цену облигации в конце трехмесячного периода, т.е. как если бы до погашения бумаги оставалось 15 лет. Как и в примере 1 данная цена равна 139200,9 долл. После этого полученную сумму с шестимесячным купоном, выплаченным в этот момент, дисконтируют под ставку процента, которая соответствует трехмесячному периоду (ставка равна 7^03 -1 = 0,014889):
(139200,9 + 5000) / 1,014889 = 142085,4долл.
Изданной цифры вычитаем сумму купонного процента за три месяца
( юооо-3 Y ---------= 2500оао .
12
142085,4 - 2500 = 139585,4г)олл.
Результат делим на номинал и получаем коэффициент конверсии 1,395854.
5.3. ХЕДЖИРОВАНИЕ ФЬЮЧЕРСНЫМ КОНТРАКТОМ НА ОБЛИГАЦИЮ
Страхование облигаций фьючерсом на облигацию осуществляют с использованием показателя дюрации. Изменение цены хеджируемой облигации при небольшом изменении ее доходности до погашения определяется по формуле:
ДР = -От/7.р-Дгг , (5.10)
где Dmp - модифицированная дюрация хеджируемой облигации;
Р - цена спот облигации;
гр - доходность до погашения облигации.
Изменение цены фьючерсного контракта при небольшом изменении доходности до погашения самой дешевой облигации определяется по формуле:
\F = -DmFF\rF , (5.11)
где DmF - модифицированная дюрация фьючерсного контракта;
F - фьючерсная цена;
rF - доходность до погашения самой дешевой облигации.
Как известно, коэффициент хеджирования равен:
Отсюда:
Д/\
АЛ1 Dmr-F^rF
(5-12)
Формулу (5.12) можно упростить, если допустить, что кривые доходности “самой дешевой” и хеджируемой облигаций сдвигаются параллельно на одну величину при изменении конъюнктуры рынка. Тогда она примет вид:
(5-13)
Формулы (5.12) или (5.13) следует использовать в случае, когда хеджируемая облигация не является “самой дешевой”. Если инвестор страхует позицию по “самой дешевой” облигации, то коэффициент хеджирования равен просто коэффициенту конверсии. Данный вывод можно получить дифференцированием формулы (5.6) или (5.8) по Р:
dF _ 1 4 Г^/база *)
dP К
или, опуская величину г
поскольку она является малой,
dF
(5-14)
Величина — в формуле (5.14) представляет собой не что иное как
dF
коэффициент хеджирования.
С учетом коэффициента хеджирования количество фьючерсных контрактов, которые необходимо открыть при страховании спотовой позиции по облигации, определяется по формуле:
количество
, хеджируемая сумма ,
фьючерсных -----------------—--------------------— н. (0.1 OJ
номинал фьючерсного иена самой дешевой контрактов контракта облигации
В формуле (5.15) цена самой дешевой облигации указывается в десятичных значениях от номинала в 100 процентов. Так, если цена облигации равна 95 долл., то в формулу следует подставить значение 0,95.
Пример.
Инвестор планирует получить через три месяца 1 млн. долл, и купить облигации, которые не являются “самыми дешевыми” для поставки по фьючерсному контракту на 6-процентную 15-летнюю облигацию номиналом 100 тыс. долл. Цена спот данных облигаций равна 95,125 долл., цена спот “самой дешевой” облигации - 95 долл., фьючерсная цена - 94,25. Модифицированная дюрация облигации составляет 11 лет, фьючерсного контракта - 9,8 года. Предполагается, что кривые доходности сдвигаются параллельно при изменении конъюнктуры. Определить количество фьючерсных контрактов, которые необходимо открыть.
Решение.
Коэффициент хеджирования равен:
Л=-'95,125 =1,1329.
9,8-94,25
Следует купить:
ЮОООООаолл. л
-------------— 1,1329 = 11,9 или 12 контрактов.
100000да7Л.0,95
При расчете коэффициента хеджирования необходимо определить, какая облигация будет “самой дешевой”. Если конъюнктура изменится, то скорее всего изменится и выбор “самой дешевой” облигации. Это потребует корректировки хеджа.
5.4. ХЕДЖИРОВАНИЕ ПОРТФЕЛЯ ОБЛИГАЦИЙ
Показатель дюрации используют для хеджирования портфеля облигаций. Коэффициент хеджирования можно рассчитать по формулам (5.12) или (5.13). В этом случае D - это дюрация портфеля облигаций. Она определяется как средневзвешенная дюрация облигаций, входящих в портфель. Р - это средневзвешенная цена облигаций в портфеле. Количество фьючерсных контрактов рассчитывается по формуле (5.15).
5.5. ДЮРАЦИЯ ФЬЮЧЕРСНОГО КОНТРАКТА
В формулах (5.12) и (5.13) присутствует показатель дюрации фьючерсного контракта. О дюрации фьючерсного контракта можно
говорить на основе его связи с “самой дешевой” облигацией. Как известно, модифицированная дюрация облигации определяется по формуле:
1
D"‘ Р dr
(5.16)
где Р - цена облигации;
г - доходность до погашения облигации.
По аналогии с формулой (5.16) можно определить дюрацию фьючерсного контракта на основе “самой дешевой” облигации как:
В,*
Найдем на основе формулы (5.6) величину —— , которая представав
ляет собой производную фьючерсной цены по доходности до погашения (у>) “самой дешевой” облигации:
dF 1 Г dP (, Т У D dr Т
---= — ----- 1-Ы-----7 + ' ~~-----7
drF К drF оаза J drF база J
ИЛИ
dF pF 1 dP (, Т \ dr Т
— = —------------1 + *---------г •
drF К Р drF база* J drF база*
(5.18)
1 dP
В формуле (5.18) величина----- = -Dm , поэтому:
Р drF
Т \ dr Т
------ ч-----------—
база ) drF база
^L.L _Dj drF К
где Dm - дюрация “самой дешевой” облигации.
dF
Подставим значение — в формулу (5.17):
drF
m
(5.19)
ИЛИ
DmF=~
т
dr T
база*J drF база
В-
К F
1 Р
база* )
dr____Т_
drr база*
(5.20)
Формула (5.20) рассчитана на основе формулы (5.6), т.е. для случая, когда по облигации купоны не выплачиваются в течение периода действия фьючерсного контракта. Если купоны выплачивают-dF ся, то для расчета дюрации следует определить величину — на drk основе формулы (5.8) или (5.9).
При использовании показателя дюрации для хеджирования спотовой позиции по облигации в формулах (5.12) и (5.13) можно вместо дюрации фьючерсного контракта взять дюрацию самой дешевой облигации. Погрешность в расчетах не будет существенной, поскольку сама методика определения коэффициента хеджирования с помощью дюрации не является точной. Как известно, дюрация является линейным приближением изменения цены облигации при изменении ее доходности до погашения. В случае значительного изменения процентной ставки ее использование приводит к погрешности, и необходимо корректировать хедж. Для упрощения расчетов часто полагают параллельность смещения кривых доходностей процентных ставок, т.е. используют формулу (5.13). На практике отношение —- скорее всего будет отличным от единицы. Как Дг,
правило, в формуле (5.20) сложно точно предсказать, как изменится
dr
отношение — при изменении процентных ставок, поскольку г - это dr;
краткосрочная процентная ставка, a rF - долгосрочная. Между ними не наблюдается большой корреляции. Кроме того, они могут изменяться даже в противоположных направлениях.
5.6. УПРАВЛЕНИЕ ПОРТФЕЛЕМ ОБЛИГАЦИЙ С ПОМОЩЬЮ ФЬЮЧЕРСНОГО КОНТРАКТА
Изменять состав портфеля облигаций можно с помощью фьючерса на облигацию. Допустим, модифицированная дюрация портфеля инвестора равна Dml. Он хотел бы изменить состав портфеля таким образом, чтобы его дюрация составила Dm2. В соответствии с формулой (3.12) запишем:
D,P&r = D . P &r + h D F F-&rF. (5.21)
Отсюда:
P(O2-Oj Ar
LCF '
(5.22)
Количество контрактов, которые необходимо открыть, определяется по формуле (5.15).
Облигации могут составлять только часть портфеля. Допустим, уд. вес облигаций в портфеле с дюрацией Dml равен . Инвестор хотел бы получить портфель, в котором уд. вес облигаций составлял бы в2, а дюрация - Dm2. В соответствии с формулой (3.12) запишем:
в2 D P &r = 0-D-P'&r + h Dm> (5.23)
z m2 I гл I ffir r \ /
Отсюда:
, p(e,D ,-PD ,) Ar
h = V m2------|_жи---- (5 24)
D fF &rF
Количество контрактов, которые необходимо купить, определяется по формуле:
количество стоимость портфеля (5 25)
контрактов стоимость фьючерсного контракта
Используя формулы (4.15) и (5.24) инвестор может одновременно изменять уд. веса акций и облигаций в портфеле с помощью фьючерсных контрактов на фондовый индекс и облигацию.
5.7. ФЬЮЧЕРСНЫЙ КОНТРАКТ НА ТРЕХМЕСЯЧНЫЙ ЕВРОДОЛЛАРОВЫЙ ДЕПОЗИТ
Рассмотрим краткосрочный процентный фьючерс на примере фьючерсного контракта на евродоллар. Контракт торгуется на Чикагской Товарной Бирже (СМЕ) с 1981 г. По объему торговли в настоящее время он занимает первое место в мире среди фьючерсных контрактов. Поэтому остановимся на его характеристике более подробно.
5.7.1. Общая характеристика контракта на трехмесячный евродолларовый депозит
Базисным активом контракта является трехмесячный (90 дней) пиродолларовый депозит, т.е. депозит в долл. США, открытый в бан
ке за пределами Соединенных Штатов7. Номинал контракта равен 1 млн. долл. Контракт котируется на базе индексной цены, которая определяется как:
Fk -100(1 -rj, (5.26)
где гф - ожидаемое значение ставки по депозиту, выраженное в процентах, на дату истечения контракта, т.е. форвардная ставка для трехмесячного депозита, который начинается с момента истечения срока действия контракта;
Fk - котировка фьючерсного контракта.
Например, доходность по депозиту ожидается на уровне 10% годовых. Тогда котировка фьючерсного контракта равна:
100-10 = 90%.
В формуле (5.26) значение гф дается в расчете на год. В то же время евродолларовый депозит является трехмесячным. Поэтому цена фьючерсного контракта определяется по формуле:
F = 10000[100 - 0,25(100 - Aj] (5.27)
Так, для фьючерсной котировки в 90% цена контракта составит:
10000(100 - 0,25(100 - 90)] = 975000долл.
Минимальное изменение цены контракта (шаг цены) составляет один базисный пункт, т.е. 0,01%. Цена одного базисного пункта для фьючерсного контракта составляет 25 долл., т.е.:8
90
1000000 долл. - 0,0001 —- = 25 долл.
360
По завершении периода обращения контракта определяется фактическая трехмесячная ставка LIBOR9 по евродолларовому
7 Изначально депозиты в долларах размещались в европейских банках, что и вызвало к жизни определение евродоллар. В современных условиях они могут размещаться и в других странах за пределами США, однако название евродоллар сохраняется.
8 Для ближайших месяцев (со 2 по 10) минимальное изменение цены может составлять 0,005%, т.е. 12,5 долл., а для последнего торгового месяца - 0,0025%, т.е. 6,25 долл.
9 LIBOR (London Inierbank Offered Rate) - ставка, по которой банки предоставляют средства на межбанковском лондонском рынке ведущим банкам, т.е. это ставка предложения денег.
LIBID (London Interbank Bid Rate) - ставка, по которой ведущие банки готовы занять средства на межбанковском лондонском рынке, т.е. это ставка спроса на заемные средства.
депозиту, который начинает действовать с момента его истечения. На основе формулы:
100 - г, где г - ставка ло трехмесячному депозиту, - рассчитывается котировочная цена. Например, на момент истечения контракта фактическая ставка по трехмесячному депозиту определена как 9%. Это означает, что котировочная фьючерсная цена равна:
100-9-91%.
Ставка L1BOR рассчитывается Британской Банковской Ассоциацией (British Bankers Association) на основе данных по ставкам, которые она получает от банков, включенных в соответствующий список.10
Контракт является расчетным. Контракты предлагаются с истечением вплоть до десяти лет вперед. Например, контракт с истечением 16 июня 2014 г. торгуется на бирже с 14 июня 2004 г. Торгуются контракты в так называемом мартовском цикле, т.е. с истечением в марте, июне, сентябре и декабре. В мартовском цикле торгуется 40 контрактов с истечением в указанные месяцы, а также контракты для четырех ближайших месяцев. Последним торговым днем считается второй рабочий лондонский банковский день перед третьей средой месяца поставки. Код контракта на СМЕ представлен буквами ED. Например, мартовский контракт с истечением 17 марта 2008 г. имеет код EDH8, где ED относится к контракту, Н обозначает месяц март, цифра 8 - 2008 год. В системе GLOBEX код контракта GE.
Контракт на евродоллроый депозит торгуется также на Сингапурской международной валютной биржей (Singapore International Monetary Exchange - (SIMEX)).11
С марта 2004 г. контракт на трехмесячный евродолларовый депозит также торгуется на бирже Euronext.life в системе электронной торговли LIFFE CONNECT. Контракт торгуется также в мартовском цикле, т.е. с поставкой в марте, июне, сентябре и декабре. В мартов
10 Ставка рассчитывается ежедневно на 11.00 лондонского времени.
11 В 1984 г. Чикагская товарная биржа вместе с Сингапурской международной валютной биржей основали совместную клиринговую систему MOS (Mutual Offset System). MOS позволяет открывать контракты на евродолларовый депозит на одной бирже, а закрывать на другой. В результате торговля контрактом может осуществляться круглые сутки. Аналогично через систему MOS на СМЕ и S1MEX торгуется контракт на грехмесячный депозит в евройенах.
ском цикле торгуется 24 контракта с истечением в указанные месяцы, а также контракты для четырех ближайших месяцев. Минимальное изменение цены контракта (шаг цены) составляет 0,005%, что соответствует 12,5 долларам. Последний торговый день определен также как и на СМЕ.
Контракт можно использовать для извлечения спекулятивной прибыли в связи с прогнозами изменения краткосрочной процентной ставки. Если ожидается падение процентной ставки, т.е. рост фьючерсной цены, то следует купить контракт. Если ожидается рост процентной ставки, т.е. падение фьючерсной цены, следует продать фьючерс.
Пример.
Котировка фьючерсного контракта на трехмесячный евродолларовый депозит равна 90%. Спекулянт ожидает падения процентных ставок и покупает фьючерс. Через три дня форвардная ставка по евродолларовому депозиту упала, и фьючерсная котировка составила 92%. Определить финансовый результат для спекулянта.
Решение.
Котировка фьючерсной цены изменилась на 2%. Разделим эту цифру на шаг цены:
2 ----= 200 шагов. 0,01
Каждому шагу цены соответствует изменение цены контракта на 25 долл. Поэтому выигрыш спекулянта равен:
25 долл.- 200 = 500()долл.
Выигрыш по контракту можно определить и другим способом.
Цена контракта в момент его открытия в соответствии с формулой (5.27) составляла:
10000[100 - 0,25(100 - 90)] = 975000долл.
В последующем она выросла до:
10000[100 - 0,25(100 - 92)] = 980000долл.
Спекулянт выиграл:
980000 - 975000 = 5000долл.
Для контракта существует понятие базиса. Он определяется как разность между фьючерсной ценой, которая соответствует текущей трехме
сячной спотовой ставке L1BOR и фактической фьючерсной ценой, т.е. котировкой фьючерсного контракта.
Пример.
Котировка фьючерсного контракта на трехмесячный евродолларовый депозит равна 90%. Текущая ставка LIBOR составляет 9%. Ей соответствует фьючерсная цена:
100-9 = 91.
Базис равен:
91-90= 1%.
5.7.2. Определение фьючерсной цены контракта и арбитраж
Фьючерсная котировка представляет собой оценку форвардной ставки для трехмесячного периода, который начнется по завершении периода обращения фьючерсного контракта. Поэтому фьючерсную цену можно определить на основе расчета форвардной ставки.12
Пример.
В настоящий момент трехмесячная ставка LIBOR равна 1,8%, шестимесячная ставка -1,99%. Определить теоретическую фьючерсную цену фьючерса на евродоллар, который истекает через три месяца.
Решение.
Теоретическая форвардная ставка равна:
^1+0,0199(180/360) УзбО 0021?
ч 1 + 0,018(90/360) ) 90
Теоретическая фьючерсная цена составляет:
100 - 2,17 = 97,83.
На практике инвестору доступны фактические цены фьючерсного контракта. Сравнивая их с теоретической, можно сделать вывод о недооценке или переоценке контракта рынком. Допустим, фактическая фьючерсная цена равна 97,80. Это говорит о том, что фьючерс
|; Определение и технику расчета форвардной ставки см. в книгах А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов”, М., 2002, глава 6 и "Управление портфелем ценных бумаг”, М., 2005, параграф 5.1.1.6.
ный контракт недооценен, так как его цена предполагает более высокую ставку доходности:
100-97,80 = 2,2%,
чем теоретическая фьючерсная цена.
Если фактическая фьючерсная цена выше теоретической, то фьючерс переоценен, так как его ставка доходности ниже теоретической форвардной ставки, определяющей теоретическую фьючерсную цену
Знание теоретической фьючерсной цены позволяет принять решение о покупке или продаже контракта, а также относительно возможностей совершения арбитражной операции. Однако в последнем случае необходимо учесть следующий момент. На практике ставки спот даются как котировки покупателя и продавца, т.е. L1BID и LIBOR. В результате, на их основе следует рассчитать две форвардные ставки, которые позволят определить возможные границы фьючерсной цены контракта в целях совершения арбитражной операции. Если котировка фьючерса выходит за эти границы, то арбитраж возможен. Рассмотрим пример.
Пример 1.
Конъюнктура процентных ставок представлена следующей таб-
лицей:
LIBID (%) LIBOR (%)
3 месяца 1,8 1,85
6 месяцев 1,99 2,04
9 месяцев 2,15 2,19
Рассчитать пограничные форвардные ставки и котировки фьючерсного контракта.
Решение.
Трехмесячный фьючерс служит для того, чтобы обеспечить инвестору в будущем по депозиту процентную ставку, соответствующую цене контракта. В то же время данную ставку можно получить за счет использования спотовых ставок LIBOR и LIBID. Для этого сегодня необходимо занять деньги на три месяца под трехмесячную ставку LIBOR и разместить их на шестимесячном депозите под ставку LTBID. Форвардная ставка, которую в этом случае обеспечит себе инвестор по депозиту, равна13:
13 Более подробно о технике совершения подобной операции см в книге А.Н.Буренина “Управление портфелем ценных бумаг", М , 2005, параграф 5116
г1 +0,0199(180/360) ч 1 + 0,0185(90/360)
-1 I—= 0,021202 или 2,12%.
) 90
Если инвестор в будущем планирует занять деньги, то он может обеспечить себе в будущем ставку равную форвардной за счет использования спотовых ставок следующим образом. Он займет сейчас средства на шесть месяцев под ставку LIBOR и разместит их на три месяца под ставку L1BID, гарантируя себе в будущем заимствование средств под ставку14:
Л 1 + 0,0204(180/360) /360 ч 1+0,018(90/360) ) 90
= 0,022698 или 2,27%.
Таким образом, в условиях представленной конъюнктуры ставок LIBOR и L1B1D, котировка фьючерсного контракта должна находится в границах 97,88-97,73, в противном случае можно совершить арбитражную операцию. В данном примере фьючерсной цене 97,73 соответствует ставка 2,27%. Поэтому, если фактическая фьючерсная цена окажется ниже значения 97,73, то ей будет соответствовать более высокая ставка, которую в будущем сможет обеспечить себе арбитражер по депозиту. Фьючерсной цене 97,88 соответствует ставка 2,12%. Если фактическая фьючерсная цена будет выше, этого значения, то арбитражер сможет обеспечить себе в будущем более низкую ставку по кредиту. Рассмотрим технику совершения операций на примерах.
Пример 2. (Сохраняются условия примера 1)
Пусть котировка трехмесячного фьючерса составляет 97,70. Она ниже нижней теоретической фьючерсной цены, т.е. фьючерс недооценен. Трехмесячная форвардная ставка, соответствующая котировке контракта, равна:
100-97,70 = 2,3%.
Она выше форвардной ставки, определяемой ставками спот, поэтому можно совершить арбитражную операцию. Суть ее состоит в следующем. Согласно рассчитанной форвардной ставке, инвестор может обеспечить себе заимствование средств через три месяца на три месяца под 2,27%. В то же время текущая котировка фьючерсного контракта позволяет обеспечить размещение средств через три месяца на три месяца под более высокую ставку 2,3%. В связи с этим
14 См. сноску 13.
арбитражер может занять деньги под 2,27% и разместить их под 2,3%. Разница в ставках даст арбитражную прибыль. Действия арбитражера сводятся к следующему. Он занимает 1 млн. долл, на шесть месяцев под ставку LIBOR 2,04%, размещает их на трехмесячный депозит под ставку LIBID 1,8% и покупает15 трехмесячный фьючерс по цене 97,70.
Через три месяца по депозиту получает сумму:
90
1000000(1 + 0,018—) - 1004500руб.
Рассмотрим два сценария развития ситуации на рынке через три месяца, т.е. случаи, когда процентные ставки выросли и когда упали.
а) Пусть через три месяца трехмесячная ставка L1BOR в день истечения контракта составила 2,34%. Следовательно котировка фьючерса равна:
100-2,34 = 97,66.
Котировка по сравнению с моментом покупки упала на:
97,70-97,66 = 0,04.
ИЛИ
0,04 л
------- 4 шага.
0,01 -
Проигрыш по контракту составляет:
25<)о.7л.'4- ЮОдолл.
Проигрыш покрывается за счет суммы, полученной по трехмесячно-
му депозиту. Оставшаяся сумма:
1004500 -100 = 1004400да7л.
размещается на трехмесячный депозит под ставку 2,34%. Еще через
три месяца арбитражер получает по депозиту сумму:
( 90
1004400 1 + 0,0234---- = 1010276долл.
I 360
По шестимесячному кредиту он возвращает сумму:
/ 180^
1000000 1+0,0204----
360)
- 1010200да7л,
15 Арбитражер покупает фьючерс, так как через три месяца он будет размещать день ги на депозите и поэтому страхуется от падения процентных ставок
Арбитражная прибыль равна:
1010276 -1010200 = Убдолл.
б) Пусть трехмесячная ставка LIBOR в день истечения контракта через три месяца составила 2,26%. Следовательно котировка фьючерса равна:
100-2,26 = 97,74.
По сравнению с моментом покупки котировка выросла на:
97,74-97,70 = 0,04.
или
°’04 л ----— 4 шага.
0,01
Выигрыш по контракту составляет:
25долл.’^ = ЮОдолл.
Данная сумма вместе с суммой, полученной по трехмесячному депозиту, размещается на трехмесячный депозит под ставку 2,26%. Еще через три месяца арбитражер получает по депозиту:
/ / 90
(1004500 +1001 1 + 0,0226— \ 360)
По шестимесячному кредиту он возвращает:
lOOOOOof 1 + 0,0204—
360)
Арбитражная прибыль равна:
1010276-1010200 = 76долл.
= 10102760олл.
= 1010200Эолл.
В приведенном примере после истечения фьючерсного контракта арбитражер размещал средства под ставку LIBOR. Однако, поскольку ио ставка предложения денег, то более реальной будет ситуация, когда ему удастся разместить средства только под ставку LIBID. Из таблицы < гаиок следует, что спрэд между трехмесячными и шестимесячными мамами LIBID и LIBOR составляет 0,05%. Поэтому арбитражеру уднмся разместить средства в первой ситуации под:
2,34-0,05 = 2,29%.
Й результате по трехмесячному депозиту он получит сумму:
1004400 1 + 0,0229--
360)
1010150долл.
По шестимесячному кредиту должен отдать:
1000000 1 + 0,0204
180Л
360;
= 1010200 долл.
Поэтому операция принесет убыток в 50 долл. Однако, если в целях совершения арбитражной операции определить теоретическую границу фьючерсной цены с учетом корректировки на спрэд ставок LIBOR и LIBID как:
97,73-0,05 = 97,68,
то это будет котировка фьючерсного контракта при которой арбитражер получит нулевую прибыль. Покажем это на цифрах.
Пусть инвестор купил фьючерс по цене 97,68 и взял кредит под 2,04%. Трехмесячная ставка LIBOR в день истечения контракта через три месяца составила 2,34%, и котировка фьючерса равна:
100-2,34 = 97,66.
Котировка по сравнению с моментом покупки упала на:
97,68-97,66 = 0,02
или
0,02
0,01
шага.
Проигрыш по контракту составил:
25дшл/2 = 50долл.
Проигрыш был покрыт за счет суммы, полученной по трехмесячном, депозиту. Оставшаяся сумма:
1004500-50 = 1004450Эолл.
была размещена на трехмесячном депозите под ставку LIBID:
2,34-0,05 = 2,29%,
Через три месяца арбитражер получил по депозиту:
( 90
1004450 1 + 0,0229--- = 1010200Эолл.
I 360)
По шестимесячному кредиту он должен вернуть:
1000000 1 + 0,0204
180 >
360)
=10102003г?™.
Таким образом, арбитражная прибыль равна нулю. Арбитражная прибыль будет положительна в том случае, если фьючерсная цена контракта в момент его заключения была ниже границы в 97,68.
Аналогично во второй ситуации, когда ставка LIBOR была определена на уровне 2,26%, арбитражер сможет разместить средства под ставку LIBID:
2,26- 0,05 - 2,21%
Тогда сумма по депозиту составит:
, / 90 Л
(1004500 + 1001 1 + 0,0221- = 10101503оо.
v \ 360)
а вернуть по кредиту следует 1010200 долл. Проигрыш по операции равен 50 долл. Однако, если котировка фьючерса была равна 97,68, то по сравнению с моментом покупки она выросла на : 97,74-97,68 = 0,06
или
0,06 ,
------- о шагов, 0,01
Выигрыш по контракту равен:
25доллгб = 1503а™.
(1004500+150
Длнная сумма вместе с суммой, полученной по трехмесячному депо-ину, размещается на трехмесячный депозит под ставку 2,21%. Еще чг^рез три месяца арбитражер получает по депозиту сумму:
90 А
1 + 0,0221— = 10102013а™.
360 J
Арбитражная прибыль практически равна нулю. Однако, если котировка контракта будет ниже уровня в 97,68, то арбитражер получит прибыль.
Таким образом для целей определения теоретической границы фьючерсной цены, соответствующей форвардной ставке по кредиту, необходимо рассчитать форвардную ставку по кредиту на основе спото-ёы* < швок LIBOR и LIBID и прибавить к ней предполагаемый спрэд Мв*ду ставками. После вычитания из 100 данной ставки получим грани
цу фьючерсной цены. В нашем примере форвардная ставка по кредиту составила 2,27%. Прибавим к ней спрэд в 0,05%:
2,27 + 0,05 - 2,32.
Граница фьючерсной цены должна составлять:
100-2,32 = 97,68.
Пример 3. (Сохраняются условия примера 1).
Пусть трехмесячный фьючерс стоит 97,93. Это выше верхней границы фьючерсной цены, поэтому можно совершить арбитражную операцию. Ее суть сводится к следующему. Фьючерсная цена 97,93 соответствует форвардной ставке:
100-97,93 = 2,07%.
Данная ставка ниже форвардной ставки по депозиту, которую можно обеспечить на основе ставок спот. Поэтому с помощью фьючерсного контракта арбитражер может обеспечить себе заимствование денег в будущем под более низку ставку 2,07%. В то же время он может разместить их под ставку 2,12%. Разница в ставках образует арбитражную прибыль. Действия арбитражера сводятся к следующему. Он занимает 1 млн. долл, на три месяца под ставку LIBOR 1,85%, размещает их на шестимесячном депозите под ставку L1B1D 1,99% и продает16 трехмесячный фьючерс по цене 97,93.
Через три месяца арбитражеру необходимо отдать кредит в размере:
90 1000000(1 + 0,0185—) - 1004625руб.
а) Пусть через три месяца ставка LIBOR составила 2,11%. Тогда котировка фьючерсного контракта равна:
100-2,11-97,89.
Фьючерсная цена снизилась на:
97,93-97,89 = 0,04
или
0,04
----~ 4 шага, 0,01
16 Арбитражер продает фьючерс, так как через три месяца он будет брать кредит и соответственно должен застраховаться от возможного роста процентной ставки.
Выигрыш по контракту составляет:
25долл.*4 = ЮОдолл.
За счет выигрыша по контракту он уплачивает 100 долл, кредита, который он брал на три месяца в момент заключения контракта, а оставшуюся часть суммы кредита в размере:
1004625 -100 = 10045250олл.
покрывает, заняв деньги на три месяца под ставку LIBOR 2,11%. Через три месяца по данному кредиту он должен вернуть сумму:
( 90 А
1004525 1 + 0,0211--- = 1009824Эолл.
I 360 J
По шестимесячному депозиту получает:
1 oooooof 1 + 0,0199—I = 1009950долл.
I 12 J
Арбитражная прибыль равна:
1009950 -1009824 = 126долл.
0) Пусть через три месяца ставка L1BOR составила 2,03%. Тогда когировка фьючерсного контракта равна:
100-2,03 = 97,97.
Фьючерсная цена выросла на:
97,97-97,93 = 0,04
ИЛИ
°,04 л
----= 4 шага.
0,01
П|иini рыш по контракту составляет:
25долл.-4 = ЮОдолл.
•>мрыш по контракту и трехмесячный кредит покрываются за счет того трехмесячного кредита, который арбитражер берет под ставку и размере:
1004625 +100 = 10047250олл.
। ри месяца по кредиту он должен вернуть:
1004725 1 + 0,0203
90 л
360;
= 10098240ОЛЛ.
По шестимесячному депозиту он получает:
( 6
1000000 1 + 0,0199 — = 1009950Эолл.
I 12
Арбитражная прибыль равна:
1009950-1009824 = 126долл.
Прибыль арбитражера будет нулевой, если в момент заключения фьючерсного контракта его котировка равна верхней границе рассчитанной цены. Покажем это для первого случая, когда ставка LIBOR составила 2,11%, а котировка фьючерсного контракта была равна 97,89.
Фьючерсная цена выросла на:
99,89-97,88 = 0,01
или
0,01
0,01
= 1 шаг.
Проигрыш по контракту составляет:
25долл.-1 = 25 долл.
Проигрыш по контракту и трехмесячный кредит он покрывает за счет нового трехмесячного кредита, под ставку 2,11%.
Через три месяца арбитражеру необходимо отдать кредит в размере:
/ / 90
(1004625 + 251 1 + 0,0211-- = 1009950долл.
v \ 360 J
По шестимесячному депозиту он получает сумму:
( 6
1000000 1 + 0,0199— = 1009950долл.
I 12)
Арбитражная прибыль равна нулю.
Подводя итог вышесказанному можно сформулировать следующий порядок действий для определения возможностей совершения арбил ражной операции. 1) На основе ставок LIBID и LIBOR вначале рассчи тываются форвардные ставки по депозиту и кредиту, как показано в примере 1. В примере были получены следующие ставки: 2,12% и 2,27%. 2) Определяется существующий спрэд между ставками LIB1I) и LIBOR. В этом случае арбитражер полагает, что такая величина спрэда сохранится и в дальнейшем. В примере спрэд равен 0,05%. 3) Данный
спрэд прибавляется к форвардной ставке по кредиту: 2,27 + 0,05 = 2,32% . 4) На основе полученных ставок определяются теоретические границы фьючерсной цены: 97,88 - 97,68.
Сделать вывод о возможности совершения арбитражной операции можно также на основе форвардной ставки, определяемой текущей котировкой фьючерсного контракта. Например, котировка фьючерса равна 97,65. Соответствующая ей форвардная ставка составляет:
100-97,65 = 2,35.
Поскольку она выше пограничной ставки в 2,32%, то можно совершить арбитражную операцию.
j 5.7.3. Использование контракта для увеличения доходности инвестиций
Фьючерсный контракт на евродолларовый депозит можно использовать для увеличения доходности инвестиций. Приведем возможный пример.
Пример.
Инвестиционный горизонт вкладчика 150 дней. Доходность облигации с погашением через 150 дней равна 10% годовых, облигации с погашением через 60 дней - 8% годовых. Котировка фьючерсного контракта на евродолларовый депозит, который истекает через 60 дней, составляет 88,4 %.
90-дневная форвардная ставка для периода, который начинается через 60 дней, равна:
1 + 0,1(150/360)
1 + 0,08(60/360)
----= 0,1118 или 11,18% годовых.
90
Поскольку котировка фьючерса 88,4%, то доходность евродолларового депозита равна 11,6%, что выше форвардной ставки. Поэтому инве- юру следует купить 60-дневную облигацию и фьючерсный контракт. После погашения облигации он размещает полученные средства на чн’хмесячном депозите. Купив фьючерс, инвестор обеспечил себе доходность по депозиту на 90 дней, которые начнутся после погашения 60-дневной облигации, на уровне 11,6% годовых. В результате Общая доходность за период его инвестиционного горизонта, составит:
60 Y, П11Г 90 ) 1 + 0,116--------
360 )
— = 0,1025 или 10,25%. 150
+ 0,08 360Л
Отмеченный вариант действий предпочтительнее простой покупки 150-дневной облигации. В заключение данного примера следует отметить, что реальная доходность инвестора окажется несколько меньше, поскольку, как отмечено в примерах с получением арбитражной прибыли, он, скорее всего, сможет инвестировать средства под ставку LIBID, которая ниже ставки LIBOR, соответствующей фьючерсному контракту.
5.7.4. Хеджирование фьючерсным контрактом на трехмесячный евродолларовый депозит
Фьючерс на евродоллар можно использовать для хеджирования краткосрочных процентных ставок. Если инвестор в будущем собирается занять деньги и опасается роста процентной ставки, то необходимо поодать фьючерс. В случае роста ставки он займет средства под более высокий процент, однако компенсирует его за счет выигрыша по контракту вследствие падения фьючерсной цены. Если инвестор в будущем планирует разместить деньги на депозите и ожидает падения процентной ставки, то необходимо купить фьючерс. В случае падения ставки он разместит средства под более низкий процент, однако компенсирует его за счет выигрыша по контракту вследствие роста фьючерсной цены. Рассмотрим технику хеджирования на примерах.
Пример 1.
Предприятие использует двухлетний банковский кредит для среднесрочного финансирования на сумму 1 млн. долл. По кредиту ежеквартально выплачивается плавающая процентная ставка LI-BOR+1%. Время выплаты процентов совпадает с временем истечения фьючерсных контрактов на евродолларовый депозит. До фиксирования уровня процента на очередной трехмесячный период остается месяц. Финансовый директор опасается роста ставки L1BOR и страхуется продажей одного фьючерсного контракта на трехмесячный евродолларовый депозит. Котировка контракта равна 97,90. Ей соответствует ставка LIBOR 2,1%. Данная ставка процента по кредиту устраивает менеджера.
Через месяц ставка LIBOR зафиксирована на уровне 2,3%. Следовательно, процентная ставка по кредиту предприятия для очередного платежа через три месяца составляет:
LIBOR +1 % = 2,3 +1 - 3,3%.
По кредиту предприятию следует уплатить проценты на сумму:
1000000 • (0,023 + 0,01) -у = 8250<3олл.
Если бы ставка LIBOR осталась на уровне 2,1%, платеж по кредиту составил:
1000000 (0,021 + 0,01)^ = 77500олл.
Разница в платеже составляет:
8250-7750 = 500долл.
Котировка фьючерсного контракта равна:
100-2,3 = 97,7.
По сравнению с моментом продажи она упала на:
97,9-97,7 = 0,2
или
°’2 on
----= 20 шагов.
0,01
Выигрыш по контракту составляет:
25 долл.'20 = 500долл.
Таким образом, увеличение суммы платежа по кредиту полностью компенсируется выигрышем по фьючерсному контракту.
Аналогично приведенному примеру инвестор может застраховаться о г снижения процентов по депозиту. В этом случае он будет покупать фьючерсный контракт.
В приведенном примере рассматривался случай полного хеджирования, когда риск возможных потерь полностью компенсировался противоположными результатами по фьючерсному контракту. Количество фьючерсных контрактов, которые необходимо открыть в этом случае, определяется по формуле (3.7),
Как известно, фьючерсная позиция ежедневно пересматривается по клирингу. Поэтому положительную вариационную маржу можно сразу же (^инвестировать, отрицательную маржу придется финансировать за inn дополнительных средств. Если хеджируемая сумма и период операции хеджирования небольшие, то финансовый эффект от ежедневного клиринга позиции будет небольшим, и им можно пренебречь. Если же юджируется большая сумма или на длительный период, то данный
эффект следует принять во внимание. Для его компенсации, как было отмечено в параграфе 3.3, необходимо дисконтировать количество полученных для полного хеджирования контрактов. В качестве ставки дисконтирования используется форвардная ставка для периода, на который берется заем или средства размещаются на депозит. Период дисконтирования равен периоду заимствования средств или размещения их на депозит.
Пример 2.
Предприятие использует двухлетний банковский кредит для среднесрочного финансирования на сумму 180 млн. долл. По кредиту ежеквартально выплачивается плавающая процентная ставка LIBOR+1%. Время выплаты процентов совпадает с временем истечения фьючерсных контрактов на евродолларовый депозит. До фиксирования уровня процента на очередной трехмесячный период остается месяц. Финансовый директор опасается роста ставки L1BOR и страхуется продажей фьючерсных контрактов на трехмесячный евродолларовый депозит. Одномесячная ставка LIBOR равна 1,73%, четырехмесячная - 1,91%. Определить количество контрактов, которое необходимо открыть.
Решение.
Для полного хеджирования, согласно формуле (3.7) надо открыть:
180 млн.долл.
-------------= 180 контрактов.
1 млн.долл.
Форвардная трехмесячная ставка LIBOR для периода времени, который начинается через месяц, равна:
f 1 + 0,0191(4/12) _ Л 4 = 0 ! %7 или 1 %
^1 + 0,0173(4/12) J
Количество фьючерсных контрактов, которые необходимо открыть, составляет:
180 контрактов
1 + 0,01967(90/360)
-179,12 или 179 контрактов.
С помощью фьючерса на евродоллар можно хеджировать заимствование денег или размещение их на депозите на сроки не обязательно равные трем месяцам. В этом случае для определения количества фьючерсных контрактов необходимо использовать коэффициент хеджирования. Рассмотрим технику хеджирования на примере
Пример 3.
Банк планирует выпустить через три месяца шестимесячные депозитные сертификаты на сумму 10 млн. долл. Чтобы застраховаться от возможного роста процентных ставок он хеджирует будущую эмиссию ' продажей фьючерсных контрактов. Необходимо определить количество 1 Контрактов, которые следует открыть.
Решение.
В данном примере представлено кросс-хеджирование, так как Страхуется шестимесячная процентная ставка с помощью контракта на Трехмесячную ставку. Поэтому определяем коэффициент хеджирования h. Как известно из главы 3, его можно рассчитать или по формуле (3.15), или получить на основе уравнения регрессии (3.19). Допустим, на основе месячных данных за последние три года было определено следующее уравнение регрессии:
г( D = 0,5 + 0,9г/г ,
где rCD - доходность шестимесячного депозитного сертификата;
rF - доходность фьючерсного контракта.
В уравнении первая цифра 0,5 говорит о том, что за рассматриваемый период ставка по шестимесячным депозитным сертификатам в среднем была выше ставки L1BOR на 0,5%. Вторая цифра 0,9 означает, что при изменении доходности фьючерсного контракта, т.е. форвардной ставки L1BOR, на 0,01% доходность депозитных сертификатов изменялась в среднем на 0,009%. Таким образом, необходимо открыть меньшее количество фьючерсных контрактов для хеджирования эмиссии депозитных сертификатов. Коэффициент хеджирования позволяет определить, как в среднем изменится процентная ставка по депозитным сертификатам, если изменится ставка I IBOR.
Для процентных инструментов в дополнение к коэффициенту хеджирования необходимо ввести еще один поправочный коэффициент -коэффициент денежной эквивалентности (money equivalent ratio). Он призван учесть разную степень реакции изменения стоимости одного фьючерсного контракта и эквивалентной стоимости будущего займа или депозита при изменении процентной ставки на один базисный пункт. В нашем примере заем осуществляется на шесть месяцев. Поэтому при и.1менении процентной ставки на один базисный пункт стоимость заимствования одного миллиона долларов изменится на величину:
1000000 0,0001-у = 50долл. (5.28)
В то же время изменение стоимости фьючерсного контракта составит:
1 OOOOOOdo.w. • 0,0001 — = 25долл., (5.29)
12
т.е. оно будет в два раза меньше. Поэтому для хеджирования суммы в 1000000 долл, для шестимесячного периода необходимо два трехмесячных фьючерсных контракта. Если бы заимствование осуществлялось на девять месяцев, то при изменении процентной ставки на один базисный пункт стоимость заимствования одного миллиона долларов изменилась бы на величину:
9
1000000дшл.-0,0001— = 75долл., (5.30)
12
т.е. оно в три раза сильнее по сравнению с трехмесячным периодом. Поэтому для хеджирования суммы в один миллион долларов для девятимесячного периода необходимо использовать три трехмесячных фьючерсных контракта.
Из представленных примеров следует, что коэффициент денежной эквивалентности можно определить на основе отношения временных периодов для хеджируемого актива и фьючерсного контракта, так как все остальные переменные в выражениях (5.28) - (5.30) являются одинаковыми, поэтому:
Л,=^, (5.31)
где h( - коэффициент денежной эквивалентности;
Th - время продолжительности хеджируемого займа или депозита;
TF - время, соответствующее периоду, для которого задается базисная ставка фьючерсного контракта;
Таким образом, в примере коэффициент денежной эквивалентности равен:
3 месяца
В результате количество фьючерсных контрактов, которые следует открыть, составляет:
10000000
1000000
0,9 2 = 18 контрактов.
На основе приведенных в примере рассуждений запишем формулу расчета количества фьючерсных контрактов в общем виде:
количество фьючерсных -контрактов
стоимость хеджируемой позиции стоимость фьючерсного контракта
Количество контрактов, которые необходимо открыть для хеджирования позиции по депозитному сертификату, можно также определить на основе следующих рассуждений. Депозитный сертификат имеет фиксированную доходность. Его цена в каждый данный момент времени представляет собой дисконтированную стоимость суммы, выплачиваемой при погашении. Если при погашении по активу выплачивается один доллар, то сейчас его цена равна:
1 + г(77360) ’
(5.33)
где Р - цена сертификата;
г - доходность до погашения сертификата;
Т - время до погашения сертификата.
Продифференцируем выражение (5.33) по г:
dP Г/360
dr [1+r(n360)]2
или
dP =
Г/360
[| + /-(Г/360)]2
(5.34)
Выражение (5.34) показывает, как изменится цена сертификата при вменении его доходности до погашения на небольшую величину.
Цена фьючерсного контракта на евродолларовый депозит номи-иалом 1 доллар определяется как:
F = 0,01 [100 -0,25(100 -FJ]
ИЛИ
F = 0,01 [100-0,25/;],
Или
F = 1-0,0025^. (5.35)
Продифференцируем выражение (5.35) по г:
dF
- = -0,0025 dr ф
или
dF ~ -0,0025^. (5.36)
Поскольку в выражении (5.27) котировка фьючерсной цены дана в процентах, то в формуле (5.36) размерностью значения гф также являются проценты (в то время как в формуле (5.34) величина г представлена в десятичных значениях). Поэтому формулу (5.36) можно записать как:
JF = -0,25<7r/v , (5.37)
где размерность гф дана в десятичных значениях.
Коэффициент хеджирования (/?**) равен:
~ dr
~ dF~ 0,25[1+г(г/360)Р dr* (5 38)
В формуле (5.38) отношение dr/drt> показывает зависимость между изменением доходности до погашения хеджируемого актива и форвардной процентной ставкой по евродолларовому депозиту. Коэффициент хеджирования, полученный в формуле (5.38) уже учитывает в себе коэффициент денежной эквивалентности, поэтому количество фьючерсных контрактов с его использованием непосредственно определяется по формуле (3.8), в которой роль коэффициента h выполняет найденный коэффициент А**.
Страхование будущих обязательств или заимствования средств на более длительные периоды времени можно осуществить с помощью нескольких последовательных краткосрочных контрактов. Данная техника называется стрип-хеджироеанием (strip hedge).
Пример.
Сейчас середина января. Инвестор планирует через три месяца взять шестимесячный кредит на сумму 10 млн. долл, и хеджируем будущий заем от роста процентной ставки с помощью контрактов на
__________ _ ___ Глава 5 Фьючерсные контракты на процентные ставки трехмесячный евродолларовый депозит. Он продает десять мартовских контрактов и десять июньских контрактов.
Для упрощения процесса формирования стрипа, т.е. одновременного заключения контрактов с разными сроками истечения, Чикагская товарная биржа предлагает такие инструменты как пакеты (pack) и связки (bundle). Они представляют собой ряд серийных контрактов, которые покупаются или продаются одной сделкой. В пакетах количество контрактов равно четырем. Код пакета для соответствующего года задается названием определенного цвета. Например, кодом пакета первого года, который содержит контракты в серии от первого до четвертого, является белый цвет, кодом второго пакета, в который входят контракты с пятого по восьмой месяцы, - красный цвет, пакета третьего года - зеленый цвет и т.д. Обычно на бирже торгуются девять пакетов, охватывающих период времени от второго до десятого года. Связка одновременно включает в себя большее количество серий контрактов по сравнению с пакетом. В настоящее время биржей предлагаются связки для одного, двух, трех, пяти, семи и десяти лет Связка первого года содержит четыре контракта, связка для двух лет - восемь контрактов и т.д. Первый контракт в любой связке - это первый серийный контракт.17
Приведем возможный вариант использования стрип-хеджиро-вания банком.
Пример.
В середине сентября предприятие обратилось в Банк за годичным кредитом в 5 млн. долл, с фиксированной процентной ставкой. Банк собирается предоставить кредит, занимая средства у другого банка на трехмесячный период под ставку LIBOR, и в последующем рефинансировать свой долг за счет заимствования средств под ставку LIBOR на следующие трехмесячные периоды в рамках года. Таким образом, он планирует получить дополнительную прибыль за счет разницы между более высокой долгосрочной годичной ставкой и краткосрочными трехмесячными ставками. Выдача кредита и последующее рефинансирование задолженности практически совпадает по времени с истечением фьючерсных контрактов.
Банк использует фьючерсный рынок, чтобы определить уровень процентной ставки, которую он может назначить по кредиту, а также
17 По фьючерсным контрактам на евроиену предлагаются пакеты для второго и Ничьего года и связки для одного, двух и трех лет
для хеджирования будущих трехмесячных заимствований при рефинансировании краткосрочного долга.
Трехмесячная ставка LIBOR равна 2,03%, цены декабрьского, мартовского и июньского контрактов составляют 97,62, 97,34 и 97,16. Соответственно их доходности равны 2,38%, 2,66% и 2,84%. Если банк возьмет трехмесячный кредит под ставку 2,03% и продаст трехмесячные, шестимесячные и девятимесячные контракты, он обеспечит себе расходы по заимствованию денег на уровне:
90 Г I + 0,0203---
360 Д
90 I + 0,0238----
90 Y
1 + 0,0266----
360 А
90 I
1 + 0,0284--- I - ! - 0,025
360 J
или 2,5% годовых.
Таким образом, издержки банка по обеспечению годичного кредита составят порядка 2,5% годовых. Поэтому данная цифра выступает как отправной ориентир для определения процентной ставки по кредиту предприятию. Например, банк определяет ставку по кредиту предприятию в 3,25%. В целом, операция банка по выдаче кредита предприятию будет включать следующие действия. Он занимает сумму в 5 млн. долл, на три месяца под ставку LIBOR, предоставляет их предприятию под 3,25% на год. Одновременно банк продает пять декабрьских, мартовских и июньских контрактов. Через три месяца он занимает под текущую ставку L1BOR деньги для рефинансирования трехмесячного займа и закрывает декабрьские фьючерсы. Еще через три месяца он рефинансирует долг, заняв деньги на следующие три месяца, и1 закрывает мартовские фьючерсы. Еще через три месяца занимает средства для рефинансирования долга и закрывает июньские фьючерсы. В результате банк обеспечил себе прибыль по операции на уровне 0,75%. На практике величина прибыли может колебаться в некотором диапазоне в зависимости от спрэда между ставками LIBOR, под которые банк рефинансировал задолженность, и ставками, под которые ему удалось закрывать фьючерсные контракты.
При страховании будущих заимствований или обязательств инвестор может столкнуться с проблемой ликвидности дальних контрактов. В этом случае используется техника роллинг-хеджирования (rolling hedge). Она состоит в страховании будущих периодов времени с помощью последовательного заключения краткосрочных контрактов.
Пример.
Сейчас начало января. Банк планирует через три, шесть и девять месяцев выпустить депозитные сертификаты на 10 млн. долл, в каждой эмиссии, и хеджирует будущий заем от роста процентной ставки контрактами на трехмесячный евродолларовый депозит. Допустим, июньский и сентябрьский контракты слабо ликвидны. Поэтому банк продает сейчас 30 мартовских контрактов. В начале марта выпускает ‘Сертификаты на 10 млн. долл, и закрывает мартовские контракты. Одновременно продает 20 июньских контрактов. В начале июня выпускает сертификаты еще на 10 млн. долл, и закрывает июньские контракты. Одновременно продает 10 сентябрьских контрактов. В начале сентября выпускает сертификаты еще на 10 млн. долл, и закрывает сентябрьские контракты.
5.7.5. Хеджирование соглашений о форвардной ставке и процентных свопов
Фьючерсный контракт на трехмесячный евродолларовый депозит можно использовать для получения арбитражной прибыли или хеджирования соглашений о форвардной ставке (ФРА).18 Приведем примеры.
Пример 1.
Сейчас середина февраля. Банк заключает с предприятием трехмесячное ФРА через четыре месяца номиналом 10 млн. долл. Форвардный период начинается в середине июня и совпадает с моментом истечения июньского фьючерсного контракта. Банк рассчитывает получить спекулятивную прибыль за счет роста процентной ставки, поэтому покупает ФРА.19 В ФРА фиксируется твердая трехмесячная форвардная ставка LIBOR 3,32%. Через месяц процентные ставки выросли, и банк решил зафиксировать прибыль хеджированием позиции фьючерсами на трехмесячный евродолларовый депозит. Котировка июньского фьючерса равна 96,48, что соответствует форвардной ставке 3,52%. Банк покупает 10 контрактов.20
Характеристику и расчеты выплачиваемых сумм по ФРЛ см. в книге А.Н. Буренина Рынок ценных бумаг и производных финансовых инструментов", М., “Научно-грхническое общество им. академика С.И. Вавилова”, 2002, параграф 15.9.
,ч В случае роста процентной ставки предприятие должно будет выплатить банку < («нветствующую сумму от номинала контракта.
Как было отмечено выше и проиллюстрировано в примере 2 параграфа 5.7.4, для учета вариационной маржи, начисляемой по контракту, количество контрактов, соот-
В результате, выигрыш банка должен составить порядка:
3,52-3,32 = 0,2%
от номинала контракта.
Рассмотрим возможные результаты по операции банка для разных условий конъюнктуры к моменту истечения ФРА в середине июня.
I. В последний день торгов котировка июньского фьючерса равна 96,88, т.е. трехмесячная ставка LIBOR составила 3,12%. Так как спотовая ставка L1BOR упала по сравнению со ставкой, зафиксированной в ФРА, то по ФРА банк выплачивает предприятию сумму:
10000000долл.(0,0332 -0?Q312X90/360) = 4%
1+~0?0312(90/360)
По фьючерсу банк выигрывает:
25^о। контрактов - 1 ООООдао.
0,01
Прибыль банка равна:
10000 - 4961,3 5038,7 долл.
II. В последний день торгов котировка июньского фьючерса равна 96,28, т.е. трехмесячная ставка L1BOR составила 3,72/о. По ФРА банк получает от предприятия сумму:
10000000долл.(0,0372 - 0,0332^90/360) = 9907>86доД1.
1 + 0,0372(90/360)
По фьючерсу банк проигрывает:
96,48-96,28 25б)шл. 1 Оконтрактов = 5000дсшл.
0,01
Прибыль банка равна:
9907,86 - 5000 = 4907,86долл.
ветствующее полному хеджированию, следует дисконтировать под форвардную став ку. Таким образом, в рассматриваемом примере количество контрактов должно составлять:
__22____________= 9,9.
l+0,0352(90/360)
Однако округление дает 10 контрактов.
Пример 2.
Сохраняется ситуация примера 1, однако банк теперь покупает шестимесячное ФРА через четыре месяца номиналом 10 млн, долл. Через месяц процентные ставки выросли, и банк хеджирует свою позицию фьючерсом на трехмесячный евродолларовый депозит. Поскольку хеджируемый период по ФРА больше срока действия фьючерсного контракта, то при определении количества покупаемых контрактов необходимо учесть коэффициент денежной эквивалентности (5.31), как было показано в примере 3 параграфа 5,7.4. Поэтому количество фьючерсных контрактов равно:
10000000 6
----------= 20 контрактов.
1000000 3
Фьючерс на евродолларовый депозит можно использовать для хеджирования позиции по свопу.21
Пример.
В середине марта банк заключил с компанией процентный своп номиналом 10 млн. долл, сроком на два года. В свопе банк обязался выплачивать ежеквартально плавающую ставку. Через год (в марте) по мнению банка стала складываться ситуация к возможному росту ставок, поэтому он принимает решение хеджировать позицию по свопу на оставшийся период времени с помощью фьючерсов на евродоллар. Он продает по 10 контрактов июньских, сентябрьских и декабрьских.
5.8. ФЬЮЧЕРСНЫЙ КОНТРАКТ НА КАЗНАЧЕЙСКИЙ ВЕКСЕЛЬ США
5.8.1. Общая характеристика контракта на казначейский вексель США
Контракт торгуется на СМЕ. В его основе лежит казначейский вексель США, до погашения которого остается 13 недель, т.е. три месяца, номиналом 1 млн. долл. Контракт поставочный. По контракту может быть поставлен вновь эмитированный вексель, до погашения которого остается 13 недель (90 дней), или уже обращающийся на
Характеристику свопов см. в книге А.Н.Буренина "Рынок ценных бумаг и производных финансовых инструментов", Научно-техническое общество им. академика С.И. Ва-нипова, М.,2002, глава 15.
рынке вексель, выпущенный на более длительный период, но к моменту поставки которого до погашения также осталось 13 недель. Котировка фьючерсной цены дается на индексной базе как:
100-d ,
где d - ставка дисконта по векселю в расчете на год.
Например, ставка дисконта равна 10%, тогда котировка фьючерсной цены будет представлена как:
100-10 = 90.
На основе котировки фьючерсной цены можно определить стоимость фьючерсного контракта. Поскольку срок обращения векселя 90 дней, то в приведенном примере цена фьючерсного контракта равна:22
( 90 1
1000000 1-0,1--- = 975000дао.
I 360)
В финансовой прессе котировка фьючерсной цены дается для бумаги номинальной стоимостью 100 долл. Для удобства определения стоимости фьючерсного контракта по его котировке, между ними можно установить следующее соответствие:
PF = 10000[100 - 0,25(100 - FJ], (5.39)
где PF - цена фьючерсного контракта; Fk - котировка фьючерсной цены.
Пример.
Котировка фьючерсной цены равна 90. Стоимость фьючерсного составляет:
= 10000[100 - 0,25(100 - 90)] = 975000долл.
Для определения фьючерсной котировки на основе стоимости' контракта из формулы (5.39) можно получить следующую формулу:
Fk = 100-4 100
PF 10000 J
22 Подробно об определении курсовой стоимости и доходности векселя см. в книге А.Н.Буренина "Рынок ценных бумаг и производных финансовых инструментов”, М., “Научно-техническое общество им. академика С.И.Вавилова", 2002, параграф 5.3.
Пример.
Стоимость контракта составляет 975000 долл. Котировка фьючерсной цены равна:
Fk = 100-4 100
_ 975000^1
10000 J
Последним торговым днем считается рабочая среда третьей недели месяца поставки. В этот день проходит аукцион по 91-дневным казначейским векселям США. Котировочная фьючерсная цена в этот день определяется как 100 минус самая высокая ставка дисконта, принятая на аукционе Казначейством США.
Минимальный шаг цены контракта 0,005%, что соответствует 12,5 долл.:
90
1000000 0,00005---= 12,5 долл.
360
Контракт торгуется в мартовском цикле с истечением контрактов в марте, июне, сентябре и декабре. Кроме этого торгуются два текущих контракта не в мартовском цикле.
Контракт можно использовать для извлечения спекулятивной прибыли в связи с прогнозами изменения процентной ставки по казначейским векселям. Если ожидается падение процентной ставки, т.е. рост фьючерсной цены, то следует купить контракт. Если ожидается рост процентной ставки, т.е. падение фьючерсной цены, следует продать фьючерс.
Пример.
Котировка фьючерсного контракта на трехмесячный казначейский вексель равна 90%. Спекулянт ожидает падения процентных ставок и покупает фьючерс. Через три дня фьючерсная котировка составила 92%, и спекулянт закрыл свою позицию. Определить финансовый результат для спекулянта.
Решение.
Котировка фьючерсной цены изменилась на 2%. Разделим эту цифру на шаг цены:
2 ------= 400 шагов. 0,005
Каждому шагу цены соответствует изменение цены контракта на 12,5 долл. Поэтому выигрыш спекулянта равен:
12,5 Эол.?.• 400 - 5000Эолл.
Выигрыш по контракту можно определить и другим способом.
Цена контракта в момент его открытия в соответствии с формулой (5.39) составляла:
10000[100 - 0,25(100 - 90)] = 975000долл.
В последующем она выросла до:
10000[100 - 0,25(100 - 92)] = 980000е)<мл.
Спекулянт выиграл:
980000-975000 = 5000Эолл.
5.8.2. Определение фьючерсной цены и арбитраж
Казначейский вексель - это финансовый инструмент, который продается со скидкой и погашается по номиналу. Поэтому цену векселя можно определить дисконтированием номинала к настоящему моменту времени под ставку без риска для периода, остающегося до его погашения:
1000000 (5.40)
1 + гг(Т/360)
где Р - цена векселя;
гТ - ставка без риска для периода времени Т;
Т - время до погашения векселя.
Цену фьючерсного контракта можно определить на основе формулы форвардной цены акции, по которой не выплачиваются дивиденды в течение действия контракта (2.1).
Пусть время с момента заключения фьючерсного контракта до момента погашения векселя, поставляемого по контракту равно , и до истечения контракта остается время . Тогда:
„ 1000000 f < А
=----т—:-----d 1 + t\ —-
1 + r2 (t2/база) база /
где - спотовая процентная ставка для периода ;
г2 - спотовая процентная ставка для периода /2.
Пример 1.
Фьючерсный контракт истекает через 30 дней, до момента погашения векселя, поставляемого по контракту, 120 дней. Процентная ставка для 30 дней 1,84%, для 120 дней - 2,09%. Процентные ставки заданы для базы 360 дней. Определить цену фьючерсного контракта.
Решение.
п 1000000 Л пЛ1О,30^
Р =---------т------г 1 + 0,0184-- = 994604, Здолл.
F 1 + 0,0209 120/360Д 360)
Цену фьючерсного контракта можно также определить, дисконтируя номинал контракта под форвардную ставку для периода времени с момента его истечения до момента погашения векселя, поставляемого по контракту:
1000000
( 90
I. + ---
^360
где гф- форвардная ставка,
или
1000000
1 + 0,25г^
(5.41)
Пример 2.
Для условий примера 1 определить цену фьючерсного контракта на основе форвардной ставки.
Решение,
Форвардная ставка для периода времени составляет:
+ 0,0209(120/360) ч 1 + 0,0184(30/360)
1 2Ё2.... -0,0217 или 2,17%. J120-30
Стоимость фьючерсного контракта равна:
1000000
1 + 0,25 0,0217
= 994604,Здолл.
Если фактическая фьючерсная цена контракта не равна теоретической, можно совершить арбитражную операцию. Рассмотрим пример.
Пример 3. (Сохраняются условия примера 1).
Котировка фьючерсного контракта равна 97,68, что соответствует фьючерсной цене контракта:
Pf = 10000[100-0,25(100-97,68)] =99420(Ю<мл.
Контракт стоит дешевле теоретически рассчитанной цены. Поэтому арбитражер: а) покупает контракт; б) занимает казначейский вексель, до погашения которого остается 120 дней и продает его по спотовой цене; ставка для 120 дней составляет 2,09% годовых, поэтому он продает его за:
1000000
1 + 0,0209(120/360)
= 993081,5до.м.
в) размещает данные средства на 30-дневном депозите под 1184% годовых.
Рассмотрим два сценария на момент истечения срока действия контракта через 30 дней.
I. Фьючерсная котировка равна 98,00. Это соответствует цене векселя:
PF = 10000[100 - 0,25(100 - 98)] = 995000долл.
По контракту арбитражер выиграл сумму:
98-97,68
---------П,5долл. ~ ъООдолл.
0,005
По депозиту получил сумму:
993081,5 1 + 0,0184
30
360;
~ 994604,Здолл.;
Общая сумма полученных средств составила:
800 + 994604,3 = 995404,3<kw.
По контракту уплачивает 995000 долл., получает вексель и возвращает его кредитору. Арбитражная прибыль равна:
995404,3 - 995000 - 404,Здшл.
II. Фьючерсная котировка равна 97,00. Это соответствует цене векселя:
PF = 10000[100 - 0,25(100 - 97)] = 992500долл.
По контракту арбитражер проиграл сумму:
—— 12,5долл, = ПООдолл. 0,005
По депозиту получил сумму:
( 30
993081,5 1 + 0,0184---
= 994604, Ъдолл,
I 360J
/4
-Общая сумма полученных средств составила:
994604,3 -1700 = 992904, Ъдолл.
По контракту уплачивает 992500 долл., получает вексель и возвращает его кредитору. Арбитражная прибыль равна:
992904,3 - 992500 = 404,3долл.
5.8.3. Хеджирование фьючерсным контрактом на казначейский вексель
Фьючерс на казначейский вексель можно использовать для страхования от изменения краткосрочных процентных ставок. Если инвестор страхуется от падения процентной ставки, следует купить контракт. Если инвестор страхуется от роста процентной ставки, необходимо продать фьючерс. Рассмотрим технику хеджирования на примерах.
Пример.
Менеджер компании должен получить через четыре месяца сумму в 975000 долл, и планирует приобрести на нее трехмесячный казначейский вексель. Он опасается падения процентных ставок и страхует будущую покупку векселя приобретением фьючерсного контракта. Котировка фьючерсного контракта на трехмесячный казначейский вексель, до истечения которого остается четыре месяца, равна 90%. Это соответствует стоимости контракта в 975000 долл.
Через четыре месяца фьючерсная котировка составила 92%. По контракту менеджер должен уплатить за вексель:
10000[100 - 0.25(100 - 92)] = 980000<1олл.
Котировка фьючерсной цены выросла на 2%. Поэтому по контракту он выиграл:
------12,5 долл. = 5000долл.
0,005
Вместе с полученной в этот момент суммой в 975000 долл, это как раз и составляет:
5000 + 975000 = 980000Эатл.,
которые он уплачивает по контракту.
Момент завершения операции хеджирования может не совпадать с моментом истечения фьючерсного контракта, или хеджируется продажа или покупка векселя, срок погашения которого не равен трем месяцам. В этом случае для определения количества контрактов, которые необходимо открыть, следует рассчитать коэффициент хеджирования. Количество контрактов, как и в случае фьючерса на евродолларовый депозит, можно определить по формуле (5.32).
Количество контрактов, которые необходимо открыть для хеджирования позиции по векселю, можно также на основе следующих рассуждений. Цена векселя в каждый данный момент времени представляет собой дисконтированную стоимость его номинала. В расчете на один доллар номинала, согласно формуле (5.40), его цена в начале периода Т равна:
1+гг(Т’/360)’
(5-42)
Продифференцируем выражение (5.42) по гт : dP _ Г/360 drT ~ (1 + rT (Т / 360)]2
или
dP =
77360
[1 + г7(77 360)]2 Гт'
(5.43)
Выражение (5.43) показывает, как изменится цена векселя при изменении его доходности до погашения на небольшую величину.
Цена фьючерсного контракта на вексель номиналом 1 доллар, согласно формуле (5.41), определяется как:
1 + 0,25гф
(5.44)
Продифференцируем выражение (5.44) по г. :
dPF _ 0,25
<1гф (1 + O,25rj
ИЛИ
02 5 Jr.
(1 + 0,25гД
Коэффициент хеджирования (&**) равен:
„ = = _ (7’/360)/[1 + 'г(77360)]2 сЛу
dP? 0,25/(1 + 0,25^ <1гф
ИЛИ
г(1 + 0,25г < J2 J,-90[1 + гг(Г/360)Р^
В формуле (5.45) отношение drT / dt^ показывает зависимость между изменением доходности до погашения хеджируемого векселя и форвардной безрисковой процентной ставкой. Коэффициент хеджирования, полученный в формуле (5.45) уже учитывает в себе коэффициент денежной эквивалентности, поэтому количество фьючерсных контрактов с его использованием непосредственно определяется по формуле (3.8), в которой роль коэффициента h выполняет найденный коэффициент //*.
5.9. ФЬЮЧЕРСНЫЙ КОНТРАКТ ФОНДОВОЙ БИРЖИ РТС НА РУБЛЕВЫЕ ОБЛИГАЦИИ ГОРОДСКОГО ВНУТРЕННЕГО ОБЛИГАЦИОННОГО ЗАЙМА г. МОСКВЫ
Фьючерсный контракт на трехлетние облигации г. Москвы заключается на Фондовой бирже РТС. Контракт включает десять облигаций г. Москвы любого выпуска, отвечающего следующим требованиям. До погашения поставляемых облигаций на дату исполнения контракта должно оставаться от 28 до 40 месяцев, объем эмиссии составляет не менее 4 млрд, руб., дата первичного размещения облигации не позднее 1 месяца перед датой исполнения контракта, отсутствует право досрочного выкупа или погашения облигаций, номи
нальная стоимость одной облигации 1000 руб. Список выпусков облигаций, которые можно поставить по контракту, публикуется на сайте биржи РТС. На момент написания данной книги на бирже обращались два контракта: первый с исполнением 19 сентября 2005 г., второй-19 декабря 2005 г. По контрактам можно было поставить облигации выпусков RU25029MOS и RU25036MOS.
Контракт является поставочным. Последний торговый день -это рабочий день, предшествующий 17 числу месяца окончания контракта.
Исполнение осуществляется в первый торговый день после последнего дня обращения контракта путем передачи продавцом 10 облигаций покупателю. Покупатель уплачивает продавцу цену исполнения. На участника, не выполнившего обязательства по исполнению контракта, налагается денежный штраф в размере базового гарантийного обеспечения, установленного на начало последнего торгового дня. Покупатель и продавец по взаимному согласию вправе не исполнять контракт поставкой облигаций, а осуществить взаимозачет обязательств. Для этого они должны не позднее 19.15 последнего торгового дня предоставить в Клиринговый центр Акт о взаимозачете обязательств по исполнению контракта.
Цена контракта указывается как чистая цена за 10 облигаций. Минимальный шаг цены 1 рубль. Минимальный размер начальной маржи установлен в размере 10% от стоимости контракта. За 5 торговых дней Клиринговый центр вправе увеличить лимит колебания фьючерсной цены и/или величину гарантийного обеспечения.
Для каждого выпуска облигаций, которые могут быть поставлены по контракту, Президентом биржи устанавливаются коэффициенты конверсии. Они рассчитываются на день исполнения контракта и остаются постоянными в течение всего времени его действия. Коэффициенты публикуются на сайте биржи. Например, по контракту с исполнением 19.09.05 коэффициенты конверсии для облигаций выпусков RU25029MOS и RU25036MOS соответственно равны 1,0053 и 1,0062. По контракту с исполнением 19.12.05 - 1,0050 и 1,0060.
Коэффициент конверсии облигации рассчитывается по формуле:
где К - коэффициент конверсии;
Р - чистая цена облигации;
У - номинал облигации.
В свою очередь цена облигации рассчитывается по формуле:
p = V —______+___-____С
2-(1+г)' + (1+гу с-
где С, - купон, выплачиваемый по облигации в момент t;
N - номинал облигации;
С(ф - купон, накопившейся по облигации на день исполнения фьючерсного контракта;
1 г - доходность до погашения облигации; ее величина устанавливается решением Президента биржи;
Т - срок до погашения облигации.
Коэффициенты конверсии приводят цены облигаций всех выпусков на день исполнения контракта к таким уровням, чтобы их доходности до погашения были одинаковыми.
Цена исполнения контракта рассчитывается по формуле:
цена цена облигации количество облигаций ( с = L . (5.46)
исполнения ! - го впуска 1 - го выпуска
Формула (5.46) предполагает, что по контракту инвестор может одновременно поставить облигации не только одного, но и разных выпусков, разрешенных в рамках данного контракта. Например, по контракту с исполнением 19.12.05 можно поставить четыре облигации выпуска RU25029MOS и шесть облигаций выпуска RU25036MOS или иные их комбинации.
В формуле (5.46) цена облигации i -го выпуска определяется следующим образом:
цена облигации котировочная цена
=---------------------К ( + С . ,
I - го выпуска 10
।де С1ф - купон, накопившейся по облигации на день исполнения фьючерсного контракта;
Л, - коэффициент конверсии облигации i -го выпуска.
По контракту инвестор имеет право поставить разные облигации. Однако он будет стремиться к тому, чтобы поставить “самую дешевую облигацию". Как мы определили в параграфе 5.1 выбор “самой дешевой” облигации можно сделать на основе расчета отношения
цена спот коэффициент конверсии
(5.47)
для всех облигаций, которые можно поставить по контракту. "Самой дешевой” будет бумага с наименьшим значением этого отношения.
Пример 1.
Сегодня 19 июля 2005 г. Фьючерсный контакт истекает 16.09,05 г„ исполнение состоится 19.09.05. По контракту могут быть поставлены облигации выпусков RU25029MOS и RU25036MOS. Их коэффициенты конверсии соответственно равны 1,0053 и 1,0062. Цена спот облигации RU25029MOS равна 107,85, облигации RU25036MOS - 108,30. Определить “самую дешевую” облигацию для поставки по контракту.
Решение.
Согласно формуле (5.47) отношения цен к коэффициентам конверсии для облигаций RU25029MOS и RU25036MOS соответственно составляют:
107,85 mn.ow Ю8,3
-----— = 107,2814; — = 107,6327.
1,0053 1,0062
Таким образом, самой дешевой для поставки по контракту является облигация выпуска RU25029MOS.
Техника расчета фьючерсной цены контракта на трехлетние облигации г. Москвы аналогична технике ее определения для фьючерсного контракта на казначейскую облигацию США (см. параграф 5.2). Поэтому приведем здесь только пример расчета фьючерсной цены для случая, когда в период действия контракта по облигациям купоны не выплачиваются.
Пример.
Сегодня 19 июля 2005 г. Фьючерсный контакт истекает 16.09.05 г., исполнение состоится 19.09.05. До исполнения контракта остается 62 дня. Инвестор определил (см. пример 1), что по контракту будет поставлена облигация выпуска RU25029MOS. Ее коэффициент конверсии равен 1,0053. Цена облигации на спотовом рынке равна 107,85%. Купоны выплачиваются два раза в год. Предыдущий купон был выплачен 5 июня 2005 г. Следующий купон выплачивается 5 декабря 2005 г. Величина купона равна 50 руб. 14 коп. Продолжительность купонного периода составляет 183 дня (с 5 июня по 4 декабря 2005 г.). Процентная ставка для периода 62 дня равна 4% годовых. Определить цену фьючерсного контракта.
Решение.
С момента выплаты купона 5.06.2005 г. до определения фьючерсной цены 19.07.05 г. прошло 45 дней.23 За это время по облигации накопился купон в размере:
50,14pyg. 45 = 12 5 j
183
Полная цена облигации на момент расчета фьючерсной цены равна:
1000руб. 1,0785 +12,32951 = 1090,83 руб.
Поскольку по облигации купон в период действия контракта не выплачивается, то для расчета фьючерсной цены используем формулу для актива, по которому не выплачиваются доходы:
( 62
1090,83 1 + 0,04—
I 365
1098,241руб.
Котировка дается на основе чистой цены. Поэтому из полученной цифры надо вычесть сумму купонных процентов, которая накопится по облигации к моменту истечения контракта. С момента выплаты последнего купона 5.06.05 г. до 19.09,05 г. пройдет 107 дней.
Соответственно сумма купонных процентов за этот период равна: 50J4p.yg. j07 = 29 3j6g3 б 183
С учетом корректировки на сумму процентов получим фьючерсную цену:
1098,241 - 29,31683-1068,924руб.
Мы рассчитали фьючерсную цену одной облигации. Контракт насчитывает 10 облигаций. Коэффициент конверсии облигации выпуска RU25029MOS равен 1,0053. Поэтому цена фьючерсного контракта равна:
1068,924 10
1,0053
-10632,89руб. или 10633 руб.
На основе рассмотренного пример можно записать общую формулу определения фьючерсной цены контракта для случая, когда по облигациям не выплачиваются купоны в период действия контракта.
у оаза )
-С — \база
Ю ,
По условиям эмиссии облигации следующий купонный период начинается со дня выплаты купона за предыдущий период
где F - фьючерсная цена контракта;
С - купон за текущий полугодовой период;
Р - полная цена “самой дешевой облигации”, т.е. с учетом суммы накопленного купонного процента за период t;
t - количество дней, которые прошли с даты выплаты последнего купона до момента определения фьючерсной цены;
Т - период действия фьючерсного контракта, или более точно, количество дней до даты поставки облигации по контракту;
база * - 365 дней;
база - фактическое количество дней в текущем купонном периоде;
г - ставка без риска для базы 365 дней;
К - коэффициент конверсии.
Если фактическая фьючерсная цена не равна теоретической, то можно получит арбитражную прибыль. Техника совершения операции аналогична примерам, рассмотренным в параграфах 5.2.1 и 5.2.2 для фьючерса на казначейскую облигацию.
КРАТКИЕ ВЫВОДЫ
Коэффициент конверсии - это коэффициент, который приводит цену поставляемой облигации на первый день месяца поставки к такому уровню, чтобы ее доходность до погашения соответствовала требованиям фьючерсного контракта.
“Самой дешевой" облигацией для поставки по фьючерсному контракту является бумага с наименьшим значением отношения:
цена спот коэффициент конверсии
При хеджировании облигаций фьючерсом на облигацию используют показатель дюрации. Дюрацию фьючерсного контракта определяют на основе “самой дешевой” облигации.
При хеджировании спотовой позиции по облигации с помощью дюрации можно вместо дюрации фьючерсного контракта использовать дюрацию самой дешевой облигации.
Краткосрочные процентные фьючерсы котируются на базе индексной цены.
Коэффициент денежной эквивалентности учитывает разную степень реакции изменения стоимости фьючерсного контракта и экви-
Гпава 5 Фьючерсные контракты на процентные ставки валентной стоимости хеджируемой позиции при изменении процентной ставки на один базисный пункт.
Страхование на более длительные периоды времени с помощью нескольких последовательных краткосрочных контрактов называется стрип-хеджированием.
Пакеты и связки представляют собой ряд серийных контрактов, которые покупаются или продаются одной сделкой.
ЧАСТЬ II. ОПЦИОННЫЕ РЫНКИ
ГЛАВА 6. ОРГАНИЗАЦИЯ И ФУНКЦИОНИРОВАНИЕ ОПЦИОННОГО РЫНКА
В настоящей главе приводится общая характеристика опционных контрактов и рассказывается об организации торговли опционами. Мы остановимся на понятиях типов и видов опционов, рассмотрим опционы на покупку и продажу, дадим определение категорий опционов и премии.
6.1. ОБЩАЯ ХАРАКТЕРИСТИКА ОПЦИОННЫХ КОНТРАКТОВ
Опцион - это срочный контракт, который дает право одному из его участников отказаться от исполнения сделки. В контракте участвуют два лица. Одно лицо покупает опцион, т. е. приобретает право выбора исполнить или не исполнить контракт. Другое лицо продает или, как говорят, выписывает опцион, т. е. предоставляет право выбора. Покупатель опциона уплачивает продавцу вознаграждение, называемое премией. Премия уплачивается в момент заключения контракта. Продавец опциона обязан исполнить свои контрактные обязательства, если покупатель (его еще называют держателем) опциона решает его исполнить. Если покупатель не исполняет опцион, то контракт истекает для продавца без наступления обязательств. Покупатель имеет право исполнить опцион, т. е. купить или продать базисный актив по цене, которая указана в контракте. Она называется ценой исполнения.
С точки зрения сроков исполнения контрактов опционы подразделяются на три типа: американские, европейские и бермудские. Американский опцион можно исполнить в любой день до истечения срока действия контракта, европейский - только в день истечения контракта. Бермудский опцион дает право исполнить его в определенные моменты времени в течение действия контракта.
Термины американский и европейский опцион имеют исторический контекст. В США опционы на акции традиционно можно было исполнить в любой день в течение действия контракта. Когда в Евро-ле в 1977 г. в Амстердаме возникла первая биржа опционов - Европейская биржа опционов (European Option Exchange) - на ней стали торговаться опционы с одним единственным возможным сроком исполнения. В современных условиях понятия американский и евро
пейский опцион представляют собой только термины без географической привязки к месту их обращения.
Существует два вида опционов: опцион на покупку или опцион колл; и опцион на продажу или опцион пут. Опцион колл дает право держателю опциона купить или отказаться от покупки базисного актива. Опцион пут дает право держателю опциона продать или отказаться от продажи базисного актива. Для лучшего понимания такого инструмента как опцион, следует не забывать, что вначале инвестор покупает опцион, т. е. само право на покупку или продажу базисного актива. После этого он исполнит опцион, если ему это выгодно, т. е. купит или продаст базисный актив в зависимости от вида опциона. Если конъюнктура окажется для него неблагоприятной, он оставит опцион без исполнения. Опционы используются для хеджирования, получения спекулятивной и арбитражной прибыли.
Выписывая опцион, продавец открывает по данной сделке короткую позицию, а покупатель - длинную позицию. Соответственно понятия 'короткий колл" или "короткий пут" означают продажу опционов колл или пут, а “длинный колл" или “длинный пут" - их покупку. Рассмотрим подробно существо каждого вида опциона.
6.1.1. Опцион колл
Опцион колл дает право покупателю опциона купить базисный актив у продавца опциона по цене исполнения в установленные сроки или отказаться от этой покупки. Инвестор приобретает опцион колл, если ожидает повышения курсовой стоимости базисного актива. Рассмотрим суть опциона колл на примере.
Пример.
Имеется трехмесячный европейский опцион колл на акцию. Цена исполнения опциона равна 100 руб., опцион стоит 5 руб. Цена спот акции составляет 100 руб. Инвестор покупает опцион. Это означает, что он уплачивает продавцу опциона 5 руб. и получает право купить через три месяца акцию по цене исполнения, т. е. за 100 руб.
Допустим, покупатель опциона спекулянт, играющий на повышение. Он ожидает повышения курса акции к моменту истечения срока действия контракта до 120 руб. Он оказался прав. Тогда через три месяца спекулянт исполняет опцион, т. е. покупает акцию у продавца опциона за 100 руб. и сразу продает ее на спотовом рынке за 120 руб. На разнице цен он выигрывает 20 руб. Общий выигрыш спекулянта следует скорректировать на уплаченную премию, поэтому он составит:
120 - 100 - 5 = 15/трб.1
Пусть спекулянт ошибся, и курс акции через три месяца упал до 80 руб. Тогда он не исполняет опцион, так как бессмысленно покупать акцию за 100 руб. по опциону, если она стоит сейчас на рынке 80 руб. Итог операции инвестора - потеря премии.
Представим возможные результаты сделки для покупателя опциона к моменту истечения контракта графически (см. рис. 6.1). По оси абсцисс показана спотовая цена акции к моменту истечения срока действия опциона. По оси ординат - потенциальные выигрыши и проигрыши. Поскольку на рисунке представлен график покупателя опциона колл, то его также могут назвать длинный опцион колл.
Рис. 6.1. Выигрыши-проигрыши покупателя европейского опциона колл к моменту истечения срока действия контракта
Как видно из графика, опцион не исполняется, если к моменту истечения контракта цена спот акции равна или ниже 100 руб. Проигрыш инвестора в этом случае равен уплаченной им премии, т. е. 5 руб. Если курс акции больше 100 руб., опцион исполняется. При цене акции 105 руб. результат по сделке нулевой, так как выигрыш в 5 руб. компенсирует уплаченную премию. При более высокой цене инвестор получает прибыль. При курсе акции больше 100, но меньше 105 руб. опцион также
1 Если быть более точным в вопросе определения издержек покупателя опциона, то следует также учесть упущенный процент, который можно получить на сумму премии опциона за период действия контракта. Например, ставка по депозиту равна 10% годовых. За три месяца по депозиту будет получена сумма:
Поэтому общий выигрыш спекулянта составит:
120-100-5,125 = 14,875руб.
исполняется, поскольку это позволяет уменьшить потери инвестора. Например, цена акции равна 103 руб. Тогда, исполнив опцион и продав акцию на спотовом рынке, инвестор выиграет 3 руб, что сократит его убыток до 2 руб.:
5-3 = 2 руб.
Сформулируем общее правило, когда исполняется европейский опцион колл. Европейский опцион колл исполняется, если спотовая цена базисного актива к моменту истечения срока действия контракта выше цены исполнения, и не исполняется, если она равна или ниже цены исполнения.
Финансовый результат для покупателя опциона можно представить следующей таблицей:
Таблица 6.1. Выигрыши-проигрыши покупателя опциона колл.
(Sr - цена спот базисного актива к моменту истечения контракта, X - цена исполнения, с - премия опциона)
Цена акции к моменту истечения контракта ST>X ST < X
Выигрыши-проигрыши по опциону S г — X — с -с
Например, выигрыш инвестора при 5Т = 120руб. согласно алгоритму таблицы 6.1 составит:
120-100-5 = 15руб.
Итоги сделки для продавца опциона противоположны по отношению к результатам покупателя и показаны на рис. 6.2. Его максимальный выигрыш к моменту истечения срока действия контракта равен величине
Рис 6.2. Выигрыши-проигрыши продавца европейского опциона колл к моменту истечения срока действия контракта
премии в случае неисполнения опциона, т. е. при цене спот акции 100 руб. или ниже. При ST = 105руб. результат сделки для него нулевой. В случае существенного роста курса акции его проигрыш может оказаться очень большим. При заключении сделки продавец опциона рассчитывает, что цена базисного актива к моменту его истечения не превысит цены исполнения. Представленный на рис. 6.2 график называют графиком продавца опциона колл или короткий опцион колл.
Финансовый результат для продавца опциона можно представить следующей таблицей:
Таблица 6.2. Выигрыши-проигрыши продавца опциона колл.
(- цена спот базисного актива к моменту истечения контракта, А7 - цена исполнения, с - премия опциона)
1 Цена акции к моменту ; истечения контракта ST> X S, <х
| ВЫИГрЬНиИ-ПрОИГрЫШИ ' по опциону -(ST-X)+c с
Например, цена акции выросла до 120 руб. Согласно алгоритму таблицы 6.2, проигрыш продавца опциона составит:
-(120-100)+ 5 = -15 руб.
Знак минус говорит о том, что это проигрыш.
В отличие от фьючерсного контракта позиции покупателя и продавца опциона не симметричны. Максимальный проигрыш покупателя равен уплаченной премии, потенциальный выигрыш не ограничен. Для продавца максимальный выигрыш равен премии, потенциальные убытки не ограничены.
Продавец опциона может понести большие потери при сильном росте курса акции, так как ему придется приобретать бумагу по текущей цене и поставлять по цене исполнения. Чтобы застраховаться от такой ситуации, он может купить акцию в момент заключения контракта. В случае последующего роста цены бумаги опцион будет исполнен. Тогда инвестор поставит акцию и не понесет потерь. В качестве итога операции у него сохранится премия.
Если инвестор выписывает опцион колл и не страхует свою пози* цию приобретением базисного актива, то такой опцион называется непокрытым. Если одновременно покупается и базисный актин, опцион именуют покрытым.
6.1.2. Опцион пут
Опцион пут предоставляет покупателю опциона право продать базисный актив по цене исполнения в установленные сроки продавцу опциона или отказаться от его продажи. Инвестор приобретает опцион пут, если ожидает падения курсовой стоимости базисного актива.
Пример.
Цена спот акции равна 100 руб. Инвестор покупает трехмесячный европейский опцион пут на акцию с ценой исполнения 100 руб. за 5 руб. Это означает, что он уплачивает продавцу опциона 5 руб. и получает право продать ему акцию через три месяца за 100 руб.
Допустим, инвестор является спекулянтом, играющим на понижение. Он ожидает падения цены акции к моменту истечения срока контракта до 80 руб. Он оказался прав. Тогда через три месяца он покупает акцию на спотовом рынке за 80 руб. и исполняет опцион, т. е. продает ее по цене исполнения. На разнице цен он получает выигрыш:
100-80 -20 руб.
Чистый выигрыш с учетом уплаченной премии равен:
20-5-15 руб.
Если спотовая цена к моменту истечения контракта оказалась равной 120 руб. опцион не исполняется, так как отсутствует возможность купить акцию по более низкой цене и продать по более высокой. Выигрыши-проигрыши покупателя опциона пут представлены на рис. 6.3. Как из него следует, при цене акции больше или равной 100 руб. опцион не исполняется, и покупатель несет потери в размере
Рис б.З. Выигрыши-проигрыши покупателя европейского опциона пут к моменту истечения контракта
уплаченной премии. При 5г<100^уб. опцион исполняется. При 8Т = 95/ml покупатель имеет нулевой результат по сделке, так как выигрыш в 5 руб. только компенсирует уплаченную премию. При более низкой цене инвестор получает прибыль. Потенциально ее величина ограничена падением курса акции до нуля. Тогда максимальный выигрыш составит величину:
Х-р ,
где р - премия опциона пут.
Сформулируем общее правило, когда исполняется европейский опцион пут. Европейский опцион пут исполняется, если к моменту истечения срока действия контракта спотовая цена базисного актива меньше цены исполнения, и не исполняется, если она равна или выше цены исполнения.
Представленный на рис. 6,3 график называют графиком покупателя опциона пут или длинный пут.
Финансовый результат для покупателя опциона можно представить следующей таблицей:
Таблица 6.3. Выигрыши-проигрыши покупателя опциона пут
Цена акции к моменту истечения контракта Sr < X ST>X
Выигрыши-проигрыши по опциону X~ST-p -р
Например, цена акции к моменту истечения контракта упала до 80 руб. Согласно алгоритму табл. 6.3 выигрыш покупателя равен:
100-80-5 = 15^6.
Рис. 6.4. Выигрыши-проигрыши продавца европейского опциона пут к моменту истечения контракта
Итоги сделки для продавца опциона противоположны по отношению к результатам покупателя и представлены на рис. 6.4. Его максимальный выигрыш равен премии в случае неисполнения опциона, т. е. при ST > 100/туб. При Sr =95 руб. он получит нулевой результат. При более низкой цене акции - понесет потери. Максимальный проигрыш ограничен падением цены акции до нуля, В этом случае он составит:
Х-р.
График на рис. 6.4 называют графиком продавца опциона пут или короткий пут. Финансовый результат для продавца опциона пут можно представить следующей таблицей:
Таблица 6.4. Выигрыши-проигрыши продавца опциона пут
Цена акции к моменту истечения контракта < X ST>X
Выигрыши-проигрыши по опциону -(Х-5Г)+ р р
Например, курс акции упал до 80 руб. Согласно алгоритму табл. 6.4 проигрыш продавца опциона составит:
-(100-80)+5 = -15дуб.
Опцион пут может быть покрытым. Это означает, что, выписывая опцион, продавец осуществляет короткую продажу базисного актива. Если опцион является расчетным, то он резервирует сумму денег достаточную для приобретения базисного актива.
6.1,3. Категории опционов
Существует классификация опционов по категориям. Выделяют три категории опционов: 1) опцион с выигрышем или ITM (in the money); 2) опцион без выигрыша или А ТМ (at the money); 3) опцион с проигрышем или ОТМ (out of the money). Для отнесения опциона к одной из категорий сравнивают только два параметра: текущую цену базисного актива (5) и цену исполнения (х). На рынке возможны следующие ситуации: цена базисного актива выше цены исполнения (S > Д'), равна ей (5 = Д') или ниже ее (s< А").
Опцион колл при (5 > А") относят к категории ITM. поскольку в случае его немедленного исполнения держатель получает выигрыш в размере (5 - X); при (5 = А") - к ATM, так как в результате его немедленного исполнения держатель получает нулевой результат; и
при (5 < х) - к ОТМ, поскольку в случае его немедленного исполнения держатель получает проигрыш в размере {5 - х).
Пример.
Цена исполнения опциона колл 100 руб. Если курс акции равен 105 руб., то данный опцион отнесут к категории “с выигрышем” или ТТМ, при 5 = 100 руб, - к категории “без выигрыша” или ATM и при 5 = 95 руб., - к категории “с проигрышем” или ОТМ.
Опцион пут при (5 < х) относят к категории ITM, поскольку в случае его немедленного исполнения держатель получает выигрыш в размере (Х-S'); при (5 = Х) - к АТМ, так как в результате его немедленного исполнения держатель получает нулевой результат; и при (5 > х) - к ОТМ, поскольку в случае его немедленного исполнения держатель получает проигрыш в размере (Х-51). Опционы исполняются, если на момент исполнения они являются выигрышными.
6.1.4. Премия
При покупке опциона покупатель уплачивает продавцу премию. Премия есть не что иное, как цена опциона. Она состоит из двух частей. внутренней стоимости и временной стоимости. Временную стоимость могут назвать еще внешней стоимостью. Для опциона колл внутренняя стоимость - это разность между текущим курсом базисного актива и ценой исполнения опциона, если эта величина положительная. Если она отрицательная или равна нулю, то внутренней стоимости у опциона нет. Для опциона пут - это разность между ценой исполнения и текущим курсом базисного актива, если эта величина положительная. Если она отрицательная или равна нулю, то внутренней стоимости нет. Временная стоимость для обоих опционов представляет собой разность между величиной премии и внутренней стоимостью.
Пример 1.
Цена исполнения опциона колл 100 руб., текущий курс акции 105 руб., опцион стоит 7 руб. Внутренняя стоимость опциона равна:
105-100 = 5руб.
Временная стоимость составляет:
7-5 = 2руб.
Пример 2.
Цена исполнения опциона колл 100 руб., текущий курс акции 95 руб, опцион стоит 1 руб. Внутренняя стоимость опциона равна:
95-100 = ~5руб.
Поскольку результат отрицательный, то внутренней стоимости у такого опциона нет. Его премия целиком состоит из временной стоимости, которая равна 1 руб.
По своей сути временная стоимость - это надежды рынка на то, |Что данный опцион принесет прибыль к моменту истечения контракта. Чем больше надежд, тем больше временная стоимость. Временная стоимость будет тем больше, чем больше времени остается до истечения опциона, так как в этом случае больше неопределенности и, соответственно, надежды (вероятности) на благоприятное развитие конъюнктуры рынка. Она максимальна для опционов АТМ и убывает по мере того, как они становятся все с большим проигрышем или выигрышем. Если опцион с большим проигрышем, то надежды на получение в будущем прибыли невысоки, поэтому и временная стоимость также невелика. Если опцион с большим выигрышем, то цена базисного актива и так уже сильно выросла, поэтому надежды на ее дальнейший значительный рост также малы. Кроме того, существует вероятность потерять часть внутренней стоимости в результате возможного неблагоприятного изменения курса базисного актива. В результате временная стоимость тоже небольшая. Если это опцион А ТМ, то надежды на получение прибыли наибольшие, так как уже при небольшом движении цены базисного актива в благоприятном направлении он принесет держателю выигрыш. Поясним сказанное с помощью графиков. Для простоты иллюстрации допустим, что цена базисного актива имеет нормальное распределение. Случай опциона колл А ТМ представлен на рис. 6.5. Если цена спот равна цене исполнения, то вероятность получить положительный результат от исполнения опциона колл равна 50%. На рис. 6.5 это соответствует заштрихованной области. Для опциона колл ГТМ (см. рис. 6.6) вероятность принести инвестору еще больший результат равна площади, заштрихованной косыми чертами. Она лежит справа от линии, соответствующей цене спот актива. В то же время вероятность потерять часть существующей в данный момент внутренней стоимости равна площади фигуры слева от цены исполнения. Она заштрихована вертикальными линиями. Данный факт влияет в направлении уменьшения временной стоимости. Для опциона колл
ОТМ (см. рис. 6.7) вероятность принести положительный результат равна заштрихованной площади под кривой распределения справа от цены исполнения.
вероятность
Рис 6.5. Вероятность получить в будущем положительный результат от исполнения опциона колл ATM
Рис. 6.6. Вероятность получить в будущем положительный результат от исполнения опциона колл ITM
Рис. 6.7. Вероятность получить в будущем положительный результат от исполнения опциона колл ОТМ
Временная стоимость зависит от стандартного отклонения доходности базисного актива. Чем оно больше, тем больше риск, связанный с данным активом, и, следовательно, больше временная стоимость. Временная стоимость также является функцией процентной ставки.
Для опционов колл на акции временная стоимость положительна. Для европейских опционов пут с большим выигрышем она может быть отрицательной величиной. Европейские опционы колл и пут на фьючерсный контракт с большим выигрышем также могут иметь отрица-| тельную временную стоимость. Это говорит о том, что по мере при-| ближения срока истечения контракта, при неизменной конъюнктуре рынка, цена опциона будет расти. Данный случай будет показан аналитически в параграфах, посвященных границам премии опционов.
На рис, 6.8 графически представлено деление премии опциона колл на внутреннюю и временную стоимость. Кривая восходящая линия представляет собой график премии опциона в зависимости от цены спот базисного актива. При цене акции премия опциона равна и и состоит только из временной стоимости. При цене акции премия равна с и включает внутреннюю стоимость (отрезок Ьо) и временную стоимость (отрезок cb). Косыми линиями заштрихована область временной стоимости. Как было отмечено выше, и следует из графика, наибольшее значение временной стоимости имеют опционы ATM.
премия опциона
Рис. 6.8. Внутренняя и временная стоимость премии опциона колл
По мере приближения срока истечения контракта величина временной стоимости будет уменьшаться, так как будет умень
шаться неопределенность в отношении результата по опционному контракту. Поэтому цена опциона будет приближаться к его внутренней стоимости.
Опционы без выигрыша и с проигрышем не имеют внутренней стоимости, их премия целиком состоит из временной стоимости. Соответственно исполняются только те опционы, которые имеют внутреннюю стоимость.
6.2. ОРГАНИЗАЦИЯ ОПЦИОННОЙ ТОРГОВЛИ.
ОПЦИОНЫ НА ФЬЮЧЕРСЫ ФОНДОВОЙ БИРЖИ РТС
Существует биржевая и внебиржевая опционная торговля. Внебиржевые контракты не являются стандартными и заключаются с помощью брокеров или дилеров. Биржевая торговля опционами была открыта в апреле 1973 г. на Чикагской Бирже Опционов (СВОЕ) и организована по типу фьючерсной. Биржевые опционы по своей разновидности преимущественно являются американскими. Контракты именуют по месяцу их истечения. Поэтому опцион, истекающий в июне, назовут июньским опционом. Биржевые опционы в основном являются краткосрочными контрактами. С момента открытия торговли контрактом биржей до момента его истечения обычно проходит девять месяцев. Однако существуют и долгосрочные опционы, которые заключаются на срок до трех лет. Они получили название LEAPS (long term anticipation securities). LEAPS являются американскими опционами. Биржевые опционы подобно фьючерсам являются стандартными контрактами для каждого базисного актива. Это означает, что участники торгов согласовывают только цену опциона. Все остальные условия устанавливает биржа. В последнее время конкуренция между биржами привела к появлению биржевых не стандартных опционов. Например, участники контракта могут согласовать отличную от стандартных условий цену исполнения или время истечения опциона. Такие контракты получили название флекс опционы (flex options).
Покупатель опциона при открытии позиции уплачивает премию. Продавец обязан внести начальную маржу. При изменении текущего курса базисного актива размер маржи будет меняться, чтобы обеспечить гарантии исполнения опциона со стороны продавца. При исполнении опциона расчетная палата наугад выбирает лицо с короткой позицией по данному опционному контракту и предписывает ему осуществить действия в соответствии с условиями контракта.
На многих биржах существует система маркет-мейкеров, которые 1 на постоянной основе дают котировки опционных контрактов, В любое время они готовы купить и продать опционы по данным ценам. , Такой механизм повышает ликвидность опционной торговли. Биржа i устанавливает ограничения на величину спрэда между котировками ’ продавца и покупателя, которые могут назвать маркет-мейкеры.
На один и тот же базисный актив биржа может одновременно Предлагать несколько опционных контрактов, которые могут отли-’ Маться друг от друга как ценой исполнения, так и сроками истечения, i Все опционы одного вида, т. е. колл или пут, на один базисный актив называют опционным классом. Опционы одного класса с одинаковой ценой исполнения и датой истечения контракта образуют опционную серию.
' Инвестор, купивший или продавший опцион, может закрыть свою Позицию офсетной сделкой. Когда заключается новый контракт, число существующих на бирже контрактов возрастает на одну единицу. При совершении офсетной сделки только одним инвестором число заключенных контрактов остается прежним. Если два лица, которые имеют противоположные позиции, заключают офсетные сделки, то число контрактов уменьшается на единицу.
Для того чтобы уменьшить влияние какого-либо инвестора на конъюнктуру рынка, биржа устанавливает для опционов каждого вида два ограничения: позиционный лимит и лимит исполнения. Позиционный лимит определяет максимальное число контрактов, которые может открыть инвестор с каждой стороны рынка. В данном случае одной стороной рынка считаются длинный колл и короткий пут, другой стороной - короткий колл и длинный пут. Лимит исполнения устанавливает максимальное число контрактов, которые могут быть исполнены инвестором в течение определенного времени.
При заключении опциона клиент уплачивает брокеру комиссионные. При исполнении опциона инвестор вновь уплачивает брокеру комиссию.
Базисным активом опционного контракта может выступать фьючерсный контракт. В этом случае при исполнении опциона колл на фьючерс у покупателя открывается длинная позиция по фьючерсному контракту, и он получает выигрыш за счет разницы между котировочной фьючерсной ценой текущего дня и ценой исполнения. У продавца опциона открывается короткая позиция по фьючерсному контракту, и с него списывают проигрыш равный разности между котировочной фьючерсной ценой и ценой исполнения.
Пример.
Цена исполнения опциона на фьючерсный контракт на акцию равна 100 руб. Котировочная фьючерсная цена сегодня равна 120 руб. Покупатель исполнил опцион. Это означает, что ему была открыта длинная позиция по фьючерсному контракту на акцию, и он получил 20 руб. положительной вариационной маржи на каждую акцию, входящую в контракт. Если фьючерс включает 100 акций, то держатель опциона получил 2000 руб. вариационной маржи. Продавцу опциона была открыта короткая позиция по фьючерсу, и с него списали указанную сумму вариационной маржи. После этого инвесторы могут обычным образом закрыть свои фьючерсные позиции на рынке с помощью офсетных сделок или держать их открытыми до момента истечения контракта.
При исполнении опциона пут на фьючерс у покупателя опциона открывается короткая позиция по фьючерсному контракту, и он получает положительную вариационную маржу равную разности между ценой исполнения и котировочной ценой текущего дня. У продавца опциона открывается длинная фьючерсная позиция и с него списывается указанная величина вариационной маржи.
Пример.
Цена исполнения опциона на фьючерсный контракт на акцию 100 руб. Котировочная фьючерсная цена 80 руб. Покупатель исполнил опцион. Это означает, что ему была открыта короткая позиция по фьючерсному контракту н!а акцию, и он получил 20 руб. положительной вариационной маржи на каждую акцию, входящую в контракт. Продавцу опциона была открыта длинная позиция по фьючерсу, и с него списали указанную сумму вариационной маржи. После этого инвесторы могут обычным образом закрыть свои фьючерсные позиции на рынке с помощью офсетных сделок или держать их открытыми до момента истечения контракта.
При исполнении опциона на фьючерсный контракт следует не забывать о следующей возможной ситуации, которую мы проиллюстрируем на примере.
Пример.
Инвестор купил американский опцион колл на фьючерсный контракт на 100 акций. Текущая фьючерсная цена равна цене исполнения и составляет 100 руб. Премия опциона равна 5 руб. за одну акцию или 500 руб. за контракт.
На следующий день (вторник) фьючерсная цена выросла, поэтому держатель опциона отдал брокеру приказ исполнить контракт. Опцион исполняется по завершении торгового дня по котировочной фьючерсной цене вторника, которая равна 120 руб. Таким образом, покупатель опциона получил выигрыш в размере:
120руб. -100руб)- 500руб. = 1500руб. (
Данные средства реально появятся у него на счете на следующий день, т. е. утром в среду. Также в среду у него будет открытая длинная позиция по фьючерсному контракту.
Предположим, что во вторник после закрытия биржи произошли события, которые должны привести к сильному падению цен на рынке. Поэтому утром в среду фьючерс на акции открылся по цене 80 руб. В итоге вместо выигрыша по опциону в 1500 руб. инвестор несет потери по фьючерсному контракту за счет падения фьючерсной цены.
Чтобы избежать подобной ситуации, держатель опциона во вторник должен поступить следующим образом: отдать приказ исполнить опцион и продать фьючерс. В результате исполнения опциона у него откроется длинная позиция по фьючерсу, однако она сразу же будет закрыта, поскольку продажа фьючерса явилась в этом случае офсетной сделкой. Соответственно вариационная маржа будет определена на основе цены продажи фьючерса и цены исполнения. Пусть во вторник фьючерс был продан по цене 122 руб. Тогда выигрыш инвестора составил:
100шауш}(122руб. - 100руб) - 500руб. = 1700руб.
При заключении контракта покупатель опциона должен уплатить премию. Такой порядок организации торговли является наиболее характерным. Однако для опционов на фьючерсные контракты, как и во фьючерсной торговле, существует также система внесения начальной маржи со стороны и продавца и покупателя.
В отечественной практике ведущей биржей, на которой заключаются опционные контракты, является Фондовая биржа РТС. Опционы заключаются на фьючерсные контракты. На момент написания данной книги на бирже предлагались опционы на фьючерсные контракты на акции РАО ЕЭС, Газпрома, Лукойла, Ростелекома, фьючерсный контракт на доллар США. Наиболее активно торгуются опционы на фьючерс на акции РАО ЕЭС.
Опционные контракты на фьючерсы на акции имеют аналогичную структуру, поэтому в качестве примера приведем основные условия опциона на фьючерс на акции РАО ЕЭС.
Опцион включает один фьючерсный контракт и является американским. Контракт поставочный. Минимальное изменение премии по контракту составляет 1 руб.
Когда биржа открывает торговлю новым временным контрактом, то в его рамках она предлагает участникам рынка заключать контракты с разными ценами исполнения. Между ценами исполнения выдерживается постоянный интервал. Например, в момент написания данной книги для опционов на фьючерсный контракт на акции РАО ЕЭС он составлял 500 руб., для опциона на фьючерс на акции Ростелекома 250 руб. Так, для опциона на сентябрьский 2005 г. фьючерсный контракт на акции РАО ЕЭС биржа предлагала сентябрьские опционы, начиная с цены исполнения 6000 руб. и так далее с интервалом 500 руб. до 10000 руб. В общем случае интервал между ценами исполнения зависит от уровня цены базисного актива. К примеру, в США для опционов на акции интервал между ценами исполнения составляет 2,5 долл, для акций стоимостью 25 долл, и ниже, 5 долл, при курсе бумаги больше 25 и до 200 долл включительно и 10 долл, при цене акции свыше 200 долл.
В течение действия данного временного контракта спотовый курс базисного актива может превысить или стать ниже заявленных соответственно самой высокой или низкой цен исполнения Тогда биржа в рамках данного временного контракта добавляет новые цены исполнения.
6.3. ХЕДЖИРОВАНИЕ ОПЦИОНАМИ
С помощью опционов можно страховаться от повышения и понижения цены базисного актива. При хеджировании от роста цены базисного актива покупают опцион колл, при страховании от падения цены базисного актива покупают опцион пут. Проиллюстрируем сказанное на примерах.
Пример 1.
Инвестор планирует купить через три месяца акцию. Он опасается, что к этому моменту цена бумаги может вырасти, поэтому покупает трехмесячный опцион колл с ценой исполнения 100 руб. за 5 руб.
К моменту истечения срока действия контракта курс акции равен 120 руб. Тогда инвестор исполняет опцион, т.е. покупает акцию за 100 руб. С учетом уплаченной за опцион премии фактическая цена покупки бумаги составила 105 руб.
Допустим, к моменту истечения срока действия контракта курс акции равен 80 руб. Инвестор не исполняет опцион и покупает акцию на спотовом рынке. Фактическая цена покупки составляет 85 руб.
Пример 2.
Инвестор владеет акцией, курс которой равен 100 руб. Он опасается падения ее цены в течение следующих трех месяцев и покупает трехмесячный опцион пут с ценой исполнения 100 руб. за 5 руб. Через три месяца курс акции составил 80 руб. Тогда инвестор исполнил опцион, т. е. продал акцию за 100 руб. С учетом уплаченной премии он фактически получил за акцию 95 руб.
Если цена акции выросла до 120 руб., он не исполнил опцион, а продал акцию на спотовом рынке по этой цене. С учетом премии фактически полученная цена составила 115 руб.
Как видно из примеров, хеджирование с помощью опционов позволяет инвестору застраховаться от неблагоприятной конъюнктуры, но оставляет возможность воспользоваться благоприятным развитием событий.
Страхование от роста цены базисного актива можно осуществить продажей опциона пут, а хеджирование от падения цены - продажей опциона колл. Однако в отмеченных случаях страховка ограничивается только величиной полученной премии
Пример 3.
Инвестор планирует купить через три месяца акцию. Опасаясь роста цены акции в будущем, он страхуется продажей трехмесячного опциона пут с ценой исполнения 100 руб. за 5 руб. Страховка сработает, если курс акции не превысит 105 руб.
Пример 4.
Инвестор владеет акцией, курс которой равен 100 руб. Он опасается падения ее цены в течение следующих трех месяцев и страхуется продажей опциона колл с ценой исполнения 100 руб. за 5 руб. Страховка сработает, если курс акции не опустится ниже 95 руб.
Инвестор может использовать опцион колл для страхования короткой продажи базисного актива.
Пример 5.
Курс спот акции 100 руб. Инвестор ожидает в течение следующих пяти дней падения цены акции до 80 руб. и осуществляет короткую продажу акции. Поскольку существует вероятность роста курса бумаги, он страхуется покупкой американского опциона колл с ценой исполнения 100 руб. за 5 руб.
Пусть инвестор оказался прав: курс акции снизился до 80 руб. Он закрыл короткую позицию. Прибыль с учетом уплаченной по опциону премии составила 15 руб.
Пусть инвестор ошибся в прогнозе: курс акции вырос до 120 руб. Тогда он исполнил опцион, т.е. купил бумагу за 100 руб. и вернул кредитору. Его проигрыш равен только величине уплаченной премии, т.е. 5 руб,
6.4. КОТИРОВКА ОПЦИОННЫХ КОНТРАКТОВ
Рассмотрим котировки опционов, приводимые в деловой прессе, В таблице 6.5 представлена котировка из газеты Уолл Стрит Джор-нел за 10 июня 2002 г. (стр. М10).
Таблица 6.5. Котировка опционов
OPTION STRIKE EXP -CA VOL. LL-LAST -Pt VOL П» LAST
[ Intel 15 Jan 81 8.10 2450 0.85
22.0 17.5 Oct 297 5.70 1954 1
I 22.0 20 Jun 1320 2.50 4540 0.40
В ней сообщается информация о торгах за предыдущий день. В первой колонке слева указывается название компании и цена акции при закрытии на спотовом рынке. Она составила 22 долл. Во второй и третьей колонках дается цена исполнения опционов по месяцам окончания сроков обращения контрактов. В четвертой и пятой колонках приводится информация об опционах колл, а в шестой и седьмой об опционах пут. Соответственно в четвертой и шестой колонках указан объем торговли, а в пятой и седьмой - цена последней сделки.
В мировой практике премия опциона дается в расчете на единицу базисного актива. Контракт может насчитывать определенное количество единиц актива. Поэтому премия за весь контракт определяется по формуле:
премия за количество
премия за контракт = х
единицу актива единиц актива.
Например, в США контракт на акцию включает 100 акций. Поэтому согласно таблице 6.5 стоимость последней сделки с июньским опционом колл составила 250 долл.
В отечественной практике котировка опциона относится к одному фьючерсному контракту. Например, цена сентябрьского 2005 г. оп
циона колл на фьючерс на акции РАО ЕЭС с ценой исполнения 8500 рублей равна 75 руб.
Инвестор, торгующий опционами, должен не забывать, что, как и по другим активам между ценами покупателя и продавца существует некоторый спрэд, который отражает риск и ликвидность рынка. Например, котировки сентябрьского 2005 г. опциона колл на фьючерс на акции РАО ЕЭС с ценой исполнения 8500 руб. в середине дня 13.05.2005 г. составляли: цена покупателя 75 руб., цена продавца -85 руб. Таким образом, инвестор в этот момент мог продать контракт за 75 руб. и купить за 85 руб. В зависимости от цен исполнения спрэд между ценами может быть весьма существенным. Например котировки сентябрьского 2005 г. опциона колл на фьючерс на акции РАО ЕЭС с ценой исполнения 8000 руб. в середине дня 13.05.2005 г. были следующими: цена покупателя 251 руб,, цена продавца - 298 руб.
КРАТКИЕ ВЫВОДЫ
"’Существует три типа опционов: американский, европейский и бермудский. Американский опцион можно исполнить в любой день в течении срока действия контракта, европейский - только в день его окончания. Бермудский опцион дает право исполнить его в определенные моменты времени в течение действия контракта. Различают два вида опционов: колл и пут. Опцион колл дает право держателю опциона купить или отказаться от покупки базисного актива. Опцион пут дает право держателю опциона продать или отказаться от продажи базисного актива. Инвестор приобретает опцион колл, если рассчитывает на повышение курса базисного актива, опцион пут - когда ожидает его понижения.
Европейский опцион колл исполняется, если к моменту истечения контракта курс спот базисного актива выше цены исполнения, европейский опцион пут - если курс спот актива ниже цены исполнения.
Выделяют три категории опционов: с выигрышем (УГЛУ), без выигрыша (ATM), с проигрышем (ОТМ).
Покупая опцион, инвестор уплачивает продавцу премию. Она состоит из двух частей: внутренней и временной стоимости.
Организация торговли опционными контрактами в своей основе аналогична торговле фьючерсными контрактами. При открытии позиции продавец контракта обязан внести гарантийный залог. При торговле опционами на фьючерсные контракты оба участника вносят начальную маржу.
При страховании от роста цены базисного актива надо купить опцион колл, при страховании от падения - опцион пут.
ГЛАВА 7. ОПРЕДЕЛЕНИЕ ГРАНИЦ ПРЕМИИ ОПЦИОНОВ НА АКЦИИ
В настоящей главе на примере опционов на акции рассматривается вопрос определения границ премии опционов. Мы ответим на вопрос о стоимости опционов перед истечением срока действия контрактов и выведем формулы для верхних и нижних границ премии опционов, проанализируем целесообразность раннего исполнения американских опционов.
7.1. ГРАНИЦЫ ПРЕМИИ ОПЦИОНОВ НА АКЦИИ, ПО КОТОРЫМ НЕ ВЫПЛАЧИВАЮТСЯ ДИВИДЕНДЫ
7.1.1. Стоимость американского и европейского опционов колл к моменту истечения срока действия контрактов
Непосредственно перед истечением срока действия контрактов стоимость европейского и американского опционов колл может принимать только два значения. Если 5 < X, (где S - цена спот базисного актива к моменту истечения контракта, X - цена исполнения опциона), то премия равна нулю, поскольку покупка опциона не принесет инвестору выигрыша. Если S > X , то премия составит 5-%. При нарушении данного условия возникает возможность совершить арбитражную операцию. Поясним сказанное на примерах.
Пример 1.
Перед истечением срока действия контракта цена опциона колл равна 5 руб., цена исполнения - 100 руб., цена акции - 110 руб.
Указанное выше условие нарушено, поэтому арбитражер покупает опцион за 5 руб., так как он стоит дешевле чем должен стоить, и осуществляет короткую продажу акции на спотовом рынке за 110 руб. Исполняет опцион, т. е. приобретет акцию по контракту за 100 руб., и возвращает ее кредитору. Его выигрыш равен:
-5-100 + 110 = 5руб.
Пример 2.
Перед истечением срока действия контракта цена опциона колл равна 15 руб., цена исполнения - 100 руб., цена акции - 110 руб.
Указанное выше условие нарушено, поэтому арбитражер продает опцион, поскольку он стоит дороже чем должен стоить, занимает
деньги и покупает на спотовом рынке акцию. При исполнении контрагентом опциона, арбитражер поставляет ему акцию за 100 руб. Его выигрыш равен:
15-110 +100 = 5руб.
минус процент за кредит.
Таким образом, к моменту истечения срока действия контракта цена опциона колл равна его внутренней стоимости, т.е. нулю, если 5 < X , или 5' - X, если 5 > X . Г рафик цены опциона колл к моменту истечения действия контракта представлен на рис. 7.1. ломаной линией оХа.
Рис. 7.1. Цена опциона колл к моменту истечения срока действия контракта
Следует подчеркнуть, что до окончания периода действия контракта график премии опциона колл будет иметь выпуклую форму, как показано на рис. 7.2. По мере приближения срока окончания контракта график все ближе будет подходить к ломаной линии оХа, пока не сольется с ней непосредственно перед моментом истечения опциона.
Рис. 7.2. График премии опциона колл за 6, 3 месяца и перед моментом истечения срока действия контракта
7.1.2. Стоимость американского и европейского опционов пут к моменту истечения срока действия контрактов
Непосредственно перед истечением срока действия контрактов цена европейского и американского опционов пут может принимать только два значения. Если 5 > X , премия равна нулю. Если 5 < X , она составит Х-S. При нарушении последнего условия можно совершить арбитражную операцию.
Пример 1.
Перед истечением срока действия контракта цена опциона пут равна 5 руб., цена исполнения - 100 руб., цена акции - 90 руб.
Указанное выше условие нарушено, поэтому арбитражер покупает опцион, поскольку он стоит дешевле чем должен стоить, и акцию, заняв для этого деньги. Исполняет опцион, т, е. поставляет акцию по контракту за 100 руб. Его прибыль равна:
-5-90 +100 = 5руб.
минус процент за кредит.
Пример 2.
Перед истечением срока действия контракта цена опциона пут равна 15 руб., цена исполнения - 100 руб., цена спот акции - 90 руб.
Указанное выше условие нарушено, поэтому арбитражер продает опцион, поскольку он стоит дороже чем должен стоить, и осуществляет короткую продажу акции на спотовом рынке за 90 руб. При исполнении контрагентом опциона арбитражер покупает акцию по контракту за 100 руб. и возвращает ее кредитору. Его выигрыш равен: 15-100 + 90 -5руб.
Рис. 7.3. Цена опциона пут к моменту истечения срока действия контракта
Графически цена опциона пут к моменту истечения срока действия контракта представлена на рис. 7.3 ломаной линией аХв.
До окончания периода действия контракта график премии опциона пут имеет выпуклую форму, как показано на рис. 7.4. По мере приближения срока окончания контракта он все ближе будет подходить к ломаной линии аХв, пока не сольется с ней непосредственно перед моментом истечения опциона.
Рис. 7.4. График премии опциона пут за 6, 3 месяца и перед моментом истечения срока действия контракта
7.1.3. Верхняя граница премии американского и европейского опционов колл
Верхняя граница премии европейского и американского опционов колл в любой момент времени действия контракта не должна быть больше цены спот акции, т. е. с < 5, (где с - премия опциона колл). При нарушении данного условия инвестор может совершить арбитражную операцию: он купит акцию и выпишет на нее опцион.
Пример.
Цена акции 100 руб. Некоторый инвестор готов купить опцион на данную акцию с ценой исполнения 50 руб. за 120 руб. Тогда арбитражер продает опцион за 120 руб. и покупает на рынке акцию за 100 руб. Если опцион исполняется, он поставляет акцию по цене исполнения. Его прибыль равна:
120 -100 + 50 = 10 руб.
Если опцион не исполняется, то в последующем он продает акцию по текущей цене спот (5Г), и его прибыль равна:
120-100 + 5..
Минимальная прибыль арбитражера при падении цены акции до нуля составит 20 руб.
Инвестор может разместить 20 руб., т.е. сумму разности между величиной премии и ценой, уплаченной за акцию, на депозите и получить дополнительную прибыль.
7.1.4. Верхняя граница премии американского и европейского опционов пут
7.14.1 Верхняя граница премии американского опциона пут
Цена американского опциона пут в любой момент времени действия контракта не должна быть больше цены исполнения, т. е. pa < X , (где ра - цена американского опциона пут). В противном случае можно получить прибыль без риска, продав опцион.
Пример.
Цена исполнения американского опциона пут равна 100 руб. Некоторый инвестор готов купить его за 120 руб. Тогда арбитражер продает опцион за 120 руб. В случае исполнения контракта арбитражер покупает акцию по цене исполнения, т, е. за 100 руб. и продает ее на спотовом рынке по текущей цене (5/), Его прибыль равна:
120 -100+ 5Г.
Если опцион не исполняется, то в качестве прибыли остается полученная премия.
7.14.2. Верхняя граница премии европейского опциона пут
К моменту истечения срока действия контракта европейский опцион пут должен стоить не больше цены исполнения. Иначе можно получить арбитражную прибыль как в приведенном выше примере. Поэтому в момент его приобретения он должен стоить не больше приведенной стоимости цены исполнения, т.е.:
1 + г(Т / база)
(7-1)
где ре - премия европейского опциона пут;
X - цена исполнения;
г-ставка без риска;
Т - время до истечения срока действия контракта;
база - финансовый год.
В противном случае арбитражер получит прибыль. Он продаст опцион и инвестирует сумму премии под процент без риска на период действия контракта.
Выражение (7.1) можно записать с использованием непрерывно начисляемого процента. Тогда оно примет вид:
Р..<Хе\
где г - непрерывно начисляемая ставка без риска.
7,1,5. Нижняя граница премии европейского опциона колл
Нижняя граница премии европейского опциона колл на акции, по которым не выплачиваются дивиденды, составляет:
I + г(Г / база) ’
где се - премия европейского опциона колл;
Т- период действия контракта;
г-ставка без риска.
Аналогичное выражение для непрерывно начисляемого процента имеет вид:
ce>S-Xe~rT. (7.3)
Докажем утверждение (7.3).
Имеется два портфеля. В первый входит длинный европейский опцион колл (cj и сумма денег равная приведенной стоимости цены исполнения (ле '7). Данная сумма инвестируется под ставку без риска г на период времени ТУ Второй портфель состоит из акции, цена спот которой равна 5. К моменту истечения контракта сумма денег (ле7) выросла на депозите до величины X, т. е. цены исполнения. Если цена спот акции в этот момент выше цены исполнения, то опцион колл исполняется. Держатель опциона уплачивает сумму X и получает акцию. Таким образом, первый портфель состоит из одной акции. Во второй портфель по-прежнему входит акция. Поэтому в конце периода Т стоимости портфелей равны.
1 Вместо суммы денег в портфель можно включить безрисковую облигацию, номинал которой равен X, погашаемую в конце периода Т .
Если в конце периода Т цена спот акции меньше или равна цене исполнения, то опцион колл не исполняется, и стоимость первого портфеля равна X. Второй портфель состоит из акции. Так как в этот момент времени ST<X(ST - стоимость акции в момент окончания контракта), то стоимость первого портфеля больше или равна стоимости второго портфеля.
В конце периода Т цена первого портфеля равна или больше цены второго портфеля. Следовательно, аналогичное соотношение должно выдерживаться и в начале периода, чтобы исключить возможность совершить арбитражную операцию. Поэтому можно записать:
се + Хе rT >S
или
ce>S~Xe~rT.
Таким образом, величина премии европейского опциона колл на акции, по которым не выплачиваются дивиденды, не должна быть меньше разности цены спот акции и дисконтированной стоимости цены исполнения. Если премия опциона колл меньше отмеченной величины, можно совершить арбитражную операцию.
Пример.
Цена спот акции 110 руб., цена исполнения 100 руб., ставка без риска для 180 дней 10% годовых. Определить нижнюю границу премии опциона, который заключается на 180 дней. (В примере используем простую процентную ставку и финансовый год равный 360 дням -формула (7.2)).
Решение.
110----------------г = 14,76 руб.
1 + 0,1(180/360)
Предположим, что фактическая цена опциона меньше нижней границы и равна 14 руб. Тогда можно совершить арбитражную операцию. Арбитражер занимает акцию2, продает ее за 110 руб. и покупает опцион за 14 руб. В результате данной операции он получает 96 руб. и размещает их на 180 дней под 10% годовых. В конце периода он получает по счету сумму:
9б[1 + 0,1(180 / 3 60)] = 100,8 руб.
2 Для упрощения примера мы предполагаем, что можно занять акцию у брокера без процентов
Если к моменту истечения срока действия контракта цена акции выше цены исполнения, арбитражер исполнит опцион, получит акцию по контракту и вернет ее брокеру. Его прибыль составит:
100,8 -100- 0,8 руб.
Если цена акции будет меньше 100 руб., арбитражер купит ее на спотовом рынке и получит еще большую прибыль.
Представим алгоритм рассуждений арбитражера в общей форме. Условие, не допускающее арбитраж, соответствует выражению (7.3). Следовательно, арбитраж возможен, если сложилась ситуация:
с <S~Xe ,т. (7.4)
Неравенство (7.4) состоит их двух портфелей: первый портфель -это левая часть неравенства, второй портфель - правая часть неравенства. Первый портфель дешевле второго, поэтому его необходимо купить. Второй портфель дороже первого, поэтому его следует продать. Покупку актива показывают знаком плюс, продажу - знаком минус. Так как второй портфель продается, то это запишем как:
-(5-Хе"т)
или
-S + Xe'1. (7.5)
Выражение (7.5) показывает, какие действия необходимо совершить, чтобы продать второй портфель. Знак минус перед 5 говорит о том, что следует продать акцию. Поскольку арбитражер не располагает акцией, то ее предварительно надо занять. Знак плюс перед Хе~,т показывает, что полученную сумму денег надо разместить на депозите под ставку без риска. На полученные от продажи второго портфеля деньги арбитражер также покупает первый портфель, т. е, опцион колл. Оставшиеся средства он размещает на депозит на время Т под ставку г,
Чтобы лучше понять результат данного алгоритма, представим выражение (7.4) как равенство:
с =S-Xe гТ. (7.6)
Равенство (7.6) соответствует безарбитражной ситуации. Преобразуем его следующим образом:
S-ce = Хе ’ г. (7.7)
Выражение (7.7) показывает, что разность между ценой акции и премией опциона равна дисконтированной стоимости цены исполнения. Таким образом, если арбитражер продаст акцию и купит опцион, то у него останется сумма денег равная приведенной стоимости цены исполнения. Разместив ее на депозите на время Т под ставку г, он получит в конце этого периода сумму равную цене исполнения. В такой ситуации арбитраж невозможен. Однако, если:
S-ce>Xe,T,
то после продажи акции и покупки опциона у арбитражера останется сумма денег, превышающая дисконтированную стоимость цены исполнения. Разместив данные средства на депозите на время Т под ставку г, он получит в конце периода сумму, превышающую цену исполнения. Это превышение и образует арбитражную прибыль.
7.1.6. Нижняя граница премии европейского опциона пут
Нижняя граница премии европейского опциона пут на акции, по которым не выплачиваются дивиденды, равна:
А ------Д-------x-S- (7-8)
1 + / база)
Для непрерывно начисляемого процента выражение (7.8) принимает вид:
ре>Хе '7 -У (7.9)
Докажем утверждение (7.9).
Рассмотрим два портфеля. В первый входит длинный европейский опцион пут (/? .) и акция (5), во второй - сумма денег равная (хе~гТ\ которая инвестируется под ставку без риска г на период Т. Если в конце периода Т курс акции ниже цены исполнения, то опцион пут исполняется: инвестор поставляет акцию и получает сумму денег равную X. Это стоимость первого портфеля в данный момент. Стоимость второго портфеля также равна X. Таким образом, стоимости портфелей равны.
Если курс акции выше или равен цене исполнения, то опцион пут не исполняется, и стоимость первого портфеля равна ST (ST- цена акции в момент окончания контракта). Стоимость второго портфеля равна X. Поэтому в конце периода Т стоимость первого портфеля больше или равна стоимости второго портфеля. Данное соотноше
ние должно выдерживаться и в начале периода, иначе можно совершить арбитражную операцию. Отсюда:
ре + 5 > Хе,т или
Таким образом, премия европейского опциона пут не должна быть меньше разности между приведенной стоимостью цены исполнения и ценой спот акции.
Пример.
Цена спот акции 90 руб., цена исполнения 100 руб., ставка без риска для 180 дней 10% годовых. Определить нижнюю границу премии опциона, который заключается на 180 дней. База составляет 360 дней.
Решение.
--------------г - 90 = 5,24руб. 1 + 0,1(180/360)
Предположим, что фактическая цена опциона в примере меньше нижней границы и равна 5 руб. Тогда можно совершить арбитражную операцию. Арбитражер занимает 95 руб. и покупает опцион и акцию. Через 180 дней он должен вернуть по кредиту:
95[1 + 0,1(180/360)] = 99,75 руб.
Если к окончанию контракта цена спот акции ниже цены исполнения, он исполнит опцион и поставит бумагу по 100 руб. Его прибыль равна:
100 -99,75 -0,25руб.
Если курс акции превысит цену исполнения, он продаст ее на спотовом рынке по более высокой цене и получит еще большую прибыль.
Представим алгоритм рассуждений арбитражера в общей форме. Условие, не допускающее арбитраж, соответствует выражению (7.9). Следовательно, арбитраж возможен, если сложилась ситуация:
pt <Xe~rT -S. (7.10)
Левая часть неравенства (7.10) - это первый портфель, правая часть - второй портфель. Первый портфель дешевле второго, поэтому его
необходимо купить. Второй портфель дороже первого, и его следует продать. Продажу второго портфеля запишем как:
-(xe~rr-s)
или
-Хе гТ + S. (7.11)
Выражение (7.11) говорит о том, что продажа второго портфеля означает заимствование денег и покупку акции. В целом в рамках данной стратегии арбитражер занимает средства и покупает акцию и опцион пут.
Чтобы лучше понять результат данного алгоритма, представим выражение (7.10) как равенство:
pe=Xe~'7-S. (7.12)
Равенство (7.12) соответствует безарбитражной ситуации. Преобразуем его следующим образом:
pe + S = Xe~r1\ (7.13)
Равенство (7.13) говорит о том, что, если цена опциона пут и акции равна дисконтированной стоимости цены исполнения опциона, то инвестор может занять данную сумму под процент г на период Т и купить опцион и акцию. От исполнения опциона, т. е. поставки акции по цене X , он получит сумму, которая покроет его заем с процентами. В такой ситуации арбитраж невозможен. Однако, если:
Pe + S'<Xe'T, (7.14)
то заимствованная сумма окажется меньше дисконтированной стоимости цены исполнения. В таком случае арбитражер заработает прибыль на разнице между суммой X, полученной от исполнения опциона, и меньшей суммой, которую он вернет по кредиту.
В главе 6 мы отметили, что европейский опцион пут на акции с большим выигрышем может иметь отрицательную временную стоимость. Покажем это аналитически, используя условие для нижней границы премии опциона.
Допустим, премия опциона пут равна ее нижней границе, т. е.:
pe = XerT-S.
Тогда внутренняя стоимость составляет:
X-S,
а временная стоимость по определению равна:
P'-(x-s\
Отсюда:
Хе~,т -S-(X-S) = Xe~r1 -X <0 , так как X>Xe~f/. График премии европейского опциона пут представлен на рис. 7.5. линией выпуклой к началу координат.
Рис. 7.5. Гоафик премии европейского опциона пут
7.1.7. Нижняя граница премии американского опциона колл. Раннее исполнение американского опциона колл
Американский опцион колл обладает всеми характеристиками европейского опциона, но также позволяет держателю исполнить его в любой момент времени до истечения срока действия контракта. Поэтому американский опцион колл должен стоить по крайней мере столько же, сколько и европейский опцион колл с той же ценой исполнения и датой истечения контракта. Отсюда можно заключить, что для американского опциона верна формула (7.2). Она и принимается в качестве его нижней границы. Если премия опциона окажется меньше, то можно совершить арбитражную операцию. Действия арбитражера аналогичны случаю с европейским опционом.
Если держатель американского опциона колл исполнит его в свя-1и с ростом цены акции, он выиграет сумму равную S - X. Однако данная величина меньше, чем нижняя граница премии, которая определяется по формуле (7.2). Таким образом, не оптимально исполнять американский опцион колл досрочно, так как в этот момент его выгоднее продать, поскольку он стоит дороже. Можно также сказать, чго при досрочном исполнении контракта его держатель реализует юлько внутреннюю стоимость опциона, но теряет временную стоимость. Получается, что право раннего исполнения опциона не имеет
никакой ценности. Поэтому американский опцион колл на акции, по которым не выплачиваются дивиденды, будет стоить столько же, сколько и европейский.
7.1.8. Нижняя граница премии американского опциона пут. Раннее исполнение американского опциона пут
Американский опцион пут можно исполнить досрочно. В этом случае держатель опциона получит сумму равную X-S. Поэтому американский опцион пут в любой момент времени действия контракта должен стоить не меньше чем X-S. Если данное условие нарушается, то последует арбитраж. Арбитражер купит опцион, поскольку он стоит дешевле, чем должен стоить, купит акцию и исполнит опцион. Прибыль по операции составит:
Раннее исполнение американского опциона пут может оказаться оптимальной стратегией, особенно, если цена акции сильно упадет и ее дальнейшее снижение будет маловероятным. Поэтому американский опцион пут должен стоить больше аналогичного европейского опциона.
7.2. ГРАНИЦЫ ПРЕМИИ ОПЦИОНОВ НА АКЦИИ, ПО КОТОРЫМ ВЫПЛАЧИВАЮТСЯ ДИВИДЕНДЫ
Выплата дивидендов в течение действия опционного контракта влияет на его цену. Премия опциона колл будет падать, так как при выплате дивиденда цена акции уменьшается. Соответственно уменьшается и потенциальный выигрыш от исполнения опциона. Для опциона пут наблюдается противоположная ситуация, поскольку падение курса акции увеличивает его внутреннюю стоимость. Отмеченные факты отражаются и на величине нижней границы премий опционов.
7.2.1. Верхняя граница премии европейских и американских опционов колл и пут
Для европейского опциона колл верхняя граница премии равна:
ce<S-D,
где D - приведенная стоимость дивиденда к моменту заключения контракта; дивиденд дисконтируется под ставку без риска г.
Для американского опциона колл и европейского и американского опционов пут верхние границы аналогичны рассмотренным случаям, когда по акциям не выплачивались дивиденды.
7.2.2. Нижняя граница премии европейского и американского опционов колл
Получим формулу для нижней границы премии европейского опциона. Вначале рассмотрим случай, когда дивиденд выплачивается на акцию в последний день действия контракта, т.е. в момент Т .
Рассмотрим два портфеля. Первый включает европейский опцион колл, сумму денег Хе~гТ 3 и сумму денег D , равную дисконтированной под ставку г стоимости будущего дивиденда к моменту заключения контракта, т.е.:
D = diverT. (7.15)
Суммы Хе~гТ и D инвестируются на время Т под ставку г, Второй портфель состоит из одной акции (5).
Если к моменту окончания срока действия контракта цена акции больше цены исполнения > Д'), то опцион колл исполняется, и первый портфель стоит:
S, + DerT
или с учетом (7.15):
+ div.
Если Sr < X, он стоит:
X 4- div.
Стоимость второго портфеля в обоих случаях равна:
Sr 4- div.
Следовательно, стоимость первого портфеля больше или равна стоимости второго портфеля. Данное соотношение должно выдерживаться и в начале периода Т, чтобы арбитраж был невозможен.
’ Вместо суммы денег в портфель можно включить безрисковую облигацию, номинал которой равен X , погашаемую в конце периода Т.
Поэтому можно записать:
ce + Xe~rT + D>S ,
ИЛИ
с >S-Xe rT -D.
Таким образом, премия европейского опциона колл должна быть не меньше, чем разность между ценой спот акции и суммой приведенных стоимостей цены исполнения и дивиденда, который планируется выплатить по акции.
Рассмотрим второй случай, когда дивиденд выплачивается в момент t в ходе действия контракта, t < Т.
Сравним два портфеля. Первый включает европейский опцион колл, сумму денег Хе гТ и сумму денег D , равную дисконтированной под ставку г стоимости будущего дивиденда к моменту заключения контракта, т.е.:
D = dive rt. (7.16)
Суммы Хе~,т и D инвестируются на время Т под ставку г. Второй портфель состоит из одной акции (5).
Если к моменту окончания срока действия контракта цена акции больше цены исполнения (S7 > Лг). то опцион колл исполняется, и первый портфель стоит:
Sr + DerT.
।
Если Sr < X, он стоит:
X + De,T.
Во втором портфеле на акцию в момент t был выплачен дивиденд div. Он инвестируется до окончания контракта под ставку г. Поэтому стоимость второго портфеля в обоих случаях равна:
ST+div-e*T(7.17)
Из (7.16) следует, что:
div = De". (7.18)
Подставим значение дивиденда из (7.18) в (7.17):
S, +De“ -er{T '^S' +DeX
Таким образом, стоимость первого портфеля больше или равна стоимости второго портфеля4. Данное соотношение должно выдерживаться и в начале периода Т, чтобы арбитраж был невозможен. Поэтому можно записать:
се + Хе'т + D>S,
ИЛИ
се> S - Xe~rT ~ D. (7,19)
Если условие (7.19) нарушается, можно совершить арбитражную операцию.
Представим алгоритм действий арбитражера для случая, когда дивиденд выплачивается в момент Т. Запишем условие, допускающее арбитраж:
с <S-XerT-D
е
или
S-ce>Xer! + R (7.20)
Примем в неравенстве (7.20) левую часть за первый портфель, правую - за второй. Поскольку первый портфель стоит дороже второго, его следует продать, второй - купить. Чтобы определить действия арбитражера по продаже первого портфеля умножим левую часть неравенства (7.20) на минус единицу и раскроем скобки:
-(S-c;)=-S + c . (7.21)
Следовательно, арбитражер осуществляет короткую продажу акции и покупает опцион колл. Полученные по операции средства (S c ) он размещает на депозите до момента окончания контракта. В этом
4 В рассмотренном доказательстве ставка г предполагается одинаковой для всех периодов, в том числе и для форвардного, т.е. (T-t). Картина принципиально не изменится, если она будет различной. В этом случае можно поступить следующим образом: в первом портфеле инвестировать величину D на время t. Полученная сумма будет эквивалентна размеру дивиденда. Далее инвестировать ее на период (г -1) под новую ставку. Под эту же ставку инвестируется и дивиденд во втором портфеле.
Можно воспользоваться другим приемом: инвестировать в первом портфеле величину D на все время действия контракта под ставку г, а для дивиденда во втором портфеле обеспечить соответствующую форвардную ставку для периода (T-t) на (юнове текущих спотовых. Технику обеспечения инвестирования под форвардную ставку < помощью спотовых см. в книге А.Н. Буренина ‘'Управление портфелем ценных бумаг", М, Научно-техническое общество им. акад. С.И. Вавилова, 2005, параграф 5.1.1.6.
состоит суть операции по покупке второго портфеля. В конце периода Т по депозиту инвестор получает сумму (5-с )егТ.
Если по истечению срока действия контракта S7 > X, арбитражер исполняет опцион, возвращает акцию и выплачивает дивиденд кредитору. Его прибыль равна:
(5-с k” -x-div. (7.22)
Прибыль возникает за счет того, что согласно (7.20) в начальный момент:
S-c > Хе т +D,
поэтому на момент окончания контракта:
(5-с>" АХе1 +D\“ = X + div.
Отсюда следует результат (7,22).
Если на момент окончания контракта ST < X, арбитражер опцион не исполняет, а покупает акцию на спотовом рынке и получает еще большую прибыль.
Дивиденд может выплачиваться на акцию в ходе действия контракта во время t. В этом случае действия арбитражера аналогичны представленным выше, но с поправкой на дивиденд. Продав акцию и купив опцион, он должен разместить сумму равную дисконтированной стоимости дивиденда на депозите на время t, За счет полученных по депозиту денег он возвратит дивиденд. Оставшиеся средства инвестируются до истечения срока действия контракта.
Американский опцион предоставляет инвестору больший диапазон возможностей по сравнению с европейским, следовательно формула (7.19) верна и для него.
7.2.3. Нижняя граница премии европейского и американского опционов пут
Получим формулу для нижней границы премии европейского опциона. Рассмотрим только случай, когда дивиденд выплачивается на акцию в последний день действия контракта, т.е. в момент Г5
Рассмотрим два портфеля. Первый состоит из одного европей
5 Если дивиденд выплачивается в ходе действия контракта в момент t, то доказательство строится аналогично такому же случаю для опциона колл
ского опциона пут и одной акции ($), второй - включает суммы денег ХегТ и D . (D - это приведенная стоимость дивиденда, который выплачивается по акции. Она получена дисконтированием дивиденда под непрерывно начисляемую ставку без риска г на время Г). Суммы Хе 11 и D инвестируются на время Т под ставку г.
К моменту истечения срока действия контракта стоимость второго портфеля при любой цене акции равна:
X + Derr = X + div,
Стоимость первого портфеля в этот момент при ST >Х составляет:
St + di v,
поскольку опцион не исполняется. Следовательно, стоимость первого портфеля больше или равна стоимости второго.
Если Sr < X , опцион исполняется, т.е. инвестор продает акцию по цене исполнения X и стоимость портфеля составляет:
X + div.
В этом случае стоимости портфелей равны. Таким образом, в конце периода Т стоимость первого портфеля равна или больше стоимости второго портфеля. Данное соотношение должно выдерживаться и в начале периода Т, чтобы арбитраж был невозможен. Поэтому можно записать:
pe + S> Xe~rT + D
или
А >Xe~rT + D-S, (7.23)
Таким образом, премия европейского опциона пут должна быть не меньше разности между суммой дисконтированных стоимостей цены исполнения и дивиденда, который планируется выплатить по акции, и ценой спот акции. Если условие (7.23) не выдерживается, можно получить арбитражную прибыль.
Чтобы определить действия арбитражера, запишем условие, допускающее арбитраж:
ре< Xe~rT + D-S
или
pe + S<Xerl +D. (7.24)
Левую часть неравенства (7.24) примем за первый портфель, правую
- за второй. Первый портфель стоит дешевле второго, поэтому первый портфель покупаем, второй продаем. Покупка первого портфеля означает покупку опциона и акции. Для этого занимаем средства на период Т под ставку г в размере (ре + £). В этом состоит суть продажи второго портфеля. В момент Т на акцию выплачивается дивиденд.
Если по истечении контракта, ST <Х, арбитражер исполняет опцион, т.е. продает акцию по цене исполнения, возвращает кредит. Прибыль равна:
X + div~{p +s\''.
Прибыль возникает за счет того, что по кредиту арбитражер должен вернуть сумму (р( +5')ег7 . От исполнения опциона и за счет дивиденда он получит сумму (x + l/zv). Величина (x + div) больше
Это следует из (7.24), если умножить обе части неравенства на ет:
(р, + S)e" <(Xerl + Dp
ИЛИ
(у? + S)err < X + div.
Если на момент истечения опциона ST > X, арбитражер не исполняет контракт, а продает акцию по спотовой сделке и получает еще большую прибыль.
Дивиденд может выплачиваться на акцию в ходе действия контракта во время t. В этом случае действия арбитражера аналогичны представленным выше, но с поправкой на дивиденд. Для покупки акции и опциона он занимает сумму + Поскольку на акцию будет выплачен дивиденд, то занимаемые средства разбиваются на две части. Сумма равная D занимается на время t. Эта часть кредита погашается с помощью будущего дивиденда. Оставшаяся сумма (sp -D) занимается на весь период действия контракта.
Американский опцион предоставляет инвестору больший диапазон возможностей по сравнению с европейским, поэтому формула (7.23) верна и для него.
Американский опцион пут можно исполнить в любой момент времени в течение действия контракта. Поэтому для него также должно выдерживаться условие:
pa>X-S,
Отсюда общее условие для нижней границы премии опциона можно записать так:
pa > max (X- S; XerT + D-S).
7.2.4. Раннее исполнение американского опциона колл
Как было показано выше, раннее исполнение американского опциона колл на акции, по которым в течение действия контракта нв выплачиваются дивиденды, не является оптимальной стратегией. Однако нельзя настаивать на этом утверждении, если базисным активом опциона являются акции, по которым выплачиваются дивиденды. Выплата дивидендов приводит к падению курса акций, и следовательно, прибыли от исполнения опциона. Поэтому исполнение американского опциона колл на такие акции может оказаться оптимальным. В качестве возможного момента исполнения следует рассматривать день непосредственно перед датой учета.6
Пусть - Дни в рамках действия опционного контракта перед датами учета. Соответственно по акции выплачиваются дивиденды div^div2,...divn. Период действия опционного контракта равен Т.
Если инвестор исполнит опцион перед последней датой учета, т.е. в момент tn, он получит внутреннюю стоимость опциона, которая равна:
После выплаты дивиденда цена акции упадет до уровня:
У -div . fn п
Если инвестор не исполнит опцион, то нижняя граница премии опциона составит:
\ - div„ - Хе-г(т-‘" ’. (7.25)
Поэтому, если (минимальная) премия опциона после выплаты дивиденда равна или больше его внутренней стоимости, которую инвестор получит от исполнения контракта перед датой учета, т.е.:
S, - div - Хе~г^т~‘^ > S. -X
® Дата учета - это дата закрытия реестра акционеров. С этого дня акция начинает гирговаться без дивиденда.
Часть II. Опционные рынки
ИЛИ
или
divn < X - Хе~г{Т1'-} ,
divn < -^[l -е Г'Т
опцион не оптимально исполнить на дату tn. Если
divn >X\i-e r{T
(7.26)
(7.27)
опцион оптимально исполнить на дату tn, особенно, когда курс акции высок, ожидается большой дивиденд, и до истечения контракта остается мало времени.
Рассмотрим момент , т. е. дату перед выплатой предпоследнего дивиденда. От исполнения опциона в этот день инвестор получит сумму равную:
Сразу после момента tn_x цена акции падает до уровня:
S, ~ div ..
"-1
Если опцион не был исполнен на дату tn_{, его цена в следующий момент времени должна быть больше величины:
~divnX-Xe н. (7.28)
Выражение (7.28) представляет собой нижнюю границу премии опциона сразу после наступления даты учета для предпоследнего дивиденда. Нижняя граница премии опциона рассчитывается здесь относительно даты tn, так как теоретически это наиболее оптимальный ближайший момент возможного досрочного исполнения опциона. Поэтому, если
S, -div„ .-Хе-г(,’-‘^ >S. -X bl I П 1 1п I
ИЛИ
или
div„_, < Х Хе-'1'--’'"' '1 ,
divn , < X ,
(7.29)
опцион не оптимально исполнять на дату , так как его цена в следующий момент будет по крайней мере не меньше внутренней стоимости, которую может получить инвестор от исполнения. Если
(7.30)
опцион оптимально исполнить на дату tn^.
Аналогичные рассуждения можно провести и для других моментов перед датами учета, чтобы определить оптимальность исполнения опциона.
Пример.
Период действия американского опциона колл на акции 5 месяцев. Через 1 и 4 месяца по акциям выплачиваются дивиденды по 2 руб. каждый. Цена исполнения опциона 100 руб., ставка без риска 10%, цена акции 120 руб. Определить, оптимально ли исполнить опцион перед выплатой первого или второго дивиденда. (Для простоты полагаем, что дата выплаты дивиденда и дата учета - это один и тот же момент времени).
Решение.
Определим, оптимально ли исполнить опцион перед выплатой первого дивиденда:
1Оо[1(мк”)] = 2,41руб.
Так как величина дивиденда (2 руб.) меньше полученного результата, то, согласно формуле (7.29), опцион не оптимально исполнить перед выплатой первого дивиденда.
Для второго дивиденда получаем результат:
1 оо[1 -е 04|'”-°335,)] = 0,83руб.
Так как величина дивиденда больше расчетной цифры, то, согласно формуле (7.27), опцион целесообразно исполнить в этот момент.
КРАТКИЕ ВЫВОДЫ
К моменту истечения срока действия контракта стоимость американского и европейского опционов колл и пут должна равняться нулю или внутренней стоимости.
Премия американского и европейского опционов колл на акцию не должна превышать цену спот акции.
Премия американского опциона пут на акцию не должна быть больше цены исполнения, европейского опциона пут - больше приведенной стоимости цены исполнения.
Премия американского и европейского опционов колл на акцию, по которой не выплачиваются дивиденды, не должна быть меньше разности между ценой спот акции и приведенной стоимостью цены исполнения.
Премия европейского опциона пут на акцию, по которой не выплачиваются дивиденды, не должна быть меньше разности между приведенной стоимостью цены исполнения и ценой спот акции.
Премия американского опциона пут на акцию, по которой не выплачиваются дивиденды, не должна быть меньше разности между ценой исполнения и ценой спот акции.
Премия американского и европейского опционов колл на акцию, по которой выплачиваются дивиденды, должна быть не меньше разности между ценой спот акции и суммой приведенных стоимостей цены исполнения и дивидендов.
Премия американского и европейского опционов пут на акцию, по которой выплачиваются дивиденды, должна быть не меньше разности между суммой дисконтированных стоимостей цены исполнения и дивидендов и ценой спот акции.
Раннее исполнение американского опциона колл на акцию, по которой не выплачиваются дивиденды, не является оптимальной стратегией. Поэтому американский и европейский опционы колл на такую акцию должны иметь одинаковую цену.
Раннее исполнение американского опциона колл на акцию, по которой выплачиваются дивиденды, может оказаться оптимальной стратегией.
Раннее исполнение американского опциона пут может оказаться оптимальной стратегией. Поэтому американский опцион пут должен стоить дороже аналогичного европейского опциона.
ГЛАВА 8. ОПРЕДЕЛЕНИЕ ГРАНИЦ ПРЕМИИ ОПЦИОНОВ НА ФЬЮЧЕРСНЫЕ КОНТРАКТЫ
В отечественной практике на Фондовой бирже РТС торгуются опционы на фьючерсные контракты. Поэтому остановимся на определении границ премий опционов на фьючерсы.
8.1. СТОИМОСТЬ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ КОЛЛ К МОМЕНТУ ИСТЕЧЕНИЯ
СРОКА ДЕЙСТВИЯ КОНТРАКТОВ
Непосредственно перед истечением срока действия контрактов стоимость европейского и американского опционов колл может принимать только два значения. Если F < X , (где F - фьючерсная цена к моменту истечения контракта, X - цена исполнения опциона), премия равна нулю. Если F > X , премия составит F-X . При нарушении данного условия можно совершить арбитражную операцию. Поясним сказанное на примерах.
Пример 1.
Непосредственно перед истечением срока действия контракта цена опциона колл на фьючерсный контракт равна 5 руб., цена исполнения - 100 руб., фьючерсная цена - 110 руб.
Указанное выше условие нарушено, поэтому арбитражер покупает опцион за 5 руб., продает фьючерс и исполняет опцион. Продав фьючерс, он открыл короткую позицию по 110 руб., исполнив опцион, он купил фьючерс по 100 руб. Покупка контракта закрыла его короткую позицию. Выигрыш равен:
-5-100 +110 = 5руб.
Пример 2.
Непосредственно перед истечением срока действия контракта цена опциона колл на фьючерсный контракт равна 15 руб., цена исполнения - 100 руб., фьючерсная цена - 110 руб.
Указанное выше условие нарушено, поэтому арбитражер продает опцион и покупает фьючерс. При исполнении контрагентом опциона у арбитражера открывается короткая позиция по фьючерсу, однако она является офсетной по отношению к его длинной позиции. Таким образом, он купил фьючерс по 110 руб., при исполнении опциона контрагентом продал фьючерс по 100 руб. Его выигрыш равен:
15-110 +100 - 5руб.
8.2. СТОИМОСТЬ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ ПУТ К МОМЕНТУ ИСТЕЧЕНИЯ
СРОКА ДЕЙСТВИЯ КОНТРАКТОВ
Непосредственно перед истечением срока действия контрактов цена европейского и американского опционов пут может принимать только два значения. Если F > X, премия равна нулю. Если F < X , она составит X - F . При нарушении последнего условия можно совершить арбитражную операцию.
Пример 1.
Непосредственно перед истечением срока действия контракта цена опциона пут на фьючерсный контракт равна 5 руб., цена исполнения - 100 руб., фьючерсная цена - 90 руб.
Указанное выше условие нарушено, поэтому арбитражер покупает опцион и фьючерс и исполняет опцион.
Он купил фьючерс по 90 руб., в результате исполнения опциона продал фьючерс по 100 руб. Продажа фьючерса явилась офсетной сделкой по отношению к покупке. Его прибыль равна:
-5-90+100 = 5^6.
Пример 2.
Непосредственно перед истечением срока действия контракта цена опциона пут на фьючерсный контракт равна 15 руб., цена исполнения - 100 руб., фьючерсная цена - 90 руб.
Указанное выше условие нарушено, поэтому арбитражер продает опцион и фьючерс. При исполнении контрагентом опциона у арбитражера открывается длинная позиция по фьючерсу.
Он продал фьючерс по 90 руб., в результате исполнения опциона контрагентом купил фьючерс по 100 руб. Покупка контракта явилась офсетной сделкой по отношению к продаже. Выигрыш равен:
15 -100 + 90 = 5руб.
8.3. ВЕРХНЯЯ ГРАНИЦА ПРЕМИИ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ КОЛЛ
Верхняя граница премии европейского и американского опционов колл в любой момент времени действия контракта не должна быть больше фьючерсной цены, т. е. c<F, (где с - премия опциона
колл). При нарушении данного условия инвестор может совершить арбитражную операцию: он купит фьючерсный контракт и выпишет на него опцион.
Пример.
Фьючерсная цена равна 100 руб. Некоторый инвестор готов купить опцион колл на фьючерс с ценой исполнения 50 руб. за 120 руб. Тогда арбитражер продает опцион за 120 руб. и покупает фьючерс за 100 руб. Премия за опцион вносится в качестве начальной маржи по счету. Если опцион исполняется, то у арбитражера открывается короткая фьючерсная позиция. Она является офсетной по отношению к его длинной позиции. Арбитражер купил фьючерс по 100 руб., в результате исполнения опциона контрагентом продал фьючерс по 50 руб. Его прибыль равна:
120-100 + 50 - 10руб.
Если опцион не исполняется, то в последующем он продает фьючерс по текущей цене (/\ ). Прибыль равна:
120+(Л, -100)
Контрагент не исполнит опцион, если фьючерсная цена окажется меньше или равной цене исполнения, т.е. 50 руб. По длинной позиции максимальный проигрыш арбитражера может составить 100 руб, если фьючерсная цена опустится до нуля. Тогда его прибыль равна 20 руб.
Как известно, по фьючерсным контрактам начисляется вариационная маржа. Поэтому, при падении фьючерсной цены со счета инвестора будут списываться деньги. Однако премия, полученная по опциону, полностью покрывает данные издержки, поскольку она больше стоимости фьючерсного контракта.
При совершении арбитражной операции в подобной ситуации для опциона на акции1 инвестор покупал акцию, поэтому дополнительную прибыль он мог получить только на сумму разности между премией опциона и стоимостью акции, разместив ее на депозите. Для опциона на фьючерс в качестве начальной маржи за счет полученной премии необходимо внести сумму, которая составляет часть стоимости контракта. Поэтому оставшуюся сумму инвестор также может разместить на депозите.
1 См. параграф 7.1.3.
8.4. ВЕРХНЯЯ ГРАНИЦА ПРЕМИИ АМЕРИКАНСКОГО И ЕВРОПЕЙСКОГО ОПЦИОНОВ ПУТ
8.4.1. Верхняя граница премии американского опциона пут
Цена американского опциона пут в любой момент времени действия контракта не должна быть больше цены исполнения, т. е. pa < X , (где ра - цена американского опциона пут). В противном случае инвестор может получить прибыль без риска, продав опцион.
Пример.
Цена исполнения американского опциона пут на фьючерсный контракт равна 100 руб. Некоторый инвестор готов его купить за 120 руб. Тогда арбитражер продает опцион. В случае исполнения контракта контрагентом у арбитражера открывается длинная фьючерсная позиция по 100 руб. Он закрывает ее по текущей фьючерсной цене (ft) . Прибыль равна:
120+ (/7-100}
Минимальная прибыль будет равна 20 руб. для случая падения фьючерсной цены до нуля. Если опцион не исполняется, то прибыль равна полученной премии.
8.4.2. Верхняя граница премии европейского опциона пут
К моменту истечения срока действия контракта европейский опцион пут должен стоить не больше цены исполнения. Иначе можно получить арбитражную прибыль как в приведенном выше примере. Поэтому в момент его приобретения он должен стоить не больше приведенной стоимости цены исполнения, т.е.:
1 + г(Т / база) ’
где ре - премия европейского опциона пут;
X - цена исполнения;
г - ставка без риска;
Т - время до истечения срока действия контракта;
база - финансовый год.
В противном случае арбитражер получит прибыль. Он продаст опцион и инвестирует сумму премии под процент без риска на период действия контракта.
8.5. НИЖНЯЯ ГРАНИЦА ПРЕМИИ ЕВРОПЕЙСКОГО И АМЕРИКАНСКОГО ОПЦИОНОВ КОЛЛ
Рассмотрим два портфеля. В первый входит длинный европейский опцион колл на фьючерсный контракт с и сумма денег равная приведенной стоимости цены исполнения Хе гТ. Она инвестируется под ставку без риска г на период времени Т2. Второй портфель состоит из одного длинного фьючерсного контракта, открытого по цене Fn, и суммы денег F^e ,l. Она инвестируется под ставку без риска до момента истечения опциона
Если к моменту истечения срока действия опциона фьючерсная цена Ff выше цены исполнения, в первом портфеле исполняется опцион колл. Держатель опциона получает вариационную маржу в размере:
F; -X.
Сумма денег Хе~гТ выросла на депозите до величины X, поэтому стоимость первого портфеля равна:
FT-X + X = FT.
Во втором портфеле по фьючерсному контракту получается вариационная маржа в размере:
Сумма денег F^e~rl выросла до величины Fo. Стоимость портфеля равна:
~ ^0 + Л) " •
Таким образом, стоимости портфелей равны.
Если к моменту истечения срока действия опциона FT < X , то в первом портфеле опцион колл не исполняется. Сумма денег Хе гТ выросла до величины X, поэтому стоимость первого портфеля равна X.
Во втором портфеле по фьючерсному контракту получается вариационная маржа в размере:
2 Вместо суммы денег в портфель можно включить безрисковую облигацию, номинал которой равен X, погашаемую в конце периода Т
Сумма денег Fe~rT выросла до величины Fo. Стоимость портфеля равна:
Fr-F0 + F0 = Fr.
Поскольку FT < X , то стоимость первого портфеля больше или равна стоимости второго портфеля. Данное соотношение должно выдерживаться и в начале периода Т, иначе можно получить арбитражную прибыль. Поэтому:
се + Xe~rT > Fo + Г()е~гГ
ИЛИ
се~> F$ +F§e~rT - Хе~гТ. (8.1)
В момент заключения фьючерсного контракта его стоимость равна нулю, в результате неравенство (8.1) принимает вид:
се > Fae-rT - Хе~гТ (8.2)
ИЛИ
с^-хУ",
или для простого процента
L Х + г^/база)
Таким образом, премия европейского опциона на фьючерсный контракт не должна быть меньше дисконтированной стоимости разности меоду текущей фьючерсной ценой и ценой исполнения. В противном случае можно совершить арбитражную операцию.
Пример.
Фьючерсная цена 110 руб., цена исполнения трехмесячного опциона на фьючерсный контракт 100 руб., ставка без риска для трех месяцев 10% годовых. Определить нижнюю границу премии опциона.
Решение.
110-100 г
----------г = 9,756руб.
1 + 0,1(3/12)
Предположим, что в примере фактическая цена опциона меньше нижней границы и равна 9 руб. Тогда можно совершить арбитражную
операцию. Алгоритм действий арбитражера определим на основе неравенства (8.2). В случае возможности совершения арбитражной операции оно принимает вид:
с <F(}e’! -Хе Г1 . (8.4)
%
Ьевая часть неравенства это первый портфель, правая часть неравенства второй портфель. Первый портфель дешевле второго, поэтому его следует купить, второй продать. Таким образом, арбитражер продает фьючерс по 110 руб., занимает 9 руб. и покупает опцион. В конце периода он должен вернуть по кредиту сумму:
9[1 +0,1(3/12)] = 9,225 руб.
Если к моменту истечения срока действия контракта FT > X , арбитражер исполняет опцион и получает вариационную маржу в размере:
FT -100.
У него также открывается длинная фьючерсная позиция. Она является офсетной относительно проданного им фьючерса. По короткой позиции он получает:
110-Fr.
Общий результат равен:
Fr-100 + 110-Fr =10.
Из этой суммы арбитражер возвращает кредит. Прибыль равна:
10-9,225 = 0,775руб.
Если к моменту истечения срока действия контракта FT < X, опцион не исполняется, арбитражер закрывает короткую фьючерсной позицию офсетной сделкой, отдает кредит и получает еще большую прибыль.
Мы рассмотрели вопрос определения нижней границы премии для опциона на фьючерсный контракт с одним допущением: не учитывали возможное перечисление вариационной маржи в ходе действия фьючерсного контракта, т.е. фактически рассматривали его как форвардный контракт. С учетом начисления процента на положительную маржу и финансирования под процент отрицательной маржи финансовый результат на практике может несколько отличаться от полученного, т.е. арбитраж с использованием фьючерсных контрактов не является абсолютно безрисковым. В то же
время, как было показано в приложении 1 к главе 3, если процентная ставка постоянна и одинакова для всех периодов времени, то результаты по форвардному и фьючерсному контрактам будут аналогичными.
Американский опцион колл можно исполнить в любой момент действия контракта. Поэтому его цена не должна быть меньше внутренней стоимости опциона, т.е.:
(8.5)
В противном случае можно совершить арбитражную операцию.
Пример.
Фьючерсная цена 110 руб., цена исполнения трехмесячного опциона колл на фьючерсный контракт 100 руб. Опцион стоит 9,9 руб. Указанное выше условие нарушено. Арбитражер покупает опцион, продает фьючерс и исполняет контракт. Его прибыль равна:
-9,9+ (110-100)= 0,1руб.
Согласно формулам (8.2) и (8.5) нижняя граница премии американского опциона колл больше премии европейского. Поэтому американский опцион должен стоить больше европейского.
В главе 6 мы отметили, что европейский опцион колл на фьючерсный контракт может иметь отрицательную временную стоимость. Покажем это аналитически, используя условие для нижней границы опциона.
Допустим, премия опциона колл равна ее нижней границе, т. е.:
С = Fe'T-XerT.
4-
Внутренняя стоимость составляет:
F-X >
а временная стоимость равна:
Отсюда:
(F-X)e-rT-(F-X)<0 , так как F-X >(F-x]e"‘.
8.6. НИЖНЯЯ ГРАНИЦА ПРЕМИИ ЕВРОПЕЙСКОГО И АМЕРИКАНСКОГО ОПЦИОНОВ ПУТ
Сравним два портфеля. В первый входит длинный европейский опцион пут (pj, длинный фьючерсный контракт (fo) и сумма денег, равная дисконтированной стоимости текущей фьючерсной цены (fo<?Она инвестируется под ставку г на период времени Т.
Второй портфель состоит из суммы денег равной дисконтированной стоимости цены исполнения [хе г7). Она инвестируется под ставку г на период времени Т .
Если к моменту истечения контракта FT < X, в первом портфеле опцион пут исполняется, и инвестор получает выигрыш в размере:
X-Fr.
Подлинной фьючерсной позиции получен результат:
Сумма денег (^ое~гГ) к моменту истечения опциона доросла до величины F[} Поэтому стоимость первого портфеля эквивалентна цене исполнения'
^-Fr+(F,-F0)+F„=X.
Во втором портфеле сумма денег Хе гТ доросла до величины X. Таким образом, стоимости портфелей равны.
Если к моменту истечения контрактов F; > X опцион пут в первом портфеле не исполняется. Сумма денег (Foe"rr) к моменту истечения опциона доросла до величины FQ. По длинной фьючерсной позиции получен результат:
F -F.
J г 1 о
Поэтому стоимость портфеля равна котировочной фьючерсной цене:
1 Г 1 О 1 О Т'
Стоимость второго портфеля доросла до величины X . Таким образом, стоимость первого портфеля больше или равна стоимости второго портфеля. Данное соотношение должно выдерживаться и в начале периода Т, иначе можно получить арбитражную прибыль. Поэтому:
p^F^Foe~rT>Xe-T
или
p^Xe^-F^. (8.6)
В момент заключения фьючерсного контракта его стоимость равна нулю, т.е. Fo = 0, поэтому формула (8.6) принимает вид:
ре > XerT ~F.e rJ (8.7)
или
л >(%-F0>-'r, (8.8)
или для простого процента
\ + г(т/база)
Таким образом, премия европейского опциона пут не должна быть меньше дисконтированной стоимости разности меоду ценой исполнения и текущей фьючерсной ценой. В противном случае можно совершить арбитражную операцию.
Пример.
Фьючерсная цена 90 руб., цена исполнения трехмесячного опциона на фьючерсный контракт 100 руб., ставка без риска для трех месяцев 10% годовых. Определить нижнюю границу премии опциона.
Решение.
100-90 г
-----7----г = 9,756руб. 1+0,1(3/12)
Предположим, что в примере фактическая цена опциона меньше нижней границы и равна 9 руб. Тогда можно совершить арбитражную операцию. Алгоритм действий арбитражера определим на основе неравенства (8.7). В случае возможности совершения арбитражной операции оно принимает вид:
pe<Xe"-F^.
Левая часть неравенства это первый портфель, правая часть неравенства - второй портфель. Первый портфель дешевле второго, поэтому его следует купить, второй продать. Продажу второго портфеля запишем как:
- (Хе’7 - Fe'1) = -Хе" + Foe "'.
Поэтому арбитражер покупает фьючерс по 90 руб., занимает 9 руб. и покупает опцион. В конце периода он должен вернуть по кредиту сумму:
9[1 + 0,1(3/ 12)] = 9,225/ж5.
Если к моменту истечения срока действия контракта F; < X , арбитражер исполняет опцион, т.е. продает фьючерс по 100 руб. и получает вариационную маржу в размере:
loo-л;.
У него открылась короткая фьючерсная позиция. Она является офсетной относительно купленного им фьючерса. По длинной позиции он получает вариационную маржу:
F, -90.
Общий результат равен:
100-/*' + F, -90 = 10.
Из этой суммы арбитражер возвращает кредит. Прибыль равна:
10-9,225= 0,775 руб.
Мы рассмотрели вопрос определения нижней границы премии для опциона на фьючерсный контракт с одним допущением: не учитывали возможное перечисление вариационной маржи в ходе действия фьючерсного контракта, т.е. фактически рассматривали его как форвардный контракт. С учетом начисления процента на положительную маржу и финансирования под процент отрицательной маржи финансовый результат на практике может несколько отличаться от полученного, т.е. арбитраж с использованием фьючерсных контрактов не является абсолютно безрисковым. В то же время, как было показано в приложении 1 к главе 3, если процентная ставка постоянна и одинакова для всех периодов времени, то результаты по форвардному и фьючерсному контрактам будут аналогичными.
Американский опцион пут можно исполнить в любой момент действия контракта. Поэтому его цена не должна быть меньше внутренней стоимости опциона, т.е.:
P>-X-F. (8.9)
В противном случае можно совершить арбитражную операцию.
Пример.
Фьючерсная цена 90 руб., цена исполнения трехмесячного опциона пут на фьючерсный контракт 100 руб. Опцион стоит 9,9 руб. Указанное выше условие нарушено. Арбитражер покупает опцион, покупает фьючерс и исполняет контракт. Его прибыль равна:
-9,9+ (100-90) = 0,1 дуб.
Согласно формулам (8.8) и (8.9) нижняя граница премии американского опциона пут больше премии европейского. Поэтому американский опцион должен стоить больше европейского.
В главе 6 мы отметили, что европейский опцион пут на фьючерсный контракт может иметь отрицательную временную стоимость. Покажем это аналитически, используя условие для нижней границы опциона.
Допустим, премия опциона пут равна ее нижней границе, т. е.:
Pl=(X-F^'T.
Внутренняя стоимость составляет:
X-F <
а временная стоимость равна:
Отсюда:
(x-F)e ,т-(x-f)<q , так как Х-F >{Х -F)e~'T.
КРАТКИЕ ВЫВОДЫ
Непосредственно перед истечением срока действия контрактов стоимость европейского и американского опционов колл и пут на фьючерсный контракт должна равняться нулю или внутренней стоимости.
Премия европейского и американского опционов колп на фьючерсный контракт не должна быть больше фьючерсной цены.
Премия американского опциона пут на фьючерсный контракт не должна быть больше цены исполнения, европейского - не больше приведенной стоимости цены исполнения.
Премия европейского опциона колл на фьючерсный контракт не должна быть меньше дисконтированной стоимости разности между текущей фьючерсной ценой и ценой исполнения.
Премия американского опциона колл на фьючерсный контракт не должна быть меньше его внутренней стоимости.
Американский опцион колл на фьючерсный контракт должен стоить больше европейского.
Премия европейского опциона пут на фьючерсный контракт не должна быть меньше дисконтированной стоимости разности между ценой исполнения и текущей фьючерсной ценой.
Премия американского опциона пут не должна быть меньше его внутренней стоимости.
Американский опцион пут на фьючерсный контракт должен стоить больше европейского.
ГЛАВА 9. СООТНОШЕНИЯ МЕЖДУ ПРЕМИЯМИ ОПЦИОНОВ
В настоящей главе рассматриваются ценовые соотношения, которые должны выдерживаться между премиями опционов. Вначале мы проанализируем зависимости между опционами с разными ценами исполнения, сроками истечения и стандартными отклонениями. После этого остановимся на соотношениях между премиями опционов с одной датой истечения контрактов и докажем паритетные взаимосвязи для европейских опционов колл и пут.
9.1. СООТНОШЕНИЯ МЕЖДУ ПРЕМИЯМИ ОПЦИОНОВ С РАЗНЫМИ ЦЕНАМИ ИСПОЛНЕНИЯ, СРОКАМИ ИСТЕЧЕНИЯ И СТАНДАРТНЫМИ ОТКЛОНЕНИЯМИ
9.1.1. Соотношения между премиями опционов с разными ценами исполнения
Опцион колл
Если два опциона колл отличаются только ценами исполнения, то опцион с более низкой ценой исполнения должен стоить не меньше опциона с более высокой ценой исполнения, иначе можно получить арбитражную прибыль.
Пример.
Имеется два трехмесячных европейских опциона колл на акцию А с ценами исполнения 100 руб. и 105 руб. Первый стоит 5 руб., второй - 8 руб. Отмеченное выше условие нарушено, поэтому арбитражер продает второй опцион за 8 руб. и покупает первый опцион за 5 руб., и получает на разности премий 3 руб.1
Если к моменту истечения срока действия контрактов 5 < 100/ж5., оба опциона не исполняются, и прибыль арбитражера равна 3 руб.
Если 100 руб. <S < 105руб., инвестор исполняет первый опцион. Второй опцион не исполняется. Прибыль равна 3 руб. плюс доход от исполнения первого опциона.
1 Полученную премию можно разместить на депозит до момента окончания срока действия опционов.
Если 5 > 105/луб., исполняются оба опциона. Арбитражер покупает акцию по первому опциону за 100 руб. и поставляет ее контрагенту по второму опциону за 105 руб. Общая прибыль равна 8 руб.
Для американских опционов действия арбитражера аналогичны с одной только разницей. В случае досрочного исполнения контрагентом второго опциона арбитражер сразу исполнит первый опцион, получит по нему акцию и поставит ее контрагенту.
Обычно опцион с более низкой ценой исполнения дороже опциона с более высокой ценой исполнения. Однако при очень низком курсе акции относительно цен исполнения опционов вероятность их исполнения мала. Поэтому их цены будут одинаковыми или почти одинаковыми.
Опцион пут
Опцион пут с более высокой ценой исполнения должен стоить не меньше аналогичного опциона с более низкой ценой исполнения, иначе можно получить арбитражную прибыль.
Пример.
Имеется два трехмесячных европейских опциона пут на акцию Л с ценами исполнения 100 руб. и 95 руб. Первый стоит 5 руб., второй - 8 руб. Отмеченное выше условие нарушено, поэтому арбитражер продает второй опцион за 8 руб. и покупает первый за 5 руб., и получает на разности премий 3 руб.2
Если к моменту истечения срока действия контрактов S > 100/туб., оба опциона не исполняются, и прибыль арбитражера равна 3 руб.
Если 95руб. < S < 100/туб., инвестор исполняет первый опцион. Второй опцион не исполняется. Прибыль равна 3 руб. плюс доход от исполнения первого опциона.
Если 5 <95/ш5., исполняются оба опциона. Арбитражер покупает акцию по второму опциону за 95 руб. и поставляет ее по первому опциону за 100 руб. Прибыль равна 8 руб.
Для американских опционов действия арбитражера аналогичны с одной только разницей. В случае досрочного исполнения контраген
2 Полученную премию можно разместить на депозит до момента окончания срока действия опционов.
том второго опциона арбитражер купит у него акцию за 95 руб. и сразу исполнит первый опцион, т.е. продаст акцию за 100 руб.
Обычно опцион с более высокой ценой исполнения дороже опциона с более низкой ценой исполнения. Однако, если курс акции довольно высок относительно цен исполнения опционов, то вероятность их исполнения мала, и они будут иметь одинаковую или почти одинаковую цену.
9.1.2. Соотношения между премиями опционов с разными сроками истечения
Опцион колл
Опцион колл с более поздней датой истечения контракта должен стоить не меньше аналогичного опциона с более близкой датой истечения, иначе можно получить арбитражную прибыль.
Пример.
Имеются трехмесячный и шестимесячный европейские опционы колл на акцию А с ценой исполнения 100 руб. Первый стоит 8 руб., второй - 5 руб. Отмеченное выше условие нарушено, поэтому арбитражер продает трехмесячный опцион за 8 руб. и покупает шестимесячный опцион за 5 руб., и получает на разности премий 3 руб.3
Если к моменту истечения срока действия трехмесячного опциона S < 100руб., он не исполняется. Арбитражер продает в этот момент шестимесячный опцион. Его прибыль равна 3 руб. плюс доход от продажи шестимесячного опциона.
Если 5 > 100руб., трехмесячный опцион исполняется, и арбитражер продает акцию контрагенту за 100 руб., купив ее по спотовой цене 5. Одновременно он продает шестимесячный опцион. Минимальная цена опциона согласно неравенству (7.3) равна:
5-ЮОе '°5.
В случае нулевой процентной ставки она составит:
5-100,
т.е. компенсирует разницу между спотовой ценой акции и ценой исполнения. Поэтому в этом случае прибыль арбитражера составит 3 руб. Если г >0, шестимесячный опцион стоит дороже чем
3 Полученную премию можно разместить на депозит до момента окончания срока действия опционов
S -100 , и прибыль арбитражера равна 3 руб. плюс дополнительный доход от продажи опциона.
Для американских опционов действия арбитражера аналогичны.4
Опцион пут
Американский опцион пут с более поздней датой истечения контрактов должен стоить не меньше аналогичных опционов с более близкой датой истечения, иначе можно получить арбитражную прибыль.
Пример.
Имеются трехмесячный и шестимесячный американские опционы пут на акцию А с ценой исполнения 100 руб. Первый стоит 8 руб., второй - 5 руб. Отмеченное выше условие нарушено, поэтому арбитражер продает трехмесячный опцион за 8 руб. и покупает шестимесячный опцион за 5 руб., и получает на разности премий 3 руб.
Если в течение срока действия трехмесячного опциона S > 100 руб., он не исполняется. Тогда после его истечения арбитражер продает шестимесячный опцион. Его прибыль равна 3 руб. плюс доход от продажи шестимесячного опциона.
Если 5 < 100руб., трехмесячный опцион исполняется, и арбитражер покупает акцию у контрагента за 100 руб. Одновременно он исполняет шестимесячный опцион, т.е. продает полученную акцию за 100 руб. Его прибыль равна 3 руб.
Для европейского опциона пут долгосрочный опцион не обязательно стоит дороже краткосрочного. Чем больше времени до истечения опциона, тем потенциально больше благоприятных возможностей в отношении конъюнктуры акции. Поэтому долгосрочный опцион должен быть дороже. Однако долгосрочный опцион дает держателю право продать акцию по той же цене (цене исполнения), что и краткосрочный опцион, но позже. Поэтому, исполнив краткосрочный контракт, инвестор может разместить полученные средства на депозит до момента истечения долгосрочного опциона и получить дополни
4 Для американских опционов возможен и другой порядок действий. В случае досрочного испопнения трехмесячного опциона арбитражер исполнит шестимесячный опцион, т е. купит акцию за 100 руб. и поставит ее контрагенту за 100 руб. Однако тогда он теряет временную стоимость шестимесячного опциона в качестве дополнительной прибыли.
тельный процент. В связи с этим краткосрочный опцион привлекательнее для инвестора и соответственно должен стоить больше долгосрочного.5 Цена опциона пут будет определяться соотношением значимости данных факторов в конкретных условиях. Если первый фактор весомее второго, то долгосрочный опцион дороже краткосрочного, и наоборот.
9.1.3. Соотношения между премиями опционов с разными стандартными отклонениями
Опционы колл и пут с большим стандартным отклонением доходности акции должны стоить не меньше аналогичных опционов на акции с меньшим стандартным отклонением. Это объясняется тем, что потенциально опционы на акции с большим стандартным отклонением предоставляют инвестору возможность получить большую прибыль вследствие большего диапазона колебаний цены акции при ограниченном уровне риска.
9.2. РАЗНОСТЬ МЕЖДУ ПРЕМИЯМИ ОПЦИОНОВ КОЛЛ НА ОДИН БАЗИСНЫЙ АКТИВ С ОДНОЙ ДАТОЙ ИСТЕЧЕНИЯ
9.2.1. Разность между премиями европейских опционов
Разность между премиями европейских опционов колл с одной датой истечения контрактов не должна превышать разности между дисконтированными стоимостями их цен исполнения. В противном случае возможен арбитраж.
Пример.
Имеется два годичных опциона колл. Цена исполнения первого 95 руб., второго - 100 руб. Первый стоит 10 руб., второй - 5 руб. Ставка без риска 10% годовых. Дисконтированная стоимость цены исполнения первого опциона равна: 95 /1,1 = 86,36руб., второго - 100/1,1 -90,90руб. Разность между данными величинами составляет 4,54 руб. в то время как разность между пре
5 Можно рассуждать еще следующим образом Покупатель опциона получает при исполнении контракта цену исполнения Чем больше времени до истечения опциона, тем меньше сегодня дисконтированная стоимость цены исполнения, т.е. тем меньше цена той суммы денег, которую покупатель получит в будущем Поэтому более долгосрочный опцион пут должен стоить дешевле более краткосрочного.
миями опционов равна 5 руб. Поэтому можно совершить арбитражную операцию.
Арбитражер продает первый опцион за 10 руб. и покупает второй за 5 руб. Полученную разность в 5 руб. размещает на безрисковый депозит на год под 10%. В конце года сумма на депозите составит:
5-1J = 5,5 руб.
Финансовый результат операции зависит от цены спот акции к моменту истечения действия контрактов и сводится к следующим вариантам:
1. Курс акции меньше или равен 95 руб. - Оба опциона не исполняются и прибыль арбитражера равна 5,5 руб.
2. Курс акции равен или больше 100 руб. - Контрагент исполняет первый опцион. Это означает, что арбитражер обязан продать ему акцию за 95 руб. Чтобы выполнить свое обязательство, арбитражер исполняет второй опцион, т. е. покупает акцию за 100 руб. Его прибыль равна:
5,5 -100 + 95 = ^,5 руб.
3. Курс акции больше 95 руб., но меньше 100 руб. - Контрагент исполняет первый опцион. Чтобы выполнить свое обязательство, арбитражер покупает акцию на спотовом рынке, например, за 98 руб., и поставляет ее по опциону за 95 руб. Его прибыль равна:
5,5 -98 + 95 = 2,5руб.
9.2.2. Разность между премиями американских опционов
Разность между премиями американских опционов колл с одной Артой истечения контрактов не должна превышать разности между йх ценами исполнения. В противном случае возможен арбитраж.
Пример.
Имеется два трехмесячных опциона колл. Цена исполнения первого 95 руб., второго - 100 руб. Первый стоит 10 руб., второй -4 руб.
Разность между премиями опционов равна 6 руб. Разность между ценами исполнения составляет 5 руб. Отмеченное выше условие нарушено. Поэтому арбитражер продает первый опцион за 10 руб., покупает второй за 4 руб. и получает разницу в 6 руб. Финансовый результат операции зависит от цены спот акции в течение действия контрактов и сводится к следующим вариантам:
1. Курс акции меньше или равен 95 руб. - Оба опциона не исполняются и прибыль арбитражера равна 6 руб.
2. Курс акции равен или больше 100 руб. - Контрагент исполняет первый опцион. Это означает, что арбитражер обязан продать ему акцию за 95 руб. Чтобы выполнить свое обязательство, арбитражер исполняет второй опцион, т. е. покупает акцию за 100 руб. Его прибыль равна:
6-100 + 95 = 1руб.
3. Курс больше 95 руб., но меньше 100 руб. - Контрагент исполняет первый опцион. Чтобы выполнить свое обязательство, арбитражер покупает акцию на спотовом рынке, например, за 98 руб., и поставляет ее по опциону за 95 руб. Его прибыль равна:
6-98+95 = 3руб.
9.3. РАЗНОСТЬ МЕЖДУ ПРЕМИЯМИ ОПЦИОНОВ ПУТ НА ОДИН БАЗИСНЫЙ АКТИВ С ОДНОЙ ДАТОЙ ИСТЕЧЕНИЯ
9.3.1. Разность между премиями европейских опционов
Разность между премиями европейских опционов пут с одной датой истечения контрактов не должна превышать разности между дисконтированными стоимостями их цен исполнения. В противном случае возможен арбитраж.
Пример.
Имеется два годичных опциона пут. Цена исполнения первого 95 руб., второго - 100 руб. Первый стоит 5 руб., второй - 10 руб. Ставка без риска 10% годовых. Дисконтированная стоимость цены исполнения первого опциона равна: 95/1,1 = 86,36р_уб., второго - 100/1,1 = 90,90 руб. Разность между данными величинами составляет 4,54 руб. в то время как разность между премиями опционов равна 5 руб. Поэтому можно совершить арбитражную операцию. Арбитражер продает второй опцион за 10 руб. и покупает первый за 5 руб. Полученную разность в 5 руб. размещает на безрисковый депозит на год под 10%. В конце года сумма на депозите составит:
5 1,1 = 5,5 руб.
Финансовый результат операции зависит от цены спот акции к моменту истечения действия контрактов и сводится к следующим вариантам:
1. Курс акции выше или равен 100 руб. - Оба опциона не исполняются и прибыль арбитражера равна 5,5 руб.
2. Курс акции меньше или равен 95 руб. - Контрагент исполняет второй опцион. Это означает, что арбитражер обязан купить у него акцию за 100 руб. Одновременно он исполняет первый опцион, т. е. продает акцию за 95 руб. Его прибыль равна:
5,5 - 100 + 95 - 0,5руб.
3. Курс больше 95 руб., но меньше 100 руб. - Контрагент исполняет второй опцион. Арбитражер покупает у него акцию за 100 руб. и продает ее на рынке, например, за 98 руб. Его прибыль равна:
5,5 - 100 + 98 - 3,5руб.
9.3.2. Разность между премиями американских опционов
Разность между премиями американских опционов пут с одной датой истечения контрактов не должна превышать разности между их ценами исполнения. В противном случае возможен арбитраж.
Пример.
Имеется два трехмесячных опциона пут. Цена исполнения первого 95 руб., второго - 100 руб. Первый стоит 4 руб., второй - 10 руб. Разность между премиями опционов равна 6 руб. Поэтому можно совершить арбитражную операцию. Арбитражер продает второй опцион за 10 руб., покупает первый за 4 руб. и получает на разности премий 6 руб.
Финансовый результат операции зависит от цены спот акции в течение действия контрактов и сводится к следующим вариантам:
1. Курс акции выше или равен 100 руб. - Оба опциона не исполняются и прибыль арбитражера равна 6 руб.
2. Курс акции меньше или равен 95 руб. - Контрагент исполняет второй опцион. Это означает, что арбитражер покупает у него акцию за 100 руб. Тогда он исполняет первый опцион, т. е. продает акцию за 95 руб. Его прибыль равна:
6-100 + 95 = 1руб.
3. Курс больше 95 руб., но меньше 100 руб. - Контрагент исполняет второй опцион. Арбитражер покупает у него акцию за 100 руб. и
продает ее на рынке, например, за 98 руб. Его прибыль равна:
6-100 + 98 -4руб.
9.4. ПАРИТЕТ ЕВРОПЕЙСКИХ ОПЦИОНОВ КОЛЛ И ПУТ
9.4.1. Паритет европейских опционов на акции, по которым не выплачиваются дивиденды
Между премиями европейских опционов колл и пут на одни и те же акции с одинаковой ценой исполнения и сроком истечения контрактов можно установить равенство, получившее название паритета опционов колл и пут. Оно имеет следующий вид:
с + Ле^ = pe+S (9.1)
при использовании непрерывно начисляемого процента и
1 + г(Т / база)
для случая простого процента. Равенство (9.1) можно получить следующим образом.
Сравним два портфеля. В первый входит длинный опцион колл (ct) и сумма денег равная дисконтированной стоимости цены исполнения (Ав"'7). Данная сумма инвестируется под ставку без риска г на период до окончания срока действия опционов (71). Второй портфель состоит из длинного опциона пут (д,) и акции (s).
Если к моменту окончания действия контрактов курс акции (S7) больше X, то в первом портфеле исполняется опцион колл. Сумма денег (хе‘гГ) выросла до величины X и уплачивается в рамках опциона за акцию. Таким образом, первый портфель состоит из акции. Во второй портфель также входит акция, так как опцион пут истек не исполненным. Поэтому стоимости портфелей равны.
Если курс акции меньше X, то опцион колл не исполняется, и стоимость первого портфеля равна X. Во втором портфеле исполняется опцион пут, т. е. акция продается по цене X . Таким образом, и в этом случае стоимости портфелей равны.
Если курс акции равен цене исполнения, то оба опциона не исполняются и стоимости портфелей вновь одинаковы, так как X = ST.
Стоимости портфелей равны в конце периода Т. Следовательно, они должны быть одинаковыми и в момент заключения опционных контрактов. В противном случае последует арбитраж.
Как видно из формулы (9.1), зная величину премии опциона колл, можно определить стоимость опциона пут, и наоборот.
Пример.
Цена исполнения европейских опционов колл и пут на акции равна 100 руб. Цена опциона колл 3 руб. Срок действия контрактов три месяца. Цена спот акции 100 руб. Ставка без риска 10% годовых. Определить величину премии опциона пут.
Решение.
р = с. +------------г -5 = 3 +----т----- -100 = 0,56руб.
]+г(Т/база) 1 + 0,1(3/12)
а) Допустим, что цена опциона пут завышена и равна 1 руб. Тогда арбитражер покупает опцион колл, продает опцион пут и акцию, заняв ее у брокера. В результате он получает сумму:
1-3+ 100 = 98 руб.
Размещает ее на депозите на три месяца под 10% годовых и получает по истечении данного периода сумму:
98[l + 0,1(3/12)]= 100,45руб.
Если к моменту окончания срока действия контрактов цена спот акции больше 100 руб, арбитражер исполняет опцион колл, т. е. покупает акцию за 100 руб. и возвращает ее брокеру. Его прибыль равна:
100,45-100 = 0,45 руб.
Если курс акции ниже 100 руб, то контрагент исполняет опцион пут. В этом случае арбитражер также покупает акцию за 100 руб, возвращает ее брокеру. Его прибыль вновь равна 0,45 руб.
б) Допустим, что цена опциона пут занижена и составляет 0,5 руб. Тогда арбитражер продает опцион колл и покупает опцион пут и акцию. Для этого он занимает на три месяца под 10% годовых сумму в размере:
3-0,5-100 =-97,5 руб.
(Знак минус означает, что арбитражер занимает эту сумму.) К моменту истечения срока действия контрактов он должен вернуть кредитору:
97,5[1 + 0,1(3 /12)] = 99,94руб.
Если в это время цена спот акции меньше 100 руб., арбитражер исполняет опцион пут и его прибыль равна:
100-99,94 = 0,06/^6.
Если курс акции выше 100 руб., контрагент исполняет опцион колл. Арбитражер продает акцию по цене исполнения, и его прибыль вновь равна 0,06 руб.
Рассмотрим алгоритм действий арбитражера в примере в общем виде. Если опцион пут стоит дороже, чем предполагается условиями паритета, то равенство (9.1) превращается в неравенство:
c^Xerl <pc+S
или
с -pt -S<-Xe rT. (9.2)
В этом случае можно получить арбитражную прибыль.
Представим левую часть неравенства (9.2) как первый портфель, правую часть - как второй. Так как первый портфель дешевле второго, его следует купить, второй - продать. Покупка первого портфеля означает, что арбитражер покупает опцион колл, продает опцион пут и осуществляет короткую продажу акции. Полученные от операции средства он размещает на депозите до момента истечения опционов. В этом состоит суть операции продажи второго портфеля.
Если опцион пут стоит дешевле равновесной цены, то возникает следующее неравенство:
+ Xe~rT > pe + S
или
с -$>-Хе~гГ. (9.3)
В этом случае первый портфель следует продать, так как он стоит дороже второго портфеля. Соответственно второй портфель надо купить. Продажу первого портфеля представим как:
- (с - ре - S) - -ci + pt + S ,
т. е. инвестор продает опцион колл, покупает опцион пут и акцию. Для этого он занимает деньги. В этом состоит суть операции покупки второго портфеля.
Паритет опционов показывает, что если S = X , то опцион колл должен стоить больше опциона пут. Чтобы увидеть это, перепишем формулу (9.1) следующим образом:
с ~Р< -S-XerT. (9.4)
Если S = X, правая часть уравнения (9.4) будет положительной величиной. Это говорит о том, что се > р€.
9.4.2. Паритет европейских опционов на акции, по которым выплачиваются дивиденды. Взаимосвязь между премиями американских опционов
Если в течение действия контрактов на акции выплачиваются дивиденды, то паритет европейских опционов колл и пут имеет следующий вид:
с^ + Хе'1 + D = pe + S , (9.5)
где D - дисконтированная стоимость дивиденда, выплачиваемого по акциям. Дивиденд дисконтируется под ставку без риска г к началу периода Т .
Паритет существует только для европейских опционов пут и колл. Для американских опционов можно установить только определенную взаимосвязь. Для опционов на акции, по которым не выплачиваются и выплачиваются дивиденды, она соответственно имеет вид:
S-X <ca-p,1<S-Xe rT
и
S-X-D<c -р <S-Xe".
a i a
9.4.3. Паритет европейских опционов на фьючерсные контракты
Сравним два портфеля. В первый входит европейский опцион колл (cj и сумма денег равная дисконтированной стоимости цены исполнения (Ae j. Она инвестируется под ставку г на период времени Т. Во второй - европейский опцион пут (ре), длинный фьючерсный контракт (fo) и сумма денег, равная дисконтированной стоимости текущей фьючерсной цены (Foe“r7). Она инвестируется под ставку г на период времени Т ,
Если к моменту истечения контрактов котировочная фьючерсная цена (ft) больше цены исполнения, то в первом портфеле опцион колл исполняется, и инвестор получает выигрыш в размере:
F, -X.
Сумма денег (Ле'7) к моменту истечения опциона доросла до величины X. Поэтому стоимость первого портфеля эквивалентна котировочной фьючерсной цене:
FT -АЧX = Ft.
При FT > X опцион пут во втором портфеле не исполняется.
Сумма денег к моменту истечения опциона доросла до величины F$. По длинной фьючерсной позиции получен результат:
Поэтому стоимость второго портфеля также эквивалентна котировочной фьючерсной цене:
F.-F^F^F,..
Таким образом, стоимости портфелей равны.
Если Ff < X, опцион колл в первом портфеле не исполняется и его стоимость равна X.
Во втором портфеле опцион пут исполняется, и инвестор получает выигрыш в размере:
X~FT.
По длинной фьючерсной позиции получен результат:
Сумма денег (/^F77) к моменту истечения опциона доросла до величины Fo. Поэтому стоимость второго портфеля эквивалентна цене исполнения:
X-Ft+(Ft-Fi})+Fa = X.
Таким образом, стоимости портфелей равны.
Если FT = X , опцион колл в первом портфеле не исполняется и стоимость портфеля равна X. Во втором портфеле опцион пут также не исполняется. По длинной фьючерсной позиции инвестор получает результат:
ft-fq = x~fq.
Сумма денег (Foe"r7) к моменту истечения опциона доросла до величины Fn. Поэтому стоимость второго портфеля составляет:
F. + X~F{) = X.
Таким образом, и в этом случае стоимости портфелей равны. Поскольку они равны в конце периода Т, они должны быть одинаковыми и в начале этого периода, чтобы исключить возможность арбитража. Поэтому можно записать:
с + Хе " - рс + F0 + /ye гГ. (9.6)
'Ь момент заключения фьючерсного контракта его стоимость равна нулю, т. е. Fo = 0 , поэтому формула (9.6) принимает вид:
се + Xe~rT = ре + F^e~rT
или
се-А.=(Л,-^И-
9.4.4. Паритет европейских опционов на валюту
Имеется два портфеля. В первый входит длинный опцион колл (cj на покупку единицы иностранной валюты и сумма денег равная дисконтированной стоимости цены исполнения (а?'7). Данная сумма инвестируется под ставку без риска г на период до окончания срока действия опционов (г), Второй портфель состоит из длинного опциона пут (д) на продажу единицы иностранной валюты и суммы денег равной дисконтированной стоимости единицы иностранной валюты где S - обменный спот курс в прямой котировке,
/у - ставка без риска по иностранной валюте. Сумма Se~rfT конвертируется в иностранную валюту по курсу S и инвестируется под ставку на период Т.
Если к моменту окончания действия контрактов валютный курс (5Г) больше X, то в первом портфеле исполняется опцион колл. Сумма денег (хе>т) выросла до величины X и уплачивается в рамках опциона за единицу иностранной валюты. Таким образом,
первый портфель состоит теперь из единицы иностранной валюты. Опцион Пут во втором портфеле истек не исполненным. Дисконтированная стоимость единицы иностранной валюты доросла до единицы иностранной валюты. Поэтому во второй портфель также входит единица иностранной валюты. В результате стоимости портфелей равны.
Если валютный курс меньше X, то опцион колл не исполняется, и стоимость первого портфеля равна X, Во втором портфеле исполняется опцион пут, т. е. единица иностранной валюты в рамках опциона обменивается на сумму X . Таким образом, и в этом случае стоимости портфелей равны.
Если валютный курс равен цене исполнения, то оба опциона не исполняются и стоимости портфелей вновь одинаковы, так как X = Sr.
Стоимости портфелей равны в конце периода Т. Следовательно, они должны быть одинаковыми и в момент заключения опционных контрактов. В противном случае последует арбитраж. Поэтому можно записать:
с + Хе ,г ~ pt + Se >fl.
Данное равенство представляет собой паритет европейских опционов на валюту.
КРАТКИЕ ВЫВОДЫ
Опцион колл с более низкой ценой исполнения должен стоить не меньше аналогичного опциона с более высокой ценой исполнения. Опцион пут с более высокой ценой исполнения должен стоить не меньше аналогичного опциона с более низкой ценой исполнения.
Цена американских опционов колл и пут и европейского опциона колл возрастает по мере увеличения периода действия контрактов. Отмеченная закономерность не является обязательной для европейского опциона пут.
Опцион на акцию с большим стандартным отклонением доходности должен стоить не меньше опциона на акцию с меньшим стандартным отклонением доходности.
Между ценами европейских опционов колл и пут на один и тот же актив с одинаковой ценой исполнения и временем окончания контрактов существует взаимосвязь, которая именуется паритетом опционов колл и пут. Если она нарушается, то можно получить арбитражную прибыль.
ГЛАВА 10. МОДЕЛИ ОПРЕДЕЛЕНИЯ ЦЕНЫ ОПЦИОНОВ
В настоящей главе рассматриваются модели определения премии опционов. Вначале мы остановимся на вопросе формирования портфеля без риска и оценки величины премии с помощью простой биномиальной модели. После этого перейдем к моделям, которые используются на практике, а именно, биномиальной модели Кокса, Росса и Рубинштейна и модели Блэка-Шоулза.
10.1. БИНОМИАЛЬНАЯ МОДЕЛЬ
10.1.1. Простая биномиальная модель
10.1.1.1. Портфель из акций и заемных средств эквивалентный опционному контракту
Один из подходов к оценке премии опциона состоит в создании портфеля из акций и заемных средств1, который полностью копирует суммы выплат по опциону к моменту окончания действия контракта, Поэтому стоимость опциона при заключении контракта должна равняться стоимости портфеля, иначе можно совершить арбитражную операцию. Поясним сказанное на примере простой биномиальной модели. Модель охватывает один временной период. В ее рамках курс акции может принимать только два значения: пойти на известную величину вверх или вниз, как показано на рис. 10.1. В первом
Рис. 10.1. Динамика курса акции в рамках простой биномиальной модели
1 Вместо заемных средств можно включить в портфель безрисковую облигацию.
случае в конце периода стоимость акции составит величину Su , во втором - Sd , где 5 - курс акции в начале периода; и = 1 + процент прироста цены акции; d = 1 - процент падения цены акции.
Пример 1.
Цена спот акции 100 руб. Инвестор определил, что через три месяца ее цена может составить 80 руб, или 120 руб. Предполагается, что акция делима. Трехмесячная ставка без риска 10% годовых. На акцию торгуется европейский опцион колл с ценой исполнения 100 руб. Если через три месяца курс акции составит 120 руб., то от исполнения опциона будет получено 20 руб., если цена составит 80 руб., результат составит ноль руб., поскольку опцион не будет исполнен. Необходимо определить, сколько должен стоить опцион колл.
Для ответа на этот вопрос рассмотрим портфель из акций и заемных средств, который бы копировал результаты по опциону. Пусть инвестор покупает акцию в количестве п единиц, используя собственные и заемные средства. Дополнительные средства он занимает на три месяца под ставку без риска в сумме к руб. Стоимость опциона равна с руб. По условиям задачи сформированный из акций и заемных средств портфель через три месяца должен принести такие же результаты, как и опцион колл. Поэтому, чтобы найти величины п и к , приравняем стоимости портфеля и опциона в конце периода для первого и второго вариантов конъюнктуры. Получим систему уравнений:
или
Г120« +1,025^=20
[ 80и + 1,025£ = 0.
Решение системы уравнений (10.1) дает ответ:
(10-1)
п - 0,5акций; к = —39,02руб.
Это означает, что инвестор покупает 0,5 акции за 50 руб. Для этого он занимает сумму 39,02 руб. на три месяца под 10% годовых и дополнительно использует свои средства в размере:
50-39,02 = 10,98руб.
Если через три месяца цена акции вырастет до 120 руб., стоимость портфеля с учетом погашения средств по кредиту составит:
120 03 акции - 40 = 20руб.
(40 руб. - это сумма кредита с начисленными за три месяца процентами). Если цена акции упадет до 80 руб,, портфель будет стоить:
80 • 0,5акции -40 = 0 руб.
Таким образом, результаты портфеля полностью копируют выплаты по трехмесячному европейскому опциону колл на акцию с ценой исполнения 100 руб. Стоимость портфеля и опциона колл через три месяца одинаковы. Следовательно, они должны быть равны и в начале периода. Стоимость портфеля инвестора с учетом заемных средств в начале периода составляет:
50-39,02 = 10,98руб.
Поэтому премия опциона также равна 10,98 руб. Если она будет выше или ниже найденной величины, можно совершить арбитражную операцию. Рассмотрим возможные варианты.
а) Цена опциона занижена и равна 10 руб. Тогда арбитражер берет взаймы 0,5 акции и продает ее за 50 руб., покупает опцион за 10 руб. и размещает оставшиеся 40 руб. на трехмесячном депозите под 10% годовых. Если через три месяца курс акции 120 руб., он продает опцион в последний день его действия и получает 20 руб. (Цена опциона перед моментом истечения контракта равна его внутренней стоимости). По депозиту ему выплачивают:
( 3
401 + 0,1 — = 41дуб.
I 12)
Из полученных сумм он уплачивает 60 руб. за половину акции и возвращает ее владельцу. Прибыль арбитражера равна:
20 + 41 - 60- \руб.
Если курс бумаги через три месяца 80 руб., он не исполняет опцион, По депозиту арбитражер получает 41 руб. За 40 руб. он покупает половину акции и возвращает ее владельцу. Прибыль равна:
41 - 40 - \руб.
б) Цена опциона завышена и составляет 11 руб. Тогда арбитражер продает опцион, занимает 39 руб, под 10% годовых на три месяца и покупает половину акции за 50 руб.
Если цена акции через три месяца 120 руб., арбитражер продает 0,5 акции за 60 руб., выкупает колл в последний день действия контракта за 20 руб., возвращает сумму кредита в размере:
( 3
39 1 + 0,1— = 39,98 дуб.
V 12 J
Его прибыль равна:
60 -20 -39,98 = 0,02 руб.
Если курс акции 80 руб., опцион не исполняется, арбитражер продает половину акции за 40 руб., возвращает кредит в сумме 39,98 руб. Его прибыль составляет:
40 -39,98 = 0,02 руб.
Таким образом, опцион должен стоить 10,98 руб., чтобы исключить возможность получить арбитражную прибыль.
В данном примере следует обратить внимание на следующие важные моменты. Определяя премию опциона, мы не использовали ни одной переменной, которая бы говорила об отношении инвестора к риску. Нам не потребовалось знания ставки дисконтирования, которая бы соответствовала риску инвестирования средств в опционный контракт. Также не потребовалось знания вероятности, с которой курс акции мог пойти вверх или вниз. Для вычисления величины премии опциона инвестору было безразлично, будет ли курс акции высоким (120 руб.) или низким (80 руб.), будет ли он расти или падать. Это означает, что инвестор не принимал во внимание величину ожидаемой доходности акции. Размер премии зависел только от выполнения условия невозможности совершить арбитражную операцию. Поэтому ожидания инвестора в отношении роста или падения курса акции не имели значения. Отсюда можно сделать вывод: при оценке премии опциона мы не должны принимать во внимание отношение инвесторов к риску.
Всех инвесторов можно разделить на три группы: склонных к риску, не склонных к риску и нейтральных к риску.2 Согласно трем группам инвесторов можно представить и три типа экономик, в которых действуют только или склонные, или не склонные, или нейтральные к риску инвесторы. Поскольку при оценке стоимости оп
2 Более подробно о склонности инвесторов к риску см. в книге А.Н.Буренина “Управление портфелем ценных бумаг”, М., Научно-техническое общество им. акад. С.И.Вавилова, 2005 г., гл.8,
циона отношение инвесторов к риску не учитывается, то цена одного и того же опциона должна быть одинаковой в любой из этих экономик. Поэтому неважно, в какой из них определять премию опциона. В то же время, наиболее просто найти ее в экономике, где инвесторы нейтральны к риску. Такие инвесторы не требуют вознаграждения в соответствии с риском финансовых активов. Нейтральный к риску инвестор безразличен в выборе между активом, который гарантированно приносит ему доходность равную ставке без риска, и активом, ожидаемая доходность которого равна ставке без риска.3 В нейтральной к риску экономике инвесторы обращают внимание только на ожидаемую доходность актива и не принимают в расчет его риск. Так как риск не учитывается, то не требуется и адекватное ему вознаграждение. Поскольку не требуется вознаграждения за риск, то все активы должны оцениваться таким образом, чтобы их ожидаемая доходность была одинаковой и равной ставке без риска. Соответственно цена любого актива в такой экономике будет равняться ожидаемым по нему выплатам, дисконтированным под ставку без риска.
При оценке премии опциона не играет роли вероятностное распределение курса акции и величина ее ожидаемой доходности, но имеет значение стандартное отклонение доходности акции. Так, если известно, что возможные значения цены акции к моменту истечения опциона составят не 120 руб. и 80 руб., а 140 руб. и 60 руб., т.е. акция характеризуется большим стандартным отклонением, то премия опциона в примере составит уже не 10,98 руб., а 20,74 руб.
Отмеченные особенности оценки премии опциона могут показаться несколько нелогичными, так как опцион - это довольно рискованный финансовый актив. Однако нелогичность исчезнет, если подчеркнуть следующую особенность представленного подхода. Стоимость опционного контракта определяется не самостоятельно, а опосредованно через оценку стоимости безрискового портфеля, который инвестор может сформировать из опционов и базисных активов. Поэтому рассмотрим концепцию формирования портфеля без риска.
1 Нейтральный к риску инвестор - это инвестор, который не принимает во внимание риск по инвестициям, Он безразличен в выборе между активом с гарантированным уровнем доходности и активом с неопределенной доходностью, ожидаемое значение которой равно доходности первого актива, Такой инвестор одинаково отнесется к ценной бумаге, по которой будет точно выплачено 50 руб, и бумаге, по которой существует 50% вероятность получить 100 руб, и 50% вероятность ничего не получить.
10.1.1.2. Формирование портфеля без риска
В основе моделей оценки премии опционов лежит посылка о том, что инвестор может сформировать портфель из опционов и базисных активов, нейтральный к риску изменения цены актива. Например, инвестор сформировал безрисковый портфель из опционов и акций. Для такого портфеля падение цены акций компенсируется ростом стоимости опционов, и наоборот, рост цены акций нейтрализуется падением цены опционов. Изменения цены акции и опциона колл направлены в одну сторону, т.е, при росте цены акции опцион колл дорожает, при падении ее цены - дешевеет. Поэтому при формировании портфеля без риска из опционов колл и акций инвестору следует купить опционы колл и продать акции или продать опционы колл и купить акции.
Изменения цены акции и опциона пут направлены в противоположные стороны. Поэтому, формируя портфель без риска из акций и опционов пут, инвестору следует купить опционы пут и купить акции или продать опционы пут и продать акции.
Для формирования портфеля необходимо рассчитать пропорцию, в которой изменяется цена опциона при изменении цены акции. Например, инвестор определил, что при изменении цены акции на 1 руб. цена опциона колл изменяется на 0,5 руб. Это означает, что, формируя портфель, он должен на каждые два проданных опциона колл купить одну акцию. Тогда при росте цены акции на 1 руб. инвестор выиграет 1 руб. на акции. Цена двух опционов в сумме также увеличится на 1 руб. Инвестор продавал контракты. Поэтому, если он будет закрывать позицию по опционам, ему придется выкупить их по цене выше в совокупности на 1 руб. Таким образом, он потеряет 1 руб на опционах. В результате стоимость портфеля останется неизменной: выигрыш по акции компенсируется проигрышем по опционам.
При падении цены акции на 1 руб. он потеряет 1 руб. на акции. Цена двух опционов также понизится в сумме на 1 руб. Инвестор продавал контракты. Поэтому, если он будет закрывать позицию по опционам, то выкупит их по цене ниже в совокупности на 1 руб. Таким образом, он выиграет 1 руб. на опционах. В результате стоимость портфеля останется неизменной: проигрыш по акции компенсируется выигрышем по опционам,
Портфель нейтрален к риску только для небольшого роста или падения цены акции, т.е. пока отмеченная ценовая пропорция остается практически неизменной. При более значительном изменении курса бумаги изменится и ценовая пропорция между акцией и преми
ей опциона. Поэтому, чтобы сохранить нейтральность портфеля к риску, необходимо постоянно корректировать его состав, Например, курс акции вырос, и новое ценовое соотношение равно 1:1, т.е. при изменении цены акции на 1 руб. цена опциона также изменяется на 1 руб. Тогда для поддержания нейтральности портфеля к риску инвестору необходимо купить еще одну акцию. В этом случае при росте цены акции на 1 руб. он выиграет по акциям в сумме 2 руб., однако по опционам проиграет также 2 руб. Соответственно при падении цены акции на 1 руб, он проиграет по акциям 2 руб., но выиграет эту сумму по опционам.4
Допустим, что акция является делимой на части. Тогда можно сформировать портфель из опциона и части акции, который будет нейтрален к риску. Например, инвестор продал опцион колл и купил 0,5 акции, поскольку ценовое соотношение между курсом акции и премией опциона равно 1:0,5. В следующий момент цена акции выросла, и новая пропорция составила 1:0,6. Тогда инвестор покупает дополнительно 0,1 часть акции, чтобы сохранить нейтральность портфеля к риску, В следующий момент цена акции упала, и новая пропорция равна 1:0,55. Инвестор продает 0,05 часть акции, и т.д. Чем чаще будет инвестор корректировать портфель, т.е. пересматривать его при малейшем изменении ценовой пропорции, тем более нейтральным он будет к риску. Если предположить, что можно осуществлять непрерывную корректировку состава портфеля при изменении цены акции, то портфель будет абсолютно нейтрален к риску изменения цены акции, и стоимость его будет оставаться неизменной. Если допустить, что издержки по корректировке состава портфеля равны нулю, то инвестор в течение всего периода действия опционного контракта без каких-либо затрат может поддерживать нейтральность портфеля. В условиях равновесия на рынке безрисковый портфель должен приносить доходность равную ставке без риска. В противном случае последуют арбитражные операции, что восстановит отмеченное условие.
Таким образом, инвестор может сформировать из опционов и базисных активов портфель нейтральный к риску и поддерживать его нейтральность в течение действия контракта, покупая и продавая базисные активы в зависимости от изменений конъюнктуры рынка.
Выше мы отметили, что цену опциона можно определить для экономики, в которой инвесторы нейтральны к риску, и она будет
4 Для поддержания нейтральности портфеля инвестор в данном примере может не покупать еще одну акцию, а купить один опцион, закрыв таким образом позицию по одному опциону.
одинаковой для всех трех типов экономик. Такой прием мы вправе использовать в отношении любых финансовых инструментов, если существует возможность сформировать безрисковый портфель, так как в этом случае цена этого инструмента определяется не отдельно, а через оценку стоимости безрискового портфеля, содержащего данный инструмент и базисный актив.
Рассмотрим на примере, каким образом можно применить технику формирования портфеля без риска применительно к простой биномиальной модели.
Пример 2.
Цена спот акции 100 руб. Через три месяца ее цена может составить 80 руб. или 120 руб. Предполагается, что акция делима. Трехмесячная ставка без риска 10% годовых. Инвестор продает трехмесячный европейский опцион колл на акцию и приобретает п акций. Данный портфель будет безрисковым, если к моменту истечения срока действия опциона стоимость его окажется одинаковой, независимо от конкретного значения цены акции. При падении курса акции до 80 руб., стоимость портфеля окажется равной 80л руб. Если курс поднимется до 120 руб., цена портфеля составит (120л-20) руб. Чтобы сформировать портфель без риска, инвестор должен купить такое число акций, которое бы удовлетворяло уравнению:
120л-20 = 80л.
Решив его, получим: л = 0,5 акции. При таком условии портфель через три месяца и в первом и во втором случае будет стоить 40 руб.:
1) 80руб. 0,5акции = 40руб.
2) 120руб. 0,5акции - 20руб. = 40руб.
Стоимость портфеля в момент заключения опционного контракта равна:
100 -0,5-с = 50-с.
Портфель без риска должен приносить инвестору доходность равную ставке без риска. Поэтому стоимость портфеля в начале периода должна соответствовать его дисконтированной стоимости через три месяца, т.е.:
Отсюда с = 10,98руб.
Таким образом, опцион должен стоить 10,98 руб., иначе можно получить арбитражную прибыль. Действия арбитражера будут аналогичны действиям, рассмотренным в примере 1.
10.1.1.3. Риск-нейтральная вероятность
Как показано в примере 1, для одного временного периода выплаты аналогичные выплатам по опциону можно получить, сформировав портфель из акции и заемных средств. Стоимость такого портфеля в начальный момент времени должна равняться цене опциона, а именно:
nS~B=c^ (10.2)
где с0 - стоимость опциона в момент его заключения;
п -количество акций;
5- цена акции в момент заключения опционного контракта;
В -сумма кредита.
В конце периода портфель может стоить или nSu-RB = cu, (10.3)
или
nSd-RB = cd, (10.4)
где си - стоимость опциона (и соответственно портфеля) в случае роста цены акции;
с / - стоимость опциона (и соответственно портфеля) в случае падения цены акции;
и = 1 + процент прироста цены акции;
d= 1 - процент падения цены акции;
R = 1 + ставка без риска.
Чтобы сформировать эквивалентный портфель из акции и заемных средств, необходимо знать величины п и В. Из формул (10.3) и (10.4) получим:
и
dc„ ~uct/ (u-d)R
(10.6)
Подставив значения п и В из формул (10.5) и (10.6) в формулу (10.2), находим стоимость опциона в начале периода:
с —с . de — ис .
_ и a _ и a u-d (и - d)R
или
о —
(W.7)
Числитель в формуле (10.7) стоимость опциона к моменту истечения контракта, где весами вы-(R d\ ( и-
представляет собой ожидаемую
ступают значения
. Поэтому можно сказать, что
и
цена опциона в начале периода равна дисконтированной стоимости средневзвешенных выплат по контракту в конце периода.
Как следует из формулы (10.7), она не включает ни одной переменной, которая бы учитывала отношение инвестору к риску. Таким образом, мы можем определить цену опциона в экономике, в которой действуют нейтральные к риску инвесторы. Такой подход к определению премии опциона получил название риск-нейтральной оценки. Она попросту означает, что мы предполагаем нейтральное отношение к риску всех инвесторов. В то же время, полученная стоимость опциона одинакова для всех трех типов экономик.
В формуле (10.7) в явном виде не присутствуют вероятности роста и падения цены акции, поскольку они не учитывались при определении премии опциона. Однако о вероятности можно говорить в неявном виде, а именно, за вероятность того, что цена опциона в конце первого периода составит си можно принять величину ------- .
Обозначим ее через р. Данную величину можно также принять за вероятность роста цены акции. Тогда вероятность получить значение
cd составляет
. Легко заметить, что:
и -R_ J R-d u-d и-d
Поэтому обозначим
через (1 - р). Данную величину мож-
k и -d )
но принять за вероятность падения курса акции. Таким образом, выполняется необходимое условие для представления указанных ве
личин в качестве вероятностей: сумма вероятностей акции пойти вверх и вниз равна единице. В результате премию опциона можно рассматривать как дисконтированную под ставку без риска средневзвешенную стоимость опционного контракта к моменту его истечения, где весами выступают вероятности роста и падения цены акции.
Выше мы отметили, что при оценке стоимости опциона инвестор не принимает во внимание фактические вероятности роста или падения курса акции. Поэтому необходимо конкретизировать, что представляют собой найденные вероятности р и (1-р) применительно к цене акции.
Ожидаемое значение цены акции в следующий момент времени является средневзвешенной величиной ее значений при росте и падении, а весами выступают вероятности. Поэтому можно записать, что:
E{ST)= pSu + (\-p)Sd , (10.8)
где e(st ) - ожидаемое значение цены акции в конце периода Т. Подставим в формулу (10.8) значения р и (1-/»):
E(ST} = —-Su + ——Sd, (10.9)
и-d и ~d
получим:
e(s^ = SR. (10.10)
Уравнение (10.10) говорит о том, что ожидаемое значение цены акции определяется на основе ставки без риска. Как известно, ожидаемая доходность актива равна ставке без риска в условиях, когда инвесторы нейтральны к риску. Таким образом, если полагать, что вероятности роста и падения цены актива соответственно равны р и (1 - р), то его ожидаемая доходность должна равняться ставке без риска. Это, в свою очередь, означает, что мы действуем в экономике с нейтральными к риску инвесторами. Тогда вероятности роста и падения цены акции р и (1- р) можно рассматривать как вероятности, существующие в экономике с нейтральными к риску инвесторами, или риск-нейтральные вероятности.
Таким образом, премия опциона равна дисконтированной стоимости его средневзвешенных цен к моменту истечения контракта, где весами выступают риск-нейтральные вероятности роста и падения цены акции.
10.1.2. Двухпериодная биномиальная модель
Рассмотрим случай, когда до истечения срока действия опциона два периода. Как видно из рис. 10.2, цена акции может принять в конце второго периода три значения: Su2,Sud, Sd2. Она может подняться за первый период до уровня Su и затем вырасти до Su2; упасть за первый период до Sd и далее опуститься до Sd2; вырасти до Su в первом периоде и упасть до Sud во втором; или вначале упасть до уровня Sd , а затем подняться до Sud. Опцион колл, соответственно ценам акции, принимает в конце второго периода три значения: син, cdu = clld, cdd.
Проанализируем вначале второй период. Можно увидеть, что он состоит из двух однопериодных моделей. В первой из них цена опциона в начале периода равна си, а в конце периода принимает значения сии или cud Во второй из них цена опциона в начале периода равна сd , а в конце cdu или cdd . Значения си и cd можно определить таким же образом, как в случае с одним временным периодом:
Си = [рСии +С-РКА/К
и
Su2
cdd
Рис. 10.2. Деухпериодная биномиальная модель
^=[рсЛ+(1-р)см]/^. (10.12)
Подставив значения с’„ и сЛ из формул (10.11) и (10.12) в формулу (10.7), получим:
с = [р'р,,. + 2Р(1 - Р)с^ + О - P)'C,J /р.- (Ю.13)
Формула (10.13) определяет цену опциона для двухпериодной модели. Согласно данной формуле вероятность того, что опцион к моменту срока его истечения будет стоить сШ( равна р1, cdd -(1 - р)2 и cud = cdu - 2р(\- р). Сумма всех вероятностей равна 1. Формула (10,13) вновь показывает, что цена опциона равна дисконтированной стоимости суммы его ожидаемых значений к моменту истечения контракта.
10.1.3. Многопериодная биномиальная модель
Рассуждения, которые были использованы при определении стоимости опциона для двухпериодной модели, можно использовать и в случае деления времени обращения опциона на любое число периодов. Тогда биномиальная формула примет следующий вид:
С= У ----------- р‘(У-рУ / . .
Формула (10.14) говорит о том, что цена опциона равна дисконтированной стоимости суммы ожидаемых выплат по контракту к моменту его истечения. Весь срок обращения опциона разбит на п периодов. Соответственно в знаменателе R" - это коэффициент дисконтирования, который учитывает ставку без риска и количество периодов. Числитель показывает ожидаемое значение суммы выплат по опциону с учетом вероятности каждого конкретного исхода. Поскольку мы рассматриваем биномиальный процесс, то в каждом периоде цена акции может пойти либо вверх с вероятностью р, либо вниз с вероятностью (|-д). Индекс j показывает количество периодов, когда цена акции возрастала из общего числа периодов п. Величина (n-j) соответственно говорит о количестве периодов, в течение которых цена акции падала. Знак суммы в формуле показывает, что количество возможных вариантов роста цены акции имеет диапазон от / = 0 до j = п.
При j = 0 оценивается вероятность падения цены акции в каждом периоде. При j = n оценивается вероятность роста цены акции в каждом периоде. Оцениваются все возможные комбинации движений цены акции за п периодов. Как мы видели в случае двухпериодной модели при п - 2, величина Sud могла быть получена двумя способами. Первый: значение S вначале выросло до Su, а затем упало до Sud . Второй: значение £ вначале понизилось до Sd, а затем выросло до Sdu. Так как Sud = Sdu , то в обоих случаях был получен одинаковый результат. Когда к состоит из еще большего числа периодов, то таких сочетаний, которые дадут одно и то же значение цены акции вне зависимости от последовательности роста и падения цены, становится больше. В формуле (10.14) выражение
как раз и показывает количество различных комбинаций движения цены акции, которые дают одну и ту же цену к моменту истечения контракта. Выражение и! - это и-факториал. Оно определяется как и!= п(п - 1)(л - 2)... 1.5 Значение 0! равно единице.
Выражение //(1-р)" ' говорит о вероятности события, когда курс акции вырастет j раз и упадет n-j раз.
n't
Выражение-------:— р'(1 - p)n~J показывает вероятность того,
что цена акции будет расти в j периодах из п периодов и падать в (и - /) периодах с учетом всех возможных комбинаций роста и падения цены акции.
Выражение тах(0,;г7Г 'S-A') дает выплату по опциону к моменту истечения контракта, если цена акции росла в j периодах на величину и и падала в п- j периодах на величину d .
Пример 3.
S' = 100 руб., п = 3 периода, X - 105руб., и = 1,2; d = 0,8, ставка без риска для одного периода равна 2%. Определить стоимость опциона.
Решение.
Вначале найдем значения р и (1 - р).
5 Например, 51= 5 4 3 • 2 1 = 120.
R-d 1,02-0,8 _ __ р --------=-------------- 0,55 ,
u-d 1,2-0,8
1-р=0,45.
Премия опциона равна:
31 о 3 0 3 3- 2 2
0 55 0 45 inax(0 12 0.8’ 100-105) + 0 55 045 тах(0 12 0 8 100-105) + O’li----------------------------------------------1'2'
+ —O.552 0,45max(0. 1 22 0,8 100 - 105) + —-0.55* 0,45° max(0 1 23 0,8° 100-105) 241 3'0’
з
1,02
= [0,091 0 + 0,334 0 + 0,408 10,2+0,166 67,8]//^ = 14,53 руб
Как видно из примера, при расчете премии имеют значение лишь слагаемые, когда опцион оказывается выигрышным к моменту истечения контракта, поскольку остальные слагаемые обращаются в ноль. Пусть к - это число подъемов цены акции, чтобы опцион оказался с выигрышем. Тогда формулу (10.14) можно переписать как:
п\
fl *
(10-15)
В формуле (10.15) суммирование значений в числителе начинается с периода А, Опцион будет выигрышным к моменту его истечения, если:
u*d" kS> X, (10.16)
Запишем неравенство (10.16) следующим образом:
и
или
- >—• (Ю.17)
{d) Sd"
Чтобы определить значение А, возьмем натуральный логарифм от обеих частей неравенства (10.17). Получим:
j . X / и к > In---/ In — .
Sd" / d
Из неравенства (10.18) следует, что А должно быть целым числом, большим чем:
(10.18)
1 л /1 и
In-— / In —.
Sd" / d
Если к больше п, то с = 0, так как курс акции за все периоды п не превысит цену исполнения (А},
Полученную модель можно применить и для определения премии опциона пут. Она имеет вид:
и!
Mn-jV
р’Ц-рУЛХ-и'сГ JS)
Rn. (10.19)
По сравнению с формулой (10.15) здесь учтены следующие изменения. Стоимость опциона пут перед моментом истечения равна Х-и\Г 'X. Через к мы обозначили количество движений цены акции вверх, в результате которых опцион колл становится выигрышным. Следовательно, опцион пут будет выигрышным, если количество движений цены акции вверх не превысит величину к -1.
В биномиальной модели мы воспользовались приемом риск-нейтральной оценки, т. е. изменили риск финансовых активов, чтобы в качестве ставки дисконтирования взять ставку без риска. Подобное изменение риска правомерно, если вместо действительных вероятностей роста и падения цены актива перейти к риск-нейтральным вероятностям. Такой переход всегда правомерен, если можно сформировать портфель, эквивалентный выплатам по опциону.
Биномиальную модель оценки премии опциона обычно называют моделью Дж. Кокса, С.Росса и М.Рубинштейна, которые опубликовали свою работу по этому вопросу в 1979 г. Однако впервые биномиальный подход был предложен У.Шарпом в 1978 г. Мы рассмотрели вычислительную часть модели. Теперь подведем итог по общей схеме построения модели.
Весь период действия опционного контракта разбивается на ряд интервалов времени, в течение каждого из которых курс акции может пойти вверх с вероятностью р или вниз с вероятностью I - р. В начале первого периода цена акции равна 5 . В конце первого периода курс акции может составить соответственно Su или Sd (см. рис. 10.3). В целях упрощения модели, поскольку период действия контракта делится на большое число интервалов, можно сделать допущение,
1 т
что и = —. Тогда в конце второго периода Д/2 цена акции может
d
принять значения Su2, Sd2 или S и т.д.6 для следующих периодов.
6 Поскольку мы полагаем, что и - — , то Sud - S d
К моменту истечения срока действия контракта цена опциона может принимать только два значения, а именно, 0 или ST-X для опциона колл и 0 или X-Sr для опциона пут. Чтобы рассчитать стоимость опциона, необходимо вначале определить его цены в конце периода Т для каждого возможного значения цены акции, т.е. для каждого узла дерева распределения. На рис. 10.3 для четырехпериодной модели это будут узлы со значениями курса акции Su4, Su2, S, Sd2, Sd4. Далее определяют цены опционов для начала последнего периода путем дисконтирования под ставку без
Рис. 10.3. Дерево распределения цены акции для четырех временных периодов
риска средневзвешенных цен опционов в конце периода Т , где весами выступают риск-нейтральные вероятности роста и падения цены акции. В примере это будет начало периода Л/4. Пусть цена опциона для узла Su4 равна с41 для узла Su2 - с2. Тогда цена опциона в начале периода Л/4 или, что то же самое, в конце периода Д/3 равна:
рс4 +(1-р)с2
(10.20)
где - цена опциона в начале четвертого периода, т.е. в узле Su3. Таким образом, последовательным дисконтированием цен опциона определяют его значение в начальный момент времени.
На практике при определении премии опциона период Т необходимо разбить на большое число периодов. Обычно деление времени опционного контракта на 30-50 интервалов уже дает приемлемый результат. Проиллюстрируем представленную схему определения цены опциона на примере.
Пример 4.
Цена исполнения европейского опциона колл 100 руб. Время его действия разбивается на три периода. Цена акции в начальный момент 100 руб., темп роста курса акции в каждом периоде равен 1,05, темп падения цены 0,95. Ставка без риска для каждого периода составляет 2%. Определить цену опциона.
Решение.
Определяем риск-нейтральные вероятности:
R-d 1,02-0,95 р =------=-----------= 0,7 ,
u-d 1,05-0,95
1-р - 0,3.
К моменту истечения действия опциона цена акции может принять следующие значения:
Sz/3 = 115,76руб.; 5м = 105руб.; Sd = 95py6.\ Sd" = 85,74руб.
Значения цен акции для каждого узла дерева распределения представлены на рис. 10.4.
Для узла Su3 цена опциона равна:
115,76-100-15,76руб.
Для узла Su:
105-100-5руб.
Для узлов Sd и Sd3 она равна нулю, так как цена спот акции меньше цены исполнения. Для узла Su2 премия опциона равна:
15,76 0,7 + 5 0,3 г
----------------- 12,29 руб.
1,02
Для узла 5:
5-0,7 + 00,3 ... . --------------- 3,43 руб.
1,02
Для узла Sd2 она равна нулю.
Для узла Su:
12,29 0,7+3,43 0,3
1,02
= 9,44руб.
Для узла Sd:
3,43-0,7 +0 0,3
1,02
= 2,35 руб.
Премия опциона в начальный момент времени составляет:
9,44-0,7 + 2,35-0,3
1,02
= 7,17 руб.
10.1.4. Биномиальная модель оценки премии американских опционов на акции, по которым не выплачиваются дивиденды
Метод использования биномиальной модели для американских опционов аналогичен приему, проиллюстрированному в примере 4. В то же время, существует некоторое отличие. Оно связано с тем, что американский опцион можно исполнить в любой момент времени в ходе действия контракта. Поэтому для каждого узла дерева распределения необходи
мо сравнить цену опциона, полученную расчетным путем, с внутренней стоимостью опциона в этот момент и выбрать наибольшее из полученных значений для продолжения процесса дисконтирования. Поясним сказанное на примере. Рассмотрим последовательно определение премии европейского и американского опционов пут.
Пример 5.
Цена исполнения европейского опциона пут на акции 100 руб. Время его действия разбивается на три периода. Цена акции в начальный момент 100 руб., темп роста цены акции в каждом периоде равен 1,05, тем падения цены 0,95. Ставка без риска для каждого периода составляет 2%. Определить цену опциона.
Решение.
Значения риск-нейтральных вероятностей и курсов акций в каждом узле дерева распределения были определены в примере 4.
Для узла &/3 (конец третьего периода) цена опциона равна:
100-85,74= 14,26^6.
Для узла Sd (конец третьего периода):
100- 95 = 5 руб.
Для узлов Su и она равна нулю, так как цена спот акции больше цены исполнения.
Для узла Sd2 (конец второго периода) премия опциона составляет:
5 0,7 +14,26-0,3
1,02
=7,63руб.
Для узла 5 (конец второго периода):
Для узла Su2 она равна нулю.
Для узла Sd (конец первого периода):
1,47-0,7+7,63-0,3 _
-------------------= 3,25 руб.
1,02
Для узла Su (конец первого периода):
0-0,7 + 1,47 0,3 ----------------= 0,43 руб.
1,02
Премия опциона в начальный момент времени равна: 0,43-0,7 + 3,25'0,3 . _ = 1,25/луб.
1,02
Для наглядности цены акции и рассчитанная премия для каждого узла дерева распределения представлены на рис. 10.5. Цена акции представлена верхней цифрой, премия опциона - нижней. Мы получили результат: европейский опцион пут должен стоить 1,25 руб.
Рис. 10.5. Трехпериодная биномиальная модель
Допустим теперь, что данный опцион является американским. Тогда на рис.10.5 внимания заслуживает узел Sd2 (конец второго периода). Расчетная цена опциона равна 7,63 руб. Однако, если держатель опциона исполнит его в этот момент, он получит сумму равную внутренней стоимости опциона, т.е.:
100-90,25 - 9,75 руб.
Поэтому цена опциона в данном узле принимается равной 9,75 руб. В результате расчетная цена опциона в узле Sd (конец первого периода) составит не 3,25 руб., как в случае с европейским опционом, а будет равна:
1,47-0,7+9,75-0,3
------------------= 3,88 руб.
1,02
В то же время, для данного узла цена акции равна 95 руб. Если инвестор исполнит опцион в этот момент, он получит 5 руб. Поэтому премия опциона для этого узла принимается равной не 3,88 руб., а 5 руб. В результате цена американского опциона в начальный момент времени должна быть равна:
0,43 0,7+ 5 0,3
Ц02
= 1,77 руб.
Чтобы воспользоваться биномиальной моделью для практических целей, необходимо ответить на вопрос, каким образом определить значения роста и падения цены акции, т.е. и и d. Процесс, которому следует динамика цены акции, является винеровским7. Биномиальное распределение должно быть построено таким образом, чтобы при делении периода действия опционного контракта на большое количество периодов, биномиальный процесс сходился к винеровскому. Мы получим такой результат, если и и d будут иметь следующие значения:
и = естЛ'; J = (10.21)
и
гД/ j в — d
u — d
(10.22)
где <т стандартное отклонение доходности акции;
А/ - период времени, представленный в долях года.
10.1.5. Вычисление стандартного отклонения доходности акции
В формуле (10.21) стандартное отклонение доходности акции представлено на основе непрерывно начисляемого процента. Для такого случая техника расчета стандартного отклонения остается такой же, как и при использовании простого процента, т. е. определяется по формуле:8
7 Определение винеровского процесса см. в книге A H. Буренина "Рынок ценных бумаг и производных финансовых инструментов”, М., 2002, параграф 10.1.
8 Подробное объяснение понятия стандартного отклонения см. в книге А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов”, М., 2002, параграф 9.1.
/7-1
(10.23)
Корректировка касается только исходных данных, которые подставляются в формулу (10.23). В данной формуле величина х{ рассчитывается как:
S
X' = In ——
где S, - значение цены акции в конце i -го периода;
Sl+1 - значение цены акции в конце i +1 -го периода.9
Величина х является средним арифметическим значений х{ за период наблюдений. Используя свойства логарифмов, ее можно определить по формуле:
< ‘S'o у и -1
где 50 - первое наблюдение значения цены акции;
ST - последнее наблюдение цены акции;
п - количество наблюдений переменной S, (поэтому количество
переменных х{ = In равно /?-1.)
Рассмотрим пример расчета стандартного отклонения доходности акции. В качестве наблюдаемой величины выступает цена акции при закрытии. Ее значения приведены в таблице 10.1. На основе данных таблицы:
<50,0 J 10
— = 0,00198 ,
9 В формуле (10.23) величина п относится к количеству значений хг.
Полученный результат показывает стандартное отклонение доходности акции за один день. Чтобы получить значение стандартного отклонения за год, необходимо умножить его на корень квадратный из количества торговых дней в году. В году порядка 250 торговых дней, поэтому:
0,018055 >/250 =0,2855 или 28,55%.
Таблица 10.1. Расчет стандартного отклонения доходности акции
День Цена (руб.) (S In Is,) Отклонение от средней Квадрат отклонения
0 50,0
1 51,0 0,0198 0,01782 0,000318
2 52,0 0,0194 0,01742 0,000303
3 51,5 -0,0097 -0.01168 0,000136
4 50,5 -0,0196 -0,02158 0,000466
5 49,0 -0,0302 -0,03218 - 0,001036
6 48,5 -0,0103 -.01228 0,000151
7 49,0 0,0103 0,00832 0.000069
8 49,5 0,0102 0,00822 0.000068
9 50,5 0,0200 0,01802 0,000325
10 51,0 0,0099 0,00792 0,000063
сумма 0,002934 _ _ - .. — — — —
10.1.6. Биномиальная модель для акций, по которым выплачиваются дивиденды
Рассмотрим биномиальную модель для опциона на акции, по которым в течение действия опционного контракта выплачиваются дивиденды. Информация о дивиденде может быть задана в двух формах: 1) в виде ставки дивиденда; 2) и как абсолютная величина ожидаемого дивиденда. Рассмотрим оба варианта.
1) Курс акции на дату учета снижается на величину выплачиваемого дивиденда. Поэтому дерево распределения цены акции принимает вид, как представлено на рис. 10.6. Данный рисунок характери
зует случай, когда известна ставка дивиденда. Ее величина равна q. Начиная с даты учета, и для всех последующих точек пересечения ветвей дерева, курс акции корректируется на величину 1 - q . Если в течение действия контракта дивиденд выплачивается несколько раз, данная корректировка проводится соответствующее число раз. В остальном техника определения премии опциона аналогична рассмотренной выше схеме для акции, по которой не выплачиваются дивиденды.
Рис. 10.6. Дерево распределения цены акции, для которой известна ставка дивиденда: дивиденд выплачивается один раз
2) Инвестор располагает данными об абсолютной величине ожидаемого дивиденда. На дату учета стоимость акции падает на эту величину. Сделаем допущение о том, что цена акции в каждый момент времени состоит из двух частей: чистой цены, т.е. цены без дивиденда, и приведенной стоимости будущего дивиденда. После такой посылки для определения премии опциона можно воспользоваться построением дерева распределения, как и для акции, по которой не выплачиваются дивиденды. В расчетах стандартное отклонение доходности акции берется для ее чистой цены. Значение цены акции в каждой точке пересечения ветвей дерева, за исключением даты учета, представляет собой сумму ее чистой цены и приведенной стоимости дивиденда для соответствующего момента времени. Поясним сказанное на примере.
Пример.
Инвестор планирует купить четырехмесячный американский опцион пут на акции. Цена спот акции составляет 48 руб., стандартное отклонение доходности акции - 35%, цена исполнения опциона - 45
руб., ставка без риска -10%. Дата учета наступает через три месяца, дивиденд равен 3 руб. Определить премию опциона, если время действия контракта разбивается на четыре периода (месяца).
Решение.
Один месяц составляет 0,0833 часть года. Таким образом, А/ = 0,0833 . Рассчитаем темпы роста и падения цены акции и риск-нейтральные вероятности:
и = е(1ДЧ^ =1,1063; d = e ° =0,9039; = е"1(1 (,М1 =1,0084;
1,0084-0,9039 л р =--------------= 0,5163;
1,1063-0,9039
1-р = 1-0,5163 = 0,4837.
Рассчитаем приведенную стоимость дивиденда на дату заключения контракта:
Зе’0'10’25 = 2,93 руб.
Чистая цена акции в этот момент составляет:
48 -2,93 = 45,07 руб.
Чистая цена акции в точке Su (конец первого периода) равна:
45,07 1,1063 = 49,86руб.
Приведенная стоимость дивиденда в этот момент составляет:
Зе’0''о-'667 = 2,95 руб.
Полная цена акции в точке Su:
49,86+ 2,95 = 52,81руб.
Чистая цена акции в точке Su2 (конец второго периода) равна:
45,07 1Д0632 = 55,16руб.
Приведенная стоимость дивиденда в этот момент:
Зе”0,10,0833 = 2,98руб.
Полная цена акции в точке Su2 равна:
55,16+ 2,98 = 58,14руб.
В точке Su' (конец третьего периода) чистая цена акции составляет:
45,07 • 1,10633 = 61,02 руб.
К данной цене дивиденд не прибавляется, так как в этот день он выплачивается акционерам. Цена акции в точке Su4 (конец четвертого периода) равна:
45,07 - Ц10634 =67,5\руб.
Аналогичным образом рассчитывается цена акции для каждой точки пересечения ветвей дерева (см. рис. 10.7). Необходимо обратить внимание на точку Sd3. Согласно расчетам, опцион стоит в этот
Рис. 10.7. Дерево распределения цены акции и премии американского опциона пут на акцию с выплатой известного дивиденда: верхние числа - курс акции, нижние - премия опциона
момент 11,15 руб. Однако, в случае его исполнения в это время инвестор получит 11,71 руб., поэтому его цена должна равняться этой величине. Аналогичная ситуация и с точкой Sd (конец третьего периода), в которой цена опциона должна составить 4,26 руб. Последовательным дисконтированием цен опциона для каждого узла дерева распределения находим: в момент заключения контракта его цена равна 2,18 руб.
Биномиальная модель используется для оценки премии американских опционов. Премии европейских опционов рассчитываются с помощью аналитических формул. Основополагающей из них является формула Блэка-Шоулза, которую мы рассмотрим в следующем параграфе.
10.2. МОДЕЛЬ БЛЭКА-ШОУЛЗА
В начале 70-х годов Ф.Блэк и М.Шоулз разработали модель оценки премии европейского опциона колл на акции, по которым не выплачиваются дивиденды. Полученная формула явилась результатом решения ими дифференциального уравнения Блэка-Шоула. Данное уравнение мы рассматриваем в следующем параграфе.10
10.2.1. Дифференциальное уравнение Блэка-Шоулза
Сформируем портфель без риска из производного актива и базисных акций: продадим производный актив и купим акции. Изменение цены акции за время dt определяется уравнением:11
dS = iiSdt + aSeJdt , (10.24)
где 5 - цена акции;
и - мгновенная ожидаемая доходность акции;
<т - мгновенное стандартное отклонение доходности акции;
е - стандартная нормально распределенная случайная переменная;
t -время;
E^dt = dW - винеровский процесс.12
Изменение цены производного актива на акцию, согласно лемме Ито, определяется формулой:13
dG ав 1
---JjS +---+------г
dS dt 2 dS2
1 firl —
cr252 dt + ^-aSsJdt , (10.25) j 65
где G - цена производного актива.
10 Интересно отметить следующий факт. Как пишет М.Шоулэ "...Фишер Блэк и я столкнулись с большими трудностями в опубликовании нашей статьи о ценообразовании опционов. Многие рецензенты полагали, что она была слишком неясная (arcane) и представляла интерес только с технической точки зрения.” (M.S Scholes. “Merton H.Miller: Memories of a Great Mentor and Leader.” //The Journal of Finance, August 2001, Vol.56, №4, p.1180), И только такие известные экономисты в области финансов как М.Миллер и Е. Фама убедили руководителей журнала “The Journal of Political Economy" напечатать статью.
11 Вывод уравнения см. в книге А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов", М., 2002, глава 10.
12 Определение винеровского процесса см. в книге А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов", М., 2002, глава 10.
13 Вывод уравнения см. в приложении 1 к настоящей главе.
Оба уравнения содержат один и тот же стохастический элемент -винеровский процесс. Чтобы сформировать портфель без риска, необходимо исключить его из динамики стоимости портфеля. В формуле (10.24) винеровский процесс представлен величиной oSsyfdt, в формуле (10.25) - величиной — aSzy/dt . Таким образом, если dS
мы продаем один производный актив, то для исключения процесса Винера из динамики стоимости портфеля надо купить акции в про-порции —. Поэтому стоимость портфеля без риска (л) равна:
dS
„ 3G О
П - -G +--5.
as
За время dt стоимость портфеля изменяется на величину:
dn = -dG +—dS. dS
(10.26)
Подставим в уравнение (10.26) значения dS и dG соответственно из уравнений (10.24) и (10.25):
jrT (dG с QG 1 d2G 2о2^ 6G гг dGt гг\
dll =----uS + — +------т-сг 52 dt---oSsddt +---\uSdt + oSsddt I
55 dt 2 dS2 dS dS f
ИЛИ
dn =
dG dt
1 d2G
2 as2
cr2S2 dt.
(10.27)
Уравнение (10.27) не включает стохастический элемент и, следовательно, риск. Поэтому за (мгновенный) период dt портфель является безрисковым и должен приносить инвестору доходность на уровне ставки без риска.14 В результате можно записать:
1 d2G
2 ds2
cr2S2 dt = r\-G + — S dt
или
14 Если доходность портфеля будет выше или ниже ставки без риска, то откроется возможность совершить арбитражную операцию. В результате равновесие восстановится.
dG dG 1 d2G 2 2
---ч-rS— +-------ra S = rG. 10.28)
dt dS 2 dS~
Уравнение (10.28) - это дифференциальное уравнение Блэка-Шоулза. С его помощью можно определить стоимость любых производных активов на акцию, по которой не выплачиваются дивиденды. Для разных типов производных инструментов уравнение имеет разные решения в зависимости от граничных условий. В частности для европейского опциона колл к моменту истечения контракта это с - max(S - Х,0), а для пут - р = max(.V - S\o).
Уравнение (10.28) не включает параметр р. Это означает, что при оценке стоимости производного инструмента не учитывается ожидаемая доходность базисной акции. Таким образом, если два инвестора имеют разные оценки ожидаемой доходности акции, но их мнения относительно дисперсии ее доходности совпадают, то они должны одинаковым образом оценить стоимость производного инструмента на эту акцию.15 Уравнение не содержит параметр р, а значит и не учитывает предпочтения инвесторов в отношении риска.16 Поэтому при оценке стоимости производного актива правомерно использовать модель, в которой инвесторы нейтральны к риску. Следовательно, для целей дисконтирования ожидаемой стоимости производного инструмента можно использовать ставку без риска.
10.2.2. Формула Блэка-Шоулза для опционов на акции, по которым не выплачиваются дивиденды
Ф.Блэк и М.Шоулз вывели формулу оценки премии европейских опционов колл, решив дифференциальное уравнение (10.28). В данном параграфе мы приводим характеристику формулы, а ее вывод даем в приложении 3. Формула Блэка-Шоулза для европейского опциона колл на акцию имеет следующий вид:
С< = S0N(dx)-Xe~rTN(d2) , (10.291
где се - премия европейского опциона колл;
- курс спот акции;
X - цена исполнения опциона;
15 Данную особенность мы уже наблюдали в простой биномиальной модели
16 Отношение к риску задается ожидаемой доходностью акции чем менее склонен к риску инвестор, тем большую ожидаемую доходность он требует на акцию
1пГУхгг7’
-А—2—+%7г, (Ю.30)
(ЗуГГ 2
(10.31)
а - мгновенное стандартное отклонение доходности акции;
г - непрерывно начисляемая ставка без риска;
Т - время до истечения контракта;
N{d) - функция нормального распределения; величину x(d^ можно рассматривать как риск-нейтральную вероятность того, что опцион принесет выигрыш, a N(d2) - как вероятность того, что он будет исполнен.
Модель Блэка-Шоулза предполагает следующие ограничения: рынок функционирует непрерывно, возможна короткая продажа акций, транзакционные издержки и налоги равны нулю, процентная ставка постоянна, доходность акций имеет логнормальное распределение, стандартное отклонение доходности акции является константой, цена акции следуют процессу Ито.17
Пример.
£ = 50/пб., X = 45руб., г -10%, Т - ^месяцев, a = 0,525.
Определить премию европейского опциона колл.
Решение.
О ln(5%J+O,l-O,5
A = z — + 0,5-0,525Jo,5 =0,6041,
0,525 -JO,5
d, = 0,6041 - 0,525 • д/о7 = 0,2329.
Из таблицы значений функции Лапласа или с помощью программы Excel находим:18 19
17 Определение логнормального распределения и процесса Ито см. в книге А Н. Буре-
нина “Рынок ценных бумаг и производных финансовых инструментов”, М., 2002, параграфы 9 3 и 10 1.4
19 Использование программы Excel для расчета вероятности наступления события приводится в приложении 5.
=0,7271 ; TV(c/2)= 0,5921.
Тогда:
= 50 • 0,7271 - 45е’010’5 • 0,5921 = 11,01 руб.
Цену опциона пут на акции, по которым не выплачиваются дивиденды, получим на основе формулы паритета опционов:
Ре = Се + Т ~ S0
ИЛИ
Р. =SaN(d,)-Xe rTN{dyXe 'r-S„=Xe " [1 - M^)]-S„[l - Ф, )] = ^Xe^N^ays^-dS
Таким образом, цена опциона пут равна:
pt = Хе-’ У(-с1г)-S„N(- dt)
10.2.3. Оценка премии европейских опционов на акции, по которым выплачиваются дивиденды
Как отмечалось выше, информация о дивиденде может быть представлена в двух формах, в виде: 1) ставки дивиденда и; 2) абсолютного значения дивиденда. Рассмотрим определение премии для первого варианта. Ставку дивиденда (q) учитываем как непрерывно начисляемый процент.
Сравним динамику роста курсовой стоимости двух одинаковых акций за период Т. По первой в конце периода выплачивается дивиденд, по второй - не выплачивается. Тогда темп прироста курсовой стоимости первой акции ниже темпа прироста цены второй акции на величину q, так как после выплаты дивиденда в конце периода Т ее цена уменьшилась на величину дивиденда.
Если в начале периода Т цена акции, по которой выплачивается дивиденд, равна $0, то в конце периода она будет стоить столько же, сколько и акция, по которой дивиденд не выплачивается, но цена которой в начале периода Т стоит S^e~q[. Поэтому премии европейских опционов на такие акции должны быть одинаковыми, поскольку одинаковыми являются и их цены к моменту истечения контактов. Выше мы привели формулы Блэка-Шоулза для оценки премии европейских опционов на акции, по которым не выплачивались
зю
дивиденды. Данные формулы можно использовать и для опционов на акции, по которым выплачиваются дивиденды, заменив 50 на V":
с = )- XerTN(d2) ;
ре = Xe rTN(~ d2)- SQe ‘<r У(- dt);
dx и d2 принимают указанный вид вследствие следующего преобразования:
1 1 | ] цТ I т
In —--= In — + Ine 4 = \n — -qT.
XX X
Данный результат в 1973 г. получил Р.Мертон.
Если инвестор имеет информацию об абсолютном размере дивиденда, то величина 50 уменьшается на приведенную стоимость дивиденда, а значение сг принимается как стандартное отклонение чистой цены акции. Полученные цифры подставляются в формулу Блэка-Шоулза.
10.3. ОЦЕНКА ПРЕМИИ ЕВРОПЕЙСКИХ ОПЦИОНОВ НА ИНДЕКСЫ, ФЬЮЧЕРСНЫЕ КОНТРАКТЫ И ВАЛЮТУ
10.3.1. Оценка премии опциона на индекс
На финансовых рынках ведется торговля опционами на фондовые индексы. Индексы обычно насчитывают большое количество акций. Поэтому их исполнение подразумевает не поставку бумаг, а осуществление взаиморасчетов в денежной форме. При исполнении опциона колл положительная разница между котировочной ценой индекса и ценой исполнения, а для опциона пут - между ценой исполнения и котировочной ценой индекса - умножаются на множи
тель, установленный для данного опционного контракта. Вычисленная таким образом сумма уплачивается покупателю опциона и списывается со счета продавца опциона.
При оценке премии европейского опциона на индекс его можно представить как акцию, по которой выплачиваются дивиденды. Поэтому премию опциона можно рассчитать по формулам Блэка-Шоулза для акций, по которым выплачиваются дивиденды. При расчете учитываются только дивиденды, выплачиваемые в период действия опциона. Если мы используем формулы со ставкой дивиденда, то ставка дивиденда на индекс определяется как средняя ставка дивиденда. Если инвестор располагает данными об абсолютном значении выплачиваемых дивидендов, то в этом случае начальное значение индекса уменьшают на величину приведенной стоимости дивидендов.
Пример.
Инвестор покупает трехмесячный европейский опцион колл на индекс А с ценой исполнения 245. В момент заключения контракта значение индекса равно 250. Стандартное отклонение доходности индекса составляет 20%. Ожидается, что дивиденды будут выплачиваться на ряд акций в первом месяце, других - во втором, и на оставшиеся акции - в третьем. Для первого месяца непрерывно начисляемая ставка дивиденда равна 1%, второго - 2%, третьего - 3%. Ставка без риска - 10%. Множитель контракта равен 100. Определить стоимость опциона.
Решение.
Ставка среднего дивиденда в расчете на год равна:
1% + 2% + 1э5%
I Аг 1 о /о j
/ \ I О 22
1п25%._ + 0,1-0,18 + —— 0,25
\ /245/ 2
d, =-----------------==---------4---= о,О52 ,
0,2^0,25
d, = 0,052-0,2-7^25 = -0,048.
Из таблицы значений функции Лапласа или с помощью программы Excel находим:
N(d^= 0,5207,
=0,4809.
се = 25Оеч)'180’25 • 0,5207 - 245е-010 25 • 0,4809 = 9,5355/?гб.
Контракт стоит:
9,5355 100 = 953,55 руб.
Американские опционы на индекс стоят больше европейских, так как их досрочное исполнение может оказаться оптимальной стратегией.
10.3.2. Формулы Блэка оценки премии опциона на фьючерсный контракт
Премии европейских опционов колл и пут рассчитываются с помощью формул, предложенных Ф.Блэком. Предполагается, что фьючерсная цена также как и цена акции имеет логнормальное распределение. Для определения премии опциона фьючерсный контракт рассматривают как акцию, по которой выплачиваются дивиденды. Ставка дивиденда принимается равной ставке без риска г. Такую аналогию можно провести, например, если сравнить дифференциальные уравнения (П.10.12) и (П.10.15) приложения 2. Уравнение (П.10.12) примет вид уравнения (П.10.15), если принять q = r . Поэтому формулу оценки премии опционов на фьючерсный контракт получают на основе формулы для акций, по которой выплачиваются дивиденды, заменив величину S{y ч/ на величину F^e~rT:
и
где
<т - мгновенное стандартное отклонение фьючерсной цены.
Фьючерсная цена равна цене спот к моменту истечения срока действия контракта. Поэтому премии двух опционов - опциона на фьючерс
ный контракт и опциона на актив, лежащий в основе фьючерсного контракта, будут одинаковыми, если фьючерсный и опционный контракты имеют одну и ту же цену исполнения и дату истечения.
10.3.3. Биномиальная модель оценки премии опциона на фьючерсный контракт
В рамках биномиальной модели за каждый данный отрезок времени курс фьючерсного контракта может с вероятностью р пойти на известную величину вверх или с вероятностью (1 - р) вниз, как показано на рис. 10.8. В первом случае в конце периода стоимость фьючерса составит величину Fu , во втором - Fd, где F - курс фьючерса в начале периода; и = 1 + процент прироста цены контракта; d = 1 - процент падения цены контракта.
Рис. 10.8. Динамика цены фьючерсного контракта в рамках простой биномиальной модели
Сформируем портфель без риска из опциона колл и фьючерсных контрактов: продадим один опцион колл и купим h единиц фьючерсных контрактов. Стоимость портфеля в начальный момент времени равна:
c(]-hF, (10.32)
где с0 - премия опциона в момент его заключения;
h - количество фьючерсных контрактов;
F- фьючерсная цена при заключении опционного контракта.
Если пренебречь условием внесения начальной маржи, то открытие фьючерсной позиции ничего не стоит инвестору. Поэтому стоимость портфеля просто равна цене опциона, т.е. с0.
В конце периода в случае роста фьючерсной цены стоимость портфеля составит:
с„ - h(Fu - F),
в случае падения цены будет равна:
где см и С/ - стоимость опциона соответственно в случае роста и падения фьючерсной цены;
h(Fu - f) и h(Fd - F) - вариационная маржа по фьючерсным контрактам соответственно в случае роста и падения цены.
Сформированный портфель является безрисковым, если к моменту истечения срока действия опциона стоимость его одинакова независимо от значения фьючерсной цены. Следовательно, в конце периода:
- h(Fu - F) = cd - h{Fd - F).
(10.33)
Отсюда находим значение h :
В условиях равновесия на рынке портфель без риска должен приносить инвестору ставку без риска. Поэтому премию опциона находим дисконтированием под ставку без риска стоимости портфеля в конце периода:
с; - h^Fu - F)
cd-h(Fd-F)
(10.35)
(10.36)
Подставив значение h из (10.34) в (10.35) или (10.36), получим:
1 17 ( w-1 1
С, = ----- с + ------ с, ,
где R = 1 + ставка без риска.
Будем рассматривать величины
---- и ------
u~d) \u—d)
как риск-
Часть II Опционные рынки нейтральные вероятности, обозначив их соответственно через р и (1 - р). С учетом сказанного формула (10.37) принимает вид;
к
Мы получили оценку стоимости европейского опциона на фьючерсный контракт в рамках однопериодной биномиальной модели.
Рассмотрим случай, когда до истечения срока действия опциона два периода. Фьючерсная цена в этом случае может принять е конце второго периода три значения: Fu2, Fud, Fd~ (см. рис. 10.9). Проанализируем вначале второй период. Он состоит из двух однопериодных моделей. В первой из них цена опциона в начале периода равна си, а в конце периода принимает значения с{т ипи cud. Во второй из них цена опциона в начале периода равна cd, а в конце cdu или cdd. Значения су и cd можно определить таким же образом, как в случае с одним временным периодом:
С = тг 1^- + <’ “ ] (1 °-39)
IX.
И
Рис. 10.9. Двухпериодная биномиальная модель
= -7 + 0 - РУМ ] • (10.40)
К
Подставив значения си и cd из формул (10.39) и (10.40) в формулу (10.38), получим:
с = тт +2р(1~ рУ'Ш1 + 0 - рУ ] • (1 °-41)
К
Формула (10.41) определяет цену опциона для двухпериодной модели. Согласно данной формуле вероятность того, что опцион к моменту срока его истечения будет стоить cillt равна р2, cdd -(1 - р)1 и c}ld = cdH - 2/?(1 - р). Сумма всех вероятностей равна 1. Формула (10.41) вновь показывает, что цена опциона равна дисконтированной стоимости суммы его ожидаемых значений к моменту истечения контракта.
Рассуждения, которые были использованы при определении стоимости опциона для двухпериодной модели, можно использовать и в случае деления времени обращения опциона на любое число периодов. Тогда биномиальная формула примет следующий вид:
с
и!
р!(\-рУ 'тах(0;и^/" F-X)
/Г
(10.42)
где индекс j показывает количество периодов, когда цена фьючерса возрастала из общего числа периодов п.
Формула (10.42) говорит о том, что цена опциона равна дисконтированной стоимости суммы ожидаемых выплат по контракту к моменту его истечения. Весь срок обращения опциона разбит на п периодов. Соответственно в знаменателе Rn - это коэффициент дисконтирования, который учитывает ставку без риска и количество периодов. Числитель показывает ожидаемое значение суммы выплат по опциону с учетом вероятности каждого конкретного исхода. Выражение и!
----------PJ(\- р)п ' показывает вероятность того, что фьючерсная цена будет расти в j периодах из п периодов и падать в (п - /) периодах с учетом всех возможных комбинаций ее роста и падения.
Выражение шах(0,м'<яГ !F-X) дает выплату по опциону к моменту истечения контракта, если фьючерсная цена росла в J периодах на величину и и падала в n-j периодах на величину d .
При расчете премии имеют значение лишь слагаемые, когда опцион оказывается выигрышным к моменту истечения контракта, поскольку остальные слагаемые обращаются в ноль. Поэтому, если через к - обозначить число подъемов фьючерсной цены, чтобы опцион оказался с выигрышем, то формулу (10.42) можно переписать как:
pJ(\-p)n J(u}dn }S-X)
(10.43)
В формуле (10.43) суммирование значений в числителе начинается с периода к. Опцион будет выигрышным к моменту его истечения, если:
(10.44)
\d) Fd"
(10.45)
Чтобы определить значение к, возьмем натуральный логарифм от обеих частей неравенства (10.45). Получим:
(10.46)
Из неравенства (10.46) следует;, что к должно быть целым числом, большим чем:
Если к больше п, то с = 0, так как фьючерсная цена за все периоды п не превысит цену исполнения (Д').
Полученную модель можно применить и для определения премии опциона пут. Она имеет вид:
Г п\
p'ii-pY'^d^S-X)
R\ (Ю.47)
По сравнению с формулой (10.43) здесь учтены следующие изменения. Стоимость опциона пут перед моментом истечения равна X ~u !d" JF . Через к обозначено количество движений фьючерсной цены вверх, в результате которых опцион колл становится выигрышным. Поэтому опцион пут будет выигрышным, если количество движений фьючерсной цены вверх не превысит величину к -1.
Чтобы воспользоваться биномиальной моделью для практических целей, необходимо определить значения роста и падения фьючерсной цены, т.е. величины и и d. Процесс, которому следует динамика фьючерсной цены, является винеровским.19 Биномиальное ‘распределение должно быть построено таким образом, чтобы при делении периода действия опционного контракта на большое количество периодов, биномиальный процесс сходился к винеровскому. Мы получим такой результат, если и и d будут иметь следующие Значения:
d = e-cr4H (10.48)
И
и-d
где ст - стандартное отклонение доходности, рассчитанной на основе фьючерсной цены, т.е. величины dFj F\
At - период времени, представленный в долях года.
Биномиальную модель можно использовать для оценки премии американских опционов на фьючерсные контракты. Различие моделей для европейских и американских опционов аналогично случаю американских и европейских опционов на акции, рассмотренном в параграфе 10.1 4.
10.3.4. Оценка премии опциона на валюту
Иностранную валюту можно рассматривать как акцию, для которой известна ставка дивиденда. Иностранная валюта приносит владельцу доходность, т. е. ставку дивиденда (rz), равную ставке без риска в иностранной валюте. Поэтому для оценки премии опционов на валюту можно воспользоваться формулами для акции, по которой выплачиваются дивиденды, заменив величину S(ie'4T на величину
се = S!se r, TN(d{) - Хе rTN(d2)
И
19 Определение винеровского процесса см в книге А.Н. Буренина “Рынок ценных бумаг и производных финансовых инструментов”, М., 2002, параграф 10.1.
Ре =Xe-'TN(-d2)-S0e-r'TN(-dl),
где
S - курс иностранной валюты в прямой котировке.
КРАТКИЕ ВЫВОДЫ
При оценке премии опциона не играет роли вероятностное распределение курса акции и величина ее ожидаемой доходности, но имеет значение стандартное отклонение доходности акции.
Стоимость опционного контракта определяется не самостоятельно, а опосредованно через оценку стоимости безрискового портфеля, который инвестор может сформировать из опционов и базисных активов.
Премия опциона на акцию равна дисконтированной стоимости его цен к моменту истечения контракта, где весами выступают риск-нейтральные вероятности роста и падения цены акции. В качестве ставки дисконтирования выступает ставка без риска.
Дифференциальное уравнение Блэка-Шоулза не включает параметр ожидаемой доходности акции. Это означает, что при оценке стоимости производного инструмента данная переменная не учитывается. Если два инвестора имеют разные оценки ожидаемой доходности акции, но их мнения относительно дисперсии ее доходности совпадают, то они одинаковым образом оценят стоимость производного инструмента на эту акцию.
Модель Блэка-Шоулза предполагает, что процентная ставка и стандартное отклонение доходности акции являются константами, доходность акции имеет логнормальное распределение, цена акции следует процессу Ито.
ПРИЛОЖЕНИЕ!.
Лемма Ито
Лемма Ито показывает зависимость между небольшим изменением значения случайной переменной и небольшим изменением функции этой случайной переменной. Для случайной переменной она выполняет такую же роль как и формула Тейлора для детерминированной переменной.
Пусть функция G - это непрерывная, дифференцируемая функция двух не стохастических переменных х и у. Тогда изменение ее значения можно представить с помощью ряда Тейлора как:
dG dG L 1 d2G J , d2G J , 1 d2G J 2
dG ----dx 4---dy +------— dx‘ +---dxdy +----— dy +
dx dy 2 dx2 dxdy 2 dy (П 10 1)
слагаемые более высоких
+
порядков относительно dx и dy.
При dx -> 0 и dy -> 0 можно пренебречь слагаемыми более высоких порядков чем dx и dy , и уравнение (П.10.1) примет вид:
dG , dG , dG ~ dx +--------dy.
dx dy
(П.10.2)
Пусть теперь функция G - это функция стохастических переменных дг и /, следующих процессу Ито:
dx- a(x,t)dt + b(x,t)gyfdt(П.10.3)
Перепишем уравнение (П.10.1) для данного случая:
_ dG . Ж 1 &G } . d"G 1 d2G J 2
dG =-----dx А--dt A---—dx~ + ----dxdtA-----—dt +
dx dt 2 dx* dxdt 2 dt (П10 4)
слагаемые более высоких + порядков относительно dx и dt.
Если переменные функции G не следуют процессу Ито, то при стремлении dx и dt к нулю мы получим такой же результат как и в формуле (П.10.2), опустив слагаемые более высоких порядков. Однако, когда переменная х(/) не определена четко, а следует процессу Ито, то нельзя непосредственно использовать приведенное выше правило дифференцирование, а надо использовать лемму Ито. Лемма Ито - это стохастический эквивалент существующему правилу дифференцирования. В рамках про
цесса Ито переменная dx2 имеет размерность dt, и ее уже нельзя исключать. Это можно показать следующим образом. Возведем уравнение (П.10.3) в квадрат, опустив для удобства запись аргументов:
dx2 = a2dt2 + labE^didt + b2s2dt . (П.10.5)
Как видно из уравнения (П.10.5), элемент dx2 включает в себя слагаемое b2s2dt, которое имеет порядок dt, и поэтому его следует учесть в уравнении (П.10.4).
Дисперсия стандартной нормально распределенной величины равна единице. Используя формулу определения дисперсии, можно записать:
Е(^2)Чад2=1. (П.Ю.6)
где символ Е0 означает ожидаемое значение или математическое ожидание величины, стоящей в скобках.
Ожидаемое значение стандартной нормально распределенной переменной равно нулю, поэтому E[(i’)]2 = 0, и из уравнения (П.10.6) Е(£*2)-1. Отсюда следует, что величина e2dt имеет ожидаемое значение равное20 dt и дисперсию порядка21 dt2. При dt -> 0 величину z2dt можно рассматривать уже как нестохастическую и равную ее ожидаемому значению dt, так как ее дисперсия в этом случае стремится к нулю. Поэтому нестохастической становится и сама величина dx2. На основании уравнения (П.10.5) ее значение при dt 0 равно b2dt. В результате уравнение (П.10.4) принимает вид:
20 Возьмем математическое ожидание от величины sdt и вынесем dt как константу для определенного интервала времени за знак математического ожидания. Учитывая, что E(s2) = I, получим:
£(й,г(У/)= dtE^s1 ) = dt \-dt.
21 Возьмем дисперсию величины e2dt как уаг(^2(У/). где var означает дисперсию. Возьмем отрезок времени dt как константу. Тогда по свойству дисперсии постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат, или: var(f2t/z)= dt2 var(£2). Отсюда видно, что размерность дисперсии переменной е2dt имеет порядок dt2.
cGJ dG 152Gk2j
JG =---dxA---dt ч-----—b dt.
dx dt 2 5x‘
(П.10.7)
Уравнение (П.10.7) представляет собой лемму Ито.
Подставим в уравнение (П.10.7) уравнение (П.10.3), получим формулу изменения цены производного актива:
dG ( J , dG J 1 d2G ,2 j dG =-----(adt + bdW) +------dt +------7- о dt
dx v 7 dt 2 dx2
или
где dW - процесс Винера.
Если в качестве базисного актива выступает акция, изменение цены которой задается формулой (10.24), то формула (П.10.8) принимает вид:
(dG n dG 1 d2G
\dS dt 2 dS2
a2S2 dt + ^-oS£y[dt. dS
ПРИЛОЖЕНИЕ 2.
2.1. Дифференциальное уравнение для производного актива на акцию, по которой выплачивается непрерывно начисляемый дивиденд
Сформируем портфель без риска: продадим один производный
dG
актив (G) и купим базисную акцию (S') в количестве —-. По акции выплачивается непрерывно начисляемый дивиденд (<?). Изменение цены производного актива за время dt определяется уравнением (10.25), цены акции - уравнением (10.24). Изменение цены производного актива за более длительный период А/ составляет:
(dG о dG 1 d2G 2o2Y dG r— n.
AG = —zaS +-— +---------ст S А/ + — aSsdAt , (П.10.9)
[dS dt 2 dS2 ) dS v
цены акции:
AS = ^/SAt + oSgyfAt + qSAt, (П.10.10)
поскольку за этот период на акцию выплачивается дивиденд.
Изменение стоимости портфеля &П за период Д? равно:
A 6G o dG Ml---------juS + — +
as at 2
1 ^-^-сг'52 |Д/-—± — (uSXt + oSs^At as2 as as^ 7
или
AZ7 =
dG 1 d2G 2_,2 dG ।
-----------~cr S + — qS Л/.
dt 2 dS2 6S
(П.10.11)
Из уравнения (П.10.11) исключен винеровский процесс, поэтому портфель является безрисковым за короткий период времени А/ и должен приносить инвестору доходность на уровне ставки без риска. В результате можно записать:
dG J
dG I d2G 2е2 dG Г
--------<7 S +—qS dt=r - G +-S dt
dt 2 dS2 dS I dS
as )
или
dG dG / \ 1 d^G , ? /л 4Л
---+----(r-<7)S + ~cr~S~ = rG. (П.10.12 dt dSV ' 2 as2 v
Уравнение (П.10.12) - это дифференциальное уравнение для цены производного инструмента на акцию, по которой выплачивается непрерывно начисляемый дивиденд.
2.2. Дифференциальное уравнение для производного актива на валюту
Дифференциальное уравнение для производного актива на валюту получим на основе формулы (П.10.12). На иностранную валюту инвестор может получать процент без риска rf . Поэтому валюту правомерно рассматривать как акцию, по которой выплачивается известный непрерывно начисляемый дивиденд со ставкой . Тогда, заменив в формуле (П.10.12) q на , получим:
cGJGi у i 1 d2G 2 2 /П1Л17\
---1 lr-г.пч----------— с S - rG, (П.10.13)
dt dS ' 2 dS2
где 5- спот курс иностранной валюты.
2.3. Дифференциальное уравнение для производного актива на товар
Дифференциальное уравнение для производного актива на товар можно получить на основе формулы (П.10,12). Если инвестор владеет товаром, ему приходится оплачивать расходы по его хранению и страхованию. Поэтому товар можно представить как акцию с отрицательной ставкой дивиденда. Пусть z - это расходы по хранению и страхованию товара, представленные как непрерывно начисляемый процент от спотовой цены товара. Тогда формула (П.10.12) принимает вид:
dG dG / х 1 d2G 2 .
— +-----(r + z)S +-----ст S' = rG. (П.10.14
dt dS 7 2 dS2
2.4. Дифференциальное уравнение для производного актива на фьючерсный контракт
Дифференциальное уравнение для производного актива на фьючерсный контракт можно получить на основе уравнения (10.28) с помощью простой замены переменных.
G является функцией F и /. В свою очередь F - это функция 5 и /, поскольку определяется по формуле F = Se^14V Учитывая дан-dG dG d2G
ныи факт, запишем производные —, — , —г : dt dS dS2
dG _ dG dG dF dG dG dF dt ~ dt * dF dt ' ~dS~dF~dS'
g2G _ ds2 ~ d dS ( dG dF' ^dF dS, }d2G J dF2 (dFy 2 dG d2F dF dS2
= -t SF F , — = er<r 'at =e^r-) ,^=o.
idt dS \8S) oS2
Подставим полученные значения производных в формулу (10.28):
с ^G dG г(Г dG r[r,) 1 d G 2г(т
rG-------rr-----+ rFe -------e ' +-------~e г e
dt dF dF 2 dF2
После сокращения одинаковых членов получаем:
(П.10.15)
Уравнение (П.10.15) является дифференциальным уравнением для производного актива на фьючерсный контракт.
ПРИЛОЖЕНИЕ 3.
Вывод формулы Блэка-Шоулза
Ф.Блэк и М.Шоулз получили формулу для европейского опциона колл на акции, по которым не выплачиваются дивиденды, на основе решения дифференциального уравнения (10.28). Мы докажем ее в данном приложении с помощью вероятностного подхода.
Согласно общему принципу определения цены финансового актива, премия опциона равна дисконтированной стоимости ожидаемого дохода, который он может принести к моменту окончания контракта, а именно:
с; = е гГ£[тах(5 - Л'.О)] , (П.10.16)
где се - цена европейского опциона колл;
S - цена акции к моменту истечения контракта; г - непрерывно начисляемая ставка без риска, Т - время действия контракта;
/:[тах(5- А\())] - ожидаемое значение стоимости опциона к моменту истечения контракта. Оно может принимать только два значения: S -X , если S > X, или 0, если S < X .
Рассчитаем ожидаемое значение премии опциона к моменту истечения контракта. Оно равно:
E[max(S-X,0)]= J(5 - , (П.10.17)
X
где /(5)-плотность распределения переменной 5.
Цена акции (s) имеет логнормальное распределение, в то же время величина In 5 распределена нормально.22 Поэтому в интеграле (П.10.17) целесообразно перейти от переменной 5 и плотности логнормального распределения /(S') к переменной in 5 и плотности нормального распределения /(inS'). Обозначим:
In S’ = 7/ (П.10.18)
22 О логнормальном распределении см в книге А Н Буренина “Рынок ценных бумаг и производных финансовых инструментов”, М , 2002, параграф 10.2.1.
и соответственно плотность нормального распределения как f(u). Из формулы (П.10.18) получаем:
S = ec. (П.10.19)
Из однозначности функциональной зависимости между 5 и U вытекает: вероятность того, что цена акции S будет меньше некоторого значения 5, т.е. Р(5<д’) эквивалентна вероятности того, что р(и < 1ns). Поэтому:
Т(5’)= p(S <j)= P(U <lns)= , (П.10.20)
(П.10.21)
где - функция распределения переменной 5.
Найдем плотность распределения /(S'). Для этого продифференцируем 'T'(S) по 5:
В интеграле (П.10.17) сделаем замену переменной 5 на U и вместо плотности вероятности /'(5) подставим ее эквивалент /(с/)—:
1S
Г(е" - x)f(u)dU =
Л (П.10.22)
In X In X
Мы разбили интеграл на два интеграла. Вычислим их последова-тельно, учитывая, что f(u)=—т=е 2b2 , где а - математиче
ское ожидание, а 62-дисперсия переменной U .
«= . (и dV2 '* 2Ь2Ь' U24-2Ga-o2
{euf(u)dU = f е' - ,— е “3 dU = —== (е “3 dU. (П. 10.23)
Дополним показатель степени при е в интеграле (П. 10.23) до полного квадрата:
В формуле (П. 10.24) под знаком интеграла стоит плотность нормально распределенной величины со средним значением а + Ь2 и дисперсией Ь2. Поэтому он равен:
~1пХ-(а + 62)~
b
ь
где n(x) - функция нормального распределения, которая говорит о вероятности того, что случайная величина X будет меньше чем х. Таким образом, первый интеграл в выражении (П.10.22) равен:
'еи f(lJ )dU = е*2 N ^Х + (а + Ь )
(П.10.25)
Величина U = In 5 распределена нормально со средним:
а = In So + г Т и стандартным отклонением b = а^/т ,
о
где 5(J - цена акции в момент заключения контракта.23
Подставим эти значения в формулу (П.10.25):
23 Вывод данных параметров см. в книге А.Н.Буренина “Рынок ценных бумаг и производных финансовых инструментов", М., 2002, стр 183.
328
(П.10.26)
Обозначим
тогда:
otj
р f(u\lU = S„e'T N(dy
In У
(П 10.27)
Решим второй интеграл в выражении (П. 10.22). Он представляет собой интеграл плотности нормально распределенной величины U :
d, =
сгл/Г
Таким образом, ожидаемая величина премии опциона равна:
£[тах(5 - Х,0)] = S„erTN(d})- XN(d2) (П. 10.28)
Подставим значение £’[max(.S'~ А",0)] из формулы (П.10.28) в выражение (П.10.16). Тогда цена опциона колл равна:
SQerTN(dt)- XN(d2)] = S0N(dt)- Xe~el N(d2)
ce=S0N(d,)-Xe ‘TN(d2).
ПРИЛОЖЕНИЕ 4.
Определение премии европейского опциона колл на акции, по которым не выплачиваются дивиденды, с помощью программы Excel
Программа Excel позволяет легко рассчитать премию европейского опциона колл с помощью формулы Блэка-Шоулза. Рассмотрим технику расчета на примере из параграфа 10.2.2.
Пример.
S' = 50 руб., X - 45руб., г - 10%, Т - 6 месяцев. a = 0,525.
Заносим в ячейки А2, В2, С2, D2 и Е2 рабочего листа исходные данные примера как показано на рис.П.10.1. В ячейке А5 размещаем формулу для значения d}:
С учетом адресов ячеек печатаем в ней следующий алгоритм:
=((LN(B2/A2)+C2*D2)/(E2*D2A0,5))+0,5*E2*D2A0,5
В ячейке В5 размещаем формулу N(d{ ):
=НОРМСТРАСП(А5)
В ячейке С5 размещаем формулу для значения d2:
d2 ~ d - ay/т.
С учетом адресов ячеек печатаем в ней следующий алгоритм: =А5-Е2*О2Л0,5
В ячейке D5 размещаем формулу /v(t72):
=НОРМСТРАСП(С5)
В ячейке Е5 печатаем формулу (10.29) Блэка-Шоулза:
=B2*B5-A2*EXP(-C2*D2)*D5
Решение задачи получаем как представлено на рис. П.10.1.
- ! 6 J с, 1 ' Р j i цена время до це на | спот ста вка мете че ния 1 ш попнения акции без риска, контракта 45 so : „ °-5 4 ci, _ 1 N(d.) ! а,'"Г_м(с1г) 5 | 0.604116384! 0,727117 0^32895] 0,5920747 С "Е "I стандартное f отклонение | доходности акции j 0,525 - г I премия опциона! 11.01199536 ' -I
Рис. П. 10.1. Определение премии европейского опциона колл.
ПРИЛОЖЕНИЕ 5.
Определение значений вероятности нормально распределенной стандартной случайной величины с помощью программы Excel
Рассмотрим использование программы Excel для определения вероятности нормально распределенной стандартной величины на основе данных примера из параграфа 10.2.2.
Пример.
Определить вероятность события, что стандартная нормально распределенная случайная величина примет значение меньше чем 0,6041.
Решение.
Получим решение в ячейке А1, поэтому выделяем ее. Для этого наводим на нее курсор и щелкаем левой клавишей мыши. На панели
инструментов наводим курсор на значок £ и щелкаем левой клавишей мыши. Появилось окно “Мастер функций”. В окне два поля. Левое называется “Категория”. В поле “Категория” наводим курсор на строку “Статистические" и щелкаем левой клавишей мыши. Строка высветилась синим цветом, а в правом поле окна под названием “Функция” появился перечень статистических функций. Наводим курсор на строку “НОРМСТРАСП” и щелкаем левой клавишей мыши. Строка высветилась синим цветом. Наводим курсор на кнопку ОК и щелкаем левой клавишей мыши. Появилось окно “НОРМСТРАСП”. В окне одна строка, которая называется “z”. Печатаем в ней цифру 0,6041 и щелкаем мышью кнопку ОК В ячейке А1 появился ответ -цифра 0,727111.
ГЛАВА 11. КОЭФФИЦИЕНТЫ ЧУВСТВИТЕЛЬНОСТИ ПРЕМИИ ОПЦИОНА
* В настоящей главе рассматриваются коэффициенты чувствительности премии опционов: дельта, гамма, вега, тета и ро. Мы охарактеризуем каждый из показателей, остановимся на вопросах формирования дельта-нейтральной, гамма-нейтральной, вега-нейтральной позиций, а также дельта- и гамма-нейтральной позиции и формирования позиций с заданной дельтой и вегой.
11.1. ДЕЛЬТА
11.1.1. Общая характеристика дельты
Для опционов разработан ряд характеристик, которые позволяют лучше представить динамику премии опциона в зависимости от изменения конъюнктуры и используются для хеджирования и в спекулятивной практике. Первая характеристика - это дельта. Дельта представляет собой отношение изменения цены опциона, к изменению цены базисного актива. Она показывает, в какой мере изменится премия опциона при изменении цены базисного актива на один пункт. Дельта представляет собой первую производную премии опциона по цене базисного актива. Поэтому дельту опциона колл можно определить как:
дс
dS’
а дельту опциона пут как:
А =
р ds ’
где А( - дельта опциона колл;
А - дельта опциона пут;
дс-небольшое изменение цены опциона колл;
др - небольшое изменение цены опциона пут;
dS - небольшое изменение цены базисного актива.
Графически дельта - это угол наклона касательной к кривой зависимости цены опциона от цены базисного актива (см. рис. 11.1). На рис. 11.1 при цене актива А дельта равна тангенсу угла a . Дельта длинного опциона колл является положительной величиной, по
скольку премия опциона и цена базисного актива изменяются в одном направлении.
Допустим, дельта опциона колл равна 0,6. Это означает, что при небольшом изменении цены базисного актива цена опциона изменится на 60% от этого изменения. Пусть цена акции выросла на 1 рубль. При дельте опциона на акцию 0,6 его цена выросла на 60 копеек. Соответственно при падении курса акции на 1 руб. его премия уменьшилась на 60 коп.
цена опциона колл
Рис. 11. /. Дельта опциона колл
Теоретически цена опциона не может измениться в большей степени, чем стоимость базисного актива. Поэтому максимальное значение дельты длинного опциона колл равно единице (опцион с большим выигрышем). Нижней границей дельты является ноль (опцион с большим проигрышем). Если дельта равна единице, то премия опциона изменится на один пункт при изменении цены актива на один пункт. При дельте равной нулю премия опциона не изменится при изменении курса актива. Опционы без выигрыша (ATM} обычно имеют дельту равную 0,5 (см. рис. 11.2.). Это означает, что их цена изменяется в два раза медленнее цены базисного актива. Дельта короткого опциона колл учитывается со знаком минус.
Дельта опциона пут отрицательна, так как при росте цены базисного актива премия опциона уменьшается, а при падении цены воз
растает. Ее значения лежат в пределах от нуля (опцион с большим проигрышем) до минус единицы (опцион с большим выигрышем). Опцион без выигрыша имеет дельту порядка минус 0,5 (см. рис. 11.3). Дельта короткого опциона пут учитывается со знаком плюс.
дельта
Рис. 11.2. Дельта опциона колл
Л&с. 11.3. Дельта опциона пут
Дельты опционов на один базисный актив можно складывать. Например, инвестор купил 100 опционов колл (один опцион на одну акцию) с дельтой 0,6. Тогда общая дельта его позиции (портфеля) равна:
100’ 0,6 -60.
Если инвестор купил опцион колл на акцию с дельтой 0,6 и купил опцион пут на эту акцию с дельтой -0,4 , то дельта его портфеля равна:
0,6+ (-0,4) = 0,2. (11.1)
Дельта не является постоянным числом. Как видно из графиков 11.2 и 11.3, ее величина изменяется с изменением цены базисного актива. Дельта длинного опциона колл возрастает по мере роста курса базисного актива и уменьшаться при ее падении. Дельта длинного опциона пут уменьшается (по абсолютной величине) при росте цены базисного актива и увеличивается при его падении. Значение дельты изменяется с наибольшей скоростью, когда цена базисного актива расположена близко к цене исполнения опциона. По мере удаления цены актива от цены исполнения скорость изменения дельты уменьшается. Значение дельты зависит от времени до истечения опциона. По мере его приближения оно стремится к нулю для длинного опциона колл ОТМ и к единице для длинного опциона колл ITM. Для длинного опциона пут она соответственно будет приближаться или к нулю или к минус единице. Уменьшение времени до истечения опциона ATM увеличивает его дельту. Рост волатильности ведет к росту дельты и наоборот.
Если рассматривать значение дельты только по абсолютной величине, то в каждый данный момент ее можно интерпретировать как меру вероятности того, что опцион принесет прибыль его держателю. Например, дельта опциона колл равна 0,5. Это говорит о существовании 50%-ой вероятности того, что опцион принесет прибыль. Если дельта опциона колл равна 0,1, то это опцион с большим проигрышем, и, соответственно, вероятность того, что он принесет прибыль, очень мала. Согласно дельте она составляет 10%. Вероятность получить прибыль по опциону с дельтой 0,9 велика, потому что он уже является с большим выигрышем. Соответственно вероятность получить прибыль составляет 90%.
Положительный знак дельты позиции инвестора говорит о том, что он будет выигрывать от роста цены базисного актива и проигрывать от ее падения. Отрицательная дельта означает, что инвестор
Гпава 11. Коэффициенты чувствительности премии опциона будет выигрывать от падения курса базисного актива и проигрывать от его роста.
Для европейских опционов колл и пут на один и тот же базисный актив с одинаковыми ценами исполнения и датами истечения контрактов справедливо равенство:
дельта опциона колл - дельта опциона пут = /. (11-2)
Его можно получить из формулы паритета опционов. Продифференцируем формулу (9.1) по 5 :
дс„ дХе rl дре 8S
8S 8S ~ 8S + 8S
ИЛИ
=Др + 1, (11.3)
или
Д -Ар=1. (11.4)
Если известна дельта опциона пут, то по формуле (11.3) можно определить дельту опциона колл с той же ценой исполнения и датой истечения контракта. Соответственно дельта опциона пут равна:
А,=Дг-1. (11-5)
Американский опцион пут стоит дороже европейского, поэтому для американских опционов равенство (11.2) несколько больше единицы.
Значение дельты рассчитывают на основе формул определения премии опциона. Продифференцировав формулы Блэка-Шоулза по 5, получим: дельта европейского опциона колл на акции, по которым не выплачиваются дивиденды, равна величине европейского опциона пут - N(d{)-1.
11.1.2. Дельта-хеджирование
Дельту можно рассматривать в качестве коэффициента хеджирования для страхования опционной позиции. Значение дельты говорит о числе единиц базисного актива, которые инвестор должен купить или продать на каждую позицию по опциону. Зная величину дельты, инвестор может сформировать портфель из опционов и базисных активов, который будет нейтрален к риску в течение следующего короткого периода времени, поскольку изменение цены опциона бу-
дет компенсироваться аналогичным, но противоположным по знаку, изменением цены базисного актива. На каждый выписанный опцион колл инвестор должен купить количество единиц базисного актива равное значению дельты. На каждый длинный опцион колл ему следует продать данное количество единиц актива. Покупая опцион пут, инвестор должен купить количество единиц базисного актива равное дельте, продавая опцион пут, - продать данное количество единиц актива.
Пример 1.
Инвестор продал 100 опционов колл (один опцион на одну акцию) с дельтой 0,6. Общая дельта его позиции равна:
100(-0,б) = -60.
Знак минус говорит о том, что инвестор открыл короткую позицию по опционам. Для хеджирования опционной позиции он покупает акции в количестве равном общей дельте его позиции, т е. 60 акций.
Допустим, что в следующий момент цена акции снизилась на 1 рубль. Тогда по акциям инвестор теряет 60 руб. Однако цена опциона упала на 0,6 рубля, и общая стоимость опционов также уменьшилась на 60 руб. Таким образом проигрыш инвестора по акциям компенсируется выигрышем по опционам, поскольку в случае закрытия опционной позиции он выкупит контракты на 60 руб. дешевле.
Допустим теперь, что цена акций выросла на 1 рубль. Тогда вкладчик выиграл 60 руб. по акциям, но проиграл данную сумму по опционам. Чтобы закрыть опционную позицию ему придется выкупать опционы на 60 руб. дороже.
В примере инвестор купил 60 акций. Дельта акции равна единице, поскольку она определяется как отношение изменения цены акции к нему же самому. Поэтому дельта позиции вкладчика по акциям составляет 60. В результате, общая дельта его портфеля из опционов и акций равна нулю. Позицию с дельтой равной нулю называют дельта-нейтральной или дельта-хеджированной.
На практике значение дельты постоянно меняется, поэтому позиция будет оставаться дельта-нейтральной только в течение относительно короткого времени. Чтобы сохранять дельта-хеджированную позицию, вкладчик должен периодически пересматривать портфель, покупая или продавая базисные активы в зависимости от изменения величины дельты.
Пример 2.
Вернемся к условиям примера 1. Допустим, что через некоторое время дельта опциона выросла на 0,01 пункта и составила 0,61 пункта. Это означает, что для сохранения дельта-нейтральной позиции необходимо приобрести дополнительное количество акций, чтобы компенсировать увеличение дельты на 0,01. Следует купить:
0,0Ы00 опционов = 1 акцию.
По мере приближения срока истечения опциона величина дельты убывает для опционов колл ОТМ и увеличивается для опционов ITM. Поэтому поддержание дельта-нейтральной позиции из опционов ОТМ потребует уменьшения количества единиц базисного актива при неизменном курсе, для опционов ITM- их увеличения.
Наиболее удобно рассматривать вопрос хеджирования, когда дельта опциона колл близка к единице или к нулю. Если дельта близка или равна единице, то на каждый проданный опцион покупается акция. Если дельта близка к нулю, то можно выписать непокрытый опцион, так как цена опциона практически не чувствительна к изменению курса акции. Наибольшей корректировки для поддержания дельта-нейтральной позиции требуют опционы А ТМ.
Дельту можно использовать для хеджирования позиции по базисному активу с помощью опционов. Для этого необходимо определить количество опционных контрактов, которые следует открыть на каждую позицию по базисному активу, чтобы общая дельта позиции инвестора равнялась нулю. В результате, изменение стоимости базисного актива будет компенсироваться аналогичным, но противоположным по знаку изменением стоимости опционов. Требуемое количество опционных контрактов можно найти, разделив дельту базисного актива (она равна единице) на дельту опциона:
1
количество опционных контрактов =----------.
дельта
Пример.
Дельта опциона колл равна 0,6. Инвестор покупает 60 акций. Чтобы хеджировать с помощью опциона одну акцию, ему необходимо продать:
1:0,6 = 1,667 опционов.
Для хеджирования позиции по 60 акциям ему следует продать:
1,667 60 = 100 опционов.
На практике опционный контракт на акции включает не одну, а много акций, например 1000 или 100 единиц. С учетом этого можно следующим образом представить формулу определения коэффициента хеджирования позиции по базисному активу с использованием дельты опциона:
комффициснт _ количество единиц хеджируемого актива (1 1 -0)
хеджирования дельта опциона количество единиц актива в опционном контракте
Произведение дельты опциона на количество единиц базисного актива в опционном контракте в знаменателе формулы (11.6) дает величину дельты одного опционного контракта.
Пример.
Инвестор страхует покупку 10000 акций с помощью опциона колл. Дельта для одной акции равна 0,25. Один опционный контракт включает 100 акций. Для хеджирования спотовой позиции ему следует продать:
10000
--------= 400 контрактов.
0,25 100
Если цена акции упадет на 1 руб., то он потеряет по ним 10000 руб. Однако по одному опционному контракту выиграет сумму:
0,25 100акции 1 руб. = 25руб.
По четыремстам контрактам его выигрыш составит:
25руб. 400 = 10000руб., что компенсирует потери по акциям.
Дельта говорит о количестве единиц базисного актива, которые следует купить или продать хеджеру для поддержания дельта-нейтральной позиции. Поэтому дельту можно определить в единицах базисного актива. Такое представление дельты удобно для целей хеджирования. Если дельта опциона на акции равна 0,5, можно сказать, что она равна 0,5 акции.
Пример.
Опционный контракт включает 100 акций. Тогда дельта 0,5 эквивалентна для контракта 50 акциям:
ЮОакций 0,5 = 50акций.
Это означает, что на один проданный опционный контракт хеджеру следует купить 50 акций. Если в последующем цена акции упадет на 1 руб., то по 50 акциям на спотовом рынке инвестор потеряет:
50акций • 1 руб. ~ 50руб.
Одновременно по опциону он выиграет согласно дельте, выраженной в акциях:
акций I руб. = 50 дуб., что компенсирует убыток по спотовой позиции.
На практике дельта обычно задается в процентах. Тогда дельта длинной позиции по базисному активу равна 100, короткой - минус 100. Дельта опциона 0,6 будет представлена как 60.
11.2. ГАММА
Дельта опциона не является постоянной величиной. Поэтому инвестору важно знать, как изменится ее значение при изменении цены базисного актива. С этой целью рассчитывают коэффициент чувствительности опциона, получивший название гамма. Гамма показывает, в какой мере изменится значение дельты опциона при изменении цены базисного актива на один пункт. Гамма представляет собой отношение изменения дельты опциона к изменению цены базисного актива:
ад • до
где у - гамма опциона;
ад - изменение дельты опциона.
Гамма - это вторая производная премии опциона по цене базисного актива. Графически гамма представляет собой кривизну графика дельты, т.е. показывает, насколько быстро меняется кривизна графика дельты при изменении цены опциона. Поэтому ее еще именуют кривизной опциона. Небольшое значение гаммы говорит о том, что дельта опциона изменится на малую величину при изменении цены базисного актива, и наоборот. Большое значение гаммы свидетельствует о высоком риске изменения цены опциона при изменении конъюнктуры рынка. Поэтому неопытному инвестору следует избегать опционов с большой гаммой. Гамма измеряется в дельтах на один пункт изменения цены базисного актива. Она является положительной величиной для длинных опционов
колл и пут. Для коротких опционов колл и пут она отрицательна. При повышении цены базисного актива значение гаммы прибавляется к значению дельты, при падении цены - вычитается.
Пример.
Дельта опциона колл равна 0,6, гамма - 0,02. Это означает, что для длинной позиции по опциону при повышении цены базисного актива на один пункт дельта вырастет на 0,02 пункта и составит 0,62 пункта. Напротив, при падении цены базисного актива на один пункт дельта опциона составит 0,58 пунктов. Если инвестор выписал опцион, то дельта его опционной позиции равна минус 0,6, а гамма - минус 0,02. При росте цены базисного актива новое значение дельты составит:
-0,6 + (-0,02) = -0,62;
при падении:
-0,6-(-0,02) =-0,58.
Зная величину гаммы, инвестор может поддерживать свою позицию дельта-нейтральной, покупая или продавая базисные активы в соответствии с гаммой опциона.
Пример.
Инвестор сформировал дельта-нейтральную позицию, купив 60 акций и продав 100 опционов колл с дельтой 0,6. Гамма опциона равна 0,02. В следующий момент цена акции выросла на 1 руб. и дельта опциона стала равной 0,62. Для поддержания дельта-нейтральной позиции инвестору необходимо купить дополнительно:
ЮОопг/ионов 0,02 = 2акцшк
Величина гаммы не является постоянной и изменяется с изменением рыночной конъюнктуры. Она достигает максимума для опционов без выигрыша и уменьшается по мере того, как они становятся с большим выигрышем или проигрышем (см. рис. 11.4). Гамма зависит от времени до истечения опциона. Она является наименьшей для опционов, до истечения которых много времени. Когда опционы приближаются к их истечению, то для опционов А ТМ гамма сильно возрастает, а для ОТМ и 1ТМ - стремится к нулю. Для опционов А ТМ и близких к ним гамма начинает возрастать по экспоненте за 30-40
дней до окончания контрактов. Рост значения гаммы для опционов, которые скоро истекают, можно представить на основе следующего примера.
Пример.
Опцион колл на акцию истекает через несколько минут. Цена исполнения 100 руб. Цена акции 99,8 руб. Поскольку это опцион ОТМ, его дельта равна нулю. Как только цена спот акции превысит 100 руб., пусть вырастет до 100,2 руб., его дельта сразу станет равной единице. Таким образом, при небольшом изменении цены акции наблюдается большое изменение дельты. Это говорит о том, что такой опцион имеет большую гамму.
Л/с. 11.4. Зависимость гаммы от цены актива (график симметричен относительно цены исполнения)
Гамма зависит от волатильности. Для опционов ATM с ростом волатильности гамма уменьшается, а для опционов ОТМ- немного возрастает.
Знак гаммы имеет большое значение для понимания инвестором динамики своих выигрышей и проигрышей в связи с изменением конъюнктуры рынка. Если цена базисного актива идет в благоприятном направлении для держателя длинного опциона колл или пут, то он выигрывает деньги в возрастающем темпе, так как дельта за счет корректировки ее на величину гаммы возрастает по абсолютной величине. Когда
цена идет в неблагоприятном направлении, инвестор теряет средства с уменьшающейся скоростью, так как дельта по абсолютной величине убывает. Для продавца опционов возникает обратная ситуация. Он выигрывает деньги с замедляющейся скоростью, когда цена базисного актива идет в благоприятном для него направлении, поскольку дельта по абсолютной величине уменьшается. Он теряет средства с ускорением при движении цены базисного актив в неблагоприятном направлении, так как дельта по абсолютной величине возрастает.
Для акций, по которым не выплачиваются дивиденды, значение гаммы можно получить как вторую производную уравнений Блэка-Шоулза по S , или продифференцировав по 5 формулы для дельты опционов колл и пут:
Л^ф,), (11.7)
Др=У(4)-1. (11.8)
Как видно из дифференцирования уравнений (11.7) и (11.8), гамма европейского опциона колл равна гамме европейского опциона пут и составляет:
”(^1)
r~sajr'
I ^1 где n(d}) = е 2.
Выше мы рассмотрели вопрос формирования дельта-нейтральной позиции. При изменении цены базисного актива необходимо пересматривать состав портфеля, чтобы сохранить его дельта-нейтральность. Инвестору тем чаще придется пересматривать портфель, чем больше значение его гаммы (по абсолютной величине). Поэтому возникает задача формирования гамма-нейтрального портфеля. Ее можно решить следующим образом. Допустим, инвестор имеет дельта-нейтральный портфель с гаммой . Он открывает позиции еще по п опционам. Тогда гамма нового портфеля равна:
Yv = Xi + № ,
где /2 - гамма дополнительной опционной позиции;
yv - гамма портфеля.
Чтобы получить гамма-нейтральный портфель, должно быть равно нулю:
Xi +/2w = 0.
Поэтому инвестор должен открыть позиции по опционам в количестве:
« = -21 /2
На практике гамму также как и дельту обычно выражают в процентах или в количестве дельт. Например, дельта опциона равна 60 и гамма 2 или 2 дельты.
11.3. ВЕГА
Цена опциона зависит от оценок степени рискованности будущей конъюнктуры рынка. Применительно к опционам изменение оценок в отношении риска находит отражение в изменении величины их внутреннего стандартного отклонения1 и, соответственно, изменении цен опционов. Поэтому инвестору важно знать степень изменчивости премии опциона при изменении внутреннего стандартного отклонения. Для этой цели рассчитывается коэффициент вега. Вега представляет собой отношение изменения величины премии опциона к изменению внутреннего стандартного отклонения опциона, т. е.
для опциона колл и
дс до
др
для опциона пут, где v - вега опциона, до- - малое изменение внутреннего стандартного отклонения.
Вега говорит о том, на какую сумму изменится премия опциона при изменении внутреннего стандартного отклонения на один процент. В литературе помимо термина вега также используют термины каппа, омега, звта, сигма. При увеличении внутреннего стандартного отклонения премия опциона возрастает, поэтому вега положительна для длинных опционов колл и пут. Вега коротких опционов учитывается со знаком минус.
1 Определение и характеристика внутреннего стандартного отклонения опциона дается в главе 12.
Пример.
Стоимость опциона колл равна 5 руб, вега составляет 20 копеек, внутреннее стандартное отклонение опциона - 20%. При росте внутреннего стандартного отклонения до 21% премия опциона увеличится до 5,2 руб, а при падении до 19% - уменьшится до 4,8 руб.
Вегу могут задать в процентах от денежной единицы - рубля или доллара. Например, вега равна 20%. Это означает, что при изменении внутренней волатильности на 1% цена опциона изменится на 20% от рубля (доллара), т. е. на 20 коп. (центов). Наибольшее значение веги имеют опционы без выигрыша (см. рис. 11.5).
Рис. 11.5. Зависимость веги от цены базисного актива (график симметричен относительно цены исполнения)
Следует отметить, что для опционов ATM величина веги остается постоянной на протяжении большого диапазона изменения внутренней волатильности. Для опционов ОТМ и ITM вега уменьшается по мере падения волатильности и растет по мере ее увеличения. Поэтому величина потерь и выигрышей при изменении внутренней волатильности для длинных и коротких опционов А ТМ относительно устойчива. Для длинных опционов ОТМ и ITM темп прироста выигрышей нарастает при росте волатильности, а проигрыши увеличиваются с убывающей скоростью при ее падении. Напротив, короткие опционы ОТМи ITMприносят доход с уменьшающейся скоростью при падении волатильности, а потери нарастают с возрастающим темпом при ее росте.
Величина веги уменьшается по мере приближения срока истечения контракта. Поэтому наиболее важно не совершить ошибку прогноза в отношении внутренней волатильности долгосрочного опциона. Изменение внутренней волатильности краткосрочного опциона не сильно скажется на величине его премии.
Опционы ATM наиболее чувствительны к изменению веги по абсолютному изменению величины премии. Но более рискованными с точки зрения веги являются опционы ОТМ и ITM, так как для них характерно большее процентное изменение премии и, соответственно, большее изменение суммы стоимости позиции при изменении внутренней волатильности.
Пример.
Опцион колл ATM стоит 5 руб., вега равна 0,2 руб., премия опциона ОТМ составляет 2,5 руб., вега 0,15 руб. Тогда при росте внутренней волатильности опционов на 1% по первому контракту процентное изменение премии составит 0,2:5 = 0,04 или 4%, а по второму 0,15:2,5 = 0,06 или 6%. Если инвестор купил первый опцион, то его выигрыш составил 20 коп. Если же он выбрал второй опцион, то на 5 руб. он открыл позицию по двум опционам. Соответственно его прибыль составила 30 коп.
Из приведенного примера видно, что реально инвестора интересует не абсолютная величина веги, а коэффициент, определяемый как отношение веги к премии опциона. Данный показатель называется нормированной вегой Нормированная вега измеряет процентное изменение стоимости опциона при изменении внутреннего стандартного отклонения на 1%.
Для европейских опционов на акции, по которым не выплачиваются дивиденды, вегу можно получить как производную уравнений Блэка-Шоулза по <т. Европейские опционы колл и пут с одной ценой исполнения и датой истечения контрактов имеют одинаковое значение веги:
дет дет v 17
Стратегия инвестора может предполагать формирование вега-нейтрального портфеля, т.е. портфеля, стоимость которого не зависела бы от изменений значения внутренней волатильности опционов. Чтобы получить такой портфель, можно рассуждать следующим образом. Допустим, инвестор имеет портфель с вегой . Он открывает позиции еще по п опционам. Тогда вега нового портфеля равна:
К = Vl + V2n ,
где v2 - вега дополнительной опционной позиции;
- вега портфеля.
Для вега-нейтрального портфеля v, должна быть равна нулю:
V| + v2n ~ О-
Поэтому инвестор должен открыть позиции по опционам в количестве:
vi п = —
Ъ
11.4. ТЕТА
При неизменной конъюнктуре рынка опцион с каждым днем будет дешеветь, так как надежды на то, что он принесет прибыль (или что она еще увеличится) будут слабеть. Поэтому инвестору важно знать коэффициент, который бы показал степень уменьшения премии опциона по мере приближения срока окончания контракта. Для этой цели рассчитывается показатель тета. Тэта говорит о том, с какой скоростью падает цена опциона по мере приближения срока истечения контракта при сохранении прочих условий рынка неизменными. Тета опциона представляет собой производную премии опциона по времени.
Тета измеряется в денежных единицах за один день. Для длинных опционов тета является отрицательной величиной, для короткой - положительной. Следует, однако, отметить, что для длинных европейских опционов пут с большим выигрышем и европейских опционов колл и пут на фьючерсы с большим выигрышем тета может быть положительной. Такие опционы имеют отрицательную временную стоимость, и поэтому будут дорожать по мере приближения срока окончания контракта. Опционы имеют отрицательную тету, когда эффект процентной ставки превышает возможности более существенного выигрыша в будущем.
Пример.
Тета опциона колл равна минус 0,2 руб., цена опциона 5 руб. Это означает, что при неизменной конъюнктуре рынка через день его цена должна составить 4,8 руб., еще через день 4,6 руб.
Значение теты возрастает по абсолютной величине по мере приближения срока истечения контракта. Она является максимальной по абсолютной величине для опционов ATM. так как они имеют наибольшую временную стоимость. Цена опциона с большим проигрышем - она целиком состоит из временной стоимости - близка к нулю, поэтому и его тэта близка к нулю. Цена опциона с большим выигрышем практически полностью состоит из внутренней стоимости, поэтому его тэта также близка к нулю. Зависимость теты опциона колл от цены базисного актива представлена на рис. 11.6. Большое значение теты говорит о том, что существует высокий риск обесценения опциона по мере приближения срока истечения контракта. Вместо термина тета могут использовать также термин эпсилон.
На основе формул Блэка-Шоулза тета опционов колл и пут определяется следующим образом:
6С = -— = -rXe-rTN(d2), (11.9)
дТ 24т
Рис. 11.6. Зависимость значения теты опциона колл от цены актива
(11.10)
Формулы (11.9) и (11.10) дают величину теты в расчете на год. Для получения теты в расчете на один день необходимо разделить найденное значение на количество торговых дней в году, т.е. на 250.
11.5. РО
Премия опциона реагирует на изменение ставки без риска на рынке Поэтому рассчитывают показатель ро, который говорит о том, как изменится премия опциона при изменении процентной ставки на один процент Ро - это производная премии опциона по процентной ставке. Премия опциона колл положительно зависит от процентной ставки, опциона пут - отрицательно. Поэтому для длинных опционов колл ро положительна, а для длинных опционов пут отрицательна На практике показатель ро важно учитывать для долгосрочных опционов, так как для коротких периодов времени влияние процентной ставки на премию опциона незначительно Ро измеряется в денежных единицах.
На основе формул Блэка-Шоулза ро опционов колл и пут определяется как:
pc=^ = XTe-rTN(d2)
dr
и
or
11.6. ЗАВИСИМОСТЬ МЕЖДУ ДЕЛЬТОЙ, ГАММОЙ И ТЕТОЙ
В главе 10 мы получили дифференциальное уравнение Блэка-Шоулза:
dG cdG 1 dG ......
— + rS------+-------<t S' = rG. (11.11)
dt dS 2 dS2
Пусть G - это европейский опцион колл. Тогда уравнение (11.11)
примет вид:
de о ос 1 д2с — + rS— +----------
dt ds 2 ds2
В уравнении (11.12) — = 0; — = Д; dt dS
том данных коэффициентов:
сг252 - гс.
d 2с
—- = у. Запишем его с уче-dS2
^4-г5Д + — сг252/ = гс . 2
(11.13)
Формула (11.13) показывает зависимость между дельтой, гаммой и тетой. Если позиция инвестора дельта-нейтральна, то из уравнения (11.13) получаем:
0 + ^-сг2А2^ = гс. (11.14)
Уравнение (11.14) показывает зависимость между гаммой и тетой опционной позиции: большой положительной гамме соответствует большая отрицательная тета; небольшой гамме соответствует небольшая тета. Эффекты гаммы и теты являются противоположными по своему влиянию на премию опциона
Уравнение Блэка-Шоулза является верным не только для любого производного актива, но и для портфеля, состоящего из таких активов. Поэтому сделанные выше замечания относительно зависимости между дельтой, гаммой и тетой верны и для портфеля опционов.
11.7. ФОРМИРОВАНИЕ ПОЗИЦИИ С ЗАДАННОЙ ДЕЛЬТОЙ И ВЕГОЙ
Инвестор хотел бы сформировать позицию с определенными значениями дельты и веги, включив в нее европейские опционы колл и пут. В этом случае дельта и вега позиции соответственно равны:
Ах + А„и„ = А„
р р , (11.15)
=v,
где пс, пр - количество опционов колл и пут;
Ad, v -дельта и вега опциона колл;
Ар, Ур - дельта и вега опциона пут;
Av, vp -дельта и вега портфеля.
Для европейских опционов А = А, -1 и у. = vp. Подставив данные значения в систему уравнений (11.15), получаем:
+ (ас ~ Av
КЛ + vcnp = vv
или
пр=^-\
Vc . (11.16)
wc=Av+—(1-Ас|
Таким образом, для формирования позиции с требуемыми значениями дельты и веги, следует открыть позиции по опционам колл и пут в количестве, заданном системой уравнений (11.16). Если инвестор формирует дельта-нейтральную позицию с определенным значением веги, то система уравнений (11.16) принимает вид:
11.8. ДЕЛЬТА-ГАММА-НЕЙТРАЛЬНАЯ ПОЗИЦИЯ
Инвестор может поддерживать дельта-нейтральный портфель, пересматривая его в соответствии с изменением конъюнктуры рынка. Портфель придется пересматривать тем чаще, чем большее значение его гаммы (по абсолютной величине). Чтобы исключить риск гаммы, можно сформировать гамма нейтральный портфель. Однако в этом случае портфель уже не будет дельта-нейтральным. Для получения одновременно дельта-гамма-нейтрального портфеля инвестору придется открыть позиции уже по новым опционам. Задачу формирования дельта-гамма-нейтрального портфеля можно решить следующим образом.
Пусть портфель инвестора включает опционы колл с ценой исполнения X, и Х4, дельта и гамма которых соответственно равны:
Др А4, у4. Общая дельта и гамма портфеля составляют:
A^j 4- А4«4 = А ,
где п{, п4 - количество опционов с ценами исполнения Хх и Х4. Чтобы сделать портфель дельта- и гамма-нейтральным, требуются уже другие опционы. Пусть это будут опционы колл на данный базисный актив с ценами исполнения X2 и Х3, дельта и гамма кото
рых соответственно равны: А2, А3, р2, у3. Дельта- и гамма-нейтральную позицию получим, определив значения п2 и п3 из следующей системы уравнений:
А2л2 + А,^ = -А
У2П, = -у
где п2, п3 - количество опционов с ценами исполнения Х2 и Х3, по которым необходимо открыть дополнительные позиции;
-А - дельта первоначального портфеля, взятая с противоположным знаком;
-у - гамма первоначального портфеля, взятая с противоположным знаком.
Дельта-гамма нейтральный портфель страхует инвестора от больших изменений цены базисного актива.
КРАТКИЕ ВЫВОДЫ
Дельта представляет собой отношение изменения цены опциона к изменению цены базисного актива. Дельта длинного опциона колл изменяется от нуля до единицы, опциона пут - от нуля до минус единицы.
Значение дельты изменяется с наибольшей скоростью, когда цена базисного актива расположена близко к цене исполнения опциона. По мере удаления цены актива от цены исполнения скорость изменения дельты уменьшается.
Значение дельты зависит от времени до истечения опциона. По мере его приближения оно стремится к нулю для длинного опциона колл ОТМ и к единице для длинного опциона колл ITM. Для длинного опциона пут она соответственно приближается или к нулю или к минус единице.
Положительный знак дельты позиции инвестора говорит о том, что он будет выигрывать от роста цены базисного актива и проигрывать от ее падения. Отрицательная дельта означает, что инвестор будет выигрывать от падения курса базисного актива и проигрывать от его роста.
Значение дельты говорит о числе единиц базисного актива, которые инвестор должен купить или продать на каждую позицию по опциону, чтобы сформировать дельта-нейтральный портфель.
Гамма показывает, в какой мере изменится значение дельты опциона при изменении цены базисного актива на один пункт. Она по
ложительна для длинных и отрицательна для коротких опционов. При повышении цены базисного актива значение гаммы прибавляется к значению дельты, при падении цены - вычитается. Гамма достигает максимума для опционов без выигрыша и уменьшается по мере того, как они становятся с большим выигрышем или проигрышем. Долгосрочные опционы имеют наименьшую гамму. Ее значение увеличивается по мере приближения срока окончания контракта. Для опционов ATM и близких к ним гамма начинает возрастать по экспоненте за 30-40 дней до окончания контрактов. Европейские опционы колл и пут с одной ценой исполнения и датой истечения контрактов имеют одинаковую гамму.
Вега показывает, в какой мере изменится премия опциона при изменении внутреннего стандартного отклонения опциона на один процент. Вега положительна для длинных опционов и отрицательна для коротких. Наибольшее значение веги имеют опционы без выигрыша. Величина веги уменьшается по мере приближения срока истечения контракта. Опционы колл и пут с одной ценой исполнения и датой истечения контрактов имеют одинаковое значение веги.
Тэта говорит о скорости обесценения опциона по мере приближения срока истечения контракта при сохранении прочих условий рынка неизменными. Для длинных опционов тета отрицательна, для коротких - положительна. Для длинных европейских опционов пут и европейских опционов колл и пут на фьючерсные контракты с большим выигрышем тета может быть положительной. Значение теты возрастает по абсолютной величине по мере приближения срока истечения контракта. Она является максимальной по абсолютной величине для опционов А ТМ.
Ро говорит о том, как изменится премия опциона при изменении процентной ставки на один процент. Для длинных опционов колл ро положительна, для длинных опционов пут отрицательна. Показатель ро важно учитывать для долгосрочных опционов.
ГЛАВА 12. ВНУТРЕННЯЯ ВОЛАТИЛЬНОСТЬ
В настоящей главе рассматривается понятие внутренней волатильности опциона. Вначале мы остановимся на методах расчета данного показателя. После этого охарактеризуем понятие “улыбки волатильности”.
12.1. ОПРЕДЕЛЕНИЕ ВНУТРЕННЕЙ ВОЛАТИЛЬНОСТИ ОПЦИОНА
При расчете цены опциона на основе аналитической формулы, например, Блэка-Шоулза, неизвестной переменной выступает премия, а в качестве одной из известных величин & . Переменная су является историческим стандартным отклонением доходности базисного актива.
В каждый данный момент на рынке представлены котировки опционов, по которым инвесторы готовы торговать контрактами. Поэтому формулу Блэка-Шоулза можно использовать в обратном порядке, т. е. определить из нее величину параметра су , приняв его за неизвестную переменную для определенного значения премии опциона. Полученное таким способом значение волатильности называют внутренней волатильностью или внутренним стандартным отклонением опциона. Данный показатель представляет собой прогноз рынка относительно волатильности доходности базисного актива к моменту окончания срока действия опционного контракта.
Непосредственно выразить переменную а из формулы Блэка-Шоулза нельзя. Поэтому значение внутренней волатильности определяют методом подстановки. Это означает, что в формулу подставляют разные значения волатильности и определяют для каждой из них величину премии. Операцию продолжают до тех пор, пока полученная на основании формулы цена опциона не станет равной его рыночной стоимости. Значение су для данной цены и является внутренним стандартным отклонением опциона. Непосредственно внутреннюю волатильность вычисляют с помощью методов бисекций или Ньютона. Рассмотрим оба метода.
12.1.1. Метод бисекций
Возьмем некоторое значение сг0, которое больше внутренней волатильности, и определим для него премию опциона. (Обозначим
это как нулевой шаг). Цена опциона выше рыночной, поскольку сг0 больше внутренней волатильности. Делим значение сг0 пополам и вычитаем его из <т0 (первый шаг). Полученная величина (crj равна:
Подставляем ее в формулу Блэка-Шоулза и определяем премию опциона. Если она выше рыночной цены, то это означает, что ст, еще выше значения внутренней волатильности. Поэтому на втором шаге величину опять делим пополам и вычитаем а, /2 из о] :
сг. = ст, -сг, /2. (12.1)
На основе значения сг2 вновь рассчитываем премию опциона. Если на первом шаге полученная премия опциона ниже рыночной цены, то значение сг2 находим, прибавив ст, /2 к ст,:
сг2 = ст, + crt / 2 , (12.2)
и рассчитываем премию опциона. Формулу (12.1) можно записать как: _ _ _ СТ, = СТ---------------------------------—----,
2 2 4 4
а формулу (12.2) как:
сг2 = <т, + сг() / 4.
Если на втором шаге премия опциона для сг2 все еще выше рыночной цены, то величину сг2 = сг0/4 вновь делим пополам, вычитаем из величины сг2:
и рассчитываем премию опциона на основе значения сг3 = —. Если
8
она оказалась ниже, то величину сг3 находим, прибавив сг0 /8 к сг2:
СТ 3 — СГ2 ^0
и рассчитываем премию опциона.
Аналогичные действия продолжают до тех пор, пока премия опциона, вычисленная по формуле Блэка-Шоулза, не станет равной рыночной цене опциона. Полученное значение а является внутренней волатильностью опциона.
Значение внутренней волатильности будет тем точнее, чем больше расчетных шагов, представленных выше, мы предпримем. Любой расчет требует только определенного уровня точности. Поэтому следует задать интервал точности оценки внутренней волатильности. Это можно сделать на основе следующих рассуждений.
В рамках представленного алгоритма действий на первом шаге мы поделили величину сг0 на 2, на втором - на 4, третьем - на 8, на четвертом - на 16, и т.д. Таким образом, корректировка значения внутренней волатильности на /-м шаге осуществлялась на величину сг0 /2'. Чтобы определить, на каком шаге закончить расчет для точности оценки в пределах требуемого интервала <р, необходимо определить i из неравенства:
сг() / 2’ < (р
или
а0/^<2\ (12.3)
Возьмем натуральный логарифм от обеих частей неравенства (12.3): 1п(сг(} / (р)< In 2' или
' (12.4)
In 2
Таким образом, количество корректировок должно быть целым чис-, 1п(сг /с?)
лом большим, чем значение
In 2
Пример.
Определить количество шагов, чтобы получить внутреннюю волатильность опциона с точностью оценки в пределах интервала 0,001%; сг0 принимаем равной 35%.
Решение.
Количество требуемых шагов равно:
In 2
Согласно формуле (12.4) величина i должна быть больше 15,095. Поэтому для получения точности оценки в рамках заданного интервала требуется осуществить 16 расчетных шагов.
12,1.2. Метод Ньютона
На рис. 12.1 показана зависимость между волатильностью и премией опциона колл. По горизонтальной оси представлена волатильность, по вертикальной - цена опциона. Рыночная котировка опциона равна ст. Необходимо определить значение внутренней волатильности сгм, которая бы соответствовала стоимости опциона ст .
сг, сг(
Рис. 12.1. Метод Ньютона
Вначале делаем предположение о значении внутренней волатильности - пусть это <т0 - и определяем для нее по формуле Блэка-Шоулза цену опциона и вегу. Соответственно, они равны с0 и v0.
Угол наклона касательной к графику зависимости между волатильностью опциона и его ценой в точке а представляет собой не что иное как вегу опциона (v0) для волатильности сг0. Значение веги можно определить из треугольника abd, оно равно величине угла abd:
СГП (Т,
(12.5)
Из формулы (12.5) находим значение волатильности :
По формуле Блэка-Шоулза определяем цену опциона (q) и вегу (vj для значения .
Рассмотрим рисунок 12.2. Из треугольника efb можно найти вегу для волатильности , она равна величине угла е/Ь:
(12.6)
Рис. 12.2. Метод Ньютона
Из формулы (12.6) находим значение волатильности сг2:
и определяем для нее цену и вегу опциона и т.д. На z-м шаге получим значение crt. Подстановка его в формулу Блэка-Шоулза дает цену опциона равную ст. Следовательно, сг! является искомым значением внутренней волатильности ат.
Метод Ньютона позволяет быстрее определить внутреннюю волатильность опциона чем метод бисекций. Однако, в отличие от метода бисекций, он подходит не для всех опционов.
12.2. УЛЫБКА ВОЛАТИЛЬНОСТИ
Согласно допущениям модели Блэка-Шоулза, базисный актив характеризуется постоянным уровнем волатильности. Если эта посылка верна, то опционы на данный актив должны обладать одинаковой внутренней волатильностью вне зависимости от цен исполнения и сроков истечения контрактов. Однако практика показывает, что опционы на один и тот же актив с одинаковой ценой исполнения, но разными сроками истечения контрактов имеют разные внутренние стандартные отклонения. Аналогично разной внутренней волатильностью характеризуются опционы с одинаковым сроком истечения, но разными ценами исполнения.
Если для опционов с одним сроком истечения контрактов построить график зависимости между ценой исполнения и внутренней волатильностью, то он покажет, что эта зависимость является или квадратичной или монотонной. График квадратичной зависимости напоминает улыбку (см. рис. 12.3). Поэтому такая зависимость между ценой исполнения и внутренней волатильностью получила название ‘улыбки волатильности . Улыбка волатильности говорит о том, что будущее вероятностное распределение цены базисного актива не логнормально. До финансового кризиса октября 1987 г. улыбка волатильности была не сильно выражена. После кризиса она приобрела более выпуклую книзу форму и для ряда рынков перестала быть симметричной.
Условия паритета европейских опционов колл и пут предполагают, что они имеют одинаковое значение внутренней волатильности. Иначе открывается возможность совершить арбитражную операцию. Приблизительное равенство внутренних волатильностей выдерживается и для американских опционов. Поэтому график улыбки волатильности является одинаковым для опционов колл и пут.
Для опционов на валюту характерна улыбка волатильности, представленная на рис. 12.3, т. е. она достаточно симметричена относительно опциона ATM. Внутренняя волатильность возрастает по мере того как опционы становятся все с большим выигрышем или все с большим проигрышем. По сравнению с логнормальным распределением вероятностное распределение валютного курса с учетом данной формы улыбки волатильности характеризуется более толстыми хвостами и большей островершинностью. Это говорит о том, что валютный курс в большей степени испытывает сильные и слабые колебания, чем изменения средней степени. Улыбка волатильности также свидетельствует о том,
что инвесторы в равной степени страхуются как от роста, так и падения курса валюты.
Улыбка волатильности валютных опционов показывает, что опционы с большим выигрышем и большим проигрышем стоят на рынке дороже, чем это предполагается формулами, основанными на логнормальном распределении.
О !
ATM
Рис. 12.3. Улыбка волатильности (а- внутренняя волатильность, X- цена исполнения, А ТМ- опцион без выигрыша)
Объяснение формы графика улыбки волатильности можно связать с действиями центрального банка, который стремится поддерживать курс валюты своей страны на определенном уровне с помощью валютных интервенций. В то же время, при активном давлении игроков на валюту действия ЦБ могут оказаться безуспешными. В этом случае валютный курс качнется в одну сторону. Если же ЦБ выстоит, то курс может отклониться в противоположную сторону. Поэтому существует большая вероятность как стабильности курса, так и его значительных изменений.
Г рафик улыбки волатильности для опционов на акции и индексы характеризуется нисходящей кривой (см. рис. 12.4). Вследствие его формы график могут назвать 'ухмылкой волатильности". Такой форме улыбки волатильности соответствует вероятностное распределение цены базисного актива, которое имеет более толстый левый хвост, более тонкий правый хвост и оно более островершинно по сравнению с логнормальным распеределением. Это говорит о том, что опцион колл с большим выигрышем и опцион пут с большим проигрышем будут стоить больше, чем это предполагается формулой Блэка-Шоулза, а опционы колл с большим проигрышем и пут с большим выигрышем соответственно меньше. Данная форма улыбки
волатильности свидетельствует о том, что продавцы опционов считают более вероятным понести потери от продажи опционов пут с проигрышем, чем от опционов колл с проигрышем.
По мнению М. Рубинштейна возможное объяснение такой формы графика улыбки волатильности состоит в том, что после финансового кризиса 1987 г. участники рынка в большей степени стали опасаться повторения подобной ситуации. Поэтому они дороже оценивают опционы с более низкой ценой исполнения. Эту причину он назвал "кра-шофобией" - от английского слова “crashphobia’’, т. е. боязнь краха.
Рис. 12.4. Ухмылка волатильности для акций и индексов
Еще одно объяснение можно связать с эффектом финансового рычага, т. е. соотношением между заемным и собственным капиталом компании. При росте курса акции финансовый рычаг уменьшается. В результате акция становится менее рискованной, и стандартное отклонение ее доходности падает. В случае падения цены бумаги финансовый рычаг возрастает, и увеличивается рискованность акции. Волатильность акции растет. Таким образом, в рамках данного подхода волатильность акции можно рассматривать как убывающую функцию ее цены.
Форма графика улыбки волатильности зависит от времени, которое остается до истечения опционов. В большинстве случаев она становится менее выраженной по мере увеличения срока действия контрактов.
Угол наклона кривой волатильности может служить для прогноза будущего направления движения цены базисного актива. Если кривая характеризуется сильным отрицательным наклоном, существует большая вероятность цены пойти вниз. Если наклон кривой положительный, то ожидают роста цены. Если форма кривой близка к прямой линии, то существенного движения цены не ожидается.
Для опционов ATM строят график зависимости между сроком истечения контрактов и внутренней волатильностью - он называется графиком временной структуры волатильности. В долгосрочном плане динамика стандартного отклонения доходности базисного актива характеризуется возвращением его к определенному устойчивому среднему долгосрочному уровню (процесс mean reversion)1. Поэтому, если текущее стандартное отклонение доходности базисного актива ниже уровня его исторического среднего значения, то временная структура внутренней волатильности будет иметь восходящий характер. Если оно выше этого значения, то временная структура будет иметь нисходящий характер.
Обычно внутренняя волатильность для краткосрочных опционов больше, чем для долгосрочных, т. е. внутренняя волатильность краткосрочного опциона в большей степени зависит от движения цены базисного актива в течение торгового дня. Поэтому кривая временной структуры волатильности обычно имеет отрицательный наклон. Чем круче кривая, тем больше вероятность того, что в краткосрочном периоде возможно более сильное колебание цены базисного актива.
В динамике внутренней волатильности опционов замечен такой интересный факт. Она растет в преддверии важных экономических событий, которые ожидаются на рынке, например, сообщениях о макроэкономических показателях развития страны. После их обнародования она имеет тенденцию к уменьшению. Это можно объяснить тем, что до момента сообщения информации на рынке возрастает степень неопределенности по сравнению с обычными торговыми днями, а значит и риск торговли опционами. После сообщения информации неопределенность снижается, что вызывает уменьшение и внутренней волатильности опционов. Иногда это может сопровождаться ростом фактического стандартного отклонения доходности базисного актива.
В начале данной главы мы отметили, что внутренняя волатильность представляет собой прогноз рынка относительно стандартного отклонения доходности базисного актива к моменту окончания срока действия опционного контракта. Однако насколько верен такой прогноз. Можно ожидать, что в среднем внутренняя волатильность будет переоценивать фактическую будущую волатильность актива, поскольку она включает в себя еще премию за риск для участника опционного контракта.
1 Более подробно о процессе mean reversion см. в книге А.Н, Буренина “Рынок ценных бумаг и производных финансовых инструментов”, М., 2002, глава 9.
КРАТКИЕ ВЫВОДЫ
Внутренняя волатильность представляет собой прогноз рынка относительно волатильности доходности базисного актива к моменту окончания срока действия опционного контракта. В основе ее расчета лежит метод подстановки.
Опционы на один и тот же актив с одинаковой ценой исполнения, но разными сроками истечения контрактов имеют разные внутренние стандартные отклонения. Разной внутренней волатильностью характеризуются и опционы с одинаковым сроком истечения, но разными ценами исполнения.
Зависимость между ценой исполнения для опционов с одним сроком истечения и внутренней волатильностью назвается “улыбкой волатильности". Улыбка волатильности говорит о том, что будущее вероятностное распределение цены базисного актива не логнормально. График улыбки волатильности является одинаковым для опционов колл и пут.
Для опционов на валюту улыбка волатильности достаточно симметрична относительно опциона ATM. Внутренняя волатильность возрастает по мере того как опционы становятся все с большим выигрышем или все с большим проигрышем. График улыбки волатильности для опционов на акции и индексы характеризуется нисходящей кривой.
Зависимость между сроком истечения опционов ATM и внутренней волатильностью называется графиком временной структуры волатильности.
ГЛАВА 13. СИНТЕТИЧЕСКИЕ АКТИВЫ
В настоящей главе рассматривается понятие и техника формирования синтетических позиций с помощью опционов. Мы остановимся на синтетических опционах, синтетической акции, синтетической фьючерсной позиции и синтетической облигации.
13.1. СИНТЕТИЧЕСКИЕ ОПЦИОНЫ
На финансовом рынке существует понятие синтетического актива. Синтетический актив можно определить как портфель, состоящий из разных активов. Такой портфель обладает определенными характеристиками риска и доходности. Характеристики синтетического актива могут копировать характеристики какого-либо существующего финансового инструмента, например, акции или облигации. Тогда такой синтетический актив назовут соответственно синтетической акцией или облигацией.
С помощью комбинирования позиций по базисному активу и опциону можно создать синтетические опционы колл и пут. Синтетическая позиция приносит инвестору такой же финансовый результат как и соответствующий опцион. Рассмотрим возможные варианты синтетических опционов, базисными активами которых являются акции. Для построения позиций используем опционы без выигрыша.
Синтетический длинный опцион колл можно создать за счет покупки акции и опциона пут. График выигрышей-проигрышей по данной позиции к моменту истечения контракта представлен на рис. 13.1 сплошными линиями.
Рис. 13.1. Синтетический длинный колл
Рис. 13.2. Синтетический короткий колл
Рис. 13.3. Синтетический длинный пут
выигрыши
проигрыши
Рис. 13.4. Синтетический короткий пут
Синтетический короткий опцион колл включает продажу акции и продажу опциона пут (рис. 13.2). Синтетический длинный пут создается продажей акции и покупкой опциона колл (рис. 13.3). Синтетический короткий пут включает покупку акции и продажу опциона колл (рис. 13.4). Синтетические опционы используются в нескольких случаях.
а) Если на рынке отсутствует интересующий инвестора опцион, но ведется торговля противоположным опционом, то можно получить необходимую позицию синтетически. Например, биржевая торговля опционами была открыта на Чикагской бирже опционов в 1973 г. Вначале на бирже были представлены только опционы колл на акции. Поэтому те лица, которые были заинтересованы в опционах пут, могли формировать их синтетически.
б) Синтетические позиции создаются для целей хеджирования. Например, инвестор купил акцию по 100 руб. и вскоре ее курс вырос до 120 руб. Он полагает, что цена бумаги продолжит рост, однако вероятность этого не велика. Поэтому инвестор покупает опцион пут с ценой исполнения 115 руб. Таким образом, он застраховался от падения курса акции ниже 115 руб. и одновременно сохранил возможность получить прибыль от дальнейшего роста ее цены. Сформированная позиция представляет собой не что иное как синтетический длинный колл. В рассмотренном примере инвестор мог бы просто продать акцию и купить опцион колл. Однако, если он заинтересован в сохранении акции, то решением проблемы является именно синтетический колл. Кроме того, синтетический колл делает позицию инвестора более гибкой. Допустим, ожидания вкладчика изменились, и он полагает, что курс акции начнет падать. Тогда он продает акцию, оставив опцион пут в надежде, что выиграет от роста премии опциона в случае понижения цены бумаги.
в) Возможность формировать синтетические позиции позволяет участникам рынка совершать арбитражные операции с европейскими опционами. Арбитражер сравнивает стоимость опциона со стоимостью его синтетического аналога. Если они не равны, то можно получить прибыль без риска. Такой анализ проводят на основе формулы паритета европейских опционов колл и пут:
с +----Д-------г - р + 5. (13.1)
I + r\t / база)
Формула паритета позволяет увидеть, какие действия должен осуществить инвестор, чтобы получить синтетическую позицию. Перепишем формулу (13.1) следующим образом:
c = p + S- (13.2)
1 + г(/ / база]
Формула (13.2) представляет собой алгоритм создания синтетического длинного опциона колл, т. е. необходимо купить опцион пут и акцию, предварительно заняв для этого средства. Умножив формулу (13.2) на минус единицу, получим алгоритм формирования короткого синтетического опциона колл:
-c = -p-S+--------------г. (13.3)
I + r\t / база)
Следует продать акцию и опцион пут и разместить полученные средства на депозите.
Пример 1.
Европейский трехмесячный опцион колл стоит 3 руб., пут - 0,56 руб., цена исполнения опционов 100 руб., курс акции -100 руб. Ставка без риска 10% годовых. Определить, возможна ли арбитражная операция.
Решение.
Стоимость синтетической позиции составляет:
0,5 6 +100-----—г = 3 руб,
1 + 0,1(3/12)
Поскольку она равна цене опциона колл, то арбитраж невозможен.
В приведенном примере цена опциона колл и его синтетического аналога равны. Поэтому инвестор может или просто купить опцион или сформировать его синтетически. Финансовый результат в обоих случаях будет одинаковым. Покажем это на примере.
Пример 2.
Инвестор формирует синтетический колл: покупает опцион пут и акцию. Для этого он занимает на три месяца под 10% сумму:
0,56 +100-3 - 97,56руб.
Инвестор занимает на 3 руб. меньше, так как располагает данной суммой для открытия позиции (в случае покупки просто опциона колл он истратил бы именно 3 руб.). По кредиту он должен вернуть:
97,5 б[1 + 0,1(3 /12)] = 100дуб.
Если через три месяца Sr > 100 руб. например, 110 руб., то от продажи акции он получит 110 руб., из них 100 руб. вернет по кредиту. Его финансовый результат равен 10 руб., которые он получил на 3 руб. собственных средств.
При S7 = 100руб. он теряет 3 руб., так как обязан отдать 100 руб. от продажи акции за кредит.
Если У,. < 100руб., например 90 руб., он исполняет опцион пут, т.е. продает акцию за 100 руб. Данную сумму он отдает кредитору. Его потери составляют 3 руб.
Таким образом, финансовые результаты инвестора по синтетической позиции полностью совпадают с результатами покупателя опциона колл.
Пример 3 (сохраняются условия примера 2).
Инвестор формирует короткий синтетический колл, т.е., согласно формуле (13.3), занимает и продает акцию, продает пут и получает:
100 + 0,56 = 100,56 руб.
Размещает деньги на депозите под 10% и через три месяца получает сумму:
100,5б[1 + 0,1(3/12)]= 103,074/^6.
Если через три месяца ST > 100 руб., например, 110 руб., он купит акцию на споте, чтобы вернуть ее кредитору. Его потери составят:
1 10 — 103,074 = 6,926 руб.,
т.е. они меньше на величину премии опциона колл с процентами, которые можно получить на 3 руб., разместив их на три месяца под 10%. (В случае продажи опциона колл инвестор получил бы от его продажи 3 руб.)
При ST=X инвестор купит акцию на споте за 100 руб. и его выигрыш составит 3,074 руб.: премия плюс процент на 3 руб.
Если S, < X , например, 90 руб., контрагент исполнит опцион пут. Поэтому инвестор купит акцию за 100 руб. и вернет ее кредитору. Его выигрыш равен:
103,074 -100 = 3,074руб.,
т. е. равен премии опциона колл в случае его неисполнения плюс процент на премию. Таким образом, финансовые результаты инве
стора по синтетической позиции совпадают с результатами продавца опциона колл.
Из формулы (13.1) получаем следующие алгоритмы для длинного (13.4) и короткого (13.5) синтетических опционов пут:
Р = с +---7“----а"5 -
1 + / у / оаза)
- р--с-
(13.4)
(13.5)
Пример 4.
На основе цифр примера 1 создать синтетический длинный пут.
Решение.
Занимаем акцию, продаем ее и покупаем колл. В результате получаем:
100-3 - 41 руб.
Размещаем на депозите средства в сумме:
97 4-0,56 = 97,56руб.
(Напомним: инвестор готов был купить пут, т.е. имел 0,56 руб. Поэтому их необходимо учесть при формировании синтетической позиции). Через три месяца получаем пр депозиту:
97,5 б[1 + 0,1 (3 /12)] = 100 руб.
Если в этот момент ST < X , покупаем акцию на споте и возвращаем ее кредитору. Прибыль равна:
(100 - Sr - 0,5б)руб.,
что соответствует результату для длинного опциона пут.
При ST = X покупаем акцию на споте и возвращается кредитору. Потери инвестора равны премии по опциону пут, т. е. 0,56 руб.
Если ST> X , инвестор исполняет колл, т.е. покупает акцию за 100 руб. и возвращает ее кредитору. Его потери, как и в случае с прямой покупкой опциона пут, равны 0,56 руб. Таким образом, финансовые результаты инвестора по синтетической позиции полностью совпадают с результатами покупателя опциона пут.
Пример 5.
На основе цифр примера 1 создать синтетический короткий пут.
Решение.
Инвестор продает колл, занимает деньги на три месяца и покупает акцию. Он занимает сумму:
100 - 3 = 91руб.
Через три месяца он должен отдать по кредиту:
97[1 + 0,1(3/12)]= 99,425 руб.
Если в этот момент ST <Х , инвестор продает акцию на спотовом рынке. Его убыток равен:
(99,425 - S, )руб.,
т. е. он уменьшен на величину премии опциона пут плюс процент, который можно получить на премию за три месяца.
При ST=X акция продается на споте за 100 руб. и прибыль равна:
100-99,425 = 0,575 руб.,
т.е. премия опциона плюс процент на премию.
Если Sr> X, контрагент исполняет опцион колл, и инвестор продает ему акцию за 100 руб. Его прибыль также равна премии плюс процент. Таким образом, финансовые результаты инвестора по синтетической позиции совпадают с результатами продавца опциона пут.
Мы рассмотрели примеры для условий паритета между опционами колл и пут. Если паритет нарушен, то можно совершить арбитражную операцию. Примеры действий арбитражера в таком случае рассмотрены в параграфе 9.4.1, посвященном паритету опционов.
13.2. СИНТЕТИЧЕСКАЯ АКЦИЯ
Паритет опционов позволяет создать синтетическую акцию. Алгоритм формирования длинной синтетической акции представлен формулой (13.6):
5 = с +-----Д----г -р. (13.6)
1 + r(t / база)
Для получения синтетической акции необходимо купить колл, продать пут и иметь сумму денег, равную дисконтированной стоимости цены исполнения опционов.
Пример 6.
Инвестор располагает 100 руб., но решает сформировать синтетическую длинную акцию для условий примера 1. Он покупает колл и продает пут. Это требует денег в сумме:
3 - 0,56 = 2,44/?уб.
Данную сумму он затрачивает из 100 руб. Оставшуюся сумму:
100-2,44 = 97,56руб.
размещает на трехмесячный депозит под 10% годовых. По окончании опционного контракта он получает по счету:
97,5б[1 + 0,1(3/12)]= ЮОр^б.
Если через три месяца S, > X, например, 120 руб., инвестор исполняет колл и получает акцию, цена которой на споте равна 120 руб.
При ST = X опционы не исполняются и стоимость портфеля инвестора равна цене акции и составляет 100 руб.
Если <Х , например, 80 руб., контрагент исполнит пут, т.е инвестор купит акцию потеряв 20 руб. Таким образом в любом случае цена портфеля инвестора эквивалентна цене акции.
В случае нарушения равенства (13.6) возникает возможность получить арбитражную прибыль. Для определения действий арбитражера равенство (13.6) удобно рассмотреть как равенство стоимости двух портфелей. Первый портфель - левая часть равенства, второй портфель - правая часть равенства. При нарушении равенства один портфель стоит дороже другого. Поэтому действия арбитражера заключаются в том, чтобы продать более дорогой портфель и купить более дешевый Поясним сказанное на примере.
Пример 7.
Пусть в примере 1 акция стоит 101 руб. Условие (13.6) нарушено:
5 >с +-------------г-р.
1 + г(Г / база)
Арбитражер продает первый портфель и покупает второй, т.е. занимает и продает акцию, покупает опцион колл, продает опцион пут. От операций он получает сумму:
101 -3 + 0,56 = 98,56 руб.
Данные средства размещает на трехмесячный депозит под 10% годовых и получает сумму:
98,5б[1 + 0,1(3 /12)] = 101,024 руб.
Если через три месяца ST > X, например, 120 руб., инвестор исполняет колл, т.е. покупает акцию за 100 руб., возвращает ее кредитору. Его прибыль равна:
101,024 - 100 = 1,024 руб.
При S{ = X арбитражер покупает акцию за 100 руб. на спотовом рынке, возвращает ее кредитору. Его прибыль вновь равна 1,024 руб-
Если 57. <Х , например, 80 руб., контрагент исполняет пут. Поэтому арбитражер покупает у него акцию за 100 руб., возвращает ее кредитору. Прибыль равна 1,024 руб.
Пусть акция стоит 99 руб. Тогда:
Арбитражер покупает первый портфель и продает второй, т.е. продает колл, покупает пут, занимает дополнительно средства на три месяца под 10% и покупает акцию. В общей сложности арбитражер занимает сумму:
0,56 + 99-3 = 96,56 руб.
Через три месяца он должен вернуть по кредиту:
( 3 1
96,56 1 + 0,1— = 98,97 руб.
\ 12 J
Если в этот момент 5Г > X , например, 120 руб., контрагент исполняет колл, т.е. арбитражер продает ему акцию за 100 руб., возвращает кредит. Его прибыль равна:
100-98,97 = 1,03 руб.
При S, = X арбитражер продает акцию за 100 руб. на спотовом рынке, возвращает кредит. Прибыль равна 1,03 руб.
Если например, 80 руб., арбитражер исполняет пут,
т.е. продает акцию за 100 руб., возвращает кредит. Прибыль равна 1,03 руб.
В формуле паритета величину X можно рассматривать как безрисковую бескупонную облигацию с номиналом X, погашаемую в момент истечения опционных контрактов. Цена облигации в момент
Y
заключения контрактов равна --?т. Поэтому из формулы
1 + ц//база)
паритета можно получить алгоритм формирования синтетической безрисковой бескупонной облигации:
----7-7---Т - S + р - С . (1 3.7) 1 + r\t/ база)
Формула (13.7) говорит о том, что синтетическая покупка облигации представляет собой покупку акции, опциона пут и продажу опциона колл. Если равенство не будет выдерживаться, можно совершить арбитражную операцию.
13.3. СИНТЕТИЧЕСКАЯ ФЬЮЧЕРСНАЯ ПОЗИЦИЯ
С помощью опционов на фьючерсные контракты можно формировать синтетические фьючерсные позиции. Длинная синтетическая фьючерсная позиция включает покупку опциона колл и продажу опциона пут с одной ценой исполнения и сроком истечения контрактов. Ее график к моменту срока истечения контрактов представлен на рис. 13.5.
Рис. 13.5. Длинная синтетическая фьючерсная позиция; синтетическая позиция представлена сплошной линией
Короткая синтетическая фьючерсная позиция формируется с помощью короткого опциона колл и Длинного опциона пут с одной ценой исполнения и датой истечения контрактов (рис. 13.6).
Рис. 13.6. Синтетическая короткая фьючерсная позиция; синтетическая позиция представлена сплошной пинией
Алгоритм формирования синтетической фьючерсной позиции можно получить на основе формулы паритета опционов. Если не принимать в расчет процентную составляющую, поскольку она представляет собой незначительную величину, то паритет опционов на фьючерсные контракты можно записать следующим образом:
c-p = F-X. (13.8)
Перегруппировав переменные в формуле (13.8), получим:
= + (13.9)
Формула (13.9) соответствует длинному синтетическому фьючерсу: покупается колл и продается пут с ценой исполнения X. Синтетический фьючерс открыт по цене с - р + X.
Пример 1.
Опцион колл на фьючерс стоит 6 руб, пут - 4 руб, цена исполнения опционов 100 руб. Определить, по какой цене открыта длинная синтетическая фьючерсная позиция.
Решение.
с-р-Х = 6-4 +100 = 102pj6.
Чтобы получить алгоритм для короткого синтетического фьючерса, формулу (13.9) следует умножить на минус один:
-F = -c + p-X. (13.10)
Это означает, что надо продать колл и купить пут с ценой исполнения X.
Формула (13.8) имеет важное значение для определения арбитражных возможностей. Левая часть равенства (13.8) показывает стоимость синтетической фьючерсной позиции. Если равенство выдерживается, то прямая фьючерсная и синтетическая позиции эквивалентны. Если с - р > F - X , то синтетическая фьючерсная позиция дороже прямой фьючерсной. Поэтому следует продать синтетический фьючерс и купить фьючерсный контракт. Прибыль арбитражера составит разность между стоимостью первой и второй позиций.
Пример 2.
Опцион колл стоит 6 руб., пут - 3,5 руб, цена исполнения опционов-100 руб., фьючерсная цена - 102 руб. При такой конъюнктуре равенство (13.8) не выдерживается:
6 - 3,5 > 102-100.
Поэтому арбитражер продает колл, покупает пут и покупает фьючерс по цене 102 руб. На разности премий он получает 2,5 руб. Если к моменту истечения опционов фьючерсная цена Ff будет больше 100 руб., контрагент исполнит колл. Это означает, что арбитражер получит короткую фьючерсную позицию и отрицательную вариационную маржу в размере (Fr-lOO). По фьючерсной позиции его выигрыш равен (FT -102). Длинный фьючерс закрывает полученную короткую позицию. Итог операции составляет:
-(FT -100) + (-102) + 2,5 - 0,5 руб.
Если к моменту истечения опционов F, < 100 руб., арбитражер исполняет пут, т.е. он получает короткую фьючерсную позицию и положительную вариационную маржу в размере (100-/7). По фьючерсу у него проигрыш равный (102 - Г,). Длинный фьючерс закрывает короткую позицию. Итог операции составляет:
(IOO-/7 )+(Fz -102)+2,5 = 0,5 руб.
Если к моменту истечения опционов F} = 100 руб., опционы не исполняются. Арбитражер закрывает длинный фьючерс офсетной сделкой по цене 100 руб. Проигрыш по фьючерсу равен:
102 -100 = 2руб.
Итог операции составляет:
2,5 - 2 — 0,5 руб.
Данный результат можно получить, рассуждая иначе. Арбитражер купил фьючерс по цене 102 и продал синтетической фьючерс, согласно алгоритму (13.10), по цене:
-6 + 3,5-100 = -102,5 руб.
(Знак минус говорит о продаже по цене 102,5 руб.) Поэтому его прибыль равна разности данных цен:
102,5 - 102 = 0,5 руб.
Если на рынке возникнет ситуация, когда с - р < F - X , то следует продать более дорогой фьючерсный контракт и купить более дешевый синтетический фьючерс.
Пример 3.
Пусть в примере 2 опцион пут стоит 4,5 руб. Равенство (13.8) нарушено:
6-4,5 < 102-100.
Арбитражер покупает колл, продает пут с ценой исполнения 100 руб. и продает фьючерс по цене 102 руб,
В данном примере арбитражер купил более дешевый синтетический фьючерс по цене:
6-4,5+ 100 = 101,5руб.
и продал фьючерсный контракт по цене 102 руб. Следовательно, его прибыль к моменту истечения опционных контрактов составила:
102 -101,5 = 0,5руб.
Стратегия, в рамках которой продается синтетический актив и покупается базисный актив (в нашем случае фьючерс), называется конверсией. Для такой ситуации синтетический актив стоит дороже. Стратегия, в рамках которой покупается синтетический актив и продается базисный актив, называется реверсией или обратной конверсией. В такой ситуации синтетический актив стоит дешевле.
В рассмотренных выше случаях в формуле паритета мы не учитывали процентную ставку. Если принять ее во внимание, то равенство (13,8) примет вид:
с - р _ F — X - цена доставки. (13.11)
Применительно к опционам на фьючерсы цена доставки равняется той сумме кредита, которую возьмет арбитражер для покупки более дешевой синтетической фьючерсной позиции или процентам по депозиту, которые он получит на сумму от продажи более дорогой синтетической фьючерсной позиции. Арбитражер осуществит конверсию, если:
с — р > F — X -цена доставки (13.12)
и реверсию в случае:
с- р < F - X - цена доставки.
(13.13)
Пример 4.
Трехмесячный колл стоит 6 руб., пут - 4 руб., цена исполнения -100 руб., фьючерсная цена - 102 руб., ставка по безрисковому депозиту - 12% годовых, ставка по кредиту - 20% годовых. Для случая конверсии, когда формируется короткий синтетический фьючерс, инвестор получает 2 руб. на разности премий и инвестирует их на три месяца. Цена доставки равна:
2-0,12 2. = 0,06 дуб.
Равенство (13.11) не выдерживается, так как:
6-4 > 102 -100 - 0,06
или
2 > 1,94.
Синтетический фьючерс стоит дороже, поэтому арбитражер продает его и покупает фьючерсный контракт. Для безарбитражной ситуации фьючерсная цена из формулы (13.11) должна была бы составить: 6-4+100 + 0,06 - 102,06руб.
Арбитражер покупает фьючерс по 102,06 руб. и продает синтетический фьючерс с ценой исполнения 100 руб. К моменту истечения контракта стоимость его позиции равна:
-102,06 +100 = -2,06 руб.
Его проигрыш по позиции полностью компенсируется за счет полученной разности премий опционов и процентов по депозиту на данную разность. Таким образом, чтобы конверсия принесла арбитражную прибыль, должно выдерживаться неравенство (13.12):
Для реверсии в примере цена доставки равняется:
3
2 0,2— = 0,1 дуб.
12
Данную сумму инвестор должен занять, чтобы купить синтетический фьючерс. Поэтому для безарбитражной ситуации разность между фьючерсной ценой и ценой исполнения должна покрыть процентные издержки. В примере синтетический фьючерс стоит 2 руб., сумма процента по кредиту равна 0,1 руб. Отсюда фьючерсная цена для безарбитражной ситуации должна равняться:
F = 6- 4+100 + 0,l = l 02,1 руб.
В случае формирования реверсии инвестор продает фьючерс по цене 102,1 руб. и покупает синтетический фьючерс с ценой исполнения 100 руб. Стоимость его позиции к моменту истечения опционов равна:
102,1 -100= 2,1руб.
По кредиту он также должен вернуть сумму 2,1 руб. Поэтому, реверсия принесет арбитражную прибыль, если выполняется неравенство (13.13).
Соотношения (13.8) и (13.11) позволяют установить равновесные цены для каждого из опционов, а также фьючерсных контрактов.
Конверсия и реверсия считаются арбитражными стратегиями. Однако в определенных ситуациях по ним может возникнуть риск. Риск появится в том случае, если после истечения срока действия опционов у арбитражера останется открытая позиция по фьючерсному контракту. Такой случай возможен, если на момент окончания опционных контрактов фьючерсная цена равна цене исполнения. Тогда на следующее утро арбитражер может обнаружить у себя открытую позицию по фьючерсному контракту. Поясним это на примере. Допустим, арбитражер сформировал конверсию. Чтобы исключить фьючерсную позицию он должен отдать приказ исполнить опцион пут. Тогда его длинная позиция по фьючерсу будет погашена коротким фьючерсом, который появится в результате исполнения опциона. Однако арбитражер, отдавая приказ исполнить пут, не может быть до конца уверен, что контрагент не исполнит проданный им колл (например в целях закрытия своей фьючерсной позиции по реверсии). В результате, если будет исполнен колл, то арбитражер получит открытую короткую фьючерсную позицию. Когда арбитражер сформировал большое количество конверсий, то наверняка какое-то количество опционов колл будет исполнено контрагентами, а какое-то нет. Чтобы избежать подобной ситуации, можно закрыть позиции
по конверсии и реверсии до момента истечения опционов, если ожидается, что фьючерсная цена будет равна цене исполнения. Однако и в этом случае возможны убытки, так как существует спрэд между ценой продавца и покупателя. Арбитражеру придется покупать проданные опционы по более высокой цене продавца и продавать купленные опционы по более низкой цене покупателя. Если спрэд отсутствует или является небольшим, то при досрочном закрытии позиции арбитражер получит прибыль.
Пример 5.
Трехмесячный опцион колл стоит 6 руб., пут - 4 руб, цена исполнения опционов - 100 руб., фьючерсная цена 101,5 руб Ставка по депозиту 12% годовых
Для данных условий:
6-4 > 101,5-100-0,06.
Поэтому арбитражер сформировал конверсию. За 10 дней до истечения опционов у него возникли опасения, что фьючерсная цена будет равна цене исполнения в момент их истечения. Поэтому он решает закрыть свою позицию. В этот момент F = 100,5pjV7.; с = \руб.\ р = 0,4руб. По депозиту он получает за 80 дней, которые прошли с
момента открытия позиции,
2 1 + 0,12
80
365?
= 2,0526. Арбитражер
покупает опцион колл, продает опцион пут и продает фьючерс. Его финансовый результат равен:
-1 + 0,4 - (101,5 -100,5) + 2,0526 = 0,4526руб.
Приведем пример построения синтетической фьючерсной позиции на основе реальных котировок опционов на фьючерсный контракт на акции РАО ЕЭС, торгуемых на Фондовой бирже РТС. Будем учитывать, что на практике котировки даются как котировки продавца и покупателя. Поэтому инвестор, желающий купить опцион, сможет это сделать по цене продавца, а инвестор, желающий продать опцион, - по цене покупателя. Данный факт следует учитывать и при определении возможностей совершения арбитражной операции.
Пример.
Сегодня середина дня 20 июля 2005 г. Фьючерсная цена контракта на акции РАО ЕЭС с истечением 14.09.05 г. равна 9122 руб. Коти
ровки сентябрьских опционов с истечением 12.09.05 г. представлены в следующей таблице.
Таблица 13.1. Котировки сентябрьских опционов на фьючерс на РАО ЕЭС
цена исполнения (руб.)
9000 9500
колл цена покупки 337 135
цена продажи 360 157
пут цена покупки 220 499
цена продажи 241 536
Согласно формуле (13.9) на основе опционов с ценой исполнения 9000 формируем длинный синтетический фьючерс: покупаем колл за 360 руб. и продаем пут за 220 руб. Синтетическая позиция открыта по цене:
F = 360 - 220 + 9000 = 9140 руб.
Согласно формуле (13.10) формируем короткий синтетический фьючерс: продаем колл с ценой исполнения 9000 за 337 руб. и покупаем пут за 241 руб. Синтетическая позиция открыта по цене:
F - 337 - 241 + 9000 - 9096руб.
Аналогично на основе опционов с ценой исполнения 9500 формируем длинный синтетический фьючерс: покупаем колл за 157 руб. и продаем пут за 499 руб. Синтетическая позиция открыта по цене: Л = 157-499 + 9500 = 9158^6.
Формируем короткий синтетический фьючерс: продаем колл с ценой исполнения 9500 за 135 руб. и покупаем пут за 536 руб. Синтетическая позиция открыта по цене:
F =135-536 + 9500 = 9099 руб.
Определим, возможен ли арбитраж. Выводы сделаем на основе нарушения равенства (13.8) с учетом использования котировок покупателей и продавцов. Для опционов с ценой исполнения 9000 руб.:
F-X = 9122-9000 = \22руб.
Если мы рассматриваем ситуацию: c-p<F-X , (13.14)
то в этом случае для получения арбитражной прибыли инвестор должен купить колл и продать пут. Поэтому величину с-р опреде
ляем на основе цены продавца опциона колл (360 руб.) и цены покупателя опциона пут (220 руб.). Она равна:
360-220 = 140/туб.
Вывод: на основе текущих котировок опционов арбитраж не возможен, так как 140 > 122 и условие (13.14) не выполняется.
Вывод о невозможности арбитража можно также сделать, если сравнить текущую фьючерсную цену и цену синтетической фьючерсной позиции. При существовании условия (13.14) инвестор должен открыть длинную синтетическую позицию. Как мы определили выше, это можно сделать по цене 9140 руб. Одновременно арбитражер должен продать фьючерс. В настоящий момент его можно продать по цене 9122 руб. Если инвестор купит фьючерс синтетически по 9140 руб. и продаст фьючерсный контракт по 9122 руб., то он получит убыток. Поэтому арбитраж не возможен.
Если мы рассматриваем ситуацию:
c-p>F-X , (13.15)
то в этом случае для получения арбитражной прибыли инвестор должен продать колл и купить пут. Поэтому величину с~р определяем на основе цены покупателя опциона колл (337 руб.) и цены продавца опциона пут (241 руб.). Она равна:
337-241 = 96/^6.
Вывод: на основе текущих котировок опционов арбитраж не возможен, так как 96 < 122 и условие (13.15) не выполняется.
Вывод о невозможности арбитража можно также сделать, если сравнить текущую фьючерсную цену и цену синтетической фьючерсной позиции. При существовании условия (13.15) инвестор должен открыть короткую синтетическую позицию. Как мы определили выше, это можно сделать по цене 9096 руб. Одновременно арбитражер должен купить фьючерс. В настоящий момент его можно купить по цене 9122 руб. Если инвестор продаст фьючерс синтетически по 9096 руб. и купит фьючерсный контракт по 9122 руб., то он получит убыток. Поэтому арбитраж не возможен.
КРАТКИЕ ВЫВОДЫ
Синтетический актив - это портфель, состоящий из разных активов.
С помощью комбинирования позиций по базисному активу и опциону можно создать синтетические опционы колл и пут. Синтети
ческий длинный опцион колл включает покупку базисного актива и опциона пут; синтетический короткий опцион колл - продажу базисного актива и продажу опциона пут. Синтетический длинный пут создается продажей базисного актива и покупкой опциона колл; синтетический короткий пут - покупкой базисного актива и продажей опциона колл.
С помощью опционов на фьючерсные контракты можно формировать синтетические фьючерсные позиции. Длинная синтетическая фьючерсная позиция включает покупку опциона колл и продажу опциона пут. Короткая синтетическая фьючерсная позиция включает короткий опцион колл и длинный опцион пут.
Стратегия, в рамках которой продается синтетический актив и покупается базисный актив, называется конверсией. Стратегия, в рамках которой покупается синтетический актив и продается базисный актив, называется реверсией или обратной конверсией.
ГЛАВА 14. ОПЦИОННЫЕ СТРАТЕГИИ
В настоящей главе рассматриваются основные стратегии, которые инвесторы могут формировать с помощью опционных контрактов. Глава начинается с простейших стратегий, представляющих собой покупку и продажу отдельных опционов. После этого мы переходим к более сложным сочетаниям, а именно, комбинациям и спрэдам. В последних параграфах главы раскрываем понятие волатильных стратегий и бокс-арбитража.
14.1. ПОКУПКА И ПРОДАЖА ОТДЕЛЬНЫХ ОПЦИОНОВ
Существует много опционных стратегий. Простейшими являются покупка и продажа опционов. При выборе стратегии необходимо сделать прогноз динамики цены базисного актива на период заключения контракта. Это позволит ответить на вопрос, следует ли купить или продать контракт. Если ожидается значительное изменение цены базисного актива, целесообразно открыть длинную позицию. Прогноз динамики внутренней волатильности опционов также ответит на вопрос покупать или продавать контракты. Ожидая роста волатильности, надо открыть длинную позицию. В результате увеличения волатильности опционы подорожают, и их можно продать с прибылью. Если базисный актив по мнению инвестора недооценен, предпочтительнее купить колл, а в случае переоценки - пут. Прогнозируя падение внутренней волатильности, целесообразно открыть короткую позицию. Если также ожидается падение курса базисного актива, следует продать колл, если рост - продать пут. О прогнозе волатильности можно судить на основе ее прошлой статистики. При высокой волатильности по сравнению с ее обычным уровнем, следует продать контракты, при низкой - купить. При прогнозах спокойного рынка надо выписать или колл или пут.
Следующий вопрос - это выбор цены исполнения. Наибольшие изменения гаммы, веги и тэты, а следовательно изменения премии опционов в связи с данными факторами риска, наблюдаются для опционов без выигрыша. Поэтому, чем более уверен инвестор в динамике цены и волатильности (сильно изменятся или останутся прежними), тем в большей мере следует выбирать опционы ATM. Если ожидания слабо определены, целесообразно остановиться на опционах с проигрышем.
Важно определить, на какой месяц открыть контракт. Краткосрочный опцион сильнее реагирует на изменение цены базисного
актива, чем долгосрочный. Поэтому при прогнозе существенного изменения курса в ближайшие несколько дней целесообразно остановиться на краткосрочных опционах. За 30-40 дней до окончания контракта опцион начинает дешеветь с ускорением. Следовательно, в случае покупки опциона необходимо определить период времени, в течение которого можно держать позицию открытой, если прогноз конъюнктуры не оправдается. Временной период удобно рассчитать на основе тэты опциона. Инвестор определяет сумму допустимого проигрыша. После этого с учетом значения тэты контракта рассчитывает количество дней, в течение которых его можно держать открытым.
Пример.
До истечения опциона колл на акцию 30 дней. Опцион стоит 2 руб. Тэта равна 0,05 руб. Инвестор ожидает, что курс акции вырастет в ближайшие пять дней, и покупает контракт. Максимальный проигрыш, который он готов допустить, если курс бумаги не изменится, равен 0,4 руб. Допустимое количество дней сохранения позиции открытой равно:
0,4 : 0,05 - 8 дней .
Если инвестор ожидает существенного изменения цены в средне-или долгосрочной перспективе, можно открыть длинную позицию по опциону. Так как до истечения контракта много времени, то эффект тэты сказывается незначительно. Однако в случае медленного изменения цены базисного актива волатильность обычно будет падать. Поэтому держатель длинной позиции может выиграть за счет изменения курса базисного актива, но в целом проиграть вследствие эффектов тэты и веги.
При прогнозе спокойного рынка надо продать контракт, до истечения которого остается 30-40 дней, так как он начинает терять временную стоимость с ускорением. Временная стоимость долгосрочного опциона больше краткосрочного, однако его тета меньше. Соответственно, он дешевеет медленнее. Поэтому, если инвестор продает долгосрочный контракт в надежде получить больший выигрыш за счет временной стоимости, он рискует в большей степени по сравнению с потенциальным выигрышем.
Для игры на веге следует использовать долгосрочные контракты, поскольку их премия в большей степени реагирует на изменение внутренней волатильности опционов.
При игре на понижение курса акции на спотовом рынке инвестор осуществляет ее короткую продажу. Альтернативой является покупка опциона пут Такая стратегия имеет следующие положительные черты. Во-первых, в случае ошибки прогноза будущей конъюнктуры максимальные потери инвестора ограничиваются только уплаченной премией. При короткой продаже они теоретически не ограничены. Во-вторых, короткая продажа акции требует маржевого обеспечения, которое резервируется на счете инвестора В случае роста цены величина маржи будет возрастать. Недостаток средств может привести к преждевременному закрытию позиции с убытками, несмотря на то, что по мнению инвестора она еще сохраняет потенциал прибыльности. При покупке опциона премия уплачивается сразу, и от инвестора не требуется внесения дополнительных средства в случае роста цены акции. Поэтому позицию по опциону можно держать открытой в течение более длительного времени. Таким образом, инвестор может играть на понижение на более длительных промежутках времени, не подвергая себя дополнительному риску. В-третьих, при ошибке прогноза инвестор может закрыть опционную позицию, продав его, и тем самым уменьшить размер потерь.
14.2. ПОКРЫТЫЙ КОЛЛ И ПОКРЫТЫЙ ПУТ
Более сложной стратегией является покрытый опцион колл. Инвестор выписывает опцион и покупает базисный актив для страховки от возможного роста его курса. Обычно выписывают опцион с проигрышем. Продавец надеется выиграть за счет падения временной стоимости контракта в условиях спокойного рынка. Чтобы уменьшить риск потерь в связи с падением цены базисного актива, позицию целесообразно открыть незадолго до истечения срока действия контракта. Следует подчеркнуть, что данную стратегию активно используют инвестиционные фонды, выписывая опционы на акции, которые они держат в своих портфелях. Такие действия приносят им в среднем более высокие результаты, чем простое владение базисными акциями за счет полученных премий. Если опцион будет исполнен, фонд поставит акцию по цене исполнения. Его прибыль равна премии плюс разность между ценой исполнения и более низкой ценой покупки бумаги (как было отмечено, обычно выписываются опционы с проигрышем). Если курс бумаги упадет, фонд может понести потери. Однако все равно его позиция более выигрышна по сравнению с простым владением акцией на величину премии. Если опцион не будет исполнен, то в качестве прибыли
фонд сохранит премию и может выписать новые опционы колл на данную акцию.
Чтобы уменьшить вероятность потерь от падения цены базисного актива, можно выписать колл ОТМ и оставить его непокрытым до того момента, пока курс актива ниже цены исполнения. Как только он превысит цену исполнения, следует купить актив и сделать опцион покрытым. При дальнейшем падении цены спот ниже цены исполнения надо продать актив и т.д. покупать и продавать базисный актив в зависимости от того, превысил ли его курс цену исполнения или опустился ниже ее. Если цена актива испытывает частые колебания вокруг цены исполнения, то инвестор может понести значительные комиссионные издержки вследствие покупок и продаж актива. Кроме того, дополнительные издержки возникают за счет того, что актив покупается по курсу выше цены исполнения, а продается по курсу ниже цены исполнения.
В качестве другого способа страховки от падения цены базисного актива можно выписать опцион колл ГТМ. Потери инвестора страхуются на величину полученной премии. Поскольку это опцион с выигрышем, он стоит существенно дороже опционов АТМи ОТЛ/и соответственно предоставляет больший диапазон страховки. Недостатком стратегии является то, что покупатель может с большей вероятностью исполнить контракт. Однако, если рынок оставался спокойным в течение срока действия опциона, продавец все равно получит прибыль за счет падения его временной стоимости.
Покрытый колл удобно использовать для покупки акции по более низкой цене чем текущая, если инвестор заинтересован держать ее длительное время, т. е. не будет обращать внимания на возможное падение курса бумаги в ближайшем будущем. В этом случае цена покупки уменьшается на величину полученной премии. Если курс акции вырастет, и опцион будет исполнен, инвестор поставит бумагу, сохранив премию.
Для покупки акции по цене ниже текущей также подходит покрытый пут: инвестор выписывает опцион и резервирует средства, необходимые для покупки акции в случае исполнения контракта контрагентом. Если опцион будет исполнен, инвестор купит ее по цене исполнения. Реальная цена покупки уменьшается на величину полученной премии.
Покрытый пут можно использовать для извлечения спекулятивной прибыли. В этом случае инвестор выписывает опцион и осуществляет короткую продажу базисного актива. Если продается пут ATM, то преследуется цель получить прибыль за счет падения вре
менной стоимости опциона. В случае роста цены актива позиция застрахована только на величину премии опциона.
Можно продать опцион ОТМ. Тогда при падении цены актива контрагент исполнит контракт. Прибыль инвестора равна премии опциона плюс разность между ценой продажи актива и ценой исполнения опциона, В случае роста курса актива позиция инвестора имеет меньшую страховку, поскольку опцион ОТМдешевле опциона А ТМ.
Для хеджирования от более существенного роста цены актива можно продать опцион пут ITM.
14.3. КОМБИНАЦИИ И СПРЭДЫ
Более сложные стратегии включают одновременно продажу и (или) покупку нескольких опционов. Их можно подразделить на две группы: комбинации и спрэды.
Комбинация - это портфель, состоящий из опционов разного вида на один и тот же актив с одним сроком истечения контрактов, которые одновременно являются длинными или короткими, цена исполнения может быть одинаковой или разной.
Спрэд - это портфель, состоящий из опционов одного вида на один и тот же актив, но с разными ценами исполнения и (или) датами истечения, причем одни из них являются длинными, а другие - короткими. В свою очередь спрэд подразделяется на вертикальный (цилиндрический или денежный), горизонтальный (календарный или временной) и диагональный.
Вертикальный спрэд объединяет опционы с одной датой истечения контрактов, но разными ценами исполнения. Горизон-тальный спрэд включает опционы с одинаковыми ценами исполнения, но разными датами истечения контрактов. Диагональный спрэд строится на основе опционов с разными ценами исполнения и сроками истечения контрактов. Когда спрэд формируется на базе опционов, которые имеют противоположные позиции по сравнению со стандартным сочетанием, его именуют обратным спрэдом.
Каждый вид спрэда имеет две разновидности: повышающуюся (спрэд быка) и понижающуюся (спрэд медведя). При создании вертикального спрэда быка покупаемый опцион имеет более низкую цену исполнения по сравнению с продаваемым. У горизонтального спрэда быка покупаемый опцион имеет более позднюю дату истечения контракта. У повышающегося диагонального спрэда покупаемый опцион имеет более низкую цену исполнения и более позднюю дату истечения контракта по сравнению с продаваемым опционом.
Для вертикального спрэда его повышающаяся или понижающаяся разновидности связаны с надеждами инвестора получить прибыль соответственно от роста или падения курса базисного актива. Для горизонтального и диагонального спрэда такая закономерность будет наблюдаться не всегда. Рассмотрим последовательно возможные комбинации и спрэды.
14.3d, Комбинации
14.3.1.1. Стеллажная сделка (стрэддл)
Стеллажная сделка или стрэддл представляет собой комбинацию опционов колл и пут на один и тот же базисный актив с одинаковой ценой исполнения и датой истечения контрактов, которые одновременно являются длинными или короткими. Если инвестор купил опционы колл и пут, то говорят, что он купил стрэддл, а позиция называется длинный стреддл (стеллаж). Если он продал опционы колл и пут, то говорят, что он продал стрэдцл, а позиция называется короткий стрэддл (стеллаж). Рассмотрим длинный и короткий стеллаж на примерах.
Пример (длинный стрэддл).
Инвестор купил трехмесячные опционы колл и пут на акцию компании А с ценой исполнения 100 руб. Колл стоит 3 руб., пут - 2 руб. Цена спот акции 100 руб. График выигрышей-проигрышей инвестора д моменту истечения контрактов представлен на рис. 14.1.
Рис. 14.1. Выигрыши-проигрыши покупателя стрэддла к моменту истечения срока действия контрактов
Как следует из графика, если к моменту истечения контрактов цена спот акции не сильно отклонится от цены исполнения, инвестор понесет убыток. Максимальные потери равны сумме уплаченных премий (/ = 3 + 2 = 5 руб,, где / - сумма двух премий) при равенстве цены спот и цены исполнения. Точки безубыточности можно определить по следующим формулам:
Х + / = правая точка безубыточности , (14.1)
X-i-левая точка безубыточности. (14.2)
В примере правая точка равна:
100 + 5 = 15^5.,
левая точка:
100-5 = 95руб.
Таким образом, если к моменту истечения контрактов цена спот акции больше 95 руб., но меньше 105 руб., инвестор проигрывает. Если акция стоит меньше 95 руб. или больше 105 руб., инвестор выигрывает. Величина выигрыша потенциально не ограничена (при росте цены акции). Для расчета выигрышей-проигрышей покупателя стеллажа к моменту истечения контрактов можно воспользоваться таблицей 14.1.
Таблица 14.1. Результаты покупателя стеллажа к моменту истечения контрактов (S - курс акции в день истечения контрактов; X - цена исполнения; / - сумма уплаченных премий)
Цена акции Финансовый результат
s<x X-S-i
s = x -i
S> X S-X-i
Для формирования стрэддла используют опционы без выигрыша. Дельта опциона колл АТМравна примерно +0,5, опциона пут ATM-минус 0,5, поэтому позиция по спрэду является дельта-нейтральной. Это означает, что при небольшом изменении цены акции стоимость портфеля инвестора практически не изменится. Так, при росте курса акции повысится цена опциона колл, но снизится стоимость опциона пут. Если инвестор закроет позицию в этот момент, то проиграет на выкупе опциона колл по более высокой цене, однако выиграет прак
тически эту же сумму на выкупе опциона пут. В результате общая сумма средств инвестора не изменится. Аналогично, если курс акции упадет, опцион колл подешевеет, но дороже станет опцион пут. Однако общая стоимость портфеля инвестора останется прежней, так как данные изменения компенсируют друг друга.
Как видно из графика, инвестор рассчитывает на сильное движение рынка, именно в этом случае он будет выигрывать. Это говорит о том, что гамма позиции положительна (она положительна для длинных опционов колл и пут). Поскольку стрэддл состоит из длинных опционов, то он имеет положительную вегу, и, следовательно, инвестор также заинтересован в росте внутренней волатильности опционов. В этом случае они будут дорожать.
Таким образом, формируя стрэддл, инвестор ожидает или роста фактической волатильности акции, т.е. роста или падения ее курса (об этом говорит положительная гамма) или внутренней волатильности опционов (на это указывает положительная вега). Если рынок остается спокойным, то покупатель стеллажа несет потери за счет падения временной стоимости опционов, так как их тета отрицательна.
Опционы без выигрыша имеют наибольшую тету, и соответственно наиболее быстро теряют временную стоимость вследствие убывания времени опционного контракта. Поэтому не целесообразно держать стрэддл в течение длительного времени, особенно в последние 30 дней до истечения срока контрактов, когда величина теты начинает возрастать (по абсолютной величине) с ускорением. Оптимально купить стрэддл незадолго до наступления значимых экономических или политических событий, например, опубликования важных макроэкономических показателей развития страны. Непосредственно перед ними внутренняя волатильность опционов будет возрастать вследствие увеличения неопределенности будущей конъюнктуры. В этот момент следует закрыть позицию, продав подорожавшие опционы.
Пример (короткий стрэддл).
Инвестор продал трехмесячные опционы колл и пут на акцию компании А с ценой исполнения 100 руб. Колл стоит 3 руб., пут - 2 руб. Цена спот акции 100 руб. График выигрышей-проигрышей инвестора к моменту истечения контрактов представлен на рис. 14.2.
Как следует из графика, если к моменту истечения контрактов цена спот акции не сильно отклонится от цены исполнения, инвестор получит прибыль. Ее максимальная величина равна сумме полученных премий (/ — 3 + 2 = 5 руб.) при равенстве цены спот и цены исполне-
Рис. 14.2. Выигрыши-проигрыши продавца стрэддла к моменту истечения срока действия опционов
ния. Точки безубыточности можно определить по формулам (14.1) и (14.2), как и для длинного стеллажа. В примере правая точка равна:
100 + 5 = 15руб.,
левая точка:
100-5 = 95руб.
Таким образом, если к моменту истечения контрактов цена спот акции больше 95 руб., но меньше 105 руб., инвестор выигрывает. Если акция стоит меньше 95 руб. или больше 105 руб., он проигрывает. Величина проигрыша потенциально не ограничена (при росте курса акции).
Для формирования короткого стрэддла используют опционы без выигрыша. Поэтому позиция инвестора дельта-нейтральна. Гамма позиции отрицательна. Это значит, что инвестор рассчитывает на спокойный рынок, именно в этом случае он будет выигрывать. Вега позиции отрицательна. Следовательно, инвестор заинтересован в падении внутренней волатильности опционов. В этом случае они будут дешеветь.
Таким образом, формируя стрэддл, инвестор ожидает или падения фактической волатильности акции (об этом говорит отрицательная гамма) или внутренней волатильности опционов (на это указывает отрицательная вега). Если курс акции сильно изменится, то продавец стрэддла понесет потери вследствие роста стоимости одного из опционов.
Тета позиции положительна. Опционы без выигрыша имеют наибольшую тету и наиболее быстро теряют временную стоимость вследствие убывания времени опционного контракта. Поэтому целе
сообразно продать стрэддл за 30 дней до срока истечения опционов, когда значение теты начинает быстро возрастать. Если продать стрэддл до этого момента, то потенциальный риск будет перевешивать возможный выигрыш.
Приведем примеры длинного и короткого стреддла на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС на бирже РТС.
Пример.
Июньские опционы на фьючерс на акции РАО ЕЭС с ценой ис-
полнения 8000 руб. имеют следующие котировки:
колл пут
продажа покупка продажа покупка
200 180 150 130
а) Длинный стрэддл.
Формируя длинный стрэддл, инвестор покупает колл по цене продавца, т.е. за 200 руб. и пут за 150 руб. В сумме он уплачивает премию в 350 руб. Инвестор получит прибыль, если: 1) сильно изменится фьючерсная цена или 2) вырастет внутреннее стандартное отклонение опционов.
В первом случае за период действия контракта фьючерсная цена должна превысить значение верхней точки безубыточности:
8000 +350 = 8350руб.
или опуститься ниже нижней точки безубыточности: 8000-350 = 7650 руб.
Во втором случае опционы подорожают вследствие роста неопределенности на рынке, поэтому их можно будет продать с прибылью.
б) Короткий стрэддл.
Формируя короткий стрэддл, инвестор продает колл по цене покупателя, т.е. за 180 руб. и пут за 130 руб. В сумме он получает премию в 310 руб. Инвестор получит прибыль, если: 1) фьючерсная цена сильно не изменится или 2) уменьшится внутреннее стандартное отклонение опционов.
В первом случае фьючерсная цена не должна превысить значение верхней точки безубыточности:
8000 + 310 = 8310 руб.
или упасть ниже нижней точки безубыточности:
8000-310 = 7690руб.
Во втором случае выигрыш получится за счет падения стоимости опционов вследствие наступления более спокойной конъюнктуры рынка. Инвестор получит прибыль, выкупив опционы по более низкой цене.
Комбинацию, аналогичную стеллажной сделке, можно получить также за счет покупки (продажи) одной акции и покупки (продажи) двух опционов колл или пут. Рассмотрим возможные сочетания.
1. Инвестор покупает одну акцию и два опциона пут (см. рис.
14.3). Стратегия аналогична длинному стеллажу.
Рис, 14.3. Покупка одной акции и двух опционов пут
2. Инвестор продает одну акцию и два опциона пут. (см. рис.
14.4). Стратегия аналогична короткому стеллажу.
выигрыши
позиция
проигрыши
Рис. 14,4. Продажа одной акции и двух опционов пут
3. Инвестор продает одну акцию и покупает два опциона колл (см. рис. 14.5). Стратегия аналогична длинному стеллажу.
выигрыши
Рис. 14.5. Продажа одной акции и покупка двух опционов колл
4. Инвестор покупает одну акцию и продает два опциона колл (см. рис. 14.6). Стратегия аналогична короткому стеллажу.
покупка
Рис. 14.6. Покупка одной акции и продажа двух опционов колл
14.3.1.2. Стрэнгл
Стрэнгл представляет собой сочетание опционов колл и пут на один и тот же базисный актив с одним сроком истечения контрактов, но разными ценами исполнения. Оба опциона являются или длинными или короткими. Если инвестор покупает опционы, то говорят, что он покупает стрэнгл, а позицию называют длинный стрэнгл. Если он продает опционы, то он продает стрэнгл, и позицию называют короткий стрэнгл. Рассмотрим длинный и короткий стэнгл на примерах.
Пример (длинный стрэнгл).
Цена спот акции 100 руб., инвестор покупает колл с ценой исполнения 105 руб. за 1,5 руб. и пут с ценой исполнения 95 руб. за 1 руб. До истечения опционов три месяца. График выигрышей-проигрышей по стрэнглу к моменту истечения срока действия опционов представлен на рис. 14.7.
Как следует из графика, инвестор понесет потери, если к моменту истечения срока действия опционов цена спот акции не сильно отклонится от 100 руб. Однако диапазон, в котором он будет проигрывать, больше, чем у покупателя стрэддла, так как опционы имеют разные цены исполнения. Поэтому цена спот должна сильнее измениться, чтобы позиция принесла прибыль к моменту истечения срока действия опционов. Максимальные потери инвестора равны сумме уплаченных премий (/ = 1,5 + 1 = 2,5 руб.). Данный проигрыш реализуется в ситуации, когда Х{ < S < Х2. Точки безубыточности можно определить по следующим формулам:
Х2 + / = правая точка безубыточности , (14.3)
X{-i - левая точка безубыточности . (14.4)
В примере правая точка беубыточности равна:
105+ 2,5 = 107,5 руб. ,
левая точка:
95 -2,5 = 92,5 руб.
Таким образом, инвестор проигрывает в ситуации, когда:
92,5 < 5 < 107,5 руб.
Если 5 < 92,5 руб. или 5 > 107,5 руб., держатель опционов получит выигрыш, причем он потенциально не ограничен при сильном росте курса акции. Возможные результаты покупателя стрэнгла к моменту истечения контрактов можно определить по таблице 14.2. 396
Рис. 14.7. Выигрыши-проигрыши покупателя стрэнгла к моменту истечения срока действия опционов
Таблица 14.2. Результаты покупателя стрэнгла к моменту истечения контрактов
Цена акции Финансовый результат
S<X<
х} <s<x2 -i
s>%2 S~X2~i
При формировании стрэнгла обычно покупают опционы с проигрышем, отстоящие на одинаковом расстоянии от текущей цены спот акции. Поэтому позиция является дельта-нейтральной. Гамма и вега позиции положительны, тета - отрицательна. Курс акции должен сильно измениться, чтобы держатель стрэнгла получил прибыль. Поэтому покупатель стрэнгла прежде всего рассчитывает не на изменение цены акции, а на рост внутренней волатильности опционов (положительная вега). В такой ситуации они будут дорожать и позицию можно закрыть с прибылью. Так как стрэнгл формируют из опционов с проигрышем, то для них характерен более высокий процентный прирост стоимости при увеличении волатильности.
При спокойном рынке инвестор несет потери вследствие падения временной стоимости опционов (отрицательная тета). Поэтому стрэнгл целесообразно продать до того момента как тета начнет существенно возрастать (по абсолютной величине). В любом случае данную позицию не следует держать длительное время. В основном она рассчитана на получение прибыли за счет роста внутренней
волатильности опционов в связи с событием, на которое ориентируется инвестор, После роста волатильности и, соответственно удорожания опционов, позицию надо закрыть.
Приведем пример длинного стрэнгла на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 3 мая 2005 г. на бирже РТС.
Пример.
Цена июньского фьючерса на акции РАО ЕЭС равна 8250 руб. Июньские опционы на данный контракт с ценами исполнения 8000 руб. и 8500 руб. имеют следующие котировки:
колл (% = 8500руб.) пут (Л= 8000руб.)
продажа покупка продажа покупка
200 180 150 130
Формируя длинный стрэнгл, инвестор покупает колл с ценой исполнения 8500 руб. по цене продавца, т.е. за 200 руб. и пут с ценой исполнения 8000 руб. за 150 руб. В сумме он уплачивает премию в 350 руб. Инвестор получит прибыль, если: 1) сильно изменится фьючерсная цена или 2) вырастет внутреннее стандартное отклонение опционов.
В первом случае за период действия контракта фьючерсная цена должна превысить значение в:
8500 + 350 = 8850руб.
или опуститься ниже:
8000-350 = 7650^6.
Во втором случае опционы подорожают вследствие роста неопределенности на рынке, поэтому их можно будет продать с прибылью.
Сравнивая длинные стрэддл и стрэнгл, можно отметить, что при первой стратегии инвестор ожидает как роста действительной волатильности рынка (положительная гамма), так и внутренней волатильности опционов (положительная вега). Во втором случае он в основном рассчитывает на рост внутренней волатильности опционов, так как гамма стрэнгла меньше гаммы стрэддла. Более того, по мере приближения срока истечения опционов при спокойном рынке гамма стрэддла будет возрастать, а стрэнгла - падать. Вега стрэнгла меньше веги стрэддла, однако он и стоит дешевле. Обе стратегии
при формировании дельта-нейтральны. Поэтому их целесообразно использовать, когда для инвестора не ясна тенденция движения рынка, но он ожидает роста неопределенности. Поскольку стрэнгл объединяет опционы с разными ценами исполнения, он более нейтрален к изменению курса базисного актива, чем стрэддл, т.е. для поддержания его дельта-нейтральности требуется меньше пересматривать портфель, чем стрэддл.
Стрэддл и стрэнгл относят к так называемым чистым волатильным стратегиям. Это означает, что инвестор в первую очередь рассчитывает на получение прибыли за счет изменения волатильности, а не вследствие движения цены базисного актива. При их формировании получается дельта-нейтральная позиция, и инвестор в одинаковой мере будет выигрывать от роста или падения курса базисного актива. Стратегии являются краткосрочными: или инвестор выигрывает вследствие движения рынка и/или внутренней волатильности или позицию следует вскоре закрыть, чтобы не проиграть на падении временной стоимости опционов.
Пример (короткий стрэнгл).
Цена спот акции 100 руб., инвестор продает колл с ценой исполнения 105 руб. за 1,5 руб. и пут с ценой исполнения 95 руб. за 1 руб. До истечения опционов три месяца. График выигрышей-проигрышей по стрэнглу к моменту истечения срока действия опционов представлен на рис. 14.8.
Как следует из графика, инвестор получит прибыль, если к моменту истечения срока действия опционов цена спот акции не сильно отклонится от 100 руб. Однако диапазон, в котором стратегия будет прибыльной больше, чем у стрэддла, так как проданы опционы с разными ценами исполнения. Поэтому цена спот акции должна сильнее измениться, чтобы позиция принесла убыток. Максимальный выигрыш инвестора равен сумме полученных премий (г = 1,5 +1 = 2,5руб.). Выигрыш реализуется в ситуации, когда
< 5 < Х2 .Точки безубыточности можно определить как и в случае с длинным стрэнглом по формулам (14.3) и (14.4). В нашем примере правая точка безубыточности равна: 105 + 2,5 = 107,5 руб. Левая точка: 95-2,5 = 92,5руб. Таким образом, инвестор выигрывает в ситуации, когда 92,5 < S < 107,5 руб. Если S' < 92,5 руб. или 5 > 107,5 руб., он проигрывает, причем проигрыш потенциально не ограничен при росте курса акции.
Рис. 14.8. Выигрыши-проигрыши продавца стрэнгла к моменту истечения срока действия опционов
Приведем пример короткого стрэнгла на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 3 мая 2005 г. на бирже РТС.
Пример.
Цена июньского фьючерса на акции РАО ЕЭС равна 8250 руб. Июньские опционы на данный контракт с ценами исполнения 8000 руб. и 8500 руб. имеют следующие котировки:
колл (X = 8500руб.) пут (% “ 8000/губ.)
продажа покупка продажа покупка
200 180 150 130
Формируя короткий стрэнгл, инвестор продает колл с ценой исполнения 8500 руб. по цене покупателя, т.е. за 180 руб. и пут с ценной исполнения 8000 руб. за 130 руб. В сумме он получает премию в 310 руб. Инвестор получит прибыль, если: 1) фьючерсная цена сильно не изменится или 2) уменьшится внутреннее стандартное отклонение опционов.
В первом случае фьючерсная цена не должна упасть ниже: 8000-310 = 7690 руб.
или превысить:
8500 + 310-8810^6.
Во втором случае выигрыш получится за счет падения стоимости опционов вследствие наступления более спокойной конъюнктуры рынка. Инвестор получит прибыль, выкупив опционы по более низкой цене.
Короткий стрэнгл формируется как дельта-нейтральная позиция: цены исполнения опционов расположены на одном расстоянии от цены спот акции и поэтому имеют приблизительно одинаковые дельты, но с разным знаком. Поскольку опционы продаются, то гамма позиции отрицательна. Поэтому инвестор заинтересован в сохранении спокойного рынка (уменьшении действительной волатильности базисного актива), Гамма стрэнгла меньше гаммы стрэддла, поэтому данная позиция менее уязвима для движений курса базисного актива, т. е. она остается дельта-нейтральной в большем диапазоне колебаний стоимости базисного актива и в меньшей степени требует пересмотра. Гамма стрэнгла практически не будет меняться при колебаниях курса актива в диапазоне от Х} до Х?. Кроме того, по мере приближения сроков истечения контрактов гамма стрэнгла падает (по абсолютной величине), так как он состоит из опционов с проигрышем, а гамма стрэддла растет (по абсолютной величине). Таким образом, стрэнгл по сравнению со стрэддлом более гамма-нейтрален. Вега позиции отрицательна, тета - положительна. Соответственно инвестор выигрывает от падения внутренней волатильности опционов (отрицательная вега) и уменьшения времени до истечения контрактов (положительная тета). Поскольку выбираются опционы с проигрышем, то для них характерно более высокое процентное падение в стоимости при падении волатильности.
Величина падения стоимости опционов вследствие убывания времени более линейна для стрэнгла, так как он состоит из опционов с проигрышем, чем для стрэддла. Поэтому, если инвестор надеется выиграть за счет падения волатильности, т.е. использует фактор отрицательной веги, то вначале, когда до истечения опционов более 30 дней, целесообразно продать стрэнгл. Это связано с относительно меньшим риском изменения курса базисного актива и более линейной зависимостью падения временной стоимости от времени до истечения опционов. За 30 дней до истечения контрактов следует закрыть позицию по стрэнглу и продать стрэддл.
Прибыль по позиции определяется падением внутренней волатильности и истечением времени действия контрактов. Если наблюдаются оба эффекта, прибыль может быть существенной. Однако возможен и рост волатильности. В такой ситуации инвестор получит
прибыль, если эффект теты перекроет эффект веги. Недостаток данной стратегии, как и стрэддла, состоит в том, что потенциальные потери не ограничены. Поэтому, если инвестор часто будет открывать такие позиции, не страхуясь, то, с точки зрения теории вероятностей, можно с большой уверенностью сказать, что в один “прекрасный” момент он понесет значительные потери.
14.3.1.3. Стрэп
Стрэп - это комбинация из одного опциона пут и двух опционов колл. Даты истечения контрактов одинаковые, а цены исполнения могут быть одинаковыми или разными. По всем опционам инвестор занимает или короткую или длинную позицию. Стрэп похож на стеллаж (единая цена исполнения опционов) или стрэддл (разные цены исполнения опционов), но только с более крутой правой ветвью вследствие открытия позиции по двум опционам колл. Стрэп покупателя именуют длинным стрэпом, продавца - коротким стрэпом. Покупатель использует такую комбинацию, если полагает, что курс базисного актива должен с большей вероятностью вырасти, чем упасть.
Пример.
Инвестор покупает два опциона колл и один пут с ценой исполнения 100 руб. Колл стоит 3 руб., пут - 2 руб. Цена спот акции 100 руб. Графики выигрышей-проигрышей покупателя и продавца стрэпа к моменту истечения контрактов представлены соответственно на рис 14.9 и 14.10.
выигрыши |
цена акции
проигрыши
Рис. 14.9. Выигрыши-проигрыши покупателя стрэпа к моменту истечения срока действия контрактов
Рис. 14.10. Выигрыши-проигрыши продавца стрэпа к моменту истечения срока действия контрактов
Покупатель выиграет, если 5 <92 руб. и S> 104 руб., проиграет при 92 руб. < 5 < 104 руб. Соответственно продавец стрэпа получит прибыль при 92 руб. <S < \04руб. Возможные выигрыши-проигрыши покупателя стрэпа (единая цена исполнения опционов) можно рассчитать по таблице 14.3.
Таблица 14.3. Результаты покупателя стрэпа к моменту истечения контрактов
Цена акции Финансовый результат
8<Х X-S-i
S = X -i
S>X 2(5 -X)-i
Определим точки безубыточности для стрэпа на основе условий таблицы 14.3. В случае S < X должно выполняться равенство:
X-S-'i-O.
Поэтому стратегия принесет нулевой результат при цене базисного актива равной:
S = X-i. (14.5)
В случае S > X должно выполняться равенство:
2(5-Ar)-z=0.
Поэтому стратегия принесет нулевой результат при цене базисного актива равной:
S = X + (i/2} (14.6)
Приведем пример стрэпа на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС.
Пример.
Июньские опционы на фьючерс на акции РАО ЕЭС с ценой исполнения 8000 руб. имеют следующие котировки.
колл пут
продажа покупка продажа покупка
200 180 150 130
а) Длинный стрэп.
Формируя длинный стрэп, инвестор покупает два опциона колл по цене продавца, т.е. за 200 руб. и один пут за 150 руб. В сумме он уплачивает премию в 550 руб. Инвестор получит прибыль, если: 1) сильно изменится фьючерсная цена или 2) вырастет внутреннее стандартное отклонение опционов.
В первом случае за период действия контракта фьючерсная цена согласно формулам (14.6) и (14.5) должна превысить значение в:
8000 + 225 = 8225 руб.
или опуститься ниже:
8000-550 = 7450 руб.
Инвестор заинтересован больше в росте цены, чем в падении, поскольку куплены два опциона колл.
Во втором случае опционы подорожают вследствие роста неопределенности на рынке, поэтому их можно будет продать с прибылью.
б) Короткий стрэп.
Формируя короткий стрэп, инвестор продает два опциона колл по цене покупателя, т.е. за 180 руб. и один пут за 130 руб. В сумме он получает премию в 490 руб. Инвестор получит прибыль, если: 1) фьючерсная цена сильно не изменится или 2) уменьшится внутреннее стандартное отклонение опционов.
В первом случае фьючерсная цена не должна упасть ниже:
8000-490 = 7510руб.
или превысить:
8000+245 =8245 руб.
Во втором случае выигрыш получится за счет падения стоимости опционов вследствие наступления более спокойной конъюнктуры рынка. Инвестор получит прибыль, выкупив опционы по более низкой цене.
14.3Л.4. Стрип
Данная комбинация включает один опцион колл и два опциона пут. Даты истечения контрактов одинаковые, цены исполнения могут быть одинаковыми или разными. Инвестор занимает по опционам или длинную или короткую позицию. Стрип похож на стеллаж (единая цена исполнения опционов) или стрэддл (разные цены исполнения опционов), но только с более крутой левой ветвью вследствие открытия позиции по двум опционам пут. Стрип покупателя именуют длинным стрипом, продавца - коротким стрипом. Покупатель использует такую комбинацию, если полагает, что курс базисного актива должен с большей вероятностью упасть, чем вырасти.
Пример.
Инвестор покупает два опциона пут и один колл с ценой исполнения 100 руб. Колл стоит 3 руб., пут - 2 руб. Цена спот акции 100 руб. Графики выигрышей-проигрышей покупателя и продавца стрипа к моменту истечения контрактов представлены соответственно на рис. 14.11 и 14.12.
Рис. 14.11. Выигрыши-проигрыши покупателя стрипа к моменту истечения срока действия контрактов
Рис. 14.12. Выигрыши-проигрыши продавца стропа к моменту истечения срока действия контрактов
Покупатель выиграет, если 5<96,5/ж5. или S>]Q7py6., проиграет при 96,5 руб. < S <\07 руб. Соответственно продавец стрипа получит прибыль при 96,5 руб. < 5 < 107 руб. Возможные выигрыши-проигрыши покупателя стрипа (единая цена исполнения опционов) можно рассчитать по таблице 14.4.
Таблица 14.4. Результаты покупателя стрипа к моменту истечения контрактов
Цена акции S<X Финансовый результат
S-X
S> X S-X-/
Определим точки безубыточности для стрипа на основе условий таблицы 14.4, В случае S < X должно выполняться равенство:
2(^-5)-/= 0.
Поэтому стратегия принесет нулевой результат при цене базисного актива равной:
S = X-(i/2). (14.7)
В случае 5 > X должно выполняться равенство:
Поэтому стратегия принесет нулевой результат при цене базисного актива равной:
S = X + i. (14.8)
Приведем пример стрипа на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС.
Пример.
Июньские опционы на фьючерс на акции РАО ЕЭС с ценой исполнения 8000 руб. имеют следующие котировки:
колл пут
продажа покупка продажа покупка
200 180 150 130
а) Длинный стрип.
Формируя длинный стрип, инвестор покупает один опцион колл по цене продавца, т.е. за 200 руб. и два опциона пут за 150 руб, В сумме он уплачивает премию в 500 руб. Инвестор получит прибыль, если: 1) сильно изменится фьючерсная цена или 2) вырастет внутреннее стандартное отклонение опционов.
В первом случае за период действия контракта фьючерсная цена согласно формулам (14.8) и (14.7) должна превысить значение в:
8000 + 500- 8500руб.
или опуститься ниже:
8000 -250 = 7750руб.
Инвестор заинтересован больше в падении цены, чем в росте, поскольку куплены два опциона пут.
Во втором случае опционы подорожают вследствие роста неопределенности на рынке, поэтому их можно будет продать с прибылью.
б) Короткий стрип.
Формируя короткий стрип, инвестор продает один опцион колл по цене покупателя, т.е. за 180 руб. и два опциона пут за 130 руб. В сумме он получает премию в 440 руб. Инвестор получит прибыль, если: 1) фьючерсная цена сильно не изменится или 2) уменьшится внутреннее стандартное отклонение опционов.
В первом случае фьючерсная цена не должна упасть ниже:
8000 -220 = 7780руб.
или превысить:
8500 + 440- 8940руб.
Во втором случае выигрыш получится за счет падения стоимости опционов вследствие наступления более спокойной конъюнктуры рынка. Инвестор получит прибыль, выкупив опционы по более низкой цене,
14.3.2. Спрэд
14.3.2.1. Вертикальный спрэд
14.3.2.1.1. Спрэд быка
Спрэд быка состоит из опционов одного вида, т. е. или колл или пут, с одной датой истечения контрактов, но разными ценами исполнения. Опцион с более низкой ценой исполнения покупается, с более высокой ценой исполнения - продается. Рассмотрим спрэд из опционов колл.
Пример.
Цена спот акции 100 руб. Опцион колл с ценой исполнения 100 руб. стоит 3 руб., опцион колл с ценой исполнения 105 руб. стоит 1 руб. График выигрышей-проигрышей по спрэду к моменту истечения контрактов представлен на рис. 14 13.
Рис. 14.13. Выигрыши-проигрыши по спрэду быка из опционов колл к моменту истечения срока действия контрактов
Как видно из графика, к моменту истечения срока действия контрактов инвестор получит небольшой выигрыш, если курс акции вырастет, или проигрыш, если он упадет. Максимальный проигрыш равен разности между уплаченной за первый опцион премией и полученной премией от продажи второго опциона, а именно:
*—3-1=2 руб.
Данный проигрыш возникнет при цене акции меньше или равной 100 руб., т. е. цене исполнения первого опциона, так как ни один контракт не будет исполнен. Максимальный выигрыш получается при цене спот акции больше или равной 105 руб. т. е. цене исполнения второго опциона. Его можно рассчитать по формуле:
максимальный выигрыш = X2-Xx-i. (14.9) В нашем примере он равен:
105 —100-2 = 3руб.
Формула (14.9) получается на основе следующих рассуждений. Если к моменту истечения опционов цена спот базисного актива равна цене исполнения второго опциона, т.е. 5 = , выигрыш от первого опциона составит S - , но поскольку 5 = Х2, то он равен
Х2 - . В издержках учитываем уплаченную за спрэд сумму /. Отсюда получается формула (14 9). Если в этот момент 5 > Х2, то будет исполнен и первый и второй опционы. В сумме исполнение опционов дает инвестору результат:
(S-A'i)-(S-X2) = A'2-X1.
Скорректировав его на уплаченную премию, вновь получаем формулу (14.9).
Нулевой результат по сделке расположен на отрезке между ценами исполнения. В такой ситуации будет исполнен только первый опцион. Поэтому цену спот акции для нулевого результата по спрэду найдем из равенства:
S - х{ -1' = 0 или
(14.10)
В примере она равна:
100+2 = 102 руб.
Выигрыши-проигрыши по спрэду быка можно рассчитать на основе таблицы 14.5,
Таблица 14.5. Результаты покупателя спрэда быка к моменту истечения контрактов (опционы колл; Х} - цена исполнения первого опциона; Х2 - цена исполнения второго опциона)
Цена акции Финансовый результат
5 < а;
%, <s<%? S-X-i
s> х2 X2-Xt-i
Инвестор выигрывает от роста цены акции, поэтому совокупная дельта позиции положительна. Выигрыш и проигрыш инвестора ограничены, поэтому при значительном росте или падении цены акции дельта позиции падает до нуля. Гамма, вега и тета позиции близки к нулю. Поскольку вега и тета мало отличаются от нуля, то спрэд быка защищает инвестора от эффектов веги и теты, т.е. изменения стоимости портфеля вследствие изменения внутренней волатильности и уменьшения срока действия контрактов. Это результат объединения опционов с противоположными позициями - длинной и короткой. Поэтому спрэд быка можно держать длительное время без существенных потерь в связи с эффектами теты или веги. Спрэд целесообразно использовать в ситуации, когда инвестор ожидает роста цены базисного актива, но хотел бы застраховаться от потерь вследствие изменения внутренней волатильности и падения временной стоимости опционов. С помощью такой стратегии можно играть на повышение в течение относительно длительного периода времени, поскольку спрэд нейтрален к эффекту теты. Однако он начинает заметно сказываться, когда до истечения опционов остается порядка 30 дней. Поэтому, если инвестор ошибся в прогнозах роста цены, ему следует закрыть позицию не позже этого момента, чтобы избежать потерь за счет уменьшения временной стоимости.
Приведем пример спрэда быка на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 3 мая 2005 г. на бирже РТС.
Пример.
Цена июньского фьючерса на акции РАО ЕЭС равна 8250 руб. Июньские опционы колл на данный контракт с ценой исполнения 8000 руб. и 8500 руб. имеют следующие котировки:
колл А-850фуб. колл Х=8000руб.
продажа покупка продажа покупка
200 180 450 430 .. — - - -
Формируя спрэд быка, инвестор покупает опцион колл с ценой исполнения 8000 руб. по цене продавца, т.е. за 450 руб. и продает опцион колл с ценой исполнения 8500 руб. за 180 руб. В сумме он уплачивает премию в 270 руб. Инвестор получит нулевой результат-если к моменту истечения контракта фьючерсная цена, согласно формуле (14.10), составит:
8000 + 270 = 8270руб.
Если за период действия контракта фьючерсная цена окажется больше 8270 руб., инвестор получит прибыль. При этом максимальный выигрыш согласно формуле (14.9) составит:
8500 - 8000 - 270 = 230 руб.
Если за период действия контракта фьючерсная цена не превысит 8270 руб., инвестор получит убыток. При этом максимальный проигрыш равен разности между уплаченной и полученной премиями, т.е.;
450-180 = 270 руб.
Еще одна сторона привлекательности спрэда быка состоит в том, что он позволяет создать практически такой же результат как и по базисному активу, но при ограничении величины проигрыша.
Пример.
Инвестор ожидает роста цены акции. Он может купить акцию, однако риск ошибки прогноза является большим. Можно купить опцион колл. Однако инвестор проиграет, если цена не вырастет, и опцион потеряет временную стоимость. Лучшим вариантом действий будет спрэд быка, поскольку он нейтрален к эффекту теты, но выигрыш по спрэду ограничен. Чтобы создать результат аналогичный покупке одной акции, необходимо общую дельту позиции по спрэду сделать равной единице. Это требует открыть несколько позиций спрэда быка. Пусть дельта спрэда составляет 0,21. Дельта акции равна единице. Тогда инвестор должен открыть 5 позиций по спрэду быка. В совокупности пять позиций имеют дельту близкую к единице и дают эффект равный покупке одной акции. Если прогнозы инвестора не оправдаются в отношении роста цены, он закроет свои позиции npatf-
тически без потерь (при условии, что до истечения опционов остается больше чем 30 дней).
Наиболее простой стратегией при повышении цены базисного актива является покупка опциона колл. Однако следует оценить возможную величину ее роста. Если прогнозируется значительный подъем, то целесообразно купить колл. Падение временной стоимости опциона перекроется выигрышем от роста цены актива. Если инвестор не уверен в сильном повышении цены и волатильности базисного актива, то лучше открыть спрэд быка, чтобы уменьшить риски веги и теты. Кроме того, спрэд дешевле прямого опциона колл и, следовательно, имеет более низкую точку безубыточности. Поскольку спрэд дешевле, то это означает, что он предлагает в случае выигрыша более высокий уровень доходности.
Спрэд быка можно использовать для извлечения арбитражной прибыли, если инвестор полагает, что опцион с более высокой ценой исполнения переоценен или опцион с более низкой ценой исполнения недооценен. Инвестор ожидает, что после открытия позиции разница между премиями опционов уменьшится. Арбитражную стратегию можно строить на основе значений внутренней волатильности опционов.
Пример.
Внутренняя волатильность опциона с более низкой ценой исполнения равна 20%, опциона с более высокой ценой исполнения - 18%. Инвестор полагает, что волатильность первого опциона вырастет до 22%, а второго упадет до 16%. Тогда целесообразно сформировать спрэд быка: купить опцион с более низкой ценой исполнения и продать опцион с более высокой ценой исполнения. В результате изменения внутренней волатильности опционов их цены изменятся и инвестор получит прибыль, закрыв позиции.
Спрэд быка можно сформировать из опционов пут. Конфигурация графика выигрышей-проигрышей аналогичена графику на рис. 14.13.
Спрэд быка можно получить как на основе опционов колл так и пут. Поэтому возникает вопрос, в пользу каких опционов сделать выбор. Ответ на него можно дать, сравнив соотношение риска и доходности и точки безубыточности для каждого спрэда.
Пример.
Цена спот акции 100 руб. Спрэд быка можно сформировать, купив опцион колл с ценой исполнения 95 руб. за 7 руб., и продав колл
с ценой исполнения 100 руб. за 3 руб. Альтернативно, можно образовать спрэд из опционов пут, купив пут с ценой исполнения 95 руб. за 1 руб. и продав пут с ценой исполнения 100 руб. за 2,5 руб.
Максимальная прибыль по спрэду из опционов колл равна:
Х2 -X, -/ = 100-95-4 = 1руб., максимальный проигрыш:
7-3 = 4 руб.
Точка безубыточности составляет:
X,-И = 95+ 4 = 99руб.
прибыль I Q риск 4
По спрэду из опционов пут максимальный выигрыш составляет:
2,5 -1 = 1,5 руб., максимальный проигрыш:
Х2 - X, -/ = 100 - 95 -1,5 = 3,5руб.
Точка безубыточности:
Х3-z = 100-1,5 = 98,5руб.
прибыль 1,5 Л —-------= — = 0,43.
риск 3,5
В данном примере следует сформировать спрэд быка из опционов пут, так как точка безубыточности наступает раньше (98,5 руб.), чем для спрэда из опционов колл (99 руб.); в спрэде из опционов пут на каждую единицу риска приходится 0,43 единицы потенциальной прибыли, в спрэде из опционов колл только 0,25 единиц. Надо также учесть, что при формировании спрэда из опционов пут инвестор сразу получает сумму 1,5 руб. на разности премий. В случае спрэда из опционов колл он сразу уплачивает 4 руб. на разности премий. Кроме того, если принять во внимание процентные начисления на суммы премий, то полученную премию по опционам пут можно сразу разместить под процент. Напротив, уплатив премию по опционам колл, инвестор упустит возможность получить на них процент.
Инвестор может сформировать спрэд быка не сразу, а после того, как изменятся его ожидания в отношении роста цены базисного актива.
Пример.
Инвестор прогнозирует существенный рост цены акции и покупает колл без выигрыша на акцию с ценой исполнения 100 руб. за 2 руб. Цена бумаги выросла до 105 руб. Теперь он полагает, что дальнейший рост будет небольшим, поэтому продает колл А ТМ с ценой исполнения 105 руб. за 2 руб. Таким образом, вследствие роста курса акции инвестору удалось продать второй опцион по более высокой цене, и потенциал прибыльности спрэда возрос. В то же время такие действия являются более рискованными, так как, если до момента продажи второго опциона упадет внутренняя волатильность опционов, то инвестор может и проиграть.
14.3.2Л.2. Спрэд медведя
Спрэд медведя состоит из опционов одного вида, т. е. или колл или пут, с одной датой истечения контрактов, но разными ценами исполнения. Опцион с более низкой ценой исполнения продается, с более высокой ценой исполнения - покупается. Рассмотрим спрэд из опционов колл.
Пример.
Цена спот акции 100 руб. Опцион колл с ценой исполнения 95 руб. стоит 7 руб., опцион колл с ценой исполнения 100 руб. стоит 3 руб. График выигрышей-проигрышей по спрэду к моменту истечения контрактов представлен на рис. 14.14.
Рис. 14.14. Выигрыши-проигрыши по спрэду медведя из опционов колл к моменту истечения срока действия контрактов
.___________ _______ Глава 14. Опционные стратегии
К моменту истечения срока действия контрактов инвестор получит небольшой выигрыш, если курс акции упадет, или проигрыш, если он вырастет. При формировании спрэда инвестор получает денежные средства в сумме разности между премиями опционов. Она составляет возможный максимальный выигрыш равный:
/ - 7-3 - 4руб.
Данный выигрыш инвестор получит при цене акции меньше или равной 95 руб., т. е. цене исполнения проданного опциона, так как ни один контракт не будет исполнен. Максимальный проигрыш возникнет в ситуации, когда цена спот акции равна или больше цены исполнения второго опциона, т. е. 100 руб. Его можно определить по формуле:
максимальный проигрыш = -(Х2 - Хх) +1. (14.11)
Он составит:
-(100- 95) + 4 = ~\руб.
Формула (14.11) получается следующим образом. Если к моменту истечения контракта цена спот базисного актива равна более высокой цене исполнения, т.е. 5 = Х2, то проигрыш от проданного опциона составит S - Л ,, но поскольку 5 = Х2, то он равен Х2-Х}. Данный проигрыш уменьшается на величину полученной премии. Если S > X,, будет исполнен и первый и второй опционы. В сумме их исполнение принесет инвестору убыток в размере:
Скорректировав его на полученную премию за спрэд, приходим к формуле (14.11).
Нулевой итог по сделке расположен на отрезке между ценами исполнения. В такой ситуации исполняется только первый опцион. Поэтому цену спот акции для нулевого результата можно найти из следующего равенства:
-(5- %,) + /- О
или
S = X}+i. (14.12)
В примере она равна:
95 + 4 = 99^6.
п
* ?
Таким образом, при 5 <99 руб. инвестор выигрывает, при S >99 руб. проигрывает. Выигрыши-проигрыши по спрэду медведя можно рассчитать на основе таблицы 14.6.
Таблица 14.6. Результаты покупателя спрэда медведя к моменту истечения контрактов (опционы колл; Х{ - цена исполнения первого опциона; Хг - цена исполнения второго опциона)
Цена акции Финансовый результат
S< X, -Н
X, < 5 < -(•S-AJ-h
S > Х2
Приведем пример спрэда медведя на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 3 мая 2005 г. на бирже РТС.
Пример.
Цена июньского фьючерса на акции РАО ЕЭС равна 8250 руб. Июньские опционы колл на данный контракт с ценой исполнения 8000 руб. и 8500 руб. имеют следующие котировки:
колл Х=8500руб колл Х=8000руб
продажа покупка продажа покупка
200 180 450 430
Формируя спрэд медведя, инвестор покупает опцион колл с ценой исполнения 8500 руб. по цене продавца, т.е. за 200 руб. и продает опцион колл с ценой исполнения 8000 руб. по цене покупателя, т.е. за 430 руб. В сумме он получает премию в 230 руб. Инвестор получит нулевой результат, если к моменту истечения контракта фьючерсная цена, согласно формуле (14.12), составит:
8000 + 230 = 8230 руб.
Если за период действия контракта фьючерсная цена окажется меньше 8230 руб., инвестор получит прибыль. При этом максимальный выигрыш равен разности полученных премий, т.е. 230 руб.
Если фьючерсная цена превысит 8230 руб., инвестор получит убыток. При этом максимальный проигрыш согласно формуле (14.11) равен:
-(8500 -8000) + 230 - -270руб.
Спрэд можно построить с помощью опционов пут. Конфигурация графика выигрышей-проигрышей аналогична графику на рис. 14.14. Формирование спрэда требует первоначальных затрат от инвестора, так как покупаемый опцион стоит дороже продаваемого. Чтобы ответить на вопрос, из каких опционов создать спрэд, необходимо, как и в случае спрэда быка, сравнить точки безубыточности и соотношение прибыль/риск по двум позициям.
По спрэду медведя инвестор выигрывает от падения цены базисного актива, поэтому совокупная дельта позиции отрицательна. Выигрыш и проигрыш ограничены. Это означает, что при значительном росте или падении цены базисного актива дельта позиции падает до нуля. Гамма, вега и тета спрэда близки к нулю. Спрэд целесообразно использовать, когда инвестор ожидает падения цены базисного актива, но хотел бы застраховаться от изменения внутренней волатильности и падения временной стоимости опционов. Инвестор может играть на понижение в течение длительного времени, поскольку спрэд нейтрален к эффекту теты. Однако он начинает заметно сказываться, когда до истечения опционов остается порядка 30 дней. Поэтому в этот момент позицию целесообразно закрыть. Спрэд медведя привлекателен еще тем, что он позволяет создать практически такой же результат как и по базисному активу при ограниченной величине проигрыша.
Пример.
Инвестор ожидает падения цены акции. Можно осуществить короткую продажу акции, однако велик риск ошибки прогноза. Можно купить опцион пут, однако существует риск потерять временную стоимость опциона. Лучшей стратегией будет спрэд медведя, поскольку он нейтрален к эффекту теты. Выигрыш по спрэду ограничен. Поэтому, чтобы создать результат аналогичный продаже одной акции, необходимо общую дельту позиции по спрэду сделать равной минус единице. Это потребует открыть несколько позиций по спрэду медведя. Пусть дельта спрэда равна -0,21. Дельта короткой акции равна минус единице. Инвестор должен открыть 5 позиций по спрэду. В совокупности пять позиций имеют дельту близкую к минус еди
нице и дают эффект равный продаже одной акции. Если прогнозы инвестора не оправдаются в отношении падения цены, он закроет позиции практически без потерь (при условии, что до истечения опционов остается больше 30 дней).
Если сравнить построение спрэда быка и медведя, то внимательный читатель заметит, что покупка спрэда быка аналогична продаже спрэда медведя, и наоборот.
14.3,2.1.3. Обратный спрэд быка
Обратный спрэд быка включает короткий опцион пут с более низкой ценой исполнения и длинный опцион колл с более высокой ценой исполнения При таком сочетании премия опциона пут должна быть больше премии опциона колл. Поэтому при формировании спрэда инвестор получает средства в сумме разности премий опционов. Конфигурация спрэда показана на рис. 14.15.
Инвестор использует такую стратегию, когда рассчитывает на определенное повышение курса базисного актива, однако его главная цель состоит в получении прибыли на отрезке А'|Л'-,. Выигрыши-проигрыши по спрэду можно рассчитать с помощью таблицы 14.7
Таблица 14.7 Результаты покупателя обратного спрэда быка к моменту истечения контрактов (Х{ - цена исполнения опциона пут; - цена исполнения опциона колл)
Цена акции Финансовый результат
s <х}
x.<s< х2 +Z
s>x2 S-X2+i
14.3.2,1.4. Обратный спрэд медведя
Обратный спрэд медведя включает длинный опцион пут с более низкой ценой исполнения и короткий опцион колл с более высокой ценой исполнения. Конфигурация спрэда показана на рис.14.16. Инвестор использует данную стратегию, когда рассчитывает на понижение курса базисного актива, но главная его цель состоит в получении прибыли на отрезке XtX2. Выигрыши-проигрыши по спрэду можно рассчитать с помощью таблицы 14.8.
।
выигрыши
I
проигрыши
Рис. 14.16. Обратный спрэд медведя
Таблица 14.8. Результаты покупателя обратного спрэда медведя к моменту истечения контрактов (Xt - цена исполнения опциона пут; Х2 - цена исполнения опциона колл)
Цена акции - - Финансовый результат - .
5 < X, А , - .S' 4 /
1 2*? IA Со 1Л 1 + i
s>x2 -(S-X,) + /
14.3,2.1.5. Бэкспрэд
Бэкспрэд создают за счет продажи и покупки или опционов колл или пут с одной датой истечения контрактов, но разными ценами исполнения. Покупают больше опционов чем продают.
Бэкспрэд из опционов колл
Рассмотрим бэкспрэд из опционов колл, в котором продается один опцион, а покупаются два. Продаваемый опцион имеет более низкую цену исполнения.
Пример.
Цена спот акции 100 руб. Инвестор продает опцион колл с ценой исполнения 100 руб. за 3 руб. и покупает два опциона колл с ценой исполнения 105 руб. по 1 руб. за каждый. График выигрышей-проигрышей покупателя бэкспрэда к моменту истечения срока действия контрактов представлен на рис. 14.17. Инвестор понесет убыток, если к моменту истечения контрактов цена спот акции не сильно отклонится от цены исполнения длинных опционов, т. е. 105 руб. При существенном снижении или повышении цены акции инвестор получит прибыль. Величина ее ограничена при падении курса и не ограничена в случае роста стоимости бумаги. При открытии позиции инвестор получает денежные средства, так как премия продаваемого опциона больше суммы премий покупаемых опционов. В примере сумма равна: i = 3-2 = 1руб. Она составляет выигрыш инвестора на момент истечения срока действия опционов, если цена спот акции будет ниже или равна цене исполнения проданного опциона, т.е. 100 руб., поскольку ни один контракт не будет исполнен.
выигрыши
проигрыши
Рис. 14,17. Выигрыши-проигрыши покупателя бзкспрэда к моменту истечения срока действия опционов
Найдем точки безубыточности позиции. Правую точку можно определить из равенства:
2(S-X2)~(S-X}) + i = 0,
так как будут исполнены все опционы. Отсюда:
5-2%2-Xj ~i. (14.12)
В примере правая точка безубыточности равна:
2-105-100-1 = 109/туб.
Левую точку безубыточности найдем из равенства:
-(5-%,) + / =0,
так как будет исполнен только проданный опцион. Отсюда:
S = X}+i. (14.13)
Левая точка равна:
100 + 1 = 101/туб.
Таким образом, инвестор получит убыток, если цена акции больше 101 руб., но меньше 109 руб. Максимальный проигрыш соответствует цене акции 105 руб. (это цена исполнения купленных опционов), так как будет исполнен только проданный опцион. Он равен:
X2-X\+i (14.14)
ИЛИ
105-100 +1 = 4руб.
При S < 101/туб. и 5 > 109/туб. инвестор получит прибыль.
Выигрыши-проигрыши по спрэду можно рассчитать с помощью таблицы 14.9.
Таблица 14.9, Результаты покупателя бэкспрэда к моменту истечения контрактов (опционы колл; Х} - цена исполнения короткого опциона; Х2 - цена исполнения длинных опционов)
Цена акции - Финансовый результат
S<X, +/
X, < S < х2
s>x2 2(5 - Х2) - (5 - Xt) + i - 5 - (2 Х2 - Xt) + /
Бэкспрэд формируется как дельта-нейтральная позиция. Продаваемый опцион, поскольку он является без выигрыша, имеет дельту -0,5, а каждый покупаемый опцион дельту порядка +0,25. Инвестор
ожидает в большей степени роста цены акции, чем падения, поэтому покупает два опциона и продает один. Из графика видно, что результаты по спрэду не симметричны как в случае стрэддла или стрэнгла. Гамма и вега позиции положительны, следовательно, инвестор выигрывает от роста действительной волатильности акции и внутренней волатильности опционов. Тета бэкспрэда отрицательна.
Чтобы лучше представить динамику потенциальных выигрышей и проигрышей по бэкспрэду, разделим его на два компонента: спрэд медведя и длинный опцион колл. Продавая опцион колл с ценой исполнения X, и покупая колл с ценой исполнения Х2, инвестор формирует спрэд медведя, и, следовательно, выигрывает от падения цены акции. Одновременно он покупает опцион колл с ценой исполнения Х2 и поэтому выигрывает от роста цены акции.
Приведем пример бэкспрэда на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 3 мая 2005 г. на бирже РТС.
Пример.
Цена июньского фьючерса на акции РАО ЕЭС равна 8250 руб. Июньские опционы колл на данный контракт с ценой исполнения 8000 руб. и 8500 руб. имеют следующие котировки:
КОЛЛ Х=д500руб. колл Л-8000руб.
продажа покупка продажа покупка
200 180 450 430
Формируя бэкспрэд, инвестор покупает два опциона колл с ценой исполнения 8500 руб. по цене продавца, т.е. за 200 руб. и продает один опцион колл с ценой исполнения 8000 руб. по цене покупателя, т.е. за 430 руб. В сумме он получает премию в 30 руб. Инвестор получит нулевой результат, если к моменту истечения контракта фьючерсная цена, согласно формулам (14.12) и (14.13), составит:
5 - 2Х2 - А; - i - 2 • 8500 - 8000 - 30 = 8970руб.
и
S = а; + i - 8000 + 30 = 8030руб.
Если за период действия контракта фьючерсная цена окажется меньше 8030 руб., инвестор получит прибыль. При этом максимальный выигрыш равен разности полученных премий, т.е. 30 руб.
Если фьючерсная цена превысит 8970 руб., инвестор получит прибыль. Ее величина потенциально не ограничена. При 8030 <5 < 8970руб. возникнет убыток. Его максимальная величина согласно формуле (14.14) равна:
Х2 - X, + / = 8500 - 8000 + 30 = 470руб.
при фьючерсной цене 8500 руб.
Бэкспрэд из опционов пут
Бэкспрэд из опционов пут включает короткие опционы с более высокой ценой исполнения и длинные опционы с более низкой ценой исполнения. Как отмечалось выше, покупается больше опционов, чем продается.
Пример.
Цена спот акции 100 руб. Инвестор продает опцион пут с ценой исполнения 100 руб. за 3 руб. и покупает два опциона пут с ценой исполнения 95 руб. по 1 руб. каждый. График выигрышей-проигрышей покупателя бэкспрэда к моменту истечения срока действия контрактов представлен на рис. 14.18. Как из него следует, покупатель проиграет, если цена акции не сильно отклонится от цены исполнения длинных опционов (X,), и выиграет при существенном росте или падении курса бумаги. При формировании бэкспрэда инвестор получает положительную премию, равную разности цен опционов. Она равна: /^3-2 = 1 руб. Правую точку безубыточности определяем из равенства:
-(Х2-5) + /-0 ,
так как будет исполнен только второй опцион. Отсюда:
S = X2-i. (14.15)
Она равна:
IOO-1 - 99руб.
Левую точку безубыточности находим из равенства:
-(Х2-5) + 2(Х|-5) + /-0,
так как будут исполнены все опционы. Отсюда:
8 = 2Х{-Х2+1. (14.16)
Она составляет:
2-95 -100 +1 = 91руб.
Если к моменту истечения срока действия опционов 91руб. <S < 99 руб,, инвестор несет убыток. Максимальный проигрыш будет при 5 = Х{, так как в этом случае исполняется только проданный опцион. Он равен:
X2-Xx-i (14.17)
или
100-95-1 = 4руб.
Рис. 14.18. Выигрыши-проигрыши покупателя бэкспрэда из опционов пут к моменту истечения срока действия контрактов
Если $<9\руб. или 5 >99руб. инвестор получает прибыль. При5 <9\руб. она максимальна при падении курса бумаги до нуля. При 5 > 99руб. выигрыш равен разности премий, т.е. 1 руб.
Бэкспрэд формируется как дельта-нейтральная позиция. Инвестор в большей степени ожидает падения цены базисного актива, чем роста, и покупает два опциона пут. Гамма и вега позиции положительны. Поэтому инвестор выигрывает как от роста волатильности акции, так и внутренней волатильности опционов. Тета бэкспрэда отрицательна.
Чтобы лучше представить потенциальную динамику выигрышей по бэкспрэду, его можно разделить на два компонента: спрэд быка и длинный опцион пут. Покупая пут с ценой исполнения Х} и продавая с ценой исполнения^, инвестор формирует спрэд быка, и, следовательно,
должен выигрывать от роста цены акции. Приобретая опцион пут с ценой исполнения А\ он будет также выигрывать от ее падения.
Приведем пример бэкспрэда на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 20 июня 2005 г. на бирже РТС.
Пример.
Цена сентябрьского фьючерса на акции РАО ЕЭС равна 9122 руб. Сентябрьские опционы пут на данный контракт с ценой исполнения 9000 руб. и 9500 руб. имеют следующие котировки:
колл Х=9500руб колл Х'9000руб
продажа покупка продажа покупка
536 499 241 220
Формируя бэкспрэд, инвестор покупает два опциона пут с ценой исполнения 9000 руб. по цене продавца, т.е. за 241 руб. и продает один опцион пут с ценой исполнения 9500 руб. по цене покупателя, т.е. за 499 руб. В сумме он получает премию в 17 руб. Инвестор получит нулевой результат, если к моменту истечения контракта фьючерсная цена, согласно формулам (14.15) и (14.16), составит:
- / - 9500 - 17 - 9483руб.
и
2%! - Х2 + / - 2 9000-9500 + 17-8517руб.
Если за период действия контракта фьючерсная цена окажется больше 9483 руб., инвестор получит прибыль. При этом максимальный выигрыш равен разности полученных премий, т.е. 17 руб.
Если фьючерсная цена будет ниже 8517 руб., инвестор получит прибыль. Ее величина ограничена падением фьючерсной цены до нуля. При 8517 < 5 < 9483руб. возникнет убыток. Его максимальная величина согласно формуле (14.17) равна:
Х2 - Х( - / - 9500 - 9000 -17-483руб.
при фьючерсной цене 9000 руб.
f4.3.2.16. Рейтио спрэд
Рейтио спрэд создают за счет продажи и покупки или опционов колл или пут с одной датой истечения контрактов, но разными ценами исполнения. Продается больше опционов, чем покупается.
Рейтио спрэд из опционов колл
Рассмотрим рейтио спрэд из опционов колл, в котором продается два опциона, а покупается один. Продают опционы с более высокой ценой исполнения.
Пример.
Цена спот акции 100 руб. Инвестор продает два опциона колл с ценой исполнения 105 руб. по 1 руб. каждый и покупает один опцион колл с ценой исполнения 100 руб. за 3 руб. График выигрышей-проигрышей покупателя бэкспрэда к моменту истечения срока действия контрактов представлен на рис. 14.19. Как из него следует, инвестор проиграет, если к моменту истечения контрактов цена спот акции существенно отклонится от цены исполнения проданных опционов, т. е. 105 руб. В случае роста цены потенциальный проигрыш не ограничен, при падении цены - ограничен. Если курс акции не сильно отклонится от цены исполнения коротких опционов, инвестор получит небольшую прибыль. Открывая позицию, инвестор уплачивает сумму денег равную разности премий опционов, так как премия длинного опциона больше суммы премий коротких опционов. В примере она равна: / = 3 — 2 = 1 руб. Данная сумма составит проигрыш инвестора на момент истечения срока действия контрактов, если цена спот акции будет равна или ниже цены исполнения длинного опциона, т.е. 100 руб., поскольку ни один контракт не будет исполнен.
Рис. 14.19. Выигрыши-проигрыши покупателя рейтио спрэда к моменту истечения срока действия опционов
Найдем точки безубыточности позиции. Правую точку можно определить из равенства:
-2(5-*2)+(5-^)-/ = 0, поскольку все опционы будут исполнены. Отсюда:
S = 2X2-Xl-i. (14.18)
Она равна:
2-105-100-1-109^6.
Левую точку безубыточности найдем из равенства: (S-X,)-/ = 0, так как будет исполнен только купленный опцион. Отсюда:
+ /. (1419)
Левая точка равна:
100 +1 — 101 руб.
Таким образом, инвестор получит прибыль, если цена акции будет больше 101 руб., но меньше 109 руб. Максимальный выигрыш соответствует цене акции 105 руб. (цена исполнения проданных опционов), так как будет исполнен только приобретенный опцион. Прибыль составит:
Х2 - Х{-i (14.20)
или
105 -100-1 - 4руб.
При S<10l/7y6. и 5 > 109руб. инвестор понесет убыток. Выигрыши-проигрыши по спрэду можно рассчитать с помощью таблицы 14.10.
Таблица 14.10. Результаты покупателя рейтио спрэда к моменту истечения контрактов (опционы колл; Х{ - цена исполнения длинного опциона; Х2 - цена исполнения коротких опционов, i - сумма двух премий)
Цена акции Финансовый результат
5 < -i
xt<s<x2 S-X}-i
s>x2 - 2(5 - Х2) + (5 - X,)- i = -S + (2Х2 - X,)- /
Рейтио спрэд формируется как дельта-нейтральная позиция. Покупаемый опцион, поскольку это опцион ATM, имеет дельту +0,5, а
каждый продаваемый опцион дельту порядка -0,25. Инвестор ожидает, что рынок останется спокойным, и курс акции не выйдет из диапазона 101-109 руб. В случае ошибки прогноза, он больше опасается падения курса бумаги, поэтому ограничивает свои потери для такой ситуации. Гамма и вега позиции отрицательны. Инвестор выигрывает от уменьшения действительной волатильности акции и внутренней волатильности опционов. В то же время он заинтересован в росте курса акции до уровня цены исполнения проданных опционов. Тета бэкспрэда положительна.
Чтобы лучше представить потенциальную динамику проигрышей по рейтио спрэду, разделим его на два компонента: спрэд быка и короткий опцион колл. Покупая колл с ценой исполнения Х} и продавая с ценой исполнения Х2, инвестор формирует спрэд быка, и, следовательно, проигрывает от падения цены акции. Продавая колл с ценой исполнения Х2, он проигрывает от роста цены акции.
Приведем пример рейтио спрэда на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 3 мая 2005г. на бирже РТС.
Пример.
Цена июньского фьючерса на акции РАО ЕЭС равна 8250 руб. Июньские опционы колл на данный контракт с ценой исполнения 8000 руб. и 8500 руб. имеют следующие котировки:
колл А-8500руб колл А-8000руб
продажа покупка продажа покупка
200 180 450 430
Формируя рейтио спрэд, инвестор покупает один опцион колл с ценой исполнения 8000 руб. по цене продавца, т.е. за 450 руб. и продает два опциона колл с ценой исполнения 8500 руб. по цене покупателя, т.е. за 180 руб. В сумме он уплачивает премию в 90 руб. Инвестор получит нулевой результат, если к моменту истечения контракта фьючерсная цена, согласно формулам (14.18) и (14.19), составит:
2 Х2 - Х{ - i - 2 ’ 8500 - 8000 — 90 — 8910руб.
и
Xt + i = 8000 + 90 + 8090/туб.
Если за период действия контракта фьючерсная цена окажется больше 8910 руб. или меньше 8090 руб. инвестор получит убыток.
Если фьючерсная цена окажется в диапазоне 8090 < 5 < 8910руб. возникнет прибыль. Ее максимальная величина согласно формуле (14.20) равна:
-i = 8500-8000-90-410руб.
при фьючерсной цене 8500 руб.
Рейтио спрэд из опционов пут
Рейтио спрэд из опционов пут включает короткие опционы с более низкой ценой исполнения и длинные опционы с более высокой ценой исполнения. Продается больше опционов чем покупается.
Пример.
Цена спот акции 100 руб. Инвестор покупает опцион пут с ценой исполнения 100 руб. за 3 руб. и продает два опциона пут с ценой исполнения 95 руб. по 1 руб. каждый. График выигрышей-проигрышей покупателя рейтио спрэда к моменту истечения срока действия контрактов представлен на рис. 14.20. Как из него следует, покупатель проиграет, если цена акции сильно отклонится от цены исполнения коротких опционов , и выиграет, если она изменится не существенно. В случае снижения цены акции потери инвестора могут быть большими, величина их ограничена падением курса бумаги до нуля. При росте курса проигрыш ограничен. Формируя спрэд, инвестор уплачивает сумму, равную разности премий опционов. Она составляет: 3-2-1руб. Правую точку безубыточности определяем из равенства:
(х2-5) + (2/1-/2)=0, поскольку будет исполнен только купленный опцион (/' - премия проданного опциона; /2 - премия купленного опциона). Отсюда:
S~ Х2+(2/| -z2) (14.21)
Она равна:
100-1 ~99руб.
Левую точку безубыточности находим из равенства: (zV2-5)-/2-2(x1-S)+2/,=0, так как исполняются все опционы. Отсюда:
5 = 2Х|-Х2+(/|-2/2). (14.22)
Она составляет:
2-95-100-И = 91руб.
Если к моменту истечения срока действия опционов 91 < 5 < 99 руб., инвестор получит прибыль. Она максимальна при 5 = , так как
исполняется только длинный опцион. Прибыль равна:
^2 +0i _2/2) (14.23)
или
100-95 -1 - 4руб.
Если S<9lpy6. или 5>99 руб., инвестор несет убыток. При S < 91руб. его величина ограничена падением курса акции до нуля. В случае 5 > 99 руб. он равен премии, уплаченной инвестором при формировании позиции, т. е. 1 руб.
Рис. 14.20. Выигрыши-проигрыши покупателя рейтио спрэда из опционов пут к моменту истечения срока действия контрактов
Рейтио спрэд формируется как дельта-нейтральная позиция. Инвестор ожидает, что курс акции снизится до цены исполнения проданных опционов. В случае ошибки прогноза он больше опасается роста стоимости акции, поэтому ограничивает свои потери для такой ситуации. Поскольку продается больше опционов, чем покупается, то инвестор выигрывает как от падения волатильности акции, так и внутренней волатильности опционов. Вследствие этого гамма и вега позиции отрицательны. Тета положительна.
Чтобы лучше представить потенциальную динамику проигрышей по рейтио спрэду, разделим его на два компонента: спрэд медведя и
короткий опцион пут. Продавая пут с ценой исполнения Х} и покупая пут с ценой исполнения Х2, инвестор формирует спрэд медведя, и, следовательно, проигрывает от роста цены акции. Продавая опцион пут с ценой исполнения Xt, он также проигрывает от ее падения.
Приведем пример бэкспрэда на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 20 июня 2005 г. на бирже РТС.
Пример.
Цена сентябрьского фьючерса на акции РАО ЕЭС равна 9122 руб. Сентябрьские опционы пут на данный контракт с ценой исполнения 9000 руб. и 9500 руб. имеют следующие котировки:
колл Х=9500руб колл ,¥=9000руб
продажа покупка продажа покупка
536 499 241 220
Формируя рейтио спрэд, инвестор покупает один опцион пут с ценой исполнения 9500 руб. по цене продавца, т.е. за 536 руб. и продает два опциона пут с ценой исполнения 9000 руб. по цене покупателя, т.е. за 220 руб. В сумме он уплачивает премию в 96 руб. Инвестор получит нулевой результат, если к моменту истечения контракта фьючерсная цена, согласно формулам (14.21) и (14.22), составит:
9 5 00 + (2 • 2 20 — 5 3 6) = 9404 руб.
и
2 • 9000 - 9500 + (536 - 2•220)= 8596 руб.
Если за период действия контракта фьючерсная цена окажется больше 9404 руб. или меньше 8596 руб., инвестор получит убыток. Если фьючерсная цена будет в диапазоне 8596 <S <9404руб. возникнет прибыль. Ее максимальная величина согласно формуле (14.23) равна:
9500 - 9000 + (2 220-536) = 404 руб.
при фьючерсной цене 9000 руб.
14.3.2.1.7. Спрэд бабочка (сэндвич)
Спрэд бабочка состоит из опционов с тремя разными ценами исполнения, но одинаковым сроком истечения контрактов. Он включает
длинный опцион колл с более низкой ценой исполнения Х{, опцион колл с более высокой ценой исполнения Х3 и два коротких опциона колл с ценой исполнения Х2, которая находится посредине между Az, и А\. Поэтому Х3 - Х2 = Х2 - Х1. Обычно цена Х2 лежит близко к текущему курсу базисного актива. Такой спрэд требует небольших начальных затрат. График выигрышей-проигрышей покупателя спрэда представлен на рис. 14.21.
Рис. 14.21. Спрэд длинная бабочка
Как следует из графика, инвестор проиграет, если к моменту истечения контрактов цена базисного актива существенно отклонится от цены X' вправо или влево. Если рынок останется спокойным, покупатель спрэда получит небольшой выигрыш. Выигрыши-проигрыши инвестора можно рассчитать с помощью таблицы 14.11.
Таблица 14.11. Результаты покупателя спрэда бабочка к моменту истечения контрактов (опционы колл; - цена исполнения длинного опциона; Х2 - цена исполнения коротких опционов; Х3 - цена исполнения длинного опциона, i - сумма премий)
Цена акции Финансовый результат
S<X^
। i I । I । VI V S-X'-i
Х2 < 5 < Х3 X3-S-i*
S > Х3 -1
*(S-Xx)-2(S-X2)-i = X3-S-i
** (S - %|) - 2(s - Х2) + (5 - %з) -i = -/
Правую точку безубыточности можно найти из равенства: (5-Л'|)-2(5-А'2)-/ = 0
ИЛИ
S = 2X2-X}-i = X3-L (14.24)
Левую точку безубыточности найдем из равенства:
S-X{ -/ = 0
или
S = X\+i. (14.25)
Спрэд бабочку можно создать с помощью опицонов пут: инвестор покупает один опцион с ценой исполнения Х{, один опцион с ценой исполнения X, и продает два опциона с ценой исполнения Х2, лежащей посередине между Х} и Х}. Конфигурация графика аналогична спрэду из опционов колл. Спрэд длинная бабочка похож на короткий стеллаж, однако имеет то преимущество, что ограничивает риск, связанный с существенным повышением или понижением цены базисного актива.
Рис. 14.22. Спрэд короткая бабочка
Спрэд может быть коротким. Его формируют в обратном порядке, т.е. продают опционы с ценами исполнения и Х3 и покупают два опциона с ценой исполнения Х2. График спрэда представлен на рис. 14.22. Как из него следует, к моменту истечения опционов инвестор получит небольшой выигрыш при существенном росте или падении цены базисного актива и понесет небольшой убыток при спокойном рынке. Спрэд короткая бабочка похож на длинный стеллаж, но имеет тот недостаток, что ограничивает выигрыши инвестора.
Спрэд бабочку можно представить как одновременное сочетание спрэдов быка и медведя, у которых один из опционов имеет одинаковую цену исполнения (см. рис. 14.23 и 14.24).
Рис, 14.23. Спрэд длинная бабочка
Рис. 14.24. Спрэд короткая бабочка
14.3.2.1.8. Спрэд кондор
Спрэд кондор формируют из четырех опционов колл с одной датой истечения контрактов, но разными ценами исполнения. Длинный кондор включает покупку опциона с ценой исполнения , продажу опционов с ценами исполнения Х2 и Хъ и покупку опциона с ценой исполнения Х4. При этом Х4 - Х3 = Х2- Х}. При открытии позиции обычно первый и второй опционы являются с выигрышем, второй и третий - с проигрышем. График спрэда к моменту срока истечения опционов представлен на рис. 14.25.
Рис. 14.25. Спрэд длинный кондор
Как из него следует, к моменту истечения контрактов инвестор понесет небольшой убыток, если курс базисного актива сильно упадет или вырастет. При спокойном рынке он получит небольшой выигрыш. Выигрыши-проигрыши инвестора можно рассчитать с помощью таблицы 14.12.
Правую точку безубыточности найдем из равенства:
ИЛИ
+ х2 - - / = Х4 - 5 - /. (14.26)
Левую точку безубыточности найдем из равенства:
5 - X, - I - О
или
5 — X [ 4- Z .
(14.27)
Таблица 14.12. Результаты покупателя спрэда кондор к моменту истечения контрактов (опционы колл; Х]7 Х4 - цены исполнения длинных опционов колл; Х2, Х3 - цены исполнения коротких опционов колл, i - сумма премий)
Цена акции Финансовый результат
-/
Х,<5<Х2 5-Х,-/
X2<S< X,
X, < 5 < Х4 Х4-5-/”
5 > Х4 ~ /
‘(5- X,)-(5- X2)-z = Х2 - X,-/.
**(5-Х,)-(5-Х2)-(5-Х3)-/ = Х4-5-/.
“•(5-Х1)-(5-Х2)-(5-Х3)+(5-Х4)-/ = -/.
В обратном порядке создают спрэд короткий кондор, т.е. продают опционы колл с ценами исполнения Х} и Х4 и покупают опционы с ценами исполнения Х2 и Х3. График спрэда к моменту истечения времени действия контрактов представлен на рис. 14.26.
проигрыши
Рис. 14.26. Спрэд короткий кондор
Длинный и короткий кондор можно создать с помощью опционов пут. Конфигурация графиков будет аналогична рис. 14.25. и 14.26.
Длинный кондор похож на короткий стрэнгл, однако с ограниченной величиной возможных потерь; короткий кондор похож на длинный стрэнгл, но с ограниченным потенциалом выигрыша.
14.3.3. Временной спрэд
Временной спрэд состоит из опционов или колл или пут с одной ценой исполнения, но разными датами истечения контрактов. Один опцион продается, другой - покупается. Если продается опцион с ближней датой, а покупается с дальней датой истечения контракта, позицию именуют длинным временным спрэдом или горизонтальным спрэдом быка. Если покупается опцион с ближней датой и продается с дальней датой истечения, то коротким временным спрэдом или горизонтальным спрэдом медведя.
14.3.3.1. Длинный временной спрэд
Рассмотрим длинный временной спрэд на примере опционов колл.
Пример.
Цена спот акции 100 руб. Инвестор продает трехмесячный опцион колл на акцию с ценой исполнения 100 руб. за 3 руб. и покупает четырехмесячный опцион с этой же ценой исполнения за 4 руб. Конфигурация спрэда представлена на рис. 14.27.
Рис. 14.27. Выигрыши-проигрыши по длинному временному спрэду к моменту истечения срока действия первого опциона
Как следует из графика, если к моменту истечения первого опциона цена спот акции не сильно отклонится от цены исполнения, инвестор
получит небольшую прибыль. Если курс бумаги существенно упадет или вырастет, он понесет небольшие убытки. Такой результат можно объяснить следующим образом. При S = X проданный опцион истечет не исполненным, и инвестор в качестве прибыли получит его временную стоимость. До окончания срока действия второго (длинного) опциона остается один месяц. За прошедшие три месяца он также терял временную стоимость, но с меньшей скоростью, чем первый. Поэтому на день истечения первого опциона второй сохранит еще часть временной стоимости. Продав его, инвестор закроет позицию и получит выигрыш на разнице временных стоимостей опционов. Если цена акции чуть ниже 100 руб., первый опцион не будет исполнен. Цена второго несколько упадет Инвестор получит прибыль, хотя и в меньшем размере. Если цена акции несколько превысит 100 руб., то первый опцион будет исполнен Поэтому прибыль по позиции также уменьшится. При сильном росте курса акции оба опциона практически теряют временную стоимость, и их цена равна внутренней стоимости, независимо от того, что первый опцион истекает в одном, а второй - в другом месяце. В результате инвестор получит убыток на разности премий опционов. Формируя позицию, он продал первый контракт за 3 руб., а купил второй за 4 руб. Таким образом, потери инвестора составят чуть меньше 1 руб., так как второй опцион возможно сохранит незначительную временную стоимость. При сильном падении курса бумаги оба опциона также теряют временную стоимость. Возможно, второй опцион сохранит небольшую временную стоимость, поэтому инвестор потеряет чуть меньше 1 руб.
Держатель длинного временного спрэда заинтересован в спокойном рынке, чтобы воспользоваться быстрым падением временной стоимости первого опциона. При росте внутренней волатильности опционов временная стоимость вырастет. Для более долгосрочного опциона она увеличится в большей степени. Поэтому инвестор выиграет от роста внутренней волатильности. Это говорит о том, что вега позиции положительна. Кроме того, по мере приближения срока истечения первого опциона его временная стоимость будет падать в большей степени, чем у второго, и, следовательно, вега (по абсолютной величине) также будет уменьшаться быстрее по сравнению со вторым опционом. Поэтому вега спрэда будет расти. Если курс бумаги не меняется, но уменьшается внутреннее стандартное отклонение, то вместо выигрыша инвестор может понести убыток, поскольку цена опциона более долгосрочного контракта упадет в большей степени, чем краткосрочного.
Значение гаммы короткого опциона отрицательно, длинного -положительно. Ее величина максимальна для опционов АТМ. Гамма
тем больше, чем ближе время истечения контракта. Поэтому можно предположить, что гамма позиции должна быть отрицательной, поскольку ее абсолютная величина больше для проданного опциона. Если инвестор не закроет позицию в момент истечения срока действия первого контракта, то в следующий момент гамма позиции станет положительной, поскольку у него останется длинный опцион колл. Такая динамика гаммы говорит о том, что вначале инвестор заинтересован в снижении действительной волатильности акции и спокойном рынке. После окончания срока действия первого опциона он заинтересован в существенном росте курса бумаги. Временной спрэд дельта-нейтрален, так как дельта длинного опциона приблизительно равна +0,5, а короткого -0,5. Тета позиции положительна.
Сравнивая длинный временной спрэд с другими стратегиями, следует подчеркнуть его особенность: знаки гаммы и веги позиции противоположны. Инвестор выигрывает как в связи с убыванием времени действия контрактов, так и вследствие роста внутренней волатильности опционов. Поскольку гамма позиции отрицательна, то инвестор, с одной стороны, заинтересован в уменьшении действительной волатильности акции, а, с другой стороны, росте внутренней волатильности. Такая ситуация встречается на рынке не часто. Ее можно проиллюстрировать на следующем примере. Наступает день, когда компания объявит о своих доходах за истекший период. В преддверии этого момента курс акций не испытывает существенных колебаний, поскольку еще не известен точный результат деятельности предприятия. Курс изменится только после обнародования соответствующих цифр. Однако неопределенность ситуации увеличивается, т.е. растет риск, связанный с акцией. Это вызывает рост внутреннего стандартного отклонения опционов.
Временной спрэд главным образом позволяет выигрывать на падении временной стоимости краткосрочного опциона, поэтому позицию целесообразно открыть, когда до истечения продаваемого опциона остается 30 дней и ожидается спокойный рынок. Однако возможна следующая ситуация. Когда до истечения краткосрочного опциона остается 30 дней, инвесторы, владевшие опционами, и заинтересованные держать свои позиции длительное время, начнут закрывать истекающие контракты и покупать более долгосрочные контракты. Поэтому увеличение спроса на долгосрочные опционы потребует от инвестора, открывающего позицию, уплатить более высокую премию за длинный временной спрэд. Если инвестор уже имеет позицию по спрэду, то продажи краткосрочных опционов приведут к более сильному падению их цены и возможному увеличению прибыли инвестора.
Для временного спрэда на фьючерсные контракты существуют две разновидности. Первая из них представлена опционами с разными сроками истечения на один и тот же фьючерсный контракт. Вторая включает опционы на два отличных по времени истечения фьючерсных контракта, хотя и на один базисный актив. Для второй разновидности возникает ряд особенностей, которые необходимо подчеркнуть.
Во-первых, фьючерсы для разных сроков истечения имеют разную фьючерсную цену. Их цены не обязательно одинаковым образом изменяются при изменении цены базисного актива. Поэтому ценовой спрэд между фьючерсными ценами может расширяться или сужаться. Выше было сказано, что временной спрэд дельта-нейтрален. Однако для спрэда на фьючерсные контракты второй разновидности это не следует понимать буквально, так как дельта каждого опциона измерена относительно фьючерсной цены для своего месяца. Поскольку фьючерсные цены не изменяются в строгой зависимости, то и позиция не является строго дельта-нейтральной.
Во-вторых, фьючерсные цены для разных месяцев не одинаковы. Поэтому и опционы ATM на фьючерсы для разных месяцев имеют разные цены исполнения (для опционов на акции это единая цена). В связи с этим длинный временной спрэд на фьючерсные контракты целесообразно формировать из опционов без выигрыша относительно фьючерсной цены каждого месяца.
В-третьих, инвестор может получить дополнительный выигрыш или убыток вследствие изменения ценового спрэда между фьючерсами. Если он увеличится, инвестор выиграет, поскольку или вырастет цена дальнего фьючерсного контракта, и, соответственно цена длинного опциона, или упадет цена ближайшего фьючерса, что вызовет падение стоимости проданного опциона Если ценовой спрэд сузится - упадет цена дальнего фьючерса или вырастет цена ближайшего фьючерса, - инвестор понесет убыток. Поэтому при формировании длинного временного спрэда следует прогнозировать динамику цен фьючерсных контрактов. Чтобы воспользоваться сужением спрэда между фьючерсными ценами, надо создать временной спрэд из опционов пут. Рост цены ближайшего фьючерса приведет к падению цены проданного опциона. Падение цены дальнего фьючерса вызовет увеличение стоимости длинного опциона.
Приведем пример длинного временного спрэда первой разновидности на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 20 июля 2005 г. на бирже РТС.
Пример.
Цена сентябрьского фьючерса на акции РАО ЕЭС равна 9122 руб. Сентябрьские и августовские опционы пут на данный контракт с ценой исполнения 9500 руб. имеют следующие котировки:
сентябрьский колл 9500руб. августовский колл Х=9500руб.
продажа покупка продажа покупка
157 135 64 51
Формируя длинный временной спрэд, инвестор покупает сентябрьский опцион колл, по цене продавца, т.е. за 157 руб. и продает августовский колл по цене покупателя, т.е. за 51 руб. В сумме он уплачивает премию в 106 руб.
14.3.3.2. Короткий временной спрэд
Рассмотрим короткий временной спрэд на примере опционов колл.
Пример.
Цена спот акции 100 руб. Инвестор покупает трехмесячный опцион колл на акцию с ценой исполнения 100 руб. за 3 руб, и продает четырехмесячный опцион на данную акцию за 4 руб. Конфигурация спрэда к моменту истечения срока действия первого опциона представлена на рис. 14.28.
Как следует из графика, если к моменту истечения первого контракта цена спот акции не сильно отклонится от цены исполнения опционов, инвестор понесет небольшой убыток. Если курс бумаги существенно упадет или вырастет, он получит небольшую прибыль. Данную
выигрыши
проигрыши'
Рис. 14.28. Короткий временной спрэд
динамику выигрышей и проигрышей можно объяснить следующим образом. При S = X длинный опцион истечет не исполненным, и инвестор потеряет его временную стоимость. До истечения времени второго (проданного) опциона остается один месяц. За истекшие три месяца он также терял временную стоимость, но с меньшей скоростью, чем первый. Поэтому в день истечения первого опциона второй сохранит еще некоторую цену. Купив его, инвестор закроет позицию и получит проигрыш на разнице временных стоимостей опционов. Если цена акции опустится чуть ниже 100 руб, первый опцион не будет исполнен. Стоимость второго несколько снизится. Инвестор получит убыток по той же причине, что и в предыдущем случае. Если цена акции немного превысит 100 руб, то первый опцион будет исполнен. Поэтому убыток по позиции несколько уменьшится. При сильном росте курса акции оба опциона практически теряют временную стоимость, и их цена определяется внутренней стоимостью. Поэтому инвестор получит прибыль на разности премий опционов. Формируя позицию, он получил от продажи второго опциона 4 руб. и купил первый за 3 руб. Таким образом, прибыль составит чуть меньше 1 руб, так как второй опцион возможно сохранит незначительную временную стоимость. При сильном падении курса бумаги оба опциона также теряют временную стоимость. Возможно, что второй опцион сохранит незначительную временную стоимость, поэтому инвестор получит прибыль, которая будут чуть меньше 1 руб. Таким образом, держатель короткого временного спрэда заинтересован в сильном движении рынка, чтобы воспользоваться быстрым падением временной стоимости опционов.
При росте внутренней волатильности опционов временная стоимость увеличится. Для более отдаленного опциона она вырастет в большей степени. В результате инвестор проиграет от роста внутренней волатильности и выиграет от ее падения. Это говорит о том, что вега позиции отрицательна. По мере приближения срока истечения первого опциона его временная стоимость будет падать с большей скоростью, чем у второго, и, следовательно, его вега (по абсолютной величине) также будет падать быстрее веги второго опциона. Поэтому позиция инвестора характеризуется ростом отрицательного значения веги. Гамма спрэда должна быть положительной, поскольку ее абсолютная величина больше для длинного опциона, так как он является более краткосрочным. Если инвестор не закроет позицию в момент истечения срока действия первого опциона, то в следующий момент гамма позиции станет отрицательной, поскольку у него останется короткий опцион колл. Такая динамика гаммы говорит о том, что вначале инвестор заинтересо-
Гпава 14. Опционные стратегии ван в росте действительной волатильности акции, после окончания срока действия первого опциона - в ее падении.
Спрэд дельта-нейтрален, так как дельта длинного опциона равна приблизительно +0,5, а короткого -0,5. Тета позиции отрицательна. Поэтому инвестор будет проигрывать по мере приближения срока истечения контрактов.
Сравнивая короткий временной спрэд с другими стратегиями, следует подчеркнуть его особенность: знаки гаммы и веги позиции противоположны. Поскольку гамма положительна, а вега отрицательна, то инвестор, с одной стороны, заинтересован в росте действительной волатильности акции, а, с другой стороны, уменьшении внутренней волатильности. Такая ситуация встречается на рынке не часто.
Инвестор покупает краткосрочный опцион, поэтому спрэд следует формировать на временном отрезке, когда эффект теты для него сказывается еще не сильно, т.е. до истечения контракта должно быть значительно больше 30 дней.
Для временного спрэда на фьючерсные контракты существуют две разновидности. Первая из них представлена опционами с разными сроками истечения на один и тот же фьючерсный контракт. Вторая включает опционы на два отличных по времени истечения фьючерсных контракта, хотя и на один базисный актив. Для второй разновидности возникает ряд особенностей, которые необходимо подчеркнуть.
Во-первых, позицию инвестора нельзя считать строго дельта-нейтральной, так как продаются и покупаются опционы без выигрыша на фьючерсные контракты с разными сроками истечения и, следовательно, разными фьючерсными ценами. В связи с этим короткий временной спрэд на фьючерсные контракты целесообразно формировать из опционов без выигрыша относительно фьючерсной цены соответствующего месяца. Во-вторых, инвестор может получить дополнительный выигрыш или проигрыш вследствие изменения ценового спрэда между фьючерсами. Если спрэд сузится, инвестор выиграет, поскольку или упадет цена дальнего фьючерсного контракта, и, соответственно цена проданного опциона, или вырастет цена ближайшего фьючерса, что вызовет рост стоимости длинного опциона. Если спрэд увеличится - вырастет цена дальнего фьючерса или упадет цена ближайшего фьючерса, - инвестор понесет убыток. Поэтому при формировании короткого временного спрэда следует прогнозировать возможную динамику цен фьючерсных контрактов. Чтобы воспользоваться расширением величины спрэда между фьючерсными ценами, надо создать временной спрэд из опционов пут. Рост цены дальнего фьючерса вызовет падение цены проданного
опциона. Падение цены ближнего фьючерса приведет к увеличение стоимости длинного опциона.
Приведем пример короткого временного спрэда первой разновидности на основе котировок опционов на фьючерсный контракт на акции РАО ЕЭС за 20 июля 2005 г. на бирже РТС.
Пример.
Цена сентябрьского фьючерса на акции РАО ЕЭС равна 9122 руб. Сентябрьские и августовские опционы пут на данный контракт с ценой исполнения 9500 руб. имеют следующие котировки:
сентябрьский копл Х~9500руб. августовский колл Х=9500руб.
продажа покупка продажа покупка
157 135 64 51
Формируя короткий временной спрэд, инвестор покупает августовский опцион колл по цене покупателя, т.е. за 64 руб. и продает сентябрьский колл по цене покупателя, т.е. за 135 руб. В сумме он получает премию в 71 руб.
14.4. ТОРГОВЛЯ ВОЛАТИЛЬНОСТЬЮ
Одно из преимуществ опционных стратегий состоит в том, что в ряде случаев инвестору нет необходимости знать направление изменения цены базисного актива, а достаточно ответить на вопрос, ожидаются ли сильные или слабые колебания его цены. На этой основе возникли стратегии, получившие название волатильных, и соответственно появился термин “торговля волатильностью”. В данной терминологии имеется в виду стандартное отклонение цены базисного актива. Волатильными называют стратегии, в рамках которых инвестора в первую очередь интересует факт возможного изменения курсовой стоимости базисного актива или его неизменности и только во вторую очередь - направление этого изменения.
Каждая стратегия имеет свои характеристики дельты, гаммы, теты и веги. Для волатильных стратегий дельта приблизительно равна нулю. Если какая-либо стратегия имеет большое значение дельты, то она уже не является волатильной. В этой ситуации инвестора в первую очередь интересует ожидаемое направление движения курсовой стоимости актива, а не сам факт движения в ту или иную сторону. Волатильные стратегии, для которых инвестор рассчитывает 444
на движение курса базисного актива, имеют положительные значения гаммы и веги. К ним относятся длинный стеллаж, стрэнгл, короткая бабочка, короткий кондор, бэкспрэд, короткий временной спрэд1. Стратегии, для которых инвестор рассчитывает на неизменность состояния рынка, имеют отрицательную гамму и вегу. К ним относятся короткий стеллаж, стрэнгл, длинная бабочка, длинный кондор, рейтио спрэд, длинный временной спрэд. Любая стратегия с положительной гаммой будет иметь отрицательную тету, и наоборот.
Выше мы дали характеристику волатильным стратегиям, которые представлены комбинациями и спрэдами. Сейчас остановимся на волатильных стратегиях, объединяющих опционы и базисные активы.
14.4.1. Покупка волатильности
Стратегия “покупки волатильности” используется в том случае, если ожидаются сильные колебания цены базисного актива. Инвестор формирует дельта нейтральный портфель из опциона и базисных активов. Такой портфель обладает следующими качествами, а) Поскольку он дельта-нейтрален, то при небольшом изменении цены актива его стоимость практически не изменится, так как выигрыши (проигрыши) по опциону будут компенсированы проигрышами (выигрышами) по активу, б) При изменении цены актива его дельта остается постоянной, а дельта опциона изменяется с ускорением. Поэтому при росте курса актива дельта портфеля автоматически становится положительной. Это говорит о том, что инвестор будет выигрывать при росте цены актива, и чем больше рост, тем больше выигрыш. В случае падения цены актива дельта портфеля автоматически становится отрицательной. Это означает, что инвестор будет выигрывать от падения цены актива, и чем больше падение, тем больше выигрыш. Таким образом, инвестор выигрывает при существенном изменении курса актива в любую сторону. В этом заключается суть стратегии покупки волатильности. Поясним сказанное на примере. Вначале рассмотрим случай роста цены базисного актива.
Пример 1.
Имеется опцион колл на акции. Один контракт включает 100 акций. Премия опциона в расчете на одну акцию составляет 5 руб., на контракт - 500 руб. Цена исполнения опциона равна цене спот акции
1 Как было сказано выше, гамма и вега временных спрэдов имеют противоположные знаки
и составляет 100 руб. Это означает, что дельта опциона равна 0,5. Инвестор формирует дельта-нейтральную позицию’ покупает один опционный контракт и осуществляет короткую продажу 50 акций. Дельта опционного контракта равна плюс 50:
100-0,5 -50.
Дельта каждой акции равна минус единице, поэтому общая дельта позиции по акциям составляет минус 50. Дельта портфеля равна нулю.
Пусть цена бумаги выросла на 5 руб. Потери по акциям увеличились линейно, т.е. в пропорции один к одному с ростом цены акции и составили:
50акций • 5руб. - 250руб.
Поскольку цена бумаги выросла, то выросла и дельта опциона, причем ее рост произошел не линейно, а с ускорением. Поэтому стоимость опциона также увеличивалась с ускорением. Пусть дельта опциона имела следующую динамику:
Таблица 14.13. Динамика дельты опциона
Цена акции (руб.) 100 101 102 103 104 105
Дельта 0,5 0,52 0.54 0,57 0,6 0.64
Суммируем дельты и получим изменение стоимости опциона на одну акцию:
0,52 + 0,54 + 0,57 + 0,6 т 0,64 - 2,87.
Оно равно 2,87руб. Следовательно, стоимость опционного контракта выросла на:
100ягкг/ш7 • 2,87руб. ~ 287руб.,
и премия равна теперь 787 руб. Таким образом, выигрыш инвестора на разности изменений стоимости акций и опционного контракта составил:
287-250 = 37/туб.
Чтобы получить данный выигрыш, его необходимо реализовать. Один вариант - это закрыть позиции. Однако инвестор полагает, что курс акции и дальше будет испытывать значительные изменения, и поэтому хотел бы фиксировать прибыль, не закрывая позиции. Для этого требуется сделать портфель вновь дельта-нейтральным, скорректировав в нем количество акций. В случае роста цены акции до
105 руб. дельта опциона составила 0,64. Следовательно, новая дельта опционного контракта равна:
100 0,64 = 64.
Это означает, что для поддержания дельта нейтральной позиции инвестор дополнительно продает 14 акций. Дельта позиции по акциям равна теперь минус 64, по опционному контракту плюс 64. Дельта портфеля равна нулю.
В результате восстановления дельта-нейтральности портфеля инвестор фиксирует 37 руб. выигрыша, сохраняя позиции открытыми.
Пусть в следующий момент курс бумаги понизился на 5 руб. т.е. упал до 100 руб. По акциям инвестор выиграл:
Макций • 5руб. = 320руб.
Новая дельта опциона равна 0,5. Поэтому стоимость опционного контракта в соответствии с таблицей 14.13 уменьшилась на 287 руб. Выигрыш на разности изменений стоимости акций и опционного контракта составил:
320 -287 = ЪЪруб.
Инвестор закрывает позиции и реализует прибыль от всей операции.
В результате роста цены акции до 105 руб. инвестор выиграл 37 руб., в результате ее дальнейшего падений до 100 руб. - 33 руб. Общий выигрыш составил 70 руб. Таким образом, восстановление дельта-нейтральности портфеля при цене акции 105 руб. позволило инвестору фиксировать прибыль от роста курса акции в размере 37 руб. и затем получить прибыль от его падения в сумме 33 руб.
Инвестор каждый раз будет получать прибыль при росте цены и дальнейшем ее снижении. Возникает вопрос, за счет какого механизма она возникает. Ее фактическим источником является покупка акций по более низкой цене и продажа по более высокой. Когда курс акции вырос до 105 руб., инвестор сделал портфель дельта-нейтралным, продав 14 акций по 105 руб. При падении курса до 100 руб. он вновь делает портфель дельта-нейтральным, покупая 14 акций по 100 руб. Таким образом, прибыль от данных действий составляет:
1 Дакций • 5 руб. = 70руб.
Как видим, она равна прибыли, полученной в результате стратегии покупки волатильности. Инвестор мог бы получить 37 руб. прибыли, закрыв позиции при цене акции 105 руб. В этом случае выигрыш по опционному контракту равен 287 руб., т.е. он купил контракт по 500
руб. и продал его по 787 руб. Проигрыш по акциям равен 250 руб.: он осуществил короткую продажу 50 акций по 100 руб.: (50бш/ий • 1 00 руб. = 5000руб.); и выкупил их по 105 руб.: (50акций 105 руб. = 5250руб.). Общий результат:
287-250 = 37 руб.
Чтобы получить прибыль от дальнейшего движения цены акции ему вновь необходимо сформировать дельта нейтральный портфель, т.е. купить опционный контракт по 787 руб. и осуществить в соответствии с дельтой опциона короткую продажу 64 акций. Тогда при понижении цены акции до 100 руб. он проиграет на опционном контракте:
787-500 = 287 руб.
От продажи акций он выиграет:
• 5 руб. = 320руб.
Прибыль равна:
320-287 = 33руб.
Таким образом, инвестор мог бы получить прибыль в сумме 70 руб., закрыв полностью позицию при цене акции 105 руб. и вновь сформировав дельта-нейтральный портфель при этой цене. Однако такие действия не являются оптимальными, так как они связаны с дополнительными комиссионными расходами. Поэтому единственное, что требуется от инвестора в случае роста цены акции, это фиксировать прибыль за счет восстановления дельта-нейтральности портфеля при ее новой цене, продав бумаги в таком количестве, чтобы дельта позиции по акциям стала равной дельте опционного контракта.
Рассмотрим случай падения цены акции.
Пример 2.
Курс бумаги упал со 100 руб. до 95 руб. Выигрыш по акциям равен:
ЗОакций 5руб. = 250руб.
Пусть дельта опциона имела следующую динамику:
Таблица 14.14. Динамика дельты опциона
| Цена акции (руб.) юо 99 98 97 96 95 - —
j Дельта 0.5 0,49 0,4? 0,44 0,41 0,38
Суммируем дельты и получим изменение стоимости опциона на одну акцию:
0,49 + 0,47 + 0,44 + 0,41 + 0,38 - 2,19.
Оно равно 2,19 руб. Следовательно, стоимость опционного контракта снизилась на:
ЮОакций • 2,19 руб. -219 руб.,
и равна теперь:
500-219 - 281^6.
Выигрыш инвестора на разности изменений стоимости акций и опционного контракта составил:
250-219 = 3\руб.
Чтобы фиксировать выигрыш необходимо вновь сделать портфель дельта нейтральным, т.е. купить 12 акций. Тогда дельта по акциям равна минус 38, дельта опционного контракта - плюс 38. Дельта портфеля равна нулю. Пусть курс акции вновь вырос до 100 руб. По опционному контракту инвестор выиграл 219 руб., а по акциям проиграл:
З&акций 5 = 190/туб,
Общий выигрыш равен:
219-190 = 29^6,
Таким образом, выигрыш от падения и последующего роста курса акции составил:
31 + 29 = 60/туб.
За счет чего фактически получена данная прибыль. Вначале инвестор продал акции по 100 руб., а затем выкупил 12 акций по 95 руб. Поэтому выигрыш возник за счет короткой продажи данных 12 акций по 100 руб. и покупки их по 95 руб.:
12акций 5 руб. = 60руб.
Данный выигрыш можно было бы получить в два этапа, закрыв полностью позицию при падении курса акции до 95 руб., и вновь открыв дельта-нейтральный портфель по этой цене. Тогда при падении цены инвестор закрывает опционный контракт по цене 287 руб. и теряет:
500-287 = 2 \9руб.
Выкупает 50 акций по цене 95 руб. и выигрывает:
5000руб. ~ 50акций 95руб. = 250руб.
Общий выигрыш равен 31 руб. После этого инвестор вновь открывает дельта нейтральную позицию, т.е. покупает опционный контракт по 287 руб. и продает в соответствие с дельтой контракта 38 акций. В результате роста цены бумаги до 100 руб. выигрыш по опционному контракту равен 219 руб., а проигрыш по акциям:
ЗЯакций 5 = 190руб.
Общий выигрыш равен 60 руб. Таким образом, инвестор мог бы получить прибыль в сумме 60 руб., закрыв полностью позицию при цене акции 95 руб. и вновь сформировав дельта-нейтральный портфель при этой цене. Однако такие действия не оптимальны, так как они связаны с дополнительными комиссионными расходами. Поэтому единственное, что требуется от инвестора в случае падения цены акции, это фиксировать прибыль за счет восстановления дельта-нейтральности портфеля при ее новой цене, купив бумаги в таком количестве, чтобы дельта позиции по акциям стала равной дельте опционного контракта. Чем сильнее будет изменяться цена акции, и чем большее количество колебаний она испытает, тем большую прибыль получит инвестор в результате стратегии покупки волатильности.
Рассмотренная стратегия обладает хорошей ликвидностью, поскольку инвестор продает и покупает бумаги, восстанавливая дельта-нейтральность портфеля, на противоположных тенденциях движения рынка. При росте цены акции он продает бумаги, так как дельта опциона выросла. При падении курса акции он покупает бумаги, так как дельта опциона уменьшилась.
В примере мы рассмотрели один шаг движения цены вверх (первый случай) и один шаг движения цены вниз (второй случай). На практике после восстановления дельта нейтральности портфеля, цена акции может продолжить движение в прежнем направлении, а не изменить его на противоположное. Рассмотрим случай только роста цены, так как ситуация будет аналогична и при ее падении.
Пример 3.
Допустим, курс акции вырос до 105 руб. Инвестор восстановил нейтральность портфеля, т.е. дополнительно осуществил короткую продажу 14 акций. После этого цена бумаги выросла еще на 3 руб. Тогда инвестор фиксирует дополнительную прибыль, так как вновь стоимость опциона выросла в большей степени, чем стоимость акций. Пусть дельта опциона имела следующую динамику:
Таблица 14.15. Динамика дельты опциона
Цена акции (руб.) 105 106 107 108
Дельта 0,64 0,68 0,73 0,78
Цена опциона выросла на:
0,68 + 0,73 + 0,78 = 2,19руб., соответственно опционный контракт подорожал на 219 руб. По акциям инвестор проиграл:
64акции • 3 руб. = 192 руб.
Общий выигрыш на разности изменений стоимости опционного контракта и акций составил:
219-192 - 15руб.
Аналогично инвестор будет выигрывать и в случае возможного дальнейшего роста цены и в случае ее падения. Каждый раз, когда инвестор полагает, что движение курса изменится на противоположное, необходимо только восстанавливать дельта-нейтральность портфеля.
В примере мы рассматривали один опционный контракт. Поэтому корректировали состав портфеля за счет изменения количества акций. На практике инвестор может купить несколько опционных контрактов. Тогда восстановить дельта-нейтральность можно за счет изменения количества контрактов. Решение зависит от того, комиссионные по каким сделкам меньше.
Стратегия приносит прибыль до тех пор, пока дельта опциона не станет равной единице или нулю. Если дельта опциона вырастет до единицы, то нейтральный портфель должен включать короткую продажу 100 акций. Это означает, что при дальнейшем росте цены бумаги стоимость опционного контракта и стоимость позиции по акциям будут изменяться в пропорции один к одному, и никакого выигрыша инвестор больше не получит. Если дельта будет равна нулю, то нейтральный портфель уже не должен включать ни одной акции, цена опциона будет равна нулю. От дальнейшего снижения цены бумаги также не будет никакого выигрыша.
Для покупки волатильности надо выбрать опцион ATM, так как он имеет наибольшую гамму. Гамма говорит о кривизне дельты. Чем больше кривизна, тем большую прибыль зафиксирует инвестор при восстановлении дельта-нейтральности портфеля. По величине гаммы можно судить о перспективах прибыльности стратегии. Надо выбрать наиболее дешевый опцион с наибольшей гаммой.
Недостатком стратегии является то, что длинный опцион имеет отрицательную тету. Поэтому с течением времени временная стоимость опциона падает. По этой причине для осуществления стратегии не следует выбирать краткосрочной опцион, так как его тета начинает нарастать с ускорением. Наибольшую (по абсолютной величине) тэту имеет опцион ATM. Стратегия принесет прибыль при частых колебаниях курса акции в течение короткого периода времени. Вследствие эффекта тэты прибыль инвестора может сократиться вплоть до убытка, если цена бумаги не будет изменяться достаточно часто. Инвестор также может понести потери за счет уменьшения внутренней волатильности опциона и получить дополнительную прибыль вследствие ее роста. Наиболее чувствительны к эффекту веги долгосрочные опционы без выигрыша. Поэтому при формировании стратегии не следует выбирать опционы, до истечения которых остается много времени. Наихудшая ситуация сложится для инвестора, если цена акции совершенно не изменится за период осуществления стратегии. Опцион потеряет свою временную стоимость. По мере приближения срока истечения контракта дельта опциона будет уменьшаться. Однако для поддержания дельта-нейтральности портфеля инвестор будет покупать акции по той же цене, по которой он их продавал.
Стратегию покупки волатильности можно осуществить, используя опцион пут. Допустим, в приведенном выше примере вместо опциона колл инвестор использует опцион пут на акции. Тогда он формирует дельта-нейтральный портфель, покупая опционный контракт пут и 50 акций. При росте цены акции дельта опциона пут уменьшается (по абсолютной величине), и дельта портфеля становится положительной. Следовательно, инвестор выигрывает от роста курса бумаги. Дельта-нейтральность позиции восстанавливается за счет продажи части акций. При падении цены дельта опциона увеличивается (по абсолютной величине), и дельта портфеля становится отрицательной. Следовательно, инвестор выиграет от падения курса за счет того, что опцион подорожал в большей степени чем уменьшилась стоимость акций. Дельта-нейтральность позиции восстанавливается за счет покупки части акций. Таким образом, как и в случае опциона колл, инвестор покупает акции при падении их цены и продает при росте их курса. Гамма опциона пут равна гамме опциона колл. Поэтому в результате изменений цены акции инвестор получает такой же выигрыш как и при использования опциона колл. Для инвестора использование в стратегии опциона пут или колл одинаково. Соответственно, он теряет при спокойном рынке за счет падения временной стоимости и внутренней волатильности опциона.
14.4.2. Продажа волатильности
Прогноз инвестора может говорить о том, что цена базисного актива в ближайшее время не изменится. Кроме того, на его взгляд стоимость опциона колл завышена. Для таких условий подойдет стратегия "продажи волатильности”. Она состоит в формировании дельта-нейтрального портфеля за счет продажи опциона колл и покупки базисных активов. Допустим, инвестор продает опцион колл без выигрыша на акции и покупает 50 акций. Если курс акций изменится не сильно, то возникший проигрыш (выигрыш) по акциям компенсируется выигрышем (проигрышем) по контракту. Если же курс существенно вырастет или упадет, то инвестор понесет убыток на разности изменения стоимости акций и опционного контракта. Причина состоит, как и в случае стратегии покупки волатильности, в не линейной зависимости изменения стоимости контракта при изменении цены акции. При изменении цены инвестор должен восстанавливать дельта-нейтральность портфеля. Однако каждый раз он будет покупать акции по более высокой цене и продавать их по более низкой, что и явится причиной потерь. Восстанавливать дельта-нейтральность необходимо, чтобы уменьшить возможные потери от изменения курса. В противном случае они будут нарастать при дальнейшем движении цены бумаги. Инвестор фиксирует убыток при восстановлении нейтральности портфеля. Если он этого не сделает, и цена акции вернется к начальному уровню, то он не понесет потерь. Однако, если курс будет расти и дальше, то возможный убыток может быть неограничен, так как инвестор продал опцион колл покрытый только на 50%. Ему следует восстанавливать нейтральность портфеля, чтобы ограничить возможные потери. Если цена акции падает, но инвестор надеется на ее возвращение к прежнему уровню и не продает бумаги, то он может потерять всю сумму, затраченную на акции.
Инвестор будет выигрывать за счет падения временной стоимости и внутренней волатильности опциона. Поэтому он заинтересован в спокойном рынке. Потенциальная прибыль стратегии ограничена, убыток неограничен.
В стратегии продажи волатильности вместо опциона колл можно продать опцион пут. Так как дельта короткого опциона пут положительна, то для формирования дельта-нейтрального портфеля необходимо осуществить короткую продажу базисных акций. Общий результат стратегии аналогичен случаю с использованием опциона колл.
14.5. БОКС-АРБИТРАЖ
Бокс-арбитраж - это арбитражная стратегия, в которой используются четыре европейских опциона. С их помощью формируются два синтетических актива с разными ценами исполнения. Одна синтетическая позиция является длинной, другая - короткой. Условия осуществления бокс-арбитража следуют из условий паритета опционов пут и колл. Определим эти условия. Имеются опционы колл и пут на акцию: ср рр с2, р2 с ценами исполнения соответственно и Х2, истекающие в одно время. Цена спот акции равна 5 . Паритет опционов сценой исполнения X, равен:
с. +----X------ = р + 5. (14.28)
' {+г{Г/база)
Паритет опционов с ценой исполнения Х2 равен:
с, +----X------ = р +S. (14.29)
‘ \ +rip база) 2
Приравняем формулы (14.28) и (14.29):
-----Г - р. - С. +-3^------г - р7
1 + г\Т/ база) }+г[Т/база)
ИЛИ
(’4301
Если существует равенство (14.30), арбитраж невозможен. Равенство (14.30) говорит о том, что разность между совокупными премиями опционов должна равняться дисконтированной стоимости разности между ценами исполнения опционов к моменту заключения контрактов. В случае нарушения формулы (14.30) можно заработать прибыль без риска. Для определения алгоритма совершения арбитражной операции обозначим в равенстве (14.30) левую часть как портфель Л, правую - как портфель В.
Пусть на рынке существует ситуация:
(с,-р,)-(с -а)< ХГХ' v (14.31) ’ ' \ + г(Т/база}
В неравенстве (14.31) А<В, поэтому необходимо купить портфель А и продать портфель В. Покупка портфеля А означает, что арбитражер покупает одну часть портфеля:
(с> - Pl)-
обозначим ее как щ, и продает другую часть портфеля:
“ (^2 ~ Рг) >
обозначим ее как а2. Покупая , инвестор покупает опцион колл ct и продает опцион пут р,. Комбинация этих действий дает синтетическую покупку акции с ценой исполнения %,. Продавая а2, арбитражер продает опцион колл с2 и покупает опцион пут р2. Комбинация этих действий дает синтетическую продажу акции с ценой исполнения Х2. Продажа портфеля В означает, что арбитражер занимает средства под процент г на время Т для покупки портфеля А. По истечении срока действия контрактов в результате исполнения опционов, акция продается по цене Х2 и покупается по цене Х{. Арбитражер возвращает кредит и получает прибыль в
Поясним данный вариант арбитража на примере.
Пример.
Имеются котировки трехмесячных европейских опционов:
Цена исполнения Колл Пут
90 12 4
100 5 7
110 3 13
Ставка без риска равна 10% годовых.
Определяем возможность совершения арбитражной операции на основе формулы (14.30). Стоимость опционной позиции равна:
(12 — 4)—(3 — 13) = 18руб.
Величина дисконтированной стоимости разности цен исполнения опционов составляет:
110-90
1 + 0,1(3/12)
= 19,51 руб.
Поскольку полученные цифры не равны, то существует возможность заработать арбитражную прибыль.
Портфель А стоит меньше портфеля В, поэтому арбитражер покупает портфель Л, т.е. покупает с, за 12 руб., продает рх за 4 руб, продает с2 за 3 руб. и покупает р2 за 13 руб.:
-12 + 4 + 3-13 = -18руб.
Знак минус говорит о том, что арбитражеру необходимо занять 18 руб, чтобы купить портфель А. Он занимает данную сумму на три месяца под 10% годовых, т.е. в нашей терминологии продает портфель В. Через три месяца он должен вернуть долг в размере:
( 3
18 1 + 0,1 —
I 12
18,45 руб.
Возможная ситуация на рынке к моменту истечения опционов.
а) Sr > 110руб. Контрагент исполняет опцион с2, и арбитражер продает ему акцию за 110 руб. В свою очередь он исполняет опцион с, и покупает ее за 90 руб. На разности цен исполнения он получает 20 руб. дохода и возвращает кредит. Прибыль равна:
20-18,45 = 1,55 руб.
б) ST <90руб. Контрагент исполняет опцион р[5 и арбитражер покупает акцию за 90 руб. В свою очередь он исполняет опцион р2, т.е. продает бумагу за 110 руб, и возвращает кредит. Прибыль равна 1,55 руб.
в) 90 руб, < ST < 110руб. Арбитражер исполняет опционы с( и р2, т.е. покупает акцию за 90 руб. и продает за 110 руб. и возвращает кредит. Прибыль равна 1,55 руб.
Если на рынке существует ситуация:
(’4-32'
то портфель А стоит больше портфеля В. Поэтому необходимо продать портфель А и купить портфеля В. Чтобы определить алгоритм действий при продажи портфеля А, умножим его на минус один:
- КС1 - Р\ )- (С2 - Pl)] = -(Cl - Р\ )+ (С2 “ Р1) >
т.е. продаем одну часть портфеля - а, и покупаем другую часть портфеля - а2. Продавая а{, инвестор продает опцион колл Cj и покупает опцион пут р}. Комбинация этих действий дает синтетическую продажу акции по цене исполнения Х{. Покупая а2, арбитражер покупает опцион колл с2 и продает опцион пут р2. Комбинация этих действий дает синтетическую покупку акции по цене исполнения X,. Покупка портфеля В означает, что арбитражер размещает на депозите под процент г на время Т сумму денег, полученную от продажи портфеля А. В результате исполнения опционов в момент их истечения, акция покупается по цене Х2 и продается по цене Х{. Прибыль арбитражера равна:
(<’, - Л )- (<•': -рХ •
1 + г\Т/база)
Поясним данный вариант арбитража на примере.
Пример.
Имеются котировки трехмесячных европейских опционов:
Цена исполнения Колл 'пут' ”4
90 12 4
100 5 7
110 3 13
Ставка без риска равна 10% годовых.
Определяем стоимость портфеля А для цен исполнения 90 руб. и 100 руб.:
(12-4)-(5-7)= 10pj<5.
Определяем стоимость портфеля В.
100-90
1 + 0,1(3/12)
= 9,76 руб.
Портфель А стоит больше портфеля В, поэтому возможен арбитраж. Арбитражер продает портфель А, т.е. продает за 12 руб., покупает Р' за 4 руб., покупает с2 за 5 руб. и продает р2 за 7 руб.:
12-4-5 + 7 = 10руб.
Размещает данную сумму на трехмесячном безрисковом депозите и к моменту истечения опционов получает по счету:
10 1 + 0,1 —
I 12
10,25 руб.
В этот момент на рынке возможны ситуации:
a) ST > 100руб. Контрагент исполняет опцион cL, и арбитражер продает ему акцию за 90 руб. В свою очередь он исполняет опцион с2, т.е. покупает ее за 100 руб. На разности цен исполнения он проигрывает 10 руб. С учетом полученной по депозиту суммы его прибыль равна:
10,25 -10- 0,25руб.;
б) ST < 90 руб. Контрагент исполняет опцион р2, и арбитражер покупает акцию за 100 руб. В свою очередь он исполняет опцион р,, т.е. продает бумагу за 90 руб., и проигрывает 10 руб. С учетом полученной по депозиту суммы его прибыль равна 0,25 руб.;
в) 90 руб. < ST < 1ООруб. Первый контрагент исполняет опцион с,, и арбитражер продает ему акцию за 90 руб. Второй контрагент исполняет опцион р2, т.е. арбитражер покупает у него бумагу за 100 руб. Прибыль равна 0,25 руб.;
г) ST= 90руб. Второй контрагент исполняет опцион р2, т.е. арбитражер покупает у него бумагу за 100 руб. и продает ее на спотовом рынке за 90 руб. (или исполняет опцион рх). Прибыль равна 0,25 руб.;
д) = 100руб. Первый контрагент исполняет опцион q, и арбитражер продает ему акцию за 90 руб. В свою очередь он покупает акцию на спотовом рынке за 100 руб. (или исполняет опцион с2). Прибыль равна 0,25 руб.
Когда арбитражер открывает длинную синтетическую позицию относительно более низкой цены исполнения, то говорят, что он покупает бокс. Если открывает короткую позицию, то продает бокс. В первом примере арбитражер купил бокс, во втором - продал. К моменту истечения опционов стоимость бокса всегда равна разности между ценами исполнения. Соответственно стоимость бокса сегодня, не допускающая арбитраж, равна его стоимости к моменту истечения контрактов, дисконтированной к сегодняшнему дню под ставку без риска. Об этом говорит формула (14.30).
14.6. ВЗГЛЯД НА ОПЦИОННЫЕ СТРАТЕГИИ
Мы рассмотрели опционные стратегии, Инвестор будет использовать их при соответствующей конъюнктуре. Однако помимо знания основных комбинаций и спрэдов, следует помнить, что их можно получить за счет разных сочетаний финансовых активов. Поэтому необходимо вырабатывать способность взглянуть на них с точки зрения синтетических аналогов. В ряде случаев такой подход может привести к пересмотру инвестором своих действий. Например, инвестор формирует покрытый колл, т.е. продает опцион колл и покупает акцию. Однако данная позиция есть не что иное как синтетический короткий опцион пут. Поступая таким образом, инвестор должен спросить себя, хотел бы он при данной конъюнктуре продать опцион пут. Не исключено, что его решение изменится.
КРАТКИЕ ВЫВОДЫ
Комбинация - это портфель, состоящий из опционов разного вида на один и тот же актив с одним сроком истечения контрактов, которые одновременно являются длинными или короткими, цена исполнения может быть одинаковой или разной.
Спрэд - это портфель, состоящий из опционов одного вида на один и тот же актив, но с разными ценами исполнения и (или) датами истечения, причем одни из них являются длинными, а другие - короткими. Спрэд подразделяется на вертикальный (цилиндрический или денежный), горизонтальный (календарный или временной) и диагональный.
Вертикальный спрэд объединяет опционы с одной датой истечения контрактов, но разными ценами исполнения. Горизонтальный спрэд включает опционы с одинаковыми ценами исполнения, но разными датами истечения контрактов. Диагональный спрэд строится на основе опционов с разными ценами исполнения и сроками истечения контрактов. Когда спрэд формируется на базе опционов, которые имеют противоположные позиции по сравнению со стандартным сочетанием, его именуют обратным спрэдом.
Волатильными называют стратегии, в рамках которых инвестора в первую очередь интересует факт, изменится ли курсовая стоимость базисного актива или нет, и только во вторую очередь - направление этого изменения.
Стратегия "покупки волатильности” используется в том случае, если ожидаются сильные колебания цены базисного актива;
стратегия “продажи волатильности" - при прогнозах спокойного рынка.
Бокс-арбитраж - это арбитражная стратегия, в которой используются четыре европейских опциона. С их помощью формируются два синтетических актива с разными ценами исполнения. Одна синтетическая позиция является длинной, другая - короткой.
Стоимость бокса сегодня, не допускающая арбитраж, равна дисконтированной под ставку без риска разности между ценами исполнения опционов, формирующих стратегию.
Опционные стратегии полезно сравнивать с их синтетическими аналогами.
ЧАСТЬ III. ЭКЗОТИЧЕСКИЕ И ПОГОДНЫЕ ПРОИЗВОДНЫЕ
ГЛАВА 15. ЭКЗОТИЧЕСКИЕ ОПЦИОНЫ
В настоящей главе рассматриваются экзотические опционы, которые зависят от динамики цены базисного актива за период действия контракта, многофакторные опционы, а также ряд других разновидностей опционов.
Современный рынок опционов насчитывает богатый арсенал торгуемых инструментов. Одни из них лишь незначительно отличаются от обычных опционов колл и пут, другие имеют довольно специфические характеристики. Поэтому их стали именовать экзотическими опционами. Рассмотрим наиболее распространенные разновидности экзотических опционов.
Экзотические опционы можно разделить на две группы разновидностей.
1) Опционы, которые зависят от динамики цены базисного актива за период их действия. В свою очередь их можно разделить на два вида: зависящие от а) среднего значения цены; б) одного или нескольких значений цены.
2) Многофакторные опционы.
Кроме того, имеются другие разновидности экзотических опционов, которые выходят за рамки отмеченной классификации.
15.1. ОПЦИОНЫ, ЗАВИСЯЩИЕ ОТ ДИНАМИКИ ЦЕНЫ БАЗИСНОГО АКТИВА
15.1.1. Опционы со средней ценой
15.1.1.1. Азиатские опционы
Азиатский опцион (Asian option), его еще могут назвать опционом средней ставки (average-rate option), отличается от обычного европейского опциона тем, что на момент истечения контракта в качестве спотовой цены, которая сравнивается с ценой исполнения, берется среднее значение спотовых цен базисного актива за весь или определенный период действия контракта. Временные моменты наблюдений для расчета средней цены обычно зависят
от структуры риска по базисному активу. Средняя цена может определяться как среднее арифметическое простое или взвешенное, когда определенные веса придаются значениям цен на особые даты. Средняя цена также может быть средней геометрической наблюдавшихся цен. В этом случае перемножаются значения всех наблюдавшихся цен - пусть их число равно п - и извлекают из произведения корень л-й степени. Обычно средние значения цен рассчитываются на основе ежедневных цен закрытия базисного актива.
Азиатские опционы находят широкое применение на валютном рынке, рынке энергоресурсов и металлов. Например, ценовой риск компании, потребляющей на постоянной основе нефть или нефтепродукты, заключается не в том, что их цена на какой-либо день составит некоторую величину, а в том, что вырастет ее средняя цена за год. Если компания занимается экспортно-импортными операциями, ее риск связан с ростом или падением среднего курса национальной валюты.
Финансовый результат держателя азиатского опциона зависит от средней цены. Среднее значение переменной всегда имеет меньшую дисперсию чем сама переменная. Кроме того, чем больше количество наблюдений, тем меньше дисперсия. Поэтому азиатские опционы дешевле своих стандартных аналогов. Цена азиатского опциона быстро уменьшается до тех пор, пока количество наблюдений для расчета средней цены не достигнет порядка 15-20. Дальнейшее увеличение количества наблюдений уже слабо сказывается на цене опциона.1
15.1.1.2. Опционы со средним значением цены исполнения (average-strike option)
У данных опционов цена исполнения определяется как среднее значение спотовых цен базисного актива за определенный период времени. Данная цена исполнения сравнивается на дату истечения опциона с ценой спот базисного актива в этот день. Такие опционы менее популярны чем азиатские.
1 п наблюдений можно рассматривать как реализации п одинаково распределенных независимых (так как наблюдения осуществляются с интервалами во времени и возможной
7
автокорреляцией можно пренебречь) случайных величин с дисперсией (7~. Дисперсия их суммы равна ст2 /п .Приросте п данная величина уменьшается.
15.1.2. Опционы, зависящие от одного или нескольких значений цены базисного актива
15,1.2.1. Барьерные опционы
Барьерные опционы (barrier option) аналогичны обычным опционам колл и пут, но включают еще одну цену исполнения, которая называется барьерной ценой (barrier или trigger price).
Существует два вида барьерных опционов: нок-аут (knock-out option) и нок-ин (knock-in option). Когда покупается опцион нок-аут, то приобретается обычный европейский опцион. Однако он прекращает свое существование, как только цена базисного актива достигает барьерной цены. Таким образом, если за период действия опционного контракта цена базисного актива не достигла барьерной цены, то графики выигрышей-проигрышей для покупателя и продавца опциона будут аналогичны графикам европейских опционов.
Когда покупается опцион нок-ин, то приобретается обычный европейский опцион. Однако он не начинает действовать до тех пор пока цена базисного актива не достигнет барьерной цены. Поэтому, если за период, на который рассчитан опцион нок-ин, цена базисного актива не достигнет барьерной цены, то европейский опцион так и не начнет своего существования. Наиболее распространенными являются опционы нок-аут. В стандартном случае для опционов нок-аут и нок-ин барьерная цена располагается в направлении противоположном выигрышной динамике, т.е. для опционов колл она ниже цены исполнения, для пут - выше. Однако может быть и противоположное расположение барьерной цены. Цена барьерных опционов меньше премии обычных европейских опционов. Чем ближе барьерная цена к цене исполнения, тем дешевле опцион нок-аут, так как тем больше вероятность, что он прекратит свое существование досрочно. Для опциона нок-ин наблюдается обратная ситуация.
Пример. (Хеджирование опционом нок-аут пут).
Инвестор располагает акцией, цена спот которой 100 руб. Он хотел бы застраховаться от падения ее курса, поэтому покупает трехмесячный нок-аут пут с ценой исполнения 100 руб. и барьерной ценой 120 руб. Если в течение действия контракта цена спот акции вырастет до 120 руб., то опцион прекратит существование. Однако инвестор продаст акцию на спотовом рынке по 120 руб. Если курс будет в диапазоне 100/птл < 51 < 120/лп , инвестор не исполнит опцион, а продаст акцию на споте по текущей цене. Если за время
действия контракта S < 100руб., то хеджер через три месяца исполнит опцион и поставит акцию контрагенту по 100 руб.
Пример. (Хеджирование опционом нок-аут колл).
Инвестор планирует купить акцию и хотел бы застраховаться от роста ее цены. Поэтому он покупает трехмесячный колл нок-аут с ценой исполнения 100 руб. и барьерной ценой 80 руб. Если в течение срока действия контракта цена спот акции упадет до 80 руб., опцион прекратит существование. Однако инвестор купит акцию на споте за 80 руб. Если курс будет в диапазоне 80руб. < S < 100руб., инвестор не исполнит опцион, а купит акцию на споте по текущей цене. Если курс акции за время действия контракта будет выше 100 руб., то через три месяца хеджер исполнит опцион, т.е. купит акцию по 100 руб.
В барьерных опционах барьерная цена может быть задана на основе как цены базисного актива (внутренний барьер), так и цены другого актива (внешний барьер). Наиболее характерным является первый вариант. Второй можно представить следующим примером: барьерный опцион на акцию компании А, но барьерная цена устанавливается относительно динамики цены акции компании В.
Существуют двойные барьерные опционы (double-barrier option). Соответственно они включают две барьерных цены. Такие опционы дешевле обычных барьерных опционов.
15.1.2.2. Опцион лукбэк (lookback option)
Существуют две разновидности опционов лукбэк: 1) опцион с плавающей ценой исполнения; 2) опцион с фиксированной ценой исполнения. В первом случае цена исполнения опциона устанавливается только в последний день его действия. В качестве цены исполнения берется наименьшая (для опциона колл) или наибольшая (для опциона пут) цена спот базисного актива, которая существовала в период действия опциона. Таким образом, опцион колл лукбэк дает возможность купить базисный актив по наименьшей цене, существовавшей в период его действия, а пут лукбэк - продать его по наивысшей цене. Если расчеты между сторонами осуществляются только в денежной форме, то для определения финансового результата цена исполнения сравнивается с ценой спот базисного актива в последний день действия контракта.
Пример.
Инвестор купил беспоставочный трехмесячный опцион колл лукбэк на акцию компании А. За период действия контракта минималь
ный курс акции составил 80 руб., поэтому она принимается в качестве цены исполнения. В последний день действия опциона цена спот акции 110 руб. Контрагент выплатил инвестору по опциону сумму:
110-80 = 30^
У опциона лукбэк с фиксированной ценой исполнения для расчетных целей в качестве спотовой цены базисного актива берется наилучшая спотовая цена, которая существовала за весь период действия контракта. Для опциона колл это наибольшая, а для пут -наименьшая цена базисного актива. Опционы лукбэк дороже обычных опционов.
15.1.2.3. Опцион лестница (ladder option)
В рамках данного опциона оговаривается, что цена исполнения периодически пересматривается при достижении ценой базисного актива определенного уровня (ступеньки). Таких пересмотров может быть несколько. При каждом пересмотре фиксируется прибыль для держателя опциона, которая равна разности между ценами исполнения опциона. Если в последний день действия контракта цена спот базисного актива выше (ниже) последней цены исполнения, то эта разность также фиксируется как прибыль по опциону колл (пут).
Пример.
Инвестор купил трехмесячный опцион колл лестницу на акцию компании А с начальной ценой исполнения 100 руб. Цена спот акции 100 руб. Цена исполнения пересматривается с шагом цены базисного актива 5 руб. Через две недели цена акции выросла до 105 руб. По опциону была установлена новая цена исполнения - 105 руб., и фиксирована прибыль держателя в 5 руб. Еще через три недели цена выросла до 110 руб. Новая цена исполнения теперь 110 руб., а общий выигрыш держателя равен 10 руб. К концу третьего месяца цена акции опустилась до 108 руб. Опцион истек, выигрыш держателя составил 10 руб.
Рассмотрим другую динамику цены для третьего месяца: к моменту истечения контракта она выросла до 114 руб. Тогда общий выигрыш держателя составил 10 руб. за предыдущие два периода пересмотра цены исполнения плюс 4 руб. от исполнения опциона в последний день его действия.
15.1.2.4. Опцион клике (clique option)
Опцион клике похож на опцион лестницу, только новые цены исполнения фиксируются в оговоренные моменты времени и равны текущей цене базисного актива.
Пример.
Инвестор купил четырехмесячный опцион колл клике на акцию компании А с начальной ценой исполнения 100 руб. Цена спот акции 100 руб. Цена исполнения пересматривается через каждые четыре недели. Через месяц цена акции выросла до 103 руб. По опциону была установлена новая цена исполнения - 103 руб., и держатель фиксировал прибыль в 3 руб. Еще через месяц цена акции выросла до 108 руб. Новая цена исполнения теперь 108 руб., а общая прибыль держателя - 8 руб. В конце третьего месяца курс акции упал до 105 руб. Новая цена исполнения теперь 105 руб. Поскольку цена акции упала по сравнению с предыдущей ценой исполнения, то за этот период прибыль держателю не была начислена. В последний день действия контракта цена спот акции составила 110 руб. Опцион был исполнен. Общая прибыль держателя по опциону равна 8 руб., полученным за предыдущие периоды, плюс 5 руб. от исполнения опциона в последний день его действия.
15.1.2.5. Опцион выкрик (shout option)
Опцион выкрик похож на опцион клике с той разницей, что держатель сам определяет время, когда он будет фиксировать (выкрикивать) новую цену исполнения. Новая цена исполнения равна цене спот базисного актива в момент выкрика. Держатель опциона фиксирует прибыль равную разности между ценами исполнения. На момент истечения контракта держатель получит дополнительную прибыль, если опцион будет с выигрышем относительно новой цены исполнения. Обычно в контрактах предоставляется право одного выкрика. Однако их может быть и больше.
Пример.
Инвестор купил трехмесячный опцион колл выкрик на акцию компании А с начальной ценой исполнения 100 руб. Цена спот акции 100 руб. Держатель имеет право одного выкрика. Через месяц цена акции выросла до 110 руб., и держатель реализовал свое право. По опциону была установлена новая цена исполнения в 110 руб., и держатель фиксировал прибыль в 10 руб. В последний день действия контракта цена акции выросла до 114 руб. Опцион был
исполнен. Общая сумма, полученная держателем, составила 10 руб. от выкрика плюс 4 руб. от исполнения опциона в последний день его действия.
15.2. МНОГОФАКТОРНЫЕ ОПЦИОНЫ
Многофакторные опционы - это опционы на несколько базисных активов. Среди них можно выделить три основные группы опционов: радуга (rainbow option), корзина (basket option) и кванто (quanto option). Кроме того, существуют и другие разновидности опционов.2 Они характеризуются тем, что их стоимость определяется ценами двух или более активов, а также корреляцией между ценами этих активов.
15.2.1. Опцион радуга
Если в основе опциона лежат два базисных актива, то его называют двухцветной радугой, и в общем случае, если это п активов -л-цветной радугой. Опцион может иметь разновидность outperformance option. Данный опцион дает право получить разницу в доходности между двумя базисными активами. На день истечения опциона рассчитывается прирост стоимости (в процентах) базисных активов за период действия контракта. Если доходность оговоренного базисного актива превысит доходность второго актива, то разница между доходностями умножается на фиксированный в контракте множитель (номинал). Полученная сумма и является выигрышем покупателя опциона. В противном случае опцион не исполняется.
Пример.
Инвестор купил трехмесячный опцион на индексы облигаций и акций. Номинал контракта 1000 руб. Опцион исполняется, если прирост индекса облигаций превысит прирост индекса акций.
За три месяца индекс облигаций вырос на 10%, а индекса акций -на 6%. Опцион был исполнен, и держатель опциона получил по контракту сумму:
(0,1-0,06)1000 = 40руб.
Если бы к моменту истечения контракта прирост индекса облигаций оказался не больше прироста индекса акций, то опцион не был бы исполнен.
2 Бинарный опцион '‘деньги или ничего” на основе двух базисных активов рассматривается в параграфе 15.3.
Другая разновидность опциона радуга - это "лучший выбор" (bet-ter-of options) или “худший выбор” (worse-of options). В качестве примера можно представить опцион на два фондовых индекса. Покупатель радуги-лучший выбор получит результат относительно индекса, доходность которого увеличилась в большей степени.
Следующая разновидность - опцион на спрэд (spread option), По данному опциону выплата определяется на основе разности (спрэда) между ценами двух активов в момент заключения и истечения контракта. Например, инвестор покупает опцион на спрэд между доходностями одногодичной и трехгодичной облигаций, если ожидает, что величина спрэда между их доходностями изменится. Положительная разность между значениями спрэдов умножается на номинал контракта. Данная сумма является выигрышем покупателя.
15.2.2. Опцион кванто
Для такого опциона величина платежа определяется на основе цены базисного актива одной страны, а выплата осуществляется в валюте другой страны. В момент заключения контракта устанавливается валютный курс, по которому будет происходить пересчет результата в случае исполнения опциона. Такой опцион позволяет инвестировать средства в иностранные активы и исключает риск изменения валютного курса.
15.2.3. Опцион корзина
Данный опцион отличается от обычного опциона тем, что его базисный актив представляет собой портфель активов, которым приданы определенные уд. веса. Примером опциона корзины является опцион на фондовый индекс.
15.3. ДРУГИЕ РАЗНОВИДНОСТИ ОПЦИОНОВ
Бинарный опцион (binary option). Существуют бинарные опционы нескольких разновидностей. Рассмотрим опционы, которые называются “деньги или ничего” (cash or nothing) и “актив или ничего” (asset or nothing). По первому опциону предусмотрена фиксированная сумма выплаты его держателю в случае, если опцион окажется выигрышным на день истечения контракта (эта разновидность называется “все или ничего” (all-or-nothing option)), или хотя бы раз в течение действия контракта (эта разновидность называется опе-
touch option). График выплаты по европейскому бинарному опциону на момент истечения контакта представлен на рис. 15.1.
выплаты
по опциону
цена акции
Рис. 15.1. График выплат по европейскому бинарному опциону
Покупатель получит фиксированную сумму Л, если курс акции превысит цену исполнения X Если курс акции будет равен или меньше цены исполнения, то он ничего не получит.
По бинарному опциону “актив или ничего" вместо выплаты фиксированной суммы предусматривается поставка актива, например, акции. Г рафик выплат по такому опциону представлен на рис. 15.2.
выплаты i
по опциону I у
цена акции
Рис. 15.2. График выплат по европейскому бинарному опциону, предусматривающему поставку акции
Бинарный опцион “деньги или ничего” может заключаться относительно двух базисных активов. Существуют четыре разновидности данного опциона. Первая - это опцион колл. По опциону выплачивается определенная сумма денег, если на момент истечения контракта цены спот базисных активов выше установленных цен исполнения. По опциону пут сумма денег выплачивается, если на момент
истечения контракта цены спот базисных активов ниже установленных цен исполнения. Выплата по разновидности опциона "вверх и вниз" (up-down) происходит, если на момент истечения контракта цена спот первого актива выше цены исполнения, а второго ниже. Выплата по опциону "вниз и вверх” (down-up) происходит, если цена спот первого актива ниже цены исполнения, а второго выше.
Опцион с условной премией (contingent option). По опциону величина премии устанавливается при заключении контракта, однако выплачивается в момент его истечения, если только он окажется выигрышным. В противном случае премия не уплачивается. Финансовый результат для держателя при исполнении опциона рассчитывается аналогично случаям для европейских опционов колл и пут.
Опцион на опцион. Опцион позволяет его держателю в определенный момент времени в будущем решить, будет ли это колл или пут. В рамках данного опциона возможны четыре разновидности: 1) колл на колл; покупатель опциона приобретает право купить в будущем колл на соответствующий базисный актив; 2) колл на пут; покупатель опциона покупает право купить в будущем пут на соответствующий базисный актив; 3) пут на пут; покупатель опциона покупает право продать в будущем пут на соответствующий базисный актив; 4) пут на колл; покупатель опциона покупает право продать в будущем колл на соответствующий базисный актив.
Опционы на опционы можно использовать для страхования от неблагоприятной конъюнктуры в ожидании наступления определенных событий. Например, компания участвует в тендере на проведение строительных работ, результаты которого станут известны через месяц. Если он будет выигран, то потребуется привлечение внешнего финансирования. Однако процентные ставки могут к этому моменту вырасти. Можно купить опцион колл на процентный инструмент, но он стоит относительно дорого и не понадобится, если конкурс не будет выигран. Решением проблемы является покупка опциона колл на колл. Опцион стоит не дорого по сравнению с простым опционом колл и гарантирует приобретение опциона колл на процентную ставку с интересующей ценой исполнения по фиксированной стоимости.
Опцион с правом выбора (chooser option). Опцион позволяет покупателю в определенный момент времени выбрать, будет ли он держателем опциона колл или пут. В простом случае цена исполнения и время истечения выбираемых контрактов являются одинаковыми. В более сложном случае цены исполнения и сроки истечения опционов колл и пут различаются.
КРАТКИЕ ВЫВОДЫ
У азиатского опциона за спотовую цену, которая сравнивается с ценой исполнения, принимается среднее значение спотовых цен базисного актива за период действия контракта,
У опционов со средним значением цены исполнения цена исполнения определяется как среднее значение спотовых цен базисного актива за период действия контракта.
Барьерные опционы аналогичны обычным опционам колл и пут, но включают еще цену исполнения, которая называется барьерной ценой. Барьерные опционы могут иметь две барьерные цены.
У опциона лукбэк в качестве цены исполнения принимается наименьшая (для опциона колл) или наибольшая (для опциона пут) цена спот базисного актива, существовавшая в период действия контракта.
Цена исполнения опциона лестница периодически пересматривается при достижении ценой базисного актива определенной величины.
У опциона выкрик держатель сам определяет время, когда он будет фиксировать (выкрикивать) новую цену исполнения. Новая цена исполнения равна цене спот базисного актива в момент выкрика.
Многофакторные опционы - это опционы на несколько базисных активов. Они характеризуются тем, что их стоимость определяется ценами двух или более активов, а также корреляцией между ценами этих активов.
ГЛАВА 16. ОЦЕНКА ПРЕМИИ НЕ СТАНДАРТНЫХ ЕВРОПЕЙСКИХ ОПЦИОНОВ1
В настоящей главе мы рассмотрим оценку премии ряда европейских опционов на основе декомпозиции формулы Блэка-Шоулза.
16.1. ДЕКОМПОЗИЦИЯ ФОРМУЛЫ БЛЭКА-ШОУЛЗА НА СОСТАВЛЯЮЩИЕ КОМПОНЕНТЫ
Оценку ряда не стандартных европейских опционов, в том числе экзотических, можно осуществить на основе формулы Блэка-Шоулза, выделив в ней соответствующие составляющие компоненты. В приложении 3 к главе 10 было отмечено, что премия европейского опциона колл представляет собой дисконтированную под ставку без риска стоимость ожидаемого дохода, которую он может принести к моменту окончания контракта:
с\, = е~'Т fifmaxfo. - %,0)]. (161)
Стоимость ожидаемого дохода равна средневзвешенной сумме возможных доходов по опциону к моменту окончания срока его действия, где весами выступают вероятности получения соответствующих доходов. Поэтому формулу (16.1) можно представить как: се = е гГ> x'\P(Sr > У)+ £(o|5j < х)р(.5г < У)] = = e~’r e(st - У|5Г > x)p(ST > X) или
ce = e~rTE(sr - X\Sr > x)p(Sr > (1g 2)
= e~rT e(st\St > x)p(st > X)-Xe~rTP(Sf > X).
Таким образом, мы преобразовали формулу (16.1) в формулу (16.2). На основе формулы (16.1) была получена формула Блэка-Шоулза (16.3):
се = SQN(d})- Xe~eTN(d2). (16.3)
Элементу Xe~eTN[d2) формулы (16.3) соответствует элемент Xe~r/P(S[ > X) формулы (16.2). Данные элементы имеют одина
1 Данный параграф написан на основе статьи Р Gray, St F Gray “A Framework for Valuing Derivative Securities” II Financial Markets, Institutions & Instruments, V 10, №5, December 2001
ковые сомножители Хе~гТ , поэтому из их сравнения следует: в рамках модели Блэка-Шоулза вероятность того, что цена акции будет выше значения X т.е. опцион будет исполнен, равна:
P[ST > x}=N(d2). (16.4)
P.Gray, St.F.Gray назвали элемент (16.4) первым строительным блоком.2 В формуле (16.3) выражение р($т > X) используется вместе с дисконтированием фиксированной величины X. Поэтому при оценке премии опциона первый строительный блок следует использовать в случае, когда по опциону выплачивается некоторая фиксированная сумма.
Элементу ) формулы (16.3) соответствует элемент e~rTE(ST\ST > X\{ST > X)
формулы (16.2):
e"rTE{sT\ST > x]p(St > x)=SnN(d}). (16.5)
P.Gray, St.F.Gray назвали элемент (16.5) вторым строительным блоком3. Величины <7| и d2 определены согласно формулам (10.30) и (10.31). Второй строительный блок используем в случае, когда по опциону предполагается увеличение выплаты с ростом курса базисного актива.
На основе полученных результатов можно легко осуществить оценку премии европейских опционов различного вида.
16.2. ОЦЕНКА СТОИМОСТИ БИНАРНЫХ ОПЦИОНОВ
16.2.1. Оценка стоимости европейского бинарного опциона с выплатой денег
Возможные результаты по бинарному опциону с выплатой денег на момент истечения контракта равны:
А если Sr > X
О если ST < X
где S7 - цена спот базисного акции;
А - выплачиваемая сумма денег.
2 P.Gray, St.F.Gray ‘A Framework for Valuing Derivative Securities.” // Financial Markets, Institutions & Inslruments, V.10, №5, December 2001, p. 259.
3 Ibid.
Премия опциона равна дисконтированной под ставку без риска стоимости ожидаемого дохода по опциону. В свою очередь ожидаемый доход равен величине выплаты по опциону, умноженной на вероятность того, что цена акции превысит цену исполнения. Поэтому для бинарного опциона можно записать:
c = Ae rrf\ST >Aj. (16.6)
В формуле (16.6) величина p(st > х) есть не что иное, как первый элемент декомпозиции формулы Блэка-Шоулза. Поэтому в соответствии с результатом формулы (16.4) получим:
с = Ae~rTN(d2).
Пример.
50руб., Х = 45руб., г = 10%, Т = бмесяцев, a = 0,525. По опциону выплачивается сумма 10 руб., если курс акции будет выше цены исполнения, в противном случае ничего не выплачивается. Определить премию европейского бинарного опциона.
Решение.
1п(50/ +0105
= V/45/ ’ ’ +0,5-0,525^5 =0,6041, 0,525/0,5
d2 = 0,6041 - 0,525 • ToJ = 0,2329.
Из таблицы значений функции Лапласа или с помощью таблицы Excel4 находим:
у(+)= 0,5921.
Тогда:
се = 1О^’1 °’5 -0,5921 = 5,63руб.
16.2.2. Оценка стоимости европейского бинарного опциона с поставкой акции
Возможные результаты по бинарному опциону с поставкой акции на момент истечения контракта составляют:
4 См приложение 5 к главе 10
$Т если ST > X О если Sr < X
где ST - цена спот базисной акции.
Поэтому премия опциона равна:
с = e~rTe{st\St > x)p(sT > %).
В соответствии с результатом формулы (16.5) получим: с = 50ф,).
Пример.
So= 50руб., /V-45руб., г = 10%, Т - бмесяцев^ сг = 0,525. По опциону поставляется акция, если ее курс будет выше цены исполнения, в противном случае акция не поставляется. Определить премию европейского бинарного опциона.
Решение.
ln(5Q/ )+0,1-0,5 t___
d{ = ,__— + 0,5• 0,525J0,5 = 0,6041.
0,525-70,5
Из таблицы значений функции Лапласа или с помощью программы Excel находим:
N(<7,) = 0,7271.
Тогда:
с =50-0,7271=36,36руб.
16.3. ОЦЕНКА СТОИМОСТИ ДРУГИХ РАЗНОВИДНОСТЕЙ НЕ СТАНДАРТНЫХ ОПЦИОНОВ
16.3.1. Оценка стоимости опциона суперакция
Опцион суперакция дает возможность покупателю получить фиксированную сумму денег, если цена базисного актива к моменту истечения контракта находится в некотором диапазоне. Выплату по опциону можно представить следующей динамикой:
О если ST < Х{ < А если X{<S<X2 О если Sr >Х2
Таким образом, если цена базисного актива окажется больше значения Х}, но меньше Х2, продавец опциона должен уплатить покупателю фиксированную сумму А . Если же цена актива будет меньше или равна Х} или больше или равна Х2, выплата по опциону не производится. График выплат по опциону представлен на рис. 16.3.
выплаты по опциону
X пена актива
Рис. 16.3. Выплата по опциону суперакция
Цена опциона равна его дисконтированной стоимости на момент окончания действия контракта. Поэтому запишем:
с — е "[0-P(S, < <ST <X2)+0P(ST >X2)]
c = AerTP(Xi <ST<X2).
(167)
В равенстве (16.7) вероятность p(xi < ST < X2) можно предста-вить следующим образом:
p(Xl<ST<X2)=p(ST>xyp{ST > Х2). (16.8)
Подставим полученный результат из правой части равенства (16.8) в равенство (16.7):
с = А е '1 [Л.8; > X,) - P(s,. > Х2)]. (16.9)
Подставим в формулу (16.9) значения вероятностей из (16.4):
с = Ae'T\_N(d2')- )]. (16.10)
Таким образом, премию опциона суперакция можно определить с помощью формулы (16.10).
Пример.
Определить стоимость европейского опциона суперакция, который характеризуется следующей динамикой выплат на момент истечения контракта:
О если S7 < 100 руб.
< 30руб. если 100руб. <£<120руб.
0 если ST >120руб.
£0 = ЯОруб.' г -- 10%, Т = 6 месяцев, a - 0,3.
Решение.
Найдем значения d^ и d*2 согласно формуле (10.31);
ln(W V f 0 1 - \ 5
пР100/ К’1 2 ’
Р =------------р=-------— = -0,92227 ,
0,Зр5
1п(8%J+ [ОД - —к5
\ /120/ 2
Р ------------Р=-------1— = -1,78174.
0,3/0,5
По таблице функции Лапласа или с помощью программы Excel находим: ///=0,178193, л/2/ = 0,037395 .
Стоимость опциона равна:
с = ЗОе'4’-'05 (0,178193- 0,037395) = А,<У1руб.
16.3.2. Оценка стоимости европейского опциона кэп
Кэп дает возможность покупателю опциона уплатить сумму денег эквивалентную цене базисного актива, но не выше установленного уровня. Возможные результаты по опциону на момент истечения контракта равны:
А если ST > X = Л Sr если S7 < X — А
где ST - цена спот базисной акции;
А - фиксированная сумма денег.
График выплат по опциону кэп на акцию представлен на рис. 16.4.
выплаты
по опциону
Х~А
цена акции
Рис. 16.4. Выплата по кэпу
Премия кэпа равна дисконтированной стоимости ожидаемого значения его цены к моменту окончания контракта:
скэ„ = AerTP{ST > х)+e-rTe(st\St < x)p(St < Х). (16.11)
Ожидаемое значение стоимости акции можно представить как:
e(st )=e[st |sr < x)p{sT < x)+ +ФтК > x)p(ST > x).
(16.12)
Отсюда:
E(sr|Sr < X)P(ST < X)=E(ST)~ > x]p(S-r > X) .(16.13)
Подставим значение E{ST\ST < X]P(ST < X) из (16.13) во второе слагаемое равенства (16.11):
e~rrE(sr^Sr < x]p(Sr < Х) = e-^IXSr)- e(s7|5V > x)p(st > X)]
ИЛИ
ее сего-
(16.15)
(16.16)
(16.17)
(16.18)
В правой части равенства (16.14) первое слагаемое есть не что иное как дисконтированная стоимость будущего курса акции, т.е. дняшняя цена. Поэтому:
e~rTE(ST)=S0.
Согласно результату формулы (16.5)
<?-'7’e(s7.|57. > x)p(Sr > X) = SQN(d}).
Подставив (16.15) и (16.16) в правую часть (16.14), получим: е r/'E(s7-|Sr < x)p(Sr < X) = Sn - SoMtZ,) = 50[1-ф|)М^(-4).
В первом слагаемом (16.11) согласно формуле (16.4)
P(ST >X)=N(d2).
Подставив результаты формул (16.17) и (16.18) в (16.11), получим:
= rTN(d2)+SuN[-d\\
Пример.
Определить стоимость европейского опциона кэп на акцию, который характеризуется следующей динамикой выплат на момент истечения контракта:
100руб. если ST > 100 руб.
ST если ST < 100руб.
= 80руб., г = 10%, Т ~ ^месяцев, ст = 0,3.
Решение.
Найдем значения dt и d2 согласно формулам (10.30) и (10.31):
По таблице функции Лапласа или с помощью программы Excel находим: )= 0,7612, N(cl2) = 0,1782.
Стоимость опциона равна:
с = 1 ООе”0,10,5 • 0,1782+ 80- 0,7612= 77,85руб.
16.3.3. Оценка стоимости европейского опциона фло
Фло позволяет покупателю опциона получить сумму денег эквивалентную цене базисного актива, но не ниже установленного уровня. Возможные результаты по опциону на момент истечения контракта равны:
А если < X - А
Sr если S> X = А
< Г Т
где ST - цена спот базисной акции;
А -фиксированная сумма денег.
Г рафик выплат по опциону фло на акцию представлен на рис. 16.5.
Рис. 16.5. Выплата по опциону фло
Премия фло равна дисконтированной стоимости ожидаемого значения его цены к моменту окончания контракта:
рфю = Ae"P(S, < X)+e~'TE(Sr\Sr > x)p(ST > %). (16.19)
Согласно результату (16.5) в формуле (16.19) второе слагаемое равно:
(16.20)
В первом слагаемом формулы (16.19) P(ST<X) можно представить как:
Р(5У <X)=\-P(ST > X) (16.21)
С учетом результата (16.4) равенство (16.21) принимает вид:
1-^(S7 (16.22)
Подставив результаты из (16.20) и (16.22) в (16.19), получим:
Пример.
Определить стоимость европейского опциона фло на акцию, который характеризуется следующей динамикой выплат на момент истечения контракта:
60руб. если ST <60 руб.
ST если Sr > 60 руб.
\ = 80руб., г = 10%, Т = бмесяцев, сг = 0,3.
Решение.
Найдем значения dx и d2 согласно формулам (10.30) и (10.31):
4%оЦ0’1+°г]0’5
d, =---------Ц=-------— = 1,6979 ,
0,3^0,5
По таблице функции Лапласа или с помощью программы Excel находим:
0,9552, N(-d2)=0,0687.
Стоимость опциона равна:
рфт = 60е 0,10,5 • 0,0687 + 80 • 0,9552 = 80,34рХ-
16.3.4. Оценка стоимости европейского опциона коллар
Коллар включает в себя два опциона: кэп и фло. Например, инвестор покупает кэп и продает фло на акцию. В результате он гарантирует себе приобретение акции по цене, которая лежит в диапазоне от цены исполнения опциона фло до цены исполнения опциона кэп. Возможные результаты по опциону на момент истечения контракта равны:
если Sr < Х}
< ST если X ST < Х2 t Х^ если Sr > Х2
где ST - цена спот базисной акции;
zV| - минимальная сумма, уплачиваемая по опциону фло;
Х2 - максимальная сумма, уплачиваемая по опциону кэп.
График выплат по коллару на акцию представлен на рис. 16.6.
Рис. 16.6. Выплата по коллару
Премия коллара равна дисконтированной стоимости ожидаемого значения его цены к моменту окончания контракта:
Сколлар “ 6 < ) +
+ e-rTE{ST\Xl <ST <Х2)р(Х1 <ST < X>)+ (16.23)
erTX2P(ST >x2).
Согласно формулам (16.21) и (16.22) p(ST < X}) = N^-d*')- По-этому первое слагаемое в (16.23) равно:
e-rTX]P(ST < X^e^X^-df'). (16.24)
Согласно (16.4) p(ST > А"2)= w(t/*2). Поэтому второе слагаемое в (16.23) равно:
erTX2P(ST > Х2) = XrrX2N(d2'-). (16.25)
Преобразуем третье слагаемое в (16.23) по элементам его сомножителей. Согласно результату (16.8):
P(Xt < ST < X2) = P(ST > X})~P(ST > x2).
В свою очередь:
или, согласно результату (16.5):
е lTE\ST <ST <Х2 )/’(а'1 < ST < Х2 ) =
= 5„,V d,
-S0X d
(16.27)
Подставив результаты (16.24), (16.25) и (16.27) в (16.23), получим:
Млк)-^оМ<2)
ИЛИ
С,..,, = е'7 [%, N(-d?)+)]+SJ47,'1)- ;V(<2)].
В заключение данного параграфа остановимся еще на одном вопросе. При оценке стоимости опционов мы рассмотрели варианты выплат по контрактам, которые представляли собой или фиксированные или возрастающие суммы с ростом курса базисного актива. Однако может возникнуть необходимость оценить опцион для случая, когда сумма выплаты уменьшается с ростом курса базисного актива как показано на рис. 16.7.
Рис. 16.7. Выплаты по опциону
Линия ab опускается под углом 45° к горизонтальной оси, поэтому треугольник ahc является равнобедренным, и стороны ас и ch равны. Данный факт можно использовать, чтобы определить величину выплаты по опциону для стоимости базисного актива на участке Х.Х.. В точке X, выплата по опциону равна А . Если курс базисного актива вырастет на AS, то выплата составит:
выплата = A-AS, (16.28)
так как треугольник ade является равнобедренным, И ed = ае = AS (см. рис. 16.7). В свою очередь величину AS на отрезке ХгХ{ можно представить как:
AS = S7 -X,, (16.29)
где ST - цена актива к моменту истечения опциона.
Подставив (16.29) в (16.28), получим:
выплата - A- ST 4- Аг[
или
выплата = А + X, - ST.
Премия опциона равна дисконтированной стоимости ожидаемого значения его цены к моменту окончания контракта. Поэтому можно записать:
премия- е "ф+%,-^1%, <S7 <хИЛ<5г<Х)
ИЛИ
премия = е rl [А + Xt )р(Х, < $г < Х2 )-е " e(s, |X, <S, <Х2 )р(Х, < ST < Х2)
Согласно результатам (16.8), (16.9) и (16.10):
^г(Л + ^)р(ЛГ,<5г<ЛГ2)=
егГ(А + Х^Х^' )~N(d^ )]
(16.31)
Согласно результату (16.27):
Подставив (16.31) и (16.32) в (16.30), получим:
премия = е~'Т(А + Xt )- Л'^'2)]-Soj/V^')- )] .
КРАТКИЕ ВЫВОДЫ
Оценку ряда не стандартных европейских опционов можно осуществить на основе формулы Блэка-Шоулза, выделив в ней два составляющих компонента:
p(ST > x)=n(cI2)
И
e~rTE(sr\sT> x)p(Sr>x)= S0N(d}Y
В рамках модели Блэка-Шоулза вероятность того, что цена акции будет выше цены исполнения, равна:
P(ST>X)=N(d2).
Кэп дает возможность покупателю опциона уплатить сумму денег эквивалентную цене базисного актива, но не выше установленного уровня,
Фло позволяет покупателю опциона получить сумму денег эквивалентную цене базисного актива, но не ниже установленного уровня.
Коллар включает в себя два опциона: кэп и фло.
ГЛАВА 17. ПОГОДНЫЕ ПРОИЗВОДНЫЕ
В настоящей главе мы рассмотрим общую характеристику производных на погоду и более подробно остановимся на контрактах, базисными активами которых выступают индексы на температуру.
17.1. ОБЩАЯ ХАРАКТЕРИСТИКА ПОГОДНЫХ ПРОИЗВОДНЫХ
Хозяйственная деятельность человека зависит от погодных условий. По оценкам, около четырех пятых всей экономической активности в мире прямо или косвенно зависит от погоды,1 в том числе около 20% экономики США непосредственно зависит от погодных факторов.2
Рынок погодных производных инструментов появился в США в 1997 г. В 1999 г. на Чикагской товарной бирже (СМЕ) были начаты торги производными контрактами на температуру для 10 городов США. В последующем их количество выросло до 15 городов США и 5 европейских городов. В дальнейшем рынок получил развитие в Европе и Азии.
В современных условиях развитию рынка способствует создание Ассоциации погодного риск менеджмента (Weather Risk Management Association WRMA) и разработка WRMA и Международной ассоциацией свопов и деривативов (International Swap and Derivatives Association ISDA) стандартных форм контрактов для погодных производных.
Производные инструменты на погоду зародились в энергетическом секторе. В результате дерегулирования рынков энергоресурсов возникли новые финансовые риски. Колебания температуры приводят к колебанию объемов потребления энергетических ресурсов. Поэтому возникает необходимость страховаться от изменения объемов потребления продукции в связи с изменением температурных условий.3 Например, более теплая погода в зимнее время уменьшает спрос на электроэнергию для отопления, а более холодная погода летом снижает спрос на энергию для кондиционирования воздуха.
1 D.van Lenner, T.Oetomo, М.Stevenson, A. de Vries. “Weather Derivatievs: An Attractive Additional Asset Class.” II The Journal of Alternative Investments, Fall 2004. p.65.
2 B.Cerrahoglu. "Financial Instruments to Weatherproof Corporate Earnings/’ // The Journal of Alternative Investments, Summer 2003, p.95.
3 В англоязычной литературе данный риск называется volumetric risk.
Для производителей энергии риск сокращения прибыли из-за “неблагоприятной погоды” преимущественно связан с уменьшением объемов потребления их продукции. В то же время наблюдается и определенный риск роста издержек производства: при сокращении потребления энергии увеличивается количество простаивающих мощностей, что влечет удорожание себестоимости продукции. Для потребителей энергии более ’‘неблагоприятная погода” вызывает увеличение расходов прежде всего в связи с ростом объемов потребления. Соответственно могут вырасти и цены на энергию в результате увеличения на нее спроса. В случае более теплой зимы сбытовая компания, торгующая топливом, может понести убытки за счет того, что не все запасы топлива будут реализованы, и возникнут дополнительные издержки по хранению. Если температура окажется ниже обычной, возможны дополнительные издержки в связи с закупками топлива по более высокой цене. Развлекательный бизнес, связанный с отдыхом, также чувствителен к изменениям температуры.
Помимо срочных контрактов, базисным активом которых является температура, существуют и другие погодные производные, например, на осадки. Производные на осадки (precipitation) позволяют страховаться от недостатка или избытка дождя или снега. Хеджерами могут выступать гидроэлектростанции, фермеры, парки отдыха, клубы для игры в гольф, горнолыжные курорты, городские власти и т. д. Так, меньший чем обычно объем осадков ведет к сокращению выработки электроэнергии гидроэлектростанциями, в сельском хозяйстве объемы производства продукции зависят от количества дождей, посещаемость парка отдыха падает при более дождливой погоде, горнолыжный курорт менее посещаем при недостатке снега, городские власти несут более значительные расходы по уборке снега в случае снежной зимы.
Приведем пример контракта, связанного с осадками. Владелец гольф клуба Gut Apeldor Gold Club, расположенного в 100 км к северу от Гамбурга, заключил контракт с французским банком Societe Generale SA на период времени с мая по сентябрь. В рамках контракта банк обязался выплатить владельцу клуба компенсацию в случае, если число дождливых дней с количеством осадков больше чем один миллиметр превысит цифру 50. Владелец клуба пошел на данный шаг после того как в 2001 г. его бизнес пострадал от дождливой погоды.4
4 М.Сао, A.U, J.Wei. "Precipitation Modeling and Contract Valuation: A Frontier in Weather Derivatieves.” // The Journal of Alternative Investments, Fall 2004, p.94.
Погодные производные можно использовать в качестве финансовых инструментов для получения прибыли, формируя из них самостоятельные портфели или объединяя вместе с традиционными активами. Особенностью погодных производных в рамках портфельного подхода является то, что они не коррелируют с другими активами, Данная черта снижает общий риск портфеля. Диверсифицированный портфель только из погодных производных также обладает низким риском в связи с не коррелируемостью погодных индексов, выступающих базисными активами контрактов.
Особенностью погодных производных является то, что базисный актив не торгуется на спотовом рынке. Это накладывает отпечаток на их спекулятивный потенциал и принцип ценообразования. Отсутствие спотового базисного инструмента исключает возможность спекулятивно создать дефицит актива с целью получить прибыль по срочным сделкам Срочная цена контракта формируется на основе ожиданий участников рынка относительно будущих погодных условий для соответствующего периода времени с учетом используемых методов их прогнозирования. В цене находит отражение спрос и предложение контрактов в соответствии с потребностями хеджирования и извлечения спекулятивной прибыли.
Подавляющая часть погодных производных в настоящее время связана с температурой. На них приходится порядка 80% всех торгуемых контрактов.5
В контрактах на температуру расчеты обычно осуществляются относительно таких показателей как “heating degree days’’ (HDD) (дни с отоплением) и “cooling degree days” (CDD) (дни с охлаждением). Понятие “degree days” появилось в связи с расчетами стоимости поддержания нормальных условий существования человека внутри помещений в течение года.
Термин degree day говорит о том, насколько среднедневная температура отличается от справочного уровня. При температуре ниже справочной потребители будут использовать больше энергии для отопления, при температуре выше справочной больше энергии пойдет на обеспечение работы кондиционеров. Средняя температура за день рассчитывается как средняя между самым высоким и самым низким значениями температуры за этот день, т.е. за период времени между 12 ночи одного дня и следующего дня для определенного географического места. Показатель HDD за один день определяется по формуле:
5 Ibid, р 93
HDD = max(o, tref-f) , (17.1)
где HDD( - значение показателя за i -й день;
/ . _ справочный уровень температуры, обычно он берется рав-
ным 65° по Фаренгейту, что эквивалентно 18° по Цельсию;
F - средняя температура за i -й день.
Таким образом, HDD за один день - это наибольшая величина из двух значений: справочная температура минус средняя температура за день или ноль. Показатель HDD отличен от нуля, когда среднедневная температура ниже справочного уровня.
Индекс HDD за определенный промежуток времени определяется как сумма ежедневных значений HDD для данного периода времени. Он показывает, насколько среднедневная температура за этот период ниже принятого справочного уровня. Таким образом, HDD является мерой относительно более прохладного уровня среднедневной температуры и говорит о дополнительных потребностях в энергии для обогрева помещений. Контракты на индекс HDD используются для холодного периода времени года.
Показатель CDD за один день определяется по формуле:
CDD=m^-tnf, О) , (17.2)
где CDDi - значение показателя за / -й день;
/ , - справочный уровень температуры, обычно он берется рав-
ГС/
ным 65° по Фаренгейту;
F - средняя температура за i -й день.
Таким образом, CDD за день определяется как наибольшая величина для двух значений: средняя температура минус справочная или ноль. Показатель CDD отличен от нуля, когда среднедневная температура выше справочного уровня. Индекс CDD за определенный промежуток времени определяется как сумма ежедневных значений CDD для данного периода времени. Он показывает, насколько среднедневная температура за этот период выше принятого справочного уровня. Поэтому CDD является мерой относительно более жаркого уровня среднедневной температуры и говорит о дополнительных потребностях в энергии для охлаждения помещений. Контракты на индекс CDD используются для теплого периода времени года.
Пример 1.
Справочная температура 18° по Цельсию. Среднедневная температура составила 15° С. Показатель HDD за день в соответствии с формулой (17.1) равен:
HDD = max(o, 18 - 15) = 3.
Показатель CDD за день в соответствии с формулой (17.2) составляет:
CDD = шах(15-18, 0) = 0.
Пример 2.
Справочная температура 18° по Цельсию. Среднедневная температура составила 20° С. Показатель HDD за день равен:
HDD = max(o, 18-20)= 0.
Показатель CDD за день составляет:
CDD = max (20-18, о)=2.
В контрактах на погоду в качестве индекса температуры вместо показателей HDD и CDD может выступать среднее значение температуры за определенный период, а также иные температурные условия, например, разность между двумя уровнями температур. Так, в сельском хозяйстве существует потребность в контрактах, в которых указываются некоторая минимальная и/или максимальная температуры. Такие условия позволяют страховаться от существенных перепадов температур.
Для производных на осадки в качестве базисных активов выступают индексы, измеряющие уровень осадков за определенный период времени.
Контракты на температуру имеют следующую наиболее общую структуру. Значение индексов HDD (CDD) рассчитывают за месяц или за несколько месяцев: зимний или летний периоды. Полученный результат сравнивают с указанным в контракте базовым уровнем. Одному градусу HDD (CDD) соответствует определенная сумма денег, например, 100 долл. Поэтому разность между указанными цифрами умножают на эту величину. Данную сумму выплачивает по контракту проигравшая и получает выигравшая сторона. Контракты также могут содержать предельную сумму выплаты. Ее величина ограничивает риск проигравшей стороны.
Среди погодных производных наиболее часто используются такие инструменты как своп, опционы и коллар. Рассмотрим существо данных контрактов.
17.2. ПОГОДНЫЙ СВОП
Погодный своп - это контракт, в котором одна сторона продает, а другая покупает погодный индекс. Стороны оговаривают в контракте некоторый базовый уровень погодного индекса, с которым сравнивается фактическое значение HDD за расчетный период. Фактическое (расчетное) значение HDD за этот период определяется как сумма их ежедневных значений. Разность между расчетным значением HDD и базовым уровнем умножается на контрактный номинал свопа. Данная сумма является величиной выплаты по контракту. Если на конец расчетного периода расчетное значение HDD больше базового значения индекса, то продавец свопа (погодного индекса) уплатит данную сумму покупателю свопа (погодного индекса). Если расчетный уровень HDD окажется ниже базового значения индекса, то эту сумму покупатель уплатит продавцу.
Таким образом, покупатель индекса HDD в свопе ожидает более холодной чем обычно погоды и более высокого расчетного значения HDD по сравнению с его базовым уровнем. Он страхуется от понижения температуры в течение контрактного периода. Продавец ожидает более теплой погоды, и более низкой величины расчетного значения HDD по сравнению с базовым уровнем. Поэтому он страхуется от более высокой температуры
Пример.
Компания А, поставляющая газ для отопительных целей, прогнозирует более теплую зиму. На основе средней температуры за последние 10 лет для области, в которой реализуется газ, она определила, что средний уровень HDD за период с октября по апрель составлял 5000 пунктов. Статистика данных также показала: изменение температуры на один пункт HDD приводит к колебаниям в доходах компании на сумму в 1 тыс. долл.
Для хеджирования возможных потерь компания А заключает своп с компанией В. По его условиям компания В должна уплатить определенную сумму компании А в случае, если величина индекса HDD окажется ниже уровня 5000. В свою очередь, компания А уплатит соответствующую сумму компании В, если значение HDD за контрактный период будет выше данной величины. Выплачиваемая
сумма определяется как произведение разности между фактическим значением HDD и величиной 5000, умноженное на 1 тыс. долл.
Допустим, что контрактный период оказался более теплым, и в конце апреля фактическое значение HDD составило 4500 пунктов. Поэтому доход компании А оказался меньше на:
(5000 - 4500)-1 ОООЛлм. = 5000000ллл.
Однако данную сумму компания В выплатила компании А в рамках свопа. Если зима оказалась более холодной, и индекс HDD вырос до 5500 пунктов, то по свопу компания А уплатила компании В сумму:
(5500 - 5000)-1 ОООдолл. = 500000rfa?.i.
Однако ее расходы были компенсированы за счет увеличения прибыли от реализации газа на эту же величину. Таким образом, компания А застраховалась от уменьшения своих поступлений в связи с более теплой зимой. В свою очередь, компания В застраховалась от роста издержек при потреблении энергии в случае более холодной зимы.
17.3. ОПЦИОН ПУТ
Опцион пут позволяет установить минимальную цену, которую производитель получит за свой товар. Опционы пут обычно покупают производители энергетической продукции.
Пример.
Энергетическая компания страхуется от более теплой зимы и покупает опцион пут с ценой исполнения 5000 HDD. Стоимость одного пункта HDD составляет 1 тыс. долл. За расчетный период фактическое значение HDD составило 4500 пунктов. Контрагент выплатил компании сумму:
(5000 - 4500) • 1 ОООдолл. = 500000дсмл.
Ее доход составил:
5()()0()(barL7. - уплаченная премия.
Если фактическое значение HDD превысило цену исполнения, то компания опцион не исполнила и получила дополнительный доход от роста объемов продаж энергии.
17.4. КОЛЛАР
Коллар ограничивает для покупателя или продавца колебания цены товара в определенных границах в обмен за отказ воспользоваться от дополнительной прибыли в случае движения цены товара в благоприятном направлении. В рамках коллара продается один опцион и покупается другой. Опцион колл имеет более высокую цену исполнения по сравнению с опционом пут. Если в рамках контрактного периода цена товара не выйдет за ценовые границы коллара, то товар будет продан по существующей спотовой цене.
Производитель или поставщик энергетической продукции в рамках коллара продает колл и покупает пут. Продажа опциона колл ограничивает его прибыль в случае роста цены выше цены исполнения, однако покупка опциона пут гарантирует продажу товара не ниже цены исполнения опциона.
Потребитель энергетической продукции в рамках коллара покупает колл и продает пут. Покупка опциона колл страхует его от дополнительных издержек в случае роста цены, однако продажа опциона пут ограничивает его возможность воспользоваться снижением цены, поскольку он должен купить товар по цене не ниже цены исполнения опциона.
Покупатели и продавцы могут обеспечить себе коллар с нулевыми издержками за счет выбора таких цен исполнений опционов, чтобы уровни премий по контрактам были одинаковыми.
Пример.
Компания А, поставляющая газ для отопительных целей, прогнозирует более теплую зиму. На основе средней температуры за последние 10 лет для области, в которой реализуется газ, она определила, что средний уровень HDD за период с октября по апрель составлял 5000 пунктов. Статистика данных также показала: изменение температуры на один пункт HDD приводит к колебаниям в доходах компании на сумму в 1 тыс. долл.
Энергетическая компания может застраховаться от более теплой зимы покупкой опциона пут. Однако, чтобы компенсировать издержки по покупке опциона пут она решает сформировать коллар. В рамках коллара компания покупает пут с ценой исполнения 4900 HDD и продает колл с ценой исполнения 5100 HDD. Премии опционов одинаковые. Стоимость одного пункта HDD в контрактах составляет 1 тыс. долл. Таким образом, если зима окажется более теплой, и фактическое значение HDD за расчетный период окажется ниже 4900
пунктов, то от реализации своей продукции компания получит меньшую прибыль. Однако она исполнит опцион пут, что компенсирует ей потери. Если зима окажется более холодной, и значение HDD за расчетный период окажется выше 5100 пунктов, то контрагент исполнит опцион колл. Это не позволит компании получить дополнительную прибыль. Таким образом, сформировав коллар, компания обеспечила себе уровень дохода от реализации продукции, который соответствует диапазону значений HDD от 4900 до 5100 пунктов. Максимальная сумма колебаний ее дохода составит порядка:
(5100 - 4900) • 1 ООООат.7. = ЮООООдолл.
17.5. БИРЖЕВАЯ ТОРГОВЛЯ ПОГОДНЫМИ ПРОИЗВОДНЫМИ
На Чикагской товарной бирже (СМЕ) можно заключать фьючерсные контракты и опционы на фьючерсы на индексы HDD и CDD. Индексы СМЕ HDD и CDD это сумма значений HDD и CDD за расчетный период. Контракт на индекс HDD или CDD - это обязательство купить или продать стоимость индекса в будущем на определенную дату. Механизм торговли погодными фьючерсами аналогичен механизму торговли фьючерсными контрактами на другие базисные активы. Контракты являются расчетными.
В момент написания книги фьючерсные контракты на HDD (CDD) на СМЕ предлагались на месячные индексы и сезонные индексы для городов Атланта, Чикаго, Цициннати, Нью-Йорк, Даллас, Филадельфия, Портланд, Туксон, Дэе Мойнес, Лас Вегас, Бостон, Хьюстон, Канзас Сити, Миннеаполис, Сакраменто.
Для холодного периода времени в контрактах используется индекс HDD, для теплого - CDD. Месячные индексы HDD торгуются для месяцев с октября по апрель включительно, месячные индексы CDD торгуются для месяцев с апреля по октябрь включительно. Контракты на сезонные индексы охватывают период с ноября по март для зимнего времени и с мая по сентябрь для летнего. Дневная температура измеряется по Фаренгейту. Минимальный шаг цены -один пункт HDD (CDD).
Окончательная котировочная цена фьючерсного контракта рассчитывается Earth Satellite Corporation. Информация о значениях HDD и CDD доступна на сайте биржи СМЕ www.cme.com.
Контракты можно использовать для целей хеджирования. Например, для страхования энергетической компании от убытков в связи с
более холодным летом и снижением потребления энергии можно продать фьючерс на индекс CDD или купить опцион пут на фьючерс на индекс CDD. Для страхования потребителя энергии от роста потребления энергии вследствие более жаркого лета можно купить фьючерс или опцион колл на фьючерс на индекс CDD. Для страхования от роста потребления энергии в период более холодной зимы потребители могут застраховаться от роста издержек покупкой фьючерсов на индекс HDD или опциона колл на фьючерс на индекс HDD. Соответственно производители энергии могут застраховаться от более теплой зимы продажей фьючерсов на индекс HDD или покупкой опциона пут на фьючерс на индекс HDD.
Фьючерсный контракт можно использовать для извлечения спекулятивной прибыли. Множитель контракта равен 100 долл, за один пункт HDD (CDD). Например, инвестор купил ноябрьский фьючерс на город Чикаго стоимостью 600 HDD и через неделю закрыл позицию с котировкой 620 HDD. Его выигрыш составил:
(620 - 600)-10(Юсмл. = 2000<)смл.
На СМЕ предлагается также ряд погодных фьючерсов на европейские и японские города.
Опционы на фьючерсы на индексы HDD (CDD) являются европейскими. Базисным активом опциона является один фьючерсный контракт. Премия опциона котируется в пунктах HDD (CDD). Стоимость опциона определяется как произведение котируемой премии опциона на сумму 20 долл. Например, премия равна 10. Тогда опцион стоит:
10 • 20долл. - 20(к)а77.
Цены исполнения контрактов на индексы для городов США могут располагаться в следующих интервалах. Для месячных индексов CDD от 1 пункта до 1500 пунктов, для месячных HDD - от 1 пункта до 3200 пунктов, сезонных CDD - от 1 пункта до 7500 пунктов, сезонных HDD - от 1 пункта до 15500 пунктов. Шаг между ценами исполнения равен 1 пункту.
Фьючерсы и опционы на индексы HDD (CDD) торгуются в системе электронной торговли СМЕ GLOBEX.
Погодные производные представлены на бирже Euronext.liffe. В основе контрактов лежат показатели средней температуры для трех географических точек - London Heathrow, Paris Orly и Berlin Tempel-hof. На основе самого высокого и самого низкого значений температуры за день рассчитывается среднее значение температуры. Его
именуют DAT (Daily Average Temperature)6. Для каждой географической точки на основе ежедневных значений DAT определяются месячные и зимний индексы. Они рассчитывается соответственно по формулам:
MI = 100 +ШТ , (17.3)
WS1 = 100 + DAT , (17.4)
где Ml - значение месячного индекса (Monthly Index);
WS1 - значение зимнего индекса (Winter Season Index);
DAT - среднее значение ежедневных значений DAT; для месячного индекса оно рассчитывается за календарное количество дней соответствующего месяца, для зимнего индекса период времени охватываете 1 ноября по 31 марта включительно.
В формулах (17.3) и (17.4) стоят цифры 100, чтобы значение индексов было всегда положительным.
Контракты для Великобритании торгуются в фунтах стерлингов, для континентальной Европы - в евро. Контракты являются расчетными. В качестве котировочной цены контрактов в последний день7 принимается значение месячного или зимнего индексов.
Контракты на месячные индексы торгуются для каждого месяца. В контрактах изменению в ГС соответствует сумма в 3 тыс. евро и 3 тыс. фунтов соответственно для контрактов в евро и фунтах. Последним торговым днем является последний рабочий день месяца поставки. Для контрактов London Heathrow и Berlin Tempelhof значение EDSP публикуется в первый рабочий день после последнего торгового дня, для контрактов Paris Orly - на второй рабочий день после последнего торгового дня. Котировка контрактов дается как 100+температура в градусах. Условия для контрактов на зимний индекс являются аналогичными, только месяцем поставки является март.
В контрактах предусмотрена основная метеостанция (Primary Station) и дублирующая метеостанция (Backup Station). Если по какой-
6 Значения DAT определяются местными метеорологическими службами. Для Великобритании - это Met Office, Франции - Meteo-France, Германии - Deutscher Wetterdienst. DAT рассчитываются в соответствии с правилами, принятыми в каждой из служб. Особенности расчета касаются временного интервала, который рассматривается как один дневной период.
7 На LIFFE котировочная цена последнего торгового дня именуется EDSP (Exchange Delivery Settlement Price).
либо причине данные по основной станции окажутся недоступными, то будут использованы данные дублирующей станции, скорректированные на определенный коэффициент.
Среднедневная температура ежедневно публикуется на сайте liffeweather.com в 14.00.
КРАТКИЕ ВЫВОДЫ
Рынок погодных производных инструментов появился в США в 1997 г. В 1999 г. на Чикагской товарной бирже (СМЕ) были начаты торги производными контрактами на температуру.
Колебания температуры приводят к колебанию объемов потребления энергетических ресурсов. Поэтому возникает необходимость страховаться от изменения объемов потребления продукции в связи с изменением температурных условий.
Погодные производные можно использовать в качестве финансовых инструментов для получения прибыли, формируя из них самостоятельные портфели или объединяя вместе с традиционными активами. Особенностью погодных производных в рамках портфельного подхода является то, что они не коррелируют с другими активами, что снижает общий риск портфеля.
Особенностью погодных производных является то, что базисный актив не торгуется на спотовом рынке.
В настоящее время порядка 80% всех торгуемых контрактов на погоду связана с температурой.
Термин degree day говорит о том, насколько среднедневная температура отличается от справочного уровня.
Индекс HDD является мерой относительно более прохладного уровня среднедневной температуры. Контракты на индекс HDD используются для холодного периода времени года.
Индекс CDD является мерой относительно более жаркого уровня среднедневной температуры. Контракты на индекс CDD используются для теплого периода времени года.
Покупатель индекса HDD в свопе ожидает более холодной чем обычно погоды, а продавец - более теплой.
ПРИЛОЖЕНИЕ.
«ИНСТРУМЕНТЫ И ТЕХНОЛОГИИ СРОЧНОГО РЫНКА РТС»
Фьючерсы на Индекс РТС
Фьючерсы на Индекс РТС - это стандартные контракты, которые исполняются не путем поставки базового актива, а путем денежных расчетов. Заключая сделки с фьючерсами на Индекс РТС, участники торгов принимают на себя обязательства оплатить или получить разницу (вариационную маржу) между ценой сделки и ценой исполнения фьючерсного контракта. Цена исполнения определяется исходя из среднего значения Индекса РТС за последний час торгов в последний день торгов по фьючерсу.
Фьючерсы на Индекс РТС предоставляют широкий набор возможностей для хеджирования рисков по портфелям акций и для игры на росте или падении фондового рынка. Эти срочные контракты одинаково доступны как для инвесторов с небольшим объемом средств, так и для крупных участников рынка.
Индекс РТС - официальный индикатор Фондовой биржи РТС - является с 1995 года общепризнанным показателем состояния российского фондового рынка. Индекс РТС рассчитывается в режиме реального времени в течение всей торговой сессии на основании данных о сделках, заключенных на Классическом рынке РТС (с 10:30 до 18:45 по московскому времени). В базу расчета этого индикатора входят 50 акций российских эмитентов. Данные о динамике Индекса РТС публикуются на web-сервере РТС, транслируются на рабочие станции и распространяются информационными агентствами.
Расширение возможностей управляющих портфелями акций при помощи фьючерсов на Индекс РТС:
• Игра на росте/падении всего фондового рынка, а не изменении котировок отдельных акций.
• Возможность хеджирования (страхования) рисков по портфелям акций.
• Выгодная альтернатива операциям на спот-рынке по созданию портфеля из акций, ориентированного на структуру Индекса РТС:
о более низкие комиссионные издержки (в частности, отсутст-' вие депозитарного сбора),
о бесплатное «плечо» (плата взимается только за открытие и закрытие позиции на срочном рынке, за поддержание открьь той позиции сборы не взимаются).
• Повышение эффективности управления портфелями акций, не совпадающими по структуре с Индексом РТС.
• Возможность «короткой» продажи сразу целого портфеля акций, т.к. продажа и покупка фьючерса - симметричные и одинаково простые операции (в отличие от «продаж без покрытия» на рынке акций — short sale).
• Возможность создания синтетического фьючерса на индекс акций «второго эшелона».
• Построение различных арбитражных и спекулятивных стратегий с использованием фьючерсов на Индекс РТС, фьючерсов и опционов на отдельные акции российских эмитентов на Срочном рынке FORTS, а также самих акций на спот-рынке.
Спецификация фьючерсного контракта на Индекс РТС
Цена (курс) контракта Указывается в базисных пунктах Индекса РТС
Стоимость одного базисного пункта Индекса РТС (лот) 2% от курса доллара США по отношению к российскому рублю, установленного ЦБ РФ, на день проведения торгов
Минимальный шаг цены (тик) 5 базисных пунктов
Способ исполнения Финансовые расчеты
Месяцы исполнения Март, июнь, сентябрь, декабрь
Последний день торгов Торговый день, предшествующий 15 числу месяца исполнения, в который НП «Фондовая биржа РТС» проводит торги акциями, входящими в расчет Индекса РТС
Дата исполнения Рабочий день, следующий за последним торговым днем
Минимальный размер гарантийного обеспечения 10% от стоимости контракта
Время торгов 10:30-18.45 по московскому времени
Код контракта RTS-<MM>.<rr>; "~ где <мм> - месяц исполнения, <гг> - год исполнения (указываются арабскими цифрами)
Краткий код контракта в биржевой торговой системе R|<M><r>, где <м> - месяц исполнения, <г> - год исполнения.
Для месяцев исполнения приняты следующие обозначения: март - Н. июнь - М, сентябрь - U, декабрь - Z. Год исполнения указывается одной цифрой, например, для 2005 года - 5.
Код контракта в системе Reuters RI<M><r>:RTS (<м> и <г> - аналогично предыдущему пункту)
Код контракта в системе Bloomberg RTSI$ СТ <GO>
Биржевой сбор (включая НДС, взимается с каждой стороны сделки)
Регистрация сделок 1 руб./контракт
Скальперские операции* 0,5 руб./контракт
Регистрация внесистемных сделок 2 руб./контракт
Организация исполнения 1 руб./контракт
* Сделки, приводящие к открытию и закрытию позиций в течение одной торговой сессии.
Стратегии использования фьючерсов на Индекс РТС
Тип стратегии Описание
Хеджирование портфеля акций от падения цен Чтобы избежать потерь от падения фондового рынка, инвесторы, владеющие портфелями акций, должны продать фьючерсные контракты. В результате потери на рынке акций будут компенсированы выигрышем на рынке FORTS. При этом с помощью фьючерсов на Индекс РТС можно захеджировать риски всего российского фондового рынка, а не специфические риски отдельных эмитентов.
Хеджирование денежного потока от роста цен акций Организации, планирующие размещение своих денежных средств на рынке акций, могут застраховать себя от преждевременного роста фондового рынка. Для этого необходимо купить фьючерсы на Индекс РТС.
Покупка/продажа всего российского фондового рынка Фьючерсы на Индекс РТС могут служить привлекательным инструментом для игры на росте/падении всего фондового рынка, а не на изменении котировок отдельных акций. При этом длинная или короткая позиция по фьючерсам будет зависеть от динамики всего российского фондового рынка, а не от котировок акций отдельных эмитентов. Размер «плеча» по операциям с фьючерсами на Индекс РТС составляет 1:10 (минимальный размер гарантийного обеспечения - 10% от стоимости фьючерсного контракта).
Покупка/продажа «портфеля» акций, ориентированного на структуру Индекса РТС Покупка фьючерса на Индекс РТС аналогична созданию портфеля из 50 акций, входящих в базу расчета Индекса РТС. При этом издержки участника срочного рынка будут намного ниже, чем на спот-рынке, за счет более низких тарифов и отсутствия необходимости
Тип стратегии Описание
платить за успуги депозитария или за маржинальное кредитование. Кроме того, с появлением фьючерсов на Индекс РТС появилась возможность «продать» портфель, идентичный по составу Индексу РТС.
Управление портфелями акций, не совпадающими по структуре с Индексом РТС Фьючерсы на Индекс РТС позволяют страховать риски не только по портфелям акций, идентичным по составу Индексу РТС. Участники рынка могут захеджировать любой портфель, ориентируясь на коэффициенты чувствительности отдельных акций к динамике Индекса РТС (коэффициенты Р).
Создание синтетического фьючерса на индекс акций «второго эшелона» Открытие противоположных позиций по фьючерсу на Индекс РТС и по фьючерсам на «голубые фишки» позволяет создать позицию синтетического фьючерса на индекс акций «второго эшелона». Такие операции можно проводить в целях хеджирования портфеля, состоящего из акций «второго эшелона». Кроме того, синтетический фьючерс можно использовать в качестве альтернативы операциям покупки/продажи портфеля акций «второго эшелона».
Календарный спрэд Наличие в обращении одновременно нескольких фьючерсных контрактов с разными сроками исполнения позволяет играть на сужении или расхождении спрэдов цен между ними.
Построение различных стратегий с использованием фьючерсов и опционов на фьючерсы С помощью комбинаций фьючерсов на Индекс РТС, производных инструментов на отдельные акции и самих акций можно создавать сложные спекулятивные и арбитражные стратегии с различным соотношением риск/доходность.
Фьючерсы на акции российских эмитентов
Фьючерсы, базовым активом которых являются отдельные акции российских эмитентов, уже много лет успешно торгуются на Срочном рынке PTC (FORTS). Список акций, на которые вводятся в обращение фьючерсные контракты, постоянно пополняется. Эмитенты акций, являющихся базовыми активами для фьючерсных контрактов, представляют практически все важные сегменты российской экономики: нефтедобыча, энергетика, связь, металлургия.
Фьючерсные контракты на отдельные акции могут использоваться для достижения различных целей при управлении портфелями акции. Высокая чувствительность цен фьючерсов на акции по отношению к ценам базовых активов обеспечивает полное хеджирование инвестиционных портфелей (страхование рисков неблагоприятного изменения цен). Фьючерсы на акции могут эффективно использовать как инвесторы с небольшим объемом средств, так и крупные участники рынка.
Расширение возможностей управляющих портфелями акций при помощи фьючерсов на акции:
• Возможность снижения риска портфеля акций.
• Возможность осуществления «коротких» продаж, т.к. продажа и покупка фьючерса - симметричные и одинаково простые операции (в отличие от «продаж без покрытия» на рынке акций -short sale).
• Использование «эффекта плеча» на акциях, которое в среднем составляет 1:5-17.
• Снижение транзакционных издержек при работе с акциями:
о более низкие комиссионные издержки (в частности, отсутствие депозитарного сбора),
о бесплатное «плечо» (плата взимается только за открытие и закрытие позиции на срочном рынке, за поддержание открытой позиции сборы не взимаются).
• Построение краткосрочных «синтетических» облигаций.
• Построение различных стратегий с использованием фьючерсов и опционов на фьючерсы.
Спецификации фьючерсов на акции российских эмитентов
Общие характеристики всех фьючерсов на акции
Способ исполнения Поставка акций
Месяцы исполнения Март, июнь, сентябрь, декабрь
Цена контракта В рублях за 1 контракт
Шаг цены (тик) 1 руб.за 1 контракт
Последний день торгов Торговый день, предшествующий 15 числу месяца исполнения, в который в ОАО «Фондовая Биржа РТС» проводятся торги акциями
Дата исполнения Рабочий день, следующий за последним торговым днем
Время торгов 10:30-18:45 ло московскому времени
Параметры фьючерсов на акции
Базовый актив Обыкновенные акции РАО «ЕЭС России» Обыкновенные акции ОАО «Газпром» Обыкновенные акции ОАО «Лукойл» Обыкновенные акции ОАО «Ростелеком» Обыкновенные акции ОАО «Сургутнефтегаз» Обыкновенные акции ОАО «ГМК «Норильский никель»
Объем контракта 1000 акций 100 акций Ю акций 100 акций 1000 акций 10 акций
Минимальный размер гарантийного обеспе- 15% 15% 15% 15% 20% 20%
КедШя-ракта1 2 EERU- <мм>.<гг> GAZR- <мм>.<гг> LKOH-<мм>.<гг> RTKM-<мм>.<гг> SNGR-<мм>.<гг> GMKR- <мм> <гг>
Краткий код контракта в биржевой торговой системе3 ЕБ<м><г> GZ<M><r> LK<M><r> RT<M><r> SN<M><r> GM<M><r>
1 В процентах от стоимости контракта.
2 <мм> - месяц исполнения, <гг> - год исполнения (указываются арабскими цифрами).
3 <м> - месяц исполнения. <г> - год исполнения. Для месяцев исполнения приняты следующие обозначения: март - Н. июнь - М. сентябрь - U, декабрь - Z. Год исполнения указывается одной цифрой, например, для 2005 года - 5.
Базовый актив Обыкновенные акции РАО «ЕЭС России» Обыкновенные акции ОАО «Газпром» Обыкновенные акции ОАО «Лукойл» Обыкновенные акции ОАО «Ростелеком» Обыкновенные акции ОАО «Сургутнефтегаз» Обыкновенные акции ОАО «ГМК «Норильский никель»
Код контракта в системе Reuters3 ES<m> <г>: RTS GZ<m> <r>:RTS LK<m> <r>:RTS RT<m> <r>:RTS SN<m> <r>:RTS GM<m> <r>:RTS
Код контракта в системе Bloomberg3 EESR= <м><г> RU <EQ-UITY> <GO> GAZP= <м><г> RU <EQ-UITY> <GO> LKOH= <м><г> RU <EQ-UITY> <GO> RTKM= <м><г> RU <EQ-UITY> <GO> SNGS= <M><T> RU <EQ-UITY> <GO> GMKN= <м><г> RU <EQ-U)TY> <GO>
Биржевой сбор, руб./контракт (включая НДС, взимается с каждой стороны сделки)
Регистрация сделок 0,5 0.5 0,5 0,5 1 1
Скаль-перские операции4 0,25 0,25 0,25 0,25 0,5 0,5
Регистрация внесистемных сделок 0,75 0,75 0,75 0,75 1,5 1,5
Организация исполнения 1 1 1 1 2 2
Стратегии использования фьючерсов на акции
Тип стратегии Описание
Хеджирование портфеля акций от падения цен Чтобы избежать потерь от падения цен на акции, инвесторы, владеющие портфелями акций, являющихся базовыми активами фьючерсов, должны заключить фьючерсные контракты на продажу (продать фьючерсы). В результате потери на рынке акций будут компенсированы выигрышем на рынке FORTS.
3 <м> - месяц исполнения, <г> - год исполнения. Для месяцев исполнения приняты следующие обозначения: март - Н, июнь - М, сентябрь - U, декабрь - Z. Год исполнения указывается одной цифрой, например, для 2005 года - 5,
4 Сделки, приводящие к открытию и закрытию позиций в течение одной торговой сессии.
Тип стратегии Описание
Хеджирование денежного потока от роста цен акций Организации, планирующие размещение своих денежных средств на рынке акций, могут застраховать себя от роста цен акций покупкой фьючерсных контрактов.
«Короткая» продажа Фьючерсы на акции позволяют участникам торгов играть на падении цен акций даже в том случае, если у них в портфеле нет ценных бумаг.
Игра «с плечом» на понижение/повышение цен акций Фьючерсы на акции могут служить привлекательным инструментом для игры на повышение или понижение цен акций. Инвесторы, рассчитывающие на рост цен акций, могут заключить фьючерсные контракты на покупку (купить фьючерсы) В связи с тем, что при заключении фьючерсного контракта необходимо внести только часть стоимости базового актива (15-20%), для работы на срочном рынке FORTS требуется значительно меньше средств, чем на рынке акций.
Покупка/продажа краткосрочной «синтетической» облигации (операции репо) С помощью комбинации операций - покупки акций и продажи фьючерсных контрактов - участники рынка могут создать позицию, аналогичную покупке «синтетических» краткосрочных облигаций, срок до погашения которых равен сроку до исполнения фьючерсного контракта. Эта операция является аналогом операции «обратное репо», когда участник дает в кредит денежные средства под залог бумаг. С другой стороны, инвесторы, владеющие портфелем акций, с помощью фьючерсных контрактов могут взять краткосрочный кредит путем продажи бумаг и покупки фьючерса. Срок кредита равен сроку до исполнения фьючерса. Эта операция является аналогом операции «прямое репо», когда участник берет кредит под залог своих бумаг.
Календарный спрэд Наличие в обращении одновременно нескольких фьючерсных контрактов с разными сроками исполнения позволяет играть на сужении или расхождении спрэдов цен между ними. При формировании календарного спрэда по многим фьючерсам на акции предусмотрены льготы по гарантийному обеспечению (начальной марже).
Построение различных стратегий с использованием фьючерсов и опционов на фьючерсы С помощью комбинации фьючерсов и опционов на фьючерсы можно создавать стратегии с различным соотношением риск/доходность.
Опционы на акции российских эмитентов
На Срочном рынке PTC (FORTS) впервые в России создан ликвидный рынок опционов на фьючерсные контракты, базовым активом которых являются отдельные акции российских эмитентов Опционы на фьючерсные контракты предоставляют широкие возможности для страхования (хеджирования) рисков на рынках акций и фьючерсов на акции, а также позволяют осуществлять операции с высокой доходностью, низкими издержками и ограниченными рисками
Особенности рынка опционов FORTS:
• Самые широкие возможности для инвесторов
• Самый удобный инструмент управления рисками, в том числе и как инструмент для хеджеров
• Возможность получения неограниченного дохода при ограниченных рисках
• Максимальный «эффект плеча»
• Построение различных стратегий с использованием фьючерсов и опционов
• Возможность клиринга внебиржевых сделок
• Опционы могут эффективно использовать как инвесторы с небольшим объемом средств, так и крупные участники рынка
* Издержки при проведении операций на срочном рынке FORTS значительно ниже, чем на рынке акций
Спецификации опционов на фьючерсы, базовыми активами которых являются акции
Общие характеристики всех опционов
Тип Call и Put
Вид Американский
Объем 1 фьючерсный контракт
Цена контракта В рублях за 1 базовый фьючерс
Шаг цены (тик) 1 руб за 1 базовый фьючерс
Последний день срока действия Срок действия опциона истекает в день который указан в коде опциона • для «длинных» опционов - за два торговых дня до дня исполнения фьючерса, являющегося базовым активом опциона • для «коротких» опционов - за месяц/2 месяца до исполнения фьючерса, являющегося базовым активом опциона
Исполнение Исполнение в любой день в течение срока действия опциона по заявлению держателя. Автоматическое исполнение опционов «в деньгах» относительно расчетной цены фьючерса в последний день срока действия контрактов не предусмотрено. При исполнении одного опциона фиксируется сделка купли-продажи одного фьючерсного контракта, лежащего в качестве базового актива опциона, по цене равной цене-страйк (цене исполнения) опциона.
Параметры опционов
Базовый актив Фьючерс на акции РАО «ЕЭС России» Фьючерс на акции ОАО «Газпром» Фьючерс на акции ОАО «ЛУКОЙЛ» Фьючерс на акции ОАО «Ростелеком»
Объем базового фьючерса 1000 акций 100 акций 10 акций 100 акций
Шаг страйка 500 руб. 500 руб. 500 руб. 250 руб.
Код контракта6 EERU-<мм>.<гг>_ <дд><мм> <гг>СА ххххх EERU-<мм>.<гг>_ <дд><мм> <гг>Р А ххххх GAZR-<мм>.<гг>_ <дд><мм><гг> СА ххххх GAZR-<мм>.<гг>_ <дд><мм><гг> РА ххххх LKOH-<мм>.<гг>_ <дд><мм><гг> СА ххххх LKOH-<мм>.<гг>_ <дд><мм><гг> РА ххххх RTKM-<мм>.<гг>_ <дд><мм><гг> СА ххххх RTKM-<мм>.<гг>_ <дд><мм><гг> РА ххххх
Краткий код контракта в биржевой торговой системе7 ESxxxxx <м><г> GZxxxxx <м><г> 1_Кххххх<м><г> RTxxxxx <м><г>
Код контракта в системе Reuters2 ESxxxxx<m> <r>.RTS GZxxxxx<m> <r>.RTS 1_Кххххх<м> <r>.RTS RTxxxxx<m> <r>.RTS
6 <мм>.<гг> - месяц и год исполнения базового фьючерса: <дд><мм><гг> - дата экспирации (последний день срока действия) опциона; СА - американский опцион Call, РА - американский опцион Put; ххххх - цена-страйк (цена исполнения) опциона.
7 ххххх - цена-страйк, <м> - месяц экспирации, <г> - год экспирации.
Для месяцев экспирации приняты следующие обозначения: _____________ _ _______
Январь Февраль Mqjr Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь
Call A В С D Е F G Н I J К L
Put M N О Р Q R S Т и V W X
‘од экспирации для опционов всех видов указывается одной цифрой, например, для 2005 года - 5.
Базовый актив Фьючерс на акции РАО «ЕЭС России» Фьючерс на акции ОАО «Газпром» Фьючерс на акции ОАО «ЛУКОЙЛ» Фьючерс на акции ОАО «Ростелеком»
Биржевой сбор, руб./контракт (включая НДС, взимается с каждой стороны сделки)
Регистрация сделок 0.5 0,5 0,5 0,5
Скальпер-ские операции8 0,25 0,25 0,25 0,25
Регистрация внесистемных сделок 0,75 0,75 0,75 0,75
Организация исполнения 1 1 1 1
8 Скальперскими операциями с опционами считаются сделки, результатом которых является:
• открытие и закрытие позиции в ходе одной торговой сессии,
• закрытие и открытие позиции в ходе одной торговой сессии,
• открытие или закрытие в ходе одной торговой сессии позиции на покупку опциона pul и на продажу опциона call,
• открытие или закрытие в ходе одной торговой сессии позиции на покупку опциона call и продажу опциона put.
Льготный тариф не распространяется на внесистемные сделки.
Стратегии использования опционов на фьючерсы, базовыми активами которых являются акции
Тип стратегии Описание
Хеджирование портфеля акций от падения или роста цен Для страхования от падения цен акций или фьючерсов можно купить опционы «на продажу» (Put), а для того, чтобы застраховать короткую позицию на акциях или фьючерсах от повышения цены можно купить опционы «на покупку» (Call) Покупка опционов обеспечивает защиту от рисков неблагоприятного движения цены и одновременно предоставляет возможность сполна получить прибыль от благоприятного движения
Спекулятивная покупка опционов Покупка опционов является привлекательной благодаря ряду характеристик • убытки при осуществлении данной операции ограничены размером выплаченной премии, • потенциальные прибыли не ограничены Точка безубыточности на момент окончания срока обращения для опциона «на покупку» (Call) равна сумме цены исполнения (страйк) опциона и выплаченной премии, а для опциона «на продажу» (Put) - разности цены исполнения и выплаченной премии
Регулирование «эффекта плеча» Размер премии опциона зависит от страйка (цены исполнения контракта), а также от цен фьючерсов и акций При этом премии опционов с разными страйками («вне денег», «на деньгах» или «в деньгах») отличаются по степени чувствительности к изменению цен на рынке базового актива Поэтому на опционах трейдеры могут строить позиции, в наибольшей степени соответствующие их рыночным ожиданиям Опционы «вне денег» имеют меньшую премию, чем опционы «на деньгах» или «в деньгах» При больших изменениях цены фьючерса, премия опциона «вне денег» может измениться в несколько раз, а при небольших, может остаться совсем без изменений
Спрэдовью стратегии Спрэд (spread) - одновременная покупка и продажа опционов одного типа (либо Call, либо Put), но с разными страйками и/или датами экспирации Спрэды бывают • вертикальными (создаются из опционов с одинаковой датой экспирации, но разными страйками), • горизонтальными (из опционов с одинаковыми страйками, но разными датами экспирации) и • диагональными (из опционов с разными страйками и датами экспирации) Такие стратегии позволяют ограничить убытки при неблагоприятном движении цен акций и фьючерсов, но и часто (но не всегда) ограничивают прибыль в случае движения цены базового актива в ожидаемом направлении.
Тип стратегии Описание
Увеличение доходностей инвестиционных портфелей продажей покрытых опционов Для получения дополнительного дохода при управлении портфелями акций и фьючерсов можно использовать стратегию продажи покрытых опционов. При наличии акций или длинных позиций по фьючерсам, трейдер продает опционы «на покупку» (Call) и получает за это премию. При наличии коротких позиций по акциям или фьючерсам продаются опционы «на продажу» (Put). Обычно трейдер проводит такие операции в расчете на то, что цены акций или фьючерсов останутся неизменными или будут незначительно изменяться в сторону, противоположную позиции, занятой по опциону. В то же самое время риск того, что опцион будет востребован, покрывается наличием позиции по акциям или фьючерсам.
Покупка/продажа волатильности Опционы - единственный финансовый инструмент, позволяющий получать прибыль при любом направлении движения цены акций и фьючерсов. При помощи опционных стратегий можно зарабатывать на увеличении или уменьшении волатильности цен базового актива. Примером такой стратегии является длинный стрэддл - одновременная покупка опционов Call и Put с одинаковыми ценами исполнения (страйками).
Арбитражные операции Комбинируя различные опционы, фьючерсы и акции можно создавать синтетические фьючерсные позиции или синтетические опционные позиции. Отличия в ценах реальных и синтетических фьючерсов и опционов можно использовать для получения арбитражной прибыли.
. Фьючерсы и опционы на доллар США
Фьючерсы и опционы на фьючерсы на курс доллара США являются важными инструментами для валютных дилеров, для управляющих портфелями ценных бумаг, для участников внешнеэкономической деятельности, а также для частных инвесторов, так как позволяют страховать (хеджировать) валютные риски, связанные с неблагоприятным изменением курса доллара США, или зарабатывать на колебаниях курса доллара США.
Расширение возможностей участников валютного рынка при помощи фьючерсов и опционов на фьючерсы на доллар США:
• Возможность снижения валютного риска.
• Использование эффекта «плеча» - аналог спекулятивных операций на рынке FOREX.
• Возможность осуществления «коротких» продаж.
• Снижение транзакционных издержек при работе с валютой.
• Проведение операций репо на валюте.
• Проведение арбитражных операций между российскими биржами и западными валютными рынками.
• Построение различных стратегий с использованием фьючерсов и опционов.
• Возможность клиринга внебиржевых сделок.
Спецификация фьючерсного контракта на доллар США
Базовый актив Курс доллара США по отношению к российскому рублю на день исполнения контракта
Объем контракта (лот) 1000 долларов США
Цена (курс) контракта Указывается в рублях за 1000 долларов США
Способ исполнения Финансовые расчеты
Месяцы исполнения Март, июнь, сентябрь, декабрь
Последний день торгов Торговый день, предшествующий 15 числу месяца исполнения, в который на спот-рынке проводятся торги по доллару США
Дата исполнения Рабочий день, следующий за последним торговым днем
Минимальный размер гарантийного обеспечения 3% от стоимости контракта
Время торгов 10 30-18 45 по московскому времени
Код контракта Si-<mm> <гг>, где <мм> - месяц исполнения, <гг> - год исполнения (указываются арабскими цифрами)
Краткий код контракта в биржевой торговой системе Si<M><r>; где <м> - месяц исполнения, <г> - год исполнения. Для месяцев исполнения приняты следующие обозначения: март - Н, июнь - М, сентябрь - U. декабрь - Z. Год исполнения указывается одной цифрой, например, для 2005 года - 5.
Спецификация опционного контракта на фьючерс на доллар США
Тип Call и Put
Вид Американский
Месяцы экспирации Март, июнь, сентябрь, декабрь
Последний день срока действия Закрытие торговой сессии в последний торговый день по базовому фьючерсу
Базовый актив 1 фьючерс на курс USD/RUR
Исполнение Покупатели могут потребовать исполнения в любой день в течение срока действия опциона. По окончании торгов в последний день срока действия опциона Клиринговый центр самостоятельно, без получения от держателей заявлений на востребование своих прав по опционам, производит исполнение опционов находящихся в состоянии «в деньгах» относительно расчетной цены фьючерсного контракта.
Код контракта Call - Si-<mm>.<гг> <дд><мм><гг>СА ххххх, Pul - Si-<mm> <гг>_<дд><мм><гг>РА ххххх; где Si-<MM>.<rr> - код базового фьючерса. <дд><мм><гг> - дата экспирации, ххххх - цена-страйк (цена исполнения) опциона.
Краткий код контракта в биржевой торговой системе Sixxxxx<M><r>; где ххххх - цена-страйк (цена исполнения) опциона, <м> - месяц экспирации, <г> - год экспирации. Для месяцев экспирации приняты следующие обозначения: для опционов Call: март - С, июнь - F, сентябрь -1, декабрь - L; для опционов Put: март - 0, июнь - R, сентябрь - U, декабрь - X. Г од экспирации для опционов всех видов указывается одной цифрой, например, для 2005 года - 5.
Стратегии использования фьючерсов и опционов доллар США
Тип стратегии Описание
Снижение риска падения курса рубля Иностранные инвесторы, покупающие ценные бумаги российских эмитентов за рубли, или компании-заемщики, кредитующиеся в допларах США, с помощью фьючерсов и опционов на фьючерсы на курс доллара США могут застраховаться от снижения курса рубля Захеджироваться от падения рубля можно покупкой фьючерсов или опционов Call
Хеджирование денежного потока от укрепления рубля Российские участники внешнеэкономической деятельности могут застраховать поток платежей в иностранной валюте от укрепления курса рубля путем продажи фьючерсов или покупки опционов Put
Игра «с плечом» на изменениях курсов валют Фьючерсы и опционы на фьючерсы на курс доллара США могут служить привлекательным инструментом для игры на повышение или понижение курса доллара США по отношению к российскому рублю поскольку предоставляют для этого большое «плечо» Размер «плеча» по операциям с фьючерсами составляет 1 33 (минимальный размер гарантийного обеспечения под каждую позицию по фьючерсу составляет 3% от его цены)
«Короткая» продажа Фьючерсы и опционы на фьючерсы на курс доллара США позволяют участникам торгов играть на понижение курса доллара даже в том случае если у них в портфеле нет американской валюты
Проведение операций репо на валюте Комбинация операций - продажа долларов на спот-рынке и покупка фьючерсных контрактов - может быть аналогом операции «прямое репо» когда участник валютного рынка берет кредит под залог валюты Наоборот, покупка долларов на рынке наличной валюты и продажа фьючерсов может рассматриваться, как «обратное репо», когда участник валютного рынка дает в кредит денежные средства под залог долларов Срок кредита равен сроку до исполнения фьючерса
Межрыночный арбитраж Кроме российских биржевых площадок фьючерсные контракты и опционы на фьючерсы на курс доллара США обращаются также на Чикагской товарной бирже (СМЕ) Наличие в обращении на нескольких биржах фьючерсных контрактов и опционов на доллар США с похожими характеристиками позволяет участникам получать безрисковую арбитражную прибыль
Комбинации фьючерсов и опционов Комбинируя различные фьючерсы и опционы на фьючерсы на курс доллара США можно создавать сложные спекулятивные или арбитражные стратегии
Фьючерсы на корзину трехлетних облигаций г. Москвы
Фьючерсы на корзину трехлетних облигаций г. Москвы являются стандартными контрактами, рассчитанными на длительный период обращения-. Поскольку сами облигации г. Москвы представляют собой эталонный инструмент для долгового рынка, фьючерсы на эти ценные бумаги позволяют хеджировать риски не только по московским бондам, но и по облигациям других эмитентов.
Расширение возможностей у участников торгов на долговом рынке при помощи фьючерсов на корзину облигаций г. Москвы:
• Возможность снижения риска портфеля облигаций.
• Возможность осуществления «коротких» продаж.
• Операции «с плечом» на облигациях.
• Построение синтетических «коротких» облигаций.
• Управление дюрацией портфеля облигаций.
• Снижение транзакционных издержек при работе с облигациями.
Спецификация фьючерсного контракта на трехлетние рублевые облигации Городского облигационного (внутреннего) займа г. Москвы
Базовый актив Облигации городского облигационного (внутреннего) займа г. Москвы любого выпуска, отвечающие следующим требованиям: • срок до погашения облигаций составляет 28-40 месяцев от даты исполнения фьючерса, • объем эмиссии - не менее 4 млрд руб.
Объем контракта (лот) 10 облигаций
Цена (курс) контракта Указывается в рублях за 10 облигаций (без учета накопленного купонного дохода)
Минимальный шаг цены (тик) 1 руб.
Способ исполнения Поставка облигаций
Месяцы исполнения Март, июнь, сентябрь, декабрь
Последний день торгов Торговый день, предшествующий 17 числу месяца исполнения, в который в ОАО «Фондовая Биржа РТС» проводятся торги облигациями
Дата исполнения Рабочий день, следующий за последним торговым днем
Минимальный размер гарантийного обеспечения 10% от стоимости контракта
Время торгов 10:30-18:45 по московскому времени
Код контракта МВЗ-<мм> <гт>; где <мм> - месяц исполнения, <гг> - год исполнения (указываются арабскими цифрами)
Краткий код контракта в биржевой торговой системе М3<м><г> где <м> - месяц исполнения, <г> - год исполнения Для месяцев исполнения приняты следующие обозначения март - Н, июнь - М, сентябрь - U, декабрь - Z Год исполнения указывается одной цифрой например для 2005 года - 5
Код контракта в системе Reuters М3<м><г> RTS (<м> и <г> - аналогично предыдущему пункту)
Биржевой сбор (включая НДС, взимается с каждой стороны сделки)
Регистрация сделок 0,5 руб /контракт
Скальперские операции* 0,25 руб /контракт
Регистрация внесистемных сделок 0,75 руб /контракт
Организация исполнения 1 руб/контракт
* Сделки, приводящие к открытию и закрытию позиций в течение одной торговой сессии
Стратегии использования фьючерсов на корзину трехлетних облигаций г. Москвы
Тип стратегии Описание
Хеджирование портфеля ценных бумаг от роста процентных ставок Инвесторы, владеющие портфелем облигаций как г Москвы, так и других эмитентов могут страховаться от роста процентных ставок на долговом рынке
Хеджирование денежного потока от падения процентных ставок Организации, планирующие размещение своих денежных средств на долговом рынке могут застраховать себя от падения процентных ставок
Хеджирование процентных ставок перед размещением Организации, осуществляющие размещение облигаций имеют возможность перейти к планированию результатов первичной продажи ценных бумаг, ориентируясь на реальную ставку доходности в будущем периоде сложившуюся на срочном рынке, а не на прогнозы состояния долгового рынка на день размещения Для этого организаторам выпуска облигаций достаточно будет провести операцию хеджирования от роста процентных ставок При этом оценка срочного рынка будет максимально объективной, потому что отразит ожидания всех игроков
«Короткая» продажа Фьючерсы на корзину облигаций позволяют участникам торгов играть на повышение процентных ставок даже в том случае, если у них в портфеле нет бумаг
Игра «с плечом» на лонижение/повышение процентных ставок Фьючерсы на корзину облигаций могут служить привлекательным инструментом для игры на повышение или понижение процентных ставок, поскольку предоставляют для этого «плечо» в размере 1 10 (Минимальный размер гарантийного обеспечения под каждую позицию по фьючерсу составляет 10% от его цены)
Тип стратегии Описание
Покупка/продажа краткосрочной синтетической облигации (операции репо) С помощью комбинации операций - покупки облигаций и продажи фьючерсных контрактов - участники рынка могут создать позицию, аналогичную покупке «синтетических» краткосрочных облигаций, срок до погашения которых равен сроку до исполнения фьючерсного контракта. Эта операция является аналогом операции «обратное репо», когда участник дает в кредит денежные средства под залог бумаг. Инвесторы, владеющие портфелем облигаций г. Москвы, с помощью фьючерсных контрактов могут взять краткосрочный кредит путем продажи бумаг и покупки фьючерса. Срок кредита равен сроку до исполнения фьючерса. Эта операция является аналогом операции «прямое репо», когда участник берет кредит под залог своих бумаг.
Календарный спрэд Наличие в обращении одновременно нескольких фьючерсных контрактов с разными сроками исполнения позволяет участникам играть на сужении или расхождении спрэдов цен между ними.
Управление дюрацией портфеля облигаций Инвесторы, владеющие портфелем облигаций, могут управлять его дюрацией. Для уменьшения дюрации необходимо заключить фьючерсный контракт на продажу облигаций, для увеличения - контракт на их покупку.
«Короткие» опционы
Специфика опционного рынка такова, что участникам торгов выгоднее не закрывать позиции досрочно, а ждать истечения срока действия опционов, что ограничивает ликвидность. Введение коротких опционов в дополнение к уже существующим контрактам расширяет возможности участников рынка и увеличивает емкость рынка.
Короткие» опционы - новые возможности:
• для продавцов: возможность получить более высокую прибыль за один и тот же период за счет последовательной продажи нескольких «коротких» опционов вместо одного «длинного»;
• для покупателей, возможность получить более высокую прибыль при краткосрочных и среднесрочных операциях, поскольку стоимость «коротких» опционов меньше стоимости «длинных» опционов с аналогичными страйками;
• для проведения арбитражных операций: наличие нескольких опционов с разными сроками действия, базовым активом для которых является один и тот же фьючерс, позволяет совершать дополнительный арбитраж синтетических позиций - «синтетику» на отдельных «ближних» опционах, на «ближних» опционах и фьючерсе, на «ближних» и «дальних» опционах;
• для построения различных стратегий: использование «коротких» и «длинных» опционов для игры на разнице их подразумеваемых волатильностей.
Варианты продажи опционов с разными сроками обращения при одинаковой цене фьючерса - 8000
Премия
Продажа 1-го «длинного» опциона call 8000 за три месяца до его исполнения 647 руб
Последовательная продажа 3-х «коротких» опционов call 8000 за месяц до исполнения каждого из них в течение того же трехмесячного периода 1056 руб
Стоимость «короткого» - апрельского опциона call 7500 Стоимость «длинного» - июньского опциона call 7500
20.03.2005 Цена фьючерса 7640 300 руб 564 руб
25.03.2005 Цена фьючерса 8140 659 руб 757 руб
Прибыль покупателя опциона от роста цены фьючерса на 6,5% 120% 34%
Арбитражные операции
1. Арбитраж синтетических позиций на «ближних» опционах
Такая арбитражная операция строится из синтетического и реального опционов.
• Можно сформировать позицию покупки синтетического опциона put за счет приобретения опциона call при одновременной продаже фьючерса:
о покупка опциона call со страйком 8500, премия - 150 руб.
о продажа фьючерса по цене 8400 руб,
о такая позиция равносильна покупке опциона put со страйком 8500 с премией 250 руб.
• При этом одновременно с этими операциями можно продать на рынке реальный опцион put со страйком 8500 и получить при этом премию 500 руб.
Таким образом, прибыль от данной арбитражной операции составит 250 руб. (без учета комиссии и других расходов).
2. Арбитраж синтетических позиций на «ближних» опционах и фьючерсе
Такая арбитражная операция строится из синтетического и реального фьючерсов.
• Позицию покупки синтетического фьючерса можно создать, купив опцион call при одновременной продаже опциона put:
о покупка опциона call со страйком 8500, премия - 150 руб.
о продажа опциона put со страйком 8500 и премией 500 руб.
о такая позиция равносильна покупке фьючерса по цене 8150 руб.
• При этом одновременно с этими операциями на рынке можно продать реальный фьючерс по цене 8400 руб.
Таким образом, прибыль от арбитражной операции составит 250 руб. (без учета комиссии и других расходов).
Приведенные для иллюстрации первых двух вариантов арбитража примеры являются абсолютно идентичными по совокупности операций, которые необходимо заключить на рынке, и по итоговому результату. Разница состоит лишь в том, какую модель расчетов выбирает трейдер для построения такой комбинации.
3. Арбитраж синтетических позиций на «ближних» и «дальних» опционах
Такая арбитражная операция строится из двух синтетических фьючерсов, сформированных из опционов с разными сроками истечения.
• Позиция покупки синтетического фьючерса:
о покупка «короткого» опциона call со страйком 8500, премия -150 руб.
о продажа «короткого» опциона put со страйком 8500 и премией 500 руб.
о такая позиция равносильна покупке фьючерса по цене 8150 руб.
• Позиция продажи синтетического фьючерса:
о продажа «длинного» опциона call со страйком 8000 и премией 650 руб.
о покупка «длинного» опциона put со страйком 8000, премия -200 руб.
о такая позиция равносильна продаже фьючерса по цене 8450 руб.
Таким образом, прибыль от арбитражной операции составит 300 руб. (без учета комиссии и других расходов).
В случае исполнения одного из «ближних» опционов у трейдера остается «длинная» позиция по реальному фьючерсу. Этот срочный контракт предстоит использовать для закрытия «короткой» позиции по синтетическому фьючерсу, сформированному из «дальних» опционов. Но если на рынке базового актива не будет какого-либо серьезного изменения цен и «ближние» опционы окажутся «на деньгах», может случиться так, что держатель опциона put не станет требовать его исполнения. При этом самому трейдеру, проводящему арбитражную операцию, нет смысла исполнять купленный опцион call: есть риск, что у него на руках окажется сразу два фьючерса, так как о решении держателя опциона put будет известно лишь после клиринга. Если исполнять обязательства по опциону put не придется, то трейдеру нужно будет просто купить фьючерс на следующий день после экспирации «ближних» опционов и таким образом покрыть позицию продажи синтетического фьючерса.
Новые стратегии
Наиболее распространенные комбинации ближних и дальних опционов подразделяются на горизонтальные и диагональные спрэды:
• горизонтальный спрэд - состоит, как правило, из опционов одного типа и одного страйка, но с разными датами истечения;
• диагональный спрэд - состоит из опционов одного типа, но с разными страйками и датами истечения.
Горизонтальные, и диагональные спрэды также подразделяются по их направленности на «медвежьи», «бычьи» и нейтральные.
Уникальность спрэдов, основанных на опционах с разными датами истечения, состоит в том, что с их помощью трейдер может зарабатывать даже в том случае, если движение цен на рынке базового актива уменьшает стоимость его позиции.
Вариант использования горизонтального спрэда
Примером стратегии, нацеленной на игру на разнице подразумеваемой волатильности (Implied Volatility, IV) опционов и волатильности базового актива является продажа «короткого» опциона call со страйком 8000 (срок до истечения - 30 дней) и покупка одного «длинного» опциона с таким же страйком (срок до истечения - 90 дней). При подразумеваемой волатильности в 32% стоимость «короткого» опциона будет составлять 352,21 руб., дальнего - 647,38 руб. Соответственно, стоимость такого горизонтального спрэда в момент создания равна 295,17 руб. (см. график).
Окончательный результат по такой позиции зависит от соотношения подразумеваемой волатильности по «ближнему» и «дальнему» опционам. При этом максимальный выигрыш трейдер получит, если через 10 дней подразумеваемая волатильность на рынке увеличится на 5 процентных пунктов - с 32 до 37% при сохранении цены
фьючерса на том же уровне. В этом случае игрок заработает 24,5%. Если при росте волатильности произойдет также увеличение цены фьючерса на 12,5%, то прибыль от такого горизонтального спрэда будет уже меньше - 15%.
Использование подобной стратегии позволит достичь максимальной прибыли, когда игрок предполагает, что в ближайшем будущем подразумеваемая волатильность на рынке увеличится или снизится без существенного изменения волатильности базового актива. Такая ситуация может сложиться, к примеру, когда на рынке ожидается какое-либо значимое событие и опционные игроки, предвидя будущие колебания рынка базового актива, активно «покупают» волатильность.
Для удобства пользователей в терминалах РТС реализована функция расчета подразумеваемой волатильности.
Срочный рынок FORTS (Фьючерсы и Опционы РТС) является лидирующей площадкой по торговле производными финансовыми инструментами в России, на долю которой приходится 98% оборота срочных контрактов. FORTS - одна из ведущих мировых площадок в сегменте производных на отдельные акции. Текущий объем открытых позиций по фьючерсам и опционам в FORTS составляет порядка 1,7 млн. контрактов, а среднедневной объем торгов превышает 200 тыс. контрактов.
Фондовая биржа РТС является ведущей фондовой биржей России по количеству обращающихся на ней ценных бумаг. Индекс РТС является общепризнанным показателем развития российского фондового рынка. К торговле в РТС допущено около 300 акций и облигаций. В информационных системах РТС представлена информация об индикативных котировках порядка 750 акций и облигаций, а также 500 векселей российских компаний РТС в партнерстве с Фондовой биржей «Санкт-Петербург» обеспечивает торги на организованном рынке акций ОАО «Газпром».
Фондовая биржа РТС
127006 г. Москва, ул. Долгоруковская, д. 38 стр. 1
Тел: (095) 705-90-31/32
Факс: (095) 733-97-03
Управление срочного рынка
E-mail: forts@rts.ru
Web: www.rts.ru или www.forts.nj
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
СПИСОК ОСНОВНОЙ ЛИТЕРАТУРЫ
Blake D Financial Market Analysis - L, 1999
Bns E, Bellalah M, Mai H, Fde Varenne Options, Futures and Exotic Derivatives - N Y , 1998
Capinski M, Zastawniak T Mathematics for Finance An Introduction to Financial Engineering - Spnnger, 2005
Chnss N Black-Scholes and Beyond Option Pricing Models - Professional Publishing, 1997
Clarke R G Options and Futures A Tutorial, 1992
Connolly К В Buying and Selling Volatility - Wiley, 2000
Cotte! Ch M Options Perceptions and Deceptions , 1996
DeRosa D F Options on Foreign Exchange 2-nd ed - Wiley, 2000
Dubil R An Arbitrage Guide to Financial Markets - Wiley, 2004
Energy Convergence The Beginning of the Multy-Commodity Market Ed by Fusaro PC- Wiley, 2002
Errera S, Brown SL Fundamentals of Trading Energy Futures & Options. 2-nd ed - Penn Well Corporation, 2002
Eydeland A, Wolyniec К Energy and Power Risk Management - Wiley* 2003
Fernandes PL, Somalo MP Opciones Fmancieras у Productos Estructura-dos 2-nd ed - McGrow-Hill, 2003
Gtdel S A Stock Index Futures and Options - Wiley, 1999
Hull J Options, Futures and Other Denvatives 4-th ed - Prentice-Hall, 2000 Kennedy M Single Stock Futures An Investor’s Guide - Wiley, 2003 Kolb R И/ The Investor's Complete Toolkit - New York Institute of Finance, 1991
Rodriguez de Castro Introduccion al Analisis de Productos Financieros De-nvados Futuros, Opciones, Fon/vards, Swaps - Editorial Limusa, 1998 Smithson Ch И/ Managing Financial Risk A Guide to Derivative Products, Financial Engineering, and Value Maximization - McGraw-Hill, 1998 Soldevilla E Opciones у Futuros Sob re Tipos de In teres a Corto PI azo -Piramide, 1997
Stephens J J Managing Interest Rate Risk Using Financial Derivatives -Wiley, 2002
The Handbook of Exotic Options Instruments, Analysis, and Applications -Professional Publishing, 1996
Van Deventer D R, Imai К, Mesler M Advanced Financial Risk Management -Wiley, 2005
Young PL, Sidey Ch Single Stock Futures A Trade’s Guide - Wiley, 2003 И/Wmott P Quantitative Finance - Wiley, 2000
Wilmott P The Theory and Practice of Financial Engineenng - Wiley, 1998 Wilmott P, Howison S, Dewynne J The Mathematics of Financial Derivatives A Student Introduction - Cambridge University Press, 1996
Алексей Николаевич Буренин
Форварды, фьючерсы, опционы, экзотические и погодные производные
Редактор А.Н. Буренин
Издатель МОО НТО им. акад. С.И. Вавилова
Подписано в печать 01.09.05 г.
Формат 125x200.
Бумага 65 г/см.
Усл.печ.л. 28,35. Уч.-изд.л. 22,9.
Тираж 1100 экз.
Отпечатано в Типографии «Лига-Принт» 105103, г. Москва, ул. 12-я Парковая, д. 11/49
БУРЕНИН Алексей Николаевич
97891631763
16643678 165546545 >51134665 945634564 146978910 ’80G206SS >44657453 135456452 131763658 701678989 280035268 747365447 156234496
7 -ведующий кафедрой Фондового рынка МГИМО(У) МИД РФ, д<)к 1 ор экономических наук, профессор.
Кандидатская диссертация посвящена деятельности |
транснациональных банков и корпораций США, докторская ди< -..•ртация - вопросам использования производных инструментов в макроэкономическом регулировании.
Введение в рынок ценных бумаг 1992 г/
• Контракты с опционами на акции» 1992 г., Фьючерсные, форвардные и опционные рынки» 1994 г., 1995 г, 2003 г
«Рынки производных финансовых инструментов» 1996 г., «Рынок ценных бумаг и производных финансовых инструментов» 1998 г, 2002 г.,
«Управление портфелем ценных бумаг» 2005 г.
’чзз^еб
785894068
986616789
«Организация торговли драгоценными металлами 1996 г.
Учебник « Курс экономической теории », подготовленный кафедрой Экономической теории МГИМ01993-2004 г., «Учебное пособие для руководителей и контролеров организаций, осуществляющих брокерскую, дилерскую деятельность и управление ценными бумагами» 1999 г, «Методическое пособие для подготовки к базовому квалификационному экзамену ФКЦБ России» 2001 г
’SBN 5902189063
dll ПИ III 11 till III
hi
ника «
Ростовкнига
|6отает на
ши
-5441
5631
6581
II
ТБК
9860 ! Ь ( 030 J13 I О . . ЪЭ f э1 6 ? Э 1 8951 06431 Вуренин А Н. Форварды.фьючер 68S3' JIfi75S&P328£8352D8887851465784671 Зь ммжао»*» ZW4 «. 10 40С» Цена 730 00 625GJ