В. П. МАСЛОВ
ОПЕРАТОРНЫЕ
МЕТОДЫ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного руководства
для студентов вузов, обучающихся '
по специальности чПрикладная математика»
издательство «наука»
главная редакция
физико-математической литературы
Москва 1973

SI 7.2
M31
УДК 517
Операторные методы. В. П. М а с л о в. Главная редакция
физико-математической литературы изд-ва «Наука», М., 1973.
. Книга написана на основе курса лекций, прочитанных авто*
ром на факультете прикладной математики МИЭМ и иа физиче-
физическом факультете МГУ.
В книге излагаются основы фуикциоиального анализа с точки
зрении приложений к задачам физики и вычислительиой матема-
математики. Развивается общий метод исчисления линейных некоммути-
рующих операторов для решения дифференциальных уравнений
с частными производными с переменными коэффициентами и диф-
ференциальио-разиостиых уравнений, подобный методу Хевисайда
для решения обыкновенных дифференциальных уравнений. Теоре-
Теоретический материал иллюстрируется иа конкретной физической
задаче, являющейся модельной задачей для этого метода, причем
формулы операторного метода сравниваются с численным ре-
решением.
Книга предназначена для студентов 3—5 курсов, специали-
специализирующихся по математике, прикладной математике и теорети-
теоретической физике. Она представляет интерес также для научных
работников.
Книга содержит 12 рис.
© Издательство «Наука», 1973.
0223-1858
М 042@2)-73 17'73

ОГЛАВЛЕНИЕ
Предисловие 5
Введение в операторное исчисление 11
§ 1. Решение обыкновенных дифференциальных уравнений операторным
методом Хевисайда A1). §2. Разностные уравнения A7). § 3. Решение
систем дифференциальных уравнений методом Хевисайда A9). § 4.
Алгебра сходящихся степенных рядов от некоммутирующих операторов
B1). § 5. Спектр пары упорядоченных операторов C1). § 6. Алгебры
с ц-структурамн C5). § 7. Пример асимптотического решения диффе-
дифференциального уравнения E1). § 8. Предельный переход уравнений
колебаний кристаллической решетки и волиоиое уравнение E3). § 9.
Понятие квазиобратимости оператора и формулироика осноииой тео-
теоремы (93).
Глава 1. Абстрактные пространства 118
§ 1. Алгебраические, системы A18). § 2. Банаховы пространства A22).
§ 3. Гильбертоиы пространства A29). § 4. Линейные функционалы и
сопряженные пространства A37). § 5. Линейные операторы A42). § 6.
Сопряженные операторы A54). § 7. Функции со значениями в банахо-
банаховом пространстве A60). § 8. Анализ в банаховом пространстве A63).
§ 9. Нормированные и банаховы алгебры A67).
Г л а в в II. Функциональные пространства 169
§ 1. Пространства Соболева A69). § 2. Двойственность пространств Собо-
Соболева A74). § 3. Некоторые пространства непрерывных функций и еиязан-
ные с ними пространства A78). § 4. Теоремы вложения A84). § 5. б^-функ-
ция Дирака в пространствах Соболева A91). § 6. Гладкие функции
в пространствах Соболева A93).
Глава III. Функции от регулярных оператором 201
§ 1. Алгебра функций от производящего оператора B03). § 2. Расши-
Расширение класса допустимых символов B17). § 3. Гомоморфизм асимптоти-
асимптотических формул. Метод стационарной фазы B24). § 4. Функции от опера-
оператора дифференцирования. Оператор Гильберта B31). § 5. Спектр произ-
производящего оператора B39). § 6. Некоторые свойства производящего
оператора B44). § 7. Самосопряженные операторы B57). § 8. Регулярные
операторы B64). § 9. Обобщенные собственные и присоединенные функ-
функции B68); § 10. Самосопряженные операторы как трансформаторы
в пространстве Гильберта—Шмидта B74).
Глава IV. Исчисление иекоммутирующих операторов 279
§ 1. Предварительные определения B79). § 2. Функции от двух неком-
некоммутирующих самосопряженных операторов B82). § 3. Функции от
иекоммутирующих операторов B86). § 4. Спектр вектор-оператора B89).
1*

4 ОГЛАВЛЕНИЕ
§ 5. Функции двух производящих наборов B91). § 6. Псевдодиффе-
Псевдодифференциальные операторы B97). § 7. Примеры C04). § 8. Дифференциро-
Дифференцирование функций от оператора, зависящего от параметра C12). § 9. Фор-
Формулы коммутации C23). § 10. Растущие символы C27). § 11. Фактор-
спектр C30). § 12. Операторнозначные символы C31). § 13. Функции от
образующих нильпотентной алгебры Ли и их представлении C36).
Глава V. Асимптотические методы 342
§ 1. Канонические преобразования псевдодифференциального опера-
оператора C42). § 2. Гомоморфизм асимптотических формул C59). § 3. Гео-
Геометрическая интерпретация метода стационарной фазы C65). § 4. Кано-
Канонический оператор на незамкнутой кривой C67). § 5. Метод стационарной
фазы C75). § 6. Канонический оператор на незамкнутой кривой, зави-
зависящей от параметров, определенный с точностью до О A/со) C78).
§7. V-объекты на кривой C84). § 8. Канонический оператор на семействе
незамкнутых кривых C89). § 9. Канонический оператор на семействе
замкнутых кривых C95). § 10. Пример на коммутацию канонического
оператора с гамильтонианом D00). § 11. Коммутация оператора Гамиль-
Гамильтона с каноническим оператором D06). § 12. Общее каноническое пре-
преобразование псевдодифференциальиого оператора D08).
Глава VI. Обобщенные уравнения Гамильтона—Якоби 415
§ 1. Основные определения и формулировки теорем D15). § 2. Решение
в малом уравнения Гамильтона — Якоби с диссипацией D26). §3. Реше-
Решение уравнения Гамильтона—Якоби с диссипацией в зоне D43). § 4. у-
перестройки как адиабатические преобразования D54). § 5. Решение
уравнения переноса с диссипацией в зоне D60). § 6. Операция обхода
фокусов и глобальное определение ростка D68).
Глава VII. Канонический оператор на лаграижевом многообразии с ком-
комплексным ростком и доказательство основной теоремы 478
§ 1. Формулы коммутации гамильтониана с комплексной экспонентой
D78). § 2. Квантовая операция обхода фокусов D82). § 3. Индекс ком-
комплексного ростка и канонический оператор D95). § 4. Доказательство
основной теоремы E09).
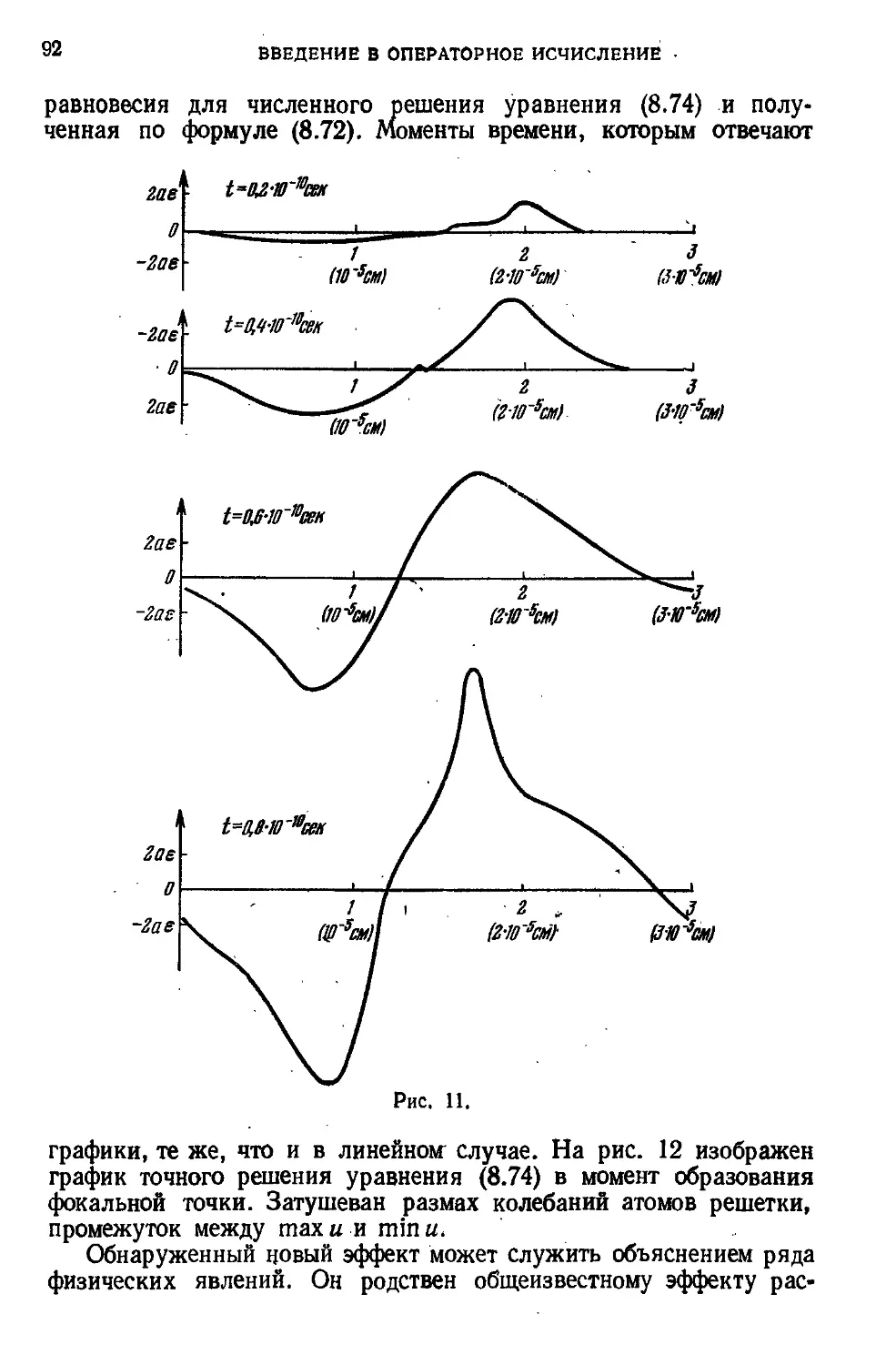
Приложение 1. Ангармонические колебания кристаллической решетки 521
Приложение 2. Вспомогательные предложения 524
Предметный указатель 539
Указатель обозначений 542

ПРЕДИСЛОВИЕ
Операторные методы — это методы, позволяющие сводить диф-
дифференциальные задачи к алгебраическим. Поэтому эти методы осо-
особенно полезны для математиков — прикладников.
Книга посвящена одному, но достаточно общему операторному
методу, который поглощает многие известные до сих пор оператор-
операторные методы и позволяет единообразно решать как классические
задачи дифференциальных уравнений с частными производными,
так и совершенно новые задачи математической физики, в том
числе и связанные с нелинейными уравнениями в частных произ-
производных.
К изложению этого общего метода мы перейдем, предварительно
изучив хорошо известные в математике методы исчисления опера-
операторов (в основном самосопряженных), источником которых послу-
послужил метод Хевисайда.
Основная теорема, изложенная в настоящей книге, относится
к теории операторов и доказывается в последней главе, но ее фор-
формулировка приводится также и во введении. Эта теорема может
привести, в частности, к теоремам существования и единственности
для гиперболических, эллиптических и параболических уравнений
с переменными коэффициентами и позволяет сводить их к интег-
интегральным уравнениям второго рода с гладкими ядрами, т. е. давать
эффективное решение этих уравнений. Имеется в виду, что выделив
из решения негладкую (или быстро осциллирующую) часть, мы
можем свести тем самым задачу к такой, которая легко решается
на ЭВМ. Сравнение же выделенной из решений быстро осциллирую-
осциллирующей части с точным решением, проводимое с помощью численного
эксперимента в одномерном примере § 8 Введения, показывает их
хорошее совпадение. При этом оказывается, однако, что проделать
такой эксперимент даже в двумерном случае машина бессильна
из-за большого объема операций. В таких случаях остается только
пользоваться подходящей асимптотикой и сведением исходной за-
задачи к интегральному уравнению. Таким образом, построенное
в основной теореме приближенное решение, выделяющее негладкую
или быстро осциллирующую часть, является как бы естественным
дополнением к ЭВМ: вместе они дают численный ответ.

6 ПРЕДИСЛОВИЕ
Предлагаемая книга по операторным, методам должна быть до-
доступной студентам старших курсов математических и физических
факультетов университетов и факультетов прикладной математики.
Имеется в виду, что для ее изучения читателю необходимо владеть
лишь классическим анализом. В нужном объеме в книге изла-
излагаются понятия группы, кольца, алгебры, основы функционального
анализа (глава I), теория обобщенных функций и пространств Собо-
Соболева (глава II), теория линейных дифференциальных и разностных
уравнений (§§ 1, 2, 3 Введения) и нелинейных дифференциальных
уравнений (§ 8 главы I), теория нелинейных уравнении первого по-
порядка с частными производными (глава VI).
Это изложение небесполезно и для читателя, знакомого с дан-
данными вопросами, поскольку оно ведется подчас не в традиционном
стиле и приспособлено для дальнейших ссылок. Читатель, изучив-
изучивший книгу целиком, будет подготовлен для проведения собственных
исследований в современной теории линейных, 'нелинейных диф-
дифференциальных и дифференциально-разностных уравнений с част-
частными производными. Кроме того, изучение изложенных здесь кон-
конкретных задач может быть хорошим трамплином для дальнейшего
изучения под некоторым определенным углом зрения теории пред-
представлений, топологии и теории пучков. Примером последних служит
теория К-объектов (глава V). Что же касается приложения изло-
изложенных мето'дов в физике, то оно, по-видимому, не исчерпывается
теми примерами, которые приводятся в книге. Так, можно допол-
дополнительно отметить асимптотику решений в зонной теории твердого
тела, в задачах о столкновении с молекулами, в теории лазерных
резонаторов, в уравнениях цепной реакции в химии, в задачах реф-
рефракции и дифракции, при выводе интегральных уравнений типа
Липмана — Швингера и Фаддеева, при вычислении квазикласси-
квазиклассических поправок к уравнению Томаса — Ферми, поправок к урав-
уравнениям электронной плазмы, асимптотику решений уравнений
Хартри, в электронной оптике, в задачах надбарьерного отражения
и во многих других задачах современной математической физики.
Эта книга построена так, чтобы она могла служить возможно
более широкому кругу читателей. В ней проводятся как бы два спо-
способа обучения. Читатель, который хочет избежать изучения тонких
оценок и предельных переходов, но который хочет овладеть практи-
практической техникой получения асимптотических решений, может про-,
пустить всю часть, посвященную функциональному анализу. Для.
этого «Введение в операторное исчисление» написано с таким рас-,
четом, чтобы можно было, изучив его, овладеть операторной техни-
техникой (пропустив главы I—IV), сразу перейдя к изучению способов
сведения конкретных задач к интегральному уравнению и выделения
негладкой части решения.
При втором способе обучения, состоящем в постепенном и
более глубоком изучении операторных методов, следует начи-

ПРЕДИСЛОВИЕ 7
нать с первой главы и лишь после главы IV прочитать Вве-
Введение.
Однако самый эффективный путь овладения предметом скорее
всего заключается в том, чтобы сначала ознакомиться с Введением,
а затем последовательно читать всю книгу.
Следует' все же предупредить читателя, что все эти способы
нелегки, ибо в книге излагается некое новое операторное исчисле-
исчисление — исчисление упорядоченных операторов. '
Настоящая книга представляет собой запись курса лекций,
читавшихся автором в течение трех лет на факультете прикладной
математики Московского института электронного машиностроения
последовательно третьему, четвертому и пятому курсам, а последние
главы также пятому курсу (в течении трех лет) выпускников ка-
кафедры математики физического факультета Московского государ-
государственного университета. Кроме того, этот курс лекций (в сокращен-
сокращенном варианте) был прочитан автором в нескольких математических
школах (на международной математической школе в Сопоте в 1971 г.,
в Пущйно в 1971 г,, в Воронеже в 1972 г. и др.).
Опыт чтения этого курса лекций показал, что, вопреки ожида-
ожиданиям, операторное исчисление при параллельном рассмотрении
сравнительно небольшого числа примеров на семинарских занятиях
воспринимается даже легче, чем вопросы, связанные с традицион-
традиционным функциональным анализом, тонкими оценками, функциональ-
функциональными пространствами и предельными переходами.
Студенты старших курсов и аспиранты могут быстро научиться
решать сложные задачи, связанные с операторными методами. В этой
книге, в частности, читатель найдет важные формулы, полученные
М. В. Карасевым (теоремы 4.4 и 6.6 Введений) и В. Г. Даниловым,
(теорема 1.1 главы V).
Если провести аналогию между изложением операторного ис-
исчисления во «Введении в операторное исчисление» с гипотетиче-
гипотетическим изложением дифференциального исчисления (см. левый стол-
столбец), то получится примерно следующее.
В §§ 1—3 излагается кольцо В §§ 1—3 излагается метод
полиномов. Хевисайда и исчисление опера-
операторов с постоянными коэффици-
коэффициентами.
В §§ 4—5 приводятся правила В §§ 4—5 выводятся правила
формального дифференцирова- нового исчисления на примере
ния полиномов и выводятся раз- формальных степенных рядов от
личные формулы дифференциро- упорядоченных операторов. Вы-
вания для полиномов: формулы водятся формулы для коммута-
Дифференцирования произведе- торов от рядов, формулы для
ния, сложной функции, раз'ло- сложной функции и разложения
жение в ряд Тейлора. в ряды Ньютона.

8
ПРЕДИСЛОВИЕ
В § б вводится система аксиом
и те же формулы выводятся для
произвольных функций в виде
теорем, и, тем самым, опреде-
определяются все формулы техники
дифференцирования.
В § 7 дается простой пример.
В § 8 с помощью введенной
техники получается новое реше-
решение классической физической за-
задачи.
В § 9 ставится задача на про-
простейшее дифференциальное урав-
уравнение. Вводится основное поня-
понятие характеристического полино-
полинома и обсуждается физический
смысл начальных условий. Фор-
Формулируется основная теорема су-
существования и приводится фор-
формула для решения уравнения в
частном случае.
В § б вводится система аксиом
и те же формулы для произволь-
произвольных функций в виде теорем, и,
тем самым, определяются все
формулы техники исчисления
упорядоченных операторов.
В § 7 дается простой пример.
В § 8 с помощью введенной-
техники получаются новые фи-
физические эффекты при изучении
классической задачи вывода вол-
волнового уравнения из уравнений
колебаний кристаллической ре-
решетки.
В § 9 формулируется основная
задача, вводится основное поня-
понятие характеристик для функции
от упорядоченного набора опера-,
торов и обсуждается физический
смысл условий поглощения. Фор-
Формулируется основная теорема и
приводится явная формула реше-
решения основной задачи в частном
случае (общая формула приво-
приводится в последней главе).
Далее (если продолжить аналогию) последовательно проводится
как бы теория пределов (глава I), затем производной как предела (гла-
(глава III) и частных производных как многократных предел'ов(глава IV).
По сути дела глава I посвящена традиционному функциональному
анализу, причем последовательно проводится концепция «пополне-
«пополнения пределами», подобно тому, как в теории Кантора действительные
числа являются пополнением последовательностей рациональных
чисел. Это позволяет полностью избежать теории меры (в частно-
частности, меры Лебега). С этой же точки зрения строится и теория функ-
функций в главе II, что согласуется с первоначальной концепцией физи-
физиков относительно б-функции Дирака как предела колоколообраз-
ных функций.
Глава III посвящена исчислению функций от одного оператора.
Вводятся понятия производящего и регулярного операторов, обоб-
обобщающих соответственно понятия самосопряженного и нормального
операторов. Для регулярных операторов доказывается теорема, по-
показывающая их общность в случае дискретного спектра: регуляр-
регулярность оператора — необходимое и достаточное условие полноты
собственных и присоединенных элементов. Как следствие выводится
известное исчисление самосопряженных операторов.

ПРЕДИСЛОВИЕ У
В главе IV вначале подробно изучается исчисление функций от
двух некоммутирующнх упорядоченных операторов, их совместный
спектр и спектральное разложение. Далее рассматриваются функ-
функции от нескольких регулярных операторов и выводятся для них
формулы, которые во введении были получены из аксиоматики. Тем
самым строится, уже на функциональной основе, вся техника исчис-
исчисления некоммутирующих операторов. На этом заканчивается соб-
собственно операторное исчисление.
Дальнейшая часть книги посвящена специальному преобразо-
преобразованию, позволяющему доказать основную теорему. Это преобразо-
преобразование называется каноническим оператором.
В главе V проводится большая подготовительная работа. Вво-
Вводится канонический оператор в простейшем действительном одно-
одномерном случае (зависящий от упорядоченных операторов).
На главе VI следует остановиться более подробно. Она необхо-
необходима для окончательного построения комплексного канонического
оператора, но, вообще говоря, совершенно обособлена и никак не
связана с техникой упорядоченных операторов. Она даже может
быть прочитана сразу. Эта глава посвящена конструкции решения
в целом уравнений, обобщающих уравнения Гамильтона — ЯкЪби.
В ней вводится^ понятие лагранжевой поверхности с комплексным
ростком. Это позволяет дать геометрическую интерпретацию решений .
уравнений типа Гамильтона — Якоби.
Можно провести следующую физическую аналогию. При падении
камня в воду вначале расходятся ровные круги, а затем, после отра-
отражения волны, получается картина, которой трудно дать геометри-
геометрическое истолкование. Точно так же и уравнение Гамильтона —
Якоби (частное решение некоторого уравнения Гамильтона — Якоби
как раа и будет дават ь эти круги) при временах, не превышающих
некоторого времени /х,имеет простое и гладкое решение. Дальше при
t > /х возникает аналог наложения многократно отражённых волн.
Чтобы разобраться вмногозначных функциях (ветвлениях решения),
необходимо провести униформизацию аналогично тому. как это
делается при помощи листов Римана для аналитических функций
с ветвлением. И именно конструкция объекта в фазовом простран-
пространстве лагранжева многообразия с комплексным ростком поз-
позволяет «распутать» многозначные решения уравнения типа Гамиль-
Гамильтона — Якоби (с поглощением). При этом введённое здесь понятие
«индекса» — целого числа — позволяет как бы пронумеровать эти
решения (листы) на лагранжевом многообразии с комплексным
ростком.
Кроме того, индексы замкнутых путей на лагранжевом много-
многообразии с комплексным ростком представляют собой важную ха-
характеристику этого объекта (характеристический класс объекта).
После этого в главе VII строится комплексный канонический
оператор и доказывается основная теорема.

10 ПРЕДИСЛОВИЕ
Результаты глав III—VII и §§ 4—9 Введения принадлежат в ос-
основном автору (за исключением теорем главы III, относящихся к са-
самосопряженным операторам, и отмеченных выше теорем Карасева
и Данилова).
Отправным пунктом для настоящего исследования послужило
замечание Р. Фейнмана *) о том, что если порядок действия опера-
операторов определяется индексами, то операторы становятся как бы
коммутирующими.
Теория лагранжева многообразия с комплексным ростком воз-
возникла в результате изучения работ Ж- Лере по задаче Коши.
Редактор книги Д. А.' Кириллов сделал ряд ценных прин-
принципиальных указаний, касающихся конструкции книги в целом.
Большую помощь мне оказали консультации А. А. Самарского и
дискуссии с Д. В. Аносовым и В. В. Кучеренко. Приношу им свою
глубокую благодарность. Я очень благодарен также, П. П. Мосо-
Мосолову, Е. А. Горину и В. Л. Дубнову, сделавшим ряд полезных
замечаний по рукописи.
Но эта книга вообще не была бы написана как учебное руко-
руководство, если бы не мои ученики,, которые записали и обработали
этот курс лекций. При этом по главам 1> II, V, VII им даже не были
предоставлены подробные конспекты. Первая глава была записана
B. Л. Дубновым, вторая Е. М. Воробьевым и В. Л. Дубновым,
III, IV главы обработал В. Л. Дубнов, V — В. Л. Дубнов и
М. В, Карасев, VI — В. Г. Данилов, VII — В. Г. Данилов и
М. В. Карасев, § 4 гл. VI — А. Г. Прудковский, который провел
также все вычисления- на машине. Кроме того, многочисленные
дискуссии с В. Л. Дубновым, М. В. Карасевым, В. Г. Даниловым,
C. Ю. Доброхотовым, А. Г. Прудковским и Г. А. Воропаевой ока-
оказали мне неоценимую помощь. При подготовке рукописи к печати
мне помогали также А. Г. Давтян и Г. Ю. Малышева. Моя призна-
признательность всем им не знает границ.
В. П. Маслов
*) В статье «Операторное исчисление, имеющее отношение к квантовой
электродинамике» (Phys. Rev., 84, 1951; рус. перев. «Проблемы современной
физики», Ms 3, 1955) в параграфе «Описание способа обозначения».
По рекомендации редактора исчисление Фейнмана в эту книгу ие вклю-
включено. Точно так же опущены и физические приложения, перечисленные иа
стр. 6.

ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
§ 1. Решение обыкновенных дифференциальных уравнений
операторным методом Хевисаида
Обозначим через C°°(R) (или С00) -множество бесконечно диф-
дифференцируемых функции ф (х), — оо < х < оо. На С00 определена
операция (оператор) дифференцирования d/dx, которую мы в даль-
дальнейшем будем обозначать через D:
Ясно, что для любого полинома Р„ (х) имеет смысл оператор Р„ (D):
С°°-*С°° вида
где а,-— комплексные числа, /=0, 1, ..., п. Иначе говоря, по
определению,
def »
2W ()
Обозначим множество операторов вида Р„ (D) через /Ci [D];
для любых двух элементов нз /Ci [D] определены их сумма
и произведение:
Через /Сх [л;] обозначим множество полиномов над- полем комп-
комплексных чисел:
i 0
Каждому полиному Рп е Кх [х] можно взаимно однозначно сопо-
сопоставить оператор Pn(D) ^ KAD P(D D D

12 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
(Для доказательства взаимной однозначности достаточно показать,
что если 2 anfM (х) = 0 для всех / е С00, то ап э= 0. Но это оче-
л=0
видно.) Будем называть полином Р (х), отвечающий оператору
Р (D), символом оператора Р (D). При таком сопоставлении сумма
двух полиномов переходит в сумму соответствующих операторов
и произведение двух полиномов переходит в произведение соот-
соответствующих операторов. Имея в виду это соответствие, будем
говорить, что Ki \x] и Ki [D] изоморфны.
Из ссновиой теоремы алгебры следует, что любой полином
Р„ (х) е Ki [x] может быть представлен в виде
т т
<=1 ¦ 1=\
где <х{ — комплексные корни полинома, ^ — кратность корня.
В силу изоморфизма между Ki\x] и Ki\D] для каждого опера-
оператора Pn(D) справедливо представление
т
где а; — операция (оператор) умножения на постоянную щ.
Теперь решим обыкновенное дифференциальное уравнение
с постоянными коэффициентами:
<=о
Предположим для упрощения, что все корни а,- полинома
Рп'(х) являются простыми. Тогда уравнение A.3) можно перепи-
переписать в виде
П (D-а,) »(*) = /(*)/а«.
Для решения уравнения A.3) нам понадобится следующая
лемма.
Лемма 1.1. Пусть Р„ (D) e Ki [D], feC". Справедлива фор-
формула:
Рп (D) в"/ (х) = <**Рп (D + a)f(x). A.4)
Доказательство проведем по индукции. Вычислим Deaxf(x)y
De**f (х) = a^xf (x) + exf (x) = <** (af (x) + /' (*)) = e°" (D + a) f (x).
Пусть теперь формула A.4) верна для оператора D". Дока-
Докажем, что она верна и для оператора D". Имеем Dneaxf (x) =
= D [Dn'l€fLxf (х)\ = DF (х), rneF(x) = Dn-1eaxf(x). По предположе-.

§ 1] РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ХЕВИСАЙДА 13
нию индукции, Dn~1eaxf(x) = eax(D + a)n~1f (х). Далее имеем
DF (х) = Deax \(D + a)»"V (*)] =
^a^x[(D + a,a-1f (х)]+еахО[(О + а)а-^ (х)] = еах (D + a)" f (x).
Таким образом, для любого целого т получена формула
DV*/ {х) = е«х (D + a)mf(x). A.5)
Из равенства A.5) сразу следует равенство A.4), что и требова-
требовалось доказать.
Рассмотрим теперь уравнение
(D-a)y(x) = f(x), /eC*. A.6)
Используя лемму, получаем
(D -а)у(х) = (р- а) е*хе' «ху (х) = ^xDe~ axy (х).
Таким образом, уравнение A.6) эквивалентно уравнению
«x. A.6')
Как известно, общее решение уравнения Dy(x) = f(x) имеет
вид у(х) = \f(x) dx-\-C, где С —константа. Введем обозначение
§/(*)d* + C = i/(*). A.7)
Отметим, что 1/D отображает элемент / s С00 в целый класс
функций д- / с: С00; если (/,Ер/, то 2?р/ тогда и только
тогда, когда г — уй — const.
Теперь можно решение уравнения A.6) (и A.6')) записать
в виде
y = e«x±-e-«xf(x). A.8)
Вернемся к уравнению A.3). Имеем
Р„ (D) у (х) = а„ П (D - а,) г/ (дг) = а„ (D - a,) f\ (D-a,) у (х) =
. 1=1 1=2
п
= an^xDe~^x \\ (D - щ) у(х) =
=... = ane«SDe-V ... e*xDe~**y (x) = /{х).
Применяя последовательно A.8), получим формулу
f*t"* ^ ^Ш^^ A.9)
Мы получили формулу, выражающую решение уравнения A.3)
через интегралы от правой части. Таким образом, существо-

14 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
вание решения установлено. Нетрудно' убедиться, что ответ
не зависит от порядка нумерации корней ох, ..., а„ полинома
Рп(х). В принятой записи видно, что общее решение уравнения
A.3), определяемое равенством A.9), зависит не более чем от п
постоянных (на самом деле ровно от п).
Формула A.9) определяет отображение элемента /еС°в неко-
некоторый класс функций. Если уравнение Р„(х) = 0 имеет простые
корни ох, ..., а„, разность двух элементов этого класса имеет
вид с^^+с^^ + .-.+Спе"*, где q, сг, ..., с„ —константы. Фор-
Формула A.9) по самому способу ее получения справедлива и в слу-
случае кратных корней: тогда разность двух элементов имеет вид
Р1 (х) eaix + Рг (х) еа*х +... + Рт(х) еат\
где Рц Р2, ..., Рт — подходящие полиномы.
Полученное отображение (или оператор) мы обозначаем 1/Рп (D).
Покажем, что для единствен ности решения уравнения
A.3) достаточно задать начальные данные Коши:
у@) = со, ..., ^(«-1)@)=с„_?. A.10)
Для этого, очевидно, достаточно показать, что задача
Pn(D)y(x) = 0, A.11)
0, .... yl»-»@)^0 A.12)
имеет единственное решение у (х) = 0. Заметим, что задача
(D—а) у (х) = 0, у @) = 0 имеет единственное решение у (х) a 0.
Преобразуем теперь уравнение A.11):
Рп (D) у (х) = П (° ~ «<)*' У (х) - (D - «0 W (х). 0.
i
Очевидно, W (х) является линейной комбинацией производных
функции у(х) порядка ^га—1. Значит, в силу условий A.12),
W@) = 0, и следовательно, W(x)s=Q. Ясно, что продолжая этот
процесс, мы получим у(х)==0.
Приведем еще один способ вычисления класса функций р (DJ,
использующий некоторое расширение рассмотренного выше ото-
отображения /Сх [х] -*¦ Ki [D] на поле рациональных функций пере-
переменного х.
Пусть R(x)=*P (x)/Q(x), где Р (х), Q(x) — полиномы. Функции
) сопоставим отображение (оператор) R(D), которое перево-
переводит функцию /еС°°,в класс функций Р (D) Q ,р. fa С°°. Функ-
Функцию R(x) будем называть символом отображения (оператора) R(D).
Убедимся, что отображение R(D) не зависит от способа представ-
представления его символа R(x) в виде дроби Р(х)/3(х). Действительно,
пусть P(x) = P(x)S(x), il(x)=Q(x)S(x), где S (х) — некоторый

5 I] . РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ХЕВИСАЙДА 15
полином. Покажем, что для любого /еС00 имеет место равенство
Пусть y&P(D)-щщf. Тогда у(х) имеет вид у(х) = Р(D)г(х),
где г (х) — решение уравнения Q (D)t (x) = f(x). Обозначим через и (х)
какое-нибудь решение уравнения S(D)u (x) = z(x). Тогда
Q (D) u(x) = Q (D) S (D) u(x) = Q (D) z(x) = f (x), так что ы е ^>.
Имеем далее; y(x)=±P (D) z(x) = P (D) S- (D) u{x) = P (D) и (х). Сле-
Следовательно.,
f
Обратно, пусть yeP(D)^f. Тогда у(х) = P (D)и (х), где
и (х) удовлетворяет уравнению Q (D) u(x) = f (x). Обозначим г (x) =
— S(D)u (x). Тогда z (x) удовлетворяет уравнению Q (D) z {x) = f (x),
и y(x) = P(D)i(x)GP(D)-^5-)f(x); значит,.у<= P(D)-~f, что
и требовалось доказать.
Обозначим множество операторов R(D) через F[D]. Введем
на множестве F[D] операцию суммы, индуцированную соответ-
соответствующей операцией в поле F[x] (F[x] — поле рациональных
функций). Положим по определению, что R(D) = R1(D)~\-R2(D)
тогда и только тогда, когда R(x)=*Ri(x)-\-R2(x). Имеет место
следующая лемма.
Лемма 1.2. Пусть Rt (x) u R2 (х) — элементы поля F [х], R (х) =
— Ri(x)-\-Ri(x)- пля того, чтобы функция у принадлежала классу
R (D) /, необходимо, чтобы она была представима в виде у (х) —
= й (*) + Уг (х), где й s Ri (D) f, y2 s R2 (D) f.
Доказательство. Пусть Ri(x)=Pi(x)/Q1(x), R2(x) =
= Pi(x)/Q3(x),. где Ptix), P2(x), <&(*), Q2(x)-полиномы. Тогда
R(x) = R1(x) + R2(x) = P(x)/Q(x), где Р (x) = P1 (x) Q2 (*) +
+ Q1(x)P2(x), Q(x) = Q1(x)Q2(x).
Будем обозначать класс функций вида у (х) через Rx (D) f (x) +
+ Ri(D)f(x). Докажем, что R(D)f<^R1(D)f + R2(D)f. Пусть
У (х) е R(D) f (х). Тогда у (х) = [^ (D) Q2 (D) + Qx (D) P2 (D))z(x),
где г(х) удовлетворяет уравнению
Q1(D)Qi(D)z(x) = f(x). A.14)
ОбозначимР! (D)Q2(D) z(x) = yi (x), P2(D)Qt (D)z(x)=y2(x). Функ-
цня иг (x) = Q2 (D) г (х) удовлетворяет уравнению Qx (D) ux (x) = f (x),
а функция u2 {x) = Qx(D)z(x) удовлетворяет уравнению Q2 (D) u2 (x) =
~ f (x). Следовательно;
yx (x) e Rt (D) f (x), уг (x) e R2 (D) f (x),
и Доказываемое включение установлено.

16 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Приведем теперь способ вычисления l/Pn'D) с помощью полу-
полученного соответствия R (х) -*¦ R (D). Для этого разложим символ
УРп(х) на простейшие дроби:
1
где «/ — комплексные корни кратности kt полинома Рп (х), а{ —
комплексные полиномы. Из леммы 1.2 следует, что
m
' fc
Это означает, что любое решение у(х) уравнения A.3) предста-
вимо в виде
т
а ж 1
¦I (D) е ' д- • • •
что непосредственно следует из A.6), A.6') и A.8). В частном
случае, когда корни простые, A.15) принимает вид
п Г х 1
у (х) = У сцеа*х. [ е~ а«р / (р) dp + Ctea'x . A.15')
Нетрудно убедиться*) в том, что общее решение уравнения A.3)
содержит ровно п констант. Отсюда следует, что A.15) дает
общее решение (т. е. любой элемент из класса р р^ Я урав-
нения A.3).
Для отыскания решения однородного уравнения также можно пользоваться
формулой A.9).
Пример'. Найти общее решение уравнения
(D - ttl) (D - а») у (х) = 0,
По формуле A.9) имеем
у (х) = еа'х~ е~а'*х е^х ^ е
*) Это немедленно следует из того факта, что любое решение уравнения
A.3) представимо в виде суммы некоторого решения этого уравнения н неко-
некоторого решения однородного уравнения. С другой стороны, любой из членов
разложения 1/Р„ (D) на простейшие дроби, примененный к нулю, удовлетво-
удовлетворяет однородному уравнению Pn(D)y=O, так как Pn(D) можно представить
ft ft
в виде Pft (D) ф — а*) *, где (D — а^) * — знаменатель этого члена.

§ 2] РАЗНОСТНЫЕ УРАВНЕНИЯ 17
Рассмотрим также на примере случай кратных корней.
Пример. Найти общее решение уравнения
(D
Из равенства A.9) получаем;
у (х) = е«* -^ е-а*е** -1 <га*ео* -I
Замечание. Рассмотрим теперь уравнение
), Рп(О)ФО, A.16)
где Pk (х)— полином степени к. Обозначим через Pa,s(x) сумму s+1 чле-
членов разложения в ряд Тейлора с центром в * = 0 функции \/Рп(х). Из ра-
равенства
немедленно следует:
Ра (ж) Ря, , (ж) - 1 + *т^л-1 (ж), A-17)
где Р„_1 (х)~— полином степени не выше п— 1.
Покажем, что
y(x) = Pats(D)Pk(x) A.18)
является решением уравнения A.16) при s^k. В самом деле, используя A.17),
получаем:
Рп (D) У (ж) = Ра (D) Pa, s (D) Pk (х) =
= A +Pn_! (D) D«-i) Pft (x) = Pft (ж) + Pn_i (D) D*+iPft (x).
Но при s^k последний член равен 0. Таким образом, при любом s^k фор-
формула A.18) дает одно из решений уравнения A.16), причем любое решение
уравнения A.16) выражается формулой
§ 2. Разностные уравнения
Рассмотрим оператор сдвига. Обозначим его через ehD\
ehDf(x)Mf(x+h),
где h — действительное число.
Это определение оправдывается следующим эвристическим рассуждением:
пусть f (х) — аналитическая функция в 2А-окрестности точки х, — сю < х < со .
Тогда
оо
А = 0
„hD
С другой стороны, разлагая е формально в степенной ряд, получим

18 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Следовательно, разложению в ряд Тейлора функции f (х -\- h) отвечает формаль-
формальное разложение в ряд экспоненты ehD.'
Рассмотрим уравнение
= f(x), /e=Cf, B.1)
где CjJ° — пространство бесконечно дифференцируемых финитных
функций на R (т. е. с компактным носителем). Перепишем это
уравнение в виде
Pn(ehD)y(x)=*f(x),
где - л
Предположим для простоты, что все корни полинома
л
Рп (х) = 2 я*** различны. Тогда справедливо равенство
2'Т^Г» B-2)
где Л, —некоторые постоянные.
Если у(х) — решение уравнения
(e"D-a)y(x) = f(x), B.3)
то у (х) есть решение уравнения
(ehD _ а) fh 1П V I 1пау {х) = / ДО.
Легко проверить, что
(««> ¦=- а) / (х) = аД lna(eftD - 1) Г т '""/ (л:).
Таким образом, B.3) можно записать в виде
00
Теперь заметим, что ряд— 2е*А?> является формальным степен-
А = 0
ным рядом для выражения (ehD'— 1)-1. Нетрудно убедиться, что

? 3] РЕШЕНИЕ СИСТЕМ МЕТОДОМ ХЕВИСАЙДА 19
где f/i (х) удовлетворяет однородному уравнению (ehD — 1) t/x = 0;
yi(x+h) = yl(x^. Значит yfi{x) есть любая периодическая функ-
функция с периодом А. Точно так же, как и в предыдущем параграфе,
можно получить, что решение уравнения B.1) представимо в виде
{2А)
Для функции у(х), определяемой B.4), положим
Тем самым задача сведена к уравнению B.3).
Задача. Найти частное решение дифференциальио-разностиого уравнения
где а удовлетворяет соотношению а
§ 3. Решение систем дифференциальных уравнений
методом Хевисайда
Любую систему линейных дифференциальных уравнений с посто-
постоянными коэффициентами можно записать в виде
B(D)Y(x) = F(x), C.1)
где Y{x) = (y1(x), .... уп(х)), F(x) = (f!(x), ..., /„ (х)) - вектор-
функции, а В (D) — пХга-матрицы, элементами которых являются
рассмотренные в § 1 операторы.
Легко видеть, что операторы В (D) образуют ^некоммутатив-
^некоммутативную) алгебру*). Мы будем обозначать ее через M[D]. Обозначим
через М [х] алгебру матриц, элементами которых являются поли-
т
номы Р(х) = 2 atx'- Очевидно, что изоморфизм P(x)-*-P(D)
( = 0
алгебр Kilx] H'KilD], определенный в § 1, можно расширить
до изоморфизма алгебр М [х] и Д1 [D].
Пусть
В^М[х], В(х) = \\Р"(х)\\.
Обозначим через Ау (х) алгебраические дополнения матрицы В (х)
и рассмотрим матрицу А^М[х], А(х) = \\Ац\\' = \\Ал\\. Из
линейной алгебры хорошо известно равенство
А:х)В(х) = Е-А(х), C.2)
*) См. <) 1 гл. 1.

20 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
где Е — единичная матрица, а А(х) = detfi (x). Из равенства C.2)
для соответствующих операторов имеем
Eb(D). C.3)
Используя равенство C.3), задачу C.1) можно преобразовать
к виду
A (D) В (D) Y(x) = A (D) F (х).
Обозначим A(D)F(x) = G(x). Тогда
EA(D)Y(x) = G х), C:4)
или
b(D)yt(x)=g,{x), /=1 п. C.4')
Такие уравнения нами уже изучены. Их решение имеет вид
i{x), « = 1, • ••> п. C.5)
Из приведенных выше рассуждений видно, что если вектор-
функция Y (х) удовлетворяет системе C.1), то ее компоненты —
функции уг (х) — удовлетворяют уравнениям C.4'). Отметим однако,
что если Hi (x) — общее решение уравнений C.4'), то функция
Y(х) — (у1(х), ..., у„{х)У вообще говоря, не удовлетворяв/ системе
уравнений C.1). Для того, чтобы функция У (х) = (у1 (х),..., уп(х)У
была решением системы C.1), необходимо наложить условия на
постоянные интегрирования, входящие в решения уравнений
C.5). Если .же
*'(*) = Ар)/«(*)'
ТО
Y(x) = A(D)Z(x),
где Z(х) = (;?!(х), ..., гп(х)), очевидно, удовлетворяет системе 3.1:
В (D) Y{x) = B (D) A (D) Z (х) = ЕА (D) Z(x)^F (x).
Нетрудно убедиться, что мы получили общее решение системы 3.1.
Пример. Решить систему уравнений
D*yx (x) - у, (х) + D"yt (x) + ft (x) = 0.
Перепишем систему в виде
(?>¦ - 1)^ (*) + (?>¦ +1) й (*) — 0.

§4] РЯДЫ ОТ УПОРЯДОЧЕННЫХ ОПЕРАТОРОВ
21
Легко видеть, что в данном случае A(D) = (D + 1J- Следова-
Следовательно, решение имеет вид
У\ (*) = ае~* + Ьхе-Х,
Подставив эти функции в первое уравнение, после сокращения
на ег* получим:
b-c-dX + d = O,
т. е. d = 0, 6 = с. Подстановка уг(х) и у% (х) во второе уравнение
дает те же условия на коэффициенты. Таким образом,, оконча-
окончательно получаем
у1{х) = ае
у2 {х) = Ье-*.
Мы убедились, таким образом, что для систем обыкновенных
дифференциальных и дифференциально-разностных уравнений
с постоянными коэффициентами операторный метод Хевисайда
позволяет сводить задачу к чисто алгебраической, связанной
с линейной алгеброй. Методы же линейной алгебры глубоко изу-
изучены и широко известны. Но если бы даже они не были известны,
то естественно было бы свести задачу к алгебраической, поста-
поставить алгебраическую задачу и далее изучать именно ее. Такой
путь был бы наиболее рационален.
В случае переменных коэффициентов дело обстоит значительно
сложнее, ибо алгебраическая задача, к которой приводит опера-
операторный метод, изложенный ниже, не была до сих пор изучена,
так что под операторным методом мы понимаем в дальнейшем
не простое сведение дифференциальной задачи к чисто алгебраи-
алгебраической, но и метод решения этой последней.
§ 4. Алгебра сходящихся степенных рядов
от некоммутирующих операторов
Операторное исчисление Хевисайда позволяет решать линей-
линейные дифференциальные уравнения с постоянными коэффициен-
коэффициентами. Обратимся к уравнению с переменными коэффициентами:
Если оператор дифференцирования снова обозначить через D, то
это уравнение естественно записать в виде
P(x,D)y(x) = f(x)<

22 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
где Р — полином по .второму аргументу:
Существенная трудность связана с тем, что операторы дифферен-
дифференцирования и умножения на х не коммутируют. Это видно уже
из следующего простейшего примера. Пусть Р (х, р) = хр\ как
понимать тогда Р (х, D), учитывая, что подстановка х и D в раз-
разном порядке дает разные результаты:
xDy (х) = ху' (х), Dxy (х) = (ху)' =у(х) + ху' (*)?
Ясно, что обозначение Р (х, D) = ^ ai (*) D', где Р (х,-1) =
= "S сц (х) I', не имеет смысла, если не подразумевать, что опера-
оператор D в обозначении Р {х, D) действует первым. Поэтому указав
номерами порядок действия операторов /и D, мы однозначно
определим оператор
Р{х, D) = 2lai(x)D'.
Естественное обобщение записи полинома от D в методе Хеви-
сайда приводит нас к определению полиномов от упорядоченных
операторов.
Для постоянных коэффициентов мы вывели правила сложения
и умножения для полиномов от оператора D. Оказалось, что эти
правила совпадают с обычными «правилами» для 'полиномов.
В этом параграфе мы введем соответствующие правила для
полиномов от упорядоченных операторов. Но эти правила приве-
приведут нас к новым алгебраическим' понятиям, которые мы аксио-
аксиоматизируем ниже.
Мы будем сразу рассматривать полиномы бесконечного порядка,
точнее, сходящиеся операторные степенные ряды. На примере
метода Хевисайда мы видели, что иногда (см. например § 2)
решение может быть представлено в виде сходящегося степен-
степенного ряда. Читатель, не знакомый с понятием ограниченных опе-
операторов, может подразумевать под операторами обычные, матрицы.
Вместе с тем, на примере §§ 1—3 мы видели, что понятия
полиномов от D, вообще говоря, недостаточно для решения диф-
дифференциальных уравнений. Значит, и здесь мы должны будем
обобщать полученные правила на случай более общих функций
от упорядоченных операторов (в § 6).
Пусть Ор —некоторая некоммутативная алгебра с единицей,
элементы А, В, С, ..., которой мы будем называть операторами.
И пусть е^ —алгебра сходящихся степенных рядов (целых
функций) переменных х, у, г, .... (этих переменных бесконечно
много, но каждый элемент алгебры &?? есть степенной ряд, содер-
содержащий лишь конечное число переменных).

§ 4J РЯДЫ ОТ УПОРЯДОЧЕННЫХ ОПЕРАТОРОВ 23
Обозначим через 3" множество сходящихся степенных рядов
от элементов алгебры Ор, если Ор нормирована (в противном
случае ^ — множество полиномов). Такие ряды определяются ана-
аналогично сходящимся степенным рядам .от коммутирующих пере-
переменных с естественными изменениями, связанными с тем, что
2 монома —например, А2В и ABA — с разным порядком сомно-
сомножителей считаются различными.
В множестве .3" естественным образом определена операция
умножения; поясним ее на примере произведения двух мономов:
2 А2ВС ¦ ЗСАВА = ЬА2ВС2АВА.
Это произведение в 3" некоммутативно.
Условимся, что буквы а, Ь, с будут обозначать числа. Для
того, чтобы формулы были более наглядными, мы будем приво-
приводить определения или правила операторного исчисления, .напри-
.например, только для случая трех некоммутирующих операторов; обоб-
обобщения на случай произвольного числа операторов будут очевид-
очевидными. ^
Здесь будут введены некоторые обозначения, а потом опреде-
определены правила действий над сходящимися степенными рядами от
операторов из алгебры Ор. Эти правила действий будут зависеть
от способа упорядочения элементов из Ор.
Снабдим операторы А, В, С номерами наверху, например,
1 2 Я
А, В, С,
¦ •
и будем при этом говорить, что оператор А действует первым,
В —вторым, а С —третьим. Рассмотрим следующее отображение ц
множества orf в &: если
со
f(x..y, z)= 2
I, I, ft
TO
V.f(x, У, z)-+f{A, B, "?) = . -2 aijkC*B'AK
•t. I, *=o
Обозначим через 31 \A, В, С) образ ®^ при отображении ц.
Алгебраические операции в && индуцируют при отображении (х
алгебраические операции в 81 \Л, В, С), относительно которых
31 \А, В, С) является, очевидно, коммутативной алгеброй.
Замечание. "Вложение 31 (л, В, с)<=3* индуцирует в
8( [А, В, С) операцию умножения, не совпадающую с умножением
в %\А, В, С), определенным выше. Умножение в 3", в отличие
от умножения в Щ [А, В, С), некоммутативно.

24 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Пример.
(А + ВJ = Л2 + 2АВ + В2 = Л2 4- 2ВЛ + &.
12 /1 а \2
Отметим, что хотя А-{-В = А + В, однако элемент \A-\-В)
алгебры %\А, В) не совпадает, вообще говоря, с (А + В)*:
= А* + АВ + ВА + В* ?±{А + В)*.
До сих пор А, В, С выступали, по существу, как формаль-
формальные символы. Теперь учтем существование в Ор соотношений:
два разных выражения, содержащие элементы из Ор, могут быть
равны друг другу как операторы. Будем говорить, что два эле-
элемента из S" эквивалентны и ставить между ними знак ~, если
один получается из другого с помощью объединения членов ряда
в некоторые конечные группы членов и замены каждой из этих групп
на другое конечное выражение, которое равно ей как оператор.
Если
К1 2 8 4 \ / 1 » 2 4\
А, В, С, d)~/U В, С, D), .
то будем писать/(Л, В^ С, D) для обозначения каждого из двух
эквивалентных рядов.
Пример (А + в)С означает АС + ВС или АС + ВС.
Отображение (л обладает следующими свойствами:
/1 2 3\ /.и, л, Л3\
1) /U. В, C)~f[A, В, С), если n1<n2<ns*).
2) Если 5 = 0, то •
0.
3) Если А п В коммутируют, то
К1 9 8\ /2 1 8\
А, В, C)~f(A, В, С)
и, стало быть, каждый из этих двух рядов можно обозначить
К1 1 »Д
А, В, С). Это обозначение не приводит к противоречию,
если В = А:
/U, A, c) = g{X, С),
где g(x, z) = f(x, x, z).
/Л! лг лЛ
*) Запись f\A, В, С) расшифровывается здесь следующим образом. Если
f(x, у, г)= 2 <4jkx'y'zk. то
I, U к
t. i. k
где единицы заполняют в каждом мономе все места, кроме %-го, пг-го и
справа.

§ 4] РЯДЫ ОТ УПОРЯДОЧЕННЫХ ОПЕРАТОРОВ 25
Пусть
оо
Мы можем подставить вместо х и z операторы А и В соответст-
соответственно, а г/ оставить в качестве формальной переменной:
/U. * *)= 2 «v*bV*.
i.l,k = O
Рассмотрим операцию подстановки операторного выражения, дей-
действующего вторым, вместо у в f\A, у, В). Пусть <р(с, D, ...
..., ?7 —элемент из 9ЦС, D, ..., ?/, где некоторые из операто-
операторов С, D, ..., Е могут совпадать между собой, а также с А или
В. Положим по определению
/С1,[ф(с, D, ..., J)], j)= 2 aijkBWA1,
i. i, ft = O
где Я —элемент из ^, равный <р(с, D, ..., ?у, Я7 —/-я степень
Я в смысле естественного (некоммутативного) умножения в о?.
Иными словами, значки, стоящие над операторами в выражении,
заключенном в скобки ([ J, ле определяют порядок действия опе-
операторов, стоящих вне этих скобок (и наоборот). По этой причине
мы будем называть скобки [ J автономными скобками.
Совершенно аналогично определяется операция подстановки
операторного выражения, действующего первым, третьим, чет-
четвертым и т. д.
Примеры. 1) Пусть ех — сходящийся степенной ряд:
1=0
Тогда
LZ
f У 1 aM.,y
i Zi / LZik\(n-k)\ D Л Zt n\
/=Oft=O . n=Ofe=O n=0
2) Разложим произведение
я! ь
в ряд по степеням однородных двучленов от Л и В при помощи

26 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
операторного метода. Имеем
Т = ев' 1е2Щ еАг =
у (А+в) =у±у
и п\ ?in\ Ат
л=0 i=0
где Съп — число сочетаний из 2п по /.
3)
)i( )j ( + )( + )
Введем, наконец, значок (операцию) исключения из автоном-
автономных скобок (операция «штриха»). Пусть
/ (дг, у, г) = 2
- h i. k
Тогда, например, под
f(A, [ч>(в, С, ЬI Е) D.1)
будем понимать сходящийся степенной ряд из S", который полу-
получается с помощью следующей процедуры. Рассмотрим сначала
f\A, [q>(,Bi, С, D)J, Б), где Вх — оператор, который считается не
коммутирующим ни с одним из операторов А, С, 'D, Е. Обозна-
Обозначим через S элемент ф [Blt С, D) е 3*. Тогда
f(A, (ФD, С, 6I &)- 2 fly*?*SM'.
••. /. k
Перенесем теперь в каждом слагаемом последней суммы оператор
fix (который входит в S1) с каждого места, на котором он стоит,
направо так, чтобы он действовал сразу вслед за А1. Получив-
Получившийся сходящийся степенной ряд мы будем Обозначать через
Для того, чтобы определить ряд D.1), остается только подста-
подставить всюду В вместо Bv
Пример.
Рассмотрим пример, где уже одно введение ц-операции позво-
позволяет получить полезную формулу. Возьмем в качестве Ор мно-
множество всех гомоморфизмов векторного пространства Cf и поло-
положим

$ 4] РЯДЫ ОТ УПОРЯДОЧЕННЫХ ОПЕРАТОРОВ 27
Пусть далее А — произвольный оператор из Ор; / (х, у), S (х, у),
g(x, у) — полиномы:
Тогда
2 1, g(x,y) = 2
eis (x. у) Ш g/s №. y)t s (x, у) е= С~.
i,
Отсюда, используя тождество
fosU. у) _eis«.>)(p+^.(x, y)J, D.2)
получим:
(Формулу D.2) для данных операторов Р и X легко получить
аналогично 1.4.) Итак, мы доказали следующую теорему.
Теорема 4.1. Пусть X, Р — операторы, введенные выше;
тогда .
,. y)])g(x, P). D.3)
Задача. Подставим в D.2) вместо у формально Р:
frets (*• ^ ~ /s W- W [Р+Ц (X, P)J. . D-4)
Применяя формально правила и обозначения для ц-операции, получить
из D.4) аналог формулы D.3).
Оператор f\X, P) в формуле D.3) называется гамильтониа-
гамильтонианом. Формулу D.3) мы будем называть формулой коммутации
гамильтониана с экспонентой.
/12 л + 1 л+.2\
Теорема 4.2. Если f[A, Си .... С„ , В )~0,
то
I 1 л+2\ / 1 2 л + 1
V\A, B)f[A, Clt..., Cn,
для любого ср (х, у). ¦

28 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Доказательство.
/ 1 я+2\ / 1 2 л + 1 л+2\
ф(Л, В )f\A, Cu ..., С„, В)~
( 1 я+4\ /2 3 л + 2 П+3\
~q>U. 5 J/U. Си ¦••, Ся, fi j~ ,
/1 3 \ 2 / 1 2 д + 1
~фИ, ад (л, сь ..., с„,
Следствие. Соотношение
{x,
эквивалентно соотношению
f{x, lP + S'(X)])g{x, i
Доказательство получается из теоремы 4.2, формулы комму-
коммутации гамильтониана с экспонентой и очевидного соотношения
~f(&,\.P+S'(X)i)g(x, А).
Приведем теперь два соотношения, играющие важную роль
в теории дифференциальных уравнений.
Предварительно заметим, что в исчислении некоммутирующих
операторов большое значение имеют разностные производные —
они как бы заменяют обычные производные в анализе. Поэтому
приведем заранее обозначения для разностных производных, кото-
которыми мы будем пользоваться.
Пусть /(*!, х2, ..., хп) — функция п переменных. Оператор
разностного дифференцирования Ьг переводит эту функцию в сле-
следующую функцию п -f 1 переменного:
KitS v" у у xgef /(Si, *г Xn)-f(xl, Хг Хп) .
Oil \Х1 > ¦*J . Х2> •«• > ¦*„; -р -;
*1 — *1
при этом первый аргумент «раздваивается». Оператор 8/ разност-
разностного дифференцирования по /-му аргументу определяется анало-
аналогично. При повторных применениях оператора бу он действует
по любому из «размножившейся» при предыдущих разностных
дифференцированиях группы /-х аргументов (предоставляем чита-
читателю убедиться, что результат не будет зависеть от выбора одного
из /-х аргументов).
Примеры. Если / — функция одной переменной х, то
ип

§ 4] РЯДЫ ОТ УПОРЯДОЧЕННЫХ ОПЕРАТОРОВ
29
если f\x, у) — функция двух переменных, то
б б И*' х- и' и-)-Пх'' M-fl*1' Л+/(*'. у')-fix'. У)
Мы будем вместо 6Ъ б2 использовать и обозначения б/блг, б/бу.
Теорема 4.3. Справедлива следующая формула изменения
порядка аргументов:
lf(A, в)]-и(А, b)j~[a!в]ьа!(а, а, в, в),
где [А, В] = [ЛВ — BAJ — коммутатор операторов А и В. бД/ —
смешанная вторая разностная производная функции f.
Доказательство. Из свойств fi-операции получаем:
BAj j-.—j-j-2—tt ~
(A-a){b-b)
B)-f(A, в)
A
k-A • A-a
.. 3/(А;д)-/(А, в) ¦u(A,h)-f(A.B)
r*~> /i j j /i ——
A —A A-A
~jfj[/U B)-f(A, B)]~lf(A, B)j
Замечание. Аналогичные формулы имеют место в случае
перестановки порядка действия двух операторов при наличии
других операторных аргументов. Например:
/U, в, c)-f{b, A, ё)~[в,*А]ш(А, а, в, в, с).
Теорема 4.4. Справедлива формула
Доказательство. Достаточно убедиться в том, что
fH+fl)~[KA+&)]+[U/a]evU+4. а+в, a+b)j
Имеем соотношение /(г)^/{x-\-y) + (z — x — yNf(x + y, z).
Подставляя вместо х, у, z соответственно операторы А, В, А + В,
получаем:
+в, a+b)j

30 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Используя теперь теорему 4.3 и замечание, получаем!
/ (А + В)
-[Лб/U + B,
-B)8f{A + B,
+1[а!а+в]&[{а+в, a+b,.a+b)i
Мы воспользовались тем, что для функции
g(x, у, г, v)=x6f(z + v, y)=x!{z+^lZfyiy) .
смешанная разностная производная do первым двум аргументам
•равна . •
i> xz> Уп Уъ г, v) =
7f
Для завершения доказательства остается заметить, что [Л,
~[А, В] и что
+ B-BNf(A+B, A + B)j-
= {A+B-BNf{A + B, A + B)-A8f(A + B, A+B) =
+ B-A'-BNf(A + B, А.+ в)~0
г
в силу теоремы 4.2 (точнее, очевидного ее обобщения). Теорема,
доказана. Полезно доказать следствие.
Следствие. Справедливо разложение'.
(А+в) + Ъ D.5)
где остаток /?2 задается формулой:
, А + В, А+В, А
, В], SB]&f(A + B, А + В, А + В, А + в) +
+ [а,°в][а,'в]8ч{А+В, А + В, А + В, А + В, А + в) +
+ [л,8в][л,вв]б*/(л + В, А + В, А + В, А + В, А + В) +
+ [А, °в] [А, "в] 6*f {А + Вх А + В, А + В, А + В, А + Ь). D.6)

I 5] СПЕКТР ПАРЫ УПОРЯДОЧЕННЫХ ОПЕРАТОРОВ 31
Нетрудно выписать следующий член разложения D.5):
j, D.7)
где остаток /?3 выражается через коммутаторы третьего порядка
аналогично D.6).
Теорема 4.5. Справедлива формула
Ц(С, А, А, А
Доказательство. Имеем тождество
^(Х1, Х2\ Х3, Уз).
6 1 5 Я
Сделаем подстановку ^j-^Cj, х2-*~С2, х3-+А-\-В, у3-+А. Тогда
для любого Т е Ор имеем
uC2, А+В)= .
f g(ft. c2; Д. л4-в)(л+в-л) =
^ ). D.8)
Отсюда, в частности, когда ф не зависит от второго аргу-
аргумента, а функция ф(л-х, у2, х2) эквивалентна f (xv x2) и Ci^C,
T~l, имеем:
/(С, A + B) = f(&, А) + В§^(С; А, А + в). '
К последнему слагаемому снова применяем формулу D.8) в слу-
случае
ф(*ъ х2, х3)=-^~(х1, х2, х3), Т~В, СХ~С, С2~А.
Тогда из D.8) сразу следует искомое разложение. Теорема
Доказана.
§ 5. Спектр пары упорядоченных операторов
Вначале остановимся на спектре матриц. Пусть А — некоторая
матрица. Обозначим через К множество всех полиномов Р с коэф-
коэффициентами в С таких, что Р(Л)=0 (нуль здесь'означает нуле-
вУю матрицу).

32 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Определение. Спектром а (Л) с: С матрицы А назовем
пересечение множеств нулей полиномов, принадлежащих К:
(г ев в) о (Р (г) = 0 для любого Рев К).
Пусть kp (К) — кратность нуля полинома Р (г) ев К в точке
Хева (А). Кратностью точки спектра X будем называть inf kp (X).
Пусть Xi, Ki •••! А» — собственные значения матрицы A, a klf
hi •••! ks — длины цепочек соответствующих им присоединенных
векторов. Из линейной алгебры известно, что для полинома
имеет место соотношение Q (А) = 0. Отсюда можно заключить,
что спектр матрицы совпадает со множеством ее собственных
значений, а кратности точек Xj равны kj. Положим для простоты
s — З. Для любого полинома Р (г) имеем
где Pi (г) — некоторый полином, коэффициенты которого зависят
от V Аналогично,
(=0
где Р2 (г) и Р3 (^ — некоторые полиномы; коэффициенты Р2 зави-
зависят от Х\ и А2; тогда учитывая, что (Л — Ai)*» (Л — ?.2)^ (А — X3)k' = 0,
имеем:
ft,-l
2 т
^^ИЛ*•)'• E-D
1=0
Мы получили, что Р(А) равен полиному порядка 12 +
и что матрица Р (А) зависит только от значений полинома и
конечного числа его производных в точках спектра. Формулу E.1)
мы будем называть спектральным разложением оператора Р (А)

§ 5] СПЕКТР ПАРЫ УПОРЯДОЧЕННЫХ ОПЕРАТОРОВ 33
Пусть А и В — некоторые элементы алгебры (операторов).
Рассмотрим множество К полиномов Р (ги z2) с коэффициентами
из С, таких, что Р (А, В) = 0.
Обобщим приведенное определение спектра и спектрального
разложения на случай упорядоченных наборов операторов. Мы
ограничимся здесь спектром пары операторов А, В.
Определение. Спектром а [А, В) а С2 упорядоченной пары
А, В будем называть пересечение множеств всех нулей полиномов
из К: (zi, ггеа(А, в)) о (Р (гъ z2) = 0) дм любого Р (zb z2) e К-
Отметим, что в силу теоремы 4.2, если Q (zi, z2) e К, то и
Q(zb Zs)P(z!, z2)e/C, где Р (zb z2) —любой полином.
Пусть Л, S, С —некоторые элементы алгебры (операторов).
Рассмотрим множество $(Zi, z2) полиномов Р (Zx, z2) с коэффи-
коэффициентами из С таких, что
ср{А,Ь)=о.
Определение. Спектром ас[А, В)сС2 пары А, В отно-
относительно С будем называть пересечение множеств нулей пощно-
„мое из #(Zx, z2):
(zb z2 еисЙ, В)) о (Р (zlt z2) = 0)
для любых Р (zx, z2)etBx, z2).
Отметим, что если Q (Zj, zg) e «(zb z2), то и Q (zlt z2) P (zx z2) e
s * (zi, z2), где P (zb z2)—любой полином.
Мы рассмотрим теперь важный пример спектрального разло-
2/1 2 \
жения функции вида Cf\A, В). Для этого обратимся к формуле
D.3) коммутации гамильтониана с экспонентой. Положим в этой
формуле X = х, Р = - id/дх; S (X, P) = S (x); g(X, P) = g (x).
Тогда в правой части получим выражение
«« Ж f {х, [р+ds/dxj) g (x)=«« w [/ (Д [
В силу теоремы 4.5 мы получаем
f[x, [p + dS/dxJ)g(x) =
(
fQ,6s,6X) g{x)+
dSjdx-dS/dx
+ f>P F«//6^)(Jr; dh/дх, dS/dx, IP + dS/dxj) g(x).
Вычислим средний член правой части равенства. Для этого вос-
воспользуемся очевидным равенством:
2 В. П. Маслов

34 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Следовательно, спектр \х, х) относительно ihd/dx в Ra лежит на
биссектрисе координатного угла. В силу теоремы 4.2 имеем
«¦—•(.*•-*)'' = О при л
Отсюда следует, что для конечного ряда Р (х, у) имеет
место спектральное разложение!
.iP (*, х)? - i [р; (х, х) х -^ - р; (х, х) -^ х]
x)
Поэтому
ft f(x, dS/dx)-f(x,
dS/dx—дЬ/д
х
Оператор Р, такой, что
Pq> = —I ^?^_J_
р р = 17 - дх
называется оператором переноса (для гамильтониана f (р, х) и
данного S(x)).
Отметим, что в спектральных разложениях мы пользуемся не только одним
понятием спектра. Нам важно знать также число членов разложения в ряд
Тейлора, которым можно ограничиться. Это число в случае матрицы было свя-
связано с. понятием кратности спектра. В приведенном примере естественно считать
кратность спектра, расположенного на биссектрисе координатного угла, равной
двум. В общем случае вопрос о кратноств спектра (т. е. вопрос о числе членов
разложения в ряд Тейлора) является весьма сложным. В главах III и IV он сво-
сводится к изучению свойств промежуточного банахова пространства Bmiu, но это
уже относится к сфере гармонического анализа, где этот вопрос в значительной
степени продвинут.
Для того, чтобы ясно было направление исследования свойств операторов
в главах III и IV, мы проведем некоторые аналогии между приведенным при-
примером н спектральным разложением матриц.
-1. Функции, на которые «действует» оператор х, должны быть дифференци-
дифференцируемы, так как вторым действует оператор Ш/дх. В пространстве дифференци-
дифференцируемых функций оператор умножения на е*-*' «растет как первая степень <», т. к.
I
? (*)) +|« 8 (*) 1^0 + 1 <|)max {\g'\ + \g I).
А ( |
2. Матрица А, у которой максимальная длина цепочки присоединенных
элементов равна 1, удовлетворяет условию
\elA'g
где g—вектор, |g|—его модуль.

§ 61 АЛГЕБРЫ С ц-СТРУКТУРАМИ 35
3. Отрезок ряда Тейлора в спектральном разложении сходящегося ряда
в обоих случаях состоит нз двух членов. Мы увидим в главе IV, что между
оценкой роста оператора eiAt н числом членов в спектральном разложении
существует глубокая связь.
Замечание. В дальнейшем будет важно для аналогии иметь в виду еще
следующие свойства матриц.
1) Всякая матрица А может быть представлена в виде суммы
А-Аг + tAt, E.2)
где Л* коммутирует с Л2, Л2—эрмитова матрица, a At имеет действительный
спектр.
2) Спектр матрицы может быть определен следующим образом. Пусть К —
множество таких полиномов Р(х, у), чюР(Ах, А^}=0. Спектром а(А) матрицы А
, назовем пересечение множеств нулей полиномов нз /С: х, у е О (А) О Р {х, у)=0
для любых Р (х, у) е /f. Собственные значения А в этом случае будут равны
x + iy, где х, у<=о(А).
Эта интерпретация спектра матрицы показывает, что можно рассматривать
лишь действительные корни полиномов от двух переменных. Правда, для раз-
разложения вида E.2) по существу уже требуется «спектральное разложение»,
однако поскольку наша задача состоит не в исследовании спектра одного опе-
оператора, а в исследовании нескольких некоммутируюпшх операторов, то мы будем
помнить, что (по крайней мере в случае матриц) каждый из операторов можно
представить как функцию двух коммутирующих операторов с действительным
спектром. Более подробно класс таких операторов будет изучен в главе III.
§ 6. Алгебры с ц-структурами
Развитого исчисления нам еще недостаточно, чтобы применить
его к решению дифференциальных уравнений с переменными
коэффициентами. Теперь мы можем ввести аксиоматически те
алгебраические объекты, которые возникают при изучении пра-
правил обращения со сходящимися рядами от упорядоченных опера-
операторов. .
Мы введем вначале а'ксиомы для наиболее простого случая,
а затем приведем более сложные формулировки аксиом ц4 и fie.
Мы выведем из них ряд теорем, и затем в § 7 продемонстрируем
на совсем простом примере, как они работают.
Далее в § 8 мы подробнейшим образом разберем классическую
задачу о выводе волнового уравнения и продемонстрируем на
этом примере силу операторного метода и его адекватность мате-
математическим и физическим явлениям, которые имеют место при
переходе системы уравнений колебаний решетки в волновое
Уравнение. . .
Для того, чтобы построить аналог исчисления для сходящихся
степенных рядов, нам удобно будет стать на аксиоматическую
точку зрения, постулировав ключевые моменты исчисления, дока-
доказав с их помощью основные формулы, а затем проверить эти
постулаты для конкретных операторов, которые нам цонадобятся
для решения дифференциальных уравнений. Такое абстрагиро-
абстрагирование весьма полезно и для выработки навыков обращения
2*

36 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
с упорядоченными операторами. Мы будем пользоваться основ-
основными элементарными понятиями алгебраических структур.
Пусть &? — произвольная, вообще говоря, некоммутативная
алгебра с единицей над полем R. Элементы алгебры <г^ будем
называть операторами.
Обозначим черкез $ю множество всех бесконечно дифференци-
дифференцируемых функций /(*), *eR* (k не фиксировано), растущих на
бесконечности вместе со всеми своими производными не быстрее \х\1
(число / — свое для каждой функции /). Функции из $°° будем
называть символами] символ, зависящий от к переменных, будем
называть k-местным.
Будем говорить, что алгебра &? наделена ^-структурой, если
для любого конечного набора At, ..., Л* операторов из некото-
некоторого множества М а &# и любого набора номеров щ, ..., nk
(удовлетворяющего условию щ Ф п}, если операторы А{ и Aj не
коммутируют), определена операция
fii (*i->- Alt ..., xk-+Ak),
которая ставит в соответствие каждому символу f (хь .,., xk)
оператор А е &#, обозначаемый
и которая удовлетворяет следующим аксиомам:
¦ Их) Аксиома однородности! если aeR, to
Й'пь\ (ni nk\
!,..., AkJl = a\j\Ai Ak)-\\
в частности, если /(д-j, ..., дг^) = О, то
\i2) Аксиома раздвигания индексов: пусты щ,..., щ,-
и тъ ..., mk — такие два семейства номеров, что, при i-ф],
(щ < nj) => (m< < mj)\ тогда
(Н nk\ (mi mk
lf\Ai, ..., Akh = lf[Ai, .... Ab
причем, если «j = «/ и Л< = Лу = A, to
(nl ni nJ
lf\Ai At Aj, ....
где
g (Xi, ДГ2, ... Xj_i, Xj+i, ..., Xk) =[f (*i, X2, ..., Xk)\Xit= xt.
*) Скобки |[ J мы' будем опускать там, где это не приводит к .путанице.

§ 6] АЛГЕБРЫ С и-СТРУКТУРАМИ 37
Пример. Пусть Л, В е М. Тогда
1 2 Я 4 1 S
4 sin Л cos Л sin В cos В = sin 2Л sin 2B.
\ia) Аксиома соответствия: символ, тождественно рав-
равный 1, ц-операция переводите единичный оператор, а [Л]= Л.
ц4) Аксиома суммы; если щфт} ни при каких «, /, то
fi6) Аксиома произведения: если m,<«y для любых
mi m
Пример. В предыдущем примере
sin2Л sin2S =[sin2S][sin 2Л].
fie) Аксиома нуля; если
и /?ь ..., рг, Г?, ..., гт — такие номера, что р/<«/, r^rij для
любых /, /, то для любого-символа g^, ..., д-,+т) и любых
операторов Вг, ..., Sj, C^ ..., Ст> Ci<=M,
r (ni nk\ (Pi Pi ri rm\
[/Ui- •••» Ал)в\В1г .... Bh Clt .... Cj]=0.
Из приведенных аксиом следует, что аксиома суммы на самом
деле выполняется для любых щ и ту. Именно, справедлива сле-
следующая теорема.
Теорема 6.1 (первая теорема 6 сумме). Для любых щ и т}
имеет место соотношение
т\
B
tf\Ai Ajj + lg^ Bj].
Доказательство. Пусть для определенности ns^.ms^
^ ns+i ^ ms + 1 при любых s. (Заметим, что если .ns = ms, то
по определению ц-структуры это означает, что Bf и А, комму-
тируют.)

38 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Рассмотрим «сумму»
UUi, .... Ak) + g[Bit..., 5j]. F.1)
По аксиоме о раздвигании эта сумма равна сумме
п\ п'Л (т\ т'Л
l \ ) F.2)
для любых п\ и tn'j, таких, что m't+i>«i+i>Щ>Щ- Кроме того,
.отдельно для каждого члена суммы имеет место равенство
/Ч ч\ (ni "Л
f\Alt ..., Ab)~f\Ai, .... AkJ,
(mt mi\ (mi тЛ
g\Bi Bj^g^, ..., BJ.
Тогда поскольку щ Ф щ ни при каких i и /, то в силу аксиомы
о сумме сумма F.2) равна
п\ п'Л 1т\ т'
)l l\Bi, .... S
F.4)
Отсюда и из F.3) следует утверждение теоремы.
Теорема 6.2 (вторая теорема о сумме).
nt-i n«
А А
и, и, , tf} +
ni ( ni ni~l ni+l nk \
(здесь А, + Я,=[!4, + В,].)
Доказательство. В силу ц2) без ограничения общности
можем считать, что |пу — «г|>2 при /#t. Тогда
/ / s \
-lAif\Ai, ..., Ли, Лг+?, ..., AkJJ-
-[ВД?> •••- Alh А'п, ...,
/ nt n{ + \ n. + 2\ /nx nfl n^ nk\
^{Ai + Bi-Ai-Bi )f[Ai, ..., Аи, Аи, •••, ЗД
Используя аксиому суммы, а -затем аксиомы раздвигания и соот-
соответствия, получаем:
, f
ft ][ -[ А, ]-[ В, ]-
== [i4i + BtJ - [Л] -Й] - Ai + В, - А, - Bi = О,
Применяем аксиому нуля, и теорема доказана.

6] АЛГЕБРЫ С ц-СТРУКТУРАМИ 39
Теорема 6.3 (теорема о произведении). Пусть щ, ..., nk,
и ••-, Pi, гъ ..., гт — такие номера, что р«-<«у, /•*>«/ для
любых i, j, и пусть ffxA^ ..., /Uj] = /\ Тогда для любого сим-
символа g(xlt ..., хи Уп ..., ут) .справедливо соотношение
\,..., Bi, с\, ...,&,
r
y
Док а за те ль ст во.' Согласно ц2) мы можем без ограничения
общности считать, что существует номер п, отличный от пъ ..., nk
и удовлетворяющий условию р( < п <. г} для любых i, у. Тогда
на основании \ij) и теоремы 6.1 имеем:
/П1 »*\ (Pi П Г1 гт\
U\Alt ..., At)g[Blt ...-, Si, Clf .... CJJ-
" ' "l / Pi Pi rl rm \
W"l "ft \ "\ / "l "/ ri rm \
Alt ..., Akj-Fjg^, ..., Bt, Clf .... CmJ].
Для завершения доказательства достаточно сослаться на це).
Теорема 6.4 (формула перестановки индексов).
4 Л, ii,, i,)]. F.5)
Эта теорема имеет место, разумеется, и в случае, когда /
зависит еще от упорядоченных операторов fi1} B2, ..., В^; отве-
отвечающие им переменные просто «замораживаются». После подста-
подстановки Ви ..., Вы в F.5) необходимо в правой части формулы
F.5) раздвинуть индексы. Стало быть, в общем случае теорема
формулируется следующим образом.
Теорема 6.5 (формула замены индексов). Если п;=П/—1 и \щ — л,-|>2
при 1ф1, j, то имеет место соотношение
V ni V
V 7 "?+1 "/V
1 Л/_1: ..., Л>, Л/+1, .... AJi—
— IL/\.i4lt ..., Ai_v Ait Ai+i A/_lt A/, A/+l
Au At A,_lt A,, A,,
?d<-' [Aj, Ai] = AjA{— A{Aj—коммутатор операторов Aj и At.
Доказательство теоремы 6.4. Пусть А1=Л, Л8==В. Нужно
Доказать тождество
ш. №-

40 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Пользуясь аксиомами цх), ц2), Ц4) и теоремой 6.3, преобразуем правую часть
к виду
—А) (Д—j§)
/cu) | fU ь)ка ^;
j L|
i—A A—A
A, b)-f(X b)J+
f(A, Ъ-tU, b)J
=lA f(A, b)-f(X
-[-,U, b)+f(A, b)}-[fU. ЬП-lfiA, k)l
Теорема доказана. На общий случай это доказательство переносится без изме-
изменений.
Мы приведем формулу для сложной функции.
Теорема 6.6 (/(-формула). Пусть / — одноместный символ,
g — двуместный символ, А, В —такие операторы из М, что
[А, В]е=М и lg{A, в)]еМ. Тогда
В отношении этой теоремы справедливо замечание к предыдущей
теореме. А именно, в очевидных предположениях справедлива
формула: ¦ _ .
/12 k k+l /1 2\ *+2 k+3 s+l
[f(d, С„ .... Сь [ gU. B/l CW) Cfc+2, ..., C
/12 * /* + l * + 2\ * + 3
¦=[/(clt c2,.... cfc, ^(л, sj, cft+i,....
dft + 5 "I « /* + 3 k + 7 ft+9\ * /* + 3 *+4
a,b]^{a, a, b)^(a, b,
/12 * /ft+1 fe+9\ *+2
x(Clt C2) ..., Cft, ffl Л, fi J, [ g
k + 8 f 1 2\ fe+10 s + 9\
[ g[A, B)l Cft+i... Cs)l F.7)
Формулу F.7 , как и более частную формулу F.6), также
будем называть К-формулой.
Доказательство теоремы 6.6. Имеем тождество:
-g(*i. *2))^(g(*i, *2): 2).
Применяя к обеим частям операцию ц: \z->~g, х^-у А, дг2

§ 6] АЛГЕБРЫ С ^СТРУКТУРАМИ 41
где g = fg\A, ВI, и используя первую теорему о сумме, полу-
получаем:
vm-иШ, в))ш(ё-Л1 ЬЩШ, в), g)i
2 S
Используя аксиому щ) и переставляя индексы у А и g по тео-
теореме 6.5, получаем далее:
Согласно ц2) и теореме 6.3,
в), fa-ig(A, &)&Ш. Ы еI
Используя эту формулу и еще раз применяя теоремы 6.3 и 6.5,
получаем:
Так как g(*b дг2) — g(^i, дг2) = 0,.то для завершения доказатель-
доказательства остается сослаться на аксиому ц±).
Теорема 6.7 (разложение в ряд Ньютона). Пусть А, (А + В),
В<=М, f—одноместный символ. Тогда
lB-BfflA, ..., А
2 ' 2т fMt / I -3 2/n—I 2m+]
5*yU ЛЛ 4 + 5Л F.8)
Замечание к предыдущим двум теоремам относится и к этой теореме.
На этот раз мы не будем приводить общей формулировки, предоставим это
читателю.
Доказательство. Прежде всего получим формулу
г2 2г / 1 2r —I 2r+l\_
[7VUА А В)] =
2/-— 1
2г 2Г + 1 2rl 2r + l 2/43 Л..
...ТГ Бr-^-U Л„ Л, Л+В)], F.9)
гДе В, Л4 Л„ А, А+В, Тх Г, е= Л1, ф— (г + 1)-местный символ.

42 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Для простоты опустим Тх Тг\ Аъ ..., Ап Т. е. докажем, что .
F.10)
Вывод общей формулы F.9) отличается от вывода формулы F.10) только более
громоздкими выкладками.
Имеем тождество
Пркменим операцию ц: \хг-~ A-j-B, xi—*A); в силу аксиомы щ) получим:
lf(A^B)-.f(A)-(A+B-Al)%(AU №=0.
Согласно а|сиомам щ_), ji2) и теореме 6.2, отсюда следует,- что
Используя еще раз теорему 6.2, приходим' к равенству
Формула F.9) доказана. Теперь, применяя последовательно формулу F.9)
к последнему члену в правой части F.8), по индукции получим искомое раз-
разложение.
Теорема доказана.
Перейдем к определению спектра для пар" операторов
в алгебре с (х-структурой, аналогично тому, как мы это делали для
случая сходящихся степенных рядов от упорядоченных опера-
операторов.
Определение. Пусть А, В.&.М. Обозначим через К мно-
множество всех символов f(xi, x2), которые операция ц: \х1-*-А,
х2-*-В) переводит в 0:
Спектром а пары А, В будем называть пересечение множеств
нулей всех функций из /О
((*!, х2)ео)о(/fa,. x2) = 0 для любого f<=K).
Теорема 6.8. Множество К является идеалом в алгебре дву-
двуместных символов.
Доказательство. Пусть f(хи лг2)еК; докажем, что
g(xi, x2)f(xlt *2)<sK для любого ge*°°(R"). Нам надо дока-

§ 61 АЛГЕБРЫ С ц-СТРУКТУРАМИ 43
зать, таким образом, что если [/(Л, в)] = 0, то и §?\А, В)Х
xf\A, BjJ — O. В силу аксиомы раздвигания индексов
ы{а, fi)'/U, B)j = ig{k, h)f(A, в)ъ F.П)
причем, поскольку в силу этой же аксиомы fj [A, b)J =
= lf[A, Sj]==Or то в силу аксиомы нуля правая часть равен-
равенства F.11) обращается в нуль. Теорема доказана.
Из этого фундаментального факта можно вывести ряд (стандартных) след-
следствий. Мы остановимся иа двух наиболее важных следствиях. Предварительно
рассмотрим следующее усиление аксиомы ц4).
HJ) Если' {fj(xi, ..., xi,)} — такая последовательность символов, что в окрест-
окрестности любой фиксированной точки (х°, ..., х?) лишь конечное число членов
00 /
ряда 2 f/(xi> -••> **) отлично от нуля н что среди операторов ?/у
/1
...,%)]
имеется лишь конечное число отличных от нулевого, то
Теорем a.6.9. Если выполнена аксиома ц^), то спектр любой пары опе-
операторов из М не пуст.
Доказательство. Предположим противное: пусть ст=ф. Тогда для
любой фиксированной точки (я}, xf) e R2 найдется функция f {хъ х%) е К,
строго положительная в некоторой окрестности U точки (х"и х°г). Любое ком-
компактное множество в R2 можно покрыть конечным числом таких окрестностей;
следовательно, существует функция из К, строго Положительная на этом
множестве. Покроем плоскость R2 квадратами Цц ¦
i, /=0, ±1, ±2, ..., e>0—фиксированное число.
Рассмотрим для каждого квадрата Цц функцию fy {хъ х%) е К, строго
положительную на q-ф Пусть далее ф(дг), «eR,-такая бесконечно дифферен-
дифференцируемая неотрицательная функция, что <р(*)=1 при 0==?Ж1 иф(х)=О
при х< — е/2 и-при z>l-f-8/2. Тогда функция
, . 00
f(*l, >*)=¦¦ 2 /(/(«I." *2) ф(*1-О Ф(^ —Л
I, / = —00
всюду положительна и fy{xlt xi)jf{x1, дг2) е К в силу теоремы 6.8. Так как
Efi/(*i» xz)lf{xi> 4)=h то в СИЛУ Рз) н 1*1) имеем
где 1 (хъ х2) — функция, тождественно равная 1, и 1 в правой части — единич-
единичный оператор. Полученное противоречие доказывает теорему.
Определение. Дополнение к спектру а будем называть резольвентным
множеством пары А, В и обозначать р(л, В).

.44 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Мы приведем теперь критерий, с помощью которого можно определять
спектр, используя лишь одномерные (т. е. обычные) функции операторов А и В.
Теорема 6.10. Для того, чтобы точка (X, ц) принадлежала р(Л, В),
необходимо и достаточно, чтобы существовали такие положительные г и Ь
и такие финитные функции р\{хг) и р^*2), положительные при
| 6
ы
ц и равные нулю при | хх — X \ > е, | х% — ц | > 6 соответственно, что
(В)р?(Л) = 0.
Доказательство. Достаточность. Из аксиомы ц6) имеем
Значит, по условию, р* (*2) р? (х{) е К, и эта функция не обращается в нуль
в точке (X, ц). Следовательно, по определению спектра, (X, ц) ? а. Достаточ-
Достаточность доказана.
Докажем необходимость. Пусть (X, ц)ер(Д, в); тогда существует функ-
функция ф е /С, положительная в точке (К, [i), а значит, положятельная н в неко-
некоторой ее Bе, 26)-окрестности. Пусть р^, р^ —функции из S00 (i?), равные
нулю соответственно вне е-окрестностн точки X и вне 6-окрестносте точки ц.
Поскольку ф(Л, В)=0, то
Пусть tf> («J, д:а) е $°°(R2) неотрицательна, равна -0 в (е, 6)-окрестности (X, ц)
и равна 1 —ф (jcj, xa) вне Bе, 26)-окрестности точки (X, ц). Очевидно, что
№ (*i. «*) + Ф («i,' х2)] р^ (х2) рх (Xl) = ф (xlt x2) рц fa) p^ (л;2)
и
»(«I. *•)+ф (*i, ^s)] e S°° (R2).
Значит,
[[th(i, в)+ФЦ в)
и, в силу аксиом цг), цв),
следовательно
и, наконец, по аксиоме (х5), Рц(В)рх,(^)=0. Теорема доказана.
Определим теперь аналогичным образом спектр а (А) и резольвентное мно-
множество р(А) одного оператора А. Очевидно, что для спектра одного оператора
будут иметь место аналогичные теоремы. Из теоремы F.10) при этом будет
непосредственно в.ытекать следующая теорема.
Теорема 6.11. Имеет 'место включение
а(А,-в)с=а(А)Ха(В).
Более содержательные результаты о спектре будут получены в главах III
и IV. Это мы Сможем сделать лишь после того, как будет введено понятие
нормированной алгебры и изучены ее свойства.
Замечание. Пусть && —топологическая алгебра и пространство симво-
символов также снабжено некоторой топологией, такой, что множество функций
от фиксированного числа аргументов xlt ..., хп образует топологическую
алгебру. В этом случае можно ввести понятие топологической алгебры с ^струк-
^структурой. Для этого аксиому ц„) надо заменить на следующую.

$ 6] АЛГЕБРЫ С ц-СТРУКТУРАМЙ 45
Т{) Для любых Ait ..., Ак, Bt В/, С%, ..., Cm e M и номеров гц,...
• •¦> "ь Ри ¦•¦> Pit гъ •••'. rmt удовлетворяющих условиям аксиомы цв), и для
любого (/ + т)-местного символа g из
[|-*0 при я—»oo,
вытекает
i, Ви Ct CJJ->0.
Кроме того, нужно добавить аксиому:
Т2) Если последовательность символов /„ (х± хп) сходится к нулю,
то и последовательность
Многие теоремы о спектре главы IV могут быть перенесены без труда
на случай топологической алгебры с ^-структурой.
Рассмотренная аксиоматика не включает операции «штриха»,
использованной в § 4. Дадим здесь аксиоматическое построение
соответствующей структуры, обобщающей [i-структуру.
Пусть /(*!, ..., xk, Xk+i, ..., xk+i) — символ. Рассматривая
хи ..., Хк как параметры и применяя операцию
получаем оператор
X{, ..., xk, Ai, ..., Ai)J = ^(xi, ..., xh),
зависящий от параметров хи ..., хк, т. е. отображение R*->&>/.
Для простоты ограничимся случаем &=1; очевидное обобще-
обобщение на случай k>\ предоставляем читателю. Пусть g(Xi, х2) —
символ, а Л—оператор. Рассмотрим упорядоченную пару <У (л^)
и А. Операция ц обобщается на этот случай. Именно, операция
ставит в соответствие функции g(xu x2) некоторый оператор, ко-
который мы обозначим через
/ 1 2 / |\\ / 1 2 / 1' nt n{
[g[A, ^W/MsU C/U, Alt .... ЛД.
Точно так же, если g — 2&-местный символ, то операция
12 к Ik
fii (хг->А, x2-^F{xx), .... x2k_i-+B, xik-+H (Хгь_{)),
где
F(*i)=
_!)=[аUft_i, Bi,.... впг

46 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
ставит в соответствие функции g оператор
! 2 / IV 2ft—! 2ft /2ft-!
A;F[Al..., В, G[B
В предлагаемой ниже -системе аксиом для того, чтобы избе-
избежать громоздких выражений,' аксиомы щ) —И-в) сформулированы
только для двуместных символов, а в аксиоме щ) символ четы-
четырехместен.
На самом деле подразумеваются естественные обобщения этих
формулировок на случай произвольных 2?-местиых символов.
цх) Аксиома однородности: если aeR, то
цг) Аксиома раздвигания:
где пх > п2, если & (я), и А ие коммутируют, и любые, если <У (х)
и А коммутируют (при любом х).
Из) Аксиома соответствия:
2 /I' • /!•¦«, ¦
U U
ц4) Аксиома суммы:
ц5) Аксиома произведения: если т,<П/ при любых /,
/, то
lg[A,
/я,- ft,/ яЛ\
ц6) Аксиома нуля: если lg[A, <?{A))J=*O, Р(>щ, r
(/, / = 1, 2), то
Пример ц - структуры. Пусть Cf (R") — векторное про-
пространство бесконечно дифференцируемых на R" функций f (х1, ...
:.., хп), равных нулю вне некоторого (для каждой функции —
своего) шара в R". Пусть Dj и */ —операторы, действующие
в C~(R") по формулам:
Мы будем обозначать также Dj через —id/dxj, а Xj—через х/,
последнее обозначение мы будем применять в тех случаях, когда
оператор Xj нельзя спутать с независимой переменной Xj.

§ 6] АЛГЕВРЫ С ц-СТРУКТУРАМИ 47
Пусть Р (xi, ..., хп; Pi, ..., рп) — полином. Рассмотрим диф-
дифференциальный оператор P[xi, ..., хп; Du ,.%, ?)„). Этот опера-,
тор легко записать с помощью преобразования Фурье. Преобра-
Преобразование Фурье ставит в соответствие функции /(%, ..., хп) ее
Фурье-образ
f (р) = Bя)~ «/» $ e-b'-'f (х) dx,
R»
где * = (*i х„), p = (Pi Рп), Р-х = р1х1 + ... + рпхп. При
этом имеет место формула обращения:
Нетрудно видеть, что Djf(x)=pjf(p). Отсюда вытекает сле-
следующая формула:
= Bя)-« I ef"-*P{x, p)dp $ e-">*f&)dt. F.15)
r" r"
Правая часть формулы F.15) сохраняет смысл, если вместо поли-
полинома подставить любую непрерывную функцию, не очень быстро,
растущую при |р|-»-оо (например, не быстрее, чем |р| в неко-
некоторой степени). Мы приходим к следующему определению.
Определение. Псевдодифференциальным оператором с сим-
символом Н (х, р) называется оператор Н (х, D], действующий по
формуле *)
Н (х, Ь) f (х) = Bя)-»$ \ е<р-(*-ЪН (х, р f (|) dl F.16)
R2»
х, D):
Н {i, Ь) f (x) = Bя)-« \ \ e""i*-QH (I, p) f ® dg.' F.17)
В множестве операторов вида Н\х, D) вводится структура ком-
коммутативной алгебры Sips (л;, D). Таким образом,
Н(х, b)L(x, b)f(x) = Vn)-» \\е<»-*-ЪН(х, p)L(x, p)f(l)dl
*) Эта "же формула определяет Н \х, Ь) на обобщенных функциях
(см. гл. IV).

48 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Аналогично определяются на f(x, h) e C™(Rn)x#°°(R) опера-
операторы р — ih д/дх и х и порожденная ими некоммутативная алгебра.
Возьмем теперь в качестве М множество операторов вида
k—l, 2, ..., Sk = Sft(x) — некоторый набор функций, принад-
принадлежащих С?(Щп).
Замечание. Вектор-оператор Ak = ihd/dx-{-dSil(x)/dx имеет компо-
компоненты A^ihd/dxj-^-dSii/dxj. Эти компоненты, как нетрудно убедиться, ком-
коммутируют между собой, поэтому над вектор-оператором А^ можно ставить
один номер.
Определим ^-операцию для Ф (я) е $°° (R"). Пусть
Fx^pf(x) = h-"Vf(p/hy, *?*P-+xg(p) = h-"'2~g(-p/h). Для про-
простоты рассмотрим случай двух переменных. Примем по опреде-
определению, при пх <Щ, фе Cf (Rn),
Теперь проверим выполнение аксиом Цх)—щ).
Все аксиомы, за исключением второго пункта аксиомы раздви-
раздвигания, выполняются очевидным образом, как это видно из самого
определения. Второй пункт аксиомы раздвигания следует непо-
непосредственно из соотношения F%.+ х Fx.+ р = 1. Выполнение цв)
см. гл. IV.
Заметим, что формула коммутации гамильтониана с экспонен-
той теперь получена по определению. Аналогично определяется
операция, включающая операцию «штриха».
Приведем еще одно обобщение ^.-структур, когда в качестве
символов можно брать функции на /n-мерном торе Мт (произ-
(произведении щ ок'ружностей). Рассмотрим бесконечно дифференцируе-
дифференцируемые функции на нем ср значениями в пространстве ^(R").
Такие функции мы будем обозначать / (а, хг,..., Х/,), где а е Мт —
угловые координаты на торе, а хх, ..., Хь — вещественные пере-
переменные, k зависит от f.
Как и ранее, рассмотрим алгебру &>/ и ее подмножество М.
Кроме того, рассмотрим еще подмножество Мт, состоящее из т
коммутирующих между собой элементов множества М; В =
= (Ви .... Вт) с Мт. Для любого конечного набора Аг ... Ак <=
еЛ1 операторов и любого набора номеров пи ..., nft + 1, удовлет-
удовлетворяющих условию tii^tij, если А{ и Aj не коммутируют, и условию
х, если Ai и Bs<sMm не коммутируют, определена one-

§ 6] АЛГЕБРЫ С ц-СТРУКТУРАМИ 49
( ni nk nk+l\
рация (г \*i-*/4i, ..., xk-+Ah, a->fi j, которая ставит в соответ-
соответствие каждому символу f(xx, ..., хп, а) оператор А ее/, обо-
обозначаемый .
я*
"к "ft+1
i, •••, Ak, В
и которая удовлетворяет всем прежним аксиомам (как если бы
'а е Rm) за исключением аксиомы соответствия, справедливость
которой мы потребуем лишь по переменной х и которую допол-
дополним зато следующим условием:
Из) Для любой вещественной бесконечно дифференцируемой
функции /(а), а<=Мт и отвечающей ей периодической функции
ftj.(x), jesRm выполняется условие >
Задача. Рассмотрим алгебру М, порожденную элементами х н р,
такнмн,- что [я, р] = й. В качестве символа f(xu а) возьмем функцию на
окружности радиуса 1 со значениями в 8е0.
Определить ц-структуру с аксиомой ц'3), выбрав в качестве множества М^
оператор х так, чтобы элементы orf были операторами, действующими на
функции на R, и выполнялось равенство
оо я
f (р, х) Ф (а) = -L ^ / («А- °)еЫа \ е~ЫуЯ (У) аУ-
В определении ^-структуры важную роль играет класс #°°
символов. Как мы увидим ниже, для наших целей класс $°°
является слишком узким. Расширение же этого класса в аксио-
аксиоматике ^-структур может привести к тому, что для алгебры,
содержащей i'^ и х, не будет существовать ^-структура.
Приведем поясняющий пример.
Пусть выбранный класс символов содержит функции вида
/(¦*!> хг)—е±и*х' и пусть Л, В—такие операторы нз М, что [А, В] =
= — i (например, А = — ij-, В — х\ Применяя к левой части
тождества
формулу коммутации F.5), переставим оператор А на первое
место. Мы получим равенство
А; В;

50 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
/13 2 «\
где символ .оператора ty\A, А; В; А) имеет вид
Ч» (А, /V. *, y) = i
Pi-Pi .
-гУУх ~t(pt-y)x
Отсюда, используя аксиомы нуля и соответствия, получим:
Значит, для данных А, ВеМи класса символов, содержащего
функции ??'*«*», (г-структура вообще не существует.
Поэтому нужно внимательно следить, чтобы в процессе полу-
получения формул неявно не использовать ц-структуры для симво-
символов более широкого класса, чем #°°. Ибо это приводит подчас
к неверным равенствам* для операторов, символы которых при-
принадлежат ?°° *).
Теперь мы дадим обобщение [г-структур, использующее рас-
расширенный класс символов.
Предположим, что алгебра && принадлежит некоторому линей-
линейному пространству «2/, причём для любых ие^ и / еX опре-
определено действие (произведение) <й^Х и la^X, линейное по /.
В этом случае говорят, что X есть двусторонний модуль над
алгеброй .Л.
Пусть X —множество, состоящее из п-\-т элементов Аъ ...
..., Л„, В алгебры &€ (п и т — фиксированные), снабженных
индексом kt<ki+1 или (ki>ki+1) и пусть С% — пространство функ-
функций ф(х, а), хеR", аеМт, растущих не быстрее степени х и
таких, что
\\
Будем говорить, что на X задана ц-структура, если для
ki kn */i-H4
набора А} ... Ah, В определена операция ц: xt-+AX, ..., хп-> А„,
а-*-В, которая ставит в соответствие каждому f(x, o)sC|
элемент L s «5?, обозначаемый
1. ••• Ak, В
*) Вопросу об определении конкретных функций от упорядочеиных опе-
операторов и выяснению границ применимости формул ц-структур посвящена гл. IV.

§ 7] ПРИМЕР 51
и удовлетворяет аксиомам цх) — jie) *). (В аксиоме ц5) левый (или пра-
правый) один из сомножителей предполагается элементом алгебры ок'.)
Модуль X с указанной операцией ц называется модулем над
алгеброй erf, наделенным ц-структурой.
§ 7. Пример асимптотического решения
дифференциального уравнения
Рассмотрим дифференциальное уравнение
Поставим задачу: найти такую функцию п(х, t), которая удов-
удовлетворяет начальному условию п(х, О) = ч|зо(лс) (где ч|з0 —произ-
—произвольная k раз непрерывно дифференцируемая функция, равная
нулю при достаточно больших 1*1), и которая при подстановке
в уравнение G.1) обращает левую часть в k раз непрерывно диф-
дифференцируемую функцию. Отметим, что подстановка в уравнение
G.1) произвольной k раз дифференцируемой функции обращает
левую часть, вообще говоря, только в k — 2 раз непрерывно диф-
дифференцируемую функцию. Поэтому искомая функция является
в некотором смысле приближенным решением уравнения G.1). Функ-
Функцию п мы будем называть асимптотикой решения по гладкости.
Обычная постановка задачи для уравнения G.1) содержит два
начальных условия. Для простоты мы ограничиваемся лишь одним
начальным условием."Предлагаемый ниже метод исследования
позволяет рассмотреть и полную постановку задачи. Мы хотим
этим примером проиллюстрировать технику вычислений с приме-
применением операторного метода.
Обозначим D = — id/дх, Do = — id/dt. Будем искать п (х, t)
в виде .
п (х, t) = e&s (I *)<p (x, t) v (x), G.2)
где
S(x, 0)=0, <р(х, О) = фо(л;), v, (poe=C™(R), шро = 1|>о.
Подставляем функцию G.2) в левую часть G.1); при этом поль-
пользуемся формулой коммутации гамильтониана с экспонентой:
Внимание: здесь L — часть операторного выражения, а не оператор.
•) Если f(xt хя,.п)бС|, g(yx ур, а) е «°°, Cv ... , СреЛ),
то /(ilf ...", 4. Bn}g[Ci 6р, "$¦)*=%. Здесь {^i, ... , АП}<=Х *
обязательно либо ?х< ... <fen+i, либо 1ц > ... > kn+i.

52 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Преобразуем выражение L. Применяя теорему 6.5, а также
учитывая, что б2/ в данном случае — единичный оператор и
г. a ds~] .ws r
\1дх' Ш \==1Ш1 МЫ можем переписать L > |;ледующем виде!
f (А
Далее, переставляем в силу теоремы 6.5 в первом слагаемом
за г г
порядок действия операторов Д Do и х, t. Получаем:
^{х, t)<p{x, t) + iD%{x,
Изменяя еще раз порядок действия тех же операторов, приходим
к формуле .
G.3)
где Lo — зависящая от S и q> функция от х, t, которая
является бесконечно дифференцируемой, если функции S
и ф бесконечно дифференцируемы. Требование, чтобы два пер-
первых члена не содержали дифференцирования по х, приводит нас
к уравнению относительно Si
которое называется D-характеристическим по' отношению к урав-
уравнению G.1). Это уравнение распадается на 2 ветви:
dt - — x \1^ dtj-
Решим уравнение со знаком — в правой части. Учитывая началь-
начальное условие S (х, 0) = 0, получаем:

§ 8] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 53
Требование, чтобы предпоследний член в G.3) не содержал диф-
дифференцирования по х, приводит, с учетом формулы G.4), к урав-
уравнению относительно ф, называемому уравнением, переноса:
Решение этого уравнения с начальным условием <f(x, 0) = щ(х)
имеет вид
2 2
Итак, имеем
V+xt/
Заметим, что
00
eihf (I) v (х\ — * С
— 00
Поэтому окончательно получаем:
п(х, t) = (
Непосредственным дифференцированием можно показать, что
в данном случае и(х, t) удовлетворяет уравнению G.1) точно.
§ 8. Предельный переход уравнения колебаний
кристаллической решетки в волновое уравнение
Мы применим теперь построенное операторное исчисление к кон-
конкретной физической задаче. Именно, рассмотрим уравнения коле-
колебаний кристаллической решетки и изучим вопрос о том, какие
его решения переходят в пределе (когда шаг решетки стремится
к нулю) в решения волнового уравнения.
Такая задача является классической и достаточно стандарт-
стандартной. Разумеется, трудно ожидать, что предложенный оператор-
операторный метод даст здесь что-либо новое. Но оказывается, этот метод
позволяет обнаружить в данной задаче довольно неожиданные
физические и математические эффекты. С помощью операторного
метода мы найдем «особые» решения уравнения колебаний решетки,
которые вообще не имеют предела. Именно такими особыми реше-
решениями обусловливаются физические эффекты, разобранные в настоя-
настоящем параграфе, из которых не все раньше были известны.
Изучаемый здесь пример показывает, что операторный метод
в некотором смысле адекватен физической задаче. Именно, мы уви-
увидим, что уравнение характеристик для функции от упорядоченных

54 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
операторов не только определяет такие фундаментальные
явления как эффект типа Черенкова (шлейф осцилляции излуче-
излучения за разрывной волной), но и дает точные границы области
«черенковского излучения». Мы увидим, что результаты хорошо
совпадают с численным экспериментом.
В остальных разделах этой книги мы не будем проводить эле-
элементарное исследование получаемых формул и тем более их срав-
сравнение с результатом численного эксперимента. Однако этот клас-
классический и простой пример будет здесь подробно разобран.
1. Переход системы колебаний решетки в волновое уравнение.
Мы .рассмотрим систему обыкновенных дифференциальных урав-
уравнений, описывающих колебания кристаллической решетки, и по-
получим из нее в пределе волновое уравнение (с частными произ-
производными). •
Рассмотрим 2N атомов массы т, расположенных на окруж-
окружности радиуса 1 на одинаковом расстоянии h = n/N друг от друга.
Предположим, что атомы взаимодействуют лишь с ближайшими
атомами. Пусть u((t) — отклонение г-го атома в момент времени /
от положениия равновесия: здесь г = 0, ±1, ..., ±N, причем
u_m — un. В линейном приближении система уравнений Ньютона
для такой решетки имеет вид
п = 0, ±1, .,,, ±N, (8.1)
def . def , fy~
^ы-лг+ь «-лг-i =«лг_1; с = у ^-
где uN = u_N, «лг-ц^ы-лг+ь «-лг-i =«лг_1; с = у ^- скорость
звука.
Систему (8.1) будем рассматривать при условии, что число N
-очень велико. Рассмотрим гладкую функцию и (х, t), которая
принимает в узлах решетки значения Uj, т. е. и (jh, t) = uj(t).
Система (8.1) приобретает при этом вид дифференциально-разно-
дифференциально-разностной задачи на окружности, или, что эквивалентно, дифферен-
дифференциально-разностной задачи на прямой с периодическим коэффи-
коэффициентом:
2«(*, h)+u(x-h1 t)),
и(х'+2л, t) = u(x, t). (8.2)
Мы будем предполагать, что, вообще говоря, скорость звука с
зависит от х, причем с(х)^Ссо есть 2п-периодическая функция,
с{х)^0.
Поскольку нас интересуют значения и (х, t) лишь в узлах ре-
решетки, то естественно рассмотреть «максимально гладкий» класс
функций, «натянутых» на значения ыу- в узлах. Пусть Mn — век-
векторное пространство, натянутое на векторы е'кх, k = 0, ±1, ...
..., db(W— 1), -\-N. Легко видеть, что для заданного набора {uj,
1 = 0, ..., ±Af, un = u_n} существует функция и е Мы, прини-

§ 8} ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 55
мающая значения иу в узлах решетки. Поэтому начальные усло-
условия для задачи (8.2) можно задать в виде
—- (х 0\ = v (х\ <= М ' /ft *W
Далее, используя соотношение
'("'* аг)и (je, t) = u(x + h, t),
И
е
перепишем задачу (8.2), (8.3) в виде псевдодифференциального
уравнения
и(х, 0) = М*), gjr(*, 0) = v2(x), и(х + 2я, f)-u(x, t).
Положим . « -
Будем писать q> е С<Ц\, если функция q> = ф (х, t, h) является s
раз дифференцируемой по х, tr 2я-периодической по х, и имеют
место оценки
sup I **%»**> I < с» < оо, *-0, 1, ......
А1|| 0Х 1
Рассмотрим вначале задачу с гладкой (равномерно по А) пра-
правой частью:
Лемма 8.1.
т+1
1
ft=4
+l
2 «*(-
IIQm<P 1 ^ст д-яп? • ak ~ некоторые фиксированные числа.
Доказательство. По формуле Тейлвра имеем:
m+l I
4 sin2 D-1 = 22+ У akzk-2z^^ [
г \
\tn-\-l)\

56 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Отсюда
Очевидно, функцию в квадратных скобках можно представить в виде линей-
линейной комбинации функций вида
±txl_ihp,
\ dx
Как нетрудно видеть, имеет место неравенство
¦ К A - i)m+1 У(х + т/г) di s? С || г|з ||.
Отсюда следует искомая оценка для Qmq>. Лемма доказана.
Первое- приближение при Л-*-0 к оператору Lh задачи (8.5)
мы будем называть волновым оператором и обозначать Qc или L.
Таким образом, по лемме 8.1 имеем:
L = U с = dydt2 - с2 (х) д*1дх*.
Уравнение Пси = / называется волновым уравнением. В этом
смысле мы будем говорить, что система обыкновенных дифферен-
дифференциальных уравнений колебаний решетки (8.1) переходит при
Л->-0 в волновое уравнение. Но мы еще ничего не знаем о пове-
поведении решений этой системы. Переходят ли они при Л-*-0 в реше-
решения волнового уравнения?
Прежде всего нужно установить, что решение задачи (8.2)
существует и что решение соответствующего волнового уравне-
уравнения существует.
Теоремы существования и единственности решений волнового
уравнения и уравнения (8.4) мы докажем здесь лишь для доста-
достаточно малого t и, главное, приведем формулы для решений.
2. Существование и единственность решения волнового урав-
уравнения. Мы докажем здесь следующую ,теорему.
Теорема 8.1. Пусть f gC^ (s достаточно большое). Тогда
при 0 < / «g Т~ где Т — любое число, существует и единственно
решение u — R0(f)^C^\ задачи
? еи-Л . (8.6)
2я, t) = u(x, t), u(x, O) = y(jr, 0) = Q. (8.6')
При этом
с,.ЛЦ\\, / = 0, 1, 2, ...,ъ,
t), где R(x, f) определено в (8.8).

§ 81 ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 57
Доказательство этой теоремы (как в дальнейшем и других
теорем такого типа) мы проведем с помощью конструкции регу-
ляризатора задачи (8.6), (8.6').
Определение. Пусть А = — id/dxе М, В = х& Ми М1 —
окружность, G (t, xlt a, s) e Cg, s=l, 2, ... —последователь-
—последовательность таких однопараметрических семейств символов, что
G@, xlt a, s)=l, G't@, xlt a, s) = 0 и что выполняется нера-
неравенство
IM*. x, a, s)\*zC(x\+l)-** {8.7)'
для символа /х е С^ оператора
h{t, А, В, s) = (dydt* + ic*(B)A*])G{t, А, В, s). (8.7')
Тогда G\t, А, В, s) называется регуляризатором задачи (8.6),
(8.6') (аргумент s мы будем опускать).
Замечание. Регуляризатор, очевидно, не единствен. Можно,
например, прибавив к G функцию, финитную по А, получить
другой регуляризатор, что мы и будем делать в дальнейшем,
так, чтобы носитель нового регуляризатора обращался в нуль
в е-окрестности ^ = 0 и, следовательно, его можно было бы
умножить на полином от х\1 или разложить по степеням х\1,
понимая под символом х[1 функцию Jtjf1 ф (л"х), где ср (х{) имеет
носитель вне е-окрестности точки х1 — 0, ср {хх) = 1 при хх > 2е.
Предположим, что такой регуляризатор построен. Покажем,
как с помощью регуляризатора можно доказать утверждение
теоремы. Подставив функцию
R(x, t) = \] G(n, А, Ь)Ф(х, x)d[idx (8.8)
в уравнение (8.6), получим:
/—т
t)+\ [ /XU А, В)Ф(х, x)dVidx. (8.8')
Таким образом, мы свели задачу (8.6), (8.6') к задаче об
определении Ф из уравнения
Ф (х, t) + $ /, (t - х, А, В) Ф (х, х) dx = / (л:, t), (8.8")
о
где
h{t, lbW\fl(x,A, B)dx
о
(начальные условия и условия периодичности (8.6') очевидно,
выполняются для функции R(x, t)).

- 58 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Уравнение (8.8") является интегральным уравнением типа
уравнения Вольтерра и решается итерациями. Именно, положим
где
Ф„(лг, /) = /(*, t),
' i s \
г, A, B)f(x, x)dx,
б
' / 2ft —I 2ft \ J> / 2ft —3 2ft — 2\
Ф*(*. *) = (-!)* W~T Л Bj /.U-t,, Л, В J...X
о о
/2U_i-Tft, A, B)f(x, xk"dxk,..dx1,
х
б'
ft-2, 3, ...
Из (8.7) для любой г|з (*, 0 €= С^ имеем оценку для
(^^TJh достаточно большого s
11/2\' — х, A, Bjijj'jf, т)||
1-х
о
где Мо = const.
Отсюда при OsSfsST имеем
Следовательно, ряд 2 Ф* сходится. Более того, из анало-
гичных оценок для производных Ф^ -следует, что ряд из произ-
производных Ф* равномерно (и притом очень быстро) сходится, сумма.
;оо . •¦
Ф=^Ф* принадлежите^, и для R0(f) = #(x, f) справедливы;
ft = O '
оценки теоремы 8.1.
Точно так же ясно, что уравнение (8.8), а следовательно, и
задача (8,6), (8.6'), имеет единственное решение, так как любое
его решение представляется единственным образом в виде ряда
00
Таким образом, чтобы доказать теорему, нам остается постро-
построить регуляризатор задачи (8.6), (8.6') (и оценить его). Мы это

§ 8J ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 59
проделаем с помощью операторного метода. Будем искать регу-
ляризатор G в виде
' G(t, A, *) = ebbG. t\(xt t, А), (8.9)
где Л = —id/dx, а функции S, <р подлежат определению (здесь
S, <р — 2л-периодические по х, S — вещественная).
Подставим оператор (8.9) в волновое уравнение и воспользу-
воспользуемся формулой коммутации; получим:
где у функций S и <р опущены аргументы (л:, /) и [х, t, А) соот-
соответственно.
Правую часть (8.10), а точнее, оператор в фигурных скобках,
мы хотели бы сделать нулевым. Точно сделать это не удастся
(в случае переменного с(х)), но для построения регуляризатора
достаточно получить справа «гладкий» оператор Д.
Регуляризатор G рассматривается нами как оператор на про-
пространстве достаточно дифференцируемых 2л-пёриодических функ-
функций v(x). Такие функции представляются в виде ряда Фурье:
/ - "О \
(Напомним, что по определению f\A, В)v (х) = 2 anf{n,x)efnx\.
V П=—00 /
def Тогда G(t, A, x)v**G0(x, t) + G{t, A, x)vu где G0(x, t)™
==G\t, A, x)a0. Функция Go является решением задачи
? cGo = fi('t A, x)a0,
t) = G0(x, t).
Очевидно, не изменяя регуляризатора, можно взять вместо Go
константу й0, которая удовлетворяет выписанной задаче, но с нуле-
нулевой правой частью.

60 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Итак, регуляризатор G достаточно рассматривать лишь на
оо
функциях вида ух (х) = ? aneinx. Но на таких функциях опре-
п= — оо
пфО
делен оператор А~г\
00
de{
Ad n
П = —00
пфО
и все его степени А~к, &—1, 2, ...
Поэтому функцию ф в (8.9) мы можем искать в виде
Подставим это разложение в (8.10) и приравняем нулю коэф-
коэффициенты при-степенях (—iA'l)k, k = —2, —1, 0', ...s—1 в фигур-
фигурных скобках (8,10). Тогда мы получим систему уравнений
где
ЩП^(§ )§, t).
При этом оператор G будет удовлетворять волновому уравне-
уравнению с правой частью (см. (8.10))
Согласно определению имеем!.
h(t, A, ^Vr^i-tY(ПоЪ (х, t)
00
71 = —СО
Отсюда видно, что ft удовлетворяет нужным оценкам (8.7).
Таким образом, нам остается решить систему*(8.11) с началь
ными условиями
G@, A. i)-l,§@, A.i)-O. (8.12
Первое уравнение (8.11) есть уравнение Гамильтона — Якоб]
для функции S(x, t):

§8J ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 61
Поставим начальное условие
S(x, 0) = 0. (8.13')
Для рещения задачи Коши (8,13), (8.13') рассмотрим соот-
соответствующую систему бихарактеристик, называемую системой
Гамильтона:
(8.14)
Эта система легко интегрируется. Пусть Х± (*в, т), Р± (х0, t) —
ее решения. Поскольку -д—- , 0=1, то при любых t (см. ниже)
имеем -х—(х0, /) ?? О и, следовательно, разрешимо уравнение:
X == Л [Xq , I),
т. е. существует гладкое решение хо = х±(х, t).
Тогда, задача (8.13), (8.13') имеет следующие 2я-периодиче-
ские по х решения (отвечающие знакам ± в (8.13)):
S± (х, t) == \ Р± (дг0, т) -г-; (дг0, т) -
-Н±(Р±(х0, т),
Заметим, что ^
Обратимся теперь ко второму уравнению (8.11). Оператор Ux
теперь распадается на два: U+ и f/j", соответствующие двум
функциям S+. Очевидно, оператор ?/± можно преобразовать к виду
где #+(*, р) = + с(*)A+р), а у функций S+ и Я± опущены
аргументы (X*, /) и (X*, P±) соответственно, -^- есть производ-
ная вдоль траекторий (8.14), т. е.
dt± ~~ dt ^ dt дх~ ~dt
В силу (8.14) •
J-[Н±(Х+ (х0, t), Р±(х0, 0)] = 0. (8.16)
Следовательно, Я+(Х+, Я+) = Я+(дг0, 0) = грс(ж0).

62 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Пусть Л- (лг0, J) = дХ~^*9' ^ ¦ Дифференцируя уравнение для
Х± (смТ (8.14))!
по переменной х0, получим:
eri±-J±[ др» dxi -r дрдх}'
Отсюда и из (8.16) для якобиана
/± (х, 0 - 2Н± (лг, ^ (дг, О) Л (*± (х, t), t) = =р 2с (дс)
получим уравнение:
dt±V\j±]
Поэтому для оператора (8.15) имеем*
-..0\
= _.' (JL _1^_ -L^^W, 0. (8-17)
где у функции Н± опущены аргументы [дг, -^(дг. 0 «'ф — любое.
\ ОХ I
Мы проделали все выкладки, используя общие обозначения,
так как в дальнейших примерах они будут повторяться дословно.
В нашем случае выражение (8.17) для оператора f/f приобре-
приобретает вид:
Поэтому второе уравнение (8.1.1) имеет два следующих решения:.
где ^f (дг) — некоторые начальные условия, подлежащие опреде-
определению.
Аналогично, при помощи представления (8.17), решаются все
остальные уравнения (8.11) и определяются 2я-периодические
функции ф^, Л = 0,-1, 2, ..., s, через некоторые интегралы щ>
траекториям Х-, Р--

§ 8] . ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 63
Окончательно, регуляризатор G имеет вид:
G (*, А, х) = ? 2 eth±<*' °«PF (х, t) (- М-*)*, (8.19)
±ft = 0
где функции S+, ф* определены выше и ?/+==/+ + /•—
Нам остается подобрать начальные условия для ф^ так, чтобы
выполнялось (8.12). Положим
Ф±(ж, 0)=1/2. (8.20)
Поскольку J+(x, Щ — 2Н±{х, 0) = qp2c(*), то из (8.18) полу-
получается следующее выражение для г|з±:
Для остальных функций ф^, к ^ 1 поставим нулевые условия:
ФГ(*. 0) = 0, А-1, 2, ..., s. (8.21)
Из (8.19) в начальный момент t = 0, учитывая (8.20), получим:
(о. A, fl-US ч*6. o)(-M-)* = 2>H*,o)=4 + !=i.
± ft=0 ±
Для производной 5G/5^ из (8.19) имеем:
-(8.22)
Но —^ (х, 0) = — Н± (х, 0) = ± с (х), поэтому первые сла-
слагаемые в (8.22) в силу (8.20) сокращаются, и остается выражение:
±
дуг
Производные —gr- выразим из (8.11). Легко видеть, что в началь-
начальный момент времени они удовлетворяют условию
Поэтому оператор G\t, А, х) удовлетворяет и второму началь-
начальному условию (8.12). Таким образом, регуляризатор для задачи
(8.6), (8.6') полностью построен, и теорема доказана.

64 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
3. Асимптотические решения системы уравнений колебаний
решетки. Мы будем различать между собой две задачи: 1) нахож-
нахождение асимптотики точного решения, 2) нахождение асимптоти-
асимптотического решения, т. е. построение функции, подстановка которой
в уравнение дает правую часть, асимптотически приближающуюся
к заданной.
Прежде чем приступать к задаче 1, мы будем строить -асимпто-
-асимптотическое решение. Р^меет место следующая почти очевидная лемма.
Лемма 8.2. Пусть заданы целые m^l, 4^2 и функция
/еС^'ь где р = р(т, k) достаточно большое. Тогда существуют
такие функции i|>y е С[%, / = 0 т.— 2, что линейная комби-
комбинация
т—2
/ = 0
является асимптотическим решением задачи (8.5). А именно,
Um(x + 2n, t)=Um(x, t),
Um(x, 0)=^(x, 0) = 0,
причем остаток t^ имеет оценку
p
Доказательство. Подставим функцию Um в уравнение
н воспользуемся леммой 8.1. Затем приравняем нулю коэффициенты
при степенях Л; тем самым получим уравнения для функций %,
/==0, ..., т — 2. Например, приравнивая нулю коэффициент при
Л2, получим уравнение для *ф0:
? Л>о + «4С2 (*) i — i-frr) Ro Ф = 0-
Отсюда в силу теоремы 8.1 найдем
4>о = - <*4#о [с2 ( - / -J^-L ^о'/)],
причем функция i|>0 удовлетворяет нулевым начальным условиям
и является 2я-периодической по х.
Аналогично получим все остальные функции фу. Оценка остатка
Fmf следует из соответствующих .оценок леммы 8.1 н теоремы 8.1.
Лемма доказана.

§ 81 ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 65
Мы получили, таким образом, что решение волнового уравне-
уравнения является асимптотическим решением системы уравнений коле-
колебаний решетки. Но, во-первых, оно является асимптотическим
•решением лишь при достаточно гладкой правой части, а во-вторых,
еще нужно доказать, что оно является асимптотикой истинного
решения. Для того чтобы найти общее асимптотическое решение
уравнения колебаний решетки и доказать, что оно является асимп-
асимптотикой истинного решения, мы прибегнем к способу уже испро-
испробованному для волнового уравнения — к построению регуляризатора.
Регуляризатором мы будем называть в этом случае аналогич-
аналогичный оператор G[t, А, В), зависящий также от h, и определение
дадим аналогичное предыдущему определению, только потребуем
дополнительно к (8.7), чтобы
|Д (хи a, t, S-, ft) |<cshs+* (х\ + \)-°1'. (8.23)
В правой части (8.7') мы-поставим, естественно, оператор
Если регуляризатор построен, то аналогично пункту 2 можно
получить интегральное уравнение типа уравнения Вольтерра
и доказать, что его решение существует, а также получить оценку
для решения," равномерную по h, при А—*0.
Заметим далее, что нам на самом деле достаточно потребовать
от /х лишь одного условия (8.7).
В самом деле, если построен такой «ослабленный» регуляриза-
регуляризатор, то далее мы можем применить результаты этого пункта -г-
лемму 8.2, которая дает способ получить настояший регуляризатор
уже с точностью до hNF, где F eCj?\ (т. е. удовлетворить (8.23)).
Таким Образом, мы свели задачу к построению ослабленного ре-
регуляризатора, такого, что соответствующая правая часть fs
удовлетворяет условию (8.7). Это мы и проделаем в настоящем
пункте с помощью упорядоченных операторов.
Построим регуляризатор для системы уравнений колебаний
решетки.
Рассмотрим задачу (8.4) при произвольных начальных данных
vlt v2 из. Mn. Очевидно, достаточно рассмотреть случай уа(л:)==0.
Кроме того, функцию Vi (х) представим в виде
N
2
n= —N+l
Очевидно, константа ав удовлетворяет задаче (8.4). Поэтому доста-
достаточно рассмотреть начальные условия вида
и(х, O) = vo(x)=S ? aj"; ^-(х, 0)=0. (8,24)
n=±l..
3 В, П, Маслов

66 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Пусть А = —i-g~. Как и выше, определим оператор А-1 на функ-
функциях v0 по формуле
Л-Ч = А-1
Под действием оператора А-1 мы получаем функцию того же типа;
следовательно, на vQ опеределены все степени A~k, k=\, 2, ...
Кроме того, очевидна оценка
Далее, -g^(A-1v0) = iv0(x, h). Поэтому
Отсюда видно, что задачу (8.4) достаточно решить с точностью
до функций вида (A-kv0).
Регуляризатор будем искать в виде (аргумент h опускаем) "
G{t, a, i)»!-е'А5 «*•'¦«> фCг, t, o»)»lf (8:25)
где (a = hA, h = n/N, S, ф — бесконечно дифференцируемые 2я-пери-
одические по х функции, S — вещественная функция.
/а 1\
Напомним, что оператор вида F \х, а) на функции о е Мм
аадается формулой
N я
F (ж, i) v = ^ 2 еШр (*•kh) \ ^v (y)dy. (8.26)
-Я
Очевидно, оператор to ограничен на Afjv:
|| toy || < л || у ||, v^MN. ¦ (8.27)
Подставим выражение (8.25) в уравнение (8.4) и воспользуемся
формулой коммутации с экспонентом. Тогда получим, что для того,
чтобы G (t, to, х) удовлетворяла уравнению (8.4), достаточно, чтобы
выполнялось равенство
i-o; (8.28)
где у функций S, ф опущены аргументы \х, t, со).

§ 8] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 67
Последнее слагаемое в этом равенстве преобразуем с помощью
/(-формулы и формулы коммутации:
+ | Ш COS (й A + ?)) ф]
(8.29)
где у функций S, ф опущены аргументы {х, t, to).
#й —некоторые дифференциальные операторы порядка k, дей-
действующие на функцию ф(лг, t, to) по переменной х (можно выпи-
выписать явный вид всех Rk). Остаток Qm и все его коммутаторы
— §У > s = 0, 1, 2, ... имеют в силу (8.27) оценки
ИЛ»1Ке,|М|, v<=MN. (8.30)
Теперь заметим, что hvo = A-1wvo. Поэтому из (8.28) и (8.29)
получаем уравнение:
от-1
-2 (-^
- 4 [с* (лг)]А-«>Й«}"оо = 0, (8.31)
2 1
где у функций ф, s опущены аргументы (х, t, to).
Будем решать (8.31), используя разложение ф по степеням А-1,
т. е. в виде
2
4=0
Подставим это разложение в (8.31) и приравняем нулю коэффи-
коэффициенты при степенях ( —г^)*, Л = 0,..., т— 1. Получим систему
з*

68 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
уравнений;
0, А— 1, 2, ..../п-2,
где
а операторы #?, А = 2, ..., m — 1 задаются формулами
Предположим, что из уравнений (8.32) мы нашли S и yk. Тогда
получим, что функция
Vm (х, t) = 2 *'is й- '¦ •) щ (х, t, i) ( - /71-0* »о + Oo
удовлетворяет уравнению (8.4) с точностью до функции
Кт (х, t) = As ft. *. •)' [^Q'mA-m+3] »Of (8.33)
где.оператор Qm задается следующей формулой:
q^=4^ (г) ]B i; (- О-*^-2 х ;.
0 = 2 ' = 0
X(/?/p«_.w)(r, ^, «)(-M-0' + Qm«m-2|. (8.34)
Дополнительно имеем
_ jas 'J. «.¦ Wft«|Q^f 2 _;-J-1 Um+a + e'^s & '••)A2Qmi-m+'} ox.
Из (8.34) и оценки (8^0) получим
I - ifx Km (X, t)
где сх = const.

5 8] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 69
Аналогично получаются оценки для всех остальных произ-
производных:
| ? ||KII> s = 0, 1, 2 m-2.
Поэтому, если sup ||fi||*^c,. то функция Vm удовлетворяет
0<А<1
уравнению (8.4) с точностью до элемента из С$72)\
Обратимся теперь к решению уравнений (8.32). Во-первых,
имеем уравнение Гамильтона — Якоби для функции S (x, t, со):
dS -+- 2 с W sin ш (\ 4 dS
Поставим начальное условие
S(x, 0, со) = О. " (8.350
Для решения такой задачи Коши рассмотрим соответствую-
соответствующую систему характеристик:
1
_ (8>3б)
± isin [f о+р±)] (х±)р± I °
± isin [f о+р±)] ж-
Эта система легко интегрируется. Пусть Х±(х0, со, t), P±(x0,
АХ—
ю, t) — ее решение (спектра (ю) е [—п, п]). Поскольку -^— |/-о= 1,
то при достаточно малых t разрешимо уравнение
х = Х±(х0, со, t), . (8.36')
т. е; существует гладкое решение a:0 = ^(^, t, со). Тогда задача
(8.35) —(8.35') имеет следующее 2я-периодическое по х решение:
S±(x, t, со)= [ {Р±(х0, со, х)^(х0, со, т)±
± 2 «(**<*«'*>> sin [f (I + Р± (х0, со, г))]} dx
Далее уравнения (8.32) решаются точно так же, как это было
сделано в пункте 2 для волнового уравнения.
В итоге «ослабленный» регуляризатор для задачи (8.4) нахо
дим в виде:
G{t, со, x)vo='z'ZetAs±{l't-i)W^, t, ^{-ib-tyoo. (8.37)
± ft=o
Теперь, учитывая замечание, сделанное в конце предыдущего
пункта, мы получаем следующую теорему.

70 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Теорема 8.2. Решение задачи (8.4) при достаточно малом t
существует, единственно и при условии (8.24) имеет вид
/ и(х, t) = G{t, A, B)v0-hr*R0(Кт) + 0(h).
Мы приведем теперь некоторые простые следствия Для этого
нам нужно представить выражение (8.37) в виде интеграла,
используя представление псевдодифференциального оператора на
окружности, и найти асимптотику при п-*-0 этого интеграла по
известному методу «стационарной фазы» (упрощенному методу
перевала для действительного случая).
Вначале приведем (оригинальный) вывод формулы метода ста-
стационарной фазы.
4. Метод стационарной фазы. Рассмотрим интеграл
/(/l)=-7=L
где Ф (у) €Е C°°(R), ф (у) €Е С" (R), -|~?- ф 0 при у е supp q> и урав-
уравнение дФ/ду = 0 имеет единственное решение ь=Уо ПРИ
г/е supp q>(t/) (стационарную точку).
Лемма 8.3. При приведенных выше условиях для любого N Э^ 1 справед-
справедливо разложение
) = е 4 е 2 ¦ с I и (иг.) 4- Z, hk ib,. (иЛ I (8.38)
где
J VJQ/,Q-
дх* YJ (у, /J
... J V J (y, tk)-^y^ Ф(y)<tti .¦• <tt»,
y = y(x, /) — решение уравнения (8.49), а якобиан
J(x, t)~J (y(x, t),t)
определен формулой (8.48). ч
Для доказательства мь! воспользуемся асимптотикой при А—<-0 решения
задачи Коши для уравнения Шредингера осциллятора
Такая асимптотика называется квазиклассической. Прямым дифференцированием

§ 8] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 71
можно показать, что решение задачи (8.39) дается формулой
.„,.. ,ч е 4 е __! х
X $ e2ftsin' ХеЛ Ф(у)ф. (8.40)
—со
Положив в формуле (8.40) х = 0, f = я/2, получим равенство
/ (Л) = 1|, @, я/2), (8.41)
а полагая в формуле (8.40) х = 0, / = — я/2, получим
/(Л)=»е-гя/?1К0, -я/2)- (8-42)
Таким образом, мы видим, что разложение в ряд функции / (Л) в силу формул
(8.41) и (8.42) совпадает с квазиклассической асимптотикой решения задачи
Коши (8.39). Решение задачи (8.39) будем искать в виде асимптотического ряда ?)
¦4 S(x, of
def T s (*• О
eh <p(x,t,h), (8.43)
где 5 (*, t) е С00, ф,- (х, t, h) е С00 — подлежащие определению функции. Под-
Подставляя функцию ф (*, t, h), определенную равенством (8.43), в уравнение (8.39),
получим уравнение
\ dS
Приравняем к 0 слагаемое, не содержащее Л. Получим уравнение Гамиль-
Гамильтона — Якоби для осциллятора:
Положим S (х, 0) = Ф (х).
Рассмотрим систему Гамильтона для осциллятора
4 = Р Я @) = У,
Легко видеть, что ее решениями являются функции
Я (t, у) = у cos t + -щ- sin t; p(t, y) = -^-cost-ysmt. (8.47)
Функции q и р называются траекториями гамильтоновой системы (8.46). Обо<
значим
Из (8.47) получим
~ д*Ф
jjraat. (8.48)
*) Последующие рассуждения аналогичны пункту 2.

72
ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Из этой формулы следует, что:
1) если даФ/3(/а > 0 при у е supp <p (у), то .
3(У- О Ф° ПРИ У е SUPP Ф(У)> °«? t «Sя/2.
2) если д*Ф/ду* < 0 при у е supp ф (у), то
3(У,ЦФ0 пр'и </ «= supp ф(у),. — y=s?
В дальнейшем мы будем предполагать, что даФ/д</а>0. В случае д*Ф/ду*<
< 0 все рассуждения сохраняются, если заменить t на (— t).
Обозначим через y=y(t, x) решение уравнения
q{t,y)=x (8.49)
(в силу теоремы о неявной функции оно существует). Аналогично пункту 2
получим, что решение уравнения (8.45) даетси формулой
t
S (х, Q=a> (у (х, Q)+y [ [ра (у, !)-*¦ (у, т)] dx \у.у(х, й. (8.50)
Рассмотрим оставшиеся слагаемые в уравнении (8.43). Введем векторное
поле
Л dl
Вычислим производную j- 7 (у (х, 0, 0- Отметим вначале, что векторное
поле d/dx совпадает с дифференцированием вдоль проекций на плоскость (*, Г)
траекторий гамильтоновой системы. Имеем | ' ¦
?Jtofc 0, 0U^A«im
где 1 (х, ДО соответствует якобиану преобразования сдвига вдоль траек-
траекторий следующей системы Гамильтона:
def
• „ _ ¦ J def
Рва~ч Р(О)=Р(*о> У(х> W)=Po-
Для вычисления J (x, &.t)=J/it заметим, что в силу системы Гамиль-
Гамильтона,
и
Легко видеть, что функция S (x, t), определенная равенством (8.50), удовлетво-
удовлетворяет условию ^- = р. Окончательно

§ 8] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 73
Обозначим теперь
Отсюда имеем для любой 6 (я, t) e С00
d /6(х, t)\ I db 16 daS
dx\ V7 ) VJdx 2 \/7dx*'
Положим теперь в формуле (8.43)
и подставим функцию if>(*, t, ft) из уравнения (8.43) в уравнение (8.39);
используя формулы (8.44) и (8.51), приравнивая члены с одинаковыми степе-
степенями. А, получаем рекуррентную систему
dx дх3 yj
Отсюда следует, что eo(*, f)=(f>(y(x, t)), а в^, k>l определяется по формуле
где У (W = У (*, t<) и интегрирование производится вдоль траекторий систе-
системы (8.46).
Докажем теперь, что функция if (*, t, h), определенная равенством (8.43),
в котором функции <pft (*, t) и S (л;, t) только что найдены нами, действительно
определяет асимптотическое разложение решения задачи (8.39). Положим
Нам нужно доказать, что функция tyN (x, t, h) мало отличается от функции
ty(x, t)—точного решения задачи (8.39). Точнее, мы докажем, что
max \)N{x, t, Щ-Ъ(х, t)\ = O(hN-^% (8.52)
(х, OeRnx[O, я/2]
Для получения оценки (8.52) заметим, что по построению, фд, (я, t, h)
удовлетворяет уравнению
ы„ и hi^N,..\ nv11—p MM) >
и, следовательно, разность ^(дс, <, ft)—if (ж, <)=^(jc, <, А) есть решение

74 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
задачи
dt 2 \ д* I
dt 2 \ дх* I дх*У'(х,*У (8-53)
Прямым подсчетом легко показать, что решение задачи (8.53) дается
формулой
t _/*_/* (l_s|gn«_f))
ж. 0= \ е—/ — х
J 1/2й|(<)
/((/, 0 , dy Л. (8.54)
dx*VJ{y, t)
Из равенств (8.51) легко видеть, что функции Ък (х, <)еС^°(х, t) k=0, ...
вместе с фувкцией у (у). Учитывая, что l/У sin г — функция, интегрируемая
в окрестности точки г = 0, из- равенства (8.54) непосредственно получаем
оценку (8.52).
Положим теперь в наших формулах х=0, /=я/2. Заметим, что
S(x, t) i/=n/2=(I)(J/@. л/2))- Это равенство легко получается из формулы (8.50).
Из равенств (8.47) получаем:
</@, я/2)=0=дФ/ду.
По условию, равенство дФ/ду = 0 возможно в единственной точке у=(/о-
Таким образом, у@, я/2)=(/0. и мы получаем разложение (8.38).
Замечание 1. Метод стационарной фазы можно применить
ь
и к интегралам вида § q> (у) е'ф W* dy. Пусть производная дФ/ду
а
отлична от нуля в некоторых окрестностях точек а и Ь. Рассмот-
Рассмотрим на [а, Ь] разбиение единицы {^(г/), ег(у), е3(у)},"подчиненное
следующим условиям: е1(у), ег(у), e3(y)^.Cf, е1 + ег + е3~\ на
[а, Ь]; е2(а) = е3{Ь) = \; дФ/дуфО при у s supp ег [} supp e3,
supple (а, Ь). Тогда
(У) Ф (У) ^ wlh dy + \ е3 (у) Ф (у) е'ф Wh dy.
—оо
—оо
Первый интеграл уже вычислен нами, а вторые два, как нетрудно
показать интегрированием по частям, являются величинами
порядка О (Л).

§ S] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 75
Замечание 2. Нам потребуются еще и суммы вида
N ,
1 , VI jr<b(nh)
п — — N — 1
Их вычисление сводится к предыдущему случаю, если восполь-
воспользоваться равенством
- N , . я
h 2j e <p(nh)= \
t
* Ф Ш Ф («/) cos BkNy) dy, (8.55)
доказательство которого элементарно проводится разложением
функции е^ ф (у) на отрезке [— я, я] в ряд Фурье с после-
последующим использованием формулы для суммы членов геометри-
геометрической прогрессии или h ? cosknh = 2nbA,ims, m — целое.
+
5. Шлейф осцилляции. Решение (8.37) есть сумма выражений
^ \ Vl
-Я rt = — /
Но в силу формулы (8.55)
= J Ф(х, /co)e('/ft>a>[s±("'"B) + j:-^dco+2 I) S Ф(х, f, co)X
Стационарная точка со0 интегралов определяется из уравнений
dS.
S±(x, t, щ)+х + щ-^(х, t, co0) = | + 2^. (8.56)
При «не очень больших» / это уравнение будет разрешимо лишь
при fe = 0, так как S±(x, t, со) |/_0 = 0.
Оценим k-& (k ф 0) член суммы. Проинтегрировав дважды
по частям (один раз вводя косинус под знак дифференциала,
а другой раз разложив косинус по формуле Эйлера)\всю экспо-
экспоненту, получим оценку вида О (h/k2). Отсюда следует, что сумма
ряда от k—\ до бесконечности имеет порядок О (К).
Теперь перейдем к решению неявного уравнения (8.56). Оказы-
Оказывается, что левая часть этого уравнения обладает замечательным

76 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
свойством. Производная от нее в силу соответствующей (плюсу
и минусу) системы бихарактеристик (8.36) (т. е. по направлению
соответствующей бихарактеристики)^ равна нулю. Проверить этот
факт (носящий на самом деле общий характер) мы предоставляем
. читателю.
Отсюда следует, что левая часть равенства постоянна вдоль
соответствующей бихарактеристики, а так как
= 0,
то при не очень больших / она равна х?(х, t, co0)— решению
уравнения (8.36): х = Х±(х0, со, /). Следовательно, уравнение (8.56)
для стационарной точки эквивалентно уравнению
X±(l, co0, t) = x.
Значит, уравнение для стационарной точки разрешимо лишь для
тех х, которые принадлежат замкнутым областям
т. е. областям, образованным концами траекторий системы биха-
бихарактеристик (8.36), выходящих из точки |.
Пусть х лежит внутри одной из областей Q+. Тогда, если
со Ф 0,. то
поскольку -Tgj- Ф 0 при t Ф 0, как это видно из системы (8.36),
если ее продифференцировать по со. Значит, производная левой
части (8.56) по со.отлична от нуля при ^^б, со#О и метод
стационарной фазы применим. Поэтому ясно, что внутри обла-
областей Q+ решение быстро осциллирует, а производные от него
неограничены при А->-0 и, следовательно, заведомо не переходят
в пределе в производные решения волнового уравнения.
- Замечание. Если х лежит на характеристиках предельного волнового
/ их—' ' \
уравнения (т. е. х=Х±&, t), где ?^--qpC(^), Xf(l,O)=lj, то ста-
ционарная точка <йо=0 является вырожденной:
Это означает на самом деле, что fосновной разр'ыв> распространяется
по характеристикам предельного волнового уравнения, а следом за ним возни-
возникает <щлейф> быстрых осцилляции. Носитель этого шлейфа определяется
характеристиками Х±.
. Мы видим на этом примере, что характеристики, определяемые
уравнением Гамильтона, зависящим от упорядоченных операторов,

S8]
ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ
77
определяют в точности носитель шлейфа осцилляции. Этот факт
на самом деле следует из общей теории для широкого класса
задач, и приведенные здесь соотношения также носят общий
характер.
Приведем теперь сравнение величины носителя этого шлейфа
осцилляции с численным экспериментом.
За единицу длины мы взяли /=10~5 см, длину интервала
(окружности) мы взяли равной 21, h—\0~8 см, скорость звука
muf-w
m<?-ffl
-т
Рис. 1.
в кристалле с=105 см/сек принята за единицу скорости. В каче-
качестве начального условия была взята периодическая функция вида
имеющая скачок в точках х = 2п, п — 0, ±1, ...
На рис. 1 представлены графики функций:
max д?(У).
обозначенный верхней границей заштрихованной области и
min <?- (и),
обозначенный нижней границей заштрихованной области.

78 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
(Сплошной линией обозначены графики точного решения, а пунк-
пунктиром — графики решений, полученных с помощью асимптотиче-
асимптотической формулы.)
6. Эффект типа Черенкова. В 1934 г. советским физиком
П. А. Черенковым был обнаружен эффект (нетормозного) излуче-
излучения света, возникающего при движении в веществе заряженных
частиц. Этот эффект был теоретически обоснован в 1937 г.
И. Е. Таммом и И. М. Франком. Но лишь в 50-х годах стала
видна исключительная широта применения этого эффекта (в 1958
году П. А. Черенкову, И. Е. Тамму и И. М. Франку была при-
присуждена Нобелевская премия).
Эффект заключается в том, что при движении электрона
в среде со скоростью, превышающей некоторую, зависящую
от среды, величину, в определенной конической области вслед
за ним излучаются быстро осциллирующие электромагнитные колеба-
колебания—световые волны (черенковское излучение). Оказывается,
математическая природа этого эффекта связана с определением
характеристик, зависящих от упорядоченных операторов. Опера-
Операторный метод позволяет обнаружить аналогичное (математическое)
свойство для широкого класса псевдодифференциальных уравне-
уравнений и, в частности, разностных схем, в том числе и для систем
уравнений кристалла. В последнем случае оно непосредственно
следует из полученных выше асимптотических формул.
Движение, «электрона» со скоростью v математически описы-
описывается введением в правой части уравнения колебаний б-образной
функции в точке x = vt (для эффекта Черенкова —электромагнит-
—электромагнитных колебаний в среде, а в нашем случае — системы колебаний
кристалла). Черенковское излучение математически означает шлейф
быстрых осцилляции решения, который следует за точкой x = vt.
Этот эффект родствен тому, который был описан в предыдущем
пункте. Мы приведем" теоретический расчет этого шлейфа и его срав-
сравнение с численным экспериментом. Так же как и в-предыдущем
примере, окажется, что этот шлейф (область черенковского излу-
излучения) полностью определяется бихарактеристиками.
Итак, рассмотрим задачу
.-> (867)
и(х, 0) = «,'(*, 0) = 0, и(х + 2л, *)==«(*. t),
N
где bh{x — vt) — -^ У eik(x-vt) и фщ|_некоторая гладкая
функция. Будем решать эту задачу при не очень больших t.
Из теоремы 8.2 следует, что решение задачи 8.57 Lhu=f

§8]
ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ
79
def
единственно: u = Lj^f. Аналогично (8.8') — (8.8*) получаем, что
/ t—x
о о
удовлетворяет соотношению
t t—x
LhR = ф (t) 6Л (*,"*)+ jj J Ь К. <». *) Ф W SA (л-, т) d/ dt,
где ^(Z, со, х) удовлетворяет оценке (8.7). Согласно лемме 8.2 и
теореме 8.1 решение уравнения
' t—x
о о
принадлежит Cf^\ где ^(т)->оо при т->оо. Значитт в силу
того, что R — Ri есть решение исходной задачи (8.57), вся неглад-
негладкая часть решения этой задачи содержится в R. Аналогично
предыдущему пункту, при вычислении асимптотики R при ft->0
мы приходим к выводу, что главный член определяется интегра-
интегралом вида (после интегрирования по частям по т'):
«'(uS_}_ (х, t — l/v, со)
»-2яА
-я о
^ix.t-1/v.a)
S_ (д:, / —S/в, 0))
Фо" (X, t — 1/V, Ш)
Применяя последовательно метод стационарной фазы сначала
по со, затем по |, получаем, что общая стационарная точка
ио, 1о (»о^=0), находится из системы уравнений
So = *?(*. t-Vv,
(8.58)
Нетрудно убедиться, что если со ф 0, |соо|<я, ||0|<я,
то вторые производные отличны от нуля, и метод стационарной
фазы применим.

80 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Рассмотрим для простоты случай с = const. Тогда система
(8.58) примет вид
. 2с . (On
t x + ct cos (iflp/2) ^8'5 ^
Решение уравнения (8.59), как это легко видеть из графика,
существует при соо Ф 0, если
(8.60)"
поскольку | со |=^ я. При выполнении- неравенства (8.60) решение
осциллирует при h-*-0 на множестве, состоящем из концов всех
траекторий, выпущенных при ^ = 0 из областей
(8.61)
где со0 определяется из уравнения (8.61). Тогда со0 = 0 является
й бй
cplth
W5
1
вырожденной, и решение имеет особый
характер («резонанс»).
Приведем сравнение ширины шлей-
шлейфа осцилляции для задачи (8.57), вы-
¦ ' ' ¦ ¦ ' )л ' f численной по формулам (8:61) с точ-
и,б и, и» но ным решением задачи (8.58), получен-
Рис. 2. ным на ЭВМдля различных и. Полагаем
в единицах предыдущего пункта длину
окружности равной 2, с=\, А=10"8. Вторая производная д*и/дР
4 i х д
аппроксимируется по формуле — ^ sin2 -у ат, т — 1,5 • 10~4:
График функции ф@ изображен на рис. 2. На рис. 3 и 4
изображены графики функций ' ¦
max J-и min f-
[х— ЮЛ. x+lOh] ох [*-10А, х+ЮА] ах
в различные моменты времени. Промежуток между графиками этих
функций закрашен. Вертикальными прямыми обозначены границы
шлейфа осцилляции, полученные из асимптотических формул.
7. Фокусировка в кристалле. Рассмотрим пример быстро
осциллирующего начального условия
ди
с, Л),
lie . ш
-J- Silly,
(8.62)
где if (х, К) — периодическое продолжение с отрезка [0, 2я] функ-

§8]
ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ
81
, supp фе @, 2я), е —некоторый пара-
парации ф (х) cos —jj-Ч S,
метр.
В силу метода Стационарной фазы коэффициенты Фурье функ-
функции t|) с номером п, \n\>N имеют порядок О (Л00), поэтому
v=0,99c
Рис. 3.
Рис. 4.
формулы, полученные в предыдущих пунктах, применимы и
в случае начальных данных (8,62).
Сравним результаты, полученные при помощи формул пункта
3, с численным решением этой задачи на ЭВМ. v
При численном расчете были выбраны: длина окружности 31,
/=Ю см, моменты времени tl = 2i-l0~u сек (i = 0, 1, ..., 5),

82 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
в единицах /
S(x) =
Ф (*)=-¦
4х
1
4 B — лг) +1
0
= хг
при х
при х
при х
при *
«з [0; 0,25]
е [0,25; 2]
е [2; 2,25]
е[2,25; 3].
Аналогично тому, как это было сделано в двух предыдущих
пунктах, решение уравнения кристалла при с = const может
быть вычислено с помощью формул (8.37) и (8.38). При этом
член, отвечающий знаку +, не будет иметь стационарной точки,
и, следовательно, может не учитываться. Нетрудно видеть, что
при ct < 1 метод стационарной фазы применим. В точке ct = 1,
х = п/2 условие дРФ/ду* Ф 0 леммы 8.3 нарушается. В этой точке,
называемой фокальной, колебания кристалла имеют большую
амплитуду, чем в соседних точках.
Заметим, что фокальная точка может быть определена непо-
непосредственно из уравнений бихарактеристик (аналогичных (8.36))
для с = const
¦§=ccosf, ?-0, (8.6Z)
начальным условиям (8.62) с S = x2 соответствуют начальные
условия для системы уравнений (8.62')
х@) = х0, рф) = ро = 2хо.
Рассмотрим фазовую плоскость р, х (в которой отождествим
точки х = 2ш так, что на самом деле можно сказать, что мы
рассматриваем цилиндр). Начальному условию ро = 2хо отвечает
прямая р = 2х, которая сдвигается вдоль траекторий системы
бихарактеристик: а именно,- в фиксированный, момент мы полу-
получаем кривую {х(х0, t), p(x0, t)}. Это изменение кривых в разные
моменты времени t = tlt ..., tb изображено на рис. 5. В момент
t = tb кривая проектируется на ось р и при р — п касательная
к ней параллельна оси р. Точка, в которой касательная парал-
параллельна оси р, и является фокальной.
На рис. 6 изображены графики max U и min U (область
между ними зачерчена) для точного решения уравнения (8.4),
отвечающего начальным данным (8.62) и t = t0, ..., tt, а на
рис. 7 — соответствующие графики для решения, полученного
по асимптотическим формулам (а =1).
На рис. 8 и рис. 9 изображены графики, отвечающие t = t&
(точному решению соответствует рис. 8). Как мы видим, в фокаль-
фокальной точке амплитуда колебаний кристалла резко возрастает.
Теперь рассмотрим нелинейное уравнение колебаний решетки.

ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ
я/2 г
B-т~5см)
3
(Ш5см)
Рис. 5.
2ае\
\ 1=0,0
Рис. 6.

84
ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Zae
~2ае ¦
Рис. 7.
гае ¦
~2ае
Рис 9.

§ 8] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 85
8. Нелинейное уравнение кристалла. До сих пор мы ограни-
ограничивались гармоническим приближением системы уравнений Нью-
Ньютона для атомов решетки. Фактически мы предполагали ампли-
амплитуды начальных отклонений малыми и пренебрегали нелинейными
членами. Теперь мы учтем поправку, которую вносят квадратич-
квадратичные члены в уравнении колебаний кристаллической решетки. Это
означает, что к уравнению (8.1) добавляется член
Ь*а [(иа+1 - илJ - (ыл - u^Y],
где а —некоторый параметр.
Подставляя в это новое уравнение Un-\-Wn, где Un — решение
линейного уравнения, мы получим для определения Wn (считая
| Wa — Wn_i | < | f/n — ип_х |) следующее неоднородное уравнение:
_ t/n)? _ {Vn _ Vnlf].
Для простоты рассмотрим случай, когда с и а —константы.
Общий случай будет рассмотрен в приложении.
Относительно зависимости начальных условий Un@) и 0п@)
от параметра Л мы сделаем одно существенное предположение.
Введем следующее определение.
Будем говорить, что семейство функций vn(h),~N+1 ^
^.n^N отвечает предельному распределению g(x, p), — п^,
=^р*^я, где g — четная обобщенная функция от -р, если для
любой функции ueC^f-n, я) выполняется предельное соотно-
соотношение
N
lim h У a (nh) t
e j \a(x)g(x, p) coskpdx dp, (8.63)
—я —я
def
+=Vi.
Физический смысл этого условия особенио нагляден при k = 0,
так как в этом случае требуется, чтобы среднее значение a(nh)
сходилось к среднему значению а (х) по некоторому распреде-
распределению. .
Мы будем рассматривать, как и ранее, вместо функций на
сетке пространство функций Mn, причем сформулируем оконча-
окончательную теорему в терминах функций Mn. Заметим, что все рас-
рассуждения этого пункта переносятся на весьма широкий класс
нелинейных псевдодифференциальных уравнений, в которых нели-
нелинейные члены можно считать малыми. Первое приближение тео-
теории возмущений в этом случае есть решение уравнения (8.4),

86 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
а второе приближение удовлетворяет уравнению
LAco = - 8ic*ah? sin -|- ((sin -|- иJ), со = © = - ih ^, (8.64)
где и удовлетворяет линейному уравнению ?Аи = 0. Для простоты
в качестве решения и линейного уравнения используем один член
суммы 2 формулы (8.37), отвечающий знаку минус. Мы предпо-
ложим, что его-начальное значение моеМ„ удовлетворяет условию
я я я
lini ^ иоа(х) (cos Ы) и odx = J \a(x)g(x, a>)coskadxda>. (8.65)
А0
Прежде всего заметим, что из условия (8.65) следует более
общее и более естественное для непрерывного случая" условие.
Обозначим
(Л q>)=
Справедлива следующая лемма.
Лемма 8.4. Пусть f (x,a>) еСм-четная периодическая функ-
функция со. Тогда, если tyh(x) отвечает предельному распределению
g(x, со), то
—Я—я
A-0
Доказательство. Разложим функцию f(x, со) в ряд Фурье по со.
Имеем
f(x, со) = 2 an(At)e'nM, (8.66)
В = — 00
где
я
f(x, со) е~'лш rfco. (8.67)
—я .
Из условий леммы следует, что для любого я выполняется неравенство
max jan (*>!==?•%-, (8.68)
к я"
ft>0—любое целое число, Cft = const. Доказательство этой оценки легко по-
получается из (8.67) интегрированием по частям.
Докажем, что lim Ц(/*(*, со) — f (jc, со)) t|>A(*)||=0, где через fk(xt ш)
мы обозначили частичную сумму ряда, (8.66):

§ 8] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 87
Заметим, что функция fk (х, со) при ft —<¦ оо равномерно сходится к f (х, со).
Имеем для любой гладкой функции и {х)
00 Г Я
п=—оо L —я
({у) e-w dy e'«* [f (x, nh) - fk (*, nh) J =
00 Г Я 1
J 2
n=—oo L —я J |/n|>A
Окончательно получаем
[f (Д со) - f* G, i) ] « W = f S fln Cr) e'^\ a (*). (8.69)
\|n|>* /
Оценим п—е слагаемое в сумме (8.69). Очевидно, справедливо неравенство
1 ап (х) е>™ и {х) || ^ max | а„ (х) \\\и\,
X
или в силу (8.68)
|k(*Vn(i«(*)lk%«(|. (8.70)
fe>0—любое целое число. Из (8.69) и (8.70) получаем
x, a)-h(x, i)]«(x)|< 2
i
ft~»oo
2 F
|n|>*
i, со)— fk{x, со)]и(дг)|=0 при fe-»
Отсюда следует, что дтГя любого б > 0 существует такое к0, что
| (i|>A, (f (i, со) -fk (x, со)) **)|<в при k 5= *о,
я я
J I If (*> со) — fk (x, со) ] g (x, со) dx dm
it w
—я —я
<6 при
наконец, в силу условия (8.63) имеем
где с (ft) = const и бА -»0 при h -»0. Фиксируя ft > ftj и устремляя h к нулю,
мы получим, что при достаточно малых h левая часть последнего неравенства
не превосходит 6. Отсюда и из предыдущих неравенств следует утверждение
леммы.
Определение. Пусть для любой финитной феС™(R")
выполняется соотношение
lim \ ф (х) Fh (х) dx= [ <р (х) г (х) dx, xе= R",
А*0

88 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
где Fj^eC — однопараметрическое семейство функций, h дос-
достаточно мало. Тогда будем говорить, что Fh(x) сходится к г(х)
обобщенно, и писать Fh(x)-*-r (х).
Найдем обобщенный предел правой части уравнения (8.64).
sin-f^-u] . Имеет место следующая лемма.
Лемма 8.5.
(О \
— c/cos-^-, cojdco.
Доказательство. Обозначим через Fx_>р и Fp_^.x преобразование
Фурье вида
я
Л p=—oo
Очевидно, что
()
С помощью этой формулы получим следующее равенство
я л л _ А ¦'
J fj(®)fidx= j fi/ (со)tfadx,
—я —л .
где fi, tfc, e С—периодические функции. Применяя это соотношение» полу-
получим для ф е С00, и = Г«о (по определению Т: «0 —* и)
ф (х) Fh (x, t)dx = —4 V ф(дг)Gш у «0J dx —
—я —up •
«=4 \ sin -|- [Щх)Т] sin -^- «ойо За:. (8.71)
Применим к выражению, заключенному в квадратные скобки, теорему
1.1 гл. V. При e=const в (8.37) <р-=1, ф?=0, ftSsl, a
Имеем
. со' . со
8S smsm
6S.
Отсюда
бсо со' —со •
sin -|-- sin
def дх
дх

$ 8) ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 89
Согласно теореме 1.1 гл. V получаем
A <
sin к—sin р-
x + 2ct i—?-*
(О—со
Отсюда, в-силу формулы коммутации следует, что выражение (8.71) отлича-
етси от интеграла
на О (А).
Последний интеграл в силу леммы 8.4 стренитси при ft —0 к
я я
¦ +4 \ \ ф (x+ct cos -|\ sin* у g (х, ©) d* d©.
—я—я
Отсюда следует утверждение леммы.
Докажем следующую теорему:
Теорема 8.3. Пусть в уравнении (8.64)а = -г> тогда реше-
решение w задачи (8.64), удовлетворяющее нулевым начальным усло-
условиям, обобщенно сходится к функции
t л
Щ{х, t) = - 2с [ J sin2<j[g{x-cxcos| +c(t-x), со) -
О —я
— g(x — cxcos j — c(t — x), cojldcodx. (8.72)
Доказательство. Примем следующие обозначения:
я
* С a I a \
r(x,t)=—4 \ 8тъ^8\х—ctcoa у, ©Jdca.
—я
(Нетрудно убедиться, что Lwt (х, /) =(?г'х {х, /), где Z, = De—волновой оператор.)
def ^ а2
Через (L%)~1 f и (L*)/ обозначим решения задач Lga*xf (х, О и L*u=f(x, I),
удовлетворяющие нулевым условиим при t=*T:

90 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
При доказательстве мы будем использовать следующие факты:
1. Для операторов Щ и L* справедлив аналог леммы 8.2. В частности,
если t|>(x, t)_e С00 не зависит от А, то
h2 (L%)~' ф (x, t) - (L*)~' i|> (x, f) = О (h).
В этом можно убедиться аналогично тому, как это было проделано в доказа-
доказательстве леммы 8.2.
2. Имеет место следующее тождество:
№ \ \ ^(x,f)L-j,1 j-=-fhdxdt =
О —Я
(8.73)
которое можно доказать, используя тождество i|> = Щ (Lfi)*11|> и интегрируя
по частям.
3. ^Fft^^^hrV2, где Ci —некоторая не зависящая от А константа.
Из 1) —3) следует, что правая часть равенства (8.73) отличается от выра-
выражения
Т
на О (Л1/2), а это выражение согласно лемме 8.5 стремится к 0 при Л т* 0.
Из леммы 8.2 следует, что
Теорема доказана.
Отметим, что на самом деле в теореме 8.3 можно заменить обобщенную
сходимость на равномерную сходимость. Это требует, однако, дополнительных
оценок. Более общаи теорема доказана в приложении 1. «
Замечание. При доказательстве теоремы мы пользовались только глад-
гладкостью функции wx (x, t), а не функции g (x, а>). Эта последняя функция может
быть, вообще говори, и обобщенной, и теорема будет верна для тех t, для
которых wt (x, t) остается гладкой.
Отметим, что наиболее ивтересные результаты получаются, когда g(x, ш)
близка к б-фуикции. (Конкретный вид «0 несуществен.)
Мы рассмотрим численный эксперимент для случая, когда
g(х, со) = е*/4ф2 (х) [6 (со + 2х) + 6 (со -2л-)],
где ф (х) определена в предыдущем пункте.
Для реализация численного эксперимента мы рассмотрим наи-
наиболее употребительный потенциал взаимодействия между атомами

$ 8] ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ
решетки, приводящий к системе
«• - $
91
(8-74)
,±1 ±3000;
Мы поставили те же начальные условия, что и в начале 7-го
пункта. При численном расчете для е=10~1 решение на ЭВМ
нелинейного уравнения (8.74) совпадает с решением линейного
2аё
В
-гае
Рис. 10.
уравнения, график которого изображен на рис. 6. При е = 2,
а=1на рис. 10 и 11 приведены соответственно деформация точек

92
ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ •
равновесия для численного решения уравнения (8.74) и полу-
полученная по формуле (8.72). Моменты времени, которым отвечают
Рис. И.
графики, те же, что и в линейном случае. На рис. 12 изображен
график точного решения уравнения (8.74) в момент образования
фокальной точки. Затушеван размах колебаний атомов решетки,
промежуток между max и и min ы.
Обнаруженный новый эффект может служить объяснением ряда
физических явлений. Он родствен общеизвестному эффекту рас-

I (Я
КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА
93
ширения кристалла при повышении температуры, свойству преобра-
преобразовывать тепловые колебания малой амплитуды, как бы складывая
их, что приводит к неосциллирующим изменениям кристау1лд
на огромную (сравнительно с амплитудой тепловых колеба-
колебаний) величину. Полученная формула распространяется на весьма
-вае
Рис. 12.
общие уравнения, в которых присутствует малый квадратичный
член. В некоторых вопросах физики наблюдается сходное явле-
явление, называемое «детектированием» —выпрямлением быстро осцил-
осциллирующих начальных условий. Поэтому можно сказать, что
в результате «детектирования» плюс «фокусировки» образуется
мощная бегущая волна большой концентрации энергии, с одной
стороны которой кристалл сильно расширяется, а с другой —
сильно сжимается.
§ 9. Понятие квазиобратимости оператора
и формулировка основной теоремы
1. Основная задача. В § 7 и § 8 мы привели примеры по при-
применению метода упорядоченных операторов подобно тому, как
в § 1 мы приводили примеры на решение уравнений оператор-
операторным методом Хевисайда.
С другой стороны, в § 3 мы видели, что задача решения
систем обыкновенных уравнений с постоянными коэффициентами
сводится к чисто алгебраической. Оказывается, что в рамках
алгебры с ^-структурой можно поставить и решить задачу,
которая по существу охватывает как уравнения с частными про-
производными с переменными коэффициентами, так и задачи на
устойчивость разностных схем, т. е. охватить решение всех этих
задач одной алгебраической теоремой. И хотя доказательство
этой теоремы завершается лишь в последней главе, мы попыта-
попытаемся здесь разъяснить ее смысл и значение.

94 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
В рассмотренных выше примерах под решением задачи пони-
понималось сведение исходного уравнения к интегральному уравне-
уравнению типа Вольтерра с гладким неосциллирующим ядром. Такого
рода редукция к интегральному уравнению (Вольтерра или
Фредгольма) с гладким ядром является основной задачей теории
уравнений с частными производными.
Приводимое ниже понятие квазиобратимости оператора позво-
позволяет распространить этот подход к решению задач для диффе-
дифференциальных уравнений на операторный случай.
Определение. Пусть X — модуль над алгеброй &#, наделен-
наделенный (а — структурой, Аг ... Ап, ВеХ, Элемент [Ее/ назовем
квазиобратимым, если существуют такие последовательности эле-
элементов SCk е «5?, Ж'ъ. е <#, что произведения fS?k и Wrf предста-
вимы в виде
1 л л + 1\
U, .... Ап, В),
4 ..., Ап, в),
где функции Rk (x, а) и R'k (x, а) убывают при | х [_->- со быстрее,
чем \х\-»; \Rb\ = Ojg(\x\-*), \R'k\ = Ox{\x\-»).
Последовательность {%"k} будем называть правой квазиобрат-
квазиобратной, a {Wk} — левой квазиобратной.
Замечание. В случае, когда алгебра &# есть алгебра неограниченных
операторов (см. гл. I —III), это определение может быть заменено на следую-
следующее. Оператор Т е ojg квазиобратим, если существуют такие последователь-
последовательности {Xk}czo^, {X'k}<=iQ??, что TXk=l + Slt X'kT=\+Slt где опера-
операторы Sj~t S^ удовлетворяют условиям
Ц A'iiSi <с> V/i: Е//=*. c=const.
В этом смысле квазиобратная последовательность., дает асимптотическое реше-
решение задачи.
На самом деле ниже всюду сами элементы /, 0Vh, 2V'k также
/ 1 п п + 1\
будут представимы в виде f = f{Au ...,' Ап, В), %k =
/ 1 п п + 1\ /«+1 2 1\
= &k[A1, ..., Ап, В), &'h = Vb{Alt ..., Ап, В).
Нашей основной задачей является отыскание квазиобратных
/1 л л + 1\
последовательностей для элемента f ^Ль ..., А„, В ). Мы решим
ее при некоторых предположениях относительно операторов
At, ..., Ап, В и символа f(x, a).
Прежде чем приступить к формулировке этих условий, есте-
естественно решить вопрос о квазиобратимости элементов в триви-

§ 9] КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА 95
альном случае —для коммутативной алгебры. В этом случае
можно рассматривать, например, операторы хг, ..., х„ и а, при-
причем символы будут совпадать с отвечающими им операторами.
И если оператор f = f(xlf ..., хп, а) имеет нули при а = а0 и
| х | -*¦ оо (например, / = х\ — х\ +ix*sin2a), то он не является квазиоб-
квазиобратимым (нельзя подобрать такой гладкой функции ^* (дгх, хъ, а), что
\х\-x\-\-ix\sin2aK?(хъхг, a) = 1 + R (хъх2, а), гдеR (хихъ а)->-0
при х\-\-xl-+co, ибо левая часть равенства обращается в нуль при
Xi = x2, a = 0). Поэтому на первый взгляд' кажется естественным по-
потребовать, чтобы символ / (х, а) не имел нулей при| х | ->- оо. Однако
это требование слишком жестко: оно лишило бы нас основных при-
приложений. Все трудности построения квазиобратных последователь-
последовательностей возникают именно в евязи с тем, что символ оператора
f[A\, ..., А„, В) обращается, вообще говоря, в нуль при
\х | -*¦ оо. Случай коммутирующих операторов в этом отношении
является особым. Чтобы понять неожиданность этого момента,
обратимся к примеру дифференциального уравнения.
Наше утверждение относительно особого случая коммутатив-
коммутативных алгебр применительно к этому примеру представляет собой
следующую парадоксальную на первый взгляд альтернативу.
Задача заведомо не имеет решения как раз в самом простом слу-
случае дифференциального уравнения с постоянными коэффициентами.
Вполне объяснимо стремление^ привести конкретную задачу (за
счет пренебрежения некоторыми факторами и известной идеали-
идеализации условий) к уравнению с постоянными коэффициентами.
Дело не только в том, что такие уравнения лучше всего
изучены, но и в том, что для решения уравнений с перемен-
переменными коэффициентами отправным пунктом, модельной задачей
часто служат уравнения с постоянными коэффициентами. Одна-
Однако, как это будет видно из основной теоремы, случай постоян-
постоянных коэффициентов оказывается весьма специальным и вырож-
вырожденным.
Например, рассмотрим символы (х{Уь У^ = у\—у\ и ft(j/i, Уъ, a) = (/f —
— У\—'Ф(а2) уЬ где функция ф(а2)^0 равна нулю при a2 < Т и больше
нуля при 2Г+б^а2^2Г. Оба символа при а2 < Т совпадают и обраща-
обращаются в нуль на бесконечности при ух = у2. Пусть А1=х, А2 = у, B=id/dx,
1 2
так что i4j коммутирует с Л2- Как уже говорилось, оператор i4f — A\, отвеча-
отвечающий символу fa (ух, (/2), не является квазиобратимым. А оператор А\ — А% —
— Щ (б2) А1 оказывается (как это будет видно из основной теоремы) квази-
квазиобратимым. Положим теперь Аг = id/at, Аг = 1д/дх, B = t. Оператор, соответ-
соответствующий символу ft (ух, Уг), будет волновым оператором d^/dt* —д*/дх2
(см. § 8). Он не является квазиобратимым. Добавление к нему члена
—1ф (/2) д*1дхг соответствует символу /2 ((/х, yit a) и отражает факт поглоще
¦ния высокочастотных иолн при Р > 27\ При этом решения уравнений
/Ui, A2)u = F(x, t) (F(x, 0 = 0 при t<0) и fs(Ax, At, b)w=F{x1 f) сов-
совпадают при /*<Г. (См. ниже пример).

96 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Замечание. Пусть совместный спектр (с учетом аксиомы jaJ)
1 л л+1
операторов Аъ ..., Ап, В принадлежит области DdRnxMm и
пусть функция Р(х, а) е*°° равна 1 при х, oeD и нулю вне
некоторой большой области. Тогда по определению совместного
/1 л л+1\
спектра Р\АЪ ..., А„, В ) = 1, и, следовательно, в этом слу-
случае в формулах (9.1) мы можем подставить вместо единицы
/1 л л+1\ /1 л л+1\
P\Ai Ая, В J,H6osupp(l-P(;c, a))naUi Ан, В )~ф.
Пример. Рассмотрим операторы
A3=x, At = y,
и пусть f(xlt хг, ха, ЛГ4) — полином от *i и х2, а х3, xt^M2, т. е.
f{ib/dx, ibldy, I у)
есть дифференциальный оператор. Построение квазиобратного
оператора сводит в этом случае задачу о решении дифференци-
дифференциального уравнения
f{mx, ibldy, *x, y)u{x, y)=F(x, у)
к решению интегрального урабнения
, id/dy, x, y)]gk(id/dx, ib/ду, х, у)щ(х, у) =
где Rk (X! хъ х3, xt) стремится к нулю быстрее, чем (| Xi |а +1 х2 |а)-*/2.
Это означает (как нетрудно убедиться непосредственно из пред-
представления псевдодифферен1*иального оператора через преобразо-
преобразования Фурье), что последнее равенство представляет собой интег-
интегральное уравнение типа Фредгольма второго рода с гладким
быстро убывающим ядром. Решение и (х, у) исходной задачи при
этом может быть представлено в виде
и(х, y)=gk{id/dx, ibldy, x, у)щ(х, у),
где <Рь(х, у)~решение интегрального уравнения
Отметим, что первый член итерации равен F, а второй равен
Rt,F. Таким .образом, второй член в силу свойств оператора Rk
является гладким. Отсюда можно заключить, что член gkF содер-
содержит негладкую часть решения исходной задачи, т. е. разность
gk4>k — gkF является гладкой.
2. Правило редукции основной задачи. Пусть Ai,..., Ап, В е X,
В —вектор-оператор, ВеМт. Предположим, что спектр At, Л*

§ 9] КВАЗИОВРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА 97
относительно .Д, .диагоналей и имеет конечную кратность, т. е.
при достаточно большом г
, = О, /,./ = 0, 1, ..., л, (9.2)
где Ао = В е Мт. Кроме того, мы предположим, что (А{ — Л)* Лу =
= — /Ak(i,j),- для тех Л, для которых \At — Atj A/ ^-const-1.
Операторы Аи ¦¦•, Ап, В мы будем называть образующими,
а алгебру &V, которую они порождают, — нильпотнтной ал-
алгеброй Ли:
Замечание. Условия (9.2),'как нетрудно убедиться, экви-
эквивалентны тому, что коммутатор n-го порядка между At и А]
равен нулю. Таким образом, можно сказать, что достаточно высо-
высокие коммутаторы между элементами Ах, ..., А„, В равны нулю.
Кроме того, для любых k, I (l^k, l^n) и любого г
S^) существуют индексы j(k, l) и s(k, r), такие, что
Теперь мы поставим каждому оператору А„ в соответствие неко-
некоторый дифференциальный оператор с частными производными
Lk\x, — io/dx, id/да), действующий в пространстве C^(R"xAfm)
(здесь а = (аь ..., <хт) — локальные координаты на Мт {xlt ...
..., *„) е R").. • •
Вектор-оператору В поставим в соответствие «оператор умно-
умножения» на о.
Операторы Lk, k=\, ..., п мы определим из соотношения
(Lm)[A A, B) = Aktv[Al, .... А, В )} (9.3)
(&=1, ..., п) для любого символа ф(дг, a) eC^(R"xMin). Опе-
Оператор Lft будем называть представлением оператора Ak.. Рассмот-
Рассмотрим вначале построение операторов Lk на простом примере.
Пусть заданы операторы Аг е М, В е Мх и
At = i[Au В], Aa = i[A1, А2], [Аг, 5] = О,
[А8, 5]= 0, [Аи Л8] = 0, [А* А3] = 0.
Пусть, кроме тою, А2, Л^М. Тогда набор Аи А2, Аа, В
удовлетворяет. всем приведенным выше условиям.
Оператор А^. коммутирует со всеми остальными операторами
набора, а оператор А2 коммутирует с В. Поэтому их. образы
La, L2 строятся тривиально:
L3 = xa, L2 = X2-
Найдем оператор Lx. Рассмотрим AxV\Ai,,A<t, A3, В*). Разлагая
4 В, П, Маслов

98 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Ф в ряд Тейлора (Ньютона) по В —В (см. § 5, § 6), получим
ь А2, Аа, в) =
л1) Аг, А3, Ь) + А1(в-в)дфа{А1, At, А» в),
так как по условию Ai\B — B) = 0 при
Итак,
Аъ А2, Д>, в).
Первое слагаемое в правой части разложим в ряд Тейлора по
А2 — Аг.'Учитывая, что ЛДЛа — А2)=0 при k5=2, получимз
, ла, ая, в
1, А„ Л3, в) + (-Д)дФ/да(л, Да, л3, в).
Отсюда видно, что для получения равенства (9.3) (при ?=1)
положить
Аналогично, для произвольного набора Ai, A2, ..., Л„, В обра-
образующих нильпотентной алгебры Ли имеется представление Lk
оператора Ak, удовлетворяющее условию (9.3). Действительно,
л+2 / 1 л л+1\
в операторе Akf\Au ...\ Ап, В) мы.стремимся поставить Ак
на место с номером k\ для этого с помощью разложения ф в ряд
Тейлора мы «протащим» Ak, коммутируя его сначала с В (при
этом возникает ряд коммутаторов [Ак, В]; [[Ak, В], В] и т. д.),
потом с Ап, с An_i и т. д. В процессе этой коммутации возник-
возникнут многочисленные коммутаторы 'Ак с Вис А„, An-i, ..., A№_i.
Эти коммутаторы по условию суть -некоторые операторы из на-
набора (Ль ..., Ап)- На следующем шаге мы каждый из этих ком-
коммутаторов будем «протаскивать» на его место с помощью ряда
Тейлора. При этом снова возникнет множество всевозможных
коммутаторов. Но все они суть нейие операторы из Аъ ..., Ап
и их мы будем снова «протаскивать» на свое место. Очевидно,
этот процесс приведет к тому, что мы получим большие комму-
коммутаторы, которые уже коммутируют со всеми Аи ..., Ап (так как
Аъ'..., Апу В —образующие нильпотентной алгебры). Эти
большие коммутаторы автоматически становятся на соответствую-
соответствующие им места. Остается только заметить, что каждое применение
формулы Тейлора к символу ф означает появление суммы нескольт
ких производных от ф. Порядок этих производных не может пре-

1 п п+1\ / 1
§ 9] КВАЗИОВРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА 99
восходить гц — длины максимального коммутатора среди Ль ....
..., Ап- Поэтому
/1 ' п я+1\ / 1- я л+1\
л*|[фИь ..-. а„, в;л-Ф*иь •¦•. ля, я/.
где ф* (*, а) есть результат применения к символу ф некоторого
дифференциального оператора Lk (х, id/dx, id/да) порядка не выше
п0. Пусть Т = 2j Cj. а^л * • • ¦ ^/А • Положим
/.а
МЛ = ?^.„A,/'*... (?,/'*.
/id
Если Tesf, то для любого символа (j>eC|g(RnxMm)
/1 я л+1\ / 1 л л+1\
Г[Фи, .... Ля, В/|-(Я;(Г)ф)и1,.-.'., Ая, В). (9.4)
Действительно, например, для T = AkAj имеем из (9.3);
1 л п+1\ / 1 п п+1\
Ц А BJ}Al(L)[A A ВД
1 я я+1\"
1. •¦-. Ая, В).
Аналогично проверяется равенство (9.4) для всех элементов Т из
алгебры ®#". Таким образом операторы Lj сами являются обра-
образующими нильпотентной алгебры Ли, которую мы будем обозна-
обозначать через П.
Построенное отображение %i ®^*т»-П называется упорядоченным
представлением нильпотентной алгебры ®^\
Из (9.4) следует, что операторы Lk, k = l, ..., п\ а удовлет-
удовлетворяют тем же соотношениям коммутации, что и операторы Ak,
В. В частности, операторы Li, ..., Ln, а являются образующими
нильпотентной алгебры П. Отсюда следует, что если Р(х, са-
салолином по х с коэффициентами, зависящими от а, то
/1 л л+1\ / 1 п л+1\
lP[Ai, ..., Ап, B/][OUi, :.., Ап, B)] =
-4>Ui, ••¦. An, B), (9.5)
/1 n n+l\
где г|з(дг, а) = Р[Ц, ..., Ln, а )G(х, а) для любого G(х, а)еС^.
Возникает вопрос, распространяется ли это равенство на слу-
случай Р (х, o)sImh0(х, а) <= С%.
По-видимому, ответ на.этот вопрос, вообще говоря, отрица-
отрицателен, если ограничиться только аксиомами цг — цв (без топо-
топологических аксиом 7\, Гг). Для того, чтобы дать положительный
ответ на этот вопрос, мы, однако, сформулируем две дополни-
дополнительные алгебраические аксиомы, которые, кроме того, удобны
тем, что позволяют получить явную формулу, выражающую
4*

100 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
функции от некоммутнрующих операторов через композицию (произ-
(произведение) функций от коммутирующих операторов.
Рассмотрим символы /(*, a, t), зависящие от параметров
<eR* (k не фиксировано), так что все производные. по этим
параметрам принадлежат <&°°.
А к с и о м а ц.7) (параметрическая аксиома). Пусть / (х, ос, /) е Cg,
/ е R* таковы, что
1 я я + 1 \
Ai, ,.., Аа, В,Щ = 0 ¦
при всех / е R*. Тогда для любой функции Ф (t) e #°° (R*) и
символов ,
выполняется соотношение
1 я я+1
Если же равенство' (|i7) выполнено при всех..* =^0, то оно
справедливо н при t = 0.
Аксиома \is) (единственности). Пусть для некоторого ЛеМ
и некоторых символов /(х, a, t) e®°° прн ieR
1 п я+1
я n-J-1 N я+2 / 1 п я + 1
А Bt)J liAf[Ai,...,An, В,
/1 я я+1 \
Тогда U\Ai, ••-. ^л, 5, Щ = 0 при всех /eR.
/ 1 я \
Задача. Доказать следующую формулу для оператора f\Ai, .... Ап):
В главе IV будет доказано, что из этих аксном следует по-
положительный ответ на поставленный вопрос.
Основная задача заключается в том, чтобы для заданной функ-
функции Р(х, а) найти такую функцию Gn(x, а), чтобы выполнялось
равенство (9.5) прн
|( ) 1+R(x, a),
где функция RN(х, а) = О# (\х\~N) для любого N. А это зна-
значит, что нужно решить задачу (9.5), т. е. основная задача
(9.1) сводится к следующей: найти такую последовательность
gN (х, ос), что
/ (li, ... ,La, "а ) gN (х, а) = 1 + Rn (x, а), (9.6)
где Rn = Ojs(\x\-n) убывает быстрее \x\~N при |х|->оо.

§ 9] КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА 101
Предположим, что для некоторых чисел р*^1, |д.^=1, Т, тH
и некоторой финитной функции р(т]), равной 1 при |т]|^т]о,' мы
построили такую функцию
*jv («, Л. *; 0 a C% (MmX R2")[ < ез [0, со),
которая при t = T убывает при х-»-со быстрее Л—*, где Л =
/Я \ 1/2 "
= B (**J/Р*+ Ч » и КотоРая удовлетворяет следующим соот-
\ft-i / ¦
ношениям:
3 1' /1 п п+1
BN(<x, id/dx, x, t), (9.7)
(Bff(<x, r\, x, t) убывает быстрее A~N при дг-»-оо равномерно по t).
Проинтегрируем уравнение (9.7) по t от 0 до Т и применим
обе части равенства ($.7) к единице; учитывая, что р (id/dx) \=Л
и обозначив *)
/ 2 г \ 1
1|Ж(сс, х, 0 = ^V«, id/dx, x, )
B'N{a, x, t)=.BN[a, i^, x, Vjk^\, (9.8)
T
§n (x, «) = + / I^'n (a, x, t) dt,
о
получим следующее равенство!
(I n n + l\
f \Ц. U, a ) gN (x, a) =
т
= l-y'N(a,x, T)-il B'N(a, x, t)dt~\+RN (a, x),
где в силу исходных условий RN убывает быстрее A~N придг-»-оо
и таким образом, мы получаем решение-основной задачи.
Иногда бывает полезно редуцировать решение основной задачи
к точному решению некоторого более. простого уравнения. Мы
видели, например, что асимптотику решения уравнения колебаний
кристалла нельзя, вообще говоря, найти с помощью одних
лишь бихарактеристик. Мы можем только редуцировать решение
2
*) Здесь %[а, К-, х, t)A-»l=pAjr \ yN(a, pt \tt)e- Л^ <1рй%.
к
Последнее рассуждение носит эвристический характер.

102 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
асимптотической задачи к более простой — точному решению вол-
волнового уравнения (см. § 8).
/ 1 п К
Пусть г [Ах Ап) s X — некоторый оператор, который мы
будем называть эталоном. И пусть
К 2 ' л + 1л+2 1/1 л \ \
Alt .... Ап, В, 1г[Аг, .... AnW&X
— оператор, к которому мы будем искать квазиобратный. Заметим,
что квазиобратный оператор в этом случае также будет зависеть
1/1 л N
от г [Аи .... Ап), а значит, сам по себе будет являться весьма
сложным оператором. Приведем в этом случае, правило редукции
основной задачи к решению задачи Коши для функции от диф-
дифференциальных операторов.
Аналогично тому, как это было проделано в начале этого
пункта, можно показать, что для любого символа g (x, a) s Cg
найдется такой символ ib/ (x, a) e Cg, что произведение оператора
/ 1 л л + 1\ /1 л л+1\
At на оператор g[Alt .... Ап, В ) равно tyA^i Ап, В )Ai.
При этом символы g(x, а) и 1|>(дг, а) связаны соотношением
^(д:, a) = G,{ib/dxt x, id/да)g(x, a), (9.9)
где Gi(id/dx, x, iд/да) —дифференциальный оператор, линейный
относительно х.
Задача. Привести явный вид оператора Gt (с помощью разложения
g(x, а) в ряд Тейлора).
Из соотношений (9.9) следует
/1 л \ / 1 ' л л+1\ • >
[rUi AnjJlg[Ai An, В ]]-
/1л л + 1\ / 1 л \
"ibiAv .... Ап, В )Жг\Аи ..., АпI
где
/1 л \
^г(л хп, <x) = r[G1, .... Gn)g(xlt ..., ха, а).
Отсюда и из (9.5) следует, в свою очередь, что' символ произве-
произведения .
/2 л + 1 л+2 1\ ' / 2 3 л + 1 л+2 1\
[f[Alt .... Ап, В, r)J[g[Alt Аг Ап, В, г]],
где g(xu .,., хп, а, х0) уже n-f/n-f 1 -местный символ, равен
/2 л+1 л+21 /1 л \ \
f[U К, *,\r\Gx Gn) + xtfg(x, а, дг,).
Таким образом, основная задача в этом случае редуцируется
к задаче (9.6), где вместо левой части (9.6) стоит
/2
2 л+1 п+21/1
kU, «, \г\рх Gj + Xojjgix, a, x0).

91 КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА 103
Далее все рассуждения, редуцирующие эту задачу к задаче Коши,
остаются прежними.
• '. / 2 л+1
Теперь рассмотрим еще более общий случай. Пусть fi=fi\Ai, ..., Ап,
Л + 2 1\
В, г) е Л1. Рассмотрим оператор
Л 2 *Л
F-F\fi.h fkh
Совершенно аналогично предыдущему .получаем, что символ произведения
„./12 *\ / 2 3 п+1 n+f 1
равен .
/1/2 -' л + 1 л + 2 1/1
>1
2 /2 П+1 П+2 1/1
[/2Ui ?«. «. [г Wi
I/a \^i> •••> ьп, <*, |i_r \кц, .... и„/ T*OJ1/J1> •<•
л+1л+2 1/1 п
™~ I . II I II I
хп. «.
Оператор в правой части, примененный к функции g, мы будем называть- гамиль-
гамильтонианом оператора Р. -
Пусть теперь r = Q, g(xu .... хп, a, Xq)=1. Тогда мы получаем формулу
для приведения сложной функции к простой функции, от тех же упорядоченных
операторов. Именно, для определения символа ty{x, а) оператора
/ 1 л п+1\
4>Ui Ап, В )=}
мы получаем формулу
Ч>(*. «0-*A/1\А. .-, ?i."« ')l -. 1ft \1* .... Ln, a )\)\, (9.10)
где справа уже сложная функция от дифференциальных операторов применяется
к элементу единица, принадлежащему пространству символов.
3. Бихарактеристики и условия поглощения. В рассмотренных
примерах мы сталкивались с понятиями характеристик и биха-
бихарактеристик. Мы видели, что негладкая и быстро осциллирующая
часть решения определяются в этих примерах решениями неко-
некоторых уравнений с частными производными первого порядка,
которые мы называли'уравнениями Гамильтона — Якоби (уравнение
характеристик) и системой (обыкновенных) уравнений Гамиль-
Гамильтона (уравнение бихарактеристик).
Выше был рассмотрен пример уравнений колебаний кристаллической решетки
на окружности, или, что то же самое, уравнения с условиями периодичности.
При этом решения системы уравнений бихарактеристик (8.36) X (х9, t), P («°, <)'
были таковы, что X (х°, <) можно было интерпретировать как координаты точки,
движущейся по окружности, а Р(х°, t) — по прямой. В целом пара X (х°, t),
P{xQ, t) определяла траекторию точки на цилиндре — произведении прямой на
окружность. Этот цилиндр называется фазовым пространством и обозначается
обычно р, х, где о—координаты на прямой, а; х— координаты на окружности (или
g-координэты). В дальнейшем мы подробнее остановимся на его свойствах и на
свойствах системы уравнений Гамильтона, которая определяет семейство кривых

104 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
в таком фазовом. пространстве. Ясно, что любому «-мерному тору Мп может
быть сопоставлено' такое фазовое пространство Т*Мп размерности 2п, что
я-координаты лежат в Ма, а р-координаты принадлежат R".
Мы' видели,' что" как уравнение Гамильтона — Якоби, так и
система Гамильтона определяется одной функцией Н (р, х), кото-
которая называется функцией Гамильтона. Эта функция в случае
кристалла имела вид •
и зависела от,параметра | со |^п. Этот параметр являлся симво-
символом оператора дифференцирования и существенно сказывался на
поведении решения.
В общем случае функции от упорядоченных образующих ниль-
потентной алгебры Ли задан Символ как функция от /ra-fn коор-
координат, где /га —размерность многообразия Мт, т. е. число компо-
компонент вектор-оператора В, а п — число операторов Аг,.;., А„. Таким
образом, область определения-символа есть пространство Af"xRm=
Пусть Т*М"+т—отвечающее ему фазовое пространство. Мы
ставим задачу о нахождении .квазиобратного оператора. На при-
примерах мы видели, что нахождение квазиобратного оператора свя-
связано с системой бихарактеристик, а значит, с функцией Гамиль-
Гамильтона. Возникает естественный вопрос об определении функции
KI п л+1\
Аи ..., Ап, В ). Мы
хотим определить бихарактеристики этого символа. Мы рассмат-
рассматриваем функцию /; вместо ее аргументов, подставляем представ-
представления Li, ..., Ln, а операторов Ах, ...., А„, В и получаем гамиль-
/1 л л+1\
тониан [\ЬЪ ..., L, а ).
После этого выделяется некоторая старшая часть полученного
выражения относительно переменных хъ ..., хп и id/да. Эта
старшая часть определяет функцию Гамильтона.
Введем определение старшей части функции. 1) Пусть (
e^o^R*) и пусть существуют такие числа р,, ..., ps
г>0, что
тогда функция называется р-квазиоднородной функцией степени г.
2) Функция а (у) называется подчиненной функции f{y), если
д1 * 'о (у)
r-i-lftl
N
¦Пусть F (у) = 2 /,• (у) + а (у), где Д (у) - р-квазиоднородные (р =
о
— Pi) •••.! Р«) функции степеней rh г;^г/+1 + б для некоторого

§ 9] КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА 105
6>0, а а (у) подчинена fo(y). Тогда будем говорить, что F(y)
асимптотически р-квазиоднородна (р = рх,.,.., ps), fo(y) будем
называть старшей частью функции F(у), a '^lfi(y)—cyuiecmeeH-
о
ной частью функции F(y).
Положим временно Xi = yt i^n, i-^— = yn+k,—г'аё = тЬ Пусть
полученная функция асимптотически р-квазиоднородна по у,
причем р„.н = 1, 0 <С i «s; m (переменные т|, а рассматриваются как
параметры; х\. принадлежит малой окрестности нуля в R", а еМ).
Старшую часть функции -f(Lx(y, r\), ..., Ln(y,.r\), а) будем
называть функцией Гамильтона, отвечающей данному гамиль-
гамильтониану, и обозначать через я (у, г\, а).
Итак, схема построений функции Гамильтона оператора
/lee/ состоит из 4-х операций: 1) (цг1) подбор Аъ ..., Ап,
/2 п п+1 \
В t=X,r = r(x, a),f(x, х0, а) е ®°° так, чтобы f\Au .... Ап, В, г) =
= Л; 2) (A-+L) построение гамильтониана с помощью упорядо-
упорядоченного представления; 3) (р) выделение старшей части я (у, г\)
гамильтониана; 4) (->р, а) определение гамильтоновых перемен-
переменных в функции я (у, т]). Итак,
/ 2 . . п + 1 п + 2 l\A->L
^f[A1 Ап, В, г) •
п + 2 1
i « . I/
->я(г/, т), а)^^Н(р, q, ю, л).
Операции (ц.) и (р), вообще говоря, неоднозначны *) и не обя-
обязательно существуют для данного А е е/. Перейдем к послед-
последней процедуре.
Пусть для определенности pt равны единице для первых s
переменных, s«?n.
Введем переобозначение переменных:
?
ai = fc+i> • • •, «m=<?«+«; р=(pi, • • •, р«); w = (мъ • • •. W
т1 = (т|т.
Обозначим
я(i/, т|, а) = е%^(р, <7, со, т]), H^Reeffl", H — Im
*) Например, для ф(хь *a)=*i+.Ki*2 при Pi=l, Рг=1 получается
) f ) 5 а при Pi= 1, р2 = 2 получается /0(хь Ar2)

106 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
Кроме того, обозначим через е%(/>. Я* ю> Tl) существенную
часть символа 1(ЬЪ...., Ln, а/. В этом пункте всегда предпол*а-
гается, что Ime%sS0.
Пусть Qe — многообразие в пространстве переменных р, q, r\,
со, определяемое условиями:
s n—s „.
2^ + 2>/ '-1
- | «ЯГ (р, 7, Л, ©) 1р-гьо I < е-
Решения системы Гамильтона.
~&T = W-(р) <7t Т1) Ю)( qj •!'-• = ^'
^Г= —щ~(р, <7. Л. ©). /»У |т=о =/?уТ -/ = 1, -..
(р°, <Д т|, ю) е Й8
/ 1 п п+1\
будем называть бихарактеристиками оператора f {Аъ ..., Ап, В ).
Чтобы избежать путаницы, мы будем в следующих примерах аргументы
символа обозначать через yt yn, а.
Примеры. Остановимся иа конструкции функции Гамильтона и проил-
проиллюстрируем ее на примере полинома от оператора iд/дх, x — xlt ..., хп, с коэф-
коэффициентами, зависящими от х. В этом случае второй коммутатор равен нулю и
представление оператора Aft = idjdXft имеет вид (/?+«д/д«ь а ВА = *? = «?.
Полином
2>|г (9.12)
имеет вид ii Щ \В) (Ml) • ^го представление имеет вид
Функция Гамильтона (для р; = 1, уО имеет вид
Н (<?, p) = Safc (Япн <Ы) (qk-Pn+kJ- (9-13)
Рассмотрим также систему Гамильтона, определяемую функцией Гамильтона
(9.14)
где q=-qi, ... , qn, P=Pi Pn-
Решения системы Гамильтона
4*-0,
fe=l, ...,n, (9.15)

§ 91 КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА 107
п
удовлетворяющие начальным условиям <7@)<=<70> р@)=0, ]?] ?»™'i
* = i
Н {qn, 0) = 0, называются бихарактеристиками оператора (9.12).
Заметим, что эти бихарактеристики можно получить из решения системы
удовлетворяющего условиям
" Qb @)=<7оя + ft.' Pk @) = Qok-
Таким, образом, данное выше определение легко приводится к определению
бихарактеристик волнового уравнении, данному в § 8.
Теперь рассмотрим оператор
л—1
2 ^Wj^ (9-16)
В этом случае функция Гамильтона будет равна
п —1
Н(q, р, т), ш)= 2 а*Йп. •••
Обозначим
п—1
Решения задачи
будем называть" бихарактеристиками оператора (9.16).
Рассмотрим теперь оператор Шредингера
Представление операторов таково:
Представление X, таким образом, имеет вид
Функция Гамильтона (при pf= I, Vt) имеет вид:
(Рй)я
^ <7о. (9.17)
2 aft (<7о. ш) P?ft + *«(%. ш) Т)=0
|2!^ (9.18)
Положим
A^ld/dt, A% = id/dx, 4>=-i-, B^i, В2=ж.
Тогда .

108 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
После замены
уравнения бихарактеристик сведутся к системе
?-0, / = 1, p=-i»'(?)> ?=
а начальные условия имеют вид
Я @) = Яю1Я*ш Р (°) = - W<7»oi
эта система отвечает функции Гамильтона
Мы получили уравнения классической механической задачи, отвечающей
той квантовой задаче, которая опнсывается оператором Шредннгера (9.18).
Задача. Рассмотреть днфференцнально-разностный оператор, определяю-
определяющий уравнение (8.4). Положив
получить в качестве бихарактеристик решения системы (8.36).
Определение. Будем говорить, что выполнены условия погло-
поглощения, если существуют такие константы Т > 0, е > 0 и такое
число т' = т'(<7°, ю, р°, т)), 0<т'<7\ что
1) при О^т^т' существует решение
q(q°, ю, р°, т|, т); р(<Д ю, р°, т|, т)
задачи (9.11), принадлежащее С00;
2) пры О^т^т' и (<7°, ю, р°, Ti)sQe выражение
— H(p(q°, ю, р°, к], т); q(q°, ю, р°, т|, т); ю; т))
неотрицательно, а при т = т' это выражение строго больше нуля.
Несколько слов относительно этого условия. Проблема постановки усло-
условнй, отвечающих явлению поглощения в электродинамике, была впервые четко
поставлена Зоммерфельдом, который решил ее в частном случае (условия Зом-
мерфельда излучения иа бесконечности). Фнзнкн пришли к заключению, что
эта проблема (проблема «черного тела») не может быть решена постановкой
одних только граничных условнй без дополнительных условнй на коэффнцненты
самого уравнения н его внд. Особенно часто с этой проблемой приходится стал-
сталкиваться в современных задачах физики (например, в теории лазерных резона-
резонаторов). Анализ физических задач показывает, однако, что зачастую поглоща-
поглощается вне некоторой области только «негладкая часть решения задачи»; неглад-
негладкая часть решения задачи определяется высокими частотами разложения реше-
иня в ряд (нлн ннтеграя) Фурье, а во многих задачах поглощаются лишь
короткие волны (высокие частоты). Известно, например, что стены дома про-
пропускают радиочастоты, а свет поглощают. Как поставить условия, которые
моделировали бы этот факт? По-видимому, не существует иного способа, кроме
введения сильного поглощающего потенциала, равного нулю внутри комнаты
и малого на низких частотах.

§ 9] КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА 109
Введенное выше условие поглощения заменяет в известной мере столь недо-
недостающие условия «черного тела», а во многих задачах даже полностью отве-
отвечает сути явления. С этой точки зрения идеализированным вырожденным слу-
случаем будет случай, когда коротковолновые лучи вообще не затухают. Это н
будет случай постоянных коэффициентов.
Основная теорема (в простейшем варианте). Пусть
Ai, ..., An., В — образующие нильпотентной алгебры Ли. Оператор
/1 л л+1\
f[Ai,.'.., An, В ) квазиобратим, если его гамильтониан таков,
что выполнено условие поглощения.
Эта теорема доказывается в последней главе и при этом (и это
главное) там дается конструкция квазиобратной последовательности.
' Замечание 1. Пусть Мп~MkxRn~k, k^n, где М* —тор;
тогда в простейшем варианте основная теорема остается справед-
справедливой, если в правой части равенства (9.1) вместо единицы стоит
функция Р (В) вектор-оператора В с компактным носителем,
равная 1 в некоторой области Q. Отметим, что когда Мп ком-
компактно, то единица есть функция от В с компактным носите-
носителем. В этом случае в условиях поглощения требуется, чтобы
<7°. е supp P (а) при i>n. . .
Замечание 2. Приведем конструкцию первого члена ква-
квазиобратной последовательности для простейшего варианта основ-
основной теоремы в частном случае. Мы не можем здесь предъявить
эту конструкцию, поскольку она требует ряда понятий тополо-
топологического характера, которые будут приведены в главе VI.
Однако, чтобы как-то ориентировать читателя, мы приведем пол-
полную конструкцию в одном частном случае и просчитаем пример.
Именно, мы дополнительно предположим следующее:
1. Гамильтониан Н — однородная функция р степени k и не
зависит от ? и- т|.
/1 л л+1\ .
2. Оператор f\Ll, ..., La, a ) не меняется, если все значки
над операторами (в том числе и внутри каждого L,) написать
в обратном порядке (т. е. п+1-*-1, я->2, ..., 1->n-f 1 *))•
Эти условия не носят принципиального характера и введены
для некоторого упрощения. Теперь мы приведем принципиаль-
принципиальные условия, отказ от которых приводит к существенному услож-
усложнению вида формулы. Эти два условия требуют отсутствия фокаль-
фокальных точек, а мы видели на примере в § 8 их принципиальное
влияние на асимптотическое поведение решения.
•3. Якобиан ^Д-Ф0 при O^/sgT1 и якобиан J(q0, t) =
= d Ф 0 на этом же интервале. Здесь функция z (a, /)
fl a n+l\
*) Иначе говоря, потребовать,• чтобы оператор (\Li, ..., Ln, a ) был
«формально самосопряжен».

НО ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
определяется из линейной системы уравнений (уравнений «ростка»)!
г = iHp (q, р) + Жп (д, р)г + Жрр (q, p)w, . (9.19)
(i> = —ifig(q, p)-<?fqq(q, p)z-<2trgp(q, p)w
и условий.
Z\t-O=W\M> = O, Z = Zi, .... 2n, W = Wlt .... Wn,
где q = q(q°, t), p = p(q°, t), q = qi, .... qn, P = Pi, .... />„-реше-
ние системы Гамильтона
.«-f-.^--v^U-^ pU=°- ' (9-20)
Приведем конструкцию символа qt {у, а) — первого члена квази-
квазиобратной последовательности. Обозначим D = — \Й dt (все интегра-
о , ¦
лы по t понимаются как интегралы вдоль траекторий,например,
\ \й{(*, t),q(q°, t))dt);
, Hq)-i{Hp, w)-
-&"•,¦ (9.21)
здесь значок (а, Ь) обозначает сумму S fli^i- Обозначим
t
Ф(9°,.0-И(^. 0 + 5* *• (9-22)
о
Из условия поглощения следует важное неравенство, называемое
неравенством диссипативносга: -
• ЫФ 2* ^D-cJD'i'-*; (9.23)
оно выполняется для некоторых Ci>0, ca(e)>0 и е>0. Пусть
М — нижняя грань таких констант са, при которых выполнено
неравенство диссипативности. Тогда
. t)}
^ (9.24)
?•=?•(«. t/t)
где 7°(а> ^0 — решение уравнения <7*(<7°, t) = at, m-\-n^i>n\
9i(9°. 0 = № «<«•
Пример. Рассмотрим оператор
^ (9.25)

§ 9] КВАЗИОВРАТИМОСТЬ" И ОСНОВНАЯ ТЕОРЕМА HI
имеющий символ
{
где ф (a) Ss 0 обращается в нуль при [ а | < 772 и строго больше
нуля при а > 772: Если операторы Ах, А2, В коммутируют," то
очевидно, что квазиобратного элемента не существует (см. стр. 95).
Положим
[Ах, B]=i, [А2, Ах] = 0, [Ла, В]=0.
Пусть спектр А2 принадлежит полуоси *) у2 > 6 > 0.
Например, пусть Ax = id/dx, В=х, A2=*k, где k — параметр
6<А<оо, и пусть F (x, k)—F(x) — функция с носителем, лежа-
лежащим в Q, так что F(x, k)P(x)=sF(x, к). Функция Я (а) опреде-
определена выше в замечании к основной теореме. Рассмотрим уравнение
относительно и(х, k):
{A1-iq>{b)X2)u(x,k)=P(B)F(x,k), \F(x, k) |<const. (9.26)
Из формулы (9.26) можно сделать вывод, что с помощью ква-
квазиобратной последовательности, примененной к F(x), получается
асимптотическое решение задачи, которое удовлетворяет уравне-
уравнению с точностью до функций, стремящихся к нулю при к-*-со
быстрее krN для любого N и N раз дифференцируемо.
Проверим это на данном примере, воспользовавшись форму-
формулой (9.24). Гамильтониан оператора (9.25) имеет вид
0i + /d/ae-fq>(a)|ft|. (9.27)
Функция Гамильтона, соответствующая гамильтониану (9.27),
имеет вид ^Т = qi — p3 — «7гФ Ш = Н + Ш.
Системы Гамильтона и ростка в данном случае следующие:
<7о, 2-0, 2@) = 0,
•Л—1. А = А = 0, р@) =0. (9.28)
Вычислим величины, входящие- в формулу (9.24). Имеем
Ф (<7о, t>- qoit+iqOi $ Ф Gоз -0 dt. ¦ (9.29)
о
Из системы ростка следует, что г (q0, f) в 0. Значит ц (q0, t) = 0.
Вычислим диссипацию D.
•) В этом случае, очевидно, достаточно, чтобы символ принадлежал
лишь при yt > б.

42 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
По определению имеем
D (q0, t) = - \ Н dt = qo2 \ Ф (<7оз - t) dU (9.30)
о о
Из .(9-29) и (9.30) следует, что неравенство диссипативности
в нашем случае выполняется при сх = 1, са = 0. Найдем реше-
решение уравнения 7з(?о» 0 —а- Из системы Гамильтона имеем
Qa=*4oa — t = a. Значит, qoa — a,-{-t. Легко видеть также, что
J (д0, 0 = 1- Подставляя найденные выражения в формулу (9.24),
получаем
a+t
?i (Уи У*, a,) = i\e « Я (а + ОЛ + О (| г/21—). (9.31)
Сделав замену a + f = p\ преобразуем интеграл, стоящий в пра-
правой части, к: следующему виду:
a
Cay, со —1$у1-\-\у,\ \<f(l)dl
е \е » P($)dfl =
a
a p
to?. + l?.l J«pF)rf6 оо -fp?i-|?,| Jф(E)rfg
= e ° Je ' о P(P)dp. . (9.32)
Применив оператор, отвечающий символу (9.32) к функции
F(x)—F(x, k), получим, учитывая, что
A J ЧР (S) rf? со — ft J ср (g) rfg
Первый член, выписанный в правой части, как нетрудно убе-
убедиться, дает точное решение уравнения (9.26). Таким образом,
в этом примере (случайно, вообще говоря) первый член асимпто-
асимптотики (квазиобратной последовательности) совпал с точностью
до O(lfka), где п любое, с точным решением задачи.
Отметим теперь следующее обстоятельство. Если F (х, й) = 0
при *<0 и мы рассматриваем интервал х<.Т, то полученное
X
выражение равно \F(x, k)dx.

§ Я КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА ИЗ
Итак, если мы хотим взять интеграл от 0 до х от функции
двух переменных F (x, k), т. е. решить задачу
i% = F{x, k), «U-o = 0 (9.33)
с помощью основной теоремы, то мы должны проделать следую-
следующую процедуру:
1. Добавить к оператору g- такой член, чтооы были выпол-
выполнены условия поглощения.
2. Вывести упорядоченное представление полученного опе-
оператора.
3. Применить формулу основной теоремы, частный случай
которой приведен выше.
И после всего этого приведенная формула основной теоремы
гарантирует лишь, что решение задачи (9.33) дается интегралом
* / ' \
\ F (х, k)dx с точностью до 0 \k 2 /* (Из формулы, приведен-
о ¦ . ¦
ной в гл. VII, следует, правда, что решение задачи (9.33) равно
этому интегралу.) Но точно такая же процедура приводит к реше-
решению широкого класса дифференциальных уравнений.
Замечание. Рассмотрим квадрат оператора вида (9.26):
*)
Здесь, очевидно, не выполняется условие поглощения в приве-
приведенном выше виде; однако ясно, что оператор L квазиобратим.
Обобщение теоремы на этот случай приведено в следующем
пункте. Это обобщение охватывает также и пример в § 8, кото-
который не попадает под условия этого пункта.
Пример. Рассмотрим волновой оператор (ср. (8.6))
Система Гамильтона, отвечающая ему, имеет вид
Л-О,
с|р|а, pl = ±c>x»)\po\,
.где х*=*х{, Хц ха; p = Pi, pa> Ра- Из уравнений (9.34) следует,
что

114 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
И
Отсюда
Добавим к волновому оператору мнимую часть вида
где q>i, 8 ((*) = 0-при |/|^7\ Фг,а(^) = а>0 при t = T+l. Тогда
условие поглощения каждой траектории будет выполнено, по-
поскольку р2 Ф О на траектории, как это следует из уравнений (9.34).
Следовательно', оператор Й + iH квазиобратим. Нетрудно
видеть, что решение задачи
[Н + Ш{р, t))u=F(x, t),
где F (x, t) — финитная, не зависит от вида ф (*а) при t2 < Г2,
Й и Н определены выше.
Таким образом, введение поглощающего члена в этом случае
вообще не сказывается на решении задачи при конечных t(t<.T).
Замечание. Добавление члена — «р(лс)/?2ф(Р). где ф(дс) = О
при. |*|<Л1 й ф(*) = а>0 при \х\ = М + \, также приводит
к условию поглощения каждой траектории, так как в силу урав-
уравнений (9.33) при достаточно большом т | х(х°, т) |>Л1 + 1.
Однако в этом случае лишь асимптотика негладкой части
решения не зависит от вида поглощающего члена. Тем не менее
в некоторых аадачах добавление такого члена имеет физический
смысл.
4. Основная теорема. Рассмотрим однопараметрическое семей-
семейство символов' f(xu ..., ха, а, х0, |) и n-местных символов
г(*х, ..., хп, I), где |-параметр, 0<|<оо. Пусть
lim /(Ла, .... хп, а, ^0. Е) = /о(%, •••, *„, а, хо)е«ю,
Пусть далее P0W — функция класса Cf(Rn), равная единице
в области 1*1=^4. где d^~некоторая константа.

га-
§ 91 КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА
/1 " \
Пусть Ai, .... А„, В<=Х, rsr Л1( ..., Аа, %J&X, а
/ 2 я+1 я + 2 1 \
мильтониан оператора /[Ai, ..., А п, В , г, %j является асимп-
асимптотически р-квазиоднородным относительно переменных yi = xt,
0<t«=?n; i/n+j = — id/даj, /s=?m; g, причем числа рь отвечаю-
отвечающие последним т+ 1 переменным, равны единице. Этот гамильто-
гамильтониан зависит также от параметров а, <р = — id/dx. Старшую часть
его символа обозначим л (у, ф, а, ?), а существенную часть обо-
обозначим по(у, ф, а, ?), где у = (у0, yxi ..., уа+т), ф = (фх, ..., Фя),
« = («!, ..., аш).
Пусть pi Ф 1 при s<.i^n, ^—Л при t^s (если это не так,
то. мы изменим нумерацию переменных у). Введем гамильтоновы
координаты. Для этого обозначим
Фг при
,_s+l при
при
при
Остальные переменные будут играть роль параметров. Для удоб-
удобства переобозначим их следующим образом. Обозначим через
« = ©о, ©1,..., «я- * переменные уй, ys+1, ya_s, а через л = Ли • • • > Л«-«
параметры ф4+1, ..., фя. Кроме того, вместо параметра ? введем
параметр v = y. Функцию я в новых переменных обозначим
через 3€ (р, qr, со, r\, v), а л0 —через 9io(p,<i; «>. Л. v).
Функцию <№ {р, q, о», v, т)) будем называть функцией Гамиль-
Гамильтона. Обозначим, как и ранее, Н = Re 3€, Й = Im <№0 и пусть й8 —
множество в пространстве переменных q, о», /?, т|, v, определен-
определенное следующей системой соотношений:
(=1 7 = 0.
s л—s
<rf; |^(p, 9, Т), и,
Сформулируем условия поглощения, обобщающие условия п. 3.
Определение. Будем говорить, что выполнены условия
поглощения, если существуют такие константы е > 0, Т > 0,
некоторое число %' =%' (а°, о», р°, tj, v), 0<т' <Т и такая функ-
функция ok (<7, о») е Сю, не равная нулю при (q, о») е {(^, со): (q, о»,
0, 0, v)e ЙоЬ

116 ВВЕДЕНИЕ В ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ
1) при Outset' и (q°, со, р°, т), v)eQt существует решение
Я (q°, «>, р°, т), v, т); р (q°, со, р°, л» v, т)
системы Гамильтона
4 = НР, q\x-o = <j°,
p=z — Hq, р\х-0 = р°,
принадлежащее классу С00;
2) при 0<;тг$т' и (q°, со, p°, tj, v)eQ8 выражение
&# (q°, со) • Н (р (q°, со, р°, т), v, т>; q (а°, со, р\ ц, v, т); со; v; т))
неотрицательно, а при т=т' это выражение строго больше нуля.
Теорема 9.1. (Основная теорема). Пусть для функции Гамиль-
Гамильтона 9ъ, отвечающей символу f (x, а, х0, ?), выполнены условия
поглощения. Тогда существует последовательность символов
gN х, а, х0, |) е C4g, зависящих от параметра |, таких, что
л+1 п+2 1 \ Г /2 3 п + 1 л + 2 1
^п, В, г, iJJtavUi, i42 Л„, В, г,
п+1 п+2 1
,..., ^4п, В, г, Ъ), (9.35)
где функция Rn(xv ..., х„, а, *0, 1) — 0а(\х\~к1 для любого N.
Равномерно по | и а *).
/ 2 п+1 п+2 \
Конструкция git\Ai, ..., Л„, В,!/ приводится в гл. VII.
При | = оо мы получим простейший вариант основной теоремы,
сформулированный ранее. Несмотря на то, что в правой части
(9.34) стоит функция Ро вместо 1, которая стояла в основной
задаче, эта теорема на самом деле дает прямой ответ на постав-
поставленный в основной задаче вопрос. Действительно, в случае, если
1 п п + 1
совместный спектр набора Аи ..., Ап, В принадлежит области
О^хЯ, вместо функции Ро в правой части (9.35) можно поставить
единицу. Это условие на спектр выполняется, как мы видели,
для задачи о кристалле (там спектр ihd/dx на Mn лежит на
отрезке [—л, я], и | = 1/А). На самом деле, оно выполняется
и для произвольных разностных схем, если заменить Mn на под-
подходящее пространство гладких функций. Аналогичная ситуация
возникает в случае, когда В — гамильтониан осциллятора, рас-
рассмотренный в § 8, и поэтому имеет дискретный спектр, располо-
*) При тех же условиях существует и левая «квазиобратная» последо-
/л+1 2 I П+2 \
Ba7wbtiOQTbg'N=gN[Alt .... Ап> В, г, %):

§9] КВАЗИОБРАТИМОСТЬ И ОСНОВНАЯ ТЕОРЕМА Н7
женный на сетке шага h, где А —постоянная Планка. Конструк-
/2 л+1 п+2\
ция gN\A, ..., Ап, В ) в этих задачах позволяет получить ква-
квазиклассическую асимптотику вторично квантованных уравнений.
По сути дела все то, что было проделано для уравнения коле-
колебаний кристаллической решетки, может быть перенесено и на
этот общий случай. При этом, если поглощающий член в перво-
первоначальном уравнении отсутствует, то его нужно ввести подобно
тому, как это было сделано в примере с волновым оператором.
И точно так же можно получить в общем виде разложение по
степеням параметра у. Роль параметра о» в уравнении кристалла
играет здесь параметр v.
Задача. Показать, проверяя условия основной теоремы, что оператор
где ф(<а) — то же, что и на стр. 95, квазиобратим, если правая часть финит-
финитна по х и t. (На самом деле из формул гл. VII следует, что если F (х, Л=0
при t < 0, то Л~1 F (x, t) совпадает при t < Т с решением задачи Коши
Qcu=F(x, t), u|,_0=u/-o=0.)
Задача. Для разностной схемы
вР (n>
. — = d = const, c(x) eC™, F (n, m) = 0 при п= — 1, — 2,'...,
апроксимирукмцей при ft—*-0 волновое уравнение, вывести эффект типа Череп-
Черепкова и получить асимптотику решения с точностью до ft^.
Указание. Приведенная функция Гамильтона имеет вид
В качестве пространства, аналогичного MNi воспользоваться простран-
пространством целых функцнй первого порядка роста типа -г- (теорема Котельникова).
Поглощающий член, не влияющий на решение уравнения при 11 \ < Т,
где Г —любое число, ввести аналогично тому, как это было сделано н в пре-
предыдущей задаче.
Замечание. В формулировке основной теоремы не участвует операция
«штриха». И иа самом деле, при доказательстве теоремы мы используем эту
операцию лишь для M = {idldx, x): правило редукции основной задачи остается
справедливым и без использования операции «штриха». Поэтому основная тео-
теорема справедлива, если структуры удовлетворяют аксиомам цх — ц8. Если же
выполнены только аксиомы \ix— Цв. то основная теорема доказывается лишь
для случая, когда символ / (х, |, а) является полиномом по х.

ГЛАВА I
АБСТРАКТНЫЕ ПРОСТРАНСТВА
§ 1. Алгебраические системы
Пусть X — множество, на котором задана бинарная операция, т. е.
правило, сопоставляющее всякой упорядоченной паре элементов
jtjeX, x,eX однозначно определенный третий элемент дгеХ.
Результат операции чаще всего обозначается через ххх2, а сама
операция называется умножением.
Определение. Множество X с заданной бинарной опера-
операцией (xlt x^-+xxx% называется группой, если выполнены следую-
следующие аксиомы:
1) операция ассоциативна, т. е. (ху)гг=х(уг);
2) существует единичной элемент е е X, т. е. такой элемент е,
что хе = ех = х для любого хеХ;
3) для любого дгеХ существует обратный элемент х~х&Х,
удовлетворяющий условию хх~1 = е.
Из приведенных аксиом' следует единственность единичного
элемента, единственность элемента х~х для любого х е X и соот-
соотношение х~1х = е, откуда в свою очередь вытекает, что (х~1)~1 = х.
Из этих свойств элемента дг1 следует, что
Группа называется коммутативной, или абелевой, если груп-
групповая операция коммутативна, т. е. ху = ух для любых х, уеХ.
В случае абелевой группы бинарная операция обычно назы-
называется сложением и записывается х-\-у. Единичный элемент назы-
называется нулевым и обозначается символом 0. Вместо х'1 пишут
— х и называют этот элемент противоположным элементу х.
Пусть К есть поле R вещественных чисел либо поле С комп-
комплексных чисел.
Определение. Абелева группа Е называется векторным
пространством (над полем К), если для любых хтХ и а е К
однозначно определено произведение адгеХ, причем выполняются
следующие аксиомы:
1) Р
2) {
3) а(Р) (Р);
4) \х = х.
Векторное пространство над полем R называется веществен-
вещественным, а над полем С — комплексным векторным пространством.

§ И АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ 119
Из аксиом векторного пространства вытекает, что —*=(— 1)дг
и Одг = О. В последнем случае 0 слева означает скаляр, а справа —
нулевой элемент из Е. ' ,
Элементы векторного пространства называются векторами. Гово-
Говорят, что векторы хх, .,., хп линейно независимы, если "
{<h.xi+.. ..+аяхя = 0) ф> (<»! =... = ая = 0).
В противном случае векторы называются линейно зависимыми.
Если Е содержит п линейно независимых векторов, но любые
его п-\-\ векторов линейно зависимы, то говорят, что ? есть
п-мерное пространство. Если пространство Е содержит сколь
угодно большое число линейно независимых векторов, то оно
называется бесконечномерным векторным пространством. Базисом
n-мерного пространства Е называется любая система {ek} из п
линейно независимых векторов еь ..., е„; каждый вектор х е Е
единственным образом представим в виде
Множество LcE' называется линейным многообразием в В,
если для любых чисел а, реК
Для 'любого множества F cz E существует наименьшее линейное
многообразие L (F) в Е, содержащее F; оно состоит из всех эле-
элементов вида 2 «л, где xi e F. Множество L (F) называется линей-
линейной оболочкой множества F.
Подмножество С векторного пространства Е называется
выпуклым множеством^ если
для любого йе[0, 1]. Для всякого множества FczE существует
наименьшее выпуклое множество, содержащее F; оно состоит из
Л Л
всевозможных элементов вида ? aft*ft, где ak &* 0, ^ ak = \,
ft=l 4=1
^ef, и называется выпуклой оболочкой множества F.
Пусть Ех, ...., Еп — векторные пространства Над одним и тем же
полем К. Произведением этих пространств называется множество
всевозможных упорядоченных наборов (хъ ..., хп), где хк^Ек;
оно обозначается через Егх...хЕп. При этом алгебраические
операции в Е%х...хЕп определяются равенствами
ахя).

120 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. t
Определение. Векторное пространство А называется алгеб-
алгеброй (над полем К), если на нем определена бинарная операция
(х, у)-*-ху, называемая умножением, причем выполняются следую-
следующие аксиомы:
Ах) умножение ассоциативно, т. е. (ху) г = х (уг);
А2) умножение дистрибутивно относительно сложения, т. е.
) (
) y + (y+) y+
А8) умножение элементов перестановочно с умножением на
числа, т. е. (ах)фу) = (а$)(ху).
Алгебра А называется алгеброй с единицей, если .выполняется
аксиома:
At) существует такой элемент е е А,*называемый единицей,
что ех = хе — х при любом Jtei
Абелевой, или коммутативной алгеброй называется алгебра е?#,
для которой выполняется аксиома:
Аъ) умножение коммутативно, т. е. ху = ух для всех х, #е А.
Иными словами, для любых элементов х, у из коммутативной,
алгебры &>? их коммутатор [х, у] = ху — ух равен 0.
Пример. Алгебра формальных степенных ря-
рядов (от коммутирующих переменных). Пусть М — множество всех по-
последовательностей {Sn}1]0 с целыми неотрицательными членами,.лишь
конечное число из которых отлично от нуля. И пусть каждой пос-
последовательности s = {sn} из М поставлено в соответствие число as
из поля К- Такое соответствие по определению задает формальный
степенной ряд с коэффициентами из К, который записывают в виде
2 «* П *л
¦GM /1=1
Здесь х{, *2,... — переменные.
00
Замечание. В записи произведения]^ л?псомножители, от-
п= 1
вечающие sn = 0, обычно опускают.
Сложение формальных степенных рядов, их умножение на скаляр
и умножение друг на друга определяются следующим образом:
2 •* Й<") + B Р. Й <-)= 2 («.+PJ П <-.
ем л = 1 ' Чем л=1 ' seM n=i
)
se м n=l / Чел n=l / se м

§ 1] ¦ АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ 121
где
Vs= 2] as' Ps",
s', s"
и суммирование в последней формуле распространяется на такие
пары последовательностей s' = {s'n}, s" = {s?}, которые удовлетво-
удовлетворяют условию s'n-[-Sn = sn для любого натурального п. Заметим,
что хотя ys и представлено в виде бесконечной суммы, однако
лишь конечное число слагаемых в этой сумме отлично от нуля.
Предоставляем читателю проверить, что множество всех формальных сте-
степенных рядов с коэффициентами из К с введенными нами операциями сложе-
сложения, умножения рядов и умножения ряда на число является коммутативной
алгеброй с единицей.
Определение. Пусть &# — алгебра. Линейное многообразие
3 в &? называется левым, (правым) идеалом алгебры ет?, если
xv ее?(vxе&) для любых nerf и ке^.
В . коммутативной алгебре понятия левого и правого идеала
совпадают, ......
Группы, векторные пространства и алгебры дают лримеры
алгебраических систем. Алгебраической системой (над полем К)
называется множество X с некоторым, набором внутренних законов
композиции (т. е. бинарных операций на X):
(х, у)-+х±у, (х, у)-+хТУ, ...
и некоторым набором внешних законов композиции (т. е. отобра-
отображений КхХ->Х):
(о, х)-*а°х, (а, х)-+а»х, ...
Пусть X, У —две алгебраические системы с множествами Nx,
Ny внутренних законов и множествами Мх, My внешних законов
композиции. Если имеются взаимно однозначные соответствия
Мх ** My, Nx ** Ny, то системы X и У называются однотипными.
Определение. Пусть X и X' — две однотипные алгебраи-
алгебраические системы. Отображение А: х-*~Ах системы X в систему X'
называется гомоморфизмом, если
А (х±у) = (Ах) ± (Ау), А(хТу) = (Ах) Т (Ау), -...,
А(а°х) = а°(Ах), A(<fx) ='a»(Ax),...
Пусть X — алгебраическая система с внутренними законами
композиции JL, Т;... и внешними законами композиции ¦>, • ,...
Пусть Y с: X — такое подмножество, что
х±у<= Y, xTy^ Y, ..., а°Хе= У, а»лте= У
для любых х, y.eY и аеЯ. Тогда законы _1_,"Т, ...,

122 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
в X индуцируют законы композиции J_f, T', „,, •', •', ,., в У
по формулам
'у — хТУ, .-.., а*'х—Ъ°х, а»'х
Относительно этих индуцированных законов композиции Y явля-
является алгебраической системой, однотипной с X. Говорят, что Y
является подсистемой системы X. Например, линейное многообра-
многообразие L в векторном пространстве Е само является векторным
пространством относительно операций сложения и умножения
на число, индуцированных из Е. Наделенное структурой вектор-
векторного пространства, L называется подпространством пространства Е.
Здесь символы J_, T, •, • обозначают соответствующие законы
композиции в X и X'. Взаимно однозначный гомоморфизм системы X
на систему X' называется изоморфизмом.
Алгебраические системы X и X' называются изоморфными,
если существует изоморфизм Х->Х'. Изоморфные алгебраические
системы обычно отождествляются, если их рассматривают только
с точки зрения их алгебраических свойств, т. е. свойств, свя-
связанных с законами композиции.
§ 2. Банаховы пространства
Определение. Вещественная функция *-»-||х||, определен-
определенная на векторном пространстве Е, называется нормой, если она
удовлетворяет следующим аксиомам:
Ni) ||*||2*0; (||*|| = 0)о(*-0);
АО ||а*||-|о.|||*||;
з) l|y||;llll+IMI
Векторное пространство, наделенное нормой, называется (век-
(векторным или линейным) нормированным пространством.
Во всяком нормированном пространстве В можно следующим
образом определить расстояние р (х, у) между элементами х, у^.В:
Р(х>. У) = \\х-у\\. .
Из аксиом нормированного пространства вытекает, что рас-
расстояние р удовлетворяет следующим условиям:
Ri) ?{х, У) ^ 0; (р (*, у) = 0) о (* = у);
#а) р(х, у) = р(у, х);
Rs) P(x, z)<p(x, y) + p(y, г).
Множество R, любой паре элементов х, у которого отнесено
число р (х, у), удовлетворяющее аксиомам Rlt R2, R3, называется
метрическим пространством.
Таким образом, нормированные пространства можно рассматри-
рассматривать как частный случай метрических. Последовательность {хп} cz R,
по определению, сходится к элементу х е Я, если lim p (х, хп) =0.

§ 2] БАНАХОВЫ ПРОСТРАНСТВА 123
Такой элемент х, когда он существует, определяется однозначно.
Последовательность {xn}czR называется фундаментальной, если
Ига р(хп, лгто) = 0. Всякая сходящаяся последовательность,
п, т-ю>
очевидно, фундаментальна. Обратное, вообще говоря, неверно.
Если же любая фундаментальная последовательность сходится*
то пространство R называется полным. Полное нормированное
пространство называется банаховым пространством.
Перечислим вкратце некоторые основные факты, касающиеся метрических
пространств (доказательства читатель найдет в любом достаточно полном учеб-,
нике функционального анализа).
Шаром (открытым) в пространстве R называется множество S(х0, r)>{«6
е R: р(*ь, х) </¦}. Прн этом точка х0 называется центром шара, а положительное
число г — его радиусом. Множество Xci? назынается открытым, если для
вейкой точки х0 s X существует такое е > 0, что S (х0, е) с: X. Объединение
любого семейства открытых множеств есть открытое множество, Множества Y,
дополнительные к открытым, называются замкнутыми. Они характеризуются
тем, что если х^е Y н х^—*х (т. е. р(х/,, х)—*0), то дсе Y. Пересечение
любого семейства замкнутых множеств есть множество замкнутое. В частности,
для любого множества AczR существует наименьшее' содержащее его замкну-
замкнутое множество Л", которое называется замыканием множества А.
Замкнутым шаром радиуса г 5* 0 с центром в точке х0 назы-
вается множество {xeR:p(x, xo)*^r}. Замкнутый шар есть мно-
множество замкнутое; он содержит замыкание шара S(x0, r) (но
может оказаться шире, например, когда пространство R содер-
содержит лишь конечное число точек).
Свойство пространства R быть полным может быть адекватно охарактери-
охарактеризовано в терминах замкнутых шаров: пространство R полно в том и только
том случае, если любая последовательность замкнутых вложенных шаров
Вх з Bj з ..., радиусы которых стремятся к нулю, имеет непустое пересече-
пересечение (состоящее, очевидно, из единственной общей нм точки). Требование стрем-
стремления к нулю радиусов (когда пространство—полное), существенное дли общих
метрических пространств, может быть опущено в случае банаховых пространств.
Из приведенного критерия полноты выводится важная теорема Бэра:
если полное метрическое пространство R представлено в виде счетного объеди-
объединения замкнутых множеств, то хотя бы одно из этих множеств целиком
содержит некоторый шар S (х0, г).
Метрическое пространство R называется компактным, если из нсякой его
последовательности {*„} можно выбрать фундаментальную последонатель-
Н0СТЬ {Ч}1
В конечномерных) евклидовых пространствах ограниченные множества,
и только они, образуют компактные подпространства (в индуцированной мет-
метрике). Если в нормированном пространстве шар {х: || х | < 1} компактен, то
пространство конечномерно, н верно обратное. Для компактности простран-
пространства R необходимо и достаточно существование конечной е-сети для любого
е>0, т. е. такого конечного набора элементов xlt ..., xN&R, где # = # (е),
что объединение шаров S(xi, е) содержит все R (нлн, как говорят, образует
покрытие R). Полное компактное пространство R называется компактом.
Пространство R тогда и только тогда является компактом, когда из любого
покрытия этого пространства шарами или любыми открытыми множествами
(открытого покрытия) можно выбрать конечную подсистему, также образующую
покрытие.

124 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. Г
Вернемся к нормированным пространствам. Пусть а н Ь—две точки
в векторном пространстве В. Множество точек же В вида at-\-(\— t)b, где
Osgf^l, называется отрезком, соединяющим точки а и Ь, н обозначается
через [а,, Ь]. Множество К с В будет выпуклым, если из а, Ь еУ вытекает
[а, Ь] с Y. Множество Y с В' называется симметричным . (относительно
точки 0), если нз леК вытекает (—а) е Y. Если В — пространство над
полем С комплексных чисел, то множество Y с В называется закругленным,
если нз asK и |^| = 1 следует, что кеУ. Ясно, что всякое закругленное
множество является симметричным. Множество Y а В называется поглощающим,
если для любого а е В существует такое %ф0, что Але Y. Ясно, что вся-
всякий шар || х || < г в нормированном пространстве В является закругленным,
выпуклым н поглощающим множеством.
Множество Y с В называется бочкой, если оно является замкнутым
выпуклым, закругленным (в вещественном случае —симметричным; и погло-
поглощающим. Всякий замкнутый шар || * || ^ г является бочкой. v ¦
Следующая лемма представляет собой удобный инструмент для доказа-
доказательства различных теорем о банаховых пространствах.
Лемма 2.1 (Лемма о бочке). Пусть В—банахово пространство. Тогда
всякая бочка Y cz В содержит некоторый шар ||*||<г.
Доказательство. Положим YN = {xeB : x=Ny, у е Y). Так как
0 е Y н так как К —выпуклое, закругленное н поглощающее, то U YN=B.
Каждое из множеств YN замкнуто (вместе с Y). Поскольку В полно, то,
по теореме Бэра, некоторое нз множеств YN содержит шар {х: \\х—xa\\<.R}i
Из выпуклости и закругленности множества YN вытекает, что тогда оно содер-
содержит шар ||ж|| < Я. Следовательно, шар ||jc||<r=./?/JV содержится в Y. Лемма
доказана.
Перечисленные выше факты уже показывают, сколь важно
свойство пространства быть полным (впрочем, это ясно и на про-
простейшем примере вещественных чисел). Мы еще неоднократно
будем иметь возможность убедиться в этом. Оказывается, суще-
существует канонический способ пополнения метрических пространств.
В применении к 'нормированным пространствам он является
одним из путей построения банаховых пространств, и мы опи-
опишем его в деталях.
Пусть Е — произвольное нормированное пространство. Фунда-
Фундаментальные последовательности {ф„} и {ф„} элементов из Е будем
называть эквивалентными, если
Ига |ф„-Ф„1 = 0.
п-юо
. Разобьем множество фундаментальных последовательностей
элементов из Е на классы, относя к одному классу эквивалент-
эквивалентные между собой последовательности. Пусть Е — возникающее
множество классов.
Введем на Е следующим образом структуру нормирован-
нормированного пространства. Пусть Фб?,?б?и пусть а, Р — комплекс-
комплексные числа. Линейной комбинацией аФ + Р^ классов Ф, ? назовем
класс &, состоящий из всех последовательностей, эквивалентных
последовательности {аф„ + Р^„}, где {ф„} еФ, {tyn} e?, Нетрудно

§ 2] БАНАХОВЫ ПРОСТРАНСТВА 125
проверить, что последовательность {афп + Р'Фл} фундаментальна
и что класс X не зависит от выбора конкретных последователь-
последовательностей {ф„} и {tyn} соответственно из Ф и Ф.
Пусть Ф е Е и {ф„} е Ф. За норму класса Ф принимается число
||Ф||-Нт||фв||. B.1)
п-*со
Предел всегда существует, так как неравенство
HI<pn!l-l!<PmllKI!<pn-<p*ll. B.2)
вытекающее из аксиомы N3, влечет фундаментальность числовой
последовательности {||<ря|!}. Легко проверить корректность опре-
определения, т. е. независимость определения от выбора представи-
представителя класса Ф и тот факт, что норма B.1) удовлетворяет аксио-
аксиомам Nx — N3.
Последовательность {ф„} называется стационарной, если
Определение. Пусть Е, F — нормированные пространства
и пусть A:E-*~F — изоморфизм векторных пространств. Отоб-
Отображение А называется изометрическим изоморфизмом, если || Ллг || =
= || л: ]| для всех д:е Е.
Определение. Пусть Е — нормированное пространство.
Множество М czE называется плотным в Е, если для любого
хеЕ найдется такая последовательность {тп\ элементов из М,
что
\\ттл — х.
п-»оо
Пусть В —банахово пространство и пусть1 множеством плотно
в В. Для доказательства того, что некоторое множество М'
плотно в В, достаточно убедиться в том, что для любого теМ
существует последовательность \m'i\ элементов из М', сходя-
сходящаяся к т.
Теорема 2.1. Пусть Е — произвольное нормированное про-
пространство и пусть Е — пространство классов эквивалентных
(фундаментальных) последовательностей. Тогда Е является бана-
банаховым пространством и линейное многообразие Е' а Е классов
эквивалентности, содержащих стационарные последовательности,
изометрически изоморфно Е и плотно в Е.
Доказательство. Для доказательства полноты простран-
пространства Е рассмотрим произвольную фундаментальную последова-
последовательность {Ф/} классов {Фу} е Е и докажем, что она сходится
к некоторой последовательности ФеЕ. Для каждого натураль-
натурального / выберем некоторую последовательность {ф</)}еФ.. Для
любого k найдется такое число nk, что для всех т~>пк справед-
справедливо неравенство
"^^И*1 B-3)

126 АБСТРАКТНЫЕ ПРОСТРАНСТВА {ГЛ. I
Рассмотрим класс Ф, состоящий из последовательностей, экви-
эквивалентных последовательности {ф^}00 •
Покажем, что эта последовательность фундаментальна (т. е.
что Ф с: Е) и что
Нт||Фу-Ф|| = 0.
/->оо
Чтобы убедиться в этом, обозначим через Ф(А) класс, содержа-
содержащий стационарную последовательность {ф<*\ ф<п*>, .. .1. По опре-
At Hi
делению нормы в Е |ФА-Ф<*>||= lim II Ф<?> - ф<*> II. Из B.3)
следует, что
||Ф*-Ф<*> |<*"V B.4)
Следовательно, для фиксированных /, /',
B.5)
при i, j-*-oo в силу фундаментальности последовательности {Ф,}.
С б {^Нф Ф Е.
р j
Стало быть последовательность {ф^Нфундаментальна, т. е. Ф
Теперь докажем • сходимость последовательности {Фу} к Ф. ^Из
неравенства B.4) вытекает неравенство
|Ф_Ф4|<|Ф-Ф(«[ + |Ф(*)-Ф4|<|Ф-Ф(*)|| + Л-1. B.6)
Из фундаментальности последовательности {ф|*Ч следует, что для
любого е>0 найдется такое po(s, k), что при р>ро(ъ, k)
а из B.5) вытекает,, что
|Ф - Ф<*> || < р~1 + кг* +1| Фр - ФА || + в... ¦ B.7)
Но последовательность {Ф/} фундаментальна., и значит, из нера-
неравенств B.6) и B.7) вытекает, что
Нт|Ф-Фь1 = 0.
Тем самым полнота пространства ? доказана.
Из предыдущих рассуждений ясно, что если Ф е Е, то суще-
существует сходящаяся к Ф последовательность {Ф(й)} элементов
из Е'. Таким образом, ?" плотно в Е, и теорема доказана.
Сужение отображения Ф-*-|Ф|| с Е на Е определяет норму
на Е', так что Е' превращается в нормированное пространство.
Отображение Е на Е, которое ставит в соответствие элементу

$ 2] БАНАХОВЫ ПРОСТРАНСТВА ' 127
фе? класс, содержащий стационарную последовательность ф,
Ф, ..., является, очевидно, изометрическим изоморфизмом. Этот
изометрический изоморфизм пространств ?* и Е позволяет в да'ль-
нейшем отождествлять их элементы, т. е. считать ? частью Е.
Пространство Е называется пополнением, пространства Е.
Пример. Пусть Q — замкнутая область в R". Обозначим
через ?2(Я) нормированное пространство непрерывных комплекс-
комплексных функций на Q (с естественным определением сложения функ-
функций и умножения их на комплексные числа), для которых
Норма в ?2(Q) определяется формулой
Нетрудно убедиться в том, что пространство L2 (QY неполно.
Его пополнение обозначается через L2(Q). Элементы пространства
L2(Q) будем называть функциями, интегрируемыми с квадратом
на п. Заметим, что, вообще говоря, элемент (peL2(Q) не явля-
является функцией в обычном смысле слова, т. е. при ф ф 1^ (Я)
может не существовать отображения ср: *-> ф (*), х е Q, ф (дг) е R,
естественным образом связанного с элементом ф.
Пусть В — банахово пространство и L — плотное в нем линей-
линейное многообразие. Пространство L является нормированным про-
пространством. Пополнение этого пространства изометрически изо-
изоморфно В. Предоставляем читателю самому доказать этот простой
факт. , ь - '
Пример. Рассмотрим в пространстве L2 (R) линейное много-
многообразие Cj°(R), состоящее лз всех бесконечно дифференцируемых
функций на R с компактными носителями*). Покажем, 4toC?°(R)
плотно в jL2(W- Сначала убедимся в том, что множество C0(R).
всех непрерывных функций с компактными носителями плотно
в L2 (R). Пусть f — непрерывная функция из L2 (R), т. е. / е L2 (R).
Рассмотрим последовательность {/>,}, где /neC0(R), /„(*) =
f()() C(R) 0(Х1 () 1
р {/>}, /0(), /„()
= f(x)an(x), aneCj°(R), причем 0<а„(*Х1, и а„(^) = 1 при
| х | ^ п. (Существование функций а„ очевидно.) Имеем
\x^>п i*i>n
при /г->оо, так что
/= Hm fn.
п-*со
*) Говорят, что функция f, определенная на R", имеет компактный'носи-
компактный'носитель, если /(*)=0 для всех *, лежащих вне некоторого шара в R".

128 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
Но поскольку L2 (R) плотно в L2(R), то отсюда следует, что C0(R)
плотно в L2(R)."
¦¦ Пусть теперь ge Co (R) — непрерывная функция с компактным
носителем. Рассмотрим последовательность таких функций ср„ е
eCj°(R), что OsScprt=sSn и
О при [jfiss-gL^.
со
Положим gn (х) = \ q>n(x — y)g (у) dy. Очевидно, gn e С? (R). Тогда
—00
\ga(x)~g(x)\= п _ J ' fe(y)-ST(*)LH-.
+ \ <Pn(x-y)g(y)dy
\/2п<\х-у\<Ч2п+\1п*
] <pn(x-y)g(y)dy <¦$!<&,(*¦
1/2п < | х-у |< 1/2П+ 1/л»
Кроме того, gn(x) = g(x) — O при |х|>с, где с —некоторая кон-
константа. Поэтому
R. I Л | « 1/2л
при /г-»-оо. Отсюда следует, что (^(R) плотно в Ь.г (R).
Итак, пространство L2(R) изометрически изоморфно попол-
пополнению линейного многообразия Cjj°(R) по норме пространства
MR).
.Мы рассмотрели процесс пополнения линейных нормирован-
нормированных пространств, приводящий к банаховым пространствам.
Другой путь построения банахозых пространств состоит
в переходе к факторпространствам. Пусть. В — банахово прост^
ранство и F — его подпространство. Будем говорить, что два
вектора хъ х2 е В эквивалентны и писать хх <->j х2, если хг — х2 е F.
На "множестве B/F классов эквивалентности естественным образом
вводятся линейные операции. Например, если X и У —два таких
класса, то Х + У есть класс, содержащий лее элементы вида
х + у, где лгеХ, </еУ. ЛегКО -видеть, что это определение
корректно. Линейное пространство B/F наделяется нормой
ЦХЦ= inf ||* ||.

$ 3] ГИЛЬБЕРТОВЫ ПРОСТРАНСТВА I29
Пространство B/F, нормированное указанным способом, явля-
является банаховым пространством (докажите). Оно называется
факторпространством пространства В по подпространству F.
Задача. Пусть В=С[0, 1] —пространство всех непрерывных функций
на отрезке [0, 1], с нормой |/||=тах|/|, и пусть F=*{f e В: /@=0 при
0/}. Докажите, что B/F изометрически изоморфно С[0, а].
§ 3. Гильбертовы пространства
В дальнейшем мы -будем, если не оговорено противное, называть
комплексные векторные пространства просто векторными прост-
пространствами (аналогично — алгебры, нормированные пространства,
банаховы пространства).
Важнейшим частным случаем банахова пространства является
гильбертово пространство.
Предгильбертовым пространством называется векторное про-
пространство Н, в котором каждой упорядоченной паре векторов
х, у поставлено в соответствие комплексное число (х, у), назы-
называемое их скалярным произведением, удовлетворяющее следующим
аксиомам:
Hi) (х,'у) = (у, х)\
Я2) (ах + ру, г)=а(лг, z) + PG/, г);
Нг) (х, х)^0;
HJ [(х, *) = 0]о(* = 0).
Положим ||*| = (*, л:)'/2 Тогда |-| удовлетворяет аксиомам Nx
и JV2.
Проверим выполнение аксиомы JVS. Для этого сначала дока-
докажем весьма важное неравенство Коши — Буняковского\
Для случая (х, у) = 0 неравенство тривиально; поэтому пред-
предположим, что (х, ,у) Ф 0. Имеем
-ау, х-ау) = (х, х)-а(у, x)-a(x, </) + |a|2(t/, у);
полагая а = (х, х)/(у, х), получаем
откуда и вытекает доказываемое неравенство. Легко видеть, что
это неравенство превращается в равенство | (х, (/)|=||д:|.|</|
тогда и только тогда, когда элементы хну линейно зависимы
(докажите). Теперь уже легко получить неравенство Af3: i x +
+ \\\\\\ + \\\\ Действительно, можно переписать JVS в виде
б В, П. Маслов

130 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ, I
т. е. в виде
или
2Re(*, у)^2\\х\\\\у\\.
Но Re (х, «/)^|(дг, у)\, и поэтому последнее неравенство следует
из неравенства Коши —Буняковского. Знак равенства в нера-
неравенстве ||* + 0||«S||*|| + 1#[| имеется тогда и только тогда, когда
векторы х и у пропорциональны с неотрицательным коэффициен-
коэффициентом пропорциональности (докажите).
Полное предгильбертово пространство называется гильберто-
гильбертовым пространством.
Пример.. В конечномерном векторном пространстве можно
ввести структуру гильбертова пространства. Поскольку все
«-мерные векторные пространства изоморфны, рассмотрим ариф-
арифметическое пространство С", элементами которого являются упо-
упорядоченные наборы дг = (дг1, ..., хп) комплексных чисел. Алгеб-
Алгебраические операции в С" определяются покоординатно. Введем
я
в С" скалярное" произведение по формуле (дг, у) = ? xi9t- Легко
проверить выполнение аксиом tfj) —#4) и полноту полученного
метрического пространства *).
Пример. Рассмотрим совокупность 12 последовательностей
00
*=(?i» Ь. •••) комплексных чисел |ft, для которых ^] |1*|2<°°.
Определим в /2 линейные операции покоординатно. Мы получим
векторное пространство. Введем в пространстве /2 скалярное
произведение, полагая для х = (%1, |2, ...), «/ = (%, %, ...)е/а
00
(х, у) = 2] 1*г|*-
Ряд сходится, так как | |*тп | =s? 1/2 (| lk |2 +1 цк f). Легко видеть,
что аксиомы предгильбертова пространства будут выполнены.
Покажем, что пространство /2 полно. Пусть ^"' — фундаменталь-
фундаментальная последовательность. Координаты вектора дг(л) обозначим |^л).
Числовые последовательности \^ при каждом k фундаментальны.
Поэтому при каждом k существует предел \к= \\m\kn\ Фикси-
п-»оо
руем е>0. Так как последовательность х(п) фундаментальна,
то найдется такое N = N(e), что при п, m>N{&) получаем
*) Скалярное произведение в R" и С" часто обозначается через х-у.

$ 31 ¦ ГИЛЬБЕРТОВЫ ПРОСТРАНСТВА 131
\\xw—x{m)l<e, т. е.
1№-1ГТ<еа-
Тем более, при любом конечном /
I№-if !*<е*.
Полагая здесь сначала т -*¦ оо, а затем / -> оо, мы получим
Поэтому A: = (ii, |2, ...)^4 и ||дг(л) — лгЦа^е при n>N(e).
Векторы х и у гильбертова пространства Я называются орто-
ортогональными, если (х, у) — 0. Легко видеть, что для таких векто-
векторов \x+yf = \xf+yf (теорема Пифагора).
Теорема 3.1. (Теорема о параллелограмме.) Банахово про-
пространство В тогда и только тогда является гильбертовым (т. е.
изометрически изоморфно гильбертову), когда норма в этом
пространстве удовлетворяет условию
}x+yf + lx-yf = 2(kxf+lyf) C.1)
для любых х, «/ е В.
Необходимость. Пусть В — гильбертово пространство.
Тогда
-y, х-у) =
= (дг, дг) + (дг, у) + (у, х) + (у, у)+(х, х) + (у, у)-(х, у)-(у, х) =
. =2\xf+2\yf.
Достаточность. Мы должны показать, что |дг|| имеет
вид (а:, хI/2 для некоторого скалярного произведения (*, у).
Пусть Б —банахово пространство и пусть выполнено условие
C.1) на норму. Определим следующую функцию (*, у) перемен-
переменных дгеВ, ysB:
(х y) \l
Покажем вначале, что эта функция удовлетворяет аксиомам ска-
скалярного произведения. Имеем
(х, x) = ±{4\xt + i\l+i\4xr-t\l-i\*\xfl*=\xr.
Отсюда следует выполнение аксиом Н3 и Ht. Соотношение Нг
следует из того, что \y-\-ix\^=\x — iy\, \y — ix\ = \x-\-iy\.
б*

132 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
Докажем Я2. Из C.1) и C.2) вытекает, что
izf - i\\x- izf + i\\y+ izf - i\y-izf) =
Положив г/ = 0, получим (дг, z) = 2fy, z\. Отсюда и из C.3) сле-
следует, что
По индукции доказывается, что для любого натурального m
справедливо равенство (тх, z) = m(x, z). Действительно, из C.4)
и из предположения (kx, z) = k(x, z) следует, что
(^+1)(д:,"г) = ^(д:, z) + (x, z) = (kx, z) + (x, z) = ((k+l)x, г).
Далее, непосредственно проверяется, что (— х, z) = — (д:, г).
Таким образом, для рациональных чисел а вида а = яг/2" выпол-
выполняется свойство (ах, г) = а х, г). Пусть теперь 0 — произволь-
произвольное вещественное число и {{$„} — последовательность. двоичных
дробей, сходящаяся к р. Тогда
(Рдг, г)-Р(дг, г) = фх, z) — р (дг, г)-(Р*х, z) + $k(x, z) =
-P)(x, г) =
так как (дг„ —¦- дг) =^> (fl дсп || —»- J дс Ц)- Следовательно, фх, z) = $(x, г).
Наконец, прямое вычисление дает: (гдг/ z) = i(x, z). Итак,
(ах+$у, г}=а(х, г) + §(у, г). Следовательно, пространство В,
наделенное скалярным произведением вида C.2), будет гильбер-
гильбертовым пространством. Теорема доказана.
Пример. ПространствоLa(Q) — гильбертово. Проверим выпол-
выполнение равенства C.1). Пусть сначала х, «/ — непрерывные функ-
функции из Lz{Q). Тогда
1* + УТ + \\х- «/112= \ \хA)+уA)\*с11+ \ \x{t)-y(l) |«dE = '

ГИЛЬБЕРТОВЫ ПРОСТРАНСТВА 133
Пусть теперь х и у — произвольные элементы из 1^@.) и
пусть {xk\ и {yk) — последовательности непрерывных функций
из L2(Q), сходящиеся соответственно к х иг/. Тогда
следовательно, по теореме 3.1, пространство Z,a(Q), наделенное
скалярным произведением по формуле C.2), является гильбер-
гильбертовым пространством, что и требовалось.доказать.
В случае, когда функции х и у непрерывны, получаем для
скалярного произведения (х, у):
- $ (х (Б) - у {%)) Й1) - Ш) dl+i\ (х (|>+iy (Б)) G® -
в в
. C.5)
Замечание. Даже в тех случаях, когда х и ^—произ-
^—произвольные элементы пространства L2(Q), не обязательно являю-
являющиеся непрерывными функциями,- будем записывать их скаляр-
скалярное произведение в том же виде:
Вернемся к общим пространствам. Если У —некоторое мно-
множество в метрическом пространстве R с метрикой р, то для лю-
любого х0 е R число р (дг0, Y) = inf p (х0, у) называется расстоянием
от х0 до У. Вообще говоря, расстояние не обязано достигаться
на каком-либо элементе i/еУ.
Задача. Доказать, что расстояние достигается, если пространство
R — полное, a Y компактно в R. Если расстояние достигается, то элемент
!/еУ, для которого р(*0, у) = р(х0, Y), не обязан быть единственным.
В случае выпуклых замкнутых подмножеств гильбертова пространства кар-
картина гораздо проще.
Теорема 3.2. Пусть У—замкнутое выпуклое множество
в гильбертовом пространстве Н. Тогда для любого хо^Н суще-
существует один и только один элемент уо^У такой, что
11*о - Уо II = Р (*о. Y) == inf || х0 - у ||. .
Доказательство. Пусть d= inf ||jf0— Vi- He ограничивая
общности, можно считать, что d>0. Пусть г/„е У — такая после-
последовательность, что ||хо — уп||-*¦ d. . Применяя теорему о паралле-

134 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
лограмме (теорема 3.1) к векторам а — хо — уп и Ь = хо — ут} мы
получаем
При п, т-»-оо правая часть равенства стремится к Ad2.
Вектор УгО/п + Ут) в силу выпуклости У принадлежит У.
Поэтому 1дг0 — 1/2(?/n + #m)|Ssd при всех п и т. Сопоставляя эти
два факта, мы видим, что
lim || уп-ут || = 0,
я, т -* оо
т. е. последовательность {«/„} фундаментальна. В силу полноты
пространства Я существует lim уп = Уо- При этом !/оеУ, так
Л-С0О
как У замкнуто. Ясно, что | дг0 — у01 = d. Тем самым установлено
существование элемента йеУ, для которого \\хо — уо\\ — р(хо, У).
Покажем, что такой элемент может быть только один. Пусть
гоеУ таков, что для этого элемента также ||х0 — г01 = d. Поло-
Положим «о^/гОУо + го). Тогда ы0 е У. Имеем
d *¦? || дг0 - ы01| = | х0 - Vi 0/о + г0) I = Vi (II (*о - У») + (хо - г0) И)
Поэтому фактически все неравенства, фигурирующие в этой
цепочке, суть равенства. В частности,
II (*о- Уо) + (Хо ~г0) || = \х0 -у01| + |х0- г0\\.
Принимая во внимание, что здесь неравенство треугольника"обра-
треугольника"обращается в равенство, мы заключаем отсюда, что xo — yo = t(xo — zo),
где ^22=0. Но так как |дг0 — «/о| = 1*о — zo\\ = d>0, то t=\.
Поэтому г0 = у0. Теорема доказана.
Те,орема 3.3. Если У — 'замкнутое линейное подмногооб-
подмногообразие' гильбертова пространства Н, то всякий вектор лей
единственным образом представим в виде
х = у + г,
где у gF, а г ортогонален к У, т. е. (г, а) = 0 для всех a^Y.
Доказательство. Единственность такого разложения оче-
очевидна: если имеется еще одно представление х = У! + г! с теми же
свойствами, то вектор y — yi = z1 — z оказывается ортогональным
самому себе, а потому нулевым. Для доказательства существова-
существования воспользуемся теоремой 3.2. Согласно этой теореме найдется
такой вектор t/e У, что |дг — у\\= inf |дг —ы||. Покажем, что век-
тор г = х — у ортогонален к У. Предположим противное. Тогда
(г, а)Ф=0 для некоторого вектора аеУ. Покажем, что при под-
подходящем подборе скаляра Я мы сможем получить \\х — (у-\-%а)\\<.
<d. Тем самым мы получим противоречие с определением

§ 3} ГИЛЬБЕРТОВЫ ПРОСТРАНСТВА 135
числа d, так как y + %a&Y. Имеем
^ г, а),
и теперь ясно, что X надо брать малым по модулю и таким,
чтобы Я (г, а)>0. Такой выбор % возможен в силу предположе-
предположения (г, а)Ф0. Следовательно, это предположение неверно, и
теорема доказана.
Вектор у в разложении вектора х, указанном в теореме 3.3,
называется проекцией вектора х на подпространство У.
Говорят, что пространство Я разлагается в прямую сумму
своих подпространств Уг и Уа, если Y1f\Yi= {0} и всякий век-
вектор дгеЯ допускает представление вида yi-\-y%, где г/.-еУ^.
В случае гильбертова пространства говорят также об ортогональ-
ортогональной прямой сумме, если подпространства У^ и Уа ортогональны,
т. е. если (уи у%) = 0 для любых ^е^ и ^еУ,,
Совокупность векторов, ортогональных к некоторому подпро-
подпространству У с: Я, образует, как легко видеть, замкнутое подпро-
подпространство в Я. Оно называется ортогональным дополнением к У.
Теорема 3.3 приводит нас к следующему результату.
Теорема 3.4. Пусть У t — замкнутое подпространство гиль-
гильбертова пространства Я. Тогда Я представляется в виде орто-
ортогональной прямой суммы подпространства Yx и его ортогональ-
ортогонального дополнения Уа, что записывается в виде H = Y1®Y2.
Задача. Докажите, что Y2 изометрически изоморфно факторпростран-
ству Н/Yi. .
Система (конечная или бесконечная) векторов е,- е Я гильбер-
гильбертова пространства Я называется ортонормированной, если
116,1=1 и (et, е/) = 0 при 1ф]. Пример ортонормированной
системы в 12 дает система gf = ,@, ..., 0, 1, 0, ...). Если дгеЯ,
i
то числа Ci = (х, et) называются коэффициентами Фурье вектора х
по системе е%. Для любой (конечной) ортонормированной системы
еъ ..., еп е Я и любого вектора х е Я имеет место следующее
важное неравенство Бесселя:
Докажем это неравенство. Пусть У—^ Ckek. Тогда (х, ei) =
* = i
= (у, ei) при ls^z'sSrt. Положим г = х — у. Тогда B, ej) = O, i =
= 1, ..., п. Поэтому (г, г/) = 0 По теореме Пифагора
4=1
что и требовалось доказать.

136 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. Г
Теорема 3.5. Пусть Н — гильбертово пространство и пусть
{ек}~ счетная ортонормированием система в Н. Пусть {Я^} —
00
последовательность комплексных чисел, для которых 21 ^* I2 < °°«
1 ¦ .
Тогда последовательность векторов
сходится в Н к вектору s, для которого (s, е,) = Я* и
i
Доказательство. Пусть п>т. Тогда, по теореме Пи-
Пифагора,
Is»-srof= 2 Iя*!2.
k = m+ 1
откуда и следуют оба утверждения.
Ортонормированная. система векторов е* е H называется пол-
полной, если из условий (х, ek) = 0 для всех k вытекает, что * = 0.
Если линейными комбинациями векторов системы \ek) можно
аппроксимировать любой вектор х е Н, то система, очевидно,
полна. Из приводимой" ниже теоремы вытекает, что в гильберто-
гильбертовом (полном!) пространстве верно и обратное.
Теорема 3.6. Пусть {ek} —полная счетная ортонормиро-
ортонормированная система в гильбертовом пространстве Н. Тогда любой
вектор х е= Н (единственным образом) представляется в виде
суммы сходящегося ряда
еде с* = (дг, ek); При этом
(равенство Парсеваля). Далее, если х и у — два любых вектора, то
00
(х, у) = ?(х, ek){y, ek).
Доказательство: В силу неравенства Бесселя имеем-
oo
для всякого п. Поэтому ряд 2lc*l2 сходится. Положим s, =
_ 1
= ciei + .'•• -\-спеп. По теореме 3.5 последовательность sn cxo-

§ 4] ФУНКЦИОНАЛЫ И СОПРЯЖЕННЫЕ ПРОСТРАНСТВА 137
дится к некоторому вектору se#. При этом (х, ek) = ck —
= lim (sn, ek) = (s, ek), так что (дг — s, ek) — 0 для всех k. По-
n * oo
n ¦* oo
n * oo
скольку система {е*} полна, отсюда следует, что * = s. Осталь-
Остальное очевидно. Теорема доказана.
Полная ортонормирования система в гильбертовом пространстве назы-
называется ортогональным базисом. Пространство, обладающее счетным ортогональ-
ортогональным базисом, называется счетномерным. Всякое счетномерное гильбертово про-
пространство Н изометрически изоморфно пространству 1% (докажите это, исполь-
используя теорему 3.6).
Нормированное пространство •/? называется сепарабельным, если в этом
пространстве существует счетное всюду плотное множество А, т. е. такое
счетное множество А, что для любого вектора *еЯ и любого е>0 имеется
вектор а е А, удовлетворяющий условию р {х, а) < 8. Другими словами,
всякий вектор из R есть предел последовательности элементов множества А.
Всякое сепарабельное гильбертово пространство Н счетномерно. Действи-
Действительно, пусть А = {щ}—счетное всюду плотное множество в Я. Выберем
такую подпоследовательность Ьх, Ь2, ... е А, чтобы: 1) при любом п векторы
Ьи ... , Ьп были линейно независимы; 2) всякий вектор из А был линейной
комбинацией векторов bt. Очевидно, такой выбор возможен. Ортогональный
базис будем строить ло нндукцнн. Положим е1=61/||61||. Допустим, что век-
векторы еъ ... , е„ таковы, что они образуют ортонормированную систему и
линейная оболочка системы {еь ... , еп\ совпадает с линейной оболочкой
системы {blt ... , bn). Положим
где %i=— Fn+i, ei), lsSfsSn. Тогда (fn+i, ег)=0 при legfsSn. Кроме
того, /л+1т^0, поскольку иначе векторы ей ... , е„, Ь^и а потому и
bi, ... , bn, bn+i, Сказались бы линейно зависимыми. Наконец, полагая
еп+1==/п+]у||/л+1|, мы совершим индуктивный переход от п к п+1. Легко
убедиться (мы рекомендуем читателю восстановить аеталн), что {e^fL, обра-
образует искомый базис.
§ 4. Линейные функционалы и сопряженные пространства
Пусть В — нормированное пространство над полем,К = R или С.
Линейным функционалом на В называется такое отображение <р:
В-+К, что <р(х + у) = у(х)+у(у) и ' ф(кх) — А,<р(дг) для любых
х, у^В и Яе/С. Если это отображение непрерывно, т. е. если
(дг„->дг)=>(ф(дг„)->ф(л;)), то оно называется линейным непрерыв-
непрерывным функционалом. Легко видеть, что непрерывность линейного
функционала во всех точках пространства В вытекает ^из его
непрерывности в точке 0.
Линейный функционал ф называется ограниченным, если
конечна величина Цф|= sup |ф(дг)|, которая называется нормой
lUii^i
функционала ф. Без труда проверяется, что непрерывность линей-
линейного функционала эквивалентна его ограниченности.
Задач а. Доказать, что линейный функционал ф тогда и только тогда
ограничен, когда не каждое число принадлежит множеству -{?С=ф (лг): ||х||< 1}.
Другим.н словами, если функционал ф не является ограниченным, то в любой

138 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
окрестности нуля он принимает всякое значение. Рассмотрите пример: сово-
совокупность дифференцируемых функций на отрезке [—1, 1]- наделяется hodmoh
||/||= max \f\ и берется функционал ф, где q>(/) = f @).
Лемма 4.1. Каждый линейный непрерывный функционал одно-
однозначно с сохранением нормы продолжается на пополнение прост-
пространства.
Доказательство предоставляется читателю. В дальнейшем мы
будем иметь дело только с линейными непрерывными функцио-
функционалами. Эпитеты «линейный» и «непрерывный» для краткости будут
опускаться. Кроме того, ввиду леммы 4.1, область определения Б
можно считать банаховым пространством.
Обилие запаса функционалов обеспечивается следующим фун-
фундаментальным фактом.
Теорема 4.1 (теорема Хана —Банаха). Пусть ф — функцио-
функционал, заданный на (замкнутом) подпространстве F пространства В.
Тогда существует такой функционал ^ на В, что сужение 1|э HaF
совпадает с ц> и ||гр|| = ||ф||.
Доказательство. Наметим основные пункты доказатель-
доказательства.
Предположим сначала, что /( = R. Допустим для простоты,
что || ф || = 1. Пусть х0 ф F. Попытаемся продолжить функционал ф
с подпространства F на подпространство Fx векторов вида %х0 -f x,
где x^F, с таким" расчетом, чтобы сохранить норму функцио-
функционала. Продолжение полностью определяется заданием числа
с = ф(дг0). Норма будет сохранена в том и только в том случае,
если для любого x&F
Это неравенство эквивалентно тому, что для любых х{,
- ф (х2) -1| х„ + х21| < с < - ф (дг2) +1| х0 + л?! ||.
Поэтому выбор числа с, обеспечивающий сохранение нормы, воз-
возможен, если
ф (Jfx) - ф (ЛГа) < | *„ + *111 +II *0 + *2 II-
Но последнее неравенство действительно выполняется!
Ф(*i)-Ф(*а)*?IФ(*i-*2)l *?||ф|Ц|*1 -*il-
+ ) + (— Ч - Х0) || < || Х0
Если F{ исчерпывает все В, то доказательство закончено, В про-
противном случае к Ft добавляется вектор х2 ф Fx и т. д. Аккурат-
Аккуратное завершение доказательства требует привлечения некоторых
специфических теоретико-множественных соображений, связанных
с аксиомой выбора, на которых мы останавливаться не будем.
Вместе с тем, случай поля К = С просто выводится из K = R.

§ 4] ФУНКЦИОНАЛЫ И СОПРЯЖЕННЫЕ ПРОСТРАНСТВА 139
Если ф (*)= а (х) -f- ф (*) — разложение ф на вещественную и мни-
мнимую компоненты, то, как легко видеть,
причем а и р — вещественные функционалы на F. Теперь надо
продолжить функционал а на Б с сохранением нормы и восста-
восстановить ty no этому продолжению в соответствии с формулой
Ф (х) = а(х) — ia{ix). Мы предлагаем читателю восполнить детали.
Теорема 4.2. Для любой точки дгоеБ
]Хо ||= SUp |q>(*o)|.
||ф||<1
Более того, существует такой функционал ф0, что [| ф01 = 1 и
)Н111
Доказательство. Очевидно, достаточно установить второе
утверждение. Рассмотрим подпространство F в В, состоящее из
векторов вида Хх0. Если на этом подпространстве задать функ-
функционал ф формулой ф(^дг0) = Л, ||лг01|, а затем продолжить его на Б
в соответствии с теоремой 4.1, то мы и получим искомый функ-
функционал ф0.
Следствие. Если хфу, то для некоторого функционала ф
имеем ф (дг) Ф ф (у).
Последнее предложение означает, что функционалы образуют весьма обшир-
обширное семейство функций на В. Семейство функций {функционалов), разделяю-
разделяющее в указанном смысле точки пространства, называется тотальным.
Задача. Построить примеры, показывающие, что продолжение функ-
функционала, указанное в теореме Хана —Банаха, вообще говоря, не единственно.
Задача. Пусть Г —единичная окружность | г | = 1. В пространстве С (Г)
всех непрерывных функций на Г рассмотрим подпространство F функций,
допускающих аналитическое продолжение в круг |z[<l. Доказать, что F —
замкнутое подпространство в С (Г). Определим на F функционал ф, полагая
Ф (f) ==f @). Показать! что |ф|=1. Пусть г|з —продолжение функционала ф
с F на С (Г), построенное с сохранением нормы. Используя тот факт, что
г1>A)=1 и ||г|з||=1, показать, что г|з{fK= 0, если f <=?(Г) и f 3=0. Вывести
отсюда, что
(т. е. продолжение единственно).
В ряде случаев полезно и важно знать, как устроены про-
произвольные линейные непрерывные функционалы на данном про-
пространстве. Особенно важен случай гильбертова пространства, и
в этом случае ответ оказывается особенно простым и красивым.
Теорема 4.3 (теорема Ф. Рисса). Всякий линейный непре-
непрерывный функционал ф на гильбертовом пространстве Н имеет вид
Ф (дг) = (дг, а),
где элемент а^Н определен однозначно. При этом ||ФJ = ||я||.

140 АБСТРАКТНЫЕ ПРОСТРАНСТВА {ГЛ. I
Обратно, если а — произвольный вектор из Н, то данная формула
задает функционал.
Доказательство. Однозначная определенность по ср эле-
элемента а&Н, утверждение о норме, а также последнее утверж-
утверждение вытекают из общих свойств скалярного произведения (нера-
(неравенства Коши —Буняковского). Основное в теореме — доказать
существование вектора а.
Пусть L — ядро функционала ф, т. е. совокупность тех д-еЯ,
для которых ф(д-) = 0. Ясно, что L есть замкнутое подпростран-
подпространство в Я. В соответствии с теоремой 3.4 представим Я в виде
Z-фМ, где М — ортогональное дополнение. Легко видеть, что
dimM=l (подпространство М одномерно). Действительно, пусть
еи г,еМ. Тогда ср(е2)е1--ср(е1)еге=?ПМ = {0}.
Пусть теперь ееМиф(в) = 1. Любой вектор ^еЯ, согласно
теореме 3.4, представим в виде x-=z-\-Xe, где zeL, При этом
Ф (х) = Ф (г) + Яф (е) = I. Поэтому (х, е) = (г, е) +1 (е, е) = ц> (х) \\ef,
так что
Ф (¦*•) = (*, а),
где ¦ а.= ур-. Теорема доказана.
Совокупность (линейных непрерывных) функционалов на дан-
данном пространстве В превращается "в линейное пространство, если
операции в нем определить соотношением
^ (х).
Далее, очевидно, что норма функционалов удовлетворяет усло-
условиям
— нулевой функционал, т. е. ф (.*¦) = 0 при всех л-eS.
Таким образом, указанная совокупность сама' становится линей-
линейным нормированным пространством. Это пространство обозна-
обозначается через В* » называется сопряженным к пространству В.
Теорема 4.4. Пространство В* полно.
Доказательство. Пусть {ф„} — фундаментальная последо-
последовательность элементов из В*. Заметим, что 8ир||фя||<оо. При
п
каждом хеВ числовая последовательность фп(х) в силу нера-
неравенства
I ф« (X) - фот (X) | = | (ф„ - фот) (X) | < || ф„ - фот I • || X ||
оказывается фундаментальной. Поэтому существует предел
Ф (х) = \\т ф„ (х).
п-»оо
Ясно, что |<p(x)|sS(sup||<pJD-||x||. Поэтому феВ*. Далее, так
как последовательность {фл} фундаментальна, то для всякого
е>0 существует такое N, что ||фя —фот|]<е при п, m>N. Если

§ 4] ФУНКЦИОНАЛЫ И СОПРЯЖЕННЫЕ ПРОСТРАНСТВА 141
теперь ||д:||<1, то
|(ф-срл)(*)|= Нт |(фт-фл)(х
т. е. ||ф — фл||^е при n>N. Теорема доказана.
Заметим, что полнота пространства В здесь не использовалась;
важно лишь то, что полно К-
Поскольку В* само представляет собой банахою пространство,
мы можем построить пространство (В*)*, которое обозначается В**
и называется вторым сопряженным к В. Процесс можно продол-
продолжить и дальше.
Имеется естественное взаимно однозначное линейное и изомет-
изометрическое отображение пространства В в В**. Именно, всякий
элемент яеВ задает функционал fx на В* по формуле
Ыф)=ф(*)-
Линейность и взаимная однозначность отображения x-*-fx оче-
очевидны, а то обстоятельство, что ||/*|| = ||я||, вытекает из теоремы 4.2.
Вообще говоря, функционалами вида fx, *еВ не исчерпывается запас
всех функционалов на В*. Если же это происходит, то пространство В назы-
называется рефлексивным.
Следующая теорема непосредственно вытекает из теоремы Рисса (тео-
(теорема 4.3).
Теорема 4.5. Гильбертово пространство рефлексивно. '
Определение. Последовательность <р„еВ* слабо сходится
к функционалу феВ*, если
Ф (х) = Нт <р„ (х)
л-»оо
для любого xeS.
Последовательность <рл е В* называется слабо фундаментальной, если каж-
каждая из числовых последовательностей срл(х), «еВ является фундаменталь-
фундаментальной. Наконец, последовательность ф„.е В* называется слабо ограниченной, если
каждая из числовых последовательностей |фл(*)!> *бВ ограничена.
Говорить о слабой ограниченности имеет смысл для любого семейства
функционалов (не обязательно последовательности).
Если фл слабо сходится к ф, то мы будем писать фп"йГФ-
Если фл-*-ф в том смысле, что ||фл — ф|-*-0, тофл-^*ф, посколь-
поскольку I (Фп — Ф) (*) I ^ II Фл — ФIIII *!• Обратное, вообще говоря, неверно.
Пусть, например, {еп} — бесконечная ортонормированная система
в гильбертовом пространстве Н. Положим фл (х) — (х, еП). Тогда,
как это вытекает из неравенства Бесселя, фЛ"^, но || ф„ || = 1.
Задача. Доказать, что если {фл} — такая последовательность функцио-
функционалов в гильбертовом пространстве, что фл—» ф и (|фя!|—*||ф||> то |]фп — ф||—>О.
Хотя сильная сходимость (т. е. сходимость по норме) функционалов не
вытекает из слабой, последний вид сходимости интересен сам по себе. Кроме

H2 АБСТРАКТНЫЕ ПРОСТРАНСТВА (ГЛ. !
того, существует простая связь иежду сильной и слабой ограниченностью.
Следующая теорема легко вытекает из леммы о бочке.
Теорема 4.6. 1) Если семейство Ф функционалов на банаховом про-
пространстве В слабо ограничено, то оно ограничено и по норме. 2) Если после-
последовательность {ф„} слабо фундаментальна, то она слабо сходится (прост-
(пространство В* слабо полно).
Говорят, что последовательность элементов х„^В слабо схо-
сходится к элементу хеб, если ср (хп) -*¦ <р (х) для любого ере В*.
Аналогично определяется слабая ограниченность, слабая фундаменталь-
фундаментальность и слабая полнота в пространстве В.
Замечание. Таким образом, в пространстве В* имеется
два различных (вообще говоря) вида слабой сходимости, и сле-
следует соблюдать осторожность, не допуская здесь путаницы!
Сформуляруем еще несколько утверждений, касающихся слабой сходимо-
сходимости (и ограниченности). Читатель может рассматривать их как набор упраж-
упражнений.
1) Есля семейство X элементов пространства В слабо ограничено, то оно
ограничено по норме. Для доказательства можно воспользоваться описанным
выше вложением пространства В в В** и теоремой 4.6.
2) Последовательность элементов % е В может оказаться слабо фунда-
фундаментальной, но не слабо сходящейся.
3) Пусть В — сепарабельное банахово пространство. Тогда из каждой огра-
ограниченной последовательности ф„ е В* можно выделить слабо сходящуюся
последовательность.
4) Согласно теореме Рисса, гильбертово пространство рефлексивно. Два
вида слабой сходимости на сопряженном пространстве совпадают. Но и само
гильбертово пространство (по той же теореме Рисса) можно отождествить
с сопряженным. Поэтому гильбертово пространство слабо полно и из каждой
ограниченной последовательности элементов (сепарабельного гильбертова про-
пространства) можно выделить слабо сходящуюся подпоследовательность.
5) Пусть последовательность элементов хпе В ограничена по норме и
Ф (хп) — Ф (*) Для любого ф из плотного в В* множества. Тогда хп слабо схо-
сходится к х.
§ 5. Линейные операторы
Пусть Вх и В2 — банаховы пространства^ Линейным оператором
называется отображение А : DA -*¦ RA, осуществляющее гомомор-
гомоморфизм линейного многообразия DA cz Вх в линейное многообразие
RAaB2. Многообразие DA называется областью определения опе-
оператора А, а многообразие RA —областью значений. Говорят, что
оператор А непрерывен в точке x^DA, если
(хп -*¦ х и хп е= DA) => (Ахп -у Ах).
Как и в случае линейных функционалов, легко проверяется,
что непрерывность оператора (слово «линейный» мы будем опус-
опускать) А в точке 0 влечет за собой его непрерывность в каждой
точке x^DA. Величина
ЦЛ||= A!

§ 5] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 143
называется нормой оператора А. Если |]Л||<оо, то оператор
называется ограниченным. Снова, как и для Линейных функцио-
функционалов, ограниченность оператора эквивалентна его непрерывности.
Имеет место следующая теорема (аналогичная лемме 4.1).
Теорема 5.1. Каждый ограниченный оператор A: DA-*~RA
однозначно, с сохранением нормы, продолжается до оператора
с областью определения DA. В частности, если DA плотно в Вь
то А продолжается до ограниченного оператора A' :Bl-*-Bi.
Ограниченные операторы А с областью определения Da — B^
мы будем называть гомоморфизмами из В1 в В2. Множество всех
гомоморфизмов обозначается через Нот(Вх, В2), а в случае,
когда В1 — В2 = В, — через Ор (В).
Замечание. Теорема, аналогичная теореме Хана —Банаха, для опера-
операторов, вообще говоря, не выполняется.
Всюду в дальнейшем (если специально не оговорено против-
противное) предполагается, что Da плотно в Вх.
Пример. Пусть Q — замкнутая область в R", U a Q — откры-
открытое ограниченное множество в R" и ф — непрерывная функция
на Q с носителем, содержащимся в U. Обозначим через ф опе-
оператор <р:Ь2(?1)-+Ь2(&), где L2 (Q) — линейное многообразие всех
непрерывных функций из L2(Q), ?2(Q) cL2(fi), действующий по
формуле
Оператор ф ограничен: ЦфЦ^тах | ф(д-) |. Следовательно, он
может быть продолжен до гомоморфизма L2(Q)->-L2(Q), который
мы снойа обозначим символом ф.
Будем говорить, что элементы fug пространства L2 (Q) сов-
совпадают на открытом множестве U, если ф/ = ф# для любой непре-
непрерывной функции ф с носителем, содержащимся в U. Будем гово-
говорить, что элемент feJL2(Q) непрерывен в точке д-0, если сущест-
существует функция geL2(Q), с которой f совпадает в некоторой
окрестности точки х0. При этом положим f (xo)^g(xo). Предо-
Предоставляем читателю убедиться в том, что /(*„) не зависит от
выбора функции g.
Теория линейных неограниченных операторов в банаховых
пространствах имеет важные приложения при изучении общих
свойств линейных дифференциальных уравнений. Приведем при-
примеры неограниченных операторов.
Пример. Пусть Т — оператор дифференцирования в про-
пространстве L2 (Q), где Q == [0, л], определенный на множестве DT.
непрерывно дифференцируемых функций на [0, л] (плотном
в L2(Q), поскольку любую непрерывную функцию на [0, я]

144 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ.
можно с заданной точностью аппроксимировать многочленом!
равномерно, а значит, и по норме пространства L2). Рассмотрим?
последовательность {ф„}:
у -|
я
2 f*
функций из DT. Имеем |] фд |]2 = — Д sin2 nxdx = 1. Щи этом
п
|Гф„|2 =2~- \ cos2nxds = n2. Поэтому
п-*оо ИфпИ
т. е. оператор Т неограничен.
Пример. Пусть S — линейное многообразие в Lg(R), состоя-
состоящее из всех бесконечно дифференцируемых функций ф, удовле-
удовлетворяющих условию: для любых целых неотрицательных тип
Множество S плотно b\L2(R), так как Cj°(R)c:S.
Пусть Т : S-*-L2 (R) — оператор умножения на независимую
переменную: Tf(x) = xf(x). Рассмотрим последовательность {ф„}:
Вычислим ||ф„| и |Тф„|. Имеем
— 00 —00
00 СО
— 00
Таким образом, оператор Т неограничен:
Определение. Оператор Т : Dr-»-В2 называется расшире-
расширением оператора A\Da-*-B%, а оператор А —сужением опера-
оператора Т на множество Da, если DaCzDt и Ах=Тх для любого
x<=DA.
Неограниченный оператор А, в отличие от ограниченного,
вообще говоря, не допускает естественного расширения до опе-
оператора, определенного на Da- Тем не менее, для некоторого

§ 5] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 145
класса неограниченных операторов существует процесс, анало-
аналогичный процессу расширения операторов по'непрерывности, и
мы опишем этот процесс, введя необходимые определения.
Определение. Оператор А называется замкнутым, если
(gn^g и %-*-/1)=>(?еОл, Ag-h).
Ясно, что ограниченный определенный на всем пространстве
оператор замкнут (ниже мы покажем," что верно и обратное).
Оказывается, не всякий оператор допускает хотя бы одно замк-
замкнутое расширение. Однако, если такие расширения существуют,
то среди них имеется наименьшее, которое мы теперь и опишем.
Рассмотрим оператор То :Dro-*-B2, DTtczBlt допускающий неко-
некоторое замкнутое расширение 7\. Пусть g^Bt есть предел после-
последовательности {gn} элементов из Dr0, для которой lim Togn=sh,
ЛеВ2. Тогда, по определению замкнутого оператора, T1gr = A.
Таким образом, g принадлежит области определения любого
замкнутого расширений оператора То. Обозначим через Т суже-
сужение оператор а. 7\. на множество
Элемент g принадлежит DT тогда и только тогда, когда сущест-
существует такая последовательность gn^Dr^ что g = \\mgn и сущест-
существует предел lim Tugn. Оператор Т замкнут. Действительно, пусть
п-юо
gn^>-g, gn^DT, и lim Tgn = h. Тогда для любого п существует
П-*0О
такая последовательность {gin)} элементов из пт„, что
№?-*.!<г пвГ-Ы<т-
Рассмотрим диагональную последовательность Ып">|. Имеем!
[g^-sl^i+^Sl^O при л-*со
^ hl^O при «-»-а>.
Таким образом, g^DT, что и требовалось доказать. Очевидно,
Т является наименьшим замкнутым расширением оператора То]
Определение. Наименьшее замкнутое расширение ^опера-
^оператора Т, если оно существует, называется замыканием этого one.
ратора и обозначается через Т.
Теорема 5.2. Оператор А имеет замыкание А тогда и
только тогда, когда (gn-*-0 и Agn-*-h).^>(h = 0).
Доказательство. Необходимость очевидна, так как если
А — замыкание оператора A, gn->-0 и Agn-+h, то h = A~0 = 0.

H6 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
Докажем достаточность. Пусть (ga-*~0 и Л?„-* Л) => (Л = 0);
построим А. Область определения оператора А должна состоять
из пределов таких последовательностей {gn} элементов из Da,
для которых последовательность {Agn} фундаментальна. Если
g^Dj и gn^g, Agn-^h, gn(=DA, то положим Ag = h. Это
определение не приводит к противоречию, ибо если /„-»-?,
Afn-*-h', fne=DA, то gn — fn-*~O, A(ga-fn)-+h — h', и следова-
следовательно, по условию теоремы, h = ti. Доказательство замкнутости
построенного оператора А совпадает с приведенным выше дока-
доказательством существования замыкания оператора, имеющего замк-
замкнутые расширения.
Нетрудно заметить наличие тесной связи между процессом
пополнения нормированного пространства и процессом замыка-
замыкания оператора.
Теорема 5.3. Оператор A:Da-*~B2, Da^Bi замкнут
тогда и только тогда, когда пространство В а, состоящее из эле-
элементов g^DA с нормой
^ E.1)
полно.
Доказательство. Пусть оператор А замкнут. Рассмотрим
последовательность {gn}, фундаментальную в В а'.
при т, n>N(e).
Из E.1) следует, что при т, n>N(e)
и
В силу полноты пространств Вх и В2 последовательности {gn} и
{Agn} имеют пределы g^Bt и h^B2, причем h = Ag, так как
оператор А замкнут. Следовательно, g е В а', кроме того, при п -*¦ оо
Обратно, пусть пространство ВА полно. И пусть gn-*-g^B-i_,
Agn-^h. Докажем, что h = Ag. Из E.1) следует, что последова-
последовательность {gn} фундаментальна в В а- В силу полноты простран-
пространства В а существует такой элемент fefl^, что | / — gn | в^-*¦ О
при л-»-оо. Так как \\f-gn\\Bl <||/—gnUA, T0 gn-^f по норме
пространства Въ так что f = g. Из E.1) следует, что \Agn—.
— Ag\\->~0 при n-»oo, т. e. h = Af — Ag, что и требовалось
доказать.
Пример. Приведем пример оператора А, не имеющего замы-
замыкания. Пусть А действует из LJ0, 1] в L2[0, 1] и пусть DA =
= С[0, 1] есть множество всех непрерывных функций на [0, 1].
Положим Ag = g(l), так что оператор А каждой функции из

§ 5] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 147
С [0, 1] ставит в соответствие постоянную функцию. Рассмотрим
последовательность {#„}, где #„(*) = *". Имеем
V2n+1
•О
при п-*-оо. Вместе с тем fl4gn|| = 1, и условие теоремы 5.2 не
выполнено.
Теоремы 5.2 и 5.3 приобретают геометрическую наглядность,
если ввести понятие графика оператора.
Рассмотрим оператор AiDA^>-RA, где DAczBt и ЯдсВа-
Произведение В = В1хВг, наделенное нормой |(*х, *2)||2 = |l-*iisi +
+ |дг2|в2, является банаховым пространством (докажите). Графи-
Графиком GA оператора А называется линейное многообразие в В:
Ясно, что GA не содержит элементов вида @, *2), где х2ф0.
Обратно, если G а В таково, что в нем нет- элементов вида
(О, *2) с *2 ф О, то G есть график в точности одного оператора.
Теперь легко убедиться, что оператор А замкнут тогда и
только тогда, когда его график GA есть замкнутое подмножество
в В (теорема 5.3). Далее, условие теоремы 5.2 тогда и только
тогда выполняется для оператора А, когда замыкание GA гра-
графика этого оператора есть снова график, т. е. не содержит эле-
элементов вида @, ж2) с Хъ Ф 6. При этом А есть оператор с графи-
графиком GA (т. е. GA = GA).
Хотя нашей главной целью является изучение произвольных
(неограниченных) операторов, мы приведем здесь ряд необходимых
для дальнейшего фактов, касающихся ограниченных операторов.
Теорема 5.4 (Теорема Банаха). Пусть Вх и В2 — банаховы
пространства. Если A i Вх-^-В^ —ограниченный оператор, для
которого DA = BX и RA — Bit причем ядро оператора А (т. е.
совокупность тех х^Ви для которых Ах = 0) не содержит нену-
ненулевых элементов, то естественно определенный обратный оператор
А'1: Въ-+Ву является также ограниченным.
Доказательство. Пусть Уц— шар в В,с центром в нуле
и радиусом N, a W^ — образ Vn при отображении А. Покажем,
что хотя бы для одного натурального N множество Wn (замыка-
(замыкание WN) содержит некоторый шар из В2. Предположим, что это
не так. Пусть ^ — произвольная точка из В2 и ?/х — шар некото-
некоторого радиуса гх с центром в точке уг. В шаре иг найдется точка
у2 из CWlt а так как CW^ — открытое множество, то и целый
шар U2 с: CWt с центром в у2 и радиусом /-2. Продолжая это
рассуждение, построим последовательность вложенных шаров
Ux з U2 -z>... zd UN zd ...

148 АБСТРАКТНЫЕ ПРОСТРАНСТВА . [ГЛ. I
с центрами в точках уг, у2, ..., Уы и радиусами rt, r2, ..., rN,,..,
причем
UN+1 с CWN.
Можно считать, что последовательность шаров {UN} выбрана так,
что Пш гп — 0. Тогда последовательность . {yN} фундаментальна,
так как \yN — yN^p\<~rN для любого /?>0. В силу полноты
оо
пространства В2 существует Нт «/#=«/• Очевидно, что г/е П Un-
ОО 00 ОО '
Но П UNcz П CWN=0, так как U' ^лг — As- Полученное
противоречие доказывает утверждение.
Итак, пусть WN содержит шар ?/ = {г/.еВ2, \ч — Уй\<г}\
иными словами, для любого г/е U и любого б>0 найдется такая
точка jcg61( что ||лг||<;# и |Ах — г/||<6. ?сли г — произвольная
точка из В2, то точка г/— 2|Гг., z-\-y0 принадлежит U. Следова-
Следовательно, для любого zeB2 и любого б >0. найдется такая точка
х е Vjf, что
Так как Ах+уо = А(х+хо), где хо = А 1у, то отсюда следует,
что для любого г/ е В2 и любого б > 0 найдется такое х е Вь что
и \\Ax-yl<8.
Пусть е = ^]е„, где е„>0. Мы можем последовательно под-
1
бирать такие хъ ..., *„, ;..efli, чтобы
1-1'
Рассмотрим ряд 2*'* Так как 21^1<о°' то РЯД сходится
к элементу хеВг При этом |^|<^ ||^|<[|1j/|| + 6] 2(А/^

§ 5] ' ЛИНЕЙНЫЕ ОПЕРАТОРЫ '49
и Ах —у. В силу произвольности е отсюда следует, что ЦЛ!^
*= ЦЛЩЫИ. Теорема доказана.
Следствие (теорема о замкнутом графике). Если оператор
A: Bi-*-B2 с DA = Bi имеет замкнутый, график (оператор зам-
замкнут), то он ограничен.
Для доказательства достаточно применить теорему 5.4 к опе-
оператору (дг, Ах)^>-х, (х, Ax)<=GA, x<=Bv Поскольку GA замк-
замкнуто, этот оператор определен на банаховом пространстве GA,
очевидно, непрерывен и взаимно однозначно отображает прост-
пространство GA на В%. По теореме 5.4, обратный оператор х-*-(х, Ах),
а с ним и оператор Л, непрерывен.
Множество Нот (Въ В2) становится линейным пространством,
если линейные операции в нем определить следующим образом:
для любых векторов х е Вх и скаляров К. Легко видеть, что
fT'i + T'ijI^IJT'il + llT'al и И^ЛЫ^ЧИЛ!- Кроме того, если ||Г| = О,
то Г —нулевой оператор, т. е. Тх = 0 для всех х^.Вг (этот опе-
оператор есть нулевой элемент линейного нормированного прост-
пространства НоггЦВл, В2)).
Учитывая, что доказательство полноты сопряженного прост-
пространства использовало лишь полноту области значений, и приме-
применяя то же рассуждение, мы получаем следующий результат:
Теорема 5.5. Если В?, —банахово пространство, то прост-
пространство Нот (Въ В2) полно при любом линейном нормированном
пространстве Bt.
Говорят,, что последовательность {Тп} операторов (из Вг в В2)
сильно сходится на множестве D с: Ви если D с: DTn для всех п
и при любом х е D последовательность элементов Тпх сходится
в пространстве В2 по норме.
Следующая теорема полезна в приложениях, ее доказатель-
доказательство весьма-просто получить, применяя лемму о бочке, и мы
снова ограничимся формулировкой.
Теорема 5.6 (Теорема Банаха—Штейнгауза). Пусть Л„е
е Нот (Въ В2) — такая последовательность, что
1) sup || Л„||<;оо,
2) на некотором плотном в Вг многообразии D последователь-
последовательность.А„ сильно сходится. Пусть далее Ах= Urn А„х, если x&D.
Тогда || Л | < со, оператор А допускает замыкание А е
е Нот (Ви В2) и последовательность А„ сильно сходится к А
всюду на Вг.
Задача. Можно ли в условиях теоремы 5.6 утверждать, что | Ап — А ||—»О?
Задача. Пусть Ф — такое семейство операторов из Нот (fit, B2), что
sup | Ax\\ = s (x) < со при любом х е Вг. Доказать, что sup | А|| <оо.
А5Ф А € Ф

150 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. Г
Пусть reHom(Blt Въ). Если ф —линейный функционал на
52, т- е. ф s^a. то формула
определяет функционал на Bj. Тем самым задано отображение
Г*: В}-»-В?. Очевидно, что Т* <= Нот (В?, B\). Так как
|(Г*ф).(^I = 1ф(Гд:)|^|Г|-||ф||-||д:|, то ||Г*|^|Г|. С другой
стороны, по теореме Хана —Банаха, для любого лгеВх сущест-
сущестй ф [|||1 \Т\ )
р, р х у
вует такой функционал фое5а, [|фо||=1, что \Тх\ = щ(Тх).
Поэтому \Тх\ = щ(Тх) = (Т^(х)^\Т*\-\х\- и ||r||<||7*||.
Таким образом, |] Т* || = |] Т |.
Пусть В1 — В2 — В. Напомним, что Нош (В, В) мы обозначаем
через Ор(В). Пространство Ор(В) обладает естественной струк-
структурой алгебры: если 7\, Г2е0р(В), то, по определению,
(T1Ti)(x) = T1(T2x), xe=B. Очевидно, что
Последнее означает, что Ор (В) является банаховой алгеброй
(подробнее о банаховых алгебрах см. в § 9).
Если ГеОр(В), то Г*<=Ор(В*). При этом (Г1Г2)* = Г|П
для любых Гь Г2<=Ор(В).
Оператор Т <= Нош (Ви В2) называется компактным (или
вполне непрерывным), если из любой последовательности вида Тх„,
где ||*я||^1, можно вкбрать сходящуюся подпоследовательность.
Задача. Если {71*} — последовательность компактных операторов и
|| Г — Г^Ц—»0, то Г — компактный оператор.
Задача. Оператор Т называется вырожденным, если многообразие
Т (Вх) с: Ва конечномерно. Доказать, что каждый вырожденный оператор явли-
ется компактным.
Задача. Оператор 7'еОр(Я), где Н — гильбертово пространство, тогда
и только тогда является компактным, когда он есть предел последовательности
вырожденных операторов.
Задача. Оператор Т е Нот (Bi, Ba) тогда и только тогда компактен,
когда компактен оператор Г* eHom(Bjjf, fif).
Задача. Компактные операторы образуют (замкнутый) двусторонний
идеал в алгебре Ор (В): если Т — компактный оператор, a SsOp(fi), то опе-
операторы TS и ST компактны.
Введем некоторые понятия, относящиеся к алгебре Ор (В).
Оператор Т е Ор {В) называется обратимым, если существует
такой оператор S е Ор (В), что TS = ST=\, где 1 означает
тождественный оператор. Оператор S в этом случае называется
обратным к Т и обозначается через Т~г.
Задача. Обратимость оператора Т эквивалентна обратимости опера-
оператора Т*.
Совокупность обратимых операторов образует группу, которая
обозначается через GL(B).

§ 5] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 151
Лемма 5.1. Если Т = 1-А, где ||Л||<1, mo T<=GL(B).
• со
Доказательство. Ряд ? Ак в силу условия |А|< 1 схо-
о
00
дится. Очевидно, что оператор S — ^A* служит обратным к Т.
о
Кроме того, мы получаем || Г!^ 1/A —1| А ||), так что Т'1-*-!,
если Г->-1.
Из леммы 5.1 вытекает, что оператор, близкий к обратимому,
обратим. Действительно, пусть T^GL(B) и S = T — А. Тогда
при ЦЛЦхСЦГ-1!-1 имеем \Т1А\<1, так что A -Г1 A) <=GL(B),
и можно записать
S = (Т - А)'1 = Г'1 A — Т-М).
Спектр в(Т) оператора ГеОр(В) по определению состоит
из тех ^еС, для которых К — T<?GL(B). Оператор RKM(K —
— Т)'1 для точек Хфа(Т) называется резольвентой оператора Т.
Из леммы 5.1 и следующего за ней замечания вытекает, что
С\(г G) — открытое множество и что функция X^-Rx непрерывна
на этом множестве. Более того, эта функция является аналити-
аналитической в том смысле, что существует предел lim ( К+НГ~ (рав-
(равный - /??). Если | К |-> | Т\, то К ф а (Т); так как тогда | Т Ц/| \ \ <
<1 и
Кроме того, ясно, что ||#»,||->--0 при | Я. | —>-оо.
Из этих замечаний легко вытекает следующая важная теорема.
Теорема 5.7. Если Т<=Ор(В), то о (Т) Ф 0.
Доказательство. Пусть а(Г) = 0. Тогда функция /?Х
аналитична при всех X. Для любых дгеВ и феВ* числовая
функция f(k) = q>(Rxx) оказывается целой. Далее, \f(K) |^||/?jjx
х IIФII1 IIх1-*~ 0 nPh IM-^00- Согласно теореме Лиувилля, f(K) — O.
Сопоставляя это с теоремой Хана —Банаха, мы приходим к про-
противоречию.
Задача. а(Г*)=о(Г).
Если % есть собственное значение оператора Т, т. е. Tx = hc
для некоторого хфО, то, разумеется, Хеа(Г). Далее, если
существует такая последовательность j;,eB, что (|лг„||=1 и
Тхп — %хп^-0, то также %<=о(Т). В последнем случае говорят,
что X —почти собственное значение оператора Т.
Задача! Используя теорему Хана — Банаха и теорему Банаха о зам-
замкнутом графике, доказать, что включение X е а (Т) влечет за собой выполне-
выполнение (по крайней мере) одной из следующих возможностей: X — собственное

!52 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
значение оператора Т; к — почти собственное значение оператора Т\ % — соб-
собственное значение оператора Т*.
Сделаем несколько замечаний по поводу ограниченных операторов в гиль-
гильбертовом пространстве Н.
По теореме Рисса, существует отображение R-.H—H*, отождествляющее
пространства Н* и Н." Именно, если а е Н, то R сопоставляет этому элементу
функционал феЯ*, для которого ф (х) = (х, а). Это отображение аддитивно
и полулинейно, т. е. R (Ка) = \ (Ra).
Каждому оператору Т е Dp (Я) сопоставляется оператор R~XT*R, дей-
действующий в исходном пространстве Н. Этот оператор R~iT*R по традиции
также называется сопряженным к Г и обозначается тем же способом — че-
через Т*. . . ¦
Обычно эти обозначения не приводят к путанице, и мы будем их.придер-
их.придерживаться. Конечно, при их употреблении следует соблюдать известную осто-
осторожность. Главное, впрочем, заключается в том, чтобы не забывать, что вместо
формулы а {Т*) = а (Т) теперь имеет место а (Т*) — а(Т).
Ясно, что для сопряженного оператора теперь выполняется соотношение
- (Тх, у) = (х, Т*у), х, у<=Н,
которое [часто "принимается за определение оператора Т* (ниже этот способ
введения сопряженного оператора используется в более общей обстановке).
Опишем один важный класс компактных операторов гильбер-
гильбертова пространства.
Пусть Я —некоторое сепарабельное гильбертово пространство,
{е,} —полная ортонормированная система в нем и Т — ограничен-
ограниченный оператор в Н. Положим
Если ряд расходится, то полагаем [|Г||г = оо. Норма ||Т||г назы-
называется нормой Гильберта — Шмидта оператора Т.
Теорема 5.8. 1) |Т||г = |Т*Цг;
2) норма Гильберта —Шмидта не зависит от выбора полной
системы {е*};
)||И||П
4) если ||Т|г<оо и R—ограниченный оператор в Н, то
5) если |T|2<oo, |S||2<co, mo || 7 + S |, < 171|2 +1S ||2.
Доказательство. 1), 2) Пусть {е\} — еще одна полная
ортонормированная система в Н. Имеем:
», E.2)
где изменение порядка суммирования' законно, поскольку все
члены ряда неотрицательны. В частности, если ег'=е,-, то из E.2)
следует 1), а общий случай теперь дает нам 2).

, 51 ЛИНЕЙНЫЕ ОПЕРАТОРЫ 153
3) Учитывая 2), получим
< sup 2\u2i
1|И|| = 1(о=1 . «=1
4), 5) Эти утверждения очевидны. Теорема доказана.
Обозначим через В2 (Н) совокупность операторов, норма Гиль-
Гильберта—Шмидта которых конечна. Из теоремы следует, что В2(Н)
образует двусторонний (ие замкнутый) идеал в банаховой алгебре
Ор (Я)> Более того, справедливо следующее утверждение.
Теорема 5.9. 1) Пространство В2(Н) становится гильбер-
гильбертовым, если скалярное произведение задается формулой
(Г', S),-|(Teh Set), E.3)
причем (Т, S)i=*(S*, T*J.
2) Все операторы из В2 (Я) вполне непрерывны.
Доказательство. 1) Ряд E.3) абсолютно сходится в силу
неравенства Коши — Буняковского. Очевидно, (Т, S)t удовлетво-
удовлетворяет всем аксиомам скалярного произведения. Поэтому для него
справедливо тождество
(Т, SJ = |
+ i(\\T + iSiy-i(lT-iS\\^}. E.4)
Эта формула показывает,, что определение скалярного произ-
произведения не зависит от выбора системы {et}.
Теперь докажем, что В2 (Н) — полное пространство. Пусть
II Тп — Тт|2->0 при п, /п->-оо. По теореме 5.8 последователь-
последовательность \Т„) сходится в Ор (Н), т. е. существует оператор Т е Ор (Я)
такой, что ||7"я-Т||->0.
Пусть е>0. Для любого Л^ имеем
21 %Тя-Т
если п, m>/io(e). Переходя здесь к пределу при т->-оо, получаем
Отсюда следует, что (Тя-Т)еВ2(Я) и || 71» — 71 ||j < e при
n^sno(e), т. е. последовательность {Тп} сходится к Те В2(Н)
по норме Гильберта — Шмидта; формула (Т, SJ = (S*, T*J сле-
следует из E.4).

154 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
2) Определим конечномерный (вырожденный) оператор Тп ра-
равенствами: Trfii — Tei при 1<:П, Tnei = 0 при />л. Пусть е>0.
оо
Тогда существует такое N (в), что ? J71ei|8<e8 при n^N(&).
Поэтому
/ оо \1/2
\Тп-Т\^\\Тп-Т\Ы ? \\TeM <е.
Ч=п+1 I
Следовательно, последовательность операторов {Тп\ сходится к Т
по норме пространства Ор (Я), и поэтому оператор Т вполне
непрерывен. Теорема доказана.
§ 6. Сопряженные операторы
Введем сначала алгебраические операции над произвольными
(не обязательно ограниченными) операторами. Мы будем пользо-
пользоваться обозначением А : Вг -*¦ В2 для оператора, действующего
из пространства Вг в пространство Вг (вместо более громоздкого
обозначения А : DA-*-Bit DA с: Bi).
Определения. Суммой операторов Аг: Bi-»- B2 и А2: Вг-^Вг
называется линейный оператор А = Аг + А2 с областью определе-
определения DA = DAt П ^а„ действующий по формуле
Ах — AtX + А2х.
Произведением, или композицией операторов А\: Вх -*¦ В2 и
Ач'.Вг-^В3 называется оператор А: Вг-*-В3, определенный во всех
векторах x<=Dau для которых Ax^DAl, и действующий по фор-
формуле
Ах=
Произведение операторов Ах и Л2 записывается в виде A2Ai.
Произведение оператора А на себя п раз называется степенью опе-
оператора и обозначается Ап.
Произведением ХА оператора А:В1-*-В2 на (комплексное) чис-
число К называется оператор А': Вг-*- В2, определенный на DA и
переводящий вектор х в К • Ах.
Единичным, или тождественным оператором 1: В-*-В называ-
называется оператор, переводящий каждый вектор xefie себя.
Нулевым оператором 0:В1-*-В2 называется оператор, перево-
переводящий каждый вектор х е Вх в нулевой вектор пространства В2.
Если К — комплексное число, 1—единичный оператор, то мы
будем обозначать оператор М через X.
Обратным оператором А'1: В2 -> Вг к оператору А: Вх-*- В2
будем называть отображение Ra на DA, обратное к отображению

§6] СОПРЯЖЕННЫЕ ОПЕРАТОРЫ 155
A'.Da-^-Ra, если это обратное отображение существует. Опера-
Оператор Л, для которого существует обратный, будем называть
обратимым.
Совокупность тех х е В1г для которых Ах = 0, называется
ядром оператора А и обозначается Кег(Л). Ясно; что существова-
существование оператора Л (обратимость в смысле приведенного опреде-
определения) эквивалентна тривиальности ядра, т. е. тому, что
Кег(Л) = {0}.
Обозначим через & (Вь В2) множество всех линейных опера-
операторов, действующих из Вг в Вг. Операция сложения в @(В1г В2),
очевидно, коммутативна, ассоциативна и обладает нейтральным
элементом. Однако &(Ви В2) не является абелевой группой отно-
относительно сложения; это связано с тем, что общая область опре-
определения двух операторов не шире областей определения слагае-
слагаемых, в то время как нейтральный элемент — нулевой оператор
Q —определен на всем пространстве Вг. Тем не менее в 0(Ви В2)
вводят вычитание:
При этом оператор 0оА = А — А есть сужение нулевого опера-
оператора на DA.
По отношению к умножению на числа в & (Вг, В2) имеют
место ассоциативность
и оба свойства дистрибутивности:
Умножение операторов в ®(В, В) ассоциативно и обладает
нейтральным элементом 1; однако обратный элемент А'1 имеется
не для каждого оператора Ле0(В, В). Наконец, заметим, что
дистрибутивность умножения по отношению к сложению имеет
место в @(В, В) только в том случае, когда оператор умножа-
умножается на сумму двух других справа:
(Л! +Л2)Л = Л1Л^-Л2Л•
Фopмyлa А(А1-\-А2) = АА1-\-АА2, вообще говоря, неверна; чита-
читателю предлагается построить соответствующий пример.
Приведем некоторые результаты, касающиеся сохранения свой-
свойства замкнутости при алгебраических операциях над операторами.
Теорема 6.1. Пусть А : Вх-> В% — замкнутый оператор,
А' i Вг -> Вг — гомоморфизм, "К — комплексное число. Тогда опера-
операторы А-\-А' и %А замкнуты.
Доказательство предоставляем читателю.
Теорема 6.2. Пусть А: Вг-> В2 — обратимый (как оператор)
гомоморфизм. Тогда оператор А'1 замкнут.

156 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
Доказательство. Пусть уп<=В2, уп~*у при л->оо и
А~хуп-*-х при я->оо. Применяя к последнему соотношению гомо-
гомоморфизм А, получаем: lim yn = lim AA~1yn = Ax. Отсюда имеем
я-»оо л-юэ
у='Ах, х — А~ху, что и требовалось доказать.
Теорема 6.3. Пусть Аг:B1-^Bi — гомоморфизм, Аг\В2->В3—
замкнутый оператор. Тогда оператор А2АХ замкнут.
Доказательство. Пусть *„ е Вх и пусть lim хп = л:; кроме
того, пусть lim Л2Л1д:л = г. Тогда, в силу того, что Лх —гомо-
я-»оо
морфизм, имеем lim Лхл;л = Л1л:. Используя теперь замкнутость
л -» оо
оператора Аг, получаем соотношение lim А^Хп — АгАхх, и тео-
рема доказана.
Теорема 6.4.. Пусть А : В -> В — замкнутый оператор и
пусть существует такое комплексное число X, что (А + К)'1 есть
гомоморфизм. Тогда для уцрбого формального полинома Р/, (х) =¦
2 оператор Рk (А) замкнут.
/о
Доказательство. Прежде в'сего заметим, что всякий поли-
полином Р (г) можно представить в виде некоторого полинома Q (г + Я)
переменной г-f-A,. Так как оператор А + X замкнут, то" можно
без ограничения общности считать, что Я = 0, т. е. что А'1 есть
гомоморфизм.
Теперь проведем доказательство по индукции; предположим,
что для .любых комплексных чисел с0, ..., ск оператор ? CjA1
/=о
замкнут и докажем замкнутость оператора ^ С/А' Для любых
/=о
ft + i
комплексных с0, ..., сА+?. Пусть хп-+х, ^ с}А!хп-*-у. Приме-
/=о
ним к обеим частям последнего соотношения гомоморфизм А'1.
Получим:
lim { 2
+ СоЛ*»? = А
Так как хп-*-х и так как оператор 2 cj+i^ замкнут, то полу-
1 = 0
ченное равенство можно переписать в виде!

§6]
СОПРЯЖЕННЫЕ ОПЕРАТОРЫ 157
Применяя теперь к обеим частям оператор А, получаем
Л + 1
что и требовалось доказать.
Следствие. Пусть А: 5 -> В — оператор, допускающий замы-
замыкание А, удовлетворяющее условиям теоремы 6.4, Р — полином. Тогда
оператор Р (А) является замкнутым расширением оператора Р (А).
Пусть Вх и Ва — банаховы пространства, В* и В% — сопряжен-
сопряженные к ним пространства. Пусть далее T'.Dt-^B^, DrCiB1 —
линейный" оператор и пусть Dr^Bi. Обозначим через L мно-
множество всех функционалов g пространства В}, для которых
-<оо,
т. е. таких, для которых существует элемент / е В*, обладаю-
обладающий свойством:
g(Tx) = f(x) при всех x<=DT.
Функционал / определяется этой' формулой однозначно, так
как Г>т плотно в Bv
Определение. Оператор Г* :L->Bf, Lc:B|, заданный
соотношением
(T*g = f)^>(g(Tx)=f(x)) для любого x(=DT,
называется сопряженным к оператору Т.
Теорема 6.5. Пусть DT —область определения оператора
Т:ОТ-^В2, DraBi, плотная в Blt.u Rr~область значений.
Тогда следующие два утверждения эквивалентны:
а) /?т- = В2; б) (Г*? = 0)=>(? = 0).
Доказательство. Пусть RT — B2 и T*g = 0. Если y<=RT,
то найдется такое х, что у = Тх, так что
А поскольку Rt плотно в В2, то отсюда следует, что g = 0.
Обратно, пусть уравнение T*g = 0 имеет только нулевое реше-
решение. Предположим, что RT не плотно в В2; и пусть уеВ2,
УФ-Rt- Рассмотрим линейное многообразие GcB2, состоящее
из элементов и, представимых в виде и —ау-\-г, где г е Rt- Опре-
Определим на G функционал g при помощи формулы
Функционал g ограничен; действительно, предположив против-
противное, мы получили бы, что существует такая числовая последова-
последовательность . {а,} и такая последовательность {zy} элементов из RT,

158 АБСТРАКТНЫЕ ПРОСТРАНСТВА ГГЛ. Г
что limay- = oo и || a,*/ -|- Zj | ^ 1 для любого натурального /. Сле-
/ — от
довательно,
й
так что
что противоречит замкнутости множества RT. По теореме Хана —
Банаха существует такой функционал g<=Bt, что g(u) = g(u)
для любого иеб. Так как ^(Тх)=0 для любого *eDr, то
f*g = O. Отсюда по условию следует, что g = 0; но это противо-
противоречит равенству g (у) =*= 1, и теорема доказана.
Рассмотрим теперь случай, когда В1 = В2 = Н, где Я —гиль-
—гильбертово пространство; при этом каждый непрерывный линейный
функционал f на Н имеет вид f(x) = (x, yj), так что Я* можно
отождествить с Я. Пусть T\DT-*-H, Drcr Я —линейный опера-
оператор с плотной в Я областью определения.
Определение. Оператор Т называется симметричным, если
(ГФ, /) = (ф, Г/)
для любых cpeDr, feOr.
Очевидно, что если Т — симметричный оператор, то оператор Т*
является расширением оператора Т:
TczT*.
Теорема 6.6. Оператор Т* замкнут, В частности, симмет-
симметричный оператор допускает замыкание.
Доказательство. Пусть
gn-+g, F.1)
T*gn-+h F.2)
при л->оо. Покажем, что h = T*g. Для любого феО7 имеем
Gф, Я„)-(ф, Т*Ы- F.3)
Переходя в F.3) к пределу при л->оо, получаем
я) = («р, Л). F.4)
По определению оператора Т*, равенство F.4) означает, что
h= T*g, и теорема доказана.
Для симметричных операторов из теоремы 6.6. вытекает соот-
соотношение Т czT*.
Определения. Оператор Т называется самосопряженным,
если

§ 6] ' СОПРЯЖЕННЫЕ ОПЕРАТОРЫ 159
Оператор Т называется существенно самосопряженным, если
Т = Т*.
Последнее определение выделяет важный в приложениях класс
симметричных операторов, которые становятся самосопряженными*
после замыкания.
Задача. Доказать, что для оператора Т, допускающего замыкание,
Пример. Пусть ff = L2(R) и пусть оператор Т с областью
определения DT = C'^(R) действует по формуле Ty(x) = iy' (х).
Оператор Т — симметричный, так как для любых ср, /eC~(R)
G>Р, Л-
Ясно, что Т* есть расширение оператора Т. Докажем, что Т
не замкнут. Рассмотрим последовательность {/„} функций из
C~(R), сходящуюся к f = ^-^ в Г, (R):
здесь О «S а„ (х) < 1, а„ е Cf (R) и а„ (д:) = 1 при | х \ < п, причем
| а'п (х) | не превосходит константы с, не зависящей от п. Имеем
^р-^гdjf4-2c2 ^ fv,_Lni-»0 при л-уоо.
1*|>я
Итак, fn-*-f, Tfn-*-T*f, однако f&DT. Следовательно, Т не замк-
замкнут.
Задача. Показать, что оператор Т из примера является существенно
самосопряженным.
Теорема 6.7. Если AiDA->H, DAa H — самосопряженный
оператор, имеющий ограниченный обратный, то DAn = H при
любом натуральном п.
Доказательство. Согласно теореме 6.5, RA = H. Если же
|] Л1| < оо, то RA = H. Действительно, расширим А до гомо-
гомоморфизма F«Н -> Н. Тогда уравнение Ах —у имеет для любого
убй решение x — Fy, В самом деле, пусть {*/J—последователь-
{*/J—последовательность элементов из RA, сходящаяся к у. Тогда AFyt = AA~1yi = yi.

160 , АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
Из ограниченности оператора F следует, что Fyi-*-Fy, а из замк-
замкнутости оператора А следует,- что AFy = y.
, Итак, DA-i = H, откуда следует, что для любого натураль-
натурального п оператор А~п является гомоморфизмом #->#. Из сим-
симметричности оператора А легко следует симметричность опера-
оператора А~п, так что оператор А~п является самосопряженным.
Применяя теорему 6.5, получаем DA" = RA-n— н> чт0 и требо-
требовалось доказать.
§ 7. Функции со значениями в банаховом пространстве
Определения. Отображение
(к *„)- { '
будем называть функцией ф со значениями в банаховом пространстве В, опре-
определенной на множестве Q с: R".
Пусть ф—функция со значениями в В, определенная на Qc R", и пусть
t0—предельная точка множества Q. Если Цq>(^)—^fЦ —> 0 при t—>t0, то будем
называть g пределом и писать g = lim ф(г) (н пользоваться обычной термино-
терминологией, относящейся к пределам).
Функция ф со значениями в нормированном пространстве. В называется
непрерывной в точке (оей, если Ф @ —» ф(t0) при t—ta.
Пример. Пуйть (х, t) —> t|) (ас, t), x e R", / e R—такая комплексная
функция (т. е. функция со значениями в С), что при каждом фиксированном t
функция ф: х —»ij) (x, t) непрерывна н интегрируема с квадратом на R". Тогда
функцию ф можно рассматривать как функцию со значениями в Ц (R"), опре-
определенную на R.
Частной производной d(f(i)/dtj функции фсо значениями в В, определенной
в окрестности точки t e R", называется предел, если таковой существует,
ф(/1( .... tj_lt tj+Mj, tj+1 tn) — <p(f)
lim r-j :
Теперь мы дадим в удобной для нас форме определение интеграла от
функций со значениями в банаховом пространстве В. Начнем с функций, за-
заданных на компактном квадрируемом множестве QcR". Напомним, что мно-
множество Q называется квадрируемым, если по этому множеству можно брать
интеграл в смысле Римана от обычных числовых функций. В частности, Q
квадрнруемо, если Q —компактная область в R" с гладкой границей (и в даль-
дальнейшем можно иметь в виду только такие множества Q).
Исходным понятием мы считаем понятие интеграла Рнмана от числовых
функций. Если теперь и: Q —> В— функция на Q со значениями в В, а ф —
непрерывный линейный функционал на В, то при любом разумном определе-
определении интеграла \ и (t) dt должно выполняться соотношение
Последнюю формулу можно использовать для определения интеграла от
функции и U).

§ 71 ФУНКЦИИ В БАНАХОВОМ ПРОСТРАНСТВЕ 161
Определение. Интегралом (Римана) [ и (t) dt от фдАкции и: Я •
.В
называется такой элемент be В, что ф (&)¦» \Ф(и(/))dt для всех г|) еВ*.
й
Из теоремы Хана —Банаха следует, что элемент Ь, если он существует,
определяется однозначно, н весь вопрос состоит в выяснении существования.
Как и в случае числовых функций, интеграл, разумеется, существует не всегда.
Однако, как нетрудно видеть, он заведомо существует, если функция и (t) не-
непрерывна. На классе непрерывных функций и (t) интеграл обладает обычными
свойствами. В частности, | С и (Q dt II < \ || и (Q Ц dt. Далее, элемент Ь = \ и (t) dt
IIQ II о а
можно получить как предел рнмановых интегральных сумм: если е>0, а
Qj, ..., Qa—достаточно мелкое разбиение'-множества Q на квадрируемые
п
подмножества, то сумма ^ tt(<|)o(Q<), где /je Qit v (Q<)—объем Q<, отлн-
чается по норме от b не более чем на е.
Сформулируем одну теорему о переходе к пределу под знаком интеграла.
Теорема 7.1. 'Пусть {Тп} последовательность непрерывных на [а, Ь]
функций со значениями в банаховом пространстве. В, причем Tn(f)-*-T(t)
при п -*¦ со по норме пространства В для любого фиксированного t e [a, b],
и Т—непрерывная на [а, Ь] функция. Тогда, если \\Tn(t)\\^c, где с—некото-
с—некоторая константа, та
. г » ь
lim [
Класс интегрируемых функций можно существенно расширить (по срав-
сравнению с классом непрерывных функций), используя идею пополнения прост-
пространства. Именно, положим ||и||«= t||w(f)M*- Тем самым определена норма на
пространстве С (В, Q) непрерывных функций на Q со значениями в В.
Пополнение L (В, Q) пространства L (В, Q) называется пространством
функций, интегрируемых по Бохнеру на Q. В случае S«=R мы получаем,
в частности, класс функций; интегрируемых в смысле Лебега на Q.
Распространение понятия интеграла на класс некомпактных множеств Q
может происходить по следующей схеме. Мы предполагаем, что пересечение Q
с каждым шаром есть *квадрируемое множество. Пусть вначале и: Q-»-B —
непрерывная функция. Функция и называется интегрируемой, если для лю-
любого в > 0 существует такое с, что 1 ( и (t) dt У < е для всякого квадрируемого
II о. 'II '
подмножества QtcQ, лежащего вне шара радиуса, с. Если это условие вы-
выполнено, то \u(t)dt определяется как предел интегралов ( и (f) dt- при
„а • anwiKi)
е->со. В частности, все условия выполняются, если конечен несобственный
интеграл Римана f у и (f) | dt.
Определение. Пусть Q—квадрируемое множество в,R". И пусть
L(B, Q)—пространство непрерывных функций на Q со значениями $ В, обла-
обладающих конечной нормой Ци||«-j||«(Q||<#. Пополнение L(B, Q) этого про-
пространства называется пространством функций, интегрируемых по Бохнеру
на Q. При атом если
Q) и uk-t-v, где
6 В, П. Маслов

162 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. »
то lim \ иь @ dt существует и обозначается через \ v dt. Элемент \vdtsB
*-<*> й й й
не зависит от выбора последовательности и^.
Интеграл Бохнера обладает обычными свойствами абсолютно сходящихся
несобственных интегралов.
В заключение рассмотрим в качестве примера функции со значениями
в банаховом пространстве решение так называемого энолюцнонного уравнения.
Пусть А — оператор в гильбертовом пространстве Я н пусть и —функция со
значениями в Н. Эволюционным уравнением называется уравнение вида
^ + Ли«=0, OsS/sgr. G.1)
Мы будем рассматривать только непрерывно дифференцируемые решения
этого уравнения. Зададим начальное условие:
и@)-(г0с=Од. G.2)
Справедлива следующая теорема.
Теорема 7.2. Пусть для любого h из плотного е Н множества М
и любого отрезка [а, Ь] с [О, Т] существует такая непрерывная на [О, Т]
функция v со значениями в Н, что
do . t /a. f А при t e (а, Ь),
-ТГ — A*V{t)=*\ Н I • /» g дч
dt \ 0 при t ф (а, Ь), 0(Г)«=О, к '
еде А*—сопряженный к А оператор.
Тогда решение задачи Коши G.1), G.2) единственно.
Доказательство. Если функции и± и и% удовлетворяют одной и той
же задаче Кошн G.1), G.2), то разность и*»иг — и% удовлетворяет уравнению
G.1) и нулевому начальному условию и @)»0. Поэтому достаточно показать,
что задача
G.4)
I и@)«=0
имеет лишь нулевое решение. Пусть и — какое-либо решение задачи G.4). Обо-
Обозначим через o/i, а, ь решение задачи G.3). Тогда
6
(и@. *><«•
а
где (•, •)—скалярное произведение. Интегрируя по частям
г
dvh, а
™ dt
о
получаем
т
(Т), vh, a, b (Т))-(и @), Oft, a, b@))-
г г
- [(%, Ч. a,b(t))dt,- [ (^,

§ 81 АНАЛИЗ В БАНАХОВОМ ПРОСТРАНСТВЕ 163
Далее, пользуясь определением сопряженного оператора, можем записать;
г г
J(b(O, A*vhia,b{t))dt=\(Au(t),
Следовательно,
6 г
(«(О, А) Л— ? (^ + Ли@. о»>в.»@)л-0.
Пусть /0—произвольная точка нз [0, Т] н е —положительное число. Тогда
найдутся такие 6>0 иЛеМ, что ||и(<0) —А||<в и || и (/) — и (t0) || < е при
|f — *0|<б. Имеем при \t — to\<6:
(и @, А) - (в @ - в (/») + в (*„), А - в (ад + в (t0)) =
III " (<о) IIе—(" @. А) | < | (и @ — и (<о), Л)
Следовательно,
.2eBe[|u(fo)|]+e»)
I/. + 8
J (в@, А)Л
<о —е
= 4е» || в {to) 1+28», || в (/о) IP ^ 2е Ц в (<„) 11+8» -*0
при 8->+0, Поэтому ||«(<o)||=»O, что н требовалась доказать.
§ 8. Анализ в банаховом пространстве
1. Гладкие отображения банаховых пространств. Пусть В1 и В2—банаховы
пространства (над полем R нли С), а/: и-*-В2 — некоторое отображение от-
открытой области О с Bv Как н в классическом конечномерном анализе, диф-
дифференциалом отображения F в топке xo^U будем называть линейную часть
приращения F(x)—F(x0)- Точнее, отображение Сбудем называть дифферен-
дифференцируемым в точке Xq&U, если существует линейное непрерывное отображе-
отображение A: B1-*Bi (производная Фреше отображения F) такое, что F (xo-\-h) —
— F (x0) = Ah-\-o(h), если xa-\-h e U. Из определения непосредственно следует,
что если А определено, то оно единственно. Обычно А обозначается F' (*0).
Соображение F дифференцируемо на открытом множестве UczBlt если F
дифференцируемо в каждой точке хщи. Отображение F: и-*-В2 принадле-
принадлежит классу С1, если F дифференцируемо на U и F'\ U -*¦ Нога (Slt Bt)
непрерывно.
Примеры, a) S1 = R", B2=R">, F—дифференцируемое отображение,
б) flj^C1, B2 = Cm, F— аналитическое отображение, в) Sj = R, B2— любое
банахово пространство, F — дифференцируемая функция со значениями в Bt.
г) Если F — постоянное отображение, F : Вх -*-у0 е В2, то F' (х) = 0, Чх е= Bv
" F' —F. е) ~
г
Если F : В1 -*¦ В2 — линейное непрерывное отображение, то F'=F. e) Если
:B1XBi-*-B3-^билинейное непрерывное отображение, то производная
отображения F в точке (*J, *j) вычисляется по формуле: F' (x^, x%) (hlt Л2) =
-Fib, xl)+F(xl fh).
Старшие производные F{k), k^2 отображения F: t/-^-S2 определяются
по индукции. Например, Я2) (дг0) определяется как производная отображения:
F'-.U-* Horn ifii, Bt), здесь F' :x-*F' {x), xei/.
Замечание. Можно дать эквивалентное определение второй производ-
производной как билинейного непрерывного отображения Я81 (х0): Вх %ВХ^-Вг, для
в*

164 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
которого при малых h справедливо равенство
Для определенных выше производвых сохраняются все обычные правила
дифференциального исчисления. Так например, правило дифференцирования
сложной функции будет формулироваться следующим образом:
Теорема 8.1. Пусть заданы отображения Fl:Ul-*-Bi,
иВ U B f() U U Тд
р у р lli, ^^,
Ft: иг-+Вг, U^cz Ba, f(*o) = </<>• *o ^ Ult y0 е U2. Тогда, если отображение
Fi дифференцируемо в точке х0, a Ft дифференцируемо в точке у0, то отобра-
отображение F=Ft'F1 дифференцируемо в точке х0, и справедливо равенство:
Доказательство. По предположению, отображения Flt Ft дифферен-
дифференцируемы в точках xq, у0 соответственно. Поэтому
) - Fi (*о) =/Г(*о)Л+ о (А)..
F.» (Уо+т) - Ft (у0) - F's ((/0) т+о (т).
Далее,
где t=F1(Jxo+h)—F1(x<l). Таким образом,
FM-Fi(</о) W (*0)h + o(Л))+о (т)=^ (у0).F[(x»)h+o(h).
Теорема 8.2. (теорема осреднем значении). Пусть F: V -v B8, U cBt —
отображение, принадлежащее классу С1. Тогда, если хг, >,е(У таковы, что
отрезок *1 + <(хг — *i), OsgfsSl лежите U, то
¦ || />•(*,) - F (^8) | <: 1| Xl- xt || sup || F' (г) ||,
где верхняя грань берется по всем- точкам г, принадлежащим указанному от-
резку.
До к.а зательст-во.- Поскольку
1
то
) - F (х8) |К 11| F' (xi+1 (xj - Xl)) {xt - Xl) \dt s? || Xi - xi || sup || F' (г) fl.
2. Сжатые отображения. Пусть F: В -*¦ В - отображение банахова прост-
пространства В в себя.
Определение. Отображение F называется сжатым, если существует
такая постоянная К,; 0 < К < 1, что
для любых векторов х, у е В.
Из определения нетрудно вывести, что отображение F является непре-
непрерывным. Если же, кроме того, F принадлежит классу С1, то для того, чтобы
F было сжатым, достаточно, чтобы sup \F' (x)||sgA,< 1.
е
Точка х е В называется неподвижной точкой отображения F, если
)
)
Теорема 8.3 (теорема о неподвижной точке). Пусть F: В-*¦ В — сжа-
сжатое отображение банахова пространства В в себя. Тогда F имеет единствен'
ную неподвижную точку, причем для любой точки х&В эта неподвижная

§ 81 АНАЛИЗ В БАНАХОВОМ ПРОСТРАНСТВЕ 165
точка является пределом последовательности
xn = Fn(x), Fn=F-...-F.
п
Доказательство. Пусть х„ = Fn (х) для некоторой точки х е В.
Покажем, что последовательность {хп} фундаментальна. Действительно, по-
скольку |IF {x)-F{y) flss А, || х- у || и xn+1 = F{xn), то || *„_,-*„ \\=\\F{xn) -
— F (xn_i) Ц =sS А, || хп - ж^ |, откуда | *„_! - *„ || =sS А," \\ хг - *01. Далее,
11*я+*—*л11== ^j (*»+i—*<) ^ ^j Л*/+1—*» II ^1~Г5Г 11*1—¦*•<> II-
Пусть у=\\тхп. Тогда, поскольку F переводит последовательность {хп\
в себя и является непрерывным, то F(y)=y.
Покажем, что F имеет единственную неподвижную точку. Пусть У\фуг
неподвижные точки- отображения 'Р. Тогда \yi—yi\=\F{y{)—F{\)?\*?.
^=^IIJ/i—УгЬ что противоречит условию, что У\ФУч-
Следствие. Пусть отображение F:B-*-B таково, что Fn для неко-
некоторого натурального п Э= 0 является сжатием. Тогда существует единственная
неподвижная точка отображения F.
Доказательство. Обозначим G = Fn. Тогда из теоремы следует, что
существует единственная неподвижная точка у е В отображения G. С другой
стороны, поскольку Fy=FGy=GFy, Fy—также неподвижная точка отобра-
отображения G. Поэтому Fy=y.
Далее, так как неподвижные точки F являютси также неподвижными точ-
точками G, то точка у единственна.
В заключение укажем несколько примеров применения теоремы о непод-
неподвижной точке. Наиболее важный для нас пример применения этой теоремы
к обыкновенным дифференциальным уравнениям будет рассмотрен в следующем
пункте".
Примеры, а) Если F : R" ->¦ R"—дифференцируемое отображение, мат-
матрица Якоби которого JX(F) удовлетворяет условию sup |/v(f)||sS A.< 1, то
существует неподвижная точка отображения F.
б) Пусть fi(xi ... *„) — дифференцируемые.функции; тогда если
то система уравнений
имеет решение (и притом единственное).
3. Обыкновенные дифференциальные уравнения в банаховой пространстве.
В зтом пункте теорема о неподвижной точке дли сжатых отображений будет
применена к доказательству существовании и единственности решений обык-
обыкновенных дифференциальных уравнений в банаховом пространстве.
Пусть F: В X R — В — непрерывное отображение. Рассмотрим обыкновен-
обыкновенное дифференциальное уравнение
dxldt=*F(x, t). (8.1)
Будем искать решение уравнения (8.1) с начальными условиями х(/0) = хо.
Возможность использования теоремы о неподвижной точке в этом случае
основана на следующем простом замечании: дифференциальное уравнение (8.1)

166 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
эквивалентно интегральному уравнению
i
x(t) = xo+\ F(x(s),s)ds. (8.2)
•о
Решения уравнения (8.2) можно интерпретировать как неподвижные точки
отображения
t
F(x(s), s)ds,
а поэтому при определенных ^словнях на F можно использовать теорему
о неподвижной точке.
Теорема 8.4. Предположим, что F удовлетворяет условиям
\\F(x,
\\F(Xl, t)-f
Тогда для любых х„^В и <о е (— со, со) уравнение (8.1) имеет определен-
определенное на всем интервале (—со, +со) единственное решение x(t), x(t0)=x0.
Доказательство. Рассмотрим отображение
' def
F (x(s P
Покажем, что & является отображеннем в себя банахова пространства С (В)
функций x(t), непрерывных по /, со значениями в В и с нормой
|*|- sup ||*@1b-
<е[а, 6]
Действительно, нз определения & н условий теоремы следует, что
Далее, оценим разность
@ - ?Ч (О К j IIF (X2 (s). s)-F (Xl (s), s) || ds <
Отсюда индукцией по п получаем
(t) || <:[Щ ' *- to']" || хг - Xl ||
нлн
Из последнего неравенства следует, что при достаточно большом л ото-
отображение 0Fn является сжатием в С[а ь] (В). Поэтому У имеет на [а, Ь)
единственную неподвижную точку x[fl ь] (t) e С[а ь, (В). Из единственности
неподвижной точкн следует, что если [аь Ь{\ с [а%, Ь21. то сужение Xra b , (t)
на отрезок [alt 6t] совпадает с х^а% ь^ (t). Поэтому существует р'ешенне
x{t)= lira xu _ , +nlW. определенное на всем интервале (—со, со).

§ д] НОРМИРОВАННЫЕ И БАНАХОВЫ АЛГЕБРЫ 167
§ 9. Нормированные и банаховы алгебры
Пусть В — алгебра над полем комплексных чисел, причем одно-
одновременно В является нормированным пространством. Мы будем
говорить, что В есть топологическая алгебра, если умножение
непрерывно по каждому из сомножителей. Другими словами, из
условий аь-*-а и Ьь-*-Ь должно следовать akb -*-ab и abk -*¦ ab.
Заметим, что соотношение akbk -*¦ ab при этом может не выпол-
выполняться. Действительно, пусть, например, В — пространство финит-
финитных последовательностей a = {|(fe)}, k^l, с нормой
и покоординатными операциями. Легко видеть, что В есть топо-
топологическая алгебра. Однако, полагая ап — Щ®\, где
О при k<.n,
?<*> =
при
О при k>2n,
получаем ||а„||-»0 и ||а&|5*с>0.
Если в алгебре В нет единицы, то ее можно присоединить,
рассмотрев алгебру Вj формальных сумм Я+a, где ЯеС, teB.
Норма в Bt определяется соотношением |А.4-а|| = | Я| + ||а||. Легко
видеть, что Вг будет топологической алгеброй, причем фактор-
пространство BJB одномерно.
Будем говорить, что В —нормированная алгебра, если суще-
существует такая константа С, что
. \\xy\\^C\\x\\.\\yl (9.1)
для всех х, у^В.
Легко показать, что пополнение нормированной алгебры
является нормированной алгеброй (содержащей В в качестве
всюду плотной подалгебры).
Нормированная алгебра В называется в дальнейшем банахо-
банаховой алгеброй, если В есть банахово пространство и
для всех х, у^В.
Мы видели, что Ор (Е) для любого банахова пространства Е
представляет собой банахову алгебру.
Теорема 9.1. Полная нормированная алгебра В путем
введения эквивалентной нормы может быть превращена в бана-
банахову алгебру.
Доказательство. Не ограничивая общности, мы можем
предположить, что В обладает единицей. Рассмотрим так назы-
называемое левое регулярное представление алгебры В в алгебре Ор (В)

168 АБСТРАКТНЫЕ ПРОСТРАНСТВА [ГЛ. I
ограниченных операторов на В. Именно, зададим отображение
а->Та, где
Легко видеть, что оператор Т е Ор (В) тогда и только тогда
имеет вид Та, когда Тху~(Тх)у. Отсюда следует, что опера-
операторы Та образуют замкнутую подалгебру в Ор (В). В частности,
{Та\ — банахово пространство. Отображение а->Та оказывается,
таким образом, взаимно однозначным гомоморфизмом банаховых
пространств. Кроме тою, по условию теоремы, оно непрерывно.
Согласно теореме Банаха, обратное отображение также непре-
непрерывно. Поэтому, беря в качестве новой нормы элемента а е В
число || ТдЦ, мы получаем норму, эквивалентную исходной. Так
как для операторов IIT'SII^IIT'II-IISII, то теорема доказана. Заме-
Заметим, что для единицы е алгебры В в новой норме |)е||=1.
Задача. Доказать, что *"в нормированной алгебре из ап —<¦ а и Ьп —> Ь
следует anbn—*ab. Обратно, если топологическая алгебра обладает этим свой-
свойством, то она является нормированной алгеброй.
Задача. Доказать, что новая норма будет совпадал» с исходной, если
В—банахова алгебра с единицей, |)е||=1.
Теорема 9.2. Пусть Е — нормированная алгебра с нор-
нормой ||.-1| и пусть А — подпространство в Е (не обязательно замк-
замкнутое), наделенное такой нормой \\, что |/||i^iCI/|| для всех
/еА Предположим, что А относительно |-|i является банахо-
банаховым пространством. Тогда, если А есть алгебра, то умножение
непрерывно по норме |-||15 т. е. || ab ||i ^ Л11| a ||i • j| & 1^ с некоторой
константой М. Другими словами, если А—алгебра, то А —пол-
—полная нормированная алгебра и, следовательно, — банахова алгебра
в некоторой норме \-%, эквивалентной норме \\.
Доказательство. Как и выше, зададим оператора Та,
полагая Та (х) = ах. Тогда Та,^Ор(А). Действительно, поскольку
Та определён всюду на А, для доказательства непрерывности
достаточно, установить, что Та — замкнутый оператор. Пусть
&„е=Л, \\Ьп-Ь1-+О и ЦГА-сЦг-О. Тогда || &„ - & |-> О,
\\abn — с|-»0 и, следовательно, ||а&„ — а&|«ёС|а||-|&п — Ъ |-»0,
так что с = аЬ — ТаЬ. Тем самым непрерывность операторов Та
установлена. Аналогично устанавливается непрерывность опера-
операторов Sa правого умножения.
Далее, если H^l, то ||ТаЬ\\х = 1 аЬ\х = ||SbaI<||Sb|• ||аЬ«?
«?!Sft||. Но мы знаем, что если семейство операторов {Та\ таково,
что |Тадг|^С(дг),. то sup||ra|<oo. Поэтому найдется, такая
константа М, что || Та || *S М, если | q \\t ^ 1. Следовательно, | аЪ \ =
= II Tat п a uJ || • || a I =ss М || ЬI ¦ || а Ц. ТеЪрема доказана.
Подпространство I cz В называется идеалом, если ах е / для
всех as/ и х еВ. Мы предполагаем, что / ФВ. Если a&GL (В),
то элементы вида ах, *еВ, образуют идеал. С другой стороны,
если а е GL(B), то, очевидно, а не содержится ни в одном идеале.

ГЛАВА II
ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА
§ 1. Пространства Соболева
Настоящий параграф посвящен введению и классификации глад-
гладких (должное число' раз дифференцируемых), разрывных и так
называемых обобщенных функций при помощи процесса попол-
пополнения векторных пространств по норме, описанного в абстракт-
абстрактной форме в § 2, гл. I. В качестве исходного пространства
берется пространство «наиболее хороших» функций, т. еГ доста-
достаточно гладких и достаточно быстро убывающих. Мы наделяем его
различными нормами, а затем, пополняя, • получаем различные
классы разрывных и даже обобщенных функций. Таким спосо-
способом мы получим важные конкретные гильбертовы пространства —
так называемые пространства Соболева. Все эти пространства
изометрически изоморфны друг другу, и поэтому можно сказать,
что они являются различными реализациями абстрактного гиль-
гильбертова пространства.
Рассмотрим векторное пространство S бесконечно дифферен-
дифференцируемых функций ф на R", удовлетворяющих. условию
aq. +...+O,
sup
<oo (I.I)
для любых целых неотрицательных рг, ..., рп, qlt ..., qn, т. е.
пространство функций, убывающих вместе со всеми своими про-
производными быстрее любой отрицательной степени | х | при | х \ -*¦ со
/ " \1/Г|
(Здесь и далее М = B]*ч • Кроме того, мы пишем х2 вместо
\ /
|*|2 при любом л^1.) В частности, пространству S принадле-
принадлежат все бесконечно дифференцируемые функции с компактным
носителем (финитные функции); векторное пространство этих
функций обозначается (^(R").
Для- того, чтобы классифицировать функции по их гладкости,
п
мы будем использовать оператор Лапласа А= У -*г-ц (точнее,
/ = i *'
— А + 1, поскольку, как мы увидим, последний обратим на S),
а для классификации функций по их росту мы будем использо-
использовать оператор умножения на функцию jcm —f—-1 -

170 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА (ГЛ. II
Заметим, что можно было бы рассматривать и другие операторы, обла-
обладающие такими свойствами. Выбор именно этих операторов диктуется лишь
соображениями удобства.
Вначале мы будем классифицировать функции по их глад-
гладкости. Для каждого целого k&sO введем в пространстве S норму,
полагая
11ф Р = S Ф (*) [- А + 1 ]' Ф (х) dx. A.2)
Определение. Пополнение пространства S по норме A.2)
называется пространством Соболева и обозначается *) U7* (Rn).
Задача. Доказать, что пространство W* (Rn) — гильбертово.
Пространство \F|(R"), можно отождествить с ^(R"), так как
множество S плотно в Ц (R"). В одномерном случае это доказано
в конце § 2 главы I.
Задача. Доказать, что при л > 1 множество S плотно в Ц (R").
Оказывается, что формуле A.2) можно придать смысл и в том
случае, когда k — отрицательное целое число. Рассмотрим вектор-
векторные, пространства S(/) (/ — натуральное число) функций i|>, пред-
ставимых в- виде
, ipeS. A.3)
Покажем, что для всякой функции if e S(/) функция ф однозначно
определяется соотношением A.3). Очевидно, достаточно рассмотреть .
случай / = 1. Случай произвольного / получается повторением этой
операции / раз. Пусть (— Д +1) ф = (— Д +1) фх. Тогда для функ-
функции / = ф —фг имеем
(-Д + 1)/ = 0, A.4)
и значит,
\}(x)(-\fl)f(x)dX = 0.
Интегрируя по частям, получаем (учитывая, что функция / и ее
производные достаточно быстро убывают при |^|->оо) равенство
I \ \f(x)\*dx-0.
R" R"
где ¦ V/ — вектор с компонентами df/dxj. Значит, $ |/(дг) ]26f;r=0,
R"
и следовательно, ф (х) = фх (*). Таким образом, определен опе-
оператор (—Д-j-l): SA)-»-S (и тем самым операторы (—Д-т-1)~'".
: S(l) -> S, I > 0). Пополняя пространство Sw по норме A.2),
•) Употребляется также обозначение Hf=Wl(Rn).

§ 1) ПРОСТРАНСТВА СОБОЛЕВА 171
где k = — /, получаем пространство W~l (R"), / > 0. Ниже будет
доказано, что S'" = S- для любого /.
Элементы, принадлежащие W*(R") при fe<0 и при этом не
принадлежащие пространству L2(Rn), принято называть обобщен-
обобщенными функциями. Элементы, принадлежащие l^, (R"), но не при-
принадлежащие C(R"), принято, называть разрывными функциями.
Заметим, что все построенные выше гильбертовы пространства содержат
функции приблизительно одного и того же порядка убывания на бесконечности.
Теперь мы перейдем к классификации функций по их поведе-
поведению при | дг | —»-оо. Заметим, что при классическом преобразовании
Фурье оператор — А +1 переходит в оператор умножения на р2 +1.
Напомним некоторые свойства преобразования Фурье.
Преобразование Фурье F функций ф из S определяется формулой
A.5)
R"
л
где р • ? = 2 P&i ~ скалярное произведение *) векторов р, % е R".
(=1
В курсах анализа устанавливаются следующие свойства пре-
преобразования Фурье F функции из S.
1) Существует обратное преобразование Фурье F'1, причем
A.6)
R"
2) I f (х) ф (дг) dx = I ШТШ № (Р) dp A -7)
R" R"
(равенство Парсеваля).
3) Пусть Dj — оператор дифференцирования по /-й координате,
Uj — оператор умножения на /-ю координату. Тогда
-iDjF = FUj, A.8)
UjF = iFD,. A.9)
Из последнего свойства непосредственно вытекает, что для любого
и^Ои для любого 1|з е S
[F(-A + l)«h|)](p) = (p« + l)-4|»(p). A.10)
Условимся обозначать через S пространство всех функций ф,
где фе S.
Исходя из рассмотренных свойств преобразования Фурье,
нетрудно установить, что пространство S инвариантно относительно
преобразования Фурье, т. е. § = S.
*) Использование двух различных форм записи для скалярного произве-
произведения диктуется лишь соображениями удобства.

172 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. II
Покажем, что если г|> е S(m) при т<0, то и равенство A.10)
справедливо при т<0. Действительно, пусть m = —k<0 и
Ф = (—A-HfV Тогда
Умножив A.11) на (р*-\-1)т, получим A.10).
Из A.10) следует, что дли любого натурального / пространство
Su) совпадает с пространством S. Действительно, пусть ф е S.
Покажем, что существует функция ifeS, удовлетворяющая усло-
условию ф = (— A + l)'i|>. Очевидно, достаточно доказать это для / = 1.
Из инвариантности S относительно преобразования Фурье, сущест-
существования F и формулы A.10) следует, что в качестве ¦$ можно
взять F'1^, где
Определение. Пространством W* (R") называется попол-
пополнение пространства S по норме
^ $ A.12)
Выше уже говорилось об изометрическом изоморфизме всех
вводимых здесь пространств. Предлагаемая ниже задача мо-
может рассматриваться как непосредственная иллюстрация этого
факта.
Задача. Пусть А : S —> S—отображение, определяемое формулой Af (x) =
= (х*-\-1)~У2 f(x). Доказать, что существует и единственно расширение А до
изометрического изоморфизма ¦ пространства ?.2(Rn) на №* (R")-
Задача. Доказать, что С? (R") плотно в ^* (R").
Теперь определим изометрический изоморфизм пространств
№* (R") и W* (R"). Как и следовало ожидать, он осуществляется
преобразованием Фурье. Именно, справедлива следующая тео-
теорема.
Теорема 1.1 Преобразование Фурье F:S^fS изометрично
относительно норм пространств W*(R") и #?(R"), т. е. для
любого ц> е S справедливо равенство
1 .»
Доказательство. Используя 1.10 и равенство Парсеваля,
получаем
k („.) ='\ Ф (х) (-Д +1)*Ф (х) dx =
2 _ я .
¦ J [(Яр) (р)] (р2 +1)* (Пр) (р) dp=||^ф iiv* (|
R" ч '

§ 11 . ПРОСТРАНСТВА СОБОЛЕВА 173
Таким образом, оператор F в силу изометричности ограничен
на плотном подмножестве S пространства W*(Rn). Следовательно,
преобразование Фурье F может быть единственным образом про-
продолжено до изометрического гомоморфизма пространства W* (R")
на IF*(Rn), который мы также будем обозначать буквой F. Итак,
мы пришли к следующему определению.
Определение. Изометрический гомоморфизм
называется преобразованием Фурьг в W* (R").
Продолжая До гомоморфизма оператор, определенный на S
формулой A.6), видим, что оператор F имеет обратный:
Действительно, если обозначить через F продолжение оператора
A.6) до гомоморфизма пространства №*(R") в W\(Rn), то для
любого ф е S
Отсюда, в силу плотности S в W* (R") и в IF* (Rn) следует, что
FF=-1, FF=\, т. е, F = F~1.
Таким образом, справедлива следующая теорема.
Теорема. 1.2. Преобразование Фурье
F: W\ (R") •-»-Щ (R«)
является изометрическим изоморфизмом.
Примечание. Для записи преобразования Фурье элементов <pe№ft(Rn),
<p^S, мы будем по-прежнему пользоваться обычной формулой преобразования
Фурье, хотя ф и <р в этом случае ие являются функциями в общепринятом
смысле. „ •
Теорема позволяет естественным образом расширить опреде-
определение пространств Соболева W\ (R") на случай дробного s. Пусть
O —любое вещественное число. ВвеДем в S норму H\ps(Rn)
по формуле
1|Ц 11^11К»)- i A-13)
Определение. Пространством Соболева Wl(Rn) называется
пополнение пространства S по норме A.13).
Этим мы заканчиваем определение пространств Соболева.
Теперь мы перейдем к доказательству важнейшего свойства про-
пространств Соболева, которое часто берется за определение про-
пространств Соболева W\ при s < 0.

174 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА
§ 2. Двойственность пространств Соболева
[ГЛ. II
В каждом из пространств Соболева, как мы видели ранее, можно
ввести естественное скалярное произведение, которое превращает
это пространство в гильбертово. Однако скалярное произведение
в L%, определенное формулой C. 5) гл. I, продолжает играть
основную роль и для пространств Соболева. Именно, оказыва-
оказывается, что «положительные» и «отрицательные» пространства Собо-
Соболева «двойственны» относительно этого скалярного произведения.
Вначале рассмотрим введенные выше пространства #* (R") и
Теорема 2.1. Пусть /е= №*(•*"). фе= №7*(R") " пусть {/,}
и {фу} — последовательности функций из S, сходящиеся соответ-
соответственно к f и ф. Тогда существует предел
lim ] f/(x)(p/(x)dx.
/-со R/l
B.1)
Доказательство. Покажем, что рассматриваемая после-
последовательность интегралов фундаментальна. Имеем:
J /р (х) ФР (яг) dx-\ fg {x) ф9 (x)dx =
R* R"
Up (x) - U (*)] ФР (дг) dx - j fg (х) [Ф? (х) - фр (дг)] dx <
R"
\ Up (x) - U (х)] Фр W dx + \fg (х) [Фв (дг) - Фр (х)] dx
R" R"
Используя неравенство Коши — Буняковского, получаем:
[fp(x)-fq(x)]<pp(x)dx =
/2 Up (х) ~ !я
Фр
m
1/2.
=1 fp—fg las* (R л) 1 Фр 1 as'-* (r»)•
Так как последовательность {fy} фундаментальна по норме про-
пространства W% (R"), а последовательность {ф^} фундаментальна по
норме пространства W~k (R") (а, следовательно и ограничена по
этой норме), то
lim $ [/р(дг)-Мдг)]ф,(дг)Жг = О;

21
ДВОЙСТВЕННОСТЬ ПРОСТРАНСТВ СОБОЛЕВА
175
аналогично получаем, что
lim \ f (*)[фр(*)-ф?(*)]^ = 0,
P,<7-*o?Rn
и теорема доказана.
Определение. Назовем предел B.1) интегралом произведе-
произведения функций / е IF* (R") ифЕ W~k (Rn) и введем обозначение
\ f (х) Ф (х) dx- li m $ /, (дг) Фу (дг) их. B.2)
Покажем, что это определение не зависит от выбора ft и ф/.
Пусть f e IF* (R"), ф е fl^—* (R") и пусть последовательности {Д}
и {/*} функций из S сходятся к /, а последовательности {ф*} и
{ф*} функций из S сходятся к ф. Так же, как при доказатель-
доказательстве теоремы 2.1, получаем
\fj(x)Vj(x)dx- ]
R" R'
<|//-/yl**(R»)NyJ»J-*(R»)+^y-^I»7*(R«)I/>li'*(R«)-
при j-*-oo, что и требовалось доказать.
Замечание. При fe=0, т. е. в случае, когда f sL2(Rn).
интеграл B.2) совпадает со скалярным произведением (f, ф); здесь ф«= lim фя,
если ф„ — ф.
Теорема 2.2. Для любых /s#*(R»), фе#7'(К")
ведлива оценка
B.3)
Доказательство. Пусть fj-*¦[', фу-»-ф, /у, ф/eS. Из
неравенства Коши — Буняковского следует, что
\ f (х) Ф (х) Лг = lim J fj (x) Фу <дг) Лг
R"
Теорема 2.3. При фиксированном /e#*iR") интеграл B.2)
определяет ограниченный линейный функционал на W~k (R").
Доказательство. Обозначим через «^ левую часть выра-
выражения B.2):
Непосредственно проверяется, что «Р, (аф + Р^)
+ Р«^/ (^Ь Ограниченность функционала «^ : W'-
из теоремы 2.2.
(ф) +
C следует

176 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА ГГЛ II
Оп ределение.-Я^сть fj-+f, фу-*ф, ft, ф/eS, f e №*(R"),
<р е №7* 0*")- Назовем интегралом произведения функций f и ф
предел
Urn J /у (дг) фУ (дг) dx Ш \f (х) Ф (дг) dx.
Задача. Используя равенство Парсеваля, доказать корректность дан-
данного определения. Получить аналоги теорем 2.2 и 2.3 для пространств №* (Rn).
Обобщить равенство Парсеваля для интеграла \ f (х) ф (лс) dx на случай, когда
{е W* (R»), ф е Wr* (R«), ft > 0.
Теорема 2.4. Я^/еть Oe[f»(R")f. Тогда найдется такой
элемент h пространства W~k (R"), что для любого
- 5 Hx)g(x)dx. B.4)
R"
Доказательство. Пусть geS, ф (д:)= 1
Тогда
Рассмотрим линейный функционал У, определенный на плотном
множестве S<zL2 (R") формулой
и ограниченный в силу B.5). По теореме Ф. Рисса существует
такой элемент /eL2 (R"), что для любого ф е L2(R")
= J /(дг)ф(дг)Жг.
Пусть /,->/, /,sS, gsS, ф(^) = A+дс1)*/2^Гх). Тогда
Ф (в) - 5 7 (*) Ф W ^ в Hm J f, (дг) Ф (х) dx - llm 5 fc/ (х) g (дг) dx,
R» /->0° R- '-*» R«
где hf(x)^(l+xi)k/2fj(x), причем из сходимости последователь-
последовательности {//} в Ц(И.п) следует сходимость последовательности {h}} к
некоторому элементу h&W—k (Rn). Таким образом, при geS
<b(g)-\h(x)g(x)dx.
R"
А поскольку S плотно в ^|(R"), то теорема доказана

§ 2] ДВОЙСТВЕННОСТЬ ПРОСТРАНСТВ СОБОЛЕВА 177
Теорема 2.5. Пусть <Pf&[W-k(Rn)]*— функционал, опре-
определенный формулой
j
Тогда \Sf\-\f\. * . •
Доказательство. Из теоремы 2.2 следует, что /
Докажем противоположное неравенство в предположении, что
f eS. Пусть ф(х) = A + х2)"/. Тогда
Поэтому 6^/1^=1/1, так что |«^/|| = ||/| при /eS.
Пусть теперь f — произвольный элемент из #* (R") и {/у} —
последовательность функций из S, сходящаяся к f. Тогда после-
последовательность функционалов «F/ сходится к &t по норме про-
пространства [W^(R")]*. Переходя к пределу в равенстве |oFfJ =
= |]/Д получаем утверждение, теоремы.
Теоремы 2.3 — 2.5 означают, что li?~*(R") можно отождест-
отождествить с пространством [W7* (R")]* ограниченных линейных функци-
функционалов на W% (R"). Именно, справедлива следующая теорема.
Теорема 2.6. Отображение А : W~k (R")-*-[r* (R")]*, опре-
определенное формулой
является изометрическим изоморфизмом.
Из теоремы 2.6 и теоремы 1.2 получаем следующую теорему.
Теорема 2.7. Отображение A: W-k(Rn)-*[W${%.*)]*, опре-
определенное формулой
U(x)g(x)dx,
является изометрическим изоморфизмом.
Оператор дифференцирования не является ограниченным ни
в одном из пространств Соболева. Однако он ограничен как опе-
оператор из одного пространства Соболева в некоторое другое, отве-
отвечающее ему пространство Соболева. Действительно, пусть
Dm: S-+S — оператор дифференцировния по m-й координате:
Справедлива следующая теорема
Теорема 2.8. Оператор ит ограничен как оператор, дей-
действующий из №*(R") в W*-'(R")-

178 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. И
Доказательство. Пусть <peS, ф"=Уф. Тогда
|Дяф||^-< (R«) - J P2 A +P2)*-1 1.Ф (P) f dp^
1 R"
Таким образом, норма оператора Dm не превосходит единицы,
и теорема доказана.
Ограниченный на плотном подмножестве S с W\ (Rn) оператор
Dm можно расширить' до гомоморфизма №*(R") в №*-' (R*).
Расширенный оператор будем обозначать тем же символом Dm.
Определение. Пусть /eW^R"). Обобщенная функция
Dmf&W*-l(Rn) называется частной производной обобщенной
функции f по т-й координате.
Замечание. Хотя и не имеет смысла говорить о значении
обобщенной функции в точке, мы иногда будем использовать
символ fix), f&Wi(Rn) (см., например, в §2 определение
интеграла
$ f (х) g (x) dx, f 6 W* (R"), g s Wr" (R»)).
R"
В таком же смысле мы будем использовать для частных про-
производных обобщенных функций обозначение
B.6)
Задача. Пусть f e W?~k(R"). Доказать, чтофункционал§е^7*~' (R*).
действующий по формуле
J «(*) ф W Лг— J »(*) Щ?гах> Ф s ^*+ ' №")» B-7)
R" R"
совпадает с Dmf.
§ 3. Некоторые пространства непрерывных функций
и связанные с ними пространства
Пространства Соболева весьма удобны для исследования свойств
дифференциальных операторов. Они являются гильбертовыми
пространствами и обладают свойством двойственности. Однако
элементы этих пространств мы не можем перемножать. (В самом
деле, если, например, ф(х)е^, то ф2 (х), вообще говоря, не при-
принадлежит L2.)
В этом отношении пространство непрерывных функций обла-
обладает преимуществом перед пространствами Соболева: произведение
двух непрерывных функций является непрерывной функцией.

§ 3] ПРОСТРАНСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 179
Это свойство будет нам особенно важно, когда будет идти речь
о пространстве операторов.
Перейдем к рассмотрению некоторых банаховых алгебр непре-
непрерывных функций. Рассмотрим сначала множество непрерывных
ограниченных комплекснозначных функций с общей областью
определения Q с R". На этом множестве обычным образом вво-
вводится структура векторного пространства. Определим норму
функции f формулой
|f|| = sup|f(x)|. C.1)
Полученное нормированное пространство функций обозначим через
C(Q). Пространство C(Q) является банаховым: его полнота выте-
вытекает из того, что сходимость функций по норме C.1) является
равномерной сходимостью. Согласно известной теореме анализа
равномерно сходящаяся последовательность ограниченных непре-
непрерывных функций имеет пределом ограниченную непрерывную
функцию. '
Аналогично C(Q) определяются нормированные пространства
(fi), k> О — целое. Норма в С(А) (Q) задается формулой
Шс*(а)= max sup[D'f(*)|, C.2)
и I/I
где / = (/i, /s, .... In), 1/1= У It, ^ = —7^ j— Элементами
пространства С() (Q) являются k раз непрерывно дифференци-
дифференцируемые на Q функции f, для которых \f\cW (а> <оо. Простран-
Пространство C(k) (Q) является банаховым пространством (полнота следует
из теоремы, аналогичной вышеупомянутой).
Пусть С* (R") — пространство, сопряженное к C(R"). Ь%-функ-
цией Дирака называется функционал на C(R"), который каж-
каждой функции g^C(R") ставит в соответствие ее значение g(|)
в точке | е R". Функционал 6g принадлежит пространству С* (R");
его ограниченность следует из неравенства
Пусть N^zO. Через C#(R") будем обозначать пространство
непрерывных функции на R", имеющих конечную норму
l= sup
g(*)
Таким образом, по определению, пространство C^(Rn) есть
пространство, в которое включаются все непрерывные функции,
растущие не быстрее 1*1^.

180 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА ¦ {ГЛ. II
В этом отношении оно является как бы «надстройкой» над
С (R"b> подобно тому как W-k(Rn) есть «надстройка» над L2(R")-
Очевидно, что функцию Дирака 8g можно рассматривать как
элемент пространства С% (Rn):
Другой пример элемента из С% (R") дает функционал е^,:
•%(*) = \<?(x)g(x)dx, C.3)
Rn
где ф —элемент векторного пространства Cg°(R") бесконечно диф-
дифференцируемых функций с компактными носителями. Действи-
Действительно,
\ <?(x)g(x)dx
Функционал a^q, удобно отождествлять с самой функцией ф (легко
видеть, что (ф Ф 0) => (^<p Ф 0)), т.е. писать ф (х) е С% (R") вместо
е^ф е С% (R"). Мы будем обозначать любой функционал «Г eCj» (Rn)
через ф (*) (хотя ф (х) может и не быть функцией в обычном
смысле слова), а значение функционала «F будем записывать
в виде ^ ф (х) g (x) dx, хотя интеграл и не существует как интег-
интеграл Римана. В частности, для функционала 6g будем, как это
принято в физической литературе, писать ^ 8 (х — |) / (х) dx.
Нам будет достаточно рассмотреть более простое и легко обо-
обозримое пространство, именно, подпространство в С% (R"), которое
является линейной оболочкой объединения 8-функций Дирака
и Cr(R")-
Итак, обозначим через С% (R") замыкание в С% (R") линейной
оболочки множества С~ (Rn) U {8s}s e Rn.
Перейдем теперь к определению преобразоваиия Фурье в про-
пространстве Cn (R"). Фурье-образом функции ipeC™ (Rn) с: С% (R")
назовем, как обычно, функцию ф, определяемую формулой
Ф (Р) = (Ff) (Р) = ~^ш- \ Ф W *-*>¦* dx. C.4)
Фурье-образом Ь^-функции назовем функцию, определяемую
формулой
(Щ (Р) \ h W *"-х ** =
C-5)

§ 3] ПРОСТРАНСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 181
Обозначим через <?®% (R") векторное пространство, состоящее
из линейных комбинаций функций вида C.4), C.5).
Формулы C.4) и C.5) задают оператор, отображающий линей-
линейную оболочку множества Cf (Rn) U {6g}geRn в <Щ^ (Rn)- Оператор F
имеет обратный; покажем это. Нужно убедиться в том, что
(F O)=>((p = O). Пусть/ф = 0, причем
Ф я-*+^] аЛл Ь Ф Ь при
). Тогда
где *ф —Фурье-образ функции ^.Следовательно,
Если хотя бы один из коэффициентов at отличен от нуля, то
функция тр не стремится к нулю на бесконечности, а это про-
противоречит тому, что if e Cf (Rn).
Введем теперь в пространстве &У (R") норму:
Обозначим через <^v(R") пополнение пространства ^8^ (Rn)
по норме C.6). Тогда оператор F может быть расширен, и при-
притом единственным образом, до изометрического изоморфизма про-
пространства Cfr(Rn) на <^v(R"). Этот изометрический изоморфизм
мы снова обозначим буквой F и назовем преобразованием. Фурье
элементов пространства Cn (R"). В дальнейшем мы увидим, что
пространство &®w(R") естественно реализуется в виде простран-
пространства непрерывных (гладких) функций.
В линейной оболочке множества
имеется коммутативная композиция (умножение), которая превра-
превращает это многообразие в алгебру, а именно,
при
8"—(So^6**115
:-l) прибег С» (Rn)..

182 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. 11
Покажем, что существует такая константа с, что
Пусть /eCw(R"). Рассмотрим интеграл
/= 5 1<𠕦](*)/(*)<**. C.7)
Интеграл C.7) можно преобразовать к виду
Bя)«/2/ = S Ч> (Q Я $ / (И- О Ф (У) dy. C.8)
Для того, чтобы убедиться в этом, достаточно рассмотреть три
частных случая (поскольку мы рассматриваем линейную оболочку
множества С? (R") U ЩУ-
а) Ф, 4>eC»(R»);
б) феС»(Г), ф = 8|;
в) ф = 86; i|j-V
В случае а)
r"
В случае б)
с другой стороны,
Rn R"
Наконец, в случае в)
Bя)„/2 /== ^ б(лг — S-T1)/(дг) Лс = /(g + П),
R"
5 в (/- J

§ 3] ПРОСТРАНСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 183
Таким образом, равенство C.8) доказано. В силу C.8)
е* (.-
+ \t |Г"
Поскольку
sup
f(y+f)
A+1
TO
Итак,
ДГ) ^ (ДГ)
I Ф * Ч3 \\C% (R-)
(Rл
Cn (r«
I Ф l
что и требовалось доказать.
В силу оценки C.9) операцию * можно, и притом единствен-
единственным образом, распространить на все пространство С% (R") с сохра-
сохранением неравенства C.9). При этом С% (R") превращается в бана-
банахову (точнее, в полную нормированную) алгебру. Поскольку
преобразование Фурье есть изометрический изоморфизм' банахова
пространства С% (R) на <3$N (Rn), то операция * индуцирует
бинарную операцию, которая превращает o%}N(Rn) в банахову
алгебру и определяется формулой
"). Пусть ф0,
Выясним, как действует операция
sCf (R") и пусть
на
Тогда
так что
~ л/2
о) (Р) + Bя)~
2

184 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. II
Легко проверить, что (/7фо»^'Фо)(Р) = фо(Р)'Фо(Р)- Поэтому
(F<f9Fty)(p) = y(p)ty(p) для любых ф, ф вида C.10), т. е. на
<5$ir(R") операция • есть поточечное умножение функций. По этой
причине мы будем опускать точку, в обозначениях этой операшш
§ 4. Теоремы вложения
Очень часто бывает непросто непосредственно установить принад-
принадлежность функций банаховой алгебре С и особенно банаховой
алгебре <?SN. Существенно проще проверить, принадлежат ли они
пространству Соболева. Поэтому нам важно установить факты
о том, что принадлежность к некоторому пространству Соболева
влечет за собой принадлежность к S3N или С. Говоря точнее,
речь идет о существовании естественного вложения пространств
Соболева в С или <$?#• Первые теоремы такого рода были дока-
доказаны С. Л. Соболевым и названы им теоремами вложения.
Теорема 4.1. При k>s имеется естественный непрерывный
оператор влоокения
W*(R")c=W|(Rn).
Доказательство. Пусть k>s, <p^S. Тогда
Стало быть всякая последовательность функций из S, фундамен-
фундаментальная по норме пространства №*(R"), фундаментальна и по
норме пространства W\ (Rn). Остается показать, что фундаменталь-
фундаментальные по норме пространства Wg(R") последовательности {фу} и
{ф/} функций из S эквивалентны в №?(R"), если они эквива-
эквивалентны в W\ (Rn). Иначе говоря, надо убедиться в том, что если
последовательность {^} с: S сходится кфв W%(Rn) и к нулю в
W\(Rn), то ф==0.
Положим tyj = Fipj', ip = Fty. Имеем
lim $
$ (
т. i-coRn
Urn
Зафиксируем е>0 и выберем такой номер /0, что при
Пусть А — столь большое число, что

f 4J
Тогда при /5=/о
ТЕОРЕМЫ ВЛОЖЕНИЯ
185
\Р\<А
\Р\>А
\р\>А
\Р\<А
Далее,
' \
\Р\<А
Следовательно,
Шп || $у IV* (R п) ^ е ^ 1 + 2 sup 1 ty ||j.
Д поскольку е произвольно, то отсюда следует, что
при
Ml^lV(R)
и теорема Доказана. ¦
Имеет место теорема, называемая теоремой вложения Соболева.
Теорема 4.2. (Теорема вложения Соболева). При
к>п/2 имеет место вложение №*(R") crC(R").
Предварительно докажем следующую лемму.
Лемма 4.1. Пусть /0: S ->• С (R") — оператор с областью опре-
определения S, действующий по формуле
/</<*)=/(*); D.1)
если k>nj2, то оператор /0 ограничен.
Доказательство. Пусть feS и пусть } — Фурье-образ
функций f, k>nl2. В силу равенства
получаем оценку
Rn
R"
D-3)
где
Af• = J (pt + 1)-*rfp = Ck\ r" (r2 + I)"*dr<oo, D.4)

186 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. II
поскольку п— 1— 2k < — 1; константа сп в D.4) равна площади
единичной (п— 1)-мерной сферы. В силу изометричности преобра-
преобразования Фурье из W*(R") в ^(R") формулу D.3) можно пере-
переписать в виде
что и требовалось доказать.
Продолжим доказательство теоремы. При k>n/2 определен
гомоморфизм
/
сужение которого на 5 есть оператор /0. Чтобы доказать, что /
есть оператор вложения, достаточно убедиться в том, что
(/ф = 0)=>(ф = 0). Пусть {фу} — последовательность функций из S,
сходящаяся к фе№*(Р"), и пусть /ф = 0. Тогда
lim /ф^ = /ф = 0.
/-со
Но /ф =/оф =ф., и значит, Пт||ф.|С(кга) =0, т. е. последова-
последовательность {фЛ равномерно сходится к нулю С другой стороны,
^(R^*); поэтому
/-¦00
Следовательно, для любой функции f e ?2 (Rn)
lim
Если /eS, то
if;(x)f(x)dx
R"
f;
\f(x)\dx-+O
R
при /-»-оо. Поэтому для любого [eS
\ <?(x)f(x)dx = O,
r"
откуда "и следует, что ф = 0. Тем самым теорема доказана.
Смысл теоремы Соболева заключается в том, что если отож-
отождествить каждый элемент пространства W*(R") с его образом при
отображении /0, то при k>n/2 элементы из W*(R") будут огра-
ограниченными непрерывными функциями.
Теорема 4.3. При k^-^+l имеет место вложение
и для любого f&W% (Rn) производная D^f совпадает с обычной
частной производной функции /.

«4J
ТЕОРЕМЫ ВЛОЖЕНИЯ
187
Доказательство. Пусть &>у+ 1, /е= №*(R"). Для дока-
доказательства того, что //eCA)(R"), достаточно показать, что /0
ограничен как оператор, действующий из №*(R") в СA) (R"). Если
/eSh J — Фурье-образ функции f, то
Следовательно,
\Pmf(p)\dp, D.5)
ffl-1 V R"
с = const.
Аналогично D.3) получаем оценку последнего члена в D.5):
причем ^ IpIO^+O kdp<oo, так как п — 2k< — 1. Итак,
r"
первая часть предложения доказана. Вторую часть предложения
можно сформулировать в виде соотношения IDm = DmI, которое,
очевидно, выполняется на множестве 5, плотном в №*(Rn), a
значит, выполняется и на всем №*(Rn). Доказательство завер-
завершено.
Задача. Доказать, что при k > -pp+zn имеет место вложение W\ (R") с
Теорема 4.4. При k~>N + y имеет место вложение
Доказательство. Пусть /eS, Тогда
114I1
SUp
С (Rn)
= 1
sup
" С (R"
) A+|*|)а»-*>-I/ J
R" Г R"
; D.6)

188 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. II
Имеем
1 V Д
D.7)
так как 2{k-N)>n. Далее, A+ |*|)а*<A+*2)*2*; поэтому
. D.8)
В силу D.6),. D,7', D.8) получаем, что 1Л1с#<с1ЛЬ(кТ где
константа с зависит от N, п и k, но не зависит от^ео. Отсюда
следует, что для любого ф е Cj° (R") *) справедлива оценка
H<PlUA,(Rn)SSSCH<Pi|^(R'1)' C "Const.
Остается показать, что если последовательность {фу} функций
(peCf(Rn) сходится к нулю в ^(Rn) и фундаментальна в
W%(Rn), то она сходится к нулю и в №§(R8). Пусть {фу} —такая
последовательность и пусть <pj*=F~lipj. Тогда фу е Cj°(R"), фу->-0
в С%(Кп) и {фу} фундаментальна в #*(R"): Нужно показать, "что
Фу->-0 в Wb(Rn). Из фундаментальности {фу} в #*(Rn) вытекает
сходимость этой последовательности в L2 (R") =э W'f (Rn). Доста-
Достаточно-показать, что R фуftc*<Rя) —*~ 0- Пусть ipsCS°(Rn). Тогда
при /-»-0. С другой стороны, если фу-»-0 в Z,2(R"), то
Inn I фу (х) ip (x) dx = (ф, \|>)tj (Rn).
Следовательно, (<p,-4|>)Ll(R«) = 0 для любого ipeCf(R"), откуда
следует, что ф = 0, и теорема доказана.
Теорема 4.5. Имеет место вложение <$н(Кп) aCiN) (Rn).
Для доказательства теоремы 4.5 нам понадобится следующая
простая лемма.
Л е м м а 4.2. Пусть fez<&PN (R«), J = F^f. Тогда
{2n)-'4* \ (—ix)ae'Px}(x)dx.
r"
Здесь
*) Через С» (R") обозначается пространство Фурье-образов функций

«fl
ТЕОРЕМЫ ВЛОЖЕНИЯ
189
Доказательство. Очевидно, достаточно проверить утверж-
утверждение леммы в двух случаях: /eCJj°(R") и /=84. В первом
случае утверждение очевидно. Пусть / = 8^. Тогда f(p) =
= Bя)~ п'Ч~ '"•&, так что
D*f {р) - Bя)~«v (- il)aer <p-t
er l"-x8 (x -1) (^ ix)a dx,
и лемма доказана.
Доказательство теоремы. Пусть f ее%% (R"), / =F~1f.
Тогда при |a|=s?.JV
F (х) (— ixfer »•* dx
sup
ап ~,lp'x
(\+\x\)N
Поэтому оператор /0 тождественного вложения <?В% (Rn) cr <?foN (R")
в С(Л/) (R") ограничен и может быть продолжен до гомоморфизма
/¦ <?SN(K")-^CW (R"). Остается доказать, что (/ф = 0)=>(ф = 0).
Пусть /ф = 0 и пусть {фу} — последовательность функций из
(Rn), сходящаяся в <?BN (R») к ф. Тогда
Обозначим ф^/7-^, ф = ^ф. Имеем Ф/-*-ф в С% (R"), откуда,
в частности, для любого / е Сл/ (R" ,
$j(x)f(x)dx.
Мы покажем, что для любой бесконечно дифференцируемой функ-
функции feCff(R»)
lim ^ ф\ (*)/(*) d* = О,
откуда и будет следовать, что ф = 0, так как С00 (R") П CN (R")
плотно в С^ (R").
Итак, пусть / — фиксированная бесконечно дифференцируемая
функция из Ctf(R") и е>0 —фиксированное число. Выберем
такой номер /„, что при />/о выполняется неравенство
|ф/— Ф/ollct, (Rn)<e- Поскольку фу0 есть линейная комбинация
функций из CS°(Rn) и буфункций, то найдется такое положи-
положительное Л, что ^ ф/0 (х)g (x) dx = 0 для любой функции g^CN(Rn),

190
ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА
[ГЛ. II
обращающейся в нуль в шаре | х | < А. Пусть /0 е Cf (R") — функ-
функция, совпадающая с / в этом шаре и не превосходящая / по
модулю. Имеем
x = \ yj(x)fo(x)dx +
r"
- + $ [ф/ (х) - Фуо (х)] U (х) - /о (х)] dx, D.9)
так как
bo(x)\f(*)-fo(x)]dx=O.
Рассмотрим первое слагаемое в правой части формулы D.9). Имеем
Фу (х) /о (х) dx
$
] (дг) dx
\[Ffo)(x)\dx-+O
йри /-voo. Второе слагаемое в правой части D.9) можно оце-
оценить следующим образом:
Значит, найдется такой номер Д.^/о, что при
А поскольку е произвольно, то отсюда следует, что
lim J фу(дг)/(дс)Ле=О,
и теорема доказана.
Таким образом, из теорем 4.4, 4.5 следует, что при
W\ (R") с &N (R«) c= Cw (R«).
Мы видим, что банахова алгебра ^^(R") находится «между»
пространством Соболева, содержащимся в CN (R"), и банаховой
алгеброй CN (Rn). Так что <#*n(R") есть банахова алгебра, более
«близкая» к пространству Соболева, чем CN (R").
Задача. Показать, что для любого феС/i (Rn) справедлива формула
Ф W

$ 51 6Е-ФУНКЦИЯ ДИРАКА 191
§ 5. 6|-функция Дирака в пространствах Соболева
Выше мы ввели функционал Ьг е С* (R"), который каждой функ-
функции g ставит в соответствие ее значение g (g) в точке ? е R".
По теореме вложения Соболева, при &>л/2 сужение функцио-
функционала б| на W\ (R") с: С (R") принадлежит пространству WTk (R").
Это сужение мы будем снова обозначать 8^ и называть Ь^-функ-
цией Дирака.
Мы знаем, что если рассматривать функцию б| как элемент
пространства O(R"), то ее Фурье-образом будет функция б6!
56(р)-Bя)-"/»«-"-в. ' E.1)
Возникает вопрос, остается ли эта формула справедливой, если
рассматривать 8^ как элемент пространства Соболева WTk (R").
Чтобы уточнить вопрос, примем следующее соглашение: если функ-
диоиал /, принадлежащий W~k(T(.n), определяется формулой
J f(x)<p(x)dx=:[g(x)<?(x)dx, 9eS,
где g — кусочно непрерывная функция, то мы будем отождеств-
отождествлять функционал f с функцией g и писать f{x)=g(x). В этом
смысле функция E.1) является элементом пространства W~k при
k>n/2.
Пусть б| есть б-функция в W^k (R") и пусть \ = F8i. Пока-
Покажем, что формула E.1) справедлива и в этом случае. Пользуясь
равенством Парсеваля и очевидным равенством (Fф) (— р) =
= (^ф) 0°). ф е 5, получаем
Ф(|)= \ b(x-l)y(x)dx=\ b%{p)y{-p)dp, .peS,
r" r"
где фягТ'ф. С другой стороны, для любого ipaS
Ф F) = Bя)-0/2 \ в""вф (р) dp = Bя)-"/2 ^ в-""8ф (- р) dp.
R" R"
Таким образом, б6 определяется как функционал на if^R"),
/г>л/2, формулой
Ь%(р)Ф(р) dp = J ^72е"""ЕФ (Р) Ф. Фе5,
и значит, формула E.1) справедлива.
Приведем теперь в одномерном случае пример так называемой
Ь-образной последовательности, т. е. последовательности кусочно
непрерывных функций* сходящейся к 6S в UV(R). Для этого

192
ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА
[ГЛ. II
мы выберем такую последовательность {6Y} функций i&'lJPj'fR),
чтобы Фурье-прообразы этих функций были кусочно непрерывны
и чтобы lim б| = Ъ\. Тогда в качестве искомой б-образной после-
довательности выберем {6i/} = {[f~16|]}. Пусть
при \р\<и
Покажем, что
Действительно,
sup
при | р | S* /.
\р\>1
2Л)
где sup берется по единичной- сфере в пространстве Щ (R).
yes
Для вычисления прообраза функции 8^ нам понадобится сле-
следующая лемма.
Лемма 5.1. Фурье-прообраз ф абсолютно интегрируемой
на R" кусочно непрерывной функции ф е Щ (R") может быть
вычислен по формуле
Ф (х) = Bя)-«/2 J е'"-*ф (р) dp. E.2)
Доказательство. Пусть {фу} — последовательность функ-
функций из S, сходящаяся к ф по норме пространства UP* (R«), и пусть
Фу = /Г~1(фу). Требуется доказать, что для любого ^eS
\ ф (х) dx \ el»-*y, (p) dp =
lim ~-j-2
r r
или, меняя в E.3) порядок интегрирования,
lim С ф, (р) ф \ —^2 е'"'•* * (*) d* -
E-3)
. E.4)

§ 61 ГЛАДКИЕ ФУНКЦИИ 193
Равенство E.4) можно переписать в виде
lim \ Ф/(р)*р(—p)dp= \ ф(р)'ф(—р) dp,
что и завершает доказательство.
Итак,
со
*,«-{;
-/
Задача. Построить 6-образную последовательность в п-мерном случае.
Задача. Показать, что последовательность Щ} функций вида
при |х-Е|<1/2/,
при |х-Ц2г1/2/
сходится к 6j по норме пространства Wp (R).
Обобщенная функция б0 называется просто 8-функцией и обоз-
обозначается символом б. Из определения б|-функции следует, чтс
ф (?) = \ &(х —
R"
для любого фе= W2 (R"), k>n/2. Если {бу} — последовательность
функций из S, сходящаяся к б-функции по норме пространства
№Т* (R")> то последовательность функций
фундаментальная по норме пространства W^k(Rn), сходится
к обобщенной функции б|:
lim \ 8i.(x)(f>(x)dx= lim \ бу (х-1)ц> {x)dx-
R
Этот факт оправдывает принятую нами запись
I 86(дг)ф'(*)<&¦= ^ 6(ДГ-Е)Ф(*)^.
R" R"
§ 6. Гладкие функции в пространствах Соболева
Каждой непрерывной функции ф: R" -*-С можно поставить в соот-
соответствие функционал на Cf(R"), который переводит элемент
fe=Cj°(R't) в число $ ф (х) f (x) dx. Этот функционал мы будем
R"
также обозначать через ф и будем отождествлять его здесь
7 В, П, Маслов

194 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. II
с функцией ф; очевидно, что различным функциям ф отвечают раз-
различные функционалы на С™ (R"). Будем рассматривать ф как функ-
функционал в W~k (R"); если этот функционал ограничен, то его можно
единственным образом продолжить до элемента пространства
[W~k (R")]* = W\ (R"). Таким образом, мы отождествляем некото-
некоторые из непрерывных функций с элементами пространства W^(Rn)
и для каждой непрерывной функции приобретает смысл вопрос,
принадлежит ли эта функция пространству HP*(R").
Лемма 6.1. На множестве S норма в пространстве №*(R").,
?S»0 эквивалентна норме
где а = (оц, ..., а„), lal ^
Доказательство. Эквивалентность норм | 1W-*(R») и || Ц*
по определению означает существование таких констант Cj и са,
что для любого ф е S . '
|ф 1V*( R")^ Cl I Ф 11*. 1|ф lift < C2
Пусть ф = ^ф. Тогда
R"
Л
R"
Очевидно, что
;=0
С другой стороны,
так что
|a|<* /=0
и лемма доказана.
Пусть теперь функция ф: R"-*-С непрерывно дифференцируема
k раз. Положим, так же как и для "функций из S:
Имеет место следующий критерий.
Теорема 6.1. Функция ф, непрерывно дифференцируемая
k раз, принадлежит пространству W\ (R") тогда и только тогда,
когда |<p'J»<oo.

г 61
ГЛАДКИЕ ФУНКЦИИ
195
Доказательство. Пусть <p&W%(Rn), т. е. существует
такое М, что для любого /eCS°(R")
\<f(x)f(x)dx
R" .
Пусть |а|<6. Тогда, интегрируя по частям, получаем, что для
любого / е= С? (R")
х)] f (х) dx
Ф (х)
dx
так как
sup
Пусть, ijj —непрерывная функция, удовлетворяющая условию
для любого /eCS°(R'1). Покажем, что
r" .
Пусть функция emeCf(R") удовлетворяет условиям
(x)^l, effl(x) = l при |д;|^т. Тогда
Следовательно,
\ 4п
Переходя в последнем неравенстве к пределу при т-+оо, полу-
получаем требуемую оценку:
,о,л<уИ.
Применяя полученную оценку к функциям Daq>, |a|^&, полу-
получаем, что II ф |* -< оо.
Обратно, пусть |ф||*<оо. Требуется получить оценку
Ф (х) f(x) dx
1_* (R«}, / s C» (R«),
*
7*

196 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. Н
Пусть функция е е Cf (R") удовлетворяет условию е (х) = 1
при |x|^l. Положим ет(х)=е(х/т) и т^\. Тогда ет(х) — 1
при |л:|ои и Daem(x) = mr^a^Dae(^)\i=x/m, так что все произ-
производные порядка sgft функций ет ограничены равномерно по т:
sup
x
Отсюда следует, что
где М2 — константа, не зависящая от т. Из леммы 6.1 следует,
что для любого / е Cj° (R")
где М8 не зависит от т. Остается заметить, что для любого /е
е С" (R") найдется такое т ^ 1, что '
и теорема доказана.
Пусть [W*(R")J° — векторное пространство всех k раз непре-
непрерывно дифференцируемых на R" комплексных функций, для кото-
которых ||ф||Л<оо. Мы получили алгебраический обратимый гомо-
гомоморфизм
[^*(R)]°^*(R)
С другой стороны, при 0«S/<k— ~ по теореме вложения
Соболева существует обратимый гомоморфизм
сужение которого на S является тождественным отображением.
Теорема 6.2. Если целое 12s 0 удовлетворяет условию k~> I +
+ л/2, то отображение h осуществляет вложение пространства
[Wi(R")]° в пространство С(/) (R").
Доказательство. Пусть ф s [W* (R")]°, ф'==Дф. Доста-
Достаточно показать, что для любого / s Cf (Rn)
Лг- S ф (л) / (дг) dr.
r"
Пусть {фя}—такая последовательность функций из S, что
sup
(
-о,

§ б] ГЛАДКИЕ ФУНКЦИИ 197
т. е. фот->1ф в W\ (R"). Но / есть гомоморфизм; поэтому срт —
= ^фот->^1ф в С(" (R"), а значит, и в C(R"). Следовательно, для
любого fe [С (R*)]*
lim J Фт (дг) / (х) dx = J [Аф (х)] / (х) их.
В частности, это верно для /eCj°(R"). Тем самым теорема до-
доказана.
Рассмотрим теперь функцию ф (х, f) двух переменных х е R",
t e (a, b) e R. Предположим, что при любом t e (а, Ь) отображе-
отображение Ф (t): *->ф(х, t) есть k раз непрерывно дифференцируемая
функция, причем .
Тогда' Ф @ есть элемент пространства W\ (R") или, иными сло-
словами, Ф есть функция на (а, Ь) со значениями в W*(R"). Будем
говорить, что функция Ф порождена комплексной функцией ф.
Приведем удобное достаточное условие непрерывности функцци Ф
со значениями в W\ (R"), порожденной комплексной функцией ф.
Теорема 6.3. Пусть функция ф: R"x(a, b)->С непрерывно
дифференцируема k раз по первому аргументу и удовлетворяет
следующим условиям:
а) для всех а =.{аг, ..., а„), удовлетворяющих неравенству
|6, функция
непрерывна по t при фиксированном х;
б) для всех а, удовлетворяющих условию |а|<;&, и для foe
s (а, Ь) сущестбует такая функция г|)а, (oeLs (R"), что при любом t
из некоторой окрестности точки t0 выполняется неравенство
Тогда функция Ф со значениями в UP*(R"), порожденная функ-
функцией ф, непрерывна.
Доказательство. Пусть fos(a> Ь). Требуется показать,
что для любого а, удовлетворяющего условию |а|^^,
lim || О°Ф (t0 + п) - О«Ф (f0) |^ (RB) = О,
Л—*оо
ибо это соотношение эквивалентно сходимости Ф(^о + Л) к Ф (t0)
по норме | |ft. Имеем:
||г, 0 _fed|g| + 'q>(*
~п dtdxa

198 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА [ГЛ. И
где 0=^6 (*)^1. Поэтому при достаточно малых h
I ?>°Ф (/. + h) - О"Ф (t0) \\ц(R.) < | Л11¦„. ,„ \\Lt(R«) +0
при й-»-0, что и требовалось доказать.
Пример. Пусть
где /5*0, т^О—целые, и пусть б >0. Легко видеть, что при
1 kl
dk<p(x,t)
дх*
dx<oo,
так что при т^>{ функция ф порождает функцию Ф со значе-
значениями в №f-'-*1 (R). При помощи теоремы 6.3 убеждаемся в том,
что при т>1-\-2 функция Ф непрерывна как функция со зна-
значениями в W^~l—3(R). В частности, для любых a, 6sR суще-
существует интеграл
который понимается как предел соответствующих римановых сумм
по норме пространства Wj*—'—8(R). Если потребовать дополни-
дополнительно, чтобы выполнялось неравенство /и>/ + 3, то будет спра-
справедлива следующая формула:
(лг) = $ф(лг, t)dt.
Действительно, в этом случае Wf-'-3(R)c:C(R); поэтому схо-
сходимость римановых сумм для интеграла в левой части влечет их
сходимость в C(R). А поскольку, интегральные суммы для обоих
интегралов совпадают как функции от х и сходимость в C(R)
влечет поточечную сходимость, то совпадают и интегралы в левой
и правой частях как функции от х.
Далее, если lQ>(t)§wm-i-3(R)*^f(t), где функция/ интегри-
интегрируема на бесконечности, то существует, в смысле сходимости по
00
норме в Wf-'-3(K) интеграл \O(t)dt, так как
при с, d->-f oo. При этом можно утверждать также, что для

§ б] ГЛАДКИЕ ФУНКЦИИ 199
любого х е R интеграл $ ф (х, f) dt сходится и справедлива фор-
о
мула
\\\) = lcp(x, t)dt,
которая доказывается предельным переходом при Ь-*~-\-со в фор-
формуле, полученной ранее для интегралов с конечными пределами;
здесь снова используется вложение W?-l~3 (R) aC (R).
Легко видеть, что рассматриваемая функция Ф при
удовлетворяет неравенству
где Р — некоторый полином. Следовательно, интеграл
существует, причем
• Из теоремы вложения Соболева теперь следует, что если сущест-
существует /0= lim /a, где предел понимается в смысле сходимости
в Wl+t(W% s^O, то
/„(*)= lim -*\
- х' Г ,л*ч*м-<?тУп х^Лтх
~ (x-i)m J 2 (дг-П» •
о
Для того, чтобы показать, что lim существует, достаточно дока-
зать, что последовательность {/а} фундаментальна по норме
в WI+1 (R), а для этого, в свою очередь, достаточно показать,
что при О^/^s+l существует предел lim dflaldx!, понима-
а + 0
а
емый в смысле сходимости в L2(R). Имеем:
dxi
Легко видеть, что —Ц^- есть линейная комбинация интегралов

200 ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА -[ГЛ. II
вида
00
Обозначим ^ twelx't2-aldt = Iv(a), Интеграл /v(a) преобра-
о
зуется к следующему виду!
/v(a) = A + 02v+1 \ i/2ve-2jcVe-w(i + « dy.
о
Используя неравенство
справедливое при у^О, получаем следующую оценку:
| /v (a) - /v @) | < 2v+1a f y*v+ie-2*'y'dy = cva
о
где cv не зависит от a к i Итак, имеем
l'( )/(O )i<^
Выберем s^l — 3; тогда / —2 + ц —/^=0 для любых
Oj/. При этих же условиях (/п + ц) — (/ — 2
/ + 2. Поэтому
где /eLj(R). Отсюда следует, что предел lim ^% по норме
«->4-0 ах'
пространства La(R) существует.
Итак, окончательно получаем следующий результат.
Пусть mSi/ + 4Ss7, Os^s^l — 3, s^m — I — 3 и и#етб
функция Фа@ есть функция со значениями в №*+' (R), индуциро-
индуцированная функцией
( O
а
Все пределы в левой части.' предел римановых сумм, предел \
о
при а-*- + оо и lim понимаются в смысле сходимости в Wt+1 (R).
аИ * ч '

ГЛАВА III
ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ
В этой главе мы строим операторное исчисление, соответст-
соответствующее ^-структуре (см. Введение) на алгебре коммутирующих
неограниченных операторов в банаховом пространстве В. Нашей
целью будет выяснить, насколько широкий класс операторов обра-
образует множество М. Кроме того, мы выясним, каким символам
отвечают ограниченные операторы в В. Это поможет нам постро-
построить расширение (по замыканию) класса символов из С00.
Для простоты здесь приводится изложение, независимое от
теории ц-структур. Однако оказывается, что введенное в этой
главе понятие символа фактически совпадает с аналогичным поня-
понятием для ц-структур.
В качестве иллюстрации к понятию функции от оператора рас-
рассмотрим функцию от оператора А умножения на независимую
переменную л: в пространстве Соболева №* = №*(Rn). Нетрудно
убедиться в том, что если ср е С* (R"), то в этом случае можно
естественным образом определить функцию ср от оператора А
умножения на ж —этот оператор будет оператором умножения на
Ф (х). Легко видеть, что ср (А) есть ограниченный оператор в №*.
Если же k-я производная от ср (х) неограничена, то и оператор
умножения на ср(лг) неограничен в №*.
С другой стороны, оператор А умножения на х в W* обла-
обладает следующими свойствами:
1) он порождает однопараметрическую группу операторов умно-
умножения на семейство функций ext; 2) этот оператор умножения
удовлетворяет условию: для любого ge Ws2(Rn), где s^k, спра-
справедливо неравенство
т. е.
2
с = const.
Если обратиться к соответствующему эволюционному уравне-
уравнению, то можно сформулировать условия 1), 2) следующим об-
образом.

202 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Существует и единственно решение «эволюционного уравнения
(как непрерывная функция от / со значениями в Bi — W\, k «s; /);
удовлетворяющее условию
И0к<еA+|<|*)||и@)|к Н
для всех и@)еВ2 = №'а.
Связь, существующая между числом s в оценке решения эво-
эволюционного уравнения вида (*) (где в качестве заданного опера-
оператора стоит в данном случае оператор умножения на х) и ограни-
ограниченностью оператора умножения на <р(*), как мы увидим ниже,
распространяется на широкий класс операторов.
Условие (**) на рост решения эволюционного уравнения, по-
порождаемого оператором А, является необходимым, если потре-
потребовать, чтобы функция от А, дифференцируемая конечное число
k раз, была ограниченным оператором. Если же отказаться от
этого требования и ограничиться рассмотрением . только беско-
бесконечно дифференцируемых функций-от оператора, то условие (••)
на рост может быть существенно ослаблено. '" - _
Рассматривая оператор дифференцирования в пространстве
C(R) непрерывны^ функций, ограниченных на бесконечности (или
в пространстве Cn непрерывных функций, рйстущих не быстрее
1*1*), нетрудно убедиться в том, что «функции щ этого опера-
оператора» образуют алгебру «$0 (соответственно, алгебру <3>n)- Этот
пример показывает, что для рассмотрения алгебры функций от
операторов класса, включающего оператор дифференцирования
в пространстве непрерывных функций, неизбежно использование
алгебры а®0 (а в случае неограниченных непрерывных функций —
и а®дг). Этими двумя примерами мы хотим подчеркнуть «необходи-
«необходимость» использования условия на рост типа (•*) и алгебры <?йц.
Наконец, рассмотрим оператор А умножения на x-\-iy
в W7* (R1). Естественно определить k раз дифференцируемую функ-
функцию от x + iy как функцию ср(*, у) от двух аргументов х и у.
Каждый из операторов * = ИеЛ и у = 1тА удовлетворяет оче-
очевидно, условию (•*), и при этом Re А коммутирует в этом случае
с 1тЛ.
Мы введем ниже операторы, удовлетворяющие -условию типа
(**), и назовем их производящими операторами степени s. Далее
мы рассмотрим операторы вида Ах + iA2, где Ах и А2 — произво-
производящие операторы степени s и где Ах коммутирует с А2. Такие
операторы мы назовем регулярными, а функции от них будем
понимать как функции от Лх и Аг.

§ 1] ФУНКЦИИ ОТ ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 203
В § 8 мы докажем теорему, которая показывает «достаточ*
ность» условия типа (**). Именно, мы докажем, что в случае
чисто дискретного спектра наличие у оператора полной системы
собственных и присоединенных элементов с не превосходящим N
числом присоединенных элементов, отвечающих данному собствен-
собственному значению, эквивалентно регулярности оператора (степени Л!).
Таким образом, мы покажем (по крайней мере для дискретного
спектра), сколь, широк класс регулярных операторов.
Для случая, когда спектр не является дискретным, в § 9 для
регулярного оператора вводится понятие системы собственных и
присоединенных обобщенных векторов и доказывается теорема о
полноте этой системы. Однако такого понятия для произвольных
операторов пока ввести не удалось, и поэтому об обратной тео-
теореме речи не идет.
§ 1. Алгебра функций от производящего оператора
Пусть Е — векторное пространство над полем С, наделенное нор-
нормами I'IIj и |-|а, причем cf-fi^HIa, c=const. И пусть Вг — попол-
пополнение пространства Е по-^норме \\, а В2 — пополнение Е по
норме ||-||2.
В этом случае условимся писать Вг^<Въ-
Пусть и (t) — функция со значениями в Е, определенная на R
и удовлетворяющая уравнению
iJw~ Au=° Aл>
и начальному условию
«(о) =5» ge-E. A.2)
Здесь А — линейный оператор А : Е-+Е, а производная -^- ё Е
понимается в том смысле, что
II du(t) u(t+h)-u(t) || Л , п
\\-зг ~ -а—nli""*0 при н~* °-
Определение. Гомоморфизм А:Е-*-Е называется произво-
производящим оператором, если для любого ge? решение u{f) e? за-
задачи A.1), A.2) существует и единственно в классе функций,
удовлетворяющих неравенству
где с>0, k^O — некоторые постоянные.
Будем говорить, что А —производящий оператор степени
с определяющей парой пространств (Вг, В*), если существует
такая константа clt что
iHoib^Mi+mnsfli ' A.3)
для любого feR ii любого

204 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Если В1 = В2 = В, то будем говорить, что А — производящий
оператор в банаховом пространстве В.
Замечание. Заменяя в случае необходимости нормы Ц-^ и
|-||а на эквивалентные нормы, можем считать, что в этом опреде-
определении с=1, что мы и будем делать в дальнейшем. .
Лемма 1.1. Отображения {U(t)}t<=R, U(t):E-+E, опреде-
определяемые равенством U (t)g = u(t), где g и 0 удовлетворяют условиям
определения, являются гомоморфизмами пространства Е и обра-
образуют однопараметрическую группу, т. е.
U (Q U № = !;& +Q.
Доказательство. Пусть u(t) = U(t)g, u1{t) = U(t) и (^).
По определению, u(t-\-t^) = U(t + t^g. Значит, нужно показать
только, что и (/х + /) = «! (/). Обозначив и (^ +1) через и (t), получим:
Так как их является решением той же задачи Коши, то в силу
единственности, v(t) = u1(t), что и требовалось доказать.
Определение. Будем называть семейство {U (t)} группой,
порожденной производящим оператороЛ А.
Лемма 1.2. AU(t) = U(t)A для любого t <= R.
Доказательство. Для любого фиксированного ^eR
0 111
Полагая / = 0 и учитывая, что U@)g = g, получаем:
. Л-»0
Применим к выражению, стоящему под |-|lt У (t); тогда из
A.3) следует, при А->0,
Следовательно,
где 1а(Д)||а->0 при А->0. С другой стороны,
где |] б (A) Hj —>- 0 при А->0. Следовательно,
UU(t) A-AU(t)]gl = lb(А)-о
при Д-»-0. Отсюда следует утверждение леммы

§ 1] ФУНКЦИИ ОТ ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 205
Лемма 1.3. Пусть А —производящий оператор степени N
с определяющей парой пространств (filt Ba), пусть {U (t)} — группа,
порожденная А, и фе^дг^)- Тогда элемент / [ф; g] простран-
пространства Щ*, определяемый формулой
оо
/[Ф; ?](ft*)--Lr § $(f)h*(U(f)g)dt,h*eBS,Q-
—оо
принадлежит В2, причем
Доказательство. Пусть й* е В*. Имеем
>
Ф t) h* (U (t) g) dt
По определению производящего оператора имеем
(l + U!Hlk; поэтому
I / [Ф! g] (h*) I <р=|фК«> 1Л* К* По-
Последовательно,
. A.4)
Остается доказать, что / [q>; g] е В3. Если ф е Cf (R), то
оо
/(ф; g] = p|= J y(t)U(t)gdt.
Здесь интеграл, понимаемый как интеграл Римана от функции со
значениями в Вг, есть элемент из В%. Если ф = б^, то снова
/ [ф; g] e Ва, так как
I[V g] U®g
Следовательно, при q>ec$^(R) имеем /[q>; gf] e Ba- Из A.4) сле-
следует, что норма оператора, действующего из <?ftN (R) в В2 и пере-
переводящего ф в /[ф; g], ограничена числом -^=|^|в,. Из замкну-
замкнутости Ва в В|* получаем, что / [ф; g] е Ва ПРИ любом ф е S3N (R).
В этом параграфе всюду дальше предполагается, что А —
производящий оператор степени # с определяющей парой про-

206 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
странств В„ Bz, a {U (t)} — группа гомоморфизмов, порожденная
оператором А.
Пусть ф ee$?#(R)- Обозначим через ф* (А) оператор ф* (A)g^L
= / [ф; g] из Вх в В2 с областью определения ?. В силу леммы
1.3 имеем
_ 1
Лемма 1.4. Я#етъ ips^(R) и «F-edfo(R), «flfe
= дсф (х). .Гогаа ф, (Л) Д «¦% (Л).
Доказательство. По определению, для любых
и q e ? имеем
Л* [Ф, (A) Aq] = pJ== J ф @ A* [i/ @ Л<?] dt,
— 00
00
°?(t)h*[U(t)q]dt,
>
где ф и а^ —Фурье-прообразы функций ф и /.
Покажем, что для любой функции g, принадлежащей про-
пространству Cat(R) вместе со своей первой производной, справед-
справедлива формула
i \ %(t)g'(t)dt= \ f(t)g(t)dt. A.5)
— 00 — 00
Сначала заметим, что формулу A.5) достаточно доказать для
случая, когда g e C°° (R) П Сдг (R), поскольку при ^еСдг (R),
g' e C/f (R) для любого 8 > 0 найдется такая бесконечно диффе-
дифференцируемая функция й, что
Итак, пусть gf^C" (R) П CN (R), g' е Сдг (R). Рассмотрим после-
последовательность {gn\ cz С™ (R), обладающую следующими свойствами:
а) ga(t) = g(t) при te=(— n, га),
б) 15.-?1^ (*>«*, ll5«-gr'llcAr(R)<C2,C1,C2=COnst.
Тогда для любого элемента Ф s Сдг (R) справедливы соотношения
? [б @ ^ (О Л, A,6)
(t)g'(t)dt=nm \ $(t)g'n(t)dt. 0.7)
п-<»_оо

§ 1]
ФУНКЦИИ ОТ ПРОИЗВОДЯЩЕГО ОПЕРАТОРА
207
Действительно, пусть Ф = lim Ф/? Ф/е/7"'«%(!*). Для лю-
/-»СО
бого е>0 найдем такой номер /0, что ||Ф, — Ф||<:е при /3s/0.
Пусть носитель функции Ф/, содержится в интервале (— щ, щ).
Тогда
(*(')-*/.('))(*(*)-ft.(9)Л <«. с = const.
Щ(Щ, ft*eC(R) справедливо равенство
f(t)h(t)dt= Г f(t)h(-t)dt, A.8)
Для любых
Парсеваля
f = Ff, h = Fh. Из включения e$# (R) с С (R) и плотности
%(R) в e%>N(R) следует, что формула (\.8) справедлива для
любого / е Ct/ (к). Значит, можно переписать формулы A.6) и
и A.7) в виде
A.9)
A.10)
&(t)g(t)dt=\im I Q>(x)gn(-x)dx,
f Ф @ ^' (t) dt = Um f Ф (x) Gn (- x) dx,
— ео
oo
где Ф = ^б, gn = Fgn, Gn = Fg'n\ при этом Gn (x) = ixgn (x). Под-
Подставляя Ф = ф, в A.10), а в A.9; Ф = в^, получим
f t)dt = -i lim
5
Л-°°-00
J(x)gn(-x)dx=-i
и формула A.5) доказана.
Пользуясь формулой A.5), получаем
dt-
Лемма 1.4 доказана.

308 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Следствие. Пусть J?<еe%N(R), где «F/(х) = х*е?0(х),
/ = 0, 1 ,...,*. Тогда <?^(А)Ак = <?к*(А).
Доказательство состоит в последовательном применении
ЛеММЫ 1.4 К фуНКЦИЯМ ф = е/2, <УЪ ... , a?~k_lt
Оценим теперь норму оператора (Л—г).
Лемма 1.5. Оператор [А — (а + ib Г1 существует при ЬфО,
и справедлива оценка
НА-{а + 1Ь)]-ц^^-±- + -ф:Т, A.11)
где с и с' —некоторые константы, ||-|||« — норма оператора, дей-
действующего из Вг в Вг.
Доказательство. Пусть ЬфО. Обозначим z = a-\-ib.
Поскольку Im г Ф 0, то функция ф : ср (х) — (х — г) принадлежит
W\ (R) при любом &eR, так что фе^A(). А так как
le^jv(R), то и функция гр : гр (х) = х(х — z)~l = z(x— z)~l-\-1
принадлежит ^jv(R)- В силу предыдущей леммы, ф* (А) А =
= Bф*)(Л) + 1?, где \Е — тождественное отображение Е на себя.
Таким образом,
т. е. оператор (Л — г) имеет обратный:
И-г) = Ф.И)км_,)
При этом
UA-zr 11;<|Ф* (Л) $< ^~
Положим Фо(^) = 7=гщТ. Тогда 11Ф1U^ (R) = II Ф
Далее, полагая ф0 = ^Фо. Ф1 (*)=¦:—г> Фг — 'г~1Фь получаем
»для любого g&Cu (R):
$ ф0 (О g () dt=
— 00
Поскольку
sup
TO
s (
sup
(±±11L\N я
откуда и следует A.11). Тем самым лемма доказана.

§ 1] ФУНКЦИИ ОТ ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 209
Аналогично доказывается следующая лемма.
Лемма 1.6. Опера/пор [А — (a + ib)]~k, k>0, удовлетворяет
оценке
^
где Ck и с\ —некоторые константы.
Доказательство. Очевидно, что при 1тгфО и 0^/<
фунйция фу (х) = л/(х — z)~k принадлежит <$кф)- Поскольку
c$?jv(R)> то отсюда следует, что и функция
принадлежит с$?# ,R). Поэтому в силу следствия из леммы 1.4
для всех ge?. Следовательно, (А — г)~к = фо* (A) \R {A_g) к,
откуда
|| (А - гГ" «I j ^ || ф, Л Л) if; < pL=«Ф
о
1 —
I
f l l 1
\"|i|F' —b-fTk-)>
at (R)maX
где фо(^) = (лг — /)"*• Таким образом, лемма доказана. Заметим,
что утверждение этой леммы непосредственно из леммы 1.5 не
вытекает.
Поставим в соответствие каждому лектору Ле? оператор
Л; gSSjv (R)-* #2 ПРИ помощи формулы
Оператор h определен на всем пространстве <&н(Щ и огра-
ограничен:
|*|- ' sup "У" <т=1*Ь- <1Л2)
Введем в ? норму |-||mid по формуле
Пополнение Е по этой норме назовем промежуточным банаховым
пространством Вт\й-
Лемма 1.7. Справедливы неравенства

210 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. Ш
так что
Доказательство. Из A.12) сразу следует, что
i'111- С другой стороны,
IIАН л-
так как || l|^(R) = ||l/2it'60Ic+(R) = V^2jt. И лемма доказана.
Лемма 1.8. Для любого /oeR справедливы равенства
2) Ф* (Л) (е-W'.), = [в-м/. ф {A)Ui уФ е «Ждг (R). .
Доказательство. Во-первых, для любого Ае? имеем
— 00
Остается показать, что
Имеем
со -
1 f y(t)U(t)U(to)hdt =
Заметим теперь, что если функция aF s е®лг (R) представлена
в виде аГ(х) = ф(л-)е-''»д:, то Z7^ = (^ф) * У^2л б/0, так что для
любого C(R)
f (F'1^) (t) § (О Л = I (F-4) @ g (/ + to) dt
— op — оо
Поэтому
что и требовалось доказать.
Лемма 1.9. Пусть ty(x)= Ц ане~"ьх. Тогда

§ 1] ФУНКЦИИ ОТ ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 211
Доказательство. Следующие неравенства очевидны
(при О)
suo Иф»(Л)/His -^ SUD
Отсюда и из леммы 1.8 следует, что
sup
sup
что и требовалось доказать.
Лемма 1.10. Функция и в определении производящего опера-
оператора удовлетворяет неравенству для любых tly ^eR
II« ft) IU ^ A+\k - k IH «
Доказательство. В силу леммы 1.1
Следовательно, по лемме 1.8, u(to-\-t) — (е~~м0*и(А>)» поэтому
согласно лемме 1.9,
|| U (/0+ 0 Imid < || б, ||С& (R) || U (/0) Imid - A +1 f | )N | И
и лемма доказана.
Повторяя рассуждения леммы 1.3, мы можем установить, что
справедлива следующая лемма-.
Лемма 1.11. Для любых фе^лгО*). Ле? элемент
'» h] пространства Вша, определяемый формулой
/mid № Л] (п*) = -т|= J «(О Л* (?/ (О Л) dt, h*
принадлежит Втц, причем
I /raid №
Обозначим через ^midM) продолжение оператора
/mid№ h] до гомоморфизма Bmid-*Bmid- Очевидно,

^l^ ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Лемма 1.12. Отображение i|) -> i|)mid (Л) есть гомоморфизм
алгебры s®;v(R) в алгебру операторов пространства Вт\й.
Доказательство. Надо доказать, что i|)mid (А) фппа (А) =
= (l|><P)mid (А) ДЛЯ ЛЮбЫХ ф, Op S g®^ (R). Для ЛЮбоГО g*^.Bmld
имеем
00
г*(фш11(Д)А) = ^= J $(t)g*(U(f)h)dt.
— 00
Поскольку tymid (Л) — гомоморфизм, то
00
g* Wmld (А) фти (Л) А) = ^ J ф @ g* ftmld (Л) t/ (*) h) dt.
Рассматривая А как производящий оператор с определяющей
парой пространств (Въ 2?mjd) и применяя лемму 1.8, получаем:
— со . — со
ОО I 00
= $ Ф@( $ {$*bt)(t')g*{U(t')h)dt'\dt.
— со \—со
С другой стороны,
Доказательство леммы будет завершено, если мы докажем сле-
следующую формулу: для любых ф, ijj e Cn (R), f ^Cn (R)
f $ (/) л f № • б,) (Г) / (/') л' = f (ф * ф) (о / (о л. A.13)
— со — со — со
Заметим, что
со со
\ ($*6t)(t')f(t)dt' = -±= \ y(T)f(T + t)dx,
— со — со
так что A.13) принимает вид:
со
5 й)! A.14)
Но формула A.14) была установлена в гл. II. Лемма доказана.
Лемма 1.13. Существует такая последовательность {ф„} е
eCS°(R), что для любых /ie5mid, А'еВ^
НтА*[(Фвш1A(Л)-1)А] = 0.

§ I]
ФУНКЦИИ ОТ ПРОИЗВОДЯЩЕГО ОПЕРАТОРА
213
Доказательство. Выберем последовательность {ф„} сле-
следующим образом:
9i(x) = l при |х|<1, фх(х)=0 при \х\>2,
Такая последовательность {ф„} ограничена в <^N{9). Действи-
Действительно, пусть фя есть Фурье-прообраз функции ф„. Тогда
Ф1
Имеем, далее, для любой функции
<pn(t)f(t)dt
n<Pi(nt)f(t)dt
М4г
. Положим %(х) =
- 0 в любом пространстве Собо-
Соботак что последо-
последоОтсюда следует, что Ik
— <~irp-- Тогда % (х) — j^j
лева W{(R). Поэтому г|)„ (х) -
вательность операторов ^„mid (А) сходится по норме к оператору
: Далее-имеем
A.15)
для любого Ае?. Заметим, что
для любого Ае?. Следовательно, для любого Ае? справедливо
следующее предельное соотношение:
1)Ь/г. A.17)

^14 ' ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Из A.17) получаем для любых Ае?, /j*
при л->-оо.
Пусть теперь h — произвольный элемент из. Bmid. h* e Bmid-
Поскольку последовательность операторов {<p»mid (Л)— 1} равно-
мерно ограничена некоторой константой М, то выбирая для дан-
данного е>0 такой элемент hе ?, что \h — A||mid<8, получаем
при Л-»-оо, а это и означает, что
lim Л*
поскольку е произвольно. Тем самым лемма доказана.
Следствие. Множество.
,. М= U
4>6C»(R)
ПЛОтНО в Bmid-
Доказательство. Предположим противное, т. е. что
Л? Ф Bmid- Тогда из теоремы Хана — Банаха следует существова-
существование такого ненулевого элемента h* e Bmid. что Л*(Л) = 0 для
любого h^M. Пусть h* {hQ)^t 0. Рассмотрим последовательность
{/*„} = {<р„т1A(Л)Ло}, где {<р„} — последовательность функций из
C™(R), введенная в лемме 1.13. Имеем: h*(hn)—O для любого п.
С другой стороны, по лемме 1.13,
lim А*(Ая)=А*.(Ао)^О.
п-*со
Полученное противоречие доказывает, что М плотно в Bmid.
Лемма 1.14. Если Imz^O, то оператор [(A— z)],^
обратим.
Доказательство. Пусть he Bmid и пусть [(А — 2)~]1midh =
= 0. Если {ф„} — последовательность функций из CS°(R), рассмот-
рассмотренная в лемме 1.13, то
для всех натуральных п. По лемме 1.13
0= НтА*
для любого h* s Bmid. Следовательно, h — Q, что и требовалось
доказать. ¦ "
Лемма 1.15. Существует замыкание А оператора А в

§ Ц ФУНКЦИИ ОТ ПРОИЗВОДЯЩЕГО ОПЕРАТОРА
215'
Доказательство. Пусть Imz^O. Тогда оператор, обрат-
обратный к [(А — г)~1]тц, замкнут; в силу леммы 1.5 этот оператор
является расширением оператора А —г. Значит, и оператор А =
= (Л — г)-\-г имеет замкнутое расширение. Лемма доказана.
Оператор А мы также будем называть производящим опера-
оператором.
Дадим теперь новую интерпретацию формулы
A.18)
Рассмотрим пространство Cjv(R", В), состоящее из непрерыв-
непрерывных на R" функций со значениями в банаховом пространстве В,
имеющих конечную норму
Пример. Для любого Ае? функция fi
f(t) = U(t)h
принадлежит пространству Cjv(R, Bmid), причем
Рассмотрим далее для каждого feC^R", В) оператор
lo[f\\F~l<?®%-*-B, определенный формулами
/о Ш б| = / (I), /о [Л ф = 5 Ф W f W djr' Ф s С (R«).
Задача. Доказать,' что || /0 [/] || ==? | f ||c^(r„_ в)
Указание. Для любого фгС^°(Rn) и любых различных вещественных
чисел ii, ...,1й
Ф+ 2аА,Ь- ,опч= ]\<P(x)\(l+\X\)Ndx+ i3|e,|(l+|5,|)W.
Расширим оператор I0[f] до гомоморфизма / [/] i C% (R")->-B.
Мы будем пользоваться обозначением
R"
которое и дает нужную нам интерпретацию равенства A.18).
Очевидно, оба рассмотренные определения оператора q>mid (А) сов-
совпадают.
Пусть /eCAr(R", В)ли пусть функция*^, определенная форму-
формулой & (x) = Cf(x), где С —замкнутый оператор в В, принадлежит

216 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Ca^R", В). Тогда для любого ф е= F'1^ (R*)
$ Ф (х) Cf (х) dx = C \ Ф (x)f (х) dx. A.19)
R" R"
Если ф — произвольный элемент из C+(R"), то выбирая последо-
последовательность {щ} с F'ioffi'k (R"), сходящуюся к ф, и переходя к пре-
пределу при А-»-оо в равенстве
$ Ф, (х) Cf (х) dx = б ] щ (х) f (х) dx,
R" R"
получаем, что и в этом случае справедлива формула A.19).
Лемма 1.16. Пусть imz^O. Тогда
Доказательство. Нужно доказать две формулы!
[(A-zf\jA-z)h = h, h<=Dj, ' A.20)
(А -г) \{А -z)]mld=l. A.21)
Формула A.20) справедлива при h&E согласно лемме 1.5;
если hn-*-h, hn^E, h^D^, то в A.20) можно перейти к пре-
пределу, так как Л — г — замкнутый оператор, a [(A — z^Jmid — гомо-
гомоморфизм. Этим формула A.20) доказана.
Пусть теперь снова fte?; обозначим через гг Фурье-прооб-
Фурье-прообраз функции гг (х) = (х — г). Имеем
00 \
h = [(А - г)'1]^ (А - г) h = -щ \ h (t) U (t) (A-z)hdt =
Af)U(t)hdt ={А-
Мы воспользовались формулой A.19). Итак, при
Из замкнутости оператора А и плотности множества Е в тц
следует, что это равенство выполняется для любого AeSmid,T. e.
формула A.21) верна, и лемма доказана.
Резюмируем основные утверждения, доказанные в этом пара-
параграфе, в виде следующей теоремы.
Теорема 1.1. 1) Производящий оператор А как оператор
в пространстве Втц имеет замыкание А-

$ 2] РАСШИРЕНИЕ КЛАССА ДОПУСТИМЫХ СИМВОЛОВ , 217
2) Существует гомоморфизм М банаховой алгебры s®at(R9
в алгебру Op (Вт1<\) гомоморфизмов Втщ -> Втиь при котором функции
1
отвечает оператор (А —гI.
Обозначение. Пусть функции ф е <$N (R) отвечает гомо-
гомоморфизм Ф: 5mid-»-fimid- Условимся обозначать Ф = ф(л). Образ
гомоморфизма М будем обозначать символом С1дг.
Функцию ф е d®N (R) будем называть символом оператора ф (Л).
§ 2. Расширение класса допустимых символов
Пусть Л — производящий оператор степени N с определяющей
парой (В1; 52) банаховых пространств, содержащих плотное
в каждом из них линейное многообразие D = DA. В предыдущем
параграфе были введены операторы вида ф(Л), где fe^(R).
Мы полагали по определению ф(Л) = фтм(Л), где ф1ш(Л) —
оператор, определенный на Е. Приведем теперь более явную
формулу для ф(Л). Именно,
со
/
для любого h e Bmid. Действительно, пусть {hn} — последователь-
последовательность элементов из Е, сходящаяся к А. Тогда
-U (t) К\=\е~ш (А-А»I ^ A +| t\)»\\h-hn\\.
Следовательно, функции U (t) hn сходятся к e~tAth в пространстве
C(R B). Поэтому
= Пт фт|а (Л) А„ = ф (Л*) А,
«0
что и требовалось доказать.
Теорема 2.1. Пусть фе«$?дг^) и пусть функция г|з:
где k — натуральное число, также принадлежит <^v(R). Тогда
¦ г|з (Л) = Л*ф (Л) = Ф (Л) А" = ф (Л) Л*.
Для доказательства нам понадобится следующая лемма.
Лемма 2.1. Для любого AsDi справедлива формула

218 функции от регулярных операторов • [гл. ш
Доказательство. Пусть {hn} — последовательность элемен-
элементов из- Е, сходящаяся к h, причем Ah= lim Ahn. Тогда
lim е~'ъ Ahn = lim
n-*co n-»oo
что и требовалось доказать.
Доказательство теоремы 2.1. Для любого Ае? спра-
справедливо равенство ipmid (A) h = фт|а (A) Akh, т. е.
. B.1)
В силу A.19) последнее равенство можно переписать в виде
Л*
4foid (Л) *--ir Л* U @ и (О Л Л = Л*фт1а (Л) А.
Здесь мы воспользовались предложением о замкнутости степени
замкнутого оператора главы I и тем фактом, что (Л + /I есть
гомоморфизм Bmid->-5mid. Мы доказали, что операторы 1|)(Л) и
Л*ф(Л) совпадают на множестве Е, плотном в Bmid- В силу
того, что ф(Л) и ф (А) — гомоморфизмы, а оператор Ак замкнут,
отсюда следует, что операторы Л*ф(Л) и if (Л) совпадают всюду.
Далее, равенство B.1) означает, что оператор ф(Л)Л* есть
сужение гомоморфизма if (Л) на всюду плотное множество Е.
-Поэтому справедлива формула
Остается доказать формулу
Иначе говоря, нужно показать, что оператор ф(Л) Ак имеет зам-
замкнутое расширение, ибо на плотном множестве Е он совпадает
с гомоморфизмом 1|>(Л). Пусть ^eDjj, А„-»-0 и последова-
последовательность ф(Л)Л*Л„ сходится. Имеем:
Ф (Л) Akhn =
-J=-
¦00

§ 2] РАСШИРЕНИЕ КЛАССА ДОПУСТИМЫХ СИМВОЛОВ 219
при п-*-оо в силу замкнутости оператора Ак, и теорема дока-
доказана.
Таким образом, мы показали, что формула [fg] {A) — f(A)g{~A)
имеет место не только в случае, когда /, ge<^&jv(R), но и в том
случае, когда / — полином, g<= <&N(R) и/ge&N(R). _
Примем теперь следующее соглашение: замыкание А произ-
производящего оператора А в Bmid будем обозначать просто через А,
оговаривая это специально в случае, возможной путаницы.
Лемма 2.2. Если q>ec$?jv(R) и если ф(х) не обращается
в нуль ни в одной точке из R, то оператор q> (А) обратим (т. е.
Ф (Л)Л??0 при hфО).
Доказательство. Пусть {е„} — такая последовательность
функций из C~(R), что
\\mh*(en(A)h) = h*(h)
П-* 00
для любых h e Bmid, h* e Вты. Существование таких последо-
последовательностей установлено в лемме 1.13. Если <р(Л)Л = О, то
где 1Мх)==е„(*-)/ф(х). Но %(А)ц>(А)=еп(А). Следовательно,
ДЛЯ ЛЮбОГО Л* S Bld
h*(h)= \imh*(en(A)h) = O.
П-+00
Отсюда следует, что h = 0, и лемма доказана.
Тебрема 2.2. Для любых /ec$?jv(R) и полинома Р сущест-
существует замыкание оператора j(A)P(A) в Bmid.
Доказательство. Пусть hn-**0 и пусть f(A)P (A)hn-*-q
при л->-оо. Покажем, что <7 = 0. Обозначим через ф функцию из
S, нигде не обращающуюся в нуль. Имеем
q.
л~»оо
Но ф/Pe«®^v(R)^ и поэтому в.силу теоремы 2.1 имеем
Отсюда в силу обратимости оператора ф(Л) следует, что G = 0,
и предложение доказано.
Теорема 2.3. Пусть f e<$N(R) и пусть Р — полином. Тогда
оператор P(A)f{A) является расширением оператора f(A)P(A).
Доказательство. Если h принадлежит области определе-
определения оператора Р (А), то
00
^ J J(t)e-iAtP{A)hdt,

220 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
где ^—Фурье-прообраз функции /. Отсюда, используя лемму
2.1 и замкнутость оператора Р(А), получаем:
00
= J= P (А) 5 } @ е-'Щ dt = P (A) f (A) h,
—00
так что оператор P(A)f(A) является расширением оператора
f(A)P(A).
Пусть теперь Л —произвольный элемент из области определе-
определения оператора f(A) P(A). Тогда существует такая последователь-
последовательность {Л„} элементов из области определения оператора Р (А),
ЧТО"
limA, = A, lim f (A) P (A) hn = f (A) P (A) h.
п-»оо я-»оо .
В силу того, что f(A) есть гомоморфизм, a f(A)P(A) есть суже-
сужение оператора P(A)f(A), получаем
Iim f (A) hn = f (A) h, Hm P (A) f (A) hn = f(A)P (A) h.
n-*<x> n-*oo
Отсюда в силу замкнутости оператора Р (А) следует, что
P(A)f(A)h = f(A)P(A)h,
и теорема доказана.
Лемма 2.3. Пусть /ь /2, /3 — функции из <^v(R) и пусть Р
и Q —полиномы, причем
/i(*)Р (*)-/.(*)Q (*) + /•(*)•
Тогда для любого heDp(A)fl(A)[\Dq(A)h(A) выполняется равенство
Доказательство. Пусть функция ipeS не обращается
в нуль ни в одной точке. Тогда согласно лемме 2.2, оператор
Ф (А) обратим, так что достаточно показать, что
V(A)[P(A)f1(A)-Q(A)f,(A)-f,(A)]h = O.
Функции фР и ф(? принадлежат <?®n (R)» кроме того,
Следовательно,
4>(A)[P(A)h(A)-Q(A)h(A)-f3(A)]h =
«= 1(РЧ>) (Л) h (А) - (QV) (A) h 'А) - Ф (A) fa (A)] h = 0,

§ 2] РАСШИРЕНИЕ КЛАССА ДОПУСТИМЫХ СИМВОЛОВ 221
так как оператор [Рср] (Л)Д (A) — [Qcp] (A)f2(A) — ф (A)f3(A) имеет
символ (p(Pfi — Qf2 — f3) = 0: Тем самым лемма доказана.
Дадим теперь определение растущих функций от производя-
производящего оператора.
Определение. Пусть g(x) = f(x)P(x)-\-f1(x), где /е=
esSjv(R)i fi^BN(R) и где Р —полином. Положим
. . . def -
Замечание. Элемент h из Вт\& принадлежит области опре-
определения оператора g(A) тогда и только тогда, когда существует
такое представление функции g в виде
где Д ^e^jvfR), P — полином, что
Из леммы 2.3 и теоремы 2.3 следует, что определение кор-
корректно в том смысле, что оператор g(A) не зависит от способа
представления функции g в виде fP-\-fi. В случае, когда ge
е «$?лг (ft), определение очевидно согласуется с определением
гомоморфизма g(A), приведенным в предыдущем параграфе.
В случае, когда g —полином, определение также согласуется
с определением полинома от оператора. Действительно, пусть
где Д Д.е^лг(Я) и где Р и g —полиномы. Прежде всего заме-
заметим, что степень полинома Р не меньше степени полинома g,
поскольку функции / и Д ограничены. Следовательно, область
определения оператора Р(А) содержится в области определения
оператора g(A). Нужно показать, что область определения опе-
оператора f(A)P(A) не шире области определения оператора g(A).
Пусть h — произвольный элемент из области определения опера-
оператора f(A)P(A). Тогда существует такая последовательность {hn}
элементов из области определения оператора Р(А), что limhn — h
п-*со
и последовательность {/ (А) Р (A) hn} фундаментальна. Но hn e
^Dg(A), и следовательно, согласно теореме 2.3 и лемме 2.3,
справедливо равенство
так что последовательность {g (A) hn] сходится. Поскольку опе-
оператор g(A) замкнут, то h^Dg(A), что и требовалось доказать.
Предположим теперь, что замкнутый оператор А обратим.
Теорема 2.4. Пусть (pe<2®w(R) и пусть функция ^i

222 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
где k — натуральное число, также принадлежит s®w(R). Тогда
^ (Л) = Л~*ф (Л).
Доказательство. Имеем: >
Ф
Следовательно,
<p(A)
Определим теперь операторы, отвечающие символам, имеющим
особенность в нуле.
Определение; Пусть g (x) =f(x)х~к, где f e &ы(R) и к—
натуральное число. Положим
Проверим корректность данного определения. Пусть /1( Д
^) x~krf1(x) = x-k>fi(x). Покажем, что
Действительно, пусть, для определенности k2~>k1. Имеем: f2(x)=
= xb-^frix); следовательно,' /2 (Л) = Л*'-**/1(Л). Умножая обе
части этого равенства слева на А~кг, получаем требуемое соотно-
соотношение. -
Лемма 2.4. Пусть /<=^\r(R), h^DA-k. Тогда
Доказательство.- Имеем:
dt=A"f <л> A'"h-
Умножая обе части полученного равенства на А *, приходим
к утверждению леммы.
Определение. Пусть g(x) = f1(x)P(x) + f2(x)x-k + f3(x),
где fv /г. /з — функция из <?®n(R), P —полином, k — натуральное
число. Положим
где 8i (x) = /i (x) P (x), g* (x) = f% (x) x~k, h — произвольный элемент
из Dul{A)[\Dgi(A),
Проверим корректность этого определения. Пусть
В М =

\
$ 21 РАСШИРЕНИЕ КЛАССА ДОПУСТИМЫХ СИМВОЛОВ 223
где ,
gi(x) = fi(x)P(xh Ы*) =/2 (*)*"*,
gt (х) - /4 (х) Q (х), gb (х) = /6 (х) х-1,
fj^&if(R), /=1, 2, ..., 6, Р и Q —полиномы, k и / — нату-
натуральные числа. Прежде всего заметим, что функции g2 и gb
можно исправить в ограниченной окрестности нуля, так, чтобы
получить функции из ^дг(Я). Поскольку
и поскольку функция gi — gt совпадает в окрестности нуля с не-
некоторой функцией из S^aKR), TO
где f7<=a®Ar(R). Следовательно, g1(A)=gi{A) + f7 (А). Далее,
справедливо равенство
где fa = fs+.h-f7^^N(Rb Пусть
Положим
q - [А (Л) - & (Л) - /, (A)) h = [Л-fcf, (Л) - А-% (А) - f, (Л)] А.
Требуется доказать, что <? = (). Проведем доказательство по сле-
следующей схеме: пусть (peS — функция, нигде не обращающаяся
в нуль, и пусть <рт(х) = хт<р (*),' /п=1, 2, ... Мы покажем, что
оператор фт (Л) обратим и что ym(A)q = 0 при достаточно боль-
большом т. Имеем фт(Л) = Лтф (Л). Поэтому
(Фт (Л) и -0) => (ЛтФ (Л) и = 0, => (ф (Л) и = 0) 4> (и = 0).
Мы воспользовались обратимостью операторов Л и ф(Л). Обра-
Обратимость оператора фт (Л) доказана.
Пусть т ^ max (Л, /). Тогда функции д:"*фт (д:) и дг~гфт (лс) при-
принадлежат пространству а®дг(Я). Пользуясь теоремой 2.4 и леммой
2.4, получаем:
(pffl (Л) q = [Лт-*ф (Л) h (Л) - Л^ф (Л) h (Л) - Л"Чр (Л) /, (Л)] h = 0,
что и требовалось доказать.
Пример. Пусть |/д: = /V|л:| при х<.0. Тогда функция
дг^+Ч/Т непрерывно дифференцируема на вещественной прямой
N+1 раз. Пусть 1=е1(х) + е2(х), где ^^^(R), e1{x) = \ при
достаточно малых д:. Положим fi{x) = el(x)xN + iyrXi /a(•*¦)=
= е2 {x)lVlc. Тогда /lt f2 e &N (R1) и

224 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
ще gi(x) = x~lv~if1(x), gi(x) = xfi{x). Следовательно, для любого
h <= Dgl {A) fl Dg, {A) спр аведлива формула
Y~Ah = A~N~>fi (A) h + Af, (A) ft.
Задача. Мы определили бесконечно дифференцируемые растущие не
быстрее степени аргумента функции от коммутирующих операторов. Показать,
что оии образуют алгебру с ц-структурой, где алгебра А есть алгебра комму-
коммутирующих неограниченных операторов, а множество М состоит из произво-
производящих операторов и действительных функций от них.
§ 3. Гомоморфизм асимптотических формул.
Метод стационарной фазы
Пусть А — замыкание в Втш производящего оператора степени N,
k— натуральное число. Из теоремы 2.1 следует утверждение:
если ф, i|je<^v(R) и ф(*)— ^(х) — О(х~^ в том смысле, что
функция xk[y(x) — xj? (лг)] принадлежит <^v(R), то для любого
geBmid вектор ф (A) g —1|> (A) g принадлежит области определе-
определения оператора Ak.
В качестве примера рассмотрим так называемый метод стацио-
стационарной фазы. Пусть ф е Cf (R), пусть /еС™ (R) — веществен-
вещественная функция, и пусть уравнение </'(?) = 0 имеет единственное
решение ?0 на носителе функции ф, причем <^" (?0) Ф 0. Рассмот-
Рассмотрим интеграл
00
"*(E)d6. C.1)
Метод стационарной фазы дает асимптотическое разложение функ-
функции / (*) по отрицательным степеням х:
/=о
где Rn+1(x) — O(x-n~3/2). Мы воспроизведем здесь вывод формулы
метода стационарной фазы, чтобы получить оценку остаточного
члена /?„+1 в нужной нам форме.
Сделаем в интеграле C.1) замену переменных
и обозначим <о = |л:|, a = sign [х^и A0)]. Получим
00
/ (х) = 4**&* \ eiaat\ it) dt, C.2)
— 00
где ф @ = Ф (I @) dl/dt, f <= Cf (R). Преобразуем формулу C.2)

§ 31 МЕТОД СТАЦИОНАРНОЙ ФАЗЫ. 225
следующим образом;
00 00
=^(O) $ ei«"dt + \
ОО
J е«°°<> ъ @ dt,
где ip! (t) = -jr ' '~^L2.; мы использовали интегрирование по
частям. Легко видеть, что вне носителя функции г|э (t) справедливо
равенство
Преобразуя интеграл § е1®0*'ifo, (t) dt так же, как это было сде-
— 00
00
лано с интегралом $ ei<aat'ty(t)dt, получим формулу
>i(O)W
где 1|з2 (t) = -~ Ф^'-^С0). Продолжая этот процесс, получаем:
1=0
00
— 00
где
Для обоснования формулы C.3) нужно еще убедиться в том, что
для любого натурального /
МЬМ) 0. C.4)
Пользуясь явной формулой для i|);t (t) при больших t, нетрудно
установить по индукции, что при t ^ suppif имеем ^ (t) = t-2P (H),
где Р — некоторый полином, зависящий от /'. Тем самым фор-
формула C.4) установлена.
8 В. П, Маслов

226 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Итак, мы получили следующее разложениег
), C.5)
00
'ИЫ)п+1 С ^«s^iw^^^ (з.б)
причем при отрицательных д:
Мы не можем подставить непосредственно в формулу C.5)
производящий оператор А вместо переменной х, так как функция
l/xJ не принадлежит пространству <?&ы (R). Подправим разложе-
разложение C.5) следующим образом. Пусть rad*—бесконечно дифферен-
дифференцируемая функция, совпадающая с Ух вне некоторой конечной
окрестности нуля, и пусть ру (д:) — бесконечно дифференцируемая
функция, совпадающая с х~* вне некоторой конечной окрестности*
•нуля. Тогда
(rad*) «-***"«•> \ е<^«> ер
!BLfliWy n+i W, C.7)
где fn+i(x) = r^-i(x) при достаточно больших |лг|.
Заметим, что все члены в C.7), кроме г„+г (х), очевидно, бес-
бесконечно дифференцируемы. Отсюда следует, что и функция гп+1(х)
также бесконечно дифференцируема.
Перейдем теперь к оценке остаточного члена г„ц(х) на беско-
бесконечности. Положим для определенности signal" (|0) = 1. Продолжая
разложение C.5), получаем для любого натурального m^
t. C.8)
Первое слагаемое в правой части C.8) есть константа, поэтому
оно принадлежит пространству <?BN (R). Далее, все слагаемые

§ 3] МЕТОД СТАЦИОНАРНОЙ ФАЗЫ 227
суммы 2 в правой части C.8) квадратично интегрируемы
/="+2 " .
в окрестности бесконечности, и тем же свойством обладают также
все их производные. Рассмотрим, наконец, функцию
оа
def
f(x) = V~x x»~m $ e'*"tfm+i (t) dt= V~x x»-m g (x).
— 00
Функция g ограничена; оценим ее производные. Имеем:
00 . 00
—00
Мы произвели здесь интегрирование по частям и воспользовались
тем, что limft|3ro+i@ = 0. Для вычисления g" (х) заметим, что
функция [%n+i (t)Y, так же как и функция i|)ro+i (if), представима в виде
произведения t~* на полином от Г1, так что
Вычисляя так же следующие производные, убеждаемся, что функ-
функция g(jr) бесконечно дифференцируема и g(k) (x) = О (\х\~*). Отсюда
следует, что при достаточно большом т функция интегрируема
в окрестности бесконечности при к <; N + 1 •
Из полученных оценок следует, что функция xnnrn+i (x) пред-
представима в виде суммы константы и функции из WJ'+^R) и сле-
следовательно, принадлежит пространству SBN (R). Сама функция /"п+1,
очевидно, также принадлежит пространству <8$ы (R)- Таким обра-
образом, ДЛЯ ЛЮбОГО g e fi
Обратимся теперь к левой части формулы C.7). Эта функция
принадлежит SbN (R), так как правая часть обладает этим свой-
свойством. Обозначим
def
rad*-/(*)=#(*).
Справедливо разложение
8*

228 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
причем область значений оператора rnJri (А) содержится в области
определения оператора АпП. Обозначим теперь
Функция g(x, I) порождает функцию G(g) со значениями
в W^+l (R) c$>n (R). Функция G непрерывна. Действительно,
справедлива оценка
-
равномерная по ?. Следовательно,
ЦА)=] g(A,
Далее, нетрудно проверить, что / е S3N (R) и значит, последнее
равенство можно переписать в виде
(A + i)-4(A)=] g(A, l)dl, l(A) = (A+tf f g(A, l)dl.
— 00 . —00
Покажем, что К (А) = rail A • I (А). Пусть heE. Тогда для
любого натурального k и любого % е <?®ц (R) имеем
оо
X (А) (А + ifh = г— J % (О (А + i)k V @ h dt = (А + 0*х (A) h.
—00
Отсюда, в частности, следует, что х(^) h принадлежит области
определения любой степени оператора А. Положим
j / . rad х
при достаточно больших k имеем radft e <?Вц (R). Для любого /ie?
rad A ¦ 1 (A) h = radft (A) (A + i)k I (A) h = radft (A) 1 (А) (А + i)k ft.
С другой стороны,
поэтому
radi4-
Пусть теперь ft — произвольный элемент из Втц, hj e E, hj—~h
при /"—>схэ. Тогда
К (А) hj — К (A) h, I (A) hj — / (A) ft при / — оо,
следовательно,
-l (A)h,
/-»оэ

§ 31 МЕТОД СТАЦИОНАРНОЙ ФАЗЫ 229
что и требовалось доказать. Мы можем теперь записать формулу
K(A) = radA-(A + i)* $ g(A, g)dg.
— 00
Отсюда следует, что для любого /ig?
+ i)* f g(A, g)Adg =
— 00
\g{A,l){A + ifhdi = radA $ <p (g) e"*«> A dg.
— 00 —00
Для того, чтобы распространить полученное при Ае? равенство
K(A)h = radA J <p
— 00
на случай произвольного ЛёВтш, покажем прежде всего, что
функция
6 —<p(g)e"*-<DA C.9)
со значениями в Вты непрерывна на вещественной прямой. Доста-
Достаточно показать, что отображение
непрерывно, что, в силу ограниченности оператора eiAi, равно-
равносильно следующему: для любого е > 0 найдется такое положитель-
положительное 6> что при |т|<6 ,'
\\eiMh —
Выберем такое h0 e E, чтобы неравенство
Ao)||<| C.10)
выполнялось для любого т из фиксированной ограниченной окре-
окрестности нуля. Положим <70 = (А + iJh0. Тогда.
II (е"т - 1 ho || = || (А + О («"'- 1) q0 II - О
при т—'0, так как функция G со значениями в W^+1 (R),
определенная формулой
непрерывна. Выберем такое б>*0, чтобы при |т|<6 выполня-
выполнялись неравенство C.10) и неравенство
Тогда при |т|<6

230 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ, Ш
Тем самым непрерывность функции C.9) доказана. Следовательно,
интеграл
понимаемый как предел интегральных сумм по норме простран-
пространства Bmid, существует.
Далее, если hn-+h при га-»-оо, то Цффе^^ (ha-h)\\Bmld-+
->0 при п-*-оо стремится к нулю равномерно по |, так как •
Пусть h — произвольный элемент из Вт\& и {пт} — сходящаяся
к h последовательность элементов из Е. Тогда
lim I (A) hm = I (A) h,
lim Г
Но 5 ф A) е'Л^ «> Am dg = / (А) hm\ поэтому
отсюда следует, что
—00
Обозначим
ау (ф, S) = VH <**»W У в.)
где функции Ч>/ построены по функциям фи/ описанным выше
образом. Числа ау(ф, «У) зависят только от значений функций
Ф, / и их производных в точке g0 до некоторого порядка, за-
зависящего от /.
Итак, получаем следующее предложение.
Теорема 3.1. Пусть ф ёCJj°(R) м га«/сть «^" — бесконечно диф-
дифференцируемая на R вещественная функция, имеющая на носителе
функции ф единственную критическую точку |0, причем <f" (?0) ^ 0.
Пусть далее radA: — бесконечно дифференцируемая функция, совпа-
совпадающая вне некоторой ограниченной окрестности нуля с функцией
(|°> при х<0,
U пусть, наконец, pj (х) — бесконечно дифференцируемые функции,

§ 41 ФУНКЦИИ ОТ ОПЕРАТОРА ДИФФЕРЕНЦИРОВАНИЯ 231
совпадающие вне некоторой ограниченной окрестности нуля с функ-
функциями x~j.
Тогда для любого целого га^=0 справедливо разложение
rad А I ф © е1^ «> A dg = е"*<е> J] а} (Ф, *f) р, (Л) А + qn+i,
-со / = 0
C.11)
где qn+i принадлежит области определения оператора АаП.
Замечание. Пусть оператор А обратим. Тогда можно в фор-
формуле C.11) заменить pj(A)h на A~fh при условии, что h^DA-n.
Для того, чтобы убедиться в этом, достаточно показать, что для
любого h e DA-j
[ру (Л)-Л"-/] А «=?>„
Обозначим [pj(A) — A~J]h = q. Тогда AJ'q=[Afpj(A) — l]h. Функ-
Функция xfpj (x) принадлежит SBN (R) и тождественно равна 1 в окре-
окрестности бесконечности. Следовательно, для любого натурального
т функция Xм (xfpj (х) — 1) принадлежит пространству S3N (R),
так что область значений оператора AJPj (A) — 1 содержится в DAm.
Значит, для любого т имеем q^DAj+m; в частности, g^DAa+i.
§ 4. Функции от оператора дифференцирования.
Оператор Гильберта
Пусть, в обозначениях предыдущего параграфа,
и пусть оператор А действует по формуле
Лемма 4.1. Оператор А является производящим оператором
нулевой степени.
Доказательство. Рассмотрим задачу Коши
^ D.1)
Решение задачи D.1) существует; именно, функция
удовлетворяет данному уравнению. В самом деле, прежде всего,
[/i4« (*)](*) =-А'
Далее,
h(x+t+8)-h(x+t) -h' (x+t) = h' (x + t + Щ-Ь' (x+t),

232 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. Ш
где |8|«sl; поскольку функция Н' равномерно непрерывна, раз-
разностное отношение
h(x+.t+&)-h(x+f)
е
сходится при 8'->-0 к h' (x-\-t) равномерно по х. Следовательно,
так что -? = — iAu, если понимать дифференцирование по t
в смысле сходимости в L2 (R) и тем более — в смысле сходимости
в W^1 (R).
Докажем теперь единственность решения задачи D.1). Заме-
Заметим прежде всего, что оператор А симметричен: Л*г>Л. Дейст-
Действительно, для любых ф, 1|з е DA
оо
= 5 (— Р) Ф (Р) Ф (Р) 0 + Р2)"* dp = (ф, /4д|з) w,- $ (ю-
— 00
Здесь Ф, ij> — Фурье-образы соответственно функций ф, \|з.
Согласно теореме 4.1 гл. I, для доказательства единственности
решения задачи Коши D.1) достаточно показать, что для любого
fteCS°(R) и для любых вещественных a, b, T существует непре-
непрерывная по норме пространства L2 (R) функция v со значениями
в CU°(R), удовлетворяющая условиям
- + lAv-l H ПрИ /е(а>
0 при f ? [а, 6],
(дифференцирование понимается в смысле сходимости в L2(R)).
Пусть для определенности а<.Ь<Т. Положим
О при
t)dT при
Продолжим функцию v в область <<са так, чтобы она удов-
удовлетворяла задаче Коши
разрешимость последней задачи доказывается точно так же, как
разрешимость задачи D.1). Определенная нами функция v удов-

§ 41 ФУНКЦИИ ОТ ОПЕРАТОРА ДИФФЕРЕНЦИРОВАНИЯ 233
летворяет всем требуемым условиям; в проверке, очевидно, нуж-
нуждается только условие
-^-\-iAv = h при *е(а, Ь).
t
Пусть /е=(а, Ь). Тогда [Av(t)] (x) = i\h' (x-T + t)dt. С другой
ь
стороны, без труда можно установить (аналогично тому как это
было сделано ранее для функции и), что
= h(x)-i[Av
Итак, единственность решения задачи Коши D.1) доказана.
Мы выяснили, что оператор А порождает однопараметриче-
скую группу {U (t)} гомоморфизмов векторного пространства Cf (R).
Имеет место формула
U(t)<t(x)=<f(x + t);
по этой "причине группа {U (t)} называется группой сдвигов. Оче-
Очевидно, что для любого вещественного t оператор U (t): W7"s{R)->-
->Wrs(R) изометричен, и следовательно, может быть расширен
до унитарного оператора е~'А1. В частности, отсюда следует, что
А — производящий оператор нулевой степени, и лемма доказана.
Лемма 4.2. Оператор А обратим.
Доказательство. Пусть {К\— такая фундаментальная
по норме пространства W^s (R) последовательность функций из
C(R), что •
Требуется доказать, что в этом случае lim 1ft L_S(R =0. Пусть
hn e ^~s (R) есть Фурье-образ функции hn, l,sS и пусть qn
есть Фурье^образ функции Ahn. Справедлива формула
Последовательность {hn} фундаментальна в W^s (R"), а после-
последовательность {<7л} сходится к нулю в #TS(R). Нужно показать,
что последовательность {ha} также сходится к нулю в W^s (R).
Последовательность элементов из #TS(R) можно рассматривать
как последовательность ограниченных линейных функционалов на
^a(R)- Поскольку сходимость, последовательности функционалов
по норме влечет за собой ее поточечную сходимость к тому же

234 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
пределу, что нам достаточно убедиться в том, что для любого
q>sCS°(R)
00
lim [ hn(p)(f(p)dp = O;
при этом мы знаем, что для любого <р е С™ (R)
— 00
при п-+ оо. Зафиксируем функцию <р е СТ (R). Для любого 8 > О
найдется такой номер N, что при n^N выполняется нера-
неравенство
00
I |(Mp)-Uv(p)b(p)|dp<e.
— 00
Далее, найдется такое число б > 0, что
в
5 \hN(p)<p(p)\dp<e.
-6
И.меем
[ lMpW(p)|dp<| \ \pha(p)<p(p)\dp-+O
|p|>e |р|>в
при п-+оо. Следовательно, найдется такое NX^N, что
|р|>в
Так как при n^N
00
$ \(hn{p)-hN{p))<f{p)\dp^ \ \(hn(p)-hN(p))<p(p)\dp<&,
|р|>в -оо
ТО .
08 I8,.
J hN(p)q>(p)dp < ^ lMp|
I
—6
5
lp|>a
Следовательно, при n
$ ha(p)<p(p)~dp
00
— 00
Ллг (р) ф (p) I dp < 48,
и лемма доказана.

§ 41 • ФУНКЦИИ ОТ ОПЕРАТОРА ДИФФЕРЕНЦИРОВАНИЯ 235
Пусть ф—функция из C™(R), равная 1 в окрестности нуля.
Положим /х (х) = [1 — ф (х)] sign х, /а (х) = хаф (х) sign x. Тогда
sign * = М
причем flt f2e«S&0(R). Следовательно, корректно следующее опре-
определение.
Определение. Оператором Гильберта (по отношению к А)
называется оператор
Лемма 4.3. Пусть f ев <&0(R), уевС^Щ, $ = /(Л)ф, ф =
= Ftp, ij5=/"ty. Тогда ty(p) = f (— р) Ф (р).
Доказательство. Предположим сначала, что / есть Фурье-
образ функции из C^°(R). Имеем
=-4, \f(t)U(t)<fdt,
где интеграл понимается как предел интегральных сумм для не-
непрерывной функции со значениями в HVS(R). Но функция
непрерывна также и как функция со значениями в №a(R)> Дей-
Действительно,
f |ф
при б-»-0. В силу теоремы вложения Соболева получаем
D.2)
Здесь интеграл понимается как обычный интеграл от числовой
функции, зависящей«от параметра х. Из формулы D.2) непосред-
непосредственно следует, что
$/(-р)Ф>). . D-3)
Пусть теперь 7 = б&» так что

236 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. 111
Тогда ¦^(р) = —=ге1р^ц>(р), и стало быть формула D.3) верна
и в этом случае.
Пусть, наконец, / — произвольная функция из ^0(К). Суще-
Существует такая последовательность {/„} функций из <MQ (R), что
[Ffn (А) Ф] (р) -/. (-р) [F<p] (p). D.4)
Ffa(A)<p-*Ff(A)<p в W7S№, L(-p)-*f(-p)
равномерно в силу вложения a©0(R) <=C(R). Отметим следующий
факт. Пусть некоторая последовательность {gn} непрерывных на
R функций сводится равномерно к некоторой функции g и в то
же время сходится в №7S(R) к функции g. Тогда g = g. Дейст-
Действительно, для любого х s C~ (R)
00 00 ОО
lira \ gn(x)%(x)dx= I g(x)%(x)dx= \g(x)%(x)dx.
П-»СО_ оо _(„ _«,
Переходя к пределу при л-»-оо в формуле D.4) и пользуясь сде-
сделанным замечанием, убеждаемся в справедливости формулы
и в общем случае. Лемма доказана.
Результат леммы 4.3 может быть сформулирован еще следую-
следующим образом. Пусть A=FAF~1, так что Лф(/?) = — рф(р) для
любого ф е С^° (R), где С?° (R) — пространство Фурье-образов функ-
функций ф е С?° (R). Оператор А является производящим оператором
нулевой степени с определяющей парой пространств 1F7S(R),
$7S(R)- Для любых ф«=С?°де) и /€=^0(R) имеет место фор-
формула
При этом f(A) = Ff(A)F-1.
Сохраняя обозначения определения 4.1, рассмотрим функцию
AeCJ5°(R). Покажем, что fz{A)h принадлежит области опреде-
определения оператора Л, т. е. что fi{A)h = Aiq, где q — некоторый
элемент из WYS(R). Имеем
h =р*<р (- р) sisn (- p) ~h (р)'
Рассмотрим функционал
«ч- I <p(-p)sign(-p)h(p)g(p)dp^(q, g), ge=(%№. D.5)

§ 41 ФУНКЦИИ ОТ ОПЕРАТОРА ДИФФЕРЕНЦИРОВАНИЯ 237
Имеет место следующая оценка:
j
Из этой оценки вытекает, что функционал D.5) определяет эле-
элемент q пространства #7S(R)- Покажем, что q^D^. Для этого
заметим прежде всего, что функционал
g-+ f sign(-p)h(p)g(p) dp 2L<qi, g), geC0°°(R).
— 00
определяет элемент qr пространства. $Y S(R)- Пусть теперь {^l"*}—
последовательность функций из C^°(R), сходящаяся к qr в про-
пространстве W^s (R). И пусть <7(л) (р) = ф (— р) 91П) (р)- Тогда q(n)-^q
в W7S(R)- Далее, пусть гя (р) = р2<7(л) (р). Так как функция
Ф1(р) = р2ф(р) принадлежит пространству C~(R), то г„ сходится
в fl^~s(R") к функции г(р) = р2ф(—p)sign(—р)Л(р). Таким об-
образом,
что и требовалось доказать. Одновременно мы получили фор-
формулу
А'% ('А) h (р) = q (р) = ф (-jb) sign (- p)h(p),
из которой следует, что
(sign^) h(p) = - (sign p) h (p). D.6)
Заметим, что для любой кусочно непрерывной функции
<7^$VS(R), убывающей быстрее любой степени р, справедлива
обычная формула обращения преобразования Фурье:
00
(F+q) {x)=~ \ e^q (p) dp. D.7)
— 00
Действительно, для любого ty e S
00 Г 00 1
TIT ^
— оо L оо
00

238 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ . [ГЛ. III
что и означает, в силу формулы Парсеваля, справедливость соот-
соотношения D.7). В частности, из формулы D.6) следует, что для
любого heC(R)
00
/А (*)=-— J e"«sign(-p)A(p)dp, D.8)
— 00
где й есть Фурье-образ функции А. Подставляя в D.8) явное вы-
выражение для А, получаем
00
= ~ J sign(-p)dp
— ОО — ОО
оо
= ~ lira ^ sign(— p)dp [ e'"<*-»AF)dg =
^ Д- + 00 J J
— a —oo
оо а
= Hm i- [ h(l)dt
Здесь v. p. —сокращенная запись для главного значения.
Преобразуем последний интеграл:
v.p. j
— 00
Интегрируя по частям, получаем
00

§ 51 СПЕКТР ПРОИЗВОДЯЩЕГО ОПЕРАТОРА ' 239
где функция hy (g) убывает на бесконечности как g. Следова-
Следовательно,
— 00
при а-»-со. Далее,
так как подынтегральная функция нечетна. Итак, мы получили
следующий результат.
Оператор Гильберта I является интегральным оператором
с ядром типа Коши: ¦ ¦ .
*W-вг ?
— 00
последний интеграл понимается в смысле главного значения.
§ 5. Спектр производящего оператора
Пусть А — производящий оператор степени N.
Определение. Резольвентным множеством р (А) оператора А
назовем минимальное открытое подмножество вещественной оси,
обладающее тем свойством, что
Множество б (А) = R \ р (Л) назовем спектром оператора А.
Задача. Доказать, что о {А) Ф а.
Теорема 5.1. Пусть Л,ер(Л). Тогда оператор (Л—А)
существует, определен на всем Вт\& и удовлетворяет оценке
где d —расстояние от точки % до спектра оператора A, a f —
некоторая невозрастающая (числовая) функция.
Доказательство. Пусть <р — бесконечно дифференцируемая
функция и ф(х) = (л; — X)'1 при \х — Х\^е, где'е<й. Покажем,
что
фA)-A-Х)-1, К^-Я.П</D). E.1)
Из равенства
Ф(х) (*->.) = 1-xW,

240 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ 1ГЛ. III
где suppxcr[X —e, X + e]czp(A), следует, что
_
q>(A)(A-X)h=*h V/ieD
Последние два равенства показывают, что
Оценим норму оператора (А — X)'1 = (р(А). Имеем:
Норма функции ф в \F^ + '(R) зависит от е и от способа про-
продолжения функции (х — X)'1 на интервал \х — Я|<е. Пусть Ф8 —
множество всех возможных ф при фиксированном е. Тогда
Теорема доказана.
Теорема 5.2. Пусть X е R. Если (Л — X)'1 — гомоморфизм,
то X ер (Л).
Доказательство. Пусть 0<б<,гр—г^-я.Покажем, что
ф(Л) = 0 для любой функции феС^ (R), удовлетворяющей усло-
вию--эиррф с: (Я —б, Я + б). Пусть ф —такая функция. Тогда
жЦк() ()у().
Легко получить следующую оценку:
Следовательно,
ХГ\\у]-+0 при * + оо.
Это означает, что [|ф(Л)[| = 0, и теорема доказана.
Из теорем 5.1 и 5.2 вытекает, что спектр производящего
оператора совпадает со спектром (в обычном смысле) его замы-
замыкания в Bmid (т. е. X ер (Л)) о [(Л — Я) — гомоморфизм].
Теорема 5.3. Для любой функции /e^(R) с носителем
в р(Л) справедливо равенство
Доказательство. Предположим сначала, что носитель
функции / компактен. Пусть {/„} — последовательность бесконечно

§ 5] СПЕКТР ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 241
дифференцируемых функций, сходящаяся к / в <$u(R), g — функ-
функция из С°° (R) с носителем в р (А), равная 1 на supp /. Тогда
gfneCfiH), supp to/») с р (Л) и gfH-+f в ^(R). Так как
g(A)fn(A) = 0, то и /(Л) = 0.
Снимем предположение о компактности множества supp/.
Пусть {фп} — такая последовательность функций из CjJ°(R), что
для' любого /i*eB* и любого АеВ справедливо соотношение
lim h*{y
Положим fn(x) = f(x)<fn(x). Тогда supp/,, cr p (А), так что
/„(Л) = 0. Для любых /i*<=B* и fteB имеем
0= lim h*(fn(A)h)= lim h* (<pa(A)f(A)h) =h* (f(A)h),
л-»оо n-*co
откуда и следует, что /(Л) = 0.
Рассмотрим подалгебру S3.N{p(A)) банаховой алгебры s®w(R),
получаемую замыканием множества функций из e®w(R), обращаю-
обращающихся в 0 в окрестности (своей для каждой функции) множества
а (А). Очевидно, что <$?лг(р(А)) — замкнутый идеал в ^^(R).
Факторалгебру <?fcN (R)/^^ (p (А)) с обычной нормой
]= inf
обозначим через еян(())
Ясно, что теорема 5.3 сохранится, если s®w(R) заменить
на SiN (а (А)). При этом улучшается оценка сверху нормы опе-
оператора ф(Л) и сужается ядро гомоморфизма М. Однако и это
отображение не является мономорфизмом (т. е. взаимно одно-
однозначным) даже когда fimid конечномерно и N —точная степень
оператора А. Дело в том, что разные жордановы клетки матрицы А
могут порождать группы гомоморфизмов с разным порядком роста.
Пример. Пусть Хг, Х% — различные вещественные числа и пусть
Д 0 0
Тогда
\0 . 0
так что А является производящим оператором первой степени,
но не является производящим оператором нулевой степени. Для
любой функции фей, (R) имеем
/ф(^) 0 0
Ф(Л)= о
\0 0

242 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ 1ГЛ. III
Спектр о = а(А) оператора А состоит из двух точек? ^ и Х2.
Пусть ф е= С? (R), Х2 <ф supp ф, ф (А,:) = 0, ф' (А,:) =? 0. Тогда
Ф (А) = 0, но || ф(л, (а) > 0 (здесь через || ф |#, (а) обозначена, как обычно,
норма класса эквивалентности, которому принадлежит функция ф).
Несмотря на то,' что гомоморфизм Ма:<?®н(о(А))-*-Ч1.ы не
является мономорфизмом, мы получаем для ||ф(Л)| достаточно
хорошую оценку сверху.
Определение. Собственным элементом оператора А
в точке X называется такой вектор g&Dj, что (A — X)g = 0.
Присоединенным элементом степени k оператора А в точке X
называется такой вектор g e D-^k, что (А — X)k g = 0, но
(A — X^g^O. Собственные и присоединенные элементы опера-
оператора А называются его с. п.-элементами.
Если оператор А имеет только изолированные точки спектра,
а число 'линейно независимых с. п.-элементов, отвечающих каждой
точке спектра, конечно, то говорят, что оператор А имеет диск-
дискретный спектр.
Задача. Пусть h—собственный вектор оператора /Г в точке А,. Доказать,
что е~ath =ё~ш h при h e D-.
Лемма 5.1. Пусть К — изолированная точка спектра произ-
производящего оператора А степени N. Если g — t. п.-элемент опера-
оператора А в точке X, то (A — X)N + l g = 0.
Доказ а те л ьствго. Пусть g — c. п.-элемент оператора А
в точке Я. Тогда для некоторого k •
(A-X)"g = 0. E.2)-
Покажем, что если k>N-\-l, то из E.2) следует, что
(А — v)* g == (Г- Предположим, что k>N + l. Пусть {%„} — такая
последовательность бесконечно дифференцируемых функций, что
Хп(А,) = 1 и что suppXn содержится в интервале (к — —, Х+— \,
так что носитель функции %п при достаточно большом п содержит
только одну точку спектра оператора А; пусть, кроме того,
где 4>д (*) = (*.— k)* %«(*)• Легко видеть, что такая последова-
последовательность существует. Имеем:
hn(A)(A-X)"-ig\\-*0 при п-+со: E.3)
С другой стороны, вектор
h = (A-X)"-ig
является собственным элементом оператора А, так как

§ 5] СПЕКТР ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 243
Значит,
00
Из E.3). следует, что (A-~X)k~1 g^O; no индукции получаем, что
(A-X)N + lg = O. ' ¦ . .
Теорема 5.4. Пусть спектр производящего оператора А'
состоит из изолированных точек Яг, 1=1, 2, ... Тогда множество
всех с. п.-элементов- оператора А полно, т. е. линейная оболочка
этого множества является плотной в В mid-
Доказательство. Пусть %1 — произвольная функция из
Cs°(R), с, носителем, содержащим лишь одну точку Я,- спектра
оператора А, и такая, что %'(#) = 1 в некоторой окрестности
точки К{. Тогда (А — h)N + l/x! (Л) = 0. Действительно, пусть, при
фиксированном i, / Х«} есть рассмотренная в лемме 5.1 последо-
последовательность при (k = N-\-2, % = %{), причем %'п(х) = 1 в некоторой
(зависящей от п) окрестности точки Xt. Имеем, при достаточно
большом и, •
О при п-^оо,
чем и доказано требуемое равенство.
В § 1 было доказано, что линейная оболочка множества всех
векторов вида y(A)h, cpeC~(R), Ae5mid является плотной
в Bmid. Значит, для доказательства теоремы достаточно убедиться
в том, что при любых AeBmid, 9eCS°(R) вектор q>(A)h пред-
представим в виде конечной суммы ^gt, где gi удовлетворяет равен-
равенству (Л — %i)u+lgi = O. Пусть {&t\ — открытое покрытие носителя
функции ф, причём %j ф Qi при i Ф у, Xt <= Q(. И пусть \х'} —
С°°-разбиение _ единицы^ подчиненное покрытию *) Ш,}. Тогда
Ф (A) h = 2 ф (А) х1 (A) h. Положим gt = ф (А) хг {А~) h. Имеем
(А - %t)N+ *8, = <р (А) (А - Я,)"+ • х' (Л) h = 0.
Теорема доказана.
*) Это означает, что %' еС00,' %*=0 вне Q,-, О^х'^Ь и 2k>es1 на
supp ф. В курсах анализа доказывается, что такой набор функций существует.

244 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Из доказательства теоремы 5.4 следует также, чтодля каждой
изолированной точки Я,- спектра производящего оператора А
существует ненулевой собственный вектор оператора А в этой
точке (т. е. Яг — собственное значение оператора А). Действительно,
достаточно убедиться в том, что существует ненулевой с. п.-эле-
п.-элемент оператора А в точке Я*. Пусть ф е С? (R) — такая функция
с носителем, содержащим ровно одну точку Яг спектра оператора А,
что ф (Л) Ф О (такая функция существует согласно определению
производящего оператора). Тогда найдется такой вектор h s Bmid.
что g^<р(А)пфО. Если %'^функция, рассмотренная в доказа-
доказательстве теоремы 5.4, то %1 (А) ф (Л) = ф (А), так что g = %l(A) X
X<p(A)h, откуда й следует, что (А — Kt)N + lg = O.
Если Я — собственное значение оператора Л, то 1/(^I^1/(^I
для любого /e(g^(R). Действительно, если g— ненулевой собст-
собственный элемент оператора А в точке Я, то f(A)g = f(%)g. Таким
образом, в случае, когда спектр оператора состоит из изолиро-
изолированных точек, мы получаем следующую оценку снизу для !/(•/!) ||:
sup \f(k)\. E.4)
§ 6. Некоторые свойства производящего оператора
Теперь уточним некоторые свойства производящего оператора.
Лемма 6.1. Пусть А —производящий оператор в банаховом
пространстве В, причем \er-tA'\^,c(l -f \t\f. Тогда при \
и т=\, 2... справедлива оценка
Доказательство. Положим г%(х)= \/(К — х). По теореме
1.1 § 1 главы III
(X - А)~т = г?(А) = —1-щ J [h.*...*h] (t) е- "' dt, F.2)
где * означает свертку функций:
— Фурье-прообраз функции
Легко видеть, что
где
( 1 при ^>0, ( 1
= \0 при ^<0, s^ = \— 1
при 1тЯ>0,
при 1тЯ<0.

§ 6] СВОЙСТВА ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 245
Отсюда непосредственным вычислением получаем
Подставив этот результат в F.2), получим оценку!
—00
00
*=0
VI с f,k{fn + k— 1)!
Тем самым лемма доказана.
Для произвольного гомоморфизма Т банахова пространства В
00
обозначим, через e~lTt оператор У ^~ '.—:. Легко видеть, что
т=0
т=0
ряд сходится по норме и определяет однопараметрическую группу
гомоморфизмов пространства В:
для любых вещественных tlt tt. Будем говорить, что оператор Т
порождает группу {е~т}. Оператор Т является производящим
тогда и только тогда, когда |е~г7"'| растет при t-+oo не быстрее
некоторой степени t.
Непосредственно проверяется, что для любых двух коммути-
коммутирующих гомоморфизмов T-l и Т2 пространства В справедлива
формула
е-' (Г.+ г,) / _ e-nlte-iTjtt
Лемма 6.2. Пусть выполнены условия леммы 6.1 и пусть
с^1. Тогда для всех вещественных е и t таких, что e?s=O,
справедлива оценка:
le>^ + ^Ar^l^c(l+Rl(e)\t\)i, F.3)
где
Е»0
Доказательство. Из леммы 6.1 получаем оценку для
Л)
Положим

246 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. ИГ*
При мейд имеем и — 1еи = ШьАи. Поэтому оператор 1еА
ограничен и его -замыкание порождает группу, которая задается
следующим рядом:
Используя оценку для 1?, получим
/п=1
Теперь учитывая, чтос^1 и что справедливо/очевидное нера-
венство (при k^l): '
fc—1I <
продолжим оценку следующим образом:
2 <*1«г-?Й
(
\n=0
где Ri (e) — некоторая положительная функция, причем число
Ri(O) подчинено единственному условию [#i (О)]1* ^ (m + I)**,
т = 0, ..., /. Для наших целей достаточно выбрвть Rt @) = 1 + /.
Лемма доказана.

§ 6] СВОЙСТВА ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 247
С помощью этой леммы можно доказать лемму о том, что
группы eriAi могут быть аппроксимированы семейством групп
g-i(i + teA)-tAt^ порожденных ограниченными производящими опера-
операторами.
Лемма 6.3. Пусть А — производящий оператор в банаховом
пространстве В. Тогда при вещественных е, < (е/^0) и в->-0
векторы e-«(i + e^r1'* и сходятся для любых и^В к e~iAt и по
норме пространства В равномерно относительно значений t, при-
принадлежащих любому компактному множеству.
Доказательство. Пусть снова /е = A+/еЛ). Оценим раз-
разность:
s i{e-t7^{t-x) (UA -UI)e-iT^Ax Л. F.4)
о
Поскольку операторы 1ВА и ё~"е'Ах коммутируют, то исполь-
используя лемму 6.2, получим для ие?)д оценку
\\е-иеА<и-е-1'°'А1и\\^ . '
1 A +11 ~ * II A +1 * II dtjil (/, - /..) Ли |, F.5)
const
в предположении, что Л имеет степень /.
Покажем, что /еи сходится к и при е-»-0 для любого иёВ.
Действительно, для неЬд имеем
¦ | и — 1еи |=| ШЪА и | < ecj | А и |,
где с-у — константа из оценки для |/е| Итак, /еи-»-и при u^.DA
и |]/е| ограничена при е-»-0. Следовательно, по теореме
Банаха — Штейнгауза, 1еи-*-и при любом и^В.
Далее, в силу F.5), имеем: е~"еА'и сходится для любого
ueB (не зависящего от t) при е-»-0 (е*^=0) к некоторому век-
вектору v = T(t)u, где Т (t) — некоторый гомоморфизм, причем схо-
сходимость равномерна относительно teK, где /( — компактное мно-
множество. Переходя в F.3) к Пределу при е-»-0, получим:
IT(t)\\^c(l + (l+l)\t\I ^c(l+\t\I, c = const. F.6)
Далее, аналогично F.4), получаем формулу
i
е~1 'вА'и = u-i\e-ll'AxIeAudx, и е= DA. F.7)
о
При фиксированном т подынтегральное выражение сходится

248 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
к Т (т) Аи; кроме того, оно ограничено (см. F.3)):
||<Гг7й* 1ЕАиI<с A + /?! (е) | т |)'с, | Аи[| <с2 A +1 т |)<|| Ли|.
Переходя к пределу в F.7) при е-»-0 (et^O) получаем
T(t)u = u-i\T{x)Audx,
о
и поэтому
i±T(t)u = T @ Аи, Т @ и |<=о = и, и еОд. F.8)
Этой же задаче Коши и оценке F.6) удовлетворяет группа е~ш.
Докажем единственность решения задачи F.8) при условии
F,6). Пусть D таково, что его пересечение с Da есть плотное
множество в В. Пусть семейство гомоморфизмов t (t) удовлетво-
удовлетворяет оценке F.6) и уравнениям F.8) для «eD. Тогда для
D[D имеем
_ f (t) и = §^ {e-iJ^x f(t-x) и) dx =
- -i \ e-iT^Ax (J7A) f (t-x)udx + i{ <Гг Vй f (t - т) Аи dx.
о о
Из F.8) следует, что для mgD справедливо равенство
f (t) Аи = At (t) и; стало быть, f(t — x) коммутирует с Т^А.
Поэтому, учитывая оценки F.3), F.6), получаем при e?s=0
\\e-il*Aiu-f (t)u\\^c3(j(l+\t-x\)l(l+\x\)ldx\\\(l-Ie)Au\\.
Но выше было доказано, что IBv-+v для любого sgB при
е ->- 0; следовательно, T(t)u = t (t) и на плотном множестве D f| Da.
Это означает, что T(t)==T (t). Единственность доказана, и тем
самым показано, что T(t) = e~lAt.
Пусть теперь заранее не обусловлено, что А — производящий
оператор.
Лемма 6.4. Пусть А—замкнутый оператор с плотной
областью определения DA в банаховом пространстве В и пусть
для всех вещественных уьфО операторы (i\i — А)'1 являются гомо-
гомоморфизмами и удовлетворяют неравенству типа
^ 1|tLn m = \, 2, .... F.9)
где / ^ 0 — некоторое целое число.

§ 6] СВОЙСТВА ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 249
Тогда А есть производящий оператор степени I в простран-
пространстве В, причем
te-iA<\^c(l + (l + t)\t\I. F,10)
Доказательство. Доказательство леммы 6.2 опирается
лишь на оценку F.1); поэтому с помощью F.9) точно так же,
как в лемме F.2), получим оценку F.3). Далее, повторяя дока-
доказательство леммы 6.3, построим семейство Т (t), удовлетворяю-
удовлетворяющее оценке F.6). Как и в лемме 6.3, доказывается единственность
решения задачи F.8) при условии F.6).
Далее, можно выбрать в В такое плотное множество D cz. DA,
что A (D) czD, A(D) = {y\y = Ax, xeD}. Действительно, положим
?>= U U {] f(t)T(t)udt\. F.11)
Из того, что на области определения оператора А уравнение
F.8) имеет решение, следует, что
Т @ (DA) cz DA и / ± Т @ и = Т @ Аи = AT (Q и F.12)
при и е DA. Отсюда легко получить включение A (D) cz D. Дей-
Действительно, пусть
о= ] f(t)T(t)udt,
—оо
где / — Фурье-прообраз некоторой функции из Cjj°(R), а и —
вектор из DA. Тогда
Лу= I f(t)AT(t)udt=
00 ,
±dt = -i J f'At)T(t)udte=D,
поскольку Фурье-образ функции —//' принадлежит Cf (R).
Кроме того, для u^DA, ft*eB* имеем (см. F.6))
h*(] f(t)T(t)udt)
\-00 / -00
^ЭПЛ* S||]«|| Y \f(t)\(l+\t\)ldt,
—00
При помощи этого неравенства, точно так же, как в лемме 1.13,
доказывается существование такой последовательности дп(() b
что для всех й*еВ* и u^.DA
h*i\ dn(t)T(t)udt\-yh* (и) при л->оо.

250 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ (ГЛ. Ш \
Отсюда, как и в следствии из леммы 1.13, получаем, что мно-
множество D плотно в В. Итак, оператор А имеет сужение Ао на
плотное в В инвариантное относительно А линейное многообра-
многообразие D. Из F.11) следует, что D инвариантно относительно' Т (t).
Поэтому Ао есть производящий оператор степени /. Оператор
(^о + г) совпадает с (Л-И) на области значений оператора-
A0 + i, плотной в В. Кроме того, так как (Ло+i) и (A + i)'1-—
гомоморфизмы, то они обязаны- совпадать, откуда следует, что
А — Ао, и лемма доказана.
Замечание. Легко видеть, что лемма 6.4 остается справед-
справедливой, если потребовать выполнения оценки F.9) лишь при
IЦI Ss Цо> гДе Цо — произвольное положительное число.
Итак, мы получили следующий критерий.
Теорема 6.1. Пусть А—замкнутый оператор с плотной
областью определения в банаховом пространстве В. Оператор А
является производящим оператором степени I в В в том и только
том случае, если при всех вещественных ц, | ц | ^ fi0 > 0, опера-
операторы (i]x — А)'1 являются гомоморфизмами и удовлетворяют оценке
F.9) для m = I, 2
Рассмотрим теперь частный случай самосопряженного опера-
оператора.
Лемма 6.5. Пусть А — самосопряженный оператор в гильбер-
гильбертовом пространстве Н. Тогда, если ImA,^0, то Я, ер (Л) и
• FЛЗ)
Доказательство. Пусть и еDA. Тогда (Аи, и) — (и, Аи)
= (Аи, и) — вещественное число. Поэтому
1т {(К-А)и, и) = \\uf 1т%
|(Я-гЛ)и|^|1тЯ||и|, мейх. - F.14)
Отсюда следует, что при ImA,^0 существует обратный оператор
(к —А)'1, определенный на области значений оператора к —А.
Область значений оператора к —А является плотной в Я, так
как оператор (к— Л)*=Я, — А обратим. Итак, оператор (к —А)'1
определен на плотном множестве и в силу F.14) ограничен:
' HS*| Im Я ||| (А,-ЛГН ve=(k-A)(DA).
Ограниченный определенный на всюду плотном множестве опера-
оператор продолжается до гомоморфизма. Поэтому к е р (А) и спра-
справедлива оценка F.13).
Следствие. Самосопряженный оператор А в гильбертовом
пространстве является производящим оператором степени 0, при-
причем группа eriAt состоит из унитарных операторов.

§ 6] СВОЙСТВА ПРОИЗВрДЯЩЕГО ОПЕРАТОРА 251
Доказательство. Из оценки F.13) следует, что выпол-
выполняются условия леммы 6.4 при 1 = 0, т. е. что А есть производя-
производящий оператор степени 0.
Из оценки F.10) имеем: ||e-M/|ssl, т. е. |е-'л/ы(|^ы для
всех ыеВ, ieR. Далее, \u\ = \eAte-iAtu\^\er'Atu\. Это озна-
означает, что ||е~м'ы| = |ы|| для всех ыеВ, /eR, т. е. все опера-
операторы ertAt- являются изометрическими (сохраняют норму).
Их области определения совпадают с В. То же самое отно-
относится и к областям значений, так как {е~1М}-~ группа. Поэтому
операторы егш — унитарные, и следствие доказано.
Изучим теперь устойчивость свойств производящего опера-
оператора А„ относительно перехода к пределу по параметру п, кото-
который для простоты мы будем считать дискретным (целочисленным).
Пусть последовательность {А„} состоит из производящих опера-
операторов и поточечно сходится к некоторому оператору А. Ответ
на вопрос о том, когда этот оператор будет производящим, дает
следующая лемма.
Лемма 6.6. Пусть |ег'Ап11 < с A +111)', где Ап — замкнутые
производящие операторы в банаховом пространстве В. Пусть после-
последовательность {А„} поточечно сходится к. А на плотном в В мно-
множестве D = Da, причем оператор А имеет замыкание. Кроме того,
пусть для некоторых чисел (klt Я^), удовлетворяющих условию
(Im Xi) (Im Я2) < 0, области значений операторов Кх — АиХ^ — А
плотны в В. Тогда:
1) спектр оператора А лежит на вещественной оси и при
lmk-фО последовательность {(К—An)'1} поточечно сходится к
(К-А)'1; _ ¦ .
2) оператор А является производящим степени-1 а В. .
Доказательство. Докажем 1). По лемме 6.1
при
где
_i!
(/—ft)l | Im Л. Iе •
Справедливо следующее общее утверждение: если последова-
последовательность операторов Fn поточечно сходится к F на всюду плот-
плотном множестве D = Df, причем F? — гомоморфизмы, ||F^||^C и
область значений оператора F является всюду плотной, то опе-
оператор F имеет обратный, ЦУ7"х || ^ с и последовательность {Fn1}
поточечно сходится к У7.
Действительно, при и е D
Следовательно, если Fu = 0, то и = 0, т. е. оператор/ обратим.

252 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. Ill i
Оператор F'1 определен на всюду плотном множестве. Далее, при 1
oeDri справедливо равенство F~1v — F-1v = F-l(F — Fn)F-^v, I
Поэтому F^1v-+F~1v. По теореме Банаха — Штейнгауза, последо- :
вательность {/V} поточечно сходится к F'1, что и требовалось ;
доказать.
В нашем случае имеем: (Xi — А„) -*¦ (К — А) поточечно на D и
1(^1 — Ап)~1\\^с\1. Поэтому существует оператор (Xj —Л), удов- ,
Летворяющий условию \\(Х1 — Л)!^^,, и последовательность ;
{(К — АпУ1} поточечно сходится к (Xj —Л). Аналогичное рас- ;
суждение проводится для оператора (Х2 —Л).
Пусть S(X) есть круг: S(X) = \р <= С; |(х — X\<:d1}. Положим ¦}
Rn(X) — (X-An)-^, R{X1) = (X1-A)~1. При \e~Sfa) имеем :
Rn(X) = Rn fa) A - (V - Я) Rn (K))-\ F.15) j
где обратный оператор в правой части задается рядом, сходя- ',
щимся по норме операторов: ';
< 2 К*!-*) 1*1 я»
ft = 0 fe = 0
Заметим теперь, что область значений оператора 1 — (к{ — )()
есть все пространство В. Действительно, для любого /еВ •
вектор
удовлетворяет уравнению
Поскольку Rn (Xj) -+ R (Xi) поточечно, то из оценки для ||A—
— (Xi — X)Rn(k1))~1\\ и общего утверждения, доказанного выше,
следует, что при XeS(Xj) существует гомоморфизм A — (Xi — X) X
X R (Xi) )~v и последовательность {A — (^ — X) Rn (Xj) )"r} пото-
чечно сходится к нему. Тогда из F.15) следует, что при Я,е S^)
последовательность {Rn (X)} поточечно сходится к оператору R' (X),
R'(X)dJLR(X1)(\-(X1-X)R(X1))-K
Очевидно,
R' (X) - R (Х{) = fc -K)R (V) R' (X) = (Л, - Я) R' (X) R (^). F.16)

§ 6] СВОЙСТВА ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 253
Далее, при А, ц <= S (Аг) получаем
R' (A) -R(h) = (K-v)R(MR' (Ц + (v-b)R(XI)R' (А);
R' (A) = R (Ax) A - (Ar — i*)
+ Oi -A) R (M A - (Ar - n) Л (AJ Г tf' (A) =
Из этого неравенства следует, что область значений оператора
R' (А) при ^eS (А^ не зависит от X, и в частности,
Далее, из того же равенства получаем, что все операторы R' (А)
обратимы, если [R' (ц) ]-1 существует хотя бы для одного значе-
значения це5(У. Покажем, что оператор R(ki) обратим. Пусть и —
произвольный вектор из В, ы„-^ы, «nS= D^,—л>->. Тогда ип =
= (А,! — A) R (Xj) ип -+ (Xi — A)R (кг) и, так что •
Пусть теперь и — произвольный вектор из Вд и {ып} —такая
последовательность, что ип-»-ы, Лы„->-Лы. Тогда un = R(X'i)X
X CK — A)un^-R(Xi)(X — A)u, так что
Значит, справ'едлива формула /? (АО = (X — Л), и все /?'(А) обра-
обратимы при Ае= SiXx).
Пользуясь обратимостью R (А) и уравнением F.16), получим
для heD:
#' (A,) R (V) ([Я' (*) I -
= I? (Aa) u - /?' (А) и = (Xi - X) R' (A) R (Ar) u,
откуда следует, что
([R' (X) Г1 - [R (Хд Г1) и = (Х- Аг) ы,
ИЛИ
[Я' (А) ]-хы = (А- А и, ue=D, А «ее S (Аг).
Из последнего равенства заключаем, что оператор А имеет замк-
замкнутое расширение А — [Я (А)] с областью определения D', а так
как область определения оператора А_ есть также D', то А —
-[/?(А)]-1 = Л, а значит, Я' (А) = (А - А)'1 при Ae=S(A!). Таким
образом, последовательность {(А — An)'1} поточечно сходится к
(А-Л) при XeS(Xi).
Теперь можно повторить все предыдущее доказательство, заме-
заменив точку Ах на любую точку ц_ круга S (А^. Действительно,
областью значений оператора \i~ А служит все пространство В,
поэтому область значений оператора ц. — А будет плотной в В.

254 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ (ГЛ. Ш 1
i
Отсюда вытекает следующее общее утверждение: резольвенты j
(к — АпУ1 поточечно сходятся к (А, —Л) на В при всех Я, таких,J
что 1тХфО. :>
Действительно,- пусть знак ImA, совпадает со знаком Im A.?. |
Тогда, точки Я, и Хх можно соединить последовательностью кругов |
5Ы, S(His),..., S(\im) с центрами в точках Х = ц1,..., цт, где]
S (иг) П 5 (им) ^ 0. Переходя от S (Hi) к S (и2), от S (u2) к S (u8) н
и т. д., мы получим, что (и — АпУ1 -»-(и — Л) поточечно на В?
при neS(uffl). В частности, это верно и для точки X. ;!
Таким образом, утверждение* 1) этой леммы распространяется^
на всю полуплоскость, в которой лежит точка Яг. Но по уело- i
вию имеется ещё точка Х2 из. другой полуплоскости, для которой ;
также проходит все доказательство. Утверждение 2) следует из ;
1) и леммы 6.4. Тем самым лемма доказана. J
Оказывается, операторы _е~Мл' поточечно сходятся к егш j
при п-*-оо. - j
Лемма 6.7. Пусть\е~1Ап1\^с(\-\-\г\I и пусть производя-,
щие операторы Ап поточечно сходятся к производящему опера-\
тору А в В на всюду плотном множестве D, инвариантном]
относительно А. Тогда операторы е~1Ап1 поточечно сходятся к
erlAi при h-уоо на В равномерно относительно значений t из\.
компактного множества. Ц
В частности, Je-M'|<c(l+|/|)'. " • ц
Доказательство. Положим Int = (l+teAn)~1, /, = A + '^
+ /8/4). Выберем любое 6>0. По лемме 6.3 для любых и е В"|
и 4>0 найдется такое Xi = x1F,,«, to)>0, что при |e|«SXi,|
tO, 111 s^ t0 выполняется неравенство •
\\e-il°Atu-e-'A'ul<6/3. ¦ F.17I
Аналогично F.4) получим формулу \
0
Отметим, что
'мАп — ItA=j^(Il — /„,).
Используя это равенство и оценку (е/^0), получаем!
1
о
По лемме 6.6 подынтегральное выражение при фиксированном т

§ 6] СВОЙСТВА ПРОИЗВОДЯЩЕГО ОПЕРАТОРА 255
сходится к нулю. Кроме того, это выражение имеет оценку
(см. F.1) и F.3)).
Используя предельный переход (что здесь законно), получаем,
что рассматриваемый интеграл сходится к нулю при n-voo. Это
значит, что для любых 6>0, иеВ, to>O, ее# существует
такое Ni = Ni (б, и, t0, е), что при n^=JVi, \t\<,t0, e/>0 выпол-
выполняется неравенство -
в/3. F.18)
Далее, как и в лемме 6.3, получим:
!(/„.- \)AnuI, F.19)
6
где usD, e/s&0.
При ы s D' имеет место тождество
(/n,- \)Апй = (Int- \)(An-A)u- ШпеА* - ielns (An -А) Аи.
Отсюда, учитывая оценку 1/л.Ц^С]. и F.19), получаем, что для '.
любого 6>0 и всех ней', ?0>0 существуют такие числа щ =
= и2(б, и, tQ)>Q, N2 = N2{b, и, t0), что при |е|<и2,
n^N2, 111^/0 выполняется неравенство
b/3. F.20)
Из оценок F.17), F.18) и F.20) легко вывести искомый резуль-
результат. Положим so:=min{yiiF, ы, /0), ха(б, ы, /0)} и N = N(b, и,
to) = max{Nt (б, ы, t^0), N^F, и, t0)}. Пусть б>0, иеО,4>0,
111 sg^0, п^N (б, и, t0). Тогда из неравенств F.17), F.18) и F.20)
непосредственно получаем неравенство
Пусть теперь и — произвольный вектор из В и v — такой век-
вектор из D, что ||ы — у|<б. Тогда при |^|^/0. n^N(8, v, t0)
имеем
Последняя лемма позволяет установить непрерывную зависи-
зависимость функций от производящих операторов относительно этих
операторов.

256 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. 111 ;
Теорема 6.2. Пусть An\D-+D, n=\, 2, ... — производящие ¦
операторы в банаховом пространстве В, причем
Предположим, что последовательность {Ап} поточечно сходится
на D по норме В к производящему оператору A i D -> D. Тогда,
для символа f е SBS (R) последовательность операторов f (Ап) схо- j
дится при п-^-оо к f(A) поточечно на В.
Доказательство. По лемме 6.7 операторы e~iAn* пото-'¦
чечно сходятся к е~ш на В равномерно относительно t из любого;
компактного множества. .:
Пусть символ / принадлежит «®J (R), т. е. j
[F-1/] @ = E c*6 (* - 5(fc)) + ф 0). ф e c" (R)-
*-1
Тогда при п-*¦ oo для любого ueB.
m
supp ф
Далее, имеем оценку для всех /ее®,(R), л=1, 2, ...:
Та же оценка справедлива и для оператора / (А), Пусть /s
s^S(R) и./.-*-/ пр: е->0 в <#,(R)- Тогда
-/.(А))и
Пусть задано 8>0. Выберем е так, чтобы первое слагаемое
из последней суммы было меньше 6/2. Далее при этом фиксиро-
фиксированном е найдем такое N F), чтобы при n^N второе слагаемое
было меньше 6/2 (это можно сделать, так как /se^
В итоге получим, что при n^N(Ь)
lf(Anyu-f(A)u\\<8.
Тем самым теорема доказана.

§7] САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 257
§ 7. Самосопряженные операторы
Пусть А — некоторый самосопряженный оператор в сепарабельном
гильбертовом пространстве Н и пусть имеется отображение M:f->
-yf(A), заданное на функциях /ea9c(R) формулой
-^dt. G.1)
Теорема 7.1. Для любого символа fea®0(R) справедлива
оценка
\f(A)K\fU*)- G.2)
Доказательство. Можно [считать, что Н реализовано в
виде пространства /2 последовательностей y = {y,}?Ii комплексных
со
чисел, имеющих конечную норму fw|)f> = 21и<12-
Предположим сначала, что А — ограниченный оператор. Пусть
е(/)_ вектор, определяемый формулой е\п = 8A, где б(/ —символ
со
Кронекера, и пусть Ле(/) = ? Л,-/('\ где Ai} — элементы матрицы
оператора А.
Обозначим через А„ оператор, действующий по формуле
п
(Anv)i= 2 Aiflj, i=\ п,
Оператор Ап можно отождествить с матрицей (Лу)? . ,. Пусть
{Л1 — ортонормированный базис в евклидовом пространстве С",
состоящий из собственных векторов матрицы
Дополнив нулями последовательность координат вектора %, отож-
отождествим его с соответствующим элементом пространства /2.
Пусть
2
1 = 1
Тогда
i=n+i
9 В. П.

258
так как
Отсюда
ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ
[ГЛ. Ill
»VW при />«.
так что
Далее,
?>у1' + |] >i!2)=llflPc(R)I4|2,
,/=1 /=л+1 /
G.3)
1 = 1
2
/=л +
2 со
п+1
где
/ = 1
при
при
Очевидно, Рл->-0 поточечно при п->-оо. Следовательно,
А — /4„-»-0 поточечно при п-»-оо, Тогда по теореме 6.2 имеем
при п -*¦ оо для любого v е Н и любого символа / е а®0 (R). Далее,
из G.3) следует оценка
||/(Л)И|Л|С(К). G.4)
Освободимся теперь от предположения об ограниченности опе-
оператора А. Пусть А — произвольный самосопряженный оператор
в Н. Рассмотрим последовательность самосопряженных операторов
их ограниченность следует из оценки
II л i|<:' l 1 *
II лл || ^= iAS- j.
(R)
Последовательность {Ап\ поточечно сходится к оператору Л на
множестве DA. В самом деле, пусть К,п = A + - Л2] . Тогда
¦I«P+

§ 7] САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 259
так что II Кп 1*^1, и — КпА2и = A — /С„)ы для и е Од1. Поэтому
на всюду плотном множестве DA> имеем A — Кп)и -> 0. По тео-
реме Банаха—Штейнгауза последовательность {Кп} поточечно
сходится к 1 • всюду и следовательно, {Л„} поточечно сходится
к Л на DA.
По теореме 6.2 последовательность f(An) поточечно сходится
к f(A) для любого символа fe=a®0(R). Но для операторов Л„
справедлива оценка G.4): ||f (Л„)|^||/||с(Я), следовательно,
||/(ЛI1^11Лк(ЯI и теорема доказана.
Замечание. Оценка G.2) означает, что гомоморфизм М :/->
->/(Л), определенный формулой G.1), расширяется на замыкание
«0Bo(R) в C(R).
Следствие. Пусть А — ограниченный самосопряженный опе-
оператор в сепарабельном гильбертовом пространстве Н. Тогда суще-
существует такой гомоморфизм Mi'. С {а (Л)) -*¦ Horn (H, Н), что для
любого / е= а®0 (R) справедливо равенство
f(A)=MJ\aiA).
Доказательство. Множество а (А) содержится в отрезке
[—\\A\\, || Л |]. Действительно, если л.>|Л|, .то (I — Л) есть
гомоморфизм:
(л.-Л) =|] Л*лг*-1/ .
Таким образом, а (Л) — компактное множество.
Напомнимтеперь,что?(Л) = Одлялюбойфункции|ге=а$0(р(Л ).
Пусть {g} — класс всех функций из ^0(R) с носителями в р (Л).
Для любогр g s {g} имеем
f(A)+g(A) = f(A).
Нетрудно видеть, что
inf \\f-\-g\\c№ = sup |f(*)|.
Отсюда получаем, что
If (A I< sup |/(jf) |=| /|в (Л) ||с (а (Л».
ХШО(А)
Отсюда следует, что оператор /(Л) однозначно определяется суже-
сужением f\0(A) функции / на спектр оператора А и что оператор,
переводящий /Цд) в f\A), ограничен как оператор, действующий
из С {а (А)) в Нот (Я, Н). Остается заметить, что множество'
функций- вида /|о(л), где /e=^80(R), плотно в С (а (А)). Действи-
Действительно, пусть g — произвольная непрерывная функция на а (А),
Продолжим g до непрерывной на R. функции G с компактным
9*

260 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
носителем. Тогда последовательность {Gn} функций из Cf (R), опре-'
деляемая формулами
1
W/i W —. tn \ « (.5/e
равномерно сходится к G, так что Gn]a{A)-+g в С (а (Л)).
Следствие. Пусть А — самосопряженный оператор в сепа-
рабельном гильбертовом пространстве. Тогда для любого вещест-
вещественного Я и любого Д>0 существует такой проектор ?х(А), что
Подпространства Е{(А)Н и A—?я(Д))# инвариантны относи-
относительно /(Л) для любого [еК,(R) и ортогональны друг другу,
причем для любой функции 7^<^o(R) с носителем в (Я, Я-fA)
справедливо равенство f (А) =} (А) ЕЦА) ~ Е\ (A) f (А) и для любой
функции [еД(R) справедлива оценка .
sup \f(x)\.
¦Доказательство. Пусть ц> (х) = 6. (дг — К) 6 (Я, + А—л-). Поло-
Положим g(х) = (х — Я) (Я + А—х)ф(л:). Тогда существует такая после-
последовательность gn функций из <й?0(К)» сходящаяся равномерно
к g, что gn(x) — 0 в (зависящих от п) окрестностях точек Я и Я А
и \gn(x)\<g(x) всюду. Пусть h<=DA*. Имеем
где Ф«(х) = (х-^1+д_х) • Поэтому
-Л) А].
Переходя в этой оценке к пределу при п -+¦ оо и используя нера-
неравенство \gn(x) | <g(x), получаем
Пусть Л^: ((А - Я) (Я + А - А) hx = 0) => hx e= N. Учитывая послед-
последнее соотношение, положим по определению
Мы определили оператор <р (А) на области значений оператора
(Л — Я)(Я+А — А), причем на этом множестве [|ср(Л)||<1.
Убедимся в том, что область значений оператора (Л — Я) (Я +
+ А —Л) является плотной в H/N. Для этого прежде всего заме-
заметим, что если f e g$?o (R) — вещественная функция, то^ оператор
/(Л) будет .самосопряженным.

§ 7] САМОСОПРЯЖЕННЫЕ.ОПЕРАТОРЫ 261
Действительно, для любых h, q ей имеем
00
(/ (А) К Я) = ~= \ (F- 7) (t) (е- iA% q) dt =ь
' —00
(F-Ч) (О (А, в'^)Л
$(Л, e-t"q)dt = (h, f(A)q).
Положим f(x) — ^x~ * ГГ ~ . Тогда область значений опера-
х*-\-1
тора f(A) является плотной в H/N и входит в область значений
оператора (Л —Я)(Я +А —Л).
Итак, оператор ф (Л) определен на всюду плотном множестве,
и поэтому его можно расширить до гомоморфизма Е\(А): Н-+Н,
полагая E\(A)h—0 при h^N.
Покажем, что оператор Е{(А) коммутирует с /(Л) для любого
fe^0(R). Действительно, пусть h — (A — Я) (Я + А — A)q. Тогда
Далее, пусть h принадлежит (плотной в H/N) области значений
оператора (Л-ЯJ(Я + А-ЛJ, т. е. А = (Л -ЯJ(Я + А- Af q.
Тогда
(А)]2 /г - g2 (Л) с? =Нт ф„ (Л) ^ (Л) (Л - Я) (Я + А - Л) q =-
так как <png-vg в C(R).
Таким образом, Е'% (А) есть ортогональный проектор. Отсюда,
очевидно, следует доказываемое утверждение.
Построенный проектор Е'% (А) отвечает символу ф (дг) = 9 (дг — Я) х
XS (Я + А — дг), доопределенному в точках разрыва условием полу-
полунепрерывности снизу. Легко получить проектор ?>,(А) с анало-
аналогичными свойствами, отвечающий символу (р(х), доопределенному
условием непрерывности слева. Именно, пусть Ai > А; тогда
положим
Е(А) ЕЦЪ)
Справедлива формула
Ек (А) + Ек+ д (Ах) = ?х (А + А,).

262 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Если символ / йриблизить равномерно с точностью е кусочно
постоянной функцией вида
где Ял+1 = А,4-}-Д>, то будет справедлива оценка
Теорема 7.2. Существует гомоморфизм М с.'С (R)->-Ор (Я),
совпадающий на «$?<> (R) с гомоморфизмом М i «$?0 (R) -+¦ Ор (Я)
ы удовлетворяющий оценке [[MC|<;1.
Доказательство. Обозначим через Еп (А) проектор ?1„ Bм).
Пусть / — произвольная функция из C(R). Положим по опреде-
определению
f(A)En(A)=fn(A)En(A),
где fn (x) — произвольная непрерывная функция с компактным
носителем, совпадающая с f(x) в окрестности отрезка [— п, п].
Тем самым оператор f(A) определен на плотном в Н множестве
оо
U
Еп(А)Н
и справедливы оценки
\№)Е.(А)\<, sup |/
l—n, л]
Значит, оператор f (А) можно расширить до гомоморфизма Н-+Н,
который мы снова обозначим через }{А). Для гомоморфизма f(A)
справедлива оценка
И
Если мы положим по определению
то тем самым теорема будет доказана.
Теорема 7.3. Для любой непрерывной вещественной функции
f на Я оператор fl(A) является унитарным.
Доказательство. Пусть {ej\f=i такая полная ортонорми-
рованная система в Я, что ej&DA, /==1, 2, ... Обозначим
Пусть Ап — гомоморфизм в Я, действующий по формулам
я
2] Anej, i=\, .... п;
0, 1 = я+1, я + 2, ...

§ 7] САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 263
Пусть //„ — подпространство в Н, натянутое на еи ..., еп,
и яр!, ..., tf>,, — ортонормированный базис в Н„, состоящий из соб-
собственных векторов оператора Ап'
АпЬ**^» i=U .-., п.
Для произвольного вектора ЛеЯ имеем
2] Vy.
/=1 /=n+l
откуда следует, что
Далее, для любого вектора А == bjhj имеем
ПтЛяА=ЛА.
/1-»оо
Предположим вначале, что /e^80(R). Тогда по теореме 6.1
имеем
откуда следует, что
•\\eiHA)h\=
для любого h из плотного в Н множества конечных линейных
комбинаций векторов еь е2, ... Значит, и для любого ЛеЯ опе-
оператор е''(Л) сохраняет норму:
Это равенство легко переносится также на случай, когда f —
произвольная непрерывная функция с компактным носителем. '
Пусть теперь / — произвольная непрерывная вещественная
функция. Тогда для любого Ле?л(Л)Я (см. доказательство
теоремы 7.2) имеем
где fn— некоторая непрерывная функция с компактным носите-
носителем. Следовательно, снова 1е"<Л>А| = |А| для любого А из плот-
плотного в Н множества, а стало быть и для любого ЛеЯ.
Остается заметить, что оператор е"<Л> имеет обратный опера-
оператор е-"*'4), определенный всюду на Н, и теорема доказана.

264 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
§ 8. Регулярные операторы
В этом параграфе мы распространим результаты предыдущих
параграфов на случай «-параметрических групп.
Пусть Е — векторное пространство и пусть {(J (t)}, /eR" есть
м-параметрическая группа гомоморфизмов Е-+Е:
U(t + x)=U(t)U(T).
Пусть далее Е наделено двумя нормами | [|, и || ||а, причем || [|х ^
5*с| Ц2, с = const, и пусть
dU (t)h ,. ,, ,,. ,
-±L- = -tAjU(t)h,
где производная понимается в смысле || d и где Aj :E-+E — ли-
линейные операторы. Назовем А = (Л1( ..., Ап) производящим набо-
набором операторов степени N — Nlt ..., Nn (по отношению к группе
{U (t)} и нормам | I, | ||2), если
Теорема 8.1. Если А — производящий набор степени N по
отношению к группе {U (t)} и нормам \\ \\и [| %, то в Е сущест-
существует такая норма || ||m[d, что А есть производящий набор сте-
степени N по отношению к той же группе и нормам \\-\\mu, |]• ||mid-
. Доказательство. Определим ||-|mid по формуле
Очевидно, что аксиомы нормы выполнены, причем
Из A.3) следует, что
й
Поэтому производная любой функции со значениями в ? в смысле
нормы II ||х является одновременно производной в смысле нормы
|| (mid. Далее,
llmid_ сц
l)"(l+m>\
Поскольку последний множитель не превосходит 1, то
что и требовалось доказать.

§8]
РЕГУЛЯРНЫЕ ОПЕРАТОРЫ 265
Пусть. Bmid — пополнение пространства Е по норме ||-j|mid- Рас-
Расширение оператора U (t) до гомоморфизма 5mid-»-5mid будем обоз-
обозначать через e4At, где At = A1t1 + ... + Antn. Через Л = (А Л„>
будем обозначать набор замыканий операторов Л; в пространстве
Bmtd. Заметим, что операторы At существуют (см. теорему 1.1).
Опр©деление. Пусть <р е<^SN(R") и пусть_А — производя-
производящий набор степени N. Определим гомоморфизм <р (A): Bmid-+Bm\<i
при помощи формулы
ф(Л)/г=Bя)~"/2 liu
где ф = /Г;1ф. Функцию ф будем называть символом оператора
Ф(Л).
Очевидно, справедлива оценка:
Л(к/1), с = const,
где SBN (R») = ^ лгл (R»).
Таким образом, отображение М : (р-^ (р (А) есть гомоморфизм
банахова пространства <^v(R") в банахово пространство Op Emid)
ГОМОМОрфИЗМОВ Bmid-*-5m|d.
Теорема 8.2. Гомоморфизм М является гомоморфизмом алгебр.
Доказательство аналогично доказательству теоремы 1.1. Анало-
Аналогично теорему 7.1 получается следующая теорема.
Теорема 8.3. Пусть (Ах, Л2) — производящий набор в сепа-
рабельном гильбертовом пространстве Н, состоящий из самосопря-
самосопряженных операторов. Тогда
Определение. Резольвентным множеством р (А) производя-
производящего набора А назовем минимальное открытое множество в R",
обладающее тем свойством, что
Множество а {А) = R"\p (Л) назовем спектром производящего
набора.
Определение. Регулярным оператором степени N назовем
оператор_вида T = A! + iA2, где (Аь Л2)—производящий набор
степени N = {N, 0}, причем
Лемма 8.1. Существует замыкание Т регулярного оператора
Т в Bmid.
Доказательство. Пусть f(х) = l2 t , i;eR!, и пусть
Л М где Л = (Л}, Л2) — производящий набор. Оператор

266 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
f(A) имеет обратный. Действительно, пусть {ф„} —такая после-
последовательность функций из C"(R2), что
lim h* (ф„ (Л) h) = h* (h)
для любых А е Bmid, h* = B*mid. Если f(A)h = O, то
Но %(x)f(x) = (pn(x), поэтому qn(A)f(A) = (pn(A). Следова-
Следовательно, ДЛЯ ЛЮбоГО h* e Bmid
откуда и вытекает, что /г==0.
Рассмотрим теперь оператор / (А) Т. Этот оператор имеет зам-
замкнутое расширение g(A), где g(х) =,Xl7,X?¦ Таким образом,
1*1 I *
(хп-+0 и f(A) Гл-„-^г)=>B = 0).
Пусть дс„->0 и Тхп-+у. Тогда /(Л) Гдг„->/(Л)г/ = О. По-
Поскольку оператор f(A) является обратимым, то отсюда следует,
что у = 0, и лемма доказана.
Теорема 8.3. Спектр замыкания Т регулярного оператора
71 = v4i + /i42 e Bmtd совпадает со спектром производящего набора.
Доказательство' аналогично доказательствам теорем 5.1 и 5.2.
Теорема 8.4. Пусть Т — регулярный оператор и пусть
спектр его замыкания Т в Вты состоит из изолированных точек.
Тогда система с. п.-элементов оператора Т является полной
в Bmld-
Доказательство аналогично доказательству теоремы 5.4.
Лемма 8.2. Пусть Т —оператор в нормированном прост-
пространстве В и {Вех}—такое семейство векторных подпространств
пространства В, что
а) Ва конечномерны, dim Ba^N-\-\, причем любая система
{go} такая, что ga e Ba, ga Ф 0, линейно независима,
б) В<х инвариантны относительно Т.
Тогда сужение То оператора Т на Е = \) Ва есть регулярный опе-
оператор степени N (относительно некоторой пары норм).
Доказательство. Пусть Та — сужение оператора Т на
Bd'-Ta = TPa, где Ра- Е->Ва — проектор из Е на Ва. Без огра-
ограничения общности можно считать, что нормальная жорданова
форма матрицы Та состоит из одной жордановой клетки
(в противном случае можно представить Ва в виде прямой суммы
инвариантных подпространств оператора Та. Итак, пусть Га

§8]
РЕГУЛЯРНЫЕ ОПЕРАТОРЫ
267
приводится к виду:
к
0
0
1
к
0
0
1
о
... 0
... 0
. . л
Рассмотрим (N+ 1)Х(/У + 1)-матрицы Аа и
же представлении имеют соответственно вид
Reia 1 0 ... О
О ReXa 1 ¦....
КОТОрые в этом
О
О
1
Очевидно, что Аа есть производящий оператор степени N, a Аа —
скалярный оператор, так что Аа коммутирует с Аа и Аа — про-
производящий оператор нулевой степени. Производящий набор (А'а,
Аа) порождает группу
-tAat _ e-iA'at'-Uai' _e-lAai'-tAai'
e-tAat _ e
_e
Действительно, пусть ц — вещественное число, А — жорданова
клетка размера N +1: .
h 1 0 ... 0\
О ц 1 0 ... О
. . . о
Тогда вектор-функция u(t)=e~iAih, АеС+' является реше-
решением задачи Коши
f-—Ми, ы@) = А,
или, в развернутой форме,
du
dt
л
— = — ШЦ. — II
dt

268 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ ГГЛ.-1И
где Uj, hj компоненты векторов и и h.' Решая последовательно
уравнения этой системы начиная с нижнего, получаем
N+¦1-1
«И0= 2] e-^Pj,k{t)hj^
где Pj, ь (t) — полиномы степени k (которые нетрудно вычислить
точно). Отсюда следует, что
\\e-iAa'h\\B^ca(l+\t\f\\h\\B, ¦ •
где са — константа, зависящая от а. Кроме того, Та — Aa + iAa-
Этому разложению соответствует разложение оператора Т„:
где А' = 2 2
Пара (А', А") порождает группу
U (Г, Г)Л = 2:е-г(л
Введем в Е норму | ||х:
Ясно, что | li^l \\в- Справедлива оценка
Таким образом, (А', А") есть производящий набор степени (N, 0)
по отношению к нормам | \ъ [| ||в, и теорема доказана.
Непосредственно из этой теоремы вытекает следующая тео-
теорема.
Теорема 8.5. Пусть Т — замкнутый оператор в банаховом
пространстве В с дискретным спектром, и обладающий полной
системой с. п.-элементов, причем у оператора Т нет присоеди-
присоединенных элементов порядка выше чем N. Тогда сужение опера-
оператора Т на некоторое плотное в В, линейное многообразие есть
регулярный оператор.
§ 9. Обобщенные собственные и присоединенные функции
Начнем с физического примера. Состояние системы частиц с п
степенями свободы в квантовой механике описывается функцией
из пространства L2 (Rn), а физическим величинам отвечают опе-
операторы в L2(Rn). При этом логическая схема квантовой механики
предполагает возможность разложения произвольного элемента
из Z.2(Rn) по «собственным функциям» оператора, соответствую-
соответствующего любой физической величине. (Кавычки поставлены здесь
потому, что те функции, которые в физической литературе при-
принято называть собственными, не обязательно принадлежат L2(Rn).)

§ 9] ОБОБЩЕННЫЕ ПРИСОЕДИНЁННЫЕ ФУНКЦИИ 269
Пусть, например, га=1 и пусть Л —оператор умножения на
независимую переменную в L^ (R). Этот оператор отвечает одной
из важнейших физических величин — координате частицы. Урав-
Уравнения
для собственных функций оператора А не имеют обычных реше-
решений; однако в физике считают, что 8^ является обобщенной собст-
собственной функцией оператора умножения на независимую Перемен-
Переменную и пишут '
х8(х-Х) = Х8(х-Х). (9.1)
Равенство (9 1) можно интерпретировать следующим образом.
Рассмотрим замыкание А — X оператора А — Х как оператора,
действующего из пространства W^S(R) B пространство
причем s достаточно велико. Тогда
Заметим, что равенство А8х — Х8к не имеет места, так как 8^ф
^L2(R). Тот факт, что А— Хф А — X, обусловлен тем, что опе-
оператор умножения на скаляр не ограничен как оператор, дейст-
действующий из WTS (R) в U (R).
Далее (в физике) пишется разложение
ф (*) =i $г|) (X) б (х - X) dX, (9.2)
или, в более общей форме, разложение
]x)dX, (9.3)
где {tyx (x)} -~семейство обобщенных собственных функций опера-
оператора какой-нибудь физической величины. Поскольку фх (•*) входит
в (9.3) как функция параметра X, то естественно считать, что
оператор (А — X) действует в пространстве функций аргумента X,
т. е. рассматривать X как оператор умножения на независимую
переменную.
В настоящем параграфе именно с этих позиций будет полу-
получено обобщение формулы (9.2) на случай разложения произволь-
произвольного вектора из Bmjd по обобщенным с. п.-функциям регулярного
оператора.
Перейдем к определениям и обозначениям.
Рассмотрим Нот (<?®N (R"), С). По определению, Нот (<ffiN (R"),
С) есть пространство ограниченных функционалов на <?®N (R"),
т. е. пространство Sd% (R") для элементов которого было принято
обозначение:
X, f е= Нот [&„ (R»), C],ge S3N. (•)

270 функций от регулярных операторов [гл. и!
Как мы уже условились вцше, этот интеграл, имеющий смысл
лишь для непрерывных f(k), записывается формально для любого
функционала /, и f(k) называется обобщенной функцией.
Пусть G (к) — непрерывная функция от Я, со значениями в В.
Тогда интеграл
Я"
определяет элемент пространства 5, так что оператор Gi
Rn . ¦ ¦
является элементом пространства Нот(<з®лг(К"). В). Условимся,
по аналогии с (*), для любого элемента G e Horn (SSN (Rn), В)
писать формально
и называть G(X) обобщенной функцией от к со значениями в В.
Обычные обобщенные функции являются в силу этого определе-
определения обобщенными функциями со значениями на комплексной
плоскости.
Пусть Т — регулярный оператор степени N, Bmi<j — отвечающее
ему промежуточное банахово пространство и пусть Х = Я,1 + /Я2 еС.
Рассмотрим оператор
который действует из Втц в Bmid. Мы будем его рассматривать
как оператор, действующий из пространства обобщенных функ-
функций от Я, со значениями в Bmid в пространство непрерывных
функций от к со значениями в Вт\д. (для того, чтобы значения
оператора (Т — Х)к принадлежали 5mid для любого фиксирован-
фиксированного Я).
Итак, мы будем рассматривать (Т — Я,) = Т , где К = Х.х -\- /Х2 = (к1г Х^)
как оператор, действующий из Нот (<$л^2)' ^mid) в С (R2> ^mid). Уточним,
что понимается под этим. Обозначим через Т^:
Нот seN(W), Bmli)~C(W, Smid)
оператор, определенный иа таких, непрерывных функциях со значениями
в Bmid, что отображение
есть непрерывная функция в R2 со значениями в Вт{й, и действующий по
формуле
Расширим оператор Т^ до оператора Г(*' следующим образом. Пусть
{/„} — такая последовательность функций из D (ft) что существует обобщен-

§9] ОБОБЩЕННЫЕ ПРИСОЕДИНЕННЫЕ ФУНКЦИИ 271
ная функция / со значениями в Bmidi обладающая тем свойством, что для любой
функции о(з s C^° (R2)
lim $ fn (X) $(k)d\= U (К) ij> (К) dX.
"^«R» ¦ R*
Пусть при этом lim rjft) L=g. Тогда положим T(k) f = g.
п-юо
Проверим корректность даииого определеиия. Пусть fn&D ik) и пусть
'о
для любого ф <= С%> (R2)
lim J fn(X)$(k)dk=O.
Пусть, далее, существует
lim 7fV«=g-
л-»со
Нужно показать, что g=0. Имеем, для любого t|> e C?° (R2):
lim J (Г-Л,)* /n (X) *(ЧА=1« (X) if (X) Л.
Пусть Я —гладкая достаточно быстро убывающая строго положительиая
функция и пусть 7'=i41 + «j4»i гДе (А1г А2) = А производящий набор, опреде-
определяющий регулярный оператор Т- Положим
2
/=о
Тогда оператор [Р (А)]~* q (А) является замкнутым расширением оператора
(Т — %)к, причем оператор [Р (А)] замкнут как оператор, обратный к гомо-
гомоморфизму. Поэтому -
Нш ] (
л-»со
для любого \j>eC^°(R2). Отсюда следует, что g=0.
Определение, fldpo оператора 7(*' назовем системой обоб-
обобф д k Т
р p рр
щенных с. п.-функций порядка ^k оператора Т.
Определение. Систему S обобщенных с. п.-функций по-
порядка sg? оператора Т назовем полной, если для любого вектора
he 5mid найдутся такая обобщенная функция Ge^ и такая
функция /e<2®jv(R2)> что
R2 •
Теорема 9.1. Система обобщенных с. п.-функций порядка
^N + 2 регулярного оператора Т степени N полна.
Лемма. Пусть ул(х), хе R2 — следующая 8-образная последо-
последовательность:
R3
lim 1 (х, + С/дг2)лг+2 фя (х) UN („., = 0.

272 ФУНКЦИИ ОТ РЕРУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Доказательство. Обозначим ¦$„ (x) — (x1-\-Cix2)N+2yn(х).
Имеем: %(х) = п-^(пх). Следовательно, %(P) — n-(N+2^1(^Y
где т?„ = F'ityn. Пусть / — произвольная непрерывная функция на
R2, удовлетворяющая условию sup — и ^1- Тогда
peR' (l+!Pi|)
1 К, 0(r.) p ^/Д
Отсюда следует, что
I^IU^ofR^^^ltilU^otR2)-^0
при n-voo.
И лемма' доказана.
Доказательство теоремы. Рассмотрим в пространстве
^аг, о (R2) оператор f с областью определения D = Cf(R2), дейст-
действующий по формуле 7'/(дс) = (л:1Ч-/дса)/(дс).
Нетрудно видеть, что оператор f регулярен, причем простран-
пространство Bmid для него совпадает с <3bN% 0(R2). Покажем теперь, что
тождественный оператор .
/ е Op №v, о (R2)) = Нот (^, 0 (R2), .^, „ (R2)) .
принадлежит ядру оператора 7<ЛГ+1). Пусть ф—монотонно не-
возрастающая бесконечно дифференцируемая функция, определен-
определенная на [0, со) и обращающаяся в 0 вместе со всеми производными
С 1
на [1, оо); пусть \|ф(|)^ = п-. Положим
Поставим в соответствие каждому Я е R2 отображение
Ф„(Я,): х-+ч>п(х-Х).
Очевидно, Фя — непрерывная функция со значениями в о®^ 0(R2).
Пусть, далее, {е„} —такая последовательность функций из Cf(R2),
что е„(л:) = 1 при |х|<п и 0^еп(х)^1. Положим
1а(к) = еа(к)Фа(к).
Пусть ip — произвольная функция из Cj°(R2). Рассмотрим по-
последовательность интег ралов
^ /„ (X) ф (X) (И=\Фп (X) еп (X) у (X) dX,

§ 9] ОБОБЩЕННЫЕ ПРИСОЕДИНЕННЫЕ ФУНКЦИИ 273
При достаточно больших п
R» R»
Покажем, что ||\)з„ —^I^/v+Ijr»)-* ПРИ п-+оо; это будет,
в частности, означать, что \fa->-\j3 в <$n, o(R2)- Имеем
$ Я = $ Фя (г/) г|з (* - у) dy: (9.5)
R» R2
Из (9.5) видно, что 1ря(дг) сходится к \р(дг) равномерно вместе со
всеми своими производными. Поскольку носители функций \)зя
лежат в некотором компактном множестве, не зависящем от п,
то отсюда следует, что г|5„ —>--ф в любом пространстве Соболева.
Рассмотрим теперь последовательность обобщенных функций
или, более подробно,
Gn (Я) (х) = (хг + ix2- Ях - &2)"+2 еп (Я) Фя (д: - Я).
Очевидно, что
| Gn (К) UN> o(R*) < 1 Gn @) IUjv, o <R*> = IIЛ» 1*дт, о <R2>-
где Ля(д:) = (д:1 + 'л:2)л'+2Фп(л:)- Легко проверить, что |] А„ ||->¦ 0 при
О || G (Л) Ц 0 Я
д я() A + 2)Фп() рр |] „ ||р
п->-оо. Отсюда следует, что || GB (Л) Ця^ 0(r»)-^-0 равномерно по Я
при n-voo, так что
Таким образом, система обобщенных с. п.-функций порядка
^N + 2 оператора f полна; действительно, для любого /е
e^.0(R2)
/= \f(l)I(X)dl.
R2
Пусть теперь Т — произвольный регулярный оператор, Т = А1-1Г
+ 1Аг, где A — (Ai, A2) — производящий набор, и пусть А —вектор
из 5mid. Рассмотрим отображение
Фя: Я->-фяД(Л)Л, где фя>я (д:) = фя(д: — Я).
Очевидно, что Фя — непрерывная функция со значениями в Втц.
Положим Кп(Ь) = епA)ФпA).
Пусть i|>, как и раньше —произвольная функция из C~(R2).
Рассмотрим последовательность интегралов
J Кп (Я) 1|з (Я) dk = \ Фя (Я)

274 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЕРАТОРОВ [ГЛ. III
Пусть К —следующая обобщенная функция со значениями в Bmtd:
. • (9.6)
R!
Покажем, что
gn = НпГ $ ф„ (К) -ф (Я,) а"к = J /С (Я.) -ф (Я.) <& = Ч> {Л) К.
Имеем
Л-00 """"цП Rn
R» • LR
где • % (х) = $ Ф« (а: - Я,) if (Я,) а^., так что
R»
Мрп^Мр в ^,o(R2) и Ч
в Bmid.
Рассмотрим теперь последовательность обобщенных функций
gn (X) = (Г - ^)^+2 еп (X) Ф„ (X) = (Т-Х)»+>еп (I) Фп> х (Л) h.
Очевидно, что
Ч,М ( (
Поэтому
)U<\hUAh\u^'0 ПРИ
Значит, Т^+1)К = 6 и /( принадлежит семейству обобщенных
с. п.функций.
Вектор h можно представить согласно (9.6) в виде
R»
и теорема доказана.
§ 10. Самосопряженные операторы как трансформаторы
в пространстве Гильберта—Шмидта
Пусть А и G—самосопряженные операторы в сепарабельном
гильбертовом пространстве Ji и пусть Т—оператор Шмидта, т. е.
7еВ2(Я), где В2 (Я) — совокупность операторов, норма Шмидта
которых ограничена. Можно сопоставить А и G операторы в про-
пространстве Вг{Н) (обозначим их через А и G), действующие по
правилу:

§ 10] ТРАНСФОРМАТОРЫ В ПРОСТРАНСТВЕ ГИЛЬБЕРТА-ШМИДТА 275
Теорема 10.1. Операторы А и G являются самосопряженными
в гильбертовом пространстве В2(Н) и коммутируют на некотором
плотном множестве.
Доказательство. Покажем сначала, что D-^f\D^ плотно
в В2(Н). Пусть Еп (А) — оператор с символом 6 (x-\-ri)Q (n — x)f
построенный при доказательстве теоремы 7.2 (??(Д) приЯ = — п,
Д = 2л), и пусть ie\n)\ — полная ортонормированная система
в Еп (А) Н, причем Мя+ °} содержит Ыя)} в качестве подсистемы.
Пусть Е„ (G) и {g\n)\ — такие же проекторы и ортонормированные
системы для оператора G. Тогда множество {е*} всех векторов
вида е\п) образует полную ортонормированную систему в Я и то
же самое справедливо для векторов gf\ Действительно, любой
вектор из Н мож-но приблизить по норме линейными комбина-
комбинациями векторов вида q> (A) h, где ф е Q° (R), а вектор вида ф (Л) h
принадлежит Еп (А) Н при достаточно больших п.
Имеем для любого Т^В2(Н):
при rt ->-oo. Аналогично,
\\En(A)T-T\bt{H)^0,
при п -*¦ оо, -ибо это последовательность остатков сходящегося ряда
21 (Те/, в/) |2. Таким образом, множество К операторов вида
E'n(A)TEm(G), Tc=B2(H) плотно в В2(Н). Но множество D со-
содержится в D-fiODfi, так как операторы АЕп(А) и Em(G)G огра-
ограничены. Тем самым плотность Dj[]D^ в Вг(Н) доказана.
Пусть {TjjJLi — такая полная ортонормированная система
в В2(Н), что Tj^Djf\Ds, /=1, 2, ... Очевидно, что AGTj =
= GATj, так что А- и G коммутируют на плотном в В2 (Н) мно-
п
жестве линейных комбинаций вида ^]
Докажем, что А и G—самосопряженные операторы. Пусть
TgeD^. t- е- АТ<=В2(Н). Тогда для Se% имеем (AS, TJ =
= (Л5, TJ = (S, ATJ = (S, АТJ, т. e.TeD|,, и А*Т = АТ.
Докажем обратное включение: D-%, с Dp
Пусть Г е D^., т. е. существует такой оператор W е 52 (Я),
что (Л5, TJ = (S, WJ для любого SeD^. Выберем в Н такую
полную ортонормированную систему {е,}, что ej^DA, /=1,

276 функции от регулярных операторов (гл. nt
2, ... Положим'TijU = (и, eijej. Тогда Tijek = bikeh так что
Легко видеть, что операторы Ttj, Tki с несовпадающими парами
индексов ортогональны в В2(Я).Итак, {Tt}} — ортонормированная
система в В2 (Я). Легко проверить, что эта система полна в В2 (Я).
Имеем: || Л7^||2 = || Леу||<оо, так что r^eDj, Далее, имеют
место соотношения
(АТФ TJ=(TU, W)t, i, 1=1, 2, ...
По определению скалярного произведения в В2 (Н) последние
равенства можно переписать в виде
(Aej, Tei) = (ej, Wei);
отсюда следует, что
т. е. AT — W^B2{H). Этим доказана-самосопряженность опера-
оператора Л. ¦ ^_
Для доказательства самосопряженности оператора (? рассмот-
рассмотрим полную ортонормированную систему {е)} в Я, состоящую из
векторов, принадлежащих Do, и пусть
T'ijii = (u, e'i)ej, \fu e Я.
Найдем сопряженный оператор (T'ijG)* произведения T'i/G.
Поскольку область значений оператора П/ содержится в Do, то
Поэтому если T^D0*, то существует такой оператор W^
еВг(Я), что
Отсюда
(e'h TGe'i) = (e'hWe\), i, /=1, 2, ...
т. е.. оператор TG имеет замыкание, равное W е 52 (Я). Это озна-
означает, что jTgDj. Докажем обратное включение Dg-cD^-, и ра-
равенство G*S = GS для SeDg-. Этим будет доказано, что G —
самосопряженный оператор.
Пусть T<=Dn, т. е. fG<=B2(H); при этом (TG)* <= В2(Н).
Определим, как действует оператор (TG)* на вектор г\. Имеем,
для любого «еЯ:
(TGu, el) = (u, {TG)*e?).

§ 10] ТРАНСФОРМАТОРЫ В ПРОСТРАНСТВЕ ГИЛЬБЕРТА-ШМИДТА 277
Поэтому для u^Dq получаем: (Gu, Т*е1) = (и, (TG)* el). Отсюда
T*e'i^D0 и (TG)* e'i = GT*e'i. Используя эти соображения для
любого S e Dfi, получаем
(S,
= 2((TG)*e'k, S*e'k) = 2l(GT*ek, S*ek);
k k
(GS, TJ = (SG,,TJ = (T*, (SG)*J =
e'k, (GS*)e'k).
Отсюда вытекает, что TeD^, и G*T = GT, и предложение до-
доказано.
Операторы Аи G порождают группы {ё~1^} и {e~iSi}; которые
действуют по формулам
е-Шт = е-шт< e-CoiT=Te-iQtt (ЮЛ)
Докажем, например, второе равенство. Рассмотрим две функции:
ы2 @ = (Те40* )*h, T*h<=Da.
Имеем Uj @) = и2 @) = T*h. Далее,
^ = (— iGe-'Z'T)* h = i [(e~iSiT) G]* h = iG (e~&T)* h = Ющ (t)\
du2 d
так что .функции их и щ, удовлетворяющие одному и тому же
уравнению -г = iGu и одному и тому же начальному условию,
совпадают. Так как множество операторов Т, удовлетворяющих
условию T*h e DQ для плотного в Н множества векторов К, плотно
в В2(Н), то формула
справедлива для любого Т^В2(Н).
Из формул (ЮЛ) следует, что плотное в В2(Н) множество К
операторов вида En(A)TEm(G), где Еп(А), Em(G) — рассмотрен-
рассмотренные выше проекторы, инвариантно относительно групп {e"iAt\,
{ё~'°1}, причем
g-iGxg-iAt
Рассмотрим двупараметрическую группу {е~ш-1°х}:
g— tit—tax Ё? g- iAtg- йзт

278 ФУНКЦИИ ОТ РЕГУЛЯРНЫХ ОПЁРАТОРОб {ГЛ. lit
Для любого Т е К имеем
от
Таким образом, (A, G) есть производящий набор операторов.
Теорема 10.2. Пусть f e=<^0(R2), J = F~1f. Тогда
Доказательство следует из формулы
^y(t,^)e-^Te-^dtdx =
и теоремы 7.2.
Задача. Мы определили бесконечно дифференцируемые растущие не
быстрее степени аргумента функции от коммутирующих операторов. - Пока-
Показать, что они образуют алгебру с ц-структурой, где алгебра о% есть алгебра
коммутирующих неограниченных операторов, я множество М состоит из про-
производящих операторов и действительных функций от них.

ГЛАВА IV
ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ
В этой главе мы построим ц-структуру для случая, когда
множество М состоит всего из двух некоммутирующих произво-
производящих вектор-операторов Лх и Л2,*). Обобщить эту конструкцию
на случай, когда М состоит из большего числа некоммутирую-
некоммутирующих неограниченных производящих операторов, оказывается
невозможным без дополнительных предположений. Поэтому основ-
основные «рабочие» формулы теории ц-структур (формулу коммутации
и /С-формулу) приходится доказывать специально и при допол-
дополнительных предположениях даже для случая двух некоммутирую-
некоммутирующих операторов, т. к. эти формулы содержат также и их ком-
коммутатор.
Эти затруднения, разумеется, отсутствуют для ограниченных
операторов. В этом случае приведенные здесь конструкции функ-
функций от упорядоченных операторов являются ^-структурами.
Из тех же соображений, что и в главе III, мы приводим
независимое построение функций - от упорядоченных операторов
и лишь в § 10 строим растущие символы, что и приводит
к ц-структурам.
§ 1. Предварительные определения
Пусть {Вх} (где х пробегает множество всех целых чисел) есть
семейство банаховых пространств, удовлетворяющее следующим
условиям:
а) существует линейное многообразие D, плотное в Вх при
любом т;
' б) (т < т') => Вх -> Вг, т. е. |• ||вх ^| • |Bt,. -
Семейство {Вх} назовем банаховой шкалой; норму в Вх будем
обозначать || ||t.
Линейное отображение A; D-+D назовем производящим опе-
оператором степени s с шагом k в банаховой шкале ВХ1 если при
любом х оператор А является производящим оператором степени s
*) Более того, речь идет на самом деле о небольшом обобщении ц-струк-
туры, так как будут определены лишь операции р. (*j,—> А^ х%,—> А%) и
у.: (д^ — Ар х% — Ах).

280 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
с определяющей парой пространств (Bt, Bt+)r); обозначим через
{UA (t)} группу гомоморфизмов порожденную А, а через V'а, т @ —
замыкание оператора UA(t): Bx-*-Bx+k.
Пусть {Тх} — такое семейство гомоморфизмов Вх-+Вхн, что
TxDc:D и Txh = Tx>h при AeD для любых т, т'. Назовем
семейство Т = {Тх} переводящим оператором с шагом /
в шкале {Вх}. В тех случаях, когда это не ведет к недоразу-
недоразумению, будем вместо Txh писать Th.
Пусть Ль ..., AN — производящие операторы в шкале {Bt}
с шагом соответственно ku ..., k^ и степенью sx, ..., sN и пусть
Т<1\ ..., T^-V — переводящие операторы с шагом соответственно
/ь ..., In-i- Припишем операторам Ль ..., AN, T<1\ ..., Т^-^
номера (которые будем ставить над буквами, обозначающими
операторы)Гследующим образом:
1 2 3 2Л/-2 2Л/-1
Аи ТЫ, Аг, ..., T<N-X\ А„; A.1)
при этом будем говорить, что оператор А\ действует первым,
оператор Т{1) — вторым, оператор AN действует BN — 1)-м.
Набор A.1) будем называть вектор-оператором. Заметим, что
некоторые из компонент вектор-оператора могут, вообще говоря,
коммутировать между собой или даже быть равными.
Поставим в соответствие вектор-оператору A.1) следующий
гомоморфизм Ux(t), зависящий от параметра < e.R*:
U(tlt U, ..., tN) =
= UAn(tN)T(»-V UAN_l(tN-l) .¦ • UAi(U)r<«>UAl(h) A.2)
(здесь и в дальнейшем, где это возможно, индекс т в обозначе-
обозначении Ux(t) опускается).
Теорема 1.1. Для любого h^.Bx функция
непрерывна.
Доказательство. ПриЛГ=1 утверждение очевидно, До-
Доказательство проводится по индукции; однако во избежание гро-
громоздких выкладок мы покажем только переход от ЛГ=1 кЛГ = 2,
так как переход от произвольного N к ЛГ-|-1 принципиально
не отличается от этого более простого случая.
Пусть ЛГ==2; обозначим ТA) через Т. Имеем
= U-a2 (t, + б2) TUAl (h + 81)h- UAl 'U) TUAl (tj h =
= UAl & + 62) T[UAl (tt + 8,) - UAl (ti)\h +
+ [UAa (t, + 6J ~ Ua, № TUAl fa) h.
Очевидно, что каждое из двух последних слагаемых стремится
К нулю по норме пространства Bt-t-fc, + ... + iN_, ПРИ 8;, б?->0.

§ 1] ПРЕДВАРИТЕЛЬНЫЕ ОПРЕДЕЛЕНИЯ 28]
Обозначим через Cs,..., sN (Rw) банахово пространство непре-
непрерывных функций на R^, имеющих конечную норму
SNR
Очевидно, что 6^-функция Дирака и функции из С" (RN) могут
рассматриваться как элементы сопряженного пространства
Cs* sN (Rw). Мы будем пользоваться для значений функциона-
функционалов из. Ctt sN интегральными обозначениями:
$ /(*) Ф (х) dx, f е=С,* SN (R"), ф е С§1 1ДГ(R").
Задача. Показать, что при1 <р s Cf (RN)'i ф = ф
IIЧР110* /,*)=$ \VW\(l+lxl\)h...(\ + \xN\yNdx.
h SN ' дЛ^
N
Решение. Положим /== J | ф(д;)| JJ A + | xi\)Sidx. Очевидно,
RN 1=1 ¦
||ФI-,*/ м\^1- Докажем обратное неравенство. Пусть е>0, F=max\(p(x)\,
c=max {| x | : x e supp ф}. Существует такое открытое множество С7е cr supp ф,
что замыкание Ue лежит внутри носителя ф и
mes[suppq>-t/e]< " ( где ^[^s^.-.+V
Построим теперь такую финитную непрерывную фувкцию фе (х), что <рв (д;) =
= sigr^(*) . при x<=Ue, фе(д;)=О при дг^Биррф, |фе(ж)|<1,
фе (х) • ф W 56 0. Пусть фе (дс) = Фе (х) Д A +1 xt |) *'. Тогда фе е Cf (Rw)
i = l
и | фе ||с = 1. Далее, имеем
$
N
\ *
N
5*/- J ' 1ф(*)|
supp ф - Ue i —
следовательно,
ll<plL*= sup \^(x)y(x)dx\^\i<p(x)-\
для любого 8 > 0. Поэтому || ф || # , w. ^ /.
Обозначим через «S? линейную оболочку множества
С (R") U {^ е ra/, б6 е= Cs* 1ДГ (Rw).
Через С^ s^CR^) обозначим замыкание «S? в С? sW(RJV)-

282 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Построим по пространству Ctv..-..sN изометричное ему бана-
банахово пространство функций e%>Sy...,sN(RN) точно так же, как
мы построили в гл. II <&)S(RN) no Ct(KN). Используемый при
этом изометрический изоморфизм будем называть преобразованием
Фурье и обозначать буквой F.
Определим пространство W**- SN (Rw) как пополнение про-
пространства C^(RN) по норме
где q) = /4p. Пусть через CSl- •"" ' >W(RW) обозначено пространство
функций /:Rw-»-C, для которых при Os^&^Si непрерывны
производные т / ' и конечна норма
dxti ... dxNN
U\ch NU»)= max
c уя ' 0« ft,-«s. x e Rw
J
Теорема 1.2. Пусть «,->s,- + у; тогда имеют место вло-
вложения
Доказательство аналогично доказательству теорем 4.4, 4.5
главы II.
§ 2. Функции от двух некоммутирующих
самосопряженных операторов
Пусть. А и В — самосопряженные операторы в сепарабельном
гильбертовом пространстве Я, а Т — некоторый оператор из
класса Гильберта-Шмидта В%{Н).
В § 10 гл. III паре операторов (А, В) была поставлена
в соответствие пара (А, В) коммутирующих на всюду плотном
множестве операторов, действующих в гильбертовом пространстве
Въ{Н). Имеется гомоморфизм
•*Х в :C(R2)-+Op (B,(H)),
который переводит функцию /eC(R2) в оператор f(A, В),
|/(Л, B)|b,(«)<I/1c(R')- Гомоморфизм о^хв индуцирует для
фиксированного Т отображение

§ 2] ФУНКЦИИ ОТ ДВУХ ОПЕРАТОРОВ 283
с помощью формулы
°*lf jf = f(A,B)T.
Мы будем обычно писать просто <Л вместо <Л 3 a i и пользо-
пользоваться обозначением
Очевидно, имеет место оценка
If/(A,
где | || — норма оператора в Я. Таким образом, <^ является
гомоморфизмом нормированных пространств. Заметим, что опре-
определение оператора Tf [А, В) согласуется с определениями пре-
предыдущего параграфа: если fee®0(R2), то , имеет место формула
Г/ {A, B)h=±;\{F-lf) (tlt 't2)e-'At< Те-™* h dt, dtt
R2
для любого fte/f. Кроме того, справедливо равенство -
Лемма 2.1. Имеет место оценка
|tyU, в)у{А, B){^
Доказательство. Имеем
и-» 17Ч|> .
Из леммы 2.1 следует, что ядро гомоморфизма <^ является идеа-
идеалом в С (R2).
Определение. Точку X е R2 будем называть точкой резоль-
резольвентного множества р(л, Т, В) пары операторов А, В относи-
2
тельнс оператора Т, если существует такая окрестность U этой
точки, что любая функция ty e Cf (R2) с носителем, лежащим
в U, принадлежит ядру гомоморфизма <Л.
US 1 \
, Т, В) в R2 назовем спектром
а (А, Т, В) пары операторов А, В относительно Т.
Теорема 2.1. 1) Любая функция из С(R2) с носителем
в р\А, Т, В) принадлежит ядру гомоморфизма aS.
2) Если ф принадлежит ядру гомоморфизма "<*#, то любая
точка AeR!, для которой ф(А)=^0, принадлежит р [А, Т, В).

284 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Доказательство. Пусть 'eC(R!), supp/c=p [А, Т, В).
C 2 1 \
А, Т, В) является максимальным открытым мно-
множеством в R2, удовлетворяющим условию
и suppcpcpU, Т,
Предположим, что носитель / компактен. Тогда найдется такая
последовательность {/„} функций из Cf, что supp/ncp(y4, Т, В)
и lim lfn(x)-f(x)\\ciR') = 0. Поэтому
Tf(A, Ь)= lim 77»
Откажемся от предположения компактности supp/\ Рассмот-
Рассмотрим плотное в Я линейное многообразие. L векторов вида
i|>e=C?(R).
Очевидно, достаточно доказать, что сужение оператора Tf [А, В)
на L равно нулю. Пусть q = ty(B)h, ty^C?(R) и пусть {ф„}—
такая последовательность функций из C~(R), что ф„(Л) поточечно
сходится к единичному оператору. Имеем:
77 (Л, h)q = tf(A, В)^(в)/г= lim T<pn{A)f{A, в
п-»'оо
так как носитель функции ф„ (#i)/(#i, лга) if) (лга) компактен и
лежит в р(л, Т, В). Пункт 1 доказан.
а / з 1 \
Пусть теперь Ту [A, B) — Q и ф(Х)#О, к — некоторая точка
из Ra. Рассмотрим функцию e^eC~(R2), обращающуюся в Овне
е = окрестности точки к. При достаточно малом е >> 0 функция
F = ejjq> принадлежит C(Ra). Но e^ — ^F и функция ф принадле-
принадлежит ядру гомоморфизма «^. Так как ядро гомоморфизма «^ есть
2 /3 1 \
идеал в C(Ra), то Те%\А, В)=0. Теорема доказана.
Теорема 2.2. 1) Точка к = (Къ К2) принадлежит р(А, Т, В)
тогда и только тогда, когда существуют функции фь ф2 е CJ° (R)
такие, что ф! (ki) Ф 0, ф2 (Х2) ф 0 и щ (А) Ту2 (В) = 0.
Доказательство. Пусть k — (ku X^) e R2 и существуют
такие функции фь ф2 s С" (R), что fi^J^O, ф2 (^2)^=0 и
/3 2 1 \
ф!(Л)Гф2 (В) = 0. Докажем, что k^p{A, T, В); обратное
утверждение следует непосредственно из определения. Очевидно,
что существует такая окрестность U точки к, в которой функция
9i(^i)9a(M не обращается в 0. Пусть ty — произвольная функция
из C~(R2) с носителем в U. Обозначим ,х(*) = —(J\*1 <ху Тогда

ФУНКЦИИ ОТ ДВУХ ОПЕРАТОРОВ 285
и .ty(x) = %(x)yl(x1)qi2(x2). Так как ядро гомомор-
veC() p() %()piA)f() р р
2 / 8 1 \
физма aS является идеалом в C(R2), то Tty[A, B) = 0. И теорема
доказана.
Следствие. 1) а (А, Т, в) а а (А) X а (В);
I % 2 1 \
2) точка (Къ %^ принадлежит о [А, Т, В) тогда и только
/82 1\
тогда, когда точка (Х^, %,} принадлежит а [В, Т*, А).
Пусть С (р).— множество всех непрерывных на R2 комплексных
функций с носителями в открытом множестве pcR8. С (р) яв-
является идеалом в C(R2). Рассмотрим банахову фактор-алгебру
C(R2)/C(p). Обозначим через а дополнение к р в R2. Пусть С (а) —
алгебра непрерывных комплексных функций на о с обычной нормой
Р
Если /, и /2 —две функции из C(R2), которым отвечает один и
тот же "элемент из C(Ra)/C(p), то сужения функций ft и f2 на а
совпадают. Значит, отображение сужения
индуцирует отображение л0: C(R2)/C(p) -> С (а), которое является
отображением на все С (а), так как любую непрерывную на а
функцию можно продолжить до функции, непрерывной на R2.
Лемма 2.2. Отображение л0 сохраняет норму.
Доказательство предоставляется читателю.
Из леммы 2.2 следует, что п0 —изоморфизм. Отождествим
с помощью этого изоморфизма алегбры C(R2)/C(p) и С (а).
Теорема 2.3. Пусть n:fl~*'f\en f ^—проекция C(R2)
на С {а [А, Т, В)). Тогда имеет место разложение
U2 1\ \ • /
, Т, В)-+ В2 (#) — гомоморфизм банаховых про-
пространств, определяемый единственным образом формулой B.1).
Имеют место оценки:
Доказательство предоставляем читателю.
Наконец, приведем следующую важную для некоторых при-
приложений теорему.
Теорема 2.4. Пусть <р — вещественная непрерывная функция
8 2 1
на а (А, Т, В). и 2 /» i\ м
Тогда \\т^(л.в)\\ v
Эта теорема непосредственно следует из унитарности опера-
оператора e'f &• в) (см. предыдущую главу и теоремы 2.3).

286 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
§ 3. Функции от некоммутирующих операторов
Пусть пространство Csv.... sN (RN, В) определено аналогично
тому, как было определено в гл. III пространство CS(R, В).
Если /еЦ Sfj (Rw) и GeC,li.,.|Sj/(R"l В), то интеграл
\ f(x)G(x)dx.
r"
будет пониматься в том же смысле, что и в случае N = 1.
Пусть имеется вектор-оператор A.1). Положим для любого
2 4.. 2N — 2 /I 3 2N — l\ de(
~l)y\Ai, Аг AN )h —
Cj. \ $(t)U(t)hdt, C.1)
где ф = /7ф, а (/@ —операторная функция A.2).
Лемма 3.1. Справедлива оценка
2Л/-2 [\ ЯЛГ —
IT2
N
где с зависит только от г и от операторов Alt .... AN.
Доказательство сразу следует из неравенства
1 $ f(x)G(x)dx\ <l/|bv...,iy(R")|G|cv..'fiw(R« в).
1 *N \\в
Замечание. Очевидно, что в приведенных выше конструк-
конструкциях можно считать степени Si производящих операторов
Л*:Вт-»-Вт+^ функциями от т. Мы не делали этого, чтобы
не загромождать записи. В каждой конкретной формуле ясно,
в какой точке т нужно взять st. Другой подход состоит в том,
чтобы рассматривать банаховы шкалы {Вх}, где т пробегает лишь
конечное множество значений. Тогда можно выбрать степени Si,
не зависящее от т, но оператор
2N—2 /1 2ЛГ —1\
. T^-'M^ Aa):Bx^B,+kl+... + kN+l.+...+lN_l
будет определен уже не для всех, а только для некоторых т.

i 3] ФУНКЦИИ ОТ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ 287
Пример. Пусть
Л2ф (х) = лгф (х), А& (х) = — V (х),
00
1
ГФ (х) = ~- \ e'p*Vl+p*m ф (р) dp, Ф е Cf (R).
У2л _Joo .
Тогда
|—т при т<0,
1—а~' ~~ ' 1—> 2^~| 0 при
Нетрудно убедиться в том, что
где ij^fijj. Мы будем обозначать
h (A,, Ai)* (дг) = L Ос, - i д/дх) ф (дг),
где L(p, x) — y(p, х)У \-\-ргт. В силу леммы 3.1 имеем
\l{x, -<
где
Задача. Пусть ф е ^/,0 (Ra),
Lj(x, Р) =
Положим
оо i
L(i)t/()
Пусть S—бесконечно днфференцируемая вещественная финитная функция.
Определим оператор 7' = Kl+(P + S')im следующим образом. Рассмотрим
производящий оператор A =p-f-S':
AU(x)*=—ihU'(x) + S'
Положим Т„ (?) = фя (|) К1 + Ъш> гДе {фл} — последовательность функций из
C<»(R), определенная в лемме 1.13 главы III. Пусть TU= Jim f ^
л-»оо п
1) Доказать, что Г —переводящий оператор шага т в IW— T(RI,
2) Доказать равенство
-4-S (Ж) /, iv is(*) /2 I v
е * L{x,p)eh U(x)=L{x,p+S')U(x),
где . .
j
L(x, p + S') =

288 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
3) Доказать, что это равенство остается справедливым и для произвольной
фу нкции .S s С°°, если рассматривать его на финитных функциях U.
Обозначение. Если % = ф^, то будем писать
2 2N — 2 /1 2JV —1\
()
2JV-2 /1 1N — 1\ [I 2JV —
. т^-Мл л*)хч>и Лдг
Лемма 3.2. ##сть f(x) = fi(Xi)f2(*2)---fw(*w)> где ф,
<?8Si(K).'Toada
2JV —2 /1 2Л/-П
^! А
= фдг (Лдг) 7-<W " »фдг_1 (ЛаГ-1) • - • ТЫ ф1
Доказательство легко получить из C.1).
Лемма 3.3. Линейная оболочка множества функций ty вида
Tp(x)=q1(x1)...yJpN(xN), ^e^.(R). C.2)
шляется плотной в «$Sl, .... *N (Rw)-
Доказательство. Достаточно показать, что линейными
комбинациями функций вида C.2) можно приблизить в простран-
пространстве <^Sl sN(RN) Фурье-образы функций из C^R^), а также
экспоненты
х -*¦ е~ '°л- ••• —'° nxn.
Для экспонент это очевидно, так как
е -ta1x1-...-taNxN _ e-ialXle-iaNxNi
Пусть теперь ф —Фурье-образ функции из Q°(R"). Тогда
Ф е W[ (RN) при любом /. Всякую функцию из пространства
Соболева можно сколь угодно точно приблизить- по норме этого
пространства линейными комбинациями произведений вида C.2),
где все % принадлежат C~(R) (докажите это). Для завершения
доказательства остается воспользоваться теоремой вложе-
вложения 4.4 гл. II и 1.2.
Леммы 3.1 и 3.2 означают, что существует гомоморфизм бана-
банаховых пространств:
М : <&h ,д, (Rw) -> Нот (Вх, Вц.*1+...+*Дг+<1+...+<Дг_1),
который определяетря формулой C.1) и который переводит функ-
функцию ф в оператор
2 2Л/-2 /1 2JV — 1 \
Г««... Г^-^ф'Л! AN)
кроме того, он обладает тем свойством, что
2 2Л/-2 /1 \ /3 \ /2ЛГ-П
^ А'(Л]И]( А)
= фл- (An) ^(Л/-" Флм (An.,) .. .Г<» ф1 (А). C.3)

§ 4J СПЕКТР ВЕКТОР-ОПЕРАТОРА 289
Этот гомоморфизм, как следует из леммы 3.3, определяется
свойством 3.3 однозначно.
Итак, справедлива следующая теорема.
Теорема 3.1. Существует, и притом единственный, гомо-
гомоморфизм
2 2Л/-1 /1 2N — \\
[lt ..., AN)
банахова пространства я%}$1 % (Rw) в банахово пространство
всюду определенных линейных ограниченных операторов из Вх •
в BT+k1+...+kN+i1+...+iN_v обладающий свойством C.3).
§ 4. Спектр вектор-оператора
Примем дальнейшие соглашения относительно обозначений. Если
переводящий оператор Т является тождественным, то будем
опускать его в обозначениях функций от вектор-оператора и
будем нумеровать подряд все оставшиеся операторы. Например,
вместо 1ф(л, А') будем писать ср(л, А').
Пусть О: Do^>Вх, причем DoгэD. Тогда норму сужения 0\о,
рассматриваемого как оператор из .Вт- в Вт», будем обозначать
через ЦО^-г"-
Следующая лемма следует непосредственно из определений.
Лемма 4.1. Пусть At, i—\, ...» N — производящие опера-
операторы степени st с шагом ki-в шкале {Вх\, a T(l), i=\, ..., N — I —
переводящие операторы. И пусть А\ —оператор At, рассматри-
рассматриваемый как производящий оператор с шагом кс\-щ. Тогда для
любых if <= $й*х sN (Rw) и fteO имеет место равенство
2 2Л/-2 /I 2А/-П 2 2Л/-2 /1 2А/-1\
ГШ... 7W-'><pUi, •.., AN)h = TW... rw-')i|»Ui' A'N)h.
Лемма 4.2. Пусть
\\Т(т)<р{Ат, i4m + i)||t + *1 + ... + *m + /1+...+/m_l-T+-*1+...+*m+;l+...+;m =
= М < оо.
Тогда справедлива оценка
2 2JV-2 /2т-1 2т + 1 \ /1 2Af — I\
( ( JH )
Доказательство. Мы докажем эту лемму для N = 2.
Именно, докажем следующую оценку:
\\т(щ>){Аъ <
Ю В. П. Маслив

290 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Пусть V : Вт+*.-> Вх+ *,+/, есть замыкание сужения опера-
оператора Ту\Аъ Л°2) на D. Тогда
Действительно, если AeD, то
S1 \
R
* ^ dt \ * ^
Ra
S(ф * ^{tlt k) Ua' {k) TUai {tl) hdt=T (^ Уь лУ h-
Для завершения доказательства остается воспользоваться лем-
леммой 3.1.
Точно так же, как и лемма 4.2, доказывается следующая
теорема.
.Теорема 4.1. Для любого целого V справедлива оценка
Лемма 4.3. Множество функций фе^,, s-(R2) таких, что
(л, Л') = °. является идеалом в алгебре <&s, S-(R2).
Доказательство. Пусть АеВт. Тогда для любого
=^(R2)
Следовательно,
ДЛЯ ЛЮбоГО ф е g55s, s' (R2).
/12 3 2JV-2 2Af-I\
Пусть JT = [аь Г»), /1Я, ..., r<" - «>, Лл, ) - вектор-опе-
вектор-оператор. В этом случае обозначим через X идеал в алгебре
&@$1 sN (RN), состоящий из всех таких функций ф> что
2 2N-2 /I 2N — l\
( l[ )
Лемма 4.3 означает, что в случае N = 2 идеал X совпадает
с ядром гомоморфизма
(Л, А).

§ 5] ФУНКЦИИ ДВУХ ПРОИЗВОДЯЩИХ НАБОРОВ 291
Определение. Толку leR" будем называть точкой резоль-
резольвентного множества вектор-оператора
12 3 2JV-3 2JV-2 2N -1\
^, Л,, .... Л„-1, 1 )
существует такая окрестность V этой тонки, что любая
функция ф е Cj° (Rw) с носителем, лежащим в U, принадлежит
идеалу X, построенному по гомоморфизму
2 2JV-2 /1 2JV —1
Дополнение к резольвентному множеству назовем спектром о
вектор-оператора X.
Лемма 4.4. Пусть функция феС00!^) принадлежит
идеалу X, построенному по гомоморфизму
2 2W - 2 /1 2JV - I \
Ц-+ТЫ ... r^-HUi, .... AN).
Тогда любая точка, в которой функция ф отлична от нуля, при-
принадлежат резольвентному множеству вектор-оператора
2N -\\
..., An).
Доказательство. Пусть ф (X) Ф 0 и пусть ^ — функция
из Cf(KN), равная единице в б^окрестности точки X и обра-
обращающаяся в нуль вне 62-окрестности этой точки. При доста-
достаточно малом б2 функция в^=е^/ф принадлежит Co°(Rvv)'. Но
ex = (f-<^, и функция ф входит в идеал X; следовательно, е*, е X.
Пусть х s Cf (R2) и пусть носитель функции % лежит в бгокрест-
ности точки X. Тогда %(х) = %(х)ег1(х), т. е. %^Х, что и требо-
требовалось доказать.
В случае N = 2 следствием лемм 4.3 и 4.4 служит следующий
критерий.
Теорема 4.1. Для того чтобы точка X е R2 принадлежала
резольвентному множеству вектор-оператора (А, Т, А'), необхо-
необходимо и достаточно, чтобы существовали такие функции фх и ф2
usCf (R), что ф, (kt) Ф 0, ф2 (А,2) Ф 0, м пры этож ф2 (Л') Гф^Л) =0.
§ 5. Функции двух производящих наборов
Пусть А = (Ль .... Ak) — производящий набор степени s с опре-
определяющей парой пространств (Ви В2), Т — гомоморфизм Т\ В2-*-В3
и А' — (А[, ..., Л А-) —производящий набор степени s' с опреде-
определяющей парой пространств (В3, Bt). Мы будем предполагать, что
имеют место вложения Вх с: Вг и В3 с ВЛ.
Пусть {U (t)} есть ^-параметрическая группа, порожденная
набором Л, a {V(/')} есть k'-параметрическая группа, порож-
10*

292 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ (ГЛ. IV
денная набором А'. Определим, аналогично предыдущему, бана-
банахову алгебру е®а, S' (R* x R*') исходя из пространства Cs, $' (R* X R*')
непрерывных на R*xR*' функций, имеющих конечную норму
Если фее®5, S'(R*xR*') и ЛеВ], то положим по определению
k-\-k'
7\р(л, Л')л = Bя) ~ J 4(t,x)e-lA'*Te-lA'hdtdx,
где егш ! Вг -*- В2 — замыкание оператора V (/); e~lA'w i Bs -*¦ Bt —
замыкание оператора V{t).
Определение. Точку (A., |i)eR'x R*' будем называть точ-
точкой резольвентного множества пары производящих наборов А, А'
относительно переводящего оператора Т, если существует такая
окрестность U этой точки, что любая функция феС™^*+*')
с носителем, лежащим в U, принадлежит следующему идеалу X
алгебры <$$. $'(Rft + ft')> построенному по гомоморфизму
банаховой алгебры <3)s, s' (R*+*') в банахово пространство
Нот (Bi, B4)!
X — {ф| &#ф\|) = 0, Уф е= s®s> s» (R*+*')}.
Пополнение к резольвентному множеству назовем спектром о
IS 2
пары А, А' относительно оператора Т.
Пусть (К, ц) — точка резольвентного множества пары А, А',
относительно Т, а ф —функция, бесконечно дифференцируемая
всюду, кроме точки (А,, ц). Пусть далее (/ — окрестность точки
(Я,, |х), фигурирующая в определении, и пусть бесконечно диффе-
дифференцируемые в U функции ф и ф из s®s, s< (R* + *') совпадают
с функцией ф вне некоторого замкнутого множества, лежащего
в U. Тогда ф — (peCf(Rft+*') и suppfo —ф)с U, так что функ-
функция ф — ф принадлежит идеалу X. Для краткости будем обозна-
обозначать элемент {ф} = {ф} факторалгебры <$s, s< (R* + *')/X через {ф}
(а иногда даже — через ф), хотя ф может не принадлежать
«^s, s' (Rft+*')). Для гомоморфизма е? имеет место разложение
еМ = яе^о, где
Я М„
Поэтому

§ 5] ФУНКЦИИ ДВУХ ПРОИЗВОДЯЩИХ НАБОРОВ 293
9 { l s \
Мы будем обозначать этот оператор также через Ту [А, А'), а
функцию ф называть его символом.
Лемма 5.1. Пусть носитель функции i|> е qS®s, S' (R* x R*')
18' »
лежит в резольвентном множестве пары А, А относительно Т.
Тогда i|> принадлежит идеалу X, построенному по гомоморфизму <Л.
Доказательство. Заметим сначала, что если точка (Я, ц)
принадлежит резольвентному множеству пары А,'А' относи-
относительно Т, то любая функция из qS®s, s- (R* x R*') с носителем
в достаточно малой окрестности точки (X, ц) принадлежит X.
Это следует из того, что такую функцию можно сколь угодно
точно аппроксимировать в <?®в, s' (Rft, R*') функцией из Cf(R*x R*')
с носителем в малой окрестности точки (X, ц),
Предположим сначала, что функция i|) имеет компактный носи-
носитель. Тогда она представима в виде суммы конечного числа функ-
функций из X и следовательно, сама принадлежит X.
Пусть теперь ^ — произвольная функция, удовлетворяющая
условиям леммы. Существует такая последовательность {/„} с:
dCs°(RfexRft'), что
lim Bл) 2 ^ (F-4n)(t)g(t)dt =
для любого g^Cs. S'(RftxR*')- Положим % = tln. Имеем
9 /1 8 \
supp 1|злсsuppt|j; поэтому Т^„[А, А') = 0. Далее,
lim Bл) ~ J (F-ЧЫ (О g @ dt =
k-\-k'
= lim {2nf 2 J [{F-i^ * {F- iin)] {t) g (t) dt =
ft +
Отсюда следует, что для любых h e Bt, h* e В*
, i')A] = li*[^(i, А')].
Значит, Г1)з(л1, Л') = 0.
Заменяя в этом рассуждений if на i|)/, получаем, что
для любого /ec$?s> S'(Rft.+*'),"a это и означает, что i|>eX, и
лемма доказана.
Теорема 5.1. Пусть А = (А1..., Ak) производящий набор степе-
степени s с определяющей парой пространств {Вх, В2), А' = (Ai,..., A'i)—>

294 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV .
производящий набор степени s' с определяющей парой пространств
(В3, В4), Т: В2-*-В3 — гомоморфизм. Пусть Хо е R*, fioeR' и
существует такая окрестность U точки (Я,о, ц0) в R*+/, что для
некоторого б > 0 при (К, ft)e(/ и е < е0 справедлива оценка
Т [{А — аJ + [А — \kJ + e2j 2 1в,-в,<с
точка (Я,о, ц0) принадлежит резольвентному множеству век-
вектор-оператора &-={А, Т, А') (с не зависит от е).
Доказательство. Пусть феCjJ°(R*+/) и supptyc U. Нам
нужно доказать, что i|) (#*)=(). Без ограничения общности поло-
положим Цо = О. Л«о = 0.
Пусть ц>(х, у), ^eRJ, yeR' —такая функция H3Cf(R*+')»
что
00 СО СО СО
Е ••• И Е ••• Е ф(^-'. »-л-1.
^ = -оо /4 = —00^ = —со /1=—со
i = (h, .... /*), / = (/i /,).
Тогда найдется такая константа clt что для достаточно больших п
. У)= Е *(*• y)V(nx-i, ny-jp. 2] *Jf>(jK, у).
где число элементов множества Мп не превосходит сгпк+1 и
D-4)^^ при (t, })еМя.
Обозначим '
R,(x, y)=(V^+y2+^+l+s+s'+6. .
Имеем:
Ф (пх -i,ny- j) Ri/n (x - -jjp, у - 4) =
= ф(пдг — /, n^ —/) Ri(nx—i, ny — j)-n-k-l-s-s'-6.
Отсюда следует оценка:
Из тождества
и оценки для оператора

§ 5) ФУНКЦИИ ДВУХ ПРОИЗВОДЯЩИХ НАБОРОВ 295
следует, что
где са —некоторая константа. Значит,
И (•*") II < сг ¦ /Г*-'-*. с1Пк+' = с&п,-6 -*- О
при п-»-оо. Теорема доказана.
Теорема 5.2. Пусть Л = (Л1,..., Ak) — производящий набор
степени s с определяющей парой пространств (Ви В2), А' =
= (Ль..., A'i) — производящий набор степени s' с определяющей
парой пространств {В3, Bt), T: В2-+В3 —гомоморфизм. Предполо-
Предположим, что для любого достаточно малого вещественного е > 0 имеет
место оценка
где с— константа, N — любое натуральное число. Тогда точка (К, ц)
принадлежит резольвентному множеству вектор-оператора 2? =
= \А, Т, А'), (с не зависит от г).
Доказательство. Предположим (без уменьшения общности),
что Х=0, ц = 0. Обозначим хе{х, у) = Ух2 + у2-\-в2 .
Пусть %(х, у) eCf(R*+') — произвольная функция с носите-
носителем в б-окрестности нуля. Тогда
Н(х, у)[гй(х, y)lwl,|f
Выберем 6<1/с. Тогда
у)[хй(х, y)r\\Bst s,(R*+')^0 при yV-^oo.
2
Здесь скобки [[ ] означают, что нумерация операторов, стоя-
стоящих внутри этих скобок, не распространяется на операторы,
стоящие вне: все выражение в скобках рассматривается как оператор,
действующий вторым (см. Введение). Теорема доказана.
Теорема 5.3. Пусть /„ — функция из <з%ъ, $- (R* x R*'), равная
единице на спектре о пары производящих наборов А, А' относи-
относительно переводящего оператора Т. Тогда выполняется неравенство
Доказательство. Пусть <?fc.s> ,-(Rk+k'/a) — подалгебра
алгебры «$?s, S'(R*+*'), явл мыканием алгебры функций

296
ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ
[ГЛ. IV
из s®s s'(R*+*') с носителем из R*+*'\o. Для любой функции
/€=<#;, ,.(R*+*'\0)
Tf{A, Л') = Р-
Поскольку «$,, S'(R*+*'\o)- идеал в s®s, S'(Rk+k'), то при /е
e=^s. S'(R*+*'\o) имеем
Следовательно,
Остается заметить, что функция /„— 1 принадлежит алгебре
# Kk+k'\)
Следствие. Пусть а —спектр пары А, А' относительно Т.
Справедливо неравенство
Определение. Пусть последовательность {Ф„} сходится
в 4,i'(R*XRs') к функции Ф, пг/стб функции $„ :х-*-[Фп(х)]~1
также принадлежат s®,,,(R*xR*') « пг/стб при этол выполня-
выполняется условие
б«/бел называть функцию Ф спектральным весом.
Будем говорить, что спектральный вес Ф подчинен спектраль-
спектральному весу «F, если ограничена последовательность норм
Введем в 4,s'(R'xR{') норму
IMk=ef|
и произведение
E.2)

§ 6] ПСЕВДОДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ 297
имеем
^I Ф1Ф IUSi s- (RftXR*') I Ф2Ф I*,,,. (R*XR*') = i Ф11
Таким образом, норма E.1) и произведение E.2) индуцируют
в s®s, s'(R* X R*') структуру нормированной алгебры.
Банахова алгебра, получаемая пополнением этой нормирован-
нормированной алгебры, будет обозначаться e$s,S'.<?(RftxR*').
Пусть <$s,S',a>(Rk+k'\o) — замыкание в ^S|S',o(R'xR*') под-
подалгебры, состоящей из финитных функций с носителями в R*+*'\a.
Факторалгебру ^s,s', ф (R* x R*')/Д, S', ф (R*+*'\a) обозначим через
Теорема. 5.2. Справедливо неравенство
Доказательство. Имеем
ыХл)'| ^
y
где е„->-0 при п->оо.
Если носитель функции <р е s®s, S' (R* X R*') лежит в R*+ft'\a,
то 7>(/4, А') = т[ц(а, Л')-фп, -4')], так что
Переходя в последнем неравенстве к точной нижней грани
по <р, получаем утверждение теоремы.
§ 6. Псевдодифференциальные операторы
Пусть Ат, т — 1, 2, —, п — оператор в W* (R") с областью
определения DAm:=S, действующий по формуле
Ату{х) = 1Ц^-. F.1)
Набор операторов А = {АЪ Аг, •-., Ап) является производящим
набором нулевой степени. Действительно, пусть h — произволь-
произвольный элемент из S. Положим
[U@] (x) = h{x1-t1,...,xn-tn),t(=R>' F.2)
и будем считать, что функция U принимает значения в W|(R").

298 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Имеем:
где Ai — оператор с областью определения D% —S, действующий
по формуле
<4i<p(*)=*icp(*), F.3)
и где U(t) = FU(t). Из F.2) следует, что
[U(t)}(x) = h(x)e-itx. F.4)
Поэтому
, <а in) , .л ritff
1 lAU V) |* (Rn) =
1ДГЖЙ (Д
(l+x*)kdx-.
М*I'A + *1)»?Б(дг, в)Л,
R
где |?(*, 6I=^1. Поскольку функция h(x)-? принадлежит про-
пространству W* (R"), то
a' ^ tn)-V{() i
т. е. функция f/ является решением уравнения
Аналогично показывается, что
F.5)
для любого / = 1, 2, ..., п. Кроме того, функция V удовлетво-
удовлетворяет начальному условию
U@) = h. F.6)
Докажем, что решение задачи F.5), F.6) единственно. Повторяя

§ 6] ПСЕВДОДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
рассуждение § 1 в гл. III, рассмотрим функцию
т
Ъ
где те [a, b], *eR", /ieCj°(Rn), и покажем, что
где dv/dx — предел соответствующего разностного отношения, по
норме в L2(R"). Для этого достаточно убедиться лишь в том, что
Имеем:
т+в
т
Далее,
в
Т
т+6
;б2 max
ал
если х не принадлежит б-окрестности носителя функции Л. Имеет
место следующая оценка:
*, 8, т)|^
., дг„
; {b — а) 8 max

300 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
и f(x, б, т) = 0, если х не принадлежит (Ь —а + 6)-окрестности
носителя функции А. Из приведенных оценок следует, что
Таким образом, доказано, что решение задачи
|| + гЛ1Ы = О, ы@, /а /») = «!С. »
единственно, так что
[U (*)] (X) = [Ыз. (t2 /„)] (ДГ! - tt, *2, ..., Хп).
Если и — решение задачи F.5), F.6), то функция
.«i(*2, -.., ta) = u(O, t2, .... tn)
является решением задачи
§^ + /AUl = o, Ml@, h, ..., /п)=и2(/з,.... tn),
где ы2(^3, .... tn) = u@, 0, ^S, ..., tn). Отсюда следует, что
x2-U, x3, .... xn),
Повторяя приведенное рассуждение, мы получаем, что всякое
решение задачи F.5), F.6) должно иметь вид F.2).
Итак, набор операторов А порождает я«параметрическую
группу {?/д@Ь действующую по формуле
UA(t)h(x) = h(x-t). F.7)
Очевидно, что при любом / оператор UA(t) изометричен. Итак,
доказано* что А есть производящий набор нулевой степени.
Пусть теперь k ^0 — целое число. Рассмотрим набор А =
= (Alf ..., Ап) операторов, определенных на S формулой
Набор А является производящим по отношению к определяющей
паре пространств (№* (Rn), №*(Rn)). Действительно, при k = 0
так что для любою fteS существует решение и задачи Коши
(/=1, •••,«):
e~oll 6
u@) = h.
.л 11
J Mr") ' F.

4 6] ПСЕВДОДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ 301
Функция и, являющаяся решением задачи F.8), подавно явля-
является решением задачи (/ = 1 п):
и„\и(к, ...,tj_lt tj+t, thl, .... tn)-u(f) % I
lirnj j- = + ^@|w* («•)-<>. F9)
при любом
. Покажем, что решение задачи F.9) единственно. Для этого
достаточно доказать единственность решения следующей задачи
Коши:
^ + М1«(т) = 0, F.10)
M@) = ft;
здесь и — функция со значениями в W*(R"). Воспользуемся тео-
теоремой 7.2 гл. I. Выберем в качестве фигурирующего в этой тео-
теореме множества М пространство 6g°(R"). Для определенности
докажем единственность решения задачи F.10) на положительной
полупрямой. Пусть ft —произвольный элемент из C™(Rn) и пусть
а, Ь, Т — числа, удовлетворяющие условиям Q*^a<Zb^ Т. Доста-
Достаточно убедиться в том, что существует функция v со значени-
значениями в CS°(R"), непрерывная на, [0, Т] по норме пространства
L2(Rn) и удовлетворяющая условиям
h при t е (а, Ь),
0 при te?(a, Ь), F.11)
где dv/dx понимается как производная функции со' значениями
в W*(Rn). Пусть ф, \|> — произвольные функции из S. Тогда
[^ ^т]- .F.12)
R"
Из формулы F.12) следует, что для любого
Стало быть, переходя к Фурье-образам, мы можем вместо задачи
F.11) рассмотреть следующую задачу:
е(а'&)' F.13)
0 при %ф(а, Ь),
а»(Т)-0;

302 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
здесь dw/dx понимается как производная функции со значениями
в #* (Rn), q есть произвольный элемент из C°°(Rn), а В —опера-
—оператор в Cf (Rn), действующий по формуле
Покажем, что решение w задачи F.13) существует. Для этого
сделаем замену неизвестной функции:
1а> (т)](*) = [г(т)] (*)(*»+1)-*.
Для функции г получаем следующую задачу!
q при те(а> 6)> 19, ш
zG) = 0;
здесь dz]dx понимается как производная функции со значениями
в La(Rn), a g^Cf(R"). Существование решения задачи F.14),
принадлежащего при каждом фиксированном т пространству Cf (Rn),
было доказано ранее. Единственность решения задачи F.10)
доказана.
Из формулы F.7) следует, что решение задачи F.9) имеет
вид:
[и (*)](*) = Г'*Л(лг). F.15)
Следовательно, набор А порождает «-параметрическую группу
u(tr
= e-'xt(f(x). F.16)
Имеем:
Отсюда следует, что А — производящий набор степени |/г|.
Если k — натуральное число, то А является, по отношению
к определяющей паре (W*(Rn), №?(Rn)), производящим набором
степени k. Действительно, для любого натурального />1
и любого AeS
[ \
Rn ' R"
при б->-0. Кроме того,
h W A
R"

§ 6] ПСЕВДОДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
при 6->-0. Отсюда следует, что функция
303
удовлетворяет задаче Коши (/ = 1, ..., п)
где du/dtj — производная в смысле нормы пространства №*(R"),
так что А, как и при неположительных k, порождает группу
Оценим норму оператора U% (t) в №* (R"). Поскольку
дх'«
х-
дх'п •»
где / =
i /„), / = (/i, .. •, jn), Pj
= cj*... c?, то
при t-*-0Q. Итак, доказано, что А — производящий набор сте-
степени k в W*(Rn).
Обозначим снова замыкания операторов A/, Aj в W*(R") соот-
соответственно через Лу, Aj. Легко видеть, что справедливо следую-
следующее утверждение:
где DAm — множество векторов Л из W*(Rn), для которых суще-
ствует Л"»Л1 *.. ¦ i4"iA, m, +... + тя =-m.
Определение. Операторы вида f\A, А) и /(Л, Л) «азы-
ваются псевдодифференциальными операторами.
Употребляются следующие обозначения:
(x)^f(-id/dx, x)u(x),
i A)u(x)=f(-id/dx, x)u(x).

ЗЭ4 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Задача. Доказать для псевдодифференциальных операторов в La (R")
формулу
Задача. Доказать, что оператор умножения на функцию /е &s (Rn),
определенный на S, ограничен в В7* (R/1) при s :> | ft | и что для любого я е S
справедлива формула
f (*)*(*)-/$) А (х).
Задача. Доказать, что для любого AeS справедливы следующие фор-
формулы:
/ {-id/дх, x)h(x)=—L
Bл) '
f{-id/dx, x)A(x)--JL
Пример.
exP I" 1 дх7
Можно рассматривать также1 псевдодифференциальные опера-
операторы с растущими символами. Именно, пусть
g(p, x) = f(p, x)P(p)Q(x),
где /e^0.ft(R")> P и Q —полиномы. Тогда для любого AeS
g{-id/дх, х) к(х) = Q(x)f (- ih/dx, х) Р (- id/дх) h(x),
g{—id/дх, х) h(x)=P (- id/дх) f (- id/дх, х) Q (x) h (x).
§ 7. Примеры
1) Пусть
Функция
удовлетворяет уравнению
.ди .ди

§ 7] ПРИМЕРЫ 305
Поэтому
;max
— 00
Очевидно, что
Имеем, для любого feS:
00
i = r7— \ e-lAt$(t)f(x)dt:
Л S
5
— 00
Поэтому для любых Ф, p
Если Я -ф ц и носитель функции ф лежит в малой окрестно-
окрестности точки к, а носитель функции Ф лежит в малой окрестности
точки ц, то оператор
равен нулю. Поэтому спектр пары \А', А) лежит на диагонали
прямого произведения RxR.
С другой стороны, спектр пары [А, А') заполняет все про-
пространство R2, так как для любых е>0, XeR, jisR найдутся
такие функции Ф, ф е Cf (R) с носителями в е-окрестиости точки
% и е-окрестноста точки ц, соответственно, что
(оператор A—cP/dp2) — нелокальный).
Таким образом, спектр пары иесамосопряженных операторов
зависит от порядка, в котором рассматриваются эти операторы:
спектр пары \А, В) неравен, вообще говоря, спектру пары {В, А);
в то же время можно показать, что для самосопряженных

306 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
операторов эти спектры совпадают (с точностью до отражения
относительно биссектрисы координатного угла).
2) Пусть В — пополнение пространства Cf (R) по норме
]/(*№=! \e**f(x)\4x,
— 00
а В' — пополнение С? (R) по норме
1/(*)||Ь'=°$ \e-"*f(x)\4x.
— 00
Очевидно, В cz В'. Возьмем в качестве Т оператор вложения
1:В-*-В'. Рассмотрим операторы «рождения» и «уничтожения»:
А==*ш+*' A' = ii-ix-
Справедлива следующая теорема.
Теорема-7.1. а) А есть производящий оператор степени О
с определяющей парой (В, В), А' есть производящий оператор
степени О с определяющей парой (В', В');
I Ч 2 \
б) спектр пары \А, А') заполняет всю плоскость R2;
в) функция
Ф: (х, у) -+с A + (х-уУУ^е-с-У^2
при достаточно большом с является спектральным весом вектор-
оператора \А, А'), так что
Доказательство, а) Решение уравнения
i^ = ip±ixu
dt дх
имеет вид и (х, t) = e+x'^(x-\-t). Поэтому
е- iMf (х) = е- 'VV*+W2/ (х + 0,
так что
1 e-***f (х) \\в = [К/2<г-/л7 (*) ||ц (RJ =
II *+W2f ( +1) \\ 1 #i*f (x)
для любого /eC»(R). Значит, \\e-iAi\\=\.
б) Аналогично, для любого ф е С? (R)
[ -11/2
\l/2
Ц \ е-хЧ*\ч>(х)\Чх) =|ф|в..
-со /

§ 7] ПРИМЕРЫ 307
Пусть Ф, fe=C~(R).
Аналогично примеру 1, получаем, что
Пусть Ф, f, 9eC~(R). Тогда
Пусть fp-* :l2(Rp)->- L^, (R*) — преобразование Фурье и
F~XLpiUiRx)-*-U(Rp) — обратное преобразование Фурье; обозна-
обозначим Fx^pfiix) через h(p). Тогда
. Ф (А') Ф (Л) f (*) =е*2/2/^ф (р) е^/^ф (р) ^ (р).
Выражение ф (р) e^'/rfp'tjj (p) не обращается в нуль ни при каких
финитных ф и tjj; поэтому спектр вектор-оператора \А, А') запол-
заполняет всю плоскость.
в) Пусть Ф (х, г/) = ф(дг — у). Нетрудно проверить, что в этом
случае Ф(-4( А') есть оператор умножения на некоторую функ-
функцию, а именно,
00
фЦ А')Нх) = ±е*Нх) ^ Ф@<г-<*-'>'Л,
— оо
где ф = /7~1ф.
Пусть
Ф„ (*, g) = 0 + (х + У)I/2 [<г-с«-»>'/» +1] = Фп (х - у).
Тогда
R»
2л/2
Нетрудно убедиться в том, что
где dn->-0 при п-*-оо, так что последний интеграл ограничен

308 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
как функция от п. Отсюда следует утверждение в), так как опе-
оператор умножения на е** ограничен как оператор, действующий
из В в В'.
Задача 1. Пусть
. . d , . Jtcosх—sinx
dx xsm Jt+лс* '
Л dx*' ' ''
Показать, что спектр вектор-оператора \А, А') лежит в области
Решение. Заметим, что A = —i v- + « -^:МП (l+——)\, так что в
силу задачи § 3
Пусть ф, ty e С» (R); тогда
\ vTp
Рассмотрим подробнее функцию
. '. d
an i -rr
dp I
dp
CO CO
1
— CO —CO
Заметим, что
или
Отсюда
Если suppx<=[«. b], то suppt) с [a—1, 6 + 1].

§ 7] ПРИМЕРЫ
309
Вернемся к оператору <f(A')ty(A). Из приведенных рассуждений видно,
что если suppip с [а, 6] и supp ф(—р8) сК\[о-1, 6+1]. т° (А')$(АH
Отсюда
а(А, /!')<
Задача 2. Пусть
A=*id/dxlt
Показать, что в этом случае
||ФЦ а-) хч (I ЛОЫфМ A')\\-h(A, «I-)!!,
т. е. алгебра, индуцированная в Нот (CSi Si (Rftf R^), CSi Sj (R^, R^)
гомоморфизмом ft#, является нормированной алгеброй.
Решение. Имеет место неравенство
где t—(tlt /2), *=(*i, хг), * = («!, sf) ф е Cs (R!). Следовательно, набор
(А, А') является производящим набором степени s. Далее, если
sC»(R8), то
| ф (Л, A') х lc, -sup A +| X! |Г5' A +| xt | Г" | $Ф (/) ос (.
WIO + l'ii)II(l+l'il)'1d
X
Такая же оценка получается, если ср (/) = 6 (/—/0)- Поэтому из определения
пространства ,#, (R2) следует, что для всех ipe^, (R") справедлива оценка
||ФЦ Х')\с _с ^||ф||да.
s s s
С другой стороны, для ф е ,^s при любом е > 0 нагдется такое /8 е С^
llXellc =1- что
li.1
Тогда
IIФ U, A') xe \\cs 5* | [ф @ Хв @ 15s || ФЦ-е.
так что || ф \А, Л')|| с -»с ^ИфНй • Отсюда получаем
S S S
1ф(Л. i') 11с -.с НфЦ."
с ..с 1фИ».
S S S
Теперь несложно вывести окончательные неравенства:
Задача 3. Пусть B1=Bt = Ba=-B4=B, T = l, н пусть А — А' — огра-
ограниченный оператор. Показать, что функция г~г при достаточно боль-
Xi—X2-\-l
шом К является спектральным весом вектор-оператора (А, <!')•

310 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ ГГЛ. IV
Решение. Пусть еп е С°° (R), еп-*1 в ^ (R) для всех /. Рассмотрим
последовательность функций
le (*) « (*) (* *) + «J е= ,#, (R2),
где s = (slt s2), sx — степень А, % — степень Л'. Имеем
f/5??k!faI& 1(R2)-
Далее,
Ik (к, Щ = ±-\\(А А А') еа {к) еа (к') + ,-l
\\
Пусть М = sup '' \А' А ™ . Выберем K~:M(d*\\A-A'[\+l). Тогда
Ф И1Ь
Итак, последовательность фп удовлетворяет всем условиям определения спект-
спектрального веса, т. е. функция —. . является спектральным весом для
\Х1 — хг) -г *
а, а).
3) Одним из самых важных частных случаев теоремы 5.3
является следующая оценка. Пусть А и А' — производящие наборы '
соответственно степеней s и s' и пусть В2 с Ва. Тогда
4) Пусть {#t} — банахова шкала, 7\ и Т2—регулярные опера-
операторы степени s с определяющей парой (Вх, Вт+т,), где т—любое
целое число. Пусть оператор 7\ — Т2 ограничен как оператор,
действующий из Вт в Бт-т,. где т2>2т1. Пусть T1 = A1 + iA2,
Тг = Вх-\-1Вг, где (Ai, Л2), (Вь В2) —производящие наборы. Пусть
функции Фх (дгх, дга) и Фа (ylt yz) таковы, что функция
г?!?"^ принадлежит Л„ ,(a(TJXo{TJ>). Тогда оператор
Oi(/41> А2) — Ф2(В1, В2) ограничен как оператор ИЙ Вт в Бт+2Т1-т»..
5) Пусть Г—гладкая кривая в R2. Введем в окрестности Г
координаты г, t, где г —длина нормали, t—параметр на кривой.
Пусть
9eC(Rz), ф(дс, ^)-ф(г,,

§7] ПРИМЕРЫ 311
A 2 \
А, Т, А') лежит на Г и сумма
степеней производящих операторов Л и Л' не превосходит N, то
ftp {A, 4')-fcp*U, А').
6) Пусть Р(х, у) = 2 aijx'xJ — полином от двух переменных, А, А' произ-
производящие операторы в некотором банаховом пространстве В. Положим
Задача. Пусть А н Л' —операторы в La(R), рассмотренные в п. 1:
А = I — Л' = i — 4- i 2X
dx' dx ' 1 -)-дс2 '
Показать, что 'А' — А) =0 тогда и только тогда, когда k ^ 3.
Решение. Легко видеть, что (л — А') ф 0 прн ft = 0, 1,2. Пусть k ^ 3.
Очевидно, Л — производящий оператор степени вд = 0. Далее,
следовательно, А' — производящий оператор степени sA, = 2. Для <р, \|)
eCJ5°(R) имеем
Поэтому, если supp ф П supp \|)=^ ф, то i|) (Л') <р (Л) = 0, т. е. спектр а (л, Л')
лежит на диагоналя в R2.
В силу предыдущего пункта оператор f{A, А') равен нулю, если функ-
функция F имеет на диагонали в R2 нуль порядка ~^sA-\-sA, + 1 =3. Следова-
Следовательно, при k^-Ъ
ш, n-*oo
, geZ,2(R)({en}— последовательность функций из леммы 1.13
гл. Ш). Отсюда (л — Д') =0 прн ft ^3.
7) Пусть B1 = B2 = L2(/?), B3 = B4 = ^1(R), T = id/dx и пусть
А и Л' —операторы умножения на гладкую вещественную функ-
функцию f(x). Нетрудно убедиться в том, что спектр вектор-оператора
{А, Т, А') лежит на диагонали.
Из равенства
легко получить формулу
где F — производная функции F по первому аргументу, ф е CJ° (R).

312 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
§ 8. Дифференцирование функций от оператора,
зависящего от параметра
Теорема 8.1. Пусть А\п), А{п) — производящие операторы с опре-
определяющими парами пространств (Въ Вг) и (В2, В2) соответ-
1(Ы! II <Ы1
1
в ' 1<М1 + 1<1) *. \\е ||( |1)
где си Si, с2, s2 — константы, не зависящие от п. И пусть-
Тп: Вх -*• В2 гомоморфизмы, ограниченные по норме одной и той
же константой. Пусть далее последовательность {Лл} сходится
поточечно на некотором плотном в Bt множестве к производящему
оператору Аъ последовательность {А{а)} сходится поточечно на
плотном в Вг множестве к производящему оператору А2, а после-
последовательность {Т„} сходится поточечно к гомоморфизму Т: Вг->¦ В2.
Тогда для любой функции f e «®Sl, ss (Rz) последовательность
|t ./ 1 (n) 8 (П)\1 2 / 1 » \
\Tnf\Ai , Ai )) сходится поточечно к гомоморфизму Tf\Alt A2) t
Доказательство. Предположим сначала, что функция f-
имеет вид / (х, у) = Д (д) /2 (у), где h e Л„ (R), f2 e Л„ (R). Тогда
справедливы формулы
Для любого h^BL по теореме 6.2 гл. Ill имеем:
lim h(A\a))h = f1(A1)h.
Так как Та-+Т поточечно и | Тп\^const, то
по норме пространства В2. Так как f2 (Aln)) -*- f2 (A2) поточечно
наВ2 и1/2(лПИ-|%11/2К(кь то
/ (Ain)) Та f (А\п)) h —• / (А2) Tf Ш!г
по норме пространства В2. Теорема 8.1 в рассматриваемом част-
частном случае доказана.
Пусть теперь h — фиксированный элемент из Bv Тогда
ЫаТ, X?)h — tf(Au A2)h
по. норме пространства В2 для любого / из плотного в <?®Su s, (Rz)
множества Р функций вида
fix, y)=Z

§ 8] ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОТ ОПЕРАТОРА 313
Обозначим через Ап :«$„„ s, (Rz)->-B2 оператор, действующий по
формуле
а через Л —оператор:
Тогда последовательность \Ап) поточечно сходится к Л на всюду
плотном множестве Р и ограничена по норме:
По теореме Банаха — Штейнгауза, Л„->- Л поточечно на <?®Hi s, (R2).
Теорема доказана.
Замечание. В этой теореме можно заменить производящие
операторы на производящие наборы. -
Пусть Л — производящий набор из k коммутирующих опера-
. торов с определяющей парой пространств (Ви BJ, А' — анало-
аналогичный производящий набор k' операторов с определяющей парой
пространств (В2, В2), Т — гомоморфизм В1-^-В^. Пусть Р (х, у)—
полином от переменных xeR', г/е R*:
Р(х, у) =
где
J = /i !k'\ x = xi ...xk, У =yS ...ук*
i
Положим
Лемма 8.1. Пуст /e=^s, s<(R*xR*'), /Pe^8,s-(R»)
Если оператор ТР\А, Л') ограничен как оператор; действующий
из Bt в В2, то
. . Ьр(а,а')=Ь(а,а>),
где Т — расширение оператора ТР (Л, Л') до гомоморфизма Вх -»- В2.
Доказательство. Пусть {/„} — последовательность функ-
функций вида
h(х, у) = «„(х)vn{ц), х<= R*. ye R*'.
Легко видеть, что если операторы Л и Л' ограничены, то утверж-
утверждение леммы справедливо для функций /„:
h, Л') = ПП(Л, А'). (8.1)
Если /„->-/ и faP-+fP в «$,,,' (R*+*'), то переходя к пределу
при п->ся в (8.1), получим требуемое утверждение. Доказатель-
Доказательство существования такой последовательности предоставляется
читателю. Лемма доказана в случае ограниченных операторов Л, Л'.

314 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Пусть теперь А и А' — произвольные производящие опера-
операторы. Полежим
А * Л'
**Я = 1 ' ^
Тогда Л„ и An — ограниченные оператрры, сходящиеся на всюду
плотных множествах к операторам А и А' соответственно. При
этом найдутся такие константы с, d, N, N', что
Обозначим: Тп = (р(А'п) Т(р(А„)._ Тогда Тп-+Т поточечно на Вх
и ЦГпЦв.-в, ^ const. Следовательно, по теореме 8.1, для любой
функции f^<?@°(R2) и для любого п<=Вх справедлива формула
lim Tnf(Xn, А'п)р(ап, k)h=ff(A, A')p{a, A')h.
л-»оо
С другой стороны, последовательность операторов
Т'п = Р (А, А') Ф [к) h {Ап) = Ф (ЛУГф (Л„),
действующих из Вх в В2, ограничена по норме и сильно схо-
сходится к Т. Поэтому
lim Л/(А«, А'»)й=.^7(А, А')/г.
Лемма доказана.
Рассмотрим теперь семейство {Т (?)} регулярных операторов
где (Aid), А2(|)) == Л(|) — производящий набор степени s с опре-
определяющей парой пространств (В, В), причем область определе-
определения D оператора Т (|) не зависит от I,
и спектр оператора Т (|) содержится в замкнутом множестве а с R2,
не зависящем от |.
Лемма 8.2. Яг/сть f^<$s(o), пусть семейство {Т (|)} обла-
5ае/п определяющей парой пространств (В1, В'), причем В а В',
и пусть для любых ?', |" мз области определения функции Т (|)
спектр пары производящих наборов А (|'), Л (|") относительно
вложения В в В' содержится в замкнутом множестве 2 ci с X
X а с: R4. Пусть далее
I —» So

§ 8] ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОТ ОПЕРАТОРА 315
Тогда, если множество функций вида
плотно *) в <?®s (?), mo
lim у / (Л (I)) - / (Л (Ы) 11в-*в- = 0.
Доказательство. Пусть функции /«(¦*)> *^Ra таковы,
что
Пусть Т%, &, — расширение оператора Г (?) — Г(|о) до гомомор-
гомоморфизма В -*¦ В'. Тогда, согласно предыдущей лемме, имеем
/. (А (?)) - /. И «.)) = П. 6. ф« U (?)
Следовательно,
при g-*-g0-
Пусть /»->/в^(аха). Тогда
. (А (I)) - /«(Л 01в-,В' +1|/»(А (|о)) -/ (Л (|о)) \\в-.в
Зафиксируем е>0 и выберем такое п, чтобы выполнялось нера-
неравенство ||/ —/„|^(R!)<e/2. Для данного п найдется такое б>0,
что
при |5 —?ol<6. Следовательно, при || —50|<S выполняется
неравенство
и лемма доказана.
Задача. Сформулировать и доказать многомерный аналог леммы 8.2.
Теорема 8.2. Пусть параметрIпробегает интервал вещест-
вещественной оси, пусть семейство регулярных операторов {Т (I)} обла-
обладает (кроме (В, В)) определяющей парой пространств (В', В'),
причем BczB', и пусть для любых |', I" из данного интервала
спектр пары производящих наборов А (?'), А (|") относительно вло-
вложения В в В' содержится в замкнутом множестве J
*¦) Заметим, что это условие выполнено, если {Г(|)} —семейство пронз-
. водящих операторов. В этом случае можно положить a = R, E = R2.

316 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Пусть далее существует производная 7" (?) в следующем смысле;
причем || Т' (I) \\в - в- < со. Пусть \^SBS (ст). Тогда, если
mo существует производная ^*f(A (?)) в топологии пространства:
Нот E, В'), причем имеет место формула
d
Следствие. Справедлива оценка
je-«ACft)*B
где с зависит только от sup —A , . „^— ы о/п
Доказательство. Из существования и ограниченности
оператора Т'(I) следует, что ||Т(| + е)~7'(?)||в^в<<оо. В силу
леммы 8.1 имеем
2
- Т ®
где 7' (ё + е) — Т (I) — расширение оператора ТA + е) — Г(|) до
гомоморфизма В-*-В'. Переходя в (8.3) к пределу при е->0
и пользуясь многомерным аналогом леммы (8.2), получаем утвер-
утверждение, теоремы.
Многомерный аналог теоремы 8.2 мы сформулируем и дока-
докажем для функций от нескольких производящих наборов.. Опре-
Определение таких функций почти дословно переносится из § 4.
Пусть Ak^i^A^ ^Г^) — производящие наборы степеней
S* на определяющих парах пространств (Вк, B'k), Л — 1, ..., N;
Ть — гомоморфизм Вk->flft+ll k= 1, ..., N — 1. Предположим, что
имеют место вложения BkczB'k, k=l N. Через Vk(t) обо-
обозначим nk-параметрическую группу, порожденную • набором Ak,
t e R"*.
Определим, как обычно, банахову алгебру «^(R|n|), |я| =
"+"wi s = (sl) ,.., Sfl), исходя из пространства C^(R|nl)

§ 8] ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОТ ОПЕРАТОРА 317
непрерывных функций на RI, имеющих конечную норму
где х-(ль JfAr) ( )
Если фее%(R1"!) и Аеfilt то положим по определению
2 2JV-2 /1 2JV —1\
где fjsR?, dt=*dtto...dfyN\ e~iAh\Bj-+ В)-замыкание опе-
оператора {//(/)•
. Определение. Точку К &K]ni будем называть точкой резоль-
Г 1 2 2ЛГ-2 2W-li
вентного множества вектор-набора Ж = \AU Tlt...r .Tn~i, An )»
если существует такая окрестность «*, зтой точки, что любая
функция ф е Cf (Riя') с носителем, лежащим в и.%, принадлежит
идеалу X, построенному по гомоморфизму
2 2JV-2
банаховой алгебры «®S(RIB|) в банахово пространство Нот E1( fijy)
(так же, как в определении из § 5). Дополнение к резольвентному
множеству назовем спектром а (&) производящего вектор-набора SC.
Пусть А, —точка резольвентного множества SC и ф —функция,
бесконечно дифференцируемая всюду, кроме точки X. Пусть_да-
леё и% — окрестность из определения. Пусть наконец, ф, фе
es®s(Ri) и функции ф~ и ф бесконечно дифференцируемы
в и% и совпадают с функциейф вне некоторого замкнутого мно-
множества, лежащего в м^Тогда ф — ф"е С"(R'лГ) и supp (ф — ф)сиь
так чтофункция ф — ф принадлежит идеалу X, т. е. элементы
{ф| и {ф} факторалгебры «®s(Ri"l)/X совпадают. Допуская неко-
некоторую неточность в обозначениях, будем писать при этом {ф} =
= {ф} = {ф}. Для гомоморфизма <Л имеет место разложение <*# =
Ж где
a, (Ri»I) -Ь <ms (Ri»i)/X -а Нот (Bit B'N).
Поэтому
2 2JV-2 _¦/ 1 Ш — \\ 2 2N — 2 =/ 1 2N —1
71 ^U AiT TMAA
Мы будем в дальнейшем обозначать этот оператор также через

318 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
2 2ЛГ-2 / 1 2JV —1\
Ti... Tx_iq>\Au ..., An) и будем называть функцию ф его
символом.
Лемма 8.3. Пусть носитель функции \|3S^(R|n|) лежит
в резольвентном множестве вектор-набора SC. Тогда •§ принадле-
принадлежит идеалу X, построенному по гомоморфизму М.
Доказательство. Заметим сначала, что если точка К при-
принадлежит резольвентному множеству SC, то любая функция из
<s$?4(Ri"i) с носителем в достаточно малой окрестности точки К
принадлежит X. Это следует из того, что такую функцию можно
аппроксимировать в <^(R|n|) функциями из CS°(R|n|) с носите-
носителями в малой окрестности точки К.
Предположим вначале, что функция я|) имеет компактный но-
носитель. Тогда она представима в виде суммы конечного числа
функций из X и, следовательно, сама принадлежит X.
Пусть теперь я|> — произвольная функция, удовлетворяющая
условиям леммы. Существует такая последовательность {еп} с
cC~(Ri"i), что
lira ,Bл)~ I«I/* \ {F~4n.) (О g (t) dt = g @)
для любой функции geCjfR1). Положим tyn' — tyen'. Имеем
2 2N — 2 / I 2ЛГ-П
suppя|>„<с:suppя|>; поэтому Тх... Тм_$п-[А1г ..., AN)=0.Далее,
lim Bя)~ i»I/» \ (F-^n.) (t) g (t) dt =
Отсюда следует, что для любых h^Blt h*^(Bk)*
f 2 2ЛГ — 2 / 1 2ЛГ —i\ 1
0 - lim h* [Тг... TN_$n [Alt ...., AN ) h\ -
"~*°° 2 2ЛГ-1 / 1 2ЛГ-1Х 1
... ^.^(^ AN)h\.
2 2ЛГ-2 / 1 2N—l
Значит, Ti... TN_tf[Ai. Л^;
Заменяя в этом рассуждении if на ij;/, получаем, что
2 2JV-2 / 1 2W —1\
)
для любого / s аЗЭ, (R1" I), а это и означает, что я|) е X. Тем самым
лемма доказана.
Пусть набор Ak(l)={Af&) А^) (|)} для всех \ в окре-
окрестности «|„ точки |) является производящим на парах (Bk, Bk)
и (Sft, Bk), k=l Л^. Предположим, что для всех k выпол-
выполнены следующие условия:

§ 8] ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОТ ОПЕРАТОРА . 319
(Ai): Bk с Bk; область определения Dk операторов А™ (?) не
зависит от |;
при всех ? е «|0,
Далее, пусть ТкA): Dk ->¦ Dk+1 — линейный оператор для всех
I е И|, и Л = 1, .... W — 1, причем 7\ (?) удовлетворяет условиям:
(Л2): Tk (?) — ограниченный оператор из 5А в ВЛ+1,
I?1*© fee *^с*« гДе с* не зависит от Е-
Аналогом леммы 8.2 является следующая лемма.
Лемма 8.4. Пусть /е= <^s(Ri"'), s-=(su .... s^), !«! = «! +
+... + rif/. Если семейства операторов .Tjfe), k=\ N —\
непрерывны в точке ?0 по норме Нот (Bk, Bk+1), а семейства
l'Ail} (%) - А^ (?,„)], / = 1 nk, k=l N непрерывны в
точке lo wo норме Нога (Bk, Bk), то семейство операторов
2 2ЛГ —2 / 1 2ЛГ-1 \
Тх(& ... Т ©/Uid), .... Лл? (Ъ)) непрерывно в точке |»
по «о^эже Нот FX, Вл?).
Доказательство. Отметим следующее тождество:
2(у*0-**')(s*.*ф) х
X (^, ..., $\ .... 4°. У?> • • •. ^1"А), ..-. Удг), (8.4)
где
/ A) @
ф(*г .... хx
— разностная производная функции ф по переменной
Пространство <=$?(м+1).(R|n|). где
Bs1+l> .... 2Sl+l 2s^+l, .-;, 2
плотно в ^(Ri"i). Поэтому для данного символа /e^s(Ri"i)
существует такая последовательность fm e <^Bs+d (R1"'), что
ZU*0 ПРИ /П^°°-
Для /т имеем соотношение: Sft) ifm^^(S,sk) (R|n| + I), где
(S, Sft) = (Sx, Sx Si, ... , Sft, ... ^Jk, ... , Sn> • • • , S.y).

320 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
В силу условия [Д1Р(?) —j4^(?o)]eHom(?ft, Bk) и леммы 8.1,
из (8.4) получаем равенство
2 2ЛГ-2 /1 2ЛГ-1
U
2 2N — 2 /1 2ЛГ — 1 \
- 7\ &) • • • 7V_X do) /» Ui do) 'AN Qo)J = „
*.,.. 2ft ... v 2 2*-2 2ft + 2 2ЛГ-2
S UP E) ~ ЛР (lo)) ?\ © . . . Tft_x (I) T* (I) ... 7^ © X
2ft —1
8ЛА+1- Л' 2 2*
4(D+5] Ti(&»).•¦ [ПF)-П(бе)].-
*=1
2ЛГ-2 / 1 ¦ 2ЛГ-1 \
. • • TVi (I) /» Ui (lo) AN (|0)J, TN = To ~ 1. (8.5)
Отсюда, в силу предположений леммы и оценки леммы 3.1, сле-
следует, что
2 2ЛГ-2 / 1 2N—X .
f{
,2ЛГ-2 / 1 2ЛГ-1
o) • • • Ts-x do) /.. (Al do) ЛN do)J |в
N nk ¦
t
при |->-?o-
Но поскольку |/m —/lUi"*"^ ПРИ /n-*-°°. то как и в Доказа-
тельстве леммы 8.2, из (8.6) получим, что семейство
2 2ЛГ-2 / 1 .2ЛГ-1
непрерывно по ? в точке ?0, и лемма доказана.
Из этой леммы сразу получается многомерный аналог теоре-,
мы 8.2.
Теорема 8.3. Пусть производящие наборы Ак (I), k=l, ...,N
в окрестности точки ?0 удовлетворяют условию (Лх) и пусть Tk:
Dk ->• ?>ft+i — линейные операторы, причем Tk е Нот (Вь, Bk+1) и Тк
не зависит от l(k=l N — 1). Пусть семейства А[Лd).
у = 1, ..., пк, k—l,...,N дифференцируемы в HomEfc, Bk)
в точке %0. Символ f принадлежит пространству ^(Sni)(R|n|),
где
Bs -f 1) = BsirH. .... 2sx + l, ..., 2sN+\, .... 28ДГ+1).
2f Й^

§ 8] ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОТ ОПЕРАТОРА 321
2 2ЛГ — 2 /1 ' 2У—1 \
Тогда семейство операторов 7у... Т^Д/М!) Аы_A))
дифференцируемое точке |о по норме пространства Horn (Bt, Bn) и
^ 2 2ЛГ —2 / 1 2ЛГ — 1
-з= 7\... Tjf_i f \A\ (D, ..., A/f (
*=1f=l
2*-l 2*+l 2*+l 2ЛГ+1
Доказательство. Разделим обе части равенства (8.5) на
| —1о. Тогда в силу той же леммы 8.4 предел правой части при
1-*-|о существует, и мы получаем утверждение теоремы.
Пример. Рассмотрим разложение оператора
1 dS\ ~1TS fs l\ I1
jf- =e L[x, hpje
где p = — { д/дх, до второй степени параметра h, S — гладкая
функция от х. В силу предыдущей теоремы
dS/dx~dS/dx
В этой формуле имеется в виду следующий выбор определяю-
определяющих пар пространств: Вх = S2 = W{, В[ = В'г — L2, Лр + dS/dx имеет
определяющие пары (Вх, В2) и (Б!, В^), р — ограниченный опера-
оператор из Да в В[.
Поскольку спектр вектор-оператора \dS/dx, p, dS/dx) лежит
на диагонали, dS/dx есть производящий оператор порядка 1,
до/дх — производящий оператор порядка 0, то
dS/dx-dS/dx
где Р (х; |, т|) — сумма нулевого и первого членов разложения
Тейлора по | функции ¦ (х' >~ в точке | = t]i т. е.
Р (х\ 1, Л) = ?Р (*, Л) +1 ^рр (*, Л) (I - Л)
11 В. П, Маслов

322 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
(Lp — производная функции L по второму аргументу). Далее:
, dS/dx)=-id/dx{Lp(x, dSjdx) +
+ у Lpp (х; dS/дх) (dS/дх - dS/дх)} =
= - iLp (x, dSidx) §-x-^Lpp (*
Итак, окончательно получаем формулу
е h L\x,—lholdx)eh <p(*)=*
= L(x, dSldx)<f(x)-ih[Lp(x, dS/дх) дфх +
+ Tlpp(x> dS{dx)d*S/dx*<p(x)l (8.7)
Задача. Пусть выполнены условия п. 4 § 7 и пусть fe,jSJ/-(R2), где г
достаточно велико. Найти условия, при которых разность
есть ограниченный оператор из В% в Sx—(лг + 1)(т2 —2тО-
Решение. Достаточно выполнение следующего условия: все функции
принадлежат пространству Ж^^ (P(Tk0) X...XO (Tkm)), где fe/= I, 2. Дей-
ствительио, с помощью леммы 8.1, так же как и в доказательстве теоремы 8.3,
получим разложение типа (8.5):
2 2N — 2 /1 2N — 1 \ 2 2Л — 2 /1 2W — I \
«1- «лг-1*(г1 TN)-Ri... RN_^\Klt..., /Сдг) =
^ 2/ \ 2 2/-2 2W . / 1 2/-1 2/4-1 2N+1
где ^ ^?лг_1—переводящие операторы, Tf, K{— регулярные операторы
степени sf, (Г, — /С,-)— переводящие операторы при ( = 1, ..., N в шкале {Вт},
Si )S)(R2X...XR2), 64s^(s s)(a(/f,)X.
Применяя последовательно эту формулу к правой части равенства

§ 91 Ф0РМУЛЫ КОММУТАЦИИ 323
получим искомое разложение:
f{Blt еа)
2N 1\ 2ЛГ + П
где оператор 2^, как легко проследить, является ограниченным оператором
ИЗ Вх В Вт_
§ 9. Формулы коммутации
Пусть А, В — производящие операторы соответственно степеней s
и s', действующие в банаховом пространстве В, содержащем всюду
плотное линейное многообразие Е, инвариантное относительно А,
В, еш, е~ш.
Мы будем предполагать в этом параграфе, что выполнено сле-
следующее условие согласования операторов А.л В\ для любой
функции ф е Cf (R) операторы ф (А) В и Вц> (А) определены на Е
и замкнуты.
Лемма 9.1. Пусть оператор А ограничен и коммутатор
[А, В] ограничен. Тогда для любого /es$?s+1(R) справедлива фор-
формула
[В,
где черта означает замыкание.
Доказательство. Пусть феCf (R) — вещественная функ-
функция, заключенная между 0 и 1 и равная 1 в окрестности нуля.
Обозначим ф„ (х) — ф (х/п). Положим Ап = ф„ (В) Лфя (В) и докажем
сначала формулу
[В, /W] = /(y~^)[В~Ц. (9.1)
Имеем
[Ап, В] = <?
Значит, правая часть формулы (9.1) равна
t<fn(B)[B,
Ап—Ап
Обозначим Вт = Вут(В). Тогда при фиксированном п и доста-
11*

324 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ " [ГЛ. IV
точно больших m
- А в f^n)-f(An) .
Ллит г 5 "г
А А
Г11УйЬШ- А в
Ап — Ап Ап — Ап
+ BjJ^-f^n) = Bm{-f{An) + f{An)) = [Bm, f(An)].
An — An
Итак, при фиксированном п и достаточно больших т спра-
справедлива формула
?ШШ = [Вт, f(An)];
в частности, это означает, что правая часть этой формулы не
зависит от т. Если h=±ty(B)q, где i|)eQ°(R), то
При достаточно больших т. Следовательно, Bmf(An)h не зависит
от т при достаточно больших т и так как <р„ (В) ->¦ 1 поточечно,
5 = Вфт(В)и В — замкнутый оператор, то
при достаточно больших т. Это означает, что формула (9.1) спра-
справедлива на всюду плотном множестве, а следовательно, и всюду.
Перейдем в формуле (9.1) к поточечному пределу.при п->оо,
предположив дополнительно, что Фурье-прообраз функции f имеет
компактный носитель. Для любого h
e-iAn'h-+e-iA'h (9.2)
равномерно по t на любом отрезке a^t^b и
|e-'V|<c ^ (9.3)
при ie[a, b]. Это следует из того, что
II ЛГ II
где 0/(е) не зависит от п. Переходя к пределу в правой
части (9.1) при я-»-оо, получаем в силу (9.2) и (9.3):
lim \ЪТТп]
„ А — А
Что же касается предела левой части формулы (9.1), то
f(An)^-f(A) поточечно, так что f(An)B-*-f(A)B на Е. Следова-

§ 9] ФОРМУЛЫ КОММУТАЦИИ 325
тельно, последовательность {Bf (Ап)Н} сходится для любого /ie?,
В силу замкнутости оператора В имеем при /ie?i
lim Bf(An)h = Bf(A)h.
я-»оо
Итак, для любого h e E справедлива формула
'[В, f(A)]h=[BT^]fiA)A~fjA)h.
Лемма доказана для функции /, имеющей Фурье-прообраз с ком-
компактным носителем. Так как множество таких функций плотно
в s$?s+i (R), то лемма верна и в общем случае.
Следующая теорема утверждает, что можно отказаться от пред-
предположения об ограниченности оператора А.
Теорема 9.1. Пусть коммутатор [А, В] ограничен. Тогда
для любого f e &s+i (R) справедлива формула
Доказательство. Пусть {ф„} — последовательность функ-
функций, рассмотренная при доказательстве леммы 9.1. Положим
Вп= Ч>п(А) Вф„(Л), А„ = Ауп(А). Рассмотрим коммутатор
[Вп, Ат] = Ф„ (А) Вф„ (А) ЛФя (А) - Ац>т (Л) Ф„ (А) Вщ (А).
Пусть п фиксировано; тогда для достаточно больших т получаем
[Вп, Ат]к =
Следовательно, при достаточно больших т оператор [Вп, Ат\
не зависит от т и ограничен по норме числом \\[В, А]\\.
Применяя, лемму 9.1, получаем
Для .достаточно больших т эту формулу можно переписать
в виде - . ' ¦
[Вп, f(Am)] - Ф„ (А) [ВГА] Ф„ {А) 1Щ=М. (9.4)
А — А
Пусть Ае?. Тогда f(Am)Bnh-f(Am)vH(A)B<pn(A)h~
= f (А) ф„ (А) Вф„ (A) h = f(A) Bnh, если т достаточно велико при
фиксированном п. Аналогично, Bnf(A^)h = Bnf{A)h при доста-
достаточно больших т. Следовательно, справедлива формула
=ф. Ц) Пга] t!j=pi. ф, U).

326 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Перейдем в этой формуле к пределу при л-»-оо. Правая часть
поточечно сходится к
, ЛJ -г 5 .
А —А
Что касается левой части, то при /te?, q = ty(A)h, i|)eCf(R)
имеем: •
[Вп, f (A)] q = Фп (А) ВФл (A) f (A)* (Л) А -
Если п достаточно велико, то <р„(ЛI|>(Л) h = ty(A) h=q, так что
lim [Bn, f(A)]q= lim уя(А)[В, f(A)]q=[B, f{A)]q.
Я-»ОО П-» 00
Так как линейная оболочка множества элементов вида i|) (A) h, где
ipeC^R), h&E, является всюду плотной, то теорема доказана.
Теорема 9.2. Пусть коммутатор [А, В] ограничен. Тогда
для любого f(x, у) ea®s+i. s'+i (R2) справедлива формула
f{X, B)-f(l B) = [ATB]-?L-{A, А, В, В). (9.5)
Доказательство. Достаточно рассмотреть случай, когда
-f(*i y)=h(x)fi(y)> поскольку множество таких функций плотно
в a©s+i, s'+i (R2). Тогда формула (9.5) получится переходом
к замыканию. Имеем
Далее,
[мл),
Поэтому
А—А В—В
И теорема доказана.
Теорема 9.3. Пусть f(x)e
s s, s
и коммутатор [А, В] ограничен. Тогда справедлива формула
^г ^A в, в)х
-j^(g{lA, b), lg{A, % ig(k, В)Ш*). (9.6)
*) Запись [[|г(л, б)]] означает, что мы рассматриваем g(A, в) как опе-
оператор, а не как часть более широкого выражения (см. Введение). Мы опускаем
скобки всюду, где это не приводит к путанице.

10] РАСТУЩИЕ СИМВОЛЫ
327
Доказательство. Если оператор А ограничен, то дока-
доказательство совпадает с доказательством теоремы 9.2.
Пусть оператор А неограничен. Положим Ап = -^-. Тогда
1
оператор А„ ограничен и ||е 'л»'||^сA + М1)*> где с и s — кон-
константы, не зависящие от п (см. гл. III). Кроме того,
\\{Ап
где М*)=—^-
н-J-
Имеем
62/« (x, У) = -
откуда следует, что
у)Ik,tMK
Значит, коммутаторы [Л„, В] ограничены равномерно по п. Если
подставить в формулу (9.6) А„ вместо А, то полученная формула
будет справедлива. Переходя., в ней к поточечному пределу при
л->оо, получим формулу (9.6) в общем случае. Тем самым
теорема доказана.
§ 10. Растущие символы
Пусть 4 и Л2-производящие операторы степеней sx и s2 соответ-
соответственно, действующие, в банаховом пространстве В. Как обычно,
предполагаем, что Лх и А2 определены на одном и том же всюду
плотном множестве Е. Замыкания операторов Лх и А2 в В снова
будем обозначать через Ах и A.t соответственно.
Определение. Пусть для функции f(x, у) найдутся такие
целые неотрицательные числа k, l, что функция
принадлежит пространству &suSi (R2). Тогда положим
f{
Alt Aj
для любого вектора /ге?, Зля которого g{AxA2)(At-\-i)kh при-
принадлежит области определения оператора А[.
Теорема 10.1. Пусть, в обозначениях определения,
k'^k, I'^l, g' (х, у) = f(x'y)

328 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ 1ГЛ, IV;
h —такой вектор на Е, что
Тогда
Доказательство. Имеем:
g (х, у) = g' (х, у) (х+/)*'-* (у + iY -«.
Пусть последовательность {<р„} функций вида
тп
Ф« (х, у) - .? а/п (х) hn (У), «jn e= <®Sl (R), P/n e ^s, (R)
сходится к g(x, у) в e%lSls, (R2). Тогда послеповательность функций.
ir' сходится к
в <^SlSi (R2). Для любого ^е? имеем:
4ь Л2/)G= 2] Р/« Иг) а/п (Л) <7 =
Переходя к пределу при п->оо, получаем:
g{kX)q = (Л + О''"'g' (К, к) (Ai
(здесь мы воспользовались замкнутостью оператора (Лг +./)''"')•
Подставляя </ —О^ + О*/! и применяя к обеим частям равенства
A0.3) оператор (Л2-ИУ> получаем формулу A0.2).
Теорема 10.1 показывает, что элемент f[Alt Л2)Л'не зависит
от выбора показателей k, l в A0.1). Заметим еще, что если пра-
правая часть формулы A0.2) существует, то и левая существует;
это непосредственно следует из формулы A0.3).
Теорема 10.2. Пусть f\Au A^) —оператор, всюду опреде-
определенный на Е и ограниченный в В, ц пусть Т —замыкание этого
оператора в В. Тогда для любой функции g e BHS, (R2) и любого

10] РАСТУЩИЕ СИМВОЛЫ 329
e? справедлива формула
Доказательство. Пусть
/ (in,) h = (At + tffQ (L к) (А, + if h,
где
fo(x,y)=-f(x, y)/(x+i)k(y+W, Д,е=#.л(R2).
Тогда для любого Ае? имеем:
T'g{Au Л\)Ъ-
= (Л, + О1 [^eff] (ii, it) Mi + 0* * =
Следствие. Справедлива оценка
г5г с—норма гомоморфизма *М\ <$Sl,s, (R2)->HomE, 5), постро-
построенного по упорядоченной паре операторов Alt'АЛ.
Далее нам понадобятся символы f(xit ..., х„), удовлетворяю-
удовлетворяющие условию
f (xi> ••• ' хп) —, <%> /пп\
для некоторого натурального числа k. Если Alt ..., Л„~набор
производящих операторов степеней sx sn соответственно,
действующих в банаховом пространстве В и определенных
на всюду плотном линейном многообразии Е, то мы положим
для любого йе?;
1 « \ w /I
где g(xu •", xn) = f(xlt .... л:,)/(л:+ «')*• Так же, как и в теореме
10.1, устанавливается, что это определение не зависит от выбора k.
Нетрудно убедиться в том, что и в этом случае справедлива
оценка, аналогичная A0.4); если \\АХ Ап)~оператор, огра-
ограниченный в В и g e <$>sv ..., в (R"), то
g)\Au ...,

330 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
где с —норма гомоморфизма <Л\ <^Sv ...,, sn (R")-> Нот (В, В),
1 п
построенного по упорядоченному набору операторов Лх Ап.
Задача. Мы определили бесконечно дифференцируемые растущие
не быстрее степени аргумента функции от двух некоммутирующих произво-
производящих операторов. Показать, что они образуют алгебру с ц-структурой,
(с той же оговоркой, что и в сноске на стр. 279).
Определим, наконец, и растущие функции от многих неком-
некоммутирующих операторов. В этом случае необходимы дополнитель-
дополнительные предположения. Именно, пусть \ВХ)—банахова шкала, причем
BtczBX' прит-<т'. Пусть Аъ ..., Ап — производящие операторы
в шкале {Вх), причем эти операторы являются и переводящими
в той же шкале. Обозначим через #°° пространство функций
/(*! х„), растущих вместе со всеми своими производными
не быстрее \x\k (показатель k — свой для каждой функции /).
Для любой функции /(*] хп) из $°° найдутся такие
натуральные числа kx kn, что
/ \ I (^ > ' * * * %п)
8(XlXn)==
принадлежит «й?^ in (R") для любых /х /„. Положим
/1 п \def/2 \ki f2n \kn (x 2n-l\
f[A1 AjHAi+V—(AM+l)ug[A1 An), A0.5)
где операторы (Ax + i)^ (Л„ + 0*п рассматриваются как
переводящие. Предлагается проверить корректность определения.
Задача. Проверить, что формула A0.5) задает в алгебре операторов^
производящих и переводящих в шкале {Вх}, ц-структуру с операцией
/1 п \
\i(x1-»Ai хп — Ап), которая переводит /fa *„) в f\Au ..., Ап).
§11. Факторспектр
Пусть {Вх\ — банахова шкала, А и А' — производящие операторы в
этой шкале соответственно степени s и s' и шагом kx и k^, a T — пе-
переводящий оператор с шагом I. Пусть Sx и S2 — операторы, оп-
определенные на D и действующие в пространстве Вх при любом т.
Назовем операторы Si и S2 эквивалентными, если для любых т, т'
Определение. Будем говорить, что точка А,е R2 при-
принадлежит факторрезольвентному множеству вектор-оператора
[А, Т, А'), если существует такая окрестность V точки К,
что для любой функции f e s®s,s' (R2) с носителем в U и любых х, т'
Tf\A, А')
т. е. оператор Tf\A, А') эквивалентен нулю.

§ 12] ОПЕРАТОРНОЗНАЧНЫЕ СИМВОЛЫ 331
Дополнение в R2 к факторрезольвентному множеству назовем
/1 2 а \
факторспектром о вектор-оператора [А, Т, А').
Лемма 11.1. Пусть f — финитная функция из e%>s.s' (R2)
и оператор Tf\A, А') эквивалентен нулю. Тогда любая точка X,
для которой f Ш Ф О, принадлежит факторрезольвентному мно-
I \ 8 8 \
жесту вектор-оператора \А, Т, А').
Доказательство. Пусть i/ —такая окрестность точки Я,
что f(X) ФО при ^е(/ и пусть ф —функция из ^s,s'(R2) с носи-
носителем в U. Тогда существует такая функция 't|)e^s,s'(R2), что
Ф = 1|}/. Согласно теореме 4.1 имеем для произвольного ц
Тем самым лемма доказана.
Следующий критерий является следствием леммы 11.1.
Теорема 11.1. Для того чтобы точка к0 принадлежала
факторрезольвентному множеству вектор-оператора [А, Т, А'),
необходимо и достаточно, чтобы для достаточно малого е>0
нашлись такие функции ф, 1|з е Cf (R) с носителями в г-окрест-
ности соответственно точек №> и A^j, чтобы выполнялось условие
и чтобы оператор
был эквивалентен нулю.
§ 12. Операторнозначные символы
Пусть А — производящий оператор степени s с определяющей
парой банаховых пространств Вг а В2. Пусть дано банахово про-
пространство В3, В3^Вг. Пусть L = Нот(Въ В2), Lx = Нот(В2, В3),
L2 = Hom (Blt В3)- Определим операторнозначные функции от А.
По аналогии со скалярным случаем введем следующие про-
пространства: C^R, ?) —пространство непрерывных на R функций
со значениями в L и нормой Цф|сл(к, d = max A + \t \)~s\\y @|i;
Cf(R, Li) — пространство бесконечно дифференцируемых функций
со значениями в Lx с компактными носителями (т. е. если фЕ
eCf(R, Li), то ф(А.) при всех достаточно больших А, равно нуле-
нулевому оператору); W^(R, ^—пополнение Cf (R, Lx) по норме
где f{l)=-r~ \ e~&f(t)dt—преобразование Фурье элемента из
]/2я J

332 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ (ГЛ, IV
Cj°(R, Li); C(s)(R, Li) —пополнение C°°(R, Lj) no норме
C's (L-*-La) — пространство ограниченных отображений из С, (R, L)
в L\; Cg(R, La)—пространство ограниченных отображений из
C,(R) в L2.
Имеется естественное вложение j\\ Cs (R)-*-Cs (R, L):
A[fl
где /i: Bx -»- B2 — оператор вложения.
Отсюда следует вложение J: C^L-^L^-^-C^R, Ц}, задава-
задаваемое формулой
(J(f), ф) = /0\[ф]), fe=C's(L-+L2), ?e
Положим
(Ff)(l) (J(f)e-M) для fszC's(L-+L
Тогда /7—это обобщенная функция ее значениями в Ц, т. е.
(Ff, ф> е Lj для ф е S (R). Очевидно, обратное преобразование
урье F переведет Ff ъ f\
(JF-* (Ff), Ф> - </7, F> - (J (Л. Ф>.
, что f
,(R, L).
Если /EGf(R, Li), то можно считать, что f
положив
Далее, определим аналог 6-функциш
Очевидно, что б/, 'еС'г(Ь-*-Ь2). Более того, как и в скалярном
случае, можно доказать, что
II N
A2.1)
где feCy>(R1 Li), с* —комплексные числа, &=1, .... N.
Рассмотрим теперь линейную оболочку объединения С? (R, Li) U
U| U 6Д в Cs (L->La) и ее Фурье-образ &l(R, U)- Аналогично
скалярному случаю определим пространство «58$ (R, Lx) как по-
пополнение <^(R, Li) по норме

§ 12] ОПЕРАТОРНОЗНАЧНЫЕ СИМВОЛЫ 333
Тогда точно так же, как и в главе II, получим вложения:
Г+Т+е (R, U) с &s (R, 1д <= С<*> (R, Li):
Теперь можно определить операторнозиачные функции от про-
производящего оператора А степени s на паре 5Х сг В2.
Пусть fe&t(H, U), т. е. /= е= C,(L->L2). Поскольку
M'||Cl |D*, то rM'eC5(R, L), и можно положить
или, символически,
A2-2)
Будем говорить, что оператор А здесь действует первым, а сим-
символ f—вторым.
Оператор f\A) принадлежит L2 = HomEi, Вя). Оценим его
норму. Если /e^2(R, L), Г*/-ф + 2«Л- гДеФеС?(R. ^i),
то
Поэтому в силу A2.1)
По замыканию эта оценка распространяется на все символы /е
ee^s(R, Z-x). Таким образом, мы построили непрерывное отобра-
отображение из Л, (#, Li) в La = Нот (Вх, Вь)\ f-+f(A).
Аналогично строится отображение f->-f(A), задаваемое симво-
символически интегралом:
(сравните с A2.2)). Будем говорить, что символ / здесь действует
первым, а оператор А — вторым.
Для отображения / (X) е Нот (Б2, B8) = LU входящего в про-
пространство a®, (R, Lj), и для производящего оператора А степени s
на паре В1аВ2 мы построили оператор / (л) е Нот (Blf Bs).

334 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
Пусть теперь f(k) = g(k, В), где В — производящий оператор
степени / на паре В2аВа- Точнее, пусть функция g(X, ц.) при
каждом фиксированном^ принадлежит пространству s®;(R). Тогда
определен оператор f(X)=g(h, B)&LV Мы хотим изучить опе-
оператор /(л)е Нот(В1, В8)=^2' Для его существования нужно,
чтобы /s*,(R, Lx).
Лемма. Если ge^,i(R!), то f<=<^s(R, Lx).
Доказательство. Пусть F~*g = бД|)( <0, т. е. g(k, г) =
^. Тогда для <pe=S(R)
= (g(K В),
т. e.
(F-VlW^e-'^W, <peC,(R. L), L-Hom^, B2). A2.3)
Тогда
т.е. /s^(R.^i)h
ll/b^R.^^l^Vlca^^^-j^llglk.^R^ A2.4)
Пусть теперь ^"^^^(R2). Тогда
(JF+f, Ф> = <^(Я, В),
, г), (F*tp) (X)) e-<Bf dt
, О, Ф, (l*)> e~lBt dt =
= pi=^ (F-ig) Oi, 0 Г^'ф (ц) Л ф.
Поэтому
(F-V) (Ф) = р= J J (^g) 0*. 0«-""ФЫ*^ фе.С,(Я, q. A2.5)
Отсюда получаем оценку

§ 12) ОПЕРАТОРНОЗНАЧНЫЕ СИМВОЛЫ 335
т. е. A2.4) имеет место и в случае, когда rigeCf(RJ). Из
этой оценки следует утверждение леммы. Лемма доказана.
Пусть g e a^j.'f (R2). Тогда имеем по определению:
НА)-
где fm = g(X, В).
Если F~1g = 6^, t<t или F^g e= Cf (R2), то формулы A2.3), A2.5)
показывают, что
в) и к,«
По замыканию эти соотношения распространяются на все
СИМВОЛЫ g e a^j, i (R2).
Доказанноэ равенство позволяет преобразовывать оператор
g\A, В) следующим способом: рассмотреть семейство операторов
g(k, В), зависящее от параметра Я; провести для него нужные
преобразования, а затем подставить Я->Л (при этом В —В).
Заметим, что мы, по существу, доказали ограниченность }\А)
при условии, что g(X, z)e^j(Rb ^/(R*))— пространству функ-
функций от Я, со значениями в ^(R*) — и заодно использовали тот
факт, что ^S(R. ^i(R)) = ^s,i(R2)-
Пусть теперь А, В—самосопряженные операторы в гильбер-
гильбертовом пространстве Я. Если /еС(R), то f(А) и /(В) ограни-
ограничены в Я. Мы можем, конечно, определить ограниченный опера-
оператор g\A, В) для ge'^ofR1). Однако, проделанные выше постро-
построения позволяют это сделать и для более широкого класса
символов, а именно, для g {X, г) е ^0 (R?u С (Rz)) и <03О (Rz, С (R*)),
а, следовательно, и для g, принадлежащего линейной оболочке
этих двух пространств.
Задача 1. Пусть ge^5,i(R!); /4 — производящий оператор степени s
на паре Bj cz B2, В—производящий оператор степени / на паре В2сВа.
Пусть и — собственный вектор оператора А, отвечающий собственному зиаче-
, ?) u^gCk, В) и.
Задача 2. 1) Пусть f e^ft(R")i гДе k—достаточно большое. Вещест-
Вещественная функция S e C2° (R"). Пусть далее, А — производящий оператор
в шкале {№7T(R")b Тогда в некотором пространстве Нот {W~xt W^~x~m)
справедливо' равенство \
2) Пусть О ф. а (А). Тогда
(об одинаковых номерах над некоммутирующими операторами см. соответствую-
соответствующее соглашение об обозначениях в § 4 Введения).
Указание: заменить оператор А параметром \.

336 ИСЧИСЛЕНИЕ НЕ КОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
§ 13. Функции от образующих нильпотентной алгебры Ли
и их представления
Параграф будет посвящен в основном изучению функций от диф-
дифференциальных операторов, которые являются упорядоченным
представлением Lu ..., Ln, а образующих некоторой нильпотент-
нильпотентной алгебры Ли (Введение, § 9). Мы покажем, что эти операторы
являются -производящими и переводящими в подходящей шкале,
и докажем соотношения (9.5) Введения для случая, когда вместо
полинома стоит произвольная функция из С%. Мы докажем здесь
также и формулу (9.10), нужную для доказательства основной
теоремы; кроме того, мы получим здесь формулы приведения
1 2 п л+1
функции от упорядоченных операторов Llt La, ..., Ln, a
к псевдодиффереициальному оператору.
Вначале укажем некоторые свойства упорядоченных представ-
представлений.
Пусть X—множество образующих Лх Ап нильпотентной
алгебры Ли (Введение, § 9). Поскольку по условию любой ком-
коммутатор длины N равен нулю, то коммутатор длины N — 1 ком-
коммутирует со всеми элементами множества X. По условию в число
операторов Аъ ..., Ап входят все коммутаторы между ними.
Пусть Xi—подмножество в X элементов, коммутирующих со всеми
элементами из X. Пусть Х2—множество таких элементов, комму-
коммутатор которых с любым элементом из X принадлежит Xt. Вообще,
пусть Xi с X — подмножество таких элементов, коммутатор кото-
которых с любым элементом принадлежит сумме X* при k <. i. Оче-
Очевидно, что число таких множеств Xt не превосходит N. .
Теперь остановимся на конструкции упорядоченного представ-
представления множества X. Процедура его построения описана в § 9
п+1 /1 п \
Введения. «Протаскивая» в Aiq[Ai, .... А„) оператор А1 с
л+Ьго на 1-е место, мы -разлагаем q\A А„) в ряд Тей-
п п + 2
лора относительно Ап в точке Ап; получим члены вида
) *?
/ 1 3 \* 2
Пусть ЛеХц,); тогда \Ап — Ап) At (правый коммутатор
&-го порядка) принадлежит некоторому классу Xj, такому, что
j «S / (л) — k. Из аналогичных соображений можно заключить, что
вообще коэффициент при производной -^ ^— оператора Ц
ox/1...axfk
есть константа или линейная однородная функция такого хг,
что *'(/•)< max i(/4).

§ 131 ФУНКЦИИ ОТ ОБРАЗУЮЩИХ 337
Отметим, что это же замечание относится и к конструкции
представления G{, определенного в § 9.
. /2 i \
Л е м м а 13.1. Пусть L = L[x,—i д/дх) — упорядоченное предста-
представление одной из образующих нильпотентной алгебры Ли. Тогда для
любых целых к, I найдутся такие целые s (k, I), m (k), n (I), что
\L\~k <const
где Cf — пространство k раз непрерывно дифференцируемых функ-
функций, имеющих конечную норму
llc* = suPn 2I- 0+1*1)' ^rvW-
Доказательство. Обозначим через Щ пополнение про-
пространства S по норме
Имеют место вложения
Следовательно, достаточно доказать оценку
Ь-11Лнщк)^нн <const
Пусть Fx-*% — преобразование Фурье. Обозначим *L = Fx^^\
Так как Фурье-образ пространства Щ есть Hlk, то достаточно
получить оценку
m(k) h
Оператор I, имеет (при, соответствующей нумерации координат)
следующий вид:
L = - i 2] ajdldtj-i 21 pJ(Si Бг.)
-/ I] Pjfa lrp)dldlj-.
n
... - I] P/{li,.'-.. i
где Pj — полиномы с вещественными коэффициентами, а, — вещест-
вещественные числа. Если i|)(g)eS, то функция г|з(|, /) ===е—*^''»|з (|) есть

338 ИСЧИСЛЕНИЕ НЕКОММУТИРУЮЩИХ ОПЕРАТОРОВ
решение следующей задачи Коши:
[ГЛ. IV
Выпишем характеристические уравнения для этой задачи:
f ~
n>
1@)=1°,
Решая последовательно первые п уравнений, получаем
^t /to
где. Qy — некоторые полиномы. Отсюда имеем:
A3.1)
где Rj — некоторые полиномы. Пусть г|з (|°, /) — функция г|з(|, /),
выраженная через координаты |°, /. Из последнего уравнения
характеристической системы имеем явную формулу для ^E°, /):
, 0 = Ф
-i\Po (IA°, т))
Заметим, что г^=1; следовательно,
A3.2)
Подставляя в A3.2) ^° = |°(|, /). применяя к обеим частям опера-
оператор вида I^(^)Y и используя A3.1), получим, аналогично оценке
в L2, требуемую оценку \e-llt\ i „«<;> для случая /^0; при
m(h)~* к
этом даже можно положить п (/) = /. Кроме того, по данному in (k)
всегда можно подобрать k = k(m). Используем теперь тот факт,
что пространства Н'т и Hz'm сопряжены друг к другу относительно
скалярного произведения в L2, иными словами, норма
= ,„ sup
11*3
,-1
= 1

$ 131 ФУНКЦИИ ОТ ОБРАЗУЮЩИХ 339
эквивалентна норме в Н1т. Сопряженный к оператору е-*1-' в?2
есть оператор е'^', так как L симметричен в L^. Следовательно,
|е-'Е'ф|г'- sup |(в-'?'ф, ip)i,l = sup |(q>, e
|Ч||/1 1№11^
Если / > 0, то по доказанному выше найдутся такие целые числа
К и s, что при \ty\Hi = 1
— *
fle-'^L < const A+ |*|)*.
"к
Поэтому
||е-'г'Ф tl = sup |] фIP'\еГиУ Li < const |]ФГ*- A +1' I У-
Лемма доказана.
Перейдем к доказательству формул (9.5) и (9.10) и аналогич-
аналогичных им, приведенных в § 9 Введения, в пункте «правило редук-
редукции основной задачи».
Это доказательство, как уже говорилось, опирается на акси-
аксиомы ц,7) и ц8). Оно состоит из двух этапов.
1) Пусть g(*)eC°°; тогда оператор
П + 2
/L) = eM*'*Mi Aa) A3.3)
I 2 n \
равен оператору ty[Ai, A2, •••» Aa,tJ, символ которого вы-
выражается через символ g (х) следующим образом: г|> (х, f)=e' k'g (x),
где LA —упорядоченное представление оператора ЛА. Послед-
Последний существует в силу того, что мы установили относительно
свойств Li,.
Доказательство. Рассмотрим производные символов
«"»+*'g(*)= h и \р(х, t) по t, т. е. символы ixn+2h и ^(х, t) =
= iLkty (x, t). Очевидно, что для первого из них выполняется соотно-
соотношение (р,*) аксиомы щ. (Напомним, что операция ц, ставит в соответст-
п + 2 k
вие дг„+2 оператор Ак, a Xk~оператор Ak). Поскольку Lk есть
упорядоченное представление Ak, то [iLkty(x, t)] i л
xi = Ai,...,xa=An
/12 n \
равно iAkf$\Ai, A2 An)J. Отсюда следует, что соотноше-
соотношение (ц,*) выполняется и для символа ty {x, t). При t = 0 оба опера-
оператора г|) и е' k'g равны g. Поэтому их разность удовлетворяет соотно-
соотношениям (ц?) и (ц?), а значит, операторы равны, что и требовалось.
Из второй части аксиомы |а,) легко следует распространение
равенства (9.5) на символы класса С^.

340 ИСЧИСЛЕНИЕ («КОММУТИРУЮЩИХ ОПЕРАТОРОВ [ГЛ. IV
2) Рассмотрим операторы
п n+1+k
' Ii Ak 'k I 1 я \ / 1 я \
eft=1 gUi Л„) и 4>Hi, ..., A,, flt ..:, *J, A3.4)
n k
1 S V*
где \|>(дг, <) = e fcs=1 g(*). Из предыдущего пункта следует, что
они равны.
Подействуем на символы обоих операторов псевдодифферен-
псевдодифференциальным оператором
. а .д_
где / € ^°°. В силу свойств оператора Lk имеем
, я k
Для символа A3.4), очевидно, имеем
я
В силу аксиомы fx7) операторы, им отвечающие, равны при всех/,
в том числе и при t = 0. Именно, при ? = 0 мы получаем равенство
Jlf.... iJi^U ij,
причем \|)(л;) выражается через ?(*) в следующем виде:
что и требовалось.
Аналогично (с использованием уже доказанных соотношений)
доказываются и другие равенства, приведенные в § 9. Обобще-
л + 1
ние на случай, когда имеется аргумент В , очевидно.
Приведем вновь формулу (9.10) для сложной функции от упо-
I \ п \
рядоченяых операторов. Пусть ft\А 1( ..., Ап)&М, /=1,...., k;
тогда f\)lt ..., }и) может быть представлена в виде функции
lt ..., Аа), причем символ ty(x) определяется по формуле

§ 131 ФУНКЦИИ ОТ ОБРАЗУЮЩИХ 341
где 1—единица, принадлежал пространству символов $°°. Эту
формулу мы применим для того, чтобы функцию от самих пред-
1 л
ставлений Lu ..., Ln представить как сложную функцию обра-
образующих другой нилЬпотентной алгебры, а именно, -^-id/dx, х, то
1 п
есть, иначе говоря, записать функции от 1^, ..., Ln в виде псев-
псевдодифференциального оператора. Итак, найдем упорядоченное
представление операторов — id/дх, х. Очевидно, что
М4 $*( 4
ММ-4. $-*(- 44
где ty(y *) ( 1
Следовательно, операторы \~^х-\-У> х) являются упорядо-
ченным представлением набора I — /g-, x). Из формулы A3.5)
тогда следует, что
где
i
. д
есть символ псевдодифференциального оператора.

ГЛАВА V
АСИМПТОТИЧЕСКИЕ МЕТОДЫ
§ 1. Канонические преобразования
псевдодифференциального оператора
Мы видели уже в § 1 и 2 Введения, что формула коммутации
дифференциального оператора с экспонентой играет в исчислении
Хевисайда существеннейшую роль. В построении в гл. IV исчис-
исчисления упорядоченных операторов формула коммутации гамильто-
гамильтониана с экспонентой также является ключевой. В теории [г-струк-
тур, точнее в применении этой теории к псевдодифференциальным
операторам, эта формула по существу была принята за опреде-
определение функций от операторов ihd/dx+dS/dx.
Отметим однако, что формула коммутации дифференциального
* S (х)
оператора с экспонентой е h , имеющая вид
е h P[ih-jr-)eh =P[ih-jr + -jr-
\ дх j \ дх дх.
может быть трактована двояким образом. Понимая Т = е h
— S(x)
как оператор умножения на функцию е Л , приходим к тому,
что
или
2)
rr, -r- S (хг р) si
До сих пор для случая, когда T = eh ф(л:, р), мы
обобщали формулу 1) и получали формулу коммутации гамиль-
гамильтониана с экспонентой. Этот параграф мы посвятим исследованию
оператора Т*р[х, ihd/dx)T, где Г*=е~т ф(лг, р).
Преобразование такого типа мы будем называть каноническим
/2 1\
преобразованием оператора Р\х, р). Оказывается, во многих слу^
чаях удобнее использовать каноническое преобразование, а не

§ 1] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 343
преобразование 1) над дифференциальным (или псевдодифферен-
псевдодифференциальным) оператором Р\х, ihb/dx).
Прежде всего, рассмотрим композицию (здесь 5 — веществен-
вещественная функция)
Т*Т=*е *
Из теоремы 1.1 (см. ниже) следует, что
у*у ._ Ф С* (*. Р. р)> h) ф (¦% (*. Р. Р, р)
| / (л (х, р, р); р; р) |
где % (х, р, р') есть решение уравнения
.(Ър,р) = х
и предполагается, что якобиан J не обращается в нуль:
J(x; p; p')Si+^^.(jj; р,р')фО.
Оператор Т*Т имеет следующий символ:
^-[S(*. P)-S(x, р')]- -
е * 9(Jf, p)9(Jf, P).
Оказывается, что с точностью до О f/г00) оператор Т*Т зависит
лишь от значений своего символа на диагонали р = р'. Если
отбрасывать члены дорядка О (Л00), то можно также ослабить
условие на якобиан /.
Сформулируем точно и докажем эти утверждения.
Лемма 1.1. Пусть Ф е C°°(R" x R"x R") и растет небыст-
небыстрее полинома; тогда
Ф{Р, X, pj^—g
X / (X') dx' dp-dp' \ e* {"'~Р)'Х'ф(р, x\ p') dx' -
Здесь Fx-*p i /(*)->? (p) = /2 J e~ ? "¦"*/ (x) dx - так «азьиае-
l/h-преобразование Фурье.
Доказательство очевидно.
' В пространстве L2 (R") зададим оператор
где q>eCjj°(Ran), SsCJD0(Ra"), S — вещественная функция.

344 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
с О
Определим вектор г- (х; р', р) е R", /-я компонента которого
есть разностная производная
en
-g^-(x; р[, .... pl-i; p'i, pa pi+i pn),
где р, p' s R". Рассмотрим уравнение
x + ^-(x; p', p)~y A.2)
относительно вектора X s Rn. Обозначим через J якобиан этого
уравнения
J(x, р', р) = <ы|бг/+^Ц(*; р[, ..., pi, Pl р
Теорема 1.1. При условии JФО имеет место тождество
= ф(^(х, р, р), р)Ч>(х{х, р, р), р) х
xl^Wi, p, р), р, р)\,
где Л (у, р', р) — решение уравнения A.2).
Доказательство. В силу леммы 1.1
x^e рПу^, р')ф(х', p)dx>.
Перейдем во внутреннем интеграле к новой переменной у по
формуле х' = % (у, р', р), где %(у,р',р) -решение уравнения A.2).
В силу условия /=^0 решение A.2) %(у, р', р) существует и
принадлежит С00^3"). Учитывая тождество
, p')-S(Z, p),
получим:
, р', р), р', р)Х
ХЧ>(*(У, Р', Р), Р')Ф(ХО/, р', р), p)dy,
где феС^(Я2в), SeC°°(R2n), S - вещественная функция.
Тогда из леммы 1.1 следует утверждение теоремы 1.1.

§ 1] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 345
Пример. Пусть S(x, р) = — (х — х2)р\ р, дгеЯ, Л = 1 и
Ф(дг, р)з=ср(лг). Тогда
(здесь р = — id/dx, так как А = l).
В этом случае^уравнение A.2) имеет вид
._l + t?k2j?t±k*UL „ли у-Л
Якобиан / = 2?. Поэтому, если ц>(х) равна нулю в окрестности
точки х = 0, то
Этим же способом, т. е. аналогичной заменой переменных, мы
выведем соответствующую формулу для оператора Тц
def 1 С 1 [S (|, р) - 111
символ которого равен 1/Л-преобразованию Фурье от символа
оператора Т. Формула, которую мы получим, поможет нам выяс-
выяснить важную роль, которую играет 1/Л-преобразование Фурье
в канонических преобразованиях псевдодифференциальных опе-
операторов.
Пусть ЛA, Р'. р) — якобиан уравнения
у=Щ(Ь р!, р)+ЦA+р-р', I; р), A.3)
рассматриваемого относительно | (вектор 6S/fi? определяется ана-
аналогично вектору 8S/8p). Таким образом,
Теорема 1.2. При условии ^фО имеет место тождество
/« / i 1 8\ 1\ — /~ / 2 1 8\ 8 1 8\'
Ti — <p\i{x, р, р), р)<р\Л\х, р, р)+р^-р, р)х -
xUr'dU P. р)> Р. р)\. A.4)
' \iy> p't p) —решение уравнения A.3). '
Доказательство. С помощью леммы 1.1 получим
Сделаем во внутреннем интеграле замену переменных |-»-«/ по

346 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
формуле A.3). В силу условия /х#0 решение \(у, р', р) суще-
существует и принадлежит C0O(R3"). Учитывая тождество
получим, как и в теореме 1.1, искомое равенство A.4). Теорема
доказана.
Теперь рассмотрим общую ситуацию, включающую в себя
формулы из теорем 1.1 и 1.2. Для простоты ограничимся дву-
двумерным случаем: х = (хи х2), р = {Ръ pi)- Рассмотрим оператор
(&, x2, p)d%1f{x). A.5)
Г
J
Аналогично теоремам 1.1 и 1.2 получим
-s^ + Pi-Pl *. p)} x
-p'i, г, р)ф(|ь z,
Мы хотим показатель экспоненты во внутреннем интеграле заме-
заменой переменных (|i, z)->(«/1( y2) привести к виду:
Для этого положим
Е о ' is о
«/i = -g^-(?il г; р\, р{, p2) + ^(li+Pi-p[, Ь.1 г; рг; р2), A.6)
ел
6— (Ь; г; р[; p'it p2).
Тогда справедливо тождество:
«/•(p'-p) = (Pa-p2)-z + S(i1, z, p,', pS)-S(b + Pi-Pi. it Pi, л).
Предположим, что отличен от нуля якобиан У2 системы A.6)!
A.7)
Тогда существуют гладкие решения ^(г/, р', р) и z(y, р', р)
системы A.6). Аналогично теоремам 1.1 и 1.2, после замены
переменных (&, z)->Q/b г/2). получим:
J 1 «\ / 8 1 8\ 1
- Л / S 1 8\ 8 1 / S 1 8\ S\
ф^Дл:. Р' PJ + Pi-Pi! «VJf, Р, РЛ PJX
X 1 Л1 [к [х, р,- р); г [х, р, р); р; р) \. • A.8)

§ 1] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 347
Итак, мы доказали теорему:
Теорема 1.3. Пусть оператор 72 определен формулой A.5) и
пусть выполнено условие A.7). Тогда имеет место тождество A.8).
Замечание. В теоремах 1.1 и 1.2 достаточно потребовать,
чтобы якобианы J и Л были отличны от нуля лишь при
(х, p)esuppq>(*, p) и, соответственно, (?, p)esuppq>(g, p).
Кроме того, теоремы 1.1 и 1.2 обобщаются на случай оператора
T*ty\p — р) Т. При этом, если якобиан J отличен от нуля при
(р, p')eR2" таких, что р — p'ssuppip, то имеет место соот-
соотношение:
, р, р), р)х
хф(*У, р, р), p)\j^{i{i, р, р), р, р)|ч>(р-р),
где %(у, р', р) —решение уравнения A.1).
Прн аналогичных условиях обобщается теорема 1.2:
Д р, р), р)х
2 1 8\ 8 1 8\| /~/3 1 8\ 1
г,-р, pj + p-p, pj|/rlUU. P. P). P.
где |(y, p\ p) —решение уравнения A.3) и якобиан- J1ф0 при
(р'( p)eR"° таких, что р' — pesuppT|3.
Аналогичное утверждение имеет место и в ситуации, описан-
описанной в теореме 1.3. .
Лемма 1.2. Пусть функция \|эв (г) == 0 в Ь-окрестности точки
г = 0, ty6(z)—l вне 28-окрестности точки г = 0 и i|)ee C^R").
Далее, nf/c/пь (peC^R2"), S (*, p)eC°°(R2n). S - вещественная
функция и якобиан
любого N и
Доказательство. В силу условия A.9) уравнение
dS(x',p) n_dS(x', p') ,
3? ^^ a? f"P
имеет единственное решение относительно р е R", а именно:
р = р'. Поэтому при |р —р'|^б вектор
A.10)
Представляя 7'*'фв(р —р) Tf в виде интеграла, аналогично тео-
теореме 1.1 нетрудно убедиться, что полученный интеграл будет
отличаться от интеграла в доказательстве теоремы 1.1 лишним

348 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
множителем Ц>6(р — р'). Поскольку на носителе г|зв(р — р') произ-
производная от показателя экспоненты во внутреннем интеграле не
обращается в нуль (см. A.10)), то внутренний интеграл можно
проинтегрировать по частям любое число раз (вводя экспоненту
под знак дифференциала). Это немедленно приведет к утвержде-
утверждению леммы.
Можно показать, что условие A.9) здесь является существен-
существенным.
Смысл леммы 1.2 состоит в том, что в оператор Т*Т основ-
основной вклад (с точностью до О (Л00)) вносят значения его символа
eh ц> (х, р)ц>(х, р) на диагонали р — р.
Итак, если ослабить условие /#0 в теореме 1.1, заменив
его условием A.9), то в силу замечания 1.1 и леммы 1.2 полу-
получим следующее утверждение.
Теорема 1.4. Пусть tf—функция из леммы 1.2 и выпол-
выполнено условие A.9). Тогда для достаточно малого б имеет место
равенство!
Т*Т = ц> (%(х, р, р), р)ф(х(х, р, p)i p)x
X |/J(*(i р\ р), Р, р)|A-^(р-р))'+Л, A.2')
где
\A\vn_vN<*cNtkhk для всех N, k^zQ.
Последние лемма и теорема могут быть сформулированы и
для операторов Tlt 7Y В случае оператора 7\ заметим, что
уравнение
имеет единственное решение р = р', если якобиан
4
не обращается в нуль. Поэтому аналогично предыдущему при
тех же предположениях на S, q> получается следующая теорема.
Теорема 1.5. Пусть /}^0. Тогда для достаточно малого б
имеет место, равенство
U Р. р)+р-р, р)х
x\j?(t(x,p,p),p,p)\(l-tf{p-p))+A,
k для всех N,
Точно так же можно переформулировать и теорему 1.3.
В приведенных формулах относительно операторо.в Т*Т и
Т*Тг можно усмотреть некоторую двойственность. Прежде всего

§ 1] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 349
заметим, что с точностью до 0(h) мы можем положить р = р и
тогда вместо якобианов J и Jx можно /будет подставить якобианы
J0 и У?. И если обозначить фх»=-^, ц>г = -^=, то полученные
формулы будут иметь вид
i, р), p)+O(h),
где %(х, р) есть решение уравнения
а |(ж, р) есть решение уравнения
далее выясним геометрический смысл наблюдаемой двойствен-
двойственности. Для этого рассмотрим однопараметрическое семейство
бесконечно гладких кривых в фазовой плоскости (?, х):
g=SG/, p), х = Х{у,'р), A.11)
где параметр peR, у — текущая координата.
Условие однопараметричности имеет вид:
/дК дХл
ду др
Заменой координаты у мы всегда можем добиться, чтобы в но-
новых переменных D=l*). Поэтому, не уменьшая общности,
положим
Р-1. A.12)
Из этого условия следует, что в точках вырождения проектиро-
проектирования на ось х, т. е. в точках, Где дЕ/ду = О, отлична от нуля
производная дВ/др. А в точках вырождения проектирования на
ось I, напротив, дХ/дрФО. В остальных точках либо дХ/дрФО,
либо дВ/дрфО.
Поэтому семейство кривых A.11) мы можем покрыть системой
перекрывающихся окрестностей, в каждой из которых отличны
от нуля либо дХ/ду и дЕ/др, либо дХ/др и дЕ/ду. Первые мы
будем называть неособыми картами, вторые — особыми картами.
Совокупность карт называется каноническим атласом семейства
кривых.
*) Это утверждение доказывается в гл. VI.

350
АСИМПТОТИЧЕСКИЕ МЕТОДЫ
[ГЛ. V
D(y,
5I
P) \y=
следовательно,
У(Х, p)
D
(*.
D
6(*.
(*. P)
P»
D
D
(X.
(</.
P)
P)
=
1
d?
0
r)?
dp
дХ
dy
0
ax
dp
1
Наряду с A.11) будем рассматривать также «сдвинутое» се-
семейство кривых:
1=Е(у, р)-р, х*=Х(у, р).
Рассмотрим финитную вещественную функцию <р {у, р) е С00
с носителем в одной из карт канонического атласа.
Мы изучим два случая, когда носитель ф лежит в неособой
и в особой карте.
а у
I случай. Неособые карты. Поскольку згт^О в этой карте,
то можно сделать замену переменных х = Х(у, р), откуда у =
= у(х, р)^Ст. Обозначим %(х, р) = Е(у(х, р), р). Имеем:
= 1;
или
§(х,Р)=ЦЙ- A-13)
Пусть рассматриваемая карта содержит точку (уо{р), р) и
пусть хй(р) = Х{уй(р), р). Обозначим
S(x, р)= \ [|(х'( p)-p]dx'+S0(p),
где
•яг 0°) — Уо (Р) — х0 (р) + (S (у0(р), Р) — р)^ (р)« A-И)
Покажем, что
3j(Xt p)+x-y(x, р). A.15)
Из определения функции S следует, что.~-=%(х, р) — р. Тогда
в силу A.13)
ду(х,Р)_д%. v_, .
(х, р) _ д I , dS
т air+a7
dS
т. е. qz(x, р)—х — у(х, р) = f(р) — функция только от р. Имеем:
ds(х, р) I _^dso(p) as, . . ча^) =
ар U=^0(pj ар аж^oW> "> др
> Р)-Р)Щ^-

§ 1] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 351
Поэтому из A.14) получим
откуда следует A.15).
Обозначим через 7" оператор вида
Из A-15) следует, что l+J^ = g = (<|) '. Поэтому из (*)
следует, что
На самом деле имеет место более точная теорема (в форму-
формулировке которой, как и в дальнейшем, мы опускаем значки' ' и
v, что не может привести к путанице).
Теорема 1.6. В сформулированных выше предположениях
имеет место равенство:
Т*Т = <р(х, р)у{х, р) + ЛМ(Л), A.16)
где | A (h) \\wn_* wn «? cN для всех N^O.
Прежде чем переходить к доказательству этой теоремы, мы
рассмотрим случай, когда носитель ф принадлежит особой карте.
II случай. Особые карты. В этом случае -^ Ф 0 ц следова-
следовательно, уравнение
t + p = E(y, p)
имеет решение уA, р)^^. Положим *(!•, р)~Х(уA, р), р).
Как и в I случае, имеем
Е. Р), 6+р))Р(В(у. р)-р. Р)\
дх
дЪ
1
дх
1
дЕ
ду
0
дЗ
др
1
• 1
_ дЗ 1дх дх
ду \д\ др
Отсюда
Определим функцию
где
л с 1гл ГЗЕа lift . -1
¦Уо(р) A.18)

352 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
(считаем, что карта содержит точку (у0 (р), р)\ %0 (р) =
= Е(уо(р), р) — р). Отметим, что на пересечении особой и неосо-
неособой карт функция S (?, р) есть преобразование Лежандра функ-
функции S(x, p) по аргументу х, т. е.
'&& р)~6*<&, P)-S(x(l, p), р).
Покажем, что
'§ & Р) У& Р>- AЛ9>
Из определения функции S имеем
Ц& р)=х& р).
Отсюда и из A.19) следует, что
ду &S ,>S _ д (д§ ds\
dl~ dpdi^d^ ~ дЬ\Щ dp}'
значит, .
-% + %-у& р)Ч(р).
Но в точке 1 = Ь>(р) имеем:
Поэтому в силу A.18)
f(p)=-d-§jt+X(yn(p), p)^- + X(yo(y), р)-уо(р) = О,
откуда следует A.19).
Равенство A.19) можно переписать иначе:
J(B(*/, P)-P, p)-g(S(f/, p)-p, Р) = у, A.19')
поскольку
?+p = S@(g, p), у), или у'^у(Е{у', р)-р, р).
Обозначим
с\&»(W (ИД)
где А, —некоторая константа, по модулю равная 1, вводимая
для удобства. Ее смысл будет ясен из дальнейшего. '
В силу 1.19,

§ 1] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 353
Поэтому из (*) следует, что
На самом деле имеет место более точное соотношение. Именно,
справедливы следующие теоремы (мы вновь опускаем ' и v).
Теорема 1.7. Имеет место равенство
ПП = Ф (*, р) Ф (*, р) +-АМ (Л), A.20)
где A (h) —такой оператор, что | A (h)\wN_wn^cn для любого
ssO. .
Доказательство этой теоремы мы приведем позже, а сейчас
сформулируем результат, относящийся к каноническому преобра-
преобразованию псевдодифференциального оператора f[x, p), символ
которого принадлежит C°°(Ra) и растет не быстрее некоторой
степени своих аргументов. Для иеособой карты имеет место соот-
' ношение
T*f{x, pO=|<p|4f. p)f(x(},p), s(i, p))+o(h).
Для особой карты имеет место аналогичное соотношение
Ttf (i, р) Т, = | Ф |« (Зс, р) f {Х (*,. р), В (i, Д) + О (А). .
На самом деле имеет место более точное утверждение. Именно,
справедлива следующая теорема.
Доказательство этой теоремы мы приведем позже.
Теорема 1.8. Пусть /eC°°(R3), причем
fip, х, p') = f(p', х, р) и
для некоторых k>0, ck не зависит от х. Пусть Т —оператор,
определенный формулой A'Л). Тогда
х, р)]г-ф(Зг, Д/(в(Зс, р);
Д р1)]; В(*', р))Ф(Д й+АМ,(А), H.21V
где A2(h) —оператор, удовлетворяющий следующему соотношению:
\Ai(h)\^N_^wN^cN для всех JV^sO. Пусть 7^ — оператор, опре-
деленный формулой A.Г). Тогда
Д р), •
Д Д], В(Д р)
где Aa(h).~ оператор, удолетворяющий следующему соотношению:
iA9(h)lWN^.WN^QN для всех N^0.
Доказательство этой теоремы мы приведем в конце параграфа.
12 В. П. Маслов

354 АСИМПТОТИЧЕСКИЕ МЕТОДЫ (ГЛ. V
Замечание. В дальнейшем будет встречаться следующая
конструкция семейства кривых S (у, р), X (у, р). Пусть х (х°, р°, t),
р (х°, р°, t) — решение системы Гамильтона
= др ' * ' ) ~ х »
Р Р(°) Р°
О
Н (х, р) е= О
Тогда по теореме Лиувилля (см. гл. VI)
Ч Р« _| в любой момент времени
Уравнения
х = х(х°, р\ t), р = р(дг°, р°, t)
при фиксированном t определяют семейство (р° — параметр) кри-
кривых, удовлетворяющих предъявленным выше требованиям..
Доказательство теоремы 1.6. По теореме 1.4 имеем
Т*Т = ф(у (х, р), р)у(у(х, р), р)х
~3п' р
fti д,Л* для всех k,
Напомним, что х (у, р, р') является решением уравнения
/2 1 8 \ дх /2 ' 8 \ II / ~,\ и
J 1\х, р, р) =--- \х, р, р), \\О (А°°)||
A2з)
Теперь заметим, что из A.15) мы имеем:
Л о
Х- (У, Р) + jp- (^ {У, Р), Р) = У.
Поэтому решение уравнения A.23) естественно искать в виде:
х {У, р, р') = X (у, р) + (р1 - р) Хг (у, p) + O{pf~ pf. A.24)
Отметим, что в силу леммы 1.2 можно рассматривать все функции лишь
в малой полоске около диагонали р = р'. Здесь и ниже символом 0{р' — р)г
мы обозначаем функции вида (р' — рJ Ф (у, р, р'), где Ф е С03-
Подставляя A.24) в уравнение A.23) н разлагая все функции по р'
в окрестности р, легко найдем коэффициент Х^.
1 32S
Xi (у, р) = - т /о (У, Р) -^ (X (у, р), р), A.25)

§ 1] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 355
где
J-XI \ _ j_ ^ ' / у _ ду (х, р)
дх х = X (у, р)'
Л У
Или иначе: /0(у, Р) = -д— (У> Р)^° (в неособой карте).
Докажем, что
Xi(y, Р)-^Щ<И> Р). 0-26)
т. е. разложение A.24) имеет вид
х(у, р, р') = Х(у, p)+lu(p'-p)^L{y, p) + O(p'-p)\ A.27)
Действительно, из A.15),
ду (х, Р) _ &S ¦
~~Тр W{
Однако,
(Ь28)
Поэтому из A.25) имеем
s J , , чГ 1 дХ , Л 1 дХ
. р) = - т Го (у, р) [- 7Ж^~др-{у' Т
т. е. доказано A.26).
Дифференцируя A-27) по у, получим разложение якобиана J'1 (у, р, р') =
= -=—((/, р, р'), а именно:
ПЦ +V)
у(Р'-Р)-^-0/. р) + О(р'-р)К A.29)
Теперь разложим по степеням (р' — р) якобианы -^— (у(х, р), р) и
-^—{у(х, р'), р'). Аналогично'предыдущему, после несложиых преобразований,
учитывая A.26), получим (здесь х = х(у, р, р')) из A.27)
Для второго якобиана имеем:
+ (о' - »["'?
¦g- (s С, rt pi -'.», />> + (о' - »["'?/'
Из этих двух выражений и A.29) получим"
1/~ЧУ. Р. Р'I
A.30)
12*

356 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
Из функций, входящих в правую часть A.22), осталось разложить
!)(у(х, р), р) и <р(у(х, р')> р')- С учетом A.28) их разложения- по степеням
Р' — Р) буДУ1 иметь вид:
<р(у& р), р)-ф(у, р)]+ ^.(у, р) ыопР)Р) 1?Ы
и
Ф (у & р'), Р') - ф (у, Р")-^- (У. р)^Рр) fr <»• Л + ° 0/ - Р)а.
Заметим^ что во втором случае мы не разлагаем <р(у, р') по аргументу р'}
кроме того, остатки О (р' — рJ здесь имеют вид
(р' - p)s Ф 0/, р, р'), где Ф s Cf.
Из этих равенств и A.30) получим, что символ оператора в правой части
A.22) равен
Ф (*, р) Ф (х, р') [1 - 1|зв (р - р')] + (Р' - РJ Ф (*. Р. Р'). A -31)
где Ф е С^3. (В A.30) вместо-аргумента у в символ подставляется оператор х,
поэтому мы в A.31) заменили у на х.)
Рассмотрим оператор
-4' -4.* -'аж. -4).
где
; em в, p, *, p', I') -(E-ET V..-7&' Ф C*. p) ф (*, p') -
m—любое целое положительное.
Очевидно, имеем оценку
№ (р-р)фA. рМ*. рI^^^<А'п«9т«Лл,(Л.)<сЛ,.тАт. о-32)
Т. е. этот оператор есть О (А00) в наших обозначениях.
Аналогично,
(р-р)гф(х, р, р) wmJflAt, где
Поэтому из A.32) и A.33) следует искомое равенство A.16). Теорема доказана.
Доказательство теоремы 1.7. В силу теоремы 1.5 имеем
<?(y(b p); р)ф(у(|+р —р, р); р)х
. kr'gp.p)i
~), A.34)
где *
I — I U Р. РЛ ^j U, Р>Р'=дх- V*' Р- Р/
||О (А°°)|глг_^« <cWj ftA* для всех W

§ 1] КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 357
Здесь функция |(i/, р, р'\ есть решение уравнения
S (I + Р- Р, р') -§ (?, р') 5 (Г, рО - 5 (I, Р) а
р-р' р'-р у- \ ¦ >
-Учитывая равенство A.19), решение A.35) естественно искать в виде
\{у, р, p') = Z(y, p)-p + (p'-p)S1(y, p) + O(p'-p)*.
Подставим это разложение в A.35). Как ив теореме 1.6, получим коэффи-
коэффициент В],:
где
или
/(l/ ) ^
Из A.19') (дифференцируя по |, по р и складывая полученные равенства)
имеем:
Из тождества g+p = S (j/(|, p), у) также получим
Эти два равенства с учетом A.36) дадут
Si (у, P)=YTP{y' p)-
Таким образом, разложение функции %{у, р, р') по степеням (р'—р)
имеет вид: .
1(у, р, р') = Е<$, р)-Р+^(р'-р)Щ)(у, р) + 0(р'-р)\ A.37)
Дифференцируя это равенство по у, получим разложение якобиана:
V (У/ftP') ^^0/. Р. Р') =
= /i(y. P) + y(p'-p) д'Х^Р) +О(р'-р)*. A.38)
Далее, аналогично доказательству теоремы 1.6, разлагаем. якобианы
д|(И!. Р): Р) и -щ{у(%+Р-р', Р'У, Р'), а также амплитудыф (у (|, р); р)
))
и ф(уШ+Р—Р'. Р')?'Р') п0 степеням (р' — р).
В итоге получим, что символ оператора в правой части A.34) есть.
. <р(к, p)tf(x, P')V -У6 (j>-p')] + <J>'-р)*Ф (х, р,у),
где Ф-еС?°.

358 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
Повторяя рассуждения теоремы 1.6, получим, что оператор с таким сим-
символом равен
(
где|И2| N .„w^c для всех N^0. Отсюда вытекает A.20). Теорема
доказана.
Прежде чем переходить к доказательству теоремы 1.8, сделаем замечание,
аналогичное замечанию 1.1.
Замечание. Пусть /еС*(R3) —функция, определенная в теореме 1.8.
Тогда для оператора Т, определенного формулой A.1), аналогично тому, как
это было сделано в доказательстве теоремы 1.6, получим
T*f(p, х, р)г = Ф (х, p)f(p; х (х, р, р); р)Ф(*, р)+ЛМ„
где х решение уравнения A.23). Поскольку х (у, р\ р)=х (у, р, р') то из
A.27) имеем
*<Я. Р'. P) = jl*(y< Р') + Х(У, р)\ + О(р'-р?.
Тогда аналогично тому, как это было сделано в доказательстве теоремы
1.6, получим:
T*f(p, х, p)f = <?(x, p)f(p; ~[x(x, p) + x(x, p)]; pjtf(x, p
где \\A'Ah)\\wN^wN^cN Для всех N^°-
Точно такое же равенство получается из теоремы 1.7 для оператора
4 /5 3 1 \ 2
Щ{р, х, р)^.
Доказательство теоремы 1.8. Обозначим
)
-(!/(*. P). P)
Используя формулу коммутации с экспонентой, получим:
5 /4 8 2\ 1 —-гЬ\Х,Р) /в 7\
T*f\p, х, р)Т=е h q{x, p) X
dS ( т\-ь 4 8 д$ . „.
\х, p)eh ' .
Далее воспользуемся /(-формулой и формулой коммутации, т. е. переста-
переставим оператор ps— ih g- на первое и, соответственно, седьмое место. Получим:
5 /4 8 2\ 1 jrS (Х, р) / 8 2 1\ Т ^ '*• Р/ Л1 I о
T*f{p, х, р)Т=е h <bN{p, х, p)eh +hN+2RNt A.39)
В этом равенстве функция Фд, имеет вид: ^
Фд, (р, х, p') — ty(x, р)/г|з (х, р') +
др' дх ' 2 др'% дх2 ' ' J •"
+ (Л) I Т (*• Р) t + 4 * (*• Р) S (Х- Р) ш\ + J Л^*&»• *• Р')г (>-40)

$ 2] ГОМОМОРФИЗМ АСИМПТОТИЧЕСКИХ ФОРМУЛ 359
где у функции f и ее производных опущены аргументы
(p+ff (*, р); *; />'+§!<*. р')); ^^^(R3), *=2 n+l
Остаток RN в A.39) имеет оценку:
IiPRnUn-wN^'n Для любого yv^.O. A.41
Поскольку p + -jr-(x, р) — 3(у(х, р), р), то из теоремы 1.6, учитывая A.40)
для члена нулевого порядка по Л в A.39), получим выражение:
= <р(*, р)/(в (х, р), ~[х(х, р) + х(х, р)], з(х, р))ФЦ р)
A.42)
Член первого порядка по Л в A.39) преобразуется точно так же; учиты-
учитывая симметричность символа /, приведем его к виду h(p—p),Q\p, х, р), где
Q^C^1 (R3).' Как и в доказательстве теоремы 1.5, получим оценку:
I h (p-p)Q (р, х, р) || wn_wn =
II / h Л \ II
l^ *' ^Цй^и^^сд,. A.43)
Остальные члены в A.39) (порядка Л2, Л8, ..., Aw+') также преобразуем
с помощью теоремы 1.5 и получим для них оценку |...|| N .„^^AV .
Поэтому из A.39), A.42) и оценок A.41), A.43) следует искомое равенство
для оператора Т.
Равенство для случая оператора Т\ устанавливается аналогично. Теорема
4.8 доказана.
§ 2. Гомиморфизм асимптотических формул
Пусть Л, и А2 — производящие операторы степени sx и s2 соот-
соответственно с одной и той же определяющей парой банаховых
пространств (В, В), определенные на одном и том же линейном
многообразии D. Замыкания этих операторов обозначим снова
через Ai и А2.
Теорема 2.1. Пусть q> ea®Sl, ss (R2) и функция t|>:
1, х2),
где k — натуральное число, также принадлежит <ffiSu Sl(Ra). Тогда
4>Ui, A2) = A^(AU A2).
JXo к а з а т ел ь <уг в о. Пусть е е Cf (R), е @) ^ 0._ Положим
f где ф(хь ^2) = ф(х1, х2)е(х2), ^{хъ хг) =
!, хг). Пусть {ф„} — сходящаяся к ф в а5Э5ь Sl последова-

360 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
тельность функций вида
т(п)
фп (*1, Х%) = 2 «я, (*l) *»«, (*ii),
/-1 .
где каждая из функций и„, vn/ либо принадлежит Cf (R), либо
является Фурье-образом б-функции. Аналогично, пусть {%} —
сходящаяся к i|r в «$?,,, s, (R) последовательность функций вида
Цп)
% (хи x2)=2l wn (jcj) г„ (х2),
где функции а>П/,-г„ берутся из того же класса, что и и„, vn/.
Положим
4>in.(^i» ^2)==ф»(^1, хг)е(хг), Ч>1Я(*1> xd='<pla
bn(Xt, b)=$(xi, x^j(\-e(x%))t Фал^х, хг)
Тогда имеют место следующие соотношения сходимости в &BHt S,.(R2):
Таким образом,
Hl'» B-1)
причем ^m(Xi, х2)+Ьп(х1, x^-x^lfpinixi, ^) + ф2»(^1, *2)]. При-
Применяя к предельным соотношениям A.1) гомоморфизм aS, полу-
получаем
B.2)
i, Л)] =*Ui, Л);
соответствующие последовательности сходятся по норме опера-
операторов.
Пусть h — произвольный элемент пространства В. Из теоремы
2.1 главы III следует, что
Л.
B.3)
Так как оператор Л? замкнут, то из B.2) и B.3) следует, что
ft)Ub Л) Л,
что и требовалось доказать.
Теорема 2.1 показывает, в частности (см. замечание в § 9),
что по существу в основной задаче мы ищем асимптотику «по

§ 2J ГОМОМОРФИЗМ АСИМПТОТИЧЕСКИХ ФОРМУЛ 361
некоторым операторам»: в данном случае по оператору Л2. То есть,
зная поведение символа «остатка» при лг2-»-оо, мы можем сделать
заключение, чтр «остаток» принадлежит области определения опе-
оператора А$.
Точнее, теорема 2.1 влечет следующее утверждение. Пусть <р
и \|з принадлежат пространству «®Sl, S,'(R*) и ф(*ь **) —Ф(*1> *г) =
= О (х^к) в том смысле, что функция
принадлежит е#?,ьSl(Ra). Тогда для любого gefi вектор
Ф\Аь At)g~ty\Ai, At)g принадлежит области определения опе-
оператора А\.
В качестве примера рассмотрим метод стационарной фазы
в том случае, кргда фаза линейно зависит от параметра. Пусть
Ф е= Cf (R),. «F — бесконечно дифференцируемая на R веществен-
. ная функция и пусть уравнение #'(|)=р имеет для любого
р её R в точности одно решение I = В (/>) на носителе функции ф,
причем в?" (Е(р))ф:0 ни в одной точке peR. Рассмотрим
интеграл
/(*, Р)-Х(Р) ] Ф(Ю^[-5ГE)-'"И4, B-4)
rflexe=CS°.(R).
Перейдем в интеграле B.4) к новой переменной интегрирова-
интегрирования t по формуле
Обозначим, как и в § 3 главы III,
Получим:
/lv ft\ «. fn\ Jxi^(S(P)) P(S(p))] Г alfDOtKu It n\ /It 10 K\
[X, p) — A V"/" J " tO \ft P)Q''i \r"")
—CO
где M>o(*i Р)==фA('« P)) ^ • Функция \|з0 бесконечно диффе-
дифференцируема по совокупности аргументов, причем существуют
такие положительные непрерывные функции с(р), d(p), что
%(t> Р) = 0 ПРИ *ф[~С(Р)> d(p)\. Построим последовательность
функций \|з/ (t, p) по следующей рекуррентной формуле:
0. W
V* Р)=ш 1 •
Очевидно, что при t#[— c(p), d(p)\
\j(t, p) = t*Pj(n, p),
где Р/(т, р)—некоторый полином от переменной т с бесконечно
дифференцируемыми коэффициентами, зависящими от р. В § 3

362 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
главы III показано, что имеет место следующее разложение:
, р)=.
2[й5Ь *• р). B.6)
где
00
Лм (М) = >^[?]"+1Х (р) S ^"^«+1С Р) dt, B.7)
—оо
функция У1с определена в § 3 главы III. В разложении B.6)
можно заменить ]/* на radx и a~r=x~J(— l/signx на pj(x)X
х(—l)'signx, где функция rad и p^ также определены в § 3
главы III. При этом остаточный член гп+1 (х, р) заменяется на
функцию г„+] (х, р) совпадающую с fn+i(x, p) при |х|>а, где
а — некоторое положительное число, не зависящее от р. Заметим,
что в B.6) sign <У" (S (р))=0о = const, так как функция *?" (В (р))
нигде не обращается в нуль. При х^О все члены разложения
B.6) кроме fn+i(x, p), очевидно, бесконечно дифференцируемы по
х и р; значит, этим свойством обладает и функция /*„+1 (х, р).
Пусть е (х) — функция из Q4R1) тождественно равная 1 при
|дг|<а. Положим
rn+i (х, р) е (х) = \i (х, р), r'n+ъ (х, р) [ 1 - е (х) ] = v (x, р).
Имеем:
'п+Л*. P) = l*(*. p) + v_(*. р).
Функция (* принадлежит C~(R2) ce©Sl. s, (R2). Поэтому" функция
(х, р)->хл>(х, р)
также принадлежит Cf(K2)cz^Sl, s, (R2). Покажем, что функция
(х, р) -+хп+1\ (х, р)
принадлежит a®Slj S,.(R2) (это будет означать также, что v e
е <^s>. s, (R2))- Положим для определенности signaF" (S (p)) = 1.
Так же, как и в §3 главы III, получим, для любого натурального
(х, р) = УПе% (у)"+V+i @, P) X (p) A - e (a:)) +
to
[ 1 -e (x)]({)m+1 J ^'ipm+] (/, p)t (p) d/. B.8)
—OO
Первое слагаемое в правой части B.8), очевидно, принадлежит

2] ГОМОМОРФИЗМ АСИМПТОТИЧЕСКИХ ФОРМУЛ ЗбЗ
s,, s, (R2)i то же относится "и к каждому из слагаемых суммы
т
2] ¦ Рассмотрим последний член в B.8). Положим
f (х, р) = У~х^~т [ 1 - е (х) ] [ e^'lw ('- Р) 1 (Р) dt =
= Vx'x»-mll-e(x)]yi(p)gm(x, p),
где
—оэ
Так же, как и в § 3 главы III, устанавливаем, что при х Ф О функ-
функция g бесконеяно дифференцируема и
где О — оценка, равномерная по р при р е supp %. Следовательно,
при m^n + 2 для любых целых неотрицательных kt и ?2
R,, дх**др*
dx dp < oo,
так что /<~ №!« + '• s»+'(R2)cr<^SliSa(R2). Итак, мы- показали,
что функции г„+1 (х, р) и дг"+1г„+1 (х, р) принадлежат пространству
<^««. s. (R2)- Обозначим
:, р).
Из разложения
Я (х, р) = УНв 4а« 2 (т")УРу W ¦/ (О, Р) X (Р) + г„+1 (х, р) B.9)
/=о
следует, что К cz &BSlt s, (R2). Применяя теорему 2.1, получаем
следующий результат! для любого h e 5 вектор
^(тУ B.10)
/=0
где 1) (Р) — Ч3; @» p)t(P)> принадлежит области определения опе-
оператора А?+}.
Теорема 2.2. Пусть Ах и Аг — производящие операторы
степеней st и s2 соответственно с одной и той же определяющей
парой (В, В) и одной и той же областью определения Da1 = Da%=
= D. Пусть функции <р, \|з е a®Sl_ 8г (R2) связаны соотношением
Х2) = Р (Xi) ф (Хи Хг),

364 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ, V
где Р — полином. Тогда
МО-
Доказательств о. Так же, как и при доказательстве тед-
ремы 2.1, построим последовательности {ф1л}, {фг„}, {ф1л}, {i|>2n}
функций вида 2 ип] (*j) vnJ (х2), обладающие следующими свой-
ствами:
lim (ф^ + Фгл) = ф, Hm (ij?ln + фг«) = f.
Л-+ОО П-*ОО
*|>1Л (*1. Х2) = Р (Xj) Ц)Ы (Xlt Хг), Ij32n (XU Xi) = P (Xt) фая (Х1г Хг).
Пусть he.D. Тогда из теоремы 2.1 гл. III следует, что
ь A2)]p(A1)h.
Переходя к пределу при.я-»-со, полу чаем:
Теорема доказана.
Теорема 2.2 влечет следующее утверждение. Пусть ф и я|? при-
принадлежат пространству e®Sl>Sl(Ra) и ф(^1» ^2) — V.(xlf хг) = О(х-^)
в том смысле, что функция
' (*1, *2)->-*?[ф(*1. X2)-q(Xv X2)]
принадлежит e3SSli s, (R.2). Тогда оператор
ограничен. i
Мы можем теперь написать аналог разложения B.10) метода
стационарной фазы в том случае, когда оператор At действует
первым, а оператор Д2 — вторым. Именно: оператор
inaa n J
()^ B.11)
inaa n -J
К {К, А) - V*e 4 ^ (х)^/ Ш PJ (Аг) А?+*
ограничен.
Применим полученные результаты о методе стационарной
фазы к псевдодифференциальным операторам. Разложение B.10)
в данном случае принимает вид
-i?,x)hW-yHe 4 2( 2 )
/=о
где ^л+1 е U7* + я +' (R), если h e U7* (R).

§ 3] ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ 365
Разложение B.11) для псевдодифференциальных операторов
имеет, вид
то, п
4 2 Ath(x) Pi (~' ?)h w+r-
/ i 2\
где псевдодифференциальный оператор гя+1(— t-j-, jr) обладает
\ сие /
тем чсвойством, что для любого k оператор re+if — t -^-, дг] X
X (—i-fa) ограничен в W*(R). Следовательно, для любого
h U7f1 (R) ф
h e= U7f-«-1 (R) функция
.'к Л / . d , -ля+i / . d , л-я-1
1 Х)[Ч + 1) +l)
принадлежит
§ 3. Геометрическая интерпретация метода
стационарной фазы
Рассмотрим интеграл
гдер, ш — вещественные переменные, ря=еы/*, фх е Cf (R); rad ш —
бесконечно дифференцируемая функция, определяемая при доста-
достаточно больших | да | формулой
Отметим, что функция 0^1 (р, ш) при достаточно больших | оэ |
является 1/сэ-фурье-образом функции е'ю^(дс'ф1(л"), зависящей от
параметра ю. .
К интегралу / (р, ш) применим метод стационарной фазы,
используя только первый член асимптотического разложения.
Предполагая, что <f'(x) ^0 на носителе функции фх(х) и что
уравнение —p + <f(x) = Q имеет единственное решение х=х(р)

366 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
при дгевиррфх, получаем:
= Ф1 (* (Р)) gfa [- р* (р) + ff" (*(р))] -L g (n, со),
где функция g(p, со) обладает следующим свойством: для любого
t&Cf (R) и любых slf s2
),, со) e^SX(Sj (R2).
В дальнейшем мы будем писать Д(р, a)~f2{p, со), если ^ —f2s
е «И.,. s, (R2) и со [/i (р, со) - f2 (р, со)] е ^Sl, Ss (R2). Таким образом,
>gn • rado f eto[
В пространстве точек (х, р), которое в физике принято назы-
называть фазовым пространством, уравнение
^'(*) = Р C-3)
задает некоторую линию. Введем на кривой C.3) параметр а:
х = х(а), р = р(а).
Условие of* (х) Ф 0 означает, что уравнение р = р (а) относительно
а имеет единственное решение а = а(р), причем функция а(р)
бесконечно дифференцируема. В этом случае говорят, что кривая
C.3) диффеоморфно проектируется на ось р. Таким образом, лю-
любую функцию на кривой C.3) можно рассматривать как функцию
от х, р или а. Допуская неточность в обозначении, мы иногда
будем писать равенства типа
Ф(дг)=Ф(р) = Ф(а),
а также а == а (х) — решение уравнения х — х(а), а = а(р) реше-
решение уравнения р = р(а) (разумеется, в тех случаях, когда не
возникает опасность путаницы). Имеем
«F (г) = <? (х (о0)) + $ S' (х) dx = <f(x (a0)) + ]pdx, C.4)
X (Оо) " О0
рх (р) + <? (х (р)) = - рх (р) + ] р dx + S (х
а
= - ^ xdp - р (а„) х (а0) + eF (х (а0)),

§41
КАНОНИЧЕСКИЙ ОПЕРАТОР НА НЕЗАМКНУТОЙ КРИВОЙ
367
где § xdp, $ р dx — криволинейные интегралы вдоль кривой C.3).
do
Интеграл § pdx вдоль кривой в фазовом пространстве будем
называть действием (это название принято в физике).
В сравнении C.2) положим
da
1/8
Учитывая C.4) и равенства
получим
со
da
C-5)
где а = i(l -signg
§ 4. Канонический оператор на незамкнутой кривой
Пусть М1: х = х(а), р = р (а) — незамкнутая бесконечно гладкая
кривая без самопересечения в фазовом пространстве с координа-
координатами (х, р), а ф (а) — бесконечно дифференцируемая функция
с компактным носителем. Определим на М1 вещественные функции
a a
S(a) = $ pdx, S(a) = $ x dp + x (a0) p (a0) = - S (a)+p(a)x(a).
do <Zo
Пусть открытая дуга U кривой М1, содержащая носитель
функции ф, диффеоморфно проектируется на оси х и р, т. е.
^-фО, -J-фЪ на ^- Тогда вместо а в качестве параметра на U
можно выбрать х или р:
a = a(x), a = a(p).
Справедливы соотношения

368
АСИМПТОТИЧЕСКИЕ МЕТОДЫ
[ГЛ. V
т. е. переход от х, S (х) к р, § (р) является преобразованием
Лежандра.
Меняя в (З.б) ролями переменные х и р и переходя к ком-
плексносопряженным величинам, получим для любой бесконечно
дифференцируемой функции р(оэ), равной нулю в окрестности
.нуля и 1 в окрестности бесконечности,
-i/a
ф(а)
¦0(P)
^X(*)pH(tsrgnu>)a|^| \(a)
при условии, что носитель функции % содержится в проекций
дуги U на ось х. Если же носитель бесконечно дифференцируемой
функции х (х) не пересекается с носителем функции ф (а (х)) и
X (х) = 1 в окрестности со, то функция
g(x,
:-/@S (а)|(*Р
Ida
-l/s
фа)
а-а(р)
принадлежит пространству W|(R2) при-любом s, и этим же
свойством обладает функция a>*g(x, ю), где k — произвольное
натуральное число. Следовательно, справедливо равенство
1\ ф.<«)
-X WРН
а-а(р)
(«)
(a<*»gi(*, ©) + &(*. <»), DЛ)
где g,, g2 — бесконечно дифференцируемые функции, gi(x, ю) = 0
при хе5иррф(а(х)), функции Щх(х, ю), ю^2(^, <») принадлежат,
пространству sffi)Sl, s, (R2) для любых целых неотрицательных sx, S2.
В правой части равенства D.1) функция
aiatS (a) djL
da
бесконечно дифференцируема на U, но вне дуги С/ она может
потерять гладкость в тех точках, где j^ — O; такие точки мы
будем называть фокальными. В то же время левая часть DЛ)
с точностью до множителя есть ю-Фурье-прообраз функции
v
-»/а
Ф(а)
Ida
а-а(р)'

§ 4]
КАНОНИЧЕСКИЙ ОПЕРАТОР НА НЕЗАМКНУТОЙ КРИВОЙ
369
причем множитель е~'»?<<»> j^
I и(Х
является бесконечно дифферен-
I
цируемой функцией в окрестности фокальной точки. Это соображе-
соображение наводит на мысль определить следующий оператор К —ка-
—канонический оператор, переводящий бесконечно дифференцируемые
финитные функции на М1 в функции от переменных со и х.
Пусть семейство {t//}/g/ открытых дуг покрывает М1:
Ml = U Uj
(в М1 не включены 1сонцы), причем каждая из дуг Uj пересе-
пересекается лишь с конечным числом дуг Uj. Пусть, далее, на каждой
дуге Uj
%ФО или !
Выберем на каждой дуге Uj в качестве параметра (локальной
координаты) х или р. Если на V, выбрано х в качестве Локальной
координаты, то мы назовем Uj неособой картой кривой М1;
в противном случае Uj будет называться особой картой. Каждой
карте Uj отвечает функция а = а1 (х) или ос = осу (p). Совокупность
{Uj}/^i неособых и особых карт иа М1 назовем каноническим
атласом кривой М1. Пусть дана функция ф(а) с компактным
носителем supp ф е Л11. Возьмем разбиение единицы, отвечающее
каноническому атласу, т. е. бесконечно дифференцируемые функ-
функции \е} (а)}, удовлетворяющие условиям:
s supp ф, supply с: С/у.
ПРИ
Тогда
Пусть *для определенности UJX — неособая карта, содержащая
выделенную точку осо. Положим для функции т|з(а) с носителем
в Un .
D.2)
L
da
'a Ax)'
Пусть Ujt — особая карта
канонический оператор K
лем в Uji, формулой
пересекающаяся с Ufl. Определим
действующий на функции С носите-
носитеdp,
где константа с будет определена ниже. Потребуем, чтобы для
любой бесконечно дифференцируемой финитной функции t|> (a)
с носителем, содержащимся в ?/д f) Uj%, было справедливо соот-
соотношение

370
АСИМПТОТИЧЕСКИЕ МЕТОДЫ
[ГЛ. V
каковы бы ни были функция xsC0°°(R) с носителем, содержа-
содержащимся в проекции Uп П U& на ось х, и функция peC°°(R),
равная 0 в окрестности нуля и 1 в окрестности бесконечности.
В силу D.1) имеем:
х, ш) с*
*.(/sign ©)eu/»n
где
Следовательно, мы должны положить
, ©),
Аналогично для неособой карты Uj3, пересекающейся с
положим
(а) = (/ sign ш) Л
, + °Ui0(\U
здесь supp ty e f/3.
Вообще, пусть t/x, t/2, ..., {/„ — конечная последовательность
карт из данного канонического атласа, причем неособые и особые
карты в этой последовательности чередуются и любые две карты,
стоящие в этой последовательности на соседних местах, пересе-
пересекаются. Тогда положим
X
da.
-J/2
при нечетном п и
ВД (х) = (i sign шГ Ос/Д п
+in УУ
X
Vm
X
fa
-1/4
Определим индекс и канонический оператор при четном п.
Назовем число
п—\
ind (/х, ...,/„) Ш 2 (- 1)* aUjk п uJM
k=i
индексом цепочки карт UJX Ujn. Для того, чтобы данное
нами определение канонического оператора К/ в карте было
непротиворечивым, необходимо и достаточно, чтобы индекс
ind (/х, ..., /„) зависел только от jt и /„ или, что то же самое, —
чтобы индекс замкнутой цепочки карт Un, •¦-, Ujz равнялся
нулю. Этот факт имеет место для незамкнутой кривой Щ1.

§ 41 КАНОНИЧЕСКИЙ ОПЕРАТОР НА НЕЗАМКНУТОЙ КРИВОЙ 371
Действительно, пусть {/ — дуга кривой М1, диффеоморфно проек-
проектирующаяся на ось р, а', а" —две точки на дуге U, не явля-
являющиеся фокальными (т. е. -^-ФО в этих точках). Положим
Y(a\ a-) = -^signg(a')-signg(a
Если же точки а' и а" лежат на дуге, диффеоморфно проекти-
проектирующейся на ось х, то положим
у (а', а")-0.
Легко видеть, что эти два определения дают одинаковый результат
в тех случаях, когда они применимы одновременно. Пусть теперь
/ — путь на кривой М1, имеющий концы Р', Р", т. е. непрерывное
отображение
отрезка [0, 1] в М1, удовлетворяющее условиям
а@) = р\ аA) = Р".
Пусть точки Р' и Р" не являются фокальными. Положим
1!т («('»). »('»+i)). D-3)
где p'=a@), P' = a(l), 0 = to<t1<...<tn_1<tn = \, причем
числа tu ..., tnlx выбраны так, чтобы в праюй части формулы
D.3) каждый участок пути с концами a(tk), a(^n-i) либо не
содержал фокальных точек, либо целиком лежал на дуге, диф-
диффеоморфно проектирующейся на ось р (такой выбор всегда
возможен. Назовем у[1] индексом пути /. Такое название оправ-
оправдано тем, что a (t) не зависит от выбора промежуточных течек
a (ti), ..., a (^„_x) на пути /. Чтобы убедиться в этом, достаточно
заметить, что у[1] не изменится, если между tk и tk+i вставить
промежуточную точку f. При этой процедуре к у [/] добавляется
слагаемое
y(a(tk), a(f')).+ Y(«(O, a(tk+1))-y(a(tk), a(tk+1)),
которое, как это следует непосредственно из определения, всегда
равно 0.
Пусть два пути /: a = f(t) и /': a = g(t) на М1 гомотопны,
т. е. существует такая непрерывная функция sF(t, s), O^^^l,
0<s<l со значениями в М1, что &(t, O)=f(t)n & (t, l)=g(t).
Если при этом для любого se[0, 1] точки <У @, s) и /AР s)
не являются фокальными, то индексы путей / и /' совпадают.
Доказательство этого факта предоставляем читателю. Теперь нам
уже нетрудно убедиться в том, что индекс замкнутой цепочки

372 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
карт на М1 равен 0. Действительно, для любой цепочки карт
Up. Ujn число ind (ji /„) равно индексу некоторого
пути /, начальная точка которого лежит в Ujlt а конечная —
в пересечении Vin_x П Ujn- Пусть fn = j\. Тогда можно считать,
что начальная и конечная точки пути / совпадают, например,
с точкой а0, т. е. путь / замкнут. Но любой замкнутый путь
на незамкнутой крнвой можно непрерывно деформировать в путь I':
'а = const (в точку). Очевидно, что у[1'] = 0. Следовательно у [I] =
== ind (>*! Л) = 0.
Понятие индекса пути на М1 становится особенно наглядным,
если в каждом компактном подмножестве М1 имеется лишь конеч-
конечное число фокальных точек и в каждой из них производная —
меняет знак (если эти условия выполнены, то говорят, что кри-
кривая М1 находится в общем положении относительно проектиро-
проектирования на ось х). В этом случае можно ввести функцию на-М1
с целочисленными значениями — индекс у (а) точки а — следующим
образом: у (а0) — 0; прн переходе через фокальную точку в направ-
направлении уменьшения -?- индекс у (а) скачком увеличивается на
единицу, а при переходе в направлении увеличения dx/dp умень-
уменьшается на единицу; в фокальных точках функция у(а) не опре-
определена, в остальных точках — непрерывна (следовательно, локально
постоянна). Подчеркнем, что начальная точка а0 не должна быть
фокальной. Для любого пути / на М1, начинающегося в точке а0
и кончающегося в точке а, имеем:
у[1] = у(а). D.4)
В случае, когда кривая М1 не находится в общем положении,
будем рассматривать формулу D.4) как определение функции у (а).
Определим, окончательно, канонический оператор . формулой
2
/ел
dp
^ki J е1в""х~te>s (а) х
X
da
ej (а) ф (а)
а=а/(р)
dp,
где /х — множество номеров неособых карт, /9 —множество номе-
номеров особых карт;
Yy = Y(a), at&Uj, -
если Uj — неособая карта. Если же Uj — особая карта, то индекс
у (а.) может принимать различные значения в разных, точках

§ 41 КАНОНИЧЕСКИЙ ОПЕРАТОР НА НЕЗАМКНУТОЙ КРИВОЙ 373
дуги 11/, в этом случае
у,= min y(«)-
o€fy
Сглаженным каноническим оператором $% будем, называть опе-
оператор, удовлетворяющий следующим условиям:
а) [a^"cp](*, ш) = [/Сф] (х, ш), если |ш| больше некоторой кон-
константы, не зависящей от ср;
б) [аг<р](*, и)бО»A^.
Пусть y4i, A2 — производящие операторы, действующие в бана-
банаховом пространстве В. Так как [$ц>](х, ю) —гладкая функция
от х и ю, то можно рассматривать операторы [a^cpJHi, А) и
[<з%?ср] (лх, Л2). Введем следующие обозначения:
—
Л.
Определение. .Б^дел говорить,' что пара производящих
операторов Аи Л2 (соответственно, Alt A%) действующих в В,
согласуется с кривой М1, лежащей в фазовой плоскости (х, р),
если для любой неособой карты U кривой М1 и любой бесконечно
дифференцируемой функции х (х) с носителем, содержащимся в про-
проекции дуги U на ось х, оператор x(^i)e'^l4>^«' (Соответственно,
%\Ai)e ф •> г&е Ф(') = 5(а(х)), ограничен в В. . - ¦
Теорема. Пусть Ж и Ж' —два канонических оператора на
М1, отвечающие различным каноническим атласам {Uj}j?i и
{U'ihei'i разбиениям единицы -{в,-} и {е'/} и различным способам
«сглаживания» по а, но одной и той же начальной точке а0. Тогда:
а) если пара Alt A2 согласуется с М1, то оператор
Аг [Ж (А, А) Ф («) - *' (А. А) Ф (а)]
ограничен в В;
б) если пара А1г А2 согласуется с М1, то оператор
к (А, А)ф(а)-^'(А, А)ф(«)]л.
ограничен в В.
Доказательство. Рассмотрим сумму {УЛ/е./» канониче-
канонических атласов {Uj\jei, {Uj\/er, т. е. множестю /" есть (дизъюнкт-
(дизъюнктная) сумма множеств / и /', Vj = Uj при /е/ и Vj = Uj при
/е"/'. Продолжим разбиения единицы {ej} и {e'j\ следующим об-
образом: ¦>
^г(а)=хО при /е/', е;(а) = 0 при /е/;

374 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
здесь / и /' рассматриваются как непересекающиеся подмно-
подмножества множества /". Тогда <% и $?' можно рассматривать как
два канонических оператора, отвечающих одному и тому же кано-
каноническому атласу {V,}, но различным разбиениям единицы {е^,
{в}}. Поэтому без уменьшения общности можем считать, что с са-
самого начала канонические атласы {?/,} и {U}} совпадали.
Имеем при достаточно больших по модулю ю
He уменьшая общности, можно предположить, что никакие
две различные неособые карты атласа {Uj\ не пересекаются, и
никакие две различные особые карты этого атласа также не пе-
пересекаются. Действительно, пусть Uj0 — неособая (соответственно,
особая) карта данного атласа и пусть /0 — множество номеров
всех неособых (соответственно, особых) карт, пересекающихся
с UJe. Тогда дугу U Ujcx (соответственно р) в качестве ло-
кальной координаты можно выбрать в качестве карты некоторого
канонического атласа на М1. Вообще, назовем два элемента /'
и /" множества / эквивалентными, если карты Vу и U/» являются
одновременно неособыми или особыми и пересекаются. Пусть 7 —
фактормножество множества / по данному, отношению эквива-
эквивалентности. Для каждого класса эквивалентности /е/ положим
причем в качестве локальной координаты на Uj выберем х, если
Uj — неособая карта при / е /, и р — в противоположном случае.
Тогда Ш-W е 7 — канонический атяас на Мии |е-\-е7 —разбие-
—разбиение единицы, отвечающее этому атласу. При этом никакие две
различные неособые (или особые) карты атласа Шу\ не,пересе-
не,пересекаются и канонический оператор, отвечающий атласу {Uj} и раз-
разбиению единицы {в/}-, очевидно, совпадает с каноническим опера-
оператором, отвечающим атласу \Uj\ и разбиению единицы ie-A.
Итак, предположим, что атлас {Uj} совпадает с атласом WA.
Тогда [е;- (а) — е] (а)] ф (а) = 0, если точка а не попадает ни в одну
неособую (особую) карту этого атласа, так как в этом случае
е, (а) ф (а) = е) (а) ф (а) = ф (а). Пусть Uj — особая карта атласа

§ 5] МЕТОД СТАЦИОНАРНОЙ ФАЗЫ 375
{Uj\ и Uki, ..i, Ukm — неособые карты, пересекающиеся с Uj.
Тогда носитель функции [еу(а)— е/(а)]<р(а) содержится в
т .
U (U;OUk), причем в любой точке aet/, f\Uj справедливы
равенства
е, (а) ф (а) + е^ (а) ф (а) = 1, е) (а) ф (а) + е^ (а) ф (а) = 1,
так что в пересечении Uj П Ut выполняется равенство
Ф (а) [Ф,- (а) - в; (а) + е^ (а) - е'к[1 (а)] = 0.
Заметим еще, что так как функции ек^ и e'k равны нулю в не-
некоторой окрестности концов дуги, то носитель функции.[еу(а) —
— е} (а)] ф (а) содержится на самом деле в некоторой открытой
дуге, диффеоморфно проектирующейся на ось х. Применяя фор-
формулу D.1), получаем, что разность [(К — К') ф] (х, ю) является
суммой конечного числа слагаемых вида
где gu gi-~бесконечно дифференцируемые функции gl(x, ш)=0
вне некоторого замкнутого множества, содержащегося в проекции
неособой карты Uj на ось х, и функции (agx{x, ш), щ^{х\ ш)
принадлежат пространству «$?,,,,, (R2) для любых целых неотри-
цательных sx и s2. Операторы А&^Ах, Аг), gi[Ai, Лг)Аг,
U2 \ - / 2 1 \
1. Аг), g^yAu Л2) Аг ограничены в В. Утверждение тео-
теоремы теперь непосредственно следует из теоремы 10.2 главы IV.
§ 5. Метод стационарной фазы
Пусть /tsR, yeR", Ф —бесконечно дифференцируемая /вещест-
венйая, ф — комплексная функция из CJJ°(Rn+2), носитель которой
содержится в (a, b) x Y X (—с, с), где а<Ь, с>0 — веществен-
вещественные числа, К —некоторый шар в R". Рассмотрим интеграл
ИЦ, Л)= \ ДФ(Р'">А)ф(Р, У, h)dp. E.1)
— 00
Предположим, что уравнение
™(p,y,h)=O, pe(a,b), y<=Y, \h\<c
имеет единственное решение р = р(у, Л), причем
${Р(У, h), у, ЩФО;
сделаем в интеграле E.1) замену переменных:
Ф (р, У, Щ - Ф (р (у, h), у, h) - Лг, E,2)

376 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
где а = sign -^ (p (у, А), у, А). Получим:
"А) \.Т"»«.У.Н)&, E.3)
— 00
где р (t, у, А) — решение уравнения E.2),
У, h) = y(p(t, y,h), у,к
Функция ty принадлежит CS°(Rn+2), причем ее носитель содер-
содержится в (d, ё) х Y X (—с, с), где d, e — некоторые вещественные
числа. Применяя к интегралу E.3) результаты § 3 гл. III, по-
получаем следующее разложение:
±. A). i/,h) ¦ r~ \ (iah\J
НУ. h)-Vn 2\T)
2t\)
i=o
0, у. h) + rN+1(y, h), E.4)
где
rN+I(y, ^-^Г'т — ^р J .>^»*, E.5)
Sh(t, У, h)=*y(t, у, h),
*. А) E-6)
dt1
Заметим, что при достаточно больших по модулю t каждая из
" 1 /1 \
функций ty(/, ^, А) имеет вид. jj-P^jilyj, где Pj,, д — полином, коэф-
коэффициенты, которого суть бесконечно дифференцируемые функции от
у, h, носители которых содержатся вУх(-с, с). Кроме того, функции
Xj(y, Л)*Ч(О. y,h)
принадлежат С?° (Rn+1) и их носители содержатся вУх (—с, с).
Оценим остаточный член. Положим А= 1/ю и рассмотрим
функцию Rft+iiy, <»)~r/v+iU/, — J. &га функция отлична от нуля
лишь пр»-|и|> 1/с. Покажем, что функция <aN + lRN+1(y, ©) при-
принадлежит пространству <ffiSu s, (R" x R) для любых slt s2. Дейст-
Действительно, для 'любого натурального т > N + 1 имеем:
-'« J *—¦*¦,(*. *i)Л. E-7)

§ 5] МЕТОД СТАЦИОНАРНОЙ ФАЗЫ 377
Первое слагаемое в правой части E.7) принадлежит
«Я... ч (R" х R),
так как
[у,^) = шЛу, 0)+i
/, А) — бесконечно дифференцируемая функция, так что
функция —%(у, —) принадлежит любому пространству Соболева.
со Л\-" со
. т
Далее, все слагаемые суммы V в правой части равенства
J+ .
E.7) интегрируемы с квадратом, и этим свойством обладают
также все их производные. Рассматрим, наконец, функцию
f(y, ш)=/Я^'то^"<вшлг-я, $<A*«'W(f, у
,def
Функция g(y, ш) отлична от нуля лишь при уеК и ограни-
ограничена, оценим ее производные. Для любого мультиндекса k =
= (klf ... kn) и любого номера / имеем:
1\ 2со/
Из формулы E.8) вытекает, что функция g(y, ш) бесконечно
дифференцируема ,и все ее производные ограничены. Следова-
Следовательно, при достаточно большом т функция f (у, <о) принадле-
принадлежит любому наперед заданному пространству Соболева. Этим до-
доказано, что остаточный член rN+1 в разложении E.4) удовлетво-
удовлетворяет условию
В заключение параграфа рассмотрим случай, когда критиче-
критическая точка фазы Ф (р, у, И) > отсутствует. Рассмотрим интеграл
E.1), и пусть функции Ф и ф удовлетворяют всем прежним
условиям, кроме разрешимости уравнения =- = 0.
Вместо этого предположим, что
при р&(а, b), yt=Y, |A|<c. В этом случае мы можем сделать

3?8 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
в интеграле E.1) следующую замену переменных:
ф (Р, У, h) = t, p = p (t,- у, К).
Получим:
Т —t
НУ> h)= \ eh y(t, у, h)dt,
— 00
где , ,, ,.
Ч> (t, V, h) = Ф (р (t, у, Л), у, h)dp{tJ'h) .
Снова, как и прежде, функция ty принадлежит C?°(Rn + 2), причем
ее носитель содержится в (d, е) X У X (—с, с), где d, e — неко-
некоторые вещественные числа. Интегрируя по частям N раз, полу-
получаем:
/ (у, h) = (ih)N \ eh — Ny' dt. E.9)
— 00
Положим ft=l/ft). Из формулы E.9) следует, что если в инте-
интеграле E.1) g- ф 0 на носителе функции ф, то для любого нату-
натурального т функция (йт1 (у, .1/ю) принадлежит любому простран-
пространству Соболева, а значит, и любому пространству e%)Su St (Rn x R).
§ 6. Канонический оператор на незамкнутой кривой, зависящей
от параметров, определенный с точностью до О A/ю)
1. Рассмотрим семейство' незамкнутых' кривых М1 ф, ю) на фа-
фазовой плоскости (х, р). Пусть PeR", ю принадлежит расширен-
расширенной числовой прямой и уравнения кривых М1 ф, ю) суть
х = х(а, р, (а), F.1)
. р=р(а, р,-©), F.2)
где а — (один и тот же) параметр на кривых рассматриваемого
семейства, х(а, р\ ю), р(а, Р, ш) — бесконечно дифференцируемые
(в том числе и при ш — со) функции.
Введем следующие функции S (а, Р, ю) и S(a, P, ю):
dS = р (ct, p, w) dx (ct, p, (в),
S@, p, <в) = 0, F.3)
(а, р, ю) = — о (а, р, (») + дг(а, р, (»)/7(а, р^ ю).
Пусть {(/(Р, <»)}рев. «оеа —семейство дуг кривых М1 ф, ю), отве-
отвечающих интервалу (а, Ь) изменения параметра а, Я —открытая
область на' расширенной числовой прямой, не содержащая нуля,
В —область в R". Предположим, что каждая из дуг 11ф, ю)
диффеоморфно проектируется как на ось х, так и на ось р, так

КАНОНИЧЕСКИЙ ОПЕРАТОР НА НЕЗАМКНУТОЙ КРИВОЙ
379
что уравнения F.1) и F.2) относительно а имеют на (а, Ь) X
X В х Q единственные решения
а = а(дг, р, ю), а = а(р, р, ю).
Пусть ф(а, р, ю) — бесконечно дифференцируемая функция
с компактным носителем, содержащимся в (а, Ь) X В х Q. Рас-
Рассмотрим интеграл
, Р, ю) =
Ф(а, р, а,)
р, р, и)
dp.
Для вычисления этого интеграла можно применить метод стацио-
стационарной фазы.Если х (ft)) — произвольная функция из CJ°(R), то
с, р, ю) =
С -1/2
= х (*) (/ sign
«¦
да
ф(«, Р,
а = а(дс. р, «о)
*, Р,
где функции ^(^, Р, ш), й(д:, Р, ч>) отличны от нуля лишь при
iiieQ, причем функции (ng1(x, P, a), a>g2(x, P, ft)) принадлежат
пространству «$?Sl> Sli s, (R x R" X R) для любых
Пусть теперь % (х) — бесконечно дифференцируемая функция,
равная 0 на объединении проекций дуг f/(P, ю) на ось х и рав-
равная 1 в окрестности бесконечности. Тогда мы можем применить
результаты предыдущего параграфа, касающиеся случая отсут-
отсутствия критических точек фазы, положив
Получим, что для любого JV и любых slf s2, ss
ю^Х W / (Jf, P, ft)) e ^Sl, „, s, (R x R" x R).
Представляя единицу в виде 1=х(*) + (!— Х(х)), где
е CJ° (R), получаем окончательно следующее соотношение:
1(х, р, «) =
>(а, Р, ю)| _
|а = а(ж:, р,
-1/2
«о)
ж, р, а», р,
, В, ©), F.4)
где функции gt и ^г обладают теми же свойствами, что и выше.

380 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
2. Определение индекса. Формула F.4), являющаяся обобще-'
нием формулы D.1), позволяет определить канонический оператор
на семействе кривых М1 ф, ю). Пусть С —компактное множество
в пространстве параметров а, р, со, не содержащее точек, в ко-
которых со =0. Пусть далее {Uj}, /=1, ..., N — семейство откры-
открытых связных множеств в пространстве параметров, покрывающее
Ct {ej\, j — 1, .... N — разбиение единицы, отвечающее покры-
покрытию {?//}: „ '
е} (а, Р, со)е=С~; j[]e/(a, р, <о)=1 при (а, 0, ю)е=С.
/«=1
Очевидно, покрытие {Uj} компактного множества Q можно вы-
выбрать так, чтобы для любого / выполнялось одно из следующих
двух условий:
а) g(a; P, со)#О при (a, p, <a)e=Uft
б) % (а, Р» ») Ф 0 при {а, р, а) е Uj.
Разобьем множество номеров 1, 2, ..., N на два класса Д и /2,
так, чтобы при /e/i выполнялось условие а), а при /е/а вы-
выполнялось условие б). Семейство {?/,} вместе с парой {1и /а} мы
будем называть каноническим атласом окрестности- множества С
в пространстве параметров; множество Uj при /еД будем на-,
зывать неособой картой этого атласа, а прн / е /2 — особой картой.
Каждой неособой карте ^.отвечает функция ау(х, р, со) —ре-
—решение уравнения
х = х(а, р, со), (а, р, со) <= Uj
относительно а, а особой карте Ur — функция а} (р, р, со) — реше-.
ние уравнения . .
р = р(а, р, ©), (a, p, cojeiV,'.
Канонический атлас {Uj}, It, I2 окрестности компактного
множества С в пространстве параметров всегда можно выбрать
так, чтобы для любых ]\ е /, /2 е /2 пересечение Uh f) Uit было
связно; мы будем предполагать, что это условие выполнено. На-
Назовем индексом пересечения неособой карты GЛ и особой карты
Uj,, имеющих непустое пересечение, число
[(a. p. »)е!/лПУ/,
Положим по определению:
Если же обе карты Ujt и с7/, являются неособымн или особыми,

§ ы КАНОНИЧЕСКИЙ ОПЕРАТОР НА НЕЗАМКНУТОЙ КРИВОЙ 381
ТО ПОЛОЖИМ
Пусть Uj, ..., Ujm — такая конечная последовательность карт
канонического атласа, что любые две последовательные карты
этой последовательности пересекаются. Такую конечную последо-
последовательность назовем цепочкой карт. Индексом этой цепочки карт
назовем число
ind(/x, .... i»u==aU
С помощью индекса цепочки карт введем индекс произвольного
пути / в пространстве параметров (а, р\ со), начинающегося и кон-
кончающегося в точках, лежащих в некоторых неособых картах.
Пусть Uj, ..., Oj — такая "цепочка карт, начинающаяся и кон-
кончающаяся неособыми картами, что путь / разбивается на сумму
сегментов
удовлетворяющих условию /ц-с: UjVt. Тогда назовем индексом
пути / число
Y [*] *-ind (/г, .... /ж).
Данное определение индекса пути / корректно, т. е. не зависит
от выбора цепочки карт Ujx, ..., Ujm и разбиения пути I на-
сегменты 1г, ..., 1т.
Для того, чтобы убедиться в этом, прежде всего предположим,
что при том же разбиении пути / на сегменты мы используем
для определения его индекса другую цепочку карт Uyi, .... ?//'»>•
Тогда
, F.5)
Действительно, пусть М^ — конец сегмента /й. Положим
1 / Ш
-s-1 1 — sign
V
если ^ (Мц) Ф 0, ^ (Мц) ФО и Оц=0 в противном случае. Пред-
Представим себе путь / в виде дороги, на каждом участке ^ которой
имеется шоссе (иеособая карта) или канал (особая карта) (или
и то и другое). В.точках находятся станции пересадки с авто-
автомобиля на теплоход (если из этой точки выходят и шоссе и ка-
канал). Путник начинает и оканчивает свой путь на автомобиле.
В каждом пункте пересадки он имебт право пересесть на другой
вид транспорта. При пересадке на теплоход ему выплачивают
сумму Оц за потерю скорости, а при пересадке на автомобиль он

382
АСИМПТОТИЧЕСКИЕ МЕТОДЫ
[ГЛ. V
платит сумму сг^. Величина выплаты не меняется вдоль каждого
участка, где проходят совместно шоссе и канал. Ясно, что сум-
суммарная выплата за весь путь не зависит от того, какую схему
пересадок изберет путник, а это и означает, что равенство F.5)
справедливо. Остается заметить, что индекс пути не изменяется
при дроблении сегмента /^ на части, так как при этом можно
в цепочке карт несколько раз повторить особую или неособую карту.
Из определения индекса пути следует, что у[1] не изменяется
прн непрерывной деформации /, если концы пути остаются непод-
неподвижными. Поскольку в нашем случае параметр а изменяется на
некотором отрезке вещественной прямой, то любой замкнутый
путь I в пространстве параметров а, Р, со можно непрерывной
деформацией перевести в точку. Значит у f/] = 0 для любого
замкнутого пути /, откуда следует, что индекс пути зависит
только от его начальной н конечной точек.
Отсюда следует, что индекс цепочки карт, начинающейся
и кончающейся неособыми картами, зависит только от первой
н последней карт цепочки. Аналогично доказывается этот же
факт для произвольной цепочки карт.
3. Определение канонического оператора. Теперь мы можем
определить канонический оператор К на семействе кривых
{Мгф, со)}. Зафиксируем точку Ро в пространстве параметров,
и пусть эта точка лежит в некоторой неособой карте UJQ. Для
любой функции ф (а, р, со) с носителем, содержащимся в множе-
множестве С, положим по определению
Р, со)= У. (isignafie"*^*-*-^
х
X
дх
— 1/2
в/ (а, р, со) ф (а, р, со)
, F.6)
где yj— индекс цепочки карт, начинающейся картой Uj0 и кон-
кончающейся картой Uj.
Определенный формулой F.6) канонический оператор К зави-
зависит (кроме выбора начальной точки Ро и произвола в опреде-
определении действия S, связанного с возможностью перепараметри-
перепараметризации семейства кривых) от выбора канонического атласа {?/,}
и разбиения единицы {еу}.
Пусть Аи .... An+i — производящие операторы, действующие
в банаховом пространстве В. Рассмотрим оператор _^
k 2 k — \ k-\r\ л+ 2 \
Аи Аг, ¦¦•, Ак-х> Ak, ..-, Ля+i, An+

§ 6] КАНОНИЧЕСКИЙ ОПЕРАТОР НЛ НЕЗАМКНУТОЙ КРИВОЙ 383
Определение. Будем говорить, что упорядоченный набор
I k 2 *-1 fc-H л+2 1 \
производящих операторов А = \АЪ Л2, ..., Ak-i, Ak, ¦•¦,An+i An+2J,
действующих в В, согласуется с семейством кривых М1 (Р, со),
лежащих в фазовой плоскости (х, р), если для любой неособой кар-
карты U в пространстве параметров а, р, со — семейства кривых
М1 (Р, со) — и любой бесконечно дифференцируемой функции % (а, р, со)
с носителем, содержащимся в U, оператор Ф(Л), отвечающий
символу
Ф(х, р, со) =*= х (а (*, Р, со), р, ш)«*««<«<*. В. «>. Р. «>,
ограничен в В.
Теорема 6.1. Пусть К и К' — два канонических оператора
на семействе {М1 (Р, со)}, отвечающие различным каноническим
атласам {?/,}/<=/, Ilt /2 и {Uj}jer, \l\, /? окрестности компакт-
компактного множества С в пространстве параметров) и разбиения еди-
единицы {ej}J(=i, {e'jjiezr соответственно. Пусть далее набор произ-
производящих операторов
/k+l 2 k k + 2 n + 2 1 \
A=\Ai, Л 2, ..., Л ft, Л^+1, ..., Л„+1, Ля^2/»
действующих в банаховом пространстве В и таких, что опера-
операторы Аъ ..., Ak коммутируют друг с другом и с операторами
Ля+2. я операторы Ak+i, ¦¦¦, Л„+1 коммутируют друг с другом
и с оператором Аъ согласован с семейством {М1 ф, со)}. Тогда
для любой бесконечно дифференцируемой функции ср (а, р, со) с но-
носителем, содержащимся в С, оператор
ограничен в В.
Доказательство этой теоремы опирается на соотношение F.4)
и проводится аналогично доказательству теоремы § 4. ч
Замечание. В дальнейшем нам понадобится зависимость и
от переводящего оператора. Этот случай аналогичен рассмотрен-
рассмотренному. Пусть для простоты и=1. В теореме 6.1 можно заменить
вектор-оператор Л на вектор-оператор
1 2 3 4 \
t. А, Т, AJ,
где Л2 коммутирует с Л3, а Т: В ->• В — переводящий оператор,
или —на вектор-оператор "" ~
/1 2 3 4
U», т, л2, л
где Л2 коммутирует с Av

•*v* АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
§ 7. У-объекты на кривой
1. Определение пространств La и Lz. Пусть М1'— бесконечно.
гладкая кривая в плоскости R2 и пусть на этой плоскости фик-
фиксированы декартовы координаты х, у. Если открытая дуга U
кривой М1 диффеоморфно проектируется на ось х, то на этой
дуге можно выбрать х в качестве параметра; если такой выбор
сделан, то мы будем называть V неособой картой кривой М1.
Аналогично, дуга кривой М1, на которой выбрано у в качестве
параметра, будет называться особой картой кривой М1.
Назовем полным каноническим атласом а^ю кривой М1 сово-
совокупность всех неособых и особых карт этой кривой. Назовем
конечным каноническим атласом кривой М1 любое конечное се-
семейство {?//}/= 1 n карт полного канонического атласа а^"»,
покрывающее М1. Будем предполагать, что конечные атласы кри-
кривой М1 существуют (например, М1 — компактная кривая).
Пусть е?&н — множество неособых карт атласа &#<х,, ®^о — мно-
множество особых карт этого атласа. Каждая карта Сfea/д опреде-
определяется уравнением
У = Уи(х),
а каждая карта U е ®^0 определяется уравнением
х = Хи(у).
Очевидно, задание двух семейств функций
эквивалентно заданию кривой .М1.
Пусть для любых двух пересекающихся карт U е Ан, V' е ®^0
задан линейный оператор Vu, w, действующий на бесконечно диф-
дифференцируемые функции or у с носителем в проекции пересече-
пересечения U{]U' на ось у и переводящий'их в бесконечно дифферен-
дифференцируемые функции от х с носителем в проекции пересечения
UDU' на ось х. Потребуем выполнения следующих двух аксиом.
Vt (локальность операторов Vu, и1)- Значение функции Vu, и'Ч
в точке х зависит только от ростка функции <р в точке уи (х)
(т. е. только от сужения функции ф на сколь угодно малую
окрестность точки уи (х)).
Vi (условия согласования)
для любой функции ф с носителем, лежащим в проекции пересе-
пересечения U'i(]U't на ось у, и любой точки Xq из проекции пересече-
пересечения Ui()U2 на ось х.
Пусть ®^ = {t/y}—конечный атлас кривой М1, /г — множество
номеров неособых карт, /2 —множество номеров особых карт этого

§ 71 V-ОБЪЕКТЫ НА КРИВОЙ 385
атласа. Рассмотрим тройку:
Ф = (®^, {<р/(х)}/е/„ {ьШ/siX GЛ)
где фу (х) — функция из С? (R) с носителем, содержащимся в про-
проекции Uj на ось х, фу (у) — функция из Cf(R) с носителем,
содержащимся в проекции Uj на ось у. Множество всевозможных
элементов ф вида G.1) становится при фиксированном &? век-
векторным пространством, если ввести на нем линейные операции
по формулам
}, {Фу («/) + Ь (У)})-
Полученное векторное пространство обозначим через L*. Обозна-
Обозначим через Lj объединение всевозможных множеств L*.
. 2. Определение V-объектов. Пусть
— два элемента из Lj. Рассмотрим следующие 4 функции на М1:
/е/, /е/
(jc. jlsUj (jc, )
, ^= 2
Будем говорить, что. элементы ф и т|з эквивалентны и писать фн=1}1,
если эти элементы удовлетворяют следующим условиям:
а) существует такое конечное множество А пар (U, U'), где
U е ®^я> U' s s^o. чт0 для двух различных пар (t/j, U[), (U2, Ui)
из А пересечение Ux f\ V\ fl иг П ^а пусто, и
фя-^я== 2 «у. V' Фо — 'Фо = 2 Ри, и1,
(У. У')ед (У. У
где ау, у, Ри, у — бесконечно дифференцируемые функции с но-
носителями, лежащими в U[\U';
б) для любой пары (U, V) е Д имеет место равенство
«У. У (*, Уи (*)) + У U. У [Ру. У (XI/' (У), у)] (X) = 0.
Обозначим через X фактормножество Lx по отношению эквива-
эквивалентности -S3.
Введем на =5? структуру векторного пространства. Для этого
прежде всего заметим, что если ф, tyeLs, то найдутся такие ф',
т|з' е Z.2, что ф^ф', itsf и атласы, отвечающие элементам ф'
13 П. В. Маслов

386 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
и 1|Л совпадают. Такие элементы ф' и i|/ можно складывать.
Определим сумму классов эквивалентности {ф} и {i|)} формулой
Легко видеть, что определение G.2) не приводит к. неоднознач-
неоднозначности суммы. Произведение класса {ф} на скаляр определим
обычным образом:
Мф} = ЙР}.
Введенное нами векторное пространство % будем называть про-
пространством V-объектов на кривой М.
Пример. Функции на кривой как V-объекты.
Рассмотрим на М' V-объект, отвечающий следующему семей-
семейству «операторов перехода» Vu, w- если U — неособая карта
атласа &>?«> и U'—пересекающаяся с ней особая карта, то
Уи.и'Ч>(У) = Ч>(Уи(х)),;. VU:Uq>(x) = q>(xU'(y)). G.3)
Пусть ф — V-объект, отвечающий ' семейству операторов пере-
перехода G.3) и являющийся классом эквивалентности, содержащим
элемент ¦)
множества Lj. Поставим в соответствие объекту ф функцию ф
на М1, определенную формулой
Ф («о. Уо) =Цф/ (х0) + 2 Ф^ Ы. G-4)
где Ki — множество номеров неособых, а 7B — множество номеров
особых карт атласа <з^, содержащих точку (х0, у0) е М1. Из фор-
формул G.3) следует, что определение функции ф не зависит от вы-
выбора представителя объекта ф в Lj.
Обратно, пусть ф — бесконечно дифференцируемая функция с
компактным носителем на М1 и пусть &? — конечный атлас на М1.
Рассмотрим какое-нибудь разбиение единицы [в]}, подчиненное
атласу s^j
N
^еС°°(М), suppeyCt/y, 2^ = 1;
тогда каждая функция фу = гу-ф имеет-носитель, содержащийся в
Uj. Если Uj — неособая карта атласа &4, то положим
Уи,{*)), G.5)
а если Uj — особая карта, то
Ъ(у) = Ь(хи,(у), У). G.6)
Формулы G.5) — (ГЩ^ряаят в соответствие функции <р такой эле-

§ 7] V-ОБЪЕКТЫ НА КРИВОЙ 387
мент (®^, {фу (л;)}, {ф^ (у)}) множества Is, что справедливо равен-
равенство G.4). Тем самым установлено взаимно однозначное соот-
соответствие между пространством 35 V-объектов, отвечающих
операторам перехода G.4), и пространством C^iM1). В дальнейшем
мы будем отождествлять V-объект ф и соответствующую ему
функцию ф.
3. Линейные операторы на пространстве V-объектов. Опишем
теперь способ, которым мы будем задавать линейные операторы
на пространстве V-объектов 35. Так как 35 — фактормножество,
то естественно сначала задать некоторый оператор Ао на мно-
множестве Lz, а затем поставить ему в соответствие, как обычно,
оператор А на 35 па формуле
AW~{Af\. G.7)
Разумеется, для того, чтобы формула G.7) действительно опреде-
определяла оператор А на 35, необходимо, чтобы оператор Ао был
согласован с отношением эквивалентности as:
Если мы хотим задать линейный оператор на 35, то обычный
подход состоит в том, чтобы сначала задать линейный оператор
Ао на Lz- Однако L% не имеет структуры векторного пространства.
Поэтому назовем оператор Ао, действующий в Is, линейным,
если для каждого конечного атласа &# кривой М1 сужение
оператора AQ иа L^ есть линейный оператор, действующий в L^.
Структура векторного пространства на 35 введена таким образом,
что линейному в вышеописанном смысле оператору Ао на Is отве-
отвечает линейный оператор А на X.
Описанный способ задания линейных операторов на 35 явля-
является еще недостаточно гибким. Можно рассматривать также^ опе-
операторы Ао, определенные не на всем Lj. Достаточно предположить,
что оператор AQ определен на объединении такого семейства A^}
линейных подпространств AJJ^g с 1^, что L'^ с L^, причем
для любого ffcz35 найдется представитель в одном из подпрост-
подпространств L'^.
Пример. Дифференциальные операторы'"на кривой.
Снова рассмотрим пространство CfiM1) как пространство
V-объектов на М1. Зафиксируем произвольный конечный атлас &?
на МгЪ разбиение единицы {еу}, подчиненное этому атласу, кото-
которое мы будем называть весовым разбиением единицы.
Рассмотрим в пространстве L^g линейное подпространство
//^•, состоящее из элементов вида
{в/ (X, Уц. (X)) ф (X, yUf (X))}, [в] (XUj (у), у) ф (xUf (У), У)}),
где ф — произвольная функция из Cf^M1). Очевидно, что для любой
13*

388 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
функции феС™(М'), найдется ее представитель в L'^. Пусть
)х — множество номеров неособых карт, /2 —множество номеров
особых карт атласа о/ё'. Дифференциальный оператор L, Действую-
Действующий в Cf (M1), мы определим с помощью наборов операторов {L,}ye/,,
{Lj}jSll с дифференцируемыми коэффициентами по формулам
}, {*/ (у)}) = LИ?, {Фу (х)}, {Ф,- (у)}), ' G.8)
^(</) L,%Q,), /е/,.
Для того, чтобы определить псевдодифференциальные операторы
на М1, мы введем Соболевские пространства W^M1). Пусть снова
зафиксированы конечный атлас о/g и весовое разбиение единицы
{ej\. Положим для любой функции (peCj°(M1):
^ 2 И фу (¦«) Dw*(R) + 2 11фу(уIуг*(»)' GЛ0)
2
где ф;(лс), ф; (у) — компоненты представителя функции ф в под-
подпространстве L'^.
Задача. Доказать, что в случае, когда кривая М1 компактна, нормы
вида G.10), отвечающие различным конечным каноническим атласам и различным
весовым разбиениям единицы, эквивалентны.
Пример. Псевдодифференциальные операторы на кривой.
Определим пространство W^iM1) как пополнение векторного
пространства CfiM1) по норме G.10). Элементы пространств
W\{M}) будем называть обобщенными функциями на М1.
Пусть феС^СМ1), (а^, {фу-(х)}, {ф; (у)}) — представитель ф в
L'^- Рассмотрим два семейства псевдодифференциальных
операторов:
-4L.- <7-">
символы которых Hj удовлетворяют условию
R2) G.12)
для любого %eCf(R). Операторы этого семейства переводят
пространство S в себя. Предположим еще, что операторы
Hj (х, — id/dx), Hj \y, — idjdy) не расширяют носителя функции, на
которую они действуют (например, дифференциальные операторы;
не годится оператор с символом Я(|, г\) = е^). Поставим в соот-
соответствие семействам функций {ф/(*)}/<=/„ {<t>j(y)}mi, новые два
семейства {% (х)}jei» {V/0/)}/e/, по формулам

§ 81 КАНОНИЧЕСКИЙ ОПЕРАТОР НА СЕМЕЙСТВЕ КРИВЫХ 389
Тогда
принадлежит пространству Ьл- Тем самым определен некоторый
оператор Я: С? (М1) — Cf {M1). Из условий G.12) следует, что Я
ограничен как оператор, действующий из Щ+т{Мг) в W'^M1),
где | /1 «g s. Расширение оператора Я до гомоморфизма W{+m (M1) —->
— W's (М1) естественно рассматривать как псевдодифференциаль-
псевдодифференциальный оператор, отвечающий семейству символов Яу(?, ц).
§ 8. Канонический оператор на семействе незамкнутых кривых
В этом параграфе будет построен класс канонических операторов
с точностью до 0A/@^), где Л/ —любое число.
1. V-объекты для канонического оператора. Пусть уравнения
х = х(а, р\ со), р = р(а, Р, со)
'определяют семейство {М}ф, со)} бесконечно гладких кривых,
в фазовой плоскости х, р, удовлетворяющее условиям, описанным
в § 6. Пусть С —компактное множество в пространстве парамет-
параметров а, р, со, не содержащее точек, в которых со = 0. В § 6 мы
ввели понятие канонического атласа окрестности множества С
в пространстве параметров. Назовем полным каноническим атла-
атласом пространства параметров множество всех неособых и особых
карт всех канонических атласов, отвечающих всевозможным ком-
компактным множествам С.
Перейдем теперь к определению объектов, к которым будет
применяться канонический оператор $%i. Это будут некоторые
V-объекты в пространстве параметров. Мы допустим некоторые
отклонения от общих определений, данных в предыдущем параг-
параграфе, что связано с желанием не загромождать определения § 7
излишними подробностями, чтобы они не потеряли наглядности.
Опишем упомянутые отклонения. В определениях предыдущего
параграфа нужно заменить полный канонический атлас кривой
на полный канонический атлас пространства параметров, конеч-
конечный канонический атлас кривой — на канонический атлас окрест-
окрестности компактного множества С в пространстве параметров.
Элементы пространства Ьл будут иметь в качестве компонент
функции
Ф, (х, р, со), / <= /ь
Ф/ (р, Р, со), / е= /2,
где 1Х — множество номеров неособых карт, /2 —множество номе-
номеров особых карт атласа А. При этом мы будем отождествлять,
такие функции (8.1), которые отличаются только на О (со"'),
т. е. такие, разность которых есть произведение со"' на

390 АСИМПТОТИЧЕСКИЕ МЕТОДЫ 1ГЛ. V
бесконечно дифференцируемую функцию; для карты, содержащей
точку со == оо, отождествлять любые две функции (8.1), если точки,
в которых (о = оо, в карте отсутствуют. Иными словами, мы про-
производим соответствующую факторизацию в каждом пространстве
La- В силу этой предварительной факторизации нужно очевидным
образом видоизменить условия, которые определяют отношение
эквивалентности». .
Определим операторы перехода Vu, u>> которые переводят
функции от х, Р, со в функции переменных р, р, со, если V —
неособая, a U — особая карта, и функции от р, Р, ео —в функции
от х, Р, (о, если ?/' — особая, a U — неособая карта. Пусть U —
неособая, О' — особая карта атласа &?«>. Карте # отвечает функ-
функция аи (х, Р, со), которая удовлетворяет уравнению х = х(а,и(х,
Р, со), р, ©), а карте U— функция ац> (р, р\ со), удовлетворяющая
уравнению>р(ац>(р, р, со), р, со) = р. Пусть ф(<х, Р, со) —беско-
—бесконечно дифференцируемая функция с носителем, содержащимся
U'OU
Рассмотрим интеграл
09
' \Х) Р» / <у —2nl J ' .
—оо
Х -1 Ш Ф (а> Р' ffl) |се=ау-(р, Э. ®) dp,
где действие S (а, р, со) определено формулами F.3). Вычисляя
интеграл I (х, р, со) по методу стационарной фазы (при х =
= *(<х, р, со), (а, р, со) е U[\У'), получаем
/ (х, р, co) = (/sign соH 2J {(^УеШ$(аи (х-?'<*)'Ь<й) X
/=о
где
и функция со/+1Г/,х (х, р, со) принадлежит любому из пространств
«®s1.....s /.(R"+2). Что же касается функций %j, то в силу метода
стационарной фазы %j(x, р, со) прн фиксированной функции S
зависит только от значении функций ф и ее производных по a
до /-го порядка включительно в точке (av (х, Р, со), р, со).

§ 8] КАНОНИЧЕСКИЙ ОПЕРАТОР НА СЕМЕЙСТВЕ КРИВЫХ 391
Мы определим оператор Vu.w так, чтобы было выполнено
равенство
X [Vu, и'ф] (X, Р, <о) + Г,+1 (*, Р, @) } .
Иными словами, положим
Йг)'х/(*. P. »)•
/
2. Построение канонического элемента. Рассмотрим простран-
пространство X V-объектов в пространстве параметров а, р,^в, отвечающих
определенному в данном параграфе семейству операторов пере-
перехода Vu,w- Векторы из пространства X мы будем называть кано-
каноническими элементами.
Опишем стандартный способ построения канонического эле-
элемента. Пусть ф(а, р, (о) — бесконечно дифференцируемая функция
с носителем, содержащимся в компактном множестве С, ©^ =
= (?/у)/е/ — канонический атлас окрестности множества С, {в/} —
разбиение единицы, подчиненное атласу <&?', которое мы будем
называть весовым:
еуеС00, suppejezUj, Sey(a, р, ш)=1, (a, p, u)sC.
Функции ф, атласу &? и весовому разбиению единицы fa]
поставим в соответствие канонический элемент с помощью сле-
следующей процедуры: пусть е^'= {?/'/}/8=/- — произвольный канони-
канонический атлас окрестности множестйа С, {е)} — разбиение единицы,
подчиненное атласу &>?'; положим
Фу(*. Р,'«в)=в/(а, р, «о)в,(а, р, (о)ф(а, р, ?0Iа=а1/;(*.э,а»./е/;,
(8.3)
ФУ(р, р, <o) = e'i(a, Р, (о)ео(а, р, (о)ф(а, р, (o)|a=otfi(p,p.e),/e/;t
где
/3 —множество номеров неособых карт атласа е^, /2 множество
номеров особых карт атласа ©^, /1, /г —множество номеров
соответственно неособых и особых карт атласа &?'. Таким обра-
образом, мы для каждого канонического атласа &#' окрестности С
определили элемент
пространства L^'. Предоставляем читателю убедиться в том, что
для любых канонических атласов &#¦', о/?" имеет место эквива-
эквивалентность qu' ^ фл"» так что все элементы вида ф^< определяют
один и тот же класс {ц>^>} е «5Р.

392 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
Пусть &i,.... knAr2 — такие целые неотрицательные числа, что
kn+1. Введем в пространстве бесконечно дифференци-
дифференцируемых функций от х, р, со следующее отношение эквивалентности
яа: ф (х, р, со)я»г|)(х, р, со) тогда и только тогда, когда
С0'~*1~ — ~*в+1[ф (ДГ, Р, СО) — г|5 (ЛГ, Р, СО^'еа®*! kn-ti (R"+2)-
Соответствующее отношению эквивалентности *=« факторпростран-
ство обозначим через S*1 *n+a-'t Допуская обычную неточность
обозначений, мы будем обращаться с элементами пространства
S*1 *п+2>/ как с функциями от х, р, со, имея при этом в виду
их представители в C°°(Rn+2). Точно так же мы будем часто поль-
пользоваться такими обозначениями и выражениями, будто компо-
компоненты ф/(лс), Фу(р) элемента из L^ являются функциями, а не
классами эквивалентных функций.
3. Определение канонического оператора. Теперь мы можем
определить канонический оператор Kt на семействе кривых
/И1 (Р, со) с фиксированной параметризацией и фиксированной
«начальной» точкой Ро в пространстве параметров, действующий
из Z.2 в S*1 *»+*•'. Пусть а^ — канонический атлас окрестности
компактного множества С в пространстве параметров, ^ — мно-
множество номеров неособых карт атласа а^, /г —множество номеров
особых карт этого атласа. Пусть Ро принадлежит неособой карте
Uj, e е^, а у — индекс цепочки карт атласа а^, начинающейся
картой Ujt и кончающейся картой Uj.
Определение. Для любого элемента
Ф = (<&=/, {фу (дс, р.
пространства L^ положим
С Р,со)= У
дх -1/2
=?? J ^((^-§(а-р'щ)) |S Ги, iP,t,^j(P)dp. (8.4)
-00 /
Задача. Показать, что определение корректно в том смысле, что если
ф/-(*. Р. ш)}, {Ф}' (Р. Р> ш)}
—два представителя одного и того же элемента фЕЦ то
Теорема 8.1. Пусть ф,л|5е/,2 и ф==1|5.
Доказательство. Прежде всего заметим, что без умень-
уменьшения общности можно считать, что ср и. ф принадлежат одному

§ 8] КАНОНИЧЕСКИЙ ОПЕРАТОР НА СЕМЕЙСТВЕ КРИВЫХ
и тому же пространству L^. Пусть
393
Тогда
, P,
. P.
> Р.
, Р,
причем ф —\|з = 0. Значит, нужно показать, что
(фз=о
Пусть
ф = (<2^, {фу- (JC, Р, to)}/e/l, {фу(р, Р, to)}/e/,), фзО.
Согласно определению отношения эквивалентности з= рассмотрим
следующие две функции:
фн(а, Р, <о)= Цф/(*(а. Р. «о), Р, <о),
Фо(а, Р, со) = 2фу(р(а, Р, со), р, со).
mi,
Тогда найдется такое конечное множество А пар (U, W), где U —
неособая карта, U' — особая карта атласа а#?г для которого
выполнены следующие условия:
а) для любых двух различных элементов (UltU[), (U2, U'2)
множества А пересечение Ui [\-U\ f) U2 П ^2 пусто;
б) Ф„(а, р, ш)= ,2] Ци.и' (а> Р, и).
(С/, ?/')еД
Фо(«. Р. и)= 2 vy, у'(а, Р, (о),
(?/,?/') еД
где ji?/, ?/'. vy, ?/' —бесконечно дифференцируемые функции с носи-
носителями, содержащимися в t/fl^'l'
в) для любой пары (U, W) cz A
Ц?/ .?/' («У (*> P. ffl). Р. °>) + I Vu.U' V?/-,?/' («?/' (р, Р, СО) Р, СО)] (ДС, Р, СО) = 0.
Пусть v (U) — индекс цепочки карт,, начинающейся картой ?/у-0
и кончающейся картой U. Тогда
, Р, <о)=
(С/,
-1/2
,^(а, р, соI
(г sign со)т <и')
I J
Pl ш) X
-1/2
,, у (а, р, со) а=аи,{р^^р}. (8.5)
В силу метода стационарной фазы каждое слагаемое в правой

394 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
части (8.5) имеет вид
(/sign.co
дх
да
-1/2 x
a=«a(/(*. p, w)
fL, (о), Р, t») + [Vt/, у-7у. с/'(«У'(Р. Р> <°)> Р. «)] X
Х(х, р, (о)} + е'Ча5^(''Э'<аIЭ-<в)/-1^ Р, «) + М*, Р, «»),
" где функция /^ (дг, Р, w) имеет носитель, лежащий в области
определения функции «у (х, р, <о),.и функции r^ r2 удовлетворяют
условию
<оМ0 (ДГ| р, а) е Sd4<..., Vs (Rti), /=1,2
для любых &х, ..., &л+2. Значит, функция
Э.«).Э.«)Г1 (лг> р> 0)) + г8(лг, р, со)]
принадлежит пространству ^lf ..., k, (Rn+a), т. е. эквивалентна
нулю. Теорема доказана.
'Из этой теоремы следует, что оператор Ki индуцирует неко-
некоторый оператор из X в Sh> ••• • kn+v '. Этот оператор мы и назо-
назовем каноническим оператором S%i.
Пусть теперь Ах Аа+г— производящие операторы сте-
степеней k^, ..., kn+2 соответственно, действующие в банаховом про-
пространстве _б и определенные на всюду плотном линейном много-
многообразии D. Оператор . . '
2 s—I s+1 ,л+2 1 N (_k _.. _k
i. ^2, • • •, As-i, As, .,., An+i,-A^i) An+i ' \n+1
ограничен в В, если ф = 0. Пусть Ор — пространство линейных
операторов в В, определенных на D, факторизованное по сле-
следующему отношению эквивалентности ^: А' с^. А" тогда и только
тогда, когда оператор (А' — A") Al~?*~"'~kn-i ограничен.. Если
элементы ф' и ф" из Ls суть представители одного и того же
класса ф е «5Р, то
/s 2 s—1 s + 1
[Ki(p'][Alt А2 As_i, As, ....
л + 2
2 s—I s — \ s+I п+2 1 \
i, А2, ..., Л2, .... /4s_i, As, .... An+i, Ап+г). (8.6)
Класс эквивалентных операторов, из 6р, которому принадлежат
левая и правая части равенства (8.6), мы будем обозначать
/ s 2 s—I s + 2
[Ki4>][A\, Аъ ..., As_lt As, ...,
я+2
A

§ 9] КАНОНИЧЕСКИЙ ОПЕРАТОР НА ЗАМКНУТЫХ КРИВЫХ 395
§ 9. Канонический оператор на семействе замкнутых кривых
1. Определение канонического оператора Kt на L^. Рассмотрим
семейство замкнутых кривых М1 ф, <о), лежащих в фазовой
плоскости (х, р), задаваемое уравнениями
х = х(а, р, (о), р=р(а, р, (о),
где а —точка на окружности, р е R", ю принадлежит расши-
расширенной числовой прямой; функции х(а, р, (о), р(а, р,(о) предпола-
предполагаются бесконечно дифференцируемыми, в том числе н при (о = оо.
Для читателя, незнакомого с теорией многообразий, сделаем
пояснения, касающиеся некоторых топологических понятий, отно-
относящихся к рассматриваемому в этом параграфе пространству
параметров <х, р, ю. Сходимость последовательности точек
на окружности понимается как сходимость этой последователь-
последовательности на плоскости, на которой лежит данная окружность.
Сходимость последовательности точек расширенной числовой пря-
прямой к оо понимается очевидным образом. Будем говорить, что
последовательность {(ат, pm, (om)} точек пространства параметров
сходится к точке (а, р, ю), если
lim<xm = <x, lim pm = P, lim a>m — ca.
m-*oo m-»oo m-»oo
После этого понятия замкнутого множества и замыкания мно-
множества в пространстве параметров (а, р, ю) определяются так же,
как и в R". Компактное множество в пространстве параметров
(а, р, (о)—это замкнутое множество, содержащееся в некотором
множестве вида | Р | < const. Открытое множество — дополнение
замкнутого. Если ввести на окружности 6 Окрестности точки <х0
параметр t, то' в окрестности точки (<х0, р0, (оо) пространства
параметров каждую функцию от а, Р, ю можно рассматривать
как функцию от t, P, (о; это позволяет ввести понятие дифферен-
дифференцируемой функции, определенной на пространстве параметров
а, р» (о. В дальнейшем считаем, что из пространства параметров
удалены точки, в которых <а = 0;
Так же, как и раньше, вводятся полный канонический атлас
е^оо и канонический атлас о/? окрестности компактного мно-
множества.
Пусть (а0, Ро, <оо) — фиксированная точка в пространстве пара-
параметров, С = (Uu ..., Um) — цепочка карт, причем (<х0, р0, (оо) е Ux.
Рассмотрим в карте Ux функцию S1(a, p, (о), определенную
формулами
dS1(a, Pi ш)=р(а, Р, (о) -—¦ (а, р, (o)da, Sj (а0, Ро. «о)=О;
для того, чтобы интерпретировать символы -х-, da, мы здесь и далее
ОСЬ

396 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
будем отождествлять текущую точку а на окружности с поляр-
полярным углом этой точки.
Пусть (а1( plt (Oj) e(/j fl еУ2. Определим в карте U2 функцию
S2 (a, P, со) по формулам
dS2(a, р, со) = р(<х, р, co)Jj(<x, р, со) da, S^a,, fc, со,) =
= S](a1) Pi, coj).
Продолжая эту процедуру, придем к функции Sm (а, р, со) в Um,
которую мы будем обозначать через Sf(<x, P, to). Определим
функцию S (а, Р, со) с помощью формулы
Sc(a, P, to) = -Sc(<x, p, со) + р(<х, р, со)дг(<х, р, со).
Определим индекс Yc цепочки карт С так же, как и раньше,
в § 6. Кроме того введем V-объекты в пространстве параметров
точно так же, как в предыдущем параграфе.
Поставим в соответствие каждой карте Uj атласа в?? цепочку
С] карт этого атласа, начинающуюся с карты UJtX содержащей
точку (а0, р0, too), и кончающуюся картой Uj. Обозначим
Yc;- = Y/> 5C; = S;, Scf = Sj, Определим на L^ канонический
оператор Kt следующим образом: пусть
Ф = (а^, {ф/(дг, Р, co)}/e/l, {фу(р, Р, со)}/е/2);
тогда
, Р, со)^ ^ (is
felt
Х
дк
-1/2
a = at/. (х. р, а) фу (х, Р, со) + ^ (' Sign co)v/ X
1 /е/«
i/
dp
-1/2
г,
, Р,
2. Условие квантования. Справедлива следующая лемма.
Л е м м а 9.1. Пусть С — (Ult..., Um), где Um = Uu —замкнутая
цепочка карт атласа в^^. Тогда ус кратно 2.
Доказательство. Индекс замкнутого пути в простран-
пространстве параметров равен индексу окружности
Р = const, to = const, [х(а, р, со)-лг0]8+ [/>(«. Р, со)-р0р = ^)
проходимой на фазовой плоскости целое число раз по или против
часовой стрелки. Вычислим индекс окружности; он равен 2.
Лемма доказана.
Предположим теперь для простоты, что Р—одномерный
параметр. Из леммы следует, что функция
(х, Р\ со)

§ 9] КАНОНИЧЕСКИЙ ОПЕРАТОР НА ЗАМКНУТЫХ КРИВЫХ 397
не зависит от выбора цепочек карт Cj в точках, удовлетворяю-
удовлетворяющих условию
(о $ pdx— я==0 (mod2rc). (9.1)
Уравнение (9.1) связывает при заданном семействе {М1^, <о)}
переменные Р и ю. Уравнение (9.1) известно под названием
«условие квантования».
Пример. Пусть кривая /кгф, <о) имеет уравнениедг2 + Р2 = Р-
Тогда условие квантования принимает вид
сояр-л = 0 (тос!2я). (9.2)
Пусть е — произвольное вещественное число. Положим
Р((о) = —-—ii—, где [ею] — целая часть ею.
Если подставить р = р (ш) в (9.2), то это условие тождественно
удовлетворится. Заметим, что Р (ю) — ограниченная функция,
терпящая скачки в изолированных точках. Эта ситуация является
типичной.
Перейдем к общему случаю. Пусть уравнение
относительно неизвестной р имеет единственное решение
где Р (а, (о) — бесконечно дифференцируемая функция, причем
производные всех порядков от Р по со ограничены. Положим
-. в (в, т)= ^ ,
где [ею] — целая часть числа ею, и обозначим:
Р(е, (о) = Р@(е, (о), (о).
Тогда подстановка р = Р(е, (о) обращает условие квантования (9.1)
в тождество.
Оператор /Скв» определенный формулой
[ЛГквф] (х, е, (о) = [/Сгф] (дс, Р(е, со), ш),
назовем квантованным каноническим оператором. Квантованный
канонический оператор не зависит от выбора цепочек С/.
3. Регуляризация канонического оператора. Функция [/Сквф]
(дг, е, со) не является гладкой функцией. Поэтому ее нельзя
использовать для построения функции от операторов. Для того
чтобы обойти эту трудность, регуляризу.ем канонический оператор.
Пусть г — целое число. С элементом ф е Ls свяжем функцию

398 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
» заданную в R3 равенством:
S е', ©)&', (9.3)
где p(e)eCf (R). Оператор Крег назовем регуляриэованным кшю-
ническим оператором.
Лемма 9.2. Пусть r^Sj+Se+l. Тогда
Доказательство. Обозначим f(x, е, ю) = [Ккв ф] (дг, е, ю),
00
f(x, е, <о) = [Крегф](*, ё, ю)=-^г ^ p(e~e')f(x, е\ to)rfe\
Функция f(x9 e, со) имеет вид
/(«.•.»)-*(*. Р. •»I11_|№^. (9-4)
вде Л(дг, Р, «о) = [»!ф](ж. Р, о),
где функции h и Р удовлетворяют следующим условиям:
а) Л бесконечно дифференцируема;
б) h(x, Р, (о) = 0 при достаточно большом |Р|, h(x, Р, (о) = 0
при достаточно малом | со |;
в) для любой функции e(x)eCS°(R), равной 1 в достаточно
большой окрестности нуля, функция [1 —e(x)]h(x, $, (о) при-
принадлежит любому соболевскому пространству;
г) для любой функции е (х) s Cj° (R) функция
д \г(д\г,(д y.e(x)h(x, р, а»
\г(д\г,(д y.e(
при г ^ /"i + rs -J- 1 и любом г8 (с = const зависит только от ги гй,
г9, г);
д) функция Р (?, (о) бесконечно дифференцируема;
е) Р ([em], ю)-*-оо при е-»-оо равномерно по F;
ж) производные всех порядков от Р (?, (о) по (о ограничены
на любом множестве, на котором ограничено | (g, со).
Сделаем в интеграле (9.3) замену переменных | = е'ю. Получим
g (*, е, о) = -j^r J р (е —|) h (х, j* ([Б], о), ш) 4- (9.5)
Дифференцируя правую часть (9.5) под знаком интеграла и
используя свойства а)—ж), получаем утверждение леммы.
Заметим, что g(x, e, ю) = 0 при достаточно большом |е|.

§ 9] КАНОНИЧЕСКИЙ ОПЕРАТОР НА ЗАМКНУТЫХ КРИВЫХ 399
Рассмотрим также оператор /Срег. определенный формулой
-> 00 .
[К'регф] (х, е, ш) = -^- \ e-(e-e'Jw2s КквфК-ft е'. <o)de', (9.6)
— 00
где х (е) е Cf (R).
Лемма 9.3. Пусть /•^s1 + rss2 + rss3-f rs—r3-f 1, если
м r^Sx + Ss+l, еслм s = 0. Тогда
Доказательство. Сделаем замену переменной интегриро-
интегрирования:
? = е'со.
Получим: ' ,
%\ ts
»Г. A(jf.IT([g,iD],iD),iD)d|, (9.7)
00—
где функции h и ft — те же, что и в доказательстве предыдущей
леммы. Дифференцируя правую часть (9.7) под знаком ннтеграла,
получаем
[Крегф] s и^- ¦¦'. >> т,
где sf>S/+ .1/2, /=1, 2, 3. Отсюда следует утверждение леммы.
Рассмотрим в пространстве «S8St. st, s, (R8) следующее отношение
эквивалентности:
i
Ф(*, е, (о)^ф(д:, е, а)
тогда и только тогда, когда
Теорема 9.1. Писть ф, ifcrL^ м ф^т|). ТогЗа лрм t
+ s3+l ' /
при /•^max{s1+s3+l, Si + rssa + /-ss3+rs — s^}
/Срегф «»* /Срег'Ф-
Доказательство. Следуя доказательству теоремы 8.1,;
достаточно показать, что если фэгО, то Крегф^О и /СрегФ
Пусть ф = 0. Рассуждая, как в предыдущем параграфе, получим:
[/СРегФ] (дг, е,- a^srw $ е"(8"Й ^А (х, f ([|], со), to) dg,
—оо

400 АСИМПТОТИЧЕСКИЕ МЕТОДЫ . [ГЛ. V
где функции h и |Г удовлетворяют условиям а) —ж), сформули-
сформулированным раньше. Отсюда получаем утверждение теоремы.
Пусть теперь Аг, А2, А3 — производящие операторы степеней
s]( s2, s3 соответственно, действующие в банаховом пространстве В
и определенные на всюду плотном линейном многообразии D.
Введем в пространстве Нот (В, В) отношение эквивалентности ~:
А' ~ А" тогда и только тогда, когда оператор (А' — А") А[+1
ограничен. Факторпространство Нот (В, В) |а обозначим через
бр (В).
Из теоремы 9.1 следует, что если элементы <р' и <р" из Ls
суть представители одного и того же класса <ре<5? и г удовлет-
удовлетворяет условиям теоремы 9.1, то
L А,)^[Крегф"](А, L А3), (9.8)
l, L Л3) ^ [/CPer9"TUb L Л3).. (9.9)
Класс эквивалентных операторов из Ор (В), которому принадле-
принадлежат левая и правая части равенства (9.8), обозначим через
[^регф] \Ац А%, А3)', класс, которому принадлежат левая и пра-
правая части равенства (9.9) — через [в^регф] \Аи Л2) Л3).
Аналогично определяются регуляризованные канонические опе-
операторы, отвечающие другим способам упорядочения тройки Аъ
А%, А3, например,
[^"регфКЛ, к, Аа), [^^](i1( Л2, Аа),
где <р — произвольный канонический элемент.
§ 10. Пример на коммутацию канонического оператора
с гамильтонианом
В этом параграфе рассматривается простейший случай, когда
кривая М1ф, ш) не зависит от параметров Рим. Для удобства
обозначений мы полагаем со = 1//г. Чтобы проиллюстрировать
общую ситуацию, рассмотрим сначала следующий пример.
in
Пример. Найдем «почти» решение уравнения -^ у" + ху — 0,
А>0 в области |xj<a с точностью до O(hs), т. е. найдем такую
функцию у(х), которая после подстановки в данное уравнение
дает невязку O(h2).
Эта задача тривиальна, так как после 1/А-Фурье-преобразо-
вания приходим к уравнению ~у—Ш~ = 0, которое является
линейным уравнением 1-го порядка. Тем не менее, мы построим
ее решение с помощью канонического оператора, для того, чтобы

§ 101 ПРИМЕР 401
проиллюстрировать общую ситуацию. По той же причине мы
будем использовать не простейший из канонических атласов.
Будем искать у в виде y = Ki4, где Ki — канонический опера*
тор (mod О (Л2)) на кривой А = \х = %, Р = а\, ассоциированной
с гамильтонианом ~ -nzrt — x- (В каноническом операторе делаем
подстановку ш = -г.) Рассмотрим на Л канонический атлас, состоя-
состоящий из неособых карт Ult U2 и особой карты U3, где карта (У,
отвечает области а>1, i/a — области а<—1, U3 — области
| а | < 2; рассмотренный случай по существу является общим.
Канонический элемент ср, на который действует оператор К,
задается тремя функциями: cpi(a), Фг(а), фз(а)> зависящими также
и от Л, с носителями в картах Ult t/2, Ua соответственно; эти
функции определяются с точностью до О (Л2). Другая тройка функ-
функций ij>i(a), ij>2(a), ifo(a) определяет тот же канонический эле-
мент ф, если выполнены следующие условия (по mod О (Л2)):
Ф1(а) = г|I(а) при а>2,
ф2(а)=г|J(а) при а< —2,
Фз (а) = \JK (а) при |а|<1,
Ф1 («) + Vi, зфз (а) = Ь (а) + Vh з^з (а) при аЕ^П U3,
Ф2 (а) + V2>дфз (а) = ijJ (а) + V2,з^з (а) при а е= U2 П ^з.
где Vi,3> V2|3 —операторы перехода из карты U3 в карты Uy и ?/2
соответственно, которые в данном случае согласно (8.2) имеют вид:
j
Канонический оператор имеет вид:
где
Обозначим Н = — -п j-з. Имеем:
где
n n d ., [ 5

402 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
Тройка операторов Ри Рг, Ps определяет оператор Р, действую-
действующий в пространстве канонических элементов, так как выпол-
выполнены условия
VP, = PtV mod О (Л8), VPt=PiV mod 0 («•).
Таким образом, имеет место следующая формула коммутации кано-
канонического оператора с гамильтонианом:
Значит, нужно решить уравнение Р<р = 0 в окрестности области
aa«g2o, т. е. найти такой канонический элемент <р, чтобы эле-
элемент л|) = /)ф определялся функциями i|>i(a), ^a(a), tya(a), где
\|),(а)=^0 при |а| = 1/2а+е, е —произвольное положительное
число. Элемент q> определяется тремя_функциями: фх(а), ф?(а),
Ф8(а). Уравнение Яф = 0при \a\<.V2a-{-e будет удовлетворено,
если функции <р/ удовлетворяют ^следующим условиям:
a) P^i(a)=O
б) р!фх (а) + VPs(fs (о
в) Рзфз (а) = 0
г) Р2фг (а) + ^Я3фз (а
Д) РаФа(а)=О
при 2<а<У2а+е,
i) = 0 при 1 <а<2,
, при | а | < 1,
;) = 0 при — 2<а<—1,
при —Y2a — е<Са< —2
Так как Ри Р%, Ря определяют оператор Р, то условия б) и г)
можно переписать в виде:
б') Р1(ф1(а)+^ф3(а)) = 0 при 1
г') Р2(фг(а) + Уф3(а)) = 0 при -
Начнем с уравнения в):
фН«)=о.
Решение этого уравнения (с точностью до произвольного постоян-
постоянного множителя) есть
Фз(а) = 1 при |а|<1.
Обозначим теперь
Уравнение б') принимает

§ 101 ПРИМЕР 403
Решаем это уравнение по теории возмущений!
х=х@)+ЛхA),
^=0, Х(о)(а)^Х(о)A) = 1.
da ~~ + ' 18а4 a8 da + 2a2 da») X W>
da 8a*' * ^'"~ 24'
Отсюда получаем:
5CA)(a) ХИ1
Пусть e(a) = l в окрестности 1, e(a) = 0 в окрестности 2. Можем
положить ,
(a)=e(a)x(a), ф1(а)=-A-в(а))х(а), Г<а<2.
Отсюда находим ф8 (а) при 1 < а < 2:
¦ При а = 2 получаем следующее начальное условие для
ФхB)=ХB)-1—§-.
Далее решаем задачу Коши:
«-0, «2)-!,
Получаем
yi v/— ч yi v~/ 24a8
Ф1(°0 = 1 — <jZZJT при
Аналогично находим:
*"(а)-^*'(а)] при -
где ё (а) = 1 в окрестности 1 и ё (а) = 0 в окрестности — 2,
при -21
~ прн —/2о -е<а<-2.

404
АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
Теперь легко выписать ответ и выяснить, как он связан с точ-
точным решением, которое можно написать в этом примере?
Пусть теперь М1 — произвольная гладкая кривая в фазовой
плоскости (х, р), К — канонический оператор mod О (А'+1) на кри-
кривой М1 — {х(а), р(а)}. Оператор действует на канонические эле-
элементы. Пусть &? — {С/у}/ g / — канонический атлас кривой М1.
Канонический элемент ф задается семейством функций {фу (а)},- € /,
где supp(fj-sUj. Функции фу определены modO(hl+*), ф/S
еСГ(?/у).
Пусть &?' = {U'i}i<z /' — другой канонический атлас. Семейство
функций % (а) е= С" (Щ), j e /' определяет тот же элемент ф,
что и семейство {фу (a)},- g /, если выполнены следующие условия:
а) в достаточно малой окрестности любой нефокальной точки
на М' выполняется равенство
/6/. /6/2 /6/1 /6/2
где
Jt — множество номеров неособых карт атласа &#,
1[ — множество номеров неособых карт атласа &&',
/2—множество номеров особых карт атласа ет?,
/g —множество номеров особых карт атласа e/Z'.
V — оператор перехода от особых карт к неособым (он опре-
определен в окрестности любой нефокальной точки и имеет вид
V =* 1 + 2 (thy Lk mod О (hl+l),
где Lb — дифференциальный оператор порядка 2k);
б) в достаточно малой окрестности любой фокальной точки
на М1 выполняется равенство
I] Фу(«)= 2 Фу («).
/€/s /6/s
Канонический оператор К действует по формуле
2
/6/
где
У[
da

101 ПРИМЕР 405
при /е/| и
dp
a=«/(pb
при / e /2-
Пусть Я — гамильтониан, т. е. псевдодифференциальный опе-
оператор вида
¦и °)г(* i h)
Н = @Л \х, р, hj,
где р = — Ж-гГ (оператор h коммутирует с х и р, поэтому
неважно, каким по порядку он действует), и пусть кривая М1
ассоциирована с гамильтонианом Я, т. е.
е%^(^(а), р(а), 0)=0,
•и параметр а выбран так, чтобы на М1 выполнялись соотношения
da=- dx - dp
Нр (х, р, 0) Яж(д, р, 0) •
Тогда для любого / е / имеем:
где Яу имеет вид
где Я/*'—дифференциальные операторы, причем
где /(а) не зависит от /; легко видеть, что в окрестности любой
точки на М1 оператор Pj зависит только от того, является ли Uj
неособой картой или особой.
Семейство операторов {Pj} определяет некоторый оператор Р,
действующий в пространстве канонических элементов, иными
словами, если Ujl — неособая карта, а Uj, — особая карта, то
для любой функции х е С^° (Ufl f| Ujs) справедливо равенство
PhV% = VPh%.
Действительно, имеем
Я/Сф = — ihKty,
где канонический элемент. \J) определяется семейством функций
tyj — Pj4j. Остается показать, что канонический элемент if опре-
определяется каноническим элементом ф однозначно, или, что то же
самое, что канонический оператор мономорфен:

406 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
Пусть канонический элемент ty отличен от нуля; докажем, что
/Сф Ф 0. Пусть, например, ty (а) Ф 0. Обозначим х = х (а) и рас-
рассмотрим функцию Kty в достаточно малой окрестности точки X.
Выберем на М1 такой канонический атлас &&, что любые две
карты этого атласа, проекции которых на ось х содержат точку X,
имеют непересекающие проекции на ось р. Существует такой
канонический элемент ?, определяемый семейством функций {Ч^},
отвечающим атласу е/?', что выполнены следующие условия:
а) % = 0, если проекция карты 11 j на чось х не содержит
точки х.
б) /ОР = /<Чр в окрестности точки X. Достаточно убедиться,
что КЧ?ФО. Обозначим К^(х) — Ф(х). Имеем в'достаточно малой
окрестности точки X
Sr mod О (Л00),
I Ja=aj(p)
где Uj — карта, содержащая точку а. Таким образом,
что и требовалось доказать.
Рассмотрим задачу: найти такую функцию у(х), чтобы урав-
уравнение Ну = 0 удовлетворялось при | х | < а с погрешностью 0 (Л'+2).
Будем искать у в виде
Для канонического элемента <р при этом получаем условия:
supp Ру(\Ма = ф,
где Мв —прообраз отрезка 1*|<о при проектировании М1 на
Кй й
рр р 1| р рр
ось ^.Канонический элемент <р, удовлетворяющий этому условию,
можно построить с помощью теории возмущений так же, как это
было сделано в рассмотренном выше конкретном примере.
§11. Коммутация оператора Гамильтона
с каноническим оператором
Пусть {pi(a), р4(а)} — весовое разбиение единицы на М1, т. е.
р1( р2 е С00, supp px не содержит точек, не входящих ни в одну
неособую карту полного канонического атласа е^м кривой М1,
supp pa лежит в объединении особых карт атласа е^ю; Pi + P2= 1.
Весовому разбиению единицы {рх, ра} отвечает оператор ?, пере?
водящий функцию ф (определенную mod О (hl+1)) на М1 в кано-
канонический элемент на М1, задаваемый в каноническом атласе
erf = {Uj\i g / формулами
Фу (а) = е, (а) ра (а) <р (а) + Ve, (а) р2 (а) Ф (а),
если С/у —неособая карта,
Ф; (а) = V^ej (а) pt (а) <р (а) + ej (а) р2 (а) ф (а),

§111 КОММУТАЦИЯ С ГАМИЛЬТОНИАНОМ 407
если Uj—особая карта; здесь {ej} — разбиение единицы, подчи-
подчиненное атласу &#.
Обозначим: S = KX>.
Лемма 11.1. Оператор S обратим.
Доказательство аналогично доказательству обратимости кано-
канонического оператора К-
Лемма 11.2. Пусть кривая М1 ассоциирована с гамильтониа-
гамильтонианом Н. Тогда для любой функции <р из области определения опе-
оператора S функция #Sq> имеет вид —ihSty, где ty —некоторая
функция на М1. -
Доказательство. Имеем HS(p — HKx,q> = — ihKP'&f).
Пусть в атласе а^ = {^у}/'«'/ канонический элемент Я^ВФ опреде-
определяется семейством функций {^(а)}. Достаточно показать, что
для любого /s/ существует такая функция %j на М1, что эле-
элемент 'з^ЗС,- определяется семейством функций
Пусть Uj — неособая карта. Тогда функция X/ определяется
из уравнения
(Pi + Vpo)%j = b. A1.1)
Оператор V имеет вид
Поэтому уравнение A1.1) переписывается в виде
Функция %j находится теперь по теории возмущений. В случае,
когда Uj — особая карта, функции %}- находится аналогично. Лемма
доказана.
Теорема 11.1. В условиях леммы 11.2 имеет место следую-
следующее коммутационное соотношение:
A1.2)
где г (а) некоторая функция, Р$ — дифференциальные операторы
на М1.
Доказательство. Согласно леммам 11.1, 11.2 имеет место
..соотношение коммутации A1.2) с некоторым оператором Рф, дей-
действующим на функции, определенные на М1 по модулю О (Л'+1).
Остается показать, что Рф имеет вид A1.3). Для этого достаточно
рассмотреть действие этого оператора на функцию с носителем

408 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
в одной карте канонического атласа. Пусть, например, ф (а) —
функция с носителем в неособой карте [/,-. Тогда канонический
элемент 3?ф можно задать набором функций: фй(а) = 0 при кф\,
Ь (а) = Pi (о) ф (а) + Vp2 (а) ф (а).
Применяя к элементу 3?ф оператор Р, получим элемент Я^ВФ»
который можно задать следующим семейством функций {% (а)}:
tyft(a) = 0 при k-ф],
i
Ь («) = -^Г1 + г И <Ма) + 2 (- Wp^Vj (a),
где г (а) — некоторая функция, Pf* — дифференциальные операторы.
Вычисляя теперь функцию ф = Яфф = ^Pi&p по теории возму-
возмущений так же, как при доказательстве леммы 11.2, получаем
формулу A1.3) для данного случая.
Случай, когда ф (а) —функция с носителем в особой карте,
рассматривается совершенно аналогично. Теорема доказана.
Теорема 11.1 позволяет свести уравнение Ну — Ок уравнению
Яфф = 0. Решение последнего уравнения легко построить по тео-
теории возмущений.
§ 12. Общее каноническое преобразование
псевдодифференциального оператора
Пусть (a = ih-^, Т = [/Сф]{х, to), где К. — канонический оператор
на семействе кривых, зависящем от параметра ш, ф —некоторая
вещественная функция. Рассмотрим преобразование псевдодиффе-
псевдодифференциального оператора L = f\x, ш, со) по формуле
L-+T*LT. A2.1)
Это преобразование содержит в качестве частных случаев кано-
канонические преобразования § 1. В этом параграфе будет получено
асимптотическое разложение преобразования A2.1) с точностью
до О (Л2).
Лемма 12.1. Пусть М1: {х = х(а), р = р (а)} — гладкая кривая
в фазовой плоскости (х, р), К — канонический оператор (с точ-
точностью до О (и-1) на М1, f(x) —гладкая функция. Тогда для любых
функций ф!(а), ф2 (a) s Cf (Ml) имеет место равенство
(/ (х) [Kq>J (х, со), [Кф2] (х, co))L, {х) =
°=<f(x («)) Ф1 (о), Ф2 (o))tl (а) + О A
Доказательство., Очевидно, достаточно рассмотреть слу-
случай, когда носитель функции / достаточно мал. На кривой М1

§ 121 ОБЩЕЕ КАНОНИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ 409
можно тогда выбрать такой канонический атлас ©^, что если
проекции двух карт Uj, Uk, j^k атласа о/Z на ось х пересе-
пересекаются с носителем функции /, то проекции этих карт на ось р
не пересекаются. Пусть {Uj\iej0—семейство карт атласа &>?,
проекции которых на ось х пересекаются с supp/. Обозначим
через U'j множество л [(supp/) (\(nU/)], гДе л — проектирование
на ось х. Тогда с точностью до 0(со-00)
где supp фу с Uj, supp ф2у с: <Л, фу (а) = ф2у- (а) при ое(/;,
Фу (а) = ф2; (а) при а е ?//. Если ¦ j^k, то (f(x (а)) фу (а),
ф2* (а))*., (а) = 0. Кроме того,
(/.(*) [Кфу] (Jf, <в), [Куи] (х, ш)) = 0 (от1). A2.2)
Действительно, обозначим:
фу (х) = [/Сфу] (х, ш), bk(x) = [K<ptk](x, <o), ifi/(x)/(x) = Yy(x)
(функции фу, ф2* зависят от ш как от параметра). Имеем:
где функции %i/ и Хг* имеют непересекающиеся носители. Обо-
Обозначим: Sj(p)=S(a,j(p)). Имеем:
так что на носителе функции ф24 функция Ту (р) равна 0 (ш).
В силу A2.1) достаточно доказать утверждение леммы в том
случае, когда ф!(а) = фу(а), ф2 (а) = ф2;- (а). Но в этом случае
утверждение леммы непосредственно следует из определения кано-
канонического оператора.
Лемма 12.2. Пусть М1:{х = х(а), р — р (а)} — гладкая кривая
в фазовой плоскости (х, р), Ki — канонический оператор на А
(с точностью до 0(оГ2)), f(x) —гладкая функция, ? — оператор,
стандартным образом переводящий гладкие функции на М1 в кано-
канонические элементы, отвечающий вещественному весовому разбиению
единицы. Тогда для любой вещественной функции ф (а) е Cf (M1)
имеет место равенство
(/ (х) [Ki ЬФ] (х, <»). f (х) [АГ^ф] {х, to))Ll w =
- (| / (х (о))|«ф (а), Ф (а))^ (а) + 0 (ш-«). (•)
Доказательство аналогично доказательству леммы 12.1. Отме-
Отметим только дополнительные по сравнению с доказательством
леммы 12.1 моменты.

410 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
1) Пусть функция ф имеет носитель, лежащий в неособой
карте U. Тогда, как нетрудно проверить, пользуясь определе-
определением операторов Vu, w, получаем:
где L — некоторый дифференциальный оператор (второго порядка)
с вещественными коэффициентами, |с| = 1. Утверждение леммы
справедливо в этом случае, так как -
2) Аналогичная формула имеет место для со-Фурье-образа
функции /С^ф, если (/ — особая карта.
3) Пусть (/ — особая карта. Обозначим •§ (х) = [/Ci&p] (x, со),
4yW=/Wi>M,,s1(p)=S(a(p)), ъ='гШУ-
Разлагая функцию
A2.3)
по степеням со, получаем, что в равенстве A2.3) с точностью
до О (а) можно заменить оператор /( — g- + 5i (p)) на оператор
где Z^—дифференциальный оператор, коэффициенты которого
вещественны, если вещественна функция / (последнее можем пред-
предположить без уменьшения общности). Рассмотрим множество опе-
операторов, зависящих от параметра со-»-оо вида
Л + ^а + 0(ш-2), A2.4)
где Аи А2—непрерывные операторы, действующие в Cf и пере-
переводящие вещественные функции в вещественные. Множество опе-
операторов вида A2.4) образует кольцо х относительно композиции
операторов:
(Л + { А2 + О («-•)) [А, + -^ At + О («"•)) - АХАШ + ^ Л + О (ш-«).
Следовательно,
? || |/2 (/ (^ (а)) +1 ^) Ф(а),
откуда и следует утверждение леммы в данном случае.

§ 12) ОБЩЕЕ КАНОНИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ 411
Замечание. Лемма 12.2 останется верной, если в левой
части (*) заменить f (х) на оператор / (х, ——-ц-), а в правой части —
f(x(a)) на f(x(a), р(а)). Доказательство полностью аналогично.
Теорема 12.1. ПустьТа = {(х,р): х = Х(а, ®),р = Р(а, со)} —
однопараметрическое семейство кривых в фазовом, пространстве
R?X Rj, причем D (X, P + a>)/D (a, /?) = 1.
Рассмотрим канонический оператор [Kfp] (x, со) на семействе Гш,
примененный к вещественной функции ф (а, со) е Cf.
Пусть Т — [К^]\х, со), где со = — iho/dx. Тогда в простран-
пространстве L2(R)
(e У ф (i, ш)+А2Я2 (А),
гЗе оператор /?2 ограничен в L2 равномерно по п: | /?2 (А) || ^ С.
Доказательство. Из определения канонического опера-
оператора следует, что [К<р](х, со) имеет компактный носитель Q.
Пусть Qoj —проекция Q на ось со;
Qx = {(jc, со', со): (*, cd)sQ и (лс, co')eQ}.
Рассмотрим в окрестности Qx некоторое конечное разбиение1
единицы {/й(*, со', (uJJcCf, в котором носители/^ достаточно
малы. Тогда
где черта обозначает комплексное сопряжение. Докажем, что
ДД ш, to) [/Сф] (i, ш) Ш (i, ш) -
= ф(*. м)ф(х, и)ь(?(х(х, а)+х[х, ш)), ш, ш) + О(А«).
A2.5)
Суммируя затем эти операторы по ц, получим утверждение тео-
теоремы.
Пусть я, я —проекции кривой Г^ на оси х и р соответст-
соответственно. Учтем, что носитель /ц, сколь угодно мал. Тогда если
проекции n~1^supp/(l(jc, щ, а')\ при со, co'eQa) пересекается
с картами Ult ..;, Ui канонического атласа Г^, то можно счи-
считать, что
е1(л~1{р+& — со', со), со^еДлГ1^, со'), со')=О
при i^j; со, со', co'eQu), где {et(a, со)} — разбиение единицы,
подчиненное каноническому атласу. (Если это не выполнено, то

412 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
можно для данного /й выбрать другой канонический атлас и вос-
воспользоваться инвариантностью канонического оператора при замене
атласа.)
На носителе /^ канонический оператор имеет вид
S *. со),
и поэтому
/и {х, м, м) [Kq>] {х, и) [Щ (х, со) =
= " ? [*foei)](*. *>) № (ФО)] (*. «»)/i. (i ». ш). A2.6)
Докажем, что
U ) U ) = A2i?2 (Л) при
}
A2.7)
где |/?а(А)||^с. Действительно, имеем
Fx^p [К (феО] (х, со) = е~ ^ '<Р> в) у, (р, со),
, ш'),
где
%(р, со)\|зу(р + со — ю', со') = О при ю, co'eQb,. A2.9)
Поскольку носители %, % не пересекаются, то можно считать,
что в A2.8)
5,- (р, со) = S (р, со) и Sj (p, со) = 5 (р, со),
где S (р, со) — некоторая гладкая вещественная функция. Тогда
't)] {к ш) [/< (фе/)] (i, ш) /„ (i, a,
p = T$.TXjj A2.10)
где
/n def f -u\-Px~s \P. <">/J ( l !\ >
rff = \eft g(,p, w, cojdp,

§ 121 ОБЩЕЕ КАНОНИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ 413
Разлагая оператор, стоящий в правой части, по степеням h,
получаем:
*J = h\lfrlP, «'). <">'> «>J, %(p, */) +
m—1
+ S И)*У(%(Р. (D') + (-//j)mQH(p, 0)', Ш),
/1=1
где VA\ ..., V' — известные дифференциальные операторы,
Q|b)e^(R3) для всех г.
Но в силу A2.9)
следовательно, согласно результатам § 1 имеем:
Поэтому, учитывая A2.10), для доказательства A2.7) доста-
достаточно оценить норму в <$?0(R3) символа оператора T|(.TQJm>, т. е.
норму функции
, со', <*) = (-
Имеем
®о (R.v X R(b' X
X
Этим доказано A2.7). Из A2.6) тогда получим:
/й (*, i, ш) [/<ф] (Д ш) [Щ (Д ш) =
= 2 [K№j)](x, a)[/C((pey)](i, ш)/йЛ ш, ш
По теоремам § 1, этот оператор преобразуется так:

414 АСИМПТОТИЧЕСКИЕ МЕТОДЫ [ГЛ. V
Далее имеем
(фв,)(х, a)(<?ej)(x, со') = О при ij&j; со, co'eQ,»,
поскольку мы, в частности, предположили, что
suppe,(*, a)()suppej(x, со') = Ф Щ>и 1ф}\ со, co'eQ,».
Тогда выражение A2.11) совпадает с правой частью A2.5), что
и доказывает A2.5). Теорема доказана.
Следствие. Пусть f &Cco(RxxRe)>xRe,) "
<p = <po(*, со) + (—ih) (px (x, <о)Ч-А«<р,(дг, со, А),
^ Фо» %_ —вещественные функции, ф0, <рх, <paeCS°,
SUP ЙФаHuj-i-/ю у» s<=cr при достаточно большом г.
при выполнении условий теоремы имеет место равенство
, со, ш)[[/Сф](х, со)] =
<ро(*. ш)
(А) |

ГЛАВА VI
ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА— ЯКОБИ
§ 1. Основные определения и формулировки теорем
На примерах волнового уравнения (§ 8 Введения), уравнения
колебаний кристалла (§ 8 введения) и уравнения Шредингера
для осциллятора (§8 введения) мы убедились, что проблема оты-
отыскания асимптотического решения этих уравнений приводит
«в нулевом приближении» к уравнению с частными производными
первого порядка, которое мы называем уравнением характеристик,
или иначе — уравнением Гамильтона -г Я коби Это последнее урав-
уравнение не содержало параметра, по которому искалась асимпто-
асимптотика исходной задачи. Его решение S (*, t) было действительной
функцией. В случае уравнения Шредингера, например, эта функ-
функция определяла фазу колебаний, и решение, после выделения
множителем выражения exp -^ S (*, f), можно было разложить
в асимптотический ряд по степеням h. Для ряда задач, однако
(в которых имеет место явление «поглощения»), аналогичная функ-
функция является комплексной, так что expyS(*, /) быстро затухает
при А->0 в области, где ImSt*, /)>0. Если исходная задача
решается с точностью до О (hN), то ясно, что в области, где
lmS(x, 0>°» значение величины ReS(x, t) несущественно.
Поэтому асимптотические решения такого типа приводят к более
сложной постановке задачи на уравнение первого порядка, чем
та, с которой мы сталкивались в приведенных выше примерах.
К формулировке этой задачи мы сейчас и перейдем.
Задача заключается -в том, чтобы найти не зависящие от h
вещественные функции Sx (*, t) и S2 (*, t) такие, что Sx (х, t),
S2(x,' 0 «= с°°(R"f°» Л). si(x> 0^° и Для любого е>0
на компактном множестве выполнены соотношения *)
( '
где Si (х, 0) = S10 (*), Sa (*, 0) =S20 (*) Ss 0, а функции / (p, p, x, t)
Поэтому можно считать, что все рассматриваемые функции имеют ком-
комй носитель.
пактный носитель

416 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ (ГЛ. VI
и f(P» P, х> t) при р — 0 связаны соотношениями
f~ = 1 f~ = f /~~ = f f~~=_"i
Ip I p> fp Ip» Ipp Ipp> Jpp Ipp
и выполнено условие }(g, 0, x, t)^0 (/, / не зависят от /г).
Определение. Приведенную выше систему мы будем назы-
называть диссипативной системой *) Гамильтона — Дкоби.
Основной задачей этой главы является построение глобаль-
глобального решения этой системы.
Введем следующее обозначение. Пусть f (х) 2= 0 — гладкая
функция. Мы будем обозначать через 0f(ha) функции g^eC05,
удовлетворяющие оценке
дх\1...дх'п
h
= 0 (на~Щ . при а-Ш
Нетрудно убедиться, что это соотношение эквивалентно неравенству
дх1,1...дх'п
1 п
2
> где Ci — некоторая константа.
Рассмотрим 2п-мерное евклидово пространство R"xR" с, коор-
координатами ри ..., рп, <7i ЦП' Это пространство будем называть
фазовым пространством.
Многообразие А = {р~р(а), q = q(ot,)} размерности п, удов-
удовлетворяющее условию
dPi dqi dpi dqi
называется лагранжевым многообразием и обозначается Л". Выра-
Выражение [р, q]jk мь1 будем называть скобками Лагранжа.
Пусть Н(р, q) eC°°(R2") — некоторая функция**).' Решение
\р{а, t), q(a, t)} системы Гамильтона
дН • дН • .
P Ч (L3>
где q\t=o-=q(a), /)|/=o = p(a), (p(a), q(a)) s Л" при фиксирован-
фиксированном t является лагранжевым многообразием. Выполнение условия
A.2) для решения системы A.3) может быть проверено непосред-
непосредственно. Сдвиг вдоль траекторий гамильтониана Н (р, q) мы будем
обозначать через g^; таким образом, Л<" = ^Лл,иеслиа—точка
на Л", то при сдциге она переходит в точку g(Ha на К.1}. Пре-
*) В частности, при Sau = 0, f=pHp, f = ~}l%piHppJrH, где tf =
= Н (р, х, /). она сводится к уравнению Гамильтона — Якаби.
**) В этой главе функцию Гамильтона мы будем называть гамильтонианом,
что не вызовет, разумеется, путаницы с гамильтонианом — оператором, опре-
определенным во введении и используемым в следующей главе.

5 1] ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛИРОВКИ ТЕОРЕМ 417
образование g'H мы будем называть каноническим преобразованием,
отвечающим гамильтониану Н (р, а).
Пусть а — координата точки а е Л". Очевидно, а можно рас-
рассматривать как координату точки g'Ha на Л,". Надо иметь в виду,
что в различные моменты времени один и тот же набор чисел а
служит координатами различных точек.
Пусть F(a), аеЛ"-функция на Л". При каноническом пре-
преобразовании g'H задается следующий (обычный) закон, изменения
функции: значение функции Ft {g*Ha) на А!} равно значению F (а).
Иначе говоря, ~ Ft («),= 0. Пусть (г (а)) (г = гх г„, w = wlt...
..., wn) — 2п-мерный комплекснозначный вектор на Л". При
каноническом преобразовании g'H задается следующий (обычный)
(zt (g'H (a))\
закон его изменения: вектор на -Л" есть решение
системы в вариациях
w = — Hqqz-Hpqw,
о = 2 (а),
где а — координата точки а е Л". Будем обозначать преобразо-
преобразование, отвечающее системе A.4), через dg^.
Введем важные для дальнейшего понятия диссипации, комп-
комплексного ростка, потенциала и ^.-действия.
1. Пусть на лагранжевом многообразии Лп — (р(а), q(a))
задана неотрицательная функция D (а) е С00, называемая дисси-
диссипацией. Множество ее нулей обозначим через Г.
2. Комплексным ростком называется совокупность двух комп-
комплексных вектор-функций на Л", {^(а), г (а)}, к>(а)=ш1(а), ...
..., wn(a), z(a)>=Zi(a) г„ (а), такая, что выполнены сле-
следующие условия (аксиомы комплексного ростка):
•2.1.
\г а) 1 = 0^/*), \w(а)\^0
2.2.
2.3. существует функция Е (а) на Л", называемая потенциалом,
такая, что
dE (a) = (w, dq) - (z, dp) +(W' dZ)~^ dW) + (f, da),
где/=0о(Л).
14 В, П, Маслов

418 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ (ГЛ. Vt
Замечание. Рассмотрим комплексное пространство С2"
с координатами Р, Q как 4п-мерное вещественное простран-
пространство R4". Оператору умножения на i в С2" отвечает некоторый
оператор / в R4" (выпишите его матрицу). Пусть L — подпрост-
подпространство R4", порожденное первыми п строками матрицы A.4').
Условие 2.2 означает, что Lf\lL = O. В этом случае говорят, что
подпространство L вещественноподобно.
Перейдем к определению важной квадратичной формы от
ростка, называемой ц-действием.
Определение. В тех точках, где --^ g?0, ^-действие
определяется формулой
где
' d(p+w)j
CV = да, • ВЧ= дщ '
Из аксиомы 2.3 комплексного ростка вытекает следующее
Следствие. При аеГ выполняется следующее соотношение
для скобок Лагранжа:
/*« У [
Л1ы покажем, что отсюда и условия 2.2 следует, что сущест-
существует покрытие Л" (пересекающимися) областями й/, в каждой
из которых отличен от нуля один из якобианов:
д (q +г , р- + И) )
/,-det *' 'да' 1)ФО,
где / — последовательность целых чисел /с A, ..., п), I (J / =
= A, ...', п). Через qi мы будем обозначать набор (q^, ..., qt)
такой, что ii<!i2<...<ik(h «"*) = /• Аналогично мы будем
понимать символы pi, zi, w/. Через (qt, p7) обозначим смешанный
набор координат, индексы которых также упорядочены по возра-
возрастанию. (Например, (qlt p2, qa).) .
Пару (О,* /) такую, что //=?() в Q, мы будем называть зоной.
Мы будем пользоваться обозначением (Q, /) = Q7.
Определение. Если / = A, 2 п), то зона Q7 «азы-
вается неособой зоной; в противном случае Q/ называется особой зоной.
Прежде всего отметим, что произведения (р, q) и (w, z)
определим при переходе в особую зону Q/ следующим образом:

S 1] ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛИРОВКИ ТЕОРЕМ 419
Приведем формулу для ц-действия в особой зоне Q/. По опре-
определению,
a
Положим по определению
где мы обозначили
¦ал /hi
и ^/ — матрица Якоби, определяемая равенством
а матрица €^/ определяется равенством
I да. •
Перейдем теперь к основному в этой главе определению.
Определение. Пусть Л^— лагранжево многообразие {р(а),
<7(а)}-, Do (а) — диссипация, Е (а) — потенциал, {w(a), z(a)} —
росток на нем, 9Е — совокупность зон Q,, а ц, — ц-действие в них.
Пусть выполнено следующее соотношение (неравенство диссипа-
тивности);
Существуют такие константы б>0, 7>0 " функция
с (а, е)^0, что для любого сколь угодно малого г выполняется
неравенство
Тогда совокупность {/?(а), <7(а)Ь {^(а). *(«)} называется лагран-
жевым многообразием с комплексным ростком и обозначается (Л", г").
Замечание. Чтобы доказать, что это определение не зависит
от способа разбиения окрестности Г на зоны, нам нужно будет
доказать, что из того, что это неравенство при aeQ^fl &u
выполнено в 'зоне Q/,, следует, что оно выполнено в зоне Q/,,
Определение. Выражение
Im (w, г),
f 9 \-ln\E + c(a, i
мы будем называть энтропией и обозначать буквой
14*

420 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
Энтропия, таким образом, определяется с точностью до
ODa (/М~е).
Теперь неравенство A.5) будет иметь вид
A.6)
Определение. Выражение вида
JT = H(p, q, t) + iH(p, q, t)
будем называть комплексным гамильтонианом.
Преобразование {р(а), q(a)}, {w(a), г (а)} такое, что А" =»
= gH№, a
d««+*5 {»(«)• *(«)}-{»(«. t), г (а, 0},
где d$H + lfi определяется сдвигом вдоль траектории линейной
системы
i i
w(a, 0) = ш(а), г (а, 0) = г(а),
будем называть комплексным каноническим преобразованием ростка
(Л», г»).
Если дополнительно выполнено условие Й^О, то это преобра-
преобразование будем называть диссипативным. Если же при комплексном
каноническом преобразовании, отвечающем гамильтониану <Ж, не
изменяется энтропия с точностью до О (п), то мы будем называть
его адиабатическим преобразованием.
Отметим, что в дальнейшем, если зона — неособая, то индекс /
У Qi, $i, И/, pi, q,, w,, zt мы будем опускать.
Теорема 1.1. Определение лагранжева многообразия с комп-
комплексным ростком корректно (т. е. не зависит от способа разбие-
разбиения на зоны). При диссипативном преобразовании росток (Лп, г")
переходит в (Л", г"); при этом диссипация на (Л", г") равна
Dt = D0-\Hdt,
о
а потенциал равен

§ 1J ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛИРОВКИ ТЕОРЕМ 421
где Do и Е — соответственно диссипация и потенциал на (Ля, г")
и интегралы берутся вдоль путей *) g{H.
Но, как уже говорилось, основной нашей задачей будет кон-
конструкция решения в целом системы Гамильтона — Якоби с дис-
диссипацией. Для этого введем еще одно определение.
Пусть Л" таково, что существует функция s(a), удовлетво-
удовлетворяющая уравнению ds(a).=p(a)dq(a). Положим Sj(a) = s(a) —
— (Ръ 07 )• ^ каждой зоне Q/ будем называть s-действием
функцию Si (а).
Определение. Фазой ростка (Л", г") в зоне Q/ называется
выражение вида
Мы докажем ниже, что, если неособая зона проектируется
диффеоморфно на ^-плоскость, то пара функций на (Л", г")
(a, t), S2=$(a, t), .
где а = а(х, ^ — решение уравнения q (a, f)~ x, удовлетворяет
системе Гамильтона — Якоби с диссипацией. Если же йгзона
проектируется диффеоморфно на (р-п <7/)'плоскость, то
Si ¦= Re Ф';, Sa = 9,, q, (a, t) = х„ Pj (а, t) =17
удовлетворяет другой системе Гамильтона — Якоби с диссипацией,
связанной с исходной некоторым простым преобразованием, кото-
которое мы назовем ^-преобразованием Лежандра». Возникает вопрос,
как определить решения системы Гамильтона — Якоби с диссипа-
диссипацией в окрестности Qa» точки а0 зоны Q/, не проектирующейся
диффеоморфно на соответствующую плоскость {qr pj) (/-пло-
(/-плоскость).
При построении такого классического решения в зоне Q/ мы
для простоты можем ограничиться случаем неособой зоны.
Это построение основано на следующем простом факте. Из того,
Q(L)
Q(nz)
что матрица ^ невырождена, немедленно следует
Лемма 1.1. В окрестности любой точки a°sfi, где Q — не-
неособая зона, найдутся такие функции yt (a), равные либо Im ги
либо Rezi( либо нулю, что deHa(^)8
*) Например,
[Hdt=[8(p(a, /), q{a, f), t)dt,
* ,~r ., def г
где
, i),

422 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА —ЯКОВИ [ГЛ. VI
(Доказательство см. на стр. 448.)
Определение. Разобьем зону Q на области аУ, в каждой
из которых отличен от О один из якобианов указанного выше вида.
Такое разбиение назовем каноническим покрытием (зоны).
Аналогично определим каноническое ^покрытие для особой
зоны Q/.
На пересечении областей ©° и м>ч мы перестроим решение
(произведем у-перестройку) с помощью отображения а-у а (а), где
Выразим функции, входящие в полученное ранее решение,
через а и затем разложим ИеФ и $ по степеням у (это приво~
дит к вычитанию у из г в энтропии и фазе).
В новые формулы входит функция а (х), которая есть решение
уравнения
q(a)+y(a)=x,
разрешимого во всей области ©v; оказывается, они дают решение
системы Гамильтона —Якоби с диссипацией в этой области.
Область в>у (вместе с отображением а) назовем у-картой. Ре-
Решения в разных v-картах склеим с помощью разбиения единицы.
Оказываемся", решение в vKaPTe неособой зоны получается
по таким же формулам, как и решение-в зоне ©°, если заменить
отображение а(х) на а(х) и функции Е, ц,, $, Ф —на Еу, цУ,
%у, Ф? согласно следующему определению.
Определение. В у-карте положим
Под у-диффеоморфизмом мы понимаем взаимно однозначное ото-
отображение q(a) + y (о) = х, а — а(х) с невырожденным якобианом.
Обозначим
(x) & (a (*)), ? e> (x) = 1, V^: a {x) e Q.

§ 1] ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛИРОВКИ ТЕОРЕМ 423
Аналогично определим Si(x/t ?7) и S2(xIt |7) в зоне Qt.
Именно, по определению, положим '
фу (а) = Ф, (а) + <р„ у,) - (Яп У7) +
Возьмем какое-нибудь разбиение зоны Q/ на coy-карты и фи-
фиксируем его.
Пусть ё*(хр |у) — разбиение единицы в (хг ^7)-плоскости по
¦у-диффеоморфизму coy-карт. Здесь под у-Диф^оморфизмом мы
понимаем отображение
?/ (о) + V/ (or) = x,, p-i (a) + v7 (о) = 17, от = а (х{, %7).,
Раз и навсегда фиксировав это разбиение единицы, мы будем
называть его весовым разбиением единицы по coy-картам. Положим
по определению
)
v
Пусть Af = g^A", a rj1 .= dg* « rn. Будем обозначать функции
S[ и S[ на (Л|«, г^) через S[(xn l7, t), S'% (x,, l7, t) соответственно.
Пусть функции
h(x, Уъ yt, й. Уъ, I) и h(x, уъ yt, yiy уъ, I),
х,у*,уьевК'К E, yi>0,e=Rl4 I = (ilt ..., 4), |/| = Л
удовлетворяют условиям

424 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
при у2 = уь = 0 и
V/,/ («si, 2, 4, 5; /el, 2, 4, 5; / = « + 1 либо } = i—l).
Рассмотрим диссипативную систему Гамильтона — Якоби
). A.7)
dS * / dS i OS i dS i dS ? ¦
(Напомним, что в обозначение Osi (h) уже входит условие поло-
положительности S'A. Положим
H = h(qn q-,, 0, Рц, О, р7), H = f2(q,, q-v 0, рп 0, р7),
(^•°)
и пусть е%" не зависит от /.
Мы докажем ниже следующую основную в этой главе тео-
теорему.
Теорема 1.2. Пусть (Л", г") — лагранжево многообразие
с комплексным ростком, a (gi,, dgtH,(T,)—Dgil.,.T. — duccunamue-
ное преобразование, определяемое гамильтонианом &%'(p, q, f).
Тогда функции S[(xlt l7, t) и S^(x,, lJt t), отвечающие ростку
(МЛ", dg* ,~r"\. и особой зоне Q*, удовлетворяют (для любого
\ л Н-\-1Н • I I
конечного t) диссипативной системе Гамильтона — Якоби A.7).
Замечание. Для' достаточно малого t очевидно, что для
всех точек а е= Q/ якобиан | Jt (a, t) \ при сдвиге вдоль траекто-
траектории диссипативного гамильтониана не обращается в нуль. И
таким образом, мы можем написать, что для достаточно малого /
A.9)
Из леммы 3.1 следует, что любой отрезок времени (О, Т)
может быть разбит на такое конечное число отрезков @, tx, ti7 ...
..., tk, T), что для каждого tt можно выбрать такое разбиение
(Aj1, r$\ на зоны {Q/}', чтобы для каждой зоны выполнялось
условие A.9) при ^sgi=sg^+1. Но в силу теоремы 1.1 переход
рт разбиения {й/}' к (Q/)'+1 при фиксированном tt сохраняет все
величины на (Л™, г*\
Поэтому если доказать справедливость утверждения теоремы
1.2 для малого отрезка времени, такого, при котором имеет
место условие A.9), то из такого рассуждения немедленно сле-
следует справедливость утверждения теоремы 1.2 в целом, т. е. на
любом конечном интервале времени t.

§ 1] ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛИРОВКИ ТЕОРЕМ 425
Таким образом, нам остается лишь доказать теорему 1.2
в малом для отдельной зоны й/. Совершенно очевидно, что мы
не уменьшим общности, если докажем ее лишь для неособой
зоны.
Доказательство теоремы 1.2 для неособой зоны изложено
в § 2 и § 3. Для доказательства теоремы 1.1 нам потребуется
знание решения уравнения переноса с диссипацией. Исследова-
Исследование этого уравнения проводится в § 5. В § 6 на основе резуль-
результатов § 3, § 4 и § 5 осуществляется операция обхода фокусов —
важная конструкция, которая позволяет переносить неравенство
диссипативности из зоны в зону. Этот факт, как легко видеть, —
единственное, что требуется для доказательства теоремы 1.1.
В силу сделанных выше замечаний, таким образом, из результа-
результатов § 6 следует доказательство теоремы 1.2 в целом.
Пусть теперь Ап = {р = р(а), q = q(a)} — лагранжево много-
многообразие с комплексным ростком. Напомним, что через Dg? . мы
обозначаем комплексное каноническое преобразование, соответ-
соответствующее гамильтониану е%"(р, q, t) = H(p, q, t)-\-iH(p, qf t).
Предположим, что наше преобразование обладает свойством дис-
диссипативности (т. е. — #^0).
Рассмотрим в фазовом пространстве R2n+2 переменных (q, t,
р, р0) многообразие, задаваемое уравнениями
Л™+1 = (<?(«, t), р(а, О, U ро(а, 0).
где р(а, t), q(a, t) — решение системы Гамильтона ¦
= Hp(p, q, t), p@)=p(a),
= -Ня(р, q, t), <7@) = <7(а).
Функция ро(а, t) определяется равенством
ро(а, t) = H(p(a, t), q(a, t), t).
Непосредственным дифференцированием можно показать, что
скобки • Лагранжа
[р, Q)],k, [p, Pob.k, [q, Poh.k и т. д.
обращаются в 0, т. е. Ап+%— лагранжево многообразие в фазо-
фазовом пространстве R^.
Определим на А"+1 комплексный вектор (z, г0, до, доё), где
z = z(a, t),w=-w(a, t), (w(a, t), г (a, t)) = dtfH+(~(w(a), г (а)),
го = О, а>0 = -|«а>, Яр> + <г, Hq)-\-H).
Определим еще диссипацию D(a, t):
D(a, t) = D{a)-\H(p(а, т), q(a, t))di

426 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
и потенциал
t
Е(а, f) = E(a)--lr[((w
Из результатов §§ 2 — 6 следует, что лагранжево многообразие
с определенными на нем только что функциями удовлетворяет
аксиомам комплексного ростка. Именно, справедливость аксиомы
2.1 следует из лемм 2.1 и 2.4, аксиомы 2.2 —из лемм 3.1 и 3.2,
справедливость аксиомы 2.3 следует из леммы 2.5.
Таким образом, мы получаем, что Ал+1 есть лагранжево мно-
многообразие с комплексным ростком. Обозначим (Лл+1, гл+1) =
= &н ш^"' г^' теоРемы * -2 следует, что функции S[ (x,, ?7, t)
и S,(*/, lj, t), определенные соответственно как действительная
и мнимая часть фазы ростка (An+1, гл+1) в зоне Q*+1crAn4V
являются решениями (для любого конечного f) системы Гамиль-
Гамильтона— Якобн A.7).
§ 2. Решение в малом уравнения.Гамильтона — Якоби
с диссипацией
Наша задача — получить в явном виде решение уравнения
Гамильтона —Якоби с диссипацией A.7), выразив их через реше-
решения системы Гамильтона и системы уравнений для ростка. В пре-
предыдущем параграфе уже были приведены явные формулы, и теперь
задачей является их доказательство. На эвристических сообра-
соображениях, при помощи которых они были получены, мы останав-
останавливаться не будем. Очевидно, можно доказать, что предъявлен-
предъявленная функция удовлетворяет уравнению, подставив ее в уравне-
уравнение и произведя дифференцирование н приведение подобных чле-
членов. И в данном случае мы поступим именно таким образом.
Однако, поскольку уже само определение уравнения Гамиль-
Гамильтона—Якоби с диссипацией содержит оценку, то эта процедура
будет еще сопряжена с некоторыми оценками. Поэтому мы. пред-
предварительно докажем несколько элементарных оценок, которыми
будем пользоваться в дальнейшем.
Лемма 2.1 (неравенство Гординга). Пусть F(x)^0,
е= С00(R»). Тогда \VF(x)\2^c-F(x)max[F^J.
Доказательство. Имеем
i, ..., xk+t, xk+1, .... *„)<
¦ **F(Xl
Известно, что, условием положительности квадратного трехчлена

§ 2] . РЕШЕНИЕ В МАЛОМ УРАВНЕНИЯ С ДИССИПАЦИЕЙ 427
является положительность его дискриминанта, т. е.
. glf^maxJF^W. B-1)
Из неравенства B.1) непосредственно следует утверждение леммы.
Неравенство Гординга имеет важное
Следствие. Пусть F(*)=sO, F(*)e=C°°(Rn). Тогда
Доказательство. Элементарные выкладки показывают,
что
max | *"<?-'/" | = О (/г"). B.2)
В силу неравенства Гординга имеем:
| VF (х) \NerF w/* ^ с -. (F (x))N'*erFwih,
с = const.
Обозначая теперь F(x) — t и используя оценку B.2), мы полу-
чаем, что | VF (дг) 1^ exp f jp-Wc/zW2, с = const. Следствие дока-
доказано.
Пусть р(р0, ft, f),, q(p0, q0, <) б См (R2(!+1). Рассмотрим функ-
функцию Н(р, q, <)^0,Яе С00, р, q, t принадлежат компакту^
Лемма 2.2. Для любого е>0 выполнены неравенства
о
5
о
t
Ш^сь(е)D1-8, где D = \H{p, q, x)dx.
о
Доказательство. 1) Предположим вначале, что не все
коэффициенты разложения функции Й (р, q, t) по формуле Тей-
Тейлора no t в точке rf = O равны 0. Тогда
H(p(Po,qo,t), g(p,,.qo,t),t) = c
где s—целое неотрицательное число, и
t ¦
о
^CytHip, q, t), cx — const.
Значит, в этом случае

428 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ, VI
В силу леммы 2.1
\Нр(р, q,
\Н9(р, q,
, /= 1, ..., 6.
Из последних неравенств и следует утверждение леммы в этом
случае.
2) Пусть все коэффициенты разложения функции Н (р, q, t)
по формуле Тейлора равны 0, т. е. H = O(tN), где N — любое
целое число, и пусть точка t0 такова, что D (tQ) = 0. Для любого
е>0 имеем
где N (е) 5= 0 — любое целое число, поскольку, если to = O, то это
следует из предположения, а если t0 Ф 0, то, в силу монотонно-
монотонности, ?>(?) = 0 при /=^о и. следовательно, все ее производные
в точке t0 равны 0. Поэтому производная ' J '* ограничена,
и, значит, ГУ (t) «=?с (е) (D (ОI"8, т. е. Я<с(е)рI"8. Из этого
неравенства и леммы 2.1 получаем утверждение леммы в этом
случае. Аналогично доказывается последняя оценка леммы.
Получим еще нужные для дальнейшего оценки решений линей-
линейных уравнений первого, порядка .в частных производных.
Пусть Х = 2Х (х)^- — векторное поле на R", трансверсальное
некоторой бесконечно дифференцируемой я —1 -мерной поверхно-
поверхности М"'1. Тогда решение задачи
где f (x) — финитная бесконечно дифференцируемая функция, су-
существует и единственно в некоторой окрестности М"'1.
Если мы введем криволинейную систему координат — а ==
= (аъ ..., а„_!) на М"'1 и «длину» / траектории векторного поля
X, то
и (х) = и {х (а, /)) = {f (х (а, /)) dl. B.3)
о

$ 2] РЕШЕНИЕ Б МАЛОМ УРАВНЕНИЯ С ДИССИПАЦИЕЙ 429
Интеграл B.3) мы будем сокращенно писать в виде
uJ\f(x)dl.
Имеет место следующая элементарная лемма.
Лемма 2.3. Пусть функции ut(x), /==1, 2, такие, что
«г 1^/1-1 = 0, удовлетворяют неравенству:
\, B.4)
где cit / = 1, 2, ..., 7 —некоторые положительные числа, /,-, i —
= 1, 2, ..., 5 — бесконечно дифференцируемые функции. Тогда
где
и с0 —некоторая константа.
Доказательство. Используя неравенства 2а6<а2 + 62,
и неравенство
(поскольку функция б фигурных скобках не убывает вдоль тра-
траекторий векторного поля), получаем из B.3)
\и,(х)\-.
k-l
x
+c
To есть
tl\ui(x)\dl+c/l\f,(x)\dl+ctf[l\ft(x)\dl+l\ui(x)\dt
¦I«i(x) I +1«2 (*) I <c0(F (x) + J (IUl (x) I +1u,
Из неравенства B.5) немедленно получаем:
B.5)

430 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
Продолжая этот процесс и учитывая," что для неубывающей
получаем для любого N>0
\иЛх)\ + \щ(х)\^Г(х)^^^- + ^ ^(\ul(x)\+\ui(x)\)dl.
Устремляя теперь N к бесконечности, получим утверждение
леммы.
Используя следствие леммы 2.1, преобразуем систему A.1)
к более удобному для нас виду. Для этого разложим функции
fip.'p, х, t) и f(p, р, х, fj по формуле Тейлора в точке р = 0;
}{р, Р, х, t) =/ (р, 0, х, t) + (р, }р (р, 0, х, 0) +
' +(P hl °
f(p, Р, х, t)=f(p, 0, х, f) + <j>, fp(p, 0, x,
+ i<P>'fp~P<P, 0, x,t),
n
Здесь мы обозначили (a, b) = ^a/bj. Заметим, что в силу след-
ствия из,, леммы 2.1 система уравнений A.1) эквивалентна следую-
следующей системе:.
Положим
Н(р, х, O = jf(P, 0, х, 0, #(Р, х,ъЩ(р, 0, х, 0
и введем функцию <?? (р, х, t) = H (p, x, t) + tH(p, x, t). Теперь
умножим на i второе уравнение системы и сложим первое урав-
уравнение со вторым. Вспоминая свойства функций f{p, p, x, t) и
f (P, Pi x, t), мы приходим к соотношению

§ 2] РЕШЕНИЕ В МАЛОМ УРАВНЕНИЯ С ДИССИПАЦИЕЙ 431
Таким образом, мы свели поставленную в § 1 задачу к следую-
следующей: иайти функции Si(x, f) и S2(x, t) такие, что 5i(*, t),
S2(x, 0eC°°(R"x[0, T]), S2(x, f)^0 и для любого е>0 выпол-
выполнено соотношение B.7).
Легко видеть, что пара функций, удовлетворяющих соотноше-
соотношению B.7), удовлетворяет также и соотношениям B.6). Кроме
того, соотношение B.7) будет играть важную роль в гл. VII.
Определение. Соотношение B.7) мы,будем называть урав-
уравнением Гамильтона —Якоби с диссипацией, соответствующим
гамильтониану <?%" (р, q,t).
Рассмотрим задачу Коши для системы Гамильтона
f=-Hq(p,q,t) рф)=ро(а).
' Условия на действительный гамильтониан Н (р, q, t), при которых
4 существует решение в целом системы Гамильтона, приводятся
в главе I, §8. ~
Решения системы B.8) обозначим
q = q(a,t), p=p(a,t).
Предположим далее, что на Л" заданы комплекснозначные функ-
функции гм (а), ..., гол(а); г<у01 (а), ..., wOn(a). Обозначим точкой
дифференцирование по t в силу системы B.8) (т. е. при фикси-
фиксированном а) и рассмотрим задачу Коши:
z = lHp(p{a, t), q(a, t), t) + ^rpq{p(a, t), q(a, t), t)z +
+ <?Fpp(p(a,'t),q(a,,t),t)w,
ib^ — iHgip (a, t), q (a, t), t) - ?Tqq (p (a, t), q (a, t), t)z-
-a5r?p(P(a. t), q(a, t), t)w
г |/uo = z0 (a), w \t=o = w0 (a).
Здесь sSFpq, ®%Грр, а%"?? — матрицы. Например, (аУСpq)i} =±= <??Piq
Систему уравнений B.9) мы называем уравнениями {комплексного)
ростка. Условимся, что всюду в дальнейшем, если аргумент
у функции а5Г опущен, то подразумевается подстановка р=
=p(a,t), x = q(a, t), z = z(a, t), w = w(a, t). Мы будем называть
полным лагранжианом ростка- функцию
ХЩ ((Нр, р) + (Hq, q) - i <//p, w) - / (Hq, z) +
. - +1[<P, q)-(w, г)))-JT. B.10)
Предположим далее, что на отрезке времени O^t^to не

432 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОВИ .(ГЛ. VI
обращается в нуль ни один из якобианов:
Dq def . II dq, II
Тогда по теореме о неявной функции при O^t*^to система урав-
уравнений
) = xh l = \, .... п B.11)
имеет единственное бесконечно дифференцируемое решение а =
= а(х, t). Введем функцию Sa(x, t), которую мы будем называть
полным ростковым действием:
l 12)
(х, t) = Son (a (a:, t)) + \{z(p (a, t), q (a, т), т) dxl . B.
Здесь SOn = Eo (a) - Va (г, w). .
Теорема 2.1. Пусть при
Тогда соотношеншо B.7) t/довлетворяют функции St (x, t) и S2 (x, t),
определяемые равенствами
S1 (x, t) = Re Ф (a (x, t), t), S2 (x, t) = S(a (x, t), t),
где Ф(а, г) — фаза, а $(а, t) —энтропия на лагранжевом много-
многообразии Л{* с комплексным ростком, полученном при сдвиге за время t,
OsS^sST начального лагранжева многообразия вдоль траекторий
системы B.8), B.9), а = а(д:, f)— решение уравнений B.11).
Замечание 1. Мы будем иногда говорить также, что функция
S (x, t)==Si(x, t) + iS2(x, t) удовлетворяет соотношению B.7).
Замечание 2. Легко видеть, что фазу Ф(а, /) можно еще
определить равенством
Ф(а, t) = Sn(a, 0 + |i(«, О,
где Sn(a, ^ — полное ростковое действие,- определяемое равен-
равенством B.12).
Изложим кратко план доказательства теоремы. Вначале мы
будем вычислять и оценивать производные функции Sn (дг, /) 4-
+ ц (х, t) по аргументам tax, используя леммы 2.1 —2.3 и вводя
для удобства промежуточные функции. Итогом этой, части дока-
доказательства является лемма'2.8. Затем мы покажем, что из усло-
условий теоремы следует, .что функция Sn(x, t)-\-\i(x, t) удовлетво-
удовлетворяет неравенству диссипативности при t > 0. Этот факт позволит

РЕШЕНИЕ В МАЛОМ УРАВНЕНИЯ С ДИССИПАЦИЕЙ
433
нам завершить доказательство теоремы. Мы получаем в первой
части доказательства оценки через диссипацию D(x, f), так как,
во-первых, через функцию D (x, t) удобно оценивать росток
(г (a, t), ay (а, t)), a во-вторых — неравенство диссипативности
позволяет легко перейти от оценок вида ОофР) к нужным нам
оценкам вида Os, (ha).
Мы начнем с доказательства простого, но важного неравен-
неравенства—оценки решений системы B.9). По лемме 2.3 имеем
\w(a,
Но по лемме 2.1
t
^ const f 120 (а) | + | w0 (а) \ + \ (| Нр | + | Hq |) dx).
\ о /
и, аналогично,
t-\Hdx
о
1/2 '
1/2
Из этих неравенств, а также из аксиомы 2.1 комплексного ростка
и определения диссипации, немедленно следует
Лемма 2.4. Справедливо неравенство
| w (a, t) | +1 г (а, t) \ < с (Ш (а, 0I/2. с = const.
Рассмотрим функцию
t
F (a, t) = Ео (а) + $ {- Ш -\ <ЯР; w) -1 <Я?; г>} dt,
о Р=Р(а, т)
ш=ш(а, т)
г=г(а, т)
B.13)
где Ео(а)— потенциал на начальном лагранжевом многообразии.
Вычислим Fa . Для этого преобразуем подынтегральное выра-
выражение в B.13). Введем функцию
'qqz) + 2(w,
; w) - {Жч, г) -1 «
+ <ш, ^Гррш». B.14)
Используя теперь системы уравнений B.8) и B.9), подынтеграль-
подынтегральное выражение в равенстве B.13) можно переписать в виде
-{{Щ, г) =

434
ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
Поэтому в силу аксиомы 2.3 (стр. 417)
<* аУ^ +
-1 (г, waj) + i <a^, z) +1 <ш, га/
dr.
Интегрируя по частям, получаем
у (г0,
4- [<ю, <7ау> - <г, рау> - у <г, ша/> + у <ш, га
,}dT = /у («) + <»1 <7а,> - <г, рЛ)).
+ у (а», 2а/> + J Лу (а, т) dx,
где через Лу обозначено подынтегральное выражение, оставшееся
в интеграле после интегрирования по частям. Преобразуем Л,:
r Hq </ц
Дифференцируя B.14) по а,, получим;
- (<Ж~Р, waj) - (г,
- (г,
j
, га/> -
— (г,
гда hj> /W> h] ~ некоторые гладкие матричнозначные функции.
Отсюда получаем, что
t
w,
Так как
и поскольку диссипация D (a, t) есть 'неубывающая функция t,
то
а, x)dx
= OD(h).

§2} РЕШЕНИЕ В МАЛОМ УРАВНЕНИЯ С ДИССИПАЦИЕЙ 435
Сформулируем полученные результаты в виде отдельного утверж-
утверждения:
Лемма 2.5. Пусть F(a, t) — функция, определенная равенст-
равенством B.13). Тогда F (a, t) есть потенциал на Л"+1 (см. стр. 426):
^а, = (®, <7ау> - (г, paj) - j (z, waj) + j (w, zaj) + OD (ft),
(
Введем теперь функцию FCT = F(a, i) — 2 ¦ Подставляя г и
xb из системы уравнений B.9) и используя лемму 2,4, получаем
FCr iH-i фр, w) - i (w, *%rppw) +1 (г, 3?qqz) + OD (W>*).
B.15)
Кроме того, в силу леммы 2.5
(F*)*, = (w, qaj) - <г, paj+wap + OD(h). B.16)
Вычислим производные от ц(а, t) по переменным ау и t. Имеем:
И«, = |<г; C-1Bza/) + ^ (brC*Bz) + OD (Л). B.17)
Обозначим теперь
S«o6^ct + H. B.18)
Тогда
(ЯдобЦ = (и*. xap — (z, paj+waj) +
+ \ (г, С-гВгар +1 {zy C-iBz) +'OD (h). B.19)
Сейчас мы докажем, что матрица С^В «почти» симметрична. Это
позволит нам упростить формулы B.17) и B.19).
Лемма 2.6. Обозначим С~ХВ = Ш. Тогда %* — Ш =е, и элементы
матрицы е удовлетворяют неравенствам
Доказательство. Так как при фиксированном t
dF = (w, dq) - (г, dp) - 1 (z, dw) +'i (w, dz) + (f, da),
то для скобок Лагранжа
справедлива оценка
\[p + w, q + z]jk\ = OD(hW) i,k = \,...,n
(здесь мы учли еще, что [р, q]jk = Q, /» k — \, ..., п). Но
=у;

436 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОВИ [ГЛ. VI
Умножая последнее равенство на Cj/Cmk и суммируя по k и /,
получаем равенство
i.k
из которого и вытекает утверждение леммы.
В силу только что доказанной леммы можно переписать равен-
равенство B.17) в виде
Равенство B.19) примет вид
= (w, qap - (г, paj + waj) +
+ (z, C-1Bza/) + OD(h) = (w, qaj)-(z,
где |f (a, t)\^c[D(a, t)], с = const.
Вычислим теперь t. Дифференцируя уравнения B.8) и B.9)
по ау, получим:
+ ipjipp + zj€qp + wJ*pp+OD{W*),
tba = - iqaHqq - ipaHpq - z<№qq-wJ€pq-\.OD(h}l*
Из последних равенств получаем по mod 0о(Л1/г):
Имеем:
р рр] - С q pq
ew* со со cvy* <р аьу» с
= —зл дрё —&ял рро> —&л дд — ёзл pq.
Таким образом, окончательно,
Ш = - ?fqq - ЗГдрШ - Ш.Жрч - Ш?ГРРШ + Оо (НЧ>). B.20)
Равенство B.20) позволяет вычислить производную fi:
Используя полученную формулу, вычислим производную Eдо6)!
Sso6 = - Ш - i (Нр, ш) -1 <ю, ^Гррш> + i (г,
= -iH-i (Нр, хю-Шг)-
-~(w- Шг, ?ГРР (w - *2)> + Oc (AH"

§ 2] РЕШЕНИЕ В МАЛОМ УРАВНЕНИЯ С ДИССИПАЦИЕЙ 437
мы здесь воспользовались следующими тождествами!
в силу симметричности матрицы
в силу симметричности «скалярного произведения» ( , );
в силу леммы 2.6. Итак, нами получены важные формулы;
Лемма 2.7. Справедливы равенства
где |/|^c-D(a, t), с = const.
Пусть s0 (a) — s-действие на Ля, а решения системы B.8) при
Osg^s^o удовлетворяют условию det qi? " \фО- Обозначим
через а = а(ж, /) решение системы уравнений.
qt(a, t)=xh i = \, .... п
и введем новую функцию
а(х, t)MSAo6(a(x, t), t).
Введем также вещественное действие s(x, t), полагая
s(x, O = k(«) + J «Р, Нр)-Н)\р=р{а, t)dt|a=a(,( 0. B.21)
L о 9=</(а, т) J
Заметим, что определенная таким образом функция s(x, t) удов-
удовлетворяет уравнению Гамильтона — Якоби — -f H (sx, x, t) = 0.
Теперь вычислим и оценим функцию g(x, t), равную
g(x, t)^% + (^rp(sx, x, t), ax) +
+ Y (а* Жрр (sx, x, t) ax) + ifi (sx, x, t). B.22)
Имеем;
*. 0 = <7« (SAo6)a.
Используя лемму 2.7, последнее равенство можно переписать
в виде
i f. B.23)

438 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
Подставляя вычисленные значения производных функции а (х, /)
в равенство B.22), получаем (используя лемму 2.4)!
g(x, t) = — iH(sx, x, f)-i(Hp(sx, x, t), w-Шг)-
-\{w- Пг, Жрр(w - Пг)) + OD (Л*'») - (w -ёг + qjf, Hp) +
x,
Изучим подробнее слагаемое (Hp, q?f). Из определения функ-
функции / видно, что (см. стр. 436)
г(а, 0Р + 1^(«. *)\*\ c = const.
Из системы уравнений комплексного ростка B.9) можно получить
оценку
\w(a, /)|<с(о;Л(о) +
dx , с = const,
или
t
|г(а, t)\2-{-\w(a, t)\2^cDl(a)^-c^(\Hp\-^-\Hq\)dxy, c = const.
о
Из оценки для f, последнего неравенства и леммы 2.2 оконча-
окончательно получаем
Применяя теперь лемму 2.4, получаем
\g(x, t)\=OD {№*-*). B.24)
Обозначим теперь:
и
? = V*M*. 0. i) = VxOi(x, t). B.25)
Из равенства B.22) очевидным образом получаются неравенства
+ (Нр, ц) |<с2 (| л | +111 +1 Нр | +1 Я? | + OD (Л1/.)), Cl, Са = const.
Из этих неравенств и леммы 2.3 получаем, что
H*=OD(ftV.), ||| = 0о(Л'/.). B.26)

§ 2] РЕШЕНИЕ В МАЛОМ УРАВНЕНИЯ С ДИССИПАЦИЕЙ 439
Здесь мы использовали еще неравенство
IЛ + Ъ11,_0 < с (| (FCT)a 11,_0 +11411,_0) = ODo (Л1/,), с = const.
В самом деле, по определению, t
а(х, t)\M, = S№6(a(x, t), t)\t-Q = F„(x0(a)) + (i(x, 0).
Отсюда в силу формул B.13), определения ji-действия и аксиомы
2.1 ростка и следует нужное неравенство.
Введем теперь функцию S(x, i):
S(x, t)Ms(x,t)+o(x, t), . B.27)
где s (x, t) — действительное действие, определенное равенством
B.21).
Замечание. Из равенства B.12), B.13), замечания 2, сде-
сделанного после теоремы 2.1, и определений функций Sflo6(a, t),
FCT (a, f) и a (x, t) легко видеть, что функция S (дг, t), определен-
определенная равенством B.27), является фазой в неособой карте неособой
зоны ростка (Л", г"), полученного сдвигом начального ростка
(Л", г") за .время t вдоль траекторий системы B.8), B.9).
Обозначим р = р + ц, р = ds/dx.
Лемма 2.8. Справедлива оценка:
х,
Доказательство. Напомним вначале, что действительное
действие s(x, t) по построению удовлетворяет уравнению
= 0.
Поэтому выполняется равенство (ср. B.22))
, x, f)t )
)). B.28)
Разложим теперь функции а5Г(р, дг, t), <?%'р(р, х, t), ppp)
по первому аргументу по формуле Тейлора в точке р—р-\.ц.
Имеем:
, х, 0 = ^Г(р-Л, х, t)=<%T(t, х, t)-{<3rp(j!>, x, t),

440 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ. VI
Аналогично
», х, t)=?>rpip, х, t)-Jrpp(p, х,
Подставляя полученные выражения в равенство B.28), получим
~ + ^ф, х, *)-<<ДГр(р, х, t), т)> + 1<ть <%Грр(р, х,
+ <^Гр(р, х, t), г\ + Ц)-(<ЯГ„ф, X,
откуда
-% + Ж(Р, х, t) + i(?Tp(P, х, t), Б>—J-<6,
= 0(|r,|3 + |r,||gp + |g||r,P)+g(A:, t).
Вспоминая неравенства B.24) и B.26), получаем, что
^- + ^Г(р, х, f) + i{Wp(Jit х, t), %)-
-\(\, Жррф, х, t)l) = OD(hW-'). B.29)
Лемма доказана.
Таким образом, функция S(x, t) = S1(x, t)-\-iS2{x, t) есть
«почти» решение (по модулю Од(Л3/2~е)) поставленной выше
задачи, так как пока неизвестно, выполнено ли условие S2 (x, t) 5г
^=0. Ответить на поставленный вопрос нам позволит
Лемма 2.9. Для всякого е>0 найдется такое число v>0
и гладкая функция с (a, t)^=0, удовлетворяющая оценке с (a, t)^
^сх(а) (l-fO> что выполнено неравенство
yD(a(x, t), t)^S2(x, t) + c(a(x, t), t)D(a(x, f),fL»—.
Доказательство. Запишем мнимую часть равенства B.28)
в виде
\nPp дх' дх^Т^РРЦх
|1) + 1<Ярр^, *g)-\mg(x. t). B.30)
Вспомним теперь, что мы обозначали т| = V^Oj (x, t), \ = Vxo2 (x, t)
(см. формулы B.25)).
Введем векторное поле d/dl по формуле:
didt^p' Тх(ррЧ' й>т2^я& d
Обозначим правую часть равенства B.30) через G,
1 r, t).

§ 21
РЕШЕНИЕ В МАЛОМ УРАВНЕНИЯ С ДИССИПАЦИЕЙ
441
В силу оценки для |т|| B.26) и разложения Я(р + т|, х, t), по
формуле Тейлора имеем:
, х, t)-8(p, х, t)-{Bp(p, x,t), т,>-
B,31)
Значит, в силу неравенства B.31) найдется такая постоянная Ме,
что
Ог(х, t) = G(x, 0 + Ме(ДK/2-е5г-Я(р + т)> х, О^О.4
Пусть функция г|) (х, f) есть решение задачи
^ = Gt(x, t), i|>U = YA>,
где у —постоянная из неравенства диссипативности на начальном
'многообразии. Очевидно, что i|i (x, t) Ss 0. Заметим теперь, что
х, t) + c[D(x, t)],
где с —некоторая постоянная, а также (см. лемму 2.1)
-Н(р, *Нт)Яр(р + ть х, D^G^x, 0+<aD(*, 0-
Применяя последнее неравенство, получаем
— Й(р,х, 0<<Мл:, t) + c1D + c2VDV— Я(р + т), х, Q
tUp, х, 0-т)Яр(р, х,
По определению D(*, 0 имеем j7 D = —Н, где через ^ мы обозна-
обозначили векторное поле ^ = 7й + (#р> дх^' Учитывая» что в силу
леммы 2.1 | V^D | <; с уТ5, с = const, получаем
_
dl
+т
и в силу леммы 2.3
, t), B.32)
с = const.
Теперь заметим, что по определению функции S (x, f)
S( о 15( о
Значит, в силу равенства B.27) и определения векторного поля

442 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
d/dl функция S2(*> 0 есть решение задачи
dS^x, V=G{Xt t)> §г(х, 0U = 5M = ImO(a).
Тогда разность 1|э (х, t) — S2 (х, t) есть решение задачи
|(t|)-S2) = G1(^ t)-G(x, t),
(¦'-$i)U = Y
Таким образом,
o - $<я! + MJL (D3/2-e), B.33)
где L — длина траектории векторного поля d/dl, Me = const.
Покажем, что L^const/. В самом деле,
||l|<1+c(|t)| + | g|)< const,
откуда и следует требуемое неравенство. Заметим еще, что
из неравенства диссипативности на начальном многообразии
следует
| y?>o - S02 К сг (а, е) Я3/*-". B.34)
Подставляя B.34) в B.33) и учитывая, что I <; const ¦ t, получаем,
что
D(x, 0<<?Ф(*. 9<
(S( 0 + ( )D3/2 + (a( e,
откуда и следует утверждение леммы.
Докажем теперь, что если выполнены условия леммы, то
функция
At
ic(a(x, t), t)D(a(x, t), QV*-
удовлетворяет соотношениям B.7). Обозначим
S^x, 0=*ReS(x, t), St(x, 0 = ImS(x, 0-
Отметим, что в силу леммы 2.9 S2(x, t)^0. Покажем теперь,
что выполнена оценка
-?<«• ^"(f ¦ *• iffi-OA*»-). B.35)
ftp
Заметим, что ReS = ReS и, следовательно, -д^—Р- Поэтому,

§ 3} . РЕШЕНИЕ УРАВНЕНИЯ С ДИССИПАЦИЕЙ В ЗОНЕ 443
в силу леммы 2.9 достаточно показать, что
р, х, t),
dSn
2-8( c = const. B.36)"
Очевидно, что для доказательства этой оценки достаточно показать,
что
2-е)( с — const.
Имеем*
е)==?K/2-е_
но в силу леммы 2.2, — Ш^с^фI 8 и, значит,
Для завершения доказательства теоремы нам нужно доказать, что
Но это. неравенство немедленно следует из B.36) и доказанного
в лемме 2.9 неравенства (оценки) OD(ha)*=LOs,(ha) (а^О —
любое число). Далее, заметим, что $2 = ®.
Таким образом, теорема 2.1 доказана.
§ 3. Решение уравнения Гамильтона —Якоби
с диссипацией в зоне
Этот параграф будет посвящен у-перестройкам. Основным момен-
моментом, на который мы- опираемся здесь, является следующее
соображение. Пусть aoeQ, где Q (для простоты) — неособая
зона, и якобиан dq/da равен нулю в этой точке. Тогда, сдвинув
окрестности точки а0 вдоль траекторий осциллятора на время
t = O(h°°), мы получим, что в сдвинутой точке этот якобиан уже
отличен от нуля, хотя и имеет порядок О (А00). Вместе с тем этот
сдвиг вдоль траекторий всей зоны нечувствителен для решения,
которое мы получаем лишь с точностью до О (№/2~в). Поэтому
мы всегда можем как бы считать, что в данной точке а„ якобиан

444 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ. VI
не равен нулю, а равен лишь О (Л00). Значит, q(a)=x в О(Л°°)-
окрестности точки а = а0 разрешимо относительно а. Но мы
должны, следовательно, внимательно следить за оценками и их
зависимостью от поведения якобиана dq/da.
Теперь мы построим решение уравнения Гамильтона — Якоби
с диссипацией на отрезке времени [О, Г] таком, что
Приведем вначале некоторые вспомогательные рассуждения.
Лемма 3.1 (о локальных координатах). Пусть р (о), q(a),
w(a), z(а) таковы, что [p,q]j, = [w,z]i +[p, zj/ +[w, ^J/-==0, и
** k k k
= n в точке ао =
тогда существует такой набор попарно неравных индексов (ix, ...
i i /п) = A. ..-, п), что
Доказательство леммы 3.1. Условимся, что слово
«ранг» будет означать ранг над полем R. Аналогичное соглаше-
соглашение примем относительно выражений типа «линейная зависимость»,
«линейная комбинация».
Пусть ранг матрицы А со строками
да ' •'"' 5а
равен k. Если k = n, то утверждение леммы верно. Пусть k<.n.
Без уменьшения общности предположим, что базисный минор
матрицы А находится в левом верхнем углу. Пусть, далее, В —
матрица со строками
d{pn+wn)
да ' ••'» да
Покажем, что ранг матрицы С, составленной из k первых строк
матрицы А и n — k последних строк матрицы В, равен п (это
означает, что утверждение леммы верно). Предположим противное:
rang C = m<n.

§ 3] РЕШЕНИЕ УРАВНЕНИЯ С ДИССИПАЦИЕЙ В ЗОНЕ 445
Тогда rang(cj = m, так что можно (изменяя, если нужно, выбор
локальных координат) считать выполненными условия
да, -0> —55;—U|
По условию леммы для любого 1=\, ..., k
доч дап
(d(q/+Zj)\k
Так как det(—^—) ?? О, то отсюда следует, что последний
столбец матрицы („) равен 0, что неверно, так как rangf6j = n.
Лемма доказана.
Обозначим теперь через Рь (р, q, t), Qk (p, q, t), Wk (p, q, w, г, t),
Z/t(P> Q> w> z> 0» 1*^?*S" решения системы уравнений комп-
комплексного ростка с гамильтонианом <№ = H-\-iH:
. дН . дН /о 1 \
и начальными условиями Р*(р, 7i 0) = Pft» Q»(P. <7>
Wft(p, 7, о», г, 0) = wft, Zft(p, 7, t», z 0) KA
Лемма 3.2. Пусть
d(P + W)
существуют такие гладкие функции фй G, р, г, ш,
0 К*, что

446 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ. VI
Доказательство. Для простоты выкладок ограничимся
моментом времени tf=X). В силу C.1) имеем:
Pk(p, q, Q«>*
Wk(p, q, w, z, ti~wk-i^
Qk(p, q, 0 = <7* + ||
Zk(p,q, w, z, /) = :
Далее, обозначив, для простоты вычислений,
Ph(q, P, /) = j
Qk(q, P,
Wk(q, p, w, z, t) = i
Zk(q, P, w, z, t) =
получим
л
dt \t-o
Подставляя выражения Ak, Bk, Ck, Dk через производные, получаем
лемму.
В качестве непосредственного следствия леммы 3.2 получаем
следующий классический результат.
Теорема (Лиувилль). Пусть Р(р, q,t), Q(p, q,t) —решения
гамильтоновой системы :
f4 s? C-2)
PkiP, q, 0) = pk, Qk(p, q, 0) = <7A;
тогда, если Qt с: R2/t — область, получаемая сдвигом на время t
вдоль решений системы C.2) измеримой области Qo, то
- \dql... dqndpi... dpn^\dq1...dqndp1...dpn.
Пусть теперь Л" с: R2" — лагранжево многообразие, ГоСгЛ",—
множество ростка; соответственно Л,я — лагранжево многообра-
многообразие, полученное сдвигом вдоль гамильтоновой системы с гамиль-
гамильтонианом Н на время /, Г, с А? соответствующее множество ростка.
Далее, пусть Pk(q, p, t), Qk(q, p, t), Wk(q, p, 0, 0, t), Zk(q, p,
О, 0, 0 —решение системы C.1) такое, что в любой момент вре-
времени t, (P, Q, W, Z) е Г/. При сделанных выше предположениях
справедлив также следующий результат.

$ 31 РЕШЕНИЕ УРАВНЕНИЯ С ДИССИПАЦИЕЙ В ЗОНЕ 447
Теорема 3.1. Пусть
/ d(Q+Z)\
rang %
при t = 0, где ах... а„ — некоторая система локальных координат
в окрестности точки ростка (Р (q, p, 0), Q(q, p, 0))<гГо; тогда
<3-3»
в любой точке (Р (q, p, t), Q(q, p, t))^rt.
Доказательство. Система C.1) с начальными условиями
Р @) = Ро, Q @) = <7о. Z @) = t%, W @) = tv0, %, wae R" определяет
семейство отображений
Ut s (Ро + iv0, 7o+ ft|o> -* (Р @ + ^ @, Q @ + 2 @)
фазового пространства С2" в себя. Дифференциал (при фиксиро-
фиксированном t)
dUti (dp0 + Шо, dq0 + /dry -* (dP + afr, dQ + dZ)
этого преобразования в точке р, q есть линейный оператор в R4/t.
Покажем, что оператор dUt невырожден. Обозначим i R
IZ RW lW
На Г< выполняются следующие условия Коши — Римана: a, (if) = 0,
i = 1 8. Действительно, прежде всего at @) = 0. Вычислим, напри-
например, ах. Учитывая, что на I\ Z (t) = W (t) = 0, получаем из
системы C.1) . ¦
-jjj ax = Нрраъ — НрРав + Hpqax — Нрда2.
Аналогичные вычисления показывают, что функции at удовлет-
удовлетворяют системе линейных однородных уравнений с нулевыми
начальными условиями, откуда и следует, что a/ssO.

448 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
Из условий Коши — Римана вытекает, что оператор d(Jt дейст-
действует следующим образом:
Невырожденность оператора dUt следует теперь из леммы 3.2.
Пусть Lt — подпространство R4", порожденноэ строками матрицы
C.3) (от t). Справедливо соотношение Lt = dUtL0. Из условий
Коши — Римана следует, что IUt = UtI. Поэтому
Ц П Щ = dUtL0 n IdUtU = dUt (Lo ПII*) = 0.
Теорема доказана.
Предположим, что det (dqt (a)/daj) = 0 в некоторой точке а0.
- Лемма 3.3. Пусть det С (а) ^ 0; тогда существует окрест-
окрестность Uat точки а0 и вещественная вектор-функция у {а), такая,
что ее компоненты равны либо 0 либо рдной из компонент действи-
действительной или мнимой части вектора г (а) и
det
Доказательство. Пусть rang <7<х = #. Преобразованием
системы координат в й преобразуем матрицу qa так, чтобы пер-
первые k строк ее были линейно независимы в окрестности точки а0,
а остальные п — k строк были нулевыми. Из невырожденности
(Re г \
а) найдется п — k столбцов
Im га/
('¦ft+i) (гп), где @)
таких, что матрица G1а qea, rkn, ..., гп)' будет невырождена
в некоторой окрестности Uaa точки а0. Для завершения дока-
доказательства осталось положить
Тогда по построению det {^a + Ya} Ф 0 при а е Uat>. Лемма дока-
доказана.
Введем некоторые новые объекты.
Определим функцию а (х) как решение уравнения
x=<7(a)+Y(a). C.4)
По только что доказанной лемме решение уравнения C.4) суще-
существует и единственно в некоторой окрестности точки а0. Пусть

§ 3] РЕШЕНИЕ УРАВНЕНИЯ С ДИССИПАЦИЕЙ В ЗОНЕ 449
в окрестности i/Qo задана функция
Зу (о) Ш Wo (с) - (р (с) + w (с), г (а)-у (о)> +
+ j(z-y, С-*В(г-у)), C,5)
где W0(a) удовлетворяет условию
^ + w(o)). C.6)
Определение. Функцию Wo(о), удовлетворяющую условию
C.6), будем называть энтальпией (комплексного) ростка.
Положим
W — ° \° \х))> v3''}
где а (х)~ решение уравнений C.4).
Пусть теперь U1c:Q — некоторая окрестность, пересекающаяся
с ?/<*„, и
. . II fins (аЛ II . _
при
Введем функцию S (х):
S(x) = W0(a)-(p(u).+ w(a), г(а)> + |(г, C^Bz)\ C.8)
** ICC ОС \Х)
где функция" a (x) есть решение уравнений
x = q(a), C.9)
а Wo (a) — энтальпия комплексного ростка.
Определение. Функцию Sy(x)
Sv (х) = Wo (а) - (р (а) + w (а), г (а)-у (а)) +
где а (х) решение уравнений C.4), будем называть у-перестройкой
функции S(x), определенной формулой C.8).
Сравним теперь функцию S (х) с ее V"nePeCTP0HK0H Sv (x)
и вычислим производные функции Sy(x).
Лемма 3.4. Пусть функция Sy(x) есть у-перестройка функ-
функции S (х). Тогда равномерно по а на пересечении окрестностей
Ui П ^а„ выполняются оценки
**L = \p + w-tz\+OD(h), (Sv (х) - S (х)) = OD
Доказательство. Оценим сначала разность
^1 (X) = | S/x Sv (X) - yxS (X) | и(в)-*(„) + у(а).
Мы пелагаем D(x) = D (а (х)) в Ux и D (х) = D (а (х)) в ?/„„). Обо-
Обозначим
16 В, П, Маслов

460 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
и пусть а(а) —решение уравнений
C.10)
0 по
ям у:
C.11)
которое существует и единственно, так как det Do (а) Ф 0 по
лемме 3.3. Разложим а (а) в асимптотический ряд по степеням у:
где «1 = -? _
DkDilt, i'¦— 1» •. • i Я,
и повторение индексов при умножении здесь и в дальнейшем
означает суммирование. _
Вычислим производную
(y)(p ) ((y) + D()
<- (С (а) - (г, - Та)) (p + w)-[C- (г, - Та)] С~ХВ (z-y) + OD (A) =,
= Do (а) {р + w) -DoC"^ (г- v).+OD (A). C.12)
Воспользовавшись разложением C.11), можно получить равен-
равенство
Подставляя выражение для а из C.13) в формулу для производ-
производной ЩР- C.12), получим
aSY?(a)) = ^о (о (а)) (Р (а) + w (а)) + Do (о (а)) В<а1 -
-Do (а) С"* (а)В (а) (г (а) - Y(«)) -D^ (а) В (а) (га (а) -
-Та(а))'«1 +
Напомним, что (C~1B) = Bt (C-1)' + OD(A1/2). Таким образом,
(CT4(Za-Ya)'- С] • a, + OD (A) = D0 (a) (p + w) (a) -
- Do^Bz+DoC-^By+D0Bt (CO^DJOi + OD (A).
Но в силу (З.Н)
DJOi —y(«).
Окончательно получаем равенство:
a)) =?>о(р)[р + к>_с-хВг1+00(А). C.14)

S 3] РЕШЕНИЕ УРАВНЕНИЯ С ДИССИПАЦИЕЙ В ЗОНЕ 451
Заметим, что равенство C.14) выполняется равномерно в обла-
области (/«,. Это следует из C.13).
Легко проверить, что из уравнения C,4) следует равенство
до(х) 1
¦ ¦' ¦ - SB —— ¦
Таким образом, на пересечении окрестностей Ua, и Uu произ-
dSV (x}
водная функция——^ равна, в силу C.14),
¦д. =д7-яГ „, =[P + W — ez]\a~a{x) + OD(n), C.15)
С/А С/А (/О Of-OtlJtl
-* v ' I •
причем эта оценка равномерна при а е iVo,, det с7а Ф 0^ Для дока-
доказательства оценки C.15) мы воспользовались только двумя пер-
первыми членами разложения C.11). Используя все члены разложе-
разложения, можно записать
+ | (<Cfi'a1( a,> + (^ К, (p + w), а,> «хЛ + О о (А3/2),
р + w = (р + w) (а) + В' («1 + «г) + OD (A),
(г - Y) (о) = (г - У) (а) + (г« - Та) (<*i + «г) + - .
C.16).
Здесь мы обозначили через га — уа матрицу с элементами
(Za— Уа) Jl Щ ,
а через (za — ya)ak — матрицу с элементами
Аналогично определяется матрица Сак. Подставляя выраже-
выражения C.16) в определение функции Sy (а) и производя вычисле-
вычисления, аналогичные предложенным для доказательства равен-
равенства C.14), получим оценку
' (SyM-SWUw-iw+yw^Oom. C.17)
причем оценка равномерна в области, где
Замечание. Можно показать, что разность Sv(x) — S(x),
обозначаемая нами OD (A3/2), есть сумма членов типа fi-zrWf Re zJ%
/IRYi и т. д., где /ь /а —гладкие функции.

452 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ (ГЛ. VI
Пусть теперь Л" — лагранжево многообразие с комплексным
ростком, det С (а) -ф 0 на Л". По определению, на Л" задана
функция Е (а) с дифференциалом
dE (a) = (w, dx) - (z, dp) -1 (г, dw) + \- (w, dz) + </, da).
Из этого факта легко следуют существование на Л" функции
Wo (a) — энтальпии ростка — и равенство:
где Ф (а) —фаза ростка, ц. (а) — ^.-действие.
По лемме 3.3 существует покрытие многообразия Л" атласом
coj1!, таким, что в каждой карте определена функция у1 (а) и
да, Г
Предположим, что в некоторой карте
Определим в ней функцию Ф(л:) равенством
В («^-картах определим (см. определение, стр. 449) функции Ф? (х)
как ^-перестройки функции Ф(^). По функциям Ф^1(х) можно
определить функцию Ф' (х) с помощью разбиения единицы {е1 (х)},
подчиненного атласу {м/}:
^^1е1(х). C.18)
Функцию Ф' (х),. определенную равенством C.18), будем назы-
называть х-фазой на многообразии Л" с комплексным ростком.
В силу неравенства диссипативности и леммы 3.4 найдется
такая функция С(а)>0, что мнимая часть функции S0(x), опре-
определенной равенством
5„ (х) = Ф' (х) + iC (а (х)) DJ/2- * (х), C.19)
неотрицательна.
Имеет место теорема
Теорема 3.2 Пусть при t<=[0, T]
det| ' «fa, ' ~
Тогда решение S (x, t) задачи B.7), удовлетворяющее условию
S(x, O) — So(x), где функция S0(x) определена равенством C.19)
при любом t е [О, Т], определяется формулой
$(Х> Ц = Ф'(Х, t) + iC(x, АПЗ/2-е

§ 3] РЕШЕНИЕ УРАВНЕНИЯ С ДИССИПАЦИЕЙ В ЗОНЕ 453
где Ф' (х, t) — х-фаза на многообразии Л" с комплексным ростком,
которое получено сдвигом начального многообразия Л" вдоль траек-
траекторий системы B.8), B.9) за время t, С(х, t) > 0~некоторая
функция, причем ImS(x, t)^sO и С(х, t)^ const.
Доказательство. Пусть {coj} —атлас многообразия Л?,
такой, что в каждой карте eoj определена функция У (а, *)"и
^° при ае@/-
Пусть в некоторой карте eoj выполнено неравенство
Определим в со$ функцию Ф (х, t)^O(a (х, /). 0. где Ф(а. 0 —
фаза ростка (Л", г?). Определим функции Ф^ (х, t) в картах oof
как ^-перестройки функции Ф(я, t).
Непосредственным дифференцированием равенства C.17) можно
показать, что в силу замечания, сделанного нами после доказа-
доказательства равенства C.17), оценок решений уравнений ростка и
леммы 3.4, равномерно по а при det <7а 9^0 выполняется оценка
| (d>v' (х, t) - Ф (х, 0) = OD (AV2- •), C.20)
где через -jt мы обозначили дифференцирование вдоль траекторий
системы Гамильтона B.8)
Из формул § 2 следует равенство (см. лемму 2.7)
Ф-МГ(р,Ч,()- i{Hp (p, x,t),w-Шг) -
^ C.21)
где | f |< const D3'2.
Анализируя вычисления, приводящие к формуле C.21), легко
усмотреть, что выражение, обозначенное через /, равномерно огра-
ограничено по а (не содержит слагаемых или сомножителей вида (<7а)"х).
Таким образом, из C.20) и C.21) получаем, что
| <l>v' (*, 0 = Н (р, q, t) -i(Hp(p, q, t), w-Шг)-
- i (w -1г, <2Vpp (W - Шг)) + OD(W*)
и функция; обозначенная нами через OD(h3/2), равномерно по а
ограничена при detect9^0.
Заметим теперь, что если мы будем подставлять в соотноше-
соотношение B.7) производные функции Ф(х, t) без слагаемых вида0о(Ав),
то оценки B.29), B.35) также будут выполняться. Значит,

454 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ. VI
функции Фу1 (х, t) всюду в точках, где det qa Ф О, удовлетворяют соот-
соотношению B.7), причем оценка выполняется равномерно по а.
По непрерывности заключаем, что функции Ф">1 (х, t) всюду
в картах coj удовлетворяют соотношению B.7). Кроме того, в силу
леммы C.4), функции Ф' (х, t) удовлетворяют неравенству дисси-
пативности; точнее, в силу замечания, сделанного после доказа-
доказательства оценки C.17) и оценок решений уравнений комплексного
ростка, найдется такая функция C(a,t), что 0<С(а, *)<const
и в каждой карте а>\ выполнено условие
ytD (х, *).< Im Ф?' (х, t) + C (о', t) 0D (А»/»~е).
Таким образом, функции Ф^ (х, t)
Ы{х, г)^Фу1(х, t) + iC(al(x, t), tHD(№-*)
суть решения уравнения, Гамильтона —Якоби с диссипацией,
каждая в своей карте. Рассмотрим теперь вещественное разбиение
единицы \е\(х, t)\, подчиненное покрытию |и{|, и определим функцию
5 (х, t) = Z Ф7' (х. t) et(x. t). C.22)
i
По построению функций Фч'(х, 0 функция S(x, t), определен-
определенная равенством C.22), является решением задачи B.7) в момент
времени t.
Таким образом, нами указан способ построения решения задачи
уравнения Гамильтона —Якоби с диссипацией до комплексной
фокальной точки, т. е. в моменты времени от 0 до Т, в которых
Замечание. Можно былЪ бы, рассмотрев в расширенном
фазовом пространстве (q, t, р, Е) лагранжево многообразие Лг,
которое получается при движении начального многообразия Л
вдоль траекторий системы Гамильтона B.8) способом, совершенно
аналогичным изложенному, построить решение задачи сразу для
всего отрезка времени до комплексной фокальной точки.
§ 4. у-перестройки' как адиабатические преобразования
В этом параграфе мы установим связь у-перестройки с адиабатическими преоб-
преобразованиями. Именно, мы покажем, что для всякой у-перестройки фазы
существует адиабатическое преобразование, задаваемое гамильтонианом, кото-
который определяется этой у-перестройкой.
Пусть снова Л" — лагранжево многообразие комплексным ростком. Через
D0(a) обозначим диссипацию на Л".
Пусть в карте 0)Y определена функция у (а) такая, что

5 41 7-ПЕРЕСТРОЙКИ 455
Определим а (х) как решение уравнений
x=q(a)+y(a).
Пусть, кроме того, в карте a>Y выполнено условие
Определим еще функцию а=а(дс) как решение уравнений
</(а)~*.
Положим
" |'Г1(г(а)-7(а))Р!<т^<Т(?). D.1)
Определение. Гамильтониан <?$Г (р, q), определенный равенством D.1),
будем называть собственным.
Для удобства вычислений введем функции'
Ф(Р. Я)=Р~Р(a)-Re[ш(о)+В< (С'Г1 {у(a)-z (а))] |С1иС(Й1
Ч>=4> (<7)= - 1ш [ю (о)+В' (С<)~1 (v (о)-г (а))] !<,=<„„).
Представим гамильтониан <?%* (р, </) в виде
р, q)=H(p, q)+i7Hp, q).
где
Я(р, <7) = Re^T(P, <7)=y(cp2-^),
Отметим, что из определения функций <р (р, </) и ^ (</) следует, что
Ф=О (р-р {o))+0D<) (Vh), ^ = 00o (/Л).
Оценим величину
Но в силу леммы 2.6
Таким образам, окончательно получаем
(T) D.3)
Напишем систему Гамильтона, соответствующую гамильтониану <?%" (р, q).
Легко видеть, что в силу D.1) она имеет вид
р=р-р0+00о(КЛ")(р-Ро)+00о(Л), р|,=0=р(а) =ро,
i=p-Po+0D, (Vh) (Р-Ро)+О0о (Л) <7|/=0=</(а)- ' D-4)
Система уравнений комплексного ростка имеет вид:
z = ihp +<Жрцг +6ЙГррю z Iм,=z (a). D.5)
Так как
| р (а) -р (a)e (a) =

456 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ. VI
в силу леммы 3.3, то из D.4) следует, что
¦p(a,f)-p(a) + ODt(VH), D.6)
q(a, Q"=<Ta) + 0D(>(KT)
я, кроме того, на решениях системы D.4)
Ф(Р, Q)=ODo (Vh), JT (p, q) = ODa (А).
Оценим теперь производные гамильтониана <?%* (р, q) no р и q на решениях
системы уравнении D.4):
^1), D.7)
°Da (V*), Йрр- 0Do (/A) ( = 0),
Из системы 4.5) и оценок D.7) получаем, что
w (о, г = ODo (Vh), г = ODo (/A). 14.8)
Покажем теперь, что сдвиг вдоль траекторий системы за произвольно
малое время переводит карту <оУ в карту ш^, днффеоморфно проектирующуюся
на плоскость q.
Лемма 4.1. Пусть det qo=0 в точке а0 е Q^; тогда существует такое
е > 0, что det 7ст (а, /) ф 0 при < е [0, е], а = а (а).
Доказательство. Пусть -»
rang(/a=ft, 0^ft<n.
Выберем такую систему координат, в которой первые k строк матрицы </а
линейно независимы, а остальные равны нулю.
Рассмотрим производные по t от функции / (f) = det {qa (a, t)} в точке
<=0. В силу того, что матрица qa{a, 0) имеет N— ft строк тождественно рав-
равных нулю, (Л/— ft — 1) производная по t от функции f (f) равна нулю при t=0.
Докажем, что
где
IQiaj \/=o I =ё ft,
Предположим противное: пусть матрица {оу} вырождена. В силу того,
что по построению первые ft строк матрицы ау линейно независимы, нз усло-
условия detay=O следует, что 3s(ft<s=s;A0 такое, что

§ 4]
Y-ПЕРЕСТРОЙКИ
457
Подставим в D.10) значения ац, найденные из D.9):
_*_ • N I N k
Di \ Piai — Re ? Bim
1 I m=»i
для у. /=1 ЛГ,
= — 1; но из D.11) следует, что матрица
D.11)
Яка;
Pk+laj
а
вырождена, что противоречит лемме о локальных координатах. Следовательно:
• /@)=0,...,— . , =0, —jj—-/@)^0
дГ~*-1 дГ~к
и в некоторой е-окрестности точки /=0 функция f (()ФО при t^.0. Лемма
доказана.
Докажем еще одну вспомогательную лемму
Лемма 4.2. Пусть функция S (q) = Si+iS^ удовлетворяет условию
¦^-«р [o)+w{o)+B'{C-i)< (a) [z-
S2((?)^cD0((/); с = const.
Тогда выполняется оценка
dS e>r(dSl A.i/tyfdSiXdS^ 1 ,dS
t (A),
D.12)
где <3%Г (Р. Я) —собственный гамильтониан.
Доказательство. Имеем
^~p (o) ~w {а)-с~1в [г
~у (о))Г
Аналогично
и ^fppsl. Подставляя полученные выражения для производных гамильто-
гамильтониана d%"(p, Я) в D-12)- получаем утверждение леммы.
Теперь мы можем выяснить геометрический смысл у-перестройки.
Теорема 4.1. Обозначим, через
преобразование исходного
ростка (Ля, г") с помощью собственного гамильтониана
ствует 6 > 0 такое, что при 0 < / ^ б выполнена оценка
,q). Тогда суще-
сущегде через Ф' (*) мы обозначили фазу на ростке
, q) (Л", г").

458 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБЙ (ГЛ. VI
Доказательство. Предположим для простоты, что многообразие Л"
покрывается одной неособой зоной, т. е.
\
a det 1ДI обращается в 0 в некоторых точках многообразия Л». Нам нужно
II <**/ И
показать, что решение диссипативиой задачи Гамильтона — Якоби, соответ-
соответствующей собственному Гамильтониану ?//? (р, q), взятое в некоторый момент
времени t (обозначим его St (x)), мало отличается от функции Ф (х), т. е.
справедливо равенство см. теорему 3.2)
C/2e). D.13)
Отметим одно важное обстоятельств/}. Так как мнимая часть собственного
гамильтониана Ж (р, q), очевидно, не удовлетворяет условию Im Ж (р, q) —
= Н (р, q) 3: 0, то мы не можем прямо использовать ранее Доказанные теоремы,
в которых определялось решение диссипативной задачи Гамильтона — Якоби.
Однако, анализируя доказательство теоремы 2.1, мы покажем, что в силу
специального вида собственного гамильтониана Ж (р, q) и начального условия
<l>(q) функция St(q), построенная по формулам теоремы 2.1, удовлетворяет
соотношению B.7).
В случае, когда гамильтониан Ж{р, q, I) не удовлетворяет условию
Й (р, q, Ц—\хпЖ(р, q, f)-^0, мы ие можем проводить оценки с помощью
диссипации D (x, t), определенной в § 1. Однако свойства собственного гамиль-
гамильтониана Ж (р, q) таковы, что все нужные оценки можно получить через Do (x) —
диссипацию на начальном лагранжевом многообразии с комплексным ростком.
В самом деле, нетрудно заметить, что во всех формулах, полученных при
доказательстве теоремы 2.1, вплоть До оценки функции g(x, t) B.24), оценки
можно получать через соответствующие степени ростка | г (a, t) |-f-| w (а, 01-
Но в силу D.8) росток в нашем случае оценивается через диссипацию Do
иа начальном лагранжевом многообразии.
Для проведения оценок во всех остальных случаях достаточно заметить,
что в силу D.7) Нр(р, q, f) = OD»{Vh). Таким образом, функция St, постро-
построенная по формулам теоремы B.1), удовлетворяет соотношению
Представим теперь функцию St (x) в виде, уже использовавшемся нами ранее:
St(x)-W{a, 0-<Р(«. 0+да(а. 0. * («. 0> +
+ ±(z(a, 0, С-1вг(а, 0>\а=,ат,
где W (а, 0 — энтальпия комплексного ростка на лаграижевом многообразии
AJ1, полученном из начального многообразия Л" сдвигом за время. / вдоль
траекторий системы D.4), a,(q, f) — решение уравнений q{a, t)=q, которое
существует в силу, леммы 4.1.
Вычислим производную -к-^. Имеем

5 41 7-ПЕРЕСТРОЙКИ 459
В силу оценок решений системы D.5)
Заметим, что диссипация Do в оценках решений системы D.5) определена
на иачальном лаграижевом многообразии.
Подставляя теперь S(=S1+iSi в выражение
г гч n\^w(dS^ Л-t-i /w ( dSl Л dS*\
L(St, q)-ye{-^-, «,j-H <afp(-^-, q), -щ-)-
2 \ dq ' ^рр\ dq- '
и производя вычисления, совершенно аналогичные проделанным при доказа-
доказательстве леммы 4-2, получим
Обозначим теперь ш(</, f) разность
«to. 0
Очевидно, что ш {q, f) удовлетворяет соотношению
Следовательно, |ш| = 0Ов(А), I »^l = OD,()
Разложим теперь функцию L(St, q) по формуле Тейлора:
L(S,, <7) y
+/<«fp+»pPReeJ, 1ш-^-Ч-1ш«^>-
1< (' )>C/2) D-14)
Здесь функции Ж, Жр, ЖрР вычисляются в точке (ЯеФ^, q).
Приводя в DЛ4) подобные члены и учитывая, что в силу леммы 4.2
получаем из D.1)
* (S/, q) = <ш^. ^ррй)J) +0^ (Аз/2).
Таким образом, получаем соотношение
-^+<»^ррЦ> = 00о(А^),
D.15;
• l/.o-O.
Дифференцируя D.15) по q, получаем соотношение вида
-щ (щ) + Жрр&ддЩ = ODt (А),
Из D.16) следуют оценки ,
|»?|=0о,(А), |ш|=б>й.(А3/2-Л
Из последней оценки и следует утверждение теоремы.

460 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
§ 5. Решение уравнения переноса с диссипацией в зоне
Роль якобиана и уравнений переноса в асимптотических форму-
формулах и геометрических конструкциях была уже ясна нам из мно-
многочисленных примеров. Здесь мы приведем решение уравнения
переноса для общей ситуации, отвечающей лагранжеву много-
многообразию с комплексным ростком.
Будем называть решением уравнения переноса с диссипацией
функцию ф (я, t), удовлетворяющую соотношению
-), E.1)
где Si (х, t), S2 (x, f) — решения диссипативной задачи Гамиль-
Гамильтона — Якоби, соответствующей гамильтониану а%" (р, q, t), G (x, t) —
гладкая функция S(x, ^) = 51(jr, t) + iS<i(x, t).
Обозначим, как и раньше, через -п- векторное поле вида
Кроме того, обозначим через Ja и 1 х определители
V\\, E.3)
Напомним, что функции qt (a, f) являются решениями системы
Гамильтона B.8) и г* (a, t) — решение системы уравнений
ростка B.9), ^(а(*), 0) = *.
Мы докажем теорему.
Теорема 5.1. Пусть
det
при O^t^T. Тогда решение уравнения переноса с диссипацией
при t е [0, Г] имеет вид
а=а (х, I)'
= г4=-(фИ-<г(а, 0, С (а, 0^„ф(а)>) X
V Ja
X exp U W (р (а, т), q (а, т), i)di\
1 J
Ф (а) —гладкая функция, г (a, t) — решение системы уравне-
уравнений ростка B.9), функция W (p, q, t) определена равенством E.19)
и а = а(д:, t) — решение уравнений q(a, t) = x.

§5]
РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА
461
Замечание. Из доказательства теоремы легко следует, что
формулу для решения ф(я, t) можно записать в виде
Ф (х, 0 = у=г- (ф (а) - (г (а, t),
аф (а)» X
(а, т), q{a, т), т) dx\\
Вначале получим лемму. В силу системы Гамильтона B.8)
B9) \
у у у
и комплексного ростка B.9) имеем для i=\ п
qi-\-2i = &%"p(p, q, f) + ^pqz-\-
По правилу дифференцирования определителей
d i - i -
E.5)
dan '" dan
Используя равенство E.5),' имеем
dan
E.6)
да/
pi4 да/
E.7)
Приводя в E.7) подобные члены, получим (по modOD (/г1/>))
ав/
E-8)
Заметим, что выражение в квадратных скобках в E.8) не зави-
зависит от / (номера строки определителя Ja). Поэтому при подста-
подстановке выражений E.8) при i, /=1 п в равенство E.6),
как легко видеть, получим
~
E.9)
ik
Воспользуемся формулой B.23), выведенной в § 2.
Vxa(x, t) = w

462 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ. VI
Имеем'
Кроме того, справедливо равенство для матриц
Вспоминая, что по определению (см.стр.421) действия g-jp = WW
н учитывая, что в силу определения B.26)
, t) = s(x, t) + o(x, t),
получаем
). E.12)
Нам остается напомнить, что решениями диссипативной задачи
Гамильтона — Якобн, соответствующей гамильтониану «ЯГ(/»", q, t),
являются действительная н мнимая части функции <§ (х, t), опре-
определяемой равенством
S(*( 0 = 3(*. t) + i[Cl(a, e)(D3/2-e) + C2(a, t,
Очевидно, что
Из формул E.12), E.13) получаем
EЛ4)
Таким образом, нами доказана лемма.
Лемма 5.1. Якобиан Ja, определенный равенством E.3),
удовлетворяет соотношению
. E.15)
Лемма 5.1 имеет очевидное следствие, которое мы будем
в дальнейшем использовать.
Следствие. Якобиан Jx, определенный равенством E.4),
удовлетворяет соотношению
). E.16)

5 5J РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА 463
Доказательство. Легко видеть, что Jx=JaL-3^A и
повторяя дословно доказательство леммы 5.1, мы получим
равенство E.16).
Доказательство теоремы. Для преобразования суммы
(dSi у Ал-'нЖ (dSi у
воспользуемся снова равенством B.23). Разлагая функции
в точке P = g- и учитывая, что U- U^cD'/2, с = const получим
) щ
, х, t) + Jrpp(p, х, f)(w-*z) + OD(#<*-*). E.17)
Теперь мы можем переписать соотношение E.1) в виде
$ (Р, х, 0 + <Жрр (р, xt t) (w
Положив теперь
получим, что функция if удовлетворяет соотношению
{Шр 0{, х, 0 + бЭГрр (р, д;, 0 (ю - *г). ^> +
; (Р,.«, 0(ю-«г), V,
{
п
- т 2 ^w(p> x>
i=l J
Обозначим через ? сумму в фигурных скобках из соотношения
E.18):
-4{p,qtt)=VTa(iHp(p,q, 0 + «ЯГда(р. <?, *)(»-*z), V -^>-
п
Г '>• EЛ9)
Обозначим через П «оператор переноса»
П =^ + <<#р(Р, ^. 0 + ЗГррЬ, х, t)(ш-Шг), Чх).

464 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ (ГЛ. VI
Предположим теперь, что W = 0. Покажем, что в этом случае
функция
\М*. Q = Ф («)-<*(«. t), СУаФ>|а-а(*.*) E.20)
удовлетворяет соотношению E.1).
Вычислим вначале производную (~. Имеем
= <& (С - га) С-^аФ +/ = С^Уаф + /, E.21)
где |/|^с|г|, с = const.
Кроме того,
E.22)
Здесь мы использовали выражение для С, полученное при
вычислении f (см. B.20)).
Подставляя E.21) и E.22) в E.18), получим, учитывая, что
- ± (г, С-^аф) + (Шр + Жрр (w - Шг), ^
Яр, C-^^)-{^pp(w-Uz), С^ф> + (гЯр,
^^ = /, E.23)
где |/|<cD'/2-e( с = const.
Таким образом, доказано, что при х? = 0 функция %(х, t),
определенная равенством E.20), удовлетворяет соотношению E.1).
Легко видеть, что в общем случае соотношению E.1) удов-
удовлетворяет функция
HxF(p, q, x)dx\.
Для завершения доказательства теоремы осталось заметить, что
в силу неравенства диссипативности (см. лемму 2.9) справедлива
оценка '
Ss (х, t)
Е>\/2-ге h =0(/г1/2-е).
Замечание. Учитывая, что в силу леммы 2.2 и оценок
решений уравнений ростка B.13) выполняется неравенство
Яр | • | г | =ss cD12, с = const,

§ 5] РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА 465
из доказательства теоремы легко усмотреть, что функция /
в равенстве E.23) имеет вид
где ' .
I ft I, I ft I < с&х~г' I ft К <ьРхп-г, Ci, c2 = const, / > б > 0.,
Рассмотрим теперь уравнение с правой частью
E.24)
(Обозначения здесь те же, что и в E.1).)
Из теоремы 5.1 непосредственно вытекает
Следствие. Пусть выполнены условия теоремы 5.1. Тогда-
функция ф (х, t), определяемая равенством
ф(*. 0 =
1 (f 1
= 77у=(ф1 («. 0 - <z> С^уаф1 («. 0»ехр{ V W (p, q, т) dz\
VJa U )
где функция W(р, ^» 0 определена равенством E.19),
о
и а = а (я, f) — решение уравнений q (а, ^) = д:, удовлетворяет соот-
соотношению E.24).
Для доказательства этого утверждения достаточно заметить,
что в этом случае
^Фг(а(*. 0. 0 = ^(<7. 0-
Все же остальные формулы для производных, которые вычислены
для доказательства теоремы 5.1, сохраняются с заменой Ф (а) на
ф1 (a, t). Пусть L*q> (а) = <р (а) - (z (a, t)-y (a, t), С (с, t) ?Ф (с)>.
Обозначим через coj особую карту в неособой зоне Qt, полу-
полученную при сдвиге карты а>у вдоль траекторий системы Гамиль-
Гамильтона B.8) за время t. Мы построим решение i|>Y (x, t) уравнения
переноса с диссипацией E.1), удовлетворяющее начальному условию
ф(х, 0) = W(ff)|e=ff7w, E.25)
где ф (сг) — гладкая финитная функция, supp ф (сг) cz o)Y, a = оу (х) —
решение уравнения q (а) -\- у (сг) = х, а е а>у.
Теорема 5.2. Пусть
det

466 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ. VI
при Os^t*s?.T. Тогда решение уравнения переноса с диссипацией
¦ф7 (дг, t), удовлетворяюще начальному условию E.25) при O^t^T
определяется равенством
Г(х, t) = :4^Ф(о)ехр(т(р@, /), q(or, t)т)dx)
Ф(о)ехр(
где функция W(p, q, t) определена равенством E.19) и функция
<х ф= о^ (х, t) — решение уравнения q (a, t) + y (a, J)=x.
Доказательство. Прежде всего напомним, что уравнение
Гамильтона — Якоби с диссипацией, соответствующее гамильтони-
гамильтониану е%" (р, q, t) в особой карте, имеет решение, определяемое
по формуле
S (х, 0 = OV (а, 0 + 1С (а, е, t) ?>»/»-• |c=<jY(JCt ty .
В силу B.23)
Дифференцируя равенство E.26) по дг, получим
= (Г1 (с - г„+у0) С*В + OD (Л1/2) = С/? + OD (Л).
Таким образом, как_и в теореме 5.1, мы получаем, что замена
ф(лг, t) на ф(дг, t)lVJ0 в уравнении E.1) приводит его к виду
(р (a, t), х, t) + i^rpp (p (a, t), x, t) (w (a, t) - ,
-Ш (г (a;t)-r(a, t))), V^>] + ?(p, x, t)<p(x, t) =
= Os, (Л1/2"е), • E.27)
где a = <fl(x, t), функция ^(р, x, t) определена равенством E.19).
(М фй %" %" ф
гд a (, ), фуц (р, , ) рд рт E.19).
(Мы произвели здесь разложение функций а%"р и s%"pp по фор-
формуле Тейлора, в точке p — ds/dxi воспользовавшись равенством
E.26) аналогично тому, как это было сделано при доказательстве
теоремы 5.1). •
Предположим теперь, как и при доказательстве теоремы 5.1,.что
^(р, х, 0 = 0. Обозначим через Ш «оператор переноса в особой
карте»—дифференциальный оператор, стоящий в квадратных скоб-
скобках в равенстве E.27). Положим
(х, 0 = Ф (о)-(г-у, С-ЧаЧ>(о))|c=cv(JCt 0 = i*p. E.28)
Мы покажем, что выполняется соотношение
П^(^. 0 = Os,(A1/2-e). E.29)
Доказательство этой оценки мы проведем, используя продолжение

§ 5] РЕШЕНИЕ УРАВНЕНИЯ ПЕРЕНОСА 467
по непрерывности, точно так же, как это было сделано при дока-
доказательстве теоремы C.2) о решении уравнения Гамильтона—Якоби
с диссипацией, до комплексной фокальной точки.'
Заметим, что на множестве точек « карты о>у, в которых одно-
одновременно разрешимы уравнения
q(a,t)=x и q(a, t) + y(a, t) = x,
справедливо-равенство
8), yvezC™, E.30)
где П — оператор переноса в неособой карте. Эту оценку легко
получить, если воспользоваться разложением C.11). Если мы до-
докажем теперь, что. функция 1ЭД (х, f) на множестве « удовлетво-
удовлетворяет равномерно по а оценкам
E.31)
где %(х, t) определена равенством E.20), то тем самым мы дока-
докажем, что на множестве х выполнена оценка E.29), которая непо-
непосредственно следует из оценок E.30), E.31) и доказанной в тео-
теореме 5.1 оценки .
Щ0(х, t) = O
Для доказательства оценки E.31) мы воспользуемся равенст-
равенством C.11) и разложим функцию
Uv(<x)M<p (а) - (г (а) - Y (а), С"» (а) V<p (<x)>
по формуле Тейлора в точке а = а.
Получим
Ф (а) - <'?>о 'у, Vcp> - (г (а) - у (a),
о1 (za -
- <'ZVY. ^Ф> + OD (h) = Ф (a) - {г (a), C^Vcp (a)> + OD (A). E.32)
Совершенно аналогично лемме 3.4 доказывается, что функция
Od (h) равномерно ограничена в окрестности тех точек, в которых
^ = 0. Из равенства E.32) диффереицированием получаем первую
из оценок E.31). Для получения второй оценки достаточно раз-
разложить по формуле Тейлора в точке a = a производную Ф-
точно так же, как это было только что проделано. Таким обра-
образом, оценка E.31) доказана.

468 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
Совершенно очевидно теперь, что функция
V(x, 0 = W(*. 0ехрПЧ'(р(G, т), q(a, т), г) dx\a=ay(х< Л E.33)
удовлетворяет в ту уравнению переноса. Таким образом, тео-
теорема доказана.
Пусть теперь Л" —лагранжево многообразие с комплексным
ростком, полученное сдвигом начального лагранжева многообра-
многообразия Л" вдоль траектории гамнльтоновой системы B.9) за время t.
Пусть й, — некоторая неособая зона на А?. Мы построим сейчас
формулу, дающую решение уравнения переноса с диссипацией
в зоне Qf
Пусть {шу'} — покрытие зоны й< картами. Обозначим через
af образы coy' при отображении
Я (о, 0 + Y'>. *)=>х, стешу*.
Пусть теперь {et (x, t)} — разбиение единицы на множестве Ut =
= (J ту'*. Положим
i
i|>(x, 0 = 2>(*. t)w'(x, t), 'E.34)
i
где функция tyyi (дг, /) определена в теореме 5.1 в случае, если
карта ©у' неособая, а в случае особой карты функция ¦ф/у' (х, t)
определена в теореме 5.2. Из теорем 5.1 и 5.2 легко получается
следующее утверждение.
Теорема 5.3. Решение уравнения переноса в момент времени t
в неособой зоне лагранжева многообразия Л" определяется форму-
формулой E.34).
Из вычислений, проведенных для доказательства теорем 5.1
и 5.2, следует еще одно важное для нас утверждение.
Следствие. Справедлива следующая формула:
+ oD (Л'/2-е). E.35)
§ 6. Операция обхода фокусов
и глобальное определение ростка
Пусть g^ — каноническое преобразование, заключающееся в пово-
повороте некоторых осей фазового пространства на угол л/2. При
этом преобразовании qi переходит в ри a Z/ переходит в wt. Его
можно описать с помощью системы Гамильтона для осциллятора.
Это преобразование можно получить с помощью другой гамнль-
гамнльтоновой системы, лишь бы в конечном счете указанный поворот
был совершен.

§ 6] ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 469
Но если для данной неособой (для простоты) зоны Qq при
повороте с помощью осциллятора встречаются фокальные точки
(в которых —во" ~ в)- то их нельзя избежать и выбором дру-
другой гамильтоновой системы, с помощью которой мы производим
преобразование.
Это обстоятельство затрудняет проведение доказательства не-
неравенства диссипации, которое мы получим лишь для случая,
когда фокальная точка отсутствует для произвольного времени.
В этом параграфе будет описан прием, позволяющий обойти
указанную трудность. Этот прием мы называем операцией обхода
фокусов.
В случае, когда / — строго возрастающая подпоследователь-
подпоследовательность последовательности A, ..., п), мы обозначаем через / упо-
упорядоченную последовательность, дополнительную к /. Под
pi, например, мы понимаем такой набор {ри р,^}, что
"(<!, ..., ik—I> Через (рр р,) (или (р,, <7;)) обозначаем смешан-
смешанные наборы координат, индексы у которых также упорядочены
по возрастанию.
Введем теперь последовательности индексов /jC/, /2 с /
и обозначим
Предположим для простоты, что лагранжево многообразие Л"
покрывается двумя зонами Q/ и QK так, что
; +Q при eeQ/ .
да F.1)
= det —¦?—Sj-* Z-фО при
Предположим дополнительно, что в зоне Q/ отличен от нуля
якобиан det
'(«/• Pi)
да
, а в зоне Q# якобиан det
д («к: рк) 1
да
Обозначим через a7 (qn p}) решение уравнений
<7/Н = <7/. P/(a)=P7- aeQ>- F-2)
а через ак (qK, p-^ — решение уравнений
Я.к(.а) = Як, Рк(а)-Рк, «ейЛ, F.3)
Пусть В/—диагональная матрица, состоящая из 1 и —1.
В дальнейшем знаки при ее элементах будут выбраны в зависи-
зависимости от зоны ?2/. Пусть А — некоторая ортогональная матрица.
Обозначим через х набор координат x=(qIt, p^), | = (p/t, <7/2)-

470 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ. VI
Рассмотрим функцию Гамильтона
Н (х, |) = 1 & А*В,Ах) + ^ (I, А*В1А1). F.4)
Имеет место следующий факт, частный случай которого был
использован в п. 8 § 9 Введения. Оказывается, можно так подо-
подобрать матрицы А н Bi, что при преобразовании g'H, dg'H пересе-
пересечения зон Q/flQ/f, отвечающем гамильтониану F.4), при
2 отсутствуют фокальные точки, т. е. якобиан
при
Обозначим через а1к число отрицательных диагональных эле-
элементов матрицы В/. Пусть S (a, t, blt, а7>) — решение уравнения
Гамильтона —Якоби с диссипацией, отвечающего* гамильтониану
F.4), такое, что
S (о,0, blt, aJt) = (qlt (ос), bt) - (ah, p/t(o)> + ReO, (a) + it, (a), F.5)
где Ф/ и #/—фаза и энтропия ростка в зоне Q/. Условию F.5)
отвечает зависящее от параметров, лагранжево многообразие
A"(&/i( ajt), которое получается из многообразия Л" с помощью
отображения gb/it ai,, переводящего
*t *i i\ ' i% * ъ * i'
а остальные координаты фазового пространства оставляющего без
изменений. Обозначим
'• »V a7.)\ ^
\р(о, t, bIt, ah))'
Иначе говоря, функции q(a, t, &Л, a7j, p(a, /, &л, a7>) удовлет-
удовлетворяют следующей задаче Коши для системы Гамильтона:
Б = |
F.6)
При некотором выборе знаков элементов матрицы Bt и для не-
некоторой матрицы А, зависящей от параметров (ph, a7j, справед-
справедливы соотношения:

§ 6] ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 471
Теорема 6.1. Существуют такие матрицы А и BJt что
при осеЙ/ПЙ/с. и таком, что 9/,(а» f". */»» aj,J = Pj, (а> |r.
*v а7 ) ~ ^ выполняются соотношения
1) У (а, 0^=0 при
. 2) У (а, я/2) = (—1
3) qh (а, я/2, рл (а), ^ (а)) = 0, р/§ (а, я/2, рл (а), q-u (а)) = 0;
?/\Л (а< я/2> рл ^' ?7.(а)
р7ч7>(а, я/2, рл(а), 9г,(а)
4) S(oc, я/2, рл(а), 97§(а)) =
где Фк и $к — фаза ростка и энтропия в зоне QK.
Доказательство. Предварительно докажем вспомогатель-
•ную лемму.
Лемма 6.1. Пусть А и В — вещественные симметрические ма-
матрицы, причем А диагонально, а В неотрицательна. Пусть С —
вещественная диагональная матрица, диагональные элементы кото-
которой равны ±1, и пусть AC^sQ. *-
Тогда матрица (А + iB) С не имеет отрицательных собствен-
ньи значений.
Доказательство. Предположим противное. Пусть А —
комплексный вектор, такой, что ACh-{-iBCh = — a2h. Тогда
CACh-\-iCBCh = — агСп и, следовательно,
(А~, CACh) + i(h, CBCh) = — a*(h~, Ch).
Значит (А, СВСА) = 0. Но поскольку СВС^О, то CBQA = O,
то есть BCh = 0. Поэтому ACh = — a2h, что невозможно. Лемма
доказана.
Первое утверждение теоремы мы для упрощения выкладок дока-
докажем в случае / = (Ц п), К*=0.
Равенство F.5) в рассматриваемом случае имеет вид
S(oc, 0, b) = {q(a), 6) + ReO/(a) + t#/(a).
Рассмотрим задачу Коши для системы Гамильтона, соответ-
соответствующей гамильтониану Н (р, q) (ср. F.6)):
p().
р A*B,Aq. F'8)
Система уравнений комплексного ростка имеет вид
z@) = z(a),
F9)

472 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА — ЯКОБИ [ГЛ. VI
Решение системы F.8) легко найти, сделав замену переменных
вида Ар = р', Aq — q'.
В новых переменных получим систему уравнений
<T=V'. q'@) = Aq@),
p'—BJ, p'@) = Ap@). F-10)
Из F.10) следует, что решение системы F.8) имеет вид
q(a, t, b) = A*UlAq(a) + A*UiA{p{a)-b),
р(а, t, b) = A*U1A(p(a)-b)-A*UiAq(a). (blU)
Здесь Ux и иг—диагональные матрицы, причем
(t/a)« = siny,Y, /=1, ..., n,
Yi = ±l —диагональные элементы матрицы Б/. Аналогично F.11)
можно написать решения уравнений F.9):
г (a, t)^1() + i(),
a»(a, t)^A*UlAw(a) — A*UtAz(a). FЛ2)
Из формул F.11) следует, что для любых невырожденных
матриц А и Bj из условий f = rt/2, q(a, я/2, &) = 0 следует соот-
соотношение р(а) = Ь.
Обозначим теперь через a (q, t, b) решение уравнения
q (a, t, b) = q, где q(a, t, b) — решения системы F.8). Выберем
ортогональную матрицу А (раз и навсегда) так, чтобы матрица
fr, я/2, Ь), 0, 6) II ,
|
была диагональной в точке ^ = 0. В силу ^сделанного здесь заме-
замечания о свойствах решений системы F.8) определение матрицы А
корректно, т. е. она существует.
Матрицу Bj выберем так, чтобы выполнялось неравенство
ReS (в(g, я/2, Ь), 0, Ъ) АВ^ъ F.13)
а/
9-0
Вычислим теперь якобиан J (a, t, b),
j (a, t, О) ^ .
Из равенств F.11) и F.12) следует, что
(«, t, Ь)+г(*, Q)_
F

S 6] ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 473
Преобразуем равенство F.14), используя определение матрицы Ux
dfa(q, t, Ь) + г(а, Q)_ д(д(а) + г(а)) „ d(p(a)+w(a)) .„. . __
a(g(B) + z(B))\-^ao»(B) + a>(B)) .„.
(«)) /,,
\ 1
a (g (в) + г (в)) \1 а (р (в) + а> (в)) .
5^ J ^ Л
Напомним теперь, что в § 5 гл. 6 доказано равенство
/ PS(a(q),0,b) \(d(q(a) + z(a))\-i(d(p(a)+w(a))\n (hm_e,
\ dqidq/ Г\ da [ да -Гио(П )¦
F.15)
Из равенств F.15), F.13), определений матриц А и U2 следует-,
что при условии «7(«, J, b)~0 к матрице /(a(g(ct^'(ct)) j^X
¦ х (р(«Н-щ(«)) ^*^/2 применима лемма 6.1. В силу этой леммы
матрица (при а е Г)
не имеет отрицательных собственных значений. Следовательно,
при условии д(а, у, 6j = 0 справедливо неравенство
У (a, f, 6)9^=0 при 0</<-j-
Таким образом, утверждение 1) теоремы доказано в случае / =
= A п), К = ф- Аналогично оно доказывается и в случае
перехода из любой зоны Q/ в любую зону пк, ^[]^кфф.
Пусть снова Н (х, ?)—функция Гамильтона вида
Я (дг,- ?) = | (х, А*В,Ах) + ± F, А*В,At).
Здесь x = (qli, р1г), ^ — {р^, qlt). Предположим, что матрицы А
и Bj выбраны так, что справедливо утверждение 1) теоремы.
Рассмотрим систему Гамильтона, соответствующую Н (х, I)
х = А*В1А%
% = -А*В,Ах F.16)
&=«, А = 0, J^/xU/i
с начальными данными
qi V-o = <7< («). Pi \м> = Pi (а) - 6,-, ig/,,
=?iW-fli. ftk^PiW. «e/,, F.16')

474 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОВИ [ГЛ. VI
Из F.16), F.16') следует, что pi(a, 0 = Р/(«), /е/\/2,
{ t)() /\/
qi{ )qi(), \x
Преобразуем оставшиеся уравнения системы F.16) с помощью
замены переменных А% = г\, Ах — Х,- Получим
= Ах(я, 0) = U
Л= В? г)@) = Л?(а, 0) = %.
Обозначим через Ux и ?/2 диагональные матрицы, элементы
которых суть
(?/i)« = cos/, (U2)u = sin-fit, i = l, ...
Здесь yi = ± 1 — диагональные элементы матрицы В/. Решение
системы F.17) есть
С = (/,?о+ ?/*%, *«=«/Ло-«/&. F.18)
Поэтому решение системы F.16) имеет вид:
Полагая ^ = т> ^ = 0» получим i4*t/2Tlo = O. Так как матрица
A*U2 невырождена, то отсюда следует, что т10 = Л?(а, 0) = 0
или ?(а, 0) = 0. Из последнего равенства и системы уравнений
F.16), F.16') непосредственно следует утверждение 3) теоремы.
Для доказательства утверждения 4) теоремы рассмотрим
систему комплексного ростка, соответствующую функции Гамиль-
Гамильтона Н (х, I)
z' = A*BjAw', , Zi\t-0 = zi{<x), i = l, .... п.
ti>' = —A*B,Az',
Из системы уравнений комплексного ростка следует, что
гг (а, 0==гг(а),. ш<(а, t) = Wi(a) при г ^ /г U /a. Для решения
оставшихся уравнений- в системе ростка положим
w" = Aw', z" = Az', F.20)
В новых переменных получим
Г = BjW', z' (а, 0) = Az' (а, 0) = г0' (а),
*' «= - BjZ', w' (а, 0) = Aw' (а, 0) = w; (а). ( '
Решение системы F.21) можно записать в виде
)" (a, fi^

S 6] ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 475 .
Используя равенства F.20), получим
г' (a, t) = A*UtAz' (а, 0) + A*U2Aw' (а, 0),
w'(a, ty=A*U1Aw'(a, 0)- A*U2Az' (а, 0). * " '
Полагая t = n/2, из равенств F.23) получаем
г'(а, л/2)'= A*BtAw'(а, 0),
да'(а, я/2) = - Л*В7Лг'(а, 0). . F<24)
Из формул F.19) и F.23) для решения систем Гамильтона и комп-
комплексного ростка следует, что
(a, t) + z (а, (), р; (a, t) + w (а, 0)
J(a, t)-^
Ho detB/ = (— l)"'K, где Ощ — число отрицательных диагональ-
диагональных элементов матрицы В/. Таким образом, утверждение 2) тео-
теоремы доказано.
D(q. (a, t)+z' (a, t), p (a, t)+w'- (a, M
Мы уже показали, что —^-^ р, . * i2 '-Ф
^0при0<^<я/2, 9/,(«. я/2, &Л, a,t) = plt{a, я/2, ft/t, a7>) =
= 0. Кроме того, в силу наших предположений и равенств F.19)
D(я. (а, 0. Р-, (а, 0)
Kh Da '\ '-Ф0 при *е[я/2-в, я/2],
где б > 0 — достаточно малое число. Таким образом, в силу тео-
теоремы 2.1 при ?е[я/2 — 6, я/2] решение уравнения Гамильтона —
Якоби с диссипацией, соответствующего функции Гамильтона
Н(х, |>, определяется по формуле
•S («/(<?/. Рп «). '• bit> «/,)=¦
/(а, т), p7(a, ^lf^
^(a)Vt-ile-e/(VP7. <), F.26)
где по условиям теоремы,
Я/2
Рассмотрим интеграл J «5? (9/ (а< 0» Р? (а> Щ &• ^ СИЛУ ве1Дест-
о
венности гамильтониана Н (х, |) и определения лагранжиана
ростка B.10)
F.27)

476 ОБОБЩЕННЫЕ УРАВНЕНИЯ ГАМИЛЬТОНА - ЯКОБИ [ГЛ, VI
Вычислим теперь выражение
я/2
О а~, "Я-, (а)
'з 'г
имеем
я/2 Я/2
/
= ± § «6, Л*5М|>-<лг, Л «В/Ас» Я.
Сделав замену A% = i\, Ax = ^, получим
Я/2 п/2
[ «6. Я6>-Я)Л = |\ «ri, Ял>-<С, 5/0) Я. ¦
О 0 -
Очевидно, достаточно рассмотреть интеграл
я/2 я/2
j (Г1!-Й)Л=5 (Лог cos ^ — So/sin YiO2 ^ —
о о
я/2
— I (?Oj cos t + % sin уЮ2 dt.
о
Легко проверить, что из условия b, —Pj (а), а7 =<// (а) и
последнего равенства следует
я/2
5 (Г1?-Й)Л = О.
о
Таким образом,
<*(я, я/2), w(a, я/2));
, P)dt\bli^pli(a) 2 1
<)
«7.
Но из равенств F.24) следует, что
(г (к, я/2), а» (я, я/2)); _ ^ (а), аи(я))у
То есть
1
Заметим еще, что из определения ^.-действия с помощью
канонических преобразований следует равенство
a =q (а)

6] ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 477
Подставляя F.28) и F.29) в F.26), получим
,, Р/1 w - s° <g> -<г (а\w{a))
а7 = ?7 (а)
Отсюда непосредственно следует тождество 4). Таким образом,
теорема доказана.
Обратимся теперь к неравенству диссипативности.
Теорема 6.2. Пусть в зоне Й/ выполняется неравенство
диссипативности, т. е. для любого сколь угодно малого е>0
существует такая константа Yi(e)>0 и такая гладкая функция
сх (а, е) :э= 0, что
I (w,(a), г,(а)\ \
yt(e)D(а)< Im[ix, (а) + к " \ lK >;+E(a)+ct (а, г)D(a)V.-«j.
Тогда при а е Й/ П &к существует такая константа у2 (е) «
такая гладкая функция с2 (а, г) ^ 0, что выполняется неравенство
Тг(е)?>(«)< 1тЦ (а) + <а>(я)'2'(я)>1С + ?(а) +с,(а, е)?)(а)'/.-«).
Операция обхода фокусов позволяет переносить неравенство
диссипативиости из зоны в зону. Действительно, пусть в карте
©J с: Q/ выполняется неравенство ytD (a) ^ $t (a); тогда на
пересечении карт со? П <»?< (предполагается, что
выполнено неравенство диссипативности
Это непосредственно следует из доказанной в § 2 леммы 2.9
о сохранении неравенства диссипативности при решении задачи
Коши для уравнения Гамильтона — Якоби с диссипацией и тео-
теоремы 6.1. Из теоремы 3.2 и операции обхода фокусов следует,
что неравенство диссипативности сохраняется и при переходе из
особой карты coycrQ/ в неособую карту ю^сгЙ^.
Для перенесения неравенства диссипативности из карты
со/ cr Q/ (при этом несущественно, является карта со; особой или
неособой) в особую карту ю^ cr QK мы можем воспользоваться
теоремой C.2). В самом деле, неравенство диссипативности выпол-
выполняется в силу операции обхода фокусов в тех точках карты ю?,
где
Переходя к у-перестройке и используя теорему 3.2, мы полу-
получаем, что неравенство диссипативности по непрерывности пере-
переносится во все точки пересечения карт со/ (] ®\- Теорема доказана.

ГЛАВА VII
КАНОНИЧЕСКИЙ ОПЕРАТОР НА ЛАГРАНЖЕВОМ
МНОГООБРАЗИИ С КОМПЛЕКСНЫМ РОСТКОМ
И ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ
§ 1. Формулы коммутации гамильтониана
с комплексной экспонентов-
В соболевской шкале {WJ(R")} рассмотрим производящие наборы
* = (*! хп), р = (Ри ¦••» Рп), где *, — оператор умножения
на /-ую независимую переменную, pj ¦» — ih д/dxj, 0 <; А — пара-
параметр. Пусть
00
«ЯГ (х, р) е ^со (R2") =
Далее, пусть S(x, со), ф(*, <о) — бесконечно дифференцируемые
функции, причем ImS(*, co)^O, ф —финитная функция, со eR".
Рассмотрим коммутацию гамильтониана а%*\х, р) и экспоненты
eft . Для этого применим оператор &С \х, р) к функции
[g-imSix. о»/йф(<уг (й)]еЛ ' . Очевидно, без ограничения
общности можно предполагать, что S — финитная функция.
Обозначим
Ф (х, со) = erIm s <*• "»/'«ф (л:, со).
По формуле коммутации (9.5) гл. IV имеем;
Применяя повторно ту же формулу коммутации, получим
|а|=о
где обозначено а = (аь ..., а„), ау = 0, 1,2,...; | а | = ах +...+ а„
*" def

§ 1] ФОРМУЛЫ КОММУТАЦИИ 479
остаток /?л(Ф) есть некоторая функция от упорядоченных опера-
операторов pj — — ihd/dx/ и Xj, (/=1, ..., п).
Выпишем здесь формулу для #й(Ф) (ниже в подобных раз-
разложениях мы уже не будем приводить явных формул для оста-
остаточных членов, ввиду их громоздкости):
X \, рх pit, р/г . Pjkt Plkl,
•••i P/ft-b Р/*> P/ft- P/ft+ь •••. Pn)l A.2)
Используя формулу A.1), Мы теперь рассмотрим коммутацию
гамильтониана «5Г (х, р) и функции ен . Прежде всего, если
S — вещественная функция (ImS=0), то по 4юрмуле коммутации
ё вещественной экспонентой (8.7) гл. IV имеем:
-ih)NLN(S\ A)q>\.
)
где L*(S), Ln(S, А) —некоторые операторы, причем, Lk(S) имеют
вид
MS)
Ф^*'. (S) — полиномы относительно производных ' -.^*' - \ у'\ =
= 2 7к*). Например, Ц(S)-*2Г(лг, ^-(лг, со)).
Остаток [L^ (S, А)ф](*, со) в формуле A.3) имеет следующую
оценку
IILn(S, h)ф\vk(R2n)^cn. k
где константа Cn, * не зависит от А.
Для случая комплексной функции S, удовлетворяющей усло-
условию ImS(Af, со) 5=0, имеет место формула коммутации, аналогич-
аналогичная A.3).
Лемма 1.1. в сформулированных выше условиях имеем:
N — 1
Дв 21 (-^ГE)Ф + ^Ф, A.4)
*) Здесь и далее буквами а, 0, v. ••• обозначаются мультииидексы из л
целых неотрицательных чисел, например v = (Yn •••» Yn)> Vy=O» ^i 2i •¦••

480
КАНОНИЧЕСКИЙ ОПЕРАТОР
[ГЛ. VII
где L<M(S), QN —некоторые операторы, причем Lf> (S) строятся
исходя из соответствующих операторов Lk (S) следующим образом:
2Л
| V|=0 L|a | = 4 | |3 1 = 0
x
Остаток (Qn<p)(x, со) в формуле A.4) имеет оценку:
||^(Q^)||w.ft(R2n)<cAf,4AW*. ^0,
Доказательство. В выражении
A.6)
, p)\eh <р)
2 1
произведем вначале коммутацию гамильтониана е%" (а-, р) с функ-
функцией Ф(х, в>) = <р(х, ш) е-Im s <*• «>/л A + 1 Jf J2")' по формуле A.1):
2N — 1 ,„, 2
«ЯГ
* 1 /is \_ V
ж, рДе* ф)~ 2
В этой сумме каждое выражение
преобразуем с помощью формулы A.3):
-~
i-Res
(-ih)»LN(ReS,
, ,8
. A.8)
После подстановки выражения A.8) в' формулу A.7) для
доказательства леммы остается совершить некоторые тождествен-
тождественные преобразования и привести правую часть A.7) к виду, ука-
указанному в формуле A.4). При этом возникнут остаточные члены,
сумма которых образует остаток QN в формуле A.4). Трудность
представляет лшиь оценка остатка
(L9)
Оценим норму \\h2NR2N D>)\\wk^wk- Из формулы A.2) следует
что достаточно оценить U:a|-^arL*_,»-* при \a\ = 2N. Индук-

§ 1]
ФОРМУЛЫ КОММУТАЦИИ
циеи по | а | легко устанавливается, что выражение я
является суммой слагаемых вида
д Тгп S д Im S |„(|, ,.wfc
481
I a I (РФ
где г|> е= С? (R2n) и
Тогда из неравенств
' д Im S \ / a Im S
Im S (x, ш)/А
.. /=1, 2,
следует оценка
,; ее
i даф
дх*
.A|a|-ft
Поэтому остаток A.9) оценивается нужным образом;
Лемма доказана.
Аналогично рассматривается действие гамильтониана
на преобразование Фурье от экспоненты:
f
х, р)
где S, феС^Я2»), ImS(g,
•^fv
Внесем оператор <?%" (х, р) под знак интеграла A.10); получим
следующее выражение:
Далее под интегралом остается воспользоваться уже получен-
полученной формулой типа A.4).
В заключение этого параграфа отметим, что в лемме 1.1 фун-
функция е%" (х, р), а также функция ср (х, со) по переменной со могут
принадлежать классу $°°, т. е. классу таких функций /(г/), все
производные которых растут не быстрее некоторой степени \у\к
при у-+со (см. гл. IV, § 10). При этом соответственно изменя-
изменяется норма в оценке A.6) по переменной со.
16 В. П, Маслов

482 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ. Vtl
§ 2. Квантовая операция обхода фокусов
В этом параграфе мы приведем асимптотику преобразования
Фурье от выражения типа (9.24), которое было приведено во
Введении в § 9. Это нам нужно сделать для'той же цели, что
и в главе V, в которой мы вычисляли асимптотику преобразова-
преобразования Фурье от осциллирующей экспоненты C.1) с тем, чтобы
потом определить канонический оператор.
В нашем случае экспонента может, вообще говоря, содер-
содержать быстро затухающий член, и на первый взгляд казалось бы,
что нам нужно применить для получения асимптотики интеграла
метод, аналогичный методу перевала4. Трудность, однако, заклю-
заключается в том> что аналогично тому, как это было сделано в гл. V,
мы хотели бы получить асимптотику преобразования Фурье выра-
выражения (9.24) (см. § 9 Введения) в таком виде, чтобы диссипация,
fi-действие, якобиан и фаза преобразовались бы по законам пере-
перехода комплексного ростка из неособой зоны в особую. Мы уже
видели на примере главы V, что именно подобная геометрическая
интерпретация асимптотики преобразования Фурье приводит
к определению канонического оператора, и тем самым глобаль-
глобального решения уравнений. С помощью формул метода перевала
это сделать, по-видимому, чрезвычайно трудно из-за того, что
комплексная функция неоднозначно. представима в виде сум-
суммы s-действия, ц-действия и потенциала. Поэтому мы для вычис-
вычисления такого интеграла применим прием, аналогичной операции
обхода фокуса и подобный тому, который был приведен в п. 4 § 8
Введения. Этот прием естественно называть квантовой операцией
обхода фокусов. Часто, впрочем, мы будем его снова называть
методом стационарной фазы.
Пусть Л" — лагранжево многообразие с комплексным ростком.
Предположим, что оно покрывается двумя особыми зонами Q; и
QK, в которых дополнительно' выполнены условия
д (q p-\
V'' /; yfc'O aegQffVQ
det
yfcO,. aegQffVQ/c,
• BЛ)
Обозначим через <*,Xqi, pi) решение уравнений
?/(a) = <7/. P7(a) = P7>
а через aK(qK, р^) —решение уравнений
В силу наших предположений функции
«/(<//, Pi) и ак(Як,

$ 2] КВАНТОВАЯ ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 483
определены на пересечении карт Q; f) &к- Пусть К = (/\Л) U h, где
/jcz/, /jjcz/ и Ф; (а)— фаза ростка в зоне Q/, 11х\ + \ /а|== /п.
Обозначим через L/ оператор, определенный на функциях,
носители которых принадлежат неособой карте со0/ cz Q;:
^ r^v. B-2)
|V|=/V
где р = - [(а^/+г^7+Ш/^)~' ]' С,) ПРИ SUPP Ф («) G ю?- Че-
Через LJ' обозначим оператор B.2), где вместо Р поставлены p*V;
пр„ supp,,„,в,7. B.3)
Определение. Будем говорить, что дифференциальный опе-
оператор iP порядка k с гладкими коэффициентами принадлежит
классу 56a,k если для любой функции (f(x, h), бесконечно диффе-
дифференцируемой по х и равномерно ограниченной по h со всеми про-
производными, и для всех мультииндексов I таких, что | /1 ^ 2<х,, выпол-
выполняется соотношение
в ^
а при |/|>2а функция ~tj—тт^~ or'ф равномерно ограничена поп.
I '" я
Если оператор or — не дифференциальный, то индекс k мы
будем опускать.
Фиксируем такую ветвь функции \fz, что — л/2 < arg Уг ^ л/2.
Вычислим асимптотическое разложение при h-^О интеграла
B-4)
x(J,) 2L,<p(a,h)
(ь)
Здесь через F, F обозначены прямое и обратное -^--преобразо-
-^--преобразования Фурье, функция ф(а, h) е С~ (Л" х [О, 1J) имеет носитель
suppф(а, h)czQi(]Qi(, функции ФЛ f/f У/— соответственно
а
фаза, энтропия ростка и комплексный якобиан в зоне Q;; диф-
дифференциальный оператор Л^-го порядка Lj определен в B.2).
Рассмотрим функцию Гамильтона Н из F.4) гл. VI, отве-
отвечающую операции обхода фокусов при переходе из зоны Q,
в зону Q^, и пусть В, —соответствующая этой функции Гамиль-
Гамильтона матрица (см. § 6 гл. VI). Обозначим через в,к(а) число
отрицательных диагональных элементов матрицы Ви
16*

484 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ VII
Пусть J (a, t) — комплексный якобиан, соответствующий сдвигу
вдоль траекторий операции обходи фокусов при переходе из Q;
в йк (см. теорему 6.1, гл. VI). Обозначим через Д;дг(а) количе-
количество оборотов, которое совершает комплексная точка J (a, t)
оро
argj(a,t)]
*
. Далее обозначим
Лемма 2.1 Пусть выполнены условия B.1). Тогда справедливо
асимптотическое разложение:
+ Rw(hN'2), B.5)
=*к (*к, рк)
/=о
где % е= С» (Л"х [0, 1]),ф,е0о (Л'/2-'8) (е> 0 -достаточно малое
число; Фя> <^к» Jk — соответственно фаза, энтропия и ^якобиан
в зоне Qk', остаток RN (ft^/2) имеет оценку
Функции ц>1 (a, h) определяются по формулам:
Фв(а,-А)*=ф(а, h), ф1(а, h) = (hP[*' + P<? + Ff)<p(a, А) = <^1ф,
Ф, (a, ft) = (ftA,11 + Pi1' + Р'Г) (ft?x + >, + Ps)'^ (йД01 + Д0' +
+ >,") Ф а, А)-^|Ф, / = 2,-3 Л^,B.&')
где Ри РТ, Л1', f,2'ecS?0; />„ />«», ^', PifeX^ Р„ Pf,
Рз11, P32'e<5?i/9_E> ^*, ^^i/2-ie,kN, kN —целое. (Способ вычис-
вычисления операторов Р)А) приводится в приложении 2, /шша 7; коз0-
фициенты этих дифференциальных операторов не зависят от N
и бесконечно дифференцируемы по параметру h.)
Доказательство. Применим уже использованный во Вве-
Введении прием для вычисления асимптотики при п-*-0 интеграла
/ (Л). Рассмотрим задачу Коши
Ф(<//, Р/; о) =*"(</„ Pi),
где Я(|, дс)— функция Гамильтона, отвечающая операции обхода
фокусов при переходе из зоны Q/ в зону Q#; здесь, как и
в § 6 гл. VI, мы обозначаем x — {ph> р-^} g = (p, , fl'/J- Выберем

§ 2] КВАНТОВАЯ ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 485
начальные данные в B.6) следующим образом:
р, >—<р 7 «; >l/f -i
' " ' '(Ji)
ад?/> р?) B.6')
Сделаем замену переменных Ах — %. Функцию if G,, p-h /) в новых
переменных обозначим через %/(?, t); соответственно, функцию
\|з° G/( р,) обозначим через \|зояШ-
Задача B.6) в новых переменных примет вид
«• B.7)
¦я(С, 0)=i|HW(S),
где'Hi (л, 0 = -g- 21 Yi ("Пг? + С/). Y< — диагональные элементы мат-
i
рицы В/. •
Во Введении приведена следующая точная формула для реше-
решения задачи B.7) в одномерном случае:
—i-j—'-у A- sinQ
Для решения многомерной задачи B.7) достаточно последовательно
решить одномерные задачи Коши, соответствующие гамильтониа-
гамильтонианам y<(—2~Ш"^~2 Щ Тогда для точного решения задачи B.7)
при />0 получим формулу:
Из этой формулы, а также из вида начальных данных B.6')
следует, что для вычисления асимптотики интеграла /(/^доста-
/(/^достаточно вычислить асимптотическое решение задачи B.6) при
O * /2
Докажем, что это асимптотическое решение имеет вид
gN (х, t)^e*S ix' ° ? ф* (*, t, h), B.8)
где S е С00, Im S ^ 0; ij)ft е С00, А = 0, ..., N, и вычислим функ-
функции S, г]>о, ... ^w в точке * = 0, t = n/2.

486 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ. VII
Применяя оператор —ih^- — H[ — ih-^, ~XJ к функции gN,
учитывая явный вид оператора Н (см. F.4) гл. VI) и производя
„/ .. д 2 \ „ is{x,t)
коммутацию гамильтониана nl-ifty, xj с экспонентои ел ,
получим:
A=0
). B.9)
Пусть функция S есть решение уравнения Гамильтона — Якоби
с диссипацией, вида A.6') гл. VI при еЗГ = #(?, х). Имеем
где*) ^[е<5?з • Решение такого уравнения, удовлетворяющее
начальному условию
S (х, t) 1,-с = [Re Ф, (а) + »*/ (а)] |«-в/ (?ь р.} +
уже было вычислено нами в точке х = 0, t = n/2 при доказа-
доказательстве формул операции обхода фокусов (гл. VI, § 6). Напом-
Напомним, что
S @, я/2) = [Re Ф*
Теперь построим функции ipk из B.8) так, чтобы правая часть
равенства B.9) имела порядок О (hNI2): пусть \|з0 удовлетворяет
уравнению переноса с диссипацией:
и начальному условию
^о (*. 0 !/-о = {(^/ («))-v» ^/Ф («. Щ \а=а;(9/> „7), B.12)
В силу предположений 36>0 такое, что D(qi (a, t), pi (a, t))/Da Ф 0
при /е[л/2 —6, я/2]. Поэтому из формул § 5 гл. VI следует,
' *) Оператор $[ легко вычисляется явно с помощью подстановки в урав-
уравнение Гамильтона — Якоб» с диссипацией решения, достроенного по форму-
лам §§ 1, 2 гл. VI,

* 2] КВАНТОВАЯ ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 487
что решение задачи B.11), B.12) в точке х = 0, t = ~ имеет вид
Кроме того, из результатов § 5 гл. VI следует равенство
fh (? 4) /*—>, &= ^'г,. B.14)
где*) ^|'е^] е 0, Тг^Х (, а через П обозначен оператор
переноса,
Обозначим также
р _д Mi* /JL А*В,А д \
Из B.10), B.14) следует, что правая часть B.9) равна
B.15)
где
(
Теперь определим функцию i^ как решение уравнения пере-
переноса с правой частью:
h AYt|>o + 44>о + ^Л = OD
. 01-0.
В силу леммы 6 приложения 2 функция % в неособой карте
может быть представлена в виде
где
I, B.17)
••) Вычисление явного вида операторов $' и #2 эквивалентно вычислению
невязки, получающейся при подстановке в уравнение переноса с диссипацией
решения, построенного по формулам § 5 гл. VI, Вш0^' =ga ^CM' CTD- 465).

488 КАНОНИЧЕСКИЙ ОПЕРАТОР ' [ГЛ. VII
причем интегрирование производится вдоль траекторий системы
Гамильтона, отвечающей функции Гамильтона Н Ц, х).
В особой карте
т К/(о, О
где
{ }, B.18)
о
(операторы L] были определены выше).
Обозначим
ф*(а, 0 =¦*(</#(«. 0. Р/(«. 0. Я. * = 0, 1, 2 #,
где ^/ (а, 0> Р/ (а. 0 — решение системы Гамильтона F.6) гл. VI.
Из формул B.17),- B.18) и теоремы 5.3 гл. VI следует, что
функцию \|)! (a, t) можно представить в виде
0)('))ф(а, h). B.19)
где операторы РЧ, Р\, Н определяются через операторы AY, ^lt
R2 соответственно и удовлетворяют условиям-леммы.
Рассмотрим tifa, yj; используя доказанное в теореме 6.1
гл. VI равенство
получим:
Отсюда и из формулы B.19) имеем:
h),
где линейный оператор G переводит начальные условия для
уравнения переноса в решение этого уравнения, а Pju —опера-
—операторы, удовлетворяющие условиям леммы и связанные с операто-
операторами Pj0> равенствами:
г
1 2 VJK
для у (a, t, Л)еС»(Лл х [0, а?) X [0, 1]).
Для остальных функций \|з„ / = 2, 3,..., N аналогично предыду-
предыдущему получим уравнение:

§2] КВАНТОВАЯ ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 489
решение которого задается формулой:
ф, а, 0 = (hPt (t) + Рг @ + Ра (t) )*-» (hP{0) +
причем
Отсюда вытекает формула B.5') для фг (а, А), приведенная
в формулировке леммы. Из B.5') непосредственно следует оценка
Ф,(о, h) = OD(h42-6), гдебга/е.
Кроме того, при указанном выборе функций \|)г, / = 0, 1, ,.., Л'
равенство B.9) приобретает вид:
где ¦ - .
GN (х, 0 = (- /А) ег S ("- ° [
Функция Gw в силу приведенных выше формул, для грлг удовлет-
удовлетворяет оценке:
\GN(x, t)\^Cfrh 2
где б > 0 — некоторое малое число, cN — константа.
Используя эту оценку и точную формулу для решения задачи
B.6), можно аналогично тому как это было сделано во Введении,
показать, что функция gN, определенная равенством B.8), является
асимптотическим разложением решений задачи B.6). Поэтому и левая
часть B.5) является асимптотикой при Л-^0 интеграла B.4).
Лемма доказана.
Следствие. Пусть на пересечении зон
det да 7^0, «gQ/fiQ^. B.19)
Пусть I (A) — интеграл, определенный равенством
B.20)
(обозначения здесь те же, что и в равенстве B.4)),

490 КАНОНИЧЕСКИЙ ОПЕРАТОР (ГЛ. VII
Тогда интеграл B.20) разлагается в асимптотический ряд B.5).
Доказательство. Для доказательства Достаточно принять
во внимание утверждение теорем 3.2 и 5.3 гл. VI, в силу кото-
которых вид решения уравнений переноса и Гамильтона — Якоби
с диссипацией при t —10 не зависит от того, в какой —особой или
неособой — карте была задана начальная функция.
d(q , р-\
Далее, в случае, если det -^—— обращается в нуль в неко-
некоторых точках пересечения зон й7 П &к> мы можем сделать ка-
канонический поворот на угол t = OD\h°), который приведет к тому,
что такие точки исчезнут. В этом случае на пересечении Q/П &к
зон, полученных в результате поворота, будут . выполнены
условия вида B.1). Однако при этом в некоторых точках карты
со* с &j П &к может быть,
det
И несмотря на то, что мы можем применить операцию обхода
фокусов, для выполнения которой достаточно разрешимости си-
системы уравнений
производные от решений соответствующих уравнений перено-
переноса и Гамильтона — Якоби с диссипацией могут в некоторых
точках со^ иметь порядок 0о(Л—°°). Но мы можем после получения
решений этих уравнений перейти к их уперестройкам, как мы
уже поступали, например, при доказательстве теорем 3-.2
и 5.2 гл. VI.
Совершив затем канонический поворот на угол —t, мы полу-
получим следующую формулу для асимптотического разложения интег-
интеграла / (h) (мы предположили здесь, что пересечение зон Q7 f| QK
покрывается одной особой картой aj,):
' X
4- О (Л00), B.21)
где Ф^ есть у-перестройка фазы ростка в зоне Q#; С\ (а) — глад-
гладкая функция, для которой выполнено неравенство
YiD (о) < Im Ф^ (а) + сг (o)D(aK/2-8,
с некоторой константой у%. Под О (Л°°) мы понимаем 0 (hN/2), где

§2]
КВАНТОВАЯ ОПЕРАЦИЯ ОБХОДА ФОКУСОВ
491
N —любое, а верхний предел суммы равен N;
Фо (a, h) = Ф (а, h), ф1 (а, h) = (ЛР{2)
if,(а, Л) =
Ф (а, h),
где ?rt — дифференциальные операторы с коэффициентами, не зави-
зависящими от N и бесконечно гладкими по А, причем
J
е> 0 —малое число.
Используя B.5) и B.21), дадим определения операторов, пере-
переводящих функции от аргументов (qn p7) в функции от аргу-
аргументов (qK, р%).
Пусть Лп —лагранжево многообразие с комплексным ростком,
jo} неособая карта в зоне Q/, <о°к — неособая карта в зоне QK.
Предположим, что со} f| а°к Ф Ф и что задана гладкая функция
Ф(а), supp ф (а) с: со" П <йд-. По лемме 2.1 имеем (мы сохраняем
здесь прежние обозначения):
р
X
1=0
'X
где (/\/i) U /j = К- Определим оператор VfK равенством
Из леммы 2.1 следует, что
где
B.22)
B.23)
з<_1 B.24)
Нетрудно показать, что операторы [УГк]г не увеличивают но-
носитель функции ф (а).
С помощью формулы B.21) определим операторы перехода
из неособой карты в зоне й7 в особую карту зоны QK. Пусть
(о? П й)( =^ О. Ф (а) —гладкая функция, supp ф (а) с со1} П ®\-
Определим оператор У^ из условия
(а)|-^(.Л.'й B'25)

492 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ. VII
Из B.21) следует, что
где операторы [V0,^ олределяются аналогично операторам [VJ^ji
(см. B.24)). • •
Аналогично, с помощью следствия из леммы 2.1 определяются
операторы V]^, VfJ. Они также являются локальными (не уве-
увеличивают носителя функции).
Из теоремы о решении уравнений переноса и Гамильтона —
Якоби с диссипацией следуют соотношения
(mod 0o (А'/—)),
Из обратимости преобразования Фурье и единственности
асимптотического разложения вытекают следующие соотношения:
V?KV%,.-1 (mod 0o (*»)).
= 1 (mod 0D(A-)). ,
Определим еще операторы перехода из особой в неособую и
из неособой в особую карты одной и той же зоны. Предположим
вначале, что для карт со° и coy выполнено условие со° П
со° П соус со^. Тогда мы положим
B.29)
Если же аЧ (] <л^ cz.ayK, то положим
V%=V%-V%. B.30)
Легко видеть, что оператор V0* определен корректно, т. е.
не зависит от зоны Q#, которой принадлежит пересечение карт
со° П ИУ- Для определения операторов перехода V°v и Vy° в об-
общем случае мы используем метод, аналогичный операции обхода
фокусов (другое определение см. в приложении 2).
Мы не доказали в гл. VI единственности (в каком-либо классе
функций) решений уравнений Гамильтона —Якоби и переноса
с диссипацией. Однако из формул, дающих решения этих урав-
уравнений, легко получить следующее утверждение. Рассмотрим дис-
сипативное уравнение Гамильтона —Якоби, соответствующее неко-
некоторому вещественному гамильтониану, не зависящему от времени.
Будем обозначать решение этого уравнения через S (я, /). Пусть
S(x, 0) = S0(x). Через Sla (x) обозначим решение нашего уравне-
уравнения в момент времени t = t0 (мы предположили для простоты, что

$ 21 КВАНТОВАЯ ОПЕРАЦИЯ ОБХОДА ФОКУСОВ 493
начальное условие задано в неособой карте со неособой зоны Я
и что карта со остается неособвй при сдвиге за время t, O^t^to
вдоль траекторий соответствующей системы Гамильтона. Это пред-
предположение несущественно; важно лишь, чтобы зона оставалась
неособой),.
Положим теперь S (х, 0) = St, (x) и будем решать задачу КЬши
для нашего уравнения «назад», т. е. рассмотрим функцию 5 (х, t)
при t = —10. Тогда
Доказательство этого факта следует из теоремы 2.1, если учесть,
что соответствующие системы уравнений Гамильтона и комплекс-
комплексного ростка обратимы во времени. Аналогичный факт справедлив
и для уравнения переноса с диссипацией.
Для определения операторов V"}v мы теперь поступим следую-
следующим образом. Пусть «ЯГ(|, *) —гамильтониан вида
«ЯГ (Б. *)=4
где Y; = — U чер63 х обозначен набор x'=(qIo, pj0) /os
а 6 = (Pi., qit).
Рассмотрим квазиклассическую асимптотику задачи Коши:
± [ф/ <о) + е (a) D
, pi, 0, h)=eh X
B.32)
где ф (а) — гладкая функция, supp <p (a) cz ю^ П ©?•
Асимптотическое решение задачи B.32) находится аналогично
асимптотике решения уравнения тина Шрёдингера, использован-
использованной в методе стационарной фазы.
Обозначим через (qi (a, t), pi (a, t)) решение соответствую-
соответствующей-системы Гамильтона, а через (Z/ (a, t), wj (a, t)) — решения
системы уравнений ростка. Предположим, что
rfpf II д{4{ (a, n+Z^a, t), p?(a, Q-f»y(a, Q) II
II ~ fa '. II
при О^^^^о, /0>0 некоторое число (очевидно, что существует
хотя бы один гамильтониан, для которого это условие выполйё-
но). Вычисляя асимптотику задачи B.32), так же, как в методе

494 КАНОНИЧЕСКИЙ ОПЕРАТОР (ГЛ. V1J
стационарной фазы, получим
Рп U h) = e^S^'">1''o)^tei(qn р7, t)Lf(to)x
i
Здесь мы обозначили через S(q,, pj, *0) решение диссипатив-
ной задачи Гамильтона — Якоби, соответствующей Я (?, *),
[ei(Qi> Pi> ^)} — разбиение единицы, подчиненное разбиению на кар-
карты области со1} (^0) П ю) (^0)> ТДе через ю1} (/), ю) (t) мы обозначили
карты, полученныеv при сдвиге карт ю^ и ©у вдоль траекторий
системы Гамильтона, с гамильтонианом B.31) за время t, V\ —
некоторые операторы (не увеличивающие носитель функции ф(а)),
и Lf определены равенством B.3) на со^ (^0).
Рассмотрим теперь решение задачи Коши
lt р-п 0, h)=*(qr, pj. tQ, h) B.33)
в момент времени t = —10. Известно, что решения задач вида
B.33) обладают групповым свойством. Именно, если мы положим
p,, 0, h),
то операторы Е (t) удовлетворяют равенству Е (^) Е D) = Е
т. е. ;
*(?/. Рп —'о. А) =*(?,, /3/, О, И).
Теперь, вычисляя квазиклассическую асимптотику задачи B.33)
' точно так же, как при доказательстве формул метода стационарной
фазы, и считая, что при t = —10 мы находимся в карте ю],
получим:
.4-г
„V/ . B.34)
Легко доказывается, что функция фх (<?,, pj, —10, К) действи-
действительно является асимптотическим разложением функции ty(qn pj,
— t0, h). Таким образом, '
Р/, —19, /i)-if(9/( pj, 0, h)=*OD(hN'2). B.35)

§ 3] ИНДЕКС КОМПЛЕКСНОГО РОСТКА 495
Мы можем определить оператор Vf из равенства B.34) формулой
V/v = l+2>2 e[Vi°4]t. B.36)
i
Оператор V?Y, определенный равенством B.36), не зависит от
выбора гамильтониана е%"(р, q) и момента времени t0. Это сле-
следует из сделанных выше замечаний о решении уравнений Гамиль-
Гамильтона — Якоби и переноса с диссипацией и групповых свойств
решений уравнений типа B.33). Легко видеть также, что опре-
определение B.36) является непосредственным обобщением определений
B.29), B.30).
Из определения операторов перехода следуют равенства
W (n*dOD0hy,
(mod ОD (Л00)),
и т. д.
Кроме того, из определения операторов перехода B.22), B.25),
B.30), B.36) следует, что для каждого из них существует квази-
квазиобратный оператор (по модулю OD(h°°)), который легко строится
методами теории возмущений.
§ 3. Индекс комплексного ростка и канонический оператор
Для того, чтобы определить индекс на Г, введем некоторый
класс многообразий, который включает в себя класс вещественных
лагранжевых многообразий.
Пусть С2" —фазовое пространство комплексной размерности
2п с координатами Р = {Рг Р„), Q = (Qi, ..., Qn), а Лу :
{р = Р(а), Q = Q(a)}, (a = a! ая) — вещественное «-мерное
многообразие, вложенное в С2я (локальные координаты а веще-
вещественны, а Pj(ol), Qj(a) — комплексные функции).
Предположим, что для Р(а), Q(a) выполняется условие равен-
равенства нулю скобок Лагранжа:
> чс v n datda) дацдац
и касательные плоскости к Л^, вещественноподобны. Обозначим:
Нетрудно видеть, что при фиксированном а матрица В( невырож-
невырождена при достаточно малых положительных t,

496 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ VH
Потребуем, чтобы многообразие Лу удовлетворяло следующему
условию:
\m(BjlCh, А)<0 C.1)
при 0 < t sg ^0 (а) для любого h е Ся.
Многообразие Лу, удовлетворяющее этому дополнительному
условию, будем называть У-лагранжевым.
Для определения индекса замкнутого пути У-лагранжева
многообразия напомним, что, если путь на Г лежал целиком
в неособой карте, то индекс пути определялся через приращение
аргумента (фазы) якобиана D(q + z)/Da.
Пусть е —достаточно малое положительное число,
Q = Q-ieP, Р=Р C.2)
отвечает сдвигу на t = e вдоль гамильтоновой системы с гамильтониа-
гамильтонианом — iP2. Покажем, что это преобразование переводит У-лагран-
жево многообразие
Ляу: {Р = Р(а), Q = Q(a)}
в У-лагранжево многообразие
АУ: {Р = Р{а), Q = Q(a)), C.3)
для которого матрица dQ/da невырождена при всех а.
Действительно, обозначим
U C.4)
Тогда
(Bj'Ch, h) = (BT1Ch,h)-iE(BTlBh, h) =
= (BjlCh, h) - it (A,- h) - it (Вт1 (В - Bt) h, h) =
= (B7'CA, A)(l-eO-»(A, h),
так что Im (BjlCh, h) sg 0 при достаточно малых t.
Следовательно, Ля есть У-лагранжево многообразие.
¦> аЛ ал ар
Далее, j~ = ~ — ie^ = C — ieB. Предположим, что матрица
C — ieB вырождена. Тогда существует такой ненулевой вектор
АеС», что (С-/еВ)А = 0. При этом СкфО, ВкфО, так как
п) имеет ранг п. Обозначим gt = Bth\ g/фО при доста-
W
точно малых t.
"Имеем:
llm ((СВГ - ie) gt, g,) = lim ((С - ieBt) h, gt) = ((C - fefl) A, g) = 0.
С другой стороны,
Im ((CBj1 - ie) gt, gt) = Im (CB?gt, gt) -*\&tf<>-*Ut IP,

§ 3] ИНДЕКС КОМПЛЕКСНОГО РОСТКА 497
откуда следует, что
lim Im ((CBp - fe) gt, ^)^e||^|p<0.
Полученное противоречие доказывает невырожденность матрицы
dQ/da.
Задача. Пусть Ж (р, q) = H (р^ q) + iH (р, q) р <= R", q<=Rn — голо-
голоморфная функция от р и q и пусть Н(р, q)^0. Доказать, что сдвиг вдоль
траекторий этого гамильтониана переводит У-лагранжево многообразие в У-
лагранжево; т. е. &чр(р,ч) ^-у У-лагранжево, где
Ay = {Q(a), P(a)}, g^^ Q) A»'. \Q(a, t), P (a, t)},
Q(a, 0)=Q(a), P (a, 0) = P(a),
^, 0. Q(«. 0).
P(a, q«_-g-(P(a,;o. Q(o. 0)-
Рассмотрим гамильтониан Н — рг-\-ф, peR*, ^eR*. Сдвиг
вдоль траекторий такого гамильтониана У-лагранжева много-
многообразия Ay = {Q(a), P(a)} осуществляется следующим преобра-
преобразованием:
Qi (a, t) = Qi (a) cos * + Pi (a) sin t, i < ^,
Qj(*, 0 = Qy(e), ^(e, 0 = ^(o) при n^/>A C<5)
Нетрудно убедиться, аналогично тому, как это было проделано
выше, что якобиан
D(Q( Q-teP(a, Q) nfi.
щ (jo)
не равен нулю при е>0 для любых действительных t. При
I = я/2 мы получим, очевидно, что
(о). Q7(o)
iij C.7)
где / = A k).
Теперь мы можем определить индекс пути, лежащего на Лу.
Пусть сначала путь / целиком лежит в одной координатной
окрестности.
Пусть Аф (I) — приращение аргумента (фазы) якобиана
J C.8)
вдоль этого пути. Положим:
Inde/ = [M], C.9)
где скобки [ ] означают целую часть числа.

498 канонический оператор [гл. vii
Очевидно, что Inde/ не зависит от выбора локальных коор-
координат, так как при переходе к другим локальным координатам
det [С (а) — ie5 (а)] умножается на положительную функцию.
Если путь / не лежит целиком в одной координатной окрестности,
то Inde/ определим по аддитивности. Очевидно, что для замкну-
замкнутого пути у. Ind у не зависит от е при достаточно малых е>0.
В этом случае мы положим Indv=Indev. Справедлива формула
D(Q-teP)
(ЗЛ0)
Da.
Легко видеть, что если замкнутый путь у можно стянуть в точку,
то Indv = 0; таким образом, Ind есть одномерный класс когомо-
логий многообразия Лу (характеристический класс).
Заметим, что индекс Ind можно определить и для некоторых
незамкнутых путей /. Именно, если при достаточно малых в
дробная часть Аф (/) превосходит некоторую положительную
константу, то положим
Ind/= lim Inde/. C.11)
е-* + 0
Кроме того, если концы пути / являются неособыми точками,
т. е. в них отличен от нуля якобиан jy , то
= Jim Л, Arg D(Q~JeP) C.12)
существует, и мы можем определить индекс пути / как [Афо/я].
Предположим теперь, что на Лу все индексы замкнутых
циклов равны нулю (т. е. целочисленный класс когомологий,
введенный выше, тривиален). Тогда индекс пути из неособой
точки ах в неособую точку а2 не будет зависеть от пути, а будет
зависеть лишь от точек аг и аг. Пусть а0 —некоторая точка
на Лу, которую мы назовем начальной. Для определенности бу-
будем считать, что она неособая, а аргумент якобиана -~ (а0) в ней
будем считать заключенными между 0 и 2я. Теперь мы можем
по непрерывности однозначно определить Arg (фазу) якобиана
DQ/Da в любой другой неособой точке а е Лу, поскольку измене-
изменение фазы якобиана Аф0, определенное в C.12), не зависит от пути.
В силу леммы о локальных координатах многообразие Лу
можно покрыть областями й/, в каждой из которых отличен
от нуля якобиан
D(Q.(<x), P7(<x))
1 ' р«' • C-13)

§ 3] ИНДЕКС КОМПЛЕКСНОГО РОСТКА 499
Мы можем определить однозначно по непрерывности и Arg этих
якобианов с помощью преобразования C.5) и перехода к пределу,
при е-»-0, Arg Je(a. л/2) в формуле C 7).
Нетрудно убедиться, что, если определить Arg якобианов
с помощью сдвига вдоль траекторий гамильтониана Н (р, q),
отвечающего операции обхода фокусов (или какого-либо* другого
(действительного) гамильтониана, приводящего к тому же конеч-
конечному каноническому преобразованию поворота на угол я), то
в силу того, что индекс не зависит от пути, мы получим то же
самое определение Arg якобиана C.13).
Множество Г комплексного ростка зачастую является пере-
пересечением лагранжева многообразия Ля и У-лагранжева много-
многообразия Лу : {Р (a), Q(a)}, причем, с точностью до 0o,{h),
Р (a) = /j(a)-ftt>(a), Q (a) = q(a) -f г (a). В этом случае все опре-
определения Arg якобианов непосредственно переносятся на лагранжево
многообразие с комплексным ростком. Если же это не так, то
нетрудно убедиться, что вообще все предыдущие рассуждения
переносятся без изменений, если вместо \Р (a), Q(a)} рассматривать
p(a) + a>(a), q(a)-\-z(a) в достаточно малой окрестности мно-
множества Г.
Перейдем к определению канонического оператора.
Пусть Ля — лагранжево многообразие с комплексным ростком.
Рассмотрим некоторое покрытие его картами {со,}, которое в даль-
дальнейшем будем называть весовым атласом. Обозначим через {ру}
разбиение единицы, подчиненное покрытию {coy}:
1; C.14)
/
это разбиение единицы будем называть весовым.
Весовой атлас" и весовое разбиение единицы будем считать
фиксированными.
Пусть {ик} — некоторое покрытие Ля картами, причем карта ик
имеет тип coy *, <р е Cj° (Ля х [0, 1])ив4еС™- разбиение единицы,
подчиненное покрытию {ик} проекции носителя <р на Ля. Положим
C.15)
где Vjk — определенные выше операторы перехода из карты и}
в карту ик.
Определим предканоншеский оператор $С с помощью формулы
i[0 (o) + ic(o)O(oK/2-e]
* '*
е

500 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ. VII
где Jb — якобиан, отвечающий карте ик, Arg Jk — определенный
выше аргумент этого якобиана, ak(x. , \-. ) — решение системы
уравнений:
я к к я я я ' -
Фк, Lk — соответственно Ф) * и L) h в карте uk.
Введем теперь в пространстве Cf (Л"х[0, 1]) отношение экви-
эквивалентности ~ следующим образом: <р (а, А)~ф(а, А) тогда и
только тогда, когда <р(а, h)~ф(а, h) — OD(hN/2-B). В частности,
Ф ~ ф( если проекция носителя разности <р — ,-ф на Л" не пересе-
пересекается с Г (напомним, что «юрез Г мы обозначили множество
нулей комплексного ростка).
Обозначим через [Cf (Лл х [0, 1])]г факторпространство
С5°(Лях[0, 1]) по отношению эквивалентности ~..
Обозначим через C°°(Rn, C(o, п) пространство бесконечно глад-
гладких функций на R" со значениями в пространстве непрерывных
функций на полуинтервале @,1] и введем в нем отношение экви-
эквивалентности «w, полагая
(/«*?)<=> (/-? = о(/^~е))- C.16)
Обозначим через [С00 (R", C<0. i])] фактррпространство 0е0 (Rn, C(o, i])
по введенному отношению эквивалентности. Учитывая локальность
V-операторов перехода, получаем, что предканонический оператор
индуцирует оператор
^Л„ : [С? (Л«о> п)]г-^ [С» (R», С(о п)], (з.17)
который мы и будем называть каноническим оператором, на лагран-
жевом многообразии с комплексным ростком (сокращенно —к. о.).
(Иногда, чтобы подчеркнуть, что асимптотические разложения
ведутся по параметру h-*- + Q, мы будем писать &РЛп = Ждп.)
Элементы пространств [С?(АПх[0, 1])]г и Cf (R", C@. i]) мы
также будем называть функциями, там, где это не вызовет
путаницы.
Лемма 3.1. Канонический оператор КАп не зависит от выбо-
выбора покрытия {uk} и разбиения единицы {eh}.
Доказательство этой леммы аналогично доказательствам соот-
соответствующих теорем гл. V. Достаточно убедиться в справедли-
справедливости следующего факта.
Пусть проекция носителя функции <р еСол(Л"х[0, 1]) ле-
лежит в пересечении карт соУ и со]? и пусть /х с /, /а сг /,

S 3] ИНДЕКС КОМПЛЕКСНОГО РбСТКА 501
2. Тогда
где V^. и У/; — ^-операторы перехода из карты шу в карты ш^
и ©у соответственно.
Этот факт проверяется с помощью метода стационарной фазы.
Замечание 1. Случай зависимости лагранжева многообра-
многообразия с комплексным ростком от параметров может быть рассмот-
рассмотрен аналогично тому, как это было сделано в гл. V. Если интег-
интегралы от pdq по циклам с на Г не равны нулю и Ind по этим
циклам также не равен нулю по mod 4, то для определения
канонического оператора требуется выполнение условий кранто-
вания
^= Ind с (mod 4). C.18)
Если вместо параметров в этом случае, нужно подставлять
упорядоченные операторы, то можно использовать регуляризо-
ванный канонический оператор совершенно аналогично тому, как
это было проделано в гл. V.
Замечание о дальнейших обозначениях. Во избе-
избежание громоздкости формул мы иногда будем (без уменьшения
общности) предполагать, что на Л" имеется всего по одной карте
каждого типа шу*. При этом мы будем писать aif вместо ик, е\
вместо ек; аналогичным образом будут изменены индексы при
других буквах. Обозначим у/ == Arg У/, набор, A,..., л) — через 0.
Перейдем теперь к коммутации гамильтониана с каноническим
оператором. Рассмотрим гамильтониан вида
И = — ih d/dt + е?Г (р\ х, i,h), p = — ihd/дх
и пусть «Я^О», q, t) = ?T{p, q, t, 0) = Hi(p, q, 0 + ^,(p, q, t)
гладкая комплексная функция, причем Д^ (р, q, t) «S 0.
Пусть (Л"+1, r"+1) — лагранжево многообразие с комплексным
ростком, определенное в гл. VI § 1. Обозначим через {«?*} атлас
на Ая+1 и пусть фе[С~(Л"+1Х/?)]г.

502 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ. VII
Теорема 3.1, Для любого целого N>0 справедливо равенство
НШ Х„+,Ф = ihPC-^xRH^ + О (hN),
где Rh — оператор вида
2N N
RH = ± + R(o,t) + 2GlH + 2 (ih)nRb.
В этом равенстве через -^ обозначена производная вдоль траек-
траекторий гамильтонова векторного поля, отвечающего функции Гамиль-
Гамильтона Я, (р, q, t),
GlH<=%t /ss*+l, k=\, 0; RnHe=Z0,n.
функция R (a, t) бесконечно дифференцируема по a, t и не зави-
зависит от h, e >0 — достаточно малое число.
Доказательство. Предположим, что supptyczu^. Рас-
Рассмотрим оператор tfC-^+x'. [О(Л")]г-> [С00(R", С@, 1])], опре-
определенный равенством
Рассмотрим сначала одно слагаемое в сумме C.19), соответствую-
соответствующее неособой карте неособой зоны. Положим el (a, t) \|з (a, t) ~
= я|зо(а, t). По формуле коммутации гамильтониана с комплекс-
комплексной экспонентой имеем:
s
ав,ч1
х, t)+iJrlpp(%, х, /)* v> +
1N
C.20)
где \иьц f=°oi
у-е, *

§ 3] ИНДЕКС КОМПЛЕКСНОГО РОСТКА 503
остаток в формуле коммутации гамильтониана с экспонентой.
Его оценка приведена в § 1. Здесь через s{x, t) мы обозначили
функцию s{x, 0 = [ф(<7, t) + ic(a, f)D(a, 03/2~е] |о-о ,*, о и
Siix, t) = Res{x, t), s2(x, t) = lms{x, t). ^
Заметим, что первое слагаемое в фигурных скобках в C.20)
(обозначим его Qx) есть уравнение Гамильтона — Якоби с дис-
диссипацией. В силу . результатов гл. VI Qi = Os, (А3'2~е) • (е&ф) х
X {о{х, f), t). Второе слагаемое в фигурных скобках в C.20)
(обозначим его Q2) в силу следствия из теоремы 5.3 гл. VI
можно записать в виде
Й-(е81>) И*. 0. 0 +
./о (а (*, О, О
+ V (а (х, t), t) (еЭД) (а {х, t),
где У (о, t) — гладкая функция (см. следствие из теоремы 5.3
гл. VI), F1e«5PJ__go, F2eX^v
Таккм образом, мы получаем соотношение
Здесь Р1— оператор вида
где
2N
= jf + 4 (о, 0+2 (S&)< + 2 т" (р®' C<22)
Таким образом, мы получим равенство *):
Д V Д !*<О)+'С <О) °3/2"е] ^о И]" •/» X
2ЛГ ЛГ
х \{чГ ^ 0 2 2()()Uol(.o
C.23)
Напомним, что по определению при N = 1
1 да
Рассмотрим оператор Li
*) Так как все рассмотрение производится в фиксироваииой карте, индексы
у оператора Ц мы в дальиейшем опускаем.

504 КАНОНИЧЕСКИЙ ОПЕРАТОР (ГЛ. VII
Вычислим оператор LLX. Для любой гладкой функции v (а) спра-
справедливо равенство
Ща И = A - <г, (<7о + гоГ1 V>) (» + <Л, q7' V»)-) =
где Lx г <S?i>3. Далее покажем, что LL1
(г, q7lVv)-(z, Go + 20rV) = B.
В лемме 6 Приложения 2 мы построим оператор Lx для лю-
любого N, причем оператор Z,x будет равен сумме операторов клас-
классов Lft/2-e, ft, k^N. ,
j Положим теперь L2 = Lx — lJ.^ Легко видеть, что справедливо
равенство ¦/
Очевидно, что продолжая этот процесс, мы можем для любого
целого А/>0 построить оператор Ln, такой, что
LLn = 1 + Ln,
где
LN^Xf^ ^, Ln^.% Af+i n .
Таким образом, мы показали, что существует оператор, обратный
к оператору L по модулю функций вида 0D (Л00). Обозначим
его Щ1.
Используя равенство C.23), можем записать
Здесь через Pg мы обозначили оператор вида
2N N
(Qb)i + 2 № №, C.25)
л=1
где (G§),^fL^'(Go)/ei?t , l^k+l, k = 0,1 в силу указан-
•и" — в# Я
ных выше свойств операторов (Go)/ и вида оператора L, (Ро)п =
Аналогично для любой карты и\ зоны Q/f доказывается
равенство
И [*А-и1ф]^ = /Л [*А«+1Р«я>]^ + О (А"), C-26)

S 3] ИНДЕКС КОМПЛЕКСНОГО РОСТКА 505
где Р% — оператор вида
2JV
Ъ=it + * (°. о + 2 «&)< +
/=1 п=1
где (Gfc),ei ,
2 ~е' *
Получим теперь соотношения коммутации между У-опера-
торами перехода и определенными только что операторами Р%.
Пусть ф (a) е С^° (А") и supp ф (а) а икК Пи)'. Используя опре-
определение ^-операторов перехода, можно получить равенства
=ih [я^чАк=ih
С другой стороны,
Н [Ж~Ап^]>к -1» [*x^K]fA]* - Л [*x«J>iVt/vfr C.28)
Нетрудно убедиться, что оператор ЗС'-,,+1 является мономор-
мономорфизмом. Из этого факта и равенств C.27) и C.28) получаем сле-
следующее соотношение:
iftf ' C.29)
Рассмотрим теперь функцию E?-л+1ф)(х, /), где 5?*n+i — канони-
канонический оператор на лагранжевом многообразии с комплексным
ростком, фе[С$°(Лп)]г. Мы предположим вначале, что существует
такой представитель г|з класса ф,.\|)еС?(Л"), что носитель г|У
целиком содержится в некоторой карте и^. Тогда б силу C.26)
и определения канонического оператора
[х B2 у^Ур +(). C.30)
Определим оператор RkK равенством
Тогда, очевидно, равенство C.30) можно переписать в виде
Покажем, чтоЛна пересечении карт ^?\и\ выполняется
равенство
* _ Dm
к *м

506 КАНОНИЧЕСКИЙ ОПЕРАТОР [Гл. Vft
В самом деле, используя равенства B.37) и C.29), имеем (mod О (/г00))
i i ) \ 1 i I
22 rff *)-«%• с3-33)
Обозначим теперь через RH оператор на An+l, определенный в карте
м^ равенством C.31). (В силу C.33) это определение инвариантно
относительно выбора атласа на Ля.) Тогда
? C.34)
Доказательство равенства C.34) следует непосредственно из опре-
определения оператора /?//• Заметим теперь, что оператор Ян имеет вид
2N N
2 л>"/??л C-35)
где Оя, /?я — операторы на Лп+1, причем
^ k = 0,
С^неХ1_ , l
2 в, в
Доказательство равенства C.35) легко следует из определения
оператора /?я и возможности представить любой F-оператор
в виде
Пусть
-ihd/dty + ^ip, х, t, A)ip=-O, 1|»|мвЯГА«Ф. C-35')
где в#"лп — канонический оператор на многообразии с комплексным
ростком г", ф е [Cf (Ля)]г, Ж е С00 —функция, удовлетворяющая
условию
lm^r(p,g,t,O) = H(p, «7,0^0.
Обозначим еще Re «ST (р, <7, ^, 0) = Н (р, q, t) и введем лагранжево
многообразие с комплексным ростком (An+1, rn+l), построенное
с помощью комплексного канонического преобразования f?H.(i,
аналогично § 1 главы VI.

§ 3] ИНДЕКС КОМПЛЕКСНОГО РОСТКА 507
Непосредственно из теоремы 3.1 получаем:
Теорема 3.2. Асимптотическое решение задачи C.35') опре-
определяется равенством
г|>(*. U А) = ^хп+1ф,
где ф удовлетворяет соотношениям
/?яф = 0, ф |,_0 = ф.
Аналогично тому, как это было сделано в гл. V, можно опреде
лить канонический оператор на семействе лагранжевых многооб-
многообразий с комплексным ростком, зависящим от параметра. Мы рас-
рассмотрим здесь лишь частный случай, однако только он и понадо-
понадобится нам в дальнейшем.
Пусть Л" = {р = р(а), q = q (а)} — лагранжево многообразие с
комплексным ростком и
<W(P, Q, U а) = Н(р, q, t, a) + iR(p, q, t,a)
— некоторая комплексная бесконечно дифференцируемая функция
в фазовом пространстве, зависящая от параметров (щ, ..., сош) и
удовлетворяющая условию Im^T(p, q, t, co) = tf (p, q, t, co)sgO.
Для построения нужного нам семейства лагранжевых многообра-
многообразий с комплексным ростком мы используем тот же прием, что и
при построении лагранжева многообразия Лл+1 с комплексным
ростком в § 1 гл. VI.
Определим вначале многообразие Ля+1 (со) в пространстве пере-
переменных (t,~q, p0, р), полагая
Ал+1 (со) = {/, q = q(a, t, со), ро = Н(р(а, t, со), q(a, t, со), t, со),
р = р(а, t, со)},
где р(а, t, со), ^(а, t, со) —решения системы Гамильтона
= Яр(р, q,t, со), q@) = q(a),
= -Hq(p, q,t, со), р@) = р(а).
Аналогично § 1 гл. VI можно проверить, что при каждом фикси-
фиксированном со Лп+1 (со) есть лагранжево многообразие. Определим
на Лп+1 (ш) комплексные функции г (a, t, со), ш(а, t, со) как реше-
решения следующей системы уравнений
= — iEq — ^qpW — eXTqqZ, W{Q)~W (а).
Здесь у функций Н и <Ж опущены аргументы (р, q, t, со).
Определим еще диссипацию
?>(а, t, a>) = D0(a)-

508 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ. VII
и потенциал
Я(а,и) = ?о (а) - 4 J ««*. Я я) + <*. # р> + Н) dt.
о
Введем, наконец, фазу на Ал+1(ю) по формуле (мы рассмотрим
здесь лишь случай неособой карты неособой зоны. В остальных
картах фаза определяется аналогично):
Ф(а, t, ю) = — у<г(а, t, со), ш(а, t, co)>-f|i(a, /, (o) + s(a, t, со) +
Легко проверить, что многообразие Ая+1(со) с определенными на
нем функциями г, w, D и Е удовлетворяет аксиомам ростка
(см. § 1 гл. VI).
Аналогично § 1 гл. VI мы будем говорить, что лагранжево
многообразие с комплексным ростком Ал+1 (и) построено с помощью
семейства комплексных канонических преобразований g*H + 1.й(со).
Дословно повторяя все приведенные нами рассуждения, опре-
определим канонический оператор в^хл+1<«>) аналогично равенствам
C.12), C.13), C.14). '
Легко видеть, что определенный таким образом оператор есть
непрерывное отображение
А ". С @,1])],
где через Г (со) мы обозначили множество точек многообразия
Ая+1(со), в которых функции г (a, t, ы) и w(a,t,a) обращаются
в нуль.
Рассмотрим теперь задачу Коши
0.
где р = — ih -3-, &%" {р, Я, t, w, А) —гладкая функция, удовлетво*
ряющая условию
. Ime%"(p,,<7, /, со, 0) = Й(р, q, t, ©)<0,
5Рдп — канонический оператор на начальном лагранжевом много-
многообразии Л". Обозначим через Ая+1(со) семейство лагранжевых
многообразий с комплексным ростком, определенное выше.
Аналогично теореме 3.2 доказывается утверждение:
Теорема 3.3. Асимптотическое разложение решения задачи
C.36) определяется равенством
г|>(х, t, а, Л)=5Рхя+1(и)ф,
где ф удовлетворяет условиям

§ 4] ДОКАЗАТЕЛЬСТВО' ОСНОВНОЙ ТЕОРЕМЫ 509
§ 4. Доказательство основной теоремы
Прежде чем переходить к доказательству основной теоремы
в ее простейшем варианте, мы отметим несколько простых обстоя-
обстоятельств.
Поскольку при р — 0 функции Ц(х, р) обращаются в дг,- (что
дледует из их построения), то -функция f(L(x, p), а) (где L —
=(/,!, ..., Ln)) при р = 0 равна f(x, а). Следовательно, из усло-
условий асимптотической р-квазиоднородности (p = (pi, .... pn+m)) для
гамильтониана следует асимптотическая р'-квазиоднородность сим-
символа f(x, а), где p' = (pi р„).
Лемма 4.1. Пусть fo(x, а)—старшая часть f(x, а) и пусть
р'-квазиоднородная функция F(xi а) на многообразии .
обращается в нуль в окрестности нулей функции fQ(x, а). Тогда
существует последовательность vp/&$co(RnxMm), удовлетворяю-
удовлетворяющая соотношению
и[Аг Ап, B-)llvN{Al Ап, fl J] =
( 1 n n+l\ . /1 ^ n n+l\
"F\A1 An, В ) + RN{A1, .... An, В ),
где /?же«°°(Я"хМт), RN(x\ xn\ a)=0{\x\~N), т. е. стре-
стремится к нулю быстрее \x\~N при х-*-со со всеми производными.
Доказательство этой леммы приведено в Приложении I.
Из этой леммы следует, что, не уменьшая общности, вместо
единицы в правой части ((9.1), стр. 94) можно рассматривать опе-
оператор, носитель символа которого лежит в окрестности нулей
функции fQ(x, a).
Отметим также следующее. Выберем любое конечное покрытие
многообразия Мх === I ? (xk) -/р* = 1 >х Мт открытыми множествами
Ш/, i=\ s}, возьмем отвечающее е»чу разбиение единицы
\е{, t = l s}, ei = ei{xl хп; а) и затем рассмотрим набор
р'-квазиоддородных функций F{(x, a) =e((x]Ao(x)~pi,.. .^^{ху"";
. . I 1 \ 1/2 s
а), где Ло (х) Ч 2 (*>J/Р* • Очевидно, ^F,(x,a)^].
Тогда, если мы найдем такие функции v$ (x, a), R§ (x, а),
i=\, ...,s, где R<$-Oj.(|x|"*), что
) a, в),

510 КАНОНИЧЕСКИЙ ОПЕРАТОР 1ГЛ. VII
s
то их сумма vN= 2 0$ Даст решение исходной задачи!
П/U. b)Mvn{a, в)в=1+1]/г(й(и, в).
t=i
Покрытие {Ui\ многообразия Мх мы выберем с учетом условий
поглощения (Введение, § 9, пункт 3). Пусть множества ?/; и
константы Ti таковы, что 0< Т;^т'(д0, со, 0, 0) и
Й(р(Я°, <о, р°, л, Ti); q(q°, <о, p°, i\, T,); <о;
при (<Д а, р°, у\) s йе, (<Д a) G [/,-,! = 1 s (см. формулировку
условий поглощения). В силу непрерывности функций Н, р, q
такое покрытие {Uit i = 1,..., s} и набор констант {7\, / = 1,..., s\
существуют при достаточно малом е.
Тем самым, в силу предыдущих рассуждений, мы сводим
задачу о квазиобращении к решению уравнения вида
И/W, B)UvN{A, b)l = F(X. b) + ?>N{A, В), D.1)
где функция F(x, a) — квазиоднородна степени 0 по переменным
х, равна нулю в окрестности нулей функции Гамильтона Н @, q,
(о, 0) и для некоторого Т > 0 справедливо неравенство
H{p{q\ со, р°, л, Т); q(q°, а, р°, т|, Т); со; тО<0,
при (q°, со, р°, л)еОв, (с?°,со)е supp F^, a).
( а)еМ
/1 г\ /1 n n-i\
Обозначим через [L, а.)ва\Ьх, ..., Ln, a / набор упорядочен-
упорядоченных операторов, являющихся представлением образующих ниль-
/ 1 п п + 1\
потентной алгебры [Alt .... Ап, В ). В силу правил редукции
решение указанного выше уравнения сводится к задаче Коши
(см. стр. 101) для гамильтониана
«) = / tt^i У. &/дх, - id/d
п+1
Ц a
По предположению этот гамильтониан является асимптотически
р-квазиоднородной функцией степени г относительно переменных
yi = xh 1 < / < п, yn+J = — id/da,, 1 < / ^ m, где р = (р1( .... )
причем р^х = ря+j = ... = рч+ш = 1.
Мы должны найти такую функцию \pw(ot, r\, x, t), \|3/v
которая удовлетворяла бы следующим условиям:
{-гЛ'-1-| + {L a)]^(a, Wx, x, t) = BN(k, id/dx, x, t),
фл, ^o, id/дх, x,0) = P [x, a) ¦ p [id/dx).

§ 41 ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ 511
Здесь BN(a, r\, х, *) —некоторая функция класса С^, убыва-
убывающая при х-ь-оо быстрее 1*1"^, гДе ^V —сколь угодно большое;
функция р такова, что peQ°(Rn), носитель р содержится в
шаре радиуса е, р (у\) = 1 в окрестности точки у\ = 0.
Операторы в задаче D.1) рассматриваются в шкале {#* (Rn x Мт)}
с нормами
}
(ср. гл. IV, § 13).
Очевидно, для любой ограниченной функции ueCc0(R"xMm)
функция Вци убывает быстрее |*|"w при *->-оо и, кроме того,
5C(RMm). Мы возьмем и (х, a) si.
Если носитель функции ^(а, tj, x, t) по переменным х =
xi х„) компактен, то функция
4» х. t)uOc, а)
убывает при *->-оо быстрее любой степени \х\~^. Поэтому,
не уменьшая общности, мы можем предполагать, что носитель
флг(а, г\, х, t) принадлежит области |лг|>с>0.
Обозначим через А = Л(^) функцию
при |дг|>с
Тогда в задаче Коши D.2) вместо оператора Ло можно поставить
оператор Л.
Преобразуем теперь гамильтониан f\L, а). Прежде всего отме-
отметим, что условия асимптотической р-квазиоднородности некоторой
функции ф(?), ? = (?i, ..., In) можно записать следующим обра-
образом: для любого Х>0 справедливо представление:
( Ч) 1 'E, X),
где ло>Л1> ••• >rk, 4>j есть р-квазиоднородная функция сте-
степени rJt 1тф,-^0, / = 0,1 k, 9ft+1eta>(Rnx@, oo)), функ-
функция фй+1 (I, X) и все ее производные по | ограничены по Я.
Поэтому асимптотически р-квазиоднородную функцию ф (|)
можно представить, в виде
где обозначено
=Ы 2 к Г Ч №4) + г1ф*« (я"р1ЛI D.3)
l/ = o J

512 канонический оператор [гл. vtt
Числа ro — rj при /=1, 2, ..., k будем обозначать через е,-
и с каждой р-квазиоднородной функцией будем ассоциировать
набор е==(еь ..., eft) (очевидно, е/>0, /=1, .... п).
С помощью представления D.3) оператор f\L, а) записывается
в виде:
4-
п + 2 А 1
а, Л/А', D.4)
где через A~pjc обозначен вектор \A~f>ix1, ..., A~p«jen), а функ-
функция fo(L(a>, г], р0), а, А) рт аргументов
pf))eR'»,Ae[-|-, oo)
имеет вид:
fo(L(a, tj, р0), а, A) = s5T1(a, tj, p0, со, хх) +
+(~гА~1)^!Г1(о, л, Ро, о), Л). D.5)
В последней формуле е%( а2Г2е$°°, ImsJTj^O, функция
*(а. Л. Poi ©» Л) ограничена вместе со всеми производными
при А-»-со, X!^(A~ei Л~е*), где e = (ei, .... ek) набор,
ассоциированный^ р-квазиоднородной функцией /0.
Из равенств D.4), D.5), используя лемму 2, стр. 526, получим
выражение для гамильтониана:
, 4- -'*-?•
где функция ^"зs ^°° выражается явно через е%^1, е%^2 с помощью
указанной леммы, е% ограничена с производными при Л-»-со.
Задачу D.2), в которой гамильтониан f\L, а) имеет вид D.6),
мы решим с помощью теории канонического оператора на лагран-
жевом многообразии с комплексным ростком, развитой в этой
главе.
Обозначим .
^Г0(Х0, X; Ро, Р; 0, и1( щ)Ш?Г1{Хо, X, Ро,
где
k^IA-% .... A8*), x2^(A'-pi, .... А1'"-).

§ 4J ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ 513
Функция е% зависит гладко от параметров со, щ и и2 ПРИ
(DER" и Ki-»-0, Xa->0. При Xi-»-0, щ-+О функция е% схо-
сходится к функции Гамильтона s2T, отвечающей оператору
( 1 п п + 1\
f\Au ..., Ап, В ) (см. определение функции Гамильтона в § 9
Введения).
Функцию е% будем рассматривать в фазовом пространстве
{(Хо, X; Ро, P)} = (MmxRn)x
Обозначим Мт х R" через Мт+п, а фазовое пространство —
через Т*Мп+т. Очевидно, что Мт+п — лагранжево многообразие.
Из условия асимптотической р-квдзиоднородности гамильтониана
следует, что Ime^^O и, следовательно,
Обозначим #0 ==s Re e% и рассмотрим систему бихарактеристик
dX.Q дНо /у у d _i_ d \ v
V-Afe OtlQ , у у JJ |^ р » у
= о,
D.7)
= 0,
о*
Л п;
t—o
В силу условий поглощения, наложенных на предельную
функцию Гамильтона ©%"= lim eS^oi когда параметры систе-
А-*оо
мы D.7) лежат в области Qe, решение этой системы существует
при х1 = и2 = 0. Поэтому по теории возмущений легко построить
асимптотическое решение системы D.7), т. е. такие функции Хо, X,
Ро, Р е С00, которые удовлетворяют системе D.7) по mod Л~ N,
где N — сколь угодно большое.
Обозначим через g* » (и, х1( ха) сдвиг вдоль этого асимп-
Яо + Ш
готического решения.
Очевидно, что все свойства комплексного ростка сохраняются,
если решение системы Гамильтона заменить на указанное асимп-
асимптотическое решение системы D.7).
Следовательно, семейство
построенное из Мт+п с помощью преобразований g^o + i^ (со,
o +
будет семейством лагранжевых многообразий о комплексным
17 В, П, Маслов

614 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ. VII
ростком (здесь число Т определено в условии теоремы) и будет гладко
зависеть от параметров © = (@! со„), <е@, Т) и хь х2. Как
доказано выше, семейству (Mj? + n, г{"+") отвечает лагранжево
многообразие (Мот+П^1, г™***1) (с краем при * = 0 и t = T)
с комплексным ростком в B(п+/п) + 2)-мерном фазовом про-
пространстве 7"*Mm+nxR2. Это многообразие, очевидно, при доста-
достаточно малых к, и Хг будет гладко зависеть от параметров со.
Пусть е/?"л — канонический оператор на (Мш+П+1, rm + " + 1),
отвечающий параметру А = Л~1.
Как видно из формул D.2), D.6) мы должны рассмотреть сле-
следующую задачу Коши;
f _ Д-i1 + ЯГХ + (_ Л-i)^3]г|> (а, /|' *¦ <)-°. D.8)
4>(о, А/адг, i, 0)=p(id/dx)p(x, о),
где у операторов «S^, e% опущены аргументы, указанные
в формуле D.6).
Покажем, что приближенное решение задачи D.8) имеет вид
j /|, №. А*"*, Л"е, ^, D.9)
х, /)=
где фдг — некоторая функция из fa>(Mm+n+1), со = [л:Л~р]|.
Прежде всего отметим, что в силу выбора начального мно-
многообразия Мш+П
(е5ГАф/у)(а> Лэ @( Ai-P| а-«, Око = Ф/^(а. л, в>,7)|<-о-
Поэтому оператор D.9) удовлетворяет начальным условиям задачи
Коши D.8), если положить
Флг(а, т|, со, 0)=р(л)Р(со, а). D.10)
Применив к обеим частям уравнения D.8) преобразование Фурье
FxUy, получим
W (-1?) <Ж3)(а, у, - ihд/да, - ikd/dy, fc)] x
{а,у, —ifoy, t) = Q, D.11)
где ^-оператор ^^)^ ( JI/P
Докажем вспомогательную лемму.
Пусть канонический оператор &>tl/h задан mod (Л00) на лагран-
жевом многообразии М с комплексным ростком, зависящим от
параметра coeR" так, что (e%l/hy)(y, co)eC^(R2"). ТогДа

§ 41 ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ 61 б
t
где Н е #°° (R") — некоторая функция Гамильтона, Rh—оператор
на многообразии М (см. теорему 3.1).
Лемма 4.2. В сформулированных условиях справедлива формула
коммутации (mod О (А00))
[я(;,- A?)( 4)( 4
Доказательство. Пара вектор-операторов Ax^ih-g-,
Аъ = у являются образующими нильпотентной алгебры. Их упо-
упорядоченное Представление (см. Введение, § 9) имеет вид [Llt Д),
уде L1 = —ih~-\-x1, и = Хг- ~
Тогда для /e*00(R2"), geC|(R2;0 имеет место формула
(см. § 13, гл. IV):
I/Wi. A\)i-Ig(Alt Л2)]=[х(л,
где %(хи X2)=f(Llt U)g'
Отсюда, учитывая условие леммы, получим:
^ 2 ) ( - /А
Г1—1НЩ'У«
Лемма доказана.
Рассмотрим теперь построенный выше канонический оператор
А; заменим Л на 1/А.
Из теоремы 3.1 следует формула
hl, -гА|- +
oL, у, со, АР"*, /г8,
+ AwX)v(a, У, со, h, t), D.12)
где xv — иекоторая бесконечно'дифференцируемая функция, огра-
ограниченная при h-*-0, а оператор RN имеет следующий вид;
2W — 1
2 (-^/2^, D.13)
где ^ —гладкая функция на многообразии Мш+Я+1, ^'—опе-
^'—операторы на этом многообразии (см. теорему 3.1).
17*

516 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ. VII
Заметим, что остаток Хлг(а, у, <о, A, t) в формуле D.12) по
аргументу у вместе со всеми производными убывает быстрее любой
степени \у\~к при у-+со. Действительно, преобразование Фурье
переводит функции из Cf в класс S функций, убывающих со
всеми производными быстрее любой степени \у\~к при у-*-оо.
Поэтому канонический оператор &СХ1Н на лагранжевом многооб-
многообразии М переводит функцию ср eQ°(M) в функцию p'kip)G5,
Поскольку гамильтониан ©%"[у, — ^д~) ПРИ s^*(¦*• р) е^т пере-
переводит пространство 3 в себя, то утверждение об убывании остатка
Хлг (а, у, ©, A, t) по аргументу у доказано.
Теперь подставим в D.11) оператор
ib^la ы, ——/Ад— ?) = (e^"'/"ro^) 1 а, ы, —ihP^- hP~*t Ae, i/.
Учитывая лемму 4.2 и формулу D.12), получим
Подставим сюда А = Л f — /=- j и совершим преобразование Фурье
Fy^x- Получим
«, 4-
D.14)
где (ой = Л~р*^й, А=1, ..., п, а у операторов a%"lf s5T8 опущены
следующие аргументы;
(S Я 1/ Я
В силу D.14) и D.6) для приближенного решения задачи
Коши D.2) достаточно найти функцию <р#, удовлетворяющую
соотношению
/?дгф» = 0 (mod OD (Л-*)).

§ 4] ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ 617
Учитывая формулу D.13), из этого уравнения и условия D.10)
функция флг находится по теории возмущений (ср. стр. 403).
Тем самым найдено искомое приближенное решение задачи
L, а) (см. лемму 4 Приложения 2).
Действительно, остается лишь проверить, что при t = T функ-
функция
ть со, Л™, Л"е, f) D.15)
убывает быстрее любой степени \x\~N при л;->-оо.
Бихарактеристики (X, Р), отвечающие функции Но (см. D.7)),
зависят от параметров ни х2, причем, в пределе при х1 = и2 = 0
эти бихарактеристики совпадают с бихарактеристиками, отвечаю-
отвечающими функции #==Ree%" (системы (9.11), см. Введение, § 9).
По условию теоремы для последних выполнены условия погло-
поглощения. Следовательно, они выполнены и на бихарактеристиках,
отвечающих Но, если число с достаточно велико *). Именно, при
t = T и достаточно большом с справедливо неравенство:
Im«aro(Xo, X; Р0) Р; со, ни ха)<-б<0.
Отсюда и из построения канонического оператора (см. § 3)
А следует, что при дс->-оо функция e%Aq>tf\t-T убывает при
*->-оо быстрее любой степени A~N. Непосредственно прове-
проверяется, что формула (9.8) Введения дает решение задачи D.1),
если tyu определяется формулой D.15).
Доказательство основной теоремы в общей форме, сформули-
сформулированной в пункте 4 § 9 Введения, проводится аналогично. Здесь
мы подробно рассмотрим лишь сведение более общих условий
поглощения (пункт 4) к обычным условиям (пункт 3 § 9 Введе-
Введения), а также наметим аналог предыдущего доказательства для
случая оператора f\A, A, %), зависящего от параметра ? (но не
зависящего от эталона г).
Общие условия поглощения пункта 4 § 9 Введения сущест-
существенно отличаются от обычных условий лишь в случае, когда мно-
множество Qo является несвязным, т. е. состоит из замкнутых непе-
непересекающихся частей Q('>, t=l, ..., s. Им отвечают непересекаю-
непересекающиеся части множества Qe, на каждой из которых функция
U(p{q\ и, р°, ц, v, т'); q(q°, и, р°, \\, v, т'); со; v, л)
по условию строго больше или строго меньше нуля. Поэтому,
как уже было продемонстрировано в начале этого параграфа,
можно выбрать некоторое покрытие многообразия Mi и соответ-
соответствующее ему разбиение единицы так, что задача о квазиобра-
*) В силу замечания, сделанного в начале доказательства теоремы,
Л0/2

618 КАНОНИЧЕСКИЙ ОПЕРАТОР HVI. VII
щении сведется к уравнениям fg$=FW+R$, /=1, ..., s, где
на носителе F^ мнимая часть функции Гамильтона Я (р\х*,Х'\
q\x-=x'\ ®> v, ц) отрицательна (если она положительна, то все
уравнение умножаем на — 1 и получаем уравнение с отрицатель-
отрицательной мнимой частью). Таким образом, общий случай сводится
к случаю обычных условий поглощения.
Рассмотрим теперь гамильтониан /(|X(jc, id/dx, — id/da,)}, a, g),
не зависящий от эталона и являющийся (р0, р1( ..., р„, Pn+J-
квазиоднородной функцией степени г по аргументам (— ig- = x0,
Xi,'.., хп\ gj, причем ро = рл+1=1. Тогда оператор f\L, а, ?)можно,
аналогично предыдущему, представить в виде суммы (ср. D.6)):
4. -^4.
V \r 1
где оператор Л = Л (я) определен выше, а через Л~е, А~рх, как
и выше, обозначаются векторы
-е=(Л-
Л*), г}>0, У=1, ...,п,
Тогда в предположении, что пространство функций, на котором
def
действует гамильтониан, таково, что оператор v3!"^ ограничен
(см. ниже), функция <&"s(a, у\, р0, со, v, Л) будет ограничена
при Л->-оо, равномерно по всем параметрам.
По правилу редукции задача о квазиобращении оператора
KI п л+1 \
Ai Ап, В , \) сводится к задаче Коши вида D.2) для
гамильтониана /(/., а, %). Гамильтониан затем представляется
в виде D.16) и весь дальнейший ход решения задачи Коши не
отличается от приведенного выше. В частности, строится функ-
функция Гамильтона
О(Х„, X; Ро, Р, (о, v, Д1-Р, Л"«) =
= «%"i(X0, X, Л» со + Л*-РД v, А-%
где co = (coi, ..., со„) — параметры, отвечающие операторам хА~**=>
Функция <^Го при Л->- оо переходит в функцию Гамильтона
отвечающую оператору f[L, а, |) (см. Введение, §9).

$ 4] ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ 619
Исходя из функции e%» как и выше, строится приближенное
решение задачи Коши D.2) в виде
4 ) ( §x A A ) 17)
где иА = л:АЛ~р*, v = |~'A.
Символ gn элемента квазиобратной последовательности имеет
вид
%(«, 4- *• '• l) = (^N)(a, i§-x, ю, v, A"*, A™, t), D.
gff(x, a, g)-i Ji|*(a, /|, х, t, ijk^-^dt, D.18)
о
где
где Р0(х, а) определена в условиях теоремы.
Носитель эиррф(л;; а; |), очевидно, содержится в области
Л (л;) =4с|. Следовательно, на носителе q> функция v имеет оценку
||
||
Мы построили правую квазиобратную последовательность.
¦Построение левой квазиобратной последовательности проводится
аналогично, с использование^ той же функции Гамильтона. Для
этого достаточно заметить, что произведение.
/ч + 1 2 1\ / 1 п ч+1
[gir\Al Ап> Bj}tf\Alt ..., Ап, В
равно
In +1
[A
1 2 1 \
! An, В), rN(x, a
n + l 2 1 \ de{
Lf : L%, a)gN, Lf(i\, x, po) = L,(—i\,x, — po>.
Теорема доказана.
В заключение рассмотрим следующее обобщение основной задачи — задачу
об отыскании приближенного решения уравнений
где
* / i п n+i\
/I п n+l\ -
t>=F\Ait ... An, Sjee/
произвольная функция, носитель символа которой сосредоточен в фиксирован-
фиксированной области AeAlj. Элемент vsjg будем называть- правым А-обратиым,
а ю—левым А-обратным.
Под приближенным решением мы понимаем такие последовательности
что
vN=vN\Ai Ап, В ) и wN=wN\ Alt .... Л„, б Д

520 КАНОНИЧЕСКИЙ ОПЕРАТОР [ГЛ, VII
где Ajf и /?]у е «5? имеют символы, убывающие быстрее \y\~N- Последова-
Последовательность vN будем называть правой Д-квазиобратной, a wN — левой Д-
квазиобратной.
Справедлив аналог основной теоремы для Д-квазиобратных элементов.
Основная теорема о Д-квазиобратных элементах отличается от основной
теоремы о квазиобратных элементах лишь тем, что начальные условия a0, q°
в условиях поглощения (Введение, § 9) здесь принадлежит пересечению обла-
области Д и окрестности нулей f0.
Теперь рассмотрим вопрос о носителе Д-квазиобратного элемента. Из фор-
формулы для Д-квазиобратного элемента, частный" случая которой мы привели
во Введении, немедленно следует, что носитель ^Д-квазиобратного элемента
(как левого, так и правого) принадлежит проекции пленки, образованной
траекториями (Введение, (9.11)) с начальными условиями a0, g°ei f] Oe
Q^t^T, на многообразие Mv Символически это можно записать так:
Sllpp VN С пр^ х мт U $ИД Л
где nPsn-ixMm—проекция иа Mlt а ?^(др|йе) сдвиг области е
по траекториям системы Гамильтона, отвечающей функции Гамильтона Н.
Задача. С помощью квантовой операции обхода фокусов получить фор-
формулу (9.14) Введения из формул D.17), D.18) для правой квазиобратиой
последовательности (в предположениях, сформулированных иа стр. 109).
Отметим, далее, что основная теорема может быть обобщена на случай,
когда операторы Alt ... , Ап, В являются порождающими операторами произ-
произвольной (не иильпотеитной) алгебры Ли. Точнее, в произвольной алгебре Ли
можно выбрать базисные элементы Лх, ... , Ап, В так, чтобы отвечающие им
элементы упорядоченного представления были псевдодифференциальными про-
производящими операторами.

ПРИЛОЖЕНИЕ 1
АНГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ
Рассмотрим нелинейную задачу о колебаниях кристалла
(ипП - 2ип + ип_1) + а [(«л+1 - ип)* - («„ - н„+1J] ^ 0, A)
где
f
От последовательностей vn и wn потребуем, чтобы последова-
последовательность (vn-\-wn) отвечала предельному распределению g+(x, ю),
а последовательность (vn — wn) отвечала предельному распределе-
распределению g_(x, со) (условия предельности). Переходим к псевдодиффе-
псевдодифференциальному уравнению
| of, B)
u\t-o = v(x, h),
ihdujdt |,_0 = 2с {х) sin -у w (x, h), v (x, h), w (x, h) g= MN, C)
w(x, A)->0, v(x, A)->0
с условием предельности (аналогично Введению): для любой
а (х) е С00 (S) (S — единичная окружность)
Ига $ (ф)())^)((
л-*о _я
= \ \ g± (х> и) cos та {х) dx dco.
Пусть ф(д:, ^)еСа, ф(д;, Т) = 0, ф^д:, 0 = 0- Умножив обе части
уравнения B) на ф (д:, t) и проинтегрировав по частям, получим
г
$ J № (х, t) и (х, t) dxdt + \ q>J (*, 0) о (х, h) dx -
0
"~ J Tsin T (c (*) Ч5 (*• °» w (x> h) dx =
г
= 8^ j J [sin А ф (*, t)] (sin 4 и)' dx A; D)

522 АНГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
пусть «0 —решение задачи B), C) с правой частью в B), равной
нулю. Предположим, что а (А) таково, что
где сх не
зависит от А и sin-y(«—ио) сильно сходится к нулю при А-»-0.
Последнее условие означает, что амплитуды начальных данных
таковы, что главным членом, определяющим осцилляции в задаче
B), C) является решение соответствующего линейного уравнения.
В высказанном предположении
г
j { \ [sin у ф (х, t)](sin |- и)'dxdt-
т
где ста->-0 при й->-0.
Тогда из равенства D) будет следовать .соотношение
т
\ \ Ь*у (х, 0 « (х, 0 dxdt+hfa (х, t, h) и dxdt+
т А
\ (J) eA. E)
где г|ф, t, /г)еС°°(Я3), L* =d*!dt*-d*c2(x)/dx* и бА->0 при
А0
\ о
0.
Вычислим теперь предел при /г->-0 интегралами, стоящего
в правой части этого равенства. Система бихарактеристик для
линейного уравнения имеет вид -
гр с (Х±) cos ^, X @) = х°,
Обозначим v± = и ± w. Из основной теоремы, примененной к этому
случаю, следует, что
sin -| «0 =21 sin А /С±ф±У± + О (hj.
±
Здесь ^ — канонический оператор, отвечающий семейству (пара-
(параметр р°) лагранжевых поверхностей вида М gj (x°, /7°), где
g± —сдвиг вдоль траекторий, определяемый бихар актер исти.
ками F), а
W

АНГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ 523
(См. § 9 гл. V). Используя формулы § 1 гл. V и лемму 8.4. Вве?
дения получим аналогично тому, как это было сделано в п. 8
§ 8 Введения,
т
lim ^А = У Wnx* (*V Р°, 0, 9 х
X sin' "* <*°/' * * iX±J^f' *> fa (*>, p°) a* dp* dt (!)
Здесь учтено также, что произведение членов, отвечающих плюсу
и минусу, стремится к нулю в силу метода стационарной фазы.
Пусть F(x, f)sC°°, а ф(д:, $—решение задачи L*<p = F,
ф|/=г = ф' \t=T = 0. Правая часть соотношения (б) после интег-
интегрирования по частям приводится к виду
l \), t-x)X
fy (8)
где G'(x, I, t — т) — функция Римана решения волнового уравне-
уравнения. Из (8) следует, что
. t
^«(*, О-
при А->-0.
Задача. При t>tb кривая на рис. 5 будет «выгибаться», причем точка
«выгиба» (фокальная точка) будет при t — co приближаться к оси q, а ско-
рость у (/) движения (/-координаты точки выгиба —к скорости звука. Пока-
Показать, что Сформировавшийся при t = tb «фронт волны» (рис. 9, 10) будет дви-
двигаться по оси q с той же скоростью v (t).

ПРИЛОЖЕНИЕ 2
ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
В этом приложении мы докажем некоторые факты, которые
используются при доказательстве теорем в §§ 2, 3 и 4 гл. VII.
Все обозначения соответствуют введенным в гл. VI и VII и в § 9
Введения.
Напомним, что через Lj\id/dx, х, —id/да), j—\ п обо-
обозначаются операторы упорядоченного представления нильпотент-
ной алгебры Ли. Кроме того, мы используем следующие сокраще-
сокращения:
АИ. <*) = №:] ЦЛ <* )
Ш,^.,-,»^,-^) L.(i x-Uf^-ikgj.i). A)
Справедлива следующая лемма.
Лемма 1. Пусть f(g)^8°°(R.nXMm) и р^Э*1, / = 1 п.
Тогда
= f (L (ч, дс - ЙР |, -Л 4). «
где /?i есть некоторая функция класса S<=° от упорядоченных one-
роторов ц, x — ihPjr-, —^~^> а> ВД1» ограниченная по h (при
/г->-0) вместе со всеми производными.
Доказательство. Ниже через \Lj\ будем обозначать
оператор [Ly(r], х — ^щ, — ^щ)]- С помощью /С-формулы

ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 525
получим:
+ 2 (-'*•») §
6 8 Я + 6 » + 7\
[LJ; [LJ, .... [ LJ, а).
В первом слагаемом правой части этой формулы поменяем
порядок операторов т^ и |Х2], пользуясь формулой коммутации и
тем фактом, что
где Фу,ft — некоторый моном (см. § 13 гл. IV, где приводится
вид операторов Lk). Получим:
Д л+1 я+2\
4 6
л*, п
ft=i
Ы; M [ ?J, aj, B)
где через 2,х обозначено выражение
def
Первое слагаемое в правой части формулы B) преобразуем,
применяя /(-формулу по отношению к аргументу [ZJ и меняя
затем в первом слагаемом результата порядок действия опера-
операторов т) и [L3].
Повторяя эту процедуру, получим формулу, приведенную
в формулировке леммы, с остаточным членом

626 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
где
—^^(ль •••» ч». ^1 i; x~ihP§^ ~ihik)
, *-*>!. -/4).
9 в Л + 7—ft П+8 — ft\
IM [U][ L\ )
Л + 7—ft П+8 — ft\
] [ Ln\ a ),
/= I i=l
и через I обозначено выражение LI-%, ..., tij-j, %, T]ft+1, ...
.... Цп, x — i^az, —ihfa)- Отсюда непосредственно следует утвер-
утверждение леммы.
Используя оценки § 13 гл. IV, получаем следующее след-
следствие.
"" Следствие. Оператор /?j ограничен равномерно по h (при
А-»-0) в норме С* для некоторого г и всех к.
Как было показано в § 13 гл. IV, оператор
f{[L(id/dx, xhP, —ihd/daj, a)
представим в виде псевдодифференциального оператора i|)(a, id/dx,
xhP, —ihd/da) с символом
$ (a, ti,. х, ро) = f ([L (т), х - iffib/dri, po)l a) 1. C)
Лемма 2. Пусть fel»(R»xMm). Тогда
f(lL(idjdx, xffi, —ihb/da)l a)==
-/(l'(«9/d*, hPx, -ihd/да), a) +
+ (—/A)/iM/aJe, APx, —ihd/да, a, h),
где ft e *°° есть некоторая функция, ограниченная по h (при h-*-0)
со всеми производными.
¦ Доказательство. Достаточно применить операторы, сто-
[щие в формуле леммы 1, к функции ф(а) —т. е. к функции,

ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 627
зависящей только от а. Очевидно, имеем:
/(l(ti, x-ihPdldi\, — ihb/da), а)ф(а) =
= /(l(ti, x, —ihblda), а)ф(а).
Поэтому
/(Z-fi. x-iffid/ди], р0), a)l =f(L(r\, х, р0), а), D)
где 1 — единичная функция на R".
" Утверждение леммы вытекает из формулы леммы 1 и C), D).
Лемма доказана.
Теперь приведем доказательство основной теоремы в ее про-
простейшем варианте (см, лемму 4.1 гл. VII).
Напомним, что через fo(x, а) обозначается главная часть
асимптотически р-квазиоднородной по переменным х функции
f(x, а) (здесь р = (рх, ..., р„)).
Лемма 3. Пусть & (х, а) есть р-квазиоднородная функция
от х степени $, причем & (х, а) = 0 в окрестности нулей функ-
функции fo(x, а). Тогда существует функция ^e*0O(R''xM'n) такая,
что
f{L, a)gN
где .
А 4 / " \ 1/2
»(х), Л= ? (J'р*)
Доказательство. Как уже было отмечено в § 4 гл. VII,
/(*, a)^f(L@, x,0), а),
поскольку Lj\io/dx, х, —го/da) есть полином относительно
id/dx, —id/да со свободным членом xj.
По условию основной теоремы функция f(L(r\, x, р0), а)
является асимптотически (рь ..-., р„, р„+1, ..., р^^-квазиодно-
родной степени г по переменным (х1г ..., хп, /jj», ..., pjm>),
причем ря+от = ... = ря+т=1- Следовательно, при Х>0 имеем!
¦ f(L(r\, х, ро), a) = \rF(L(i\, Х-ох, Х^р»), а, Ц, - E)
F(L(r\, \-ex, X-ip0), a, Х) =
~2>Fj (Л. A--PJC, Г1?,,, а) Л," e/+F4+1 (л. ^'"х, Х^р0, а, X) Я"». F) .
Здесь Fj(r\, х, р0, а), / = 0 k, есть р-квазиоднородная функ-
функция степени г, по переменным (я, р0), причем го = г>гх>...>• г*;
fio = 0» бу = /-о-г^, / = 1, ..., ft; функция/"ft+1 (т), д:, р0, Я)е«°°
ограничена по % со всеми производными. Главная часть F0(r\, x,
р0, а) при т)=ро = 0, очевидно, совпадает с функцией fo(x, a):
Fo@, x, 0, a)-/„(*, a). G)

528 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
Используя эти формулы, преобразуем оператор f\L, а). Имеем
в силу E);
f{L, i)-A'tF(i i X)j, (8)
где LjLjitfydx, A-Px, —&r*b/da).
Выражение в правой части этой формулы преобразуем с по-
помощью леммы 2 к виду;
, a, a)] = [f(l(/^, Л-р*. -iA^d/da), а, л)]+
+ A~1iB(i()/dx, A-p*x, —iA^d/da, a, X)], (9)
где В (т), х, р0, а, X) — некоторый символ, ограниченный по к
со# всеми производными.
'Теперь заметим, что оператор вида i\>(id/dx), tye*00 можно
всегда представить в виде разложения по формуле Тейлора;
I Р 1=0 I P I = N
где Р = (Рх Р„), |P| = Pi + ...+P«, P7 = Pi!...P,!; (^f =
^(О^1—r F* ^р е *°° ~ некотоРая Функция, которая выра-
выражается явно через производные от i|> порядка iV. Пользуясь
формулой A0), разложим оба оператора в правой части (9) по
переменным id/dx и —iA^d/da, Тогда из (9) получим:
If(L, a, A)] = tF(L@, ЛЧ, о), а, л)]+
+ 2
21 "Т'
lvl=o
где Фу. Р^» а» *-) и фу^(л> а» Л. Ро. Я)—функции класса *°°,
ограниченные по X со всеми производными; v—(Vi» •••» Ут),
P = (Pi. .... Р»)-
Обозначим через р оператор iko/dx. Имеет место оценка:
А"» (дс) Ф (*) |с(г) ^ с* | Ф [|c(s) А = 1, 2, .... A2)
О О
где /е*°°, феС^1 для любого /n, s = s(r).

ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 529
Обозначим ® — (®и ..., <в„), <Bft = .KA--
(и , „), ft ft
С помощью A1), (8) оператор f\L, а) можно записать в виде:
, *)]={F(L(O, ш, 0), а,
2<А-( "l <*
=i \iei,ivl = o
-^(й, а, p, -fA, A), A3)
где ty*'^, \J3W — некоторые функции класса S^, ограниченные по Л
со всеми производными.
Главный член в формуле A3) в силу F), G) имеет вид:
¦F(L@, a, 0), а, Л) =
«/оК «) + 2^@, со, 0, а)Л-в/+Л"^+1 @, со, 0, а, Л). A4)
В силу р-квазиоднородности функции af, нам нужно найти функ-
функцию ^.удовлетворяющую уравнению
±f (L, a)jgN = As"^ (ш, a) + Л"^. A5)
С помощью A3), A4) это уравнение решается по теории.возмуще-
теории.возмущений. Функцию gN ищем в виде
¦ gN (х, а) = Л*"' L (ш, а) + 2 Л""^ К Л> аI.
\ т=0 /
Подставляя это разложение для g/v, а также A3), A4) в урав-
уравнение A5), получим для каждого из коэффициентов gm уравнение
вида: ' ¦ '
Ыи. a)gm = Pm{k <в, a, Iff о, р, д/да)^, A7)
/2222 11 \
где Рт\А, a, a, l/f0, p, д/да) —дифференциальный оператор,
полиномиально зависящий от 1//0. Очевидно, правая часть "A7)
есть функция класса ^°°, равная нулю в окрестности нулей
функции /„(со, а). Поэтому решение уравнения A7) существует.
Оператор р, очевидно, ограничен в С на функциях вида
Л*ф(сй, а); поэтому \gm(a, Л, а)|^ст. Из этого же соображения
следует оценка остатка R^, который получится в A5) после всех
указанных вычислений. Лемма доказана. -;

530 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
Перейдем еще к одному предложению, использованному в пос-
последнем параграфе главы VII. Пусть *eR", ? e R", g (?, х) —
бесконечно дифференцируемая функция, обращающаяся в 0 при
\1\>10. Пусть, далее, -р,3*1, /=1, ..., п, Л (*) = / ? *J/PA \
toj {х) = X] [А (х)]~р/, S (I, а) — бесконечно дифференцируемая функ-
функция, Ф(&, *) = A(a:)S(?, <а(х)). Обозначим ReQ = O!, 1тФ = Ф2.
Будем говорить,, что функция f(x) принадлежит классу СГ>
если / (я) — бесконечно дифференцируемая' функция,
M sup
<oo
для любого натурального s.
Лемма 4. Пусть g(|, я) принадлежит по совокупности пере-
переменных классу С%, функция Фх удовлетворяет условию
при li'l^lo» IS'l^lo» а функция Ф2 неотрицательна.
Тогда оператор
TMe19^»^ g(p,x), p=* — id/dx
переводит любую функцию /е^Г8, s^O в функцию из класса
С00. „ 7 ,Ve>0.
8_2m__i__e
Доказательство. 1) Обозначим Т0 = е1ф1^" *'g(p, x),
* „ — ' x'g\p, х). Рассмотрим оператор
где фгеС~, 0^фг(д;)^1, фг(д;) = 1 при | х | < г. Справедлива
формула
Ai.r = Qi,r{x, р, р), A8)
где
Qi,r(x, I', t')=g(?, x(x, 1', Г))г(Г, ^(а;. Г, Г))х
¦ . , хA+>(*, Г, ?'))Ч(*(*. S', ?')I^(Г, Г, ^(^, Г, 6')I.
>*(•«» I'» |') —решение уравнения
^+-^-A', I', *) = х.
Действительно, для любого AeCf
l \ M\.-x"l"+x'l'
'. JOgA%
)-Ф, (S".

ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 631
Производя в последнем интеграле ту же замену переменных, что
и при доказательстве теоремы 1.1 главы V, получаем формулу A8).
2) Символ Qi,r можно оценить следующим образом: при k>l +
+ /п+л
HQ'. '!»„. k, *(RnxRnXR'lM*C'>*»
где ci k не зависит от г. Поэтому V/ieCj0, получаем,-учитывая,
что (Т*и, v)L, = (u, Tv)Li\
-| (Л, Ai,
\ \Tth(x)\*(l+x*)<er(x)dx
Переходя в этом неравенстве к пределу при г->оо, получим
так что Г0*еНот(^а, &{) при k>l + m + n. Пусть и,
Тогда
| (Го«, v) \и = | («, 7» \Li <\и 1 ^
так что
| Тои I^-ft < | Tt 1 ^*_, jj,/1 и 1 $,_/
2 2 2 8
и, значит, То е= Нот ($7"'» ^Р7*) при
3) Справедлива формула
где е(?, д;) — бесконечно дифференцируемая функция, е(?, лг) == 1
при 111<go и <?(|, *) = 0 при 11|>210л^_Оператор ГоA + х*)г
принадлежит пространству Нот (W^l+Sr, W^*) при
Оценим символ
l, x).
Пусть ц = (Hi, ..., Ц.п), v = (vlt ..., vn). Тогда
k 3
откуда следует, что h&Bk0 при г>~т-{--ап- Поэтому из B)
следует, что Vs^O, е>0
. r^,—2s—2m— ~n— e\
Г1, ^2 2 У*

532 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
4) Продифференцируем функцию Tf(x); если сР (g) — полином,
то
<r(p)Tf(x) = #>(p)Ml,*)g(J>, l)fW-**&S)gl(it x)f(x),
где функция gid, x) = <iP(l)g(l, х) наряду с функцией g(l,x)
удовлетворяет условиям леммы. Поэтому если f^W~s, то
и значит, функция dP(p)Tf для любого / принадлежит простран-
пространству Н1 _ _т_ _ (см. § 13, гл. IV). Для завершения доказа-
доказательства остается сослаться на вложение
Лемма доказана.
Построим почти обратный оператор для оператора
где
и N — фиксированное целое число.
Лемма 5. Справедливо равенство:
1 + U, B1)
где
N
v4i
Po
Доказательство. Во избежание громоздкости в вычисле-
вычислениях докажем равенство B1) для одномерного случая при N = 2
в неособой карте неособой зоны.

ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 633
Имеем:
= 1 + tfrlz д/да + 1/2 (<?'гJ дг/даг - (С" 1г) д/да —
— С'^агад/да - Cr'q^z^ д'/да* - С1 (q^zy.zadVdaa -f
+ 1/2 (С" ЧУ д2/даа + (С*J q^za дуда* +
- + 1/2 (С-^У №У г'а 02/да2 + Тг + Тг
= 1 + 1/2 (^' - СJ 22 г
+ 1/2
где операторы 7^ 7*2 и 71B) удовлетворяют утверждениям леммы,
что и требовалось доказать.
Построим оператор R]f такой, что ?/#&= I + Rn, где Rj/ e
g^Af + i- Положим #2 = #iO —Rd- Тогда
Аналогично, полагая
Rn = Rn-i~Ri(Ri)n-1, B2)
получим L/i?jv= 1 — (^1)^. Из леммы 5 следует, что $7 <=
2
Используя равенство B2) и определения операторов Rx и Rlt
по индукции легко доказать, что
RN~ 1 + 2 ЯЬ + Я<">; ЯЦ, s **_ /?(^><=Хн±\.
k=l 2* - ~
Пусть иу' и <ау> — карты зоны Q, ростка (Л", г"), ay f| а^^ф.
Дадим определение F-оператора, действующего на функции
Ф(а, Л) е= С?°((а?1 П <йУг)х[0, 1]) (зависящего от iV, N>0 —
любое целое число). Пусть ф(а, Л) еС^° ((<»?' П ®?)х?0, 1]),
а а (а) —решение уравнений
qi (a) + Yi/ (а) = 9/ (^) + Ya/ (о),
Уравнения B3) разрешимы относительно а на носителе функции
ф(а, И), причем ст(а) = а + OD (М/2) (ср. 3.11) гл. VI). Разложим
функцию ф(с(а), Н) по формуле Тейлора в точке в = а:
Ф (а (а), h) = Ф (а, Л) + 2 (Р«Ф) (а. Л) + 0D (/^2), B4)

534 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
где Pt&Xifai. Из результатов § 3 главы VI следует равенство
Re Ф? (а)+ /«? (а) !„=„<«) = НеФУ' +W(a) + OD(A8/*~8),
где ФУ и ШУ — соответственно фаза и энтропия в карте ©У зоны Q/.
Кроме того,
J( J
Разлагая функции е* и {г)~х>г по формуле Тейлора, получим
Д [Re Ф ] I
B5)
где ^i^<^i/2~ie, i- Используя построенный выше почти обратный
оператор к оператору L], перепишем равенство B5) в виде
а •= а (а);
Положим
JV
[ 1
ф (а. Щ + 2 (<^ф)(а, А) . B6)
Из B6) следует:
а, А) = ф(а, А) +
2
где .&1&%1/г-1е,1.
Пусть ф (а) —гладкая функция с носителем в неособой карте
неособой зоны goJ. Положим
n
B7)

ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 635
(
Пусть Rn—оператор, почти обратный к оператору L. Из ре-
результатов § 5 главы VI следует, что функция
t
—L\RNF(q(a,T),x)dx ,o j
Ч>(*. О ' лт—:я г«р{\ *(/»(«.*). <?(<*, т), x)dx B7')
при JV=>1 удовлетворяет уравнению переноса E.24) (см. теоре-
теорему 5.1), причем при подстановке ее в_уравнение E.24) правая
часть принимает вид
РХ S Z-I/2 _8, 0 , Р2 6= ^1 -8, 1» Ps S Z-1 _8, 2.
Лемма 6. Я
. О -м л Д(|?(«, 0+г(а, 0)
Da
при /s[0, Г]. Тогда после подстановки в левую часть уравнения
E.24) главы VI функции •$ (х, t), определенной равенством B7'),
П+ 2j Tk-\-T'N]F, где
Доказательство. Во избежание громоздких выкладок
докажем утверждение .леммы в случае N = 2. Аналогично § 5
главы VI преобразуем уравнение переноса с диссипацией к виду
(ср. E.18))!
х, t) + JTpp(p, х, t)(w-$z),Vxf)~
B8)
где I {x, t) =i|) (a (*, t), t) У Ja (a (*, t), t) и Q1et1/2,0) Q2eL,, i.
Предположим, что Y = 0 и докажем, что в этом случае утвержде-
утверждение леммы справедливо для функции
= ЙР (а, 0|а_а(*. 0 =
'']а(я0, B9)
Ф (а, 0 = - $ /?jvF (<? (а, т), т) dr.
о
Пусть

536 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
I
Вычислим производные функции % (х, t) по х и /. Имеем
-
'(С) Z + g2q>
где gi e L^ , g2 <= Z^, 2) gs e= Lb 8.
2' '
Произведя несложные преобразования, получим (ср. E.21)
гл. VI)i
fe
'(С) г + fa + g2 + ft) ф
Вычислим производную -yrtyo (x, t):
%(х, t) = -LR2F(x, t)-{i, С-»фв>-
'(С^)г V'(C-»J> + <'(C^)*, Ф«в'(^)г>. C0)
С помощью равенств B.9), B.20), E.22) .главы VI преобразуем
C0) к виду
~ % (х, t) = - LR2F (x, f) - (Шр,
• + (''(С)Hp + 'iC-1) <ЖрЧг+'(С-1) <2Tppw, ф„„'(С-1) г) -
-('(С-1)(?Гр(>'С + ?Грр<В)'(С-1)г,<раа'(С-1)г). C1)
Подставим найденные значения производных tf>0 (я, /) в левую
часть B8). В силу равенства E.23) главы VI достаточно рас-
рассмотреть выражение
(F - LR2F) +1 ± ('((Г*) г, Фаа '(С) г) -
- (iHp+ Жрр (w-%г)> С-^фаЛС) г) +
+ (Ш + ?ГРР (w - %г)ч fa + g2 + g3) Ф>. C2)
Сумма первых трех слагаемых в C2) в силу C1) и определе-
определения оператора R2 равна
(i '(С) Нр + '(С) «ДГиг+'(С) <%Гррхю, Фаа.^С) г) -
- ('(С-1) (*%V С + <?ГРР 'В) '((Г1) г, Фаа '(С) г) -
- (Шр - <ЖРР (w - Шг), C-4aa '(С) г) + giF = g5F, C3)
где &> ёъ е %4i. k, k — некоторое целое число (здесь мы исполь-
использовали лемму 2.6 главы VI).
Из леммы 2.2 главы VI следует, что справедлива оценка
t\Hp\<;Dxl2-*. Поэтому из формулы E.23) главы VI, а также
из B9'), C2), C3) следует, что при подстановке в B8) функции

ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 537
я|H (я, t), определенной равенством B9), правая часть B8) примет
вид
где Т\ <= #i/2-e( о, Tk e= %k_+± _e k, T'% <= Xil2i „, п - целое число.
Доказательство завершается теперь так же, как доказательство
теоремы 5.1 главы VI.
Аналогично, в случае особой зоны, Р в формуле B7) заменяется
на (J?, и, при условии необращения в нуль соответствующих
якобианов, остается справедливым утверждение леммы 5.
Пусть (Л{>, г7) —росток, полученный из начального ростка
(Л", г") с помощью канонического преобразования, отвечающего
функции Гамильтона операции обхода фокусов Н (х, |). Обозна-
Обозначим через й'сА" пересечение зон Q/Пйх на Л" и пусть й'с
' с: Л{* — образ п° при этом каноническом преобразовании. Из
результатов § б главы VI следует, что |_Ш' при 0^<^я/2 при-
принадлежит некоторой зоне Q'; ростка 1)(Л?, /¦"). Пусть |<aj'} —
покрытие Q'j Y-картами. Обозначим через {eyi(qn p-,, t)\ раз-
разбиение единицы по образам карт ш^' при 7-ДиФФеоморфизме.
. 0. Pi'(«. 0 + Ут(а. 0, 0-
Положим
v'@
Пусть $х и ^2 — операторы, введенные на стр. 487, R0 = —iAy.
Карте ш^* сопоставим операторы
Ли @ о = - eVfe W (^ («, 0)"и2Цк \ RNJl/2RuiV dt. C3'}
i=l,2,3,t)eCco(A'1x[01n/2]). •
В правой части равенства C3') интегрирование ведется вдоль
траекторий системы Гамильтона, соответствующей функции Н (х, |).
Лемма 7. Операторы Pit Pf\ Pf> в лемме 2.1 главы VII
имеют вид
pt (о - Е Ам @. ? J0) w - А (О 2 <^~ ¦**.;•.
A ft
Я/2

538 . •ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
Доказательство. В силу результатов § 5 главы VI и
леммы 5 решение уравнения B.16) главы VII можно представить
в виде
Ъ(Ч„ Рр 0 = S №".1 + им + Р».г]% I v
k |a=oT* (qt> р-/( <)
где функция i|>o = iMa> 0 определяется равенством
tfo («, 0 = 1] еу* @ (У (а, 0)" 1/21)Ч (а,Л).
k
Из условий леммы 2.1 главы VII следует, что при <е[я/2-
— б, я/2] (б > 0 — достаточно малое число) область п* покрыва-
покрывается одной неособой картой со*. Из равенства B.2) главы VII
и доказательства теоремы 6.1 главы VI следует, что Li\t=n/2 =
= L/f|/=o. В силу выбора ветви функции У~г и теоремы 6.1
главы VI из предыдущих равенств следует, что операторы Pi(t)
в области Q*/2 можно представить в виде
Pt = ein'21* it—14 {jk)- u*LKP ,<".
Отсюда, из результатов § 5 главы VI, леммы 5 и равенства B.5)
главы VII нетрудно получить утверждения леммы.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксиомы Ц-Структуры 36, 37, 43, 45, 46, 49,
100, 120, 122, 129
Алгебра 120
— банахова 167
— коммутативная 120
— Ли иильпотентиая 97
— нормированная 167
— операторов 36
— степенных рядов 22
— с ц-структурой 36, 44
— с единицей 120
¦— топологическая 167
— формальных степенных рядов 120
Асимптотика квазиклассическая 51, 64, 70,
JI7 --.
— по гладкости 51
Атлас канонический 349, 369, 384
— — весовой 499
Базис 119, 137
Бихарактеристики 106, 107, 116
Бочка 124
Вектор-оператор 280
Веществеииоподобиая плоскость 418
Гамильтониан 27, 103, 104
— для операции обхода фокусов 469
— комплексный 420
— собственный 455
Гомоморфизм 121, 143
График замкнутый 149
— оператора 147
Группа 118
— двупараметрическая 277
— обратимых операторов 150
— порожденная производящим оператором
204
г- сдвигов 233
Действие вещественное 437
— ростковое 432
«-действие 421
и-действие 418. 452
Диссипация ПО, 407, 425, 427, 507
V-диффеоморфизм 422, 423
Дополнение ортогональное 135
Замыкание оператора 145
Значение собственное 151
Зона (иеособая, особая) 418
Идеал 121, 150, 168
Изоморфизм 122
— изометрический 125
Индекс пути 371, 382
« на У-лаграижевом многообразии 498
.— цепочки карт 370, 381
Интеграл несобственный 161
— Рнмаиа 160
Карта 343; 369
7-карта 422
Квазиобратимость 94
Д-квазиобратимость 519
0-квазиодиородиость 104
— асимптотическая 105, 511
•— — старшая часть 105
существенная часть 105
— степень 104
Класс характеристический 498
— эквивалентности 428
Коммутатор 29, 120
Компакт 123
Композиция операторов 154
Кратность спектра 32, 34, 97
Кривая, ассоциированная с гамильтонианом
Лагранжиан ростка полный 431
Лемма о бочке 124
— о локальных координатах 444
Метод стационарной фазы 70, 74, 224, 361.
365, 375. 482
— Хевисайда 11, 19
Многообразие лаграижево 416
•— У-лаграижево 496
•— линейное 119
<— с комплексным ростком 419
Множество выпуклое 119, 124
— нулей ростка 417
— плотное 125
•— резольвентное 43
<~ факторрезольвеитиое 330
Набор производящий 264
Неравенство Бесселя 135
—| Гординга 426
— диссипативности НО. 419
— Коши — Буняковского 129
Норма 122
— в промежуточном пространстве 209
•- Гильберта •- Шмидта 152
*- оператора 143
— функционала 137
— эквивалентная 194
Носитель ивазиобратиого элемента 520
•— компактный 127
Область значений 142
<-> определения 142
Оболочка выпуклая 119 ,
<¦* линейная 119
Образующие иильпотеитиой алгебры Ли 97
V-объекты 384
Оператор-вполне непрерывный 150
— волновой 56, 113, 117
•— вырожденный 150
•- Гильберта 235
_ дифференцирования 143, 387
¦— единичный 154
— замкнутый 145
•— канонический (к, о.) 367, 372, 379, 392,
396, 397
— -= на многообразии с ростком 500

540
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ'
Оператор канонический регуляризованный
398
—¦ — сглаженный 373
— компактный 150
— конечномерный 154
— Лапласа 169
— линейный 142
— непрерывный 142
— нулевой 154
— обратимый 150, 154
— обратный 150, 154
— ограниченный 143
— переводящий 280
— переноса 34, 53, 463, 466
— перехода из карты в карту 390
— порождающий группу 245
— предканоннческий 499
— производящий 203, 215
¦ в банаховом пространстве 204
, степень, шаг 203, 279
— псевдодифференцнальный 47, 303
на кривой 388
¦ на окружности 49
— регулярный 265
— —, степень 265
— рождения, уничтожения 306
— самосопряженный 158
— сдвига 15.
— симметричный 158
— существенно самосопряженный 158
•— тождественный 150, 154
— умножения 144
— унитарный 262
— упорядоченный 22
— Шмндта 274
— Шредингера 107
V-оператор 491, 506
Операция бинарная 118
— обхода фокусов 469
— квантовая 482
— подстановки 25
— «штриха» 26, 45
М.-операцня 23, 36, 49, 50
Отображение дифференцируемое 163
— полулинейное 152
— сжатое 164
Перестройка (гамма) 422, 443, 449, 454
Покрытие 123
— каноническое 422
Поле векторное 428, 440
Пополнение 127
Последовательность квазнобратная 94
~- слабо ограниченная 141, 142
— I- сходящаяся 141, 142
— »- фундаментальная 141, 142
— стационарная 125
— сходящаяся 122
— фундаментальная 123
Потенциал 417, 508
Правила редукции 96, 100—102
Представление (упорядоченное) нильпо-
тентной алгебры Ли 97, 99, 336
— алгебры левое регулярное 167
Преобразование адиабатическое 420, 454
— днсснпатнвное 420
— каноническое 417
псевдоднфференциального оператора
342, 408
— Лежандра 352, 368
— ростка каноническое комплексное 420
— Фурье 47, 171, 282
обратное 171
/-преобразование Лежандра 421
Проекция вектора 135
Произведение оператора иа число 154
— операторов 154
Произведение пространств 119
— скалярное 129
Производная вдоль траекторий 61, 72
•— обобщенной функции 178
— разностная 28, 319
•— семейства операторов 316
— функции со значеинямн в банаховом
пространстве 160
¦- Фреше 163
Пространство банахово 123
¦ промежуточное 209
— бесконечномерное 119
— векторное 118
— гильбертово 130
— компактное 123
— метрическое 122
— л-мерное 119
— нормированное 122
— полное 123
— предгильбертово 129
— рефлексивное 141
— сепарабельное 137
— Соболева 170, 173
— сопряженное 140, 179
— счетномерное 137
— фазовое 103, 416
— функций, интегрируемых по Бохнеру 161
--впо Лебегу 161
— Фурье-образов 188
Равенство Парсеваля 136, 171
Разбиение единицы весовое 423, 499
Разложение спектральное 32, 34
Разностная производная 28
•" схема 117
Расширение оператора 144
•• — наименьшее замкнутое 145
Регулярнзатор 57, 65
— ослабленный 65
Резольвента оператора 151
Решение асимптотическое 51, 64, 65
'По гладкости 51
Росток комплексный 417
Ряд формальный степенной 120
Свертка функций 244
Символ ^-местный 36, 49
— на торе 48, 49
— оператора 12, 14, 50. 217, 265, 293, 318
— операторнозначный 331
<— растущий 327, 330
Система алгебраическая 121
— бихарактеристик 61, 69, 71, 103, 106, 116
— в вариациях 417
— Гамильтона 61, 69, 77, 103, 106,'116, 416,
425, 431
<— Гамильтона р- Якобн дисснпатнвная 416,
424
— дифференциальных уравнений 19
— колебаний решетки 54, 521
— обобщенных собственных и присоединен-
присоединенных (с. п.) функций 271
— ортонормированная 135
—1 полная 136
— ^ обобщенных с. п. функций 271
— уравнений ростка 431
Скобки автономные 25, 295
— Лагранжа 416, 418, 425, 435, 495
Спектр дискретный 242
— вектор-оператора 291
>-н матрицы в С 32
— - в R» 35
— оператора 151
— пары в С 33
В R2 42, 44
операторов
ов А, В

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ'
541
Спектр пары производящих наборов Л, А
относительно Т 292
— производящего вектор-иабора 317
— — набора 265
—.— оператора 239
Степень оператора 154
— производящего оператора 203, 279
Ц-структура 36, 48, 50
Сужение оператора 144
Сумма операторов 154
"- прямая 135
Сходимость в метрике 122
¦— обобщенная 88
— сильная 141
— слабая 14J, 142
Теорема Банаха 147
— Банаха ¦— Штейнгауза 149
— Бэра 123
— вложения 184
Соболева 185
— Лнувилля 446
— о замкнутом графике 149
— о неподвижной точке 164
— о параллелограмме 131
— основная 109, 116, 117, 519
— Ф. Рисса 139
*- Хана •¦ Банаха 138
Точка неподвижная 164
— резольвентного множества 282, 291 292,
317
— стационарная 70
— фокальная 82
Траектории гамильтоиовой системы 71
Уравнение волновое 56
•- Гамильтона«Якобн 52, 60, 69, 71, 103
— ~ — с диссипацией 431
— диффереициальио-разиостиое 54
— кристалла 54
» нелинейное 85, 521
— переноса 53
-с диссипацией в зоне 460
— разностное 17
— ростка ПО, 417
— с постоянными коэффициентами 95, 109
— характеристик 52, 60, 69, 71. 103
— Шредннгера 107
лля осциллятора 70
Условия квантования 396, 501
— поглощения 108, 116
Фаза на многообразии с ростком 452, 508
«- ростка 421, 452
Факторпростраиство 128
Факторспектр 331
Фокусировка в кристалле 82, 93
Формула коммутации (перестановки ин-
индексов) 25, 29, 32, 39, 326
канонического оператора с гамильто-
гамильтонианом 402, 407
— 1" с экспонентой 27, 48, 321, 322, 335, 342,
479, 481
— Ньютона 31, 41, 323
— Тейлора 55, 98, 102
К-формула 29, 30, 40
Функционал линейный 137
•— непрерывный 137
е- ограниченный 137
Функция Гамильтона 104, 105
— Дирака 179, 191
— интегрируемая 161
» по Бохнеру 161
— — по Лебегу 161
— обобщенная 171
— порожденная комплексной функцией 197
— разрывная 171
— со значениями в банаховом простран-
пространстве 160
б функция 193
Черное тело 108, 109
Шаг оператора 203, 279
Шар 123
Шкала банахова 279
Шлейф осцилляции 76
Элемент единичный 118
— канонический 391
— квазиобратимый 94
— нейтральный 155
— нулевой 118
— обратный 118
— присоединенный 242
— собственный 242
— с. п. 242
Энтальпия ростка 449
Энтропия 419
Эталон 102
Эффект типа Черепкова 78, 117
Ядро 140
— оператора 147, 155
— тривиальное 155
Якобиан 62, 343, 344, 347, 460, 484

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
R", Сп—n-мерные (вещественное и комплексное) арифметические, простран-
пространства.
б, -s—разностная производная 28.
[•..J—автономные скобки 25, 295.
[..., ...] —коммутатор 29.
[..., ...]yfe —скобки Лагранжа 416.
II • - - flmid норма в пространстве ВтЫ 209, 264.
А
{a, 6>=Sa&.
f*g — свертка функций fug 244.
бу—символ Кронекера.
ind fa /„) — индекс цепочки карт 370, 381.
у[1] — индекс пути на лагранжевом многообразии 371, 381.
Ind Y—индекс пути на У-лагранжевом многообразии 498.
g//— каноническое преобразование, отвечающее гамильтониану Я 417.
g* ~—комплексное каноническое преобразованве 420, 425.
&gllh — канонический оператор (к. о.), отвечающий параметру А-»0 500.
gffA—K. о., отвечающий параметру Л-*оо 514.
Ккв—квантованный канонический оператор 397.
Крег—регулярнзованный канонический оператор 398.
?Х,(Д), ?^(Д) —ортогональные проекторы, отвечающие интервалу 260, 261.
?/л(/) — группа гомоморфизмов, порожденная операторе i A 204, 280.
Тф(Да, fli)—функция от трех упорядоченных операторов 2872 293.
Qc^gp—с* (ж) g-j—волновой оператор 56.
def
Sa3—оператор Лапласа.

УКАЗАТЕЛЬ ОБОЗНАЧЕНИИ 543
J—матрица Якоби.
dhr,
\дхп"'дхп
Л*—матрица, сопряженная к А.
(Л, Л' —матрица, транспонированная по отношению к Л.
fa, .... хп)', 'fa ж„)—вектор-столбец.
?*(?}) —пространство функций, ии
интегрируемых о квадратом иа Q c-R"
127, 132.
<®t i ...'i s (^"i X ... X Rnw)— банахова алгебра символов 282.
S-^-пространство быстро убывающих гладких функций 169.
JP*(R«)—пространство Соболева 170, 173.
&ка (R") —образ пространства Соболева при преобразовании Фурье 172.
Cj (Rn)—пространство k раз непрерывно дифференцируемых функций,
имеющих конечную норму C37):
I |Y|
1 . lYl-0
^—потолнение. пространства S по норме C37):
MN—.векторное пространство, натинутое на функции elk'x, k=*0, ± 1, ...
.... ±N; *eR 64.
Cj^f—пространство s раз дифференцируемых по х, /eR, 2л-периодиче-
ских по х функций ф таких, что E5):
sup
sup С
0<h<l J
— я
. ,>-0. 1
—пространство символов ц-структуры на алгебре 36.
(R" X Мт) — пространство символов ц-структуры на модуле X 60.
^A*1"^)—функция класса C^(Rn хМт), для которой .60):
. М, IYI-0, 1, 2, ...
(ft*)—гладкая функция на R», такая, что D16):

Виктор Павлович Маслов
ОПЕРАТОРНЫЕ МЕТОДЫ
М., 1973 г., 544 стр. о нлл,
Редакторы А, А, Кириллов, Е. И. Стечкина
Техн. редактор А. П. Колесникова
Корректор Е, Я.Строева
Сдано в набор 2/Х 1973 г. Подписано к печати
28/ХИ 1973 г. Бумага 60Х907и. тип. № 2. Физ.
печ. л. 34. Условн. печ. л. 34. Уч.-изд. л. 33,72.
Тираж 20 000 экз, Т-20429. Цена книги 1 р, 28 к,
Заказ № 1038.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинград-
Ленинградская типография № 1 «Печатный Двор» имени
А. М. Горького Союзполиграфпрома при Государ-
Государственном комитете Совета Министров СССР по
делам издательств, полиграфии и книжной тор-
торговли. 197136, Ленинград, П-136, Гатчин-
Гатчинская ул,, 26,