Author: Салмин В.В. Ишков С.А. Старинова О.Л.
Tags: физика космос астрофизика полет в космос освоение космоса издательство снц ран
Year: 2006
Text
В.В. Салмин
С.А. Ишков
О.Л. Старинова
МЕТОДЫ
РЕШЕНИЯ ВАРИАЦИОННЫХ ЗАДАЧ
МЕХАНИКИ КОСМИЧЕСКОГО ПОЛЕТА
С МАЛОЙ ТЯГОЙ
Самара
Издательство СНЦ РАН
2006
В.В. Салмин
С.А. Ишков
О.Л. Старинова
МЕТОДЫ
РЕШЕНИЯ ВАРИАЦИОННЫХ ЗАДАЧ
МЕХАНИКИ КОСМИЧЕСКОГО ПОЛЕТА
С МАЛОЙ ТЯГОЙ
Под общей редакцией заслуженного
деятеля науки Российской Федерации
В.В. Салмина
Самара
Издательство СНЦ РАН
2006
УДК
Монография издана при поддержке Губернского гранта в области
науки и техники № 102 «Подготовка и издание монографии «Методы
решения вариационных задач механики космического полета с малой
тягой»
Рецензент член корр. РАН, д-р техн, наук, профессор Г.П. Аншаков
С164 В.В. Салмин, С.А. Ишков, О.Л. Старинова
Методы решения вариационных задач механики космического полета с
малой тягой. - Самара: Издательство Самарского научного центра
РАН, 2006, 164 стр.
В книге систематизированы существующие и развитые
авторами методы решения вариационных задач механики полета с
малой тягой. Представлены математические модели, описывающие
движение КА с энергодвигательными установками малой тяги.
Описаны результаты решения серии прикладных задач, полученные с
помощью описанных методов.
Монография может быть полезна для инженеров и научных
сотрудников, заинтересованных в решении задач оптимального
управления и проектирования космических аппаратов с малой тягой, а
также работающих в смежных отраслях аэрокосмической науки и
техники.
Печатается по решению издательского совета Самарского
научного центра Российской академии наук
ISBN - 978-5-93424-282-5
© В.В. Салмин, С.А. Ишков, О.Л. Старинова
Введение
Содержание
Введение....................................................5
1. Методы оптимизации космических перелетов с малой тягой...10
1.1. Математические постановки задач оптимизации...16
1.1.1. Критерии оптимальности...................16
1.1.2. Выделение динамической задачи............18
1.1.3. Учет неопределенных факторов.............20
1.2. Методы решения задач оптимального управления ... 21
1.2.1. Необходимые и достаточные условия
оптимальности....................................21
1.2.2. Способы задания синтезирующей функции....25
1.2.3. Оценки приближенно-оптимальных решений...27
1.3. Метод усреднения в задачах оптимального управления
...........................................28
1.4. Численные методы решения краевых задач
оптимального управления.............................31
1.5. Метод разбиения пространства состояний........35
1.6. Метод последовательных расширений.............36
1.7. Итерационная процедура поэтапной оптимизации...37
2. Математические модели задач оптимизации................39
2.1. Основная задача оптимизации.................39
2.2. Математическая модель задачи оптимального
управления околоземными эллиптическими орбитами.....49
2.3. Математическая модель задачи оптимизации перелетов
между орбитами с большими эксцентриситетами.........52
2.4. Математическая модель задачи оптимизации
управления относительным движением космических аппаратов56
2.5. Математическая модель задачи оптимизации
совместного управления траекторным и угловым движением..58
2.6. Математическая модель задачи совместной
оптимизации траекторий и ориентации солнечных батарей.67
2.7. Математические модели задач оптимизации
межпланетных перелетов с малой тягой................73
2.8. Математическая модель, описывающая движение КА в
системе Земля-Луна..................................77
2.9. Математические модели, описывающие движение КА с
солнечным парусом...................................78
3. Прикладные задачи оптимизации перелетов с малой тягой..81
3.1. Оптимальное управление элементами эллиптических
орбит ..............................................83
3
Введение
3.2. Приближенный метод расчета энергетики маневра и
параметров управления элементами орбиты..............89
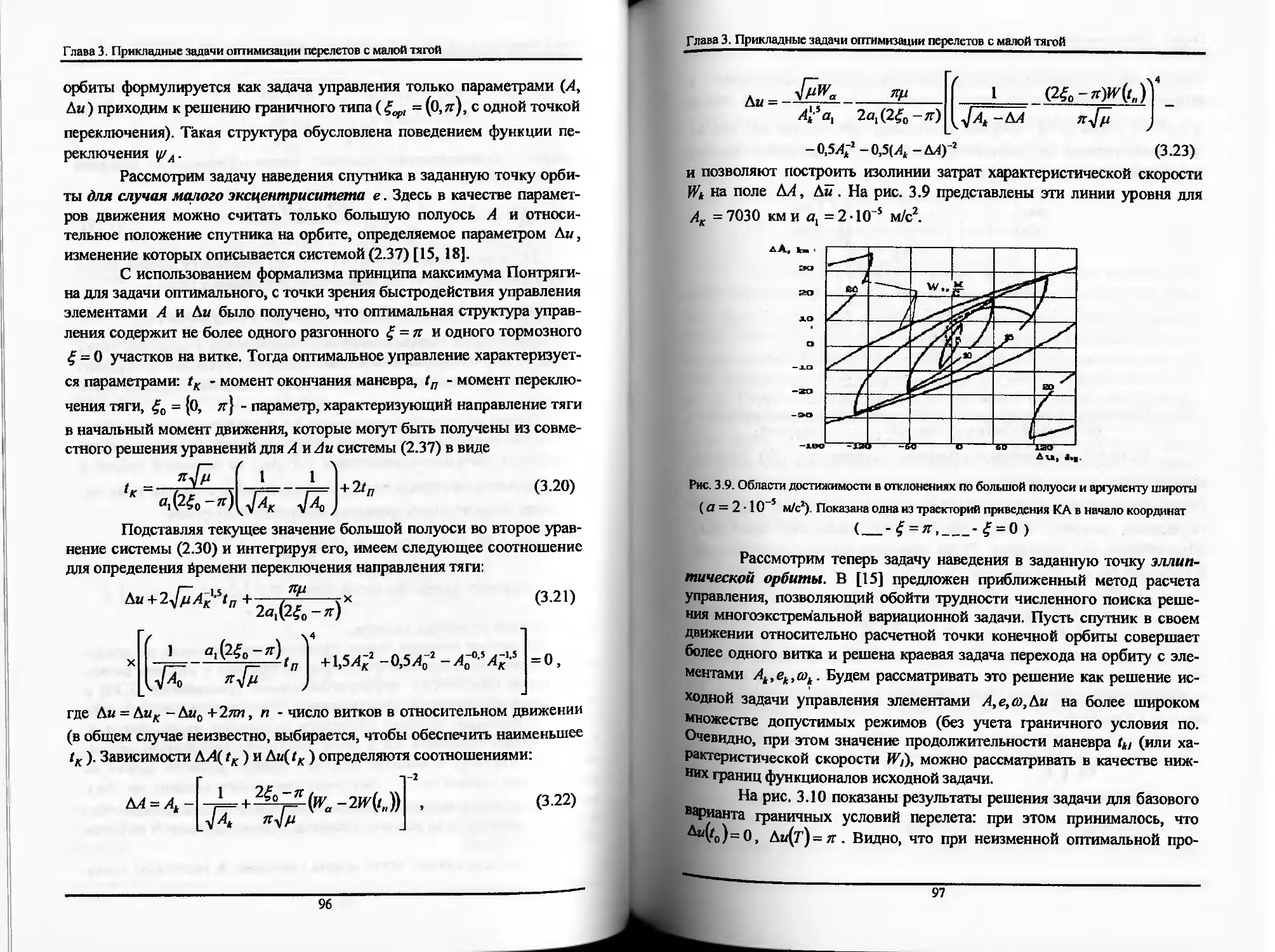
3.3. Задача наведения КА в расчётную точку орбиты.95
3.4. Оптимальное управление относительным движением
космических аппаратов с двигателями малой тяги.........99
3.5. Расчет оптимальных перелетов между орбитами с
большими эксцентриситетами.............................103
3.6. Задача коррекции орбиты спутника Земли с учетом
неопределенности силы сопротивления верхних слоев атмосферы
105
3.7. Задача оптимального набора параболической скорости
и торможения КА с учетом ограничений на угловую скорость
поворота вектора тяги..............................110
3.8. Оптимизация траекторий перелета с непрерывной
тягой между круговыми некомпланарными орбитами......113
3.9. Совместная оптимизация траекторий и проектных
параметров межорбитальных транспортных аппаратов с
двигателями малой тяги..............................122
3.10. Расчет оптимальных дат старта при перелете на
геостационарную орбиту КА с солнечной ЭРДУ..........132
3.11. Синтез приближенно-оптимальных алгоритмов
управления при перелетах КА на геостационарную орбиту.... 135
3.12. Оптимизация замкнутых межпланетных перелетов с
малой тягой.........................................142
3.13. Оптимизация траектории перелетов с малой тягой
между Землей и Луной................................146
3.14. Оптимизация движения КА с солнечным парусом .151
Заключение...............................................159
Список использованных источников.........................161
4
Введение
ВВЕДЕНИЕ
В настоящее время механика космического полета с малой тя-
гой выделилась, по существу, в новый раздел механики космического
полета, рассматривающий в совокупности проблемы оптимизации тра-
екторий и законов управления движением, а также выбора оптимальных
соотношений масс основных компонентов космического аппарата (КА)
с электрореактивным двигателем (ЭРД). Облик типичного КА с ЭРД
(проект SMART-1) показан на рис. В.1.
Физические и технические основы электрореактивных двигате-
лей широко освещены в специальной литературе [1]. К настоящему
времени в России, (а ранее в СССР) и ряде других стран - США, Герма-
нии, Франции, Англии созданы и испытаны серийные образцы двигате-
лей, которые активно используются в космическом пространстве для
решения целого ряда практических задач космонавтики. В основном
ЭРД использовались в околоземном космосе для управления орбитами
ИСЗ. Источником энергии для ЭРД служат солнечная или (в перспекти-
ве) ядерная энергетическая установка.
Рис. В. I. Экспериментальный аппарат с ионным двигателем ESA SMART-1
Космические эксперименты последнего десятилетия (Deep
Space 1, SMART-1, КА «Ямал», «Монитор») показали хорошее соответ-
ствие расчетно-теоретических и экспериментальных характеристик
ЭРД, показали пути дальнейшего повышения их эффективности и воз-
можность создания перспективных космических аппаратов, целиком
ориентированных на использование электрореактивных двигательных
установок.
Главное направление теоретических исследований в области
динамики космических перелетов с малой тягой заключается в развитии
аналитических и численных методов решения вариационных задач для
5
Введение
поиска оптимальных траекторий. В последнее время большее значение
приобретают вопросы, связанные с учетом дополнительных факторов в
математических моделях движения космических аппаратов, а также
дополнительных ограничений на возможности управления двигатель-
ной установкой.
Например, следует заметить, что в подавляющем большинстве
работ КА рассматривают как точку переменной массы, сводя проблему
выбора оптимальной траектории к оптимизации управления вектором
тяги. Однако если двигатель жестко закреплен относительно корпуса
КА, любая программа изменения вектора тяги может осуществляться
только разворотом КА в пространстве с помощью управляющего мо-
мента, величина которого ограничена. В этом случае следует выбирать
оптимальную траекторию из условия минимума суммарных затрат на
управление движением центра масс и программный разворот корпуса
космического аппарата или с учетом ограничений на ориентацию век-
тора тяги. При этом существенно усложняется математическая модель
задачи оптимизации.
Дополнительные проблемы возникают при рассмотрении во-
просов управления аппаратами с солнечными энергетическими уста-
новками. Основная причина трудностей заключается в наличии боль-
ших панелей солнечных батарей с системой индивидуального наведе-
ния на Солнце, ограничивающих возможность оптимального управле-
ния вектором тяги. С другой стороны, ограничения на управление ори-
ентацией солнечных батарей не позволяют реализовать максимальный
уровень тяги ЭРД. Поэтому необходима совместная оптимизация не
только траекторного и углового движений, но и ориентации батарей и
начального положения плоскости орбиты относительно Солнца.
Таким образом, традиционный подход к задачам механики по-
лета с малой тягой, при котором КА рассматривается как материальная
точка с «идеальным» управлением вектором тяги, в ряде случаев оказы-
вается несостоятельным.
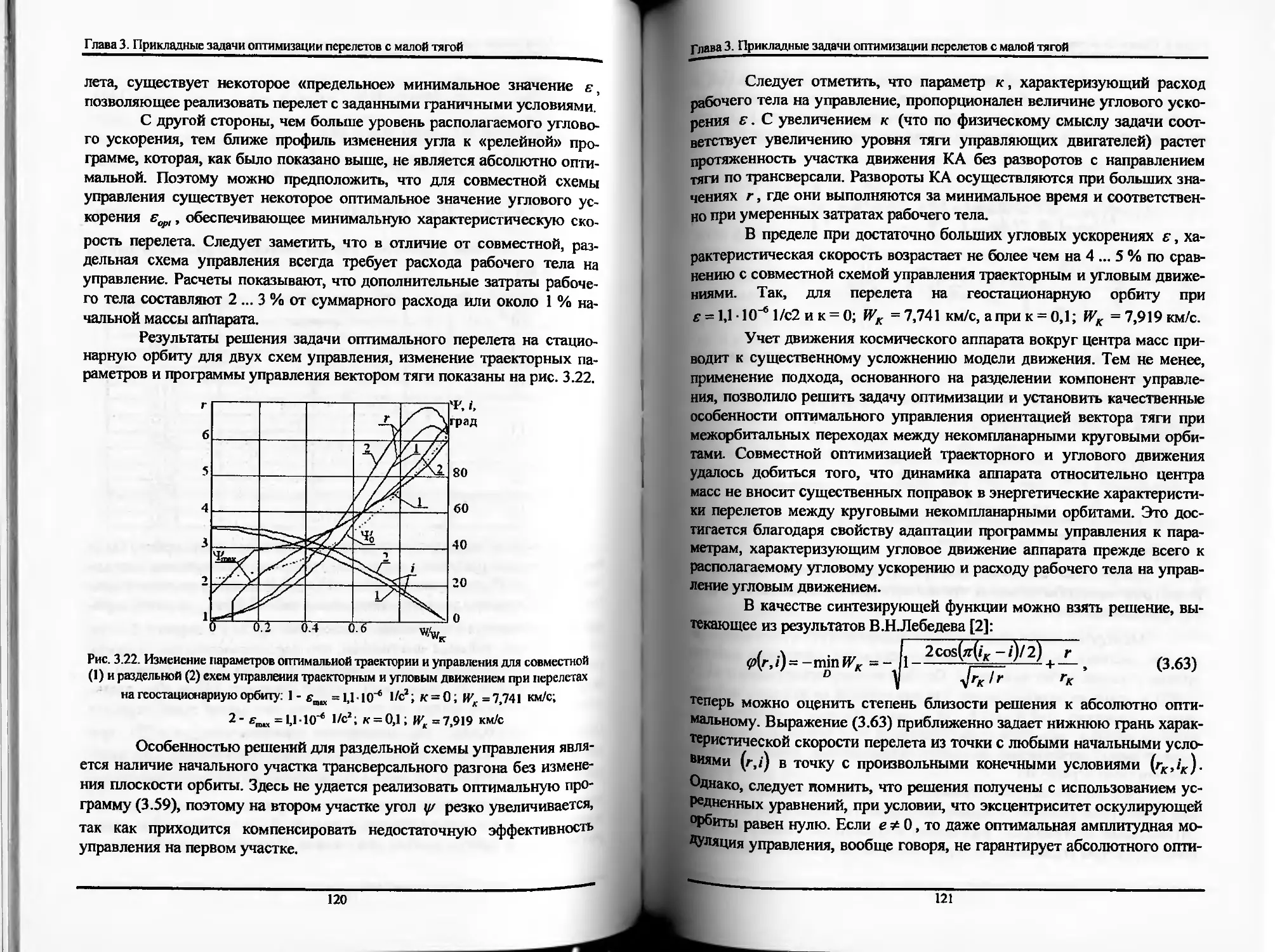
Еще одна проблема заключается в трудности решения задач оп-
тимизации многовитковых траекторий полета в «сильных» гравитаци-
онных полях планет. Блестящий подход к решению этой проблемы был
предложен В.Н.Лебедевым [2]. Он основан на разделении переменных
на «быстрые» и «медленно меняющиеся» и усреднении уравнений дви-
жения. В настоящей монографии этот подход получил дальнейшее раз-
витие.
Существенные трудности содержат также задачи оптимизации
замкнутых межпланетных перелетов. Отдельные участки перелетов
(припланетные, гелиоцентрические) сравнительно легко оптимизируют-
6
Введение _______________________________________________________
ся однако при их объединении в схему замкнутого перелета необходи-
мо решать задачу стыковки участков на основе параметрической опти-
мизации. Алгоритм решения вариационной задачи носит ярко выражен-
ный двуцикленный характер, а его устойчивость становится проблема-
тичной.
При решении задач оптимизации движения КА с солнечным па-
русом существующая взаимосвязь между величиной и направлением
управляющего ускорения и положением паруса требует совместного
моделирования движения центра масс КА и его расположения относи-
тельно центра масс. Дополнительные трудности создает необходимость
учета светотеневой обстановки на орбите, деградирующего влияния
температуры и радиации на поверхность солнечного паруса, а также
ограничений на управление, связанных с большими габаритами и невы-
сокой прочностью конструкции.
В данной монографии предлагается также новый подход к про-
блеме поиска оптимального управления для КА с малой тягой, движу-
щегося в системе двух гравитирующих тел. Такое движение, например,
осуществлялось КА SMART-1 (задача перелета на орбиту спутника Лу-
ны) на участке между сферами действия Земли и Луны. Оптимизация
этого движения в рамках проекта SMART-1 не проводилась, больше
того, на этом участке вообще осуществлялось пассивное движение, так
как оптимальное управление не было определено. Сложности оптими-
зации этого участка движения связаны с громоздкостью и большой раз-
мерностью математической модели движения, а также необходимостью
оптимальной стыковки с другими участками траектории.
Усложнение математической модели движения КА ведет к по-
явлению новых трудностей при решении задач оптимизации. По сути
дела, происходит сужение класса допустимых траекторий и управлений.
В этих условиях существенно возрастает роль приближенных методов
решения задач оптимизации. Поэтому актуальной проблемой становит-
ся разработка методов отыскания приближенно-оптимальных траекто-
рий и управлений и их оценки. Эти методы базируются на известном
принципе расширения класса допустимых состояний и управлений и
достаточных условиях абсолютного минимума [3,4].
Авторами предложен и теоретически обоснован следующий
подход к решению проблемы оптимизации перелетов с малой тягой.
Сначала формулируется задача в наиболее общей постановке. Затем
анализируются физическая сущность задачи и ее особенности, позво-
ляющие провести редукцию математической модели движения, напри-
мер усреднение движений, носящих циклический характер (движение
аппарата вокруг центра масс, орбитальное многовитковое движение и т.
7
Введение
п.) отбрасывание ряда связей и ограничений. В результате модель дви-
жения существенно упрощается, сохраняя, однако, все важнейшие осо-
бенности исходной модели.
Для отыскания приближенно-оптимальных траекторий предло-
жен метод, основанный на разбиении пространства состояний на от-
дельные области, где возможные упрощения модели движения позво-
ляют получить аналитические результаты для количественных оценок.
После получения приближенно-оптимальных решений по участкам
осуществляется их стыковка на границах областей и оптимизация по
фазовым координатам - параметрам точек стыковки. При таком подхо-
де приходится сознательно отказываться от получения универсального
решения для априори заданной области допустимых состояний.
Следующий шаг заключается в отыскании структуры оптималь-
ного управления в рамках упрощенной модели движения. Здесь приме-
няются как методы теории оптимальных систем, так и эвристические
приемы отыскания приближенно-оптимальных управлений. Последние
обладают теми достоинствами, что позволяют выбрать рациональные
управления, заведомо удовлетворяющие ограничениям и содержащие
необходимое число свободных параметров для решения краевой задачи.
Третий этап заключается в оценке степени оптимальности вы-
бранных приближенно-оптимальных управлений и траекторий. Специ-
альные процедуры оценки позволяют установить, насколько близки
найденные управления к абсолютно оптимальным, и указать способы их
улучшения.
Совместную оптимизацию траекторий и проектных параметров
КА предлагается проводить итерационным методом, с использованием
последовательности усложняющихся динамических и проектных моде-
лей. В соответствии с этим подходом, решение задачи оптимизации в
рамках упрощенной модели рассматривается как первое приближение.
На последующих итерациях, по мере усложнения модели, уточняется
динамическая характеристика маневра, под которой подразумевается
мера затрат на его реализацию, зависящая от совокупности баллистиче-
ских и проектных параметров, а также уточняются параметры, задаю-
щие облик проектируемого космического аппарата.
На основе описанного подхода получены результаты для ряда
новых задач механики полета с малой тягой:
• управления параметрами низкой околоземной эллиптической орбиты,
в том числе с учетом возмущающего воздействия атмосферы;
• межорбитального перехода с малой тягой на высокоэллиптическую
геоцентрическую орбиту;
• выбора оптимальных траекторий и параметров межорбитального
8
Введение
транспортного аппарата (МТА), совершающего перелеты между низкой
и геостационарной орбитами;
. сближения и маневрирования близколетящих КА;
• межпланетного перелета на Марс с возвращением к Земле с использо-
ванием солнечной энерго двигательной установки;
• межорбитального перелета к Луне с учетом гравитации Земли и Луны;
• перелета КА с солнечным парусом.
Эти результаты публиковались в течение многих лет в серии
статей в журнале «Космические исследования», а также частично изло-
жены в монографии В.В.Салмина «Оптимизация космических переле-
тов с малой тягой».
В настоящей монографии обобщаются результаты исследований
авторов в области механики космического полета с малой тягой. Полу-
ченные решения подкрепляются большим объемом численных расчетов.
Ограниченность объема настоящей книги не позволила полно-
стью описать технологию решения прикладных задач. При необходимо-
сти читатель может найти все необходимые сведения в публикациях,
приведенных в списке литературы.
9
Глава 1. Методы оптимизации космических перелетов с малой тягой
1. МЕТОДЫ ОПТИМИЗАЦИИ КОСМИЧЕСКИХ
ПЕРЕЛЕТОВ С МАЛОЙ ТЯГОЙ
Исследования в области теории космических полетов с двигате-
лями малой тяги ведутся с середины 50-х годов. Уже в ранних работах
отмечалась необходимость совместной оптимизации траекторий и зако-
нов управления движением, с одной стороны, и основных проектных
параметров (мощности энергоустановки, тяги двигателя, скорости исте-
чения рабочего тела, соотношения масс основных компонентов КА), с
другой. Трудности решения подобной задачи неизбежно требуют её
упрощения, как за счет приближенного описания динамики движения и
процесса управления, так и за счет упрощения проектной модели КА.
Одной из важнейших задач оптимизации является обеспечение
максимальной полезной массы тп динамического маневра при задан-
ной начальной (стартовой) массе т0 КА.
Под динамическим маневром обычно понимают переход из на-
чального состояния, характеризующегося вектором положения г0 и век-
тором скорости Ко в конечное состояние, заданное соотношениями:
rK е RK, VK е Vk где Rt, Vk - конечные многообразия координат и ско-
ростей. Продолжительность динамического маневра Т = (tK ~tD) либо
задается, либо не фиксируется и тогда служит параметром задачи
оптимизации.
Во многих известных работах вводится в рассмотрение про-
стейшая проектная модель КА с двигателем малой тяги, в которой пола-
гается, что его масса состоит из трех основных компонентов: полезной
массы тп, массы рабочего тела тРТ, массы энергодвигательной уста-
новки (ЭДУ) тэду . Последняя включает в себя источник энергии, пре-
образователь, устройство, создающее тягу (собственно электрореактив-
ный двигатель), теплообменник, элементы системы управления векто-
ром тяги, и может быть представлена в виде источника энергии, тэу и
массы двигательной установки, тду Масса источника энергии (наибо-
лее тяжелого элемента ЭДУ) считается преобладающей. В полезную
массу тп входят масса экипажа, научной аппаратуры, системы жизне-
обеспечения, а также конструкции КА и его систем. При многоцелевом
назначении КА и многоразовом характере его функционирования целе-
сообразно включать в полезную массу также массу энергодвигательной
установки.
При фиксированной массе т0 максимальная полезная масса
10
Глава t
Методы оптимизации космических перелетов с малой тягой
обеспечивается при минимальных затратах рабочего тела на выполне-
ние маневра. В дальнейшем будем называть траектории и управления,
обеспечивающие минимум затрат рабочего тела, энергетически опти-
мальными.
Подобная модель была впервые введена в [2] и успешно исполь-
зовалась в проектно-баллистических исследованиях.
В более поздних работах используются более сложные проект-
ные модели КА, обладающие большей степенью полноты и детализа-
ции, учитывающие специфику и функциональное назначение отдельных
компонентов КА; применяются также «экономические» (стоимостные)
модели, в той или иной степени отражающие затраты на доставку еди-
ницы полезной массы.
Важнейшими техническими параметрами электрореактивной
энергодвигательной установки являются: электрическая мощность, вы-
рабатываемая энергоустановкой N3y; электрическая мощность, по-
требляемая двигателем N; величина развиваемой двигателем тяги Р и
реактивная мощность N струи истекающего рабочего тела; тяговый
коэффициент полезного действия, показывающий эффективность пре-
образования электрической энергии в кинетическую энергию реактив-
ной струи, r) = Np/N\ эффективная скорость истечения реактивной
струи с; секундный расход массы рабочего тела на различных режимах;
q=P/c\ так называемая «цена тяги», равная отношению мощности, под-
водимой к двигателю, к создаваемой им тяге, у = NIP ; удельная масса
источника энергии (масса энергоустановки, приходящаяся на единицу
мощности), а = тЗУ / N3y.
По сложившейся терминологии двигатель малой тяги называет-
ся «идеально регулируемым» [1], если потери рабочего вещества и
электрической мощности отсутствуют, ограничение наложено только на
мощность N, а масса тЗДУ пропорциональна максимальной мощности
источника энергии: тЭДУ - aNmtx. В этом случае вся подведенная
электрическая мощность превращается в мощность реактивной струи:
(«7 = 1,^ =^„)
N --c-.qcl
Р 2 2 ’
можно получить соотношение:
9 ~_ 27V,., _ Р1 а2(0
dt сг 2Am„ 2A_ ’
II
Глава 1. Методы оптимизации космических перелетов с малой тягой
где m(t) - текущая масса КА, a(t) - реактивное ускорение, а=Р/т.
Полезная масса динамического маневра, выполняемого КА с
идеально регулируемым двигателем малой тяги, выражается:
( т Т Y*
'яп='”о ~тэду и™
1-1
-•Пэду. (1.1)
Здесь время t отсчитывается с момента t0 = 0, продолжитель-
ность маневра обозначена через Т. При фиксированных параметрах КА
максимум полезной массы соответствует минимуму интеграла
l=]a2dt. (1.2)
о
= т0\
и достигается при мощности энергоустановки
В данной постановке задача о максимуме полезной массы раз-
деляется на две независимые: динамическую и параметрическую.
Динамическая задача - отыскание оптимальной программы,
обеспечивающей минимум интеграла I для заданных граничных усло-
вий маневра. Последний, в дальнейшем будем называть динамической
характеристикой маневра с «идеально регулируемым ЭРД».
Параметрическая задача - выбор оптимального соотношения
масс тэду / т0, обеспечивающего максимум полезной массы тп, явля-
ется задачей оптимизации проектных параметров КА с ЭРД.
Известно, что при практической реализации оптимальных зако-
нов управления, полученных для «идеально регулируемых» двигателей,
возникает ряд технических трудностей, учет которых заставляет перей-
ти к другой предельной постановке задачи, вводя понятие «нерегули-
руемого» двигателя малой тяги [1].
Двигатель называется «нерегулируемым», если он может быть
либо включен, и тогда тяга Р, скорость истечения с и расход массы q
постоянны, либо выключен, и тогда эти параметры принимают нулевые
значения. В дальнейшем будем использовать более точный термин:
«ЭРД с нерегулируемой тягой».
В качестве критерия оптимальности перелетов с нерегулируе-
мой тягой часто используется характеристическая скорость W\
12
я 1 Методы оптимизации космических перелетов с малой тягой
W =fadt = y^- = cln-^- = cln(l-^-TM) . (1.3)
О о rn m(r) \ С J
Конечная характеристическая скорость WK зависит в общем
случае, как от граничных условий маневра, так и от проектных парамет-
ров (а0,с)- С использованием формулы (1.3) выражение для массы по-
лезной нагрузки приводится к виду
тп — — тЭду — т0 ехр[
^(а0,с)
с
аса0
2
(1.4а)
Определенное неудобство использования характеристической
скорости в качестве параметра, характеризующего перелет, состоит в
том, что ее значения при решении одних и тех же баллистических задач
для перелетов с двигателями малой и большой тяги не одинаковы.
Вследствие так называемых гравитационных потерь, имеющих место
для перелетов с малой тягой, характеристическая скорость оказывается
большей, чем при импульсных перелетах, однако более высокая ско-
рость истечения обеспечивает выигрыш в полезной массе.
В наиболее общем случае в качестве критерия оптимальности
используется время полета с включенным двигателем Тм - так назы-
ваемое моторное время. Принимая, что и в этом случае масса тэду
пропорциональна мощности источника энергии, масса полезной нагруз-
ки определяется согласно формуле:
=т0
} аса0 а0
2 с
(1.46)
где а0 = Р1т0 - начальное реактивное ускорение. Если в выражении
(1.46) принять, что Тм не зависит от с, то оптимальная скорость исте-
чения будет равна
С^~- 0-5)
Однако эту формулу надо рассматривать как приближенную,
поскольку Тм является функцией тяги и скорости истечения, а опти-
мальное значение с определять в ходе итерационной процедуры.
Для ЭРД с нерегулируемой тягой общая задача оптимизации в
чистом виде не разделяется на динамическую и параметрическую.
Минимальное моторное время при фиксированном общем вре-
мени перелета будет функцией параметров ЭДУ ( N, с ) или ( а0, с ). Для
13
Глава 1. Методы оптимизации космических перелетов с малой тягой
отыскания оптимальных для данного маневра тяги и скорости истече-
ния необходимо сначала решить серию динамических задач оптимиза-
ции маневра по критерию минимума моторного времени Тм, опреде-
лить зависимость 7^^ = /(а0,с) и только потом приступить к реше-
нию параметрической задачи: отысканию (по, с) = arg max mn
(«о. О
В качестве «классической» математической модели движения
космического аппарата с малой тягой обычно используются уравнения
движения центра масс КА в инерциальной системе отсчета под действи-
ем реактивной тяги в центральном гравитационном поле [1]:
г = Й,
• V=—e + g(r) + f, (1.6)
m
m = ~Q>
где m - масса KA; г, V - радиус-вектор и вектор скорости КА;
Р- величина тяги; е - единичный вектор ориентации тяги;
g(r) = —zrF - вектор гравитационного ускорения; q- секундный рас-
г
ход массы рабочего тела; // - гравитационный параметр притягивающе-
го центра; f - вектор возмущающих ускорений.
Добавляя к этим уравнениям граничные условия маневра
гОо) = го. Г('о) = ^ }
r(‘K)=rK, v(tK)~vK,
и вводя критерий оптимальности: /, Тм или WK, получим классиче-
скую постановку задачи оптимизации траекторий перелета с двигателем
малой тяги в центральном гравитационном поле. Здесь управлениями
служат величина тяги Р или реактивного ускорения а=Р/т и единичный
вектор направления тяги е(Г).
В современных ЭРД величина тяги регулируется либо плавно,
что обеспечивается изменением параметров электрической цепи; либо
ступенчато, что достигается компоновкой двигательной установки из
отдельных идентичных блоков (модулей). Отметим также, что тяга, раз-
виваемая ЭРД с солнечным источником энергии, зависит как от рас-
стояния до Солнца, так и от ориентации панелей солнечных батарей в
той степени, в какой зависит от этих факторов электрическая мощность,
подводимая к двигателю. При попадании в тень Земли из-за недостатка
14
рлава 1 Методы оптимизации космических перелетов с малой тягой
мощности солнечных батарей ЭРД обычно выключается.
Большое разнообразие регулировочных характеристик тяги оп-
равдывает введение моделей «идеально регулируемого ЭРД» и «ЭРД с
нерегулируемой тягой», которые оказались чрезвычайно полезными для
получения предельных оценок критериев эффективности космических
систем с малой тягой.
Для случая планетоцентрического движения центра масс в сис-
теме уравнений (1.6) учитываются следующие возмущающие ускорения
f — 1н + ?а+ 1л + fc + /сд (1 -8)
Здесь fH - вектор гравитационного ускорения, обусловленный
нецентральностью гравитационного поля планеты, fA - вектор аэроди-
намического ускорения, fc и /л возмущающие ускорения, вызванные
притяжением Солнца и Луны, - ускорение, обусловленное влияни-
ем силы светового давления.
Возмущающее ускорение от аэродинамических сил описывается
(1-9)
С S
где = —-----баллистический коэффициент КА, зависящий от време-
2т
ни, Сх - коэффициент лобового сопротивления, S - характерная пло-
щадь, VA - вектор скорости КА относительно воздуха,/? - текущая
плотность атмосферы, рассчитывается согласно статической или дина-
мической модели.
Возмущающие ускорения, вызванные притяжением Солнца и
Луны, принято записывать в единой форме
Рс.л
(1.10)
где цсл t соответственно, гравитационные параметры Солнца и Луны,
гс • гл> г - векторы положения соответственно Солнца, Луны и КА в
геоцентрической системе координат.
Ускорение, обусловленное влиянием силы светового давле-
ния> fcg определяется согласно.
1е cos 1(п{, )ej
(1.11)
15
Глава 1. Методы оптимизации космических перелетов с малой тягой
Здесь - солнечное давление на удалении 1 а.е. от Солнца, rij - еди-
ничный вектор нормали к характерной площади S, i - единичный век-
тор направления солнечного светового излучения, £ - коэффициент
отражения (0 < £ < 1). Направление ускорения заключено между
нормалью к отражающей поверхности и направлением солнечного све-
тового излучения i.
1.1. Математические постановки задач оптимизации
1.1.1. Критерии оптимальности
Сформулируем проблему совместной оптимизации баллистиче-
ских параметров и траекторий динамического маневра и проектных па-
раметров КА с двигателем малой тяги.
Введем множество динамических маневров Z. Под динамиче-
ским маневром z из множества маневров Z понимается переход КА из
начального состояния х(/о)еА'о в конечное x(tK) 6 Хк , начинающий-
ся в момент времени t0 и заканчивающийся в момент tK . Маневр зада-
ется набором чисел (баллистических параметров маневра), определяю-
щих начальное Хо и конечное Хк многообразия и его продолжитель-
ность Т = tK - Го, а также характеризующих баллистическую схему ма-
невра, внешние условия и ограничения. Вектор баллистических пара-
метров маневра z включает m компонент: начальное Хе и конечное Хк
многообразия в пространстве состояний, внешние условия и ограниче-
ния и определяет схему и продолжительность маневра. Вектор парамет-
ров маневра z включает ш компонент:
z = (z,,22,’..,z„)reZcE”,
X0=X0(z), r0=r0(z), (1.12)
Обозначим символом р вектор проектных параметров
р = (р,, р2,......р,)т сРсЕ1, характеризующих принятую конструктив-
но-компоновочную схему КА. К компонентам вектора проектных пара-
метров могут относиться и предельные значения управляющих функ-
ций. Здесь Р - множество допустимых проектных параметров, размер-
ности /.
Динамику движения КА будем описывать системой обыкновен-
ных дифференциальных уравнений:
x~ = f(t,x,u,p,u),
at
16
Глава 1. Методы оптимизации космических перелетов с малой тягой____
x(/o)e^o(z),x(rj6^(z), (1.13)
u = u(t,x)eU(p), (x,u)=yeY(p)cD,
реР, zeZ, ueftfz).
Здесь x = (х1,х2,...,х„У eXczE" - вектор состояния (фазовых
координат) системы; w(r,x)=(w1,u2,...,ur)r eU(p)cE' - вектор функций
управления; и(р) - множество допустимых управлений; для любого
момента Ге[/О,/Л] пара (x,u(r,x))=y принадлежит множеству допус-
тимых, которое будем обозначать через D. veQ(z) - вектор случайных и
неопределенных параметров, учитывающий неполноту информации об
условиях реализации отдельных маневров; множество Q(z) задает ап-
риори границы, в которых заключены неопределенности.
Среди управлений следует выделить так называемые параметры
настройки или «уставки» 9 = (9[,92,..q5)T eQ, которые либо не мо-
гут меняться по времени в процессе выполнения маневра, но могут быть
изменены перед выполнением маневра в ходе настройки системы (же-
сткая схема управления), либо меняются в ходе выполнения маневра по
заданному алгоритму, гибко приспосабливающемуся к реальным усло-
виям полета.
Задачей совместной оптимизации будем называть задачу оты-
скания проектных параметров ре Р и совокупности функций
(u(t,x,z\ x(r,z)) из множества допустимых D = u(p,z)x X(p,z), обес-
печивающих реализацию диапазона динамических маневров Z при ми-
нимальном (максимальном) значении заданного критерия эффективно-
сти р. Для определенности будем считать, что задачей оптимального
синтеза является обеспечение максимума р:
р= max /r(z,p,x(f),w(f,x)) (1.14)
н(Г,х)е(7(р),ре/>
Очевидно, в этом случае каждому маневру z из диапазона Z со-
ответствует свое оптимальное проектное решение, характеризующееся
вектором параметров p(z) и управлений й(г,х,г). Сформулируем не-
сколько определений.
1. Основной задачей оптимизации КА, предназначенного для
выполнения единичного маневра z е Z, назовем задачу отыскания век-
тора проектных параметров р е Р и вектор-функций x(t,z),u(t,x,z),
задающих состояние и управление из допустимого множества D и дос-
тавляющих максимум критерию р\
17
Глава 1. Методы оптимизации космических перелетов с малой тягой
(х,и,р) = argmax p(z, p,x(t),u(t,x)) (1.15)
(х,»)еГ(р),ре/>
2. Вектор параметров р е Р будем называть оптимальным
для диапазона динамических маневров Z, если:
• КА с параметрами р может выполнить любой маневр Z из заданного
диапазона Z;
• максимальная степень неоптимальности p(z,p) на множестве Z дос-
тигает минимального значения при р= р.
Здесь под степенью неоптимальности p(z,p) понимается
мера проигрыша в критерии эффективности р(г,р), получающаяся при
замене вектора оптимальных проектных параметров p(z) на некоторый
другой р:
p(z,p} = \p(z,p)-p(z,p)\
Степень неоптимальности можно задавать в виде [5]:
max p(z, р)
или [1]
max p(z.p)- p(z,p)
p(z,p)=-^----------------- (1.17)
max p(z, p)
Мера неоптимальности проектного решения на множестве ди-
намических маневров Z характеризуется критерием
R = min max p(z, р)
/кР teZ
Вектор р, получаемый в результате операции
p = argminmaxp(z,p) (1.18)
называется вектором универсальных для множества Z проектных
параметров.
1.1.2. Выделение динамической задачи
Сложность задачи оптимизации в постановке (1.14, 1.15) состо-
ит в том, что оптимальные траектории существенно зависят от проект-
ных параметров, и наоборот, оптимальные проектные параметры КА во
многом определяются выбранными траекториями и режимами управле-
ния.
Введем интегро-терминальный критерий (функционал) 1, зави-
сящий от траектории х(г), управления и(/, х), баллистических параметров
18
Глава 1. Методы оптимизации космических перелетов с малой тягой
маневра z и проектных параметров КА р, а также неопределенных фак-
торов и:
/[z,p,x(r),w(r,x),u]=F[x(r0)>x(rA.)]+ ] f0{f,x,u,v)dt. (1.19)
*0
Задачу отыскания экстремума функционала 1 при заданных па-
раметрах z и р назовем динамической задачей оптимизации. Пусть
существует траектория x(f) и управление w(r,x), доставляющие мини-
мум функционалу 1 при фиксированных векторах z и р для некоторой
принятой модели неопределенностей и е Q
(x(r),w(/,х)) = argmin /[z,р,x(t)u(t,х),u] (1.20)
х(/)е Л,
»(<,х)еУ(р)
Минимальное значение функционала I, соответствующее этой
траектории будем называть динамической характеристикой маневра
S(z,p,u). Конечным результатом решения динамической задачи опти-
мизации является семейство оптимальных или близких к ним траекто-
рий, структура закона управления и динамическая характеристика S,
определенная для всей совокупности задач из данного класса динамиче-
ских маневров на множестве проектных параметров Р.
Задачу о максимуме критерия оптимальности p(z,p,x,u) назо-
вем разделяющейся на динамическую и параметрическую, если в кри-
терии р удается выделить критерий низшего уровня - функционал /,
зависящий только от траекторий и управления, но не зависящий от про-
ектных параметров. Минимум I для каждого фиксированного маневра
достигается на паре (x(;),u(/,x))eD и обеспечивает локальный макси-
мум критерия р при любом выборе вектора параметров р е Р:
р = p(z, р, Z[z, х,«]). Если в соответствии со сказанным выше
min/[z,x{t\u(t,х)] = S(z), \fpeP, тогда p(z,р,х,й) & p(z,р,S(z)).
Очевидно, если — < 0, то решение задачи оптимизации реали-
. <95
зуется в форме двух, выполняемых независимо друг от друга операций
1) (x,w) = argmin/[z,x,и]; /(z,x,w) = S(z) (1.21)
(x,u)eD
2) p = argmax^(z,p,S(z)) (1-22)
peP
Выше уже отмечалось, что описанное «чистое» разделение за-
дач оптимизации справедливо лишь для идеально регулируемого двига-
теля малой тяги, когда его динамика описывается простейшей моделью
точки переменной массы с идеальным и «бесплатным» управлением. В
19
Глава I. Методы оптимизации космических перелетов с малой тягой
общем случае динамическая характеристика S не обладает инвариант-
ностью по отношению к параметрам КА, поэтому разделение задач оп-
тимизации часто носит условный характер.
Задачу о максимуме критерия p(z,p,x,u) будем называть ус-
ловно разделяющейся на динамическую и параметрическую части, если
минимум функционала l(z,p,x,u) обеспечивает локальный максимум
критерия р. Отыскание глобального максимума р, реализуется в форме
двух последовательных операций:
1) (x,w) = argmin/[z,p,x,w], J(z,p,x,u) = S(z,p), (1-23)
(x,u)gD
2) p(z)=argmax^(z,p,S(z,p)). (1-24)
реР
Решение этой задачи связано с большими трудностями, обу-
словленными необходимостью иметь зависимость S(z, р), определенную
на множестве Р во всем диапазоне маневров Z. Сложный характер по-
добных зависимостей приводит к необходимости упрощений как за счет
сокращения размерности вектора р так и за счет упрощения модели ди-
намической задачи.
1.1.3. Учет неопределенных факторов
Наличие факторов, не поддающихся строгому математическому
описанию в рамках принятой модели, делает функционал £ (динамиче-
скую характеристику), неоднозначно зависящим от параметров маневра
Z. Сформулируем вспомогательную задачу - отыскания верхних и ниж-
них границ изменения динамической характеристики на множестве £2:
SR = min max/; SH = min min/ (1.25)
(x,i/)eD ven " (x.u)eB reO
Влияние неопределенных факторов не только приводит к ошиб-
кам в решении динамической задачи, но и осложняет задачу параметри-
ческого синтеза, так как косвенным образом, через динамическую ха-
рактеристику маневра, эти факторы влияют на выбор проектных пара-
метров.
Введем новый показатель
max max/z(z, и,и)
p(ztp) = -^^----------г- (1.26)
min/Xz, p,v)
vgQ
Здесь величина р характеризует степень неоптимальности
объекта с параметрами р, реализующего динамический маневр z при
«наихудшем» (с точки зрения критерия р ) сочетании неопределенных
факторов v по сравнению с объектом, специально спроектированным
для выполнения маневра z при некотором «наилучшем» сочетании не-
20
Глава
I Методы оптимизации космических перелетов с малой тягой
определенных факторов.
Справедливо следующее утверждение.
Если задача о максимуме критерия p(z,p,v) разделяется на ди-
намическую и параметрическую, то степень неоптимальности р может
быть представлена в виде:
max p(z,p,SH)
(1.27)
где р > Р > причем при отсутствии неопределенности выражение для
р (1.27) совпадает с (1.16) и тогда р = р > 1. Докажем это.
При выполнении условий разделения задач, очевидно, что «наи-
худший» случай сочетания неконтролируемых факторов соответствует
верхней границе динамической характеристики: SB(z,p), а «наилуч-
ший» - нижней ее границе, 8н(г,р). Если неопределенности внешних
факторов нет, то SH = SB = S: и степень неоптимальности р полно-
стью определяется выражением (1.16). Пусть, далее v * 0 , а множество
Z состоит из единичного маневра z; поскольку всегда
p(z,p,SH)>p(z,p,SB), то числитель в формуле (1.27) больше знаме-
нателя при любом выборе р.
Задание функции р* в виде (1.27) означает, что даже при вы-
полнении одной задачи аппаратом, рассчитанным на «экстремальные»
внешние условия, степень неоптимальности р' будет завышена по
сравнению с некоторым «расчетным» случаем. Это является результа-
том априорной неопределенности внешних факторов (плата за незна-
ние) и влияет на результаты параметрического синтеза, который строит-
ся теперь в соответствии с операцией
р = arg min max р* (z,p) (1-28)
р^Р zeZ
1-2. Методы решения задач оптимального управления
1-2.1. Необходимые и достаточные условия оптимальности
Основы современной теории оптимального управления были
заложены в 50-х годах нашего столетия. Важнейшими результатами
теоретических поисков явилась формулировка принципа максимума
Л.С. Понтрягина [6] и принципа оптимальности Р. Веллмана [7]. Однако
в настоящее время более или менее регулярные алгоритмы отыскания
оптимального управления существуют лишь для линейных систем с
21
Глава 1, Методы оптимизации космических перелетов с малой тягой
критерием оптимальности (функционалом) специального вида (напри-
мер, так называемым, квадратичным). Ряд скрытых особенностей прак-
тических задач (в большинстве своем нелинейных), в том числе наличие
нескольких решений, удовлетворяющих необходимым условиям опти-
мальности, вызывают значительные трудности и требуют разработки
специальных подходов к решению.
С этой точки зрения определенные перспективы открывает тео-
рия, основанная на принципе расширения - сужения класса допустимых
состояний и управлений. Достаточные условия оптимальности, сформу-
лированные В.Ф. Кротовым [4], позволяют построить алгоритмы поис-
ка, улучшения и оценки приближенно-оптимальных управлений. Изло-
жим основные положения этой теории.
Задача оптимизации в самых общих терминах формулируется
следующим образом. На некотором множестве D с элементами у=(х,и),
называемом множеством (классом) допустимых состояний и управле-
ний, состояний и управлений, задан функционал I. Требуется найти
элемент у eD, на котором достигается наименьшее значение /:
/(у) = d = nun /
Как правило, во многих задачах оптимизации множество допус-
тимых D задается посредством некоторых условий, выделяющих его из
более широкого множества Е. Задачу оптимизации в этом случае можно
рассматривать на указанном более широком множестве при некоторых
дополнительных условиях.
Один из путей получения необходимых и достаточных условий
оптимума состоит в применении принципа расширения - сужения клас-
са допустимых. Путем сужения класса D получены известные необхо-
димые условия минимума функций и функционалов и принцип макси-
мума Понтрягина. Принцип расширения состоит в том, что функционал
доопределяется на более широкое множество Е, но так что наименьшее
значение он принимает в D.
Принцип расширения - сужения был применен В.Ф. Кротовым
для получения общих достаточных условий оптимальности: задания
такого множества Е, включающего у, чтобы задача о минимуме на нем
имела простое, но не тривиальное решение, и до определения функцио-
нала 1 на множестве Е.
В задачах оптимального управления элементами класса допус-
тимых D являются управляемые процессы, точнее их математические
модели. Рассмотрим систему, которая в каждый момент времени харак-
теризуется вектором состояния х=(х/х2, ...,х„)т, являющимся элементом
некоторого множества X, называемого фазовым или пространством со-
22
Глава 1. Методы оптимизации космических перелетов с малой тягой__
стояний. Изменение состояния х во времени называется процессом х(1).
Управляемые процессы принято описывать путем указания закономер-
ности перехода от предыдущего состояния к последующему в зависи-
мости от управляющего воздействия, которое характеризуется вектором
управлений w=(mi w2,.wr)T, являющимися элементом некоторого мно-
жества U (множества управлений).
Математическая модель управляемого процесса представляет
собой, как правило, уравнение, связывающее последующее состояние с
предыдущим состоянием и управлением.
Следует подчеркнуть, однако, формальный смысл понятий со-
стояния и управления, связанный с принятой формой математической
модели, которая для реального управляемого объекта может быть не-
единственной. Например, в задачах оптимизации космических траекто-
рий в качестве состояния принято рассматривать положение и скорость
центра масс космического аппарата, а в качестве управления — направ-
ление вектора тяги. Как уже отмечалось, изменение направления тяги
космического аппарата часто достигается путем его поворота с помо-
щью устройств, создающих моменты относительно центра масс, что
заставляет учитывать и динамику вращательного движения. Это несоот-
ветствие отражает тот факт, что математическая модель зависит от тех
задач, которые должны решаться с ее помощью.
Помимо управления, на переход из предыдущего состояния в
последующее могут оказывать влияние другие факторы, которые не
поддаются строгому учету. Они характеризуются так же, как и состоя-
ние и управление, некоторым вектором а, который принято называть
возмущением.
В том случае, когда возмущающие факторы настолько несуще-
ственны, что ими можно пренебречь, вектор v не содержится в уравне-
ниях математической модели управляемого процесса, а последний на-
зывается процессом с полной информацией.
Если изменение состояния рассматривается в каждый момент
времени на каждом промежутке, говорят о непрерывном процессе. Если
состояние рассматривается в дискретные моменты времени, процесс
называется дискретным.
Рассмотрим постановку задачи оптимального управления для
случая непрерывного процесса с полной информацией.
На отрезке [годк] задается множество D как множество пар
функций (х(/),п(О), удовлетворяющих условиям
x = f(t,x,u),
1*ШхеХ, иеС/,(х(/),и(О)€К(Г), (1.29)
23
Глава 1. Методы оптимизации космических перелетов с малой тягой
х(10)еХ0, x(lt)EXt.
Минимизируемый функционал зададим в виде
Ч
1 = jf0(t,x,u)dt + F(x(t0),x(tky), (1.30)
А)
причем функции u(t) считаются кусочно-непрерывными; x(t) - кусоч-
но-дифференцируемыми функциями.
Построим функции
G(x0, xt) = F0+<?(Z*,xt)~ «5(/0,х0); (1.31)
R = <PTxf(t,X,u) + <p, -f0(t,X,u) =
= • f(J,x,u) + j~fo ('. x, и),
i=\ OXj Ct
где <p(t,x)- непрерывная и дифференцируемая функция; а ее частные
производные непрерывны для всех (/, х), кроме конечного числа точек.
Основная теорема (В.Ф. Кротов). Для того чтобы функционал
(1.30) достигал абсолютного минимума на (х,и) е D, достаточно суще-
ствования [3] такой функции <p(t,x), чтобы
1) R(x, и, t) = max R(t, х, и) = p(t), (1-32)
2) G(x(z0),x(zt)) = minG(x(/0),x(/t)). (1.33)
Здесь Kx — проекция множества K(Z) на пространство X; K„(z,x) - сечение
V(t) при каждом фиксированном х. Предполагается, что ju(t) - кусочно-
непрерывная функция времени.
Для доказательства теоремы положим, что множество Е вклю-
чает пары (х,и), не связанные дифференциальным уравнением (1.29) и
допускающие разрывы функции x(t) в конечном числе точек. Опреде-
лим на Ефункционал
L = G(x(Z0),x(Zj)-} R(t,x,u)dt (1.34)
fo
Нетрудно показать, что на исходном множестве D функционалы
L и 1 совпадают. Действительно, при (х, и) е D
R(t,x,u) = -f0(-) + <p, (1.35)
Подставляя это выражение в L и учитывая непрерывность
х G D, получим L=I
24
Глава 1 Методы оптимизации космических перелетов с малой тягой
Так как на множестве Е допускаются разрывы функции x(t), то
слагаемые в L можно рассматривать независимо друг от друга. Поэтому
minL = minG(x(/0),*(/*))- max l/?(r,x,«)J/ (1-36)
(Х.в)€Е
*(<*)№(<*)
Если теперь предположить, что (х,и) е D и выполняются усло-
вия (1-32, 1.33), то согласно (1.36) L достигает абсолютного минимума
на £ и одновременно при этом достигается min I.
Теорема сводит задачу о минимуме функционала к более про-
стой задаче об экстремуме функций многих переменных. Проблема сво-
дится теперь к следующему: так задать неопределенный элемент -
функцию qXtjc) (синтезирующую функцию или функцию Кротова), ко-
торая доопределяет функционал 1 на Е так, чтобы минимум 1 принадле-
жал D. Оказываемся, задать функцию <р можно различными способами,
и это дает возможность приспосабливаться к специфике задачи. Один из
способов (формализмов) приводит к процедуре принципа Понтрягина,
другой - к процедуре динамического программирования, а третий (ме-
тод кратных максимумов) пригоден для решения так называемых выро-
жденных задач [4].
1.2.2. Способы задания синтезирующей функции
Пусть проекция множества V(t) на пространство X - множество
Кх(/) есть открытая область при всех t е , а при t=t0 и t=tk - фикси-
рованная точка: х(/0), х(/к) и терминальный член в функционале (1.30)
отсутствует. Далее, пусть множество Vu не зависит от х. Потребуем,
чтобы <гХ/>х) была дважды дифференцируема вдоль оптимальной траек-
тории. Тогда необходимое условие (или условие 1-го порядка) макси-
мума функции R(t,x,u) по х будет иметь вид
df У д<р _ д2<р
дх
df0 | &<Р
дх дх2
dR
дх
(1.37)
= 0
дх dtdx _
Введем функцию
, тогда вдоль минимали x(f)
дх -
д2д>
dxdt
Г?,]
Sr2 7)-'
Тогда из (1.33) легко получить
25
Глава 1. Методы оптимизации космических перелетов с малой тягой
|г дН
ио=
(1.38)
= -f0(t,x,u)+pTf(t,x,u)
(1.39)
(1-40)
где Н - функция Гамильтона:
H(x,u,t,y/) = Hl х,и,1,—
Условие максимума R(t,x,u) по управлению может быть теперь
представлено в виде
Н (х, и, t, у/) = max Н(х, и, t, у/).
Система уравнений (1.38) носит название сопряженной системы
уравнений и может быть решена совместно с исходной системой (1.29).
Обычно эти уравнения представляют в канонической форме
-х^', у,-™ (1.41)
ду/ дх
Таким образом, необходимые условия максимума функции Н
совпадают с известными условиями оптимальности принципа мак-
симума Понтрягина [6] (формализм Лагранжа-Понтрягина). Если су-
ществует такая функция <p(t,x), что на решении x(t),u(t) удовлетво-
ряются не только необходимые, но и достаточные условия максимума
R(t,x,u) при каждом Ге(Г0,/А), то в силу теоремы Кротова решение
(х,и) задает искомую минималь, т.е. обеспечивает абсолютный мини-
мум функционала 1 на множестве D. В частности, (1.37), (1.40) являются
необходимыми и достаточными условиями оптимальности линейных
систем с линейным и квадратичным (выпуклым) функционалом.
Опишем теперь способ задания функции Кротова, приводящий
к процедуре динамического программирования. Этот способ принято
называть формализмом Гамильтона - Якоби - Веллмана [3].
Рассмотрим непрерывный процесс (1.29) с функционалом (1.30).
Пусть X- открытое множество при всех t е , а при t = t0 совпада-
ет с точкой х(/0) = х0, а функция F в функционале I не зависит от x(Z0).
Выберем <p(t,x) так, чтобы max R(t,x,u) не зависел от х, т.е. имело
место соотношение
шах -Л(М«)+Н;| + ~ =C(t)-
(дх J Bt
(1.42)
26
Глава 1 Методы оптимизации космических перелетов с малой тягой
Тогда будет автоматически выполнено условие (1.32). Для вы-
полнения условия (1.33) потребуем, чтобы G не зависела от x(/t):
F(x(t*))+«’O*>x(t*)) = C, = const. (1.43)
Указанный способ задания функции (p(t,x) приводит к необхо-
димости решения уравнения (1.42) с граничным условием (1.43). Если
положить С(г) = 0, С,=0 и ввести обозначение S(t,x) = -<p(t,x), то
уравнение (1-42) принимает классический вид уравнения Беллмана для
непрерывных систем
(8S У .
— f(t,x,u)
J
8S
----- mm
dt «И,
/0(Г,х,м) +
(1.44)
с граничным условием
S(tk,x) = F(x(tk)) (1.45)
Как следует из (1.44, 1.45), решение уравнения (1.42) ^(/,х)
можно интерпретировать как функцию «будущих потерь»
S(t, х) = min / [х(0, п(/)], взятую с обратным знаком.
1.2.3. Оценки приближенно-оптимальных решений
Рассмотрим величины m,rvil, которые для непрерывных систем
определяются соотношениями
т = mm [F0 + <зО*,х(/*))-р(/0,х(/0))],
(ч>л)
г = ] fj(t)dt, (1.46)
'о
I = min L = т- г .
Е
Очевидно, I зависит от <p(f,x). Так как КФ) - нижняя граница 7,
то d = minl >1(ф)- При удачном выборе р(7,х) l(<p) = d. Таким обра-
зом, в задачах, где функция ср, удовлетворяющая условиям основной
теоремы (1.32, 1.33), существует, она соответствует наибольшему зна-
чению функционала КФ). Очевидно разность
д6>> Ф) = 1(у)~ КФ) Ку) ~ min I (1.47)
^сть верхняя оценка приближенно-оптимального решения
У = (х,п)е£>. Теперь можно искать последовательность приближен-
ных решений (пар) {<ps,ys} такую, что ys е D, а разность
= 1G')-K<ps) = Hy,)-K<ps) -> 0. (1.48)
27
Глава I, Методы оптимизации космических перелетов с малой тягой
По достижении достаточно малого значения Дг процесс поиска
можно прекратить, поскольку поиск идеально точного (абсолютно оп-
тимального) решения зачастую не оправдан практической постановкой
задачи, связанной с неизбежным упрощением модели.
При практическом решении задач оптимального управления на
основе принципа расширения и достаточных условий оптимальности
основная проблема помимо выбора функции ^заключается в отыскании
д(Г) = max R(t,x,u) и т = min G(x(z0),x(/4)), т.е. в отыскании экстре-
(х,и)еГ(О
мума функции многих переменных. Если управления в данной задаче
удовлетворяют априорно заданным условиям принадлежности множе-
ству допустимых U, то для вектора состояния целесообразно построить
так называемую область достижимости, т.е. область, содержащую толь-
ко те функции x(Z), которые удовлетворяют условиям х = f(t,x,u),
(х,к) е D. Получающиеся при этом множество фактически достижимых
состояний К/ (/) уже, или по крайней мере не шире, чем априорно за-
данное множество Vx(t).
Заметим, что точное определение K^(z) в общем случае бес-
смысленно, так как требует решения серии задач оптимального управ-
ления того же порядка, что и поставленная задача.
Поэтому реальный смысл имеет задача о построении К^(г), ко-
торое удовлетворяет условию Vx (t) с Vx (t) с Vx (z).
1.3. Метод усреднения в задачах оптимального управления
При решении динамических задач оптимизации в механике по-
лета с малой тягой используются асимптотические методы, предпола-
гающие разделение параметров движения на быстрые и медленные
компоненты [2]. Это обусловливается, во-первых, наличием в явном
виде малого параметра - реактивного ускорения от тяги, которое мень-
ше гравитационного на несколько порядков; во вторых, присутствием
циклической переменной - угловой координаты, характеризующей по-
ложение КА на орбите относительно линии узлов или перицентра.
Запишем уравнения движения в общем виде, придерживаясь
общепринятых в задачах такого рода обозначений [8].
х = а- Х(х,<р, w(z)),
<р = а>(х,<р)+ а Y(x,<p,u(t)), (1.49)
где х - вектор «медленных» фазовых координат системы размерности и;
а - малый параметр; <р - быстрая скалярная переменная (фаза); w(0e U
28
Глава 1 Методы оптимизации космических перелетов с малой тягой
- вектор управлений размерности г.
В общем случае в управление могут входить как быстрые, так и
медленные составляющие. В связи с этим задачу выбора оптимального
управления удобно разделить на две:
• определение управления как функции быстрой переменной (выбор
структуры управления на витке);
• определение «медленных» законов изменения параметров этой про-
граммы от витка к витку.
В итоге реализуется схема «расщепления» управляющей функ-
ции на быстрые и медленные компоненты. Задача определения структу-
ры управления на витке представляет самостоятельный интерес и может
быть или задана априори, на основе эвристических подходов с учетом
технических ограничений или выбираться из соображений локальной
оптимальности.
Система (1-49) при определенных условиях может быть упро-
щена, учитывая, что в большинстве случаев а>(х,ср)» a-Y и вторым
членом в уравнении для быстрой переменной можно пренебречь.
Критерий оптимальности представим в следующем виде:
I = a\f>(x,u)dt. (1.50)
о
Перейдем'в системе (1.49) от времени t к быстрой переменной <р
в качестве независимой переменной:
= аХ{х, ср, со 1 (х, <р),
dtp
— = аш'(х,<р). (1.51)
Здесь т - так называемое «медленное» время, ? = a-t. В соот-
ветствии с принципом максимума Понтрягина введем вектор сопряжен-
ных переменных у/и запишем Гамильтониан системы (1.51)
Н = у/ т (а • «Г* (х, (/>) х(х, ср, «(<)))+ у\ а • со(х, <р) -
- а • со’ (а, <р) • /0 (х, ср, и) = aF(x, <р, у/, и). (1.52)
Определим локально-оптимальное управление и из условия
максимума Гамильтониана на отрезке <р е [о,2я] (на витке)
w = argmax н(х,у/,и,<р)~ и(х,у/,<р) (1.53)
ugU
Запишем исходную и сопряженную системы, с учетом решения
29
Глава I. Методы оптимизации космических перелетов с малой тягой
dtp
^- = aFx(x,p,u{x,ip,p^,
dtp
(1-54)
— -aco *(x,0>).
dtp 4 '
Проведем затем процедуру усреднения исходной и сопряженной
систем по быстро меняющейся переменной ср. Усредненная система
уравнений будет иметь вид
dx а 2? _|/ \ (л Л Yk
----= —J® HiW'aI х,р,и х,р,р I dp,
dtp о \ v Д/
dip а 2г-,(л ~(л л Y) , ,,
— = — \FI\x,y,u\x,p,p \\dp, (1.55)
dtp 2,7t о \ \ J J
dr a 2F .(л > ,
— = —Jo \x,p\dp,
dtp £,71 о \ )
а усредненный критерий оптимальности
а ?2Л (л ( * л
J =—J JFO x,wl 11 «Й. (1.56)
о О \ X
Интегралы в правых частях системы (1.55) образуют совокуп-
ность так называемых «усредняющих интегралов»
Ф = У()</<р, Ф = (фу)г, у = 1,2и + 1. (1.57)
О
После усреднения правые части системы (1.55) не содержат
циклической переменной <р. Поэтому модель «медленной» эволюции
вектора состояния и вектора сопряженных переменных может быть
представлена в виде системы интегро-дифференциальных уравнений, с
«медленным» временем в качестве независимой переменной
,Л Ф)|Х| z -у
ад. А ) л /л л? ---------------------
где g = l х,^ I , у = 1,2и + 1,
ЯГ я, I л ] к )
Ф2,1+1Ы
Ф2„+1 = (L58)
ох/
Исходная оптимизационная задача, сводится, таким образом, к
30
г- „о» 1 Методы оптимизации космических перелетов с малой тягой
1 i —МИ».———
решению краевой задачи для системы (1.55, 1.56). Однако, вычисление
усредняющих интегралов (1.57) представляет самостоятельную пробле-
му и требует разработки специальных процедур.
Дальнейшее решение задачи оптимизации может идти по двум
направлениям. Первое заключается в попытке получения точных или
приближенных аналитических решений для усредняющих интегралов.
Разумеется, это возможно лишь в исключительных случаях. Второе на-
правление предполагает параметризацию структуры управления на вит-
ке и представление интегралов Ф} в виде функций ограниченного чис-
ла переменных.
Например, пусть для оптимальной структуры управления на
витке, имеет место представление й = й[К,<р\ где К - вектор парамет-
ров размерности г 2 л, задающих структуру управления, которые мед-
ленно меняются от витка к витку. Причем, как уже упоминалось, струк-
тура управления, на витке может задаваться из эвристических сообра-
жений или соображений локальной оптимальности.
Интегралы в (1.58) могут быть приведены к виду:
2х
Фу = К-^= \С^К,(рУ<р = Ф]{к,^. (1.59)
о о
В этом случае вариационная задача формулируется для системы
вида:
^=ф^,х)ф-;+1 (1.60)
где управляющими параметрами являются компоненты вектора К. Оп-
тимальный вектор К определяется из условия:
К = argmax/7 = argmax^z Ф"^,-Ф0(К,х)^,
где Фо =2JF0|x,u[ К,х,<Р И dtp (1.61)
1-4. Численные методы решения краевых задач оптималь-
ного управления
В соответствии с принципом максимума Понтрягина оптималь-
ное управляемое движение КА описывается системой дифференциаль-
ных уравнений
dx, / —\
31
Глава 1. Методы оптимизации космических перелетов с малой тягой
= i = l,n, (1.62)
at
где и - оптимальное управление в неявной форме, получен-
ное из условия максимума гамильтониана Н.
Фазовые координаты КА в начальный момент времени являют-
ся определенными, а начальные значения сопряженных множителей -
неизвестными:
t = t0, х(/0)= х0, (у(/0) - не определено. (1.63)
В конечный момент времени требуется выполнение некоторых
условий, определяемых целью перелета
' = j = О-64)
Значения переменных х(/^), при t-tK можно рассмат-
ривать как функции не заданных начальных значений сопряженных пе-
ременных ^(/0). Решение краевой задачи (1.62 - 1.64) сводится к оты-
сканию корней системы уравнений
j = \,m. (1.65)
где - векторная функция невязок, зависящая от значений
сопряженных множителей ^(/0) в начальный момент времени. В зави-
симости от цели .динамического маневра, рассматриваемого участка и
выбранной модели движения функция невязок может иметь различный
состав, в простейшем случае ее можно описать линейной зависимостью
<>*>
При решении задач оптимизации, требующих учета условий
трансверсальности на концах траектории зависимость (1.66) может но-
сить более сложный, нелинейный характер. Однако, в любом случае
функция невязок (1.66) определяется результатами моделирования дви-
жения КА при заданных начальных условиях и управлении.
Задача оптимизации считается решенной, если определено на-
чальное значение вектора удовлетворяющее уравнению (1.65) с
заданной погрешностью.
Функция невязок системы (1.65) очень чувствительна к началь-
ным значениям подбираемых параметров (Z/(z0) и имеют многоэкстре-
мальный, «овражистый» характер.
Одним из наиболее эффективных методов решения системы не-
линейных уравнений (1.65) является модифицированный метод Ньюто-
32
Глава 1. Методы оптимизации космических перелетов с малой тягой
на с автоматической оценкой сходимости и изменением шага вычисле-
ния производных и ограничений на приращения.
Применение этого метода для решения этой системы уравнений
сводится к следующему итерационному процессу (s - номер итерации)
И^о)=Ло)+лИ’)(<о) • (1-67)
Приращения &y/s\t0) находятся путем решения системы ли-
нейных уравнений
7 = (168)
/=| ду/,
Здесь значения функций и ее частных производных
вычисляются в точке численно. Близость значений к
решению будем характеризовать величиной
А(4 = Е|^(^»Ло)]- (1-69)
Краевая задача считается решенной, если величина стано-
виться меньше заданной погрешности е . Если значения частных произ-
водных в (1.68) больше единицы, то итерационный процесс (1.67, 1.68)
может расходиться. Его сходимость можно обеспечить, уменьшая вели-
чины Д^\10), найденные из (1.68), если окажется, что величина по-
грешности на следующей итерации больше, чем на предыдущей
д(«')>дб) (1>70)
Для этого заменим соотношение (1.67) соотношением
V'(,+,)Go)=H,)0o)+*(l) • ДИ’Х'о)- (1.71)
Очевидно, что при к = 1 соотношения (1.67) и (1.71) совпадают.
Итерационный процесс начинается с этого значения. При выполнении
условия (1.70) будем полагать
*W = *W/2 (1.72)
и вновь вычислим значения к/И)(г0), А(,+1) по формулам (1.71), (1.69).
Если вновь условие (1.70) выполняется, то опять уменьшаем величину
по (1.72) до тех пор пока не получим уменьшение величины по-
грешности . Ддя того, чтобы не вызывать замедление сходимости
процесса вблизи решения, на каждом шаге итерационный процесс на-
чинается с к = 1.
Ускорить процесс сходимости можно выбирая параметр к,
ечивающий наибольшее уменьшение погрешности. Для этого рас-
33
Глава I, Методы оптимизации космических перелетов с малой тягой
считывается уменьшение погрешности Д^-А^ при к=1, к=0.5, к=2.
По этим значениям строится квадратичная аппроксимация функции
дЮ_д(ж)
и определяется точка минимума этой параболы [9].
Однако даже при использовании такой модификации метода
Ньютона существуют случаи, когда происходит бесконечное уменьше-
ние параметра к без уменьшения величины погрешности А^. Поэто-
му в программной реализации этого метода предусмотрен «аварийный»
выход при некотором значении числа дроблений приращений к (обычно
выбирается значение 20), т.е. при конкретном числе обращений к фор-
муле (1.72).
dtp.
Частные производные ------находятся путем и —кратного
интегрирования системы (1.62) с поочередным варьированием началь-
ных значений по формуле правой разностной производной
-----2-Г W --------------------------- . I 1 . / J 1
Хорошо известно, что вычисление производных по формуле
(1.73) не является корректным численным методом, т.е. точность вы-
числения производной не всегда улучшается при уменьшении значений
приращения переменных А^,. Это не позволяет априори определить
значения этих приращений для наиболее точного вычисления производ-
ных.
В работе [10] для преодоления этого обстоятельства предложена
следующая модификация итерационного процесса. При осуществлении
«аварийного» выхода (отсутствии сходимости процесса) предлагается
изменить величину приращений для вычисления производной
А = д / ю. (1.74)
Для того, чтобы эффект от изменения значения приращений для
вычисления производной сохранялся, на каждом шаге итерационный
процесс (1.68, 1.7-1, 1.73) продолжается до его успешного завершения
или «аварийного» выхода. Если процесс все же не завершается успеш-
но, опять воспользуемся формулой (1.74). Через d обращений к (1.74)
величина А у/, должна быть восстановлена:
A{y/(s) = A^(s)10". (175)
Таким образом, если значение приращений для вычисления
производных является «удачным» для итерационного процесса, то оно
сохраняется. Если «неудачным», то изменяется, может быть несколько
34
Глава 1 Методы оптимизации космических перелетов с малой тягой
раз, пока «удачное» значение не будет найдено. Для того, чтобы итера-
ционный процесс при отсутствии сходимости не имел зацикливаний он
останавливается при конечном обращении к формулам (1.74 - 1.75).
Использование таких модификаций метода Ньютона позволило
в автоматическом режиме решать большинство краевых задач, связан-
ных с поиском оптимального управления при движении КА с двигате-
лями малой тяги.
1.5. Метод разбиения пространства состояний
Получение приближенных аналитических задач оптимизации
является весьма заманчивой целью. Однако, получить подобные реше-
ния чрезвычайно трудно. Одним из путей достижения результатов явля-
ется разбиение области X пространства состояний. Наиболее известным
применением этого метода является использование классической тео-
рии сфер действия при расчете межпланетных перелетов.
Пусть движение КА описывается системой (1.13). Откажемся от
получения универсального решения для всего пространства переменных
и поставим цель определить ряд упрощенных решений для каждой от-
дельной выделенной области X пространства состояний. Разобьем об-
ласть X на т подобластей X с.Х} и/, и...и/я. Заменим исходную
двухточечную краевую задачу на последовательность переходов:
х0 -> xt xm_j -> хк, где xR - {х,.хтЧ} - граничные условия
промежуточных (нефиксированных) состояний:
х, е X, пХ2,..., x„_, е^и_, сХ„. (1.76)
Таким образом, межорбитальный переход представим в виде
последовательности более простых динамических маневров с неизвест-
ными координатами промежуточных точек и управлениями К|(0, w2(0>
•••» «л, (О (рис. 1.1).
zi ={*о>*1}Г. •••. ={хи-„хк}г. (1.77)
Функция управления для единичного маневра z, определяется
из Условия минимума функционала
35
Глава I. Методы оптимизации космических перелетов с малой тягой
и,, = arg min J.(z. Х,и), (1-78)
(u,x]eD, 1 *»
где Dj cU (JX. - допустимая область управлений и состояний. При опре-
делении оптимального управления для единичных маневров возможно
использование следующих упрощений:
• отбрасывание второстепенных связей;
• линеаризация уравнений в окрестности опорного движения;
• асимптотическое разделение движения на быстрые и медленные ком-
поненты и использование процедуры усреднения.
Если указанные способы не приводят к получению необходи-
мых решений, то проводятся нелинейные преобразования и осуществ-
ляется переход к другим переменным. При этом процесс разделения
может быть продолжен и далее в новом пространстве фазовых коорди-
нат.
В результате получается динамическая характеристика единич-
ного маневра
S, = min Jf(zt,x,u). (1.79)
(«,x)eD(
Затем реализуется процедура минимизации глобального крите-
рия по координатам промежуточных точек. Для определения степени
неоптимальности осуществляется сравнение полученного решения с
точным решением, соответствующим модели без упрощений.
1.6. Метод последовательных расширений
Метод последовательных расширений заключается в редукции
математической модели задачи оптимизации в сторону упрощения мо-
дели движения КА. Это упрощение производится за счет отказа от не-
которых связей и ограничений; придания некоторым переменным фик-
сированных значений; усреднения уравнений движения, носящих цик-
лический характер; линеаризации движения в окрестности опорной ор-
биты и т.д. Такое- последовательное упрощение позволяет получить по-
следовательность моделей различного уровня сложности, сохраняющих,
однако, все важнейшие особенности исходной модели. Переход от бо-
лее простой модели к более сложной сужает область переменных и
управлений, в которой ищется оптимальное решение. В дальнейшем
производится отыскание синтезирующей функции и ее частных произ-
водных по компонентам вектора состояния в аналитическом виде и по-
строение оценочной функции режимов управления.
В первом приближении оптимизация траекторий и управлений
осуществляется с использованием простейших динамических моделей,
например, представляющих КА точкой постоянной массы движущейся
36
гппка I Методы оптимизации космических перелетов с малой тягой
t
в центральном поле тяготения с «бесплатным» управлением. После-
дующие приближения используют более сложные модели, учитываю-
щие, например, динамику углового движения КА, возмущающие уско-
рения от гравитационных, аэродинамических и иных сил.
1.7. Итерационная процедура поэтапной оптимизации
Поскольку проектные параметры КА влияют на динамическую
характеристику маневра, и наоборот, баллистическая схема и траекто-
рии перелета существенным образом влияют на выбор проектных пара-
метров, процесс оптимизации параметров КА и семейства оптимальных
траекторий необходимо вести совместно.
Ключевая идея предлагаемого подхода состоит в условном раз-
делении общей проблемы оптимизации на динамическую и параметри-
ческую части, с последующим их объединением через динамическую
характеристику маневра, являющуюся мерой затрат на его реализацию,
зависящей от граничных условий, проектных параметров и неопреде-
ленных факторов и уточняемую по мере перехода от простых моделей
динамической задачи к более сложным.
Зададим тюследовательность математических моделей {a/s},
s=l,2,... динамической задачи для конкретного маневра z из подмноже-
ства Z. В рамках каждой из моделей Ms определим критерий опти-
мальности динамической задачи - функционал J(z,p,x,u,v), а также мно-
жество допустимых траекторий и управлений Ds и получим динамиче-
скую характеристику маневра, S<s)(z, р,ь>.). Пусть в результате решения
совокупности динамических задач с применением моделей {л/5} полу-
чена последовательность значений глобального критерия оптимально-
сти^:
{uw}= {^W(z> P,S(s\z, p,u))j, s=l,2,... (1.80)
и определен вектор оптимальных проектных параметров согласно вы-
ражению
р'} = argmax ^(я,р,5<ж)(г, p,t>.)). (1-81)
Процесс оптимального синтеза назовем устойчивым, если сколь
угодно малым приращениям вектора проектных параметров соответст-
вУЮт малые изменения критерия р. Процесс заканчивается, когда при-
менение модели более высокого уровня не приводит к заметному изме-
нению критерия оптимальности р и вектора проектных параметров р .
В результате реализуется схема, основанная на использовании
ПослеД°вательности усложняющихся моделей управляемого движения:
37
Глава 1. Методы оптимизации космических перелетов с малой тягой
в качестве первого приближения используются приближенно оптималь-
ные решения для упрощенных моделей, приближенный синтез управле-
ния, затем модель,динамической задачи последовательно усложняется, а
решение, полученное на предыдущей итерации, используется для оце-
нок и сравнения различных режимов управления.
Влияние неконтролируемых факторов приводит к неопределен-
ности динамической характеристики маневра в пределах нижних и
верхних границ ее изменения, SH , SB которые в свою очередь опреде-
ляются размерами области неопределенности £3. Сначала анализируют-
ся пределы изменения динамической характеристики
S (z, р) < S(z, p,u)<S (z,p) и выбираются проектные решения з-го
н в
приближения р^, р^, соответствующие предельным оценкам SH, SB:
Pi0) = argmaxp(z,p,S„(z,p)),
peP
p^ =argmaxp(z,p,SB(z,p)). (1-82)
Соответственно, будем иметь и критерии оптимальности для
двух вариантов решений:
=p(z,p1G)), =p(z’Pi})-
Сравнение компонентов векторов р^, р^ и критериев р^,
р^ позволяет установить влияние неопределенности на облик проек-
тируемого объекта и показатель его эффективности.
На следующих итерациях уточнение проектных параметров
приводит к необходимости повторного расчета семейства оптимальных
траекторий и режимов управления, а также баллистических параметров.
38
Глава 2. Математические модели задач оптимизации
2 МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЗАДАЧ
оптимизации
Решение динамических задач оптимизации ведется с использо-
ванием двух видов математических моделей: теоретических и имитаци-
онных. Последние должны достаточно полно и точно описывать как
динамику движения КА, так и процесс управления. Поэтому общая ма-
тематическая модель управляемого движения как некоторого физиче-
ского процесса будет включать в себя:
• математические зависимости, описывающие проектный облик КА и
отражающие взаимодействие КА с другими физическими объектами
или внешней средой;
• уравнения движения КА;
• математическую модель формирования управляющих воздействий в
рамках принятой степени приближения и детализации.
2.1. Основная задача оптимизации
Одной из важнейших проблем оптимизации в механике косми-
ческого полета с малой тягой считается обеспечение максимальной мас-
сы полезной нагрузки в конце перелета при заданной начальной массе
КА. Уравнения, описывающие зависимости массы полезной нагрузки в
простейших случаях линейной зависимости массы энергодвигательной
установки от ее мощности для идеально регулируемых и нерегулируе-
мых ЭРД приведены в разделе 1.1 (1.1 - 1.5).
Если цель маневра доставка максимально возможной полезной
нагрузки с исходной на рабочую орбиту (рис. 2.1), то в начальный мо-
мент времени масса КА равна фиксированной стартовой массе, а в ко-
нечный момент времени Т
(2.1)
Если целью перелета является доставка ПН с исходной на рабо-
чую орбиту и возвращение КА на исходную орбиту (рис. 2.2), то фазо-
вые координаты должны удовлетворять граничным условиям.
В момент.старта с исходной орбиты (t = 0):
'(0) = г0, Г(0) = Ёо, m(0) = т0. (2.2)
В момент достижения рабочей для ПН орбиты (t = 7\):
'(Г.) = гк, Г(Т;)= VK, m(Tt)= ma-mm. (2.3)
В момент отлета с рабочей орбиты (t = Т?):
^2)= гк, VK , m(r2)= m0 - mPTl-mnH . (2.4)
В момент окончания маневра (t~T)‘.
г(7’)=''о> >/(7’)=К>, 'п(т)=тс-т„1-тпн-трт1. (2.5)
39
Глава 2. Математические модели задач оптимизации
Здесь г - вектор положения КА, V - вектор скорости КА.
Рис. 2.1. Баллистическая схема межорбитального перелета без возвращения
Рис. 2.2. Баллистическая схема межорбитального перелета с возвращением
Для проектно-баллистического анализа динамического маневра
и КА будем использовать обозначения:
• д(<) - вектор ускорения от тяги, на его величину и направление могут
быть наложены ограничения, связанные с конструктивными
особенностями КА;
• х(/) = j - вектор фазовых координат КА в пространстве, определя-
ется граничными условиями перелета (2.2 - 2.5);
* р — вектор основных оптимизируемых проектных параметров КА.
В этих обозначениях задача оптимизации сводится к определе-
нию закона управления вектором тяги КА а(/) и проектных параметров
аппарата р таких, чтобы при фиксированной стартовой массе КА на
40
рдава 2 Математические модели задач оптимизации
рабочую орбиту была доставлена полезная нагрузка наибольшей массы:
"h, = = flXe^ (26)
Задачу оптимизации полезной нагрузки в общем случае принято
разделять на динамическую и параметрическую части.
Динамическая задача — отыскание оптимальной программы
управления вектором тяги a(t), обеспечивающей минимальные затраты
рабочего тела на прямой и обратный перелеты для заданных параметров
исходной и рабочей орбиты и длительности движения. Меру этих затрат
в дальнейшем будем называть динамической характеристикой пере-
лета. Этой мерой может быть характеристическая скорость или мотор-
ное время перелета. Целью решения динамической задачи является по-
строение зависимости динамической характеристики перелета от гра-
ничных условий перелета и проектных параметров КА. Уравнения тра-
екторного движения описываются системой (1.6)
Параметрическая задача - это задача выбора оптимальных
проектных параметров КА, обеспечивающих при заданной динамиче-
ской характеристике перелета максимум полезной нагрузки.
Если в качестве критерия оптимальности использовать характе-
ристическую скорость перелета, то решение динамической задачи сво-
дится к построению зависимости
WK -» min (2.7)
а параметрическая - в определении таких параметров р , чтобы
тп -> max . (2.8)
Задачи динамической и параметрической оптимизации могут
решаться с использованием моделей различной степени точности. Есте-
ственно чем точнее решение, тем больших затрат на свое осуществле-
ние оно требует.
Рис. 2.3. Системы координат с началом в центре масс аппарата
Для описания движения КА относительно центра масс введем
системы координат (рис. 2.3): «инерциальную» OXYZ и связанную
41
Глава 2. Математические модели задач оптимизации
с аппаратом Oi-X^Z, с центром в центре масс КА и вращающуюся от-
носительно первой с угловой скоростью со . Обозначим через /,, у,, к,
единичные векторы, направленные вдоль связанных осей.
Запишем векторные уравнения, отражающие результаты из-
вестных теорем механики об изменении количества движения Q и ки-
нетического момента К «фиктивного» твердого тела
dt dt °’
—+ ®хК=^^+юх(/0ЙГ)=л70. (2.9)
dt dt
Здесь Fo , Mo - соответственно, главный вектор и главный
момент относительно центра масс внешних, реактивных и кориолисо-
вых сил, I0(t) - тензор инерции КА, компоненты которого изменяются
по мере изменения массы аппарата, йГ - вектор угловой скорости. В
первом приближении можно не учитывать перемещение центра масс
относительно корпуса КА, а также кориолисову силу FK, возникающую
при перемещении масс внутри КА при его вращении и момент этой си-
лы МК . Влияние указанных факторов на параметры движения КА мало
вследствие малости секундного расхода рабочего тела.
Присоединяя к уравнениям (1.6) кинематические соотношения
(2.9) и уравнение, выражающее расход массы с учетом управления, по-
лучим систему векторных дифференциальных уравнений описывающих
движение центра масс и угловое движение КА с учетом ограничений на
ориентацию вектора тяги, зависимость тяги двигателя от расстояния КА
до Солнца и от ориентации солнечных батарей, влияние возмущений:
dr — dV __ 7 Р _ 7
— = К, —— =a+g+f=— 6-e + g + f,
dt dt m
^ = Ц'(мо-а*1осо),
at
— = co-x.~i., — = ^-=axklt (2.Ю)
dt ' dt dt '
~T~= _(? + Уулр ) = ~ + Яупг^упр I •
dt \c )
Нетрудно проследить связь данной постановки задачи с други-
ми традиционными постановками задач. Использование вместо уравне-
ний (2.10) системы (1.6) (из системы, описывающей движение КА, ис-
42
Глава 2. Математические модели задач оптимизации
ключаются уравнения, описывающие его угловое движение) расширяет
множество допустимых траекторий и управлений D до некоторого мно-
жества Е. Очевидно, mjn I < min I.
Общей тенденцией развития перспективных КА с ЭРД является
увеличение их масс и моментов инерции, что в свою очередь, создает
ряд проблем в управлении движением. Конструктивные схемы тяжелых
КА, как правило, предусматривают жесткое закрепление связки двига-
телей относительно корпуса. Изменение направления тяги реализуется
при этом путем разворота корпуса КА в пространстве с помощью
управляющего момента, величина которого ограничена.
Главный момент внешних сил Мо представим в виде суммы
M0=MvnP+H, (2.11)
где МуПР - вектор управляющего момента, Н - суммарный вектор мо-
ментов от гравитационных, аэродинамических и иных внешних сил.
В свою очередь вектор управляющего момента является суммой
управляющего момента, не связанного с созданием ускорения центра
масс КА Л/,, момента от тяги маршевых двигателей Мг и момента,
создаваемого управляющими ЭРД М3
М = Л7( -F Мг + М3, (2.12)
__ п ________ ___ М _
мг = zР„, X Р,6,, w, = х PynpJ • SmJ (2.13)
/=1 y=l
где Рм< " вектор, задающий положение точки крепления маршевого
двигателя с тягой Р, в связанной системе координат, р^ - вектор, за-
дающий координаты точки крепления управляющего ЭРД с номером j.
Для эффективного управления вектором тяги необходимо изме-
нять положение КА в пространстве с помощью управляющего момента.
При этом необходимо выполнение следующего условия реализации
программных разворотов КА:
Мупг >10 — -Н+0)к100)
at
(2-14)
Производная единичного вектора направления тяги в инерци-
альной системе кцординат выражается формулой
de (_
—-I —I +д>хе (2.15)
х /OX^Zt
где । de )
- производная вектора в связанной системе координат. При
' '«ад
43
Глава 2. Математические модели задач оптимизации
отсутствии ограничений на направление вектора тяги е(г) в связанной
системе координат ориентация вектора тяги в пространстве не зависит
от углового положения аппарата, и управление траекторией осуществ-
ляется независимо от его движения относительно центра масс.
В ряде задач целесообразно рассматривать КА как твердое тело
с ограниченной угловой скоростью поворота вектора тяги. Для обосно-
вания такой модели достаточно предположить, что КА постоянно сба-
лансирован по моментам, и угловая скорость а поворота вектора тяги,
жестко связанного с корпусом КА, является независимым управлением.
Векторные уравнения движения (1.6) дополняются уравнением, описы-
вающим поворот вектора тяги:
^-=£}к*ё. (2.16)
Здесь к - единичный вектор угловой скорости поворота вектора тяги,
причем а> = £>к,(к,ё) = О. Частным случаем этой модели, удобной для
описания движения вращающихся КА с искусственной гравитацией,
является случай постоянной ориентации КА и вектора тяги в простран-
стве ( Q = 0, ё - const), здесь управление осуществляется только путем
изменения величины реактивного ускорения и реверса тяги.
Если вектор тяги фиксирован в связанной системе координат
(двигатель жестко закреплен относительно корпуса КА), то изменение
направления тяги осуществляется за счет разворота корпуса КА. В этом
случае удобно считать, что тяга направлена вдоль одной из связанных
осей, например, ОХ} Тогда
f—) =0, => — = ёГхё (2.17)
dt
В рамках модели (2.10), представляющей КА твердым телом пе-
ременного состава и учитывающей взаимосвязь траекторного и углово-
го движений, общая задача оптимизации не разделяется на динамиче-
скую и параметрическую части. Действительно, условием разделения
задач оптимизации, как это следует из постановок (1.1 - 1.6), являлось
отсутствие в явном виде составляющих полной массы КА в правых час-
тях уравнений движения. Однако, в постановке (2.10) компоненты тен-
зора инерции /0 зависят от массы КА, поэтому в правых частях уравне-
ний траекторного движения реактивное ускорение а не является
управлением, независимым от проектных параметров, что и определяет
взаимосвязь динамической и параметрической задач оптимизации. Ис-
ключение составляет случай, когда моменты инерции КА постоянны, а
44
Глава 2. Математические модели задач огтгимизации
так)Ке, когда любая траектория г (/) и программа a(t) «бесплатно» реа-
лизуется системой регулирования углового движения аппарата. Следо-
вательно, в рамках указанной модели динамическая и параметрическая
задачи должны решаться совместно.
В реальных конструкциях КА практически всегда имеют место
ограничения на управление вектором тяги, выраженные либо в форме
ограничений на угловые скорости поворота, либо на углы отклонения
тяги в связанной системе координат.
Проектную модель КА с двигателями малой тяги будем строить
на основе уравнения баланса масс его компонентов и систем на старто-
вой орбите. Анализ работ в области оптимизации КА с ЭРД малой тяги
позволяет записать это уравнение в следующем виде [11]:
тд = тп + тэ + тд + тРТ + тспх + тпк, (2.18)
где «л - масса полезного груза; тэ - масса энергоустановки, состоящая
из источника и преобразователя энергии; тд - масса двигательной уста-
новка, включающая маршевые и управляющие двигатели вместе с ис-
полнительными органами; тРТ - масса рабочего тела, необходимого для
прямого и обратного перелета с учетом расхода на управление; тслх -
масса системы подачи и хранения рабочего тела (баки, трубопроводы и
пр.); тк - корпус и конструкции МТА.
Наиболее простыми и часто использующимися зависимостями
массы отдельных компонентов КА от проектных параметров являются
линейные зависимости масс от номинальной мощности энергоустанов-
ки N и тяги двигателей на стартовой орбите Р:
m3=a3-N, тд=уд-Р, (2.19)
тК — ак + ' Р > тспх ~ ^СПХ ' тРТ >
где аэ - удельная массовая характеристика энергоустановки, кг/Вт; ак
- удельная масса конструкции по мощности, кг/Вт; уд - удельная мас-
са двигательной установки, кг/Н; ук — удельная масса конструкции по
тяге двигателей, кг/Н; .- отношение массы системы подачи и хра-
нения рабочего тела к массе рабочего тела.
Масса израсходованного рабочего тела на перелет выражается
через моторное время или характеристическую скорость перелета
Р„ ( (
трт =-Ти = mJ 1-ехр------. (2.20)
с I I с))
Подставляя эти выражения в формулу (2.18) с учетом зависимо-
м°щности от проектных параметров и с учетом КПД
45
Глава 2. Математические модели задач оптимизации
(2.21)
N = —
27
получим новый вид уравнения баланса масс на начальной орбите:
т0 = тп+ <ХЭ-— + Уд'Р + TM(l + kcnx) +
27 с
Рс
+ 'Ъ]+Гк
или для массы полезной нагрузки
Pc _ Р _ \
тп - то- <хэ — Уд- Р-----7^(1 + кСпх) -
2г] с
Рс
Анализ уравнения для массы полезной нагрузки (2.23) как
функции двух переменных Рис показывает, что при фиксированной
стартовой массе КА максимум тп достигается при скорости истечения
(2.24)
(2.22)
(2.23)
~ рм 0 + ^спх)^ .
%' ~
аэ +ак
Значение тяги двигателей Р должно быть минимальным с точки зрения
возможностей выполнения маневра.
Реальная зависимость стартовой массы от проектных парамет-
ров аппарата имеет более сложный нелинейный вид и уравнение балан-
са масс (2.22) значительно усложняется. В любом случае можно гово-
рить о том, что стартовая масса аппарата является функцией тяги двига-
телей, скорости истечения рабочего тела, массы рабочего тела, требуе-
мого на выполнение целевой задачи и ограничений, наложенных на фа-
зовые координаты, законы управления и проектные параметры КА.
Если управляющий момент создается маршевыми двигателями,
например, за счет рассогласования тяг отдельных блоков ЭРД, поворота
двигателя в кардановом подвесе или перемещения связки ЭРД по спе-
циальным направляющим, перпендикулярным направлению тяги, рас-
ход рабочего тела на управление отсутствует. При использовании дви-
гателей-маховиков также не требуется дополнительный расход рабочего
тела. Назовем такую схему совместного управления траекторным и уг-
ловым движением «совместной». В отличие от нее, «раздельная» схе-
ма управления траекторным и угловым движением предполагает ис-
пользование специальных управляющих двигателей, создающих только
управляющий момент. Создание управляющих моментов приводит к
дополнительным Затратам рабочего тела.
46
Глава 2. Математические модели задач оптимизации
Для оценки расхода рабочего тела на разворот корпуса КА
включим соответствующие затраты в приведенную характеристическую
скорость перелета W'K - теперь она является мерой энергетических за-
трат на управление траекторным и угловым движением [12]:
К =И(1 + ^Ы)ИЛ- (2-25)
о т
а
Здесь kt = , б. - функция включения-выключения маршевого двига-
теля (равна 0 или 1), бу пр - функция включения-выключения управ-
ляющих двигателей (принимает значение +1, 0, -1), qynp - секундный
расход массы маршевых и управляющих двигателей кг/с. Получим:
ти0 = тт + a3N + (1 + 'успхХ^рп + mpri)+®пэ "О - +
+ У к Н1 + )+ <*KN + + MJ > (2.26)
где Aj = , с - скорость истечения рабочего тела управляющих
с
двигателей; с - скорость истечения рабочего тела маршевых двигателей,
- относительная масса конструкции КА, апэ — удельная масса пре-
образователя энергии, кг/кВт. т]пэ — к.п.д преобразователя энергии.
Мощность ЭУ связана с тягой:
^эУ=Т-'Р-^- (1 + Мг), (2-27)
*-'Чт 'Чпэ
где т]т - тяговый КПД.
m0 = т„ + (аэ + а„э(1 - т]пэ)+ аК )N + (1 + уСпх Х"1™ + туп )+
+ (Гх + Гду И1 + к,кг )+ АЛ > (2.28)
Суммарные затраты рабочего тела на прямой и обратный пере-
лет с учетом формулы Циолковского получим
wn+'»rJ = m0(zl+z1-z1za + ^zJ), (2.29)
( ( W' V) ( ( W' W
z,= 1-exp , za = [l-expl-^- . (2.30)
k \ c )) k \ c ))
В качестве главного критерия оптимальности примем теперь
относительную массу полезной нагрузки р = Подставляя (2.27),
7И0
(2-28) в (2.26) учитывая, что P = qc после приведения подобных чле-
в°в, получим
47
Глава 2 Математические модели задач оптимизации
l-/j(z, + z,-z,z2)-/fr (2.31)
1- Az2
^(l + ^Ja + cQ + V.)/ (2.32)
+ Успх + * ’
_ аэ + апэ 0 ~ 7лэ) + ак , у = ук + у„ .
^ПтПпэ
Вектор проектных параметров р обобщенно характеризующий
облик КА и схему.управления движением запишем в виде:
Р = ’ (2.33)
где гм, Гу,,р — векторы характеризующие расположение относительно
центра масс точек крепления маршевых и управляющих двигателей.
Компонентами вектора р являются составляющие тензора
инерции 70 КА, тяги маршевых и управляющих двигателей и координа-
ты их размещения (задаваемые векторами гм, Гу»р ) скорость истечения
рабочего тела, мощность энергоустановки, максимальные управляющие
моменты по соответствующим осям. Размерность вектора р велика,
однако часть параметров задаётся априори из технических требований к
системе и поэтому может быть исключена из процедуры оптимизации.
Компонентами вектора управлений могут быть углы ориента-
ции вектора тяги в пространстве, функции включения-выключения дви-
гателей, управляющие моменты относительно связанных осей и др.:
и = {е,еУПР,3,3УпруМ . (2.34)
Основная задача оптимизации формулируется теперь сле-
дующим образом: определить вектор проектных параметров ре Р и
вектор функций управления й(г)е U, доставляющие при заданной мас-
се полезного груза и заданном времени перелета Т максимум относи-
тельной массе полезной нагрузки р, при выполнении граничных усло-
вий:
(u, р)= argmin p{p,u(t),T,M„H ). (2.35)
rM’.ofou
На этапе баллистического проектирования задача оптимизации
решается для каждого из альтернативных вариантов схемы управления
движением, причём в вектор оптимизируемых параметров включаются
только те независимые компоненты полного вектора р, влияние кото-
рых является определяющим.
48
Глава 2. Математические модели задач оптимизации
Описанная постановка задачи оптимизации ориентирована на
случай доставки на заданную орбиту вполне определённого и постоян-
ного для всех рейсов полезного груза. Однако в ряде случаев следует
учитывать многоцелевое назначение КА (1].
2.2. Математическая модель задачи оптимального управ-
ления околоземными эллиптическими орбитами
Характерной особенностью задач управления движением спут-
ника с двигателем малой тяги на низкой орбите является наличие воз-
мущающих ускорений (1.8 - 1.11), обусловленных нецентральностью
гравитационного поля Земли и сопротивлением верхних слоев атмосфе-
ры, сравнимых с величиной реактивного ускорения. Модель задачи оп-
тимизации становится при этом достаточно сложной, а эллиптичность
орбиты требует аккуратного описания «медленной» эволюции орбиты
иа больших интервалах времени. Критерием оптимальности динамиче-
ского маневра здесь обычно является моторное время или продолжи-
тельность динамическаго маневра.
В силу малости возмущающих и управляющих ускорений наи-
более удобной формой записи уравнений, описывающих эволюцию ор-
бит, оказываются уравнения в оскулирующих элементах вида
= (2.36)
at
где Э - вектор оскулирующих элементов (обычно включает большую
полуось орбиты А, эксцентриситет е, аргумент перигея со, долготу вос-
ходящего узла £2, наклонение орбиты к плоскости экватора i, время про-
хождения перигея т), & - циклическая «быстро меняющаяся» перемен-
ная (истинная аномалия, аргумент широты или другой угловой пара-
метр), по которой удобно проводить ускорения уравнений, переходя к
исследованию «медленной» эволюции орбиты.
Уравнения движения спутника в центральном гравитационном
поле под действием трансверсальной ах, радиальной ау и бинормаль-
ной аг составляющих реактивного ускорения [13] и возмущающего
Ускорения f =
49
Глава 2. Математические модели задач оптимизации
da) Гр( I .\cosi9 (а + Г)Г, г) . „ (°,+/,)r . • )
---= , — I —(а + /,)—+" 14— SinJ-^—'-^ctgismu ,
Л | р е е \ р) р J
— = J- + К + Л)-2----------- ----- 1 + — Sin J , (2.37)
dt \p\j е е V р) J
du Гр( р к+/,У . . •
--------------------
_ Гр (а, 4-/7)rsinH di _ Гр (а, + /,)rcosw
dt ур psinz ’ dt у р р
Здесь р = л(1 -ег) - фокальный параметр орбиты, и - аргумент широты
(рис. 2.4). В качестве критерия оптимальности примем моторное время
Тм (или продолжительность перелета Т).
Рис. 2.4. Системы координат, используемые при описании перелетов
между околоземными орбитами
Будем считать, что изменение элементов Ли/ малы по сравне-
нию с их начальными значениями, радиальное управляющее ускорение
равно нулю ( ау = 0 ). То есть компоненты управляющего ускорения на-
правлены по трансверсали или бинормали к орбите и не связаны между
собой (существует два вида управляющих двигателей). Предположим,
что величины аж/е и аж малы по сравнению с гравитационным ускоре-
50
Глава 2. Математические модели задач оптимизации
лием. Эти допущения позволили воспользоваться методом усреднения
движения, и для задачи совместного управления всеми оскулирующими
элементами орбиты (А, е, «а, Х2 0. а также относительным угловым по-
ложением Ди спутника, обеспечивающего минимум моторного времени,
получить структуру оптимального управления на отдельном витке ор-
биты [14, 15], показанную на рис. 2.5.
Рис. 2.5. Полученная структура оптимального управления на витке
Оптимальная по быстродействию структура совместного
управления элементами (А, е, <о) эллиптической орбиты трансвер-
сальным реактивным ускорением в пределах витка в общем случае
включает два активных участка противоположного направления
ускорения, центры которых разнесены на угол п по эксцентрической
аномалии.
Оптимальная по быстродействию структура совместного
управления элементами (£2, i) эллиптической орбиты бинормальным
ускорением в пределах витка включает два активных участка про-
ншвоположного направления ускорения, центры которых разнесены
на угол л по аргументу широты.
Для этой структуры управления в [15] получена математическая
модель эволюции орбиты в поле земного сфероида, с учетом возму-
Щающего влияния атмосферы и малой тяги с оптимальной структурой
Управления:
d4_4ax EFf a-я-) /—
51
Глава 2 Математические модели задач оптимизации
at
di аг [лТ . ( р\ р .( р п}
— = —, — 2sin <р+— cos—cos^-ЗЯ) (р+-----------
dt я у V 2) 2 V 2 2)
(2.38)
3 ( В А
sin 2l lcos/7-(/l1cos2^' + Za sin2^) ,
d£l а ГЙТ . ( РУ Р г Р
— = —-— — 2sin (3+— cos—sin£-З/Ц <р+----------------
dt л-sin» VAL \ 2) 2 \ 2 2)
3 .
—sin
2
2^<p + -^Jcos/?-(^ cos 24” +Л, sin 2^")
еcos i -1
а0>5л3-5 ’
Здесь Т] - эксцентрическая аномалия центра разгонного участка
трансверсальной тяги ( аж > 0 ), £ - половина ширины разгонного участ-
ка для трансверсальной тяги, а - ширина одного пассивного участка
трансверсальной тяги; - аргумент широты центра участка с az > 0, <р -
половина ширины рабочего участка бинормальной тяги аг > 0 , Р - ши-
рина одного пассивного участка для бинормальной составляющей тяги.
Уравнения (2.37 - 2.38), описывающие изменение фазовых ко-
ординат е, со пригодны для описания орбит с отличным от нуля эксцен-
триситетом. Для анализа околокругового движения вместо этих элемен-
тов следует использовать компоненты вектора Лапласа
д,=есо8й>, g2=esin<w.
2.3. Математическая модель задачи оптимизации перелетов
между орбитами с большими эксцентриситетами
Для задач оптимизации плоских перелетов между орбитами с
52
Глав» 2 Математические модели задач оптимизации
движение к
темы (2.38).
большим11 эксцентриситетами можно рассматривать два варианта ори-
ентации вектора тяги: свободная ориентация и ориентация по трансвер-
сали. Если тяга направлена только по трансверсали, то усредненное
” \ может быть описано первыми четырмя уравнениями сис-
Критерием оптимальности служит конечная характеристи-
ческая скорость или моторное время перелета.
Для описания оптимального движения со свободной ориентаци-
ей тяги для оскулирующих элементов кеплеровской орбиты А,е,<о ис-
пользовались уравнения (2.37). В этих уравнениях положим а2 =0,
fl = a-cos#, ау = asin#, где в - угол отклонения вектора тяги от
трансверсали. Увеличение ускорения, связанное с уменьшением массы
КА в ходе маневра (из-за расхода рабочего тела), учитывается форму-
/ и/А
лой а=а0 ехп — Так как двигатель работает без выключения и являет-
ся нерегулируемым, то единственным параметром управления в рас-
сматриваемой задаче будет угол в.
Используя замену
= J-5-(l-ecos£)',c& можно перейти в
уравнениях (2.37) к новой независимой переменной - эксцентрической
анамалии Е. Учитывая малую величину реактивного ускорения по срав-
нению с гравитационным (пренебрегая членами содержащими а2) и
а ц
полагая — «~- получим [16]:
е А
clA А3 (IV V Г----Т
— = 2а0—ехр — esin#sin£ + yl-e cos#
«Е р (с Д
(2.39)
л [ w Wl-e / . \
- а0 —expl— I-----sin^(cos “е)+
, l-ecos£^ г 2 . _
+ cos # I я-----— Ml - е sin Е
I 1-е2 J
dw (W Y
dE -а0^—ехр|—JQ-ecos
бы new Фазовые координаты (2.39) можно разбить на две группы, что-
едовательно корректировать элементы А, е и затем — со.
53
Глава 2. Математические модели задач оптимизации
Рис. 2.6. Приближенно-оптимальноя программа управления вектором тяги на витке,
согласно зависимости (2.41)
Структура оптимального управления на витке для коррек-
ции большой полуоси и эксцентриситета. Найдем управление, обес-
печивающее переход из точки Ао, е0 в точку Ак, ек с минимальными за-
тратами характеристической скорости WK. В данном случае задача на
минимум WK эквивалентна задаче на быстродействие, т.к. характери-
стическая скорость однозначно связана со временем перелета в соответ-
ствии с формулой Циолковского. С использованием формализма прин-
ципа максимума Понтрягина, получен закон изменения 6(f):
п V^Aeip. + (1 -е2 V)sin Е п
= arCtg~(----\ - --------Г \ \ К 2 (2 40)
-b^cosf-ecos E-ep/tyJi-e
Здесь ц/А и \ре - переменные, сопряженные фазовым координа-
там А и е. Если в (2.40) эксцентриситет считать достаточно малым
(е<0.8), то структура оптимального управления будет иметь простой
параметрический вид:
к’^ (2'4|)
Программы управления вектором реактивного ускорения на
витке по (2.41) для различных значений К показаны на рис. 2.6.
Использование этих законов управления на витке (2.40 - 2.41) и
стандартной процедуры усреднения позволило получить уравнения ус-
редненного изменения элементов Л, е.
d А а0 А3 ( _ Г г Л W
---= —т— eJt +2Vl-e J2 exp—,
dE n p \ J c
= + 2(2J3 -e(A + J2))lexp—, (2‘42)
dE In p L J c
54
Глава 2. Математические модели задач оптимизации
где усредняющие интегралы для оптимального управления 0ор1 с уче-
том эксцентриситета (2.40) имеют вид:
2х 2л-
J, = J sin ввр1 sin EdE, J2 = J cos 6Bpl dE,
0 0
2jt 2x
J3 = Jcos#^, co&EdE, JA = Jcos#^ cos2 EdE.
о 0
Неудобство полученной модели состоит в том, что интегралы
Jt ... JA не выражаются через аналитические функции. В случае ис-
пользования оптимального управления (2.41), пренебрегающего эксцен-
триситетом орбиты усредняющие интегралы соответственно упрощают-
ся и принимают вид
J, = Jsin2£A"'d£, J2 = j(/C + cos£)A“ltZ£,
о о
J3 = + cos£)cos£A 'dE,
о
JA = J(£ + cos E)cos2 £A"'dE, A = -^sin2 £ + 4(k + cos e)2 .
0
В [16] было показано, что управление (2.40 - 2.41) не влияет на
вековое изменение других параметров оскулирующей орбиты. Если в
усредненных уравнениях (2.42) перейти к характеристической скорости
в качестве независимой переменной, то уравнения движения дополни-
тельно упростятся и примут вид:
~ , (2.43)
— ~e~Jx +2(j3 e(jА +-/г))1.
агг 2.П L J
Структура оптимального управления на витке для коррек-
ции аргумента перицентра. Применяя аналогичную процедуру к эле-
менту со получим оптимальное управление, обеспечивающее наиболь-
шУю скорость изменения аргумента перицентра за виток:
1-ecosE
1-е2
Если приближенно считать эксцентриситет малым, то можно
Ущественно упростить структуру оптимального управления
&ор1 = -arctg (cos £ - е
1-е2 sin £
. (2.44)
55
Глава 2. Математические модели задач оптимизации
(2.45)
Используя (2.45), процедуру усреднения и переходя к характе-
ристической скорости в качестве независимой переменной, получим
уравнение для описания векового изменения аргумента перицентра
= + 2~е2}^±~4р/^ <2-46)
dW 2е ' ' 2е
Таким образом, усредненная модель приближенно-
оптимального движения КА содержит уравнения (2.43, 2.46) и позволя-
ет определить оптимальное управление для варианта «свободной» ори-
ентации вектора тяги для задач оптимизации перелетов между орбитами
с большими эксцентриситетами. Подробный вывод уравнений этой мо-
дели приведен в [16,17]
2.4. Математическая модель задачи оптимизации управле-
ния относительным движением космических аппаратов
Задачи управления относительным движением космических ап-
паратов на околоземных орбитах, возникают при выполнении маневров
сближения, орбитального сопровождения одного КА другим, при под-
держании требуемой конфигурации спутниковых систем, управлении
орбитой геостационарного спутника. Эти задачи заключаются в целена-
правленном изменении параметров, характеризующих относительное
движение двух или нескольких космических аппаратов, образующих
орбитальную систему. В общем случае возмущенное относительное
движение аппаратов будет описываться системой из 6п нелинейных
дифференциальных уравнений, где п - количество аппаратов.
Решение задачи осуществляется поэтапно. На первом этапе про-
водится анализ математической модели движения, и определяются об-
ласти фазового пространства, где возможно получение аналитических
решений. Существенное упрощение модели в рассматриваемых задачах,
возможно при введении допущения о малости координат относительно-
го движения по сравнению с координатами абсолютного движения. Это
позволяет сократить размерность системы и перейти к линеаризованной
модели движения.
В качестве основной будем рассматривать схему управления
относительным движением двух КА, один из которых считается пас-
сивным (КА]), другой активным (КАи), снабженным ЭРД.
Рассмотрим возмущенное движение КА в цилиндрической сис-
теме координат г и z, где г - расстояние от центра Земли до проекции
спутника на плоскость невозмущенной круговой орбиты, и - угол, от-
считываемый в плоскости невозмущенной орбиты от некоторой началь-
56
Глава 2. Математические модели задач оптимизации
ной оси по направлению полета спутника, z - расстояние от плоскости
г
невозмущенной орбиты до спутника. Считая, что величина — мала,
запишем уравнения движения в виде:
— = V, — = Yjl
dt r’ dt г
dt г гг Х’
Q-AT)
dV
II _
dt
dV г
dt
Н
= -—z + аг .
г
где Vr - радиальная скорость, Vu - трансверсальная скорость, V, - нор-
мальная скорость (проекция скорости на перпендикуляр к плоскости
невозмущенной орбиты.
Рис. 2.7. Относительное движение КА
При анализе динамики относительного движения будем исполь-
зовать линейную теорию возмущений, предполагающую малость от-
клонений по параметрам. После процедуры линеаризации относительно
кеплеровской невозмущенной орбиты модель относительного движения
принимает вид:
d&r
----=
dt ’
d&L dkz
---= АК-лДг, ----= ДК
dt * ’ dt г
= -Л2Лг+^-Ьг + ах,
dt г/
d&V V V.
~~ = -ЛЛУг ——bV„ + — AAr + aY,
d‘ r, r,
(2.48)
57
Глава 2. Математические модели задач оптимизации
. 1Д1-е2)
где л = ' —1 - средняя угловая скорость движения КА по опорной
V Р
орбите КАь - проекция расстояния между космическими
аппаратами на дугу невозмущенной орбиты (рис. 2.7).
В большинстве практических задач эксцентриситет опорной ор-
биты невелик, поэтому уравнения относительного движения записыва-
ются в следующем виде:
Дг = ДКг, Д£ = Д^(-ЯДг, Дг = ДГ,,
Д Vr = 2ЯД Vu - Л2 Дг + ах, (2.49)
Д = -ЛДГ, + ау, ДР, = -Л2Дг + az.
Записанные уравнения пригодны и для описания относительно-
го движения в случае, когда оба КА движутся по околокруговым орби-
там, поскольку параметры движения входят в них линейно [18].
В качестве критерия оптимальности в данной задаче примем
моторное время перевода КА из некоторой области начальных отклоне-
ний в заданную конечную область.
2.5. Математическая модель задачи оптимизации совмест-
ного управления траекторным и угловым движением
Пространственное движение КА можно представить как резуль-
тат сложения двух движений: перемещения ценктра масс аппарата в
мгновенной плоскости орбиты и вращения этой плоскости вокруг при-
тягивающего центра. Систему уравнения движения удобно записывать в
с использованием в качестве координат векторов Лапласа вместо пара-
метров А и е [20] (см. рис. 2.4):
dA 2Л3(1-^-^) ( +а flsinff-frcosjp \
dtp l + <7(cos^ + <72sin(p^ х Г l + eftcos^ + ^sin^J ’
dgi ^2(l-g2 -9») (а 2cos<a + q,cos2<p + gasinpcosp + g, |д sinJ;
dtp l + 9jCosp + 02sinp( х 1 + cosp + q2 sinp r )
= ^2(l-q2-gz) (a 2cos p + q2 sin2 p + g, sin <3 cos tp + q2 _ 0 cos J;
dip 1 + qt COSp + ga sinp^ x 1 + q} cosp + q2 sinp ’ J
— = —rj- a7 cos(^> + to'); (2.50)
dtp (1 + q{ cos tp + q2 sin tp)
58
Глава 2. Математические модели задач оптимизации
сЮ _ A2(l-q2-q2) sin((o + t»')
---— — —- ,
dtp (1 + qy cos tp + q2 sin tp) sin i
do' Л (1— qf ~ q2) . t л
- = 7---i----1---az sinfa + о )ctg 1;
dtp (1 + q} cos tp + q2 sin tp)
Л ^fa-qt-qlY1
dtp (1 + qt cos tp + q2 sin tp)2
Здесь все обознаяения соответствуют введенным ранее, о' можно счи-
тать условным аналогом аргумента перицентра, a qt = ecostw' и
q2 = esin o' - соответствующие аналоги множителей Лагранжа.
Пусть тяга двигателя постоянна и направлена так, что ее радиаль-
ноя составляющая аг равна нулю. Тогда направление вектора тяги за-
дается всего одной величиной - углом у между вектором тяги и оску-
лирующей плоскостью орбиты. Составляющие реактивного ускорения
представим в виде
a0cosu/ W
ax=acosip=----------= a0cosy/exp—, ау =0,
С
с
aosin^ . W м
az =-asmtp = — -------= -o0sin^exp—, (2.51)
c
c
При помощи составляющей реактивного ускорения az, нормаль-
ной к оскулирующей плоскости орбиты, можно изменять наклонение i.
Если в точках, где аргумент широты и = <р + о' принимает значения
я/2, Злг/2,... , изменить направление бинормальной составляющей az
на противоположное, то наклонение орбиты i будет изменяться моно-
тонно. Следовательно, при помощи управления
— i = 0; (2.52)
с J
az = ±а0 sin|y/| • ехр^—• sign(cos и)
в принципе можно осуществить перелет между некомпланарными орби-
тами разного радиуса [2].
При малых значениях угла i правые части системы (2.50) могут
неограниченно возрастать по модулю. Поэтому будем считать, что угол
1 в нашей задаче не меньше некоторого значения; этого всегда можно
59
Глава 2. Математические модели задач оптимизации
добиться соответствующим выбором плоскости отсчета, например, со-
вмещая ее с плоскостью эклиптики.
Подставим значения компонент реактивного ускорения (2.52) в
исходные уравнения (2.50). Полагая, что а0 «1 и с»1 (масштабом
измерения скорости истечения служит скорость движения по круговой
начальной орбите), систему уравнений можно привести к стандартному
виду систем с малым параметром и быстро (фазовый угол (р )и медленно
меняющимися переменными.
Траектория движения КА с малым реактивным ускорением в
«сильном» гравитационном поле обычно имеет многовитковую струк-
туру, в которой сочетаются как периодические, так и вековые измене-
ния элементов оскулирующей орбиты. Разумно предположить, что и
управление - угол ориентации тяги ip(t) содержит как периодическую,
так и вековую составляющие.
Особый интерес представляет случай, когда начальная орбита -
круговая. Получим условия, при которых орбита остается близкой к
круговой. Обращаясь ко второму и третьему уравнениям системы (2.50),
видим, что для этого необходимо выполнение равенств
0, = = 0; Q2 = = 0. (2.53)
о dtp йа<р
Учитывая, что компоненты реактивного ускорения имеют вид
(2.52) и <710 = qK = 0, условие (2.63) представляется:
2г 2ж
Qt = J cosy/cosy? d(p = O; Qi~ J cos у/sin у? d<p = Q. (2.54)
о о
Из уравнений (2.50) следует, что при выполнении условий
(2.54) О = Qo = const; <о' = = const. Примем, не нарушая общности,
&>' =0, что соответствует направлению оси Ои£ по линии узлов. По-
скольку (р + а>' = и (и — текущий аргумент широты) в дальнейшем вме-
сто угловой координаты <р будем использовать обозначение и.
В результате операции усреднения уравнения околокругового
движения КА с малой тягой принимают следующий вид [12, 19]:
«о V з ГИ'Л,
— = —-Jr •cosy'-exp— aw;
du 2л 'о \с )
— = — (г2 sinly/l • coslwl -expf—\lu ; (2.55)
du 2л о V с )
60
Глава 2. Математические модели задач оптимизации
dW а0 г? у (W\
----- — г 2 -exp — du = exp — ;
du 2л Jo \с/
dt
—= r .
du
Здесь вместо большой полуоси А введен радиус «круговой» ор-
биты г, символом « » обозначены усредненные величины. Дополним
уравнения траекторного движения (2.55) уравнениями, описывающими
динамику движения КА относительно центра масс. В данном случае
угловое движение КА осуществляется только вокруг нормальной оси
аппарата OYt, совпадающей с направлением радиуса-вектора центра
масс г (см. рис. 2.8):
= (2.56)
du У| du IYt
Здесь a>Y{ - скорость вращения КА вокруг связанной оси OYt; MYi -
управляющий момент; /у> - момент инерции КА относительно оси OYt;
е - угловое ускорение.
Рис. 2.8. Схема управления вектором тяги при некомпланарных перелетах
В дальнейшем в уравнениях (2.55) перейдем к новому аргумен-
ту - характеристической скорости:
dr г% 2?
— = — (со,,, Л;
d/
^F=^7'fsinMIC0SMl
du.
(2.57)
_ В среднем влияние управления вектором тяги на траекторию
характеризуется интегралами:
61
Глава 2. Математические модели задач оптимизации
7, = jcos^ du-, /2 = jsin|i//| • |cosw| du. (2.58)
о о
Задачу оптимизации перелета разделим на две самостоятельные
задачи. Задачей локальной оптимизации назовем задачу отыскания
программы изменения угла ц/ и соответствующего углового ускорения
е, обеспечивающей минимум затрат характеристической скорости в
пределах каждого витка траектории. Задачей оптимальной парамет-
рической модуляции программы управления назовем задачу отыскания
оптимального закона изменения интегралов 7,, 12 вдоль всей траекто-
рии перелета, илй по существу в оптимальном программировании мед-
ленно меняющейся составляющей управления.
Для учета дополнительных затрат рабочего тела на управление
угловым движением будем использовать последнее уравнение системы
(2.10), описывающее изменение массы КА.
Предположим для простоты, что скорость истечения рабочего
тела управляющих двигателей такая же, как и у маршевых. В этом слу-
чае задача о минимуме суммарного расхода рабочего тела эквивалентна
задаче о минимуме условной характеристической скорости W'K :
(2-59)
/0 й»
где т - текущая масса КА; а0 = const - начальное ускорение от марше-
вых двигателей; Рупр - тяга управляющего двигателя; дупр - функция
включения-выключения управляющих двигателей; А/Г| -e-IYi -Рупр^
- управляющий момент, h - плечо управляющей силы.
_ Рупр _ „ с _ кИи ГТ
«о ------= Чупр — = -Г-
' то h
Введем параметр к, которым будем в дальнейшем характеризо-
вать дополнительный расход рабочего тела на управление:
= (2.61)
«о аоЛ
Ясно, что для совместной схемы управления к = 0, если управ-
ление осуществляется по раздельной схеме, то:
(1 + ЫУПР) dt. (2-62)
to
Дифференциальное уравнение изменения условной характери-
стической скорость имеет вид
62
Глав* 2. Математические модели задач оптимизации
(2.63)
— = —, fj =1(1 +А<5У/7Р) .
dW Fi f УЯР/
Переходя к аргументу W' в уравнениях (2.57), получим (сим-
вол «'» опущен)
</г _ 2г^ .
dW' Fi ”
Интегралы I, и 12
di rh
dW' ~ Fi'
здесь определяются выражениями (2.58).
Отметим, что для совместной схемы управления к = 0, Ft = In,
(2.64)
jy' = W. В этом случае управлением является угол ориентации тяги у/,
который можно считать функцией двух переменных: аргумента широ-
ты, характеризующего положение КА на орбите, и текущей характери-
стической скорости W. Легко показать, что уравнения системы (2.64)
интегрируются, если угол у/ является функцией только аргумента ши-
роты. Пусть F, = const, тогда решение этих уравнений, соответствую-
щее граничным условиям перелета между круговыми некомпланарными
орбитами, имеет вид
z х-2
/_/0=^1ПГ; Г=(,-^П ‘ (2’65)
(2.66)
Решение (2.65, 2.66) справедливо и для случая, когда iK = iB.
Однако, если rK = r0 = 1, конечная характеристическая скорость переле-
та определяется путем непосредственного интегрирования второго
уравнения системы (2.64):
(2.67)
*2
Рассмотрим «релейную» программу управления [2] причем по-
ложим Fi = 2я, Л = 0:
М = const = у/0 ; signy/ = —sign(cosu). (2.68)
Тогда решение (2.65) с учетом интегралов У, и 1г примет вид
/, = 2л cos у/0, У2 = 4 sin ув. (2-69)
'-»о=^^-1пг; г = (1-^005^,, У2. (2.70)
л
Перелет с орбиты единичного радиуса на орбиту радиуса гК,
63
Глава?. Математические модели задач оптимизации
плоскость которой повернута относительно плоскости орбиты на угол
&iK =iK-iB, можно осуществить с помощью управления (2.68), если
положить
ДЛ.
y/0=arctg—
lnrK
В этом случае конечная характеристическая скорость и про-
должительность перелета определяется формулами
Г Y
1-ехр------—
I
(2.71)
1¥г =
secv'o J
с
«о
В частном случае, когда у/в = 0, получим изменение радиуса
орбиты при перелете с трансверсальной тягой
7*=— 1-ехр -
ccos^JJ
(2.72)
, 1
1—т= secy/0 =
к
(2.73)
(2.75)
г=(1-И')2 = l-cln]l-—/
\ Xе.
Если, а = const то W = at и решение еще более упрощается:
r = (l-at)2. (2.74)
Решения, соответствующие случаю уменьшения радиуса орби-
ты, получаются при что приводит к смене знаков в формулах
(2.73) и (2.74). '
Если ц/в — л/2, имеем задачу поворота плоскости орбиты би-
нормальной тягой. При этом гк = гс -1. Согласно решению (2.67)
- т ^‘к
i = z0+---; FF„=----
п 2
Найдем локально-оптимальную программу изменения угла
которая обеспечивала бы минимум характеристической скорости
при заданных приращениях радиуса и наклонения орбиты. Пусть при
этом не[о,2?г]. Согласно решению (2.66), будем искать максимум
функционала It (2.58) при выполнении изопериметрического условия
2(4 -iB)lt= /2 In гк, которое с учетом (2.58) преобразуется к виду:
-z0)cos^-lnrK sin |^||cos w|)c/w = 0. (2.76)
О
Без учета изопериметрической связи (2.76) получим, согласно
64
Глава 2. Математические модели задач оптимизации
принципу расширения, верхнюю грань функционала Z,
max 7, = 7IS = 2л-. (2.77)
Для отыскания оптимальной программы у/(и), дающей макси-
мум /] с учетом связи (2.76), исследуем на экстремум функцию
Н - cos^zz + A(2(iK -/0)cos^ - InrK sin|^||cosw|)- (2.78)
Здесь A = const г множитель Лагранжа. Локально-оптимальная про-
грамма у/(и) получается в следующем виде:
<gy(«)=- хcosh = £ cosh. (2.79)
, 1 + 2Л(/л 10)
Параметр L можно интерпретировать как тангенс угла у/^ , со-
ответствующего аргументу широты и=0, тогда
И«) = arctg(tgcosh), tgу/^ = L = - Д1?** ,. (2.80)
1 + ZA(IK -10)
Выражение (2.80) показывает, что угол ориентации тяги на вит-
ке дважды меняет знак. Характер изменения управления у/ (и) на витке
траектории показан на рис. 2.10.В. Интегралы 7, и 72 для локально оп-
тимальной программы у/ (и) (2.80) приводятся к виду
= 42; cos^ du ,
° Vcos2 V'nux +sin V™ COS2 и
, .2? sin w cos2 u ,
7, = 4 J y du. (2.81)
° VCOS Vnux + sin V™ COS1 «
Интегралы (2.81) через элементарные функции не выражаются
и сводятся к полным эллиптическим интегралам первого и второго рода
и Е(у^):
А = 4 Kk™ )cos у/^ = I,B = max 7,; (2.82)
1г = 4£(^х) _ 4^(^)cos^n,M
SW№ tgy^
Зависимость интеграла 71в от параметра L, который, будучи от-
ношением интегралов 7,/7, (см. (2.65)), в свою очередь, зависит от угла
> показана на рис. 2.9. Там же даны и соответствующие значения
УГла • В отличие от IIS, 11С можно считать точной верхней гранью
Функционала 7, в сформулированной задаче локальной оптимизации и
65
Глава 2. Математические модели задач оптимизации
использовать для оценки других программ управления. Отметим, что
для весьма широкого класса перелетов, когда параметр L>5, точная гра-
ница 11В отличается от lls не более чем на 3...5%, что позволяет ис-
пользовать и гарантированную оценку /и.
Рис.2.9. Предельная оценка Ih и верхняя грань /,в функционала Ц.
Дадим оценку эффективности некоторых программ управления.
Простейшей «релейной» программе управления вектором тяги (2.68),
показанной на рис. 2.10.а, соответствуют решения (2.69 - 2.72).
Заметим, что эффективность поворота плоскости орбиты в ок-
рестности точек, где u-nfl, Зя/2 , наименьшая. Здесь целесообразно
ориентировать вектор тяги точно по трансверсали. Вид программы
управления с таким изменением показан на рис. 2.10.6. Ее параметрами
являются угол отклонения тяги от плоскости орбиты и ширина уча-
стка 8 (в угловой мере), где тяга ориентирована точно по трансверсали:
Рис. 2.10. Программы управления вектором тяги: а) «релейная»;
6) «релейная» с участком трансверсальной тяги; в) оптимальная
В табл. 2.1 приведены значения критерия локальной оптимаДЬ'
66
Глава 2. Математические модели задач оптимизации
ности перелета - функционала /,, рассчитанного для трех описанных
программ управления и для фиксированных граничных условий, соот-
ветствующих перелету с низкой круговой орбиты (г0* = 6771 км) на эк-
ваториальную орбиту стационарного ИСЗ: Д(а.=0.9, ^=6.2319 км.
Здесь же даны значения конечной характеристической скорости, как
безразмерной, так и в км/с.
Таблица 2.1. Сравнение локально-оптимальных программ управления
Программа управления А/Дв WK, безр. (км/с)
(2.80) рис. 2.10.В 1.00 1.0640(8.163)
(2.68) рис. 2.10.а 0.9666 1.1038 (8.465)
(2.83) рис. 2.10.6 0.9851 1.0831 (8.306)
Результаты расчета показывают, что локальная оптимизация
программы управления вектором тяги позволяет улучшить критерий
оптимальности /, на 2...3%. Подробнее с описанными результатами
можно познакомиться в [12,19].
2.6. Математическая модель задачи совместной оптимиза-
ции траекторий и ориентации солнечных батарей
Дальнейшим развитием модели (2.10) является модель, пред-
ставляющая КА твердым телом с присоединенными элементами и по-
зволяющая учесть влияние условий освещенности КА и ориентации
панелей его солнечных батарей на величину и направление вектора тя-
ги, а следовательно, на форму траекторий и энергетику перелетов.
В этой модели величина тяги Р представляется следующим вы-
ражением
Р = cq<p(r ,пСБ) (2.84)
где р(г,иС£)- функция, устанавливающая зависимость тяги от вектора
положения центра масс КА в пространстве г и вектора ориентации
нормали пСБ к плоскости панелей солнечных батарей (на теневых уча-
стках орбиты = 0 ). Для КА с автономным источником энергии можно
считать p(r,wCfi) = l) . Кинематика движения нормали описывается вы-
ражением
^сб _ — —
& ~ аСБ Х ПСБ »
гДе оС5- вектор угловой скорости вращения панелей солнечных бата-
РеЙ- Максимальная электрическая мощность (а значит, и тяга ЭРД) реа-
лизуется при совпадении нормали псв с вектором положения Солнца
67
Глава 2. Математические модели задач оптимизации
rc(f) в орбитальной системе координат OXYZ.
Электрическая мощность, вырабатываемая солнечными бата-
реями (СБ) на освещенных участках траектории, зависит от угла р меж-
ду направлением на Солнце и нормалью к поверхности батарей:
N-NmaxCosp. Задачей управления ориентацией СБ является обеспечение
максимального значения cosp. При отсутствии ограничений максималь-
ная электрическая мощность вырабатывается при cos р = 1.
Рис. 2.10. Параметры углового положения КА и солнечных батарей
Положение солнечных батарей относительно корпуса КА будем
характеризовать двумя углами (рис. 2.10): уСв * Угол крена оси батареи,
который составлен осью вращения батареи OZCe и поперечной осью КА
OZi', (рсв - угол собственного вращения батареи, характеризующим по-
ворот нормали ОУсб к плоскости батареи вокруг ее собственной оси
OZCE. Очевидно, с, помощью последовательных поворотов на углы усвк
(Реп можно добиться постоянного направления нормали УСб на Солнце.
При этом следует учитывать, что сам КА одновременно осуществляет
программу разворота по углу у/.
Запишем .выражения для проекций единичного вектора OYcs
нормали к плоскости солнечной батареи на оси орбитальной системы
координат OXYZ:
пх = cos <рСБ cos - sin уСБ sin <рСБ sin (// ,
=cos/CTsin^C£, (2-85)
п? - cos (рСБ sin + sin yCfi sin <рСБ cos ц/.
Будем считать, что в каждый момент известны компоненты
единичного вектора rs =(%, rsr, гж) направления на Солнце в ор
тальной системе координат. Максимальная мощность реализуется пРи
68
Глава 2. Математические модели задач оптимизации___________________
cosp - n-rs =1. Для этого случая выражения для программных углов
ориентации солнечных батарей таковы:
<рСБ ~ arccos(riv s*n Vх + rsz cosy/),
arccosr™/ zo ост
/» - ' <2'86’
Однако двухканальное управление ориентацией солнечных ба-
тарей в сочетании со сложной программой изменения положения кор-
пуса КА в пространстве может оказаться трудным для реализации. В
этом случае рассматриваются альтернативные варианты одноканально-
го управления:
• батареи вращаются только вокруг оси OZCe, постоянно совпадающей с
поперечной осью 0Z, ( уСБ - 0); угол <рСБ в этом случае обозначим (рр,
• ось вращения батарей совпадает с направлением связанной оси ОУ,, а
значит, и оси ОУ; уСБ = я/2; угол собственного вращения обозначим
Очевидно, для,этих двух вариантов сояД;; < 1.
Получим выражение для cos Д. Для этого в (2.86) положим
Усб ~ 0.
cos Д = cosy?, cosy/ + г1Г sin у?, + cosy?, sin у/.
Для обеспечения максимума cos Д найдем оптимальное значе-
ние у?;:
у?^ = arctg-------;--------- (2.87)
Гу. cos у/4^ sin у/
при этом
COS Amaz = + (гхг cos + <sz sin ^)2 (2.88)
Для второй схемы управления, очевидно, cos Д, не зависит от
углового положения самого аппарата. Положим в (2.62) уСБ = л/2, то-
гда
Vuop, = arctg - у/ ; cos Д 1т(и = у/г^+г^ (2.89)
rsx
С учетом возможности выключения двигателя при попадании
Рата в тень Земли целесообразно анализировать поведение среднего
ло*ИТ°К косинУСа УГЛа Д Освещенность КА зависит от взаимного по-
ил Солнца и оскулирующей плоскости орбиты.
^Ная вект°ры направления на Солнце rs и на аппарат г в пла-
У» о&^ИЧеСК°^ бальной СК, можно оценить текущую светотене-
тановку. Аппарат находится в тени, если выполняется условие
69
Глава 2. Математические модели задач оптимизации
|^хг|<-|^-,и <0, (2.90)
где Rlu - радиус планеты.
С учетом возможности выключения двигателя при попадании
аппарата в тень Земли целесообразно анализировать поведение среднего
за виток косинуса угла р. Освещенность КА зависит от взаимного по-
ложения Солнца'и оскулирующей плоскости орбиты. Поскольку оно
меняется в процессе полета, на отдельных этапах перелета может ока-
заться более выгодной первая схема одноканального управления сол-
нечными батареями, а на других - вторая. Поскольку целью управления
солнечными батареями является обеспечение максимальной мощности,
можно рассмотреть также комбинированную схему, при которой воз-
можны развороты аппарата по креиу на ±90° при смене знака разности
(cos/?, - cos/?,,).
Рассмотрим задачу совместной оптимизации траекторного дви-
жения аппарата и управления ориентацией панелей солнечных батарей
для некомпланарного перехода между околокруговыми орбитами [12].
Запишем уравнения околокругового движения
dr ~ з — = 2r acosy/ ; du = or2|cosw|sin|^|; (2.91)
dW _ х. dt _ *
du du
Примем, что реактивное ускорение а изменяется в зависимости
от косинуса угла Между направлением на Солнце и нормалью к плоско-
сти солнечных батарей а = ав cos р, причем ав = const.
Если критерием оптимальности межорбитального перелета счи-
тать конечную характеристическую скорость WK, легко показать, что
оптимум дает локально-оптимальное управление (2.60). В самом деле,
приводя уравнения (2.91) к аргументу W, получим систему уравнений,
инвариантную по отношению к реактивному ускорению а\
= 2г^ cos^, = r^lcoswIsinM. (2.92)
dW dW 1 1 1 1
Отсюда следует, что минимум характеристической скорости
достигается при той же программе управления углом ц/, что и в задаче
без ограничений.
Рассмотрим теперь задачу на минимум времени перелета. При*
ведем систему (2.?1) к аргументу t (уравнение для характеристической
70
Глава 2. Математические модели задач оптимизации
скорости не учитывается):
= 2ав cospr*1 cosy/, = аоcosPrlcosм|sin|y/| (2.93)
Пусть реализуется первый вариант управления ориентацией СБ,
когда ось OZce, постоянно совпадает с осью OZh В этом случае cos/?lmB
определяется выражением (2.88) или
cos/?lna, = (1 -(cosy/cos<5-siny/sin<5cos(w + м0)))\ (2.94)
где д - угол между направлением на Солнце и нормалью к плоскости
орбиты OZ зависит от оскулирующих элементов орбиты и определяется
cos 8 = cos i sin eb sin в - sin i cos eb cos Q sin 0 +
+sin j sin £2 cos 0 (2.95)
где £B - угол наклона плоскости эклиптики к плоскости экватора; О -
угол между направлением на точку весеннего равноденствия и линией
Земля - Солнце. При расчете 8 необходимо учитывать движение Солн-
ца по эклиптике (изменение в) и прецессию восходящего узла орбиты
Q. Сформулируем задачу о минимуме конечного значения аргумента t
системы уравнений (2.93) с учетом связи в форме (2.94 - 2.95). Управ-
лениями в данной задаче служат углы у/ и р. Введем в рассмотрение
функцию R:
Л = —(2а cos
дгу °
+л(1 - (sin 8 cos(w + u0 )sin у/ + cos 8 cos у/ )2),
где X - неопределенный постоянный множитель.
d<p dtp
Упростим задачу, полагая — = const, = const (это соответ-
дг di
ствует допущению о малости приращений г, i в пределах выделенного
витка). Такой подход приводит к отысканию локально-оптимального
Управления ( у/, р ), которое определяется условиями первого порядка
максимума R по г, г.
-=о.
dp
~^,авгУ1со^ч/зт cosnsiny/sin Р-2|cos/?]sin р = О
~ ^У/гаог^ siny/cosР + y/,aBr^ cosh cosy/cos/? +
+ 2(sin 8 cos(h + u„ )sin у/ + cos 8 cos у/ Xsin 8 cos(u + h0 )cos у/ - cos 8 sin у/),
Pr% cosy/)+ —(а0 co&Pr^ cosHsiny/)
di
(2.96)
71
Глава 2. Математические модели задач оптимизации
(2.97)
1 да> 1 др
где V, =-7-^’
X дг л di
Выражая из первого уравнения cos/? (тривиальное решение
sin /? = 0 исключается) и подставляя его во второе уравнение, после
преобразований получаем следующие решения:
cos/? = -^r^cos^-^-r^coswsin^ а0 ;
Zg|2^| _ V/rV/iaor* cosu + 2sin<5 cos <5 cos(zz + ц0)
y/2a2r3 -—a^r cos2 и - sin2 Scos2(w + «0)cos2 8
4
Решения (2.97) содержат две произвольные постоянные: рг и
у/, которые, строго говоря, надо рассматривать как медленно меняю-
щиеся переменные. Их можно определить, решая задачу оптимального
управления «медленным» движением. Решение этой задачи, однако,
связано со значительными трудностями, обусловленными вычислением
интегралов
2я 1я
I,p = jcos/7cos^ du , 1г = Jcos/?sin|^||cosw| du .
о с
Поэтому для выявления качественных закономерностей реше-
ния был использован следующий прием: начальное приближение для
медленно меняющихся переменных рг, задавалось решением зада-
чи оптимизации без ограничений; вдоль траектории фиксировались ха-
рактерные значения этих переменных, рассчитывались текущие значе-
ния угла <5; затем по формулам (2.97) рассчитывались (3 и у.
Рис. 2.11. Характер изменения параметров 41 и соф на траектории перелета на геостаи»
парную орбиту при одноканальном управлении СБ (оо = 10‘3 м/с1; с = 60 км/с)>
— начальный участок: г = 6700 км; / = 51°;_конечный участок: г = 43 000 км;»" >
72
Глава 2. Математические модели задач оптимизации
Результаты расчета показаны на рис. 2.11. Параметры расчета
подобраны так, что они соответствуют переходу с низкой круговой ор-
биты с наклонением 51° на стационарную орбиту. На начальном участке
траектории перелета cosfi мал, поэтому уровень реактивного ускорения
недостаточен и процесс разгона аппарата затягивается. В средней части
траектории значение cos/? увеличивается, профиль угла ориентации тяги
у>(и) становится близким к оптимальному в задаче без ограничений; на-
конец, на заключительном аппарат движется в плоскости, близкой к
плоскости экватора, поэтому удается достигнуть близких к единице
значений cosfi. С физической точки зрения, полученные решения соот-
ветствуют компромиссу между достижением максимальной электриче-
ской мощности солнечных батарей и оптимальной программой разворо-
тов вектора тяги космического аппарата в плоскости орбиты [12].
2.7. Математические модели задач оптимизации межпла-
нетных перелетов с малой тягой
Траектория межпланетного перелета КА с малой тягой разбива-
ется на участки движения в сферах действия планет и Солнца, и опти-
мальное движение рассчитывается по участкам. На границах участков
необходимо осуществлять стыковку траектории по фазовым координа-
там и массе аппарата.
Особенностью оптимизации замкнутых межпланетных переле-
тов (с возвращением КА на планету старта) является дополнительное
условие равенств^ угловых перемещений аппарата и планеты старта в
конечный момент времени.
(Г2 + Г4)-й>3 -(^2 + ^4)+ Т3(а)сг-аф)=2л п, (2.98)
где (рг и срА - угловые дальности прямого и обратного гелиоцентриче-
ских перелетов, сист и аф - средние угловые скорости движения планет
старта и назначения, п - произвольное целое число. В связи этим появ-
ляется неоднозначность решения целевой задачи, в зависимости от
г = Тг / Г4 - соотношения длительностей прямого и обратного перелетов
и * Даты старта экспедиции. Это приводит к необходимости введе-
НИя и последующей оптимизации дополнительных параметров, описы-
““ощих баллистическую схему перелета b = {DQ, т}г.
Задача проектно-баллистической оптимизации межпла-
ого перелета формулируется следующим образом. Требуется оп-
ределить вектор проектных параметров р = (Р0, с)7 еР, вектор бал-
ЛВС1Ических параметров b = (£>0, г)7 6 В и вектор функций управле-
73
Глава 2. Математические модели задач оптимизации
НИЯ е U, доставляющие при заданных массе полезно-
го груза тп и длительности перелета Tz минимум стартовой массе КД
и обеспечивающие выполнение целевой задачи проекта, описываемой
множеством допустимых фазовых координат аппарата X:
тв = Мтт0{р,Ь,и{(\тп,Тг = fixe,xeX). (2.99)
Задачи оптимизации пилотируемых экспедиций наиболее
сложны, так как множество допустимых фазовых координат кроме гра-
ничных условий прямого и обратного перелетов содержат специфиче-
ские ограничения, связанные с обеспечением безопасности экипажа
(ограничения на суммарную длительность экспедиции Тх < ТПРЕД , ми-
нимально-допустимое расстояние от КА до Солнца [я| > RnpEJ], дли-
тельность нахождения в радиационных поясах Земли и др.).
Для разделения задачи оптимизации на параметрическую и ди-
намическую части вводится промежуточный критерий оптимизации -
приведенное моторное время:
= (2.100)
О
где /(/?) коэффициент, учитывающий падение мощности энергоуста-
новки, а, следовательно, тяги двигателей и расхода рабочего тела в за-
висимости от расстояния от КА до Солнца, для аппаратов с ядерными
источниками энергии /(/?)= 1, а для аппаратов с солнечной энергоус-
тановкой
(зло»
Ро No Я,л
Этот критерий непосредственно определяет суммарные затраты
рабочего тела (р)-—Т’(р) на перелет и, следовательно, является
с
динамической характеристикой маневра.
Динамическая часть задачи оптимизации состоит в опреде-
лении вектора функций управления п(/) = (е(/), <?(/))г и вектора балли-
стических параметров b = (£>0, г)г (для замкнутых перелетов), обеспе
чивающих выполнение целевой задачи с минимальными затратами Ра.
бочего тела при фиксированных проектных параметрах КА и постро®
ния зависимости
74
рлава 2. Математические модели задач оптимизации
dVr 1 х 3
dt г г2
dV„ VV
—- = —-?-+ aSsin Л,
dt г
а^аМ
1-д '
(2.103)
Т’(р)= ЙГ'Л’ “^Р = fixe, Тъ= fixe, хе х). (2.102)
r pit fSr JDGtJ
Параметрическая часть задачи оптимизации состоит в вы-
боре вектора проектных параметров р = (Р0, с)г обеспечивающих ми-
нимум стартовой массе КА с учетом полученной зависимости.
Баллистическая часть задачи оптимизации решалась в соответ-
ствии с разработанным подходом связанным с использованием после-
довательности усложняющихся моделей [21].
Модель А описывает движение аппарата в рамках теории сфер
действия в центральном поле притяжения Солнца и планет, без учета
возмущений от других притягивающих центров в плоской полярной
системе координат:
± = р
dt г'
dtp
dt г
dm а _
— ——о
dt с
Здесь т - текущая относительная масса израсходованного ра-
бочего тела, отнесенная к стартовой массе аппарата та; г , <р - поляр-
ные координаты аппарата; Vr, V9 - радиальная и трансверсальная ком-
поненты скорости КА; Я - угол между направлением тяги и гелиоцен-
трическим радиус-вектором КА; а - текущее ускорение от тяги двига-
телей; а0 - ускорение от номинальной тяги двигателей при стартовой
массе КА.
Компоненты скорости и координаты аппарата, скорость истече-
ния рабочего тела и ускорение от тяги двигателей - безразмерные и от-
несены к круговой скорости, радиусу орбиты Земли и центростреми-
тельному ускорению на орбите Земли. Орбиты планет считаются круго-
ВЫМи и компланарными. Стыковка плането- и гелиоцентрических уча-
СТ1СОВ осуществляется только по массе аппарата.
В рамках модели Б, движение КА разделяется, в соответствии с
сфер Действия, на гелио и планетоцентрические участки, при
рий 113 границах сфер действия проводится точная стыковка траекто-
дд, даижения по координатам, скорости и массе аппарата. Орбиты пла-
Женад10^10™ аллиптическими и некомпланарными; при расчете дви-
Ппмп В С^>еРах Действия планет учитываются участки затенения, грави-
ИНЫе возмущения от других небесных тел и нецентральности гра-
75
Глава 2. Математические модели задач оптимизации
витационного поля планеты. Уравнения движения КА с учетом про-
странственного движения и управления записываются в виде
dt
dtp _Vv cosisin^sin^j-a0 cosisintp
sin>-K,(l-m) 2 sinf-K,
1 । cos^-cosZ, a0-<5 •/(?•) ।
dt г г2 (1-л?)
dv9 = _ + cos^sinZj-no-g-^r) +
dt r (1-m)
dt г
dVr _ кр2
(2.104)
sin<£>
sini-Kp ’
cos^>
dt с
сК1 _ sin^-sin^ а0-д-%(г)
dt sinz-Гр (1-от)
di cos^-sin^ a0-d-^(r)
~dt~ J‘ Vv '
Здесь fr, f , fz - компоненты возмущающего ускорения, действующе-
го на КА.
Модель В использует уравнения движения в поле притяжения
нескольких тел (Солнце и планеты Солнечной системы), учитывается
эллиптичность и ^компланарность орбит планет, деградация солнеч-
ных батарей и другие факторы. Воздействие радиации на панели сол-
нечных батарей приводит к возникновению дефектов кристаллической
решетки полупроводников, что приводит к снижению коэффициента
собирания солнеч'ных элементов и падению фототока:
^)=^(1-ЛдЛ(0), (2.105)
где а(г) - мощность энергоустановки в текущий момент времени, кД -
коэффициент деградации Солнечных батарей (принимался равным
5 10 9
данный момент времени. При решении динамической части задачи учи-
тываются ограничения на проектные и баллистические параметры и
вектор управления, траектория рассматривается как непрерывная с оп-
тимальной стыковкой участков.
/Бэр -суммарная доза радиации, полученная аппаратом на
76
Глава 2. Математические модели задач оптимизации
2.8. Математическая модель, описывающая движение КА в
системе Земля-Луна
Движение космических КА в системе Земля-Луна традиционно
рассчитывалось в рамках теории сфер действия. Это оправдано при ис-
пользовании двигателей большой тяги в рамках импульсной постановки
баллистических задач. Однако, при расчете движения в системе Земля-
Луна КА с малой тягой, реактивное ускорение от двигательной системы
сравнимо с возмущающими ускорениями Земли и Луны. В таких усло-
виях некорректно полагать, что оптимальное управление не зависит от
гравитационных воздействий второго притягивающего центра. Будем
рассматривать проблему оптимального управления и соответствующих
ему траекторий движения в рамках плоской круговой ограниченной
задачи трех тел.
В наиболее простом случае можно считать, что орбиты Земли и
Луны относительно барицентра системы - круговые, возмущения от
нецентральности гравитационного поля притяжения Земли и других
небесных тел не учитываются. Также не учитываются возмущения, свя-
занные с работой двигательной установки, например падение мощности
при воздействии радиационных поясов Земли или ограничения на
управление, из-за особенностей углового движения КА.
Движение аппарата будем описывать в инерциальной полярной
барицентрической системе координат (рис. 2.9). Основная плоскость
совмещена со средней плоскостью движения Луны, полярная ось на-
правлена в этой плоскости в сторону точки весеннего равноденствия,
центр координат находится в центре тяжести системы Земля - Луна.
Положение центра масс КА относительно барицентра определяется ра-
диус-вектором г и полярным углом <р. Расстояние от КА до Земли и
Луны соответственно задается векторами г3 и гл .
Вектор реактивного ускорения от тяги двигателей лежит в ос-
77
Глава/. Математические модели задач оптимизации
новной плоскости, его величина зависит только от массы КА. Направ-
ление ускорения задается углом управления Aft), который отсчитывается
от радиус-вектора против часовой стрелки. Положение Земли и Луны
определяется постоянными по величине радиус-векторами R3 и и
углом <9, имеющем постоянную скорость изменения а>, равную средней
угловой скорости движения Луны по орбите.
Безразмерные уравнения движения имеют вид [10]:
dt r dt г
У J
6 р у+ R3 C°s(A9>) Цл (г - Ял cos(&ff)) t а
dt г Л rl г2
dV9 VrVv . 6 .. ^3sin(A^) pjjRjjsm^tp)
j ’’"V Г*ЛJ з 3
dt r r3 гл
, (2.106)
+ а
<р
at = a0 cos A av = aD sin A
9
Здесьцл~0.0123 — отношение массы Луны к суммарной массе системы
Земля-Луна, &<р = <р-3 - угол Луна - барицентр - КА. Расстояния от
КА до Земли и Луны равны соответственно:
r3 = -Jr2 + R3 +2rR3 cos(Ap),
г„ =^r2 + Ял - 2гКл cos(A^).
Граничные условия оптимальных перелетов определяются в за-
висимости от задач выполняемых КА в системе Земля-Луна. В качестве
критерия оптимальности может использоваться минимальная длитель-
ность перелета или мимимальный расход рабочего тела.
(2.107)
2.9. Математические модели, описывающие движение КА с
солнечным парусом
При использовании солнечного паруса в качестве движетеля,
для описания движения используется система дифференциальных ураВ'
нений, включающая в себя уравнения плоского движения аппарата в
полярной системе координат и уравнения, характеризующие положение
плоскости орбиты относительно базовой, аналогичная (2.104), но
изменения массы КА [22].
Для идеально отражающего солнечного паруса направление у
корения совпадает с нормалью к поверхности паруса. Величина ус* ™
ния определяется по формуле:
78
Глава 2. Математические модели задач оптимизации
а =4~cos2 9, (2.108)
г т
где Ра ю 9,1-Iff6 Н/м2 - сила светового давления на один квадратный
метр поверхности паруса на орбите Земли, S - площадь паруса, & - угол
межДУ направлением на Солнце и нормалью к поверхности паруса, г -
расстояние от паруса до Солнца, выраженное в а.е.
Для определения точной величины и направления тяги, созда-
ваемой солнечным парусом и положения теневого участка на витке вве-
дем в рассмотрение следующие системы координат (рис. 2.10):
• OXYZ- геоцентрическая орбитальная СК (ось ОХ - направлена по
линии узлов);
• О'X’ Y’ Z’ - объектоцентрическая орбитальная СК (ось ОХ' - направ-
лена по радиус-вектору).
ХЛтоскрсть орбиты
Рис.2.10. К определению угла между нормалью к парусу и направлением на Солнце
Единичный вектор направления на Солнце в геоцентрической
орбитальной системе координат определяется следующим образом:
= cosficos0 + sinficosesin0,
= -cos/sinficos# +
+cos i cos ficos e sin в + sin isin e sin 0, (2.109)
= sin/sinficos#- sin»cos fi cose sin 0 +cos isinesin в.
Здесь 0 - угол между точкой весеннего равноденствия и поло-
Солнца (отсчитывается в плоскости эклиптики), е «23.45° -
Между экватором и плоскостью эклиптики.
В объектоцентрической орбитальной СК
=eIcosn+rJ,sinw, =-rrsinn + ^cosn, (2.110)
79
Глава 2. Математические модели задач оптимизации
где и - аргумент широты. Компоненты вектора ускорения от солнечно-
го паруса при этом имеют вид:
о'= acos^cos^, а'у = acos^sin^, (2.111)
а\ - acos2 i9sin^2.
Угол между нормалью к парусу и направлением на Солнце оп-
ределяется зависимостью
COSi9 = «' r's = r^COS/ljCOS/lj +
+r'Sy cossin Л, . (2.112)
Условие (2.90) позволяет учитывать попадание в тень планеты при пла-
нетоцентрическом движении. Естественно при этом ускорение от сил
светового давления отсутствует.
Граничные условия в задачах оптимизации формируются по-
разному в зависимости от цели динамического маневра, критерием оп-
тимальности обычно является минимальная длительность.
80
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
3 ПРИКЛАДНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ
ПЕРЕЛЕТОВ с малой тягой
Анализ баллистических задач, выполняемых космическими ап-
паратами с ЭРД, позволяет выделить четыре основных класса объектов,
имеющих как общие черты, так и характерные отличия.
К первому классу относятся КА, двигающиеся на сравнительно
низких (от 300 до 900 км) околоземных орбитах, выбранных на основе
требований к функционированию спутниковой системы прикладного
назначения. Динамические маневры этой группы аппаратов заключают-
ся в формировании рабочих орбит, поддержании орбит и трасс на боль-
ших интервалах времени, маневрировании в окрестности заданной точ-
ки рабочей орбиты. Управление ориентацией КА, как правило, опреде-
ляется требованиями, вытекающими из их целевого назначения (напри-
мер, постоянная ориентация одной из связанных осей на Землю, или
фиксированное положение спутника в орбитальной вращающейся сис-
теме координат и т.п.) Масса и габаритные размеры низкоорбитальных
КА не очень велики, поэтому управление их, как правило, осуществля-
ется с помощью электромеханических исполнительных органов (гиро-
динов) без затрат рабочего тела.
Направление вектора тяги для таких КА обычно фиксировано в
орбитальной системе координат, а управление движением осуществля-
ется за счет включения-выключения двигателя и переключения направ-
ления тяги с разгонного на тормозное (реверса).
Ко второму классу КА будем относить межорбитальные транс-
портные аппараты (космические буксиры), предназначенные для транс-
портировки и доставки на удаленные околоземные орбиты тяжелых, а
иногда и крупногабаритных полезных грузов. Динамические маневры
этих КА заключаются в многократном совершении перелетов между
околокруговыми или эллиптическими орбитами; диапазон рабочих ор-
бит весьма широк и включает геостационарную орбиту, сильноэллипти-
ческую орбиту (типа спутника связи «Молния») и т.п. Энергетические
затраты на выполнение подобных маневров велики. Возможности эф-
фективного управления вектором тяги во многом определяются массо-
во-инерционными характеристиками КА (или, точнее, системы «КА -
полезный груз»). Выбор оптимальных траекторий здесь, как правило,
бедует осуществлять с учетом динамики движения КА относительно
Центра масс.
Третий класс космических аппаратов составляют межпланет-
НЬ1е зонды для исследовательских полетов к астероидам, ближним и
Дальним планетам Солнечной системы, а также межпланетные экспеди-
81
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ционные комплексы (МЭК), предназначенные для пилотируемых экспе-
диций. Использование в перспективных программах освоение космоса
ЭРД малой тяги позволяет значительно снизить стартовую массу по-
добных космических комплексов на околоземной орбите за счет высо-
кой скорости истечения и малого расхода рабочего тела. Продолжи-
тельность замкнутых пилотируемых перелетов с возвращением МЭК на
околоземную орбиту до 1,5 - 2 лет, что является приемлемым с точки
зрения ограничений на пребывание человека в космосе.
Оптимальные проектные параметры межпланетных аппаратов
существенно зависят от выбранной баллистической схемы полета, дат
старта и возвращения, а также от траекторий, определяющих энергетику
перелетов. Такая зависимость значительно усложняет оптимизацию
проекта в целом, требует совместного решения задач баллистического
проектирования и выбора законов управления движением, и определе-
ния основных проектных параметров КА. Корректное решение динами-
ческой задачи требует аккуратного описания движения на всех участках
многоэтапного перелета (плането- и гелиоцентрических, участках пер-
турбационных маневров и т.п.), при условии точной стыковки кинема-
тических параметров движения на соседних участках.
При оптимизации маневров в системах «планета - спутник»
возникает необходимость учитывать влияние взаимодействующих по-
лей притяжения нескольких гравитирующих тел на законы управления
КА с малой тягой. Дополнительного исследования требуют проекты
межпланетных КА с солнечными источниками энергии. Здесь необхо-
димо учитывать падение электрической мощности батарей по мере уда-
ления от Солнца,, а также вследствие деградации фотоэлементов под
действием радиации.
При выборе модели движения межпланетного КА на гелиоцен-
трическом участке траектории можно не учитывать вращательное дви-
жение аппарата, рк как угловые скорости поворота связанных осей на
оптимальной траектории (а значит, и вектора тяги) малы и не превыша-
ют 1 град/сутки (это примерно соответствует угловой скорости враще-
ния Земли, относительно Солнца).
Четвертый класс рассматриваемых аппаратов представляют
собой аппараты, использующие для создания ускорения световое давле-
ние от Солнца. Аппараты этого класса всегда привлекали инженеров
своей фантастической способностью совершать различные маневры в
пространстве без необходимости расходовать рабочее тело. Однако рас-
чет и оптимизация таких перелетов объединяют сложности оптимиза-
ции аппаратов с солнечными батареями (зависимость ускорения от рас-
стояния до Солнца, светотеневой обстановки на орбите, деградации п°'
82
ГПЯва 3. Прикладные ^адачи оптимизации перелетов с малой тягой
рерхности солнечного паруса и т.д.) с необходимостью учитывать вза-
лмное влияние траекторного и углового движения крупногабаритных
конструкций в космосе.
Описанные классы космических аппаратов, особенности их
конструктивно-компоновочных схем и схем управления движением
требуют различных подходов к формулировке динамической задачи
оптимизации, выявлении определяющих и отбрасывания несуществен-
ных факторов при записи уравнений движения. Поскольку при первона-
чальной постановке задачи неясно, какие факторы надо учитывать, а
какие можно отбросить, целесообразно применять итерационную схему
решения оптимизационной задачи, с использованием последовательно-
сти усложняющихся динамических и проектных моделей.
3.1. Оптимальное управление элементами эллиптических
орбит
В соответствии с методом последовательных расширений мно-
жества допустимых состояний и управлений, задачу оптимального
управления элементами орбиты (Л, е, со, Z2, i, Ди) сформулированную в
рамках модели «медленной» эволюции орбиты (2.38), разобьем на ряд
задач меньшей сложности, сводящихся к управлению группами элемен-
тов, слабо влияющих друг на друга. Выделим две основные задачи:
• управление элементами А, е, со и положением спутника на орбите от-
носительно заданного Ди;
• управление элементами Q, i.
С использованием модели (2.34 - 2.35) можно исследовать зада-
чи оптимального управления «медленными» плоскими элементами ор-
биты на больших интервалах времени. Управление осуществляется с
помощью трансверсально направленной тяги и обеспечивает оптималь-
ное быстродействие. На каждом витке имеются пассивные участки,
суммарная продолжительность которых на витке 2а. считается задан-
ной, а их расположение на орбите произвольно. Расширим множество
Допустимых состояний и управлений, исключив из рассмотрения урав-
нение, описывающее изменение параметра Ди. Тем самые множество
допустимых Et заменится другим, более узким Е, с Е,. Сформулируем
^Дачу об оптимальном по быстродействию управлении орбитой сле-
ДУклцим образом; определить параметры £(/), которые обеспечи-
Вают коррекцию элементов А , е, со.
Проведенный в [15] анализ позволяет сделать следующий вы-
*РД- струКТура оптимального управления для рассматриваемой задачи
^лфекции орбиты должна предусматривать два рабочих участка (раз-
83
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
гонный и тормозной), центры которых разнесены на угол п по эксцен-
трической аномалии. Если на витке должен быть предусмотрен пассив-
ный участок протяженностью 2а, то два пассивных участка шириной
а должны разделить разгонный и тормозной участки. Расположение
рабочих участков на витке будем характеризовать тремя параметрами:
г/ - центр разгонного участка; £ - половина его ширины; а - ширина
одного пассивного участка. Таким образом, для оптимальной структуры
управления имеем: . Суммарная ширина пассивных уча-
стков 2а,, поэтому г]_=г) + л. После подстановки в
уравнения (2.35) получаем систему уравнений движения, описывающую
вековую эволюцию плоских элементов орбиты при оптимальной струк-
туре управления в пределах витка:
< 14 4 л [A f _ а я-А
— =— l^-acos—sinf^-P— Icos^ ; (3.1)
d t 2 ( 2)
d o 4 IA a . (. a} . n.y,
— =— —a cos—sm £ +— sm^ + ВЯ .
dt яеу,р 2 < 2 J
Эта модель движения дает достаточную точность для продол-
жительности маневра порядка 60 - 90 сут (см. рис. 3.1).
Рис. 3.1. Оценка методической погрешности модели движения (3.1)
— - численное интегрирование точных уравнений,
-— - расчет по усредненным уравнениям
С использованием формализма принципа максимума Понтряги-
на в [14] получены оптимальные законы изменения параметров управ-
ления 7^, и
84
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Чор, = «gw(v/„)-erc/g
0^Ф+ — <л,
2
Ф + — £ л,
2
где O = arccos
Ул’А
а уа а .
у/, COS — COS >7 +-COS — Sin Г)
(3.2)
(3.3)
- сопряжен-
ные переменные, соответствующие большой полуоси, ексцентриситету
и долготе восходящего узла соответственно.
Вариационная задача сведена к двухточечной краевой задаче
для системы шести дифференциальных уравнений (с учетом уравнений
для сопряженных множителей) первого порядка. Сформулированная
краевая задача решалась модифицированным методом Ньютона. На рис
3.2, 3.3 показаны результаты решения задачи управления элементами А,
е, <о для одного из вариантов граничных условий. Начальная орбита
имела параметры, лежащие в пределах: Лв=7025±60 км; е0 <0,017;
й>0=(11...83°). Параметры конечной орбиты соответствуют так называе-
мой «стабильной» солнечно-синхронной орбите с наклонением 98°.
корректирующее ускорение принималось равным а = 0,175-10"’ м/с2,
пассивный участок отсутствовал ( а = 0 ).
Анализ полученного решения позволяет установить следующее
свойство оптимальной по быстродействию коррекции орбиты: в цен-
тральном поле расположение рабочих участков относительно восходя-
щего узла орбиты не изменяется по всей траектории, т.е. ич = const.
Это свойство позволяет находить оптимальное управление в результате
решения двухпараметрической краевой задачи для системы уравнений
(3.1) без привлечения сопряженной системы уравнений.
В результате решения параметрической краевой задачи рассчи-
тываются следующие параметры управления: = const, характери-
зующий расположение середины разгонного рабочего участка относи-
Щльно восходящего узла орбиты, и £ =const , определяющий протя-
Женность разгонного рабочего участка на витке. Рассчитав по прибли-
»енной методике параметры управления для проведенных выше гра-
Крных условий, получим: 7 = 162,1°; £ = 123°; t'K = 60,45 сут. Таким
образом, приближенное решение дает погрешность по функционалу
85
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
(времени маневра) на 0,6 сут, что составляет всего 1% от общего време-
ни межорбитального перелета.
Расчет последовательного управления элементами орбиты по
схеме А —» е —* со (эффективность управления аргументом перигея уве-
личивается при малых значениях эксцентриситета) дал следующие ре-
зультаты: Г=64,44 сут из которых коррекция большой полуоси длится
10,98 сут, коррекция е - 48,39 сут, коррекция со - 5,07 сут. Таким обра-
зом, совместное оптимальное управление элементами орбиты дает вы-
игрыш в функционале для этого варианта граничных условий ~7%.
Рис 3.2. Изменение элементов орбиты для а = 0.175-10"< м/с2 на оптимальной
траектории: — для центрального поля,____с учетом несферичности Земли
Рис 3.3. Изменение параметров управления для а = 0.175- 104 м/с2 на оптимальной
траектории:-------для центрального поля,_с учетом несферичности Земли
Из рис. 3.’2, 3.3 видно, что сжатие Земли оказывает существен-
ное влияние на характеристики оптимального процесса. Минимальное
время коррекции здесь равно t'K = 67,2 сут. Зависимость co(t) представ-
ляет собой монотонную функцию, близкую к линейной. Это объясняет-
86
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ся тем, что при заданном уровне корректирующего ускорения домини-
рующим фактором, определяющим изменение со, является прецессия
орбиты, обусловленная влиянием 2-й зональной гармоники в разложе-
нии потенциала гравитационного поля Земли. Поскольку I = 98°, то
В<0, и аргумент перигея уменьшается. Как показали расчеты, для опти-
мальной по быстродействию коррекции элементов орбиты с учетом
прецессии характерно, что аргумент широты центра разгонного участка
изменяется по закону, близкому к линейному; иГ1 « + ВА~\ [12].
Следует отметить, что на изменение аргумента перигея одно-
временно воздействуют два фактора: реактивное ускорение и возмуще-
ние, обусловленное несферичностью Земли. Влияние реактивного уско-
рения является доминирующим, если
(3-4)
——J^-sin^sinT? >|ВЛ 3,5|
п е у ц 1 1
(3-5)
или
а тге15cos2 i-1
- > ---------;-------
е 8Л4
В окрестности так называемых «критических наклонений
i=63,4o и г=116,6° прецессия орбиты отсутствует, и для решения задачи
оптимизации можно использовать более простую модель центрального
поля. Для этого варианта граничных условий доминирует вращение пе-
ригея в сторону, противоположную движению по орбите (по крайней
мере, пока эксцентриситет достаточно велик). Поэтому продолжитель-
ность интервала управления в основном определяется временем, кото-
рое требуется, чтобы обеспечить выполнение граничных условий по
параметру со. На рис. 3.4, 3.5 приведены решения для другого варианта
граничных условий с учетом несферичности Земли
(а = 0.175-10-4 м/с2).
Оказалось, что для всех вариантов закон изменения большой
полуоси А близок к линейному; координаты разгонного участка при-
мерно на % интервала управления практически не изменяются (здесь
управление воздействует на параметр е), а затем - резко изменяется,
способствуя изменению со. Аргумент перигея сначала изменяется по
почти линейному закону под действием прецессии, но в конце перелета
изменяется нелинейно, с учетом совместного воздействия тяги и пре-
цессии. Эксцентриситет е на большей части траектории уменьшается
по закону, близкому к линейному, а в конце стабилизируется около ко-
нечного значения.
Оказалось также, что введение на витке определенным образом
87
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
расположенного пассивного участка (что может быть продиктовано
техническими соображениями, связанными, например, с недостатком
энергии) незначительно увеличивает время маневра. Это объясняется
тем, что при коррекции параметров е, а на витке имеются участки, где
воздействие управления на эти параметры неэффективно, и выключение
двигателя здесь слабо влияет на продолжительность маневра.
Рис 3.4. Изменение элементов орбиты на оптимальной траектории
Рис 3.5. Изменение параметров управления на оптимальной траектории
Ряд решений задач оптимизации был получен для сравнительно
больших изменений А порядка (300-700 км). С увеличением АЛ суще-
ственно меняется характер оптимального управления, в частности ши-
рины разгонного 'участка £. Параметр не остается постоянным, а
изменяется, достигая для некоторых вариантов табличного значения тс
или 0 (это означает, что граничные условия по е и (о уже выполнены и
управление воздействует лишь на величину большой полуоси.
88
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
3.2. Приближенный метод расчета энергетики маневра и
параметров управления элементами орбиты
Управление элементами А,е,<о. Рассмотрим сначала движе-
ние в центральном поле тяготения с учетом влияния сопротивления ат-
мосферы. Вектор управлений для этой задачи включает в себя функции
£(t), 4(0- Из условий принципа максимума Понтрягина с учетом огра-
ничения 0 < £ + а‘< л найдено оптимальное управление (3.2), (3.3).
Качественный анализ результатов расчетов серии краевых задач
показал, что для большой группы граничных условий оптимальные за-
коны управления ^,(0, 77^(0 можно аппроксимировать постоянными
значениями g=const, rj=const. В математической модели движения
(2.35) пренебрежем членами содержащими малый множитель е. Учиты-
вая малость изменения большой полуоси (ДЛ«Л0) на интервале
управления, можно теперь проинтегрировать первые три уравнения сис-
темы (2.35). В результате получим три уравнения для требуемого изме-
нения орбитальных параметров с тремя неизвестными tK] [15]:
(3.6)
где Аа, = Ак - 0,5ЛЛо , А^,е0,а0 - значения большой полуоси, экс-
центриситета и аргумента перигея на начальной орбите. В (3.6) учиты-
вается изменение большой полуоси от действия атмосферы, а также
смещение перигея вследствие нецентральность гравитационного поля
Земли, которое определяется зависимостью:
Лл> ^(Scosa/~1X^-Лр-4)
g 1б[а/Л0'5(2£ +а-л)-яорр°‘5Аёр]’
Из системы (3.6) можно определить половину ширины разгон-
ного участка £,/
а ( ст А
ЛА cos—sin £ Н— I cos ту,
f + +------2_1-----2)-----
1 2 2 2аАСР ЛеАСР
89
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
которое уточняется с помощью итерационной схемы Ньютона
(CW+£_£_^_Asin^(0 + £>|
2 2 2aA_f V* 2)
l-*cos|£(<)+—|
I 2 J
(3-9)
* . а
ДА COS — СО5Т);
где к =-------—------, i - номер итерации. Как показал анализ, при
АеЛс;
определении можно ограничиться тремя-четырьмя итерациями, если
в качестве нулевого приближения выбирать значения:
^ = л/4-а/2 При ДА<0 или = Зя/4-а/2 при ДА>0.
Расположение рабочих участков на витке относительно перигея
определяется из третьего уравнения системы (3.6):
= arctg
А®,
, sign(cosr]l)= sign&e,
(3.10)
In 1 + —
.К е° Л
Здесь Аюо учитывает изменение аргумента перигея только от
трансверсального реактивного ускорения. При этом расчет необхо-
димо проводить итерационно совместно с расчетом .
Зная величину , продолжительность маневра коррекции мож-
но определить из первого уравнения системы (3.6):
" +а-л)~ '
Для затрат характеристической скорости Wxl при условии не-
прерывной работы двигателей (а = 0 ) получим
4М Г7~ 1+
4sin£ |Лр[_
На рис. 3.6 показана зависимость (3.12), в виде изолиний «при-
(З.П)
Лч2
1п2(1+Д^е0)
(3.12)
веденной» характеристической скорости
И\ в ко-
ординатах Л®„ и Ae/e0 . Полученная зависимость является универ-
сальной и может быть использована на стадии проектно-
90
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
баллистических расчетов при определении затрат рабочего тела на ма-
невр коррекции. По существу это изолинии функции «будущих потерь»
- критерия оптимальности W в задаче оптимизации плоских маневров в
центральном поле.
Для нецентрального гравитационного поля величина изменения
аргумента перигея Ла должна быть уточнена с помощью поправки
ztogfeX где начальное приближение для продолжительности маневра
tKI рассчитывается по формуле (3.11), а затем уточняется итерационным
методом. В табл. 3.1 приведены результаты расчетов, иллюстрирующие
точность приближенного метода.
Рис. 3.6 Изолинии затрат характеристической скорости для маневра коррекции А,е,а
Таблица 3.1 Оценка точности приближенного метода расчета энергетики манев-
ра и параметров управления с учетом нецентральности гравитационного поля Земли.
Исходная работа Конечная о □бита а, м/с2 10*5 /, град Приближ. методика Краевая задача
Ло, км е0 <Уо, град Лк. км «К &к. град град град W "t' м/с град *7. град м/с
7080 .0213 29 7030 .0013 69 1.7 98 71.3 196.6 130 714 196.5 129.1
6980 .0213 109 7030 .0013 69 1.7 98 108.8 210.0 142.2 107.2 210.3 141.2
7080 .0213 109 7030 .0013 69 1.7 98 71.3 210.6 1434 73.2 210.1 142.8
6980 .0213 29 7030 .0013 69 1.7 98 108.8 197.0 128.4 108.9 196.6 128.3
6970 .020 70 7030, .0015 30 2.0 98 109.4 148.9 109.5 - 149 1
6970 020 70 7030 .0015 30 8.0 98 113.8 121.1 114.1 - 120.8
676]_ 6761 .010 40 6791 .002 0 2.0 62 114.8 210.4 61.2 II4.8 210.7 61.5
.010 40 6791 .002 0 6.0 62 115.7 205.6 59.41 115.8 205.9 59.3
6691_ 6691 .012 0 6721 .002 30 2.0 51 104.2 104.9 104.7 - 105 5
.012 0 6721 .002 30 6.0 51 113.0 192.5 67.05 113.0 192.8 67.39
Зависимость характеристической скорости Wt от а для некото-
рых классов маневров показана на рис. 3.7. Здесь высота базовой орби-
91
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ты составила 660 км, ликвидировалась погрешность в величине боль-
шой полуоси порядка 60 км, отклонения от эксцентриситета — до 0,02,
диапазон корректируемых отклонений аргумента перигея и фазового
угла не ограничивался. Сплошная горизонтальная линия на графике
соответствует модели центрального поля (опорное решение). Расчет с
учетом нецентральное™ гравитационного поля Земли (показан точка-
ми) приводит к зависимости затрат характеристической скорости не
только от приращений элементов орбиты, но и от уровня реактивного
ускорения. Уточнение энергетики маневра при выполнении гра-
ничного условия по угловому положению спутника приводит к допол-
нительным затратам, зависящим от уровня реактивного ускорения. При
достаточно малых а (случай многовиткового относительного движе-
ния) они пренебрежимо малы; с увеличением реактивного ускорения
дополнительный расход на фазирование увеличивается.
Рис. 3.7. Зависимость характеристической скорости маневра
от величины реактивного ускорения для различных моделей движения:
__- модель центрального поля тяготения, • - учтены возмущения от нецентральное™
гравитационного поля, х - учитывается граничное условие по угловому положению
Управление элементами Я, i. Медленное изменение долготы
восходящего угла (1 и наклонения орбиты / под действием постоянного
бинормального ускорения описывается последними двумя уравнениями
системы (2.30). Углы /2и / изменяются под действием £(J).
Будем аппроксимировать оптимальный закон управления £ за-
висимостью (,-const. Тогда при монотонном изменении параметров
движения на интервале управления t е [0,/д] из последних двух уравне-
ний системы (2.30) можно получить [15]
А. ./ т . 2дз [A (J г
Д» = 'V * ) - 'о =-Л ~ cos - cos ,
71 у Ц L
92
Глава 3 Прикладные задачи оптимизации перелетов с малой тягой
iB + А/ /-
tg~^~L ° 2
etk [sin(i0 + A/) - sin i0 ]
Л5,5А/7Д
где i0, Qo - начальные значения наклонения и долготы восходящего
узла, причем AQ учитывает смещение линии узлов вследствие прецес-
сии. Используя (3.13) положения рабочего участка положительным би-
нормальным ускорением можно определить как
АП
+ arctg —,
AQ = Q(rJ-Q0 =
'о I Р г
ctg— I cos у sin -
(3.13)
AQg
Vad2 +b2
sign cos = signAi,
, , ( i0 + Ai
где b = Inl/g 2 i.o 2 .
£ = arcsin
(3.14)
АО - g4in(<o+Ap-sin/o
g 7 ’ g ~ В
' 2а, Л4 cos—
2 2
Здесь АП* — приращение Q и вследствие прецессии от нецен-
тральности гравитационного поля Земли. Необходимо также учитывать
неоднозначность определения параметра £ из (3.15) так как в качестве
АП можно брать как значение AQ=Q-&0+27msign(Qk-&a), так и АП=£?Г
£20 -27msignCQk-U0) (4&к - заданное конечное значение долготы восхо-
дящего узла, (ПА - По) е [- п = 0,1,2,...). Это обусловлено тем, что
долгота восходящего узла может совершать несколько оборотов вокруг
притягивающего центра и что возможны два способа формирования
управления: а) действие бинормального реактивного ускорения совме-
стно с действием второй зональной гармоники; б) «противодействие»
гравитационным возмущениям. Окончательно выбирается значение £,
для которого существует решение (3.15) |AQJ=|/2-£^| и наименьшее, что
соответствует наименьшим затратам характеристической скорости Wj.
Получим формулу для затрат характеристической скорости на
маневр Wj. при условии непрерывной работы двигателей (Р=В). Jipa
этого перепишем уравнения (3.13) в виде
«о+А/ t i0 .
ctg^ sin
AQ„ =AQ-AQg
Выразим W2 из этих уравнений
(3.15)
93
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
= £
1+-------
In2 tg
АО2
AQ^sin2/^
М1
'о+А« . »0
-----dg —
2 2
(3-16)
На рис. 3.8 зависимость (3.16), представлена графически в виде
„ - 2
ИЗОЛИНИЙ IV 2 =--------
п sin/.
• W2 = const в координатах Д£2а и
А/ sin 1 iCP. Полученная графическая зависимость является универсаль-
ной (не зависит от конкретного вида граничных условий) и может быть
использована на стадии гфоектно-баллистических расчетов при опреде-
лении затрат рабочего тела на маневр коррекции для конкретного вида
двигательной установки малой тяги.
Рис. 3.8. Изолинии затрат характеристической скорости для маневра коррекции £2,/
Из формул (3.12, 3.16) можно получить аналитическое выраже-
ние для оценочной функции <р
- (О) - (0) - (0)
<р (х,г)=^! (я,е,®)+р2 (/,п), (3.17)
где первое слагаемое соответствует приближенному решению задачи о
минимуме характеристической скорости плоского межорбитального
маневра
94
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
а второе - приближенному решению задачи оптимального поворота
плоскости орбиты
На основе зависимостей (3.17 — 3.19) проводится оценка допус-
тимых управлений u(t,x) согласно схеме, описанной в главе 1.
3.3. Задача наведения КА в расчётную точку орбиты
Рассмотрим таперь межорбитальный переход в заданную точку
орбиты, то есть потребуем выполнения граничного условия по парамет-
ру дй е [- я-, я], характеризующему текущее положение спутника отно-
сительно точки выведения (условие «фазирования»).
Одним из способов приведения КА в расчетную точку орбиты
является так называемый пассивный способ, который сводится к выбору
оптимального начального положения КА Аи0 на исходной орбите и
расчету времени ожидания. Выбор Аи0 проводится с учетом того, что
КА в своем относительном движении совершает N оборотов:
Ап0 - u(t0 )-ик = Аик - Ф 4- 2лЕ
Ф
’
где [ ] - оператор выделения целой части, Ф = 3/2 -/1^3/2) dt -
полная угловая дальность маневра.
Численное решение задачи «фазирования» основано на приме-
нении формализма принципа максимума Понтрягина к системе, движе-
ние которой описывается дифференциальными уравнениями (2.30) и
осложняется неединственностью решения. Многоэкстремальность про-
блемы оптимизации является следствием различного числа оборотов,
которые может совершать КА в своем движении относительно расчет-
и°й точки. Поэтому в качестве опорного бралось решение задачи на
расширенном множестве Ег (без учета граничного условия по Aw),
затем определялось минимально возможное число относительных обо-
ротов N, и окончательно искалось решение, отличающееся от N не более
чем на один оборот.
В частном случае, когда задача наведения в расчетную точку
95
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
орбиты формулируется как задача управления только параметрами (А,
Ли ) приходим к решению граничного типа ( = (О, я-), с одной точкой
переключения). Такая структура обусловлена поведением функции пе-
реключения \р А.
Рассмотрим задачу наведения спутника в заданную точку орби-
ты для случая малого эксцентриситета е. Здесь в качестве парамет-
ров движения можно считать только большую полуось А и относи-
тельное положение спутника на орбите, определяемое параметром Aw,
изменение которых описывается системой (2.37) [15, 18].
С использованием формализма принципа максимума Понтряги-
на для задачи оптимального, с точки зрения быстродействия управления
элементами Л и Aw было получено, что оптимальная структура управ-
ления содержит не более одного разгонного £ = тг и одного тормозного
£ = 0 участков на витке. Тогда оптимальное управление характеризует-
ся параметрами: tK - момент окончания маневра, tn - момент переклю-
чения тяги, £0 = {О, я} - параметр, характеризующий направление тяги
в начальный момент движения, которые могут быть получены из совме-
стного решения уравнений для А и Ли системы (2.37) в виде
(3.20)
Подставляя текущее значение большой полуоси во второе урав-
нение системы (2.30) и интегрируя его, имеем следующее соотношение
для определения йремени переключения направления тяги:
Aw + 2^% ---тх (3.21)
2аД2&-я-)
где Aw = AwK - Aw0 + 2ли, п - число витков в относительном движении
(в общем случае неизвестно, выбирается, чтобы обеспечить наименьшее
tK ). Зависимости АЛ( tK ) и Aw( tK ) определяютя соотношениями:
AA = At
- + ^=^(^-2^,,))
At я^р
(3.22)
96
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Ли = _ (2£o-ffMc,)Y _
^*’а1 2а,(2£0 -Я-) ^Д, —ЛА 7Гу[р
- 0,5л;1 - 0,5(Л„ - АЛ) 2 (3.23)
и позволяют построить изолинии затрат характеристической скорости
Wt на поле ЛА, Ли . На рис. 3.9 представлены эти линии уровня для
Ак = 7030 км и а, = 2 • 10~5 м/с2.
Рис. 3.9. Области достижимости в отклонениях по большой полуоси и аргументу широты
(а = 2 • 10-5 м/с2). Показана одна из траекторий приведения КА в начало координат
(_-£ = *,___________________________-^ = 0)
Рассмотрим теперь задачу наведения в заданную точку эллип-
тической орбиты. В [15] предложен приближенный метод расчета
управления, позволяющий обойти трудности численного поиска реше-
ния многоэкстремальной вариационной задачи. Пусть спутник в своем
движении относительно расчетной точки конечной орбиты совершает
более одного витка и решена краевая задача перехода на орбиту с эле-
ментами Ai,ek,cot. Будем рассматривать это решение как решение ис-
ходной задачи управления элементами А, е,со, Ли на более широком
множестве допустимых режимов (без учета граничного условия по.
Очевидно, при этом значение продолжительности маневра ttl (или ха-
рактеристической скорости И2;), можно рассматривать в качестве ниж-
них границ функционалов исходной задачи.
На рис. 3.10 показаны результаты решения задачи для базового
варианта граничных условий перелета: при этом принималось, что
Мо) = О, Аи(т) = я. Видно, что при неизменной оптимальной про-
97
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
грамме r](t) происходит перераспределение ширины «разгонных» и
«тормозных» участков: в начале маневра g<^°\t), а в конце
£ > (здесь озгачает программу, полученную для тех же
граничных условий без учета координаты Ан). Общее время маневра
при этом увеличивается на 5,1 суток.
Рис. 3.10. Параметры управления в задаче формирования орбиты (базовый вариант).
------------без коррекции углового положения КА,__- с коррекцией
Изменим .незначительно программу управления £(0 следую-
щим образом: введем приращение A £(/), малое по сравнению с £ и,
считая отклонения элементов 8А,8е,&о, вызванное такой вариацией
управления, малыми, линеаризуем исходные уравнения; программу
Fj(t) оставим без изменения. Тогда линеаризованные уравнения для
отклонений 8А и &\и примут вид (а=О)
— = dteu = _ 3 (3.24)
dt л\ ц ' dt
Найдем приращение обеспечивающее выполнение гранич-
ных условий по угловой координате Aw и отклонению большой полуоси
от номинальной траектории 8&u(tk) - Q,8A{tk) = 0. Введем замену пере-
менных. Обозначим
8А. = 1^84 , 8и. = S-Z»Aw . (3.25)
При такой замене система уравнения (3.24) примет вид
^^- = Д£, -^- = <54. (3.26)
dt dt
98
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Система уравнения (3.26) представляет собой каноническую
модель линейной системы второго порядка, содержащую управление
д£(0. (А£ е [-А^га,+А^т], где А£т - параметр). Цель управления: пе-
ревести систему из начального состояния &4,(to) = O, в <5и,(/о)*О в
конечное М(4) = 0, <5u.(/t) = 0. Нетрудно найти решение этой вспо-
могательной задачи в форме синтеза
А£ = -Assign 8и, +~^ . (3.27)
2£»
Структура управления в данном случае релейная и имеет одну
точку переключения с -Afm на +А£т или наоборот, поэтому для реше-
ния задачи необходимо выбрать знак управления в начальный момент
£(/0), момент переключения t„ и момент окончания маневра /*. Пусть в
первом приближении при многовитковом относительном движении мо-
мент tk определяется из решения задачи без учета углового положения:
4= 4/- Тогда момент переключения находится из уравнений (3.26) как
t„=O,5tk. Знак приращения управления в начальный момент определяет-
ся из (3.27) signA^(t0) = signAu{0}(tkl),где signAu(0}(tki)значение фазо-
вого угла, характеризующего положение спутника относительно конеч-
ной точки в момент /*, при номинальной программе управления (конеч-
ный промах). Результаты расчетов для такого управления и различных
вариантов граничных условий представлены в табл. 3.2.
Таблица 3.2.
№ вар Аи0 д«(о) (/*>)> град 4/> сут А^о) > град град град сут
1 0 104,23 86,065 1,586 -1,330 3,05-10"6 0,265 86,090
2 180 -3,097 94,610 - 0,039 0,063 -6,010-’ 0,033 94,623
3 20 - 36,90 35,664 -2,764 0,699 9,0-Ю"6 0,154 35,696
5 30 55,31 39,059 2,279 -1,037 6,710-* 0,177 38,994
3-4. Оптимальное управление относительным движением
космических аппаратов с двигателями малой тяги
Представим исходную задачу, описанную моделью (2.42) в виде
последовательности менее сложных задач, допускающих аналитические
решения.
Система (2.42) с помощью замены х, =Г|-1(дг + Л]‘ДГи),
= —}(Дч-2Л11г1',дкг), г = Л,г приводится к канонической форме, ис-
пользование которой позволяет получить решение задачи об оптималь-
99
Глава 3 Прикладные задачи оптимизации перелетов с малой тягой
ном по быстродействию переводе системы (2.42) из произвольного на-
чального состояния в начало координат:
ах = —а • sign
(3.28)
Структура оптимального управления содержит лишь одно пере-
ключение. Для этого случая имеем точную оценку продолжительно-
сти маневра ( ДК, = О и ДКИ = 0 ), являющуюся по существу функцией
будущих потерь
Для продольного относительного движения характерным явля-
ется наличие периодических и вековых составляющих. При отсутствии
возмущений один аппарат будет двигаться относительно другого в
плоскости ( Аг, AZ ) по эллипсу, центр которого смещается с постоянной
скоростью. Параметры, характеризующие смещение эллипса и размер
его полуоси, можно считать вековыми, а характеризующие положение
КА на эллипсе - периодическими [18].
Введем переменные: Д г9 - среднее смещение вдоль радиуса;
Д!^, - среднее смещение вдоль орбиты; I - малая полуось эллипса
относительного движения КА в плоскости орбиты; 1г - амплитуда вза-
имных колебаний аппаратов в боковом направлении; <р , <р г - углы,
характеризующие положения КА на эллипсе относительного движения.
Дифференциальные уравнения относительного движения примут вид:
• 2 *3 2
Л.гср=—ах, Л.ЬсР =— ЯЛлл--аг,
Л Х 2 Ч А
(р = Я +—(ак cos <р-2ах sin <р),
Я/
/ = ^-(ar sin (р + 2ах cos<р],
Л
• 1 • , 1 .
I, =y«zcos^, <р, = Л —— a2sm<pz.
Л Al
Для системы (3.30) получено оптимальное по быстродействию управле-
ние для совместного изменения элементов продольного движения:
(3.30)
100
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ta - +y/<sin<g+/ ly/t>cos<3 (3 31)
°р‘ 2ц/r + 2y/t costp- 2Г1ц/9 sin <р
Стратегия управления вековыми и периодическими составляю-
щими состоит из следующих этапов с соответствующими граничными
условиями:
• управление вековыми составляющими Агср и AZc/) = тт-^^,
• коррекция амплитуды боковой составляющей относительного движе-
ния: /,(<*)= О,
• коррекция амплитуды периодической составляющей
Arq,(rJt)=O, ДДГд,(г4)=0,г AZ,g,(rJ=O.
Некоторые иллюстративные результаты имитационного моде-
лирования по этой стратегии представлены на рис. 3.11, где для ряда
расчетных случаев показана пространственная траектория относитель-
ного движения и ее проекции на продольную и боковую плоскости [18].
Рис. 3.11. Результаты моделирования
Перейдем теперь к задаче оптимизации проектных парамет-
ры
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ров маневрирующего КА. Представим полную массу активного КА в
виде суммы масс отдельных его компонентов в соответствии с массовой
моделью, описанной в главе 2. В качестве критерия оптимальности бу-
дем использовать относительную массу полезного груза
д = = 1 _ а рай - -^(1 + у) .
w0 2 с
Стратегию гарантирующего управления выбираем в следующем
виде. Пусть КАП находится в заданном диапазоне смещений вдоль ор-
биты с отклонением по среднему радиусу Дг ф 0. Активный аппарат в
относительном движении эволюционирует, смещаясь вдоль орбиты
(рис. 3.12). В точке «1» ( Ы = Д£и ), находящейся внутри заданного диа-
пазона, включается двигательная установка аппарата, и он переводится
в точку «2» с гарантированным изменением знака Лгс/,. После этого
КАЦ начинает дрейфовать в противоположную сторону. В точке «3»
( л/. = ) тяга двигателей включается на торможение и КАП переходит
на орбиту с меньшим, чем у пассивного аппарата средним радиусом.
Затем процесс повторяется. В процессе дрейфа, при необходимости,
осуществляется коррекция полуоси эллипса взаимного движения.
Рис. 3.12. Управление относительным движением
Ставится задача определения проектных параметров ( ав, с) ма-
неврирующего КА, осуществляющего функцию «сопровождения» пас-
сивного КА. Весь процесс управления разделяется на этапы формирова-
ния заданного относительного положения продолжительтостью ТФОрм и
поддержания заданного относительного положения продолжительно-
стью Тп, причем Тп» Тформ-
Проведено моделирование работы алгоритмов управления на
различных режимах полета. Выбор оптимальных параметров, опреде-
ляющих проектный облик КА, будем проводить поэтапно, используя на
каждом следующем этапе более полную и точную модель объекта син-
теза. Результаты изменения проектных и баллистических характеристик
102
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
по итерациям для орбиты со средней высотой 660 км приведены в табл.
3.3. Для завершения процесса синтеза оказалось достаточно 3 итераций;
при этом критерий оптимальности // изменяется не очень существенно
(на З...6%), но основной проектный параметр а0 меняется на 10-12% по
сравнению с первоначальным значением.
Таблица 3.3. Изменение оптимальных параметров по итерациям Ак = 7030 км, i = 98° ;
= ±60 КМ, Детах=0,02, 7’иг = 104 час, 7’форм ^31=30 сут, 4^= 1,2 км,
Л/.*^ =125 км, Уэу=50 кг/кВт, уду=48 кг/Н, успх=0,05
Итерации Расчет энергети- ки манев- ра по верхней оценке W Центральное грав. поле. «Иде- альный» пре- дельный цикл поддержания Аг^ =1.5 км, =150 КМ Учет несфе- ричности Зем- ли. Синтез циклограммы с учетом ампли- туды колебаний Численное моделир. динамики движения и процесса управления
а„ 10s, м/с2 9,91 10,72 8,08 8,08
с, км/с 38,7 38,9 38,9 38,9
д 0,85 0,83 0,803 0,817
Продолжительность формирования /форм, сут 18,0 17,6 19,8 19,7
Число коррекций, п (Г„=1сут) - - 2 2
Моторное время этапа поддержания Т мт, час 9570 9580 9574 9163
Общее число включ. ЭР Д, Пвкл 2129 2303 2166 2220
Средняя продолж. одного включения, А/ вкл, час 4,49 4,16 4,42 4,13
Средняя прод. паузы, А/ п, час 16,1 14,87 15,82 15,61
3.5. Расчет оптимальных перелетов между орбитами с
большими эксцентриситетами
В [16, 17] с использованием моделей движения (2.39, 2.42, 2.43,
‘•46) подробно рассмотрены оптимальные с точки зрения минимума
характеристической скорости перелеты между орбитами с большими
эксцентриситетами. Для трансверсальной ориентации вектора тяги было
Показано, что оптимальная структура управления на витке должна со-
юз
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
держать не более двух активных участков разного знака, разделенных
равными пассивными участками.
Функция включения тяги S определяется следующим образом
S = {sig4(E - Ч - £ - а\Е - т] - 2 л + а + £)]-
(3.32)
где f - протяженность в угловой мере половины разгонного участка; а -
протяженность в угловой мере одного пассивного участка; ч - угловое
а) б)
Рис.3.13. Оптимальные параметры управления и изменение оскулирующих элементов
для перехода на высокоэллиптическую орбиту
Проводилось численное решение оптимизационных задач прин-
ципом максимума Понтрягина для свободной и трансверсальной ориен-
тации вектора тяги. На рис. 3.13.а и 3.13.6 представлены результаты
решения задачи о переходе КА с низкой круговой орбиты на орбиту
спутника «Молния» при трансверсальной ориентации вектора тяги для
трех различных значений общего времени перелета.
Рис. 3.14. Области достижимости для начальной орбиты с параметрами А-26621 км, e-OJ'*-
-----свободная ориентация вектора тяги, - трансверсальная ориентация вектора тяги
104
Г пава 3. Прикладные задачи оптимизации перепетой с малой тягой
Полученные решения позволили также построить для ряда бал-
листических задач области достижимости при фиксированных затратах
характеристической скорости.
Для орбиты спутника «Молния» построены области корректи-
руемых параметров в координатах большая полуось - эксцентриситет.
Показано, что выигрыш в характеристической скорости при свободной
ориентации вектора тяги по сравнению с трансверсальной ориентацией
может достигать 10% (рис. 3.14).
3.6. Задача коррекции орбиты спутника Земли с учетом не-
определенности силы сопротивления верхних слоев атмо-
сферы
Как уже отмечалось, особенностью движения ИСЗ на низких
орбитах является неопределенность возмущающей силы аэродинамиче-
ского сопротивления, обусловленная неточностью знания баллистиче-
ского коэффициента спутника и плотности атмосферы [23]. Для оценки
возмущающего ускорения использовалась изотермическая модель плот-
ности, где высота однородной атмосферы Н изменяется в зависимости
от уровня солнечной активности, а баллистический коэффициент в за-
висимости от текущего аргумента широты и .
Л
Средняя за виток величина реактивного ускорения а, компен-
сирующего влияние аэродинамических возмущений, определяется пу-
тем взятия интеграла от |/о| на интервале, равном периоду обращения.
Результаты расчета а для <тх =0.002 м2/кг приведены в табл. 3.4.
В [24] получены приближенные аналитические решения для
расчета параметров «корректирующего импульса», создаваемого двига-
телем малой тяги. Показано, что одновременная коррекция большой
полуоси и перигейного расстояния при одном активном участке на вит-
ке принципиально возможна в ограниченной области параметров, ха-
рактеризуемой отношением корректируемых ошибок.
Твб; gua 3.4. Результаты расчета среднего «компенсирующего» реактивного ускорения
Параметр высота перигея #,.км ы орбиты высота апогея, На , км Минимальный уровень солнечной активности fro=7510-“ -4^-1 м Гу) Максимальный уровень солнечной активности (\ = 250 1(Г“ -^-1’ ( мГц) Л « , ая-10 м/с
250 350 0.68 1.556
350 350 0.035 0.325
105
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Рассмотрим более подробно коррекцию элементов орбиты
трансверсальным реактивным ускорением ( а = const, a = 0 ). Исследу-
ем принципиальную возможность одновременной коррекции двух эле-
ментов орбиты при одном активном участке на витке. Для примера рас-
смотрим одновременную коррекцию оскулирующего периода Т и пе-
ригейного расстояния гя. В этом случае необходимо решить систему
уравнений относительно £ и т]:
[(4 - е0 )^] - 4sin£cos?7+-у sin2£ cos2^,
ДГ = 12лф’^/АлД1-е02У. (3.33)
Выражая ускорение из (3.29) после преобразований получим
£ = В (4-e0)£-4sin£cos77 + -^-sin2£cos27; ,
где В =------является функцией отношения корректируемых ошибок.
4Агх
Тривиальное решение £ = О соответствует отсутствию коррекции.
Если параметр В известен, то можно определить предельную
координату середины активного участка т]ПРЕД , при которой коррекция
таких ошибок возможна:
(3.34)
1
пред ~ arccos
Le<>
Показано, что одновременная коррекция оскулирующего перио-
да (большой полуоси) и перигейного расстояния при одном активном
участке на витке принципиально возможна в ограниченной области па-
раметров, характеризуемой отношением корректируемых ошибок. Если
В < %, такая коррекция невозможна. Если Be—, '
Leo
, располо-
4-е0
жение активного участка должно выбираться в области cos г] < cos 7..
Этот результат легко объяснить следующим образом. Если соотношение
между корректируемыми ошибками таково, что преобладает ошибка по
большой полуоси, то активный участок следует располагать ближе к
перигею, чтобы большая ошибка АЛ ликвидировалась за счет увеличе-
ния апогейного расстояния. Если же преобладает ошибка в перигейном
расстоянии, то целесообразно исправить ее, располагая активный уча-
сток ближе к апогею. Это хорошо согласуется с известными результа-
рлава 3. Прикладные задачи оптимизации перелетов с малой тягой
тами по импульсной коррекции эллиптических орбит. Наконец, если
ошибка в перигейном расстоянии превосходит некоторый «критиче-
ский» уровень по отношению к ошибке АЛ, то решение задачи в рам-
ках одного активного участка невозможно.
Рассмотрим теперь задачу выбора универсальных параметров
двигателя малой тяги, предназначенного для поддержания низкой ор-
биты спутника Земли [25]. Задачу поддержания орбиты будем форму-
лировать как задачу ликвидации вековых возмущений периода обраще-
ния Т, возникающих из-за действия силы аэродинамического
сопротивления.
Весь интервал управления разобьем на Y равных частей, каждая
из которых состоит из т пассивных и п активных витков. На на актив-
ных витках ЭРД создает постоянное по величине реактивное трансвер-
сальное ускорение aj. В результате за (т+п) витков период обращения
восстанавливается с некоторой избыточностью (рис 3.15).
Рис. 3.15 Циклограмма включения ЭРД при поддержании периода обращения (т=5, л=1)
В качестве критерия оптимальности выберем относительную
полезную массу р, а оптимизируемыми параметрами ЭРД будем счи-
тать скорость истечения рабочего тела с и реактивное ускорение щ. В
работе [25] предложен метод выбора ограниченного числа з двигатель-
ных установок малой тяги, предназначенных для гарантированного
поддержания некоторого множества орбит Y. Орбита характеризуется
высотой перигея hx, высотой апогея ha и наклонением i.
Систему двигательных установок Г= {рь р2,..., ps} будем считать
универсальной для поддержания диапазона орбит Y, если:
• система двигателей Г может решить задачу поддержания любой орби-
ты yeY,
максимальная степень неоптимальности для любого двигателя систе-
мы Минимальна (см. гл. 1).
Величина
107
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
max//(y,p,vH)
р(у,р')=-Ч—г-Г" (3-35)
P\y,P,vB)
характеризует степень неоптимальности двигателя с параметрами р’,
поддерживающего орбиту у при высоком уровне плотности (v = vB),
по сравнению с двигателем, специально спроектированным для выпол-
нения этой задачи при низком уровне плотности (v = vH ).
За цикл коррекции управление должно полностью компенсиро-
вать действие возмущающей аэродинамической силы. Уровень реактив-
ного ускорения а/, необходимый для поддержания орбиты:
а, = а,(Лж,и) = l2(w.+ $7 <ST(^,v) (3.36)
24тггпА3^А(1-е2)
Характеристическая скорость на маневр составит
|2(/и + л)-1 lu-Jx"
=WK^,V) = - 7 -W) (3.37)
24№иЛ3 у] Л(1 - е2 )(т + л)
Оптимальное значение скорости истечения при коррекции пе-
риода обращения определяется только циклограммой работы двигателя
и не зависит от орбиты и внешних условий полета. Это существенно
облегчает решение задачи универсализации, так как позволяет выбрать
скорость истечения, оптимальную для всего множества орбит Y.
Конкретизируем выражение для степени неоптимальности
(3.35). С учетом выражений (3.36), (3.37) получим
(3.38)
1-J/c-y—
2
где d = ~^+г^з 1цК3 /2п(т + л)л(1 - ег). (3 39)
Максимальное значение функции р при гарантированном вы-
полнении диапазона задач Y зависит от границ области Y и будет равно
р= max Ah„a,c)^ X~dSr^\. (3.40)
^жЧ^гпшЛгш»] | _ J J
Изменение периода на одном витке пропорционально величине
баллистического ах, зависит от плотности атмосферы и параметров
орбиты. Для расчета падения периода обращения на одном витке
^(Л^) можно использовать аналитические аппроксимационные фор'
мулы.
108
рлава 3. Прикладные задачи оптимизации перелетов с малой тягой
На рис. 3.16 приведены «предельные» зависимости: 3T„(h^) со-
ответствует минимальной плотности атмосферы, a STa(h^ - максималь-
ной плотности атмосферы, полученные путем обработки результатов
численного моделирования движения ИСЗ с использованием модели
плотности по ГОСТ 22721-77 и соответствуют баллистическим коэффи-
циентам стх=0,001 м2/кг и стк=0,002 м2/кг, высоте апогея Ла=35О км и на-
клонению i=51 °.
Рис. 3.16. Границы изменения периода обращения на одном витке
В рассматриваемом примере минимальная гарантированная сте-
пень неоптимальности F® = 1,0696 при применении двух разнотипных
ЭРД. При этом весь диапазон высот перигея разбивается на два поддиа-
пазона. При hx е [160, 173] км двигатель первого типа должен обеспе-
чить реактивное ускорение а, = 7,9-10"“ м/с2, при hn е[173, 240] км
двигатель второго типа должен обеспечить реактивное ускорение
°2 = 6,22 • 104 м/с2. Оптимальное значение скорости истечения для рас-
смотренного примера равно с^, - 36,25 км/с. Отметим, что при исполь-
зовании для всего диапазона маневров одного типа двигателя, распола-
гающего реактивным ускорением а, = 7,9 10 4 м/с2 степень неопти-
мальности равна F® = 1,091. В результате анализа оказалось, что даль-
чейшее увеличение числа двигателей s > 2 практически не уменьшает
^рантированную'степень неоптимальности.
109
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
3.7. Задача оптимального набора параболической скорости
и торможения КА с учетом ограничений на угловую скорость
поворота вектора тяги
Рассмотрим задачу об оптимальном управлении траекторным и
угловым движением КА при межорбитальных перелетах [26]. Вектор
состояния х включает в себя компоненты (г, V, в, &, и). Здесь &
- угол между вектором тяги (ось OXt КА) и трансверсалью. Вектор
управления и - компоненты (б, Q), причем <У = {-1, 0, +1} - функ-
ция переключения двигателей, -Пти < Q < Пт|х - угловая скорость
поворота вектора тяги, ограниченная значением .
В качестве критерия оптимальности примем время перелета
Плоское движение КА с постоянной по величине тягой в цен-
тральном поле описывается системой дифференциальных уравнений:
. Kcos0
и —-----,
г = V sin в,
г =2^4
——— cos(i9 - 0),
l-o0r/c v ’
COS0 V2 1 ' +——— sin (.9 - б), l-aot/c
V 1r г)
(3.41)
Используя формализм принципа максимума Понтрягина, полу-
чено оптимальное управление:
-signVa,
(3.42)
где y/s - сопряженная переменная. Если 0, структура управления
содержит особый режим:
= {яо>{яо>^}} = L. ^8sin.9-r^f cos .9
{^5 > }} r
В данном случае особый режим имеет простой смысл. Это ре-
шение первого порядка для той же задачи, но без учета одной диффе-
ренциальной связи, т.е. на некотором расширенном множестве EzjD -
Если оно оптимально на Е, то оно оптимально и на множестве D.
Следовательно, особый режим должен быть включен в состав
искомого решения, структуру которого естественно представлять из
трех участков:
по
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
• движение из начальной точки в фазовом пространстве до особой по-
верхности;
• особый режим;
• сход с особой поверхности и достижение конечной точки. Система
уравнений (3.41) допускает решение такой структуры, которое оконча-
тельно находится в ходе решения краевой задачи. Таким образом, осо-
бые экстремали в> задаче управления с ограничением на угловую ско-
рость поворота вектора тяги совпадают с экстремалями традиционной
задачи оптимизации, когда движение КА вокруг центра масс не учиты-
вается и ограничения на угловую скорость поворота вектора тяги отсут-
ствуют. Этот результат вытекает из анализа задачи управления в общей
постановке, где вывод об особых участках был сделан на основании
замены исходного множества D на более широкое Е (иными словами,
исключая уравнения углового движения).
Необходимое условие оптимальности особого режима заключа-
ется в неотрицательности скобки Пуассона
a0|cos(.9+(£
Последнее условие выполняется, если всюду на особом участке
20.
(3-44)
траектории сопряженный множитель y/v неотрицателен.
На рис. 3.17 - 3.19 показаны характер изменения угловой скоро-
сти П и угла а между вектором тяги и касательной к траектории и
особый режим управления Q [26]. Интересно отметить, что согласно
полученным решениям управление Q стремится удержать тягу в окре-
стности касательной к траектории (примерно в диапазоне - 40° < 9 <
40°). Если вектор тяги выходит из этого диапазона, угловая скорость
меняет знак, т.е. способствует быстрейшему перевороту КА и приходу
вектора тяги в указанную окрестность «с другой стороны».
Естественно, что разгон КА с ограничением на скорость пово-
111
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
рота вектора тяги занимает большее время, чем без этого ограничения
(когда угол ориентации тяги а является независимым управлением).
Проигрыш во времени увеличивается с уменьшением Г2тах. Время дос-
тижения параболической скорости на «экстремальной» траектории, т.е.
без ограничений на О, может, таким образом, служить оценкой нижней
границы функционала Т. Интересно отметить, что время Т' разгона по
траектории с локально-оптимальным режимом управления
П = -Qmix • «g«[sin 2(5 - 6*)] незначительно превышает минимальное.
Рис. 3.18. Характер изменения угловой скорости поворота вектора тяги П и угла а на оп-
тимальной траектории с=5.2) для /^<„=0.51/- момент реверса тяги, г - момент
перехода на особый режим
При ограниченной величине Q на начальном этапе оптималь-
ное управление стремится удержать вектор тяги все более продолжи-
тельное время в окрестности касательной к траектории (см. рис. 3.18,
3.19). С увеличением радиуса орбиты угловая скорость орбитального
движения со0 уменьшается настолько, что управление способно обеспе-
112
Глава 3, Прикладные задачи оптимизации перелетов с малой тягой
чить оптимальную ориентацию тяги вплоть до точки набора параболи-
ческой скорости. Время разгона зависит от начального направления
вектора тяги, т.е. от угла 30, но эта зависимость проявляется довольно
слабо.
Совершенно аналогично исследуется задача о минимальном
времени торможения КА при переходе на круговую орбиту спутника
планеты. Начальный участок движения здесь является участком особого
управления, а конечный - регулярным, с максимальной по модулю уг-
ловой скоростью поворота вектора тяги.
3.8. Оптимизация траекторий перелета с непрерывной тя-
гой между круговыми некомпланарными орбитами
При оптимизации траекторий перелетов между некомпланар-
ными орбитами решающее значение приобретают два фактора. Первый
связан с различными схемами управления угловым движением аппарата
и связанными с ними дополнительными затратами рабочего тела на раз-
ворот корпуса аппарата. Второй фактор - невозможность решения зада-
чи оптимизации для достаточно сложной математической модели дви-
жения, включающей уравнения как траекторного, так и углового дви-
жений.
Принцип расширения допустимых состояний и управления
здесь позволяет свести решение общей задачи оптимизации перелета к
последовательности решений частных задач оптимизации меньшей раз-
мерности, получаемых путем отбрасывания некоторых связей. При этом
решение каждой задачи меньшей размерности дает гарантированную
оценку критерия оптимальности для «последующей» более сложной
задачи.
Задача перелета между круговыми некомпланарными орбитами,
описываемого усредненными уравнениями (2.57), формулируется те-
перь следующим образом: перейти с орбиты, параметры которой
(го.'о), на орбиту с параметрами (rK,iK), обеспечивая минимальное
значение характеристической скорости WK. Предполагается, что мар-
шевый двигатель работает без выключения; управлением в данной зада-
че является момент Му> (или угловое ускорение а), который, вообще
Говоря, ограничен по величине некоторым значением Мшх (£<. ешх ).
Угол ориентации тяги у/ является теперь одной из компонент вектора
с°стояния, причем включает как вековую, так и периодическую состав-
Л’пощие. Соответственно в управлении е целесообразно выделить веко-
ВУ*° и периодическую компоненты.
Получим необходимые и достаточные условия оптимальности в
113
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
задаче о минимуму характеристической скорости перелета между кру-
говыми некомпланарными орбитами в классе допустимых траекторий и
управлений, выбранных без учета динамики углового движения аппара-
та и затрат на управление. Движение КА описывается уравнениями
(2.57 - 2.58) в которых интегралы It, 12 играют роль управлений и яв-
ляются функциями угла ориентации вектора тяги {//[19, 12].
Введем функцию ^>(г,/), частные производные которой по ра-
, д<р dq> .г,
диусу и наклонению обозначим через ——, — и составим функцию R:
dr di
(3.45)
дг 'я 1 di 2л 1 dW '
Зададим функцию <p(r,i) так, чтобы тождественно выполнялось соот-
ношение
+ (3.46)
dr ' di 2 2 7
При таком выборе <p(r,i) функция R не зависит от управлений /,, /2 и
условия максимума R выполняются автоматически. Составим характе-
ристическое уравнение для линейного уравнения в частных производ-
ных (3.46)
dr _ 2di
l\r I2
(3.47)
решение которого имеет вид
' I /
г = гоехр,2М-Л .
<. <0 l2 J
Для того, чтобы траектория r(t), i(t) и управление y/(l)
обеспечивали минимум характеристической скорости на перелет
между круговыми некомпланарными орбитами, достаточно выпол-
нения соотношения
lndQ = 2j-^Jf. (3.48)
го »о Л
Как всякое достаточное условие, оно не позволяет программи-
ровать оптимальное управление, то есть находить оптимальную зависи-
мость отношения интегралов /,//2 вдоль траектории перелета, но тем
не менее пригодно для проверки любых допустимых управлений, най-
денных, например, с помощью необходимых условий оптимальности.
В частном случае, когда программа управления {//(«) остается
114
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
неизменной вдоль траектории, интегралы Z, и 12 постоянные, а соот-
ношение (3.48) переходит в полученное ранее (2.65), что говорит о
единственности, а значит и об оптимальности последнего.
Сформулируем теперь задачу оптимизацию параметра <//тах -
максимального отклонения угла ориентации тяги от трансверсали в
программе (2.80) - как функции текущей характеристической скорости
при перелете между круговыми орбитами. Траекторное движение аппа-
рата описывается уравнениями (2.57 - 2.58). Исследуем на максимум
функцию R (3.45), соответствующую задаче о минимуме конечной ха-
рактеистической скорости. Необходимые условия первого порядка мак-
симума R по координатам (г, г) и управлению у/тах:
У',' —Л(^)+^^тах)+-^г = 0. (3.49)
я 4я dW
у/, = consf, У'.мх (^) = arg max R.
Здесь частные производные синтезирующей функции <p(r,i,w)
8<р 8<р
y/r = , у/, = -4- - вычисляются в точках предполагаемой минимали
dr di
(г, i). Поскольку y/t = const, из условия нормировки можно положить
=1.
Особенностью данной задачи является то, что оптимальное
управление ^/тах (И7) в явном виде не выражается из последнего условия
(3.49), поскольку входит достаточно сложным образом в интегралы и
1г. Отыскание оптимальной зависимости сводится к решению
двухточечной краевой задачи для системы
dr _гУг , \ di _гУг
dW ~ л '^тахdW~ 2л
^ = -~гУ1у/г1Ху/та)-~-1г{у/,!т). (3.50)
dW 2л 4я
с граничными условиями, соответствующими перелету между неком-
Планарными круговыми орбитами.
Окончательно оптимальная программа управления на множест-
Допустимых Ел получается в результате объединения вековой и пе-
риодической составляющих
У7^ >") = arctgitgy/^ (H')cosn). (3.51)
Десь выступает в роли функции, осуществляющей оптималь-
Му7™»).
115
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ную амплитудную модуляцию периодической составляющей управле-
ния. Оптимальная, программа управления вектором тяги (3.51) не выра-
жается аналитически. Между тем, если в пределах витка траектории
использовать простую «релейную» программу переключения угла у
(2.68), незначительно (в смысле интеграла Z,) уступающую локально-
оптимальной прокрамме (2.80), то сравнительно просто удается полу-
чить аналитическое решение. Для релейной программы (2.68) интегра-
лы /1 и 12 выражаются формулами (2.69). Функция Я; в задаче о ми-
нимуме характеристической скорости принимает следующий вид:
7?! =^.2r^cosv/o+-^-^—sin^0+^- (3.52)
or Ol n cW
Оптимальное управление ^(И7), удовлетворяющего необходи-
мым условиям первого порядка максимума R, по координатам и управ-
лениям, сводится к решению краевой задачи для следующей системы
уравнений
dr _ 2тгу/гг^г di _ 2г
4W ф + я2р2г2 dW Яу/1 + я2ц/2г2
dw ' Злт^ц/2 1
'................. (3.53)
dW -^\+л2у/2г2 лг^2 J\ + лгу/2г2
Проинтегрируем систему (3.53) и приведем решения к следую-
щему виду:
I1-—W + W2 ,
I Wk J
/0 + — arctg^A W- BW)~'),
яг ~ 4 4 ' >
(3.54)
(3.55)
(3.56)
'о •
sm----— cos-----------—
где А = ——, В - 1-------------pj , А/д. = iK
Минимальная характеристическая скорость перелета WK Д|,я
данной постановки получается в виде
(3.57)
116
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
между некомпланариыми круговыми орбитами
Решение (3.57) позволяет «в первом приближении» построить
изолинии критерия оптимальности динамического маневра - зависи-
мость WK от требуемого приращения радиуса и наклонения орбиты
(рис. 3.20). Исключая W из решений (3.54 - 3.55), получим уравнение
фазовой траектории перелета r(i) в виде
где в - tg(?r(i - i0)/2). Соответственно, заменяя W в выражении для угла
\у(3.56), получаем закон управления в форме синтеза, то есть зависимо-
сти от текущих координат г, i
A + Btg-^—^
V'o = arctg---- /: . т - (3.59)
' B-Atg^^
Результаты расчета оптимальной траектории перелета на орбиту
стационарного спутника Земли приведены на рис. 3.21. Максимальный
Угол отклонения вектора тяги от трансверсали у/тт возрастает по мере
приближения к конечной орбите. Характерно, что радиус орбиты снача-
ла увеличивается до некоторого значения гтя>гк, а затем уменьшается
До значения гк. При достижении rmax угол ^тах равен 90°, а затем тяга
Начинает тормозить аппарат и уменьшать радиус орбиты. Такая струк-
1УРа оптимальной траектории хорошо согласуется с известными зако-
117
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
нами механики космического полета, согласно которым поворот плос-
кости орбиты более эффективен на большем удалении от центра притя-
жения. Поскольку на участке торможения угол ориентации тяги превы-
шает 90°, интеграл характеризующий среднее значение трансвер-
сальной компоненты тяги, становится отрицательным.
Рис. 3.21. Параметры оптимальной траектории перелета иа стационарную орбиту:
гк =6,2319; Мк =0,9
Рассматривая задачу совместной оптимизации траекторного и
углового движений считаем, что двигатели жестко закреплены относи-
тельно корпуса, а разворот КА происходит только вокруг связанной оси
OY}. При этих допущениях, необходимые условия реализации про-
грамм управления вектором тяги с помощью управляющего момента
имеют вид:
₽m«x ~ таХ ~2~ • (3.60)
UL ' dt
С учетом ограничений на управляющий момент выбрана при-
ближенно оптимальная структура управления угловым движением и
получена новая «асимптотическая» модель пространственного движе-
ния:
^7 = К*" а>'cos+ а'7< '•
aW п + 2ка
118
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
4r^ / r v „
-------------(cos« sintzz + al, I, (3.61)
dW n +2ka
где усредняющие интегралы имеют вид:
A^fcos^tl-z2)^, 'c = H-/rZft
О ' о
/° = f sin y/max (1 - z1 )• sin a • (1 - z)dz. (3.62)
о
Здесь W" - текущая характеристическая скорость с учетом затрат на
разворот КА.
_____Таблица 3.5. Результаты оптимизации перелетов на геостационарную орбиту
1 о-6,1/с2 К Вариант граничных условий WK , км/с
о,1 0 1 Г“ 8,031
2 -
1,0 0 1 -
Г 2 5,912
1,1 0 1 8,119
2 5,915
0,1 1 8,429
2 6,111
1,5 0 1 8,153
2 5,925
2,0 0 1 8,183
2 5,935
Расчеты некоторых перелетов на геостационарную орбиту были
выполнены для различных вариантов граничных условий, как для со-
вместной (к = 0), так и для раздельной (к = 0,1) схемы управления дви-
жением. Результаты расчетов приведены в табл. 3.5 (y^miX = const, вари-
ант 1 соответствует изменению наклонения на 51,5°, вариант 2 - на
25,5°). Данные таблицы показывают, что характеристическая скорость
перелета определенным образом зависит от уровня располагаемого уг-
лового ускорения. Эту зависимость можно объяснить двумя обстоятель-
ствами. При очень малых значениях е на начальном этапе перелета
(вариант 1, е =0,1 10"® 1/с2) реализуется движение с у/тях , при
котором аппарат совершает непрерывные развороты в плоскости мест-
ного горизонта ( а = у ). В результате наиболее интенсивное изменение
наклонения орбиты происходит на большем удалении от центра притя-
*ения, что энергетически гораздо выгоднее. Ясно, что при Е = 0 пово-
рот плоскости орбиты вообще невозможен. Поэтому для каждого пере-
119
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
лета, существует некоторое «предельное» минимальное значение е,
позволяющее реализовать перелет с заданными граничными условиями.
С другой стороны, чем больше уровень располагаемого углово-
го ускорения, тем ближе профиль изменения угла к «релейной» про-
грамме, которая, как было показано выше, не является абсолютно опти-
мальной. Поэтому можно предположить, что для совместной схемы
управления существует некоторое оптимальное значение углового ус-
корения Еор, , обеспечивающее минимальную характеристическую ско-
рость перелета. Следует заметить, что в отличие от совместной, раз-
дельная схема управления всегда требует расхода рабочего тела на
управление. Расчеты показывают, что дополнительные затраты рабоче-
го тела составляют 2 ... 3 % от суммарного расхода или около 1 % на-
чальной массы аппарата.
Результаты решения задачи оптимального перелета на стацио-
нарную орбиту для двух схем управления, изменение траекторных па-
раметров и программы управления вектором тяги показаны на рис. 3.22.
Рис. 3.22. Изменение параметров оптимальной траектории и управления для совместной
(1) и раздельной (2) схем управления траекторным и угловым движением при перелетах
на геостационарную орбиту: 1 - ет„ = 1,1 1 О'* 1/с1; к = 0; И7*. =7,741 км/с;
2 - = 1,1 W* 1/с2; к = 0,1; 1ГК = 7,919 км/с
Особенностью решений для раздельной схемы управления явля-
ется наличие начального участка трансверсального разгона без измене-
ния плоскости орбиты. Здесь не удается реализовать оптимальную про-
грамму (3.59), поэтому на втором участке угол у/ резко увеличивается,
так как приходится компенсировать недостаточную эффективность
управления на первом участке.
120
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Следует отметить, что параметр к, характеризующий расход
рабочего тела на управление, пропорционален величине углового уско-
рения е . С увеличением к (что по физическому смыслу задачи соот-
ветствует увеличению уровня тяги управляющих двигателей) растет
протяженность участка движения КА без разворотов с направлением
тяги по трансверсали. Развороты КА осуществляются при больших зна-
чениях г, где они выполняются за минимальное время и соответствен-
но при умеренных затратах рабочего тела.
В пределе при достаточно больших угловых ускорениях е , ха-
рактеристическая скорость возрастает не более чем на 4 ... 5 % по срав-
нению с совместной схемой управления траекторным и угловым движе-
ниями. Так, для перелета на геостационарную орбиту при
с = 1,1 КГ61/с2 и к = 0; WK = 7,741 км/с, а при к = 0,1; WK =7,919 км/с.
Учет движения космического аппарата вокруг центра масс при-
водит к существенному усложнению модели движения. Тем не менее,
применение подхода, основанного на разделении компонент управле-
ния, позволило решить задачу оптимизации и установить качественные
особенности оптимального управления ориентацией вектора тяги при
межорбитальных переходах между некомпланарными круговыми орби-
тами. Совместной оптимизацией траекторного и углового движения
удалось добиться того, что динамика аппарата относительно центра
масс не вносит существенных поправок в энергетические характеристи-
ки перелетов между круговыми некомпланарными орбитами. Это дос-
тигается благодаря свойству адаптации программы управления к пара-
метрам, характеризующим угловое движение аппарата прежде всего к
располагаемому угловому ускорению и расходу рабочего тела на управ-
ление угловым движением.
В качестве синтезирующей функции можно взять решение, вы-
текающее из результатов В.Н.Лебедева [2]:
-min WK . - , (3.63)
D У ylrKlr ГК
теперь можно оценить степень близости решения к абсолютно опти-
мальному. Выражение (3.63) приближенно задает нижнюю грань харак-
теристической скорости перелета из точки с любыми начальными усло-
виями (r,i) в точку с произвольными конечными условиями
Однако, следует помнить, что решения получены с использованием ус-
редненных уравнений, при условии, что эксцентриситет оскулирующей
орбиты равен нулю. Если е 0, то даже оптимальная амплитудная мо-
дуляция управления, вообще говоря, не гарантирует абсолютного опти-
121
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
мума в исходной задаче. Используя синтезирующую функцию (3.63),
можно оценить степень близости решения к абсолютно оптимальным,
не прибегая к громоздкой процедуре отыскания последних в рамках
модели движения. В итоге получим общее выражение для оценки в виде
IV к - min W к <А;
в
„„ r/,(v/max) a^
max.---------7----
2/2(v/mJ di
dtp 2л ~
-F—
di ~n \
(3-64)
max
Здесь /Л y/max и /з Vхmax -усредняющие интегралы, соответ-
ствующие оцениваемому режиму управления г, i - соответ-
ствующие параметры траектории.
ц = _______^y/^du_________,
°7С’082^т«х +SmVmaxCOS2«
12 = *1 S™ ^„ux COS2 И
O^COS2 V'max+SinVm» COS2 И
(3.65)
3.9. Совместная оптимизация траекторий и проектных па-
раметров межорбитальных транспортных аппаратов с двига-
телями малой тяги
Межорбитальные транспортные аппараты (МТА) предназначе-
ны для доставки полезных грузов на достаточно удаленные рабочие
орбиты с низких орбит выведения. Особый интерес представляют МТА
с ЭРД в плане их использования для размещения на высоких орбитах
крупногабаритных конструкций, таких как солнечные электростанции,
антенны радаров, элементы радиотелескопов. Все эти конструкции об-
ладают малой жесткостью и имеют существенные ограничения на
транспортную перегрузку
При выборе опорных траекторий и последующем формирова-
нии алгоритмов управления будем использовать достаточно близкие к
оптимальным программные управления и траектории, однако выберем
такие структуры управления, которые заведомо допускают возможность
122
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
их практической реализации. Такой подход позволяет избежать трудно-
стей, связанных с неоправданным усложнением вычислительных про-
цедур синтеза траекторий и управлений.
Зададим структуру управления вращательным движением так,
что в окрестности точек с координатами = л^/2 (j = 1,3,...), где U-
аргумент широты КА, максимальный по модулю управляющий момент
Мупр производит разворот КА из положения +y/j, в положение —t//j,
(или наоборот), а на остальной части витка равен нулю. Таким образом,
управлением в данной задаче служит параметр ^тах — амплитуда ко-
лебаний угла ориентации тяги. Такая структура хорошо аппроксимирует
оптимальную программу управления вектором тяги (2.80)
ц/ = arclg(tgipmvi cosh), незначительно уступая последней по энергети-
ке, и в то же время обладает свойствами, удобными для ее технической
реализации [2, 19, 11].
Дальнейшее упрощение модели движения связано с тем, что ор-
бита считается околокруговой. В сочетании с малостью реактивного
ускорения это позволяет применить метод усреднения уравнений дви-
жения и использовать для описания эволюции параметров орбиты г, i
уравнения (2.58,2.63,2.64).
1х гх
Усредняющие интегралы Jt = Jcos^ dtp, J2 = jsin|^||cos<p\ dtp
о о
характеризуют «в среднем» управление ориентацией вектора тяги, ин-
теграл F = f(l + |^yOT|z) характеризует дополнительные затраты на
о
управление вращательным движением в пределах витка. Здесь % - па-
раметр, характеризующий расход рабочего тела специальными управ-
ляющими двигателями (для «совместной» схемы % = 0 ). В простейшем
случае МУПР = Pyhph = ЕУПР1У, тогда
= *-£. <з.«»
где Еупр _ управляющее реактивное ускорение, 1У — момент инерции
КА относительно связанной оси ОУ, направленной вдоль радиуса, h —
плечо силы тяги управляющего двигателя.
Введем параметр а, обозначающий половину протяженности
Участка разворота КА и зададим программу изменения углового уско-
рения в виде:
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
. t \ 1 + s/gnlsin2 <р - cos2 а) ..
Е = ~Еynpsign\cos (з)--S-S—-------------1. (3.67)
На участке разворота углы у/ и а изменяется согласно уравнени-
ям
где v'max - постоянный для данного витка параметр. При фиксирован-
ных V'max и еупр Угол а , характеризующий протяженность участка
разворота, будет тем меньше, чем больше радиус орбиты. Очевидно,
а < яг/2, отсюда получаем предельные значения угла , соответст-
вующие еупр , г
W„np =----(3.69)
О
С учетом выражений (3.68) интегралы J,, J2, F приводятся к
виду:
y-alcos^
J2 = 4 sin^m cos a + aj sin ^/m(l - z2)sin a(l - z) dz ,
о
Время работы управляющих двигателей вычисляется
1 7 2а (
1упр ~ J 9 ехР
л'ао о 1 + х— V
п
dW.
(3.70)
(3.71)
(3.72)
(3.73)
Сформулируем вариационную задачу о перелете между круго-
выми некомпланарными орбитами (г0> /0) и iK) с минимальными
затратами характеристической скорости WK. Уравнения движения за-
даны в виде (2.64), а входящие в них интегралы — соотношениями (3.79
-3.72).
В принципе при фиксированных параметрах %, еупр можно
подобрать параметр (z/max обеспечивающий выполнение граничных ус-
ловий перелета. Однако большой интерес представляет отыскание оп-
124
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
тимальной программы у/тгх opl(w)- В соответствии с формализмом
принципа максимума Понтрягина составляется функция Гамильтона
Н=2Л Л
+ r^2F~l(a,y)j2(a,y/m) = maxH. (3.74)
V'm
Здесь Л-Л((У) определяется решением дифференциального
уравнения
= (3.75)
аг, иг
Оптимальное управление „Дй7) в явном виде из функции
Гамильтона не выражается. Это существенно усложняет процесс реше-
ния краевой задачи. Для упрощения вычислительной процедуры значе-
ния интегралов (3.70 - 3.72) предварительно вычислялись как функции
параметров а и (//тах табулировались с достаточно малым шагом. Вы-
борка из таблиц производилась с использованием процедуры линейной
интерполяции.
Численные результаты были получены для задачи перелета с
низкой орбиты высотой /7=400 км и наклонением Iq=51,0 и 28,5° на
геостационарную орбиту (гк =42164 км). Расчеты позволили установить
характерные особенности оптимальных программных траекторий [11].
Проведенные для «совместной» схемы управления (% = 0 )
расчеты показали, что при малых значениях располагаемого углового
ускорения еУПр на начальном участке траектории перелета угол у/тах
выходит на предельный уровень (у/тах = у/ттГ1р ) - при этом а = Я/2 и
сохраняет его до достижения такого радиуса, при котором возможен
переход на «регулярный» режим. Характерным является изменение угла
а : если сначала а = л/2 (здесь КА совершает непрерывные развороты
с периодом, равным периоду обращения), то затем а плавно уменьшает-
ся, однако на заключительном этапе перелета, где радиус орбиты
уменьшается, а снова несколько возрастает. При малых еупр поворот
плоскости орбиты при г, близких к г0 неэффективен, поэтому на малых
высотах тяга ориентируется в основном на увеличение радиуса орбиты;
изменение наклонения происходит на заключительном этапе перелета.
При достаточно больших значениях £ут> переориентация КА выполня-
^я быстро, профиль программы ориентации тяги близок к «релейно-
125
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
му». Расчеты показывают, что при еупр = е , наблюдается слабый ми-
нимум характеристической скорости.
При раздельной схеме управления ( % * 0 ) имеется начальный
участок трансверсальной ориентации тяги; движение происходит без
поворота плоскости орбиты, угол у поддерживается равным нулю. На
втором участке амплитуда колебаний угла у/ резко увеличивается, чтобы
компенсировать недостаточную эффективность управления на первом
участке. С увеличением х растет протяженность участка движения КА
без разворотов, с цу = 0. Зависимость WK от £ для раздельной схемы
управления показана на рис. 3.23.
Рис. 3.23. Результаты решения при раздельной схеме управления
Зависимость характеристической скорости перелета WK, от па-
раметров Ет,х удобно представить в форме аппроксимационных поли-
номов. Так для случая % - 0 (совместная схема управления) предлага-
ется следующая формула:
= WK + ЬеУщ> + c£y}jp, (3.76)
где характеристическая скорость при оптимальной релейной про-
грамме, которая выражается известной формулой
W*K =^1 -2г/ cos^ + г-'^2. (3.77)
Здесь rK, WK даны в безразмерном виде; радиус отнесен к начальному
радиусу г0, а характеристическая скорость — к круговой скорости при
г = го-
126
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой___
Для раздельной схемы управления ( % 0 ) аппроксимационная
формула усложняется
WK = М'к +~^ + ск£’>/пр + ^кгЕугПР+ек£-2пр+^-. (3.78)
Л Л
Коэффициенты аппроксимационных формул определялись из
условия наилучшего согласования с результатами расчетов методом
наименьших квадратов.
Приведенный анализ и расчеты показывают, что для задачи пе-
релета на геостационарную орбиту дополнительные затраты на управ-
ление вращательным движением КА могут составить до 4—5% мини-
мально достижимой характеристической скорости. Такой уровень за-
трат оправдывает усложненную постановку задачи оптимизации пере-
лета с учетом вращательного движения КА и вместе с тем нацеливает на
поиск оптимальной схемы и параметров управления вращением тяже-
лых МТА с ЭРД.
Вектор основных проектных параметров, задающих проектный
облик МТА, содержит мощность энергоустановки N3y, уровень тяги
маршевых ЭРД Р и скорость истечения рабочего тела с. Размерность
базового вектора параметров существенно меньше, чем полного вектора
р (не включаются sm, % и т.п.). Далее процесс оптимизации ведется
итеративно.
На начальном этапе выбор параметров, задающих базовый про-
ектный облик МТА, ведется по расчетному значению характеристиче-
ской скорости . Одновременно оцениваются диапазон изменения
параметров и критерия оптимальности р с учетом верхний границы
W° = .
Затем проводится анализ условий реализации выбранных про-
граммных траекторий с точки зрения возможности управления угловым
движением КА: оценивается уровень потребных управляющих момен-
тов и угловых скоростей разворота, дополнительных затрат рабочего
тела и т.п.
Если учет динамики углового движения не вносит принципи-
альны корректив в структуру программных траекторий и управлений и
незначительно увеличивает затраты энергетики на реализации маневра,
то дальнейшее решение проектной задачи можно вести, основываясь на
прежней динамической модели. Например, при повороте плоскости ор-
биты на небольшие углы требуются малые управляющие моменты; оп-
тимальная программа управления вектором тяги реализуется практиче-
ски бесплатно. При обратном перелете МТА с высокой на низкую орби-
127
Глава 3, Прикладные задачи оптимизации перелетов с малой тягой
ту его моменты инерции уменьшаются в несколько раз по сравнению с
прямым перелетом, в такой же пропорции уменьшаются затраты на
управление угловым движением.
Если учет углового движения КА при реализации динамическо-
го маневра необходим, поскольку он вносит принципиальные измене-
ния в структуру программных траекторий и режимов управления, в
энергетику маневра, динамическая задача оптимизации решается зано-
во. Результат ее решения зависит теперь от параметров ет, %, с.
Процедуру поиска оптимальных параметров еп, % целесооб-
разно разделить на два шага: на первом эти параметры выбираются из
условия минимума только характеристической скорости перелета; а на
втором уточняются, обеспечивая максимум по глобальному критерию
т„ X
ц - —— - относительной массе полезного груза:
«о
= arg max ,х\ WK1 (г„,х\ Wvnf (е„ ,х\с,х,Ет,Т)- (379)
Здесь И^,’, WK1 берутся из решения динамической задачи как
функции параметров ет, х, параметр Т варьируется в диапазоне
(7min, Ттгх ]. Подобная процедура реализуется для каждого динамическо-
го маневра z из указанного множества Z.
После определения оптимальных значений, , х^ > ОСУ"
ществляется расчет проектных параметров МТА и параметров, характе-
ризующих баллистическую схему перелета: тяги маршевых двигателей
(I IV
1-ехр ——
к с
(3.81)
мощности энергоустановки
сХ(»+х)
С ) С J
продолжительности прямого и обратного перелетов
128
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
_ ^тп f| _ expf _
fjP [ V C J C
Т2=Т-1\. (3.82)
На заключительном этапе уточняются дополнительные затраты
энергетики на реализацию перелета и задается закон управления в фор-
ме обратной связи. Здесь учитываются основные возмущения, методи-
ческие погрешности и ошибки исполнения программы управления.
В результате определяется окончательная баллистическая схема
перелета, прогнозируется распределение коррекций. Окончательное
значение характеристической скорости служит для синтеза
оптимальных параметров МТА третьего приближения.
Результат^! оптимизации проектно-баллистических характери-
стик и параметров МТА приведены в табл. 3.4. и на рис. 3.24.
Таблица 3.4. Результаты оптимизации проектно-баллистических характеристик МТА для
Го =6870 км, гк =42164 км, /0=51°, 1'х=0° <Хэу =20 кг/кВт, уЯУ =60 кг/Н,. Ycnx=®^
Итерация Оптимальные параметры перелета и МТА
сут т z > суг км/с А С, кмк. «_10‘ с2 X
Оценка энергетики перелета, с учетом 10%-иого запаса на управ- ление 152.2 47.8 8.406 0.445 30.4 - 0,05
1. Энергетика перелета оптимизи- руется (первая строка - совместная схема, вторая - раздельная) 158.4 41.64 7.580 0.528 32.4 0,325 -
157.0 43.0 7.693 0.511 31.7 0,260 0,026
2. Совместная оптимизация пара- метров МТА и траекторий перелета 157.3 42.7 7.713 0.514 31.9 0,135 0,014
3. Учет дополнительных затратна реализацию траектории 155.8 44.2 7.819 0.499 31.1 0,180 0,018
Данные табл. 3.4 показывают степень зависимости критериев
оптимальности перелета WK, ц , и параметров, характеризующих облик
МТА, от принятой математической модели задачи оптимизации. Грубые
оценки энергетики перелета в рамках модели, не адекватной физиче-
ской сущности задачи, приводят к существенному занижению массовой
.отдачи транспортной операции. В таблице показан процесс пошагового
Улучшения критерия ц в ходе реализации итеративной процедуры и
[Наглядно подтверждается эффективность итеративной процедуры со-
вместной оптимизации параметров МТА и режимов управления его
аижением, основанной на использовании усложняющихся динамиче-
Рих моделей и процесса управления. Применение сложных моделей
Инамики, управления движением, массовых соотношений МТА приве-
129
Глава 3. Прикладные Задачи оптимизации перелетов с малой тягой
ло к существенному уточнению, как законов управления, так и парамет-
ров МТА. Для завершения процесса оптимизации практически требует-
ся три итерации, причем критерии оптимальности ц изменяется суще-
ственно (на 10 - 12%).
Рис. 3.24. Изменение относительной массы полезной нагрузки и
программы управления по итерациям
Окончательные результаты синтеза проектных параметров МТА
и их изменение по итерациям показаны на рис. 3.25 - 3.28 для перелетов
различной продолжительности.
Рис. 3.25. Оптимальные проектные параметры «универсального» МТА с СЭРДУ
(ач.= 12,44 кг/кВт, уду=35 кг/Н). Перелет на ГСО с возвращением г0=6871 км, Гк =42164
км, /0 =51°, /^=0°
130
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Рис. 3.26. Оптимальные проектные параметры МТА с СЭР ДУ, предназначенного
для транспортировки «стандартной» полезной нагрузки а,,= 12,44 кг/кВт, уд = 35 кг/Н.
Перелет на ГСО с возвращением
возвращением (Д/ =51 °)
131
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
I I —1__________I-----L.
0 100 200 300 ООО 500
Т.Сут
Рнс. 3.28. Зависимость относительной массы полезной назгузки
от суммарной продолжительтости перелета
Корректная постановка динамической задачи оптимизации по-
зволила уточнить энергетику перелета и показала принципиальную воз-
можность улучшения массовой отдачи программ космической транс-
портировки. Начальная масса МТ А, тй = ц'т,,, определенная согласно
приближенным оценкам энергетики перелета, оказалась завышенной,
оптимизация показала также возможность уменьшения потребной мощ-
ности энергоустановки и тяги блока маршевых ЭРД.
3.10. Расчет оптимальных дат старта при перелете на гео-
стационарную ррбиту КА с солнечной ЭРДУ
Как уже отмечалось, для МТА с солнечной ЭРДУ имеет значе-
ние длительность пребывания в тени Земли и закон управления солнеч-
ными батареями. Приближенный расчет суммарной продолжительности
теневых участков при перелете между заданными орбитами ведется с
использованием усредненных уравнений, дополненных уравнениями,
учитывающими прецессию орбиты и годовое движение Солнца в плос-
кости эклиптики [12].
Протяженность Ф теневого участка на витке определяется по
формуле
Ф = 2arcsin
(3.81)
где 8 - угол между направлением на Солнце и нормалью к плоскости
орбиты определяемый (2.59) cos<5 = cos/sin«r0sin£?-sin/cos£0cosQ +
132
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
+sin/sin Qcos# . Причем угол в между направлением наточку весенне-
го равноденствия и линией Земля-Солнце изменяется
ва ~ 0,0172(7^ -8о), где Т^т - число суток с начала года до момента
старта.
Для расчета суммарной длительности теневых участков запи-
шем уравнения околокругового орбитального движения с учетом пре-
цессии долготы восходящего узла орбиты.
dr . j dt % dlV %
du du du
z \2
z/z" 21 I i I 3 r 3/f Rn 1 .
— ~ ar cosw smM, — = — ЦсГ/г\ — cosz. (3.82)
du 1 1 11 du 2 20 I r J
Примем, что реактивное ускорение а изменяется в зависимости
от косинуса угла между направлением на Солнце и нормалью к плоско-
сти солнечных батарей а - а0 cos/?.
В зависимости от даты старта, которая определяет начальную
ориентацию плоскости орбиты относительно Солнца, траектория ме-
жорбитального перелета аппарата с солнечным ЭРД будет характеризо-
ваться различным временем затенения. Поставим задачу отыскания та-
ких дат старта, при которых суммарное время т пребывания КА в тени
минимально.
Серия расчетов перелетов в окрестность геостационарной орби-
ты, выполненных для различных значений параметров С10, Тст позволяет
построить линии равных времен пребывания аппарата в тени и выбрать
оптимальные дату старта и положение восходящего узла орбиты. Ре-
зультаты расчетов для перелета на геостационарную орбиту с низкой
орбиты высотой 400 км и наклонением 51° показаны на рис. 3.28 - 3.30.
в виде изолиний продолжительности теневых участков. Начальное ре-
активное ускорение варьировалось в пределах: ао=1О'3 м/с2, скорость
истечения принималась равной 60 км/с. Здесь характерно сочетание
оптимальных дат старта с резко неблагоприятными датами, где продол-
жительность теневых участков достигает 20% от общего времени пере-
лета.
Изолинии, показанные на рис. 3.29 показывают, что при одина-
ковом моторном времени перелета 7* = 86,4 сут время пребывания в
тени составляет от 0,7 до 18,6 сут. Оптимальные и неоптимальные даты
старта повторяются с периодичностью 6 месяцев. При фиксированной
дате старта можно добиться уменьшения времени пребывания КА в те-
ни за счет оптимального выбора начальной ориентации плоскости орби-
ты (угла Па).
133
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Дата старта, месяцы
Рис. 3.29. Линии равной продолжительности теневых участков для перелета КА с СЭРУ
иа геостационарную орбиту а<г=0,82 КГ3 м/с2, io =51°
Дата старта, месяцы
Рис. 3.30. Линии равной продолжительности теневых участков для перелета КА с СЭРДУ
иа геостационарную орбиту ао=1,О 10’5 м/с2, io =51 °
134
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Дата старта, месяцы
Рис. 3.31. Линии равной продолжительности теневых участков для перелета КА с СЭРДУ
на геостационарную орбиту а</=1,16 10"’ м/с2, >0=51°
Оказалось, что для любого варианта граничных условий можно
в принципе добиться постоянной освещенности КА Солнцем, то есть
существует такое реактивное ускорение aos, что при at > ats время
пребывания КА в .тени может быть сведено к нулю. В этом случае реа-
лизуются сравнительно «быстрые» перелеты, и плоскость орбиты пре-
цессирует таким образом, что КА не успевает зайти в область тени и
постоянно опережает Солнце в его годовом движении по эклиптике.
Оптимальная дата старта ( т -> min ) повторяется приблизительно через
каждые полгода.
Описанная приближенная методика позволяет существенно су-
зить границы области поиска оптимальных дат старта для космических
аппаратов с солнечными двигателями ограниченной мощности.
3.11. Синтез приближенно-оптимальных алгоритмов управ-
ления при перелетах КА на геостационарную орбиту
Условием решения задачи терминального управления является
перекрытие области достижимости Х'к образующейся в конце этапа
дальнего наведения в результате влияния неучтенных факторов, возму-
щений и ошибок реализации программы, областью гарантированного
приведения г(Д^д), соответствующей определенному уровню затрат
135
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
на участке точного наведения A WH = fixe.
Проверка выполнения условия перекрытия
может быть осуществлена только численно, так
как Х'к и г(д^7„) - суть многообразия в шестимерном пространстве
Е6, не обладающие четкой, аналитически описанной конфигурацией.
В рамках данного подхода решение задачи перекрытия области
достижимости областью гарантированного приведения может быть по-
лучено разными путями. Первый путь заключается в увеличении разме-
ров области Г за счет дополнительных затрат энергетики, выделяемой
ни проведение заключительного этапа точного наведения.
Второй подход состоит в коррекции программы управления на
участке дальнего наведения. Наиболее простой способ ликвидации на-
копившихся ошибок по радиусу и наклонению орбиты, заключается в
периодическом пересчете программы управления сохраняющей базо-
вую структуру. Обновление модулирующей функции ^тах(И/) произво-
дится по следующей схеме:
(3.83)
Здесь параметры (гj, ij, Wj) - средние значения параметров
движения, соответствуют некоторому моменту , к которому приведе-
ны текущие навигационные измерения, уточняющие вектор состояния.
Для решения задачи фазирования введем новый контролируемый пара-
метр, которым будем характеризовать положение КА относительно за-
данной точки конечной орбиты - «условную» долготу Лс, совпадаю-
щую с геоцентрической долготой КА при нулевом наклонении плоско-
сти орбиты
4 = П + и - So - a>3(t - tso). (3.84)
Здесь So - звездное время в гринвичскую полночь, tso - соот-
ветствующий So момент времени, - угловая скорость вращения
Земли. В общем случае на момент tK величина Лс определяется со-
136
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
гласно выражению
'«А™ /
(3.85)
которое используется для формирования невязки в процедуре решения
краевой задачи.
Из всех решений, получаемых в ходе этой процедуры, выбира-
ется решение, обеспечивающее абсолютный минимум характеристиче-
ской скорости (или продолжительности) маневра. При этом относитель-
ная угловая дальность полета до достижения заданной долготы висения
на стационарной орбите определяется выражением
Г - (о) - (°)
Ф + nsign<t> + Лс
2тс
(3.86)
Ф = 2С - 2лЕ
-(о)
где Ф - относительная угловая дальность, соответствующая решению
задачи пространственного наведения без учета граничного условия по
угловое положение КА на конечной орбите, Е - оператор выделения
целой части числа.
Частота обновления программы управления определяется в ходе
численного моделирования движения с использованием точных уравне-
ний, содержащих, возмущения и ошибки и служащих для имитации на-
вигационных измерений. Однако возможности метода ограничены в
силу несоответствия реального динамического процесса его упрощен-
ной математической модели, заложенной в основу программы. Метод
последовательных коррекций программы управления в общем случае не
может обеспечить требуемой точности по всем компонентам вектора
состояния и пригоден только для околокруговых орбит.
Рассмотрим алгоритм совместного управления траекторным и
угловым движением КА, настраивающийся на ликвидацию конечного
промаха по компонентам вектора состояния. Базовая программа изме-
нения модулирующей функции определяется на каждом шаге
управления в результате решения краевой задачи (рис 3.32). Для удоб-
ства зависимость ^тах(0 аппроксимируется участками прямых, пара-
метрами которых являются i//lt где i - номер очередной перекладки
вектора тяги. Таким образом, зависимость включает следующие харак-
терные участки:
• участок быстрой переориентации КА с постоянным по модулю управ-
ляющим моментом,
• участок медленных разворотов КА с постоянной ц/,.
137
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Рис. 3.32. Формирование управления ориентацией вектора тяги в алгоритме пространст-
венного наведения. 1 - номинальная программа управления; 2 - фактическая реализация.
Логика управления угловым движением предусматривает расчет
величин , в момент окончания переориентации аппарата и, соот-
ветственно, моменты включения двигателей ориентации, реализующих
оптимальный по быстродействию перевод КА из положения
у/1Ч), в положение (^, ). Далее, на отрезке [г(,/,+1] аппарат сохраня-
ет «остаточную» угловую скорость , переводящую его в положение
у/)+1. Такая логика переключении в канале управления углом рыскания
соответствует оптимальному регулятору «со смещенным нулем».
На участке быстрой переориентации КА управляющее угловое
ускорение меняется по закону
= ~emsignK(<p,&), (3.87)
где К = <р+—- функция переключения, <р, ф - рассогласованию по
т
углу и по угловой скорости в канале рыскания. В силу «асимметрии»
программы управления p(w), «левые» и «правые» развороты КА вы-
полняются на разные углы:
(з = А^(/) = ^(/)-^л(/),
^ = АЙ)=^лр(0-^л(г)- (3-88)
На участке поворота КА с «остаточной» угловой скоростью
WjlJIP (3.89)
Вследствие движения центра масс КА по орбите, начало орби-
тальной системы координат OXYZ совершает вращение вокруг центра
притяжения с угловой скоростью <о0 . При этом возникают компоненты
угловой скорости по осям связанной системы координат OXlYiZl:
соХ1, оГ1, <»Z1. Рассматривая уравнения движения КА относительно
138
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
центра масс, легко получить выражения для компонент угловой скоро-
сти, соответствующие, ( у == 0, <9^0):
dw
n dt
V cos G
ZD0 =------
60х\ ~ s^n У7 9
юг, = -z»0cos^,
(3.90)
Учитывая эти соотношения, получены выражения для управ-
ляющих моментов по связанным осям
Л/Х1 =/a-i®oCOSv<-^,
at
=/n4f + Qzi-^i)ft,o2sin^cos^,
at
= 7zi«o sin ig + (lri - IXI )®0 sin у/ ,
dt dt
и программных управляющих ускорений по этим же осям
Л/г. dw
= —^- = z»0-f-cos^,
Лч dt
Му. d2w г .
еУ1 = —— = —~ + ш0 smy/cos^ ,
/Г1 dt
Mz[ dy/ .
ezl = —= 2<a0 —y-sm Ц/.
/Z1 at
Программа управления может быть описана выражениями
^(w, /) = -y/„fs7gri(cos(w + Yi ))*
х
(3.91)
(3.92)
и jszgnsinl
Т2
(3.93)
£msign (cos(zz + Yi )l 1 + sign I sin2 и - sin'
21 n ]
i----a
\2 ))
Эта программа имеет следующий набор параметров: у/1Л, ф1Л,
соответствующие’ «левому» развороту вектора тяги; i// 1ПП, ц/1ПП, соот-
ветствующие «правому» развороту, у, - фазовый угол, смещающий
точку переключения бинормальной составляющей тяги. Задача синтеза
управления на каждом шаге управления заключается теперь в решении
пятипараметрической краевой задачи с незаданным моментом оконча-
ния решения; условием останова является выполнение одного из гра-
139
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ничных условий задачи, например, приведение КА в плоскость конеч-
ной орбиты (i = iK ).
Последовательность формирования управления пространствен-
ным наведением такова:
• на момент tj дается оценка вектора состояния хуизм ;
• производится расчет совокупности параметров управления из условия
приведения системы в конечное состояние (при i = iK );
• после решения краевой задачи ведется расчет фактического движения
КА, на базе точных уравнений движения в оскулирующих элементах, с
учетом возмущений от нецентральное™ и аномалий гравитационного
поля Земли, притяжения Луны и Солнца, силы солнечного давления,
ошибок реализации программы управления вектором тяги, ошибок оп-
ределения фактических параметров движения;
• по достижении момента f ,+1, процесс повторяется, если норма про-
гнозируемого промаха превышает максимально допустимое значение.
Для решения задачи неполной коррекции может применяться
упрощенная логика управления, когда часть параметров на конце траек-
тории жестко не фиксируется. Так, для управления совокупностью
«плоскостных» параметров ( А , е, Дм ) и наклонениям орбиты i доста-
точно подбирать набор постоянных; у/,л, У'щп, -WjAl)’
Wmn = с переключением бинормальной составляющей тяги стро-
го при и =—к, А =1,2,..
Эффективность разработанных алгоритмов управления для ме-
жорбитальных перелетов исследовалась путем математического моде-
лирования на ЭВМ динамики движения КА и процесса управления.
Таблица 3.5. Ошибки выведения иа стационарную орбиту со стартовой орбиты
г0 =6771 км, /0 =51° и скоростью истечения рабочего тела с=20 км/с
а0 -10-3 м/с2 Г^.суг Ы-грвд ек104
0,328 236 0,173 9,0 13,5
0.563 138 0,221 16,0 14,9
0.645 121 0,236 18,0 15,0
0,83 93 0,313 22,8 15,1
1,0 70,1 0,337 28,1 16,0
1,47 48 0,382 35,3 18,6
В табл. 3.5 и на рис. 3.33, 3.34 приведены некоторые результаты
расчетов выведения КА на геостационарную орбиту; процесс интегри-
140
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
рования заканчивался в момент достижения заданного периода обраще-
ния (Тд = 86164 с). При этом фиксировались затраты характеристиче-
ской скорости и ошибки выведения по наклонению орбиты |Д/Л-|, экс-
центриситету ек, а также отклонение характеристической скорости от
расчетного значения (решение задачи на второй итерации).
JI Лв'м*
п
Рис. 3.33. Изменение параметров траектории и управления на заключительном этапе вы-
ведения иа ГСО ае = 1 • 10“3 м/с2, с = 20 км/с, Го =6771 км, Гк =42164 км, /0 =51°,
jK=0,l°, £m=10010'6 с-2
Рис. 3.34. Трасса КА на заключительном этапе выведения на геостационарную орбиту
(указаны номера витков) а0 = 1 • Ю3 м/с2, С = 20 км/с, Лгкон — 90°
141
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
3.12. Оптимизация замкнутых межпланетных перелетов с
малой тягой
Оптимальное управление КА на гелиоцентрических участках
определяется по уравнениям (2.103) или (2.104) в зависимости от ис-
пользуемой модели движения согласно принципу максимума Понтряги-
на. Для расчетов, проводимых врамках модели А угол направления тяги
Z и функция включения-выключения двигателей определяются соот-
ношениями [28]:
sinA^,
2 - 2> COSA^
. +¥Ч
Wv,
I 2 2
Д<0 * V'm + V4
, где Д = —-+-— --.
Д>0 c 1-m
6 =
(3.94)
0,
1,
Для расчетов, проводимых в рамках моделей Б, В оптимальные
углы направления тяги Л,, и функция включения-выключения дви-
гателей определяются соотношениями [21,29]:
\ = arcsin
<4
2 2
. + Vv.
(cos<p-sini-y/t -cosi-smtp-v/v +sin<p-y/n
Л? = arcsin---------------------------------------------
(3-95)
D
ё =
где
0, Д <0
1, Д>0
I (cos<p • sin / • у/, - cosi - sin• 1(/р+sin$? • y/n j2 г sin2 Л Kj 2 + 2) >
^m-K(S-sin/ D
Д =-----r—— +-------.
c \-tn
В формулах (3.94 - 3.95) , ^Vr , - со-
пряженные множители, соответствующие фазовым координатам.
В зависимости от граничных условий перелетов и целевого
функционала возможны различные постановки краевых задач: опти-
мальные по быстродействию или расходу; с фиксированной угловой
дальностью перелета или нет.
Вариационная задача об оптимальных, по критерию минимума
приведенного рабочего времени или быстродействию, гелиоцентриче-
142
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ских перелетах сводится к двухточечным четырехпараметрическим (для
модели А) или шестипараметрическим (для модели Б) краевым задачам.
Получены оптимальные законы управления и баллистические парамет-
ры для различных межпланетных перелетов. На рис. 3.35 показаны оп-
тимальные гелиоцентрические траектории достижения планет Солнеч-
ной системы для КА с солнечной энергодвигательной установкой, по-
лученные для модели А.
а) 6)
Рис. 3.35. Примеры оптимальной пролетной гелиоцентрической траектории (а) и
траектории с выравниванием скоростей (б)
Расчет планетоцентрических маневров набора скорости и тор-
можения КА, в рамках модели А, проводился с использованием транс-
версального закона управления и эмпирических зависимостей расхода
рабочего тела и длительности маневра от проектных параметров КА,
полученных в [21].
Планетоцентрическое движение аппарата в рамках модели Б
рассчитывалось в комбинированной системе координат (2.104), с уче-
том возмущений от нецентральности поля сил тяготения планет, воз-
действия атмосферы и зате-
нения панелей солнечных
батарей (рис. 3.36). Для рас-
чета пространственного ма-
невра набора параболической
скорости использовался
трансверсальный закон
управления тягой двигателей
с отклонениями тяги от плос-
кости орбиты с переключени-
ем знака бинормальной со-
Рис. 3.36. Траектория планетоцентрического
участка набопа паоаболнческой скопости
ставляющей тяги дважды за
виток.
143
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
В процессе моделирования движения на планетоцентрических
участках траектории было установлено, что наиболее существенное
влияние на баллистические характеристики маневров набора параболи-
ческой скорости и торможения оказывает время пребывания КА в тени
планеты. Значительное увеличение длительности маневра (более чем на
20%) приводит к 'изменению гелиоцентрических координат аппарата в
момент выхода из сферы действия планеты, что, в свою очередь, суще-
ственно влияет на траекторию и проектно-баллистические параметры
межпланетного перелета (оптимальное управление, расход рабочего
тела и др.).
Алгоритм оптимизации замкнутых межпланетных перелетов
основан на последовательном моделировании участков плането и ге-
лиоцентрических участков движения со стыковкой участков, преду-
смотренной в рамках используемой модели движения при заданных
значениях проектных и баллистических параметров и последующем
решении задачи математического программирования для определения
их оптимальных значений.
Рис. 3.37. Изолинии стартовой массы КА на поле баллистических параметров (р, т и иа
поле проектных параметров р = {с, Ро}
Результаты проектно-баллистической оптимизации замкнутого
перелета Земля-Марс-Земля, выполняемого КА с солнечной энергетиче-
ской установкой и двигателями малой тяги представлены на рис. 3.37.
На рис. 3.38 показана соответствующая оптимальная баллистическая
схема перелета Земля-Марс-Земля в проекции на плоскость эклиптики
для оптимальных дат старта с учетом эллиптичности и некомпланарно-
сти орбит планет [21]. В табл. 3.6 показано изменение результатов про-
ектно-баллистической оптимизации перелета, полученные для различ-
ных моделей движения (см. также рис. 3.39)
144
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Рис. 3.38 Оптимальная баллистическая схема экспедиции Земля-Марс-Земля
Таблица 3.6. Результаты поэтапной проектно-баллистической оптимизации пилотируемой
экспедиции Земля-Марс-Земля с двигателем малой тяги______________________________
Использованная модель Оптимальные даты т, безр Тх. сут Масса КА, тонн Опт. пара- метры
старта финиша старт финиш расход Р, н с, км/с
Планетоцентри- ческое и гелио- центрическое движение рас- считывалось по приближенным зависимостям 06.07. 2017 05.08. 2019 .456 770 371.0 130.0 181.0 350.2 72
Модель А 08.07. 2017 07.08. 2019 456 770 361.8 129.9 171.9 350.1 70
Модель Б (без оптимизации точек стыковки злането и гелио- центрических участков) 08.07. 2017 07.08.20 19 .454 770 316.8 129.9 126.9 350.0 70
Модель Б (опти- (альная стыковке тлансго и гелио- центрических участков) 09.07. 2017 08.08.20 19 .456 770 309.7 129.9 119.8 350.0 70
Модель В (ими- тационное моде- лирование) 09.07. 2017 10.08.20 19 - 772 309.7 129.9 119.8 350.0 70
145
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Рис. 3.39. Зависимость приведенного моторного времени от дат старта с учетом эллиптич-
ности и некомпланарности орбит планет
Используя последовательность описанных моделей, можно ус-
тойчиво решать вариациионные задачи оптимального управления и ав-
томатизировать процесс получения оптимального проектного решения.
3.13. Оптимизация траектории перелетов с малой тягой меж-
ду Землей и Луной
Применяя формализм принципа максимума Понтрягина к дина-
мической системе, движение которой описывается системой (2.106 -
2.107) определим оптимальное направление вектора ускорения и
функции включения-выключения двигателей обеспечивающие выпол-
нение маневра за минимальное время :
Sjn^=7../ ,
-
СО8Лч>-=-г=Т5==7
А<0
Д>0’
л2+^,2
где А = — + --=-Х-
с 1-т
(3.96)
(3.97)
Таким образом, задача об оптимальном по быстродействию
плоском движении в системе Земля-Луна сводится к следующей двух-
точечной четырехпараметрической краевой задаче. Требуется найти
• у I 2 2
такие начальные значения Ло = arctg—B = +1//у ,
(y/r = +1 - из условия нормировки), чтобы на концах оптимальной тра-
ектории выполнялись начальное и конечное условия X(t0)=X0,
Х(Т) = ХТ.
146
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Если стартовая орбита круговая с радиусом г0, и положение КА
относительно Луны в начальный момент Д<з0, то начальный вектор фа-
зовых координат задается значениями
(3.98)
В зависимости от цели перелета конечные значения вектора фа-
зовых координат задаются следующим образом:
1) для задачи достижения устойчивых точек либрации системы
X \г
Jr=h, Д%=±у, Krt=0, Vn = 11 ; (3.99)
2) для пролета Луны на заданном угловом расстоянии &<рк с не фикси-
рованным вектором скорости VT = (КгГ, , с учетом условий транс-
версальности для вектора скорости
Jr=(l, Д%, РУг =0, PVr=tf (3.100)
Так как < 0, при всех t е [/0, г], и для задачи на опти-
dt
мальное быстродействие расход рабочего тела в конечный момент вре-
мени не фиксирован, то, согласно условиям трансверсальности,
(т) = 0 . При t е [О, Т) \рт (/) > 0, поэтому для задачи на оптимальное
быстродействие функция включения-выключения двигателей,
то есть двигатель работает без выключений. Кроме того, в силу моно-
тонного убывания функции удобно использовать эту сопряжен-
ную переменную для выхода из интегрирования. Остальные сопряжен-
ные переменные и фазовые координаты могут изменяться немонотонно,
а длительность перелета неизвестна.
Для решения краевых задач был использован модифицирован-
ный метод Ньютона с автоматической оценкой сходимости и изменени-
ем шага вычисления производных и ограничений на приращения, опи-
санный в разделе 1.3.
В [10] подробно описывалась процедура решения задачи дос-
тижения точки либрации системы Земля-Луна L4 (КА движется по
круговой орбите радиусом равным среднему радиусу орбиты Луны,
опережая ее на 60°). Проектные параметры аппарата выбраны близкими
к параметрам исследовательского КА Европейского космического
агентства SMART-1: т0 = 400 кг, Р = 0,5 Н, с = 15 км/с. В качестве стар-
товой рассматри. вается круговая орбита с большой полуосью
147
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Со = 100000 км.
Рис. 3.40 Оптимальное достижение точки либрации L4 системы Земля-Луна
На рис. 3.40 показана траектория оптимального по быстродей-
ствию достижения точки либрации L4, с учетом гравитации Луны.
На рис. 3.42 - 3.43 показаны зависимости компонент скорости
КА и закона управления на оптимальной траектории от угловой
дальности перелета. Для сравнения приведены аналогичные зависимо-
сти для задачи пролета орбиты Луны без учета гравитации Луны ис-
пользованные в качестве начального приближения (штриховые линии).
Наибольшее влияние на оптимальное управление и изменение
фазовых координат Луна оказывает на последних витках орбиты в мо-
менты своего максимального сближения с КА. Однако в целом дли-
тельность и угловая дальность перелета, оптимальное управление и тра-
ектории движения оказались близки к решению, использованному в
качестве начального приближения.
Рис. 3.41. Зависимость безразмерной составляющей скорости
от угловой дальности перелета для задачи достижения точки либрации L4
148
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
Рис. 3.42. Зависимость безразмерной составляющей скорости V?
Рис. 3.43. Оптимальная программа управления, соответствующая достижению
точки либрации L4 системы Земля-Луна
В [10] рассматривается задача пролета Луны при фиксирован-
ном угловом расстоянии KA-Луна в конечный момент времени. Началь-
ные значения проектных параметров (кроме тяги двигателей) и старто-
вой орбиты выбраны такими же, как для задачи достижения точек либ-
рации. Номинальная тяга двигательной установки увеличена до Р = 1 Н.
Показано, что гравитация Луны оказывает существенное влия-
ние на оптимальный закон управления и соответствующую траекторию
движения. Например, на рис. 3.44 изображены оптимальные траектории
для пролета Луны на угловом расстоянии от нее 5° при старте с круго-
вой орбиты с а0 =100000 км. Сплошной линией показано движение с
включенным двигателем и оптимальным законом направления тяги.
Пунктиром - траектории пассивного движения КА после завершения
целевой задачи и отключения двигателей.
Задача оптимизации имеет многоэкстремальный характер. Во-
первых, существуют различные классы решений, показанные на рис.
3.44а и 3.446: траектории с монотонным изменением радиуса орбиты
КА и траектории с увеличением радиуса траектории существенно боль-
ше радиуса орбиты Луны. Кроме того, в пределах одного класса воз-
можны траектории, угловая дальность которых отличается на целое ко-
личество витков. Естественно, значение критерия оптимальности полу-
149
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
ченное для всех этих траекторий различно.
На траекториях с монотонным изменением радиуса орбиты
(рис. 3.44а), КА после выключения двигателей оказывается захвачен-
ным гравитационным полем Луны и выходит на замкнутую селеноцен-
трическую траекторию. Эти траектории могут использоваться для фор-
мирования орбиты вокруг Луны с заданными параметрами. Траектории
с немонотонным изменением радиуса орбиты (рис. 3.446) характеризу-
ются большой относительной скоростью КА — Луна в момент отключе-
ния двигателей и могут быть использованы для формирования траекто-
рии возвращения к Земле.
На рис. 3.45. показана программа оптимального управления для
монотонных и немонотонных оптимальных траекторий.
Рис. 3.44. Оптимальные по быстродействию траектории пролета Луны, &<рк = 5°.
а) монотонное изменение радиуса орбиты (Т = 39.31 сут, Д$90 = —43° );
б) текущий радиус орбиты превышает радиус орбиты Луны (Т = 68.13 сут, Д^?о = 87°)
Рис. 3.45 Оптимальная программа управления, для задачи пролета Луны Д^ = 5°
а) монотонное изменение радиуса орбиты (Т = 39.31 сут, Д^>0 = —43’ );
б) текущий радиус орбиты превышает радиус орбиты Луны (Т = 68.13 сут, Д<р0 = 87°)
Таким образом, предложенная методика показала свою эффек-
150
Глава 3, Прикладные задачи оптимизации перелетов с малой тягой
тивность для оптимизации сложных многовитковых траекторий движе-
ния КА с двигателями малой тяги в поле притяжения двух тел. Полу-
ченные оптимальные законы управления и соответствующие ему траек-
тории движения могут быть использованы для решения задач формиро-
вания заданных селеноцентрических орбит.
3.14. Оптимизация движения КА с солнечным парусом
Исследование межпланетных маневров КА с солнечным пару-
сом проводилось в рамках теории сфер действия с кинематической сты-
ковкой участков. Задача условно разделялась на расчет многовитковой
траектории набора параболической скорости в сфере действия Земли и
гелиоцентрический маневр с заданными граничными условиями [22].
Выбор программы управления парусом на планетоцентрическом
участке движения для задачи набора параболической скорости и выхода
КА из сферы действия Земли представляет собой сложную математиче-
скую проблему. Колебательный характер изменения фазовых перемен-
ных, описывающих движение КАСП, и значительная продолжитель-
ность маневра делает невозможным применение классического метода
оптимизации управления на основе принципа максимума Понтрягина.
При этом реализация двухканального управления по 2, (/) и ^(t) явля-
ется сложной технической задачей. Естественным путем получения
приемлемого управления является упрощение задачи путем фиксации
одного из управляемых параметров.
Рассмотрим локально-оптимальные программы управления
парусом имеющие аналитический вид.
Пусть Л, (0s О, т.е. вектор ускорения лежит в плоскости орби-
ты, а парус ей перпендикулярен. Определим локально-оптимальную
программу для Л1 (/), обеспечивающую максимизацию проекцию тяги
на трансверсаль (ось OY'):
Лчр/ 2
S,
arcsin
-arc/g-f-
(3.101)
Подобное управление применимо, если орбита КАСП лежит
вблизи плоскости эклиптики. На рис. 3.46 показана реализация данного
закона управления для круговой стартовой орбиты, лежащей в плоско-
сти эклиптики.
151
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
..... । —" 1 1 1
Рис. 3.46. Локально оптимальный закон управления (3.101)
при начале движения по круговой орбите в плоскости эклиптики.
Пусть теперь Я, = 90°, т.е. ось вращения паруса направлена по
местному радиус-вектору. В этом случае
.arcsin
S'
-arctg-^
2
(3.102)
Данное управление удобно для реализации полета гравитацион-
но-ориентированного паруса (аппарат представляет собой конструкцию
вытянутую вдоль оси ОХ’). При этом плоскость орбиты должна нахо-
дится как можно ближе к терминатору ( S'x = « 0 ).
Проведенное моделирование движения КА с учетом возмуще-
ний от нецентральное™ гравитационного поля Земли, годового движе-
ния Земли и затенения показало, что прецессия плоскости орбиты
вследствие влияния этих возмущающих факторов и большой длитель-
ности маневра приводит к значительному отклонению реальной плоско-
сти орбиты от плоскости эклиптики, что делает невозможным использо-
вание закона управления Цандера в чистом виде. Полученные локально-
оптимальные законы управления (3.101, 3.102) в этом случае примени-
мы и использовадись для моделирования траекторий геоцентрического
движения КАСП с различными проектными параметрами.
На рис. 3.47 приведен пример траектории набора параболиче-
ской скорости КАСП при старте с орбиты лежащей в плоскости эклип-
тики и законе управления (3.101). Для этого закона управления проис-
ходит быстрое увеличение эксцентриситета орбиты за счет поднятия
апогея.
152
Глава 3 Прикладные задачи оптимизации перелетов с малой тягой
Рис. 3.47. Траектория геоцентрического движения КАСП при движении
с локально оптимальным законом управления (3.101)
Так как при движении вблизи эклиптики аппарат попадает в
тень планеты, где ускорение от паруса отсутствует, то в процессе ма-
невра возможно уменьшение перигея орбиты. Такое уменьшение может
вызвать приближение КАСП к плотным слоям атмосферы и разрушение
конструкции. Оказалось, что на этот процесс существенное влияние
оказывает положение перицентра орбиты старта относительно направ-
ления на Солнце.. При оптимальном выборе положения линии апсид
управление поднимает перицентр орбиты и опасного сближения с атмо-
сферой не происходит. Такое положение линии апсид стартовой орби-
ты, относительно направления на Солнце, автоматически определяется
в зависимости от даты старта и используется при моделировании гео-
центрического маневра набора параболической скорости.
При моделировании движения с законом управления парусом
(3.102), вблизи плоскости терминатора, эксцентриситет орбиты практи-
чески не изменяется, до тех пор пока плоскость орбиты значительно не
отклонится от плоскости терминатора (за счет прецессии плоскости ор-
биты и годового движения Земли). На начальном участке движения ор-
бита не затенена, что позволяет непрерывно увеличивать кинетическую
энергию КА и позволяет сократить суммарную длительность маневра.
При уменьшении парусности КА (отношение площади паруса к массе
аппарата) длительность маневра по закону управления (3.102) увеличи-
вается быстрее, чем по закону (3.101). Это связано с быстрым уходом
плоскости терминатора и существенным отклонением управления
(3.102) от оптимального. Управление (3.101) менее чувствительно к
возмущениям и при значении парусности менее 54 м2/кг суммарные
длительности манрвров примерно одинаковы.
Результаты моделирования маневров набора параболической
скорости, с локально-оптимальными законами управления (3.101) и
153
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
(3.102) для массы КА 100 кг, площади паруса 20 тыс. м2 и круговой
стартовой орбиты высотой 1000 км приведены на рис 3.48. В процессе
моделирования рассчитывались угловые скорости вращения паруса.
Этот параметр важен при определении конструктивной схемы, обеспе-
чения требуемого закона управления. Для маневра набора скорости по
локально-оптимальному закону управления (3.101) максимальная угло-
вая скорость вращения паруса составила 0,0035 град/с, а при управле-
нии (3.102) 0,0078 град/с, что является приемлемой величиной для па-
русных систем любой конструкции.
Рис. 3.48. Зависимость геоцентрического расстояния от времени при движении с локально
оптимальными законами управления (1 - 3.102) и (2 -3.101)
Задача оптимизации гелиоцентрического межпланетного пере-
лета опирается на модельную задачу о плоском движении КАСП в не-
возмущенном гравитационном поле Солнца. Используются следующие
допущения: движение КАСП начинается с орбиты Земли, с ее скоро-
стью, вне сферы ее действия; солнечный парус считается идеально от-
ражающим и двусторонним. В этом случае движение КА может быть
описано системой (2.103), но ускорение, получаемое аппаратом от сол-
нечного давления изменяется согласно закону
Р *?
а = -±—cos2 Я), (3.103)
г т
так как энергия солнечного излучения уменьшается обратно пропор-
154
Глава 3. Прикладные Задачи оптимизации перелетов с малой тягой
ционально квадрату гелиоцентрического расстояния, а угол & = \ .
Рассматриваются задачи определения закона управления пару-
сом, обеспечивающего минимум времени гелиоцентрического маневра
для следующих вариантов граничных условий:
• доставка полезной нагрузки в заданную точку пространства с форми-
рованием заданной гелиоцентрической орбиты (задача «встречи»),
возможно совпадающей с орбитой планеты назначения (рис. 3.49);
• доставка полезной нагрузки в заданную точку пространства без фор-
мирования заданной орбиты, когда вектор скорости в конечный момент
времени не фиксируется (задача «пролета»).
Следуя принципу максимума Понтрягина [6], системе исходных
уравнений движения (2.103) ставится в соответствие гамильтониан
V
г
Уг г
(р 1 Л
+ у/Уг------+a-cosZ, +Wyt
+ а • sin Z,
7
(3.104)
и соответствующая система сопряженных уравнений.
Рис. 3.49. Оптимальная по быстродействию траектория «встречи» с Марсом
Искомый оптимальный закон управления углом установки па-
руса в плоскости орбиты Z, должен доставлять абсолютный максимум
Гамильтониану (3.104) и в рассматриваемом случае имеет вид:
+8^ -3^„
tg\ = V ' - ------------- (3-105)
tyv.
Граничные условия в задаче оптимизации гелиоцентрического
155
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
перелета формируются по-разному в зависимости от цели динамическо-
го маневра.
Для задач «встречи» граничные условия, с учетом условий
трансверсальности имеют вид:
/ = 0, <3 = 0, r = r9, Vr=Vr№,
7~>min, Pv=0, r = rt, Гг = Гг1, = (3.106)
Для задач «пролета» граничные условия, с учетом условий
трансверсальности выглядят следующим образом:
Г = 0, <р = 0, r = r№, Vr = Vr№, Г =Гв,
Г —> min, Р,=0, r-г., Д =0, Ру=0. (3.107)
Вариационные задачи с граничными условиями (3.106, 3.107)
сводятся к решению трехпараметрических двухточечных краевых задач,
которые решались модифицированным методом Ньютона. Достижение
аппаратом планеты назначения, при нефиксированной конечной угло-
вой дальности перелета, обеспечивается выбором даты старта от Земли.
Разработана процедура приближенного определения начальных значе-
ний сопряженных множителей, позволяющая регулярно решать задачи
для широкого диапазона параметров аппарата и баллистических схем
перелетов, в том числе, и гравитационных маневров в сферах действия
планет.
Рис. 3.50. Решение задачи «пролетов» Марса и Венеры с использованием гравитационного
маневра в сфере действия Марса
Для полетов к дальним планетам и выхода из Солнечной систе-
мы рассматривается возможность моделирования гравитационных ма-
невров в сфере действия одной или нескольких промежуточных планет
156
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
с последующим решением целевой задачи с новыми граничными усло-
виями. Например, на рис. 3.50 показано решение задачи «пролета» Мар-
са с последующим гравитационным маневром, позволяющим осущест-
вить «пролет» Венеры.
Установлено, что аппараты с солнечным парусом позволяют
осуществлять «пролет» мимо всех планет Солнечной системы. Напри-
мер, для аппарата с относительно небольшой парусностью 100 м2/кг
перелет к Юпитеру продлится менее года. Было показано, что, для
КАСП с 50...100 м2/кг и менее, перелеты с выравниванием скоростей
аппарата и планет осуществимы только к планетам земной группы, а к
Юпитеру и Сатурну только при очень большой длительности. При пе-
релетах к Урану, Нептуну и Плутону выравнивание скорости аппарата и
планеты невозможно, ввиду недостаточного уровня ускорения на орби-
те планеты назначения.
Другой интересной проблемой, стало определение парусности
КАСП, позволяющей аппарату набрать параболическую скорость в ге-
лиоцентрической СК и выйти из сферы действия Солнца. Вариационная
задача определения оптимальной программы управления для достиже-
ния аппаратом максимальной полной энергии за фиксированное время
формулируется следующим образом. Необходимо определить програм-
му управления X/Z), доставляющую максимум критерию оптимально-
2
сти: V2-----> max (гиперболический избыток скорости). Начальные
г
фазовые координаты аппарата равны координатам Земли
t = t0, X = Хо - конечные координаты не фиксируются.
В соответствии с принципом максимума Понтрягина, вводится
дополнительная фазовая координата (безразмерная отрицательная пол-
2
ная энергия КА) х0 = — V2 - V2, закон изменения которой можно запи-
сать:
= -^-cos2X (у cos Л + К sin я).
dt г2 v >
(3.108)
Применяя формализм принципа максимума Понтрягина, уда-
лось получить оптимальное управление в аналитическом виде:
Л, =— ^-arcsin
+2^
з^+зк^ + ^+гк/)2
(3.109)
157
Глава 3. Прикладные задачи оптимизации перелетов с малой тягой
где д, - arccos-^=— ' —=== •
Из условий трансверсальности в конечный момент времени
=°>а V'x» =-1Таккак и у/= const, то ^Дг) = О,
а
Таким образом, вариационная задача сводится к двухточечной
трехпараметрической краевой задаче. Необходимо подобрать начальные
значения сопряженных множителей таким образом, чтобы при заданных
уравнениях движения (2.103, 3.108), сопряженной системе и оптималь-
ном управлении (3.109), выполнялись граничные условия и условия
трансверсальности.
Рис. 3 51. Начальный участок траектории оптимального набора скорости
Краевая задача решалась модифицированным методом Ньютона
для различных уровней парусности КАСП и длительностей перелета.
Были проанализированы возможности КАСП с различными техниче-
скими характеристиками по достижению максимально возможной ско-
рости. Для аппаратов с различной парусностью были получены траек-
тории оптимального набора гиперболического избытка скорости (рис.
3.51). Интересно отметить, что для совершения маневра оказывается
оптимальным сначала приблизить КАСП к Солнцу, а затем начать на-
бор скорости. Было установлено, что при парусности 206 ± 1 м2/кг аппа-
рат набирает параболическую скорость на расстоянии 123 а.е. от Солн-
ца. Дальнейшее увеличение парусности ведет к быстрому увеличению
скорости и для аппарата с парусностью 300 м2/кг на том же расстоянии
от Солнца избыток гиперболической скорости составит 15,8 км/с.
158
Список использованных источников
ЗАКЛЮЧЕНИЕ
Механика космического полета с малой тягой, основы которой
были заложены более полувека назад, явилась благодатной почвой для
развития приближенных методов решения вариационных задач.
Первоначально эта книга задумывалась как непосредственное
продолжение монографии «Оптимизация космических перелетов с ма-
лой тягой». Однако, оказалось, что простое дополнение ранее изложен-
ного материала не годится - необходимо было переосмыслить заново
все результаты, связать их единой нитью и насытить содержательными
задачами.
Описанные методы и алгоритмы решения вариационных задач
механики космического полета с малой тягой позволяют эффективно
определять энергетику маневра, оптимальное управление, соответст-
вующие ему траектории движения и проектно-баллистические парамет-
ры околоземных и межпланетных миссий. Эти методы и алгоритмы
легли в основу информационно-вычислительного комплекса, позво-
ляющего автоматизировать процессы моделирования, оптимизации и
отображения полученных траекторий и законов управления. Высокая
информативность графического отображения движения КА позволяет
эффективно решать и наглядно представлять результаты решения ши-
рокого комплекса задач, возникающих при проектировании полетов КА
с двигателями малой тяги. Все отображения траекторий движения, при-
веденные в данной книге, получены с помощью этого комплекса.
Авторы, отдавшие много лет исследованиям в области вариаци-
онных задач механики полета с малой тягой, искренне благодарят всех
коллег, вместе с которыми обсуждались проблемы оптимизации траек-
торий и управлений, своих аспирантов и учеников, выполнивших ог-
ромный объем вычислительной работы. Далеко не все материалы, полу-
ченные в ходе исследований, удалось включить в ограниченный объем
этой монографии, некоторые интересные задачи изложены здесь весьма
фрагментарно. Немало проблем еще остаются нерешенными. Поистине
можно утверждать, что механика полета с малой тягой неисчерпаема,
поскольку новые проекты космических миссий, новые технические дос-
тижениякосмонавтики будут постоянно стимулировать новые постанов-
ки задач и заставлять искать эффективные методы их решения.
Авторы надеются, что эта книга позволит пробудить интегес
молодых ученых к этой области космических исследований, а результа-
том этих усилий будут создание принципиально новых типов космиче-
ских аппаратов, способных расширять наши знания о Вселенной.
Молодежь, пробующая свои силы в науке в начале XXI столе-
159
Список использованных источников
тия слегка отравлена компьютерными технологиями, но иногда догады-
вается, что за ними стоит огромная работа аналитиков. Порой с изумле-
нием молодые люди берут в руки научные журналы и понимают, что
наука существовала задолго до эпохи ИНТЕРНЕТ. И многие из них на
подсознательном уровне уже испытывают потребность в получении
своих аналитических решений и вычислительных схем.
Авторы надеются, что читатели простят им неточности в тексте
и в формулах, погрешности в доказательствах и не всегда убедительные
выводы. А кто-то из читателей исправит ошибки и пойдет дальше, до-
полняя и улучшая наши результаты. Ибо «...конечная цель - ничто,
движение — все!».
160
Список использованных источников
СПИСОК ИСПОЛЬЗОВАННЫХ источников
1. Гродзовский Г.Л., Иванов Ю.Н., Токарев В.В. Механика космического по-
лета (проблемы оптимизации). М., Наука, 1975. - 704 с.
2. Лебедев В.Н. Расчет движения космического аппарата с малой тягой.- М.:
ВЦ АН СССР, 1968. - 108 с.
3. Кротов В.Ф., Гурман В.И. Методы и задачи оптимального управления. М.:
Наука, 1973.-446 с.
4. Гурман В.И. Принцип расширения в задачах управления. М.: Наука, 1985. -
284 с.
5. Брусов В.С., Салмин В.В. Комбинированная двигательная система, универ-
сальная для диапазона маневров //Космические исследования - 1974. Т. 12,
№3, С. 368 - 373.
6. Математическая теория оптимальных процессов / Понтрягин Л.С., Болтян-
ский А.Г. и др.; под ред. Понтрягина Л.С./ М.: Наука, 1976.392 с.
7. Беллман Р. Динамическое программирование, ИЛ, 1960.
8. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории
нелинейных колебаний. М.: Физматгиз, 1958.
9. Исаев В.К., Сонин В.В. Об одной модификации метода Ньютона численного
решения краевых задач // Журнал выч. математики и матем. физики - 1963,
№6, С. 102-117.
10. Старинова О.Л. Оптимизация движения космического аппарата с двигате-
лем малой тяги в системе Земля-Луна. Известия Самарского научного цен-
тра РАН, 2006, Т.8, №2, С. 144-152.
11. Ишков С.А., Салмин В.В. Оптимизация траекторий и параметров межорби-
тальных транспортных аппаратов с двигателями малой тяги //Космические
исследования - 1989. Т.27, №1, С.42-53.
12. Салмин В.В. Оптимизация космических перелетов с малой тягой: Пробле-
мы совместного управления траекторным и угловым движением.- М.: Ма-
шиностроение, 1987.- 208 с.
13. Основы теории полета космических аппаратов / Под ред. Г.С. Нариманова,
М.К.Тихонравова. М.: Машиностроение, 1972
14. Юрин В.В. Оптимальная коррекция параметров орбиты космического ап-
парата с двигателем малой тяги //Космические исследования - 1983.- Т.21,
№5. - С.666 - 674.
15. Салмин В.В., Соколов В.О. Приближенный расчет маневров формирования
орбиты спутника Земли с двигателем малой тяги //Космические исследова-
ния - 1991. Т.29, № 6, С.872-888.
16. Ишков С.А. Расчет оптимальных межорбитальных перелетов с малой
трансверсальной тягой на эллиптическую орбиту //Космические исследова-
ния - 1997. Т.35, №2, С. 178 - 188.
17. Ишков С.А., Романенко В.А. Формирование и коррекция высокоэллипти-
ческой орбиты спутника Земли с двигателем малой тяги //Космические ис-
следования - 1997. Т.35, №3, С. 287 - 296.
18. Ишков С.А. Сближение космических аппаратов с малой тягой на околокру-
161
Список использованных источников
говых орбитах //Космические исследования - 1992. Т.ЗО, № 2, С. 165 - 179.
19. Салмин В.В., Ишков С.А. Оптимальные программы управления в задаче
межорбитального перелета с непрерывной тягой //Космические исследова-
ния - 1984. Т. 22, № 5. - С. 702 - 711.
20. Кузмак Г.Е., Копнин Ю.М. Новая форма уравнений движения спутника и
приложения ее к исследованию движений, близких к круговым // ЖВМ и
МФ. 1963. Т. III, №4. С. 730-741.
21. Салмин В.В., Старинова О.Л. Оптимизация межпланетных перелетов КА с
двигателями малой тяги с учетом эллиптичности и некомпланарности ор-
бит планет//Космические исследования - 2001. Т.39, №1, С. 51 - 59.
22. Ишков С.А., Старинова О.Л. Оптимизация и моделирование движения кос-
мического аппарата с солнечным парусом. Известия Самарского научного
центра РАН, 2005, Т.7, №1, С.99-106.
23. Салмин В.В. Многошаговые алгоритмы управления движением космиче-
ских аппаратов //Космические исследования - 1979. Т. 17, № 6. - С. 835 -
845.
24. Васильев В.В., Салмин В.В. Многошаговые алгоритмы коррекции орбиты
спутника Земли двигателем малой тяги //Космические исследования - 1984.
Т.22, №4, С. 507-519.
25. Васильев В.В., Салмин В.В. Выбор универсальных параметров двигателя
малой тяги, предназначенного для поддержания орбиты спутника Зем-
ли//Космические исследования — 1984. Т.22, № 6. - С. 858 - 866.
26. Гурман В.М., Попов Ю.Б., Салмин В.В. О возможности реализации траек-
торий аппаратов с малой тягой с учетом их движения вокруг центра масс
//Космические исследования - 1970. Т.8, № 5, С.684-692.
27. Васильев В.В., Салмин В.В. Оптимальный разгон космического аппарата с
электрореактивным двигателем при ограниченной скорости поворота век-
тора тяги //Космические исследования -1976. Т. 14, № 3, С. 336 - 342.
28. Ишков С.А., Милокумова (Старинова) О.Л., Салмин В.В. Оптимизация
замкнутых межпланетных перелетов Земля-Марс-Земля с малой тягой
//Космические исследования - 1995. Т.ЗЗ, №2, С. 210 - 218.
29. Старинова О.Л. Оптимальное по быстродействию движение космического
аппарата между круговыми компланарными орбитами. Известия Самарско-
го научного центра РАН, 2005, Т.7, №1, С.92-98.
162