Теория графов - Дистель Р.

2.2. Паросочетания в произвольных графах

3.5. Не пересекающиеся по ребрам остовные деревья

4.4. Планарные графы. Теорема Куратовского

4.5. Алгебраические критерии планарности

6.5. Двойственность между потоками и раскрасками

Глава 8. Подструктуры в разреженных графах

10.2. Гамильтоновы циклы и степенные последовательности

10.3. Гамильтоновы циклы в квадрате графа

11.4. Пороговые функции и вторые моменты

Глава 12. Миноры, деревья и правильные квазиупорядочения

12.2. Теорема о минорах графов для деревьев

12.4. Древесная ширина и запрещенные миноры

Author: Дистель Р.

Tags: комбинаторный анализ теория графов теория вероятностей математическая статистика дискретная математика

ISBN: 5-86134-101-Х

Year: 2002

Similar

Теория графов

Эйлеровы графы и смежные вопросы

Дискретная математика (2-е издание)

Text

Рейнгард Дистель
ТЕОРИЯ ГРАФОВ
НОВОСИБИРСК
2002

Graduate Texts in Mathematics
Reinhard Diestel
Graph Theory
Second Edition
Springer

Рейнгард Дистель
Теория графов
Новосибирск
Издательство Института математики
2002

УДК 519.17
ББК 22.17
Д48
Перевод с английского О. В. Бородина
Дистель Р.
Теория графов: Пер. с англ. — Новосибирск: Изд-во Ин-та
математики, 2002. — 336 с.
ISBN 5-86134-101-Х.
В книге отражено ядро современной теории графов как
самостоятельной математической дисциплины. Это учебник
углубленного типа, выводящий читателя на передний край исследований.
Дан обзор последних достижений в теории графов, включая
доказательства ряда глубоких теорем. Впервые в доступном изложении
представлены такие актуальные разделы, как миноры графов,
предписанная раскраска, случайные графы и применение леммы
регулярности. Все упражнения снабжены указаниями.
Для студентов вузов и специалистов по дискретной математике
и информатике.
•G&H
Издание осуществлено при финансовой поддержке
Российского фонда фундаментальных исследований
(код проекта 99-01-14094)
Z^lSyW1 Без об^явл- © Бородин О. В., 2002
ISBN 5-86134-101-Х © Институт математики
им. С. Л. Соболева СО РАН, 200

Посвящается Дагмар

Сведения об авторе
Рейнгард Дистель получил Ph. D. в Кембриджском
университете после работы в 1983-1986 гг. в Тринити-колледже под
руководством Белы Боллобаша. Был стажером в колледже Св. Джона,
Кембридж, с 1986 по 1990 г. Затем занимался научной работой в Би-
лефельде (Германия), Оксфорде и США. С 1994 г. — профессор
в Кемнице, Германия, с 1999 г. заведует кафедрой в Гамбурге.
Основные научные интересы Рейнгарда Дистеля связаны с
теорией графов, особенно бесконечных графов. Им опубликовано
большое число статей и научная монография «Разложения графов»
(Оксфорд, 1990).

Оглавление
Предисловие 10
Глава 1. Основные понятия 15
1.1. Графы 16
1.2. Степень вершины 19
1.3. Пути и циклы 20
1.4. Связность 24
1.5. Деревья и леса 26
1.6. Двудольные графы 29
1.7. Стягивание и миноры 31
1.8. Эйлеровы обходы 33
1.9. Немного линейной алгебры 35
1.10. Другие виды графов 40
Упражнения 41
Примечания 43
Глава 2. Паросочетания 44
2.1. Паросочетания в двудольных графах 44
2.2. Паросочетания в произвольных графах 50
2.3. Покрытия путями 55
Упражнения 57
Примечания 58
Глава 3. Связность 59
3.1. 2-Связные графы и подграфы 59
3.2. Структура 3-связных графов 61
3.3. Теорема Менгера 66
3.4. Теорема Мадера 72
3.5. Не пересекающиеся по ребрам остовные деревья 74
3.6. Пути между заданными парами вершин 78
Упражнения 80
Примечания 82
Глава 4. Планарные графы 84
4.1. Топологические предпосылки 85
4.2. Плоские графы 87
4.3. Изображения 94
4.4. Планарные графы. Теорема Куратовского 98
4.5. Алгебраические критерии планарности 103
4.6. Двойственность на плоскости 105
Упражнения 108
Примечания 110

8 Оглавление
Глава 5. Раскраска 112
5.1. Раскраска карт и плоских графов 113
5.2. Раскраска вершин 115
5.3. Раскраска ребер 121
5.4. Предписанная раскраска 123
5.5. Совершенные графы 129
Упражнения 136
Примечания 139
Глава б. Потоки 142
6.1. Циркуляции 143
6.2. Потоки в сетях 144
6.3. Потоки со значениями в группе 147
6.4. й-Потоки для малых к 152
6.5. Двойственность между потоками и раскрасками 155
6.6. Гипотезы Татта о потоках 159
Упражнения 163
Примечания 165
Глава 7. Подструктуры в плотных графах 166
7.1. Подграфы 168
7.2. Лемма Семереди о регулярности 172
7.3. Применение леммы регулярности 180
Упражнения 185
Примечания 187
Глава 8. Подструктуры в разреженных графах 188
8.1. Топологические миноры 189
8.2. Миноры 198
8.3. Гипотеза Хадвигера 200
Упражнения 204
Примечания 205
Глава 9. Теория Рамсея для графов 207
9.1. Первоначальные теоремы Рамсея 208
9.2. Числа Рамсея 212
9.3. Индуцированные теоремы Рамсея 215
9.4. Рамсеевские свойства и связность 227
Упражнения 229
Примечания 230
Глава 10. Гамильтоновы циклы 232
10.1. Простые достаточные условия 232
10.2. Гамильтоновы циклы и степенные
последовательности 235
10.3. Гамильтоновы циклы в квадрате графа 237
Упражнения 246
Примечания 247
Глава 11. Случайные графы 249
11.1. Понятие случайного графа 250
11.2. Вероятностный метод 256
11.3. Свойства почти всех графов 258
11.4. Пороговые функции и вторые моменты 263
Упражнения 268
Примечания 270

Оглавление 9
Глава 12. Миноры, деревья и правильные
квазиупорядочения 272
12.1. Правильное квазиупорядочение 272
12.2. Теорема о минорах графов для деревьев 274
12.3. Древесные разложения 276
12.4. Древесная ширина и запрещенные миноры 285
12.5. Теорема о минорах графов 297
Упражнения 301
Примечания 304
Указания ко всем упражнениям 306
Список основных обозначений 321
Предметный указатель 323

Предисловие
Почти два десятилетия прошло с момента появления тех
текстов по теории графов, которые и по сей день определяют
содержание большинства начальных курсов. Утвержденный этими книгами
канон помог выделить некоторые основные области в обучении и
исследовании и несомненно будет и в обозримом будущем оказывать
влияние на развитие данной дисциплины.
Однако за эти 20 лет произошло немало, и в теории графов не
меньше, чем где-либо еще: были найдены глубокие новые теоремы;
на первый взгляд совершенно разнородные методы и результаты
оказались взаимосвязанными и возникли совершенно новые
направления. Достаточно упомянуть о том, что новое понятие предписанной
раскраски связало такие далекие инварианты, как средняя степень
и хроматическое число, что вероятностные методы и лемма о
регулярности завоевали экстремальную теорию графов и теорию Рам-
сея и что в рамках совершенно новой проблематики миноров в
графах и древесных разложений удалось решающим образом приложить
стандартные методы топологии поверхностей к давно стоявшим
алгоритмическим задачам на графах.
Ясно поэтому, что наступило время для переоценки: каковы на
сегодняшний день те существенные области, методы и результаты,
которые должны составлять основу начального курса по теории
графов, призванного готовить слушателей в соответствии с
современными тенденциями ее развития?
В этой книге я попытался предложить материал для такого
курса. Ввиду нарастающей сложности и зрелости предмета я нарушил
традицию попыток отразить и теорию, и приложения: книга
предлагает введение в теорию графов как часть (чистой) математики;
она не содержит ни явных алгоритмов, ни «практических»
приложений. Я надеюсь, что потенциальная глубина, достигаемая за счет
сужения охвата, принесет пользу как студентам-информатикам, так
и их коллегам-математикам. Полагая, что они предпочитают
алгоритмы, но выиграют от встречи с чистой математикой любого рода,
кажется идеальной возможность искать ее вблизи области их
интересов.
При отборе и изложении материала я преследовал две
противоречивые цели. С одной стороны, я считаю, что начальный курс

Предисловие
11
должен быть скупым и сосредоточенным на главном, чтобы
послужить руководством для новичков в этой области. В качестве текста
для продолжающих он кроме того должен быстро приводить к
пониманию сути материала; в конечном счете была идея дать хотя бы
представление о глубине материала и методах. С другой стороны,
моей особой заботой было излагать материал достаточно подробно,
чтобы сделать текст приятным и легко читаемым: наводящие
вопросы и идеи будут даны в явном виде, а все приводимые
доказательства будут строгими и полными.
Поэтому, как правило, глава начинается с краткого обсуждения
ключевых вопросов рассматриваемой области, далее кратко
перечисляются ее классические результаты (часто с упрощенными
доказательствами), а-затем приводятся одна или две более глубоких
теоремы, хорошо передающие ее специфику. Обычно доказательствам
последних предшествует (или сопутствует) нестрогое описание их
основных идей, но в итоге доказательство получается строгим и на
том же уровне детализации, что и для их более простых
предшественников. Я вскоре заметил, что вследствие этого некоторые
доказательства в печатном виде получились длиннее, чем они могли
бы быть при своих замечательно простых идеях. Все же надеюсь,
что даже читателю-профессионалу такая детализация поможет хотя
бы сократить время при чтении ...
При желании данный текст можно использовать в качестве
лекционного курса с минимальной переработкой или даже без нее.
Проще всего будет следовать порядку изложения, глава за главой; за
исключением двух явно указанных случаев все используемые в
доказательствах результаты будут к тому моменту уже доказаны.
Однако лектор может также разбить материал на легкий
начальный и более амбициозный последующий односеместровые курсы.
Чтобы помочь в подготовке курсов с измененным порядком
изложения, я перечисляю на полях рядом с доказательством номера
используемых в нем результатов. Эти ссылки даны в круглых скобках; так,
ссылка (4.1.2) на полях рядом с доказательством теоремы 4.3.2
показывает, что в нем будет использована лемма 4.1.2. Соответственно
на полях рядом с леммой 4.1.2 есть ссылка [4.3.2] (в квадратных
скобках) на то, что данная лемма будет использоваться в доказательстве
теоремы 4.3.2. Отметим, что эта система действует только между
разными разделами (одной или разных глав), разделы же написаны
как блоки, и их лучше читать подряд.
Математическая подготовка для этой книги, как и для
большинства текстов по теории графов, требуется минимальная: первое
знакомство с линейной алгеброй предполагается в разделе 1.9 и один раз
в разделе 5.5, некоторые начальные топологические понятия о
евклидовой плоскости и 3-мерном пространстве используются в главе 4,
а предварительное знакомство с элементарной теорией вероятности
поможет в главе 11. (Даже в этом случае нужно лишь знание
основных определений; все те немногие вероятностные инструменты, ко-

12
Предисловие
торые требуются, вводятся по ходу дела.) Есть две области теории
графов, которые я нахожу и увлекательными, и важными, особенно
с точки зрения заложенной в них чистой математики, но которые не
представлены в книге — это алгебраическая теория графов и
бесконечные графы.
В конце каждой главы имеются упражнения и примечания исто-
рико-библиографического характера. Многие из упражнений
выбраны с целью дополнить основной материал; они иллюстрируют
новые понятия, показывают связь новых инвариантов с более
ранними или то, в каком смысле сформулированный результат не
улучшаем. Особенно легкие упражнения отмечены значком ", а более
трудные — значком +. Примечания призваны сориентировать
читателя в последующем чтении; в частности, даются монографии и
обзорные статьи по теме главы. Также приводятся комментарии
исторического и другого рода.
Конец доказательства помечается символом D . Если этот знак
стоит сразу после формального утверждения, то доказательство
считается излишним, но так ли это — еще нужно убедиться! Если
нетривиальная теорема приводится лишь для сведения читателя, то
это можно понять по отсутствию доказательства и знака D .
Почти в любой книге есть ошибки, и вряд ли данная будет
исключением. Я постараюсь сообщать по сети Web обо всех
необходимых исправлениях. Соответствующий сайт может со временем
изменяться, но будет всегда доступен по адресам:
http://www.springer-ny.com/supplements/diestel/
http://www.springer.de/catalog/html-files/deutsch/math/3540609180.html
Пожалуйста, сообщайте мне о любых найденных ошибках.
В учебнике мало действительно оригинального, даже стиль
написания и изложения неизбежно подвергся влиянию примеров.
Книга, которая повлияла на меня в наибольшей степени, — это
несомненно классическая работа по теории графов Боллобаша; именно по
курсу, записью которого и стала эта книга, я познакомился с теорией
графов будучи студентом. Всякий, кто хорошо знает эту книгу,
почувствует ее влияние здесь, несмотря на все различия в содержании
и изложении.
Я хотел бы поблагодарить всех, кто так щедро дарил мне свои
время, знание и советы в связи с этой книгой. В особенности
помогли мне Н. Алон, Г. Брайтвел, П. Вальтр, Р. Джиллет, И. Лидер,
Т. Лучак, В. Мадер, В. Рёдл, П. Д. Сеймур, А. Д. Скотт, Р. Томас,
К. Томассен, Р. Халин, М. Хинц, А. Хук, Г. Шимони и М. Шковьера.
Я особенно благодарен также Томми Р. Иенсену, который научил
меня многому в раскраске и всему, что я знаю о ^-потоках, и кто
затратил массу настойчивости и энергии на вычитывание гранок
предварительного варианта этой книги на немецком языке.
Март 1997 г.
Р. Д.

Предисловие
13
О втором издании
Разумеется, я счастлив, что пишу это добавление через столь
короткий срок после выхода книги летом 1997 г. Мне особенно
приятно, что все больше людей используют ее не только в своей работе,
но и как материал для лекций; именно это, в конечном счете, и было
моей целью при написании книги, а также оправданием более
значительных усилий в работе над изложением, чем если бы она
предназначалась лишь специалистам.
Крупных изменений два. В последней главе о минорах теперь
дается полное доказательство одного из главных результатов в
теории Робертсона и Сеймура: их теоремы о том, что исключение
любого графа как минора ограничивает древесную ширину, если
и только если граф план арен. Этого короткого доказательства еще
не было, когда я писал первое издание, поэтому в него я включил
короткое доказательство следующей по важности теоремы —
аналогичного результата для цепной ширины. Теперь эта теорема из
главы 12 исключена. Еще одно изменение в этой главе состоит в том,
что теорема двойственности для древесной ширины (теорема 12.3.9)
теперь также дается с доказательством (коротким).
Второе важное изменение состоит в добавлении полного списка
указаний к упражнениям. Эта работа в основном сделана Томми
Иенсеном, которому я благодарен за потраченное на это время.
Указания должны помочь тем, кто самостоятельно изучает теорию
графов по этой книге, но не лишить их удовольствия совсем.
Упражнения, вместе с указаниями, по-прежнему предназначены для работы
в классе.
Кроме этих двух изменений есть еще несколько добавлений.
Наиболее значительное из них состоит в формальном введении деревьев
поиска в глубину в разделе 1.5 (что привело к некоторым
упрощениям в последующих доказательствах) и в новом оригинальном
доказательстве теоремы Менгера, принадлежащем Беме, Герингу и Ха-
ранту (и нигде больше не опубликованном).
Наконец, есть еще масса мелких упрощений и уточнений в
рассуждениях, которые были замечены мною, когда я вел занятия по
книге, либо были указаны мне другими. Всем этим лицам я
выражаю сердечную благодарность.
Страница Web перекочевала вместе со мной в
http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/
Думается, что этот адрес будет какое-то время сохраняться.
Еще раз благодарю всех, кто внес вклад в эту книгу, особенно
указав на ошибки в первом издании или предложив улучшения. Буду
благодарен и за последующие замечания!
Декабрь 1999 г.
Р. Д.

14
Предисловие
От переводчика
В книге Рейнгарда Дистеля «Теория графов» впервые удалось
представить широкому читателю такие важные современные
аспекты этой теории, как миноры графов, предписанная раскраска,
случайные графы, лемма о регулярности и др. Эти активно
развивающиеся направления будут, по-видимому, определять лицо теории
графов в ближайшей перспективе. Автор рассматривает теорию
графов как самостоятельную ветвь чистой математики, прослеживает
объединяющие ее задачи и методы. Ему удалось, с одной стороны,
дать сжатое введение в эту область для студентов в рамках двухсе-
местрового курса, а с другой — удовлетворить потребности
специалистов (информатиков и математиков) в доступном изложении
последних достижений в теории графов, включая доказательства ряда
глубоких теорем. Преследуя казавшуюся ранее недостижимой цель
охватить в учебнике объемом чуть более 300 страниц содержание
ядра современной теории графов, автор направляет внимание
читателя на принципиальную, математическую сторону дела, оставляя
за бортом технические вопросы алгоритмизации результатов, иногда
доходящие до записи их на формальном алгоритмическом языке.
Эта перспективная книга пользуется заслуженным успехом
на Западе; в частности, первое немецкое издание 1996 года было
мгновенно раскуплено. В 1997 году она была опубликована на
английском языке издательством «Шпрингер» в ведущей в мире учебной
серии «Graduate Texts in Mathematics» и вскоре была переведена на
многие языки мира. Ожидается, что это будет новый стабильный
учебник по теории графов на ближайшее десятилетие.
Рейнгард Дистель любезно предложил мне перевести книгу на
русский язык, и я счел своим приятным долгом взяться за эту
работу, считая, что публикация данной книги в России поможет
широкому кругу отечественных читателей не отстать от развития
событий в теории графов, поддержит достигнутый в нашей стране
уровень в преподавании и исследованиях в данной области.
Издательство «Шпрингер» уступило мне права на издание перевода в России,
а Российский фонд фундаментальных исследований выделил грант
на покрытие расходов по изданию. Выражаю также свою
глубокую признательность за помощь в работе над данным проектом
профессору Рейнгарду Дистелю, доктору Томми Иенсену, аспирантке
А. Э. Фрид и директору Издательства Института математики СО
РАН профессору В. Л. Бересневу.
Предлагаемый перевод соответствует 2-му англоязычному
изданию книги Р. Дистеля «Теория графов», вышедшему в издательстве
«Шпрингер» в мае 2000 г. Замечания прошу направлять по адресу:
brdnoleg@math.nsc.ru.
Май 2001 г. О. В. Бородин, д. ф.-м. н.
зав. лабораторией теории .графов
Институт математики СО РАН
Новосибирск, 630090

Глава 1
Основные понятия
В этой главе дается деликатное, но сжатое введение в основную
часть терминологии, используемой далее в книге. К счастью,
большинство стандартных теоретико-графовых терминов столь
наглядны, что легко запоминаются. Те же немногие понятия, что лучше
понимаются в соответствующем контексте, вводятся в дальнейшем
по мере необходимости.
Раздел 1.1 предлагает краткую, но представительную сводку
основных теоретико-графовых определений, примыкающих к
понятию графа. Для большинства читателей они уже знакомы или
будут объяснены в процессе чтения книги. Поэтому в разделе 1.1 мы
не останавливаемся на этих определениях дольше, чем нужно для
достижения ясности; главная цель здесь собрать большую часть
основных терминов в одном месте для облегчения ссылок в дальнейшем.
Начиная с раздела 1.2 все новые определения будут сразу же
иллюстрироваться несколькими простыми, но важными
утверждениями. Часто они будут связывать вновь определенные понятия друг
с другом; вопрос о том, как одни величины влияют на другие,
пронизывает большую часть теории графов, так что будет полезно
привыкать к этому стилю мышления с самого начала.
Через N мы обозначаем множество натуральных чисел, включая
ноль. Множество TLjnTL целых чисел по модулю п обозначается
через 7Ln\ его элементы записываются в виде г := i+nZ. Для
вещественного числа х мы обозначаем через [х\ наибольшее целое < ж, а через
\х\ наименьшее целое > х. Подразумевается, что логарифмы,
записанные как log, берутся по основанию 2, а натуральный логарифм
обозначается через In. Множество А = {А\,..., Ak} попарно
непересекающихся подмножеств множества А образует разбиение множе-
к
ства А, если А = (J А{ и Д\ф 0 для всех г. Разбиение {А[,..., А±}
t=i
множества А измельчает разбиение «с/, если каждое из А'{
содержится в некотором Aj. Через [А]к мы обозначаем множество всех
fc-элементных подмножеств в А. Множества с к элементами суть
к-множества; подмножества с к элементами суть к-подмножества.

16
Глава 1. Основные понятия
1.1. Графы
Граф есть пара множеств G — (V,E), где Е С [V]2] таким
образом, Е состоит из 2-элементных подмножеств множества V. Чтобы
избежать двоякого понимания обозначений, мы будем всегда
молчаливо предполагать, что V П Е = 0.
Элементы множества V называются вершинами (или узлами,
или точками) графа G, а элементы из Е — его ребрами (или
линиями). Рисуя граф, обычно изображают каждую вершину точкой
и соединяют линиями такие пары точек, которым в графе
соответствует пара вершин, образующая ребро. Как именно нарисованы
эти точки и линии, считается несущественным, важно лишь, какие
пары вершин образуют ребро, а какие — нет.
Рис. 1.1.1. Граф на множестве вершин V = {1,... , 7} со множеством ребер
Я={{1,2},{1,5},{2,5},{3,4},{5,7}}
О графе со множеством вершин V говорят, что он задан на V.
Множество вершин графа G обозначается через V(G), а множество
его ребер — через E(G). Эти договоренности не зависят от того,
какие имена присвоены этим двум множествам. Так, множество
вершин W графа Н = (W,F) по-прежнему обозначается через V(H),
а не через W(H). Мы не всегда будем строго различать граф и его
множества вершин и ребер. Например, мы можем говорить о
вершине v £ G (вместо v £ V{G))) ребре е £ G и так далее.
Число вершин графа G называется его порядком и записывается
как |G|; число его ребер обозначается через ||G||. Граф конечен или
бесконечен вместе со своим порядком; за исключением явно
оговариваемых случаев все рассматриваемые графы конечны.
Вместо пустого графа (0,0) мы пишем просто 0. Граф
порядка 0 или 1 называется тривиальным. Иногда, например, когда
нужно начать индукцию, пустые графы могут быть полезны; в
других случаях они дают вырожденные контрпримеры и становятся
помехой. Во избежание засорения текста оговорками о
нетривиальности мы обычно будем пренебрегать тривиальными, а тем более
пустыми графами.

1.1. Графы
17
Вершина v инцидентна ребру е, если v £ е; тогда еще говорят,
что е есть ребро при v. Две вершины, инцидентные ребру, суть его
концевые вершины или концы, ребро соединяет свои концевые
вершины. Ребро {х,у} обычно записывается как ху (или ух). Если
ж £ X и у £ Y, то ху есть X-Y ребро. Множество всех X-Y
ребер во множестве Е обозначается через E(X,Y); вместо E({x},Y)
и Е(Х, {у}) мы пишем просто E(x,Y) и Е(Х,у). Множество всех
ребер из Е при вершине v обозначается через E(v).
Две вершины х, у в G смежны или являются соседями, если
ху есть ребро в G. Два ребра е ф f смежны, если у них есть
общий конец. Если все вершины в G попарно смежны, то граф G
называется полным. Полный граф на п вершинах обозначается Кп\
К3 называется треугольником.
Попарно несмежные вершины графа называются независимыми.
Более строго, множество вершин или ребер независимо (или
внутренне устойчиво), если никакие два его элементы не смежны.
Пусть G = (V, Е) и G = (V, Е1) — два графа. Назовем G и G'
изоморфными и запишем это как G ~ G', если существует биекция
(р: V —► V, где ху £ Е <$> <р{х)<р(у) £ Е' при всех х, у £ V.
Такое отображение <р называется изоморфизмом, причем если G = G1',
то автоморфизмом. Чаще всего различий между изоморфными
графами не делается. Так, обычно пишут G = G' вместо G ~ G',
говорят о единственном полном графе на 17 вершинах и так далее.
Отображение, аргументами которого являются графы, называется
графовым инвариантом, если оно приписывает изоморфным графам
одинаковые значения. Числа вершин и ребер графа являются
простыми графовыми инвариантами; другой пример — наибольшее
число попарно смежных вершин.
3 •-
-• 5
GuG'
G-G'
GDG'
Рис. 1.1.2. Объединение, разность и пересечение;
вершины 2, 3, 4 индуцируют или порождают треугольник в G U G', но не в G

18
Глава 1. Основные понятия
Положим G U G' := (V U V, Е U Е') и G П G' := (7 ПГ,£П £')•
Если GflG' = 0, то G и G' we пересекаются. Если V С V и £' С £,
то G' называется подграфом графа G (a G — надграфом для G'),
и это записывается как G' С G. Менее строго можно сказать так:
G содержит G'.
Если G' С G и G' содержит все ребра iy G ^ с х,у G ^', то
G' — индуцированный подграф в G. Будем говорить, что V
индуцирует или порождает G' в G, и писать G' =: G[V;]. Таким образом,
если С/ С V — множество вершин, то через G[U] обозначается граф
на С/, ребрами которого являются в точности те ребра из G, оба
конца которых лежат в U. Если Н — подграф в G, не обязательно
индуцированный, мы сокращаем G[V(H)] до G[H]. Наконец, G' С G
является остовным подграфом в G, если V' заметывает G, т. е. если
V = V.
0П0
G G' G"
Рис. 1.1.3. Граф G с подграфами G' и G":
G' является индуцированным подграфом графа G, a G" — нет
Если U — произвольное множество вершин (обычно в G), то
вместо G[V \ U] мы пишем G — U. Другими словами, G — U
получается из G удалением всех вершин множества Uf)V и инцидентных
им ребер. Если U = {v} состоит из одной вершины, то будем вместо
G — {v} писать G — v. Вместо G — V(G') будем писать просто G — G'.
Для подмножества F в [V2] пишем G — F := (V,E\ F) и G + F :=
(V, Е U F)\ как и выше, G — {е} и G -f {е} сокращаются до G — е
и G + е. Будем называть G реберно-максимальным относительно
данного теоретико-графового свойства, если G этим свойством
обладает, а ни один граф вида G -\- ху для любых несмежных вершин
х,у £ G уже не обладает.
Более общо, когда мы называем граф минимальным или
максимальным с некоторым свойством, но не описываем конкретно
порядок, то подразумеваем просто вложенность подграфов. Говоря же
о минимальных и максимальных множествах вершин и ребер, мы
имеем в виду обычное теоретико-множественное включение.
Если G и G1 не пересекаются, мы обозначаем через G*G' граф,
получающийся из G U G' соединением всех вершин из G ребрами со
всеми вершинами из G'. Например, К2 * К3 — Къ. Дополнением G
к G называется граф на том же множестве вершин V со множеством
ребер [V]2 \ Е. Реберный граф L(G) к G задан на Е, а его вершины
х,у £ Е смежны тогда и только тогда, когда они смежны как ребра
графа G.

1.2. Степень вершины
19
Рис. 1.1.4. Граф, изоморфный своему дополнению
1.2. Степень вершины
Пусть G = (V, Е) — (непустой) граф. Множество соседей
вершины v в G обозначим через Nq(v) или кратко1) через N[y). Более
общо, для U CV соседи в V \U вершин из U называются соседями
множества £/; их множество обозначается через N(U).
Степень (или валентность) dc(v) = d(v) вершины v есть
число \E(v)\ ребер при v; по нашему определению графа2) она равна
числу соседей вершины v. Вершина степени 0 изолирована.
Число 6(G) := mm{d(v) \ v £ V} называется минимальной степенью
графа G, а число A(G) := ma,x{d(v) \ v £ V} — его максимальной
степенью. Если все вершины графа G имеют одну и ту же степень k,
то он k-однороден или просто однороден. 3-0днородный граф
называется кубическим.
Число
rf(G):= ш £ w
есть средняя степень графа G. Ясно, что
6(G) < d(G) < A(G).
Средняя степень оценивает глобально то, что локально измеряется
степенями вершин — число ребер графа G, приходящихся на одну
вершину. Иногда будет удобно выражать это отношение напрямую
Kaxe(G):=\E\/\V\.
Величины d и е, конечно же, тесно взаимосвязаны. В самом деле,
если мы сложим степени всех вершин в G, то учтем каждое ребро
ровно дважды, по одному разу с каждого конца. Таким образом,
|£| = J Е^) = ^снн
и поэтому
e(G) = \d{G).
1> Здесь индекс опускается, как и везде, где понятно, о каком графе идет речь.
2) Но не мультиграфа; см. раздел 1.10.

20
Глава 1. Основные понятия
Предложение 1.2.1. Число вершин нечетной степени в любом
графе четно.
Доказательство. Граф на V имеет | ^ d(v) ребер, поэтому
число J2 d(v) четно. □ v^v
Если граф имеет большую минимальную степень, т. е.
повсеместно много ребер на одну вершину, то в нем много ребер
приходится на одну вершину и глобально: e(G) = \d{G) > \8(G).
Обратное, конечно же, неверно: средняя степень может быть большой,
даже если минимальная степень мала. Однако вершины большой
степени не могут быть полностью затеряны среди вершин малой
степени. Как показывает следующее предложение, в графе G есть
подграф, средняя степень которого не меньше средней степени самого G
и чья минимальная степень больше половины его средней степени.
Предложение 1.2.2. Каждый граф G, имеющий хотя бы одно
ребро, содержит подграф Н с 6(H) > е(Н) > e(G).
Доказательство. Для построения Н по G будем пытаться
удалять вершины малой степени одну за другой, пока не останутся
только вершины большой степени. До какой степени d(v) мы можем
позволить себе удалять вершину v, не понижая при этом е? Ясно,
что до d(v) = е: ведь тогда число вершин уменьшается на 1, а число
ребер — не более чем на £, так что соотношение е между числом
ребер и вершин не уменьшается.
Формально, мы строим последовательность G = Go D G\ D ...
индуцированных подграфов графа G следующим образом. Если в G,
есть вершина V{ степени d(v{) < £(Gt), полагаем Gt-+i := Gt- — г/,-;
в противном случае заканчиваем построение и полагаем Н := G,.
По выбору V{ имеем e(G{+i) > e(G{) при всех г и, следовательно,
е(Н) > e(G).
Что еще можно сказать о графе HI Поскольку е(К1) — 0 <
£(G), ни один из графов в нашей последовательности не тривиален,
в частности, Я ф 0. Тот факт, что в Я нет вершин, пригодных
к удалению, означает, что S(H) > е(Н), что и утверждалось. □
1.3. Пути и циклы
Путь — это непустой граф Р — (V, Е) вида
V - {а?0,я?1,.. .,3*}, Е = {x0xi,xix2, ...,хк-1Хк}>
где все Х{ различны. Вершины xq и хк соединены путем Р и
называются его концами] вершины х\}..., Xk-i суть внутренние
вершины пути Р. Число ребер в пути есть его длина] путь длины к
обозначается через Рк. Отметим, что к может быть равным нулю,
а именно, Р° — К1.

1.3. Пути и циклы
21
Рис. 1.3.1. Путь Р = Р6 в G
Мы часто задаем путь как последовательность его вершин3),
т. е. пишем, например, Р — xo^i ...Xk и называем Р путем из xq
в Xk (а также между xq и ж*).
При 0 < г < j < к пишем
Рх{
Х{Р
X{PXj
— Xq .
= X{.
= X{.
••xi}
•Xk,
.Xj
P°Xi
lip
°.p°
= X\ . . .Ejfc-i,
= Xq . . .Ж,-_1,
= Х{+1...Xk,
— Xi + i . . .Xj-i,
имея в виду соответствующие под пути в Р. Аналогичные
наглядные обозначения используются и для объединений путей. Так, если
объединение Рх U xQy U yR трех путей есть снова путь, мы можем
обозначить его просто через PxQyR.
Рис. 1.3.2. Пути Р, Q и xPyQz
3) Точнее, как одну из двух последовательностей xq .. .х^ или х^. .. .xq,
обозначающих один и тот же путь. Но все же иногда полезно зафиксировать
одно из этих упорядочений множества V(P) в обозначениях; тогда можно
говорить о таких вещах, как «первая» вершина на Р с некоторым свойством
и так далее.

22
Глава 1. Основные понятия
Для множеств вершин А, В назовем Р — хо .. .Xk А-В путем,
если V(P) Г\А— {хо} и V(P) Г\В — {хк}. Как и раньше, пишем а-В
путь вместо {а}-В пути и т. д. Два или больше путей независимы,
если ни один из них не содержит внутренней вершины другого.
Например, два а-Ь пути независимы, если и только если общими в них
являются лишь вершины а и Ь.
Для графа Я назовем Р Н-путем, если Р нетривиален и
пересекается с Я только своими концами. В частности, ребро Я-пути
длины 1 никогда не принадлежит Я.
Если Р — хо .. .Xk-i есть путь и к > 3, то граф С := Р + Xk-iXo
называется циклом. Как и путь, мы часто задаем цикл
(циклической) последовательностью его вершин; только что упомянутый
цикл С может быть записан как хо .. .Хк-\Хо. Длина цикла есть
число его ребер (или вершин); цикл длины к называется к-циклом
и обозначается через Ск.
Наименьшая длина цикла в графе G есть его обхват g(G),
наибольшая длина цикла в G называется его периметром. (Если G
не содержит циклов, то полагаем обхват равным оо, а периметр —
нулю.) Ребро, соединяющее две вершины цикла, но ему не
принадлежащее, есть хорда этого цикла. Таким образом, индуцированный
цикл в G, т. е. цикл, образующий в G индуцированный подграф, —
это в точности цикл без хорд (рис. 1.3.3).
Рис. 1.3.3. Цикл С8 с хордой ху и индуцированные циклы С6, С4
Если граф имеет большую максимальную степень, то в нем есть
длинные цепи и циклы.
Предложение 1.3.1. Каждый граф G содержит путь длины
6(G) и цикл длины не менее 6(G) -f 1 (при условии, что 6(G) > 2).
Доказательство. Пусть xo...Xk — длиннейший путь в G.
Тогда на нем лежат все соседи вершины Xk (рис. 1.3.4). Отсюда
к > d(xk) > 6(G). Если г < к минимально при Х{Хк G E(G), то
Х{... XkXi есть цикл длины не менее 6(G) + 1. □
Минимальная степень и обхват, с другой стороны, не связаны
друг с другом (если только число вершин не зафиксировано). Как
мы увидим в главе 11, существуют графы, сочетающие произвольно
большую минимальную степень с произвольно большим обхватом.

1.3. Пути и циклы
23
• • 9h • +■ 9^ • -^
Хо Х{ Хк
Рис. 1.3.4- Длиннейший путь xq .. .х^ и соседи вершины х^
Расстояние da(x, у) в G между вершинами х, у есть длина
кратчайшего х-у пути в G; если ни одного такого пути нет, мы полагаем
d(x,y) := оо. Наибольшее расстояние между двумя вершинами в G
есть диаметр графа G, обозначаемый diam(G). Диаметр и обхват,
конечно же, взаимосвязаны.
Предложение 1.3.2. Каждый граф G, содержащий цикл,
удовлетворяет условию g(G) < 2 diam(G) -f 1.
Доказательство. Пусть С — кратчайший цикл в G. Если
g(G) > 2diam(G) -f 2, то в С найдутся две вершины с расстоянием
по С не меньше diam(G) -f 1. В G расстояние между этими
вершинами меньше, поэтому никакая кратчайшая цепь Р между ними не
является частью С. Таким образом, Р содержит некоторый С-путь
хРу. Вместе с более коротким из двух х-у путей в С этот путь хРу
образует более короткий цикл, чем С; противоречие. □
Вершина центральна в G, если наибольшее расстояние от нее
до всех остальных вершин минимально. Это расстояние есть радиус
графа G, обозначаемый rad(G). Таким образом, формально rad(G) —
min max do(x, у). Как нетрудно убедиться (упражнение), имеем
xev(G)yev(G)
rad(G) < diam(G) < 2rad(G).
Диаметр и радиус не связаны напрямую с минимальной или
средней степенью: граф может сочетать большую минимальную
степень с большим диаметром, а также малую среднюю степень с
малым диаметром (примеры?).
Максимальная степень ведет себя по-другому: граф большого
порядка может иметь малые диаметр и радиус, лишь если его
максимальная степень велика. Эту связь очень приблизительно можно
оценить следующим образом.
Предложение 1.3.3. В графе G радиуса не более к с
максимальной степенью не более d имеется не более 1 + kdk вершин.
Доказательство. Пусть z есть центральная вершина в G, а
Di обозначает множество вершин в G на расстоянии i от z. Тогда
к
V(G) = U D{ и |Д)| = 1. Поскольку A(G) < d, имеем |Д| < d|A_i|
t = 0
при г = 1,... , к, а значит, по индукции имеем |Д| < dl. Складывая

24
Глава 1. Основные понятия
эти неравенства, получаем
к
\G\< 1 + ХУ< ! + Ы*- D
t=i
Маршрут (длины к) в графе G есть непустая чередующаяся
последовательность uoeoi/iei .. .e^-iVk вершин и ребер в G такая, что
d = {vt,i;t-+i} при всех г < к. Если г/о = и*, то маршрут замкнут.
Если все вершины в маршруте различны, то он, очевидно,
определяет путь в G. Вообще говоря, каждый маршрут между двумя
вершинами4) содержит путь между этими вершинами
(доказательство?).
1.4. Связность
Непустой граф G называется связным, если любые две его
вершины соединены путем в G. Если U С V(G) и G[U] связен, мы также
называем множество U связным (в G).
Предложение 1.4.1. Вершины связного графа G можно
занумеровать так (например, v\,... ,vn), что подграф G{ := G[vi,... , V{]
будет связным при всех г.
Доказательство. Возьмем любую вершину за v\ и
предположим по индукции, что вершины fi,... , V{ уже выбраны для
некоторого i < \G\. Теперь возьмем вершину v £ G — G{. Поскольку
граф G связен, он содержит v-vi путь Р. Выберем в качестве ut-+i
последнюю на Р вершину из G — G{\ тогда u,-+i имеет соседа в G{.
Связность каждого G{ легко получается индукцией по г. □
Пусть G = (V,E) — граф. Максимальный связный подграф
в G называется компонентой (связности) графа G. Отметим, что
компонента, будучи связной, всегда непуста; тем самым пустой граф
не имеет компонент.
Рис. 1.4.1. Граф с тремя компонентами
и минимальный связный остовный подграф в каждой из компонент
) Мы будем часто употреблять термины, введенные для графов, также по
отношению к маршрутам, если их смысл остается очевидным.

1.4. Связность
25
Если A.BCVnXCVUE таковы, что каждый А-В путь в G
содержит вершину или ребро из X, мы говорим, что X разделяет
множества А и В в G. Отсюда, в частности, следует, что АС\В С X.
Более общо, будем говорить, что X разделяет граф G, и называть X
разделяющим множеством в G, если X разделяет в G какие-нибудь
две вершины из G — X. Вершина, разделяющая две другие вершины
своей компоненты, называется разделяющей вершиной (или точкой
сочленения), а ребро, разделяющее свои концы, есть мост. Иначе
говоря, мосты в графе суть те и только те ребра, которые не лежат
на цикле.
Рис. 1.4-2. Граф с разделяющими вершинами v, а;, т/, w и мостом е = ху
Граф G называется к-связным (при некотором к Е N), если
\G\ > к и G — X связен для любого множества X С V с \Х\ < к.
Другими словами, никакие две вершины в G не разделены меньше, чем
к другими вершинами. Каждый (непустой) граф 0-связен, а 1-связ-
ные графы суть нетривиальные связные графы. Наибольшее целое к,
при котором G является й-связным, есть его связность k(G). Таким
образом, «(G) = 0, если и только если G несвязен или G = К1,
а к(Кп) = п — 1 при всех п > 1.
Если \G\ > 1 и G — F связен для любого множества F С Е
с менее чем I ребрами, то G называется (.-реберно-связным.
Наибольшее целое I такое, что G является ^-реберно-связным, есть
реберная связность A(G) графа G. В частности, имеем A(G) = 0, если
G несвязен.
Рис. 1.4-3. Октаэдр G (слева) с k(G) — A(G) = 4
и граф Я с к(Н) = 2, но Л(Я) = 4

26
Глава 1. Основные понятия
Для любого нетривиального G выполняется неравенство
k(G) < X(G) < 6(G)
(упражнение), так что, в частности, высокая связность требует
большой минимальной степени. Напротив, большая минимальная
степень не обеспечивает ни высокой связности, ни даже высокой
реберной связности (примеры?). Однако она влечет существование
подграфа большой связности.
Теорема 1.4.2 (Мадер, 1972). Каждый граф средней степени
не менее 4к содержит к-связный подграф.
Доказательство. При к Е {0,1} утверждение тривиально;
рассмотрим к > 2 и граф G — (V, Е) с |V| =: п и \Е\ =: т. Для
облегчения индукции докажем более сильное утверждение, а именно,
что G имеет fc-связный подграф при любых
(i) п > 2к - 1 и
(ii) m> (2k-3)(n-k + 1) + 1.
(Это утверждение действительно сильнее, так как (i) и (ii) следуют
из нашего предположения d(G) > 4к: (i) следует, поскольку п >
A(G) > d(G) > 4&, a (ii) следует непосредственно из m = \d(G)n >
2kn.)
Доказываем индукцией по п. Если п = 2к — 1, то к = ^(n-fl),
и поэтому m > т;п(п— 1) ввиду (ii). Таким образом, G = Кп Э Kk+l,
и утверждение доказано. Теперь допустим, что п > 2к. Если
вершина v имеет d(v) < 2к — 3, достаточно применить индукционное
предположение к G — v. Поэтому допустим, что 5(G) > 2к — 2. Если
G является ^-связным, доказывать нечего. Поэтому допустим, что
G имеет вид G - G\ U G2, где \G\ П G2\ < к и |Gi|, |G2| < п.
Поскольку каждое ребро графа G лежит либо в G\ либо в G2, то в G
нет ребер между G\ — G2 и G2 — G\. Из того, что у каждой вершины
в этих подграфах есть не менее 6(G) > 2к — 2 соседей, получаем
|Gi|, |G2| > 2fc — 1. Но тогда хотя бы один из графов Gi, G2
должен удовлетворять индукционному предположению (завершая
доказательство). В противном случае имеем
l|Gi||<(2*-3)(|G,-|-*+l)
при i — 1, 2 и, следовательно,
™<l|Gi|| + ||G2||
<(2Jb-3)(|Gi| + |G2|-2Jb + 2)
< (2Jb - 3)(п - к + 1)
(так как \G\ Г) G2| < к — 1), что противоречит (ii). □

1.5. Деревья и леса
27
1.5. Деревья и леса
Ациклический граф, т. е. не содержащий циклов, называется
лесом. Связный лес называется деревом. (Таким образом, лес —
это граф, компоненты которого суть деревья.) Вершины степени 1
в дереве называются листьями. Каждое нетривиальное дерево имеет
не меньше двух листьев, например таковы концы длиннейшей цепи.
Этот простой факт часто оказывается удобным, особенно в
индуктивных доказательствах о деревьях: если мы удаляем из дерева лист,
то остается дерево.
Рис. 1.5.1. Дерево
Теорема 1.5.1. Для графа Т следующие утверждения
равносильны:
(i) Т является деревом]
(ii) любые две вершины в Т соединены единственным путем]
(iii) Т — минимальный связный, т. е. Т связен, ноТ — е несвязен
для любого ребра е Е Т;
(iv) Т — максимальный ациклический, т. е. Т не содержит
цикла, ноТ + ху содержит цикл для любых несмежных вершин
x,yGT. D
Доказательство теоремы 1.5.1 прямолинейно и послужит
хорошим упражнением для тех, кто еще не вполне освоился с понятиями,
которые в ней фигурируют. Обобщая наши обозначения для путей из
раздела 1.3, будем под хТу понимать единственный путь в дереве Т
между вершинами х, у (см. (ii) выше).
Часто используемое приложение теорем 1.5.1 состоит в том, что
всякий связный граф содержит остовное дерево: из равносильности
(i) и (iii) всякий минимальный остовный подграф является деревом.
На рис. 1.4.1 в каждой из трех компонент графа выделены остовные
деревья.

28
Глава 1. Основные понятия
Следствие 1.5.2. Вершины дерева можно занумеровать так
(например, v\,... ,vn), что каждая вершина V{ при г > 2 будет иметь
единственного соседа в {vi,... , Vi-i}.
Доказательство. Применяем нумерацию, построенную в
предложении 1.4.1. □
Следствие 1.5.3. Связный граф с п вершинами является
деревом, если и только если в нем в точности п — 1 ребер.
Доказательство. Индукция по г показывает, что подграф,
порожденный первыми г вершинами из следствия 1.5.2, содержит г— 1
ребер; при г = п это доказывает прямую импликацию. Обратно,
пусть G есть связный граф с п вершинами ип-1 ребрами, и пусть
G' — остовное дерево в G. Поскольку G' имеет п— 1 ребер по первой
импликации, то получаем G — G1. □
Следствие 1.5.4. Если Т есть дерево, a G — любой граф с
S(G) > \Т\ — 1, то Т С G, т. е. G содержит подграф, изоморфный Т.
Доказательство. Находим копию дерева Т в G индуктивно,
следуя нумерации из следствия 1.5.2. □
Иногда удобно считать одну из вершин дерева особой; такая
вершина называется корнем этого дерева. Дерево с зафиксированным
корнем называется корневым деревом. Выбор корня г в дереве Т
задает частичный порядок на V(T) (считаем, что х < у, если х Е гТу).
Это — древесный порядок на V(T), определяемый Т и г. Отметим,
что г является в этом частичном порядке наименьшим элементом,
всякий лист х ф г в Т является наибольшим элементом, концы
любого ребра сравнимы, а любое множество вида {х \ х < у} (где у —
любая фиксированная вершина) есть цепь, т. е. состоит из попарно
сравнимых элементов (доказательства?).
Корневое дерево Т, содержащееся в графе G, называется
нормальным в G, если концы любого Т-пути в G сравнимы
относительно древесного порядка, задаваемого посредством Т. Если Т
покрывает G, это равносильно требованию, что любые две вершины
из Т должны быть сравнимы, если они смежны в G (см. рис. 1.5.2).
г
Рис. 1.5.2. Дерево поиска в глубину с корнем г

1.6. Двудольные графы
29
Нормальные остовные деревья также называются деревьями поиска
б глубину из-за способа их применения в компьютерном поиске по
графу (упражнение 17).
Нормальные остовные деревья являются простым, но мощным
инструментом в теории графов. И они всегда существуют.
Предложение 1.5.5. Каждый связный граф содержит
нормальное остовное дерево, причем в качестве корня можно взять
произвольную вершину.
Доказательство. Пусть граф G связен, а г Е G — любая его
вершина. Рассмотрим его максимальное нормальное дерево Т с
корнем г в G; покажем, что V(T) = V(G).
Предположим противное, и пусть С — компонента в G — Т.
Поскольку Т нормально, N(C) является цепью в Т. Пусть х — ее
наибольший элемент, а вершина у £ С смежна с х. Пусть дерево Т'
получается из Т соединением у с х; задаваемый по Т' древесный
порядок тогда содержит порядок, задаваемый Т. Мы придем к
противоречию, показав, что Т' также нормально в G.
Пусть Р является Т'-путем в G. Если оба конца пути Р
лежат в Т, то они сравнимы в древесном порядке, индуцированном Т
(а значит, и индуцированном Т"), поскольку тогда Р также является
Т-путем, а Т нормально в G по предположению. Если нет, то у
является концом для Р, поэтому Р лежит в С, за исключением другого
конца z, который лежит в N(C). Значит, z < х ввиду выбора х. Для
нужной нам сравнимости у и z достаточно показать, что х < у, т. е.
что х G гТ'у. Но это уже очевидно, поскольку у есть лист в Т;,
смежный с х.
1.6. Двудольные графы
Пусть г > 2 — целое число. Граф G — (V, Е) называется
г-дольным, если V допускает такое разбиение на г классов, при
котором концы каждого ребра лежат в разных классах; вершины из
одного класса разбиения должны быть попарно несмежны. Вместо
«2-дольный» обычно говорят двудольный.
Рис. 1.6.1. Два 3-дольных графа

30
Глава 1. Основные понятия
г-Дольный граф, в котором каждые две вершины из разных
классов смежны, называется полным] полные г-дольные графы для
всех г вместе называются полными многодольными графами.
Полный г-дольный граф КП1 * ••• * КПг обозначается через ](П11111)Пр;
если щ = • • • = пг =: 5, то пишем короче: Krs. Так, Krs есть
полный г-дольный граф, в котором каждый класс разбиения состоит из
s вершин5). (На рис. 1.6.1 изображен октаэдр К^\ сравните его вид
с приведенным на рис. 1.4.3.) Графы вида Ki>n называются
звездами.
Рис. 1.6.2. Три изображения двудольного графа/<з,з = А'|
Ясно, что двудольный граф не содержит нечетных циклов, т. е.
циклов нечетной длины. На самом же деле двудольные графы
описываются этим свойством однозначно.
Предложение 1.6.1. Граф двудолен, если и только если он не
содержит нечетных циклов.
Доказательство. Пусть граф G = (V,E) не содержит
нечетных циклов; покажем, что G двудольный. Ясно, что граф двудолен,
если все его компоненты двудольны или тривиальны, поэтому можно
предположить, что G связен. Пусть Т — остовное дерево в G;
выберем корень г £ Т и обозначим отвечающий им древесный порядок
на V через <т. Для любой v £ V единственная цепь rTv имеет либо
нечетную, либо четную длину. Это задает разбиение множества V
на две доли; покажем, что G является двудольным с этим
разбиением.
Пусть е — ху является ребром в G. Если е £ Т, причем х <т у,
то гТу = гТху, и поэтому х и у лежат в разных классах разбиения.
Если е ф Т, то Се := хТу+е есть цикл (рис. 1.6.3) и, как мы уже
видели, вершины вдоль хТу попеременно принадлежат двум классам.
Поскольку цикл Се по предположению четен, то х и у также лежат
в разных классах. □
') Отметим, что A'J получается заменой каждой вершины в КГ на
независимое 5-множество; наше обозначение К% содержит намек на эту связь.

1.7. Стягивание и миноры
31
Рис. 1.6.3. Цикл Се в Т + е
1.7. Стягивание и миноры
В разделе 1.1 мы встретили два фундаментальных отношения
включения на графах: включение по подграфам и включение по
«индуцированным подграфам». В этой главе мы рассмотрим еще одно:
отношение стягивания.
Пусть е = ху есть ребро в графе G — (V, Е). Обозначим через
G/e граф, полученный из G стягиванием ребра е в новую
вершину ve, которая становится смежной со всеми соседями вершин х и у.
Формально, G/e есть граф (V,,E/) со множеством вершин V : —
(V \ {ж, у}) U {ve} (где ve есть «новая» вершина, т. е. ve £ V U Е)
и множеством ребер
Е' := {vw е Е \{v,w}D {х, у} = 0}
М{иек; | xw G Е \ {е} или yw £ Е\ {е}}
Более общо, если X — еще один граф и {Vx \ х £ V(X)} является
таким разбиением множества V на связные подмножества, что для
любых вершин ж, у £ X в G существует Vx-Vy ребро, если и только
если ху £ Е(Х). Мы называем G графом MX и пишем6) G = MX
6) То есть формально выражение MX, где М называется «минором» (см.
ниже), обозначает целый класс графов, a. G — MX означает (немного
неуклюже), что G принадлежит этому классу.

32
Глава 1. Основные понятия
(рис. 1.7.2). Множества Vx суть в emeu этого MX. Нестрого
говоря, X получается из G стягиванием каждой ветви в одну вершину
и удалением возможно возникающих при этом «параллельных
ребер» и «петель».
Рис. 1.7.2. Y Э G = MX, поэтому X есть минор графа Y
Если Vx = U С V — ветвь, а все остальные ветви состоят из
одной вершины, мы иногда пишем G/U вместо графа X и v\j вместо
вершины х £ X, на которую стягивается £/, а оставшуюся часть
графа X считаем индуцированным подграфом графа G.
Описанное выше стягивание одного ребра ии' может рассматриваться как
частный случай с U = {и, и'}.
Предложение 1.7.1. Граф G есть MX, если и только если X
может быть получен из G последовательным стягиванием ребер, т. е.
если и только если существуют графы Go,..., Gn и ребра е,- £ d
такие, что Go = G, Gn с^ X, a Gt-+i = G,-/e,- для всех i < п.
Доказательство. Индукция по \G\ - \Х\. □
Если G = MX является подграфом графа У, мы называем X
минором графа У и пишем X =^ У. Отметим, что каждый подграф
графа является его минором; в частности, каждый граф является
своим собственным минором. По предложению 1.7.1 любой минор
графа может быть получен из него сначала удалением вершин и
ребер, а затем стягиванием ребер. Наоборот, любой граф, полученный
из другого повторными удалениями и стягиваниями (в любом
порядке), является минором последнего. Это очевидно для одного
удаления и стягивания, а для нескольких вытекает из транзитивности
отношения быть минором (предложение 1.7.3).
Если заменить ребра в X на непересекающиеся пути между их
концами (чтобы ни один из путей не имел внутренней вершины на
другом пути или в X), то полученный граф G мы называем
подразбиением графа X и записываем как G = ТХ7\ Если G = ТХ
7) Итак, снова ТХ обозначает целый класс графов — тех, которые гомеоморф-
ны X, если рассматривать их как топологические пространства. Буква Т
в ТХ заменяет слово «топологический».

1.8. Эйлеровы обходы
33
является подграфом графа Y, то X называется топологическим
минором графа У (рис. 1.7.3).
Рис. 1.7.3. Здесь Y DG=TX,
поэтому X есть топологический минор графа Y
Если G — ТХ, мы рассматриваем V(X) как подмножество
множества V(G) и называем эти вершины вершинами ветвления в G;
остальные вершины в G суть его подразбивающие вершины. Таким
образом, все подразбивающие вершины имеют степень 2, тогда как
вершины ветвления сохраняют свою степень из X.
Предложение 1.7.2.
(i) Всякий ТХ является также MX (рис. 1.7.4); таким
образом, всякий топологический минор графа является также
его (обычным) минором.
(ii) Если А(Х) < 3, то любой MX содержит ТХ; таким
образом, всякий минор с максимальной степенью не более 3
графа является также его топологическим минором. □
Рис. 1.7.4- Подразбиение графа А'4, рассматриваемое как МА'4
Предложение 1.7.3. Отношение быть минором =4 н отношение
быть топологическим минором являются частичными порядками на
классе всех конечных графов, т. е. они рефлексивны,
антисимметричны и транзитивны. □
1.8. Эйлеровы обходы
Любой математик, которому пришлось бы оказаться в восточно-
прусском городе Кенигсберге (и в 18 веке), подобно великому
Леонарду Эйлеру немедленно задал бы себе вопрос о существовании
замкнутого маршрута по старой части города, проходящего через
каждый мост на рис. 1.8.1 ровно один раз.

34
Глава 1. Основные понятия
Рис. 1.8.1. Мосты Кенигсберга (1736 год)
Вдохновившись этим рисунком8), назовем замкнутый маршрут
в графе эйлеровым обходом, если он проходит каждое ребро графа
ровно один раз. Граф эйлеров, если он допускает эйлеров обход.
Рис. 1.8.2. Граф, формализующий задачу о мостах
Теорема 1.8.1 (Эйлер, 1736). Связный граф эйлеров, если
и только если каждая его вершина имеет четную степень.
Доказательство. Очевидно, что условие на степени
необходимо: вершина, встречающаяся в эйлеровом обходе к раз (или к + 1
раз, если это начальная и конечная вершина, учитываемая дважды),
должна иметь степень 2к.
8) Тот, кому такое вдохновение окажется недоступным даже после созерцания
рис. 1.8.2, может найти утешение в мультиграфе на рис. 1.10.1.

1.9. Немного линейной алгебры
35
Обратно, пусть в связном графе G степени всех вершин четны,
и пусть
W - v0e0 .. .ei-ivi
есть длиннейший маршрут в G, использующий каждое ребро не
более одного раза. Поскольку расширить W нельзя, он уже включает
все ребра при vi. По предположению, число таких ребер четно.
Значит, vi = г/о, т. е. маршрут W замкнут.
Предположим, что W не эйлеров. Тогда в G есть ребро е, не
входящее в W, но инцидентное вершине из W, например, е — uv{.
(Здесь мы используем связность графа G, как и при доказательстве
предложения 1.4.1.) Тогда маршрут
ueviei.. .et-ivteo ...et-_iv»
длиннее, чем W\ противоречие. □
1.9. Немного линейной алгебры
Пусть в графе G — (V,E) имеется п вершин и т ребер,
скажем, V = {г/i,.. . ,г/п} и Е — {ei,...,em}. Пространство вершин
y(G) графа G есть векторное пространство над 2-элементным
полем F2 = {0,1} всех функций V —» F2. Каждый элемент из y(G)
естественным образом отвечает некоторому подмножеству в V —
множеству тех вершин, которым он приписывает 1, а каждое
подмножество в V однозначно представимо в y(G) своей индикаторной
функцией. Можно считать V(G) множеством всех подмножеств
множества V, преобразованным в векторное пространство: сумма U Л-U'
двух множеств вершин С/, U' С V есть их симметрическая разность
(почему?), a U = —U для любых U С V. Нулем в ^(G),
рассматриваемом таким образом, является пустое множество (вершин) 0.
Поскольку {{г/i},..., {г/п}} является (стандартным) базисом в ^(G),
то имеем dim(T(G)) = п.
Таким же образом, как выше, функции Е —> F2 образуют
пространство ребер <*(G) графа G. Его элементы суть подмножества
множества Е, сложение векторов равносильно симметрической
разности, 0 С Е есть нуль, a F — — F для всех F С Е. Как и раньше,
{{ei}> • • •) {em}} есть стандартный базис в <^(G), a dim(<f (G)) = т.
Поскольку именно ребра графа задают его структуру, мы в
основном будем иметь дело с пространством ребер. Для заданных
множеств ребер F, F' £ y(G) и их коэффициентов Ai,..., Am и Х[,..., А^
в стандартном базисе полагаем
(F,F/):=A1A/1 + ... + AmA/mGF2.

36
Глава 1. Основные понятия
Заметим, что (F, F') = 0 может иметь место даже при F = F' ф 0.
Действительно, (F, F') — 0, если и только если F и F' пересекаются
по четному числу ребер. Для подпространства & в ^(G) полагаем
&*- := {i>e <?(G) | (F, D) = 0 для всех F G ^}.
Это снова подпространство* в <*(G) (пространство всех векторов,
удовлетворяющих некоторому множеству линейных уравнений;
какому?), откуда имеем
dim^ + dim^-1) = m.
Пространство циклов tf = ff(G) есть подпространство в <^(G),
состоящее из всех циклов в G, точнее, из множеств их ребер9).
Размерность пространства ^(G) называется цикломатическим числом
графа G.
Предложение 1.9.1. Индуцированные циклы графа G
порождают все пространство циклов.
Доказательство. По определению ^(G) достаточно показать,
что индуцированные циклы в G порождают любой цикл С С G с
хордой е. Это легко получается индукцией по \С\: два цикла вС + е,
пересекающиеся только по е, короче, чем G, а их симметрическая
разность в точности равна С. □
Предложение 1.9.2. Множество ребер F С Е лежит в ^(G),
если и только если каждая вершина из (V, F) имеет четную степень.
Доказательство. Прямая импликация получается индукцией
по числу циклов, требуемых для порождения F, а обратная —
индукцией по числу циклов в (V, F). D
Если {Vi, Vb} есть разбиение множества вершин V, то
множество E(Vi,V2) всех ребер в G, пересекающих это разбиение,
называется разрезом. Напомним, что при V\ — {v} этот разрез
обозначается через Е(у).
Предложение 1.9.3. Вместе с 0 разрезы в G образуют
подпространство ff* пространства <f (G). Это подпространство
порождается разрезами вида Е(у).
Доказательство. Пусть ^* обозначает множество всех
разрезов в G вместе с 0. Для доказательства того, что ^* является
подпространством, покажем, что вместе с любыми D, D' £ ^* также
и D + D' (= D - D') лежит в <*?*. Поскольку D + D = 0 Е <*?*
9) Для простоты мы обычно не будем, говоря о пространстве циклов,
различать циклы и их множества ребер.

1.9. Немного линейной алгебры
37
hD + 0 = DG^*, можно считать, что D и D' различны и
непусты. Пусть {Vi, V2} и {V/, V2} — соответствующие разбиения
множества V. Тогда D -f D' состоит из всех ребер, пересекающих одно
из этих разбиений, но не пересекающих другого (рис. 1.9.1). Но это
в точности ребра, соединяющие (Vi П V/) U (Vb П V2') с (Vi П V2') U
(V2 П V/), а так как D ф D', эти два множества образуют еще одно
разбиение множества V. Следовательно, D -f -D' £ ^*, и ^* в самом
деле является подпространством в <?(G).
Рис. ^.5Л. Ребра разрезов в .D + £)'
Наше второе утверждение, что разрезы вида -E(v) порождают
целиком ^*, следует из того факта, что каждое ребро ху £ G
лежит в двух и только двух таких разрезах (в Е(х) и Е(у))\ значит,
для каждого разбиения {Vi, V2} множества V имеет место равенство
E(VUV2)= £ ВД. п
Подпространство ^* =: ^*(G) в <f (G) из предложения 1.9.3
будет называться пространством разрезов графа G. Нетрудно найти
среди разрезов вида E(v) явный базис для ^(G) и тем самым
определить его размерность (упражнение); вместе с теоремой 1.9.5 это
дает независимое доказательство теоремы 1.9.6.
Следующая лемма пригодится нам при изучении
двойственности плоских графов в разделе 4.6.
Лемма 1.9.4. Минимальные разрезы в связном графе
порождают его пространство разрезов.
Доказательство. Заметим сначала, что разрез в связном
графе G = (V, Е) минимален, если и только если оба множества в
соответствующем разбиении множества V связны в G. Теперь
рассмотрим любой связный подграф С С G. Если D является компонентой
bG— G, toG — D также связно (рис. 1.9.2), поэтому ребра между
D и G — D образуют минимальный разрез. По выбору D этот разрез
совпадает с множеством E(C,D) всех C-D ребер в G.
Для доказательства леммы возьмем разбиение {Vi, V2}
множества V и рассмотрим компоненту С графа G[Vi]. Тогда Е(С, V2) =

38
Глава 1. Основные понятия
Е(С, G — С) является объединением непересекающихся множеств
ребер Е(С, D) по всем компонентам D в G — С, а значит,
объединением непересекающихся минимальных разрезов (см. выше). Теперь
непересекающееся объединение всех этих множеств ребер Е(С, Vo),
взятое по всем компонентам С в G[Vi], есть в точности наш разрез
E(Vi,V2). Значит, этот разрез порождается минимальными
разрезами, как и утверждалось. D
Рис. 1.9.2. G — D связно, a E(C,D) — минимальный разрез
. Теорема 1.9.5. Пространство циклов *£ и пространство
разрезов ff* любого графа связаны соотношениями
Доказательство. Рассмотрим граф G = (V,E). Ясно, что
каждый цикл в G содержит в любом разрезе четное число ребер.
Отсюда <*? С ^*±.
Обратно, согласно предложению 1.9.2 для любого множества
ребер F £ *£ существует вершина г/, инцидентная нечетному числу
ребер в F. Отсюда (E(v),F) — 1, поэтому из Е(у) £ ^* следует
F £ <ё>*±. Утверждение ^ = <^*-L доказано.
Для доказательства равенства^7* = <^7-L теперь достаточно
показать, что^* = (<^*-L)-L. Здесь ^* С (<^*-L)J- следует непосредственно
из определения _L. Но поскольку
dim(«") + dimOT^) = m = dim^^) + dim((tir±)±),
ff* имеет ту же размерность, что и ((^*±)±, а значит, ^* = (<^7*-L)-L,
как и утверждалось. □
Теорема 1.9.6. Для любого конечного графа Gen вершинами
и m ребрами выполняются соотношения
dim(V(G)) = m-n+l и dim(V(G)) = n - 1.

1.9. Немного линейной алгебры
39
Доказательство. Пусть G = (V,E). Поскольку по
теореме 1.9.5 dim(^)?-b^dim(^*) = га, достаточно найти га — п -f 1
линейно независимых векторов в?ип-1 линейно независимых
векторов в ^*: раз сумма этих чисел равна га, ни размерность ^, ни
размерность ^* не могут быть строго больше.
Пусть Т — остовное дерево в G. По следствию 1.5.3 в Т имеется
п — 1 ребер, поэтому га — п -f 1 ребер графа G лежат вне Т. Для
любого из этих m — п + 1 ребер е £ Е \ Е(Т) граф Т + е содержит
цикл Се (см. рис. 1.6.3 и теорему 1.5.1(iv)). Поскольку ни одно из
ребер е не лежит на Се> для е' ф е, эти га — n + 1 циклов линейно
независимы.
Для любого из п — 1 ребер е £ Т граф Т — е имеет ровно две
компоненты (теорема 1.5.1(iii)), а множество De ребер из G между
этими компонентами образует разрез (рис. 1.9.3). Поскольку ни одно
из этих ребер е £ Т не лежит в Д./ при е' ф е, эти га — 1 разрезов
линейно независимы. □
Рис. 1.9.3. Разрез De
Матрица инцидентности В — (bij)nxm графа G — (К, Е) с V —
{г/i,..., vn} и Е — {е\,..., ет} определяется над F2 следующим
образом:
Г 1, если V{ £ ej,
bij :— <
I О в противном случае.
Как обычно, В% обозначает транспонированную матрицу для В.
Тогда В и В* задают линейные отображения В: <^(G) —+ V(G)
к В*: y(G) —± <^(G) в стандартных базисах.
Предложение 1.9.7.
(i) Ядром отображения В является ^(G).
(ii) Множеством значений отображения В% является ff*(G). □
Матрица смежности А — (a>ij)nXn графа G задается правилом
Г 1, если V{Vj £ Е,
aij :== ^
^0 в противном случае.

40
Глава 1. Основные понятия
Наше последнее предложение устанавливает простую связь между
А и В (которые теперь рассматриваются как вещественные
матрицы*), л. Пусть D есть вещественная диагональная матрица (dij)nXn
с da ~ d(v{) и d{j = 0в противном случае.
Предложение 1.9.8. ВВ* = А +D. П
1.10. Другие виды графов
Для полноты перечислим ряд разновидностей графов, которые
встречаются в этой книге реже или совсем не встречаются.
Гиперграф есть пара (V) Е) непересекающихся множеств, где
элементами Е являются непустые подмножества (произвольной
мощности) множества V. Таким образом, графы суть гиперграфы
специального вида.
Ориентированный граф (или орграф) есть пара (V, Е)
непересекающихся множеств (вершин и ребер)10^ вместе с двумя
отображениями init: Е —+ V и ter: Е —+ V, приписывающими каждому
ребру е его начальную вершину init(e) и его концевую вершину ter(e).
Говорят, что ребро е ведет из init(e) в ter(e). Заметим, что
ориентированный граф может иметь несколько ребер между какими-то
двумя вершинами ж, у. Такие ребра называются кратными ребрами]
если они направлены одинаково (скажем, из х в у), то называются
параллельными. Если init(e) = ter(e), то дуга е называется петлей.
Ориентированный граф D является ориентацией
(неориентированного) графа G, если V(D) = V(G) и E(D) = E(G) и при этом
{init(e), ter(e)} = {х,у} для любого ребра е = ху. Говоря
содержательно, такой направленный граф получается из некоторого
неориентированного графа заданием на каждом ребре направления от
одного конца к другому. Иначе говоря, направленные графы суть
ориентированные графы без петель и кратных ребер.
Мультиграф есть пара (V, Е) непересекающихся множеств
(вершин и ребер) вместе с отображением Е —+ F U [F]2,
приписывающим каждому ребру одну или две вершины — его концы. Таким
образом, в мультиграфах тоже могут быть петли и кратные ребра;
можно считать мультиграф орграфом, в котором ориентации ребер
«забыты». Чтобы указать, что х и у являются концами ребра е, мы
по-прежнему пишем е = ху, хотя этим е уже однозначно не
определяется.
По существу граф есть мультиграф без петель и кратных ребер.
Быть может, немного удивительно то, что иногда бывает проще
доказать более общую теорему о мультиграфах, чем исходную теорему
10) В отечественной литературе применительно к орграфам чаще вместо ребер
говорят «дуги». — О. Б.

Упражнения 41
о графах. Более того, в некоторых разделах теории графов (таких,
как план арная двойственность; см. разделы 4.6 и 6.5) мультиграфы
возникают более естественно, чем графы, и сужение вопроса до
графов там кажется искусственным и приводит к техническим
трудностям. Поэтому мы в таких случаях будем рассматривать
мультиграфы, но без особых технических оговорок. Ранее введенная
терминология для графов будет просто использоваться применительно
к мультиграфам.
Все же стоит указать на два различия. Во-первых, в мультигра-
фах возможны циклы длины 1 и 2: петли и пары кратных (или
двойных ребер). Во-вторых, понятие стягивания ребра в мультиграфах
проще, чем в графах. Если стянуть ребро е = ху в мультиграфе G —
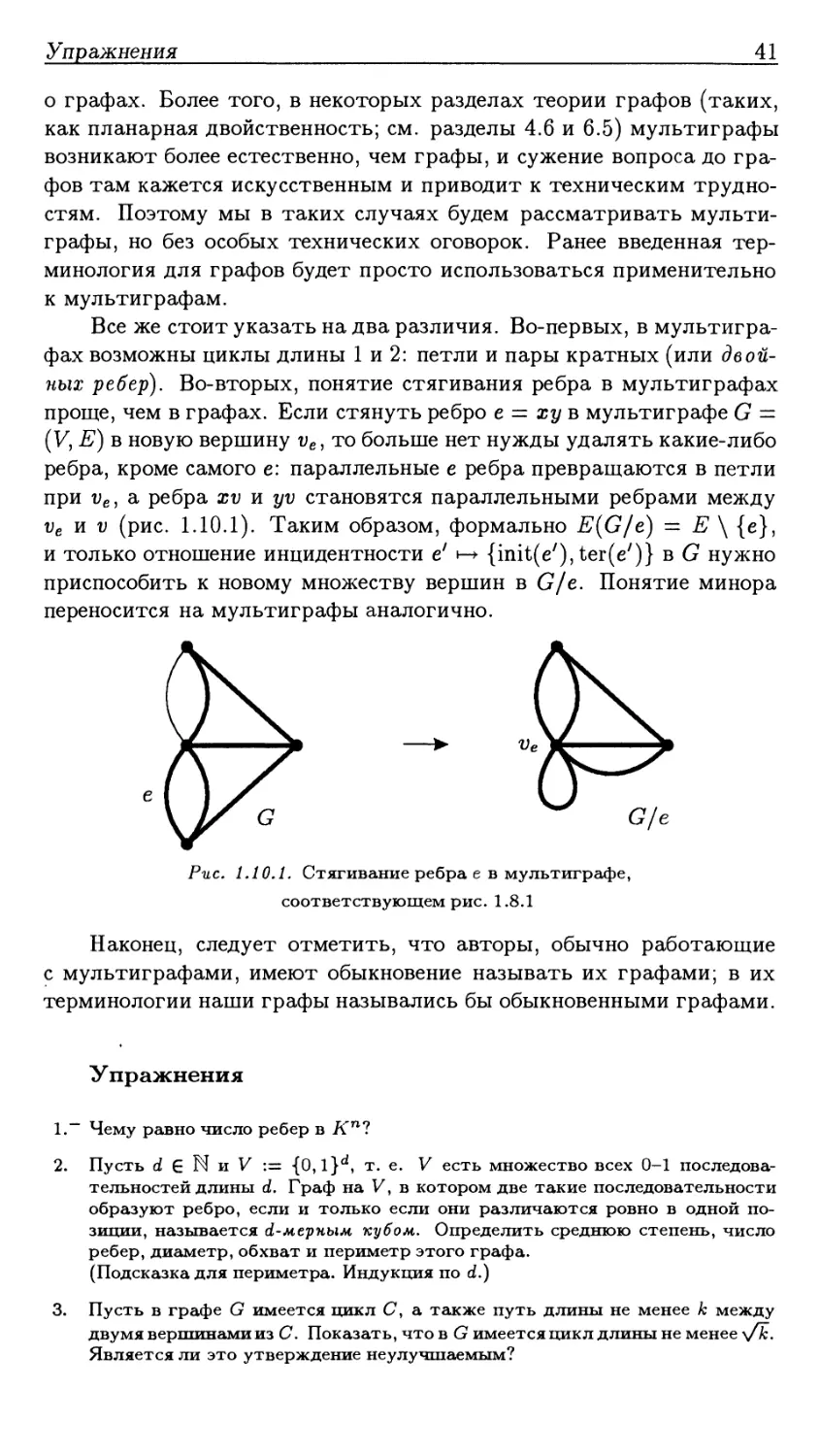
(V, Е) в новую вершину ие, то больше нет нужды удалять какие-либо
ребра, кроме самого е: параллельные е ребра превращаются в петли
при ие, а ребра xv и yv становятся параллельными ребрами между
ve и v (рис. 1.10.1). Таким образом, формально E(G/e) — Е \ {е},
и только отношение инцидентности е! н-» {init(e/), ter(e')} в G нужно
приспособить к новому множеству вершин в G/e. Понятие минора
переносится на мультиграфы аналогично.
Рис. 1.10.1. Стягивание ребра е в мультиграфе,
соответствующем рис. 1.8.1
Наконец, следует отметить, что авторы, обычно работающие
с мультиграфами, имеют обыкновение называть их графами; в их
терминологии наши графы назывались бы обыкновенными графами.
Упражнения
1.~ Чему равно число ребер в А'п?
2. Пусть d G N и V := {0,l}d, т. е. V есть множество всех 0-1
последовательностей длины d. Граф на V, в котором две такие последовательности
образуют ребро, если и только если они различаются ровно в одной
позиции, называется d-мерным кубом. Определить среднюю степень, число
ребер, диаметр, обхват и периметр этого графа.
(Подсказка для периметра. Индукция по d.)
3. Пусть в графе G имеется цикл С, а также путь длины не менее к между
двумя вершинами из С. Показать, что в G имеется цикл длины не менее
Является ли это утверждение неулучшаемым?

42
Глава 1. Основные понятия
4.~~ Является ли оценка в предложении 1.3.2 неулучшаемой?
5. Показать, что rad(G) < diam(G) < 2rad(G) для любого графа G.
бЛ Считая, что d > 2 и к > 3, улучшить оценку в предложении 1.3.3 до dk.
7.~~ Показать, что компоненты графа разбивают его множество вершин.
(Другими словами, показать, что каждая вершина принадлежит ровно одной
компоненте.)
8.— Показать, что каждый 2-связный граф содержит цикл.
9. (i)" Определить k(G) и A(G) для G = Рк,Ск, Кк, Km,n (k,m,n > 3).
(ii)+ Определить связность n-мерного куба (введенного в упражнении 2).
(Подсказка для (ii). Индукция по п.)
10. Показать, что k(G) < A(G) < 6(G) для любого нетривиального графа G.
II.- Существует ли такая функция /: N —* N, что для всех к Е N любой граф
с минимальной степенью не меньше f(k) является Аг-связным?
12. Пусть с*,/3 — два инварианта с целыми положительными значениями.
Сформулируйте строго приведенные ниже утверждения и покажите, что
каждое из них влечет другое:
(i) а ограничено сверху некоторой функцией от /3;
(ii) /3 становится произвольно большим при достаточно большом се.
Показать, что утверждение
(iii) /3 ограничено снизу некоторой функцией от a
не равносильно (i), (ii). Какое небольшое изменение позволило бы добиться
этого?
13."*" Какова более глубокая причина того, что доказательство теоремы 1.4.2
основано на допущении вида m > en — 6, а не просто на нижней оценке
для средней степени?
14. Доказать теорему 1.5.1.
15. Показать, что любое дерево Т имеет не менее А(Т) листьев.
16. Показать, что «древесный порядок», связанный с корневым деревом Т,
действительно частичный порядок на У(Т), и проверить утверждения об этом
частичном порядке в тексте.
17. Пусть граф G связен, а г £ G — вершина. Начиная с г будем двигаться по
ребрам графа G, пытаясь по мере возможности идти в еще не пройденную
вершину. Если таковой нет, возвращаемся по ребру, по которому когда-
то впервые зашли в текущую вершину (если текущая вершина не г, иначе
алгоритм закончен). Показать, что пройденные ребра образуют нормальное
остовное дерево в G с корнем г.
(Эта процедура дала таким деревьям название деревьев поиска в глубину.)
18. Пусть У есть множество поддеревьев дерева Т. Предположим, что деревья
в 2? попарно пересекаются. Доказать, что их общая часть П^" непуста.
19. Показать, что каждый автоморфизм дерева оставляет на месте вершину
или ребро.
20. Всегда ли доли однородного двудольного графа равномощны?
21. Показать, что граф двудолен, если и только если в нем каждый
индуцированный цикл имеет четную длину.
22. Найдите такую функцию /: N —* N, что для любого k Е N всякий граф со
средней степенью не менее f(k) содержит двудольный подграф с
минимальной степенью не менее к.

Примечания
43
23. Покажите, что отношение =^ быть минором задает частичный порядок
на любом множестве (конечных) графов. Верно ли это для бесконечных
графов?
24." Показать, что элементами пространства циклов графа G являются
объединения множеств ребер реберно-непересекающихся циклов в G и только они.
25. В графе G найти среди разрезов вида E(v) базис пространства разрезов в G.
26. Доказать, что циклы и разрезы вместе порождают все пространство его
ребер, либо найти контрпример.
27. Дать прямое доказательство того факта, что циклы Се, определенные в
доказательстве теоремы 1.9.6, порождают пространство циклов.
28. Дать прямое доказательство того факта, что разрезы De, определенные
в доказательстве теоремы 1.9.6, порождают пространство разрезов.
29. Каковы размерности пространств циклов и разрезов графа с к
компонентами?
Примечания
Используемая в этой книге терминология в основном стандартна.
Альтернативы, конечно, существуют и некоторые из них даются при первом
определении понятия. Есть одна деталь, в которой наши обозначения отличаются от
стандартных. Хотя полные графы, пути, циклы и т. п. заданного порядка
обычно обозначаются через Кп, Р^, Ci и т« Д«> мы используем верхние индексы
вместо нижних. Преимущество состоит в том, что переменные Л', Р, С и др.
высвобождаются для использования применительно к той или иной конкретной
ситуации: можно теперь нумеровать компоненты как С\, С2,. •., говорить о
путях Р\,..., Pk и т. д. без боязни внести путаницу.
Теорема11^ 1.4.2 получена в работе: Mader W. Existenz n-fach zusammenhan-
gender Teilgraphen in Graphen gemigend grofter Kantendichte // Abh. Math. Sem.
Univ. Hamburg. 1972. 37. P. 86-97. Теорема 1.8.1 взята из: Euler L. Solutio prob-
lematis ad geometriam situs pertinentis // Comment. Acad. Sci. I. Petropolitanae,
1736. 8. P. 128-140.
Что касается обширной области алгебраических методов в теории графов,
раздел 1.9 не претендует на отражение ее сколько-нибудь исчерпывающим
образом. Общепризнанной на эту тему является монография: Biggs N. L. Algebraic
Graph Theory. 2nd ed. Cambridge: Univ. Press, 1993. Еще одно
исчерпывающее изложение содержится в: Godsil С. D., Royle G. F. Algebraic Graph Theory
(готовитсяМгечати). Обзоры по алгебраическим методам можно найти также
в: Handbook of Combinatorics j Ed. by R. L. Graham, M. Grotschel, L. Lovasz.
Amsterdam e. a.: North-Holland Publ., 1995.
' Для удобства чтения заключительные примечания к главам дают ссылки
только на теоремы, причем лишь тогда, когда такой ссылки нет в
монографии или обзоре, упоминаемых в соответствующей главе.

Глава 2
Паросочетания
Предположим, требуется найти максимально возможное число
независимых ребер в заданном графе. Как это сделать? Возможно
ли разбить множество всех вершин графа на пары смежных
вершин? Если нет, то как убедиться, что это действительно
невозможно? Несколько удивительно, но эта общая проблема не только
лежит в основе многочисленных приложений, но и позволяет
построить весьма интересную теорию.
Пар о сочетанием называется множество М независимых ребер
графа G — (V,E). Если каждая вершина из множества U С V
инцидентна какому-то ребру паросочетания М, то говорят, что М
покрывает множество U. Вершины из U в этом случае называются
покрытыми (паросочетанием М); вершины, не инцидентные
никакому ребру из М, называются непокрытыми.
Остовный ^-однородный подграф называется k-фактором.
Таким образом, подграф Н С G является 1-фактором в графе G тогда
и только тогда, когда Е{Н) — паросочетание, покрывающее
множество V. Основной темой этой главы будет проблема характеризации
графов, имеющих 1-фактор, т. е. паросочетание, покрывающее
множество всех вершин.
2.1. Паросочетания в двудольных графах
На протяжении этого раздела предполагается, что G — (V, Е) —
заданный двудольный граф, разбивающийся на доли {Л, В].
Предполагается, что вершины, обозначаемые через а, а' и т. п., лежат
в А, а вершины, обозначаемые через Ь и т. п., — в В.
Как найти в G паросочетание с наибольшим возможным
количеством ребер? Начнем с рассмотрения произвольного
паросочетания М в графе G. Путь в G, начинающийся с непокрытой вершины
в А и содержащий по очереди ребра из Е \ М и из М, называется
путем, чередующимся относительно М. Чередующийся путь Р,

2.1. Паросочетания в двудольных графах
45
оканчивающийся непокрытой вершиной из В, называется
увеличивающим путем (рис. 2.1.1), поскольку его можно использовать для
превращения М в большее паросочетание — симметрическую
разность множеств М и Е(Р). Чтобы убедиться, что эта разность снова
является паросочетанием, достаточно рассмотреть ребра при данной
вершине. Покрытых же вершин в новом паросочетании стало на две
больше: прибавились концы пути Р.
*\ Р
\^^ —►
М
ш •
А В
Рис. 2.1.1. Увеличение паросо
с помощью чередующегося
Чередующиеся пути играют важную роль в практической
задаче поиска больших паросочетании. Действительно, начав с
любого паросочетания и применяя увеличивающие пути до тех пор,
пока это возможно, всегда можно получить оптимальное
паросочетание — паросочетание с максимальным возможным числом ребер
(упражнение 1). Алгоритмическая задача нахождения таких
паросочетании, следовательно, сводится к алгоритмической задаче
нахождения увеличивающих путей — задаче интересной и поддающейся
решению.
Следующая теорема характеризует максимальную мощность
паросочетания в G с помощью своего рода условия двойственности.
Множество U С V назовем покрытием (или вершинным покрытием)
множества ребер Е в графе G, если каждое ребро графа G
инцидентно некоторой вершине из U.
Теорема 2.1.1 (Кёниг, 1931). Максимальная мощность
паросочетания в двудольном графе равна минимальной мощности его
вершинного покрытия.
Доказательство. Пусть М — паросочетание максимальной
мощности в двудольном графе G. Выберем по одному концу для
каждого ребра из М: конец из В, если в соответствующей вершине
заканчивается какой-то чередующийся путь, и конец из А в
противном случае (рис. 2.1.2). Докажем, что множество U этих \М\
вершин покрывает G. Поскольку каждое вершинное покрытие графа G
должно покрывать и М, вершинных покрытий меньшей, чем |М|,
мощности существовать не может, из чего и будет следовать
утверждение теоремы.
В
ания М
шР

46
Глава 2. Паросочетания
ипв
UnA J/^^*
Рис. 2.1.2. Вершинное покрытие U
Рассмотрим ребро ab £ Е и покажем, что либо а, либо Ъ
лежит в U. Если а& £ М, то это так по определению множества U\
поэтому предположим, что ab £ М. Поскольку М —
максимальное паросочетание, оно содержит ребро a'b', где a =: а' или b = b'.
Можно предположить, что а — а!\ ведь если вершина а не покрыта
(и b — b'), то ab — чередующийся путь, и, таким образом, конец
ребра а'Ь' £ М, принадлежащий U, — вершина Ь' — Ь. Далее, если
а' — а не принадлежит U, то b' £ U и некоторый чередующийся
путь Р заканчивается в вершине Ь'. Но тогда существует и
чередующийся путь Р', заканчивающийся в вершине 6: либо Р' := Р6
(при 6 £ Р), либо Р; := Pb'a'b. Однако в силу максимальности М
путь Р' не является увеличивающим. Значит, вершина b покрыта
и была включена в U благодаря содержащему ее ребру из М. □
Вернемся к нашей основной проблеме — поиску необходимых
и достаточных условий существования 1-фактора. В данном случае
для двудольного графа можно также задаться более общим
вопросом: когда G содержит паросочетание, покрывающее А! Это
паросочетание и будет 1-фактором, если \А\ = \В\, а это условие в любом
случае должно выполняться, чтобы 1-фактор в G существовал.
Ясно, что для существования паросочетания на А необходимо,
чтобы у каждого подмножества множества А было достаточно
соседей в Б, т. е. чтобы выполнялось условие
|W(S)|>|S| для всех SCA.
Следующая теорема о свадьбах утверждает, что это очевидное
необходимое условие является и достаточным.
Теорема 2.1.2 (Холл, 1935). Двудольный граф G содержит
паросочетание, покрывающее А, тогда и только тогда, когда \N(S)\ >
\S\ при любом S С А.
Мы дадим три доказательства нетривиальной части этой
теоремы, т. е. того, что из «условия паросочетаемости» вытекает
существование паросочетания, покрывающего А. Первое доказательство
основано на теореме Кёнига; во втором непосредственно приводится

2.1. Паросочетания в двудольных графах
47
конструкция через увеличивающие пути; третье доказательство
использует только основные понятия.
Первое доказательство. Если Gне содержит паросочетаний,
покрывающих множество А, то по теореме 2.1.1 в нем есть
покрытие U, состоящее менее чем из \А\ вершин. Пусть U — A' U В', где
А' С An В' С В. Тогда
\A'\ + \B'\ = \U\<\A\,
\В'\<\А\-\А'\ = \А\А'\
(рис. 2.1.3). Однако, по определению U в G нет ребер, соединяющих
А \ А' и В \ В', так что
\N(A\A')\<\B'\<\A\A'l
и для S := А \ А' условие паросочетаемости не выполняется. П
Рис. 2.1.3. Покрытие менее чем \А\ вершинами
Второе доказательство. Рассмотрим паросочетание М в G,
оставляющее какую-то вершину из А непокрытой, и построим путь,
увеличивающий М. Пусть ао, &i, ai, &2> «2, • • • — максимальная
последовательность различных вершин аг- £ А и 6г- £ 5, которая при
любом г > 1 удовлетворяет следующим условиям (рис. 2.1.4):
(i) ао непокрыта;
(ii) каждая из Ъ{ смежна какой-то вершине Q>j(i) £ {ао,..., at_i};
(iii) аг-6г- £ М.
По условию паросочетаемости эта последовательность не может
заканчиваться вершиной из А: ведь все вместе г вершин ао,..., a,-_i
имеют по меньшей мере г соседей в В, так что всегда можно найти
новую вершину Ь{ ф &i,..., &t-_i, удовлетворяющую (ii). Пусть
bk € В — последняя вершина последовательности. Ввиду (i)-(iii)
путь
Р :- bjba/(A.)b/(jb)a/2(jb)b/2(jb)a/3(jb) .. .a/r(jb),
где fr(k) — 0, является чередующимся.

48
Глава 2. Паросочетания
а° *\ ^* ^1
а4 *г * Ь5
Рис. 2.1.4- Доказательство теоремы о свадьбах
с помощью чередующихся путей
Что мешает нам продолжить последовательность ao&iai .. .6*?
Если бы bk было соединено ребром из паросочетания, скажем, с а, то
последовательность действительно могла бы быть продлена
вершиной ajb := а, если только а уже не равно некоторому аг-, где 0 < г < к.
Однако в последнем случае из (iii) следовало бы, что bk — Ь{\
противоречие. Таким образом, вершина bk не покрыта, а значит, Р —
увеличивающий путь между ао и 6*. D
Третье доказательство. Применим индукцию по \А\. При
\А\ =. 1 утверждение верно. Теперь зафиксируем \А\ > 2 и
предположим, что условия паросочетаемости достаточно для существования
паросочетания, покрывающего А, при меньших \А\.
Если |N(S)| > |5|+1 для любого непустого подмножества S С Л,
то выберем какое-то ребро ab £ G и рассмотрим граф G' := G—{а, 6}.
Тогда всякое непустое множество S С А\{а} удовлетворяет условию
\NG'(S)\ > \NG(S)\ - 1 > \S\,
так что по предположению индукции G' содержит паросочетание,
покрывающее А\{а}. Добавив ребро аб, мы получаем паросочетание,
покрывающее А в G.
Теперь предположим, что в А есть такое непустое собственное
подмножество А', что \В'\ = \А'\, где В' :— N(A'). По
предположению индукции граф G' :— G[A'{JB'\ содержит паросочетание,
покрывающее А!. Но G — G' также удовлетворяет условию
паросочетаемости, иначе для всякого множества S С А\А', в котором \N'g-g'(S)\ <
|5|, мы вопреки предположению имели бы \Nq(S U А')| < |SUj4'|.
Снова используя предположение индукции, мы получаем, что G — G'
содержит паросочетание, покрывающее А \ А!. Объединяя эти два
паросочетания, мы получаем паросочетание, покрывающее
множество А в G. D
Следствие 2.1.3. Если \N(S)\ > \S\-d для каждого множества
S С А и какого-то фиксированного d £ N, то G содержит
паросочетание мощности \А\ — d.

2.1. Паросочетания в двудольных графах
49
Доказательство. Добавим к В еще d новых вершин, соединив
каждую из них со всеми вершинами в А. По теореме о свадьбах
новый граф содержит паросочетание, покрывающее А, причем не
менее чем \А\ — d ребер этого паросочетания должны быть ребрами
графа G. □
Следствие 2.1.4. Если граф G k-однороден, где к > 1, то в G
есть 1-фактор.
Доказательство. Ясно, что если G fc-однороден, то \А\ = \В\;
таким образом, достаточно посредством теоремы 2.1.2 показать, что
G содержит паросочетание, покрывающее А. Каждое множество
S С А соединено с N(S) в общей сложности k\S\ ребрами, а всего
имеется й|7У(5)| ребер G, инцидентных N(S). Таким образом, k\S\ <
k\N(S)\, т. е. G действительно удовлетворяет условию паросочетае-
мости. D
Несмотря на кажущуюся узость формулировки теорема о
свадьбах находится в числе теорем о графах, наиболее часто применяемых
как в самой теории графов, так и вне ее. Однако часто
переформулировка проблемы в терминах двудольных графов требует усилий.
В качестве простого примера мы применим теорему о свадьбах для
вывода одного из самых ранних результатов теории графов —
результата, исходное доказательство которого было отнюдь не таким
простым и далеко не коротким.
Следствие 2.1.5 (Петерсен, 1891). Каждый однородный граф
четной положительной степени имеет 2-фактор.
Доказательство. Пусть G — 2&-однородный граф (к > 1),
без ограничения общности связный. По теореме 1.8.1 G содержит
эйлеров обход voeo .. .ei-ivi, где vi — vq. Заменим каждую
вершину v парой (г>~ ,!>+), а каждое ребро ег- = U:Ut+i — ребром v^v^+1
(рис. 2.1.5). Получающийся двудольный граф G' fc-однороден и по
следствию 2.1.4 содержит 1-фактор. Объединяя каждую пару
вершин (v~ ,v+) обратно в вершину г>, мы превращаем этот 1-фактор
графа G' в 2-фактор графа G. □
X - ^
Рис. 2.1.5. Расщепление вершин в доказательстве следствия 2.1.5

50
Глава 2. Паросочетания
2.2. Паросочетания в произвольных графах
Пусть дан граф G. Обозначим через % множество его
компонент, а через q(G) — число его нечетных компонент, т. е. компонент
нечетного порядка. Если в G есть 1-фактор, то ясно, что
q(G -S)< \S\ для всех S С V(G)}
поскольку каждая нечетная компонента графа G — S посылает в S
ребро из фактора.
Рис. 2.2.1. Условие Татта q(G - S) < \S\ при q = 3
и стянутый граф Н§ из теоремы 2.2.3
И снова это очевидное необходимое условие существования
1-фактора оказывается и достаточным.
Теорема 2.2.1 (Татт, 1947). Граф G содержит l-фактор тогда
и только тогда, когда q(G — S) < \S\ для всех S С V(G).
Доказательство. Пусть G — (V,E) — граф без 1-фактора.
Наша задача — найти плохое множество S С V, для которого
нарушается условие Татта.
Можно предположить, что G — реберно-максимальный граф без
1-фактора. Действительно, если G' получен из G добавлением ребер,
а множество S С V плохое для G7, то S плохое и для G: всякая
нечетная компонента графа G — S является объединением компонент
графа G — S и одна из этих компонент должна быть нечетной.
Как выглядит граф G? Ясно, что если G содержит плохое
множество S, то из его реберной максимальности и тривиальной прямой
части теоремы следует, что
все компоненты графа G — S полны, а каждая
(*)
вершина s £ S смежна со всеми вершинами из G — s.
Но и обратно, если множество S С V удовлетворяет (*), то либо 5,
либо пустое множество должны быть плохими. Если S не плохое,

2.2. Паросочетания в произвольных графах
51
мы можем присоединить к нему как непересекающиеся множества
нечетные компоненты графа G — S и сгруппировать по парам все
оставшиеся вершины. Это невозможно лишь тогда, когда порядок
\G\ нечетен, а в этом случае пустое множество 0 является плохим.
Таким образом, достаточно доказать, что в G есть множество
вершин 5, удовлетворяющее (*). Пусть S — множество вершин,
смежных со всеми остальными вершинами. Если S не удовлетворяет
условию (*), то в какой-то компоненте графа G — S есть несмежные
вершины а и а'. Пусть а, 6, с — первые три вершины кратчайшей
а-а! цепи в этой компоненте; тогда ab, be £ Е, но ас £ Е. Поскольку
6^5, существует такая вершина d £ V, что bd £ Е. По
максимальности G в G + ас существует покрывающее V паросочетание М\,
а в G -f bd — покрывающее V паросочетание М2.
Пусть Р — d.. .v — максимальный путь в G, начинающийся с d
ребром из Mi и содержащий по очереди ребра из М\ и Мъ (рис. 2.2.2).
Если последнее ребро пути Р лежит в Mi, то v — 6, поскольку иначе
Р мог бы быть продолжен. В этом случае положим С :— Р -f bd.
Если же последнее ребро пути Р лежит в Мг, то по
максимальности Р Mi-ребром при вершине v должно быть ас, т. е. v £ {а, с};
тогда пусть С — цикл dPvbd. В обоих случаях С — четный цикл,
ребра которого через одно лежат в Мг, а единственное его ребро,
не принадлежащее Е} — это bd. Заменяя ребра Мг, входящие в С,
на ребра из С — Мч, получаем паросочетание, покрывающее
множество V и лежащее в Е\ противоречие. □
Рис. 2.2.2. Вывод противоречия при 5, не удовлетворяющем (*)
Следствие 2.2.2 (Петерсен, 1891). Всякий кубический граф
без мостов имеет 1-фактор.
Доказательство . Покажем, что всякий кубический граф G без
мостов удовлетворяет условию Татта. Пусть дано подмножество
S С V(G); рассмотрим нечетную компоненту С графа G — S.
Поскольку граф G кубический, сумма степеней вершин в С нечетна,
но только какая-то четная часть этой суммы соответствует ребрам
из С. Значит, G имеет нечетное число 5-С-ребер, а раз в G нет
мостов, то таких ребер по меньшей мере три. Всего ребер между
S и G — S не меньше чем 3q(G — S). Но поскольку G кубический,
таких ребер не больше чем 3|5|. Значит, q(G — S) < |5|, что и
требовалось. □

52
Глава 2. Паросочетания
Чтобы лучше осветить используемую в теории паросочетаний
технику, дадим теперь второе доказательство теоремы Татта. На
самом деле будет доказан несколько более сильный результат,
вычленяющий в произвольном графе структуру, интересную с точки
зрения паросочетаний. Если при этом граф удовлетворяет условию
Татта, то получающаяся структура сразу дает 1-фактор.
Граф G — (V, Е) называется фактор-критическим, если G ф 0
и для любой вершины v £ G граф G — v имеет 1-фактор. Заметим,
что сам граф G в этом случае имеет нечетный порядок, а значит, не
может содержать 1-фактора. Рассмотрим множество вершин S С V
и (двудольный1)) граф #s, получающийся из G стягиванием каждой
компоненты С Е %-5 в одну вершину и удалением всех ребер
внутри S. (Формально #s — это граф с множеством вершин S U %-s
и множеством ребер {sC \ Зс £ С: sc £ Е}\ см. рис. 2.2.1.) Если
Hs содержит паросочетание на S, то будем говорить, что S связано
паросочетанием с G — S.
Теорема 2.2.3. Всякий граф G — (V, Е) содержит множество
вершин S со следующими двумя свойствами:
(i) S связано паросочетанием с G — S;
(ii) каждая компонента графа G — S фактор-критична,
причем для любого такого множества S граф G содержит 1-фактор
тогда и только тогда, когда \S\ — \^g-s\-
Из этого результата для любого G легко вытекает
утверждение теоремы Татта. Действительно, из (i) и (ii) следует, что \S\ <
\ct>G-s\ — q(G — S) (поскольку фактор-критические графы имеют
нечетный порядок); поэтому условие Татта q(G — S) < \S\ влечет
|5| = |%-s|j и существование 1-фактора следует из последней
части теоремы 2.2.3.
Доказательство теоремы 2.2.3. Сначала заметим, что
последнее утверждение теоремы сразу же вытекает из утверждений
(i) и (ii): если в G есть 1-фактор, то q(G — S) < \S\ и |5| = |%-s|j
как описано выше; обратно, если |5| = |%-5|3 то существование
1-фактора напрямую следует из (i) и (ii).
Докажем существование множества S, удовлетворяющего (i)
и (ii). Применим индукцию по \G\. Если \G\ — 0, то можно взять
5 = 0. Теперь рассмотрим граф G с \G\ > 0 и предположим, что
для графов с меньшим числом вершин утверждение верно.
Пусть d — наименьшее целое неотрицательное число такое, что
q(G -T)<\T\ + d для всякого TCV. (*)
Существует множество Т, для которого (*) обращается в равенство:
это следует из минимальности d, если d > 0, и из того, что q(G—0) >
) Кроме (возможного) случая, когда 5 или ^g—S пусто.

2.2. Паросочетания в произвольных графах
53
|0| + 0, если d = О. Пусть S — такое множество Т максимальной
мощности, а ^ := %-s-
Сначала покажем, что всякая компонента С £ ff нечетна. Если
порядок |С| четен, то выберем вершину с £ С и положим S' : =
S U {с} и С7 := С —с. Тогда порядок множества С нечетен, а значит,
в С есть хотя бы одна нечетная компонента. Значит, q(G — S') >
q(G — S) + 1. Поскольку неравенство (*) на Т := S обращается в
равенство, мы получаем, что
q(G -S')>q(G-S) + l = \S\ + d+l = \S'\ + d>q(G- S'),
(*)
т. е. имеет место равенство, что противоречит максимальности S.
Теперь докажем утверждение (ii), т. е. что всякая компонента
С G ^ фактор-критична. Предположим, что существуют такие
С £ ^ и с £ С, что С \— С — с не содержит 1-фактора. По
предположению индукции (и из того факта, что, как показано ранее, для
фиксированного G теорема Татта вытекает из нашей теоремы)
существует такое множество Т' С V(C), что
q{C -Т')> \Т'\.
Поскольку порядок |С| нечетен, а значит, \С'\ четен, числа q(C — Т')
и \Т'\ четны либо нечетны одновременно, т. е. они не могут
отличаться ровно на 1. Поэтому мы можем усилить последнее
неравенство до
q(C -Т')> 17*1 + 2.
Тем самым для Т :— S U {с} U Т' мы получаем, что
' q(G-T) = q(G-S)-l + q(C'-r)
> |S| + d-1 + 17*1 + 2
= \T\ + d
>q(G-n
О)
т. е. выполняется равенство, что противоречит максимальности S.
Остается показать, что S связано паросочетанием с G — S. Если
S = 0, то это очевидно, поэтому пусть S ф0. Поскольку (*)наТ:=5
обращается в равенство, множество ^ также непусто. Теперь
применим кЯ:= Hs следствие 2.1.3 «в обратную сторону», т.е. сЛ:=^.
Для <£' С ^ положим S' := NH(^') С S. Поскольку каждая С £ #'
является также нечетной компонентой графа G — S', имеем
\NH(V')\ = |S'| > q(G -S')-d> \V\ - d.
(«О

54
Глава 2. Паросочетания
Тогда по следствию 2.1.3 граф Н содержит паросочетание мощности
\tf\-d = q(G-S)-d=\S\,
которое и является искомым паросочетанием на множестве S. □
Рассмотрим еще раз множество S из теоремы 2.2.3 и вместе
с ним — любое паросочетание М в G. Как и раньше, полагаем
^ := %-5- Обозначим через ks число ребер в М, у которых по
меньшей мере один конец лежит в 5, а через к<# — число ребер в М,
у которых оба конца лежат в G — S. Поскольку каждая компонента
С Е ^ нечетна, по меньшей мере одна из ее вершин не инцидентна
ни одному ребру второго типа. Поэтому каждое паросочетание М
удовлетворяет условиям
*5<|s| и kv<l-{\v\-\s\-№). (1)
Более того, в G есть паросочетание Мо, для которого в обоих случаях
имеет место равенство: сначала выберем \S\ ребер между S и (J^7
согласно (i), а потом с помощью (ii) найдем подходящее множество
из |(|С| — 1) ребер в каждой компоненте СЕ^. Значит, Мо содержит
в точности
\M0\ = \S\ + $\V\-\S\-\V$ (2)
ребер.
Из выражений (1) и (2) следует, что любое паросочетание М
максимальной мощности обращает обе части (1) в равенства.
Поскольку \М\ > \Мо\ и по (2), М имеет по меньшей мере \S\ -f
|(| V| — \S\ — \<£\) ребер, откуда ни одно из неравенств в (1) не может
быть строгим. Но из равенств в (1), в свою очередь, вытекает, что
М имеет описанную выше структуру: поскольку ks — |5|, каждая
вершина s £ S является концом ребра st £ М, где t £ G — 5, а
поскольку к<£ — \i\V\ — \S\ — |^|), то для каждой СЕ^вС лежит
в точности \{\С\ — 1) ребер из М. Наконец, ребра этого последнего
вида не покрывают только по одной вершине в каждой компоненте С,
а значит, концы t ребер st для разных s лежат в разных
компонентах С.
Таким образом, в технической, на первый взгляд, теореме 2.2.3
скрыто богатство структурной информации: она содержит основу
подробного описания всех наибольших по мощности паросочетаний
в произвольных графах2).
2) В примечаниях в конце главы будет дана ссылка на полную
формулировку этого структурного результата, известного как теорема Галлаи —
Эдмондса о паросочетаниях.

2.3. Покрытия путями
55
2.3. Покрытия путями
Вернемся ненадолго к теореме 2.1.1 — теореме Кёнига о
двойственности для двудольных графов. Если сориентировать каждое
ребро графа G по направлению от А к В, то эта теорема
сообщит нам, как много нужно непересекающихся ориентированных
путей, чтобы покрыть все вершины графа. Каждый такой путь имеет
длину 0 или 1, и очевидно, что число элементов в таком покрытии
путями принимает наименьшее значение, когда покрытие содержит
наибольшее количество путей длины один, другими словами, когда
оно содержит паросочетание наибольшей мощности.
В этом разделе мы задаемся более общим вопросом: какого
наименьшего числа путей в ориентированном графе достаточно, чтобы
покрыть всё множество вершин? Конечно, с тем же успехом мы
можем рассматривать и неориентированные графы. Однако, как
оказывается, в неориентированном случае результат, который мы
докажем, более тривиален (и вынесен в упражнение); в ориентированном
же случае он, кроме всего прочего, имеет интересное следствие.
Ориентированным путем называется ориентированный граф
Р ф 0, состоящий из различных вершин xq, ... , Xk и ребер ео,...
. ..,е*_1, где для каждого i < к ребро ег- направлено от Х{ к ж,-+1.
Последнюю вершину Хк пути Р мы обозначаем через ter(P).
Термин путь в этом разделе всегда будет означать «ориентированный
путь». Покрытие путями ориентированного графа G — это
множество попарно непересекающихся путей в G, содержащих в
совокупности все вершины графа G. Через a(G) мы будем обозначать
максимальную мощность независимого множества вершин графа G.
Теорема 2.3.1 (Галлаи, Мильграм, I960). Всякий
ориентированный граф G можно покрыть не более чем a(G) путями.
Доказательство. Для двух заданных покрытий путями ^i,
3*2 будем писать &\ < 0*2, если выполняется {ter(P) | Р £ 2?\) С
{ter(P) | Р £ ^2} и \&\\ < \&ч\* Докажем следующее утверждение.
Если & — покрытие графа G путями, минимальное
в смысле отношения < , то G содержит независимое
(*)
множество вершин {vp \ Р £ £Р}, где vp £ Р для любого
Р £&>.
Ясно, что из (*) вытекает утверждение теоремы.
Докажем (*) индукцией по \G\. Пусть & — {Pi,... , Pm} —
покрытие из условия (*), и пусть V{ := ter(Pt) для каждого г. Если
множество {v{ | 1 < г < т) независимо, то доказывать нечего;
значит, можно предполагать, что в G есть дуга из i>2 в vi. Поскольку

56
Глава 2. Паросочетания
P2V2V1 — тоже путь, из минимальности & вытекает, что v\ не
единственная вершина в Р\\ обозначим через v вершину,
предшествующую в Pi вершине v\. Тогда З?1 := {Piг/, Р2, • • • > Рт} — покрытие
путями графа G' := G - v\ (рис. 2.3.1). Покажем сначала, что
покрытие £?' минимально в смысле отношения < .
V1\
Pi
■
>
>
>
>
P2
v2
Puc. 2.3.1. Покрытие путями &*' графа G'
Пусть £?" < SP1 — другое покрытие графа G' путями. Если
путь Р £ &" заканчивается вершиной и, то можно заменить Р в SP11
на Pvv\ и получить покрытие графа G, меньшее чем ^, что
противоречит минимальности Р. Если путь Р £ SP" заканчивается
вершиной г>2 (но не и), мы заменяем Р в &" на Рг^ь что опять
противоречит минимальности £?. Значит, {ter(P) | Р £ £?"} С
{г/3, •.. , vm} и, в частности, \0Р"\ < \£?\ - 2. Но теперь <Р" и
тривиальный путь {i>i}, взятые вместе, образуют покрытие графа G
путями, противоречащее минимальности SP.
Значит, как и утверждалось, покрытие SP1 минимально. По
предположению индукции {V(P) \ Р £ &'} содержит независимое
множество представителей. Но это множество является
одновременно и множеством представителей для ^, и (*) доказано. □
Сейчас, в качестве следствия из теоремы 2.3.1, мы выведем
классический результат из теории частичных порядков. Напомним, что
подмножество частично упорядоченного множества (Р, <)
называется цепью в Р, если все его элементы попарно сравнимы, и
антицепью, если они попарно несравнимы.
Следствие 2.3.2 (Дилворт, 1950). В любом частично
упорядоченном множестве (Р, <) минимальное число цепей, покрывающих
множество Р, равно максимальной мощности антицепи в Р.
Доказательство. Если А — антицепь максимальной
мощности в Р, то очевидно, что Р не может быть покрыто менее чем \А\
цепями. Тот факт, что \А\ цепей достаточно, следует из теоремы 2.3.1,
примененной к ориентированному графу на Р с множеством ребер
{{х,у)\х<у}. □

Упражнения 57
Упражнения
1.~ Пусть М — паросочетание в двудольном графе G. Показать, что если
М содержит меньше ребер, чем какое-то другое паросочетание в G, то G
содержит увеличивающий путь по отношению к М. Обобщается ли этот
факт на паросочетания в недвудолъных графах?
(Подсказка. Симметрическая разность.)
2. Описать алгоритм, который как можно более эффективно находил бы в
произвольном двудольном графе паросочетание максимальной мощности.
3. Найти бесконечный контрпример к утверждению теоремы о свадьбах.
4. Пусть к — целое число. Показать, что любые два разбиения конечного
множества на /:-подмножества имеют общую систему различных
представителей.
5. Пусть А — конечное множество с подмножествами Ai,...,An, и пусть
d\,..., dn G N. Показать, что непересекающиеся множества D}~ С А^, где
\Dk\ = dki существуют для всех к < п тогда и только тогда, когда
LN>£*
%ei ' iei
для всех 1С {1,... ,п}.
6."*" Доказать лемму Шпернера: в п-множестве X не существует больше чем
(, П12\) подмножеств, ни одно из которых не содержит другого.
(Подсказка. Построить (1J/21) цепей, покрывающих решетку всех
подмножеств множества X.)
7. Описать множество S из теоремы 2.2.3 для случая, когда G — лес.
8. Используя (лишь) теорему 2.2.3, показать, что всякий Aj-связный граф
с не менее чем 2к вершинами содержит паросочетание размера к.
Наилучшая ли это оценка?
9. Граф G называется (вершинно-)транзитивным, если для любых двух
вершин v,w G G существует автоморфизм на G, переводящий v в w.
Используя те же соображения, что и в доказательстве теоремы 2.2.3, показать, что
всякий транзитивный связный граф либо фактор-критичен, либо содержит
1-фактор.
(Подсказка. Рассмотреть отдельно случаи S = 0hS^0.)
10. Показать, что граф G содержит к независимых ребер тогда и только тогда,
когда q(G — S) < \S\ -f \G\ — 2к для всех множеств S С V(G).
(Подсказка. Для утверждения «тогда» предположить, что G не содержит
к независимых ребер, и применить теорему Татта об 1-факторе к графу
G * A'lGl-2fc или воспользоваться теоремой 2.2.3.)
11.~ Найти кубический граф без 1-факторов.
12. Вывести теорему о свадьбах из теоремы Татта.
13.~ Доказать неориентированный вариант теоремы Галлаи — Мильграма (не
используя ориентированный вариант).
14. Вывести теорему о свадьбах из теоремы Галлаи — Мильграма.
15.~ Показать, что всякое частично упорядоченное множество из не менее чем
rs -f 1 элементов содержит либо цепь размера г + 1, либо антицепь размера
5 + 1.

58
Глава 2. Паросочетания
16. Доказать следующий двойственный вариант теоремы Дилворта: во всяком
конечном частично упорядоченном множестве (Р, <) минимальное число
покрывающих Р антицепей равно максимальной мощности цепи в Р.
17. Вывести теорему Кёнига из теоремы Дилворта.
18."*" Найти частично упорядоченное множество, не содержащее бесконечной
антицепи, но не покрываемое конечным числом цепей.
(Подсказка. N X N.)
Примечания
Существует легко читаемая и исчерпывающая монография о паросочета-
ниях в конечных графах: Lovdsz L., Plummer М. D. Matching Theory // Ann.
Discrete Math. 29. Amsterdam e. a.: North-Holland Publ., 1986. В этой книге
можно найти все ссылки на результаты данной главы.
Как мы увидим в главе 3, теорема Кёнига 1931 года — это двудольный
случай более общей теоремы Менгера, опубликованной еще в 1929 году. В то же
время оба эти результата гораздо менее известны, чем теорема Холла о свадьбах,
доказанная даже позже (в 1935 году). И по сей день теорема Холла остается
одним из наиболее активно применяемых результатов теории графов. Ее частный
случай, когда оба подмножества разбиения имеют один и тот же размер, был
в неявной форме доказан еще Фробениусом (1917) в работе о детерминантах.
Приведенное нами доказательство теоремы Татта об 1-факторе основано на
доказательстве Ловаса (1975). Обобщение теоремы Татта (теорема 2.2.3,
включая следующее за ней неформальное ее обсуждение) представляет собой
облегченный вариант структурной теоремы о паросочетаниях, принадлежащей Галлаи
(1964) и Эдмондсу (1965). Формулировку и обсуждение деталей этой теоремы
можно найти в книге Ловаса и Пламмера.
Теорема 2.3.1 была опубликована в: Gallai Т., Milgram А. N. Verallgemeine-
rung eines graphentheoretischen Satzes von Redei // Acta Sci. Math. (Szeged).
1960. 21. P. 181-186.

Глава 3
Связность
Определение ^-связности, данное в разделе 1.4, носит
недостаточно интуитивный характер. В нем не слишком подробно
обсуждаются «связи» в ^-связном графе — утверждается лишь, что
требуется удалить по меньшей мере к вершин, чтобы сделать граф
несвязным. Возможно, более наглядно следующее определение,
влекущее за собой, в частности, уже приведенное: граф называется
к-связным, если любые две его вершины могут быть соединены к
независимыми путями.
В действительности эти два определения эквивалентны и
являются двойственными друг к другу формулировками одного и того
же свойства. В разделе 3.3 мы довольно подробно изучим этот
классический результат теории графов — теорему Менгера (1927).
В разделах 3.1 и 3.3 исследуется структура 2-связных и 3-связ-
ных графов. Для этих малых значений к еще возможно дать простое
общее описание того, как могут быть построены такие графы.
В остальных же разделах этой главы рассматриваются другие
определения связности, более поздние, чем стандартное определение,
но не менее важные: число Я-путей в графе для данного подграфа Я,
число непересекающихся по ребрам остовных деревьев и
существование непересекающихся путей, соединяющих несколько данных пар
вершин.
3.1. 2-Связные графы и подграфы
Блоком называется максимальный связный подграф без точек
сочленения. Таким образом, всякий блок графа G представляет собой
либо максимальный 2-связный подграф, либо мост (вместе со своими
концами), либо изолированную вершину. Обратно, каждый такой
подграф является блоком. Разные блоки в графе G благодаря своей
максимальности могут пересекаться только по одной вершине,
которая в этом случае является точкой сочленения в G. Таким образом,

60
Глава 3. Связность
всякое ребро графа G принадлежит единственному блоку, а сам G
является объединением блоков.
В этом смысле блоки — 2-связныё аналоги компонент, т. е.
максимальных связных подграфов. В то же время структура графа G не
определяется полностью структурой его блоков, как это было в
случае компонент. Поскольку блоки могут пересекаться, способ их
пересечения определяет еще одну структуру, своего рода
приблизительный вид графа G при взгляде на него издалека.
Грубая структура графа G, образуемая его блоками,
описывается в следующем предложении. Пусть А — множество точек
сочленения графа G, а 38 — множество его блоков. Тогда естественным
образом возникает двудольный граф на A U 33 с ребрами вида аВ,
где a £ В. Этот граф блоков графа G показан на рисунке 3.1.1.
Рис. 3.1.1. Граф и его граф блоков
Предложение 3.1.1. Граф блоков связного графа —дерево. □
Предложение 3.1.1 сводит строение данного графа к строению
его блоков. Но что можно сказать о самих блоках? Следующее
предложение дает простой метод, в принципе позволяющий составить
список всех 2-связных графов.
Предложение 3.1.2. Граф 2-связен тогда и только тогда,
когда он может быть построен из цикла последовательным добавлением
Н-путей к уже построенному графу Н (рис. 3.1.2).
Рис. 3.1.2. Строение 2-связных графов

3.2. Структура 3-связных графов
61
Доказательство. Ясно, что каждый построенный по
описанному методу граф 2-связен. Обратно, пусть дан 2-связный граф G.
Очевидно, что он содержит цикл, а значит, имеет максимальный
подграф Я, который можно построить описанным образом.
Поскольку всякое ребро ху £ E(G) \ Е(Н), где х,у £ Я, определяло бы
Я-путь, то Я — индуцированный подграф графа G. Значит, если
Я ф G, то из-за связности G существует ребро vw, где v £ G — Я,
а и; £ Я. Так как G 2-связен, G — w содержит v-H путь Р. Но
тогда wvP есть Я-путь в G, и подграф Я UiuuP, строго больший Я,
можно построить описанным методом. Противоречие с
максимальностью Я. □
3.2. Структура 3-связных графов
Мы начнем этот раздел с аналога предложения 3.1.2 для 3-связ-
ности. Первая наша теорема описывает, каким образом всякий
3-связный граф может быть получен из К4 последовательностью
элементарных операций, сохраняющих 3-связность. Затем мы докажем
глубокий результат Татта об алгебраической структуре
пространства циклов 3-связного графа; этот результат сыграет важную роль
в разделе 4.5.
Лемма 3.2.1. Если G 3-связен и \G\ > 4, то в G есть такое
ребро е, что граф G/e снова 3-связен.
Доказательство. Предположим, что такого ребра не
существует. Тогда для всякого ребра ху £ G граф G/xy содержит
разделяющее множество из не более чем двух вершин. Поскольку «(G) > 3,
стянутая вершина vxy графа G/xy (см. раздел 1.7) лежит в S и
|5| = 2, т. е. в G есть такая вершина z £ {х,у}, что {vxy,z}
разделяет G/xy. Тогда любые две вершины, разделенные
множеством {vxy,z} в G/xy, разделены в G множеством Т := {х, у, z}.
Поскольку никакое собственное подмножество множества Т не
разделяет G, каждая вершина из Т имеет соседа в каждой компоненте С
графа G — Т.
Выберем ребро ху, вершину z и компоненту С так, чтобы
мощность \С\ была минимальной. Выберем соседа v вершины z в С
(рис. 3.2.1). По предположению, G/zv опять не является 3-связным,
так что снова существует такая вершина iu, что {z} v} w} разделяет G
и, как и раньше, каждая из вершин {z,v,w} имеет соседа в каждой
компоненте графа G — {z} г/, w}.
Поскольку вершины х иу смежны, в G — {z, г/, w} есть такая
компонента D, что D П {х, у} — 0. Тогда каждый сосед вершины v в D
лежит в С (поскольку v £ С), так что D ПС ф 0 и, следовательно,
D С С из-за выбора D. Противоречие с выбором ху, z и С. □

62
Глава 3. Связность
Рис. 3.2.1. Разделяющие вершины из доказательства леммы 3.2.1
Теорема 3.2.2 (Татт, 1961). Граф G S-связен тогда и только
тогда, когда существует последовательность Go,..., G„ графов со
следующими свойствами:
(i) Go = К4 и Gn = G;
(ii) для всякого i < п в графе G,-+i есть такое ребро ху, что
d(x),d(y)>3HGi = Gi+i/xy.
Доказательство. Если G 3-связен, то последовательность из
условия теоремы существует по лемме 3.2.1. Заметим, что все графы
в этой последовательности 3-связны.
Наоборот, пусть Go,..,G„ — последовательность из условия
теоремы. Покажем, что для каждого г < п, если Gt = G{+\/xy
3-связен, то 3-связен и G,-+i. Предположим, что это не так. Пусть
S — разделяющее множество из не более чем двух вершин в Gt+i,
а С\ и С2 — две компоненты графа Gt>i — S. Поскольку вершины
х и у смежны, мы можем считать, что {х, у}ПУ(С\) — 0 (рис. 3.2.2).
Рис. 3.2.2. Положение ребра ху Е G;_j.i в доказательстве теоремы 3.2.2
Тогда С2 не может содержать ни обе вершины ж, у, ни вершину
v £ {х,у}: в противном случае либо vxy, либо v были бы отделены
от С\ в Gi не более чем двумя вершинами; противоречие. Но, значит,
С2 содержит ровно одну вершину: либо ж, либо у. Это противоречит
предположению о том, что d(x), d(y) > 3. □
Теорема 3.2.2 является основой принадлежащего Татту
результата, известного под названием теоремы о колесе1). Подобно
предложению 3.1.2 для 2-связных графов она дает возможность строить
произвольные 3-связные графы с помощью простого индуктивного
*) Граф вида Сп * К1 называется колесом; таким образом, А'4 — наименьшее
колесо.

3.2. Структура, 3-связных графов
63
процесса, зависящего только от локальной информации об уже
построенном графе: начав с К4, мы выбираем в уже построенном графе
вершину и, расщепляем ее на две смежные вершины г/ и v" и
соединяем их с бывшими соседями v каким угодно способом — лишь бы
и у г/, и у v" было не менее чем по три инцидентных ребра и каждый
бывший сосед v был смежен по крайней мере с одной из г/, v".
Теорема 3.2.3 (Татт, 1963). Пространство циклов 3-связного
графа порождено его неразделяющими индуцированными циклами.
Доказательство. Применим индукцию по порядку графа G.
В КА каждый цикл представляет собой треугольник или
симметрическую разность треугольников (в смысле ребер). Поскольку
треугольники индуцированы и не являются разделяющими, то для
\G\ — 4 предположение верно.
Для шага индукции рассмотрим такое ребро е — ху графа G, что
G' :— G/e — снова 3-связный граф; оно существует по лемме 3.2.1.
Тогда каждое ребро е' £ E{G') \ E(G) имеет вид е1 — uve, где по
меньшей мере одно из ребер их и иу лежит в G. Выберем из них
лежащее в G (либо их, либо иу) и отождествим его в обозначении с е'\
начиная с этого момента е1 обозначает и ребро uve графа G' и одно
из ребер их, иу. В этом смысле мы можем рассматривать E(G') как
подмножество E(G), a <f (G') — как подпространство <^(G); в
частности, на <f (G7) однозначно переносятся все векторные операции.
Рассмотрим индуцированный цикл С С G. Если е £ С и С — G3,
мы называем С фундаментальным треугольником; тогда С/е — К2.
Если е £ G, но С ф G3, то С/е — цикл в G'. Наконец, если е ^ С,
то в С лежит не более чем одна из вершин ж, у (иначе ребро е было
бы хордой), так что вершины цикла С образуют по порядку цикл
и в G', если заменить х или у на ие; получающийся цикл тоже
будет обозначаться через С/е. Таким образом, если С — не
фундаментальный треугольник, то С/е всегда обозначает единственный
цикл в G'. Заметим, однако, что в случае, когда е ^ G, множество
ребер в G/e, рассматриваемое как подмножество E(G), не обязано
совпадать с Е(С) или даже вообще быть циклом (пример показан на
рис. 3.2.3).
С С/е E(C/e)QG
Рис. 3.2.3. Одна из четырех возможностей для С/е в случае е ^ С

64
Глава 3. Связность
Будем называть базисными неразделяющие индуцированные
циклы в G и G'. Элемент ^(G) назовем хорошим, если он
является линейной комбинацией базисных циклов G. Мы хотим показать,
что всякий элемент ^(G) хорош. Основная идея нашего
доказательства— стянуть данный цикл С £ ff(G) к С/е, по индукции породить
С/е в *£{&) и попытаться вернуться от порождающих его элементов
к базисным циклам в G, порождающим С.
Начнем с доказательства трех вспомогательных фактов.
Всякий фундаментальный треугольник — базисный цикл в G. (1)
Ясно, что всякий фундаментальный треугольник wxyw индуцирован
в G. Если бы он был разделяющим в G, то {ve,w} разделяло бы G',
что противоречит выбору е. Тем самым (1) доказано.
Если С С G — индуцированный цикл, но не
фундаментальный треугольник, то С -f С/е -f D £ {0, {е}} (2)
для некоторого хорошего D £ ^(G).
Суть (2) состоит в том, что в терминах «порождаемое™» С и С/е
различаются лишь немного: после добавления допустимого
ошибочного члена D отличие состоит максимум в одном ребре е. Тогда
в каких еще ребрах могут различаться С и С/е? Ясно, что не
более чем в двух ребрах eu — uve и ew — vew, инцидентных ve в С/е
(см. рис. 3.2.4). Но эти различия между множествами ребер С/е и С
выравниваются в точности добавлением соответственно
фундаментальных треугольников иху и xyw, базисных согласно (1).
Действительно, пусть Du обозначает треугольник иху, если еи £ С, и 0
иначе, и пусть Dw обозначает xyw, если ew (£ G, и 0 иначе. Тогда
D := Du -f Dw удовлетворяет (2), что и требовалось.
Далее, покажем, как перенести базисные циклы графа G'
обратно на G.
Для любого базисного цикла С' С G' существует
базисный цикл С = С(С') С G, где С/е — С'.
Если ve £ С, то (3) выполняется для С := С. Предположим
поэтому, что ve £ С. Пусть и и w — два соседа вершины ve вС,
и пусть Р — u-w путь в С, избегающий ve (рис. 3.2.4). Тогда Р С G.
х
и „-- •.г* --„ W
Рис. 3.2.4. Поиск базисного цикла С, где С/е — С

3.2. Структура, 3-связных графов
65
Предположим сначала, что {их, иу, wx, wy} С E(G), и
рассмотрим в качестве кандидатов на роль С циклы Сх := uPwxu и Су :=
uPwyu. Оба они — индуцированные циклы в G (поскольку С
индуцирован в G'), и ясно, что Сх/е — Су/е — С. Более того, ни один
из этих циклов не разделяет двух вершин из G — (V(P)U {х,у}) в G,
поскольку С не разделяет таких вершин в G'. Значит, если, скажем,
Сх — разделяющий цикл в G, то одна из компонент графа G — Сх
состоит только из вершины у. Таким же образом, если Су разделяет G,
то одна из получающихся компонент содержит только х. Однако это
невозможно для Сх и Су одновременно, иначе Nc({x,y}) С V(P),
и, таким образом, поскольку в С нет хорд, Nq{{x, у}) — {и, w}, что
противоречит тому, что «(G) > 3. Значит, по меньшей мере один из
циклов Сх и Су — базисный в G.
Остается рассмотреть случай, когда {их, иу, wx, wy} <jL E(G),
например, их (fc E(G). Тогда, как и выше, либо uPwyu, либо uPwxyu
есть базисный цикл в G в зависимости от того, является ли wy
ребром G. Это завершает доказательство (3).
Перейдем теперь к основной части доказательства —
доказательству того, что каждый цикл С £ ^(G) хороший. Как следует
из предложения 1.9.1, мы можем предположить, что С —
индуцированный цикл в G. Далее, в силу (1) мы можем также предположить,
что С не фундаментальный треугольник, значит, С/е — цикл. Суть
остального состоит в следующем. По (2) С отличается от С/е самое
большее в хорошем ошибочном члене D (и, возможно, в е). По (3)
базисные циклы С[ графа G, дающие в сумме С/е, по индукции
могут быть стянуты из базисных циклов графа G, которые также
отличаются от С[ только на соответствующие хорошие ошибочные
члены Д- (и, возможно, на е). Значит, эти базисные циклы графа G
вместе с ошибочными членами дают в сумме С — и лишь ребро е
требует особого внимания.
По предположению индукции С/е допускает представление
С/е = С[ + • • • + с;
в пространстве ^(G;), где все циклы С- базисные вС Из (3) мы
для каждого г получаем базисный цикл С(С±) С G, где С{С^)/е —
С[ (в частности, C{Cf) — не фундаментальный треугольник), а из
утверждения (2) — хороший Д- £ ^(G) такие, что
С(С?)+С? + А-е{0,{е}}. (4)
Положим
Ci-.= C{Ct) + Di.
Тогда С{ хороший и по (4) он отличается от С[ не более чем ребром е.
Снова пользуясь (2), мы имеем
C + C/e + DE{0,{e}}

№
Глава 3. Связность
для некоторого хорошего D £ ^(G), т. е. С -\- D отличается от С/е
не более чем ребром е. Но тогда С -f D -f С\ -f • • • -f Ск отличается
от С/е + С{ + Ь С'к — 0 не более чем ребром е, т. е.
С + D + d + ".+ С*Е{0,{е}}.
Поскольку C+D + Ci + hCjbG ^(G), но {е} <£ ^(G), это значит,
что на самом деле
С Л- D + Gi-f ••■ + Ск =0,
так что цикл G = D -f С\ -f Ь С* хороший. □
3.3. Теорема Менгера
Следующая классическая теорема Менгера является одним из
краеугольных камней теории графов.
Теорема 3.3.1 (Менгер, 1927). Пусть дан граф G = (V, Е)
и подмножества А, В С V. Тогда минимальное число вершин,
отделяющих А от В в G, равно максимальному числу непересекающихся
А-В путей в С
Мы приводим три доказательства этого результата. Пусть G,
А и В заданы, как в формулировке теоремы; через k = k(G,A,B)
обозначим минимальное число вершин, отделяющих А от В в С
Ясно, что G не может содержать более чем к непересекающихся
А-В путей. Наша задача — показать, что к таких путей
существуют.
Первое доказательство. Докажем следующее более сильное
утверждение.
Пусть & — произвольное множество из менее чем к
непересекающихся А-В путей в G. Тогда существует
множество £} из \£Р\ + \ непересекающихся А-В путей,
множество концов которых включает в себя множество
концов путей из 0*.
Зафиксировав G и А, будем менять В и применим индукцию по
\G — В\. Пусть R — А-В путь, избегающий вершин из В,
лежащих на путях из 3? (таких вершин менее к). Если R не пересекается
с путями из ^, то множество £1 := & U {R} искомое. (Именно
это произойдет при \G — В\ — 0, когда все А-В пути тривиальны.)
В противном случае пусть х — последняя вершина пути Я, лежащая
в некотором Р е & (см. рис. 3.3.1). Положим В' := В U V(xPUxR)

3.3. Теорема Менгера
67
и 3* := {9 \ {Р}) U {Рх}. Тогда |3»'| = \&\ и k(G,A,B') >
k(G,A,B), поэтому по предположению индукции существует
множество £2! из \£?\ -f 1 непересекающихся А-Б' путей, среди концов
которых лежат все концы путей из &'. Тогда £1' содержит путь Q,
кончающийся в вершине ж, и единственный путь Q', последняя
вершина у которого не лежит среди последних вершин путей из £?'.
Если у £ хР, мы получаем £1 из £2! добавлением хР к Q, и
добавлением 2/Я к Q', если у £ В. В противном случае у £ хР, и мы
получаем i2 из £1' добавлением xR к Q и уР к Q'. □
Рис. 3.3.1. Пути в первом доказательстве теоремы Менгера
Второе доказательство. Покажем индукцией по \G\ -f ||G||,
что G содержит к непересекающихся А-В путей. Если к £ {0,1},
то для любых G, А, Б это верно. Для шага индукции рассмотрим
G, А, В с к > 2 и предположим, что для графов с меньшим числом
вершин или ребер условие теоремы выполняется.
Если существует вершина х £ А О В, то G — х по
предположению индукции содержит к — 1 непересекающихся А-В путей
(почему?). Вместе с тривиальным путем {х} они образуют искомый
набор из к путей в G. Предположим поэтому, что
АПВ = 0. (1)
Сначала построим пути из утверждения теоремы для случая,
когда А и В разделены множеством X CV, где \Х\ = к и X ф А, В.
Пусть С а — объединение компонент G — X, пересекающихся с А.
Заметим, что С а ф 0> поскольку \А\ > к = \Х\, но А ф X.
Аналогичным образом определенный подграф Св также непуст, и С а П
Св = 0. Обозначим GA := G[V{CA)UX] и GB := G[V(CB)UX].
Поскольку всякий А-В путь в G содержит какой-либо А-Х путь в G^,
мы не можем отделить А от X в G^ менее чем & вершинами. Значит,
по предположению индукции Ga содержит к непересекающихся А-Х
путей (рис. 3.3.2). Подобным же образом мы находим к
непересекающихся Х-В путей в Gb- Поскольку \Х\ = к, мы можем соединить
эти пути попарно и получить к непересекающихся А-В путей.

68
Глава 3. Связность
GA
Рис. 3.3.2. Непересекающиеся А-Х пути в G^
В общем случае пусть Р — произвольный А-В путь в G.
Благодаря (1) в Р есть такое ребро ab, что a £ В, &Ь £ А. Пусть У —
множество вершин минимальной мощности, отделяющее А от В в G — ab
(рис. 3.3.3). Тогда и Уа := У U {а}, и У6 := У U {6} отделяют А от Б
в G, и по определению числа & мы имеем
|Уа|,|П|>*.
Если здесь имеет место равенство, то, так как противный случай
уже был рассмотрен, можно предположить, что {Уа,Уб} С {А, Б},
т. е. {Ya)Yb} = {А, В}, поскольку a <£ В и b <£ А. Значит, У = АС\В.
Так как |У| > к — 1 > 1, это противоречит (1).
a s-\ у\ Ъ
Р
vV
Рис
■ ab
3.3.3. Отделение А от В в G -
Таким образом, у нас либо \Ya\ > &, либо |У{,| > к, а значит,
|У| > к. Тогда по предположению индукции даже в G — ab С G
существует к непересекающихся А-В путей. □
Примененная к двудольному графу теорема Менгера сводится
к теореме Кёнига (2.1.1). В качестве третьего доказательства к
более общему условию теоремы 3.3.1 приспосабливается
доказательство теоремы Кёнига через чередующиеся пути. Пусть опять даны
G, А, Б, и пусть & — множество непересекающихся А-В путей в G.
Обозначим
V[&\ := \J{V(P) \Ре&},

3.3. Теорема Менгера
69
Маршрут W — х^е^х\е\ .. .en-ixn в G, где ег- ф е;- при г ^ j,
называется чередующимся относительно ^, если для всех г < п
выполняются следующие три'условия (рис. 3.3.4):
(i) если е,- = е Е Е[£Р]} то И^ проходит по ребру е в обратном
направлении, т. е. Х{+\ Е Рх{ для некоторого Р Е 3?\
(ii) если жг- = Xj, где г ^ j, то жг- Е V\3P\\
(iii) если э^ Е V[^], то {ег_ь ег} П Я[^] ^ 0 2).
Рис. 3.3.4. Чередующийся маршрут из А в В
Рассмотрим маршрут W — х^х^ .. . еп_1Ж„ из А \ V[^]
вБ\ V[£&], чередующийся относительно SP. По (ii) всякая вершина
не из V\&*\ встречается в W не более одного раза. Поскольку все
ребра ег- маршрута W различны, из (iii) вытекает, что всякая
вершина из V[&*] встречается в W не более чем дважды. Возможны
два случая: если, допустим, Х{ — х^ где 0 < г < j < п, то
либо ct-_i,c;- Е #[^], aet-,e;-_i ^ #[^],
ли£о ег-,е;-_1 Е Я[^], аег-_ье;- £ £[^>].
Лемма 3.3.2. Если такой маршрут W существует, то G
содержит \£?\ -f 1 непересекающихся А-В путей.
Доказательство. Пусть Я — граф на V[&\ U {ж0,.. .,»„},
множество ребер которого является симметрической разностью
множеств Е\ЗР\ и {ео,.. .,en_i}. Концы путей из & и маршрута И^
имеют в Н степень 1 (или 0, если этот путь или маршрут W
тривиален); все остальные вершины имеют степень 0 или 2. Таким
образом, для каждой из \£?\ -f 1 вершин a Е (АО V[&]) U {xq} компонента
графа Я, содержащая а, является путем (например, Р — vq .. . i>fc),
который начинается с а и заканчивается на А или В. Используя
условия (i) и (iii), легко показать индукцией по г = 0,..., А; — 1, что Р
проходит по каждому из своих ребер е = иг-иг-+1 в прямом
направлении по отношению к & или W. (Говоря точнее, если е Е Р', где
Р' Е ^, то ы Е P'vi+i] а если е — еу Е W, то иг- = ж;- и иг-+1 = жу+ь)
2) Для i = 0 мы полагаем {e,_i, е,} := {ео}.

70
Глава 3. Связность
Значит, Р заканчивается в множестве В. Поскольку всего в Р
имеется |^| -f 1 таких непересекающихся путей, лемма доказана. □
Третье доказательство теоремы Менгера. Пусть 5* —
множество независимых А-В путей в G, имеющее наибольшую
мощность. По умолчанию, под чередующимися маршрутами мы всегда
понимаем маршруты, чередующиеся относительно &. Положим
Аг :=ACiV[&\, А2 :=А\Аи
В1 := ВПУ[3*], В2 :=В\Вг.
Для каждого пути Р £ £? обозначим через хр последнюю
вершину из Р, лежащую в каком-либо чередующемся маршруте,
начинающемся в А2. Если таких вершин не существует, то пусть хр —
первая вершина пути Р. Ясно, что мощность множества
X := {хР | Р е &}
равна |^|, значит, достаточно показать, что X отделяет А от В.
Пусть Q — какой-то А-В путь в G; покажем, что Q пересекается
с X. Предположим, что это не так. По максимальности & путь Q
пересекается с V[£?\. Поскольку A-V[&] путь в Q, очевидно,
является чередующимся маршрутом, то Q пересекается и с множеством
вершин V[&>']i где
&' := {РхР \Ре&>}.
Пусть у — последняя вершина пути Q, принадлежащая V\2?'\, Р —
путь из ^, содержащий у, и х := хр. Наконец, пусть W —
чередующийся маршрут из А2 в х из определения вершины хр. По
предположению, Q не пересекается с X и, следовательно, не содержит х, так
что у £ Рх и WUxPyQ — маршрут из А2 в В (рис. 3.3.5). Если этот
маршрут чередующийся и оканчивается на В2, то по лемме 3.3.2 в G
содержится |^| + 1 непересекающихся А-В путей, что противоречит
максимальности SP.
Рис. 3.3.5. Чередующиеся маршруты
из третьего доказательства теоремы Менгера

3.3. Теорема Менгера
71
Каким же образом W U xPyQ мог бы не быть чередующимся
маршрутом? Прежде всего W мог бы уже использовать ребро из
хРу. Но если х' — первая вершина из W в хРу, то W :— WxJРу —
чередующийся маршрут из А2 в у. (Под Wx' мы понимаем
начальный отрезок маршрута W, заканчивающийся первым вхождением
в W вершины х'\ начиная с этого момента W следует вдоль Р
обратно к у.) Даже этот новый маршрут W'yQ не обязан быть
чередующимся: W все еще может пересекаться с yQ. Однако из
определения £?' и W и выбора вершины у в Q следует, что
V(W) П V[&\ С V[&>'] и V(yQ) П У[3"] = 0.
Таким образом, W7 и yQ могут пересечься только вне &.
Если W действительно пересекается с yQ, то пусть z —
первая вершина маршрута W, лежащая в yQ. Поскольку z лежит
вне V[&], в маршруте W она встречается только один раз
(условие (ii)), обозначим W" := W'zQ. Если же W П yQ — 0, обозначим
W" \— W \JyQ. В обоих случаях маршрут W" чередуется
относительно ^', поскольку таковым является W, a yQ не пересекается
с V[£P'\. (Заметим, что во втором случае W" удовлетворяет
условию (iii) в вершине у, в то время как в первом случае (iii) к z не
применимо.) Таким образом, по определению £?' маршрут W" не
пересекается с V\&\ \ V[£?'], в частности, V(yQ) П V\&\ — 0. Значит,
W" чередуется и по отношению к & и заканчивается в В^.
(Заметим, что у не может быть последней вершиной W", поскольку у £ Рх
и, следовательно, у £ В.) Далее, W" начинается в Аг, поскольку там
начинается W. Значит, чтобы получить требуемое противоречие
с максимальностью ^, можно использовать W" и лемму 3.3.2. □
Множество a-В путей называется а-В веером, если любые два
из этих путей пересекаются только в вершине а.
Следствие 3.3.3. Пусть В CV и а £ V \В. Тогда
минимальное число отличных от а вершин, отделяющих а от В в G, равно
максимальному числу путей, образующих a-В веер в G.
Доказательство. Теорема 3.3.1 применяется к А := N(a). О
Следствие 3.3.4. Пусть а и b — две различные вершины в G.
(i) Если ab £ Е, то минимальное число вершин, отличных от
a, b и отделяющих а от b в G, равно максимальному числу
независимых a-b путей в G.
. (ii) Минимальное число ребер, отделяющих а от b в G, равно
максимальному числу a-b путей в G, не пересекающихся по
ребрам.

72
Глава 3. Связность
Доказательство, (i) Теорема 3.3.1 применяется к А := N(a)
и В := АГ(6).
(ii) Теорема 3.3.1 применяется к реберному графу графа G и
к А := Е(а), В := £(&). П
Теорема 3.3.5 (глобальный вариант теоремы Менгера).
(i) Граф к-связен тогда и только тогда, когда он содержит к
независимых путей между любыми двумя вершинами.
(ii) Граф к-реберно-связен тогда и только тогда, когда он
содержит к непересекающихся по ребрам путей между любыми
двумя вершинами.
Доказательство, (i) Если граф G содержит к независимых
путей между любыми двумя вершинами, то \G\ > к и G не может
быть разделен менее чем к вершинами, значит, G &-связен.
Напротив, предположим, что G &-связен (в частности, в нем
более к вершин), но содержит вершины а, 6, не связанные к
независимыми путями. По следствию 3.3.4(i) а и 6 смежны; пусть G1 := G—ab.
Тогда G' содержит не более чем к — 2 независимых a-b путей. По
следствию 3.3.4(i) мы можем разделить а и b в G' множеством X из
не более чем к — 2 вершин. Поскольку \G\ > к, в G есть еще по
крайней мере одна вершина v £ X U {а, 6}. Множество X отделяет v
в G' от одной из вершин а и 6, скажем, от а. Но тогда X U {6} —
множество из не более чем к—\ вершин, отделяющее v от а в G, что
противоречит ^-связности графа G.
(ii) Напрямую вытекает из следствия 3.3.4(ii). □
3.4. Теорема Мадера
По аналогии с теоремой Менгера можно рассмотреть следующий
вопрос: сколь много независимых Я-путей можно найти в графе G
для данного индуцированного подграфа Я?
В этом разделе приводится без доказательства глубокая теорема,
доказанная Мадером и разрешающая этот вопрос в стиле теоремы
Менгера. Как и теорема Менгера, эта теорема утверждает, что
естественная верхняя граница для числа таких путей, выражаемая через
размер разделителей определенного вида, действительно достигается
на некотором подходящем множестве путей.
Как может выглядеть такая верхняя оценка? Ясно, что если
каждый Я-путь в G содержит вершину из какого-то множества X С
V(G — Я) или ребро из множества F С E(G — Я), то в G может быть
не более чем \Х U F\ независимых Я-путей. Значит, наименьшая
мощность такого множества X U F представляет собой
естественную верхнюю оценку для числа независимых Я-путей. (Заметим,

ЗА. Теорема Мадера
73
что поскольку Я — индуцированный подграф G, а его ребра не
считаются Я-путями, каждый Я-путь пересекается с G — Я.)
В отличие от теоремы Менгера эта оценка может быть
улучшена. Ясно, что мы можем исключить из F ребра, имеющие концы
в X, так как в качестве разделителей они не используются. Пусть
У := V(G -Н)\Х] обозначим через &f множество компонент
связности графа (У, F). Поскольку всякий Я-путь, не пересекающийся
с X, содержит ребро из множества F, для какого-то С £ ^f он
содержит по меньшей мере две вершины из дС — множества вершин из С,
смежных с G — X — C (рис. 3.4.1). Таким образом, число независимых
Я-путей в G ограничено сверху величиной
MG(H):= min f\X\+ £
где минимум берется по всем X и F, описанным выше, а именно,
X С V(G - Я), a F С E(G - Я - X), причем всякий Я-путь в G
содержит вершину или ребро из X U F.
Рис. 34.1. Я-путь в G - X
Именно эта верхняя граница согласно теореме Мадера всегда
достигается на каком-либо множестве независимых Я-путей.
Теорема 3.4.1 (Мадер, 1978). Для всякого индуцированного
подграфа Я графа G в G найдутся Mq{H) независимых Я-путей.
Чтобы получить прямую аналогию с вершинным и реберным
вариантами теоремы Менгера, рассмотрим два частных случая
вышеописанной задачи, в которых соответственно F и X пусты.
Обозначим через кс(Н) наименьшую мощность множества вершин X С
V(G — Я), пересекающегося с каждым Я-путем в графе G.
Аналогично, через Л^(Я) обозначим наименьшую мощность множества
ребер F С E(G), пересекающегося со всяким Я-путем в G.
Следствие 3.4.2. Для всякого индуцированного подграфа Я
графа G в G найдутся не менее ^кс(Н) независимых Н-путей и не
менее ^Хс(Н) не пересекающихся по ребрам Я-путей.
:\9С\

74
Глава 3. Связность
Доказательство. Пусть к — максимальное число
независимых Я-путей в G. По теореме 3.4.1 существуют такие множества
X С V(G - Н) и F С E(G - Н - X), что
\\*с\
и всякий Я-путь в G содержит вершину из X или ребро из F. Для
каждой С £ ^f, для которой дС ф 0, выберем вершину v £ ЗС
и положим Ус := ЗС \ {г/}; если же <9С = 0, то положим Ус := 0.
Тогда [||3C|J > ||Ус| Для всех С £ ^р- Более того, всякий Я-путь
содержит вершину из X U У, где У := (J Ус- Значит,
k>\X\+ Y, \\Yc\>\\XUY\>LG(H),
что и доказывает первую часть следствия.
Вторая часть следствия вытекает из первой, примененной к
реберному графу графа G (см. упражнение 16). □
Это может показаться удивительным, но оценки из следствия
3.4.2 в общем случае неулучшаемы. Можно найти примеры графов
G и Я, в которых G содержит не более чем |/с^(Я) независимых
Я-путей или не более чем ^А^(Я) Я-путей, не пересекающихся по
ребрам (упражнения 17 и 18).
3.5. Не пересекающиеся по ребрам остовные деревья
Реберная версия теоремы Менгера говорит о том, в каких
случаях граф G содержит к не пересекающихся по ребрам путей между
любыми двумя вершинами. В действительности такие пути могут
существенно зависеть от выбора этих двух вершин: нахождение
независимых путей для одной пары вершин-концов совершенно
необязательно может помочь в нахождении их для другой пары.
В ситуации, когда требуется быстро находить множество из к
не пересекающихся по ребрам путей между двумя вершинами, имеет
смысл требовать от графа большего, чем просто fc-реберная
связность. Например, если в G есть к не пересекающихся по ребрам
остоепых деревьев, то между любыми двумя вершинами есть к
канонических независимых путей (по одному в каждом дереве).
Когда существуют такие деревья? Ясно, что прежде всего для
этого граф должен быть &-реберно-связным. Обратное же, как
нетрудно заметить, неверно. Не понятно даже, может ли
существование к не пересекающихся по ребрам остовных деревьев вытекать

3.5. Не пересекающиеся по ребрам остовные деревья 75
из какой-либо большей реберной связности. Изучение условий
существования k не пересекающихся по ребрам остовных деревьев —
первая задача этого раздела.
Как и раньше, нетрудно выписать несколько очевидных
необходимых условий существования к таких остовных деревьев.
Рассмотрим разбиение множества V(G) на г подмножеств и назовем
ребрами-переходами ребра, концы которых лежат в разных
подмножествах. Ясно, что в любом остовном дереве содержится не менее
чем г — 1 ребер-переходов (почему?). Значит, если в G есть к не
пересекающихся по ребрам остовных деревьев, в нем есть и не менее
чем к (г — 1) ребер-переходов.
И снова это очевидное необходимое условие оказывается также
и достаточным.
Теорема 3.5.1 (Татт, 1961; Нэш-Уильямс, 1961). Мультиграф
содержит к не пересекающихся по ребрам остовных деревьев тогда
и только тогда, когда для всякого разбиения Р множества его
вершин он содержит не менее чем к(\Р\ — 1) ребер-переходов.
Прежде чем доказывать теорему 3.5.1, заметим следующее ее
удивительное следствие: чтобы обеспечить существование к не
пересекающихся по ребрам остовных деревьев, достаточно увеличить
реберную связность всего лишь до 2k.
Следствие 3.5.2. Всякий 2к-реберно-связный мультиграф G
содержит к не пересекающихся по ребрам остовных деревьев.
Доказательство. Всякое подмножество из разбиения
множества вершин графа G связано с остальными подмножествами этого
разбиения не менее чем 2k ребрами. Значит, для всякого разбие-
г
ния на г подмножеств в G есть не менее чем | ]И 2k — кг ребер-
t=i
переходов. Таким образом, утверждение следствия вытекает из
теоремы 3.5.1. □
Переходя к доказательству теоремы 3.5.1, предположим, что
даны мультиграф G — (V, Е) и число к £ N. Пусть & — множество
всех наборов F — (Fi,...,Fjb) из k не пересекающихся по ребрам
остовных лесов в G с наибольшим в совокупности числом ребер, т. е.
таких, что мощность \\F\\ := \E[F]\, где E[F] := £(Fi) U • • • U E(Fk),
максимальна.
Если^ = (Fi,...,Fk) E^aeG E\E[F], то для всех i = 1,.. ., &
граф F{ -f e содержит цикл; в противном случае в F можно было
бы заменить F,- на F,- -f е и получить противоречие с
максимальностью ||F||. Зафиксируем г и рассмотрим ребро е' ф е из этого
цикла. Пусть F{ := F{ -f е — е' и Fj := Fj для всех j ф i. Очевидно,
что F' \— [F{,..., Fj£) — снова элемент &. Говорят, что F' получен
из F замещением ребра е' ребром е. Заметим, что компонента связ-

76
Глава 3. Связность
ности леса F{, содержащая е', превращаясь в компоненту связности
леса F{, сохраняет множество вершин. Значит, для всякого пути
х ... у С F( в F{ существует единственный путь xFiy; позже этот
факт нам понадобится.
Рассмотрим фиксированный набор F° = (i^0,..., F%) G &.
Множество всех наборов из J£", которые могут быть получены из F0
серией замещений ребер, будет обозначаться через J£"°. Наконец,
положим
Е°:= (J (E\E[F})
Лемма 3.5.3. Для всякого e° G E\E[F°] существует множество
U С V, связное в каждом из F{° (г = 1,.. ., к) и содержащее концы
ребра е°.
Доказательство. Поскольку F° G ^°, то е° G Е°. Пусть
С0 — компонента графа G0, содержащая е°. Докажем утверждение
для U := У(С°).
Пусть дано г G {1,..., к}. Надо показать, что U связно в F?.
Для этого сначала докажем следующее.
Пусть F = (Fu...,Fk)e&°,M пусть набор (F[,..., Ffi
получен из F замещением ребра из F{. Если х, у — (1)
концы пути в F( Г) С0, то и xFiy С С0.
Пусть е — vw — новое ребро в E(^F[) \ E[F]; это единственное ребро
из F-, не лежащее в F{. Можно считать, что е G xF-y, иначе
выполнялось бы равенство xF{y — xF^y и доказывать было бы нечего.
Достаточно показать, что vF{W С С0, тогда (xFly—e)\JvFiW — связный
подграф графа Ft- П С0, содержащий ж, у, а значит, и xF{y. Пусть
е' — произвольное ребро из vF{W. Поскольку в F G ^° ребро е'
можно заменить на е и получить не содержащий е' элемент J*"0, то
е' G Е°. Таким образом, vF{W С G°, а значит, vF{W С С0, поскольку
v, w G я^/з/ С С0. Тем самым (1) доказано.
Чтобы доказать, что U = V(C°) связно в F®, покажем, что для
всякого ребра ху G С0 существует путь xF®y, лежащий в С0.
Поскольку граф С0 связен, объединение всех этих путей будет связным
остовным подграфом графа F-*[U].
Итак, пусть дано ребро е — ху G С0. Поскольку е G Е°,
существуют такое число s G N и такие s наборов Fr = (Ff,..., F£), где
г = 1,...,5, что каждый набор Fr получен из Fr~l замещениями
ребер, и е G E\E[FS]. Полагая в (1) граф F := Fs, можно считать е
путем длины 1 в F- Г)С°. Затем последовательные применения (1)
к F — F5,..., F0 дают xF^y С С0, что и требовалось. □

3.5. Не пересекающиеся по ребрам остовные деревья 77
Доказательство теоремы 3.5.1. Докажем неочевидную часть
теоремы индукцией по |G|. Для \G\ = 2 утверждение верно.
Теперь, для индукционного шага, предположим, что для каждого
разбиения Р множества V существует не менее чем k(\P\ — 1) ребер-
переходов, и построим в G к не пересекающихся по ребрам остовных
деревьев.
Выберем набор F° = (F?,..., Fj>) G &. Если каждый из
лесов F{° — дерево, то наша цель достигнута. Если же это не так, то
imi = EH°|<*(iGi-i)
t=i
по следствию 1.5.3. С другой стороны, по предположению ||G|| >
k(\G\ — 1): достаточно рассмотреть разбиение V на отдельные
вершины. Значит, существует ребро е° £ Е \ E[F°]. По лемме 3.5.3
существует множество U С V, связное в каждом из F{° и содержащее
концы ребра ео, в частности, \U\ > 2. Поскольку каждому
разбиению стянутого мультиграфа G/U соответствует разбиение мульти-
графа G с теми же ребрами-переходами3), то в G/U есть не менее чем
к(\Р\ — 1) ре б ер-переходов относительно любого разбиения Р.
Значит, по предположению индукции в G/U есть к не пересекающихся
по ребрам остовных деревьев Т\,..., Т*. Заменяя в каждом из Т{
вершину vu, стянутую из U, на остовное дерево F? П G[U] в G[U], мы
получаем к не пересекающихся по ребрам остовных деревьев в G. □
Говорят, что подграфы Gi,..., G* графа G разбивают G, если
множества их ребер образуют разбиение множества E(G). Наша
задача об остовных деревьях в этих терминах может быть
переформулирована следующим образом: на какое наибольшее количество
связных остовных подграфов можно разбить данный граф?
Обоснованием такой сложной переформулировки нашей задачи
может служить то, что теперь задача имеет очевидную
двойственную к ней (см. теорему 1.5.1): на какое наименьшее количество
ациклических (остовных) подграфов можно разбить данный граф? Или
если задано к: какие графы могут быть разбиты на не более чем
к лесов?
Очевидным необходимым условием здесь будет то, что каждое
множество U С V(G) индуцирует самое большее k(\U\ — 1) ребер: не
более чем по \U\ — 1 на каждый лес. И снова это необходимое условие
оказывается и достаточным. Что неожиданно, доказать это можно
с помощью леммы 3.5.3, назначением которой было доказательство
теоремы о не пересекающихся по ребрам остовных деревьях.
) О стягивании мультиграфов см. раздел 1.10.

78
Глава 3. Связность
Теорема 3.5.4 (Нэш-Уильямс, 1964). Мультиграф G = (V, Е)
может быть разбит на не более чем к лесов тогда и только тогда,
когда 11G [U] 11 < k (| U \ — 1) для любого непустого подмножества U С V.
Доказательство. Прямая импликация была доказана выше.
Покажем теперь, что любой набор F = {F\,..., Fk) £ & разбивает G,
т. е. что E[F] = Е. Если это неверно, пусть е £ Е \ E[F]. По
лемме 3.5.3 существует множество U С V, связное в каждом из F,-
и содержащее концы ребра е. Тогда G[U] содержит по \U\ — 1 ребер
из каждого F{ и кроме того ребро е. Получается, что ||G[[/]|| >
k(\U\ — 1), что противоречит условию теоремы. □
Наименьшее число лесов, образующих разбиение графа G,
называется его древесностъю. По теореме 3.5.4 древесность является
мерой максимальной локальной плотности. Древесность графа мала
тогда и только тогда, когда граф «нигде не плотен», т. е. в нем нет
подграфа Н с большим е(Н).
3.6. Пути между заданными парами вершин
Говорят, что граф с не менее чем 2к вершинами к-сцеплен, если
для всяких его 2к различных вершин s\,..., s^, t\,..., t* он содержит
к непересекающихся путей Pi,..., Р*, где Рг- = S{.. Л{ для всех г.
Здесь в отличие от теоремы Менгера речь идет не просто о
существовании к непересекающихся путей между двумя множествами
вершин: требуется, чтобы каждый из этих путей связывал
конкретную пару вершин.
Ясно, что всякий fc-сцепленный граф &-связен. Обратное,
однако, далеко не верно: в общем случае &-сцепленность — свойство
гораздо более сильное, чем ^-связность. Тем не менее эти два
свойства связаны между собой. Цель этого раздела — доказать
существование такой функции /: N —+ N, что всякий /(&)-связный граф
&-сцеплен.
В качестве леммы нам нужен результат, который в противном
случае был бы приведен в главе 8.
Теорема 3.6.1 (Мадер, 1967). Существует функция h: N —+ N
такая, что для любого г £ N всякий граф со средней степенью не
менее h(r) содержит как топологический минор полный граф Кг.
Доказательство. Если г < 2, то h(r) существует и равно 1.
Предположим теперь, что г > 3. Индукцией по m = г,..., Q
покажем, что всякий граф G со средней степенью d(G) > 2m содержит
топологический минор X с г вершинами и m ребрами. Значению
m — (П соответствует граф Кг, из чего вытекает утверждение
теоремы для h(r) — 2v2).

3.6. Пути между заданными парами вершин
79
Если m — г, то по предложениям 1.2.2 и 1.3.1 G содержит цикл
длины не менее e(G) -f 1 > 2r_1 -f 1 > r-f 1, и утверждение верно для
X = СГ.
Теперь пусть г < m < (г2). Предположим, что утверждение
верно для меньших т. Пусть дан граф G с d(G) > 2m, значит,
e(G) > 2m_1. Поскольку в G есть компонента С с е{С) > e(G),
можно предположить, что G связен. Рассмотрим такое
максимальное множество U С V(G), что U связно в G, a e{G/U) > 2m_1. Такое
U существует, потому что сам G имеет вид G/U, где \U\ — 1.
Поскольку G связен, N(U) ф 0.
Пусть Н := G[N(U)]. Если в Н есть вершина v степени (1h{v) <
2m_1, добавление ее к U дает противоречие с максимальностью U.
Действительно, при стягивании ребра vvu в G/U теряется одна
вершина и dn(v) -f 1 < 2m_1 ребер, так что е останется не менее 2m_1.
Поэтому d(H) > 8(H) > 2m_1. По предположению индукции Н
содержит TY, где |У| = г и ||У|| = m — 1. Пусть х, у — две вершины
ветвления этого ТУ', которые в У не смежны друг с другом.
Поскольку х и у лежат в N(U), a U связно в G, граф G содержит х-у
путь, внутренние вершины которого лежат в U. Добавление в ТУ
этого пути дает требуемое ТХ. □
Каким образом теорема 3.6.1 может помочь показать, что
высокая связность способна обеспечить &-сцепленность графа?
Поскольку высокая связность с необходимостью увеличивает среднюю
(и даже минимальную) степень, по теореме можно предположить,
что наш граф содержит подразделение К большого полного графа.
Теперь осталось использовать теорему Менгера, чтобы взаимно
однозначно связать данные вершины S{ и t{ с вершинами ветвления К,
а затем соединить эти правильные пары вершин внутри К.
Теорема 3.6.2 (Юнг, 1970; Ларман, Мани, 1970). Существует
такая функция /: N —>• N, что для всех к £ N любой f(к)-связный
граф к-сцеплен.
Доказательство. Докажем утверждение для f(k) = h(Sk) -f 2&,
где h — функция из теоремы 3.6.1. Пусть G — /(&)-связный граф.
Тогда d(G) > 6(G) > k(G) > h(Sk). Выберем К = ТКзк С G, как
в теореме 3.6.1, и пусть U есть множество его вершин ветвления.
Пусть даны вершины si,..., s^ и £i,... ,£* графа G. Докажем,
что для них существуют пути из определения &-сцепленности. По
определению функции f(k) верно равенство k(G) > 2к. Значит,
по теореме Менгера (3.3.1) в G есть такие непересекающиеся пути
Pi, • • , Pk, Qit • • •, Qk, что каждый из Рг- начинается с st-, каждый Qi
начинается с t{ и все эти пути заканчиваются в U (но не содержат
в U внутренних вершин). Пусть множество 3? этих путей выбрано
так, чтобы общее число ребер вне Е(К) было наименьшим.

80
Глава 3. Связность
Пусть щ,..., Uk — те & вершин из U, которые не являются
концами путей из &. Пусть Lt- для каждого г — 1,...,& обозначает
[/-путь в К (соответствующий ребру в Кзк), проходящий от щ до
конца Р{ в U, и пусть V{ — первая вершина пути Lt-, принадлежащая
какому-либо пути Р £ 3*. По определению & в пути Р содержится
не больше ребер, не принадлежащих Е(К)} чем в Ру{Ь{Щ, поэтому
ыР — V{Li, а значит, Р — Р{ (рис. 3.6.1). Точно так же если Мг-
обозначает [/-путь в К, проходящий из щ в конец Qi в U, a W{ —
первая вершина М», принадлежащая пути из ^, то этот путь
равен Q{. Тогда пути SiPiViLiUiMiWiQiU для разных г не пересекаются
и показывают, что G &-сцеплен. □
Рис. 3.6.1. Построение Si~tt пути через иг
В доказательстве теоремы 3.6.2 мы не старались найти какую-
либо хорошую оценку на связность, обеспечивающую &-сцепленность
графа: использованная нами функция / растет экспоненциально
по &. Не удивительно, что это далеко не наилучшая оценка. Тем
не менее достойно упоминания то, что на самом деле / может быть
линейной функцией. Как показали Боллобаш и Томасон (1996),
всякий 22&-связный граф &-сцеплен.
Упражнения
В первых трех упражнениях дан граф G и его вершины а, 6 Е V(G).
Предположим, что множество X С V(G)\{a,6} отделяет а от 6 в G. Говорят, что X
отделяет а от 6 минимально, если никакое собственное его подмножество а от 6
в G не отделяет.
1.~ Показать, что X отделяет а от 6 минимально тогда и только тогда, когда
каждая вершина из X смежна какой-либо вершине из компоненты Са графа
G — X, содержащей а, и другой вершине из компоненты Сь графа G — Xу
содержащей 6.
2. Пусть X' С V(G) \ {а, 6} — другое множество, отделяющее а от 6; С'а и С'ь
определяются соответственно. Показать, что оба множества
Ya := (X П С'а) U {X П X') U (X' П Са),
П := (X П С'ь) U {X П X') U (X1 П Сь)
тоже отделяют а от 6 (см. рис.).

Упражнения
81
3. Если иХ,иХ' отделяют а от 6 минимально, то можно ли сказать то же
самое об Ya и Уь? Если \Х\ и \Х'\ минимальны для множеств вершин,
отделяющих а от 6, то всегда ли минимальны \Ya\ и |Уь|?
4. Пусть X и X' — такие минимальные разделяющие множества вершин в G,
что X пересекается с не менее чем двумя компонентами графа G — X'.
Показать, что X' пересекается со всеми компонентами G — X, а X — со
всеми компонентами графа G — X'.
5.~ Доказать элементарные свойства блоков, упомянутые в начале раздела 3.1.
6. Показать, что граф блоков всякого связного графа — дерево.
7. Не применяя теоремы Менгера, показать, что всякие две вершины 2-связно-
го графа принадлежат общему циклу.
8. Будем писать е ~ е;, где е, е' Е E(G), если либо е = е;, либо е и е'
лежат на одном и том же цикле в G. Показать, что ~ является отношением
эквивалентности на E(G), причем его классы эквивалентности совпадают
с множествами ребер нетривиальных блоков графа G.
9. Пусть G — 2-связный граф, но не треугольник, а е — ребро в G. Показать,
что один из графов G — е и G/e снова 2-связен.
10. Пусть G — 3-связныйграф, а. ху — его ребро. Показать, что G/xy 3-связен
тогда и только тогда, когда G — {х, у} 2-связен.
11. (i) Показать, что всякий кубический 3-реберно-связный граф 3-связен.
(и) Показать, что граф является кубическим и 3-связным тогда и только
тогда, когда он может быть построен из /С4 последовательными
применениями следующей операции: подразделить два ребра вставкой в каждое из
них по новой вершине и соединить две эти новые вершины ребром.
12." Показать эквивалентность теоремы Менгера следующему утверждению.
Для всякого графа G и для любых множеств вершин А, В С V(G)
существуют такие множество 9* непересекающихся А-В путей в G и множество
X С V(G), отделяющее А от В в G, что X имеет вид X = {хр \ Р Е 9},
где хр Е Р Для всех Р Е &.
13. Проработать детали доказательства следствия 3.3.4(H).
14. Пусть к > 2. Показать, что всякий Aj-связный граф порядка не менее 2к
содержит цикл длины не менее 2к.
15. Пусть к > 2. Показать, что любые к вершин /с-связного графа принадлежат
общему циклу.
16. Вывести утверждение о ребрах следствия 3.4.2 из утверждения о вершинах.
(Подсказка. Рассмотреть Я-пути в графе, полученном из
непересекающегося объединения Н с реберным графом L(G) добавлением всех таких
ребер /ie, что h — вершина графа Н, а е Е E(G) \ Е(Н) — инцидентное ей
ребро.)
17.~ К непересекающемуся объединению графа Н — K2rn+l с к копиями /f2m+i
добавляются ребра, взаимно однозначно связывающие Н с каждым из
^2m+i. Показать, что получающийся граф G содержит не более km —
^kq(H) независимых Я-путей.

82
Глава 3. Связность
18. Найти такой двудольный граф G с долями А и В, что для Н := G[A] в G
существуют не более ^Xq(H) не пересекающихся по ребрам //-путей.
19.+ Вывести теорему Татта об 1-факторе (2.2.1) из теоремы Мадера.
(Подсказка. Расширить граф G до графа G' добавлением к каждой
вершине v G G новой вершины t>;, смежной с v. Выбрать Н С G' так, чтобы
1-факторы в G соответствовали достаточно большим множествам
независимых Н-путей в G'.)
20. Найти ошибку в следующем коротком «доказательстве» теоремы 3.5.1.
Назовем разбиение нетривиальным, если в нем не менее двух классов и по
меньшей мере в одном из них содержится более одного элемента. Покажем
индукцией по \V\ -f \Е\, что если всякое нетривиальное разбиение
множества V на г подмножеств (допустим) содержит не менее к(г — 1) ребер-
переходов, то G = {V,E) разбивается на к не пересекающихся по ребрам
остовных деревьев. Индукция начинается с тривиального графа G = К1,,
а в качестве к не пересекающихся по ребрам остовных деревьев
рассматриваются к копий графа К1. Теперь займемся индукционным шагом. Если
во всяком нетривиальном разбиении множества V на г подмножеств
(допустим) есть более к(г — 1) ребер-переходов, мы удаляем из G любое ребро
и таким образом заканчиваем индукционный шаг. Поэтому пусть
существует нетривиальное разбиение {Vj,. .., Vr} множества V с ровно к(г — 1)
ребрами-переходами. Предположим, что |Vi | > 2. Если в графе G' := G\V\]
имеется к непересекающихся остовных деревьев, мы можем скомбинировать
их с А: непересекающимися остовными деревьями, существующими в G/V\
по индукции. Поэтому предположим, что в G' нет к непересекающихся
остовных деревьев. Тогда по индукции существует его нетривиальное
вершинное разбиение {V{, •.. , Ve'} с менее чем k(s — 1) ребрами-переходами.
При этом {V{, • • •, Vgt V2,. .., Vr} — нетривиальное вершинное разбиение
графа G на г-j-5 — 1 множество с менее чем к(г — l) + k(s — 1) = k((r + s — 1) — 1)
ребрами-переходами; противоречие.
21.— Показать, что всякий /:-сцепленный граф (2А: — 1)-связен.
Примечания
Хотя теоремы о связности, без сомнения, принадлежат к наиболее
естественным и потому наиболее востребованным результатам теории графов,
исчерпывающей монографии по этой теме до сих пор не существует. Некоторые
разделы описаны в: Bollobds В. Extremal Graph Theory. London: Acad. Press,
1978; Halin R. Graphentheorie. Darmstadt: Wissenschaftliche Buchgesellschaft,
1980 — и в главе А. Франка в: Handbook of Combinatorics / Ed. by R. L.
Graham, M. Grotschel, L. Lovasz. Amsterdam e. a.: North-Holland Publ., 1995. Обзор,
специально посвященный технике работы с минимально Aj-связными графами
(см. ниже) и результатам о них дан в: Mader W. On vertices of degree n in mini-
maDy n-connected graphs and digraphs // Combinatorics, Paul Erdos is eighty j Ed.
by D. Miklos, V. T. Sos, T. Szonyi / Bolyai Soc. Math. Studies. V. 2. Budapest:
Janos Bolyai Math. Soc, 1996.
Доказательство теоремы Татта 3.2.3 дается по: Thomassen С. Planarity
and duality of finite and infinite graphs //J. Combin. Theory. Ser. B. 1980. 29.
P. 244-271. В этой же работе содержатся лемма 3.2.1 и ее короткое независимое
доказательство. (Конечно же, утверждение леммы вытекает из теоремы Татта
о колесе, но ее независимое доказательство ценно тем, что значительно
сокращает доказательства обеих теорем Татта.)
В главе не затронут еще один подход к изучению связности —
исследование минимальных Aj-связных графов, теряющих свою Аг-связность при удалении
любого ребра. Их минимальная степень, как и у всех Аг-связных графов, больше
или равна А:, а согласно фундаментальному результату Халина (1969) их
минимальная степень в точности равна А:. Существование вершины малой степени

Примечания
83
в Aj-связном графе может быть особенно полезно в индуктивных доказательствах.
Теорема Халина была отправной точкой для ряда все более и более
усложненных исследований минимальных /с-связных графов; см. вышеупомянутые книги
Боллобаша и Халина и в особенности обзор Мадера.
Первое доказательство теоремы Менгера дается по: Bohrne Т., Goring F.,
Harant J. (рукопись 1999 года); второе — по: Рут J. S. A proof of Menger's
theorem // Monatsh. Math. 1969. 73. P. 81-88; третье—no: Grunwald Т. (позже
Т. Gallai). Ein neuer Beweis eines Mengerschen Satzes // J. London Math. Soc.
1938. 13. P. 188-192. Глобальный вариант теоремы Менгера (теорема 3.3.5)
впервые был сформулирован и доказан Уитни (1932).
Теорема Мадера 3.4.1 взята из: Mader W. Uber die Maximalzahl kreuzungs-
freier Я-Wege // Arch. Math. 1978. 31. P. 387-402. Эта теорема может
быть рассмотрена как совместное обобщение теоремы Менгера и теоремы Татта
об 1-факторе (упражнение 19). Теорема 3.5.1 была независимо доказана Нэш-
Уильямсом и Таттом; обе работы содержатся в J. London Math. Soc. 1961. 36.
Теорема 3.5.4 была доказана в: Nash-Williams С. St. J. A. Decompositions of finite
graphs into forests // J. London Math. Soc. 1964. 39. P. 12. Приведенные здесь
доказательства принадлежат Мадеру (частные сообщения). Оба результата
могут быть изящно сформулированы и доказаны в терминах матроидов; см. § 18 в:
В о Hob as В. Combinatorics. Cambridge: Univ. Press, 1986.
В разделе 8.1 мы докажем, что для обеспечения существования в графе G
топологического минора Кг не обязательно требовать, чтобы средняя степень G
(А
была столь велика, как h(r) = 2 w (значение, использованное в
доказательстве теоремы 3.6.1); в действительности требуемая средняя степень может быть
ограничена сверху функцией, квадратичной по г (теорема 8.1.1). Упомянутое
усиление теоремы 3.6.2 доказано в: Bollobds В., Thomason A. G. Highly linked
graphs // Combinatorica. 1996. 16. P. 313-320. В работе: Robertson N.,
Seymour P. D. Graph Minors. XIII: The disjoint paths problem // J. Combin. Theory.
Ser. В 4995. 63. P. 65-110 — показано, что для каждого заданного к
существует алгоритм сложности О (п3), устанавливающий, является ли данный граф
порядка п /г-сцепленным. Если же к рассматривается как часть входных данных,
задача становится NP-трудной.

Глава 4
Планарные графы
Когда мы рисуем граф на листе бумаги, то, конечно, стараемся
сделать его как можно более обозримым. Одним из очевидных
способов добиться уменьшения хаоса, создаваемого множеством линий,
является попытка избежать их пересечения. В частности, естествен
вопрос о возможности нарисовать граф так, чтобы никакие два
ребра не пересекались нигде, кроме как в их общей концевой вершине.
Графы, нарисованные подобным образом, называются плоскими
графами] абстрактные же графы, которые могут быть так
нарисованы, называются плаиарными. В этой главе мы изучаем как
плоские, так и планарные графы, а также связи между ними, т. е.
вопрос о том, как абстрактный граф может быть изображен
принципиально разными способами. Предварительно накопив в разделе 4.1
ряд основных топологических фактов, которые в дальнейшем
позволят нам доказывать результаты строго, не слишком заботясь при
этом о технических тонкостях, мы приступаем в разделе 4.2 к
изучению структурных свойств плоских графов. В разделе 4.3 мы
рассматриваем вопрос о том, как сильно могут различаться два
изображения одного и того же графа. Основной результат этого раздела
состоит в том, что 3-связные планарные графы имеют, по существу,
единственное изображение в некотором весьма сильном и
естественном топологическом смысле. Два следующих раздела посвящены
доказательству всех классических критериев планарности, т. е.
условий, при которых абстрактный граф является план арным. Глава
завершается разделом о плоской двойственности — понятии,
имеющем интереснейшие связи с алгебраическими, раскрасочными и
потоковыми свойствами графов (разделы 1.9 и 6.5).
Традиционный способ изображения графа состоит в том, что его
вершины представляются точками на евклидовой плоскости, а
ребра — соединяющими их жордановыми кривыми, причем различные
кривые пересекаются только в своих концевых точках. Во
избежание ненужных топологических осложнений мы, однако, будем
рассматривать только кривые, являющиеся ломаными. Нетрудно
показать, что любое изображение можно привести к такому виду, так
что эти два понятия фактически совпадают.

4.1. Топологические предпосылки
85
4.1. Топологические предпосылки
В этом разделе мы вкратце рассмотрим некоторые
топологические определения и факты, используемые в дальнейшем. Все эти
факты имеют (к настоящему времени) простые и хорошо известные
доказательства; ссылки можно найти в примечаниях к этой главе.
Так как доказательства не касаются теории графов, мы не будем их
приводить; наша цель — лишь собрать требуемые топологические
факты, a we доказать их. В дальнейшем все доказательства будут
строго следовать из определений и сформулированных здесь фактов
(и будут направляться геометрической интуицией, но не
основываться на ней), поэтому представленный далее материал поможет
свести топологические рассуждения в этих доказательствах к
минимуму.
Отрезок прямой на евклидовой плоскости есть подмножество
в Е2 вида {р -f X(q — р) | 0 < А < 1}, где точки р, q £ Е2 различны.
Многоугольник есть подмножество в Е2, являющееся объединением
конечного числа отрезков прямой и гомеоморфное единичной
окружности. Здесь и далее предполагается, что подпространство
топологического пространства несет топологию подпространства. Дуга
многоугольника есть подмножество в Е2, являющееся объединением
конечного числа отрезков прямой и гомеоморфное замкнутому
единичному интервалу [0,1]. Образы 0 и 1 при таком гомеоморфизме
называются концами этой дуги многогранника, которые она
соединяет и которыми она ограничена. Вместо «дуга многогранника»
мы будем говорить просто дуга. Если Р есть дуга между х и у, мы
обозначаем множество точек Р \ {х,у} — внутренность дуги Р —
о
через Р.
Пусть ОСЕ2 — открытое множество. Связанность дугой,
лежащей в О, задает отношение эквивалентности на О.
Соответствующие классы эквивалентности также открыты; они суть области
множества О. Говорят, что замкнутое множество X С Е2
разделяет О, если 0\Х содержит более одной области. Границей
множества ХСШ2 называется множество Y всех таких точек у ЕЖ2, что
любая окрестность точки у пересекает и X, и Е2 \ X. Заметим, что
если X открыто, то его граница лежит в Е2 \ X.
Граница области О в Е2 \ X, где X — конечное объединение
точек и дуг, обладает двумя важными свойствами. Первое —
достижимость: если х £ X лежит на границе О, то ж можно соединить
с некоторой точкой из О отрезком прямой, внутренние вершины
которого целиком лежат внутри О. Как следствие, любые две точки на
границе О можно соединить дугой, внутренние точки которой лежат
внутри О (почему?). Другое существенное свойство границы
области О состоит в том, что она отделяет О от остальной части Е2.
В самом деле, если ф: [0,1] —► Р С Е2 непрерывно, причем ф(0) £ О

86
Глава 4. Планарные графы
и ф(1) (£ О, то Р пересекает границу области О по крайней мере
в точке ф(у) вида у := inf{x | ф(х) £ О} — первой точке из Р
в!2\0.
Теорема 4.1.1 (теорема Жордана о кривой для
многоугольников). Для любого многоугольника Р С Ж2 множество Ж2\Р состоит
из двух областей, причем в точности одна из них ограничена.
Границей каждой их этих двух областей является многоугольник Р.
С помощью теоремы 4.1.1 нетрудно доказать следующую лемму.
Лемма 4.1.2. Пусть три дуги Р\, Р2, Рг имеют одинаковые
концы и попарно не имеют других общих точек.
(i) Ж2 \ (Pi U Р2 U Рз) состоит из трех областей, границами
которых являются Pi U Рг, Р2 U Рз и Р\ U Рз.
о о
(ii) Если дуга Р соединяет точку из Р\ с точкой из Рз, а ее
внутренность лежит в области множества Ж2 \ (Р\ U Рз),
О 0 0
содержащей Р2, то Р П Р2 ф 0.
Рис. 4..1.1. Дуги в лемме 4.1.2(ii)
Следующая наша лемма дополняет теорему Жордана о кривой
утверждением, что дуга не разделяет плоскость. Для удобства
использования в дальнейшем мы сформулируем этот факт более общо.
Лемма 4.1.3. Пусть непересекающиеся множества Xi, Х2 С Ж2
являются объединениями конечного числа точек и дуг, а внутрен-
0
ность Р дуги Р, соединяющей точку из Х\ с точкой из Хч, лежит
о
в области О множества Ж2\(Х\ UХ2). Тогда 0\Р является областью
множества Ж2 \ (Хг U Р U Х2).
Рис. J^.1.2. Дуга Р не разделяет область О множества Ж2 \ (Х\ U Хг)

4.2. Плоские графы
87
Остается ввести несколько терминов и фактов, которые будут
использоваться только однажды, при рассмотрении понятий
эквивалентности изображений графов в разделе 4.3.
Как обычно, мы обозначаем через Sn сферу размерности п —
множество точек в En+1 на расстоянии 1 от начала координат.
2-Сфера без своего «северного полюса» (0,0,1) гомеоморфна
плоскости; выберем фиксированный гомеоморфизм тг: S2\ {(0, 0,1)} —>Ж2
такого вида (например, стереографическую проекцию). Если Р С
Ж2 — многоугольник, а О — ограниченная область в Ж2 \ Р, то
назовем С := 7Г_1(Р) окружностью на S2, а множества 7Г_1(0)
и S2 \ 7Г_1(Р U О) — областями С.
Наш последний инструмент — теорема Жордана и Шенфлайеса,
опять-таки слегка видоизмененная для наших целей.
Теорема 4.1.4. Пусть ф: С\ —► Съ — гомеоморфизм между
двумя окружностями на S2, и пусть 0\ — область С\, а О2 — об-
ласть Съ- Тогда отображение ф можно продолжить до
гомеоморфизма Ci U Oi -»с2 и о2.
4.2. Плоские графы
Плоский граф есть пара (V, Е) конечных множеств со
следующими свойствами (элементы множества V опять называются
вершинами, а множества Е — ребрами):
(i) V С Ж2]
(ii) каждое ребро является дугой между двумя вершинами;
(iii) разные ребра имеют разные множества концевых точек;
(iv) внутренность ребра не содержит ни вершин, ни точек
никакого другого ребра.
Плоский граф (V, Е) естественным образом задает граф G на V.
Пока не возникает разночтений, мы употребляем обозначение G этого
абстрактного графа также применительно к плоскому графу (V, Е)
и к множеству вершин V U ([)Е)\ аналогичные договоренности
действуют для сопоставления абстрактных и плоских ребер, подграфов
и так далее1).
Для любого графа G множество Ж2 \ G открыто; его области
называются гранями графа G. Поскольку G ограничен, т. е. лежит
внутри достаточно большого диска D, в точности одна из его граней
не ограничена — та, которая содержит Ж2\И. Эта грань называется
внешней гранью графа G; остальные суть его внутренние грани.
' Однако мы и далее будем обозначать символом \ разность точечных
множеств и символом — разность графов, что поможет различать их.

88
Глава 4. План арные графы
Множество граней в G обозначается через F(G). Заметим, что если
Я С G, то каждая грань графа G содержится в грани графа Н.
Чтобы заложить основы для (легкого, но) строгого введения
в плоские графы, обещанного в данном разделе, еще раз спустимся
в царство действительно элементарной топологии плоскости и
докажем то, что кажется и без того очевидным2); граница грани плоского
графа G всегда является подграфом в G, а не, скажем, половиной
ребра. Следующая лемма утверждает это формально и указывает
на два кажущихся «очевидными» свойства плоских графов.
Лемма 4.2.1. Пусть G — плоский граф, а е — ребро в G.
(i) Если X является границей грани в G, то либо еСХ, либо.
ХО°е = 0.
(ii) Если е лежит на цикле С С G, то е лежит на границе в
точности двух граней из G, и эти грани содержатся в разных
гранях цикла С.
(Ш) Если е не лежит на цикле, то е лежит на границе в точности
одной грани графа G.
Доказательство. Мы доказываем все три утверждения
вместе. Начнем с рассмотрения одной точки xq £ е. Покажем, что xq
лежит на границе в точности двух или одной грани в зависимости
от того, лежит ли е на цикле в G или нет. Далее мы покажем, что
о
всякая другая точка из е лежит на границе тех и только тех граней,
что и хо. Тогда концы ребра е будут также лежать на границе
этих граней, просто потому что любая окрестность концевой точки
ребра е является также и окрестностью некоторой внутренней точки
ребра е.
Граф G является объединением конечного числа отрезков;
можно считать, что любые два из них пересекаются не более чем в одной
о
точке. Около любой точки х £ е можно найти открытый диск Dx
с центром х, пересекающийся только с этими (одним или двумя)
отрезками, содержащими х.
Выберем внутреннюю точку xq отрезка S С е. Тогда DXQ C\G =
DXQ П S, поэтому DXQ \ G является объединением двух открытых
полудисков. Поскольку эти полудиски не пересекаются с G, каждый
из них лежит в некоторой грани графа G. Обозначим эти грани
через /i и /2; они — единственные грани в G, на границе которых
лежит xq, и они могут совпадать (рис. 4.2.1).
) Заметим, что даже самая лучшая интуиция может лишь иногда быть
«точной», т.е. совпадать с тем, что следует из точных определений, в той мере,
в какой эти определения действительно формализуют то, что интуитивно
подразумевалось. Ввиду сложности определений в элементарной топологии
это вряд ли можно считать не требующим доказательства.

4.2. Плоские графы
89
Рис. Ji.%.1. Грани /i, /2 графа G в доказательстве леммы 4.2.1
Если е лежит на цикле С С G, то DXo пересекает обе грани этого
цикла (теорема 4.1.1). Грани Д, Д графа G поэтому содержатся
в разных гранях цикла С; поскольку С С G, любая грань графа G
является подмножеством грани цикла С и, в частности, Д ф Д.
Если е не лежит на цикле, то е является мостом, а значит, связывает
два непересекающихся точечных множества Х\, Х2, где Х\ U Х^ —
G \ е. Ясно, что /i U е U /2 есть подмножество грани / из G — е
(почему?). По лемме 4.1.3 /\е является гранью в G. Но/\е содержит
Д и /2 по определению /, поэтому Д = / \ е = /2, так как и Д, и Д,
и / суть грани в G.
Рассмотрим теперь любую другую точку х\ £ е. Пусть дуга Р
из жо в а?! содержится в е. Поскольку множество Р компактно,
некоторое конечное множество дисков Dx с х £ Р покрывают Р.
Занумеруем их как Do,..., Dn в порядке следования их центров вдоль Р.
Добавляя по необходимости DXo или DXl, можно считать, что Do = DXo
и Dn = DXl. Индукцией по п легко доказать, что любую точку
у £ Dn\e можно соединить ломаной, содержащейся в (DoU- • -UD„)\e,
с некоторой точкой z £ Do \ е (рис. 4.2.2); тогда у и z эквивалентны
в 12\G. Значит, любая точка из Dn \ е лежит в Д или в Д, так
что х\ не может лежать на границе никакой другой грани графа G.
Поскольку оба полудиска из Do \ е можно соединить с Dn\e таким
образом (поменяв ролями Do и Dn), мы получаем, что х\ лежит на
границе как Д, так и Д. □
Рис. J^.2.2. Дуга из у в Dq вблизи Р
Следствие 4.2.2. Граница грани всегда есть множество точек
некоторого подграфа. D
Говорят, что подграф графа G, множество точек которого
является границей грани /, ограничивает /, и называют его границей
этой грани; мы обозначаем его через G[f]. Говорят, что грань
инцидентна вершинам и граням своей границы. Заметим, что если
Я С G, то любая грань / из G содержится в некоторой грани f
из Я. Если G[f] С Я, то / = f (почему?); в частности, / — всегда
грань своей собственной границы G[f]. Эти основные факты будут
часто использоваться в последующих доказательствах.

90
Глава 4. Планарные графы
Предложение 4.2.3. Плоский лес имеет в точности одну грань.
Доказательство. Воспользуемся индукцией по числу ребер
и леммой 4.1.3. □
За единственным исключением границы различных граней
плоского графа различны.
Лемма 4.2.4. Если в плоском графе границы разных граней
совпадают, то этот граф есть цикл.
Доказательство. Пусть G — плоский граф, и пусть Я С G
является границей различных граней Д, /г в G. Поскольку Д и Д
являются также и гранями в Я, предложение 4.2.3 влечет, что Я
содержит цикл С. По лемме 4.2.1(ii) Д и /2 содержатся в разных
гранях цикла С. Поскольку границей и /i, и /2 является целиком Я,
то имеем Я — С: любые другие вершина или ребро из Я лежали бы
в одной из граней цикла С, а значит, не на границе другой из них.
Таким образом, Д и /2 суть разные грани цикла С. Но С имеет
лишь две грани, следовательно, Д U Си /2 = Ж2, а значит, G — С. □
Предложение 4.2.5. В 2-связном плоском графе любая грань
ограничена циклом.
Доказательство. Пусть / — грань 2-связного плоского
графа G. Покажем индукцией по |G|, что G[f] является циклом. Если
сам G — цикл, это следует из теоремы 4.1.1, поэтому допустим, что
G не есть цикл.
По предложению 3.1.2 существуют 2-связный плоский граф
Я С G и такой плоский Я-путь Р, что G = Я U Р. Внутренность
пути Р лежит в грани /' из Я, которая по индукционному
предположению ограничена циклом С.
Если / — также грань из Я, то все уже доказано ввиду
индукционного предположения. В противном случае граница грани /
пересекается с Р \ Я, поэтому / С /'. Отсюда / является гранью
для С U Р, а значит, ограничена циклом (лемма 4.1.2(1)). D
Плоский граф G называется максимально плоским или просто
максимальным, если к нему невозможно добавить ни одного нового
ребра так, чтобы получился плоский граф G'DGc V(G') — V(G).
Граф G называется плоской триангуляцией, если каждая из граней
в G (включая внешнюю грань) ограничена треугольником.
Предложение 4.2.6. Плоский граф порядка не менее 3
является максимально плоским^ если и только если он есть плоская
триангуляция.
Доказательство Пусть плоский граф G имеет порядок не
менее 3. Легко видеть, что если каждая его грань ограничена
треугольником, то G максимально плоский. В самом деле, любое добавочное
ребро е лежало бы своей внутренностью в некоторой грани графа G,

4.2. Плоские графы
91
а своими концами на границе этой грани. Следовательно, эти концы
уже смежны в G, так что G U е противоречит условию (iii) в
определении плоского графа.
Обратно, допустим что G является максимально плоским, а
/ £ F(G) — грань; положим Н := G[f]. Поскольку G максимален
как плоский граф, то G[H] является полным: любые две вершины
из Я, которые не смежны в G, могли бы быть соединены дугой
через / с получением из G большего плоского графа. Таким образом,
G[H] — Кп для некоторого п, но мы пока не знаем, какие ребра
из G[H] лежат в Я.
Покажем сначала, что Н содержит цикл. Если не содержит,
то G\ Н ф 0, поскольку G Э Кп при п > 3 и \G\ > 3 в противном
случае. С другой стороны, мы знаем, что /U# = Ж2 по предложению
4.2.3, а следовательно, G — Н\ противоречие.
Поскольку Н содержит цикл, достаточно показать, что п < 3.
Тогда Н — К3, что и утверждается. Предположим, что п > 4,
и пусть цикл С — viV2V^va^\ лежит в G[H] (= Кп). Так как С С G,
грань / содержится в грани /с цикла С; пусть f'c — другая грань
для С'. Поскольку вершины v\ и 1/3 лежат на границе грани /, их
можно соединить дугой, внутренность которой лежит в /с и
избегает G. По лемме 4.1.2(ii) плоское ребро 1/2U4 в G[H] проходит
через fc, а не через /с (рис. 4.2.3). Аналогично, поскольку v2,v^ Е
G[f], ребро vi 1/3 проходит через f'c. Но ребра v\v^ и и2и4 не
пересекаются, что противоречит лемме 4.1.2(ii). □
Рис. J^.2.3. Ребро г>2г>4 графа G проходит через грань j'c
Следующий классический результат Эйлера (1752),
формулируемый здесь в простейшем виде для плоскости, является одним
из общих источников зарождения как теории графов, так и
топологии. Эта теорема связывает числа вершин, ребер и граней плоского
графа; сумма таких чисел с подходящими знаками всегда равна 2.
В общем виде теорема Эйлера утверждает то же самое для графов,
соответствующим образом вложенных и в другие поверхности:
получаемая сумма всегда есть число, зависящее только от
поверхности, а не от графа, и это число меняется от одной (ориентируемой
замкнутой) поверхности к другой. Таким образом, любые две
такие поверхности можно различить посредством простого арифмети-

92
Глава 4. Планарные графы
ческого инварианта вложенного в них графа3)!
Теперь докажем теорему Эйлера в ее простейшем виде.
Теорема 4.2.7 (формула Эйлера). Пусть G — связный
плоский граф с п вершинами, m ребрами и £ гранями. Тогда
п- т + £ = 2.
Доказательство. Зафиксируем п и воспользуемся индукцией
по т. При т < п— 1 граф G является деревом, а т — п—\ (почему?),
так что утверждение следует из предложения 4.2.3.
Пусть теперь т > п. Тогда в G есть ребро е, лежащее на цикле;
пусть G' \— G — е. По лемме 4.2.1 (ii) е лежит на границе в точности
двух граней Д, /2 графа G; положим /i^ :=/iUeU/2. Мы докажем
равенство
F(G)\{fuf2} = F(G')\{flt2}, (*)
не предполагая, что /i^ £ F(G'). Однако поскольку е должно
лежать в некоторой грани графа G' и эта грань не может быть гранью
графа G, то ввиду (*) этой гранью может быть только Д^. Снова
ввиду (*) в графе G' граней на одну меньше, чем в G. Так как в G'
и ребер на одно меньше, чем в G, утверждение следует из
индукционного предположения для G'.
Для доказательства (*) сначала рассмотрим любую / £ F{G) \
{/ь /г}- По лемме 4.2.l(i) имеем G[f] С Ge = G1. Поэтому /
является также гранью в G' (но, очевидно, отличной от /1,2), а значит,
лежитв^(С/)\{Л12}.
Обратно, пусть задана грань /; ф f\t2 в G'. Поскольку е лежит
на границе /i и /г, любые две точки из /^2 можно соединить дугой
в Е2\ G7, поэтому /1,2 лежит внутри грани /{2 графа G'. Из нашего
предположения /; ф /lj2 теперь следует, что /; С /1>2 (так как иначе
/' С /1,2 С /{ 2, и поэтому /; = /1>2 = f[i2)- Пусть точка х находится
в /; \ /i|2, тогда х лежит в некоторой грани / ф /i, /2 графа G. Как
показано выше, / — также грань в G''. Следовательно, х £ / П /'
влечет / = /;, т. е. /; £ F(G)\{/i, /2}, что и требовалось доказать. □
Следствие 4.2.8. Плоский граф с п > 3 вершинами имеет не
более Зп — б ребер. Плоская триангуляция с п вершинами имеет
Зп — б ребер.
Доказательство. Ввиду предложения 4.2.6 достаточно
доказать второе утверждение. В плоской триангуляции G граница любой
грани содержит в точности три ребра, а каждое ребро лежит в
границе в точности двух граней (лемма 4.2.1). Двудольный граф на
3) Эта фундаментальная связь между графами и поверхностями лежит в
основе доказательства знаменитой теоремы Робертсона и Сеймура — теореме
о минорах графов; см. раздел 12.5.

4.2. Плоские графы
93
E(G)UF(G) с множеством ребер {е/ | е С G[f]} имеет поэтому в
точности 2|#(G)| = 3|F(G)| ребер. Согласно этому тождеству мы
можем заменить £ на 2т/3 в формуле Эйлера и получить т = Зп — б. □
Формула Эйлера может быть полезна при доказательстве того,
что граф не планарен. Граф К5, например, имеет 10 > 3-5 — б ребер,
т. е. больше, чем допускается следствием 4.2.8. Аналогично, Кз,з
не может быть плоским графом. Иначе, поскольку Кз,з 2-связен и не
содержит треугольников, любая грань плоского графа Кз,з была бы
ограничена циклом длины не менее 4 (предложение 4.2.5). Как в
доказательстве следствия 4.2.8, это влечет 2т > 4£, что дает т < 2п—А
при подстановке в формулу Эйлера. Но в Кз,з имеется 9 > 2 • б — 4
ребер.
Очевидно, что наряду с самими Къ и Кз,з их подразделения
также не могут быть плоскими графами.
Следствие 4.2.9. Плоский граф не содержит в качестве
топологического минора ни Къ, ни Кз,з- П
Удивительно, что это простое свойство плоских графов,
оказывается, выделяет их среди всех остальных графов. Как будет
показано в разделе 4.4, произвольный граф можно нарисовать на
плоскости, если и только если в нем нет (топологических) миноров Къ и Хз,з-
Как мы видели, граница каждой грани в 2-связном графе есть
цикл. В 3-связном графе эти циклы можно охарактеризовать
комбинаторно.
Предложение 4.2.10. Границами граней 3-связного плоского
графа являются его неразделяющие индуцированные циклы, и
только они.
Доказательство. Пусть плоский граф G 3-связен, а С С G —
цикл. Если С — неразделяющий индуцированный цикл, то по
теореме Жордана о кривой две его грани не могут обе содержать точку
из G\C. Поэтому он ограничивает грань графа G.
Обратно, предположим, С ограничивает грань /. По
предложению 4.2.5 С — цикл. Если С имеет хорду е = ху, то компоненты
множества С — {х,у} соединены С-путями в G, так как G 3-связен.
И этот путь, и е проходят через другую грань цикла С (не /), но не
пересекаются; противоречие с леммой 4.1.2(ii).
Остается показать, что С не разделяет никаких двух вершин
х,у £ G — С. По теореме Менгера (3.3.5) х и у соединены в G тремя
независимыми путями. Ясно, что / лежит внутри некоторой грани
их объединения, и по лемме 4.1.2(1) эта грань ограничена только
двумя из этих путей. Поэтому третья избегает / и его границу С. □

94
Глава 4. Планарные графы
4.3. Изображения
Вложением в плоскость или планарным вложением
(абстрактного) графа G называется изоморфизм между G и плоским графом G.
Последний будет называться изображением графа G. Мы не всегда
будем различать в обозначениях вершины и ребра графов G и G.
В этом разделе мы исследуем вопрос, как сильно могут
различаться планарные вложения графа. Чтобы он имел смысл, мы
должны прежде договориться о том, когда два вложения следует
считать одинаковыми. Например, если мы подвергаем вложение
простому вращению вместе с плоскостью, то полученное вложение вряд
ли можно считать существенно иным способом изображения этого
графа.
Для подготовки почвы сначала рассмотрим три возможных
понятия эквивалентности плоских графов (уточняющие абстрактный
изоморфизм) и посмотрим, как они связаны. Пусть G — (V, Е) и G' —
{V',E') — два плоских графа с множествами граней F(G) —\ F
и F(G') =.; F1. Допустим, что G и G' изоморфны как абстрактные
графы, и пусть а\ V —» V — изоморфизм. Полагая ху »—► а(х)а(у),
мы можем естественным образом расширить а до биекции V U Е —>
V U Е', отображающей V в V, а Е в Е' и сохраняющей
инцидентность (и неинцидентность) между вершинами и ребрами.
Наше первое понятие эквивалентности между плоскими
графами, возможно, самое естественное. Интуитивно, мы хотели бы
назвать изоморфизм а «топологическим», если он индуцируется
гомеоморфизмом плоскости Ж2 на себя. Чтобы избежать
предоставления особого статуса внешним граням, мы делаем обходной
маневр через гомеоморфизм 7г: S2 \ {(0,0,1)} —+ Ж2, введенный в
разделе 4.1; назовем а топологическим изоморфизмом между плоскими
графами G и G7, если существует такой гомеоморфизм ф: S2 —> 52,
что ф := 7Г о ф о 7Г-1 индуцирует а на V U Е. (Более строго, мы
требуем, чтобы ф был согласован с а на V и чтобы он отображал
каждое плоское ребро е £ G на плоское ребро а(е) £ G1. Если
только ф не фиксирует точку (0, 0,1), отображение ф будет не
определено в 7г(0_1(О, 0, 1)).)
Рис. 4-3.1. Два изображения графа,
не являющиеся топологически изоморфными (почему?)

4.3. Изображения
95
Можно показать, что с точностью до топологического
изоморфизма внешние и внутренние грани больше и в самом деле не
различаются: если'мы выберем в качестве ф вращение сферы S2,
отображающее 7г_1-образ точки некоторой внутренней грани из G в
северный полюс (0, 0,1) в S2, то ф будет отображать остальную часть
этой грани во внешнюю грань в ip(G). (Однако чтобы ребра в ^(G)
были по-прежнему ломаными, требуется немного подправить ф.)
Если сг, как и выше, топологический изоморфизм, то за
исключением, быть может, пары точек, где ф или ф~1 не определено, ф
отображает грани графа G на грани графа G' (доказательство?). Так,
а естественным образом продолжается до биекции сг, т. е. VUEUF —>
V U Е' U F', сохраняющей инцидентность вершин, ребер и граней.
Выделим это последнее свойство топологического изоморфизма
как определяющее для второго понятия эквивалентности плоских
графов и назовем изоморфизм а между абстрактными графами G
и G' комбинаторным изоморфизмом плоских графов G и G', если
его можно продолжить до биекции а: V U Е U F —» V U Е' U F',
сохраняющей не только инцидентность между вершинами и ребрами,
но и инцидентность вершин и ребер с гранями. (Формально мы
требуем, чтобы вершина или ребро х £ G лежали на границе грани
/ £ F, если и только если а(х) лежит на границе грани сг(/).)
G'
Рис. 4-3.2. Два изображения графа,
изоморфные комбинаторно, но не топологически (почему?)
Если а является комбинаторным изоморфизмом плоских графов
G и G7, то он отображает границы граней из G на такие же в G'.
Возьмем это свойство за основу нашего третьего определения
эквивалентности плоских графов и назовем изоморфизм а абстрактных
графов G и G' теоретико-графовым изоморфизмом плоских графов
G и G7, если
{a(G[f}) : / € F} = {G'[f] : f G F'}.
Таким образом, мы больше не следим за тем, какая грань
ограничена данным подграфом; единственное, что мы принимаем во
внимание, — это ограничивает подграф некоторую грань или нет, и мы
требуем, чтобы а отображало ограничивающие грань подграфы
друг в друга. На первый взгляд это третье понятие
эквивалентности может показаться немного менее естественным, чем
предыдущие два. Однако практическое преимущество его в том, что оно

96
Глава 4. Планарные графы
формально слабее, а потому легче проверяемо, и к тому же оно
в большинстве случаев оказывается эквивалентным двум другим
понятиям.
Как мы уже видели, каждый топологический изоморфизм между
двумя графами является также и комбинаторным, а каждый
комбинаторный является также и теоретико-графовым. Следующая
теорема показывает, что для большинства графов обратное также верно.
Теорема 4.3.1.
(i) Каждый теоретико-графовый изоморфизм между двумя
плоскими графами является также и комбинаторным. Он
однозначно продолжается до биекции граней, если и только
если граф не является циклом.
(ii) Каждый комбинаторный изоморфизм между двумя 2-связ-
ными плоскими графами является также и топологическим.
Доказательство. Пусть G = (V,E) и G' - (V',E') — два
плоских графа. Положим F(G) =: F и F(G') = : F'', и пусть a: V U
Е —> V' U Е' является изоморфизмом между соответствующими
абстрактными графами.
(i) Если G — цикл, то утверждение следует из теоремы о жор-
дановой кривой. Предположим теперь, что G не является циклом.
Пусть Ж и Ж' — множества границ граней в G и G'
соответственно. Если а есть теоретико-графовый изоморфизм, то
отображение Н »—► (т{Н) есть биекция между Ж и Ж1. По лемме 4.2.4
отображение / »—► G[f] является биекцией между F и Ж, и то же
верно для F1 и Ж'. Композиция этих трех биекций является
биекцией между F и F', и ее мы выбираем в качестве a: F —» F'. По
построению, это продолжение отображения а на V U Е U F
сохраняет инцидентность (и является единственным с этим свойством),
поэтому а действительно является комбинаторным изоморфизмом.
(ii) Допустим, что G 2-связен и что а есть комбинаторный
изоморфизм. Мы должны построить гомеоморфизм ф: S2 —> 52,
который для любых вершины или плоского ребра х £ G отображает
7г_1(ж) в тг~1(а(х)). Поскольку а является комбинаторным
изоморфизмом, а : 7Г-1 о сг о 7Г есть сохраняющая инцидентность биекция
вершин, ребер и граней4) из G := 7r_1(G) в вершины, ребра и грани
графа G1 ^tt-^G7).
) Под «вершинами, ребрами и гранями» графов G и G' мы подразумеваем
образы при 7г-1 вершин, ребер и граней графов G иС (плюс (0,0,1) в
случае внешней грани). Будем обозначать эти множества через V(G), E(G),
F(G) и V(G'), E(G')} F(G'), а инцидентность определять по наследству из
Си G'.

4.3. Изображения
97
S2DG —?—> G' С S2
"I I-
12DG ► G" с m2
a
Puc. 4-3.3. Определением через a
Построим ф в три этапа. Сначала зададим ф на множестве
вершин графа G, полагая ф(х) := <т(ж) для всех х £ V"(G). Очевидно,
что это гомеоморфизм между V(G) и V{G').
На втором этапе продолжим ф до гомеоморфизма между G и G',
который индуцирует <т на V(G) U E(G). Мы можем это делать,
перебирая ребра одно за другим, следующим образом. Каждое ребро ху
в G гомеоморфно ребру сг(ху) — ф(х)ф(у) из G' посредством
гомеоморфизма, переводящего х в ф(х), а у в 0(у). Тогда объединение всех
этих гомеоморфизмов, по одному для каждого^ребра из G,
действительно является гомеоморфизмом между G и G' — искомым
продолжением отображения ф на G. Всё, что мы должны проверить — это
непрерывность в вершинах (где реберные гомеоморфизмы
накладываются друг на друга), но это сразу следует из нашего
предположения, что оба графа, и по отдельности их ребра, несут топологию
подпространства в!3. _
На третьем этапе мы продолжаем наш гомеоморфизм ф: G —* G1
на всю сферу S2. Это можно сделать аналогично второму этапу —
грань за гранью. По предложению 4.2.5 границы всех граней в G
и в G' суть циклы. Далее, если / есть грань в G с границей G,
то сг(С) := (J{^(e) I е £ Е(С)} ограничивает грань <?(/) в G'. По
теореме 4.1.4 мы можем продолжить уже построенный гомеоморфизм
ф\ С —> 5(G) до гомеоморфизма из С U / в 5(G) U ?(/). Наконец,
берем объединение всех этих гомеоморфизмов, по одному для каждой
грани / из G, в качестве искомого гомеоморфизма ф: S2 —> S2. Как
и раньше, непрерывность проверяется без труда. D
До сих пор мы рассматривали способы сравнения плоских
графов. Перейдем теперь к нашей истинной цели — определению
эквивалентности для вложений графов. Назовем два план арных
вложения o"i, fi2 графа G топологически (соответственно комбинаторно)
эквивалентными, если сг2 о crj"1 является топологическим
(соответственно комбинаторным) изоморфизмом между v\{G) и cr2(G).
Если G 2-связен, то эти два определения совпадают по теореме 4.3.1,
и мы говорим просдго об эквивалентных вложениях. Ясно, что это
действительно отношение эквивалентности на множестве всех пла-
нарных вложений любого заданного графа.
Отметим, что два изображения графа G, получающиеся из
неэквивалентных вложений, вполне могут оказаться топологически эк-

98
Глава 4. Планарные графы
Бивалентными (упражнение): для эквивалентности двух вложений
мы не только требуем, чтобы существовал некоторый изоморфизм
(топологический или комбинаторный) между их образами, но чтобы
канонический изоморфизм сг2 о сг^1 был соответственно
топологическим или комбинаторным.
Даже в этом сильном смысле 3-связные графы имеют
единственное вложение с точностью до эквивалентности.
Теорема 4.3.2. (Уитни, 1932). Любые два планарных
вложения 3-связного графа эквивалентны.
Доказательство. Пусть G — 3-связный граф с планарными
вложениями (Т\: G —+ G\ и &2 '• G —» G^- По теореме 4.3.1 достаточно
показать, что &2 оа^1 является теоретико-графовым изоморфизмом,
т. е. что (Т\{С) ограничивает грань в Gi, если и только если (Тп(С)
ограничивает грань в G2 для любого подграфа С С G. Это сразу
следует из предложения 4.2.10. □
4.4. Планарные графы. Теорема Куратовского
Граф называется планарным, если его можно вложить в
плоскость, т. е. если он изоморфен плоскому графу. Планарный граф
максимален или максимально планарен, если он планарен, но не
может быть расширен до большего планарного графа добавлением
ребра (но не вершины).
Ясно, что изображения максимальных планарных графов суть
максимально плоские графы. Обратное утверждение, однако, не
очевидно: когда мы начинаем рисовать планарный граф, не может ли
случиться, что мы застрянем на полпути на собственном подграфе,
который уже является максимально плоским? Наше первое
предложение утверждает, что этого никогда не может случиться, т. е.
плоский граф никогда не является максимально плоским лишь
потому, что он плохо нарисован.
Предложение 4.4.1.
(i) Каждый максимально плоский граф максимально планарен.
(ii) Планарный граф с п > 3 вершинами максимально планарен,
если и только если в нем в точности Зп — б ребер.
Доказательство. Применяем предложение 4.2.6 и следствие
4.2.8. □
Какие графы являются планарными? Как мы видели в
следствии 4.2.9, никакой планарный граф не содержат ни Къ, ни Кз,з
в качестве топологического минора. Наша цель в этом разделе
состоит в том, чтобы доказать удивительное обратное утверждение —
классическую теорему Куратовского: любой граф без
топологического минора Къ или Хз,з планарен.

4.4. Планарные графы. Теорема Куратовского
99
Прежде чем доказывать теорему Куратовского, заметим, что
достаточно рассматривать обычные миноры, а не топологические.
Предложение 4А.2. Граф содержит Къ или Кз,з как минор,
если и только если он содержит Къ или Кз,з как топологический
минор.
Доказательство. По предложению 1.7.2 достаточно показать,
что каждый граф G с минором Къ содержит или Къ как
топологический минор, или Кз,з как минор. Так что предположим, что G £= Къ,
и пусть К С G минимален с условием К — МКЪ. Тогда каждая
ветвь в К индуцирует дерево в К и между любыми двумя ветвями
в К имеется в точности одно ребро. Если взять дерево,
индуцированное ветвью Vx, и добавить к нему четыре ребра, соединяющие
его с остальными ветвями, то получится дерево, скажем, Тх. Ввиду
минимальности К в Тх имеется в точности четыре листа, четыре
соседа ветви Vx в других ветвях (рис. 4.4.1).
Рис. 4-4-1- Каждый МКЬ содержит ТКЬ или МА'з,з
Если каждое из этих пяти деревьев Тх есть ТК\^ то К есть
ТКЪ, и предложение доказано. Если одно из Тх не является TKi^,
то в нем в точности два вершины степени 3. Стягивая Vx на эти две
вершины, а каждую другую ветвь — в единственную вершину, мы
получаем граф на б вершинах, содержащий Кз,з- Таким образом,
G ^= Xз,з j что и требовалось. D
Сначала докажем теорему Куратовского для 3-связных графов.
В этом заключается суть доказательства; отсюда легко следует
общий случай.
о£ , И
Лемма 4.4.3. Каждый 3-связный граф G без миноре К иЯи
Кз,з план арен.
Доказательство. Применим индукцию по \G\. При \G\ — 4
имеем G = К4, и утверждение верно. Теперь пусть \G\ > 4, и
предположим, что утверждение верно для меньших графов. По лемме
3.2.1 в G есть такое ребро ху, что G/xy является 3-связным. Так

100
Глава 4. Планарные графы
как отношение быть минором транзитивно, в G/xy также нет
миноров К5 и Кз,з- Таким образом, по индукционному предположению
G/xy имеет плоское изображение G. Пусть / — грань в G — vxy,
содержащая точку vxy, а С — граница грани /. Пусть X := Nc(x)\{y}
и У := NG(y) \ {х}, тогда X UY С 7(C), поскольку vxy G /•
Очевидно, что
G1 :=G-{vxyv\veY\X}
можно рассматривать как изображение графа G — у, в котором
вершина х представлена точкой vxy (рис. 4.4.2). Наша цель состоит
в том, чтобы добавить к этому изображению вершину у и получить
изображение графа G.
Рис. 4>4'%- G' как изображение графа G — у\
вершина х представлена точкой vxy
Так как G 3-связен, то G — vxy 2-связен, т. е. С — цикл
(предложение 4.2.5). Пусть Ei,..., Xk — нумерация по этому циклу вершин
из X, а Р{ — Х{ .. .Ж{+1 — Х-пути по С между ними (г = 1,..., fc,
xjc+i := xi). Для каждого г множество С \ Р% содержится в одной
из двух граней цикла С{ :— хх{Р{Х{+\х\ обозначим другую грань
цикла С{ через /{. Так как /г- содержит точки из / (вблизи ж), но не
из С, имеем /г- С /. Кроме того, плоские ребра xxj при j £ {г, г + 1}
пересекаются с Сг- только в ж и заканчиваются вне /г- в С\Р{} так что
fi не пересекает ни одно из этих ребер. Следовательно, /г- С E2\G;,
поэтому fi содержится в грани графа G'. (На самом деле /,• — грань
в G', но это не существенно.)
Чтобы превратить G' в изображение графа G, попробуем найти
такое г , что Y С V{Pi)\ тогда можно будет вложить у в /{ и связать
ее с соседями дугами внутри /{. Предположим, что такого г нет.
Как тогда вершины Y могут быть распределены относительно С?
о
Если бы вершина у имела соседа в некотором Рг-, то она имела бы
его также в С — Pi, так что G содержал бы ТКз.з (с вершинами
ветвления х, у, Xi, жг-+1 и двумя соседями вершины у). Следовательно,
У С X. Теперь если \Y\ = \Y П Х\ > 3, то имеем ТКЪ в G, поэтому
\Y\ < 2. На самом же деле \Y\ = 2, поскольку d(y) > «(G) > 3. Так
как две вершины из У не лежат ни на каком общем Р;, мы опять
можем найти ТКзлз в G; противоречие. D

4.4. Планарные графы. Теорема Куратовского
101
По сравнению с другими доказательствами теоремы
Куратовского вышеупомянутое доказательство имеет ту привлекательную
особенность, что при небольшом изменении может давать
изображение, в котором каждая внутренняя грань является выпуклой
(упражнение), в частности, каждое ребро может быть нарисовано прямым.
Заметим, что 3-связность здесь существенна: 2-связный планарный
граф не обязан иметь изображения со всеми выпуклыми
внутренними гранями (пример?), хотя он всегда имеет прямолинейное
изображение (упражнение 12).
В принципе нетрудно свести общую теорему Куратовского к
3-связному случаю, комбинируя частичные изображения,
существующие по индукционному предположению. Так, если «(G) = 2 и
G = Gi U G2 с V(Gi П G2) = {х, у}, a G не содержит ТКЪ или ТК3)3
как подграф, то ни G\ -f ху, ни G2 + ху не содержат такого
подграфа, и можно попытаться составить из изображений этих графов
изображение всего G -f ху. (Если ху — уже ребро из G, то же самое
можно сделать с G\ и G2.) Для «(G) < 1 все становится даже проще.
Однако используемые при этом геометрические операции требуют
довольно громоздкого согласования, даже если все встречающиеся
плоские ребра предполагаются прямыми.
Следующий более комбинаторный способ столь же прост и
может быть подходящей альтернативой.
Лемма 4.4.4. Пусть 36 — множество 3-связных графов. Пусть
G — граф с «(G) < 2, и пусть Gi, G2 — такие собственные
индуцированные подграфы в G, что G — G\ U G2 и \G\ П G2| = «(G). Если
G реберно-максимален без топологического минора в 3£, то такими
же являются G\ и G2, a G\ П G2 = К2.
Доказательство. Заметим сначала, что каждая вершина v £
S :=: V{G\ П G2) имеет соседа в каждой компоненте Gt- — S, i — 1,2,
иначе 5\{г/} разделял бы G вопреки \S\ — «(G). Ввиду
максимальности графа G каждое ребро е, добавленное к G, лежит в ТХ CG + e,
где X G ЗС. При любом выборе рассматриваемого ниже ребра е
из-за 3-связности X все вершины ветвления этого ТХ лежат в
одном и том же G{, скажем, в G\. (Положение ребра е будет всегда
симметричным относительно G\ и G2, так что это предположение
не влечет за собой потери общности.) Тогда ТХ пересекается с G2
разве что по пути Р, соответствующему ребру из X.
Если 5 = 0, мы сразу же получаем противоречие, выбирая е
с одним концом в Gi, а другим в G2. Если S — {v} —
одноэлементное множество, то пусть е соединяет соседа v\ вершины v в G\ — S
с соседом V2 вершины v в G2 — S (рис. 4.4.3). Тогда Р содержит
как г/, так и ребро i>ii/2. Заменяя vPv\ на ребро vv\, мы получаем
ТХ в Gi С G; противоречие.

102
Глава 4. Планарные графы
Рис. 4-4-3- Если G+e содержит ТХ, то и G\ либо С?2 содержит ТХ
Итак, \S\ — 2, скажем, S — {х,у}. Если ху £ G, то положим
е := ху, и в полученном ТХ заменим е на х-у путь через Gi- Это
дает ТХ в G; противоречие. Следовательно, ху £ G и G[S] — К2,
что и требуется.
Остается показать, что G\ и Gi реберно-максимальны без
топологического минора из X. Пусть е' —дополнительное ребро,
например, для G\. Заменяя в случае необходимости хРу ребром ху,
получаем ТХ в G\ -f е' (что показывает реберную максимальность
графа Gi, которую и требовалось доказать) или в G2 (что
противоречит включению G2 С G). D
Лемма 4.4.5. Если \G\ > 4 и G реберно-максимален при
условии ТК5,ТК3>3 £G,toG 3-связея.
Доказательство. Применим индукцию по \G\. При \G\ = 4
имеем G = К4, и утверждение верно. Теперь пусть \G\ > 4, a G
реберно-максимален по свойству не содержать ТКЪ и ТКз.з-
Предположим, что «(G) < 2, и выберем Gi и G2, как в лемме 4.4.4. При
X := {К5,Кз}з} лемма утверждает, что G\ П G2 есть К2, скажем,
с вершинами х, у. По леммам 4.4.4, 4.4.3 и индукционному
предположению G\ и Gi планарны. Для каждого i — 1, 2 по отдельности
выберем изображение графа G;, грань /; с ребром ху на границе и
вершину Z{ ф х,у на границе грани /;. Пусть К есть ТКЪ или ГКз.з
в абстрактном графе G + z\z2 (рис. 4.4.4).
Рис. 44-4- ТА'5 или ТА'з.з в G + z^z2
Если все вершины ветвления из К лежат в одном и том же Gt-, то
или Gi+xzi, или Gi+yzi (или же сам G;, если z-% уже смежна с х или ?/
соответственно) содержит ТКЪ или ТКз.з- Это противоречит
следствию 4.2.9, так как эти графы планарны по выбору Z{. Поскольку
G -f Z1Z2 не содержит четырех независимых путей между (G\ — G2)

4.5. Алгебраические критерии планарности
103
и (G2 — Gi), эти подграфы не могут оба содержать вершину
ветвления из ТКЪ и не могут оба содержать двух вершин ветвления из
ТКз.з- Следовательно, К есть ТК3уз только с одной вершиной
ветвления v, допустим, в G2 — Gi. Но тогда и граф G\ -f v -f {vx, vy, vzi},
который является планарным ввиду выбора z\, содержит TK3f3. Это
противоречит следствию 4.2.9. □
Теорема 4.4.6 (Куратовский, 1930; Вагнер 1937). Следующие
утверждения для графа G эквивалентны:
(i) G план арен;
(ii) G не содержит в качестве минора ни Къ, ни K3f3]
(iii) G не содержит в качестве топологического минора ни К6,
ни K3t3.
Доказательство. Объединяем следствие 4.2.9 pi предложение
4.4.2 с леммами 4.4.3 и 4.4.5. D
Следствие 4.4.7. Каждый максимальный планарный граф с не
менее чем четыремя вершинами 3-связен.
Доказательство. Применяем лемму 4.4.5 и теорему 4.4.6. □
4.5. Алгебраические критерии планарности
В этом разделе мы показываем, что план арность может быть
охарактеризована в чисто алгебраических терминах некоторым
абстрактным свойством его пространства циклов. Теоремы,
связывающие такие кажущиеся далекими друг от друга свойства графа,
редки, и их значение простирается за пределы их непосредственной
применимости. В известном смысле они указывают на то, что
некоторые два способа рассмотрения графа — в нашем случае
топологический и алгебраический — не сводятся лишь к любопытным
формальным построениям. Если оба они достаточно естественны
и неожиданно выясняется, что каждый может быть выражен в
терминах другого, то они позволяют глубже понять строение графов
и поэтому достойны внимания.
Пусть G = (V, Е) — граф. Назовем подмножество & его
пространства ребер ${G) простым, если каждое ребро из G лежит не
более чем в двух множествах из &. Например, пространство
разрезов ^*(G) имеет простой базис. Согласно предложению 1.9.3 оно
порождается разрезами E(v), состоящими из всех ребер при данной
вершине г/, и ребро ху Е G лежит в E(v) только для v = х и v — у.
Теорема 4.5.1 (Маклейн, 1937). Граф планарен, если и только
если его пространство циклов имеет простой базис.

104
Глава 4. Планарные графы
Доказательство. Так как утверждение очевидно для графов
порядка не более 2, рассмотрим граф G порядка не менее 3. Если
K(G) < 1, то G — объединение двух собственных индуцированных
подграфов Gi, G2 с |GinG2| < 1. Тогда^(G) — прямая сумма ^(Gi)
и ^(G2) и, следовательно, имеет простой базис, если и только если
его имеют и ^(Gi), и ^{G-i) (доказательство?). Кроме того, G пла-
нарен, если и только если такими же являются G\ и Gi\ это сразу
следует из теоремы Куратовского, а также и из простых
геометрических соображений. Утверждение для G, таким образом, следует
индуктивно из справедливости его для G\ и G2. В остальной части
доказательства теперь можно считать, что G 2-связен.
Сначала предположим, что G планарен и выберем его
изображение. По лемме 4.2.5 границы грани G суть циклы, так что они
являются элементами ^(G). Покажем, что границы грани
порождают все циклы в G. Тогда ^(G) будет иметь простой базис по
лемме 4.2.1. Пусть С С G — любой цикл, и пусть / — его внут-
о
ренняя грань. По лемме 4.2.1 каждое ребро е с е С / принадлежит
границам в точности двух граней G[f] с /' С / и каждое ребро из С
находится на границе в точности одной такой грани. Следовательно,
сумма в ^(G) всех границ таких граней равна С.
Обратно, пусть {Gi,...,Gfc} — простой базис в ^(G). Тогда
для каждого ребра е Е G пространство ^(G — е) также имеет
простой базис. Действительно, если е лежит в точности в одном из
множеств G{, скажем, в С\, то {G2, Сз,. ■ •, Ск} — простой базис
для ^(G — е); если же е лежит в двух из С{, скажем, в С\ и G2, то
\С\ +G2, Сз,..., С к} — такой базис. (Заметим, что эти два базиса —
действительно подмножества ^(G—e) ввиду предложения 1.9.2.)
Таким образом, каждый подграф графа G имеет пространство
циклов с простым базисом. Для доказательства того, что G является
план арным, таким образом, достаточно показать, что пространства
циклов графов Къ и Кз,з (а следовательно, и пространства циклов их
подразбиений) не имеют простого базиса. Тогда G не может
содержать ТКЪ или ТКз.з, а значит, планарен по теореме Куратовского.
Рассмотрим сначала Къ. По теореме 1.9.6 dim(^(K5)) = 6.
Пусть & — {Gi,..., Cq) — простой базис, и положим Go := С\ -f .. •
-\-Cq. Так как 33 линейно независимо, ни одно из множеств Go,..., Се
не пусто, а значит, каждое из них содержит не менее трех ребер (см.
предложение 1.9.2). Простота^ поэтому влечет
18 = 6-3 < |Ci| + ...+ |C6|
<2||K5||-|G0|
< 2-10-3= 17;
противоречие. Для обоснования среднего неравенства заметим, что
каждое ребро из Go находится лишь в одном из множеств Gi,..., Се-

4.6. Двойственность на плоскости
105
Для Кз,з теорема 1.9.6 дает сИт(^(Кз,з)) = 4. Пусть £8 =
{Ci,..., С4} — простой базис, и положим Со := С\ -f • • -+6*4. Так как
#з,з имеет обхват 4, каждый С; содержит не менее четырех ребер,
поэтому
16 = 44 < |Ci| + -.. + |C4|
<2||К3>з||-|Со|
< 2 • 9 - 4 = 14;
противоречие. □
Один из ярких и глубоких результатов в теории планарности
заключается в том, что два таких абстрактных и интуитивно
неочевидных результата о порождающих множествах в пространствах
циклов, как теорема Маклейна и теорема Татта 3.2.3, в совокупности
приводят к очень естественному критерию планарности 3-связных
графов.
Теорема 4.5.2 (Татт, 1963). 3-связный граф планарен, если
и только если каждое его ребро лежит на не более чем (или в
точности на) двух неразделяющих индуцированных циклах.
Доказательство. Прямая импликация следует из
предложений 4.2.10 и 4.2.1 (и предложения 4.2.5 для варианта «в точности
на»); обратная импликация следует из теорем 3.2.3и4.5.1. D
4.6. Двойственность на плоскости
В этом разделе мы с помощью теоремы Маклейна обнаружим
еще одну связь между планарностью и алгебраическим строением —
связь между двойственностью плоских графов, определяемой ниже,
и двойственностью пространств циклов и разрезов. Намек на это
содержится в разделах 1.9 и 3.5.
Плоский мулыпиграф — это пара G = (V, Е) конечных
множеств (вершин и ребер соответственно), удовлетворяющая
следующим условиям:
(i) FCE2;
(ii) каждое ребро является или дугой между двумя вершинами,
или многоугольником, содержащим в точности одну
вершину (свою концевую точку)]
(iii) кроме своей концевой точки (точек) ребро не содержит ни
вершин, ни точек никакого другого ребра.
Мы будем свободно использовать применительно к плоским мульти-
графам термины, определенные для плоских графов. Заметим, что,
как и в абстрактных мультиграфах, петли и двойные ребра
считаются циклами.

106
Глава 4. Планарные графы
Рассмотрим плоский мультиграф G, показанный на рис. 4.6.1.
Поместим новую вершину внутрь каждой грани графа G и соединим
эти новые вершины между собой с образованием другого плоского
мультиграфа G* следующим образом: для каждого ребра е в G мы
соединяем ребром е*, пересекающим е, две новые вершины в гранях,
инцидентных е. Если е инцидентно лишь одной грани, мы
прикрепляем петлю е* к новой вершине в этой грани, также пересекая
ребро е. Плоский мультиграф G*, полученный таким образом, является
двойственным к G в следующем смысле: если применить только
что описанную процедуру к G*, то получается плоский мультиграф,
очень похожий на G. В действительности и сам граф G можно вновь
получить таким способом из G*.
е "'• е*
G А "Р
Рис. J^.6.1. Плоский граф и двойственный ему граф
Чтобы выразить эту идею более точно, рассмотрим любые два
плоских мультиграфа G = (V, Е) и (V*,E*) и положим F(G) =: F
и F((V*,E*)) =: F*. Назовем мультиграф (V*, Е*) плоско
двойственным к G и будем писать (V*, Е*) =: G*, если имеются биекции
F->V\ Е->Е\ V-+F\
f*-+v*(f), ен-+е*, v*-+f*(v),
удовлетворяющие следующим условиям:
(0 v*(f)ef для всех feF;
(ii) |e*HG| = |е*Пе| = \е П G*\ = 1 для всех е Е Я;
(iii) v Е /*(и) для всех v Е V.
Существование таких биекций влечет связность G и G*
(упражнение). Обратно, каждый связный плоский мультиграф G имеет
плоскодвойственный мультиграф G*: если выбрать в каждой грани / в G
точку v*(f) как вершину для G*, то всегда можно соединить эти
вершины независимыми дугами, как требуется условием (ii), и всегда
имеется биекция V —» F*, удовлетворяющая условию (iii)
(упражнение).
Если G* и G£ — два плоскодвойственных мультиграфа к G, то,
очевидно, G* ~ G^. На самом же деле можно показать, что
естественная биекция и*(/) ь-+ ^з(/) есть топологический изоморфизм

4.6. Двойственность на плоскости
107
между G* и GJ. В этом смысле можно говорить о единственном
плоскодвойственном мультиграфе G* к G.
Наконец, G, в свою очередь, является плоскодвойственным к G*.
Действительно, об этом свидетельствуют обратные отображения к
биекциям из определения G*. Полагая v*(f*(v)) :—vvi f*(v*(f)):— f
для f*(v) G F* и v*(f) G V*, мы видим, что условия (i) и (iii) для G*
превращаются в (iii) и (i) для G. При этом условие (ii) симметрично
по G и G*. Таким образом, термин «двойственный» находит
формальное оправдание.
Плоская двойственность не менее привлекательна и в том
отношении, что она устанавливает связь между двумя естественными,
но очень разными видами множеств ребер в мультиграфе, а именно,
между его циклами и разрезами.
Предложение 4.6.1. Для любого связного плоского мульти-
графа G множество ребер Е С E(G) есть множество ребер цикла
в G, если и только если Е* := {е* | е £ Е} — минимальный
разрез в G*.
Доказательство. По условиям (i) и (ii) в определении G* две
вершины u*(/i) и и* (/2) из G* лежат в одной и той же компоненте
графа G* — Е*, если и только если Д и /2 лежат в одной и той
же области из Ж2 \ [JE: каждый и*(fi)-v*(/2) путь в G* — Е* —
это дуга между /i и /2 в Е2 \ (J Е. И обратно, каждая такая дуга Р
(cPC\V(G) — 0) определяет маршрут в G*—E* между u*(/i) и ^(/з)-
Далее, если С С G — цикл и Е = Е(С), то ввиду теоремы Жор-
дана о кривой и вышеупомянутого соответствия мультиграф G* — Е*
имеет в точности две компоненты, поэтому Е* — минимальный
разрез в G*.
Обратно, если Е С E(G) таково, что Е* является разрезом в G*,
то по предположению 4.2.3 и вышеупомянутому соответствию Е
содержит ребра цикла С С G. Если Е* минимален как разрез, то Е
не может содержать никаких других ребер (ввиду показанной выше
импликации), а значит, Е = Е(С). □
Предложение 4.6.1 подсказывает следующее обобщение плоской
двойственности на понятие двойственности для абстрактных муль-
тиграфов. Назовем мультиграф G* абстрактно-двойственным к
мультиграфу G, если E(G*) = E(G) и минимальные разрезы в G* —
в точности множества ребер циклов в G. Заметим, что абстрактно-
двойственный мультиграф к любому мультиграфу связен.
Предложение 4.6.2. Если G* абстрактно-двойствен к G, то
пространство разрезов в G* есть пространство циклов в G, т. е.
V*(G*) = V(G).

108 Глава 4. План арные графы
Доказательство. По лемме 1.9.45) ^*(G*) есть
подпространство в ^(G*) = <*(G)} порожденное минимальными разрезами в G*.
По предположению они представляют собой в точности множества
ребер циклов в G и, значит, порождают ^(G) в <?(G). □
В заключение рассмотрим один из ярких результатов
классической теории план арности: план арные графы можно
охарактеризовать тем свойством, что они имеют абстрактно-двойственный граф.
Хотя эта двойственность менее интуитивно очевидна, она
представляет собой свойство столь же фундаментальное, как и сама планар-
ность. Действительно, следующая теорема вполне может
рассматриваться как топологическая характеризация графов, имеющих
двойственный граф.
Теорема 4.6.3 (Уитни, 1933). Граф планарен, если и только
если он имеет абстрактно-двойственный мультиграф.
Доказательство. Пусть дан граф G. Если G плоский, то
каждая компонента С в G имеет плоскодвойственный мультиграф С*.
Рассмотрим эти С* как абстрактные мультиграфы, выберем
вершину в каждом из них и отождествим эти вершины. В полученном
связном мультиграфе G* множество минимальных разрезов является
объединением множеств минимальных разрезов в мультиграфах С*.
По предложению 4.6.1 эти разрезы — в точности множества ребер
циклов в G, так что G* абстрактно-двойствен к G.
Обратно, предположим, что G имеет абстрактно-двойственный
мультиграф G*. По теореме 4.5.1 и предложению 4.6.2 достаточно
показать, что ^*(G*) имеет простой базис, но это следует из
предложения 1.9.3. □
Упражнения
1. Показать, что любой граф можно вложить в Ж3 так, чтобы все ребра были
отрезками прямой.
2.~ Вывести непосредственно из леммы 4.1.2, что А'з.З непланарен.
3.~~ Найти формулу Эйлера для несвязных графов.
4. Показать, что любой связный планарный граф с п вершинами, m ребрами
и конечным обхватом g имеет m < —^{п — 2).
5. Показать, что любой планарный граф есть объединение трех лесов.
6. Пусть G\, G2,... — бесконечная последовательность попарно
неизоморфных графов. Показать, что если limsupefGt) > 3, то графы Gt имеют
неограниченный род, другими словами, не существует (замкнутой)
поверхности, в которую можно вложить все графы Gt.
5) Хотя лемма формулируется только для графов, ее доказательство
применимо и для мультиграфов.

[Упражнения
109
' (Подсказка. Можно использовать тот факт, что для каждой поверхности 5
i существует такая константа х(^) < 2, что любой граф, вложенный в 5,
удовлетворяет обобщенной формуле Эйлера п — т + I > х(^)-)
, 7. Найти прямое доказательство для плоских графов теоремы Татта о
пространстве циклов 3-связных графов (теорема 3.2.3).
J 8.~ Показать, что два плоских графа на рис. 4.3.1 не являются комбинаторно
(а значит, и топологически) изоморфными.
I 9. Показать, что два графа на рис. 4.3.2 являются комбинаторно, но не
топологически изоморфными.
,10.— Показать, что наше определение эквивалентности планарных вложений
действительно задает отношение эквивалентности.
11. Найти 2-связный планарный граф, у которого все изображения
топологически эквивалентны, но не все планарные его вложения эквивалентны.
12.+ Показать, что любой плоский граф комбинаторно эквивалентен некоторому
плоскому графу с прямыми ребрами.
(Подсказка. Для данной плоской триангуляции постройте по индукции
теоретико-графово изоморфный плоский граф, все ребра которого суть
отрезки прямой. Какое дополнительное свойство внутренних граней может
помочь в индукции?
Не используйте теорему Куратовского в следующих двух упражнениях.
13. Показать, что любой минор планарного графа планарен. Выведите отсюда,
что граф планарен, если и только если он является минором некоторой
решетки. (Решетки определяются в главе 12.3.)
14. (i) Показать, что в принципе планарные графы могут быть
охарактеризованы, как в теореме Куратовского, т. е. существует такое множество ЭС
графов, что граф G планарен, если и только если G не имеет
топологического минора из SC'.
(ii) Более общо, какие свойства графа можно охарактеризовать таким
образом?
15.- Каждый ли планарный граф имеет изображение, в котором все внутренние
грани выпуклы?
16. Изменить доказательство леммы 4.4.3 так, чтобы все внутренние грани
стали выпуклыми.
17. Всякий ли минимально непланарный граф G (т. е. непланарный, все
собственные подграфы которого планарны) содержит такое ребро е, что G — е
является максимально планарным? Изменится ли ответ, если определить
«минимальный» относительно миноров, а не подграфов?
18. Показать, что добавление нового ребра к максимально планарному графу
порядка не менее 6 всегда создает ТА'5 и ТАз,з как подграф.
19. Вывести общий вид теоремы Куратовского из 3-связного случая, работая
с плоскими графами, т. е. не пользуясь леммой 4.4.5.
(Это не предлагается как упражнение по элементарной топологии; для
топологических частей доказательства будет достаточно грубого наброска.)
20. Граф называется внешнепланарным, если он имеет изображение, в котором
каждая вершина лежит на границе внешней грани. Показать, что граф
внешней л анарен, если и только если он не содержит в качестве минора
ни А'4, ни А2,з-
21. Пусть G = G\ U G2, где \G\ П G2I < 1. Показать, что ^(G) имеет простой
базис, если его имеют и ^(G\), и ^(G'z)-

110 Глава 4. Пленарные графы
22."*" Найти простой базис пространства циклов среди границ граней 2-связного
плоского графа.
23. Показать, что 2-связный плоский граф является двудольным, если и только
если каждая его грань ограничена четным циклом.
24." Пусть G — связный плоский мультиграф, a G* — его плоскодвойственный
мультиграф. Доказать для каждого ребра е £ G следующие утверждения:
(i) если е лежит на границе двух различных граней f\, /2 в G, то
e* = V(h)v*(f2);
(ii) если е лежит на границе ровно одной грани / в G, то е* является
петлей при v*(f).
25." Как выглядит плоскодвойственный мультиграф к плоскому дереву?
26." Показать, что плоско двойственный мультиграф к плоскому мультиграфу
связен.
27."*" Показать, что плоский мультиграф G имеет плоскодвойственный, если и
только если G связен.
28. Пусть G, G* — взаимно двойственные плоские мультиграфы, ае£ E(G).
Доказать следующие утверждения (при соответствующем
определении G/e):
(i) если е не мост, то G*/e* является плоскодвойственным к G — е;
(ii) если е не петля, то G* — е* является плоскодвойственным к G/e.
29. Показать, что любые два двойственных мультиграфа к плоскому
мультиграфу комбинаторно изоморфны.
30. Пусть G, G* — два взаимно двойственных плоских графа. Доказать
следующие утверждения:
(i) если G 2-связен, то и G* 2-связен;
(ii) если G 3-связен, то и G* 3-связен;
(iii) если G 4-связен, то G* может не быть 4-связным.
31. Пусть G, G* — взаимно двойственные плоские графы. Пусть В\%... ,Вп
являются блоками в G. Показать, что 5*,..., 5* — блоки графа G*.
32. Показать, что если G* абстрактно-двойствен к мультиграфу G, то G
абстрактно-двойствен к G*.
33. Показать, что связный граф G = {V,E) планарен, если и только если
существует такой связный мультиграф G' = (V,Е) (т. е. с тем же
множеством ребер), что для каждого множества F С Е верно следующее
утверждение: граф (У, F) является деревом, если и только если деревом является
(V',E\F).
Примечания
Имеется превосходная монография о вложении графов в поверхности,
включая плоскость: Mohar В., Thomassen С. Graphs on Surfaces. Baltimore: Johns
Hopkins Univ. Press, 2001. Там можно найти доказательства результатов,
цитируемых в разделе 4.1, а также все ссылки для этой главы. Хорошее изложение
теоремы Жордана о кривой (и случай многоугольника, и общий) дается также в:
Stillwtll J. Classical topology and combinatorial group theory. N. Y. e. a.: Springer-
Verl., 1980.
Короткое доказательство следствия 4.2.8 использует прием, который
заслуживает специального упоминания — это так называемый двойной подсчет
пар, показанный в тексте на примере двудольного графа, ребра которого можно
пересчитать двояко, по очереди суммируя его степени слева и справа.
Двойной подсчет — широко используемая в комбинаторике методика; далее в книге
встречаются еще примеры на эту тему.

Примечания
111
Материал раздела 4.3 не является стандартным для вводного курса теории
графов, и остальную часть главы можно читать независимо от этого раздела.
Однако результаты раздела 4.3 ни в коем случае нельзя считать
незначительными. В некотором смысле они пали жертвой собственного успеха: переход от
топологической к комбинаторной постановке проблем планарности, который они
обеспечивают, сделал развиваемые в них топологические методы
необязательными для большей части теории планарности.
В своем первоначальной варианте теорема Куратовского была
сформулирована только для топологических миноров; версия для общих миноров была
добавлена Вагнером в 1937 г. Наше доказательство для 3-связного случая
(лемма 4.4.3) можно легко усилить так, чтобы все внутренние грани были
выпуклыми (упражнение); см.: Thomassen С. Planarity and duality of finite and infinite
graphs // J. Combin. Theory. Ser. B. 1980. 29. P. 244-271. Существование
таких «выпуклых» изображений 3-связных плоских графов следует уже из
теоремы Штейнина (1922) о том, что эти графы являются в точности 1-скелетами
3-мерных выпуклых многогранников. См. также: Tutte W. Т. How to draw
a graph // Proc. London Math. Soc. 1963. 13. P. 743-767.
Как легко видеть, добавление любого ребра к максимальному планарному
графу (порядка не менее 6) порождает не только один из топологических
миноров Къ пли Кз,з> но и оба сразу. В разделе 8.3 мы увидим, что, более общо,
каждый граф с п вершинами и более чем Зп —6 ребрами содержит и ТК5, и (с
одним легко описываемым классом исключений) ТА'з з • Сеймур предполагает, что
любой 5-связный непланарный граф содержит ТА (личное сообщение).
Простой базис пространства циклов, построенный в доказательстве
теоремы Маклейна и состоящий из границ внутренних граней, каноничен в
следующем смысле: для любого простого базиса 38 пространства циклов 2-связного
плоского графа существует изображение этого графа, в котором 38 является
в точности набором границ внутренних грани. (Это доказано в упомянутой
книге: Mohar В., Thomassen С. Graphs on Surfaces — где также приводятся
некоторые другие критерии планарности.) Наше доказательство обратного
утверждения в теореме Маклейна основано на теореме Куратовского. Более
прямой подход, в котором плоское вложение фактически строится из простого
базиса, принят в книге: Wagner К. Graphentheorie. Mannheim е. a.: Hochschul-
taschenbucher, 1970.
Явления двойственности между разрезами и циклами в абстрактных графах
(и в более общих ситуациях) глубоко исследуются в теории матпроидов; см.:
Oxley J. G. Matroid Theory. Oxford: Univ. Press, 1992.

Глава 5
Раскраска
Как много цветов потребуется для того, чтобы раскрасить
страны на карте так, чтобы каждые две смежные страны были окрашены
по-разному? Сколько дней нужно отвести для встреч
парламентского комитета, если каждый комитет намерен заседать в течение
одного дня, а некоторые члены парламента служат в нескольких
комитетах? Как составить школьное расписание минимальной длины,
зная как часто каждый преподаватель должен преподавать в каждом
классе?
Вершинная раскраска графа G — (V, Е) есть такое отображение
с: V —* S , что с(у) ф c(w) всякий раз, когда v и w смежны.
Элементы множества S называются цветами. Все, что интересует нас
относительно S — его мощность. Обычно мы будем искать
наименьшее целое число к, при котором G имеет к-раскраску, т. е.
вершинную раскраску с: V —► {1,...,&}. Такое к называется (вершинным)
хроматическим числом графа G и обозначается через x(G). Граф G
с x{G) — к называется к-хроматическим', если x{G) < к, то граф G
к-раскрашиваем. 2
Рис. 5.0.1. Вершинная раскраска V —» {1,... ,4}
Заметим, что fc-раскраска есть не что иное, как вершинное
разбиение на к независимых множеств, называемых цветовыми
классами] нетривиальными 2-раскрашиваемыми графами, например,
являются двудольные графы, и только они. Исторически раскрасочная
терминология пришла из сформулированной выше задачи раскраски
карты, которая сводится к проблеме определения максимального хро-

5.1. Раскраска карт и плоских графов
113
матического числа плоских графов. Задача о расписании работы
комитета также может быть перефразирована как проблема вершинной
раскраски (как?).
Раскраска ребер графа G = (V, Е) есть отображение с: Е —± S
с с(е) ф c(f) для любых смежных ребер е, /. Наименьшее целое
число к, при котором существует к-раскраска ребер, т. е. раскраска
ребер с: Е —+ {1,...,&}, называется реберным хроматическим числом
или хроматическим индексом1^ графа G и обозначается через x'{G)-
Третий из наших вступительных вопросов может быть
сформулирован как задача раскраски ребер в двудольном мультиграфе (как?).
Ясно, что раскраска ребер графа G есть вершинная раскраска
его реберного графа L(G) и наоборот, в частности, x'{G) — x(L(G)).
Задача обнаружения хороших реберных раскрасок может,
следовательно, рассматриваться как сужение более общей задачи
вершинной раскраски на этот специальный класс графов. Как мы увидим,
соотношение между этими двумя задачами раскраски
характеризуется заметным различием в нашем знании относительно их
решений: для х имеются лишь очень грубые оценки, а родственное ему х!
всегда принимает одно из двух значений: А или A -f 1.
5.1. Раскраска карт и плоских графов
Если какой-то из результатов в теории графов и претендует на
известность во внешнем мире, то это следующая теорема о четырех
красках (из которой следует, что каждая карта может быть
окрашена не более чем в четыре цвета).
Теорема 5.1.1 (теорема о четырех красках). Каждый плоский
граф 4-раскрашиваем.
Некоторые замечания относительно доказательства теоремы
о четырех красках и ее истории можно найти в примечаниях в конце
этой главы. Здесь мы доказываем следующее ее ослабление.
Предложение 5.1.2 (теорема о пяти красках). Каждый
плоский граф Ъ-раскрашиваем.
Доказательство. Пусть G — плоский граф с п > б
вершинами и т ребрами. Предположим по индукции, что каждый
плоский граф с менее чем п вершинами может быть 5-раскрашен. По
следствию 4.2.8
d(G) = 2т/п < 2(3п - б)/п < 6.
Пусть v G G — вершина степени не более 5. По индукционному
предположению граф Н := G — v имеет вершинную раскраску с: V(H) —+
{1,...,5}. Если раскраска с использует не более четырех цветов
) А также хроматическим классом.— О. Б.

114
Глава 5. Раскраска
для соседей вершины г/, то мы можем продолжить ее до 5-раскраски
графа G. Поэтому допустим, что v имеет ровно 5 соседей и что все
они имеют различные цвета.
Пусть D — открытый диск вокруг г/, настолько маленький, что
пересекает только те пять отрезков ребра G, которые содержат г/.
Занумеруем эти отрезки согласно их циклическому порядку в D как
si,..., 55, и пусть W{ будет ребром, содержащим S{, г — 1,...,5
(рис. 5.1.1). Без ограничения общности можно считать, что с(г/:) = г
для любого г.
Рис. 5.1.1. Доказательство теоремы о пяти красках
Покажем сначала, что каждый г/1-г/з путь Р С Н отделяет
г/2 от г/4 в Я. Ясно, что это утверждение равносильно тому, что
цикл С \— vv\Pv^v отделяет г/2 от г/4 в G. Мы доказываем его как
следствие того, что г/2 и г/4 лежат в разных гранях цикла С.
Рассмотрим две области в D \ (si U S3). Одна из этих областей
пересекает $2, а другая — 54. Поскольку С П D С si U 53, каждая
из этих двух областей содержится в грани цикла С. Кроме того,
эти грани различны; иначе D пересекался бы только с одной гранью
цикла С вопреки тому, что v находится на границе обеих граней
(теорема 4.1.1). Таким образом, D П s^ и D П s$ лежат в различных
гранях цикла С. Но раз С пересекает ребра г/г>2 D S2 и г/г>4 D s$
только в г/, то же самое имеет место для г/2 и г/4.
При заданных i,j Е {1,...,5} пусть H{j — подграф Я,
индуцированный вершинами цвета г или j. Можно считать, что
компонента С\ подграфа Я^з, содержащая v\, содержит и г/з-
Действительно, если поменять цвета 1 и 3 во всех вершинах из Ci, то
получается другая 5-раскраска графа Я. Если г/3 ^ Ci, то v\ и г/з
окрашены в 3 при этой новой раскраске, и тогда можно покрасить v в
цвет 1. Таким образом, Я^з содержит у\-уз путь Р. Как
показано выше, Р отделяет г/2 от г/4 в Я. Поскольку Р П Я2,4 = 0, это
означает, что г/2 и г/4 лежат в разных компонентах подграфа Я2,4-
В компоненте, содержащей г/2, меняем цвета 2 и 4, перекрашивая г/2
в 4. Теперь г/ больше не имеет соседа цвета 2, и можно покрасить ее
в этот цвет. □

5.2. Раскраска вершин
115
Для сравнения с этими двумя широко известными теоремами
приведем еще один известный результат.
Теорема 5.1.3 (Грёцш, 1959). Каждый плоский граф, не
содержащий треугольника, 3-раскрашиваем.
5.2. Раскраска вершин
Как определить хроматическое число данного графа? Как
найти вершинную раскраску в как можно меньшее число цветов? Как
хроматическое число связано с другими инвариантами графа
такими, как средняя степень, связность или обхват?
Прямо из определения хроматического числа можно получить
следующую верхнюю оценку.
Предложение 5.2.1. Каждый граф Gem ребрами имеет
X(G) <\ + фт+\.
Доказательство. Пусть с — вершинная раскраска графа G
в к — x(G) Цветов. Тогда G содержит по меньшей мере одно
ребро между любыми двумя цветовыми классами; если нет, то можно
было бы использовать один и тот же цвет для обоих классов. Таким
образом, т > ^к(к — 1). Решая это неравенство относительно к,
получаем требуемое утверждение. □
Один из очевидных способов раскрасить граф G в не слишком
большое число цветов — следующий жадный алгоритм: начиная
с фиксированной вершинной нумерации v\,..., vn графа G
рассматриваем вершины по очереди и раскрашиваем каждую V{ первым
наличным цветом, например наименьшим положительным целым
числом, не использованным еще в раскраске ни одного соседа
вершины V{ среди вершин v\,..., i>t-i- Таким образом, никогда не
понадобится больше, чем A(G) -f 1 цветов, даже при неблагоприятном
выборе нумерации v\,..., vn. Если G — полный граф или нечетный
цикл, то эта оценка даже точна.
Однако в общем случае эта верхняя оценка A-fl весьма
избыточна даже для жадных раскрасок. Действительно, для окраски
вершины V{ при этом алгоритме требуется лишь наличие dG[Wl>...>Wi](vt)+lj
а не dc(vi) -f 1 цветов, чтобы можно было двигаться дальше.
Вспомним, что в этот момент алгоритм игнорирует любых соседей Vj
вершины V{ с j > г. Следовательно, для большинства графов есть
возможность улучшения оценки A -f 1 за счет выбора подходящего
начального упорядочения вершин — такого, в котором вершины
большой степени выбираются на раннем этапе (когда большинство
соседей еще игнорируется), а вершины малой степени последними. В
оставшемся подграфе число dG[Vl)...)vi](vi) + 1 требуемых цветов будет

116
Глава 5. Раскраска
наименьшим, если V{ имеет минимальную степень в G[v\,..., v,-]. Но
добиться этого легко: нужно лишь выбрать сначала vn с d[yn) —
5(G), затем взять в качестве vn-i вершину минимальной степени
в G — vn и так далее.
Наименьшее число к, при котором G имеет такую нумерацию
вершин, что любой вершине предшествует менее к ее соседей,
называется раскрасочным числом col(G) графа G. Рассматриваемая
выше нумерация показывает, что col(G) < max 6(H) -f 1. Но для
Я С G очевидно также, что col(G) > со1(Я) и со1(Я) > 6(H) -f 1,
поскольку «обратная степень» последней вершины в любой
нумерации подграфа Н есть просто ее обычная степень в Я, которая не
меньше 6(H). Таким образом, мы доказали следующее
Предложение 5.2.2. Каждый граф G удовлетворяет
неравенству
X(G) < col(G) = max{<5(#) | Я С G} + 1. □
Следствие 5.2.3. Каждый граф G имеет подграф
минимальной степени не меньше x(G) — 1. □
Раскрасочное число графа тесно связано с его древесностью
(см. замечание после теоремы 3.5.4).
Как мы видели, каждый граф G имеет x(G) < A(G) + 1 с
равенством для полных графов и нечетных циклов. Во всех остальных
случаях эта общая оценка может быть немного улучшена.
Теорема 5.2.4 (Брукс, 1941). Пусть G — связный граф. Если
G не является ни полным графом, ни нечетным циклом, то
X(G) < A(G).
Доказательство. Применим индукцию по \G\. Если A(G) < 2,
то G — путь или цикл, и утверждение тривиально. Поэтому
предположим, что А := A(G) > 3 и что утверждение выполняется для
графов меньшего порядка. Допустим, что x(G) > А.
Пусть v G G — вершина и Я := G — v. Тогда х(Н) ^ А. По
индукции каждая компонента Н' из Я имеет х(Н') < А(Я;) < А,
если Н' не полон или не является нечетным циклом. В этих случаях
х(Н') = А(Я') -f 1 < А, поскольку каждая вершина Н' имеет
максимальную степень в Я7 и одна такая вершина к тому же смежна
с v в G.
Так как Я может быть А-раскрашен, a G не может, имеет место
следующее утверждение.
Каждая А-раскраска графа Я использует все цвета
1,..., А на соседях вершины v, в частности, d(v) = А.

5.2. Раскраска вершин
117
Для любой А-раскраски графа Н обозначим соседа вершины и,
имеющего цвет г, через и;, г = 1,...,А. Для всех г ф j пусть Hij
обозначает подграф Н из вершин цветов г или j.
Для всех i ф j вершины V{ и Vj лежат в общей
компоненте С,-,/ графа Hij.
Иначе мы могли бы поменять цвета г на j и наоборот в одной из этих
компонент; тогда V{ и Vj были бы окрашены одинаково вопреки (1).
Cij — всегда V{-Vj путь. (3)
Действительно, пусть Р есть v,—Vj путь в dj. Так как d#(i/t) <
А — 1, соседи вершины V{ имеют попарно различные цвета; иначе
мы могли бы перекрасить V{ вопреки (1). Следовательно, сосед
вершины v{ на Р есть его единственный сосед в dj, и аналогично
для Vj. Таким образом, если Cij ф Р, то в Р есть внутренняя
вершина с тремя одинаково окрашенными соседями в Я; пусть и —
первая такая вершина на Р (рис. 5.2.1).
Рис. 5.2.1. Доказательство утверждения (3) в теореме Брукса
Поскольку на соседях и используются не более А — 2 цветов, мы
о
можем перекрасить и. Но это превращает Ри в компоненту графа
Hi j вопреки (2).
Для любых различных i, j, к пути Cij и С,-,*
пересекаются только в V{.
Действительно, если i/t- ф u Е Cij П Ct-,jb, то и имеет двух соседей
цвета j и двух цвета к, так что мы можем перекрасить и. В
новой раскраске вершины Vi и vj лежат в различных компонентах
графа Hi j вопреки (2).
Доказательство теоремы теперь заканчивается легко. Если
соседи v попарно смежны, то каждый имеет А соседей уже в N(v)U{v},
поэтому G = G[N(v)U{v}] = KA+1. Поскольку G полон, доказывать
нечего. Мы можем, таким образом, предполагать, что v\V2 £ G,

118
Глава 5. Раскраска
где v\,..., ид получают свои названия по некоторой фиксированной
А-раскраске с графа Н. Пусть и ф v2 — сосед вершины v\ на пути
6*1,2, тогда с(и) = 2. Меняя цвета 1 и 3 в С^з, мы получаем
новую раскраску с1 для Я. Пусть v\, H{j, С[ j и так далее определены
для с' очевидным образом. Будучи соседом вершины v\ — v'3 наша
вершина и теперь находится в С^з, посколькУ с'{и) — с(и) — 2.
Однако ввиду (4) для с путь viC\t2 сохранил исходную раскраску,
поэтому и G v\Cit2 С С[2- Следовательно, и £ С2 3 П С{ 2 вопреки (4)
для с7. □
Как мы видели, граф G с большим хроматическим числом
должен также иметь большую максимальную степень, по крайней мере
x(G) — 1. Что еще можно сказать о структуре графов с большим
хроматическим числом?
Одна из очевидных возможных причин для х(^) > & —
присутствие Кк как подграфа. Это локальное свойство графа G
совместимо с произвольными значениями глобальных инвариантов типа
е и к. Следовательно, предположение о x(G) > & не сообщает нам
ничего об этих инвариантах для самого G. Однако оно влечет
существование подграфа, в котором данные инварианты велики. По
следствию 5.2.3 G имеет подграф Н с S(H) > к — 1, и, следовательно,
по теореме 1.4.2 подграф Н' имеет «(Я7) > \_\{к — 1)J.
Итак, является ли присутствие этих относительно плотных
подграфов единственной причиной того, что \ велико? В свою очередь,
обязательно ли они содержат граф с большим хроматическим
числом, может быть, даже один из некоторого небольшого набора
канонических графов таких, как Кк1 Оказывается, что это не так.
Подграфы большой, но «постоянной» средней степени —
ограниченной снизу только функцией от к, а не от \G\ — далеко не настолько
плотны, чтобы обязательно содержать какой-либо конкретный граф
с большим хроматическим числом, не говоря уже о Кк2\
Но даже если вышеупомянутые локальные структуры, как
выяснилось, не помогают, могло бы еще оказаться, что каким-то
образом большое хроматическое число вынуждает наличие некоторых
канонических подграфов с большим хроматическим числом. Что это
не так, будет основным результатом главы 11: согласно
классическому результату Эрдеша, доказанному вероятностным методом,
существуют графы с произвольно большим хроматическим числом,
имеющие к тому же произвольно большой обхват (теорема 11.2.2).
) Это с очевидностью следует из примера КП)П, который является 2-хрома-
тичным, но у которого связность и средняя степень равны п, т. е.
превышают любую константу. Какая в точности (не равная константе) средняя
степень будет вынуждать существование в графе заданного подграфа,
является темой главы 7.

5.2. Раскраска вершин
119
Таким образом, для любого графа #, не являющегося лесом,
и каждого k Е N существуют графы G с x(G) > к и Н <£ G3\
Таким образом, вопреки нашему начальному предположению
о том, что единственной причиной большого хроматического числа
является присутствие в графе некоторой плотной локальной
подструктуры, на самом деле это явление может носить сугубо
глобальный характер: ведь локально, вблизи каждой вершины, граф
большого обхвата является деревом, а значит, в частности, 2-раскраши-
ваем там!
Пока что мы задавались вопросом, что является следствием
большого хроматического числа. Оно заставляет быть большими
инварианты 8, d, А и к в некотором подграфе, но не влечет
существования какого-либо конкретного подграфа с большим хроматическим
числом. Теперь рассмотрим обратный вопрос: из каких
предположений мы могли бы вывести, что хроматическое число данного графа
велико?
За исключением конкретного подграфа, известного как высоко
хроматический (типа Кк), в поле зрения почти ничего нет:
никакие значения инвариантов, изучавшихся до сих пор, пока не влекут
того, что рассматриваемый граф должен иметь большое
хроматическое число. (Вспомним о КП)П.) Поэтому, что именно может быть
причиной высокой хроматичности как глобального явления, в
значительной степени остается тайной!
Однако имеется простая — хотя не всегда короткая —
процедура для построения всех графов с хроматическим числом > к. Для
каждого к Е N определим рекурсивно класс к-конструируемых
графов следующим образом:
(i) полный граф Кк является ^-конструируемым;
(ii) если G ^-конструируемый и х,у Е V(G) не смежны, то
и (G -f ху)/ху ^-конструируемый;
(iii) если Gi, Gi ^-конструируемые и имеются такие вершины
х, 2/i, ?/2, что Gi П G2 = {х}, хуг Е E{G\) и ху2 Е E(G2), то
и (G1UG2) — xyi — ХУ2 + У1У2 ^-конструируемый (рис. 5.2.2).
X X
Рис. 5.2.2. Конструкция Хайоша (iii)
3) Согласно следствиям 5.2.3 и 1.5.4, конечно, каждый граф с достаточно
большим хроматическим числом будет содержать любой заданный лес.

120
Глава 5. Раскраска
Легко проверить по индукции, что все &-конструируемые графы
и, следовательно, их надграфыпо меньшей мере fc-хроматичны.
Действительно, если (G + xy)/xy, как в (ii), имеет раскраску в менее чем
к цветов, то она годится и для G; противоречие. Аналогично, в
любой раскраске графа, построенного в (iii), вершины у\ и у2 не могут
обе иметь тот же цвет, что и ж, так что эта раскраска индуцирует
раскраску или Gi, или G2, а значит, использует по крайней мере
к цветов.
Замечательно то, что обратное утверждение также верно.
Теорема 5.2.5 (Хайош, 1961). Пусть G — граф и к G N.
Тогда x(G) > к, если и только если G имеет к-конструируемый
подграф.
Доказательство. Пусть G — граф с x(G) > к. Мы
показываем, что G имеет ^-конструируемый подграф. Пред поло жим
противное; тогда к > 3. Добавляя при необходимости ребра, сделаем G
реберно-максимальным со свойством, что ни один из его подграфов
не ^-конструируем. Теперь G не является полным г-дольным
графом ни для какого г: иначе x(G) > & влекло бы г > к и G содержал
^-конструируемый граф Кк.
Так как G не является полным многодольным графом,
несмежность не является отношением эквивалентности на V(G). Поэтому
имеются такие вершины 2/ъ ж, 2/2> что угх,ху2 $. E{G), но 2/12/2 Е
E(G). Поскольку G реберно-максимален без ^-конструируемого
подграфа, каждое ребро xyi лежит в некотором ^-конструируемом
подграфе Hi графа G -f xyi (г = 1,2).
Пусть #2 — изоморфная копия графа Яг, которая содержит
х и Яг — #i, но в остальном не пересекается с G, вместе с
изоморфизмом v *-+ v' из Яг до Н2, который фиксирует Яг П Н2 поточечно.
Тогда Н\С\ Н2 — {х}, поэтому
Я := (Hi U Н'2) - xyi - ху'2 + 2/i2/2
является ^-конструируемым согласно (iii). Будем отождествлять
последовательно в Я каждую вершину v' £ Н2 — G с ее партнершей v;
поскольку vv' не является ребром из Я, каждое из этих
отождествлений составляет шаг конструкции типа (ii). В итоге мы получаем
граф
(Hi U Я2) - xyi - ху2 + 2/12/2 С G;
это и есть искомый ^-конструируемый подграф графа G. □

5.3. Раскраска ребер
121
5.3. Раскраска ребер
Ясно, что каждый граф G имеет x'{G) > A(G). Для двудольных
графов здесь имеет место равенство.
Предложение 5.3.1 (Кёниг, 1916). Каждый двудольный граф
G имеет X'(G) = A(G).
Доказательство. Применим индукцию по ||G||. Для ||G|| = О
утверждение верно. Теперь предположим, что ||G|| > 1 и что
утверждение верно для графов с меньшим числом ребер. Пусть А :=
A(G); выберем ребро ху £ G и возьмем какую-нибудь А-раскраску
ребер в G — ху, существующую по индукционному предположению.
Ребра, окрашенные в а, будем называть а-ребрами и так далее.
В G — ху каждая изхиу инцидентна не более чем А — 1
ребрам. Следовательно, имеются такие а,/3 £ {1,..., А}, что х не
инцидентна а-ребру, а у — /3-ребру. Если а — /3, мы можем покрасить
ребро ху этим цветом и получить искомую раскраску; поэтому
предположим, что а ф (3 и что х инцидентно /?-ребру.
Расширим это ребро до максимального маршрута W, ребра
которого окрашены поочередно в /? и а. Так как никакой такой
маршрут не содержит одну и ту же вершину дважды (почему?), W
существует и является путем. Кроме того, W не содержит у. Иначе он
закончился бы в у на а-ребре (по выбору (3) и, таким образом, имел
бы четную длину, так что W -f ху был бы нечетным циклом в G
(ср. предложение 1.6.1). Теперь перекрасим все ребра на W, меняя
а на, /3 и наоборот. По выбору а и ввиду максимальности W любые
смежные ребра в G — ху по-прежнему окрашены по-разному. Таким
образом, мы нашли реберную А-раскраску графа G — ху, в которой
ни ж, ни у не инцидентны /?-ребру. Окрасив ху в /3, мы продолжаем
эту раскраску до реберной А-раскраски графа G. □
Теорема 5.3.2 (Визинг, 1964). Каждый граф G удовлетворяет
неравенству
A(G)<X'(G)<A(G)+1.
Доказательство. Мы доказываем второе неравенство
индукцией по ||G||. Для ||G|| = 0 оно тривиально. Для шага индукции
предположим, что задан граф G = (V, Е) с А := A(G) > 0, и
допустим, что утверждение имеет место для графов с меньшим числом
ребер. Вместо «реберная (A -f 1)-раскраска» будем говорить просто
«раскраска». Ребро, окрашенное в а, будем называть а-ребром.
Для каждого ребра е £ G по индукционному предположению
существует раскраска графа G —е. В такой раскраске ребра при любой
вершине v используют не более d(v) < А цветов, так что некоторый
цвет /3 £ {1,..., A -f 1} отсутствует при v. Для любого другого
цвета а имеется единственный максимальный маршрут (возможно,

122
Глава 5. Раскраска
тривиальный), начинающийся в и, ребра которого окрашены
поочередно в а и /3. Этот маршрут — путь; мы называем его af/3-путем
из вершины v.
Предположим, что G не раскрашиваем. Тогда имеет место
следующее.
Для любых ху £ Е и раскраски графа G — ху, в которой
цвет а отсутствует в х, а цвет (3 отсутствует в у, (1)
a/P-путь из у заканчивается в х.
Действительно, иначе мы могли бы поменять цвета а и /3 па, этом
пути, покрасить ху в а и получить раскраску графа G;
противоречие.
Пусть хуо £ G — ребро. По индукционному предположению
Go := G — хуо имеет раскраску cq. Пусть a — цвет, отсутствующий
при х в этой раскраске. Далее, пусть уо, yi,..., у* — такая
максимальная последовательность различных соседей х в G, что со(жуг)
отсутствует в cq при yt-_i для каждого г = 1,..., к. Для каждого из
графов G{ :— G — xyi мы определяем раскраску с:-, полагая
/ч f co(s%4i) Для е = xyh если j G {0,..., г- 1},
с»(е) •= i , v (2)
^ со(е) в противном случае.
Заметим, что в каждой из этих раскрасок при х отсутствуют те же
цвета, что и в cq .
Пусть теперь /3 — цвет, отсутствующий при вершине ук в
раскраске со. Ясно, что /3 по-прежнему отсутствует при у к bq. Если
бы /3 отсутствовал и при х, то можно было бы окрасить хук цветом (3
и тем самым расширить с* до раскраски графа G. Следовательно,
х инцидентна /?-ребру (в любой раскраске). Поэтому ввиду
максимальности к найдется такое г Е {1,...,&— 1}, что
CQ(xyi) = /?.
Пусть Р есть а//3-путъ из у к в графе Gjb (относительно с*;
рис. 5.3.1). По утверждению (1) Р заканчивается в х, причем на
/?-ребре, так как а отсутствует при х. Поскольку /3 = co(xyi) =
Ck(xyi-i), это ребро есть ху{-\. Но в со, а следовательно, также
в ct_i цвет /3 отсутствует при у{-\ (по (2) и выбору у,-). Пусть Р' —
а//?-путь из yt_i в графе G,-i (относительно ct_i). Поскольку Р'
определен единственным образом, он начинается с yt_iPyjb.
Заметим, что ребра в Рх окрашены в раскраске ct_i так же, как и в с*.
Но в со, а следовательно, в ct_i нет /3-ребра при yjt (по выбору /?),
поэтому Р; заканчивается в у к вопреки (1). D

5.4. Предписанная раскраска
123
Рис. 5.3.1. a/Р путь Р в Gk
Теорема Визинга делит конечные графы на два класса согласно
их хроматическому индексу. Графы, имеющие х' — Д> относятся
к классу 1, а имеющие х' = Д -f 1, — к классу 2.
5.4. Предписанная раскраска
В этом разделе мы рассмотрим относительно недавнее
обобщение ранее изучавшихся понятий раскраски. Это обобщение может,
на первый взгляд, показаться немного искусственным, но в
действительности оно устанавливает фундаментальную связь между
классическими (вершинным и реберным) хроматическими числами графа
и другими его инвариантами.
Предположим, что дан граф G = (V, Е) и для каждой вершины G
задан список цветов, разрешенных в этой вершине. Когда можно
раскрасить G (в обычном смысле) так, чтобы каждая вершина
получила цвет из ее списка? Более формально, пусть (SV)V£V —
семейство множеств. Мы называем вершинную раскраску с графа G,
где c(v) £ Sv для всех v £ V, раскраской, выбранной из списков4^ Sv.
Граф G называется предписаний k-раскрашиваемым или к-выбирае-
мым, если для каждого семейства (Sv)V£V с \SV\ = к для всех v
имеется вершинная раскраска G из списков Sv. Наименьшее целое число к,
для которого G является fc-выбираемым, есть предписанное
хроматическое число или число выбираемости ch(G) графа G.
Предписанные раскраски ребер определяются аналогично.
Наименьшее целое число к, при котором G имеет раскраску ребер из
любого семейства списков размера к, есть предписанный
хроматический класс ch'(G) графа G. Формально, мы просто полагаем ch'(G) :=
ch(L(G)), где L(G) — реберный граф графа G.
4) Или предписанной. — О. Б.

124
Глава 5. Раскраска
В принципе доказать &-выбираемость заданного графа труднее,
чем его &-раскрашиваемость; последнее свойство — лишь частный
случай, когда все списки равны {1,..., к}. Таким образом,
ch(G)>X(G) и cti(G)>X'(G)
для всех графов G.
Несмотря на эти неравенства многие из известных верхних
оценок для хроматического числа, оказывается, имеют место и для
числа выбираемости. Примерами этого явления служат предложение
5.2.2 (с тем же самым доказательством) и теорема Брукса. С другой
стороны, легко строятся графы, для которых эти два инварианта
сильно различаются (упражнение 25). Вместе взятые эти два факта
указывают, как далеки от точных могут быть общие верхние оценки
хроматического числа.
Следующая теорема показывает, что по своим связям с
другими инвариантами графа число выбираемости существенно
отличается от хроматического числа. Как уже упоминалось, существуют
2-хроматические графы произвольно большой минимальной степени,
например графы КП)П. Число выбираемости, однако, будет с
необходимостью возрастать при больших значениях инвариантов типа 6, е
или к.
Теорема 5 АЛ (Алон, 1993). Существует функция /: N —* N
такая, что для любого целого числа к все графы G со средней
степенью d(G) > f(k) удовлетворяют неравенству ch(G) > к.
Доказательство теоремы 5.4.1 использует вероятностный метод,
объясняемый в главе 11.
На практике иной характер числа выбираемости подчеркивается
еще одним явлением: даже в тех случаях, когда известные оценки
для хроматического числа удается перенести на число
выбираемости, их доказательства, как правило, существенно различаются.
Один из самых простых и наиболее впечатляющих примеров
тому — предписанная версия теоремы о пяти красках: каждый
плоский граф 5-выбираем. Предположение было известно почти 20 лет,
пока Томассен не нашел очень простого доказательства по индукции.
Это доказательство не использует теорему о пяти красках, которая
в результате получает принципиально новое доказательство.
Теорема 5А.2 (Томассен, 1994). Каждый плоский граф Ь-вы-
бираем.
Доказательство. Мы докажем следующее утверждение для
всех плоских графов G с не менее чем тремя вершинами.

5.4. Предписанная раскраска
125
Предположим, что каждая внутренняя грань графа G
ограничена треугольником, а его внешняя грань —
циклом С = vi .. .VkVi. Предположим далее, что v\
уже окрашена цветом 1, a v2 окрашена в 2. Предположим
наконец, что каждой из остальных вершин цикла С (*)
сопоставлен список из не менее чем 3 цветов, а каждой
вершине из G — С — список из 5 или более цветов.
Тогда раскраска вершин v\ и v2 может быть продолжена
до раскраски всего графа G из заданных списков.
Проверим сначала, что (*) влечет утверждение теоремы. Пусть
задан произвольный плоский граф вместе со списком из 5 цветов
для каждой вершины. Будем добавлять ребра к этому графу, пока
он не станет максимальным плоским графом G. Ввиду
предложения 4.2.6 G есть триангуляция плоскости; пусть 1/1U21/31/1 — граница
его внешней грани. Теперь окрашиваем v\ и v2 в разные цвета из их
списков и продолжаем эту раскраску согласно (*) до раскраски G из
заданных списков.
Докажем (*) индукцией по \G\. Если \G\ — 3, то G — С, и
утверждение тривиально. Пусть теперь \G\ > 4, и допустим, что (*) верно
для меньших графов. Если С имеет хорду vw, то vw лежит на двух
циклах С\,С2 С С + vw с v\v2 G С\ и v\v2 £ С2. Для г = 1,2
пусть G{ обозначает подграф в G, индуцированный вершинами,
находящимися на С{ или в его внутренней грани (рис. 5.4.1). Применяя
индукционное предположение сначала к Gi, а затем к G2 (с цветами,
предписанными v и w), получаем искомую раскраску графа G.
Рис. 5.4-1. Шаг индукции с хордой vw; здесь w — г>2

126
Глава 5. Раскраска
Если С не имеет хорд, пусть v\, иь ..., um, Vk-\ — соседи Vk в их
естественном циклическом порядке вокруг и*5); по определению
цикла С все соседи щ лежат во внутренней грани цикла С (рис. 5.4.2).
Рис. 5.4-2. Щаг индукции без хорды
Поскольку внутренние грани С ограничены треугольниками,
Р := viUi ... umVk-\ есть путь в G, а С := Р U (С — Vk) — цикл.
Теперь выбираем два различных цвета j, £ ф 1 из списка
вершины Vk и удаляем эти цвета из списков всех вершин щ. Тогда
каждый список вершин на С по-прежнему содержит не менее трех
цветов, так что по индукции можно раскрасить С и его внутреннюю
область, т. е. граф G — v^. По меньшей мере один из двух цветов
j, £ не используется на Vk-i, так что можно окрасить в него и*. D
Как часто случается в доказательствах по индукции, суть
приведенного только что доказательства — в изящно сбалансированном
усилении доказываемого утверждения. Заметим, что
доказательство не использует ни традиционных приемов раскраски (типа
двухцветной перекраски вершин вдоль пути), ни формулы Эйлера,
неявно присутствующей в стандартном доказательстве теоремы о пяти
красках. Это наталкивает на мысль, что и в других, нерешенных
задачах раскраски, возможно, имеет смысл попытаться доказать сразу
их предписанную версию, т. е. утверждение вида ch(G) < к вместо
формально более слабого х(^) < к. К сожалению, этот подход
терпит неудачу для теоремы о четырех красках: плоские графы в общем
случае не 4-выбираемы.
Как уже говорилось, хроматическое число графа и его числа вы-
бираемости могут сильно различаться. Удивительно, однако, что ни
одного такого примера не известно для раскраски ребер. Высказано
предположение, что их и не существует.
Гипотеза о предписанной раскраске ребер. Каждый граф
G имеет ch'(G) = X'(G).
') Как в первом доказательстве теоремы о пяти красках.

5.4. Предписание раскраска
127
Докажем гипотезу о предписанной раскраске ребер для случая
двудольных графов. В качестве инструмента будем использовать
ориентации графов, определенные в разделе 1.10. Если D —
ориентированный граф и v £ V(D), то обозначим через N+(v) множество,
а через d+(v) — число таких вершин w, что D содержит дугу,
ориентированную от v к w.
Чтобы увидеть, как ориентации начинают действовать в
контексте раскраски, вспомним жадный алгоритм из раздела 5.2. Чтобы
применить этот алгоритм к графу G, сначала нужно выбрать
вершинную нумерацию v\,..., vn графа G. Выбранная нумерация
определяет ориентацию графа G — просто ориентируем каждое ребро
V{Vj «в обратном направлении», т. е. от V{ к Vj, если г > j. Тогда
при окраске каждой вершины V{ алгоритм рассматривает только те
дуги при V{, которые исходят из V{\ если d+(v) < к для всех
вершин v, то будет использовано не более к цветов. Кроме того,
первый цветовой класс U, найденный алгоритмом, обладает следующим
свойством: он является независимым множеством вершин, в которое
из каждой остальной вершины ведет хотя бы одно ребро. Второй
цветовой класс имеет то же самое свойство в G — U и так далее.
Следующая лемма обобщает это на ориентации D графа G, которые
не обязательно получаются из вершинной нумерации и могут
содержать контуры. Назовем независимое множество U С V(D) ядром D,
если для каждой вершины v £ D — U имеется дуга в D, ведущая из v
в некоторую вершину из U. Заметим, что ядра непустых
ориентированных графов сами непусты.
Лемма 5.4.3. Пусть Я — граф, a (Sv )vev(H) — семейство
списков. Если Н допускает такую ориентацию D с d+(v) < \SV\ для
любой вершины v, что в каждом индуцированном подграфе графа D
есть ядро, то Н может быть раскрашен из списков Sv.
Доказательство. Применяем индукцию по |#|. При |#| = 0
берем пустую раскраску. Для шага индукции допустим, что \Н\ > 0.
Пусть a — цвет, встречающийся в каком-то из списков Sv, и пусть
D — подходящая ориентация в Я. Вершины v с a £ Sv заметывают
непустой подграф D' в D\ по предположению, D' имеет ядро U ф 0.
Раскрасим вершины в U цветом а и удалим а из списков всех
остальных вершин в D'. Так как каждая из этих вершин является
началом дуги, ведущей в U, измененные списки S'v для v £ D — U
снова удовлетворяют условию d+(v) < \S'V \ в D — U. Поскольку D — U
есть ориентация в Н — U, то можно раскрасить Н — U из новых
списков по индукционному предположению. Так как ни один из этих
списков не содержит а, полученная раскраска расширяет нашу
раскраску U —► {а} до требуемой предписанной раскраски всего Я. D
Теорема 5.4.4 (Галвин, 1995). Каждый двудольный граф G
имеет ch'(G) = X'(G).

128
Глава 5. Раскраска
Доказательство. Пусть G =: (X U У,Е), где {X,Y} —
вершинное 2-разбиение графа G. Будем говорить, что два ребра G
пересекаются в X, если они имеют общий конец в X, и соответственно
говорим об У. Пусть x'{G) = ' к, и пусть с есть реберная й-раскраска
графа G.
Ясно, что ch (G) > k\ докажем, что ch'(G) < А;. Наш план
состоит в том, чтобы с помощью леммы 5.4.3 показать, что реберный
граф Н графа G является fc-выбираемым. Чтобы применить лемму,
достаточно найти такую ориентацию D графа Я, что d+(v) < к для
каждой вершины v, а каждый индуцированный подграф в D имеет
ядро. Чтобы определить D, рассмотрим смежные ребра е, е' £ Е,
и пусть с(е) < с(е'). Если еие' пересекаются в X, мы ориентируем
ребро ее7 £ Н от е' к е; если еие7 пересекаются в У, мы ориентируем
его от е к е' (рис. 5.4.3).
1 \3 •
Рис. 5.4'3. Ориентация реберного графа графа G
Вычислим d+(e) для заданного е £ Е = V(D). Если, скажем,
с(е) = г, то каждое ребро е; £ N+(e), пересекающееся с е в X, имеет
цвет из {1,...,г— 1}, а каждое е' £ 7V+(e), пересекающееся с е в У,
имеет цвет из {г-fl, ...,&}. Поскольку любые два соседа е' ребра е,
пересекающиеся с е или оба в X, или оба в У, в свою очередь смежны
и, следовательно, раскрашены в разные цвета, это влечет d+(e) < к,
что и требовалось доказать.
Остается показать, что каждый индуцированный подграф D'
графа D имеет ядро. Покажем это индукцией по \D'\. При D' = 0
пустое множество есть ядро, поэтому пусть \D'\ > 1. Положим
Е' := V{D') С Е. Для каждой вершины х £ X, при которой Е'
имеет ребро, пусть ех £ Е' — ребро при х с минимальным цветом
в раскраске с, и пусть U обозначает множество всех таких ребер ег.
Тогда каждое ребро е' £ Е' \ U пересекается с некоторым е £ U
в X и дуга ее7 £ D' направлена от е' к е. Если U независимо, то
оно — ядро в D7, и требуемое доказано; поэтому допустим, что U не
является независимым.
Пусть е,е; £ U смежны, и допустим, что с(е) < с(е;). По
определению множества U ребра еие7 пересекаются в У, так что дуга

5.5. Совершенные графы
129
ее' £ D' направлена от е к е'. По индукционному предположению
D' — е имеет ядро U'. Если е' £ U'', то С/7 — также ядро в D\
и теорема доказана. Если нет, то существует такое е" £ [У7, что D'
имеет дугу, ориентированную из е' в е". Если е' и е" пересекаются
в X, то с(е") < с(е') по определению графа D вопреки тому, что
е' £ U. Следовательно, е1 и е" пересекаются в У и с(е') < с(е/;).
Поскольку еже1 пересекаются в У, то и е с е" пересекаются в У,
откуда с(е) < с{е') < с(е"). Значит, дуга ее" направлена из е в е",
и поэтому снова U' — ядро в D'. □
Ввиду предложения 5.3.1 мы теперь знаем предписанный
хроматический класс двудольных графов.
Следствие 5.4.5. Каждый двудольный граф G имеет ch'(G) =
A(G). □
5.5. Совершенные графы
Как уже говорилось в разделе 5.2, высокое хроматическое число
может выступать как чисто глобальное явление: даже когда граф
имеет большой обхват, а значит, локально напоминает дерево, его
хроматическое число может быть произвольно большим. Поскольку
с такой «глобальной зависимостью», очевидно, трудно иметь дело,
вызывают интерес графы, в которых такого явления не наблюдается,
т. е. хроматическое число которых велико, только когда для этого
есть локальная причина.
Прежде чем уточнить сказанное, введем два определения для
графа G. Наибольшее целое число г, при котором Кг С G,
называется плотностью u(G) графа G, а наибольшее целое число г, при
котором (индуцированный) Кг С G, называется числом
независимости ct(G) графа G. Ясно, что ct(G) = u(G) и u(G) = a(G).
Граф называется совершенным, если каждый индуцированный
подграф Н С G имеет хроматическое число х(Ю — и{Н), т. е. если
тривиальная нижняя оценка в ш{Н) цветов для раскраски вершин
графа Н достижима. Таким образом, в то время как доказательство
утверждения вида x{G) > & для данного графа G в общем случае
может быть трудным даже в принципе, для совершенного графа оно
сводится к установлению наличия подграфа Kk+l как единственной
причины нераскрашиваемости в к цветов.
На первый взгляд структура класса совершенных графов
кажется несколько надуманной: хотя он замкнут относительно
индуцированных подграфов (если пользоваться явным определением), он не
замкнут относительно взятия произвольных подграфов или надгра-
фов, не говоря уже о минорах (примеры?). Однако совершенность —
важное понятие в теории графов. Отчасти, указанием на это может

130
Глава 5. Раскраска
служить тот факт, что несколько фундаментальных классов графов
являются (как будто по счастливой случайности) совершенными6^.
Какие же графы являются совершенными? Например,
двудольные. Менее очевидно, что дополнения двудольных графов также
совершенны — факт, эквивалентный теореме 2.1.1 Кёнига о
двойственности (упражнение 34). Совершенны и так называемые графы
сравнимости, как и графы интервалов (см. упражнения); и те и
другие часто встречаются в приложениях.
Чтобы изучить хотя бы один такой пример более подробно,
докажем, что хордальные графы являются совершенными: граф хор-
дален (или триангулирован), если каждый из его циклов длины не
менее 4 имеет хорду, т. е. если граф не содержит индуцированных
циклов, отличных от треугольника.
Чтобы показать, что хордальные графы являются
совершенными, сначала изучим их строение. Если G — граф с
индуцированными подграфами G\, Gi и S такой, что G — G\ U Gi и S = G\ П Go,
мы говорим, что G получается из G\ и Gi склейкой этих графов
по S.
Предложение 5.5.1. Граф хордален, если и только если его
можно построить рекурсивно склейками по полным подграфам
начиная с полных графов. Q\fiu itilh
Доказательство. Если G получен от двух хордапьных
графов Gi, Go склейкой их по полному подграфу, то G, очевидно, снова
хордален: любой индуцированный цикл в G находится в ^каждом из
G\ и G2, а значит, является треугольником в соответствии с
предположением. Так как полные графы хордальны, это доказывает, что
все графы, построенные такими склейками, хордальны.
Обратно, пусть граф G хордален. Покажем индукцией по |G|,
что G может быть построен, как описано выше. Это очевидно,
если G полон. Поэтому предположим, что G неполон, в частности
\G\ > 1, и что все меньшие хордальные графы получаются такими
склейками. Пусть a,b £ G — две несмежные вершины, и пусть
X С V(G)\ {а, 6} есть минимальное множество вершин, отделяющее
а от 6. Пусть С обозначает компоненту в G — X, содержащую а;
положим G\ := G[V(C) U X] и Gi := G - G. Тогда G является
результатом склейки G\ и Gi по S := G[X].
Поскольку G\ и Gi являются оба хордальными (как
индуцированные подграфы графа G) и, следовательно, конструируемы по
индукционному предположению, достаточно показать, что граф S
полон. Предположим, что s,t £ S несмежны. Из-за минимальности
6) Класс совершенных графов обладает свойствами двойственности, глубоко
связанными с оптимизацией и теорией сложности и еще далеко не до конца
понятыми. Теорема 5.5.5 показывает лишь верхушку айсберга; за
дальнейшим отсылаем читателя к обзору Ловаса, цитируемому в примечаниях.

5.5. Совершенные графы
131
X = V(S) как a-b разделителя s и t имеют по соседу в С.
Следовательно, имеется Х-путь из s в t в G\\ пусть Р\ — самый короткий из
таких путей. Аналогично, G2 содержит самый короткий Х-путь Р^
из s в I. Но тогда Р\ U Р2 — цикл без хорд длины > 4 (рис. 5.5.1)
вопреки предположению, что G является хордальным. □
Рис. 5.5.1. Если G\ и G2 хордальны, то хордален и G
Предложение 5.5.2. Каждый хордальный граф является
совершенным.
Доказательство. Так как полные графы совершенны,
достаточно ввиду предложения 5.5.1 показать, что любой граф G,
полученный из совершенных графов G\, G2 склейкой их по полному
подграфу 5, снова совершенен. Итак, пусть Я С G — индуцированный
подграф; покажем, что х{Н) < и(Н)-
Пусть Н{ := НГ\ d при г = 1, 2, и пусть Т := Я П S. Тогда Т
снова полон, а Н является результатом склейки Н\ и if2 по Т. Как
индуцированный подграф графа G,- каждый Я,- может быть окрашен
в и(Н{) цветов. Поскольку Т полон и, следовательно, раскрашен
инъективно, раскраски графов Hi и Яг можно объединить в
раскраску графа Я в тах{о;(Я1),а;(Я2)} < ^(Я) цветов, при
необходимости меняя цвета в одном из Яг-. D
Мы подходим к основному результату в теории совершенных
графов— теореме о совершенных графах.
Теорема 5.5.3 (Ловас, 1972). Граф является совершенным,
если и только если его дополнение совершенно.
Мы дадим два доказательства теоремы 5.5.3. Первое из них —
исходное доказательство Ловаса, которое является по-прежнему
непревзойденным по своей ясности и «ощущению» задачи, которое оно
передает. Наше второе доказательство, принадлежащее Гаспаряну
(1996), фактически является очень коротким и изящным линейно-
алгебраическим доказательством другой теоремы Ловаса (теорема
5.5.5), из которой легко следует теорема 5.5.3.
Предварим наше первое доказательство теоремы о совершенных
графах леммой. Пусть G — граф, а х £ G — вершина, и пусть

132
Глава 5. Раскраска
С получается из G добавлением вершины х' и соединением ее с ж
и всеми соседями вершины х. Мы говорим, что G получен из G
расширением вершины х до ребра хх' (рис. 5.5.2).
Рис. 5.5.2. Расширение вершины х в доказательстве леммы 5.5.4
Лемма 5.5.4. Любой граф, полученный из совершенного графа
расширением вершины, также совершенен.
Доказательство. Проведем индукцию по числу вершин
рассматриваемого совершенного графа. Расширение вершины в К1
дает полный граф К2, который является совершенным. На шаге
индукции пусть G — нетривиальный совершенный граф, и пусть G'
получен из G расширением вершины х £ G до ребра хх'. Для
доказательства того, что G' является совершенным, достаточно
доказать неравенство x(G') < w(G'): каждый собственный
индуцированный подграф Н графа G' или изоморфен индуцированному подграфу
графа G, или получен из собственного индуцированного подграфа
графа G расширением вершины х. В любом случае граф Н
совершенен по индукционному предположению и может, следовательно,
быть окрашен в и{Н) цветов.
Пусть u(G) =: ш\ тогда u(G') £ {и, и -f 1}. Если u(G') — и -f 1,
то
X(G') < x(G) + 1 = ш + 1 = w(G'),
и мы уже имеем требуемое. Поэтому предположим, что w(G;) = ш.
Тогда х не лежит ни в одном из Ки С G: вместе с х' это дало бы
Кш+1 в G'. Раскрашиваем G в ш цветов. Так как каждый Кш С G
пересекает цветовой класс X вершины х, но не саму х, граф Н :=
G — (X \ {х}) имеет плотность ш(Н) < ш (рис. 5.5.2). Поскольку
G совершенен, можно, таким образом, раскрасить Н в и — 1 цветов.
Теперь X независимо, так что множество (Х\{ж})и{ж/} = V(G' — H)
также независимо. Поэтому можно продолжить (и — 1)-раскраску
графа Н до w-раскраски всего G7, откуда x(G') < ^ — w(G;), что
и требовалось. D
Доказательство теоремы 5.5.3. Индукцией по \G\ покажем,
что дополнение G любого совершенного графа G — (V, Е) снова
совершенно. Для \G\ — 1 это очевидно, так что пусть \G\ > 2 для шага

5.5. Совершенные графы
133
индукции. Пусть <Ж обозначает множество всех множеств вершин
полных подграфов из G. Положим a(G) =: а, и пусть я/ —
множество всех независимых множеств вершин А в G с \А\ — а.
Каждый собственный индуцированный подграф G есть
дополнение собственного индуцированного подграфа в G и, следовательно,
совершенен по индукции. Для доказательства совершенности G
достаточно доказать, что x{G) < w(G) (= а). Для этого найдем такое
множество К £ ЛГ, что К С\ Аф 0 для всех А £ £?. Тогда
u(G -K) = a(G-K)<a = w(G),
поэтому по индукционному предположению
X(G) <X(G-K) + l = w(G-K) + l< u(G),
что и требуется доказать.
Предположим, что такого К нет; иначе говоря, для каждого
К £ <Ж существует множество Ак £ £? с К Г\Ак — 0- Заменим в G
каждую вершину х полным графом Gx порядка
k(z) := \{К е JT \ х е Ак}\,
соединяя все вершины из Gx со всеми вершинами из Gy всякий раз,
когда х и у смежны в G. Граф G', полученный таким образом, имеет
множество вершин (J V(GX), и две вершины v £ Gx и w £ Gy
смежны в G', если и только если х — у или ху £ Е. Кроме того,
G' может быть получен из графа G[{x £ V \ к(х) > 0}]
вершинными расширениями. Будучи индуцированным подграфом графа G
этот граф совершенен по предположению, так что G' совершенен по
лемме 5.5.4. В частности,
X(G')<u(G'). (1)
Чтобы получить противоречие с (1), вычислим теперь w(G')
и x(G')- По построению G1 каждый максимальный полный подграф
в G' имеет вид G'
U G.
Lxex
ствует такое множество X £ J*T, что
для некоторого X £ JT. Поэтому суще-
= \{(х,к):хех,Ке^,хеАК}\
= J2 \ХПАК\
< \x\-\.

134
Глава 5. Раскраска
Последнее неравенство следует из того, что \Х П Ак\ < 1 для всех К
(так как Ак независимо, a G[X] является полным) и \Х П Ах\ — О
(по выбору Ах)- С другой стороны,
\G'\ = 4£k(x)
xev
= \{(х,к)-.хе v, келс,хеАк}\
= £ i^i
= \Jtr\-ct.
Так как a(G') <апо построению G', это влечет соотношения
Х(С) > Jgjr > ^ = МП- (3)
а(Сг) а
Сопоставляя (2) и (3), получаем
x(G') > |Jf| > |Jf| - 1 > w(G');
противоречие с (1). □
Так как следующая характеристика совершенности
симметрична относительно G и G, она с очевидностью влечет теорему 5.5.3.
Поскольку наше доказательство теоремы 5.5.5 будет строиться на
первичных понятиях, мы тем самым получим второе и независимое
доказательство теоремы о совершенных графах.
Теорема 5.5.5 (Ловас, 1972). Граф G является совершенным,
если и только если
\H\<a(H)-u(H) (*)
для всех индуцированных подграфов Н С G.
Доказательство. Обозначим V(G) =: V =: {vi,...,vn} и
положим a := ct(G) и и :— w(G). Необходимость (*) очевидна: если
G совершенен, то каждый индуцированный подграф Н графа G
может быть разбит на не более чем и{Н) цветовых классов, каждый из
которых содержит не более а(#) вершин, откуда и следует (*).
Чтобы доказать достаточность, применяем индукцию по п —
\G\. Предположим, что каждый индуцированный подграф Н графа G
удовлетворяет (*), но G не совершенен. По индукционному
предположению каждый собственный индуцированный подграф G
совершенен. Следовательно, каждое непустое независимое множество U С V
удовлетворяет условию
x(G-U)=u(G-U)=u. (1)

5.5. Совершенные графы
135
Действительно, первое равенство сразу следует из
совершенности G — U, а второе доказывается тоже просто: неравенство <
очевидно, a x(G — U) < w влекло бы x(G) < и> так что G был бы
совершенен вопреки нашему предположению.
Применим (1) к одноэлементному множеству U — {и} и
рассмотрим w-раскраску графа G — и. Пусть К — вершинное множество
какого-либо полного графа Кш в G. Ясно, что
если и £ К, то К пересекается с каждым , .
цветовым классом графа G — щ ^
если и £ К, то К пересекается со всеми, кроме ,~.
ровно одного, цветового класса в G — u. ^
Пусть Ао — {щ,..., иа} — независимое множество в G
порядка а. Пусть А\,..., Аш — цветовые классы некоторой w-раскраски
графа G — щ, и пусть Аы+1, • • •, А^и — цветовые классы w-раскраски
графа G — U2 и так далее; вместе это дает aw -f 1 независимых
множеств Ао, А\,..., Ааи) в G. Для каждого г = 0,..., аи ввиду (1)
существует Кш С G — А{; обозначим его множество вершин через К{.
Заметим, что если К есть множество вершин любого Кш в G,
то
К П А{ = 0 для ровно одного i £ {0,..., aw -f 1}. (4)
Действительно, если К П Ао = 0, то К П А{ ф 0 для всех г ф О
по определению А{ и по условию (2). Аналогично, если К Г\ Аоф0,
то |# П Ао| = 1, поэтому К (Л А{ — 0 для ровно одного г ф 0.
Применим (3) к единственной вершине и £ К П Ао, а (2) — ко всем
остальным вершинам и £ Ао.
Пусть J — вещественная (aw -f 1) х (aw -f 1) матрица с
нулевыми элементами на главной диагонали и всеми остальными
элементами, равными 1. Пусть А — вещественная (aw -f 1) х п матрица,
строки которой суть векторы инцидентности подмножеств А{ С V.
Если ац,..., din — элементы г-й строки в А, то аг-;- = 1 при Vj £ А{
и dij = 0 в противном случае. Аналогично, пусть В — вещественная
п х (aw -f 1) матрица, столбцы которой суть векторы инцидентности
подмножеств i£t- С V. Теперь, хотя \К{ П А{\ = 0 для всех г по
выбору #г-, имеем К{ C)Aj ф 0, а следовательно, ввиду (4) |А,- C)Aj\ = 1
для любых i ф j. Таким образом,
AB = J.
Так как J неособая, это влечет, что А имеет ранг aw -f 1. В
частности, n > aw -f 1, что противоречит (*) для Н := G. □
По определению, каждый индуцированный подграф
совершенного графа снова совершенен. Свойство совершенности поэтому
может быть охарактеризовано запрещенными индуцированными
подграфами: существует такое множество Jf несовершенных графов,

136 Глава 5. Раскраска
что любой граф является совершенным, если и только если он не
имеет индуцированного подграфа, изоморфного элементу из Ж.
(Например, можем взять в качестве Ж множество всех несовершенных
графов с вершинами из N.)
Естественно, было бы желательно иметь как можно меньшее Ж.
Одна из наиболее известных гипотез в теории графов говорит, что
Ж содержит всего два типа графов: нечетные циклы длины > 5 и их
дополнения. (Ни один из них не совершенен (почему?).) Или, слегка
перефразируя:
Гипотеза о совершенных графах (Берж, 1966). Граф G
является совершенным, если и только если ни G, ни G не содержат
в качестве индуцированного подграфа нечетного цикла длины не
менее 5.
Ясно, что данная гипотеза влечет теорему о совершенных
графах. На самом деле эта теорема также предполагалась Бержем: до
своего доказательства она была известна как «слабая» версия
гипотезы о совершенных графах, а вышеупомянутая гипотеза
представляла собой «сильную» версию.
Графы G, для которых ни G, ни G не содержат индуцированного
нечетного цикла длины не менее 5, называются графами Бержа.
Таким образом, все совершенные графы являются графами Бержа, а
гипотеза о совершенных графах состоит в том, что все графы Бержа
совершенны. Она была «приближенно» проверена Премелем и Ште-
гер (1992), которые доказали, что отношение числа совершенных
графов к числу графов Бержа на п вершинах стремится к единице
при п —+ оо.
Упражнения
1.~ Показать, что теорема о четырех красках действительно решает задачу
раскраски карты, сформулированную в первом предложении этой главы.
Обратно, влечет ли 4-раскрашиваемость каждой карты теорему о четырех
красках?
2.~ Показать, что в предыдущей задаче раскраски карт достаточно
рассмотреть такие карты, где никакая вершина не находится на границе более чем
трех стран. Как это влияет на доказательство теоремы о четырех красках?
3. Попробуйте превратить доказательство теоремы о пяти красках в
доказательство теоремы о четырех красках следующим образом. Определяя v и Н,
как и раньше, предположите индуктивно, что Н имеет 4-раскраску, и идите
по тексту. Где доказательство терпит неудачу?
4. Вычислить хроматическое число графа в терминах хроматических чисел
его блоков.
5.~ Показать, что каждый граф G имеет упорядочение вершин, при котором
жадный алгоритм использует всего лишь x(G) цветов.
6. Для каждого п > 1 найдите двудольный граф с 2п вершинами,
упорядоченными таким образом, что жадный алгоритм использует п цветов вместо
двух.

Упражнения 137
7. Рассмотрим следующий подход к вершинной раскраске. Сначала находим
максимальное независимое множество вершин и раскрашиваем их в цвет 1,
затем находим максимальное независимое множество вершин в оставшемся
графе и раскрашиваем их в 2 и так далее. Сравните этот алгоритм с
жадным алгоритмом: какой из них лучше?
8. Показать, что оценка в предложении 5.2.2 никогда не хуже, чем в
предложении 5.2.1.
9. Найти такую функцию /, что каждый граф древесности не менее f(k) имеет
раскрасочное число не менее к и такую функцию д, что каждый граф с рас-
к'расочным числом не менее д(к) имеет древесность не менее к при всех
к Е N. (Древесность графа определена в разделе 3.5.)
10.~ Ar-Хроматический граф называется критическим k-хроматическим или
просто критическим, если x(G — v) < к для каждого v Е V{G). Показать,
что всякий Аг-хроматический граф содержит критический Аг-хроматический
индуцированный подграф и что любой такой подграф имеет минимальную
степень не менее к — 1.
11. Описать все критические 3-хроматические графы.
12.+ Показать, что каждый критический Аг-хроматический граф (к — 1)-реберно-
связен.
13. Для любого к Е N найти такую константу с^ > 0, что каждый граф G
с \G\ > ЗА; и cx(G) < к содержит цикл длины не менее c/j|G|.
14. ~ Найти граф G, для которого теорема Брукса дает значительно более слабую
оценку для x(G), чем предложение 5.2.2.
15.+ Показать, что при доказательстве теоремы Брукса для графа G = (V,E)
можно считать, что «(G) > 2 и A(G) > 3. Доказать теорему при этих
предположениях, доказав сначала следующие две леммы.
(i) Пусть v\,..., Vn — нумерация множества V. Если каждая vi (г < п)
имеет соседа Vj с j > г и если v\vn,V2Vn Е Е, но v\ г>2 i Е, то жадный
алгоритм использует не более A(G) цветов.
(ii) Если G не полон и vn имеет максимальную степень в G, то vn смежна
с vi, г>2, как в (i).
16. Для графа G и числа к Е N обозначим через Pg(^) число вершинных
раскрасок V(G) —» {!,..., к}. Показать, что Pq есть многочлен от к
степени n := \G\, в котором коэффициент при кп равен единице, а
коэффициент при кп~1 равен —||G||. (Pq называется хроматическим многочленом
графа G.)
(Подсказка. Примените индукцию по ||G||. На шаге индукции сравните
значения PG(^)> PG-e(k) и PGfe(k).)
17.+ Определить класс всех графов G, для которых Ро{к) = к(к — l)n_1. (Как
и в предыдущем упражнении, n := |G|, a Pq — хроматический многочлен
графа G.)
18. В определении /с-конструируемых графов замените аксиому (ii) на:
(ii); Каждый надграф к-конструируемого графа также к-конструируем\
а аксиому (iii) — на:
(iii); Если G — такой граф с вершинами х, у\, у2, что у\У2 Е E(G), но
ХУ\,ХУ2 £ E(G), и если G + ху\ и G + ху2 k-конструируемые, то G
также к-конструируем.
Показать, что граф является /^-конструируемым относительно этого нового
определения, если и только если его хроматическое число не менее к.

138 Глава 5. Раскраска
19.~ Матрица п X п с элементами из {1,..., N} называется латинским
квадратом, если каждый элемент {1,..., п} встречается ровно один раз в каждом
столбце и в каждой строке. Сформулировать проблему построения
латинских квадратов как задачу раскраски.
20. Не пользуясь предложением 5.3.1, показать, что x'{G) = ^ для каждого
/г-однородного двудольного графа G.
21. Вывести предложение 5.3.1 из формулировки предыдущего упражнения.
22."*" Для каждого k Е N построить /:-хроматический граф без треугольников.
23." Не пользуясь теоремой 5.4.2, показать, что каждый плоский граф
предписание 6-раскрашиваем.
24. Для каждого целого к найти 2-хроматический граф с числом выбора не
менее к.
25." Найти общую верхнюю оценку для ch'(G) через x'(G).
26. Сравнить число выбираемости графа с его раскрасочным числом: какое из
них больше? Можно ли доказать аналог теоремы 5.4.1 для раскрасочного
числа?
27.+ Доказать, что число выбора графа A'J равно г.
28. Тотальное хроматическое число x"(G) графа G — (V,Е) есть
наименьшее количество цветов, необходимое для такой раскраски вершин и ребер
графа G, чтобы любые смежные или инцидентные элементы из V U Е были
окрашены по-разному. Гипотеза о тотальной раскраске утверждает, что
x"(G) < A(G) -f 2. Оценить тотальное хроматическое число сверху в
терминах предписанного хроматического класса и с помощью этого вывести
ослабление гипотезы о тотальной раскраске из гипотезы о предписанной
раскраске ребер.
29." Найти ориентированный граф, не имеющий ядра.
30.+ Доказать теорему Ричардсона: каждый ориентированный граф без
нечетных контуров имеет ядро.
31. Показать, что каждый двудольный плоский граф предписанно 3-раскраши-
ваем.
(Подсказка. Примените предыдущее упражнение и лемму 5.4.3.)
32." Показать, что совершенность не замкнута ни по удалению, ни по
стягиванию ребра.
33."~ Вывести теорему 5.5.5 из гипотезы о совершенных графах.
34. С помощью теоремы Кёнига 2.1.1 показать, что дополнение любого
двудольного графа совершенно.
35. Используя результаты этой главы, найти доказательство в одну строчку
следующей теоремы Кёнига, двойственной к теореме 2.1.1: в любом
двудольном графе без изолированных вершин минимальное число ребер,
покрывающих все вершины, равняется максимальному числу независимых
вершин.
36. Граф называется графом сравнимости, если существует такое частичное
упорядочение его вершин, что две вершины смежны, если и только если они
сравнимы. Показать, что каждый граф сравнимости совершенен.
37. Граф G называется графом интервалов, если существует такое множество
{Iv | у Е ^(^)} вещественных интервалов, что 1и П /„ ф 0, если и только
если uv Е E(G).

Примечания 139
(i) Показать, что каждый граф интервалов хордален.
(ii) Показать, что дополнение любого графа интервалов есть граф
сравнимости.
(Обратно, по теореме Гилмора и Хофмана (1964) хордальный граф будет
графом интервалов, если его дополнение — граф сравнимости.)
38. Показать, что х{Н) Е {ш(Н),и>(Н) -f- 1} для каждого реберного графа Н.
39.+ Охарактеризовать графы, реберные графы которых совершенны.
40. Показать, что граф G совершенен, если и только если каждый непустой
индуцированный подграф Н в G содержит такое независимое множество
А С V{H), что ш(Н - А) < ш(Н).
41.+ Рассмотрите графы G, в которых каждый индуцированный подграф Н
обладает тем свойством, что каждый максимальный полный подграф Н
пересекает каждое максимальное независимое вершинное множество в Н.
(i) Показать, что такие графы G совершенны.
(ii) Показать, что эти графы G суть графы, не содержащие
индуцированной копии Р3.
42.+ Показать, что в каждом совершенном графе G можно найти такое
множество £/ независимых множеств вершин и такое множество б множеств
вершин полных подграфов, что [J&f = V(G) = [J б и каждое множество
из £? пересекает каждое множество из б'.
(Подсказка. Лемма 5.5.4.)
43.+ Пусть G — совершенный граф. Как в доказательстве теоремы 5.5.3,
заменим каждую вершину х из G на совершенный граф Gx (не обязательно
полный). Показать, что получившийся граф G' также совершенен.
44. Пусть Ж\ и 3%2 суть два множества несовершенных графов и каждое
минимально с тем свойством, что граф совершенен, если и только если он не
имеет индуцированного подграфа в Ж% (г = 1,2). Верно ли, что Ж\ и Жъ
содержат одни и те же графы с точностью до изоморфизма?
Примечания
Авторитетным справочником по всем вопросам раскраски графа является
книга: Jensen Т. R., Toft В. Graph Colouring Problems. N. Y.: John Wiley &;
Sons, 1995. Начинаясь с краткого обзора наиболее важных результатов и
областей исследования по этой тематике, данная монография содержит детальный
обзор более чем 200 нерешенных задач раскраски вместе с обширным обзором
связанного с ними материала и многочисленными ссылками. Большинство
приведенных ниже замечаний подробно обсуждается в этой книге, и в ней можно
также найти все ссылки по этой главе.
Проблема четырех красок — может ли каждая карта быть окрашена в
четыре цвета так, чтобы смежные страны имели различные цвета — была
поставлена неким Франсисом Гатри в 1852 г. Он задал этот вопрос своему брату
Фредерику, в то время студенту-математику в Кембридже. Проблема была впервые
предложена вниманию общественности в выступлении Кэли на заседании
Лондонского математического общества в 1878 г. Годом позже Кемпе опубликовал
неправильное доказательство, которое было в 1890 г. переделано Хиву дом в
доказательство теоремы о пяти красках. В 1880 г. Тейт анонсировал «дальнейшие
доказательства» гипотезы четырех красок, которые так и остались нематериа-
лизованными; см. примечания к главе 10.

140 Глава 5. Раскраска
Первое общепризнанное доказательство теоремы о четырех красках было
опубликовано Аппелем и Хакеном в 1977 г. Доказательство основано на идеях,
восходящих еще к статье Кемпе и далеко продвинутых Биркгофом и Хеешем.
Говоря очень приблизительно, доказательство сводится, во-первых, к
утверждению, что каждая триангуляция плоскости должна содержать по крайней мере
одну из 1482 «неизбежных конфигураций». На втором этапе с помощью
компьютера показывается, что каждая из этих конфигураций «сводима», т. е. что
любая плоская триангуляция, содержащая такую конфигурацию, может быть
4-раскрашена, исходя из 4-раскрасок меньших триангуляции. Вместе взятые эти
два шага составляют индуктивное доказательство того, что все плоские
триангуляции, а следовательно, и все плоские графы можно раскрасить в четыре
цвета.
Доказательство Аппеля и Хакена не было обойдено критикой, и не только
из-за использования ими компьютера. Авторы ответили 741-страничной
алгоритмической версией доказательства, которая учитывает различные
критические замечания и исправляет множество ошибок (например, ими добавлено ещё
несколько конфЕЕгурапий к «неизбежному» списку): Appel К., Haken W. Every
Planar Map is Four Colorable. Providence: Amer. Math. Soc, 1989.
(Contemporary Mathematics; 98). Гораздо более короткое доказательство, которое основано
на тех же идеях (и, в частности, использует компьютер таким же образом), но
более доступно проверке как в текстовой, так и в компьютерной части, дано
в статье: Robertson N., Sanders D., Seymour P. D., Thomas R. The four-colour
theorem // J. Combin. Theory. Ser. B. 1997. 70. P. 2-44.
Относительно короткое доказательство теоремы Грешна было получено
в работе: Thomassen С. Grotzsch's 3-color theorem and its counterparts for the
torus and the projective plane // J. Combin. Theory. Ser. B. 1994. 62. P. 268-279.
Хотя задачи раскраски для графов, вложенных в поверхности, отличные от
плоскости, и не затрагиваются в этой главе, они составляют существенную и
интересную часть теории раскраски; см.: Mohar В., Thomassen С. Graphs on Surfaces.
Baltimore: Johns Hopkins Univ. Press, 2001.
Доказательство теоремы Брукса, приводимое в упражнении 15, где жадный
алгоритм применяется к тщательно выбранному упорядочению вершин,
принадлежит Ловасу (1973). Также Ловас (1968) впервые построил графы с
произвольно большими обхватом и хроматическим числом; существование таких
графов доказал вероятностным методом Эрдеш десятью годами раньше.
Эркхарт в статье: The graph constructions of Hajos and Ore // J. Graph
Theory^ 1997. 26. P. 211-215 — показал, что графы с хроматическим числом не
менее к не только содержат /^-конструируемый граф (как следует из теоремы
Хайоша), но и сами /г-конструируемы. Алгебраические средства для
доказательства того, что хроматическое число графа велико, были разработаны Клейтма-
ном и Ловасом (1982), а также А лоном и Тарси (1992); см. цитируемую ниже
статью Алона.
Предписанная раскраска была впервые введена в 1976 г. Визингом. Среди
прочего Визинг доказал обобщение теоремы Брукса на случай предписанной
раскраски. Маргит Фогт (1993) построила плоский граф порядка 238, который не
является 4-выбираемым; таким образом, принадлежащая Томассену
предписанная версия теоремы о пяти красках неулучшаема. Стимулирующий обзор по
предписанному хроматическому числу и его связям с более известными
инвариантами графа (включая доказательство теоремы 5.4.1) дается в статье: A Ion N.
Restricted colorings of graphs // Surveys in Combinatorics / Ed. by K. Walker.
Cambridge: Univ. Press, 1993. (London Math. Soc. Lecture Notes; 187). И
гипотеза о предписанной раскраске, и принадлежащее Галвину доказательство ее
двудольного частного случая первоначально формулировались для мультигра-
фов. Кан (1994) доказал, что гипотеза асимптотически правильна в следующем
смысле: для любого е > 0 каждый граф G с достаточно большой максимальной
степенью имеет ch'(G) < (1 -f- б)^(^)«
Гипотеза о тотальной раскраске была предложена примерно в 1965 году
Визингом и Бехзадом; подробности см. в книге Т. Иенсена и Б. Тофта.

Примечания
141
Доступное введение в основные факты относительно совершенных графов
и их приложений дается в книге: Gohmbic М. С. Algorithmic Graph Theory and
Perfect Graphs. N. Y.: Acad. Press, 1980. Наше первое доказательство теоремы
о совершенных графах следует обзору Л. Ловаса в книге: Selected Topics in Graph
Theory 2 I Ed. by L. W. Beineke, R. J. Wilson. London; New York: Acad. Press,
1983. Теорема была также доказана независимо и лишь немного позже Фал-
керсоном. Наше второе доказательство теоремы 5.5.5 заимствовано из статьи:
Gasparian G. S. Minimal imperfect graphs: a simple approach // Combinatorica.
1996. 16. P. 209-212. «Приближенное» доказательство гипотезы о
совершенных графах дано в статье: Prom el Н. J., Sieger A. Almost all Berge graphs are
perfect // Combin. Probab. Comput. 1992. 1. P. 53-79.

Глава 6
Потоки
Будем рассматривать граф как сеть: его ребра несут некоторый
поток — воды, электричества, данных и т. п. Как смоделировать эту
ситуацию в точных терминах?
Для начала мы должны знать, какое количество потока
проходит через каждое ребро е — ху и в каком направлении. В нашей
модели мы можем приписать паре (х,у) целое положительное
число к, выражая этим, что поток в к единиц проходит через е от х
к у, или приписать —к ребру (х,у), выражая этим, что к единиц
потока проходят через е в обратном направлении от у к х. Для такого
предписания /: V2 —» Ъ имеем f(x,y) — —f(y,x) всякий раз, когда
х и у — смежные вершины из G.
Как правило, сеть будет иметь только несколько узлов, где
поток входит или покидает ее; для всех других узлов сумма входящих
потоков равняется сумме выходящих. Для нашей модели это
означает, что в большинстве узлов х функция / удовлетворит закону
Кирхгофа
£ /(*,») = о.
y£N(x)
В этой главе будем называть любое отображение f:V2 —► %
с вышеупомянутыми двумя свойствами «потоком» на G. Иногда мы
будем заменять 7L другой группой, и, как правило, мы
рассматриваем мультиграфы вместо графов1). Оказывается, что теория таких
«потоков» не только полезна как модель для реальных потоков, но
и прекрасно взаимодействует с другими частями теории графов,
обнаруживая ряд глубоких и удивительных связей с ними, особенно
с задачами о связности и о раскрасках.
) Чтобы быть последовательными, мы будем формулировать некоторые
утверждения только для графов, а именно, те, доказательства которых опи*
раются на факты, ранее доказанные (для графов) в книге. Однако все эти
результаты верны и для мультиграфов.

6.1. Циркуляции
143
6.1. Циркуляции
В контексте потоков мы должны иметь возможность говорить
о «направлении» ребра. Поскольку в мультиграфе G — (V, Е) ребро
е = ху не определяется однозначно парой (ж, у) или (у, ж), определим
ориентированные ребра как тройки:
Ё := {(е, x,y)\eeE;x,yeV; е = ху}.
Таким образом, ребро е — ху с х ф у имеет два направления (е, х, у)
и (е,у, ж); петля е — хх имеет только одно направление — тройку
(е, х, х). Для заданного е = (е, х,у) £ Е полагаем е := (Е, у, х), а для
произвольного множества F С Е мы полагаем
F := {е | ё*£ F}.
Заметим, что само Е симметрично: Е — Е. Для X,Y С V и F С Е
определяем
F(X, У) := {(£, *, у) € F | * € X; у € У; * ^ у},
сокращаем F({x}, У) до F(x, У) и т. д. и полагаем
F(x):=F(x,K) = F({x},{7}).
Здесь, как и ниже, X обозначает дополнение V \ X множества
вершин X С V. Заметим, что любые петли при вершинах х £ X П У
в определениях множеств F(X, У) и F(x) игнорируются.
Пусть Н — абелева полугруппа2), записанная аддитивно с
нулем 0. При заданных множествах вершин X, У С V и функции
/': Е —► Я полагаем
ДХ,У):= £ Ле").
еб^(Х.У)
Вместо /({ж}, У) мы опять пишем f(x, У) и т. д.
Далее предполагается, что if — группа. Назовем / циркуляцией
на G (со значениями в if) или Н-циркуляцией, если для /
выполняются следующие два условия:
(F1) /(е, ж, у) = -/(е, у, ж) для всех (е, х, у) £ £ с х ф у;
(F2) f(v, V) = 0 для всех и £ К.
2) В этой главе теория групп почти не затрагивается. Единственные
полугруппы, которые мы будем рассматривать для Н — это натуральные
числа, целые числа, вещественные числа, циклические группы 7L^ и (в одном
месте) четверная группа Клейна.

144
Глава 6. Потоки
Если / удовлетворяет (F1), то
f(X,X) = 0
для всех X С V. Если / удовлетворяет (F2), то
f(X,V)=^f(x,V) = 0.
Вместе эти два основных наблюдения показывают, что в циркуляции
суммарный поток через любой разрез равен нулю.
Предложение 6.1.1. Если f — циркуляция, то f(X,X) — О
для каждого множества X С V.
Доказательство. f(X, X) = f(X, V) - f(X} X) = 0 - 0 = 0. □
Поскольку мосты являются разрезами, предложение 6.1.1
влечет, что циркуляция через мост всегда равна нулю.
Следствие 6.1.2. Если f — циркуляция, а е — ху — мост в G,
то /(е, х, у) — 0. □
6.2. Потоки в сетях
Здесь мы даем краткое введение в ту часть теории потоков в
сетях, которая является теперь стандартной методикой доказательства
в таких областях, как паросочетания и связность. Для примера мы
докажем классический результат этой теории — так называемую
теорему Форда и Фалкерсона о максимальном потоке и
минимальном разрезе. Из данной теоремы без труда следует теорема Мен-
гера (упражнение 3), что отчасти указывает на мощь, заключенную
в данном подходе.
Рассмотрим задачу моделирования сети с одним источником s
и одним стоком t, в которой количество потока через данную связь
между двумя узлами ограничено некоторой пропускной
способностью этой связи. Наша цель состоит в том, чтобы определить
максимальное количество потока через сеть, идущего из s в t.
Оказывается, что ответ зависит и от строения сети, и от пропускных
способностей ее связей, а как именно — мы и хотим выяснить.
Пусть G — (V,E) — мультиграф, s,t £ V — две выделенные
вершины, а с: Е —> N — функция; назовем с функцией пропускной
способности на G, а кортеж N := (G,s,t,c) — сетью. Заметим,
что с определена независимо для двух направлений ребра. Функция
/: Е —> Ж есть поток в N, если она удовлетворяет следующим трем
условиям (рис. 6.2.1):

6.2. Потоки в сетях
145
(F1) /(е, х, у) - -/(е, у, х) для всех (е, х, у) £ Я с х ф у\
(F2') f(v,V) = 0 для всех veV\{s,t};
(F3) /(e) < с(е) для всех ее Ё.
Назовем поток / целочисленным, если все его значения являются
целыми числами.
Рис. 6.2.1. Сетевой поток в краткой системе обозначений;
все значения относятся к указанному направлению
(пропускные способности не показаны)
Пусть / — поток в N. Если S С V таково, что s £ S и t £ 5,
то назовем пару (5, 5) разрезом в N, а с(5, 5) — пропускной
способностью этого разреза.
Поскольку / теперь должно удовлетворять только (F27), а не
(F2), то равенство f(X,X) = 0 уже не выполняется для всех 1С К
(как в предложении 6.1.1). Однако это значение неизменно для всех
разрезов.
Предложение 6.2.1. Любой разрез (S,S) в N удовлетворяет
равенству /(5, S) - /(s, V).
Доказательство. Как и в доказательстве предложения 6.1.1,
имеем
f{S,S) = /(S,V)-f(S,S)
ves\{s}
- f(s,V). П
(F2')
Общее значение f(S,S) в предложении 6.2.1 называется величиной
потока f и обозначается через |/|3^. Поток, показанный на рис. 6.2.1,
имеет величину 3.
Из (F3) имеем
\f\ = f(S,S)<c(S,S)
3) Таким образом, формально |/| может быть отрицательной. На практике,
однако, можно изменить знак у |/|, просто поменяв ролями s и t.

146
Глава 6. Потоки
для каждого разреза (S,S) в N. Следовательно, величина потока
в N никогда не больше, чем наименьшая пропускная способность
разреза. Следующая теорема о максимальном потоке и
минимальном разрезе утверждает, что эта верхняя оценка всегда достигается
на некотором потоке.
Теорема 6.2.2 (Форд, Фалкерсон, 1956). В любой сети
максимальная величина потока равняется минимальной пропускной
способности разреза.
Доказательство. Пусть N = (G,s,t,c) — сеть и G =: (V,E).
Мы далее определим последовательность /о, /i, /г, • • • целочисленных
потоков в N строго увеличивающейся величины, т. е. таких, что
|/o|<|/i|<|/2|<....
Ясно, что величина целочисленного потока — снова целое число, так
что на самом деле |/n+i| > |/n| -f 1 для всех п. Так как все эти
числа ограничены пропускной способностью любого разреза в TV, наша
последовательность закончится некоторым потоком /„. По этому
потоку мы найдем разрез с пропускной способностью сп — |/п|.
Поскольку никакой поток не может иметь величину больше, чем сп,
а никакой разрез не может иметь пропускную способность меньше,
чем |/п|, это число — одновременно максимум и минимум,
упомянутый в теореме.
Для /о полагаем /о(е) := 0 при всех е£ Е. Определив
целочисленный поток fn в N для некоторого п £ N, мы обозначаем через
Sn множество всех таких вершин г/, что G содержит s-v маршрут
х0е0 .. .ei_ixi, где
/n(ci) < с(е{)
для всех i < £] здесь ё{ \— (ег-, жг-, £{+i) (и, конечно, хо — s и xi — v).
Если t £ 5„, то пусть W — жоео • • -Q-i^ — соответствующий
s-t маршрут; без потери общности можно считать, что W не
проходит через одну и ту же вершину дважды. Пусть
6 := min{c(ei) - /„(£) | г < £}.
Тогда б > 0, а поскольку /п (как и с) целочисленна по
предположению, то б — целое число. Пусть
[fn{z) + e для е = ei, г = 0, ...,£-1;
/n+i: е^ < fn(e) -е для е = е,-, г = 0,... ,£ - 1;
[ Fn(e) для е £ W.
Нестрого говоря, /п+1 получается из /п пропусканием
дополнительного потока величиной е по W из s в t (рис. 6.2.2).

6.3. Потоки со значениями в группе
147
Рис. 6.2.2. «Увеличивающий путь» W с приращением е = 2
для постоянного потока /п = 0 и пропускных способностей с = 3
Ясно, что /n+i — снова целочисленный поток в N. Вычислим
его величину |/n+i| = fn+i(s,V)- Так как W содержит вершину s
только один раз, ё*о — единственная тройка (е,х,у) с х = s и у Е V,
для которой величина / изменилась. Эта величина, а следовательно,
и величина /n+i(s, V) возросли. Поэтому |/n+i| > |/п|, что и
требовалось.
Если t $ 5„, то (Sn,Sn) — разрез в N. Из (F3) для /п и
определения Sn имеем
/„(e) = с(е)
для всех е £ E(Sn,Sn), поэтому
|/п | — Jnybn j »Ьп j — с(»Ьп) »Ьп))
что и требовалось доказать. □
Так как поток, построенный в доказательстве теоремы 6.2.2, це-
лочислен, получаем
Следствие 6.2.3. В каждой сети (с целочисленной функцией
пропускной способности) существует целочисленный поток
максимальной величины. □
6.3. Потоки со значениями в группе
Пусть G = (V, Е) — мультиграф, а Я — абелева группа. Если
/ и g — две Я-циркуляции, то ясно, что (/ -f g): е ь-+ f(e) -f g(e)
и —/: ё*н-*- — /(e) — снова Я-циркуляции. Итак, Я-циркуляции на G
естественным путем образуют группу.
Функция /: Е —► Я называется нигде не нулевой, если /(e) / О
для всех е £ Е. Я-Циркуляция, которая является нигде не нулевой,
называется Я-потоком^. Заметим, что множество Я-потоков на G
не замкнуто по сложению: если два Я-потока на некотором ребре е
4) Эта терминология кажется самой простой для наших целей, но не является
стандартной; см. примечания.

148
Глава 6. Потоки
дают в сумме нуль, то их сумма уже не Я-поток. По следствию 6.1.2
граф с Я-потоком не может иметь моста.
Для конечных групп Я число Я-потоков на G и, в частности,
их существование удивительным образом зависят только от порядка
группы Я, а не от Я как таковой.
Теорема 6.3.1 (Татт, 1954). Для каждого мультиграфа G
существует такой многочлен Р, что для любой конечной абелевой
группы Я число Я-потоков на G равно Р(\Н\ — 1).
Доказательство. Пусть G —: (V,E); применим индукцию по
m := \Е\. Предположим сначала, что все ребра в G — петли. Тогда,
для любой конечной абелевой группы Я всякое отображение Е —>
Я \ {0} является Я-потоком на G. Поскольку \Е\ — \Е\, если все
ребра — петли, то имеется (|Я| — 1)т таких отображений, а значит,
Р \— хт — искомый многочлен.
Допустим теперь, что имеется ребро ео — ху £ Е, не
являющееся петлей. Пусть ё*0 •= (ео,х,у) и Е' := Е \ {во}. Рассмотрим
мультиграфы
Gi:=G-e0 и G2 := G/e0.
По индукционному предположению имеются такие многочлены Рг-
для г = 1, 2, что для любых конечной абелевой группы Я и к := |Я| — 1
число Я-потоков на G{ равно Р{(к). Докажем, что число Я-потоков
на G равняется Рг(^) — Pi (к)] тогда многочлен Р :— Р2 — Pi будет
искомым.
Пусть задана группа Я, а множество всех Я-потоков на G
обозначается через F. Мы хотим показать, что
\F\ = P2(k)-P1(k). (1)
Я-Потоки на Gi — это в точности сужения на Е' тех Я-циркуляций
на G, которые являются нулевыми на ео, но нигде больше.
Обозначим множество этих циркуляции на G через F\\ тогда
Рг(к) - |Fi|.
Мы покажем, что Я-потоки на Gi аналогичным образом взаимно
однозначно соответствуют тем Я-циркуляциям на G, которые не
являются нулевыми нигде, кроме как, быть может, на ео- Множество Еъ
этих циркуляции на G тогда удовлетворяет условию
ад = \ч,
a F2 есть непересекающееся объединение F\ и F. Этим мы
докажем (1), а следовательно, и саму теорему.
Пусть vq := veo — вершина в G2, полученная стягиванием ео
(рис. 6.3.1; см. раздел 1.10). Мы ищем биекцию / ь-, g между Fn

6.3. Потоки со значениями в группе
149
и множеством Я-потоков на G2. При заданном / пусть д есть
ограничение / на Е' \ Е'(у,х). (Так как х-у ребра е £ Е' становятся
петлями в G2, они имеют там только одно направление (e,i>o,i>o);
в качестве его ^-величины мы выбираем /(е,ж,у).) Тогда д —
действительно Я-поток на G2- Заметим, что (F2) выполняется в vq по
предложению 6.1.1 для G при X := {х,у}.
Рис. 6.3.1. Стягивание дуги ео
Остается показать, что отображение / t—>• д является взаимно
однозначным. Если задан Я-поток д на G^ и мы пытаемся найти
/ £ ^2 с / »—> д, то f(e) уже определено как f(e) — д(е) для всех
е £ Е' \ Е'(у,х). Ввиду (F1) имеем далее f(e) — — /(e) для всех
е £ Е'(у}х). Таким образом, отображение / \-+ д биективно, если
и только если для заданного д всегда имеется единственный способ
определить оставшиеся величины /(ёо) и /(ео) так, чтобы /
удовлетворял условию (F1) для ео и (F2) для х и у.
Но это действительно имеет место. Пусть V := V \{х,у}. Уже
фиксированные /-величины удовлетворяют условию
f(x,V') + f(y,V') = g(vo,V') = 0 (2)
согласно (F2) для д. При
ёеЁ'(х,у) е£Е'(х,у)
(F2) для / влечет
0 = f(x,V) = f(eo) + h + f(x,V)
И
0 = F(y,V) = F(eo)-h + f(y,V').
Следовательно, мы должны положить
№):=-f(*,V')-h и f(e0):=-f(y,V') + h.
Тогда /(ёо) + /(е"о) = 0 согласно (2), поэтому / также
удовлетворяет (F1) на ео. О
Многочлен Р в теореме 6.3.1 известен как потоковый многочлен
мультиграфа G.

150
Глава 6. Потоки
Следствие 6.3.2. Если Н и Н' — конечные абелевы группы
равного порядка, то G имеет Н-поток, если и только если G имеет
Н'-поток. □
Следствие 6.3.2 имеет фундаментальное значение для теории
алгебраических потоков: оно показывает, что главные трудности
при доказательстве существования Я-потока вряд ли имеют
теоретико-групповой характер. С другой стороны, возможность выбирать
удобную группу может быть весьма полезной; хороший пример тому
мы увидим в предложении 6.4.5.
Пусть к > 1 — целое число, a G — (V} Е) — мультиграф. Всякий
Z-поток / на G, удовлетворяющий условию 0 < |/(е)| < к для всех
е £ Е, называется k-потоком. Ясно, что любой &-поток является
также ^-потоком для всех £ > к. Возникает вопрос, каково
наименьшее целое к, при котором G допускает &-поток в предположении, что
такое к существует. Назовем это наименьшее к потоковым числом
графа G и обозначим его через <p(G). Если G не имеет fc-потока ни
при каком к, то полагаем <p(G) := оо.
Задача определения потоковых чисел сразу приводит к
некоторым из самых глубоких нерешенных проблем в теории графов. Мы
рассмотрим их позднее в данной главе. Сначала же посмотрим, как
fc-потоки связаны с более общим понятием Я-потоков.
Имеется тесная связь между ^-потоками и 7L*-потоками. Пусть
fjjb обозначает естественное гомоморфное отображение i \-» г из 7L
в Z*. Посредством композиции с <т* каждый &-поток определяет
Zjfc-поток. Как показывает следующая теорема, обратное
утверждение также имеет место: по каждому Zjb-потоку на G можно
построить &-поток на G. Ввиду следствия 6.3.2 это означает, что
общий вопрос о существовании Я-потоков для произвольных групп Я
сводится к соответствующему вопросу для ^-потоков.
Теорема 6.3.3 (Татт, 1950). Myльтиграф допускает к-поток,
если и только если он допускает Ъ^-поток.
Доказательство. Пусть g есть Zjb-поток на мультиграфе G —
(V, Е)\ построим &-поток / на G. Без ограничения общности можно
считать, что G не имеет петель. Пусть F — множество всех функций
/: Е —+ 7L, которые удовлетворяют трем условиям: (F1), |/(ё*)| < к
для всех еЕЕисгк0/ — 9- Заметим, что, как и д, любой поток
/ G F является нигде не нулевым.
Покажем сначала, что F ф 0. Поскольку можно выразить
каждую величину д(е) £ Zk как г с |г| < к и затем положить f(e) := г, то
с очевидностью имеется такое отображение /: Е —► Z, что \f(e)\ < к
для всех е£ Е и (Tk о f = д. Для каждого ребра е £ Е выберем одно
из двух направлений и обозначим его через е. Тогда можно
определить /'': Е —► Z, полагая f'(e) := f(e) и f'{e) := -f(e) для каждого

6.3. Потоки со значениями в группе
151
е £ Е. Теперь функция /' удовлетворяет (F1) и принимает значения
в нужном диапазоне. Остается показать, что о> о/' и д согласуются
не только на выбранных направлениях е} но и на обратных им е. Так
как a к — гомоморфизм, это действительно имеет место:
('к о Я(е) = <тк(-№) = -К о /)(ё) = -д(е) = д(е).
Следовательно, /' £ F, так что F действительно не пусто.
Наша цель состоит в том, чтобы найти отображение / £ F,
удовлетворяющее закону Кирхгофа (F2), а следовательно, являющееся
^-потоком. В качестве кандидата рассмотрим / £ F, для которого
сумма
ВД:=£|/(*,Щ
всех отклонений от закона Кирхгофа минимальна. Мы докажем, что
K(f) = 0. Тогда очевидно, что f(x, V) = 0 для каждого ж, что
и требуется доказать.
Предположим, что K(f) ф 0. Поскольку / удовлетворяет
условию (F1), а следовательно, YL /(ж> Ю — f{V, У) — 0, то существует
вершина х с rGV
/(*,V)>0. (1)
Пусть ХС7 — множество всех вершин х', для которых G содержит
такой маршрут жоео .. . е£_1Ж£ из ж в ж7, что/(ег-, жг-, Жг+i) > 0 для всех
i < £. Кроме того, положим X' := X \ {ж}.
Сначала покажем, что X' содержит вершину х' с f(x', V) < 0.
По определению X имеем /(е, ж7, ?/) < 0 для всех таких ребер е = х'у,
что х1 £ X и у £ X. В частности, это имеет место для х' = х.
Таким образом, (1) влечет /(ж, X') > 0. Отсюда f(X'} х) < 0 по (F1),
а также f(X\ X') — 0. Следовательно,
£ /(*', Ю = /(*', Ю = ^Х*',X) + /(*',*) + f(X',X') < о,
х'еХ'
поэтому существует х' £ X' с
/(*', V) < 0. ■ (2)
Поскольку х' £ X, существует такой ж-ж' маршрут И^ = жо^о ■ ■ ■
.. .ei-ixi, что f(e{,X{, Жг+i) > 0 для всех г < ^. Изменим /, посылая
некоторый поток вдоль W в обратном направлении, где f': Е —> 7L
задается следующим образом:
f:e>
f(e)-k при е = (ei,Xi,xi+i), i = 0,...,£-l;
f(e)+k при е = (е,,ц+1,Х{), i = 0, ...,£-1;
{ /(e) при е i W.

152
Глава 6. Потоки
По определению W имеем |/'(е)| < к для любого е £ Е.
Следовательно, /', как и /, находится в F.
Как модификация потока / затрагивает К! Во всех
внутренних вершинах v из W, так же как и вне W, отклонение от закона
Кирхгофа остается неизменным:
f'(v, V) = f(v, V) для всех vGV\{x,x'}. (3)
Для ж и ж7, с другой стороны, имеем
f'(x,V) = f(x,V)-k и f'(x',V) = f(x',V) + k. (4)
Поскольку д есть Zfc-поток и, следовательно,
ak(f(x,V))=g(x,V) = OeZk,
<rk(f(z',V))=g(x',V) = OeZk,
то и f(x, V), и /(х', V) кратны к. Таким образом, f(x, V) > к
и f(x', V) < —к ввиду (1) и (2). Но тогда из (4) следует, что
\f'(x,V)\<\f(x,V)\ и \f(x',V)\<\f(x',V)\.
Вместе с (3) это дает K(f) < K(f) в противоречие с выбором /.
Поэтому K(f) — 0, что и утверждалось, а / — действительно
&-ПОТОК. П
Так как сумма любых двух Zjb-циркуляций — снова
TL^-циркуляция, то Zjb-потоки часто строить легче (суммированием подходящих
частичных потоков), чем й-потоки. Таким образом, теорема 6.3.3
может оказать значительную помощь при определении того,
действительно ли заданный граф имеет &-поток. В следующих разделах мы
встретимся с несколькими подтверждениями сказанному.
6.4. ^-Потоки для малых к
Очевидно, что граф имеет 1-поток (пустое множество), если
и только если в нем нет ребер. В этом разделе мы рассмотрим
несколько простых достаточных условий того, что граф имеет
2-, 3- или 4-поток. Другие примеры можно найти в упражнениях.
Предложение 6.4.1. Граф имеет 2-яоток, если и только если
все его степени четны.
Доказательство. По теореме 6.3.3 граф G — (V,E) имеет
2-поток, если и только если он имеет 2^2-поток, т. е. если и только
если постоянное отображение Е —> Ж,2 со значением 1 удовлетворяет
условию (F2). Но это имеет место, если и только если все степени
четны. D
В оставшейся части этой главы будем называть граф четным,
если степени всех его вершин четны.

6.4. к-Потоки для малых к
153
Предложение 6.4.2. Кубический граф имеет 3-поток, если
и только если он двудолен.
Доказательство. Пусть G = (V, Е) — кубический граф.
Предположим сначала, что G имеет 3-поток, а следовательно, также и
^з-поток /. Покажем, что любой цикл С — xq...xiXq в G имеет
четную длину (см. предложение 1.6.1). Рассмотрим два
последовательных ребра на G, например et-_i := Х{-\Х{ и е,- := Х{Х{+\. Если /
приписывает этим ребрам одно и то же значение в направлении
прямой ориентации цикла G, т. е. если /(et_i, ж»-ь жг-) = /(е», ж», Et+i)j
то / не мог удовлетворять (F2) в ж,- ни при каком ненулевом
значении третьего ребра при Х{. Поэтому / приписывает значения 1 и 2
ребрам из С поочередно, и, в частности, С имеет четную длину.
Обратно, пусть G двудолен и имеет вершинное 2-разбиение
{X, У}. Так как граф G кубический, отображение Е —► 2з,
определяемое условиями /(е, ж, у) := 1 и /(е, у, х) :— 2 для всех ребер
е = хусх€Хиу£У, есть 22з-поток на G. По теореме б.3.3 тогда
G имеет 3-поток. D
Каковы потоковые числа полных графов Кп? Для нечетных
п > 1 имеем <р(Кп) — 2 по предложению 6.4.1. Кроме того, <р(К2) = со
и <р(К4) = 4; это легко видеть непосредственно (и это же следует
из предложений 6.4.2 и 6.4.5). Интересно, что К4 — единственный
полный граф с потоковым числом 4.
Предложение 6.4.3. Для всех четных п > 4 имеем <р(Кп) = 3.
Доказательство. Из предложения 6.4.1 следует, что <р(Кп) > 3
для четных п. Покажем индукцией по п, что каждый G — Кп с
четным п > 4 имеет 3-поток.
За базу индукции возьмем п — 6. Тогда G —
реберно-непересекающееся объединение трех графов G\, G^ и G3, где G\,G2 = #3
и G3 — ^з,з- Очевидно, что каждый из Gi и G2 имеет 2-поток, a G3
имеет 3-поток по предложению 6.4.2. Объединение всех этих потоков
дает 3-поток на G.
Пусть теперь п > 6, и предположим, что утверждение имеет
место для п — 2. Ясно, что G есть реберно-непересекающееся
объединение Кп~2 и графа G' = {V, Е'), где G' = Кп~2 * К2. Но Кп"2 имеет
3-поток по индуктивному предположению. По теореме 6.3.3, таким
образом, достаточно найти йз-поток на G'. Для каждой вершины z
из Кп~2 С G' пусть fx есть 22з-поток на треугольнике zxyz С G',
где е = ху — ребро графа К2 в G'. Пусть /: £У —► TLz — сумма
этих потоков. Ясно, что / нигде не нулевой, кроме как, быть
может, в (е, ж,у) и (е,у,х). Если /(е, ж, у) ф 0, то / — искомый
2з-поток на G'. Если /(е, ж, ?/) = б, то /-ЬД (для любого г) является
^з-потоком на G'. D
Предложение 6.4.4. Каждый А-реберно-связный граф имеет
4-поток.

154
Глава 6. Потоки
Доказательство. Пусть G — 4-реберно-связный граф. По
следствию 3.5.2 G имеет два реберно-непересекающихся остовных
дерева Т{, i — 1,2. Для каждого ребра е £ Т{ пусть Ct)e —
(единственный) цикл в Т{ -f е и пусть Де есть ^-поток величины г
вокруг Ct)e, точнее, ^-циркуляция на G со значениями г и —г на ребрах
из С{>е и нуль в противном случае.
Положим /i := Y2 /i,e- Поскольку каждое е £ Т\ лежит на
единственном цикле Ci>e/ (а именно, при е — е'), то /i принимает
вне Т\ только значения 1 и — 1 (= 3). Пусть
F:={eZE{T{)\h{e) = Q}
и h '•— Y1 /2,е- Как и выше, /2(е) = 2 = -2 для всех е £ F-.
Отсюда / := Д-Ь/г — сумма ^-циркуляции и, следовательно, в свою
очередь, ^-циркуляция. Кроме того, поток / нигде не нулевой: на
ребрах из F он принимает значение 2, на ребрах Т\ — F он совпадает
с /i (а значит, является ненулевым ввиду выбора F) и на всех ребрах
вне Т\ принимает одно из значений 1 или 3. Следовательно, / есть
2£4-поток на G, и утверждение следует из теоремы б.3.3. D
Следующее предложение описывает графы с 4-потоком в
терминах графов с 2-потоком.
Предложение 6.4.5.
(i) Граф имеет 4-яоток, если и только если он является
объединением двух четных подграфов.
(ii) Кубический граф имеет 4-яоток, если и только если он
3 -ре б ер но-р аскр ашиваем.
Доказательство. Пусть 7L\ — Z2 х 22 — четверная группа
Клейна. (Таким образом, элементы 7L\ суть пары (а, 6) с а, b £ TL-i
и (а, 6) -f (а', Ь') = (а -f а', 6-f б7).) По следствию 6.3.2 и теореме 6.3.3
граф имеет 4-поток, если и только если он имеет 2^-поток.
Теперь (i) следует непосредственно из предложения 6.4.1.
(ii) Пусть G = (V, Е) — кубический граф. Предположим
сначала, что G имеет ^-поток /, и зададим раскраску ребер Е —>
Ъ\\ {0}. Так как a = —а для всех a £ 7L\, имеем f(e) — /(e) для
каждого е £ Е; раскрасим ребро е этим цветом /(ё). Теперь если
два ребра с общим концом v имели бы один и тот же цвет, то эти
два значения / давали бы в сумме нуль; по (F2) / тогда
приписывал бы нуль третьему ребру при v. Поскольку это противоречит
определению /, построенная раскраска ребер правильная.
Обратно, так как три ненулевые элемента в 7L\ дают в сумме
нуль, каждая 3-раскраска ребер с: Е —» 7L\\\§) определяет 2£|-поток
на G, если положить f(e) = /(e) = с(е) для всех е£ Е. □
Следствие 6.4.6. Никакой кубический 3-реберно-раскраши-
ваемый граф не имеет мостов. □

6.5. Двойственность между потоками и раскрасками 155
6..5. Двойственность между потоками и раскрасками
В этом разделе мы увидим удивительную связь между
потоками и раскраской: каждый &-поток на плоском мультиграфе
порождает вершинную fc-раскраску двойственного ему мультиграфа,
и наоборот. Таким образом, исследование ^-потоков предстает как
естественное обобщение уже знакомых нам задач раскраски карт на
плоскости.
Пусть G = (V, Е) и G* = (V*,E*) — двойственные плоские
мультиграфы. Для простоты допустим, что G и G* не имеют ни
петель, ни мостов и нетривиальны. Для множества ребер F С Е
положим
F* := {е* е Е* | е G F}.
Обратно, если задано подмножество множества Е*, мы будем обычно
записывать его сразу в виде F* и, таким образом, задавать F С Е
неявно через биекцию еие*.
Предположим, что задана циркуляция g на G*. Как можно
воспользоваться двойственностью между G и G*, чтобы получить
по g какую-либо информацию о G? Наиболее общее свойство всех
циркуляции указано в предложении 6.6.1, которое утверждает, что
д(Х,Х) = 0 для всех X С V*. По предложению 4.6.1 минимальные
разрезы Е*(Х,Х) в G* в точности соответствуют циклам графа G.
Таким образом, если мы возьмем композицию / отображений е^е*
и д и просуммируем ее значения по ребрам цикла в G, то эта сумма
снова будет нулевой.
Конечно, здесь все же имеется одна техническая помеха: так как
д принимает значения пе в Е*, а, в Е*, мы не можем определять /
так просто, как раньше. Сначала мы должны уточнить биекцию
е |—► е* до биекции из Е в Е*, т. е. приписать канонически каждой
дуге е G Е одно из двух направлений ребра е*. Это будет целью
нашей первой леммы. Затем мы покажем, что / действительно дает
в сумме нуль по любому циклу в G.
Если С = vq ... vi-ivo — цикл с ребрами ег- = г/гг/г+1 (и vi := vq),
то назовем
С :- {(ei,Vi,Vi+i) \i<£}
циклом с ориентацией. Заметим, что это определение цикла С
зависит от вершинной нумерации, выбранной для обозначения С:
каждый цикл имеет две ориентации. И наоборот, конечно, С может быть
восстановлен по множеству С. На практике поэтому мы можем
говорить о цикле С даже несмотря на то, что формально был определен
только С.
Лемма 6.5.1. Существует биекция * : е*—> е* из Е в Е* со
следующими свойствами.

156 Глава 6. Потоки
(i) Опорным ребром дуги е* является е*, т. е. е* — одда из
двух ориентации е*, е* ребра е*.
(ii) Если С С G — цикл, то F := Е(С), а если X С V* таково,
что F* = Е*(Х} X), то существует ориентация С цикла С,
при которой {е* | ее С} - Ё*(Х, X).
Доказательство леммы 6.5.1 не вполне очевидно; оно основано на
так называемой ориентируемости плоскости, и мы не можем дать
его здесь. Однако утверждение леммы кажется интуитивно
правдоподобным. Действительно, если определим для е = vw и е* = ху
предписание (e,v,w) ь-> (e,i/,u>)* £ {(е*, х, у), (е*, у, х)}, просто
поворачивая е и его концы по часовой стрелке на е* (рис. 6.5.1), то
получающееся отображение е »—► е* удовлетворяет обоим
утверждениям леммы.
Рис. 6.5.1. Ориентируемая двойственность между разрезами и циклами
Если Н — абелева группа, то пусть /: Е —> Н и g: Е* —> Н —
такие два отображения, что
для всех е£ Е. Для F С Е полагаем
ёеР
Лемма 6.5.2.
(i) Отображение g удовлетворяет условию (F1) вместе и только
вместе с /.
(ii) Отображение g — циркуляция на G*, если и только если f
удовлетворяет условию (Fl), a f(C) = 0 для каждого цикла
С с ориентацией.

6.5. Двойственность между потоками и раскрасками 157
Доказательство. Утверждение (i) следует из леммы 6.5.l(i)
и того факта, что ё*н-> е* является биекцией.
Для доказательства прямой импликации в (ii) допустим, что g —
циркуляция на G*, и рассмотрим цикл С С G с некоторой заданной
ориентацией. Пусть F \— Е(С). По предложению 4.6.1 F* —
минимальный .разрез в G*, т. е. F* — Е*(Х,Х) для некоторого
подходящего X С V*. По определению / и g лемма 6.5.1(H) и предложение
6.1.1 дают
f(C) = £ № = £ 9(d) = g(X, X) = о
е£С d£E*(X,X)
для одной из двух ориентации С цикла С. Тогда, поскольку /(G) —
—/(С), соответствующее значение для нашей заданной ориентации
цикла С также должно быть нулевым.
Для доказательства обратной импликации достаточно ввиду (i)
показать, что g удовлетворяет (F2), т. е. что д(х, V*) = 0 для
каждой х £ V*. Мы докажем, что g(x,V(B)) = 0 для каждого блока
в графе G*, содержащего х. Так как каждое ребро G* при
вершине х находится ровно в одном таком блоке, это даст равенство
g(x,V*) = 0.
Итак, пусть задана жЕГ,и пусть В — любой блок графа G*,
содержащий х. Поскольку граф G* — нетривиальный
плоскодвойственный, а следовательно, связный, то имеем В — х ф 0. Пусть
F* — множество всех ребер из В при х (рис. 6.5.2), и пусть X —
множество вершин компоненты G* — F*, содержащей х. Тогда 0 ф
V(B — х) С X ввиду максимальности В как подграфа, свободного от
разделяющих вершин. Следовательно,
F* = £*(X,X) (1)
по определению X, т. е. F* — разрез в G*. Будучи двойственным,
G* связен, так что G*[X] также связен. Действительно, каждая
вершина в X связана с х путем Р С G*, последнее ребро которого
находится в F*. Тогда Р — х есть путь в G*[X], пересекающий В.
Поскольку х не разделяет В, это показывает, что G*[X] связен.
X
Рис. 6.5.2. Разрез F* в G*

158
Глава 6. Потоки
Таким образом, X и X оба связны в G*, так что F* — это даже
минимальный разрез в G*. Пусть С С G — цикл с Е(С) — F,
который существует по предложению 4.6.1. По лемме 5.5.1(H) С имеет
такую ориентацию G, что {е* | еЕ С} — Е*(Х, X). Однако ввиду (1)
Ё*(Х, X) = Ё*{х, V(B)), поэтому
g(x,V(B)) = g(X,X) = f(C) = 0
по определению fug. □
С помощью леммы 6.5.2 теперь можно доказать теорему о
двойственности раскрасок и потоков для плоских мультиграфов. Если
Р = vq ... vi — путь с ребрами ег- = г/гг/г+1 (i < t), то положим (в
зависимости от выбранной вершинной нумерации Р)
P:={(ei,Vi,v+i) \i<£}
и будем говорить, что Р есть vo —+ vi путь. Опять-таки Р может
быть задан неявно через Р.
Теорема 6.5.3 (Татт, 1954). Для каждой двойственной пары
G, G* плоских мультиграфов имеет место равенство
X(G) = <p(Gm).
Доказательство. Пусть G =: (V,E) и G* =: (V*,E*). Для
\G\ G {1,2} утверждение легко проверяемо. Допустим, что \G\ > 3,
и применим индукцию по числу мостов в G. Если е £ G — мост,
то е* — петля и G* — е* плоскодвойствен к G/e (почему?).
Следовательно, по индукционному предположению
X(G)=x(G/e) = <p(G*-e*) = <p(G*).
Для первого и последнего равенств мы используем то, что е не
единственное ребро в G, так как \G\ > 3.
Остается проверить лишь базу индукции. Допустим, что G не
имеет мостов. Если в G есть петля, то G* содержит мост и x{G) —
со = (p(G*). Поэтому можно считать, что в G нет петель.
Тогда x(G) конечно. Докажем для заданного к > 2, что G является
^-раскрашиваемым, если и только если G* имеет &-поток. Так как G,
а следовательно, и G* не имеют ни петель, ни мостов, к G и G* можно
применить леммы 6.5.1 и 6.5.2. Пусть е у-+ е* — биекция между Е
и Е* из леммы 6.5.1.
Допустим сначала, что G* имеет &-поток. Тогда G* также имеет
Zjb-поток g. Как и раньше, пусть f:E —+ 7L^ задано равенством

6.6. Гипотезы Татта о потоках
159
/(e) := <?(е*). Будем использовать / для построения вершинной
раскраски с: V —*• Zjb мультиграфа G.
Пусть Т — нормальное остовное дерево в G, скажем, с корнем г.
Положим с(г) := б. Для каждой другой вершины v £ V положим
c{v) := f(P), где Р есть г —+ г/ путь в Т. Чтобы проверить,
получилась ли правильная раскраска, рассмотрим ребро е = vw £ Е. Так
как Т нормально, можно считать, что v < w в древесном порядке,
задаваемом Т. Если е — ребро в Т, то с(ю) — c(v) = /(е, г/, iu) по
определению с, так что c(v) ф c(w), поскольку д (а следовательно,
и /) нигде не нулевой. Если е (£ Т, то пусть Р обозначает v —+ iu
путь в Т. Тогда
c(tu) - c(v) = f(P) = -/(е, w, v) ф б
по лемме 6.5.2(ii).
Обратно, допустим, что G имеет fc-раскраску с. Зададим
функцию /': Е —+7L равенством
f(e,v,w) := c(iu) - с(и),
а, д: Е* —± Ъ — условием flf(e*) := /(e)- Очевидно, что /
удовлетворяет (F1) и принимает значения в {±1,..., ±(fc — 1)}, поэтому по
лемме 6.5.2(i) то же самое верно и для д. По определению / имеем
теперь /(С) = 0 для каждого цикла С с ориентацией. Следовательно,
по лемме 6.5.2(ii) д является ^-потоком. □
6.6. Гипотезы Татта о потоках
Как определить потоковое число графа? Каждый ли граф (без
мостов) имеет потоковое число, т. е. &-поток при некотором к?
Могут ли потоковые числа, подобно хроматическим числам, быть
произвольно большими? Можно ли охарактеризовать графы,
допускающие fc-поток для заданного к?
Из четырех вопросов мы ответим в этом разделе на второй и
третий, доказывая, что каждый граф без мостов имеет б-поток. В
частности, граф имеет потоковое число, если и только если он не имеет
мостов. Вопрос о характеризации графов с ^-потоком остается
открытым для к — 3,4, 5. Частичные ответы предложены в следующих
трех гипотезах Татта, заложившего основы алгебраической теории
потоков.
Самая старая и наиболее известная из гипотез Татта —
гипотеза о 5-потоке.
Гипотеза о 5-потоке (Татт, 1954). Каждый мультиграф без
мостов имеет Ъ-поток.

160
Глава 6. Потоки
Какие графы имеют 4-поток? Ввиду предложения 6.4.4 к таким
относятся 4-реберно-связные графы. С другой стороны, граф Петер-
сена (рис. 6.6.1) является примером графа без мостов, не имеющего
4-потока. Так как он кубический, но не 3-реберно-раскрашиваемый,
он не может иметь 4-потока в силу предложения 6.4.5(ii).
Рис. 6.6.1. Граф Петерсена
Принадлежащая Татту гипотеза о ^-потоке утверждает, что
граф Петерсена должен присутствовать в каждом графе без
4-потока.
Гипотеза о 4-потоке (Татт, 1966). Каждый мультиграф без
мостов, не содержащий графа Петерсена как минор, имеет 4-поток.
Ввиду предложения 1.7.2 можно заменить слово «минор» в
гипотезе о 4-потоке на «топологический минор».
Даже если гипотеза о 4-потоке верна, она не будет самой сильной
из возможных: К11, например, содержит граф Петерсена как минор,
но имеет 4-поток и даже 2-поток. Гипотеза кажется более
естественной для разреженных графов, и, действительно, кубические графы
образуют ее важный частный случай (см. примечания).
Кубический граф или мультиграф без мостов, не имеющий
4-потока (или, что то же самое, не имеющий 3-раскраски ребер)
называется снарком. Гипотеза о 4-потоке для кубических графов
утверждает, что каждый снарк содержит граф Петерсена как минор; в этом
смысле граф Петерсена является наименьшим из снарков. Снарки
образуют ядро как теоремы о четырех красках, так и гипотезы о
5-потоке. Теорема о четырех красках эквивалентна утверждению,
что никакой снарк не является план арным (упражнение), и нетрудно
свести гипотезу о 5-потоке к случаю снарков5). Однако хотя снарки
и представляют собой очень узкий класс графов, ни одна из
упомянутых проблем, по-видимому, не становится проще от этого сужения6).
Гипотеза о 3-потоке (Татт, 1972). Каждый мультиграф без
разрезов, состоящих ровно из одного или трех ребер, имеет 3-поток.
5) То же самое относится к еще одной известной гипотезе — гипотезе о
двойном покрытии циклами; см. упражнение 13.
6) То, что снарки неуловимы, математикам известно уже довольно давно; см.
Lewis Carroll. The Hunting of the Snark. N. Y.: Macmillan, 1876.

6.6. Гипотезы Татта о потоках
161
Опять-таки гипотеза о 3-потоке не является наилучшей из
возможных: легко построить графы с разрезами из трех ребер, которые
имеют 3-поток (упражнение).
В силу теоремы двойственности (6.5.3) все три гипотезы о
потоках верны для план арных графов и этим мотивированы. Гипотеза
о 3-потоке сводится к теореме Грёцша (5.1.3), гипотеза о 4-потоке —
к теореме о четырех красках (так как граф Петерсена не план арен,
он не является минором планарного графа), а гипотеза о 5-потоке —
к теореме о пяти красках.
Мы заканчиваем этот раздел основным результатом главы.
Теорема 6.6.1 (Сеймур, 1981). Каждый граф без мостов имеет
6-поток.
Доказательство. Пусть G = (V,E) — граф без мостов. Так
как б-потоки на компонентах G составляют б-поток на G, можно
считать, что G связен; так как G не содержит мостов, он 2-реберно-
связен. Заметим, что любые две вершины в 2-реберно-связном графе
лежат в некотором общем четном связном подграфе, например в
объединении двух реберно-непересекающихся путей, связывающих эти
вершины по теореме Менгера (3.3.5(ii)). Мы будем неоднократно
использовать этот факт.
Построим последовательность Но,..., Нп непересекающихся
связных четных подграфов графа G вместе с последовательностью
Fi,...,Fn непустых множеств ребер между ними. Каждое из
множеств F{ будет содержать только одно или два ребра, а именно,
между Н{ и Но U ■ • • U #г-_1. Положим Н{ =: (К', #;),
Н{ := (Но U • • • U Н{) + (Fi U • • • U F{)
и #* =: (V\E{). Заметим, что каждый #' = (#i_1 U Hi) + F{
связен (индукция по г). Наше предположение, что Hi является четным,
влечет ввиду предложения 6.4.1 (или непосредственно по
предложению 1.2.1), что Hi не имеет мостов.
В качестве Но выберем любой К1 в G. Допустим теперь, что
Но, • •., #г-1 и Fi,..., Ft-_i уже определены для некоторого г > 0.
Если Vx~l — V, мы заканчиваем построение и полагаем г— 1 =: п.
В противном случае пусть множество Xi С V1'1 минимально при
условии, что Xi ф 0 и
|ВД,^-1\Х,-)1<1 (1)
(рис. 6.6.2); такое Xi существует, потому что таковым является
V*-"1. Поскольку G 2-реберно-связен, (1) влечет, что E(Xi, У1~1)ф0.
Ввиду минимальности Xi граф G[X,] связен и не имеет мостов, т. е.
он 2-реберно-связен или совпадает с К1. В качестве элементов Ft- мы

162
Глава 6. Потоки
выбираем одно или два ребра из Е(Х{, V1'1), по возможности два.
В качестве Н{ выберем любой связный четный подграф графа G[A';],
содержащий концы в Х{ ребер из F{.
VF7rr\Xt
Хх
Рис. 6.6.2. Построение Н{ и F,
Когда построение завершено, мы полагаем Нп =: Н и Е1 :=
Е \ Е{Н). По определению п Н — остовный связный подграф в G.
Определим теперь «обратной» индукцией последовательность
/п,..., /о из ^з-циркуляций на G. Для каждого ребра е £ Е1 пусть
Се — цикл (с ориентацией) в Н -f е, содержащий е, а /е —
положительный поток по Се. Формально мы полагаем, что /е — такая
^з-циркуляция на G, при которой fe~1{0) = Е\ (Се U Се). Пусть fn
есть сумма всех этих /е. Поскольку каждое е' £ Е1 лежит лишь на
одном из циклов Се (а именно, на Се/), имеем /„(е) ф 0 для всех
ее Е'.
Допустим теперь, что ^з-циркуляции /п,..., /г- на G уже
определены для некоторого г < п и что
fi(e) ф 0 для всех ее Ё' U (J F;-, (2)
;>*
где Fj := {ё* £ Е \ е £ Fj}. Наша цель — определить /t_i таким
образом, чтобы (2) имело место также и для г — 1.
Рассмотрим сначала случай |Ft| = 1, допустим, Ft- = {е}. Тогда
полагаем /;_i := /г-, а значит, нужно показать, что поток /г-
ненулевой на (обоих направлениях) ребра е. Наше предположение \F{\ — 1
влечет по выбору Ft-, что G не содержит ребер из Xi-V1"1, кроме е.
Поскольку G 2-реберно-связен, он имеет по меньшей мере одно, а
значит, в силу (1) ровно одно ребро е' между Х{ и Vx~l \Х{. Покажем,
что fi ненулевой на е1. Поскольку {е, е'} — разрез в G, по
предложению 6.1.1 отсюда будет следовать, что /г- является также ненулевым
на е.
Чтобы показать, что /г- ненулевой на е', воспользуемся (2).
Покажем, что el е E'\J (J Fj, т. е. что е' не лежит нивЯ^, ни в Fj при
;>*
j < г. Так как ребро е' имеет оба конца в V1'1, оно с очевидностью

Упражнения 163
не лежит в Fj при j < г и в Нк при к < г. Но каждый Hk при к > г
есть подграф графа GfF1"1]. Поскольку е' — мост в G[Fl_1], но Нк
не имеет мостов, это означает, что е' £ Нк- Следовательно, в
рассмотренном случае /t-_i действительно удовлетворяет условию (2)
для г — 1.
Остается рассмотреть случай, когда |Ft| = 2, скажем, F{ —
{61,62}. Так как и Яг-, и Я"1 связны, можно найти цикл С в Нг =
(Hi U Hl~l) -f F{, который содержит в\ и ез- Если /г- ненулевой на
обоих этих ребрах, мы опять-таки полагаем /t_i : = /t-. В противном
случае имеются такие ориентации ё\ и ез ребер t\ и 62, что, без
потери общности, fi(e\) = 0 и /г(е2) £ {0,1}. Пусть С — ориентация
цикла С, при которой ё*2 £ С, и пусть <? — поток величины 1 по С.
(Формально, пусть д — такая ^з-циркуляция на G, что д(ео) = 1
и <7_1(0) = E\(CUC)). Затем положим /t-_i : = fi+g. По выбору
направлений ё\ и ё*2 поток /г_1 ненулевой на обоих ребрах. Поскольку
/г-_1 согласуется с /г- на всем E'iJ (J F;-, а для г имеет место (2), то (2)
верно и для г — 1. •7>г
Наконец, /о будет ^-циркуляцией на G, которая является
нигде не нулевой, кроме, быть может, как на ребрах из Но U • • • U Нп.
Объединяя /о с отображением h t—► 2/i из TLz в 2£б (/i £ {1,2}), мы
получаем ^-циркуляцию / на G со значениями в {б, 2, 4} для всех
ребер, расположенных в некотором Яг-, и со значениями в {2,4} для
всех остальных ребер. Добавляя к / 2-поток на каждом Яг-
(формально, ^-циркуляцию на G со значениями в {1, — 1} на ребрах из Яг-
и 0 в противном случае; такая циркуляция существует по
предложению 6.4.1), получаем 2£б-циркуляцию на G, которая является нигде
не нулевой. Следовательно, G имеет б-поток по теореме 6.3.3.
Упражнения
1.~ Доказать предложение 6.2.1 индукцией по \S\.
2. (i)~ При заданном n Е N найти такую функцию пропускной способности
для указанной ниже сети, что алгоритму из доказательства теоремы о
максимальном потоке и минимальном разрезе потребуется более чем п
увеличивающих путей W', если они выбираются неудачно.
(ii)"*" Показать, что если все увеличивающие пути выбираются как можно
более короткими, то их число ограничено функцией от размера сети.
3. Получить теорему Менгера 3.3.4 из теоремы о максимальном потоке и
минимальном разрезе.
(Подсказка. Реберную версию получить легко. Для вершинной версии
примените реберную версию к подходящему вспомогательному графу.)

164
Глава 6. Потоки
4.~ Пусть / — Я-циркуляция на G, а д: Я —> Я' — гомоморфизм группы.
Показать, что д о / есть Я'-циркуляция на G. Верно ли, что д о / является
Я'-потоком, если / есть Я-поток?
5.~ При заданном к > 1 показать, что граф имеет Aj-поток, если и только если
каждый из его блоков имеет /г-поток.
6.~ Показать, что y>(G/e) < <p(G) для любых мультиграфа G иребрае в G.
Следует ли отсюда, что для любого к класс всех мультиграфов, допускающих
/г-поток, замкнут по взятию миноров?
7.~ Определить потоковое число графа /\4 непосредственно, без использования
каких-либо результатов из текста.
8. Пусть имеются конечная абелева группа Я, граф G и остовное дерево Т в G.
Показать, что каждое отображение из ориентации множества E(G) \ Е(Т)
в Я, удовлетворяющее (F1), однозначно продолжается до Я-циркуляции
наС.
В следующих трех упражнениях не используйте теорему 6.6.1 о 6-потоке.
9. Показать, что y>(G) < оо для каждого мультиграфа G без мостов.
10. Предположим, что граф G имеет такие m остовных деревьев, что никакое
ребро G не лежит сразу во всех этих деревьях. Показать, что y>(G) < 2m.
11.+ Пусть G — связный граф без мостов с п вершинами и m ребрами.
Рассматривая нормальное остовное дерево на G, показать, что y>(G) < m — п -f 2.
12. Показать, что каждый граф с гамильтоновым циклом имеет 4-поток. (Га-
милыпонов цикл G — это цикл в G, который содержит все вершины из G.)
13. Семейство (не обязательно различных) циклов в графе G называются
двойным покрытием циклами в G, если каждое ребро в G принадлежит ровно
двум из этих циклов. Гипотеза о двойном покрытии циклами утверждает,
что каждый мультиграф без мостов имеет двойное покрытие циклами.
Доказать эту гипотезу для графов с 4-потоком.
14."~ Определить потоковое число графа С5 * А'1 — колеса с 5 спицами.
15. Найти такие графы без мостов G и Я = G — е, что 2 < y(G) < у (Я).
16. Доказать предложение 6.4.1, не пользуясь теоремой 6.3.3.
17.+ Доказать теорему Хивуда: плоская триангуляция 3-раскрашиваема, если
и только если все ее вершины имеют четную степень.
18." Найти граф без мостов, который имеет и 3-поток, и разрез ровно из трех
ребер.
19. Показать, что гипотеза о 3-потоке для планарных мультиграфов
эквивалентна теореме Грёцша 5.1.3.
20. (i)~ Показать, что теорема о четырех красках эквивалентна
несуществованию планарного снарка, т. е. утверждению, что каждый кубический пла-
нарный мультиграф без мостов имеет 4-поток.
(ii) Можно ли условие «без мостов» в (i) заменить на «3-связный»?
21.+ Показать, что граф G = (V, Е) имеет Aj-поток, если и только если он
допускает ориентацию D, при кото£ой для каждого X С V не менее l/А: ребер
в Е(Х, X) направлено из X в X.
22.~ Обобщить теорему 6.6.1 о 6-потоке на мультиграфы.

Примечания
165
Примечания
Теория потоков в сетях — приложение теории графов, которое оказывает
глубокое воздействие на ее развитие на протяжении нескольких десятилетий.
Как показывает уже тот факт, что теорема Менгера может легко быть выведена
из теоремы о максимальном потоке и минимальном разрезе (упражнение 3),
взаимодействие между графами и сетями может происходить в обоих направлениях.
В то время как «чистые» результаты в таких областях, как связность, паросоче-
тания и случайные графы, нашли приложения в сетевых потоках, наглядность
последних способствовала развитию методов доказательства, которые, в свою
очередь, привели к новым теоретическим достижениям.
Стандартный источник по сетевым потокам — книга: Ford L. R., Fulker-
son D. R. Flows in Networks. Princeton: Univ. Press, 1962. Более современный
и полный обзор дается в работе: Ahuja R. К., Magnanii Т. L., Orlin J. В. Network
Flows. New Jersey: Prentice-Hall, 1993. Другие теоретические аспекты можно
найти в написанной А. Франком главе книги: Handbook of Combinatorics / Ed.
by R. L. Graham, M. Grotschel, L. Lovasz. Amsterdam e. a.: North-Holland Publ.,
1995. Общее введение в алгоритмы на графах дается в книге: Gibbons A.
Algorithmic Graph Theory. Cambridge: Univ. Press, 1985.
Если переформулировать задачу о максимальном потоке в терминах
линейного программирования, можно вывести теорему о максимальном потоке и
минимальном разрезе из теоремы двойственности линейного программирования; см.:
Schrijver A. Theory of integer and linear programming. N. Y.: John Wiley &: Sons,
1986.
Более алгебраическая теория потоков со значениями в группе и /г-потоков
была разработана в значительной степени Таттом; он дает подробное
изложение ее в своей монографии: Tuite W. Т. Graph Theory. Massachusetts е. а.:
Addison-Wesley Publ., 1984. Гипотезы Татта о потоках приводятся также в
обзоре: Jaeger F. Nowhere zero7) flow problems // Selected Topics in Graph
Theory 3 I Ed. by L. W. Beineke, R. J. Wilson. London; New York: Acad.
Press, 1988. Гипотезы о потоках см. также в книге: Jensen Т. R., Toft В. Graph
Coloring Problems. N. Y.: John Wiley &: Sons, 1995. Теорема Сеймура о 6-потоке
доказана в статье: Seymour P. D. Nowhere-zero 6-flows // J. Combin. Theory.
Ser. B. 1981. 30. P. 130-135. В этой статье также показано, как гипотеза Татта
о 5-потоке сводится к снаркам. В 1998 г. Робинсон, Сандерс, Сеймур и Томас
объявили о доказательстве ими гипотезы о 4-потоке для кубических графов.
Наконец, Татт обнаружил связанный с графом многочлен от двух
переменных, который обобщает как его хроматический многочлен, так и потоковый. То
немногое, что известно об этом многочлене Tamma, по-видимому, представляет
собой лишь верхушку айсберга: это понятие имеет далеко идущие и пока мало
исследованные связи со столь отдаленными областями, как теория узлов и
статистическая физика. См.: Welsh D. J. A. Complexity: knots, colourings and counting.
Cambridge: Univ. Press, 1993. (London Math. Soc. Lecture Notes; 186).
) В литературе термин «поток» часто используется для обозначения того,
что мы назвали «циркуляцией», т.е. по умолчанию от потоков не
требуется, чтобы они были нигде не нулевыми.

Глава 7
Подструктуры в плотных графах
В этой и следующей главах мы изучаем зависимость
глобальных параметров графа таких, как его реберная плотность или
хроматическое число, от присутствия в нем тех или иных локальных
подструктур. Сколько ребер, например, должны мы дать графу на
п вершинах, чтобы быть уверенными, что независимо от того, как
эти ребра расположены в графе, он будет содержать подграф Кт
для заданного г? Или хотя бы минор Кг? Или топологический
минор Кг? Будут ли достаточно высокие средняя степень или
хроматическое число гарантировать, что одна из этих подструктур
обязательно встретится?
Вопросы такого рода относятся к наиболее естественным в
теории графов, и на эту тему имеется много глубоких и интересных
результатов. Вместе взятые, они составляют экстремальную
теорию графов.
Экстремальные в этом смысле задачи на графах распадаются
на две категории следующим образом. Если мы ищем способ
гарантировать посредством некоторых глобальных предположений, что
граф G содержит некоторый заданный граф Я как минор (или
топологический минор), то достаточно будет увеличивать ||G|| выше
значения некоторой линейной функции от \G\ (в зависимости от Я),
т. е. сделать e(G) достаточно большим. Существование такой
функции было уже установлено в теореме 3.6.1. Точная необходимая для
этого скорость роста будет исследована в главе 8, где мы
изучаем подструктуры таких «разреженных» графов. Так как
достаточно большое значение е вынуждает существование минора Я
для любого заданного графа Я, его возникновение можно вынудить
по-другому, увеличивая некоторые другие глобальные инварианты
(типа к или х), которые, в свою очередь, заставляют повышаться е,
по крайней мере в некотором подграфе. Это также будет одной из
проблем, рассматриваемых в главе 8.
С другой стороны, если мы задаемся вопросом, какие
глобальные предположения могли бы повлечь существование некоторого за-

Глава 7. Подструктуры в плотных графах
167
данного графа Я как подграфа, то увеличение ни одного из
инвариантов е, к или х не поможет, не говоря уже о любом из других
инвариантов, обсуждавшихся в главе 1. Действительно, как
упоминалось в разделе 5.2, для любого графа Я, который содержит хотя
бы один цикл, существуют графы произвольно большого
хроматического числа, не содержащие Я как подграф (теорема 11.2.2). По
следствию 5.2.3 и теореме 1.4.2 такие графы имеют подграфы
произвольно большой средней степени и связности, так что эти
инварианты также могут быть большими в отсутствие Я как подграфа.
Таким образом, если Я не лес, то единственный способ
вынудить существование подграфа Я в произвольном графе G
посредством глобальных предположений о G состоит в том, чтобы поднять
||G|| существенно выше любого значения, вытекающего из больших
значений вышеупомянутых инвариантов. Если Я не двудолен, то
любая функция / такая, что f(n) ребер в п-вершинном графе
вынуждают подграф Я, должна расти даже квадратично по п. Так как
полные двудольные графы могут иметь \п1 ребер, то f(n) должна
превышать \п2.
Графы с числом ребер, примерно1) квадратичным от числа
вершин, обычно называются плотными, а число ||G||/( 2 ) — реберной
плотностью графа G. Вопрос о том, какая в точности реберная
плотность необходима для вынуждения заданного подграфа —
типичная экстремальная задача на графах в ее первоначальном (более
узком) смысле. Это и есть тема данной главы. Вместо того, чтобы
пытаться дать обзор столь широкой области, как (плотная)
экстремальная теория графов, мы сосредоточим внимание на двух ее
наиболее важных результатах и дадим представление об одном мощном
и общем методе доказательства.
Этими двумя результатами являются классическая
экстремальная теорема Ту рана для Я = КТ (результат, который послужил
образцом для бесчисленных подобных теорем при других графах Я)
и фундаментальная теорема Эрдеша — Стоуна, которая дает
точную асимптотическую информацию сразу для всех Я (раздел 7.1).
Метод доказательства, важность которого в экстремальной теории
плотных графов всё возрастает, состоит в использовании леммы
регулярности Семереди. Эта лемма формулируется и доказывается
в разделе 7.2. В разделе 7.3 мы даем набросок общего метода
применения леммы регулярности и иллюстрируем его доказательством
теоремы Эрдеша — Стоуна, отложенным в разделе 7.1. Другое
приложение леммы регулярности будет дано в разделе 9.2.
) Заметим, что формально понятия разреженных и плотных имеют смысл
только для семейств графов, порядок которых стремится к бесконечности,
а не для отдельных графов.

168
Глава 7. Подструктуры в плотных графах
7.1. Подграфы
Пусть Я — граф и п > \Н\. Сколько ребер будет достаточно
для того, чтобы вынудить подграф Я в любом графе на п вершинах
независимо от того, как эти ребра расположены? Или, перефразируя
задачу: какое наибольшее возможное число ребер может иметь граф
на п вершинах, если он не содержит копию Я как подграф? Как
выглядит такой граф? Является ли он единственным?
Граф G 2 Н на п вершинах с наибольшим возможным числом
ребер называется экстремальным для п и Я; число его ребер
обозначается через ex(n, Я). Ясно, что любой граф G, который
является экстремальным для некоторых пиЯ, будет также реберно-
максимальным при Н <£. G. Однако, наоборот, реберная
максимальность не влечет экстремальность: G вполне может быть реберно-
максимальным для Н <£. G при наличии меньшего, чем ех(п, Я),
числа ребер (рис. 7.1.1).
Рис. 7.1.1. Два графа, которые являются реберно-максимальными для Р3 %-G.
Является ли правый граф экстремальным?
Как особенно важный частный случай рассмотрим нашу задачу
при Н — Кг (с г > 1). Здесь сразу приходят на ум некоторые
очевидные кандидаты на экстремальность: все полные (г — 1)-дольные
графы реберно-максимальны по свойству не содержать КТ'. Но
какие из них имеют наибольшее число ребер? Ясно, что те, в которых
множества разбиения равны, насколько это возможно, т. е.
отличаются по размеру не более чем на 1. Если Vi, V2 — два множества
разбиения с |Vi| — IV2I > 2, то можно увеличить число ребер в нашем
полном (г — 1)-дольном графе, переместив вершину из V\ в V2.
Единственный полный (г — 1)-дольный граф на п > г — 1
вершинах, множества разбиения которого отличается по размеру не
более чем на 1, называется графом Турана; мы обозначаем его
через Тг_1(п), а число ребер в нем — через tr_i(n) (рис. 7.1.2). При
п < г — 1 мы формально продолжаем использовать эти определения
в предположении, что вопреки нашей обычной терминологии
множества разбиения могут теперь быть пустыми; в последнем случае
ясно, что Tr~l{n) = Кп для всех п < г — 1.

7.1. Подграфы
169
Рис. 7.1.2. ГрафТуранаТ3(8)
Следующая теорема сообщает нам, что Тг~1(п) действительно
является экстремальным для п и Кг, причем единственным. В
частности, ex(n, Kr) = tr-i(n).
Теорема 7.1.1 (Туран, 1941). Для всех целых чисел г, п, где
г > 1, любой граф G ~£ Кг сп вершинами и ех(п, Кг) ребрами есть
Т-\п).
Доказательство. Применим индукцию по п. При п < г — 1
имеем G = Кп = Тг_1(п), что и утверждалось. Для шага индукции
пусть теперь п > г.
Поскольку G реберно-максимален без подграфа Кг, то G
содержит подграф К = Кг~1. По индукционному предположению G — К
имеет не более tr_i(n — г -f 1) ребер, а любая вершина G — К имеет
не более г — 2 соседей в К. Следовательно,
l|G|| < tr-i{n -r+l) + (n-r+ 1)(г - 2) +
tr-i(n); (1)
равенство справа следует непосредственно из графа Турана Тг 1(п)
(рис. 7.1.3).
г-2
*r-i(™ -*•+!)
Рис. 7.1.3. Уравнение из (1) при г = 5 и п =■ 14

170
Глава 7. Подструктуры в плотных графах
Поскольку G экстремален для Кг (и Tr~l(n) 2 Кг), в (1) имеет
место равенство. Таким образом, любая вершина из G — К имеет
роено г — 2 соседей в К — точно так же, как вершины zi,..., zr_i
из самого К. При г = 1,..., г — 1 пусть
Vi := {и G 7(G) | ух{ £ E(G)}
есть множество всех вершин G, чьи г — 2 соседей в К — в точности
вершины, отличные от Х{. Поскольку Kr <£ G, все множества К'
независимы и они разбивают V(G). Следовательно, граф G является
(г — 1)-дольным. Так как Tr~l(n) — единственный (г — 1)-дольный
граф с п вершинами и максимальным числом ребер, наше
утверждение, что G = Тг_1(п), следует из предположения об
экстремальности G. □
Графы Турана Tr~l(n) плотны: они имеют по порядку
величины примерно п2 ребер. Точнее, для любого п и г имеем
1 г — 2
*r-i(*0< ^2 г,
z г — 1
причем равенство выполняется всякий раз, когда г — 1 делит п
(упражнение 8). Поэтому замечательно, что лишь на en2 большее
количество ребер (для любого фиксированного е > 0 и большого п) дает
нам как подграф не только Кг (по теореме Турана), но и Щ, сам
изобилующий Кг подграфами, для любого заданного целого числа s.
Теорема 7.1.2 (Эрдеш, Стоун, 1946). Для любых целых чисел
г> 2hs> 1 и любого е > 0 существует такое целое число по, что
любой граф с п > по вершинами и не менее чем
tr_i(n) -f en2
ребрами содержит Krs как подграф.
Мы докажем эту теорему в разделе 7.3.
Теорема Эрдеша — Стоуна интересна не только сама по себе,
она также имеет чрезвычайно интересное следствие. На самом деле,
именно это совершенно неожиданное следствие сделало данную
теорему своего рода метатеоремой для экстремальной теории плотных
графов, и тем самым сделало ее знаменитой.
Для графа Н и целого числа п рассмотрим hn := ех(п, Я)/^);
это максимальная реберная плотность, которую может иметь п-вер-
шинный граф, не содержащий Я. Может ли случиться так, что эта
критическая плотность по существу лишь функция от Я, т. е. что
hn сходится при п —*• оо? Теорема 7.1.2 влечет и это, и нечто
большее: предел hn определяется очень простой функцией естественного
инварианта графа Я — его хроматического числа!

7.1. Подграфы
171
Следствие 7.1.3. Для любого графа Н с не менее чем одним
ребром выполняется равенство
Для доказательства следствия 7.1.3 нам потребуется лемма,
утверждающая, что tr_i(n) не может сильно отклоняться от значения,
которое эта величина принимает при г — 1, делящем п (см. выше),
и что tr-i{n)/(^) сходится соответствующим образом.
Доказательство этой леммы оставляем в качестве легкого упражнения с
подсказкой (упражнение 9).
Лемма 7.1.4. Имеет место равенство
limtr_i(n)( ) =-—-.
п — оо \2J Г — 1
Доказательство следствия 7.1.3. Пусть г := х(Щ-
Поскольку Н не может быть покрашен в г — 1 цветов, имеем Н $£
Tr~l{n) для всех n £ N, а следовательно,
tr_i(n) < ex(n, Н).
С другой стороны, Н С Щ для всех достаточно больших s, поэтому
ех(п, Я) < ex (n, Krs)
для всех таких s. Зафиксируем такое s. Для любого е > 0
теорема 7.1.2 влечет то, что с какого-то момента (т. е. для достаточно
больших п)
ех (п, К5Г) < tr_i(n) + en2.
Следовательно, для больших п
<tr_1(n)/("j+46 (прип>2).

172
Глава 7. Подструктуры в плотных графах
Поэтому так как tr-i(n)/(^) сходится к ^f (лемма 7.1.4), то
сходится и ех(п, Я)/("). Таким образом,
(п\ ~ * г — 2
2 J г — 1
что и утверждалось. □
Для двудольных графов Я следствие 7.1.3 утверждает, что для
вынуждения подграфа Я достаточно существенно меньше, чем Q),
ребер. Оказывается, что
сщ2-2^1 < ех(щКг>г) < с2п2-^г
при подходящих константах ci, с2, зависящих от г. Нижняя граница
получена с помощью случайных графов2), верхняя оценка
вычисляется в упражнении 13. Если Я — лес, то Я С G, как только e(G)
достаточно велико, поэтому ех(п, Я) не более чем линейно по п
(упражнение 5). Эрдеш и Шош в 1963 г. предположили, что ex(n,Т) <
\{к — \)п для всех деревьев с к > 2 ребрами; как общая оценка для
всех п она достижима для любого Т. Подробности см. в
упражнениях 15-18.
7.2. Лемма Семереди о регулярности
Более 20 лет назад в ходе доказательства важного результата
о рамсеевских свойствах арифметических прогрессий Семереди
разработал теоретико-графовый инструмент, фундаментальная
важность которого все глубже осознается в последние годы — это так
называемая лемма о равномерности или о регулярности. В очень
общих чертах лемма утверждает, что все графы могут быть
приближены случайными графами в следующем смысле: любой граф можно
разбить на ограниченное число равных частей так, чтобы
большинство его ребер соединяли различные части, а ребра между любыми
двумя частями распределялись весьма равномерно, так же как мы
могли бы ожидать при порождении их случайным образом.
Чтобы сформулировать лемму регулярности в точных
терминах, нам нужны некоторые определения. Пусть G — (V,E) — граф,
а подмножества X, У С V не пересекаются. Тогда обозначим через
\\Х, У || число Х-У ребер в G и назовем
d(X у) - Ы
2) См. главу 11.

7.2. Лемма Семереди о регулярности
173
плотностью пары (X, У). (Это вещественное число находится
между 0 и 1.) Для заданного е > 0 назовем пару (А, В) непересекающихся
множестве, В С V е-регулярной, если все ХСАиУСВс
\Х\>е\А\ и |У|>б|В|
удовлетворяют условию
\d(X,Y)-d(A,B)\<e.
Ребра в б-регулярной паре, таким образом, распределены весьма
равномерно: чем меньше б, тем более равномерно их распределение.
Рассмотрим разбиение {Vb, Vi,..., Vk) множества V, в котором
одно множество Vq выделяется как исключительное множество.
(Это исключительное множество Vq может быть и пустым3).)
Назовем такое разбиение е-регулярным разбиением графа G, если оно
удовлетворяет следующим трем условиям:
(i) |Vo| < e\V\;
(ii) |v^| = -.. = |v*|;
(iii) все, кроме не более чем ek2 из пар (Vi,Vj) с 1 < i < j < к,
являются е-регулярными.
Роль исключительного множества Vq состоит лишь в удобстве:
оно позволяет потребовать, чтобы все остальные множества
разбиения имели один и тот же размер. Поскольку условия (iii) влияют
только на множества V\,..., Vk, можно рассматривать Vb как своего
рода мусорную корзину — его вершины при оценке равномерности
разбиения игнорируются, но вершин в нем мало.
Лемма. 7.2.1 (лемма регулярности). Для любого е > 0 и
любого целого числа т > 1 существует такое целое число М, что
любой граф порядка не менее m допускает е-регулярное разбиение
{Vo,Vu ... ,Vk} при m < к < М.
Лемма регулярности, таким образом, утверждает, что для
любого б > 0 любой граф имеет 6-регулярное разбиение на ограниченное
число множеств. Верхняя оценка М на число множеств разбиения
гарантирует, что для больших графов множества разбиения также
велики. Отметим, что 6-регулярность очевидна, когда все множества
разбиения одноэлементны, и является мощным свойством, когда они
большие. Кроме того, эта лемма позволяет определить нижнюю
границу га на число множеств разбиения. Выбирая m большим, можно
увеличивать долю ребер между различными множествами
разбиения (уменьшая долю внутренних ребер), т. е. долю ребер, которые
подчиняются условию регулярности.
3) Поэтому Vq может также быть исключением из нашего терминологического
правила, что множества разбиения обычно непусты.

174
Глава 7. Подструктуры в плотных графах
Заметим, что лемма регулярности предназначена для работы
с плотными графами4^. Для разреженных графов она становится
очевидной, потому что все плотности пар, а следовательно, и их
разности стремятся к нулю (упражнение 22).
Оставшаяся часть этого раздела посвящена доказательству
леммы регулярности. Хотя доказательство нетрудное, читатель,
встречающийся с леммой регулярности впервые, вероятно, извлечет
больше пользы из примера ее использования, чем от изучения
технических особенностей его доказательства. Такой читатель может
перейти сейчас к началу раздела 7.3 и обратиться к доказательству на
досуге.
Нам понадобится следующее неравенство для вещественных чи-
сел>1,...,/1д. > 0 и ei,...,e* > 0:
Оно следует из неравенства Коши — Шварца ^ af ^ Щ > (^ at-6t-)w
при at- := у/Щ и 6,- := вг/^Дц.
Пусть G — (V, Е) — граф и n := |V|. Для попарно
непересекающихся множеств А, В С V положим
\А\\в\*1А оч_ UM
q(A,B):=^^d2(A,B)
\А\\В\п*-
Для разбиений я/ множества А и 3$ множества В полагаем
а для разбиения 3* = {Ci,..., С*} на ]/ положим
*(^):=£*(С.-,С,).
Однако если 3* = {Со, Ci,..., Ск} — разбиение наУс
исключительным множеством Со, мы рассматриваем Со как множество
одноэлементных множеств и полагаем
q(3>) := q(&\
где &:= {Ci,...,Ck}U {{v} \ v G C0}.
) Хотя версии для разреженных графов существуют; см. примечания.

7.2. Лемма, Семереди о регулярности
175
Функция q{3?) играет ведущую роль в доказательстве леммы
регулярности. С одной стороны, она измеряет равномерность
разбиения 3*: если в 3? слишком много нерегулярных пар (Л, Б), то
можно взять пары (X, У) подмножеств, нарушающих регулярность
пар (А, В), и переделать эти множества X и У в самостоятельные
множества разбиения. Как мы докажем, это под разбивает 3? до
такого разбиения, для которого q является существенно большим, чем
для 3*. Здесь «существенно» означает, что увеличение q(3*)
ограничено снизу некоторой константой, зависящей только от 6. С другой
стороны,
<z(^) = I>(a-,Q)
=Y*№m#{CiiCi)
<^£|C.-|IQI
< 1-
Число возможных увеличений q{3?) на константу, таким образом,
также ограничено константой. Другими словами, после некоторого
ограниченного числа утончений наше разбиение будет 6-регулярным!
Поэтому все, что нужно сделать для завершения доказательства
леммы регулярности — это заметить, сколько множеств может
иметь последнее разбиение, если мы начинаем с разбиения на m
множеств, и выбрать это число в качестве искомой оценки М.
Следуя этому плану, проведем строгое доказательство леммы
регулярности. Начнем с доказательства того, что при утончении
разбиения значение q не уменьшается.
Лемма 7.2.2.
(i) Пусть множества С, D С V не пересекаются. Если *£ —
разбиение С, а @ —разбиение D, то выполняется неравенство
q(V,9)>q(C,D).
(ii) Если 3*, 3*' — разбиения V, а 3?' утончает 3?, то
выполняется неравенство q(3*') > q(3?).
Доказательство, (i) Пусть
V=:{Cu...,Ck}, 9=:{Du...,Dt}.

176
Глава 7. Подструктуры в плотных графах
Тогда
q(V,9) = '£iq(Ci,Dj)
1 уЧ|с,-,ду||2
, (Е1|с*,1>у||)!
(t)^ EIG-II^I
1 ||C,D||2
>
"2 (£|с«|)(Е1г>,-|)
= ?(C,D).
(ii) Пусть ^ =: {Ci,..., С*}, и для г = l,...,fc пусть % —
разбиение Сг-, индуцированное 2Р1. Тогда
поскольку q(&>') = £<z(^) + Е 9(«S,*5)- D
t i<J
Покажем далее, что утончение разбиения посредством
подразбиения нерегулярных пар множеств разбиения немного
увеличивает q. Поскольку мы здесь имеем дело лишь с единственной
парой, это увеличение будет по-прежнему меньше любой константы.
Лемма 7.2.3. Пусть е > 0, и пусть С, D С V
непересекающиеся. Если пара (С, D) не е-регулярна, то существуют такие
разбиения *ё — {С\, С2) множества С и Q> — {D\, D2) множества D, что
qiV,®)>qiC,D) + Sl-W.
Доказательство. Предположим, что пара (С, D) не £-регуляр-
на. Тогда имеются такие множества С\ С С и D\ С D с |Ci| > е\С\
и |Di| > e\D\, что
Ы > £ (2)
при r]:=d(Ci,Di)-d(C,D). Пусть <af := {Ci,C2} и 0 := {£>i,£>2},
гдеС*2:=С\С1 и D2 :=D\D!.

7.2. Лемма Семереди о регулярности
111
Покажем, что ^ и @ удовлетворяют заключению леммы.
Положим a := |Ci|, di := |Д-|, e{j := ||С*, £>у||, с := |С|, <i := \D\ и е : =
||С, D\\. Как и в доказательстве леммы 7.2.2,
D2
,2
1 '^L + у А
> 1 (iL_ + (е-е"Н
(Т) ^2 \cic?i cd — c\d\ )
По определению 77 имеем ец = c\d\ejcd-\- r\c\d\, поэтому
n2q(V,@)>^r(C-^ + r]c1d1
cidi \ cd
1 ( cd — c\d\
cd — c\d\ \ cd
c\d\e2 1er\c\d\ 2
cd — c\d\ 2 2e7]C\d\ r]2c\d\
c2d2 cd cd — c\d\
>
>
(2)
e2
cd
e2
cd
+ r]2cidi
+t4cd,
поскольку ci > бе и di > 6d по выбору C\ И Di. □
Наконец, покажем, что если разбиение содержит достаточно
нерегулярных пар множеств разбиения, чтобы нарушить определение
б-регулярности разбиения, то подразбиение всех таких пар сразу
приводит к увеличению q на константу.
Лемма 7.2.4. Пусть 0 < е < 1/4, а & = {С0, Ci,..., С*} —
разбиение множества V с исключительным множеством Со мощности
\Со\ < еп и \С\\ — • • • — \Ск\ —'- с. Если £? не е-регулярно, то имеется
разбиение 2Р1 — {С0, С[}..., С'£} множества V с таким
исключительным множеством С0, где к < £ < Ык, что \С0\ < |Со| -f п/2к, все
остальные множества С- имеют равную мощность, и
q(&>') >?(^) + е5/2.
Доказательство. Для всех 1 < г < j < к определим
разбиение %j множества Сг и разбиение ^}г- множества Cj следующим

178
Глава 7. Подструктуры в плотных графах
образом. Если пара (Ci,Cj) 6-регулярная, мы полагаем %j := {Сг}
и ffji := {Cj}. Если нет, то по лемме 7.2.3 имеются разбиения %j
множества С% и ^ множества Cj с \%j\ = \^ji\ = 2 и
q{%j,%i) > Я(Ъ,Ц) + <4Щ^ = q{Ci, Cj) + ^-. (3)
Для любого i — 1,..., к пусть ^ — единственное минимальное
разбиение множества Сг, которое утончает каждое из разбиений %j
с j ф г. (Другими словами, если считать два элемента из Сг
эквивалентными всякий раз, когда они лежит в одном и том же
множестве разбиения %j для любого j ф г, то % — множество классов
эквивалентности.) Таким образом, |^| < 2к~1. Теперь рассмотрим
разбиение
к
<€ := {Со} U [J %
г = 1
множества V с Со в качестве исключительного множества. Тогда ^f
утончает 3? и
*< Щ<к2к. (4)
Пусть % •'= {{и} : v G Со}. Теперь если 3* не 6-регулярно, то для
более чем ек2 пар (Cf, Cj) с 1 < г < j < к разбиение ^ нетривиально.
Следовательно, по определению q для разбиений с исключительным
множеством и леммы 7.2.2(i)
«(*) = Е *(*s.^) +Ел**)+ £«<*«)
1<г<; 1<г 0<г
> J2 ^.^)+Е5^-^})+?(я
1<г<; 1<г
> ?(^) + б5/2.
(Для обоснования последнего неравенства вспомним, что |Со| < en <
^п, так что кс > |п.)
Чтобы превратить ^ в искомое разбиение 3*', теперь остается
лишь разрезать его множества на части некоторого одного размера,
настолько малого, чтобы все оставшиеся вершины можно было
собрать в исключительное множество, не сделав его слишком
большим. Пусть С[,..., С[ — такой максимальный набор
непересекающихся множеств размера d := |_C/4*J, что любое С[ содержится в
некотором Се <*f \{С0}, и положим С0 := V \ \JC[. Тогда 3»' =

7.2. Лемма Семереди о регулярности
179
{Co,i С,..., С[) — действительно разбиение множества V. Более
того, 8Р1 утончает ^, поэтому
q{^')>q{^)>q{^)^e^/2
по лемме 7.2.2(ii). Поскольку каждое множество С[ ф С'0 также
содержится в одном из множеств С\,..., Ск, но не более чем Ак
множеств С/ могут лежать внутри одного и того же Cj (по выбору d),
то имеем также к < £ < к4к, что и требуется. Наконец, множества
С(,..., С[ используют все, кроме, быть может, d вершин из каждого
множества С ф Со разбиения Ч>. Следовательно,
|C£|<|Co| + d|*1
<|Со| + ^*2*
(4) 4*
= \С0\ + ск/2к
<\С0\ + п/2к. П
Доказательство леммы регулярности теперь легко получается
многократным применением леммы 7.2.4.
Доказательство леммы 7.2.1. Пусть заданы е > 0 и m > 1;
без ограничения общности е < 1/4. Положим s := 2/б5. Число s —
верхняя оценка на число итераций леммы 7.2.4, применяемой к
разбиению графа до тех пор, пока оно не станет 6-регулярным;
вспомним, что q(£?) < 1 для всех разбиений £?.
Есть одно формальное требование, которому должно
удовлетворять разбиение {Со, Ci,..., Ск) с \С\\ — • • • = |Cjb|, прежде чем к нему
можно будет (повторно) применить лемму 7.2.4: размер |Со| его
исключительного множества не должен превышать еп. Однако с
каждой новой итерацией леммы размер его исключительного множества
может увеличиваться не более чем на п/2к. (Точнее, не более чем на
п/2£, где £ — число остальных множеств в текущем разбиении, но
£ > к ввиду леммы, так что п/2к заведомо является верхней оценкой
этого приращения.) Таким образом, мы хотим выбрать к настолько
большим, чтобы даже s приращений по п/2к составляли в сумме
не более ^бп, а п настолько большим, чтобы для любого
начального значения |Со| < к выполнялось неравенство [Со| < ^еп. (Если
мы придаем нашему начальному разбиению к неисключительных
множеств Ci,..., Ск, то мы должны позволить начальному размеру
множества Со достигать к, чтобы добиться выполнения равенств
|Ci| = --- = |C*l-)
Итак, пусть к > m настолько велико, что 2к х > s/e. Тогда
s/2k < б/2, а следовательно,
& + -^п < еп (5)
всякий раз, когда к/п < б/2, т. е. для всех п > 2к/е.

180
Глава 7. Подструктуры в плотных графах
Теперь выберем М. Оно должно быть верхней оценкой
числа (неисключительных) множеств в нашем разбиении после не
более s итераций леммы 7.2.4, где на любой итерации это число
может возрасти по сравнению со своим текущим значением г не
более, чем на г4г. Пусть / — функция х t—► хАх, и возьмем М \—
max{/5(&), 2k/e}. Второй член в этом максимуме гарантирует, что
любое п > М достаточно велико, чтобы удовлетворять условию (5).
Наконец, нужно показать, что любой граф G = (V, Е) порядка не
менее m имеет 6-регулярное разбиение {Vb, Vi,..., V*} с m < k < M.
Итак, пусть задан G и n := \G\. Если п < М, то мы разбиваем G
на к := п одноэлементных множеств, выбирая Vq := 0 и |Vi| =
• • • = |Vib| = 1. Это разбиение G, очевидно, является 6-регулярным.
Предположим теперь, что п > М. Пусть Со С V — такое
минимальное множество, что к делит \V \ Со|, и пусть {Ci, • • -, C*jt} —
любое разбиение множества V \Cq на подмножества равной
мощности. Тогда [Со| < к, а следовательно, [Со| < сп ввиду (5). Начиная
с {Со, Ci,..., С*} применяем лемму 7.2.4 снова и снова, пока
полученное разбиение графа С не станет 6-регулярным. Это случится
не позднее s-й итерации, поскольку ввиду (5) размер
исключительного множества в разбиении все время меньше бп, так что лемму
действительно можно снова применять, вплоть до теоретического
максимума в s раз. □
7.3. Применение леммы регулярности
Цель этого раздела состоит в демонстрации того, как лемма
регулярности обычно применяется в контексте экстремальной
теории «плотных» графов. Предположим, мы хотим доказать, что
некоторая реберная плотность графа С достаточна, чтобы вынудить
возникновение некоторого заданного подграфа Я, и что мы имеем
6-регулярное разбиение графа С Ребра внутри почти любой пары
(Vi, Vj) множеств разбиения распределены равномерно, хотя их
плотность может зависеть от этой пары. Но поскольку в G ребер много,
эта плотность не может быть нулевой для всех пар: некоторая
значительная доля пар будет иметь положительную плотность. Теперь
если граф С большой, то велики и пары; вспомним, что число
множеств разбиения ограничено и они имеют одну и ту же мощность.
Но любой достаточно большой двудольный граф с равными
множествами разбиения, фиксированной положительной реберной
плотностью (произвольно малой!) и равномерным распределением ребер
будет содержать любой заданный двудольный подграф5), что будет
5) Читатели, уже знакомые со случайными графами, могут найти
поучительным сравнение этого утверждения с предложением 11.3.1.

7.3. Применение леммы регулярности
181
уточнено ниже. Таким образом, если в нашем разбиении G
достаточно много пар имеют положительную плотность для того, чтобы
Я'можно было записать как объединение двудольных графов,
каждый из которых возникает в одной из этих пар, то мы можем
надеяться, что Н С G, как и требуется.
Эти идеи будут формализованы ниже в лемме 7.3.2. Затем мы
воспользуемся ею и леммой регулярности, чтобы доказать теорему
Эрдеша — Стоуна из раздела 7.1; еще одно применение будет дано
позже при доказательстве теоремы 9.2.2.
Прежде чем мы сформулируем лемму 7.3.2, отметим простое
следствие 6-регулярности пары (А, В): для любого подмножества
У С 5, которое не слишком мало, большинство вершин А имеет
примерно среднее число соседей в У.
Лемма 7.3.1. Пусть (А, В) —е-регулярная пара, скажем,
плотности d, и пусть У С В имеет мощность \Y\ > е\В\. Тогда каждая
из вершин в А, кроме, быть может, е\А\ вершин, имеет не менее
(d — e)\Y| соседей в У.
Доказательство. Пусть X С А — множество вершин с менее
чем (d - e)\Y\ соседями в У. Тогда \\Х, Y\\ < \X\(d - e)\Y\, так что
*&,Y)=ll^<d-e = d(A,B)-e.
Пара (А, В) 6-регулярна, и отсюда следует, что \Х\ < е \А\. □
Пусть G — граф с б-регулярным разбиением {Vq, V\,..., Vk} при
исключительном множестве Vq и |Vi| = • • • = |VJb| — \£. При
заданном d £ (0,1] пусть R — граф с вершинами V\,..., Vjb, в котором две
вершины смежны, если и только если они образуют 6-регулярную
пару в G плотности > d. Назовем R графом регулярности графа G
с параметрами е, £ и d. При заданном sGN заменим теперь каждую
вершину V{ в R множеством V* из s вершин, а каждое ребро —
полным двудольным графом между соответствующими ^-множествами.
Полученный граф будем обозначать через Rs. (При R = Кг,
например, имеем Rs — Krs.)
Следующая лемма утверждает, что подграфы графа Rs могут
быть найдены также и в G при условии, что е достаточно мало, a V{
достаточно велико. На самом деле, требуемые значения е и £ зависят
только от (d и) максимальной степени подграфа.
Лемма 7.3.2. Для всех d £ (0,1] и А > 1 существует бо > О
со следующим свойством: если G — любой граф, Н — граф с
Д(#) < A, s£N, a R — любой граф регулярности графа G с
параметрами е < €q, £ > s/cq и d, то
яа^ясс

182
Глава 7. Подструктуры в плотных графах
Доказательство. При заданных d и А выберем во < d
настолько малым, что
Д + 1
JcTTo)*60^1' (1)
такой выбор возможен, поскольку (А + l)6/(d — е)А —► 0 при
б —»■ 0. Теперь пусть G, Н, s и R заданы, как сказано выше. Пусть
{Иъ V\, . •., Vk} — б-регулярное разбиение G, которое породило R.
Таким образом, е < е0, 7(Д) = {7i,...,Vi} и |7i| = ■■■ = |V*| = £
Допустим, что на самом деле Н — подграф графа Rs (а не только
изоморфен его подграфу), скажем, с вершинами ui,...,u^. Любая
вершина щ лежит в одном из s-множеств Vf в Я5; это определяет
отображение <т: г»—► j. Наша цель — определить вложение иг- i—► «£ G
Кт(г) графа Н в G. В итоге i>i,..., i^ будут различны, a V{Vj будет
ребром G всякий раз, когда U{Uj — ребро Н.
План состоит в том, чтобы выбрать вершины i>i,..., Vh
индуктивно. В процессе индукции мы будем иметь «целевое множество»
Yi Я: K7(t)» приписанное каждому г; оно содержит вершины,
которые продолжают оставаться кандидатами на выбор г/,-.
Первоначально Yi — это все множество Va(i)- По ходу вложения У*
становится все меньше и меньше (пока оно не сожмется в {г/г}, когда
Vi будет уже выбрано). Всякий раз, когда выбирается вершина Vj
с j < г и UjU{ G Е(Н), мы удаляем все те вершины из Уг-,
которые не смежны с Vj. Тогда множество YJ- сворачивается следующим
образом:
Va(i) = Y{° D ■ ■ ■ D Yl = {«,-},
где Y/ обозначает версию Y{, ставшую текущей после определения Vj
(и удаления соответствующих вершин из Y?~l).
Чтобы реализовать данный подход, мы должны гарантировать,
что целевые множества Y{ не становятся слишком малыми. Когда
мы вкладываем вершину Uj, то рассматриваем все индексы i > j
с UjU{ G Е(Н); имеется не более А таких г. Для любого из этих г мы
хотим выбрать vj так, чтобы
Y> =N(vj)nY/-1 (2)
было велико, т. е. ненамного меньше, чем Y/'1. Теперь ЭТО можно
сделать по лемме 7.3.1 (с А = Va(j), В = Va(i) и У = Y-~ ): если
Y?~ не слишком мало (порядка меньшего, чем е£), то все, кроме,
быть может, е£ выборов vj, будут таковы, что (2) влечет
|^|>(d-c)|^-i|.
(3)

7.3. Применение леммы регулярности
183
Делая это одновременно для всех из не более чем А значений г, мы
находим, что все, кроме, быть может, Ае£ выборов Vj из Va(j) и, в
частности, из Yj~~ С Va(j), удовлетворяют условию (3) для всех г.
Чтобы гарантировать существование подходящего выбора для
Vj, остается показать, что рассмотренные выше для леммы 7.3.1
множества У действительно не могут быть очень малы и что \Y-~ | —
Ае£ > s. Поскольку cr(j') — a(j) для не более чем s — 1 вершин uji
с f < h то выбор из s подходящих кандидатов на роль Vj будет
достаточен, чтобы Vj была отлична от i>i,..., ity-i. Но все это следует
из сделанного нами выбора во. Действительно, начальные целевые
множества Y{° имеют мощность £} а из любого Y; вершины
удаляются, только когда определяется некоторая Vj с j < г и UjU{ G Е(Н),
что происходит не более А раз. Таким образом,
\Y-j \-Ae£>(d- е)А£ - Ае£ > (d - е0)А£ - Ае0£ > е0£ > s
(3) (1)
при любых j < г, поэтому, в частности, |Y^ | > €q£ > е£ и |^_1| —
Ае£ >s. □
Теперь мы готовы доказать теорему Эрдеша — Стоуна.
Доказательство теоремы 7.1.2. Пусть г > 2 и s > 1 заданы,
как в утверждении теоремы. Для s = 1 утверждение следует из
теоремы Турана, поэтому предположим, что s > 2. Пусть задана
7 > 0; эта j будет играть роль е из теоремы. Пусть G — граф
с \G\ —\ п и
||G||><r-i(n) + 7"2-
(Таким образом, 7 < 1-) Мы хотим показать, что Krs С G, если
п достаточно велико.
Наш план состоит в использовании леммы регулярности для
нахождения в G столь плотного графа регулярности R, чтобы по
теореме Турана он содержал Кг. Тогда Rs содержит Krs, поэтому
можно надеяться, что с использованием леммы 7.3.2 удастся
установить включение Krs С G.
Получая на входе d := j и А :— А(К[), лемма 7.3.2 выдает
бо > 0. Поскольку утверждение леммы относительно во становится
более слабым при уменьшении бо, можно считать, что
б0<т/2<1. (1)
Чтобы применить лемму регулярности, положим m > I/7 и
выберем б > 0 настолько малым, что е < во и
6 :=2у-е2 -4e-d > 0;
m

184
Глава 7. Подструктуры в плотных графах
это возможно, поскольку 27 — d — ~ > 0. Получая на входе бит,
лемма регулярности дает на выходе целое число М. Допустим, что
Ms
Поскольку это число не меньше т, лемма регулярности обеспечивает
существование 6-регулярного разбиения {Vo, 14,..., 14} графа G, где
m< к < М\ пусть |Vi| = ■■■ = |14| = : L Тогда
n > k£, (2)
и
n— \Vq\ n— en 1-е s
к M M е0
по выбору п. Пусть R — граф регулярности для G с параметрами
б, £} d} отвечающий вышеупомянутому разбиению. Поскольку е < во
и £ > s/cq, граф регулярности R удовлетворяет посылке леммы 7.3.2,
а по определению А имеем Д(К[) = А. Таким образом, чтобы
заключить по лемме 7.3.2, что Krs С G, остается лишь проверить, что
Кг СЕ(а следовательно, Krs С Rs).
Мы хотели показать, что Кг С R по теореме Турана. Таким
образом, нужно проверить, что R имеет достаточно много ребер,
т. е. что достаточно много 6-регулярных пар (Vi,Vj) имеют
плотность не менее d. Это должно следовать из нашего предположения,
что G имеет не менее tr_i(n) -f jn2 ребер, т. е. реберную плотность
примерно ^5f + 27- Такая оценка существенно выше
приблизительной реберной плотности ^5у графа Турана Тг~1 (к) и, следовательно,
существенно выше любой плотности, которую мог бы иметь G, если
не более чем £r_i(&) из пар (Vi.Vj) имело бы плотность > d, даже
если бы все эти пары имели плотность 1!
Теперь оценим ||Д|| точнее. Сколько ребер из G лежит вне
6-регулярных пар? Не более ('^°') ребер лежит внутри Vq, а по
условию (i) в определении 6-регулярности это дает не более \(еп)2
ребер. Не более |Vo|H < епк£ ребер соединяют Vq с другими
множествами разбиения. Не более ек2 других пар (K',V/), которые не
6-регулярны, содержат не более £2 ребер каждая, все вместе не более
ек2£2, а 6-регулярные пары недостаточной плотности (< d) содержат
не более d£2 ребер каждая, все вместе не более \k2d(? ребер.
Наконец, имеется не более (2) ребер внутри любого из множеств
разбиения Vi,..., 14, всего не более \£?к ребер. Все остальные ребра из G
лежат в 6-регулярных парах плотности не менее d, а значит, вносят
вклад в ребра графа R. Поскольку любое ребро из R соответствует
не более чем £2 ребрам из G, мы, таким образом, имеем в общей
сложности
||С|| < 1-<?п2 + епк£ + ек2£2 + ]-k2d£2 + ]-£2к + ||Я||^2.

Упражнения 185
Следовательно, для всех достаточно больших п
„ „ 1,ЛС\\-\е2п2-епМ-екЧ2-Ш2(.2-Ш2
\\Щ\ > ^к2^-^ р^ 2 2_
. 1 l2 ftr-i(n) + yn2 - \e2n2 - enkl 1
^> —fC I 7T~TZ — ^^ — (" — T"
(i72) 2 V ™72 *
>^2f!!:i#-b2T-^-4,-^-i
(2) 2 V "72 ' m
(Строгое неравенство следует из леммы 7.1.4.) Поэтому Кг С R
по теореме 7.1.1, что и требовалось доказать. □
Упражнения
1."" Показать, что К^з экстремален без Р3.
2.~ Для данного А: > 0 найти экстремальные графы с хроматическим числом
не более /:.
3. Определить значение ех(п, К\}Г) для всех r^n Е N.
4. Существует ли граф, который является реберно-максимальным без
минора К3, но не экстремальным?
5. Показать, что для любого леса F значение ex(n, F) ограничено сверху
линейной функцией от п.
бЛ Пусть А: > 0. Найти экстремальные графы без паросочетания порядка /:.
(Подсказка. Теорема 2.2.3 и упражнение 10 главы 2.)
7. Не пользуясь теоремой Турана, показать, что максимальное число ребер
в графе порядка п > 1 без треугольников есть [n2/4j.
8. Показать, что
1 .г- 1
ir_i(n) < -п
2 г - 1
причем равенство выполняется всякий раз, когда г — 1 делит п.
9. Показать, что ir_i(n) J("J сходится к (г — 2)/(г — 1) при п —► со.
(Подсказка. *г_2 ((г - 1) [^J ) < *r_2 (n) < *r-i ((г - 1) f^] ).)
10.+ Для данных несмежных вершин u, v в графе G обозначим через G[w —* г>]
граф, полученный из G сначала удалением всех ребер при и, а затем
соединением и со всеми соседями вершины v. Показать, что Kr g G[u —»■ г>],
если А'г 2 £*• Многократно применяя эту операцию к данному
экстремальному графу для п и Кг, докажите, что ex(n,i\r) = ir_i(n). На каждом

186
Глава 7. Подструктуры в плотных графах
итеративном шаге выберите и и v так, чтобы число ребер не уменьшалось,
а значит, чтобы в конечном итоге получился полный многодольный граф.
11. Показать, что удалением из Кт)П не более чем (т — s)(n — t)/s ребер нельзя
уничтожить все его подграфы Ks,t-
12. Для 0 < s < t < п пусть г(п, s, t) — максимальное число ребер в двудольном
графе, оба множества разбиения которого имеют порядок п и который не
содержит Ks,t' Показать, что 2 ex(n, KSft) < z(n, s,t) < ex(2n, A's.t).
13.+ Пусть 1 < г < n — целые числа. Пусть G — двудольный граф с 2-разбие-
нием {А, В}, где \А\ = \В\ = п, и допустим, что Кг,г 2 G. Показать, что
хел
Используя предыдущее упражнение, вывести отсюда, что ех(п,/\Г)Г) <
сп2~1'т для некоторой константы с, зависящей только от г.
14. Верхняя плотность бесконечного графа G есть точная нижняя грань всех
таких вещественных чисел а, что конечные графы HCGc||H||f'2'J >а
имеют ограниченный порядок. Показать, что это число всегда принимает
одно из счетного множества значений |0,1,^,^, £■,... |.
(Подсказка. Теорема Эрдеша — Стоуна.)
15. Доказать следующее ослабление гипотезы Эрдеша — Шош
(сформулированной в конце раздела 7.1): для данных целых чисел 2 < k < п любой
граф с п вершинами и не менее чем (к — \)п ребрами содержит как подграф
каждое дерево с к ребрами.
16. Показать, что в качестве общей оценки для произвольного п оценка на
ex(n, Т) в гипотезе Эрдеша — Шош есть наилучшая из возможных для
любого дерева Т. Является ли она наилучшей из возможных даже для
каждого п и каждого Т?
17.~ Доказать гипотезу Эрдеша — Шош для случая, когда рассматриваемое
дерево — звезда.
18. Доказать гипотезу Эрдеша — Шош для случая, когда рассматриваемое
дерево есть путь.
(Подсказка. Применить результат следующего упражнения.)
19. Показать, что каждый связный граф G содержит путь длины не менее
min{2<S(G),|G|-l}.
20.~ Для чего в определении б-регулярной пары требуются условия \Х\ > е\А\
и|У|>£|В|?
21.~ Показать, что любая б-регулярная пара в G является е-регулярной и в G.
22. Доказать лемму регулярности для разреженных графов, т. е. для каждой
такой последовательности (Gn)nGj\j графов Gn порядкап, что ||Gn||/n2 —* 0
при п —► со.

Примечания
187
Примечания
Общепринятым справочником по результатам и нерешенным задачам в
экстремальной теории графов (в очень широком смысле) до сих пор является:
Bollobds В. Extremal Graph Theory. London: Acad. Press, 1978. Нечто вроде
новой версии этой книги дается автором в его главе из: Handbook of
Combinatorics J Ed. by R. L. Graham, M. Grotschel, L. Lovasz. Amsterdam: North-
Holland Publ., 1995. Поучительный обзор экстремальной теории графов в более
узком смысле нашей главы дается М. Шимоновичем в: Selected Topics in Graph
Theory 2 I Ed. by L. W. Beineke, R. J. Wilson. London; New York: Acad. Press,
1983. Эта статья, в частности, подчеркивает важную роль графов Турана.
Более свежий обзор того же автора можно найти в: The Mathematics of Paul Erdos /
Ed. by R. L. Graham , J. Nesetfil. V. 2. Berlin: Springer-Verb, 1997.
Теорема Турана не просто один из результатов в экстремальной теории
графов — это результат, открывший целое направление исследований. Наше
доказательство этой теоремы фактически следует оригиналу; доказательство
в упражнении 10 принадлежит Зыкову.
Наша версия теоремы Эрдеша — Стоуна немного упрощает оригинал.
Прямое доказательство, не использующее лемму регулярности, дано в: Lovdsz L.
Combinatorial Problems and Exercises. 2nd ed. Amsterdam: North-Holland Publ.,
1993. Ее наиболее фундаментальное приложение — следствие 7.1.3 — было
найдено Эрдешеми Шимоновичем (1966) уже спустя 20 лет после публикации самой
теоремы.
Из двух приведенных нами оценок для ех(п, КГ)Г) именно первая считается
дающей правильный порядок роста. Для сильно внедиагональных полных
двудольных графов это было проверено в работе: Kolldr J., Ronyai L., Szabo Т.
Norm-graphs and bipartite Turan numbers. Combinatorica. 1966. 16. P. 399-406,
где доказано, что ex(n, Kr>3) > crn2~1'r при s > r!.
Подробности относительно гипотезы Эрдеша— Шош, включая
приближенное решение для больших к, можно найти в упомянутом ниже обзоре Комлоша
и Шимоновича. Случай, когда дерево является путем, доказан Эрдешем и Гал-
лаи в 1959. Именно этот результат наряду с легким частным случаем звезд
(упражнение 17) вызвал к жизни данную гипотезу как возможный
объединяющий результат.
Лемма регулярности доказана в: Szemeredi Е. Regular partitions of graphs //
Problemes Combinatoires et Theorie des Graphes: Colloques Internationaux CNRS,
Orsay. 1976. 260. P. 399-401. Наше изложение следует наброску Скотта (личное
сообщение). Широкий обзор по лемме регулярности и ее приложениям дается
Комлошем и Шимоновичем в: Combinatorics, Paul Erdos is eighty / Ed. by
D. Miklos, V. T. Sos, T. Szonyi / Bolyai Soc. Math. Studies. V. 2. Budapest:
Janos Bolyai Math. Soc, 1996; понятие графа регулярности и лемма 7.3.2 взяты
из этой работы. Адаптация леммы регулярности к разреженным графам
разработана независимо Кохаякавой и Рёдлем; см.: Kohayakawa У. Szemeredi's
regularity lemma for sparse graphs // Foundations of Computational Mathematics: Selected
papers of a conference held at IMPA in Rio de Janeiro, Jan. 1997 / Ed. by F. Cucker,
M. Shub. Berlin: Springer-Verl., 1997.

Глава 8
Подструктуры в разреженных графах
В этой главе мы изучаем, как глобальные предположения
относительно графа — о его средней степени, хроматическом числе или
даже (большом) обхвате — могут вынуждать существование в нем
заданного графа Я в качестве минора или топологического минора.
Нам уже известно из теоремы 3.6.1 Мадера, что существует такая
функция h, для которой средняя степень d(G) > Н(г) достаточна
для появления в G подграфа ТКГ, а следовательно, и
(топологического) минора Я, если г > |#|. Поскольку граф с п вершинами
и средней степенью d имеет ^dn ребер, это показывает, что для
любого Я имеется такая «константа» с (зависящая от Я, но не от п),
что топологический минор Я присутствует в любом графе с п
вершинами и не менее чем сп ребрами. Такие графы с числом ребер,
приблизительно линейным1) относительно его порядка, называются
разреженными, так что в этой главе изучаются подструктуры в
разреженных графах.
Первый вопрос, следовательно, будет об аналоге теоремы Ту-
рана: для заданного положительного целого числа г найти
минимальное значение вышеупомянутой «константы» с при Я = Кг, т. е.
о наименьшей скорости роста функции h(r) из теоремы 3.6.1. Это
было крупной нерешенной проблемой вплоть до совсем недавнего
времени. В разделе 8.1 мы излагаем ее решение, основанное на
некоторых интересных методах, которые вызвала к жизни эта задача за
время своего существования.
Если при увеличении средней степени с неизбежностью
возникает некоторый минор, то это же происходит и при увеличении
любого другого инварианта, который, в свою очередь, повышает
среднюю степень. Например, если d(G) > с влечет Я =^ G, то так же
будет и при x(G) > с-f 1 (по следствию 5.2.3). Однако является ли
это условие наилучшим из возможных? Даже если указанное
значение — наименьшее из возможных для d(G) > с, дающих Я =^ G,
J) Сравните со сноской в начале главы 7.

8.1. Топологические миноры
189
условие x{G) > с -f 1 уже не обязано быть самым слабым из
гарантирующих включение Н =4 G. Одна из наиболее известных гипотез
в теории графов — гипотеза Хадвигера — предполагает, что здесь
действительно имеется зазор. В то время как значение с = с'гл/log г
(где с1 не зависит ни от п, ни от г) есть наилучшее из возможных
для того, чтобы d(G) > с влекло Н =^ G (раздел 8.2), эта гипотеза
утверждает, что x(G) > г гарантирует то же самое! Таким
образом, если гипотеза Хадвигера верна, то она показывает, что влияние
большого хроматического числа на возникновение миноров каким-то
образом выходит за пределы того, что уже вполне понято, а именно,
его влияние лишь через реберную плотность. Мы рассмотрим
гипотезу Хадвигера в разделе 8.3.
8.1. Топологические миноры
В этом разделе мы доказываем, что средняя степень сг2
достаточна для вынуждения в графе топологического минора КТ. Полные
двудольные графы показывают, что с точностью до константы с это
значение наилучшее из возможных (упражнение 5).
Следующая теорема была доказана в 1996 г. независимо Болло-
башем и Томасоном, а также Комлошем и Семереди.
Теорема 8.1.1. Существует такое с ЕЖ, что для любого г £ N
любой граф G средней степени d(G) > сг2 содержит Кт как
топологический минор.
Доказательство этой теоремы, в котором мы следуем Боллобашу
и Томасону, займет всю оставшуюся часть раздела. Множество
U С V(G) будет называться сцепленным (в G), если для любых
различных вершин i*i,..., U2h £ U имеется h непересекающихся путей
Pi — U2i-i.. .v>2i в G, i = 1,.. .,h2\ Сам граф G (k,£)-сцеплен, если
любое ^-множество его вершин содержит сцепленное ^-множество.
Как мы собираемся находить ТКГ в G, существование которого
утверждается в теореме 8.1.1? Основа нашего подхода состоит
сначала в построении некоторого г-множества X как множества вершин
ветвления и выборе для любого х £ X некоторого множества Ух из
г — 1 его соседей, по одному для любого инцидентного х ребра в Кт'.
Если константа с из теоремы достаточно велика, то г -f г (г — 1) = г2
вершин множества X U (|J Ух) можно выбрать различными: по
предположению 1.2.2 G имеет подграф минимальной степени не менее
e(G) — \d(G) > \cr2, так что можно выбирать X и его соседей
внутри этого подграфа. Зафиксировав X и множества Ух, мы затем
должны соединить правильные пары вершин в У :— [JYX
непересекающимися путями в G — X, чтобы получить искомый ТКГ.
2) Таким образом, в Аг-снепленном графе (см. раздел 3.6) любое множество из
не более чем 2к -\- 1 вершин сцеплено.

190
Глава 8. Подструктуры в разреженных графах
Это было бы возможно сразу, если бы У было сцеплено в G — X.
К сожалению, надеяться на это не приходится: никакая средняя
степень, сколь угодна большая, не заставит каждое г (г — 1)-множество
быть сцепленным (почему?). Однако если мы выбираем для X
значительно больше, чем г, вершин, необходимых в конечном счете,
а для любого х £ X значительно больше, чем г — 1 соседей в
качестве Уг, то У могло бы стать настолько большим, чтобы высокая
средняя степень графа G гарантировала существование некоторого
большого сцепленного подмножества Z С У. Это имело бы место,
если бы G был (&,^)-сцеплен для некоторых k < \Y\ и £ > \Z\.
Как и выше, достаточно большая константа с будет легко
гарантировать, что X и У можно выбрать с большим запасом. Другая
проблема, однако, является более серьезной: оказывается,
недостаточно сделать £ (а значит, и Z) большим в абсолютном
выражении. Действительно, если к (и У) будут все еще гораздо больше,
может случиться, что Z, хотя и большое, состоит из соседей лишь
нескольких вершин в XI Таким образом, мы должны гарантировать
что £ велико также относительно к. Это будет целью нашей первой
леммы (8.1.2) — она устанавливает достаточное условие для того,
чтобы G был {к, [&/2~|)-сцепленным.
В чем состоит это достаточное условие? Оно — в
предположении, что G имеет особенно плотный минор Я, в котором
минимальная степень превышает \\Н\ на положительную долю от к. (В
частности, Н будет плотен в смысле главы 7.) Ввиду теоремы 3.6.2 не
удивительно, что такой плотный граф Н имеет высокую сцеплен-
ность. При достаточно высокой связности графа G (которая опять-
таки легко получается при достаточно большом с) можно будет
затем попытаться связать вершины любого У, как и выше, с
различными множествами ветвления в Н непересекающимися путями в G,
избегающими большинства остальных множеств ветвления, и тем
самым, следовательно, перенести свойства сцепленности из Н на
некоторое \к/2]-множество Z С У (рис. 8.1.1).
Однако еще более удивительно то, что существование такого
плотного минора Н может быть выведено из нашего предположения
о d(G) > сг2. Это будет показано в еще одной лемме (8.1.3);
утверждение самой теоремы после этого получится уже легко.
Лемма 8.1.2. Если граф G к-связен и содержит минор Н такой,
что 28(H) >\Н\ + |&, то G является (к, \к/2])-сцепленным.
Доказательство. Пусть У := {Vx \ х £ V(H)} — множество
множеств ветвления в G, соответствующих вершинам из Н. Для
доказательства того, что G является (к, [&/2~|)-сцепленным, допустим,
что заданы к различных вершин vi,...,Vk £ G. Назовем
последовательность Pi,...,Pjb непересекающихся путей в G сцепкой, если
каждое Р{ начинается в V{ и заканчивается в попарно различных

8.1. Топологические миноры
191
множествах V G У] сами пути Рг- будут называться цепями.
Поскольку наши предположения относительно Н влекут, что \Н\ > к
и G &-связен, такие сцепки существуют: просто выбираем к вершин
из попарно различных множеств V € У и связываем их с {vi,..., и*}
независимыми путями по теореме Менгера.
Теперь пусть SP — (Pi,..., Pjb) — сцепка, у которой общее число
ребер вне (J G[V] минимально. Таким образом, если /(Р) обозна-
чает число ребер в Р, не лежащих ни в каком G[Vr], то выберем
3* так, чтобы минимизировать J^ /(Рг)- Тогда для любого V G У,
t=i
которое пересекает путь Pt- G ^, существует единственный путь,
который заканчивается в V. Иначе мы могли бы закончить Р,- в V
и уменьшить f(P{). Следовательно, ровно к множеств ветвления
из Н пересекаются с цепью. Разделим эти множества на два класса:
<%У := {V £ У \ V пересекает ровно одна цепь},
W \— {V G У | V пересекает более чем одна цепь}.
Поскольку Н плотен, а любое U G <%£ пересекает только одна цепь,
то будет легко показать, что начальные вершины V{ этих цепей
образуют сцепленное множество в G. Следовательно, наша цель —
показать, что |^| > fA?/2"|, т. е. что W не меньше, чем W. (Вспомним,
что \%/\ -f \W\ = к.) Для этого сначала докажем следующее.
Любое V G W пересекается некоторой цепью, которая
покидает V еще раз и затем сразу пересекает некоторое (1)
множество из °М (где она и заканчивается).

192 Глава 8. Подструктуры в разреженных графах
Предположим, что Vx G ^ — контрпример к (1). Поскольку
26(H) >\H\ + ^k> 8(H)+ ^k,
имеем S(H) > |&. Так как \^/ U W\ = к, это влечет наличие у х
соседа увНсУу£У\ (<%/ U W). Пусть wxwy — ребро из G с wx G Vx
и wy G Vy. Пусть Q = w .. .wxwy — путь в G[VX U {iuy}], из
вершин которого только w лежит на какой-либо цепи, скажем, на Рг
(рис. 8.1.2). Замена Р,- в 2? на Р/ := PjiuQ тогда дает другую сцепку.
Рис. 8.1.2. Если Pi не заканчивается в Vx, то заменяем Рг и Р на Р' и Р'
Если Pi не есть цепь, заканчивающаяся в Vx, то /(Р/) < /(Д)-
Выбор ^ тогда влечет, что /(Р/) = f{Pi), т. е. что Рг
заканчивается в том множестве ветвления W, в которое она заходит сразу
после Vx. Поскольку Vx — контрпример к (1), имеем W £ <%У, т. е.
W € W. Пусть Р ф Р{ — другая цепь, пересекающая W. Тогда
Р не заканчивается в W (потому что там заканчивается Рг). Пусть
Р' С Р — (минимальный) начальный сегмент из Р, который
заканчивается в W. Если мы теперь заменим Р; и Р на Р/ и Р' в ^, то
получим сцепку, противоречащую выбору &>.
Допустим теперь, что Р, заканчивается в Vx; тогда /(Р/) =
f(Pi) -f 1. Поскольку 14 G >^, существует цепь Р,, которая
пересекает Vx и затем покидает это множество. Пусть Pj —
начальный сегмент в Ру, заканчивающийся в Vx (рис. 8.1.3), тогда f(Pj) <
f(Pj) — 1. На самом деле, поскольку замена Р* и Pj на Р/ и Р.- в &
дает другую сцепку, выбор & влечет, что f(Pj) — /(Pj) —1, поэтому
Pj заканчивается в том множестве ветвления W, в которое она
входит сразу после Vx. Тогда W EW, и можно определить Р и Р', как
и раньше. Заменяя Pt, Pj и Р на Р/, Р' и Р' в ^, мы наконец
получаем сцепку, которая противоречит выбору &. Этим завершается
доказательство утверждения (1).

8.1. Топологические миноры
193
Рис. 8.1.3. Если Pi заканчивается в V^, то заменяем Р^, Pj, Р на Р/, Р', Р'
С помощью утверждения (1) можно определить инъективное
отображение W —+ ^ следующим образом: при заданном Ж £ W
выберем цепь, которая проходит через W, а затем сразу пересекает
множество U £ ^, а также отображение W »—► {/. (Это
действительно инъективное отображение, потому что различные цепи
заканчиваются в различных множествах ветвления.) Таким образом,
\Щ > |^|, а следовательно, \<&\ > [А/2].
Предположим, что нумерация «i,..., Vk такова, что первые и :=.
\°1/\ цепей Pi,..., Pk заканчиваются во множествах из <%У. Поскольку
28(H) > \Н\ -f |&, можно найти для любых двух множеств VX) Vy £
<%У не менее -^к таких множеств Vz, что xz,yz £ Е(Н). Не менее
А/2 из этих множеств Vz не лежат в °М U >^. Таким образом,
всякий раз, когда C/i,..., С/2/1 — различные множества в Щ (и поэтому
h < и/2 < 2/к), можно найти индуктивно h таких различных
множеств Vх' £ Г \ (^ U W) (г = 1,..., ft), что Vх' соединено в G с C/2,_i
и [/2г- Для любого г любая вершина из С/2г —i может быть сцеплена
путем через Vх с любой нужной вершиной из {/2,-; эти пути будут
непересекающимися для различных г. Соединяя соответствующие
пары путей из ^, мы видим, что множество {i>i,..., vu} сцеплено
в G, и лемма доказана. □
Лемма 8.1.3. Пусть к > б — целое число. Тогда любой граф G
с e(G) > К имеет такой минор Я, что 28(H) > \Н\ + ^к.
Доказательство. Начнем с выбора (=^-) минимального
минора Go графа G с e(Go) > к. Минимальность Go влечет, что 8(Go) > к
и £(Go) = к (в противном случае мы могли бы удалить из Go
вершину или ребро), и, следовательно,
к + 1 < «(Go) < d(G0) = 2k.
Пусть xq £ Go — вершина минимальной степени.
Если к нечетно, положим m := (к -f 1)/2 и
Gi:=G0[{*o}UWg0(z0)].

194
Глава 8. Подструктуры в разреженных графах
Тогда |Gi| = «(Go) + 1 < 2А + 1 < 2(А + 1) = 4m. Ввиду
минимальности Go стягивание любого ребра хоу в Go приведет к потере не
менее k -f 1 ребер. Вершины xq и у, следовательно, имеют не менее
к общих соседей, поэтому S(Gi) > к -f 1 = 2m (рис. 8.1.4).
Ng0(x0)
Рис. 8.1.4- Граф G\ =^ G: первое приближение к искомому минору Н
Если к четно, то полагаем m := к/2 и
G1 := Go[^Go(x0)].
Тогда |Gi| = «(Go) < 2k — Am и 6(Gi) > к — 2m, как и раньше.
Таким образом, в каждом случае мы нашли такие целое число
m > к/2 и граф G\ =^ G, что
|Gi|<4m
и ^(Gi) > 2m, поэтому
e(Gi) > m> к/2 > 3.
(1)
(2)
Поскольку 26(G\) > 4m > |Gi|, наш граф G\ — уже хороший
кандидат на роль искомого минора Н в G. Чтобы увеличить его
значение 28 на ^к (как требуется для Я), мы повторно применим
вышеупомянутый процесс стягивания к Gi, причем немного более
строго, чем прежде: будем стягивать ребра одно за другим, пока это
приводит к потере не более чем |т ребер на одну вершину.
Другими словами, мы допускаем потерю ребер немного большую, чем,
казалось бы, требуется для сохранения неравенства е > т.
(Вспомним, что когда мы стянули G на Go, мы положили этот порог
равным e(G) — к.) Если этот второй процесс стягивания заканчивается
непустым графом #о, то е(#о) будет не меньше |т: больше, чем
для G\\ Этой дополнительной ^т будет достаточно, чтобы
обеспечить графу #i, полученному из #о, так же как G\ был получен
из Go, требуемую высокую минимальную степень.
Но как нам убедиться в том, что этот второй процесс
стягивания действительно закончится на непустом графе? Хотя это может
показаться парадоксальным, причина состоит в том, что даже
допускаемая потеря до |т ребер (и одной вершины) на любом шаге

8.1. Топологические миноры
195
стягивания не может уничтожить m|Gi| или большее количество
ребер в G\ за |Gi| возможных шагов: графы с менее чем т
вершинами к концу процесса были бы просто слишком малы, чтобы суметь
потерять |т ребер, а согласно (1) такие малые графы встречались
бы на протяжении примерно четвертой части процесса!
Формально, мы будем управлять графами Н в процессе
стягивания не заданием верхней оценки на число ребер, которые будут
ликвидированы на каждом шаге, а фиксацией нижней оценки для ||#||
в терминах |#|. Эта оценка растет линейно от значения, немного
большего (™) при |#| = т, до значения, меньшего Am2 при \Н\ — Am.
Ввиду (1) и (2) Н = G\ удовлетворяет этой оценке, но ясно, что ей не
может удовлетворять ни один Н с |#| = т. Таким образом, процесс
стягивания должен закончиться где-то раньше, при |Я| > т.
Чтобы реализовать этот подход, положим
/(тг) := -т(п — т — 5)
6
Ж := \ Н 4 Gi : ||Я|| > т\Н\ + /(|Я|) - ( ™
Согласно (1)
/(|G1|)</(4m) = im2-^m<M,
поэтому G\ G Ж ввиду (2).
Для любого Н G Ж любой граф, полученный из Н одной из
следующих трех операций, будет снова лежать в Ж:
(i) удаление ребра, если ||#|| > т\Н\ + Д|#|) - (^) + 1;
(ii) удаление вершины степени не более |т;
(iii) стягивания такого ребра ху £ Н, что х и у имеют не более
чем 17п — 1 общих соседей в Н.
Начиная с G\ будем применять эти операции как можно большее
число раз, и пусть #о £ Л? — граф, полученный в конечном итоге.
Поскольку
\\Кт\\ = т\Кт\-т- (™^
и
*, ^ 5
f(m) = -^™> ~т,
то Кт не имеет достаточно ребер, чтобы быть в Jf; таким образом,
Jt? не содержит графов на т вершинах. Следовательно, |#о| > т

196
Глава 8. Подструктуры в разреженных графах
и, в частности, Но ф 0. Пусть х\ Е Яо — вершина минимальной
степени; положим
#i:=#o[{*i}UW*0(*i)].
Докажем, что минимальная степень Н \— Н\ так велика, как
требуется в лемме.
Заметим сначала, что
8{НХ) > 7-т. (3)
Действительно, поскольку Яо минимален относительно (ii) и (iii),
имеем d{x\) > |m в Яо (а следовательно, в #i), и любая вершина
у ф х\ из Hi имеет более |т— 1 общих соседей с х\ (а следовательно,
более ^т соседей в Hi в целом). Чтобы преобразовать (3) в искомое
неравенство вида
2<5(#i) > |#i| + c*m,
нам нужна верхняя оценка для |#i| в терминах т. Поскольку Но
лежит в Jf, но является минимальным относительно (i), имеем
||#о|| < т\Н0\ + (\т\Н0\ - \т2 - \т^ - (™) + 1
= -т\Н0\--т2--т+1 (4)
7 4
< -го|#о|- -т2.
(2) 6 О
По выбору Х\ и определению Hi, следовательно,
\Н1\-1 = 6(Н0)
< 2е(Я0)
<\т-\т2/\Нй\
s 7 1
< -т т
(1) 3 3
= 2т,
поэтому |#i| < 2т. Следовательно,
261НЛ > 2т+ -т
(з) 3
>\Hi\+l-m
> |#i|+J*,
(2) 6
что и утверждалось. D

8.1. Топологические миноры
197
Доказательство теоремы 8.1.1. Мы доказываем
утверждение при с := 1116. Пусть G — граф с d(G) > Шбг2. По теореме 1.4.2
G содержит такой подграф Go, что
k(G0) > 279г2 > 27бг2 + Зг.
Выберем в Go множество X := {х\,..., хзг} из Зг вершин и положим
G\ \— Go — X. Для любого г = 1,...,3г выберем множество У{
из Ъг соседей Х{ в G\. Пусть эти множества У{ не пересекаются при
разных г. (Это возможно, поскольку 6(Gq) > «(Go) > 15r2 -f \Х\.)
Так как
6(d) > /c(Gi) > «(Go) - \Х\ > 27бг2,
имеем e(G\) > 138г2. По лемме 8.1.3 G\ содержит минор Н с 26(H) >
\Н\ + 23г2 и поэтому (15г2, 7г2)-сцеплен по лемме 8.1.2. Пусть Z С
Зг
(J У{ — множество из 7г2 вершин, сцепленное в G\.
t=i
При всех г = 1,..., Зг положим Z{ :— Z C\Y{. Поскольку Z
сцеплено, достаточно найти г индексов г с \Z{\ > г — 1. Тогда
соответствующие Х{ будут вершинами ветвления для ТКГ в Go- Если найти
г таких г невозможно, то |Zt-| < г — 2 для всех, за исключением не
более чем г — 1, индексов г. Но тогда
Зг
|Z| = ]Г |Z,.| < (г - 1)5г + (2г + 1)(г - 2) < 7г2 = |Z|;
i=i
противоречие. D
Хотя теорема 8.1.1 уже дает хорошую оценку, кажется очень
трудным определить точную среднюю степень, необходимую для вы-
нуждения подграфа ТКГ, даже при малых г. Мы вернемся к случаю
г — 5 в разделе 8.3; другие результаты и гипотезы даны в
примечаниях.
Приведенный ниже почти противоречащий интуиции результат
Мадера говорит нам, что существование топологического минора Кт
может быть вынуждено фактически уже большим обхватом. В
следующем разделе мы докажем аналог этого результата для обычных
миноров.
Теорема 8.1.4 (Мадер, 1997). Для любого графа Н
максимальной степени d> 3 существует такое целое число k, что любой граф G
минимальной степени не менее d и обхвата не менее к содержит Н
как топологический минор.
Как уже говорилось в разделе 5.2 и во введении к главе 7,
никакая постоянная средняя степень, сколь угодно большая, не заставит

198
Глава 8. Подструктуры в разреженных графах
произвольный граф содержать заданный граф Н как подграф при
условии, что Н содержит по меньшей мере один цикл. По
предположению 1.2.2 и следствию 1.5.4, с другой стороны, любой граф G
содержит все деревья вплоть до (s(G) -f 2)-вершинных. Большая
средняя степень поэтому гарантирует возникновение любого
фиксированного дерева Т как подграфа. Что можно сказать, однако, если
мы хотим, чтобы Т встречался как индуцированный подграф?
Здесь большая средняя степень может приносить столько же
вреда, сколько и пользы, даже для графов ограниченной
плотности. (Рассмотрим, например, полные двудольные графы.) Тем более
замечательно, что предположение о большом хроматическом числе
вместо большой средней степени, по-видимому, меняет ситуацию:
согласно гипотезе Дьярфаша любой граф с достаточно большим
хроматическим числом содержит в качестве индуцированного подграфа
или большой полный граф, или любое заданное дерево. (Формально,
для любого целого числа г и любого дерева Т существует такое
целое число &, что любой граф G с x(G) > & и ^(G) < г содержит
индуцированную копию дерева Т.)
Более слабая топологическая версия этого предположения в
самом деле верна.
Теорема 8.1.5 (Скотт, 1997). Для любого целого числа г и
любого дерева Т существует такое целое число &, что любой граф
с x(G) > & и u(G) < г содержит индуцированную копию
некоторого подразделения дерева Т.
8.2. Миноры
Согласно теореме 8.1.1 средняя степень сг2 достаточна для
существования в заданном графе топологического минора Кт'. Если
нас устраивает любой минор, топологический он или нет, то
подойдет даже меньшая средняя степень. В основополагающей статье
1968 года Мадер доказал, что любой граф со средней степенью не
меньше cr log г содержит минор Кг. Следующий результат,
аналогичный теоремам 7.1.1 и 8.1.1 для общих миноров, устанавливает
точную необходимую среднюю степень как функцию от г с
точностью до константы с.
Теорема 8.2.1 (Косточка, 1982; Томасон, 1984). Существует
такое с £ Ж, что при любом г £ N любой граф G средней степени
d(G) > cry/log г содержит минор Кг. С точностью до значения с эта
оценка — наилучшая из возможных как функция от г.
Более легкое утверждение этой теоремы — что в общем случае
средняя степень cry/log г необходима для вынуждения минора Кг —
следует из рассмотрения случайных графов, вводимых в главе 11.

8.2. Миноры
199
Обратная импликация — что такая средняя степень достаточна —
доказана методами, похожими на описанные в разделе 8.1.
Вместо доказательства теоремы 8.2.1 мы посвящаем
оставшуюся часть этого раздела другому впечатляющему результату по
выну ждению миноров. На первый взгляд этот результат настолько
удивителен, что кажется почти неправдоподобным: всего лишь при
условии, что мы не подразделяем ребер, можно вынудить в графе
минор Кг просто за счет увеличения его обхвата (следствие 8.2.3)!
Теорема 8.2.2 (Томассен, 1983). При заданном целом числе к
любой граф G с обхватом g(G) > Ак — 3 и 6(G) > 3 имеет минор Н
с 6(H) > к.
Доказательство. Так как 6(G) > 3, любая компонента
графа G содержит цикл. В частности, утверждение очевидно для к < 2,
поэтому пусть к > 3. Рассмотрим множество вершин V компоненты
в G вместе с разбиением {Vi,...,!^} множества V на как можно
большее число связных множеств V* как минимум с2к — 2 вершинами
в каждом. (Такое разбиение существует, поскольку \V\ > g(G) >
2k — 2 и V связно в G.)
Сначала покажем, что любой подграф G[V{] есть дерево. Для
этого возьмем остовное дерево Т% в G[K*]- Если G[V{] имеет ребро
е £ TJ, то Т{ + е содержит цикл С; по предположению С имеет длину
как минимум 4А? — 3. Ребро, (приблизительно) противолежащее е
на С, поэтому делит путь С — е, а следовательно, также и Т{ на две
компоненты с не менее чем 2к—2 вершинами в каждой. Вместе с
множествами Vj, j ф г, эти две компоненты образуют разбиение
множества V на га -f 1 множеств, что противоречит максимальности га.
Поэтому любой граф G[V{] — действительно дерево, т. е.
G[Vi] = Т{. Так как 6(G) > 3, степени в G вершин из V{ дают в сумме
по меньшей мере 31V51, в то время как ребра из Т{ вносят в эту сумму
только 2|К*| — 2. Следовательно, для любого г граф G имеет как
минимум \V{\ + 2 > 2к ребер, соединяющих Vi с V \V{. Докажем, что
любое V{ посылает не более двух ребер в любое другое Vj. Тогда Vi
должно посылать ребра не менее чем в к таких множеств Vj,
следовательно, Vi суть множества ветвления для МИ С G с 6(H) > к.
Предположим, без ограничения общности, что G имеет три
V1-V2 ребра. Тогда найдутся такие вершины v\ £ V\ и i>2 G V2,
что G[Vi U V2] содержит три независимых ui-i/2 пути Pi, Р2, Рг
(рис. 8.2.1). Не более одного из этих путей может быть короче,
чем ^g(G). Предположим, что Pi имеет длину по меньшей мере
о
|"f0(G)l > 2А - 1, и пусть Р[ := Рц тогда \Р{\ >2к-2. Поскольку
Рч U Рз — цикл длины как минимум 4А: — 3, можно далее найти
непересекающиеся пути Р2, Рз С Р2 U Рз с 2к — 2 вершинами в каждом.
Поскольку G[V\ U V2] связен, существует такое разбиение V\ U V2 на
три связных множества V/, К2, V^, что V(P() С V/ при г = 1,2,3.

200
Глава 8. Подструктуры в разреженных графах
Заменяя эти множества Vi, V2 в разбиении V на три множества
К/, V27, V3, получаем разбиение множества К, которое противоречит
максимальности m. D
Рис. 8.2.1. Три ребра между V\ и V2
Следующая комбинация теорем 8.2.1 и 8.2.2 показывает
парадоксальный характер последней из них особенно ярко.
Следствие 8.2.3. Существует такое с & Ж, что для любого
г £ N любой граф G с обхватом g(G) > cry/log г и 6(G) > 3 содержит
минор Кт.
Доказательство. Докажем следствие для с := 4с', где с' —
константа из теоремы 8.2.1. Пусть граф G удовлетворяет условию.
По теореме 8.2.2 G имеет минор Н с 6(H) > c'r>/logr. По теореме
8.2.1 Н (а следовательно, и G) имеет минор Кг. □
8.3. Гипотеза Хадвигера
Как мы видели в предшествующих двух разделах, средняя
степень cry/log г достаточна для того, чтобы произвольный граф имел
минор Кт, а средняя степень сг2 вынуждает его иметь
топологический минор Кт. Если мы заменим «средняя степень» на
«хроматическое число», то с почти теми же константами с эти два утверждения
остаются верными. Это следует из того, что любой граф с
хроматическим числом к имеет подграф средней степени не меньше к — 1
(следствие 5.2.3).
Хотя обе вышеупомянутые функции cry/\og г и сг2 являются
наилучшими из возможных (с точностью до константы с) для
упомянутых импликаций со «средней степенью», возникает вопрос,
являются ли они все еще наилучшими из возможных с «хроматическим
числом» или же для этой цели подошла бы и несколько медленнее
растущая функция. Что скрывается за этой задачей о скоростях
роста, несомненно является фундаментальным вопросом относительно

8.3. Гипотеза Хадвигера
201
природы инварианта х- может ли этот инвариант иметь какое-либо
прямое структурное влияние на граф в терминах вынуждения
конкретных подструктур или же его влияние не больше, чем у
«неструктурного» свойства иметь где-нибудь большое количество ребер,
которое оно влечет с очевидностью?
Ответ на этот вопрос не известен ни для общих, ни для
топологических миноров. Для общих миноров, однако, следующая
гипотеза Хадвигера предполагает положительный ответ; она
рассматривается многими как одна из самых глубоких нерешенных проблем
в теории графов.
Гипотеза (Хадвигер, 1943). Следующая импликация имеет
место для любого целого числа г > 0 и любого графа G:
x(G)>r=> G^KT.
Гипотеза Хадвигера очевидна для г < 2, легко доказывается
для г = 3иг = 4 (упражнения) и эквивалентна теореме о четырех
красках для г = 5 и г = 6. Для г > 1 гипотеза открыта.
Перефразированная как G )р KX(G\ она верна для почти всех графов3).
В общем случае гипотеза для г -f 1 влечет ее для г (упражнение).
Гипотеза Хадвигера для любого фиксированного г эквивалентна
утверждению, что любой граф без минора Кт имеет (г—1)-раскраску.
В этой формулировке гипотеза ставит вопрос о том, как выглядят
графы без минора Кт'. Любое достаточно подробное структурное
описание таких графов позволило бы нам решить, действительно ли
они могут быть (г — 1)-раскрашены.
Для г = 3, например, графы без минора Кт — в точности леса
(почему?), и они действительно 2-раскрашиваемы. Для г = 4 также
имеется простая структурная характеризация графов без минора Кт.
Предложение 8.3.1. Граф с не менее чем тремя вершинами
является реберно-максимальным без минора К4, если и только если
он может быть построен рекурсивно из треугольников склейками4^
по К2.
Доказательство. Вспомним сначала, что любой МК4
содержит ТК4, поскольку А(К4) = 3 (предложение 1.7.2); графы без
минора К4, таким образом, совпадают с графами без
топологического минора К4. Доказательство того, что любой конструируемый
описанным образом граф является реберно-максимальным без
минора К4, оставляем в качестве легкого упражнения. Чтобы вывести
гипотезу Хадвигера для г = 4, нужна, по существу, только обратная
импликация. Докажем ее индукцией по \G\.
3) Понятие «почти все» вводится в главе 11.
4) Формально это было определено в главе 5.

202 Глава 8. Подструктуры в разреженных графах
Пусть дан граф G, реберно-максимальный без минора К4. Если
\G\ = 3, то G — треугольник, поэтому пусть \G\ > 4 для шага
индукции. Тогда G не полон. Пусть S С V{G) — разделяющее множество
с |5| = «(G), и пусть С\, Съ — различные компоненты в G — S.
Поскольку 5 — минимальный разделитель, любая вершина в S имеет
соседа в С\ и еще одного в Сч- Если |5| > 3, то G содержит три
независимых пути Pi, Р2, Р3, соединяющих вершину v\ Е С\ с вершиной
V2 £ С*2. Поскольку «(G) = |5| > 3, граф G — {1/1,1/2} связен и
содержит (кратчайший) путь Р между двумя различными Р,-. Тогда
Р U Pi U Р2 U Р3 = ТК4\ противоречие.
Следовательно, «(G) < 2 и утверждение следует из леммы 4.4.45)
и индукционного предположения. D
Одно из интересных следствий предложения 8.3.1 состоит в том,
что все реберно-максимальные графы без минора К4 имеют одно
и то же число ребер и, таким образом, все они «экстремальны».
Следствие 8.3.2. Любой реберно-максимальный граф G без
минора К4 имеет 2|G| — 3 ребер.
Доказательство. Индукция по \G\.
Следствие 8.3.3. Гипотеза Хадвигера верна для г = 4.
Доказательство. Если G получается из Gi и Gi склейкой по
полному графу, то x(G) = max{x(Gi),x(G2)} (см. доказательство
предложения 5.5.2). Следовательно, предложение 8.3.1 влечет
индукцией по |G|, что все реберно-максимальные (а следовательно, все)
графы без минора К4 3-раскрашиваемы. D
Следствие 8.3.3 можно также доказать простым прямым
рассуждением (упражнение 12).
Ввиду теоремы о четырех красках справедливость гипотезы
Хадвигера для г = 5 вытекает из следующей теоремы о строении
графов без минора Къ так же, как она следует из предложения 8.3.1
для г = 4. Доказательство теоремы 8.3.4 похоже на доказательство
предложения 8.3.1, но значительно длиннее. Поэтому мы приводим
ее без доказательства.
Теорема 8.3.4 (Вагнер, 1937). Пусть G —
реберно-максимальный граф без минора Къ. Если \G\ > 4, то G может быть
построен рекурсивно, склейками по треугольникам и К2, из
плоских триангуляции и копий графа W (рис. 8.3.1).
') Доказательство этой леммы элементарно и может читаться независимо от
остальной части главы 4.

8.3. Гипотеза Хадвигера 203
Рис. 8.3.1. Три представления графа Вагнера W
С помощью следствия 4.2.8 можно легко вычислить, какие из
графов, построенных как указано в теореме 8.3.4, имеют больше
всего ребер. Оказывается, что эти экстремальные графы без
минора Къ имеют не больше ребер, чем те, которые являются
экстремальными относительно {МКЪ, М#з,з}> т- е- максимальные пла-
нарные графы.
Следствие 8.3.5. Граф с п вершинами без минора К5 имеет
не более Зп — б ребер. □
Поскольку x(W) = 3, теорема 8.3.4 и теорема о четырех красках
влекут гипотезу Хадвигера для г = 5.
Следствие 8.3.6. Гипотеза Хадвигера верна для г = 5. D
Гипотеза Хадвигера для г = б опять-таки существенно труднее,
чем случай г = 5, и она в этом случае снова опирается на теорему
о четырех красках. Ее доказательство сводится (без
использования теоремы о четырех красках) к тому, что любой минимальный
контрпример получается из планарного графа добавлением одной
вершины, поэтому ввиду теоремы о четырех красках он все-таки
не может быть контрпримером.
Теорема 8.3.7 (Робертсон, Сеймур и Тома^Л^ЙЗ). Гипотеза
Хадвигера верна при г = б.
По следствию 8.3.5 любой граф с п вершинами и более чем Зп —б
ребрами содержит МКЪ. На самом деле он даже содержит ТКЪ. Это
неприметное уточнение — еще один глубокий результат, который
существовал в виде гипотезы более 30 лет.
Теорема 8.3.8 (Мадер, 1998). Любой граф с п вершинами и
более чем Зп — б ребрами содержит Къ как топологический минор.
Никакой теоремы о строении графов без ТКЪ, аналогичной
предложению 8.3.1 и теореме 8.3.4, не известно. Однако Мадер недавно
охарактеризовал такие графы с наибольшим возможным числом
ребер.
Теорема 8.3.9 (Мадер, 1997). Граф является экстремальным
без ТКЪ) если и только если его можно построить рекурсивно из
максимальных планарных графов склейкой по треугольникам.

204 Глава 8. Подструктуры в разреженных графах
Упражнения
1. Доказать, опираясь лишь на основные понятия, теорему Вагнера (1964)
о том, что каждый граф с хроматическим числом не меньше 2Г содержит
Кг как минор.
(Подсказка. Примените индукцию по г.)
2. Доказать, опираясь лишь на основные понятия, результат Мадера (1967)
о том, что каждый граф средней степени не менее 2Г~2 содержит Кг как
минор.
(Подсказка. Индукция по г.)
3.~~ Вывести теорему Вагнера (упражнение 1) из теоремы Мадера
(упражнение 2).
4.+ Для заданного целого г > 0 найти такое целое к, что любая решетка с к
добавленными ребрами содержит минор Кг при условии, что все концы
новых ребер находятся на расстоянии не меньше к по решетке как друг от
друга, так и от границы решетки. (Решетки определены в разделе 12.3.)
5.+ Показать, что любая функция h в теореме 3.6.1 удовлетворяет неравенству
h(r) > g-r2 для всех четных г, а следовательно, что теорема 8.1.1 является
наилучшей из возможных с точностью до константы с.
6. Доказать утверждение леммы 8.1.3 для к < 6.
7. Объяснить, как именно член ^к из заключения леммы 8.1.3 используется
в доказательстве теоремы 8.1.1. Можно ли заменить его на /г/1000 или на
ноль?
8. Объяснить, как именно возникло число g- в доказательстве леммы 8.1.3.
Можно ли заменить его на |?
9.+ Для каких деревьев Т существует такая функция /: N —► N, стремящаяся
к бесконечности, что каждый граф G с x(G) < /(^(G)) содержит
индуцированную копию дерева Т? (Другими словами: можно ли заставить
хроматическое число повышаться за счет увеличения средней степени, пока Т не
встречается как индуцированный подграф? Или, как в гипотезе Дьярфаша,
вынуждает ли большая средняя степень индуцированную копию дерева Т,
если хроматическое число остается малым?)
10."" Вывести теорему о четырех красках из гипотезы Хадвигера для г = 5.
II.- Показать, что гипотеза Хадвигера для г + 1 влечет эту гипотезу для г.
12."" Используя результаты этой главы, доказать следующее ослабление
гипотезы Хадвигера: для любого б > 0 любой граф с хроматическим числом не
меньше г1_*"€ содержит минор Кг при условии, что г достаточно велико.
13.+ Доказать гипотезу Хадвигера для г = 4, опираясь лишь на основные
понятия.
14.+ Доказать гипотезу Хадвигера для реберных графов.
15. (i)~ Показать, что гипотеза Хадвигера эквивалентна утверждению, что
G )£= KX(G) для всех графов G.
(ii) Показать, что любой контрпример G минимального порядка к
гипотезе Хадвигера (перефразированной, как выше) удовлетворяет условию
/fx(<?)-l g G и имеет связное дополнение.
16. Показать, что любой граф, построенный как в теореме 8.3.1,
реберно-максимален относительно свойства не содержать минора А'4.
17. Доказать импликацию 6(G) > 3 =» G Э ТА'4.
(Подсказка. Теорема 8.3.1.)

Примечания 205
18. Мультиграф называется параллельно-последовательным, если его можно
построить рекурсивно из А'2 посредством операций подразделения и
удвоения ребра. Показать, что 2-связный мультиграф
параллельно-последователен, если и только если он не имеет (топологического) минора А'4.
19. Доказать следствие 8.3.5.
20. Охарактеризовать графы с п вершинами и более чем Зп — 6 ребрами,
которые не содержат ТА'з.з- В частности, определите ех(п, ТА'з,з)-
(Подсказка. По теореме Вагнера всякий реберно-минимальный граф без
минора А'з ,з можно построить рекурсивно из максимальных плоских графов
и копий графа А'5 склейкой по К2.)
21. По теореме Пеликана каждый граф минимальной степени не меньше 4
содержит подразделение графа А'^_, т. е. А'5 без ребра. Используя эту
теорему, докажите результат Томассена (1974), что каждый граф с п > 5
вершинами и по меньшей мере 4п — 10 ребрами содержит ТА'5.
(Подсказка. Покажите индукцией по |G|, что если ||G|| > 4п — 10, то для
каждой вершины х £ G имеется ТКЪ С G, в котором х не вершина
ветвления.)
Примечания
Изучение графов, не содержащих заданного графа в качестве минора или
топологического минора, имеет длинную историю. Оно, по-видимому, началось
с диссертации Вагнера (1935), в которой он попытался «детопологизировать»
проблему четырех красок путем классификации графов без минора А'5. Он
надеялся независимо показать, что все такие графы 4-раскрашиваемы. Поскольку
графы без минора А'5 включают планарные графы, это дало бы доказательство
гипотезы четырех красок без привлечения топологии. Результат усилий Вагнера
(теорема 8.3.4) находится в заманчивой близости от цели, но не достигает ее:
хотя она дает классификацию графов без минора А'5 в структурных терминах,
планарность заново появляется как один из критериев, использованных в
классификации. С этой точки зрения поучительно сравнить теорему Вагнера о А'5
с подобными ей теоремами классификации, в частности с ее аналогом для А'4
(предложение 8.3.1), в котором графы разбиваются на части, принадлежащие
некоторому конечному множеству несводимых графов. Другие примеры теорем
классификации см. в: Diestel R. Graph Decompositions. Oxford: Univ. Press,
1990.
Несмотря на то что структурная теорема Вагнера о А'5 не позволяет
решить проблему четырех красок, она повлияла на развитие теории графов как
очень немногие другие результаты. Упомянем лишь два примера: она
натолкнула Хадвигера на его знаменитую гипотезу и вызвала к жизни понятие
древесного разложения, которое является фундаментальным в работе Робертсона
и Сеймура по минорам (см. главу 12). Сам Вагнер ответил на гипотезу
Хадвигера доказательством того, что для вынуждения минора А'г достаточно
увеличить хроматическое число графа до некоторого значения, зависящего только
от г (упражнение 1). Кроме того, эта теорема наряду с ее аналогом для
топологических миноров, доказанным независимо Дираком и Юнгом, подсказала вопрос
о том, какая средняя степень достаточна для вынуждения искомого минора.
Самый глубокий вклад в эту область исследования был, без сомнения,
сделан Мадером в ряде статей с конца шестидесятых годов. Наше доказательство
леммы 8.1.3 намеренно представлено пошаговым способом, чтобы показать
некоторые из идей Мадера. Собственное доказательство Мадера, не говоря уже
о доказательстве принадлежащей Томасону неулучшаемой версии леммы,
приведенном в первоначальном доказательстве теоремы 8.1.1, подается столь изящно,
что становится трудно увидеть стоящие за ним идеи. За исключением этой
леммы, наше доказательство теоремы 8.1.1 следует работе: Bollobds В., Thoma-
son A. G. Proof of a conjecture of Mader, Erdos and Hajnal on topological complete

206
Глава 8. Подструктуры в разреженных графах
subgraphs // Europian J. Combin. 1998. 19. P. 883-887. Константа с в этой
теореме, как показано в: Komlos J., Szemeredi Е. Topological cliques in graphs. II //
Combin. Probab. Comput. 1996. 5. P. 79-90 — не превосходит примерно j, что
недалеко от нижней границы |-, данной в упражнении 5.
Теорема 8.1.4 взята из статьи: Mader W. Topological subgraphs in graphs
of large girth // Combinatorica. 1998. 18. P. 405-412. Для Я = Kr эта
теорема утверждает, что любой граф G с 8(G) > г — 1 и большим g(G) содержит
ТКГ. При г = 5 Мадер предположил, что условия g(G) > 5 должно быть
достаточно и что требование 6(G) > 4 может быть еще ослаблено. Им было сделано
предположение, что любой граф обхвата не меньше 5, достаточно большого
порядка п и с 2п — 4 или более ребрами имеет топологический минор А'5. (Чтобы
увидеть, что это влечет версию гипотезы для минимальный степени даже для
малого порядка, можно рассмотреть достаточное число непересекающихся копий
заданного графа.) Для произвольного Н Мадер улучшил теорему 8.1.4,
ослабив условие на 8(G) > d до d(G) > d — 1 -f- б при произвольном б > 0 (теперь
обхват /г, требуемый для вынуждения ТН в таких графах G, зависит от б и Н)\
см.: W. Mader. Subdivisions of a graph of maximal degree n -f-1 in graphs of average
degree n + б and large girth (рукопись 1999 г.).
Теорема 8.1.5 получена в: Scott A. D. Induced trees in graphs of large
chromatic number // J. Graph Theory. 1997. 24. P. 297-311. Теорема 8.2.1 была
доказана независимо Косточкой в 1982 г.: Косточка А. В. О минимуме числа
Хадвигера для графов с данной средней степенью вершин // Сб. трудов ИМ
СО АН СССР. 1982. Вып. 38. С. 37-58 — и в статье: Thomason A. G. An
extremal function for contractions of graphs // Math. Proc. Cambridge Phylos. Soc.
1984. 95. P. 261-265. Теорема 8.2.2 взята от обзора Томассена: Paths, Circuits
and Subdivisions // Selected Topics in Graph Theory 3 / Ed. by L. W. Beineke,
R. J. Wilson. London; New York: Acad. Press, 1988.
Доказательство гипотезы Хадвигера для г = 4, подсказываемое в
упражнении 13, дано Хадвигеромв статье 1943 года, содержащей его гипотезу. В течение
некоторого времени существовал аналог гипотезы Хадвигера для
топологических миноров — гипотеза Хайоша о том, что x(G) > Т влечет даже G Э ТКГ.
Контрпример к этой гипотезе был найден в 1979 г. Катлином. Немного позже
Эрдеш и Фейтлович даже доказали, что гипотеза Хайоша ложна для почти всех
графов (см. главу 11).
Теорема 8.3.8 Мадера о том, что Зп — 5 ребер вынуждают существование
в графе топологического минора К5, была высказана как предположение
Дираком в 1964 г. Ее доказательство занимает две статьи: Mader W. Зп — 5 edges do
force a subdivision of K$ // Combinatorica. 1998. 18. P. 569-595; Mader W. An
extremal problem for subdivisions of K~ // J. Graph Theory. 1999. 30. P. 261-276.
Гипотеза Дирака была обобщена Сеймуром, который предположил, что каждый
5-связный неплоский граф должен содержать ТА'5 (не опубликовано).

Глава 9
Теория Рамсея для графов
В этой главе мы рассмотрим класс задач, в некотором
смысле сходных с изучавшимися в последних двух главах: какие
подструктуры обязательно присутствуют в каждом достаточно
большом графе?
Лемма о регулярности в разделе 7.2 дает один из возможных
ответов на этот вопрос, утверждая, что всякий (большой) граф G
содержит большие двудольные подграфы, похожие на случайные
графы. Однако если мы ищем более конкретные подструктуры
такие, как подграфы, изоморфные некоторым заданным графам Н, то
такие Н должны в достаточной мере дополнять друг друга, чтобы
охватить все многообразие, допустимое для G. Например, пусть
задано целое число г. Каждый ли достаточно большой граф содержит
или Кт', или индуцированный Кг?
Несмотря на сходство с экстремальными задачами, в которых
мы ищем локальные следствия глобальных предположений,
вышеупомянутый тип вопроса приводит к математике несколько иного
рода, имеющей свои отличительные особенности. Действительно,
теоремы и доказательства в этой главе имеют больше общего с
подобными результатами, скажем, из алгебры или геометрии, чем из
большинства других областей теории графов. Поэтому изучение
присущих им основных методов обычно рассматривается как
самостоятельный раздел комбинаторики — теория Рамсея.
В соответствии с предметом этой книги мы сосредоточимся на
результатах, которые естественным образом выражаются в
терминах графов. Однако даже с точки зрения общей теории Рамсея это
не является столь значительным ограничением, как могло бы
показаться. Язык графов естествен в рамсеевских задачах, и
материал главы показывает разнообразие идей и методов, достаточное
для того, чтобы передать обаяние этой теории в целом.

208
Глава 9. Теория Рамсея для графов
9.1. Первоначальные теоремы Рамсея
В своей простейшей версии первоначальная теорема Рамсея
утверждает, что для любого целого числа г > 0 каждый достаточно
большой граф G содержит или Кг, или Кг как индуцированный
подграф. На первый взгляд это может показаться удивительным:
в конце концов нам нужно примерно (г —2)/(г— 1) из всех возможных
ребер для вынуждения подграфа Кг в G (следствие 7.1.3), но нельзя
ожидать, чтобы G или G содержали больше половины всех ребер.
Однако, как хорошо показывают графы Турана, внесение большого
числа ребер в G без образования Кг налагает на G дополнительную
структуру, которая может помочь нам в отыскании Кг.
Как это можно доказать? Попробуем строить Кг или Кг в G
индуктивно, начиная с произвольной вершины v\ £ У\ :— V(G). Если
\G\ велико, то имеется большое множество Уч С V\ \ {v\] вершин,
которые или все смежны, или все несмежны с v\. Соответственно
можно рассматривать v\ как первую вершину Кг или Кг, все
остальные вершины которого лежат в V2. Теперь выберем еще одну
вершину V2 £ Vi Для нашего Кг или Кг. Поскольку У2 велико, имеется
довольно большое подмножество Уз вершин, которые все «одинаково
относятся» также и к и2: все они или смежны, или все несмежны
с нею. Затем продолжим наш поиск вершин внутри Уз и так далее
(рис. 9.1.1).
Рис, 9.1.1. Выбор последовательности v\, V2,...
Как долго можно действовать таким образом? Это зависит от
мощности начального множества V\\ каждое множество У{ не более
чем вдвое уступает по мощности своему предшественнику К'_ъ
поэтому мы сможем сделать s шагов построения, если G имеет порядок
примерно 25. Как показывает последующее доказательство, выбор
s — 2г — 3 вершин V{ позволяет найти среди них вершины графов Кг
или Кг.
Теорема ЭЛЛ (Рамсей, 1930). Для любого г £ N существует
такое п £ N, что любой граф порядка не меньше п содержит или Кт,
или Кт как индуцированный подграф.
Доказательство. Утверждение очевидно для г < 1;
предположим, что г > 2. Пусть п := 22г~3, и пусть G — граф порядка по

9.1. Первоначальные теоремы Рамсея
209
меньшей мере п. Определим последовательность V\,..., Vir-i
множеств и выберем вершины V{ £ Vi со следующими свойствами:
(i) |К| = 221-2-' (i=l 2г-2);
(ii) К-СКч\Ы (i = 2,...,2r-2);
(iii) Vi-i смежна или со всеми вершинам в Vi, или ни с какой
вершиной из К' (г = 2,..., 2г — 2).
Пусть V\ С V(G) — любое множество с 22г~3 вершинами, и
выберем v\ £ V\ произвольно. Тогда (i) имеет место для г — 1, в то
время как (ii) и (iii) выполняются с очевидностью. Предположим
теперь, что K'-i и u;_i £ K'-i уже выбраны и удовлетворяют условиям
(i)-(iii) для г — 1, где 1 < г < 2г — 2. Поскольку
|K_i\{^-i}| = 22r-1-»-l
нечетно, то V{_i содержит подмножество Vf, удовлетворяющее
(i)-(iii); мы выбираем V{ £ Vi произвольно.
Среди 2г —3 вершин i>i,..., 1>2г-з имеется г— 1 вершин, которые
ведут себя одинаково по отношению к i/t-_i в (iii) будучи смежными
или со всеми вершинами в Vi, или ни с одной из них. Соответственно
эти г— 1 вершин и i>2r-2 индуцируют в G или КГ, или Кг, поскольку
i>i,..., v2r-2 G Vi для всех г. □
Наименьшее целое п, связанное с г, как в теореме 9.1.1, есть
число Рамсея R(r) для г; наше доказательство показывает, что R(r) <
22г~3. В главе 11 мы с помощью простого вероятностного
рассуждения покажем, что R(r) ограничено снизу величиной 2Г'2
(теорема 11.1.3).
В теории Рамсея принято смотреть на разбиения как на
раскраски: раскраска (элементов) множества X в с цветов или, для
краткости, с-раскраска — это просто разбиение множества X на
с классов (индексированных данными «цветами»). В частности, эти
раскраски не обязаны удовлетворять какому бы то ни было
требованию несмежности, как в главе 5. Для заданной с-раскраски
множества [Х]к всех ^-подмножеств множества X назовем множество
У С X одноцветным, если все элементы в [Y]k имеют один и тот
же цвет1), т. е. принадлежат одному и тому же из с классов
разбиения множества [Х]к. Точно так же, если G = (V, Е) — граф и все
ребра в Н С G имеют один и тот же цвет в некоторой раскраске
множества Е, то назовем Н одноцветным подграфом графа G и будем
говорить о красном (зеленом и т. п.) подграфах Н графа G и так
далее.
В этих терминах теорема Рамсея может быть сформулирована
следующим образом: для каждого г существует такое п, что для
2) Заметим, что Y называется одноцветным, но именно элементы множества
[Y]k, а не У являются (одинаково) раскрашенными.

210
Глава 9. Теория Рамсея для графов
любого п-множества X каждая 2-раскраска множества [X]2 дает
одноцветное г-множество У С X. Интересно, что это утверждение
остается верным для с-раскраски множества [Х]к с произвольными
с и к, причем почти в точности с тем же доказательством!
Чтобы избежать повторения, воспользуемся случаем
продемонстрировать другую общепринятую методику доказательства: мы
сначала докажем бесконечную версию общей теоремы Рамсея
(которая проще, потому что нам не нужно заботиться о числах), а
затем выведем конечную версию посредством так называемого метода
компактности.
Теорема 9.1.2. Пусть к, с — положительные целые числа,
а X — бесконечное множество. Если множество [Х]к раскрашено
в с цветов, то X содержит бесконечное одноцветное подмножество.
Доказательство. Докажем теорему индукцией по к при
фиксированном с. Для к — 1 утверждение имеет место, поэтому
допустим, что к > 1 и наше утверждение верно для меньших значений к.
Пусть множество [Х]к раскрашено в с цветов. Будем строить
бесконечную последовательность Xq , Х\,... бесконечных
подмножеств в X и выбирать элементы Х{ £ Х{ со следующими свойствами
(для всех г):
(i) xi+i с х,-\ {*.•};
(ii) все ^-множества {х{} U Z с Z £ [Xj+i]*-1 имеют один и тот
же цвет, который мы связываем с Х{.
Начнем с Xq := X и выберем xq £ Xq произвольно. По
предположению Xq бесконечно. Выбрав бесконечное множество Х{ и Х{ £ Х{
для некоторого г, мы с-раскрашиваем множество [^tAi^t}]^-1? давая
каждому множеству Z цвет множества {x{]\JZ из нашей с-раскраски
множества [Х]к. По индукционному предположению Х{ \{х{}
содержит бесконечное одноцветное подмножество, которое мы и возьмем
за Х{+1. Ясно, что этот выбор удовлетворяет условиям (i) и (ii).
Наконец, выберем жг+1 £ ^г+i произвольно.
Поскольку с конечно, один из этих с цветов связан с бесконечно
многими Х{. Эти Х{ образуют бесконечное одноцветное
подмножество в X. □
Чтобы вывести конечную версию теоремы 9.1.2, воспользуемся
следующим стандартным теоретико-графовым инструментом в
комбинаторике.
Лемма 9.1.3 (лемма Кёнига о бесконечности). Пусть Vq, V\, ...
есть бесконечная последовательность непересекающихся непустых
конечных множеств, и пусть G — граф на их объединении.
Допустим, что каждая вершина v в множестве Vn с п > 1 имеет
соседа f(v) в Vn-i- Тогда G содержит бесконечный путь v^v\ ..., где
vn £ Vn для всех п.

9.1. Первоначальные теоремы Рамсея
211
Рис. 9.1.2. Лемма Кёнига о бесконечности
Доказательство. Пусть 3* — множество всех путей вида
vf(v)f(f(v))... , заканчивающихся в Vq. Поскольку множество Vo
конечно, а 3? бесконечно, то бесконечно много путей из 3?
заканчиваются в одной и той же вершине vq £ Vo. Среди этих путей
бесконечно многие согласуются также по своей предпоследней
вершине vi £ Vi, поскольку множество V\ конечно. А из таких путей
бесконечно многие совпадают и по вершине г>2 в Vi и так далее. Хотя
рассматриваемое множество путей уменьшается от шага к шагу, оно
остается все еще бесконечным после любого конечного числа шагов,
поэтому vn определяется для каждого п £ N. По определению,
каждая вершина vn смежна с vn-\ в одном из этих путей, поэтому путь
vqV\ ... действительно бесконечен. □
Теорема 9.1.4. Для всех к, с, г > 1 существует такое п > к,
что каждое п-множество X имеет одноцветное г-подмножество
относительно любой с-раскраски множества [Х]к.
Доказательство. Как принято в теории множеств, обозначим
через п £ N (также) множество {0,...,п— 1}. Предположим, что
утверждение неверно для некоторых к, с, г. Тогда для любого п> к
существуют такие n-множество (без ограничения общности
множество п) и с-раскраска [п]к —» с, что п не содержит одноцветного
г-множества. Назовем такие раскраски плохими] мы, таким
образом, допускаем, что для каждого п > к существует плохая раскраска
множества [п]к. Мы хотим объединить их в плохую раскраску
множества [N]*, что будет противоречить теореме 9.1.2.
Для каждого п > к пусть Vn Ф 0 — множество плохих
раскрасок множества [п]к. При п > к сужение f(g) любого g £ Vn на [п— 1]к
все еще является плохой раскраской и, следовательно, лежит в Vn-\.
По лемме о бесконечности существует такая бесконечная
последовательность 0jb,0jb+i,... плохих раскрасок дп £ Vn, что f(gn) - gn-i
для всех п > к. Для каждого m > к все раскраски дп с п > m
совпадают на множестве [т]к, поэтому для каждого У £ \Ы\к
значение дп(У) совпадает при всех п > max У. Определим g(Y) как
это общее значение всех gn{Y). Тогда д — плохая раскраска
множества [Щк: каждое г-множество S С N содержится в некотором
достаточно большом п, поэтому S не может быть одноцветным,
поскольку д совпадает на [п]к с плохой раскраской дп. □

212
Глава 9. Теория Рамсе я для графов
Наименьшее целое п, связанное с к, с, г, как в теореме 9.1.4,
называется числом Рамсея от этих параметров; обозначим его через
Д(*,с,г).
9.2. Числа Рамсея
Теорему Рамсея можно перефразировать следующим образом:
если Н — Кг, a G — граф с достаточно большим числом вершин, то
или сам G, или его дополнение G содержит копию Н как подграф.
Ясно, что то же верно и для любого графа Н, просто потому что
Н CKh для А:=|#|.
Однако если мы спросим, каково наименьшее число п
(называемое числом Рамсея R(H) графа Н) такое, что каждый граф G
с п вершинами обладает вышеупомянутым свойством, тогда этот
вопрос имеет смысл. Если в Н ребер мало, то он должен легче
вкладываться в G или в G, и можно ожидать, что R(H) окажется
меньшим, чем число Рамсея R(h) = R(Kh).
Немного более общо, пусть #(#i,#2) обозначает наименьшее
п £ N такое, что Н\ С G или #2 С G для каждого графа G
порядка п. Для большинства графов #i, #2 известны лишь очень
грубые оценки для R(H\,Hi). Интересно, что нижние границы,
полученные с помощью случайных графов (как в теореме 11.1.3), часто
точнее, чем даже лучшие оценки, даваемые явными конструкциями.
Следующее предложение описывает один из немногих случаев,
где точные числа Рамсея известны для сравнительно широкого
класса графов.
Предложение 9.2.1. Пусть s, t — положительные целые
числа, а Т — дерево порядка t. Тогда Я(Т, Ks) - (s - l)(t - 1) + 1.
Доказательство. Объединение s — 1 непересекающихся
графов К%~1 не содержит копии Т, в то время как дополнение этого
графа — полный (s — 1)-дольный граф K%Z\ — не содержит К3.
Отсюда Д(Г, Ks) >{s- \){t - 1) + 1.
Обратно, пусть G есть любой граф порядка n — {s— 1)(2— 1) + 1,
дополнение которого не содержит К3. Тогда s > 1 и в любой
вершинной раскраске G (в смысле главы 5) не более s—1 вершин могут
иметь один и тот же цвет. Следовательно, x(G) > \n/(s — 1)] — t.
По следствию 5.2.3 G имеет подграф Я с 6(H) > t — 1, который по
следствию 1.5.4 содержит копию дерева Т. □
Как основной результат этого раздела мы докажем теперь одну
из немногих общих теорем, дающих относительно хорошую верхнюю
оценку для чисел Рамсея широкого класса графов, определенного
в терминах некоторого стандартного инварианта графа. В этой
теореме речь идет о числах Рамсея разреженных графов: она
утверждает, что число Рамсея графов Н с ограниченной максимальной сте-

9.2. Числа Рамсея
213
пенью растет лишь линейно по \Н\, что дает огромное улучшение
экспоненциальной оценки из доказательства теоремы 9.1.1.
Теорема 9.2.2 (Хватал, Рёдль, Семереди и Троттер, 1983).
Для любого целого положительного числа А существует такая
константа с, что
R(H) < с\Н\
для всех графов Н с А (Я) < А.
Доказательство. Основная идея доказательства состоит в
следующем. Мы хотим показать, что Н С G или Н С G, если \G\
достаточно (хотя и не слишком) велико. Рассмотрим 6-регулярное
разбиение G, обеспеченное леммой регулярности. Если достаточно
много б-регулярных пар в этом разбиении имеют положительную
плотность, то можно надеяться, что в G найдется копия графа Н.
Если же большинство пар имеет нулевую или малую плотность, мы
пытаемся найти Н в G. Пусть R, R' и R" — «графы регулярности»2)
графа G, ребра которых соответствуют парам плотности > 0, > 1/2
и < 1/2. Тогда R — реберно-непересекающееся объединение R' и R".
Теперь для того чтобы Н С G или Я С G, достаточно по
лемме 7.3.2 гарантировать, что Н содержится в подходящем
«раздутом графе регулярности» R's или R". Поскольку х{Н) < &{Н) + 1 <
A -f 1, так будет, если s > a(H), и мы сможем найти КА+1 в R'
или в R". Этого легко добиться: нам нужно лишь, чтобы Кг С R,
где г — число Рамсея от A -f 1, а это будет следовать из теоремы
Ту рана, поскольку R плотен.
Переходя к формальному доказательству, предположим, что
задано А > 1. Получая на входе d := 1/2 и А, лемма 7.3.2
возвращает бо. Поскольку утверждение леммы относительно во становится
более слабым при уменьшении бо, можно считать, что во < 1. Пусть
га := R(A -f 1) — число Рамсея для A -f 1. Пусть е < во
положительно, но настолько мало, что для k — m (и, следовательно, для
всех к > т)
2е<-^—-\. (1)
т— 1 к
Наконец, пусть М — целое число, возвращаемое леммой
регулярности (7.2.1) при входах б и га.
Все определенные до сих пор величины зависят только от А.
Докажем теорему при
М
) Позже мы определим R" несколько иначе, чтобы это определение было
согласовано с нашим формальным определением графа регулярности.

214
Глава 9. Теория Рамсея для графов
Итак, пусть задан Я с Д(Я) < А, и пусть s \— \Н\. Пусть G —
произвольный граф порядка п > С\Н\\ покажем, что Я С G или
ЯСС.
По лемме 7.2.1 G имеет 6-регулярное разбиение {Vo, V\,..., Vk}
с исключительным множеством Vo и |Vi| = • • • = |Vjb| = : £, где т <
к < М. Тогда
^n_^>n-en=nl-e>csl-e = L
к М М М со w
Пусть R — граф регулярности с параметрами б, £, 0, отвечающий
этому разбиению. По определению, R имеет к вершин и
2 т- 1
><m-l(*)
ребер. Поэтому по теореме 7.1.1 в R есть подграф К — Кт.
Теперь раскрасим ребра графа R двумя цветами: красным, если
ребро соответствует паре (V{, Vj) плотности не меньше 1/2, и
зеленым в противном случае. Пусть R! есть остовный подграф графа R,
образованный красными ребрами, a R" — остовный подграф R,
образованный зелеными ребрами и теми, для которых соответствующая
им пара имеет плотность в точности 1/2. Тогда R' — граф
регулярности графа G с параметрами б, £ и 1/2, a R" — граф
регулярности графа G с теми же параметрами. Как легко проверить,
каждая пара (V{}Vj)} которая является б-регулярной для G, также
б-регулярна и для G.
По определению т граф К содержит красный или зеленый
подграф Кг при г := х(Ю < Д + 1. Соответственно Н С R's или
Н С R". Поскольку б < б0 и £ > s/eo по (2), то и R' и Я"
удовлетворяют требованиям леммы 7.3.2, поэтому Н С G или ЯСС, что
и требуется. D
Ранее в этом разделе мы выясняли, каков наименьший порядок
графа G, при котором любая 2-раскраска его ребер дает одноцветную
копию некоторого заданного графа Я. Вместо того чтобы делать
акцент на порядок графа G, мы могли бы пытаться
минимизировать сам G по отношению вложенности подграфов. Для заданного
2б
1 1
771—1 к

9.3. Индуцированные теоремы Рамсея
215
графа Н будем говорить, что граф G есть минимальный по Рамсею
для #, если G минимален со свойством, что каждая 2-раскраска его
ребер дает одноцветную копию графа Н.
Как выглядят такие минимальные по Рамсею графы?
Единственны ли они? Следующий результат, который мы включаем из-
за его остроумного доказательства, отвечает на второй вопрос для
некоторых Н.
Предложение 9.2.3. Если Т — дерево, но не звезда, то
бесконечно много графов минимальны по Рамсею для Т.
Доказательство. Пусть \Т\ = : г. Покажем, что для любого
n G N существует граф порядка по меньшей мере п, который
является минимальным по Рамсею для Т.
Воспользуемся утверждением теоремы 11.2.2 из главы 11,
согласно которой существует граф G с хроматическим числом x(G) > г2
и обхватом g(G) > п. Если мы раскрасим ребра G в красный и
зеленый цвета, то красный и зеленый подграфы не могут оба иметь
(вершинной) г-раскраски в смысле главы 5. В противном случае мы
могли бы раскрасить вершины G парами цветов из этих раскрасок
и получить противоречие с x(G) > г2. Поэтому пусть G1 С G
одноцветен и x{G') > г. По следствию 5.2.3 граф G' содержит подграф
минимальной степени не меньше г, который содержит копию Т по
следствию 1.5.4.
Пусть граф G* С G минимален по Рамсею для Т. Ясно, что G*
не лес: ребра любого леса можно раскрасить в 2 цвета так, чтобы
никакой одноцветный подлее не содержал путь длины 3, не говоря
уже о копии леса Т. (Здесь мы используем то, что Т не звезда и,
следовательно, содержит Р3.) Поэтому G* содержит цикл, который
имеет длину g(G) > п, поскольку G* С G. В частности, |G*| > п,
что и требуется. D
9.3. Индуцированные теоремы Рамсея
Теорема Рамсея может быть перефразирована следующим
образом. Для каждого графа Н — Кг существует такой граф G, что
каждая 2-раскраска ребер G порождает одноцветный подграф Н С G,
например, в качестве G подходит любой достаточно большой
полный граф. Теперь слегка изменим задачу и спросим, существует ли
граф G, в котором каждая реберная 2-раскраска порождает
одноцветный индуцированный подграф Н С G, где теперь Н —
произвольный заданный граф.
Эта небольшая модификация полностью меняет суть задачи.
Теперь уже требуется не простое доказательство того, что G
является «достаточно большим» (как в теореме 9.1.2), а тщательное

216
Глава 9. Теория Рамсея для графов
построение графа, который при любом 2-разбиении его ребер
содержит индуцированную копию графа Я со всеми ребрами в одном и том
же классе разбиения. Назовем такой граф графом Рамсея для Я.
Тот факт, что такой граф Рамсея существует при любом
выборе Я, является одним из фундаментальных результатов в теории
Рамсея для графов. Его доказали примерно в 1973 г. независимо
друг от друга Дойбер, а также Эрдеш, Хайнал и Поша и, наконец,
Рёдль.
Теорема 9.3.1. Каждый граф имеет граф Рамсея. Другими
словами, для каждого графа Я существует граф G, содержащий при
любом разбиении {Ех^Еъ} множества E(G) индуцированный
подграф Я с Е(Н) С Ei или Е(Н) С Е2.
Мы дадим два доказательства. Каждое из них отличается
своеобразием, и все же каждое предлагает образец истинной теории
Рамсея: используемые в них графы — не более чем кирпичи в
конструкции, но построенное здание впечатляет.
Первое доказательство. При построении искомого графа
Рамсея мы будем неоднократно заменять вершины уже построенного
графа G = (VjE) копиями другого графа Я. Для множества вершин
U С V пусть G[U —» Я] обозначает граф, полученный из G
заменой вершин u £ U копиями Н{и) графа Я и соединением каждого
Н{и) полностью со всем Н{и') посредством ребер uu' £ Е и со всеми
вершинами v £ V \ U посредством ребер uv £ Е (рис. 9.3.1).
Рис. 9.3.1. Граф G[U — Я] при Я = К3
Формально, G[U —+ Я] есть граф на
(UxV(H))U ((V\U)x{0}),
в котором две вершины (vjw) и {v\w') смежны, если и только если
м' £ Е либо v - v' £ U и ww' £ Е(Н)3\
3) Замена V \ U на (V \ U) X {0} — всего лишь формальный способ
гарантировать, что все вершины G[U —*■ Н] имеют один и тот же вид (v,w),
a G[U —* Я] является формально непересекающимся с G.

9.3. Индуцированные теоремы Рамсея
217
Докажем следующее формальное усиление теоремы 9.3.1.
Для любых графов Н\, Hi существует такой граф
G = G(#i, #2), что любая раскраска ребер G цветами 1 и 2
порождает или индуцированный подграф Н\ С G (*)
со всеми ребрами цвета 1, или индуцированный подграф
#2 С G со всеми ребрами цвета 2.
Это формальное усиление позволяет применить индукцию по |#i| -f
|#2| следующим образом.
Если в #i или в #2 нет ребер (в частности, если |#i| -f |#2| < 1),
то (*) имеет место при G — Кп для достаточно большого п. Для
шага индукции допустим теперь, что и в #i, и в Hi есть по
меньшей мере одно ребро и что (*) имеет место для всех пар (Н[, Н^)
с меньшим |Я{| -f \Н'2\.
Для каждого г = 1,2 выберем вершину ж,- £ Яг-, инцидентную
какому-нибудь ребру. Пусть Н[ := Яг- — жг-, и пусть подграф Я"
графа Я,- индуцирован соседями вершины Х{.
Построим последовательность G0,..., Gn непересекающихся
графов; Gn будет искомым графом Рамсея G(H\} Я2). Наряду с
графами d мы определим подмножества Vх С V(G%) и отображение
/: V1 U • • • U Vn -> 7° U • • • U Vn~l
такие, что
/(П = V (1)
для всех г > 1. Записывая г-кратную композицию / везде, где она
определена, как /1 := / о • • • о /, а тождественное отображение на
V0 = V(G°) — как /°, мы имеем fx(v) £ V0 для всех v £ V*. Назовем
/1(г/) прародителем вершины г/.
Подграфы G1 [Vх] отражают строение графа G0 следующим
образом.
Вершины в Vх с различными прародителями смежны
в G , если и только если их прародители смежны в G .
Утверждение (2) не будет формально использовано в
доказательстве. Однако оно помогает наглядно представлять графы G1:
каждый G1 (точнее, каждый Gl[Fl], так как будут еще некоторые
вершины х £ G1 — Vх) по существу есть раздутая копия G0, в
которой каждая вершина w £ G° заменяется множеством всех вершин
из Vх с прародителем w, а отображение / связывает вершины с
одним и тем же прародителем через различные G1.

218
Глава 9. Теория Рамсея для графов
По индукционному предположению существуют графы Рамсея
Gi:=G(#b#0 и G2:=G(#{,#2).
Пусть G0 — копия графа Gi, и положим V0 := V(G°). Пусть далее
Wq, ..., W^_i — подмножества в Vго, порождающие Н'2в G0. Таким
образом, п определяется как число индуцированных копий графа Н2
в G0, и мы будем строить граф G1 для каждого множества W(_x,
i = 1,...,п. Поскольку Hi имеет ребро, то п > 1; в противном
случае G0 не мог бы совпадать с G{Hi,H2). Для г = 0, ...,га— 1
пусть W/7 — образ множества V{Hif) при некотором изоморфизме
Допустим теперь, что G0,..., G1"1 и V0,..., Vх 1 уже
определены для некоторого г > 1, а / определено на V1 U • • • U Vx~l и
удовлетворяет условию (1) для всех j < г. Мы расширяем G1"1 до G1 за
два шага. На первом шаге рассмотрим множество С/1"1 всех вершин
v £ V1'1, чьи прародители /1~1(г') лежат в W/ii- (При г = 1 имеем
U0 = Wq .) Расширим G1"1 до графа G1"1, заменяя каждую вершину
u £ Ux~l копией G2(u) графа G2, т. е. полагая
G1'"1 :=Gt'-1[£/t'"1-G2]
(см. рисунки 9.3.2 и 9.3.3). Положим f{u') := и для всех и £ С/1"1
и и' £ G2(u) и /(и') := v для всех г/ = (и, 0) с и £ V1"1^1"1.
(Вспомним, что (г/,0) — просто нерасширенная копия вершины v £ G1"1
в G1"1.) Пусть V" — множество тех вершин v' или и' из G1"1, для
которых / уже определено таким образом, т. е. вершин, которые
либо соответствуют непосредственно вершине v в Vх'1, либо
принадлежат расширению G2(iO такой вершины и. Тогда (1) имеет
место для г. Кроме того, если предположить индуктивно
справедливость (2) для г— 1, то условие (2) выполняется также и для г (в G1"1).
Граф G1-1 составляет уже «существенную часть» графа G1 — часть,
которая напоминает раздутую копию гра^а G0.
Во втором шаге мы расширяем граф G1"1 до искомого графа G1
добавлением некоторых вершин х £ Vх. Пусть & обозначают
множество всех семейств F вида
F=(H{(u)\ueUi-1),
где каждый Н[(и) есть индуцированный подграф графа G2(u),
изоморфный Н[. (Менее формально, & — набор способов выбрать из
каждого G2(u) в точности одну индуцированную копию графа Н[.)
Для каждого F £ & добавим к G*"1 вершину x(F) и соединим ее
со всеми вершинами из Н"{и) для каждого и £ С/1"1, где Н"(и) —
образ графа Н" при некотором изоморфизме Н[ —» Н[{и) (рис. 9.3.2).

9.3. Индуцированные теоремы Рамсея
219
Рис. 9.3.2. Конструкция G1
Обозначим полученный граф через G1. Этим заканчивается
индуктивное определение графов G0,..., Gn.
Теперь покажем, что G := Gn удовлетворяет условию (*). Для
этого докажем следующее утверждение о графах G1 при г — О,..., п.
При любой раскраске ребер цветами 1 и 2 граф G1
содержит или индуцированный подграф Н\ цвета 1,
или индуцированный подграф #2 цвета 2,
или такой индуцированный подграф Н цвета 2, (**)
что V(H) С. Vх и ограничение /1 на V(H) есть
изоморфизм между Н и GQ\W'k\ для некоторого
к е {г,.. .,п- 1}.
Заметим, что третий из вышеупомянутых случаев не может
возникать при г = п, поэтому (**) для п эквивалентно (*) с G := Gn.
Для г = 0 утверждение (**) следует из выбора G0 как копии
графа Gi = G(#i,#2) и определения множества W'k. Теперь пусть
1 < г < п, и допустим, что (**) выполняется для меньших значений г.
Пусть задана раскраска ребер графа G1. Для каждой и £ С/1"1
в G1 найдется копия графа G2:
Gl'DG2(u)-G(#{,#2).
Если G2(u) содержит индуцированный подграф #2 цвета 2 для
некоторой и £ U1"1, то утверждение (**) доказано. Если нет, тогда
каждый G2(u) имеет индуцированный подграф Н[(и) ~ Н[ цвета 1.
Пусть F — семейство таких графов Н[(и), по одному для каждой
вершины и £ U1"1, и пусть х := x(F). Если для некоторой и £ С/1"1

220
Глава 9. Теория Рамсе я для графов
все x-Hi(u) ребра в G1 также окрашены в 1, то имеем
индуцированную копию Н\ в G1, и (**) доказано. Поэтому можно считать, что
каждый Н"(и) имеет вершину уи, для которой ребро хуи окрашено
в 2. Пусть
Ui-1:={yu\ueUi-1}CVi.
Тогда / задает изоморфизм из
G1'"1 := в1[и{-1 U {(и, 0)\ve V(G1-1) \ С/1'"1}]
в Gl~l: каждая уи отображается в и, а каждое (и,0) — в d.
Таким образом, наша раскраска ребер графа G1 индуцирует раскраску
ребер графа G1"1. Если эта раскраска порождает индуцированный
подграф Hi С G1"1, покрашенный в 1, или индуцированный подграф
#2 С G1, покрашенный в 2, то это же имеет место также ивб1 С G1,
и доказательство завершено.
Поэтому согласно условию (**) для г — 1 можно считать, что
G*"1 содержит индуцированный подграф Я', покрашенный в 2, где
У{Н') С V1"1, и такой, что ограничение fl~l на V(H') есть
изоморфизм из Я' в G°[H^] ~ Н'2 при некотором к £ {г—1,... ,п— 1}. Пусть
Я' — соответствующий индуцированный подграф графа G1"1 С G*
(также покрашенный в 2). Тогда V{H') С Vх,
/|"(7(Я/)) = /|"-1(^(Я/)) = ^,
а /£: Я' -> G0 [И/^] — изоморфизм.
Если к > г, то доказательство (**) заканчивается при Н := Н'.
Поэтому допустим, что к < г, а следовательно, & = г — 1 (рис.
9.3.3). По определению Ul~l и G1"1 прообраз W(/_1 при изоморфизме
/г: Н' —► G°[V^/_1] является подмножеством в /У1"1. Поскольку
вершина х смежна в точности с теми вершинами из Я7, которые лежат
в U1'1, а все эти ребра хуи имеют цвет 2, то граф Н' вместе с х
индуцирует в G* копию графа Яг, покрашенную в цвет 2, и
доказательство (**) завершено. □
Вернемся еще раз к переформулировке теоремы Рам сея,
рассмотренной в начале этого раздела: для каждого графа Я существует
такой граф G, что любая 2-раскраска ребер графа G порождает
одноцветный подграф ЯСС Граф G, для которого это сразу следует из
теоремы Рамсея — любой достаточно большой полный граф. Если
же мы хотим, чтобы G не содержал полных подграфов, больших чем
имеющиеся в Я, т. е. чтобы w(G) = ш(Н), то задача снова
становится трудной, даже если мы не требуем от Я быть индуцированным
подграфом в G.

9.3. Индуцированные теоремы Рамсея 221
Рис. 9.3.3. Одноцветная копия графа/^2 в G1
Наше второе доказательство теоремы 9.3.1 решает сразу обе эти
задачи: при заданном Н мы построим граф Рамсея для #, имеющий
ту же плотность, что и Н.
В этом доказательстве, т. е. в оставшейся части этого раздела,
будем рассматривать двудольные графы Р как тройки (Vi,V2,#),
где V\ и Vi — доли вершинного разбиения, а Е С V\ х Уг —
множество ребер. Причина для введения этой более явной системы
обозначений состоит в нашем желании добиться, чтобы вложения
между двудольными графами сохраняли их 2-разбиения. Пусть имеется
другой двудольный граф Р' = (V/, V^E'). Инъективное
отображение ф: V\ U Vi —► V[ U V2' будет называться вложением Р в Р', если
Ф(У\) Q У( Для * — 1)2, а ф{ь\)ф{ь2) есть ребро графа Р' тогда
и только тогда, когда v\V2 — ребро в Р. (Заметим, что такие
вложения являются «индуцированными».) Вместо ф: V\ U V2 —► V{ U У2;
можно писать просто ф: Р -+ Р'.
Нам понадобятся две леммы.
Лемма 9.3.2. Каждый двудольный граф можно вложить в
двудольный граф вида (X, [Х]к, Е), где Е = {xY \ х £ Y}.

222
Глава 9. Теория Рамсея для графов
Доказательство. Пусть Р — любой двудольный граф,
например, с долями {ai,...,an} и {6i,...,6m}. Пусть X — множество
с 2п -f т элементами, скажем,
х = {si,...,sn,yi,..-,yn,*i,...,*m};
тогда определим вложение ф: Р —» (X, [Х]п+1, Е).
Сначала положим ф{а,{) := Х{ для всех г = 1,..., п. Какие (п +1)-
множества У С X являются подходящими кандидатами на выбор
ф(Ь{) для заданной вершины 6г? Ясно, что в точности смежные
с образами соседей вершины &*, т. е. удовлетворяющие условию
У П {*!,...,*„} =^(JVp(&,-)). (1)
Поскольку d(bi) < п, требование (1) оставляет по меньшей мере
один из п + 1 элементов множества У неопределенным. В
дополнение к ф(Мр(Ь{)) можно поэтому включить в каждый У = ф(Ь{)
вершину Z{ как «индекс». Это гарантирует, что ф{Ь{) ф ф{Ь^) для
i Ф j, даже когда Ъ{ и bj имеют одних и тех же соседей в Р. Чтобы
определить множество У = ф(Ь{) полностью, мы под конец
заполняем их «фиктивными» элементами yj, пока не наступит равенство
|У| = п + 1. □
Вторая лемма уже покрывает двудольный случай теоремы —
она утверждает, что каждый двудольный граф имеет граф Рамсея,
причем даже двудольный.
Лемма 9.3.3. Для любого двудольного графа Р существует
такой двудольный граф Р', что для любой 2-раскраски ребер Р'
существует вложение ф: Р —>• Р', при котором все ребра ф{Р) имеют один
и тот же цвет.
Доказательство. По лемме 9.3.2 можно считать, что Р имеет
вид (Х,[Х]к,Е), где Е = {xY \ х £ У}. Докажем утверждение для
графа Р' \— {X'', [Х']к , Е'), где к' := 2k — 1, X' — любое множество
мощности
\X,\ = R(k,,2^,k\X\ + k-l)
(число Рамсея, определенное после теоремы 9.1.4), а
Е' := {х'У | х' е У'}.
Теперь раскрасим ребра графа Р' двумя цветами: а и /3. Среди
\У'\ — 2k — 1 ребер, инцидентных вершине У £ [Х']к , по меньшей
мере k имеют один и тот же цвет. Поэтому для каждого У можно
выбрать такое фиксированное ^-множество Z' С У, что все ребра

9.3. Индуцированные теоремы Рамсея
223
х'У с х' £ Z' имеют один и тот же цвет; назовем этот цвет
связанным с У.
Множества Z' могут лежать (к) способами в своих
надмножествах У следующим образом. Пусть X' линейно упорядочено. Тогда
для каждого У £ [Х']к имеется единственная сохраняющая порядок
биекция ау': У —► {1,.. •, к'}, которая отображает Z1 в один из (jj.)
возможных образов.
Теперь раскрасим [Х']к b2(J элементов множества
[{1,...,к'}}кх{а,/3}
как цвета, давая каждому У £ [Х']к в качестве его цвета пару
(сгу/(^'),7), где 7 — цвет а или /?, связанный с У. Поскольку \Х'\
было выбрано как число Рамсея с параметрами к', 2(к) и k\X\-\-k — 1,
мы знаем, что X' содержит одноцветное подмножество W мощности
fc|X|-f к — 1. Значит, все Z' с У С W лежат в своих У одним и тем же
образом, т. е. существует такое S £ [II,..., к'}]к , что ay>{Z') — S
для всех У £ [W]k , а все У7 £ [W]k связаны с одним и тем же
цветом, например с а.
Теперь построим искомое вложение ф из Р в Р'. Сначала
определяем ф на X =: {ж1,..., жп}, выбирая образы 0(жг) =: W{ £ Ж так,
чтобы W{ < Wj в нашем упорядочении множества X' всякий раз,
когда г < j. Кроме того, выберем W{ так, чтобы в точности к — 1
элементов множества W были меньше iui, в точности & — 1 лежали
бы между iu; и iu;+i для г = 1,..., п — 1 ив точности к - 1 были
больше iun. Поскольку |1У| = кп + к — 1, это действительно можно
сделать (рис. 9.3.4).
Определим теперь ф на [Х]к. При заданном Y £ [X]* мы хотим
выбрать ф(У) =: У7 £ [X7]* так, чтобы соседями У среди вершин
из ф(Х) были в точности образы соседей У в Р, т. е. вершины ф(х)
с ж £ У, причем так, чтобы все эти ребра в У были окрашены
в а. Чтобы найти такое множество У7, мы сначала фиксируем его
подмножество Z1 как {ф(х) \ х £ У} (имеется к вершин типа iut-),
а затем расширяем Z1 добавлением к1 — к дополнительных вершин
и £ W \ ф(Х) до множества У £ [И^]* таким образом, чтобы Z1
лежало в Y' правильно, т. е. так, что ayi(Z') = S. Это можно
сделать, поскольку между любыми двумя W{ лежит к — \ — к' — к
других вершин из W. Тогда
Упф(Х) = г' = {ф(х)\хеУ},
поэтому У имеет правильных соседей в ф(Х)} а все ребра между У
и этими соседями окрашены в а (так как эти соседи лежат в Z', а У
связано с а). Наконец, ф инъективно на [Х]к: образы У различных

224 Глава 9. Теория Рамсея для графов
k-1
Wi
w2
к-l I
к-l I
к-l I
x'\ : I
Puc. 9.3.4. Граф из леммы 9.3.3
вершин Y различны, потому что их пересечения с ф(Х) различны.
Следовательно, наше отображение ф — действительно вложение Р
вР'. □
Второе доказательство теоремы 9.3.1. Пусть Я задано,
как в теореме, а п := R(r) — число Рамсея для г := |#|. Тогда при
любой 2-раскраске своих ребер граф К = Кп содержит одноцветную
копию Я, хотя и не обязательно индуцированную.
Мы начинаем с построения графа G0 следующим образом.
Представим себе, что вершины К размещены в столбце, и заменим
каждую вершину строкой из (") вершин. Тогда каждый из (")
полученных столбцов можно связать с одним из (") способов вложения
V(H) в V(K)) снабдим этот столбец ребрами такой копии Я.
Возникающий при этом граф G0 состоит из (") непересекающихся копий
графа Я и (п — г)(") изолированных вершин (рис. 9.3.5).
Чтобы определить G0 формально, предположим, что V(K) =
{1,..., п}, и выберем копии #i,..., Н/п\ графа Я в К с попарно
различными множествами вершин. (Таким образом, на каждом г-мно-
жестве в V(K) получается одна фиксированная копия Hj графа Я.)

9.3. Индуцированные теоремы Рамсея
225
п-г
Затем положим
У п
Рис. 9.3.5. Граф G0
V(G°) := |(*,j) |*= 1 »;i = l,
С)
E{G0):=\J{{i,j){i!,j)\it еЕ{Н;)}.
3=1
Идея дальнейшего доказательства состоит в следующем. Наша
цель — свести общий случай теоремы к двудольному, который имел
место в лемме 9.3.3. Применяя лемму итерационно ко всем парам
строк в G0, мы построим очень большой граф G такой, что для
каждой раскраски ребер из G имеется индуцированная копия G0 в G,
которая является одноцветной на всех двудольных подграфах,
индуцированных ее парами строк, т. е. в которой ребра между одними
и теми же двумя строками всегда имеют один и тот же цвет.
Проекция этого G0 С G на {1,..., п) (как результат стягивания его строки)
тогда определяет раскраску ребер графа К. По выбору \К\ один из
Hj С К будет одноцветным. Но этот Hj встречается при той же
раскраске в j-м столбце нашего G0, где он является
индуцированным подграфом графа G0, а значит, и G.
Формально, определим последовательность G0,..., Gm
п-дольных графов G*, скажем, с n-разбиением {V*,..., V*} и положим
G := Gm. Граф G0 был определен выше. Пусть V]0,..
строки,
^:={(ifi)|i=l,...,(;
Теперь пусть ei,...,em есть нумерация ребер графа К. Для к —
О,...,т— 1 построим Gk+1 по Gk следующим образом. Если,
скажем, ejfc+i = ziZ2, то пусть Р = (V^, V^, Ё) — двудольный подграф
V0
' 1 у п
его

226
Глава 9. Теория Рамсея для графов
графа Gk, индуцированный его ii-и и г*2-й строками. По лемме 9.3.3
Р имеет двудольный граф Рамсея Р' = (Wi, W2, Е'). Мы хотим
определить G*"*"1 Э Р' так, чтобы каждое (одноцветное) вложение
Р —► Р' могло быть расширено до вложения Gk —► G*+1. Пусть
{01,..., фч) — множество всех вложений Р в Р', а
7(G*+r):=Vr1*+1U---UVrn*+1>
где
К-*+1 := <
VKi при г = zi,
Wi при г = г2,
U (К* х Ы) ПРИ *£ {*1,*2}.
(Таким образом, при г ф i\,ii мы берем в качестве V{ + просто
^ непересекающихся копий графа V^*.) Определим теперь множество
ребер G*+1 так, чтобы очевидные расширения фр на все V(Gk) стали
вложениями Gk в G*+1. При р = 1,..., q пусть ^р : V(G*) -+ V(G*+1)
определяется следующим образом:
, Г ^р(и) при и е Р,
I (f,p) при ^Р,
и пусть
£(G*+1) := UM>(i#p(i/) I ™' G E(Gk)}.
Теперь при любой 2-раскраске своих ребер граф G*+1 содержит
индуцированную копию ipp(Gk) графа G*, ребра которой в Р, т. е.
между его г*1-й и г*2-й строками, имеют один и тот же цвет: просто
выберем р так, чтобы фр(Р) был одноцветной индуцированной копией Р
в Р', которая существует по лемме 9.3.3.
Мы утверждаем, что G := Gm удовлетворяет заключению
теоремы. Итак, пусть задана 2-раскраска ребер графа G. По
построению графа Gm из Gm_1 можно найти в Gm такую индуцированную
копию графа Gm_1, что при ет = И' все ребра между г-й и г'-й
строками имеют один и тот же цвет. Таким же образом мы находим
внутри этой копии графа С71"1 индуцированную копию графа Gm~2,
ребра которой между г-й и г'-й строками имеют один и тот же цвет
также и при гг' = em_i. Продолжая таким образом, мы в конечном
итоге придем к такой индуцированной копии графа G0 в G, что для
каждой пары (г, г') все ребра между V® и Vy имеют один и тот же
цвет. Как показано выше, этот G0 содержит одноцветную
индуцированную копию Hj графа Я. □

9.4. Рамсеевские свойства и связность
227
9.4. Рамсеевские свойства и связность
Согласно теореме Рамсея каждый достаточно большой граф G
содержит или очень плотный, или очень разреженный
индуцированный подграф заданного порядка — Кг или Кг. Предполагая, что G
является связным, можно доказать несколько более сильное
утверждение.
Предложение 9.4.1. Для каждого г £ N существует такое
п £ N, что любой связный граф порядка по меньшей мере п содержит
в качестве индуцированного подграфа Кг, К\)Г или Рг.
Доказательство. Пусть d-fl — число Рамсея от параметра г,
п > 1 -f rdr и G — граф порядка по меньшей мере п. Если в G есть
вершина v степени не меньше d -f 1, то по теореме 9.1.1 и выбору d
либо N(v) индуцирует Кт в G, либо {v} U N(v) индуцирует К\^.
С другой стороны, если A(G) < d, то по предположению 1.3.3 граф G
имеет радиус > г и, следовательно, содержит две вершины на
расстоянии > г. Любой кратчайший путь в G между такими двумя
вершинами содержит Рг. □
Набор «типичных» индуцированных графов в предложении 9.4.1
является наименьшим из возможных в следующем смысле. Если Ш —
любое множество связных графов с тем же свойством, т. е. такое,
что при заданном г £ N каждый достаточно большой связный граф G
содержит или Кг, или индуцированную копию некоторого графа
порядка > г из #, то # содержит произвольно большие полные графы
и звезды и произвольно длинные пути. (Заметим, что если мы
берем в качестве G полный граф, звезду или путь, то все его подграфы
являются такими же.) Но предложение 9.4.1 утверждает, что ничего
другого нам и не требуется.
В принципе, мы могли бы искать похожее на # множество для
любой связности к. Мы могли бы попытаться найти такое
«минимальное» множество (в вышеупомянутом смысле) типичных
^-связных графов, что каждый большой fc-связный граф содержит
большой подграф из этого множества. К сожалению, ^, по-видимому,
растет очень быстро с ростом к: уже для к = 2 оно становится
совершенно бесформенным, если (как при к — 1) мы настаиваем, чтобы
эти подграфы были индуцированными. Ослабляя наше требование
к вложимости от «индуцированного подграфа» до «топологического
минора» и далее до «минора», можно, однако, дать некоторую
четкую характеризацию вплоть до к — 4.
Предложение 9.4.2. Для любого г £ N существует такое
п £ N, что любой 2-связный граф порядка по меньшей мере п
содержит Ст или Kij как топологический минор.
Доказательство. Пусть d есть то п, которое связано с г в
предложении 9.4.1, и пусть G — 2-связный граф с более чем 1 -f rdr

228 Глава 9. Теория Рамсея для графов
вершинами. По предположению 1.3.3 или G имеет вершину
степени > d, или diam(G) > rad(G) > г.
В последнем случае пусть a, b £ G — две вершины на
расстоянии > г. По теореме Менгера (3.3.5) G содержит два независимых
a-b пути. Они образуют цикл длины > г.
Допустим теперь, что в G есть вершина v степени > d.
Поскольку G 2-связен, то G — v связен, а значит, имеет остовное
дерево. Пусть Т — минимальное дерево в G — v, которое содержит
всех соседей вершины v. Тогда каждый лист в Т является соседом
вершины v. По выбору d или в Т есть вершина степени > г, или
Т содержит путь длины > г, связывающий без ограничения
общности два листа. Вместе с v такой путь образует цикл длины > г.
Вершина и степени > г в Т может быть соединена с v посредством г
независимых путей, проходящих через Т, с образованием ТК^^т- D
Теорема 9.4.3 (Опоровский, Оксли и Томас, 1993). Для любого
г £ N найдется такое п £ N, что каждый 3-связный граф порядка
не меньше п содержит в качестве минора или колесо порядка г, или
граф Кз,г-
Назовем граф вида Сп * К2 [п > 4) двойным колесом, 1-скелет
триангуляции цилиндра (как на рис. 9.4.1) — короной, а 1-скелет
триангуляции ленты Мёбиуса — короной Мёбиуса.
(Ш553) CS5S
Рис. 9.4-1- Корона и корона Мёбиуса
Теорема 9.4.4 (Опоровский, Оксли и Томас, 1993) Для любого
г £ N найдется такое n £ N, что каждый 4-связный граф с не
менее чем п вершинами имеет минор порядка > г, который является
двойным колесом, короной, короной Мёбиуса или K^yS.
Заметим, что миноры, встречающиеся в теоремах 9.4.3 и 9.4.4,
соответственно сами 3- и 4-связны и не являются минорами друг
друга. Таким образом, в каждом случае набор миноров минимален
в обсуждавшемся выше смысле.

Упражнения
229
Упражнения
1.~ Найти число Рамсея Я(3).
2. Вывести случай к = 2 (но с произвольным с ) теоремы 9.1.4 непосредственно
из теоремы 9.1.1.
3.+ Построить граф на IR, который не содержит ни полного, ни безреберного
индуцированного подграфа на |Ж| = 2N° вершинах. (Так что теорема Рамсея
не допускает обобщения на несчетные множества.)
4.+ С помощью теоремы Рамсея показать, что для любых к,£ Е N существует
такое п £ N, что каждая последовательность из п различных целых
чисел содержат возрастающую подпоследовательность длины к -f 1 или
убывающую подпоследовательность длины £ + 1. Найти пример,
показывающий, что n > к£. Затем доказать теорему Эрдеша — Секереша о том, что
п = к£ + 1 — одно из возможных значений.
5. Дать набросок доказательства следующей теоремы Эрдеша — Секереша:
для каждого к Е N существует такое n Е N, что среди любых п точек
на плоскости, никакие три из которых не коллинеарны, найдутся к точек,
образующих выпуклый /:-угольник, т.е. таких, что ни один из них не лежит
в выпуклой оболочке остальных
6. Доказать следующий результат Шура: для каждого к Е N существует
такое n Е N, что для каждого разбиения множества {1,..., п} на к множеств
по меньшей мере одно из них содержит такие числа х, у, z, что х + у = z.
7. Пусть (X, <) — вполне упорядоченное множество, a G = {У*Щ — граф на
V := [X]2 с Е := {(х,у)(х',у') | х < у = х' < у'}.
(i) Показать, что G не содержит треугольника.
(ii) Показать, что х(^) становится произвольно большим, если выбирать
\Х\ достаточно большим.
8. Семейство множеств называется Д- систем ой, если каждые два множества
имеют одну и ту же мощность пересечения. Показать, что каждое
бесконечное семейство множеств одного и того же конечного порядка содержит
бесконечную Д-систему.
9. Доказать следующее ослабление теоремы Скотта 8.1.5: для каждого г Е N
и каждого дерева Т существует такое к Е N, что любой граф G с х(^) > к
и oj(G) < г содержит подразделение дерева Т, в котором никакие две
вершины ветвления не смежны в G (если только они не смежны в Т).
10. С помощью леммы о бесконечности показать, что при заданном к Е N
счетно-бесконечный граф Аг-раскрапшваем (в смысле главы 5), если все его
конечные подграфы Аг-раскрашиваемы.
11. Пусть га, n Е N, и предположим, что п — 1 делится на га — 1. Показать, что
каждое дерево Т порядка га удовлетворяет условию Я(Т, К\}П) = га + п — 1.
12. Доказать, что 2е < Я(2,с, 3) < Зс! для любого ceN.
(Подсказка. Индукция по с.)
13."~ Вывести утверждение (*) в первом доказательстве теоремы 9.3.1
непосредственно из теоремы, т. е. показать, что (*) лишь формально сильнее, чем
сама теорема.
14. Показать, что граф Рамсея G для Н, построенный во втором доказательстве
теоремы 9.3.1, действительно удовлетворяет условию w(G) = ш(Н).

230 Глава 9. Теория Рамсея для графов
15. Показать, что для любых двух графов Н\ и #2 существует такой граф
G = G(H\, Н2), что при любой вершинной раскраске графа G цветами 1 и 2
в нем имеется либо индуцированная копия Hi цвета 1, либо индуцированная
копия Н2 цвета 2.
(Подсказка. Примените индукцию, как в первом доказательстве теоремы
9.3.1.)
16. Показать, что каждый бесконечный связный граф содержит бесконечный
путь или бесконечную звезду.
17.~ Граф Кг из теоремы Рамсея, последний из возникавших в предложении
9.4.1, таинственным образом не появляется в предложении 9.4.2 и далее.
Чем это можно объяснить?
Примечания
Из-за усилившегося взаимодействия с исследованием случайных и
псевдослучайных4) структур (источником последних служит, например, лемма
регулярности) теория Рамсея для графов в последнее время переживает период
значительной активности и успехов. Теорема 9.2.2 — ранний пример этих
достижений.
При более классическом подходе можно порекомендовать хорошо
написанный вводный текст: Graham R. L., Rothschild В. L., Spencer J. Н. Ramsey
Theory. 2nd ed. N. Y.: John Wiley & Sons, 1990. Эта книга включает главу о теории
Рамсея для графов, но этим не ограничивается. Более современный общий
обзор дан Я. Нешетрилом в: Handbook of Combinatorics / Ed. by R. L. Graham,
M. Grotschel, L. Lovasz. Amsterdam e. a.: North-Holland Publ., 1995. Теория
Рамсея для бесконечных множеств представляет собой существенную часть
комбинаторной теории множеств; она подробно излагается в: Erdos P., Hajnal А.,
Mate A., Rado R. Combinatorial Set Theory. Amsterdam e. a.: North-Holland
Publ., 1984. Привлекательный набор ярких результатов из различных разделов
теории Рамсея, включая приложения к алгебре, геометрии и топологии
точечных множеств, предлагается в книге: Bollobds В. Graph Theory. Berlin е. а.:
Springer-Verl., 1979. V. 63. (Graduate Texts in Mathematics).
Лемма Кёнига о бесконечности или, для краткости, лемма Кента
содержится в самой первой книге по теории графов: Konig D. Theorie der endlichen
und unendlichen Graphen. Leipzig: Akad. Verl., 1936. Метод компактности для
выведения конечных результатов из бесконечных (или наоборот), упомянутый
в разделе 9.1, на самом деле не является таким таинственным, как может
показаться. До тех пор пока «бесконечный» означает «счетно-бесконечный», он
есть не что иное, как искусство применения леммы бесконечности (как в
доказательстве теоремы 9.1.4), не больше и не меньше. Для бесконечных множеств
большей мощности это рассуждение становится эквивалентным известной
теореме Тихонова о том, что произвольные произведения компактных пространств
компактны, — теореме, благодаря которой метод компактности получил свое
название. Подробности можно найти в главе 6, теорема 10 книги Боллобаша
и в главе 1, теорема 4 книги Грэма, Ротшилда и Спенсера. Другая часто
используемая версия общего метода компактности — лемма Радо о выборе; см.
главу А. Хайнала по бесконечной комбинаторике в цитируемом выше Handbook
of Combinatorics.
Теорема 9.2.2 получена в статье: Chvdtal V., Rodl V., Szemeredi Е.,
Trotter W. Т. The Ramsey number of a graph with bounded maximum degree // J. Com-
bin.Theory. Ser. B. 1983. 34. P. 239-243. Наше доказательство следует
эскизу из работы: Komlos J., Simonovits М. Szemeredi's Regularity Lemma and
) Конкретные графы, строение которых напоминает строение, характерное
для случайного графа, называются псевдослучайными. Например,
двудольные графы, определяемые б-регулярной парой множеств вершин в
некотором графе, псевдослучайны.

Примечания
231
its applications in graph theory // Combinatorics, Paul Erdos is eighty / Ed. by
D. Miklos, V. T. Sos, T. Szonyi / Bolyai Soc. Math. Studies. V. 2. Budapest: Janos
Bolyai Math. Soc, 1996. Эта теорема представляет собой крупное продвижение
в гипотезе Бэра и Эрдеша (1975) о том, что числа Рамсея графов с
ограниченной в каждом подграфе средней степенью линейны. Гипотеза утверждает, что
для каждого d Е N существует такая константа с, что R(H) < с\Н\ для всех
графов Н с d(H') < d для всех Н' С Н. Эта гипотеза была проверена также для
класса планарных графов (Чен, Шелп, 1993) и, более общо, для класса графов, не
содержащих Кг (при любом фиксированном г) как топологический минор (Рёдль
и Томас, 1996). Ссылки см. в главе Нешетрила из Handbook of Combinatorics.
Наше первое доказательство теоремы 9.3.1 основано на работе: Deuber W.
A generalization of Ramsey's theorem // Infinite and finite sets / Ed. by A. Ha-
jnal, R. Rado, V. T. Sos. Amsterdam e. a.: North-Holland Publ., 1975. В этом
же томе содержится другое доказательство этой теоремы, принадлежащее Эр-
дешу, Хайналу и Поше. Рёдль доказал этот же результат в своей магистерской
работе в Карловом Университете, Прага, в 1973. Наше второе доказательство
теоремы 9.3.1, которое сохраняет плотность Н для G, взято из работы: Nesetfil J.,
Rodl V. A short proof of the existence of restricted Ramsey graphs by means of
a partite construction //Combinatorica. 1981. 1. P. 199-202.
Обе теоремы раздела 9.4 получены в: Oporowski В., Oxley J., Thomas R.
Typical subgraphs of 3- and 4-connected graphs // J. Combin.Theory. Ser. B. 1993.
57. P. 239-257.

Глава 10
Гамильтоновы циклы
В разделе 1.8 мы кратко обсуждали задачу о том, когда граф
содержит эйлеров обход, т. е. замкнутый маршрут, проходящий через
каждое ребро в точности один раз. Простая теорема 1.8.1 решает эту
задачу вполне удовлетворительно. Теперь зададим такой же вопрос
относительно вершин: когда граф G содержит замкнутый маршрут,
который проходит через каждую вершину G в точности один раз?
Если \G\ > 3, то любой такой маршрут есть цикл — гамилътонов
цикл графа G. Если G имеет гамильтонов цикл, то G называется га-
милътоновым. Аналогично, путь в G, содержащий каждую вершину
из G, есть гамилътонов путь.
Определить, имеет ли заданный граф гамильтонов цикл,
намного труднее, чем установить, является ли он эйлеровым, и ни
одной хорошей характеризации1) таких графов не известно. Мы
начнем эту главу со стандартных достаточных условий существования
гамильтонова цикла (разделы 10.1 и 10.2). Остальная часть главы
посвящена красивой теореме Флейшнера о том, что «квадрат»
каждого 2-связного графа имеет гамильтонов цикл. Это один из
основных результатов в области гамильтоновых циклов. Простое
доказательство, которое мы предлагаем читателю (принадлежащее Рихе),
все же немного длиннее, чем другие доказательства в этой книге, но
не трудное.
10.1. Простые достаточные условия
Какого рода условие могло бы быть достаточным для
существования гамильтонова цикла в графе G? Чисто глобальные
предположения, подобные высокой реберной плотности, не будут достаточны:
мы не сможем обойтись без того локального свойства, что каждая
■' Понятие «хорошая характеризация» можно сформулировать строго; см.
введение к разделу 12.5 и примечания к главе 12.

10.1. Простые достаточные условия
233
вершина имеет по меньшей мере двух соседей. Но столь же
недостаточна и сколь угодно большая (но постоянная) минимальная
степень: нетрудно найти графы без гамильтонова цикла, у которых
минимальная степень превышает любую константу.
Следующий классический результат важен в свете только что
сделанных замечаний.
Теорема 10.1.1 (Дирак, 1952). Каждый граф с п > 3
вершинами и минимальной степенью по меньшей мере п/2 имеет гамиль-
тонов цикл.
Доказательство. Пусть G = (V,E) — граф с \G\ - п > 3
и 6(G) > п/2. Тогда G связен. В противном случае степень
любой вершины в наименьшей компоненте С графа G была бы меньше
\С\ < п/2.
Пусть Р = хо .. .Xk — самый длинный путь в G. Ввиду
максимальности Р все соседи вершин xq и ж* лежат на Р. Следовательно,
как минимум п/2 из вершин хо,... ,Xk-i смежны с Xk и по
меньшей мере п/2 из этих к < п вершин Х{ таковы, что жоЯг+i G Е. По
принципу Дирихле существует вершина ж,, которая обладает обоими
этими свойствами, поэтому xqX{+\ £ Е и X{Xk Е Е для некоторого
г< к (рис. 10.1.1).
Рис. 10.1.1. Нахождение гамильтонова цикла в доказательстве теоремы 10.1.1
Мы утверждаем, что цикл С := xoXi+iPxkX{Pxo есть гамиль-
тонов цикл графа G. Действительно, поскольку G связен, то С
в противном случае имел бы смежную вершину в G — С, которая
в объединении с подходящим остовным путем цикла С давала бы
путь длиннее, чем P. D
Теорема 10.1.1 неулучшаема в том отношении, что мы не
можем заменить оценку п/2 даже на [n/2j: если п нечетно, a G —
объединение двух копий if'п'2', пересекающихся по одной вершине,
то 6(G) = 1/ь/2_|, но K(G) = 1, и поэтому G не может иметь
гамильтонова цикла. Другими словами, для обеспечения 2-связности
графа G необходим высокий уровень оценки S > п/2, если для этого
нет других средств. Последнее условие с такой же очевидностью
является необходимым для гамильтоновости, как и то, что
минимальная степень должна быть не меньше 2. Казалось бы поэтому,
что требование некоторого большого (константного) значения от /с,
а не от 5, дает несколько большие шансы на обеспечение
гамильтоновости. Однако это не так: хотя fc-связные графы содержат длинные
циклы в терминах к (упражнение 0 главы 3), графы Knjk
показывают, что их периметр не обязательно растет с ростом п.

234
Глава 10. Гамильтоновы циклы
Имеется еще один инвариант с подобным свойством: малое
число независимости a{G) гарантирует, что G имеет длинные циклы
(упражнение 13 главы 5), хотя не обязательно имеет гамильтонов
цикл. Однако в совокупности предположения о высокой связности
и малом числе независимости удивительным образом дополняют
друг друга, давая достаточное условие гамильтоновости.
Предложение 10.1.2. Каждый граф G с \G\ > 3 и k(G) > &{G)
имеет гамильтонов цикл.
Доказательство. Положим k(G) =: k, и пусть С —
длиннейший цикл в G. Занумеруем вершины С циклически, допустим, как
V(C) = {vi | i £ Zn}, где iw+i £ E(C) для всех г £ 7Ln. Если
цикл С не гамильтонов, то выберем вершину v £ G — С и v-C веер
& — {Рг- | % £ /} в G, где /CZ„h каждый Р{ заканчивается в V{.
Пусть & выбрано с максимальным количеством элементов; тогда
vvj £ E{G) для любого j £ I и
И > min{A, |С|} (1)
по теореме Менгера (3.3.3).
Для каждого г £ / имеем г -f 1 ^ /. В противном случае цикл
(С U Pi U Рг+i) — ЩЩ+1 был бы длиннее, чем С (рис. 10.1.2, левая
часть). Таким образом, \&\ < |С|, а следовательно, |/| = \&\ > к
согласно (1). Кроме того, г/г-+1^+1 t E{G) для всех hi £ ^> так как
в противном случае цикл {С U Р{ U Pj) -f Vt+ity+i ~~ vivi+i — vjvj+i
был бы длиннее, чем С (рис. 10.1.2, правая часть). Следовательно,
{vi+i | г£/}и{и} — множество из к -f 1 или более независимых
вершин в G вопреки тому, что a{G) < к. □
Рис. 10.1.2. Два цикла длиннее, чем С
Хотя при первом знакомстве это может показаться
удивительным, но гамильтоновость для планарных графов связана с
проблемой четырех красок. Как мы отмечали в разделе 6.6, теорема о
четырех красках эквивалентна несуществованию планарного снарка, т. е.
утверждению, что каждый планарный кубический граф без мостов
имеет 4-поток. Легко проверить, что «без мостов» в этом
утверждении можно заменить на «3-связный» и что каждый гамильтонов

10.2. Гамильтоновы циклы и степенные последовательности 235
граф имеет 4-поток (упражнение 12 главы 6). Для доказательства
теоремы о четырех красках поэтому достаточно было бы показать,
что каждый 3-связный планарный кубический граф имеет гамиль-
тонов цикл!
К сожалению, этот путь не ведет к цели: первый контрпример
был найден Таттом в 1946 г. Десятью годами позже Татт доказал
следующую глубокую теорему как наилучшее из возможных
ослаблений.
Теорема 10.1.3 (Татт, 1956). Каждый 4-связный планарный
граф имеет гамильтонов цикл.
10.2. Гамильтоновы циклы и степенные
последовательности
Исторически теорема Дирака явилась отправной точкой для
открытия ряда все более и более слабых условий на степени вершин,
каждое из которых является достаточным для гамильтоновости. Это
развитие в итоге завершилось единственной теоремой, которая
охватывает все ранее полученные результаты; ее мы и докажем в этом
разделе.
Если G — граф с п вершинами со степенями d\ < • • • < dn,
то n-набор (di,..., dn) называется степенной последовательностью
графа G. Заметим, что эта последовательность единственна даже
при том, что G имеет несколько вершинных нумераций,
порождающих его степенную последовательность. Назовем произвольную
последовательность целых чисел (ai,..., ап) гамилътоновой, если
каждый граф с п вершинами постепенной последовательностью,
поточечно мажорирующей (oi,...,an), гамильтонов. (Последовательность
(di,...,dn) поточечно мажорирует (ai,... ,an), если d{ > at- для
всех г.)
Следующая теорема характеризует все гамильтоновы
последовательности.
Теорема 10.2.1 (Хватал, 1972). Последовательность целых
чисел (ai,...,an), где 0 < о>\ < • • • < ап <пяп>3, является
гамильтоновой, если и только если для каждого i < п/2
выполняется следующее условие:
а,- < г => an-x > n — i.
Доказательство. Пусть (ai,...,an) — такая целочисленная
последовательность, что 0<ai<---<an<n и п > 3. Допустим
сначала, что эта последовательность удовлетворяет условию
теоремы, и докажем, что она гамильтонова. Предположим противное;

236
Глава 10. Гамильтоновы циклы
тогда существует такой граф G = (V, Е) со степенной
последовательностью {d\,..., dn), что
di > a,i для всех г, (1)
но G не имеет гамильтонова цикла. Пусть G был выбран с
максимальным числом ребер, и пусть (i>i,.. . ,un) — нумерация
множества V с d(i/,-) = d( для всех г. Согласно (1) наши предположения
о (ai,..., an) переносятся на (d^..., dn), т. е.
d,- < г => dn_,- > п — г для всех г < п/2. (2)
Пусть ж, у — различные и несмежные вершины в G с d(x) < d(y)
и как можно большей d(x) -f d(?/). Легко проверить, что степенная
последовательность графа G+xy поточечно мажорирует (di,..., dn),
а значит, и (fli,...,fln). Следовательно, ввиду максимальности G
новое ребро ху лежит на гамильтоновом цикле Н в G -f жу. Тогда
Н — ху — гамильтонов путь xit.. . ,ж„ в G, скажем, с a?i = ж и хп = у.
Как и при доказательстве теоремы Дирака, рассмотрим теперь
индексные множества
/ := {г | xxt+i € Е) и J := {j | Xjy G £}.
Тогда I U J С {1,...,п— 1}, а /flJ = 0, поскольку G не имеет
гамильтонова цикла. Следовательно,
d(x) + d(y) = \I\ + \J\ < n, (3)
откуда ft \— d(x) < n/2 по выбору x.
Поскольку Xiy £ E для всех i G /, все такие X{ были
кандидатами на выбор х (вместе с у). Наш выбор {ж, у} с максимальной
d(x) -f d(y), таким образом, влечет, что d(x{) < d(x) для всех i £ I.
Следовательно, G имеет как минимум \I\ = h вершин степени не
более ft, поэтому dh < ft. Ввиду (2) отсюда следует, что dn_h > п — ft,
т. е. все ft -f 1 вершин vn-h, • • •, и„ имеют степень по меньшей мере
п — ft. Так как d(x) = ft, одна из этих вершин, например z, не смежна
с х. Поскольку
d(x) + d(z) > ft + (п - ft) = n
это противоречит выбору ж и у ввиду (3).
Покажем теперь, что, наоборот, для каждой последовательности
(ai,..., an) из теоремы, имеющей
ah < ft и ап-л < n — ft — 1
для некоторого ft < п/2, существует негамильтонов граф со
степенной последовательностью, поточечно мажорирующей (ai,..., a„).

10.3. Гамильтоновы циклы в квадрате графа
237
Ясно, что достаточно при заданном h доказать это для наибольшей
такой последовательности (ai,..., an), т. е. последовательности
h раз
n — 2h раз
(4)
h раз
п-Л
Vn-h+l
Vh+i
Рис. 10.2.1. Любой цикл, содержащий v\,... ,Vh, избегает Vh+\
Как показывает рис. 10.2.1, действительно существует граф со
степенной последовательностью (4), но без гамильтонова цикла —
граф с вершинами vi,..., vn и множеством ребер
{v{Vj | г, j > h} U {v{Vj | г < h\ j > n- h},
т. е. объединение Kn~h на вершинах i^+i,.. .,i;n и Кд^ с долями
{иь...,ил} и {и„.л+1,...,г;п}. D
Применяя теорему 10.2.1 к G*KX, можно легко доказать
следующую ее адаптацию для гамильтоновых путей. Назовем
целочисленную последовательность путъ-гамилътоновой, если каждый граф
с поточечно мажорирующей степенной последовательностью имеет
гамильтонов путь.
Следствие 10.2.2. Целочисленная последовательность (ai,...
..., an), где n>2#0<ai<---<a„<n, является путь-гамильто-
новой, если и только если для каждого i < га/2 выполняется условие
а{ < г => an+i-t > га — г. D
10.3. Гамильтоновы циклы в квадрате графа
Для данного графа G и положительного целого числа d
обозначим через Gd граф на K(G), в котором две вершины смежны, если
и только если расстояние между ними в G не более d. Ясно, что
G = G1 С G2 С Наша цель в этом разделе состоит в
доказательстве следующего фундаментального результата.

238
Глава 10. Гамильтоновы циклы
Теорема 10.3.1 (Флейшнер, 1974). Если граф G 2-связея, то
G2 имеет гамильтонов цикл.
Мы начинаем с трех простых лемм. Будем говорить, что ребро
е £ G2 замыкает вершину v £ G, если его концы смежны с v в G.
Лемма 10.3.2. Пусть Р — v0 .. .Vk — путь (к > 1), а граф G
получен из Р добавлением двух вершин u, w вместе с ребрами uv\
и wvk (рис. 10.3.1). Тогда:
(i) Р2 содержит такой путь Q от vq до v\ с V(Q) = V(P)
и Vk-iVk £ E(Q), что каждая из вершин v\,..., vjb—i
замкнута ребром из Q;
(ii) G2 содержит такие непересекающиеся пути Q от vq до Vk
и Q' от и до w, что V(Q) U V(Q') — V(G) и каждая из
вершин vi,..., Vk замкнута ребром из Q или Q'.
Vq V\ vk
Рис. 10.3.1. Граф G в лемме 10.3.1
Доказательство, (i) Если к четно, то положим Q := vqv2...
.. .Vk-2VkVk-iVk-3 - - .из^ь если иначе, положим Q := v0v2 ...
(ii) Если к четно, то положим Q := vqv2 .. .Vk-2Vk, если иначе,
положим Q := vqV\v^ .. .Vk-2vk- В обоих случаях берем в качестве Q'
u-w путь на оставшихся вершинах графа G2. D
Лемма 10.3.3. Пусть G — (V, Е) — кубический мультиграф
с гамильтоновым циклом С. Пусть е £ Е(С) и f £ Е \ Е(С) —
ребра с общим концом v (рис. 10.3.2). Тогда существует замкнутый
маршрут в G, который проходит е один раз, каждое другое ребро
из С — один раз или дважды, а каждое ребро из Е \ Е(С) один
раз. Этот маршрут может быть выбран так, чтобы он содержал
тройку (е, г/, /), т. е. проходил е в направлении вершины г/, а затем
покидал v по ребру /.
Рис. 10.3.2. Мультиграфы GhG'b лемме 10.3.3

10.3. Гамильтоновы циклы в квадрате графа
239
Доказательство. Согласно предложению 1.2.1 С имеет
четную длину. Заменим каждое второе ребро из С двойным ребром
так, чтобы е оставалось одинарным. В возникающем 4-регулярном
мультиграфе G' мы расщепляем v на две вершины и', v", делая г/
инцидентной е и /, a v" — инцидентной двум другим ребрам при v
(рис. 10.3.2). По теореме 1.8.1 этот мультиграф имеет эйлеров обход,
который индуцирует искомый маршрут в G. П
Лемма 10.3.4. Для каждых 2-связного графа G и х Е V(G)
существует цикл С С G, содержащий х, а также вершину у ф х
cNG(y)CV(C).
Доказательство. Если G имеет гамильтонов цикл, то
доказывать нечего. Если нет, то пусть С' С G — любой цикл,
содержащий х. Такой цикл существует, поскольку G 2-связен. Пусть
D — компонента графа G — С1. Допустим, что С1 и D выбраны так,
чтобы |D| был минимальным. Поскольку G 2-связен, D имеет по
меньшей мере двух соседей на С'. Тогда С' содержит такой путь Р
о
между двумя такими соседями и и и, внутренность Р которого не
содержит ж и не имеет соседей в D (рис. 10.3.3). Заменяя Р в С' на
u-v путь через D, получаем цикл С, который содержит х и вершину
у Е D. Если бы у имел соседа z в G — С, то вершина z лежала бы
в компоненте D' С D графа G — С вопреки выбору С' и D.
Следовательно, все соседи вершины у лежат на С и С удовлетворяет
утверждению леммы. D
Рис. 10.3.3. Доказательство леммы 10.3.4
Доказательство теоремы 10.3.1. Покажем индукцией по |G|,
что для любой вершины х* Е G существует гамильтонов цикл Н
в G2 со следующим свойством.
Оба ребра из Н при вершине х* лежат в G. (*)
Для \G\ = 3 имеем G = К3, и утверждение очевидно. Поэтому
допустим, что \G\ > 4, утверждение верно для графов меньшего
порядка и пусть задана х* Е V(G). По лемме 10.3.4 имеется цикл
С С G, содержащий и ж*, и вершину у* ф х*, все соседи которой в G
лежат на С.

240
Глава 10. Гамильтоновы циклы
Если С — гамильтонов цикл графа G, то доказывать нечего,
поэтому допустим, что G — С ф 0. Рассмотрим компоненту D графа
G — С. Пусть D обозначает граф G/(G — D), полученный из G
стягиванием G — D в новую вершину х. Если \D\ = 1, то положим
3*(D) := {D}. Если |D| > 1, то D снова 2-связен. Следовательно, по
индукционному предположению D2 имеет гамильтонов цикл G, оба
ребра которого при х лежат в D. Заметим, что путь С — х может
иметь ребра, которые не лежат в G2 — ребра, замыкающие двух
соседей вершины ж, не имеющих общих соседей в G (и сами не
смежные в G). Пусть Е обозначает множество таких ребер, a 3?(D) —
множество компонент в (С — х) — Е\ это множество путей в G2, концы
которых смежны с х в D (рис. 10.3.4).
X '
Рис. 10.3.4- &*{D) состоит из трех путей, один из которых тривиален
Пусть 3* обозначает объединение множеств 3?(D) по всем
компонентам D графа G — С. Ясно, что 3? обладает следующими
свойствами:
Элементы 3? — попарно непересекающиеся пути в G ,
избегающие G, a V(G) =^V(C) U (J V(P). Каждый
Pe&> (1)
конец у пути Р £ 3* имеет соседа на С в G. Выберем
такого соседа и назовем его стопой пути Р при у.
Если Р G 3? тривиален, то Р имеет в точности одну стопу. Если
Р нетривиален, то путь Р имеет стопу при каждом из своих концов.
Однако эти две стопы не обязаны быть различными, поэтому любой
нетривиальный путь Р имеет или одну, или две стопы.
Теперь мы немного изменим 3?, сохраняя свойства,
подытоженные в (1); никакие другие свойства 3? в доказательстве далее не
будут использованы. Если вершина из С является стопой для двух
различных путей Р^Р' £ 3*, скажем, при у £ Р и при у' £ Р\ то
уу' — ребро, а Руу'Р' — путь в G2; мы заменяем Р и Р; в 3? на
этот путь. Такая модификация 3? повторяется до тех пор, пока мы
не добьемся следующего.
Никакая вершина С не является стопой
для двух различных путей в 3*.

10.3. Гамильтоновы циклы в квадрате графа
241
Для г = 1, 2 пусть 3?{ С 3? обозначает множество всех путей в 3?
в точности с г стопами, и пусть Х{ С V(C) обозначают множество
всех стоп путей из 3?{. Тогда Х\ ПХ2 = 0 ввиду (2), а у* ^ Х\ \JX%.
Теперь немного упростим G; опять-таки эти изменения не
затронут ни путей из ^, ни истинности (1) и (2). Сначала мы
предположим, что в дальнейшем все элементы 3? являются путями в
самом G, а не только в G2. Это предположение может давать нам
некоторые дополнительные ребра для G2, но мы не будем
использовать их при построении гамильтонова цикла Н. (На самом деле
Н будет содержать все пути из 3? целиком как под пути.) Таким
образом, если Н лежит в G2 и удовлетворяет (*) для измененной
версии графа G, то это будет верно также и для исходного графа.
Для каждого Р Е 3? мы далее удаляем все Р-С ребра графа G, кроме
ребер между концами Р и соответствующими им стопами. Наконец,
мы удаляем все хорды цикла С в G. Таким образом, без ограничения
общности можно считать, что:
Все ребра в G между циклом С и путем Р Е 3?
исчерпываются двумя ребрами между концами Р
и соответствующими стопами. {Если \Р\ = 1, (3)
то эти два ребра совпадают.) Ребрами графа G
с обоими концами на С являются только ребра самого С.
Мы хотим построить искомый гамильтонов цикл Н в G2 из
путей в 3? и подходящих путей в С2. В качестве первого приближения
построим замкнутый маршрут W в графе
G:=G- U3*x
— маршрут, который уже удовлетворяет условию типа (*) и
проходит каждый путь из 3?ъ ровно один раз. Позже мы изменим W так,
чтобы он проходил через каждую вершину С ровно один раз и,
наконец, чтобы включить пути из 3?\. При построения маршрута W мы
предполагаем, что 3?2 ф ®\ случай 3?ъ — 0 намного проще и будет
рассмотрен позже.
Мы начинаем с выбора фиксированной циклической ориентации
цикла G, т. е. биекции г t—► щ из TL\c\ на V(C) с г/г-г/г-+1 Е Е(С) для всех
г Е Z|c|- Будем считать ее ориентацией по часовой стрелке. Тогда
каждая вершина V{ Е С имеет правого соседа v* := V{+i и левого
соседа иг~ := г/г_1. Соответственно ребро v~~v лежит слева от г/,
ребро г/г/+ лежит от нее справа и так далее.
Нетривиальный путь Р = г;»г;»+1 • • -Vj-iVj в С такой, что V(P)0
Х2 = {vijVj}, называется интервалом с левым концом V{ и правым
концом Vj. Таким образом, С является объединением \Х2\ = 21^1

242
Глава 10. Гамильтоновы циклы
интервалов. Как обычно, мы обозначаем Р =: [v{,Vj] и т. д. и по-
0 0 0
лагаем (v{,Vj) := Р, а также [v{,Vj) := Pvj и (v{,Vj] := V{P. Для
интервалов [u,v] и [v,w] с общим концом v мы будем говорить, что
[u, v] лежит слева от [v, w], а [г/, w] лежит справа от [и, v]. Обозначим
единственный интервал [v,w] ci*G (u,iu] через /*, путь из ^2 со
стопой w через Р*, а путь I*wP* через Q*.
При построении W можно рассматривать G как мультиграф М
на ^2, ребрами которого являются интервалы на С и пути из ^2
(со своими стопами в качестве концов). Согласно (2) М кубический,
поэтому можно применить лемму 10.3JJ с е := /* и / := Р*. Лемма
дает нам замкнутый маршрут W в G, который проходит /* один
раз, каждый из остальных интервалов в С один или два раза, а
каждый путь в ^2 один раз. Кроме того, W содержит Q* как подпуть.
Два ребра при ж* из этого пути лежат в G; в этом смысле W уже
удовлетворяет (*).
Теперь изменим W так, чтобы W проходил через каждую
вершину из С ровно один раз. Одновременно мы будем готовиться
к последующему включению путей из ^i, задавая отображение
v I—► е(и), которое является инъективным на Х\ и приписывает
каждой вершине v Е Х\ ребро e(v) измененного W со следующим
свойством.
Ребро e(v) или замыкает v, или инцидентно ей.
(**)
В последнем случае e(v) £ С и e(v) ф vx*.
Для простоты мы определим отображение v н-> e(v) на всем V(C)\X2,
т. е. на множестве, которое содержит Х\ ввиду (2). Чтобы
гарантировать инъективность на Х\, мы только должны
удостовериться, что никакое ребро vw Е С не выбрано и как e(v), и как e(w).
Действительно, поскольку \Х\\ > 2, если инъективность находится
под вопросом, a 2?i ф 0 по предположению, то имеем \С — у*\ >
\Х\\ -f 2|^2| >4и, следовательно, \С\ > 5. Таким образом, никакое
ребро графа G2 не может замыкать больше одной вершины из С или
замыкать вершину из С и лежать при этом на С.
Для задуманного нами исправления W в вершинах из С
рассмотрим интервалы из С поочередно. По определению W каждый
интервал может быть одного из следующих трех типов.
Тип 1. W проходит / один раз.
Тип 2. W проходит / дважды: в одном направлении, а затем сразу
в обратном (формально W содержит тройку (е,ж,е), где
х Е Х2 и е Е Е(1)).
Тип 3. W проходит / дважды, причем в разное время (т. е. не
существует такой тройки, как выше).

10.3. Гамильтоновы циклы в квадрате графа
243
По определению W интервал /* имеет тип 1. Вершина х в
определении интервала типа 2 называется тупиком этого интервала.
Наконец, поскольку Q* — подпуть W, a W проходит иГ,иР* лишь
по одному разу, получаем следующее свойство.
Интервал справа от Г имеет тип 2,
а его тупик находится слева.
Рассмотрим фиксированный интервал / = [жьжг]- Пусть у\ —
сосед £i, а до — сосед Х2 на некотором пути из £?2- Пусть /~
обозначает интервал слева от /.
Предположим сначала, что / имеет тип 1. Тогда мы не
меняем W на /. Если / ф /*, то выберем в качестве e(v) для каждого
о
v € I ребро слева от v. Поскольку /~ ф I* согласно (4), а
следовательно, х\ ф х*, такой выбор e(v) удовлетворяет (**). Если 1 = 1*,
о
то определяем e(v) как ребро слева от v при v Е (xi,x*]C\I и как
ребро справа от v при v Е (х*,Х2). Такой выбор e(v) снова совместим
с (**).
Предположим теперь, что / имеет тип 2. Сначала допустим,
что Х2 — тупик для /. Тогда W содержит маршрут y\X\Ix2lx\I~
(возможно, в обратном порядке). Применим теперь лемму 10.3.2(i)
с Р := yix\Ix2 и заменим в W подмаршрут y\X\Ix2lx\ на у\-х\ путь
Q С G2 из леммы (рис. 10.3.5). Тогда V(Q) = V(P)\{yux1} = V(I).
Каждая из вершин v Е (xi^x^) замкнута ребром из Q, которое мы
и выбираем за e(v). В качестве е(ж^) выберем ребро слева от х^
(за исключением случая х% = х\). Ввиду леммы это ребро также
лежит на Q. Кроме того, по (4) оно не инцидентно х* (поскольку
Х2 — тупик для / по предположению), а следовательно,
удовлетворяет (**). Случай, когда х\ — тупик для /, рассматривается таким
же образом: используя лемму 10.3.2(i), мы заменяем в W подмарш-
0 °
рут у2Х21х\1х2 на У2~Х2 путь Q С G с V(Q) = V(I), выбираем за
e(v) для v Е {х^х^ ребро из Q, замыкающее вершину и, и
определяем e(xf) как ребро справа от xf (за исключением случая xf = Х2).
[W ^ -v. . .
-Y
Г xi I x-i xi e(x2) x2
Puc. 10.3.5. Как изменить W на интервале типа 2
Предположим наконец, что / имеет тип 3. Поскольку W
проходит ребро у\Х\ только один раз, а интервал /~ не более чем дважды,
то W содержит у\Х\1 и /~ U / как подпути, а /~ имеет тип 1.
Согласно (4), однако, /~ ф I*. Следовательно, когда e(v) определялось

244
Глава 10. Гамильтоновы циклы
для вершин v Е 1~~, самое правое ребро х~[х\ в /~ не было выбрано
в качестве e(v) ни для какой вершины и, поэтому теперь можно
заменить это ребро. Поскольку W проходит /+ не более чем дважды,
он должен проходить ребро Х2У2 сразу после одного из своих двух
под путей у\ х\1 и х±х\1. Возьмем начальную вершину этого под-
пути (у\ или х~[) за вершину и в лемме 10.3.2(i), а другую вершину
из {yi, ж^} — за г/о- Кроме того, положим и* := х^ и ги := г/2. Тогда
лемма позволяет нам заменить эти два подпути в W между [у\, х± }
и {^2,2/2} непересекающимися путями в G2 (рис. 10.3.6), а также
о
приписывает каждой вершине v £ I ребро e(v) одного из этих путей,
замыкающее v.
Vi . .2/2 2/i^ ^2/2
1 ' - . ГутутУ!
Рис. 10.3.6. Модификация типа 3 для случая и = у\ при нечетном А:
После описанных модификаций W становится замкнутым
маршрутом в G2. Проверим, что кроме того W содержит каждую вершину
из G в точности один раз. Для вершин путей из 0*2 это очевидно,
потому что W все еще проходит каждый такой путь один раз и
избегает его в противном случае. Для вершин из С — Хъ это следует из
сделанных нами модификаций по лемме 10.3.2. А как обстоит дело
с вершинами из Х*р.
Пусть задана вершина х Е Хъ, и пусть у — ее сосед на пути
из ^2- Пусть 1\ обозначает интервал /, который удовлетворял
условию yxl С W до модификации маршрута W, а Д — другой интервал,
заканчивающийся в х. Если 1\ имеет тип 1, то Д имеет тип 2 с
тупиком х. В этом случае х была сохранена в W, когда W изменялся
на /i, но пропускалась, когда W был изменен на Д, а значит,
содержится теперь в W ровно один раз. Если 1\ имеет тип 2, то х не
является его тупиком, а Д имеет тип 1. Подмаршрут W, который
начинался с гуж, а затем шел по Д и обратно, был заменен на у-х
путь. Теперь за этим путем по W следует прежний интервал Д,
поэтому и в этом случае вершина х теперь встречается в W в точности
один раз. Наконец, если Д имеет тип 3, то ж содержалась в одном из
замещающих путей Q, Q' из леммы 10.3.2(ii). Поскольку эти пути
были непересекающимися ввиду утверждения леммы, то вершина х
и в этом случае сохранена на W ровно один раз.
Тем самым показано, что W после модификации является
замкнутым маршрутом в G2, содержащим каждую вершину из Gb
точности один раз, поэтому W задает гамильтонов цикл Н в G2.
Поскольку W все еще содержит путь Q*, то Н удовлетворяет
условию (*).

10.3. Гамильтоновы циклы в квадрате графа
245
До сих пор мы предполагали, что £?2 не пусто. Если £?2 = 0, то
положим Я := G = С; тогда Я снова удовлетворяет (*). Остается
превратить Я в гамильтонов цикл Я графа G2 посредством
включения путей из 9*\. Чтобы иметь возможность рассматривать случай
^2 = 0 наряду со случаем ^ ф ®, определим отображение v »—► e(v)
также при 3*2 = 0 следующим образом: для каждого v £ С — у*
положим
Г vv+, если v е [х*, у*),
е[у) := <
t vv , если v G (у*, ж*).
(Здесь [ж*, у*) и (у*, ж*) обозначают пути в С, определяемые
аналогично интервалам.) Как и раньше, это отображение v »—► е(и)
инъективно, удовлетворяет (**) и определено на надмножестве
множества Х\\ вспомним, что у* не может лежать в Х\ по определению.
Пусть Р G &\ — путь, который надлежит включить в Я,
скажем, со стопой v G Х\ и концами у\,У2- (Если \Р\ — 1, то у\ — у2.)
Наша цель состоит в том, чтобы заменить ребро е := e(v) в Я на
путь Р. Таким образом, мы должны показать, что концы Р
соединены с концами ребра е подходящими ребрами из G2.
Согласно (2) и (3) вершина v имеет только двух соседей в G —
своих соседей х\, Х2 по циклу С. Если v инцидентна е, т. е. если
е — vxi с г £ {1,2}, мы заменяем е путем ьу\Ру2Х{ С G2 (рис. 10.3.7).
Если v не инцидентна ребру е, то е замыкает v ввиду (**). Тогда
е = х\Х2, и мы заменяем е путем х\у\Ру2Х2 С G2 (рис. 10.3.8).
Поскольку v н-> e(v) инъективно на Х\у утверждение (2) влечет, что все
такие модификации Я (по одной для каждого пути Р £ 3*i) могут
быть выполнены независимо, а следовательно, дать нам гамильтонов
цикл Я в G2.
Рис. 10.3.7. Замена ребра е в Н
Рис. 10.3.8. Замена ребра е в Н

246
Глава 10. Гамильтоновы циклы
Наконец, проверим, что Н удовлетворяет (*), т. е. что оба ребра
из Н при х* лежат в G. Поскольку условие (*) для Н выполняется,
достаточно показать, что любое ребро е = х*z из Я, которое не
лежит в Я (и, следовательно, имеет вид е = е(у) для некоторого
v £ Х\), было заменено на x*-z путь, первое ребро которого
принадлежит G.
Где может лежать v? Покажем, что v должна быть инцидентна
ребру е. Если нет, то 2?2 /0ие замыкает v. Теперь 3*2 Ф ® и v £ Х\
вместе влекут, что \С — у*\ > \Х\\ -f 2|^г| > 3, поэтому \С\ > 4.
Поскольку е G G (ввиду (*) для Я), тот факт, что е замыкает г/,
таким образом, противоречит (3).
Итак, вершина v действительно инцидентна ребру е.
Следовательно, v £ {ж*, z} по определению е, в то время как е ф vx* по (**).
Таким образом, v = х* и е было заменено путем вида x*y\Py2Z.
Поскольку х*2/i — ребро графа G, эта замена снова сохраняет (*).
Поэтому Я действительно удовлетворяет (*), и наша индукция
завершена. D
Мы завершаем главу гипотезой, далеко обобщающей теорему
Дирака.
Гипотеза (Сеймур, 1974). Пусть G — граф порядка п > 3,
а к — положительное целое число. Если G имеет минимальную
степень
6(G) > -^-п,
то в графе G существует такой гамильтонов цикл Я, что Нк С G.
Для к — \ это в точности теорема Дирака. Случай к — 2 уже
высказывался в виде предположения Пошей в 1963 г., а для больших п
он был доказан Комлошем, Шаркози и Семереди (1996).
Упражнения
1. Показать, что каждый однозначно 3-реберно-раскрашиваемый кубический
граф гамильтонов. («Однозначно» означает, что все реберные 3-раскраски
индуцируют одно и то же разбиение ребер.)
2. Доказать или опровергнуть следующее усиление предложения 10.1.2:
каждый /г-связный граф G с \G\ > 3 и х(^) ^ 1^1/^ имеет гамильтонов цикл.
3. Для данного графа G рассмотрим такую максимальную последовательность
Go,..., Gfc, что Go = G и G^i = G; -f xtyt при i — 0,..., A: - 1, где
xi > Vi — Две несмежные вершины из G,, удовлетворяющие условию dQ{ (xt ) +
d>Gi(y%) > |G|. Последний граф G^ в этой последовательности называется
гамильтоноеым замыканием графа G. Показать, что этот граф зависит
только от G, но не от выбора последовательности Go,..., G^.
4. Пусть х, у — две несмежные вершины связного графа G с d(x) + d(y) > \G\.
Показать, что G имеет гамильтонов цикл, если и только если его имеет
G + ху. Используя предыдущее упражнение, выведите следующее усиление

Примечания 247
теоремы Дирака: если d(x)+d(y) > \G\ для каждых двух несмежных вершин
х,у £ G, то G имеет гамильтонов цикл.
5. При заданном четном положительном к для каждого п > к построить
^-однородный граф порядка 2n -f 1.
6.~~ Найти гамильтонов граф, степенная последовательность которого не га-
ми ль тонова.
7.~ Пусть граф G имеет менее г вершин степени не более г для каждого
г < \G\/2. С помощью теоремы Хватала показать, что G гамильтонов.
(Таким образом, в частности, теорема Хватала влечет теорему Дирака.)
8. Найти связный граф G, квадрат G2 которого не имеет гамильтоновых
циклов.
9.+ Показать индукцией по |G|, что куб G3 связного графа G содержит
гамильтонов путь между любыми двумя вершинами. Выведите отсюда, что
G3 гамильтонов.
10. Показать, что квадрат 2-связного графа содержит гамильтонов путь между
любыми двумя вершинами.
11. Ориентированный полный граф называется турниром. Показать, что
каждый турнир содержит (ориентированный) гамильтонов путь.
12."*" Пусть G — граф, в котором каждая вершина имеет нечетную степень.
Показать, что каждое ребро из G лежит на четном числе гамильтоновых
циклов.
(Подсказка. Пусть задано ребро ху Е E(G). Гамильтоновы циклы,
содержащие ху, соответствуют гамильтоновым путям в G — ху, соединяющим
х и у. Рассмотрите множество Ж всех гамильтоновых путей в G — ху,
начинающихся в а;, и покажите, что четное число их заканчиваются в у. Для
этого определите граф на Ж так, чтобы искомое утверждение следовало из
предложения 1.2.1.)
Примечания
Задача нахождения гамильтонова цикла в графе имеет тот же источник,
что и аналогичный ему эйлеров обход, а также проблема четырех красок: все
три задачи возникли из математических загадок, более старых чем сама теория
графов. То, что началось как игра, изобретенная У. Р. Гамильтоном в 1857 г.,
в которой требовалось найти «гамильтоновы циклы» на графе додекаэдра,
повторно возник ло более чем через сто лет как комбинаторная задача оптимизации,
имеющая первостепенное значение, — так называемая задача коммивояжера.
В ней коммивояжер должен посетить некоторое множество клиентов, и задача
его состоит в том, чтобы упорядочить их в виде подходящего замкнутого
маршрута. (По причинам, не включенным в математическую модель, маршрут
должен быть таким, чтобы после посещения каждого клиента продавец больше уже
не попадал в тот же самый город.) Интерес к изучению гамильтоновых циклов во
многом объясняется их связью с разновидностями этой алгоритмической задачи.
Подробное обсуждение различных степенных условий для гамильтоновости,
упомянутое в начало раздела 10.2, можно найти в книге: Halin R. Graphentheorie.
Darmstadt: Wissenschaftliche Buchgesellschaft, 1980. Все важнейшие ссылки для
разделов 10.1 и 10.2 можно найти там же или в: Bollobds В. Extremal Graph
Theory. London: Acad. Press, 1978.
«Доказательство» теоремы о четырех красках, приведенное в конце
раздела 10.1 и основанное на (ложной) предпосылке, что каждый 3-связный
кубический планарный граф гамильтонов, обычно приписывается шотландскому
математику П. Г. Тейту. Вслед за ошибочным доказательством Кемпе 1879 года
(см. примечания к главе 5) и Тейт, по-видимому, также считал, что располагает

248
Глава 10. Гамильтоновы циклы
по меньшей мере еще одним «новым доказательством теоремы Кемпе». Однако
когда он выступал на эту тему перед Эдинбургским математическим обществом
в 1883 г., он, вероятно, уже знал, что в действительности не может доказать
вышеупомянутое утверждение о гамильтоновых циклах. Его отчет: Tait P. G.
Listing's topologie // Philos. Mag. 1884. 17. P. 30-46 — представляет собой
любопытное чтение.
Более короткое доказательство теоремы Татта о том, что 4-связные планар-
ные графы гамильтоновы, дано в статье: Thomassen С. A theorem on paths in
planar graphs // J. Graph Theory. 1983. 7. P. 169-176. Контрпример Татта к
предположению Тейта о том, что даже 3-связность достаточна (по меньшей мере для
кубических графов), приводится в книге Боллобаша, а также в: Bondy J. А.,
Murty U. S. R. Graph Theory with Applications. N. Y.: Macmillan, 1976 (где
ошибочное доказательство Тейта обсуждается довольно подробно).
Предложение 10.1.2 принадлежит Хваталу и Эрдешу (1972). Наше
доказательство теоремы Флейшнера основано на статье: Eiha S. A new proof of the
theorem by Fleischner// J. Combin. Theory. Ser. B. 1991. 52. P. 117-123.
Гипотеза Сеймура опубликована в: Seymour P. D. Problem 3 // Combinatorics / Ed.
by T. P. McDonough, V. C. Mavron. Cambridge: Univ. Press, 1974. ГипотезаПоши
была доказана для большого п в работе: Komlos J., Sdrkozy G. N., Szemeredi E.
On the square of a Hamiltonian cycle in dense graphs // Random Structures and
Algorithms. 1996. 9. P. 193-211.

Глава 11
Случайные графы
В этой книге мы уже неоднократно сталкивались со следующей
фундаментальной теоремой Эрдеша: для любого целого числа к
существует граф G с g(G) > к и x(G) > к. Или, попросту говоря,
существуют графы, сочетающие произвольно большой обхват с
произвольно высоким хроматическим числом.
Как можно доказать такую теорему? Стандартный подход
состоял бы в построении графа с двумя этими свойствами, возможно,
по этапам, с помощью индукции по к. Однако такое построение ни
в коем случае не очевидно: глобальная природа второго свойства,
вызванная первым, а именно то, что граф должен иметь высокое
хроматическое число «в целом», но быть ациклическим (и,
следовательно, 2-раскрашиваемым) локально, препятствует любым
попыткам строить такой граф последовательно из меньших частей,
обладающих теми же или подобными свойствами.
В своей основополагающей статье 1959 года Эрдеш предпринял
радикально иной подход: для каждого п он определил вероятностное
пространство на множестве графов с п вершинами и показал, что для
некоторых тщательно выбранных вероятностных мер вероятность
того, что n-вершинный граф обладает обоими вышеупомянутыми
свойствами, положительна для всех достаточно больших п.
Этот подход, называемый теперь вероятностным методом,
с тех пор развился в сложную и гибкую технику доказательства,
работающую как в теории графов, так и в других областях дискретной
математики. Теория случайных графов теперь является
самостоятельным предметом исследования. Цель этой главы состоит в том,
чтобы предложить элементарное, но строгое введение в случайные
графы — не более чем необходимое для понимания ее основных
понятий, идей и методов, но в достаточной мере отражающее мощь
и элегантность, скрытые за вычислениями.
Теорема Эрдеша утверждает существование графа с
некоторыми свойствами. Это совершенно обычное утверждение, не
содержащее никаких признаков хаотичности, используемой в ее до-

250
Глава 11. Случайные графы
казательстве. Но в случайных графах имеются и такие результаты,
которые являются случайными даже по своей формулировке —
теоремы о почти всех графах (с этим понятием мы встретимся в
разделе 11.3). В последнем разделе мы даем детальное доказательство
теоремы Эрдеша и Реньи, которое иллюстрирует метод
доказательства, часто используемый в случайных графах, — так называемый
метод вторых моментов.
11.1. Понятие случайного графа
Пусть V — фиксированное множество п из элементов, скажем,
V = {0,...,га— 1}. Наша цель — превратить множество <& всех
графов на V в вероятностное пространство, а затем рассмотреть
ряд типичных вопросов, возникающих по поводу случайных
объектов. Какова вероятность того, что граф G £ *& имеет то или иное
свойство? Каково ожидаемое значение заданного инварианта на G,
например, его ожидаемые обхват или хроматическое число?
Интуитивно ясно, что мы должны уметь случайно порождать G
следующим образом. Для каждой пары е £ [V]2 мы решаем
некоторым случайным экспериментом, действительно ли е будет ребром
в G. Эти эксперименты выполняются независимо, и для
каждого вероятность успеха, т. е. принятия е в качестве ребра для G,
равна некоторому фиксированному1^ числу р £ [0,1]. Тогда если
Go — некоторый фиксированный граф на V, допустим, с т ребрами,
то элементарное событие {Go} имеет вероятность pmq\^)~m (где
q := 1— р): с такой вероятностью наш случайным образом
порожденный граф G является этим конкретным графом Go- (Вероятность
того, что G изоморфен графу Go, будет, как правило, больше.) Но
если вероятности всех элементарных событий заданы таким
образом, то задана и вся вероятностная мера нашего искомого
пространства *$. Следовательно, остается лишь проверить, что такая
вероятностная мера на *3, при которой все индивидуальные ребра
встречаются независимо с вероятностью р, действительно существует2^.
Чтобы построить такую меру на *$ формально, мы начинаем
с определения для каждого потенциального ребра е £ [V]2 его
собственного маленького вероятностного пространства fie := {0е,1е},
*' Часто значение р будет зависеть от мощности п множества V, на
котором порождаются наши случайные графы. Таким образом, р есть значение
р = р(п) некоторой функции п \-+ р(п). Заметим, однако, что V (и,
следовательно, п) в определении ^ фиксируется: для каждого п по отдельности
мы строим вероятностное пространство из графов G на V = {0,..., п — 1},
и в пределах каждого пространства вероятность того, что е Е [V]2 является
ребром G, имеет одно и то же значение для всех е.
2) Читатель, готовый поверить в это, может теперь перейти в конец
предложения 11.1.1, без боязни упустить что-либо.

11.1. Понятие случайного графа
251
выбирая Ре({1е}) := р и Ре({Ое}) := q как вероятности двух его
элементарных событий. В качестве нашего искомого
вероятностного пространства <3 = ^(га,р) мы далее возьмем произведение
пространств
Q:= Д fie
ee[V)*
Таким образом, формально элемент в Q есть отображение w,
приписывающее каждому е £ [V]2 либо 0е, либо 1е, а вероятностная
мера Р на Q есть произведение всех мер Ре. На практике, конечно,
мы отождествляем ш с графом G на V, множество ребер которого
есть
S(G) = {е |w(e) = 1е},
и называем G случайным графом наУс вероятностью ребра р.
Следуя стандартной вероятностной терминологии, можно
теперь называть любое множество графов на V событием в &(п,р).
В частности, для каждого е Е [К]2 множество
Ае:={и;\и;(е) = 1е} .
всех графов G на V с е £ #(G) — это событие, заключающееся в том,
что е есть ребро графа G. Для этих событий теперь можно доказать
формально то, что нам подсказывала интуиция.
Предложение 11.1.1. События Ае независимы и происходят
с вероятностью р.
Доказательство. По определению,
Ае = {1е}х Д Пе,.
Поскольку мера Р есть произведение всех мер Ре, имеем
Р(Ае)=р.Ц1 = р.
Аналогично, если {ei,..., е*} — любое подмножество [V]2, то
Р(Ае1 П • • • ПАек) = РUlei} х .. х {lefc} х Д fie
e^{ei,...,efc}
= Рк
= P(Aei)...P(Aek).
Как уже отмечалось, Р однозначно определяется значением р
и нашим предположением, что события Ае являются независимыми.

252
Глава 11. Случайные графы
Поэтому, вообще говоря, для вычисления вероятности в У(п,р)
достаточно сделать эти два предположения. Наша конкретная модель
для ^(гс,р) уже выполнила свое назначение и больше не понадобится.
В качестве простого примера подобного вычисления рассмотрим
событие, состоящее в том, что G содержит некоторый
фиксированный граф Я на подмножестве V как подграф. Пусть \Н\ =: к и
||#|| —: £. Вероятность этого события Я С G есть произведение
вероятностей Ае по всем ребрам е £ Я, поэтому Р[Н С G] = р1.
Напротив, вероятность того, что Я является индуцированным
подграфом графа G, есть plq\^)~l. Теперь ребра, отсутствующие в Я,
должны также отсутствовать и в G, и они делают это независимо
и с вероятностью q.
Вероятность Рн того, что G имеет индуцированный подграф,
изоморфный графу Я, обычно вычисляется труднее: поскольку
копии графа Я на подмножествах множества V могут накладываться,
то события, состоящие в том, что они встречаются в G, не являются
независимыми. Однако сумма (по всем ^-множествам из U С V)
вероятностей Р[Н ~ G[U]\ всегда является верхней оценкой для Рн,
поскольку Рн есть мера объединения всех таких событий. Например,
если Я = Кк, то имеем следующую очевидную верхнюю оценку для
вероятности того, что G содержит индуцированную копию графа Я.
Лемма 11.1.2. Для любых целых чисел п, к, где п > к > 2,
вероятность того, что G £ ^(п,р) содержит множество из к
независимых вершин, не превосходит
P[a(G)>k}<(^jq&.
Доказательство. Вероятность того, что данное ^-множество
U С V является независимым в G, есть q\2). Утверждение, таким
образом, следует из факта, что существует лишь (£) таких
множеств U. □
Аналогично, вероятность того, что G £ ^(п,р) содержит Кк, не
превосходит
PHG)>k]<(^jp(").
Теперь если к зафиксировано, а п настолько мало, что эти оценки
для вероятностей P[a(G) > к] и P[u(G) > к] дают в сумме меньше 1,
то <& содержит графы, которые не обладают ни одним из данных
свойств — это графы,которые не содержат ни Кк, ни
индуцированного подграфа Кк. Но тогда любое такое п дает нижнюю оценку
для числа Рамсея от к\
Как показывает следующая теорема, эта нижняя оценка весьма
близка к верхней оценке 22к~3, вытекающей из доказательства
теоремы 9.1.1.

ILL Понятие случайного графа
253
Теорема 11.1.3 (Эрдеш, 1947). Для каждого целого числа & > 3
цисло Рамсея от к удовлетворяет неравенству
R(k) > 2*'2.
Доказательство. При к = 3 мы тривиально имеем R(3) >
3 > 23/2, поэтому пусть к > 4. Покажем, что для всех п < 2к/2
и G £ *3 (га, ^) каждая из вероятностей P[a(G) > к] и P[u(G) > к]
меньше \.
Поскольку р — q — |, лемма 11.1.2 и аналогичное утверждение
для u;(G) влекут следующие неравенства для всех п < 2к/2
(используется тот факт, что к\ > 2к при к > 4):
P[a(G)>A],P[u,(G)>A]<^)Q) '
< (n*/2*)2-5*(t-1)
<(2*2/2/2*)2-i*(*-D
= 2"*/2
4°
В контексте случайных графов каждый из знакомых
инвариантов графа (таких как средняя степень, связность, обхват,
хроматическое число и так далее) может интерпретироваться как
неотрицательная случайная величина на ^(га,р), т. е. функция
Х:^(га,р)->[0,оо).
Среднее или ожидаемое значение величины X есть число
Е(Х):= £ P({G}).X(G).
Заметим, что оператор Е — математическое ожидание — является
линейным: равенства Е(Х + У) = Е(Х) + E(Y) и Е(ХХ) = ХЕ(Х)
выполняются для любых двух случайных величин X, Y на ^(п,р)
и A G1.
Вычисление среднего значения случайной величины X может
явиться простым и эффективным способом установить
существование такого графа G, что X(G) < а для некоторого фиксированного
а > 0 и G, кроме того, обладает некоторым требуемым свойством 3*.
Действительно, если ожидаемое значение X мало, то X(G) может
быть велико разве что для немногих графов в ^(п,р), поскольку
X(G) > 0 для всех G £ ^(п,р). Следовательно, X должна быть

254
Глава 11. Случайные графы
мала для многих графов в &(п,р), и разумно ожидать, что среди
них можно будет найти граф с требуемым свойством 2?.
Эта простая идея лежит в основе бесчисленных
неконструктивных доказательств существования с использованием случайных
графов, включая доказательство теоремы Эрдеша, представленное
в следующем разделе. Выраженная количественно, она принимает
вид приведенной ниже леммы, доказательство которой сразу следует
из определения математического ожидания и аддитивности Р.
Лемма 11.1.4 (неравенство Маркова). Пусть X > 0 —
случайная величина на ^(п,р) и a > 0. Тогда
Р[Х > а] < Е(Х)/а.
Доказательство. Очевидно, что
ВД= £ P({G}).X(G)
> £ P({G}).X(G)
Gev(n,p)
X(G)>a
> J2 P({G})-a
Ge<y(niP)
X(G)>a
= P[X >a]-a. D
Поскольку наши вероятностные пространства конечны,
математическое ожидание может часто вычисляться простым применением
двойного подсчета — стандартной комбинаторной техники, с
которой мы ранее встречались в доказательствах следствия 4.2.8 и
теоремы 5.5.3. Например, если X — случайная величина на ^(га, р),
подсчитывающая число подграфов графа G в некотором фиксированном
множестве Ж графов на V, то Е(Х), по определению,
подсчитывает число таких пар (G,#), что Н С G, причем каждую с весом,
равным вероятности подграфа {G}. Алгоритмически мы вычисляем
Е(Х), проходя по графам G £ У(п,р) во «внешнем цикле» и
выполняя для каждого G «внутренний цикл», который пробегает графы
Н £ J4? и суммирует «P({G})>> по всем Н С G. Можно и
наоборот, перечислять то же самое множество взвешенных пар, имея Н
во внешнем, a G — во внутреннем циклах; это сводится к сложению
по всем Н С Ж вероятностей Р[Н С G].
Чтобы проиллюстрировать это хотя бы раз подробно, вычислим
ожидаемое число циклов некоторой заданной длины к > 3 в
случайном графе G £ ^(п,р). Итак, пусть X: &(п,р) —► N — случайная
величина, которая приписывает каждому случайному графу G число

11.1. Понятие случайного графа
255
его fc-циклов, т. е. число его подграфов, изоморфных Ск. Обозначим
через
(п)к := п(п - 1)(п - 2) • • • (п - к + 1)
число последовательностей из к различных элементов заданного
га-множества.
Лемма 11.1.5. Ожидаемое число к-циклов в G £ ^(га,р) есть
Е{Х) - ЖР '
Доказательство. Для каждого &-цикла С с вершинами в V =
{0,...,га — 1} — множестве вершин графов из &(п,р) — пусть
Хс ' &(п,р) —» {0,1} обозначает индикаторную случайную величину
цикла С:
Г 1, если С С G;
ХС: Си '
I v в противном случае.
Поскольку Хс принимает из положительных значений только 1, ее
математическое ожидание Е(Хс) равняется мере Р[Хс = 1]
множества всех тех графов в £^(га,р), которые содержат С. Но это как раз
вероятность того, что С С G:
Е(ХС) = Р[С С G] = рк. (1)
А сколько таких циклов С = vq .. .Vk-iVQ существует? Имеется
(га)* последовательностей vq .. .Vk-i различных вершин из V, и
каждому циклу отвечает 2к таких последовательностей, поэтому имеется
в точности (п)к/2к таких циклов.
Наша случайная величина X приписывает каждому графу G
число его ^-циклов. Ясно, что это сумма всех значений Xc(G), где
С пробегает (п)к/2к циклов длины к с вершинами из V:
С
Поскольку математическое ожидание линейно, то из (1) имеем
Е{Х) = е{^Хс)=^Е(Хс)={^-р\
что и утверждалось. □

256
Глава 11. Случайные графы
11.2. Вероятностный метод
Говоря очень упрощенно, вероятностный метод в дискретной
математике возник на основе следующей идеи. Чтобы доказать
существование объекта с некоторым требуемым свойством,
определяют вероятностное пространство на несколько большем — и
заведомо непустом — классе объектов, а затем показывают, что элемент
этого пространства имеет искомое свойство с положительной
вероятностью. «Объекты», населяющие это вероятностное пространство,
могут быть любого рода: разбиения или упорядочения вершин
некоторого фиксированного графа возникают столь же естественно, как
отображения, вложения и, конечно, сами графы. В этом разделе мы
проиллюстрируем вероятностный метод, дав детальное изложение
одного из его самых ранних результатов — классической теоремы
Эрдеша о большом обхвате и большом хроматическом числе.
Теорема Эрдеша утверждает, что для любого положительного
целого числа к существует граф G с обхватом g(G) > к и
хроматическим числом x(G) > &• Назовем циклы длины не более к короткими,
а множества с \G\/k или более вершинами — большими. Для
доказательства теоремы Эрдеша достаточно найти граф G без коротких
циклов и больших независимых множеств вершин. Тогда цветовые
классы в любой вершинной раскраске G будут малы (не будут
большими), поэтому для раскраски G потребуется более чем к цветов.
Как найти такой граф G? Если мы выберем р достаточно
малым, то случайный граф в &(п,р) вряд ли будет содержать какие-
либо (короткие) циклы. Если выберем р достаточно большим, то
для G наличие больших независимых множеств вершин
маловероятно. Отсюда вопрос: пересекаются ли эти два диапазона для р, т. е.
можно ли выбрать р так, чтобы для некоторого п оно было бы и
достаточно малым, чтобы Р[д < к] < ^, и достаточно большим, чтобы
Р[а > п/к] < \l Если это удастся, тогда ^(п,р) будет содержать
по меньшей мере один граф без коротких циклов и больших
независимых множеств.
К сожалению, такой выбор для р невозможен: эти два диапазона
для р не пересекаются! Как мы увидим в разделе 11.4, мы должны
держать р ниже п"1, чтобы сделать возникновение коротких циклов
в G маловероятным, но для любых таких р в G почти наверняка не
будет вообще никаких циклов (упражнение 19), поэтому G будет
двудольным и, следовательно, иметь по меньшей мере га/2 независимых
вершин.
Но еще не все потеряно. Чтобы сделать большое независимое
множество маловероятным, мы будем фиксировать р выше га-1, на
уровне га6"1 для некоторого е > 0. К счастью, оказывается, что если
6 достаточно мало, то в G возникает лишь малое число коротких
циклов, даже по сравнению с п (а не с га*, как чаще бывает). Если затем

11.2. Вероятностный метод
257
мы удалим по вершине из каждого такого цикла, то полученный
граф Н не будет иметь коротких циклов, а его число независимости
а(#) будет не более, чем у графа G. Поскольку Н ненамного меньше,
чем G, то его хроматическое число будет все еще большим, поэтому
мы получаем граф с большим обхватом и большим хроматическим
числом.
Чтобы подготовиться к формальному доказательству теоремы
Эрдеша, покажем сначала, что вероятность ребра р = гас_1
действительно всегда достаточно велика, чтобы гарантировать, что
G £ £^(га, р) «почти наверное» не имеет большого независимого
множества вершин. Точнее, докажем следующее немного более сильное
утверждение.
Лемма 11.2.1. Пусть к > 0 — целое число, а р = р(п) — такая
функция от га, что р > (6&1пга)га-1 для больших га. Тогда
= 0.
Доказательство. Для любых целых чисел га, г, где га > г > 2,
и всех G £ ^(га,р) по лемме 11.1.2 имеем
Р[а> г] < (]q($
< nrq&)
= (nqW2)r
здесь последнее неравенство следует из того факта, что 1 — р < е~р
для всех р. (Сравните функции i и еЕ и г и х + 1 при х — —р.)
Теперь если р > (б&тг^га""1 иг> \n/k, то основание степени
удовлетворяет соотношениям
ne-p(r-l)/2 = ne-Pr/2+P/2
< ne-(3/2)lnn + p/2
= у/ё/у/п —► 0.
п—юо
Поскольку р > (бЫпга)га"1 для больших га, мы тем самым получаем
для г := [|га/&] равенство
= lim Р[а > г] = 0,
п-юо
что и утверждалось. □
lim Р
п—юо
Of > -га/А;
lim Р
п—юо
а > -га/А;
~ 2 '

258
Глава И. Случайные графы
Теорема 11.2.2 (Эрдеш, 1959). Для любого целого числа к
существует граф Н с обхватом д(Н) > к и хроматическим числом
Х(Н) > к.
Доказательство. Допустим, что к > 3, зафиксируем е в
диапазоне 0 < б < l/к и положим р := п£~1. Пусть X(G) обозначает
число коротких циклов в случайном графе G £ &(п,р), т. е. число
его циклов длины не более к.
По лемме 11.1.5 имеем
к к
ВД = £ ^ * \ 5>V < |(* - 2)»V;
{=3 {=3
заметим, что (пр)' < (пр)к, поскольку пр = пе > 1. По лемме 11.1.4
Р[Х > п/2] < Е(Х)/(п/2)
<(к-2)пк-1рк
= (к-2)пк-1п^е-1)к
= (к-2)пке~1.
Так как fcf — 1 < 0 по выбору б, отсюда следует, что
lim Р[Х > п/2] = 0.
П—ЮО
Пусть п будет настолько большим, что Р[Х > га/2] < |
и Р [а > |га/&] < |; последнее возможно по выбору р и лемме 11.2.1.
Тогда существует граф G £ £^(га,р) с менее чем п/2 короткими
циклами и a{G) < ^п/к. Из каждого такого цикла удалим по вершине,
и пусть Н — полученный граф. Тогда \Н\ > га/2 и Я не имеет
коротких циклов, поэтому д(Н) > к. По определению G
Следствие 11.2.3. Существуют графы с произвольно большим
обхватом и произвольно большими значениями инвариантов к,е и S.
Доказательство. Применим следствие 5.2.3 и теорему 1.4.2. □
11.3. Свойства почти всех графов
Свойство графа — это любой класс графов, который замкнут
относительно изоморфизма, т. е. содержит вместе с каждым
графом G также все графы, изоморфные G. Если р = р(п) —
фиксированная функция (возможно, константа), а 3* — свойство графа,

11.3. Свойства почти всех графов
259
то можно задать вопрос, как вероятность P[G £ 8Р\ ведет себя для
G £ &(п,р) при п —+ со. Если эта вероятность стремится к 1, мы
будем говорить, что G £ SP для почти всех (или почти каждого)
G £ ^(п,р) или что G £ ^ почти наверное. Если она стремится
к 0, мы будем говорить, что почти ни один граф G £ &(п,р) не
обладает свойством ^. (Например, в лемме 11.2.1 мы доказали, что
для некоторого р почти ни один G £ &(п,р) не содержит множества
из более чем \njk независимых вершин.)
Чтобы проиллюстрировать это новое понятие, покажем, что для
константы р каждый фиксированный абстрактный3^ граф Н
является индуцированным подграфом почти всех графов.
Предложение 11.3.1. Для любой константы р £ (0,1) и
любого графа Н почти все графы G £ ^(п,р) содержат
индуцированную копию графа Н.
Доказательство. Пусть задан граф Я, а А; := |#|. Если п > к
и (/С {0,...,п- 1} — фиксированное множество из к вершин
графа G, то G[U] изоморфен Н с некоторой вероятностью г > 0. Эта
вероятность г зависит от р, но не от п (почему?). Далее, G содержит
набор из \п/к\ непересекающихся таких множеств U. Вероятность
того, что ни один из соответствующих графов G[U] не изоморфен Я,
есть (1 — r)l-n/*J, поскольку эти события независимы ввиду
непересекаемости множеств ребер из [U]2. Таким образом,
Р[Н <£.G как индуцированный подграф] < (1 — r)Ln/*-i —► 0,
п—-юо
откуда и следует доказываемое утверждение. □
Следующая лемма представляет собой простой механизм,
позволяющий установить, что довольно многие из естественных свойств
графа (включая перечисленные в предложении 11.3.1) присущи
почти всем графам. При заданных г, j £ N пусть 3*ij обозначает
свойство рассматриваемого графа содержать для любых
непересекающихся множеств вершин U, W с \U\ < i \\ \W\ < j вершину v £ UUW,
которая смежна со всеми вершинами из U, но не смежна ни с одной
вершиной из W.
Лемма 11.3.2. Для любых константыр £ (0,1) я чисел г, j £ N
почти любой граф G £ ^(п,р) обладает свойством &*ij.
Доказательство. Для фиксированных С/, W ии £ G-(UUW)
вероятность того, что v смежна со всеми вершинами из С/, но ни
с одной из W, равна
p>V>p'y.
3) Слово «абстрактный» использовано для указания, что известен или
существен только вид графа Н с точностью до изоморфизма, а не его
фактические множества вершин и ребер. В данном контексте это указывает, что
слово «подграф» использовано в обычном смысле — изоморфный поддрафу.

260
Глава 11. Случайные графы
Следовательно, вероятность того, что для этих U и W не существует
ни одной подходящей v, есть
(1 - pW^iyHcHK'i < (1 _ ру)»--;
(при п > i -f j), поскольку соответствующие события для
различных v независимы. Так как в V(G) имеется не более nt+J пар таких
множеств С/, W (закодируем множества U из менее чем г точек как
неинъективные отображения {0,..., г— 1} —> {0,..., п— 1} и т. д.), то
вероятность того, что некоторая такая пара не имеет подходящих и,
не превосходит
пг+'(1-рУ)п-г'Ч
и выражение стремится к нулю при п —+ со, поскольку 1— plqJ < 1. □
Следствие 11.3.3. Для любых константы р £ (0,1) и числа
& £ N почти каждый граф в&(п,р) является к-связным.
Доказательство. Ввиду леммы 11.3.2 достаточно показать,
что каждый граф в .0*2,*-1 ^-связен. Но это легко: каждый граф
из 3^2,k-i имеет порядок не меньше к -f 2, и если множество W
содержит менее к вершин, то по определению ^.Jb-i любые две другие
вершины х, у имеет общего соседа v £ W, в частности, W не
отделяет ж от у. D
При доказательстве следствия 11.3.3 мы показали существенно
большее, чем требовалось: вместо того, чтобы обнаружить для
любых двух вершин ж, у £ W некоторый х-у путь, избегающий W, мы
показали, что х и у имеют общего соседа вне W. Таким образом,
все пути, необходимые для установления искомой связности, могли
на самом деле быть выбраны длины 2. То, что можно было принять
за хитрую уловку в этом конкретном доказательстве, на самом деле
характерно для более фундаментального явления при константных
вероятностях ребра: в силу одного нетрудного факта из логики
любое утверждение относительно графов, выраженное квантификацией
только по вершинам (а не по множествам или последовательностям
вершин)4), является или почти наверное истинным или почти
наверное ложным. Все такие утверждения, или их отрицания,
являются на самом деле непосредственными следствиями утверждения, что
граф обладает свойством 3*ij при некоторых подходящих г, j.
Как последний пример результата на тему «почти все» покажем
теперь, что почти каждый граф имеет удивительно большое
хроматическое число.
) Используя логическую терминологию: любое предложение первого порядка
на языке теории графов.

11.3. Свойства почти всех графов
261
Предложение 11.3.4. Для любой константы р Е (0,1) и
любого б > 0 почти любой граф G Е ^(п,р) имеет хроматическое число
X(G) > bg(1/9) "
2 + 6 log n
Доказательство. При любых фиксированных n > к > 2
лемма 11.1.2 влечет
P[*>k]< (fjq®
< nkq(*)
к ( 21о*та 1 к l)
= q*\ iog(i/9)+/c V.
При
^:=(2 + £)-108П
bg(l/<?)
показатель этого выражения стремится к бесконечности вместе с п,
поэтому само выражение стремится к нулю. Следовательно, почти
каждый граф G Е &(п,р) таков, что в его вершинной раскраске
не может быть к вершин одного цвета, поэтому каждая раскраска
использует более чем
n _ \og(l/q) п
к 2-f6 log п
цветов. D
Согласно результату Боллобаша (1988) предложение 11.3.4 не-
улучшаемо в следующем смысле: если мы заменим е на —6, то
нижняя оценка для х превращается в верхнюю оценку.
Большинство результатов этого раздела имеет ту интересную
общую особенность, что значения р вообще не играют никакой роли:
если почти каждый граф в *$ (п, ^) обладал рассматриваемым
свойством, то это же было верно для почти любого графа в ^(п, 1/1000).
Как такое могло случиться?
Такая нечувствительность нашей случайной модели к
изменению р заведомо не была преднамеренной: в конце концов, среди всех
графов с некоторым свойством 3* часто именно обладающие
свойством 3* «едва-едва» являются наиболее интересными, поскольку
такие графы должны, скорее всего, иметь также и различные
свойства — свойства, которым & могло бы таким образом быть
поставлено в соответствие. (Доказательство теоремы Эрдеша — хороший
тому пример.) Однако для большинства свойств (и это объясняет

262
Глава 11. Случайные графы
вышеупомянутое явление) критический порядок величины р — «как
раз» около которого свойство наблюдается или не наблюдается —
лежит гораздо ниже любого значения константы р; это обычно функция
от п, стремящаяся к нулю при п —► со.
Посмотрим теперь, что происходит, если р позволено изменяться
вместе с п. Почти сразу разворачивается изумительная картина.
Для вероятностей ребра р, порядок которых лежит ниже п~2,
случайный граф G £ ^(п,р) почти наверное вообще не имеет ребер.
С ростом р граф G приобретает все более сложное строение: начиная
примерно с р = л/пп~2 и выше он почти наверное имеет компоненту
с более чем двумя вершинами, затем эти компоненты превращаются
в деревья, и около р — п~1 рождаются первые циклы. Вскоре
некоторые из них уже будут иметь несколько пересекающихся хорд,
делая граф неплоским. В то же время одна компонента перерастает
другие, пока не поглощает их все около р — (logn)n"1, делая граф
связным. Почти тут же при р — (1 -f e)(logn)n~1 наш граф почти
наверное уже имеет гамильтонов цикл!
Стало общепринятым сравнивать это развитие случайных
графов при возрастании р с эволюцией организма: можно смотреть
на свойства, присущие почти всем графам из ^(п,р) при каждом
р = р(п), как на свойства «одного» типичного случайного графа
G £ &(п,р) и изучать изменение G с ростом р. Как и у других
видов, эволюция случайных графов происходит довольно внезапными
скачками: критические вероятности ребра, упомянутые выше, суть
пороги, ниже которых почти никакой граф не обладает
соответствующим свойством, а выше которых почти каждый граф им уже
обладает. Точнее, мы называем вещественную функцию t — t(n)
с t(n) ф 0 при всех п пороговой функцией для графового
свойства ^, если для всех р — р(п) и G £ &(п,р) имеет место следующее:
Г 0, если pit —+ 0 при п —> со;
lim P[Ge&>] = \ ,
п-+оо [ 1з если p/t —+ со при п —+ со.
Если 8? имеет пороговую функцию t, то ясно, что любое
положительное кратное ct порога t — также пороговая функция для 8Р.
Таким образом, пороговые функции в вышеупомянутом смысле
единственны лишь с точностью до мультипликативной константы5).
Какие свойства графа обладают пороговой функцией?
Естественными кандидатами на эту роль являются возрастающие
свойства, т. е. сохраняющиеся при добавлении ребер. (Свойства графа
5) Наше понятие порога отражает только самый грубый среди
представляющих интерес уровней различения: для некоторых свойств таких, как
связность, можно определить более точные пороги, в которых главное значение
приобретает уже постоянный множитель. Отметим также роль
постоянного множителя в нашем сравнении связности с гамильтоновостью в
предыдущем параграфе.

11.4. Пороговые функции и вторые моменты
263
вида {G | G Э #} при фиксированном Я являются типичными
возрастающими свойствами; еще один пример дает связность.) И
действительно, Боллобаш и Томасон (1987) показали, что все возрастающие
свойства, кроме очевидных исключений, имеют пороговые функции.
В следующем разделе мы изучаем общий метод вычисления
пороговых функций.
11.4. Пороговые функции и вторые моменты
Рассмотрим графовое свойство вида
3* = {G\X{G)>0},
где X > 0 — случайная величина на ^(п,р); бесчисленные свойства
находят естественное выражение в таком виде. Например, если X
обозначает число остовных деревьев, то 3* соответствует связности.
Как можно было бы доказать, что 3* имеет пороговую
функцию t? Любое такое доказательство будет состоять из двух частей:
доказательства того, что почти никакой G Е &(п,р) не обладает
свойством 3*, когда р мало по сравнению с t, и того, что почти
каждый G обладает свойством 3*, когда р велико.
Если X целочисленна, то для первой части доказательства
можно применить неравенство Маркова и искать верхнюю оценку для
Е(Х), а не для Р[Х > 0]: если Е(Х) мало, то X(G) может быть
положительным и, следовательно, равным по меньшей мере 1 только
для немногих G Е ^(га,р). Кроме того, вычислять математическое
ожидание намного легче, чем вероятности. Не беспокоясь о таких
вещах, как независимость или несовместимость событий, можно
вычислять математическое ожидание суммы случайных величин,
например индикаторных случайных величин, просто суммированием
их индивидуальных ожидаемых значений.
Со второй частью доказательства дело обстоит сложнее. Чтобы
показать, что Р[Х > 0] велико, недостаточно оценить Е(Х) снизу.
Поскольку X не ограничена сверху, Е(Х) может быть велико уже
просто потому, что X очень велика лишь на нескольких графах G,
поэтому X может все-таки быть нулевой для большинства графов
G Е У(п,р)6\ Чтобы доказать, что Р[Х > 0] —► 1, мы,
следовательно, должны показать, что этого произойти не может, т. е. что
X не слишком часто намного отклоняется от своего среднего
значения.
6) Например, для некоторых р между п~1 и (logп)п~1 почти любой граф
G G ^(п,р) имеет изолированную вершину (и, следовательно, не имеет
остовных деревьев), однако его ожидаемое число остовных деревьев
стремится к бесконечности вместе с п ! Детали см. в упражнении 13.

264
Глава 11. Случайные графы
Следующий элементарный инструмент из теории вероятности
как раз достигает этой цели. Как это принято, мы обозначаем
М := Е(Х)
и определяем a > О, полагая
а*:=Е((Х-»П
Эта величина а2 называется дисперсией или вторым моментом
случайной величины Х\ по определению, она есть (квадратичная) мера
того, насколько X отклоняется от своего среднего значения.
Поскольку математическое ожидание Е линейно, определяющее
выражение для а2 разлагается в виде
а2 = Е(Х2 - 2рХ + /i2) = Е(Х2) - /А
Заметим, что ц и а2 всегда относятся к случайной величине на
некотором фиксированном вероятностном пространстве. В нашей
постановке, где рассматриваются пространства ^(п,р), обе величины
суть функции от га.
Следующая лемма говорит в точности то, что нам нужно: X не
может намного отклоняться от своего среднего значения слишком
часто.
Лемма 11.4.1 (неравенство Чебышева). Для всех
вещественных А > О
P[\X-fi\>\]< a2/X2.
Доказательство. По лемме 11.1.4 и определению а2
P[\X-fi\>X] = P[(X-fi)2>X2]<a2/X2. D
Для доказательства того, что X(G) > 0 для почти всех G Е
^(п,р), неравенство Чебышева может быть использовано
следующим образом.
Лемма 11.4.2. Если fi > 0 при больших га и cr2//i2 —» 0 при
га —► оо, то X(G) > 0 для почти всех G Е ^(га,р).
Доказательство. Любой граф G с X(G) = 0 удовлетворяет
равенству \X(G) — fi\ = fi. Следовательно, лемма 11.4.1 влечет при
А := /i, что
Р[Х = 0] < Р[\Х - /i| > /i] < a2/fi2 —► 0.
n—>oo
Поскольку X > 0, это означает, что X > 0 почти наверное, т. е. что
X(G) > 0 для почти всех G Е &(n,p). П
Как основной результат этого раздела докажем теперь теорему,
которая сразу же даст нам пороговые функции для нескольких
естественных свойств. Для данного графа Н обозначим через &н
свойство содержать копию графа Н как подграф. Назовем Н
сбалансированным, если е(Н/) < е(Н) для всех подграфов Н' графа Я.

11.4. Пороговые функции и вторые моменты
265
Теорема 11.4.3 (Эрдеш и Реньи, I960). Если Я —
сбалансированный граф с к вершинами и £ > 1 ребрами, то t(n) := n~kll есть
пороговая функция для &н •
Доказательство. Пусть X(G) обозначает число подграфов
графа G, изоморфных Я. При заданном n £ JV пусть Jf обозначает
множество всех графов, изоморфных Я, вершины которых лежат
в {0,..., п — 1} — множестве вершин графов G £ У(п, р):
Ж := {#' | Я' ~ Я, V(H') С {0,..., п - 1}}.
При заданных Я' £ Ж и G £ ^(гс,р) формула Я' С G будет
означать, что сам Я', а не только его изоморфная копия, является
подграфом графа G.
Через h обозначим число изоморфных копий графа Я на
фиксированном ^-множестве; ясно, что h < k\. Поскольку для графов в Jf
существует (") возможных множеств вершин, имеем
^=©k£G)i!s"'' (i)
Для р = р(п) положим 7 '•= p/t] тогда
р = 7п-*/£. (2)
Нужно показать, что почти ни один G £ ^(п, р) не лежит в &*н, если
7 —► 0 при п —► со, и что почти все G £ ^(п,р) лежат в £?н, если
7 —► со при п —► со.
Для первой части доказательства мы найдем верхнюю оценку
для Е(Х), т. е. ожидаемого числа подграфов графа G,
изоморфных Я. Как в доказательстве леммы 11.1.5, двойной подсчет дает
Е(Х)= J2 P[H'CG]. (3)
н'ьзе
Для каждого фиксированного Я' £ Л? имеем
Р[Н* С G] = р', (4)
поскольку ||Я|| = £. Следовательно,
ед = ИУ < п*(7п-*/')' = у. (5)
(3,4) (1,2)
Таким образом, если 7 —»• 0 при п —► оо, то
P[G е &н\ = Р[Х > 1] < Я(Х) < 7' —-+ о
п—*оо

266
Глава 11. Случайные графы
согласно неравенству Маркова (11.1.4), поэтому почти ни один G £
^(п}р) не лежит в &*н-
Теперь переходим ко второй части доказательства: покажем,
что почти все G Е ^(п,р) лежат в &*н, если j —► со при п —► со.
Заметим сначала, что для п > к
ЛЛ -к _ 1 fn п — к + 1\
\к)П " *! \п'" п )
Таким образом, пк превышает (") разве что на множитель, не
зависящий от п.
Мы хотим применить лемму 11.4.2 и, следовательно, оценить
сг2//22 = (Е(Х2) — /i2)//i2 сверху. Как в (3), имеем
Е(Х2)= Y, P[H'\JH"CG\. (7)
(Н',н")ея?2
Теперь вычислим эти вероятности Р[Н' U Н" С G]. При заданных
#',#"€ Л" имеем
P[H'uH"cG\=p2i-W'nH"K
Поскольку граф Н сбалансирован, е{Н' П Н") < е(Н) — £/к. При
\Н' П Н"\ =: i это дает ||#' П #"|| < И/к, поэтому 0 < р < 1 влечет
Р^иЯ"^]^2^. (8)
Итак, мы оценили индивидуальные слагаемые в (7). Что это
дает для суммы в целом? Поскольку (8) зависит от параметра i =
\Н' П #"|, мы разобьем весь диапазон Ж2 суммы в (7) на
подмножества
J*f := {(#', Я") G Ж2 : |#' П #"| = *}, г = 0,..., *,
и вычислим для каждого Ж2 соответствующую сумму
А{ :=^.P[#'U#"CG]
по отдельности. (Здесь, как и ниже, мы используем J2i Для
обозначения суммы по всем парам (Н/, Н") £ Ж2.)

11.4. Пороговые функции и вторые моменты
267
Если г = 0, то Н' и Н" не пересекаются, поэтому события Н' С G
и Н" С G независимы. Следовательно,
А0 =J2 P[H'\JH"CG\
= £oP[#'CG].P[tf"CG]
< y, р[я' £ G] • р[я" ^ G]
(#',#")е^-2
= ( ^ Р[Я'СС])-( J^ P[H"CG]
Теперь оценим А{ для г > 1. Обозначим через J2 сумму ^2н'ея?>
а через ^ — сумму ^2н"елг- Заметим, что ^ можно записать как
Е Е|Я'пЯ"|=г- ^ля фиксированного Н' (соответствующего первой
сумме ^2 ) вторая сумма пробегает
слагаемых, число графов Н" £ Ж с |#" П Н'\ = г. Следовательно,
для всех г > 1 и подходящих констант ci, С2, не зависящих от га,
At = ^.P[#'U#"CG]
(|Е'С)(;::>л-«"
s|Jf|C)(r')ftp2'(7""'"ri'"
< |Jf \ptclnk-ihpt1-itlkni
= uClnkhplj-ie'k
/ic^W""
<
(6)
(1,5)
если 7^1- По определению А{ это влечет при сз := кс2, что
** (7) \^2 f^H2 J (9)

268
Глава 11. Случайные графы
а следовательно,
а2 Е{Х2)-ц2 11к
По лемме 11.4.2 поэтому X > 0 почти наверное, т. е. почти все
G £ ^(га,р) имеют подграф, изоморфный Я, а следовательно, лежат
в &н. □
Теорема 11.4.3 позволяет получить пороговые функции для
нескольких естественных свойств графа.
Следствие 11.4.4. Если к > 3, то t(n) = п~1 есть пороговая
функция для свойства, содержать к-цикл. □
Интересно отметить, что пороговая функция в следствии 11.4.4
не зависит от длины рассматриваемого цикла к: при эволюции
случайных графов циклы всех (константных) длин появляются
примерно в одно и то же время!
Аналогичное явление имеет место и для деревьев. Здесь
пороговая функция зависит от порядка рассматриваемого дерева, но не от
его строения.
Следствие 11.4.5. Если Т — дерево порядка к > 2, то t(n) =
n-k/(k-i) есть пороговая функция для свойства содержать копию Т.
Наконец, имеем следующий результат для полных подграфов.
Следствие 11.4.6. Если к > 2, то t(n) = п~2^к~1^ есть
пороговая функция для свойства содержать Кк.
Доказательство. Граф Кк сбалансирован, поскольку е(Ю) —
\{% - 1) < \{к - 1) = е{Кк) при г < *. Для £ := \\Кк\\ = |*(* - 1)
получаем п~к11 = п~2^к~1\ D
Нетрудно приспособить доказательство теоремы 11.4.3 к
случаю, когда Н не уравновешен. Порогом тогда становится функция
t(n) = п-1/*'^, где е'{Н) := max{e(F) | F С #}; см.
упражнение 22.
Упражнения
1.~ Какова вероятность того, что случайный граф в #(п,р) имеет в точности
m ребер при фиксированном 0 < m < ("j?
2. Каково ожидаемое число ребер в G Е #(п,р)?
3. Каково ожидаемое число Кг-подграфов в G Е #(п, р)?
4. Охарактеризовать графы, которые встречаются как подграфы в каждом
графе достаточно большой средней степени.
5. В обычной терминологии пространств с мерой (и, в частности,
вероятностных пространств) фраза «почти все» используется для указания на
множество точек, дополнение которого имеет меру нуль. Вместо рассмотрения

Упражнения 269
предела вероятностей в #(п,р) при п —► оо не будет ли более естественным
определять вероятностное пространство на множестве всех конечных
графов (взяв по одному экземпляру каждого) и исследовать свойства «почти
всех» графов в этом пространстве в вышеуказанном смысле?
6. Показать, что если почти все графы G Е Sf(n,p) обладают свойством 9*\
и почти все G Е #(п,р) обладают свойством ^2> то почти все G Е &(п,р)
обладают обоими этими свойствами, т. е. свойством &*\ П &>2-
7~ Показать, что для постоянного р Е (0,1) почти любой граф в &(п,р) имеет
диаметр 2.
8. Показать, что для постоянного р Е (0,1) почти ни один граф в Sf(n,p) не
имеет разделяющего полного подграфа.
9. Вывести предложение 11.3.1 из леммы 11.3.2.
10.+ (i) Показать, что бесконечный случайный граф G Е ^(No» р) обладает всеми
свойствами ^ij (г, j Е N) с вероятностью 1.
(ii) Показать, что любые два (бесконечных) графа, обладающие всеми
свойствами ^t,j» изоморфны.
(Таким образом, существует только один, с точностью до изоморфизма,
счетно-бесконечный случайный граф.)
11. Пусть б > 0 и р = р(п) > 0, а г > (1 + б)(21пп)/р — целочисленная функция
от п. Показать, что почти ни один граф в #(п, р) не содержит г независимых
вершин.
12. Показать, что для любого графа Н существует такая функция р — р(п),
что lim р(п) = 0, но почти любой G Е #(п,р) содержит индуцированную
п—*оо
копию графа Н.
13.+ (i) Показать, что для любых 0<е<1ир=(1- б) (In n)n~1 почти любой
граф G Е ^(п,р) имеет изолированную вершину.
(ii) Найти такую вероятность р = р(п), что почти любой G Е ^(п, р)
несвязен, но ожидаемое число остовных деревьев G стремится к бесконечности
при п —*■ оо.
(Подсказка для (ii). Теорема Кэли утверждает, что Кп имеет в точности
пп~2 остовных деревьев.)
14.+ При заданном г Е N найти такое с > 0, что при р = сп~1 почти любой граф
G Е ^(п, р) содержит минор Кг. Может ли с быть выбрано независимо
от г?
15. Найти возрастающее свойство графа без пороговой функции и свойство,
которое не возрастает, но имеет пороговую функцию.
16."" Пусть Н — граф порядка /:, a h обозначает число графов, изоморфных Н на
некотором фиксированном множестве из к элементов. Показать, что h < к\.
Для каких графов Н имеет место равенство?
17."" Для каждого к > 1 найти пороговую функцию для {G \ A(G) > к}.
18." Существует ли при заданном d Е N пороговая функция для свойства
содержать d-мерный куб (см. упражнение 2 главы 1)? Если это так, то какая?
Если нет, то почему?
19. Показать, что t(n) = n—1 — пороговая функция также для свойства
содержать любой цикл.
20. Имеет ли свойство содержать любое дерево порядка к (при фиксированном
к > 2) пороговую функцию? Если это так, то какую?

270 Глава 11. Случайные графы
21."*" Для данного графа Н пусть 9 есть свойство содержать индуцированную
копию графа Н. Если Н полный, тогда по следствию 11.4.6 9 имеет
пороговую функцию. Показать, что 9 не имеет пороговой функции, если Н не
полон.
22.+ Докажите следующую версию теоремы 11.4.3 для неуравновешенных
подграфов. Пусть Н — любой граф с по меньшей мере одним ребром, и
положим s'(H) := max{£(F) | 0 ф F С Н}. Тогда пороговая функция для 9ц
ecTbt(n) = n-1fe'<<H\
(Подсказка. Следуйте доказательству теоремы 11.4.3. Вместо множеств Жх
рассмотрите множества Ж* := {(#',#") Е Ж2 \ #' П Я" = F}. Замените
различие между случаями г = 0 и г > 0 на различие между случаями \\F\\ = О
и ||F|| > 0.)
Примечания
Имеется немало монографий и текстов на тему случайных графов.
Наиболее всесторонняя из них книга: Bollobds В. Random Graphs. London: Acad. Press,
1985. Другая углубленная, но удобочитаемая монография: Janson S., Luczak Т.,
Ruciriski A. Topics in Random Graphs (готовится к изданию); она
концентрируется на областях, развитых после выхода из печати Random Graphs. Книга:
Palmer Е. М. Graphical Evolution. N. Y.: John Wiley & Sons, 1985 — покрывает
материал, подобный частям Random Graphs, но излагает его более доходчиво.
Компактные введения в предмет, выходящие за пределы того, что освещается
этой главе, даны в книге: Bollobds В. Graph Theory. Berlin е. a.: Springe г-Verb,
1979. V. 63. (Graduate Texts in Mathematics) — ив работе: Karonski M.
Handbook of Combinatorics / Ed. by R. L. Graham, M. Grotschel, L. Lovasz. Amsterdam
e. a.: North-Holland Publ., 1995.
Стимулирующее углубленное введение в использование рандомизации в
дискретной математике в целом дано в: A Ion N., Spencer J. Н. The
Probabilistic Method. N. Y.: John Wiley & Sons, 1992. Одна из привлекательных сторон
данной книги состоит в том, что она показывает применимость вероятностных
методов к доказательству полностью детерминистских теорем, чего трудно было
бы ожидать заранее. Другой пример этого явления — доказательство А лоном
теоремы 5.4.1; см. примечания к главе 5.
Вероятностный метод зародился в 1940 годы. Одним из его самых
ранних результатов является полученная Эрдешем вероятностная нижняя оценка
для чисел Рамсея (теорема 11.1.3). Лемма 11.3.2 о свойствах 9ltJ взята из
вышеупомянутой книги Боллобаша, опубликованной в издательстве «Шпрингер».
Очень доступное доказательство того, что для константы р каждое предложение
первого порядка о графах является или почти наверное истинным, или почти
наверное ложным, приведено в работе: Winkler P. Random structures and zero-one
laws // Finite and Infinite Combinatorics in Sets and Logic / Ed. by N. W. Sauer
et al. Dordrecht: Kluwer Acad. Publ., 1993. V. 411. (NATO ASI. Ser. C).
Основополагающей статьей об эволюции графов является: Erdos Р..
Renyi A. On the evolution of random graphs // Publ. Math. Inst. Hungar. Acad.
Sci. 1960. 5. P. 17-61. Эта статья включает также теорему 11.4.3 и ее
доказательство. Обобщение этой теоремы на неуравновешенные подграфы было
сначала получено Боллобашем в 1981 г. с использованием углубленных методов;
упрощение исходного доказательства Эрдеша и Реньи было найдено Ручиньским
и Вэнсом (1986) и опубликовано в написанной Кароньским статье для Handbook
of Combinatorics.
Существует еще один способ определения случайного графа G, который
является столь же естественным и общим, как и рассмотренная нами модель.
Вместо того чтобы выбирать ребра для G независимо, будем выбирать граф G
целиком, равномерно и наугад из числа всех графов на {0,. .. ,п — 1}, которые
имеют в точности М = М(п) ребер. Тогда каждый из этих графов встречается
с одной и той же вероятностью (M), где N := ("J- Так же, как мы изучали

Примечания
271
типичные свойства графов в #(п,р) для различных функций р = р(п), можно
исследовать зависимость свойств графа G во второй модели от функции М(п).
Если М близко к pN — ожидаемому числу ребер графа в #(п,р), то эти две
модели ведут себя очень сходным образом. Поэтому выбор той, которую из них
рассматривать, в значительной степени является вопросом удобства;
подробности см. в книге Боллобаша.
При более подробном изучении пороговых явлений часто рассматривают
следующее порождение случайного графа: начиная с Кп как нулевой стадии
выбирают дополнительные ребра одно за другим (равномерно и наугад), пока
граф не станет полным. Это простой пример марковской цепи, М-я стадия
которой соответствует «равномерной» случайной модели графа, описанной выше.
Обзор пороговых явлений в этой постановке дан в статье: Luczak Т. The phase
transition in a random graph // Combinatorics, Paul Erdos is eighty / Ed. by
D. Miklos, V. T. Sos, T. Szonyi / Bolyai Soc. Math. Studies. V. 2. Budapest: Janos
Bolyai Math. Soc, 1996.

Глава 12
Миноры, деревья и правильные
квазиупорядочения
Наша цель в этой последней главе — та единственная теорема,
которая затмевает любой другой результат в теории графов и
несомненно может считаться одной из самых глубоких теорем, которые
предлагает математика: в каждом бесконечном множестве графов
имеются два таких графа, что один из них есть минор другого. Эта
теорема о минорах графов (или, для краткости, теорема о
минорах), хотя и неприметная на первый взгляд, оказала
фундаментальное влияние как на саму теорию графов, так и за ее пределами. Ее
доказательство, принадлежащее Нейлу Робертсону и Полу Сеймуру,
занимает более 500 страниц.
Поэтому мы должны скромно признать, что эта глава передает
лишь очень приблизительное представление о фактическом
доказательстве теоремы о минорах. Однако, как это случается с истинно
фундаментальными результатами, ее доказательство привело к
развитию методов, самых различных по их направленности и
потенциалу. Это особенно касается использования древесного
разложения — техники, с которой мы встретимся в разделах 12.3 и 12.4.
Раздел 12.1 дает введение в правильное квазиупорядочение —
понятие, являющееся ключевым в теореме о минорах. В разделе 12.2
мы используем это понятие для доказательства теоремы о минорах
для деревьев. Глава заканчивается кратким обзором в разделе 12.5
доказательства общей теоремы о минорах графов и некоторых из ее
непосредственных следствий.
12.1. Правильное квазиупорядочение
Рефлексивное и транзитивное отношение называется
квазиупорядочением. Квазиупорядочение < на множестве X есть правильное
квазиупорядочение, а элементы в X правильно квазиупор яд очены
отношением <, если для каждой бесконечной последовательности
xq, xi, ... в X существуют такие индексы г < j, что Х{ < Xj. Тогда

12.1. Правильное квазиупорядочение
273
(xi,Xj) есть хорошая пара этой последовательности.
Последовательность, содержащая хорошую пару, — хорошая последовательность.
Таким образом, квазиупорядочение на X является правильным
квазиупорядочением, если и только если каждая бесконечная
последовательность в X является хорошей. Бесконечная последовательность
называется плохой, если она не является хорошей.
Предложение 12.1.1. Квазиупорядочение < на множестве X
есть правильное квазиупорядочение, если и только если X не
содержит ни бесконечной антицепи, ни бесконечной строго убывающей
последовательности xq > х\ > ....
Доказательство. Прямая импликация очевидна. Пусть,
обратно, xq,x\,... — любая бесконечная последовательность в X, и
пусть К — полный граф на N = {0,1,...}. Раскрасим ребра ij
(г < j) графа К в три цвета: зеленый, если Х{ < Xj, красный, если
Х{ > Xj,n желтый, если Х{, Xj несравнимы. По теореме Рамсея (9.1.2)
К содержит бесконечный индуцированный подграф, все ребра
которого имеют один и тот же цвет. Если в X нет ни бесконечной
антицепи, ни бесконечной строго убывающей последовательности, то
этот цвет должен быть зеленым, т. е. хо,х\,... имеет
бесконечную последовательность, в которой каждая пара является хорошей.
В частности, последовательность xq, х\, ... — хорошая. □
В доказательстве предложения 12.1.1 мы показали больше, чем
требовалось: вместо того, чтобы найти в xq,xi,... единственную
хорошую пару, мы нашли бесконечную возрастающую
подпоследовательность. Таким образом, имеет место утверждение.
Следствие 12.1.2. Если X — правильное квазиупорядочение,
то каждая бесконечная последовательность в X содержит
бесконечную возрастающую последовательность. □
Для теории правильного квазиупорядочения фундаментальными
являются следующая лемма и идея ее доказательства. Пусть < —
квазиупорядочение на множестве X. Для конечных подмножеств
А,ВСХ будем писать А < В, если имеется такое инъективное
отображение /: А —> В, что a < f(a) для всех a £ А. Оно
естественным образом продолжает < до квазиупорядочения на [Х]<ы —
множестве всех конечных подмножеств в X.
Лемма 12.1.3. Если множество X правильно квазиупор ядочено
отношением <, то это же верно для [Х]<ш.
Доказательство. Предположим, что < есть правильное
квазиупорядочение на X, но не на [Х]<ы. Мы начинаем с
построения плохой последовательности (Ап)п^ в [Х]<ы следующим
образом. При заданном n £ N, предположим индуктивно, что А{ уже
определено для каждого г < п и что существует плохая
последовательность в [Х]<ы, начинающаяся с Aq, ... ,Ап-\. (Это, очевидно,

274 Глава 12. Миноры, деревья и правильные квазиупорядочения
верно для п = 0: по предположению [X]<w содержит плохую
последовательность, а та имеет пустую последовательность как
начальный сегмент.) Выберем An £ [X]<w так, чтобы некоторая плохая
последовательность в [X]<w начиналась с Aq, ..., Ап и \АП\ было
минимальным.
Ясно, что (Ап)„его — плохая последовательность в [Х]<ы, в
частности, Ап ф 0 для всех п. Для каждого п выберем элемент ап £ Ап
и положим Вп := Ап \ {ап}.
По следствию 12.1.2 последовательность (ап)„ем имеет
бесконечную возрастающую подпоследовательность (a„.)tGN- Ввиду
минимальности выбора АПо последовательность
Ло,..., ЛПо_1, ВПо, ВП1, ВП2,...
является хорошей; рассмотрим хорошую пару. Поскольку (Ап)п^ —
плохая, эта пара не может иметь вид (AitAj) или (Д-,Бу), так как
Bj < Aj. Поэтому она имеет вид (Д-,Ву). Продолжая инъективное
отображение Д- —► Bj посредством аг- »—► ау, мы снова получаем, что
пара (A{,Aj) является хорошей; противоречие. D
12.2. Теорема о минорах графов для деревьев
Теорему о минорах можно сформулировать так: конечные
графы правильно квазиупорядочены по отношению =$ быть минором.
Действительно, согласно предложению 12.1.1 и тому очевидному
факту, что никакая строго убывающая последовательность миноров
не может быть бесконечной, правильная квазиупорядоченность
эквивалентна несуществованию бесконечной антицепи (формулировка
использовалась ранее).
В этом разделе мы докажем сильный вариант теоремы о минорах
графов для деревьев.
Теорема 12.2.1 (Краскал, I960). Конечные деревья правильно
квазиупорядочены по отношению быть топологическим минором.
Мы будем базировать доказательство теоремы 12.2.1 на
следующем понятии вложения между корневыми деревьями, которое
усиливает обычное вложение в виде топологического минора. Рассмотрим
два дерева ТиГ', скажем, с корнями гиг'. Будем писать Т <Т',
если существует изоморфизм ф некоторого подразбиения дерева Т на
поддерево Т" из Т", который сохраняет древесный порядок на V(T),
связанный с Т и г. (Таким образом, если х < у в Т, то ф(х) < ф(у)
в Т"; см. рис. 12.2.1). Как легко проверить, это квазиупорядочение
на классе всех корневых деревьев.

12.2. Теорема о минорах графов для деревьев
275
/ —* V /ф^
\ / * \/
\/ Т X
г'
Рис. 12.2.1. Вложение дерева Т в Т', показывающее, что Т < Т'
Доказательство теоремы 12.2.1. Покажем, что корневые
деревья правильно квазиупорядочены по определенному выше
отношению <; это с очевидностью влечет теорему.
Предположим противное. Чтобы получить противоречие, мы
действуем, как в доказательстве леммы 12.1.3. При заданном nGH
предположим индуктивно, что уже выбрана такая
последовательность To,...,Tn_i корневых деревьев, что некоторая плохая
последовательность корневых деревьев начинается с этой
последовательности. Выберем в качестве Тп такое корневое дерево
минимального порядка, что некоторая плохая последовательность начинается
с То,..., Т„. Для каждого п £ N обозначим корень дерева Т„ через гп.
Ясно, что (Тп)пел — плохая последовательность. Для каждого п
пусть Ап обозначает множество компонент в Тп — гп,
превращенных в корневые деревья выбором в качестве их корней соседей
вершины г„. Заметим, что древесный порядок этих деревьев совпадает
с тем, который индуцирован деревом Тп. Докажем, что множество
А := (J Ап всех таких деревьев правильно квазиупорядочено.
nGN
Пусть (Tk)k£N — любая последовательность деревьев в А. Для
каждого к £ N выберем п = п(к) так, что Тк £ Ап. Выберем к
с наименьшим п(к). Тогда
-*0,-..,-*n(*)-li-* )^ ,...
является хорошей последовательностью ввиду минимальности
выбора Tn(fc) и того, что Тк С Tn(jb). Пусть (Т, Т') — хорошая пара этой
последовательности. Поскольку последовательность (Тп)п^ плохая,
то Т не может находиться среди первых п(к) членов То,... ,Тп^)-1
нашей последовательности. Иначе Т' было бы некоторым Тг с г > &,
т. е.
Т <Т' = Т <Тп(г).
Поскольку п(к) < n(i) по выбору к, это делало бы (Т, Tn(j))
хорошей парой в плохой последовательности (Тп)п6^. Следовательно,

276 Глава 12. Миноры, деревья и правильные квазиупорядочения
(Т,Т') — хорошая пара также и в (Tk)k£N, что завершает
доказательство правильной квазиупорядоченности множества А.
По лемме 12.1.31) последовательность (An)nGN в [А]ш содержит
хорошую пару (A{,Aj). Пусть /: А{ —» Aj — такое инъективное
отображение, что Т < f(T) для всех Т £ А{. Теперь мы
продолжаем объединение вложений Т —» f(T) до отображения ф из V(T{)
в V(Tj), полагая 0(rt-) := г;-. Это отображение 0 сохраняет
древесный порядок на Т{ и определяет вложение, показывающее, что
Т{ < Tj, поскольку ребра Г{Г £ 7* отобралааются естественным
образом в пути rjTj ф(г). Следовательно, (7;, 7}) — хорошая пара в нашей
первоначальной плохой последовательности корневых деревьев;
противоречие. □
12.3. Древесные разложения
Деревья — это графы с очень отличительными и
фундаментальными свойствами; вспомним теорему 1.5.1 и следствие 1.5.2 или
более сложный пример теоремы Краскала. Поэтому законно спросить,
в какой степени их свойства могут быть перенесены на графы более
общего вида — графы, которые не являются сами деревьями, но
древовидны в некотором смысле2). В этом разделе мы изучаем понятие
древовидности, которое допускает обобщения всех вышеупомянутых
свойств дерева (включая теорему Краскала) и которое играет
главную роль в доказательстве теоремы о минорах графов.
Пусть G — граф, Т — дерево, а У — (Vt)teT — семейство
множеств вершин Vt С V(G), индексированных вершинами t из Т. Пара
(Т,У) называется древесным разложением графа G, если она
удовлетворяет следующим трем условиям:
(Tl) V{G) = U Vt;
(Т2) для каждого ребра е £ G существует такое t £ Т, что оба
конца е лежат в Vt;
(ТЗ) Vtl П Vt3 С Vt2 для всех таких hMM G Т, что t2 £ tiTt3.
Условия (Tl) и (Т2) вместе означают, что G является объединением
подграфов G[Vi]; назовем эти подграфы и сами множества Vt час-
тлями разложения (Т, У) и будем говорить, что (Т, У) является
древесным разложением графа G на эти части. Из условия (ТЗ) следует,
что части (Ту У) организованы подобно дереву (рис. 12.3.1).
*) Читатели, обеспокоенные тем, что мы можем нуждаться здесь в лемме для
последовательностей или мультимножеств, а не только для множеств,
пожалуйста, заметьте, что изоморфные элементы в Ап не отождествляются:
мы всегда имеем \An\ = d(rn).
2) Каким в точности должен быть этот «смысл», зависит и от
рассматриваемого свойства, и от его предполагаемого применения.

12.3. Древесные разложения
277
Рис. 12.3.1. Ребра и части, исключенные условиями (Т2) и (ТЗ)
Прежде чем обсуждать роль, которую играют древесные
разложения в доказательстве теоремы о минорах, отметим некоторые из
их основных свойств. Рассмотрим фиксированное древесное
разложение (Т, У) графа G с У = (Vt)t^T, как выше.
Возможно, наиболее важная особенность древесного разложения
состоит в том, что оно переносит свойства отделимости своего дерева
на разложенный граф.
Лемма 12.3.1. Пусть t\t2 — любое ребро в Т, а 7\,Т2 —
компоненты в Т — t\t2, где t\ £ Т\ и t2 £ Т2. Тогда Vtl П V%2 отделяет
Ux := (J Vt от U2 := (J Vt в G (рис. 12.3.2).
Рис. 12.3.2. Vtl П Vt2 отделяет U\ от U2 в G
Доказательство. И t\, и t2 лежат на каждом t-t' пути в Т,
где t £ Тх и f £ Т2. Поэтому Ux П U2 С Vtl П V%2 согласно (ТЗ), так
что требуется лишь показать, что в G нет такого ребра u\u2, что
и1 £ U\\U2 и и2 £ U2\Ui. Если щи2 — такое ребро, то согласно (Т2)
имеется t £ Т с щ, и2 £ Vt. По выбору щ и и2 не может быть ни
t £ Т2, ни 2 £ Ti; противоречие. □
Заметим, что древесные разложения переносятся на подграфы.
Лемма 12.3.2. Для каждого Н С G пара (Т, (V* П V(#))teT)
есть древесное разложение подграфа Н. □

278 Глава 12. Миноры, деревья и правильные квазиупорядочения
Аналогично для стягиваний:
Лемма 12.3.3. Предположим, что G есть МИ с множествами
ветвления Uh, h £ V(H). Пусть f: V(G) —► V(H) —
отображение, приписывающее каждой вершине из G индекс множества
ветвления, содержащего ее. Для всех t £ Т пусть Wt := {f(v) \ v £ Vt},
и положим W \— (Wt)teT- Тогда (T,W) есть древесное разложение
графа Н.
Доказательство. Утверждения (Т1) и (Т2) для (T,W)
следуют сразу из соответствующих утверждений для (Т, У). Теперь
пусть ^1,^2)^3 £ Т будут, как в (ТЗ), и рассмотрим вершину h £
Wt1 П Wt3 из Н. Покажем, что h £ Wt2. По определению Wtl и W%z
имеются вершины v\ £ Vtl П Uh и г/3 £ Vt3 ПС/д. Поскольку Uh связен
в G, a Vt2 отделяет v\ от г/3 в G по лемме 12.3.1, то Vt2 имеет вершину
в Uh- По определению Wt2 это влечет h £ Wt2. П
Приведем еще одно полезное следствие леммы 12.3.1.
Лемма 12.3.4. Для данного множества W С V{G) существуют
либо такое t £ Т, что W С V%, либо такие вершины w\, W2 £ W и
ребро tit2 £ Т, что iui, IU2 лежат вне множества Vtx C\Vt2 и разделены
им в G.
Доказательство. Сориентируем ребра в Т следующим
образом. Для каждого ребра tit2 £Т определим U\, U2, как в лемме 12.3.1.
Тогда Vt1 П Vt2 отделяет Ui от U2- Если Vtl П V%2 не разделяет
никаких двух вершин из W', которые лежат вне его, то можно найти
такое г £ {1,2}, что W С [/{, и сориентировать tit2 к t{.
Пусть t — последняя вершина максимального ориентированного
пути в Т; мы утверждаем, что W С V%. При заданном w £ W пусть
t' £ Т — такое, что w £ Vti. Если i; ф t, то ребро е при t, которое
отделяет f от t в Т, направлено к 2, поэтому ги также лежит в Vf для
некоторого t" из компоненты графа Т — е, содержащей 2. Поэтому
w G Ц ввиду (ТЗ). □
Следующий частный случай леммы 12.3.4 используется
особенно часто.
Лемма 12.3.5. Любой полный подграф графа G содержится
в некоторой части разложения (Т, У). □
Как показано на рисунке 12.3.1, части разложения (Т,У)
отражают строение дерева Т, так что в этом смысле разложенный граф G
напоминает дерево. Однако это ценно только постольку, поскольку
строением графа G в пределах каждой части можно пренебречь: чем
меньше части, тем сильнее сходство.
Это наблюдение мотивирует следующее определение. Ширина
древесного разложения (Т, У) есть число
max{|7t|-l :<GT},

12.3. Древесные разложения
279
а древесная ширина tw(G) графа G есть наименьшая ширина любого
древесного разложение для G. Как легко проверить3), сами деревья
имеют древесную ширину 1.
По леммам 12.3.2 и 12.3.3 древесная ширина графа не может
возрастать при удалении или стягивании.
Предложение 12.3.6. Если Н 4G,to tw(#) < tw(G). □
Графы ограниченной древесной ширины похожи на деревья
настолько, что становится возможным перенести доказательство
теоремы Краскала на этот класс графов. Говоря очень приблизительно,
нужно повторить рассуждение о «минимальной плохой
последовательности» из доказательства леммы 12.3.1 tw(G) раз. Это
приближает нас еще на шаг к доказательству теоремы о минорах графов.
Теорема 12.3.7 (Робертсон и Сеймур, 1990). Для каждого
целого числа к > 0 графы древесной ширины < к правильно
квазиупоря дочены по отношению быть минором.
Чтобы воспользоваться теоремой 12.3.7 для доказательства
общей теоремы о минорах, мы должны суметь сказать кое-что о
графах, которые первая из теорем не охватывает, т. е. вывести
некоторую информацию о графе из предположения, что его древесная
ширина велика. Наша следующая теорема как раз достигает этой
цели. Она описывает каноническое препятствие для малой
древесной ширины — конфигурацию, которая встречается в графе, если
и только если его древесная ширина велика.
Будем говорить, что два подмножества в V(G) соприкасаются, \
если они имеют общую вершину или если G содержит ребро меж- |
ду ними. Множество взаимно соприкасающихся связных множеств (
вершин в G называется ежевикой. Обобщая нашу терминологию ^
из раздела 2.1, будем говорить, что подмножество из V(G) покры- /
вает ежевику 3& (или является ее покрытием), если оно пересекает- I
ся с каждым элементом из 3&. Наименьшее число вершин, покры- \
вающих ежевику, есть порядок этой ежевики. j
Будет полезным следующее простое наблюдение. ^
Лемма 12.3.8. Любое множество вершин, разделяющее два
покрытия ежевики, также покрывает эту ежевику.
Доказательство. Поскольку каждое множество в ежевике
связно и пересекается с обоими покрытиями, оно также пересекается
с любым множеством, разделяющим эти покрытия. D
Типичный пример ежевики — множество пересечений в
решетке. Решетка к х к есть граф на {1,..., к}2 с множеством ребер
{{i,№,?):\i-i'\ + \j-f\ = l}.
' В действительности —1 в определении ширины не служит никакой другой
цели, кроме как сделать данное утверждение верным.

280 Глава 12. Миноры, деревья и правильные квазиупорядочения
Пересечениями этой решетки являются к2 множеств
Cir.= {{i,l)\t=l,...,k}U{(t,j)\l=l,...,k}.
Таким образом, пересечение Сг;- есть объединение г-ro столбца
решетки и ее j-й строки. Ясно, что пересечения к х к решетки
образуют ежевику порядка к: они покрыты любыми строкой или
столбцом, в то время как любое множество менее чем из к вершин минует
и некоторую строку и какой-то столбец, а следовательно, и их
пересечение.
Следующий результат иногда называют теоремой
двойственности для древесной ширины.
Теорема 12.3.9 (Сеймур и Томас, 1993). Пусть к > 0 —целое
число. Граф имеет древесную ширину > к, если и только если он
содержит ежевику порядка > к.
Доказательство. Для доказательства обратной импликации
предположим, что 38 — произвольная ежевика в графе G. Покажем,
что каждое древесное разложение (Т, (Vt)teT) графа G имеет часть,
которая пересекается с каждым множеством из 3$.
Как в доказательстве леммы 12.3.4, мы начинаем с
ориентирования ребер tit2 в Т. Если X := Vtx П Vt2 пересекает каждое В Е 38,
то все уже доказано. Если нет, то для каждого В, не
пересекающегося с X, существует такое г Е {1,2}, что В С £/»• \ X (определение
см. в лемме 12.3.1); вспомним, что В связно. Кроме того, это i одно
и то же для всех таких В, поскольку они соприкасаются. Теперь мы
ориентируем ребро ti^2 к U.
Если каждое ребро в Т ориентировано таким образом и t —
последняя вершина максимального ориентированного пути в Т, то
Vt пересекает каждое множество из 3$ так же, как в доказательстве
леммы 12.3.4.
Для доказательства прямого утверждения допустим теперь, что
G не содержит ежевик порядка > к. Покажем, что для каждой
ежевики 38 в G существует ^-допустимое древесное разложение
графа G, т. е. такое, в котором ни одна часть порядка > к не
покрывает 3&. Для 3$ — 0 это влечет, что tw(G) < к, потому что каждое
множество покрывает пустую ежевику.
Пусть 3$ задано и допустим индуктивно, что для каждой
ежевики 3&1 с большим, чем в «^, количеством множеств существует
«^'-допустимое древесное разложение графа G. (Индукция
начинается, поскольку никакая ежевика в G не содержит более чем 2'G'
множеств.) Пусть X С V(G) — наименьшее по числу вершин покрытие
для 38. Тогда £ :— \Х\ < к есть порядок ежевики 3$. Наша цель —
показать следующее.

12.3. Древесные разложения
281
Для каждой компоненты С графа G — X существует
3&-допустимое древесное разложение графа (*)
G[X U V(C)] с X в качестве одной из частей.
Тогда эти древесные разложения могут быть объединены в
«^-допустимое древесное разложение графа G отождествлением их
узлов, соответствующих X. (Если X — V(G), то древесное
разложение с X в качестве единственной части является ^-допустимым.)
Итак, пусть С — фиксированная компонента в G—X. Обозначим
Я := G[X U V(C)] и положим SS1 := SS U {С}. Если S&* не ежевика,
то С не касается некоторого элемента из 3$, а следовательно, У :—
V(C)UN(C) не покрывает 3$. Тогда древесное разложение графа Я,
состоящее из этих двух частей X и У, удовлетворяет (*).
Поэтому можно считать, что 3S1 — ежевика. Поскольку X
покрывает ^, но не покрывает 3&', то \39'\ > \39\. Наше индукционное
предположение поэтому гарантирует, что G имеет ^'-допустимое
древесное разложение (Т, (Vt)teT)- Если это разложение также
^-допустимо, то доказывать больше нечего. Если нет, тогда одна
из его частей порядка > &, например Vs, покрывает 3&. Поскольку
никакое множество из менее чем £ вершин не покрывает 3$, лемма
12.3.8 с помощью теоремы Менгера (3.3.1) влечет, что Vs и X
связаны £ непересекающимися путями Pi,..., Pi. Так как Vs не может
покрывать 38' и, следовательно, лежит в G—С, пути Р,- пересекают Я
только в своих концах i,- G I.
Для каждого г — 1,..., £ выберем U £Т с Х{ Е V%{ и положим
Wt := (Vt П (X U V(C))) U {х{ \ t Е sTU)
для всех t £Т (рис. 12.3.3). Тогда (Т, (И^)*ет) — древесное
разложение, которое (Т, (Vt)t£T) индуцирует на Я (см. лемму 12.3.2), за
исключением того, что несколько Х{ были добавлены к некоторым из
частей. Несмотря на эти добавления все еще \W%\ < \Vt\ для всех t:
Рис. 12.3.3. Wt содержит Х2 ихз) но не х\\ Wti не содержит ни одной Xi

282 Глава 12. Миноры, деревья и правильные квазиупорядочения
для каждого Х{ Е W% \ V% имеем t Е sTU, поэтому V% содержит
некоторую другую вершину из Р{ (лемма 12.3.1). Эта вершина не лежит
в Wt, так как Р,- пересекает Н только в Х{. Кроме того, (Т, (И^)*ет)
с очевидностью удовлетворяет (ТЗ), поскольку каждая Х{ добавлена
к каждой части по некоторому пути в Т, следовательно, это снова
древесное разложение.
Так как Ws = X, для (*) остается лишь показать, что
разложение является ^-допустимым. Рассмотрим любое W% порядка > к.
Тогда Wt пересекает С, так как \Х\ = £ < к. Поскольку (Ty(Vt)teT)
является ^'-допустимым и \V%\ > \W%\ > к, то V% не может
пересекаться с некоторым В Е 3$. Покажем, что W% также не пересекается
с В. В противном случае существует некоторое ж,- Е W% \ У%.
Тогда В — связное множество, пересекающееся и с Va, и с Vti, но не
пересекающееся с V%. Так как t Е sTt{ по определению Wt, это
противоречит лемме 12.3.1. D
Часто теорема 12.3.9 формулируется в терминах ежевичного
числа графа, т. е. наибольшего порядка ежевики в нем. Теорема
тогда утверждает, что древесная ширина графа в точности на
единицу меньше, чем его ежевичное число (упражнение 15).
Насколько полезным может быть даже легкое обратное
утверждение теоремы 12.3.9, можно показать еще раз на примере ежевики
пересечений в решетке к х к: эта ежевика имеет порядок к, поэтому
ввиду теоремы решетки к х к имеют древесную ширину по меньшей
мере к — 1. (Попробуйте показать это без теоремы!)
На самом же деле решетки к х к имеют древесную ширину к
(упражнение 16). Но еще более, чем это точное значение, важен
тот факт, что древесная ширина решеток стремится к
бесконечности вместе с их порядком. Действительно, как мы увидим,
миноры больших решеток создают другое каноническое препятствие
для малой древесной ширины: большие решетки (и, следовательно,
все графы, содержащие большие решетки как миноры; ср. с
предложением 12.3.6) не только имеют большую древесную ширину, но
и обратно, каждый граф большой древесной ширины содержит
минор большой решетки (теорема 12.4.4).
Еще одно каноническое препятствие для малой древесной
ширины описано в упражнении 30.
Для любых двух вершин t\, 22 Е Т лемма 12.3.1 влечет, что
каждое Vt с t Е t\Tt2 отделяет Vtl от Vt2 в G. Назовем наше древесное
разложение (Т, У) на G сцепленным, или тпощимА\ если оно
удовлетворяет следующему условию:
' В зависимости от того, который из двух двойственных аспектов в (Т4) мы
хотим подчеркнуть.

12.3. Древесные разложения
283
(Т4) для любых s £ N и ti,t2 £ Т либо G содержит s
непересекающихся Vtl-Vt2 путей, либо существует такое t £ t\Tt2,
что \Vt\ < s.
Таким образом, «ветви» в тощем древесном разложении оторваны
от любой большой части, не требующейся для поддержания их
связующих свойств: если ветвь толстая (части вдоль пути в Т велики),
то G сильно связен вдоль этой ветви.
В наших поисках древесных разложений на «малые» части мы
имеем теперь на выбор один из двух критериев: глобальный, «в
наихудшем случае», критерий ширины, который гарантирует, что Т
нетривиально (если только G не является полным графом), но не
утверждает ничего относительно древовидности G среди частей, не
являющихся наибольшими, и более тонкий локальный критерий
истощения, который гарантирует древовидность всюду по Т, но
который трудно реализовать, кроме как с тривиальным или почти
тривиальным Т. Удивительно, что тем не менее всегда можно найти
древесное разложение, которое является оптимальным относительно
обоих критериев сразу.
Теорема 12.3.10 (Томас, 1990). Каждый граф G имеет тощее
древесное разложение ширины tw(G).
Доказательство теоремы 12.3.10 не слишком длинное, но
техническое, и мы не будем излагать его. Тот факт, что эта теорема
дает нам очень полезное свойство минимальности ширины
древесных разложений «бесплатно», сделал ее ценным инструментом везде,
где применяются древесные разложения.
Древесное разложение (Т, У) графа G называется симплициалъ-
ным, если все сепараторы Vt1 П V%2 индуцируют в G полные
подграфы. Это предположение может позволить нам перенести
утверждения относительно частей разложения на сам G. Например, если
в симплициальном древесном разложении графа G все части
^-раскрашиваемы, то этим же свойством обладает и G (доказательство?).
То же самое применимо к свойству не содержать минора Кг для
некоторого фиксированного г. Нетрудно получить симплициальное
древесное разложение заданного графа на несводимые части
алгоритмически. Действительно, все, что нужно сделать, — это расщепить
граф рекурсивно по полным сепараторам; если все они выбираются
минимальными, то множество полученных частей будет даже
единственным (упражнение 22).
Обратно, если G может быть построен рекурсивно из
множества Ж графов склейкой по полным подграфам, то G имеет
симплициальное древесное разложение на элементы из Jf. Например,
по теореме 8.3.4 Вагнера любой граф без минора Кь имеет надграф
с симплициальным древесным разложением на плоские
триангуляции и копии графа Вагнера W, и аналогичное утверждение имеет
место для графов без минора К4 (см. предложение 12.4.2).

284 Глава 12. Миноры, деревья и правильные квазиупорядочения
Древесное разложение может, таким образом, приводить к
наглядным структурным характеризациям графовых свойств.
Особенно простой пример дает следующая характеризация хордальных
графов.
Предложение 12.3.11. Граф G хор дален, если и только если
G имеет древесное разложение на полные части.
Доказательство. Применим индукцию по \G\. Допустим
сначала, что G имеет такое древесное разложение (Т, У), что граф G[Vt]
полон для каждого t Е Т. Выберем (Т, У) с минимальным \Т\.
Если \Т\ < 1, то G полный и, следовательно, хордальный.
Поэтому пусть t\t2 Е Т — ребро, и для г — 1,2 определим Т{ и Gt '.—
G[Ui], как в лемме 12.3.1. Тогда G = d U G2 ввиду (И) и (Т2),
a V(G\ П G2) = Vtl П Vt2 ввиду леммы. Таким образом, граф G\ 0G2
полный. Поскольку (Т,-, (Vt)t£Ti) есть древесное разложение графа G{
на полные части, оба G,- хордальны по индукционному
предположению. (По выбору (Т, У) никакой G% не является подграфом графа
GfV^n Vi3] = GiflG2, поэтому оба Gt- действительно меньше, чем G.)
Поскольку G\ П G2 полон, любой индуцированный цикл в G лежит
в G\ или в G2 и, следовательно, имеет хорду, поэтому G также хор-
дален.
Обратно, допустим, что G хордален. Если G — полный граф,
то доказывать нечего. Если нет, то по предложению 5.5.1 G есть
объединение меньших хордальных графов Gi, G2, где граф G\ П G<i
полный. По индукционному предположению G\ и G2 имеют
древесные разложения {Т\,У\) и (Тг, ^) на полные части. По лемме 12.3.5
G\ П G2 лежит внутри одной из этих частей в каждом случае,
например с индексами t\ Е Т\ и i^ £ Т2. Как легко проверить, ((Ti UT2) +
tit2, У\ U Уъ) — древесное разложение графа G на полные части. D
Следствие 12.3.12. Имеет место равенство
tw(G) = т1п{о;(Я) - 1 | G С Я; Я хордален}.
Доказательство. По лемме 12.3.5 и предложению 12.3.11
каждый из графов Я, рассмотренных для минимума, имеет древесное
разложение ширины о;(Я) — 1. Каждое такое древесное разложение
индуцирует древесное разложение графа G по лемме 12.3.2, поэтому
tw(G) < ш(Н) — 1 для каждого Я.
Обратно, построим Я, как выше, с и;(Я) — 1 < tw(G). Пусть
(Т,У) — древесное разложение графа G ширины tw(G). Для
каждого t ЕТ пусть Kt обозначает полный граф на Vt, и положим Я :=
(J Kt. Ясно, что (Т,У) — также древесное разложение графа Я.
По предложению 12.3.11 Я хордален, а по лемме 12.3.5 и(Н) — 1 не
превосходит ширины (Т,У), т. е. не больше, чем tw(G). □

12.4. Древесная ширина и запрещенные миноры 285
12.4. Древесная ширина и запрещенные миноры
Если Jf — любое множество или класс графов, то класс
Forb^(J^) := {G | G ¥ Н для всех Н Е J?}
всех графов без минора из Jf является свойством графа, т. е.
замкнут относительно изоморфизма5). Когда имеется запись, как выше,
мы будем говорить, что это свойство выражено заданием графов
Н £ Ж в качестве запрещенных (или исключенных) миноров.
По предложению 1.7.3 Forb^(J^) замкнут относительно взятия
миноров: если G ^ G G Forb^(Jf), то G' G Forb^(Jf). Свойства
графа, которые являются замкнутыми относительно взятия миноров,
называются в этой главе наследственными. Каждое наследственное
свойство может, в свою очередь, быть выражено через запрещенные
миноры.
Предложение 12.4.1. Свойство графа 2? может быть
выражено через запрещенные миноры, если и только если оно
наследственно.
Доказательство. Часть «если» следует из того, что 3* =
Forb^(^), где & — дополнение к &. D
В разделе 12.5 мы вернемся к общему вопросу о том, как лучше
всего представить заданное наследственное свойство запрещенными
минорами. В этом разделе мы будем заниматься конкретным типом
наследственного свойства — ограниченной древесной шириной.
Итак, рассмотрим свойство иметь древесную ширину меньше
некоторого заданного целого числа к. Согласно предложениям 12.3.6
и 12.4.1 это свойство может быть выражено запрещенными
минорами. Выбирая их множество Jf минимальным, мы находим, что
Ж — {К3} для к = 2: графы древесной ширины < 2 в точности
леса. Для к = 3 имеем Ж — {К4}.
Предложение 12.4.2. Граф имеет древесную ширину < 3,
если и только если он не содержит минора К4.
Доказательство. По лемме 12.3.5 имеем tw(K4) > 3. По
предложению 12.3.6 отсюда следует, что граф древесной ширины < 3 не
может содержать К4 как минор.
Обратно, пусть G — граф без минФра К4. Предположим, что
\G\ > 3. Будем добавлять ребра к G, пока полученный граф G'
не станет реберно-максимальным без минора К4. По предложению
8.3.1 G' может быть построен рекурсивно из треугольников
склейкой по К2. Используя индукцию по числу шагов рекурсии и лемму
5) Как обычно, мы сокращаем Forb^ ({Я}) до Forb^ (Я).

286 Глава 12. Миноры, деревья и правильные квазиупорядочения
12.3.5, получаем, что каждый граф, конструируемый таким образом,
имеет древесное разложение на треугольники (как в доказательстве
предложения 12.3.11). Такое древесное разложение графа G' имеет
ширину 2, и по лемме 12.3.2 оно является также древесным
разложением графа G. D
Вопрос, обратный к вышеупомянутому, состоит в том, для
каких Н (отличных от К3 и К4) древесная ширина графов из Forb^(#)
ограничена. Интересно отметить, что нетрудно доказать планар-
ность любого такого Я. Действительно, поскольку все решетки и их
миноры планарны (почему?), то каждый класс Forb^(#) с
неплоским Н содержит все решетки. В то же время, как мы отметили после
теоремы 12.3.9, решетки имеют неограниченную древесную ширину.
Следующая глубокая и удивительная теорема утверждает, что
и, обратно, древесная ширина графов из Forb^(#) ограничена для
каждого планарного Я.
Теорема 12.4.3 (Робертсон, Сеймур, 1986). Для данного
графа Н графы без минора Н имеют ограниченную древесную ширину,
если и только если Н планарен.
Остальная часть этого раздела посвящена доказательству
теоремы 12.4.3.
Чтобы доказать теорему 12.4.3, нужно показать, что запрещение
любого планарного графа Н как минора ограничивает древесную
ширину графа. На самом деле мы должны только показать это для
частных случаев, когда Н — решетка, поскольку каждый план
арный граф есть минор некоторой решетки. (Чтобы увидеть это,
возьмем изображение графа, утолщим его вершины и ребра и наложим
достаточно ажурную плоскую решетку.) Таким образом, достаточно
доказать следующее утверждение.
Теорема 12.4.4 (Робертсон, Сеймур, 1986). Для каждого
целого числа г существует такое целое число к, что каждый граф
древесной ширины по меньшей мере к содержит минор решетки г х г.
Наше доказательство теоремы 12.4.4, которое намного короче,
чем первоначальное доказательство, выглядит следующим образом.
Пусть г задано, и пусть G — любой граф достаточно большой
древесной ширины (зависящей от г). Сначала покажем, что G
содержит большое семейство я/ = {А\у.. .уАт} непересекающихся
связных множеств вершин такое, что каждая пара Л»,Л;- £ я/ может
быть сцеплена в G семейством ^tJ- из многих непересекающихся
A{-Aj путей, избегающих все остальные множества в я/. Затем мы
рассмотрим все пары (^';> ^i'j1) этих семейств путей. Если можно
найти среди них такую пару, что многие пути из 3*ij пересекаются
со многими путями из &*i*j*, мы будем представлять себе пути из &^
горизонтальными, а пути из ^,-#у# — вертикальными и извлекать из

12.4. Древесная ширина и запрещенные миноры
287
их объединения подразбиение решетки г х г. (Это будет трудной
частью доказательства, потому что эти пути, вообще говоря,
пересекаются менее регулярным образом, чем они это делают в решетке.)
Если нет, то для каждой пары (^у, ^i'j1) многие из путей семейства
&*ij избегают многих из путей семейства ^:-/;/. Тогда мы сможем
выбрать по одному пути Р,-;- £ ^,у из каждого семейства так, чтобы
эти выбранные пути были попарно непересекающимися. Наконец,
стягивание каждого из связных множеств А £ я/ даст нам минор Кт
в G, который содержит искомую решетку г х г, если т > г2.
Чтобы реализовать эти идеи формально, нам нужны несколько
определений. Назовем множество X С V(G) внешне k-связным в G,
если \Х\ > к и для всех непересекающихся подмножеств У, Z С X
с \Y\ = \Z\ < к существует \Y\ непересекающихся Y-Z путей в G,
которые не имеют внутренних вершин и ребер в G[X]. Заметим,
что множество вершин fc-связного подграфа в G не обязано быть
внешне к-связным в G. С другой стороны, любой горизонтальный
путь в решетке г х г внешне &-связен в этой решетке для каждого
к < г (каким образом?).
Одно из первых доказываемых ниже утверждений состоит в том,
что любой граф достаточно большой древесной ширины — а не
только решетки — содержит большое внешне fc-связное множество
вершин (лемма 12.4.5). Обратно, нетрудно показать, что большие
внешне fc-связные множества (при большом к) могут существовать только
в графах большой древесной ширины (упражнение 30). Поэтому
подобно минорам больших решеток эти множества представляют собой
каноническое препятствие для малой древесной ширины: они могут
быть найдены в графе, если и только если его древесная ширина
велика.
Упорядоченную пару (Л, J5) подграфов графа G будем называть
предъячейкой в G, если G = A U В и А содержит такое дерево Т,
что:
(i) Т имеет максимальную степень < 3;
(ii) каждая вершина из А П В лежит в Т и имеет степень < 2
вТ;
(iii) Т имеет лист в А П В либо \Т\ = 1 и Т С А П В.
Порядок такой предъячейки есть число \А П J5|, и если V(A П J5)
внешне &-связен в В, то эта предъячейка есть k-ячейка в G.
Лемма 12.4.5. Пусть G — граф, a h > к > 1 — целые
числа. Если G не содержит к-ячеек порядка h, то G имеет древесную
ширину < h -f k — 1.
Доказательство. Можно считать, что G связен. Пусть
множество U С V(G) максимально при условии, что G[U] имеет
древесное разложение @ ширины < h -f k — 1 с тем дополнительным
свойством, что для каждой компоненты С из G — U соседи С в U лежат

288 Глава 12. Миноры, деревья и правильные квазиупорядочения
в одной части из 0, a (G — G, С) — предъячейка порядка < Л, где
С := G[V(C) U ЛГ(С)]. Ясно, что U ф0.
Мы утверждаем, что U — V(G). Предположим противное. Пусть
С — компонента в G — U, X := N(C), аТ — дерево, сопоставленное
предъячейке (G — G, С).
По предположению, \Х\ < h] покажем, что здесь имеет место
равенство. Если нет, то пусть и £ X — лист в Т (соответственно
{и} := V(T)), как в (iii), и пусть г/ £ С — сосед вершины и.
Положим U' := С/ U {г/} и I' := I U {г/}. Пусть Т" — дерево,
полученное из Т соединением к и, а ^' — древесное разложение графа
G[U'], полученное из & добавлением X' как новой части
(соединенной с некоторой частью из 0, содержащей X, которая существует
по выбору U] см. рис. 12.4.1). Ясно, что 0' все еще имеет ширину
< h -f k — 1. Рассмотрим компоненту С из G — U'. Если С ПС — 0,
то С7 — также компонента в G — [/, поэтому А/"(С7) лежит внутри
некоторой части из @ (а следовательно, из &), a (G — С\С') —
предъячейка порядка < h по предположению. Если С" П G ф 0, то
С'ССи TV (С") С X'. Кроме того, v £ N(C')\ в противном
случае N(C') С X отделяло бы С от г/, противореча тому факту, что
С и г/ лежат в одной и той же компоненте С графа G — Х^ Поскольку
v — лист дерева Т", нетрудно проверить, что (G — С', С") — снова
предъячейка порядка < /i вопреки максимальности [Л
Рис. 12.4-1. Расширение U и 9 при |Х| < /i
Таким образом, \Х\ — Л, поэтому, по предположению,
предъячейка (G — СУС) не может быть ^-ячейкой; пусть Y,Z С X —
множества, свидетельствующие об этом. Пусть 3* — множество
из как можно большего числа непересекающихся Y-Z путей в Н :=
G[V(C) U У U Z] — E(G[Y U Z]). Поскольку все такие пути являются
«внешними» к X в С, имеем к' := |^| < \Y\ — \Z\ < к по выбору
У и Z. По теореме Менгера (3.3.1) У и Z отделены в Н
множеством S из к' вершин. Ясно, что S имеет в точности одну вершину

12А. Древесная ширина, и запрещенные миноры 289
на каждом пути в &\ обозначим путь, содержащий вершину s £ S,
Рис. 12.4-2- S отделяет Y от Z в Н
Положим X' \— X U 5 и U' :— U U S, и пусть 07 — древесное
разложение графа G[U'], полученное из @ добавлением X' как
новой части. Ясно, что \Х'\ < \Х\ + \S\ < h -f к — 1. Покажем, что
U' противоречит максимальности U.
Поскольку YUZ С W(C) и |5| < |У| = \Z\, то 5ПС ^ 0, поэтому
U' больше, чем U. Пусть С — компонента в G—U'. Если С'ПС = 0,
мы рассуждаем, как раньше. Поэтому С" С С и N(C) С Х;. Как
и раньше, С имеет по меньшей мере одного соседа, например v,
в 5 П С, поскольку X не может отделять С" С С от S П С. По
определению S компонента С' не может иметь соседей сразу и в У \ 5,
и в Z \ 5; предположим, что их нет в У \ 5. Пусть Т' —
объединение Т и всех Y-S подпутей путей Ps с s Е N(C) П С Поскольку эти
подпути начинаются в У \ S и не имеют внутренних вершин в X',
то они не могут пересекаться с С'. Поэтому (G — С7, С7) — предъ-
ячейка с деревом Т7 и листом и; условия на степени в Т7 проверяются
легко. Ее порядок есть |N(C7)| < \Х\ - \У\ + |5| = А - \Y\ Л-к' < А;
противоречие с максимальностью U. D
Лемма 12.4.6. Пусть к >2 — целое число, Т — дерево
максимальной степени < 3, а X С V(T). Тогда Т содержит такое
множество F ребер, что каждая компонента в Т — F имеет от k до 2k — \
вершин в X, за тем исключением, что одна такая компонента может
иметь меньшее количество вершин в X.
Доказательство. Применим индукцию по \Х\. Если \Х\ <
2k — 1, мы полагаем F = 0. Поэтому допустим, что \Х\ > 2k. Пусть
е — такое ребро в Т, что некоторая компонента Т' из Т — е имеет по
меньшей мере k вершин в X и \Т'\ минимальное с этим свойством.
Так как А(Т) < 3, конец ребра е в Т7 имеет степень в Т7 не бо-

290 Глава 12. Миноры, деревья и правильные квазиупорядочения
лее двух, поэтому минимальностьТ' влечет, что \Х П V(T')\ < 2k — 1.
Применяя индукционное предположение к Т — Т', мы завершаем
доказательство. П
Лемма 12.4.7. Пусть G — двудольный граф с 2-разбиением
(A, J3), \А\ = а, \В\ — Ь, и пусть с < а и d < b — положительные
целые числа. Допустим, что G имеет не более (а — с)(6 — d)/d ребер.
Тогда существуют такие С С А и D С В, что \С\ = с, |D| = d
и С U D независимо в G.
Доказательство. Поскольку ||G|| < (a — c)(b — d)/d, менее чем
b — d вершин в В имеют более чем (а — c)/d соседей в А. Выберем
D С В так, чтобы |jD| = d и каждая вершина в D имела не более
(а — c)/d соседей в А. Тогда D посылает в А в общей сложности не
более a — с ребер, поэтому А содержит подмножество С из с вершин
без соседей в D. D
Для данного дерево Т назовем г-набор (х\,..., хг) из различных
вершин Т хорошим, если для каждого j — 1,...,г— 1, Xj-Xj+i путь
в Т не содержит ни одной из остальных вершин этого г-набора.
Лемма 12.4.8. Каждое дерево Т порядка по меньшей мере
г (г — 1) содержит хороший r-набор вершин.
Доказательство. Возьмем любую вершину х £ Т. Тогда Т —
объединение своих подпутей вида хТу, где у пробегает все листья.
Следовательно, за исключением случая, когда хотя бы один из этих
путей содержит г или более вершин, Т имеет по меньшей мере
|Т|/(г— 1) > г листьев. Поскольку любой путь из г вершин и любое
множество из г листьев порождают хороший г-набор в Т,
утверждение доказано. □
Наша следующая лемма показывает, как получить решетку из
двух больших систем путей, которые пересекаются особенно
регулярным образом.
Лемма 12.4.9. Пусть с/, г > 2 — такие целые числа, что d >
г2г+2 ]jyCTb Q — граф, содержащий множество Ж из г2 — 1
непересекающихся путей и множество У = {Vi,..., V^} из d
непересекающихся путей. Допустим, что каждый путь из У пересекает
каждый путь из Ж и что каждый путь Н Е Ж состоит из таких
d последовательных (вершинно-непересекающихся) сегментов, что
V{ пересекается с Н только в i-м сегменте для каждого i — 1,..., d
(рис. 12.4.3). Тогда G содержит минор решетки г х г.
Доказательство. Для каждого г = l,...,d рассмотрим граф
с множеством вершин Ж, в котором два пути смежны всякий раз,
когда Vi содержит под путь между ними, не пересекающий никакой
другой путь в Ж. Поскольку Vi пересекает каждый путь в Ж,
этот граф связен; пусть TJ — остовное дерево в нем. Поскольку

12.4. Древесная ширина и запрещенные миноры
291
Н
Рис. 12.4-3. Пути, пересекающиеся как в лемме 12.4.9
\Jf?\ > r(r — 1), лемма 12.4.8 влечет, что каждый из этих d > r2(r2)r
деревьев Т{ имеет хороший г-набор вершин. Поскольку имеется не
более чем (г2)г различных г-наборов на Ж', некоторые г2 из
деревьев Т{ имеют общий хороший г-набор (Я1,..., Яг). Пусть / =
{г1,...,ггг} — множество индексов этих деревьев (с ij < г* при
j < к); положим Jf?' := {Н1,...,НГ}.
Приведем неформальное описание того, как мы строим нашу
решетку г х г. Ее «горизонтальными» путями будут пути Я1,..., Яг.
Ее «вертикальные» пути будут составляться одно ребро за
другим следующим образом. Ребра первого вертикального пути (их
г — 1) берутся из первых г — 1 деревьев TJ — деревьев с
индексом г, находящимся среди первых г элементов множества /.
Точнее, его «ребром» между HJ и Я;+1 будет последовательность под-
путей в Vij (вместе с некоторыми соединяющими горизонтальными
кусками, взятыми из путей в Jf \ Jf'), индуцированных ребрами
некоторого HJ-HJ+1 пути в T{j} который не имеет внутренних вершин
в Jf"; см. рис. 12.4.4. (Вот почему нам нужно, чтобы (Я1,..., Яг)
было хорошим г-набором в каждом дереве Т{.) Аналогично, j-e ребро
второго вертикального пути берется из Н^-Н^1 пути в Tir+j и так
далее6). Чтобы слить эти отдельные ребра в г вертикальных
путей, мы далее стягиваем в каждом горизонтальном пути начальный
сегмент, который пересекается с первыми г путями V* с г £ /, затем
стягиваем сегмент, который пересекает следующие г путей V* с г £ /
и так далее.
Формально мы действуем следующим образом. Рассмотрим все
j, к £ {1,..., г}. (Мы будем считать, что индекс j перечисляет го-
6) Хотя нам нужны только г — 1 ребер для каждого вертикального пути, мы
резервируем г, а не только г — 1 путей V, для каждого вертикального пути,
чтобы сделать индексацию более наглядной. Пути Vr,V2rt... остаются
неиспользованными.

292 Глава 12. Миноры, деревья и правильные квазиупорядочения
Hj-Hj+l путь Р в Т{.
Hj-Hj+l путь Р' в G
Vh Vtj Vir+l
Я1
Hr
стягивание
***♦!
■н—
i
щ
li
1
:
1]
—к-
s
i
!
1 j
P'
j
i
|
-j—
, j
1
i
I
T < 1
i 1
Jj
Tj
il
!lj
—i—
j
1
i
1
i i
1 i
i 1
!
1
i
|
1 j
1 1
: 1
1 1
1
j
j
стягивание
стягивание
Рис.
P' как подразделенное H*-HJ+l ребро
12.4-4- Hi-H3*1 путь Р в Tij, индуцирующий сегменты Vj.
для j-ro ребра первого вертикального пути решетки

12.4. Древесная ширина и запрещенные миноры
293
ризонтальные пути, а индекс к — вертикальные пути строящейся
решетки.) Пусть Нк — минимальный подпуть в Я-7, который
содержит г-й сегмент из HJ для всех г с i(k-i)r < * < ^r (положим
г0 := 0). Пусть Я-7 получен из Я-7 сначала удалением всех вершин
после его гг2-го сегмента, а затем стягиванием каждого подпути Нк
в одну вершину vJk. Таким образом, Я7 = vJkv[ ... v{.
При заданных j £ {1,...,г—1}и&£ {1,...,г} нужно определить
путь Vk , который образует подразделенное «вертикальное ребро»
v{vi* • Этот путь будет состоять из сегментов пути V{ вместе с
некоторыми, в противном случае неиспользуемыми, сегментами путей
из 3%>\3%>1 при г := i^-i)r-\-j- Вспомним, что по определению Я7
и Я-7-1"1 этот путь Vi действительно пересекает Я-7 и Я-7-1"1 в
точности в вершинах, которые были стянуты buJ и vk соответственно.
Для определения Vk рассмотрим какой-нибудь Я^-Я-7"1"1 путь Р =
Н\ .. .Ht в Т{, который не имеет внутренних вершин в Jtf"'. (Таким
образом, Н\ = Я-7 и Н% = Я-7*1.) Каждое ребро Я5Я5+1 из Р
соответствует Я5-Я5+1 подпути пути К', который не имеет внутренней
вершины ни на одном пути в Jf. Вместе с частями i-x сегментов из
Яг,..., Я^_1 эти подпути пути К' образуют Я^-Я-7"*"1 путь Р' в G,
который не имеет внутренних вершин ни на каком из путей Я1,..., Яг
и не пересекает никакой путь из Jf вне его г-го сегмента.
Заменяя концы пути Р' на Я-7 и Я;+1 вершинами vk и г/{+
соответственно, мы получаем искомый путь Vk , образующий j-e
(подразделенное) ребро к-го «вертикального» пути нашей решетки.
Поскольку пути Р' не пересекаются для разных г, а различные пары
(j, к) порождают различные г, то пути Vk не пересекаются, за
исключением возможных общих концов vk. Кроме того, они не имеют
внутренних вершин на путях Я1,..., Яг, потому что ни один из
этих Я-7 не является внутренней вершиной никакого из путей Р С Тг,
использованных при построении Vk . □
Доказательство теоремы 12.3.4. Теперь мы готовы
доказать следующую количественную версию нашей теоремы (которая
с очевидностью влечет последнюю).
Пусть г, m > 0 — целые числа, a G — граф древесной
ширины по меньшей мере г4т (Г+2Л Тогда G содержит
в качестве минора или решетку г х г, или Кт.
2
Поскольку КТ содержит решетку гхг как подграф, можно считать,
что 2 < m < г2. Положим с := г4(г+2) и к := с2(™). Тогда с > 216 и,
следовательно, 2тп-\- 3 < ст, поэтому G имеет древесную ширину по
меньшей мере
с™2 = стк > (2т + 3)А >(т + 1)(2к - 1) + А - 1,

294 Глава 12. Миноры, деревья и правильные квазиупорядочения
достаточную по лемме 12.4.5, чтобы обеспечить наличие в G
^-ячейки (А, В) порядка (т -f l)(2k — 1). Пусть Т С А — дерево, связанное
с предъячейкой (А, В); тогда X := V(AClB) С V(T). По лемме 12.4.6
Т имеет \X\/{2k — 1) — 1 = m непересекающихся поддеревьев,
содержащих по меньшей мере по к вершин из Х\ пусть Ai,...,Am —
множества вершин этих деревьев. По определению ^-ячейки В
содержит при всех 1 < г < j < m множество 3?{j из к
непересекающихся Ai~Aj путей, которые не имеют внутренних вершин в А. Эти
множества 2?'%j немного сожмутся либо будут изменены позже в
доказательстве, но они всегда будут состоять из «многих»
непересекающихся A{-Aj путей.
Сначала в нашем доказательстве мы попытаемся найти
единственные пути Pij £ &ij, которые не пересекаются для различных
пар ij, а значит, соединяют множества А{ с образованием минера Кт
в G. Если эта попытка потерпит неудачу, мы вместо этого
предъявим два таких конкретных множества 2?ij и &pq, что многие пути
из &*{] пересекают много путей из £?pq) образуя при этом решетку
г х г по лемме 12.4.9.
Введем линейный порядок на индексных парах ij, фиксируя
произвольную биекцию a : {ij | 1 < г < j < т} —+ {0,1,..., (™) — l}.
Для £ = 0,1,... поочередно рассмотрим пару pq с cr(pq) = £ и
выберем Ар-Aq путь Ррд, который не пересекается ни с какими ранее
отобранными такими путями, т. е. с путями Pst при a(st) <£. В то же
время мы заменим все «более поздние» множества «^j
или то, что осталось от них, меньшими множествами, содержащими
только пути, не пересекающиеся с Ррд. Таким образом, для каждой
пары ij мы определим последовательность &ц — 2P\j, 2P\j,... все
меньших и меньших множеств путей, которая в конечном счете
сворачивается к 3?fj — {Pij}, когда £ возрастает до £ = cr(ij).
Более формально, пусть £* < (™) — такое наибольшее целое
число, что для всех 0 < £ < £* и всех 1 < г < j < т существуют
множества ^f,-, удовлетворяющие следующим пяти условиям.
(i) &\: — непустое множество непересекающихся A{-Aj путей
в 5, которые пересекают А только в своих концевых точках.
Всякий раз, когда множество 3?fj определено, мы записываем
объединение его путей как Hfj \— (J 2?fj-
(ii) Если cr(ij) < £} то &\- имеет в точности один элемент Pxj
и Р^ не пересекается ни с каким путем, принадлежащим
множеству 3**-Л% при ij ф st.
(iii) Если a(ij) = £, то \&\.\ - к/с21.
(iv) Если a(ij) > I, то \&f\ = к/с2£+1.
(v) Если £ = a(pq) < a(ij), то для каждого е G E(Hfj) \ Е(Н^д)
в графе (fff • U Hpq) — е не существует к/с21*1
непересекающихся Ai-Aj путей.

12.4. Древесная ширина и запрещенные миноры
295
Заметим, что согласно (iv) рассмотренные в (v) пути действительно
существуют в #/•. Цель (v) состоит в том, чтобы вынудить эти
пути повторно использовать ребра из H*q всякий раз, когда это
возможно, используя новые ребра е <fc H^q только при необходимости.
Заметим далее, что поскольку c(ij) < (™) по определению а, условия
(iii) и (iv) дают \^fj\ > с2 всякий раз, когда cr(zj) > £.
Ясно, что если £* = (™), то по (i) и (ii) мы имеем минор
(подразделенного) Кт с множествами ветвления А\,..., Ат в G.
Предположим поэтому, что £* < (™). Покажем, что I* > 0. Пусть
pq \= сг_1(0), и положим 3*^ := 3*рд. Для определения S&- при
a(ij) > 0 положим H{j := U ^V Пусть F С Е(Щ,) \ Е(Щд) —
максимально при условии, что (Я°д иЯ^) — F все еще содержит к/с
непересекающихся A{-Aj путей, и пусть 3*fj — такое множество
путей. Поскольку вершины из Ap\jAq имеют степень 1 в HpqUHij, если
только они не лежат также в А{ U Aj, то эти пути не имеют
внутренних вершин в А. Поэтому выбранные нами 3*^ удовлетворяют
условиям (i)-(v) при £ = 0.
Показав, что £* > 0, рассмотрим теперь £ \— £* — 1. Таким
образом, условия (i)-(v) выполнены для £, но не могут быть выполнены
при £+1. Пусть pq \— а~1{£). Если 3**q содержит путь Р, который
избегает множество £}{j из некоторых \ЗР\А/с путей в 3*fj для всех ij
с a(ij) > £, то можно определить З***1 для всех ij, как и раньше
(с противоречием). Действительно, пусть st := а~1(£+ 1), и
положим <3^+1 := £tX. Для a(ij) >£+1 положим Hij := \J&ij. Пусть
F С E(Hij)\E(H^1) максимально при условии, что (Я^+1иЯг;)-Р
все еще содержит по меньшей мере \3*fj \/с2 непересекающихся A{-Aj
путей, и пусть 3?^ — такое множество путей. Полагая З?*^1 : =
{Р} и ЗР\^Х := 3*fj = {Pfj} для a(ij) < £} получаем тогда семейство
множеств З*^1, которое противоречит максимальности £*.
Таким образом, для каждого пути Р £ &**q существует такая
пара ij с cr(ij) > £, что Р избегает менее чем \3*(j\/c путей в 3?\у
Для некоторых \\^рЯ\ /(*£)] этих Р пара ij будет одной и той же;
пусть 3* обозначает множество таких Р, и зафиксируем ij,
начиная с этого момента. Заметим, что \3*\ > \3*рд\/(™) = Cl^f;l/(T)
согласно (iii) и (iv).
Применим лемму 12.4.7 для нахождения таких множеств У С
^C3^qnJPC 3^fj, что
\П>\\&\ (>^|*&|).
\JP\ = г2
и каждый путь в У пересекает каждый путь в Jf. Нужно проверить,
что двудольный граф с множествами вершин 3* и 3*fj, в котором

296 Глава 12. Миноры, деревья и правильные квазиупорядочения
Р £ 2Р смежен с Q £ 3*fj всякий раз, когда Р П Q = 0, не содержит
слишком много ребер. Поскольку каждый Р £ & имеет менее чем
\&*tj\/c соседей (по определению ^), этот граф действительно имеет
не более
l^lK-|/c<|^lK-|/6r2
<im/2jK-|/2r2
<U^I/2J(K-|/r2-l)
= (|^|-[|^|/21)(|^|-г2)/г2
ребер, что и требовалось. Следовательно, У и Jf существуют, как
и утверждалось.
Хотя все («вертикальные») пути из У пересекают все
(«горизонтальные») пути из JfP, эти пути не обязательно пересекаются
таким регулярным образом, как требуется для леммы 12.4.9. Чтобы
разделить пути из Jf на сегменты и выбрать пути из У,
пересекающиеся с ними только в подходящих сегментах, мы сначала
выберем путь Q £ Jf, чтобы он служил меркой. Мы разобьем Q
на сегменты, каждый из которых пересекает большое количество
путей из У, выберем «непересекающееся» подмножество Vi,..., Vd
этих вертикальных путей, по одному из каждого сегмента (что
является наиболее тонкой задачей; здесь нам понадобится условие (v)
из определения множеств ^f.-), и, наконец, разделим остальные
горизонтальные пути на «индуцированные» сегменты, по одному на
каждый Vn-
Итак, выберем путь Q £ Jf и положим
d := Ь/^/Н = [г2г+4/т\ > г2г+2.
Заметим, что \У\ > (с/т2)\^\ > d2\^fj\.
При n=l,2,...,d—1 пусть еп — первое такое ребро в Q (если
идти от А{ к Лу), что начальная компонента Qn из Q — еп
пересекает по меньшей мере nd\£Pfj\ различных путей из У, и такое, что
еп не является ребром графа H^q. Поскольку любые две вершины
в Q, которые лежат на различных путях из У, разделены в Q
ребром не из Hpq} каждый из этих Qn пересекает в точности nd\£Pfj\
путей из У. Положим Qo := 0 и Qd '•= Q- Поскольку \У\ > d2\3*fj\,
мы, таким образом, разделили Q на d последовательных
непересекающихся сегментов Q'n := Qn — Qn-i (n = l,...,d), каждый из
которых пересекает по меньшей мере d\£Pfj\ путей из У.
Для каждого п = 1,..., d — 1 теорема Менгера (3.3.1) и условия
(iv) и (v) влекут, что HpqUHfj имеет такое множество Sn из |ЗР\^1 — 1
вершин, что (Hpq U #£•) - en — Sn не содержит путей от А{ до Aj.

12.5. Теорема о минорах графов
297
Пусть S обозначает объединение всех таких множеств 5„. Тогда
|5| < d|^f;-|, поэтому каждый Q'n пересекает по меньшей мере один
путь Vn Е У, который избегает S (рис. 12.4.5).
П
i i
*-! iQn
ч—f
-+—+-
е*~\ Qd
Р'
Sn-
л
S.
Ai
Рис. 12.4-5. Vn пересекает каждый горизонтальный путь, но избегает S
Ясно, что каждое 5„ выбирает в точности одну вершину х из
каждого пути Р е 9*j \ {Q}. Обозначим начальную компоненту
в Р — х через Рп, положим Pq := 0 и Pd := Р, и пусть Р'п \— Рп — Рп-\
при п = 1,..., d. Свойства отделимости множеств Sn теперь влекут,
что Vn П Р С Р'п для п = 1,..., d (и, в частности, что Рп ф 0, т. е.
что Pn_i С Рп)- Действительно, Кп не может пересекать Pn-i,
потому что Pn-i U Vn U (Q — Qn-i) тогда содержало бы А{-Aj путь
в (HpqUHtj) -en-i — «Sn-i и) аналогично (рассмотрим 5„), Vn не
может пересекать Р — Рп. Таким образом, для всех п = 1,..., d путь Vn
пересекает каждый путь Р £ Jf \ {Q} в точности в его n-м
сегменте Рп. Применение леммы 12.4.9 к системам путей Jf \ {Q}
и {Vi,..., Vd) теперь дает искомый минор решетки. □
12.5. Теорема о минорах графов
Наследственные графовые свойства, т. е. являющиеся
замкнутыми относительно взятия миноров, часто встречаются в теории
графов. Среди наиболее естественных примеров — свойство вложи-
мости в некоторую фиксированную поверхность, в частности пла-
нарность.
По теореме Куратовского планарность может задаваться
запрещением миноров Къ и /^3,3- Это хорошая характперизация планар-
ности в следующем смысле. Предположим, что мы хотим убедить
кого-то, что некоторый граф планарен. Это легко сделать, если мы
сможем построить изображение графа. Но как мы убедим кого-то,
что граф непланарен? По теореме Куратовского также существует
легкий способ сделать это: мы должны лишь выявить в нашем графе

298 Глава 12. Миноры, деревья и правильные квазиупорядочения
МКЪ или МКз,з как легко проверяемое «свидетельство» непланар-
ности. Наше простое предложение 12.4.2 — другой пример хорошей
характеризации: если граф имеет древесную ширину < 3, то можно
доказать это, продемонстрировав подходящее древесное разложение;
если же нет, то можно привести в качестве доказательства какой-
нибудь МК4.
Теоремы, которые характеризуют наследственное свойство 3?
множеством Ж запрещенных миноров, несомненно относятся к
числу наиболее привлекательных результатов в теории графов. Как
мы видели в доказательстве предложения 12.4.1, такая характери-
зация всегда существует — та, в которой Jf есть дополнение 3?
к ЗР. Однако естественно стремление сделать Ж как можно
меньшим. И, как оказывается, действительно существует единственное
наименьшее среди всех таких множеств Ж: множество
Jf^» := {# | Н ^-минимально в 3*}
удовлетворяет условию 3? = Forb^(Jf) и содержится в любом
другом таком множестве Jf?.
Предложение 12.5.1. 3* = Forb^(Jf^), а Ж& С Ж для
каждого множества Ж с 3? — Forb^(Jf). □
Ясно, что элементы множества Ж& несравнимы по
отношению =^ быть минором. Следующая теорема о минорах графов Ро-
бертсона и Сеймура утверждает, что любое множество
^-несравнимых графов должно быть конечно.
Теорема 15.5.2 (теорема Робертсона — Сеймура о минорах
графов). Конечные графы правильно квазиупорядочены по
отношению =^ быть минором.
Итак, каждое Jt&> конечно, т. е. каждое наследственное
свойство графа может быть представлено конечным множеством
запрещенных миноров.
Следствие 15.5.3. Каждое свойство графа, которое является
замкнутым по взятию миноров, может быть выражено как Forb^ (jtf?)
с конечным Ж. □
Как частный случай следствия 12.5.3 имеем, по крайней мере
в принципе, аналог теоремы Куратовского для каждой поверхности.
Следствие 12.5.4. Для каждой поверхности S существует
такое конечное множество графов #i,..., Я„, что Forb^ (#i,..., Hn)
содержит в точности те графы, которые не вложимы в S.
Минимальное множество запрещенных миноров было
определено в явном виде только для одной поверхности, отличной от сферы;

12.5. Теорема о минорах графов
299
для проективной плоскости известно, что оно состоит из 35
запрещенных миноров. Нетрудно показать, что число запрещенных
миноров быстро растет вместе с родом поверхности (упражнение 34).
Полное доказательство теоремы о минорах графов заняло бы
целую книгу или даже две. Однако при всей его сложности в деталях
уловить основную идею легко. Нужно показать, что каждая
бесконечная последовательность
Go, Gi, G2,...
конечных графов содержит хорошую пару — два графа Gt =^ Gj
с г < j. Можно считать, что Go ^ G,- для всех г > 1, поскольку Go
образует хорошую пару с любым графом Gj, минором которого он
является. Таким образом, все графы Gi, G2, ■ • • лежат в For b^ (Go),
и можно использовать структуру, общую для этих графов, при
поиске хорошей пары.
Мы уже видели, как это работает, когда Go план арен: в этом
случае графы в Forb^(Go) имеют ограниченную древесную ширину
(теорема 12.4.3) и поэтому правильно квазиупорядочены по
теореме 12.3.7. Вообще говоря, нам нужно рассмотреть только случай
Go = Кп. Поскольку Go =^ Кп для га :— |Go|, можно считать, что
Кп ^ Gi для всех г > 1.
Доказательство теперь следует той же схеме, что и выше: снова
графы в Forb^(Arn) могут быть охарактеризованы через их
древесные разложения, и снова их древовидное строение, как в теореме
Краскала, помогает доказать, что они являются правильно
квазиупор ядоченными. Части в этих древесных разложениях теперь уже
не ограничены в терминах порядка, но они ограничены в более
тонких структурных терминах. Говоря упрощенно, для каждого га
существует такое конечное множество 5? замкнутых поверхностей, что
каждый граф без минора Кп имеет симплициальное древесное
разложение на части, каждая из которых «почти» вложима в одну из
поверхностей S £ У («Почти» скрывает меру беспорядка, которая
зависит от га, но не от вкладываемого графа.) С помощью
обобщения теоремы 12.3.7 и, следовательно, теоремы Краскала теперь, по
существу, достаточно доказать, что множество всех частей в этих
древесных разложениях является правильно квазиупорядоченным;
тогда графы, разлагающиеся на эти части, также являются
правильно квазиупорядоченными. Поскольку У конечное, каждая
бесконечная последовательность таких частей имеет бесконечную
подпоследовательность, все члены которой (почти) вложимы в одну и ту
же поверхность S £ У. Таким образом, нужно лишь показать, что
для любой замкнутой поверхности S все графы, вложимые в S\
правильно квазиупорядочены по отношению быть минором.
Это показывается индукцией по роду поверхности S (точнее,
по 2 — x(S)} где x(S) обозначает эйлерову характеристику поверх-

300 Глава 12. Миноры, деревья и правильные квазиупорядочения
ности S) с использованием того же подхода, что и раньше: если
Но, Hi, #2,... — бесконечная последовательность графов, вложимых
в S, то можно считать, что ни один из графов Hi, Я2,... не
содержит Но как минор. Если S = S2, то мы возвращаемся к случаю,
когда Но планарен, поэтому индукция начинается. Для шага
индукции допустим теперь, что S ф S2. Снова исключение Но как
минора ограничивает строение графов Hi, #2, • ■ •» на этот раз
топологически: каждый Н{ с г > 1 имеет вложение в S, которое
пересекается с некоторой нестягиваемой замкнутой кривой С,' С 5 в не
более чем ограниченном числе вершин (и не пересекается с
ребрами), скажем, в Х{ С V(Hi). (Оценка на \Х{\ зависит от Но, но
не от Н{.) Разрезая по Сг и пришивая диск к каждой из одной
или из двух замкнутых граничных кривых, возникающих из
разреза, получаем одну или две новых замкнутых поверхности большей
эйлеровой характеристики. Если разрез порождает только одну
новую поверхность Si, то наше вложение Hi — Xi все еще считается
почти-вложением Яг- в Si (поскольку Xi мало). Если это происходит
для бесконечно многих г, то бесконечно многие из поверхностей Si
также совпадают, и индукционное предположение дает нам хорошую
пару среди соответствующих графов Яг-. С другой стороны, если
мы получаем две поверхности S[ и S[' для бесконечно многих г (без
ограничения общности те же самые две поверхности), то Я»
разлагаются соответственно на подграфы Н[ и Щ, вложенные в эти
поверхности, с V(H[ П Я/7) = Х{. Множество всех вместе взятых
таких подграфов снова правильно квазиупорядочено по
индукционному предположению и, следовательно, таковы же и пары (Яг-,Яг-;)
ввиду леммы 12.1.3. Используя усиление леммы, которое принимает
во внимание не только сами графы Н[ и Н", но также и то, как
Х{ лежит внутри них, мы, наконец, получаем индексы г, j не только
с Н[ ^4 Щ и Щ =$ Hj', но также и такие, что эти вложения
продолжаются до искомого вложения Яг- как минора в Hj, завершая
доказательство теоремы о минорах.
Наряду с ее воздействием на «чистую» теорию графов
теорема о минорах графов имеет далеко идущие алгоритмические
следствия. Используя свою теорему о древовидной структуре для графов
в Forb^(Ar"), Робертсон и Сеймур показали, что проверка для
любого фиксированного минора является «быстрой»: для каждого
графа Я существует алгоритм полиномиальной сложности7^, который
выясняет, действительно ли граф на входе содержит Я как минор.
Ввиду теоремы о минорах тогда каждое наследственное свойство
графа 3* может быть распознано за полиномиальное (даже
кубическое) время: если #!,...,#* — соответствующие минимальные
7) На самом деле кубический, хотя обычно с огромной константой, зависящей
от Я.

Упражнения 301
запрещенные миноры, то проверка графа G на принадлежность к £?
сводится к проверке к утверждений вида #г- =^ G!
Следующий пример показывает, как глубоко это
алгоритмическое следствие воздействует на теорию сложности алгоритмов на
графах. Назовем граф безузловым, если его можно вложить в Е3 так,
чтобы ни один из его циклов не образовывал нетривиальный узел. До
теоремы о минорах графов было нерешенной проблемой, является
ли отсутствие узлов разрешимым свойством, т. е. существует ли
вообще алгоритм (неважно, сколь медленный), который выясняет
для любого заданного графа, является ли этот граф безузловым.
И по сей день ни один такой алгоритм не известен. Однако, как легко
видеть, свойство отсутствия узлов является наследственным:
стягивание ребра в графе, вложенном в 3-мерное пространство, не будет
создавать узел там, где его не было прежде. Следовательно, ввиду
теоремы о минорах существует алгоритм, который распознает
отсутствие узлов — даже за полиномиальное (кубическое) время!
Но сколько бы ни были эффектными такие неожиданные
решения давно стоявших проблем, рассматривать теорему о минорах
графов всего лишь с точки зрения ее следствий будет
несправедливо. По меньшей мере столь же важны и методы, развитые для ее
доказательства, различные способы построения миноров и работы
с ними. Большинство из них даже не были затронуты здесь, но они,
по-видимому, будут влиять на развитие теории графов еще многие
годы.
Упражнения
1.~ Пусть < — квазиупорядочение на множестве X. Назовем два элемента
х,у G X эквивалентными, если х < у и у < х. Показать, что это
действительно отношение эквивалентности на X и что < индуцирует частичное
упорядочение на множестве классов эквивалентности.
2. Пусть (А, <) — квазиупорядочение. Для подмножеств X С А положим
Forb<(X) := {а Е А \ а £ # для всех х & X}.
Показать, что < есть правильное квазиупорядочение на А, если и только
если каждое подмножество В С А, замкнутое относительно > (т. е. такое,
что х<у&В=>х&В), может быть представлено как В = Forb<(X)
с конечным X.
3. Доказать предложение 12.1.1 и следствие 12.1.2 непосредственно, не
пользуясь теоремой Рамсея.
4. Для данных квазиупорядочений (X, <) и подмножеств А, В С X будем
писать А <7 В, если существует сохраняющее порядок инъективное
отображение /: А —► В с а < /(а) для всех а Е А. Остается лив силе лемма 12.1.3,
если рассматриваемое квазиупорядочение на [^]<и' есть <7?
5.~ Показать, что определенное в тексте отношение < между корневыми
деревьями — действительно квазиупорядочение.

302 Глава 12. Миноры, деревья и правильные квазиупорядочения
6. Показать, что конечные деревья не являются правильно квазиупорядочен-
ными по отношению вложенности подграфов.
7. Последний шаг доказательства теоремы Краскала рассматривает
«топологическое» вложение Тт в Тп, которое отображает корень дерева Тт в
корень дерева Тп. Предположим индуктивно, что деревья Ат вложены в
деревья Ап таким же образом, т. е. корни отображаются в корни.
Кажется, что таким образом мы получаем доказательство утверждения, что
конечные корневые деревья являются правильно квазиупорядоченными по
отношению вложенности подграфов, даже с корнями, отображающимися
в корни. В чем здесь ошибка?
8Л Показать, что конечные графы не являются правильно
квазиупорядоченными по отношению быть топологическим минором.
9.+ Является ли класс {G | G ~fr Pk} правильно квазиупорядоченным по
отношению вложенности подграфов при заданном k Е N?
10. Показать, что граф имеет древесную ширину не более 1, если и только если
он — лес.
11. Пусть G — граф, Т — множество, a (Vt)teT — семейство подмножеств
в V(G), удовлетворяющее условиям (Tl) и (Т2) из определения древесного
разложения. Показать, что существует дерево на Т, для которого (ТЗ)
верно, если и только если существует такая нумерация t\,.. ., tn дерева Т,
что для каждого к = 2,..., п существует j < к, удовлетворяющее условию
V.fcn(J Vb.-CVt,..
Кк
(Это новое условие часто удобнее для проверки, чем (ТЗ). Оно может
помочь, например, при построении древесного разложения на заданное
множество частей.)
12. Докажите следующее обратное утверждение к лемме 12.3.1: если (Т,У)
удовлетворяет условию (Tl) и утверждению леммы, то (Т, У) — древесное
разложение графа G.
13. Может ли древесная ширина подразделения графа G быть меньше, чем
tw(G)? Может ли она быть больше?
14. Пусть (Т, (Vt)teT) — древесное разложение графа G. Для каждой
вершины v G G положим Tv := {t G Т | v G Vt}. Показать, что Tv всегда
связно в Т. Более общо, для каких подмножеств U С V(G) множество
{t & Т \ Vt П U ф 0} всегда связно в Т (т. е. при всех древесных
разложениях)?
15." Показать, что древесная ширина графа на единицу меньше, чем его число
ежевики.
16. С помощью теоремы 12.3.9 показать, что решетка к X к имеет древесную
ширину не меньше к, и найти древесное разложение ширины в точности к.
17. Пусть 38 — ежевика максимального порядка в графе G. Показать, что
каждое древесное разложение минимальной ширины в G имеет единственную
часть, покрывающую 38.
18."*" Во второй половине доказательства теоремы 12.3.9 пусть Н' — объединение
Н и путей Pi,..., Р/, пусть Н" — граф, полученный из Н' стягиванием
каждого Р,, и пусть (Т, {^{')teT) — древесное разложение, индуцированное
на Н" (как в лемме 12.3.3) разложением, которое (Т, (Vt)teT) индуцирует
на Я'. Является ли оно, после очевидного отождествления Н" с Н', тем
же разложением, что использовалось в доказательстве, т. е. верно ли, что
W? = Wt для всех t G Т?
19. Показать, что любой граф с симплициальным древесным разложением на
Аг-раскрашиваемые части в свою очередь /с-раскрашиваем.

Упражнения
303
20. Пусть Ж — множество графов, а граф G построен рекурсивно из
элементов Ж склейкой по полным подграфам. Показать, что G имеет симпли-
циалъное древесное разложение в элементы множества Ж.
21. Для данных древесного разложения (Т, (Vt)t£T) на G и t G Т пусть Ht
обозначает граф, полученный из G[Vt] добавлением всех таких ребер ху, что
х, у G Vt П Vti для некоторого соседа t' вершины t в Т. Назовем графы Ht
торсами этого древесного разложения. Показать, что в G нет минора Кь.
если и только если G имеет древесное разложение, в котором каждый торс
является или планарным, или копией графа Вагнера W (рис. 8.3.1).
22."*" Назовем граф несводимым, если он не разделяется никаким полным
подграфом. Каждый (конечный) граф G может быть разбит на несводимые
индуцированные подграфы следующим образом. Если G имеет
разделяющий полный подграф 5, то разложим G на собственные индуцированные
подграфы G'hG"cG = G'U G" иС'П G" = 5. Затем разложим G' и G"
таким же образом и так далее, пока все полученные графы не станут
несводимыми. Согласно упражнению 20 G имеет симплициальное древесное
разложение на эти несводимые подграфы. Показать, что они будут определены
однозначно, если всегда выбирать полные сепараторы минимальными.
23.+ Если & — семейство множеств, то граф G на & с XY Е E{G) & X П
Y ф 0 называется графом пересечения семейства &. Показать, что граф
хорд а лен, если и только если он изоморфен графу пересечения семейства
(множеств вершин) поддеревьев некоторого дерева.
24. Древесное разложение графа называется путевым разложением, если его
дерево разложения есть путь. Показать, что граф имеет путевое
разложение на полные графы, если и только если он изоморфен графу интервалов.
(Графы интервалов определены в упражнении 37 главы 5.)
25. Путевая ширина pw(G) графа G определяется как наименьшая ширина
его путевого разложения (см. упражнение 24). Доказать следующий
аналог следствия 12.3.12 для путевой ширины: каждый граф G удовлетворяет
равенству pw(G) = minw(H) — 1, где минимум берется по всем графам
интервалов Н', содержащим G.
26.+ Имеют ли деревья неограниченную путевую ширину?
27. Пусть & — наследственное свойство графа. Показать, что усиление
понятия минора (например, до топологического минора) увеличивает множество
запрещенных миноров, требуемых для характеризации 2Р.
28. Выведите из теоремы о минорах, что каждое наследственное свойство
может быть выражено запрещением конечного числа топологических миноров.
Верно ли то же самое для каждого свойства, которое является замкнутым
по взятию топологических миноров?
29. Показать, что каждый горизонтальный путь в решетке А: X А: внешне Аг-связен
в этой решетке.
30."'" Показать, что древесная ширина графа велика, если и только если он
содержит большое внешне Аг-связное множество вершин, где А: велико. Например,
показать, что графы древесной ширины < А: не содержат внешне (А: + 1)-
связного множества из ЗА: вершин и что графы, не содержащие внешне
(А: + 1)-связного множества из ЗА: вершин, имеют древесную ширину < 4/с.
31.+ Найти такую N —* N2 функцию A: i—► (h,£), что каждый граф с внешне
^-связным множеством (см. упражнение 30) из h вершин содержит ежевику
порядка по меньшей мере А:. Выведите отсюда ослабление теоремы 12.3.9
о том, что при заданном А: каждый граф достаточно большой древесной
ширины содержит ежевику порядка не меньше к.
32. Не пользуясь теоремой о минорах, показать, что хроматическое число
графов в любой =^-антицепи ограничено.

304 Глава 12. Миноры, деревья и правильные квазиупорядочения
33. Принадлежащая Сеймуру гипотеза о само минорности утверждает, что
каждый счетно-бесконечный граф есть собственный минор самого себя.
Сформулируйте это утверждение точно и выведите из него теорему о
минорах.
34. Для заданной ориентируемой поверхности 5 рода g найдите нижнюю оценку
в терминах g для числа запрещенных миноров, необходимых, чтобы
охарактеризовать вложимость в 5.
(Подсказка. Наименьший род ориентируемой поверхности, в которую
может быть вложен заданный граф, называется (ориентируемым) родом этого
графа. Воспользуйтесь теоремой о том, что род графа равен сумме родов
его блоков.)
Примечания
Теорема Краскала о правильных квазиупорядочениях конечных деревьев
была сначала опубликована в: Kruskal J. A. Well-quasi ordering, the tree theorem,
and Vaszonyi's conjecture// Trans. Amer. Math. Soc. 1960. 95. P. 210-225. Наше
доказательство принадлежит Нэш-Вильямсу, который ввел гибкую технику
выбора «минимальной плохой последовательности». Эта техника была также
использована нами в доказательстве леммы 12.1.3 Хигмана.
Нэш-Вильямс обобщил теорему Краскала на бесконечные графы. Это
обобщение намного труднее, чем конечный случай; оно является одной из самых
глубоких теорем в теории бесконечных графов. Общая теорема о минорах графов
для произвольных бесконечных графов не имеет места, как показано в статье:
Thomas R. A counterexample to «Wagner's conjecture» for infinite graphs // Math.
Proc. Cambridge Philos. Soc. 1988. 103. P. 55-57. Можно ли распространить
теорему о минорах на счетные графы, остается нерешенной проблемой.
Понятия древесного разложения и древесной ширины были сначала
введены (под другими названиями) в статье: Halin R. 5-functions for graphs //
J. Geometry. 1976. 8. P. 171-186. Среди прочего Халин показал, что решетки
могут иметь произвольно большую древесную ширину. Робертсон и Сеймур
повторно ввели эти два понятия, очевидно, не зная о статье Халина, с прямой
ссылкой на работу: Wagner К. Uber eine Eigenschaft der ebenen Komplexe //
Math. Ann. 1937. 114. P. 570-590. (Это классическая статья, в которой симпли-
циальные древесные разложения были введены для доказательства теоремы 8.3.4;
ср. с упражнением 21.) Симплидиальные древесные разложения подробно
рассматриваются в книге: Diestel R. Graph Decompositions. Oxford: Univ. Press,
1990.
Робертсон и Сеймур сами обычно ссылаются на теорему о минорах графов
как на гипотезу Вагнера. Кажется, Вагнер действительно обсуждал эту задачу
в 1960-е годы со своими тогда еще студентами Халином и Мадером. Однако
Вагнер, по-видимому, никогда не предполагал ее положительного решения, и он
определенно отклонял любые ссылки на эту «гипотезу», когда она была доказана.
Робертсон и Сеймур привели доказательство теоремы о минорах графов
в серии из более чем 20 статей под общим названием «Миноры графов» (в
частях IV-VII, IX-XII и XIV-XX), которая публикуется в Journal of Combinatorial
Theory. Ser. В начиная с 1983 г. Из цитируемых в этой главе их теорем
теорема 12.3.7 взята из статьи «Миноры графов. IV», а теоремы 12.4.3 и 12.4.4 —
из статьи «Миноры графов. V». Наше короткое доказательство этих последних
теорем взято из: Diestel R., Gorbunov К. Yu., Jensen Т. R., Thomassen С Highly
connected sets and the excluded grid theorem // J. Combin. Theory. Ser. B. 1999.
75. P. 61-73.
Теорема 12.3.9 доказана в статье: Seymour P. D., Thomas R. Graph
searching and a min-max theorem for tree-width // J. Combin. Theory. Ser. B. 1993. 58.
P. 22-33. Наше доказательство является упрощением первоначального
доказательства. Рид дает поучительный вводный обзор по древесной ширине и
минорам графов, включая некоторые алгоритмические аспекты, в: Surveys in
Combinatorics I Ed. by R. A. Bailey. Cambridge: Univ. Press, 1997. P. 87-162. Рид

Примечания
305
также ввел в обиход термин «ежевика»; в статье Сеймура и Томаса ежевики
назывались «ситами».
Препятствиями для малой древесной ширины, фактически
использованными в доказательстве теоремы о минорах графов, были не ежевики, а так
называемые сплетения. Сплетения являются более мощными, чем ежевики, и вполне
заслуживают изучения. Для ознакомления со сплетениями и их связями с еже-
виками и древесными разложениями см. «Миноры графов. X» или обзор Рида.
Теорема 12.3.10 получена в работе: Thomas R. A Menger-like property of
tree-width; the finite case // J. Combin. Theory. Ser. B. 1990. 48. P. 67-76.
Как предварительную версию теоремы 12.4.3 Робертсони Сеймур доказали
следующий ее аналог для путевой ширины («Миноры графов. I»): исключение
графа Н как минора ограничивает путевую ширину графа, если и только если
Н — лес. Короткое доказательство этого результата, с оптимальными оценками
можно найти в первом издании этой книги или в статье: Diestel R. Graph
Minors. I: ashort proof of the path width theorem // Combin. Probab. Comput. 1995.
4. P. 27-30.
Bee 35 минимальных запрещенных миноров для графов, вложимых в
проективную плоскость, были найдены в статье: Archdeacon D. A Kuratowski theorem
for the projective plane // J. Graph Theory. 1981. 5. P. 243-246. Верхняя оценка
для числа запрещенных миноров, требуемых для произвольной замкнутой
поверхности, дана в работе: Seymour P. D. A bound on the excluded minors for
a surface // J. Combin. Theory. Ser. В. (в печати). В статье: Mohar В.
Embedding graphs in an arbitrary surface in linear time // Proc. 28th Ann. ACM STOC.
Philadelphia, 1996. P. 392-397 — описывается множество алгоритмов, по одному
для каждой поверхности, которые распознают вложимость в эту поверхность
за линейное времени. Как следствие Мохар получает независимое и
конструктивное доказательство «обобщенной теоремы Куратовского» (следствие 12.5.4).
Другое независимое и короткое доказательство этого следствия, которое
опирается на теорему 12.4.3 и «Миноры графов. IV», но ни на какие другие статьи
из серии «Миноры графов», найдено в статье: Thomassen С. A simpler proof
of the excluded minor theorem for higher surfaces // J. Combin. Theory. Ser. B.
1997. 70. P. 306-311. Обзор классических теорем о запрещенных минорах дан
в главе 6.1 книги: Diestel R. Graph Decompositions. Oxford: Univ. Press, 1990.
Более поздние результаты рассмотрены в работе: Thomas R. Recent excluded
minor theorems // Surveys in Combinatorics / Ed. by J. D. Lamb, D. A. Preece.
Cambridge: Univ. Press, 1999. P. 201-222.
Для каждого графа X статья «Миноры графов. XIII» дает явный алгоритм,
который для каждого графа G на входе решает за кубическое время, верно ли,
что X =^ G. Константы в кубических многочленах, ограничивающих время
работы этих алгоритмов, зависят от X, но конструктивно ограничены сверху.
Краткий обзор алгоритмических следствий серии «Миноры графов» см. в обзоре
Джонсона по NP-полноте в: J. Algorithms. 1987. 8. Р. 285-303.
Понятие «хорошая характеризация» свойства графа было впервые
предложено в: Edmonds J. Minimum partition of a matroid into independent subsets //
J. Research of the National Bureau of Standards. Ser. B. 1965. 69. P. 67-72. Ha
языке теории сложности характеризация является хорошей, если, она указывает
такие два утверждения о графах, что для любого графа G первое
утверждение имеет место для G, если и только если второе ложно, и при этом каждое
утверждение, если оно верно для G, предоставляет свидетельство своей
истинности. Таким образом, каждая хорошая характеризация имеет то следствие, что
проблема разрешимости, соответствующая свойству, которое она характеризует,
лежит в NP П co-NP.

Указания ко всем упражнениям
Пояснение. Эти указания призваны наставить на верный путь того, кто
уже потратил некоторое время на упражнение, но не добился успеха. Они вряд ли
будут полезными без таких начальных усилий. С другой стороны, они не смогут
отнять все удовольствие от задачи, сразу раскрыв ключевую идею. Однако они
могут помочь сосредоточить усилия на одном из возможных подходов к решению.
Указания к главе 1
1." Сколько ребер инцидентно каждой вершине?
2. Средняя степень и ребра: рассмотрите степени вершин. Диаметр: как
определить расстояние между двумя вершинами, зная их 0-1
последовательности? Обхват: есть ли в этом графе цикл длины 3? Периметр: разбейте
d-мерный куб на кубы меньшей размерности и воспользуйтесь индукцией.
3. Рассмотрите, как данный путь пересекается с С. Где видны циклы, и могут
ли все они быть короткими?
4.~" Можете ли Вы найти графы, для которых в предложении 1.3.2 достигается
равенство?
5. Оцените расстояния в G относительно центральной вершины.
6.+ Рассмотрите случаи с£ = 2ис£>2по отдельности. При d > 2 усильте
оценку для \Di\ при i > 0, данную в доказательстве предложения 1.3.3.
7.~" Допустите противное и придите к противоречию.
8."" Найдите две вершины, связанные двумя независимыми путями.
9. (i) Непосредственно из определений.
(ii) Докажите к > п индукцией по п: разбейте n-мерный куб на кубы
меньшей размерности и покажите по индукции, что удаление < п вершин
оставляет связный подграф.
10. Для доказательства первого неравенства рассмотрите концевые вершины
множества из A(G) ребер, удаление которых разъединяет G. Для
доказательства второго неравенства воспользуйтесь определением числа A(G).
11."" Попробуйте найти контрпример при к = 1.
12. Перефразируйте (i) и (ii) как утверждения© существовании некоторых двух
функций N —► N. Чтобы показать равносильность, выразите каждую из
этих функций через другую. Покажите, что (iii) может выполняться даже
если ни (i), ни (ii) не выполняются, и усильте (iii) так, чтобы исправить
это.

Указания к главе 2
307
13.+ Попробуйте следовать доказательству, предполагая e(G) > 2/с вместо
условия (и). Почему это не проходит, и почему условие (ii) исправляет
ситуацию?
14. Выведите (i) =>■ (ii) =>■ (iii) =>■ (iv) =>■ (i) из определений используемых
понятий.
15. Рассмотрите пути, выходящие из вершины максимальной степени.
16. Теорема 1.5.1.
17. Индукция.
18. Легче всего применить индукцию по \Т\. Какого вида вершину лучше всего
удалять из Т на индукционном шаге?
19. Возможна индукция по |Т|, но не только она.
20. Подсчитайте ребра.
21. Покажите, что если граф содержит нечетный цикл, то содержит и
индуцированный нечетный цикл.
22. Воспользуйтесь предложением 1.2.2. Разбейте найденный там подграф на
две части так, чтобы каждая вершина имела много соседей в другой части.
23. Постарайтесь перенести доказательство для конечных графов на
бесконечный случай. Где оно не проходит?
24."" Воспользуйтесь предложением 1.9.2.
25. Почему все разрезы E(v) порождают пространство разрезов? Будет ли это
иметь место после удаления одного из них? А двух?
26. Начните со случая, когда рассматриваемый граф есть цикл.
27. Индукция по \F \ Е(Т)\ при фиксированном F Е ^(G).
28. Индукция по \D П Е(Т)\ для фиксированного разреза D.
29. Воспользуйтесь теоремой 1.9.6.
Указания к главе 2
1.~ Сравните данное паросочетание с паросочетанием наибольшей мощности.
2. Увеличивающие пути.
3. Если в конечном случае вы имеете 5 С S' С А с \S\ = |АГ(5)|, то условие
паросочетаемости гарантирует, что N(S) С N(S'): рост 5 делает
доступным большее количество соседей. Использовать факт, что это не так, если
5 бесконечно.
4. Примените теорему о свадьбах.
5. Постройте двудольный граф, одна из долей которого равна А, а другая
состоит из подходящего числа копий множеств А{. Определите множество
ребер этого графа так, чтобы желаемый результат вытекал из теоремы
о свадьбах.
бЛ Постройте цепи в решетке подмножеств множества X следующим образом.
Для каждого к < п/2 используйте теорему о свадьбах, чтобы найти такое
взаимно-однозначное отображение ф из множества А всех /:-подмножеств на
множество В всех (к-f l)-подмножеств множества X, что Y С Ф{У) для всех
Y £А.

308 Указания ко всем упражнениям
7. Решите, куда попадут листья: в фактор-критические компоненты или в 5?
8. Рассмотрите случаи \S\ < 1 и \S\ > 2 по отдельности.
9. Случай 5 = 0 прост. Во втором случае надо искать вершину, входящую во
всякое паросочетание максимальной мощности. Каковы последствия этого
для остальных вершин?
10. Для направления «тогда» рассмотрите граф, предложенный в подсказке:
есть ли в нем 1-фактор? Если нет, то рассмотрите множество вершин,
задаваемое теоремой Татта об 1-факторе. Другой способ решения: применить
замечания о паросочетаниях наибольшей мощности, приведенные после
доказательства теоремы 2.2.3.
11." Следствие 2.2.2.
12. Пусть G — двудольный граф, удовлетворяющий условию паросочетаемо-
сти, разбитый, скажем, на доли (А, В). Сведите задачу к случаю \А\ =
\В\. Чтобы проверить посылку теоремы Татта для данного множества
5 С V(G), оцените \S\ снизу в терминах числа компонент графа G - S,
содержащих больше вершин из А, чем из В, и наоборот.
13." Рассмотрите любое наименьшее покрытие путями.
14. Направьте все ребра из А в В.
15." Дилворт.
16. Начните с множества элементов, минимальных в Р.
17. Считайте, что элементы из А меньше, чем их соседи из В.
18.+ Допустите, что (х, у) < (я:', у1) тогда и только тогда, когда х < х1 и у < у1.
Указания к главе 3
1."~ Вспомните определения терминов «компонентами «разделять».
2. Опишите словами то, что видно на рисунке.
3. Для ответа на первый вопрос используйте упражнение 1. Второй вопрос
требует элементарных вычислений, их может подсказать рисунок.
4. Доказательства требует только первая часть — вторая получается в силу
симметрии. Так что предположим, что какая-то компонента графа G — X
не пересекается с X', и обратимся к упражнению 1. Где лежит Х,Г}. Все ли
наши предположения относительно X' остаются в силе?
5.~ Каким образом блок может не быть максимальным 2-связным подграфом?
Что еще верно в этом случае?
6. Выведите связность графа блоков из связности исходного графа, а его
ацикличность — из максимальности каждого блока.
7. Докажите предложение по индукции, используя предложение 3.1.2. Либо
выберите цикл, проходящий через первую вершину и лежащий на
минимальном расстоянии от второй. Покажите, что это расстояние не может
быть больше нуля.
8. Принадлежность к одному и тому же блоку — отношение эквивалентности
на множестве ребер; см. упражнение 5.
9. Индукция согласно предложению 3.1.2.

Указания к главе 4
309
10. Предполагая, что G/xy не является 3-связным, рассмотрите по отдельности
случаи, когда vxy лежит внутри либо снаружи разделяющего множества из
не более чем двух вершин.
11. (i) Рассмотрите ребра, инцидентные меньшему разделяющему множеству,
(ii) Индукция показывает, что всякий так построенный граф кубичен
и 3-связен. Чтобы провести доказательство в обратную сторону,
рассмотрите такой максимальный подграф ТН С G, что Н можно построить
описанным образом; затем покажите, что Н = G.
12." Может ли это быть не так при произвольном выборе X и 0* согласно
теореме Менгера?
13. Выберите непересекающиеся А-В пути в L(G) минимальными.
14. Рассмотрим самый длинный цикл С. Как к нему присоединены оставшиеся
вершины?
15. Рассмотрите цикл, проходящий через наибольшее возможное количество из
этих к вершин. Если одна из вершин в него не входит, можно ли провести
цикл иначе, чтобы включить ее?
16. Рассмотрите описанный в подсказке граф. Покажите, что любое
подмножество его вершин, пересекающееся со всеми Я-путями (но не с самим Н),
соответствует подобному же подмножеству в E(G) \Е(Н). Что в G
соответствует паре Н-путей во вспомогательном графе?
17.~ Сколько путей может разместить каждый из A'2m+1?
18. Выберите подходящие степени вершин в В.
19.+ Пусть Н — граф без ребер на новых вершинах. Рассмотрите множества
XhF, которые обеспечивает теорема Мадера, если G' не содержит |Cj|/2
независимых Я-путей. Если в G нет 1-фактора, используйте их, чтобы
найти подходящее множество, которое сыграет роль 5 в теореме Татта.
20. Чуть-чуть подумайте.
21. ~ Если две вершины s, t разделяются менее чем 2к—1 вершинами, продолжите
{s} и {t} до /г-множеств 5 и Т, показывающих, что G не /с-сцеплен.
Указания к главе 4
1. Вкладывайте вершины по индукции. Куда не следует помещать новую
вершину?
2." Рис. 1.6.2.
3.~ Сделайте граф связным.
4. Это обобщение следствия 4.2.8.
5. Теорема 3.5.4.
6. Действуйте, как при доказательстве следствия 4.2.8.
7. Предложение 4.2.10.
8.~ Выразите различие между этими двумя изображениями как строгое
утверждение о вершинах, гранях и инцидентности между ними.
9. Комбинаторно: воспользуйтесь определением. Топологически: выразите
относительное положение коротких (соответственно длинных) ветвей в G'
формально как свойство графа G', которое любой топологический
изоморфизм сохранял бы, a G не может сохранять.

310 Указания ко всем упражнениям
10.~ Рефлексивность, симметричность, транзитивность.
11. Найдите граф, у которого изображения выглядят одинаково, но который
допускает автоморфизм, не продолжаемый до гомеоморфизма плоскости.
Возьмите этот автоморфизм за <?2 ° °\ •
12.+ Звездообразная форма: каждая внутренняя грань содержит точку, из
которой видна вся гранила грани.
13. Работайте с плоским, а не с пленарным графом.
14. (i) Множество ЗС может быть бесконечным.
(ii) Если Y является ТХ, то любой ТУ также является ТХ.
15." Ввиду следующего упражнения контрпример имеет разделяющее
множество из не более чем двух вершин.
16. Добавьте дополнительное условие в индукционное предположение. Это
поможет избежать многоугольников с углами в 180 градусов.
17. Число ребер.
18. Воспользуйтесь тем, что максимальные планарные графы 3-связны, а
соседи каждой вершины индуцируют цикл.
19. Если G = G\ U Gi с G\ П Gi = К2, у нас возникает затруднение. Его не
будет, если мы будем вкладывать немного больше, чем необходимо.
20. Воспользуйтесь подходящей модификацией заданного графа G,
моделирующей внешнепланарность.
21. Воспользуйтесь тем фактом, что ^(G) является прямой суммой ^(Gi)
иВД).
22.+ Эйлер.
23. Границы внутренних граней образуют базис в ^(G).
24."~ Каковы те грани, с которыми может пересекаться ребро е*
(рассматриваемое как дуга многоугольника)?
25." Сколько в нем вершин?
26."~ Соедините две заданные вершины двойственного графа прямой линией
и с помощью нее найдите путь между ними в двойственном графе.
27.+ Для доказательства существования задайте требуемые биекции F —* V*,
Е —► Е*, V —* F* последовательно в этом порядке и одновременно
стройте G*. Покажите, что для обеспечения биективности всех трех функций
необходима связность.
28. Сначала выполните предыдущее упражнение.
29. Воспользуйтесь теми биекциями, которые связаны с данными
двойственными мультиграфами, чтобы задать искомый изоморфизм и доказать, что
он является комбинаторным.
30. Воспользуйтесь теоремой Менгера и предложением 4.6.1. Для (iii)
рассмотрите 4-связный граф с 6 вершинами.
31. Примените индукцию по п начиная с части (i) предыдущего упражнения.
32. Теорема 1.9.5.
33. Для прямой импликации рассмотрите G' := G*. Для обратной —
воспользуйтесь подходящим критерием планарности.

Указания к главе 5
311
Указания к главе 5
1." Двойственность.
2.~ Всякий раз, когда больше чем три страны имеют общую вершину, сделайте
небольшое изменение карты в этом месте.
3. Где доказательство 5-раскрашиваемости использует тот факт, что у и не
больше соседей, чем имеются цветов?
4. Как могут раскраски различных блоков мешать друг другу?
5."~ Используйте некоторую раскраску G для получения подходящего
упорядочения.
6. Как удаление некоторых ребер может заставить жадный алгоритм
использовать большее число цветов?
7. Опишите точнее, как реализовать этот альтернативный алгоритм. В чем
его отличие от традиционного жадного алгоритма?
8. Сравните число ребер в подграфе Н из предложения 5.2.2 с числом т ребер
bG.
9. Для нахождения / рассмотрите граф с малым раскрасочным числом и
разложите его по индукции на небольшое число лесов. Для нахождения д
используйте простую часть утверждения теоремы 3.5.4.
10." Удаляйте вершины последовательно, пока граф не станет критически /с-хро-
матическим. Что можно сказать о степени любой из оставшихся вершин?
11. Предложение 1.6.1.
12.+ Измените раскраски по обе стороны гипотетического разреза с менее чем
к — 1 ребрами так, чтобы их объединение давало (А: — 1)-раскраску всего
графа (с противоречием).
13. Предложение 1.3.1.
14.~ Для каких графов с большой максимальной степенью предложение 5.2.2
дает особенно малую оценку сверху?
15.+ (i) Как будут окрашены v\ и V2 и как vn?
(ii) Рассмотрите подграф, индуцированный соседями вершины vn.
16. Для начала индукции вычислите явным образом Pg(^) Для \G\ = п
и ||0|| = 0.
17.+ Найдите из многочлена число ребер и число компонент в G; см. предыдущее
упражнение.
18. Следуйте доказательству теоремы 5.2.5.
19.- Кп.п.
20. Как раскраски ребер связаны с паросочетаниями?
21. Постройте двудольный А(С)-регулярный граф, который содержит G как
подграф. Может быть, нужно будет добавить некоторые вершины.
22.+ Индукция по к. На шаге к —► к + 1 индукции рассмотрите несколько копий
графа, найденного для к.
23.- Степени вершин.
24. Кп,п> Для выбора п таким, чтобы КП)П не был n-выбираемым, рассмотрите
списки /с-подмножеств к2 -множества.

312
Указания ко всем упражнениям
25. Теорема Визинга.
26. Все, что нужно — это определения, предложение 5.2.2 и стандартное
рассуждение из раздела 1.2.
27.+ Попробуйте применить индукцию по п. На шаге индукции хотелось бы
удалить некоторую пару вершин и только один цвет из списков других
вершин. Что можно сказать об этих списках, если такое невозможно? Уже
эта информация позволяет найти раскраску непосредственно, не обращая
больше внимания на граф.
28. Покажите, что x"(G) < ch'(G)-f 2, и с помощью этого выведите неравенство
x"(G) < A(G) -f 3 из гипотезы о предписанной раскраске ребер.
29." А имеют ли ядро двудольные графы?
30."*" Назовем набор 5 вершин в ориентированном графе D сердечником,, если D
содержит направленный v—S путь для каждой вершины v Е D — 5. Если,
кроме того, D не содержит ориентированного пути между никакими двумя
вершинами из 5, то назовем S сильным сердечником. Покажите сначала,
что каждое ядро содержит сильный сердечник. Затем определите
индуктивно такое разбиение множества V(D) на «уровни» Lq, ..., Ln, что для
четных г множество L, есть сильное ядро в JDt := D — (Lq U • • • U L^_i), в то
время как для нечетных г множество L{ состоит из вершин JD,, из которых
ведет дуга в Lt_i. Покажите, что если D не имеет нечетного контура, то
объединение четных уровней образует ядро графа D.
31. Постройте ориентацию, необходимую для леммы 5.4.3 поэтапно: если в
текущей ориентации все еще есть вершины v с d* (v) > 3, измените
направление дуг при v и позаботьтесь об общем эффекте этой замены. Если нужно
будет ограничить среднюю степень двудольного плоского графа, вспомните
формулу Эйлера.
32."~ Начните с несовершенных графов.
33."~ Удовлетворяют ли нечетные циклы или их дополнения условию (*)?
34. Упражнение 12 главы 3.
35. Рассмотрите дополнение.
36. Определите цветовые классы данного индуцированного подграфа Н С G
индуктивно начиная с класса всех минимальных элементов.
37. (i) Могут ли вершины индуцированного цикла содержать друг друга как
интервалы?
(ii) Воспользуйтесь естественным упорядочением вещественных чисел.
38. Сравните w(H) с A(G) (где Я = L(G)).
39.+ Какие графы обладают тем свойством, что их реберные графы не содержат
индуцированных циклов нечетной длины > 5? Чтобы доказать, что ребра
такого графа G можно раскрасить в w(L(G)) цветов, следуйте
доказательству теоремы Визинга.
40. Используйте А как цветовой класс.
41.+ (i) Индукция.
(ii) Допустим, что G не содержит индуцированного подграфа Р3.
Предположим, что некоторый Н имеет максимальный полный подграф К и
максимальное множество А независимых вершин, не пересекающееся с К. Для
каждой вершины v Е К рассмотрите множество соседей вершины v в А.
Как эти множества пересекаются? Есть ли среди них наименьшее?
42.+ Начните с кандидата на роль множества б', т. е. с множества
максимальных полных подграфов, покрывающих множество вершин графа G. Если

Указания к главе 6
313
все элементы С оказались порядка и>(Ст), то как существование £? следует
из совершенности G1 Если нет, можно ли расширить G (сохраняя его
совершенность) так, чтобы они стали таковыми и адаптировать £? для
расширенного графа к самому G?
43.+ Сведите общий случай к случаю, когда все Gx, кроме одного, тривиальны;
затем следуйте доказательству леммы 5.5.4.
44. Примените свойство Ж\ к графам из Жъ и наоборот.
Указания к главе 6
1.~ Перемещайте вершины, одну за другой, из 5 в 5. Как изменяется каждый
раз значение f(SyS)l
2. (i) Вовлеките алгоритм в многократное использование среднего ребра в
чередующихся направлениях.
(ii) Для любого фиксированного момента при работе алгоритма рассмотрите
для каждой вершины v самым короткий s-v маршрут, который является
начальным отрезком некоторого увеличивающего пути. Покажите для
каждого v, что длина этого s-v маршрута никогда не уменьшается в течение
работы алгоритма. Затем рассмотрите ребро, которое используется для
увеличивающего пути дважды в одном и том же направлении. Покажите,
что второй из этих путей должен быть длиннее, чем первый. Теперь
получите искомую оценку.
3. Для реберной версии определите пропускные способности так, чтобы поток
максимальной величины потребовал достаточно много реберно-непересе-
кающихся путей. Для вершинной версии разбейте каждую вершину х на
две смежных вершины х~, #+. Определите ребра нового графа и их
пропускные способностей таким способом, чтобы положительный поток через
ребро х~х"^ соответствовал использованию х одним из путей в G.
4.~ По определению, //-потоки нигде не равны нулю.
5.~ Используйте определение и предложение 6.1.1.
6.~ Считаются ли подграфы минорами?
7.~ Проверьте поочередно к = 2,3,.... При поиске Аг-потока попробуйте
зафиксировать значение потока через некоторую дугу и посмотреть, какие
последствия это имеет для смежных ребер.
8. Чтобы установить однозначность, рассмотрите разрезы специального вида.
9. Представьте G как объединение циклов.
10. Объедините ^2-потоки на подходящих подграфах в поток на G.
11.+ Для начала направьте малое количество потока через каждое ребро вне Т.
12. Представьте G как объединение подходящим образом выбранных циклов.
13. Следствие 6.3.2 и предложение 6.4.1.
14." Двойственность.
15. Возьмите в качестве Н ваш любимый граф с большим потоковым числом.
Можно ли уменьшить его потоковое число, добавляя ребра?
16. Эйлер.
17.+ Теорема 6.5.3.
18." Поищите среди малых кубических графов.

314
Указания ко всем упражнениям
19. Теорема 6.5.3.
20. (i) Теорема 6.5.3.
(и) Да, можно. Покажите, рассматривая наименьший контрпример, что
если каждый 3-связный кубический планарный мультиграф
3-реберно-раскрашиваем (и, следовательно, имеет 4-поток), то этим же свойством
обладает и каждый кубический планарный мультиграф без мостов.
21.+ Для импликации «только если» примените предложение 6.1.1. Обратно,
рассмотрите циркуляцию f на G со значениями в {0, ±1,..., ±(А: - 1)},
которая поддерживает заданную ориентацию (т. е. является положительной
или нулевой на направлениях ребра, приписанных JD) и равна нулю на как
можно меньшем числе ребер. Затем покажите, что / нигде не нулевая
следующим образом. Если / нулевая на е = st Е Е, a D направляет е из t
в 5, то определите такую сеть N = (G,s,t,c), что любой поток в N
положительной величины противоречит выбору /, но любой разрез в N нулевой
пропускной способности противоречит свойству D.
22.~ Превратите заданный мультиграф в граф с теми же потоковыми
свойствами.
Указания к главе 7
1.~ Прямо из определения.
2.~ При построении графов сначала зафиксируйте цветовые классы.
3. Нетрудно определить верхнюю оценку для ех(п, К\}Г). Остается лишь
доказать, что эта оценка достижима при всех run.
4. Предложение 1.7.2(H).
5. Предложение 1.2.2 и следствие 1.5.4.
6.+ Каково максимальное число ребер в графе, строение которого описано в
теореме 2.2.3, если он не содержит паросочетания порядка к? Каково
оптимальное распределение вершин между S и компонентами G — 5? Всегда
ли существует граф, в котором число ребер достигает соответствующей
верхней оценки?
7. Рассмотрите вершину х Е G максимальной степени и подсчитайте ребра
в G — х.
8. Выберите к и i так, чтобы п = (г — 1)к + г, где 0 < г < г — 1. Сначала
разберите случай г = 0, а затем покажите для общего случая что tr-\ (п) =
9. Оценки, данные в подсказке, суть порядки двух особенно простых графов
Турана; каких?
10.+ Как выбрать v так, чтобы число ребер не уменьшилось? Где в графе эта
операция может быть повторена, и что напоминает ситуация, когда ничего
нового уже не происходит?
11. Выберите среди т вершин множество из s вершин, которые все еще
инцидентны как можно большему числу ребер.
12. Для доказательства первого неравенства удвойте множество вершин
экстремального графа для Ks,t, чтобы получить двудольный граф со вдвое
большим числом ребер, но все еще не содержащий KS}t.
13.+ Для указанного неравенства подсчитайте такие пары (x,Y), что х Е А
и У С В, причем |У| = г и х смежно со всем множеством Y. Чтобы оценить

Указания к главе 8
315
ех(п,Кг,г), воспользуйтесь оценкой (s/t)* < (*) < s* и тем фактом, что
функция z ь-* zr выпукла.
14. Предположите, что верхняя плотность больше, чем 1 — fzj- Что именно
следует отсюда и из теоремы Эрдеша — Стоуна?
15. Следствие 1.5.4 и предложение 1.2.2.
16. Полные графы.
17." Средняя степень.
18. Вынуждают ли ^(к — 1)п ребер подграф с подходящей минимальной
степенью?
19. Рассмотрите самый длинный путь Р в G. Где находятся соседи его
концевых вершин? Может ли G[P] содержать цикл на V(P)?
20.~ Почему было бы неудобно включать в сравнение, скажем, одноэлементные
множества^, У?
21." Воспользуйтесь определением б-регулярной пары.
22. Разреженные графы имеют мало ребер. Как это влияет на условие для
средней степени в определении б-регулярности?
Указания к главе 8
1. На шаге индукции разбейте множество вершин графа G на два множества
V\ и V2 так, чтобы раскраски G\V\] и G[V2] могли быть объединены в
раскраску всего G.
2. Следуйте началу доказательства леммы 8.1.3.
3.~ Заставляет ли большое хроматическое число повышаться среднюю
степень? Если есть сомнения, см. главу 5.
4.+ Попробуйте взять параллельные пути в решетке в качестве множеств
ветвления.
5.+ Как лучше всего вложить ТК2г в К3,з, когда мы хотим, чтобы s было мало?
6. Разбейте рассуждение на случаи к = 0 и к > 1.
7. Как эти две леммы используются в доказательстве теоремы?
8. См. наводящие рассуждения, предшествующие определению / в
доказательстве.
9.+ Рассмотрите Ваши любимые графы с высокой средней степенью и
низким хроматическим числом. Какие индуцированные деревья они содержат?
Есть ли причина ожидать, что эти и только эти деревья всегда могут быть
найдены как индуцированные подграфы в графах с большой средней
степенью и малым хроматическим числом?
10."~ Имеет ли планарность отношение к минорам?
11." Рассмотрите подходящий надграф.
12." Средняя степень.
13.+ Покажите индукцией по |G|, что любая 3-раскраска индуцированного цикла
BG^fc К4 продолжается на весь G.
14.+ Сведите утверждение к критическим к-хроматическим графам и
воспользуйтесь теоремой Визинга.

316
Указания ко всем упражнениям
15. Пункт (i) доказывается легко. В первой части (ii) рассмотрите отдельно
случаи, когда граф разделяется или не разделяется посредством К*^)""1.
Докажите вторую часть индукцией по хроматическому числу. На шаге
индукции разбейте множество вершин графа на два подмножества.
16. Индукция по числу шагов построения.
17. Индукция по \G\.
18. Обратите внимание на предыдущее упражнение.
19. Какие из графов, построенных в теореме 8.3.4, имеют наибольшую среднюю
степень?
20. Какие из графов, построенных в подсказке, имеют наибольшую среднюю
степень?
21. Рассмотрите подграф в G, индуцированный соседями вершины х.
Указания к главе 9
1.~ Можно ли раскрасить ребра Къ в красный и зеленый цвета, не создав при
этом красный или зеленый треугольник? Можно ли сделать то же для Л'6 ?
2. Индукция по с. На шаге индукции объедините два из цветовых классов.
3.+ Выберите полный порядок на Ж и сравните его с естественным
упорядочением. Используйте тот факт, что объединение счетного числа счетных
множеств счетно.
4."*" Первый и второй вопросы легкие. Чтобы доказать теорему Эрдеша и Се-
кереша, используйте индукцию по к при фиксированном I и рассмотрите
на шаге индукции последние элементы возрастающих последовательностей
длины к. Либо примените теорему Дилворта.
5. Воспользуйтесь тем фактом, что п > 4 точек образуют выпуклый
многоугольник, если и только если его образуют любые четыре из них.
6. Переведите заданное Аг-разбиение на {1,2,..., п} в Аг-раскраску ребер
графа Кп.
7. Утверждение (i) очевидно. Для получения (ii) воспользуйтесь
существованием Я(2, к, 3).
8. Начните с обнаружения бесконечно большого числа множеств, чьи
попарные пересечения все имеют один и тот же порядок.
9. Упражнение предлагает больше информации, чем требуется. Найдите
в разделе 8.1 то, что существенно.
10. Рассмотрите вспомогательный граф, вершинами которого служат
окрашенные конечные подграфы заданного графа.
11. Следуйте доказательству предложения 9.2.1.
12. Нижняя граница доказывается легко. Имея раскраску для верхней оценки,
рассмотрите какую-нибудь вершину и тех ее соседей, которые соединены
с нею подходящим образом раскрашенными ребрами.
13." При заданных Н\ и #2 постройте граф Н, для которого граф G из теоремы
9.3.1 удовлетворяет (*).
14. Покажите индуктивно для к = 0,... , га, что w(Gk) = w(H).

Указания к главе 11
317
15. На шаге индукции постройте G(H\, Н2) из объединения непересекающихся
GffiiiH^) и G(H[,H2), присоединяя некоторые новые вершины
подходящим способом.
16. Лемма о бесконечности.
17." Почему именно становится неверным предложение 9.4.1, если
отбросить А'г?
Указания к главе 10
1. Рассмотрите объединение двух цветовых классов.
2. Будет ли доказательство предложения 10.1.2 проходить, если предположить
х(С?) > \G\/k вместо a(G) < к? На что похожи Аг-связные графы, которые
удовлетворяют первому условию, но не второму?
3. Рассмотрите ребро, которое добавляется к одной последовательности, но не
добавляется к другой.
4. Рисунок 10.1.1.
5. Индукция по к при фиксированном п; на шаге индукции рассмотрите G.
6.~ Вспомните определение гамильтоновой последовательности.
7.~ На какого рода вершины переносится условие Хватала? Для проверки этого
условия для G сначала найдите такую вершину.
8. Как произвольный связный граф отличается от тех графов, квадраты
которых содержат гамильтонов цикл по теореме Флейшнера? Как это различие
могло бы воспрепятствовать существованию гамильтонова цикла?
9.+ На шаге индукции рассмотрите минимальный разрез.
10. Условие (*) в доказательстве теоремы Флейшнера.
11. Индукция.
12.+ Как можно превратить один гамильтонов путь Р £ Ж в другой?
Сколькими способами? Как это связано со степенью в G последней вершины
пути Р?
Указания к главе 11
1.~ Рассмотрите фиксированный выбор т ребер на {0,1,...,п}. Какова
вероятность того, что G G &(п,р) имеет в точности это множество ребер?
2. Рассмотрите соответствующие индикаторные случайные величины, как
в доказательстве леммы 11.1.5.
3. Рассмотрите соответствующие индикаторные случайные величины.
4. Эрдеш.
5. Какова была бы мера множества {G} для фиксированного G?
6. Рассмотрите дополнительные свойства.
7-- ^2,1-
8. Примените лемму 11.3.2.
9. Индукция по |//| при помощи упражнения 6.

318
Указания ко всем упражнениям
10.+ (i) Для данной пары U, U' вычислите вероятность того, что каждая другая
вершина соединена с U U U' неправильно. Какова тогда вероятность того,
что это имеет место для некоторой пары U, С/'?
(ii) Занумеруйте вершины G и G' совместно и постройте изоморфизм G —► G'
по индукции.
11. Следуйте доказательству леммы 11.2.1.
12. Следуйте доказательству предложения 11.3.1. Для оценки требуемых
вероятностей воспользуйтесь неравенством 1 — х < е~х, как в доказательстве
леммы 11.2.1.
13.+ (i) Найдите ожидаемое число изолированных вершин и примените лемму
11.4.2, как в доказательстве теоремы 11.4.3.
(ii) Линейность.
14.+ Раздел 8.2, доказательство теоремы Эрдеша и немного Чебышева.
15. Для первой задачи слегка измените возрастающее свойство так, чтобы оно
перестало быть возрастающим, но сохранило свою пороговую функцию.
Для второго найдите возрастающее свойство, вероятность которого
фактически не зависит от р.
16."~ Перестановки на V(H).
17.~ Этот результат замаскирован в тексте.
18.~ Баланс.
19. Для p/t —*■ 0 примените леммы 11.1.4 и 11.1.5. Для p/t —► оо примените
следствие 11.4.4.
20. Существует лишь конечное число деревьев порядка к.
21.+ Покажите сначала, что никакая такая пороговая функция t = t(n) не может
стремиться к нулю при п —* с». Затем воспользуйтесь упражнением 12.
22.+ Исследуйте различные шаги в доказательстве теоремы 11.4.3 и заметьте,
какие требуются изменения. Как определяются суммы Ар на
заключительных этапах доказательства и почему сумма всех Ар таких, что ||F|| = 0
равняется Aq? При ||F|| > 0 вычислите оценку для Ар и покажите, что
каждое Ар/ ^i2 стремится к нулю при п —► оо, как и раньше.
Указания к главе 12
1.~ Антисимметрия.
2. Предложение 12.1.1.
3. Чтобы доказать предложение 12.1.1, рассмотрите бесконечную
последовательность, в которой каждая строго убывающая подпоследовательность
конечна. Как последний элемент максимальной убывающей
подпоследовательности сравнивается с элементами, которые идут после него? Для
следствия 12.1.2 сначала докажите, что по меньшей мере один элемент образует
хорошую пару с бесконечным числом более поздних элементов.
4. Очевидный подход состоит в попытке следовать доказательству леммы
12.1.3 для <'; если это не удается, то какова причина? Можно также
попробовать превратить инъективное отображение, возникающее в лемме 12.1.3,
в отображение, сохраняющее порядок, не теряя при этом свойство a < /(а)
для всех а.
5.~ Это и в самом деле упражнение: «легко видеть» здесь не является
доказательством ...

Указания к главе 12
319
6. Сначала найдите два дерева Т, Т' с \Т\ < |Г'|, но Т £ Г', потом проитери-
руйте.
7. Отображается ли когда-либо в исходном доказательстве корень некоторого
дерева в обычную вершину другого дерева?
8.+ Когда мы пытаемся вложить граф TG в другой граф Н, вершины
ветвления TG могут отображаться только в определенные вершины из Н.
Расширьте G до похожего графа Н, который не содержит G как
топологический минор, потому что эти вершины из Н размещены в Н неудобно. Затем
проитерируйте этот пример, чтобы получить бесконечную антицепь.
9.+ Да. Одно из возможных доказательств состоит в использовании
нормальных остовных деревьев с пометками и следует доказательству теоремы
Краскала.
10. Почему не существует циклов древесной ширины 1?
11. Для доказательства прямой импликации примените следствие 1.5.2. Для
обратного утверждения используйте индукцию по к.
12. Чтобы доказать (Т2), рассмотрите ребро е на рисунке 12.3.1. Проверить
условие (ТЗ) легко.
13. Для ответа на первый вопрос вспомните предложение 12.3.6. Для второго
попробуйте превратить древесное разложение графа G в древесное
разложение графа TG, не увеличивая его ширины.
14. Лемма 12.3.1 связывает свойства отделимости графа G и его дерева
разложения Т. Упражнение освещает это отношение с двойственной точки
зрения связности: как связные подграфы G соотносятся со связными
подграфами в Т?
15." Это всего лишь переформулировка теоремы 12.3.9.
16. Видоизмените приведенное в тексте доказательство того, что решетка к х к
имеет древесную ширину не меньше к — 1.
17. Существование доказывалось в теореме 12.3.9; задача — показать
однозначность.
18.+ Дайте явное описание множеств W(, подобное определению множеств Wt,
и сравните их.
19. Индукция.
20. Индукция.
21. Использовать предыдущее упражнение и один результат из раздела 8.3.
И не отчаиваться из-за подграфа графа W\
22.+ Показать, что этими частями являются максимальные несводимые
индуцированные подграфы графа G и только они.
23.+ Упражнение 14.
24. Для доказательства прямой импликации интерпретируйте подпути пути
разложения как интервалы. Какой подпуть естественно сопоставить
заданной вершине графа G1
25. Придерживайтесь доказательства следствия 12.3.12.
26.+ Да. Чтобы доказать это, покажите сначала, что каждый связный граф G
содержит путь, удаление которого уменьшает путевую ширину графа G.
Затем примените индукцию по подходящему множеству деревьев, удаляя
на шаге индукции подходящий путь.

320
Указания ко всем упражнениям
27. Рассмотрите минимальные множества вида ЗСср в предложении 12.5.1.
28. Чтобы ответить на первую часть, постройте для каждого запрещенного
минора X конечное множество графов, исключение которых как
топологических миноров эквивалентно запрещению X как минора. Для второй части
вспомните упражнение 8.
29. Ищите требуемые пути поочередно.
30.+ Одно направление -— лишь ослабление леммы 12.4.5. Для другого следуйте
доказательству леммы 12.3.4.
31.+ Пусть X — внешне ^-связное множество из h вершин в графе G, где h и I
велики. Рассмотрите малый сепаратор 5 в G: ясно, что X почти целиком
лежит в одной из компонент графа G — 5. Попытайтесь переделать эти
«большие» компоненты, возможно вместе с их сепараторами 5, в искомые
связные множества вершин.
32. Справьтесь в разделе 8.2 насчет подструктур, которые должны
присутствовать в графах с большим хроматическим числом.
33. Выведите теорему о минорах сначала для связных графов.
34. К5.

Список основных обозначений
Вхождения этого указателя делятся на две группы. Вхождения,
состоящие только из математических символов (т. е. не
содержащие букв, отличных от символов переменных), приводятся на
первой странице данного указателя и сгруппированы нестрого по их
назначению. Например, вхождение [ ] относится как к определению
индуцированных подграфов Н[U] на с. 18, так и к определению
границ граней G[f] на с. 89.
Вхождения, включающие фиксированные буквы как
неотъемлемую часть, приводятся на второй странице указателя группами,
упорядоченными по этим буквам. Буквы, выступающие в роли
переменных, в этом упорядочении игнорируются.
0 16
17
~ 17
С 18
< 272
=$ 32
+ 18 , 35 , 147
18 , 87 , 147
G 16
\ 87
U 18
П 18
* 18
U 15
П 15
|| 16 , 145
|| || 16 , 172
[] 18 , 89
[]' 15
[]<" 273
/ 31
( , ) 35
<gL , &x , . . . 36
0 , 1 , 2 , . . . 15
(n)t) . . . 255
E(v) , E'(w) , . . . 17
E(X , Y) , E'(U , W) , . . . 17
(e , x , y) 143
E , F , C , . . . 143 , 155
e , E , F , . . . 143
f(X , Y) , g(U , V) , . . . 143
G* , F* , e* , . . . 106 , 155 ,
*G2 , #V . . 237
G , X , & , . . . 18 , 143 , 285
(5 , 5) , . . . 145
xy , x0 . . . xk , . . . 17 , 22
xP , Px , xPy , xPyQz , . . . 21
P , xQ , . . . 21 , 85
xTy , . . . 27

322 Список основных обозначений
F2 35
N 15
Zn 15
<eG 50
V(G) 36
«"(G) 37
/(G) 35
Sf(n , p) 251
&и 259
Г(б?) 35
С* 22
E(G) 16
£(X) 253
F{G) 88
Forb^(JT) 285
G(HltH2) 217
tf" 17
•^m «r 30
K\ 30
L(G) 18
MX 31
JV(t») , JV(C/") 19
N+(v) 127
P 251
P* 20
PG 137
Ря 252
R(H) 212
R(HUH2) 212
Д(А , с , г) 212
Д(г) 209
Д . 181
5" 87
ГХ 32
Т* - 1^) 168
7(G) 16
ch(G) 123
ch'(G) 123
col(G) 116
d{G) 19
d(t>) 19
d+(t>) 127
dG{x , y) 23
rf(X , У) 172
diam(G) 23
ex(n , Я) 168
/*(«) 106
ff(G) 22
г 15
init(e) 40
log , In 15
pw(G) 303
q(G) 50
rad(G) 23
tr - i(n) 168
ter(e) 40
tw(G) 279
ve , vEy , t)[/ 31 , 32
v*(f) 106
A(G) 19
a(G) 129
6(G) 19
e(G) 19
k(G) 25
кб(Я) 73
A(G) 25
AG(tf) 73
ц 264
tt : S2\{(0 , 0 , 1)}^!2 87
(т4 : 2 - »24 150
cr2 264
<p{G) 150
X(G) 112
X'(G) 113
X"(G) 138
w(G) 129

Предметный указатель
Вхождения расположены в алфавитном порядке; символы,
обозначающие переменные, не учитываются (например, вхождение
«й-раскраска» стоит в списке на букву «р»).
абстрактно двойственный
мультиграф , 107 - 108 , 110
абстрактный граф , 16 , 84 , 94 , 258
автоморфизм , 17
алгебраическая
теория графов , 12 , 35 - 40 , 43
теория потоков , 147 — 163
теория раскраски , 140
алгебраические критерии
планарности , 103 - 105
алгоритмическая теория графов ,
165 , 300 - 301 , 304 - 305
Алон Н . , 124 , 140 , 270
антицепь , 56 , 58 , 273
Аппель К . , 140
Аркдикон Д . , 305
Ахуйа Р . К . , 165
ациклический граф (см . лес)
без дырок , см . хордальный
безузловой граф , 301
Берж К . , 136
бесконечная грань , см . внешняя
грань
бесконечные графы , 16 , 43 , 58 ,
186 , 229 , 269 , 304
Бехзад М . , 140
Бите Н . Л . , 43
Биркгоф Г . Д . , 140
блок , 59
граф как блок , 60 , 81
Боллобаш Б . , 80 , 82 , 187 , 189 , 230 ,
247 , 248 , 261 , 263 , 270 , 271
Бонди Дж . А . , 248
Брукс Р . Л . , 116 , 137
предписанная версия теоремы
Брукса , 140
теорема Брукса , 116
Бэр С . А . , 231
в (графе) , 21 - 22
(отображение) в , 276
Вагнер К . , 103 , 111 , 202 , 204 ,
205 , 304
валентность , см . степень
веер , 71
веерный вариант теоремы
Менгера , 71 - 72
величина потока , 145
вероятностный метод , 249 ,
256 - 258 , 270
верхняя плотность , 186
вершина , 16
плоского графа , 87
вершинная
раскраска , 112 , 115 - 120
связность , 25
вершинно - транзитивный , 57
ветвь , 132
вершина ветвления , 33
Визинг В . Г . , 121 , 140 , 312 , 315
вложение
в плоскость , 94 , 98 - 111
в поверхности , 91 , 110 - 111 ,
297 - 300 , 304 - 305
в S2 , 87 , 95
двудольных графов , 221 - 224

324
внешнепланарный , 109
внешне Aj - связный , 287 , 303
внешняя грань , 87 , 94 - 95
внутренне непересекающиеся ,
см . независимые
внутренне устойчивое множество ,
17
внутренность
дуги , 85
пути , 20 - 21
внутренняя вершина , 20
внутренняя грань , 87
возрастающее свойство , 262 , 269
второй момент , 263 - 268
/г - выбираемый , 123
вынуждение
большого хроматического
числа , 118 - 120
высокой связности , 26
дерева , 28 , 198
длинных путей , 22 , 186
длинных циклов , 22 , 41 , 137 ,
233 - 248
индуцированных деревьев , 198
коротких циклов , 199 - 200 , 258
минора с большой минимальной
степенью , 193 , 198
подграфа , 28 , 166 - 187
сцепленности , 78 - 80 , 82 , 189 - 193
треугольника , 138 , 229
МКГ , 198 - 203 , 205 - 206
ГА'5 , 203 , 206
ТКГ , 77 , 189 - 198 , 205 - 206
выну ж денно - гамильтоновый ,
см . гамильтонова
последовательность
выпуклое изображение , 101 ,
109 , 111
выпуклый многоугольник , 229
Вэнс А . , 270
Галвин Ф . , 127
ГаллаиТ . , 55 , 58 , 83 , 187
Гамильтон В . Р . , 247
гамильтонов
граф , 232
путь , 232 , 237
гамильтонов цикл , 232 - 248
в планарных графах , 235
в почти всех графах , 262
в G2 , 237 - 246
Предметный указатель
в G3 , 247
достаточные условия
существования , 232 - 237
и минимальная степень , 233
и 4 - поток , 164 , 234 - 235
и степенная последовательность ,
235 - 237 , 246 - 247
и теорема о четырех красках ,
234 - 235
степень г . ц . , 246
гамильтонова последовательность ,
235
гамильтоново замыкание , 246
Гаспарян Г . С , 141
ГатриФ . , 139
геометрически двойственный ,
см . плоскодвойственный
Гибонс А . , 165
Гилмор П . С , 139
гиперграф , 40
«гипотеза Вагнера» , 304
гипотеза о 3 - потоке , 160
гипотеза о 4 - потоке , 160 - 161
гипотеза о 5 - потоке , 159 - 161
гипотеза о предписанной раскраске
ребер , 126 - 127 , 138 , 140
гипотеза о самоминорности , 304
гипотеза о совершенных графах ,
136
гипотеза Хадвигера , 189 , 200 - 206
гипотеза Эрдеша— Шош , 172 ,
186 , 187
гипотезы Татта о потоках , 159 - 161
Годсил К . , 43
голова , см . концевая вершина
ГолумбицМ . К . , 141
Горбунов К . Ю . , 304
граница , 85
граница грани , 88 - 90
грань , 87
граф , 16 - 18 , 40 - 41
плоский , 87 - 93 , 105 - 108 , 113 - 114 ,
124 - 126 , 155 - 159
обыкновенный , 41
граф Бержа , 136
граф Вагнера , 202 - 203 , 283 , 303
граф интервалов , 139 , 303
граф пересечений , 303
граф Петерсена , 160
граф Рамсея , 216

Предметный указатель
325
граф регулярности , 181
раздутый , 213
граф сравнимости , 130 , 138
граф Турана , 168 - 172 , 187 , 314
графическая последовательность ,
см . степенная последовательность
ГрещпХ . , 115 , 161 , 164
Грэм Р . Л . , 230
Грюнвальд Т . , 83
двойное
колесо , 228
ребро , 41
двойной подсчет , 92 - 93 , 110 ,
133 - 134 , 254 , 265
двойственность
и связность , 110
между потоками и раскрасками ,
155 - 159 , 314
между циклами и разрезами ,
38 - 39 , 107 - 108 , 155
плоских мультиграфов , 105 - 108
двойственность на плоскости ,
105 - 108 , 110 , 155 - 159 , 311
двудольный граф , 29 - 30 , 42 ,
110 , 113
в теории Рамсея , 231 - 232
вынуждение д . г . как подграфа ,
172 , 180
и раскраска ребер , 121 , 138
паросочетание в д . г . , 44 - 49
потоковое число кубических
д . г . , 153 - 154
предписанно - хроматический
индекс д . г . , 127 - 129 , 140
двуугольник , см . двойное ребро
дерево , 27 - 29
как вынужденная подструктура ,
28 , 198 , 204
нормальное , 28 - 29 , 42 , 159 ,
164 , 319
поиска в глубину , 28 - 29 , 42
Джонсон Д . , 305
диаметр , 23 , 269
и обхват , 23
и радиус , 23
Дилворт Р . П . , 56 , 308 , 316
Дирак Г . А . , 205 , 206 , 233 , 246
дисперсия , 264
ДистельР . , 205 , 304
длина
маршрута , 24
пути , 20 , 22 - 23
цикла , 22
Дойбер В . , 216
доказательство существования
(вероятностное) , 140 , 249 - 250 ,
253 - 254 , 256 - 258
г - долъный , 29
дополнение
графа , 18
двудольного графа , 130 , 138
и совершенность , 131 , 312
к свойству , 285
древесная ширина , 279 - 297
и ежевики , 279 - 282 , 302 , 305
и запрещенные миноры , 285 - 297
минора , 279
подразделения , 302
препятствия для малой д . ш . ,
279 - 282 , 286 - 287 , 304 , 305
решетки , 282 , 302 , 304
теорема двойственности
для д . ш . , 280 - 282
древесное покрытие , 77
древесное разложение , 205 ,
276 - 284 , 302 , 305
индуцированное на минорах , 278
индуцированное на подграфах ,
277
препятствия для д . р . , 279 - 282 ,
285 - 287 , 303 - 305
симплициальное , 283 , 299 ,
302 , 304
тощее , 282
часть д . р . , 276
ширина д . р . , 278
древесность , 78 , 116 , 137
древесный порядок , 28
дуга (ребро в ориентированном
графе) , 40
дуга (ребро в плоском графе) , 85
дуга многоугольника , 85 , 86
ежевика , 279 - 282 , 305
ежевичное число (число
ежевики) , 282 , 302
порядок ежевики , 280
жадный алгоритм , 115 , 127 , 136
Жеже Ф . , 165
Жордан К . , 86 , 87

326
задача коммивояжера , 247
задача о четырех красках , 139 , 205
закон Кирхгофа , 142 - 144
замкнутый
маршрут , 24 , 34
относительно изоморфизма ,
258 , 285
относительно миноров , 138 ,
164 , 285
относительно надграфов , 262
относительно подграфов , 138
по сложению , 147
замыкать , 238
запрещенные миноры
выраженный в терминах з . м . ,
285 , 297 - 301
и древесная ширина , 285 - 297
и хроматическое число , 201 - 204
минимальное множество з . м . ,
298 , 303 - 305
планарные , 286
звезда , 30 , 186 , 215
индуцированная , 227
звездообразная форма , 310
Зыков А . А . , 187
из . . . в , 21
изображение , 84 , 94 - 98
выпуклое , 111
прямолинейное , 109
изолированная вершина , 19 , 269
изоморфизм , 17
плоских графов , 94 - 98
изоморфный , 17
инвариант графа , 17
индикаторная случайная величина ,
255 , 317
индуцированный подграф , 18 ,
129 , 135 - 136 , 312
в случайном графе , 252 , 270
в теории Рамсея , 215 - 226
всех больших связных графов ,
227
всех несовершенных графов ,
135 - 136 , 139
дерево , 198
почти всех графов , 259 , 269
цикл , 22 - 23 , 36 , 63 , 93 , 105 ,
130 , 136 , 312
интуиция , 88 , 251
Предметный указатель
инцидентность , 17
как отображение , 40 - 41
кодирование планарного
вложения , см . комбинаторный
изоморфизм
инцидентный , 17 , 89
исключенные миноры ,
см . запрещенные миноры
исключительное множество , 173
источник , 144
Йенсен Т . Р . , 139 , 165 , 304
Кан Дж . , 140
Кароньский М . , 270
Катлин П . А . , 206
квадрат
графа , 237 - 238
латинский , 138
квазиупорядочение , 272 - 273 ,
301 - 302
правильное , 272 - 275 , 299 ,
301 , 302 , 304
Кемпе А . Б . , 140 , 247 - 248
Кёниг , Д . , 45 , 58 , 68 , 121 , 138 ,
210 , 230
кёнигсбергские мосты , 34
класс 1 и класс 2 , 123
Клейтман Д . Дж . , 140
колесо , 62
теорема о колесе , 62 , 81
комбинаторная теория множеств ,
230
комбинаторный изоморфизм , 95 , 96
Комлош Я . , 187 , 189 , 206 , 230 , 248
компонента , 24
конец
дуги , 85
пути , 20
ребра , 17 , 40
конечный граф , 16
Ажонструируемый , 119 - 120 , 137
конструкция Хайоша , 119 - 120
контур , см . ориентированный цикл
концевая вершина , 17 , 40
корень , 28
корневое дерево , 28 , 274 , 301 - 302
корона , 228
Косточка А . В . , 198
КохаякаваИ . , 187
коцикл , см . разрез

Предметный указатель
327
Краскал Дж . А . , 274 , 302 , 319
кратные ребра , 40
критерий планарности
Куратовского , 103
Маклейна , 103
Татта , 105
Уитни , 108
критический , 137
критический по раскраске ,
см . критический /с - хрома -
тический
критический к - хроматический ,
137 , 315
куб
графа , G3 , 247
d - мерный , 41 , 269
кубический граф , 19
и потоковое число , 153 - 154
и связность , 81
и 1 - фактор , 51 , 57
КуратовскийК . , 98 - 103 , 297
Кэли А . , 139 , 269
ЛарманД . Г . , 79
латинский квадрат , 138
лемма Кёнига о бесконечности ,
210 , 230 , 317
лемма (о) бесконечности , 210 ,
230 , 317
лемма (о) регулярности , 167 ,
172 - 185 , 187 , 230
лемма (об) униформности ,
см . лемма регулярности
лемма Радо о выборе , 230
лемма Шпернера , 57
лес , 27
разбиения на леса , 77 - 78
линейная алгебра , 35 - 40 , 63 - 66 ,
103 - 105 , 135
линейное программирование , 165
линия (ребро) , 16
лист , 27 , 42
Ловас Л . , 58 , 131 , 134 , 140 ,
141 , 187
логарифмы , 15
ломаная , 84
Лучак Т . , 270 , 271
Мадер В . , 26 , 72 - 74 , 78 , 82 - 83 ,
197 , 203 , 205 - 206
МаклейнС , 103 , 111
максимальная степень , 19
и предписанно - хроматический
класс (индекс) , 129 , 140
и радиус , 23 , 42
и хроматический индекс (класс) ,
121 - 123
и хроматическое число , 116
и числа Рамсея , 212 - 215
ограниченная , 181 , 212 - 213
максимальный , 18
ациклический граф , 27
планарный граф , 98 , 103 , 109 ,
111 , 203 , 205
плоский граф , 87 , 90 , 98
Мани П . , 79
МаньянтиТ . Л . , 165
марковская цепь , 271
маршрут , 24
замкнутый , 24
чередующийся , 68
Мате А . , 230
математическое ожидание ,
253 - 254 , 263
матрица инцидентности , 39
матрица смежности , 39
Мёбиуса
корона , 228
лестница , 203
между , 21 , 85
Менгер К . , 58 , 66 - 72 , 81 , 163 , 307
метод компактности , 210 , 230
Мильграм А . Н . , 55
минимальная степень , 19
и вынуждение
гамильтонова цикла , 273 , 246
длинных циклов , 22
длинных путей , 22 , 186
коротких циклов , 199 - 200 , 258
деревьев , 28
и обхват , 197 - 200 , 258
и периметр , 22
и связность , 26 , 82 - 83
и средняя степень , 19
и сцепленность , 190
и хроматическое число , 116 - 116
и число выбираемости , 124
минимальное
множество запрещенных миноров
298 , 303 , 304 - 305
разделяющее множество , 80 - 81

328
Предметный указатель
минимальный по Рамсею , 216
минимальный , 18
непланарный граф , 109
разрез , 37 , 107 - 108 , 155
связный граф , 27
/с - связный граф , 82
минор , 31 - 33
(см . также топологический
минор)
бесконечный , 304
всех больших 3 - или 4 - связных
графов , 228
вынужденный , 193 , 198 - 205
граф Петерсена как минор , 160
запрещенный , 200 - 203 , 285 - 301 ,
303 - 305
и планарность , 98 - 103 , 109
и правильное квазиупорядочение ,
272 - 301
и топологический минор ,
33 - 34 , 98 - 99
мультиграфа , 41
#з , з , 111 . 205
А'4 , 201 , 285
К5 , 202 , 205
А"5 и Кз , з , 98 - 103
А'6 , 203
А"г , 200 , 201
многоугольник , 85
многочлен Татта , 165
/ : - множество , 15
момент
второй (дисперсия) , 263 - 268
первый , см . неравенство Маркова
мост , 25 , 51 , 144 , 154 , 234
Мохар Б . , 110 - 111 , 140 , 305
мультиграф , 40 - 41
и предписанный хроматический
индекс , 140
плоский , 105
Мурти У . С . Р . , 248
на , 16
над граф , 18
направление , 143
наследственное свойство графа ,
285 , 297 - 301
алгоритмическая разрешимость
н . с . г . , 300 - 301
насыщенный ,
см . реберно - максимальный
начальная вершина , 40
не покрытая паросочетанием
вершина , 44
независимые
вершины , 17 , 55 , 129 , 252
пути , 22 , 70 - 73 , 306
ребра , 17 , 45 - 54
события , 251
непересекающиеся графы , 18
неравенство Маркова , 254 , 258 ,
263 , 266
неравенство Чёбышева , 264 , 318
несводимый граф , 303
неуравновешенный подграф ,
268 , 270
нечетная
компонента , 50
степень , 20
нечетный цикл , 30 , 116 , 136 , 312
НешетрилЯ . , 230 , 231
нигде
не нулевой , 147 , 165
не плотный , 78
нормальное дерево , 28 - 29 , 42 ,
159 , 164 , 319
нулевой граф , см . пустой граф
Нэш - Уильямс , К . С . Дж . А . , 75 ,
78 , 81 , 83 , 304
область , 85 - 87
наS2 , 87
обхват , 22
и диаметр , 23
и минимальная степень , 22 ,
199 - 200 , 258
и миноры , 199 - 200
и планарность , 108
и связность , 258
и средняя степень , 258
и топологические миноры ,
197 - 198
и хроматическое число , 118 ,
140 , 256 - 258
Оксли Дж . Г . , 111 , 228
Опоровский Б . , 228
Орлин Дж . Б . , 165
объединение , 17
ограниченное подмножество
в Ж2 , 87
однородный , 19 , 49 , 247

Предметный указатель
одноцветный (в теории Рамсея)
индуцированный подграф ,
215 - 226
одноцветное (вершинное)
множество , 209 - 211
подграф , 209 , 211 - 215
окружность на S2 , 87
октаэдр , 25 , 30
орграф , см . ориентированный граф
ориентация , 40 , 127 , 164 , 311
ориентированное ребро (дуга) , 40
ориентированный
граф , 40 , 127 , 138
путь , 55
цикл , 138
ориентируемая поверхность , 304
плоскость как о . п . , 156
остовные деревья , 27 , 29
не пересекающиеся по ребрам ,
74 - 77
число о . д . , 269
остовный
подграф , 18
отношение быть минором ,
32 - 33 , 298
отрезок (сегмент) прямой , 85
Палмер Э . М . , 270
параллельно - последовательный , 205
параллельные ребра , 40
паросочетание , 44 - 58
в двудольных графах , 44 - 49 , 129
в произвольных графах , 50 - 54
и раскраска ребер , 138
покрывающее множества
вершин , 44
Пеликан Дж . , 205
первая точка на границе , 85
пересечение , 18
пересечения в решетке , 279 - 280
перешеек , см . мост
периметр , 22
и минимальная степень , 22
и связность , 80 , 233
Петерсен Ю . , 49 , 51
петля , 40
Пим Дж . С , 83
Пламмер М . Д . , 58
планарный , 98 - 108 , 297
плоская триангуляция , 90 , 92 , 283
329
плоский
граф , 87 - 93 ,
мультиграф , 105 - 108 , 155 - 159
плоскодвойственный (мультиграф) ,
106 , 109
плотность , 129 - 136 , 221 , 284
верхняя плотность , 186
пары множеств вершин , 173
пороговая функция для
плотности , 268
реберная плотность , 167
случайного графа , 252
плотные графы , 167 , 170
плохая последовательность ,
273 , 304
подграф , 18
большой минимальной степени ,
20 , 116 , 137
всех больших Аг - связных графов ,
227 - 228
вынужденный реберной
плотностью , 167 - 185
высокой (большой) связности , 26
индуцированный , 18
подразбивающая (подразделяющая)
вершина , 32 - 33
подразбиение (подразделение)
(ребра) , 32 - 33
подстягивание , см . минор
покрытие
антицепями , 58
вершинами , 45 , 279
деревьями , 77 - 78 , 108
ежевики , 279
путями , 55 - 56
ребрами , 138
цепями , 56 , 58
покрытие вершин , 45
полная часть
древесного разложения , 284
путевого разложения , 303
полный , 17
двудольный , 29
г - дольный , 30
минор , 198 - 203 , 297 - 298
многодольный , 30 , 170
подграф , 119 , 129 - 130 , 166 - 170 ,
252 , 268 , 278
сепаратор (разделяющий
подграф) , 283 , 303

330
топологический минор , 78 ,
189 - 198 , 203 - 205
пороговая функция , 262 - 268 , 271
для деревьев , 268
порожденный (индуцированный)
подграф , 18
порядок
графа , 16
древесный , 28 , 42
ежевики , 279
удаления/стягивания , 32
частичный , 28 , 33 , 42 , 56 ,
58 , 139 , 301
ячейки или предъячейки , 287
последовательная раскраска ,
см . жадный алгоритм
поток , 142 - 165 , 144 - 145
2 - поток , 152
3 - поток , 153 , 160 - 161
4 - поток , 153 - 154 , 160 - 161
Я - поток , 147 - 152
А>поток , 150 - 154 , 159 - 165
в плоских графах , 155 - 159
в сети , 144 - 147 , 313
величина потока , 145
гипотезы о потоках , 159 - 161
двойственность между потоками
и раскрасками , 155 - 159 , 313
потоковое число , 150 - 153 ,
158 - 159 , 164
потоковый многочлен , 149 , 165
со значением в группе ,
147 - 152 , 164
теорема о 6 - потоке , 161 - 163
целочисленный , 145 , 167
поточечно мажорирующий , 235
почти , 258 , 268 - 269
Поша Л . , 216 , 246
правильное квазиупорядочение ,
272 - 305
правильное квазиупорядочение
деревьев , 274 - 276
предложение первого порядка , 260
предписанная раскраска , 123 - 129 ,
140
двудольных графов , 127 - 129 , 140
предписанно /с - раскрашиваемый ,
см . /с - выбираемый
Предметный указатель
предписанное (списочное)
хроматическое число , см . число
выбираемости
предписанный вариант теоремы
Брукса , 140
предписанный хроматический
класс (индекс) , 123 , 126 - 129 ,
140
предъячейка , 287
ПремельХ . Й . , 136 , 141
препятствие
для малой древесной ширины ,
279 - 282 , 286 - 287 , 304 , 305
проективная плоскость , 299 , 305
пропускная способность , 145
функция п . с , 144
простой
базис , 85 , 103 - 111
(обыкновенный) граф , 41
пространство вершин , 35
пространство ребер , 35 , 103
процесс порождения графов , 271
псевдослучайный граф , 230
пустой граф , 16
путевая ширина , 303 , 305
путевое разложение , 303
путь , 20 - 24
а - Ь - путь , 22 , 71
Л - Б - путь , 22 , 66 - 72
Я - путь , 22 , 60 - 61 , 72 - 74 , 81 , 82
гамильтонова
последовательность , 237
длина , 20
длинный , 22
индуцированный , 227
между заданными парами
вершин , 78 - 80 , 82 - 83 , 189
независимые пути , 22 , 71 - 74 , 306
непересекающиеся по ребрам ,
71 - 74
непересекающиеся пути ,
55 , 66 - 72
ориентированный , 55
покрытие путями , 55 - 56 , 308
сцепка , 78 - 80 , 82 , 189 , 190
чередующийся , 44 - 45 , 48
радиус , 23
и диаметр , 23 , 42
и максимальная степень , 23 , 42
Радо Р . , 230 - 231

Предметный указатель
разбивать (разделять)
граф , 25 , 66 , 71 , 72
плоскость , 85
разбиение , 15 , 77 , 209
разбиение графа , 75
разделяющая вершина , 25 , 58 - 60
разделяющая вершина (см . точка
сочленения)
разделяющее множество , 25
разность графов , 17 - 18
разреженные графы , 166 ,
188 - 203 , 212
разрез , 36
в сети , 145
двойственность между разрезами
и циклами , 155 - 157
минимальный , 37 , 107
однореберный , см . мост
поток через , 144
пропускная способность , 145
пространство разрезов , 37 - 38 ,
43 , 103 , 107
разделяющее ребро , см . мост
РамсейФ . П . , 208 - 212
раскраска , 112 - 141
алгоритмы раскраски , 115 , 137
в теории Рамсея , 209 - 210
и потоки , 155 - 159
плоских графов , 113 - 115 , 155 - 159
тотальная , 138
раскраска карт , 112 - 115 , 136 ,
139 , 155
раскраска ребер , 113 , 121 - 123 , 209
и паросочетания , 138
и потоковое число , 154
раскрасочное число , 116 , 137
/^ - раскрашиваемый , 112
расстояние , 23
расширение вершины , 132
реберная плотность , 19 , 167
вынуждение
миноров/топологических миноров , 188 - 200
вынуждение подграфов , 166 - 187
и лемма регулярности , 173 , 186
и средняя степень , 19
реберная связность , 25 , 72 , 75
ре берно - максимальный , 18
без ГА"3 , з , 205
без МКЬ , 202
без ТК* , 201
331
без ГА'5 , ТА'з . з , 102
и экстремальный , 168 , 202 - 203
реберно - непересекающиеся
остовные деревья , 74 - 77
£ - реберно - связный , 25
реберное покрытие , 138
реберное хроматическое число ,
см . хроматический индекс
(класс)
реберный граф , 18 , 113 , 204
ребро , 16
X - Y ребро , 17
двойное , 41
мультиграфа , 41
ориентированное , 40
пересекающее разбиение , 36
плоское , 87
ребро - переход , 75
е - регулярная пара , 173 , 186
е - регулярное разбиение , 173
Реньи А . , 265 , 270
решетка , 109 , 279
древесная ширина решетки ,
282 , 302 , 305
минор решетки , 282 , 286 - 297
теорема о решетке , 286
Рёдль В . , 187 , 213 , 216 , 231
Рид Б . А . , 305
Риха С , 248
Ричардсон М . , 138
РобертсонН . , 83 , 140 , 203 , 205 ,
279 , 286 , 298 , 304
род
графа , 110 - 111 , 304
и раскраска , 140
поверхности , 299
Ротшильд Б . Л . , 230
Руаль Ж . Ф . , 43
Ручиньский А . , 270
Сандерс Д . П . , 140
сбалансированный , 264
свидетельство , 298 , 305
сводимая конфигурация , 140
свойство графов , 258
свойство , 258
возрастающее , 261
наследственное , 285
почти всех графов , 258 - 263 ,
268 - 269

332
связанность вершин путем ,
24 , 27 , 320
связанный паросочетанием , 52
связность , 24 - 26 , 59 - 83
внешняя , 287 , 303
и гамильтоновы циклы , 234
и минимальная степень , 26
и обхват , 258
и периметр , 80
и плоская двойственность , 110
и плоское представление , 97 - 98
' и рамсеевские свойства , 227 - 228
и реберная связность , 25
и средняя степень , 26
и сцепленность , 78 , 82
случайного графа , 260
связный граф , 24
2 - связный , 59 - 61
3 - связные графы , 61 - 66 , 98
Аг - связный , 25 , 80 - 81
внешне , 287 , 303
минимально связный , 27
минимально /с - связный , 82
Сеймур П . Д . , 83 , 111 , 140 , 161 ,
203 , 205 , 206 , 246 , 279 , 280 ,
286 , 298 , 304 , 305
Секереш Д . , 229
СемередиЭ . , 172 - 173 , 189 , 206 ,
213 , 246
см . также лемма регулярности
сердечник , 312
сеть , 144 - 147
сильный сердечник , 312
симметрическая разность , 35 ,
45 , 57 , 69
симплиниальное древесное
разложение , 283 , 299 , 302 , 304
система множеств , см . гиперграф
система различных
представителей , 57
А - система , 229
склейка , 130 , 201 - 203 , 205 , 283
Скотт Б . К . , 187 , 198 , 229
Скрайвер А . , 165
случайная величина , 253
индикаторная , 255 , 317
случайный граф , 198 , 212 ,
249 - 271 , 251
бесконечный , 269
порождение , 270 - 271
Предметный указатель
равномерная модель , 270 - 271
эволюция случайных графов , 262
смежный , 17
снарк , 160
планарный , 160 , 164 , 234
событие , 251
совершенное паросочетание ,
см . 1 - фактор
совершенные графы , 129 - 136 ,
139 , 141
содержать , 18
соединенный
дугой , 85
путем , 20
соединять , 16
соприкасающиеся множества , 279
сосед , 17 , 19
Спенсер Дж . X . , 230 , 270
сплетение , 305
средняя степень , 19
двудольного планарного
графа , 311
и вынуждение миноров , 188 ,
198 , 204
и вынуждение топологических
миноров , 78 , 189 - 198
и лемма регулярности , 173 , 186
и минимальная степень , 19 - 20
и обхват , 258
и предписанная раскраска , 124
и связность , 26
и хроматическое число , 118 - 119 ,
124 , 198 , 204
и числа Рамсея , 231
и число ребер , 19
ограниченная , 231
стандартный базис , 35
степень , 19
степенная последовательность ,
235
степень графа , 237
стереографическая проекция , 87
Стилвел Дж . , 110
сток , 144
Стоун А . X . , 170 , 181
стягивание , 31 - 33
в мультиграфах , 41
и 3 - связность , 61 - 62
и древесная ширина , 277 - 278
и миноры , 31 - 33

Предметный указатель
стягивание ребра , 31
в мультиграфе , 41
и 3 - связность , 61
и миноры , 31 - 32
сумма
множеств ребер , 35
потоков , 152
сцепленное
(тощее) древесное разложение ,
282 - 283
множество , 189
сцепленный
/г - сцепленный , 78 - 80 , 82
и Аг - связный , 78 , 81
(к , £) - сцеп ленный , 189
Тарси М . , 140
Татт В . Т . , 50 , 62 , 63 , 75 , 82 - 83 ,
105 , 111 , 148 , 150 , 158 , 165 ,
235 , 248
Тейт П . Дж . , 131 , 247 - 248
теорема Галлаи — Эдмондса
о паросочетаниях , 52 - 54 , 58
теорема Кёнига о двойственности ,
45 , 55 , 130
теорема о максимальном потоке
и минимальном разрезе , 144 ,
146 , 163 , 165
тебремао минорах , 272 , 297 - 301 ,
298
для деревьев , 274 - 276
доказательство , 299 - 300
теорема о минорах графов ,
272 , 297 - 301
теорема о 6 - потоке , 161
теорема о пяти красках , 113 ,
139 , 161
предписанный вариант , 124 , 140
теорема о свадьбах , 46 , 49 ,
57 - 58 , 310
теорема о совершенных графах ,
131 , 134 , 136 , 141
теорема о трех красках , 115
теорема о четырех красках , 113 ,
161 , 164 , 201 , 203 , 204 , 234 , 247
история , 140
теорема об 1 - факторе , 50 , 82
теоретико - графовый изоморфизм ,
95 - 96
теория матроидов , 83 , 111
теория потоков в сетях , 165
333
теория сложности , 130 , 297 , 305
теория Рамсея , 207 - 228
бесконечная , 210 - 211 , 229 , 230
и связность , 227 - 229
индуцированная , 215 - 226
теория узлов , 165
ТихоновА . Н . , 230
Томас Р . , 140 , 203 , 228 , 231 ,
280 , 304 - 305
ТомассенК . , 82 , 111 , 124 , 140 , 199 ,
205 , 206 , 248 , 304 , 305
Томасон А . Дж . , 83 , 189 , 198 ,
205 , 263
топологический изоморфизм ,
94 , 96 , 106
топологический минор , 32 - 33
А'з . з , 111 , 205
А'4 , 201 , 204 , 285
К5 , 111 , 203 , 205
К5 иА'з . з , 93 , 98 - 103
A'i , 205
Кг% 78 , 189 - 198
всех больших 2 - связных
графов , 227
вынужденный обхватом , 197
вынужденный средней степенью ,
78 , 189 - 198
вынужденный хроматическим
числом , 200
дерево (индуцированное) , 198
и обычный минор , 32 - 33 , 99
и планарность , 93 , 98 - 103 , 109
и правильное квазиупорядочение
деревьев , 274
и правильное квазиупорядочение
произвольных графов , 302
индуцированный , 198
как отношение порядка , 33
торс , 303
тотальная раскраска , 138
гипотеза , 138 , 140
тотальное хроматическое
число , 138
точка (вершина) , 16
точка сочленения , 25 , 59 - 60
точность , 318
Тофт Б . , 139 , 165
транзитивный граф , 57
треугольник , 17 - 18

334
триангулированный ,
см . хордальный
триангуляция , см . плоская
триангуляция
тривиальный граф , 16
Тротер Б . Т . , 213
Туран П . , 169
турнир , 247
увеличивающий путь
для паросочетания , 45 , 57 , 307
для потока в сети , 147 , 163
удаление , 18
узел (вершина) , 16
Уинклер П . , 270
Уитни X . , 83 , 98 , 108
утончение (измельчение)
разбиения , 15 , 175 - 179
Уэлш Д . Дж . А . , 165
фактор , 44
1 - фактор , 44 - 54
2 - фактор , 49
/ : - фактор , 44
теорема об 1 - факторе , 50 , 58 , 82
фактор - критический , 52 , 308
Фалкерсон Д . Р . , 141 , 146 , 165
Фейтлович С , 206
физика , 165
Флейшнер X . , 238 , 317
Фогт М . , 140
Форд Л . Р . , 146 , 165
формула Эйлера , 92 - 93 , 108 - 109 ,
312
Франк А . , 82 , 165
Фробениус Ф . Г . , 58
Хадвигер X . , 201 , 205 - 206
Хайнал А . , 216 , 230
Хайош Г . , 119 , 206
Хакен В . , 140
Халин Р . , 82 - 83 , 247 , 304
характеризация по Куратовскому ,
109 , 297 - 298 , 304 - 305
Харант Й . , 83
Хватал В . , 213 , 235 , 248
хвост , см . начальная вершина
Хееш X . , 140
Хивуд П . Дж . , 139 , 164
Хигман Д . Г . , 273 - 274 , 304
Холл П . , 46 , 58
хорда , 22
Предметный указатель
хордальный , 130 - 131 , 139 , 284 , 303
хорошая
пара , 273
последовательность , 273
характеризация , 297 , 305
Хофман А . Дж . , 139
хроматический индекс (класс) ,
113 , 121
двудольных графов , 121
и максимальная степень , 121 - 123
и предписанный хроматический
класс , 123 , 126
хроматический класс ,
см . хроматический индекс
хроматический многочлен , 137 , 165
/ : - хроматический , 112
хроматическое число , 112
и вынуждение коротких циклов ,
118 - 119 , 258
и вынуждение миноров , 200 - 204
и вынуждение подграфов ,
118 - 119 , 197 - 198 , 229 - 230
и вынуждение треугольника ,
138 , 229
и максимальная степень , 118
и минимальная степень , 115 - 116
и обхват , 118 , 258
и Кг - подграфы , 116 - 118 , 129 - 130
и потоковые числа , 158
и связность , 116
и средняя степень , 118 , 124 ,
197 - 198 , 204
и число выбираемости , 123 - 124
и число ребер , 115
и экстремальные графы , 170 - 171
как глобальное явление , 119 , 129
почти всех графов , 261
цветовой класс , 112
целочисленная
случайная величина , 263
функция , 145
целочисленный поток , 145 , 147
центральная вершина , 23 , 306
цепь , 28 , 56 , 57
цикл , 20 - 23
в мультиграфах , 41
гамильтонов , 164 , 232 - 248
гипотеза о двойном покрытии
циклами , 160 , 164

Предметный указатель
335
двойственность между циклами
и разрезами , 155 - 157
длина , 22
длинный , 22 - 23 , 41 , 80 - 81 , 137
индуцированный , 22 , 36 , 63 - 64 ,
105 , 130 , 136 , 312
короткий , 118 - 119 , 199 - 200 ,
256 , 258
неразделяющий , 63 , 105
нечетный , 30 , 116 , 136 , 312
ожидаемое число циклов , 255
ориентированный (контур) , 138
пороговая функция , 268
пространство циклов , 36 , 38 - 39 ,
43 , 63 - 66 , 103 - 105 , 107 , 111
с ориентацией , 155 - 158
цикломатическое число , 36
циркуляция , 143 , 156 , 165
частично упорядоченное
множество , 56 , 58
часть древесного разложения , 276
ЧенГ . , 231
чередующийся
маршрут , 69
путь , 44
четверная группа Клейна , 154
четная степень , 34 , 49
четность , 19 - 20 , 50 , 52 - 53 , 247
четный граф , 152 , 154 , 164
числа Рамсея , 209 , 212 - 215 ,
229 - 230 , 252 - 253
число внутренней устойчивости ,
см . число независимости
число выбираемости , 123
двудольных планарных
графов , 138
и средняя степень , 124
планарных графов , 124
число независимости , 129 - 136
и гамильтоновы циклы , 234
и длинные циклы , 137
и покрытие путями , 55
и связность , 234
случайного графа , 252 , 269
ШаркозиД . Н . , 246
Шелл Р . X . , 231
ШенфлайесА . М . , 87
ШимоновичМ . , 187 , 230
ширина древесного разложения , 278
Шош В . , 172 , 186 , 187
Штегер А . , 136 , 141
Штейниц Э . , 111
Шур И . , 229
эволюция случайных графов ,
262 , 270
Эдмондс Дж . , 58 , 305
Эйлер Л . , 33 - 34 , 92
эйлеров
граф , 34
обход , 33 - 35 , 313
эйлерова характеристика , 300
эквивалентность
в частичном порядке , 301
планарных вложений , 94 - 98 , 109
точек в Е2 , 85
экстремальная теория графов ,
166 , 170 , 180 , 187
эк стр ема льный
без МКЬ , 203
безТАГ3 , з , 205
без ТА"4 , 201 - 202
без ГА"5 , 203
граф , 168 - 169
двудольный граф , 185 - 186
и реберно - максимальный ,
168 , 202
Эрдеш П . , 118 , 140 , 170 , 183 , 187 ,
206 , 216 , 229 - 231 , 234 , 248 , 253 ,
256 - 258 , 265 , 270 , 318
Эркхарт А . , 140
Юнг X . А . , 79 , 205
ядро
матрицы инцидентности , 39
ориентированного графа ,
127 - 128 , 138
ЯнсонС . , 270
/с - ячейка , 287

Учебное издание
Дистель Рейнгард
ТЕОРИЯ ГРАФОВ
Перевод с английского
Бородина Олега Вениаминовича
Издание подготовлено с использованием макропакета Лд^^-Т^Х
разработанного Американским математическим обществом.
This publication was typeset using A/^S-T^.,
the American Mathematical Society's Tg]X macro system.
Подписано в печать 11.02.02. Формат 70 X 100 1/\в. Печать офсетная.
Усл. печ. л. 27,5. Уч.-изд. л. 25. Тираж 500 экз. Заказ №139.
Лицензия ЛР №065614 от 8 января 1998 г.
Издательство Института математики
пр. Академика Коптюга, 4, Новосибирск 630090
Отпечатано в ГУП РПО СО РАСХН
пос. Краснообск, 630500, Новосибирская обл., Россия