Author: Кроуэлл Р. Фокс Р.
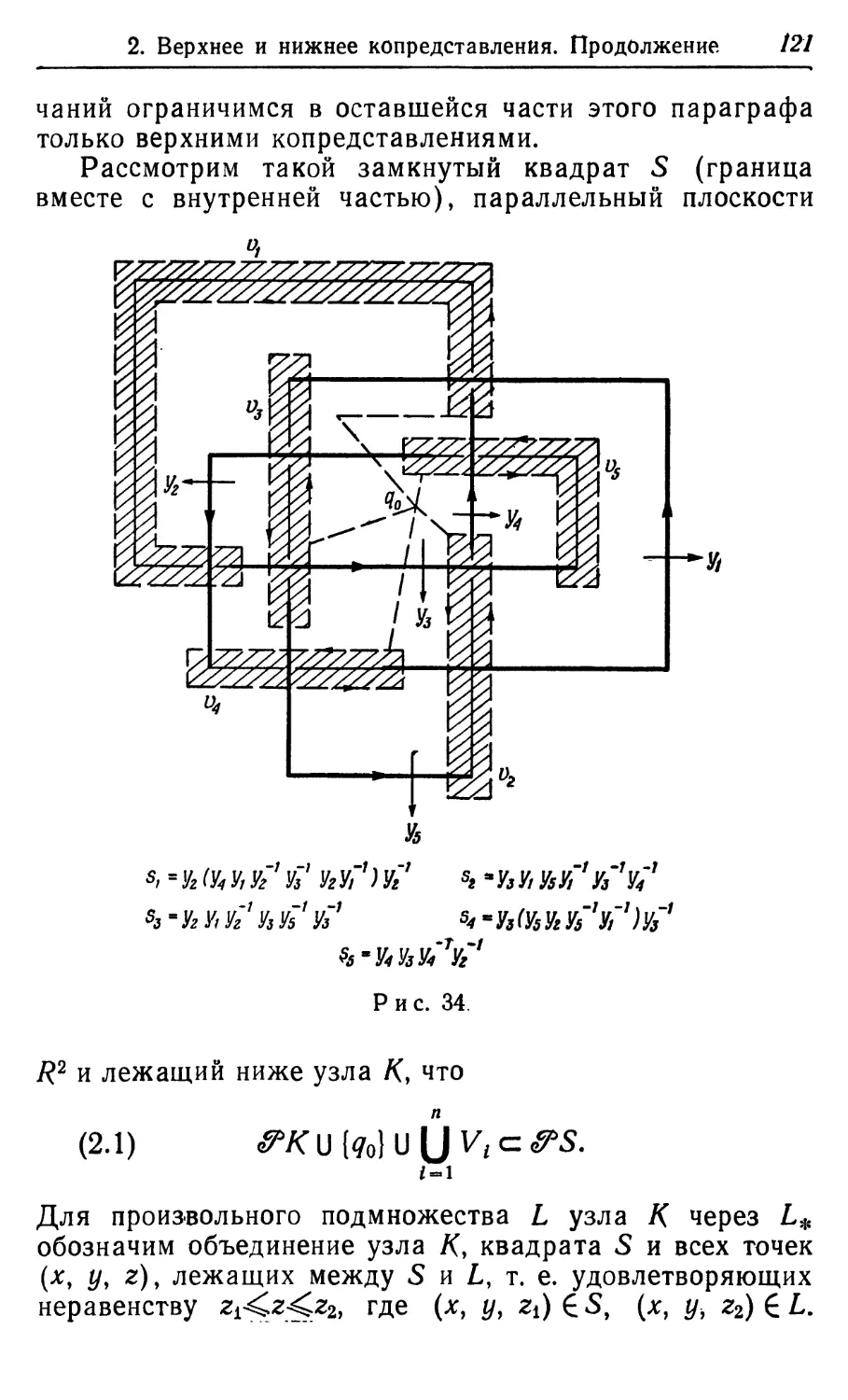
Tags: математика механика теоретическая механика переводная литература введение в теорию узлов
Year: 1967
Text
Р.Кроуэлл
Р.Фокс
ВВЕДЕНИЕ В ТЕОРИЮ УЗЛОВ
L
INTRODUCTION TO
KNOT THEORY
By
Richard H. Crowell
Dartmouth College
and
Ralph H. Fox
Princeton University
1963
QINN AND COMPANY
Boston • New York • Chicago • Atlanta • Dallas •
Palo Alto • Toronto
Р. КРОУЭЛЛ, P. ФОКС
ВВЕДЕНИЕ
В ТЕОРИЮ УЗЛОВ
Перевод с английского
А. М. ВИНОГРАДОВА
ИЗДАТЕЛЬСТВО «МИР»
МОСКВА 1967
УДК 513.83
Книга посвящена теории узлов, одной из ветвей
алгебраической топологии, отличающейся своеобразной
красотой и наглядностью, а также связями с другими
разделами математики.
В данном издании к основному тексту книги, за-
задуманной как учебник по теории узлов, добавлены пе-
переводы обзорной статьи по теории узлов Р. Фокса и
его же списка проблем. Имеется богатая библиография
и путеводитель по литературе.
Книга дает возможность начиная с простейших по-
понятий перейти к весьма тонким вопросам теории узлов
и будет поэтому интересной как студентам-математи-
студентам-математикам, так и специалистам. Она заинтересует также и
нематематиков, встречающихся в своей работе с теорией
узлов.
ПРЕДИСЛОВИЕ
К РУССКОМУ ИЗДАНИЮ
Когда книга переводится на другой язык, авторам
предоставляется возможность пересмотреть свою работу.
При этом существенная переделка книги, разумеется,
исключена и, например, привлечь теорию накрытий уже
нельзя. Мелких же ошибок, которые следовало бы испра-
исправить, в книге (как это ни странно!) нет. Поэтому мы де-
делаем только одно изменение — продолжаем библиогра-
библиографию на несколько лет вперед.
Ральф Фокс
Токио
5 июля 1966 г.
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
Теория узлов, одна из самых старых частей алгебраи-
алгебраической топологии, принадлежит к числу тех разделов
математики, где ставить «естественные» вопросы гораз-
гораздо легче, чем отвечать на них. Поэтому, несмотря на то,
что ею занимаются многие математики уже почти де-
девяносто лет, полученные в ней результаты довольно
скромны и многие основные проблемы все еще ждут
своего решения. Особенно парадоксально то, что в теории
узлов зачастую проблемы многомерной топологии ре-
решаются гораздо легче, чем аналогичные им проблемы
в обычном трехмерном пространстве. Источником алгеб-
алгебраических трудностей в теории узлов является то, что
используемая в ней алгебра по своему существу неком-
некоммутативна, причем возникающие в ней алгебраические
вопросы весьма нестандартны с точки зрения чистой
алгебры, что затрудняет применение известных алгеб-
алгебраических результатов к теории узлов.
Сейчас положение в теории узлов, по-видимому, та-
таково, что основные понятия и проблемы твердо опреде-
определены, однако методы их эффективного решения в ряде
случаев только нащупываются.
Книга Р. Фокса и Р. Кроуэлла, перевод которой пред-
предлагается вниманию советского читателя, представляется
интересной по ряду причин. Во-первых, это превосход-
превосходно написанный учебник по теории узлов, который мо-
могут читать студенты-математики первых курсов, а также
нематематики, интересующиеся приложениями теории
узлов. Хорошо подобранные упражнения, помещенные
в конце каждой из глав книги, позволят читателю про-
проконтролировать себя, а также дадут материал, расши-
расширяющий рамки основного текста. Во-вторых, подход к
теории узлов, изложенный в этой книге, будет, на наш
Предисловие переводчика
взгляд, интересен и специалисту-топологу. Мы надеемся,
что эта книга возбудит интерес к проблемам теории уз-
узлов у читателей.
В качестве Приложения I к книге дан перевод статьи
Р. Фокса «Краткий экскурс в теорию узлов», в которой
излагаются в основном без доказательств важнейшие
(по мнению автора) моменты современной теории уз-
узлов. Для понимания первых трех параграфов первого
приложения достаточно владеть основным текстом книги.
Поэтому эти параграфы могут рассматриваться как
расширение (довольно значительное) рамок основного
текста. Параграфы 4 и 5 посвящены приложениям тео-
теории накрывающих пространств к теории узлов. Для их
понимания необходимо знание основ теории накрываю-
накрывающих пространств и теории гомологии в многообразиях.
По-видимому, они будут доступны топологам с некото-
некоторым опытом. Отметим, что накрывающие пространства
весьма существенны для теории узлов в силу многих
обстоятельств. В частности, накрывающие пространства
дают ряд новых (т. е. таких, которые не получаются
методами основного текста) инвариантов узлов. Кроме
того, они проливают свет на истоки свободного диф-
дифференциального исчисления, на котором основан спо-
способ нахождения основных инвариантов узлов, но появ-
появление которого в основном тексте довольно неожиданно.
Здесь нелишне также отметить, что многие наиболее
сильные результаты трехмерной топологии связаны с
теорией накрытий. Наконец, последний параграф При-
Приложения I посвящен некоторым элементарным приемам
нахождения представлений групп узлов.
При переводе Приложения I был опущен материал,
пересекающийся с текстом книги. Кроме того, перевод-
переводчиком добавлены примечания к нему. В них набросаны
доказательства большинства результатов, упоминаемых
в тексте этого Приложения, или указаны методы их воз-
возможного получения. Для усвоения этих примечаний до-
достаточно знать материал, необходимый для понимания
соответствующих мест Приложения I. Мы надеемся, что
с помощью этих примечаний терпеливый читатель смо-
сможет восстановить доказательства всех ключевых мест
Приложения L
8 Предисловие переводчика
К качестве Приложения II помещен список проблем
теории узлов, предложенный в 1961 г. Р. Фоксом. Он до-
довольно ярко иллюстрирует положение дел, сложившееся
к настоящему времени в теории узлов и, по-видимому,
подтверждает соображения, высказанные нами ранее.
Наконец, в конце книги приведен Путеводитель по
литературе, в котором отражена почти вся основная ли-
литература по теории узлов начиная с времен Гаусса. Он
составлен Кроуэллом и Фоксом.
В заключение переводчик выражает свою благодар-
благодарность проф. Р. Фоксу, приславшему дополнительный спи-
список литературы и указавшему на неточности в переве-
переведенных текстах.
А. Виноградов
ПРЕДИСЛОВИЕ АВТОРОВ
Теория узлов представляет собой часть геометрии,
привлекательную тем, что изучаемые в ней объекты мож-
можно воспринимать и осмысливать в обычном физическом
пространстве. Она — место стыка таких разных разде-
разделов математики, как теория групп, теория матриц, тео-
теория чисел, алгебраическая и дифференциальная гео-
геометрия (мы называем лишь наиболее важные разделы).
Ее истоки лежат в математической теории электричества
и элементарной атомной физике, а недавно наметилась
возможность ее новых приложений в некоторых обла-
областях химии1). Вид современной топологической теории
теория узлов приобрела после работ Дена, Александера,
Рейдемейстера и Зейферта почти тридцать лет тому
назад. Как часть топологии она образует как бы остов
широкого круга проблем, связанных с расположением
одного многообразия внутри другого.
Эта книга, представляющая собой обработку курса
лекций, читанных Р. Фоксом в Хэйверфордском коллед-
колледже весной 1956 г., является попыткой сделать теорию
узлов широко доступной. Прежде всего, это учебник для
студентов младших курсов, но мы считаем, что она бу-
будет полезной и студентам старших курсов. Посколь-
Поскольку нужная нам алгебра не сводится к обычной комму-
коммутативной алгебре, непропорционально большую часть
книги занимают необходимые предварительные алге-
алгебраические сведения. Однако в этом есть и хорошая
сторона, потому что изучение некоммутативного случая
существенно не только в теории узлов, но важно и
само по себе; к тому же эта тема не очень широко
*) Frisch H. L., Wasserman E., Chemical Topology, /. Am.
С hem. Soc, 83 A961), 3789—3795.
10 Предисловие авторов
представлена в литературе. Возможно, наиболее краси-
красивым аспектом теории узлов является взаимодействие
геометрии и этой некоммутативной алгебры.
В последние тридцать лет книга Курта Рейдемейсте-
ра Knotentheorie, изданная в серии Ergebnisse der Ма-
thematik, была,- по-видимому, единственной книгой по
нашему предмету. За это время в теории узлов сделано
существенное продвижение и теперь комбинаторная точ-
точка зрения, преобладавшая в Knotentheorie, заменилась
строгим топологическим подходом. В связи с этим мы
везде подчеркиваем топологическую инвариантность на-
нашей теории.
Для авторов вполне очевидно, что теория узлов кон-
концентрируется вокруг понятий группы узла, матрицы
Александера и накрывающего пространства, и наше из-
изложение следует этой точке зрения. Жаль только, что,
стремясь изложить материал настолько элементарно, на-
насколько это возможно, мы не вводим и не используем
теорию накрывающих пространств. Если бы это было
сделано, то книга получилась бы более длинной, более
трудной и, возможно, более ценной. Опытные математи-
математики (например, те, кто уже изучил эту книгу) могут най-
найти обзор основных идей этой теории в статье Фокса*).
Приводимая нами библиография неполна и все же
намного больше, чем требуется для вводного изложения
теории узлов. Мы пошли на это отчасти потому, что в
такой библиографии по нашему предмету имеется сей-
сейчас большая нужда, а отчасти и потому, что, как мы на-
надеемся, этой книгой будут пользоваться самые искушен-
искушенные математики. Чтобы сделать эту библиографию бо-
более полезной, мы предпослали ей путеводитель по ли-
литературе.
Наконец, мы благодарим многочисленных математи-
математиков, читавших и критиковавших рукопись на различных
этапах ее подготовки. В особенности мы отметим Ли
Нойвирта, Дж. Ван Бускирка, Р. Ауманна и двух аспи-
аспирантов Дартмутского колледжа — С. Циммермана и
П. Розмарина.
*) Перевод статьи помещен в конце книги (см. приложе-
приложение \). — Прим. перев.
ПРЕДВАРИТЕЛЬНЫЕ УКАЗАНИЯ
Для изучения этой книги достаточно знания элемен-
элементов высшей алгебры и теории множеств. Точнее, мы
предполагаем, что читатель знаком с понятием функции
(или отображения) и примыкающими сюда понятиями
области определения, области значений, образа, прооб-
прообраза, взаимно однозначного отображения, отображения
на, композиции отображений, отображения вложения и
ограничения отображения; с понятием отношения экви-
эквивалентности и класса эквивалентности; с определением
и простейшими свойствами замкнутых и открытых мно-
множеств; с понятиями окрестности, замыкания, внутрен-
внутренности, индуцированной топологии, прямого произведе-
произведения, непрерывного отображения, гомеоморфизма, ком-
компактности, связности, открытого покрытия п-мерного
евклидова пространства Rn и, наконец, с определением
и основными свойствами гомоморфизма, автоайэрфизма,
ядра и образа, группы, нормального делителя, фактор-
факторгруппы, кольца, идеала (двустороннего), группы пере-
перестановок, определителя и матрицы.
Этот материал изложен во многих стандартных учеб-
учебниках. Мы можем, например, отослать читателя к изве-
известной книге Л. С. Понтрягина «Непрерывные группы»,
гл. I, II*). Часть вышеперечисленных понятий внесена
в указатель.
Для понимания Добавления I необходимо сверх этого
знание дифференциального и интегрального исчисления.
В книге используются стандартные символы теории
множеств: б, с, z>, =, U, П и —. Символ включения
имеет обычный смысл: А а В означает, что р£В всякий
*) Эта книга рекомендована нами вместо соответствующей ли-
литературы на английском языке. — Прим. перев,
12 Предварительные указания
раз, как р£А. Образ и обратный образ множества А
при отображении f обозначены либо выражением fA и
f~lA9 либо f(A) и f~l(A). Ограничение отображения /
на подмножество А обозначается через f\A} а компози-
композиция отображений: f : X-+Y, g.Y -+Z — через gf.
Если имеется необходимость рассмотреть одновре-
одновременно несколько отображений разных множеств, удобно
размещать их в диаграммах, подобных следующим:
X ~> У или X — ■> У — ■> Z
w
Если любой элемент произвольного множества в диаг-
диаграмме имеет не более одного образа во всяком другом
множестве диаграммы, то диаграмма называется ком-
коммутативной*). Следовательно, первая диаграмма ком-
коммутативна тогда и только тогда, когда g/=l и fg=l, a
вторая — когда bf=a и cg = b (а значит, и cgf=a).
Стоит отметить также следующую «лемму насыще-
насыщения». Ее доказательство будет дано позднее
Если h : G —* Н и k : G —► К суть некоторые гомомор-
гомоморфизмы uh — гомоморфизм на, то гомоморфизм f : Н —► К
(необходимо единственный), делающий диаграмму
Q
h/ \k
И -U К
коммутативной, существует тогда и только тогда, когда
ядро гомоморфизма h содержится в ядре гомоморфизма k.
*) Мы переводим здесь термин «consistent diagram» более при-
привычным термином «коммутативная диаграмма», — Прим, перев,
ГЛАВА I
УЗЛЫ И ТИПЫ УЗЛОВ
1. Определение узла. Почти все знакомы по крайней
мере с простейшими из узлов, т. е. с простым узлом,
(рис. 1), и восьмеркой (рис. 2).
Небольшой эксперимент с кускам веревки убедит
каждого, что эти узлы различны: нельзя перевести один
Рис. 1. Рис. 2.
узел в другой, не протаскивая один конец через петлю,
т. е. без «связывания» и «развязывания». Тем не менее
наша неудача при попытке перевести восьмерку в прос-
простой узел -после часа терпеливого кручения не является
доказательством того, что этого нельзя сделать вообще.
Проблема, которая нас интересует, как раз и состоит в
том, чтобы показать математически, что эти (и многие
другие) узлы действительно различны.
Математик может доказать что-либо только относи-
относительно математического объекта, а кусок веревки — это
объект физический. Поэтому прежде, чем думать о до-
доказательствах, мы должны позаботиться о математиче-
математическом определении узла и того, когда два узла должны
рассматриваться как одинаковые. Подобная проблема
построения математической модели возникает всякий
раз, когда математику применяют к некоторой физиче-
физической ситуации. При этом определения должны быть та-
такими, чтобы математические объекты возможно точнее
14 Гл. I. Узлы и типы узлов
аппроксимировали рассматриваемые физические объек-
объекты. Такая модель хороша или плоха в зависимости от
того, насколько близко соответствие между математиче-
математической теорией и действительностью. Однако мы не можем
доказать (в математическом смысле, т. е., по-видимому,
единственном смысле, в котором слово «доказать» имеет
точное значение), что математические определения опи-
описывают физическую ситуацию полно.
Очевидно, что восьмерка может быть преобразована
в простой узел связыванием и развязыванием (вообще
все узлы эквивалентны, если эти операции допустимы).
Поэтому связывания и развязывания следует запретить
или при определении того, когда два узла считаются
одинаковыми, или уже с самого начала, при определе-
определении узла. Последний путь проще, и мы примем его. При
этом, правда, мы должны избавиться от концов. Можно
убрать концы на бесконечность. Однако проще склеить
их. В соответствии с этим под узлом мы будем понимать
подмножество трехмерного пространства, гомеоморфное
окружности. Формальное определение таково: К являет-
является узлом, если существует гомеоморфизм единичной
окружности С в трехмерное пространство /?,3, образ ко-
которого совпадает с К\ Под окружностью С мы понимаем
множество точек (#, у) плоскости /?2, удовлетворяющих
уравнению х2 + у2=1.
Рисунки 3 и 4 показывают, как теперь выглядят про-
простой узел и восьмерка. В такой форме простой узел
чаще называют клеверным листом. Другое общеприня-
общепринятое название этого узла — трилистник. Восьмерку же
чаще называют четырехкратным узлом или же узлом
Листинга.
Теперь мы рассмотрим вопрос о том, когда два узла
/Ci и /С2 могут считаться одинаковыми. Заметим преж-
прежде всего, что вопрос не в том, являются ли эти узлы
гомеоморфными. Оба они гомеоморфны единичной
окружности и, следовательно, гомеоморфны между со-
собой. Заузленность не является'внутренним топологиче-
топологическим свойством пространства, состоящего из всех точек
узла, а характеризует способ, при помощи которого это
пространство вложено в R3. Теория узлов поэтому яв-
1. Определение узла
15
ляется частью трехмерной, а не одномерной топологии.
Если кусок веревки перевести из одного положения в
другое путем закручивания, то деформация закручива-
закручивания вполне определяет взаимно однозначное соответ-
соответствие между точками этих двух положений. Поскольку
разрезание веревки недопустимо, это соответствие не-
непрерывно в обе стороны. Добавим, что естественно счи-
считать, что движение веревки сопровождается движением
Р и с. з.
Рис 4.
окружающих молекул воздуха, которое определяет не-
непрерывное в обе стороны перемешивание точек всего
пространства. Эти соображения приводят к следующему
определению: узлы К\ и /Сг эквивалентны, если суще-
существует гомеоморфизм пространства R* на себя, отобра-
отображающий /Ci на /Сг-
Очевидно, что отношение эквивалентности узлов яв-
является и в самом деле отношением эквивалентности. Эк-
Эквивалентные узлы называются узлами одного и того же
типа, а класс эквивалентных узлов — типом узла. Узлы,
эквивалентные незаузленной окружности х2+у2=1, 2=0,
называются тривиальными и образуют тривиальный
тип1). Аналогично тип клеверного листа или восьмерки
определяется как класс эквивалентности, представленный
соответствующим узлом. Утверждение, что клеверный
*) Любой узел, лежащий на плоскости, обязательно тривиален.
Это хорошо известный, глубокий факт «плоской» топологии. См.
Newman A. H.t Elements of the Topology of Plane Sets of Points,
Sec. ed., Camb. Univ. Press, Cambridge, 1951, 173.
16 Гл. I. Узлы и типы узлов
лист и восьмерка — различные узлы, строго грво^'я, вы-
выражается тем, что они принадлежат к разнйГм типам
узлов.
2. Ручные и дикие узлы. Полигональный узел — это та-
такой узел, который является объединейием конечного чис-
числа замкнутых прямолинейных отрезков, называемых
сторонами. Концы этих отрезков называются вершинами
узла. Узел называется ручным, если он эквивалентен по-
полигональному узлу. В противном случае он называется
диким. Различие между ручными и дикими узлами имеет
первостепенную важность. Действительно, большая
часть теории узлов, развитой в этой книге, применима
(в данной формулировке) только к ручным узлам.
Важнейшие инварианты типов узлов, а именно элемен-
элементарные идеалы и полиномы узлов, определить для диких
узлов, вообще говоря, нельзя. Более того, их вычисле-
вычисление основано на полигональном представлении, которое
используется как отправная точка. Тот факт, что теория
узлов в основном ограничивается изучением полигональ-
полигональных узлов, может показаться неожиданным, особенно
читателю, который подходит к изучению узлов с точки
зрения высокой степени общности теоретико-множествен-
теоретико-множественной топологии.
Естественно спросить, какой класс узлов, отличных
от полигональных, состоит из ручных узлов. Частичный
ответ на этот вопрос дает следующая теорема.
B.1). Если узел, параметризованный длиной дуги,
принадлежит классу С1 (т. е. непрерывно дифференци-
дифференцируем), то он является ручным.
Доказательство этого дано в Добавлении I. Оно до-
довольно громоздко, но зато >прямое и использует только
обычную технику дифференциального исчисления. Пред-
Предположения относительно узла К состоят в том, что он
спрямляем и задан как образ векторнозначной функции
p(s) = (x(s), y(s), z(s)) длины дуги s, имеющей непре-
непрерывные первые производные. Следовательно, всякий до-
достаточно гладкий узел является ручным.
Совсем не очевидно, что существуют дикие узлы. На-
Например, ни один узел, расположенный на плоскости, не
3. Проекции узлов
17
является диким. Хотя изучение диких узлов лежит вне
рамок этой книги, на рис. 5 приводится пример дикого
узла2). Этот узел является замечательной кривой. Если
бы уисло петель не возрастало неограниченно в то вре-
время, как их размеры неограниченно уменьшаются (что
на рисунке указывается пунктирным квадратом вокруг
точки р), этот узел мог бы быть, очевидно, развязан.
Рис. 5.
Отметим также, что везде, кроме одной точки р, этот
узел можно считать сколько угодно раз дифференци-
дифференцируемым.
3. Проекции узлов. Узлы обычно, задаются своей про-
проекцией. Например, рис. 3 и 4 изображают проекции
«клеверного листа» и «восьмерки» соответственно. Рас-
Рассмотрим проекцию
определенную соотношением £Р (х, (/, z) = (x, у, 0). Точ-
Точка р, принадлежащая образу проекции S^K, называется
кратной, если ее прообраз #> р содержит более одной
точки узла К. Порядком точки р6<^ К называется мощ-
мощность множества (SP~lp)[\K. Поэтому двойная точка—
это кратная точка порядка два, тройная точка — точка
третьего порядка и т. д. Могут, конечно, встречаться и
точки бесконечного порядка. Вообще, образ узла S?K
может быть устроен весьма сложно относительно имею-
имеющихся на нем кратных точек и их типов. Однако
можно заменить узел К другим узлом, ему эквивалент-
2) Fox R. Н„ A Remarkable simple closed curve, Annals of
Mathematics, 50 A949), 264, 265,
2 Зак. 317
18
Гл. I. Узлы и типы узлов
ным, образ которого при проекции устроен довольно
просто. Критерий достаточной «простоты» образа для
полигонального узла состоит в том, чтобы узел был в
так называемом регулярном положении. Точное опре-
определение таково: полигональный узел К находится в ре-
регулярном положении, если: I) все его кратные точки яв-
являются двойными и их число конечно, II) никакая
двойная точка не является образом вершины узла К.
Второе условие гарантирует, что каждая двойная точка
является настоящим пересечением, как это показано на
Рис. 6а.
Рис. 6Ь.
рис. 6а. Пересечения типа, указанного на рис. 6Ь, за-
запрещены.
Всякая двойная точка проекции полигонального узла
в регулярном положении является образом ровно двух
точек узла. Та из них, у которой координата z больше,
называется переходящей, а другая соответственно про-
проходящей.
C.1) Всякий полигональный узел переводится сколь
угодно малым вращением пространства R3 в эквивалент-
эквивалентный ему полигональный узел в регулярном положении.
Доказательство. Геометрическая идея доказа-
доказательства состоит в том, что фиксируется узел /(, а ме-
меняется проекция. Каждый пучок параллельных прямых
в R3 определяет проекцию пространства Rz на плоскость,
проходящую через начало координат перпендикулярно
рассматриваемому пучку. Мы расширим очевидным об-
образом предыдущее определение регулярного положения
так, чтобы имел смысл вопрос, расположен ли узел К
в регулярном положении относительно некоторой проек-
3. Проекции узлов 19
ции. При этом удобно рассматривать пространство /?3
как подмножество действительного проективного трех-
трехмерного пространства Ргъ).
Тогда всякой проекции можно сопоставить точку пе-
пересечения любой прямой, параллельной направлению
проекции, с бесконечно удаленной проективной плос-
плоскостью Р2. Очевидно, что это соответствие взаимно од-
однозначно. Пусть Q — множество точек плоскости Р2, со-
соответствующих проекциям, относительно которых узел К
не находится в регулярном положении. Мы покажем, что
множество Q нигде не плотно в Р2. Отсюда будет следо-
следовать, что существует проекция еР0, относительно которой
узел К занимает регулярное положение и которая как
угодно близка к первоначальной проекции & вдоль
оси z. После этого для окончания доказательства доста-
достаточно рассмотреть произвольное вращение простран-
пространства /?3, переводящее прямую S^o1 (О, 0, 0) в ось z.
Для доказательства того, что множество Q нигде не
плотно © Р2, рассмотрим сначала множество всех пря-
прямых, соединяющих вершины узла К с его сторонами.
Оно пересекает плоскость Р2 по конечному числу прямо-
прямолинейных отрезков, объединение которых мы обозначим
через Qi. Всякая проекция, соответствующая точке из
Р2 — Qu должна, очевидно, удовлетворять условию II)
определения регулярного положения. Более того, она
может иметь не более конечного числа кратных точек,
из которых ни одна не имеет бесконечного порядка. Ос-
Осталось показать, что можно избавиться от кратных то-
точек порядка я^>3. Это делается следующим образом.
Рассмотрим три взаимно скрещивающиеся прямые, каж-
каждая из которых: содержит некоторую сторону узла /С.
Совокупность прямых, пересекающих все эти прямые,
образует поверхность второго порядка, которая пересе-
пересекает Р2 по некоторому коническому сечению (см. источ-
источники, указанные в примечании3)).
Пусть Q2 — объединение всех таких сечений. Ясно,
что их только конечное число. Более того, образ узла К
3) Описание понятий, используемых в проводимом доказатель-
доказательстве, можно найти в книге Делоне Б. Н. и Райкова Д. А.,
«Аналитическая геометрия»*
2*
20 Гл. I. Узлы и типы узлов
относительно любой проекции, соответствующей некото-
некоторой произвольной точке множества Р2 — (QiUQi), ие
имеет кратных 1ючек порядка я>3. Мы показали, что
Следовательно, Q есть подмножество множества QiU Q2*
которое нигде не плотно в Р2. Этим завершается доказа-
доказательство утверждения C.1).
Итак, всякий ручной узел эквивалентен полигональ-
полигональному узлу в регулярном положении. Этот факт является
отправной точкой для вычисления основных инвариан-
инвариантов, различающих типы узлов.
4. Изотопический тип, зеркальные и обратимые узлы.
Этот параграф не является необходимым для последую-
последующего изложения теории узлов в этой книге. Тем не ме-
менее он важен и заслуживает внимания уже на первых
порах.
Наше определение типа узла было мотивировано
примером перемещения веревки из одного положения
в другое, сопровождаемого перемещением окружающих
молекул воздуха. Это определение, полученное абстра-
абстрагированием упомянутого примера, все же упрощает фи-
физическую ситуацию, так как не содержит никакого упо-
упоминания о самом перемещении из начального положения
в конечное. Более развитая конструкция, дающая мо-
модель перемещения, описывается в определении изотопи»
ческого типа узла. Изотопической деформацией тополо-
топологического пространства X называется такое семейство
гомеоморфизмов hu 0</<l, пространства X на себя, что
hQ является тождественным отображением, т. е. hQ(p)=p
для любой точки р из X, и отображение Я, определяе-
определяемое соотношением //(/, р)=/**(Р)> непрерывно по сово-
совокупности переменных tup. Это определение — частный
случай более общего определения деформации, которое
будет изучено в гл. V. Узлы К\ и /С2 принадлежат к од-
одному и тому же изотопическому типу, если существует
такая изотопическая деформация {ht} пространства /?3,
что /ii/Ci = /C2. Буква / в обозначениях выбрана специаль-
специально для того, чтобы подчеркнуть аналогию со временем.
Следовательно, для фиксированной точки p€Rz точ-
4. Изотопический тип, зеркальные и обратимые узлы 21
ка ht(p) описывает, так сказать, путь молекулы, перво-
первоначально расположенной в р во время перемещения ве-
веревки из ее начального положения К{ в /С2.
Очевидно, что узлы Ki и /С2, принадлежащие одному
изотопическому типу, эквивалентны. Обратное, однако,
неверно. Понятие ориентации, изложенное ниже, иллю-
иллюстрирует разницу между этими определениями.
Всякий гомеоморфизм А пространства Rz на себя либо
сохраняет ориентацию, либо обращает ее. Хотя строгая
трактовка понятия ориентации дается теорией гомоло-
гомологии4), интуитивно его идея проста. Гомеоморфизм А со-
сохраняет ориентацию, если образ всякого право (лево)-
закрученного винта есть снова право (лево)-закрученный
винт, и обращает ориентацию, если образ всякого пра-
право (лево) -закрученного винта является лево (право) -за-
-закрученным винтом. Рассуждения, показывающие, что
других возможностей нет, основаны на непрерывности
гомеоморфизма А. Множество точек, в которых А сохра-
сохраняет вращение винта, открыто в /?3. То же самое верно
и для множества точек, в которых ориентация обра-
обращается. Так как А — гомеоморфизм, каждая точка про-
пространства R3 принадлежит одному из этих непересе-
непересекающихся множеств, а так как /?3 связно, то отсюда
следует, что одно из этих множеств пусто.
Композиция гомеоморфизмов удовлетворяет обычно-
обычному правилу четности:
сохраняет сохраняет сохраняет
обращает сохраняет обращает
сохраняет обращает обращает
обращает обращает сохраняет
4) Гомеоморфизм k я-мерной сферы Sn на себя сохраняет
ориентацию или нет в зависимости от того, является ли изомор-
изоморфизм k*:Hn(Sn) -±Hn(Sn) тождественным или нет. Пусть Sn =
=/?nU{°°} — одноточечная компактификация я-мерного действитель-
действительного векторного пространства /?п. Тогда всякий гомеоморфизм h
пространства Rn на себя допускает единственное расширение до
гомеоморфизма k сферы Sn=/?n(J{oo}, обладающего свойствами:
k\Rn = h, &(oo) = сю. Тогда h сохраняет или обращает ориентацию
согласно тому, сохраняет или обращает ориентацию гомеомор-
гомеоморфизм k.
22 Гл. I. Узлы и типы узлов
Очевидно, тождественное отображение сохраняет ориен-
ориентацию. С другой стороны, отражение (х, у, z)->(x, у, — z)
обращает ориентацию. Если h — линейное преобразова-
преобразование, то оно сохраняет или обращает ориентацию соглас-
согласно таму, положителен или отрицателен его определи-
определитель. Аналогично, если гомеоморфизм h и его обратный
принадлежат к классу С1 в каждой точке /?3, то они
сохраняют или обращают ориентацию согласно тому, яв-
является ли их якобиан всюду положительным или всюду
отрицательным.
Рассмотрим изотопическую деформацию {ht} про-
пространства /?3. Тот факт, что тождественное отображение
сохраняет ориентацию, и непрерывность отображения
H(t, p)=z^t{p) наводят на мысль о том, что и любое
отображение hu 0<^<ll, сохраняет ориентацию. Это вер-
верно и на самом деле5). Как следствие этого мы полу-
получаем, что необходимым условием изотопической эквива-
эквивалентности двух узлов является существование сохра-
сохраняющего ориентацию гомеоморфизма пространства /?3
на себя, переводящего один узел в другой.
Назовем узел К зеркальным, если существует такой
обращающий ориентацию гомеоморфизм h простран-
пространства /?3 на себя, что hK=K. В следующей лемме пред-
предлагается эквивалентное определение, более согласую-
согласующееся с геометрической интуицией. Под зеркальным
образом узла К мы понимаем образ узла К при отраже-
отражении^: (х, у, z) —► (х, у, —z)\ Имеем:
D.1) Узел К является зеркальным тогда и только
тогда, когда существует сохраняющий ориентацию го-
гомеоморфизм пространства R3 на себя, переводящий
узел К в его зеркальный образ.
Доказательство. Если узел К зеркален, то ком-
композиция Mh сохраняет ориентацию и отображает узел К
на его зеркальный образ.
5) Всякая изотопическая деформация {ht}, 0<£<l, л-мерного
векторного пространства Rn допускает единственное расширение до
изотопической деформации {kt}, 0</<l, л-мерной сферы Sn, т. е.
kt\Rn — hu kt(oo) = оо. Для всякого / гомеоморфизм kt гомотопен
тождественному, и поэтому индуцированный изоморфизм (kt)*
группы Hn(Sn) является тождественным. Отсюда следует, что ht
сохраняет ориентацию для всех t, O^t^ 1, (См. примечание4).)
4. Изотопический тип, зеркальные и обратимые узлы
23
Обратно, если h' — сохраняющий ориентацию гомео-
гомеоморфизм пространства /?3, отображающий узел К на его
зеркальный образ, то композиция МЫ обращает ориен-
ориентацию и (Mh')K=K.
Нетрудно показать, что восьмерка — зеркальный
узел. Лучший способ для этого — опыт: кусок веревки
со скрепленными концами, завязанный по восьмерке,
очень легко перекрутить в его зеркальный образ. Эта
A)
B)
D)
F)
операция иллюстрируется рис. 7. С другой стороны, кле-
клеверный лист не является зеркальным узлом. Правда, в
этом случае эксперимент с куском веревки ни к чему не
приводит, кроме как к убеждению в том, что вопрос
нетривиален. И действительно, доказать, что клеверный
лист не является зеркальным узлом, трудно, и для этого
требуется довольно развитая техника теории узлов.
Предполагая этот результат известным, мы видим, что
клеверный лист и его зеркальный образ эквивалентны,
но не принадлежат к одному изотопическому типу.
Естественно спросить, всегда ли сохраняющий ориен-
ориентацию гомеоморфизм пространства R3 на себя можно
реализовать изотопической деформацией, т. е. найдется
ли для данного / такая деформация {ht}, O^Ct^Cl, что
24
Гл. I. Узлы и типы узлов
/ = /zi? Если бы ответ был отрицателен, мы бы получили
третий вид эквивалентности узлов. Однако ответ поло-
положителен6), хотя сам вопрос не из простых.
Так же как и всякий гомеоморфизм пространства /?3
на себя, любой гомеоморфизм / узла К на себя либо
Р и с. 8.
сохраняет, либо обращает его ориентацию. Геометриче-
Геометрическая интерпретация этого аналогична, хотя и проще ин-
интерпретации в случае трехмерного пространства. Пусть
Рис. 9,
на узле указано некоторое направление обхода. Гомео-
Гомеоморфизм / сохраняет или обращает ориентацию соглас-
согласно тому, сохраняется ли или изменяется порядок точек
на К после его применения. Узел К называется обрати-
обратимым, если существует сохраняющий ориентацию гомео-
гомеоморфизм h пространства R3 на себя, ограничение h\K
6) См. Fisher G. M., On the Group of all Homeomorphisms
of a Manifold, Trans. Amer. Math. Soc. 97 A960), 193—212.
4. Изотопический тип, зеркальные и обратимые узлы 25
которого является обращающим ориентацию гомеомор-
гомеоморфизмом узла К на себя. И восьмерка, и клеверный
лист — обратимые узлы. Достаточно повернуть их на
180° (см. рис. 8).
До недавнего времени не было известно примеров
необратимых узлов. Троттер решил эту проблему, по-
построив бесконечное множество необратимых узлов, один
из которых показан на рис. 97).
УПРАЖНЕНИЯ
1. Покажите, что всякий простой замкнутый много-
многоугольник на плоскости R2 является тривиальным узлом.
2. Покажите, что всякий четырех- или пятиугольник
(пространственный) незаузлен. Какие типы узлов пред-
представляются шестиугольниками? Семиугольниками?
3. Предложите какой-нибудь способ построения таб-
таблицы узлов и найдите десять узлов, имеющих не более
шести перекрещиваний. (Вопрос о том, действительно
ли они различны, не рассматривайте.)
4. Определите экспериментально, какие из построен-
построенных выше десяти узлов зеркальны, и проверьте, что все
они обратимы.
5. Покажите, что число ручных узлов не более чем
счетно.
6. (Брунн) Покажите, что всякий узел эквивалентен
узлу, проекция которого имеет не более одной кратной
точки (возможно, весьма высокого порядка).
7. (Тэйт) Полигональный узел в регулярном положе-
положении называется альтернированным, если проходящие и
переходящие точки чередуются при обходе вокруг него.
(Тип узла называется альтернированным, если он имеет
альтернированного представителя.) Покажите, что для
любого узла К в регулярном положении найдется аль-
альтернированный узел (в регулярном положении), имею-
имеющий ту же самую проекцию, что и /С.
8. Покажите, что области, на которые плоскость R2
делится регулярной проекцией узла, можно так раскра-
7) Trotter H. F., Noninvertible Knots Exist. Top., 2 A963),
341—358.
26 Гл. I. Узлы и типы узлов
сить черной и белой краской, чтобы прилегающие
области были закрашены по-разному (как шахматная
доска).
9. Докажите утверждение,сделанное в примечании4):
всякий гомеоморфизм h пространства Rn на себя един-
единственным образом продолжается до гомеоморфизма k
сферы Sw = /?w U {оо} на себя.
10. Докажите утверждение, сделанное в примечании5):
всякая изотопическая деформация {Л*}, (Х/-<1, про-
пространства Rn на себя единственным образом продол-
продолжается до изотопической деформации {kt}, O^.t^.1, сфе-
сферы Sn. (Указание: определите функцию F(p,t) = (ht (p), /)
и, используя теорему об инвариантности области, дока-
докажите, что F — гомеоморфизм пространства /?теХ[0, 1] на
себя.)
ГЛАВА II
ФУНДАМЕНТАЛЬНАЯ ГРУППА
Введение. Элементарная аналитическая геометрия
дает нам хороший пример применения формальной ал-
алгебры к изучению геометрических объектов. Аналогич-
Аналогичная ситуация имеет место и в алгебраической топологии,
где чисто топологическим или геометрическим объектам
сопоставляются различные алгебраические объекты.
Двумя основными геометрическими концепциями топо-
топологии являются концепции топологического простран-
пространства и непрерывного отображения одного пространства
в другое. Используемая же в ней алгебра в противопо-
противоположность обычной аналитической геометрии есть то, что
часто называют «современной» алгеброй. Пространствам
и непрерывным отображениям между ними сопостав-
сопоставляют группы и гомоморфизмы групп. Однако аналогия
с аналитической геометрией полностью нарушается з
одном существенном месте. Именно, в то время как «ко-
«координатная алгебра», используемая аналитической гео-
геометрией, полностью отражает геометрию, алгебра, при-
применяемая в топологии, лишь частично характеризует
топологию. Это означает, что типичная теорема алге-
алгебраической топологии формулируется так: если тополо-
топологические пространства X и У гомеоморфны, то выпол-
выполняются такие-то алгебраические условия. Однако обрат-
обратное утверждение, как правило, бывает неверным. Следо-
Следовательно, если эти алгебраические условия не выпол-
выполняются, мы знаем, что X и У топологически различны.
Таким образом, мост от топологии к алгебре почти все-
всегда — дорога с односторонним движением. Но несмо-
несмотря на это, можно все-таки достичь многого.
Одним из важнейших понятий алгебраической топо-
топологии является понятие фундаментальной группы топо-
топологического пространства. Эта глава и посвящается ее
28 Гл. II. Фундаментальная группа
определению и изучению ее элементарных свойств.
В первой главе обсуждались основные пространства и
непрерывные отображения теории узлов: трехмерное про-
пространство #3, сам узел и гомеоморфизмы простран-
пространства R3 на себя, переводящие один узел в другой того
же типа. Другим пространством первостепенной важно-
важности является дополнительное пространство R3—К узла /С,
состоящее из всех точек пространства /?3, не принадле-
принадлежащих узлу /С. Изложение теории узлов в этой книге
посвящено изучению свойств фундаментальной группы
дополнительного пространства узла. Это, разумеется,
центральная тема в теории узлов. В этой главе, однако,
изучение фундаментальной группы проводится для про-
произвольного пространства независимо от дальнейших при-
приложений фундаментальной группы к теории узлов.
1. Пути и петли. Частица, движущаяся в простран-
пространстве в течение некоторого времени, описывает некоторый
путь. Нам будет удобно предположить, что движение
начинается в момент времени £=0 и продолжается до
времени остановки, которое может быть разным для
разных путей, но должно быть положительным или ну-
нулем. Для двух действительных чисел х и у, х^уу обо-
обозначим через [х, у] множество всех действительных чи-
чисел /, удовлетворяющих неравенству xKt^y. Путь а
в топологическом пространстве X есть непрерывное ото-
отображение
а:[0. ||а|Ц-*Л\
Число ||а|| является здесь временем остановки. Предпо-
Предполагается, что ||а||>0. Точки а@) и а(||а||) в простран-
пространстве X являются начальной и конечной точками пути а
соответственно.
Необходимо отличать путь а от множества точек
вида a(t) пространства X, когда t пробегает отрезок
[0, ||а||). Различные пути вполне могут иметь одинаковые
точечные образы. Пусть, например, X — единичная
окружность на плоскости, задаваемая в полярных коор-
координатах (г, 0) уравнением г=1. Два следующих пути
= A, t\
= A, 2/),
1. Пути и петли 29
являются разными, несмотря на то, что у них одинако-
одинаковое время остановки, одинаковые начальные и конечные
точки и одинаковые точечные образы. Пути а и b равны
тогда и только тогда, когда они имеют совпадающие об-
области определения, т. е. ||а|| = ||&||, и если при каждом /
из этой области a(t)=b(t).
Рассмотрим теперь два таких пути а и Ь в X, что
начальная точка пути Ь совпадает с конечной точкой
пути а, т. е. а(\\а\\)=Ь@). Произведение а-b путей а иЬ
определяется тогда формулой
(п m
~\b{t-\\a\\)9
Очевидно, эта формула определяет непрерывное ото-
отображение и, следовательно, а • Ь есть путь в X. Его
время остановки равно
Подчеркнем, что произведение двух путей определено
лишь тогда, когда конечная точка первого совпадает с
начальной точкой второго. Очевидно, что следующие три
утверждения:
(I) произведения а-b и b-с определены,
(II) произведение* а-(Ь - с) определено,
(III) произведение (а-Ь)*с определено,
эквивалентны и что при выполнении каждого из них
имеет место ассоциативный закон
а • (Ь • с) = (а • Ь) • с.
Путь а называется единичным путем или просто еди-
единицей, если он имеет время остановки ||а||=0. Эта тер-
терминология отражает тот факт, что множество всех еди-
единичных путей в некотором топологическом пространстве
может быть охарактеризовано как множество всех еди-
единиц относительно введенного выше умножения. Это
означает, что путь е есть единица тогда и только тогда,
когда е»а = а и b*e = b всякий раз, когда произведения
е • а и Ь • е определены. Очевидно, единичный путь имеет
своим образом только одну точку, и, обратно, имеется
30 Гл. II. Фундаментальная группа
в точности один единичный путь, имеющий своим обра-
образом любую заданную точку пространства. Мы назовем
путь, образ которого состоит из одной точки, постоян-
постоянным путем. Каждый единичный путь постоянен, однако
обратное, очевидно, неверно.
Для произвольного пути а мы через сг1 обозначим
обратный путь, образованный прохождением пути а в
обратном направлении. Это означает, что
<r4t)=a(\\a\\-t), 0<*<||а||.
Смысл употребления этого названия и обозначения
для пути яг1 выяснится в дальнейшем. Сейчас же нет
особого смысла называть путь агх обратным, так как
ясно, что путь а • сгх является единицей лишь тогда, ко-
когда а = е.
Слабая алгебраическая структура, введенная выше
в множество всех путей некоторого топологического про-
пространства, конечно, весьма далека еще от групповой
структуры. Один из путей алгебраического улучшения
этой ситуации состоит в том, чтобы выбрать произволь-
произвольную точку р в X и ограничиться рассмотрением путей,
которые начинаются и кончаются в точке р. Путь, чья
начальная и конечная точки совпадают, называется пет-
петлей, а его единственная концевая точка — его базисной
точкой. Петля с базисной точкой р будет часто назы-
называться далее р-базисной петлей. Произведение любых
двух /7-базисных петель естественно определено и являет-
является /7-базисной петлей. Единичный путь, соответствующий
точке р, является мультипликативной единицей. Сумми-
Суммируя эти замечания, получаем, что множество всех р-ба-
зисных петель пространства X образует полугруппу с
единицей.
Построение полугруппы петель является шагом в
правильном направлении, но это еще не группа. Следо-
Следовательно, нам следует сделать еще один шаг. Возвра-
Возвращаясь к множеству всех путей, определим в нем — в сле-
следующем параграфе — понятие эквивалентности путейца
затем рассмотрим новое множество, элементами кото*
рого являются классы эквивалентных путей. Фундамен*
тальная группа получится комбинированием этой кон-
конструкции с понятием петли.
2. Классы путей и петель 31
2. Классы путей и петель. Набор путей fts, 0<s<l,
пространства X будет называться непрерывным семей-
семейством путей, если
(I) время остановки \\hs\\ непрерывно зависит от s;
(II) функция h, определяемая формулой h(s, t)=*
= hs(t), непрерывно отображает замкнутую область
0<5<1, (X/<||/is|| в пространство X.
Здесь необходимо заметить, что функция двух пере-
переменных, непрерывная в каждой точке своей области оп-
определения по каждому из переменных, не обязательно
непрерывна по совокупности переменных. Функция /,
определенная на единичном квадрате 0-*Cs-<l, 0^/
формулой
1, если s — t = O,
f(s t) —
't
в остальных случаях,
дает нам пример такого рода. Поэтому семейство путей
{/s}, определенное равенством M0=f(s> Ot не является
непрерывным семейством.
Семейство путей с фиксированными концами — это
такое непрерывное семейство {/is}, 0-*Cs^l, что точки
/is@) и /is(||As||) не зависят от s, т. е. существуют такие
точки р и q пространства X, что /*s@)=/? и hs(\\hs\\)=q
для всех s из отрезка [О, 1]. Отличие «обычного» не-
непрерывного семейства путей от семейства путей с фикси-
фиксированными концами проиллюстрировано на рис. 10.
Пусть а и b — два пути в топологическом простран-
пространстве X. Тогда путь а называется эквивалентным пути Ь
(записывается а~6), если существует такое семейство
путей {hs}, OKsKU с фиксированными концами, что
Отношение ~ рефлексивно, т. е. для любого пути а
имеем а ~а, так как мы можем, очевидно, положить
М0=а@» O^s^Cl. Это отношение также симметрично,
т. е. из aczzb следует, что Ьс^а, поскольку мы мо-
можем положить ks(t)—hi~8(t). И наконец, это отношение
транзитивно, т. е. из a cz b и Ь ~ с следует, что а ~ с.
Чтобы проверить это последнее утверждение, предполо-
предположим, что hs uk3 — семейства с фиксированными концами,
32
Гл. II. Фундаментальная группа
реализующие эквивалентности ас^±Ь и b ~с соответст-
соответственно. Тогда набор путей {Д}, определяемый равенством
и является семейством путей с фиксированными кон-
концами, показывающими, что а^с. Для завершения до-
доказательства читателю рекомендуется убедиться в том,
Рис. 10.
что семейства путей, определенные выше с целью уста-
установления рефлексивности, симметричности и транзитив-
транзитивности, и в самом деле удовлетворяют всем необходимым
условиям определения эквивалентности, т. е. имеют фи-
фиксированные концы, непрерывно изменяющееся время
остановки, а также непрерывны по совокупности пере-
переменных и/.
2. Классы путей и петель 33
Итак, отношение ^ является настоящим отношением
эквивалентности, и, следовательно, множество всех пу-
путей пространства X разбивается на классы эквивалент-
эквивалентности. Класс эквивалентности, содержащий некоторый
путь а, мы обозначаем через [а]. Это означает, что класс
[а] состоит из всех таких путей 6, что а~Ь. Следова-
Следовательно, мы имеем [а]=[6] тогда и только тогда, когда
а~Ь.
Совокупность всех классов эквивалентности путей то-
топологического пространства X будет обозначаться Г (А").
Это фундаментальный группоид*) пространства X. Оп-
Определение группоида как абстрактного понятия дано в
Добавлении II.
С геометрической точки зрения пути а и b эквива-
эквивалентны тогда и только тогда, когда один из них можно
непрерывно продеформировать в другой в пространстве Х>
не двигая концевые точки. Приведенное выше определе-
определение является формальной обработкой этой интуитивной
идеи. Пусть, например, X — кольцевая область на плос-
плоскости, изображенная на рис. 11. Рассмотрим пять пе-
петель: е (единица), аи а2, а3, а4 на X с базисной точ-
точкой р. Имеем среди них следующие эквивалентности:
ах ~ а2 — е,
а3 ~ а4.
Однако неверно, что
aj ~ a3.
Рис. 11 показывает, что некоторые важные свойства
пространства X отражаются структурой классов эквива-
эквивалентности петель.
Если, например, точки области, ограниченной внут-
внутренней граничной линией кольца X, включить в состав
пространства X, т. е. заклеить дыру, то все петли с ба-
базисной точкой р станут эквивалентными единице е. Под-
Подразумевается, что стрелки на рис. 11 указывают, каким
образом параметр t пробегает путь аг-. Образ точки /
обегает цикл а{ один раз в направлении, указанном
*) Алгебраическая операция, превращающая множество Т(Х}
в группоид, будет введена ниже. — Прим. перев.
3 Зак 317
34 Гл. II. Фундаментальная группа
стрелкой. Этим подчеркивается идея того, что путь аг- —
функция. Совокупность точек, составляющих путь, не оп-
определяет путь полностью; например, а3фа3 • а3, и, более
того, даже неверно, что а3 ^ а3 • а3.
Теперь мы покажем, что умножение путей индуци-
индуцирует умножение в фундаментальном группоиде Т(Х).
В результате мы сможем перенести наше внимание с
путей и операции их перемножения на классы эквива-
эквивалентных путей и операцию умножения этих классов.
Рис. П.
Сделав это, мы получим необходимую алгебраическую
структуру для определения фундаментальной группы.
B.1) Пусть а, а', 6, bf— некоторые пути в X. Если
произведение а • b определено и а~а', b ~b\ то произ-
произведение а' • br также определено и а • b ~ а' • &'.
Доказательство. Если {hs} и {ks} — семейства
путей с фиксированными концами, осуществляющие эк-
эквивалентности а~а' и b~b' соответственно, то семей-
семейство путей {hs • ks) как раз является тем семейством пу-
путей с фиксированными концами, которое осуществляет
эквивалентность а • b~ar. br. Заметим сначала, что про-
произведения hs-ks определены для всех O^s^l, так как
2. Классы путей и петель 35
В частности, произведение а/-6/=Л1-/г1 определено. Не-
Непосредственно проверяется, что функция Л • k, опреде-
определенная соотношением
(*.*)(*, *) = (*,•*,)('). 0<5<1, 0«<||Л,||+Н*,||
непрерывна по совокупности переменных s и t. Так как
величина ||Ав • fts|| = IIAs|| + |l&sll непрерывно зависит от s,
пути hs • ks образуют непрерывное семейство. Далее
имеем
так что {hs-kg}, 0<s-<l, является семейством с фиксиро-
фиксированными концами. Но поскольку ho-ko=--a-b и h{-ki =
= а'« Ь', то доказательство закончено.
Рассмотрим теперь такие два пути а и b в простран-
пространстве Ху что произведение а • 6 определено. Тогда произ-
произведение классов эквивалентности [а] и [Ь] определяется
формулой
Теорема B.1) показывает, что такое определение умно-
умножения в Т(Х) корректно.
Так как все пути, принадлежащие к одному классу
эквивалентности, имеют одни и те же концевые точки,
мы можем определить начальную и конечную точки лю-
любого элемента а£Г(Х) как соответствующие точки лю-
любого пути, представляющего класс а. Произведение а • р
двух элементов Т(Х) определено, если конечная точка
элемента а совпадает с начальной точкой элемента р.
Поскольку отображение а-*[а] сохраняет умножение,
ассоциативный закон имеет место и в Т{Х) всякий раз,
когда все соответствующие произведения определены
точно так же, как и для путей.
Элемент е из Г(Х) называется единицей, если он со-
содержит единичный путь. Как и выше, имеем: элемент е
является единицей, если е-а = а и р«е = р всякий раз,
когда произведения е • а и р • е определены. Это утверж-
утверждение почти очевидно из соответствующего утверждения
для путей. Именно пусть е — единица. Предположим, что
произведение е • а определено. Пусть е — единичный
36 Гл. II. Фундаментальная группа
путь из класса е и а — путь из класса а. Тогда е . а = а и,
значит, е-а = а. Точно так же получаем, что р-е = р.
Обратно, допустим, что е — не единица. Чтобы доказать
существование такого класса а, что произведение е • а
определено и е • афа, возьмем в качестве представителя
класса а единичный путь, соответствующий конечной
точке элемента е. Тогда произведение е • а определено и,
так как а — единица, е*а = г. Следовательно, если
8»а = а, класс е является единицей, что противоречит
нашему предположению. Это завершает доказательство.
Заметим, что группоид Т(Х) имеет по крайней мере та-
такую же алгебраическую структуру, что и множество
всех путей в X. Замечательно здесь то, что на самом
деле структура в Г(Х) богаче.
B.2) Для любого а в X существуют такие единичные
пути ei и е2, что a- a~l~ eu a~{ -a ~ е2.
Доказательство. Пути е\ и #2, очевидно, яв-
являются единицами, соответствующими соответственно
начальной и конечной точкам пути а. Рассмотрим семей-
семейство путей {/is}, 0<s-<l, определенное формулой
a(t),
Область определения отображения А, определенного ра-
равенством A(s, t)=hs(t), заштрихована на рис. 12. На
прямой £=0, т. е. на s-оси, отображение А тождественно
равно а@). То же самое верно и для прямой £=2s||a||.
Значит, пути hs образуют семейство с фиксированными
концами.
По переменному t вдоль горизонтали 5=1 функция Л
ведет себя так же, как и функция а-а. Имеем
откуда
2. Классы путей и петель
37
Это и показывает, что a- a~l ~et. Другая эквивалент-
эквивалентность из B.2) может быть доказана точно так же; од-
однако проще, используя только что полученный резуль-
результат, заключить, что а~! • (а*1)""^^. Но так как (a~])~l = af
наше утверждение доказано.
Рис. 12.
B.3) Если пути а и b таковы, что а~Ь, то а~х с^Ь~х.
Доказательство. Этот результат следует из
B.1) и B.2). Именно
а ~ а'1 • Ь • Ь~х ~ агх • а • b~x ~ b'K
Основываясь на B.3), мы можем для произвольного
элемента а из Т{Х) определить обратный формулой
а~1=[а"], где а — любой путь из класса а.
Элемент а зависит от а и не зависит от выбора пред-
представителя а, т. е. класс а определен корректно. Смысл
этого обозначения раскрывает утверждение B.4), яв-
являющееся следствием B.2).
B.4) Для любого элемента а из Г(Х) найдутся та-
тад 1 1
()
кие единицы 8i и е2, что а • a~1 = 8i и а • а=е2.
Это утверждение выражает то свойство фундамен-
фундаментального группоида Г(Х), которое отличает его от мно-
множества всех путей пространства X. Теперь можно
38 Гл. II. Фундаментальная группа
определить фундаментальную группу пространства X с
базисной точкой р, определив аналог в Г (X) полугруппы
всех р-базисных петель; множество п(Х, р) есть множе-
множество всех элементов группоида Г(Х), имеющих в каче-
качестве начальной и конечной точек точку р, соответствие
#—►[#] определяет отображение полугруппы всех
р-базисных петель на я (Я, р), сохраняющее умножение;
следовательно, л(Х, р)—полугруппа с единицей, и в
силу B.4) имеем
B.5) Множество л(Х, р) вместе с введенным выше
умножением образует группу, которая по определению
называется фундаментальной группой1) пространства X
с базисной точкой р.
Мы закончим этот параграф полезным замечанием
о том, что с точностью до эквивалентности постоянный
путь совпадает с единичным.
B.6) Всякий постоянный путь эквивалентен некото-
некоторому единичному пути.
Доказательство. Пусть k — некоторый постоян-
постоянный путь в X, определенный равенством
где р — некоторая точка из пространства X. Очевидно,
что набор путей, определяемых равенством
является семейством с фиксированными концами, ht = k
и ho=e, где е — единичный путь, соответствующий точ-
точке р.
3. Изменение базисной точки. Фундаментальная груп-
группа п(Х, р) пространства X определена относительно ба-
базисной точки р и зависит от ее выбора. Однако мы пока-
покажем сейчас, что если пространство X линейно связно, то
1) Обычно в топологии эти группы обозначают через щ(Х, р),
так как существует последовательность групп лп(Х,р), я]>1, на-
называемых гомотопическими группами пространства X с базисной
точкой р. Фундаментальная группа является первой в этой после-
довательности*
3. Изменение базисной точки 39
все его фундаментальные группы, соответствующие раз-
различным базисным точкам, изоморфны друг другу. Топо-
Топологическое пространство X называется линейно связ-
связным, если его любые две точки можно соединить путем,
лежащим в X2).
C.1) Пусть а —некоторый элемент группоида Т(Х)
с начальной точкой р и конечной точкой р\ Тогда соот-
соответствие
Р —► а • р • а, где р пробегает группу я(Х, р)
осуществляет изоморфизм между группами я(Х, р) и
п(Х, р')-
Доказательство. Произведение а'1 • р • а, конеч-
конечно, определено, и ясно, что от1-р-а€я(Я, р'). Для лю-
любых элементов Pi, Рг€я(Аг, р) имеем
Pi-fts-*»- (Pi-p2) •а=(а-р1-а) -(a^-fe-a),
так что это соответствие является гомоморфизмом. Пред-
Предположим далее, что a-p-a=l ( = e). Тогда
откуда можно заключить, что это соответствие — изо-
изоморфизм*). Наконец, для любого элемента у группы
я{Х, р') элемент а-уа~1 лежит в п(Х, р), и очевид-
очевидно, что
a .у. a —*y*
Таким образом, рассматриваемое отображение является
отображением на и доказательство закончено.
Следствием предложения C.1) является то, что фун-
фундаментальная группа линейно связного пространства не
зависит от базисной точки в том смысле, что группы,
2) Это определение следует сравнить с определением связности.
Топологическое пространство называется связным, если оно не яв-
является объединением двух непустых непересекающихся открытых
множеств. Легко показать, что линейно связное пространство обя-
обязательно связно, но связное пространство, вообще говоря, не яв-
является линейно связным.
*) Автор различает изоморфизм в и изоморфизм на. Под изо-
изоморфизмом в понимается гомоморфизм с тривиальным ядром, что
и имеется в виду выше. — Прим. перев.
40 Гл. И. Фундаментальная группа
определенные в двух разных базисных точках, изоморф-
изоморфны. По этой причине фундаментальную группу часто оп-
определяют только у линейно связных пространств. В этом
случае обычно говорят просто о фундаментальной группе
п(Х) пространства X, опуская всякие ссылки на базис-
базисную точку. Иногда это может привести к недоразуме-
недоразумениям (если интересоваться не только теми свойствами
группы п{Ху р), которые присущи ей как абстрактной
группе). Как бы там ни было, символ п(Х) обозначает
всегда группу п(Х, р) при некотором выборе базисной
точки р в X.
4. Индуцированные гомоморфизмы фундаментальной
группы. Зададимся некоторым непрерывным отображе-
отображением f \X—*Y топологического пространства X в У. Лю-
Любой путь а пространства X определяет путь fa в про-
пространстве У, задаваемый композицией отображений
[О, ||a||]-^*-Ur,
т. е. fa(t)=f(a(t)). Время остановки пути /а, очевидно,
то же, что и у пути а, т. е. ||/а|| = ||а||. Более того, со-
соответствие a-+fa сохраняет умножение:
D.1) Если произведение а*Ь определено, то также
определено произведение fa-fb и f(a-b)=fa-fb.
Доказательство этого очень просто. Так как произве-
произведение a- b определено, то а(||а||) =6@). Следовательно,
т. е. произведение fa-fb определено. Более того,
f f(a(t))t
\f(b(t-\\a\})),
= lf*('-IIMI).
4. Индуцированные гомоморфизмы 41
Очевидно, что
D.2) Если е— единица, то fe— тоже единица. Более
того,
D.3) fa-i
Доказательство.
Для любого непрерывного семейства путей {/is},
<11, в X семейство путей {fhs} также будет непре-
непрерывным. Более того, семейство {fhs} имеет фиксирован-
фиксированные концы, если этим свойством обладает семейство
{hs}. Следовательно,
D.4) Если а~Ь,то\а~ fb.
Из сказанного следует, что отображение / определяет
отображение /# фундаментального группоида Т(Х) в
фундаментальный группоид Г (У), задаваемое формулой
Суммируем основные свойства отображения /*.
D.5) (I) Если г — единица, то /*е — тоже единица.
(II) Если произведение а-р определено, то также
определено произведение f*a • /*Р и f% (а • Р) =/* а • /# р.
(III) Если f : X —► X —* тождественное отображение,
т. е. f(x)=x, то f* —также тождественное отображение,
т. е. f*(a)=a.
(IV) Если X —-> Y -£-> Z — непрерывные отобра-
отображения и gf : X -* Z —► композиция, то (gf) % = g* • /*.
Доказательство этих утверждений следует из D.1),
D.2) и ассоциативности композиции отображений, т. е.
(f f
f) g(f)
Ясно, что при любом выборе базисной точки р в про-
пространстве X f*(n(X, /?))ся(У, fpj. Значит, ограничение
отображения /* на группу п(Х, р) (которое будет обо-
обозначаться также через /*) определяет гомоморфизм
f*:*(X, р)-*я(У, /р),
42 Гл. II. Фундаментальная группа
который называется гомоморфизмом, индуцированным
отображением f. Отметим, что, если пространство X ли-
линейно связно, алгебраические свойства гомоморфизма /*
не зависят от выбора базисной точки. Точнее, выберем
для двух любых точек р, q £Х элемент а€Г(Х) с на-
начальной точкой р и конечной точкой q. Тогда гомомор-
гомоморфизмы
D.6) P-xx-^l
я(Х, q)—^n(Y, fq)
образуют коммутативную диаграмму, в которой верти-
вертикальные отображения являются изоморфизмами на
(см. C.1)). Следовательно, если, например, один из
этих двух гомоморфизмов /* является либо гомоморфиз-
гомоморфизмом на, либо изоморфизмом в, то таковым является и
другой.
Как уже указывалось во введении к этой главе, поня-
понятие гомоморфизма, индуцированного непрерывным ото-
отображением, является фундаментальным в алгебраиче-
алгебраической топологии. Гомоморфизм фундаментальной группы,
индуцированный непрерывным отображением, является
мостом от топологии к алгебре в теории узлов. Следую-
Следующая важная теорема показывает, как топологические
свойства отображения / отражаются на гомоморфизме/*.
D.7) Теорема. Если отображение / : X -> Y есть
гомеоморфизм пространства X на Y, то индуцированный
гомоморфизм f*:n(X, р) —>я(У, fp) является изомор-
изоморфизмом при любом выборе базисной точки р.
Доказательство представляет собой простое упраж-
упражнение на использование свойств функции /#, сформули-
сформулированных в предложении D.5). Отображения
индуцируют гомоморфизмы
я(*. р)-**+*(¥, fp)-£2*+n(X, p).
6. Фундаментальная группа окружйости 43
Но композиции / • fl и f" • / являются тождествен-
тождественными отображениями. Значит, таковыми являются и го-
гомоморфизмы (Г1 • /Х-/. • /.. (/ • Г\ = К • К1- Отсю-
да следует, что гомоморфизм f# является изоморфизмом
на. Доказательство закончено.
Итак, если линейно связные пространства X и У го-
меоморфны, то их фундаментальные группы изоморфны.
Рассматривая рис. 11, мы заметили, что некоторые то-
топологические характеристики пространства X отражают-
отражаются на структуре классов эквивалентности петель в X.
Теорема D.7) является точной формулировкой этого
наблюдения.
Предположим, что имеются два узла К и /С', и мож-
можно показать, что группы л(/?3—К) и я(/?3— К') не изо-
изоморфны. Тогда в силу основной теоремы D.7) можно
утверждать, что пространства R3—К и R3—K' не яв-
являются топологически эквивалентными, так как если бы
узлы К к К' были бы эквивалентны, то должен был бы
существовать гомеоморфизм пространства R3 на себя,
переводящий К в /('. Этот гомеоморфизм, ограниченный
на R3—/(, должен определить тогда гомеоморфизм про-
пространства R3—К на ^3—К'. Отсюда уже можно заклю-
заключить, что узлы К и К' имеют разный тип. Именно таким
способом, можно различать многие узлы.
5. Фундаментальная группа окружности. При не-
небольшом навыке часто бывает сравнительно легко пра-
правильно угадать фундаментальную группу не очень слож-
сложного пространства. Однако, для того чтобы подкрепить
доказательством такого рода догадку, желательно, кро-
кроме простого знания определения, иметь еще и некоторую
топологическую технику вычисления фундаментальной
группы. Глава V посвящена описанию такой техники.
Эти замечания не относятся к вычислению фундамен-
фундаментальной группы выпуклого множества. Подмножество
n-мерного векторного пространства над действительными
или комплексными числами называется выпуклым, если
любые две его точки могут быть соединены отрезком, со-
содержащимся в этом подмножестве. Всякая /^-базисная
петля в. таком множестве эквивалентна постоянному
44 Гл. II. Фундаментальная группа
пути. Чтобы доказать это, нам достаточно положить
ha(t)=sp+(l —s)a(t), 0</<||а||, 0<s<l.
Эта деформация линейна вдоль отрезка, соединяющего
точки р и a(t). Линейно связное пространство называет-
называется односвязным, если его фундаментальная группа три-
тривиальна. В результате имеем
E.1) Всякое выпуклое множество односвязно.
Рассмотрим теперь задачу определения фундамен-
фундаментальной группы окружности. Наше решение этой задачи
подсказано теорией накрывающих пространств3), даю-
дающей как раз ту топологическую технику, о которой упо-
упоминалось в первом абзаце этого параграфа. Пусть R
ч о i г ъ 4
Рис. 13.
обозначает поле действительных чисел, а У — его под-
кольцо, состоящее из целых чисел. Аддитивную под-
подгруппу, состоящую из всех чисел, кратных трем, обозна-
обозначим через ЗУ. Окружность, фундаментальную группу
которой будем вычислять, можно рассматривать как
факторгруппу /?/ЗУ, рассматриваемую с топологией ото-
отождествления, т. е. в наиболее сильной топологии, в ко-
которой канонический гомоморфизм ф:/?-*/?/ЗУ является
непрерывным. Наглядно это можно изобразить следую-
следующим образом: рассмотрим факторгруппу R/3J как окруж-
окружность длины 3, поставленную наподобие колеса на дей-
действительную прямую, по которой она может свободно
кататься вперед и назад без трения. Возможные точки
касания определяют при этом многозначное соответ-
соответствие ф (см. рис. 13). Кстати, факторгруппа R/3J (а не
группа R/J или R/xJ для некоторого другого а:) выбрана
8) Зейферт Г., Трельфалль В., Топология, М.—Л., 1938.
5. Фундаментальная группа окружности 45
в качестве окружности, из соображений удобства, что
станет ясно в дальнейшем.
E.2) Образ открытого множества пространства R при
отображении ф является открытым множеством в /?/3/.
Доказательство. Любое подмножество В=>/?/3/
открыто тогда и только тогда, когда открыто подмноже-
подмножество у-](В). Более того, для любого подмножества
Ас/? имеем
где Зп + Х обозначает множество всех действительных
чисел вида Зп + х, х£Х. Поскольку сдвиг прямой R на
некоторое расстояние является гомеоморфизмом и объ-
объединение любого количества открытых множеств от-
открыто, наше утверждение тем самым доказано.
Ограничение отображения ф на интервал прямой R
длины меньше чем 3 является взаимно однозначным и,
значит, в силу E.2) гомеоморфизмом этого интервала.
Поэтому ф — локальный гомеоморфизм. Для любого це-
целого п определим множество Сп как образ открытого
интервала (п—-1, п+l) при отображении ф. Из E.2)
следует, что все множества Сп открыты, а из предыду-
предыдущего замечания — что отображение
фп : (п— 1, п+1) -*СП,
определенное равенством фп(*) =ф(*), п— 1<л;<я + 1,—
гомеоморфизм. Множества Сп образуют открытое по-
покрытие окружности. Однако это покрытие состоит толь-
только из трех различных множеств, так как легко видеть,
что
Сп = Ст тогда и только тогда, когда
Более того, три отличные друг от друга точки
Ро=ф(О), Р1 = фA) и р2
представляют собой множество фУ. Геометрически, ко-
конечно, точки ро, Ри Рг являются равноотстоящими друг
от друга точками окружности (см. рис. 13), а Со пред-
46 Гл. II. Фундаментальная группа
ставляет собой открытую связную дугу длины 2, иду-
идущую от pi к /?2 и содержащую точку ро, и т. д.
Определим далее последовательность непрерывных
функций г|)„, представляющих собой композицию ото-
отображения Фл1 с отображением вложения в R:
Сп— ^(лг — 1, п+\)
\ /
^п\ ь/вложение.
R
Важные свойства этих отображений приведены ниже.
E.3) (I) фг|ь(р)=Р всякий раз, когда tyn(p) опреде-
определено
(II) Если точки tyn(p) и tym(p) определены, то они
совпадают в том и только в том случае, если \п—пг\ <2.
(III) Если ф(лс) 6 Сп при некоторых х и п, то суще-
существует только одно такое целое m=n(mod 3), что
Доказательство. Так как доказательство свой-
свойства (I) тривиально, мы сразу перейдем к свойству (II).
В одном направлении результат очевиден, так как при
\п—т|>2 образы отображений г|?те и г|зт не пересе-
пересекаются. Обратное можно доказать, установив, что
*M/>)=*»Hi(P). если Р 6 Сп ПСте+1. В силу (I)
Следовательно, tyn(p) =^n+i(p) +3r для некоторого
целого г. Но так как г|>п(/?), ^n+i(p) 6 (>г— 1, я + 2),
то г=0, и доказательство утверждения (II) закончено.
Для* доказательства третьего утверждения заметим пре-
прежде всего, что единственность следует непосредственно
из (II). Существование же доказывается следующим
образом. Если ф(х)£Сп, то ф(*)=ф(у) при некотором
у€{п— 1, п+1). Тогда х=у+3г при некотором целом
г и х£(Ъг+п— 1, Зг+я+1). Значит,
5. Фундаментальная группа окружности 47
и можно положить т = п + Ъг. Этим доказательство за-
завершено.
Рассмотрим теперь два произвольных действитель-
действительных неотрицательных числа а и т и прямоугольник Е,
состоящий из всех таких пар (s, t), что О^О-^а,
0<^-<т. Основной шаг нашего вычисления фундамен-
фундаментальной группы окружности состоит в следующем.
E.4) Для произвольного непрерывного отображения
h : E^R/SJf и любого действительного числа xdR, тако-
такого, что ср(х) =Л@, 0), ^существует одна и только одна
непрерывная функция h:E^-R, такая, что 7г@, 0)=х и
Доказательство единственности. Пред-
Предположим, что существуют два непрерывных отображе-
отображения h и F, удовлетворяющих соотношениям /* = ф/г = ф/г'
и х = Л@, 0) = 7г'@, 0)^ Пусть Ео — множество всех таких
точек (s,t)£E, что h(s,t)=h'{s, t). Так как R — хаус-
дорфово пространство, то ясно, что Ео — замкнутое под-
подмножество прямоугольника Е. Более того, Ео содержит
точку @,0) и, значит, непусто. Мы утверждаем, что
множество^ Ео также и открыто. Предположим, что
%(so, A))=^'(so, to)=xo. При некотором целом пхо£
(: (п— 1, л+1), и, значит, существуют такие содержащие
точку (s0, *o) ^открытые подмножества U и (/' простран-
пространства Я, что hU и WU' являются подмножествами ин-
интервала (п—1, п+1). Тогда для любого (s, t) € U C\ U'
имеем
Я E,/), V(s,t) d{n— 1, /i+l)
и
<Vn(h(sJ))=h(s,t)=q>n(h'(s,t)).
Поскольку фте — гомеоморфизм, то h(s, t) =h'{s, t), и на-
наше утверждение доказано. Но поскольку пространство Е
связно, отсюда следует, что Е0=Е, и доказательство
единственности закончено.
Доказательство существования. Пред-
Предположим сначала, что прямоугольник Е невырождец»
48 Гл. II. Фундаментальная группа
т. е. числа а и т положительны. Рассмотрим разбиения
О = /0 < ^i < ••• <<|=т,
настолько мелкие, что каждый элементарный прямо-
прямоугольник Ец, задаваемый неравенствами s^^s-O^,
tj-i^t^tj, содержится в одном из открытых множеств
вида h~xCn. (Если бы такого разбиения не существовало,
то должна была бы найтись точка в прямоугольнике Е,
лежащая в прямоугольниках сколь угодно малого диа-
диаметра, ни один из которых не содержится ни в одном из
множеств вида h~lCn, что привело бы нас к противоре-
противоречию*).) Существует такая функция v (*',/)= 0, 1, 2, что
i№y)cCv(/<i), i=\, .... Л, 7 = 1, ..., L
Функция h теперь конструируется «по кусочкам». Ее
значение будет определяться для каждого элементар-
элементарного прямоугольника. Начиная с Eiu. имеем
Значит, согласно E.3) (III), существует единственное
целое \i(\, l)=v(l, 1) (mod 3), такое, что
Для произвольной точки E, t) ££ц положим 7г(з, t) =
==<ФдA,1)ЛE, t). Далее предположим, что функция h рас-
распространена присоединением к ее первоначальной обла-
области определения ряда элементарных прямоугольников в
некотором порядке, удовлетворяющем только тому усло-
условию, что прямоугольники Ei-ij и Z?i,j_i всегда присоеди-
присоединяются раньше, чем Е^. Для того чтобы продолжить
функцию h на £tj, мы снова воспользуемся свойством
E.3) (III) для получения единственного целого
jx(i, /)^v(i, /)(mod3), такого, что
а затем для любой точки E, t) 6 E{j положим
h(s, t)=^ll(i,j)h{s> t). To, что это расширение непрерывно
*) Это, по существу, вариант известной «леммы о вложенных
отрезках (прямоугольниках)». — Прим. перев.
5. Фундаментальная группа окружности 49
согласовано с ранее построенным, доказывается приме-
применением утверждения E.3) (II) к точке ft(si~i, /j-i) с
целью показать, что
/_ 1, у) _.,!(/, у)|<2,
Тогда опять-таки из утверждения E.3) (II) следует,
что функция h корректно определена на левом и нижнем
граничном отрез_ках прямоугольника £tj. Подобным об-
образом функция h распространяется на весь прямоуголь-
прямоугольник Е. Доказательство для вырожденного прямоуголь-
прямоугольника следует из результата, доказанного уже для невы-
невырожденных прямоугольников. Например, если а=0 и
т>0, можно выбрать произвольное о>'>0 и положить
A'(s> t) = h(O, t), 0</<т, 0<s<a'.
Так как существование функции h' уже установлено, мы
полагаем
Доказательство утверждения E.4) теперь закончено.
Рассмотрим петлю а на окружности с базисной точ-
точкой ро=ф(О). Ее область определения [0,||а||] есть вы-
вырожденный прямоугольник. Из E.4) следует, что суще
ствует один и только один путь а, накрывающий путь а
и начинающийся в точке 0, т. е. а = уа и а@)=0. Так
как фй(||а||) =ф@), то, как мы уже знаем, а(\\а\\) =3г.
Число г = га определено однозначно. Назовем его чис-
числом вращения петли а. С геометрической точки зрения
га есть алгебраическое число оборотов петли а вокруг
окружности.
E-5) 'а.ь = га + гь.
Доказательство. Пусть а и 5 — пути, начинаю-
начинающиеся в точке 0, и накрывающие пути а и b соответ-
соответственно. Функция с, определенная равенством
- Г _ a(t).
4 Зан. 317
50 Гл. II. Фундаментальная группа
очевидно, определяет путь с началом в точке 0, накры-
накрывающий произведение а • Ь. Поскольку существует лишь
один накрывающий путь, отсюда сразу следует, что
E.6) Пути с одинаковыми числами кручения экви-
эквивалентны.
Доказательство. Этот результат является пря-
прямым следствием того очевидного факта, что все пути
в R с одинаковыми концами эквивалентны. Пусть а и
Ь — две /?0-базисные петли на окружности, числа враще-
вращения которых равны и определяются с помощью путей а
и 5 в R. Образы hs = q>hs, 0<s<l, произвольного семей-
семейства путей {hs} с фиксированными концами, с помощью
которого устанавливается эквивалентность путей а и 5,
образуют непрерывное семейство, с помощью которого
устанавливается эквивалентность путей а и Ь.
E.7) Эквивалентные пути имеют одинаковые числа
вращения.
Доказательство. Именно в этом месте утвер-
утверждение E.4) используется в полном объеме. Рассмотрим
непрерывное семейство ^-базисных петель fts, 0<^s<I,
на нашей окружности. Пусть т — верхняя грань множе-
множества действительных чисел ||Ав||, 0<5<1. Определим
непрерывную функцию h равенством
Тогда имеем
где h — единственная функция, накрывающая h, т. е.
ф7г = Л и й@,0)=0. Следовательно, множество точек
h(s, Hftsll), 0<5<l, содержится в дискретном множе-
множестве 3/. Но непрерывная функция, отображающая связ-
связное множество в дискретное, должна быть постоянной
на этом множестве. Используя это, а также свойство
5. Фундаментальная группа окружности 51
единственности накрывающего пути, имеем
и доказательство закончено.
В силу E.7) мы можем однозначно сопоставить
каждому элементу группы я(/?/3/, р0) число вращения
некоего его представителя. Определение умножения в
фундаментальной группе и утверждение E.5) показы-
показывают, что это сопоставление является гомоморфизмом
в аддитивную группу целых чисел. Из E.6) следует, что
этот гомоморфизм в действительности не имеет ядра.
Заметив, что существуют петли с наперед заданным
числом вращения*), получаем доказательство следую-
следующей теоремы.
E.8) Фундаментальная группа окружности есть
бесконечная циклическая группа.
УПРАЖНЕНИЯ
1. Вычислить фундаментальную группу объединения
двух кубов, имеющих общую вершину и нигде более не
пересекающихся.
2. Вычислить фундаментальную группу пятиконеч-
пятиконечной звезды (граница вместе с внутренностью).
3. Доказать, что если а, р€я(^, р) и а€а, 6 6 р, то
петли а и Ь свободно эквивалентны (также говорят —
свободно гомотопны) тогда и только тогда, когда эле-
элементы аир сопряжены в п(Х, р). (Определения «со-
«сопряженности» и «свободной гомотопии» даны в указа-
указателе.)
4. Показать, что если пространство X односвязно и
/ и g — пути из точки р € X в точку q 6 X, то / и g при-
принадлежат к одному и тому же семейству путей с фикси-
фиксированными концами.
*) Именно, петля hh : R/3J -> R/3J, индуцированная отображе-
отображением x->kx прямой R в себя, имеет своим числом вращения k,—
Прим. перев,
4*
52 Гл. II. Фундаментальная группа
5. Пусть /: X-+Y — непрерывное отображение и
f* :n(Xy/?)->л(У, fp) —индуцированный гомоморфизм.
Верны ли следующие утверждения?
(a) Если / — отображение на, то /* — гомоморфизм
на.
(b) Если отображение f взаимно однозначно, то го-
гомоморфизм /# также взаимно однозначен.
6. Доказать, что если X, У и X П У — непустые, от-
открытые, линейно связные подмножества пространства
X\j Y и X и Y односвязны, то пространство л U Y также
односвязно.
7. Ослабим понятие непрерывного семейства путей,
потребовав, чтобы функция h была непрерывна по ка-
каждому переменному отдельно (вместо непрерывности
по совокупности переменных). Определим «особую фун-
фундаментальную группу» я(Х, /?), используя это слабое
определение эквивалентности. Показать, что «особая
фундаментальная группа» окружности тривиальна.
ГЛАВА lit
СВОБОДНЫЕ ГРУППЫ
Введение. Во многих приложениях теории групп и
особенно в нашем последующем анализе фундаменталь-
фундаментальной группы дополнительного пространства узла группы
описываются при помощи «определяющих соотношений»,
или, как мы будем говорить дальше, «копредставле-
нием»*). Здесь мы снова имеем аналогию (но уже со-
совсем другую) с аналитической геометрией. В аналити-
аналитической геометрии выбирается система координат и изу-
изучаемые геометрические конфигурации определяются
множеством из одного или более уравнений. В теории
копредставлений групп роль системы координат в ана-
аналитической геометрии играет свободная группа. Поэто-
Поэтому изучение копредставлений групп следует начать с
подробного описания свободных групп.
1. Свободная группа F[<A]. Предположим, что мы
задались некоторым множеством JL мощности а. Эле-
Элементы а, Ь, с множества Л могут быть просто абстракт-
абстрактными символами или же объектами из некоего матема-
математического контекста. Мы будем называть далее множе-
множество ji алфавитом, а его элементы — буквами. Под сло-
слогом мы будем понимать символ ап, где а — буква алфа-
алфавита <А, показатель, п — целое число, а под словом —
конечную упорядоченную последовательность слогов.
Например, выражение Ь'3а°а{с2с2а°с1 есть слово из семи
слогов. В слове слоги записываются друг после друга
в виде формального произведения. Каждый слог сам
*) Так мы переводим английский термин «presentation», не
имеющий аналога в русской математической терминологии, учиты-
учитывая, что русский термин «представление» используется в другом
смысле, a «representation» в некотором смысле двойственно «pre-
«presentation». — Прим. перев.
54 Гл. III. Свободные группы
является односложным словом. Слог может повторяться
или следовать за другим слогом, образованным с по-
помощью той же буквы. Существует единственное слово,
не имеющее слогов. Оно называется пустым словом и
обозначается символом 1. Слоги в слове считаются сле-
слева направо. Так в только что приведенном примере а1
есть третий слог. Для краткости слог вида а1 обычно
записывается просто как а.
Во множестве W {А) всех слов алфавита Л есте-
естественным образом определено умножение: произведение
двух слов образуется просто приписыванием одного
слова за другим. Число слогов в этом произведении есть
сумма числа слогов в каждом из исходных слов. Оче-
Очевидно, что введенное умножение ассоциативно и пустое
слово 1 является и леьой, и правой единицей. Следова-
Следовательно, W (Л) есть полугруппа.
Однако полугруппа W {JL) не является группой, так
как только один элемент из W (JL) имеет обратный,
и этот элемент 1. Для того чтобы образовать группу, со-
соберем слова в классы эквивалентности аналогично тому,
как мы строили фундаментальную группу из полугруппы
р-базисных петель.
Если слово и имеет вид W\a°w2, где Wi и w? — неко-
некоторые слова, то говорят, что слово v = WiW2 получено из
слова и при помощи элементарного сокращения типа I,
или что слово и получено из слова v при помощи эле-
элементарного расширения типа I. Если а0 есть п-й слог
слова и, то сокращение происходит на п-м слоге.
Если слово и имеет вид WiOPcflw^ где Wi и w2 — не-
некоторые слова, то говорят, что слово v = wiaP+Qw2 полу-
получено из слова и элементарным сокращением типа II или
что слово и получено из слова v элементарным расши-
расширением типа II. Сокращение происходит на п-м слоге,
если ач есть n-й слог.
Слова и u v называются эквивалентными (что запи-
записывается u~v), если одно из них может быть получено
из другого конечной последовательностью элементар-
элементарных сокращений и расширений. Очевидно, что это дей-
действительно отношение эквивалентности. Таким образом,
множество W (<Л) разбивается на классы эквивалент-
эквивалентности. Как и выше, мы обозначим через [и] класс экви-
2. Свободные группы 55
валентности, представляемый словом и. Следовательно,
равенство [#]=[&] означает то же, что и u~v. Множе-
Множество классов эквивалентности слов мы обозначим через
]
Нетрудно проверить, что если слово и' получается из
v элементарным сокращением, то слово uv' также полу-
получается из слова uv элементарным сокращением, и что
если слово и! получается из слова и элементарным со-
сокращением, то слово u'vr также получается из слова uv'
элементарным сокращением. Отсюда легко вывести, что
если и~и' и v~v\ то uv~u'v'. Другими словами, мно-
множество Р{Л) получает умножение, имеющееся в W (Л)\
это умножение определяется следующим образом:
[w][0]=(wi>]. Ассоциативность полученного умножения в
Р(Л) следует непосредственно из ассоциативности
умножения в W (Л)\ класс эквивалентности [1] является
одновременно правой и левой единицей. Следовательно,
F[dl] получает от W (Л) также и структуру полу-
полугруппы. Однако в Р[Л] каждый элемент имеет также
и обратный: обратный элемент [и]"{ для класса [и] пред-
представляется словом й, которое получается из слова и на-
написанием всех слогов в обратном порядке и изменением
знака показателя у каждого из слогов на обратный.
Например, если u = b~3a°alc2c2cflcl9 то п = с-1а°с-2с-2а-{а°Ь3.
Это показывает, что полугруппа Р\Л\ на самом деле
является группой, которая называется свободной груп-
группой над алфавитом Л. Заметим, что мы допускаем и
пустой алфавит. Соответствующая ему свободная груп-
группа тривиальна. Свободная группа над алфавитом, со-
состоящим ровно из одной буквы, является бесконечной
циклической группой. Абстрактное понятие свободной
группы будет дано в следующем параграфе, где будет
показано, что группа Р[Л] действительно свободна.
Термин «свободная группа над алфавитом Л» предвос-
предвосхищает этот результат.
2. Свободные группы. Представим себе некоторую
группу бив ней какое-либо подмножество Е. Набор
подгрупп группы G, содержащих множество £, непуст,
так как в него входит несобственная подгруппа G. Лег-
Легко проверить, что пересечение этого набора подгрупп
56 Гл. III. Свободные группы
является опять-таки подгруппой, содержащей Е. Она
называется подгруппой, порожденной множеством Е.
Нетрудно также убедиться в том, что эта подгруппа со-
составлена из всех элементов группы G, имеющих вид
ВхЧ*2 ' • • £/"'' где Su gb ..., gi€E и пи л2, ..., Щ —
целые числа. Если подгруппа, порожденная множест-
множеством £, совпадает со всей группой G, множество Е назы-
называется множеством образующих элементов группы G.
В группе F\JL\ всякий элемент может быть записан
(многими способами) как произведение целых степеней
классов [4 [Ь], [4 .... Например, [а2Ь*с~2] = [а]2[Ь]*[с]-2.
Следовательно, совокупность элементов [а], [6], [с], ...
является множеством образующих элементов группы
F[<A\. Мы обозначим это множество образующих через
И].
Назовем множество Е образующих группы G сво-
свободным базисом, если для всякой группы Н отображе-
отображение ф : Е->Н может быть продолжено до гомоморфизма
группы G в Н (так как множество Е порождает груп-
группу G, такое продолжение необходимо единственно).
Группа, обладающая свободным базисом, называется
свободной. Простейшей свободной группой является три-
тривиальная группа 1; пустое множество Е = 0 есть ее
свободный базис.
B.1) Группа свободна тогда и только тогда, когда
она изоморфна группе вида F[Ji] при некотором А.
Доказательство. Группа F[ot] свободна, так
как множество [Л] является ее свободным базисом.
Чтобы доказать это, рассмотрим произвольное отобра-
отображение <р: [<А]->Н и обозначим через фг соответствую-
соответствующее отображение алфавита^ в Н. Продолжим отобра-
отображение фг до гомоморфизма полугруппы W (Л) в Я,
полагая
и заметим, что <р'(и)—ф'^)» если и~v. Отсюда следует,
что отображение ф' индуцирует гомоморфизм группы
F[JL\ в Н. Этот гомоморфизм является, очевидно, рас-
расширением исходного отображения ф: [Л\->Н, и, следо-
следовательно, множество [Ж\ является свободным базисом
2. Свободные группы S7
группы Z7^]. Если теперь G-—некоторая группа, изо-
изоморфно отображаемая на F\Jt\ изоморфизмом К, то
множество Е = АГ1 \<А\ является, очевидно, свободным
базисом группы G, так что группа G должна быть сво-
свободной группой.
Обратно, пусть G — свободная группа и £ — ее сво-
свободный базис. Пусть F[A\ — свободная группа над ал-
алфавитом Л, мощность которого совпадает с мощностью
множества Е. Пусть х: £-> [Л] — отображение, уста-
навливающее взаимно однозначное соответствие между
Е и \<А\. Так как Е — свободный базис, соответствие х
продолжается до гомоморфизма ф группы G в F[ul].
Так как [ol]~- свободный базис группы Z7^], отобра-
отображение и: [сА]-> Е можно продолжить до гомоморфиз-
гомоморфизма г|) группы F\ol\ в G. Композиции гомоморфизмов
q4*. F\<A]->F[di\ и г|мр : G -> G являются расширения-
расширениями отоб!ражен'ий юг1 : [ot] -> [Л\ и тсЫ : Е->Е. По-
Поскольку эти отображения тождественны, они продол-
продолжаются до тождественных автоморфизмов групп F\<A)
и G соответственно. Но поскольку такие продолжения
единственны, гомоморфизмы ф-ф и г|)ф являются тожде-
тождественными автоморфизмами. Значит, ф изоморфно ото-
отображает группу G на F[<A] и г|? = ф~1. Таким образом,
группа G изоморфна группе F[JL\ и доказательство за-
закончено.
Приведенное доказательство показывает, что мощ-
мощность свободного базиса Е группы G равна мощности
а алфавита Л. Следовательно, свободные группы G
и G' изоморфны, если они обладают свободными бази-
базисами Е и Ег соответственно одинаковой мощности. Да-
Далее будет показано обратное (см. D.2) гл. IV); свобод-
свободные группы, имеющие базисы разной мощности, не изо-
изоморфны. Отсюда вытекает, что каждой свободной груп-
группе G соответствует такое число я, что всякий свободный
базис этой группы имеет мощность п. Это кардинальное
число п называется рангом свободной группы G.
B.2) Любая группа есть гомоморфный образ сво-
свободной группы.
Это утверждение очень важно для теории копредста-
влений групп. Оно означает, что можно использовать
Гл. III. Свободные группы
свободные группы как «системы координат» для того,
чтобы ввести «координаты» в любой группе. Доказатель-
Доказательство его чрезвычайно просто. Пусть Е — некоторое мно-
множество образующих рассматриваемой группы G, и
F\di\— свободная группа над алфавитом Ж% мощность
а которого не меньше мощности множества Е. Пусть
Я:[с^]-> Е — любое отображение, образ которого состоит
из всего множества Е. Так как [<А\ — свободный базис
группы F[ui]9 отображение X продолжается до гомо-
гомоморфизма свободной группы F[JL\ на G.
3. Приведенные слова. Иногда бывает важно опре-
определить, являются ли заданные слова и и v эквивалент-
эквивалентными. Конечно, если попытка преобразовать слово и в
слово v путем элементарных расширений и сокращений
приведет к успеху, вопрос будет исчерпан. Однако в
случае неудачи вопрос останется открытым. Нужен не-
некий стандартный прием решения этого вопроса. Про-
Проблема нахождения такого стандартного приема обычно
называется проблемой слов для свободной группы Т7^].
Она очень проста и решается следующим образом.
Слово w назовем приведенным, если к нему нельзя
применить никакого элементарного сокращения, т. е.
если ни один слог слова w не имеет показателя, равного
нулю, и никакие два последовательных слога не явля-
являются степенями одной и той же буквы. Очевидно, по-
поскольку всякое элементарное сокращение уменьшает
число слогов, то каждый класс эквивалентности слов
содержит по меньшей мере одно приведенное слово.
Покажем теперь, что такое слово единственно.
С этой целью определим стандартную редукцию
слова w, т. е. последовательность слов
определенных следующим образом.. Для всякого /=О,
1, ... , /и—1 слово ку<г'+1> получается из слова w№ эле-
элементарным сокращением на первом возможном слоге
(т. е. w(i+l) получается из слова w^ элементарным со-
сокращением /-го слога, причем в слове w& нельзя про-
произвести сокращение ft-ro слога при k<j). Последнее
слово w* этой последовательности приведено (т. е. по-
3. Приведенные слова 59
следовательность обрывается, когда уже нельзя произ-
произвести никакого элементарного сокращения). Заметим,
что иногда возможно применить к /-му слогу слова wW
элементарные сокращения обоих типов. Однако это не
усложняет приведение, так как тогда слово w№ должно
иметь вид w№ = uaPa°v, где и — слово длины /—2, по-
последний слог которого отличен от степени а, и оба типа
сокращений приводят к слову w^i+^ = ua^v. Теперь заме-
заметим, что
C.1) слово и приведено тогда и только тогда, когда
и = и*.
Основное утверждение при нашем решении проблемы
слов таково:
C.2) u~v тогда и только тогда, когда u* = v#.
Доказательство. Поскольку каждое слово стан-
стандартной редукции эквивалентно любому предшествую-
предшествующему или последующему слову, то, очевидно, u~v>
если u* = v%. При доказательстве обратного мы можем
считать, что слово v получено из слова и элементарным
сокращением. Предположим сначала, что v получено
из и элементарным сокращением типа I на /-м слоге.
Так как сокращаемый слог а0 не может появиться в
слове и*, найдется такое целое i, что и^ является по-
последним словом из последовательности стандартной ре-
редукции слова и, в котором появляется слог а0. Тогда
где w — приведенное слово. Значит,
Стало быть, u(i+2) = v(i+V и т. д., u% = v%.
Предположим, что слово v получено из слова и эле-
элементарным сокращением II на /-м слоге. Значит, /-й
слог слова и есть a?, a (/—1)-й слог есть а*\ Пусть
i — индекс последнего слова последовательности стан-
стандартной редукции слова и, в котором рядом встреча-
встречаются слоги а? и я?. Тогда
60 Гл. III. Свободные группы
где w — приведенное слово. Если слово w пусто, или
если его последний слог не есть степень буквы а, то
и, значит, и*«&*. Если, с другой стороны, w = w"aT, то
= w"a'ap+'w.
где переход ^г'+1)->а(г'+2>— сокращение типа I или II
в соответствии с равенством или неравенством нулю
г+/7, а переход у(») —> уО'+о — сокращение типа I или
II в соответствии с равенством или неравенством
нулю г. Как и выше, мы делаем отсюда вывод, что
w# = i>#, и доказательство утверждения C.2) закончено.
Итак, мы доказали следующее:
C.3) Каждый класс эквивалентности слов содержит
ровно одно приведенное слово. Более того, всякая по-
последовательность элементарных сокращений слова и
оканчивается одним и тем же приведенным словом и*.
Следовательно, найден конечный алгоритм для выяс-
выяснения того, определяют или нет слова и и v один и тот
же элемент группы Т7^]: достаточно найти слова и*
и v* и сравнить их слог за слогом.
УПРАЖНЕНИЯ
1. Сколькими способами можно привести слово
ar2hb'xa1bb"xarx к слову а^ элементарными сокраще-
сокращениями?
2. Найти конечный алгоритм для определения, пред-
представляют ли два заданных слова сопряженные элементы
в группе F\ol\.
3. Найти конечный алгоритм для определения, пред-
представляет ли данное слово п-ю степень некоторого эле-
элемента группы F\Jt].
4. Доказать, что элементы г/, хух~\ х2ух~2 образуют
свободный базис подгруппы группы F[x, y\ которую они
порождают. Вывести отсюда, что свободная группа лю-
любого конечного ранга п может быть изоморфно отобра-
3. Приведенные слова 61
жена внутрь свободной группы любого заданного ранга
т>2.
5. Доказать, что свободная группа ранга п не может
порождаться менее чем п элементами.
6. Известно (Нильсен, Шрейер и др.1)), что всякая
подгруппа свободной группы свободна. Используя этот
факт, доказать, что в свободной группе:
a) нет элементов конечного порядка (отличных от
единицы);
b) если два элемента коммутируют, то они являются
степенями некоторого третьего элемента;
c) если umd = vndf где тип взаимно просты, то су-
существует такой элемент wt что u~wn, v~wm\
d) если uvu = v, то м = 1.
7. В упражнении 6 доказать утверждения а), Ь), с)
и d) непосредственно, не используя теорему Нильсена.
8. Показать, что если u, v, u\ v' — такие элементы
свободной группы, что uvu-lv-l = u'v'(u')-l(v')-l=t=l1 то
элементы и и и* могут не коммутировать.
х) Fox R. H., Free Differential Calculus III. Subgroups, Ann.
Math., 64 A956), 40&
ГЛАВА IV
КОПРЕДСТАВЛЕНИЯ ГРУПП
Введение. В этой главе будет дано обоснование за-
задания групп образующими и соотношениями. Это важ-
важный момент. Если, например, не различать четко эле-
элементы группы и слова, описывающие их, можно почти
наверняка прийти к курьезам.
Основная проблема здесь состоит в определении
того, когда два множества образующих и соотношений
определяют одну и ту же группу. Теоретически этот во-
вопрос решается теоремой Титце. Однако она дает прак-
практические результаты лишь тогда, когда уже имеется ка-
какой-либо метод упрощения рассматриваемых групп.
Здесь полезны упрощения при помощи так называемых
до-подгрупп, которые будут введены в конце главы.
1. Развитие понятия копредставления. Понятие аб-
абстрактной группы развилось из понятия группы пере-
перестановок (или подстановок, как она вначале называ-
называлась), которая, естественно, конечна. Поэтому исследова-
исследователи, поначалу развивавшие теорию абстрактных групп,
концентрировали свое внимание почти исключительно на
конечных группах, так что группы обычно описывались
при помощи групповой таблицы Кэли. Конечно, исполь-
использование таблиц Кэли невозможно для бесконечных
групп и нецелесообразно даже для конечных групп
большого порядка. Более того, эти таблицы содержат
излишнюю информацию, так что еще и по этой причине
такие таблицы не являются достаточно эффективным
описанием групп. Например, таблица
1
а
Ь
1
1
а
Ь
а
а
Ь
1
Ь
b
1
а
1. Развитие понятия копредставления 63
имеет девять клеток, но, используя тот факт (см. цен-
центральную клетку), что Ь = а2, можно свести описание
группы к трем элементам 1, а, а2 и соотношению а3=1.
Поэтому рассматриваемая группа будет описана более
эффективно, если мы укажем, что элемент а порождает
эту группу и что равенство а3=1 имеет место, а равен-
равенства а2=1 или а=1 не выполняются.
Сказанное приводит к методу описания группы при
помощи образующих и определяющих соотношений.
Введенный в 1882—1883 гг. Диком, этот метод состоит
в следующем: группа G определена полностью, если за-
заданы множество gu gz> ... порождающих ее элементов,
называемых образующими, и множество уравнений
h(gu £2, ...) = 1, Mgi, #* ...) = 1, ... , называемых
определяющими соотношениями, которые обладают тем
свойством, что всякое соотношение между элементами
£ь #2, • • • является алгебраическим следствием входя-
входящих в него уравнений.
Однако, строго говоря, такое определение содержит
некоторую неясность, поскольку левые части уравнений
не имеют точного смысла. Какого рода объект выраже-
выражение fi(gu gi> ...)? Оно не может быть элементом группы
G, так как в этом случае это был бы попросту еди-
единичный элемент. Чтобы записать такое уравнение, мы
должны постулировать существование такого объекта,
в котором выражение fi(gu #2, . •.) имеет точный смысл.
Ясно, что объектом такого рода как раз и является сво-
свободная группа. Это приводит нас к следующей модифи-
модификации предыдущего метода описания группы.
Пусть F — свободная группа со свободным базисом
#ь *2, элементы которого находятся во взаимно одно-
однозначном соответствии с образующими gu #2, ... груп-
группы G. Пусть ф — гомоморфизм группы F на G, опреде-
определенный равенствами q>Xj=gj9 /=1, 2, .... Для каждого
из определяющих соотношений fi(gu gz* ...) = 1 поло-
положим
Гг = 1г(хи Х2у ...), /=1, 2, ... ,
т. е. гх есть элемент группы Z7, полученный заменой эле-
элементов gj, /=1, 2, ... , в выражении fi(gu g2, ...) эле-
элементами Xjy /=1, 2, .... Например, если i-e соотноше-
Гл. IV. Копредставления групп
ние имеет вид .g^f1^1 = 1, то г.=ххх2х-1х-К
Утверждение, что соотношение fi{gu £2, . ..) = 1 имеет
место в G, эквивалентно тогда утверждению, что эле-
элемент Г{ принадлежит ядру гомоморфизма ф, т. е.
l=ep/*i=Mgi, £2, ...)•
Элементы ги г2, ... называются соотношениями.
Теперь нетрудно точно сказать (учитывая, что каж-
каждое уравнение U{gu gz, ...) = 1 заменено элементом гг),
что означают слова: уравнение является алгебраическим
следствием некоторых других. Элемент / некоторой
группы Q называется следствием множества элементов
fu /2, • • • группы Q, если при любом гомоморфизме г|з
группы Q в любую другую группу Ну переводящем эле-
элементы fu f2, ... в 1, элемент / также отображается в 1.
Поскольку всякий гомоморфизм группы Q определяет
нормальный делитель в Q, т. е. ядро этого гомомор-
гомоморфизма, и, обратно, всякий нормальный делитель груп-
группы Q определяет ее гомоморфизм, ядром которого он
является, предыдущее определение можно сформулиро-
сформулировать следующим образом. Элемент / группы Q является
следствием элементов fu /2, ... , если он содержится во
всяком нормальном делителе, содержащем элементы
fu /2, ... • Назовем множество всех следствий элементов
fu /2, ... оболочкой этих элементов; таким образом, мы
установили, что оболочка элементов /i, /2, ... является
пересечением всех нормальных делителей группы Q, со-
содержащих элементы fu f2i ... . Так к^к пересечение лю-
любого множества нормальных делителей есть снова нор-
нормальный делитель, оболочка элементов fu /2, ... пред-
представляет собой наименьший нормальный делитель
группы Q, содержащий элементы fu /2, ... .
" Оболочку элементов flt /2, ... можно, однако, опре-
определить более наглядно. Заметим, что всякое произведе-
произведение элементов, сопряженных степеням элементов fu
/2, ... , т. е. элемент вида
Д h
1. Развитие понятия копредставления 65
отображается в 1 всяким гомоморфизмом, переводящим
в 1 все элементы fiy f2, ... . Значит, всякий такой эле-
элемент k есть следствие элементов fiy /2, • • • . Нетрудно
видеть, что совокупность всех таких элементов образует
нормальный делитель К группы Q, который, следова-
следовательно, содержится в оболочке элементов fu /2, ... .
С другой стороны, К есть нормальный делитель, содер-
содержащий все элементы fu f2, ... , т. е. К принадлежит
к совокупности подгрупп, пересечение которых дает
оболочку элементов fu f2y ... . Отсюда следует, что обо-
оболочка элементов fu \2> ... в точности есть К. Таким об-
образом, мы показали, что элемент группы Q тогда и
только тогда является следствием элементов fu f2y ... ,
когда он имеет вид
ДА fn
пЩ-1
В дальнейшем нам понадобится следующая теорема.
A.1) Пусть gu £2» ... — некоторое множество эле-
элементов группы G и ф — гомоморфизм группы G на груп-
группу Н. Тогда гомоморфизм ф отображает оболочку эле-
элементов gu g2, ... иа оболочку элементов ygu yg2, ...
группы Н.
Доказательство. Обозначим через Kg оболочку
элементов giy g2, ... , а через Кн — оболочку элементов
/*1 = Ф£ь ^2=Ф^2, .... Так как подгруппа ф/Са содержит
все элементы Аь h2i ... и, кроме того, является нор-
нормальным делителем, то ф/Со содержит Кн- Для доказа-
доказательства обратного включения рассмотрим произволь-
произвольный элемент h из ф/С0 и выберем такой элемент ^€A"g,
что yg = h. Если г|) — некоторый гомоморфизм Я, пере-
переводящий все элементы hu h2> ... в 1, то гомоморфизм
\|?Ф должен перевести элементы gi, £г, *•• в 1. Но так
как g€KG, то \|)ф£=1, что равносильно тому, что
г|)/г=1. А раз элемент h отображается в 1 всяким таким
гомоморфизмом, он должен принадлежать подгруп-
подгруппе Кн- Этим показано, что Кн содержит ф/Со и, значит,
Кн = Ч>Ко- Доказательство закончено.
5 Зак 317
66 Гл. IV. Копредставления групп
Возвращаясь теперь опять к гомоморфизму/7—->G,
обозначим через R оболочку соотношений ги г2, ... .
Утверждение, что уравнения
fdgu £2, ...) = 1, /=1, 2
образуют множество соотношений группы G, из которых
следуют все другие, равносильно утверждению, что обо-
оболочка R совпадает с ядром гомоморфизма ф. В этом
случае группа определяется свободным базисом х^
х2, ... и элементами ги г2, ... , так как она изоморфна
факторгруппе F/R.
2. Копредставления и типы копредставлений. В сле-
следующих определениях формализованы понятия предыду-
предыдущего параграфа. Пусть F — свободная группа со сво-
свободным базисом £, который предполагается достаточно
обширным, чтобы обеспечить неисчерпаемый запас ба-
базисных элементов. Множество Е называется базисным
множеством образующих. Обозначим через (х: г) ко-
представление, состоящее из подмножества х базисного
множества образующих и подмножества г подгруппы
F(x), порожденной в F множеством х. Заметим, что
группа F(x) изоморфна свободной группе F[x] над алфа-
алфавитом х. Здесь важно отметить, что группа F(x) сама
является свободной группой со свободным базисом х. Это
непосредственно вытекает >из определения свободного ба-
базиса (без ссылок на весьма тонкую теорему Нильсена-—
Шрейера, утверждающую, что всякая подгруппа сво-
свободной группы свободна). Множество х называется мно-
множеством образующих, а множество г—множеством со-
соотношений копредставления. Группа копредставления
(х : г) или группа, определяемая этим копредставлением,
есть факторгруппа |х : r| =F(x)//?, где R — оболочка
множества г в группе ^(х).
Копредставление группы G состоит из копредставле-
копредставления (х:г) и некоторого изоморфизма i группы |х:г|
на G. Ясно, что любой гомоморфизм ф свободной груп-
группы F(x) на G, ядро которого совпадает с оболочкой
множества г, определяет копредставление группы G.
Обратно, всякое копредставление группы G определяет
такой гомоморфизм. Точнее, любой из гомоморфизмов
2. Копредставления и типы копредставлений 67
Ф или i определяется другим однозначно, если у — кано-
канонический гомоморфизм группы F(x) на F(x)/R в комму-
коммутативной диаграмме:
F(x)
Когда понадобится особая точность, мы будем писать
(х: г)ф, подчеркивая, что (х:г) есть копредставление
группы G, осуществляемое гомоморфизмом ф.
Термин «копредставление» был выбран для описания
такого способа изучения группы G, при котором на нее
отображается хорошо известная группа (свободная
пруппа f(x)), так как этот способ в некотором смысле
дуален такому, при котором группа G изучается с по-
помощью отображения ее в известную группу (например,
группу перестановок). Эти последние отображения есть
то, что называют «представлениями» группы G.
Введем еще раз понятие соотношения, хотя в этом
и нет логической необходимости. Причина этого в том,
что обращение с соотношениями привычнее для нашего
мышления, чем обращение с элементами, задающими
эти соотношения. Например, нетрудно убедиться в том,
что если элементы а и b коммутируют, то из того, что
(abJ=ly следует, что a2b2—\y однако то, что элемент
a2b2 есть следствие элементов abcrlb~l и (abJ, далеко
не так очевидно. (а2Ь2 = Ь'1(аЬа~1 Ь-1)-1ЬЬ~1(аЬJЬ.) По-
Понятие «соотношения» нетрудно сделать точным: фор-
формула u — v будет обозначать то, что следовало бы за-
записывать как u=v (modi?), т. е. uv-l£R. При этом,
разумеется, всегда имеется в виду заданное копред-
копредставление (х:г). Иногда можно "даже писать
(х : uv~l = l9 ...) или (x:u = vy ...), имея в виду то же,
что и (х: uv~\ ...). Бесполезно пытаться быть более
точными, поскольку выгода от использования соотноше-
соотношений вместо элементов, задающих эти соотношения, со-
состоит в достигаемой таким образом неформальности.
Понятие копредставления может быть соответствую-
соответствующим образом использовано и тогда, когда множество
5*
68 Гл. IV. Копредставления групп
соотношений пусто; так, (х: ) есть копредставление
свободной группы F(x).
Можно даже обозначить через (:) простейшее ко-
копредставление тривиальной группы, хотя вряд ли нам
придется часто сталкиваться с таким случаем.
Коп'редставлемие (х: г) называется конечно порож-
порожденным, если множество х конечно, и с конечным чис-
числом соотношений, если конечно множество г.
Копредставление называется конечным, если оба
эти свойства выполняются одновременно. Говорят, что
группа конечно порождена, если она обладает по мень-
меньшей мере одним конечно порожденным копредставле-
нием, что группа имеет конечное число соотношений,
если имеется хотя бы одно ее копредставление с конеч-
конечным числом соотношений, и что группа конечно пред-
ставима, если она обладает хотя бы одним конечным
копредставлением. Хотя бесконечные копредставления
встречаются довольно часто и вовсе не являются пато-
патологическими, мы будем в основном рассматривать толь-
только конечные множества х и г.
Так же, как и уравнения кривой или поверхности в
разных системах координат имеют разный вид, так и
группа имеет много разных копредставлений. Напри-
Например, можно показать, что
|лг, у: хух = уху\ж\ау Ь\ а? = Ь2\У
а также, что
\х9 у: ху2 = у*х, ух2
Задача о том, определяют ли два разных копред-
копредставления изоморфные группы, называется проблемой
изоморфизма: Общее решение этой проблемы не суще-
существует1), но можно найти весьма важные для нас част-
частные решения. Как правило, они имеют вид условий, на-
!) Имеется ряд похожих проблем, относительно которых из-
известно, что они не имеют общего решения, например: установить
является ли группа, определенная заданным копредставлением, три-
тривиальной (проблема тривиальности); конечной, абелевой, свободной
и т. д., или определить, является ли данное слово следствием за-
заданного множества слов (проблема слов), а также много других.
См. статью Рэбина (Rabin M. A., Recursive unsolvability of group
theoretic problems, Ann. of Math., 67 A958), 172—194).
2. Копредставления и типы копредставлений 69
кладываемых на копредставления условий, которые
должны выполняться, если эти копредставления опре-
определяют изоморфные группы. Такие условия весьма важ-
важны, так как они позволяют устанавливать, что те или
иные группы неизоморфны. Далее будут рассмотрены
методы нахождения подобных частных решений про-
проблемы изоморфизма.
Отображение копредставлений f : (х : г) -> (у : s) со-
состоит из двух копредставлений (х : г) и (у : s) и гомо-
гомоморфизма /: F(x)->F(y), удовлетворяющего условию:
образ f(r) множества г при этом отображении является
следствием множества s.
Каждое отображение копредставлений /:(х:г)->-
->(y:s) однозначно определяет гомоморфизм групп
/* : |х: г| —►|у : si, удовлетворяющий условию f*y=yf,
где канонические гомоморфизмы F(x)-->|x:r| и
f)Hy:s| обозначены символом у.
Композиция отображений копредставлений опреде-
определяется естественным образом. Если заданы отображе-
отображения /: (х: r)->(y : s) и g : (у : s)->(z : t), то компози-
композиция gf этих отображений будет состоять из копредстав-
копредставлений (х:г) и (z:t) и гомоморфизма gf: F(x)->f(z).
При этом справедлив ассоциативный закон и, кроме
того, существуют тождественные отображения. Таким
образом, набор всех представлений и их отображений
образует категорию. Более того, 1*=1 и (^/)*=^*Дх-
Отображения копредставлений fu f2: (x:r)->(y : s)
называются гомотопными (запись: /i~/2), если для
каждого #£х элемент fi(x) $г{х~1) является следствием
множества s.
Условие гомотопности отображений копредставлений
можно записать как yfi(u)=yf2(u) для любого u£F(x).
Поскольку по определению индуцированного гомомор-
гомоморфизма fi^y(u)=yfi(u)} f=l, 2, то тем самым доказано
B.1) /i^/г тогда и только тогда, когда /i* = /2*.
70 Гл. IV. Копредставления групп
Более того,
B.2) Если ft~/2 и gi^g2, то gifi^g2f2.
Мы видели, что отображение копредставлений /
определяет гомоморфизм /*. Обратно,
B.3) Для каждого гомоморфизма 9 : | х : г I -> | у : s |
существует такое отображение копредставлений
f: (х: r)->(y: s), что /* = 9. Более того, два любых та-
таких отображения гомотопны.
Доказательство. Рассмотрим диаграмму
F(x) /Чу)
v!
vl
Так как гомоморфизмы у являются отображениями на,
мы можем каждому элементу х£х сопоставить некото-
некоторый элемент f(x) £F(y) таким образом, что yf(x) =
= Qy(x). Но поскольку F(x)—свободная группа с ба-
базисом х, это сопоставление может быть продолжено до
гомоморфизма /:/7(x)->F(y), так что yf=Qy. Образ /г
содержится в оболочке множества s, и, значит, f —
отображение копредставлений и /* = 9- Единственность
отображения / с точностью до гомотопии следует из
B.1).
Итак, гомотопические классы отображений копред-
копредставлений находятся во взаимно однозначном соответ-
соответствии с гомоморфизмами определяемых ими групп. Бо-
Более того, это соответствие сохраняет композиции.
Копредставления (х : г) и (у: s) имеют одинаковый
тип, если существуют отображения (х : г) ^z± (у : s), та-
такие, что gf ~ 1 и fg ~ 1. Пара отображений /, g
(или отдельно одно из них) называется эквивалент-
эквивалентностью копредставлений (или гомотопической эквива-
эквивалентностью).
B.4) Два копредставления имеют один и тот же тип
тогда и только тогда, когда определяемые ими группы
изоморфны.
3. Теорема Титце 71
Доказательство. Если /, g — эквивалентность
копредставлений, то
Значит,/* изоморфно отображает |х:г| на |y:s|
(и gr* = /*1)- Обратно, если 9 изоморфно отображает
|х:г| на |y:s| и/* = 9, g^G'1 *), то
= ^ = e-1e = l==l#f значит gf~\.
= fA = ee-1 = l = l,f значит fe~l.
3. Теорема Титце. Среди эквивалентностей ^пред-
^представлений особую роль играют эквивалентности Титце I,
Г, II, 1Г, которые мы и рассмотрим сейчас.
Пусть (х: г) — некоторое копредставление и s —
следствие множества г. Рассмотрим новое копредстав-
копредставление (y:s), полагая у=х, s = rUs. В этом случае обо-
оболочка множества г совпадает с оболочкой множества s.
Следовательно, пара (х : г), (у : s) и тождественный
автоморфизм l:F(x)->F(y) определяют отображение
копредставлений I:(х: г) ->(у: s). Аналогично пара
(у: s), (х : г) и тождественный автоморфизм опреде-
определяют отображение копредставлений Г : (у : s)->(x: г).
Очевидно, что пара отображений I и Г является экви-
эквивалентностью копредставлений.
Исходя опять-таки из произвольного копредставле-
ния (х:г), выберем в базисном множестве образующих
любой элемент у, не содержащийся в х. Пусть также
I — произвольный элемент группы F(x). Рассмотрим те-
теперь копредставление (y:s), где у=х[} у и s = r[}yl.
Гомоморфизм II: F(x)->F(y), определяемый правилом
П(х)=х для любого х£х, отображает г в оболочку
множества s, так что пара (x:r), (y:s) и гомоморфизм
II: /7(х)->/7(у) определяют отображение копредставле-
копредставлений II: (х : r)->(y : s). Далее, гомоморфизм 1Г:/7(у)->
->F(x), определяемый правилами: 1Г(х)=х, если х£х,
и IV (у) =£> отображает множество s на г U 1 и, следова-
следовательно, в оболочку множества г. Отсюда следует, что
*) Существование таких / и g следует из B.3). — Прим. перев.
72 Гл. IV. Копредставления групп
пара (y:s), (х.т) и гомоморфизм 1Г: F(y)->F(x)
определяют отображение копредставлений II':(y:s)->
->(х:г). Композиция 1Г II является тождественным
отображением. Кроме того, для х£х, II W(x) -х~х = 1 и
llll'(y)-y-{ = U(t)y-l = ly-l= (ytl)~l\ последний эле-
элемент принадлежит оболочке множества s, так что
1П1'~1. Следовательно, пара отображений II, 1Г яв-
является эквивалентностью копредставлений. Отметим,
что гомоморфизм II: F(x) —>F(y) является вложением, а
гомоморфизм ll':F(y) -+F(x) —ретракцией*).
Хотя теоретически отображения I и Г определяются
тривиально, а отображения II и 1Г—не совсем, при
конкретных вычислениях получается обратное. Действи-
Действительно, проверка того, что некий элемент (или соотно-
соотношение) является следствием некоторых других, может
быть крайне затруднительной. (Это частный случай
проблемы слов, см. сноску1) на стр.68.) Та же самая
трудность встречается и в доказательстве фундамен-
фундаментальной теоремы Титце, которую мы собираемся дока-
доказать. Следующая лемма необходима для того, чтобы
оправдать употребление отображений I и V в этом до-
доказательстве.
C.1) Пусть х и у — непересекающиеся подмножества
базисного семейства образующих и 9 — ретракция груп-
группы F(x U у), на F(x). Пусть (х:г)ф — копредставле-
ние группы G. Тогда ядро гомоморфизма ф8: F(x[)y)-+G
представляет собой оболочку С множества, являющего-
являющегося объединением множества г и всех элементов вида
Доказательство. Ясно, что ф8(г) =ф(г) = 1 при
любом г 6 г. Так как 6 — ретракция, то 82 = 6 и, значит,
фв(# -9(У))=фF(у) • в(^)) =фA) = >- Следовательно,
множество С содержится в ядре гомоморфизма фб.
Для того чтобы доказать обратное, рассмотрим ка-
канонический гомоморфизм у группы ^(xUy) на фактор-
*) Если G является подгруппой группы G\ то гомоморфизм /
группы О' в G называется ретракцией, если f(g)—gt при любом
g £ G. — Прим. перевг
3. Теорема Титце 73
группу F(x\Jy)/C и его ограничение у' на подгруппу
F(x). Имеем
X У
F(x[)y)!C
Тогда y'Q(x)=y'(x)=y(x), если х€х. Более того, если
у£у, то у(у) -/В(у)-1=у(у) -уВ(у)-1=у(ув(у)-*) = \,
а, значит, y'Q(y)=y(y)- Тем самым показано, что y'^y-
Предположим теперь, что элемент и €F(x U у) таков, что
ф9(и) = 1. Тогда
и, таким образом, ^^(м)^^. Но ф6(м) = 1, поэтому
0(м) является следствием множества г и, значит, лежит
в С. Отсюда мы заключаем, что и = и • б(м) • Q(u) £C.
C.2) теорема титце. Предположим, что(х : r)^±(y : s) —
эквивалентность копредставлений; (х: г) м (у: s) /co-
нечны. Тогда существует конечная последовательность
Т\, Гь ..., Г/, Г/ эквивалентностей Титце, такая, что
f=Tx...Th g=Ti ...Т[.
Доказательство. Докажем сначала теорему в
предположении, что множества х и у не пересекаются.
Рассмотрим следующую диаграмму:
/у
F(x[}y)
|x:r| < ^—±|y:s|
74 Гл. IV. Копредставления групп
где гомоморфизмы i и о —вложения, а р и а—ретрак-
а—ретракции, определенные так, что р(у) =g(y), */€у и о(х) =
= f(x), х£х.
Легко видеть, что эквивалентность копредставлений
(x:r)^±(xUy:rUb),
где Ъ = {у • р(у)}, можно разбить в произведение экви-
валентностей Титце Т\, Т\, ..., Tmt Tm типа II, где
m — число элементов множества у, так что i^=jTi ... Гт,
р = Т'т ... Ту Аналогично эквивалентность копредста-
копредставлений
(у: S)<|±(xUy :sl)a),
где а={х-а(х)}, можно разбить в произведение экви-
валентностей Титце Si, S\ Sn, 5« типа II, где п —
число элементов множества х, так что o=Sl ... Sn,
Из C.1) следует, что ядро гомоморфизма YP содер-
содержится в оболочке множества г lib. Но yp=g*yo и
ya(s U а) = 1. Значит, множество s U а лежит в оболочке
множества r|Jb. По тем же соображениям множество
r|Jb лежит в оболочке множества sUa. Следовательно,
эквивалентности копредставлений
определяемые тождественным автоморфизмом группы
F(x\Jy), могут быть разложены в произведение эквива-
лентностей Титце типа I соответственно U\, U[, ...
. . . ,Uq+n, U'q+n И Vu V'l, • • • » Vр+тУ р+т> ГДе /7 — ЧИСЛО
элементов множества г и q — число элементов множе-
множества S. Тогда а = £А ... t/g+n, а' = 6/д+л ... U[,
р = Vi ... Vp+m, pr= Vfp+m ... Vu так что
f =o$'ai = S'n ... S'y'p+m • • • V\U\ ... Uq+nT\ ... Tm,
g = pa'po = T'm ... T[U'q+n ... U[Vi ... Vp+mSx ... Sn.
3. Теорема Титце 75
Если множества х и у пересекаются, мы выберем в
базисном м«ожестве образующих подмножество г, не пе-
пересекающееся cxUy» элементы которого находятся во
взаимно однозначном соответствии с элементами мно-
множества х. Это соответствие индуцирует изоморфизм fti
группы F(x) на F(z) и обратный изоморфизмАг = Af1
группы F(z) на F(x). Пусть t = /i±(г), k{=fh2 и k2 h
Тогда f=kihu g = h2k2.
(z : t)
(У = 8)
Ясно, что hi и h2 являются эквивалентностями копред-
ставлений. Мы утверждаем, что kt и k2 — также экви-
эквивалентности копредставлений. Обозначим оболочки мно-
множеств г, s и t соответственно через R, S и Т. Тогда
*i(t)=/Mt)=/(r)cS и k2(s)=hig(s)czhl(R)=T, так
что k\ и k2 — отображения копредставлений. Более того,
k2kl = hlgfh2~ hiIh2=l и kik2 = fh2hig = fg~l. Теперь
можно дважды применить первую часть доказательства
и теорема доказана.
Важность теоремы Титце состоит в том, что она сво-
сводит проверку того, что заданная функция на копредстав-
лениях групп зависит только от самих групп, к проверке
тогд, что функция не меняется операторами Титце I и II.
Например, в гл. VII мы покажем, как вычислять после-
последовательности так называемых элементарных идеалов,
исходя из конечных копредставлений группы. Так как
будет показано, что копредставления, отличающиеся
лишь на два оператора Титце, определяют изоморфные
последовательности идеалов, то можйо будет сделать
вывод, что элементарные идеалы являются групповыми
инвариантами.
В качестве иллюстрации того, как эквивалентности
Титце используются для получения одних копредставле-
копредставлений из других, мы покажем сейчас, что группы
76 Гл. IV. Копредставленйя групп
|*, у, г : xyz=yzx\ и \х, у, а : ха = ах\ изоморфны
(х, у, z-.xyziyzxy1)
I II
(х, у, z, a:xyz(yzx)~\ a(yz)~l)
I I
(x, у, z, a:xa(ax) \ a(yz)~\ xyz{yzx)~l)
I Г
(x, y, z, a:xa(ax) \ a(yz)~l)
I I
(x, y, z, a:xa(ax)~\ z(y~xa)~\ a{yz)~l)
l Г
(x, y, a, z:xa(ax)~\ г{у-^а)~х)
(x, у, а : xa(ax)).
В качестве другого примера покажем, что группа
\х, у :хух=уху\ изоморфна группе \а, b:az = b2\. За-
Заметим сначала, что, умножая обе части равенства
хух=уху слева на хух, получаем (хух)(хух) =
= (ху) (ху) (ху). Потом обозначим а=ху и Ь=хух,отме-
Ь=хух,отметив, что эти два уравнения можно разрешить относи-
относительно х и (/. Эти соображения приводят нас к следую-
следующей последавательности эквивалентностей Титце (в не-
неформальной записи):
(л:, у : хух = уху)
| II (дважды примененная)
х, у, at b:xyx = yxy, а = ху, Ь — хух)
\ I (трижды примененная)
(л:, (/, а, Ь : хух = уху, а3 = й2, а — ху, b = хух, х =
= a~lb, y = b~la2)
| V (трижды примененная)
(л:, у у a, 6:ad==62, x = a~lb, у = Ь~1а2)
| IF (дважды примененная)
(a, b\a? = b\
4. до-подгруппы и ассоциированные гомоморфизмы 77
4. до-подгруппы и ассоциированные гомоморфизмы.
При нахождении необходимых условий в проблеме изо-
изоморфизма просто необходимо найти некий общий метод
упрощения групп. С этой целью мы собираемся исполь-
использовать «до-подгруппы».
Для того чтобы определить до-пэдгруппу, выделим
сначала подмножество W некоторой свободной группы
^(х). (Элементы множества W являются словами в ба-
базисном множестве образующих, что объясняет термин
«до-подгруппа» *).) Зафиксировав некоторую группу G,
рассмотрим множество Q = Q(G) всех возможных гомо-
гомоморфизмов со группы F(x) в группу G и обозначим че-
через W(G) подгруппу группы G, порожденную всеми эле-
элементами вида со(до), w£W, (об й. Эта подгруппа W(G),
которая и называется w-подгруппой, является обяза-
обязательно нормальным делителем, так как она не меняется
при любом внутреннем автоморфизме группы G. В дей-
действительности же подгруппа W(G) обладает еще более
сильным свойством — она отображается в себя любым
эндоморфизмом группы G (такие подгруппы называются
вполне нормальными). Так как а —некоторый эндомор-
эндоморфизм группы G и <o£Q, то a<o£Q и, таким образом,
a(W{G))cW(G).
Простейшими примерами до-подгрупп являются ком-
коммутант и степень. Для определения коммутанта мы рас-
рассмотрим множество х = {х, у} и выделим в качестве под-
подмножества W группы F(x, у) единственный элемент
[xt y]—xyx"xy~x. Получающаяся при этом до-подгруппа
W(G) и называется коммутантом и может быть обозна-
обозначена через [G, G]. Она является подгруппой группы G,
порожденной всеми элементами вида g^ST1^1- Фак-
Факторгруппа G/[Gy G] называется прокоммутированной
группой, а канонический гомоморфизм G -> GI[G, G] —
коммутированием. Прокоммутированная группа являет-
является всегда абелевой группой. Коммутирование как раз и
делает все элементы перестановочными.
Для построения п-й степени группы G(n>0) рассмот-
рассмотрим множество х = {х}, а подмножество W группы F(x)
*) Термин до-подгруппа соответствует здесь английскому word
subgroup. — Прим. перев.
78 Гл. IV. Копредставлейия rpynrt
составим из единственного элемента хп. Соответствую-
Соответствующая до-подгруппа называется п-й степенью группы G и
может быть обозначена через Gn. Она является под-
подгруппой группы G, порожденной всеми элементами
вида gn. Пожалуй, ясно, что если т делится на пу то
G°=l, Gl = G и GmczGn. Отметим также, что [G, G]czG2.
В самом деле, ggg^g*1 = (Л ?2J * (в^ЯГ1^J^-
Это означает, что группа G/G2 всегда абелева.
Если ф : Gi —► G2 есть некоторый гомоморфизм, a W—
подмножество свободной группы, то yW(Gi) czW(G2),
поскольку ф<о6£2(О2) для любого <d£Q(Gi). Следова-
Следовательно, при этом индуцируется единственный гомомор-
гомоморфизм ф#, такой, что диаграмма
Ох -^+ G2
коммутативна. Непосредственно доказывается, что
D.1) (а) Если гомоморфизм ф тождествен, то также
тождествен гомоморфизм q>#. (b) Если дана композиция
гомоморфизмов G{ — ->G2— ->O3, то (^)*=\|)^#. (с) Если
Ф — гомоморфизм на, то таковым является и гомомор-
гомоморфизм ф*. (d) Если ф — изоморфизм на, то <р* также изо-
изоморфизм на.
Например, если свойства (а) и (Ь) уже проверены,
то свойство (d) следует из того, что
Заметим, что если утверждение (d) изменить, опустив
слово «на», то оно перестанет быть верным.
Используя D.1), можно доказать одно утверждение,
обещанное в гл. III.
D.2) Если тип — различные кардинальные числа,
то свободные группы рангов т и п не изоморфны.
Доказательство. Рассмотрим свободные группы
Fm и Fn рангов тип соответственно и предположим,
что они изоморфны. Тогда, согласно D.1), группы FmjF2m
4. до-подгруппы и ассоциированные гомоморфизмы 79
и Fn/Fl> должны быть изоморфизмами на. Но элементы
этих групп могут быть выписаны в явном виде и сосчи-
сосчитаны. Так как Fm\F2m— абелева группа, ее элементы
являются произведениями л:*1 ... л:*т, где хи • • •> *т —
базис группы Fm, 6; =0 или 1 и только конечное число
показателей бг- отлично от нуля*). Следовательно, чис-
число элементов группы FmlFli равно в точности числу
конечных подмножеств множества мощности тп. Оно
равно 2 m , если тп конечно, и пт, если тп бесконечно.
Если Fm/Fm ж Fn/Fl, то мощности m и и должны быть
одновременно либо конечными, либо бесконечными и,
значит, тп = и.
Из D.1) вытекает наиболее элементарное из всех не-
необходимых условий в проблеме изоморфизма.
D.3) Для того чтобы группы Gi и G2 были изоморф-
изоморфными, необходимо, чтобы были изоморфны их проком-
мутированные группы GJ[Gi, G\] и G2/[G2, G2].
Прокоммутированная группа G/[G, G], соответствую-
соответствующая некоторой группе G, есть наибольшая абелева
группа, являющаяся гомоморфным образом группы G.
Более строго это можно выразить следующим образом.
Рассмотрим произвольный гомоморфизм 9 группы G в
абелеву группу /С. Тогда существует единственный го-
гомоморфизм 9Г группы G/[G, G] в /(, который вместе с 9
и гомоморфизмом коммутирования а : G ~> G/[G, G] об-
образует коммутативную диаграмму
ai[Q, G]
Чтобы доказать это, рассмотрим произвольный комму-
коммутатор
*) Точнее, каноническая проекция Fm->Fm/F<^n осуществляет
взаимно однозначное отображение множества этих элементов груп-
группы Рщ "а группу Рщ/Рщ- —Прим. перев,
80 Гл. IV. Копредставления групп
Так как группа К— абелева, то
6fei, g2\=№gu 9g2]=l
и, таким образом, оболочка множества коммутаторов G
содержится в ядре гомоморфизма 9. Группа [G, G], по-
порожденная коммутаторами группы G, автоматически со-
содержится в их оболочке. Следовательно, гомоморфизм 8'
корректно определен равенством
e'ag = 9£, g£G.
Единственность гомоморфизма 9' очевидна. Заметим, что
так как подгруппа (G, G] — нормальный делитель груп-
группы G, то она совпадает на самом деле с оболочкой ком-
коммутаторов группы G. Доказанный результат коротко вы-
выражается следующим утверждением:
D.4) Всякий гомоморфизм произвольной группы в
абелеву можно профакторизовать через прокоммутиро-
ванную группу.
D.5) Если группа G порождается элементами
gu §2, . •., то ее коммутант [G, G] совпадает с оболоч-
оболочкой коммутаторов [gu gj], /,y=l,2,....
Доказательство. Оболочка К коммутаторов
[gi, gj] содержится во всяком нормальном делителе G,
содержащем множество {[gu gj]}. Отсюда Kc[G, G]. Для
доказательства обратного нужно показать, что коммута-
коммутатор [и, v] любых двух элементов группы G лежит в К
Для каждого элемента g£ G обозначим через l{g)
наименьшее неотрицательное число л, для которого
существуют такие числа еь е2, ... , еп=±1, что
п
g = W g\k. Очевидно, l{g)=0 тогда и только тогда,
когда g=l. Далее проведем индукцию по l(u)+l(v).
Если либо /(и>=0, либо /(а)=0, то [и, v]=l£K Если
l(u)=l(v) = l, то коммутатор [и, v] совпадает с одним
из следующих коммутаторов:
[8Tl> 8-jl\ = 8Tl8]l[8i> 8j]8j8
5. Свободные абелевы группы 81
Каждый из этих элементов принадлежит К. Предпо-
Предположим далее, что либо 1(и), либо l(v) больше единицы.
Вследствие тождества
[и, v] = [v, и]
можно предположить, что именно 1(и) больше единицы.
Тогда и = ихиь где l(ui)<l(u) и 1{и2)<1(и). Согласно
индуктивному предположению,
[ихи2, v] = ul[u2, v]u~l[av v]£K,
чем завершается доказательство.
D.6) Если (х : г) — некоторое копредставление, то
(х : г U {[хи хд], i, /= 1, 2, ... ,}) является копредставле-
нием прокоммутированной группы, соответствующей
группе |х : г|.
Доказательство. Пусть у обозначает канониче-
канонический гомоморфизм свободной группы F(\) на ее фактор-
факторгруппу |х:г|. Гомоморфизм коммутирования, как и
выше, обозначим через а. Нужно показать, что ядро го-
гомоморфизма а^ лежит в оболочке К множества^
г U {[хи Xj]}. To, что оболочка содержится в этом ядре,
очевидно. Для доказательства обратного утверждения
выберем такой элемент и группы ^(х), что ауи=1. Со-
Согласно D.5), элемент уи содержится в оболочке множе-
множества {[ухи yXj]} — {y[Xu Xj]}. Но, согласно A.1), эта обо-
оболочка является образом оболочки множества {[хи х$
при гомоморфизме у. Следовательно, yu=yv, где v —
следствие множества {(хг-, Xj]}. Поэтому u = vw, где w —
следствие множества г, и доказательство закончено.
5. Свободные абелевы группы. В теории абелевых
групп встречается другой тип свободных групп, пол-
полностью аналогичных свободным группам («о все же от-
отличных от них), так как oihh определены в нашей книге.
А именно, свободная абелева группа ранга п есть груп-
группа, изоморфная прокоммутированной свободной группе
ранга п. Так как коммутативными из свободных групп
являются только группы рангов 0 и 1, т. е. тривиальная
и бесконечная циклическая группы, то ясно, что эти два
понятия пересекаются, но те совпадают. Вообще говаря,
6 Зак 317
82 Гл. IV. Копредставления групп
свободная абелева группа не является свободной груп-
группой. Однако оба этих типа групп полностью опреде-
определяются своим рангом.
Итак,
E.1) Две свободные абелевы группы изоморфны то-
тогда и только тогда, когда они имеют одинаковый ранг.
Нетрудно доказать этот факт, основываясь на ана-
аналогичном результате для свободных групп D.3) и ис-
прльзуя технику доказательства утверждения D.2) (см.
упражнения 2, ниже).
Существует абстрактное определение свободной абе-
левой группы, вполне аналогичное определению свобод-
свободной группы. Множество Е образующих абелевой груп-
группы G называется базисом, если для произвольной абе-
левой группы Н всякая функция ф : Е —► Н может быть
продолжена до гомоморфизма группы G в Н. Имеем
E.2) Абелева группа является свободной абелевой
группой тогда и только тогда, когда она имеет базис.
Доказательство этого, основанное на D.4), очевидно.
Используя утверждение D.6), нетрудно описать про-
простое капредставление свободной абелевой группы. На-
Например, копредставления (#, у:ху = ух) и (#, у, z :ху =
— ух, yz=zy, zx=xz) являются копредставлениями
свободных абелевых групп рангов 2 и 3 соответ-
соответственно.
УПРАЖНЕНИЯ
1. Доказать следующее добавление к теореме D.1).
Если ф — изоморфизм в, то ф# может не быть таковым.
(Одно из решений: G{= (x :), G2=(w, v :),ф(#) =uvu~lv-\
1F(G)=[G, О].)
2. Если Fn — свободная группа ранга я, а Ап — сво-
свободная абелева группа ранга я, то FnlF\ ~ An/Al. Вы-
Вывести отсюда утверждение E.1).
3. Доказать утверждение E.2).
4. Сколько существует различных гомоморфизмов
свободной группы ранга 2 на циклическую группу по-
порядка 4?
5. Свободные абелевы группы 63
5. Показать, что копредставления (а, 6:а2=1, 63=1,
ab = ba) и (с:с6=\) описывают одну и ту же группу.
6*. Показать, что группа, определяемая копредстав-
лением (х, у: ху2 = у3х, ух2=х3у), тривиальна.
7. Проверить, что в копредставлении (а, 6, с, d:b =
= c~lac, c = dbd'\ d=a-lca, a = bdb~l) всякое соотношение
является следствием остальных.
8. Показать, что копредставление (а, 6 : а3= 1, 62=1,
ab = ba2) описывает симметрическую группу порядка 3.
9. Описать до-подгруппы W(G) произвольной груп-
группы G, если (I) W=xy9 (II) U7=*V. (Ill) W=xyxy~K
10. Верна ли теорема A.1), если ф не есть гомомор-
гомоморфизм на?
11. Показать, что теорема D.5) неверна, если в ней
слово «оболочка» заменить фразой «подгруппа, порож*
денная элементами»...
б*
ГЛАВА V
ВЫЧИСЛЕНИЕ ФУНДАМЕНТАЛЬНОЙ
ГРУППЫ
Введение. В гл. II было уже отмечено, что только в
редких случаях точное вычисление фундаментальной
группы пространства X основывается на определении
группы п(Х). Пока набор топологических пространств,
фундаментальную группу которых читатель мог бы под-
подсчитать (пользуясь теорией, изложенной ранее в этой
книге), состоит из пространств, топологически эквива-
эквивалентных окружности или выпуклому множеству. Это, ко-
конечно, не очень много, и целью гл. V является расшире-
расширение этого класса пространств. Техника, рассматриваемая
здесь, будет развиваться в двух направлениях. Первое
относится к тому, что можно считать пространствами
одинаковой формы. Рисунки 14—16 дают примеры того,
что имеется в виду. Бели понимать фундаментальную
группу, как группу, образованную множеством классов
эквивалентности путей с базой в данной точке, то гео-
геометрически ясно, что пространства, показанные на рис. 14,
имеют одинаковые или изоморфные фундаментальные
группы. То же самое имеет место и на рис. 15 и 16.
Примеры эти специально выбраны так, <Ггобы никакие
два пространства не были топологически эквивалентны.
(Этот факт не очевиден1).) Тем не менее все простран-
пространства, изображенные на одном и том же рисунке, имеют
изоморфные фундаментальные группы и в некотором
смысле одинаковую форму. В первых двух параграфах
этой главы изучается математическая терминология, ис-
1) Большая часть пространств одного и того же рисунка может
быть отличима друг от друга в силу того факта, что размерность
топологического пространства в окрестности точки является тополо-
топологическим инвариантом, т. е. при гомеоморфизме локальная размер-
Введение
Окружность
Заполненный тор
Ущемленный заполненный
тор
Рис. 14.
Сфера
Колючая сдзера
Рис. 15.
пользуемая для точного описания понятия и его связи
с фундаментальной группой. Вводится определение ре-
тракции, деформации, деформационного ретракта и го-
гомотопического типа. Понятие гомотопического типа дает
ность пространства для любой точки такая же, как и у ее образа.
См. В, Гуревич, Г. Воллмен, Теория размерности, ИЛ, М.,
1948. [Возможно и совсем элементарное доказательство, основанное
на том, что пространство, полученное из исходного выбрасыванием
вб Гл. V. Вычисление фундаментальной группы
строгую формулировку нашего интуитивного понятия
Пространств одинаковой формы.
Вторая основная тема этой главы — это вычисление
фундаментальной группы пространств, построенных оп-
определенным образом из более простых пространств, фун-
фундаментальная группа которых известна. В качестве про-
простого примера рассмотрим пространство, являющееся
Эллипсы с одной общей
точкой
Оправа ow/(oe
Дбойное плоское кольцо
Рис. 16.
объединением двух окружностей X и У, имеющих един-
единственную общую точку р. Весьма естественно (а также
и правильно) предположение, что группа n(X[}Y) яв-
является свободной группой с двумя образующими: одна
из них порождает группу п(Х), а другая я (К). Однако
это заключение не следует явно из развитой до сих пор
техники. Ясно, что было бы очень важно иметь доста-
достаточно общую процедуру «склейки» фундаментальных
точки, — также топологический инвариант. Например, у сферы вы-
выбрасывание любой точки дает нам связное пространство. Если же
у колючей сферы выбросить внутреннюю точку какой-либо иглы, то
получится несвязное пространство, таким образом, сфера и колючая
сфера негомеоморфны. Аналогично можно разобрать остальные слу-
случаи, если вдобавок учитывать фундаментальную группу пространства
без точки*. — Прим, перев.]
1. Ретракции и деформации 87
групп пространств, объединяемых в одно. Для широкого
класса пространств подобная процедура существует, что
следует из теоремы ван Кампена. Большинство про-
пространств, встречающихся в топологии, в особенности так
называемые комплексы, описываются как объединение
структурно простых подмножеств. Последовательное при-
применение теоремы ван Кампена к этим компонентам зна-
значительно расширяет выбор пространств, фундаменталь-
фундаментальная группа которых легко вычислима. В § 3 дается
точная формулировка этой важной теоремы и рассма-
рассматривается ее применение на некоторых примерах. Дока-
Доказательство дано в Добавлении III.
1. Ретракции и деформации. Ретракцией топологиче-
топологического пространства X на подпространство Y называется
непрерывное отображение p:X-+Y, такое, что р(р)=р
для любой точки р 6 Y. Пространство Y называется ре-
трактом пространства X, если существует ретракция
р : X — У.
В качестве примера рассмотрим квадрат Q в дву-
двумерном евклидовом пространстве, определяемый нера-
неравенствами 0-<х-<1, 0<СуК1. Ретракция квадрата Q на
его основание Е, определяемое условиями 0<j^<1, (/ = 0,
задается равенством
*/) = (*, 0),
Ограничивая область определения этой функции на мно-
множество Q, состоящее из всех точек (#, у) квадрата Q,
удовлетворяющих уравнению ху{\ — х) A — у) =0 (по
крайней мере один из сомножителей должен обращаться
в нуль), получаем ретракцию границы этого квадрата
на основание Е. Добавим, что начало координат @,0)
является ретрактом квадрата, его границы, а та:кже ос-
основания Е. Ретракция при соответствующим образом вы-
выбранной области определения задается формулой
*/) = @, 0).
Вообще для любой точки р произвольного топологиче-
топологического пространства X постоянное отображение р:Х-*р
является ретракцией. Следовательно, точка является ре-
ретрактом любого содержащего ее пространства.
88 Гл. V. Вычисление фундаментальной группы
Из вышесказанного следует, что любая внутренняя
точка р замкнутого круглого диска D является ретрак-
том всего диска. Проектируя точки вдоль лучей, выходя-
выходящих из точки р на границу D этого диска, мы видим,
что D является ретрактом дополнения D—р точки р.
Аналогичный результат имеет место и в трехмерном
случае. Если р — центр диска D и трехмерный шар В
получен вращением диска D вокруг диаметра, то р есть
ретракт шара В, а граничная сфера—-ретракт В —р.
Если диск' D вращается вдоль линии, проходящей вне
его, то oih описывает заполненный тор V, а точка р —
окружность С. Мы видим, что окружность С, образую-
образующая остов заполненного тора V, есть ретракт V. Анало-
Аналогично тор, образующий поверхность тела V, является
ретрактом пространства V—С.
Конечно, не менее важно дать примеры подпро-
подпространств, которые не являются ретрактами содержащих
их пространств. Это тоже нетрудно сделать. Граница
квадрата не есть ретракт всего квадрата. Точно так
же Ь не есть ретракт диска D. Невозможна ретракция
всего пространства ни на заполненный тор V, ни на его
остов С. Экватор не является ретрактом земной поверх-
поверхности. Все это так, но как мы узнали это? Как вообще
можно доказать, что ретракции не существуют? Ответ
на это дается следующей теоремой:
A.1) Если р : X -* Y есть ретракция и пространство X
линейно связно, то тогда для любой базисной точки
р£Х гомоморфизм р*:я(Х, р)-*я(У, рр) является го-
гомоморфизмом на.
Доказательство. В гл. II было уже замечено
(см. D.6) и сопровождающее обсуждение), что алгеб-
алгебраические свойства всякого гомоморфизма, индуциро-
индуцированного непрерывным отображением линейно связного
пространства, не зависят от выбора базисной точки. По-
Поэтому достаточно прорерить утверждение A.1) для ба-
базисной точки р 6 Y. Рассмотрим индуцированные гомо-
гомоморфизмы
я (К, p)-iz+n(X, p)-*+n(Y, p),
1. Ретракции и деформации 89
где i: Y-+X есть вложение. Так как р — ретракция, то
композиция pi" — тождественное отображение. Следова-
Следовательно (см. D.5) гл. II), (рО* = Р*''* есть тождественный
эндоморфизм, откуда и следует, что гомоморфизм р*
является отображением на. Доказательство закон-
закончено.
Непрерывный образ линейно связного пространства
линейно связен. Следовательно, пространство У в тео-
теореме A.1) линейно связно. Без предположения о ли-
линейной связности пространства X утверждение A.1) не-
неверно.
Квадрат, диск, пространство /?3 — выпуклые множе-
множества и, следовательно, имеют тривиальную фундамен-
фундаментальную группу. Доказательство того факта, что фун-
фундаментальная группа сферы тривиальна, будет да«о
только в конце этой главы. Тем не менее то, что все
петли на сфере, имеющие общую базисную точку, могут
быть стянуты в точку, правдоподобно (кстати, слово
«сфера», взятое одно, всегда означает поверхность шара).
Следовательно, во всех примерах, перед предложением
A.1), фундаментальная группа объемлющего простран-
пространства X всегда тривиальна. Подпространство же У в ка-
каждом примере имеет бесконечную циклическую фунда-
фундаментальную группу, а группа, содержащая только один
элемент, не может, конечно, быть отображена на группу,
содержащую более одного элемента. Поэтому утвержде-
утверждения вышеприведенных примеров доказаны.
Перейдем теперь к понятию деформации. Объяснение
здесь почти интуитивно. Топологическое пространство X
деформируемо в подпространство У, если его можно не-
непрерывно «сжать» в подпространство У. Слова «на» и «в»
имеют здесь обычный смысл. Если результат сжатия не
только содержится в У, но и совпадает с ним, то мы го-
говорим, что X деформируется на У. Например, квадрат
можно деформировать на его основание. Соответствую-
Соответствующее точное определение таково: деформация топологиче-
топологического пространства X — это такое семейство отображе*
ний: hs:X —* X, O-O-^l, что hQ—тождественное отобра*
жение, т. е. ho(p)=p для всех р£Х, и отображение Л,
определяемое равенством h(s, p)=h8(p), непрерывно по
90 Гл. V. Вычисление фундаментальной группы
совокупности переменных 5 ир2). Деформация простран-
пространства X в (или на) подпространство Y — это такая де-
деформация {fts}, что hiX содержится в (или совпадаете) Y.
Говорят, что X деформируемо в (или на) подпростран-
подпространство У, если существует подобная деформация.
Можно, например, деформировать квадрат на его
основание. Эта деформация в R2 задается семейством
(I) M*. </) = (*> V-s)y), 0<х, у, 5<1.
Семейство функций
(II) ha(x, y) = ((l-s)x, (l-s)y), 0<х, у, 5<1,
является деформацией квадрата на угол @, 0). Диск Д
определяемый в полярных координатах неравенством
0<г<1, деформируется в свой центр семейством отобра-
отображений
@<r, <?<1,
(III) Мг.в) = И1-*).в), (о<9<2я.
Пространство, состоящее из всех точек диска Д кроме
его центра, можно продеформировать на границу D
диска. Эта деформация определяется семейством
(IV) *,(г, e) = (r(i —s)+s, е),
0<9 <2я.
Читатель может проверить, что при 0<г-<1, 0-О-<1 вы-
выполняется неравенство r<r(l—5)+s<l. Отметим, что
деформация (IV) не может быть продолжена до дефор-
деформации всего диска D на D. Ка>к и выше, мы можем наши
рассмотрения на диске перенести на трехмерный случай.
Напри-мер, заполненный тор V можно деформировать в
его остов, окружность С, или V — С можно деформиро-
деформировать на тор, образующий границу тела V.
2) Обобщением этого определения является определение дефор-
деформации пространства X в содержащее его пространство Z как се-
семейства отображений h8:X-*Z, 0<s<l, такого, что ho(p)=p для
всех р £ X, и выполнено условие непрерывности по совокупности
переменных. Данное выше более ограниченное понятце деформации
вполне достаточно для дальнейшего изложения.
1. Ретракции и деформации
91
Можно построить следующую деформацию диска на
его границу. Диск D в полярных координатах задан как
множество точек (г, 9), удовлетворяющих неравенству
0<r-<sdn 9. (См. рис. 17.) Граница диска D есть тогда
множество точек, удовлетворяющих соотношению r=sin 9.
D
х
Рис. 17.
Деформация осуществляется в два шага. Сначала в ин-
интервале 0<5<V2 сожмем весь диск в начало коорди-
координат р. Затем при 72-0^1 заставим точки двигаться по
границе Ь в направлении против часовой стрелки с воз-
возрастающими г и s. Точнее, для упорядоченной пары
(г, 9), удовлетворяющей условию 0-O-<sin 9, положим
(r(l—2s), 9),
(sinnr{2s— 1), nrBs — 1)), ~
0<s<
1
1
7'
Нетрудно убедиться, что это семейство функций удовле-
удовлетворяет тем условиям непрерывности по обоим перемен-
переменным, которые предписываются определением деформа-
деформации. Этот пример интересен еще и тем, что, как извест-
известно, A.1) граница диска D не является ретрактом всего
диска D,
92
Гл. V. Вычисление фундаментальной группы
Таким образом, имеется пример топологического про-
пространства Ху которое можно деформировать на подпро-
подпространство, не являющееся его ретрактом. Естественно
Рис. 18.
возникает вопрос, справедливо ли обратное, существуют
ли ретракты, которые нельзя получить деформацией?
Рис. 19.
Да, существуют, и хорошим средством построения при-
примеров является теорема A.3). Докажем сначала лемму:
A.2) Если {hs}y 0 < 5 < 1, — некоторая деформация
пространства X, то для произвольной базисной точки
р£Х гомоморфизм (fti)* : тс(Х, р)-+л(Х, h\(p)) являет-
является изоморфизмом на.
1. Ретракции и деформации 93
Доказательство. Определим путь а с началь-
начальной точкой р и конечной точкой q = hi(p) формулой
a(t)=ht(p)y 0</<1.
Обозначим через а класс эквивалентных путей, содер-
содержащий путь ау и покажем, что для любого р 6 я(ЛГ, р)
Наш результат будет тогда следовать из теоремы C.1)
гл. II. Итак, рассмотрим произвольный элемент
р£я(Х, р) и представляющую его петлю Ь в р. Мно-
Множество
Набор {ks} является, конечно, непрерывным семейством
петель. Его область определения изображена на рис. 18.
Другое непрерывное семейство путей представлено на
рис. 19 и определено следующим образом:
q, 0</<s<l.
Последнее непрерывное семейство путей представлено
на рис. 20 и определено формулой
Произведение этих семейств {/s • ks • /s} определено и
является непрерывным семейством путей. Оно изобра-
изображено на рис. 21. Так как семейство {js-ks-ls} имеет фи-
фиксированные концы, справедлива эквивалентность
яг1 • b • а~с • кф -су
где с — постоянный путь, отвечающий точке q. Класс
эквивалентности, содержащий постоянный путь, является
единицей (см. B.6) гл. II). Отсюда
а • р • а=[а-1 • Ь . а]=[М>]= (Л^р,
что завершает доказательство.
Произвольное непрерывное отображение f:X-+Y
топологического пространства X на подпространство Y
94
Гл. V. Вычисление фундаментальной группы
реализуемо деформацией пространства Ху если суще-
существует такая деформация {/is}, 0<5<<1, пространства Ху
что hx = if, где /: Y-*X есть отображение вложения. Как
Рис. 20.
S
I
W
а-'
|
b
а
Ш
ц
1
t
Рис. 21.
следствие леммы A.2) получаем следующую теорему:
A.3) Если непрерывное отображение f : X ~> У реали-
реализуется деформацией пространства X, то при произволь-
произвольной базисной точке р£Х индуцированный гомоморфизм
f*:n(X, p)—я (У, fp) является изоморфизмом в.
Доказательство. Пусть i\Y-*X есть отобра-
отображение вложения и {hs} — такая деформация простран-
пространства X, что hi = if. Поскольку (Ai)* = i'**f* и (fti)# —
изоморфизм, согласно лемме A.2), можно сделать вы-
вывод, что /* — также изоморфизм. Отметим, что /*, во-
1. Ретракции и деформации 95
обще говоря, не является изоморфизмом на, хотя тако-
таковым является (fti)*.
Очевидно, что пространство X деформируемо в под-
подпространство У тогда и только тогда, когда существует
отображение f : X —> У, реализуемое деформацией про-
пространства X. Следовательно, используя теорему A.3),
нетрудно найти примеры ретракции, которая не может
быть получена деформацией. Как мы видели, основа-
основание Е квадрата Q является ретрактом границы Q этого
квадрата. Однако пространство Q нельзя деформиро-
деформировать в Е. Фундаментальная группа n(Q) является бес-
бесконечной циклической, а группа п(Е) тривиальна, так
что никакое отображение n(Q) в п(Е) не может быть
изоморфизмом. Аналогично пространство Q нельзя де-
деформировать в точку. В противоположность соответ-
соответствующему утверждению для ретракций произвольное
пространство X нельзя деформировать в точку.
Теперь уже можно объединить понятия ретракции и
деформации в одно новое. Подпространство У топологи-
топологического пространства X называется деформационным ре-
ретрактом пространства X, если существует ретракция
р : X -* У, реализуемая деформацией пространства X.
Поскольку отображение hu определяемое любой из
формул (I), (II), (III) и (IV), является ретракцией,оно
описывает также' соответствующие деформационные ре-
тракты. Так и сторона квадрата и его угловая точка —
его деформационные ретракты. Внутренняя точка р
диска D является деформационным ретрактом диска D,
а граница этого диска является деформационным ре-
ретрактом дополнения D — р. В следующей теореме, яв-
являющейся прямым следствием теорем A.1) и A.3), ука-
указывается одно весьма важное свойство деформационных
ретрактов.
A.4) Если подпространство У является деформа-
деформационным ретрактом линейно связного топологического
пространства X, то группа п(Х) изоморфна группе я (У).
Отметим, что в этой теореме пространство У автома-
автоматически линейно связно. Более содержательная форму-
формулировка утверждения A.4) такова:
96 Гл. V. Вычисление фундаментальной группы
Если X — линейно связное пространство, ретракция
р : X -* Y реализуема деформацией и i: Y -* X есть ото-
отображение вложения, то для любых точек р£Х, q£Y ин-
индуцированные гомоморфизмы
р*:п(Х, /?)->л(Г, р/7),
/,:я(Г, q) ->n{X,q)
являются изоморфизмами на.
Первое утверждение является прямым следствием
теорем A.1) и A.3). Для доказательства второго рас-
рассмотрим гомоморфизмы л (Л", q)-&->n(Y, q)—+n(X, q).
Мы уже заметили, что р# — изоморфизм на. Более
того, известно, что существует такая деформация {hs}
пространства X, что hi = ip. Согласно A.2), гомоморфизм
(Ai)* = t'*p* является изоморфизмом на, откуда сразу
следует, что f* — также изоморфизм на. Существенное
различие -между двумя приведенными формулировками
теоремы A.4) состоит в том, что в последней не просто
утверждается изоморфность двух групп, но и указывают-
указываются в явном виде соответствующие изоморфизмы.
Понятия ретракции, деформации и деформационного
ретракта можно хорошо иллюстрировать примером квад-
квадрата Q. Так как существует гомеоморфизм квадрата Q
на круговой диск Д переводящий границу Q на гра-
границу диска D, то квадрат, как и диск, может быть де-
деформирован на свою границу. Следовательно, имеем
следующую диаграмму:
Q (квадрат)
\ деформация, но
\ не ретракция
деформационный
ретракт
Q (граница квадрата)
ретракция, / \ ретракция, но
но ^деформация \не деформация
р (угловая точка) деформационный ретракт Е (основание)
Обозначим замкнутый диск, задаваемый в полярных
координатах неравенством 0<г<Л, буквой D, а его
h,(r. 9) = {(Г(
1. Ретракции и деформации 97
центр —р. Открытый диск, определяемый неравенством
0О<1, обозначим через D. Заметим, что D=D—D. Де-
Деформация (IV) пространства D—р на D может быть
продолжена следующим образом. Для любых г, s и 9,
таких, что О О, O^s^l, 0-^9-Оя, положим
-s) + s, 9), 0<г<1,
(г, 9), 1 < г.
Эта продолженная деформация показывает, что допол-
о
нение R2 — D открытого диска на плоскости является
деформационным ретрактом плоскости без точки, т. е.
R2— р. Вращая диск D вокруг какой-дибо оси, лежащей
вне его, получим заполненный тор V, поверхность и внут-
• о
ренность которого обозначим через V и V соответствен-
соответственно. При вращении точка р описывает окружность С, и
тор 1/, очевидно, является деформационным ретрактом
дополнения V—С. Рассмотрим далее топологическое вло-
вложение замкнутого тора V в трехмерное пространство /?3.
Образ окружности С при вложении представляет собой
некоторый узел К. Заузленный тор, являющийся обра-
образом заполненного тора V и содержащий в качестве
остова узел /С, обозначим через W, а его поверхность и
внутренность через W и W соответственно. Можно пока-
показать, что вложение V в /?3 переводит V в W и V в W.
Следовательно, поверхность W является деформацион-
деформационным ретрактом пространства W—K.
Но так как точки поверхности W остаются неподвиж-
неподвижными во время деформации, то можно распространить
эту деформацию на все пространство R3 и сделать вы-
вывод, что пространство Rz—W является деформационным
ретрактом пространства R3—/(. Следовательно, простран-
пространства R3—K и R3—W имеют изоморфные фундаменталь-
фундаментальные группы3). Очевидно, что всякий ручной узел
3) Однако фундаментальные группы пространств R3 — К и
R3 — W могут и не быть изоморфными (тор W может быть «рога-
«рогатым»). См. Alexander J. W.; An example of a simply connected
surface bounding a region wich is not simply connected, Proc. Nat
Acad. Sci USA, 10 A924), 8—10.
7 Зак 317
Гл. V Вычисление фундаментальной группы
является остовом своей открытой тороидальной окрестно-
окрестности. Доказано4) обратное: всякий узел, обладающий то-
тороидальной окрестностью такого рода, ручной.
Следующая теорема, которой мы завершаем этот па-
параграф, возможно, несколько неожиданна. Во всяком
случае, на первый взгляд она может показаться невер-
неверной, доказательство же ее почти тривиально.
A.5) Если пространство X деформируемо в Y и если
существует ретракция р пространства X на У, то У яв-
является деформационным ретрактом X. Более того, ре-
ретракция р может быть реализована деформацией.
Доказательство. Пусть {hs} — деформация про-
пространства X на У. Определим новую деформацию!^} X
на У следующим образом. Для любой точки р£Х по-
положим
*,(/>) Н
Тогда ko(p) =ho(p) ~p. Условие совместной непрерывно-
непрерывности по переменным sup здесь выполнено, так как оба
определения отображения k ± совпадают. Используя
2
первую часть формулы, находим, что k±(p)= hx(p).
1
Поскольку по предположению точка Л± (/?) лежит в У,
используя вторую часть формулы, получаем, k\ (/?) =
1
= phl(p) = hl(p). Ретракция р реализуется деформацией
kSi потому что ki(p) =pho(p) =p(p).
2. Гомотопический тип. Топологические пространства
X и У имеют одинаковый гомотопический тип, если су-
существует конечная последовательность топологических
пространств
X = Хо, Xit ..., Хп = У,
4) См. Moise P., Affine structures in 3-Manifolds, V. The
triangulation theorem and hauptvermutung, Ann. Math., 56 A952),
96-114.
3. Теорема ван Кампена 99
такая, что при каждом /=1, ..., п пространство Х{ либо
топологически эквивалентно пространству Хг-_1, либо есть
деформационный ретракт пространства Хг-_1 или наобо-
наоборот5). Отношение принадлежности к одному и тому же
гомотопическому типу, очевидно, является отношением
эквивалентности. Используя только что доказанную тео-
теорему A.4) и теорему D.7) гл. II, мы видим, что
B.1) Если линейно связные пространства X и Y
имеют одинаковый гомотопический тип, то группа
л(Х) изоморфна группе я (У).
Произвольная точка выпуклого множества С являет-
является его деформационным ретрактом. Отсюда следует, что
всякое выпуклое множество имеет гомотопический тип
точки. Следовательно, набор пространств, фундамен-
фундаментальную группу которых мы уже знаем, можно охарак-
охарактеризовать как совокупность пространств, имеющих
гомотопический тип точки или окружности. Гомотопиче-
Гомотопический тип — одно из важнейших отношений эквивалент-
эквивалентности в алгебраической топологии. Большинство алгеб-
алгебраических инвариантов является инвариантами гомото-
гомотопического типа. Это отношение значительно слабее, чем
отношение топологической эквивалентности. Каждое из
пространств, изображенных на рис. 14—16, имеет тот
же гомотопический тип, что и остальные пространства
на том же рисунке.
3. Теорема ван Кампена. Формулировка этого важ-
важного результата, данная в C.1), на первый взгляд не
является полезной для вычисления фундаментальной
груплы. Однако абстрактный подход имеет значительные
преимущества. Одно из них — структурная простота:
утверждение C.1) отражает только существенную алгеб-
алгебраическую структуру теоремы, и по этой причине оно яс-
яснее и легче доказывается, чем все остальные. Кроме
того, важные следствия C.2), C.4), необходимые для
5) Обычное определение гомотопического типа см. в книге Ху
Сы-цзяна, Теория гомотопий, Изд-во «Мир», М., 1964. Доказатель-
Доказательство того, что наше определение совпадает с обычным в статье:
Fox R. К, On Homotopy Type and Deformation Retracts, Ann.
Math.,M A943), 40—50.
7*
100 Гл. V. Вычисление фундаментальной группы
следующей главы, наиболее прямо и просто вытекают
из абстрактного подхода. Классическая формулировка
теоремы ван Кампена в терминах образующих и соотно-
соотношений выводится отсюда и приведена в C.6).
Пусть X — топологическое пространство, являющееся
объединением X = XiU^2 открытых подмножеств Xi
и Х2, таких, что пространства Хи Х2 и X0=Xt П %2 ли-
линейно связны и непусты. Так как их пересечение Хо не-
непусто, пространство X линейно связно. Выберем базис-
базисную точку р(Х0 и положим G = jt(X, p), Gi=*n(Xh p),
* = 0, 1, 2. Гомоморфизмы, порожденные отображениями
включения, образуют коммутативную диаграмму
e,/
g>o G2 0H = (д$1 = @2Э2.
C.1) теорема ван клмпЕна. Образы toiGi групп Gt-,
t = 0, I, 2, порождают группу G. Более того, если #—-
произвольная группа и \|?г-: G{-+H, 1=0, 1, 2, — гожо-
морфизмы, удовлетворяющие условию гр0=xpi9i = г|?2в2, то
существует единственный гомоморфизм К : G ~> Я, та-
/сой, что г|)г- = Х(Ог, i = 0, 1,2.
Доказательство этой теоремы приведено в Добавле-
Добавлении III. Отметим, что в силу соотношений коммутатив-
коммутативности (Do = (Oi9i = 00262 утверждение о том, что подгруппы
coiGi и 002G2 порождают группу G, полностью эквива-
эквивалентно первому утверждению теоремы C.1) и может его
заменить. В качестве непосредственного следствия по-
получаем:
C.2) Если пространства Х4 и Х2 односвязны, то тако-
таковым является также и пространство X=Xi\$ X2*).
*) Здесь имеется в виду, что пространства Хх и Х2 удовлетво-
удовлетворяют условиям теоремы C.1). — Прим. перев.
3. Теорема ван Кампена
101
Как будет подробно показано на примерах, приведен-
приведенных в конце этой главы, нижеследующая теорема (след-
(следствие из теоремы ван Кампена) решает задачу вычисле-
вычисления фундаментальной группы двух окружностей, соеди-
соединенных в одной точке (см. рис. 22).
C.3) Если группа Go тривиальна, a Gt и G2 — сво-
свободные группы с базисами {ai, 0&2, ...} и {Pi, P2, • • } со-
соответственно, то группа G также является свободной и
{ г, • • •, co2Pi, 02P2, .. } — ее свободный базис.
Доказательство. Пусть Н — свободная группа
со свободным базисом {хи х2, ..., Уи Уг, • • •}, причем
функции г|?1 и г|?2, определенные равенствами
ф1ау = Ху, 7=1, 2, . .,
осуществляют взаимно однозначное соответствие между
множествами {аь аг, ...} и {хи х2, . ..} и между {рь р2,. • •}
и {#ь #2, • • •} соответственно. Так как группы Gi и G2
свободны, эти функции можно продолжить до гомомор-
гомоморфизмов
102 Гл. V. Вычисление фундаментальной группы
Поскольку группа Go тривиальна, существует тривиаль-
тривиальный гомоморфизм \|)O:Go-*#, причем гро=it>i6i = гр2в2.
По теореме ван Кампена существует такой гомоморфизм
Я: G-*#, что \|)г = А,(Ог, J = 0, 1, 2. Следовательно,
Ал^а, == iftay = лгу, у=1, 2, ...,
tobfo = W* = y*. ft=l, 2, ... .
Так как группа Я свободна, существует гомоморфизм
(х : Н —»• G, определенный соотношениями
у = 1, 2, ...,
k=\, 2,
Очевидно, что обе композиции \хХ и А,|л определяют тож-
тождественные отображения. Поэтому гомоморфизмы X я \х
являются взаимно обратными изоморфизмами. Доказа-
Доказательство тем самым завершено.
C.4) Если пространство Х2 односвязно, то гомомор-
гомоморфизм (Oi является отображением на. Более того, если
элементы {аи аг, ...} порождают группу Go, то ядро
гомоморфизма он является оболочкой множества
{ }
Доказательство. Так как группа G2 тривиальна,
образ группы coiGi порождает группу G, ибо группа не
может порождаться собственной подгруппой. Итак,
co1Gi = G. Относительно второго утверждения заметим,
что
l, /=1, 2, ... .
Следовательно, оболочка {0iai, бюсг, ...} содержится
в ядре гомоморфизма щ. Обратно, рассмотрим произ-
произвольный элемент р из ядра гомоморфизма coi и канони-
канонический гомоморфизм ipiiGi—♦//, где Н — факторгруппа
О1/(оболочка множества {0iai, 0ia2, ...}). Композиция
ipiBi, обозначаемая через \|H, конечно, тривиальна. Обо-
Обозначая тривиальный гомоморфизм группы G2 в Н через
•ф2, получаем соотношения коммутативности гр0=грiвi =
=г|J02- Согласно теореме ван Кампена, существует та-
такой гомоморфизм X\G-*H, что \|)i = A(Oi. Следовательно,
3. Теорема ван Кампена 103
откуда и следует, что элемент р является следствием
элементов {Bicci, 9ia2, ...}. Доказательство закончено.
Теперь можно вычислить фундаментальную группу
некоторых интересных топологических пространств. При
этом, однако, должны выполняться условия, наклады-
накладываемые на подпространства Х{ и Х2 теоремой ван Кам-
Кампена, т. е. Х\ и Х2 должны быть открытыми. Обычно
большинство примеров не являются таковыми, так что
необходимо небольшое разъяснение. В самом деле, при
некоторых условиях теорема ван Кампена верна и для
замкнутых подмножеств Хх и Х2 и может быть в таком
виде непосредственно использована в наших примерах6).
Однако без введения довольно обширной терминологии
трудно сжато описать соответствующее обобщение. Что
нужно делать в каждом отдельном случае, станет ясно
по мере изложения.
(I) я-лепестковая роза. Это пространство, обозначае-
обозначаемое С(П), является объединением п топологических окруж-
окружностей Хи ..., Хп, соприкасающихся в некоторой точ-
точке р и нигде более не пересекающихся (см. рис. 22).
Фундаментальная группа пространства С(гг) является
свободной группой ранга п. Полнее, если дсг- — образую-
образующий элемент бесконечной циклической группы я(Хг-) и
(Oi:jt(Xi)—я(С(П)) есть гомоморфизм, порожденный
вложением, то
Доказательство этого проводится индукцией по п. Про-
Пространство C(i) есть окружность, фундаментальная группа
которой, как было показано в гл. II, бесконечная ци-
циклическая, т. е. свободная группа ранга 1. Рассмотрим
пространство
= £(л) U Хп+1, {/?} = С(Л) Л ^л + 1-
Если бы подмножества С(П), Xn+i и {р} являлись бы от-
открытыми в С(П+1), желаемое утверждение непосредственно
6) van К a m p e n E. R., On the connection between fundamen-
fundamental groups of some related spaces, Amer. Journ. Math., 55 A933),
261—267; Olum P, Nonabelian cohomology and van Kampen's
theorem, Ann. Math., 68 A958), 658—668.
104
Гл. V. Вычисление фундаментальной группы
вытекало бы из C.3). Чтобы обойти эту трудность,
рассмотрим открытую окрестность N точки р в C(n+i), со-
состоящую из точки р и объединения 2(п+1) непересе-
непересекающихся открытых дуг, каждая из которых имеет в
качестве одного из своих концов точку р (см. рис. 23).
Рис. 23.
Тогда пространства C(n), Xn+i и {р} являются деформа-
деформационными ретрактами пространств C(rt)l)N» ^d+iUA/'
и {р} U N соответственно. Последние являются открыты-
открытыми подмножествами в С(п+1), и можно применить след-
следствие C.3)'для завершения доказательства. В частности,
при я = 2 получаем ответ на вопрос, поставленный во
введении к этой главе: как вычислить фундаментальную
группу двух окружностей, соединенных в одной точке?
(II) Сфера. Пусть Хо — открытая полоса вдоль эква-
экватора, делящая сферу X на северную и южную полярные
шапки. Пусть Х{ есть объединение северной полярной
шапки и полосы ХОу а Х2— объединение южной поляр-
полярной шапки и Хо. Ясно, что множества Хи Х2 и Хо = Х1(\Х2
линейно связны, непусты и открыты в X = Xi\}X2k. Кроме
того, пространства Х{ и Х2 гомеоморфны выпуклым дис-
дискам и, следовательно, односвязны. Отсюда следует в
силу C.2), что и сфера односвязна.
3. Теорема ван Кампена
105
(III) Сфера с п>1 дырками. Растягивая одну из
дыр к экватору и проектируя затем результат на пло-
плоскость, видим, что сфера с гС&\ дырками, обозначаемая
через 5(П), топологически эквивалентна диску с п — 1
дырками. Если я>1, то такой диск содержит (п—1)-
лепестковую розу в качестве деформационного ретракта
(см. рис. 24). Отсюда делаем вывод, что группа яE(П))
Рис. 24.
является свободной группой ранга п—1. (Тривиальная
группа является свободной группой paiHra 0.)
(IV) Тор. Можно представить тор как объединение
двух таких открытых множеств А\ и Х2, что Х2 является
диском, a Xi содержит 2-лепестковую розу в качестве
деформационного ретракта. Такое разбиение изображено
на рис. 25. Подпространство А\ представляет собой тор
без замкнутого диска D (или тор с дыркой), а Х2 — ка-
какой-либо открытый диск X, содержащий D. Тогда пере-
пересечение X0=Xi П Х2 является открытым кольцом и его
фундаментальная группа является, следовательно, беско-
бесконечной циклической. То, что пространство Х^ имеет го-
гомотопический тип 2-лепестковой розы, можно заметить,
растягивая дыру D так, как указано на рис. 26. Следо-
Следовательно, группа n(Xi) является свободной группой
ранга 2. Образующий элемент группы л(Х0) представ-
представляется путем с, проходящим по кромке областей Xi\\X%.
Рис. 25.
Р ** С. 26,
3. Теорема ван Кампена
107
Из рис. 26 видно, что такой путь эквивалентен в ^ пути,
проходящему сначала вокруг а, потом вокруг 6, потом
вокруг а в обратном направлении и, наконец, вокруг Ь
в обратном направлении. Следовательно,
где скобки означают класс эквивалентных в Xt путей.
Другой хороший способ сделать наглядным это соотно-
соотношение состоит в том, чтобы разрезать тор вдоль путей
а и b и развернуть его на плоскость, как это показано
на рис. 27. Подмножества Х{ и Х2 на нем заштрихованы,
и предыдущее соотношение читается прямо с третьей
фигуры рис. 27. Подводим итог: я^) —свободная груп-
группа и *=[а], у=[Ь] — ее свободные образующие; про-
пространство Х2 односвязно, а группа к(Х0) порождается
элементом, образ которого в группе п(Х{) при гомомор-
гомоморфизме, порожденном вложением, совпадает с хух~1у~1.
Из C.4) следует, что индуцированный вложением
108 Гл. V. Вычисление фундаментальной группы
гомоморфизм coi: n(Xi) —*п(Х) и есть гомоморфизм на,
ядро которого — следствие хух~1у~К Следовательно, фун-
фундаментальная группа тора обладает копредставлением
(х, у :хух~1у-{)у
или, на языке соотношений,
(*, у :ху = ух).
А эта группа является свободной абелевой ранга 2.
Последняя задача этой главы— вывести из тео-
теоремы C.1) формулировку теоремы ван Кампена в тер-
терминах копредставлений. Предполагается, что простран-
пространства X и Xiy /=0, 1, 2, удовлетворяют всем условиям,
которые были наложены на них в абзаце, предшествую-
предшествующем C.1). Обозначения соответствующих фундаменталь-
фундаментальных групп и гомоморфизмов, порождаемых вложения-
вложениями, оставим прежними. Кроме того, заданы копредстав-
ления
01 = |х:г|ф1,
C.5) О2 == | у : s |ф2,
Go = | z : t |ф0.
Нужно найти копредставление группы G; решение сфор-
сформулировано в C.6).
Обозначим через Fu F2 и Fo свободные группы, ко-
которые являются областями определения гомоморфиз-
гомоморфизмов фь фг и ф0 соответственно. Удобно предположить, что
множества х и у не пересекаются и их объединение яв-
является свободным базисом свободной группы F. Так, Ft
и F2 — подгруппы F. Существует единственный гомомор-
гомоморфизм ф : F -* G, такой, что
ф|/7г = СО1ф^ 1=1, 2.
Отметим, что фГ = ф8=1. Поскольку группа Fo свободна,
гомоморфизмы 9i и 9г можно поднять до свободных
групп, т. е. существуют такие гомоморфизмы 9*:Fo-+ F{y
i=l, 2, что диаграмма
Fl Л- Fo ^ F2
1ф1 |ф0 1ф2
^ + +
3. Теорема ван Кампена 109
коммутативна. Пусть z = {zu z2, ...}. Рассмотрим множе-
множество элементов б^Д^-1^/7, А=1, 2, .... Ясно, что
1) = СОоФо (ZkZ~*) = 1.
Следовательно, оболочка множества г U s U {®\гь®я*к1}
содержится в ядре гомоморфизма ф. Утверждаем, что
верно и обратное. Чтобы доказать это, рассмотрим про-
произвольный гомоморфизм ty;F-+Hy переводящий множе-
множество г U s U {®izk®^k1} Ha I- Тогда, очевидно, существуют
такие гомоморфизмы г^ : G* —► Я, t=l, 2, что следующая
диаграмма коммутативна:
A
a/'_
Кроме того, так как фб^ — фбгЗА, ft=l, 2, ..., из про-
проверки диаграмм следует, что
и 1 о
Поскольку элементы фо^ь фо-^2» • • • порождают группу
Go, можно отсюда заключить, что гомоморфизм \|>о, зада-
задаваемый равенствами
определен корректно. По теореме ван Кампена C.1) най-
найдется такой гомоморфизм XiG-^Я, что \|)i = A,(Df,
t = 0, I, 2. Рассмотрим, наконец, произвольные элементы
tii£Fu i=l, 2. Тогда
и, следовательно,
г|) = Адр.
Отсюда следует, что всякий элемент, лежащий в ядре
гомоморфизма ф, лежит также и в ядре гомомор-
гомоморфизма \|>, и наше утверждение доказано. Значит, ядро
110 Гл. V. Вычисление фундаментальной группы
гомоморфизма ф совпадает с оболочкой множества
rusu^z^z-i}.
Итак, мы доказали следующую теорему.
C.6) ДРУГАЯ ФОРМУЛИРОВКА ТЕОРЕМЫ ВАН КАМПЕНА.
Если группы Gu G2 u_ Go имеют копредставления C.5),
то G = \x, у: г, S, {6^ • ва2*1}^
УПРАЖНЕНИЯ
1. Рассмотрим замкнутый круглый диск D с цент-
центром р и границей Д указанный на рис. 17. Мы видели,
что дополнение к открытому диску D—D—D в плоско-
плоскости R2 является деформационным ретрактом плоскости
без точки R2— р. Доказать, что дополнение R2— D не
является деформационным ретрактом плоскости без точ-
точки, но что пространства R2 — D и R2 — р имеют один
и тот же гомотопический тип.
2. Доказать, что если X — деформационный ретракт
пространства У, а У — деформационный ретракт про-
пространства Z, то X — деформационный ретракт простран-
пространства Z.
3. Найти копредставление фундаментальной группы
(а) «бутылки Клейма», (Ь) «сферы с двумя ручками».
4. Доказать, что пространства, изображенные на
рис. 16, имеют одинаковый гомотопический, но разный
топологический тип*).
5. Какова фундаментальная группа дополнения
/?3 — X: (а) если Х = окружность; (Ь) если Аг = объеди-
нение двух незацепленных окружностей; (с) если
Х = объединение двух просто зацепленных окружностей?
(Имеются в виду незаузленные окружности.)
*) Здесь можно воспользоваться сноской на стр. 85.—Прим. перев.
ГЛАВА VI
КОПРЕДСТАВЛЕНИЯ ГРУПП УЗЛОВ
Введение. В этой главе мы возвращаемся к теории
узлов. Основное здесь — это описание и обоснование
процедуры, которая позволяет сопоставить всякому по-
полигональному узлу К в регулярном положении два ко-
представления его группы, называемых соответственно
верхним и нижним копредставлениями. Классическое ко-
представление Виртингера получается при этом как
частный случай верхнего копредставления.
Далее вычисляется полностью верхнее копредставле-
ние групп четырех узлов разных типов и последний па-
параграф содержит доказательство существования нетри-
нетривиальных узлов, где показано, что клеверный лис г не
может быть развязан. Тот факт, что основное построение
проводится для пары копредставлений, объясняется
дальнейшим развитием теории. В этой главе он ника-
никакого значения не имеет. Одного копредставления вполне
достаточно, и поэтому в четвертом параграфе мы огра-
ограничиваемся примерами верхних копредсгавлений. Суще-
Существование пары верхнего и нижнего копредставлений
является основой некоторой теории двойственности, ко-
которая будет применена в гл. IX для доказательства од-
одной из важнейших теорем.
Если К — узел в пространстве/?3 иро — какая-нибудь
точка в /?3— /(, то фундаментальная группа я(/?3—/С, Ро)
называется группой узла /(. Так как пространство
/?3 — К связно, различные выборы базисной точки при-
приводят к изоморфным группам. Поэтому, как правило,
говорят просто о группе n{Rz — K) узла /С, не упоминая
базисную точку. Тем не менее точное значение фразы
«группа узла» — это «группа я(/?3— К, Ро) при некото-
некотором выборе базисной точки р0». Ниже будет ясно, что
112 Гл. VI. Копредставления групп узлов
конкретные верхнее и нижнее копредставления, построен-
построенные для данного узла в регулярном положении, зависят
не только от самого узла, но также и от некоторого про-
произвола в выборе. Поэтому фраза «верхнее и нижнее ко-
копредставления узла К» служит примером даже большей
степени неточности языка, чем фраза «фундаменталь-
«фундаментальная группа пространства X». Узел в регулярном положе-
положении имеет много пар верхних и нижних копредставле-
ний. Все они, как будет видно, принадлежат к одному
и тому же типу.
1. Верхнее и нижнее копредставления. Пусть К —
полигональный узел в регулярном положении и <&* —
проекция: &(х, у, z) = (x, у, 0) (см. гл. I, § 3). Для
некоторого целого п выберем на К множество Q, состоя-
состоящее ровно из 2п точек, ни одна из которых не является
ни переходящей, ни проходящей. Эти точки делят узел К
на два класса замкнутых связных дуг, переходов и про-
проходов, которые чередуются вдоль узла, т. е. каждая
точка множества Q принадлежит ровно одному переходу
и одному проходу. Это подразделение надо выбирать
так, чтобы ни один переход не содержал проходящих
точек и никакой проход не содержал переходящих то-
точек. Такое построение может быть осуществлено мно-
многими способами, хотя, как правило, мы будем стараться
выбрать наименьшее . п. Обозначим переходы через
Аи ..., Ап, их объединение Ах\] ... \]Ап через Л, про-
проходы—через Ви..., Вп и их объединение Вх\] ... U Вп
через В. Порядок произвольный. Довольно очевидно,
что существует такой кусочно-линейный гомеомор-
гомеоморфизм1) пространства /?3 на себя, сдвигающий точки
вертикально, т. е. параллельно оси г, что образ множе-
множества А — Q лежит выше плоскости ху пространства R2,
а образ множества B — Q — ниже R2. Так как сам
узел К и его образ при этом гомеоморфизме суть экви-
эквивалентные полигональные узлы, то можно сделать упро-
1) Отображение /?3->/?3 называется кусочно-линейным, если
его ограничение на любом прямолинейном отрезке является линей-
линейным везде, кроме конечного числа точек. Следовательно, при этом
многоугольник переходит в многоугольник.
1. Верхнее и нижнее копредставления 113
щающее предположение, что узел К с самого начала
лежит в таком же положении, как его образ. Отсюда
следует, что QczR2.
Всякое копредставление строится относительно неко-
некоторой ориентации узла К в пространстве /?3. Поэтому
одно из двух направлений выбирается за положитель-
положительное, например ставим стрелку на К- В R3 будет постоян-
постоянно выбрана ориентация левозакрученного винта. Выбе-
Выберем также две базисные точки. Одна, р0, лежит выше
узла, а другая, р'о, — ниже. В дальнейшем условимся
считать, что РО = (О, О, г0), а р'0 = @, О, — г0), где
г0 — некоторое положительное число. (Тогда (л:, у, г) 6 К
влечет —го<-г<го.) Следовательно, поворот на 180° во-
вокруг оси х переводит одну базисную точку в другую.
Наконец, выберем еще точку qo€R2—еРК
Назовем путь а в плоскости R2 простым, если он удо-
удовлетворяет следующим трем условиям. Путь а полиго-
полигонален, его начальная и конечная точки не принадлежат
<&*К, и он пересекает проекцию узла ff* К только в конеч-
конечном числе точек, из которых ни одна не является вер-
вершиной самого пути а или проекции #* /С Пусть F(x) —
произвольная свободная группа, свободно порождаемая
множеством \=(хи ..., хп). Каждому простому пути а
в R2— S^B сопоставим элемент а# группы F(\)y опреде-
определяемый следующим образом:
а =х^ ... Хц
где переходы, проекции которых на R2 пересекаются с пу-
путем а, это Ai[f .. ., Aiv a еь=1 или —1, согласно тому,
как путь а проходит под отрезком Л/л, слева направо
или справа налево (или, другими словами, согласно
тому, какую пару образуют &*Aik и а — левую или
правую). Отображение а-+а#, иллюстрируемое рис. 28,
очевидно, сохраняет умножение, т. е.
f#j • ^2/ ~=== ^1 ^2 '
Это отображение не является, однако, отображением на
f(x). Для любой точки p£R2 путь р идет сначала прямо-
прямолинейно из точки ро параллельно плоскости R2 в точку,
8 Зек. 317
114
Гл. VI. Копредетавления групп узлов
лежащую точно над /?, а затем опускается верти-
вертикально в точку р. Для всякого пути а в плоскости R2
положим
*а=аф)-а'п(\\а\\)-1.
Группа F(\) должна быть группой верхнего копредстав-
ления. Гомоморфизм ф : ^(х) —► я(/?3 — К, ро) опреде-
определяется следующим образом. Пусть а^ — такой простой
о
1
1
1
1
1
1
1
1
!
"',
А2
--—J
/
4
/
/
л3
путь, в R2 —
что
п — X^X^XzX^ X
Рис. 28.
я. Положим
где квадратные скобки обозначают класс эквивалентных
путей в R3 — К, содержащий /?0-базисную петлю *а;-. Оче-
Очевидно, что cpXj не зависит от выбора пути aj. Гомомор-
Гомоморфизм ф есть единственное расширение на всю группу
F(x) заданного выше на образующих хи ..., хп отобра-
отображения. Из сказанного следует, что
для любого пути в R2—S^B. Мы утверждаем, что гомо-
гомоморфизм ф является гомоморфизмом на, или, другими
словами, что элементы цхи .. ., срхп порождают группу
я(/?3 — К, Ро). Доказательство этого будет дано в сле-
следующем параграфе. Отметим только, что он весьма
естествен. Как подсказывает рис. 29, геометрически поч-
1. Верхнее и нижнее копредставления
115
ти очевидно, что всякая /?0-базисная петля в /?3 — К эк-
эквивалентна произведению путей *dj, /=1, ..., п, и об-
обратных им. Во всяком случае не видно, почему бы это
могло быть не так.
Рис. 29.
Образующие для нижнего копредставления выби-
выбираются аналогичным образом. Пусть F(y)—свободная
группа, свободно порождаемая множеством у = {уи..., уп) -
Сопоставим каждому простому пути Ъ в R2 — S^A эле-
элемент Ьь группы F(y), определяемый равенством
где проекции проходов, пересекаемые путем й, по по-
порядку таковы: ^Bj{t ..., ^Bjm> a 6ft=l или —1, со-
согласно тому, проходит ли b над Bjk слева направо или
справа налево (т. е. согласно тому, какую пару обра-
образуют Bjk и Ъ — левую или правую). Сопоставление
Ь->ЬЬ иллюстрируется рис. 30.
Гомоморфизм ф': F (У) -> я (R3 — /С, р'о) определяет-
определяется тем же самым образом. Пусть $ -—отражение:
<$(*,(/,£) = (*, у, — г), и а —некоторый путь в R2.
116
Гл. VI. КопреДсГавлеййя групп узлов
Положим *а=с$*а. Пусть Ьг — такой простой путь в
R2 — S» Л, что bf = yl$ i=\, ..., я. Тогда
ф'Ы=[*Ы 1=1, .
Л,
где квадратные скобки обозначают класс эквивалентно-
эквивалентности из л(/?3—К> р'о). Мы снова утверждаем, что рас-
распространение на всю группу этого отображения обра-
образующих является гомоморфизмом на.
в3
--г
в,
л
\
\
\
\
\ '
А
Рис. 30.
Образы проходов $*Ви ^=1, ..., ^, являются непе-
непересекающимися ломаными. Поэтому можно выбрать в
плоскости R2 такие односвязные открытые множества
Vu..., Vn, что ePBidVu '=1, ..., л, и их границы яв-
являются непересекающимися образами простых петель
Vu .. •, ^п, обегающих области Vu • • •» Уп соответствен-
соответственно против часовой стрелки (если смотреть сверху). Ана-
Аналогично выберем в R2 односвязные непересекающиеся от-
открытые множества £/1э ..., Un, такие, что ePAjCiUj,
/*=1, ..., я, и их границы являются непересекающимися
образами простых петель ии ..., ип, обегающих области
Uи • • •» Un соответственно по часовой стрелке (если
смотреть сверху). Потребуем также, чтобы первона-
первоначально выбранная точка ^о лежала вне замыканий об-
областей Vu Uj> ^ /=1. •••> л. Далее, выберем множество
простых путей cit ..., сп так, чтобы каждый путь сг имел
1. Верхнее и нижнее копредставления 117
начальную точку <7о, а конечную Vi@) и^(£) б/?2-— [J Vk
всегда, за исключением значения tf=lkdl. (Vk обозна-
обозначает замыкание области Vk-) Аналогично, выберем мно-
множество простых путей diy ..., dn так, чтобы ^@) =^0,
п
dj(||dj \\) = Uj@) и dj(t)£ R2 — (J £/*, за исключением
значения < = ||rfy||. Все эти пути могут быть выбраны
B) ^.
'E)
Рис. 31.
неоднозначно. Примеры, иллюстрирующие выбор таких
областей и путей, указаны на рис. 32, 33 и 34.
Теперь мы можем описать два копредставления.
Верхнее копредставление группы я(/?3 — /С, ро) таково:
A.1) (#ь *.., хп : г и ..., >*п)ф,
где r/ = (ct • vt • cjiy&> /= 1, ..., п. Соответствующее
нижнее копредставление группы я (/?3 — /С, /?q) таково:
(Ь2) (f/!, ..., ул:$!, ..., 5л)ф,
где Sj — (dj- tij • djl)b, y = l, ..., п. Справедливость
уравнений фг**=1 и q/sj=l, t, /=1, ..., /г, геометрически
очевидна. Имеем
118
Гл. VI. Копредставления групп узлов
=l, ..., п.
Стягивание петли * (с. • vt • cfl) передвиганием ее под
дугой Вг изображено на рис. 31. Аналогичный рисунок
можно, конечно, нарисовать и для нижнего копредстав-
копредставления. Кстати, мы вовсе не утверждаем очевидность того,
Рис. 32.
что соотношения ги ..., гп и su ..., sn образуют мно-
множество определяющих соотношений.
Описание нижнего и верхнего копредставления поч-
почти так же сложно, как и последующие доказательства.
Советуем читателю провести до конца предыдущие по-
построения на нескольких примерах. Довольно сложные
примеры вычислений даются ниже на рис. 32 и 33. Пе-
1. Верхнее и нижнее копредставления
119
реходы на них указаны жирными линиями, а проходы —
тонкими. Пути Си dj, v% и Uj даны пунктирными ли-
линиями. Удобно также обозначать образующие х\ и yi
маленькими стрелками. Дополнительные примеры верх-
верхних копредставлений приводятся в четвертом параграфе.
'ZZZZZZZZZZZZZZZZZZZZZZZ,
»>ж
, Ут" Уз ' У? У, ')У'г h = Ул У! Уь У/"' Уз'У?
*УгУ,Уг Уз Уз Уз
h ~У*УзУ4 У
Рис. 33.
Осталось доказать, что верхнее и нижнее копредстав-
копредставления являются, как мы и утверждали, копредставле-
ниями групп я(R3 — /(, ро) и яG?3 — К, pf0) соответ-
соответственно. Доказательство дано в следующем параграфе.
Важным следствием этого результата является теорема:
A.3) Во всяком верхнем копредставлении A.1) (ниж-
(нижнем копредставлении A.2)) любое из соотношений гь ...
•». * rn [s\> . •., sn] является следствием п—\ остальных,
120 Гл. VI. Копредставления групп узлов
Следовательно, в любом из таких копредставлений
одно из соотношений может быть опущено. Этот факт
очень помогает при вычислениях и имеет важные тео-
теоретические приложения.
2. Верхнее и нижнее копредставления. Продолжение.
В этом параграфе мы докажем, что верхнее и нижнее
копредставления, заданные формулами A.1) и A.2),
на самом деле являются копредставлениями групп
лG?3— /С, р0) и л(/?3 — /С, /?q) соответственно и полу-
получим в процессе доказательства теорему A.3). Заметим
прежде всего, что нет необходимости давать отдельные
доказательства для обоих копредставлений. Нижнее ко-
копредставление может быть описано в терминах верхнего,
если изменить ориентацию узла К и поменять ролями
верх и низ. Точнее, пусть h : R3 -> /?3 есть поворот на
180° вокруг оси *, определяемый равенством h(x, у', z) =
= (*. —У* ~z)' Положим K' = hK. Гомеоморфизм h ин-
индуцирует изоморфизм А# : л(ф — К', P0)->n(R* — K, p'0\
В качестве положительного направления вдоль узла К!
возьмем обратное тому, которое индуцируется гомеомор-
гомеоморфизмом h и тем направлением вдоль /(, которое было
использовано при построении копредставления A.1),
т. е. перевернем узел К и обратим стрелку на нем. Пусть
(У\> •••> Уп'-Sv •••> sn)t
некоторое верхнее копредставление группы 7i(R3—K',Po),
построенное таким же способом, что и A.1). Предпо-
Предположим, что /-й переход узла К' есть /iBj, что i'-е соотно-
соотношение получено в результате обхода вокруг области
oPhAi и что точка hq0 является общей базисной точкой
в R2 для путей, определяющих соотношения. Тогда ко-
копредставление
очевидно, совпадает с копредставлением A.2). Рассмо-
Рассмотрим один пример и убедимся, что это очевидно. На
рис. 34 показано верхнее копредставление узла, получен-
полученного вращением на 180° узла, изображенного на рис. 32
ц 33, и изменением его ориентации. В силу этих заме-
2. Верхнее и нижнее копредставления. Продолжение 121
чаний ограничимся в оставшейся части этого параграфа
только верхними копредставлениями.
Рассмотрим такой замкнутый квадрат S (граница
вместе с внутренней частью), параллельный плоскости
Рис. 34.
и лежащий ниже узла /С, что
B.1) [j
Для произвольного подмножества L узла /С через L*
обозначим объединение узла /(, квадрата S и всех точек
(х9 у, г), лежащих между S и L, т. е. удовлетворяющих
неравенству г!<г<г2, где (х, у, zt) £S, (x, у, z2)£L.
122
Гл. VI. Копредставления групп узлой
Например, множество Q* является объединением квад-
квадрата S, узла К и 2п вертикальных отрезков, соединяю-
соединяющих S и Q (Q —множество точек первоначального раз-
разбиения узла на проходы и переходы). Множество /С*для
клеверного листа изображено на рис. 35.
Доказательство будет состоять в последовательном
применении теоремы ван Кампена. Сначала будет по-
показано, что пространство R3— К* односвязно. Далее мы
присоединим множество К* —В.. к множеству R3 — К%
и докажем, что группа я(/?3 — В*, /?0) свободна и имеет
Рис. 35.
ранг п. Окончательное применение теоремы ван Кампена
после добавления множества В* —К дает верхнее ко-
представление.
B.2) Пространство R3 — К* односвязно.
Доказательство. Геометрически этот результат
очевиден (см. рис. 35), тем не менее следует дать фор-
формальное доказательство, использующее теорему ван
Кампена. Пусть X — множество всех точек пространства
R3 — /(*, которые не лежат ниже квадрата 5. Таким об-
образом, если S'— множество всех таких точек (х, t/, г'),
что (*, г/, z) £S и г'<г, то
-Y=(/?3 —/С*) -S'.
Легко доказать интуитивно ясное утверждение, что про-
пространство X односвязно. Действительно, базисная точка
pQ— @, 0, г0) является деформационным ретрактом про-
пространства X. Это вытекает из рассмотрения следующих
2. Верхнее и нижнее копредставления. Продолжение 123
двух деформаций:
hs(x, у, z) = (x, у, A—s)z-+-sz0), i
ks(x, у, zo) = ((l — s)x, A — s)уf z0), i
Первая из них, {hs}, деформирует по вертикали простран-
пространство X на горизонтальную плоскость, содержащую точ-
точку ро, а вторая стягивает эту плоскость на точку р0
(используйте упражнение 2 гл. V для обоснования ис-
использования композиции этих деформаций). Далее,
пусть У — односвязное пространство, состоящее из всех
-Я2
7| I | I | I I |~ | | | | | | | | | I I I I I I I I I I I |ч
Рис. 36.
точек, лежащих ниже горизонтальной плоскости, содер-
содержащей квадрат S. Ясно, что
Множества X, К, и X П Y не пусты, открыты и линейно
связны в пространстве X U Y. Из теоремы ван Кампена,
а точнее из ее следствия C.2) гл. V, следует, что про-
пространство X\jY односвязно, и утверждение B.2) дока-
доказано.
Множество К* — В., является объединением п не-
непересекающихся открытых топологических дисков Fu ...
..., Fn% которые мы упорядочим так, что диск Fj со-
состоит из всех точек, лежащих между ломаной Aj — Q
и квадратом S, за исключением тех точек, которые ле-
лежат на проходах или ниже их (см. рис. 36).
Пусть flj для любого /, /=1, ..., я, обозначает про-
простой путь в /?2 — <^В, однократно проходящий под пере-
переходом Aj слева направо. Путь *#j пересекает диск Fj
в одной точке; остальная его часть лежит в R3 — /С*.
Пусть Wj—некоторая открытая окрестность объединения
124 Гл. VI. Копредставления групп узлов
диска Fj и точечного образа пути *О/, выбранная
так, что:
(I) пространство Wj линейно связно, и группа
n(Wj» Po) является бесконечной циклической, порождае-
порождаемой классом эквивалентности петли *<Zj в Wj\
(II) 1Р,ПК* = РЛ
(III) пространство Wj— К* односвязно.
То, что подобные множества можно построить, гео-
геометрически очевидно. Всякую окрестность Wj можно счи-
считать объединением множества Fj и образа пути *а2
слегка расширенных до открытых в R3 множеств. Точ-
Точнее, пусть е>0 настолько мало, что открытая е-окрест-
ность Wj образа пути *CLj удовлетворяет условию
W'j П /С* cz Fj\ и пусть W) является множеством то-
точек, расстояние которых до множества Fj меньше чем е,
расположенных ближе к Fj, чем к К% — Fj. Доказать,
что окрестность Wj—W'j[)Wj удовлетворяет усло-
условиям (I), (II), (III), довольно сложно, но, вообще го-
говоря, возможно.
B.3) Пространство R3 — В* линейно связно, а группа
n(R3 — В*, ро) является свободной группой. Более того,
множество классов эквивалентности хи ..., хп, содержа-
содержащих петли *аь ..., *ап, образует ее свободный базис.
Доказательство. Положим
Так как W}[\K* = /> то
- KJ U Wj = /? - (/С, - Wj) = #» - (К.
и поэтому
(\j), j=\ п.
j
\ft-l
В частности,
Хп = {R* - К,) U (АГФ - В,) = /?з _ В.,
2. Верхнее и нижнее копредставления. Продолжение 125
так что рассматриваемая последовательность пространств
оканчивается пространством R3— В*. Более того, по-
поскольку
то
Следовательно, согласно (III), пространство Xj-iftWj
односвязно.
В лемме B.2) утверждается, что пространство Хо
односвязно; примем в качестве индуктивного предполо-
предположения следующее: пространство Х^{ линейно связно,
группа k(Xj_!, ро) свободна и классы эквивалентности
путей *аь ..., *CLj-i в Xj-{ образуют ее свободный ба-
базис. Так как множества Xj^u Wj и Xj-i П Wj линейно
связны, не пусты и открыты в Xj = Xj_l{} Wj, то вслед-
вследствие условия (I) из утверждения C.3) гл. V вытекает,
что множество классов эквивалентности путей *аь ...
..., *«j образует свободный базис группы n(Xh p0).
Доказательство леммы C.3) получается теперь по
индукции.
Элементы хи ..., хп, введенные в предыдущей лемме,
должны быть далее образующими верхнего копредстав-
копредставления. Другими словами, группа я(/?3 — В*, р0) выбрана
свободной группой этого копредставления. Отметим, что
элементы cpXj, /= 1, ..., п, где
B.4) Ф : я (Я3 - В*, ро) -* я (Я3 - К, Ро)
есть гомоморфизм, порожденный вложением, представ-
представляют собой классы эквивалентности петель *clj в про-
пространстве R3 — К. Следовательно, с точностью до изо-
изоморфизма гомоморфизм ф совпадает с гомоморфизмом,
обозначенным той же буквой в § 1. Для любого про-
простого пути а в R3 — еРВ элемент а% будет теперь пони-
пониматься как элемент группы я(/?3 — В*, pQ). В самом
деле, элемент а% как раз и является классом эквива-
эквивалентности петли *а в пространстве R3 — В*. Завершает
доказательство утверждение, что ф — гомоморфизм на
и его ядро является оболочкой любых п — 1 соотноше-
соотношений из гь ..., гпу введенных в A.1). Отметим, что это
последнее утверждение содержит также теорему A.3).
126 Гл. VI. Копредставления групп узлов
Доказательство получим из тех же соображений,
что были использованы для определения группы
я(/?3 — В*, ро). Присоединяя к пространству, фундамен-
фундаментальная группа которого известна, соответствующую от-
открытую окрестность добавляемого множества (здесь
В*— К), можно описать структуру неизвестной группы,
применяя теорему ван Кампена. Рассмотрим с этой
целью прямоугольную коробку Г, такую, что квадрат S
лежит внутри нее, а узел К — вне. Коробка Т топологи-
топологически является сферой, но нам удобно предположить,
что она тонкая и узкая и что две ее. грани параллельны
квадрату S.
Пусть W — открытая окрестность множества В* — /С,
выбранная так, что:
(IV) окрестность W односвязна и содержит точку р0,
(V) W(]K = 0,
(VI) пространство Т — В* является деформационным
ретрактом пространства W—B*.
Такая окрестность может быть построена многими
способами. Например, соединим коробку Т с точкой Ро
некоторой ломаной £, не пересекающейся с /С*. Пусть
W — объединение е-окрестности множества Т{] Е и
точек внутри Т. Пусть W" — множество точек, распо-
расположенных ближе к В* — /(, чем к /(, расстояние которых
от множества В* меньше чем е. При достаточно ма-
малом е объединение W U W" может быть принято за
множество W.
Следующая теорема — гвоздь этого параграфа.
B.5) Группа узла К имеет верхнее копредставление
я(/?3 — К, Po) = \xlf ..., xn:rl9 ..., rk9 ..., rn\r
где символ rh означает отбрасывание k-го соотношения
r/i, а ф — гомоморфизм B.4).
Доказательство. Применим теорему ван Кам-
Кампена к фундаментальным группам пространств/?3—В*, W
и (R3 — В*) П W. Заметим сначала, что
В,— W = (K\)(B>.-K))- W =
,- К)- W) = K.
2. Верхнее и нижнее копредставления. Продолжение 127
Следовательно,
т. е. объединение этих пространств и есть пространство,
фундаментальную группу которого мы ищем. Кроме
того, пространства (R3 — В..) П W= W — В* и Г —В
имеют одинаковый гомотопический тип. Пространство
Т — В* представляет собой коробку с п прорезями на
крышке; т. е. имеет гомотопический тип сферы с п ды-
дырами и, следовательно, его фундаментальная группа яв-
является свободной, ранга п— 1 (см. пример (III) гл. V,
§ 3). Более полно, пусть h — вертикальная проекция пло-
плоскости R2 на плоскость, содержащую крышку коробки Г.
Из B.1) следует, что
*
:7\
Так как замыкания Fi, ..., Vn областей Vit ..., Vn по-
попарно не пересекаются, можно выбрать множество мно-
п
гоугольных путей еи .. •, еп в Т—\J hVt с общим на*
чалом hqo, удовлетворяющих следующим условиям. Во-
первых, каждый путь в\ является дугой (т. е. гомеомор-
гомеоморфизмом) и его конечная точка совпадает с h(Vi@))
(т. е. образом при проекции h базисной точки петли,
ограничивающей область Vi). Во-вгорых, образы путей
еи ..., еП1 за исключением точки hq^ попарно не пере-
пересекаются и содержатся, за исключением концов, в
п
Т— U AF,(cm. рис. 37).
Пусть
w. = et • hvt • er\ /==1, ..., /г.
Ясно, что это объединение образов путей wu ..., wn
имеет гомотопический тип n-лепестковой розы (см. при-
пример (III) гл. V). Более того, объединение образов лю-
любых п — 1 путей из wu ..., wn является деформацион-
деформационным ретрактом множества Т — В*. Хотя строгое доказа-
доказательство не тривиально, геометрическая его идея проста.
128
Гл. VI. Копредставления групп узлов
Сначала расширим все прорези и растянем их до кри-
кривых hvi. Затем выберем одну из полученных дыр и, рас-
растягивая ее, стянем оставшуюся часть коробки на осталь-
остальные п—\ петель до4. В любом случае отсюда можно
сделать вывод, что группа я (Г —В.», hq0) свободна и
любые п—1 петель wu ..., wn образуют ее свободный
базис. Следовательно, то же верно и для группы
n(W — В*, hq0), и наконец, множество классов эквива-
эквивалентности любых п—\ путей из а-тг-агх, i=l, .,., я,
Рис. 37.
является свободным базисом группы n(W—B*, ро)у где
а — путь в пространстве W — В#, от точки р0 к точке hq0.
Тот факт, что ф есть гомоморфизм на и что его ядро
является оболочкой любых п—1 классов эквивалентно-
эквивалентности петель a»Wi»a~l, i=\, ..., я, теперь прямо вытекает
из следствия C.4) гл. V теоремы ван Кампена. Итак,
мы получаем
i = h .... ft, ..., n\r
Заметим, наконец, что для каждого i=l, ..., п эле-
элемент [а • Wi • а] сопряжен с элементом x;f и, значит, с
элементом гг. Для доказательства рассмотрим путь Ьг
(аналогичный и эквивалентный пути у*@)), который
сначала идет по горизонтальной прямой из точки р0 в
точку, лежащую точно над i>*@), а затем прямо опу-
опускается до точки hVi@). Очевидно (см. рис. 38), что в
2. Верхнее и нижнее копредставления. Продолжение 129
пространстве R3 — В% имеет место эквивалентность
*vi~bi • hvt • bj1, / = 1, ..., п.
Следовательно,
а • wr а'1 = (а • et) • hvt • (а • е^ с^
с^(а • et • б,) • 6, • hvt • 6Г1 • (а • ^ • b^-f.. \ . /Г1,
где /. = (а • ^. • 6Г1). В результате имеем
Поскольку элемент ^f сопряжен в свою очередь элемен-
элементу гг, ядро гомоморфизма ф является оболочкой элемен-
Р и с. 38.
тов ги ..., rft> ..., rn, и доказательство теоремы B.5)
закончено.
Похоже, что читатель, проработавший этот пара-
параграф, останется неудовлетворенным. Прежде всего,
доказательство является длинным и сложным. Возмож-
Возможно, еще более неприятно ощущение, что, несмотря на
9 Зак. 317
130 Гл. VI. Копредставления групп узлов
свою длину, доказательство все еще неполно. В трех ме-
местах существование довольно сложных геометрических
объектов, важных для рассуждений, предлагается без
доказательства. Возможно, было бы проще для кратко-
краткости и элегантности предположить необходимое утвержде-
утверждение и исходить из него? Наиболее честный ответ на это
состоит в том, что существуют разные степени очевидно-
очевидности. В первом параграфе этой главы оставлены откры-
открытыми два существенных вопроса: откуда мы знаем, что
элементы флсь ..., флсп порождают группу узла? И бо-
более трудный вопрос: почему любые п— 1 из элементов
гь ..., гп образуют множество определяющих соотно-
соотношений? И наоборот, утверждения, детали доказательств
которых мы опустили, являются утверждениями другого
рода. Здесь может интересовать только то, как лучше
доказать их, но не их справедливость. И все же целью
данного абзаца не является самооправдание, скорее на-
наша задача — обратить внимание на тот факт, что, хотя
опущенные детали довольно сложны, они, в сущности, не
глубоки. Это происходит из-за того, что мы пользуемся
исключительно конечными полигональными конструк-
конструкциями. Все можно разрезать на конечное число треуголь-
треугольников и тетраэдров и последовательно изучить их. Воз-
Возникает желание попытаться исключить эти ограничения
линейности хотя бы по той причине, что неестественно
рисовать узлы в виде ломаных. До некоторой степени
это возможно. Однако существование диких узлов, груп-
группы которых не обязательно конечно порождены, показы-
показывает, что здесь мы имеем дело с причинами, более глу-
глубокими, чем просто соображения удобства.
3. Копредставление Виртингера. Существенная черта
любой пары соответствующих друг другу верхнего и
нижнего копредставлений— их общая базисная точка,
обозначенная в первом параграфе через qo и 2п простых
путей в /?2, образы которых при отображениях * и b со-
составляют множества соотношений этих двух копредстав-
копредставлений. Необходимость такой общей точки станет ясной
лишь при изучении в гл. IX точной двойственности верх-
верхнего и нижнего копредставлений. Отметим, однако, что,
каковы бы ни были причины, они никак не связаны с
3. Копредставление Виртингера 131
типом копредставления. Копредставление
C.1) (xv .... xn:vf, ...,
группы n(R3 — К, Ро) получается из верхнего копредстав-
копредставления A.1) n-кратным применением операций Титце
типа I -и Г*). (Напомним, что vt — это петля в R2 — оРВ
вокруг проекции прохода S^Bi.) Главное преимущество
копредставления C.1) перед копредставлением A.1) со-
состоит в том, что его можно вычислить с гораздо мень-
меньшим трудом: нет больше необходимости находить эле-
элементы cf, ..., с#. Поэтому мы использовали исключи-
исключительно эту модифицированную форму верхнего копред-
копредставления в примерах, рассмотренных в следующем па-
параграфе. Конечно, и для копредставления C.1) по-преж-
по-прежнему верно, что любой из элементов vf, ..., v# яв-
является следствием п — 1 остальных и, следовательно, мо-
может быть опущен.
Копредставление C.1) группы узла называется ко-
копредставлением Виртингера, если всякий проход содер-
содержит только одно пересечение и каждый путь vt пересе-
пересекается с проекциями переходов ровно в четырех точках.
Эти два условия всегда можно выполнить, за исключе-
исключением того случая, когда узел не имеет проходов. О том,
что это естественные ограничения, свидетельствует тот
факт, что исторически это копредставление группы узла
было одним из первых изученных, и оно, несомненно, на-
наиболее часто встречается в литературе. Копредставления
клеверного листа и восьмерки, изучаемые в следующем
параграфе, являются примерами его использования. При-
Привлекательность копредставлений Виртингера состоит в
том, что соотношения в этом случае особенно просты;
каждое из них имеет вид (если его записать в виде ус-
условия на образующие): xk = x*xjcjz% e = ± 1 (см.
рис. 39).
*) Точнее, прибавим к соотношениям г\, ... * гп элемент vf —
следствие элемента г\ (операция типа I), а затем из множества
Tj, ..., rn, vf удалим следствие элемента vf, элемент Г\ (опе-
(операция I). Аналогично заменяются элементы г2, 4.., тп.— Прим.
перев.
9*
132 Гл. VI. Копредставления групп узлов
Отметим, однако, что, за исключением тех случаев,
когда проекция узла альтернирующая (т. е. при движе-
движении вдоль узла переходящие и проходящие точки чере-
чередуются), копредставление Виртингера не является наи-
наиболее экономичным относительно числа получающихся
образующих и соотношений.
Р и с. 39.
4. Примеры непредставлений. Ниже мы построим
верхние копредставления для нескольких узлов. Восполь-
Воспользуемся, как уже отмечалось в предыдущем параграфе,
копредставлением типа C.1) вместо A.1), так как оно
проще, и, кроме того, тем фактом, что одно произволь-
произвольное соотношение может быть опущено. Получающиеся
копредставления часто бывают довольно сложными и
могут быть упрощены использованием операций Титце.
Некоторые такие редукции проиллюстрированы на сле-
следующих примерах.
D.1) Тривиальный узел (рис.40).
Единственный его переход нарисован жирной линией,
проход — двойной тонкой, а путь — пунктирной. Копред-
Копредставление получается таким:
Следовательно, группа тривиального узла является бес-
бесконечной циклической.
4. Примеры копредставлений 133
D.2) Узел клеверный лист (рис. 41).
Здесь опять переходы показаны жирными линиями, а
петли Vi, v2y v3—пунктирными линиями вокруг проходов.
Выберем образующие х, у, z так, чтобы
x = a?t у = а§> z = a$.
Ясно, что
vf =z~lxyx~l.
Следовательно, для группы я(/?3 — К) клеверного листа
получаем копредставление
(х, yt z : x
в котором соотношение vf опущено.
Включим, однако, в это копредставление все три со-
соотношения, полученные при просмотре проходов. Запи-
Записывая их менее формально, получаем
y у, г:х=угу-\ у = гхг-\ z=xyx~l\.
Подстановка z=xyx~l в два другие соотношения дает
{R3 K)\ ly-\ у=хуху1х-\\.
134
Гл. VI. Копредставления групп узлов
Рис. 41.
Р и с. 42.
Умножая справа второе из этих соотношений на
хух~1у-\ получаем первое. Это эмпирическое обоснова-
обоснование того, что любое из соотношений верхнего копредстав-
копредставления, получаемое при просмотре прохода, является след-
следствием остальных. Итак, получили следующее известное
копредставление группы n(R3 — К) клеверного листа;
(#, у:хух=уху).
4. Примеры копредставлений
135
D.3) Узел восьмерка (рис. 42).
На рис. 42 представлена проекция восьмерки, отлич-
отличная от той, что была на рис. 4 и 7 гл. I. Нетрудно по-
показать с помощью куска веревки или карандаша и бу-
бумаги, что тип узла, представленного ниже, тот же, что
и у восьмерки.
X
*4
X
1
3
1
Ч
Рис. 43.
Соответствующее ^представление Виртингера та-
таково:
(ху уу г, w :x=zrxwzy y = wxw~\ z=x~lyx).
Подставляя z=x~lyx в остальные два соотношения, по-
получаем
n(R3 — /С) = |#, у, w :x~
y y=wxw~l\.
Первое уравнение дает нам w=x'lyxylx. Подстав-
Подставляя это во второе соотношение, находим
n{R3 — K) = \xy y:y=
Наконец, получаем
л(/?3 — /С) = |*, у : yx
136 Гл. VI. Копредставленйя групп узлов
D.4) «Турецкая чалма» (рис. 43).
я(/?3 — К) = |xv х2, х3, xA:xi =
~ (ХЦ-3Х7+2Х7+з) (Xi+2Xi +1**42) (Xi + 3
/==1, ..., £ ..., 4| =
Напомним, что элемент [а, &] есть коммутатор [а, 6] =
= aba-lb~l. Заметим, что [a, b]~l = [by a].
5. Существование нетривиальных типов узлов. Те-
Теперь мы можем показать, что существуют разные гипы
узлов. Мы докажем, что узел клеверный лист нельзя
развязать, т. е. что его тип отличен от типа тривиаль-
тривиального узла. Напомним, что если узлы К и К! имеют один
и тот же тип, то их дополнительные простраства Яъ — К
и /?3 — К' гомеоморфны и, следовательно, их фундамен-
фундаментальные группы я(/?3 — К) и n(Rz — К') изоморфны.
Тот факт, что узлы одного и того же типа имеют изо-
морфные группы, является тем принципом, с помощью
которого мы различаем в этой книге типы узлов. Нетри-
Нетривиальность клеверного листа будет доказана, если пока-
показать, что его группа \х, у :хух = уху\ не является беско-
бесконечной циклической (см. D.1) и D.2)). С этой целью
рассмотрим симметрическую группу S3 ранга 3, порож-
порожденную циклами A2) и B3). Прежде всего отметим, что
группа 53 не абелева, так как
A2) B3) = A32) =£A23) = B3) A2).
Верхнее копредставление D.2) узла клеверный лист со-
состоит из гомоморфизма ф свободной группы F, свобод-
свободный базис которой образуют элементы х и у, на группу
узла, причем ядро ф является оболочкой элемента
хух(уху)'1. Гомоморфизм 0 группы F на S3, определяе-
определяемый равенствами
= B3),
2) Индексы здесь берутся по mod 4. Следовательно
д
и т. д.
5. Существование нетривиальных типов узлов 137
индуцирует гомоморфизм группы узла на S3, если
Q(xyx)=Q(yxy). Но
е (уху) = е (у) е (х) е до = B3) A2) B3) = A3),
Следовательно, группа узла клеверный лист отображает-
отображается гомоморфно на неабелеву группу. Отсюда следует,
что сама группа узла неабелева и, конечно, не является
бесконечной циклической. Отсюда мы заключаем, что
клеверный лист нельзя развязать.
Аналогично, чтобы доказать, что клеверный лист от-
отличается от восьмерки, достаточно показать, что их груп-
группы неизоморфны. Копредставления этих групп даны в
D.2) и D.3). К сожалению, не существует общего прие-
приема решения вопроса, определяют или нет изоморфные
группы два данных копредставления. Из теоремы Титце
известно, что если две группы изоморфны, то их конеч-
конечные копредставления связаны друг с другом операциями
Титце. Однако попытки доказать прямыми методами, что
копредставления, описанные в D.2) и D.3), не связаны
операциями Титце, показывают, что это вовсе не про-
просто3). А нам нужен некий стандартный прием, позво-
позволяющий находить, исходя из копредставления группы,
некоторые легко вычислимые алгебраические величины,
одинаковые для изоморфных групп и называемые вслед-
вследствие этого групповыми инвариантами. Это значит, что
тип группы узла слишком сложен как инвариант, и, сле-
следовательно, мы должны перейти к более простым в обра-
обращении. Здесь, однако, есть опасность выплеснуть ребенка
вместе с водой из ванны: при переходе к более прос-
простым инвариантам неизбежно теряется часть информации.
3) В самом деле, можно доказать что узлы клеверный лист
(с группой G) и восьмерка (с группой G') различны, так же как
мы доказали нетривиальность клеверного листа. Если G^G\ то
должен существовать гомоморфизм £ группы G' на симметриче-
симметрическую группу 53. Используя копредставление G'— \х, у : ух-]уху~1 =
= х~1уху-1х\, можно убедиться в силу конечности числа возможных
случаев в том, что никакое отображение элементов х и у в груп-
группу S3 не продолжается до гомоморфизма группы G' на S3. (Однако
это не говорит о том, что восьмерка не может быть развязана.
Справедливость последнего утверждения будет доказана в гл. VIII.)
138
Гл. VI. Копредставления групп узлов
Мы же хотим найти простые легко отличаемые инва-
инварианты, еще достаточно тонкие,, чтобы различать груп-
группы большого числа разных узлов. Следующие две главы
посвящены именно этой проблеме.
УПРАЖНЕНИЯ
i. Для каждого из следующих узлов найти копред-
ставление его группы, имеющее ровно две образующие.
(с) узел
грузчика
Рис. 44.
2. Для каждой из пяти групп узлов, рассмотренных
в упражнении I, найти все представления в симметри-
симметрическую пруппу степени 3.
3. Торический узел КР,д типа (р, q) (р и q —-взаим-
—-взаимно простые целые числа) представляет собой кривую на
поверхности незаузленного тора (г—2J+z2=l *), кото-
которая пересекает меридиан тора в р точках, а параллель — в
q точках. Она записывается уравнением г=2 + cos (qQ/p),
z=sin(qQ/p). Разделив пространство R3 — К на части,
*) Здесь г = Ух2 -\- у2.— Прим. перев.
5. Существование нетривиальных типов узлов 139
одна из которых не внутренняя, а другая не внешняя по
отношению к тору, и применив теорему ван Кампена, до-
доказать, что (a, b'.av^bv) является копредставлением
группы узла Kv,q.
4. а) Показать геометрически, что узел клеверный
лист является торическим узлом К2,з- Ь) Нарисовать то-
рический узел /С2,5-
5. Доказать, что копредставление группы узла кле-
клеверный лист, полученное в D.2), имеет тот же тип, что
и копредставление (а, Ь : а2 = 63).
6. Скажем, что диаграмма узла обладает свойством
/, если можно так раскрасить в три цвета проекции пе-
переходов (каждый переход одним цветом), что а) три пе-
перехода в точке пересечения окрашены либо в разные,
либо в одинаковые цвета, Ь) при раскраске использо-
использованы все три цвета.
Показать, что диаграмма узла К обладает свойством
/ тогда и только тогда, когда группа узла К может быть
гомоморфно отображена на симметрическую группу сте-
степени 3.
7. Показать, что свойство / эквивалентно следую-
следующему: каждому переходу можно сопоставить целое чис-
число таким образом, что сумма этих чисел, соответствую-
соответствующих трем переходам в точке пересечения, делится на
три.
8. Показать, что группа узла не может быть гомо-
гомоморфно отображена на фундаментальную группу бутыл-
бутылки Клейна.
9. Используя то обстоятельство, что группа G кле-
клеверного листа имеет копредставление (а, 6:а2 = &3), най-
найти все классы представлений группы G на знакопере-
знакопеременную группу Л5 степени 5.
ГЛАВА VII
СВОБОДНОЕ ИСЧИСЛЕНИЕ
И ЭЛЕМЕНТАРНЫЕ ИДЕАЛЫ
Введение. В последней главе был развит метод вы-
вычисления копредставлений группы узла в регулярном
положении. К сожалению, как уже отмечалось, даже
теперь не просто различать группы узлов, а следова-
следовательно, и типы узлов. Не существует общего алгоритма
для определения того, изоморфны или нет группы, задан-
заданные своими копредставлениями, и даже в частных слу-
случаях это может быть трудной задачей. Мы, следователь-
следовательно, приходим к задаче нахождения сильных, но вместе
с тем и эффективно вычислимых инвариантов типа ко-
копредставлений группы. Таковыми являются элементар-
элементарные идеалы. В этой главе изучается необходимый для
их построения алгебраический аппарат^Применение его
к копредставлениям групп узлов, естественным образом
приводит нас в гл. VIII к понятию полиномов узла. С по-
помощью этих инвариантов можно будет легко различать
многие типы узлов.
1. Групповое кольцо. Со всякой группой G (записан-
(записанной мультипликативно) можно связать ее групповое
кольцо JG над кольцом / целых чисел. Элементами
кольца JG являются отображения v:G-W, удовлетво-
удовлетворяющие уравнению v(g)=0 для всех, за исключением не
более чем конечного числа элементов g£G. Сложение и
умножение в JG определяются соответственно форму-
формулами
(VlV2)£=
1. Групповое кольцо 141
при любых vi, V26/G и gdG. Непосредственно прове-
проверяется, что JG действительно является кольцом относи-
относительно этих двух операций. Умножение на целое число
я, определенное в любом кольце, удовлетворяет уравне-
уравнению (nv)g = n(vg) при любых v&JG, g£G.
Существует отображение G-+JG, которое элементу
gdG сопоставляет функцию g"*, определяемую следую-
следующим равенством:
?шЦи если А=*'
8 w 10, если h + g.
Это отображение сохраняет умножение и разные элемен-
элементы переводит в разные. Так как образ любого сохраняю-
сохраняющего умножения отображения группы в кольцо является
группой, то мы видим, что отображение g-+g* является
изоморфизмом группы G на ее образ. Элемент е*, где
е — единица группы, является ненулевой мультиплика-
мультипликативной единицей кольца JG.
Пусть v — произвольный ненулевой элемент кольца
/G. Пусть gu ..., gky &>1, —все элементы группы G,
для которых v(gi)=t=Q и пусть
^ = v(g'/)» '==1 к.
Тогда
т. е. образ группы G при отображении g-+g* порождает
аддитивную группу кольца /G. В силу этого будем отож-
отождествлять g и g* и записывать элементы кольца /G в
виде конечных целочисленных линейных комбинаций эле-
элементов группы G. При этом, например, становится оче-
очевидным, что
A.1) Кольцо JG коммутативно тогда и только тогда,
когда коммутативна группа G *).
Легко проверяется, что если п^+ ... +nkgk:=0 и
элементы gu ..., gh различны, то п{ = .. ,=лА=0. Отсю-
Отсюда следует, что всякий ненулевой элемент кольца JG
*) Новая запись произведения в кольце 7C, как нетрудно ви-
видеть, такова: B ml^i\ B njS'j\ = 2 nimjSiej- — Прим.перев.
142 Гл. VII. Свободное исчисление и элементарные идеалы
записывается единственным образом в виде конечной
суммы различных элементов группы G с ненулевыми ко-
коэффициентами. Это показывает, что аддитивная группа
кольца JG удовлетворяет следующему условию, анало-
аналогичному рассмотренному в гл. III характеристическому
свойству свободных групп.
A.2) Произвольное отображение ф группы G в адди-
аддитивную абелеву группу А единственным образом продол-
продолжается до аддитивного гомоморфизма ср: JG —►Л. Более
того, если А — кольцо и отображение ф сохраняет умно-
умножение, то это продолжение есть гомоморфизм колец.
Доказательство. Положим фО = О. Всякий нену-
ненулевой элемент кольца JG имеет единственную запись в
виде выражения ttigi+ ... + nkgk, где п*=£0, t=l,..., k,
и элементы gu ..., gk различны. Определим требуемое
продолжение, положив
Заметим далее, что если это равенство .имеет место цри
условиях из A.2), то оно также имеет место и при лю-
любых числах tti, ..., Пь и элементах gi, ..., gk. Но тогда
построенное отображение ф, очевидно, сохраняет сложе-
сложение. Поскольку любое расширение ф до аддитивного го-
гомоморфизма JG-+A удовлетворяет этому уравнению,
единственность несомненна. Наконец, если А — кольцо,
а отражение ф сохраняет умножение в G, то
S
и доказательство закончено.
Аддитивная группа кольца JG является, следователь-
следовательно, свободной абелевой, а подмножество G — базис (см.
§ 5 гл. IV). Другим следствием предложения A.2) яв-
является следующее:
A.3) Всякий гомоморфизм групп ф : G -*• G' един-
единственным образом продолжается до гомоморфизма ко-
колец y;JG-+JG'.
ф B ntgi 2 п)ё'}) = ф
= S nffgt S п)^ = (ф S ntg^ (ф 2 пщ
2. Свободное исчисление 143
Отметим, что если одно из условий: (I) ф — тожде-
тождественное отображение, (II) ф —отображение на или
(III) ф — взаимно однозначное отображение на свой об-
образ, имеет место для гомоморфизма групп ф: G—>G\ то
такое же условие имеет место и для гомоморфизма ко-
колец (q:JG-+JG\
Два довольно часто встречающихся гомоморфизма
группового кольца произвольной группы заслуживают
специального упоминания и названия. Первый из них,
коммутирование, был введен в § 4 гл. IV как канониче-
канонический гомоморфизм группы на ее прокоммутированную
группу. Теперь мы будем понимать под коммутированием
либо групповой гомоморфизм ct:G—*G/[G, G], как и
выше, либо его единственное расширение на групповые
кольца. Второй гомоморфизм — тривиализация. Для про-
произвольной группы G рассмотрим отображение t:G-+J,
определяемое равенством t(g) = l, g£G. Тривиализация
есть единственное расширение отображения t до гомо-
гомоморфизма колец t :/G->/. Ясно, что
*Bл/£/)=2л,
\ i I i
Закончим этот параграф замечанием, что отображе-
отображение /-*/G, определяемое соответствием п-*пе, где
e£G — единица, представляет собой кольцевой изомор-
изоморфизм. Следовательно, и группа G, и кольцо / можно рас-
рассматривать как подмножества группового кольца /G.
2. Свободное исчисление. Под дифференцированием
в групповом кольце /G будет пониматься всякое отобра-
отображение D:JG-+JG, удовлетворяющее условиям
B.1) D(v1-hv2) = Dv1 + ^2.
B.2) D(v1v2) = (Dv1)t(v2) + v1Dv2,
где I — тривиализация, a vi, V26/G. Для элементов
группы G условие B.2) принимает более простой вид
B.3) D(glg2) = Dgl + glDg2, g
В силу предложения A.2), однако, дифференцирование
может быть определено как единственное продолжение
н# JQ отображения группы G в /G, удовлетворяющего
144 Гл. VII. Свободное исчисление и элементарные идеалы
условию B.3). Очевидно, что отображение кольца JG
на нулевой элемент является дифференцированием. Во-
Вопрос о том, всегда ли существуют нетривиальные диф-
дифференцирования в произвольном групповом кольце, ре-
решается положительно, так как отображение g-*g—1,
g€ G, всегда определяет дифференцирование. Более того,
если D и Df — два дифференцирования в кольце /G, а
vo6/G — произвольный элемент, то нетрудно проверить,
что отображения D + D' и D о Vo, определяемые равенст-
равенствами
определяют также дифференцирование в JG.
Стоит отметить также некоторые следствия аксиом,
определяющих дифференцирования:
B.5) DB*ift) = 2*,0ft.
B.6) Dn = 0 при любом целом п,
B.7) Dg^^—g^Dg при любом g£G-
Первое из них следует из того, что D — аддитивный го-
гомоморфизм. Так как D\ =D(l . 1) =D1 +D1, то Dl=0,
откуда следует и более общее утверждение B.6). Нако-
Наконец, равенства O=D(g-lg)=Dg-l+g~lDg доказывают
формулу B.7). Полезно также определить для любого
g€G и целого п следующий элемент группового кольца:
О, п = О,
S £*, П > О,
S^ п<0.
В этих обозначениях имеем
B.8) Dgn = ll^
Докажем B.8) индукцией по абсолютной величине чис-
числа п. При А2 = 0, +1, —1 наше равенство сводится соот-
£>1=0, Dg=Dg и Dg-] = —g-lDg. Предпд-
2. Свободное исчисление 145
ложим далее, что |/г|>1. Если п положительно, то ин-
индуктивная гипотеза вместе с B.3) влечет за собой, что
л-1
Dg»+' = Dg" + g" Dg = ^ gt Dg + g"Dg = g"+^-* Dg.
Аналогично при отрицательном п имеем
i-n
что завершает доказательство.
Другим следствием аксиом является то, что диффе-
дифференцирование однозначно определяется своими значе-
значениями на всяком подмножестве, порождающем груп-
группу G.
Хотя понятие дифференцирования было введено для
произвольного группового кольца, здесь нас будут инте-
интересовать дифференцирования в групповом кольце сво-
свободной группы (отсюда и название этой главы). Предпо-
Предположим, что F — свободная группа со свободным базисом,
состоящим из элементов хи х2, ... . Произвольный эле-
элемент группового кольца представляет собой конечную
сумму конечных произведений степеней этих элементов,
и естественно мыслить себе такие элементы полиномами
от переменных х4, ..., хп. Конечно, они не являются
настоящими полиномами, так как в них могут встре-
встречаться отрицательные степени и, что более важно, пере-
переменные не коммутируют. Тем не менее элемент кольца
IF будет нами называться свободным полиномом и обо-
обозначаться, как правило, f(x) = 2 #А> tit£F. Действие
тривиализации t на свободный полином будет записы-
записываться так: t f(x) =f A).
B.9) Всякому свободному образующему х$ соответ-
соответствует единственное дифференцирование Dj = -g^-r в
кольце IF, называемое дифференцированием по Xj,
JO Зак. 317
146 Гл. VII. Свободное исчисление и элементарные идеалы
обладающее следующим свойством:
-~L = 60- (символ Кронекера).
Доказательство. Поскольку значения дифферен-
дифференцирования d/dXj заданы на порождающем подмножестве
группы F, единственность его очевидна. Для доказатель-
доказательства существования рассмотрим произвольное множество
Л, состоящее из элементов аи #2, . • •, находящихся во
взаимно однозначном соответствии с элементами Хи
х2, ... при отображении Qat=Xi. Из результатов гл. III
известно, что отображение 8 продолжается до сохраняю-
сохраняющего умножения отображения полугруппы слов W(A)
на группу F, при котором эквивалентные слова в W(А)
отображаются на один и тот же элемент группы F.
Предлагается определить для каждого элемента Xj ото-
отображение AjiW(A) -+JF, индуцирующее дифференци-
дифференцирование д/dXj. Это определение получается индукцией по
числу слогов слова из следующих соотношений:
(*)
Лу1=О A обозначает пустое слово),
?A.a, a£W(A).
Смысл нашего обращения к полугруппе W(A) для полу-
получения основного определения ясен. Так как в W(А) от-
отсутствует закон сокращения, отображение Aj корректно
определяется равенствами (*). Мы утверждаем, что
(••) A;(ab) = Aja + ва . Afi9 a, b£W(A).
Доказательство этого приведем индукцией по числу
слогов в произведении аЬ. Если а — пустое слово, наше
утверждение тривиально, так что мы предположим, что а
содержит хотя бы один слог. Следовательно, а = ап.с,
и в силу соотношений (*) мы имеем
Л . (ab) = Лу (аЩ = Л,а? + х»А. (cb).
2. Свободное исчисление 147
Из предположения индукции поэтому получаем
Лу (ab) = Ajui + xiAjC + xfic • Ар =
= Aja -f- в а
Мы утверждаем теперь, что если два слова эквива-
эквивалентны, то их образы при отображении Aj равны. Дока-
Доказательство этого равнозначно проверке того, что
А.(аа°.Ь) = А.
Aj (aan.+mb) = Aj
Эти соотношения легко устанавливаются с помощью ра-
равенства (**). Для первого из них имеем
Лу (ааР.Ь) = Лу (аа?) + 0 (аа°). Afi =
= Aja + ва . Ар = Aj (ab).
Перед проверкой второго заметим, что
откуда следует, что Лу(а^+/|) = Лу(а^а^). Поэтому по-
получаем
= Луа + ва • Лу(а*aj) + в(аа^а?) • А.Ь =
= Aj(aaTJlanib)>
и наше утверждение доказано. Отображение d/dXj:F-
—»JF определяется теперь следующим равенством:
'dv7' ®а == ^Уа для лю^ого а 6 W (Л).
Определение отображения d/dXj корректно, так как 8 —
отображение на, и если 8а = 8£, то слова а я b эквива-
эквивалентны, и Ajd=Ajb. (Отметим, что доказательство зави-
зависимости отображения Aj только от классов эквивалент-
эквивалентности слов основано на том, что это же верно для отобра-
отображения 8.) Из определения (***) немедленно следует, что
10*
148 Гл. VII. Свободное исчисление и элементарные идеалы
xj = 6ij. Для проверки того, что отображение д/дх^
определяет дифференцирование в /F, мы должны прове-
проверить только аксиому B.3). Но для любых элементов
и=ва и v=Qb группы F имеем
и доказательство теоремы B.9) завершено.
Предыдущая теорема представляет собой замеча-
замечательный результат, в котором в полной мере раскры-
раскрывается структура множества дифференцирований в
групповом кольце свободной группы. Точно это утвер-
утверждение сформулировано в следующем важном след-
следствии:
B.10) Для любых свободных полиномов hi(x),
h2(x), ... найдется одно и только одно такое дифферен-
дифференцирование D в кольце JF, что Dxj=hj(x), /=1, 2, ... .
Более того, для любого полинома f(x)£JF имеем
Доказательство. Единственность опять-таки сле-
следует автоматически. Далее необходимо проверить, что
предыдущая сумма конечна. Мы предоставляем чита-
читателю проверить, что df(x)/dXj = 0, если образующий Xj
не встречается в свободном многочлене f(x) (см. упр. 5).
Отсюда следует, что отображение f (х) -> 2 {dfjdxj) hj(x)
есть дифференцирование в IF (см. B.4)), обладающее
требуемыми свойствами, и доказательство закончено.
Мы уже отметили, что отображение f (#)-*/(#)—/A)
является дифференцированием в IF, Как следствие пред-
предложения B.10) получаем следующую основную формулу:
B.11) ^
Из нее следует, что свободный полином определяется
своими производными и своим значением в 1. Аналогия
3. Матрица Александера 149
с хорошо известным законом о средних здесь очевидна.
Возможны также и другие интересные обобщения.
3. Матрица Александера. Свободное исчисление бу-
будет являться основным математическим орудием при по-
построении полезных инвариантов типа копредставлений.
Рассмотрим копредставление (х:г). Множество х =
= (#ь #2, ...) является свободным базисом свободной
группы F, а группа, определяемая этим копредставле-
нием, представляет собой факторгруппу,
где R — оболочка множества г=(гь г2, ...), а Y — кано-
канонический гомоморфизм. И гомоморфизм у, и коммутиро-
коммутирование а обладают единственными расширениями до го-
гомоморфизмов соответствующих групповых колец. Обо-
Обозначая через Н прокоммутированную группу |х: г|, по-
получаем следующую композицию:
д
Матрица Александера копредставления (х: г) есть мат-
матрица ||a«j||, определяемая формулой
Результат применения гомоморфизма ау к элементу
drjdxj приводит к большим упрощениям Гомоморфизм
у переводит элементы кольца IF в элементы кольца
/|х:г|, где всякое следствие множества г равно 1. Но
даже более важным здесь является то, что коммутиро-
коммутирование ct затем отображает все в коммутативное кольцо.
В коммутативном кольце можно определить детерми-
детерминанты, и, кроме того, для группы узла кольцо /// уст-
устроено особенно просто.
Следует отметить, что определение матрицы Алек-
Александера зависит от упорядочения образующих и соот-
соотношений, в то время как определение копредставления
группы, данное в гл. IV, не зависит. На самом деле это
несущественно. В следующем параграфе мы увидим, что
две матрицы, отличающиеся только перестановкой строк
150 Гл. VII. Свободное исчисление и элементарные идеалы
или столбцов, все равно будут рассматриваться как эк-
эквивалентные.
Добавочные условия упорядоченности можно было
бы попросту ввести в описание копредставления группы.
Однако они для нас не являются существенными, а оп-
определение без них выглядит проще.
4. Элементарные идеалы. Пусть R — произвольное
коммутативное кольцо с единицей. Рассмотрим некото-
некоторую т (строки) Хп (столбцы) матрицу Л, составленную
из элементов кольца R. Для любого неотрицательного
целого числа k следующим образом определим k-и эле-
элементарный идеал Ek(A):
Если 0<п — & -< т, то Ek(A) — идеал, порожденный
всеми минорами матрицы А порядка n — k.
Если п — k>mt то Ek(A) = 0.
Если п — kKQ, то Ek(A) = /?.
Из того, что определитель произвольной матрицы
можно разложить по элементам любой ее строки или
столбца, сразу следует
D.1) Элементарные идеалы матрицы А образуют воз-
возрастающую цепочку
E0(A)czE1(A)cz ... czEn(A) = En+l(A)= ...=/?.
Пусть А и А' — две матрицы над кольцом R. Ска-
Скажем, что матрица А эквивалентна матрице А' (обозна-
(обозначение А~А'), если существует такая конечная цепочка
матриц
А. = -Aj, /i2> • • • > Ап ==:: А ,
что матрица Ai+i получается из матрицы Ах (или А{ из
Ai+i) одной из следующих операций:
(I) перестановка строк или столбцов,
Л II А ||
(II) добавление нулевой строки А->\\ п II,
II ^ II
(III) прибавление к строке линейной комбинации
других строк,
(IV) прибавление к столбцу линейной комбинации
других столбцов,
4. Элементарные идеалы
151
(V) добавление такой новой строки и такого нового
столбца, что на пересечении новой строки и нового столб-
столбца стоит элемент 1, а все остальные элементы новой
II Л 0 1
строки и нового столбца равны нулю, А-> ~ .
Нетрудно показать, что матрица А эквивалентна мат-
матрице, полученной из А добавлением такой новой строки
и такого нового столбца, что на их пересечении стоит
элемент 1, остальные элементы нового столбца равны
все нулю, а остальные элементы новой строки произ-
произвольны. Следовательно, условие (V) может быть заме-
заменено более сильным условием
И о II
(V/) HI* И!*
Для доказательства этого утверждения достаточно
применить один раз эквивалентность (V) и п раз экви-
эквивалентность (IV), где п — число столбцов матрицы Л,
А
Л
Рассматриваемое определение эквивалентности мат-
матриц наиболее заметно отличается от того определения,
которое обычно встречается в линейной алгебре, в пунк-
пунктах (II) и (V). Тем не менее распространение операции
умножения строки или столбца на единицу е кольца R *)
сохраняет эквивалентность. Это мюжно получить следую-
следующим образом:
а\
a
ea\\
A)
A
II ea ||
a
(,
A
ea
a — e~xea
и
\ea\
*) Здесь в отличие от «обычной» единицы (единичного эле-
элемента) имеется в виду элемент е £ /?, для которого найдется эле-
элемент ел € R, такой, что ее~1 = \. — Прим. перевг
152 Гл. VII. Свободное исчисление и элементарные идеалы
Необходимо отметить, что эквивалентность матриц,
определенная нами, является рефлексивным, симметрич-
симметричным и транзитивным отношением, т. е. это — настоящее
отношение эквивалентности.
D.2) Эквивалентные матрицы определяют одинако-
одинаковые цепочки элементарных идеалов.
Доказательство. Наше доказательство опирает-
опирается на хорошо известные элементарные факты относи-
относительно действий с определителями. Кстати, они имеют
чисто комбинаторный характер и верны для любого
коммутативного кольца. Мы должны доказать, что
Ek(A) =Ek(A')y если матрица А' получена из матрицы Л
с помощью одной из операций (I), ..., (V). Для опе-
операций (I), (III) и (IV) это видно сразу. Например, рас-
рассмотрим операцию (III). Тогда всякий образующий
элемент идеала Eh(A') либо уже сам совпадает с неко-
некоторым образующим идеала Eh(A), либо, что видно из
разложения миноров матрицы А' по строкам, является
линейной комбинацией образующих этого идеала. Такое
же разложение показывает, что верной обратное утверж-
утверждение.
Далее рассмотрим операцию (II). Так как п = п' и
m'=m+l, мы видим, что если 0<n — &<m, то 0<
<n' — kKm' и Ek(A)=Ek(A'). Единственный случай,
не вытекающий непосредственно из определений, полу-
получается при п — & = т'. В этом случае тривиально полу-
получаем, что Ek(A)=Oy а идеал Ek(A') порождается мино-
минорами порядка т' матрицы А'. Но так как последняя
строка в каждом из этих миноров состоит из нулей, то
равенство Еь{А') =0 также имеет место.
4. Элементарные идеалы 153
Наконец, нам осталось проверить операцию (V).
Здесь я' = А1+1, т' = т+1. Если п — k>m, то nr — k =
= (п+1) — k>m+l=m\ и равенства Ek(A)=Ek(A') =0
справедливы. Если п — k^O, то п' — k^l. В этом слу-
случае непосредственно ясно, что Ek(A)=R, и то же самое
верно и для матрицы А', кроме случая, когда п! — k=l.
Но ЕП'-\{А') — идеал, порожденный элементами мат-
матрицы А'. Так как один из этих элементов равен 1, то мы
заключаем, что Enr-\{A') = R. В остальных случаях
0<n — k^,m. Всякий минор матрицы А порядка
(п — k) может быть расширен до минора матрицы А'
порядка (n'—-k) добавлением соответствующих элемен-
элементов нового столбца и новой строки матрицы А', содер-
содержащей, следовательно, на их пересечении элемент 1.
Разложение по элементам нового столбца показывает,
что определители этих двух миноров равны с точ-
точностью до знака. Следовательно, Ek(A) cEk(A'). Об-
Обратно рассмотрим произвольный минор матрицы А'
порядка (п' — k), строки которого могут содержать,
но могут и не содержать новой строки матрицы А' (от-
(отметим, что nr — k^-2). Если содержат, то разложение
по элементам новой спроки показывает, что ее опреде-
определитель является образующим идеала Ек(А) *) и, следо-
следовательно, принадлежит Ek(A). Если же ее строки не со-
содержат новой строки матрицы А'у то ее определитель
принадлежит идеалу Ek-i{A), который, согласно D.1),
содержится в Ek(A). Отсюда заключаем, что при опе-
операции (V) Ek(A)zDEk(A')y и доказательство закончено.
Рассмотрим теперь произвольный гомоморфизм ко-
колец ф :R-*R'9 где R и R' — коммутативные кольца с
единицей. Пусть А = 1^11— матрица с элементами
из кольца R. Определим ее образ
Весьма полезен следующий результат:
D.3). Если ф — отображение на, то (pEk(A)=Ek((pA)t
*} Или нулем. — Прим. перев.
154 Гл. VII. Свободное исчисление и элементарные идеалы
Доказательство. Автоматически ф@)=0. Равен-
Равенство ф/? = /?', которое нам необходимо при я — &-<0, есть
как раз наше предположение о том, что ф — отображе-
отображение на. Очевидно, что образ множества всех миноров
порядка п — k матрицы А совпадает с множеством всех
миноров порядка п — k матрицы фЛ. Следовательно,
единственное, что нужно выяснить, это является ли об-
образ идеала, порожденного элементами аи ..., аг коль-
кольца /?, идеалом кольца /?', порожденным их образами
<p(#i)> •••> ф(яг)- Как легко видеть, ответ на это утвер-
утвердителен, но, конечно, при условии, что ф — отображе-
отображение на.
Для произвольного конечного копредставления
(х : г) и неотрицательного целого числа k мы определим
k-й элементарный идеал копредставления (х: г) как
k-й элементарный идеал матрицы Александера этого ко-
представления. В силу теоремы D.2) можно, конечно,
вычислять элементарные идеалы копредставления, ис-
исходя из матриц, эквивалентных матрице Александера.
В конкретных примерах естественно для этого использо-
использовать простейшую из эквивалентных матриц.
Элементарные идеалы, определенные для любого ко-
конечного копредставления, являются обобщениями поли-
полиномов узла, которые мы определим в следующей главе
для копредставлений групп узлов. Имеется несколько
преимуществ введения идеалов раньше полиномов. Преж-
Прежде всего, в то время как идеалы определяются для про-
произвольного конечного копредставления группы, полиномы
существуют и единственны только для более ограничен-
ограниченного класса групп, удовлетворяющих некоторым алгеб-
алгебраическим условиям. В следующей главе мы обсудим
эти условия и покажем, что всякая группа ручного узла
удовлетворяет им. Более того, легче доказывать инва-
инвариантность идеалов, чем инвафиантность полиномов. По-
Поскольку полиномы можно охарактеризовать в терминах
идеалов, мы убиваем здесь сразу двух зайцев. Наконец,
даже в тех случаях, когда полиномы существуют, идеа-
идеалы содержат большую информацию. В гл. VIII описаны
два узла, которые не различаются полиномами, но име-
имеют разные элементарные идеалы.
4. Элементарные идеалы 155
Проблема, возникающая перед нами, в первую оче-
очередь состоит в том, чтобы доказать, что элементарные
идеалы конечного копредставления являются инвариан-
инвариантами типа копредставления. Доказательство этого осно-
основано на теореме Титце, которая сводит все к проверке
инвариантности идеалов при операциях Титце I и Н.
Основная часть доказательства поэтому состоит в изу-
изучении действия каждой из этих операций на матрицы
Александера. Для ясного понимания формулировки тео-
теоремы об инвариантности, которая приводится ниже, чи-
читатель может просмотреть основные определения и ре-
результаты гл. IV, касающиеся отображения копредстав-
лений и теоремы Титце.
Пусть f : (х : г) -> (у : s) — некоторое отображение
копредставлений. Оно индуцирует гомоморфизм групп
/* : |х : г| -* |у : s|, соответствующих этим копредставле-
ниям. Это отображение в свою очередь индуцирует гомо-
гомоморфизм f** прокоммутированной группы |х:г| в про-
коммутированную группу |y:s| (см. D.1) гл. IV). Если
известно, что копредставления (х : г) и (у : s) имеют оди-
одинаковый тип, то найдется эквивалентность копредстав-
копредставлений (х: г) -U (у : s) -£> (х: г), причем
тождественное отображение = (/&)*=/*£*,
тождественное отображение = (/*if#)* = /**£**.
Аналогично отображение £«*/«* тождественно. Итак,
D.4) Если пара f> g является эквивалентностью ко-
копредставлений, то каждое из отображений /**, g^ яв-
является изоморфизмом на и обратным другому.
Отметим, что такое заключение верно и для расши-
расширений гомоморфизмов /*#, g%# до гомоморфизмов соот-
соответствующих групповых колец.
Напомним, что если пара отображений f, g является
эквивалентностью копредставлений, то каждое из ото-
отображений f, g в отдельности может быть названо экви-
эквивалентностью. Однако если речь идет об одном из них
в отдельности, то следует иметь в виду, что из его суще-
существования вытекает существование другого. Утвержде-
Утверждение, что элементарные идеалы конечного копредставле-
копредставления являются инвариантами типа копредставления, со-
составляет содержание следующей теоремы;
156 Гл. VII. Свободное исчисление и элементарные идеалы
D.5) Инвариантность элементарных идеалов. Если
(х : г) и (у : s) — конечные копредставления групп и
f : (х : г) - (у : s)
— эквивалентность этих копредставлений, то k-й элемен-
элементарный идеал копредставления (х : у) отображается изо-
изоморфизмом /#.5. на k-й элементарный идеал копредстав-
копредставления (у : s).
Доказательство. Доказательство вследствие тео-
теоремы Титце немедленно сводится только к проверке эк-
вивалентностей Титце I, Г, II и 1Г. Заметим также, что
в силу предложения D.4) если теорема D.5) верна для
одного члена пары эквивалентностей Титце, то она авто-
автоматически верна и для другого. Поэтому мы должны
проверить только эквивалентности Титце I и II.
Эквивалентность Титце I. Это такое отображение ко-
копредставлений
(х: г) --> (х : г U s)9
где х= (хи ... t дсп), г= (ги ..., гт), элемент 5 принад-
принадлежит оболочке элементов множества г и I : F(x) —► F(x)
есть тождественный гомоморфизм. Отсюда следует, что
отображения I* и I** также тождественны. Следова-
Следовательно, доказательство будет закончено, если показать,
что копредставления (х : г) и (х : г U s) имеют одинако-
одинаковые матрицы Александера. Так как элемент s принадле-
принадлежит оболочке множества г, имеем
ds д ,
~дхГ = "длГ\и1гУхи\л)~^~ Й1Г7
/'-1
Но так как у(Г/)=Ь то
4. Элементарные идеалы 157
Однако
/ ц f ,кц~j ] — —— -4— // — il f .*U~
дх i V * 'fe / <у-^/ " г,- — 1 ^лг у k дх л
J \ К / У f . У « у
Следовательно,
Полагая сьЛау(йЛ) = сЛ, окончательно получаем
Итак, матрица Александера копредставления (x:rUs)
такая же, что и матрица копредставления (х:г), за ис-
исключением того, что она имеет лишнюю строку, являю-
являющуюся линейной комбинацией других. Две такие мат-
матрицы эквивалентны*), и первая часть доказательства
закончена.
Эквивалентность Титце II. Это такое отображение ко-
представлений
где x=(*i, ..., хп), г=(гь ..., rm)cf(x), ^^(x), у —
элемент базисного множества образующих, не содержа-
содержащийся в х, и II i/^x) —►/7(x, у) —гомоморфизм вло-
вложения. Полагая
и обозначая через Н и Н' прокоммутированные группы G
и Gr соответственно, получаем следующую диаграмму
*) Именно, чтобы получить матрицу копредставления (х : г (J SK
из матрицы копредставления (х : г) достаточно применить сначала
операцию II, а затем III. — Прим, перев.
158 Гл. VII. Свободное исчисление и элементарные идеалы
гомоморфизмов:
JF (x
vj
JO
a\
JH
)—->
JF
v'l
JO
.'1
JH
(X
r
r
uy)
У
a'
II = H*Y
Обозначим матрицы Александера копредставлений
(х : г) и (х U У : г U У%~1) через А =||а | и A = \aftj
соответственно. Тогда
/ = 1, . . ., /7Z,
у = 1, -.., л,
П( дГг \ / / / E/*/ \ #
I »■■ ) — d Y I —— I — а
Очевидно, что
Поэтому если обозначим строку элементов
через а', то получим
Н^Л О II
А'= а' 1 Г
Следовательно, операция (V) (стр. 101) дает эквива-
эквивалентность
Из предложений D.2) и D.3) теперь следует, что
и доказательство теоремы об инвариантности закончено.
Особенностью техники гл. IV и нашего подхода к
теории матриц Александера и элементарных идеалов
4. Элементарные идеалы 159
было построение теории копредставлений групп незави-
независимо от тех конкретных групп, для которых эти копред-
копредставления могут возникать (например, в теории узлов —
от фундаментальных групп). Мы определили матрицу
Александера и элементарные идеалы скорее для копред-
копредставления, чем для копредставления данной группы G.
Аналогично теорема Титце утверждает существование
факторизации отображений копредставлений. Она дана
не как утверждение о копредставлениях одной и той же
группы. Мы думаем, что подход, который мы применили,
не только проще по своим идеям, но также более точно
соответствует расчетам примеров в теории узлов. Можно,
однако, без труда описать и другой подход. Рассмот-
Рассмотрим копредетавлаиие (х: г)ф группы G. Матрица Алек-
Александера группы G определяется как матрица ||а^||, со-
состоящая из элементов
(а, конечно, — коммутирование группы G), а элемен-
элементарные идеалы — как элементарные идеалы этой мат-
матрицы. Тогда теорема инвариантности принимает вид:
D.6) Элементарные идеалы являются инвариантами
группы G, обладающей конечным копредставлением, т. е.
два конечных копредставления этой группы имеют оди-
одинаковые цепочки идеалов.
Доказательство теоремы D.6) исходя из теоремы
D.5) является простым упражнением, использующим
только самые общие свойства гомоморфизмов и фактор-
факторгрупп.
УПРАЖНЕНИЯ
1. В групповом кольце свободной группы F(xy y> г)
найти следующие производные:
(а) -^ (хугЪ-гу-Ъ-*), (b) ±
160 Гл. VII. Свободное исчисление и элементарные идеалы
2. Пусть F — свободная группа со свободным бази-
базисом (хи #2, •••)• Показать, что если в кольце JF най-
найдется такое конечное число элементов аи ..., аП1 что
п
2 Я/ (•*/ — 1) = 0, то ах = ... = ап = 0.
3. Пусть элементы gu g2y ... порождают группу G.
Показать непосредственно, что для любого v£/G най-
найдется такое конечное множество элементов vi, ..., vn
п
кольца /G, что v—tv=2v/(gyj — !)• (Например,
l«ffi(ft— l) + (gi — 1).)
4. Чувствуется, что наше доказательство теоремы
B.9) не так хорошо, как могло бы быть, так как оно
существенно опирается на способ получения свободной
группы из полугруппы слов. Возникает вопрос, можно
ли дать хорошее доказательство теоремы B.9), осно-
основанное на определении свободной группы как группы,
обладающей свободным базисом. Возможный подход
к этому, например, состоит в том, чтобы доказать утвер-
утверждение упражнения 2 независимо от существования диф-
дифференцирований d/dxjy а затем скомбинировать его с ре-
результатом упражнения 3. Следовательно, исходя из
упражнения 3, получим, что f(x) — fA)= S^yC*/ — 1)
при некоторых uj^JF. Если же известно, что эле-
элементы а,} однозначно определяются полиномом /(я),
можно просто определить производную df/dxj как эле-*
мент cij.
Повозитесь немного с этим!
5. Используя только утверждения B.1), B.2) и B.9),
доказать, что если образующий элемент Xj не входит в
полином f{x)y то df/dXj = O. Отметим, что это задача об
элементах свободной группы, а не о словах.
6. Вычислить производные элементы до=[[а, &], [су d]].
Что произойдет с матрицей Александера от прибавления
к копредставлению соотношения w=U
7. Обозначим через G' коммутант группы G и соот-
соответственно через G" коммутант группы G'. Исследуйте
связь между матрицами Александера групп G и GIG".
8. Построением цепочки элементарных идеалов дать
4. Элементарные идеалы 161
другое доказательство того, что свободные группы раз-
различных конечных рангов т и п не изоморфны.
9. Предположим, что 9 гомоморфно отображает груп-
группу Gi на группу G% таким образом, что его ядро содер-
содержится в коммутанте G[ группы G\. Доказать, что инду-
индуцированный гомоморфизм 9* группы Gi/Gi на группу
G2/G2 является изоморфизмом и что для любого d
идеал Ed(Gi) содержится в идеале Ed(G2). (Ed(G) обо-
обозначает d-й идеал матрицы Алексаадера некоторого
копредставления группы G.)
10. Найти цепочку элементарных идеалов свободной
абелевой группы ранга п и вывести из этого, что при
п>1 свободная группа ранга п не абелева.
11. Найти цепочки элементарных идеалов для:
(a) фундаментальной группы «бутылки Клейна»
\а, b : abcrlb=l |;
(b) группы |а, b : b2— 11;
(c) группы |а, fe:62=l, ab = ba\ и, используя полу-
полученные результаты, показать, что эти группы не изо-
изоморфны.
12. Найти цепочку элементарных идеалов для мета-
циклической группы |а, x:av—l, л:^ = 1, xax'x—ak\,
где р — нечетное простое число, a k — первообразный ко-
корень по modp, определение этого понятия см. в указа-
указателе. Вывести отсюда, что эта группа не является абе-
абелевой.
13. Найти цепочку элементарных идеалов для фунда-
фундаментальной группы ориентируемой поверхности рода
av bv ..., ahi bh: Д \av b\ =
, и вывести из этого,
что при \О>2 эта группа не является ни свободной, ни
абелевой.
14. Найти цепочку элементарных идеалов для группы
I*. У- (хУ)п==(Ух)п\ и вывести из этого, что эта группа
при я>2 не является ни свободной, ни абелевой.
15. Найти цепочку элементарных идеалов для группы
\х, у, г:\[у-К х], г] = [[г-*, у\, х]=Цх-*9 г], у\ = \\
\\ Зак. 317
162 Гл. VII. Свободное исчисление и элементарные идеалы
и вывести из этого, что эта группа не является ни сво-
свободной, ни абелевой.
16. Найти цепочку элементарных идеалов для группы
косы *):
it ..., on:oi oulol = Gi^xaioul (/ = 1 п— 1),
17. Доказать, что если свободная группа ранга п мо-
может быть гомоморфно отображена на группу G, то
fi(G(l)
()()
18. Для данного множества целочисленных полино-
полиномов /i(/), ..., /п@, таких, что (Ml), ■ ■•» fn(l)) = l, по-
построить группу G таким образом, чтобы G/G/=(/:) и
E(G)(M0f@)
]) Artin E., The theory of braids, American Scientist. 38, № 1
A950), 112—119; Boh nenb lust F., The Algebraical Braid Group,
Ann. of Math., 48 A947), 127—136.
ГЛАВА VIII
ПОЛИНОМЫ УЗЛА
Введение. Структура теории узлов, развитой в этой
книге, представляет собой цепочку все более слабых ин-
инвариантов типа узла. Последовательность полиномов
узла, которым посвящена эта глава, является последним
звеном этой цепочки:
тип узла К
I
Тип копредставления группы я(/?3 — К)
1
Последовательность элементарных идеалов
У
Последовательность полиномов узла
Полным инвариантом является только первый из пере-
перечисленных, т. е. сам тип узла. Он полон просто потому,
что два узла имеют один и тот же тип тогда и только
тогда, когда они имеют один и тот же тип. Если ограни-
ограничиться только этим, то мы получим определение, но не
теорию и с нашими знаниями не сможем даже доказать,
что существуют неэквивалентные узлы. Следующий шаг
дает значительное продвижение. Теорема о том, что узлы
одного и того же типа имеют изоморфные группы, сво-
сводит топологическую проблему к чисто алгебраической.
Остальные инварианты нацелены уже на весьма труд-
трудную проблему распознавания того, когда два копред-
копредставления задают неизоморфные группы. Здесь важно
указать, что на каждом шагу из нашей цепи теряется
информация. В самом деле, для каждого из инвариантов
в конце этой главы приведен пример пары узлов, типы
которых различаются этим инвариантом, но уже не раз-
различаются следующим. Эти потери компенсируются при
И*
164 Гл. VIII. Полиномы узла
рассмотрении проблем распознавания, т. е. при рассмот-
рассмотрении вопроса о том, определяют ли два способа зада-
задания один и тот же инвариант или нет. Как мы уже ука-
указали, эта проблема не разрешима в целом для копред-
ставлений групп. Для полиномов узла она, однако, три-
тривиальна.
Полиномы узла можно определить посредством эле-
элементарных идеалов («см. C.22)). Однако в отличие от
идеалов, которые определены для любого конечного ко-
представления, существование и единственность полино-
полиномов узла основываются на особых алгебраических свой-
свойствах прокоммутированной группы узла. Поэтому первый
параграф этой главы посвящен доказательству теоре-
теоремы о том, что прокоммутированная группа узла всегда
является бесконечной циклической группой. Во втором
параграфе устанавливаются нужные для дальней-
дальнейшего алгебраические свойства группового кольца беско-
бесконечной циклической группы. Затем мы определяем поли-
полиномы узла, проверяем их существование, единственность
и инвариантность и изучаем некоторые их свойства. По-
Последний параграф содержит примеры различных типов
узлов, отличаемых друг от друга с помощью вычисления
их полиномов или идеалов. Особо подчеркнем, что мы
ограничиваемся здесь узлами, чьи группы обладают
верхним копредставлением. Под группой узла мы, сле-
следовательно, понимаем фундаментальную группу допол-
дополнения ручного узла *).
1. Прокоммутированная группа узла. Мы утверждаем,
что прокоммутированная группа любого узла является
бесконечной циклической. Доказательство этого осно-
основано на рассмотрении верхнего копредставления группы
узла.
Пусть G — группа узла и (хи ..., хп:ги ..., гп)ф
есть ее верхнее копредставление. Типичный пример
того, как получается соотношение гг- цри обходе про-
*) То, что узел обладает верхним копредставлением, предпола-
предполагает существование «хорошей» проекции узла на плоскость. Учиты-
Учитывая это и то, что все гомеоморфные образы окружности на пло-
плоскости — ручные, можно доказать, что первоначальный узел также
ручной. — Прим. перев.
1. Прокоммугированная группа узла
165
хода, приведен на ри-с. 45, ниже. (Хотя это, очевидно,
несущественно, но мы для простоты использовали моди-
модифицированный вариант верхнего копредставления C.1)
гл. VI вместо первоначального A.1) гл. VI.) Для лю-
любого элемента и свободной группы F, порожденной эле-
элементами Хи • • •, хп, мы определим j-to сумму показате-
показателей элемента и как сумму показателей при всевозмож-
всевозможных вхождениях элемента Xj в и. Мы уже имеем и
выражение для этой величины: /-я сумма показателей
Рис. 45.
элемента и равна образу производной dw/cbcj при гомомор-
гомоморфизме тривиализации t JF-+J. Пусть хх(г> и хщ) —
образующие, соответствующие двум переходам, между
которыми лежит проход, с помощью которого опреде-
определяется соотношение гг-. Для определенности мы предпо-
предположим, что переход, отвечающий образующему *х(г>
предшествует (в смысле ориентации узла) переходу, от-
отвечающему образующему л^(г> Пример, приведенный на
рис. 45, иллюстрирует тот факт, что х(/)-я и ХA)-я сум-
суммы показателей элемента Г\ равны соответственно 4-1
и —1, в то время как сумма показателей этого элемента,
соответствующая любому другому образующему, равна
нулю. Следовательно, если 0 — произвольный гомомор-
гомоморфизм группы G в некоторую абелеву группу, то
Так как проекция узла всегда связна, то мы заключаем,
что Q(pXi = Q(pXi для любой пары образующих хи х^
/66 Гл. VIII. Полиномы узла
Следовательно, всякий элемент образа 0G группы G яв-
является степенью единственного элемента /=0ф^-, /~ 1,...
,,., п. Итак, мы доказали, что
A.1) Каждый гомоморфный абелев образ группы
узла является циклической группой. Более того, все об-
образующие любого верхнего копредставления этой груп-
группы отображаются при этом в один образующий эле-
элемент.
В частности, прокоммутированная группа любого
узла является циклической. Остается доказать, что она
не может быть конечной. Чтобы доказать это, опять рас-
рассмотрим верхнее копредставление группы G и обозна-
обозначим через (/) бесконечную циклическую группу, поро-
порождаемую элементом t. Так как F — свободная группа,
отображение £*j = /, /=1, ..., п, можег быть продол-
продолжено до гомоморфизма группы F на (/). Легко пока-
показать, что существует такой гомоморфизм 9 группы G
на (/), что следующая диаграмма
А/
«>
коммутативна. Ясно, что ^гг = /^, t=l, ... ,п, где 5г- —
сумма по / всех /-х сумм показателей элемента гг-. Имеем
7-1 7 7-1
Следовательно, £^ = 1, /=1, ..., п, и оболочка элементов
ги ..., Г/г, ..., rn, являющаяся ядром гомоморфизма ф,
содержится в ядре гомоморфизма £. Отсюда следует, что
гомоморфизм 0 корректно определен равенством
Но поскольку гомоморфизм £ является гомоморфизмом
на, то таковым является и гомоморфизм 0. Рассмотрим
далее гомоморфизм коммутирования а : G -+ G/[Gy G].
Напомним то важное обстоятельство, что всякий гомо-
2. Групповое кольцо бесконечной циклической группы 167
морфизм некоторой группы в абелеву можно «пропус-
«пропустить» через прокоммутированную группу (см. D.4)
гл. IV). Поэтому существует такой гомоморфизм 0', что
диаграмма
— \ >
0/@, Q\
коммутативна. Так как 0 — гомоморфизм на, то 0' —
тоже гомоморфизм на. Но отображение, образ которого
бесконечен, не может иметь в качестве области опреде-
определения конечное множество. Отсюда мы и заключаем, что
группа G/[G, G] бесконечна. Комбинируя этот результат
с предложением A.1), получаем
A.2) Прокоммутированная группа произвольного уз-
узла является бесконечной циклической группой.
Можно также получить этот результат редукцией со-
соответствующего копредставления операциями Титце.
Если исходить, например, из копредставления Виртин-
гера группы G, то группа G/[G, G] имеет копредставле-
ние (см. D.6) гл. IV)
(Xv . ., Хп '-XJ+ixl {i)XtXkuy \Xi* Xj]> l* У^Ь •••» П)>
которое можно привести к следующему:
(xv ..., xn:xi + lxj-l9 /=1 n)~(t:).
Отметим, что этот подход основан на теореме (см. D.5)
гл. IV) о том, что оболочка множества коммутаторов
[gi> gjl где элементы gu #2, ... порождают группу G,
совпадает со всем коммутантом.
2. Групповое кольцо бесконечной циклической группы.
Знание некоторых фундаментальных свойств группового
кольца бесконечной циклической группы Н необходимо
для понимания природы полиномов узла. Поэтому в этом
параграфе мы сделаем обзор некоторых элементарных
понятий, касающихся делимости в кольцах и областях
168 Гл. VIII. Полиномы узла
целостности, и рассмотрим, как они применяются к груп-
групповому кольцу JH.
Пусть R — произвольное кольцо с единичным элемен-
элементом 1. Элемент и кольца R будем называть единицей,
если он имеет и левый, и правый обратные элементы,
т. е. существуют такие элементы v, w£R, что uv =
= wu=l *).
Из ассоциативности следует, что
w = w(uv) — (wu)v = v.
Следовательно, эквивалентное определение состоит в том,
что единица — это элемент, обладающий обратным, ко-
который, в силу тех же соображений, должен быть един-
единственным. Так как произведение двух единиц снова яв-
является единицей, то нетрудно видеть, что множество
единиц кольца R образует группу по умножению. На-
Например, в кольце целых чисел единицами являются
только элементы +1 и —1. В групповом кольце едини-
единицами, очевидно, являются все групповые элементы и их
аддитивные обратные. Это так называемые тривиаль-
тривиальные единицы группового кольца. Возможность существо-
существования нетривиальных единиц будет коротко рассмотрена
несколько позднее в этом параграфе.
Мы скажем, что элемент а делит элемент Ь (запись
а\Ь), где а и Ъ — элементы коммутативного кольца /?,
если существует такой элемент c£R, что Ь = ас. Элемен-
Элементы а и b назовем ассоциированными, если а\Ь и Ь\а. От-
Отношение ассоциированности является отношением экви-
эквивалентности при условии, что кольцо R обладает единич-
единичным элементом. Единственным элементом, ассоцииро-
ассоциированным нулю, является он сам. Коммутативное кольцо
называется областью целостности, если оно содержит по
меньшей мере два элемента и обладает тем свойством,
что если аФО и ЬФО, то аЬФО.
B.1) Два элемента области целостности, обладаю-
обладающей единичным элементом, ассоциированы тогда и толь-
*) Начиная с этого места, следует различать единичный эле-
элемент кольца, т. е. такой элемент 1, что 1-а=а-1 = а, а 6 R, и еди-
единицу кольца, т. е. элемент, обладающий обратными. — Прим. перев.
2. Групповое кольцо бесконечной циклической группы 169
ко тогда, когда один из них равен другому, умноженному
на единицу.
Доказательство. Если элементы а и Ь ассоции-
ассоциированы, то существуют такие элементы с и d, что а = Ьсу
b = ad. Следовательно, a — adc и а{\—dc)=0. Так как
рассматриваемое кольцо является областью целостности,
то либо а, либо A —dc) равно нулю. Если а = 0, то то-
тогда и 6 = 0, и все доказано. Если же 1 —dc=Oy то эле-
элементы d я с являются единицами, и нужное утверждение
доказано. Предположим обратное, что a = ub, где и —
некоторая единица. Тогда Ь = аи~\ и элементы а и b ас-
ассоциированы. Доказательство утверждения B.1) за-
закончено.
Коммутативное кольцо R называется ассоциирован-
ассоциированным своему подкольцу Q, если существует такое отобра-
отображение р : R —*Q, что для любых a, b^R элементы а и ра
ассоциированы и p(ab) = (ра) (р&). Отсюда сразу еле»
дует, что
B.2) Если Q — область целостности, то R — также
область целостности.
Доказательство. Рассмотрим ненулевые эле-
элементы а и b кольца /?. Всякий элемент, ассоциированный
ненулевому элементу, должен быть ненулевым. Так как
Q — область целостности, то p(ab) = (ра) (рЬ)ФО, а зна-
значит, и аЬФО.
Элемент d коммутативного кольца R называется наи-
наибольшим общим делителем (сокращенно — н. о. д.) ко-
конечного м-ножества элементов аи ..., an£R, если d\ah
f=l, ..., п, и из того, что e\aiy edR, i=l, ..., п, сле-
следует, что e\d. Очевидно, что любые два н. о. д. одного
и того же конечного множества элементов ассоцииро-
ассоциированы. Не всякое конечное множество коммутативного
кольца имеет н. о. д. Пример этому дает кольцо всех
комплексных чисел вида m-{-nY—3, где m и п — це-
целые числа. Так как это нетривиальное подкольцо поля
комплексных чисел, то оно автоматически является об-
областью целостности. Его единственными единицами яв-
являются элементы +1 и —1. Нетрудно показать, что
170 Гл. VIII. Полиномы узла
любой общий делитель чисел 4 и 2 (l -f V — 3) является
одним из чисел ±1, ±2, ±A + у=з), ±A-/33).
Так как ни одно из этих чисел не делится другими, то
числа 4 и 2(l-+- V^—3) не имеют наибольшего общего
делителя. Назовем кольцо н. о. д.-областью, если оно
является областью целостности и всякое конечное мно-
множество его элементов обладает наибольшим общим де-
делителем.
B,3) Если коммутативное кольцо R ассоциировано
подкольцу Q, являющемуся н. о. д.-областью, то кольцо R
также является н. о. д.-областью.
Доказательство. Из B.2) следует, что /? — об-
область целостности. Сохраняющее умножение отображе-
отображение кольца R в Q обозначим, как и выше, через
р : R ~>Q. Рассмотрим произвольное конечное множество
элементов aif ..., ап кольца /?, и пусть d — н. о. д. в
кольце Q элементов рай ..., рап. Мы утверждаем, что
d —н. о. д. элементов аи ..., ап в кольце R. Прежде
всего, так как d|pa* и ра^а*, то d\a\, 1=1, ..., п. Пред-
Предположим далее, что e\ai9 /=1, ..., п. Тогда а1 = Ьге и
раг-=р6*ре, так что элемент ре делит в Q элементы ра*.
Так как d — н. о. д. этих элементов, то ре делит d в
кольце Q, а значит, ив/?. Следовательно, е\ре и pe|d,
поэтому e\d. Это завершает доказательство.
В области целостности, обладающей единичным эле-
элементом, два любых н. о. д. одного и того же конечного
множества элементов получаются один из другого умно-
умножением на единицу. Поэтому для таких колец обычно
говорят о любом наибольшем общем делителе d конеч-
конечного множества элементов аи ..., ап просто как о наи-
наибольшем общем делителе и пишут d=H. о. д. (аи ..., ап).
В настоящем параграфе пойдет также речь о поня-
понятиях простого числа и единственности разложения на
простые множители. Элемент р некоторой области це-
целостности называется простым, если он не является еди-
единицей, и из равенства p=ab следует, что либо а, либо Ь
есть единица. Область с однозначным разложением —
это область целостности, обладающая единичным эле-
элементом, в которой всякий элемент, не являющийся ну-
2. Групповое кольцо бесконечной циклической группы ///
лем или единицей, имеет однозначное в существенном
разложение на простые множители. Мы здесь говорим,
что разложение на простые множители однозначно в су-
существенном, если для любых простых ри q$, '^l» •••
..., m, /=1, ..., п, таких, что рх •... -рт = qx -... -qny
имеет место следующее: т — п и при соответствующем
изменении нумерации элементы р\ и qi ассоциированы,
/=1, ..., я. Утверждение о том, что кольцо целых чисел
является областью с однозначным разложением, и есть
знаменитая основная теорема арифметики.
B.4) Всякая область с однозначным разложением яв-
является н. о. д.-областью.
Доказательство. Пусть а — ненулевой элемент
области R с однозначным разложением. Объединяя про-
простые множители, ассоциированные друг другу, можно
получить разложение
а = ир\х • ... • рп™% m > О,
где никакие из простых элементов ри ..., Рт не ассо-
ассоциированы друг с другом, rij — положительные целые
числа и и — единица. Всякий делитель элемента а до-
пускает разложение и'р • ... • рп^\ где и! — единица,
a n'j — такие целые числа, что 0 < n'j < rtf). Аналогич-
Аналогично если аи . •., ап — ненулевые элементы кольца /?, то
существуют такие простые элементы рь ... ,рт, т>0,
что никакие два из них не ассоциированы друг с дру-
другом и
где tiij — целые числа >0, а и{ — единицы. Элемент
U = Pi1 • • • • • Р mt ft • ^^ Ш1П (П. •),
* * * т J \ i J/
i
является, очевидно, наибольшим общим делителем эле-
элементов аи •.., «п. Но область целостности, в которой
всякое конечное множество ненулевых элементов имеет
*) Считается, что а°=\. — Прим. перев.
172 Гл. VIII. Полиномы узла
н.о. д., и является н. о. д.-областью, так что доказатель-
доказательство закончено.
Мы предполагаем, что читатель имеет некоторое зна-
знакомство с определением и простейшими фактами, касаю-
касающимися кольца R[t] полиномов одного переменного t с ко-
коэффициентами в области целостности R. Например1),
нетрудно показать, что если R — область целостности, то
R[t] — также область целостности, единственными едини-
единицами которой являются единицы кольца R. Более глу-
глубокий результат (идея доказательства принадлежит
Гауссу) представляет следующая теорема2):
B.5) Если R — область с однозначным разложением
на множители, то R[t] — также область с однозначным
разложением на множители.
Теперь мы возвратимся опять к групповому кольцу
бесконечной циклической группы Я. После выбора обра-
образующего / группы Н произвольный элемент а кольца Ш
будет иметь единственное представление в виде
а = 2 ant\
где все целые числа ап, кроме конечного числа, равны
нулю. Отсюда следует, что кольцо полиномов /[([являет-
/[([является подкольцом кольца JH. Для каждого ненулевого эле-
элемента а кольца JH определим число \i(a), равное та-
такому наименьшему целому я, что апФ0. Например,
Если а = 0, положим |х(а)=оо и будем, как обычно, счи-
считать, что оо + оо = оо, оо+п = п + оо = оо. Тогда имеем
B.6) (я(а&)=(я(а) +\х(Ь) при любых а, b£JH.
Доказательство. Если либо а = 0, либо 6 = 0, то
утверждение B.6) очевидно, так что мы предположим,
') См. Зарисский О., Самюэль П., Коммутативная ал-
алгебра, т. 1, ИЛ, М., 1963, стр. 39.
2) См. там же, стр. 46.
2. Групповое кольцо бесконечной циклической группы ИЗ
что оба они не равны нулю. Пусть c = ab. Тогда, если
ОО ОО UO
я = 2ап*п, 6 = 2bntn и с=2cntn,
-оо
мы имеем
Сп = 2 ulbn-l= 2 Я^я-ч.
f = -oo f «М- (fl)
Если n<^i(a)+^i(&) и/>^(а), топ — /<п — fi(a)<ji(&),
так что ai-bn-i = 0. Значит, сп = 0, если n<ji(a) +\i(b).
Если n = ji(a)+|i(&) и />|x(a), то п — i<n — \i(a) =
= ^lF) И аг&п_г==0. СлеДОВаТеЛЬНО, ^м,(а)+м,(Ь) = ^ц(а)-&м,(Ь),
так как кольцо целых чисел — область целостности. До-
Доказательство закончено.
Если считать, что /-°° = 0, то очевидно, что для лю-
любого а£Ш элемент at~^a^ является полиномом. Следо-
Следовательно, отображение, определяемое равенством
pa = a^<a>, переводит кольцо JH в подкольцо полиномов
J[t]. Тот факт, что любая степень образующего / являет-
является единицей кольца /Я, показывает, что элементы а
и pa ассоциированы. Так как ^(а)/-м<(Ь)=:/-Ма)+м,(Ь)) прИ
любых а, &6/Я, то из леммы B.6) следует, что отобра-
отображение р сохраняет умножение. Отсюда мы заключаем,
что кольцо JH ассоциировано подкольцу полиномов J[t].
Из лемм B.5) и B.4) и основной теоремы арифметики
следует, что кольцо /[/] есть н. о. д.-область. Следова-
Следовательно, в силу предложения B.3) мы приходим к нашей
основной теореме:
B.7) Групповое кольцо бесконечной циклической груп-
группы является н. о. д.-областью.
Следует отметить, что, как тривиально следует из
леммы B.6), кольцо JH является областью целостности.
Пример группового кольца, не являющегося областью
целостности, дает нам групповое кольцо циклической
группы порядка 2, в котором имеет место равенство
t— l)=t2— 1=0.
Другой важный результат состоит в следующем:
174 Гл. VIII. Полиномы узла
B.8) Групповое кольцо бесконечной циклической
группы обладает только тривиальными единицами, т. е.
степенями образующего элемента /, взятыми с коэффи-
коэффициентом ±1.
Доказательство. Пусть а — единица кольца JH
и Ь — ее обратный элемент. Тогда а&=1 и (ра) (рб) =
= pi = 1. Единственными единицами кольца полиномов
J[t] являются элементы 1 и —1. Следовательно, ра =
= а£-^а)=±1 и а=±Ма\ что и завершает доказа-
доказательство.
Для построения примера нетривиальных единиц в
групповом кольце рассмотрим групповое кольцо цикли-
циклической группы порядка 5, порождаемой элементом t.
Тогда
= A — / + t3—\ +t)P =
Наши результаты для группового кольца бесконеч-
бесконечной циклической группы на самом деле верны и для
группового кольца свободной конечно порожденной абе-
левой группы. Доказательство остается прежним. Пусть
/( — свободная абелева группа (записанная мультипли-
мультипликативно) ранга т, порождаемая элементами tu ..., tm.
Тогда произвольный элемент а кольца JK имеет един-
единственное представление вида
где все целые числа ап . п , за исключением конеч-
1 * т
ного числа, равны нулю. Для элемента аФО определим
число \ii(a) как наименьшую степень переменного ^,
встречающуюся в записи элемента а. Соответствие р,
задаваемое формулой
pa^l*'1^' ••• •^1"'(а)'
10.
2. Групповое кольцо бесконечной циклической группы 175
определяет сохраняющее умножение отображение коль-
кольца JK в кольцо полиномов от т переменных J[tit ..., /m].
Ясно, что при этом каждый элемент сопряжен со своим
образом, так что кольцо JK ассоциировано своему под-
кольцу J[tu ..., tm]. Исходя из кольца целых чисел и
применяя т раз теорему B.5), получаем, что кольцо
•Фь • • •» tm] является областью с однозначным разложе-
разложением. Аналогичные соображения показывают, что един-
единственными его единицами являются элементы 1 и —1.
Леммы B.4) и B.3) вместе с очевидным аналогом лем-
леммы B.8) дают тогда полное доказательство того, что
B.9) Групповое кольцо свободной абелевой группы
ранга тХ) является н. о. д.-областью, единственными
единицами которой являются групповые элементы, взя-
взятые с коэффициентами ±1.
Понятие наибольшего общего делителя может быть
элегантно описано в терминах идеалов. Напомним, что
в коммутативном кольце R с единичным элементом 1
идеал Е, порожденный множеством S, представляет со-
собой множество всех конечных сумм
ЦаД, a, g 5, bt£R.
i
Эквивалентная характеристика идеала Е состоит в том,
что Е — наименьший идеал, содержащий множество S.
Под этим понимается пересечение всех идеалов кольца /?,
содержащих множество S. Поскольку идеал, содержа-
содержащий множество S, должен содержать идеал, порождае-
порождаемый этим множеством, эквивалентность этих двух под-
подходов очевидна.
Идеал называется главным, если он порожден одним
элементом. Нетрудно проверить, что два любых ассо-
ассоциированных элемента порождают один и тот же идеал
в кольце R и, обратно, два любых образующих глав-
ного идеала ассоциированы. В дальнейшем окажется
полезным понятие наименьшего главного идеала, содер-
содержащего данное конечное множество элементов. Един-
Единственной неприятностью здесь будет то, что в произволь-
произвольном коммутативном кольце такого идеала, вообще го-
говоря, не существует. Под наименьшим главным идеалом,
176 Гл. VIII. Полиномы узла
содержащим элементы аи ..., ап, мы понимаем пере-
пересечение главных идеалов рассматриваемого кольца,
содержащих элементы аи ..., ап. Это пересечение, ко-
конечно, — идеал, но не обязательно главный идеал.
B.10) Пусть R— коммутативное кольцо с единицей
и аи . • •, undR. Тогда элемент d тогда и только тогда
является н.о.д. элементов аи ..., ап, когда пересечение
всех главных идеалов кольца R, содержащих эти эле-
элементы, само является главным идеалом, порожденным
элементом d.
Доказательство. Предположим сначала, что
наименьший главный идеал D, содержащий элементы
а\, ..., ап, существует и d — его образующий. Тогда мы,
конечно, имеем, что d\a^ t=l, ..., п. Рассмотрим далее
произвольный элемент e£R, такой, что е\аи /=1, ..., п.
Главный идеал £, порождаемый элементом е, содержит
тогда элементы аи ..., ап, а значит, и идеал D. Следо-
Следовательно, d£E, так что e\d, откуда мы и заключаем,
что d есть н.о.д. элементов аь ..., ап. Пусть, обратно,
d есть н.о.д. элементов аи ..., ап и порождает главный
идеал D. Так как d\a{, i=l, ..., п, то отсюда следует,
что идеал D содержит все элементы аь ..., ап. Рассмот-
Рассмотрим далее произвольный главный идеал £, содержащий
элементы а\, ..., ап. Если е — образующий элемент
идеала £, то е\аи t=l, ..., п. Следовательно, e\d, от-
откуда вытекает, что идеал Е содержит идеал D. Множе-
Множество, которое является подмножеством каждого из мно-
множеств некоторого набора, есть пересечение множеств
этого набора. Поэтому D — наименьший главный идеал,
содержащий элементы аь ..., ап, и доказательство за-
закончено. В качестве следствия получаем
B.11) В н.о. д.-области, обладающей единичным эле-
элементом, н. о. д. всякого конечного множества элементов
является образующим наименьшего главного идеала, их
содержащего.
Образующий элемент главного идеала в таком коль-
кольце определяется, конечно, только с точностью до умно-
на единицу, и то же самое справедливо для н. о. д.
3. Полиномы узла 177
Поэтому последний результат верен постольку, поскольку
ой воюбще имеет смысл: строго говоря, утверждается, что
совпадают соответствующие классы эквивалентности.
3. Полиномы узла. Групповое кольцо бесконечной
циклической группы после выбора образующего груп-
группы t становится кольцом, которое можно назвать коль-
кольцом L-полиномов от переменного t. Использование бук-
буквы «L» подсказано аналогией со степенными рядами
Лорана из теории функций комплексного переменного,
содержащими члены с отрицательными показателями.
Вообще кольцо L-полиномов от п переменных tu tn
является групповым кольцом свободной абелевой группы
ранга п, порожденной элементами tu ..., tn. Отметим,
что для одного переменного понятия L-полинома и сво-
свободного полинома, которое было введено в предыдущей
главе, совпадают. Это происходит просто потому, что бес-
бесконечная циклическая группа является одновременно и
свободной, и свободной абелевой группой. Следует под-
подчеркнуть, что кольцо L-полиномов определяется не толь-
только групповым кольцом. Всякий элемент группового коль-
кольца бесконечной циклической группы, вообще говоря,
имеет два представления в виде L-полинома (например,
3t2 — 5t + t3 и t3 — 5t~l + 3t'2) в зависимости от того,
какой из двух образующих обозначен через t. Тем не
менее обычно говорят об элементах группового кольца
свободной абелевой группы, как об L-полиномах. Приме-
Примером этого, в частности, является следующее определение
полиномов узла.
Для всякого целого k^-0 k-м полиномом Аи конеч-
конечного копредставления (х: г) = (хи ..., хп : ги ..., гт)
группы узла называется наибольший общий делитель
всех миноров порядка п — k матрицы Александера этого
копредставления, причем считается, что
Дл = о, если п — k > m,
Дл = 1, если п —
Группа |х:г| канонически изоморфна группе узла, за-
задаваемой копредставлением (х:г), и, следовательно,
согласно теореме A.2), соответствующая ей прокомму-
тированная группа является, конечно, бесконечной цик-
Зак. 317
178 Гл. VIII. Полиномы узла
лической. Отсюда следует, согласно предложениям B.7)
и B.8), что групповое кольцо прокоммутированной груп-
группы |х:г| является н.о.д.-областью с тривиальными еди-
единицами. Мы заключаем, что
C.1) Полиномы узла существуют и единственны с
точностью до ±/п, где п — произвольное целое число, а
t — образующий элемент бесконечной циклической груп-
группы, являющейся прокоммутированной группой копред-
ставления (х : г) группы узла.
Наименьший главный идеал, содержащий данное
конечное множество элементов, является наименьшим
главным идеалом, содержащим идеал, порожденный
этими элементами. Следовательно, как следствие пред-
предложения B.11) и определений полиномов узла Дл и эле-
элементарного идеала Ek мы получаем следующую харак-
характеристику полиномов узла.
C.2) Всякий полином узла Д& является образующим
наименьшего главного идеала, содержащего элементар-
элементарный идеал Ей-
Из предложения C.2) и того, что эквивалентные ма-
матрицы имеют одинаковые элементарные идеалы, выте-
вытекает весьма важное на практике следствие. Полиномы
копредставлений, как и элементарные идеалы, могут вы-
вычисляться исходя из любой матрицы, эквивалентной
матрице Александера. Естественно при этом использо-
использовать по возможности простейшую из эквивалентных
матриц
C.3) Дм-ИД*.
Доказательство. Мы воспользуемся следствием
C.2) и тем, что элементарные идеалы образуют убы-
убывающую цепочку (см. D.1) гл. VII). Пусть (Л*) и
(A&+i)—главные идеалы, порожденные элементами Д&
и Aft+i соответственно. Имеем
Так как (Д&) —наименьший главный идеал, содержа-
содержащий идеал Е^ то
(ДЛ+,)=)(ДЛ).
Следовательно, Д* = аД*+ь или
3. Полиномы узла t79
Следующая теорема представляет собой аналог для
полиномов узла теоремы инвариантности элементарных
идеалов (см. D.5) гл. VII). Она, по существу, утверж-
утверждает, что полиномы узла являются инвариантами типа
узла.
C.4) Инвариантность полиномов узла. Если (х: г) и
(у : s) — конечные копредставления группы узла и
— их эквивалентность, то с точностью до единиц k-й по-
полином Д& — копредставления (х: г) отображается гомо-
гомоморфизмом ft* на k-й полином Д* копредставления
(y:s).
Доказательство. Мы воспользуемся следствием
C.2) и теоремой инвариантности D.5) гл. VII. Напо-
Напомним, что гомоморфизм /#* представляет собой линейное
расширение на групповое кольцо индуцированного изо-
изоморфизма прокоммутированной группы |х:г| на про-
коммутированную группу |y:s| (см. D.4) и предше-
предшествующий параграф гл. VII). Обозначим через (ДЛ) и
(Д^) главные идеалы, порожденные соответственно Д&
и Д*. а через Eh и Ей —элементарные идеалы копред-
ставлений (х: г) и (y:s). Тогда
£*с(ДД £ic(Ai) и UEk = El
Далее, образ главного идеала при изоморфизме есть
снова главный идеал и f**(kk)^ f**Ek=Ek- Так как
/**\ / /**
идеал (Д*) минимален, то
По тем же самым соображениям
так что
ид*)=(д;)-
Так как идеал fx%(&k) порождается элементом /««Да,
элементы Д^ и /**Дл ассоциированы, а потому полу-
12*
ISO Гл. VIII. Полиномы узла
чаются один из другого умножением на единицу. Это
завершает доказательство.
Предыдущая теорема является фундаментальной. Из
нее непосредственно следует, что полиномы узла яв-
являются инвариантами типа узла. Напомним еще раз ос-
основные моменты: A) если два узла представляют один
и тот же тип узлов, то их группы изоморфны (см. D.7)
и последующее обсуждение в гл. II); B) два копред-
ставления изоморфных групп принадлежат к одному
и тому же типу копредставлений и, следовательно, ме-
между ними существует эквивалентность (см. B.4) и со-
сопровождающее обсуждение в гл. IV). Давайте посмот-
посмотрим, как применяется теорема инвариантности на сле-
следующем примере. Предположим, чго мы задались двумя
узлами К и К' одного и того же типа и хотим найти для
некоторого целого k соответствующие полиномы Aft и
Д*. Мы находим какое-то верхнее копредставление узла
Л", по возможности упрощаем его, вычисляем матрицу
производных, выбираем образующий элемент прокомму-
тированной группы и получаем матрицу Александера.
Затем мы ухитряемся найти н. о. д. всех миноров поряд-
порядка п — k и, наконец, приходим к некоторому L-полино-
му, скажем, Д& = 3^3— 5t2 + t. Так как полином узла оп-
определен однозначно только с точностью до единиц, то
естественно нормализовать его, получив полином
Д& = 3^2— 5^+1, т. е. полином, не имеющий отрицатель-
отрицательных степеней и содержащий константу. Заметим, однако,
что вид нормализованного полинома зависит от выбора
образующего в прокоммутированной группе копредстав-
ления. Если мы выберем другой образующий s = t~lf то
нормализованный полином примет вид А^ = 52 — 55 + 3,
который по виду отличается от полинома З/2—5/+1.
Однако этот полином ассоциирован в кольце JH перво-
первоначальному. Возникает следующий вопрос: если мы
аналогичные вычисления проделаем для узла К' и най-
найдем д£, то что можно сказать об этом полиноме? Да-
Давайте предположим, что мы выбрали соответствующий
образующий х, так что Д* является L-полиномом от х.
Так как узлы К и К' имеют один и тот же тип, то их
группы изоморфны и существует изоморфизм /** между
3. Полиномы узла 181
прокомментированными группами их копредставлений.
Отметим, что вне зависимости от того, насколько слож-
сложно описать изоморфизм между группами узлов, отобра-
отображение Z** устроено весьма просто. Существуют только
две возможности отобразить изоморфно одну бесконеч-
бесконечную циклическую группу на другую: либо /##@ =*, либо
f**(t)=xrl. В нашем примере, следовательно, либо
f**Ak = 3x2 — 5x+l, либо Злг2 — блг1+ 1.
В силу теоремы инвариантности C.4), мы имеем
/мДЛ = ± xnk'k' Следовательно, если полином Д* нор-
нормализован, то существуют только две возможности
Д^ = 3л:2 —5jc+1 или х2 — 5jc + 3.
Как мы указали выше, эти два взаимно обратных вида
полинома одинаково хороши.
Рассмотренный выше пример носит условный харак-
характер, так как мы докажем в следующей главе, что если
Дл@==£л'Я~£л-1'Я~1'4" ••• +£q—некоторый норма-
нормализованный полином узла, то * d = cn-u 1=0, ..., п.
Следствием этой симметрии является то, что нормали-
нормализованный вид полинома узла является инвариантом
типа узла. В частности, если нормализованные поли-
полиномы Д* и Д£, соответствующие узлам К и /(', не сов-
совпадают при некотором &Х), то узлы /С и /С' имеют раз-
разные типы.
Во всяком верхнем копредставлений группы узла
любое одно из соотношений является следствием других
и, следовательно, может быть отброшено (см. A.3) гл.
VII). Поэтому группа узла всегда имеет копредставле-
ние с матрицей Александера порядка (п—1)Хп. Сле-
Следовательно,
C.5) Нулевой элементарный идеал и полином груп-
группы узла тривиальны: £о = До = О.
На самом деле это утверждение представляет собой
частный случай более общего утверждения, состоящего
в том, что нулевой элементарный идеал конечного ко-
представления тривиален тогда и только тогда, когда
182 Гл. VIII. Полиномы узла
прокоммутированная группа копредставления беско-
бесконечна *).
Пусть (х : г) = (хи ..., хп:ги ..., гт) — копредстав-
копредставление заданной группы узла. Обозначим через у гомо-
гомоморфизм свободной группы, порожденной элементами
Хи • • •, хп на свою факторгруппу |х:г|, а через а —
гомоморфизм коммутирования группы |х:г|. Предполо-
Предположим, что все образующие элементы копредставления
отображаются гомоморфизмом ау в один и тот же эле-
элемент, т. е.
C.6) ayxt = ayxj9 i, j = 1, ..., п.
Это условие, в частности, выполняется для верхних ко-
представлений (см. A.1)). Элементы матрицы Алексан-
Александера A = ||a<j|| копредставления (х:г) определены равен-
равенством
*) Действительно, пусть прокоммутированная группа М конеч-
конечного копредставления (х: г) бесконечна. Тогда, очевидно, суще-
существует гомоморфизм /: Я -> У, отображающий Н на группу целых
чисел. /. Рассмотрим копредставление и= (х : г, {[*,-, Xj]}, h\, ..., hh),
где элементы hi таковы, что множество {аЛг} /=1, ..., k порождает
ядро гомоморфизма /. Ясно, что группой этого копредставления
является группа, изоморфная /, а его матрицей Александера —
матрица вида А' = ^ , Где А — матрица Александера копред-
копредставления (х:г). Очевидно, Eh(A')ZD Eh(A). Но поскольку к — ко-
копредставление группы /, Ё0(Л/)=0, а значит, и Е0(А)=0.
Обратно, пусть группа Н конечна. Рассмотрим копредставление
х= (х: г [}{[xi> хз\}) группы Н и обозначим через А' его матрицу
Александера. Непосредственно проверяется, что Ь4' = ~ , от-
II и
куда, очевидно, \Ek(A') =iEh(A). Но так как Я —конечная
абелева группа, то она допускает и такое копредставление
трица Александера этого копредставления, то Ы" =|!0 ... рт I
So ... о I
как показывает непосредственный подсчет. Стало быть, t£0 (А) =
= t£0 (A') = tE0(A") = /?, ... ртф0, значит, и £О (А) Ф 0. —
Прим. перев.
3. Полиномы узла 183
Согласно основной формуле (см. B.11) гл. VII),
Так как у^г=1, получаем
Но поскольку ayxl = uyXj1 /=1, ..., я, мы можем запи-
записать это так:
Элемент ay*i является образующим элементом беско-
бесконечной циклической группы, совпадающей с прокомму-
тированной группой |х:г|, так что (ауАг4 —1)=£0. Но
так как групповое кольцо бесконечной циклической
группы является областью целостности, то
S
т. е. сумма столбцов матрицы Александера равна нулю.
Следовательно,
C.7) Матрица Александера А всякого конечного ко-
представления группы некоторого узла, удовлетворяю-
удовлетворяющего условию C.6), эквивалентна матрице, полученной
заменой произвольного столбца матрицы А столбцом
нулей.
Предположим, что (х: г) — верхнее копредставление
с п образующими и п— 1 соотношениями. Как было за-
замечено выше, условие C.6) в этом случае выполнено,
так что предложение C.7) применимо. В этом случае
матрица А является матрицей порядка (п—1)Хп. Если
один из ее столбцов заменить нулями, то у полученной
матрицы остается по меньшей мере один отличный от
нуля минор порядка (п —- 1) X {п -— 1). Так как эквива-
184 Гл. VIII. Полиномы узла
лентные матрицы определяют одни и те же элементар-
элементарные идеалы, то отсюда следует, что первый элементар-
элементарный идеал копредставления (х: г) является главным.
Следовательно, в силу C.2) получаем
C.8) Первый элементарный идеал группы узла яв-
является главным идеалом, порожденным первым полино-
полиномом узла At.
Первый полином узла Ai является наиболее важным
в последовательности полиномов узла. Он называется
полиномом Александера группы узла и часто записы-
записывается без нижнего индекса, т. е.
Ясно, что любой минор порядка (п—1)Х(п—1)
матрицы А может быть взят в качестве полинома Ai.
4. Типы узлов и полиномы узлов. Следующие при-
примеры иллюстрируют возможности использования поли-
полиномов узла. Из них станет ясно, что эти инварианты
дают нам действенное средство различения типов узлов
в весьма широком диапазоне. Наши вычисления осно-
основаны на результатах предыдущих параграфов. Напри-
Например, следствием предложения A.1) является то, что
матрица Александера всякого верхнего копредставления
может быть получена заменой в матрице производных
всех образующих хг элементом t. С другой стороны,
обычно выгодно перед тем, как вычислять производные,
упростить верхнее копредставление. При этом, если все
образующие некоторого копредставления группы узла
отображаются при гомоморфизме а у в один и тот же
образующий элемент прокоммутированной группы, то
тем же свойством будет обладать и любое другое ко-
представление, полученное из исходного при помощи
операций Титце |, V и II'. Стало быть, мы можем заме-
заменять образующие х\ элементом t после упрощения верх-
верхнего копредставления, но при условии, что при этом мы
не вводим новых образующих. Отметим, что для этих
копредставлений справедливо утверждение C.7). Это
обстоятельство очевидно позврляет значительно сокра-
сократить вычисления,
4. Типы узлов и Полиномы узлов 185
Копредставления групп гораздо чаще записываются
при помощи соотношений, чем при помощи более фор-
формальных элементов соотношений
Соотношение ^ = 5г- соответствует элементу соотношения
г^г1. Имеем
drtsjl dr, ds;
dxj dxj i i dxj
Так как естественный гомоморфизм у переводит всякий
элемент соотношения в 1, вычисление элементов ац мат-
матрицы Александера упрощается, если заметить, что
дг1*Тх
В следующих примерах мы сначала рассмотрим те
узлы, для которых мы уже вычислили в гл. VI копред-
копредставления групп.
D.1) Тривиальный узел (рис.46).
7Г(Я3-К)=\х:\
Рис. 46.
Вместо того чтобы говорить о матрице с одним
столбцом, но без строк, мы заметим, что копредставле-
ние (х:) имеет тот же тип, что и копредставление
(х:1). Следовательно, его матрицей Александера яв-
является просто матрица Л = ||0|| и
Afc=l, k>\.
186
Гл. VIII. Полиномы узла
D.2) Клеверный лист (рис. 47).
Два элемента соответствующей матрицы Александера
А = Цацами таковы:
ХУ — У)>
1 — ух).
ап = аУ -^ (ХУХ — УхУ) =
ai2 == аУ Jf (ХУХ — УХУ) =
Полагая ayx = ayy = t$ получаем
Следовательно,
и Дл = 1,
так что клеверный лист не может быть развязан. Мы,
однако, уже доказали это в гл. VI.
Рис. 47.
D.3) Восьмерка. Копредставление Виртингера, в ко-
котором х и у соответствуют переходам, показанным на
рис. 48, можно упростить, получив копредставление
я(/?3 — К) = \х, у :yx~lyxy-{=x-lyxy-lx\.
Снова мы полагаем ayx = CLyy — t. Наши вычисления со-
сокращаются наполовину, если заметить, что (поскольку
предложение C.7) имеет место для всякого верхнего ко-
представления) любой из двух элементов матрицы Алек-
4. Типы узлов и полиномы узлов
187
сандера можно положить равным полиному Ai. Следо-
Следовательно,
1—1-1=*
После нормализации получаем
Очевидно, что Ал = 1, &>2. Мы заключаем отсюда, что
восьмерка — нетривиальный узел, тип которого отличен
от типа клеверного листа.
Рис. 48.
D.4) Турецкая чалма (рис. 49).
л \/\ i\ ) — |-^1» -^2» -^3' -^4 '
[—11 I
/ = 1, ..., 4 — целые mod4|.
Как можно увидеть из рис. 49, это копредставление по-
получено упрощением копредставления Виртингера. Обра-
Образующие хи • • •, #4 представляют собой четыре из восьми
первоначальных образующих, поэтому мы полагаем
Ki = t, t=l, ..., 4. Матрица Александера Л = ||аг;||
188
Гл. VIII. Полиномы узла
задается равенствами
— — (х —
Следовательно, имеем
а«=1
i = \y ..., 4; индексы — целые
числа по mod 4.
Любое из четырех соотношений является следствием
Рис. 49.
трех других и может быть отброшено, г. е. мож'но опу-
опустить 4-ю строку матрицы А и получить
1
3
1
1
t-2
— t + 2
-Г1 1
2
—1
1
— 24-Г1
3
__г_1_2—г1
-1
1
4
t-2 + ri
-t + 2-Г1
j
Читателю предоставляется проверка операций пере-
перехода в следующей редукции матрицы А к эквивалент-
4. Типы узлов и полиномы узлов
189
ной матрице более простой формы:
t — 2 f t
0
1
t — 2 -f t
0
0
-i
-i
,-i
0
0
-1
1
+ Г1
0
0
1 ,-1
0
0
+ Г1
T-l-l
— ^ -f-2 — t
—1
0
—/ + 2 —Г1
—1
0
—1
0
'"') 0
0
0
0
0
0
0
0
0
0
0
»
У
0 0
—1 0
t—\-+t
J
о о
г1)
о о
1-4-Г1 0
Следовательно, нормализованные полиномы таковы:
Это означает, что рассматриваемый узел не является
ни тривиальным, ни клеверным листом, ни восьмеркой.
Отметим, что элементарные идеалы Ег и Е2 являются
главными идеалами: £4 порождается полиномом Дь
а Ег — полиномом Лг-
Рис. 50.
Рис. 51.
4. Типы узлов и полиномы узлов 191
D.5) Узел грузчика (рис. 50).
Здесь х и (/ — образующие копредставления Виртин-
гера, так что мы полагаем ayx = ayy=t. Используя
C.7), получаем
= —24-2/ +t — {—2t 4 2*2) =
= -2*24 б/-2.
Старшие полиномы, очевидно, все равны 1. После нор-
нормализации получаем
Д1 = 2*2 — 5/+2,
Старшие элементарные идеалы совпадают со всем коль-
кольцом, т. е.
£\ = B*2 — 5* 4-2),
£, = A), k>2.
D.6) Узел, изображенный на рис. 51.
Здесь мы опускаем детали. Можно упростить копред-
ставление Виртингера и получить
jt(/?3 —/С) = |л:, у, г:ги г8|,
где х, у, г —образующие копредставления Виртингера,
указанные на рис. 51, а элементы соотношений г4 и гг
соответствуют следующим соотношениям:
г2: x
При гомоморфизме ау образующие х, у, z переходят в
элемент/,и матрица Александера этого копредставления
192
Гл. VIII. Полиномы узла
может быть без труда выписана. Получаем
Следовательно,
1 з*-1-
3-3* -
-1+2*
2 — * О
О
— Г: + 2 —2Г1
Г1 —2 О
-1+2* О|
1—2* О
2*
О
О
Так как полиномы 2 — * и 1—2* различны и непри-
зодимы, их н. о. д. равен 1. Следовательно,
-2*) = 2 —5* + 2*2,
Второй элементарный идеал £2 порождается элемента-
элементами 2 — / и 2/—1. То, что этот идеал не совпадает со
всем групповым кольцом JH прокоммутировадной груп-
группы копредставления, можно усмотреть, гомоморфно ото-
отображая кольцо JH на кольцо целых чисел, положив
/—*—1, /-1-*— 1. При этом гомоморфизме идеал Е2
отображается на идеал, порожденный тройкой, так как
1 — 2/ -> 3.
4. Типы узлов и полиномы узлов
193
Мы заключаем отсюда, что
£2 = B — tt 1—2t) — не главный идеал,
£, = A), k>3.
Сравнение этого примера с предыдущим показывает,
что узлы, представленные на рис. 50 и 51, имеют одина-
одинаковые полиномы, но разные элементарные идеалы. Эти
примеры оправдывают утверждение, сделанное в гл. VII
Рис. 52.
Рис. 53.
и во введении к этой главе, состоящее в том, что элемен-
элементарные идеалы являются более сильными инвариантами,
чем полиномы.
D.7) Узлы, изображенные на рис. 52 и 53.
Матрица Александера любого из этих узлов эквива-
эквивалентна матрице
Следовательно, методы, развитые в двух последних гла-
главах, недостаточны для того, чтобы их различить. Однако,
13 Зак. 317
194
Гл. VIII. Полиномы узла
как это может быть показано другими методами, их
группы неизоморфны3).
D.8) Бабушкин узел и сквер-узел (рис. 54 и 55).
Можно показать с помощью более совершенной техники,
что узлы, приведенные на рис. 54 и 55, относятся к раз-
а ха ■» ют
Р и с. 54.
Рис. 55.
ным типам узлов4). Однако методы этой книги уже с
самого начала недостаточны для различения их: они не
только имеют эквивалентные матрицы Алексавдера, но
даже обладают изоморфными группами, для каждой из
3) Например, с помощью инвариантов зацепления второго раз-
разветвленного циклического покрытия, см. S e i f е г t H., Die Ver-
schlingungsinvarianten der zyklischen Knotenuberlagerungen, Hamb.
Abh., 11 A935), 84—101*).
*) См. по этому поводу приложение I, § 5. — Прим. перев.
4) F о х R. H., On the Complementary Domains of a Certain Pair
of Inequivalent Knots, Ned. Akad. Wetensch., Indag. Math-, 14
A952),37—40; Seifert H., Verschlingungsinvarianten, S.B. Preuss.
Akad. Wiss. Berlin, 26 A933), 811—823.
4. Типы узлов и полиномы узлов
195
которых мы имеем
я (R3—К) = | х, у, а:а~1ха=хах~1, a'
= yay-i\
УПРАЖНЕНИЯ
1. Для каждого из пяти узлов, описанных в упраж-
упражнении 1 к гл. VI, найти матрицу Александера с одной
строкой и двумя столбцами. Вычислить элементарные
идеалы и полиномы этих узлов.
Р и с. 56а.
Рис. 56Ь
Рис. 56с.
Рис. 56d.
2. Вычислить элементарные идеалы и полиномы для
каждого из следующих четырех узлов:
а) узел истинной дружбы, Ь) узел ложной дружбы,
с) китайская роза, d) беседочный узел.
3. Используя копредставление группы торического
узла КР, q, приведенное в упражнении 3 к гл. VI, пока
зать, что его полином Александера
и£2=1.
13*
196 Гл. VIII. Полиномы узла
4. Доказать, что степень нормализованного полинома
Александера не превышает числа точек пересечения на
любой из его диаграмм.
5. Показать, что матрица Александера узла, пред-
представленного на рис. 57, принадлежит к тому же классу,
что и матрица тривиального узла.
Рис. 57.
6. Доказать, что группа «восьмерки» не может
быть гомоморфно отображена на группу «клеверного
листа».
7. Если мы свяжем два узла на одном и том же ку-
куске веревки, то получим так называемый составной узел.
Доказать, что полином Александера составного узла
равен произведению полиномов Александера составляю-
составляющих его узлов.
8. Пусть k и п — целые положительные числа. По-
Попытаемся сопоставить каждому переходу Xj регулярной
проекции узла целое число К] таким образом, чтобы для
каждого пересечения Xj-> j ->xJ^l выполнялось соот-
xk
ношение k(Xk— Kj)=kh — Xj+i(mod/2). Доказать что это
можно сделать нетривиальным способом тогда и только
тогда, когда A(&)=20(modn).
9. Доказать, что группа узла может быть гомо-
гомоморфно отображена на группу, приведенную в упраж-
упражнении 12 к гл. VII тогда и только тогда, когда
4. Типы узлов и полиномы узлов 197
10. Пусть /(/)—целочисленный полином. Попытаем-
Попытаемся сопоставить каждому переходу Xj некоторой регуляр-
регулярной проекции узла целочисленный полином Aj(t) таким
образом, чтобы для каждого пересечения (обозначения
упражнения 8) имело место соотношение
t(Ak(t) -ЛИ/))=Л*(/) -Лж(/) (mod/(/)).
Доказать, что это можно сделать нетривиальным спосо-
способом тогда и только тогда, когда полином f(t) делит (
ГЛАВА IX
ХАРАКТЕРИСТИЧЕСКИЕ СВОЙСТВА
ПОЛИНОМОВ УЗЛОВ
Введение. Обзор полиномов узлов А/*(/), вычислен-
вычисленных в конце предыдущей главы, показывает, что для
любого из них Л/<A) = ±1. Доказательство того, что это
равенство имеет место для полиномов любого узла, со-
составляет содержание первого параграфа данной главы.
Этот же обзор подтверждает также предположение, что
все полиномы узлов являются взаимными, т. е. для лю-
любого полинома узла Ak(t) найдется такое целое /г, что
A/i@ =/"A/i(/). Следовательно, если Д*@ =cntn +
+ cn-itn~l+ ... +Со, то коэффициенты сг- обладают сле-
следующей симметрией: Ci = cn-h * = 0, ..., я*). Как было
указано в третьем параграфе гл. VIII, это свойство су-
существенно необходимо для вывода о том, что узлы од-
одного и того же типа обладают идентичными полиномами.
Поэтому нам важно ликвидировать этот пробел в тео-
теории. Доказательство того, что полиномы узла являются
взаимными, будет осуществлено в §§2 и 3 введением по-
понятия дуальных копредставлений группы, важным при-
примером которых являются верхнее и нижнее копредстав-
ления группы узла, определенные в гл. VI. Следует под-
подчеркнуть, что наши аргументы применимы только для
ручных узлов. Поэтому в этой главе слово «узел» будет
всегда означать «ручной узел».
Известно *), что свойства
—взаимный полином,
*) Если, конечно, сп ф 0, с0 Ф О. — Прим. перев.
l) Seifert H., Ober das Geschlect von Knoten, Math. Ann.,
110 A934), 571—592; Torres G., Fox R. H., Dual Presentations
of the Group of a Knot, Ann. of Math., 59 A954), 211—218.
1. Операция тривиализации 199
вполне характеризуют первый полином, или полином
Александера Ai@- Другими словами, всякий L-поли-
ном, обладающий этими свойствами, является первым
полиномом некоторого узла*).
1. Операция тривиализации. Всякий элемент а груп-
группового кольца JH бесконечной циклической группы Н
имеет представление в виде L-полшюма
где все, за исключением конечного числа, целые ап рав-
равны нулю. Образ элемента а при гомоморфизме тривиа-
тривиализации t :/#-*/ получается подстановкой в этот
L-полином значения ^=1 (см. § 1, гл. VII). Поэтому мы
пишем ta = a(l). Последовательность целых чисел
'|Д/гA)|, k = l9 2, ..., является инвариантом типа узла,
более простым, чем сами полиномы узла Д*(/). Хотя
всякий полином узла определен только с точностью до
умножения на ±tn, абсолютное значение |АлA)| одно-
однозначно определяется классом изоморфии группы уз-
узла. Этот инвариант, однако, бесполезен как средство
различения типов узлов. В этом параграфе будет дока-
доказана интересная теорема о том, что для любой группы
узла
A.1) |Д*AI=1- *=1, 2
Следующее утверждение эквивалентно A.1).
A.2) Для всякого конечного копредставления (х: г)
группы узла и всякого целого k > 1 образ элементарного
идеала Eh копредставления (х: г) при гомоморфизме
тривиализации t совпадает со всей группой целых чи-
чисел, т. е. t Ek = J, k=l, 2, ... .
Нетрудно показать, что утверждения A.1) и A.2)
эквивалентны. Заметим прежде всего, что, так как
*) Недавно J. Levine доказал, что следующие свойства необ-
необходимы и достаточны для того, чтобы последовательность полино-
полиномов Ai@» I===l» 2, ..., была последовательностью полиномов некото-
некоторого узла: 1) Дю(/) = 1, ш>п0; 2) ДгA) = ±1; 3) Д*(t) — взаимный
полином, /=1,2, ...; 4) Ai_i@/Ai@ делит Аг(/)/Дг + i (/) в коль-
кольце QG L-полиномов с рациональными коэффициентами. См. также
примечание 27 на стр. 307. — Прим* перев.
200 Гл. IX. Характеристические свойства полиномов узлов
+| (см. C.3) гл. VIII), утверждение A.1) эквива-
эквивалентно |Ai(l)| = l. Аналогично элементарные идеалы
образуют возрастающую цепь, так что утверждение
A.2) эквивалентно тому, что tEi = J. Мы показали, что
Е{ является главным идеалом, порожденным элементом
Ai. Отсюда следует, что идеал t E\ порожден tA1 = A1(l).
Следовательно, если |Ai(l) |=1, то- tEi = J. Обратно, об-
образующий элемент всякого главного идеала в области
целостности определен однозначно с точностью до еди-
единиц. Поэтому если t Ei = J, то |Ai(l)| = l.
Докажем A.2). Пусть (х:г) = (*ь ..., хп:ги...,гп)
есть конечное копредставление группы узла и Л—его
матрица Александера. Вследствие леммы D.6) гл. IV
црокоммухированная группа узла имеет копредстав-
лен-ие (х:г, [xiy Xj], i, /=1, ,.., п). Обозначим мат-
матрицу Александера этого копредставлеиия через А'.
Так как прокоммутированная группа любого узла яв-
является бесконечной циклической, то копредставление
(х:г, [хи Xj\ i, /=1, ..., п) имеет тот же тип, что и ко-
копредставление (#:). Элементарные идеалы последнего
таковы: £l0=@), Ei = E2= ... =A). Из теоремы инва-
инвариантности элементарных идеалов (см. D.5) гл. VII)
следует, что
Идеал A), порожденный единичным элементом 1, сов-
совпадает, конечно, со всем кольцом. Заметим далее, что
образ всякой матрицы Александера при гомоморфизме
тривиализации совпадает с образом исходной матрицы
свободных производных при тривиализации. Более того,
^[хг х.\ = bikA -х.Х;Х7*) + bjk(х. -x.XjXTi*ji),
так что
Следовательно,
2. Сопряжение 201
Используя результаты этого параграфа и утверждения
D.2) и D.3) гл. VII, получаем, что
tEk (A) = Ek (tA) = Ek (tAf) = tEk (A') =
@), k = 0,
•Л & ^ *■»
так что доказательство теоремы A.2) закончено.
2. Сопряжение. Цель этого и следующего парагра-
параграфов— доказать следующую теорему:
B.1) Для всякого полинома узла Д/*(/) найдется та-
такое четное целое число п, что
Отметим, что если теорема B.1) имеет место для не-
некоторого полинома &h(t), то она также имеет место и
для произведения этого полинома на единицу.
оо
Степень L-полинома a(t)—^amtm (все числа ат>
—оо
кроме конечного числа, равны нулю) есть разность ме-
между наибольшим и наименьшим значениями индекса т,
при которых атФ0. Так как это число не меняется ни
при умножении на единицу ±th, ни при замене перемен-
переменного 5 = /, то степень полинома узла является коррек-
корректно определенным инвариантом типа узла. Если полином
Ak(t) выбран нормализованным (у него нет отрицатель-
отрицательных степеней переменного t, и свободный член положи-
положителен), то целое число п, фигурирующее выше в теореме
B.1), является, очевидно, степенью полинома Ak(t):
Таким образом, из теоремы B.1) следует не только, что
полиномы узла являются взаимными полиномами, но
и что
B.2) Всякий полином узла имеет четную степень.
Отображение ()~1:G->G, относящее каждому эле-
элементу g некоторой группы G его обратный элемент g~l,
является взаимно однозначным и отображением на, но
не изоморфизмом (если группа G не абелева). Так как
это отображение обращает умножение вместо того, чтобы
202 Гл. IX. Характеристические свойства полиномов узлов
его сохранять, т. е.
1 = h~Y\ g, k£O,
то оно называется антиизоморфизмом. Важный, но,
впрочем, тривиально проверяемый факт состоит в том,
что отображение ( ) перестановочно с гомоморфиз-
гомоморфизмами, т. е. для всякого гомоморфизма ср: G — Н следую-
следующая диаграмма коммутативна:
<pl
Единственное линейное продолжение отображения ( )"!
на групповое кольцо JG (см. A.2) гл. VII) называется со-
сопряженным и обозначается черточкой. Следовательно,
Используя теорию дуальных копредставлений, которая
будет изложена в § 3, мы докажем следующую важную
теорему:
B.3) Элементарные идеалы Ек любого конечного ко-
представления группы узла_инвариантны относительно
операции сопряжения, т. е. Ek = Ehi й = 0, 1, 2, ... .
Теорема B.1) является следствием теорем B.3) и
A.1). Доказывается это так. Обозначим через Дь глав-
главный идеал, порожденный полиномом узла Aft. Напомним,
что (А/г) —наименьший главный идеал, содержащий
идеал Eh. Так как Ekcz (Дй), то
Но в групповом кольце абелевой группы сопряжение
является кольцевым изоморфизмом, так что (Дь) = (Дь).
Так как идеал (Ak) минимален, то
и мы заключаем отсюда, что
3. Дуальные копредставления 20д
Образующие главного идеала в области целостности оп-
определены однозначно с точностью до единичных множи-
множителей, поэтому
л, (о = 8^D).
где е= ± 1. ^Конечно, здесь ДЛ(*) = ДЛ> а Д
Если й = 0, то обе части написанного равенства — нули,
так что значение, принимаемое числом е, в этом случае
не играет роли. Если й>0, то нам известно из A.1), что
A/i(l)=£0. Следовательно, подстановка /=1 немедленно
дает нам, что е=1. Записывая Л/<(/) =co + Ci/+ ... +cntn,
мы отсюда находим, что сг=сп_г-, i=0, ..., п. Если чи-
число п было бы нечетно, мы на основании A.1) получили
бы, что
что невозможно. Следовательно, число п четно. Итак,
теорема B.1) выведена из теорем B.3) и A.1).
3. Дуальные копредставления. Опередление дуаль-
дуальных копредставлений удобно формулируется на языке
сравнений. Если / : R —► /?' — гомоморфизм колец и
о-и #26^?, мы пишем ai=a2(mod/) (#i сравнимо с а2 по
модулю f) всякий раз, когда fai = fa2. (Это выражение
употребляется наиболее часто при рассмотрении гомо-
гомоморфизма кольца целых чисел J на кольцо JVклассов
вычетов.) Два конечных копредставления некоторой
группы (х : г) = {хи ..., хп:ги .. •, гп) и (у: s) =
= (У\> •••, Уп'-Su •••, sn) образуют пару дуальных ко-
копредставлений, если существует такая эквивалентность
копредставлений 8 : (х : г) —► (у : s), что
(I) ex.EE^-^modaY), / = 1, ..., /г,
Лу = 1 /г.
Здесь у — гомоморфизм, являющийся расширением на
групповое кольцо канонического гомоморфизма свобод-
свободной группы, порожденной элементами уи .. • , Уп, на ее
факторгруппу |y:sl, а a —коммутирование.
204 Гл. IX. Характеристические свойства полиномов узлов
Дуальные копредставления имеют ipso facto один и
тот же тип, так что имеет смысл говорить о дуальных
копредставлениях данной группы. Мы утверждаем, что
группа любого узла обладает парой дуальных копред-
ставлений. Точнее, мы докажем, что верхнее и нижнее
Рис. 58.
копредставления A.1) и A.2) из гл. VI взаимно дуаль-
дуальны. Мы будем предполагать, что К — полигональный
узел в регулярном положении, расположенный так, как
описано в § 1 гл. VI, и что переходы, проходы, ориен-
ориентации, образующие, базисные точки и т. д. выбраны так
же, как и там. Будут использованы те же обозначения.
Копредставления A.1) и A.2) сокращенно обозначим
(х: г) и (у : s) соответственно, а канонические гомомор-
гомоморфизмы групп F(x), F(y), на их факторгруппы |х:г|,
|y:s( будут оба обозначены через у. Пусть а — класс
эквивалентных путей в /?3—-К с началом в точке /?о и
концом в точке ро. Отображение т|, определяемое равен-
равенством
-а
для любого рбя(/?3 — /С, ро), является изоморфизмом
группы я(Я3 — /С, ро) на группу л(/?3—/С, р'о) (см. C.1)
3. Дуальные копредставления 205
гл. II). Этот изоморфизм индуцирует естественный изо-
изоморфизм 8* группы Iх:г 1 на группу ly:s|, реализуе-
реализуемый эквивалентностью копредставлений 0: (x:r)->(y:s)
(см. B.3) и B.4) гл. IV). Все эти весьма простые факты
суммируются в следующей коммутативной диаграмме:
е
X е ^
Х|«Г'~> «I'
Рассмотрим произвольный проход Bhf соприкасаю-
соприкасающийся с некоторым переходом А$. Если р—-класс экви-
эквивалентности пути, изображенного ниже на рис, 58, то
ясно, что
щХ; = (а • Г1) • (Р • Ф*у • Р) • (Р • а)
и
Следовательно,
) = (а • р) • (q/f/J1) • (р • а),
так что
Ъ*уХ; = о.(уу-1).о-\
где а —образ элемента (а-р*1) при изоморфизме
я(/?3 — К, р'о)» | у : s |. Обозначая гомоморфизмы ком-
коммутирования групп |х:г| и ly:s| одной и той же бук-
буквой а, окончательно получаем
<хуЪх} = ьв*уХ; — а [а . (уу^1) • а] = ауу~1.
Это вместе с тем обстоятельством (см. A.1) гл. VIII),
что
C.1) Xi-zBXj (moday), /, у = 1, ..., п,
влечет за собой сравнение
вхк=гуь1 mod (ay).
Итак, условие (I) определения дуальных копредставле-
копредставлений проверено.
206 Гл. IX. Характеристические свойства полиномов узлов
Следствием двух предыдущих сравнений является
сравнение
C.2) #/ = {/у (modav), /, у = Ь . ., п.
Более того (см. A.П и A.2) гл. VIII), прокоммутиро-
ванная группа ly:sl, являющаяся бесконечной цикли-
циклической группой, порождается единственным элементом
s= <хууи i=l, ..., п.
Для того чтобы проверить свойство (II), нам пона-
понадобится следующая лемма:
C.3) Пусть а и Ь —некоторые простые пути в
R2 — еРВ и R2— <&*А, имеющие одни и те же концевые
точки (г. е. а{0)=Ь@) и а(\\а\\) = Ь(\\Ь\\)). Тогда
ва% = (ЬЬу1 (mod ay).
Доказательство. Из сравнений C.1) и C.2) на-
находим
а#=х[ (mod cry) при некотором целом /,
b^^yf (mod ay) при некотором целом пг.
Выберем далее такой простой путь с в R2 — S^А с теми
же концевыми точками, что и у путей а и ft, что
cb=y[ (mod (IY).
Имеется несколько способов подобрать такой путь с
Например, можно просто идти вдоль пути а по возмож-
возможности ближе к нему, огибая всякую встречающуюся
проекцию перехода (см. рис. 59). Предположим, что
путь а проходит под переходом А^ вклад которого в
элемент а # равен х*}. Тогда, как показано на рис. 59,
вклад в элемент с^ пересечений пути с с проходами,
возникающих при огибании проекции <^Mj, имеет вид
Следовательно, суммы показателей у элементов а# и сЬ
равны. Так как cb:1 —замкнутый путь, не пересекающий
проекций переходов, то
3. Дуальные копредставления
207
£b==£b (mod cry),
у[=у™ (modcry)..
Следовательно,
так что
Так как элемент &yyi порождает бесконечную цикличе-
циклическую группу, мы приходим к выводу, что 1 = т. Окон-
Окончательно, используя условие (I), получаем
6а# = §х™ = у~т = (bb)~l (modav),
и доказательство закончено. Отметим, кстати, что лемма
C.3) в качестве частного случая содержит условие (I).
Рис. 59.
Копредставления (х: г) и (у: s) не зависят от формы
и размеров областей Vu ..., Vn и Uu • • •, Un. Следо-
Следовательно, мы можем предполагать, что точки каждой из
них расположены достаточно близко от проекций тех
проходов или переходов, которые они покрывают. Рас-
Рассмотрим произвольную пару целых чисел i, /=1, ..., п.
Мы имеем (см. A.1) и A.2) гл. VI) r.=cf • vf -(cfy1 и
(яП?)". Заметим, что
дГ:
dc
dvf dcf
dvf
208 Гл. IX. Характеристические свойства полиномов узлов
dsf
диЧ
и аналогично
Следовательно, для проверки условия (II) нам следует
выяснить, как входит элементу в vf, a yt в иЪ. Мы
скажем, что переход Aj смежен проходу Ви если они
имеют общую концевую точку, т. е. они располагаются
друг за другом при обходе вдоль узла К- Различные
встречающиеся случаи можно классифицировать сле-
следующим образом.
Случай A). Переход Aj не проходит над проходом
В{ и не смежен с ним. В этом случае vf не содержит
элемента xJt а
не содержит элемента у{. Значит,
А К .
1
и*
у
ЧА
\
ч
\
V
¥
1
-^. J
h
f\ !
v;
4 9
<
Bx
r — ~'
Aj ,/--*'
Рис. 60.
Случай B). Переход Aj проходит не менее одного
раза над проходом Bit но не смежен с ним. Мы допу-
допускаем возможность того, что Aj проходит над Вг не-
несколько раз. Вкладом каждого пересечения пути Vi с
проекцией S^Aj в производную drjdxj является некото-
некоторый одночлен, и dri/dxj в точности есть сумма таких
одночленов. Аналогично производная dsj/dt/i является
суммой одночленов, соответствующих пересечениям пути
3. Дуальные копредставления 209
Uj и проекции ePBi. Следовательно, мы можем изучать
каждое пересечение в отдельности. То, что происходит
около отдельно взятого пересечения проекций звеньев В\
и Aj, показано на рис. 60. В этом случае
Следовательно,
&гi , ,и ... ... ... . -... . ^/ — 1
vy. j J У1 А
Поэтому
J^L(xr-\)=cfeb{\—f*)(x)—\)+ ... (mod ay),
— l)+ • • • (modav).
Согласно лемме C.3), имеем
'1 (modov),
(modov),
6^ = (*b) (modoy).
Значит,
откуда вытекает, что
*) Многоточия здесь и ниже обозначают сумму такого же рода
членов, соответствующих другим пересечениям. — Прим. перев<
14 Зак. 317
210 Гл. IX. Характеристические свойства полиномов узлов
Случай C). Переход Aj смежен проходу Bt. Этот
случай изображен на рис. 61. Мы имеем здесь
г,
Следовательно,
В силу леммы C.3),
в (*?**) ^(йГ]^) (modav),
Qxej==yie (moday),
так что
Мы уже видели в случае B), что пересечение проекций
звеньев Aj и Вг дает члены, которые попарно аннули-
аннулируются по mod ay. Откуда следует, что
9
} - 1)) = IJ: (^ - 1) (mod ay).
и доказательство дуальности копредставлений (х: г) и
(у: s) закончено. Итак, мы доказали, что
C.4) Соответствующие друг другу верхнее и нижнее
копредставления группы узла являются дуальными.
Инвариантность элементарных идеалов при сопря-
сопряжении группы' узла, т. е. утверждение B.3) является
прямым следствием теоремы C.4). В силу сравнений
C.1), C.2) и условия (I) мы получаем более сильный
результат
= -^- (modav), i, у = 1, ..., п.
3. Дуальные копредставления
211
Значит, если А и В — матрицы Александера копредстав-
лений (х : г) и (у : s) соответственно, то
C.5) Q**A=B*.
(Индекс t обозначает транспонированную матрицу.)
Транспонированная матрица имеет, очевидно, те же эле-
элементарные идеалы, что и исходная матрица. Обозначим
k-e элементарные идеалы копредставлений (х: г) и
/е
Рис. 61.
(у: s) через E{k} и £*2) соответственно, а k-и идеал не-
некоторой матрицы М — через Ek(M). Следовательно,
Е^) = Ек(А)9 E{k} = Ek(B). Наконец, получаем (см. D.3)
и D.5) гл. VII)
еТ = ejsP=Ek (в<) = Ek (В) = ^7Щ
Следовательно, теорема B.3) этого параграфа дока-
доказана.
УПРАЖНЕНИЯ
1. Показать, что существует автоморфизм группы G
клеверного листа, индуцирующий отображение сопряже-
сопряжения на прокоммутированной группе G/G'.
2. Используя результат упражнения 1, непосред-
непосредственно показать (т. е. без использования дуальных
14*
212 Гл. IX. Характеристические свойства полиномов узлов
копредставлений),что элементарные идеалы группы кле-
клеверного листа инвариантны отно-сительно сопряжения.
3. Доказать непосредственно (т. е. без использова-
использования дуальных копредставлений), что элементарные
идеалы всякого обратимого узла инвариантны относи-
относительно сопряжения.
4. Показать, что полином Александера Д(/) любого
узла может быть записан в виде
-tfh
и, обратно, для данного множества целых чисел
си ..., си найдется узел, полином Александера которого
равен
5. Доказать, что не существует узла, группа кото-
которого имела бы следующее копредставление:
\х, У: хух~хух=ух~хуху\.
6. Доказать, что А(—1) всегда является нечетным
целым числом.
7. Пусть Д(/)—полином Александера некоторого
узла степени 2ft и е — комплексное число, лежащее на
единичной окружности. Показать, что число А(е)/ел дей-
действительно.
8. Пусть Д(/)—полином Александера некоторого
узла степени 2h и со — примитивный корень кубический
из единицы. Показать, что Д(о))/со/1 — целое число.
9. (См. упражнение 8.) Показать, что Д(со)/сол =
=Д((о2)/со2/1 и, значит, число Д(о)*Д(со2) является квад-
квадратом некоторого целого числа.
10. Доказать, что если (— примитивный корень чет-
четвертой степени из единицы, то Д@Д(—0—квадрат
целого числа.
ДОБАВЛЕНИЕ I
Дифференцируемые узлы — ручные. Пусть К — узел
в трехмерном пространстве /?3, спрямляемый и заданный
как образ периодической вектор-функции /?($) =
= (x(s), y(s)t z(s)) длины дуги 5, производная которой
р'(s) =* (x'(s), y'(s)t г'($)) существует и непрерывна при
всех 5. Период / является длиной узла /С. Докажем, что
такой узел К ручной, т. е. эквивалентен полигональному
узлу.
Обозначим норму, или длину, вектора /?6/?3 через
Ир||, а скалярное произведение векторов ри /?г€/?3 через
/?1«/?2. Если ни р\у ни р2 не равны нулю, то угол между
ними определяется равенством
Рассмотрим любые три значения параметра So, Si, 52,
удовлетворяющие неравенству So^si<$2. Из соотноше-
соотношения
s2 s2 s2
JV(«)<*»= / P'(so)du+ j (p'(u)-p'(so))du
St 5, 5,
следует, что
P(s2)-P(si)^(s2~sl)(p'(so)-+ Q), A)
где
Так как параметр соответствует длине дуги, то
\\p'{so)\\ = 1. Следовательно,
214 Добавление I
так что
где <7~ некоторое число, удовлетворяющее неравен-
неравенству |<7|<|Q|. Значит,
IIР (s2) - Р (Si) II = (s2 - sx) A + q). B)
Выберем некоторое положительное число е<72. Так
как производная p'(s) непрерывна, а значит, и равно-
равномерно непрерывна, найдется такое 6>0, что если
\s — s'^e, то lp'(s) — p'(s')l<e. В соответствии с
этим наложим ограничение s2 — so<6. Тогда
(S2_Sl)|Q|| = J (р'(и)-р'(so))du\<(s2-5,)е
и
£е. C)
Деля равенство A) на B), получаем
где
Так как ?> — е>—1/2, то 1/A+<7)<2. Значит,
E)
Сделаем теперь два вывода из предыдущих соотно-
соотношений. Во-первых, следствием соотношений B) и C) яв-
является хорошо известный факт:
A.1) Отношение длины хорды к длине дуги узла К
стремится к 1 при стремлении к нулю длины дуги.
Второй вывод представляет собой основную лемму,
на которую опирается наше доказательство того, что
узел К ручной.
A.2) Для любого угла а>0 существует такое 6>0,
что при любых 5, s\ uy и\ лежащих на интервале длины
б и таких, что s<s' и и<и\ имеем
)-P{s)> РМ-Р(*))«*-
Добавление I 215
Доказательство. Эта лемма является следстви-
следствием соотношений D) и E). Если
so=:min [s, s', и, uf),
то
Следовательно,
Р (s') — р (s) р(и') — р(и)
\\p(s')-p(s)\\
где
Поэтому
Правая часть может быть сделана произвольно малой.
Значит, cos ^C(pis') — p(s), p(u') — p{u)) как угодно
мало отличается от 1, откуда следует лемма A.2).
Обратимся теперь к основным соображениям, пока-
показывающим, что узел К ручной. Пусть агс(/?, /?') для лю-
любых двух точек /?, р'£ К обозначает меньшую из длин
между иими, вычисленную вдоль узла К. Заметим,
что если \s — s'\^Cl/2, где / — длина всего узла,
то arc(/?(s), p{s')) = \s — s'\. Рассмотрим функцию
f : KXK-+R, определяемую равенством
IP-p'll/arc(p, р'), РФр\
Мы показали, что отношение длины хорды к длине дуги
стремится к единице, когда длина дуги стремится к
нулю. Следовательно, функция /(р, р) непрерывна. Так
как она положительна, а ее область определения ком-
компактна, то она имеет положительный минимум т.
Значит,
\\р-р'\\>тък(р,р% р.р'еК. F)
Выберем далее положительный угол ао<я/4 так,
чтобы tgcco^w/2, и подберем для этого угла число б в
216
Добавление I
соответствии с леммой A.2). Пусть п — целое положи-
положительное число, такое, что //п<б/2. Выберем такие значе-
значения параметра {^}^-00, что si+i —■ s{ = //я. Заметим,
что p(Si) =p(Sj) тогда и только тогда, когда i=/(mod n)y
так что множество [p(si)}c^ma_oo состоит ровно из п то-
точек узла. Построим для каждого значения S{ двойной
заполненный конус*) Сг- с углом ао при вершине, ось ко-
которого совпадает с хордой, соединяющей точки p(Si) и
p(Si+i) (см. рис. 62).
Рис. 62.
Следующие четыре предложения следуют из леммы
A.2) и неравенства F).
A.3) Смежные конусы пересекаются только в общей
вершине.
Доказательство. Так как s/+2--Sj = (s/+2 —
—Sj+1)+(sj+1—5/)<6, то острый угол между осями кону-
конусов d и Сг-+1 меньше, чем угол а0, который в свою оче-
очередь меньше чем я/4. Угол при вершине конуса равен
ао, следовательно, не может быть пересечения в других
точках, кроме вершины.
A.4) Если Si^s-^Si+i, то p(s) 6 С{.
*) Здесь имеется в виду тело вращения равнобедренного тре-
треугольника вокруг его основания. — Прим. перев.
Добавление I 217
Доказательство. Имеем
— Р E)
откуда непосредственно вытекает A.4).
A.5) Для всякого сечения D любого из конусов Си
перпендикулярного оси, найдется в точности одно такое
число s из интервала [sif si+i]t что p(s) €D.
Доказательство. Существование такого 5 сле-
следует из предложения A.4) и непрерывности функ-
функции р. Для доказательства единственности предположим,
что 5/<5<5/<5/+1 и что точки р(s) и p(s') лежат на
одном и том же перпендикулярном оси сечении конуса
С{. Тогда угол *3L(p(s') — p(s), p(si+l) — p(st)) должен
с одной стороны быть равен я/2, а с другой — быть мень-
меньше чем о&о. Приходим к противоречию.
A.6) Несмежные конусы не пересекаются.
Доказательство. Предположим противное, т. е.
что существуют несмежные конусы С* и Cjt пересекаю-
пересекающиеся в точке р (см. рис. 63). Пусть p(s) — такая
точка, лежащая в плоскости, содержащей точку р и пер-
перпендикулярной к оси конуса Си что s^s-Of+i. Анало-
Аналогично выберем точку p(s) для конуса С]. Тогда
и такое же неравенство имеет место для точки p{s'). Так
как конусы Ci и Cj не смежны, то, как мы знаем,
— < arc (p (s), p (sf)). Следовательно,
||/i(s)-p(s')\\<2arc(p(s), p(s'))t§ao< marc(p(s), p(s')).
Но это противоречит неравенству F), что и доказывает
предложение A.6).
Доказательство того, что узел К ручной, в сущности,
закончено. Осталось только проверить, что для любого
двойного конуса С« существует гомеоморфизм Ы этого
конуса Ci на себя, тождественный на границе и перево-
переводящий дугу К П Ci на ось конуса. В силу предложений
218
Добавление I
A.4) и A.5) конструкция такого отображения неслож-
несложна. Рассмотрим произвольный замкнутый круглый
диск D с центром в точке /?0. Мы допускаем возможность
того, что диск D вырожден, т. е. D = {p0}. Для всякой
внутренней точки р диска D определено отображение
gDp\ D -> D, линейно отображающее всякий отрезок,
P(S)
~~~—^—-Ц/-
Phi
i /^
соединяющий точку р с некоторой точкой q, лежащей на
окружности, на отрезок, соединяющий точки ро и q так,
что р-*ро, q-*q (см. рис. 64). Очевидно, что go, v — го-
гомеоморфизм диска D на себя, оставляющий границу ди-
диска неподвижной и переводящий точку р в точку р0. Бо-
Более того, отображение gDtv(p') непрерывно по совокуп-
совокупности переменных р и р'.
Возвращаясь к двойному конусу, рассмотрим произ-
произвольную точку pdCi. Пусть p(s) — точка пересечения
узла К с плоскостью, содержащей точку р и перпенди-
перпендикулярной к оси конуса Сг-. Эта плоскость пересекает ко-
конус С{ по диску (вырожденному, если точка р совпадает
с вершинами Сг), который мы обозначим через Ds. Иско-
Искомый гомеоморфизм 1гг: Сг -> С* можмо определить теперь
Добавление I
219
равенством
„с
(/>)•
существование и единственность точки p(s) как некото-
некоторой внутренней точки диска Ds является следствием
предложения A.5) и доказательства предложения A.4).
Р и с. 64. Перпендикулярное сечение конуса.
Последний шаг состоит в продолжении гомеомор-
гомеоморфизмов hi до отображения h пространства Rz на себя,
которое определено равенством
*(/>) =
kt(p),
То, что гомеоморфизм h определен корректно, следует
из A.3) и A.6) и из того, что гомеоморфизмы /г* тожде-
тождественны на границах конусов. Итак, мы получаем
Теорема A.7). Узел К ручной.
Есть два интересных дополнения к этой теореме, о
которых стоит упомянуть. Первое состоит в том, что ко-
конусы Ci могут, очевидно, быть выбраны как угодно ма-
малыми, т. е. так, чтобы максимум их диаметров был
220 Добавление I
меньше, чем любое наперед заданное число е. В результате
получаются узлы К, которые называют е-эквивалентлыми
полигональному узлу. Для любого е>0 найдется такой
гомеоморфизм h пространства R3 на себя, что узел hK
полигонален и \\h(p) — р||<е при всех р€/?3. Более того,
гомеоморфизм h сдвигает только те точки, которые от-
отстоят от узла не более чем на е. Второе дополнение со-
состоит в том, что гомеоморфизм h реализуется изотопиче-
изотопической деформацией пространства R3. Это происходит про-
просто потому, что отображение go, p изотопно тождествен-
тождественному. Используя векторные обозначения, мы можем по-
положить
Следовательно, дифференцируемый узел (как он опреде-
определен в начале этого дополнения) является ручным в са-
самом строгом возможном смысле.
Вопрос о том, когда узел является ручным, был изу-
изучен рядом авторов. Например, Милнор1) ввел понятие
абсолютной кривизны к произвольной замкнутой кри-
кривой и доказал (вместе с другими результатами), что
если абсолютная кривизна узла конечна, то узел ручной.
Он также показал, что если замкнутая кривая С задана
как образ функции p(s) длины дуги s с непрерывной
второй производной, то абсолютная кривизна к задается
обычной интегральной формулой
*=l\\p"(s)\\ds.
l) Mil nor J. W., On the Total Curvature of Knots, Ann. Math.,
52 A950), 248-257.
ДОБАВЛЕНИЕ II
Категории и группоиды. Тенденция современной ма-
математики рассматривать почти всякое множество свойств
в отрыве от первоначального контекста, давать ему спе-
специальное название и развивать абстрактную теорию по-
породила удивительный лексикон и массу различных опре-
определений. Очевидно, что эти определения сильно отли-
отличаются и областями их приложений, и глубиной сопут-
сопутствующих им теорий. Некоторые из них, например по-
понятия группы или топологического пространства, имеют
без преувеличения фундаментальное значение для всей
математики. Другие в большой степени являются просто
удобными, а зачастую и весьма специальными обозначе-
обозначениями, преследующими в основном «сортировочные»
цели. Понятия категории и группоида настолько, на-
насколько они необходимы для этой книги, принадлежат
к последнему классу1). Интересно, что они оказы-
оказываются удобными для систематизации идей, возни-
возникающих при построении понятия фундаментальной
группы.
Некоторое множество С называется категорией, если
для некоторых пар элементов ее, р€С определено про-
произведение этих элементов, принадлежащее также С и
удовлетворяющее нижеследующим аксиомам (I) и (II).
Элемент е£С называется единицей, если для любого
а€С всякий раз, когда определено произведение е*а
х) Идея категории играет основную роль при аксиоматическом
развитии теории гомологии. И в самом деле, определение катего-
категории и последующая лемма A1.1} взяты непосредственно из гл. IV
книги Эйленберга С. и Стинрода Н., Основания алгебраической
топологии, Физматгиз, М., 1958.
222 Добавление II
(или а-е), имеет место равенство е-а=сс (или
а • е = а).
(I) Произведение а -(Р • у) определено тогда и только
тогда, когда определено произведение (сс-р)-у. Когда
определено хотя бы одно из этих произведений, имеет
место ассоциативный закон
Более того, произведение а • р • у (скобки опущены в
силу ассоциативности) определено тогда и только тогда,
когда определены оба произведения а • р и р • у.
(II) Для всякого элемента а из С найдутся в С та-
такие единицы 8i и 82, что произведения е4 • а и а • е2 опре-
определены.
Читатель заметит, что мы уже встречались с этими
свойствами выше. В самом деле, основное содержание
начала гл. II можно резюмировать следующим образом:
Как множество всех путей топологического простран-
пространства X, так и фундаментальный группоид Т(Х) являются
категориями. Отображение первой из этих категорий во
вторую, сопоставляющее каждому пути а его класс эк-
эквивалентности [а], является отображением на, сохраняет
умножение и переводит множество единиц первой кате-
категории на множество единиц второй.
Теперь мы можем проследить, как в абстрактном
виде проводятся рассуждения, соответствующие тем,
которые проводились при построении фундаментальной
группы узла.
Докажем сначала, что
(II.1) Для каждого элемента а категории С единицы
8i и е2, такие, что произведения е4 • а и а • е2 определены,
единственны.
Доказательство. Предположим, что существуют
такие единицы гГ г[ £ С, что произведения е, • а и е( • а
определены. Тогда произведение г[ • (ех • а) определено,
так как ei»a = a. Следовательно, определено произведе-
произведение e(-elf так что ej = e{«e1 = e1. Аналогично един-
единственна и единица ег.
Добавление II 223
Для всякой категории С и единицы е£С мы обозна-
обозначим через Се множество всех таких элементов а £ С, что
произведения е • а и а • е определены.
A1.2) Множество Се является полугруппой.
Доказательство. Произведение единицы на себя
определено всегда*). Следовательно,е£Сг. Рассмотрим
далее произвольные элементы аир множества Се. Так
как произведения а • е и е • р определены, то определены
произведения (а - е) - 0 и (а • е) • 0 = а • 0. Значит, опреде-
определено произведение двух любых элементов множества
Се. Поскольку при этом ассоциативный закон имеет ме-
место, наше доказательство завершено.
И множество всех /^-базисных узлов и фундаменталь-
фундаментальная группа я (х, р) являются, конечно, примерами мно-
множества Се в соответствующих категориях.
Элемент а"*1 категории С называется обратным для
элемента а, если существуют такие единицы ei и е2 кате-
категории С, что a-a~1 = ei и a~1-a = 82.
(П.З) Произведения ei • a, a • 82, 82-сг1 и а"*1 • ei
определены.
Доказательство. Так как произведение ei • ei
определено, определены и произведения ei • а • а"*1 и
а • а • ei. Отсюда следует, что определены произведе-
произведения 8i • а и а • ei. Аналогичные рассуждения справед-
справедливы и для произведений a • е2 и е2 • а".
(II. 4) Если обратный элемент существует, то он един-
единствен.
Доказательство. Предположим, что элементы
р и р' обратны элементу а. Из леммы (П.З) и (II. 1)
следует, что единицы ei и е2, существование которых сле-
следует из существования обратного для элемента а, одно-
однозначно определены элементом а. Значит,
a-p = a«p/ = 6i и р • а=р' • а = б2.
*) Действительно, из определения единицы следует существо-
существование такого а, что произведение а•ei (или ei • а) определено.
Но тогда определено произведение (a* 8j) • 8i = a«Ei (или
ei • (ei • a)=ei • а), а значит, и произведение ер г\. —Прим. перев.
224 Добавление II
Так как, согласно лемме (II. 3), определено произведе-
произведение 62 • р', мы получаем
что и требовалось.
Группоид — это категория, в которой каждый эле-
элемент имеет обратный. Из леммы B.4) гл. II ясно, что
множество Т(Х) классов эквивалентности путей в про-
пространстве X удовлетворяет всем требованиям, наклады-
накладываемым на группоид.
(II. 5) Если С —группоид и е— единица, то множе-
множество Се — группа.
Доказательство. Рассмотрим некоторый эле-
элемент а £Се. Так как С — группоид, то элемент а имеет
обратный а"*1 и существуют такие единицы ei и е2 в ка-
категории С, что a-a"*1==8i, a~1«a = 82, и произведения
ei • а, а • 82, ег • а~! и а"*1 • е4 определены. Так как а € Се.
то произведения е • а и а • е определены, и мы можем
заключить на основании леммы (II. 1), что e=8i = e2.
Следовательно, сг1 €Се, Этот вывод вместе с лем-
леммой (II. 2) завершает доказательство.
Абстрактный аналог теоремы C.1) из гл. II также
имеет место. Доказательство, по существу, то же самое.
(II.6) Пусть С — группоид, ei и 82 — некоторые его
единицы, а а — такой его элемент, что произведения
ei • а и а • 82 определены. Тогда для любого элемента
Р 6 ^е, произведение а • р • а определено и соответ-
соответствие р —* а"*1 • р • а является изоморфизмом группы Се,
на группу Се2-
ДОБАВЛЕНИЕ III
Доказательство теоремы ван Кампена. Формулиров-
Формулировка этой теоремы дана в C.1) гл. V. Нам нужно дока-
доказать две вещи. Во-первых, что
(III. 1) Образы групп озг(/г-, i' = 0, I, 2, порождают
группу G.
Доказательство. Рассмотрим произвольный не-
нетривиальный элемент а € G и /^-базисную петлю
а : [0, ||а||]—>ХУ представляющую этот элемент. Так как
а=£1, то, как мы знаем, ||а||>0. Построим такое раз-
разбиение
O = tQ<tx< ... </я = ||а||
отрезка [0, ||а||], что каждый из отрезков [t{—/ы] содер-
содержится по крайней мере в одном из прообразов а~1Хи
j = 0, I, 21). Выберем далее функцию индексов jn, ото-
отображающую целые числа /=1, ... , п на множество чи-
чисел 0, 1,2, таким образом, что
я['/-1. tt]cX»ti)> ' = Ь .... л.
Для каждой точки /г-, i' = 0,..., дг нашего разбиения вы-
выберем путь Ь{ в пространстве X так, чтобы он удовле-
удовлетворял следующим условиям:
(I) bt@) = p и А/(||А/||) = а(//),
(II) если a(ti) = pi mo bt{t)~p при всех t,
, / = 1 л—1.
Заметим, что условие (III) может быть удовлетворено,
поскольку пересечение Хи .п П Ха (/+1) совпадает с одним
1) См. П о н т р я г и н Л. С, Непрерывные группы, § 13, стр. 79.
15 Зак 317
226 Добавление HI
из пространств^, Х\ или Х2, каждое из которых линейно
связно. Рассмотрим далее пути аг:[0, ti — f<_1]-+A',
i=l, ... , nt определяемые равенством аг{г) =a(t + ti-{).
Ясно, что
\{
Так как каждое из произведений 6/_i • at • bt l опреде-
определено, а пути bo и Ьп единичны, имеем
Каждый из путей bi^\ai-bi является /^-базисной пет-
петлей, образ которой лежит целиком в пространстве X^>
и которая, следовательно, является представляющей
петлей элемента со^ос* для некоторого а* € G^i). Значит,
и доказательство утверждения (III. 1) закончено.
Вторая часть теоремы ван Кампена такова:
(III.2) Если Н — некоторая группа и i|?i: G* -* Я,
i=0, 1, 2, — гомоморфизмы, удовлетворяющие условию
^o=<ti0i=\|?202, то найдется единственный гомоморфизм
%: G-+ Н, такой, что грг-=Ясог-, * = 0, 1, 2.
Доказательство. Единственность гомоморфизма
Я доказать нетрудно. Если он существует, то соотноше-
соотношения г|>* = Я(йг, ' = 0, 1, 2, и утверждение (III. 1) показы-
показывают, что он единствен. Остается доказать его суще-
существование, которое устанавливается с помощью следую-
следующей очевидной конструкции. Пусть а — произвольный
элемент группы G. Мы показали, что
п
а = П
так что мы можем положить
п
Добавление III 227
Трудность состоит в доказательстве того, что отображе-
отображение X определено корректно. Если это установить, то до-
доказательство теоремы тем самым будет закончено, так
как предыдущие формулы показывают, что X —гомомор-
—гомоморфизм, удовлетворяющий соотношениям t|?i = tao*, /=0,1,2.
Наша задача равносильна доказательству того, что для
любого множества элементов щ £ G^, где /= 1,..., г,
а [г — некоторое отображение множества целых чисел
1, ... , г в множество чисел 0, 1,2, равенство
г г
П®14</)В/= 1 влечет за собой равенство Ц \ {1)щ = 1.
Проверка этого утверждения и является целью после-
последующего доказательства.
Выберем представляющие петли аг-£аь /=1,...,г.
Тогда произведение
эквивалентно единичному пути. (Для простоты мы бу-
будем обозначать отображение вложения и индуцирован-
индуцированный им гомоморфизм фундаментальных групп одним и
тем же символом.) Эта эквивалентность осуществляется
семейством путей {hs} с фиксированными концами, или,
что то же самое, таким непрерывным отображением
h:R-+X, где
Я=[0.||а|||Х[0. 1Ь
что
h (/, 0) = а(*),
Вертикальные линии /== 2||я*||, '=Ь •••• г» осуще-
осуществляют разбиение прямоугольника R. Мы рассмотрим
его подразбиение
0=/0</,< ... <tn = \\a\\,
O = so<s,< ... <sm = \
15»
228 Добавление HI
на прямоугольники Rij, настолько мелкие, что каждый
из этих прямоугольников содержится по меньшей мере в
одном из прообразов h~lX{y f=0, 1, 2. Каждый прямо-
прямоугольник Rij состоит из всех пар (/, s), удовлетворяю-
удовлетворяющих неравенствам
< < i = 1, . . ., П.
Так как рассматриваемое подразбиение было выбрано
достаточно мелким, существует такая функция индексов
v (*,/), что
hRijd Xvili ;), /= 1, ..., п, ]= 1, ..., т.
Для каждой точки решетки {tu Sj) выберем путь ец в
пространстве X, удовлетворяющий следующим условиям:
(IV) начальной и конечной точками пути ец являют-
являются точки р и h(tu Sj) соответственно;
(V) если h(ti, Sj) =p, то eij(t)~p при всех t\
(VI) образ пути e\j содержится в пересечении
Xyj a, j) П ^v (/+ь у) П ^v (/, y+i) П Xv (/+1> ;Ч1)
(мы предполагаем, что Xv^tj)=X, если /=0 или п+\
или если /=0 или т+\)\
(VII) если Sl|e*IK'<-i<'/<Sll^ll. то образ
й1 Л1
пути ei0 содержится в Х^у
Условия (IV), (V) и (VII) полностью аналогичны
условиям (I), (II) и (III) соответственно. Условие (VII)
вносит дополнительные усложнения. Определим далее
следующие пути (-см. рис. 65):
и положим
Из условия (VI) вытекает, что образы петель сщ, Ъ\$,
at, j_j и &f-i,j лежат в пространстве Яу(*,л- Следователь-
Добавление HI
229
но, они определяют элементы а.;., р/у, a'.J9 р,у группы
Ov(i, j) соответственно. Произведение aly ;_i • й/у • ajj • Ы\ у
путей стягиваемо (т. е. эквивалентно единичному
пути) в X. Более того, так как образ прямоугольника
Rij так же, как и образы этих четырех путей, лежит в
Х^ j), их произведение стягиваемо в Xv{i>j). Из этого
мы заключаем, что
Центральная идея нашего доказательства предложе-
предложения (III. 2) основана на том, что если элементы а (; Gi
Рис. 65.
и P6gj» *\ / = 0» '> 2, обладают общей представляющей
их петлей, то t|ha=iJ?jP.
Доказательство этого не представляет труда. Так как
Xt[\ Xj = Xk при некотором & = 0, 1 или 2, то каждое из
отображений вложения
vr tit V Лг V
Л i —-> Л ь < Л j
является либо тождественным отображением, либо од-
одним из вложений 6i или 62. Вследствие этого индуциро-
индуцированные гомоморфизмы
должны быть согласованы с гомоморфизмами \|?0, i|H и
ф2> т. е. лргг]1==1|5л =i|?7r]2. Предположение о том, что эле-
элементы ее и р обладают общей представляющей петлей,
230 Добавление III
дает нам существование такой р-базисной петли с в про-
пространстве Xhi что r\ic£ а, г|2с€р. Следовательно, если
петля с определяет элемент у€ Gk, то
r]iY = a, Л27 = Р-
Поэтому
и наше утверждение доказано.
Применяя этот результат, мы получаем
Применим теперь гомоморфизм tf^j) к равенству A).
Получаемое соотношение утверждает, что результат об-
обхода всякого прямоугольника Rij против часовой стрел-
стрелки отображается гомоморфизмом t|)v(Z-, ^ в единицу. Соот-
Соотношения B) показывают, что при этом общие отрезки
смежных прямоугольников уничтожаются. Отсюда сле-
следует (по индукции), что результат обхода вокруг гра-
границы всего большого прямоугольника R равен единице.
Более того, только элементы, соответствующие нижнему
основанию 5 = 0, нетривиальны. Следовательно, мы мо-
можем отсюда заключить, что
j
Так как каждое из чисел 2 И#*И» У=Ь •••» г» яв-
ляется элементом множества [tv ..., tn)t существует
такая функция /(/), что /@)=0 и
у
ti{))= S || a* ||f у=Ь ..., г.
Л — 1
Тогда вследствие условий (IV) и (V) мы имеем
В силу условия (VII), можно считать, что эта экви-
эквивалентность имеет место в пространстве Х^. Следова-
Добавление III 231
тельно, каждая петля аг0, * = '(/ — 1) + 1, ... , i(j), опре-
определяет элемент ^^G(A(^) и
KJ)
Так как элементы ал и а\ обладают общей предста-
представляющей петлей п{оУ из нашего основного утверждения
следует, что
Наконец, имеем
1 =
и доказательство утверждения (III. 2) закончено.
Предложенное доказательство теоремы ван Кампена
может быть использовано для доказательства более об-
общей теоремы2), копией доказательства которой является
наше доказательство. Вместо того чтобы рассматривать
пространство X как объединение двух пространств Х4
и Лг, мы рассмотрим произвольную совокупность линей-
линейно-связанных открытых подмножеств Х{ (i может про-
пробегать любое множество индексов), замкнутую относи-
относительно операции конечных пересечений и удовлетворяю-
удовлетворяющую условиям:
Х= [) Х{ и существует точка /?€ П Хг-.
Пусть Gi = n(Xiy p) и G = n(Xy p). Рассмотрим все гомо-
гомоморфизмы Qij: Gj —* Gj, о)г-: Gi — G, индуцированные вло-
вложениями (существование гомоморфизма 6ц предпола-
предполагает, что XiCiXj). Тогда имеет место теорема ван Кам-
Кампена:
2) С г о w е 11 R. Н., On the van Kampen theorem, Pacific. Л
Math., 9, № 1 A959), 43—50.
232 Добавление III
Группы (uiGf порождают группу G. Для семейства
гомоморфизмов фг-: G2 —► Н, где И — некоторая группа,
удовлетворяющих условию tyi = tyfiij, найдется единствен-
единственный гомоморфизм X:G-+H, такой, что \|?г = Ясог.
Это обобщение может быть использовано для вычис-
вычисления фундаментальной группы объединения возрастаю-
возрастающего семейства открытых множеств, фундаментальные
группы которых известны. Этот результат используется
для вычисления копредставлений групп диких узлов и
других диких вложений3).
8) Fox R. H.f Art in E.f Some Wild Cells and Spheres in
Three dimensional Space, Ann. Math., 49 A948), 979—990.
ПРИЛОЖЕНИЕ I
КРАТКИЙ ЭКСКУРС В ТЕОРИЮ
УЗЛОВ*)
1. Зацепления и графыП)
Следующий пример показывает, как видоизменяется
развитая выше теория применительно к зацеплениям.
Пример 1 (тройное кольцо).
аса
= | а,
с: cbc ]ocb
и т. д.
В случае зацеплений прокоммутированная группа
H=G/G' является не бесконечной циклической, а сво-
свободной абелевой группой, ранг которой равен числу
компонент зацепления <2>. В рассматриваемом примере
ранг равен трем, поэтому
О
Л
— | х, у, z : ху — ух, xz~ zx, yz = zy |.
*) Перевод статьи Р. Фокса: Fox R. H., A quick trip through
knot theory, Topology of 3-manifolds, Proc. 1961 Top. Inst. Univ.
Georgia, Prentice Hall. Переведены § 5—10 этой статьи. Ссылки
типа(i) относятся к примечаниям переводчика, данным з конце
Статьи. — Прим. перев.
234 Приложение I. Краткий экскурс в теорию узлов
Следовательно, матрица Александера составляется из
L-полиномов от трех переменных х, у, г, причем
О
г) A_г)A_*) о
У групп зацеплений первый элементарный идеал <fx
является произведением некоторого фиксированного иде-
идеала (в случае я = 3 этот идеал порождается L-полинома-
ми х—1, у—1, z—1)*) и некоторого главного идеала
(А (*, у, z)) <3). Соответствующий ему L-полином, который
определен только с точностью до множителя ±xfy%zh,
назовем полиномом Александера данного зацепления.
В нашем примере находим
у, г) = {х-\){у-\){г-\)9
У2 = ((^-1)(У-1). (X~l)(z-\)9 (у— 1)BГ— 1)).
У нижеследующего зацепления
очевидно, A(x,y, z) = 0. Отсюда мы заключаем, что трой-
тройное кольцо нельзя «расцепить».
Полином Александера зацепления обладает свойства-
свойствами, аналогичными свойствам A) и B) полинома узла
Л(/) (см. стр. 198). Например, для двухкомпонентного
зацепления с коэффициентом зацепления <4>, равным q,
имеем <5>
A) А(*. 1)
*) Если зацепление имеет п компонент, то этот фиксированный
идеал порождается L-полиномами t\ — 1, t2—1, ...,tn — 1,
где ti — образующий группы Я, соответствующий естественным об-
образом i-pi компоненте (см. примечание B)). — Прим. перев.
1. Зацепления и графы 235
где А (л:)—полином Александера узла, образованного
первой компонентой.
B) ДA/*, 1/у)=**-у-!Д(*,0),
если полином А нормализован умножением на соответ-
соответствующий множитель ±xuyv.
Являются ли эти свойства достаточными для того,
чтобы утверждать, что для данного полинома Д(я, у)
найдется зацепление, полиномом которого он является,
неизвестно.
В случае ориентированного зацепления, состоящего
из \х компонент (ц>1), меридианы*) этих \х компонент
определяют предпочтительный базис в кольце JH. По-
Поэтому, когда мы сравниваем полиномы двух зацеплений,
нет необходимости учитывать автоморфизмы груп-
группы Я**). Однако в случае графов может оказаться не-
невозможным выделить предпочтительный базис, что при-
приводит к дальнейшим усложнениям.
Пример 2.
\ax, а2, а3, а4» #5, blt b2, b& b4, b5
афф2 = аффъ =
*) Под меридианом здесь понимается «малая» петля, обегаю-
обегающая вокруг дуги зацепления, — Прим. перев.
**) Так как при гомеоморфизмах зацеплений меридианы пере-
переходят в меридианы, а элементы группы Я, соответствующие этим
меридианам, определяют канонический базис группы И. — Прим.
перев.
236 Приложение I. Краткий экскурс в теорию узлов
Заметим, что в случае графа дополнительные соотно-
соотношения получаются при обходах вокруг вершин*). Груп-
Группа графа, вообще говоря, имеет дефект >1 и, значит,
£\@(б)
2. Заузленные 2-сферы
Дополнительная область R4 — S2 к двумерной сфере
S2 B-сфере) в четырехмерном евклидовом пространстве
R4 имеет своей первой группой гомологии Н{ бесконеч-
бесконечную циклическую группу <7>. Следовательно, сейчас мы
можем поступить точно так же, как и в случае узлов в
трехмерном пространстве. Единственное различие в вы-
вычислениях состоит в том, что идеал Александера в этом
случае не является, вообще говоря, главным идеалом.
Рассматриваемые ниже 2-сферы будут предполагаться
не только полиэдральными, но и локально плоскими^.
Однако излагаемый нами метод легко можно перенести
на 2-сферы, имеющие особенности.
Если 2-сфера 52 в пространстве /?4 образована вра-
вращением в /?4 заузленной дуги k, расположенной в полу-
полупространстве R\> вокруг ограничивающей это полупро-
полупространство плоскости, то говорят, что она получена вра-
вращением**). Группа n(RA— 52) в этом случае изоморф-
изоморфна группе л(/?+ —k)> которая является группой
узла***). Однако, как мы увидим далее, в пространстве
R4 существуют- 2-сферы, которые нельзя получить вра-
вращением и группы которых не являются группами узлов.
Первая проблема состоит в том, чтобы найти метод
нахождения копредставлений группы сферы 52 в про-
пространстве /?4. По-видимому, здесь наиболее полезен ме-
метод гиперплоских сечений. Расположим полиэдральную
сферу S2 так, чтобы она находилась в общем положе-
положении ****) в/?4, и рассечем ее семейством параллельных ги-
*) См. примечание A). — Прим перев.
**) Точнее, концы дуги k лежат в плоскости /?2, ограничиваю-
ограничивающей полупространство /?3, причем пересечение R2f\K состоит только
из этих точек. — Прим. перев.
***) Именно группой того узла, который получится, если концы
дуги k соединить дугой, лежащей целиком в R2. — Прим. перев.
****) Это означает, что выпуклой оболочкой любых пяти ее вер-
вершин в R4 является четырехмерный симплекс. — Прим. перев.
2. Заузленные 2-сферы 237
перплоскостей /?/. —оо</<оо, перпендикулярных соот-
соответствующим образом выбранному направлению. В об-
общем случае пересечение пространства R] со сферой S2
будет представлять собой полигональный узел или за-
зацепление в /??. Будет, однако, и конечное число «осо-
«особых» значений t. Соответствующие им особые гиперпло-
гиперплоскости могут пересекаться со сферой S2 в изолирован-
изолированных точках, являющихся минимумами или максимумами
функции высоты t, или же по графу с единственной вер-
вершиной, из которой исходят четыре стороны. Эти верши-
вершины называются седловыми точками. Особые гиперпло-
гиперплоскости разрезают пространство RA на слои, и группа до-
дополнения сферы S2 в каждом таком слое совпадает в
точности с группой узла или зацепления, возникающего
в любой входящей в него гиперплоскости (если, конеч-
конечно, S2 пересекает этот слой).
Группа сферы S2 в R4 может быть склеена из групп
дополнений слоев применением теоремы ван Кампена.
Точнее, предполагая, что особая точка @, 0, 0, 0) ле-
лежит в гиперплоском сечении / = 0, нам следует применить
теорему ван Кампена дважды к трем открытым множе-
множествам U~-S2, W-S2tV-S2tme
U = {(*, y,z,t)\t> max(-е, - V*2 +У2+ **))>
W = {(x, у, z, t)\x2 + y2 + z2+t2<e2}t
V = [(x, y,z,t)\t< min(e, Yx2 + у2 + г2)}.
Нетрудно видеть, что в точках максимума или мини-
минимума новых соотношений не появляется, а в седловой
точке добавляется одно новое соотношение:
ft
238
Приложение I. Краткий экскурс в теорию узлов
новое соотношение добавляется к группе нижнего слоя:
а = й, новое соотношение добавляется к группе верхнего
слоя: c = d.
Отметим, что при переходе через седловую точку чис-
число компонент меняется на одну. В примерах, которые мы
рассмотрим, сечение при t = 0 будет обычным узлом, и
при прохождении t через седловую точку в направлении
возрастания своего абсолютного значения число компо-
компонент также возрастает. Это гарантирует нам то, что в
результате получится 2-сфера, а не какая-либо другая
замкнутая поверхность (см. следующую схему). Вопрос
о том, всякий ли тип локально-плоской заузленной
2-сфе,ры представим таким образом, открыт. (То есть
вопрос о том, является ли необходимым рассмотрение
более сложных схем, например вроде следующей, у ко-
которой нет связных сечений.)
Пример 3. «Экваториальное» сечение является сквер-
узлом. Его группа такова: (х, а, Ь : хах = аха, xbx =
= bxb). Группа заузленной 2-сферы получается из этого
копредставления присоединением соотношения а = Ь
t=-l
t»0
2. Заузленные 2-сферы 239
(дважды: один раз при / = — 1, а другой раз при *=1).
Следовательно, в результате получаем группу G =
= \х, а:хах = аха\, так что группа этой заузленной сфе-
сферы изоморфна группе клеверного листа и имеет полином
Александера Д@ = 1 — t+t2.
Из примера видно, что преобразование перехода че-
через оедловую точку следует применять к узлам с не-
некоторой осторожностью, если мы хотим получить в итоге
локально-плоскую 2-сферу. Например, после приведен-
приведенного преобразования мы безнадежно «зацепляемся».
8ь
'"О
Это говорит о том, что не всегда можно начать с про-
произвольного узла нашу процедуру задания сфер сече-
сечениями. Тип узла, который может быть представлен как
сечение локально плоской 2-сферы гиперплоскостью,
должен иметь полином Александера вида (9) А@ =
= F(t)F(tl). Милнор и автор назвали такие узлы нуль-
эквивалентными. Однако поскольку это может привести
к недоразумениям, то, по-видимому, более удачно на-
название срезанный узел, предложенное Мойзом (отметим,
что полином сквер-узла Д(/) = A—t+t2J обладает тре-
требуемым свойством, а полином клеверного листа А (О —
= 1 — t+t2 нет).
Обратное почти наверняка неверно. Бабушкин узел
имеет тот же полином, что и сквер-узел (вообще он
имеет ту же группу), но мало вероятно, чтобы бабушкин
узел был срезанным узлом. Были бы интересны также
аналогичные условия и для срезанных зацеплений. Су-
Существуют ли таковые, автору неизвестно.
Пример 4. Пусть экваториальное сечение будет узлом
грузчика. Его группа такова:
\х} а: хагха
240
Приложение I. Краткий экскурс в теорию узлов
а полином равен Д(/) = A — 2t) B — /). Группа сферы
S2 получается присоединением соотношения ах = а2ха~2,
или, что то же самое, соотношения ха2 — ах. Соотношение
я-2 t*-1 1 = 0 t = i t.2
хаъхсг2хгх=а2хсг2 является его следствием. Следова-
Следовательно,
G= |аг, а :ха2 = ах\,
Пример 5 полностью аналогичен предыдущему
хо х
G= \xya : а2х=ха\,
Последние два примера показывают, что полином Алек-
сандера заузленной 2-сферы может не быть взаимным,
так что группа заузленной 2-сферы может не быть изо-
морф'ной группе какого-либо узла. Конечно, равенство
|ДA)| = 1 все еще справедливо. Киносита показал, что
полином А @» удовлетворяющий условию
2 Заузленные 2-сферы 241
|ДA) i = l, является полиномом для некоторой локально
плоской заузленной сферы <10>. (Терасака же показал,
что если полином А(/) имеет вид F(t)' F(t~l), то он яв-
является полиномом некоторого срезанного узла*10).)
Пример 6 представляет собой комбинацию двух пре-
предыдущих примеров
GX х
G= |*t а : ха2 = ах, а?х = ха\.
Оба соотношения этого копредставления возникают
при переходе через верхнюю и нижнюю седловые точки
соответственно. Первоначальное соотношение в группе
узла грузчика является следствием каждого из них.
Рассмотрим эквивалентное копредставление
Отсюда видно, что коммутант группы G является конеч-
конечной циклической группой G'=|a:a3=l|, а группа G
представляет собой его расширение при помощи беско-
бесконечной циклической группы. Идеал c?i=B/ — 1, 2 — t)
не является главным. Представление х—► (О, 1), а-+
—►@ 12) группы G на §>з показывает, что аф\. Следо-
Следовательно, мы доказали гипотезу Кэртиса: группа локаль-
локально плоской двумерной сферы в четырехмерном простран-
пространстве может иметь элементы конечного порядка.
Следующие замечания поясняют, почему эта гипоте-
гипотеза имела смысл. В 1957 г. Папакирьякопулос доказал
лемму Дена, асферичность узлов и гипотезу Хопфа*).
*) В гипотезе Хопфа утверждается, что группа узла не имеет
элементов конечного порядка. — Прим. перев.
к. 317
242
Приложение I. Краткий экскурс в теорию узлов
Использованные им методы показали, что решения этих
трех проблем весьма тесно связаны друг с другом. По-
После этого Эндрьюс и Кэртис показали, что заузленная
2-сфера не всегда асферична; в их сообщении было от-
отмечено, что лемма Дена не допускает обобщения (в не-
некотором смысле) на четырехмерные многообразия с
краем. И Кэртис просто предположил, что гипотеза
Хопфа также не допускает обобщения на четырехмер-
четырехмерный случай (гипотеза Кэртиса).
Пример 7
Схема сечений
Здесь группа зацепления, получающегося в экваториаль-
экваториальном сечении, такова:
| х, у, z : уху1 = zxz~xt zxyx^z'1 = у |.
Полином Александера: А (х, у, z) =у — zx.
Полином Хосакавы: V(/)= |^ = 1.
Рассматриваемая сфера имеет тривиальный тип, по-
поскольку, как указал Давид Эпштейн, она ограничивает
трехмерный шар. Следующая диаграмма показывает се-
сечения этого шара (каждое сечение является частью по-
2. Заузленные 2-сферы
243
верхности сферы). Этот пример показывает, что суще-
существует сфера тривиального типа, имеющая в сечении не-
нетривиальное зацепление. Несколько труднее построить
пример сферы тривиального типа, имеющей в сечении
нетривиальный узел. Один такой пример привел Стол-
лингс.
Пример 8. Здесь мы имеем две сферы тривиального
типа. Полином Александера сечения равен нулю, однако
это зацепление нетривиально в силу того, что
^Э2:=A—х+ху)A—у+ху). Эти сферы расцепляемы;
можно построить в дополнении к одной из них трехмер-
о
о
о
о
о
о
ный шар, ограниченный другой. (В дополнении к этому
трехмерному шару мож<но построить другой трехмерный
ша,р, граница которого — первая сфера, хотя это и не
так просто доказать.)
Этот пример показывает, что существуют пары непе-
непересекающихся трехмерных шаров, таких, что сечение их
границ образует нетривиальное зацепление.
Пример 9. Этот пример обобщает пример 6. Здесь
только показано его экваториальное сечение, узел с
16*
244
Приложение I. Краткий экскурс в теорию узлов
пересечениями. Его полином таков:
— 2n(n+l)]t + n(n+l)t2.
Группа соответствующей двумерной сферы является ме-
тациклической:
О = | х% а: хап'1 — апх, апл 1х — хап \ =
где Ь = ап.
Следовательно, для любого нечетного числа 2п+1
найдется локально плоская двумерная сфера в четырех-
четырехмерном пространстве, группа которой имеет элемент по-
порядка 2п+1. Автору не удалось построить пример ло-
локально плоской сферы, группа которой имела бы эле-
элементы четного порядка.
3. Арифметика узлов
Узел, получающийся при завязывании на одном ку-
куске веревки узла / вслед за узлом к, называется компо-
композицией этих двух узлов и обозначается через £#/.
Имеются два различных способа задавать композицию.
3. Арифметика узлов
245
A) Если ориентированные полигональные простые
замкнутые кривые k и / расположены в трехмерном про-
пространстве по разные стороны от некоторой плоскости Р
и имеют общий отрезок е, на котором индуцируются про-
противоположные ориентации узлами k и /, то узел k#l
представляется ориентированной кривой (k—е) U (/—е).
B) Пусть Т — заполненный тор, узел / представлен
кривой в Т, пересекающей выбранный меридианальный
диск ровно в одной точке, V — заполненный тор, пред-
представляющий узел й, и f — точное отображение тора V
на тор Т (т. е. гомеоморфизм, переводящий ориентиро-
ориентированные параллели тора Т на ориентированные парал-
параллели тора V) A1). Тогда кривая /(/) представляет собой
узел k # /.
При изучении операции композиции удобным бывает
иногда одно, иногда другое представление. В первом
представлении удобно иногда также заменять плоскость
Р сферой.
Очевидно, что композиция является ассоциативной
операцией и тривиальный тип узлов является единицей.
Коммутативность понятна из следующего рисунка:
Следовательно, множество всех типов узлов (ручных,
ориентированных) образует коммутативную полугруппу
с единицей относительно операции #.
246 Приложение I. Краткий экскурс в теорию узлов
Шуберт доказал, что в этой полугруппе разложение
на множители единственно. Доказательство, как и в
случае разложения на множители целых чисел, опи-
опирается на две фундаментальные леммы: (а) о конеч-
конечности разложения и (Ь) о простых делителях произве-
произведения.
Для доказательства леммы (а) введем понятие рода
узла. Заметим прежде всего, что на всякий ручной узел
можно натянуть ориентированную поверхность. Это мо-
может быть сделано следующим образом. На каждое пе-
пересечение натянем «скрученный» прямоугольник так, как
это показано ниже на рисунке слева (не так, как это по-
показано справа):
Ж
Если мы выбросим внутренности этих прямоугольников
и те части их границы, которые лежат на узле, то остав-
оставшаяся часть от узла будет проектироваться в некоторое
число непересекающихся окружностей, которые можно
назвать окружностями Зейферта.
Окружность Зейферта можно описать, начав с неко-
некоторой точки узла и двигаясь вдоль него в положитель-
положительном направлении до первой точки пересечения, затем пе-
перескакивая в ней на другую ветвь и двигаясь вдоль нее
в положительном направлении до встречи со следующей
точкой пересечения и т. д. до возвращения в первона-
первоначальное положение. Окружности Зейферта не пересе-
пересекаются, однако они вполне могут быть вставлены друг
в друга. Начиная с самых внутренних окружностей, мо-
можно шаг за шагом натянуть на окружности диски таким
образом, чтобы их внутренние части не пересекались
друг с другом и с прямоугольниками. Ясно, что объеди-
объединение этих частей и прямоугольников образует ориенти-
ориентированную поверхность, натянутую на наш узел. Если
d — число точек пересечения, а / — число окружностей
3. Арифметика узлов 247
Зейферта, то мы получили ориентированную поверх-
поверхность, род которой (d—/+1)/2 с однокомпонентной гра-
границей.
Поскольку на узел k можно натянуть хотя бы одну
ориентированную поверхность, существует такое мини-
минимальное целое h(k), что на узел k можно натянуть
ориентированную поверхность рода h(k). Это число на-
называется родом узла k. Очевидно, что только тривиаль-
тривиальный узел имеет род 0. Степень полинома Д(/) узла k
не превосходит числа 2Л и равна ему для альтерниро-
альтернированных узлов*12). Представляется, что, вообще говоря,
число h весьма трудно вычислимо. Тем не менее в Acta
Mathematicae имеется длинная статья Хакена, в кото-
которой дается алгоритм вычисления рода любого узла. (В
частности, это дает нам алгоритм решения вопроса,
представляет ли заданная проекция узла тривиальный
узел или нет.)
Возвращаясь к полугруппе узлов, нетрудно пока-
показать, что h(k U 1) = А(Л) + А(/). Если F — поверхность,
натянутая на узел k Ш, а Р—плоскость в общем с F
положении, разделяющая узлы k и /, то пересечение по-
поверхности F с этой плоскостью состоит из дуги е и не-
некоторого числа простых замкнутых кривых. Натягивая
шапочки на эти кривые, можно получить поверхности
F\ и F2, натянутые на узлы k и / соответственно. Ясно,
что при этом h(Fi)+h{F2)<h{F), откуда й(*)+й(/)<
<h(knl).
Обратно, пусть F\ и F2 — поверхности, натянутые на
узлы к и / соответственно. Мы можем склеить их вместе
248 Приложение I. Краткий экскурс в теорию узлов
и получить поверхность рода h(F{)+h(F2)9 натянутую
на узел k Д I- Конечно, могут быгь пересечения Fi с F2,
мешающие осуществлению этого плана. Однако можно
сначала переместить их на бесконечность, а затем со-
соединить поверхности F{ и F2 вдоль дуги е. Таким обра-
образом, h(kttl)^-h(k) +/i(/), чем и заканчивается доказа-
доказательство того, что род является гомоморфизмом полу-
полугруппы узлов на аддитивную полугруппу неотрицатель-
неотрицательных целых чисел*). Отсюда следует, что не существует
бесконечно разложимых узлов, т. е. каждый узел разла-
разлагается в произведение простых далее уже не разложи-
разложимых узлов. Стандартные таблицы узлов являются таб-
таблицами простых узлов.
Лемма (а) доказана, осталось доказать лемму (Ь):
Если k —- простой узел, делящий узел / Д /л, то k де-
делит либо /, либо т. Для доказательства этого рассмо-
рассмотрим простую замкнутую кривую, представляющую
узел I Д m и плоскость Р, пересекающую ее в двух точ-
точках и «отделяющую / от т». (Этому нетрудно придать
точный смысл.) Так как узел k делит узел /Д т, най-
найдется двумерная сфера S2, пересекающая эту кривую в
двух точках и содержащая узел k внутри себя. Если
сфера S2 не пересекает плоскость Р, наше доказатель-
доказательство закончено. В противном случае сфера S2 пересе-
пересекает плоскость Р по некоторому числу непересекаю-
непересекающихся простых замкнутых кривых. Те из них, которые
не зацеплены с /Дт, могут быть сразу убраны
(деформацией сферы 52), а те, которые зацеплены
с /Дт, также могут быть уничтожены (опять-таки
деформацией сферы S2) по той причине, что узел k
прост.
Следствием конечности разложения на множители, в
частности, является невозможность завязать последова-
последовательно друг за другом узлы k и / на одном куске верев-
веревки так, чтобы они «съели» друг друга. В некоторых по-
популярных журналах, особенно в Scientific American,
утверждалось, что это нерешенная проблема, поэтому
*) Так как существуют узлы рода 1, например клеверный
лист. — Прим. перев.
3. Арифметика узлов 249
имеет смысл дать краткое доказательство этого факта
без использования понятия рода.
Предположим, что существовал бы гомеоморфизм f
всего пространства на себя, переводящий узел fcft / в
тривиальный. Можно было бы считать, что / тожде-
тождествен вне куба С, граница которого пересекает узел
А# I в двух точках. Рассмотрим следующий дикий
узел т:
Г^ к 1...
Тогда найдется гомеоморфизм fn всего пространства на
себя, тождественный вне куба C2n_i + C2n и заменяющий
узел kXXl тривиальным внутри C2n-i + C2ri. Определяя
гомеоморфизм / внутри куба C2n_i + C2n как fn и как
оо
тождественный вне 2 С/, находим, что узел т три-
/-1
виален. Повторяя это же рассуждение с кубами
С2ц + С2п+1, я = 1, 2, 3, ... , вместо кубов C2n-i + C2n и
замечая, что £Д/ = /Д£, видим, что m = k. Значит,
k = 0 и, следовательно, 1=0.
Нетрудно видеть, что узел k является срезанным тог-
тогда и только тогда, когда в четырехмерном полупро-
полупространстве найдется двумерный диск, ограниченный уз-
узлом k. Если узел k представляет собой пересечение ло-
локально плоской двумерной сферы с гиперплоскостью,
тогда каждое из четырехмерных полупространств пере-
пересекается с этой двумерной сферой по локально плоско-
плоскому двумерному диску. Обратно, если узел k ограничи-
ограничивает локально плоский двумерный диск, лежащий в
250 Приложение I. Краткий экскурс в теорию узлов
четырехмерном полупространстве по одну сторону от
гиперплоскости, содержащей узел &, то зеркальный об-
образ этого диска относительно этой же гиперплоскости
вместе с исходным диском дает нам двумерную сферу:
сечением которой и является узел k. В определении ло-
локально плоского диска, конечно, надо наложить некото-
некоторые условия локальной плоскости не только внутри, но
и на границе (отметим, что всякий узел ограничивает
локально плоский двумерный диск во всем четырехмер-
четырехмерном пространстве, так что ограничение определения на
полупространство необходимо).
Аналогично если k и / — ориентированные узлы, то
они называются принадлежащими к одному и тому же
классу кобордизмов {k~l)y если существует локально
плоское кольцо, лежащее в четырехмерном слое, грани-
границей которого является k — /, причем k лежит в одной
из ограничивающих слой гиперплоскостей, а / — в дру-
другой. Очевидно, что соотношение ~ является соотноше-
соотношением эквивалентности и что k~0 тогда и только тогда,
когда k — срезанный узел. Более того, нетрудно видеть,
что &# &*~0, где k* обозначает узел, полученный из
k зеркальным отражением и заменой ориентации. (Напри-
(Например, если k — клеверный лист, то k#k* есть сквер-узел.)
Отступление. Имеются две операции обращения
ориентации: обращение ориентации всего пространства
(это эквивалентно взятию зеркального образа) и обра-
обращение ориентации узла (т. е. изменение направления
обхода вдоль узла). Получаем следующую диаграмму;
Обращение ориентации
пространства
Обращение I
и \ i
узла 1
3. Арифметика узлов 251
Узел &* равен узлу op(k)=po(k). Узел k называется об-
обратимым, если узел o(k) эквивалентен k, и зеркальным,
если узел k эквивалентен либо р(&), либо op(k). (На са-
самом деле первые из них следовало бы называть + зер-
зеркальными, а вторые — зеркальными.) Клеверный лист,
как известно, не является зеркальным узлом,т.е. имеет-
имеется и правый трилистник, и левый трилистник. Восьмерка
является зеркальным узлом. Узел 817 явно (!) необра-
необратим, но это нигде не доказано. Более того, не доказано
даже существование необратимых узлов. Это очень
трудная проблема*).
Простые геометрические доводы показывают, что
если k~l, той # m — l# m. Следовательно, классы ко-
бордизмов узлов наследуют от полугруппы узлов опе-
операцию # и образуют коммутативную группу относи-
относительно нее. В этой группе обратным элементом данного
узла является его зеркальный образ с обращенной
ориентацией. Ясно, что всякий узел, являющийся обра-
обратимым и зеркальным, имеет порядок 2 в этой группе.
Неизвестно, имеются ли в этой группе элементы поряд-
порядка отличного от двух. Известно также, что эта группа
не является конечно порожденной*13). Эти два факта
представляют, собственно, все, что известно о строении
этой группы.
Третий способ задания операции # можно обоб-
обобщить следующим образом. Пусть торы Т и V такие же,
как и выше, а / — некоторый узел в торе Г, пересекаю-
пересекающий любой его меридианальный диск. Если V представ-
представляет тип узлов &, то узел k называется осью узла /(/).
(Другими словами, если узел /(/) нетривиально содер-
содержится внутри заузленного заполненного тора V, то тин
узлов, представляемый «осью» тора V, называется осью
узла /(/).)
Ясно, что любой из двух узлов является осью их
композиции. Рассмотрим другой пример. Пусть узел /
расположен внутри Т так, как (см. стр. 252) указано на
рисунке (на каждом из них имеется 2р + 2 пересечений).
Узел /(/) в этом случае называется удвоением узла k
*) Эту проблему недавно положительно решил Троттер; см,
основной текст стр. 25. — Прим» перев%
252
Приложение I. Краткий экскурс в теорию узлов
с кручением р. Пусть, наконец, / — торический узел типа
(а, 6), расположенный внутри тора Т на поверхности,
концентрической границе Т. В этом случае узел /(/) на-
называется обмоткой вокруг узла k.
Если узел k является осью узла т = /(/), а узел I
обегает а раз вокруг тора Г, то для их родов выполне-
выполнено следующее неравенство*14):
й(т)>ай(А)+А(/),
а для их полиномов — равенство <15>
ДЛ@ = Д*(О-МО-
Единственными осями произведения узлов являются его
простые множители и их оси. Удвоение всякого узла
имеет род 1 (если оно нетривиально). Осями нетриви-
нетривиального удвоения узла k являются все оси самого узла k.
Осями обмотки вокруг нетривиального узла k также яв-
являются все оси узла. Две обмотки вокруг нетривиаль-
нетривиальных узлов k и W имеют один и тот же тип только тогда,
когда k — k\ и обматывания имеют «одинаковый тип».
Удвоения узлов k и k' имеют один и тот же тип только
тогда, когда k=k', и сами удвоения имеют «один и тот
же тип» (исключая случай fe = fe/ = 0, когда имеются три-
тривиальные исключения из этого правила).
4. Накрывающие пространства
Пусть S — Ai-мерное многообразие, например трехмер-
трехмерная сфера, a L — его замкнутое нигде не плотное подмно-
подмножество. Каждому накрывающему пространству простран-
пространства S — L соответствует единственное пополнение 2, на-
называемое ассоциированным разветвленным накрываю-
4. Накрывающие пространства 253
щам пространством <16>. Пусть Л множество точек про-
пространства 2, лежащих над L. Справедлива следующая
диаграмма:
2 —Лс2
S — AdS
Следовательно, 2—Л есть неразветвленное накрытие
пространства S — L и дополнение 2 есть ассоциирован-
ассоциированное разветвленное накрытие 5.
Если многообразие 5 триангулировано, L — его под-
подкомплекс и индекс ветвления <17) конечен в каждой точке
множества Л, то тогда пространство 2 можно триангу-
триангулировать так, что Л будет его подкомплексом. Если L,
кроме того, — локально плоское {п — 2)-мерное под-
подмногообразие, то 2 также будет n-мерным многообра-
многообразием, а Л — его локально плоским (п — 2) -мерным под-
подмногообразием. (Условие конечности индекса ветвления
во всех точках множества L здесь необходимо. Нетруд-
Нетрудно видеть, что накрытие двумерного диска 5, ветвя-
ветвящееся только в одной его внутренней точке L,
а на 5 — L являющееся универсальным накрытием,
не является даже локально компактным вблизи
точюи Л.)
Хорошо известно, что неразветвленные накрытия
2 — Л пространства S — L находятся во взаимно одно-
однозначном соответствии с подгруппами Г группы яE—L),
если при этом выделяется базисная точка /?0€2—Л, ле-
лежащая над базисной точкой p£S—L. Если базисная
точка не выделена из множества точек р0, Ри ..., лежа-
лежащих над /?, то соответствие устанавливается между на-
накрывающими пространствами 2 — Ли классами сопря-
сопряженных подгрупп группы n(S — L).
Каждая подгруппа Г группы G индекса g<oo инду-
индуцирует транзитивное*) представление группы G в
*) Представление р: G -> 2g называется транзитивным, если
для любых двух элементов множества, переставляемого группой S^,
найдется такой элемент g £ <j, что перестановка p(g) переводит
первый из них во второй. — Прим. перев.
254
Приложение I. Краткий экскурс в теорию узлов
симметрическую группу Sg ранга g. Если переставляемые
этой группой символы 0, 1,..., g — 1 отождествить с
правыми смежными классами Го, Ft, ... , Tg~i по под-
подгруппе Г = Го, то это представление р будет иметь вид:
где а — некоторый элемент группы G.
Обратно, если р — транзитивное представление груп-
группы G в $g, ему соответствует подгруппа Г, состоящая из
всех тех элементов а группы G, для которых переста-
перестановка р(а) оставляет символ 0 на месте. (Отметим, что,
вообще говоря, подгруппа Г — не нормальный делитель
и отнюдь не является ядром гомоморфизма р. Отметим
также, что элемент а € G принадлежит правому смеж-
смежному классу Fft тогда и только тогда, когда перестанов-
перестановка р(а) переводит символ 0 в символ k.) Таким обра-
образом, имеется взаимно однозначное соответствие между
подгруппами группы G и транзитивными представления-
представлениями группы G. Классу сопряженных подгрупп соответ-
4. Накрывающие пространства
255
ствует класс эквивалентных представлений. Имеем:
Накрываю-
Накрывающие £-ЛИСТ-
ные про-
пространства
2—А
Классы
со-
пряженных
подгрупп
индекса
Г
g
Классы эквивалент-
эквивалентных транзитивных
представлений в сим-
симметрическую группу
ранга g.
Вложение S—Л—►S определяет гомоморфизм груп-
группы Г на яB). Его ядро состоит из тех элементов группы
Г = яB — Л), которые представляются малыми петлями,
расположенными достаточно близко от многообразия Л
(т. е. петлями вида /Л/, где / — путь от базисной точки
в малую окрестность многообразия Л, a h — путь в этой
окрестности). Иначе говоря, это ядро образовано теми
элементами группы G = n(S—L), лежащими в под-
подгруппе Г, которые представимы петлями, достаточно
близкими к многообразию L и просто зацепленными
с ним.
Пусть копредставление (хи ... ,хп : гь ..., гт) опре-
определяет заданную группу G. Теорема Рейдемейстера —
Шрейера *) позволяет построить копредставление груп-
группы Г, а отсюда и копредставление группы яB). Объ-
Объясним алгоритм построения копредставления группы Г,
исходя из заданного копредставления группы G и тран-
транзитивного представления р этой группы перестановками.
Этот алгоритм эквивалентен теореме Рейдемейстера —
Шрейера, однако по сравнению с ней он несколько про-
проще. В TeqpeMe Рейдемейстера — Шрейера мы прежде
всего должны выбрать в группе G представителей ка-
каждого смежного класса по подгруппе Г. Если мы про-
пронумеруем точки, лежащие над базисной точкой р про-
пространства S—L, индексами правых смежных классов
Го, Fi,..., IY-i, а именно /?0, ри • • •, Pg-u то такой вы-
выбор будет равнозначен выбору для каждого &=0, 1,...
..., g—1 некоторого пути в 2 — Л от точки р0 к точке /?&.
(Они должны также удовлетворять так называемому
*) Теорема Рейдемейстера — Шрейера указывает алгоритм, по-
позволяющий построить копредставление группы Г, исходя из копред-
копредставления группы G и транзитивного представления р, соответ-
соответствующего подгруппе Г. — Прим. перев.
256 Приложение I. Краткий экскурс в теорию узлов
условию Шрейера: их объединение должно быть дере-
деревом.) Этот выбор представителей связан с несимметрич-
несимметричностью и нарушением простоты алгоритма. Этого можно
избежать в предлагаемом нами алгоритме с помощью
вынесения нужных представляющих путей из простран-
пространства 2—Л. Точнее, возьмем g-penep Ф с концевыми точ-
ками pOt px pg_x и отождествим каждую точку
р'у с соответствующей точкой ру пространства 2—Л.
Фундаментальная группа полученного пространства бу-
будет, очевидно, изоморфна группе T*Fg-\. Символом
Л*5 обозначается свободное произведение групп А и
В, a Sg_i —- свободная группа ранга g—1. Наш алго-
алгоритм будет алгоритмом для нахождения копредставле-
ния группы Г*/^-4 вместо группы Г. В большинстве
случаев этого вполне достаточно, так как известно, что
здесь присутствует свободный множитель Fg-U и его,
как правило, легко учесть.
Итак, заданному копредставлению (хи ..., хп:ги ..., гт)
группы G и заданному транзитивному представлению р
группы G б $g наш алгоритм сопоставляет копредстав-
ление группы r*/v-i вида
х10, ..., хп0 г10 гт0
Смысл символов Xjp и г?а мы сейчас разъясним.
Пусть 0 — некоторый элемент группы G и /—пред-
/—представляющий его путь в 5 — L. Обозначим через 0р эле-
элемент группы r*Fg-u представляемый в B—Л) U Ф
петлей вида h&ffiy1, где Лр — путь в Ф от точки /?0 к точ-
ке Pfa f — начинающийся в р$ путь пространства 2—Л,
накрывающий путь / и оканчивающийся, скажем, в точ-
точке ру (здесь у — индекс, в который переводится индекс
4. Накрывающие пространства
257
р перестановкой /?F)), и hy — путь в Ф ог точки /?о к
точке ру.
Рассмотрим теперь свободную группу, порожденную
символами Xjp A<у</г, 0<p<g—1), и, отобра-
отобразив каждый элемент х^ в элемент (xj)&, описанный
выше*), продолжим это отображение до гомоморфизма
на группу T*Fg-i (также обозначаемого через ср, так
что х^ = (*5)р)' Этот гомоморфизм обладает следую-
следующим приятным свойством:
Если для некоторого слова и = xjxj^ ... (еЛ= ±1)
и некоторого индекса а£{0, 1, ,.. , g—1} формально
определить**)
где индексы
... хеь
, аз,... определяются по правилу:
..) еСЛИ е* = 1>
... а ... \
если ek = -г 1,
*) Здесь ф : Fn -> G есть канонический гомоморфизм, соответ-
соответствующий копредставлению (хи ..., хп : ги ..., гп)ф, а лгч>=ф(^).—
Прим. перев.
**) Здесь надо учесть, что (^у)а^(^уа)8» так что символ xBja,
строго говоря, смысла не имеет. Автор считает, что дГу-а = (д:уа)£. —
Прим. перев.
17 Зак 317
258 Приложение I. Краткий экскурс в теорию узлов
то элемент иа отображается гомоморфизмом <р в эле-
элемент (ич)а группы F*F8-u опи-саиный выше.
Например, если и-=ххх\х-хх2х, р(л:1)==@34)B5)
и р(л:2) = C12) D5), то
U0 ~ ^О^З^Л!) Х24 *
Ul ~ ХПХ2\Х22Х\0 *20 $
* И Т ^
Если Шо=1, t^i,..., ш^_1 суть такие слова из букв
*! хп, что «#=1, w? w^_x лежат в смеж-
смежных классах Го, Ft,..., Fg-i соответственно, и если вы-
выполнено условие Шрейера, т. е. если любая левая часть
слова Wi совпадает с одним из других слов Wu> что все-
всегда можно обеспечить, то элементы w^0 wg-\,o
могут быть выбраны в качестве образующих свободного
множителя Fg-i. Значит, некоторое копредставление
группы Г можно получить из нашего копредставлеиия
группы F*F^_! присоединением соотношений a>i,o=l, ...
..., хюё-и о=1. Это приводит нас к алгоритму Рейде-
мейстера — Шрейера <18>.
Пример 5 (продолжение). Группа G= |jc, a : а2х=ха\
имеет представление д:->@ 1), а->@ 1 2) в группу $3-
Если Г — фундаментальная группа соответствующего
трехкратного нерегулярного накрытия 2—Л дополни-
дополнительного пространства, то группа Г*/*2 имеет копред-
копредставление
где А2 = а2аоа1. Можно выбрать элементы доо=1, w{=a и
w2 = a2, удовлетворяющие условию Шрейера, и получить
копредставление \xv а2: а\х2 = х2а21 группы Г, присо-
присоединяя Соотношения ао=1, ai = l. Следовательно, T«G
и одномерная группа гомологии пространства 2—Л яв-
является бесконечной циклической группой.
4. Накрывающие пространства 259
Для нахождения группы я B) нужно описать соот-
соотношения ветвления, следствием которых является ядро
отображения яB—Л)—*яB). Бели v—некоторый
элемент группы G, представляемый как угодно ма-
малой петлей, расположенной вблизи L, и если p(v) =
= (Р1Р2 ... РО (...)..., то соответствующие соотношения
ветвления имеют видт^т^ ... v^ = 1, ..., геометриче-
геометрический смысл которых легко понять A9>.
Пример 5 (продолжение). Элементы х и ах группы G
представляются как угодно малыми петлями, близкими
к L Соответствующие соотношения ветвления таковы:
(два последних соотношения, конечно, являются лишни-
лишними), откуда видно, что пространство 2 односвязно. По-
Поскольку подмногообразие Л состоит из двух двумерных
сфер*) и #iB—Л) «Z, пространство 2 не может быть
четырехмерной сферой. Возможно, оно гомеоморфно
многообразию 52х52.
Найдя группы Г = яB — Л) и яB), мы можем найти
группы гомологии пространств 2—Л и 2. Причем этот
процесс можно сделать автоматическим следующим об-
образом. Пусть / — матрица Якоби
~ II дх II
группы G, а 0 — регулярное представление группы $g в
группу квадратных (gXg) -матриц, т. е.
О 1 ...*-1
Продолжим его на групповое кольцо. Тогда матрица со-
соотношений <20> группы Hi B— Л) ф Ag-U где знак ®
обозначает прямую сумму, a Ag-i — свободную абелеву
группу ранга g— 1, совпадает с целочисленной
(ngXmg) -матрицей / ер B1)-
*). Это следует из того, что всякое накрытие сферы есть сфера,
а р(*) = @1)B) (см. примечание A9)). — Прим. перев.
17*
260
Приложение I. Краткий экскурс в теорию узлов
Пример 5 (продолжение). Якобиан представления
\х, а:а2х = ха\ равен / = ||а2 — 1 1+а — р
о ооц.
1—1
=1 !
0
0
—1
1
1
0
1
1
—1
1
0
1
0
0
1
0
Матрица соотношений для группы //iB)©/4g_i полу-
получается из Уер присоединением строк, соответствующих
соотношениям ветвления. Следовательно, в нашем при-
примере матрица соотношений для группы #1B)©Л2
равна
—1 0 1 10 0
1—1 0—111
0 1—1 1 0 0 —1|0 0||.
1 1 0 0 0 0
О 0 1 0 0 0
(Если вместо представления 6р мы использовали бы
представление и —► ||8азиа||, то получили бы матрицу
Якоби для группы r*Fg-i.)
Гомоморфизм коммутирования отображает группу
узла G на бесконечную циклическую группу Z. Для ка-
каждого положительного целого числа g существует един-
единственный гомоморфизм группы Z на Zg (циклическую
группу порядка g), а следовательно, и единственный го-
гомоморфизм группы G на Zg. Накрытия 2—Л и 2, соот-
соответствующие ядру G' гомоморфизма G-*Z, называются
бесконечными циклическими накрытиями, а накрытия,
соответствующие ядрам гомоморфизмов G-+Zgi назы-
называются g-ми циклическими. Первая группа гомологии
#iB — Л) неразветвленного g-ro циклического накры-
накрытия является прямой суммой группы Z и первой группы
гомологии #iB) g-ro циклического разветвленного на-
накрытия W. Порядок 6 группы #tB) в этом случае,
как можно показать, равен
?-i
6 =
5. Циклические накрытия пространства узла 261
где со — примитивный корень из единицы степени g. Если
группа Hi B) бесконечна, то ее ранг равен числу корней
уравнения Д(/)=0, подсчитанных с учетом кратностей,
которые являются корнями g-й степени из единицы <23>.
Если #iB)—конечная группа, то прокоммутированная
группа яB—Л) является бесконечной циклической,
так что она обладает полиномам Александера <24>. Мо-
Можно показать, что этот полином Д(т) равен JJ Д(о)Л;),
где т = /*<2б>. Ясно тогда, что число ДA) есть порядок
группы Hi B).
Пример. Клеверный лист:
6 = 3, £(т) = A
6 = 4, А(т) =
= A— t-+-t2)(\
и т. д.
Замечание 1. Для нециклических накрытий группы
#tB) и #tB — А) не связаны между собой никакой
очевидной формулой. Не известны также формулы для
порядков этих групп.
Замечание 2. В некотором смысле полином А@ яв-
является порядком группы //iB — А), когда 2 — А — бес-
бесконечное циклическое накрытие. Для этого надо рассма-
рассматривать группу #iB—А) как операторную, считая опе-
операторами скольжения этого накрытия*).
5. Циклические накрытия пространства узла
Сейчас мы более подробно исследуем конечные ци-
циклические накрытия, используя упрощающий процесс,
принадлежащий Зейферту.
*) См. примечание B3). — Прим. перев.
262
Приложение I. Краткий экскурс в теорию узлов
Пусть <ЗГ — поверхность рода h с границей, состоя-
состоящей из одной окружности. Как показывает приведенная
ниже схема, поверхность <&~ можно изотопически про-
деформировать на модель, состоящую из двумерного
диска, к которому приклеено 2Л полосок.
Бели поверхность <&* вложена кусочно-линейно в трех-
трехмерное пространство, эта изотопия может быть продол-
продолжена до изотопии всего пространства. Значит, всякий
тип вложения поверхности <&* содержит представителя,
состоящего из двумерного диска, к которому приклеено
2Л полосок. Правда, эти полоски могут быть закручены,
заузлены и зацеплены.
Пусть аи 02, 0з, 04, ... , 02/1-1, 02/i — каноническое мно-
множество кривых на поверхности^"'. Оно состоит из ориен-
ориентированных замкнутых кривых, имеющих одну общую
точку, нигде более не пересекающихся и размещенных
так, как показано на схеме. Мы продеформировали
нашу поверхность^'в окрестность множества ai + a2+...
• • - + 02Л-1 + 02/1, при этом полоски подклеены к централь-
центральному диску в следующем порядке: начало полоски
вдоль аи начало полоски вдоль а2, конец полоски
вдоль аь конец полоски вдоль а2, начало полоски
вдоль а3 и т. д.
Если нам задан узел и мы натянули на него ориенти
рованную поверхность d?~ рода h методом Зейферта (ил*
каким-либо другим), мы можем отметить на ней точку
выбрать каноническую систему кривых аи ..., 02/i, про
ходящих через нее, и продеформировать поверхность^"
в окрестность этих кривых. Это можно сделать всегда
5. Циклические накрытия пространства узла
263
хотя для поверхностей большого рода необходимо не-
некоторое терпение.
Поскольку поверхность & ориентируема, число за-
закручиваний каждой полоски обязательно четно. Следо-
Следовательно, эти закручивания можно заменить завитками
(которых будет ровно вдвое меньше, чем закручиваний),
так, как показано на рисунке.
Получаемая таким образом поверхность^ имеет такой
же тип вложения, что и первоначальная, и может быть
так уложена на плоскость, что только одна ее сторона
будет видимой. Например, для трилистника имеем
Если окружности Зейферта (см. стр. 246) вложены
друг в друга, то поверхность Зейферта окажется много-
многослойной, что довольно-таки неудобно. Оказалось, одна-
однако, что во всех случаях, которые рассматривал автор,
можно избежать этого изменением диаграммы узла.
264 Приложение I. Краткий экскурс в теорию узлов
Например, следующая поверхность довольно сложна.
Но другая диаграмма «восьмарки», хотя и не
являющаяся экономичной в смысле числа пересечений,
гораздо удобнее для построения поверхности Зейферта:
Исходя из такой нормализованной поверхности, мо-
можно получить целочисленную BЛХ2Л)-матрицу V=*(vu).
Элемент иг;- определяется как алгебраическое число
переходов /-й полоски через f-ю слева направо*). Сле-
Следовательно, для построенной выше поверхности, натя-
натянутой на трилистник, имеем матрицу
v-\\~l l
v —I о —1
*) Это число равно разности чисел перехода слева направо и
справа налево. — Прим. перев*
5. Циклические накрытия пространства узла
265
а для поверхности, натянутой на восьмерку, —
ни =:
Заметим, что всегда
012—021=1, 034 — 043 «I, • • • ,
а в остальных случаях Vij = Vji, что в матричной форме
означает
у V = l,
где штрих означает транспонирование, а через / обозна-
обозначена диагональная матрица, составленная из h блоков
О —1 II
1 о г
Отметим, что / есть BhX2h)-матрица пересечений на
поверхности <ZF канонических кривых*) аи ••• » а%п\
/«II* (аи я;) II.
Определим, как и Зейферт,
*0i2 —^и vu —'
*022 — 21 *024 —'
•032 —^31 34 — '
•042 — *041 ^44 —•
Одномерные циклы аи а2,..., а2н-и а2н образуют ба-
базис одномерной группы гомологии поверхности <^\ и из-
изменение этого базиса приводит к замене матрицы V на
матрицу UVU\ где U — унимодулярная матрица. По-
Поэтому класс матриц, конгруэнтных**) V, является инва-
инвариантом типа вложения поверхности^. Однако на за-
заданный узел k можно натянуть много разных поверхно-
поверхностей df, так что класс конгруэнтности матрицы V, ко-
неч)но, не является инвариантом типа узла k. Тем не ме-
менее возможно выразить некоторые из инвариантов в
*) Символ S (а, Ь) здесь и далее обозначает индекс пересече-
пересечения цепей а и Ь. — Прим. перев.
**) Матрицы V и UVW, где матрица V унимодулярна, назы-
называются конгруэнтными. — Прим. перевь
266
Приложение I. Краткий экскурс в теорию узлов
терминах матрицы V, что приведет нас к значительным
упрощениям при работе с этими инвариантами.
Вычислим теперь матрицу Александера в терминах
матрицы V. Так как матрица Александера является ин-
инвариантом *) группы G/G"\ то можно начать с нахо-
нахождения копредставления группы G/G". Рассмотрим сна-
сначала пару полосок, где кривые аи а%, ..., такие, как и
выше. Пусть Ь{ — петля, обегающая i-ю полоску в на-
направлении, указанном на рисунке, и х— малая петля,
обегающая вокруг узла в указанном на диаграмме ме-
месте. Поскольку мы все рассматриваем по модулю вто-
второго коммутанта G", элементы аи ..., агл, bu ..., b2h,
принадлежащие, очевидно, коммутанту G', коммути-
коммутируют <26>, так что несущественно, в каком месте i-й по-
полоски расположен путь Ь\. Другие неточности на рисун-
рисунке, такие, как появление петли х в двух разных местах,
объясняются аналогично. Нетрудно убедиться в том,
что группа G\G" порождается элементами #, а4, ... , a2h,
bu • • • i b2h-
Кроме соотношений, показывающих, что коммута-
коммутаторы коммутируют, имеются еще два вида соотношений,
т. е., точнее,
и/и" = \х, а,\, ..., #2л> bv ..., b<ih • /*i> . • •> г2^,
*) Это следует из результатов упражнений 6 и 7 к гл. VI.—
Прим. перев.
5. Циклические накрытия пространства узла 267
Пытаясь поднять петлю щ прямо вверх, получим соотно-
соотношение гг. Естественно, при этом петля цепляется за по-
полоски, что и дает возможность выразить петлю аг- через
петли &i, ... , 62/i, обегающие вокруг этих полосок.
В итоге получим
2А
Соотношение Si получается при попытке передвинуть
петлю х вдоль первой полоски (по правой ее стороне).
При передвижении она также будет цепляться за другие
полоски, и в результате мы придем к сопряженному эле-
элементу. Например, на предыдущем рисунке петля х це-
цепляется прежде всего за первый завиток первой полоски
и петлю вокруг правой стороны первой полосы, /рас-
/расположенную сразу nbcjle этого завитка, т. е. за b\XbTl>
как видно из рисунка. Перенеся петлю х вдоль первой
полоски, мы получим дца выражения для ее образа, т. е.
малой петли, обегающей вокруг правой стороны этой
полоски на другом ее конце, откуда и получим наше пер-
первое соотношение
Аналогично получаем
{s2):
и вообще
В этом копредставлении мы можем либо отбросить об-
образующие п\ и соотношения гг- или же образующие Ьг и
соотношения S*. Первый способ приводит нас к матрице
а второй — к матрице
268
Приложение I. Краткий экскурс в теорию узлов
(так как /2 = —£, то вторая матрица может быть полу-
получена из первой умножением справа на —/). В соответ-
соответствующих матрицах Александера будет, кроме того,
столбец из нулей, получаемый при дифференцировании
по х. Следуя Зейферту, рассмотрим вторую матрицу
F(t)=E+(t—l)T.
Ясно, что A@=defF@B7).
Далее, ^-кратное циклическое накрытие соответст-
соответствует представлению х —■> @ 1 ... g — 1), а, -♦ единица.
Обозначим через Тй (gXg)-матрицу
О 1 0 ... О
О 0 1 ... О
О 0 0 ... О
0 0 0 ... 1
1 0 0 ... О
регулярного представления перестановки @ 1 .. .g— 1).
Тогда F(T8) есть матрица соотношений первой группы
гомологии ^-кратного разветвленного накрытия трех-
трехмерного пространства, разветвляющегося над рассма-
рассматриваемым узлом *). Переставляя столбцы и строки ма-
матрицы F(Tg), получаем
Е— Г
о
г
L
Эта матрица эквивалентна
Е
0
0
0
* ...
Е ...
0 ..
0 ...
*
*
Е
0
Г 0 ..
7 Г Г
0 0 ..
следующей
pg- /р
/о*
э
0
-Г
*) Это так, потому что матрица F(Tg) совпадает с матри-
матрицей /ер, построенной в предыдущем параграфе. — Прим. перев.
5. Циклические накрытия пространства узла
Следовательно, BЛХ2Л) -матрица
является матрицей соотношений группы Н{{2).
Для многих узлов сказанное является значительным
упрощением. Отсюда следует, например, что группа
HiB) может быть вычислена из Bhx2h)-матрицы, если
узел имеет род Л, в то время как метод, введенный ра-
ранее, приводит к матрице гораздо более высокого по-
порядка.
Для узлов рода 1 нам надо только решить ряд разно-
разностных уравнений, чтобы получить элементы матрицы Fg.
Это приводит к точному вычислению группы #iB) для
всех значений g, и некоторые из этих результатов очень
интересны. Например, для трилистника можно найти
g = 0 (mod 6),
= 0 g==± I(mod6),
= Z8, g=±2(mod6),
= Z2@Z2, £=3 (mod6).
Для восьмерки имеем следующую таблицу:
g I ^B)
1
2
3
4
5
6
7
8
9
10
0
^4 ©^4
15 Vjt/ 3
Z ff^ ^
Z40 ф Z8
^29 © ^29
^105© ^21
z76 ф z76
^275© ^55
Наличие в нечетных строках этой таблицы удвоен-
удвоенных групп не удивительно. Вообще для любого узла
группа гомологии #iB) ^-кратного циклического раз-
разветвленного на^рыгия является всегда «удвоенной»
при нечетном gBsK
270 Приложение I. Краткий экскурс в теорию узлов
Так как ^-кратное разветвленное накрытие 2 являет-
является замкнутым ориентированным трехмерным многооб-
многообразием, в нем можно рассматривать коэффициенты за-
зацепления L, являющегося примитивным билинейным
симметрическим отображением одномерной группы кру-
кручений в группу рациональных чисел по модулю 1. Оно
определяется следующим образом: пусть а и b — циклы
конечного порядка. Тогда существует двумерная цепь Л,
граница которой есть та при некотором тФО. Положим
L(a, &)=-!§(Л, b)(modi),
т
где S> обозначает индекс пересечения в 2. Если в мно-
многообразии 2 изменить ориентацию, то форма L изменит
знак. Но так как многообразие 2 наследует ориентацию
сферы 5, то форма L меняет знак, когда сфера S меняет
ориентацию.
Группа кручения 7\B) вместе с примитивным били-
билинейным симметричным отображением
L: 7\BH 7^B) -^Рац. числа modi
являются инвариантами типа узла fe, расположенного в
ориентированной трехмерной сфере. Отсюда числовые
инварианты могут быть получены следующим образом.
Пусть ть Т2,..., тп суть коэффициенты кручения много-
многообразия 2 (их можно найти с помощью матрицы Fg),
рассматриваемые в таком порядке, что xr+i делит тг, и
р— любой нечетный простой делитель числа тг, такой,
что pd делит Тг, но не делит rr+i (при этом мы считаем,
что тп+1=1). Тогда при соответствующим образом подо-
подобранных элементах конечного порядка git ... , gr груп-
группы Я] B) произведение
представляет собой целое число, взаимно простое с р,
причем число %г(р), являющееся символом квадратично-
квадратичного вычета (ti.. .тг • det \\L(gi, gj) \\/p) этого целого числа,
не зависит от сделанного выбора и является инвариан-
инвариантом типа узла в ориентированной трехмерной сфере S.
Можно показать, что матрица пересечений, соответ-
соответствующая матрице соотношений Fg, есть в точности
5. Циклические накрытия пространства узла
271
матрица
S*= (Г —£)*•/.
Теперь можно определить и соответствующую матрицу
зацеплений Lg, поскольку
Рассмотрим в качестве примера матрицу
найденную нами ранее для трилистника. Здесь
1
1
о
52 =
Tl = 3, t2=l,
четом числа
—1
О
(mod 1),
1 2
9 1
3 3
2 1
T з
%iC) является квадратичным вы-
Так как 1 есть квадратичный
вычет mod3, то xi C) = 1. С другой стороны, если изме-
изменить ориентацию на трехмерной сфере 5, то
1
-1
= 3, г=1.
3 • -g- = 1
II 1
Г =
О —1
1
1
:i
—1 -2
2 1
(mod 1),
a XiC) есть символ квадратичного вычета числа
3 • (—"з/ = ~-1# ^ак как —'—квадратичный невычет
mod3, то XiC)= — 1» откуда следует, что «трилистник»
не является зеркальным узлом.
Если g = 2, то аналогичный алгоритм можно по-
построить, основываясь на не обязательно ориентируемых
поверхностях, натянутых на узел. Такие поверхности мо-
можно получить, раскрашивая области на диаграмме узла
как клетки на шахматной доске. Правило, позволяющее
272
Приложение I. Краткий экскурс в теорию узлов
построить подобную поверхность, состоит в следую-
следующем. Раскрасим области диаграммы в черный или бе-
белый цвет, согласно тому, какое число раз пересекает
проекцию узла путь, идущий из этой области в беско-
бесконечность, четное или нечетное. (В пересечениях поверх-
поверхность так же, как и выше, закручивается.) Поставим в
соответствие каждому пересечению с целое число
т](с) = ±1, измеряющее «кручение» поверхности в этом
месте. Пусть Хо% Хи ..., Хп суть области, окрашенные в
черный цвет (где Хо обозначает, скажем, неограничен-
неограниченную область), и определим число е^ = 2ц(с) как сумму
таких чисел по всем точкам с, прилегающим одновре-
одновременно к Xi и Xj. Пусть
fix* xv ..., хп)=% еи(Х1 —X;J.
Положим
f(xu ... , xn)=j(O, хи ... , хп).
Эта функция называется квадратичной формой диаграм-
диаграммы. Ясно, что
I (Хо, Xv . . ., Хп)=
2j
5. Циклические накрытия пространства узла 273
где ац = —е{1 при /=£/, а аи = 2 *//==2Tl(£)i где с про-
пробегает все пересечения, прилегающие к Хг-. Квадратич-
Квадратичной форме f(x0, jci jcn) соответствует целочисленная
симметричная матрица ^ = |1#/Д, у^о, i,..., л' а Ф°Рме
f(*t,... ,Jcn)— ее главный минор
Можно показать, что матрица соотношений группы
#iB), где 2 —двукратное циклическое накрытие, сов-
совпадает с яХя-матрицей А и что матрица зацеплений
равна A~l(modl). (Отметим, что матрица А всегда не-
неособая, так как det А = Д(—1) =£0.)
Примеры (рисунки см. выше).
1. Трилистник (первая проекция)
f(Xl)*= — 3x\, Л = —3, Л-1 = — i(modl).
Очевидно, что она не зеркальна.
2. Трилистник (вторая проекция)
I [хх, л:2) = хх [хх лу xv
11—2 1 II .1 || —2 —1 II
3. Восьмерка
f (хх, х2) = х\ 4- 2 (х, — л2J 4-
13 21 . 1 I 3 —2
Л = |2 з||' А—В"!
Восьмерка, очевидно,—зеркальный узел; обратив его
перекрещивания так, чтобы получилось зеркальное ото-
отображение, имеем
1—3—2 1 . i I] —3 21!
Н--2 ~з|' А =1Ц 2 -3||<modl>-
В любом из этих случаев XiE) = ( ± -g-J = 1.
18 Зак 317
274 Приложение I. Краткий экскурс в теорию узлов
6. Нахождение представлений
В трех- и четырехмерной топологии часто возникает
проблема нахождения представлений группы, заданной
некоторым копредставлением: например, если нужно по-
показать, что некоторая дуга является дикой, для чего
вполне достаточно найти хотя бы какое-нибудь предста-
представление на любую нетривиальную группу, или если тре-
требуется различить два данных вложения. В этом случае
задача более тонкая и может понадобиться изучить все
представления на выбранную нетривиальную группу.
Виды групп, на которых осуществляются представле-
представления, ограничены только воображением исследователя.
Наиболее часто используются группы перестановок, од-
однако используются, например, и группы матриц, группы
движений плоскости Лобачевского и даже сами группы
узлов.
Наиболее простой способ нахождения представлений
группы G по известному копредставлению состоит в до-
добавлении новых соотношений. В удачном случае соот-
соответствующий гомоморфный образ будет достаточно про-
простым для опознания его, но и не упрощенным до три-
тривиальности. Если группа G совершенна (т. е. G =(/'),
то добиться такого положения можно лишь с помощью
довольно тонких методов, а если группа G проста, то и
вовсе невозможно. (Далее упоминается, однако, другой
подход, позволяющий иногда работать даже с простыми
группами.)
Поскольку многие встречающиеся группы являются
группами узлов или близкими к группам узлов, рассмо-
рассмотрим прежде всего представления труппы G ручного
узла k. Прежде всего замечаем, что коммутирование
отображает группу G на группу Z и что при любом g
существует единственный гомеоморфизм группы Z на Zg •
Значит, для всякого g существует единственное пред-
представление группы G на Zg. Если мы будем представлять
себе элементы группы Zg как степень перестановки
(О 1 ... g—1), то соответствующее представление по-
получится, если любой образующий элемент Xj заданного
верхнего копредставления отобразить в цикл @ 1 ...
... g—1). Описанные представления являются един-
6. Нахождение представлений
ственными конечными абелевыми представлениями груп-
группы узла.
(Изменяя нумерацию символов 0 1 .. .g— 1, скажем пе-
переставляя их, получаем представление, отличающееся от
исходного внутренним автоморфизмом симметрической
группы Sg ранга g. Представления, в §>g определены
только с точностью до таких внутренних автоморфиз-
автоморфизмов.)
Из неабелевых представлений только метабелевы мо-
могут быть получены систематически и, в частности, мета-
циклические. Покажем, как находить метациклические
представления.
Рассмотрим соотношение, возникающее в типичной
точке пересечения: xk = XjX.xjl. Единственные нену-
ненулевые элементы соответствующей строки матрицы Алек-
Александера — это
*1 X] *Ь
t 1 — t — 1
Поэтому, умножая матрицу Александера справа на сле-
следующую матрицу-столбец:
18*
276 Приложение I. Краткий экскурс в теорию узлоб
получаем нулевую матрицу, если система п линейных
однородных уравнений от п неизвестных
имеет решение. Так как сумма коэффициентов в любом
из этих уравнений равна нулю и так как любое из п
соотношений является следствием остальных, одно из
уравнений может быть отброшено и одному произволь-
произвольному неизвестному придано нулевое значение. Посколь-
Поскольку определитель оставшейся системы (п—1)Х(я—1)
линейных однородных уравнений — полином А@» имеет-
имеется по меньшей мере одно нетривиальное решение, если
равенства интерпретировать как сравнения по модулю
|Д@ |, а /, скажем, считать целым числом.
Этим сравнениям можно дать интересную интерпре-
интерпретацию. Каждое из них может быть переписано в виде
Рассмотрим п точек Ри Ръ - -., Рщ лежащих на единич-
единичной окружности некоторой плоскости, и радиусы
ОРи ОР2,..., ОРп. Будем считать, что gi, g2,..., In
суть углы наклона этих радиусов, деленные на 2я/|Д(/) |.
Тогда интерпретация нашего типичного сравнения со-
состоит в том, что угол «$- PjOPh представляет собой
/-кратный угол -*$ PjOPi. (Например, при t= — l это озна-
означает, что OPj есть биссектриса угла P%OPh, а при /=3
6. Нахождение представлений
277
радиус ОР{ осуществляет трисекцию угла PjOPk.) Сле-
Следовательно, каждое решение нашей системы линейных
уравнений определяет некоторую совокупность п точек
Рь ..., Рп на единичной окружности. Группа G может
быть теперь представлена как группа перестановок вер-
вершин правильного |Д(/) | -угольника, если, например, при
/ = —1 сопоставить каждому образующему Х\ отражение
относительно линии OPi, а в общем случае /-кратное
увеличение угла PjOPu / = 0, 1, ... , /г. Это можно, ко-
конечно, записать с помощью перестановок.
Пример 10.
= \a, by с, d, e:b =
= ece
~\
Матрица Александера такова:
t _i oi — / 0
\ — t t —1 0 0
0 0 t —11 —
0 \ — t 0 t —1
—1 0 1-/0 /
A(—1)=7. Соответствующая однородная система в этом
случае имеет вид:
— а — |i +26 =0,
2а — p — Y =0,
e=0 (mod 7),
2р —6 —е =0,
2р — е =0.
278
Приложение I. Краткий экскурс в теорию узлов
Положим 06=0 (mod 7) и выбросим одно из предыдущих
сравнений. Одно из решений таково:
а=0, р=2, у^5> S=l, e=3.
2
Следовательно, расположив символы а, Ь, с, d и е на
правильном семиугольнике, как показано, мы получаем
представление:
а ~> A6) B5) C4),
6 ~> A3) @4) E6),
с-> D6) @3) A2),
d-> @2) C6) D5),
г->B4)A5)@6),
Пример 11.
| a, b, c:b = cac
~l
«=»!— t + r. A(—2) = 7.
— 2a—|
3a —2p —y=0 (mod 7),
6. Нахождение представлений 279
Получаем представление
а->A 3 2 6 4 5),
Ь->@ 2 15 34),
<?->C 54 160).
Всякое метациклическое представление группы узла
можно получить следующим образом. Пусть M(ri, t) —
метациклическая группа \у, и : ип=1, уиу1 = иг\. Отобра-
Отобразим Х{ в ucty и попытаемся определить целые с{ так,
чтобы это отображение продолжалось до гомоморфизма.
Типичное соотношение отобразится тогда в
так что мы должны иметь tci+ A — t)cj — ck=0(mo&n).
Это такая же система сравнений, что и выше, и она
имеет нетривиальное решение всякий раз, когда A(t)
делит число т.
Пример 12. Группа \а, Ь, с : b — cac~l, c = aba~l>
a = bcb~l\ представляется на группу МG,—2) сле-
следующим образом (ср. с предыдущим примером):
b -> и6у,
с -> и?у.
В статье автора [Фокс, 1949] была получена группа
Г = |Ьо, Ьи Ь2, • • •; 1 ] |
280
Приложение I. Краткий экскурс в теорию узлов
и нужно было показать, что она неабелева, т. е. отлична
от Г/r'^Z. Если добавить соотношения &о==&2 = &4 = ...,
&1==&з = &5= ..., то эта группа отобразится гомеоморфно
на конечно копредставимую группу \bo, fa: bibobT* —
= bobibol\, так что метод, обсуждавшийся выше, при-
приводит к представлению
Ьп->(\2), если п четно,
если п нечетно,
что и было там сделано. Более того, автору неизвестны
методы решения этой задачи, отличные от приведенного.
В статье автора и Е. Артина [Фокс, Артин, 1948] воз-
возникли трудности при попытке найти представление не-
некоторой группы. К счастью, соотношения ее просто по-
получаемого гомоморфного образа были
Эти соотношения похожи на соотношения хорошо изве-
известного копредставления
/ — j\ > 2 |
группы косы Bd+u что говорит о возможности использо-
использования матриц Бюрау, которые и в самом деле являются
нужным приемом.
Матрицы Бюрау и сами по себе представляют зна-
значительный интерес, и, как показывают предыдущие за-
замечания, они могут действовать как группы перестано-
перестановок бесконечного ранга. Бюрау рассматривал группу
таких бесконечных матриц, элементы которых почти
всюду совпадают с элементами бесконечной единичной
матрицы, представляя элемент о% матрицей
Е
0
0
0
1—* t
1 0
0
0
0
Е
6. Нахождение представлений
281
Это представление имеет поясняющее его смысл толко-
толкование в терминах свободного исчисления. Как показы-
показывает приводимая ниже диаграмма, элемент а* связан с
автоморфизмом Т{
Xj->Xjy ]Ф1, / + 1,
фундаментальной группы компактифицированной пло-
плоскости с удаленными d+l точками (т. е. свободной груп-
группы ранга d). Это представление группы Bd+i автомор-
автоморфизмами свободной группы ранга d играет основную
роль в исследованиях Артина групп кос. Элементы ос-
основного 2Х2-минора соответствующей матрицы Бюрау
таковы:
дх[ dxjj ,
где ^(Xh)—t. Поэтому представление Бюрау имеет вид
г=1, 2
"-*-"|| —эг;— и > *> j = *> *
Из элементарных формул свободного исчисления сле-
следует, что матрица Бюрау, представляющая любое слово
282 Приложение I. Краткий экскурс в теорию узлов
, 02,..., ad) группы косы, имеет вид
w -
\\dT(Xi)f
где Т — автоморфизм свободной группы ранга d, соот-
соответствующий слову w.
Использование свободных произведений с объединен-
объединенной подгруппой часто является методом, более сильным,
чем представления. Некоторое копредставление опреде-
определяет свободное произведение А *б, если его образующие
распадаются на два множества, скажем, хих2,... и
Уи У2,..., а соотношения, — скажем, на ги г2,... и
Su ^2,..., причем каждое гг- есть слово только от х^ х2,...
и каждое s{ — только от уи Уъ .. • . Если, кроме того,
имеются соотношения вида Ui = vu u2 = v2,..., где ка-
каждое щ — слово от хи х2,..., а v{ — слово от у и \}ъ,...,
то соответствующее копредставление может не опреде-
определять свободное произведение с объединенной подгруп-
подгруппой А* В; нужно еще доказать, что подгруппа С\
с
группы Л, порожденная элементами иии2,..., изоморф-
изоморфна подгруппе Ci группы б, порожденной элементами
fli, v2,..., причем изоморфизм этот переводит и{ в vu
и2 в v2 и т. д. Если это удается сделать, награда бывает,
как правило, весьма значительной. Например, группы А
И В изоморфно вкладываются в А * В. Поэтому, если
одна из этих групп нетривиальна, то отсюда сразу выте-
вытекает нетривиальность группы А* В. (Это можно, на-
например, использовать при доказательстве того, что узел
k#l нетривиален, если хотя бы один из узлов k и / не-
нетривиален.) Поскольку группы Л и В не являются нор-
нормальными делителями произведения А* 5, нахожде-
нахождение нетривиальных представлений может быть весьма
затруднено, если вообще возможно. В качестве примера
приведем другие полезные свойства таких произведений:
1) если некоторый элемент группы А* В имеет ко-
конечный порядок, то он обязательно сопряжен либо с не-
некоторым элементом подгруппы Л, либо с некоторым эле-
элементом подгруппы В\
6. Нахождение представлений
283
2) если два элемента группы А * В коммутируют, то
при некотором z они принадлежат либо подгруппе zAzrx,
либо zBz~l.
В качестве простой иллюстрации использования сво-
свободных произведений с объединенной подгруппой
(здесь — просто свободных произведений) мы сейчас до-
докажем существование пары нерасцепляемых дуг. Это
означает существование таких непересекающихся дуг X
и У, что всякая область, гомеоморфная трехмерному
iiiaipy и пересекающая одну из них, пересекает также
и другую.
Если бы дуги X и У были расцепляемы, группа
G=n(S3—(Х[}У)) была бы представима в виде свобод-
свободного произведения групп n(S3 — X) и n(S3 — У) и по-
поэтому никакой элемент, сопряженный с &, не коммути-
коммутировал бы с элементом, сопряженным с с (поскольку,
как можно показать с помощью соответствующего пред-
представления, Ъ и с — нетривиальны). Но так как элементы
ft и с, очевидно, коммутируют, дуги X и У нельзя рас-
расцепить.
ПРИМЕЧАНИЯ ПЕРЕВОДЧИКА
A) Зацеплением (цепью) с п компонентами называется гомео-
морфный образ в R3 пространства, состоящего из п непересекаю-
непересекающихся окружностей. Граф — это гомеоморфный образ в R3 одно-
одномерного комплекса. На графы (а стало быть, и зацепления) непо-
непосредственно переносятся все основные определения, результаты и
доказательства из гл. I, VI и VII основного текста. И поэтому в
дальнейшем будут использованы обозначения из этих глав.
Опишем для группы графа аналог копредставления Виртингера.
Это необходимо для понимания § I данного «экскурса» и будет
использоваться далее.
Под особой точкой диаграммы графа, находящегося в регулярном
положении, будем понимать либо его вершину, либо точку пересе-
пересечения, а под элементарной дугой — ориентированную дугу, соеди-
соединяющую две особые точки графа и не содержащую других особых
точек внутри себя, кроме точек перехода. Сопоставляя /-й элемен-
элементарной дуге (некоторая нумерация дуг задана) символ *,-, получим
набор свободных образующих искомого копредставления. Соотноше-
Соотношения Г{ получаются при обходах вокруг особых точек. Именно, рас-
рассмотрим малую окружность, обходящую против часовой стрелки,—
заданную особую точку, и зафиксируем на ней начало обхода —
точку q. Точка, двигающаяся по этой окружности, пересекает
Примечания переводчика
285
встречающиеся элементарные дуги либо слева направо, либо справа
налево. В первом случае приписываем справа к слову-соотношению
соответствующий образующий хг в степени +1, во втором — обра-
образующий в степени —1. Например, обход, указанный на рисунке,
дает соотношение х$ х^ххх = 1. Как и раньше, одно из соотноше-
соотношений г, можно всегда отбросить.
B) Докажем это для простоты для двухкомпонентного за-
зацепления с помощью описанного выше копредставления Виртин-
гера. Пусть xh...,xh+m— образующие этого копредставления,
соответствующие дугам первой компоненты Si, а у\ yi+n ■—
второй, S2, причем предположим, что ориентации элементарных дуг
совпадают с ориентациями, выбранными на каждой из компонент.
Число т равно числу переходов компоненты S2 над Si, a n — числу
переходов S\ над S2. Из леммы D.6) гл. IV следует, что прокомму-
тированная группа зацепления Н является гомоморфным образом
свободной абелевой группы со свободными образующими
*!,..., х'ь + т* у'\ #/+я» пРичем ЯДР° этого гомоморфизма по-
порождается элементами Гу,где гj — аддитивно записанное соотноше-
соотношение о, в котором элементы хр, yq заменены на хр% yq.Ho при не-
непосредственной проверке видно, что всякое соотношение г j имеет
вид xfp — Je£ = O или ур— Уд = О, откуда и следует, что группа Н
свободно порождается элементами х = х[ = ... = xfk + m, у = у[ =
г
C) Проведем доказательство для двухкомпонентного зацепле-
зацепления, которое непосредственно распространяется на общий случай.
Примем обозначения примечания B) и заметим, что соотношения о
можно разбить на четыре типа:
..-е„-1
, причем [ryr2 rk+l+m + n} =
,, s. s , t. t }. Положим
. 1 m V ii\
ds.
ri v ^t II •' si*. •* T ■ /i v и
Тогда матрица Александера А рассматриваемого копрелставления
Принимает вид
Р О
л ° Q
А •
286
Примечания переводчика
Прибавим первые k+m—1 столбцов матрицы А к (&+/л)-му
столбцу, и все столбцы от (&+/л+1)-го до (k+1+m+n—1)-го —
к (k+l+m+ri)-My, получив эквивалентную матрицу А'\
Р'
О
К
о
Q'
где I-
О-у)
II =
у "*+» —
A-лг)
тлп —
где 6j=±l. Заметим, что (^ — 1I=A — </)II, откуда следует, что
всякий определитель, содержащий эти столбцы (или их частиI,
равеет нулю. Так как, удаляя из матрицы А какую-либо строку, мы
получаем эквивалентную матрицу (см. конец примечания A)), то
это же можно сделать и с матрицей А', получив эквивалентную
(&+/+/л+А1-1)Х(&+/+/л+л)-матрицу А". В матрице Л", в силу
предыдущего замечания, только два минора порядка k+1 + m+n—\
могут быть отличны от нуля, причем один из этих миноров содер-
содержит столбец I, но не содержит столбца II, а другой — наоборот,
остальные столбцы у них общие. Вынося из столбца I первого ми-
минора множитель у— 1, а из столбца II второго минора 1-х, при-
приходим к требуемому результату.
D) Определим коэффициент зацепления двух ориентированных
окружностей Si и 52, расположенных в Rz. Для этого рассмотрим
гладкую ориентированную поверхность Р в R3 (для простоты не
имеющую особенностей), краем которой является окружность Si,
т. е. Si = dP, причем будем считать, что ее ориентация согласована
Примечания переводчика
287
в обычном смысле с ориентацией ее края Sb Кроме того, предполо-
предположим, что пересечение S2 П Р состоит из конечного числа то-
точек pi, ..., рь, причем ни одна из этих точек не является точкой
касания поверхности Р и окружности 52. Конструкция Зейферта,
описываемая в § 3, стр. 246, показывает, что все эти условия
можно осуществить. Положим v(pi) = l или —1 в зависимости от
того, с какой стороны, отрицательной или положительной, подходит
к поверхности Р в точке р% точка, обегающая S2 в положительном
направлении. Теперь коэффициент зацепления v(Si,S2) можно опре-
определить как индекс пересечения v (Р, S2) = 2 v (Pi) поверхности Р
i
и линии S2. Нетрудно видеть, что если Р' — замкнутая поверх-
поверхность в /?3, то v(P',S2)=0, откуда следует, что наше определение
не зависит от выбора поверхности Р. Это же показывает, что вся-
всякая деформация окружности S\ (или S2), возможно, с самопересе-
самопересечениями, в процессе которой образы окружностей S\ и 52 не пере-
пересекаются, не меняет индекса пересечения. Совершенно аналогично
определяется коэффициент зацепления одного множества окруж-
окружностей 5ц S\m в R3 с другим 52i 52п.
E) Докажем приводимые свойства A) и B) полинома Д(*,«/),
приняв обозначения примечаний C) и D). Пусть ty:JH->JH—
гомоморфизм, определяемый равенствами ^ (•*) ^ х> ^ (#) = 1
Предположим также, что при построении матрицы А" мы отбро-
отбросили соотношение ри и обозначим через Р" результат выбрасыва-
выбрасывания первой строки из матрицы Р'. Замечая, что
получаем, что
ХуА" «
Р"
0
f Q'
1УГх
0
0
:
0
0
0
1У У
(■■)
Обозначим через Aj единственный нетривиальный минор по-
порядка Aj+/+2m —1. Очевидно, что Д(я, 1) = ±Ai/(*— 1), или
III P"
I II Г Л II I I II к
У
II р" II
Матрице , можно дать следующую интерпретацию. Нанесем
на диаграмму первой компоненты рассматриваемого зацепления т
точек 1\ 1т в тех местах, где диаграмма первой компоненты
проходит под второй. Эти точки мы будем считать вершинами
графа, телом которого является первая компонента. Построим ко-
представление группы этого графа, как указано в примечании A).
288 Примечания переводчика
Тогда, очевидно, это копредставление имеет следующий вид
(х\у ..., Xh+m : Р\ Phy S\, ..., sm), где s£- = xZfXftEy т. е. полу-
получено из Si подстановкой yg = \. Если у этого копредставления от-
отбросить соотношение pi, а в матрице Александера получившегося
копредставления все столбцы прибавить к последнему, то получится
11 Р" О
матрица | ^ . В силу теоремы инвариантности первый эле-
Р"
ментарный идеал этой матрицы, т. е. I III f о III I, совпадает с
(Д(дг))или
тируем матрицу
± л'лД (х). Аналогичным образом интерпре-
Для этого рассмотрим зацепление, со-
состоящее из двух компонент Si и S2, причем предположим, что ре-
регулярные проекции этих компонент на плоскость представляют
собой несамопересекающиеся замкнутые кривые. Предположим, что
на компоненте S2 нанесено / точек Pi р/, делящих ее на коге-
когерентно ориентированные дуги du ..., du и эти дуги находятся во
взаимно однозначном соответствии с дугами d\ dt компо-
компоненты S2, на которые ее делят проходящие точки^ Наконец, пред-
предположим, что структура переходов компоненты S{ через дугу dt
такая же, как и структура переходов компоненты З^чедез
Дугу di, /=1, ..., /. Геометрически ясно, что зацепление Ei,52),
удовлетворяющее приведенным условиям, можно получить, дефор-
деформируя исходное зацепление так, что в процессе деформации образы
компонент Si и S2 не ^пересекаются между собой. Это позволяет
нам считать, что vEi,S2)=vE1,52) (см^ примечание D)).
Рассмотрим матрицу Александера А зацепления Si, 52, соот-
соответствующую копредставлению Виртингера, которое строится как
копредставление графа, с вершинами Pi р/ (см. примеча-
II *yQ II II *1#
ние A)). Непосредственно видно, что = ^ 11, где
II ^у у II II ^у у II
матрицы Q и Гу — подматрицы матрицы А, определенные анало-
аналогично подматрицам Q и Ту матрицы А. Поэтому на основании уже
доказанного имеем
±х*-
где Д(л:, у) — полином Александера зацепления (Si, S2), а Д(я) —
полином Александера компоненты s\. Так как эта компонента по
Примечания переводчика
289
условию незаузлена, то Д(дг))=«1. С другой стороны, нетрудно ви-
видеть, что зацепление EЬ S2) имеет тот же тип (в зависимости от
знака коэффициента vEi,52)), что и одно из следующих канониче-
канонических зацеплений:
v = у > О
v =7 <0
Непосредственное вычисление полинома Д(#, 1) для любого из
этих зацеплений показывает, что он равен #? —Л. Стало быть, из
теоремы инвариантности теперь следует, что Д(*, 1)»*« —1, что
завершает доказательство свойства A).
Свойство B) вытекает из инвариантности элементарных идеа-
идеалов относительно антиавтоморфизма x->x~lt y-±y~l, что доказы-
доказывается точно так же, как и в основном тексте гл. IX, на основе
понятия пары дуальных копредставлении.
Отметим в заключение, что случай ц>2 можно исследовать
точно так же. При этом свойство (I), заменяется следующим:
*-и tt+u
где Ц] — коэффициент зацепления i-й и /-й компонент, а
Д(/ь ..., ti-u tj+i ty)—полином зацепления, полученного из
исходного выбрасыванием i-й компоненты.
F) Это означает, что группы графов, вообще говоря, допускают
копредставления, число образующих которых превосходит более
чем на единицу число соотношений. Это так, например, для приво-
приводимого ниже графа.
19 Зак 317
290 Примечания переводчика
G) Напомним, что для любого линейно связного простран-
пространства X имеет место равенство Hi(X)=n(X)/[n(X), л(Х)] (см. Ху
Сы-цзян, Теория гомотопий, «Мир», М., 1964, стр. 65).
Доказать, что группа nl(R4—S2) бесконечная циклическая
можно, исходя из копредставления группы n(R4—S2), описанного*
ниже в тексте, добавляя в него, согласно предложению 4.6 гл. IV,.
соотношения коммутирования и учитывая тот факт (см. примеча-
примечание B)), что группа всякого зацепления — свободная абелева с со-
соответствующим числом образующих.
(8) Полиэдральная поверхность 5 в R4 называется локально-
плоской в точке q% если найдется такая окрестность U точки q в S
и такой кусочно-линейный гомеоморфизм f:R4->R4, что f(U) = U\
где V1 — некоторая область плоскости R2 С R4. Особенности по-
поверхности S — это точки, вблизи которых она не является локально-
плоской. Ясно, что таковыми могут быть лишь вершины ком-
комплекса S.
Рассмотрим в R3 нетривиальный узел А' и точку q£R4, q (jjj Я3-
Соединяя всевозможными отрезками точку q с точками узла /(,
получим поверхность, гомеоморфную диску D2, не являющуюся ло-
локально плоской в точке q.
(9) Докажем это для так называемых ленточных узлов (см.
стр. 317). Является ли всякий срезанный узел ленточным, неиз-
неизвестно (проблема 25, стр. 318). Ленточный узел К можно предста-
представить как край поверхности 5 следующего вида. Рассмотрим
в /?3 попарно непересекающиеся и несамопересекающиеся диски
D\ Dp, соединенные полосками Yi» • • •» Yp-i так. что по~
лоска y* соединяет диски Dt- и Di+l. Относительно полосок
Yi Yp—1 предположим, что они также попарно непересекаю-
непересекающиеся и цесамопересекающиеся и кроме того, пересекают диски
D\ Dv (не касаясь их) только по дугам, лежащим внутри этих
дисков. Объединение описанных дисков и полосок образует поверх-
поверхность нужного нам вида, т. е.
Нетрудно видеть, что, деформируя поверхность, можно так распо-
расположить ее в /?3, что ее проекция будет иметь вид, указанный на
рисунке.
/7=2
Примечания переводчика
29Г
Нижеследующее доказательство мы проведем для случая р=2г
так как общий случай отличается от этого только более громозд-
громоздкими обозначениями.
С поверхностью 5 естественным образом связан г£аф Г, состоя-
состоящий из краев Oi=dDit дисков Df и средних линий у г полосок Yj_
(см. рисунок). Рассмотрим копредставление Виртингера группы G
этого графа, ориентировав окружности О\ и (Тг против часовой
стрелки, а дугу Yi — от ai к аг. Оно будет иметь вид (см. приме-
примечание A)):
где
!) *
••" xm:Pv
. *i 5Л,
?/ = *,
ri — xn(i)cixn(t)c
l
of *
или bPv\iy p/ = ± 1)
St —
-1 -H
p (i)xa (i
а два последних соотношения получены обходами вокруг вершин.
Непосредственно из него следует, что коммутирование а группы G
таково, что си*/ = и, / = 0 k, abj = vt j = 0, ..., /, curz=lf
/==0^. ..,_m, где и и v — базис свободной абелевой группы
HG[&G]
Копредставление группы G узла_ K=dS можно получить из
описанного копредставления группы G добавлением одного соотно*
19*
292 Примечания переводчика
V V V
шения aQz=zbu где z = dlld22... d^t ad}— элементарная дуга,
разделяющая дуги jc2--i и хи vt = \_ или —1 в зависимости от того,
как проходит в этом месте дуга уь слева направо или справа на-
налево, под дугой di. To, что добавления этого соотношения доста-
достаточно, видно из следующего.
Утолщив немного граф Г, получим тело Г, гомеоморфное запол-
заполненному кренделю и расположенное концентрично графу Г, причем
нетрудно видеть, что Rz—Г гомеоморфно R3 — T. Рассмотрим^ кривой
прямоугольник Z), составленный из всех отрезков /*, х £ Yl кото-
которые соединяют точки поверхности тела Д лежащие точно выше и
ниже точки х (прямоугольник для незаузленного тора изображен
на рисунке). Тогда, очевидно, R3—K гомеоморфно (R3 — T)\J D. Из
теоремы же ван Кампена теперь непосредственно следует, что до-
добавление диска D к пространству R9—Т соответствует добавлению
описанного соотношения при переходе от копредставления груп-
группы G к копредставлению группы G.
Матрицу Александера А полученного копредставления
можно_ сильно упростить, замечая, что a (pdst/dxj = а (pdSi/dxjt
где S/aas-*p(/)-i-*p"(V^TH Равенства показывают, что если рас-
рассмотреть новое копредставление, полученное заменой соотноше-
соотношений Si на Si, то матрица Александера этого нового копредставления
останется прежней. Но новое копредставление немедленно упро-
упрощается (ввиду соотношенийлГр^)_ 1 =лГр^)) отбрасыванием лишних
образующих. Этот упрощенный вариант нового копредставления
можно описать следующим образом. Разобьем дугу Yi на ДУГИ
Yo» • • •» Уп* проекции которых имеют своими концами проходящие
точки дуги Yi под окружностями ai и аг (таким образом, проекции
дуг Y/ могут иметь самопересечения), и сопоставим дуге Y/ обра-
образующий у г. Положим i|)Xi=#j, если дуга Xi лежит на дуге Yy •
Тогда упрощенное новое копредставление имеет вид
? = (я0' •••• а» V-- bv Уо>---Уп:Р1 Р* iv-fr
Г bQ = 1гуп, яо?= й,),
где слова ри qu riy z получены из соответствующих слов рг-, qu
rit z заменой элементов х\ на tyx^ Итак, хотя группа этого копред-
копредставления отлична, вообще говоря, от группы G, его матрица
Александера эквивалентна матрице Александера описанного выше
копредставления группы n(Rz — /С). Поэтому мы можем далее рабо-
работать с матрицей Александера А копредставления V. Отметим, что
aa^adj, i% ./ = 0, ..., К abt=* abf /, у=*0, .... /, а^ == 1, / = 0, ...л,
Примечания переводчика
293
а соотношение aoz=zbi показывает, что аа0 = abQt а зна-
значит, и что cuz/ = abj = t при любых i, /. Непосредственное вычис-
вычисление матрицы А показывает, что она имеет следующий вид:
ak V
Ч
1 -1
•;. о
о ':.
i -i
-10 1
0
0
0
1 -1
':. о
о
1 -1
-1 1
0
Эо h
Р
-to о
Q
0 0 /
i -Л
:. о
о :.
Матрица Р=||ро11 определяется так: Pa = Zit j(t—1), если
~pt = a^^yj'i at yj>ft в противном случае pij=O. Аналогично опре-
определяется матрица Q — WqaW. Совершим над матрицей А последова-
последовательно следующие эквивалентные преобразования: прибавим пер-
первые k строк к (& + 1)-й, прибавим все строки 6т (&+2)-й до
(&+/+1)-й к (k+l+ty-и, прибавим первые k столбцов к (&+1)-му,
столбцы от (£+2)-го до (&+/ + 1)-го прибавим к (&+/+2)-му, далее
(&+/+3)-й столбец, умноженный на tPx, прибавим к (Ал-/+4)-му,
полученный столбец, умноженный на t9*, к (А;+/+5)-му и т. д.
20 Зак 317
294
Примечания переводчика
В итоге придем к матрице
Ek
0
0
0
0
. . .
0
0
0
0
0
а
0
0
0
0
. . .
0
0
0
0
0
р
р
. . .
Q
. . .
. . .
:
:
•
т
О О 2а
О О S
а р w
k I
Здесь а = \] a/» P=== ^j
и, наконец, Л/ —
единичная матрица порядка i. Число e* имеет простой геометриче-
геометрический смысл: оно является индексом пересечения проекции дуги Y/
с проекцией окружности аи так что е, —±1 или 0. Аналогичный
смысл имеют числа 6*. Нетрудно видеть, что
Последний полином тождественно равен нулю при любом выборе
чисел pi = ±l, ..., рп = ±1. Непосредственный подсчет показывает
также, что а + В=0. Поэтому матрица А эквивалентна матрице
|| 0 0 1а II
и Д(/)=а2а. Индукцией по п нетрудно проверить*
I (X U W
чтоа(Г1)-*Р|+'"'+Ря+ = —
, где а = а@, 2fl == 2fl @, что
приводит нас к желаемому результату.
A0) Эти утверждения просто вытекают из результатов преды-
предыдущего примечания. Рассмотрим такую локально плоскую сферу
Примечания переводчика
295
S2 в /?4, что ее сечение при /=0 является узлом /C=dS, р=2 (см.
примечание (9)), она симметрична относительно гиперплоскости
f=0, а единственные «преобразования перехода через седловую точ-
точку» при /=±1 указаны на рисунке.
В силу симметрии сферы S2 относительно гиперплоскости /=0,.
переходы через седловые точки при /=±1 добавляют к копредстав-
лению узла К одно соотношение хп — \. Поэтому матрица Алексан-
дера группы сферы S2 имеет вид
II ^
1 0 ... О 1
(матрица А здесь такая же, как и в примечании (9)). Преобразо-
Преобразования, описанные в примечании G), переводят матрицу В в мат-
0 0 2Л
О 0 2*
а Р w
0 0 1
откуда следует, что Д(/)=а.
Далее нетрудно видеть, что граф Г можно выбрать таким об-
образом, чтобы полином 2а имел наперед заданные значения коэффи-
коэффициентов 6j=±l или 0, pj=±l (это следует из их геометрического-
смысла).
A1) Точнее, это означает, что каноническая параллель у тора Г
при гомеоморфизме / переходит в кривую /(у), незацепленную с уз-
узлом k, т. е. v(f(Y),&)=0. Если задана диаграмма узла k, то парал-
параллельная ей кривая k' (см. рисунок), вообще говоря, зацеплена с уз-
узлом. Пусть xtl ... xtk—элемент, соответствующий
20*
296 Примечания переводчика
обходу вдоль узла k по проекции узла k'. Тогда v(k,k') =
= ±@!+ ... +pfc) = p. Доказательство этого непосредственно выте-
вытекает из данного в примечании D) определения коэффициента за-
зацепления, если в качестве поверхности, натянутой на узел &, взять
поверхность Зейферта, построение которой описано несколько ниже
в тексте. Отметим, что для диаграммы узла k, представленного как
край «нормализованной» поверхности (см. § 5), р=0.
A2) Если узел k имеет род Л, то как показано ниже в § 4,
можно найти копредставление группы G/G", имеющее ровно 2/г со-
соотношений. Так как элементарные идеалы групп G и GIG" совпа-
совпадают (см. упр. 6, 7 к гл. VI), то сделанное утверждение непосред-
непосредственно вытекает из сказанного выше.
A3) Докажем это, рассматривая полугруппу Г классов ассо-
ассоциированных взаимных 1-полиномов f(t), /(l) = ±lf относительно
операции умножения. Объявляя два таких класса эквивалентными,
-если их представители fi(t) и МО связаны соотношением МО —
— МО £ @ #(*"'). заметим, что умножение в Г' индуцирует умно-
умножение в этом множестве Г классов эквивалентности, т. е. Г — полу-
полугруппа. Но так как класс полинома f(t) в Г обратен в Г
классу f(t~l)t то Г — группа. Сопоставляя каждому классу кобор-
кобордизмов узлов полином Александера (определенный с точностью до
умножения на ±tf(t)f(t-1), как это следует из примечаний (9),
A0)), получаем гомоморфизм группы кобордизмов узлов на Г (см.
стр. 241)i. Но группа Г имеет бесконечное множество образующих.
Это следует из того, что существует бесконечное число неприводи-
неприводимых взаимных L-полиномов f(t), f(l) = ±l. Поэтому и сама группа
кобордизмов бесконечно порождена.
A4) Чтобы доказать это неравенство, рассмотрим ориентиро-
ориентированную поверхность 5, натянутую на узел f(l). Можно считать,
что эта поверхность пересекает поверхность V заузленного тора V
по некоторому числу кривых, ориентация которых задается ho на-
направлению векторного произведения положительных нормалей к
поверхностям 5 и V.
Рассмотрим связный кусок S' С 5 пересечения S П V, содержа-
содержащий узел k. Его граница, кроме узла k, состоит из ориентированных
г
кривых Cj cr£V, причем P\i ±ay= 2 c/€^i (Ю» гДе Y — па-
раллель, а ц — меридиан тора V. Так как кривые сг несамопересе-
кающйеся, то их классы гомологии имеют, как известно, вид
ci~piv-irqiiL,(pi, ^) = 1, а поскольку кривые с,-, си 1ф'и не
пересекаются, то если хотя бы одна с* негомологична нулю,
(Pj.<7j)e(ep«,e?<), где е=0 или ±1. Поэтому сг~ (е*р, е*?),
Г
i==l г. Но циклы у и 2 ci = fr* ± aY гомологичны нулю в про-
*-1
странстве V[} (R3—V). Поэтому Р=0, в силу негомологичности р,
нулю в этом пространстве и приа=^0, <7» = е»#=0, i=\ г.
Примечания переводчика
297
Кривые си ..., сг разбивают поверхность 5 — S' на некоторое
число кусков Slt ..., St. Рассмотрим кусок Sj. Если бы его граница
содержала такие кривые
р у
2'1\Ф
чт0 е
то по*
верхность S была бы неориентируемой. Поэтому, если е^ или
е/з Ф 0, возможны только случаи, (а) только одна из кривых {с}
ограничивает кусок Sjt (b) кусок Sj ограничивают кривые с^ и с,-2,
причем е^ = — е/г. Отсюда следует, что кривых вида (а) должно
быть не менее а штук, а так как каждая из них имеет вид ву и,
значит, образует узел того же типа, что и &, то натянутая на нее
поверхность Sj имеет род >/и. Итак, показано, что часть поверх-
поверхности S, лежащая вне тора V, имеет род ^<xhh.
С другой стороны, если тор V незаузлен и аф О, на кривые
Сг, i=l, ..., г, можно натянуть в (R3 — V) U V попарно непересекаю-
непересекающиеся диски di, так что S'LJ^iU ... \}drбудет замкнутой ориенти-
ориентированной поверхностью, натянутой на узел k. Это показывает, что
род поверхности Sf не менее рода узла к. Возвращаясь к исходной
о
ситуации, мы видим, что род (S')^hu а род (S — S') !>- a/i/i, что
завершает доказательство.
A5) Для доказательства этой формулы заметим прежде всего,
что Я3 —т~[(/?3— V) Ц V] U /(Г — /). Из теоремы ван Кампена
и того, что [(/?3— V) U V](]f(T — /) = V, следует, что копредставле-
копредставление группы я (Я3 — т) имеет вид (х, z : г, sf ц=/#(|ы), Y==f*(Y))»rAe
(х : г) — копредставление группы п(Т — /), (z : s)— копредставление
группы я (Я3— V)=n(R3 — k), а \i и у —элементы группы я (Г — /),
определяемые каноническими меридианами и параллелью тора Т.
Для нахождения копредставления группы п(Т — 1) заметим,
что я (#3 — \i) л я (F), откуда следует, что я (Т — /) а я (Я3 - (/ |J ц) )•
Рассмотрим верхнее копредставление зацепления / U ja, разбивая
21 Зак. 317
298
Примечания переводчика
меридиан [i на один переход у и один проход (см. рисунок). Тогда
это копредставление будет иметь в качестве образующих элементы
Х\ *п+р, соответствующие узлу &, и элемент у, а его соотно-
соотношениями, кроме соотношений рь ..., рп, лежащих на узле /, будут
е, -1 -е, . .
I р, соответствующие обходам по окруж-
окружен
-1 -е, .
s, = yxk> у хг \ i
6 6 £
ностям на рисунке, и соотношение yxk ... xk9 = xk
е
*У
Р
со-
ответствующее обходу по прямоугольнику. Очевидно, что ^в/=±а.
Отбрасывая соотношение рп и считая, что алг/ = ^, ау = м, полу-
получаем следующую матрицу Александера:
кп+р
Рп-\
где R — некоторая строка.
Примечания переводчика
299
Прибавляя (л+р—1) столбцов этой матрицы к (я+р)-му, по-
получаем вторую матрицу
Из рассмотрения второй матрицы сразу следует, что
Далее, для узла k выберем такую диаграмму, что C=0 (см.
примечание A1)). Тогда, нумеруя проходы этой диаграммы Z\ zv
R — 1 ft
по порядку обхода, получаем систему соотношений ^ = ztz^ zi+lzm l
/ = 1 v, ^v+1 = z0, p = 2 Рг = 0, для копредставления группы
=i
/() /'^Cy) принимают вид z^ =
Если аг=1/, то из последних со-
соузла )fe, а соотношения м<:=/*(М'),
ei ep pi P
= лгй л:л , y = zm ... z
отношений следует, что v = tat и = v"= 1. Поэтому матрица Але-
ксандера этого копредставления имеет указанный на стр. 300 вид.
Вторая матрица получена из первой прибавлением первых (п+р — 1)
столбцов к (л+р)-му, прибавлением суммы
v l ' l~l
Qi
к (n+p+v)-Pt строке, где Qi есть («+р+/)-я строка, и,
наконец, прибавлением к (я + р+2)-му столбцу всех столбцов от
(я+р-4-3)-го до последнего. Очевидно при этом, что Дл(и) ==|Q'|.
21*
Я\
vf; ' (v)
и/;' (и)
s
0
0
0
-R
0
I-*8'
1-A>
l-/a
0
1
0
0
0
0
«431
я
1
L
0
S'
0
0
0
0
- R
0
0
0
0
0
0
6
0 1
1-/"
0
0
1
0
0 1
0
0
0
0
0
1
0
0
0
Q'
(v-l)L
L
0
Примечания переводчика
301
Вторая матрица эквивалентна следующим:
p'
s
0
0
0
0
a
0
0
0
0
0
0
p
0
1 -V
1
0
0
0
Q'
0
L
P*
S
0
0
0
0
0
0
0
0
0
e
0
1— V
i
0
0
Q
0
L
Но первый идеал последней матрицы порождается, очевидно, эле-
элементами
104 и ±(l-t/)
S'
■ | Q' |, таким образом,
Ат (t) = At (t) Ak(v) = A, (t) Ak И.
A6) Это пополнение строится следующим образом. Пусть
p:P->S — L есть данное накрытие пространства 5 — L. Рассмот-
Рассмотрим множество #={(£/, х)} всех таких пар (U, *), что U — область
пространства Р, замыкание которой О взаимно однозначно проекти-
проектируется на р(О) CZ 5 —L, а точка х $ 5 принадлежит замыканию
области р(U). Отождествим далее любые две пары (Uux) и (U2, x),
если найдется такая пара (V,x)£U, что Vczui(](J2\ полученное
таким образом фактормножество множества U обозначим через 2,
а естественную проекцию множества 2 на 5, определяемую соот-
соответствием (С/, х)->х, — снова через р. Наконец, превратим множе-
множество 2 в топологическое пространство, считая, что точка множе-
множества 2, определяемая парой (U,х), является предельной точкой
множества всех точек, задаваемых парами вида (U, х'), где
•^(iPW- Так как все пары (U,x), где точка x£S — L фиксиро-
фиксирована, очевидно, определяют одну точку пространства 2, то, сопо-
сопоставляя^ этой точке единственную точку хх£Р, такую, что р(хх)=*х
и X\£U, получаем гомеоморфизм пространства p~l(S — L)c2Ha
пространство Р. Поэтому подпространство p~l(S — L)c2 можно
отождествить с пространством Р. Кроме того, очевидно, что под-
подпространство A==2-(p-!(S — L)) является накрытием многообра-
многообразия L, а значит, и многообразием,
302 Примечания переводчика
A7) Индекс ветвления v(x) разветвленного накрытия 2 в точ-
точке х £ Л можно определить таким образом. Пусть U — связная
окрестность точки p(x),zUr ap-l(U) --связная компонента области
р~1@), содержащая точку х. Тогда кратность естественного накры-
накрытия U'—A~>U—L для достаточно малых окрестностей U не за-
зависит от U и называется индексом ветвления накрытия.
A8) Покажем, что описанное копредставление в действитель-
действительности является копредставлением группы Г. Для этого сопоставим
копредставлению (х : г) группы Г двумерный комплекс /(, одномер-
одномерный остов которого есть букет окружностей (ориентированных)
5Ь ..., 5П, а пространство К — /II SA есть объединение непересе-
кающихся открытых дисков би ..., Dn. Причем если элементу х%
поставить в соответствие петлю Si, *'=1, .... м, то путь, по кото-
которому диск Dj приклеивается к букету ^J^» равенS
где г . = х 1^х !^ , ..., J = 1, ..., п. Из теоремы ван Кампена
следует, что я(/С)=|х:г|. Рассмотрим далее накрытие /('->/(, соот-
соответствующее подгруппе Г, и комплекс /C'^/C'U® (см. стр. 256).
Тогда непосредственно видно, что элементы Xja порождают группу
я (/С"), так как из них соткан одномерный остов комплекса /С".
Соотношения, возникающие между образующими xja, соответствуют
путям, по которым диски комплекса К', накрывающие диски
Du ..., Dmy подклеиваются к одномерному остову комплекса К'.
Но это как раз и есть описанные в тексте элементы г/р. Таким об-
образом, копредставление I{xja} : {r^} \ есть копредставление группы
п(К"). Рассмотрим, наконец, такие слова t/0=l, vlt ..., vg-{ от
хи ..., хп, что набор слов v0, v0Vu ..., vov{ ... vg-\ совпадает с на-
набором слов ш0 ... Wg-\. Такие слова существуют в силу условия
Шрейера. Тогда, подклеивая диски Drk вдоль путей (vf) к комп-
k
лексу К", где а^ = рф(У1 ... ua-i), получим комплекс К!", дефор-
деформационным ретрактом которого, как видно геометрически, является
комплекс /('. Поэтому Г=я (/(')= л (К"). Но приклеивание дисков
Dfk эквивалентно добавлению соотношений (v|) =0, или, что
то же, добавлению соотношений w%0 = 0, к копредставлению
I {*/а} : (Op} I- Итак> |{^уа} : {г/р}' {wto}\ есть копредставление
группы Г.
A9) Точнее, многообразие Л состоит из некоторого числа ком-
компонент Ль Л2, ... . Индекс ветвления двух точек, лежащих на од-
одной компоненте, как это непосредственно следует из примечаний
A6), A7), один и тот же, т. е. можно говорить об индексе ветвле-
ветвления компоненты Aj. Если и — малая петля, обегающая вокруг мно-
многообразия L, то всякая малая петля м, лежащая над и (т. е.
р{п)=и)у является вдалой петлей вокруг только одной из компонент
Примечания переводчика 303
Aj, причем накрытие п->и является ^-кратным циклическим на-
накрытием-(так как над окружностью возможны только такие накры-
накрытия), где q есть индекс ветвления компоненты А}. Из сказанного
следует, что для нахождения копредставления группы я B) доста-
достаточно добавить по одному соотношению ветвления для каждой
компоненты. При этом число этих компонент равно числу циклов
в подстановке p(t;) = (Pi ... fc) (• • •) • • •, а длина каждого из этих
циклов равна индексу ветвления соответствующей компоненты.
B0) Пусть абелева группа С задана как факторгруппа Л/В
свободной абелевой группы Л с конечным числом, скажем /г, обра-
образующих. Зададим группу Л как группу целочисленных векторов
(*ь ..., хп) и выберем систему векторов bi—(xiu ..., xin),
i=l, ..., т, порождающую подгруппу ВС Л. Тогда матрица соотно-
соотношений копредставления Л/В группы С есть просто матрица ||дг,^Ц,
i= 1, ..., я, /=1, ..., т.
B1) Для того чтобы задать группу #iB — Л)+Л^_1 в виде
Л/В (см. предыдущее примечание), можно воспользоваться копред-
ставлением | {xja} : {r^} | группы T*Fg-u учитывая тот факт, что
#iB — Л)+Л^_ь есть прокоммутироваиная группа r*Fg_h Именно
такое задание мы получаем, считая, что свободная абелева груп-
группа Л свободно порождается элементами Xja, i=l, ..., /г, ос=0, ...
...,g—1,а ее подгруппаВпорождена м^-векторами г,-^,где в векторе
Г/о на месте (ky) стоит (ky) -я сумма показателей слова Г/р. Соответ-
Соответствующая матрица соотношении /' будет тогда состоять из строк ггр.
Если упорядочить элементы *;аи строки гг- р лексикографически, то
построенная нами матрица /' будет совпадать с матрицей / р. Это
проверяется непосредственным вычислением элементов обеих мат-
матриц.
B2) Чтобы установить это, заметим прежде всего, что, выбра-
выбрасывая из сферы S вместо многообразия L его трубчатую окрест-
окрестность V (открытую), мы получаем пространство, гомотопически
эквивалентное дополнению S — L. (Если L — узел, то V — это тор,
рассматривавшийся в § 3.) Поэтому пространство 2 — W, W =
=p-i (V)t где p:2->S есть проекция, гомотопически эквивалентно
неразветвленному накрытию 2 — Л. Если 2 — циклическое накры-
накрытие, то многообразие Л состоит из одной компоненты, причем W
есть ее трубчатая окрестность. Пусть D — меридианальный диск
трубчатой окрестности V= V, a D — накрывающий его диск. Тогда
Hl((S-~V)l)'D)~Hl(S) и Я, = (B- #)и/>)~#,B),так как под-
подмножества S — [(S— V)U^] и 2 — [B— U?)(j£], очевидно, гоМео-
морфны открытым шарам размерности >2. Учитывая эти изомор-
изоморфизмы, получаем, что Я2E, S — L) =Я2E, S— V) =H2(D, D) =Z и
Я2B, 2 — Л)=#2B, 2— #)=Я2E, D-)=Z, причем гомоморфизм р„
переводит образующую группы Я2B,2—А) в ^-кратную образую-
образующую группы Я2E, S — L). Отсюда следует, в силу того, что гра-
граничный гомоморфизм H2(S}S — L)->Hl{S — L) является вложе-
304 Примечания переводчика
нием, что таковым является и гомоморфизм Я2B, 2—A)->#iB — Л).
Далее, так как #оB,2 — Л) =Я0 (S, о — L) = 0, то гомоморфизм вло-
вложения #iB—A)->#iB) является гомоморфизмом на.
Таким образом, мы приходим к точной последовательности
0-*Я2B, 2 — Л)Л>Н{B — Л)->Я,B)->0. Но Я, (S — L) =
= Zzdg"Z = /?,//i B —Л), откуда следует, что композиция гомомор-
гомоморфизмов Z = tf2B, 2 — Л)Д-Я1B — A)-?+Hl(S — L) = Z не
имеет ядра, и, значит, подгруппа дИ2 B, 2 — Л) сг Нх B — Л) вы-
выделяется прямым слагаемым, дополнительным к которому является
ядро гомоморфизма /?#. Оно, в силу полученной точной последо-
последовательности, изоморфно группе Нх B).
B3) Для того чтобы установить упомянутые факты, нам нуж-
нужно выяснить связь матрицы /^ф с группой #iB—A), где 2—А есть
накрытие, соответствующее нормальному делителю Go cG, a
ф: G -> H=G/Go есть естественная проекция. Так как существует,
очевидно, отображение f:K->S — L комплекса /С, описанного в
примечании A8), в S — I, индуцирующее изоморфизм /*:я(/С)->
->n(S — L), то эту связь нам достаточно проследить для комплекса
/С Рассмотрим накрывающий согласно Go комплекс К\ клеточное раз-
разбиение которого накрывает клеточное разбиение комплекса К. Тогда
вершины комплекса /(', будучи прообразами единственной вер-
вершины р, имеют вид pQhy h^H, где Ро — произвольная фиксирован-
фиксированная вершина, a poh — результат действия элемента h£H на точку
Ро. Поэтому мы будем отождествлять вершины комплекса /С' с эле-
элементами группы Н. Пусть далее xit i=l, ..., л, — путь, начинаю-
начинающийся в точке ро и накрывающий петлю х%. Тогда одномерный
остов комплекса К' состоит из дуг (ориентированных) Хг • hy h£H.
Двумерные клетки Dili комплекса К' подклеены к одномерному
остову вдоль путей ггн> где h£H, г» — слова, вдоль которых при-
приклеиваются диски Di к одномерному остову комплекса К (см. при-
примечание A8)), а слово rih получается из гг- по следующему пра-
правилу: если г1 = х]1 ... х]\ то г = (х1 ЛЛ*1 ... Ut hs\\ где
1 S Л \ 1 / \ S /
ej=±l и
h =1 lk-\
\
Таким образом, базис одномерных цепей комплекса К\ являю-
щихся границами, состоит из цепей гш~ Jj Ej(xihj)z==
/1 7
•т-е-если 7t ^ F">то Ft=
Примечания переводчика
305
и rih = ri' h. Склеим, наконец, в комплексе К' все вершины poh
в одну вершину q. Тогда в полученном комплексе К" любая одно-
одномерная цепь будет циклом, а одномерные границы будут соответст-
соответствовать цепям rih, i= 1, ..., k, h £ Н. Стало быть, матрица из строк
rih и столбцов Xih есть матрица соотношений (может быть, беско-
бесконечная) группы Н\(К"). Но если группу Н\(К") рассматривать как
операторную над группой Н скольжений накрытия, то ее оператор-
операторными образующими будут элементы яг-, а операторными соотноше-
соотношениями — соотношения г*, т. е. матрица У^ф = i|?<p -т—^ есть матри-
матрица операторных соотношений группы Н\ (К"), или, что то же,
#(B ЛI1Ф)
(( I1)
Если H=G/G\ то i|?=a,-и мы можем получить комплекс /(«,,
гомотопически эквивалентный комплексу 2—Л, приклеивая диски
по путям xn-tk, &=0, ±1, ..., к комплексу К". Поэтому мы рас-
рассматриваем верхнее копредставление |*lt ..., хп:ги ..., гп|, и мат-
матрица операторных соотношений группы #iB—Л) имеет вид
£= П1Г где ^ — матрица Александера группы G=
— n(S — L). Но В~А\ где А' — подматрица матрицы Л, состоящая
из ее первых п—1 строк и столбцов, и A(/)=|i47|. Заметим, что
квадратная целочисленная матрица обычных соотношений абелевой
группы R=P/Q имеет в качестве образующего элемента Ai своего
первого элементарного идеала A\ZcZ порядок группы /?, а если
Ai=O, то группа R бесконечна. Поэтому естественно назвать поли-
полином А(/) операторным порядком группы #iB—Л).
Рассмотрим теперь g — циклическое накрытие 2—Л, отвечаю-
отвечающее нормальному делителю Go, т. е. Zg — G/G0. Тогда матрица опе-
операторных соотношений группы Я1(B—Л)иФ) имеет вид XgA =
= XgJa(p, где Xg:Z-*Zg — естественный гомоморфизм на, т. е. в
этом случае элементы матрицы /^ф можно рассматривать как L-no-
линомы от t, подчиняющиеся соотношению /*=1. Используя это
соотношение, мы можем всякий L-полином привести к нормальному
1
виду
Матрица V обычных соотношений группы
#i(B — A)U®) может быть получена теперь из операторной мат-
матрицы Уфф описанным в примечании B1) образом. Она состоит из
gXg-матриц Тц, t, /—1 л,
... с„
306 Примечания переводчика
*1
где 2 c*i/tk — нормальный вид полинома kgan(t), а пц(г) есть
L-полином, стоящий на (/, у)-ом месте матрицы Александера А.
При этом нумерация элементов матрицы Г'=||7\^|| соответствует
лексикографическому упорядочению элементов Xik—Xi-ih и соотно-
соотношений r~ik = 7i -tky t=l, .... /г, 6 = 0, ..., g — 1.
Так как переход от //i(B—A)U Ф) к #iB—Л) происходит
в рассматриваемом случае путем добавления соотношений
xn-th = 0, & = 0, ..., g — 2, то матрица Т соотношений группы
Hi B —Л) получается добавлением к матрице Т строки gX^-матриц
Тп+\, g, где Тп+\, g=0, ]фп, 7\j+i,/i=4 E . | • Отсюда видно,
1 0 ... 0 I
что Г- Т" ; , где Т" = \ТЦ\1%}_Х я__ь
Но эта последняя матрица есть матрица соотношений группы
вида Z+я, где я — группа с матрицей соотношений Т". Стало быть,
rt~#iB) и Т" есть матрица соотношений группы #iB). Замечая
g-\ g-_i
теперь, что | Т" \ = Д Д (<о'*), мы видим, что б = | Т" \ = Д Д (<о''),
g g
Д Д (<о'*), мы видим, что б = | Т" \ = Д
а ранг группы Я^Е) равен {g(n— 1) — (ранг матрицы Г")}={число
сомножителей Д(со^), /=0, ..., g— 1, равных нулю}.
B4) Это, очевидно, оговорка, так как (см. примечание A1))
яB—Л)/[яB—Л), яB—Л)] = £-}-Я1B). По-видимому, здесь автор
хотел сказать, что если группа Hi B) конечна, то существует
единственный гомоморфизм группы я B—Л) на группу Z. Тогда
накрытие Ху соответствующее ядру этого гомоморфизма, имеет в
качестве матрицы операторных соотношений группы Н{(Х) матрицу
L-полиномов. Первый полином этой матрицы естественно называть
полиномом Александера.
B5) Чтобы показать это, рассмотрим накрытие 2<х>—Aoo->2g—А#,
где 2ft— Aft есть й-кратное циклическое накрытие пространства S—L.
Если пространство Xg—Ag заменить комплексом Kg, полученным
из комплекса /С", соответствующего накрытию 2g—Ag->S—L (см.
примечание B3)), приклеиванием дисков вдоль путей xn»th,
&=0 g — 2, то n(Kg)=n(%g — Ag). Поэтому вместо простран-
пространства I>g — Ag можно далее рассматривать комплекс/Cg. Заметим, что
комплекс, накрывающий комплекс Kg, согласно примечанию B4),
совпадает с комплексом /(«>, построенным в примечании B3). По-
Поэтому если группу Hi(Koo) рассматривать как операторную, причем
операторами считать скольжения накрытия Коо -> Kg, то ее опера-
операторными образующими будут петли Xttk, /=1, ..., я, &=0, ...
t.., § — 1, операторными соотношениями — слова г/ • th, /= 1? ..., л,
Примечания переводчика
307
k=0 g—1, и хп • th% k=0 g—1, а операторами — умно
жения на t&.
Из сказанного теперь следует, что матрица Р операторных со-
соотношений группы Hi(Koo) относительно накрытия /(«>->/С*
имеет вид
пп • •• Р\ л-1 Р\
Pfti • • • P/1/i-i
О ... О
пп
Здесь Eg — единичная матрица порядка g, a
4'И ...<#.,И
где
обозначает (*,/)-й элемент матрицы Александера А
группы n(S-L) и
Поэтому Р
л-о
/-1, ..., п-г^Р- То' что 1^1
= Д A (®*t
проверяется
теперь непосредственно. Отметим, что tP=T" (см. примечание B3)).
B6) Если воспользоваться верхним копредставлением узла к,
то обходу вдоль пути а,- будет соответствовать элемент вида
( ei ~еЛ ( ес -еЛ
[xklxt Ч ... ухь?xt s I где ег = ±1, а каждая скобка соответ-
соответствует проходу под соответствующей полоской. Отсюда видно, что
ctfli=l, т. е. ui £Gf.
B7) Отметим, что i-й элементарный идеал матрицы Ф@ =
=/+A — 0 У совпадает с (i+1)-m идеалом узла k.
Учитывая вид матрицы Ф@. можно получать различные сведе-
сведения о строении этих идеалов и их полиномов. Например, так как
Д@=|Ф@1» то АA) = I /1 = 1- Или так как Q>(t) = V'—tV, то
ф(^~1) = ^~ \tV —V) = —1~ \V —tV\ , откуда немедленно вы-
вытекает инвариантность элементарных идеалов узла k относительно
сопряжения t-+t~l- Заметим далее, что V=X+A, где А — сим-
симметричная матрица, а матрица А состоит из блоков
о о
стоя-
щих вдоль главной диагонали, причем для любой симметричной
матрицы X можно так подобрать нормализованную поверхность <?~?
308 Примечания переводчика
чтобы ее матрица V имела вид Х+А. Учитывая это, нетрудно по-
показать, что всякий взаимный полином f(t), f(l) = l, может служить
полиномом Александера для некоторого узла k. Для этого доста-
достаточно соответствующим образом подобрать матрицу X.
B8) Это можно доказать, основываясь на результатах приме-
примечания B3). В частности, если g нечетно, то полином A(t) имеет
четное число корней, являющихся корнями g-й степени из единицы,
откуда следует, что свободная часть группы #iB) имеет четное
число образующих, т. е. представима в виде прямой суммы (см.
стр. 261).
B9) Методы вычисления групп #iB — А) и #iB), описанные
в § 4 и примечаниях B1, 23), не позволяют вычислять коэффи-
коэффициенты зацеплений. Ниже мы даем краткое описание другого ме-
метода, позволяющего, в силу своей геометричности, вычислять эти
коэффициенты.
Именно рассмотрим узел &, являющийся краем ориентирован-
ориентированной поверхности of', и разрежем сферу S3 вдоль этой поверхности.
В итоге получим многообразие Г, краем которого являются две по-
поверхности &' и с?"", гомеоморфные поверхности еГ, склеенные
вдоль линии k. Зозьмем далее g экземпляров многообразия Г,
а именно Гь ..., Tg с краями e^ill^i» •••» ^g^i^g* и склеим их
так, что поверхность еГг склеивается с <&~'2, аГ2 — с <^"з» • • •» ^'g —
с £Г ^ Полученное многообразие 2g естественным образом проекти-
проектируется на S3, причем эта проекция всюду, кроме ky является
g-кратной. Кроме того, отображение Ti->Ti+l (считается, что
g-fl=il) индуцирует на Xg гомеоморфизм порядка g, перестановоч-
перестановочный с естественной проекцией 2 -> S3. В силу единственности цик-
циклических накрытий отсюда следует, что построенное нами много-
многообразие и есть g-кратное разветвленное циклическое накрытие,
отвечающее узлу k.
Многообразие Г, очевидно, гомотопически эквивалентно допол-
дополнительному пространству графа Г, образованного каноническими
линиями au...ta2h* т. е. Г = [J а{. Поэтому Hx{T)=Hx{Sb-Y).
Эта последняя группа, как нетрудно проверить, является свободной
абелевой, образующими которой служат циклы Ь{ бгл, описан-
описанные выше в тексте. При склеивании многообразий Т{, ..., Tg в
многообразие 2 на образующие b\t ..., b\h,..., 6f, ..., b%h групп
Н\(Т\) Н{(Тё) накладываются соотношения akt=aki + l>
k — 1, ..., 2А, где a>ki(u'ki) — цикл, соответствующий циклу йкСеГ
при естественном гомеоморфизме <^-><^^(<^г;\ Выразив циклы а^,
aki через Ьу, мы получаем
пЦ1 ^~~ 2j Vkjbp a2k, i ^°2к-\ — а21г, r a2k-\l i — ~ °2k ~~ a^k-l^
Примечания переводчика
309
и придем к следующей матрице соотношений группы
о
... tf...,
— к
О
о
о
о
f + V
— V
72Л, ^ — />, 1 ' Т v
Отметим, что матрица а/ совпадает с матрицей соотношений,
приведенной на стр. 268.
Для получения коэффициентов зацепления реализуем циклы blj
как меридианы поверхности *Гt [)<^i> а пленки, осуществляющие
соотношения aktz=ak, i + \>—следующим образом. Пусть iki —
пленка, внутренность которой лежит в 7* и которая осуществляет
гомологию —'Lvjijbtj = aki. Аналогично определим пленку xkl и
положим tkl = x"ki -\- %'kt l + 1. Тогда при соответствующем соглаше-
соглашении об ориентациях числа пересечений циклов bv ..., Ь?гп с плен-
пленками Тц, . . , т2л, g даются матрицей порядка 2gh
Е —Е ... О О
О Е ... О О
О 0 ... Е
Е 0 ... О
Е
(Матрица а/, очевидно, соответствует матрице пересечений т/.)
Упрощая матрицу а/ и соответственно матрицу пересечений т/,
можно без труда получить результаты, сформулированные в тексте
относительно коэффициентов зацепления.
C0) Если поверхность еГ неориентируемая, то метод примеча-
примечания B9) можно применить только в случае g=2. Это происходит
потому, что процесс разрезания сферы S3 по неориентируемой по-
поверхности приводит нас к мноюобразию 7, границу которого кри-
кривая К не делит на два гомеоморфиых куска F{ и F2. Однако на
границе дТ действует гомеоморфизм / порядка 2. В самом деле,
так как границу дТ можно рассматривать как совокупность пар хи
х2% соответствующих точке х £оГ — /С, и кривой /С, то можно поло-
положить f{xi)=x2 и /(*)=*, х^К. Взяв теперь два экземпляра V и Т"
многообразия Т и отождествляя их границы по правилу:x'<-+f(x")%
где х' (• дТ\ х" £ дТ" — точки, соответствующие точке х £ дТч мы
получим двукратное разветвленное накрытие 2 пространства узла К.
Зацепления в многобразии 2 = 7V|J7V/ определяются методом,
изложенным в примечании B9).
ПРИЛОЖЕНИЕ II
НЕКОТОРЫЕ ПРОБЛЕМЫ ТЕОРИИ
УЗЛОВ»)
Р. Фокс
Приводимые ниже проблемы из теории узлов были предложены
проф. Р. Фоксом топологической школе при Университете штата
Джорджия, США, в 1961 г. С тех пор многие из них были, есте-
естественно, продвинуты в той или иной степени, а некоторые решены
полностью. Мы не имеем здесь возможности изложить все получен-
полученные результаты. Тем не менее нами добавлены в ряде случаев
краткие замечания, поясняющие постановку или состояние той или
иной проблемы. Кроме того, нами добавлена под № 41 интересная
старая проблема, предложенная Смитом.
Проблемой общего характера является нахождение
условий, необходимых для того, чтобы группа G была
группой некоторого узла (или группой некоторого клас-
класса вложений, например группой какого-либо зацепле-
зацепления). Одним таким условием является наличие изомор-
изоморфизма G/G'^Z (а, значит, ДA) = 1). Другое условие со-
состоит в том, что дефект группы G равен единице [см.
прим. F), стр. 289]. Наконец, еще одно условие состоит
в том, что класс соответствующих матриц Александера
является эрмитовым, т. е. матрица A(t) эквивалентна
транспонированной матрице к матрице А 1-т) • Это свой-
свойство автор назвал [Торрес, Фокс, 1954] двойственностью
в группах узла.
Проблема 1. Какие теоретико-групповые свойства
группы G обеспечивают эрмитов характер ее матрицы
Александера?
*) Перевод статьи Р. Фокса, Fox R. H., Some Problems in
Knot Theory, Topology of 3-manifolds, Proc. Top. Inst. Prentice-Hall,
1962, 168—176. Примечания переводчика даны в тексте петитом.—
Прим. перев.
Приложение II. Некоторые проблемы теории узлов 311
Эрмитов характер элементарных идеалов (даже для
узлов в произвольных ориентированных трехмерных
многообразиях) является следствием теорем двойствен-
двойственности Блэнчфилда [Блэнчфилд, 1957]. Они касаются го-
гомотопических цепочек дополнительного пространства и,
стало быть, намечают первый шаг в решении проблемы 1.
Проблема 2. Охарактеризовать среди полиномов с
целочисленными коэффициентами от \i переменных те,
которые являются полиномами зацеплений Д(/4, ..., t^).
Эта проблема решена для jlx = 1 [Зейферт, 1934] [см.
также прим. на стр. 199]. Для pi>2 известны некоторые
необходимые условия [Торрес, Фокс, 1954] [см. также
стр. 234 и прим. E), стр. 287].
Проблема 3. Верно ли, что всякая группа узла есть
свободное произведение (Fn*Fn)p свободной группы
ранга п на себя с отождествленной свободной подгруп-
подгруппой ранга 2п— 1?
Это — предположение Нойвирта, доказавшего его
для всех альтернированных узлов, а также для всех не-
альтернированных узлов с менее чем десятью пересече-
пересечениями, кроме узла 94е [Нойвирт, 1959].
Возможно, оно возникло в связи с тем, что при п=1
группа G=\x, y:xa=yb\ торического узла типа (а, Ь)
может быть представлена таким образом.
Это доказывается при помощи разбиения дополни-
дополнительного пространства торического узла на две части,
лежащие вне и внутри тора, и применением теоремы ван
Кампена. Если бы это предположение было доказано,
то из него можно было бы получить многие глубокие
свойства группы G, например уже известный факт, утвер-
утверждающий, что группа узла не имеет элементов конеч-
конечного порядка, и предполагаемый факт, состоящий в том,
что только группы торических узлов имеют нетривиаль-
нетривиальный центр [Нойвирт, 1959, 1960].
Проблема 4. Можно ли представить пару коммути-
коммутирующих элементов группы G петлями на неособой тори-
ческой поверхности, лежащей в дополнительной области
узла?
312 Приложение II. Некоторые проблемы теории узлов
Если два элемента коммутируют, то, естественно,
представляющие их петли лежат вместе на некотором
сингулярном торе дополнительной области. Поэтому эта
проблема аналогична лемме Дена.
Проблема 5. Являются ли группы узлов вычетно-ко-
нечными? То есть найдется ли для произвольного нетри-
нетривиального элемента и t G такой гомоморфизм 0 груп-
группы G на конечную нетривиальную группу, что ( l?
Проблема 6. Определяется ли топологический тип
дополнительного пространства S3 — k группой G вместе
с периферической структурой на ней?
Пусть V—тор, концентричный узлу k (см. стр. 245), а
GvczG — образ группы я(У) в группе яE3—k) = G. Перифериче-
Периферическая структура в группе G— это класс подгрупп, сопряженных
с подгруппой Gv.
Эта проблема решена Нойвиртом (Нойвирт, 1961]
для тех узлов k, группа G' которых конечно порождена.
Рапопорт [Рапопорт, 1960] показала, что группа G' не
может быть конечно порожденной, за исключением слу-
случая, когда старший коэффициент полинома Д(/) ра-
равен ±1.
Проблема 7. Определяется ли тип узла k топологиче-
топологическим типом его дополнения S3 — k?
Это доказано для торических узлов [Глюк, неопубли-
ковано]. Для зацеплений аналогичными вопрос решается
отрицательно [Фокс, 1962]. Отрицательный пример при-
приводится на рисунке. Для двумерных сфер в S4 анало-
аналогичный вопрос частично решен Глюком [Глюк, 1961].
Приложение II. Некоторые проблемы теории узлов 313
Проблема 8. Если группа дикого узла конечно поро-
порождена, то изоморфна ли она группе какого-либо [руч-
[ручного] узла?
Конечно, всякая группа узла [=группа ручного узла]
может быть реализована группой дикого узла просто
«привязыванием» этого узла к дикому узлу, группой ко-
которого является Z [=группа целых чисел].
Проблема 9. Какие пары типов узлов могут быть
представлены как компоненты зацепления рода 1?
Род зацепления определяется таким же образом, как
и род узла, но только он зависит от ориентации компо-
компонент. Изменение ориентации одной из компонент может
привести к изменению рода.
Проблема 10. Существуют ли необратимые узлы?
Эта проблема положительно решена Троттером [Троттер, 1962].
Проблема 11. Найти условия на двухкомпонентное
зацепление, при которых оно перестановочно.
Зацепление K+L перестановочно, если существует
гомеоморфизм всего пространства на себя, переводящий
К в L, a L в К. Очевидное условие этого состоит в том,
чтобы узлы К и L имели один и тот же тип. Однако
ясно, что оно не является достаточным.
Необходимым условием является также инвариантность элемен-
элементарных идеалов зацепления /C+L относительно автоморфизма
х-* У* У~+х кольца /(я(/(+£)), где х — канонический образующий
элемент, соответствующий компоненте /С, а у — элемент L.
Проблема 12. Охарактеризовать среди полиномов
узлов те, которые являются полиномами альтерни-
альтернированных узлов или специальных альтернированных
узлов.
Узел называется специальным альтернированным,
если у него такая альтернированная проекция, что со-
соответствующая шахматная поверхность [см. стр. 272] ори-
ориентируема, т. е. окружности Зейферта в этом случае не
вставлены друг в друга. Полином Александера альтер-
альтернированного узла является знакопеременным полино-
полиномом, у которого ни один член не пропущен [Мурасуги,
314 Приложение II. Некоторые проблемы теории узлов
1958"], т. е. А@=2(— 1 )'*/<' и с{>0. Изучение поли-
/-о
номов альтернированных узлов, у которых меньше 12 пе-
пересечений, приводит к предположению, что со^Сс\^С .. •
... ^Сси, причем всякий раз, когда сг=с*+1 при некото-
некотором *<А, то Ci = Ci+t= ... =£/!. Полином Александера
специального альтернированного узла обладает еще и
тем свойством [Мурасуги, 1960], что числа с0 и ДA)
имеют одинаковые знаки.
Проблема 13. Пусть 2—Л — накрытие дополнитель-
дополнительного пространства S3—L, а К — узел, стягиваемый в
S3—L. В этом случае узел К накрывается некоторым
числом кривых, которые можно перенумеровать символа-
символами смежных классов по подгруппе, определяющей исход-
исходное накрытие. Можно ли коэффициенты зацепления этих
кривых вычислить, исходя из группы зацепления K+L.
В 1937 г. Эйленберг ввел одно интересное понятие,
которое, по-видимому, в дальнейшем не исследовалось
[Эйленберг, 1937]. Назовем двухкомпонентное зацепле-
зацепление ^-зацепленным, если его коэффициент зацепления
отличен от нуля, и назовем индуктивно некоторое за-
зацепление п-зацепленным, если всякий полиэдр, лежащий
в дополнении к одной из компонент, скажем L2, содер-
содержащий другую компоненту Li и на котором некоторая
кратность цикла Li есть граница, содержит кривую,
(п—1)-зацепленную с L2. Эйленберг показал, что за-
зацепление, приведенное на рисунке, 1-зацеплено, но не
0-зацеплено.
Приложение II. Некоторые проблемы теории узлов 315,
Проблема 14. Существует ли для всякого натураль-
натурального п зацепление, являющееся д-зацепленным, но не
(п — 1)-зацепленным?
Хорошие кандидаты для этого получаются из зацеп-
зацепления, являющегося 1-зацепленным, но не 0-зацеплен-
ным, последовательным удваиванием. Например, для
Проблема 15. Симметрично ли свойство л-зацепляе-
мости?
Для п=1 это сразу вытекает из следующей характе-
характеристики 1-зацепляемое™, полученной Эйленбергом: Li и
L2 I-зацеплены, если группа зацепления Li+L2 не мо-
может быть гомеоморфно отображена на свободную груп-
группу ранга 2.
Проблема 16. Имеет ли n-зацепляемость что-либо об-
общее с тождественным исчезновением полинома Алексан-
дера Д (*,*/) или с длиной цепочки элементарных идеа-
идеалов?
Напомним в связи с этим, что если v[L{ L2]*=0, то &(х, 1)=»
A(UH
Проблема 17. Являются ли дуги 1.1, 1.1 *, 1. 3, приве-
приведенные в работе [Артин и Фокс, 1948], а также «замеча-
«замечательная простая замкнутая кривая» из работы Фокса
[Фокс, 1949] обратимыми? зеркальными?
Я/0 Приложение II. Некоторые проблемы теории узлов
Проблема 18 (Болл). Существует ли несчетное мно-
множество диких дуг, которые являются локально ручными
везде, кроме одной из концевых точек?
Проблема 19. Как индекс проницаемости (penetra-
(penetration tindex) -связая с родом обвертывания (enclosure
genus) [Болл, 1962]? Можно ли эти числа вычис-
вычислить, исходя из группы дуги или из локальных групп
дуги?
Проблема 20. Существуют ли дикие простые замкну-
замкнутые кривые, у которых максимальные периферические
подгруппы [Фокс, 1952] изоморфны группе ZxZ? груп-
группе Z? группе 1? Являются ли эти случаи единственно
возможными?
Похоже, что праща (sling) Бинга [Бинг, 1956] не
имеет нетривиальных периферических элементов.
Представляется также, что максимальная перифери-
периферическая подгруппа всякого дикого узла изоморфна Z
или 1.
Проблема 21. Существуют ли в трех- или четырех-
четырехмерном евклидовом пространстве такие дикие двумер-
двумерные диски с единственной внутренней точкой дико-
дикости р, что всякое их подмножество, гомеоморфное
диску и имеющее точку р на своей границе, является
ручным?
Это было бы естественным обобщением диких дуг,
которые являются суммой ручных дуг [Артин, Фокс,
1948]. В четырехмерном пространстве хорошие канди-
кандидаты на эту роль получаются вращением вокруг плоско-
плоскости дуги, расположенной в трехмерном полупростран-
полупространстве и представляющей собой последовательность завя-
завязанных друг за другом узлов, сходящихся к концевой
точке, находящейся в этой плоскости.
Проблема 22. Существуют ли в трех- или четырех-
четырехмерном пространстве необратимые двумерные диски?
незеркальные двумерные диски?
Приложение II. Некоторые проблемы теории узлов 317
Двумерные диски в этой проблеме предполагаются
ручными везде, кроме одной внутренней точки. В статье
Хэролда, Фокса [1962] построен пример незеркальной
дуги в трехмерном пространстве. Кроме того, в этой же
статье построена необратимая дуга при условии положи-
положительного решения проблемы 10.
Так как проблема 10 решена положительно [Троттер, 1962],
то проблема 22 для дуг также решается положительно.
Проблема 23. Является ли бабушкин узел срезанным
узлом? Предполагается, что ответ на этот вопрос отри-
отрицательный. Если ответ отрицательный, то отсюда выте-
вытекает недостаточность условия A(t)=F(t)F(t~l) для того,
чтобы узел был срезанным узлом.
Пусть Л* — минимальное значение рода локально
плоской поверхности в четырехмерном полупространстве
Я4, натянутой на узел или зацепление L. Ясно, что
Л*^Л(Л = род L), причем равенство не обязательно имеет
место.
Проблема 24. Найти условия, которым должна удо-
удовлетворять группа зацепления узла L, если h*^Ca, a —
заданное целое положительное число.
Узел является срезанным тогда и только тогда, когда
й* = 0, так что полиномиальное условие A(t)=F(t)F(tl)
дает частичный ответ на поставленный вопрос.
22 Зак 317
318 Приложение II. Некоторые проблемы теории узлов
Назовем сингулярный диск в R3 ленточным, если его
особенности имеют следующий вид:
Узел назовем ленточным, если он является границей
ленточного диска. Ясно, что всякий ленточный узел яв-
является срезанным узлом (надо только продеформировагь
окрестность линии А"В" в полупространство Я4). На-
Например, сквер-узел является ленточным узлом.
Проблема 25. Всякий ли срезанный узел является
ленточным узлом?
Пусть L—ц-компонентное зацепление. Рассмотрим
следующие четыре условия:
М
N
A) L — сечение \i локально плоских двумерных сфер
в /?4, здесь и далее сферы и диски непересекающиеся.
Приложение II. Некоторые проблемы теории узлов 319
B) L ограничивает \х локально плоских двумерных
дисков в полупространстве Я4.
C) L — сечение одной локально плоской двумерной
сферы в /?4.
D) L ограничивает поверхность рода 0 в Я4. Не-
Нетрудно видеть, чтоA)фи=фB)=фCI4>D). Зацепление М
удовлетворяет условию C), но не удовлетворяет условию
B), зацепление N удовлетворяет условию D), но не удо-
удовлетворяет условию C). Если \х^2, то B) ф==фC), а
если \i=l, то C) <£==ф D).
Назовем L срезанным зацеплением, если оно удовле-
удовлетворяет условию C), и строго срезанным зацеплением,
если оно удовлетворяет условиям A) = B).
Проблема 26. Найти необходимые условия для того,
чтобы L было срезанным зацеплением; строго срезан-
срезанным зацеплением.
Проблема 27. (Косинский). Имеются ли в S4 локаль-
локально плоские многообразия S2XS\ ни одна из (замкну-
(замкнутых) дополнительных областей к которым не совпадает
с тем, что можно предположить (т. е. с S2XEZ или
£3S')?
)
Этот вопрос — естественное обобщение одной весьма
сильной теоремы Александера [Александер, 1924]: если
тор S{XS] является ручным в S3, то по крайней мере од-
одна из его замкнутых дополнительных областей является
заполненным тором.
Если задать локально плоскую двумерную сферу в
/?4 ее сечениями, то нетрудно продеформировать ее так,
чтобы все ее минимумы были ниже максимумов. При
этом условии группа этой двумерной сферы будет гомо-
гомоморфным образом группы любого из зацеплений, высе-
высекаемого из нее между максимумами и минимумами.
Проблема 28. Если конечно копредставимая группа
является гомоморфным образом группы некоторого узла
и если ее фактор по коммутанту бесконечный цикличе-
циклический, то является ли такая группа группой некоторой ло-
локально плоской двумерной сферы в RA?
22*
320 Приложение II. Некоторые проблемы теории узлов
Так как в /?4 существуют локально плоские двумер-
двумерные сферы, группы которых не являются группами уз-
узлов (Приложение 1), то сразу же возникает следующий
вопрос.
Проблема 29. Существуют ли в пятимерном простран-
пространстве локально плоские трехмерные сферы, группы кото-
которых не являются группами локально плоских двумер-
двумерных сфер в четырехмерном пространстве.
Дж. Левин показал, что последовательность полиномов всякой
локально плоской л-мерной сферы Sn в R"+2t п>2, может быть
реализована как последовательность полиномов некоторой локально
плоской двумерной сферы в R4. Это следует из примечания A0)
стр. 295.
Проблема 30. Если группа локально плоской сферы
в jR4 изоморфна Z, то является ли эта сфера тривиаль-
тривиальной?
Ответ на аналогичный вопрос для обычных узлов положителен
[Папакирьякопулос, 1957].
Проблема 31. Существует ли более одного типа рас-
расположения проективной плоскости в RA с группой, изо-
изоморфной Z2?
Из теоремы двойственности Александера следует, что
если G — группа некоторой поверхности, расположенной
в RA, то G/G' есть либо Z, либо Z2 в зависимости от того,
ориентирована поверхность или нет. Нетрудно построить
пример локально плоской проективной плоскости, группа
G которой изоморфна Z2.
Проблема 32. Может ли группа локально плоской
проективной плоскости в /?4 быть конечной группой, от-
отличной от Z2?
Проблема 33. Существуют ли локально плоские дву-
двумерные сферы, группы которых обладают элементами
четного порядка?
Проблема 34. Существует ли локально плоская дву-
двумерная сфера, группа которой имеет вид ZxD, где D —
додекаэдрическая группа?
Приложение II. Некоторые проблемы теории узлов 321
Этот вопрос навеян примером Барри Мазура, по-
построившего локально плоскую двумерную сферу в го-
гомотопической четырехмерной сфере (т. е. многообразии,
гомотопически эквивалентном четырехмерной сфере),
группа которой есть ZxD. Е. Зиман показал, что гомо-
гомотопическая 4-сфера Мазура является стандартной сфе-
сферой, так что проблема 34 этим решена положительно.
А так как группа D имеет порядок 120, то вместе с этим
получает положительное решение и проблема 33.
Проблема 35. Существуют ли незеркальные локально
плоские двумерные сферы?
Киносита заметил, что если А(/) не является взаим-
взаимным полиномом, то не существует автоморфизма группы
G, отображающего образующие Xj в их обратные. По-
Поэтому двумерная сфера с таким полиномом необратима.
Аналогичные соображения показывают, что такая дву-
двумерная сфера не является также + зеркальной (в при-
примерах 4.5 § 3, Приложение I, полиномы невзаимные).
Следовательно, в проблеме 35 спрашивается, сущест-
существуют ли локально плоские двумерные сферы, не являю-
являющиеся зеркальными, т. е. не переводимые в свой зер-
зеркальный образ с обращенной ориентацией никаким со-
сохраняющим ориентацию гомеоморфизмом. Несколько
разъясняет постановку проблемы тот факт, что простей-
простейший способ построить срезанный узел состоит в том,
чтобы скомпанировать узел со своим зеркальным об-
образом с обращенной ориентацией.
Проблема 36. Найти алгоритм вычисления второй го-
гомотопической группы дополнительного пространства ло-
локально плоской двумерной сферы (которая рассматри-
рассматривается как операторная группа с группой двумерной сфе-
сферы в качестве группы операторов).
Проблема 37. Существуют ли асферичные локально
плоские двумерные сферы, т. е. такие сферы S2 в S4=
=/?4 U оо, что jt2-(S4—S2)=0, />2?
Имеется класс двумерных сфер в S4, асферичность
которых установлена [Кэртис, Эндрьюс, 1959], однако
они не являются локально плоскими,
322 Приложение II. Некоторые проблемы теории узлов
Проблема 38. Построить бруннову [Дебруннер, 1961]
систему локально плоских двумерных сфер в S4 (т. е.
найти такую совокупность \х непересекающихся сфер в
/?4, что любые k из них полностью расцепляемы, тогда
как любые &-Н —нет.)
Эта проблема решена. Янагава [1964].
Проблема 39. а) Какие срезанные узлы являются се-
сечениями тривиальных двумерных сфер? Ь) Какие
срезанные зацепления являются сечениями тривиальных
двумерных сфер? с) Какие строго срезанные зацепления
являются сечениями тривиального объединения три-
тривиальных двумерных сфер?
Автор высказывает предположение, что узел груз-
грузчика не является сечением никакой тривиальной дву-
двумерной сферы. Основания для такого предположения в
том, что все попытки разрушить идеал Александера ef
узла грузчика подклеиванием тривиальной двумерной
сферы, по-видимому, обречены на неудачу. По поводу
пунктов Ь) и с) проблемы 39 см. примеры 7, 8 § 2, Крат-
Краткий экскурс в теорию узлов.
Проблема 40. Сколько концов [Эпштейн, 1962] может
иметь группа локально плоской двумерной сферы?
Эта проблема обобщает вопрос, поставленный Па-
пакирьякопулосом для групп узлов. Группа узла имеет
один или два конца в зависимости от того, тривиален
узел или нет. В проблеме же 40, по существу, спраши-
спрашивается, существуют ли локально плоские двумерные сфе-
сферы, группы которых имеют бесконечно много концов.
Проблема 41. Пусть k — ручной нетривиальный узел.
Существует ли преобразование сферы S3 конечного по-
порядка р, множеством неподвижных точек которого яв-
является узел k?
Предполагаемый ответ отрицателен. Решение этой проблемы
для некоторых частных случаев, а также интересное обсуждение
см. в работе [Фокс, 1962"].
ПУТЕВОДИТЕЛЬ ПО ЛИТЕРАТУРЕ
Литература по теории узлов весьма разбросана, при-
причем часть ее трудна для чтения. Единственной подроб-
подробной книгой на эту тему является [Рейдемейстер, 1932].
Однако с тех пор литература более чем утроилась. Пред-
Предлагаемый Путеводитель призван помочь читателю найти
более доступные статьи и ориентировать его в них. В ос-
основном цитируются недавно появившиеся статьи. Ссыл-
Ссылки относятся к библиографии в конце книги, которая
дается в хронологическом порядке. Такие ссылки, как
[Фокс, 1954], [Броди, 1960'], [Мурасуги, 1958"], относятся
соответственно к первой, второй и третьей работе авто-
авторов за упомянутый год. Многие важные более ранние
работы, которые не цитируются в Путеводителе, могут
быть найдены в библиографии к этой книге, а также в
списках литературы к цитированным работам.
Основная проблема в этой книге является частным
случаем проблемы размещения: пусть заданы топологи-
топологические пространства X и У, сколько существует различ-
различных вложений пространства X в пространство У? В на-
нашем случае X — S{, У=/?3. Его значение состоит в том,
что это простейший интересный случай и что методы,
используемые для его изучения, имеют mutatis mutan-
mutandis общее значение.
Итак, мы можем всегда рассмотреть группу G =
= я(У—X) вложения XczY. Если эта группа имеет ко-
конечное копредставление, она имеет матрицу Александера
и элементарные идеалы [Фокс, 1954], но если эта группа
не имеет такового, ее матрица Александера является
бесконечной матрицей, и все становится значительно
сложнее [Броди, I960'].
324 Путеводитель по литературе
Если пространство X представляет собой цепь из \х
звеньев, т. е. объединение (ы попарно непересекающихся
простых замкнутых кривых в пространстве У=/?3, то
прокоммутированная группа G/G' является свободной
абелевой группой ранга \ху так что мы должны иметь
дело в этом случае с L-полиномами от \i переменных.
Если цепь является ручной, то полином A(tu ..., t^) мо-
может быть определен даже тогда, когда (ы>2. Он обла-
обладает свойствами, аналогичными свойствам полинома
Александера в случае одного переменного [Рейдемейстер
и Шуман, 1934; Фокс, 1954; Торрес и Фокс, 1954; Хо-
сокава, 1958; Фокс, I960']. Если X — одномерный ком-
комплекс в пространстве У=#3, то группа G/G', будучи по-
прежнему свободной абелевой, может уже не иметь «хо-
«хорошего» базиса, что приводит к дополнительным трудно-
трудностям [Киносита, 1958', 1959].
Естественным обобщением теории узлов является тот
случай, когда X есть m-мерная сфера или объединение^
попарно непересекающихся т-мерных сфер, а У егггь
Rn(n>m). Установлено, что для одной m-мерной сферы
(заузление) интересен только случай m = n—2; для не-
нескольких сфер (зацепление) все размерности, кроме
^<ая<# —2, не интересны [М. Браун, 1960; Стол-
лингс, 1961; Зиман, I960]*). Если т = п—2, то группа
G/G/ является свободной абелевой ранга \х, и теория в
этом случае очень похожа на теорию узлов и зацеплений
в R3 [Артин, 1925'; ван Кампен, 1928; Эндрьюс и Кэртис,
1959; Фокс и Мил нор, 1957; Терасака, 1959; Зиман,. 1960;
Киносита, 1961], однако при /?>3 взаимность полиномов
Д уже, вообще говоря, не имеет места. Естественно, что
случай п = А привлек наибольшее внимание. Если X —
поверхность, отличная от сферы S2, в /?4, то группа G/G'
может иметь элементы конечного порядка, что создает
новые трудности [Фокс, I960'; Киносита, 196Г]. Узлы и
*) В отличие от случая т=1 в многомерном случае гладкие
(дифференцируемые) узлы отличаются от кусочно-линейных (много-
(многогранных). Цитированные выше результаты устанавливают тривиаль-
тривиальность «многогранных» узлов при п — т > 2п > 4. Гладкие же узлы
устроены весьма нетривиально. Весьма сильные результаты о них
недавно получены Хефлигером и Дж. Левиным [Хефлигер, 1962;
Дж. Левин, 1965]. — Прим. перев.
Путеводитель по литературе 325
зацепления в произвольном трехмерном многообразии
были также рассмотрены [Бленчфилд, 1957; Броди,
1960], хотя многое еще предстоит сделать. Это особенно
интересный случай, так как его возможно использовать
для еще не решенной проблемы классификации трех-
трехмерных многообразий. Сами группы представляют собой
более сильные инварианты, чем полиномы, так что об их
свойствах, естественно, известно еще меньше [Фокс,
1948; Торрес и Фокс, 1954; Рапопорт, 1960; Нойвирт,
1959].
Ряд интересных и трудных проблем, соприкасаю-
соприкасающихся с теорией узлов, связан с расположением поверх-
поверхностей, с границей или без нее, в пространстве R3 [Алек-
сандер, 1924; Фокс, 1948; Кайл, 1955]. Особого внима-
внимания здесь заслуживает лемма Цена, доказательство
которой было одним из важных достижений в топологии
за последнее время [Папакирьякопулос, 1957; Шапиро и
Уайтхед, 1958; Папакирьякопулос, 1958]. Непосредствен-
Непосредственным следствием леммы Дена является то, что ручной
узел (в R3) тривиален тогда и только тогда, когда его
группа циклическая [Ден, 1910].
Простое и красивое построение показывает, что вся-
всякий ручной узел можно всегда расположить на ориенти-
ориентируемой поверхности. Этот факт можно использовать для
получения особенно удобной для приложений формы
матрицы Александера [Зейферт, 1934; Вендт, 1937; Фокс,
1960].
Одна из наиболее важных глав теории узлов связана
с накрывающими пространствами. Неразветвленные на-
накрытия описаны, например, в книге Зейферта и Трелль-
фаля, 1934, а описание разветвленных накрытий было
формализовано лишь недавно [Фокс, 1957]. Всякое зам-
замкнутое ориентируемое трехмерное многообразие являет-
является разветвленным накрытием сферы S3 [Алексаадер,
1919, а также Клиффорд, 1877]. Используя разветвлен-
разветвленные циклические накрытия пространства узла (или це-
цепи), можно получить геометрическое истолкование эле-
элементов матрицы Александера и даже можно сконструи-
сконструировать более сильные инварианты [Зейферт, 1933', 1935;
Бленчфилд и Фокс, 1951; Кайл, 1954, 1959; Фокс, 1956,
1960].
326 Путеводитель по литературе
Теория сочетаний узлов включает в себя умножение
(композицию), удвоение и свивание узлов [Шуберт, 1953,
1954; Уайтхед, 1937; Зейферт, 1949]. Для того чтобы пе-
перемножить два узла, надо просто завязать их один за
другим на одном и том же куске веревки. Относительно
этой операции ручные узлы образуют коммутативную
полугруппу S с однозначным разложением на множи-
множители [Шуберт, 1949]. В этой полугруппе только тривиаль-
тривиальный узел имеет обратный элемент. Это показывает, что
невозможно так завязать на одном куске веревки два
узла, чтобы они аннулировали друг друга. Проблема, со-
состоящая в том, какие типы узлов могут получиться при
пересечении (локально плоской) сферы S2 в простран-
пространстве RA гиперплоскостью /?3, приводит к такой класси-
классификации типов узлов, что классы этих типов относитель-
относительно умножения, индуцированного умножением в S, обра-
образуют группу [Фокс и Милнор, 1957; Терасака, 1959]. Об
этой группе еще мало что известно.
Имеются интересные проблемы теории узлов, связан-
связанные с диаграммами узлов, т. е. регулярными проекция-
проекциями узлов. Здесь альтернированные узлы, т. е. узлы, об-
обладающие такой проекцией, у которой пересечения свер-
сверху и снизу чередуются при обходе вдоль узла, имеют
ряд удивительных свойств [Мурасуги, 1958, 1958', 1958",
1960; Кроуэлл, 1959, 1959'], одно из которых, возможно,
звучит, как каламбур: полином Александера альтерни-
альтернированного узла сам является альтернированным. Вопрос
о том, как узнать, исходя из их диаграмм, эквивалент-
эквивалентны ли два данных узла, не решен в полной общности,
однако недавно был предложен метод установления три.
виальности узла, исходя из его диаграммы [Хакен, 1961].
Решение аналогичной проблемы для альтернированных
узлов и зацеплений уже известно [Кроуэлл, 1959]. Если
узел имеет диаграмму, обладающую только одним пере-
переходом, то он, очевидно, тривиален. Узлы, обладающие
диаграммами, у которых имеются два перехода, класси-
классифицированы полностью [Шуберт, 1956]. Известно, что
всякий ручной узел имеет особого рода диаграмму, на-
называемую планом [Рейдемейстер, 1960]. Простейшим слу-
случаем является здесь случай плана с четырьмя сплете-
сплетениями (Viergefleckte). Он привлек определенное внима-
Путеводитель по Литераторе 327
ние со стороны других авторов [Банквитц и Шуман,
1934].
Гомотопические группы nk (&=1, 2, ...) обобщают
понятие фундаментальной группы я = яь так что есте-
естественно исследовать гомотопические группы простран-
пространства У—X некоторого размещения пространства X в про-
пространстве Y. В настоящее время известно [Папакирьяко-
пулос, 1957], что группа jta(/?3—X), &>2, тривиальна для
всякого ручного узла X, а если X —некоторое зацепле-
зацепление, то группа jt2(/?3—X) тривиальна тогда и только
тогда, когда зацепление X не может быть «разделено на
две части». Более раннее исследование этой проблемы
привело к весьма интересным алгебраическим задачам,
общее решение которых не получено [Уайтхед, 1939, Хиг-
мен, 1948]. Если X есть (п—2) -мерная сфера в простран-
пространстве Rn или объединение таких попарно непересекаю-
непересекающихся сфер, то группа H2(Rn—X) может быть, а может
и не быть тривиальной. Это приводит к ряду интересных
проблем [Эндрьюс и Кэрти-с, 1959; Эпштейн, I960].
Наиболее почтенным инвариантом теории узлов яв-
является коэффициент зацепления двух компонент цепи.
Он был впервые рассмотрен свыше ста лет назад [Гаусс,
1833]. Его величину можно определить, исходя из диа-
диаграммы [Брунн, 1892] или исходя из полиномов [Рейде-
мейстер и Шуман, 1934; Торрес и Фокс, 1954]. Этот ин-
инвариант обобщался различными способами и заслужи-
заслуживает дальнейшего изучения [Паннвитц, 1933; Эйленберг,
1937; Милнор, 1954, 1957; Плэнс, 1957].
Может ли множество неподвижных точек преобразо-
преобразования конечного порядка р пространства R3 быть (руч-
(ручным) узлом? Эта проблема не решена, хотя некоторые
результаты здесь получены [Монтгомери и Самельсои,
1955; Киносита, 1958'; Фокс, 1958]. Близкая проблема
касается узлов, которые могут быть отображены на себя
периодическим преобразованием порядка р [Троттер,
1961]. Она также еще слабо разработана.
Связь между теорией узлов и дифференциальной гео-
геометрией [Фари, 1949; Милнор, 1950, 1953; Фокс, 1950], а
также между теорией узлов и алгебраической геоме-
геометрией [Зарисский, 1935; Рив, 1955] заслуживают даль-
дальнейшего изучения.
328 Путеводитель по литературе
Имеется множество самых разных работ по диким
узлам и вообще по диким вложениям, из которых мы
отметим следующие [Борсук, 1947; Фокс и Артин, 1948;
Фокс, 1949; Блэнкиншип и Фокс, 1950; Киркор, 1958,
1958'; Бинг, 1958; Дебруннер и Фокс, 1960; Броди, I960'].
Наконец, мы должны упомянуть работы по теории
кос, близко примыкающей к теории узлов [Артин, 1925,
1947, 1947', 1950; Ньюмен, 1942; Марков, 1935; Вайнберг,
1939; Фокс и Нойвирт, 1962] и несколько статей, содер-
содержащих стимулирующие идеи, окончательная ценность
которых пока не ясна [Фокс 1958'; Киносита и Терасака,
1957; Хасидзуме и Xосокава, 1958; Кэртис, 1959].
Стандартную таблицу неразложимых узлов*) с де-
девятью или менее пересечениями можно найти в книге
Рейдемейстера [1932, стр. 25, 31, 41, 70—72]. Таблицы,
приведенные на стр. 70—72, были расширены многочис-
многочисленными авторами еще в XIX в. до десяти пересечений
и до одиннадцати альтернирующих пересечений. Соот-
Соответствующее расширение таблицы, приведенной на
стр. 41 и касающейся полиномов Д(/), было осущест-
осуществлено с помощью машины, но до сих пор не опублико-
опубликовано.
Книга Эшли об узлах [Эшли, 1944] представляет со-
собой великолепное краткое руководство по узлам, напи-
написанное в терминах, понятных морякам, ткачам и т. д.
При небольшом терпении в ней можно найти все харак-
характерные примеры узлов и зацеплений.
*) То есть узлов, не представимых в* виде композиции нетри-
нетривиальных узлов. — Прим. перев.
БИБЛИОГРАФИЯ
Эта библиография содержит только наиболее важные работы
по теории узлов. Ссылки на неверные, тривиальные, весьма част-
частного или отдаленного характера работы отсутствуют. Сокращения
/. F. М., ZbL, M. R. относятся к заголовкам реферативных журна-
журналов Jahrbuch uber die Fortschritte der Mathematik, Zentralblatt fur
Mathematik и Mathematical Reviews*).
1833 Гаусс (Gauss K. F.), Zur mathematischen Theorie der
electrodynamischen Wirkungen, Werke. Koniglichen Gessel-
schaft der Wissenschaften zu Gottingen, vol. 5, 1877, s. 605.
1877 Клиффорд (Clifford W. K), On the canonical form and
dissection of a Riemann's surface, Proc. London Math. Soc.
8, 292—304; /. F. M., 9, 391.
1877—Тэйт (Tait P. G.), On knots, Scientific Paper, I, Cam-
1885 bridge University Press, London, 1898, 273—347; /. F. M,% 9,
342; 11, 362; 17, 521.
1890 Л иттл (Little С. N.), Alternate ± knots of order 11,
Trans. Roy. Soc. Edinburgh, 36, 253—255; /. F. M., 22, 562.
1892 Брунн (В r u n n H.), Topologische Betrachtungen, Z. fur
Math, und Phys., 37, 106—116; /. F. M., 24, 507.
1900 Л и ттл (Little С. N.), Non-alternate ±knots, Trans. Roy.
Soc. Edinburgh, 39, 771—778; /. F. M., 31, 481.
1910 Ден (Dehn M.), Uber die topologie des drei-dimensionalen
Raumes, Math. Ann., 69, 137—168; /. F. M., 41, 543.
1914 Ден (Dehn M.), Die beiden Kleeblattschlingen, Math. Ann.,
75t 402—413.
1919 Александер (Alexander J. W.), Note on Riemann spa-
spaces, Bull. Amer. Math. Soc, 26, 370—372; /. F. M., 47, 529.
1921 Антуан (Antoine L.), Sur rhomeomorphie des deux figu-
figures et de leurs voisinages, /. Math., ser. 8, 4, 221—325;
/. F. M., 48, 650.
1923 Шрейер (Schreier O.), Uber die Gruppen ЛаБь = 1,
Hamburg Abh., 3, 167—169; /. F. M., 50, 70.
1924 Александер (Alexander J. W.), On the subdivision of
3-space by a polyhedron, Proc. Nat. Acad., 10, 6—8; /. F. M.,
50, 659.
Александер (Alexander J. W.), An example of a sim-
simply connected surface bounding a region which is not simply
connected, Proc. Nat. Acad., 10, 8—10; J. F. M., 50, 661.
*) В большинстве случаев авторы указывают после самой ра-
работы и реферат на нее. — Прим. перев.
330 Библиография
Александер (Alexander J. W), Remarks on a point
set constructed by Antoine, Proc. Nat. Acad, 10, 10—12;
/. F. M., 50, 661.
1925 Артин (А г t i n E.) Theorie der Zopfe, Hamburg Abh., 4,
47—72; /. F. M.. 51, 450.
Артин (A r t i n E.), Zur Isotopie zweidimensionaler Flachen
im /?4, Hamburg Abh., 4, 174—177; /. F. M., 51, 450.
1926 Рейдемеистер (Reidemeister К), Knoten und Grup-
pen, Hamburg Abh., 5, 7—23; /. F. M., 52, 578.
Рейдемейстер (Reidemeister K). Elementare Be
grundung der Knotentheorie, Hamburg Abh., 5, 24—32;
J. F. M., 52, 579.
Рейдемейстер (Reidemeister К), Uber unendliche
diskrete Gruppen, Hamburg Abh., 5, 33—39;' У. F. M., 52.
112.
Шрейер (Schreier O.), Die Untergruppen der freien
Gruppen, Hamburg Abh., 5, 233—244; /. F. M., 53, 110.
1927 Александер, Бриггс (Alexander J. W.,
Briggs G. В.), On types of knotted curves, Ann. Math.,
28, 562—586; /. F. M., 53, 549.
1928 Александер (Alexander J. W.), Topological invariants
of knots and links, Trans. Amer. Math. Soc, 30, 275—306;
/. F. M., 54, 603.
ван Кампен (van Kampen E. R), Zur Isotopie zweidi-
zweidimensionaler Flachen im R^ Hamburg Abh., 6, 216; /. F. M.,
54, 602.
Рейдемейстер (Reidemeister K.), Uber Knotengrup-
pen, Hamburg Abh., 6, 56—64; /. F. M., 54, 603.
1929 К н е з e p (Kneser H.), Geschlossene Flachen in dreidimen
sionalen Mannigfaltigkeiten, Jahresbericht Deutsch. Math.
Verein., 38, 248—260; /. F. M., 55l, 311.
Рейдемейстер (Reidemeister K), Knotten und Ver-
kettungen, Math. Z., 29, 713—729, /. F. M., 552, 973.
1930 Банквитц (Bankwitz C), Uber die Torsionszahlen der
zyklischen Uberlagerungsraume des Knotenraumes, Ann.
Math., 31, 131 — 133; /. F. M., 562, Ц33.
Франкль, Понтрягин (Frankl F., Pontrjagin L.),
Ein Knotensatz mit Anwendung auf die Dimensionstheorie,
Math. Ann., 102, 785—789; /. F. M., 561, 503.
1931 Магнус (Magnus W.), Untersuchungen uber einige unend-
unendliche diskontinuierliche Gruppen, Math. Ann., 105, 52—74;
/. F. M., 57», 151.
1932 Александер (Alexander J. W.), Some problems in to-
topology, Verhandlungen des Internationallen Mathematiker-
Kongress Zurich, vol 1, s. 249-257;/. F. M., 581, 621; ZbL. 6,
421.
Бюрау (Burau W) Uber Zopfinvarianten, Hamburg Abh.,
9, Ц7—124; /. F. M., 58», 614; ZbL, 6, 34.
Бюрау (Burau W), Kennzeichnung der Schlauchknoten,
Hamburg Abh., 9, 125-133; У. F. M.t 68», 615; ZbL,
6, 34.
Библиография 331
Рейдемейстер (Reidemeister K-), Knotentheorie, сер
Ergebnisse der Mathematik, vol. 1, n. 1, /. F. M., 582, 1202;
ZbL, 5, 120.
1933 ван Кампен (van Kampen E. R.), On the connection
between the fundamental group of some related spaces, Amer.
J. Math., 55, 261—267; /. F. M., 591, 577; ZbL, 6, 415.
Г е р и т ц (G о е г i t z L.), Knoten und quadratische Formen,
Math. Z., 36, 647—654; /. F. M., 592, 1237; ZbL, 6, 422.
3 e й ф е р т (Seifert H.), Topologie dreidimensionalen ge-
faserter Raume, Ada Math., 60, 147—238; /. F. M., 592,
1241; ZbL, 6, 83.
Зейферт (Seifert H.), Verschlingungsinvarianten, Sit-
zungsbericht. preus. Akad. Wissenschaften, 26, 811—828; /
F. M., 592, 1238; ZbL, 8, 181.
Паннвитц (Pannwitz E.), Eine elementargeometrische
Eigenschaft von Verschlingungen und Knoten, Math. Ann.,
108, 629—672; /. F. M., 59l, 557; ZbL, 7, 231.
1934 Банквитц и Шуман (Bankwitz С, Schu-
Schumann H. G.), Ober Viergeflechte, Hamburg Abh., 10,
263—284; /. F. M., 601, 527; ZbL, 9, 230.
Бюрау (Burau W.), Kennzeichnung der Schlauchverkettun-
gen, Hamburg Abh., 10, 285—297; /. F. M., 601, 525; ZbL,
9, 231.
Геритц (Goeritz L.), Die Betti'schen Zahlen der zykli-
schen Oberlagerungsraume der Knotenaussenraume, Amer
J. Math., 56, 194—198; /. F. M., 601, 524; ZbL, 9, 39.
Геритц (Goeritz L.), Bemerkungen zur Knotentheorie
Hamburg Abh., 10, 201—210; /. F. M., 601, 525; ZbL, 9, 230
Зейферт (Seifert H.), Uber das Geschlecht von Knoten,
Math. Ann., 110, 571—592; /. F. M., 60', 523; ZbL, 10, 133.
Зейферт Г., Трельфалль Н., Топология, М. — Л., 1938
(перевод с немецкого издания, вышедшего в 1934 г.).
Рейдемейстер, Шуман (Reidemeister К., Schu-
Schumann Н. G.), L-Polinome von Verkettungen, Hamburg.
Abh., 10, 256—262; J. F. M., 601, 526; ZbL, 9, 230.
1935 Банквитц (Bankwitz C.), Ober Knoten und Zopfe in
gleichsinniger Verdrillung, Math. Z.t 40, 588—591; /. F. M.,
612, 1352.
Бюрау (Burau W.), Ober Verkettungsgruppen, Hamburg
Abh., 11, 171—178; /. F. M., 61*. 1021; ZbL, 11, 177.
Бюрау (Burau W.) Ober Zopfgruppen und gleichsinnig ver-
drillte Verkettungen, Hamburg Abh., 11, 179—186; /. F. M..
611, 610; ZbL, 11, 178.
Зарисский (Zariski O.), Algebraic surfaces Ergebnisse
der Mathematik, vol. 3, n. 5, Springer, Berlin, J. F. M., 61 \
704.
Зейферт (Seifert H.), Die Verschlingungsinvarianten der
zyklischen Knotenuberlagerungen, Hamburg. Abh., 11,
84—101; /. F. M., 611, 609; ZbL, 11, 178.
Марков A. A., Ober die freie Aquivalenz der geschlossener
Zopfe, Мат. сб., 1 A936), 73—78,
332 Библиография
1936 Зейферт (Seifert H.), La theorie des noeuds, L'enseigne-
ment Math., 35, 201—212; J. F. M., 621, 659; ZbL, 15, 84.
Эйленберг (Eilenberg S.), Sur les courbes sans noeuds,
Fund. Math., 28, 233—242; ZbL, 16, 138.
1937 Вендт (W e n d t H.), Die gordische Auflosung von Knoten,
Math. Zeit., 42, 680—696; /. F. M., 631, 552; ZbL, 16, 420.
Ньюмен, У а й т x e д (Newman M. H. A., White-
head J. H. C), On the group of certain linkage, Quart. J.
Math., 8, 14—21; J F, M., 63\ 552; ZbL, 16, 278.
Уайтхед (Whitehead J. H. C), On doubled knots, /.
London Math. Soc, 12, 63—71; J. F. M., 631, 552; ZbL, 16,
44.
Эйленберг (Eilenberg S.), Sur les espaces multicohe-
rents II, Fund. Math., 29, 101—122; ZbL, 17, 40.
1939 Вайнберг Н. М., О свободной эквивалентности замкнутых
кос, ДАН, 23, 215—216.
Вьеторис (Vietoris L.), Uber m-gliedrige Verschlingun-
gen, J. Deutsche Math. Vereinigung, 49, Abt. 1, 1—9; ZbL, 20,
407.
Уайтхед (Whitehead J. H. C), On the asphericity of
regions in a 3-sphere, Fund. Math., 32, 149—166; ZbL, 21,
162.
1942 Ньюмен (Newman M H. A.), On a string problem of
Dirac, /. London Math. Soc, 17, 173—177; ZbL, 28, 94; M. R.,
4, 252.
Титце (T i e t z e H.), Ein kapitel Topologie. Zur Einftihrung
in die Lehre von den verknoteteh Linien, Teubner, Leipzig
und Berlin; M. R., 8, 285.
1944 Эшли (Ashley С W.), The Ashley book of knots, Double-
day and Co. N. Y.
1947 Артин (Art in E.), Theory of braids, Ann. Math., 48,
101—126; ZbL, 30, 177; M. R., 8, 367.
Артин (А г t i n E.), Braids and permutations, Ann. Math.,
48, 643—649; ZbL, 30, 178; M. R., 9, 6.
Боненбласт (Bohnenblust F.), The algebraical braid
group, Ann. Math., 48, 127—136; ZbL, 30, 178; M. R., 8, 367.
Борсук (Borsuk K), An example of a simple arc whose
projection in every plane has interior points, Fund. Math.,
34, 272—277; ZbL, 32, 314; M. R., 10, 54.
1948 Борсук (Borsuk K), Sur la courbure totale des courbes
fermees, Ann. soc. Polon. math., 20, 251—265; M. R., 10, 60.
Фокс (Fox R. H.), On the imbedding of polyhedra in
3-space, Ann. Math., 49, 462—470; ZbL, 32, 125; M. R., 10,
138.
Фокс, Артин (Fox R. H., Art in E.), Some wild cells and
spheres in three-dimensional space, Ann. Math., 49, 979—990;
ZbL, 33, 136; M. R., 10, 317.
Хигман (Higman G.) A theorem on linkages, Quart. J.
Math., 19, 117-122; ZbL, 30, 322; M. R., 9, 606.
Ч ж о у (Chow W. L.), On the algebraical braid group, Ann.
Math., 49, 654-658; ZbL, 33, 10; H. R., 10? 98.
Библиография 333
1949 Бюргер (Burger E.), Ober Schnittzahlen von Homotopie-
ketten, Math. Z.f 52, 217—255; Zbl., 33, 207; Af. R.t 12, 43.
Зейферт (Seifert H.). Schlingknoten, Math. Z. 52, 62—80;
Zbl., 33, 137; M. #.,11, 196.
Фар и (Far у I.), Sur la courbure totale d'une courbe gauche
faisant un noeud, Bull. Soc. Math. France, 77, 128—138;
M. R., 11, 393.
Фокс (Fox R. H.), A remarkable simple closed curve, Ann.
Math., 50, 264—265; Zbl., 33, 136; M. R., 11, 45.
Шуберт (Schubert H.), Die Eindeutige Zerlegbarkeit
eines Knotens iin Primknoten, Sitzungsberichte der Heidel-
berger Akademie der Wissenschafien Mathematisch-Naturwis-
senschaftlicheKlasse, No. 3, 57—104; Zbl., 31, 286; M. R.t 11,
196.
1950 Артин (Art in E.), The theory of braids, American Scien-
Scientist, 38, 112—119; M. R., 11, 377.
Блэнкиншип, Фокс (Blankinship W. A., Fox R. H.),
Remarks on certain pathological open subsets of 3-space and
their fundamental groups, Proc. Amer.Math. Soc.,\, 618—624;
ZbL, 40, 259; M. R., 13, 57.
Бюргер (Burger E.), Ober Gruppen mit Verschlingungen,
/. Reine Ang. Math., 188, 193—200; Zbl., 40, 102; M. R., 13,
204.
Гройб (Graueb W.), Die semilinearen Abbildungen, S.-B.
Heidelberger Akad. Wiss. Math. Nat. kl, 205—272; M. R., 13,
152.
Зейферт (Seifert H), On homology invariants of knots,
Quart. I. Math., 1, 23—32; ZbL, 35, 111; Af. R., 11, 735.
Зейферт, Трельфалль (Seifert H., Threlfall W.),
Old and new results on knots, Canadian. I. Math., 2, 1—15;
ZbL, 35, 251; Af. #.,11, 450.
Милнор (Milnor J. W.), On the total curvature of knots,
Ann. Math., 52, 248—257; ZbL, 37, 389; Af. R., 12, 373.
Фокс (Fox R. M.), On the total courvature of some tame
knots, Ann. Math., 52, 258—260; ZbL, 37, 390; Af. R., 12, 373.
1951 Блэнкиншип (Blankinship W. A.), Generalization of
a construction of Antoine, Ann. Math., 53, 276—297; ZbL, 42,
176; M. R., 12, 730.
Блэнчфилд, Фокс (Blanchfield R. C, Fox R. H.),
Invariants of self-linking, Ann. Math., 53, 556—564; ZbL, 45,
443; Af. R., 12, 730.
Торрес (Torres G.), Sobre las superficies orientables ex-
tensibles en nudos, Bol. Soc. Math. Mexicana, 8, 1—14; Af. R.,
13, 375.
Чен (Chen К. Т.), Integration in free groups, Ann. Math.,
54, 147—162; ZbL, 45, 301; Af. R., 13, 105.
1952 Моиз (Moise E. E.), Affine structures in 3-manifolds. V,
The triangulation theorem and Hauptvermutung, Ann. Math.,
56, 96—114; ZbL, 48, 171; M. R., 14, 72.
Фокс (Fox R. H.)f On the complementary domains of a cer-
certain pair of inequivalent knots? Koninklijke Nederlandse
23 Зак 317
334 Библиография
Academie van Wetenschappen, Proceedings, Ser. A, 55, 37—40*
ZbL, 46, 168; M. R., 13, 966.
Фокс (Fox R. H.), Recent development of knot' theory at
Princeton, Proc. Inter. Congress of Math. Cambridge, 1950,
2, 453-457; ZbL, 49, 130; M. R., 13, 966.
Чен (Chen К. Т.), Commutator calculus and link invari-
invariants, Proc. A. M. S., 3, 44—55; ZbL, 49, 404; M. R., 13, 721.
Чен (Chen К. Т.), Isotopy invariants of links, Ann. Math.,
56, 343—353; ZbL, 49, 404; M. R., 14, 193.
1953 Гугепхейм (Gugenheim, V. К- А. М.), Piecewise linear
isotopy and embedding of elements and spheres, I, II, Proc.
London Math. Soc, ser. 2, 3, 29—53, 129—152; ZbL, 50, 179;
M. R.. 15, 336.
К н е з e p, Пуппе (Kneser M., Puppe D), Quadratische
Formen und Verschlingungsinyarianten von Knoten, Math.
Z.f 58, 376—384; ZbL, 50, 398; M. R.f 15, 100.
Милнор (Milnor J. W), On the total curvatures of closed
space curves, Math. Scandinavica, 1, 289—296; ZbL, 52, 384;
M. R., 15, 465.
Плене (Plans A.), Aportacion al estudio de los grupos de
homologia de los recubrimientos ciclicos ramificados corres-
pondientes a un nudo, Revista de la Real Academia de Cien-
cias Exactas, Fisicas у Naturales de Madrid, 47, 161 — 193;
ZbL, 51, 146; M. R., 15, 147.
Торрес (Torres G.), On the Alexander polynomial, Ann.
Math., 57, 57—89; ZbL, 50, 179; M. R., 14, 575.
Фокс (Fox R. H.), Free differential calculus, I. Derivation
in the free group ring, Ann. Math., 57, 547—560; ZbL, 50,
256.
Шуберт (Schubert H.), Knoten und Vollringe, Ada
Math., 90, 131—286; ZbL, 51, 404; M. R., 17, 291.
1954 Б инг (В i n g R. H.), Locally tame sets are tame, Ann. Math.,
59, 145—158; ZbL, 55, 168; M. R., 15, 816.
Кайл (Kyle R. H.), Branched covering spaces and the
quadratic forms of a link, Ann. Math., 59, 539—548; ZbL, 55,
421; M. R.f 15, 979.
Милнор (Milnor J.), Link groups, Ann. Math., 59, 177—
195; ZbL, 55, 169; M. R., 17, 70.
Моиз (Moise E. E.), Affine structure in 3-manifolds VII.
Invariance of the knot types; local tame imbedding, Ann.
Math., 59, 159—170; ZbL, 55, 168; M. R., 15, 889.
Торрес, Фокс (Torres G., Fox R. H), Dual presenta-
presentations of the group of a knot, Ann. Math., 59, 211—218; ZbL,
55, 168; M. R., 15, 979.
Фокс (Fox R. H.), Free differential calculus II, Ann. Math.,
59, 196—210; M. R., 15, 931.
Хомма (Но mm а Т.), On the existence of unknotted poly-
polygons on 2-manifolds in £3, Osaka Math. J., 6, 129—134;
ZbL, 55, 421; M. R., 16, 160.
Шуберт (Schubert H), Ober eine numerische Knoten-
invariante, Math. Z.t 01, 245—288; ZbL, 58, 174; M. /?., 17,29?.
Библиография 335
1955 Кайл (Kyle R. H.), Embedings of Mobius bands in 3-di-
mensional space, Proc Royal Irish Acad., Section A, 57,
131 — 136; ZbL, 66, 171; M R., 19, 976.
Монтгомери, Самельсон (Montgomery D., Sa-
Samel son H.), A theorem on fixed points of involutions in
S3, Canad. J. Math., 7, 208—220; ZbL, 64, 177; M. R., 16,
946.
Папакирьякопулос(Раракумакорои1озС. D.),
On the ends of knot groups, Ann. Math., 62, 293—299; ZbL,
67, 158; M. R., 19, 976.
Рив (Reeve J. E.), A summary of results in topological
classification of plane algebroid singularities, Rend. Sem.
Math, di Torino, 14, 159—187.
1956 Ауман (Aumann R. J.)f Asphericity of alternating knots,
Ann. Math., 64, 374—392; ZbL, 78, 164; M. R., 20, 453.
Б инг (В i n g R. H.), A simple closed curve that pierces no
disk, /. Math. Pur. AppL, ser. 9, 35, 337—343; ZbL, 70, 402;
M. R., 18, 407.
Фокс (Fox R. H ), Free differential calculus III. Subgroups,
Ann. Math., 64, 407—419; M. R., 20, 392.
Шуберт (Schubert H.), Knoten mit zwei Brucken, Math.
Z., 65, 133—170; ZbL, 71, 390; M. R., 18, 498.
1957 Б инг (В i n g R. H.), Approximating surfaces with poly-
polyhedral ones, Ann. Math., 65, 456—483; M. R., 19, 300.
Бленчфилд (Blanch field R C), Intersection theory
of manifolds with operators with applications to knot theory,
Ann. Math., 65, 340—356; ZbL, 80, 166; M. R., 19, 53.
Киносита, Терасака (Kinoshita S., Terasaka H),
On unions of knots, Osaka Math. /., 9, 131—153, ZbL, 80,
170; M. R., 20, 804.
К о н н e p (Conner P. E.), On the action of a finite group on
SnXSn, Ann. Math., 66, 586—588; M. R., 20, 453.
Ми л нор (Mil nor J.), Isotopy of links, Lefschetz sympo-
symposium. Princeton Math. Ser., 12, 280—306; ZbL, 80, 169; M. R.,
19, 1070.
Папакирьякопулос (Papakyriakopoulos C. D.),
On Dehn's lemma and the asphericity of knots, Proc. Nat.
Acad. Set., U. S. A., 43, 169—172; Ann. Math., 66, 1—26;
ZbL, 78, 164; M. R., 18, 590; 19, 761.
Плене (Plans A.), Aportacion a la homotopia de sistemas
de nudos, Revista Math., Hispano-Amer., Ser. 4, 17, 224—237;
M. R., 20, 803.
Фокс (Fox R. H ), Covering spaces with singularities, Lef-
schetz simposium. Princeton Math Ser., 12, 243—257; ZbL, 79,
165; M. R.t 23, 106.
Фокс, Милнор (Fox R H., Mil nor J. W.), Singularities
of 2-spheres in 4-space and equivalence of knots. Bull. Amer.
Math. Soc, 63, 406.
1958 Б инг (В i n g R. H.)f Necessary and sufficient conditions
that a 3-manifolds be S3, Ann. Math., 68, 17—37; ZbL, 81,
392; M. R., 20, 325.
23*
Библиография
К и н о с и т а (К i n о s h i t a S.), On Wendt's theorem of
knots II, Osaka Math. L. 10, 259—261.
Киносита (Kinoshita S.), On knots and periodic trans-
transformations, Osaka Math. J., 10, 43—52; M. R., 21, 434.
Киносита (Kinoshita S.), Alexander polynomials as
isotopy invariants I, Osaka Math. J., 10, 263—271; M. R., 21,
308.
Киркор (Kirkor A.), A remark about Cartesian division
by a segment, Butt. Acad. Polon. ScL, 6, 379—381; M. R.,
20, 580.
Киркор (Kirkor A.), Wild O-dimensional sets and the
fundamental group, Fund. Math., 45, 228—236; Zbl., 80, 168;
M. R., 21, 300.
M у р а с у г и (М u r a s u g i К.), On the genus of the alter-
alternating knot I, J. Math. Soc. Japan, 10, 94—105; M. R.f 20,
1010.
M у р а с у г и (М u r a s u g i К), On the genus of the alter-
alternating knot II, J. Math. Soc. Japan, 10, 235—248; M. R., 20,
1010.
M у р а с у г и (М u r a s u g i К.)» On the Alexander polynomial
of the alternating knot, Osaka Math. J., 10, 181 — 189; M. R.,
20, 1010.
Папакирьякопулос (Р a p a k у r i a k о р о u 1 о s C. D.),
Some problems on 3-dimensional manifolds, Bull. Amer
Math. Soc, 64, 317—335; M. P., 21, 307.
Рэбин (Rabin M. O.), Recursive unsolvability of group
theoretic problems, Ann. Math., 67, 172—194.
Уайтхед ( (Whitehead J. H. C), On 2-spheres in
3-manifolds, Bull. Amer. Math. Soc, 64 161—166; M. #.,21, 432.
Фокс (Fox R. H.), On knots whose points are fixed under
a periodic transformation of a 3-sphere, Osaka Math. J., 10,
31—35; Zbl., 84, 395.
Фокс (Fox R. R), Congruence classes of knots, Osaka
Math. J., 10, 37—41; Zbl., 84, 192.
Фокс, Чен, Лин дон (Fox R. H., Chen К. Т., Lyn-
Lyndon R. С.), Free differential calculus IV. The quotient
groups of the lower central series, Ann. Math., 68, 81—95;
M. R.t 21, 247.
X а с и д з у м е (Н a s h i z u m e Y.), On the uniqueness of
the decomposition of a link, Osaka Math. J., 10, 283—300;
11, 249; M. R., 21, 308.
Хасидзуме, Хосокава (Hashizume Y., Hoso-
kawa F.), On symmetric skew unions of knots, Proc. Ja-
Japan Acad., 34, 87—91; M. R., 20, 804.
Хосокава (Hosokawa F.), On V-polynomials of links,
Osaka Math., J., 10; 273—282; M. R., 21, 308.
Шапиро, Уайтхед (S h a p i г о A., W h i t e h e a d J. H. С),
A proof and extension of Dehn's lemma, Bull. Amer. Math.
Soc, 64, 174—178; M. R., 21, 432.
1959 Г о б л и р ш (Goblirsch R. Р.), On decomposition of 3-space
by linkages, Proc. Amer. Math. Soc, 10, 728—730; M. R., 22, 507.
Библиография 337
Кайл (Kyle R. H.), Branched covering spaces and the qua-
quadratic forms of links II, Ann. Math., 69, 686—699; M, R., 21,
1111.
Киносита (Kinoshita S.), Alexander polynomials as
isotopy invariants II, Osaka Math. J.,l\,9\—94\M. R.f 22, \70.
Ко н нер (Conner P. E.), Transformation groups on a
/((я, 1), Mich Math. J., 6, 413—417; M. R., 23, 113.
Кроуэлл (Crowe 11 R. H.), Non-alternating links, ///. /.
Math., 3, 101—120; M. R., 20, 1010.
Кроуэлл (С г о w e 11 R. H.), On the van Kampen theorem,
Рас. J. Math., 9, 43—50; M. R., 21, 713.
Кроуэлл (С rowel 1 R. H.), Genus of alternating link
types, Ann. Math.. 69, 258—275; M. R., 20, 1010.
Кэртис (Curtis M. L.), Self-linked subgroups of semi-
semigroups, Amer. J. Math., 81, 889—892; M. R., 21, 1343.
Нойвирт (Neuwirth L.), Knot groups, Princeton Ph. O.
Thesis.
Терасака (Terasaka K), On null-equivalent knots,
Osaka Math. J., 11, 95—113; M. R., 22, 1447.
Хомма (Horn ma Т.), On tame imbeddings of O-dimensio-
nal compact sets in £3, Yokohama Math. /., 7, 191—195;
M. R., 23, 241.
Энджер (Anger A. L.), Machine calculation of knot poly-
polynomials, Princeton senior thesis.
Эндрьюс, Кэртис (Andrews J. J., Curtis M.. L.),
Knotted 2-spheres in 4-spheres, Ann. Math., 70, 565—571;
M. R., 21, 1111.
1960 Браун (Brown M.), A proof of generalized Schoenflies
theorem, Bull. Amer. Math. Soc, 66, 74—76; M. R.. 22, 1441.
Броуди (Brody E. J.), The topological classification of
the lens spaces, Ann. Math., 71, 163—184; M. R., 22, 1215.
Броуди (Brody E. J.), On infinitely generated modules,
Quart. J. Math., 11, 141—150; M. R., 22, 1701.
Дебруннер, Фокс (Debrunner H., Fox R. H.), A
mildly wild imbedding of an n-frame, Duke Math. J., 27,
425—429; M. R., 22, 1939.
Зиман (Zeeman E. C), Unknotting spheres, Ann. Math.,
72, 350—361; M. R.,22, 1447.
Зиман (Zeeman E. C), Linking spheres, Hamburg Abh.,
24, 149—153; M. R., 22, 1448.
Зиман (Zeeman E. C), Unknotting spheres in five dimen-
dimensions, Bull. Amer. Math. Soc. 66, 198; M. R., 22, 1447.
Киносита (Kinoshita S.), On diffeomorphic approxi-
approximations of polyhedral surfaces in 4-space, Osaka Math. J.,
12, 191—194.
Мурасуги (Murasugi K.)» On alternating knots, Osaka
Math. J., 12, 277—303.
Ногути (Noguchi H), The smoothing of combinatorial
/i-manifolds in (n-M)-space, Ann. Math., 72, 201—215.
Нойвирт (Neuwirth L.), The algebraic determination of
the genus of knots, Amcr. J. Math., 82, 791—798; M. R., 22, 1946.
338 Библиография
Рапапорт (Rapaport E S), On the commutator sub-
subgroup of a knot group, Ann. Math . 71, 157—162; M R.. 22,
1159.
Рейдемейстер (Reidemeister K), Knoten und Ge-
flechte, Akad. Wiss. Gott. Math.-phys. Kl. Nachrichten...
Math.-phys.-chem. Abt., 5, 105—115; M. R., 22, 337.
Терасака (Terasaka H), On the non-triviality of some
kinds of knots, Osaka Math. J., 12, 113—144.
Терасака (Terasaka H.), Musubime no riron (Japan),
Sugaku, 12, 1—20.
Фишер (Fisher G. M), On the group of all homeomorp-
hisms of a manifold, Trans. Amer. Math. Soc.t 97, 193—212;
M. R.f 22, 1443.
Фокс (Fox R. H.), The homology characters of the cyclic
coverings of the knots of genus one, Ann. Math., 71, 187—
196; M. #., 22, 1702.
Фокс (Fox R. H.), Free differential calculus V. The Alexan-
Alexander matrices reexamined, Ann. Math., 71, 408—422; M. R.t
22, 444.
Хосокава, Киносита (Hosokawa F., Kinoshi-
t a S.,) On the homology group of the branched cyclic co-
covering spaces of links, Osaka Math. J., 12, 331—355.
Хотц (Hotz G.), Arkadenfadendarstellung von Knoten und
eine neue Darstellung der Knotengruppe, Hamburg Abh., 24,
132—148; M. R., 22, 337.
Эпштейн (Epstein I). B. A), Linking spheres, Proc.
Cambridge Phil. Soc, 56, 215—219; Af. R., 22, 1448.
1961 Бинг (В ing R. H), Tame Cantor sets in £3, Рас. J. Math.,
2, 435—446.
Г асе нер (Gassner M. J.), On braid groups, Hamburg
Abh., 25, 10—12.
Гэй ((Gay D. A.), A problem involying certain knots of ten
and eleven crossings, Princeton senior thesis.
Глюк (Gluck H.), The embedding of two-spheres in four-
sphere, Bull Amer. Math Soc, 67, 586—589.
Глюк (Gluck H.), Orientable surfaces in four-space, Bull.
Amer. Math. Soc, 67, 590—592.
Дебруннер (Debrunner H.), Links of Brunnian type,
Duke Math. J., 28, 17—23.
Келдыш Л. В., Некоторые проблемы топологии евклидовых
пространств, У. М. H.t 16, I—15.
Кервер, Мил нор (Kervaire J., Mi In or J.), On
2-spheres in 4-manifolds, Proc. Nat. Acad., 47, 1651—1657.
Киносита (Kino shit a S.), On the Alexander polynomial
of 2-spheres in a 4-sphere, Ann. Math., 74, 518—531.
Кроуэлл (Crowe 11 R. R), Knots and wheels, N. С. Т. М.
Yearbook.
Кроуэлл (С row ell R. H.), Corresponding group and mo-
module sequences, Nagoya Math. J., 19, 27—40.
Липшутц (Lipschutz S), On finite matrix representa-
representation of the braid group, Arch. Math., 12, 7—12.
Библиография 339
Мурасуги (М и г a s u g i К), On the definition of the
knot matrix, Proc. Japan Acad., 37, 220—221.
Мурасуги (Murasugi K), Remarks on torus knots,
Proc. Japan. Acad., 37, 222.
Мурасуги (Murasugi K), Remarks on knots with two
bridges, Proc. Japan Acad., 37, 294—297.
Нойвирт (Neuwirth L.), The algebraic determination
of the topological type of the complement of a knot, Proc.
Amer. Math. Soc, 12, 904—906.
Нойвирт (Neuwirth L.), A note on torus knots and
links determined by their groups, Duke Math. J., 28,
545-551. ,
Терасака, Хосокава (Terasaka H., Hosokawa F.),
On the unknotted sphere S* in E\ Osaka Math. J., 76, 116—
148.
Троттер (Trotter H.), Periodic automorphisms of groups
and knots, Duke Math. J, 28, 553—557.
Фаделл, ван Бускирк (Fadell E., van Buskirk J.),
On the braid groups of E2 anc[ s2t Bull. Amer. Math. Soc,
67, 211—213.
Хакен (Haken W.), Theorie der Normalflachen, Ada Math.,
105, 245—375.
Шуберт (Schubert H.), Bestimmung der Primfaktorzer-
legung von Verkettungen, Math. Z., 76, 116—148.
Эпштейн (Epstein D B. A.), Projective planes in 3-ma-
nifolds, Proc. London Math. Soc, 11, 469—484.
1962*)Браун (Brown M.), Locally flat imbeddings of topological
manifolds, Ann. Math., 75, 331—341.
Б инг (Bing R. H.), Decompositions of £3, Proc. Top. Inst.,
5—21.
Бол л (Ball В. J.), Penetration indices and applications,
Proc. Top. Inst., 37—39.
Глюк (Gluck H.), Rotational symmetry of 3-manifolds,
Proc. Top. Inst., 104—106.
Глюк (Gluck H.), The reducibility of embedding problems,
Proc. Top. Inst., 182—183.
Дам (Dahm D. M.), A generalization of braid theory, Prin-
Princeton Ph. D. thesis.
Доил (Doyle P. H.), Tame, wild and planar sets in E3,
Proc. Top. Inst., 34—36.
Зим an (Zeeman E. C), Isotopies and knots in manifolds,
Proc. Top. Inst., 187—193.
Киносита (К i n о s h i t a S.), On quasi-translations in
3-space, Proc. Top. Inst., 223—226.
Кроуэлл, Троттер (G г о w e 11 R. H., Trotter H. F.),
A class of pretzel knots, Duke Math. /.
*) В ссылках за этот год сокращение Proc. Top. Inst. обозна-
обозначает книгу Topology of 3-Manifolds and Related topics. Proceedings
of the 1961 Topology Institute at the University of Georgia, Prentice-
Hall.
340 Библиография
Мазур (М a z u г В.), Symmetric homology spheres, III. /.
Math., 6, 245—250.
Милнор (Milnor J.), A unique decomposition theorem
for 3-manifolds, Amer. J. Math., 84, 1—7.
Мойз (Moise E.), Periodic homeomorphisms of the 3-sphere,
///. /. Math., 6, 206—225.
Нойвирт (Neuwirth L). On Stallings fibrations, Proc.
Amer. Math. Soc.
Нойвирт (Neuwirth L.), A remark on knot groups with
center, Proc. Amer. Math. Soc.
Столлингс (Stallings J.), On topologically unknotted
spheres, Ann. Math.
Столлингс (Stallings J), On fibering certain 3-mani-
3-manifolds, Proc. Top. Inst., 95—100.
Tp оттер (Trotter H. F.), Homology of group systems
with applications to knot theory, Ann. Math.
Фаделл, Нойвирт (Fadell E., Neuwirth L.), Con-
Configuration spaces, Math. Scand., 10, 111—118.
Фокс (Fox R. H.), A quick trip through knot theory, Proc.
Top. Inst., 120—167 (перевод большей части этой и следую-
следующей статей помещен в этой книге).
Фокс (Fox R. К), Some problems in knot theory, Proc.
Top. Inst., 168—176.
Фокс (Fox R. H.), Knots and periodic transformations, Proc.
Top. Inst., 177—182.
Фокс (Fox R. H.), Construction of simply connected 3-ma-
3-manifolds, Proc. Top. Inst., 213—216.
Фокс, Нойвирт (Fox R. H.. Neuwirth L.), The braid
groups, Math. Scand., 10, 119—126.
Фокс, Хэрролд (Fox R. H., Harrold O. G), The wil-
wilder arcs, Proc. Top. Inst., 184—187.
Хемпел (Hampel J.), Construction of orientable 3-mani-
3-manifolds, Proc. Top. Inst., 207—212.
Хефлигер (Haefliger A.), Knotted Dk—1)-spheres in
6£-space, Ann. Math., 75, 452—466.
Хэрролд. (Harrold O. G.), Combinatorial structures lo-
local unknottedness and local peripheral unknottedness, Proc.
Top. Inst., 71—83.
Шепперд (Shepperd J. A. H.), Braids which can be plai-
plaited with their threads tied together at an end, Proc. Roy.
Soc.f A 265, 229—244.
Штёль (Stoel Т. В.), An attempt to distinguish certain
knots of ten and eleven crossings, Princeton senior
thesis.
Эдварде (Edwards С. Н.), Concentric tori and tame cur-
curves in S3, Proc. Top. Inst., 39—41; M. R., 23, 107.
Элфорд (Alford W. R.), Some «nice» wild 2-spheres in
£3, Proc. Top. Inst., 29—33.
Эп штейн (Epstein D. B. A.), Ends, Proc. Top. Inst.,
И0-И7.
ДОПОЛНИТЕЛЬНАЯ БИБЛИОГРАФИЯ1)
1962 Зиман (Zeeman E. С), Unknotted 3-spheres in six dimen-
dimension, Proc. Amer. Math. Soc, 13, 753—757.
Киносита (Kinoshita S.), A note on the genus of a
knot, P/oc. Amer. Math. Soc, 13, 451.
Мил нор (Mi In or J.), A duality theorem for Reidemeister
torsion, Ann. Math., 76, 137—147.
Мурасуги (Murasugi K.)» Non amphicheirality of the
special alternating links, Proc. Amer/ Math. Soc, 13,
771—776.
Фаделл, Нойвирт (Fadell E. and Neuwirth L.),
Configuration spaces, Math. Scand., 10, 111—118.
Хакен (Haken W.), Uber das Homoomorphieproblem der
3-Mannigfaltigkeiten IM Math. Zeitschr., 80, 89—120,
Хефлигер (Haefliger A.), Differentiate links, Topology,
1, 241-244.
Я x и м a (Y a j i m а Т.), On the fundamental groups of knot-
knotted 2-manifold in the 4-space, /. Osaka Math., 13, 63—71.
1963 Бюрд (Burde G.), Zur Theorie der Zopfe, Math. Ann., 151,
101-107.
Глюк (Gluck H.), Unknotting S1 in S\ Bull. Amer. Math.
Soc, 69, 91—94.
Зиман (Zeeman E.), Unknotting combinatorial falls, Math.
Ann., 78, 501—520.
Кроуэлл (С г owe 11 R.), The group G'/G" of a knot
group G, Duke Math. J., 30, 349—354.
Кроуэлл, Троттер (Crowell R., Trotter H.), A
class of pretzel knots, Duke Math. J., 30, 349—354.
Липшутц (Lipschutz S.), Note on a paper by Shepperd
on the braid group, Proc. Amer. Math. Soc, 14, 225—227.
Мурасуги (Murasugi K.), On a certain subgroup of
the group of an alternating link, Amer. J. Math., 85, 544—550.
Ногути (Noguchi H.), A classification of orientable sur-
surfaces in 4-space, Proc. Japan Acad., 39, 422—423.
Нойвирт (Neuwirth L), Interpolating manifolds for
knots in S3, Topology, 2, 359—365.
Нойвирт (Neuwirth L), A remark on knot groups with
a center, Proc. Amer. Math. Soc, 14, 378—379.
Столлингс (S tailings J.), On topologically unknotted
spheres, Ann. Math., 77, 490—503.
l) Составлена Р. Фоксом специально для русского издания.
342 Дополнительная библиография
Та к асе (Т a k a s e R.), Note on orientable surfaces in 4-spa-
ce, Proc. Japan Acad., 39, 424.
Троттер (Trotter H.), Non-invertible knots exist, Topo-
Topology, 2, 341—358.
X а д с о н (Hudson J. F. P.), Knotted tori, Topology, 2, 11—22.
Хаммер (Hammer G.), Ein Verfahren zur Bestimung von
Begleitknoten, Math. /.,81, 395—413.
Хефлигер (Haefliger A.), Plongement dif ferentiable
dans le domaine stable, Comtn. Math. Helv., 37, 3, 155—176.
Шмид (Schmid J.), Uber eine Klasse von Verkettungen,
Math. Zeitschr., 81, 187—205.
1964 Б и н г, Кли (В i n g R., К lee V.), Every simple closed curve
in £3 is unknotted in E\ J. London Math. Soc, 39, 86—94.
Бодмен (Boardman J.), Some embedding of 2-spheres in
4-manifolds, Proc. Camb. Phil. Soc, 60, 354—356.
Кротенхирд (Krotenheerdt 0.), Uber einen speziellen
Тур alternierender Knoten, Math. Ann., 153, 270—284.
Кроуэлл (С го well R.), On annihilator of a knot module,
Proc. Amer. Math. Soc, 15, 696—700.
Ми л нор (Mil nor J.), Most knots are wild, Fund. Math.,
54, 335—338.
Фокс, Смит (Fox R., Smythe W.), An ideal class inva-
invariant of knots, Proc. Amer. Soc, 15, 707—709.
Эндрьюс, Дристи (Andrews J., Dristy F.), The
Minkowski units of ribbon knots, Proc Amer. Math. Soc, 15,
856-864.
Яхима (Yajima Т.), On simply knotted spheres in R\ J.
Osaka Math., 1, 133—152.
Янагава (Yanagawa Т.), Brunnian system of 2-spheres
in R\ J. Osaka Math., 1, 127—132.
1965 Зиман (Zeeman E.), Twisting spin knots, Trans. Amer.
Math. Soc, 115, 471—495.
Левин (Levin J.), A characterisation of knot polynomials,
Topology, 4, 135—141.
Левин (Levin J.), A classification of dif ferentiable knots,
Ann. Math., 82, 15—51.
Мурасуги (Murasugi K.)» On a certain numerical inva-
invariant of link types, Trans. Amer. Math. Soc, 117, 387—422.
Мурасуги (Murasugi K.), On the Minkowski unit of
slice links, Trans. Amer. Math. Soc, 114, 377—383.
Мурасуги (Murasugi K), Remark on rosette knots,
Math. Ann., 158, 290—292.
Нойвирт (Neuwirth L.), Knot groups, Ann. of Math.
Study № 56, Princeton Univ. Press.
Робертелло (Robertello R.), An invariant of knot co-
bordism, Comtn. Pure Appl. Math., 18, 543—555.
Хефлигер, Штир (Haefliger A., Steer В.), Symetry
of linking coefficient, Comm. Math. Helv., 39, 259—270.
1966 Фокс (Fox R.), Rolling, Bull. Amer. Math. Soc, 72, 162—164.
Шофель (Shaufele C), A note on link groups, Bull.
Amer. Math. Soc, 72, 107—110.
УКАЗАТЕЛЬ
Абсолютная кривизна узла 220
Алфавит 53
Антиавтоморфизм 202
Ассоциированные элементы 168
Деформация 85, 89, 90
— изотопическая 20
Дифференцирование, свободное
143
Базис (свободный) 56
Базисное множество образую-
образующих 66
Буква 53
Вершина узла 16
Время остановки пути 28
Гомоморфизм, индуцированный
отображением 42
Гомотопия отображений копред-
ставлений 69
Гомотопия свободная 51
Две петли называются свобод-
свободно гомотопными, если они
принадлежат непрерывному се-
семейству петель (не обязатель
но имеющих общую точку)
Граф 233
Группа
— кобордизмов узлов 251
— конечно порожденная 68
— копредставления 66
— косы 162
— метациклическая 167
— прокоммутированиая 77
— свободная 56
над алфавитом 55
— с конечным числом соотноше-
соотношений.68
— узла 111
— фундаментальная 38
Групповое кольцо 140
Единица ( = единичный элемент)
35, 55
— категории 221
— кольца 168
— тривиальная (группового
кольца) 168
Зацепление 233, 284
— срезанное 239, 319
строго 319
— сфер 324
Зеркальный образ узла 22
Идеал
— главный 175
— элементарный матрицы 150
копредставления 154
Инварианты зацеплений 270
Индекс ветвления 253
Категория 221
Квадратичная форма диаграммы
узла 270
Класс кобордизмов узлов 250
Кольцо
— ассоциированное подкольцу
269
— групповое 140
Коммутант 77
Коммутативная диаграмма 12
Комплекс 87
Композиция
— отображений копредставлений
69
344
Указатель
Композиция узлов ( = произведе-
произведение узлов) 244
Копредставление 66
— верхнее 117
— Виртингера 131
— дуальное 203
— конечное 68
— конечно порожденное 68
— нижнее 117
— с конечным числом соотноше-
соотношений 68
Коэффициент зацепления 234
Лемма Дена 325
Матрица
— Александера 149
— Бюрау 280
Множество
— образующих элементов 56
копредставления 66
— соотношений копредставления
66
Наибольший общий делитель
169, 170
Накрывающее пространство
(== накрытие)
— бесконечное циклическое 260
— — циклическое
— разветвленное 252
Н. о. д.-область 170
Область
.— с однозначным разложением
170
— целостности 168
Обмотка узла 151
Оболочка множества элементов
64
Образующие элементы 63
Окружности Зейферта 246
Определяющие соотношения
63
Основная формула свободного
исчисления 148
Ось узла 251
Отображение
— копредставления 69
— кусочно-линейное 112
Переход 112
Периферическая структура груп-
группы узла 312
Петля 30
— базисная 30
Подгруппа
— вполне нормальная 77
— порожденная множеством
56
Полугруппа 30, 54
— узлов 245
Полином
— Александера зацепления 334
узла 184
— взаимный 198
— свободный 145
— узла 177, 178
Представление
— Бюрау 281
— транзитивное 253
— группы узла
абелево 274
метабелево 275
метациклическое 275
Проблема
— изоморфизма 68
— слов 58
— тривиальности 68
Произведение
— линейно связное 39
— односвязное 44
— путей 29
— слов 54
— узлов ( = композиция узлов)
— узла дополнительное 28
Проход 112
Путь 28
— единичный 29
— обратный 30
— постоянный 30
— простой ИЗ
Редукция слов стандартная 58
Регулярное положение узла 18
Ретракт 87
Указатель
Ретракт деформационный 85, 95
Ретракция 72, 85
Род узла 247
Свободное произведение с объ-
объединенной подгруппой 282
Семейство путей
— непрерывное 31
— с фиксированными концами
31
Сквер-узел 194
Слово 53
— приведенное 58
— пустое 54
Слог 52
Соотношение 64
Степень
— группы 77
— L-полинома 201
— полинома узла 201
Сторона узла 16
Сумма показателей слова 165
Сфера
— заузленная 236
— локально-плоская 236
— полученная вращением 236
Теорема
— ван Кампена 87
— Нильсена — Шрейера. 61
— Рейдемейстера — Шрейера 255
— Титце 72
Тип
— гомотопический 85, 98
— копредставления 70
— узла 15
изотопический 20
Топология отождествления 44
Тор
— заполненный 88
— заузленный 225
Точка
— базисная 30
— двойная 17
— конечная пути 28
— кратная 17
— начальная пути 28
— переходящая 18
— проходящая 18
Точка седловая сферы 237
Тривиализация 143
Удвоение узла 252
Умножение узлов ( = произведе-
произведение узлов)
Узел 14
— альтернированный 25
— бабушкин 194
— беседочный 195
— восьмерка 13
— грузчика 191
— дикий 16
— дифференцируемый 213
— истинной дружбы 195
— китайская роза 195
— клеверный лист 14
— ложной дружбы 195
— листинга ( = восьмерка) 13
— необратимый 25
— неразложимый 328
Узел называется неразложи-
неразложимым, если он не есть компо-
композиция двух нетривиальных уз-
узлов
— нульэквивалентный 239
— обратимый 24, 251
— простой ( = восьмерка или не-
неразложимый) 13
— ручной 16
— составной 196
— специальный альтернирован-
альтернированный 313
— срезанный 239
— торический 138
— тривиальный 15
— трилистник (клеверный лист)
— турецкая чалма 187
— четырехкратный (восьмерка)
13
Число вращения 49
Эквивалентность
— копредставлений 70
— матриц 150
— путей 31
свободная 51
— Титце 71
— узлов 15
ОГЛАВЛЕНИЕ
Предисловие к русскому изданию 5
Предисловие переводчика . . 6
Предисловие авторов 9
Предварительные указания 11
Глава I. Узлы и типы узлов 13
1. Определение узла 13
2. Ручные и дикие узлы 16
3. Проекции узлов 17
4. Изотопический тип. зеркальные и обратимые узлы . . . 20
Глава II. Фундаментальная группа 27
Введение 27
1 Пути и петли 28
2 Классы путей и петель 31
3. Изменение базисной точки 38
4. Индуцированные гомоморфизмы фундаментальной группы 40
5. Фундаментальная группа окружности 43
Глава III. Свободные группы 53
Введение 53
1. Свободная группа t \<Л\ 53
2. Свободные группы 55
3. Приведенные слова . 58
Глава IV. Копредставления групп 62
Введение 62
1. Развитие понятия копредставления , , 62
2. Копредставления и типы копредставлений 66
3. Теорема Титие 71
4. до-подгруппы и ассоциированные гомоморфизмы .... 77
5. Свободные абелевы группы 81
Оглавление 347
Глава V. Вычисление фундаментальной группы 84
Введение 84
1. Ретракции и деформации 87
2. Гомотопический тип 98
3. Теорема ван Кампена 99
Глава VI. Копредставления групп узлов 111
Введение 112
1. Верхнее и нижнее копредставления 112
2. Верхнее и нижнее копредставления. Продолжение . . . 120
3. Копредставление Виртингера 130
4. Примеры копредставлений 132
5. Существование нетривиальных типов узлов 136
Глава VII. Свободное исчисление и элементарные идеалы . . 140
Введение 140
1. Групповое кольцо 140
2. Свободное исчисление 143
3. Матрица Александера 149
4. Элементарные идеалы 150
Глава VIII. Полиномы узла 163
Введение 163
1. Прокоммутированная группа узла 164
2. Групповое кольцо бесконечной циклической группы . . 167
3. Полиномы узла 177
4. Типы узлов и полиномы узлов 184
Глава IX. Характеристические свойства полиномов узлов . . 198
Введение 198
1. Операция тривиализации 199
2. Сопряжение 201
3. Дуальные копредставления . . 203
Добавление I 213
Добавление II 221
Добавление III 225
Приложение I. Краткий экскурс в теорию узлов . . . . 233
1. Зацепления и графы 233
2. Заузленные 2-сферы 236
3. Арифметика узлов . 244
4. Накрывающие пространства 252
348 Оглавление
5. Циклические накрытия пространства узла 261
6. Нахождение представлений 274
Примечания переводчика 284
Приложение И. Некоторые проблемы теории узлов . . .310
Путеводитель по литературе 323
Библиография 329
Дополнительная библиография 341
Указатель 343
Р. Кроуэлл, Р. Фокс
ВВЕДЕНИЕ В ТЕОРИЮ УЗЛОВ
Редактор Э. Э. Пейсахович
Художник К. П. Сиро то в
Художественный редактор В. И. Шаповалов
Технический редактор М. А. Белева
Сдано в производство 17/VHI 1966 г. Подписано к печати 2/11 1967 г.
Бумага 84х 108»/82 = 5,44 бум. л., 18,27 усл. печ. л. Уч.-изд. л. 16,24, Изд. № 1/3748
* уб. 30 коп. Зак. 317. Тем. план 1967 г. Изд-во «Мир» пор. № 15
Цена 1 руб
ИЗДАТЕЛЬСТВО «МИР» Москва, 1-й Рижский пер., 2.
Ленинградская типография № 2 имени Евгении Соколовой
Главполиграфпрома Комитета по печати при Совете Министров СССР.
Измайловский проспект, 29.