Author: Мантуров В.О.
Tags: анализ монография атомы теория узлов теория натуральных узлов виртуальные узлы
ISBN: 5-93972-404-3
Year: 2005
Text
В. О. Мантурое
ТЕОРИЯ УЗЛОВ
Москва ♦ Ижевск
2005
УДК 517
Интернет-магазин · физика
^v\xRe^5
• мате матика
• биология
• нефтегазовые
http://shop.rcd.ru технологии
Мантуров В. О.
Теория узлов. — Москва-Ижевск: Институт компьютерных исследований, 2005,
512 стр.
Настоящая монография покрывает почти все направления и методы современной
теории узлов. Изложение является замкнутым, поэтому книгу можно использовать
для изучения узлов с самого начала. Особенное место в книге уделено бурно
развивающейся в последнее время теории виртуальных узлов, а также авторскому подходу
к узлам и виртуальным узлам посредством атомов.
ISBN 5-93972-404-3
© В. О. Мантуров, 2005
© Институт компьютерных исследований, 2005
http://rcd.ru
http://ics.org.ru
Моей маме Елене Ивановне Мантуровой
Gelegentlich ergreifen wir die Feder
Und schreiben Zeichen auf ein weifies Blatt,
Die sagen dies und das, es kennt sie jeder,
Es ist ein Spiel, das seine Regeln hat.
Doch wenn ein Wilder oder Mondmann кате
Und solches Blatt, solch furchig Runenfeld
Neugierig forschend vor die Augen пакте,
Ihm starrte draus ein fremdes Bild der Welt,
Ein fremder Zauberbildersaal entgegen.
Er sake A und В als Mensch und Tier,
Als Augen, Zungen, Glieder sich bewegen,
Beddchtig dort, gehetzt von Trieben hier,
Er lase wie im Schnee den Krahentritt,
Er liefe, ruhte, litte, floge mit
Und sake aller Schopfung Moglichkeiten
Durch die erstarrten schwarzen Zeichen spuken,
Durch die gestabten Ornamente gleiten,
Sah Liebe gliihen, sake Schmerzen zucken.
Er wiirde staunen, lachen, weinen, zittern,
Da hinter dieser Schrift gestabten Gittern
Die ganze Welt in ihrem blinden Drang
Verkleinert ihm erschiene, in die Zeichen
Verzwergt, verzaubert, die in steifem Gang
Gefangen gehn und so einander gleichen,
Dafi Lebensdrang und Tod, Wollust und Leiden
Zu Briidern werden, kaum zu unterscheiden...
Und endlich wiirde dieser Wilde schreien
Vor unertraglicher Angst, und Feuer schiiren
Und unter Stirnaufschlag und Litaneien
Das weifie Runenblatt den Flammen weihen.
Dann wiirde er vielleicht einschlummernd spur en,
Wie diese Un-Welt, dieser Zaubertand,
Dies Unertragliche zuriick ins Niegewesen
Gesogen wiirde und ins Nirgendland,
Und wiirde seufzen, lacheln und genesen.
Herman Hesse, "Buchstaben" (Das Glasperlenspiel).
Оглавление
Предисловие (Луис Кауфман) χ
Предисловие автора xii
Часть I. Узлы, зацепления и инвариантные полиномы
Глава 1. Введение 3
1.1. Основные определения 4
Глава 2. Движения Рейдемейстера и арифметика узлов 13
2.1. Полигональные зацепления и движения Рейдемейстера 13
2.2. Арифметика узлов и поверхности Зейферта 19
Глава 3. Зацепления в двумерных поверхностях в R .
Простейшие инварианты зацеплений 29
3.1. Узлы в двумерных поверхностях. Классификация торических узлов 29
3.2. Коэффициент зацепления 33
3.3. Арф-инвариант 35
3.4. Инвариант раскрасок 39
Глава 4. Фундаментальная группа 42
4.1. Примеры развязывания узлов 42
4.2. Фундаментальная группа 45
4.3. Вычисление групп зацеплений 51
Глава 5. Дистрибутивные группоиды и алгебры Конвея 55
5.1. Введение 55
5.2. Два определения дистрибутивного группоида 58
5.2.1. Геометрическое определение 58
5.2.2. Алгебраическое описание дистрибутивного группоида ... 59
5.3. Полнота дистрибутивного группоида узла 61
5.4. Специальные реализации 64
5.5. Алгебра Конвея и полиномы 65
5.6. Реализации алгебры Конвея 74
5.7. Полином Александера. Матричное представление 75
Глава 6. Подход Кауфмана к полиному Джонса 77
6.1. Скобка Кауфмана 77
6.2. Полином Джонса и скейн-соотношения 80
6.3. Полином Кауфмана от двух переменных 82
Оглавление ν
Глава 7. Полином Джонса. Комплекс Хованова 85
7.1. Простейшие свойства 85
7.2. Первая гипотеза Тейта и теорема Кауфмана-Мурасуги 89
7.3. Классификация альтернированных зацеплений 90
7.4. Третья гипотеза Тейта 91
7.5. Таблица узлов 91
7.6. Полином Хованова 91
7.6.1. Феноменологические гипотезы 100
7.6.2. Редуцированный комплекс Хованова 101
Часть II. Теория кос
Глава 8. Косы, зацепления и представления 105
8.1. Четыре определения группы кос 105
8.1.1. Геометрическое определение 105
8.1.2. Топологическое определение 107
8.1.3. Алгебро-геометрическое определение 107
8.1.4. Алгебраическое определение 107
8.1.5. Эквивалентность четырех определений 108
8.1.6. Стабильная группа кос 111
8.1.7. Крашеные косы 111
8.2. Зацепления как замыкания кос 117
8.3. Косы и полином Джонса 119
8.4. Представления групп кос 125
8.4.1. Представление Бурау 125
8.4.2. Контрпример 130
8.5. Представление Крамера-Бигелова 130
8.5.1. Явные формулы Крамера 130
8.5.2. Конструкция Бигелова 131
Глава 9. Косы и зацепления 135
9.1. Теорема Александера 135
9.2. Алгоритм Вожеля 137
9.3. L-Движения и алгоритм построения кос 140
Глава 10. Алгоритмы распознавания кос 144
10.1. Геометрический алгоритм 144
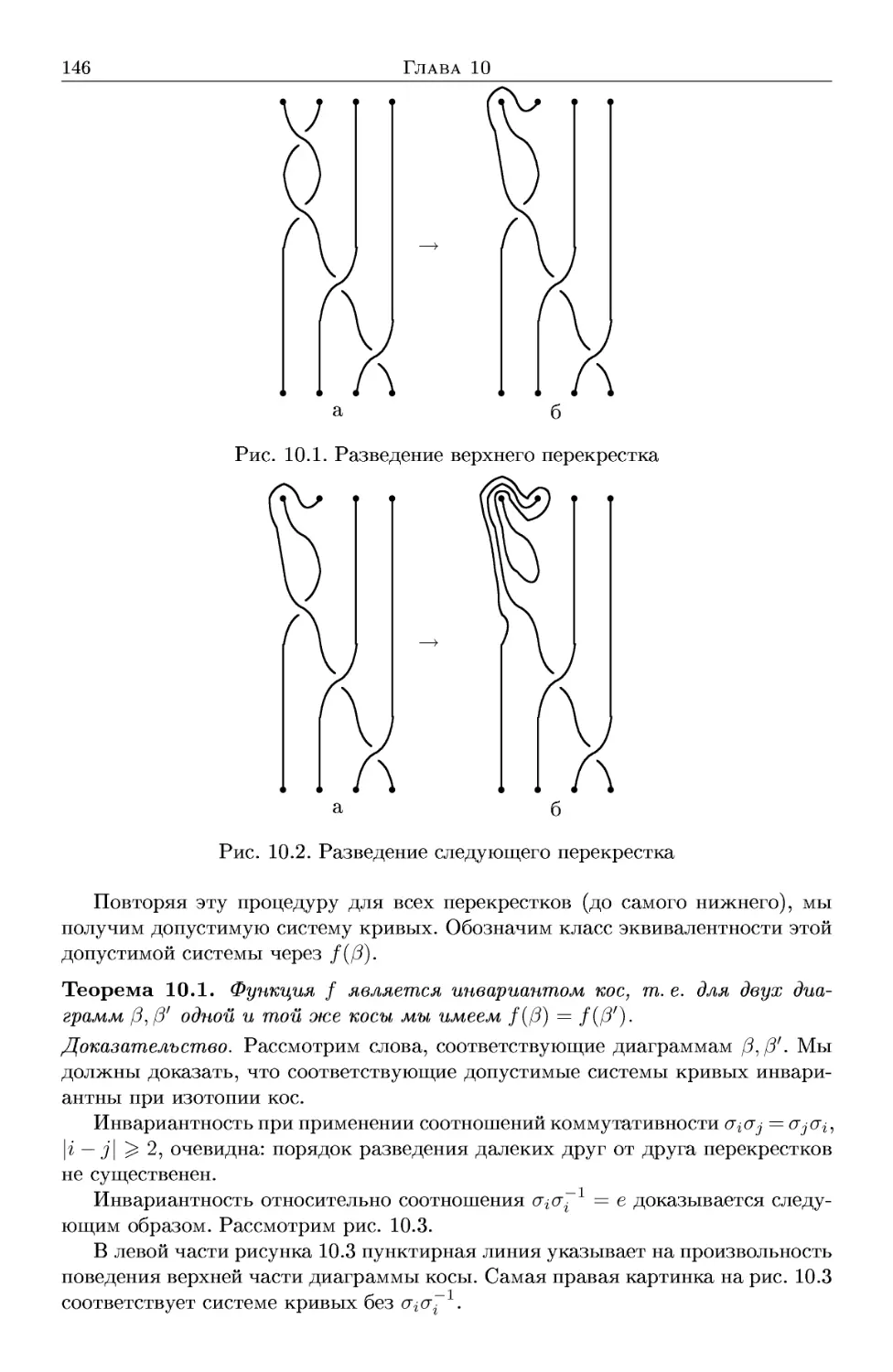
10.1.1. Введение 144
10.1.2. Построение инварианта 145
10.1.3. Алгебраическое описание инварианта / 150
10.2. L^D-системы и алгоритм Деорнуа 153
10.2.1. Почему алгоритм Деорнуа останавливается? 165
10.3. Нахождение минимального слова для Вг(3) 167
10.4. Сферические, цилиндрические и иные косы 168
10.4.1. Сферические косы 168
10.4.2. Цилиндрические косы 172
vi Оглавление
Глава 11. Теорема Маркова 177
11.1. Теорема Маркова согласно Мортону 177
11.1.1. Постановка задачи и определения. Прошивания 177
11.1.2. Теорема Маркова и прошивания 183
11.2. Обобщение Маканина. Унарные косы 191
11.3. Уравнение Янга-Бакстера 192
Часть III. Инварианты Васильева
Глава 12. Основные понятия 199
12.1. Сингулярные узлы 199
12.2. Инварианты нулевого и первого порядков 201
12.3. Примеры инвариантов старших порядков 202
12.4. Коэффициенты полинома Конвея 202
12.5. Другие полиномы и инварианты Васильева 205
12.6. Пример инварианта бесконечного порядка 210
Глава 13. Алгебра хордовых диаграмм 212
13.1. Основные структуры 212
13.2. Структура биалгебры 217
13.3. Копроизведение диаграмм Фейнмана 221
13.4. Теорема о четырех красках 223
13.5. Оценки размерностей 226
13.5.1. Историческая справка 226
13.5.2. Верхняя оценка 227
13.5.3. Нижняя граница 228
13.5.4. Таблица размерностей 230
Глава 14. Интеграл Концевича 231
14.1. Предварительный интеграл Концевича 232
14.2. Значение Z(oo) и нормализация 236
14.3. Инвариантность интеграла Концевича 238
14.3.1. Интегрирование голономии 239
14.4. Модуль Васильева 250
14.5. Теорема Гусарова 251
14.5.1. Диаграммы Гаусса 251
Часть IV. Атомы и d-диаграммы
Глава 15. Атомы, высотные атомы и узлы 255
15.1. Атомы и высотные атомы 255
15.2. Теорема об атомах и узлах 257
15.3. Задание узлов ^-диаграммами 257
15.4. Критерий реализуемости 262
15.5. Доказательство теоремы Кауфмана-Мурасуги 266
15.6. Примеры инвариантов Васильева 268
Оглавление vii
Глава 16. Скобочная полугруппа узлов 272
16.1. Задание словами в конечном алфавите 272
16.2. Представление зацеплений квазиторическими косами 275
16.2.1. Определение квазиторических кос 275
16.2.2. Крашеные косы являются квазиторическими 277
16.2.3. d-Диаграммы квазиторических кос 280
Часть V. Виртуальные узлы
Глава 17. Основные определения 285
17.1. Комбинаторное определение 286
17.2. Проекции из поверхностей с ручками 289
17.3. Гауссовы диаграммы 292
17.4. Простейшие инварианты 293
17.5. Дистрибутивный группоид 294
17.5.1. Фундаментальные группы 294
17.5.2. Странные свойства виртуальных зацеплений 295
Глава 18. Инвариантные полиномы виртуальных узлов 297
18.1. Виртуальный группоид (квандл) 298
18.2. Полином Джонса-Кауфмана 306
18.3. Представления виртуального группоида 307
18.3.1. Фундаментальная группа 308
18.3.2. Инвариант раскрасок 309
18.4. Полином VA 310
18.4.1. Свойства VA-полинома 316
18.5. Мультипликативный подход 318
18.5.1. Полином от двух переменных 318
18.5.2. Полином многих переменных 326
Глава 19. Обобщения полинома Джонса—Кауфмана 331
19.1. Введение. Основные опеределния 331
19.2. Пример 338
19.3. Проблемы минимальности и атомы 339
Глава 20. Комплекс Хованова для виртуальных узлов 345
20.1. Комплекс Хованова с коэффициентами в поле Z2 345
20.2. Комплекс Хованова удвоений узлов 348
20.3. Атомы и комплекс Хованова 354
Глава 21. Длинные виртуальные узлы 361
21.1. Введение 361
21.2. Рациональная функция ЯЗ 363
21.3. Длинный группоид 365
21.4. Инвариант раскрасок 368
21.5. Виртуальные узлы и длинные виртуальные узлы 369
21.6. Коммутируемость длинных узлов 370
viii Оглавление
Глава 22. Виртуальные косы 374
22.1. Определения виртуальных кос 374
22.2. Представление Бурау и его обобщения 375
22.3. Инварианты виртуальных кос 377
22.3.1. Построение основного инварианта 378
22.3.2. Первые следствия 381
22.3.3. Насколько силен инвариант JF? 383
22.4. Виртуальные зацепления
как замыкания виртуальных кос 386
22.5. Аналог теоремы Маркова 386
Часть VI. Другие теории
Глава 23. Трехмерные многообразия и узлы 391
23.1. Узлы в RP3 391
23.2. Введение в исчисление Кирби 394
23.2.1. Теорема Хегора 395
23.2.2. Построение многообразий по оснащенным зацеплениям . . 398
23.2.3. Изображение оснащенных зацеплений 399
23.2.4. Движения Кирби 399
23.3. Инварианты Виттена-Решетихина-Тураева 402
23.3.1. Алгебра Темперли-Либа 403
23.3.2. Идемпотент Джонса-Венцля 406
23.3.3. Основная конструкция 408
23.4. Инварианты зацеплений в трехмерных многообразиях 411
23.5. Виртуальные трехмерные многообразия и их инварианты .... 413
Глава 24. Лежандровы узлы и их инварианты 415
24.1. Лежандровы многообразия и лежандровы кривые 415
24.1.1. Контактные структуры 416
24.1.2. Плоские диаграммы лежандровых зацеплений 416
24.2. Определения, основные понятия и теоремы 419
24.3. Движения Фукса-Табачникова 421
24.4. Числа Маслова и Беннекина 424
24.5. Инварианты лежандровых узлов конечного порядка 426
24.6. Дифференциальная градуированная алгебра 428
24.7. Инварианты Чеканова-Пушкаря 429
24.8. Основные примеры 431
Приложение А. Независимость преобразований Рейдемейстера 432
Приложение Б. Инварианты Васильева виртуальных зацеплений435
Б.1. Подход Гусарова-Поляка-Виро 435
Б.2. Подход Кауфмана 436
Б.2.1. Некоторые наблюдения 437
Б.З. Инварианты Васильева виртуальных зацеплений 437
Б.4. Инварианты Васильева, происходящие от Ξ 438
Оглавление ix
Приложение В. Алгоритмическое распознавание виртуальных
зацеплений 440
Приложение Г. Энергия узла 445
Приложение Д. Максимумы критических коэффициентов
полинома Джонса—Кауфмана (Р. С. Авдеев) 449
Д.1. Коэффициент Μι 449
Д.2. Коэффициент М2 455
Д.З. Вычисление значений функции F\ 458
Приложение Е. Нерешенные проблемы в теории узлов 461
Приложение Ж. Таблица узлов 465
Литература 472
Предметный указатель 490
Preface
The research monograph you have in your hands is an excellent introduction
to the theory of knots, starting from first principles. Readers can begin this book
with only a passing acquaintance with topology, and use the first parts as a special
subject introduction to topological ideas. Learning more, this beginning reader can
go on to more specialized topics in the later chapters. The first six chapters provide
an elementary introduction to knot theory including the Kauffman bracket model
for the Jones polynomial.
At the seventh chapter the research nature of the book reveals itself, with
a concise introduction to the Khovanov categorification of the Jones polynomial
and later (Chapter 20) an exposition of Manturov's pioneering approach to using
Khovanov homology for virtual knots (the first instance of this in the literature). We
are now in the midst of current research, and Manturov guides the exposition with
an eye to current research problems. This tone is maintained throughout the rest
of the book with work on braids, braid recognition, Markov's Theorem, Vassiliev
invariants, Kontsevich integral, Manturov's connection of the theory of atoms with
virtual knots, generalizations of the Kauffman-Murasugi Theorem, virtual knot
theory and new invariants of virtual knots — including new invariants by the
author of the book, work on long virtual knots,virtual braids, recognition theorems
for virtual knots and links, three-manifold invariants, Legendrian knots and other
selected topics in knot theory.
This book is an unusual research monograph in that it is truly self-contained, it
spans a very wide road through the theory of knots, it has significant new results
by its author and it provides access to a goldmine of new research problems for the
reader.
Anyone serious about knot theory should read this book and get to work.
Louis H. Kauffman
Math UIC
851 South Morgan Street
Chicago, Illinois 60607-7045
(kauffman@uic.edu)
Предисловие
Исследовательская монография, которую Вы держите в руках, — это
отличное введение в теорию узлов, начинающееся с основ. Читатель может начать
эту книгу, лишь немного ознакомившись с топологией, и использовать
первые шесть глав как специальное предметное введение в топологические идеи.
Двигаясь далее, этот начинающий читатель переходит к более
специализированным темам в дальнейших главах. Первые шесть глав представляют собой
элементарное введение в теорию узлов, включая модель скобки Кауфмана для
полинома Джонса.
В седьмой главе исследовательская сущность книги выявляет себя,
начиная с краткого введения в категорификацию Хованова для полинома Джонса
и, позднее, (глава 20) с пионерского подхода Мантурова для построения
гомологии Хованова для виртуальных узлов (этот подход впервые публикуется
в настоящей книге). Мы находимся в центре текущего исследования, и
Манту ров проводит изложение с видом на текущие исследовательские проблемы.
Этот тон выдерживается до конца книги при работе с косами,
распознаванием кос, теоремой Маркова, инвариантами Васильева, интегралом Концевича,
подходом Мантурова к теории виртуальных узлов с помощью атомов,
обобщениях теоремы My расу ги, теорией виртуальных узлов и новыми инвариантами
виртуальных узлов, включая новые инварианты, принадлежащие автору
настоящей книги, в работе над длинными виртуальными узлами, виртуальными
косами, теоремами распознавания виртуальных узлов и зацеплений,
инвариантами трехмерных многообразий, лежандровыми узлами и иными избранными
темами из теории узлов.
Настоящая книга является необычной исследовательской монографией, ибо
она самодостаточна; она покрывает очень широкий путь, проходящий через
теорию узлов, она содержит существенные новые результаты автора и открывает
доступ к золотой жиле новых исследовательских проблем для читателя.
Каждый серьезно заинтересованный в теории узлов должен прочесть эту
книгу и сесть за работу.
Луис Кауфман
Университет штата Иллинойс в Чикаго
(kauffman@uic.edu)
Предисловие автора
Теория узлов играет видную роль в современной математике. Наиболее
яркие результаты в этой теории были получены в последние несколько
десятилетий. Одним из важных открытий в теории узлов является предложенная
Луисом Кауфманом в 1996 году теория виртуальных узлов. Настоящая
монография посвящена современному состоянию теории узлов с особенным уклоном
в сторону виртуальных узлов.
Как математическая теория, теория узлов восходит к концу
восемнадцатого века. Важный вклад в развитие теории узлов внесли К.-Ф. Гаусс, Ф.Клейн,
М.Ден и другие. При этом прорыв в теории узлов, приведший к
современному ее состоянию, решению многих открытых проблем, связан с открытиями
Дж.Х.Конвея и В.Джонса, а позднее — В.А.Васильева и других, и относится к
последней трети двадцатого века. За открытия в теории узлов Джонс, Виттен,
Дринфельд и Концевич были удостоены высшей математической награды —
филдсовских медалей.
В девяностые годы получили широкое развития несколько разветвлений,
связанных с теорией узлов, имеющих самостоятельный интерес. С одной
стороны, получила широкое распространение теория лежандровых узлов,
лежащая на стыке теории узлов и контактной геометрии. Она имеет многомерные
аналоги, а методы теории лежандровых узлов позволили решить некоторые
важные давно поставленные задачи классической теорией узлов.
Замечательным изобретением является теория виртуальных узлов, предложенная Луисом
Кауфманом в 1996 году. С ее появлением стало понятно, что классические узлы
являются малой частью более широкого объекта, изучение свойств которого
помогает лучше понять некоторые являения в теории классических узлов, а также
стимулирует постановку новых задач. Наконец, предложенная Михаилом Хо-
вановым в конце девяностых годов идея категорификации полинома Джонса,
явилась значительным шагом в понимании строения инвариантов узлов. Все
эти теории имеют связь с различными задачами комбинаторики, трехмерной и
четырехмерной топологии, теорией представлений групп и алгебр Ли.
Целью настоящей монографии является описание основных конструкций
современной теории узлов и ознакомление читателя с передним краем
научных исследований в этой области. С другой стороны, первые несколько глав
содержат все основные понятия "старой теории узлов" с полными и
подробными доказательствами, так что книга будет полезна не только профессионалам,
но и начинающим.
В настоящей книге мы описываем как "старую" теорию узлов:
фундаментальную группу, полином Александера, результаты Дена, Зейферта, Б у pay, Ар-
тина, так и новейшие результаты, принадлежащие Конвею, Матвееву,
Джонсу, Кауфману, Васильеву, Концевичу, Бар-Натану, Бирман. Книга содержит
Предисловие автора
хш
полное доказательство теоремы Маркова, алгоритмы распознавания кос в
различных пространствах, описание точного представления группы кос Крамера-
Бигелова, полученное на рубеже 20-21 веков. Приводится знаменитая
конструкция Джонса: посредством кос определяется инвариант зацеплений — полином
Джонса двух переменных. Часть книги посвящена методу кодирования узлов
посредством d-диаграмм, начатому в работах автора в [Mai, Ma2, МаЗ]. Как
оказалось, этот метод тесно связан с различными разделами теории узлов.
Центральное место в книге занимает теория виртуальных узлов,
предложенная Луисом Кауфманом в [KaulO]. Большая часть книги посвящена
результатам автора в теории виртуальных узлов.
Доказательства утверждений из теории узлов, приведенные в книге,
используют некоторые конструкции из других теорий, которые имеют
самостоятельный интерес: мультипликативный интеграл, алгебры Гекке, теория связностей
и уравнение Книжника-Замолодчикова, дистрибутивные группоиды, алгебры
Хопфа и квантовые группы, уравнения Янга-Бакстера и др.
Содержание настоящей книги не покрывается существующими
монографиями по теории узлов; некоторый материал был заимствован из лекционных
записок автора [МанО]. Последняя составляет материал лекций, которые
читались автором для студентов, аспирантов и преподавателей мех-мата МГУ с
1999 года и читаются по настоящее время.
Книга разделена на тематические части. Первая из них описывает
достижения в теории узлов, предшествующие инвариантам Васильева:
фундаментальную группу, дистрибутивный группоид, полиномиальные инварианты узлов и
их свойства, включая знаменитую теорему Кауфмана-Мурасуги о свойствах
полинома Джонса. В этой лее части (в главе, посвященной свойствам
полинома Джонса) читатель найдет современное описание одной из красивейших
конструкций современной теории узлов — комплекса Хованова.
Вторая часть посвящена теории кос. Приводятся алгоритмы построения
косы по зацеплению, алгоритмы распознавания кос, доказательство теоремы
Маркова, представление Бурау а также доказательство точности
представления Крамера-Бигелова. Описываются различные обобщения кос; косы в
различных пространствах. На основе представлений алгебры Гекке группы кос
выводится инвариантность полинома Джонса двух переменных (в духе
работы Джонса) и дается начальное представление об уравнении Янга-Бакстера и
квантовых инвариантах.
Третья часть посвящена теории инвариантов Васильева. Доказывается, что
инварианты Васильева различают узлы лучше, чем любые полиномиальные
(квантовые) инварианты. Приводится конструкция интеграла Концевича,
описывающая алгебраическую структуру инвариантов Васильева. Исследуются
алгебры хордовых и фейнмановских диаграмм и дается введение в теорию Бар-
Натана построения весовых систем (для получения инвариантов Васильева) на
базе представлений групп и алгебр Ли. В этой части также приведены
результаты, касающиеся роста размерности пространства хордовых и фейнмановских
диаграмм с ростом градуировки.
Четвертая глава посвящена способу кодирования узлов посредством атомов
и d-диаграмм, предложенному автором. Этот способ, с одной стороны,
позволяет кодировать топологические объекты (такие как узел, зацепление, хор-
XIV
Предисловие автора
довая диаграмма) словами в конечном алфавите. С другой стороны, метод d-
диаграмм оказывается тесно связанным с различными разделами теории узлов:
с его помощью молено получить простое доказательство теоремы Мурасуги и
некоторые его обобщения, связанные с изучением минимальности посредством
скобки Кауфмана и комплекса Хованова, он позволяет построить семейства
инвариантов Васильева зацеплений произвольного количества компонент исходя
из коэффициентов полинома Кауфмана, он связан с инвариантами графов и
плоских кривых.
Пятая — центральная — часть книги посвящена теории виртуальных
узлов, предложенной Кауфманом. В этой части представлены многочисленные
результаты автора, связанные с обобщением известных классических и
построением новых инвариантов виртуальных зацеплений. Так, в частности,
приведены различные модификации понятия дистрибутивного группоида, которые
иногда позволяют определять, что виртуальный узел не является
классическим. Построена теория длинных виртуальных узлов, которая сильно
отличается от теории длинных классических узлов, например, тем, что длинные
виртуальные узлы не коммутируют. Описаны некоторые обобщения полинома
Джонса с использованием "внутренней геометрии" виртуального узла, а также
приведены три различные конструкции комплекса Хованова, в основе которых
лежит кодирование узлов посредством атомов и d-диаграмм. Отдельной главой
выделена теория виртуальных кос, в которой помимо известных определений
и конструкций приведен принадлежащий автору инвариант виртуальных кос,
вопрос о полноте которого до сих пор является открытым.
Последняя часть содержит введение в теорию инвариантов трехмерных
многообразий — инвариантов Виттена-Решетихина-Тураева. Кроме того, в ней
представлено современное введение в теорию лежандровых узлов, включая
результаты Фукса и Табачникова, инварианты Чеканова-Элиашберга, Чеканова-
Пушкаря и др.
В конце книги приведены несколько дополнений. Наиболее важными из
них являются доказательство алгоритмической распознаваемости виртуальных
зацеплений, работа об инвариантах Васильева для виртуальных зацеплений,
а также работа об экстремальных коэффициентах полинома Кауфмана.
Последняя из них написана Романом Сергеевичем Авдеевым. По сути дела, это —
две самостоятельные статьи. Кроме этого, в качестве приложения в книге
доказана независимость трех классических движений Рейдемейстера, введение в
энергию узлов, а также список нерешенных задач в теории узлов и таблицы
узлов.
Математический материал подан достаточно замкнуто; монография
является вполне доступной для широкого круга читателей, желающих ознакомиться
с современным состоянием теории узлов "от самого начала". Она полезна для
специалистов по теории узлов, алгебраической топологии, комбинаторике,
теории представлений групп и алгебр Ли.
Некоторые технические детали доказательств, которые в дальнейшем не
используются в книге, либо опущены, либо приведены мелким шрифтом.
Кроме специальных курсов, которые автор читал в Московском
государственном университете, на формирование книги повлиял также семинар "Узлы
и теория представлений", работающий под руководством автора в МГУ начи-
Предисловие автора
XV
ная с 2000 года. До 2002 года автор вел его совместно с профессором Валерием
Владимировичем Трофимовым (1952-2003). Я глубоко благодарен ему за
плодотворное сотрудничество в течение многих лет и полезные советы. Для
настоящей книги были также полезны обсуждения с Хайнером Цишангом (1936-2004),
которому я также глубоко признателен.
Особенную благодарность я приношу моему отцу Олегу Васильевичу Ман-
турову за постоянную поддержку моей научной работы в течение всей жизни.
Я благодарен Луису Хиршу Кауфману и Виктору Анатольевичу Васильеву
за плодотворное сотрудничество. Во время написания этой книги для меня
были важны обсуждение и переписка с Роджером Фенном, Алексеем
Викторовичем Чернавским, Сергеем Владимировичем Матвеевым, Владимиром
Георгиевичем Тураевым, Михилем Хазевинкелем, Никитой Юрьевичем Нецветаевым,
Джоан Бирман, Патриком Деорнуа, Кентом Орром, Владимиром
Валентиновичем Вершининым, Владимиром Павловичем Лексиным, Сергеем Васильевичем
Дужиным, Сергеем Владимировичем Чмутовым, Сергеем Константиновичем
Ландо, Алексеем Валерьевичем Щепетиловым и многими другими.
Я признателен слушателям моих спецкурсов и участникам моего семинара,
особенно Роману Сергеевичу Авдееву. Им написано приложение Д.
Мне также приятно выразить благодарность моему другу и коллеге Рутвигу
Кампоамору-Штурсбергу за постоянные научные консультации и переписку.
Книга написана с использованием шрифтов knots.tex, содержащих специ-
альные символы, используемые в теории узлов такие, как Λ Г. и GO· Эти
шрифты были созданы и предоставлены мне М.М.Виноградовым и
А.Б.Сосинским, за что я им весьма признателен.
Василий Олегович Мантуров
Москва, декабрь 2004.
Часть I
Узлы, зацепления и
инвариантные полиномы
Глава 1
Введение
Теория узлов происходит из замечательной и на первый взгляд очень
простой топологической задачи. В течение более двух веков к ней обращались
А.Т.Вандермонд, К.-Ф.Гаусс (предложивший знаменитую электромагнитную
формулу для вычисления коэффициента зацеплений [Gau]), Ф.Клейн, М.Ден
[Dehn]. Оказалось, однако, что для решения (далее частичного) этой задачи
требуется сложный математический аппарат, связанный с топологией,
теорией дискриминантов, теорией групп и алгебр Ли, теорией мультипликативаного
интеграла, квантовых групп и т. д. Теория узлов быстро развивается и
стимулирует появление новых областей математики. В начале двадцатого века весомый
вклад в теорию узлов внес знаменитый американский тополог Дж. Александер.
Однако наиболее существенные достижения в теории узлов были получены
лишь в конце двадцатого века. Эти достижения связаны с именами Дж. X. Кон-
вея, В.Джонса, В.А.Васильева, М.Л.Концевича, В.Г.Тураева,
М.Н.Гусарова, Дж. Бирман, Л. X. Кауфмана, Д. Бар-Натана и других.
Но и после этих выдающихся достижений, приведших к решению многих
важных задач, теория узлов продолжает развиваться, более того,
появляются новые направления этой науки. Особенно стоит отметить замечательную
конструкцию М.Хованова [Khl], предложившего категорификацию полинома
Джонса — инвариант узлов, основанный на совершенно новых идеях.
Основной целью настоящей монографии является описание современного состояния
теории классических и виртуальных узлов. Мы также затронем теорию ле-
жандровых узлов, лежащую на стыке теории узлов и контактной геометрии
и топологии. Наиболее весомый вклад в эту (очень молодую) науку внесли за
последние несколько лет Д. Б. Фукс, С. Л. Табачников, Ю. В. Чеканов, Я. Эли-
ашберг.
Еще одним заслуживающим внимания разветвлением теории узлов
является предложенная Кауфманом в 1996 теория виртуальных узлов; многие яркие
задачи в этой теории еще ждут своего решения. Одной из главных целей
настоящей монографии является описание последних достижений в этой теории.
Теория узлов имеет и прикладное значение. Она является важным
инструментом для других теорий; ярким примером того является исчисление Кирби —
теория кодировании трехмерных многообразий оснащенными узлами.
Теория узлов имеет многомерные аналоги; кроме того, узлы являются
отправной точкой в построении объектов многомерной топологии, например, узел-
многообразий [НМ], среди которых встречаются, в частности, сферы Милно-
4
Введение
pa — многообразия, гомеоморфные, но не диффеоморфные стандартной
семимерной сфере.
1.1. Основные определения
Под узлом мы понимаем гладкое вложение окружности S1 в
ориентированное пространство R3 (или сферу S3)1; узлом также называют образ этого
отображения.
Деформируя объемлющее пространство R3, мы также деформируем и узел
(образ вложения). Два узла называются изотопными, если один из них может
быть продеформирован в другой посредством диффеоморфизма
объемлющего пространства на себя, сохраняющего ориентацию; такой диффеоморфизм
гомотопен тождественному отображению в классе диффеоморфизмов.
Основным вопросом теории узлов является следующий: как определить,
изотопны два заданных узла или нет. Эта задача носит название проблемы
распознавания узлов. Рассматривая узлы с точностью до изотопии, можно
говорить об изотопических классах узлов. Говоря "узел", мы часто будем иметь
в виду его изотопический класс, если это ясно из контекста. Ключевую роль
играют инварианты узлов, т. е. функции на множестве изотопических классов
узлов или, другими словами, функции на узлах, инвариантные относительно
изотопии.
Частным случаем проблемы распознавания узлов является проблема
распознавания тривиального узла. Под тривиальным узлом понимается
простейший узел, который может быть представлен как граница диска, гладко
вложенного в R3.
Оба вопроса являются чрезвычайно сложными. Хотя они к настоящему
моменту решены, их решение требует серьезной техники (см. [Hem, Mat]), а
алгоритм распознавания настолько сложен, что не может быть запрограммирован
для практических целей. Этот алгоритм полностью описан в [Mat], см.
также [Матв2]. Приведенный в книге Сергея Владимировича Матвеева алгоритм
основан на теории Вольфганга Хакена нормальных поверхностей.
В настоящей монографии мы опишем частичные ответы на эти вопросы.
Для того, чтобы доказать изотопность двух узлов, как правило, нужно
предъявить пошаговую изотопию, переводящую один узел в другой. Простейшими
изотопиями узлов являются так называемые движения Рейдемейстера, см.
главу 2. Известно, что всякая изотопия сводится к ним (а также диффеоморфизму
плоскости на себя; обычно он подразумевается и не вводится в список
движений).
Для того чтобы показать, что два узла не являются изотопными, достаточно
найти инвариант узлов, принимающий разные значения на этих двух узлах.
Обычно узлы кодируются следующим образом. Фиксируем узел, т. е. образ
отображения / : S1 —>· R3. Рассмотрим некоторую плоскость h С R3 (скажем,
h = Oxy) и проекцию узла на нее. Без ограничения общности можно считать,
что проекция узла на плоскость представляет собой вложенный конечный
четырехвалентный граф, являющийся образом гладкого погружения окружности
1 Эти две теории эквивалентны по причине коразмерности. В дальнейшем мы будем иметь
дело с узлами в R3, если не оговорено противное.
1.1. Основные определения 5
в плоскость. Обычно мы будем называть часть узла его ветвью. Каждая
вершина графа проекции (называемая перекрестком) оснащена следующей
структурой. Пусть а, Ъ — две ветви узла, проекции которых пересекаются в точке V.
Так как а и Ъ не пересекаются в R3, два прообраза точки V имеют различные
г-координаты. Таким образом, мы можем сказать, какая ветвь (а или Ъ)
проходит сверху (образует переход)] а какая — снизу (образует проход) (см. рис. 1.1).
Ребра переходов изображаются сплошными линиями, в то время как проход
изображается имеющим разрыв в перекрестке.
Такое изображение узла на плоскости называется плоской диаграммой узла.
Рис. 1.1. Локальная структура перекрестка
Четырехвалентный граф проекции без указания структуры проходов и
переходов называется тенью узла. Сложностью узла называется минимальное
количество перекрестков диаграмм узлов заданного изотопического типа.
Следующее утверждение остается читателю в качестве упражнения: любые
два узла, имеющие одну и ту лее комбинаторную структуру плоской
диаграммы, являются изотопными.
Приведем несколько примеров.
Пример 1.1. Узел, имеющий диаграмму без перекрестков (см. рис. 1.2.1)
называется тривиальным узлом. На рисунке 1.2.2. изображена другая диаграмма
тривиального узла. На рис. 1.2.3. изображен узел, называемый трилистником,
а на рис. 1.2.4. — узел, называемый восьмерков. Два последних узла не
тривиальны и не изотопны один другому. Таблицы узлов и компьютерную программу
изображения и (частичной) классификации узлов можно найти в [Scha].
Рис. 1.2. Простейшие узлы
У каждого узла есть зеркальное отражение, т. е. узел, полученный из него
отражением в некоторой плоскости. Диаграмма зеркального отражения может
быть получена из диаграммы исходного узла заменой всех типов перекрестков,
т. е. заменой проходов на переходы и наоборот без изменения тени узла. Узел
называется зеркальным, если он изотопен своему зеркальному отражению.
6
Введение
Так, например, трилистник не является зеркальным узлом. Это значит, что
есть два трилистника — правый и левый, см. рис. 1.3. Тот факт, что два
трилистника различны (неизотопны) впервые был доказан Максом Деном, см. [Dehn].
Рис. 1.3. а. Левый трилистник б. Правый трилистник
Упражнение 1.1. Покажите, что восьмерка является зеркальным узлом.
Молено говорить об ориентированных узлах, т. е. гладких вложениях
(образах вложений) ориентированной окружности в R3. Под изотопией в данном
случае следует понимать изотопию, сохраняющую ориентацию.
Определение 1.1. Диаграмма L узла называется восходящей (начиная с
точки А, не являющейся перекрестком), если при прохождении диаграммы L
начиная с точки А в согласно ориентации узла каждый перекресток сначала
проходится снизу, а затем — сверху. Аналогично определяется нисходящая
диаграмма.
Упражнение 1.2. Покажите, что всякая восходящая диаграмма
представляет собой тривиальный узел.
Аналогично вложениям одной окружности можно рассматривать вложения
несвязного объединения набора из нескольких окружностей; это приводит к
понятию зацепления. Зацепление — это гладкое вложение (образ вложения)
нескольких несвязных окружностей в R3. Каждый из узлов, представляющих
собой образ вложения одной из этих окружностей, называется компонентной
зацепления. Естественным образом определяется изотопия зацеплений
(посредством диффеоморфизма объемлющего пространства на себя,
гомотопного тождественному отображению в классе диффеоморфизмов, или, что то же
самое, посредством диффеоморфизма, сохраняющего ориентацию, плоские
диаграммы зацеплений и инварианты зацеплений. Под ориентированным
зацеплением мы понимаем гладкое отображение (или его образ) несвязного
объединения ориентированных окружностей.
Аналогично узлам и зацеплениям определяются длинный узел как гладкое
вложение (образ вложения) ориентированной прямой в трехмерное
пространство, совпадающее вне некоторого шара с центром в начале координат с
тождественным вложением оси Ох. От изотопии нужно потребовать, чтобы она
была постоянна вне некоторого шара с центром в начале координат. В качестве
плоских диаграмм длинных узлов будем рассматривать проекции общего
положения на плоскость, параллельную Оху. В этом случае диаграмма вне
некоторого шара будет совпадать с горизонтальной линией, а внутри него вести себя
как диаграмма обычного (не длинного) узла.
1.1. Основные определения
7
Длинные узлы получаются из обычных разрыванием в некоторой точке и
вытягиванием концов на бесконечность, см. рис. 1.4.
Рис. 1.4. Вытягивание концов узла на бесконечность
Существует другой подход к определению эквивалентности зацеплений, при
котором каждой компоненте зацепления разрешено самопересекаться, но
пересечения разных компонент запрещены. Эта теория описана в замечательной
работе Джона Уилларда Милнора [Mi], который ввел в рассмотрение так
называемые μ-инварианты для классификации зацеплений относительно такой
эквивалентности.
Тривиальным п-компонентным зацеплением называется зацепление, пред-
ставимое как граница набора из η попарно непересекающихся вложенных в R3
двумерных дисков.
Пример 1.2. На рисунке 1.5.1. изображено тривиальное зацепление из двух
компонент. На рисунках 1.5.2, 1.5.3 и 1.5.4 изображены зацепление Хопфа,
зацепление Уайтхеда и кольца Борромео соответственно. Все эти три зацепле-
Рис. 1.5. Простейшие зацепления
ния не тривиальны. Кольца Борромео обладают интересным свойством: при
удалении любой из трех компонент зацепление распадается (т. е. становится
тривиальным), в то время как в целом оно является нетривиальным.
Упражнение 1.3. Покажите, что зацепление Уайтхеда имеет симметрию
8
Введение
относительно перестановки компонент, т. е. существует изотопия,
переводящая его в себя и переставляющая компоненты.
Первым знаменитым инвариантом узлов (после электромагнитной формулы
Гаусса для вычисления коэффициента зацепления) является фундаментальная
группа дополнения к узлу {зацеплению). Этот инвариант — топологический; он
различает неизотопные узлы (в частности, он распознает тривиальный узел
и тривиальное зацепление с произвольным числом компонент). Однако такое
решение проблемы распознавания узлов не является полным, так как оно
всего лишь сводит проблему к вопросу распознавания групп; последний в общем
случае не разрешим.
В 1923 американский математик Джеймс Александер [Alel, Ale2] получил
из фундаментальной группы полиномиальный инвариант зацеплений. Этот
инвариант много слабее самой фундаментальной группы, но он много проще для
применения: полиномы легко сравнивать друг с другом в отличие от групп,
заданных копре д став л ениями.
В 1932 немецкий тополог Курт Рейдемейстер опубликовал книгу "Теория
узлов" (Knotentheorie, [Rei]), в которой он привел список локальных движений
(известных ныне как движения Рейдемейстера) и доказал, что любые две
плоские диаграммы задают одно и то лее зацепление тогда и только тогда, когда
они могут быть получены друг из друга конечной последовательностью этих
движений. Это позволило ему составить таблицу узлов вплоть до семи
перекрестков.
С тех пор доказательство инвариантности тех или иных функций на узлах
основывается как правило на проверке инвариантности относительно движений
Рейдемейстера.
Из книг, описывающих состояние узлов того времени, мы рекомендуем
книги Эшли [Ash], Кроуэлла и Фокса [КФ] и Бурде и Цишанга [BZ].
Следующим важным шагом в развитии теории узлов было открытие
полинома Джона Хортона Конвея [Con], основанное на так называемых
соотношениях типа Конвея (skein relations). Это комбинаторные соотношения,
описывающие взаимосвязь значений инварианта на "похожих" плоских диаграммах.
Полином Александера [Alel] может быть истолкован в терминах этих
соотношений, причем Александер знал об этом. Важным достижением Конвея было
то, что он первым обнаружил, что эти соотношения могут быть использованы
для аксиоматического определения инварианта узлов.
Это открытие стимулировало построение множества других, более мощных,
инвариантов, удовлетворяющих соотношениям типа Конвея. Здесь стоит
отметить полином Джонса двух переменных, [Jonl, Jon2]. С использованием этих
полиномов были решены некоторые старинные проблемы, например, проблема
Тейта [Tait].
Среди полиномов, удовлетворяющих таким соотношениям (skein-полиномов)
выделим также полином HOMFLY и полином Кауфмана.
Открытия Конвея и Джонса и последовавшие за ним работы положили
начало более общей конструкции — квантовым инвариантам; важнейший вклад
в эту науку принадлежит В.Г.Дринфельду и В.Г.Тураеву. Современное
состояние теории квантовых инвариантов освещено в книгах [KPT, Tur3, Oht].
1.1. Основные определения
9
Подход к исследованию узлов с помощью их плоских диаграмм — не
единственная возможность. Большое значение для теории узлов имеет теория кос.
Косы были предложены немецким математиком Эмилем Артином, давшим
основные определения и доказавшим важные теоремы в этой теории вплоть
до классификации кос [Artl], более подробную (англоязычную) версию см.
в [Art2]. Косы тесно связаны с полиномами без кратных корней, теорией
дискриминантов, теорией представлений и др. Под косой из η нитей понимается
множество из η восходящих простых непересекающихся кривых в R3
(обычно рассматривают гладкий, кусочно-гладкий или кусочно-линейный случаи),
называемых нитями, соединяющих точки Αι,..., Ап на одной горизонтальной
прямой линии с точками В\,..., Вп на некоторой нижней горизонтальной
линии. Аналогично узлам, косы могут быть описаны их плоскими диаграммами]
классы эквивалентности кос определяются как семейство диффеоморфизмов
объемлющего пространства, оставляющих нити восходящими. Произведением
кос а и Ъ называется коса, получающаяся приставлением косы а сверху к косе Ъ
и сжатием полученного так, чтобы верхние и нижние точки встали на нужные
позиции.
Рис. 1.6. Замыкание косы
Легко видеть, что замыкая косу самым естественным образом (т.е.,
соединяя Ai с Bi, г = 1,..., гг, см. рис. 1.6), мы получаем диаграмму зацепления.
Теорема Александера утверждает, что зацепление любого изотопического
типа может быть получено замыканием некоторой косы. Теорема Артина [Artl]
задает представление группы кос: образующие и соотношения. Теорема
Маркова [Маг] устанавливает список необходимых и достаточных преобразований,
с помощью которых можно перевести друг в друга косы, замыкания которых
являются изотопными зацеплениями. Мы также описываем алгоритмы
распознавания изотопности кос, [Deh, GM], а также точные представления групп кос
Крамера и Бигелова, [Bigl, Krai, Kra2].
10
Введение
Важным свойством кос является наличие групповой структуры (в отличие
от узлов). Это заметно упрощает проблему распознавания и сводит ее к
проблеме распознавания тривиальной косы.
Из литературы по теории узлов мы рекомендуем следующие монографии и
учебники: Кауфман [Kaul, Kau2], Адаме [Ada], Каваучи [Kaw+] и Атья [Атья].
Последняя книга является замечательным кратким введением в результаты
Джонса и Виттена о "физических" инвариантах в трехмерной топологии.
Пусть задан узел, и мы хотим изменить его изотопический класс, гладко
меняя отображение окружности в R3. Если мы допустим пересечения, то это
становится возможным, при этом самым интересным моментом при изменении
такого отображения будет момент, когда возникает пересечение (мы можем
предполагать, что таких моментов дискретное множество).
Если в некоторой момент мы имеем отображение окружности, все
особенности которого состоят лишь из конечного (быть может, нулевого) количества
трансверсальных пересечений, мы говорим, что задан сингулярный узел.
Пространство всех сингулярных узлов (имеющих по крайней мере одну точку
пересечения) называется дискриминантным пространством2.
Изучая пространства дискриминантов, Виктор Анатольевич Васильев
предложил понятие инвариантов конечного порядка, в дальнейшем известных как
инварианты Васильева. Изначально изучение инвариантов Васильева
требовало сложной техники; затем было предложено комбинаторное их определение.
В настоящей книге мы приведем доказательство того факта, что инварианты
Васильева сильнее всех (полиномиальных) инвариантов, описанных выше.
Первое доказательство существования нетривиальных инвариантов
Васильева было приведено в [Vas]; структура пространства таких инвариантов
была впервые описана Максимом Львовичем Концевичем (гипотеза была
предложена Васильевым); для описания этой структуры Концевич предложил
замечательный интеграл, впоследствии названный интегралом Концевича, [Коп].
Детальное и глубокое описание интеграла Концевича можно найти в работе
Дрора Бар-Натана [BN1]. В этой работе также описывается связь между
инвариантами Васильева и представлениями алгебр Ли. Интеграл Концевича также
является универсальной конструкцией для так называемых квантовых
инвариантов, см., например, [Oht].
Вычисление интеграла Концевича было очень сложным до появления
работы Ле и Мураками [LM]. В этой работе они предложили явное техническое
описание вычисления интеграла Концевича. См. также [Oht].
Достойна особого внимания выдающаяся работа Михаила Хованова [Khl]
1997 года, давшего обобщение полинома Джонса в терминах когомологий
некоторого формального алгебраического комплекса (комплекса Хованова):
появился принципиально новый инвариант узлов.
Заслуживает внимания также следующий способ представления узлов и
зацеплений, основанный на понятиях d-диаграммы и атома, [МаЗ]. d-Диаграмма
представляет собой хордовую диаграмму на окружности с двумя семействами
непересекающихся между собой хорд. Эта теория берет начало с так называе-
2Молено рассматривать также и другие сингулярности, такие, как потеря гладкости в
конечном множестве точек, точки касания и точки многократного пересечения. Глубокому
изучению особенностей дискриминантов посвящена монография В.А.Васильева [Ва].
1.1. Основные определения
11
мых атомов и позволяет кодировать зацепления словами в конечном
алфавите [МаЗ], состоящем из скобок ( , ) , [ , ]. В этом состоит ее превосходство,
скажем, над кодированием узлов замыканиями кос: в последнем случае для
записи произвольного зацепления требуется, вообще говоря, неограниченное
количество букв. Атомы и d-диаграммы естественным образом появляются во
многих задачах комбинаторики и маломерной топологии.
С использованием d-диаграмм молено представить все зацепления петлями
на клетчатой бумаге, исходящих из начала координат и лежащих внутри
первого квадранта.
Простейшие d-диаграммы, соответствующие левому и правому
трилистникам, показаны на рис. 1.7.
Рис. 1.7. Левый трилистник; Правый трилистник.
Соответствующие скобочные структуры выглядят как
(((([))))]
для левого трилистника и
(([[))]]
для правого трилистника.
Таким образом, на клетчатой бумаге левый трилистник кодируется
прямоугольником 1 χ 4, в то время как квадрат 2x2 кодирует правый трилистник
(см. рис. 1.8).
ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_
ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_
ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_ ι_
I I I I I I I I I I I I
(0,0) (0,0)
Рис. 1.8. Левый трилистник Правый трилистник
Кодирование узлов посредством атомов и d-диаграмм естественно связано
с различными обобщениями узлов: лежандровыми узлами и виртуальными
узлами.
Особенно стоит отметить предложенную в 1996 году Луисом Кауфманом
теорию виртуальных узлов, [KaulO]). Понятие виртуального узла (и
виртуального зацепления) возникает, если мы расширяем комбинаторное понятие плоской
12
Введение
диаграммы зацепления, разрешая новый тип перекрестка, называемый
виртуальным, расширяя при этом список движений Рейдемейстера и добавляя в них
движения, относящиеся к виртуальным перекресткам. Виртуальный
перекресток не является ни проходом, ни переходом, его можно понимать как
"случайную встречу" двух ветвей узла, изображения которых пересекаются, так как
не могут разойтись на плоскости. Эта теория может быть интерпретирована
как "проекция" теории узлов в утолщенных поверхностях вида Sg x / на
плоскость (здесь Sg замкнутая двумерная поверхность рода д, I — отрезок). Теория
быстро развивается и содержит как обобщения теорем классической теории
узлов, так и виртуальные эффекты, не имеющие места в классическом случае
(см. статьи [Ма2, Ма5, Маб, KM, FKM, Saw, SW] и др.). Этой важной части
теории узлов посвящена V часть настоящей монографии. В настоящее время
готовится к изданию монография [КМО] Луиса Кауфмана и автора
настоящей книги, посвященная современному состоянию теории виртуальных узлов.
Проблема распознавания виртуальных зацеплений является алгоритмически
разрешимой, [Ма7]; этому посвящено приложение В настоящей книги. Однако,
как и в случае классических зацеплений этот алгоритм основывается на
технически сложных утверждениях из теории Хакена и поэтому вряд ли может
быть эффективно реализован на компьютере.
Глава 2
Движения Рейдемейстера и
арифметика узлов
В настоящей главе мы обсудим плоские диаграммы зацеплений и структуру
полугруппы, возникающую на множестве узлов; последняя изоморфна
полугруппе натуральных чисел относительно умножения. Это позволяет говорить
об арифметике узлов.
Зацепления кодируются плоскими диаграммами; при изотопной
деформации зацепления в объемлющем пространстве диаграмма зацепления может
претерпевать некоторые комбинаторные изменения, проходя через сингулярные
состояния. Эти сингулярные состояния мотивируют наличие списка
простейших перестроек для плоских диаграмм. Эти перестройки называются
движениями Рейдемейстера, см. рисунки 2.1,2.2. Каждое из этих движений локальное,
т. е. представляет собой перестройку части диаграммы зацепления,
изображенной на рисунке, в то время как часть зацепления, находящаяся вне
изображенной области, может быть произвольной и остается неизменной при движении.
Заметим теперь, что версии движений Ω ι и Ω3, изображенные на рис. 2.2
(которые мы будем обозначать теми же буквами), могут быть выражены как
комбинации движений, приведенных на рис. 2.1 (и преобразований, не
меняющих комбинаторной структуры зацепления на плоскости). Этот факт
предлагаем читателю в качестве упражнения.
2.1. Полигональные зацепления
и движения Рейдемейстера
Так как узел является гладким вложением окружности S1 в пространство R3,
его можно сколь угодно точно аппроксимировать вложением замкнутой
ломаной в R3. Здесь мы имеем в виду лишь хорошие аппроксимации, т. е. такие, что
после сколь угодно малого сглаживания в окрестностях вершин ломаной, мы
получим кривую из того же изотопического класса, что и изначальная кривая.
Определение 2.1. Вложение несвязного объединения η замкнутых ломаных
линий в R3 называется полигональным (многоугольным) гг-компонентным
зацеплением. Полигональный (многоугольный) узел — это полигональное одно-
компонентное зацепление.
14 Полигональные зацепления и движения Рейдемейстера
Первое движение
Рейдемейстера Ω ι
Второе движение
Рейдемейстера Ω2
<->
Третье движение Рейдемейстера Ω;
Рис. 2.1. Движения Рейдемейстера Ωι,Ω2,Ω3
Иногда говорят о ручных зацеплениях, т. е. о (гладких) зацеплениях, как
они были определены в предыдущей главе, и диких зацеплениях, т. е. о
непрерывных вложениях окружности в трехмерное пространство, рассматриваемых
с точностью до непрерывной (не обязательно гладкой) изотопии, см.
определение далее. Классы изотопии ручных (гладких) зацеплений и полигональных
зацеплений (см. определение ниже) совпадают; подробное доказательство этого
факта можно найти в книге [КФ].
Изложение теории диких зацеплений можно найти в статье Эмиля Артина
и Ральфа Фокса [AF].
При необходимости мы будем использовать оба определения узлов:
полигональные узлы и гладкие узлы.
В дальнейшем мы всегда будем подразумевать зацепления ручными, если
не оговорено противное.
Определение 2.2. Два полигональных зацепления называются изотопными,
если одно из них может быть продеформировано в другое посредством
последовательных применений элементарной изотопии и преобразования, обратного
к ней. Здесь под элементарной изотопией понимается замена ребра АВ ломаной
L на два ребра АС и ВС при условии, что треугольник ABC не пересекается
с L\(AC U ВС), см. рис. 2.3.
Полигональные зацепления и движения Рейдемейстера 15
Первое движение Рейдемейстера
<->
Третье движение Рейдемейстера
Рис. 2.2. Движения Рейдемейстера Ωι,Ωβ
Рис. 2.3. Элементарная изотопия
Как и гладкие зацепления, полигональные зацепления обладают плоскими
диаграммами с проходами и переходами; имея такую диаграмму, можно
восстановить зацепление с точностью до изотопии.
Диаграммы полигональных зацеплений состоят из ребер, которые
соединяются в вершинах (валентности два) и пересекаются в перекрестках,
снабженных структурой проход-переход.
Замечание 2.1. Плоская диаграмма полигональных узлов определяется
аналогично плоской диаграмме гладких узлов. Однако двухвалентные вершины
16 Полигональные зацепления и движения Рейдемейстера
(образы вершин ломаной) дают излишнюю комбинаторную информацию. Так,
разбивая ребро на два ребра путем добавления новой вершины, мы получаем
диаграмму, плоско-изотопную изначальной, но имеющую другую
комбинаторику.
Упражнение 2.1. Покажите, что все полигональные зацепления с не более,
чем пятью ребрами, тривиальны.
Упражнение 2.2. Постройте полигональный трилистник с шестью
ребрами.
Определение 2.3. Под плоской изотопией гладкой плоской диаграммы
зацепления мы понимаем диффеоморфизм плоскости на себя, не меняющий
комбинаторной структуры диаграммы.
Очевидно, что плоская изотопия действительно является изотопией, т. е. она
не меняет изотопического класса зацепления в R3.
Теорема 2.1 (Рейдемейстер, [Rei]). Диаграммы Ό\ и Ό^ гладких
зацеплений представляют один и тот же изотопический класс, если и только если
диаграмма Ό\ может быть продеформирована в диаграмму Ό^ посредством
применения конечной последовательности плоских изотопии и движений
(перестроек) Рейдемейстера Ωι,Ω2,Ω3, см. рис. 2.1.
Это утверждение можно доказать с использованием соображений
коразмерности. Мы дадим доказательство с использованием полигональных зацеплений.
Доказательство. Одна импликация очевидна: легко проверяется, что ни одно
из движений Ωι, Ω2, Ω3 не меняет изотопического класса зацепления.
Обратно, пусть Di,U2 — две плоские диаграммы изотопных
полигональных зацеплений К\ и i^2· По определению изотопия между К\ и К2 состоит из
конечного набора элементарных изотопии, имеющих вид [АВ] <—> [AC] [J[CB].
Без ограничения общности будем полагать, что на каждом шаге в
треугольнике ABC ребра [DA] и [BE], выходящие из концов отрезка [АВ] не пересекают
внутренности треугольника ABC (этого можно легко добиться,
предварительно применив движение Ωι). Без ограничения общности можно считать также,
что плоскость треугольника ABC не ортогональна плоскости проекции (можно
изначально выбрать плоскости проекции так, чтобы она не была ортогональна
ни одной из конечного набора плоскостей треугольников, возникающих по
ходу изотопии). Легко видеть, что мы можем выбрать плоскость проекции так,
чтобы ортогональная проекция была общего положения.
Пусть Lo — проекция зацепления Ко "до применения элементарной
изотопии" на плоскость треугольника ABC. Разобьем компоненты пресечения
треугольника ABC и проекции Lq на два множества: верхние и нижние,
соответственно тому, как проходят ребра зацепления Kq относительно плоскости
ABC.
Разобьем треугольник ABC на малые треугольники четырех типов таким
образом, что ребра малых треугольников не содержат вершин проекции L^.
Каждый треугольник первого типа содержит ровно один перекресток
проекции Lq; при этом ребра Lq пересекают две стороны треугольника. Треугольник
Полигональные зацепления и движения Рейдемейстера 17
второго типа содержит одну вершину Lo и части исходящих ребер.
Треугольник третьего типа содержит часть ребра из Lo и не содержит вершин. Наконец,
треугольник четвертого типа не содержит ни вершин, ни ребер. Примеры
треугольников всех типов, за исключением четвертого (пустого) изображены на
рис. 2.4.
Третий тип
Рис. 2.4. Типы маленьких треугольников
Такая триангуляция треугольника ABC может быть построена следующим
образом. Сначала мы отсекаем все перекрестки и все вершины достаточно
малыми треугольниками первого и второго типов соответственно. Затем мы
разбиваем оставшуюся часть треугольника ABC и получаем треугольники двух
оставшихся типов.
После этого доказательство теоремы проходит так. Вместо применения
элементарной изотопии к треугольнику ABC мы применяем шаг за шагом
изотопии для малых треугольников, составляющих треугольник ABC. Очевидно,
что эти движения для малых треугольников являются комбинациями
движений Рейдемейстера и плоских изотопии.
А именно, изотопия для треугольника первого типа является комбинацией
второго и третьего движений Рейдемейстера, треугольники второго и
третьего типа порождают второе движение Рейдемейстера либо плоскую изотопию.
Наконец, преобразование, соответствующее четырехугольнику четвертого типа
является плоской изотопией. D
Замечание 2.2. Обычно плоская изотопия не вносится в список движений,
так как она не меняет комбинаторной структуры узла, поэтому для
доказательства инвариантности функций на узлах, строящихся комбинаторно,
нужно проверять только движения Рейдемейстера Ωι,Ω2,Ω3
Сложное упражнение 2.1. Покажите, что три движения Рейдемейстера
Ωι,Ω2,Ω3 являются независимыми.
18 Полигональные зацепления и движения Рейдемейстера
Итак, проекция зацепления в общем положении имеет, вообще говоря,
много перекрестков; все они простые и трансверсальные. Интересным является и
"противоположный" случай.
Сложное упражнение 2.2 (Г. Брунн). Покажите, что для каждого
зацепления L существует изотопное ему зацепление V и плоскость Ρ такая,
что проекция зацепления V на плоскость Ρ имеет ровно одну
многократную точку пересечения, которая является трансверсальной для всех ветвей
зацепления.
Замечательное решение этой задачи предложено в [Гай].
Определение 2.4. Узел называется обратимым если он изотопен узлу,
полученному из него заменой ориентации.
Упражнение 2.3. Покажите, что оба трилистника являются обратимыми
узлами.
Существование необратимых узлов было проблемой в течение долгого
времени. Эта проблема была решена Троттером в 1964 году [Тго]. Простейшим
необратимым узлом является узел 8ιγ, см. таблицу узлов в конце книги.
Пример, предложенный Троттером, показан на рис. 2.5.
Рис. 2.5. Необратимый узел
Определение 2.5. Диаграмма зацепления называется альтернированной,
если при движении вдоль каждой компоненты проходы чередуются с переходами.
Простейший неальтернированный узел (т. е. узел, не имеющий
альтернированной диаграммы) показан на рис. 2.6.
2.2. Арифметика узлов и поверхности Зейферта
19
Рис. 2.6. Неальтернированный узел
2.2. Арифметика узлов и поверхности Зейферта
Перейдем к описанию алгебраической структуры на множестве
изотопических классов узлов
Пусть Κι и i^2 — два ориентированных узла.
Определение 2.6. Под связной суммой (конкатенацией), узлов Κι и Къ
будем понимать ориентированный узел, полученный отождествлением концов
узла К^, разорванного в некоторой точке, с концами узла Κι, разорванного в
некоторой точке, с учетом ориентации, см. рис. 2.7. Обозначение: К1ФК2.
Рис. 2.7. Связная сумма узлов
Замечание 2.3. Важно не путать обратимость узла (в смысле замены
ориентации) с наличием обратного в смысле взятия связной суммы, см.
определение 2.6.
20 Полигональные зацепления и движения Рейдемейстера
Упражнение 2.4. Покажите, что связная сумма корректно определена,
т. е. изотопический класс узла Κχ^Κ^ не зависит от выбора мест
разрывания.
Упражнение 2.5. Покажите, что эта операция коммутативна: для любых
двух узлов Κι,Κ2 узлы К\#К2 и К2#К\ являются изотопными, при этом
изотопия может быть осуществлена в категории длинных узлов, т. е.
узлов, разорванных в одной точке с концами, вытянутыми на бесконечность
(под изотопией понимается преобразование, которое можно получить
применением движений Рейдемейстера; такая изотопия не меняет диаграммы
узла вне некоторого достаточно большого круга).
Определение 2.7. Несвязная сумма зацеплений Κι π Κ2 изпиш компонент
соответственно — это зацепление из η + т компонент, имеющее диаграмму,
состоящую из диаграмм Κι и К2-> лежащих в непересекающихся открытых
областях плоскости проекции. Обозначение: Κι U К2>
Теорема 2.2. Пусть Κι — нетривиальный узел. Тогда для любого узла К2
узел Κι#Κ2 также нетривиален.
Мы приведем три доказательства этой теоремы. Первое из них не совсем
строго, но очень наглядно. Второе (тоже наглядное и очень красивое)
доказательство принадлежит Дж.Х. Конвею. Последнее доказательство является
следствием из некоторого более сильного утверждения.
Начнем с первого доказательства.
Доказательство. Предположим, что Κι — нетривиальный узел, а К1ФК2 —
тривиальный узел. Рассмотрим последовательность узлов
КфК2,(КфК2)#(КфК2),..., (2.1)
в каждом слагаемом каждого члена которой первый узел Κι лежит внутри
круга радиуса 1, узел К2 лежит внутри круга радиуса ^, следующий узел Κι
(во всех связных суммах, содержащих не менее трех узлов) лежит внутри
некоторого круга радиуса \ и так далее.
Можно рассмотреть "предел" этой последовательности узлов, который будет
компактным, см. рис. 2.8.
Рис. 2.8. Дикий узел
2.2. Арифметика узлов и поверхности Зейферта
21
Таким образом мы получаем некоторый (быть может, дикий) узел.
Обозначим его через а. Так как узел К\^К2 тривиален, тривиальным
является и узел а. С другой стороны мы имеем следующее разложение:
а = ifi#(i^2#^i)#(^2#^i)... Так как операция взятия связной суммы
коммутативна, узел Къ^Кх — тривиален. Следовательно, тривиальный узел а
изотопен нетривиальному узлу К\. Противоречие завершает доказательство
теоремы. D
Замечательное доказательство того лее факта принадлежит Джону Хортону
Конвею.
Доказательство. Обратим внимание на рис. 2.9.
Рис. 2.9. Связная сумма двух нетривиальных узлов нетривиальна
Определение 2.8. Под стандартно вложенным (в R3) телом с g ручками
(где g — некоторое натуральное число) мы понимаем малую окрестность
произвольного графа лежащего внутри некоторой поверхности, гомеоморфной R2,
которая в свою очередь лежит в R3, см. рис. 2.10. Под стандартно вложенной
поверхностью Sg с g ручками мы понимаем край стандартно вложенного тела
с ручками.
Имеются два важных инварианта узлов. Первый из них — число заузленно-
сти U(К). Оно определяется как минимум по всем диаграммам К' количества
перекрестков, тип которых можно изменить, чтобы превратить узел К в
тривиальный. Это число всегда конечно, потому что у всякого узла имеется
восходящая диаграмма. Второе — это тоннельное число Τ {К). Оно определяется
как минимальное число г перемычек hi,..., hi вида D2 χ [0,1] — заполненных
цилиндров, которые нужно добавить к замкнутой окрестности Ν(Κ) узла К,
чтобы получить тело с ручками. Очевидно, что оба эти числа равны нулю
только на тривиальном узле.
Упражнение 2.6. Покажите, что для любого узла Τ (К) < U(K).
На рис. 2.9 изображена связная сумма узлов К1ФК2 и ее окрестность,
внутри которой узел К2 стягивается.
22 Полигональные зацепления и движения Рейдемейстера
Рис. 2.10. Граф и соответствующее тело с ручками
Из определения следует, что у узла К1ФК2 есть трубчатая окрестность Т,
эквивалентная естественной трубчатой окрестности узла К\ в смысле изотопии
в R3. Эта поверхность обладает тем свойством, что каждый меридиональный
диск D имеет гомологически нетривиальное пересечение с К\^К2-
Однако для тривиального узла U единственная возможная окрестность Т7,
обладающая таким свойством — это стандартно вложенное полноторие.
Узел Κι нетривиален, поэтому "утолщенные" узлы Г' и Г не изотопны.
Следовательно узел К\^К2 нетривиален. D
Таким образом мы показали, что никакой элемент полугруппы узлов, за
исключением тривиального, не имеет обратного. Перейдем к описанию других
свойств этой полугруппы.
Определение 2.9. Нетривиальный узел К называется простым если для
любых узлов L, Μ таких, что К = ЬфМ один из узлов L, Μ тривиален. В
противном случае узел называется составным.
Определение 2.10. Если для узлов К, L,M имеет место разложение К =
= L#M, то говорят, что узлы L, Μ делят узел К.
Упражнение 2.7. Покажите, что любой узел (зацепление) может быть
представлен как кривая (соответственно, набор кривых) на некоторой
поверхности с ручками стандартно вложенной в R3.
Дадим теперь определение поверхности Зейферта, предложенное Гербертом
Зейфертом в [Seil].
2.2. Арифметика узлов и поверхности Зейферта
23
Определение 2.11. Пусть L — ориентируемое зацепление. Поверхностью
Зейферта (Зейферт, [Seil], см. также [КФ]) для зацепления L называется
компактная ориентируемая поверхность в R3, краем которой является
зацепление L.
Теорема 2.3. Для каждого зацепления в R3 существует соответствующая
ему поверхность Зейферта.
Доказательство. Рассмотрим плоскую диаграмму D зацепления L. Будем
"сглаживать" перекрестки диаграммы так, как показано на рисунке 2.11.
Рис. 2.11. Сглаживание перекрестков диаграммы
После такого сглаживания мы получим набор замкнутых непересекающихся
простых кривых на плоскости.
Эти кривые называются окружностями Зейферта. Их можно заклеить
непересекающимися дисками в трехмерном пространстве.
К каждому перекрестку локально с разных сторон подходят два диска.
Выберем два отрезка на границе этих дисков и соединим их перекрученной лентой,
см. рис. 2.12. Компонентами края этой ленты являются (помимо двух
отрезков) две ветви зацепления, соответствующие проходам и переходам. Верхняя и
нижняя части рисунка 2.12 указывают на два возможных способа скручивания
ленты (в одном случае вертикальная линия проходит выше горизонтальной,
а в другом — ниже).
Пример поверхности Зейферта для узла восьмерки приведен на рис. 2.13.
Таким образом мы получаем некоторую поверхность, которая, вообще
говоря, может и не быть связной. Соединяя разные компоненты этой поверхности
трубками, вложенными в R3, мы получаем связную поверхность, вложенную в
трехмерное пространство и имеющую ту же границу.
Остается доказать ориентируемость этой поверхности. Рассмотрим
плоскость Ρ проекции зацепления. Выберем положительный репер на плоскости Р.
Он задает ориентацию для каждого из дисков, приклеенных к окружностям
24 Полигональные зацепления и движения Рейдемейстера
диск
J
диск
диск
диск
диск
J
диск
диск
У
диск
Рис. 2.12. Приклеивание ленты к дискам
Рис. 2.13. Поверхность Зейферта для восьмерки
Зейферта. Таким образом, ориентации двух таких дисков, лежащих в
окрестности одной вершины, являются локально противоположными (в смысле
поверхности Зейферта), так как они соединены перекрученной лентой.
Остается доказать, что для любой последовательности С\,Съ,...Сп = С\
окружностей Зейферта, в которой каждые две соседние окружности C^Q+i
примыкают к одной вершине, число η является нечетным. Другими словами,
при переходе от окружности к ней самой мы можем пройти лишь через четное
число перекручиваний. Последний факт следует из того, что для
многоугольника с нечетным числом сторон нельзя ориентировать его стороны так, чтобы
любые две соседние стороны имели противоположную ориентацию. D
Теорема 2.4. Четность числа окружностей Зейферта диаграммы к-компо-
нентного зацепления с η перекрестками совпадает с четностью числа п — к.
Доказательство. Пусть L — диаграмма /с-компонентного зацепления с η
вершинами. Рассмотрим поверхность Зейферта S(L). Построим клеточное
разбиение этой поверхности. Сначала выберем одномерный остов этого клеточного
2.2. Арифметика узлов и поверхности Зейферта 25
разбиения следующим образом: вершины остова соответствуют перекрестки
зацепления L (по две вершины рядом с каждым перекрестком), а каждому ребру
тени зацепления соответствуют два ребра диаграммы, кроме того, каждому
перекрестку соответствует по одному ребру (это ребро соединяет две
вершины, происходящие из данного перекрестка). Будем теперь приклеивать диски к
компонентам края нашей поверхности Зейферта (т. е. компонентам зацепления).
Количество двумерных клеток такого подразбиения равно количеству
окружностей Зейферта плюс количество компонент зацепления. Таким образом мы
получаем замкнутое ориентируемое двумерное многообразие. Эйлерова
характеристика этого многообразия должна быть четной; она равна 2η — 3n + S + /с,
где η — количество перекрестков диаграммы L, a S — количество окружностей
Зейферта этой диаграммы. Из этого следует утверждение теоремы. D
Рис. 2.14. Разбиение поверхности Зейферта на клетки
Поверхность Зейферта для узла К является компактной двумерной
поверхностью, границей которой является узел К. Приклеивая диски к компонентам
края этой поверхности, мы получаем сферу с несколькими ручками.
Определение 2.12. Говорят, что узел К имеет род д, если g — минимальное
количество ручек "заклеенной" поверхности Зейферта для узла К.
Понятие рода узла было предложено Зейфертом в [Seil].
Замечание 2.4. Вычисление рода узла является очень сложной задачей.
Первое ее решение было предложено Хакеном. Для этой цели он развил теорию
нормальных поверхностей — поверхностей в трехмерных многообразиях,
расположенных "нормально" по отношению к некоторому разбиению {например,
к триангуляции или к разбиению на ручки), см. [На]. Распознавание
тривиального узла {единственного узла рода ноль) является частным случаем вопроса
о вычислении рода узла.
26 Полигональные зацепления и движения Рейдемейстера
Лемма 2.1. Функция д является аддитивной, т. е., для любых узлов К\^К^
имеет место равенство д{К{) + д{К2) = д{К\фК<2).
Доказательство. Докажем сначала, что g{K\j^K2) < д{К\) + g{K<i).
Рассмотрим поверхности Зейферта F\ и F2 минимальных родов для узлов
К\ и Къ (расположенных в непересекающихся шарах в трехмерном
пространстве). Без ограничения общности можно считать, что эти поверхности не
пересекаются. Эти поверхности можно соединить лентой способом,
согласованным с ориентацией таким образом, что мы получим поверхность Зейферта узла
^ι#^2 рода д{К\) + g{K<i). Следовательно
9(Κ1#Κ2)^9(Κ1)+9(Κ2).
Покажем теперь, что д{К\^Къ) ^ д{К\) + д{Къ). Рассмотрим поверхность
Зейферта F для узла Κι#Κ2, имеющую минимальный род. Существует
(топологическая) сфера S2, отделяющая узел Κι от узла К2 в связной сумме К1ФК2
и пересекающая эту связную сумму в точках А и В.
Без ограничения общности можно полагать, что сфера S2 пересекает
поверхность F вдоль нескольких замкнутых простых кривых а\,..., а^ и одной
кривой, соединяющей точки А, В. Каждая несамопересекающаяся кривая
(окружность) делит сферу S2 на две части так, что одна из таких частей не содержит
точек кривой АВ. Окрестность каждой кривой αι в сфере представляет собой
цилиндр. Удалим малую цилиндрическую окрестность нашей кривой
(окружности) и заклеим две образовавшиеся окружности малыми дисками. Мы
получим поверхность, возможно не связную. Если она не связна, выберем ту
ее часть, которая содержит узел К\^К2- После выполнения такой операции
по отношению к каждой из окружностей, мы получим поверхность F'',
содержащую узел К1ФК2 и пересекающую сферу S2 вдоль АВ. Описанная таким
образом операция может лишь уменьшать род поверхности Зейферта.
Следовательно, g(F') ^ g(F). Так как род поверхности F минимален, мы видим, что
g(F') < g(F) = д(КфК2).
Сфера S2 разбивает F' на поверхности, которые можно рассматривать как
поверхности Зейферта для узлов К ι и К2. Таким образом
д{К{) + д(К2) > g(F') > 9{ΚλφΚ2)) (2.2)
Тем самым теорема доказана. D
В качестве следствия мы получаем теорему о том, что у нетривиального
узла не может быть обратного, так как тривиальный узел имеет род ноль, в то
время как остальные имеют положительный род. В этом заключается третье
доказательство отсутствия обратных для нетривиальных узлов.
Таким образом, каждый узел может быть разложен в связную сумму
конечного числа простых узлов. Для окончательного прояснения ситуации нам
остается доказать лемму об однозначном разложении.
Упражнение 2.8. Покажите, что род трилистника равен единице.
Лемма 2.2. Пусть L и Μ — узлы и пусть К — простой узел, делящий L#M.
Тогда одно из двух утверждений имеет место: К делит L либо К делит М.
2.2. Арифметика узлов и поверхности Зейферта 27
Доказательство. Рассмотрим узел L#M вместе с некоторой плоскостью р,
пересекающей его в двух точках А и В и отделяющей узел L от узла Μ. Если
перейти от рассмотрения R3 к S3 = R3Uoc, плоскость ρ превратится в сферу Р.
Так как L#M делится на К, то существует (топологическая) двумерная
сфера S2, пересекающая узел L#M в двух точках.
Если эта сфера не пересекает сферу Р, то проблема решена. В противном
случае без ограничения общности предположим, что сфера S2 пересекает сферу
Ρ по некоторым непересекающимся несамопересекающимися кривым
(окружностям). Каждая из этих окружностей на сфере Ρ либо разделяет точки А и В,
либо не разделяет. Окружности, не разделяющие точек А и В, легко
уничтожаются небольшой модификацией сферы: нужно начать с окружностей, не
содержащих внутри себя других кривых.
При уничтожении кривых q, разделяющих точки А и В, нужно
использовать простоту узла К. Сфера Ρ разбивает сферу S3 = R3 U ос на два
трехмерных шара. Пусть В к — шар, содержащий узел К. Рассмотрим компоненту
связности S2 Π Βχ, содержащую Q. Она может быть либо двумерным диском,
либо цилиндром. В случае цилиндра кривая q уничтожается малым
шевелением сферы 5*2 вместе с другой кривой (другим краем того же цилиндра).
В первом случае рассматриваемый диск D2 пересекает узел ЬфМ ровно в
одной точке. Из простоты узла К следует, что в В к он целиком расположен по
одну сторону от диска D2. Следовательно, мы можем уничтожить диск D2,
а вместе с ним и кривую.
Из сказанного выше заключаем, что если связная сумма ЬфМ делится на К,
то одно из зацеплений L или Μ делится наК. D
Замечание 2.5. Это основное утверждение из арифметики узлов
принадлежит Хорсту Шуберту, см. [Шу].
Таким образом, мы получаем:
1. Изотопические классы узлов образуют коммутативную полугруппу
относительно операции взятия связной суммы; единичным элементом этой
полугруппы является тривиальный узел.
2. Ни у какого нетривиального узла нет обратного элемента.
3. Разложение на простые множители однозначно с точностью до
перестановки.
4. Количество различных простых узлов счетно.
Упражнение 2.9. Докажите последнее утверждение.
Из последнего утверждения вытекает то, что количество изотопических
классов (гладких) узлов счетно. Суммируя сказанное, получаем следующую
теорему.
Теорема 2.5. Полугруппа изотопических классов узлов относительно
операции взятия связной суммы изоморфна полугруппе натуральных чисел
относительно умножения. Здесь простые узлы соответствуют простым числам.
28 Полигональные зацепления и движения Рейдемейстера
Однако такой изоморфизм не является каноническим, так как нет
канонического линейного упорядочения узлов (простых узлов),
Существует лишь одна (с точностью до изоморфизма) полугруппа,
обладающая описанными выше свойствами.
В [МаЗ] предложено чисто алгебраическое описание этой полугруппы, т. е.
задано явное описание изоморфизма между этой геометрической полугруппой
и некоторой алгебраически определенной "скобочной полугруппой."
У каждой полугруппы есть соответствующая группа Гротендика —
минимальная группа, содержащая данную полугруппу в качестве подполугруппы.
Так, для полугруппы Ζ по умножению группа Гротендика изоморфна группе
рациональных чисел по умножению. Естественным вопросом является
геометрическая (узловая) интерпретация элементов, обратных к узлам. Решение этой
задачи приведено в работе Я. Мостового [Mos].
Глава 3
Зацепления в двумерных
о
поверхностях в R .
Простейшие инварианты
зацеплений
Узлы (зацепления), вложенные в R3, могут быть рассмотрены как кривые
(наборы кривых) на двумерных поверхностях, вложенных стандартно в
трехмерное пространство. Таким образом могут быть получены все изотопические
классы узлов и зацеплений.
Мы опишем серию торических узлов и зацеплений, т. е. узлов и зацеплений,
которые можно представить лежащими на торе, стандартно вложенном в R3.
Будут построены некоторые инварианты узлов и зацеплений. С их
помощью мы докажем нетривиальность некоторых зацеплений и неэквивалентность
некоторых пар зацеплений.
3.1. Узлы в двумерных поверхностях.
Классификация торических узлов
Рассмотрим двумерную поверхность с ручками Sg, стандартно вложенную
в R3, и кривую (узел) К на ней. Какие изотопические классы узлов могут быть
получены таким образом для фиксированного д?
Заметим сначала, что при д = 0 существует лишь один узел, вложимый в
S2 С R3, а именно, тривиальный узел.
Упражнение 3.1. Покажите, что для любого изотопического класса L с R3
существует представляющее его зацепление V, лежащее в некоторой
стандартно вложенной в R3 поверхности с некоторым числом ручек.
Случай g = 1 (тор, торические узлы) дает нетривиальные примеры.
Рассмотрим тор как декартово произведение S1 x S1 с координатами φ, ψ Ε
[О, 2π], где 2π отождествлено с 0. На рис. 3.1 тор изображен в виде квадрата с
отождествленными противоположными сторонами.
Вложим этот тор стандартно в трехмерное пространство:
(φ, ψ) —> ((R + г cos ψ) cos cj),(R-\- r cos ψ) sin 0, r sin ψ) (3.1)
30
Узлы в поверхностях. Торические узлы
(2тг, 2тг)
ф\
(0,0) φ
Рис. 3.1. Тор
Здесь R — внешний радиус тора, г — внутренний радиус тора (г < R), где
φ — параллель тора, а ψ — меридиан тора; направления параллели I и
меридиана т указаны на рис. 3.2.
Рис. 3.2. Параллель и меридиан тора
Очевидно, что две несамопересекающиеся кривые, гомотопные в Т2,
являются изотопными в R3 как узлы.
Пусть дана замкнутая кривая 7 на торе. Без ограничения общности молено
предположить, что 7 не проходит через точку (0,0) = (2π, 2π) = (2π, 0) = (0, 2π)
и пересекает ребра квадрата трансверсально и конечное число раз каждое.
Посчитаем отдельно алгебраическое число пересечений кривой с горизонтальными
ребрами квадрата и отдельно — с вертикальными. При этом прохождение
через правое или верхнее ребро считается положительным, а прохождение через
левое или нижнее ребро — отрицательным.
Таким образом, каждой такой кривой мы сопоставили пару целых чисел.
Если оба этих числа равны нулю, то кривая ограничивает диск, лежащий на
торе, и, следовательно, представляет собой тривиальный узел. Перейдем к
рассмотрению таких кривых, для которых по крайней мере одно из этих двух
чисел не равно нулю.
Упражнение 3.2. Покажите, что для несамопересекающейся кривой на
торе соответствующие числа либо взаимно просты либо оба равны нулю.
Таким образом, каждый торический узел проходит ρ раз параллель тора и
q раз меридиан тора, причем (p,q) = 1. Легко видеть также , что для любой па-
Узлы в поверхностях. Торические узлы
31
ры взаимно простых чисел ρ и q такая кривая существует: можно взять линию
{ςφ — рф = a(mod 2π)} в координатах (3.1). Такой кривой соответствует то-
рический узел; обозначим его T(p,q). Поэтому изотопический тип торического
узла однозначно определяется этими числами ρ и q.
Таким образом, для классификации торических узлов нужно понять, для
каких пар (p,q) и (р1\q') соответствующие торические узлы изотопны в R3.
Простейшим является случай, когда одно из чисел р, q равно единице.
Упражнение 3.3. Покажите, что при ρ = 1 и произвольном q или при q
и произвольном ρ узел Т(р, q) является тривиальным.
1
Следующий простейший случай представляет пара ρ = 3, q = 2 (или ρ = 2,
q = 3). В каждом из этих случаев мы получаем трилистник.
(2тг,2тг)
Рис. 3.3. Трилистник как торический узел
Докажем следующий результат.
Теорема 3.1. Для любой пари взаимно простых чисел ρ и q торические узлы
типов (p,q) и (q,p) изотопны.
Доказательство. Рассмотрим сферу S3 в качестве объемлющего пространства
(вместо R3); это не влияет на изотопность узлов.
Сфера S3 может быть представлена как объединение двух полноторий
склеенных согласно следующему диффеоморфизму края. Этот диффеоморфизм
отображает параллель первого тора в меридиан второго и наоборот. Более точ-
но, S3 = {z,w £ С \ \z\ -\- \w\ =1}. Два полнотория задаются неравенствами
\z\ ^ \w\ и \z\ < \w\ ; их общая граница задается уравнением \z\ = \w\ = w^.
Легко видеть, что окружности, заданные уравнениями
№
-,ζ фиксированное, по модулю равноеу -
(3.2)
N
-,w фиксированное по модулю равноеу-,
(3.3)
представляют собой параллель и меридиан граничного тора (в смысле обоих
полноторий).
Таким образом, торический узел типа (p,q) в одном полноторий
представляет собой торический узел типа (q,p) в другом полноторий. Следовательно,
32
Узлы в поверхностях. Торические узлы
существует диффеоморфное отображение трехмерной сферы на себя,
сохраняющее ориентацию сферы и меняющее местами полнотория и, следовательно,
отображающее узел Т(р, q) в узел T(q,p). Такое отображение можно достроить
до изотопии. D
Упражнение 3.4. Опишите эту изотопию в S3 явно.
Замечание 3.1. Торический узел типа (p,q) допускает следующее описание
посредством плоских диаграмм, см. рис. 3.4-
ρ штук
Рис. 3.4. Диаграмма торического узла типа р, q
На рисунке 3.4 указан способ кодирования узла (зацепления) посредством
замыкания косы (из ρ нитей). Об этом будет рассказано позже.
Аналогично случаю торических узлов, можно определить торические
зацепления, т.е. зацепления, вложенные в тор, стандартно лежащий в R3.
Перейдем к описанию торических зацеплений. Мы знаем, как задать
торические узлы. Таким образом, чтобы получить торическое зацепление, нам
нужно рассмотреть торический узел К С Τ (можно считать, что он
представлен "прямолинейной" линией определенной уравнением (в координатах (3.1))
и добавить к ней некоторое количество замкнутых простых непересекающихся
кривых; каждая кривая должна также не пересекать узел К. Можно считать,
что все эти кривые вложены в Т\К, т. е. открытый цилиндр.
Каждая замкнутая кривая на таком цилиндре либо является стягиваемой,
либо представляет собой параллель цилиндра, см. рис. 3.5.
Следовательно, любая несамопересекающаяся кривая в Т\К либо
стягиваема внутри Т\К, либо "параллельна" узлу К внутри тора Т, т. е. гомотопна
кривой, заданной уравнением q<fi — рф = ε (mod 2π) внутри Т\К.
Поэтому имеет место следующая теорема.
3.2. Коэффициент зацепления
33
Рис. 3.5. Простые кривые на цилиндре
Теорема 3.2. Каждое торическое зацепление изотопно несвязной сумме
тривиального зацепления и зацепления, представимого набором ^параллельных"
торических узлов некоторого типа (p,q).
Пока мы не можем точно сказать о торических узлах (зацеплениях), когда
они не изотопны между собой. Для этого нужно перейти к описанию
инвариантов узлов.
3.2. Коэффициент зацепления
Будем представлять зацепления их плоскими диаграммами. Для
доказательства инвариантности той или иной функции, заданной на плоских
диаграммах, нам достаточно показать ее инвариантность относительно движений
Рейдемейстера.
Рассмотрим сначала простейший целочисленный инвариант двухкомпонент-
ных зацеплений.
Пусть L — зацепление, состоящее из двух ориентированных компонент А
и 5, и пусть V — плоская диаграмма зацепления L. Рассмотрим те перекрестки
диаграммы L7, в которых компонента А проходит над компонентой В. Есть два
возможных типа таких перекрестка с учетом ориентации: положительный /С
и отрицательный X. ·
Каждому положительному перекрестку сопоставим число (+1), а каждому
отрицательному — число (—1). Просуммируем эти числа по всем перекресткам,
в которых компонента А проходит над компонентой В. Таким образом, мы
получим некоторое целое число; обозначим его через lk(A, В).
Упражнение 3.5. Покажите, что это число является инвариантом
относительно движений Рейдемейстера.
Таким образом, //с(·,·) является инвариантом двухкомпонентных
зацеплений.
Определение 3.1. Будем называть этот инвариант коэффициентом
зацепления.
Замечание 3.2. Этот инвариант был впервые предложен Гауссом, [Gau]; он
входит в знаменитую формулу, получившую впоследствии название
электромагнитной формулы Гаусса. Коэффициент зацепления может быть обобщен
34
Узлы в поверхностях. Торические узлы
на случай многомерных зацеплений, а именно, р-мерного и q-мерного
ориентированных многообразий в Rp+g,+1.
Формула Гаусса имеет место для параметризованных замкнутых
непересекающихся несамопересекающихся кривых ji(t) и 72(^)5 которые задаются
радиус-векторами Т\ (t), г 2 (t) и имеет следующий вид
7w ^ ч 1 ( ( ([dri,dr2],(r1 -r2))
1кЫ,12) = -г- / : [з , (3.4)
где [ , ] обозначает векторное произведение, а ( , ) — скалярное произведение.
Доказательство инвариантности этой формулы остается читателю в
качестве упражнения.
Указание 3.1. Покажите, что эта функция совпадает со степенью
отображения из тора, представляющего собой декартово произведение двух
окружностей — компонент зацепления — в сферу и, таким образом, инвариантна
относительно изотопии зацепления.
Коэффициент зацепления позволяет различать некоторые пары двухкомпо-
нентных зацеплений.
Пример 3.1. Для тривиального зацепления при любой перенумеровке его
компонент все коэффициенты зацепления равны нулю. Для зацепления Хопфа (см.
стр. 7) коэффициент зацепления двух его компонент равен =Ы в зависимости от
ориентации компонент. Из этого следует нетривиальность зацепления Хопфа.
Пример 3.2. Коэффициент любых двух из трех колец Борромео равен нулю,
при этом каждая компонента зацепления (кольцо) представляет собой
тривиальный узел. Однако кольца Борромео не изотопны тривиальному трехкомпо-
нентному зацеплению. Это будет показано позже.
Для диаграмм зацеплений из одной компоненты (т. е. диаграмм узлов)
можно определить коэффициент самозацепления. Для этого нужно взять
диаграмму К ориентированного узла и нарисовать "параллельно ей" на плоскости
диаграмму К' того же узла. А именно, фиксируем ориентацию диаграммы К
и выберем в каждой точке диаграммы К нормальный вектор такой, что
пара векторов (нормальный, касательный) составляют положительный репер на
плоскости проекции. Тогда диаграмма К' представляет собой диаграмму,
полученную из К сдвигом каждой точки на малое расстояние ε вдоль
соответствующего нормального вектора. Вместо каждого перекрестка диаграммы К
мы получим четыре перекрестка; там, где ветвь а узла К проходит над ветвью
β мы имеем две ветви а, а' узлов К, К', проходящие над соответствующими
ветвями /3,/37. Пример удвоения стандартной диаграммы трилистника показан
на рис. 3.6. Аналогичным образом определяется операция утроения и, вообще,
взятия к параллельных копий. Обозначение: К —>· Dk(K).
Нетрудно проверить, что операция К —>· Dk(K) инвариантна относительно
движений Ω2, Ω3, т. е., если мы применим к диаграмме К движение Ω2 или Ω3,
диаграмма D^{K) перейдет в эквивалентную ей диаграмму..
3.3. Арф-инвариант
35
Рис. 3.6. Удвоение трилистника: параллельная копия изображена тонкой линией
После этого мы берем коэффициент зацепления компонент К и К'.
Нетрудно проверить, что этот коэффициент инвариантен относительно движений Ω2
и Ω3, но не относительно Ωι: добавление петли изменяет его значение на =Ы.
Коэффициенты зацепления молено вычислять также с помощью
поверхностей Зейферта.
Определение 3.2. Пусть F — поверхность Зейферта ориентированного
узла J. Предположим, что ориентированный узел К пересекает поверхность F
трансверсально и в конечном числе точек. Каждой точке мы сопоставим знак
Si = =Ы согласно следующему правилу.
Определим ориентацию поверхности F, считая положительным следующий
репер {βι,β2} (здесь е\ — ориентирующий вектор для J, а в2 — вектор
внутренней нормали к краю; последний перпендикулярен вектору е\ и "смотрит"
внутрь F). Пусть ез — вектор скорости узла К в точке α Ε Κ Π F, и пусть
{ei?e2l — положительный репер на поверхности F в точке а. Тогда мы
полагаем Si = +1, если ориентация репера {е^е^ез} совпадает с ориентацией
объемлющего пространства R3; и Si = — 1 в противном случае.
Сумма всех таких знаков Si называется коэффициентом зацепления узлов
J и К.
Упражнение 3.6. Покажите, что коэффициент зацепления (в смысле
последнего определения) корректно определен (не зависят от выбора
поверхностей Зейферта) и совпадает с коэффициентом зацепления в смысле
предыдущего определения.
Указание 3.2. Рассмотрите проекции на плоскость и исследуйте поведение
проекций двух узлов в окрестности перекрестка.
3.3. Арф-инвариант
Тот простой инвариант зацеплений, который мы построили, работает в
случае ориентированных зацеплений. В случае неориентированных зацеплений мы
можем лишь построить коэффициент зацепления со значениями в Z2.
Оказывается, что существует инвариант узлов, принимающий значения в Z2,
тесно связанный с коэффициентом зацепления, а именно Арф-инвариант. Есть
много способов определения этого инварианта, см., напр., [Каи4] и [Ada].
36
Узлы в поверхностях. Торические узлы
Арф-инвариант имеет многомерные аналоги и связан с изучением
гомотопических групп сфер. Заинтересованного читателя отсылаем к книге [Нов].
Определение 3.3. Два узла называются пасс-эквивалентными, если один из
них может быть преобразован в другой последовательным применений
изотопии и локальных преобразований одного из видов, изображенных на рис. 3.7.
Рис. 3.7. Пасс-эквивалентность
Отметим, что двойное перекручивание (поверхности Зейферта узла),
изображенное на рис.3.8, представляет собой пасс-эквивалентность.
Упражнение 3.7. Покажите, что правый и левый трилистники являются
пасс-эквивалентными.
Мы будем пользоваться следующим определением Арф-инварианта.
Определение 3.4. Арф-инвариант — это полный инвариант классов пасс-
эквивалентности. Иными словами, это инвариант, который сопоставляет узлу
его класс пасс-эквивалентности.
Обозначим Арф-инвариант буквой А и зададим теперь значения Арф инва-
рианта следующим образом: A(Q) = 0, А((уУ) = A(QQ) = 1 где О обозначает
тривиальный узел.
Как оказывается, Арф-инвариант может принимать на узлах ровно два
значения — единицу и ноль.
3.3. Арф-инвариант
37
Рис. 3.8. Двойное перекручивание
Теорема 3.3. Каждый узел является пасс-эквивалентным либо
тривиальному узлу, либо трилистнику {оба трилистника пасс-эквивалентны).
Тривиальный узел и трилистник не являются пасс-эквивалентными.
Сначала мы опишем основную идею доказательства того, что каждый узел
пасс-эквивалентен либо тривиальному узлу, либо трилистнику. Тот факт, что
Арф-инвариант принимает действительно различные значения на трилистнике
и на тривиальном узле, будет показан позднее.
Замечание 3.3. Пасс-эквивалентность является первым грубым
приближением к теории конкордантности узлов. Два зацепления Li,L2 Ε R3
называются конкордантными, если существует локально плоская (гладкая)
двумерная поверхность S в R3 χ {0,1} такая, что ее край совпадает с (L\ χ {0}) U
(L2 x {1}).
Условие локальной плоскости состоит в следующем. Для каждой точки χ
на поверхности S пересечение достаточно малой окрестности U(x) с любой
гиперплоскостью h Ε R3 χ {0,1} задает тривиальный узел в h = R3. Без этого
условия любой узел был бы эквивалентен (конкордантен) тривиальному.
Очевидно, что если два узла конкордантны, то значение Арф-инварианта
на них одинаково. С другой стороны, понятие конкордантности — более
грубое, чем понятие изотопической эквивалентности (любые два изотонически
эквивалентных узла конкордантны). Блестящий подход к изучению
конкордантности узлов предложен Тимом Кохраном, Кентом Орром и Петером
Тайхнером, см. [СОТ, Tei].
Замечание 3.4. Конкордантность зацеплений и инварианты зацеплений,
аналогичные Арф-инварианту узлов, являются отправной точкой для
построения узлов-многообразий. Эти многообразия связывают маломерную
топологию с дифференциальной топологией больших размерностей. Как
оказывается, среди узлов-многообразий и зацеплений-многообразий есть экзотические
сферы (сферы Милнора), см. [НМ]; [Ег1е]; [Каиб].
38
Узлы в поверхностях. Торические узлы
Заметим сначала, что каждую поверхность Зейферта (как и всякую
ориентируемую поверхность с непустым краем) можно представить как диск с
некоторым количеством лент, приклеенных к его краю. Каждая лента может
быть перекручена некоторое (целое) количество раз, ленты могут быть заузле-
ны и зацеплены между собой в трехмерном пространстве. Более точно, любая
поверхность Зейферта имеет вид D2 U^=1 Б^, где все В3■ = 13; χ {0,1}, а также D2
являются вложенными в R3 дисками. Приклейка В3 состоит в отождествлении
Jj χ {0} и /j χ {1} с некоторыми отрезками D^ и Бц на крае 0D2; все 2к
отрезков вида Dio, Dji попарно не пересекаются, а множества D2, £>ι,..., В^ не
имеют никаких общих точек, кроме поименованных выше.
Количество полных оборотов каждой ленты можно считать равным нулю
или единице в силу пасс-эквивалентности: двойное перекручивание изменяет
закрученность ленты на двойку. Кроме того, пасс-эквивалентность
позволяет менять расположение лент в трехмерном пространстве, например,
избавляться от заузленности. Суммируя сказанное, мы можем построить узел, пасс-
эквивалентный изначальному и обладающий поверхностью Зейферта очень
простого вида: она имеет вид диска, к границе которого приклеено некоторое
количество лент в некотором порядке; некоторые ленты перекручены один раз, в
то время как остальные не перекручены. После этого можно применить
некоторые упрощающие операции, которые не меняют класса пасс-эквивалентности,
и превращают узел в связную сумму некоторого набора трилистников.
Оставшееся утверждение является следствием упражнения.
Упражнение 3.8. Покажите, что связная сумма трилистника с другим
трилистником пасс-эквивалентна тривиальному узлу {здесь можно брать
любой трилистник в качестве любого из двух слагаемых).
В дальнейшем, все уравнения относительно значений Арф-инварианта,
выписываются по модулю Z2-
Оказывается, что существует простой способ вычисления Арф-инварианта.
Рассмотрим две диаграммы, не отличающиеся друг от друга вне малой
окружности и выглядящие как /\, /X внутри нее; одна из них является
диаграммой узла, другая является диаграммой зацепления из двух компонент.
Рассмотрим диаграмму, отличающуюся локально от первых двух и выглядящую
внутри этой малой окружности как j f.. Предположим, что j (■ является
диаграммой зацепления из двух компонент 1\ и Ϊ2- Тогда справедлива следующая
теорема.
Теорема 3.4. Имеет место равенство
А(^\}) ~ А(</\^ = HhM) (mod Z2). (3.5)
Это соотношение, во-первых, показывает, что трилистник и тривиальный
узел не являются пасс-эквивалентными, и, во-вторых, позволяет явно
вычислять значения Арф-инварианта на различных узлах. Для этого нам
понадобится утверждение о том, что любой узел может быть превращен в тривиальный
узел изменением некоторых перекрестков.
3.4. Инвариант раскрасок
39
Отметим, что если определить пасс-эквивалентность для зацеплений,
получится более содержательная теория (инвариант Робертелло-Арф, [Rob]).
Аналогичная ситуация возникнет, когда мы будем аксиоматически
определять полиномиальные инварианты узлов. Для этого нам понадобятся так
называемые skein-соотношения или соотношения типа Конвея, которые будут
введены позлее. Эти соотношения ведут к более сильным инвариантам узлов.
3.4. Инвариант раскрасок
Опишем теперь некоторый простой инвариант неориентированных
зацеплений, определяемый в терминах их диаграмм. Этот инвариант был известен
еще в начале развития теории узлов. Как потом будет показано, он может быть
обобщен для получения более сильных инвариантов (ориентированных) узлов
и зацеплений.
Рассмотрим неориентированное зацепление.
Определение 3.5. Под дугой плоской диаграммы этого зацепления будем
понимать связную компоненту плоской диаграммы зацепления, подразумевая,
что линия прохода имеет разрыв в окрестности перекрестка (как это обычно
изображается на плоскости).
Таким образом, каждая дуга все время проходит "сверху"; она начинается и
заканчивается проходами. В общем случае каждый перекресток "инцидентен"
трем дугам. Некоторые из них могут, вообще говоря, (глобально) совпадать.
Будем сопоставлять дугам диаграммы цвета: красный, синий, черный.
Каждое такое сопоставление будем называть раскраской.
Определение 3.6. Раскраска диаграммы зацепления называется правильной,
если в каждом перекрестке диаграммы три дуги, инцидентные этому
перекрестку покрашены либо все в один цвет, либо в три разных цвета.
Теорема 3.5. Количество правильных раскрасок является инвариантом
зацеплений.
Доказательство. Мы докажем инвариантность следующим образом.
Рассмотрим некоторое движение Рейдемейстера и две диаграммы L, L7, получаемые
одна из другой применением этого движения Рейдемейстера. Мы предъявим
явное взаимно однозначное соответствие между правильными раскрасками
диаграммы L и правильными раскрасками диаграммы V.
Случай первого движения Рейдемейстера Ω ι очевиден: два ребра
диаграммы L7, соответствующих одному "разделенному" ребру диаграммы L должны
быть покрашены в один и тот же цвет, так как одно из них примыкает к
перекрестку дважды, следовательно, в этом перекрестке трехцветная правильная
раскраска невозможна.
Таким образом, взаимно однозначное соответствие раскрасок в случае
первого движения Рейдемейстера очевидно. Существуют аналогичные случаи
локально одноцветных раскрасок для второго и третьего движений
Рейдемейстера.
40
Узлы в поверхностях. Торические узлы
В случае второго движения Рейдемейстера две дуги а, Ъ перестраиваются,
при этом дуга а разбивается на три последовательно идущих дуги с, d, е.
Очевидно, что при любой правильной раскраске дуги сие будут покрашены в
один цвет. Сопоставим этот цвет дуге а в изначальной диаграмме. Цвет
дуги Ъ оставим прежним. Тем самым правильной раскраске модифицированной
диаграммы (с дугами с, d, е) сопоставлена правильная раскраска изначальной
диаграмме. Обратно, зная правильную раскраску изначальной диаграммы, мы
сопоставим цвет дуги а дугам сие, при этом цвет дуги d будет определяться
однозначно.
На рис. 3.9 указаны раскраски для ребер, участвующих в третьем
движении Рейдемейстера. Для каждой такой пары диаграмм, отличающихся третьим
движением, раскраски вне области, указанной на рисунке, совпадают. Мы
приводим основные примеры таких раскрасок и их однозначное соответствие для
диаграмм до и после применения движения Рейдемейстера. Все остальные
возможные локально неодноцветные раскраски могут быть явно перечислены,
если применить к указанным раскраскам перестановки цветов (цвета помечены
цифрами 1, 2, 3).
Каждой правильной раскраске диаграммы однозначно соответствует
правильная раскраска диаграммы, полученной из нее применением любого
движения Рейдемейстера. Таким образом, количество правильных раскрасок
является инвариантным относительно движений Рейдемейстера. D
г
/ 1 У
г
у у
Рис. 3.9. Инвариантность числа правильных раскрасок
Назовем число правильных раскрасок инвариантом раскрасок
относительно Ω3.
Обозначение: для зацепления L число раскрасок равно CI(L).
Очевидно, что для тривиального узла мы имеем CI(О) = 3, а для
тривиального /с-компонентного зацепления CI = Зк.
3.4. Инвариант раскрасок
41
Упражнение 3.9. а) Посчитайте инвариант раскрасок для
трилистников и покажите, что они оба нетривиальны.
б) Посчитайте число раскрасок зацепления Уайтхеда и покажите, что оно
нетривиально.
в) Посчитайте значение инварианта раскрасок на кольцах Борромео и
покажите, что это зацепление нетривиально.
Однако на восьмерке все правильные раскраски одноцветные. Таким
образом, этот инвариант не способен распознать нетривиальность узла восьмерки.
Глава 4
Фундаментальная группа.
Группа узла
4.1. Отступление. Примеры развязывания узлов
Рассмотрим следующий пример (или задачу), связанный с развязыванием
узлов.
Пусть дана некоторая диаграмма тривиального узла. Попробуем развязать
ее, используя движения Рейдемейстера. В "хорошем" случае это молено сделать,
используя только движения Рейдемейстера, не увеличивающие количества
перекрестков.
Однако в общем случае это не всегда так. А именно, существуют
диаграммы тривиального узла с непустым множеством перекрестков такие, что мы
не можем применить ни "уменьшающие" версии первого и второго движений
Рейдемейстера, ни третье движение Рейдемейстера.
В общем случае актуальна задача нахождения верхней оценки f(m)
числа движений Рейдемейстера, необходимых для развязывания диаграммы
тривиального узла (зацепления) с т перекрестками. Некоторые (весьма грубые)
оценки приведены функции /(га) в работе [LH].
Это означает, что для развязывания таких узлов с помощью движений
Рейдемейстера нам потребуется сначала увеличить количество перекрестков.
Перейдем к построению таких диаграмм.
Пример 4.1. Рассмотрим диаграмму Κι узла, показанную на рис. 4.1.
Очевидно, что этот узел тривиален, поскольку диаграмма может быть перестроена в
тривиальную диаграмму последовательностью "уменьшающих" движений
Рейдемейстера Ω2 (и плоских изотопии).
Пример 4.2. Рассмотрим диаграмму К2 узла, показанную на рис. 4.2. Она
может быть получена из диаграммы, изображенной на рис. 4.1 перенесением
отрезка АВ через бесконечность (мы рассматриваем плоскость пополненную
одной бесконечно удаленной точкой). Очевидно, что перенесение через
бесконечность не изменяет изотопического класса узла. Следовательно, мы получаем
тривиальный узел на рис. 4.2.
Пример 4.3. Рассмотрим диаграмму К% узла, изображенную на рис. 4.3. Она
может быть получена из диаграммы рис. 4.2 применением второго движения
4.1. Примеры развязывания узлов
43
В
Рис. 4.1. Первая диаграмма тривиального узла.
С
D
A1
-
ι ι
в
-
[
Рис. 4.2. Вторая диаграмма тривиального узла
Рейдемейстера к отрезку CD и перенесением ее через бесконечность.
Следовательно, диаграмма узла, приведенная на рис. 4.3, также задает тривиальный
узел.
Теорема 4.1. Каждое движение Рейдемейстера, которое может быть
применено к диаграмме К%, увеличивает количество вершин диаграммы.
Доказательство. Рассмотрим диаграмму К% как четырехвалентный граф с
проходами и переходами. Для того, чтобы было возможно выполнение
второго или первого уменьшающих движений Рейдемейстера тень рассматриваемой
диаграммы должна содержать петлю или двуугольник. Далее, для того, чтобы
выполнение третьего движения Рейдемейстера было возможным, тень должна
содержать треугольник такой, что ни одна сторона его не проходит дважды
сверху. Легко видеть, что диаграмма узла, показанная на рис. 4.3 не имеет ни
петель, ни двуугольников, ни "хороших" треугольников. Таким образом, каждое
движение Рейдемейстера, примененное к этой диаграмме, увеличивает
количество ее перекрестков, что завершает доказательство. D
44
Глава 4
Рис. 4.3. Третья диаграмма тривиального узла
При этом помимо плоских диаграмм узлов (зацеплений) молено
рассматривать также сферические диаграммы, представляя сферу как одноточечную
компактификацию плоскости: S2 = R2U{*}. Без ограничения общности молено
предположить, что тень зацепления в состоянии общего положения не
проходит через добавленную (бесконечную) точку *. В этом случае появляется еще
одна "простейшая изотопия", которая заключается в том, что некоторое ребро
на диаграмме проходит через бесконечную точку. Это движение в терминах
плоских диаграмм называется заменой бесконечности.
Интуитивно очевидно, что замена бесконечности представляет собой
изотопию в обычном смысле (из чего следует, что переход к рассмотрению
сферических диаграмм корректен). Оно может быть представлено как
последовательность движений Рейдемейстера.
Упражнение 4.1. Докажите этот факт.
Таким образом, узел К% может быть развязан без использования
увеличивающих движений Рейдемейстера, если мы допускаем замену бесконечности.
Перейдем к следующему примеру. Диаграмма узла К^ приведенная на
рис. 4.4 не может быть развязана с помощью лишь не увеличивающих
движений Рейдемейстера, далее если мы разрешим замену бесконечности (на этой
диаграмме бесконечная клетка уже не представляет собой двуугольник).
Если мы рассмотрим теперь диаграмму узла, показанную на рис. 4.3 как
сферическую диаграмму, мы увидим двуугольник, содержащий бесконечную
точку. Таким образом, после замены бесконечности, мы получаем возможность
развязать диаграмму без использования увеличивающих движений
Рейдемейстера.
4.2. Фундаментальная группа
45
На рис. 4.4 показан еще один пример сферической диаграммы, не
имеющий петель, двуугольников и "хороших" треугольников, к которым возможно
было бы применить третье движение Рейдемейстера. Следовательно, для
развязывания узла, приведенного на рис. 4.4, нужно сначала применить некоторое
количество увеличивающих движений Рейдемейстера.
Другой пример такой диаграммы (И.М.Никонов) показан на рис. 4.5.
Рис. 4.4. Четвертая диаграмма тривиального узла
Рис. 4.5. Диаграмма тривиального узла,
не уменьшаемая одним движением Рейдемейстера
4.2. Фундаментальная группа.
Основные определения и примеры
Фундаментальная группа дополнения является топологическим
инвариантом узлов. Изучение свойств фундаментальной группы привело к построению
полинома Александера.
Перейдем к основной части настоящей главы. Мы определим понятие
фундаментальной группы для произвольных топологических пространств и укажем
46
Глава 4
способы вычисления фундаментальной группы в общем случае и
применительно к случаю дополнений к узлам. Мы также опишем некоторые копредставле-
ния этой группы, см. напр., [КФ].
Пусть задано топологическое пространство X и точка хо Ε X. Рассмотрим
абстрактную окружность S1 и фиксируем точку а на ней. Рассмотрим
множество непрерывных отображений / : S1 —>· X таких, что f(a) = xq. Множество
гомотопических классов таких отображений обладает естественной групповой
структурой: умножение элементов определяется как путь, полученный
прохождением одного пути вслед за другим, а обратный элемент определяется как
прохождение того же пути в обратном порядке. Эти операции, с очевидностью,
корректно определены на гомотопических классах путей.
Определение 4.1. Полученная группа называется фундаментальной группой
пространствах. Обозначение: πι(Χ, жо)·
Замечание 4.1. В случае связного пространства X для произвольных точек
x$,xi Ε X существует изоморфизм πι(Χ, xq) = πι (Χ, χ ι) (однако он не
является каноническим). Поэтому имеет смысл говорить о фундаментальной
группе пространства без выделенной точки. Обозначение: πι(Χ).
Фундаментальная группа является гомотопическим инвариантом
топологических пространств.
Пусть теперь К — зацепление в R3. Пусть Μχ = H3\N(K) — дополнение
к малой окрестности зацепления К. По определению дополнение Μ к будет
оставаться гомеоморфным самому себе в процессе изотопии зацепления К в
пространстве R3, следовательно, фундаментальная группа дополнения
является инвариантом зацеплений.
Определение 4.2. Фундаментальная группа дополнения к узлу (зацеплению)
также называется группой узла (зацепления).
В работе Гордона и Л юкке [GL] показано, что дополнение к узлу (более
точно, к его малой трубчатой окрестности в R3) является полным инвариантом
узла с точностью до зеркального отражения.
Аналогичное утверждение про зацепления, однако, неверно. Для
построения контрпримера нам понадобится следующая лемма.
Лемма 4.1. Пусть D3 — шар в R3; а Т с D3 — полноторие, см. рис. 4-6-
Тогда существует гомеоморфизм пространства R3\T на себя, отображающий
кривые АВ и CD (β том виде, как они показаны на рис. 4-в.а) в кривые АВ и
CD (на рис. 4-6.б), постоянный вне тара D3.
Доказательство. Для более наглядного восприятия представим себе, что
внутренний радиус полнотория Τ очень велик (так что "внутренняя" часть тора
представляет собой высокий цилиндр). Таким образом, у нас образуется
глубокая дыра, см. рис. 4.7.
В дополнении к высокому полноторию мы имеем цилиндр. Сделаем разрез
этого цилиндра так, как показано на рис. 4.8.а. Повернем теперь часть,
образовавшуюся после этого разреза (которая представляет собой окружность с
4.2. Фундаментальная группа
47
г&
а б
Рис. 4.6. Изменение перекрестка
Рис. 4.7. "Высокое" полноторие
двумя отмеченными точками) в направлении, указанном стрелками. Эта
операция возможна, так как полноторие вырезано из шара D3. Производя поворот
на 180 градусов, мы получим картину, изображенную на рис. 4.8.6. Повернув
еще на 180 градусов, мы получим вложение, показанное на рис. 4.8.в. Таким
образом, каждая точка разреза возвращается на свое место, и мы получаем
гомеоморфизм пространства D3\T на себя. Этот гомеоморфизм с
очевидностью может быть продолжен до гомеоморфизма пространства R3\T на себя,
тождественного вне шара D3. Последний гомеоморфизм реализует замену
перекрестка зацепления. D
Зацепления L\ и L^ (см. рис. 4.9.а и 4.9.6), очевидно, не изотопны, но
дополнения к ним гомеоморфны.
Таким образом, неизотопные зацепления могут иметь гомеоморфные
дополнения и, следовательно, изоморфные фундаментальные группы дополнения.
48
Глава 4
А , С
^Ъ
L
*&-Ч)
ι« ίΐι\ an
Ъ—е( z>—V
а б в
Рис. 4.8. Поворачиваем верхнюю часть цилиндра
Упражнение 4.2. Найдите пару неизотопных (и не зеркальных) узлов с
изоморфными фундаментальными группами.
а б
Рис. 4.9. Неизотопные зацепления с гомеоморфными дополнениями
Фундаментальная группа окружности изоморфна группе дополнения к
тривиальному узлу; они обе изоморфны группе Z. Фундаментальная группа
дополнения к тривиальному гг-компонентному зацеплению изоморфна свободной
группе с η образующими.
Фундаментальная группа дополнения к зацеплению является очень
сильным инвариантом. Так, например, она распознает тривиальный узел и
тривиальное зацепление из произвольного числа компонент. Эти результаты следуют
из теоремы Дена.
Теорема 4.2 (Ден). Зацепление L из т компонент тривиально тогда и
только тогда, когда группа 7ri(R3\7V\L)) изоморфна свободной группе с т
образующими.
Таким образом, теорема Дена сводит проблему распознавания
тривиального зацепления к проблеме распознавания свободной группы (в некотором
классе групп). В общем случае проблема распознавания групп является
неразрешимой. Более подробно о проблеме распознавания фундаментальной группы
тривиального зацепления см. в [Bir2] и [BZ].
Теорема Дена является следствием следующей леммы.
4.2. Фундаментальная группа
49
Лемма 4.2. Пусть Μ — трехмерное многообразие с краем, и пусть 7 —
замкнутая кривая на крае дМ. Тогда если существует погруженный двумерный
диск D —> Μ такой, что 0D = η, то существует вложенный диск D' с Μ
с той же самой границей dD' = 7·
Первое доказательство этой леммы было предложено Максом Деном, см.
[Dehn2], но в этом доказательстве были пробелы. Первое безупречное
доказательство было предложено полвека спустя Папакирьякопулосом [Пап]; оно
использовало красивую идею башен двулистных накрытий.
Теперь мы можем доказать теорему Дена следующим образом. Имея узел
KcR3 с его трубчатой окрестностью N(K), рассмотрим группу πι (R3\7V'(К),А),
где A G Τ (К) = ON (К). Каждую петлю можно гомотопно продеформировать
на тор Τ (К) и, таким образом, может быть проинтерпретирована в терминах
параллели (см. стр. 30) и меридиана тора Τ (К), которые являются
непересекающимися и несамопересекающимися замкнутыми кривыми. Очевидно, что
меридиан μ, т.е. простая замкнутая кривая на Τ (К), имеющая коэффициент
зацепления один с узлом К, не стягивается в дополнении к узлу. Пусть λ —
параллель, т. е. простая замкнутая кривая на Т, пересекающая меридиан ровно
один раз ("параллельная узлу К") и имеющая коэффициент зацепления ноль с
узлом К. Кривые μ и λ порождают фундаментальную группу тора Т.
Предположим, что группа узла К изоморфна группе Ζ. Эта группа
содержит в себе {μ} = Ζ. Более того, никакая степень элемента λ не может быть
равна ненулевой степени элемента μ (по причине коэффициентов зацепления).
Таким образом, кривая λ стягивается в фундаментальной группе πι(Έ13\Ν(Κ)).
Следовательно, существует сингулярный (погруженный) диск в R3\7V(К),
границей которого является кривая λ. По лемме Дена это означает, что существует
диск, вложенный в R3\7V(К) и имеющий границу λ. Стягивая Ν(Κ) на К в R3,
мы получаем диск, границей которого является узел К. Следовательно, узел
К тривиален, что завершает доказательство теоремы Дена.
Утверждение теоремы Дена показывает, что фундаментальная группа
является достаточно сильным инвариантом. Она, однако, не позволяет различать
зеркальные узлы и некоторые другие пары узлов. Первый в истории пример
распознавания двух зеркальных узлов, а именно, двух трилистников,
принадлежит Дену, см. [Dehn]. Он рассматривал фундаментальную группу вместе с
выделенным ориентированным меридианом. Этого оказалось достаточно,
чтобы отличить правый трилистник от левого. В дальнейшем мы покажем неизо-
топность правого и левого трилистников с помощью других более наглядных
инвариантов.
Согласно современной терминологии, дополнения к нетривиальным
зацеплениям принадлежат к классу так называемых достаточно больших
трехмерных многообразий, см. определение в главе 5.
Достаточно большие многообразия были классифицированы СВ.
Матвеевым, однако алгоритм их распознавания является очень сложным технически
и вряд ли может быть применен на практике (например, в виде компьютерной
программы).
В [Mat] также был построен полный инвариант узлов, называемый
дистрибутивным группоидом узла. Дистрибутивный группоид является естественным
50
Глава 4
комбинаторным обобщением понятия фундаментальной группы. Мы
определим его в следующей главе.
В дальнейшем мы будем иметь дело лишь со связными (линейно-связными)
топологическими пространствами, если не оговорено противное.
Приведем теперь методы вычисления фундаментальной группы дополнения
к узлу; первый из них — общий, он может быть применен к произвольным
топологическим пространствам; второй приводит к так называемому копредстав-
лению Виртингера: он удобен для дополнений к узлам, а также для некоторых
обобщений (например, для вычисления групп виртуальных узлов, о которых
будет сказано в дальнейшем).
Сформулируем общеизвестную теорему.
Пусть X — топологическое пространство, допускающее разложение X =
Χι U X2, где каждое из пространств Χι, Х^ Хо = Χι Π Χ^ открыто, линейно-
связно и непусто. Выберем точку А £ Хо. Предположим, что
фундаментальные группы πι (Χι, А) и πι(Χ2, А) имеют копредставления (αϊ,... |/ι = е,...} и
(6ι,... \gi = e,...} соответственно (здесь е — единица группы). Предположим,
что образующие с\, С2 ... группы πι (Хо, А) (которые как элементы
принадлежат обеим группам: πι (Χι, А) и πι(Χ2,Α)) могут быть представлены в виде
Ci = q(<2i, ...), а также в виде q = q(6i, ...) по образующим групп πι (Χι, Α)
ππι(Χ2,Α).
Имеет место следующая теорема.
Теорема 4.3. (Теорема Ван-Кампена) Группа πι (Χ, А) допускает копредстав-
ление
(a>i,bi,\fi = e,gi = e,Ci(a) = q(6)}. (4.1)
Эта теорема очевидна для случая клеточных комплексов; полное
доказательство в общем случае см. в [КФ].
Следствие 4.1. Если оба пространства Χι иХ2, описанные выше, являются
односвязными (т. е. имеют фундаментальную группу, состоящую из одного
элемента), то пространство X также является односвязным.
В качестве примера вычислим фундаментальные группы двумерных
многообразий.
Теорема 4.4. Фундаментальная группа связной ориентируемой поверхности
рода g (g > 0) без края допускает копредставление
(αϊ, 6ι,..., ag, 6^|αι6ιαι_16ι~ .. .agbgag~1bg~ = e). (4-2)
Доказательство. Рассмотрим поверхность с ручками, представленную как Ад-
угольник, у которого пары сторон отождествлены так, как показано на рис. 4.10.
Разобьем полученное многообразие на две части: одна из них находится
внутри большого круга на рис. 4.10, другая представляет собой дополнение к
малому кругу.
Первая часть является односвязной; вторая часть стягивается к букету из
2д окружностей; следовательно, ее фундаментальная группа изоморфна
свободной группе с образующими1 αϊ, 6j_,..., ад, Ъд.
1 Здесь каждое ребро 2^-угольника обозначается буквой; так как все вершины склеиваются
4.3. Вычисление групп зацеплений
51
Г
-W>
V_
"ЯГ
Рис. 4.10. Склейка поверхности с ручками
Пересечение двух вышеупомянутых областей представляет собой кольцо,
которое, будучи стягиваемым к окружности, имеет фундаментальную группу,
изоморфную Z. Таким образом, по теореме Ван-Кампена мы получаем
ровно одно соотношение, получаемое как равенство двух различных выражений
образующей группы Z.
Более точно, мы имеем:
ni(Sg) = (αι,6ι,... ,α^,^|αι6ιαι_16ι_1 .. .agbgag~1bg~1 = e). (4.3)
D
Для каждого зацепления L существует поверхность Sg с ручками,
стандартно вложенная в R3 (упражнение 3.1), и набор кривых L' с Sg С R3,
представляющий зацепление, изотопное зацеплению L в R3. Таким образом, мы можем
вычислить фундаментальную группу дополнения к зацеплению L (или, что то
же самое, к L') с использованием теоремы Ван-Кампена, разбивая дополнение
к зацеплению V на две части: внутри и вне поверхности Sg.
4.3. Вычисление групп зацеплений
Покажем, как работает эта техника на примере торических узлов. Пусть
К = T(p,q) — торический узел, вложенный в тор, стандартно лежащий в R3.
Нам удобно будет рассматривать дополнение к узлу, а не к его окрестности.
Кроме того, нам будет удобно заменить R3 на S3 (фундаментальная группа
трехмерного многообразия не меняется от удаления из него одной точки)
Рассмотрим теперь S3\K как
(Внутренне полноторие без узла К) U (Внешнее полноторие без узла К).
(4.4)
Легко видеть, что удаление некоторого множества на границе полнотория не
меняет фундаментальной группы. Следовательно, обе фундаментальные
группы, к которым мы применяем теорему Ван-Кампена, изоморфны группе Ζ
(одна из них имеет образующую λ, другая имеет образующую μ; они соответствуют
в одну, все ребра представляют собой замкнутые пути; именно эти пути и соответствуют
буквам.
52
Глава 4
параллели и меридиану тора, представляющего собой границу обоих полното-
рий). Пересечение этих частей гомеоморфно цилиндру, который получается
разрезанием тора по нетривиальной кривой. Следовательно, фундаментальная
группа пересечения изоморфна группе Z. Единственная образующая этой
группы записывается как Хр с одной стороны и как μ4 с другой стороны. Из этого
следует теорема.
Теорема 4.5. Фундаментальная группа дополнения к торическому узлу типа
(p,q) имеет копредставление с двумя образующими λ и μ и единственным
соотношением \р = μς.
Очевидно, что фундаментальная группа не меняется при переходе от узла
к его зеркальному образу.
Фундаментальные группы изотопных узлов изоморфны, что ясно видно из
копредставлений для торических узлов: так, узел T(p,q) имеет ту же группу,
что и Т(д,р), а группа тривиального узла Т(1,п) изоморфна группе Z. Тори-
ческие узлы типов (p,q) и (ρ,—q) являются зеркальными образами друг друга,
и их группы совпадают.
Во всех остальных случаях фундаментальная группа различает
неизотопные торические узлы.
Для задания копредставления фундаментальной группы дополнения к
зацеплению существует естественный способ, который состоит в следующем.
Рассмотрим зацепление L, заданное некоторой плоской диаграммой L. Рассмотрим
некоторую точку ж, "висящую" над плоскостью проекции зацепления. Будем
классифицировать гомотопические классы петель, исходящих из данной
точки. Легко видеть (этот факт остается в качестве упражнения для читателя),
что в качестве образующих элементов молено выбрать следующие. Рассмотрим
петли, исходящие из точки χ и зацепляющие дуги диаграммы L один раз в
направлении, заданном правилом буравчика, см. рис. 4.11.
Рис. 4.11. Петли, соответствующие ребрам
Перейдем теперь к описанию определяющих соотношений в такой группе.
Опишем геометрическую связь между петлями, зацепляющими соседние
дуги (т.е. дуги, отделенные друг от друга некоторым переходом). Мы имеем:
Ъ = сас~х, если с отделяет дугу а от дуги 6, см. рис. 4.12.
То, что данный набор соотношений порождает все соотношения в данной
группе, следует из геометрических рассуждений, приведенных ниже.
Рассмотрим проекцию петли на плоскость диаграммы L; будем подвергать
петлю изотопии. При изотопии петли ее запись через образующие будет
претерпевать изменения в случае, когда проекция проходит через перекрестки за-
4.3. Вычисление групп зацеплений
53
Ъ = сас
Рис. 4.12. Соотношение в перекрестке
цепления. Такая "простейшая" изотопия изображена на рис. 4.13; дуга,
соединяющая точки Ρ и Q проходит под перекрестком.
Рис. 4.13. Изотопия, определяющая соотношение
Очевидно, что петля, изображенная слева (на рис. 4.13) соответствует
элементу с~1Ъс, в то время, как петля справа в точности соответствует дуге а.
Таким образом, копредставление фундаментальной группы имеет
следующий вид: дуги соответствуют образующим, в то время как определяющие
соотношения происходят из перекрестков: мы полагаем сас-1 = Ъ для соседних дуг
а и 6, отделенных дугой с, если Ъ лежит слева от с относительно ориентации
дуги с.
Определение 4.3. Это представление фундаментальной группы дополнения
к узлу называется копр составлением Виртипгера.
Упражнение 4.3. Приведите явное алгебраическое доказательство того
факта, что копредставление Виртингера для различных диаграмм одного и того
же зацепления задают изоморфные группы.
Упражнение 4.4. Найдите копредставление Виртингера для простейшей
диаграммы трилистника и покажите, что группы, имеющие копредставле-
ния (а,Ъ\аЪа = ЪаЪ) и (c,d\c3 = d2) являются изоморфными.
Группа, задаваемая копредставлением (а, Ъ\аЪа = ЪаЪ) встречается в других
разделах теории узлов. Она изоморфна группе кос из трех нитей.
54
Глава 4
Оказывается, что не только изотопные (или зеркально-симметричные) узлы
могут иметь изоморфные группы.
Упражнение 4.5. Покажите, что для трилистников ΤΊ
фундаментальные группы дополнений к узлам Τ\ψΤ\ и ΤχψΤϊ изоморфны.
Упражнение 4.6. Вычислите представление Виртингера для:
1. Узла восьмерки;
2. Колец Борромео.
Оказывается, что инвариант раскрасок CI (см. стр. 40) для узлов
определяется по фундаментальной группе. Докажем следующую теорему.
Теорема 4.6. Для каждого узла К число С1(К) + 3 равно числу
гомоморфизмов из πι(ΐί3\Ν(Κ)) в группу перестановок S3.
Доказательство. Рассмотрим узел К и произвольную его плоскую
диаграмму. Для построения гомоморфизма из πι(ΐί3\Κ) в Ss нам нужно определить
образы образующих элементов (т.е. дуг диаграммы К).
Предположим, что элемент, соответствующий некоторой дуге (обозначим
ее через s) отображается в четную перестановку. Тогда все элементы,
соответствующие дугам, отображаются в четные перестановки (здесь мы пользуемся
тем, что К — узел, и все элементы, соответствующие дугам, сопряжены между
собой). Так как группа А% четных перестановок коммутативна, мы видим, что
все дуги отображаются в один и тот же элемент группы А%. Следовательно,
существуют ровно три таких отображения.
Если хотя бы один элемент, соответствующий дуге, отображается в
нечетную перестановку, то элементы, соответствующие всем дугам, отображаются в
нечетные перестановки, т.е. в транспозиции (12), (23), (31). Если сопрячь одну
из этих из транспозиций посредством некоторой другой, мы получим третью
транспозицию. Эта операция как раз согласована с правилом раскраски (если
считать образы элементов, соответствующих дугам, цветами).
Таким образом, все гомоморфизмы из πι(ΐί3\Κ) в Ss, за исключением трех
"четных", находятся в однозначном соответствии с правильными раскрасками
выбранной диаграммы зацепления К. D
Таким образом мы получаем следующее утверждение.
Следствие 4.2. Инвариант раскрасок принимает одинаковые значения на
узле и его зеркальном образе.
Это утверждение не следует явно из определения инварианта раскрасок.
Глава 5
Дистрибутивные группоиды и
алгебра Конвея
5.1. Введение
Целью настоящей главы является описание универсального (полного)
инварианта узлов, независимо открытого Сергеем Владимировичем Матвеевым
[Матв2] и Дэвидом Джойсом [Joy]. В русскоязычной литературе этот
инвариант называется дистрибутивным группоидом; в литературе на других языках
он известен как квандл (quandle).1 Этот инвариант является полным
(относительно эквивалентности, чуть более слабой, чем обычная изотопия), однако
его значения трудно поддаются сравнению. В настоящей главе, помимо
общей конструкции дистрибутивного группоида, мы построим некоторые более
слабые инварианты, происходящие из дистрибутивного группоида; эти
инварианты поддаются легкому описанию и сравнению. Во второй части настоящей
главы мы опишем конструкцию так называемых алгебр Конвея, восходящих к
оригинальной работе Конвея (определение впервые предложено в [РТ]). Оба
направления — и дистрибутивные группоиды, и алгебры Конвея, — позволяют
строить различные (в том числе полиномиальные) инварианты узлов.
Рассмотрим простейший инвариант узлов — инвариант раскрасок. Почему
возможно построить инвариант узлов такими простыми средствами?
Попробуем использовать большее множество цветов (палитру). Пусть Г —
произвольное конечное множество (конечность нам нужна для того, чтобы
иметь возможность посчитать количество раскрасок); все элементы
множества Г называются цветами.
Предположим, что множество Г снабжено бинарной операцией а : ГхГ —>· Г;
эту операцию мы будем также обозначать кружочком: а о Ъ = а(а, Ь).
Определение 5.1. Под правильной раскраской диаграммы D
ориентированного зацепления К будем понимать способ сопоставления цветов дугам
зацепления D таким образом, чтобы для каждого перекрестка переход (имеющий
некоторый цвет 6), дуга прохода, лежащая справа (цвет а) и дуга прохода,
лежащая слева (цвет с), удовлетворяли соотношению а о Ь = с см. рис. 5.1.
Заметим, что нам не важна ориентация дуг, которым сопоставлены цвета а
и с.
1 Встречаются также и другие названия того лее самого и похожих на него объектов:
например, кристалл и рэк (rack).
56 Дистрибутивные группоиды и алгебра Конвея
с = а о h
Ъ а
Рис. 5.1. Правило для раскрасок
Какими условиями должна обладать операция о, чтобы количество
правильных раскрасок было инвариантным относительно движений Рейдемейстера?
Легко показать, что (локальной) инвариантности такой функции при
движении Ωι соответствует соотношение идемпотентности а о а = а для всех
элементов a Ε Г, которые могут быть сопоставлены дуге и играть роль цвета. Однако,
для упрощения ситуации мы потребуем, чтобы идемпотентность имела место
всегда: Va Ε Γ : а о а = а.
Аналогично, инвариантность относительно движения Ω2 требует левой
обратимости операции о, а именно, для любых элементов а и Ъ из Г уравнение
χ о а = Ъ должно иметь в точности одно решение χ Ε Γ (в случае трехцветной
палитры обратная к операции о совпадает с ней самой).
Наконец, для инвариантности относительно движения Ω3 нам
потребуется правая самодистрибутивность операции о, которая означает, что для всех
а, 6, с Ε Г имеет место равенство (а о Ь) о с = (а о с) о (Ъ о с) В дальнейшем будем
называть любое множество, снабженное операцией о, которая удовлетворяет
перечисленным выше условиям, дистрибутивным группоидом.
Каждый дистрибутивный группоид задает правило правильной раскраски
диаграмм зацеплений, как это было описано выше.
Из сказанного выше следует
Предложение 5.1. Количество правильных раскрасок элементами
фиксированного конечного дистрибутивного группоида является инвариантом
зацеплений.
Для любого дистрибутивного группоида обозначим операцию, обратную к
операции о, через /. Более точно, элемент Ъ/а определяется как единственное
решение уравнения χ о а = Ъ.
Упражнение 5.1. Покажите, что любой дистрибутивный группоид Τ (с
операцией о) является дистрибутивным группоидом также и относительно
операции /.
Докажите также следующие соотношения для Г; (а о Ъ)/с = (а/с) о (Ъ/с),
(α/b) о с = (а о с)/(Ь о с).
Существует общий способ задания дистрибутивных группоидов
образующими и соотношениями.
Пусть А — алфавит (т.е. множество, состоящее из букв). Словом в
алфавите А назовем произвольную конечную последовательность элементов из А и
5.1. Введение
57
символов (,), о, /. Определим теперь индуктивно множество D(A) допустимых
слов согласно следующим правилам:
1. Для каждого а Ε А слово, состоящее из единственной буквы α и не
содержащее других символов, допустимо.
2. Если два слова Wi, W2 допустимы, то слова (Wi) ° (И^) и
(Wi)/(W2) так лее допустимы.
3. Не существует других допустимых слов, кроме тех, которые получаются
индуктивно согласно правилам 1 и 2.
Иногда мы не будем писать скобки, когда смысл слова понятен из контекста.
Так, например, для букв αϊ, а2 мы будем писать слово а\ о а2 вместо (αϊ) ο (а2)
и считать первое слово также допустимым.
Пусть R — множество соотношений, т. е. тождеств типа ra = sa, где ra, sa E
D(A), а а пробегает некоторое множество X индексов. Введем отношение
эквивалентности для D(A), предполагая, что W\ = W2 если и только если
существует конечная цепочка преобразований, начинающаяся с W\ и заканчивающаяся
словом W2, построенная по правилам 1-5, описанным ниже:
1. Ж ο χ <^> ж;
2. (хоу)/у ^=> ж;
3. (х/у) о у ^^ ж;
4. (ж о у) о ζ <^> (ж о ζ) о (у о г);
О. Г^ < )* 5^·
Каждое преобразование в этой цепочке представляет собой замену подслова,
стоящего в левой части одного из пяти перечисленных выше правил, на слово,
стоящее в его правой части, или наоборот.
Обозначим множество таких классов через T(A\R). Очевидно, что это
множество является дистрибутивным группоидом по отношению к операции о.
Рассмотрим следующий пример конечного дистрибутивного группоида
(обозначаемого G±)· Пусть G4 — множество из четырех элементов αϊ, α2, «з? &4·
Замечание 5.1. Пример, который мы строим, происходит из
универсальной конструкции группоидов, соответствующих группам. В дальнейшем эта
конструкция будет описана более подробно.
Определим операцию о по следующему правилу:
о
αϊ
а2
а3
CL4
а\
ах
CL4
а2
а3
а2
а3
а2
С14
а\
а3
а4
αϊ
а3
а2
CL4
а2
а3
αϊ
а4
Здесь результат применения операции щ о clj находится в таблице на j-м
месте в г-ж строке.
58
Дистрибутивные группоиды и алгебра Конвея
Упражнение 5.2. Проверьте, что для этой операции выполняются аксиомы
дистрибутивного группоида.
Легко проверить, что узел восьмерка допускает неодноцветную раскраску
элементами дистрибутивного группоида G^· To же самое молено сказать и о
трилистнике.
Для тривиального узла любая раскраска элементами любого конечного
группоида является одноцветной. Тем самым показана нетривиальность узла
восьмерки.
Из предложения 5.1 мы видим, что дистрибутивные группоиды полезны
для построения инвариантов узлов. Если применить ту же конструкцию с
другой точки зрения, молено построить инвариант, сопоставляющий каждому узлу
(зацеплению) дистрибутивный группоид, являющийся универсальным и (почти
полным2). Для простоты мы будем описывать этот инвариант для случая
узлов. Универсальный дистрибутивный группоид узлов может быть описан
двумя способами: геометрическим и алгебраическим.
5.2. Геометрическое и алгебраическое
определения дистрибутивного группоида
5.2.1. Геометрическое определение
Пусть К — ориентированный узел в R3, и пусть N(K) — его малая
трубчатая окрестность. Положим Ε (К) = (R?\N(K)) — замкнутое дополнение к этой
окрестности в трехмерном пространстве. Фиксируем точку отсчета χ к в Ε (К).
Обозначим через Τ к множество гомотопических классов путей в пространстве
Ε (К) с начальной точкой χ к и конечной точкой на dN(K) (эти условия
должны сохраняться во время гомотопии). Заметим, что ориентации пространства
R3 и узла К определяют ориентацию трубчатой окрестности узла (по правилу
буравчика). Пусть ть — ориентированный меридиан, обходящий вокруг
некоторой дуги Ъ. Определим а о Ъ = \bmbb~1 а], где для χ Ε Γ& буква χ обозначает
некоторый путь, а [х] означает гомотопический класс эквивалентности этого
пути, см. рис. 5.2.
Аксиомы дистрибутивного группоида в этом случае проверяются
непосредственно. Также легко показать, что группоиды, соответствующие разным
выборам точки отсчета χ&, изоморфны. Последнее утверждение остается читателю
в качестве упражнения.
Существует естественное отображение ("морфизм") из дистрибутивного
группоида Τ (К) в группу πι(ΐί3\Ε(Κ)). Оно описывается следующим
образом. Фиксируем точку χ вне трубчатой окрестности узла. Каждому элементу
7 дистрибутивного группоида (т.е. пути в точку χ в дЕ(К)) мы сопоставим
петлю 7^ж7-1> гДе тх — меридиан в окрестности точки х.
Отсюда мы видим, что фундаментальная группа может быть
восстановлена по дистрибутивному группоиду: все меридианы узла могут играть роль
2В дальнейшем мы упомянем, насколько не полным в обычном смысле слова является
этот инвариант.
5.2. Два определения дистрибутивного группоида
59
Рис. 5.2. Наглядное описание операции о дистрибутивного группоида
образующих фундаментальной группы, в то время как соотношения для
группоида вида аоЪ = с преобразуются в групповые соотношения баб-1 = с, которые
составляют полный список порождающих соотношений группы.
Отметим, что такое отображение группоида в группу не является эпиморф-
ным: в группоиде нет операции, соответствующей групповому умножению. Так,
например, группоид из одного элемента {а} порождает группу, изоморфную Z,
образующей в которой будет образ элемента а.
Кроме того, фундаментальная группа естественным образом действует на
дистрибутивном группоиде: для каждой петли д и элемента 7 дистрибутивного
группоида путь gj также является элементом дистрибутивного группоида.
5.2.2. Алгебраическое описание
дистрибутивного группоида
Пусть D — диаграмма ориентированного узла К. Обозначим множество дуг
диаграммы D через Ар. Пусть Ρ — перекресток этой диаграммы, инцидентный
двум дугам α и с, составляющим проход, и дуге 6, образующей переход.
Выпишем соотношение а о Ъ = с, считая, что а — та из дуг прохода, которая лежит с
правой стороны от 6, а с — дуга, лежащая с левой стороны от дуги Ъ. Обозначим
множество всех таких соотношений для всех перекрестков через Rd-
Рассмотрим теперь дистрибутивный группоид Г\Ad\Rd), определенный образующими
Ad и соотношениями Rd-
Теорема 5.1. Дистрибутивные группоиды Υ к и T(Ad\Rd) изоморфны.
Перед тем, как доказывать эту теорему, сделаем следующие важные
замечания. С одной стороны, эта теорема показывает, как описывать образующие и
соотношения для геометрически определенного дистрибутивного
группоида Υ к- С другой стороны из нее следует независимость T(Ad\Rd) от выбора
60
Дистрибутивные группоиды и алгебра Конвея
конкретной диаграммы узла. Далее, предложение 5.1 (о числе раскрасок)
очевидным образом следует из теоремы 5.1 так как число правильных раскрасок
диаграммы узла элементами некоторого дистрибутивного группоида Г
совпадает с числом гомоморфизмов T(Ad\Rd) в Г.
Доказательство теоремы 5.1. Сопоставим каждой дуге а диаграммы D путь
sa в Ε (К) таким образом, что
1. Путь sk соединяет точку отсчета с точкой части тора ΟΝχ,
соответствующей дуге а;
2. Во всех точках проекция пути sa на плоскость проекции диаграммы D
узла, где она пересекает путь sa, проходит выше узла, см. рис. 5.3.
Рис. 5.3. Определяем путь sa
Очевидно, что этими условиями гомотопический класс пути sa определен
однозначно.
Следовательно, каждой образующей дистрибутивного группоида Y(Ad\Rd)
соответствует некоторый элемент группоида Υ к- Таким образом, мы
определили гомоморфизм φ : T(Ad\Rd) —>· Υ к- Для того, чтобы определить обратный
гомоморфизм ψ : Υ к —>· Г (До | До), выберем элемент s G Υ к- Без ограничения
общности можно выбрать путь, представляющий элемент s, таким образом,
что его проекция пересекает диаграмму D трансверсально и не содержит
перекрестков диаграммы.
Обозначим через αη, ап-ъ · · · ? αι ДУГИ диаграммы D, проходящие сверху
пути s в порядке их пересечения. Обозначим через ао дугу, соответствующую
концу пути s. Далее, сопоставим пути s G Υ к элемент ((... (αο^ι^ι)^2 · · · ^η-ι)^η^η
дистрибутивного группоида Y(Ad\Rd), где ε ι означает / в случае, если s
проходит под α,ΐ слева направо (относительно ориентации а^иов противном случае,
см. рис. 5.4.
5.3. Полнота дистрибутивного группоида узла
61
^(з) = (аооа)/а2
Рис. 5.4. Построение отображения ψ : Г& —> Y{ADlRD).
Легко видеть, что это отображение корректно определено (т. е. не зависит от
выбора представителя s элемента Г&), а так лее, что отображения φ ж ψ являются
взаимно обратными. D
Дистрибутивный группоид, соответствующий узлу, является полным
инвариантом узла (с некоторой оговоркой). Однако с помощью этого инварианта
трудно распознавать узлы, так как трудно понять, являются ли два
дистрибутивных группоида, заданных образующими и соотношениями, изоморфными,
или нет.
5.3. Полнота дистрибутивного группоида узла
Грубо говоря, дистрибутивный группоид является полным инвариантом
узлов, поскольку он содержит всю информацию о группе узла, а также "несколько
больше". Для доказательства факта о полноте дистрибутивного группоида мы
воспользуемся очень сильным топологическим результатом Фридхельма Валь-
дхаузена [Wal].
Согласно определению Матвеева, два (вообще говоря неизотопных) узла
эквивалентны, если можно получить один из них из другого одновременной
заменой ориентации узла и объемлющего пространства (R3 или S3). В этом смысле
два трилистника (левый и правый) являются эквивалентными; они имеют
изоморфные дистрибутивные группоиды.
62
Дистрибутивные группоиды и алгебра Конвея
Далее в этой главе под полнотой дистрибутивного группоида мы будем
понимать, что он различает узлы с точностью до эквивалентности по Матвееву.
Отправными пунктами доказательства полноты являются следующие:
1. Для тривиального узла ситуация очевидна: фундаментальная группа
распознает тривиальный узел согласно теореме Дена.
2. Если узел не тривиален, то его дополнение является достаточно большим
трехмерным многообразием по теореме Дена, см. стр. 49.
3. Для класса достаточно больших трехмерных многообразий
фундаментальная группа плюс "несколько больше" является полным инвариантом.
4. По дистрибутивному группоиду узла восстанавливается структура
фундаментальной группы дополнения плюс "несколько больше."
Для простоты мы будем иметь дело лишь с узлами. Те же результаты
остаются верными и для зацеплений.
Фундаментальная группа дополнения к узлу восстанавливается (с
точностью до изоморфизма) по дистрибутивному группоиду: за образующие группы
берутся образующие группоида, а определяющие соотношения группы
получаются из определяющих соотношений группоида, где аоЪ преобразуется в баб-1,
а а/Ъ преобразуется в Ь~гаЬ.
Введем некоторые определения.
Двумерная поверхность F в трехмерном многообразии Μ называется
собственной, если F Π дМ = OF.
Определение 5.2. (Двумерная) поверхность F в (трехмерном) многообразии
Μ называется сжимаемой в одном из следующих случаев:
1. Существует нестягиваемая простая замкнутая кривая к на поверхности
F и диск D в Μ (внутренность которого лежит в М), таких что D Π F =
dD = k.
2. Существует шар (связная компонента) Ε в Μ такой, что Ε Π F = дЕ.
В противном случае поверхность называется несжимаемой.
Таким образом, несжимаемая поверхность — это поверхность, не
содержащая тривиальных сфер (которые можно заклеить шаром, вложенным в
многообразие), а также нетривиальных кривых, которые можно затянуть вложенным
(сжимающим) диском, лежащим в многообразии. Для выполнения последнего
условия достаточным является то, что отображение фундаментальной группы
tti(F) в 7Γι(Μ), порожденное вложением поверхности, является
мономорфизмом.
Определение 5.3. Трехмерное многообразие Μ называется неприводимым,
если любая сфера S2 С Μ является сжимаемой, т. е. ограничивает шар.
Трехмерное многообразие Μ с краем называется гранично неприводимым,
если его край дМ является несжимаемым.
5.3. Полнота дистрибутивного группоида узла
63
Определение 5.4 ([Матв]). Компактное ориентируемое трехмерное
многообразие (быть может, с краем) называется достаточно большим если оно
содержит собственную несжимаемую гранично несжимаемую двумерную
поверхность, отличную от сферы и диска.
Пусть К — ориентированный узел. Рассмотрим фундаментальную группу
π пространства H3\N(K) (или его замыкания, что то же самое), где N —
трубчатая окрестность узла К. Очевидно, что ON = Τ является тором; рассмотрим
ориентированный меридиан т этого тора.
Если узел К нетривиален, то фундаментальная группа π(Τ) является
естественным образом вложенной в π. Это следует из теоремы Дена.
Определение 5.5. Для нетривиального узла К тройка m G πι (Τ) С π
называется периферической системой.
Теорема Вальдхаузена утверждает следующее:
Теорема 5.2. [Wal] Пусть Μ, Ν — неприводимые и гранично неприводимые
трехмерные многообразия. Пусть Μ — достаточно велико и пусть φ: πι (TV) —>
πι (Μ) — изоморфизм фундаментальных групп, сохраняющий периферическую
структуру. Тогда существует гомеоморфизм f : TV —> Μ, индуцирующий
отображение φ.
Покажем теперь, что дистрибутивный группоид является полным
инвариантом узлов.
Пусть К\,К2 — два ориентированных узла. Предположим, что φ —
изоморфизм Τ (Κ ι) —>· Τ (К2) соответствующих дистрибутивных группоидов.
Обозначим дополнения к трубчатым окрестностям узлов Κι, Къ через Εχ1, Εχ2
соответственно.
Заметим, что если узлы Κι и К2 не тривиальны, то многообразия Екг, Εχ2
являются гранично-неприводимыми, достаточно большими и неприводимыми
(по теореме Дена, см. стр. 48).
Предположим, что один из двух узлов (например, Κι) тривиален. Тогда
группа π (Κ ι) изоморфна группе Ζ. Так как группа узла может быть
восстановлена по его дистрибутивному группоиду, мы заключаем, что группа π (К 2)
изоморфна группе Ζ. Следовательно, узел К2 также тривиален.
Рассмотрим теперь случай, когда узлы Κι, К2 нетривиальны.
В этом случае группа каждого из узлов восстанавливается по
дистрибутивному группоиду, следовательно, группы узлов изоморфны; кроме того,
меридиан также восстанавливается из дистрибутивного группоида (в качестве
меридиана можно выбрать образ (в группе) любого элемента из дистрибутивного
группоида при естественном отображении). Заметим, что меридиан в
фундаментальной группе не единственен: для любых двух меридианов μι, /i2
существует автоморфизм группы, переводящий μι в μ2 и оставляющий на месте
периферическую систему.
Фундаментальная группа естественно действует на группоиде слева: если
g — петля (элемент фундаментальной группы), а 7 — путь (из начальной
точки в точку на торе, то gj — также элемент группоида, который проходит
сначала вдоль ^ а до начальной точки, а затем идет вдоль 7· Выберем элемент
64
Дистрибутивные группоиды и алгебра Конвея
а из группоида. Докажем теперь, что нормализатор элемента а в
фундаментальной группе в точности совпадает с фундаментальной группой трубчатой
окрестности узла πι(Τ2) = Ζ2. Действительно, каждый элемент группы πι(Τ2)
представляет собой путь вида ana-1, где а обозначает путь в дистрибутивном
группоиде из начальной точки в точку на торе Т2, а п — некоторая замкнутая
петля на торе Т2. Таким образом мы имеем ana-1 -a = an, что гомотопно пути
а согласно геометрическому определению дистрибутивного группоида.
Предположим теперь, что для некоторого д пути да ία а гомотопны. Тогда
эта гомотопия порождает путь на торе (путь, который проходит конечная
точка во время гомотопии) Обозначим этот путь через х. Мы имеем: дата-1 = е,
таким образом, путь д гомотопен пути вида ап~1а~1, т.е. принадлежит
фундаментальной группе тора Т^.
Итак, по дистрибутивному группоиду можно восстановить периферическую
структуру. Пусть К\, i^2 — нетривиальные узлы с одной и той же
периферической структурой га Ε Ζ2 С π. Рассмотрим изоморфизм групп узлов,
сохраняющий эту структуру. По теореме Вальдхаузена он порождает гомеоморфизм
между Екг и Ек2 и отображает меридиан первого пространства в некоторый
меридиан второго пространства. Таким образом, мы имеем одинаковую
информацию о том, как приклеивать полнотория к пространствам Εχ1 и Εχ2 для
получения объемлющего пространства R3 для узлов. Параллели этих полното-
рий представляют собой как раз узлы Κι и К^. Следовательно, узлы являются
изотопными. Для осуществления этого плана нам нужно лишь фиксировать
ориентации пространств Εχλ и Εχ2. В таком случае мы получаем информацию
об ориентации меридианов. При выборе противоположных ориентации
объемлющего пространства и меридиана мы получим узел, эквивалентный
исходному.
При этом в случае, если ориентация меридиана фиксирована, узел может
быть однозначно восстановлен.
5.4. Специальные реализации
дистрибутивного группоида:
инвариант раскрасок,
фундаментальная группа,
полином Александера
Рассмотрим свободный дистрибутивный группоид с образующими а\,..., а&
и без соотношений Г (αϊ,... ,αη|).
Ему естественным образом соответствует свободная группа с теми лее
образующими.
Пример 5.1. Рассмотрим свободную группу с бесконечным (счетным) числом
образующих. Определим на ней дистрибутивный группоид по следующему
правилу: а о Ь = баб-1, а/Ъ = Ъ~1аЪ. Все аксиомы дистрибутивного группоида
проверяются непосредственно. В этом случае мы получаем естественный морфизм
из свободного дистрибутивного группоида в свободную группу. Как и в случае
дистрибутивных группоидов, в случае групп любая (конечно определенная)
группа получается добавлением конечного числа определяющих соотношений
5.5. Алгебра Конвея и полиномы
65
к свободной группе. Нас интересуют лишь группы узлов; они все являются
конечно определенными.
Молено показать, что образом дистрибутивного группоида узла является
фундаментальная группа дополнения к узлу (это следует непосредственно из
сравнения определяющих соотношений для фундаментальной группы и
дистрибутивного группоида).
Пример 5.2. Рассмотрим отображения дистрибутивного группоида в
свободный модуль над кольцом полиномов Лорана (от переменной t) Для этого
положим
а о Ъ = ta + (1 - t)b, a/b = -а + И - - ) Ъ. (5.2)
В этом случае дистрибутивному группоиду узла будет соответствовать фак-
торкольцо, задаваемое квадратной матрицей соотношений на образующие αϊ,
(22,... (см. далее). Эта матрица называется матрицей Александера диаграммы
узла. Полином Александера узла определяется следующим образом: мы
добавляем новое уравнение сц = 0, а затем решаем оставшуюся систему из η
уравнений с η — 1 переменной. В результате мы получаем некоторое соотношение для
элементов кольца, имеющее вид f(t) = 0, где / — некоторый полином Лорана.
Функция / (определенная с точностью до умножения на ±tfc), называется
полиномом Александера. Она также получается, если взять любой минор матрицы
Александера.
У полинома Александера есть аналог — полином многих переменных. Здесь
мы его определять не будем, см. [Тог].
5.5. Алгебра Конвея
и полиномиальные инварианты
Мы опишем конструкцию, которая позволяет систематизировать подход к
разным инвариантам узлов (в том числе полиномиальным, таким как
полиномы Джонса-Кауфмана, Конвея и HOMFLY). В частности, мы докажем
инвариантность и корректную определенность полинома HOMFLY. 3 Мы будем
придерживаться подхода, предложенного в статье [РТ].
Основная идея заключается в следующем. В отличие от предыдущего
инварианта (дистрибутивного группоида), где мы сопоставляли особый
алгебраический объект каждому зацеплению, мы собираемся построить некоторый
алгебраический объект и сопоставлять зацеплениям элементы этого объекта
(которые и будут значениями нашего инварианта).
Предостережение. Мы собираемся ввести операции о и /, которые имеют
совсем другой смысл и несколько иные свойства, нежели операции,
обозначаемые теми же буквами, введенные ранее.
Пусть А — алгебра с бинарными операциями о и /, для которых имеют место
следующие свойства: для любых a, b Ε А справедливо (aob)/b = а, (α/b) о Ь = а.
3HOMFLY является аббревиатурой фамилий шести авторов, предложивших этот полином
[HOMFLY]: Hoste, Ocneanu, Millett, Freyd, Lickorish и Yetter. Этот полином был также открыт
Йозефом Пржитицким и Павлом Трачиком, см. [РТ].
66
Дистрибутивные группоиды и алгебра Конвея
Для каждой плоской диаграммы L зацепления будем строить элемент W(L)
алгебры А следующим образом. Зафиксируем набор элементов {αη}5 η= 1,2,...
алгебры А, которые мы будем сопоставлять гг-компонентным тривиальным
зацеплениям.
Потребуем также, чтобы для каждой тройки Конвея (т. е. тройки диаграмм,
совпадающих везде, за исключением некоторого маленького круга и
выглядящих как '/\:, у\ , Λ Γ внутри него) имело место равенство
^(Х)) = ич(х)) ° wo (ρ· (5-3)
Под единственностью обратного будем понимать существование и
единственность такой бинарной функции /, что W(y^.)/W(.^ ^:) = W(y<^■) и, даже
более общо, для каждых ж, у существует единственный элемент ζ = χ/у такой,
что zoy = χ. Итак, мы строим отображение W из множества зацеплений в
некоторый алгебраический объект. В дальнейшем мы увидим, что частным
случаем уравнения (5.3) являются соотношения типа Конвея. Обратим внимание на
следующее обстоятельство: так как каждое зацепление может быть доведено до
тривиальной (восходящей) диаграммы изменением некоторых типов
перекрестков (упражнение 1.2), значение функции W на произвольном т-компонентном
зацеплении с η перекрестками может быть выражено через значение функции
W на тривиальном m-компонентном зацеплении и значения функции W на
зацеплениях с меньшим числом перекрестков (которые, в свою очередь, также
вычисляются через значения на тривиальных диаграммах); в этом выражении
могут участвовать операции о и /. Следовательно, для каждой плоской
диаграммы зацепления мы можем определить значение функции W как-нибудь,
быть может, различными способами. На данный момент мы не знаем,
определена ли функция W корректно на диаграммах зацеплений и, если так,
инвариантна ли она относительно движений Рейдемейстера. Рассмотрим алгебру А
и попробуем найти ограничения, которые ведут к корректному определению
инвариантной функции W.
Рассмотрим диаграммы тривиального гг-компонентного зацепления ровно
с одним перекрестком на одной компоненте. Таких диаграмм существует две.
Значение функции W на обеих диаграммах должно быть равно ап.
Следовательно, из уравнения (5.3) мы получаем
ап = апо αη+ι (5 А)
ап = ап/ап+1. (5.5)
Эти два условия должны выполняться для произвольного натурального п.
Кроме этого, есть еще соображение "порядка замены перекрестков".
Рассмотрим некоторую плоскую диаграмму L и выберем два перекрестка ри^на
этой диаграмме, см. рис. 5.5.
Обозначим через Lap (для α,β Ε {+,—,0}) диаграмму зацепления,
совпадающую с L вне малых окрестностей Up, Uq перекрестков ρ, q и имеющую тип
а в Up и тип β в Uq (здесь плюс означает наличие положительного
перекрестка '/С:·) минус — наличие отрицательного перекрестка ,у\ , а нуль — отсутствие
перекрестка, т.е. случай, когда диаграмма локально имеет вид Λ г:).
5.5. Алгебра Конвея и полиномы
67
Рис. 5.5. Два способа разрешения перекрестков
Применим соотношение (5.3) к перекрестку р, а затем к перекрестку q.
Мы имеем: W(L++) = VT(L_+) о W(L0+) = (W(L—) о W(L-0)) о (W(L0-) о
W(Loo)).
Рассмотрим теперь то же самое соотношение сначала для q, а затем для ρ
(в обратном порядке). Мы получаем: VF(L++) = H/(L+_)oH/(L+o) = (W(L )о
W(L0-)) о (W(L_0) oW(L00)).
Сравнивая полученные уравнения, мы имеем:
(а о Ь) о (с о d) = (а о с) о (6 о d),
(5.6)
где а = W(L__),h = W(L0-),c = W(L-0),d = W(L00).
Потребуем, чтобы соотношение (5.6) выполнялось для произвольных
четверок элементов а, 6, с, d алгебры, которую мы строим.
В случае, когда оба перекрестка ρ и q находятся в диаграмме L в
отрицательном состоянии, мы получаем аналогичное уравнение
(a/b)/(c/d) = (a/c)/(b/d). (5.7)
Аналогичным образом, если один из перекрестков был положительным, а
другой — отрицательным, то мы получаем уравнение
(a/b)o(c/d) = (aoc)/(bod).
(5.8)
Таким образом, мы нашли некоторые необходимые условия для того, чтобы
функция W(L) была корректно определена. Докажем теперь достаточность
этих условий.
Определение 5.6. Алгебра А с двумя бинарными операциями о и /,
обратными друг другу слева, и фиксированной последовательностью элементов αη,
68
Дистрибутивные группоиды и алгебра Конвея
η = 1, 2,..., называется алгеброй Конвея, если для нее выполняются
соотношения (5.4)-(5.8).
Теорема 5.3. Для каждой алгебры Конвея существует единственная
функция W(L) на диаграммах ориентированных зацеплений, принимающее
значение ап на произвольной диаграмме тривиального η-компонентного зацепления
и удовлетворяющая соотношению (5.3). Эта функция является инвариантом
ориентированных зацеплений.
Доказательство. Покажем сначала, что построенная таким образом функция
является инвариантом зацеплений с перенумерованными (крашеными)
компонентами. Будем использовать индукцию по количеству перекрестков
диаграммы.
Пусть Ck — класс зацеплений, представимых диаграммами, имеющими не
более к перекрестков (таким лее образом будем обозначать и само множество
таких диаграмм).
Основное предположение индукции. Существует корректно
определенная функция W(L) на множестве С&, которая инвариантна относительно тех
движений Рейдемейстера, которые не выводят диаграмму зацепления из
класса Ck', эта функция удовлетворяет соотношению (5.3) для всех троек Конвея,
лежащих в С&.
База индукции (к = 0) очевидна, так как в этом случае класс Ck состоит
только из тривиальных зацеплений, и в этом случае нельзя применять
движения Рейдемейстера, при этом соотношения Конвея также проверять не на
чем: в каждой тройке Конвея по крайней мере два элемента имеют непустое
множество перекрестков.
Чтобы провести шаг индукции, зафиксируем сначала некоторый
канонический способ сопоставления W(L) диаграмме зацепления L Ε С&+1,
упорядочивая компоненты зацепления и выбирая начальную точку (отличную от
перекрестка) на каждой из них.
После этого, мы докажем независимость функции W(L) от выбора точек
отсчета, затем инвариантность относительно движений Рейдемейстера и,
наконец, независимость от перенумерации компонент.
Построение функции W. Перенумеруем компоненты зацепления L.
Фиксируем точку Ъ\ на первой компоненте, точку 62 на второй компоненте, и так
далее, так, чтобы фиксированные точки не являлись перекрестками. Опишем
теперь построение элемента Wb(L) (здесь индекс Ъ обозначает набор 6ι, 62,...
выделенных точек). Начнем обходить компоненты зацепления вдоль
ориентации. Начнем с первой компоненты и точки Ъ\ и пройдем всю первую компоненту
вплоть до &i, затем возьмем 62 и пройдем вторую компоненту, и так далее.
Перекресток ρ назовем хорошим, если мы сначала проходим его снизу, а после —
сверху (при проходе по очереди всех компонент зацепления). Все остальные
перекрестки назовем плохими.
Введем теперь вторую индукцию (по количеству плохих точек). Мы
утверждаем, что можно корректно определить функцию Wb на диаграммах
зацеплений. База индукции очевидна: если все точки — хорошие, то диаграмма
зацепления является восходящей и, следовательно, тривиальной. В этом случае мы
имеем по определению Wb(L) = αη, где η — количество компонент зацепления.
5.5. Алгебра Конвея и полиномы
69
Предположим, что мы определили Wb для всех диаграмм зацеплений с к-\-1
перекрестками, из которых не более т — плохие. Пусть L — зацепление с к + 1
перекрестком, из которых т + 1 перекресток плохой.
Зафиксируем первый плохой перекресток, который встречается при нашем
обходе всего зацепления. Без ограничения общности молено предположить, что
этот перекресток положительный (/\:)· Применим соотношение (5.3) к этому
перекрестку. Мы получим две диаграммы зацеплений: L_, имеющее на один
плохой перекресток меньше, чем диаграмма L (следовательно, Wb(L-)
корректно определено по предположению индукции) и диаграмму Lo, принадлежащую
Ck (поэтому W(Lq) (и, следовательно, Wb(Lo)) также корректно определено).
Для диаграммы L зададим
Wb(L) = Wb(L_)oW(L0). (5.9)
Тем самым мы корректно определили значение функции Wb на множестве
Cfc+i·
Докажем теперь, что функция Wb удовлетворяет соотношению
ИЪ(()<ф) = ИЪ(фф о W0 (j) (5.10)
в случае, если диаграмма /\ принадлежит множеству (7&+ι.
Мы уже использовали это соотношение, чтобы определить значение W.
Однако мы еще не доказали, что такое определение не приводит к
противоречию. Таким образом, соотношение (5.3) еще нужно доказать для всех троек
Конвея из Ck+i, а не только для тех, которые участвуют в определении
функции Wb.
Рассмотрим диаграмму L = L+ и перекресток q этой диаграммы.
Предположим сначала, что перекресток q плохой. Если это первый плохой перекресток,
появляющийся при нашем обходе, то соотношение (5.3) выполняется по
построению.
Применим теперь индукцию (третье предположение индукции) по
порядковому номеру N этой точки среди плохих точек, встречающихся при обходе
компонент зацепления. Предположим, что для некоторого т при N < т
соотношение Конвея имеет место. Пусть ρ — первый плохой (скажем,
положительный) перекресток. По определению значения Wb (i), по второму предположению
индукции (И) и по основному предположению индукции (Hi), в силу (5.6) (iv), и,
опять, по второму предположению индукции (ν) и основному предположению
индукции (vi), мы получаем:
Wb(L++) L Wb(L_+) о W(L0+) "i" (Wb(L__) о W(L-0)) ° (W(L0-) о W(L00))
*= (Wb(L__) о W(Lo-)) о (W(L-o) ° W(L00)) v= Wb{L+.) о W(L+0).
(5.11)
Здесь мы использовали следующие обозначения: первый индекс в Lap
относится к перекрестку р, а второй индекс относится к перекрестку q. Это и есть
соотношение (5.10).
70
Дистрибутивные группоиды и алгебра Конвея
Если перекресток q — хороший (скажем, положительный) для L+, то он
является плохим для зацепления L_. Как уже было показано, равенство Wb(L-) =
Wb(L+)/W(Lo) имеет место в этом случае, поэтому Wb(L+) = Wb(L-) о W(Lq)
является простым следствием. Таким образом, соотношение (5.10) доказано.
Покажем теперь, что функция Wb на зависит от выбора точек
отсчета (порядок компонент остается фиксированным). Для этого
достаточно рассмотреть лишь случай, когда одна точка отсчета (скажем, Ьк)
проходит через перекресток (обозначим его через q), в позицию Ъ'к, см. рис. 5.6.
Рис. 5.6. Изменение точки отсчета
Предположим, что перекресток q положительный. Если он хороший как
для Ъ = (Ьь ..., Ъп) , так и для Ъ' = (Ьь ..., bfc_b Ъ'к, bfc+b ..., Ъп) , то
равенство Wb(L) = Wb'(L) имеет место по определению. Если перекресток q —
плохой в обоих случаях, то мы имеем Wb(L+) = Wb(L-) о W(Lo),Wb'(L+) =
Wb'(L-) о W(Lq). Так как q является хорошим для зацепления L_ в обоих
случаях, мы видим, что Wb(L-) = Wb'(L-) и, следовательно, Wb(L+) = Wb'(L+).
Остается рассмотреть лишь случай, когда перекресток q является хорошим для
Ъ и плохим для Ь' (или наоборот). Это случается лишь тогда, когда обе ветви
зацепления, проходящие через перекресток д, лежат на одной и той лее
компоненте.
Можно предположить теперь, что как по отношению к 6, так и по
отношению к б7 у зацепления L больше нет плохих точек; если бы таковые были, их
все можно было превратить в хорошие, используя соотношение Конвея
(которое оставляет инвариантным равенство Wb(L) = Wb'(L)).
Итак, предположим, что зацепление L не имеет плохих точек по отношению
к 6, следовательно, Wb(L) = ап. Зацепление L имеет единственную плохую
точку q по отношению к Ъ' (по определению, Wv(L) = Wb'(L-)oW(Lo)). Нам
остается заметить, что зацепления L_ и Lq также не имеют плохих точек
относительно Ъ'. Следовательно, W(L-) = an,W(Lo) = αη+ι· Принимая во внимание
0"п — ап° йп+ъ мы получаем Wb(L) = Wb'(L).
Дока^сем теперь, что функция Wb(L) инвариантна относительно
тех движений Рейдемейстера, которые оставляют диаграмму
зацепления в классе Ck+i>
Основная идея состоит в следующем: предположим, что мы применяем
движение Рейдемейстера внутри некоторой области U. Мы имеем две картины
внутри U: до применения преобразования и после применения. Вне области U,
обе диаграммы выглядят одинаково. Если мы можем расставить перекрестки
вне области U таким образом, чтобы получить две восходящие (согласно задан-
5.5. Алгебра Конвея и полиномы
71
ной перенумерации компонент) диаграммы, соответствующие положению до и
положению после внутри области U, то инвариантность очевидна: мы можем
представить две изначальные диаграммы одинаковым образом через
диаграммы тривиальных зацеплений (отличающихся только внутри области U). В
противном случае нужно применить соотношение (5.3) и перейти к рассмотрению
случая описанного выше.
Опишем эту ситуацию более подробно. Прежде всего рассмотрим движение Ωι.
Точки, возникающие или исчезающие при движения Ω ι можно изначально выбрать
хорошими. В этом случае существование петли не влияет на результат
вычисления Wb. По тем же причинам значение Wb не изменяется под действием движения
Ω2, если обе возникшие (исчезнувшие) точки являются хорошими. Если обе
появившиеся (исчезнувшие) точки плохие и не могут быть превращены в хорошие
изменением точки отсчета (это может случиться, если в движении Ω2 участвуют
точки двух различных компонент), следует применить соотношение Конвея к обеим
точкам и учесть, что L_o = Lq- и W(L-o) = W(Lo-), см. рис. 5.7. Поскольку
/
\
V
ι
Рис. 5.7. Различные способы разрешения двух перекрестков
Wb{L.+) = Wb(L—)°W(L-o) = (Wb(L+-)/W{Lo-))oW{L-o) = Wb(L+-), процедура
превращения всех плохих точек в хорошие не влияет на поведение Wb под действием
Ω2. Рассмотрим, наконец, случай Ω3. Предположим, что все точки отсчета лежат вне
области действия движения Ω3. Обозначим через χ точку пересечения верхней и
нижней ветвей, через у — точку пересечения верхней и средней (образующей один проход
и один переход) ветвей, через ζ — точку пересечения средней и нижней ветвей, см.
рис. 5.8
Обозначим зацепление, полученное после выполнения движения Ω3, через L'.
Заметим, что χ не может быть единственной плохой (или единственной хорошей) точкой
из множества {х,у, ζ}. Если к примеру χ хорошая точка, точки у и ζ — плохие, то
отрезок χζ предшествует отрезку ху относительно ориентации, отрезок ху предшествует
yz, и yz предшествует χζ, что содержит противоречие.
Таким образом, если χ является хорошей точкой, то хорошей точкой является
72
Дистрибутивные группоиды и алгебра Конвея
Рис. 5.8. Третье движение Рейдемейстера
также по крайней мере одна из точек у, ζ. Предположим, что такой точкой будет у.
В этом случае перекидывание дуги ху через точку ζ не меняет значения инварианта
Wb по определению. Если точка χ плохая, то одна из точек множества у, ζ (пусть это
будет, ζ) также является плохой. Выпишем соотношения Конвея для точек ζ, χ. Без
ограничения общности будем считать, что обе точки ζ, χ положительны (остальные
случаи рассматриваются аналогично). Получим:
Wh{L++) = Wh{L-+) о W(L0+) = (Wb(L—) о W(L-0))) о W(L0+),
Wh{L'++) = Wh{L'_+) о W{L'0+) = {Wh{L'__) о W(L'_0)) о W{L'0+).
Первый индекс у I.. относится κ ζ, а второй — к х. Поскольку для зацепления
L-- точки χ, ζ хорошие, то Wb(L--) = Wb(L'__) (этот случай был уже рассмотрен).
Диаграммы L_o и Lf_0 совпадают, a Lq+ может быть получено из Lo+ применением
движения Ω2 дважды, что не изменяет Wb. Следовательно, VFb(L++) = Wb(L'++).
Таким образом, мы построили функцию W, которая является инвариантом
зацеплений с отмеченными компонентами.
Покажем, что эта функция является инвариантом зацеплений (не
зависит от отмеченных точек). С этой целью введем операцию замены
перекрестка у( —> [У\ (будем обозначать ее через Ωο). Обозначим частные
случаи движений Ω ι, Ω2, уменьшающих количество перекрестков через Ω^, Ω^".
Нам потребуется следующая лемма.
Лемма 5.1. Всякая диаграмма зацепления может быть преобразована в
диаграмму тривиального зацепления без перекрестков применением движений
Ωο, Ω^ , Ω2 , Ω3·
Мы докажем эту лемму позже.
Заметим, что уравнение Wb(L) = Wb'(L) инвариантно относительно Ωο, т.е.
если L т. е. если V получается из L заменой перекрестка, то Wb(L) = Wy (L) <^>
Wb{Lf) = Wb'{Lf). Как было доказано ранее, оно инвариантно также
относительно движений Ωι, Ω2, Ω3.
5.5. Алгебра Конвея и полиномы
73
Из инвариантности W относительно движений движений Рейдемейстера в
классе Ck+i следует, что для любой стандартной диаграммы Ln тривиального
зацепления из η компонент справедливо Wb(Ln) = Wb'(Ln). Поскольку любая
диаграмма L может быть сведена к тривиальной движениями Ωο, Ω^, Ω^~, Ω3,
то Wb(L) = Wb>(L). Π
Доказательство леммы 5.1. Пусть L — диаграмма зацепления. Отрезок I этой
диаграммы называется петлей, если его начальная и конечная точки совпадают. Петля
называется простой, если она не имеет самопересечений и если в области,
ограниченной этой петлей нет других петель. Будем называть две ветви h,h D L границей
двуугольника, если эти дуги не имеют самопересечений, имеют общие начальную и
конечную точки. Двуугольник называется простым, если он не содержит внутри
себя других двуугольников или петель. На рисунке 5.9 показано, что если L содержит
простой двуугольник, то количество точек пересечения может быть уменьшено
применением движений Ωο, Ω3 (это позволяет сделать двуугольник пустым) и последующим
удалением самого двуугольника движением Ω^~.
Рис. 5.9. Удаление двуугольника
В случае простой петли мы имеем аналогичную ситуацию. На последнем шаге
петля удаляется движением Ω^~. Осталось заметить, что если диаграмма
зацепления имеет по крайней мере одну точку пересечения, то она содержит либо простой
двуугольник, либо простую петлю. Доказательство последнего утверждения является
легким упражнением для читателя.
D
Покажем теперь, что полиномы Джонса, Конвея и HOMFLY являются
частным случаем инварианта W для некоторых алгебр А.
Мы уже доказали, что для каждой алгебры Конвея А существует инвариант
ориентированного зацепления W(-) Ε А со значениями А. Среди всех таких
алгебр существует универсальная алгебра Ац. Она порождена соотношениями
ап,п^ 1 и не имеет других соотношений за исключением (5.4-5.8).
Универсальный инвариант зацеплений, соответствующий универсальной
алгебре, является сильнейшим по сравнению со всеми инвариантами,
получаемыми таким путем. При этом распознавание, т. е. решение вопроса о том,
совпадают ли два элемента алгебры Конвея, является довольно трудным делом.
Приведем примеры алгебр Конвея. Инварианты, которые будут построены,
являются более удобными, чем универсальный инвариант: с их помощью лег-
74
Полиномы Александера, HOMFLY и Кауфмана
че распознаются элементы алгебры А. Приведем способ построения семейства
алгебр Конвея.
Пусть А произвольное коммутативное кольцо с единичным элементом а\ Ε
А и α, β некоторый обратимый элемент в кольце А.
Определим о,/ формулами:
χ о у = ах + Ру (5.12)
и
х/у = оГхх — οΓλРу, (5.13)
где
ап = (Р~\1 - α))η_1αι,η ^ 1. (5.14)
Следующее утверждение непосредственно вытекает из определения алгебры
Конвея:
Предложение 5.2. При любом выборе обратимых элементов а, Р и
элемента а\, кольцо А, снабженное операциями о, / определенными выше, и
элементами ап {см. {5.12,5.13,5.14)), является алгеброй Конвея.
5.6. Реализации алгебр Конвея.
Полиномы Александера,Конвея, HOMFLY
и Кауфмана
Приведем примеры простых инвариантов,происходящих из алгебры Конвея.
Пример 5.3. Пусть А кольцо полиномов от переменного χ с
целочисленными коэффициентами . Пусть а = 1,/3 = ж, αϊ = 1. Тогда W(L) совпадает с
полиномом Конвея (называемым также потенциальной функцией Конвея).
Полином Конвея был первым среди полиномов, удовлетворяющих
соотношениям Конвея. Он был предложен в оригинальной работе Конвея [Con]. Все
другие полиномы и их модификации появились много позже
На рисунке 5.10, изображен знаменитый узел Киношиты-Терасаки. Этот
узел нетривиален. Однако, как легко проверить, полином Конвея для этого
узла равен единице. Так что полином Конвея не всегда отличают тривиальный
узел от нетривиального.
Этот узел имеет нетривиальный полином Джонса. До сих пор неизвестно,
отличает ли полином Джонса нетривиальные узлы от тривиальных. Мы
коснемся этой проблемы ниже.
Пример 5.4. Пусть А кольцо полиномов Лорана от ^/д, где а = q2, Ρ = q{^/q —
-/=), «ι = 1. В этом случае W{L) совпадает с полиномом Джонса от q.
Пример 5.5. Пусть А — кольцо полиномов Лорана с целочисленными
коэффициентами от переменных га, Z. Пусть а = — у, /3 = y,&i = 1. Тогда построенный
инвариант V(l,m) называется полиномом HOMFLY.
Упражнение 5.3. Напишите соотношения типа Конвея для этих
полиномов.
5.7. Полином Александера. Матричное представление 75
Рис. 5.10. Узел Киношиты-Терасаки
5.7. Еще о полиномах Александера.
Матричное представление
Опишем другой способ определения полиномов Александера.
Мы не будем давать доказательства инвариантности этого полинома. С
одной стороны они следуют из свойств дистрибутивного группоида с операцией
а о 6, определенной посредством равенства ta + (1 — t)b. С другой стороны
читатель может проверить все утверждения прямым вычислением.
По данной диаграмме L ориентированного зацепления построим
инвариантный полином следующим образом. Пусть дана ориентированная диаграмма
зацепления L с η вершинами. Построим соответствующую ей матрицу
Александера M(L) следующим образом. (Мы вернемся к таким матрицам в
дальнейшем, когда будем рассматривать виртуальные узлы).
Перенумеруем все перекрестки диаграммы натуральными числами 1,..., п.
В общем случае из каждого перекрестка исходит ровно одна дуга (если
только в диаграмме нет отдельных циклических дуг). Легко видеть, что в каждом
изотопическом классе есть диаграмма без отдельных циклических дуг. В этом
случае сопоставим каждой дуге номер г того перекрестка, из которого она
выходит. Теперь можно построить матрицу инцидентности, в которой перекрестки
соответствуют строкам, а дуги соответствуют столбцам.
Допустим, что ни один перекресток не соответствует одной и той же дуге
дважды (нет петель).Тогда каждое пересечение принадлежит ровно трем
дугам: дуга, образующая переход (номер j), исходящая дуга (номер г), и входящая
дуга (номер к).
При этом г-ж ряд матрицы Александера состоит из трех ненулевых
элементов, расположенных на местах г, j, к. Если г-ж перекресток положителен, то
гпц = 1, rriik = —t, rrtij = t — 1. В противном случае полагаем тпц = t, rrtik = — 1,
rriij = 1 — t.
Очевидно, что определитель этой матрицы равен нулю, поскольку сумма
элементов в каждой строке равна нулю.
Обозначим алгебраическое дополнение к элементу га^/ через Δ^.
Справедлива следующая теорема.
76
Матричное представление
Теорема 5.4. Все Δ^ совпадают между собой с точностью до умножения
на ±tk.
Полином Δ молено нормировать относительно так, чтобы старшая и
младшая степень входящих в него мономов отличались знаком. Более того,
естественным образом молено определить знак естественным образом молено
определить естественным образом так, чтобы получить инвариантный полином
ориентированных зацеплений. Тем самым мы получаем полином Александера,
который мы также обозначим через Δ.
Теорема 5.5. Функция А, определенная на зацеплениях, удовлетворяет
следующему скейн-соотношению:
Αό^ζϊ) - Δ(φ<*)) = (ί1/2 - ί-ϊ/χφ (':). (5.15)
Легко проверить, что для тривиального узла О выполняется Δ (О) — 1·
Таким образом, получаем, что полином Δ совпадает с полиномом Конвея
с точностью до замены переменной χ = t1'2 — t-1'2 . Так что он является
корректно определенным инвариантом зацеплений.
Замечание 5.2. Такой способ построения полиномов типа полинома Алек-
сандера можно найти, например, в [КФ, Сг].
Полином Конвея [Con] может быть получен из полинома Александера
посредством замены переменной: χ = (t* — t~^). Таким образом этот полином,
(обозначенный через С), удовлетворяет скейн-соотношению С( /\·) — ^(у\') =
χ · С( j Г'.). Конвей был первым, кто доказал, что это соотношение (вместе с
С (О) — 1) может быть положено в основу аксиоматического определения
инвариантов узлов. Подход Пржитицкого и Трачика, описанный в этой главе,
является обобщением подхода Конвея.
Глава 6
Подход Кауфмана к полиному
Джонса
В настоящей главе исходя из диаграмм зацеплений мы опишем другой
подход к построению инвариантных полиномов. Он был предложен Кауфманом.
Этот подход очень удобен и позволяет довольно просто строить инвариантные
полиномы. Один из них — скобка Кауфмана — приводит к построению
полинома Джонса от одной переменной. После соответствующей нормировки эти
два полинома совпадают, так что говорят о полиноме Джонса-Кауфмана или
полиноме Джонса в форме Кауфмана. Второй полином — более сильный. Он
носит название полинома Кауфмана (двух переменных)
Второй полином связан с более причудливой, чем первый, техникой. Так,
полином Кауфмана двух переменных является более сильным, чем полином
Джонса.
6.1. Скобка Кауфмана
Вначале попытаемся построить инвариантный полином для
неориентированных зацеплений. Пусть L диаграмма неориентированного зацепления с η
пересечениями. Каждое пересечение может быть "сглажено" (разведено)
двумя способами.
Эти способы L —>· La hL^ Lb показаны на рис. 6.1.
L La Lb L'
Рис. 6.1. Два способа сглаживания диаграммы
Теперь попробуем построить некоторую функцию (в дальнейшем будем
называть ее скобкой Кауфмана) от трех коммутирующих друг с другом
переменных а, 6, с, удовлетворяющую следующим соотношениям:
(L) = a(LA)+b(LB)
(6.1)
78
Глава 6
(LuO) = c(L) (6.2)
(О) = ι. (б.з)
Здесь мы рассматриваем произвольные диаграммы L = у/ , V = /(·> La =
и L^ = .) (■, которые совпадают между собой вне малого круга; внутри
круга диаграммы отличаются так, как показано на рисунке 6.1.
Здесь О означает тривиальный узел, a U означает несвязную сумму.
Попытаемся найти условия на а, 6, с , чтобы получить инвариантный
относительно движений Рейдемейстера полином.
Сначала проверим инвариантность относительно второго движения
Рейдемейстера. Используя (6.1) и (6.2), мы выводим следующие свойства нашей
гипотетической функции:
<(jSh> = «<()(}> + Ь<(JT)> = («2 + ^((Х)) + ab<Qf)> + аЬ0 (}>
= (а2 + б2 + а&с)<(Х)> + αδ(() (':)
Таким образом,
<(^Г)> = (а2 + ^ + «Ьс)((Х)> + ^0 (;)· (б·4)
Из инвариантности функции относительно движения Ω2, мы вывели
равенство (6.4) для всех троек, имеющих вид Ъ , ^^ ОС ВНУТРИ малого круга и
совпадающих вне его. Так что инвариантность полинома, который мы строим,
относительно Ω2 влечет за собой выполнение следующих соотношений: аЪ = 1
и а2 + Ъ2 + абс = 0 и далее Ъ = а-1 и с = —а2 — а-2.
Таким образом, если существует полином в Ζ [α, α-1], инвариантный
относительно Ω2, то он удовлетворяет свойствам, описанным выше и определен
однозначно.
Оказывается, что здесь из инвариантности относительно Ω2 следует
инвариантность относительно Ω3. Обсудим это обстоятельство более подробно.
Рассмотрим две диаграммы ^/^~ и г^-, где одна получается из другой
третьим движением Рейдемейстера. Сглаживая их в одном перекрестке, имеем:
и
■/у / у ■/ у
Сравним правые части этих равенств. Получим: ^?У- = 1-^£. Далее,
применяя Ω2 дважды, имеем:
6.1. Скобка Кауфмана
79
Тем самым "доказана" инвариантность скобки относительно движения Ω3.
Однако при изучении вопроса об инвариантности гипотетического
полинома относительно первого движения Рейдемейстера мы встречаемся с одним
неприятным обстоятельством: добавление (удаление) петли умножает полином
на —а3 или на —а-3. Действительно, применяя (6.1), получаем линейную
комбинацию значений скобок двух диаграмм. А именно, (о } = а{ О } + а_1(. О } =
[а(—а2 — а~2) + а-1]; о = (—а3)(; о } для положительного перекрестка.
Аналогичным образом, ( о } = (—α_3)(; ο ■).
Взяв сумму этих двух слагаемых, получаем (—a )(L).
Таким образом мы доказали, что скобка Кауфмана должна бы
удовлетворять некоторым свойствам, т. е. мы вывели эти свойства из аксиом. Однако мы
до сих пор не установили главное, т. е. существование такой скобки. Докажем,
что она существует.
Теорема 6.1. Существует единственная функция на диаграммах
неориентированных зацеплений со значениями в Ζ[α,α_1]; удовлетворяющая
соотношениям (6.1-6.3) и инвариантная относительно Ω2,Ω3·
Доказательство. Рассмотрим диаграмму L неориентированного зацепления L
с η перекрестками. Перенумеруем все перекрестки диаграммы L целыми
числами от 1 до гг.
Подобно предыдущему мы можем сгладить каждый перекресток двумя
способами, А : // -►.)(■ или В : ^χΛ —>· .) (·· Сгладив каждый перекресток
одним из способов, мы получим набор непересекающихся окружностей на
плоскости.
Определение 6.1. Под состоянием перекрестка мы понимаем одно из двух
возможных его сглаживаний. Под состоянием диаграммы мы понимаем
совокупность из η состояний перекрестков, полученных некоторым сглаживанием
каждого перекрестка.
Таким образом, диаграмма L имеет 2П возможных состояний. Выберем
состояние s диаграммы L. Очевидно, сглаживания превращают L в множество
непересекающихся кривых на плоскости, гомеоморфных окружностям. Это
будет тривиальное зацепление из некоторого количества к компонент; по
определению, значение полинома Джонса-Кауфмана на нем полагается равным
(-α2-α"2)*"1.
Пусть a(s) и β(β) означают количество перекрестков в состоянии А ж В,
соответственно. Пусть 7 означает количество окружностей диаграммы L в
состоянии s.
Если мы сгладим все перекрестки диаграммы L посредством (6.1) и затем
применим соотношения (6.2) и (6.3), то получим
(L) = ^аа^-^\-а2 - а-2)^-1, (6.5)
S
где сумма берется по всем состояниям s диаграммы L.
80
Глава 6
Тем самым мы показали единственность полинома, удовлетворяющего
свойствам (6.1)-(6.3): если такой полином определен, то он выражается по
формуле (6.5).
Осталось показать, что формула (6.5) устанавливает не только
единственность (L), но также и его и существование
Действительно, мы можем определить полином (L) формулой (6.5).
Так определенный скобочный полином удовлетворяет соотношениям (6.2)
и (6.3). Инвариантность построенного полинома относительно Ω2,Ω3 может
быть выведена непосредственно из аксиом. Теорема доказана. D
6.2. Полином Джонса в форме Кауфмана
и скейн-соотношения
Итак, мы имеем корректно определенный скобочный полином [скобка
Кауфмана). Этот полином определен на диаграммах неориентированных зацеплений
и является инвариантным относительно Ω2 и Ω3. Оказывается, что его можно
превратить в инвариантный полином на ориентированных зацеплениях, т. е. в
функцию на диаграммах ориентированных зацеплений инвариантную
относительно всех движений Рейдемейстера.
Рассмотрим диаграмму ориентированного зацепления L Определим w(L)
следующим образом. Сопоставим каждому перекрестку L знак +1 или —1 как
показано на рис. 6.2. Такое число называется локальным числом закрученно-
сти. Взяв сумму таких чисел по всем перекресткам, получаем число закручен-
ности w(L).
-1 \ / -1
Рис. 6.2. Локальное числа закрученности
Легко видеть, что это число является инвариантом относительно Ω2, Ω3, но
не Ωι: под действием этого движения локальное число закрученности
умножается на =Ы. Это обстоятельство позволяет нам нормализовать скобку. Можно
определить инвариантный полином следующим образом:
X(L) = (-a)-^L\\L\), (6.6)
где L — диаграмма ориентированного зацепления и \L\ — диаграмма
неориентированного зацепления, полученного из L "забыванием" ориентации.
Определение 6.2. Назовем инвариантный полиномом X определенный
равенством (6.6) полиномом Джонса-Кауфмана.
Покажем, что полином Джонса-Кауфмана удовлетворяет некоторому скейн-
соотношению. Действительно, пусть L+ = /\ , L- = у\^ and Lq = *) Г: тройка
6.2. Полином Джонса и скейн-соотношения
81
Конвея. Без ограничения общности можно считать, что w(L+) = l,w(L_) =
— l,w(Lo) = О.1 Рассмотрим неориентированные диаграммы К+ = \/\\ =
У(^.,К- = [у\] = \\,Ка = | ) { | = ) (·, а также Кв = ^ . Из
соотношений (6.1) и (6.6) следует, что
*0/О = (-а)-3(а(КА) + α~ι{ΚΒ)) = -а-2(КА) - α~Α{ΚΒ) (6.7)
и аналогично
XI
ν/
(=/у) = ~а2(КА) - а4(Кв), (6.8)
X(Q (:) = (КА). (6.9)
Чтобы исключить К в из (6.7) и (6.8), умножим (6.7) на a4, a (6.8) — на
—а-4 и рассмотрим их сумму. Получим
a^Xi^^J) - αΓΑΧ(^ζ^) = (α"2 - α2)Χ(φ f}). (6.10)
Это и есть искомое скейн-соотношение для полинома Джонса-Кауфмана.
Ясно, что значения полинома Кауфмана для каждого зацепления содержат
только четные степени а.
После замены переменной q = α-4, получаем другой инвариантный
полином, обозначаемый через V и называемый полиномом Джонса, впервые
предложенный Джонсом [Jonl]. Очевидно, что он удовлетворяет следующим скейн-
соотношениям
9_м(Х)) - «nOXy) = (я1* - «г V(() (;)· (6Л1)
Упражнение 6.1. Докажите, что полином Джонса никогда не обращается
тождественно в нуль.
По определению значение полинома Джонса на гг-компонентном
тривиальном зацеплении равно (—<р — g~2)n_1.
Полином Джонса позволяет различать некоторые зеркальные узлы.
Например, можно доказать, что правый трилистник не изотопен левому трилистнику.
Действительно, из (6.11) получаем:
v{(SO) = ч2 ■ по)+«(«* - rtncSb) =
(здесь соотношения Конвея применяются к верхнему левому перекрестку)
= q2 + (q*-qhV((]l)).
1Ή.ά самом деле они равны η + 1,п — 1 и η соответственно; при этом (—α)_3η молено
выносить за скобку.
82
Глава 6
Принимая во внимание
v\yy) = q2(-q~^ -qh + viq1* -q~h = -qi -яК
мы видим, что
&
^(ОО) = q2 + q(q2 -я. 2)(-q2 -q2) = -q4 + q3 + q-
Аналогичным образом доказывается V((5Q) = —q~4-\-q~3-\-q.
Следовательно, правый и левый трилистники не изотопны.
Ниже мы приведем замечательное доказательство Джонса-Кауфмана
инвариантности (более сильного) полинома от двух переменных, называемого
полиномом Кауфмана двух переменных.
6.3. Полином Кауфмана от двух переменных
Подход Кауфмана позволяет построить еще один сильный инвариант —
полином от двух переменных.
Для того, чтобы построить его придется рассмотреть более сложные
соотношения по сравнению с теми, которые приводят к обычному полиному
Кауфмана.
Именно, рассмотрим сначала четыре диаграммы L = ^/,L' = \? ,La =
^(,,Ьв = ^^ неориентированных зацеплений, отличающихся друг от друга
только лишь внутри малого круга.
Мы хотим построить полином D(z,a), который удовлетворял бы локальному
соотношению, в котором участвуют все четыре диаграммы L, L/', La, Lb-
Классический полином Кауфмана от двух переменных α, ζ задается сначала
для оснащенных зацеплений, а затем нормируется с помощью числа закручен-
ности. Его аксиомы таковы:
K(L) + K(L') = z(K(LA) + K(LB));
КЮ) = 1;
K(X# %.)=aK(X);
К{Х# £) = а-1К(Х).
Нормализация очевидна.
Оказывается, что этот полином эквивалентен с помощью замены
переменных полиному с другой аксиоматикой, изобретение которого также
принадлежит Луису Кауфману, а утверждение об их эквивалентности — Раймонду
Ликоришу. Опишем его более подробно.
Положим сначала
D(0) = 1 (6.12)
Выберем в качестве такого соотношения следующее:
D(L) - D(L') = z(D(LA) - D(LB)) (6.13)
6.3. Полином Кауфмана от двух переменных
83
Замечание 6.1. У этого полинома имеется еще "близнец"!), который
удовлетворяет соотношению V(L) + T)(L') = z(V(La) + V(Lb))
Далее, мы используем переменную а "для закручивания" петель. По
определению полагаем
£>(*#{ Π )) = aD(X),D(X#- (^ }) =a-1D(X). (6.14)
Полином D называется полиномом Дубровник.
В дальнейшем нам придется нормировать полином по переменной а, чтобы
он был инвариантен относительно второго движения Рейдемейстера.
Еще нужно определить, как должен изменяться полином D при добавлении
отдельно стоящей окружности. Применяя формулу (6.13) к D(: Q ■) — D( Q .),
мы получаем:
D(LUO)=(l + ^f^JD(L) (6.15)
для любой диаграммы L.
Полином D (также как и скобка Кауфмана) инвариантен относительно Ω2, Ω3
Как и в случае полинома Кауфмана от одной переменной мы нормализуем
эту функцию с помощью w(L), а именно положим
Y(L)=a-w^D(\L\),
где \L\ является неориентированной диаграммой, полученной из L "забыванием
ориентации". Это согласуется со смыслом введенной нами переменной а.
Полученный полином называется полиномом Кауфмана от двух
переменных.
Теперь докажем существование, единственность и инвариантность
относительно движений Рейдемейстера полинома, определенного выше
аксиоматически.
Что касается единственности, то доказательство весьма простое. Сначала
мы определим значения полинома на тривиальных зацеплениях.
Затем для определения полинома на всех зацеплениях применим индукцию
по количеству классических перекрестков. База индукции очевидна: для
тривиальных зацеплений полином Кауфмана двух переменных определяется
согласно формулам (6.12) и (6.15). Шаг индукции использует соотношение (6.13): мы
можем поменять проход и переход и выразить искомое значение через значения
на тривиальных зацеплениях и зацеплений с меньшим числом перекрестков.
Доказательство корректной определенности полинома Кауфмана двух
переменных (версии Дубровник) проводится в том же духе, что и доказательство
для алгебр Конвея: сначала он определяется на восходящих диаграммах с
фиксированными точками, затем доказывается его независимость от выбора этих
точек и инвариантность относительно движений Рейдемейстера. Подробное
доказательство можно найти в оригинальной книге Кауфмана [Каи2].
Имеет место несложное утверждение, которое мы оставляем читателю в
качестве упражнения.
84
Глава 6
Теорема 6.2 (Ликориш). Для каждого фиксированного зацепления У имеет
место следующее тождество для значений полиномов Ό и К:
D(a,z) = -Г™(У)(-1)с(У)К(ш,-гг), (6.16)
где г — корень из —1, а с(У) — число компонент зацепления У.
Совсем недавно используя подход Кауфмана к изучению статистических
сумм, Б.Болобаш, Л.Пебодь, и Д. Вайнрайх [BPW] нашли замечательную
явную формулу для вычисления полинома HOMFLY. Эта формула далее проще,
чем формула для вычисления полинома Кауфмана от двух переменных.
Глава 7
Свойства полиномов Джонса.
Комплекс Хованова
7.1. Простейшие свойства
В настоящей главе мы опишем некоторые свойства полиномов Джонса и
способы их применения к решению некоторых задач теории узлов.
Мы сформулируем также три знаменитые задачи о диаграммах
зацеплений, которые почти сто лет просуществовали в виде гипотез и лишь благодаря
появлению полинома Джонса были решены. Затем мы опишем обобщение
понятия полинома Джонса, так называемый комплекс Хованова, — более сильный
инвариант узлов, обладающий весьма интересными свойствами.
Докажем сначала некоторые свойства полинома Джонса и сделаем из них
некоторые выводы.
Теорема 7.1. 1. Значение полинома Джонса V(L) не изменяется при
изменении ориентации компонент диаграммы.
2. Значения полинома Джонса на зеркальных узлах получаются друг из
друга заменой q —>· q~x.
Доказательство. Первое утверждение очевидно и оставляется читателю в
качестве легкого упражнения (нужно применить индукцию по количеству
перекрестков). Доказательство второго утверждения также требует индукции по
числу перекрестков. База индукции очевидна. Проведем шаг индукции. Пусть
L+ = /\ ,L- = ΛνΓ , Lo = ) Π тройка Конвея и L+,L'_,Lq три диаграммы,
полученные из первых трех заменой всех перекрестков на противоположные.
Очевидно, что {Z/_,Z/|_,Lo} является также тройкой Конвея.
Согласно предположению индукции мы видим, что V(Lq) получено из V(L'0)
посредством замены q —>· q~x. Применим соотношение (6.11) к тройке Конвея
{L+,L_,Lo}. Получим:
V(L+) = q2V(L_) + q(qi - q-^)V(L0),
Учитывая, что {V!_, V+, Vq} представляют собой тройку Конвея, мы
получаем:
V(L'+) = q-2V(L'_) - q-Hq* ~ <Г*)П4) = 4~2V{L'_) + q-^qS - q*)V(L'0).
86
Глава 7
Отсюда видно, что если утверждение теоремы верно для (Lo, L'0) и (L_, Ζ/_),
то оно же верно и для (-L+, £+)· Утверждение верно для Lo по предположению
индукции. Таким образом, если утверждение верно для некоторой диаграммы,
то оно выполняется и для всех диаграмм с той же тенью.
Поскольку утверждение теоремы верно для каждой диаграммы
тривиального зацепления (следовательно для всякой диаграммы тривиального зацепления
с любой тенью), то утверждение верно для каждой диаграммы с любой
заданной тенью. Принимая во внимание, что тривиальные зацепления могут иметь
любые тени, получаем лее лаемый результат
D
Теорема 7.2. Для произвольных ориентированных зацеплений Κι и К2
справедливо равенство
V(K1#K2) = V(K1).V(K2).
Доказательство. Докажем этот факт для полиномов Джонса-Кауфмана.
Достаточно заметить, что скобка Кауфмана мультипликативна
относительно операции связной суммы, а функция w(L) - аддитивна. Первое утверждение
следует из (6.5), а второе — из определения функции w(L).
Π
Замечание 7.1. Тем самым мы доказали мультипликативность для
произвольной связной суммы двух зацеплений.
Аналогичным образом можно доказать следующее.
Теорема 7.3. Для произвольных ориентированных узлов Κι и К2
справедливы следующие равенства
V{KX U К2) = -(q-* + 3*)ΗΚΊ) · V(K2).
Пример 7.1. Рассмотрим два зацепления, представленные на рис. 7.1.
Согласно 7.1, полиномы Джонса этих зацеплений совпадают. Однако эти зацепления
не изотопны, поскольку не изотопны их компоненты.
S
Рис. 7.1. Два неизотопных зацепления с одинаковым полиномом Джонса
Этот пример показывает, что полином Джонса не всегда различает
неизотопные зацепления. Причина состоит в том, операция связной суммы
определена "не вполне корректно". Оказывается, что полином Джонса не является
7.1. Простейшие свойства
87
полным инвариантом и для узлов, см. рис. 7.2. Действительно, пусть L —
диаграмма зацепления на плоскости Р. Допустим, что существует область (7сР,
симметричная относительно линии I так, что dU является прямоугольником,
стороны которого параллельны координатным осям. Допустим, что U
пересекает стороны L трансверсально в четырех точках: две из них лежат на верхней
стороне прямоугольника, а другие две — на нижней. Внутри области U
находится некоторая часть зацепления (обозначенная через R на рис. 7.3).
Предположим, что эти точки симметричны относительно прямой /. Пусть V —
диаграмма, совпадающая с L вне U, и с поворотом диаграммы L относительно I
на 180 градусов внутри области U (при котором R переходит в Я, см. рис. 7.3.
На рис. 7.2 приведен конкретный пример.
Рис. 7.2. Левая диаграмма L; правая диаграмма L'
Лемма 7.1. В этом случае V(L) = V(L').
Доказательство. При отражении части диаграммы Z, знак ε = =Ы
перекрестка не изменяется. Таким образом, w(L) = w(Lf). Надо сказать, что скобка
Кауфмана также не изменяется. С каждым состоянием L естественным образом
связано состояние V'. Осталось заметить, что после сглаживания всех
перекрестков диаграмм L и U согласованным образом количество окружностей
будет одинаковым. Остальное очевидно. D
Такого рода преобразования узлов называются мутациями. Общий вид
мутации изображен на рис. 7.3. Распознавание мутаций — очень важное свойство
инвариантов узлов.
Пример 7.2. Можно показать, что узлы, представленные на рис. 7.2 не
изотопны. Таким образом, полином Джонса не является полным инвариантом.
Глава 7
180"
H
Рис. 7.3. Мутация
Замечание 7.2. К настоящему времени остается открытой проблема о
том, распознает ли полином Джонса тривиальный узел, т. е. верно ли, что
из V(K) = 1 вытекает тривиальность узла К, см. список нерешенных
проблем в Приложении Е. Эта проблема связана с проблемой точности
представления Бурау для кос из четырех нитей (см. работу С. Бигелова [Big2]).
Проблема точности представления Бурау будет сформулирована ниже.
Проблема распознавания тривиального зацепления среди гг-компонентных
зацеплений посредством полинома Джонса была решена недавно отрицательно.
Серия соответствующих примеров (нетривиальных двухкомпонентных
зацеплений с полиномом Джонса, равным — q1'2 — q~x'2, построена Шаломом Элиаху,
Луисом Кауфманом и Морвеном Тистлтуэйтом в [ЕКТ].
Таким образом по полиному Джонса невозможно судить об обратимости
узла.
Полином Джонса удовлетворяет соотношениям типа Конвея, в которых в
качестве слагаемых участвуют только целые и полу целые степени q. В
действительности, полином Джонса является полиномом от q^z. Более точно, имеет
место теорема.
Теорема 7.4. (а) Если ориентированное зацепление L имеет нечетное число
компонент (например, если зацепление является узлом), то V(L) содержит
только целые степени переменной q.
(б) Если количество компонент зацепления L четно, то V(L) содержит
только слагаемые вида q
,/ceZ.
Доказательство. Сначала заметим (это следует явно из определений), что
полином Джонса, вычисленный для m-компонентного тривиального зацепления
равен
(-q-* -q^)m-\ (7.1)
7.2. Первая гипотеза Тейта и теорема Кауфмана-Мурасуги 89
Следовательно, утверждение теоремы справедливо для тривиальных
зацеплений.
Мы можем вычислить значения полинома Джонса для произвольных
зацеплений, используя соотношения типа Конвея (6.11) для полиномов Джонса,
зная их значения для тривиальных зацеплений.
Применим индукцию по количеству перекрестков. База индукции очевидна.
Согласно предположению индукции утверждение верно для диаграмм
зацеплений с меньшим, чем η количеством перекрестков. Пусть L — диаграмма с
η перекрестками. Мы можем превратить диаграмму в диаграмму
тривиального зацепления (например, восходящую) с помощью замены типов перекрестков.
Каждой операции замены перекрестка соответствует тройка Конвея. Выпишем
соотношения (6.11).
Пусть даны три диаграммы L+,L_,Lo (первые две имеют η перекрестков,
а последняя имеет η — 1 перекресток); утверждение теоремы верно для Lq и
для одного из L+,L_. Без ограничения общности можно считать, что это L_.
Для завершения доказательства нужно только установить, что:
1. Количества компонент зацеплений L+ и L_ одинаковы (и поэтому имеют
одинаковую четность);
2. Количества компонент зацеплений L+ и Lo имеют различную четность.
D
Упражнение 7.1. Докажите по аналогии с предыдущим, что в случае
нечетного количества компонент зацепления (е частности, для узлов) полином
Конвея содержит члены только четной степени, а в случае четного числа
компонент члены только нечетной степени.
7.2. Первая гипотеза Тейта
и теорема Кауфмана-Мурасуги
Около ста лет тому назад знаменитый английский физик и исследователь
узлов Петер Гьютри Тейт сформулировал три весьма интересные гипотезы. На
протяжении многих лет они оставались нерешенными. В конце концов две из
них были решены положительно, а одна отрицательно.
Замечание 7.3. Все эти гипотезы формулируются ниже для зацеплений со
связной тенью.
Определение 7.1. Длиной полинома Лорана Ρ от одной переменной
называется разность между старшей и младшей степенью его членов. Обозначение:
spanP.
Под точкой распадения диаграммы L зацепления понимается такой
перекресток диаграммы L, при удалении которого из тени L тень перестает быть
связной.
Первая гипотеза Тейта (1898) гласит: Если диаграмма зацепление L со
связной тенью и с η перекрестками альтернирована и не имеет точек распадения,
90
Глава 7
то не существует диаграммы зацепления L с меньшим, чем гг, числом
перекрестков.
Эта теорема была доказана независимо Кауфманом, Мурасуги [Murl] и
Тистлтуэйтом [Th] в 1987 году.
Теорема 7.5 (Теорема Кауфмана—Мурасуги). Длина полинома Джонса
для зацеплений со связной тенью и η перекрестками меньше или равна п.
Равенство достигается только для альтернированных диаграмм без точек
распадения или для связных сумм таких диаграмм.
В главе 15 мы дадим доказательство теоремы Кауфмана-Мурасуги,
основанное на понятии атома и приведем некоторые обобщения этой теоремы.
Утверждение первой гипотезы Тейта вытекает непосредственно из теоремы
Кауфмана-Мурасуги. Предположим противное, т. е. что у некоторого
зацепления имеется альтернированная без точек распадения диаграмма L с η
перекрестками и некоторая диаграмма L' с менее чем η перекрестками. Тогда
диаграммы L,Z7 не имеют точек распадения, и L' представляют одно и то же
зацепление, причем V имеет перекрестков строго меньше, чем п. Получаем
противоречие: spanV(L) = η > spanV(L').
7.3. Теорема Менаско-Тистлтуэйта и
классификация альтернированных зацеплений
Теорема Кауфмана -Мурасуги явилась важной вехой в проблеме
классификации альтернированных зацеплений. Проблема классификации
альтернированных (простых) зацеплений сведена к случаю зацеплений с фиксированным
числом перекрестков.
Последний шаг был сделан Уильямом Менаско и Морвеном Тистлтуэйтом
[МТ], когда они доказали вторую гипотезу Тейта. Эта гипотеза (известная как
Tait fly ping conjecture) имеет давнюю историю; она была решена лишь в 1993
году.
Будем рассматривать диаграммы зацеплений с точностью до замены
бесконечности или, что то же самое, сферические диаграммы.
В действительности Менаско и Тистлтуэйт доказали следующую теорему.
Теорема 7.6. Любые две диаграммы одного и того же альтернированного
зацепления могут быть получены друг из друга последовательным
применением серии переворачиваний; т. е. движений, показанных на рис. 7.4-
V
Рис. 7.4. Переворачивание
Очевидно, что теорема Менаско-Тистлтуэйта вместе с теоремой Кауфмана-
Мурасуги дает полное решение проблемы классификации альтернированных
7.4. Третья гипотеза Тейта
91
зацеплений. Алгоритм решения задачи состоит в следующем. Сначала
нужно рассмотреть простые альтернированных диаграммы без точек распадения.
Пусть L, U — две такие диаграммы. Посмотрим имеют ли эти диаграммы
одинаковое количество η перекрестков. Если количества перекрестков различны,
то зацепления не изотопны. В противном случае следует применить все
возможные переворачивания (см. рис. 7.4) с целью получить из зацепления L
зацепление U. Так как количество перекрестков при этом не будет меняться,
количество различных диаграмм, которые могут быть получены из L таким
образом, конечно. Следовательно, за конечное число шагов мы можем
установить, изотопны L и U или нет.
Для больших подробностей мы отсылаем читателя к [МТ], где он найдет
точное доказательство, основанное на некоторых индукциях и трехмерном
воображении.
7.4. Третья гипотеза Тейта
Гипотеза звучит следующим образом.
Если количество перекрестков диаграммы узла минимально по сравнению
с другими диаграммами того же узла, и это количество нечетно, то такой узел
не является зеркальным.
Если диаграмма узла является минимальной альтернированной
диаграммой (без точек распадения), то полином Джонса не может быть инвариантным
1 _ 1
при замене qz —>· q 2 из-за его нечетной длины.
Так что узел не может быть зеркальным. Поэтому контрпример третьей
гипотезе Тейта следует искать среди неальтернированных узлов.
Эта гипотеза была опровергнута Тистлтуэйтом в 1998 году, см. [HTW].
7.5. Таблица узлов
Ниже мы приводим таблицу узлов с простыми диаграммами с количеством
перекрестков меньшим или равным семи (с точностью до зеркальной
симметрии). Оказывается, что полином Джонса различает все узлы этой таблицы, так
что по сути дела мы построили начальную таблицу простых узлов, см. рис. 7.5.
7.6. Категорификация Хованова
для полинома Джонса
Перейдем к описанию очень интересного обобщения полинома Джонса,
принадлежащего Михаилу Хованову, [Khl, Kh2], см. также [Viro]. Наше описание
близко к статье [BN3]. Автор этой статьи дает прозрачное объяснение теории
Хованова, вычисляет различные примеры и показывает, что гомологии
комплекса Хованова представляют собой инвариант более сильный, чем полином
Джонса.
Этот инвариант обладает свойством функториальности (впервые доказано
Магнусом Якобсоном [Jac] и Михаилом Ховановым). А именно, рассмотрим
гладкий кобордизм зацеплений L\ и L2, лежащих в двух копиях трехмерного
92
Глава 7
Рис. 7.5. Простые узлы с количеством перекрестков меньше восьми
пространства: R3 χ {0} и R3 χ {1}, представляющий собой двумерную
поверхность в R4 = R3 χ /tG[0;i]. Тогда ему соответствует (с точностью до знака =Ь)
отображение гомологии Хованова зацеплений L\ и L2. В частности, если
зацепления пусты, комплекс Хованова задает (с точностью до знака =Ь) инвариант
двумерных узлов — двумерных поверхностей в четырехмерном пространстве.
Это наблюдение оказалось чрезвычайно полезным; с его помощью Якоб Рас-
муссен [Ras] решил задачу о срезанном роде торических узлов.
Приводимое ниже описание комплекса Хованова алгебраическое: по
диаграмме зацепления строится некоторый алгебраический объект, а затем
доказывается, что он инвариантен при движениях Рейдемейстера; совсем недавно
Бар-Натан (см. [BN5]) обнаружил, что с помощью теории кобордизмов можно
сопоставить диаграммам узлов некоторый топологический объект, который,
рассмотренный с точностью до некоторой факторизации, даст инвариант
узлов; после этого полученный топологический инвариант можно реализовать
в той форме, которую предложил Хованов. Этот подход Бар-Натана сильно
упрощает как доказательство инвариантности, так и его функториальности.
Хованов предложил следующую идею: обобщить понятие скобки Кауфмана,
при помощи некоторых формальных комплексов и их гомологии.
В начале мы опишем некоторое обобщение полинома Джонса и скобки
Кауфмана, следуя Хованову. При этом (ненормированный) полином Джонса
является эйлеровой характеристикой градуированного комплекса Хованова. [КЫ].
Версия полинома Джонса, используемая Ховановым немного отличается от
той, которую мы использовали ранее. Они связаны между собой заменой
переменной.
Сделаем перенормировку скобки Кауфмана согласно следующим аксиомам:
1. Скобка Кауфмана пустого множества (зацепления из нуля компонент)
равна 1.
7.6. Полином Хованова
93
2. (LUO) = (q + q-1)(L).
3. Для всяких трех диаграмм L = ^/.,La = Л (~>Lb — /-N неориентируе-
мых зацеплений, имеет место
(L) = (LA)-q(LB).
Назовем состояние А перекрестка 0-сглаживанием, а состояние В
перекрестка 1-сглаживанием. Если перекрестки перенумерованы, то каждое состояние
может быть рассмотрено как вершина п-мерного куба {0, 1}^j , где X есть
множество перекрестков диаграммы. Высотой вершины куба называется
сумма ее координат.
Пусть диаграмма L имеет гг+ положительных перекрестков и гг_
отрицательных перекрестков; обозначим сумму гг+ +гг_ через η (что равно числу всех
перекрестков).
Обозначим ненормированный полином Джонса через
J(L) = (-l)n-qn+-2n-(L). (7.2)
Определим полином Джонса (обозначенный через J, согласно [BN3])
следующим образом:
Имеем
J(L) = (_l)»-g»+-2«- ^(-g^Wfa + g-1)^8)-1,
s
где 7(s) означает количество окружностей в состоянии s, a(s) — количество
О-сглаживаний, a /?(s) — количество 1-сглаживаний; a(s) -\- P(s) = п.
Этот нормализованный полином J отличается от полинома
Джонса-Кауфмана простой заменой переменной а = γ (—g-1)· А именно,
(_α)-3(η+-η_) £у(в)-/3(в)(_а2 _ а-2)7(.)-1 =
S
(-1)"α-3("+-"-) ^ α-2β{Β)+η ■ (q + q-1)^)-1 =
S
(-1)"α4"—2"+ ^ (-9)^W(9 + д"1)^"1 =
S
(-1)"- qn+~2n- ^(-g)^W(g + g-1)^»)-!.
S
Идея категорификации Хованова состоит в замене полиномов
градуированными векторными пространствами. Это превращает полиномы Джонса в
некоторый гомологический объект.
Замечание 7.4. Так как дифференциалы комплекса Хованова увеличивают
высоту, правильно было бы называть соответствующий комплекс
когомологическим. Однако мы будем говорить "гомологии Хованова", как это
сложилось в литературе. Мы также будем говорить "цепи, циклы, границы"
вместо "коцепи, коциклы, кограницы".
94
Глава 7
С другой стороны это позволяет рассматривать инварианты, которые будут
построены как полиномы от двух переменных.
Мы построим "скобку Хованова" (ненормированную), которая будет играть
ту лее роль для комплекса Хованова, что и скобка Кауфмана для полиномов
Джонса). Мы обозначим ее двойными квадратными скобками.
Начнем с основных определений и введения обозначений.
Определение 7.2. Пусть W = ®mWm градуированное векторное
пространство с однородными компонентами Wm. Назовем градуированной размерностью
W полином qdimVF = J2m У™ ^m Wm.
Определение 7.3. Назовем сдвигом градуировки -{1} : W \-^ W - {1}
операцию на векторном пространстве W = фт1Ут, заданную формулой: [И/{/}]т =
Wm-i. Так что qdim(W · {1}) = qlqdimW.
Клеточный комплекс С = · · · —>· Сг —>· (7r+1 ... состоит из пространств Сг
высоты г.
Определение 7.4. Назовем "сдвигом по высоте" операцию на цепных
комплексах, оставляющую теми лее линейные пространства, но меняющую их
высоту. А именно, для "сдвинутого комплекса" С = C[s], то Cr = Cr~s\ все
дифференциалы сдвигаются соответствующим образом.
Пусть L, η и п± определены так, как указано выше. Пусть X означает
множество всех перекрестков L. Пусть V векторное пространство, порожденное
двумя базисными элементами ν+ и V- градуировки +1 и —1 соответственно.
По определению qdim V = q + q-1. С каждой вершиной куба а Ε {0,1}^^
мы связываем градуированное векторное пространство Va(L) = V®k{r}, где к
(прежнее 7) есть количество окружностей в сглаживании L согласно состоянию
се, а г есть высота \а\ = Σι аг состояния — вершины куба — а (таким образом,
чтобы qdimVa(L) являлся полиномом, соответствующим вершине а куба).
Определим группу цепей комплекса Хованова как Θ(ae{o,i}{*})^a(L) ·
Определим r-ю группу цепей [[L]]r как прямую сумму всех векторных пространств
ВЫСОТЫ Г, Т.е. Фа:|а|=г
Va(L).
Забудем на время о том, что на [[L]] не определен дифференциал. Положим
C:=[[L]][-n_]{n+-2n_}.
Определение 7.5. Градуированной эйлеровой характеристикой
градуированного комплекса С называется альтернированная сумма градуированных
размерностей его групп гомологии. xq(L) = ^2i qdim Нг (С).
Замечание 7.5. Можно показать, что для градуированного комплекса С
градуированная размерность xq(C) равна альтернированной сумме
градуированных размерностей соответствующих групп цепей как и в случае обычных
(ко) гомологии.
Таким образом, можно вычислить эйлерову характеристику комплекса С
(принимая во внимание только градуированные размерности цепей);
дифференциалы будут введены позже.
7.6. Полином Хованова
95
Теорема 7.7. Градуированная эйлерова характеристика комплекса C(L)
совпадает с ненормированным полиномом Джонса J зацепления L, см. (7.2).
Доказательство. Для доказательства нужно лишь взять альтернированную
сумму градуированных размерностей групп цепей и заметить, что qdim(V®n) =
(qdim(y))(g)n. Оставшаяся часть доказательства очевидна. D
Определим теперь структуру комплекса Хованова. Для этого нужно
описать его дифференциалы.
Сопоставим ребрам куба {0,1} последовательности из {0,1,*} длины η
ровно с одним элементом *. Каждое такое ребро соединяет две вершины,
получающиеся подстановкой единицы или нуля вместо *.
Определение 7.6. Высотой \ξ\ ребра ξ называется меньшая из двух высот его
концов.
Таким образом, если мы обозначим отображение, соответствующие ребру ξ
через άξ, то дифференциал будет иметь вид dr = E{i£i=r}(~^)^^·
Нам теперь нужно объяснить, что означает знак (—1)^ и определить
отображения άξ. Для того, чтобы корректно определить дифференциальный оператор
d, чтобы выполнялось условие d о d = 0, достаточно показать, что "частичные
дифференциалы" άξ на двумерных гранях куба представляют собой
антикоммутативные диаграммы.
Куб с дифференциалами, идущими вдоль ребер в направлении возрастания
координаты, называется коммутативным, если каждая двумерная грань
этого куба представляет собой коммутативную диаграмму, и
антикоммутативным, если каждая двумерная грань представляет собой антикоммутативную
диаграмму.
Коммутативный куб может быть преобразован в антикоммутативный
следующим образом. Сначала нужно построить отображения на ребрах таким
образом, чтобы каждая двумерная грань представляла собой коммутативную
диаграмму, а затем снабдить эти отображения άξ знаками. Знак определяется по
следующему правилу. Каждой вершине куба сопоставим номера всех ее
координат в возрастающем порядке: ζι, Z2,..., ik и формальное внешнее произведение
Xi1 Л Xi2 Л · · · Л Xik. Так, например, при η = 3 мы сопоставляем вершине {1,0,1}
внешнее произведение х\ Л х%. Каждое ребро куба, увеличивающее некоторую
j-ю координату, можно рассматривать как внешнее умножение на Xj. Если в
результате применения такого внешнего умножения к "нижней" вершине мы
получаем внешнее произведение, сопоставленное верхней вершине, мы ставим
на ребре знак "плюс", а если нет — то знак "минус". Так, например, на ребре
{1, *, 1} мы имеем знак минус, так как (х\ Л х%) Л Х2 = —х\ Л Х2 Л х$.
Упражнение 7.2. Покажите, что такой выбор коэффициентов
действительно делает коммутативный куб антикоммутативным.
Перейдем теперь к описанию отображений άξ на ребрах куба.
Каждое ребро соответствует изменению состояния в некотором
перекрестке. Геометрически это означает, что либо одна окружность перестраивается в
две окружности, либо наоборот: две окружности сливаются в одну. В первом
96 Глава 7
случае мы будем использовать операцию "коумножения" Δ : V —>· V ® У, а во
втором случае — операцию "умножения" га : V ® V —>· У; эти отображения
будут относиться лишь к тем окружностям, которые возникают при перестройке
данного перекрестка. Если мы имеем, скажем η не меняющихся окружностей,
то наше отображение будет иметь вид Δ ® (Id)®n · {1} или га ® (Id)®71 · {1}, где
тождественное отображение /<i®n относится ко всем не меняющимся
окружностям.
Эти операции определяются следующим образом.
Отображение га:
Г г;+ 0 ί>_ ι—> г;_, г;+ 8) г;+ ι—> г;+,
\ г;_ 8) г>+ ι—» г;_, г;_ 8) г;_ ι—» О
Отображение Δ :
Г г;+ ι—> г;+ 8) г;_ + г;_ 8) ^+
\ г;_ ι—» г;_ 8) г;_.
Отметим, что отображение Δ является мономорфизмом, а отображение μ
является эпиморфизмом.
По причине того, что вершины куба имеют сдвиг градуировки, отображения
га и Δ выбраны сдвигающими градуировку на (—1). Результирующее
отображение сохраняет градуировку.
Тот факт, что все двумерные грани нашего куба являются
коммутативными для отображений άξ (без коэффициентов ±1) проверяется непосредственно.
Следовательно, добавив соответствующие знаки =Ы, мы получим
антикоммутативный куб; тем самым корректно задав дифференциал и, вместе с ним, цепной
комплекс.
Замечание 7.6. Введенное нами определение дифференциала (точнее, знаков
=Ы на ребрах куба) зависит от нумерации вершин. Отметим, что
градуированные группы гомологии не меняются при такой перестановке вершин. Это
утверждение остается читателю в качестве упражнения.
Наиболее важным является доказательство того факта, что все группы
гомологии комплекса Хованова являются инвариантными относительно
движений Рейдемейстера. Поговорим об этом более подробно.
Рассмотрим диаграмму зацепления L. Обозначим через Kh(L) выражение
^2trqdimHr(L). (7.5)
г
Замечание 7.7. Если мы хотим подчеркнуть, что имеется в виду некоторое
поле (или кольцо) F, будем писать Khp(L).
Теорема 7.8 (Основная теорема). Все группы гомологии комплекса Hr(L)
являются инвариантами зацеплений; в частности, таковым является и
полином KHr(L) (от переменных t,q над любым кольцом R); его значение при
t = — 1 совпадает с ненормированным полиномом Джонса J(L).
(7.3)
(7.4)
7.6. Полином Хованова
97
Доказательство. Рассмотрим по одному случаю каждого из трех движений
Рейдемейстера Ωι, Ω2, и Ω3. Остальные случаи рассматриваются аналогично.
Как и в доказательстве инвариантности скобки Кауфмана и полинома
Джонса, инвариантность может быть доказана "локально", с использованием правила
разведения ((L) = (La) — д(Ьв}). Здесь мы будем делать почти то же самое, но
не с полиномами, а с комплексами, и, вместо сокращения подобных слагаемых,
нам понадобится некоторый аналог для гомологии, называемый "принципом
сокращения".
Пусть С — цепной комплекс, и пусть С а С — подкомплекс комплекса С.
Тогда имеет место следующее утверждение.
Лемма 7.2 (Принцип сокращения). 1. Если комплекс С ацикличен, то
Н(С) = Н(С/С).
2. Если комплекс С /С ацикличен, то Η (С) = Η (С).
Оба утверждения очевидным образом следуют из точной
последовательности
> НГ(С') -> НГ(С) -> НГ(С/С) ->..., (7.6)
которая связана с короткой точной последовательностью
О -> С -> С -> С/С -> 0. (7.7)
Докажем теперь инвариантность гомологии относительно движений
Рейдемейстера. Фиксируем некоторое кольцо R коэффициентов.
Инвариантность относительно движения Ωι.
Рассмотрим произвольную тройку диаграмм Q , О и Q , совпадающих
внутри малого круга.
При вычислении 7ί(Ρ), мы получаем следующий комплекс
с = [[■' о"',]] = (isf О ';]] ™ [[■: о ":]]{1>У (7.8)
ЯЛ = ([РО;]]^[[:Я
Это означает, что весь гг-мерный куб, соответствующий диаграмме Q ,
разбивается на два (п — 1)-мерных куба, соответствующих двум
сглаживаниям в выделенном перекрестке (один из этих кубов-комплексов имеет
сдвинутую градуировку); "частичные" дифференциалы между этими двумя кубами по
определению представляют собой отображение т (с точностью до тензорного
умножения на тождественное отображение).
Как легко видеть, все цепи в комплексе для О , у которых малой окруж-
ности о соответствует v+ G V, "убивают" все цепи во, так как v+ играет
роль единичного элемента в V по отношению к умножению га. Таким
образом, все гомологии, которые мы можем иметь в [[ О ]], порождаются цепями,
в которых малый круг помечен как г>_. После нормировки эти гомологии
совпадают с гомологиями (нормированного) комплекса [[ Q ]]. Иными словами,
98
Глава 7
в С(- Q ) мы выделили ацикличный подкомплекс, факторизация по которому
дает комплекс, изоморфный С( О ).
Докажем теперь инвариантность гомологии Хованова относительно
относительно второго движения Рейдемейстера Λ {. —>· ' Ъ . Если мы рассмотрим
ситуацию, возникающую при применении движения Ω2, мы получим
следующие комплексы.
Изначальный комплекс С выглядит так:
О :]]{1} -^ [[■ 0 ]]{2}
?
Δ Τ _ Τ (7.9)
[00]] ■" [[00]]{ι}
Этот комплекс содержит подкомплекс С:
[[^]].Д1} ^ [[:' 0 ']]{2}
С' = О' '<V' (7.10)
0 —> 0
Ацикличность комплекса С7 очевидна.
После факторизации комплекса С по комплексу С, мы получим
Δ Τ Τ (7.11)
w
ОС
]]{!}
Последний комплекс (после соответствующей нормировки) дает те же
гомологии, что и [[" ?Г ]]. Тем самым инвариантность относительно Ω2 доказана.
В случае третьего движения Рейдемейстера Ω3 доказательство
инвариантности гомологии Хованова является более сложным, чем аналогичное
доказательство инвариантности скобки Кауфмана.
Изменение комплекса Хованова при третьем движение Рейдемейстера
выглядит так, как показано на рис. 7.6.
Напомним доказательство инвариантности полинома Джонса от одной
переменной относительно движения Рейдемейстера Ω3. Мы разводим один
перекресток для двух диаграмм, после чего видим, что получившиеся диаграммы
либо совпадают, либо получаются друг из друга применением движения Ω2. Мы
будем действовать аналогичным образом: рассмотрим трехмерный куб
(каждая вершина которого представляет собой куб коразмерности три); два таких
куба, отличающихся третьим движением Рейдемейстера, имеют совпадающие
нижние уровни и отличающиеся вторым движением Рейдемейстера верхние
уровни. Вернемся к доказательству инвариантности гомологии Хованова
относительно Ω2-
7.6. Полином Хованова
99
Рис. 7.6. Изменение комплекса Хованова при движении Ω3
Рассмотрим теперь специальный случай, изображенный на верхнем уровне
рис. 7.6. Соответствующий комплекс С /С содержит подкомплекс
(7.12)
Последний является ацикличным, так как отображение Δ является
мономорфизмом.
Замечание 7.8. Здесь стрелка τ не является дифференциалом. В
дальнейшем стрелка по диагонали вида β = τβ означает, что мы отождествляем
два элемента в кубе.
β
а
—>
\
с£*оч
0
Τ
τβ,
После этого мы видим, что
(С/С')/С"
β
τ
о
—> о
\ τ
—> 7·
(7.13)
В силу принципа сокращения, мы можем применить эту операцию (фак-
торизуя верхнюю грань трехмерного куба по соответствующим ей комплексам
С и по С") для двух кубов показанных на рис. 7.6 (только для их верхних
граней). В итоге получим кубы, показанные на рис. 7.7.
100
Глава 7
γΕ -л/^
Рис. 7.7. Инвариантность относительно Ω3
Полученные два комплекса являются в действительности изоморфными
(изоморфизм устанавливается посредством отображения 2), которое
оставляет неизменными нижние уровни, показанные на рис. 7.7. и отображает пару
(/?ι?7ι) β паРУ /^2,72 на верхнем уровне).
Тот факт, что 2) в действительности является изоморфизмом линейных
пространств очевиден. Для того, чтобы доказать, что он является изоморфизмом
также и на уровне комплексов, нам необходимо установить его
коммутативность с отображениями на вертикальных ребрах. Доказательство этого факта,
а именно, того, что т\ о d\*§\ = ^2*01 и ^ι*ιο = ^2 ° £?2*ιο? остается читателю в
качестве упражнения. D
Как было сказано ранее, полином Хованова (для рациональных гомологии)
строго сильнее полинома Джонса. Пример двух узлов с совпадающим
полиномом Джонса, различаемых комплексом Хованова, показан на рис. 7.8.
Упражнение 7.3. Проделайте эти вычисления явно.
7.6.1. Феноменологические гипотезы
Недавно были сформулированы и доказаны следующие
феноменологические гипотезы ([ΒΝ3]), принадлежащие Дрору Бар-Натану, Ставросу Гаруфа-
лидису и Михаилу Хованову.
Гипотеза 7.1. Для любого простого узла L существует четное числа s = s(L)
7.6. Полином Хованова
101
т
Рис. 7.8. Рациональные гомологии Хованова сильнее полинома Джонса
и полином Kh'(L) от t±1,q±1 с неотрицательными коэффициентами такой,
что
Г KhQ(L) = q*-1 (1 + q2 + (1 + tq4)Kh'(L))
\ KhZ2(L) = <г-1(1 + q2)){l + tq2)Kh'(Lj). ^i4j
Гипотеза 7.2. В случае простого альтернированного узла L число s(L) равно
сигнатуре узла L, а полином Kh'(L) является полиномом от (tq2).
Эти две гипотезы были проверены Б ар-Натаном для узлов со сравнительно
небольшим количеством перекрестков (с семью для Q и одиннадцатью для Z2).
Легко видеть, что из этих гипотез следует, что для альтернированных
простых узлов полином Хованова восстанавливается по полиному Джонса.
В работе Гаруфалидиса [Gar] сформулированы еще некоторые
феноменологические гипотезы. Более подробную информацию о двух сформулированных
гипотезах можно найти на домашней страничке Бар-Натана [BNh].
Гипотеза об альтернированных диаграммах была решена (в случае поля Q
Эун-Су Ле, см. [Leel]. В работе Ле показано, что комплекс Хованова (над Q)
можно рассматривать как начальный член спектральной последовательности,
гомологии которой над Q имеют размерность 2П, где η — количество компонент
зацепления.
7.6.2. Редуцированный комплекс Хованова
Градуированная эйлерова характеристика полинома Хованова равна
ненормированному полиному Джонса, который отличается от нормированного
умножением на (<2 + <2-1)· Оказывается, что можно построить так называемый
редуцированный комплекс Хованова, гомологии которого также инвариантны, при
102
Глава 7
этом его градуированная эйлерова характеристика равна нормированному
полиному Джонса (в той нормировке, которая используется в настоящей главе).
А именно, пусть L — диаграмма ориентированного зацепления. Рассмотрим
соответствующую ей неориентированную диаграмму \L\. Выберем точку χ на ее
ребре, отличную от вершины. В каждом состоянии s диаграммы \L\ имеется
одна окружность, содержащая точку s. Будем теперь рассматривать только такие
цепи в комплексе Хованова, в которых окружности, содержащей ж,
сопоставлен элемент г>+. Соответственно мы переопределим дифференциал, игнорируя
те его члены, в которых окружности, содержащей ж, сопоставлен элемент г>_.
Доказательство инвариантности всех гомологии редуцированного
комплекса Хованова аналогично доказательству инвариантности для обычного
комплекса Хованова. Доказательство см. в оригинальной работе Хованова [Kh3].
С помощью редуцированного комплекса Хованова можно доказывать
важные свойства полинома Джонса.
В [Kh3] доказана следующая
Теорема 7.9. Для альтернированного простого зацепления L без точек
распадения гомологии Хованова занимают ровно одну диагональ q — 2t = const.
Почти альтернированным называется полином вида ±</* Σΐ=ο Ci(~^У ^ гДе
t — некоторое целое или полуцелое число, а все коэффициенты q
неотрицательны.
Так, например, полином —q4-\-q3-\-q является почти альтернированными,
а полином — q2 + q + 1 — нет.
Следствие 7.1. Полином Джонса зацепления, имеющего простую
альтернированную диаграмму без точек распадения, является почти
альтернированным.
Часть II
Теория кос
Глава 8
Косы, зацепления
и представления
групп кос
8.1. Четыре определения группы кос
В предыдущих главах мы рассматривали лишь один способ кодировки
зацеплений (посредством плоских диаграмм)г. Настоящая глава посвящена
введению в теорию кос. С одной стороны, теория кос дает новую точку зрения на
теорию узлов. С другой стороны, косы имеют некоторые внутренние свойства,
которые представляют интерес сами по себе. Так, например, косы, в отличие
от узлов, обладают структурой группы, и эта группа связана с различными
разделами математики и физики.
8.1.1. Геометрическое определение
Рассмотрим прямые {у = 0, ζ = 1} и {у = 0, ζ = 0} в R3 и выберем по га
точек на каждой из этих линий с абсциссами — натуральными числами от 1 до
га.
Определение 8.1. Косой из га нитей называется множество из га
непересекающихся гладких (или кусочно-гладких) путей, соединяющих точки первого
семейства с точками второго семейства (в произвольном порядке) таким
образом, что проекция каждого из этих путей на ось О ζ представляет собой взаимно
однозначное отображение.
Эти гладкие пути называются нитями косы.
Замечание 8.1. Определение косы как набора кусочно-гладких путей удобно
для определения умножения в группе кос. С другой стороны, каждую кусочно-
гладкую косу можно однозначным образом сгладить.
Пример косы показан на рис. 8.1.
Естественно рассматривать косы с точностью до изотопии в трехмерном
пространстве.
ХВ дальнейшем мы также опишем способ кодировки посредством d-диаграмм, который
был упомянут во введении.
106
Глава 8
Рис. 8.1. Коса
Определение 8.2. Две косы Во и В\ называются равными, если они
изотопны, т.е. если существует непрерывное семейство кос Bt,{t E [0,1]},
начинающееся с косы Во и заканчивающееся косой В\.
Определение 8.3. Множество всех кос из т нитей имеет структуру группы.
Произведением АВ двух кос А ж В является приставление косы В снизу косе
А и изменение масштаба вдоль координаты ζ так, чтобы концы кос совпадали
с фиксированными наборами точек.
Единичным элементом {единицей) группы кос служит коса, представимая
вертикальными нитями, параллельными друг другу.
Обратной к заданной косе является коса, получающаяся из данной взятием
зеркального отражения в плоскости ζ = ^, см. рис. 8.2.
е А В АВ С С'1
IIИII
Рис. 8.2. Единичный элемент и операции в группе кос
Упражнение 8.1. Проверьте, что описанная выше групповая структура
корректно определена.
Определение 8.4. Группой кос (Артина) из т нитей2 называется группа,
определенная выше. Обозначение: Вг(т).
2Есть также и другие группы кос, например, косы Брискорна. Они тесно связаны с
диаграммами Кокстера-Дынкина и группами симметрии, см. [Bril, Bri2].
8.1. Четыре определения группы кос
107
Молено рассматривать лишь косы, каждая нить которых соединяют точки
с одинаковыми абсциссами.
Определение 8.5. Такие косы называются крашеными. Крашеные косы
образуют подгруппу в группе кос. Обозначение: Группа крашеных кос из га
нитей РВ(т).
8.1.2. Топологическое определение
Определение 8.6. Пусть X топологическое пространство. Неупорядоченным
га-конфигурационным пространством для X называется пространство всех
подмножеств из га попарно различных точек пространства X (снабженное
естественной топологией). Обозначение: В(Х,т).
Аналогичным образом можно определить упорядоченное
т-конфигурационное пространство.Опо состоит из всех упорядоченных наборов га различных
точек Обозначение: F(X,m).
Пусть теперь X = R2 = С1.
Определение 8.7. Группа кос из га нитей есть группа, изоморфная
фундаментальной группе πι(Β(Χ,τη)).
Определение 8.8. Группа 7Ti(F(X, га)) называется группой крашеных кос из
т нитей.
8.1.3. Алгебро-геометрическое определение
Рассмотрим пространство полиномов степени га с комплексными
коэффициентами от переменного ζ со старшим коэффициентом равным единице.
Очевидно, что это множество (вместе с естественной топологической структурой) го-
меоморфно комплексному пространству Сп: коэффициенты многочленов
можно толковать как комплексные координаты).
Исключим теперь из нашего множества множество Σ7η всех полиномов с
кратными корнями (по крайней мере с двумя совпадающими корнями).
Получится множество Cm\Em.
Определение 8.9. Группа кос из га нитей изоморфна фундаментальной труп-
петп(Сго^т).
8.1.4. Алгебраическое определение
Определение 8.10. Группа кос из га нитей есть группа, заданная (га — 1)
образующими σι,..., сгш-\ и следующими соотношениями:
GiGj = GjGi (8.1)
при \г — j\ ^ 2 (так называемая дальняя коммутативность) и
(ГгСг+гСг = СГг+1^г^г+1 (8.2)
при 1 ^ г ^ га — 2.
Эти соотношения называются соотношениями Артина.
108
Глава 8
Определение 8.11. Слова в алфавите из букв σι и σί будут рассматриваться
как слова в группе кос.
Мы будем также употреблять термин слово-коса — слово в алфавите из
σι, σ ~ , задающее ту или иную косу.
8.1.5. Эквивалентность четырех определений
Теорема 8.1. Четыре определения группы кос, приведенные выше,
эквивалентны.
Доказательство. Самой легкой частью доказательства теоремы является
установление эквивалентности топологического и алгебро-геометрического
определений. В самом деле, пространство всех полиномов без кратных корней со
старшим коэффициентом единица и пространство всех неупорядоченных наборов
из т комплексных чисел (т.е. элементов из С1) гомеоморфны
(соответствующий гомеоморфизм сопоставляет каждому полиному множество его корней).
Так что фундаментальные группы этих пространств изоморфны.
Докажем теперь эквивалентность геометрического и топологического
определений. Как известно, фундаментальная группа не зависит от выбора
начальной точки в связном пространстве. Выберем в качестве начальной точки А
пространства неупорядоченных наборов из т точек набор (1, 2,... ,га).
Рассмотрим пространство R3 как произведение С1 χ R1.
Каждой замкнутой петле, исходящей из А и лежащей в ^(С1,/^),
сопоставим набор кривых в R3 следующим образом. Петля представляет собой
изменение набора точек в зависимости от параметра. При этом точка из набора
описывает при изменении параметра кривую в С1. Каждая из этих кривых
порождает кривую в R3, если к С1 добавить третью вещественную ось,
координата которой задается параметром t кривой. Обратно, набор непересекающихся
кривых, начала и концы которых принадлежат множеству (1,2,..., т), задает
петлю в неориентируемом конфигурационном пространстве, см. рис. 8.3.
Рис. 8.3. Коса из трех нитей
8.1. Четыре определения группы кос
109
Таким образом, с каждой геометрической косой мы связали одну
единственную топологическую косу, при этом изотопным геометрическим косам мы
сопоставили одну и ту же топологическую косу.
Замечание 8.2. Аналогично определяются и косы для произвольного
двумерного многообразия М2: как элементы конфигурационного пространства точек
на М2 или посредством нитей в Μ2 χ /.
Остается показать эквивалентность геометрического и алгебраического
определений. С этой целью мы введем понятие плоской диаграммы косы, аналог
плоской диаграммы зацепления.
Для построения плоской диаграммы косы спроектируем косу на плоскость
Οχζ.
В общем случае мы получим диаграмму, описываемую следующим образом.
Определение 8.12. Плоская диаграмма косы (для случая косы из т нитей)
есть граф, лежащий внутри прямоугольника [1,га] x [0,1], снабженный
следующей структурой и имеющий следующие свойства:
1. Точки [0, г] и [1, г], г = 1,...,га являются вершинами графа валентности
один, остальные точки типа [0, t] или [1, t] не являются вершинами графа.
2. Все другие вершины графа имеют валентность четыре. Противоположные
ребра в таких вершинах образуют угол в 180 градусов.
3. Нити косы, т. е. линии, составленные из ребер графа, проходящие от ребра
к противоположному и идущие от вершины с ординатой один к вершине
с ординатой ноль, должны быть монотонно убывающими относительно
координаты t.
4. Каждая вершина валентности четыре снабжена структурой
"проход-переход".
По аналогии с плоской изотопией диаграмм зацеплений можно определить
плоскую изотопию диаграмм кос, потребовав при этом, чтобы все нити косы
были убывающими на протяжении всей изотопии.
Ясно, что все изотопические классы геометрических кос могут быть
представлены их плоскими диаграммами. Более того, несложными
преобразованиями можно достичь регулярности: того, что все перекрестки (вершины
валентности четыре) будут иметь различные ординаты.
Поэтому всякий элемент геометрической группы кос может быть разложен
в произведение следующих образующих σι: элемент σι для г = 1,..., т — 1
состоит из т — 2 отрезков, соединяющих [/с, 1] и [/с, 0] для всех к ^ г,к ^ г -\- 1,
и двух отрезков [г, 0] — [г + 1,1], [г + 1, 0] — [г, 1], таких, что последний проходит
над первым, см. рис. 8.4.
Различные диаграммы кос могут порождать одну и ту же косу. Перейдем к
описанию соотношений на σι,..., ат.
Пусть нам даны две равные геометрические косы В\ иБ2- Представим
процесс их изотопии в терминах их плоских диаграмм.
по
Глава 8
ι ι+ 1 г ι+ 1
ΥII НУ
Рис. 8.4. Образующие группы кос и их обратные
Каждый конечный промежуток времени в нашей изотопии либо не меняет
расположение (порядок) перекрестков или, по крайней мере, два перекрестка
имеют (на один миг) одинаковые ординаты; в последнем случае диаграмма
перестает быть регулярной.
Мы интересуемся теми моментами, в которых алгебраическое строение
нашей косы изменяется. Легко видеть, что при этом возможны только три случая.
В первом случае (см. рис. 8.5.а) только одна пара перекрестков имеет
одинаковые ординаты. Во втором случае (см. рис. 8.5.6) две нити касаются. В третьем
случае (см. рис. 8.5.в) мы имеем тройную точку пересечения.
X
Ά
<->
<->
<->
<->
Рис. 8.5. Наглядное описание изотопии диаграммы косы
Первый случай описывается соотношением σ^σ^ = σ^-σ^, \г — j\ ^ 2 (это
соотношение называется дальней коммутативностью) или эквивалентным ему
соотношением σί σ ■ = σ ■ σί , \i — j\ ^ 2. Во втором случае мы имеем: аа~х = 1
(или а~га = 1), а в третьем случае получаем одно из следующих трех
соотношений:
ViCi+iCi = Ci+iCiCi+i, (8.3)
(8.4)
8.1. Четыре определения группы кос
111
Очевидно, что второе и третье соотношения могут быть выведены из
первого. Это простое наблюдение оставляется читателю как упражнение.
Доказательство теоремы завершено. D
В группе кос из га нитей естественным образом выделяется подгруппа РВ(гп)
крашеных кос.
Упражнение 8.2. Покажите, что подгруппа РВ(т) является нормальным
делителем в Вг(т), а фактор-группа Вг(т)/РВ(т) изоморфна группе
перестановок S(m).
8.1.6. Стабильная группа кос
Для натуральных чисел га < п, существует вложение Вг(т) С Вг(п): коса
из Вг(т) может рассматриваться как коса из группы Вг(п), в которой
последние (п — га) нитей вертикальны и отделены от остальных.
Определение 8.13. Стабильная группа кос Вт (ос) есть предел групп В г (ή)
при η —>· ос по отношению к этим вложениям.
Группа Вг (оо) имеет копредставление с образующими σι, σ2,..., и
соотношениями GiGj = GjGi для \i — j\ ^ 2,GiGi+iGi = σ^+ισ^+ι для всех
натуральных г.
8.1.7. Крашеные косы
С каждой косой из η нитей связана перестановка из элементов 1,..., щ эта
перестановка переводит каждое к в та, если нить, начинающаяся в /с-й верхней
точке и заканчивается в га-й нижней точке. Крашеные косы — те, которым
соответствует единичная перестановка.
Имеется и другие интерпретации группы крашеных кос РВ(п). Например,
вместо конфигурационного пространства неупорядоченных наборов точек в R2
можно рассмотреть пространство упорядоченных наборов точек.
Фундаментальная группа этого пространства изоморфна РВ(п).
Интересной задачей является нахождение копредставлений группы
крашеных кос из η нитей.
Различные копредставления группы крашеных кос приведены, напр., в [Bir2,
Мака, Sta].
Крашеные косы из η нитей соответствуют петлям в пространстве
упорядоченных наборов точек на плоскости. Они образуют подгруппу конечного
индекса в группе кос.
Существует алгебраический метод Рейдеместера-Шрейера, который
позволяет построить копредставление подгруппы Η группы G конечного индекса
по копредставлению группы G, если G является конечно определенной (см.,
напр., [КФ]).
Справедлива следующая теорема.
Теорема 8.2. Группа РВ(т) порождена косами
bij,l < г <j < гг (8.5)
(см. рис. 8.6).
112
Глава 8
Рис. 8.6. Образующая Ьц группы крашеных кос
Будем доказывать эту теорему индукцией по числу η нитей косы. При η = 2
утверждение теоремы очевидно: каждая крашеная коса из двух нитей является
степенью косы Ъ\ъ — σ\· Допустим, что утверждение теоремы верно для
некоторого п. Рассмотрим крашеную косу dn+i из (п + 1) нити. Если мы удалим
первую нить, мы получим крашеную косу ап из η нитей. Используем тождество
dn+i — \dn+i&n )θ"π·
Согласно предположению индукции коса ап может быть разложена по
образующим (8.5). Последние η нитей косы <in+ian-1 не зацеплены. Выпрямим
их, т. е. сделаем их вертикальными. В этом случае первая нить завивается
вокруг них. Эта коса может быть представлена как произведение Ьц, Ь~- . Это
можно сделать следующим образом: каждый раз, когда первая нить идет под
какой-либо нитью, она должна быть протянута подо всеми нитями до крайнего
левого положения, затем повернута и возвращена в прежнее положение подо
всеми нитями, см. рис. 8.7.
^
с
<J\<J2^2^\
D
bl2bl3
D
Рис. 8.7. Разложение крашеной косы
Таким образом, коса dn+i может быть представлена в виде произведения
кос вида Й1.
8.1. Четыре определения группы кос
113
Одно из копредставлений группы крашеных кос имеет такой вид ([Sta]):
образующие 6^, соотношения
bijbki = bkibij при к < I < г < j или г < к < I < j
bijhkbjk = bjkbijbik = bikbjkhj при г < j < к
bjibkibikbjk = bkihkbjkbji при г < j < к <1.
Доказательство необходимости этих соотношений см. на рис. 8.8,
доказательство достаточности см. в оригинальной статье [Sta].
Рис. 8.8. Соотношения в группе крашеных кос
Крашеные косы и классы отображений
Приведем еще одно описание группы крашеных кос.
Обозначим через Нп группу классов изотопии гомеоморфизмов диска
(круга) с отмеченными η точками на себя при которых все точки граница диска
неподвижны (с точностью до композиции с изоморфизмом, гомотопным
тождественному). Оказывается, группа крашеных кос тесно связана с группой Нп.
Рассмотрим сначала Щ.
Теорема 8.3 (Теорема Александера о гомеоморфизме). Группа Но
изоморфна единичной группе, т. е. каждый гомеоморфизм диска {круга),
постоянный на границе, гомотопен тождественному отображению. Более того,
такая гомотопия может быть выбрана среди тех гомотопий, которые
постоянны на границе.
Доказательство. Рассмотрим диск \ζ\ ^ 1 в одномерном комплексном
пространстве пространстве С1. Пусть ho — тождественное отображение, и пусть
114
Глава 8
hi произвольное отображение диска на себя, постоянное на границе. Согласно
известной теореме отображение hι имеет неподвижную точку внутри круга.
Без ограничения общности можно считать, что эта точка совпадает с центром
круга. Построим теперь искомую гомотопию. Для t Ε (0,1), построим
гомеоморфизм ht следующим образом: ht тождественен внутри кольца {t ^ \z\ ^ 1}.
Внутри круга \z\ ^ t полагаем ht(z) = ί(/ΐι(|)). Очевидно, ht является гомото-
пией, удовлетворяющей условиям теоремы. D
Диск с удаленным конечным множеством точек гомотопически
эквивалентен диску с удаленными малыми кругами с центрами в этих точках (с дырами).
Рассмотрим группу Ηп. Пусть д Ε Нп — гомеоморфизм диска с η отмеченными
точками, который тождественен на границе диска с отмеченными точками, т. е.
на границе круга и на границах дыр.
Этот гомоморфизм может быть продолжен до гомеоморфизма всего
диска, поскольку отображение д может быть продолжено с границы всякой
дыры на всю дыру. (Это можно сделать, полагая отображение тождественным
внутри дыры). Обозначим полученный гомеоморфизм через hi. Из теоремы
Александера следует, что существует гомотопия ht, соединяющая hi с ho = id.
Фиксируем точки χι,..., хп внутри дыр. Для каждого г = 1,..., η множество
(£, ht(xi)),0 ^ t ^ 1 есть дуга, соединяющая точки на верхнем и нижнем
основаниях цилиндра Ι χ D, где / означает интервал времени, a D — диск. На
рисунке 8.9 показаны следы фиксированных точек.
Рис. 8.9. Утолщенная коса
Таким образом мы получили крашеную косу. Эта коса "знает" почти все
об /ι, но не все. При движении окружности мы можем наблюдать за
фиксированной точкой на ней; след этой точки описывает цилиндр. Чтобы описать h с
точностью до изотопии, достаточно рассмотреть цилиндры, соответствующие
всем нитям косы, и отметить следы движения точек по их краям. Крашеная
коса с такой дополнительной информацией называется утолщенной косой.
8.1. Четыре определения группы кос
115
Очевидно, что классы гомеоморфизмов диска с η дырами, постоянных на
границе (с точностью до гомеоморфизмов, изотопных тождественному),
находятся в однозначном соответствии с утолщенными косами. Этот факт остается
читателю в качестве упражнения.
Группа утолщенных кос Нп является расширением группы крашеных кос
Ρ Β (ή). Из приведенных выше рассуждений следует, что группа Нп является
прямой суммой РВ(п) и Ζη (каждое из слагаемых Ζ соответствует
скручиваниям вдоль границ дыр).
Пусть М2 — ориентируемое двумерное многообразие (с краем или без
оного), и пусть 7 — кривая, лежащая внутри М2. Рассмотрим малую окрестность
U кривой 7? гомеоморфную S1 χ [0,1]. Пусть 7ι и 72 — края этой окрестности.
Определение 8.14. (Однократным) скручиванием Депа двумерной
поверхности М2 вдоль кривой 7 называется гомеоморфизм М2 на себя, постоянный
вне области U, который представляет собой полный оборот кривой 72 по
отношению к кривой 7ι? которая, в свою очередь, неподвижна при гомеоморфизме
внутри области U. На рис. 8.10 показано, как скручивание Дена действует на
кривой, соединяющей точку, лежащую на 7ъ с точкой, лежащей на 72 '· мы
показываем куда переходит прямолинейный отрезок.
Также можно рассматривать скручивания Дена произвольной
(положительной или отрицательной) кратности, т. е. степени однократного скручивания
Дена.
Рис. 8.10. Скручивание Дена
Типичным примером скручивания Дена является гомеоморфизм тора,
получаемый скручиванием вдоль меридиана, см. рис. 8.11.
Замечание 8.3. Можно толковать группу кос как группу классов
отображений диска с фиксированными точками в себя. А именно, можно
рассматривать все гомеоморфизмы проколотого диска Рп на себя, которые
тождественны на границе и затем факторизовать их по отношению
эквивалентности.
Такой подход обсуждается в книге [Bir2]. Это позволяет конструировать
различные представления группы кос и решать некоторые специальные
задачи.
Чтобы прояснить ситуацию докажем следующую теорему.
Теорема 8.4. Группа Нп порождена скручиваниями вдоль конечного числа
замкнутых кривых в круге.
116
Глава 8
Рис. 8.11. Скручивание тора вдоль меридиана
Доказательство. Как было доказано выше, группа Нп изоморфна группе
утолщенных кос. Допустим, что гомеоморфизм h Ε Ηη соответствует утолщенной
косе а4, которая является суммой ап + се, где ап Ε Кп, и α Ε Ζη. Здесь мы
используем аддитивную запись, так как имеем дело с прямой суммой. Крашеная
коса ап может быть выражена через образующие 6^, которые соответствуют
скручиванию вдоль кривых обходящих по одному разу точки г и j, см. рис. 8.12.
Рис. 8.12. Петля вокруг двух отмеченных точек
Утолщенная коса а порождена скручиванием Дена вдоль кривой,
обходящей а.
Суммируя сказанное выше, получаем утверждение теоремы.
D
Скручивания Дена играют ключевую роль в теории гомеоморфизмов
двумерных ориентированных поверхностей. А именно, имеет место следующая
теорема
Теорема 8.5 (Теорема Дена—Ликориша). Пусть М2 — двумерное
ориентированное замкнутое многообразие. Тогда любой сохраняющий ориентацию
8.2. Зацепления как замыкания кос
117
гомеоморфизм многообразия М2 па себя может быть представлен как
композиция скручиваний Дена и гомоморфизмов, гомотопных тождественному.
Первое безупречное доказательство этой теоремы (сформулированной Де-
ном) было дано Раймондом Ликоришем в 1962 (см. [Lic2])
Эта теорема нам понадобится для изучения трехмерных многообразий.
8.2. Зацепления как замыкания кос
С каждой диаграммой косы можно связать плоскую диаграмму узла (или
зацепления) следующим образом.
Определение 8.15. Замыканием косы Ъ называется зацепление С 1(b),
полученное из Ъ соединением нижних концов косы с верхними концами так как
показано на рис. 8.13.
Рис. 8.13. Замыкание косы
Очевидно, что изотопные косы порождают изотопные зацепления.
Замечание 8.4. Замыкание косы обычно рассматривается как
ориентированное зацепление: все нити косы ориентируются сверху вниз.
Некоторые косы порождают узлы, а некоторые — зацепления. При
вычислении количества компонент зацепления полезно иметь в виду следующее простое
наблюдение. Существует естественный эпиморфизм группы кос на группу
перестановок Σ : В г (η) —>· Sn, определенный следующим правилами σι —>· s^, где Si
означают образующие группы перестановок — транспозиции, переставляющие
г-й и г + 1-й элементы.
Рассмотрим косу В. Очевидно, что для всех чисел р, принадлежащих к
одной и той же орбите естественного действия (элемента Σ (В)) на множестве
1,..., п, соответствующие верхние точки косы с абсциссами ρ тоже
принадлежат одной и той же компоненте зацепления.
Следствием этого является следующее утверждение.
118
Глава 8
Предложение 8.1. Количество компонент замыкания зацепления С 1(B)
равно количеству орбит действия группы, порожденной Σ (Б).
Упражнение 8.3. Постройте косы, замыкание которых представляют
собой оба трилистника и восьмерку.
Неизотопные косы могут, вообще говоря, порождать изотопные зацепления.
Этот вопрос будет рассмотрен в дальнейшем.
Интересным вопросом является определение минимального количества
нитей косы, замыкание которой порождает заданный класс изотопии L.
Обозначим это число через Braid(L).
Важная теорема на этот счет принадлежит Джоан Бирман и Уильяму Ме-
наско.
Теорема 8.6. Для любых двух узлов Κι и К2, справедливы следующие
равенства:
Braid(K1#K2) = Вгага(Кг) + Braid(K2) - 1.
На рис. 8.14 показано, что если Κι может быть представлен косой с η
нитями, и К2 косой с т нитями, то К\фК2 может быть представлена косой с
(п + т — 1) нитями. Это доказывает неравенство "^".
Рис. 8.14. Связная сумма кос
Систематическое изучение зацеплений посредством представления их
замыканиями кос (включая теоремы Маркова и Александера, которые мы обсудим
ниже) было проведено в серии работ Бирман и Менаско [Birl, BM2, ВМЗ, ВМ4,
ВМ5, ВМ6].
8.3. Косы и полином Джонса
119
8.3. Косы и полином Джонса
В начале мы сформулируем знаменитые теоремы Александера и Маркова,
которые будут использоваться ниже.
Теорема 8.7 (Александера, доказательство см. в главе 9). Для каждого
зацепления L существует коса В такая, что С 1(B) = L.
Теорема 8.8 (Маркова, доказательство см. в главе 11). Замыкания двух
кос βι и β2 представляют собой изотопные зацепления тогда и только тогда,
когда βι может быть преобразована в β2 последовательностью
преобразований (движений Маркова), показанных на рис. 8.15 (на правом рисунке снизу
добавляемый перекресток может иметь любой тип).
А
1 1 1
в-1
1 1 1
А
I I 1
в
1 I 1
А
А
\
X
/ \
Рис. 8.15. Движения Маркова
Главная идея построения полинома Джонса от двух переменных такова.
Можно рассматривать функции, похожие на те, которые используются в
теории представлений групп и изучать их свойства. Оказывается, что некоторые
такие функции (так называемый след Окнеану) очень хорошо ведут себя при
движениях Маркова.
Замечание 8.5. В работе [Jon2] Джонс использует нестандартное
обозначение для образующих групп кос, а именно, в качестве образующей σι он
выбирает образующую, переставляющую нити с номерами г и г + 1 так, чтобы
они образовывали положительный перекресток (то, что мы ранее
обозначали через сг"1). На протяжении настоящего раздела будем придерживаться
обозначений Джонса.
Ниже будет нам понадобится следующее замечание. Если добавить
соотношения σ\ = 1 к стандартным соотношениям группы кос Вг(п), то получится
группа перестановок Sn.
Определение 8.16. Алгеброй Гекке H(q,n) называется алгебра над полем С
от формальной переменной q, заданная следующим копредставлением:
(9i,---,9n-i\9i
(Я ~ V)9i + q,
Ι,.,.,η- l,gigi+igi = 9%+ι9%9%+ΐιί = 1,2,...,η
9i9j = 9j9i,\i-j\ > 2).
2,
(2)
120
Глава 8
Имеется естественное вложение алгебр Гекке ··· С H(q,n — 1) С H(q,n) С
H(q,n+l).
Сформулируем теорему о следе Окнеану.
Теорема 8.9 (Окнеану, [HOMFLY]). Для каждого ζ Ε С существует след —
линейная функция tr от переменных z,q — на H(q,n), определенная
следующими аксиомами:
1.
tr(ab) = tr(ba);
2.
tr(l) = 1;
3.
tr{xgn) = ztr(x)
для каждого
χ Ε H(q,n).
В случае п = 0 последняя формула означает, что ti(gi) = ζ.
Ниже мы приводим доказательство этой теоремы, принадлежащее
Джонсу, [Jonl]. Оно слегка отличается от оригинального доказательства Окнеану и
приводит к построению полиномов Джонса.
Доказательство. Главная идея доказательства состоит в следующем. Если к
соотношениям группы кос добавить соотношения af = e, мы получим группу
перестановок. Эта группа конечна, и с ней удобно работать.
В частности, каждый элемент этой группы с образующими pi,... ,ρη_ι, где
Pi транспозиция г-го и (г + 1)-го элементов, единственным образом
представляется в виде
{(PiiPh-l · · -Pii-fci)(Pi2 · · -Pi2-k2) · · · (Pi3 · · -Pi3-k3)} (8-6)
для некоторых if
1 < ϊχ < i2 < - - - < ip < η - 1. (8.7)
Алгебра Гекке имеет квадратичные соотношения, отличные от д? = 1, а
именно:
9г =(Я~ 1)& + Q· (8-8)
Оказывается, что они ничуть не хуже, чем соотношения в группе
перестановок. Именно, каждая коса может быть сведена к "базисной косе" с некоторыми
коэффициентами, для которых легко определяется след Окнеану.
Множество "базисных" кос задается теми же самыми словами, что и
элементы группы перестановок группы перестановок.
{(9ii9ii-i · · · 0ii-fci)(0i2 · · · 9i2-k2) · · · (9iP · · · 9iP-kp)} (8.9)
8.3. Косы и полином Джонса
121
при
1 < i\ < %2 < · · · < гр < η — 1.
Достаточно показать, что для каждого слова W типа (8.9) и для любой
образующей д^, слова Wgi и W д~ могут быть представлены линейными
комбинациями слов типа (8.9).
В силу соотношений gf = (q—l)gi-\-q, достаточно рассмотреть только первый
случай.
Допустим, что W разложено в произведение W\ · · · И^, где образующие gi
в каждом Wj имеют убывающий порядок, а первые буквы в словах W^s имеют
возрастающий порядок (в смысле (8.9)). Идея состоит в следующем.
Дополнительная образующая gi может быть "протащена сквозь" Wk- Затем ее можно
"протащить сквозь" Wk-i,... и так далее до конца.
Для простоты будем считать, что слово Wk имеет вид:
(0ii0ii-1...0ii-fci)· (8·10)
Тогда в случае г = i\ — к\ — 1, новая образующая просто добавляется к слову
Wk-> тем самым рассматриваемое слово имеет искомый вид.
Если г > ζι, то слово Wgi уже имеет тип (8.9) поскольку gi может быть
истолковано как новое слово Wk+i.
Если г <i\ — к\ — 1,то мы переставляем gi со словом Wk и не делаем ничего
со словом Wk: работаем только с W\... Wk-\g%-
В случае г = i\ — к\ — 1 ситуация опять простая: в конце слова мы получим
gf, что может быть преобразовано в линейную комбинацию элементов gi ia е.
Таким образом, все слово представляет собой (q - 1)W + qW\ ... Wk-iW^ где
под W'k подразумевается д^ .. .^i-fci-i (если /ci=0, это слово пусто).
В случае ii—ki — 1 ^ г ^ i\ имеет место следующая ситуация: мы
переставляем gi с последними буквами слов Wk до тех пор, пока это возможно и получаем
при этом следующее подслово в Wk'· gigi-igi, которое равно gi-igi9i-i- Все
буквы в слове Wk, расположенные до этого под слова перестановочны с gi-i- Так
что мы можем переместить <^-ι влево относительно Wk·
Таким образом, мы получили линейную комбинацию слов W\ ... Wk-ig^Wk
и W\... Wk-igiW^ для некоторого г'. Во всех случаях г' меньше, чем индекс
первой буквы в слове Wk-
Следующий шаг таков же как и предыдущий: мы протаскиваем ду сквозь
Wk-i- Затем мы проделываем то же самое с Wk-2 и так далее. Стоит лишь
заметить, что индекс буквы, которую мы протащили, меньше индекса начальной
буквы последнего пройденного слова Wj. Благодаря этому конечный
(пройденный) отрезок изменяемого слова всегда имеет вид конечного отрезка некоторого
слова вида (8.9), причем длина такого "хорошего отрезка" постоянно
увеличивается.
Теперь мы видим, что размерность H(q,n) не превышает п\ (количество
перестановок). Доказательство того, что алгебра не вырождается до тривиальной
хорошо известно и может быть найдено в [Bourb].
Вышеприведенная конструкция показывает, что для кос из (п + 1) нити
достаточно рассматривать только те образующие, которые содержат
образующую дп ровно один раз. Теперь мы готовы определить след Окнеану явным
122
Глава 8
образом (используя метод индукции по числу нитей) посредством следующих
начальных формул:
tr(l) = 1
и
tr(xgny) = ζ · tr(xy)
для всех x,yG H(q, n).
Главной трудностью является доказательство свойства ti(ab) = tr(ba).
Применим индукцию по п. Допустим, что свойство верно для χ,ί/G H(q,n).
Единственным утверждением, которое не вытекает непосредственно из определения,
является ti(gnxgny) = ti(xgnygn). При доказательстве того, что для
некоторого элемента а Ε Н(п -\- 1) и для произвольного Ъ Ε Η (η + 1) имеет место
tr(ab) = tr(ba) достаточно проверить это лишь для Ъ = дп и Ъ Ε i/n. Остальное
следует из определения.
Проверку достаточно провести для случая, когда одним множителем
является элемент дп а другой принадлежит Нп-\- Очевидно, что для этого
достаточно рассмотреть следующие три случая:
1. х,у Ε #η_ι;
2. один из элементов х,у принадлежит i/n_i, другой равен адп-\Ь\
3. χ = адп-хЬ,у = cgn-id„ где a,b,c,d Ε #η-ι·
Первый случай тривиален, поскольку образующая дп коммутирует со всеми
элементами из Нп-\.
Во втором случае (мы рассматриваем лишь случай, в котором у Ε i/n-i? и У
коммутирует с дп\ случай χ Ε ϋη-\ полностью аналогичен рассматриваемому):
tr(gnagn-ibgny) = tr(a#n#n_i#nfo/) = tr(a#n_i#n#n_ifo/) =
ζ · tr^^fo/) = (q- l)z · tr{agn-iby) + qz · tr(afo/) =
((^-l)z2 + ^)tr(a6y)
и
^{адп-хЪдпудп) =
^(agn-xbgly) = (q - 1) tr(a#n6#n_i?/) + qtr(agn-1by)
= z(q - 1) tr(a#n_ifo/) + gz · tr(afo/) =
(ς — l)z2 ti(aby).
Наконец, в третьем случае имеем:
tr(gnagn-ibgncgn-id) =
tr(agngn-ignhcgn-id) = tr(agn-igngn-ihcgn-id) =
ζ-ti(agl^bcgn-xd) =
z(q - 1) ti(agn-ihcgn-id) + zq · ti(ahcgn-id) =
z(q — 1) ti(agn-ibcgn-id) + z2q · ti(abcd)
8.3. Косы и полином Джонса
123
tr(agn-ihgncgn-idgn) =
tr(agn-ihcgngn-ignd) = tr(agn-ibcgn-igngn-id) =
ζ · tiiagn-ibcgl^d) =
z(q - 1) ti(agn-ihcgn-id) + zq · ti(agn-ibcd) =
z(q — 1) ti(agn-ibcgn-id) + z2q · ti (abed).
Таким образом шаг индукции завершен, и след Окнеану определен
корректно.
Теорема доказана.
D
Как следует из теоремы, свойства 1, 2, и 3 позволяют нам вычислить след
для любого элемента из H(q,n). В самом деле, сначала мы можем
преобразовать его в линейную комбинацию "базисных" элементов. Затем,
воспользовавшись ti(xgny) = ztr(xy), свести задачу к случаю кос с меньшим числом нитей.
И потом применить метод индукции по числу нитей.
Пример 8.1. Вычислим tT(gig29392)· Имеем:
tr(#i#2#3#2) = ζ · tr(£i02) = z(q - 1) tr(0i02) + zq · ti(gi) =
z3(q- l) + z2q.
Рассмотрим ориентированное зацепление как замыкание косы. Для
построения инварианта зацеплений в виде функции, заданной на косах, следует
изучить поведение этой функции под действием движения Маркова.
Функция tr является инвариантом относительно первого движения Маркова
(сопряжения). Кроме того, она ведет себя достаточно хорошо при втором
движении Маркова. Для завершения построения инварианта нам осталось лишь
провести нормализацию.
Нормализуем сначала все образующие gi таким образом, чтобы оба типа
второго движения Маркова (т. е. умножения элемента из H(q, η) на дп и на д^1)
действовали на след Окнеану одинаковым образом. Для того, чтобы это
сделать, введем переменную θ такую, что tr(B^) = tr((©#z)-1)·
Простое вычисление дает:
θ2 = I д ) = z-q+1
ζ qz
Положим λ = θ2. Тогда qz\ = ζ — q + 1 =^> ζ = -^Егр
Теперь мы готовы определить инвариантный полином.
Определение 8.17. Полином Джонса от двух переменных Xl(</, λ)
ориентированного зацепления L определен равенством
XL(q,X) = (%~^Х (x/A)e(a)tr(7r(a)),
124
Глава 8
где a G В г (ή) означает косу с замыканием L, е — длина косы се, т. е. количество
букв вида σι минус количество букв σ~ в записи косы а. Очевидно, что это
число не зависит от выбора слова, представляющего косу а. Далее, π(σ^) = gi.
Обозначение. Значение полинома X на зацеплении L будем обозначать
через Xl] переменные будем писать в скобках.
Инвариантность X относительно сопряжения очевидна (следствие
инвариантности следа и длины е относительно сопряжения). Покажем инвариантность
полинома X относительно второго движения Маркова.
Пусть а — коса из η нитей, χ — соответствующий ей элемент из H(n,q).
Пусть е — длина косы а. Обозначим через L замыкание С 1(a), а через V —
С1(аап). Имеем:
^ = (^))n(VX)"ltr(^) =
\y/X(l-q)J '[ \V\(l-q)
= xL^±Vx-^- = xL.
q\ - 1 VA(1 - q)
Инвариантность функции Х при умножении косы а на σ"1 доказывается
аналогично.
Теорема 8.10. Для каждой тройки Копвея полином Джонса от двух
переменных удовлетворяет следующим соотношениям Конвея:
1 X .--. -ybqX, -, =^Х.
vm .-ν/. ν :··\λ ^ λ λ;
Доказательство. Действительно, рассмотрим три диаграммы, отличающиеся
только в одном перекрестке. Диаграмма /\ имеет перекресток σ^, ,у\
имеет перекресток σ~ , а : V. не имеет перекрестка; в остальном эти диаграммы
совпадают.
Из соотношений алгебры Гекке имеем:
</<D)=(* - xx) (/)+^УО-
Имеем, Х^ = V\ti(gt)M,X = -±= И(дГг)М,Х, f = Μ, где Μ об-
/V У\ У У
щая часть всех диаграмм.
Выписывая соотношения в алгебре Гекке gi = (q — 1) + qg~ , получаем
желаемый результат. D
Проводя замену переменных, мы получим скейн-соотношение для полинома
HOMFLY. Пусть t = yf~\yf~q, х = (л/Я ~ 7f )· Замена
переменных превращает
XL(q,X) в PL(t,x). Это и есть знаменитый полином HOMFLY, [HOMFLY].
8.4. Представления групп кос
125
Теорема 8.11. Справедливы следующие соотношения Конвел:
ГХР .--.. -tP --., =хР,
/\ ■■■/>" у у
Доказательство полностью аналогично приведенному выше.
8.4. Представления групп кос
8.4.1. Представление Бурау
Наиболее естественным путем для поиска представлений группы кос
является следующий. Молено рассмотреть группу кос Вп {= Вг(п)) и попытаться
представить косы матрицами η χ п. Более точно, молено связать с элементом
σι блочно-диагональную матрицу с блоком 2x2, расположенным в двух
строках (г, г + 1) и двух столбцах (г, г + 1) и остальными блоками размера (1 χ 1),
равными 1 и расположенными на главной диагонали. Очевидно, что для
такой матрицы должны выполняться некоторые соотношения коммутирования
между образами σ^,σ^ где \г — j\ ^ 2. Если взять матрицы, соответствующие
σι с одинаковыми (2 χ 2)-блоками (но на разных местах), то останется только
проверить соотношения g\G2(J\ = 02(У\(У2 для матриц размера 3x3. На этом
пути легко получается представление, в котором блок матриц размера 2x2
выглядит так:
(ж7* S)· (8Л1)
Это представление называется представлением Бурау группы кос. Оно было
предложено Бурау, [Bur].
Точность (т. е. мономорфность) этого представления была открытым
вопросом на протяжении долгого времени. В работе [Bir2] Джоан Бирман доказала
точность этого представления для группы кос из трех нитей.
В работе [Моо91] Муди построил первый пример нетривиального элемента
из ядра представления Бурау (группы кос с большим, чем три, количеством
нитей).
К настоящему времени проблема точности представления Бурау решена
положительно для η ^ 3 и отрицательно для η ^ 5; см., например, [Bigl]. Случай
η = 4 до сих пор открыт. В [Big2] Стивен Бигелов указал на связь между
проблемой распознавания тривиального узла полиномом Джонса одной
переменной и точностью представления Бурау для кос из четырех нитей.
Более того, по причине сложности проблемы распознавания Бигелов
считает, что проблема точности представления Бурау при η = 4 неразрешима с
помощью современных компьютерных средств.
Мы приведем доказательство точности представления Бурау при η = 3 и
дадим контрпример для η = 5 следуя Бигелову [Bigl, Big2].
Заметим сначала, что представление Бурау приводимо: оно имеет
тривиальный собственный вектор (1,..., 1) с собственным значением 0. Таким образом,
существенным является приведенное представление Бурау, которое отображает
126
Глава 8
группу кос из η нитей в матрицы размера (п — 1) х (п — 1). Дальнейшая
геометрическая интерпретация относится именно к приведенному представлению
Бурау.
Сначала рассмотрим следующую интерпретацию группы кос и
представления Бурау. Обозначим через Dn единичный круг на комплексной плоскости
с η отмеченными точками в нем χι,..., жп, расположенными подряд на
вещественной оси. Множество всех автоморфизмов с точностью до изотопии, как
известно, представляет собой интерпретацию группы кос Вп. Выберем в
качестве начальной точки do точку —г.
При этих соглашениях представление Бурау можно толковать следующим
образом. Для каждого β Ε Вп можно рассмотреть количество полных оборотов
элемента β в направлении против часовой стрелки или, что эквивалентно,
количество образующих в любом слове, представляющем этот элемент. Тем самым
определен гомоморфизм h : Вп —>· Z. Можно построить накрытие Вп —>· Вп с
действием группы Ζ на Вп. Эта группа порождена образующей (q). Рассмотрим
группу Ηι(Βη). Согласно вышеприведенным аргументам эта группа допускает
структуру модуля над Ζ [ς, ς-1]. Пусть do — прообраз точки do при
отображении h.
Представление Бурау возникает из гомоморфизмов модулей. Более точно,
пусть β означает гомоморфизм, представляющий косу β Ε Βη. Индуцированное
действие β на πι (Αι) удовлетворяет условию h о β = h. Поэтому существует
единственное поднятие β косы β такое, что следующая диаграмма
коммутативна:
(Dn,d0) -> (Dn,d0)
I I
(Αι, do) -► (Αι, d0).
Далее, β коммутирует с q. Таким образом, β индуцирует гомоморфизм Ζ^1]-
модулей, обозначаемый /3*. Итак, мы можем определить представление Бурау
посредством
Вигаи(Р) = /3*.
Нетрудно проверить, что такое определение представления Бурау совпадает
с редуцированным.
Проверим теперь, что это представление точно в случае трех нитей. Сначала
введем обозначения из [Big2].
Определение 8.18. Вилкой называется дерево F с четырьмя вершинами do,
Pi, pj, z и тремя ребрами, вложенное в D такое, что:
1. В F нет отмеченных точек, кроме Pi,Pj]
2. F пересекается с dDn только в точке do;
3. Все три ребра дерева F имеют ζ в качестве вершины.
Определение 8.19. Ребро дерева F, содержащее do, называется ручкой
вилки F. Объединение оставшихся двух ребер можно считать одним ребром;
назовем его зубцом вилки F и обозначим его через T(F). Ориентируем зубец T(F)
таким образом, чтобы ручка вилки F располагалась справа от зубца T(F).
8.4. Представления групп кос
127
Определение 8.20. Стеблем называется ориентированное ребро N в Dn
такое, что
1. Стебель N ориентирован от do к некоторой другой точке X из dDn\
2. NndDn = {d0,X};
3. Одна из двух связных компонент множества Dn\N содержит ровно одну
отмеченную точку.
Рис. 8.16. а) Вилка; б) Стебель.
Пусть F и N — вилка и стебель соответственно. Определим спаривание
(N,F) G Z[g±:L] следующим образом. Без ограничения общности можно
считать, что T(F) пересекает стебель N трансверсально. Пусть ζι,... ,Zk —
точки пересечения T(F) и N (порядок нумерации несущественен). Для каждого
г = 1,..., к обозначим через 7г ДУГУ в Dn, которая идет от do к ζι вдоль F и
затем обратно к do вдоль N. Пусть а^ означает число такое, что h(ji) = qa\
a Si есть знак пересечения N и F в точке ζι. Положим
к
(N,F) = ^2eiqa\ (8.12)
г=1
Можно легко проверить, что введенное отношение не зависит от
предварительной изотопии (которая позволяла считать пересечение зубца T(F) и стебля
N трансверсальным). Впрочем, это вытекает из основной леммы.
Доказательство точности представления Бурау следует из двух лемм.
Лемма 8.1 (Основная лемма). Пусть коса β : Dn —>· Dn лежит в ядре
представления Бурау. Тогда (N,F) = (TV, P(F)) для любого стебля N и
вилки F.
Лемма 8.2 (Ключевая лемма). В случае η = 3 равенство (N,F) = 0
имеет место в том и только в том случае, если зубец T(F) изотопен дуге, не
пересекающей N.
Выведем теперь точность представления Бурау для кос из трех нитей из
этих двух лемм. Предположим, что коса β лежит в ядре представления Бурау.
Покажем, что β — тривиальная коса.
128
Глава 8
Пусть TV — стебель. Без ограничения общности молено выбрать N
горизонтальной линией в Dn такой, что выколотые точки р\ и р^ лежат выше 7V, а рз
лежит ниже N. Пусть F — вилка такая, что T(F) представляет собой отрезок
прямой от pi до р2, не пересекающий стебля N. Тогда (N,F) = 0. По
основной лемме мы имеем (TV, P(F)) = 0. По ключевой лемме дуга P(T(F)) изотопна
некоторой дуге, не пересекающей N. Применяя изотопию к /3, можно считать,
что p(T(F)) = T(F).
Аналогичным образом можно доказать, что каждое из трех ребер
треугольника с вершинами р\, р2, Рз сохраняется под действием β. Таким образом, если β
нетривиальна, то она представляет собой некоторое количество полных
оборотов диска D. Однако легко проверить, что такие косы (представляющие собой
центр группы кос из трех нитей) не лежат в ядре представления Б у pay. Таким
образом, представление Бурау для кос из трех нитей точно.
Для интересующихся подробностями, мы приводим внизу доказательства
основной и ключевой лемм.
Доказательство основной леммы. Основная идея состоит в следующем. Мы
переделаем определение (8.12) так, чтобы оно работало для случая петель, а не вилок.
В этом случае инвариантность для петель немедленно следует из того факта, что
коса лежит в ядре представления Бурау.
Мы можем предполагать, что зубцы вилок Τ и β(Τ) пересекают стебель N транс-
версально.
Пусть F — поднятие вилки F на Dn согласно накрытию /г, содержащее точку
do, a T(F) — соответствующее поднятие для T(F). Тогда для каждого а £ Ζ все
пересечения T(F) с qaN (если таковые имеются) трансверсальны. Пусть (qaN,T(F))
обозначает алгебраическое число пересечения этих двух дуг. Тогда следующее
определение спаривания эквивалентно определению (8.12):
{N,F) = J2(qaN,f(F))qa. (8.13)
aGZ
Предположим теперь, что T(F) соединяет точки pi и pj. Обозначим через v(pi) и
v(jpj) малые непересекающиеся окрестности точек pi и pj соответственно. Пусть 7 —
часть дуги T(F), начинающаяся в v(pi) и заканчивающаяся в v(pj), а Si — петля в
iy(pi) с начальной точкой 7(0)? обходящая против часовой стрелки вокруг точки pi.
Обозначим через Тг(.Р) следующую петлю:
T2(F)=153l-15i-\
Пусть Тг(-Р) — поднятие для Тг(.Р), которое совпадает с (1 — q)T(F) вне малых
окрестностей выколотых точек. Тогда следующее определение (8.14) эквивалентно
определениям (8.12) и (8.13):
{NjF) = _L· J2(QaN,f2(F))qa- (8.14)
^ aGZ
Так как β лежит в ядре представления Бурау, петли Тг(.Р) и ТЬ(/3(^))
представляют один и тот же элемент группы гомологии Hi(Dn). Таким образом, они имеют
одно и то же алгебраическое число пересечений с любым поднятием qaN элемента N.
Утверждение леммы следует таким образом из (8.14). D
8.4. Представления групп кос
129
Доказательство ключевой леммы. Основной идеей является нахождение вилки,
зубец которой пересекает N в минимальном (ненулевом) количестве точек. Мы
покажем, что это невозможно.
Напомним, что, согласно определению (8.12), мы имеем (N,F) = Σί=ι £iQai·
Применяя при необходимости гомеоморфизм, можно считать, что N — это
горизонтальный отрезок прямой, проходящий через Ds, с двумя выколотыми точками с
верхней стороны и одной выколотой точкой с нижней стороны (таким образом, вилка
является перекрученной). Здесь мы немного отошли от прежней договоренности
считать, что выколотые точки лежат на действительной оси, продеформировав слегка
наше множество D% С D. Пусть D~%, D% обозначают верхнюю и нижнюю части
множества Ds\N соответственно. Перенумеруем выколотые точки таким образом, чтобы
D^ содержало точки ρι,ρ2, а множество D% содержало точку рз- Рассмотрим
теперь пересечение T(F) с D$ . Оно состоит из несвязного набора дуг с концами в N
(возможно, что у одной дуги одна конечная точка совпадает с рз). Дуга T(F) Π D^,
у которой оба конца лежат в Ν, должна отделять (вместе с частью
горизонтального диаметра, расположенной между концами дуги) точку рз': в противном случае ее
можно удалить вместе с парой точек пересечения (что противоречит предположению
о минимальности). Таким образом, множество T(F) Π D% должно состоять из набора
"параллельных" дуг, отделяющих точку рз и, возможно, одной дуги, имеющей конец
в точке рз-
Аналогичным образом, всякая дуга в T(F) Π D% либо отделяет одну из точек
Ρι,Ρ2, либо имеет конец в одной из точек р\ или р2. Не может быть дуги в T(F) ΠD^,
отделяющей обе точки: в противном случае самая внешняя такая дуга вместе с самой
внешней дугой в нижней части образовывали бы замкнутую петлю.
Рис. 8.17. Зубцы вилки и стебель в Ds
Посчитаем аккуратно число пересечения и убедимся, что все слагаемые, взятые
при q = — 1, имеют один и тот же знак.
Действительно, пусть z% и Zj — две точки пересечения между T(F) и N,
соединенные дугой в T(F) Π D^ или в T(F) Π D% . Эта дуга вместе с частью дуги N
ограничивает область, содержащую выколотую точку. Таким образом, a,j = а% ± 1.
Кроме того, два знака точек пересечения противоположны: Sj = —Si. Следовательно,
130
Глава 8
Sj{ — l)aj = Si{ — 1)αί. Рассуждая также и впредь, мы заключаем, что все слагаемые
для (N, F): взятые при q = — 1, имеют один и тот же знак. Следовательно, (N, F) не
равно нулю. D
8.4.2. Контрпример
На самом деле доказательство точности представления Бурау не работает
при η > 3. Грубо говоря, ключевая лемма использует внутренние свойства
группы кос из трех нитей.
Идея построения контрпримера состоит в следующем. Каждая кривая а с
концами в выколотых точках задает косу, которая порождает автоморфизм та
группы гомологии Hi(Dn). Этот автоморфизм порожден "половинным"
скручиванием Дена вокруг а (переставляющим концы).
Явное вычисление показывает, что, если (α, β) = 0, то т(а), и т(/3)
коммутируют.
Для того, чтобы показать неточность представления Бурау достаточно
предъявить пример вложенных дуг α, β Ε Dn с концами в выколотых точках
таких, что (α, β) = 0, но соответствующие косы та и Τβ не коммутируют.
При η ^ б, простейший известный пример выглядит следующим образом.
Мы полагаем φι = σ\σ^ σ§ σ^ и φ^ = σ^ σ2σ^σ^ . Пусть 7 — простейшая
дуга, соединяющая точку xs с точкой х^.
Непосредственная проверка показывает, что при а = φι (7), β = 02 (τ)
соответствующие косы имеют вид та = φισ^Φϊ и τ β = ф2&зФ2 ·> и мы получаем
(α, β) = 0. Таким образом, коса τ^ΤβΤ^τ^1 принадлежит ядру представления
Бурау. Чтобы доказать нетривиальность этой косы, можно воспользоваться,
скажем, одним из алгоритмов распознавания кос, приведенных в настоящей
книге.
Эта коса имеет запись из сорока четырех букв в стандартном алфавите для
группы кос Вг(6). Аналогичным образом может быть найден элемент ядра
представления Бурау для кос из пяти нитей. Длина соответствующей косы
равна ста двадцати.
8.5. Представление Крамера-Бигелова
Поиск точного линейного представления группы кос из произвольного числа
нитей был важной алгебраической задачей, которая была решена лишь к концу
двадцатого века. Точное представление дает явный полный инвариант группы
кос. В развитие той идеи, что представление Бурау происходит из
некоторого накрытия, Стивен Бигелов предложил более изощренное накрытие, которое
порождает другое представление. Бигелов доказывает точность этого
представления, используя технику "вилки и стебля". Мы начнем с формального
определения, следуя работе Даана Крамера [Krai]. После этого мы опишем работу
Бигелова [Bigl] в главных чертах.
8.5.1. Явные формулы Крамера
Пусть η — натуральное число, a i? — коммутативное кольцо с единицей
над R, порожденное элементами q, t E R. Пусть V линейное пространство
Конструкция Бигелова
131
над кольцом R размерности п^п~ >; порожденное некоторыми элементами Xij,
1 ^ г < j ^ п.
Определим действие группы кос Вг(п) на пространстве V по следующему
правилу:
Xij к < г — 1 или к > j;
Xi-ij + (1 - q)Xij к = г - 1;
I tq(q - tyxij+i + qxi+ij к = г < j - 1;
<rk(xi,j) = { tq2Xij k = i=j-l; (8.15)
xi;J· + tqk~z(q - l)2xfc,fc+i г < A; < j - 1
Zij-i + 43~\q ~ 1)xj-iJ г < к = j -1
(1 - ^)xi;J· + qxij+i к = j;
где ak,k = 1,..., (n — 1), — образующие группы кос. Непосредственно
проверяется, что указанные формулы действительно задают представление группы
кос.
Обозначим пространство представления Крамера-Бигелова группы кос
В г (ή) через Ln. Поскольку базис пространства Ln является частью базиса
пространства Ьп+ъ мы имеем Ln с £η+ι· Из формул (8.15) следует, что Ln
является инвариантным пространством относительно действия представления
(8.15) группы Вг(п + 1) в пространстве Ln+i-
При переходе от матриц представления группы Вг(п) к матрицам
представления группы Вг(п-\-1) верхний блок стабилизируется. Таким образом, молено
говорить о бесконечномерном линейном представлении стабильной группы кос.
Мы не будем доказывать точность этого представления, поскольку такое
доказательство требует рассмотрения многих причудливых конструкций. Детали
см. в оригинальной работе Крамера [Кга2].
8.5.2. Конструкция Бигелова
и основные идеи доказательства
Мы опишем результаты Бигелова, следуя [Bigl, Tur2]. Он строит более
хитроумное, чем Бурау, накрытие. Это накрытие порождает точное представление,
совпадающее с представлением Крамера.
В действительности представление Бигелова имеет дело с самой группой
кос, а не с группой классов отображений. Следует отметить работу Ло-
уренса [Law], в которой он обобщает идею построения представления Бурау
с использованием накрытия конфигурационного пространства Dn, и
получает все так называемые представления Темперли-Либа. Именно представления,
предложенные Лоуренсом, оказались точными (согласно Крамеру и Бигелову).
Доказательство Бигелова точности представления основано на тех лее
идеях, которые использовались при доказательстве точности представления Бурау
для группы кос из трех нитей. Именно, оно разделяется на три шага.
1. Основная лемма.
2. Ключевая лемма.
3. Вывод точности представления из этих двух лемм.
132
Конструкция Бигелова
Мы несколько видоизменим определенное выше спаривание для кривых
используя более остроумное накрытие; в данном случае базой будет черырехмер-
ное пространство, при этом будут рассматриваться его двумерные гомологии.
Как мы показали ранее, основная лемма, работает для всех η далее для
представления Бурау. Мы приведем новое спаривание и модифицируем основную
лемму. Для доказательства оставшихся двух шагов мы будем использовать
новое накрытие и новое спаривание.
Пусть D,Dn определены как прежде, выколотыми точками будут точки
χι,... ,хп: —1 < х\ < · · · < хп < 1.
Пусть С — пространство всех неупорядоченных пар точек в Dn. Ясно, что
С является некомпактными четырехмерным многообразием с краем. Оно
имеет естественную ориентацию, индуцированную ориентацией пространства Dn.
Пусть d = — г и пусть d! = —ге~^~ для некоторого малого положительного е.
Выберем cq = {d, df} в качестве точки отсчета для С.
Замкнутая кривая а : [0,1] —>· С может быть записана в виде {cei(s), 0^(5)},
где s Ε [0,1], a, ai,0i2 — дуги в Dn такие, что {cei(0), «2(0)} = {αι(1), ^(l)}
в С. В этом случае дуги cei, «2 либо обе являются петлями, либо имеют общие
концы и могут быть присоединены друг к другу. Таким образом, они образуют
замкнутое ориентированное 1-многообразие а в Dn. Пусть а(а) Ε Ζ — общее
число оборотов кривой а вокруг выколотых точек в Dn.
Рассмотрим отображение s : [0,1] —> S1, заданное как s \-^ ^Гы^ГыТ'
и естественную проекцию S1 —>· RP1 = S1, отождествляющую
противоположные точки. Мы получим петлю в RP1. Соответствующий элемент группы
гомологии ^(RP1) обозначим через Ь(а). Формула а —> qa(a)tb(a"> определяет
таким образом гомоморфизм φ из Н\(С) в свободную коммутативную группу,
порожденную элементами q,t. Пусть R = Z^^1,^1] — групповое кольцо этой
группы.
Пусть С —>· С — регулярное накрытие, соответствующее ядру
отображения ф. Образующие q, t действуют на С как коммутирующие преобразования,
тем самым превращая группу гомологии #2(С, Z) в ^-модуль.
Всякий гомеоморфизм h пространства Dn на себя индуцирует
гомеоморфизм С —> С по формуле h({x,y}) = {h(x),h(y)} (мы используем то же
обозначение: К).
Легко проверяется, что h(co) = со, и что действие h на гомологиях Н\(С)
коммутирует с ф. Таким образом, гомеоморфизм h : С —>· С может быть поднят
единственным образом до отображения С —>· С, сохраняющего слой над со
поточечно и коммутирующего с преобразованиями, порожденными t и q.
Рассмотрим представление Вп —>· Aut(H2(C)), отображающее
изотопический класс h в R-линейный автоморфизм h* of H2(C).
Теорема 8.12 ([Bigl]). Представление Вп —> Aut(H2{C)) является точным
для всех η ^ 1.
Доказательство использует технику вилок и стеблей.
Для дуг α, β : [0,1] —> Dn таких, что s Ε [0,1] a(s) φ /?(s), обозначим через
{a(s), β(β)} дугу в С, заданную как {ce,/3}(s) = {a(s),/?(s)}. Фиксируем точку
со Ε С, лежащую над cq Ε С.
Конструкция Бигелова
133
Мы слегка модифицируем понятие стебля. А именно, под стеблем будем
понимать вложенную дугу N С Dn с концами в точках d и d!. Для любого
стебля N множество Σ^ν = {{ж, у} Ε С\х,у Ε TV, ж ^ у} является поверхностью
в С, содержащей точку с$. Эта поверхность гомеоморфна треугольнику с одним
удаленным ребром. Ориентируем N от d к d! и ориентируем Στν следующим
образом: в точке {ж, у} = {у, ж} Ε Στν такой, что χ ближе к d, чем у вдоль 7V,
ориентация поверхности Στν задается как произведение ориентации стебля N в
точках хну.
Пусть Στν — поднятие поверхности Στν на С, содержащее точку со-
Ориентация поверхности Σ^ν естественным образом определяет ориентацию для Σ^ν.
Очевидно, что, Σ^ν Π 5С = ΟΈν
Для вилки F = TU Η с конечными точками d = do,Xi,Xj и вершиной г, мы
можем произвести малое шевеление (оставляя х^ и Xj на месте и двигая d к df)
и получить параллельный экземпляр F' с зубцом Т7 и ручкой ff7. Обозначим
Tf DHf через ζ'. Мы можем предположить, что F' пересекает F только в общих
вершинах {а^, Xj} и еще в одной точке Η П Τ7, лежащей рядом с ζ и г7.
Мы будем использовать Στν и Σ^? для установления двойственности между
N и D. Без ограничения общности можно предположить, что N пересекает
зубец Τ вилки F трансверсально в га точках ζι,..., zm. Выберем параллельную
вилку Т7 = Т7 U Н' как и раньше таким образом, чтобы зубец Т7 пересекался
с N трансверсально в га точках z[,...,zfm, где каждая пара Zi,z\ соединена
короткой дугой в 7V, лежащей в узкой полосе, ограниченной TUT7, и не
пересекает других Zi, Zj. (здесь нумерация произвольна). Таким образом, поверхности
Σ^,Στν пересекаются трансверсально в га2 точках {zi,z'j} при i,j = 1,...,га.
Следовательно, для любых а, Ъ Ε Ζ образ qatbT>N при преобразовании
расслоения пересекает Σ^? трансверсально.
Перейдем к определению спаривания.
Определение 8.21. Рассмотрим алгебраическое число пересечения
qat ΣιΝ-Έρ Ε Ζ и положим
(TV, F)= Σ (qatbtN · tF)qatb. (8.16)
a,b£Z
Опишем теперь основные идеи доказательства теоремы.
Для любой пары i,j E {1,2,...,га} существуют единственным образом
определенные числа caj^bij Ε Ζ такие, что qai'jtbi'jJ^N пересекает Σ^ в
точке, лежащей {^, Zj} E С.
1. Сначала нужно проверить, что это спаривание корректно определено
(инвариантно при гомотопии).
2. Можно заметить, что знак Sij точки пересечения {i,j} задается
формулой Eij = -(-1)6^+6^+6^.
3. Ключевая лемма
Лемма 8.3. Если гомеоморфизм h пространства Dn на себя
представляет собой элемент в ядре отображения Вп —> Aut(H2(C), то для
любого стебля N и для любой вилки F мы имеем (N, h(F)) = (TV, F).
134
Конструкция Бигелова
Доказательство следует из рутинной проверки аналогичной случаю
представления Бурау для трех нитей.
4. Основная лемма:
Лемма 8.4. (N,F) = 0 тогда и только тогда, когда зубец Τ может
быть произотопирован так, чтобы он не пересекался с N.
Для представления Бурау мы использовали тот факт, что выколоты лишь три
точки, и что в случае минимального пересечения все точки пересечения имеют
один и тот-же знак при q = — 1. В данном случае работает другой аргумент:
дву мерность.
Предположим, что (N,F) = 0. Допустим, что пересечение между Л^иТне
может быть удалено с помощью изотопии; рассмотрим минимальное пересечение.
Будем упорядочивать мономы лексикографически: qat > qct , если а > с или
а = c,b > d. Пара {г, j} является максимальной, если qai>Hbi>j ^ qak,itbk,i дЛЯ
любых /с, I £ {1,..., га}.
Тогда имеет место следующее утверждение.
Если пара (i,j) максимальна, то £>г,г = bjj = Ь^%.
Таким образом, все вхождения максимального монома, скажем, qat , в (8.16)
имеют один и тот же знак —( — 1) · Таким образом (N, F) φ 0.
5. Из ключевой леммы и основной леммы мы видим, что любой элемент
ядра сохраняет заранее выбранные линии, соединяющие выколотые
точки. Следовательно, единственная возможность для этого элемента быть
нетривиальными — это быть степенью скручивания Дена вдоль кривой,
параллельной границе. Однако такое скручивание в представлении Кра-
мера-Бигелова задается умножением на q2nt2.
Таким образом мы построили точное представление группы кос,
коэффициентами матриц которого являются полиномы от двух переменных. Из
классических теорем теории чисел следует, что существует пара вещественных чисел,
при подстановке которых вместо переменных мы получим точное
представление с вещественными коэффициентами. Следовательно, все группы кос Вг(п)
линейны.
Глава 9
Алгоритмы построения
косы по зацеплению
В настоящей главе мы приведем три алгоритма построения косы В по
заданному (ориентированному) зацеплению L так, что С 1(B) = L.
9.1. Теорема Александера
В настоящем разделе мы считаем все зацепления ориентированными; в
случае, если дано неориентированное зацепление, мы можем задать на нем
произвольную ориентацию.
Упражнение 9.1. Постройте косу, замыканием которой являются кольца
Борромео (с какой-нибудь ориентацией).
Теорема 9.1. (Теорема Александера [А1еЗ]) Каждое зацепление представимо
в виде замыкания ориентированной косы.
Мы приведем три доказательства этой теоремы (три алгоритма построения
косы по зацеплению): оригинальное доказательство Александера, алгоритм Во-
желя [Vogel] и алгоритм, основанный на L-движениях.
Начнем с доказательства Александера.
Доказательство. Мы будем доказывать эту теорему для случая
полигональных зацеплений.
Рассмотрим диаграмму L многоугольного зацепления на плоскости Ρ и
точку О G Ρ (эта точка не должна принадлежать ребру диаграммы или совпадать
с каким-либо из перекрестков). Без ограничения общности можно считать, что
каждое ребро нашего зацепление содержит не более одного перекрестка (этого
можно добиться дополнительным подразбиением ребер). Будем говорить, что
L заплетается вокруг О, если каждое ребро диаграммы L видно из точки О
ориентированным против часовой стрелки.
Определение 9.1. Для каждой диаграммы L и точки О назовем ребро /
диаграммы L, которое ориентировано против часовой стрелки, если смотреть из
точки О, положительным. В противном случае назовем ребро
отрицательным.
136
Глава 9
Если найдется такая точка О, что диаграмма зацепления заплетается
вокруг нее, то утверждение теоремы Александера становятся вполне очевидным:
мы просто разрежем нашу диаграмму вдоль луча, идущего из точки О и
"выпрямим" часть диаграммы вне малого угла, не содержащего перекрестков так,
как показано на рис. 9.1.
Рис. 9.1. Построение косы по заплетающемуся зацеплению
Таким образом, чтобы доказать эту теорему в общем случае, нам
достаточно уметь преобразовывать произвольную диаграмму зацепления к диаграмме,
заплетающейся как коса вокруг некоторой точки О.
На плоскости диаграммы зацепления фиксируем точку О, не
принадлежащую тени зацепления. Мы будем использовать Трюк Александера, который
состоит в следующем. Рассмотрим отрицательное ребро АВ диаграммы нашего
многоугольного зацепления и выберем точку С на плоскости проекции Ρ
такую, что треугольник ABC содержит точку О. Теперь заменим АВ на АС
и ВС. Очевидно, что два ребра будут положительными, см. рис. 9.2.
Мы будем использовать эту операцию, чтобы получить диаграмму,
заплетающуюся вокруг О.
Опишем эту конструкцию более подробно. В случае когда отрицательное
ребро АВ не содержит перекрестков, трюк Александера может быть применен
непосредственно, см. рис. 9.2.а. Действительно, можно разделить ребро АВ на
две части и протащить их над точкой О.
То же самое можно сделать и в том случае, когда АВ содержит
единственный перекресток, являющийся переходом по отношению к другому ребру. 9.2.6.
Наконец если АВ содержит единственный перекресток, являющийся
проходом по отношению к другому ребру, мы можем протащить его снизу, как
показано на рис. 9.2.в.
Упражнение 9.2. Используя трюк Александера, постройте косу, замыкание
которой представляет собой связную сумму двух правых трилистников.
Метод доказательства теоремы Александера, предложенный выше, дает
некоторый явный алгоритм построения косы по зацеплению. Однако этот алго-
9.2. Алгоритм Вожеля
137
, >
Рис. 9.2. Трюк Александера
ритм является очень медленным. Мы изложим более быстрый алгоритм
построения косы, замыканием которой является данное зацепление.
9.2. Алгоритм Вожеля
Мы опишем алгоритм, предложенный Пьером Вожелем, см. [Vogel].
Определение 9.2. Ориентированная диаграмма зацепления является
заплетенной, если существует точка на плоскости этой диаграммы, вокруг которой
она заплетается как коса.
Заплетенная диаграмма зацепления, с очевидностью, представляет собой
замыкание диаграммы косы.
Замечание 9.1. Свойство диаграммы быть заплетенной не зависит от
структуры перекрестков. Таким образом, можно сказать, что мы
работаем лишь с тенями зацеплений. В дальнейшем до конца главы мы не будем
пользоваться информацией о проходах и переходах.
Рассмотрим ориентированную замкнутую диаграмму D зацепления L;
рассмотрим операцию сглаживания перекрестков, показанную на рис. 9.3. В итоге
мы получаем набор окружностей Зейферта. Обозначим это сглаживание
через σ.
Определение 9.3. Скажем, что все окружности Зейферта некоторой плоской
диаграммы образуют гнездо если все они индуцируют одну и ту лее ориентацию
на плоскости и ограничивают вложенную систему дисков.
Очевидно, что если все окружности Зейферта некоторой плоской
диаграммы зацепления образуют гнездо, то соответствующая диаграмма является
заплетенной. Более того, количество нитей соответствующей косы равно
количеству окружностей Зейферта.
Фиксируем некоторую диаграмму зацепления D и рассмотрим ее тень. Эта
тень делит сферу проекции (одноточечную компактификацию плоскости) на
138
Глава 9
г *
ч
ί 1
г
к
> )
CDD
CD
Рис. 9.3. Сглаживание перекрестков и окружности Зейферта
двумерные клетки, называемые гранями. Внешней называется грань,
содержащая бесконечную точку.
Определение 9.4. Грань S называется неупорядоченной, если у нее есть два
ребра а, 6, принадлежащие различным окружностям Зейферта Αι, Α^ и
индуцирующим одну и ту же ориентацию для S\ в противном случае грань
называется упорядоченной.
В первом случае мы говорим, что окружности Зейферта А\,А^ образуют
неупорядоченную грань S.
К неупорядоченной грани можно применить движение Ω2 так, как показано
на рис. 9.4. В этом случае грани в целом становятся "более упорядоченными".
Имеет место следующее.
Предложение 9.1. Если все ребра грани Σ принадлежат двум окружностям
Зейферта, то эта грань является упорядоченной.
Доказательство. Рассмотрим ребра этой грани. Легко видеть, что все ребра,
принадлежащие одной и той же окружности Зейферта, имеют одну и ту же
ориентацию. Рассмотрим два соседних ребра, принадлежащих к различным
окружностям Зейферта. Они должны иметь противоположные ориентации.
Таким образом, любые два ребра данной грани, принадлежащие различным
окружностям Зейферта, имеют противоположные ориентации, из чего следует,
что грань является упорядоченной. D
Предложение 9.2. Если диаграмма D зацепления L не имеет
неупорядоченных граней, то она может быть преобразована в заплетающуюся диаграмму
посредством замены бесконечности.
Доказательство. Предположим, что у диаграммы D нет неупорядоченных
граней. Рассмотрим некоторую грань; любые два соседних ребра этой грани
либо имеют одну и ту же ориентацию (и в этом случае принадлежат одной
и той же окружности Зейферта), либо разные ориентации (и тогда
принадлежат разным окружностям Зейферта). Если мы рассмотрим
последовательности соседних ребер, принадлежащих одной и той же окружности Зейферта
как "длинное" ребро, то мы получим некоторый многоугольник Μ (или
одну целую окружность Зейферта). Ориентации ребер (если таковых по
крайней мере два) многоугольника Μ чередуются. Таким образом, количество его
9.2. Алгоритм Вожеля
139
ребер (если не все они принадлежат одной окружности Зейферта) четно. Так
как грань является упорядоченной, количество окружностей Зейферта,
связанных с данным многоугольником, не превосходит двух. Следовательно, каждая
окружность Зейферта, соответствующая многоугольнику М, соседствует либо
с одной окружностью Зейферта, либо с двумя (лежащими по разные стороны
от М). В противном случае это привело бы к неупорядоченной грани.
Оставшаяся часть доказательства предлагается читателю в качестве легкого
упражнения.
D
Алгоритм Вожеля работает следующим образом. Сначала мы удаляем все
\> , А>- \Л , А/, зател
ОС
ОС·
эм, исполь-
перекрестки по следующему правилу: /v —г , ί ■■,-./
зуя движение Ω2, мы удаляем неупорядоченные грани. После этого если
окружности Зейферта не образуют гнезда, мы применяем замену бесконечности.
Опишем этот алгоритм более подробно.
Сгладим сначала все перекрестки диаграммы. Обозначим число
получившихся окружностей Зейферта через s. Некоторые пары этих окружностей
могут образовывать неупорядоченные грани. Построим граф, вершины которого
соответствуют окружностям Зейферта, при этом две вершины соединены
ребром, если соответствующие окружности Зейферта образуют неупорядоченную
грань. Обозначим полученный граф через Γι. Обозначим окружности Зейферта
через Ai,A2,...,As таким образом, что окружность А^\ образует
неупорядоченную грань с одной из предыдущих окружностей. Этого можно добиться в
том случае, если наш граф Γι связен. Легко видеть, что в случае несвязного
графа можно применить алгоритм к каждой связной его компоненте; в этом
случае он будет работать еще быстрее.
Будем применять следующую операцию. Рассмотрим неупорядоченную
грань, порожденную окружностями А\ и А^, и применим к ней Ω2 как
описано выше. Вместо окружностей А\ и А2 мы получим две окружности Зейферта,
одна внутри другой. Они уже не образуют неупорядоченной грани, см. рис. 9.4.
Неупоря доч енная
грань
Рис. 9.4. Удаление неупорядоченной грани
140
Глава 9
Обозначим внутреннюю из полученных окружностей через Αι, а внешнюю —
через А^. Так как "бывшая А^ образовывала неупорядоченную грань с
окружностью Аз, новая окружность А\ также образует неупорядоченную грань с As
(для которой обозначение не меняется).
Применим операцию Ω2 к окружностям Αι и Аз и снова изменим
обозначения: полученную внешнюю окружность обозначим через Αι, а внутреннюю —
через Аз- И так далее. В конце (после применения s — 1 операции Ω2) мы
получим одну внешнюю окружность Αι, которая не образует неупорядоченных
граней. После этого мы не будем трогать окружность А\\ мы применим ту же
самую процедуру для пар (А.2, A3), (A.2, Aj) и так далее. Затем мы проделаем
то лее самое для пар (Аз, А^),г > 3, и так далее. Таким образом, мы
применили s з ' вторых движений Рейдемейстера. Мы получили набор окружностей
Αι, Α.2,..., As, где каждая следующая лежит внутри предыдущей.
После этого, если понадобится, сделаем замену бесконечности. Таким
образом получим заплетающуюся диаграмму. Всего мы применили C2S вторых
движений Рейдемейстера (в случае связного графа) или меньшее число в
случае несвязного графа.
Таким образом, мы доказали следующую теорему.
Теорема 9.2. Если диаграмма D имеет η перекрестков и s окружностей
Зейферта, то
1. Алгоритм Вожеля требует не более C2S движений Рейдемейстера.
2. Общее количество нитей получившейся косы равно s, а количество
перекрестков не превосходит η + s(s — 1).
Применим алгоритм Вожеля к узлу 52 (согласно стандартной
классификации, см. таблицы в конце книги).
Для этого применим второе движение Рейдемейстера Ω2 дважды и один раз
замену бесконечности, см. рис. 9.5. Таким образом, двух движений
Рейдемейстера Ω2 достаточно.
В конце мы получим заплетающуюся диаграмму, показанную на рис. 9.5.
Таким образом мы имеем возможность строить косы по зацеплениям еще
быстрее, чем с помощью алгоритма Александера.
9.3. //-Движения и алгоритм построения кос
Последний приводимый в настоящей главе алгоритм использует идеи Софии
Ламбропулу и Колина Рурка [LR]; основная идея этого алгоритма может быть
использована при доказательстве теоремы Маркова и при обобщении на случай
виртуальных кос.
Скажем, что диаграмма зацепления на плоскости Оху находится в общем
положении, если она не содержит горизонтальных отрезков и представляет
собой объединение восходящих и нисходящих (относительно координаты у)
ветвей; каждая ветвь имеет ровно один максимум и один минимум. Идея заплете-
ния косы состоит в том, чтобы оставить дуги, направленные вниз, а дуги,
направленные вверх представить в виде объединения ветвей, направленных вниз
и частей диаграммы, представляющих собой замыкание косы.
9.3. L-Движения и алгоритм построения кос
141
I замена ос
Рис. 9.5. Плоские диаграммы узла и окружности Зейферта
142
Глава 9
Скажем, что диаграмма зацепления L смотрит вниз, если в каждом
перекрестке обе ее ветви направлены вниз относительно координаты у.
Любое зацепление имеет диаграмму, смотрящую вниз. Этого легко
добиться, применив к произвольной диаграмме плоскую изотопию так, как показано
на рис. 9.6.
Рис. 9.6. Диаграммы, смотрящие вниз (справа)
Диаграмма, смотрящая вниз, уже имеет задатки замыкания косы. Все, что
нам остается сделать для построения диаграммы косы, — это преобразовать
ветви, направленные вверх, в ветви, соответствующие замыканиям нитей косы,
т.е., мы стремимся к тому, чтобы зацепление L имело вид замыкание косы
L = В U (U/г), где В — коса, а ϊι — "замыкающие" ветви зацепления.
Так как диаграмма смотрит вниз, то каждая ветвь, направленная вверх,
не содержит перекрестков. Пусть L — диаграмма зацепления общего
положения, смотрящая вниз. Рассмотрим две горизонтальные линии / и га, такие, что
вся диаграмма L лежит между этими линиями. Рассмотрим все ее ветви,
направленные вверх. Каждая такая ветвь начинается в некотором локальном
минимуме Ai (выше /) и заканчивается в некотором локальном максимуме В ι
(ниже га). Обозначим через V наименьший из таких минимумов, а через га/ —
наибольший из таких максимумов. Мы заменяем рассматриваемую ветвь
двумя ветвями: AiCi, и DiBf, точки С ι и Ό ι лежат на линиях / и га одна под
другой, при этом ветвь AiCi направлена вниз, а ветвь ΌιΒι направлена тоже
вниз, см. рис. 9.7. При этом будем считать, что обе эти ветви образуют
переходы при пересечении с другими ветвями, а каждая ветвь, встречаемая на пути
данной, ориентирована вниз. Последнего условия можно добиться ввиду того,
9.3. L-Движения и алгоритм построения кос
143
что ветви, ориентированные вверх, не содержат перекрестков, и концы нитей,
ориентированные вверх, находятся между парой горизонтальных линей V,mf,
где I < V < т' < т.
В
<
Рис. 9.7. L-преобразование
Будем называть это преобразование I-движением.
Если мы теперь замкнем получившуюся диаграмму, соединив С ι с Ό ι так,
как показано в правой части на рис. 9.7, мы получим диаграмму, зацепления,
изотопную изначальной, так как не содержащая перекрестков ветвь ΑιΒι была
произотопирована в ветвь AiCiDiBi, содержащую только переходы.
Проделав эту операцию для всех ветвей, направленных вверх, мы получим
косу, замыкание которой будет изотопно изначальному зацеплению L.
Глава 10
Алгоритмы распознавания кос
В настоящей книге мы у лее описали один алгоритм распознавания кос, а
именно, точное представление группы кос Крамера-Бигелова. К настоящему
времени известны несколько алгоритмов распознавания кос. Первый из них
содержался в оригинальной статье Артина [Artl] (и, более детально, в [Art2]). Из
более поздних работ по распознаванию кос отметим работы Бирман [Bir2], Гар-
сайда [Gar], Терстона и других. В настоящей главе мы опишем два алгоритма
распознавания кос: геометрическое построение полного инварианта кос,
состоящее в модификации работы Артина, см. [GM]) и алгебраический алгоритм,
предложенный Деорнуа.
В работе [Gar] Гарсайд предложил метод нормальных форм; с
использованием этого метода он решил не только проблему распознавания (слов в группе)
кос, но также и проблему распознавания сопряженности кос — гораздо более
сложную алгебраическую проблему. В настоящей книге мы не приводим
решения проблемы сопряженности. Помимо упомянутых алгоритмов, приведенных
в настоящей книге, мы дадим описание алгоритма М. Бергера, решающий
проблему нахождения минимального слова, соответствующего заданной косе из
трех нитей.
10.1. Геометрический алгоритм
Ниже мы приведем доказательство полноты некоторого инварианта кос,
предложенного Артином (в модификации [GM]).
10.1.1. Введение
Для произвольного η мы построим инвариант группы кос из η нитей.
Этот инвариант имеет простое геометрическое описание как отображение
(не гомоморфное) из группы кос Вг(п) в набор из η копий свободной группы
с η образующими.
Мы также опишем некоторые обобщения этого инварианта на случай
цилиндрических и сферических кос. Основная идея доказательства полноты этих
инвариантов состоит в том, что косы кодируются некоторым набором классов
кривых, при этом изотопический класс косы может быть однозначно
восстановлен по этим кривым.
Отметим, что цилиндрические косы из η нитей (т. е. косы в утолщенном
цилиндре S1 χ (0,1) χ (0, ос)) могут быть рассмотрены как косы в R3\Oz, что
10.1. Геометрический алгоритм
145
равносильно рассмотрению кос с η + 1 нитью, одна из которых вертикально
идет по оси Οζ. Тем самым крашеные цилиндрические косы из η нитей
образуют подгруппу в группе крашеных кос из η нитей, что сводит проблему
распознавания цилиндрических кос к проблеме распознавания обычных кос. В
настоящей главе мы приведем иной способ распознавания цилиндрических кос,
не использующий этого соображения.
10.1.2. Построение инварианта
Начнем с определения понятий и введения обозначений.
Определение 10.1. Под допустимой системой из η кривых мы понимаем
семейство из η непересекающихся несамопересекающихся кривых в верхней
полуплоскости {у > 0} плоскости Оху такое, что каждая кривая соединяет точку
с ординатой ноль с точкой с ординатой единица, а абсциссы концов всех
кривых — это натуральные числа от 1 до п. Все точки (г, 1), где г = 1,..., п,
называются верхними точками, а все точки (г, 0), г = 1,..., гг, называются нижними
точками.
Определение 10.2. Две допустимые системы А и А' из η кривых А назовем
эквивалентными, если существует гомотопия между А и А' в классе кривых
с фиксированными концами, лежащими в верхней полуплоскости такая, что в
процессе гомотопии ни одна внутренняя точка ни одной кривой не совпадает с
верхней или нижней точкой.
Аналогичным образом, эквивалентность определяется для каждой
отдельной кривой (возможно самопересекающейся) с фиксированными верхними и
нижними концами: в процессе гомотопии в верхней полуплоскости никакая
внутренняя точка этой кривой не может совпадать ни с одной верхней или нижней
точкой.
В дальнейшем будем рассматривать допустимые системы кривых с
точностью до эквивалентности.
Замечание 10.1. Заметим, что в процессе гомотопии кривые могут
пересекаться.
Замечание 10.2. В дальнейшем, будем обозначать число нитей
рассматриваемой косы через п, если не оговорено противное.
Пусть β — диаграмма косы на плоскости, соединяющая набор нижних
точек {(1, 0),..., (гг, 0)} с набором верхних точек {(1,1),..., (гг, 1)}. Рассмотрим
самый верхний перекресток С диаграммы β и протянем нижнюю его ветвь
вдоль верхней так, как это показано на рис. 10.1.
Естественно, что это преобразование портит диаграмму косы:
получившийся результат, изображенный на рис. 10.1.6 уже не является диаграммой косы.
Преимущество этой "диаграммы" состоит в том, что у нее меньше перекрестков.
Проделаем ту же операцию со следующим перекрестком (считая сверху),
а именно, протянем его нижнюю ветвь вдоль верхней до верхней точки. Если
верхняя ветвь уже была продеформирована в предыдущем перекрестке, мы
будем протаскивать нижнюю ветвь вдоль продеформированной верхней ветви,
см. рис. 10.2.
146
Глава 10
а б
Рис. 10.1. Разведение верхнего перекрестка
а б
Рис. 10.2. Разведение следующего перекрестка
Повторяя эту процедуру для всех перекрестков (до самого нижнего), мы
получим допустимую систему кривых. Обозначим класс эквивалентности этой
допустимой системы через /(/3).
Теорема 10.1. Функция f является инвариантом кос, т. е. для двух
диаграмм β, β' одной и той же косы мы имеем /(β) = ί(β')·
Доказательство. Рассмотрим слова, соответствующие диаграммам /3,/37. Мы
должны доказать, что соответствующие допустимые системы кривых
инвариантны при изотопии кос.
Инвариантность при применении соотношений коммутативности σ^σ^ = σ^σ^,
\i — j\ ^ 2, очевидна: порядок разведения далеких друг от друга перекрестков
не существенен.
Инвариантность относительно соотношения σ%σ~[ = е доказывается
следующим образом. Рассмотрим рис. 10.3.
В левой части рисунка 10.3 пунктирная линия указывает на произвольность
поведения верхней части диаграммы косы. Самая правая картинка на рис. 10.3
соответствует системе кривых без (у%(у~ .
10.1. Геометрический алгоритм
147
Рис. 10.3. Инвариантность функции / при втором движении Рейдемейстера
Наконец, инвариантность относительно преобразования σ^+ισ^σ^+ισ^+1
показана на рис. 10.4. В верхней части (выше горизонтальной линии) показано
поведение /(Ατ^+ισ^), а в нижней части — поведение /(Ατ^+ισ^+ι) для
произвольного слова-косы А. На среднем рисунке в верхней части, часть кривой
изображена пунктирной линией. Удаляя (стягивая) эту кривую, мы получим
картинку, изображенную справа сверху; она совпадает с картинкой,
изображенной справа снизу.
Поведение диаграммы в верхней части А диаграммы косы произвольное.
Для простоты изобразим это тремя вертикальными линиями.
Таким образом, мы доказали, что /(Ατ^+ισ^) = /(Ατ^+ισ^+ι).
Этим завершается доказательство теоремы. D
Докажем теперь следующую лемму.
Лемма 10.1. Если для двух кос а иЪ имеет место f(a) = f(b), то для любой
косы с мы получаем f(ac) = f(bc).
Доказательство. Утверждение f(ac) = f(bc) следует явно из построения.
Действительно, нам нужно лишь "добавить" косу с к допустимой системе кривых,
соответствующей косе а (или 6), а затем развести все перекрестки,
соответствующие косе с. D
На самом деле имеет место и более сильная теорема.
Теорема 10.2 (Основная теорема). Функция f является полным
инвариантом.
148
Глава 10
Рис. 10.4. Инвариантность функции /
относительно третьего движения Рейдемейстера
Для доказательства этого утверждения нам понадобятся некоторые
вспомогательные определения и леммы. Нам нужно уметь восстанавливать косу по
соответствующей допустимой системе кривых.
В дальнейшем мы будем иметь дело с косами, у которых концы имеют вид
(г, 0, 0) и (j, 1,1), а все нити идут вверх относительно координаты ζ. Такие
косы получаются можно получить из обычных кос наклоном плоскости Οχ ζ, на
10.1. Геометрический алгоритм
149
которой расположена диаграмма косы, переводящим ось О ζ в линию {у = ζ}.
Очевидно, что такие косы однозначно соответствуют стандартным косам (у
которых верхние точки имеют координаты (j, 0,1)). Для преобразования
такой косы в стандартную достаточно соединить точки (j, 1,1) с точками (j, 0, 2)
прямыми линиями, а затем сжать получившийся набор нитей в два раза
относительно оси Oz.
Рассмотрим косу Ъ и плоскость Ρ = {у = ζ} в пространстве R3 = Oxyz.
Расположим косу Ъ в малой окрестности плоскости Ρ таким образом, чтобы
ее нити соединяли точки (г, 0,0) и (j, 1,1), г, j = 1,...,гг. Проекции этой
косы на оси Оху и Oxz являются диаграммами косы. Обозначим диаграмму на
плоскости Оху через β.
Нашим следующим шагом будет изменение проекции на плоскость Оху,
которое не меняет изотопический тип косы. Оказывается, что можно изменить
абсциссы и ординаты некоторых кусочков нитей косы Ъ таким образом, чтобы
проекция измененной косы на ось Оху представляла собой допустимую систему
кривых для β.
Действительно, так как коса лежит в малой окрестности плоскости Р,
каждый перекресток в проекции Оху соответствует перекрестку на Oxz. Таким
образом, процедура протаскивания одной нити вдоль другой нити в плоскости,
параллельной плоскости Оху, задает изотопию кос.
В этом и заключается геометрическое значение инварианта /: этот
инвариант сопоставляет "наклонной" косе ее проекцию на плоскость Оху, не имеющую
точек самопересечения.
Определение 10.3. Под допустимой параметризацией (в дальнейшем все
параметризации предполагаются гладкими) допустимой системы кривых мы
понимаем набор параметризаций для всех кривых (мы используем
параметры £]_,... ,£п) такие, что в верхних точках все ti равны единице, а в нижних
точках — нулю.
Любая допустимая система А из η кривых с допустимой параметризацией
Τ задает некоторую косу: каждая кривая на плоскости становится нитью косы,
если рассмотреть ее параметризацию как г-координату в трехмерном
пространстве. Соответствующая коса имеет концы в (г, 0, 0) и (j, 1,1), где г, j = 1,..., п.
Обозначим ее через д(А,Т).
Лемма 10.2. Изотопический класс д(А,Т) не зависит от выбора
параметризации Т.
Доказательство. Действительно, рассмотрим две допустимые
параметризации Τι и Т^ допустимой системы А из η кривых. Пусть Ts, s G [1,2], —
непрерывное семейство допустимых параметризаций между Τι и Тг, заданное по
формуле Ts = (s — 1)Т2 + (2 — s)Ti. Для каждого s G [1,2] кривые из Ts не
пересекают друг друга, при этом для каждого s G [1,2] набор кривых
(нитей) g(A,Ts) представляет собой косу, следовательно, g(A,Ts) задает изотопию
кос. D
Таким образом, функция д(А) = д(А,Т) корректно определена.
Теперь мы готовы доказать основную теорему (о полноте инварианта /).
Докажем сначала лемму.
150
Глава 10
Лемма 10.3. Пусть A,Af — две эквивалентные допустимые системы из η
кривых. Тогда д(А) = д(А').
Доказательство. Пусть At,t Ε [0,1] — гомотопия, соединяющая А с А'. Для
каждого £ Ε [0,1] At представляет собой систему кривых (возможно не
допустимую). На каждой кривой {ciiit, г = 1,..., n, t Ε [0,1]} выберем точки X^,t и Yi,t
таким образом, чтобы отрезок, соединяющий верхнюю точку с X^,t (верхний
отрезок) и отрезок, соединяющий нижнюю точку с Y^t (нижний отрезок) не
содержали точек пересечения ни при каком значении t. Обозначим оставшуюся
часть (средний отрезок) между X^,t и Y^t через Sij- Параметризуем теперь все
кривые для всех значений t параметрами {sij Ε [0,1], г = 1,..., η} следующим
образом: для каждого t верхняя точка на каждой кривой имеет параметр s = 1,
а нижняя точка имеет параметр s = 0. Кроме того, потребуем, чтобы для г < j
для каждого χ Ε Sij,y E Sjj выполнялось неравенство Si^(x) < Sj,t(y)· Это
возможно, потому что мы можем изменять параметризации верхнего и
нижнего интервалов внутри [0,1]; например, можно сделать так, чтобы средний
интервал j-й нити соответствовал значениям параметра на отрезке [^4^, й^]·
Очевидно, что при t = 0 и t = 1 эти параметризации допустимы для А и
для А'. Для каждого t Ε [0,1] параметризация s порождает косу Bt в R : мы
рассматриваем параметры s^t в качестве z-координат для нитей αι^. В этом
случае нити не пересекают друг друга, поскольку значения параметров на среднем
интервале для разных нитей не могут совпадать.
Таким образом, семейство кос Bt представляет собой изотопию между Bq
и Вх. U
Следовательно, функция д является корректно определенной на классах
эквивалентности допустимых систем кривых.
Для завершения доказательства основной теоремы нам остается доказать
лишь следующую лемму.
Лемма 10.4. Для каждой косы Ъ мы имеем g(f(b)) = Ъ.
Доказательство. Действительно, расположим Ъ в малой окрестности
наклонной плоскости Ρ таким образом, чтобы концами этой косы были точки (г, 0, 0)
и (j, 1,1), г J = 1,...,п.
Рассмотрим допустимую систему кривых /(6), лежащую в плоскости Оху.
Существует допустимая параметризация для /(6), которая восстанавливает
косу Ъ. По лемме 10.2, каждая допустимая параметризация для f(b) порождает Ъ.
Следовательно, g(f(b)) = b. D
10.1.3. Алгебраическое описание инварианта /
Значения некоторых инвариантов иногда представляют собой сложные
(алгебраические) объекты, распознавание эквивалентности которых часто
представляют собой трудную задачу, едва ли более простую, чем задача
классификации исходных объектов (на которых инвариант принимает значения). К
таковым относятся, например, фундаментальная группа и дистрибутивный
группоид узлов.
Мы опишем построенный нами инвариант алгебраическим образом.
Оказывается, что полученный результат очень прост для распознавания. А именно,
10.1. Геометрический алгоритм
151
проблема распознавания кос в нашем случае оказывается сведенной к проблеме
распознавания слов в свободной группе. Таким образом, имеется инъективное
отображение из множества изотопических классов кос в набор из η копий
свободной группы из η образующих (это отображение, однако, не является
гомоморфизмом).
Каждая коса β задает перестановку. Эта перестановка может быть
однозначно восстановлена из любой допустимой системы кривых, соответствующей
косе β. Действительно, для допустимой системы А кривых соответствующая
перестановка отображает г в j, где j — ордината нижнего конца нити, имеющей
верхний конец (г, 1). Обозначим эту перестановку через р(А).
Пусть η — целое число. Рассмотрим свободное произведение G η групп,
изоморфных группе Ζ, с образующими αϊ,... ,αη. Обозначим через Ει левые
смежные классы G по {cti}, т.е., #ι,#2 G G представляют собой один и тот же
элемент в Ει если и только если д\ = о^дъ для некоторого к.
Определение 10.4. Под п-системой будем понимать набор элементов {е\ G
Ει,... ,en G Еп}.
Определение 10.5. Под упорядоченной п-системой будем понимать пару: п-
система и перестановка из Sn.
Предложение 10.1. Существует инъективное отображение из множества
классов эквивалентности допустимых систем кривых во множество
упорядоченных п-систем.
Так как перестановки для эквивалентных допустимых систем кривых
совпадают, мы можем выбрать перестановку s G Sn и рассматривать лишь
допустимые системы кривых с перестановкой s. Таким образом, достаточно показать
лишь, что существует инъективное отображение из множества всех
допустимых систем из η кривых, у которых фиксировано соответствие нижний конец —
верхний конец, во множество п-систем.
Дальнейшее доказательство вытекает из следующей очевидной леммы.
Лемма 10.5. Кривые с концами в точках (г, 1) и (j, 0), рассмотренные с
точностью до неподвижной на концах гомотопии, при которой внутренние
точки кривых не могут совпадать с верхними точками, находятся во взаимно
однозначном соответствии с элементами из Ει.
Таким образом, для фиксированной перестановки s допустимые системы
кривых могут быть однозначно закодированы п-системами, что завершает
доказательство предложения 10.1.
Теперь мы видим, что построенный инвариант является таким объектом,
значения которого легко сравнивать.
Опишем теперь, как следует вычислять функцию / по слову-косе шаг за
шагом.
Пусть β — слово-коса, записанное как произведение образующих группы кос
(и обратных элементов) β = σ^1 ... σ\^, где каждая переменная Sj равна либо
+ 1, либо —l,ij = 1,..., гг — 1 а σι,..., ση_ι — стандартные образующие группы
кос Вг(п).
152
Глава 10
Мы будем строить п-систему шаг за шагом при чтении слова β. Сначала
выпишем η пустых слов (в алфавите αϊ,..., αη). Предположим, что первой буквой
слова β является Gj. Тогда все слова, за исключением слова e^+i, не
изменяются (т.е. остаются пустыми), а слово e^+i становится равным а~ . Если первый
перекресток отрицателен, т.е соответствует σ~ , то слова, за исключением е^,
остаются неизменными и е^ превращается в α^+ι. При рассмотрении каждого
следующего перекрестка мы поступаем следующим образом. Пусть ρ и q —
номера нитей, идущих с левой и правой сторон соответственно. Если перекресток
положителен, т.е. соответствует образующей σ^, то все слова, за исключением
слова eq, остаются прежними, a eq преобразуется в eqe~1a~1ep. Если
перекресток отрицателен, то все перекрестки, за исключением ер, остаются прежними,
и ер переходит в epe~laqeq. После прохождения всех перекрестков мы получаем
желаемую гг-систему.
Пример 10.1. Для тривиальной косы, представленной в виде σισ2σισ^" σ^ σ^
построение операции происходит следующим образом:
(е,е,е) —> (β,α^,β) —> (е, а^1, а^1) —> (е, а^1, a^"1aj"1) —>
-> (β,β,α^α^1) -> (β,β,α^Γ1) -> (е,е,е).
A priori эти слова могут быть и нетривиальными, они только должны
представлять тривиальную косу, например, мы могли бы получить тройку (αϊ ,ο^,α^ )
Однако, на самом деле это не так.
Предложение 10.2. Для тривиальной косы вышеописанный алгебраический
алгоритм дает тривиальное слово.
Доказательство. В самом деле, алгебраическое число вхождений образующей
αϊ в слово ei равно нулю. Это может быть легко установлено индукцией по числу
перекрестков. В начальном положении все слова тривиальны. Шаг индукции
очевиден. Таким образом, конечное слово е^ равно а^, где ρ = 0. D
Из описанного подхода можно легко получить инвариант (действие)
следующим образом. Вместо множества {ei,..., еп} можно рассмотреть множество
{βιαιβ^ , ... ,βηαηβ"1}. Поскольку слова е^ определены с точностью до
умножения на элементы а^ слева, полученные элементы корректно определены в
свободной группе. Кроме того, элементы ^ = е^е" являются
образующими в свободной группе. Это следует из пошаговой проверки. Таким образом,
для каждой косы Ъ мы получаем множество образующих Q(b) группы кос.
Поэтому коса Ъ определяет преобразование, равное композиции преобразований,
соответствующих образующим. Легко проверить, что преобразование,
соответствующее произведению двух кос равняется композиции преобразований,
соответствующих этим косам. Можно говорить о действии косы на свободной
группе. Поскольку / является полным инвариантом, это действие имеет пустое
ядро.
Определение 10.6. Это действие называется действием Гурвица группы кос
Вп на свободной группе Z*n.
10.2. LD-СИСТЕМЫ И АЛГОРИТМ ДЕОРНУА
153
10.2. Х£)-системы и алгоритм Деорнуа
Для распознавания кос есть и чисто алгебраический алгоритм. Он
предложен французским математиком Патриком Деорнуа [Deh]. Этот алгоритм
является довольно быстрым.
Его идея очень близка к той, которая используется в дистрибутивных
группоидах. Мы рассматриваем некоторое (конечное) множество цветов и
связываем цвета с дугами косы. Затем мы определяем некоторый способ сведения косы
к тривиальной и, если коса не является тривиальной, мы указываем отчего коса
нетривиальна (причина нетривиальности выражается в терминах цветов).
Более точно, для "хороших" цветовых систем, каждая коса определяет оператор
цветовой системы, и этот оператор нетривиален для нетривиальной косы.
Напомним сначала, что косы обладают групповой структурой. Так что для
сравнения двух α, β кос достаточно решить вопрос о том, является ли коса
θίβ~χ тривиальной.
Пусть дана коса /3, записанная в виде слова W в алфавите σί , г =
= 1,2...,п- 1.
Определение 10.7. Назовем косу β I-положительной если коса может быть
представлена словом W', в котором буква σι встречается только в
положительных степенях (и не встречается в отрицательных степенях). Аналогично
определяется 1-отрицательная коса.
Если коса может быть записана словом W без σι и σ^ , то мы скажем, что
эта коса 1-нейтральна.
Замечание 10.3. Каждая коса может быть представлена различными
словами; при этом заранее не ясно пересекаются ли описанные выше классы
положительных, отрицательных и нейтральных кос. Ниже мы покажем, что
эти классы не пересекаются и вместе составляют множество всех кос.
Теорема 10.3. Каждая 1-положительная (соотв., 1-отрицательная) коса
нетривиальна.
Замечание 10.4. В действительности справедливо более сильное
утверждение: каждая коса, представляемая словом, содержащим of и не содержащим
Gi~e для некоторого е = ±1, нетривиальна. Это утверждение мы доказывать
не будем, см. [Deh].
Первой нашей целью является доказательство того, что вышеупомянутые
классы кос не пересекаются. Мы собираемся описать алгоритм, преобразующий
каждую косу в ей эквивалентную, которая при этом либо тривиальна, либо 1-
положительна, либо 1-отрицательна (множество 1-нейтральных кос
подразделяется на 2-положительные, 2-отрицательные и 2-нейтральные косы в
зависимости от наличия вхождений σ2 или σ^~ в запись косы, далее 2-нейтральные
косы подразделяются на 3-положительные, 3-положительные и 3-нейтральные
косы, и т.д.).
Для доказательства теоремы 10.3, нам понадобятся предварительные
определения и леммы.
Рассмотрим положительную косу β и все ее дуги.
154
Глава 10
Мы хотим построить множество Μ и пометить диаграмму косы элементами
из Μ следующим образом: свяжем с каждой дугой элемент из Μ так, что:
1. Все дуги, выходящие из верхних концов косы, помечаются переменными,
могущими принимать значения в М;
2. Каждая метка однозначно определяется метками, над ней стоящими;
3. Оператор /, выражающий нижние метки через метки, стоящие выше,
является инвариантным относительно изотопии кос.
Для установления такой разметки нам придется рассматривать перекрестки
диаграмм. Допустим, что перекресток образован дугами а, 6, и с. Положим
с = а * 6, см. рис. 10.5.
Рис. 10.5. Соотношение
Проанализируем инвариантность оператора / относительно изотопии.
Каждая элементарная изотопия связана с одной из следующих формул:
σ^σζ_1 = е,г = 1,... ,гг - 1,
(движение Ω3):
σισι+ισι = σ^+ισ^+ι,ζ = 1,...гг — 2,
(дальняя коммутативность):
GiGj = σ^σ^, \г — j'\ ^ 2,1 ^ г, j ^ η — 1.
Соотношение σ%σ~[ = ε будет рассмотрено ниже (сейчас мы рассматриваем
только слова с положительными степенями образующих).
Функция, которую мы строим, должна быть инвариантной относительно
дальней коммутативности.
Для инвариантности этой функции относительно движения Ω3 нам
требуется левая самодистрибутивность структуры (в случае дистрибутивного
группоида — нам была нужна праводистрибутивная структура):
а * (6 * с) = (а * Ь) * (а * с). (Ю-1)
Определение 10.8. Множество Μ с левой самодистрибутивной структурой *
называется LD-системой или LD-множеством.
10.2. LD-СИСТЕМЫ И АЛГОРИТМ ДЕОРНУА
155
Замечание 10.5. Очевидно, что соотношения (10.5) f недостаточно для
определения f в случае произвольных слов: мы не знаем, что делать с
буквой σ"1.
Продолжая начатое, мы введем еще две операции V и Λ на Μ так, как
показано на рис. 10.7
Очевидно, что отображение / инвариантно относительно соотношений
дальней коммутативности (переставляющих σι и Gj для \г — j\ ^ 2).
Осталось проверить инвариантность отображения / относительно Ω3, т.е.
относительно преобразования а^г+1&г ~^ &г+1^г&г+1· Легко видеть, что (см.
рис. 10.6) инвариантность относительно Ω3 означает левую дистрибутивность
операции *.
(a*b)*(a*c) a*b a a*(b*c) a*b a
Рис. 10.6. Инвариантность относительно Ω3 влечет левую дистрибутивность
Таким образом, имея £1}-множество М, мы можем пометить дуги
положительных кос элементами из М. Множество элементов в нижних точках
однозначно определено множеством элементов в верхних точках.
Обозначим последние через pi, где г пробегает значения от 1 до щ элементы
при верхних точках обозначим через qi. Например, для тривиальной косы мы
получаем pi = q^
Для всякого Ь1}-множества можно определить отношение частичного
порядка <. Именно, для любых а, Ъ Ε Μ мы имеем а < а*Ъ.
Определение 10.9. Частично упорядоченное LZJ-множество Μ называется
упорядоченным если частичное отношение < ациклично, т. е. не существует
последовательности а\ < а2 < · · · < ап < а\.
Пример 10.2. Множества R и Q допускают некоторые леводистрибутивные
(но не ацикличные) операции:
156
Глава 10
1. α * Ъ = тах(а,6)
2. а * Ъ --
(а+Ь)
3. а*Ь= (α + 1).
Приведем пример ацикличной L^D-системы. Для того, чтобы сделать это
нам придется рассмотреть более сложные структуры, включающие в себя LD-
структуры. Обозначим полугруппу неотрицательных кос через Вг(п)^~.
Замечание 10.6. Такие полугруппы (моноиды) играют ведущую роль в
теории нормальных форм Γαρ сайда.
Определение 10.10. Пусть (Μ, Λ) — множество с бинарной операцией.
Определим с помощью индукции правое действие полугруппы Вг(п)^~ на Мп =
Μ χ · · · χ Μ. Сначала для а = (αϊ,..., ап) положим по определению для
любой косы w
где ε
(α)ε = α, (α)σ^ = (αϊ ..., α» Λ α*+ι, ai? ai+2,
единичный элемент группы кос.
,an)w,
(10.2)
Для того, чтобы раскрашивать произвольные диаграммы кос (не только
положительные) операции * не достаточно. Изменим обозначения:
переобозначим операцию * через Л и рассмотрим новые операции V и о. Теперь мы можем
раскрашивать диаграммы кос по правилу, указанному на рис. 10.7.
α Л Ъ аоЪ
Рис. 10.7. Определение нижних меток
ЪУ а
Как и прежде, мы выражаем метки нижних точек через метки верхних
точек; так определяется оператор /.
Лемма 10.6. Пусть (Μ, Λ, ο, ν) — множество с тремя бинарными
операциями. Тогда определенный выше оператор f инвариантен относительно
изотопии, порожденных третьим движением Рейдемейстера если и только если
на множестве Μ выполняются следующие соотношения:
Vx, у G Μ хоу = у,хЛ(х\/у) = х\/(хЛу) = у.
Доказательство. Утверждение непосредственно вытекает из рис. 10.8.
D
10.2. LD-СИСТЕМЫ И АЛГОРИТМ ДЕОРНУА
157
аЛЬ
аоЪ
(α Λ Ь) о а
aV (ЪЛа)
(а о Ъ) Λ (Ъ V а
ЪУ а
аоЪ
Рис. 10.8. Инвариантность относительно Ω2
Определение 10.11. L^D-система Μ (относительно операции Λ), снабженная
операцией V, называется LD -квазигруппой если соотношение
ж Л (ж V у) = ж V (ж Л у) = у
имеет место для произвольных ж, у £ М.
(10.3)
Замечание 10.7. В отличие от дистрибутивных группоидов, для
LD-квазигрупп может не выполняться соотношение идемпотентности.
Замечание 10.8. Изотопия, порожденная движением Ω2, ne меняет
оператора f по определению. Таким образом, если Μ является LD-квазигруппой,
то оператор f инвариантен относительно изотопии кос.
Следующее утверждение проверяется непосредственно.
Предложение 10.3. Пусть G — группа. Тогда бинарные операции χ Λ у =
хух~г, χ V у = х~гух, χ о у = у, задают структуру LD-квазигруппы на G.
Таким образом, для заданной группы G мы можем использовать (G, Λ,ν)
(где χ о у = у для любых ж, у) для раскрашивания кос. В частности, пусть
FGn — свободная группа, порожденная элементами {ж1,... ,жп}. Для слова-
косы Ъ (из η нитей) определим Ъ как слово-косу, полученную из Ъ написанием
букв в обратном порядке. Так, например, σ\σ^ сгз^Г |—>> σϊ σ3σ2~ σι·
Для заданных элементов ж ι,..., хп определим элементы у ι,..., уп
согласно следующему правилу: (yi,... уп) = (ж1,... хп)Ъ. Пусть ф(Ъ) — автоморфизм
группы FGn, отображающий (ж1,..., хп) в (yi,..., уп). Тогда φ является
эндоморфизмом группы кос Вг(п) в Aut(FGn), так как ф(Ь~г) совпадает с ф(Ъ)~
по построению.
158
Глава 10
Обозначим через FGoq прямой предел вложений FG\ С FG2 С FGs С
Таким образом, мы получаем эндоморфизм φ : В^ —>· Aut(FGOQ).
Обозначим φ(σι) через щ.
По построению мы имеем:
iXk к < г или к > г + 1
XiXi+ix'1, к = г (Ю-4)
Xi, к = г + 1.
Замечание 10.9. Это действие совпадает с действием образующей σι на
цвета дуг, см. рис. 10.7, ср. с определением действия Гурвица.
У нас есть операция сдвига sh, действующая на образующие: sh(xi) = Хг+i·
Определим теперь сдвиг sh на FG^^ отображая χι в χ^+ι для каждого г.
Действие сдвига sh на Aut(FGOQ) определяется по следующему правилу. Для
φ G Aut(FGOQ), положим sh^)(xi) = χι и s/i(0)(x^+i) = sh^(xi)) для г ^ 1,
где действие кос определено по формуле (10.2).
Определим теперь Λ по правилу
0 Λ φ = φ о sft(^) о он о s/i(0_1), (10.5)
где φ — гомоморфизм из (Бг(оо), Λ) в (Aut(FGос), Λ). Покажем, что операция,
определенная равенством (10.5), является самодистрибутивной слева.
Заметим, что а\ коммутирует со всяким автоморфизмом в образе sh2. Для
завершения доказательства левой самодистрибутивности операции Λ,
достаточно доказать следующее.
Предложение 10.4. Пусть G — группа, а — элемент группы G, a s —
автоморфизм группы G. Пусть элемент а коммутирует с образами отображения
s2 и пусть имеет место уравнение
as(a)a = s(a)as(a). (10.6)
Тогда формула хАу = xs(y)as(x~1) определяет левую самодистрибутивную
операцию.
Доказательство. Так как s является изоморфизмом группы G, мы имеем
χ Λ (у Λ ζ) = xs(y)s2(z)s(a)s2(y~1)as(x~1), (Ю-7)
(χ Λ у) Λ (χ Λ ζ) = xs(y)as2(z)s(a)s2(x~1)as2(x)s(a~1)s2(y~1)s(x~1). (10.8)
Если операция Λ является самодистрибутивной слева, то, полагая χ = у =
ζ = 1, мы получаем s(a)a = as^asi^a-1).
Легко проверить, что обратное утверждение также верно.
Наконец из формулы (10.6) и предположения о том, что а коммутирует со
всеми элементами вида s2(z) следует тот факт, что отображение /,
определенное как ί(σι) = sz_1(a), порождает гомоморфизм из В^ в G. D
Таким образом мы определили левую самодистрибутивную систему на
множестве Aut(FGOQ) с операцией Λ.
10.2. LD-СИСТЕМЫ И АЛГОРИТМ ДЕОРНУА
159
Теорема 10.4. Эта система (Aut(FGOQ),A) ациклична.
Доказательство следует из двух вспомогательных лемм о свободной
редукции; свободная редукция появляется при вычислении oti{x) и состоит в
следующем.
Обозначим множество слов в алфавите {хг , х2 , · · · } через Woo·
Скажем, что слово из W^ является свободно редуцированным если оно не
содержит под слов вида Х{Х~ и х~ χ ι. Для каждого w Ε W^ обозначим через
red(w) слово, полученное из w последовательным удалением таких под слов.
Таким образом, мы можем отождествить свободную группу FG^ с множеством
всех свободно редуцированных слов; операция на этом множестве имеет вид
и · ν = red(uv).
Определение 10.12. Для буквы χ из алфавита {хг , х2 ·,···} обозначим
через Е(х) подмножество множества FG^oo, состоящее из всех свободно
редуцированных слов, заканчивающихся на х.
Рассмотрим образ множества Е{х^[ ) относительно действия ai .
Лемма 10.7. Пусть φ — произвольный элемент из Aut(FGOQ). Тогда
автоморфизм sh{4>) отображает множество Е(х^г) в себя.
Доказательство. Пусть / — автоморфизм множества W^, отображающий
каждые элемент χι в некоторое редуцированное слово ф{х%). Пусть w —
произвольный элемент из Е(х± ). Тогда w = их^ , где и — некоторое
редуцированное слово, не принадлежащее множеству Е(х\). В этом случае мы имеем
sh(f)(w) = sh(f)(u) ■ sh(f)(x^), т.е. red(sh(f)(u)x^).
Пусть последнее слово не принадлежит множеству Е{хх ). Это означает,
что его последняя буква х± сокращается с некоторой буквой х\ из sh(f)(u). Но
буква χι в sh(f)(u) может происходить только от некоторой буквы х\ в и. Таким
образом, мы имеем разложение и = u\X\U2 такое, что red(sh(f)(u2)) является
пустым словом, т.е. sh(f)(u2) = 1. Так как sh(f) является автоморфизмом
FGoc, то U2 = 1. Это означает, что и^ Ε Е(х\). Противоречие изначальному
предположению завершает доказательство. D
Лемма 10.8. Автоморфизм а\ отображает Е(х^г) в себя.
Доказательство. Пусть w — некоторый элемент из Е(х^1). По определению
w = их^1, где и — некоторый редуцированный элемент, не принадлежащий
множеству E(xi), a a\(w) совпадает red{a\{w)). Более точно,
Oii(w) = red{ai{u)x\X21Xi1)· (10.9)
Предположим, что слово в правой части не принадлежит множеству Е(х^ ).
Это означает, что последняя буква х^ сокращается с некоторой буквой х\ в
конце слова а\{и). Эта буква происходит либо из некоторого Х2, либо из
некоторого xf1 в слове а\{и).
В первом случае выпишем букву Ж2> которая участвует в сокращении, и
представим и в виде U1X2U2, где U2 — некоторое редуцированное слово, начальная
буква которого не совпадает с х% · Таким образом, мы имеем
ol\{w) = red(ai(ui)xiai(u2)xiX21Xi1), (10.10)
160
Глава 10
и изначальное предположение может быть переформулировано следующим
образом: red{a\(u2)x\x^ ) является пустым словом (так как ot\(u2) = χ^Χχ )·
Пусть теперь а\ будет автоморфизмом, а хъх^1 — образом элемента х^хх\
под действием ol\. Таким образом, мы имеем и = х^ х\- Но это ведет к
противоречию: слово и не должно начинаться с χ2 ·
Во втором случае мы можем аналогично записать и = и\х\и2 для е = =Ы.
Таким образом мы получаем:
ol\(w) = red(ai(ui)xiX2Xi1ai(u2)xiX21Xi1)- (10.11)
Теперь наше предположение состоит в том, что red{x\x^ а\(и2)х\х^)
является пустым словом.
В этом случае мы видим, что ol\{u2) — Х\Х2 Хл . Последнее слово равно
слову а\(х1~е). Следовательно, и^ должно быть равно слову хг~е. Если е = +1,
то слово U2 является пустым. Если е = -1, то W2 = xf. В обоих случаях U2
принадлежит множеству Е(х\), что ведет к противоречию. D
Лемма 10.9. Предположим, что φ является автоморфизмом множества
FGос, который может быть представлен как композиция образов
отображений sh uoli, причем последнее встречается хотя бы один раз. Тогда ф(х\)
принадлежит множеству Е(х^г). В частности, отображение φ не является
тождественным.
Доказательство. Предположение леммы состоит в том, что φ имеет
представление следующего вида:
φ = s/i(0o) ° Οίι ° ^Η(φι) ο α\ о · · · о а\ о sh^p). (10.12)
В этом случае мы имеем sh^p)(xi) = х\ и, следовательно, oi\{x\) = х\Х2Х^ ,
т.е., ol\{x\) G Е(х± ). Поэтому каждое следующее отображение sh^k) (так лее,
как и οίι) отображает Е(х^г) в Е(х^1).
Π
Докажем теперь теорему 10.4. Нам нужно показать, что в Aut(FGOQ)
равенства вида
ф=(...(фАф1)А...)Афр) (10.13)
не могут иметь места.
Используя определения Λ, мы получаем представление для φ в виде
φ = φ о нечто (10.14)
Здесь "нечто" содержит α ι и sh.
Таким образом, оператор Id должен быть выразим через sh и α ι, причем
α>ι должно встретиться по крайней мере один раз. Это противоречит последней
лемме.
Завершим теперь доказательство теоремы 10.2. Пусть Ъ является 1-поло-
жительной косой (словом-косой). Рассмотрим автоморфизм ф(Ъ). Он
удовлетворяет условиям леммы 10.9, следовательно, он не является тождественным,
поэтому коса Ъ не тривиальна.
10.2. LD-СИСТЕМЫ И АЛГОРИТМ ДЕОРНУА
161
Молено привести также следующее "наглядное" доказательство.
Пусть имеется L^D-квазигруппа Q, которая является ацикличной LD-qvl-
стемой с частичным отношением порядка <. Покажем, что существование
такой квазигруппы Q влечет утверждение теоремы 10.2. Рассмотрим элементы
αϊ, аг,..., flfe, соответствующие "самым левым" перекресткам, а также элементы
6ι, 62,..., лежащие справа от сц, см. рис. 10.9.
6°
Рис. 10.9. 1-положительная коса нетривиальна
Легко видеть, что α^+ι = сц /\ bi > αι. Следовательно, α& > а\. Так как
отношение < является ацикличным, мы имеем: а^ φ α\.
При этом для тривиальной косы элементы множества М, соответствующие
верхним точкам, совпадают с элементами, соответствующими нижним точкам
(в том числе это относится и к левой верхней и левой нижней точкам).
Противоречие доказывает теорему.
Отсюда сразу получаем несколько следствий.
Следствие 10.1. Обратная к 1-положительной косе является 1-отрица-
тельной; обратная к 1-нейтральной косе является 1-нейтральной.
Следствие 10.2. Каждая коса В принадлежит не более, чем к одному типу:
1-положителъных, 1-отрицательных и 1-нейтральных кос.
Эти следствия остаются читателю в качестве легкого упражнения.
Итак, 1-положительные и 1-отрицательные косы не являются тривиальны-
162
Глава 10
Все 1-нейтральные косы молено подразделить на 2-положительные, 2-отри-
цательные и 2-нейтральные в соответствии с тем, встречаются ли в некоторой
их записи только G2 или только σ^ .
Аналогично теореме 10.5, молено доказать следующее
Предложение 10.5. Все 2-положительные и 2-отрицательные косы
нетривиальны.
Аналогично 1- и 2-положительным (отрицательным, нейтральным) косам
можно определить /с-положительные (соответственно, нейтральные) косы
(слова-косы). Рассуждая как и прежде, можно показать, что все положительные и
отрицательные косы нетривиальны.
Следовательно, согласно нашей классификации, существует ровно одна (п —
1)-нейтральная коса из η нитей, а именно, тривиальная коса.
Покажем теперь, что все косы могут быть классифицированы таким
образом, а именно, имеет место следующая теорема.
Теорема 10.5. Каждая коса является либо I-положительной, либо 1-отри-
цательной, либо 1-нейтральной.
Обсудим сначала эту теорему.
Предположим, что имеется некоторое слово-коса, представляющее косу из
η нитей К, и мы хотим использовать соотношения σ^σ^ = σ^σι при \г — j\ ^ 2,
GiGi+iGi = σ^+ισ^+ι для удаления либо σι, либо σι-1.
Предположим, что L является подсловом в К, имеющим вид a\vwa\~v', где
ρ = =Ы, а слово w содержит только образующие σ , где j > г.
Определение 10.13. Такое слово называется 1-ручкой.
Наглядно г-ручка выглядит так как показано на рис. 10.10.
Рис. 10.10. Ручка
К такой ручке можно применить редукцию, т. е. движение, протягивающую
г-ю нить над соседними перекрестками, как показано на рис. 10.11. Этот
рисунок схематично изображает набор блоков (в которых коса может иметь
произвольный — но одинаковый для правой и левой части — вид и разделяющих их
перекрестков — в данном случае двух — каждый из которых может быть как
проходом так и переходом).
Редукция, очевидно, не меняет изотопический тип косы.
10.2. LD-СИСТЕМЫ И АЛГОРИТМ ДЕОРНУА
163
Рис. 10.11. Редукция ручки
Предложение 10.6. В этом случае слово σ\νσϊ е переходит в слово ν',
полученное из ν заменой всех σί+\ β ν на σ^1σί Vf+1.
Доказательство. Действительно, рассмотрим ручку, изображенную на
рис. 10.11. Все перекрестки, лежащие справа от σ2, не меняются. Начальный
и конечный перекрестки σ1 исчезают. Перекрестки, в которых "подвижная"
нить проходит сверху, меняют свой тип так как указано в утверждении. D
Рассмотрим теперь слово-косу К и будем последовательно редуцировать
ручки в ней. Если процесс остановится (т.е. мы избавимся от всех ручек), то
полученная коса будет иметь либо 1-положительную, либо 1-отрицательную,
либо 1-нейтральную форму.
На самом деле такой "наивный" подход работает не всегда.
Соглашение. Для удобства (из за малого числа нитей в рассматриваемых
примерах) будем использовать строчные латинские буквы а, 6, с,... вместо
образующих σι, σ2, · · · и заглавные буквы А, В, С,... вместо σ^ , σ% ,....
Пример 10.3. Рассмотрим слово аЪсВА. Оно содержит 1-ручку. Применяя
редукцию ручки, мы получим слово B(abcBA)b, содержащее изначальное слово
в качестве под слова. Таким образом, применяя редукцию ручек многократно,
мы всегда будем заново получать ручки и увеличивать длину слова.
Дело в том, что что "внутри" рассматриваемой 1-ручки находится 2-ручка;
после редукции 1-ручки эта 2-ручка появляется снаружи и становится 1-ручкой.
Для этого слова-косы можно сначала редуцировать "внутреннюю" ручку,
а затем — внешнюю. Таким образом мы получим а(ЬсВ)А —>· (аСЬсА) —>· СЬАВс;
из этого можно заключить, что коса является 1-положительной.
Оказывается, что наличие /с-ручек внутри j-ручек (k > j) является
единственным препятствием к тому, чтобы редуцировать слово-косу к слову-косе
без 1-ручек.
164
Глава 10
Докажем следующую лемму.
Лемма 10.10. Если j-ручка не имеет (j+Ι)-ручек внутри (в качестве подсло-
ва, заключенного между концами j-ручки), то после редуцирования j-ручки
новых ручек не появляется.
Доказательство. Без ограничения общности предположим, что j' = 1. Пусть
и = a\eva\~e — 1-ручка, е = =Ы. Так как ν не содержит 2-ручек, мы видим,
что внутри υ есть только либо только положительные степени σ^·, либо только
отрицательные степени.
То лее самое можно сказать и о степенях σ\ в слове и'', получающихся из и
посредством редукции ручки.
Следовательно, слово и' не содержит ручек. D
Определение 10.14. Ручка, содержащая внутри себя другие ручки в качестве
под слов, называете гнездом.
Определение 10.15. Редукция г-ручки, не содержащей (г + 1)-ручек внутри,
называется собственной.
Опишем теперь действие алгоритма.
Сначала мы редуцируем все внутренние ручки (которые не могут являться
гнездами), затем мы редуцируем ручки, которые содержали ручки, которые мы
уже редуцировали, и так далее. В конце мы получим слово, представляющее
1-положительную, 1-отрицательную или 1-нейтральную косу.
В первых двух случаях алгоритм останавливается. В третьем случае мы
забываем о первой нити и повторяем ту же операцию для последующих нитей.
Пример 10.4. Рассмотрим слово АВасВСВаСЪаа. Применим к нему
описанный выше алгоритм.
АВасВСВаСЪаа
ЬАВсВСВаСЬаа
ЪЪАВсЪАВСЪАВСЪаа
ЬЬАВсЬАВСЬАсВСаа
ЪЪАВсЪАВСЪсЪАВСа
ЪЪАВсЪАВСЪсЪЪАВС
Выше мы подчеркивали под слово, содержащее ручку, которую мы
редуцировали.
Полученное слово является 1-отрицательным. Следовательно,
рассматриваемая коса нетривиальна.
Таким образом, мы получили простой и эффективный алгоритм для
распознавания кос. Этот алгоритм носит название алгоритма Деорнуа.
Мы еще не доказали, что алгоритм Деорнуа останавливается (количество
букв в слове-косе, вообще говоря, растет, поэтому мы не можем точно сказать,
остановится ли алгоритм за конечное время.)
Упражнение 10.1. Докажите, что алгоритм Деорнуа останавливается для
кос из трех нитей.
Далее мы приводим краткое доказательство того факта, что алгоритм
Деорнуа останавливается. С более полным доказательством можно ознакомиться в
[Deh].
10.2. LD-СИСТЕМЫ И АЛГОРИТМ ДЕОРНУА
165
10.2.1. Почему алгоритм Деорнуа останавливается?
Определение 10.16. Слово-коса называется положительной (соответственно
отрицательной), если она содержит только σι (соответственно только σ~ ).
Оказывается, что, применяя собственные редукции ручек wo^wi^W2^...,
мы можем представить Wk как путь в специальном конечном графе. Стартуя
со слова w = wo, мы можем попасть только в конечное число слов.
Опишем эту конструкцию более подробно. Дадим сначала несколько
определений.
Назовем слово-косу положительной, если в ее записи встречаются
только положительные степени образующих σ^; аналогично, слово-коса называется
отрицательной, если в ее записи встречаются только отрицательные степени
образующих σι.
Определение 10.17. Под положительной {отрицательной)
эквивалентностью двух слов будем понимать равенство а = Ъ двух положительных (соотв.,
двух отрицательных) слов-кос.
Пример 10.5. a\G2(J\ = (У2&\&2 является положительной эквивалентностью;
σϊ σ3 = σ3 σϊ является отрицательной эквивалентностью;
σισ2σ]~ = σ^ (J\(J2 не является ни положительной, ни отрицательной
эквивалентностью .
Определение 10.18. Под переворачиванием слова мы имеем в виду
эквивалентность cr~1aj —>· (JjG^1 если \г—j\ ^ 2 или cr~1aj —>· σ^σ:/·σ~1σ~1 если \г—j\ = 1
(правое переворачивание).
Аналогично определяется левое переворачивание.
Легко проверить, что, повторно применяя левое переворачивание, можно
каждую слово-косу w привести к виду NlD^ , где Nl и Dr —
положительные слова-косы. Они называются левым числителем и правым знаменателем
соответственно.
Аналогичным образом, применяя правое переворачивание, каждую косу
можно привести к форме D~[ Nr с левым знаменателем Dl и правым
числителем Nr.
Для каждой косы и мы имеем Dl(u)Nr(u) = Nl(u)Dr(u).
Определение 10.19. Под абсолютным значением слова-косы w мы понимаем
DL(w)NR(w).
Обозначение: \w\.
Определение 10.20. Для положительной косы X графом Кэли называется
следующий граф: его вершинами являются тривиальная коса е, коса X, а также
положительные косы Υ, для которых существует положительная коса Ζ такая,
что Υ Ζ = X. Две вершины Ρ и Q соединены ребром если существует г такое,
что Ρ = Qai или Q = Ρσι. В этом случае ребро ориентировано от "меньшей
косы" к "большей".
Пример 10.6. Рассмотрим положительную косу Δ4 = о\02(У\(Уъ02&\-
Соответствующий ей граф Кэли показан на рис. 10.12.
166
Глава 10
Δ4
Рис. 10.12. Граф Кэли для Δ4
Определение 10.21. Пусть и — положительная коса и пусть С (и) — граф
Кэли для косы и. Тогда каждый путь в (с любым началом и концом) на графе
Кэли может быть выражен в образующих группы кос и их обратных;
следовательно, он порождает слово в группе кос. Такие пути называются словами-
следами для и.
Сформулируем теперь некоторые вспомогательные леммы, из которых
будет следовать, что алгоритм Деорнуа останавливается за конечное время.
Лемма 10.11. Каждая собственная редукция ручки может быть сведена к
переворачиванию слов, положительной эквивалентности и отрицательной эквивалент-
ностям.
Лемма 10.12. Для произвольного слова w все слова, получаемые из w (правым и
левым) переворачиванием слов, а также положительной и отрицательной
эквивалентностью, являются словами-следами в \w\.
Из этих двух лемм вытекает следующая лемма.
Лемма 10.13. Каждое слово, получаемое из w собственными редукциями ручек,
является словом-следом в \w\.
Определение 10.22. Пусть w — слово-коса. Высотой слова w называется
максимальное число букв σι, которое может встречаться в слове, не содержащем σ"1, и
являющемся словом-следом в графе Кэли для \w\.
Предположим, что w = wo,wi,W2, · · · — последовательность собственных
редукций ручек для w. Заметим сначала, что количество σι-ручек в Wi не превосходит
числа σι-ручек в w.
Определение 10.23. Критическим префиксом (номер р) prefp(wk) называется коса,
представленная префиксом в Wk: которая кончается первой буквой р-й σι-ручки Wk-
10.3. Нахождение минимального слова для Вг(3) 167
В дальнейшем будет использовано то обстоятельство, что для каждого ρ префикс
"не возрастает" при переходе от wк к Wk+i и на самом деле убывает, при собственной
редукции ручки. Более точно, справедлива следующая лемма.
Лемма 10.14. Допустим, чтор-я σι-ручка редуцирована omwk KWk+i· Тогда
существует слово-коса uPjk являющаяся словом-следом в графе Кэли для w от prefp(wk)
к prefp(wk+i), которая содержит одну букву σ\ и не содержит σι.
Теперь нетрудно доказать следующую лемму.
Лемма 10.15. Пусть w — слово-коса длины I и высоты h. Тогда количество
редукций ручек, необходимых для w, не превышает lh.
Эта лемма показывает, что любая слово-коса может быть редуцирована либо к
1-положительной, либо к 1-отрицательной, либо к 1-нейтральной слову-косе.
Следовательно, алгоритм Деорнуа останавливается за конечное время.
10.3. Нахождение минимального слова для Вг(3)
Среди множества алгебраических проблем, возникающих в теории кос, есть
проблема нахождения минимального слова, задающего данную косу.
Естественно, решение такой проблемы содержит проблему распознавания тривиальной
косы (единственной косы длины нуль) и, следовательно, любых кос.
Мы приводим решение этой проблемы для случая трех нитей,
принадлежащее Митчелу Бергеру, см. [Вег].
Для группы кос Вг(3) существует естественный автоморфизм,
переставляющий σι и σ2. Пусть Τ — слово-коса из трех нитей; обозначим образ этой
слова-косы Τ под действием этого автоморфизма через Т.
Определение 10.24. Положим Δ = σισ2σι = σ2σισ2.
Заметим, что Δ "почти коммутирует" со всеми косами. А именно, имеет
место следующее
Предложение 10.7. Для произвольной косы А мы имеем А А = Δ А.
Определение 10.25. Назовем кирпичом каждое из четырех слов:
σισ2, σ2σι, σ]~1σ2"1, σ2"1σ]~1. (10.15)
Алгоритм, который будет описан ниже, состоит из трех шагов.
Первый шаг. Рассмотрим слово-косу Bq. Будем искать вхождения Δ или
Δ-1 и переносить их влево, используя равенство А А = А А.
Продолжаем процесс до тех пор, пока Bq не превратится в слово вида Δη£>ι,
где В ι не содержит ни одного Δ.
Второй шаг позволяет освободиться от кирпичей. Мы читаем слово слева
направо и, обнаружив кирпич в В ι, мы заменяем его указанным ниже способом:
σισ2 = Δσ^"1,
σ2σι = Δσ2
168
Глава 10
a^V^1 = Δ_1σι,
a^Vf1 = Δ_1σ2.
После каждого такого преобразования мы отправляем Δ^1 налево
указанным выше способом. Таким образом, мы получаем В = АРВ2 или В = Δρ£>2,
где
Б (71 —Γι <72 — <72 <7гтг — Г™
где все qi и г^ являются положительными целыми числами.
Наконец, третьим шагом мы частично повторяем второй шаг в обратном
порядке. Для определенности пусть ρ > 0 и В = Δρ£>2·
Выберем вхождение Δ слева и перенесем ее направо до встречи с σ2 · После
этого мы заменяем Δ · σ2 на кирпич σ2(Τ\· Каждый раз, когда это происходит
длина слова уменьшается на 2.
Затем мы повторяем эту операцию до тех пор, пока в слове не останется
ни одного вхождения Δ (если ρ ^ г) или ни одной σ2 (ρ ^ г). Обозначим
полученное слово-косу через Bmin.
Главная теорема в работе Бергера может быть сформулирована следующим
образом.
Теорема 10.6. Для заданного слова В, слово Bmin имеет минимальную длину
среди всех слов-кос, эквивалентных слову В.
10.4. Сферические, цилиндрические и иные косы
На самом деле инвариант /, описанный выше, см. стр. 146 (посредством
допустимой системы кривых) допускает обобщение на случай кос в различных
пространствах, [GM].
10.4.1. Сферические косы
Напомним, что а сферической косой из η нитей называется элемент из πι (Χη) ?
где Хп — конфигурационное пространство неупорядоченных наборов из η
точек на стандартной сфере S2.
Как и в случае обычных кос, сферические косы допускают простое
описание в пространстве.1 Нити косы в S% x It идут вниз с убыванием t (высоты)
и соединяют фиксированные точки Αι χ {1} и Aj χ {0}, где Αι,... ,Ап
фиксированные точки на сфере S2. Подобно обычным косам, сферические косы
рассматриваются с точностью до изотопии; мы рассматриваем изотопные
косы как одинаковые. Сферические косы образуют группу. Обозначим ее через
SB(n).
Рассмотрим сферическую косу. Молено предположить без ограничения
общности, что существует точка X £ S2 такая, что ни одна нить данной
сферической косы не содержит Χ χ t при любом t E [0,1].
1 Здесь / единичный отрезок ; ζ и t означают координаты на сфере S2 и отрезке /,
соответственно.
10.4. Сферические, цилиндрические и иные косы 169
Это значит, что каждая сферическая коса происходит от некоторой обычной
косы. Более точно, существует гомоморфизм h из В г (ή) на SB (ή),
определенный следующим образом: каждая коса Ъ в R3 = R2 x R порождает
сферическую косу б7, если мы компактифицируем плоскость R2 одной точкой, тем
самым отобразив R3 to S2 x R. Гомоморфные свойства такого отображения
группы кос очевидны.
Известно, (см., например, [Fr]) что ядро гомомофизма h порождено одним
элементом Ση = (σι ... ση_ι)η для любого η > 2.
Докажем это утверждение. Доказательство того, что элемент Ση
коммутирует со всеми элементами группы Вг(п) очевидно. Действительно, к косе Ση
можно добавить ленту такую, что первая и последняя нить являются частями
границы этой ленты, и все другие нити делят ленту на более мелкие ленты, см.
рис. 10.13.
Рис. 10.13. Στν коммутирует с образующими
Теперь каждая образующая σι группы кос может быть взята вдоль
соответствующей меньшей ленты, идущей с верху до низу как показано на рис. 10.13.
Это значит, что Ση действительно лежит в центре группы кос.
Оставшаяся часть доказательства может также быть изложена на языке
лент. Мы сделаем это, используя индукцию по по количеству нитей (начиная с
трех). Мы слегка изменим базис индукции: каждая крашеная коса, которая
коммутирует со всеми элементами группы кос является степенью элемента Ση.
Мы делаем так для того, чтобы начать индукцию со случая двух нитей. Для
двух нитей базис индукции очевиден.
Теперь шаг индукции может быть выполнен следующим образом: возьмем
170
Глава 10
нашу косу из η нитей, которая перестановочна со всеми косами из η нитей. По
причине перестановок она является крашеной. Затем мы рассмотрим η
крашеных кос, полученных из нее поочередным удалением одной из η нитей. По
предположению индукции каждая такая коса должна равняться Σ^_1 для
некоторого целого числа к. Оставшаяся часть доказательства предоставляется
читателю.
Очевидно, что инвариант / (см. стр. 146) отличает Στν от тривиальной косы,
поэтому он не является инвариантом для Вг(п). Более того, имеет место
Теорема 10.7. Ядро отображения Вг(п) —> SB (ή) совпадает с центром
группы Вг(п).
Главная идея доказательства (см. например, [Fr]) такова. Рассмотрим
тривиальную косу, представленную самым естественным образом в R3 с S2 x R.
Добавим к ней ленту самым простым образом. Будем следить за тем, что
происходит с лентой в процессе изотопии косы. Единственное, что может
случиться, — это перекручивание ленты. Это происходит, когда мы проходим через
точку компактификации X £ S2 = R2 U X, см. рис. 10.14.
Рис. 10.14. Перекручивание ленты
Теперь очевидно, что после некоторого количества перекручиваний наша
коса (в смысле Вг(п)) становится некоторой степенью косы Ση. Таким обра-
10.4. Сферические, цилиндрические и иные косы 171
зом мы доказали, что никакая другая коса, кроме степеней косы Ση, не может
лежать в ядре отображения В г (ή) —>· SB (n). С другой стороны, коса Ση
действительно является тривиальной в SB(n).
Мы собираемся "поправить" инвариант / для случая сферических кос.
Будем делать это следующим образом. Возьмем сферическую косу Ъ и ее
прообраз Ъа при отображении h (состоящий из бесконечного числа элементов).
Рассмотрим образы точек множества Ьа при отображении f. Они, возможно,
отличаются друг от друга. Построим отображение /(·), которое будет
постоянно на всех элементах f(ba). На этом пути будет построен полный инвариант
группы сферических кос.
Обозначим через Е[,..., Е'п множества, полученные факторизацией
множеств Ei по единственному определяющему соотношению эквивалентности
(αϊ ... ап) = е. Имеем отображение ϊ) : (Е\,..., Εη) ι—> (Е[,..., Е'п).
Определение 10.26. Назовем сферической η-системой множество элементов
{е[ G E[,...,e'n G Е'п} и упорядоченной п-системой сферическую гг-систему
вместе с некоторой перестановкой из Sn.
Определим отображение fs из обычных кос в сферические п-системы
следующим образом. Для каждой косы Ъ упорядоченная п-система f(b) состоит из
перестановки s, соответствующей косе 6, и множеств е^ G Ei,i = 1,... ,η. При
этом упорядоченная сферическая гг-система fs(P) состоит из перестановки s
и множества i) (ei),..., Ь(ег)· Очевидно, что / является инвариантом группы
обычных кос и таковым же является fs.
Теорема 10.8. Функция fs является полным инвариантом сферических кос,
т. е., две косы 6, Ъ' G Вп порождают одну и ту же сферическую косу тогда и
только тогда, когда fsib) = fsib')·
Доказательство. Прежде всего заметим, что утверждение леммы 10.1
справедливо также и для инварианта fs. (Доказательство остается буквально тем
же самым).
Так что для каждой косы Ъ имеем fs(b) = fs(^b) и, следовательно, fs
является инвариантом кос и Σ коммутирует с 6, /^(^Σ) = fs(T>b) = fs(b). Таким
образом, если b и Ь' порождают одну и ту же сферическую косу, то fs(b) = fs(bf).
Поэтому fs является инвариантом.
Докажем теперь обратное утверждение, т.е., что инвариант fs является
полным инвариантом сферических кос.
Действительно, нам нужно доказать, что если β\^β^ — две сферически
эквивалентные косы, то fs(Pi) = /s(/?2)· По лемме 10.1 для fs мы видим, что для
этого достаточно показать, что fs распознает тривиальную сферическую косу.
Пусть β — коса из Вг(п), и пусть Η(β) — соответствующая ей сферическая коса.
Предположим, что fs(h(P)) = е. По определению значение /(/3) вычисляется
следующим образом. Перестановка, соответствующая косе /3, тривиальна, и
соответствующая гг-система равна ((αϊ ... an)kl,..., (αϊ ... an)kn) для некоторых
целых /ci,..., kn. Напомним, что гг-система происходит из допустимой системы
кривых (не пересекающихся). Таким образом, мы видим, что к\ = &2 = ... кп.
Пусть к = к\ = · · · = кп.
172
Глава 10
Единственное, что остается проверить, это то, что если гг-система имеет вид
{((αϊ... ап)к,..., (αϊ ... ап)к)} при некотором /с, а соответствующая
перестановка — тривиальна, то β = Efe.
Но в этом случае β собой тривиальную сферическую косу, т.е. Η(β) = е.
Этим завершается доказательство теоремы.
D
10.4.2. Цилиндрические косы
Рассмотрим цилиндр С = S1 χ I.
Определение 10.27. Цилиндрической косой из η-нитей называется элемент
из группы 7Ti(Cn), где Сп — конфигурационное пространство неупорядоченных
наборов из η точек на цилиндре С. Цилиндрические косы рассматриваются с
точностью до естественной изотопии. Обозначим группу цилиндрических кос
из η нитей через СВ(п).
Построение инварианта цилиндрических кос еще проще, чем в случае со
сферическими косами. Эта простота следует из того, что С является
произведением отрезка / на одномерное многообразие (окружность).
Цилиндрическая коса из η нитей может быть рассмотрена как множество из
η кривых в CxIt, нисходящих οτί = 2κί=1 таким образом, что концы кривых
образуют множество {Yi х {1},^ х {2}, г, j = 1,...,η,Υί £ С}. Множество
С = С χ It = S^ χ /s χ It можно рассматривать как подмножество в R3 = Oxyz:
координата t соответствует ζ Ε [1,2], a, φ Ε [0,2π),5 Ε [1,2] образуют систему
полярных координат на плоскости Оху.
Для каждой кривой в С мы можем рассмотреть ее проекцию на цилиндр
S1 х It- Таким образом, для цилиндрической косы β мы имеем систему кривых
на цилиндре S1 x It с координатой t, убывающей от двух до единицы. В случае
общего положения эти кривые имеют лишь двойные точки трансверсального
пересечения, соответствующие разным уровням координаты t. Для каждого
перекрестка нужно указать, какая кривая имеет большую координату (образует
переход); другая кривая образует проход.
Выберем точку χ £ S1. Сингулярное значение — это такое значение t, что
уровень S1 χ {t} содержит либо перекресток, либо пересечение одной из нитей
косы с линией χ χ R.
Потребуем, чтобы перекрестки не лежали на линии χ χ R, а все пересечения
нитей с χ χ R были трансверсальными, при на каждом сингулярном уровне
лежал ровно один перекресток либо ровно одна точка пересечения.
Определение 10.28. Назовем такой набор кривых, снабженный структурой
проходов и переходов диаграммой цилиндрической косы.
Замечание 10.10. Очевидно, что все обычные косы порождают
цилиндрические косы посредством вложения R1 в S1 и, соответственно, R^^xR1.
Обратное утверждение, с очевидностью, неверно: если некоторая нить
представляет собой нетривиальный элемент в πι (5 х R1), то коса не может
происходить их обычной косы. Например, СВ(1) = Ζ.
10.4. Сферические, цилиндрические и иные косы 173
Как и обычная группа кос, группа С В (ή) имеет простое копредставление.
Действительно, пусть β — диаграмма косы на цилиндре S1 x Rt- Тогда мы
можем выписать по ней слово следующим образом. Обозначим множество / х
R = (5'1\х) χ R через Т. Каждый регулярный (не сингулярный) уровень косы
β состоит из η точек. Следовательно, каждому перекрестку можно сопоставить
номер ai ,г = 1,..., η таким же образом, как и в случае обычных кос.
Точке пересечения мы сопоставляем г если, проходя сверху вниз, мы
пересекаем "правый край разворота" Τ и возвращаемся слева, и г-1 в противном
случае.
Здесь г является дополнительной образующей (по отношению к уже
имеющимся образующим σ^ стандартной группы кос).
Очевидно, что σ\ ..., ση_ι вместе с τ порождают всю группу
цилиндрических кос из η нитей.
Пример построения слова по диаграмме цилиндрической косы общего
положения показан на рис. 10.15.
τσ-, σ2τ
Рис. 10.15. Диаграмма цилиндрической косы и соответствующее слово
Как и в случае обычных кос, мы можем легко построить набор
преобразований (и, соответственно, соотношений) для группы цилиндрических кос. Они
выглядят следующим образом:
1. Движения, не меняющие комбинаторной структуры перекрестков и
пересечений (но, возможно, меняющие порядок их расположения по высоте),
см. рис 10.16.
2. Второе движение Рейдемейстера, см. рис. 10.17.
3. Третье движение Рейдемейстера, см. рис. 10.18.
Кроме соотношений обычной группы кос {σ^σ:/=σ:/σ^, \г— j\ > 1} и {σ^+ισ^ =
σ^+ισ^+ι}, мы имеем также следующие соотношения: τσ^+ι = σ^τ при г =
1,... ,п — 2 и ση_ιτ2 = τ2σ\.
174
Глава 10
Геометрический смысл дополнительных соотношений состоит в следующем.
Первая серия соотношений относится к изменению нумерации перекрестков под
действием τ: σι переходит σ^+ι, в то время как самая правая нить появляется
слева. Вторая дополнительная серия (из одного соотношения) означает оборот
двух нитей, образующих правый крайний перекресток.
Легко проверяется, что эта система соотношений является определяющей
системой соотношений для группы цилиндрических кос.
Замечание 10.11. Элемент тп лежит в центре группы цилиндрических кос.
Рис. 10.16. Преобразование диаграммы цилиндрической косы
Рис. 10.17. Применение второго движения Рейдемейстера
к диаграмме цилиндрической косы
Замечание 10.12. Второе и третье движения Рейдемейстера локальные;
они выглядят точно так же, как и в классическом случае.
Имея диаграмму β цилиндрической косы 6, построим инвариант fc(b) =
/(β) (далее мы покажем, что он корректно определен).
Рассмотрим цилиндр 5ΐ χ R1.
10.4. Сферические, цилиндрические и иные косы 175
ч
ч
Рис. 10.18. Применение третьего движения Рейдемейстера к диаграмме
цилиндрической косы
Определение 10.29. Под допустимой цилиндрической системой из η
кривых назовем набор из η непересекающихся и несамопересекающихся кривых в
верхней половине цилиндра S1 x R+ такой, что каждая кривая соединяет точку
с абсциссой нуль с точкой с абсциссой единица, причем координата φ для всех
концов кривых пробегает множество
f 2π 2(η-1)π)
\ ' η ' η J
Все точки
2*3
η
,1
при j = 1,...,п называются верхними точками, а точки (j,0) называются
нижними точками.
Обозначим
М?}
через Сп.
Рассмотрим диаграмму косы β на цилиндре. Будем подвергать все
перекрестки косы /3, начиная с самого верхнего, протягиванию нижней ветви под
верхней, как и в случае обычной косы.
Таким образом мы получим допустимую цилиндрическую систему кривых.
Следующее определение полностью аналогично случаю обычных кос.
Определение 10.30. Две допустимые цилиндрические системы А ж А!
кривых называются эквивалентными, если существует гомотопия между А и А' в
классе кривых с фиксированными концами, лежащих в верхней половине
цилиндра при том, что во время гомотопии никакая внутренняя точка кривой не
может совпадать ни с одной верхней или нижней точкой.
Имея диаграмму β косы 6, можно построить допустимую цилиндрическую
систему Α(β) кривых, ей соответствующую. Рассмотрим класс эквивалентности
для Α(β) и обозначим его через fc(P)·
176
Глава 10
Докажем следующую теорему.
Теорема 10.9. 1. Отображение fc является инвариантом
цилиндрических кос, т. е. для различных β\,βι, представляющих одну и ту же косу
Ъ, мы имеем /ο(βι) = /с(/?2)·
В этом случае мы будем писать просто f(b).
2. Инвариант fc является полным, т. е. fc(bi) = fc(^2) влечет Ъ\ = &2·
Доказательство. Для доказательства первой части теоремы нам достаточно
проверить инвариантность функции fc под действием второго и третьего
движений Рейдемейстера. Доказательство выглядит точно так же, как и в случае
классических кос, см. рис. 10.3 и рис. 10.4.
Доказательство полноты также аналогично классическому случаю. По
допустимой цилиндрической системе кривых мы можем восстановить
цилиндрическую косу (несколько сдвинутую с нижними концами г = 1, φ = -^ и верхними
концами г = 2,φ = 2^)5 параметризуя каждую кривую параметром,
принимающим значения от 1 до 2. Докажем теперь, что эквивалентные допустимые
цилиндрические системы кривых задают одну и ту же косу.
Для этого фиксируем сначала перестановку s £ Sn (очевидно, что две
допустимые системы кривых могут быть эквивалентны, только если
соответствующие перестановки совпадают). Далее, выберем две эквивалентные допустимые
системы А и А' из η кривых и выберем допустимые параметризации для них.
Получим искомую изотопию кос. D
Как и значения инварианта /, значения инварианта fc легко поддаются
сравнению. Действительно, вместо кривых в Рп мы рассматриваем кривые
в Сп. Следовательно, наш инвариант полностью описывается следующим
объектом.
Пусть Gt — свободная группа с образующими а\,..., an, t. Обозначим через
Gi, г = 1,..., п, левый класс смежности G по а^.
Определение 10.31. Под цилиндрической η-системой будем понимать
множество g\ Ε Gi,..., дп Ε Gn вместе с перестановкой s Ε Sn.
Очевидно, что значения инварианта fc полностью описываются
цилиндрическими гг-системами. Перестановка берется из допустимой цилиндрической
системы кривых, а элементы gi соответствуют гомотопическим классам кривых
в Сп с фиксированными концами, а буква t соответствует образующей
фундаментальной группы цилиндра.
Глава 11
Теорема Маркова.
Уравнения Янга-Бакстера
и квантовые инварианты
В своей знаменитой работе 1936 года [Маг] Андрей Андреевич Марков
описал набор движений, доставляющих необходимое и достаточное условие для
того, чтобы замыкания классических кос, полученных друг из друга
цепочкой простейших преобразований, задавали изотопные классические
зацепления. Его доказательство, однако, было не безупречным. Он оставил эту задачу
своему ученику Н.М.Вайнбергу, который погиб на войне вскоре после своей
первой публикации [Wei] на эту тему. Первое точное доказательство теоремы
Маркова принадлежит Джоан Бирман, [Bir2]. Новейшие доказательства
теоремы Маркова принадлежат Павлу Трачику [Тга], а также Джоан Бирман и
Уильяму Менаско [ВМ].
Мы будем доказывать теорему Маркова основываясь на работе Хью Мор-
тона [Мог].
Далее мы приведем некоторые уточнения теорем Александера и Маркова,
предложенные Геннадием Семеновичем Маканиным.
Отметим, что "обычный" способ замыканий кос для получения узлов — не
единственный. Интересный подход к построению узлов "замыканиями"
крашеных кос был предложен в работе Якова Мостового и Теда Стэнфорда [MS]; на
основе этого подхода Михай Стаич [Sta] построил инварианты узлов исходя из
их заданий косами.
В заключительной части настоящей главы мы обсудим уравнения Янга-
Бакстера, которые связаны с представлениями групп кос и построениями
инвариантов узлов.
11.1. Теорема Маркова согласно Мортону
11.1.1. Постановка задачи и определения. Прошивания
Теорема Маркова дает частичный ответ на вопрос, когда замыкания кос
задают изотопные зацепления. При этом она не ведет к алгоритму,
устанавливающему изотопность зацеплений, а лишь описывает необходимый и
достаточный набор преобразований для установления такой изотопии, но не указывает,
178
Глава 11
в каком порядке применять эти преобразования и когда нужно
остановиться.
В своей работе Мортон предложил оригинальную идею прошивания —
альтернативный способ построения косы по зацеплению (отличный от алгоритмов,
описанных в предыдущей главе).
Замечание 11.1. Мы будем рассматривать каждое замыкание косы как
набор кривых внутри цилиндра D2 χ I, не пересекающих ось цилиндра * χ Ι;
под осью косы будем понимать замыкание кривой, совпадающей с осью
цилиндра. Эту ось удобно представлять себе в полнотории S2 χ I, стандартно
вложенном в R3 и содержащем внутренность цилиндра.
Определение 11.1. Пусть К — ориентированное зацепление в R3 и пусть L —
незаузленная кривая. Скажем, что К заплетается вокруг L или что К U L
образуют зацепление-косу , если К и L представляют собой замыкание
некоторой косы и ось этой косы соответственно (т. е. К лежит внутри полнотория
Si х D, при этом координата t (определенная вдоль окружности S1) возрастает
вдоль движения по К, a L представляет собой ось (параллель) полнотория),
см. рис. 11.1.
Рис. 11.1. Коса в понотории
Имея плоскую диаграмму замыкания косы, мы можем получить
соответствующее зацепление-косу прошиванием исходной диаграммы, см. рис. 11.2.
Пусть К — плоская диаграмма некоторого ориентированного зацепления.
Рассмотрим кривую L на плоскости проекции Ρ зацепления К такую, что L
пересекает диаграмму К трансверсально и не проходит через перекрестки
диаграммы К.
Определение 11.2. Под выбором переходов диаграммы зацепления К будем
понимать два множества S = {si,..., s^}, F = {Д,..., Д} точек на диаграмме
К (отличных от перекрестков) таких, что при движении вдоль зацепления К
в соответствии с ориентацией точки из S чередуются с точками из F; кроме
того, каждый интервал вида [s, /] не содержит проходов, а интервал вида [Д s]
не содержит переходов.
11.1. Теорема Маркова согласно Мортону
179
Рис. 11.2. Прошитое замыкание косы
Определение 11.3. Скажем, что кривая L, проекция которой на плоскость
диаграммы К является простой (несамопересекающейся) кривой, прошивает
К согласно выбору переходов (S,F), если она делит плоскость на две части,
одна из которых целиком содержит все точки из S, а вторая — все точки из F,
при этом отрезок диаграммы К проходит над L, когда он начинается в
области, содержащей точки из S, и под кривой L, если он начинается в области,
содержащей точки из F, как показано на рис. 11.3.
Замечание 11.2. В последнем определении не предполагается, что этот
отрезок кривой L содержит элементы одного из множеств S или F.
К
F
К
Рис. 11.3. Пересечения с L
Для заданной диаграммы зацепления К и кривой L на плоскости проекции
такой, что L отделяет точки из S от точек из F мы можем расставить проходы
и переходы между К и L таким образом, чтобы полученная из L кривая V
(уже не лежащая в плоскости проекции) прошивала зацепление К. Кривая
L' совпадает с L всюду, кроме малой окрестности точек пересечения К и L. В
окрестности точек пересечения точки V проектируются в точки на L, находясь
выше или ниже соответственно проходу или переходу.
Докажем следующую теорему.
Теорема 11.1. Если L прошивает К, то К заплетается вокруг L.
Доказательство. Выберем (S, F) для диаграммы К (произвольным образом)
и некоторую простую замкнутую кривую L общего положения на плоскости
180
Глава 11
проекции Ρ диаграммы К, отделяющую точки из S от точек из F.
Выпрямим кривую L на плоскости Ρ с помощью гомеоморфизма плоскости Ρ на
себя: мы потребуем, чтобы пересечение преобразованной кривой (которую мы
также обозначим через L) с некоторым достаточно большим диском D с Р,
содержащим диаграмму К, представляло собой прямолинейный отрезок.
Следовательно, точки из множества S лежат по одну сторону от кривой L, а точки
F — по другую. Такое преобразование показано на рис. 11.4.
i
ϊ
2
3
S2
Si
S3
гт
_/l
J
J
3
2
S2
Si
S3
fr
Рис. 11.4. Выпрямление кривой L
Без ограничения общности можно считать, что все проходы и переходы
диаграммы L лежат в двух плоскостях, параллельных плоскости Ρ (как раз над и
под образами соответствующих проекций). Изменим точку зрения будем
считать, что Ρ = Οχ ζ, а прямолинейная часть кривой L идет по оси Οζ.
Будем считать линию L (без ее "бесконечной" замыкающей части) осью
цилиндрических координат. При этом плоскость Ρ разделится на две
полуплоскости; одна из них задается уравнением {Θ = 0}, а другая — уравнением {θ = π}.
Здесь подразумевается, что на полуплоскости {ζ = 0, ж > 0} имеет место θ = 0;
точки над этой полуплоскостью имеют положительную координату Θ.
Построим теперь зацепление, изотопное зацеплению К, следующим
образом. Расположим все нижние ветви узла К (т.е. все отрезки вида [/, s\) на
полуплоскостях {θ = —ε}, {θ = π + ε}, а все верхние ветви — на
полуплоскостях {θ = ε}1{θ = π — ε}, где ε достаточно мало. При этом над точками из
множеств S и F построим отрезки, проецирующиеся в одну точку плоскости
Οχζ.
Дуги, в которых проекция К пересекается с прямой L, изобразим дугами в
вертикальных плоскостях. У полученного таким образом зацепления (которое
мы также будем обозначать через К) полярная координата θ не убывает при
движении вдоль ориентации.
Этот процесс изображен на рис. 11.5 и 11.6. Приведенный узел изотопен
узлу, изображенному на рис. 11.4.
После малого шевеления полученного зацепления можно достичь того,
чтобы полярная координата строго возрастала. Таким образом преобразованное
зацепление (которое мы по-прежнему обозначаем через К) будет представлять
собой косу относительно L. D
Из теоремы 11.1 следует, что если некоторое зацепление К является косой
11.1. Теорема Маркова согласно Мортону
181
Рис. 11.5. Диаграмма зацепления, пересекающаяся с L
-ГГ^
-ГТ^
Рис. 11.6. Полярная координата возрастает при движении вдоль зацепления
относительно некоторой незаузленной кривой L, то К представимо посредством
замыкания косы.
Теорема 11.2. Любое замыкание К косы В можно прошить кривой L так,
чтобы К являлось косой относительно L.
Доказательство. Пусть D2 χ Ι — цилиндр. Рассмотрим В в качестве косы,
соединяющей точки, лежащие на верхнем основании цилиндра с точками на
нижнем основании цилиндра. Замкнем теперь косу следующим образом. Соединим
нижние точки с верхними линиями, идущими горизонтально вдоль оснований
и вертикально в некоторые дискретные моменты как показано на рис. 11.7.
182
Глава 11
Рис. 11.7. Коса и зацепление-коса
Применим изотопию, выпрямляющую нити кос и гомеоморфно
изменяющую верхнее основание цилиндра. Получившиеся зацепление, изотопное
исходному, легко прошить следующим образом.
Пусть /ιо — уровень, на котором лежат "нижние" вершины зацепления-косы,
a fti — уровень , на котором лежат "верхние" вершины. Обозначим множество
нижних концов косы В через А\ и множество верхних концов через А2, см.
рис. 11.7.
Можно считать, что на уровнях ho и hi лежат также и другие вершины, с
помощью которых происходит замыкание косы, а именно, точки множества А\
соединяются параллельными линиями с точками множества А2, и точки
множества В ι соединяются с точками множества В2. Рассмотрим теперь окружность,
лежащую в плоскости на уровне h = °^ г и разделяющую наборы прямых
АХА2 и В1В2.
Спроектируем нашу диаграмму на основание цилиндра и выберем в
качестве S множество Αι, а в качестве F — множество А2.
Легко видеть, что в таком случае проекция нашей окружности
действительно будет представлять собой прошивание диаграммы нашего зацепления.
D
Из теорем 11.1 и 11.2 следует теорема Александера. Доказательство этих
теорем дает нам конкретный алгоритм (отличный от приведенных ранее
алгоритмов) для представления всякого зацепления замыканием косы.
Напомним главную теорему этой главы. Она уже была сформулирована в
главе 8.
Теорема 11.3. Замыкания кос А и В изотопны тогда и только тогда, когда
В может быть получена из А последовательностью следующих
преобразований (движений Маркова):
1. сопряжение Ъ —> а~гЪа с помощью косы а с тем же самым количеством
нитей, что и Ъ,
2. преобразование Ъ —> Ьа^1, где Ъ коса из η нитей, а полученная коса Ьа^1
имеет η + 1 нить,
3. преобразование, обратное к 2.
11.1. Теорема Маркова согласно Мортону
183
Необходимость этих условий очевидна. Изотопии между соответствующими
косами показаны на рис. 11.8.
На рис. 11.8.6 представлено первое движение Рейдемейстера. Это движение
не принимало участие в изотопиях кос, и появляется здесь, когда разговор
заходит об изотопиях узлов.
η
о
|
b
|
а-1
L
-J
η
α"1
I
о
I
b
L
J
a
b
η
b
Рис. 11.8. Два движения Маркова
11.1.2. Теорема Маркова и прошивания
Переформулируем теперь трудную часть теоремы Маркова.
Для того, чтобы сделать это нам будут нужны некоторые определения.
Определение 11.4. Скажем, что две зацепления-косы KUL и K'VJL' просто
марковски эквивалентны если существует изотопия второго из них,
переводящая U в L, а К' — в зацепление, совпадающее с К, за исключением одной дуги
а для К и дуги а' для К' (концы дуги а совпадают с концами дуги а') такая,
что:
1. угловая координата постоянна на дуге а и монотонно возрастает на
дуге а'.
2. дуги а, а' ограничивают диск, пересекающий L трансверсально в
единственной точке.
Определение 11.5. Два зацепления-косы являются Марковски
эквивалентными если одно переводится в другое посредством многократного
последовательного применения изотопии и простой марковской изотопии.
Упражнение 11.1. Покажите, что замыкания двух кос из η нитей
изотопны в классе замыканий кос из η нитей тогда и только тогда, когда эти две
косы сопряжены.
Замечание 11.3. В дальнейшем при изображении на плоскости диаграммы
зацепления-косы К U L все перекрестки, в которых L проходит выше
компонент зацепления К, будут обозначены как обычные пересечения (без переходов
и проходов).
184
Глава 11
Лемма 11.1. Если зацепления KUL и K'UL' просто марковски
эквивалентны, то они являются прошитыми замыканиями некоторых кос, которые
изотопны косам β G Br (η) и βσ^1 Ε Br (n + 1).
Доказательство. Обозначим значение угловой координаты на дуге а через #о·
Рассмотрим дугу а$. Без ограничения общности молено считать, что ее
координата почти везде равна #о & в некоторой малой окрестности зацепления V
делает петлю, а также то, что эта петля соответствует гг-й (последней) нити косы а.
Мы можем произотопировать наши косы К и К' в окрестности {а = θ о =Ь ε}
таким образом, чтобы конечные точки дуг а и а$ лежали в малой окрестности
зацепления V. После этого утверждение леммы становится очевидным. D
Принимая во внимание лемму 11.1 вместе с утверждением упражнения 11.1
можно сформулировать трудную часть теоремы Маркова следующим образом:
Теорема 11.4. Пусть β и j — две косы, замыкания которых В и Τ изотопны
как ориентированные зацепления. Тогда их прошитые замыкания являются
марковски эквивалентными.
Для дальнейшего нам необходимы некоторые предварительные леммы и
теоремы.
Лемма 11.2. Рассмотрим ориентированную диаграмму зацепления К на
плоскости Ρ с фиксированным выбором переходов (S,F). Тогда прошивания К
различными кривыми L и V', разделяющими множества S и F, являются
марковски эквивалентными.
Доказательство. Основная идея доказательства заключается в следующем:
сначала мы рассматриваем случай, когда кривые L и V изотопны в дополнении
P\(S UF). В таком случае они переводятся друг в друга набором движений,
каждое из которых является марковской эквивалентностью.
В общем случае добавляется одно движение, при котором диаграмма L
двумя ветвями проходит через точку из S (или F). Такое движение является
марковской эквивалентностью.
Приведем доказательство более подробно.
Случай а). Предположим, что L и L' изотопны в P\(S U F). Тогда К U L и
KOL' получаются друг из друга последовательностью преобразований первого
и второго типов, показанных на рис. 11.9 (отметим, что здесь не предполагается,
что пересечения кривой L с К являются переходами, как это было обговорено
раньше).
Первый тип представляет собой или второе движение Рейдемейстера или
движение, при котором добавляются две точки пересечения альтернированным
образом (т. е. с на одной ветви кривой имеется один переход и один проход). Как
будет показано ниже, это движение представляет собой простую марковскую
эквивалентность.
Второй тип движения является изотопией во всех случаях, за исключением
того, который показан на рис. 11.10.
В этом случае первое прошивание переводится во второе
последовательностью движений первого и второго типа и изотопии см. рис. 11.11.
11.1. Теорема Маркова согласно Мортону 185
Рис. 11.9. Композиция преобразований двух типов
Рис. 11.10. Марковская эквивалентность
При этом нужно заметить, что проходы К под L чередуются с переходами
К над L при движении вдоль К. Осталось показать, что два прошивания,
получающиеся друг из друга движением первого типа, являются просто марковски
эквивалентными.
Таким образом, часть зацепления К, изображенная на диаграмме,
принадлежит либо к одной верхней ветви, либо к одной нижней ветви. В конструкции
прошивания мы можем предположить, что две части зацепления К на одной
стороне кривой L лежат на одном и том же уровне рь (угол θ может быть равен
π =Ь ε или ±ε в зависимости от стороны, с которой он расположен). Соединим
их дугой так, как показано на рис. 11.12.
Дуги а и а' ограничивают диск. Таким образом, мы получаем простую
марковскую эквивалентность двух прошиваний.
Случай б). В общем случае заметим, что если кривая М' с Р, отделяющая
множество S от множества F, может быть изотопирована к кривой Μ С Ρ
посредством композиции (локальных) преобразований, каждое из которых
состоит в локальном протаскивании двух дуг зацепления К через некоторую
точку из множества S или F (как показано на рис. 11.13), то Μ и М' являются
186
Глава 11
Рис. 11.11. Композиция марковских эквивалентностей
Рис. 11.12. Кривая, проходящая через диск
изотопными прошиваниями. На рис. 11.13 преобразуемая (от Μ κ Μ') кривая
изображена жирной линией.
Изотопия "криволинейной" части L (или, эквивалентно, передвижение точек
из множества S или из множества F) может быть разбита на несколько шагов,
внутри каждого из которых изменение расположения L по отношению к S и F
носит непрерывный характер. Между ними происходят некоторые дискретные
движения, меняющие комбинаторный тип расположения L по отношению к
множествам S и F. Нашей задачей является описание возможных дискретных
шагов.
Без ограничения общности предположим следующее.
Пусть множества S и F состоят из точек {(—1, сц)} и {(1, сц)}
соответственно для некоторых αϊ,... а&. Пусть L — часть оси Оу, замкнутая большой
полуокружностью так, что внутренность L содержит F. Можно предположить,
11.1. Теорема Маркова согласно Мортону
187
s
Прошивание
ян-
Рис. 11.13. Пара ветвей кривой, проходящая через точку
что К проходит параллельно оси Ох вблизи от каждой точки si,..., s&
множества S.
Пусть L' — произвольная простая замкнутая кривая, разделяющая
множества (S'hFh ограничивающая область, содержащую множество F. Без
ограничения общности можно считать, что кривая V пересекает лучи у = α,ΐ,χ < — 1
трансверсально в конечном числе точек, см. рис. 11.14. Перенумеруем точки
пересечения кривой с каждым из лучей по убыванию абсциссы. Для каждого луча
количество пересечений, очевидно, четно. Для каждого луча сгруппируем эти
точки пересечения парами: (1, 2), (3,4),.... Для этого мы сначала изотопируем
U внутри P\(S (J F) так, что между каждой парой точек не будет перекрестков
диаграммы К.
Будем теперь двигать линию L' направо так, чтобы в конце оставить все
точки слева от (преобразованной) кривой L'. Такое передвижеие будет
разбиваться на этапы, когда V не содержит точек из S и моменты, когда L' содержит
такие точки. В первом случае мы применяем марковскую эквивалентность, как
в случае а). Во втором случае предположим, что точки пересечения кривой L'
с каждым лучом исчезают парами, т. е. кривая L' по очереди проходит двумя
своими ветвями через одну и те лее точку si. Это движение также является
марковской эквивалентностью, см. рис. 11.13.
Таким образом, прошивание посредством U марковски эквивалентно
прошиванию посредством кривой, лежащей справа от всех точек s^. Эта кривая
изотопна кривой L внутри множества P\(S[JF), таким образом, прошивание
посредством этой кривой марковски эквивалентно прошиванию посредством
кривой L, см. пункт а). Следовательно, прошивание посредством L' также
марковски эквивалентно прошиванию посредством L. Этим завершается
доказательство леммы.
Лемма 11.3. Если для диаграммы К задан выбор переходов (S,F), и точка
s на диаграмме К не принадлежит множеству F, то существует выбор
переходов (S, F) такой, что s Ε S,S С S, F С F.
188
Глава 11
Рис. 11.14. Прохождение кривой через точки
Доказательство. Идея доказательства довольно проста: мы добавляем
элементы из S или F там, где мы хотим компенсировать их соответствующими
элементами из F или S. Если s лежит на верхней дуге разбиения (S, F), то мы
можем выбрать / непосредственно перед s относительно ориентации К таким
образом, чтобы отрезок [/, s] С К не содержал переходов. В случае, если s
лежит на нижней дуге, мы можем добавить / сразу после точки s; в этом случае
[s, /] С К не содержит проходов. D
Теорема 11.5. Любые два прошивания К U L и К U L' одной и той же
диаграммы К являются марковски эквивалентными.
Доказательство. Выберем переходы (S,F) для прошивания К U L и (Sf,Ff)
для прошивания К U V. Согласно лемме 11.3, существует выбор переходов
(S , F ) такой, что (S, F), (S", F7) С (5 , F ), и два прошивания с одинаковым
выбором переходов, первое из которых марковски эквивалентно К UL и второе
марковски эквивалентно К U V'. Согласно лемме 11.2, эти два прошивания
марковски эквивалентны между собой. D
Теорема 11.6. Всякие две диаграммы изотопных зацеплений имеют
марковски эквивалентные прошивания.
Доказательство. Для доказательства теоремы нам достаточно показать, как
строить марковски эквивалентные прошивания для диаграмм, получающихся
друг из друга посредством движений Рейдемейстера.
11.1. Теорема Маркова согласно Мортону
189
Согласно теореме 11.5, мы можем установить произвольный выбор
переходов. Идея состоит в том, чтобы перестроить выбор переходов после
каждого движения Рейдемейстера. Для первых двух движений Рейдемейстера без
ограничения общности можно выбрать отделяющую кривую вне малого круга,
в котором будет происходить деформация. В случае первого движения внутри
круга выбираем одну вершину s, в случае второго движения все вершины из
(S,F) находятся вне круга.
Мы показали, что диаграммы зацеплений, получаемых друг из друга
первым и вторым движениями Рейдемейстера, допускают марковски
эквивалентные прошивания.
Для третьего движения Рейдемейстера можно выбрать одну вершину s и
одну вершину / внутри круга, а остальные — вне его, см. рис. 11.15.
Рис. 11.15. Изменение меток при применении движений Рейдемейстера
На рис. 11.16 показано, что прошивания, соответствующие диаграммам,
отличающимся третьим движением Рейдемейстера, являются изотопными и,
следовательно, марковски эквивалентными. (Показан только один случай; другие
случаи Ω3 с ориентацией и расположением L и К в левой части рисунка вполне
аналогичны).
В верхней части этого рисунка мы показываем, как линия L может быть
трансформирована относительно движения Ω3. В нижней части рисунка мы
показываем проходы и переходы между L и К в реализации конкретной
трансформации.
D
Теперь мы готовы доказать сложную часть теоремы Маркова.
Доказательство теоремы 11.4· Пусть К U L, К' U L' — две зацепления-косы,
причем диаграммы К и К' определяют изотопные зацепления.
190
Глава 11
Рис. 11.16. Изотопные прошивания диаграмм, связанных движением Ω3
По теореме 11.2 зацепление К U L является прошиванием для К, а К' U V
является прошиванием для К'. По теореме 11.6 молено выбрать марковски
эквивалентные прошивания для К и К'. По теореме 11.5 первое из них марковски
эквивалентно прошиванию К U L, а второе — марковски эквивалентно
прошиванию К' U V.
Следовательно прошивание К U L марковски эквивалентно прошиванию
К' U L7, что завершает доказательство теоремы Маркова. D
Покажем теперь, как можно применять теорему Маркова.
Как мы показали ранее, для взаимно простых чисел ρ и q торические узлы
Т(р, q) и T(q,p) изотопны. Покажем это для случая трилистников Т(2, 3), Т(3, 2)
с помощью теоремы Маркова.
Пример 11.1. Коса, соответствующая Т(2,3), имеет вид erf3; вторая коса
(соответствующая Т(3, 2)) имеет вид σ^ σ^ ο~ϊ σ^ · Выпишем
последовательность движений Маркова, переводящих первую косу во вторую:
2 движение
σΛ σ9
сопряжение
(Τι (То (Τι
σ1 1(σ1 1(J21(J\ X)
]ч ИЗОТОПИЯ КОС
(Τι (То (Τ л <J'
ι~-ι
Упражнение 11.2. Проделайте аналогичные вычисления для торических уз-
лоеТ(2,2гг+1) ι*Τ(2η+1,2), а также для Τ'(3,4),Τ'(4,3).
11.2. Обобщение Маканина. Унарные косы
191
11.2. Обобщение Маканина. Унарные косы
В своей работе [Мак] Г.С.Маканин предложил обобщения теорем Алексан-
дера и Маркова: он доказал, что все узлы (не зацепления) могут быть получены
как замыкания так называемых унарных кос и показал, что две унарные косы
задают один и тот лее узел в том и только в том случае, когда существует
последовательность марковских преобразований от одной косы к другой, такая что
все промежуточные косы являются унарными. Кроме того, он нашел систему
кос (называемых гармоническими), действие которых сопряжением оставляет
инвариантным множество унарных кос, подробное изложение см. в
оригинальной статье [Мак].
В настоящем разделе все узлы предполагаются ориентированными.
Определение 11.6. Коса из (п + 1) нити называется унарной , если нижний
конец нити, верхний конец которой имеет абсциссу, равную единице, имеет
номер (абсциссу) (п + 1), причем после удаления первой нити мы получаем
тривиальную косу из η нитей.
Очевидно, что унарным косам соответствуют лишь узлы (не зацепления).
Теорема 11.7 ([Мак]). Для каждого изотопического класса узла К
существует унарная коса В такая, что замыкание С 1(B) изотопно узлу К.
Первое, что нужно заметить, это то, что узел К может быть задан косой /3,
которой соответствует перестановка Ρ = (1^2^3···^η+1^ Ι).
Далее нужно показать, что каждая коса (напр., β с перестановкой Р)
сопряжена некоторой унарной косе β'. Таким образом, по теореме Маркова,
замыкание ΟΙ(β') изотопно узлу К.
Ключевая лемма заключается в следующем.
Лемма 11.4. Пусть К — коса из группы Вг(п + 1), а Р —
соответствующая перестановка. Тогда существует унарная коса Υ, сопряженная косе К
посредством косы из В г (ή) С Вг(п + 1).
Эта лемма использует конструкцию "чистых кос", предложенную Артином
в его оригинальной статье [Artl]. Доказательство см. в [Мак].
Теорема 11.8 ([Мак]). Пусть K,L — два изотопных узла. Пусть В,В' — две
унарных косы, замыкания которых изотопны К и L соответственно. Тогда
существует цепочка унарных кос В = £>ι, £>2,..., В^ = В' такая, что коса Βι
получается из косы £>г-1 одним из движений Маркова (для г = 2,..., к).
Доказательство. Стратегия состоит в следующем. Сначала мы находим
цепочку преобразований Маркова от Б к Б7, а затем деформируем ее посредством
некоторых дополнительных движений Маркова, чтобы получить цепочку из
унарных кос.
Пусть К — унарная коса из Вг(р + 1), a L — унарная коса из Br(q + 1).
Тогда существует последовательность кос К = Qi, Q2, · · ·, Qt — L, в которой
каждая коса Q^+i получается из предыдущей косы Qi посредством движения
Маркова. Без ограничения общности можно предположить, что сопряжения не
применяются одно после другого (иначе можно последовательное применение
192
Глава 11
двух сопряжений трактовать как одно сопряжение). Кроме того, между
каждыми двумя движениями Маркова второго типа мы можем поместить сопряжение
посредством единичной косы. Следовательно, мы можем считать, что каждое
преобразование Q 2.7-1 -^ Qij является сопряжением, а каждое преобразование
Q2j —> Q2.7+1 представляет собой второе движение Маркова (добавление или
удаление нити и перекрестка).
Основная идея состоит в том, что операция сопряжения косы из Вг(п)
посредством косы из Вг(п — 1) коммутирует со вторым движением Маркова
(добавлением (п + 1)-й нити и перекрестка).
Построим теперь цепочку унарных кос. Для каждой косы Qi из щ нитей
пусть Yi — унарная коса, сопряженная косе Qi посредством косы из (щ — 1)
нити.
Очевидно, что каждая коса Y2j-i сопряжена косе Y^ посредством некоторой
косы Br(ri2j). Далее, рассмотрим переход Y^j —> ^27+1- Коса Y^j G Br(ri2j)
сопряжена косе Q2J G Br(ri2j) посредством некоторой косы δ из Br(ri2j — 1).
В случае, если преобразование Q2j —► Q23+1 состоит в добавлении нити, мы
можем проделать ту же операцию для Y^j. Получим косу У2*7 (добавление нити с
перекрестком). Очевидно, что косы Y^j и Q 2.7+1 сопряжены посредством косы δ.
Следовательно, косы Υζ- и l^j+i также сопряжены.
В случае, когда Q2j —► Q 2.7+1 является удалением нити, обратное
преобразование Q2J+1 -^ Q2j добавляет нить. Рассуждая как ранее, мы видим, что косы
Y2j и У27+1 связаны движениями Маркова, в которых участвуют лишь унарные
косы.
Таким образом, мы построили цепочку преобразований Маркова для
унарных кос, соединяющих В с В'. Этим завершается доказательство теоремы. D
Работа Маканина позволяет кодировать узлы словами в конечном алфавите.
А именно, чтобы задать унарную косу из η нитей, нам нужно лишь описать
поведение первой ее нити, т. е. указать, когда она идет направо, а когда —
налево, а также когда она образует проход, а когда — переход. Для этого нам
достаточно будет использовать четыре символа: —►,—►,<— и <—.
Единственным условием для получения унарной косы является то, что
общее число стрелок —>· минус общее число стрелок <— всегда положительно и не
превосходит η для всех начальных под слов, при этом в точности равно η для
всего слова.
Другой подход к описанию узлов и зацеплений словами в конечном
алфавите (скобочное исчисление) будет описан в части IV настоящей книги.
11.3. Уравнение Янга-Бакстера,
представления кос и инварианты узлов
Уравнение Янга-Бакстера было изначально предложено физиками, однако
нашло применение в различных разделах математики. В частности, оно тесно
связано с представлениями группы кос. Детальное обсуждение связи уравнений
Янга-Бакстера с теорией узлов и кос см., напр., в [Tur3, KPT, Kau2, Oht].
После выдающихся работ Джонса [Jonl, Jon2] стало понятно, что полином
Джонса и его обобщения (например, полином HOMFLY) являются частными
11.3. Уравнение Янга-Бакстера
193
случаями некоторого широкого семейства инвариантов узлов — квантовых
инвариантов, см. [Jon3, RT1, Turl].
Имея диаграмму узла (зацепления) на плоскости, молено разрезать ее
(точнее, сколь угодно близкую к ней диаграмму) горизонтальными линиями на
простейшие кусочки — танглы. Каждый простейший тангл представляет собой
перекресток либо точку локального максимума или минимума, см. рис. 11.17.
Основная идея построения квантовых инвариантов состоит в том, чтобы
сопоставить перекресткам и экстремумам тензоры валентности (2, 2), (2,0) и (0, 2) с
тем, чтобы после сверток этих тензоров по диаграмме узла мы получили
некоторое число, которое не менялось бы при движениях Рейдемейстера (или, более
точно, при движениях Тураева, см., напр., [Oht], которые помимо движений
Рейдемейстера описывают взаимное расположение перекрестков и
экстремумов). Нахождение таких тензоров является важной и интересной задачей.
Рис. 11.17. Разложение узла на танглы
Важным частным случаем такого разложения является замыкание кос.
В этом случае все экстремумы находятся сверху и снизу, в то время как во
"внутренней" части диаграммы имеются лишь перекрестки. В этом случае самым
важным является нахождение четырехвалентных тензоров, свертка которых
задает представление группы кос, после чего свертка (удачно подобранных)
тензоров, соответствующих верхним и нижним экстремумам, приводит к
инварианту узлов.
Пусть V — конечномерное векторное пространство с базисом ei,..., еп над
некоторым полем F. Пусть R : V ®V ^ V ®V некоторый эндоморфизм
пространства V ® V. Рассмотрим эндоморфизм
Rt:Id®---(g)Id(g)R(g)Id(g)---(g)Id: V®n -► V®71, (11.1)
где V®71 означает п-ю тензорную степень пространства V, Id — тождественный
оператор, a R действует на произведении V® V, находящихся на местах (г, г +1).
194
Глава 11
Определение 11.7. Говорят, что оператор R является R-матрицей, если он
удовлетворяет следующему условию:
RiRi+lRi = Ri+lRiRi+1, г = 1, . . . , 71 — 1 (И-2)
Это уравнение переписывается в терминах матрицы R, более точно, мы
имеем уравнение для матриц над V®3:
(R ® Idv) · (Idv ®R)-(R® Idv) = (Idv ®R)-(R® Idv) · (Idv <8> Д). (11.3)
Уравнения (11.3) называются уравнениями Янга-Бакстера. Заметим, что
очевидным образом имеет место уравнение
RzRj=RjRu \i-j\ ^2. (11.4)
Уравнения Янга-Бакстера очень похожи на соотношения Артина для
группы кос: последнее получается из первого подстановкой σ вместо R\ уравнения
(11.4) соответствует дальней коммутативности в группе кос.
Имея ^-матрицу, мы сразу получаем инвариант кос (и, при некоторых
возможных модификациях, также и инвариант зацеплений).
Общие инварианты зацеплений, получающиеся таким образом, были
предложены Тураевым и носят названия квантовых инвариантов.
Представление группы кос В г (ή) в тензорном произведении V®71 получается
по формуле ρ(ai) = Ri, где σι — стандартные образующие группы кос.
После этого для заданного зацепления L мы находим косу 6, замыкание
которой С 1(b) изотопно зацеплению L.
Можно положить T(L) = trace(p(b)). В этом случае T(L) является
инвариантом относительно изотопии кос и первого движения Маркова (сопряжения),
но, вообще говоря, может не являться инвариантом относительно второго
движения Маркова. Для этого вместо обычного следа используются более
сложные конструкции, как, например, след Окнеану в случае полинома Джонса или
свертка тензоров с помощью локальных экстремумов в случае общих
квантовых инвариантов.
Замечание 11.4. Все коэффициенты полинома Джонса являются
квантовыми инвариантами.
В квантовой механике также рассматривается квантовое уравнение Янга-
Бакстера, которое выглядит следующим образом
η12π13π23 = η23π13π12. (п.5)
Здесь IZij получаются из некоторой матрицы ΊΖ, задающей автоморфизм ΊΖ :
у®п _^ у®п д именно, представив ΊΖ в виде ΊΖ = Σαΐν ® β\ζ·> мы записываем
матрицу IZij как сумму тензорных произведений &k,Pk и единичной матрицы,
где ak стоит на месте г, а β^ — на месте j.
Легко проверяется, что квантовая ^-матрица ΊΖ соответствует обычной R-
матрице R по правилу R = Ρ о 7£, где Ρ — оператор перестановки компонент
на V χ V, определенный по правилу Р(х ® у) = у ® х.
11.3. Уравнение Янга-Бакстера
195
Каждое решение уравнения (11.5) называется квантовой R-матрицей.
Глубокие и важные результаты связаны с нахождением i^-матриц
посредством квантовых групп, групп и алгебр Ли, вычисления монодромии уравнений
Книжника-Замолодчикова (о которых речь пойдет позлее) и др. Эти
результаты принадлежат Тураеву, Дринфельду, Виттену и многим другим. Для
знакомства с ними мы рекомендуем монографии Владимира Георгиевича Тураева
[ТигЗ] и Томотады Отсуки, [Oht].
Русскоязычное введение в теорию ^-матриц можно прочесть в обзоре
Михаила Арсеньевича Семенова-Тянь-Шанского [Сем]. Мы также рекомендуем
обзор Михиля Хазевинкеля, см. [Haz].
Часть III
Инварианты Васильева
Глава 12
Основные понятия теории
инвариантов Васильева
Инварианты узлов, получившие название инвариантов Васильева, были
впервые предложены в 1989 Виктором Анатольевичем Васильевым [Vas] при
изучении топологии дискриминантного множества отображений S1 —>· R3.
Немногим позже Михаил Николаевич Гусаров [Гус] независимо предложил
комбинаторное описание этих инвариантов.
12.1. Сингулярные (особые) узлы
и определение инвариантов
конечного порядка
На протяжении этой части книги все узлы предполагаются
ориентированными, если не оговорено противное. Кроме того, мы будем иметь дело с узлами,
а не с зацеплениями. Теория инвариантов конечного порядка для зацеплений
строится абсолютно аналогично, но определения несколько более громоздки.
Как известно, каждый узел может быть переделан в тривиальный
заменой некоторых перекрестков. Можно считать, что такая замена перекрестков
представляет собой непрерывный процесс в трехмерном пространстве, причем
в некоторый момент узел перестает быть узлом; в этот момент возникает точка
самопересечения.
Пусть Ао — множество всех изотопических классов узлов и пусть задан
инвариант узлов / : Ао —>· А со значениями в некоторой абелевой группе А.1
Можно рассмотреть его значения на паре узлов, которые отличаются в одном
перекрестке. Рассмотрим теперь непрерывный процесс деформации от одного
узла к другому и погруженную окружность с одной точкой трансверсального
самопересечения, возникающей в процессе изотопии. Назовем такое погружение
сингулярным узлом порядка один. Под сингулярным или особым узлом
порядка η (где η — натуральное число или нуль) мы понимаем иммерсию окружности
S1 в R3, с η различными точками самопересечения, причем самопересечение в
каждой из этих точек простое и трансверсальное. Под сингулярным (особым)
зацеплением мы понимаем погружение несвязного набора окружностей в R3,
имеющее конечное число точек пересечения, при этом все точки пересечения
1А может быть полем или кольцом. Нас будут интересовать случаи Q,R и С.
200
Глава 12
являются простыми и трансверсальными. Допускаются как самопересечения
некоторой компоненты, так и пересечения разных компонент.
Сингулярные узлы рассматриваются с точностью до изотопии, которая
определяется аналогично изотопии классических узлов. Множество (пространство)
сингулярных узлов порядка η (при η = 0 мы имеем множество классических
узлов) обозначается Хп. Множество всех сингулярных узлов (включая Х$) будем
обозначать через X = Xq U ΛΊ U ^2 U · · ·.
Таким образом, при замене перекрестка для классического узла мы в
некоторый момент получим сингулярный узел порядка один.
В этом случае мы можем определить производную f инварианта / согласно
следующему соотношению:
/,(ί·Χ)}=/(-Х;) - /(νΦ· (ΐ2·ι}
Это соотношение задает определение производной для всех троек диаграмм
(две классические и одна /Х| сингулярная порядка гг), которые совпадают вне
малого круга. Оно называется соотношением Васильева.
Очевидно, что функция f является корректно определенной на множестве
сингулярных узлов порядка один (аккуратное доказательство остается
читателю в качестве упражнения). Тем самым f представляет инвариант
сингулярных узлов порядка один рассмотренных с точностью до изотопии.
Пусть теперь задан инвариант /. Можно определить его производные
высших порядков по следующему правилу. Нужно рассмотреть формулу (12.1)
применительно к тройкам диаграмм, у которых, быть может, есть сингулярные
перекрестки вне малого круга. Таким образом, эта формула ведет к
определению производной порядка гг + 1 на особых узлах η + 1-го порядка, если задано
значение производной порядка η на особых узлах порядка п. Обозначение:
/(П+1)((Х)) = /(п)((Х';) - /(n)((X.D· (12.2)
Таким образом, имея инвариант узлов, мы получили инвариант на
множестве X, который называется расширением инварианта f на множество
сингулярных узлов.
Аналогичным образом определяется расширение инварианта зацеплений на
множество сингулярных зацеплений.
Определение 12.1. Инвариантом (Васильева) конечного порядка называется
инвариант узлов / для которого найдется такое натуральное гг, что
производная j(n+1) равна тождественно нулю на сингулярных узлах порядка η + 1. В
этом случае говорят, что / имеет порядок не больше п.
Определение 12.2. Инвариантом Васильева порядка η называется
инвариант Васильева порядка не больше гг, не являющийся инвариантом Васильева
порядка не больше η — 1.
Обозначим через Vn пространство всех инвариантов Васильева порядка, не
превосходящего п.
12.2. Инварианты нулевого и первого порядков
201
Пример 12.1. Посчитаем значение расширения полинома Джонса на
простейшем сингулярном узле порядка два. После применения соотношения Васильева
мы получаем q + q3 — q4 — 1, см. рис. 12.1.
=V((Q))-V((Q))=q+q -Ч4 -1
Рис. 12.1. Вычисление производной по Васильеву
12.2. Инварианты нулевого и первого порядков
Из определения инвариантов Васильева непосредственно следует, что
инвариант порядка нуль принимает одинаковые значения на любых двух
диаграммах узлов, отличающихся заменой перекрестка, следовательно, он постоянен
на всех узлах.
Оказывается, что инвариантов порядка один не существует, т. е. что все
инварианты порядка не более одного также являются константами.
Действительно, рассмотрим простейший сингулярный узел U,
изображенный на рис. 12.2.
Рис. 12.2. Простейший сингулярный узел
Пусть S — тень сингулярного узла порядка один, в которой выделена
проекция сингулярной вершины.
Упражнение 12.1. Покажите, что можно расставить проходы и переходы
в остальных перекрестках диаграммы S, чтобы получить сингулярный узел,
изотопный сингулярному узлу U.
202
Глава 12
Легко видеть, что для любого инварианта Васильева / порядка не более
единицы мы имеем I'(U) = 0. Действительно, I'(U) = ДОО) ~~ АОО) — 0·
Покажем, что всякий инвариант / порядка не больше единицы является
константой. Пусть К — диаграмма ориентируемого узла. Изменяя некоторые
перекрестки, мы можем трансформировать диаграмму К в диаграмму
тривиального узла. Таким образом, 1(К) = /(О) + Σ ±Ι'{Κΐ)·> гДе Κΐ ~ сингулярные
узлы порядка один (множество этих сингулярных узлов может быть пустым,
если исходная диаграмма была тривиальной). Но, как было сказано ранее,
каждый особый узел Ki может быть переделан в некоторую диаграмму особого
узла U заменой перекрестков. Следовательно, I'(Ki) = I'(U) + Σ±Ι"(Κ^),
где Kij — сингулярный узлы второго порядка. По определению имеем I" = 0,
следовательно, I'(Ki) = 0, поэтому 1(К) = /(О)· Таким образом мы видим,
что функция / является константой; таковы все инварианты порядка не более
единицы.
12.3. Примеры инвариантов старших порядков
Рассмотрим полином Конвея С = Σι сгх% и ег0 коэффициенты сп.
Теорема 12.1. Для каждого натурального η функция сп является
инвариантом узлов порядка не большего, чем п.
Доказательство. В самом деле, надо только сравнить соотношение Васильева
и определяющее соотношение для полинома Конвея:
<0<у) = с«0X.;) -сп(-д)) = χ■ сп(ф {.:)· (12·3)
Напомним, что полином Конвея С принимает значения в кольце Ζ [ж]. Мы
видим, что первая производная от С делится на ж; аналогичным образом, гг-я
производная от С делится на хп. Так что (гг+ 1) дифференцирование приводит
сп к нулю.
D
Это дает нам первый нетривиальный пример. Второй коэффициент с^
полинома Конвея является инвариантом второго порядка (можно легко убедиться
в том, что он не является константой, а именно, его значение на трилистнике
не равно значению на тривиальном узле). Этот инвариант не различает левый
и правый трилистники, поскольку сам полином Конвея их не различает. В
следующей главе мы покажем как инвариант третьего порядка может различить
эти трилистники.
12.4. Символы инвариантов Васильева,
порожденные полиномом Конвея
Как уже отмечалось, каждый коэффициент сп полинома Конвея имеет
порядок не превосходящий п.
12.4. Коэффициенты полинома Конвея
203
Пусть ν — инвариант Васильева порядка п. По определению имеем г;(п+1) =0.
Это значит, что для всяких двух сингулярных узлов Κι, Κ<ι п-го порядка,
диаграммы которых отличаются друг от друга только одним перекрестком (у
первого узла имеет место переход, а у второго — проход), справедливо равенство
ν^η\Κι) = ν^η\Κ2). Таким образом, в сингулярном узле n-го порядка молено
заменять переход на проход и наоборот без изменения значения ν^ηΚ
Следовательно, значение ν^ не зависит от заузленности, которую порождает
классические перекрестки. Это значение зависит только от комбинаторной структуры
расположения точек пересечения на узле.
Определение 12.3. Функция ν^ называется символом инварианта v.
Определение 12.4. Хордовой диаграммой называется конечный
трехвалентный граф состоящий из одного ориентированного цикла (окружности) и
неориентированных хорд (ребер, соединяющих различные точки этого цикла).
Порядком хордовой диаграммы называется количество его хорд.
Замечание 12.1. Хордовые диаграммы рассматриваются с точностью до
естественного изоморфизма графов, переводящего хорды в хорды, цикл —
в цикл, и сохраняющего ориентацию цикла.
Замечание 12.2. Обычно хордовые диаграммы изображаются на плоскости в
виде окружности и прямолинейных {пересекающихся между собой) хорд. Мы
не будем оговаривать ориентацию окружности хордовой диаграммы, всегда
считая, что цикл ориентирован против часовой стрелки.
Вышеприведенные замечания, касающиеся сингулярных узлов, могут быть
переформулированы на формальном языке хордовых диаграмм. Именно,
каждому сингулярному узлу сопоставим хордовую диаграмму, получаемую
следующим образом. Мы предполагаем, что узел задан как образ стандартно
ориентированной евклидовой окружности S1 в R3. Хордовая диаграмма получается
из S1 соединением хордами тех пар точек, которые переходят в одну точку
в R3 (т.е. соответствуют перекрестку сингулярного узла).
Таким образом, каждый инвариант порядка η порождает функцию на
множестве хордовых диаграмм с η хордами. Можно рассматривать формальное
линейное пространство хордовых диаграмм с коэффициентами, скажем, в Q,
и линейные функции на этом пространстве, порожденные символами n-го
порядка инвариантов Васильева (вместе с постоянной функцией, равной нулю,
которая имеет порядок ноль).
Теперь ясно, что пространство Vn/Vn-i изоморфно пространству символов,
рассмотренных на формальном языке диаграмм.
Докажем, что для четного η коэффициент сп имеет порядок в точности
равный п. Более того, мы вычислим их символы, следуя [CDL].
Рассмотрим хордовую диаграмму D порядка п. Продублируем каждую
хорду и сотрем малые дуги между концам параллельных хорд. Полученный объект
(ориентированная окружность без 2η малых дуг, но с η парами параллельных
хорд) допускает обход вдоль самого себя. Действительно, начиная с
произвольной точки окружности мы достигаем начало какой-либо хорды (после которой
мы удалили малую дугу), затем поворачиваем и идем вдоль по этой хорде.
После того, как хорда кончилась, мы снова идем по окружности (по тому участку,
204
Глава 12
который не был удален) и так далее. Очевидно, что мы вернемся к начальной
точке. Здесь мы имеем две возможности.
В первом случае мы обойдем весь объект. Во втором случае мы пройдем
только часть объекта.
Выполнив некоторое малое преобразование в R3 мы можем сделать все
хорды непересекающимися. Тогда объект превратится в одномерное многообразие
m(D). Первая возможность, описанная выше, соответствует связному
многообразию, вторая соответствует несвязному одномерному многообразию.
Предложение 12.1 ([CDL]). Значение п-й производной сп на D равно
единице, если m(D) имеет только одну компоненту связности и равно нулю в
противном случае.
Доказательство. Пусть L — сингулярный узел, которому соответствует
хордовая диаграмма D. Расщепим узел в некоторой вершине, пользуясь скейн-
соотношением для полинома Конвея С и соотношением Васильева:
C'(^^j)=x-C0(j). (12.4)
После применения этого соотношения η раз видим, что значение n-й
производной инварианта С на L (на D) равно значению С на диаграмме, полученной
из D разведением всех сингулярных перекрестков способом *Х* —>· Λ Г.,
умноженному на хп. При этом коэффициент сп n-й производной полинома Конвея
для сингулярного узла равен значению коэффициента со на полученной
разведенной диаграмме. Это значение не зависит от типа перекрестков: оно равно
единице на тривиальном узле и равно нулю на тривиальном зацеплении с
числом компонент, большим единицы. Так что оно равно единице на любом узле
и нулю на любом зацеплении количеством компонент, не меньшим двух. Это
завершает доказательство. D
Оказывается, что для узлов (также как и для зацеплений с нечетным
числом компонент) коэффициент сп равен нулю при нечетных п. Аналогично, для
зацеплений с четным числом компоненты сп = 0 при четных п.
Этот факт может быть доказан при помощи предложения 12.1. Пусть D —
хордовая диаграмма с нечетным количеством хорд, равным п. Предположим,
что у кривой m(D), соответствующей диаграмме D, ровно одна компонента
связности. Заклеим ее диском. Получим некоторое ориентированное (докажите
это!) двумерное многообразие с вырезанным диском. Его эйлерова
характеристика должна быть четной. С другой стороны, она равна: 2п — Зп + 1 = — η + 1.
Принимая во внимание, что η четно, получаем противоречие, которое
завершает доказательство.
Очевидно, что при четном гг, существуют хордовые диаграммы, на которых
сп не обращается в ноль.
Пример 12.2. Значение инварианта С4 на диаграмме НН (см. рис. 12.3,
верхняя часть), равно нулю; значение С4 на 6ν\) (см. рис. 12.3, нижняя часть), равно
единице.
12.5. Другие полиномы и инварианты Васильева
205
Рис. 12.3. Превращение хордовой диаграммы в систему кривых
Упражнение 12.2. Покажите, что для любого четного η значение п-й
производной инварианта сп на диаграмме, у которой всякие две хорды
пересекаются, равно единице.
Из этого упражнения следует существование инвариантов Васильева
произвольного четного порядка.
Вышеприведенные рассуждения показывают, что полином Конвея слабее
инвариантов Васильева, т. е. если какие-либо два узла различаются полиномом
Конвея, то существует инвариант Васильева, принимающий различные
значения на этих узлах, при этом нетрудно показать существование двух
неизотопных узлов, различаемых инвариантами Васильева, значения полинома Конвея
на которых совпадают.
Впрочем, то же самое можно сказать о полиномах Александера, которые
получаются из полинома Конвея простой заменой переменной.
12.5. Другие полиномы
и инварианты Васильева
Если мы попытаемся в поисках инвариантов конечного порядка применить
формальное дифференцирование к коэффициентам других полиномов, то
потерпим неудачу. Например, коэффициенты полинома Джонса не являются
инвариантами Васильева. Дело в том, что полином Джонса не является
полиномом в строгом смысле этого слова, он содержит члены отрицательных степеней
и является полиномом Лорана. Таким образом, при многократном
дифференцировании некоторые члены полинома Джонса (а именно члены с
отрицательными степенями) не исчезают.
В работе [JJP] дан критерий ответа на вопрос когда коэффициенты
полиномиального инварианта узлов являются инвариантами Васильева. Там лее
показано, как построить полиномиальный инвариант по заданному инварианту
Васильева.
Несмотря на то, что не все полиномы получаются из полинома Конвея
(Александера) заменой переменного, инварианты Васильева оказываются
более сильными, чем описанные выше полиномиальные инварианты узлов (за
исключением, быть может, полинома Хованова). Более того, инварианты
Васильева сильнее всех квантовых инвариантов узлов, доказательство см., напр.,
206
Глава 12
в [Oht]. Результаты, приводимые ниже, восходят к работе Джоан Бирман и
Сяо-Сон Линя [BL] (препринт этой работы появился в 1991 году), см. также
[BN1].
Рассмотрим сначала полином Джонса V от переменной q. Напомним, что
этот полином удовлетворяет следующим скейн-соотношениям:
Сделаем замену переменной q = ех. Получим:
Выпишем теперь формальный степенной ряд по χ для вышеприведенного
выражения и перенесем все члены, делящиеся на χ в правую часть равенства.
В правой части мы имеем сумму, делящуюся на ж, а в левой части получаем
производную полинома Джонса плюс нечто, делящееся на х:
у((Х}}=^Х;) - ν0Φ=х<нечт°>- (12·5)
Рассуждая так лее, как и раньше, мы видим, что после второго
дифференцирования в правой части равенства остаются только члены, делящиеся на х2.
Следовательно, после (п + 1) дифференцирования п-й член ряда,
выражающего полином Джонса через ж, становится равным нулю. Таким образом, все
члены этого ряда являются инвариантами Васильева. Мы получаем
следующую теорему.
Теорема 12.2. Полином Джонса от одной переменной слабее инвариантов
Васильева.
Замечание 12.3. Мы доказали часть "не сильнее", в то время как легко
построить примеры узлов, не различаемых полиномом Джонса, но различаемых
инвариантами Васильева.
Можно проделать ту же работу с полиномом Джонса от двух переменных
(обозначаемого через X)).
Выпишем скейн-соотношения для него:
VAV<2 '■ · ^ У Л/Ч '<■ ■
(12.6)
сделаем замену переменной уд = еж, у λ = еу и выпишем разложение в ряд
Тейлора по χ и у.
В правой части равенства мы получим нечто, делящееся на χ и в левой
части нечто, делящееся на ху плюс производная полинома Джонса.
Наконец, мы имеем
*0 Χ.Ο - ^Ο',Χ;) = *<нечто}.
12.5. Другие полиномы и инварианты Васильева
207
Таким образом, после (п + 1)-кратного дифференцирования все члены
степени ^ η по χ исчезают.
Следовательно, справедлива теорема:
Теорема 12.3. Полином Джонса от двух переменных слабее инвариантов
Васильева.
Поскольку полином HOMFLY получается из полинома Джонса двух
переменных заменой переменной, справедлива.
Теорема 12.4. Полином HOMFLY слабее, чем инварианты Васильева.
Наиболее интересным и трудным является случай полинома Кауфмана от
двух переменных потому что этот полином не удовлетворяет соотношениям
Конвея. Этот полином может быть выражен через степени функций ζ, α,
и ^^—. Для того, чтобы представить полином Кауфмана в виде ряда из
инвариантов Васильева, нужно выразить все эти функции с помощью рядов от
положительных степеней двух переменных.
Напомним, что полином Кауфмана (версия Дубровник) от двух переменных
задается формулой
Y(L) = a-w^D(L),
где D — функция на неориентированных диаграммах узлов, удовлетворяющая
следующим соотношениям:
Как и в случае полинома Джонса-Кауфмана, в полиноме двух
переменных мы переходим от неориентированной диаграммы к ориентированной, а
затем нормируем (с помощью a~w<yL)). Здесь мы обозначили ориентированные и
неориентированные диаграммы одной и той же буквой L.
£>(; V)) - £>о: д)) = ^(ί'Χ'ί) - D0 (.;)); (12·7)
D(0)=(i + ^—); (12.8)
£>(Х#{ Π }) = aD(X),D(X#: £)) = a^D^X). (12.9)
Перепишем соотношение (12.7) для Υ. Получим:
а~1у(СЯу) - ау(:'Х;)=*(у(£0 - γό (?) ■аК <12·10)
для некоторого к.
Применим замену переменной ρ = 1п(^^). Тогда ζ,α, ^^— выражаются
через положительные степени и ряды от положительных степеней переменных
ζ и р. А именно:
Ζ = Ζ,
а = zev + 1 = z(l+p + ...) + 1,
208
Глава 12
α"1 = 1-ζ(1+ρ+...) + ζ2(1+ρ+...)2 + ...,
Каждая из правых частей равенств выражается как ряд от положительных
степеней переменных риг.
Таким образом, значение полинома Кауфмана от двух переменных на
каждом узле может быть выражено через положительные степени переменных
ρ и ζ. С другой стороны, принимая во внимание, что а = 1 + г(нечто1) и
а-1 = 1 + г(нечто2), мы можем вывести из (12.10) и (12.9), что
Υ' = ζ (нечто).
Таким образом, все члены в нашем двойном ряде, имеющие степень не
больше η по переменной г, обращаются в нуль после (п-\- 1)-го дифференцирования.
Следовательно, все они являются инвариантами Васильева. Таким образом, мы
доказали следующую теорему.
Теорема 12.5. Полином Кауфмана от двух переменных не сильнее
инвариантов Васильева.
Покажем теперь, как считать производную произведения двух функций (по
Васильеву).
Для функций / и д, заданных на диаграммах узлов можно формально
определить производные f и д' на диаграммах сингулярных узлов порядка один и,
далее, производные высших порядков на соответствующих диаграммах
сингулярных узлов.
Рассмотрим функцию f-g и диаграмму сингулярного узла К порядка п. Под
разбиением будем понимать выбор г сингулярных вершин η узла К. Выберем
разбиение s. Пусть K2S — диаграмма, полученная разрешением г выбранных
вершин узла К положительно, a K\s — диаграмма, полученная разрешением
оставшихся (п — г) (невыбранных) вершин разбиения s отрицательно.
Аналогично можно определить разбиение для хорд хордовой диаграммы,
соответствующей узлу К.
Лемма 12.1. Пусть К — хордовая диаграмма порядка п. Имеет место
формула Лейбница:
η
{fg)(n\K) = ΣΣ f(i){Kls)^\K2s). (12.11)
г=0 s
Доказательство. Будем использовать индукцию по п.
Установим сначала базу индукции (случай η = 1). Пусть дан особый узел
порядка один. Рассмотрим его диаграмму и сингулярную вершину А. Выпишем
12.5. Другие полиномы и инварианты Васильева
209
в ней соотношение Васильева:
= g^y^Mf^y^i) - д(Хш+/((X;o(^(=X"o - 9(·, y(j))
=/,(i^^( ·Χ-°+^^УР^У^'
(12.12)
Равенство (12.12) следует из определения производных f и д1'. Отсюда
следует утверждение теоремы для η = 1. Эта лее формула применима не только к
обычным, но и к сингулярным узлам, при этом следует считать, что некоторые
сингулярные перекрестки находятся вне малой окру лености, отображенной в
формуле, и все изображенные диаграммы совпадают вне этой окружности.
Рассмотрим теперь сингулярный узел К порядка п. Выберем сингулярную
вершину А диаграммы узла К. Значение (fgpn' на К равно разнице
значений (fg)^n~^ на двух сингулярных диаграммах К1 и К2; эти две диаграммы
имеют порядок η — 1 и представляют собой положительное и отрицательное
разрешения в перекрестке А соответственно.
По предположению индукции мы имеем:
п-1
{f9)(n-i){Kr} = YtYifU(K3ls)gin-1-i\Kia),j = 1,2, (12.13)
г=0 s
где s пробегает все разбиения порядка (п — 1).
Далее,
(fg)in\K) = (fgfn-l\Kl) - (fg^-^iK2) =
ЕЕ[/(1)(^)9(П"И(^) - /(<)(*?.)9(п-1-<)(*2.)] =
г=0 s
п-1
г=0 s
+ ^(KDg^-^HKL) - ^\к1)д^-^\к1)
п-1
Σ Σ \!{г+1\к,а)д{п-1-г\к1) + ^\к1)9(п-'\к28)
η
ΣΣ/(<)№«)3(,"0№·)·
г=0 s
г=0 s
Π
Из леммы 12.1 вытекает
Следствие 12.1. Пусть fug — две функции, заданные на диаграммах узлов
(не обязательно являющиеся инвариантами узлов) такие, что /(n+1) = 0,
g{k+l) = 0> Т()гда ^(n+fc+i) Ξ 0>
В частности, произведение инвариантов Васильева порядков пик
является инвариантом Васильева порядка не больше (п + к).
210
Глава 12
12.6. Пример инварианта бесконечного порядка
Все явно полиномиальные инварианты (кроме полинома Хованова), с
которыми мы имели дело до сих пор, являются либо инвариантами Васильева, либо
явным образом сводятся к последним.
Приведем пример инварианта узлов, имеющего бесконечный порядок, [BL].
Определение 12.5. Числом заузленности (ср. с определением на стр. 21)
U(K) ориентированного зацепления К называется минимальное число η Ε Ζ+
такое, что К может быть продеформирован в тривиальное зацепление
прохождением η через сингулярные зацепления порядка один или, что то же самое,
заменой η типов перекрестков.
По определению наш инвариант равен нулю для тривиальных зацеплений.
Теорема 12.6. Инвариант U имеет бесконечный порядок.
Доказательство. Выберем произвольное г Ε N. Мы приведем пример
сингулярного узла, для которого U^ φ 0. Фиксируем целое число т > 0 и
рассмотрим узел К4т с 4т сингулярными вершинами (расположенными одна за другой
так, что две соседние сингулярные вершины соединены двумя отрезками узла),
показанный на рис. 12.4.
4т вершин
Рис. 12.4. Сингулярный узел, на котором U1 φ 0.
По определению производной значение и^ш> на этом узле равно
знакопеременной сумме 2 слагаемых; каждое из них равно значению U на узле,
полученном некоторым разрешением диаграммы К^т.
Заметим, что на каждом из этих узлов значение U не превосходит
единицы: изменяя тип перекрестка в А, мы получаем тривиальный узел. С другой
стороны, узел, полученный из К/^т разрешением всех сингулярных вершин
тривиален если и только если число положительных разрешений равно количеству
отрицательных разрешений.
В случае q положительных и 4т — q и отрицательных перекрестков мы
получаем (—l)q.
12.6. Пример инварианта бесконечного порядка
211
Таким образом, £/(4т) (К^т) равно
u(4m\Kim) = 2[с°4т - с\т + ■ ■ ■ - clz-1].
Эта сумма, очевидно, отрицательна, поэтому U^m\K4m) φ 0. Таким
образом, для т > |, мы получаем U^ φ 0. Следовательно, инвариант U не
является инвариантом порядка не большего г. Так как г выбрано произвольным
образом, U не является инвариантом конечного порядка. D
Замечание 12.4. Мы не утверждаем, что U не может быть выражен через
инварианты конечного порядка.
Число заузливания является некоторой "мерой сложности" узла. Таким
образом, естественно было бы предполагать, что оно может быть реализовано
минимальными (по числу перекрестков) диаграммами узлов. Однако это неверно.
Первый результат в этом направлении был получен Блейлером и Наканиши
[В1, Nak]. После этого бесконечная серия таких узлов была построена Гари-
ти [Gar].
Глава 13
Алгебра хордовых диаграмм
13.1. Основные структуры
В настоящей главе мы будем обсуждать алгебраические структуры,
возникающие на пространстве инвариантов Васильева.
В предыдущей главе мы определили символы инвариантов Васильева на
языке хордовых диаграмм.
Основным является следующий вопрос: какие функции на хордовых
диаграммах могут играть роль символов?
Простое наблюдение ведет к следующему. Если имеется хордовая диаграмма
С = { ) с произвольным числом хорд, из которых одна является отдельно
стоящей, то любой символ инварианта Васильева соответствующего порядка на
этой диаграмме равен нулю. Это уже было показано в терминах сингулярных
узлов.
Это соотношение называется IT -соотношением (или одночленным
соотношением).
Легко вывести также обобщенное IT -соотношение, в котором мы выбираем
диаграмму С = LllllJ, где одна из хорд не пересекается ни с одной из оставшихся
хорд. Тогда каждый символ инварианта Васильева соответствующего порядка
принимает значение нуль на диаграмме С. Доказательство остается читателю.
Справедлива следующая
Теорема 13.1 (Четырехчленное соотношение). Для каждого символа v^
инварианта Васильева ν порядка η имеет место:
ν(η4 ΓνΟ) - ν^(Γ\ Α) - «<»>(Г7Ч) + v^CT)) = °· (13-1)
В этом соотношении участвуют хордовые диаграммы порядка п; при этом
все хорды, не изображенные в формуле (13Л) являются неподвижными (они
одинаково расположены на всех диаграммах).
Доказательство. Рассмотрим четыре сингулярных узла 5Ί, #2, S%, S^
порядка гг, диаграммы которых совпадают вне некоторого малого круга, так, что
внутри этого круга их фрагменты si, S2, S3, S4 имеют вид:
13.1. Основные структуры
213
Рассмотрим инвариант ν порядка η и значения его символа на этих четырех
сингулярных узлах. Из соотношения Васильева следуют соотношения,
изображенные на рис. 13.1.
) =«("-1)(-
) =«(»-1)е
Л;
) =„("-!)(-
.,(η-1)ί
) -W("-1)(-
) -υ(η-1)(-\
) _„(»-!)(-
>е
)= α — 6
)= с — d
)= с — α
)=d-b
Рис. 13.1. Одинаковыми буквами обозначены значения г/п ^ на изотопных
узлах
Мы имеем
(a-b)-(c-d) + (c-a)-(d-b) = 0.
Чтобы получить сингулярные узлы, нужно замкнуть их фрагменты si, S2, S3 ? S4.
Имеются две возможности сделать это, см. рис. 13.2.
В каждом из двух случаев соотношение
,(п)
vw(Si) - i7w(S2) + vw(53) - г^Ч^) = 0.
W/
,Wi
(13.2)
в точности представляет собой четырехчленное соотношение: на
фиксированных участках соответствующие хордовые диаграммы отличаются
предписанным образом.
Принимая во внимания произвольность расположения оставшихся (п — 2)
сингулярных вершин на диаграммах 5Ί, #2, 5з, *$4, мы получаем утверждение
теоремы.
D
И одночленное, и четырехчленное соотношения могут быть рассмотрены
на хордовых диаграммах, а также на двойственном пространстве линейных
функций на хордовых пространствах (эти два пространства можно очевидным
214
Глава 13
Рис. 13.2. Замыкания фрагментов диаграмм и 4Т-соотношение
образом отождествить). Таким образом, под четырехчленным соотношением
мы будем понимать два соотношения. Одно из них относится к функции
(элементу двойственного пространства) и утверждает, что линейная комбинация
значений такой функции на любой четверке диаграмм, указанных в
формуле (13.1), равна нулю, а второе из них относится к алгебре хордовых диаграмм
и утверждает, что сама линейная комбинация каждой такой четверки хордовых
диаграмм дает ноль. И то, и другое соотношение мы будем называть
четырехчленным соотношением.
Определение 13.1. Каждая линейная функция на хордовых диаграммах
порядка гг, удовлетворяющая одночленному и четырехчленному соотношениям,
называется системой весов порядка п.
Обозначение: Система весов порядка η обозначается через Лп (мы также
будем использовать обозначение Δη).
Из сказанного выше следует, что каждый инвариант Васильева порядка η
задает систему весов порядка п.
В случае инвариантов Васильева порядков не более двух ситуация ясна:
существует ровно одна нетривиальная (не равная нулю по модулю одночленного
соотношения) диаграмма из двух хорд, при этом все четырехчленные
соотношения тавтологичны. Символ инварианта Васильева порядка два реализуется
как второй коэффициент полинома Конвея, таким образом, dim Л2 = 1. В
размерности три мы имеем две нетривиальные диаграммы СдО и Οτν: любая из
оставшихся диаграмм имеет отдельно стоящую хорду. Оказывается, что они
линейно зависимы. Для нахождения линейной зависимости выпишем
четырехчленное соотношение (здесь хорда, одинаковая для всех четырех диаграмм,
13.1. Основные структуры
215
обозначена пунктирной линией):
Учитывая одночленное соотношение, получаем (жЗ = 2ζ
Таким образом, если существует инвариант порядка три, то его символ
однозначно определен значением на СЖЗ· Предположим, что имеется такой
инвариант У, при этом ^"(СжЗ) = 1. Тогда этот инвариант различает правый и
левый трилистники, см. рис. 13.3
v(Q)-v(Q)=
Рис. 13.3. Инвариант Васильева порядка три
различает правый и левый трилистники
При этом первое равенство на рис. 13.3 вытекает из следующих
соображений: из всех узлов, имеющих ту же тень, что и стандартный трилистник,
только два — левый и правый трилистники — являются нетривиальными. Поэтому
вторая производная на соответствующих сингулярных узлах равна значению
инварианта на соответствующем трилистнике минус его значению на
тривиальном узле.
Существование такого инварианта будет доказано позднее.
Рассмотрим теперь пространство Δ4.
Имеют место следующие четырехчленные соотношения:
216
Глава 13
Отсюда легко следует, что dim Δ4 = 3 и что три диаграммы
ι vw' θΐθ' (/Ю Г можно выбрать в качестве базиса.
Оказывается, что хордовые диаграммы, профакторизованные по
четырехчленному соотношению (с одночленным соотношением или без оного) образуют
алгебру. А именно, имея две хордовые диаграммы С ι и Сг, молено разорвать их
в точках с\ G С\ и С2 G Съ (не являющихся концами хорд) и соединить их в
одну диаграмму способом, согласованным с ориентацией. Полученную хордовую
диаграмму молено рассматривать как произведение С\ · С^· Такое определение
произведения зависит от выбора точек с\ и С2, следовательно, различный
выбор мог бы привести к получению различных элементов в Ас. Однако это не
так из-за четырехчленного соотношения.
Теорема 13.2. Произведение хордовых диаграмм в Лс корректно определено,
т. е. не зависит от выбора начальных точек.
Для доказательства этой теоремы будет удобно перейти к дуговым
диаграммам.
Определение 13.2. Дуговой диаграммой называется диаграмма, состоящая
из (ориентированной) прямой линии и нескольких дуг, соединяющих точки на
этой прямой так, чтобы никакая точка прямой не была инцидентна двум дугам.
Как и хордовые диаграммы, дуговые диаграммы рассматриваются с
комбинаторной точки зрения.
Разрывая хордовую диаграмму в некоторой точке и вытягивая окружность
на прямую, мы получаем дуговую диаграмму. При этом разрывая одну и ту
лее диаграмму в разных точках мы получаем, вообще говоря, разные дуговые
диаграммы.
Рассмотрим теперь четырехчленное соотношение применительно к дуговым
диаграммам. А именно, соотношение для четверок дуговых диаграмм, которые
получаются из хордовых диаграмм, участвующих в четырехчленном
соотношении, разрыванием последних в "одной и той лее" точке.
Пусть D — некоторая хордовая диаграмма, а А\ и А^ — дуговые диаграммы,
получающиеся из А разрыванием в разных точках. Оказывается, что
диаграммы А\ и ^2 являются эквивалентными по модулю четырехчленного
соотношения. Этого наблюдения достаточно для доказательства теоремы 13.2.
Очевидно, что диаграмма А2 молеет быть получена из диаграммы А\ многократным
"перебрасыванием крайнего конца дуги через бесконечность". Таким образом,
для доказательства теоремы 13.2 нам достаточно доказать следующую лемму.
Лемма 13.1. Пусть А\,Аъ — две дуговые диаграммы, отличающиеся
только расположением одной дуги I, а именно, один {правый) конец дуги I
занимает самую правую позицию в А^, в то время как соответствующий ему
{левый) конец соответствующей дуги V в А\ является самым левым концом;
все остальные концы дуг в А\ и А2 расположены одинаково. Тогда Αι и А2
являются эквивалентными по модулю четырехчленного соотношения.
Доказательство. Обозначим порядок диаграмм Αχ и А^ через п. Обозначим
общие (неподвижные) концы дуг в А\ и А2 через Χι,Χ2? · · · 5^2η-ι Β
перенумеровке слева направо. Они разбивают прямую линию на 2 η интервалов
13.2. Структура биалгебры
217
h ? · · · ? hn (также перенумерованных слева направо). Обозначим через Dj
дуговую диаграмму имеющую те лее неподвижные концы дуг, как и А\, и А 2 и один
"подвижный" конец хорды, находящийся в Ij. Таким образом, А\ = D\,A2 =
D2n. Очевидно, что Ак = Ак+1.
Рассмотрим следующее выражение
Мп-М = А2п-А2п-1+А2п-1-А2п-2 + ' ' • + Ак+2-Ак+1+Ак-Ак-1+. . . А2~АЪ
В нем 4п — 4 слагаемых. Легко видеть, что их можно разбить на п— 1 группу
по четыре слагаемых в каждой, так что слагаемые из одной группы образуют
четырехчленное соотношение.
Таким образом, А2П = Αι, что завершает доказательство теоремы. D
Таким образом, умножение хордовых диаграмм корректно определено в Лс.
Продолжая умножение по линейности, мы получаем алгебраическую
структуру на пространстве хордовых диаграмм Лс.
13.2. Структура биалгебры на Лс и Л^.
Хордовые диаграммы и диаграммы Фейнмана
Алгебра хордовых диаграмм Лс имеет еще одну структуру, более
интересную, чем описанная выше. Оказывается, что Лс является также биалгеброй
(определение будет дано позднее). Структура коалгебры на Лс вводится
следующим образом.
Пусть С — хордовая диаграмма порядка п. Обозначим множество всех хорд
диаграммы С через X. Определим коумножение Δ : Лс —>· Лс (8) Лс как
Си ^С5(8)СЖ_5,
где сумма взята по всем подмножествам s множества X, а Су обозначает
хордовую диаграмму, множество хорд которой содержит все хорды из С,
принадлежащие множеству у. Продолжим коумножение Δ по линейности на все Лс.
Проверим теперь, что эта операция корректно определена. Для этого нам
нужно показать, что для каждой четверки диаграмм А = (Ν/Ί, В = (\/), С =
, D = Cj) (таких, что А—В-\-С—D = 0 представляет собой четырехчленное
соотношение) выполняется равенство Δ (Α) — Δ(Β) + Δ (С) — Δ(Ό) = 0.
Действительно, пусть A,B,C,D — четыре диаграммы, обладающие
вышеуказанными свойствами. Рассмотрим коумножение Δ. Мы видим, что все
слагаемые, в которых две "основные" хорды находятся в разных подмножествах, не
дают разницы между А, 5, и разницы между С, D. В том же случае, когда две
основные хорды расположены по одну сторону от операции коумножения, мы
получаем сокращение в силу четырехчленного соотношения. Следовательно,
коумножение Δ корректно определено.
Дадим теперь формальное определение биалгебры1.
ХВ [О] определяемый объект также называется Алгеброй Хопфа. Обычно в определении
алгебры Хопфа требуется также понятие антипода, см., напр. [Кае]; однако биалгебра хордовых
диаграмм также является и алгеброй Хопфа. Мы не будем использовать понятие антипода
и его свойства.
©
218
Глава 13
Определение 13.3. Градуированная алгебра А с алгебраической операцией
μ и единичным отображением е, а также с коалгебраической операцией Δ и
коединичным отображением ε называется биалгеброщ если:
1. е является гомоморфизмом градуированных алгебр;
2. ε является гомоморфизмом градуированных алгебр;
3. Δ является гомоморфизмом градуированных алгебр.
Алгебра Хопфа Ас является, очевидно, коммутативной и ко коммутативной.
Определение 13.4. Элемент χ биалгебры В называется примитивным, если
Δ(χ) = x(g)l + l(g)x.
Очевидно, что для алгебры Ас с естественными операциями е, ε и
операциями умножения и коумножения, определенными выше, операции Δ, е и ε
являются гомоморфизмами, сохраняющими градуировку. Отображение Δ мо-
номофно: оно имеет пустое ядро, поскольку при χ φ Ο, Δ (χ) содержит слагаемое
ж® 1.
Таким образом, Ас является биалгеброй.
Рассмотрим еще одну интересную алгебру Аь, которая в последствии
окажется изоморфной алгебре Ас.
Определение 13.5. Диаграммой Фейнмана2 называется конечный связный
граф кратности три в каждой вершине, в котором выделен ориентированный
цикл (окружность)3. Все вершины графа, не лежащие на окружности,
называются внутренними вершинами. Вершины, лежащие на окружности,
называются внешними. Каждая внутренняя вершина снабжена также циклическим
порядком исходящих полу ребер.
Замечание 13.1. Предполагается, что диаграммы Фейнмана на плоскости
имеют ориентацию окружности против часовой стрелки; против часовой
стрелки задается и порядок исходящих ребер в каждой внутренней вершине.
Мы будем пользоваться этим правилом и не будем указывать каждый раз
ориентацию и циклический порядок, изображая диаграмму на плоскости.
Определение 13.6. Порядком диаграммы Фейнмана называется половина
общего числа ее вершин.
Все хордовые диаграммы являются диаграммами Фейнмана; в этом случае
два определения порядка согласуются.
Рассмотрим формальное линейное пространство всех диаграмм Фейнмана
порядка п. Профакторизуем это пространство по всем так называемым STU-
соотношениям, см. рис. 13.4.
Как и четырехчленное соотношение, STU-соотношение является
схематичным: предполагается, что оно выполняется для всех троек диаграмм, локально
2Также называется китайской диаграммой.
3Эта окружность называется также петлей Уилсона; мы не будем использовать это
название.
13.2. Структура биалгебры
219
Рис. 13.4. STU-соотношение
(в окрестности некоторой внешней вершины) отличающихся так, как показано
на рис. 13.4.
Обозначим полученное пространство через Агп.
На диаграммах Фейнмана молено определить умножение как и на хордовых
диаграммах (разрывая диаграммы и склеивая их в одну). Оказывается, что
получающаяся таким образом структура алгебры определена корректно. Более
того, имеет место
Теорема 13.3. Существует естественный изоморфизм f : Afn —> Асп,
задающий структуру алгебры на А1, являющийся тождественным на Асп. Кроме
того, STU-соотношение влечет следующие соотношения на А1:
1. Антисимметрию, см.. 13.5.
2. IHX-соотношение, см. рис. 13.6.
-О
Рис. 13.5. Соотношение антисимметрии
Рис. 13.6. Соотношение ШХ
Доказательство. Докажем сначала, что линейные пространства Ль и As
изоморфны. Очевидно, что из STU-соотношения для А* следует 4Т-соотношение
для Ас. Построим теперь изоморфизм /. Для всех элементов из Ас С Аг
положим изоморфизму / быть тождественным. Чтобы определить / на всех
остальных диаграммах Фейнмана, будем использовать индукцию по количеству χ
внутренних вершин. При χ = 0 доказывать нечего.
220
Глава 13
Предположим, что / корректно определено для всех диаграмм Фейнмана,
имеющих не более d внутренних вершин. Пусть К — диаграмма Фейнмана
порядка d + 1.
Очевидно, что существует внутренняя вершина V диаграммы К, которая
соединена ребром ν с некоторой внутренней вершиной. Таким образом, мы
можем применить STU-соотношение к этой вершине и получить разницу двух
диаграмм с d внутренними вершинами; продолжим операцию / по
линейности. Однако эта операция формально зависит от выбора вершины V и ребра v.
Покажем, что на самом деле эта операция не зависит от выбора U,V,u,v. Пред-
пол ожим, что есть две такие пары вершин V,v и U,u, причем V φ U, ν φ и.
В этом случае доказательство корректной определенности следует из
двукратного применения соотношения STU, см. рис. 13.7.
Рис. 13.7. Применяем соотношение STU дважды
В случае U = V и и φ ν, можно взять некоторую другую пару, а именно,
пусть W, w — такая пара, где внутренняя вершина W соединена с некоторой
внешней вершиной ребром w. Применяя STU-соотношение для U, и мы
получим тот же результат, как и в случае W, w, а последний результат совпадает с
результатом разведения для U, v.
Рассмотрим, наконец, случай, когда U = У, и Φ ν, a U является
единственной внутренней вершиной, которая соединяется ребром с некоторой внешней
вершиной. Покажем, что в этом случае наша диаграмма Фейнмана равна нулю
по модулю STU-соотношения.
Зафиксируем некоторую область, содержащую все внутренние вершины
графа, кроме одной. Эта область соединяется со внешними вершинами только
через вершину U и одну из хорд и, v. В этом случае имеются две возможности
применять STU-соотношение. По предположению индукции произведение фей-
нмановских диаграмм с общим количеством вершин, не превосходящим <i,
корректно определено и коммутативно. Используя коммутативность, мы видим,
что можно переместить внешнюю вершину вместе со всей "внутренней"
областью из одного места в другое, см. рис. 13.8. Таким образом, каждый из двух
способов в итоге дает нуль.
13.3. Копроизведение диаграмм Фейнмана
221
.® -® -
Рис. 13.8. Диаграмма особого вида эквивалентна 0 по модулю STU-соотноше-
ния
Докажем теперь, что из STU-соотношения следует соотношение
антисимметричности.
Применяя STU-соотношение многократно, молено свести соотношение
антисимметрии к случаю, когда все хорды, исходящие из рассматриваемых
внутренних точек, заканчиваются во внешних точках. В этом случае соотношение
антисимметрии проверяется непосредственно, см. рис. 13.9.
Рис. 13.9. STU-соотношение влечет соотношение антисимметрии
Доказательство IHХ-соотношение может быть сведено к случаю , когда
одна из концевых вершин (скажем, левая нижняя) является внешней. Этого
можно добиться, рассматривая левую нижнюю вершину всех диаграмм,
участвующих в IHХ-соотношении и разрешая последовательно все внутренние
вершины, находящиеся между данной вершиной и окружностью. В конце мы
получим 2П троек диаграмм (если η — количество промежуточных вершин), для
каждой из которых нужно проверить ΙΗХ-соотношение в том виде, как
проделано на рис. 13.10.
Замечание 13.2. Заметим, что одночленное соотношение не портит
структуры биалгебры; соответствующая биалгебра получается простой
факторизацией.
13.3. Копроизведение диаграмм Фейнмана
Вернемся к алгебрам Ас и At хордовых и фейнмановских диаграмм.
Замечание 13.3. В этом разделе мы не будем факторизовать
рассматриваемые пространства по одночленному соотношению.
222
Глава 13
φν^-^^-^-^νυ^
+
+
Рис. 13.10. STU-соотношение влечет ШХ-соотношение
Как было показано ранее, две алгебры изоморфны, следовательно, At имеет
структуру алгебры Хопфа. Опишем эту структуру подробно.
Пусть D — диаграмма Фейнмана и пусть V(D) — множество связных
компонент этой диаграммы, т. е. множество связных компонент графа,
получаемого из диаграммы D удалением ориентированного цикла. Пусть J С V(D) —
подмножество множества V(D). Это множество определяет диаграмму
Фейнмана Cj, связные компоненты которой лежат в V(D), т. е. диаграмму
Фейнмана, состоящую из ориентированного цикла диаграммы D и связных компонент
графа V(D), принадлежащих множеству J.
Определим копроизведение fi(D) по правилу
£С°) = Σ CJ®CV(D)\J,
JCV(D)
см. рис. 13.11.
Рис. 13.11. Копроизведение диаграммы Фейнмана
Теорема 13.4. Копроизведение, определенное таким образом, согласуется с
копроизведением, определенным на Ас, т.е. μ = μ.
13.4. Теорема о четырех красках
223
Доказательство. Нам нужно показать, что для каждой диаграммы Фейнма-
на D, ее копроизведение совпадает с линейной комбинацией копроизведений
хордовых диаграмм, на которые разлагается D.
Докажем это индукцией по числу к внутренних вершин диаграммы. При
к = 0 доказывать нечего.
Предположим, что утверждение верно для диаграмм Фейнмана с η
внутренними вершинами. Рассмотрим диаграмму Фейнмана D с (гг+1) внутренней
вершиной. Нам нужно показать, что μ(Ό) = μ(Ό). Согласно STU-соотношению,
диаграмма D представима как разница D+ — Ζ}_, см. рис. 13.12; в этом
случае связной компоненте диаграммы D может соответствовать одна связная
компонента диаграммы Ό\ (как и Ό^)^ а могут соответствовать и две связные
компоненты (на которые изначальная компонента разбивается при разведении
вершины). В первом случае шаг индукции очевиден.
Рис. 13.12. Применяем STU-соотношение
Во втором случае выберем компоненты (α+, 6+) и (α_, 6_) на диаграммах D+
и D-. Они получаются разрешением внутренней точки диаграммы D. Каждая
из диаграмм D± имеет η внутренних вершин. Таким образом, для них
верно утверждение теоремы: μ(Ό±) = fi(D±). Выпишем теперь μ(Ό) = μ(Ό+) —
μ(Ό-). В каждом из этих копроизведений остаются (не сокращаются) только
те члены, в которых компоненты (а+,6+) (соответственно, (а_,6_)) лежат по
одну сторону от знака тензорного произведения. Очевидно, что такие члены,
взятые вместе, дают fi(D) (в предыдущем смысле копроизведения).
Суммируя сказанное выше, получаем утверждение теоремы.
D
13.4. Представления алгебр Ли,
хордовые диаграммы
и теорема о четырех красках
Замечательная идея, связывающая теорию представлений алгебр Ли и
теорию узлов была рассмотрена в [BN1]; см. также [BN4, CV, Oht].
Идея: свертывать трехвалентные тензоры вдоль ребер графов.
Замечание 13.4. В настоящем разделе мы не будем учитывать одночленное
соотношение. Мы будем работать только с четырехчленным соотношением
(или соотношением STU в случае диаграмм Фейнмана).
224
Глава 13
Более подробно, идея заключается в следующем. Имея трехвалентный граф
и трехвалентный тензор, мы можем сопоставить этот тензор каждой вершине
графа, а затем свертывать имеющиеся тензоры вдоль ребер графа.
Естественно, что нам понадобится некоторая метрика, с помощью которой мы должны
поднимать и опускать индексы у тензоров. Для этого удобно рассмотреть
полупростые алгебры Ли: мы рассматриваем тензор структурных констант С^
(со всеми нижними индексами) и метрику gv/, которая в этом случае является
невырожденной. В качестве трехвалентного графа мы рассматриваем
диаграмму Фейнмана с ее циклическим порядком ребер в вершинах.
Замечательное наблюдение состоит в том, что STU-соотношение (равно как
ШХ-соотношение) для диаграмм Фейнмана соответствует тождеству Якоби
для алгебр Ли. Таким образом, если мы посчитаем свертку тензоров согласно
некоторой диаграмме Фейнмана, мы получим функцию, инвариантную
относительно STU-соотношения.
Эта конструкция является частным случаем общей конструкции; описанная
конструкция имеет дело с присоединенным представлением. В общем случае
нужно рассмотреть ориентированный цикл на диаграмме Фейнмана и
произвольное представление R алгебры Ли G. Затем мы располагаем вдоль цикла
элементы пространства представления таким образом, чтобы два соседних
элемента отличались друг от друга действием элемента алгебры Ли,
соответствующего ребру, исходящему из точки, разделяющей эти две дуги.
Рассмотрим случай присоединенного представления алгебры Ли so(3).
В этом случае подсчет сверток очень прост. А именно, в so(3) имеются три
базисных элемента а, 6, с, которые коммутируют по правилу: [а, Ь] = с; [6, с] = а;
[с, а] = Ъ.
Определение 13.7. Под плоской картой мы понимаем трехвалентный граф,
вложенный в плоскость. Этот граф делит плоскость на связные компоненты,
которые мы называем областями.
Предположим, что мы хотим правильно раскрасить карту (т. е. ее области)
четырьмя красками. Мы будем использовать палитру из четырех элементов
Z2eZ2,T.e. (0,0), (0,1), (1,0) и (1,1).
Определение 13.8. Карта называется раскрашиваемой в четыре цвета, если
можно сопоставить каждой области цвет, так чтобы области, соседствующие
по ребру, были раскрашены в разные цвета.
Теорема о четырех красках утверждает, что любая плоская карта
раскрашиваема в четыре цвета.
Эта замечательная задача оставалась нерешенной в течение долгого
времени. Ее первое решение [АН] является технически очень запутанным. В
настоящей главе мы продемонстрируем как свертки тензоров структурных констант
алгебр Ли могут дать некоторое достаточное условия для раскраски плоской
карты в четыре цвета [BN4].
Предположим, что имеется некоторая раскраска плоской карты в четыре
цвета (рассматриваемые как элементы группы Z2 Θ Ζ2. Тогда можно
раскрасить каждое ребро графа элементом из Ζ2 Θ Ζ2, равным разнице (или сумме)
элементов, соответствующих областям, соседствующих по данному ребру.
13.4. Теорема о четырех красках
225
Очевидно, что карта является раскрашиваемой в четыре цвета, если и
только если ребра можно раскрасить в три цвета (0,1), (1,0) и (1,1) таким образом,
чтобы соседние ребра имели различные цвета.
Каждую плоскую карту Μ можно естественным образом рассматривать как
диаграмму Фейнмана. Таким образом, ей можно сопоставить число,
соответствующее свертке структурного тензора для so(3). Обозначим соответствующее
число через 1%(М).
Теорема 13.5 (BN5). Если h(M) φ 0; то карта Μ раскрашиваема в четыре
цвета.
Доказательство. Используем базис а,Ъ,с для вычисления 1^{М). Так как
1з(М) φ 0, то существует по крайней мере одна расстановка элементов а,Ъ,с
на ребрах графа такая, что соответствующая свертка дает ненулевой элемент.
Принимая во внимание закон сверток для so(3), мы видим, что для такой
расстановки каждым трем соседним ребрам сопоставлены все три элемента а,Ь,с,
т. е. ребра раскрашиваемы в три цвета, следовательно, вся карта Μ
раскрашиваема в четыре цвета. D
Назовем d-диаграммой хордовую диаграмму, хорды которой могут быть
разбиты на два семейства хорд так, что хорды из одного семейства не
пересекаются, d-Диаграммы можно вложить в плоскость, расположив хорды одного
семейства внутри окружности, а хорды другого семейства — вне окружности.
Отметим, что хордовые диаграммы, не являющиеся d-диаграммами, не
вкладываются в плоскость.
Пусть дана d-диаграмма, вложенная в R2. Тогда соответствующая карта
является раскрашиваемой в четыре цвета. Действительно, вся плоскость делится
на две части окружностью d-диаграммы, а области каждой из этих двух частей
можно покрасить в два цвета. Следовательно, вся карта допускает раскраску
в четыре цвета, см. рис. 13.13.
В связи с этим уместным является рассмотрение следующего вопроса.
Рассмотрим карту (или вложенную в плоскость диаграмму Фейнмана). Можно ли
распознать в ней d-диаграмму? Другими словами, можно ли выбрать
замкнутый цикл таким образом, чтобы оставшаяся часть диаграммы представляла
собой несвязное множество ребер, соединяющих пары вершин на этом цикле.
Эта проблема является знаменитой, и она до сих пор не решена. Она была
впервые поставлена Уильямом Роуаном Гамильтоном. Соответствующий цикл
носит название гамильтопова цикла. К настоящему моменту решены
некоторые частные случаи этой проблемы.
Легко видеть, что положительное решение проблемы нахождения гамиль-
тонова цикла ведет к положительному решению проблемы четырех красок
посредством d- диаграмм.
Способ, предложенный в [BN3], не является критерием. Действительно, имея
диаграмму Фейнмана D, для которой Iz(D) = 0, соответствующая карта
может иметь гамильтонову кривую и быть раскрашиваемой в четыре цвета. Дело
в том, что при вычислении Iz(D) некоторые члены (соответствующие
правильным раскраскам в четыре цвета) дают положительный вклад, а другие члены —
отрицательный, так что суммарный вклад равен нулю.
226
Глава 13
Рис. 13.13. Каждая карта, соответствующая d-диаграмме
раскрашиваема в четыре цвета
13.5. Оценки размерностей пространств Λά·
Таблица известных размерностей
В настоящем разделе мы собираемся дать некоторые оценки размерностей
пространств Δη. В дальнейшем будет показано, что Δη — изоморфно
пространству Vn/Vn-b
13.5.1. Историческая справка
Очевидно, что мощность множества всех хордовых диаграмм из d хорд не
превосходит (2d - 1)!! = 1 · 3 · · · (2d - 1).
Это дает очевидную верхнюю оценку. Результаты (дальнейшие оценки),
приведенные ниже, позаимствованы из [CDBook]).
1. (1993) Сергей Владимирович Чмутов и Сергей Васильевич Дужин [CD1]
доказали, что dim Ad < (d — 1)!.
2. (1995) К. Инь в [Ng] добился замены (d - 1)! на ^^.
3. (1996) Александр Стойменов [St] доказал, что dim^ растет медленнее,
г/' -1-1
чем р, где а = 1.1
4. (2000) Бэла Болобаш и О. Риордан [BR] получили ассимптотическую
верхнюю оценку (21n(2)d|o(1))^ (примерно χ^).
5. (2001) В [Zag] Дон Загир улучшил результат до 6 ^2dddl, чт° ассимптоти-
чески мажорируется функцией -j для любого значения константы а <
^ = 1.644...
История нахождения нижних оценок такова.
13.5. Оценки размерностей
227
1. (1994) С.В.Чмутов, СВ. Дужин и С.К.Ландо [CDL] привели нижнюю
оценку для числа примитивных элементов Vn ("леса"): dimVd ^ 1 for
d > 1.
2. (1995) dimVd ^ [§] (см. Мельвин-Мортон [МеМ] и Чмутов-Варченко [CV]).
3. (1996) dimVd ~ ^, см. Дужин [Dul].
4. (1997) dimPd - dz°0d, см. Чмутов-Дужин, [CD2].
5. (1997) (М. Л. Концевич) dimPn > e^v^
6. (1997) dimPn > ес^ для любой постоянной С < πγ^2/3 (Оливье Дасбах,
[Da]).
Далее мы собираемся доказать простейшую верхнюю оценку из работы
[CD1] и описать идею, ведущую к более тонким оценкам [CD2]. Идеи работы
[Da] обобщают технику, предложенную в работе [CD2], добавлением некоторых
идей маломерной топологии. Более детальное обсуждение см. в [CDBook].
13.5.2. Верхняя оценка
Обсудим сначала верхнюю оценку из [CD1], а именно dim Δη ^ (η— 1)!. В
работе приводится набор из (п — 1)! хордовых диаграмм, линейно порождающих
пространство Δη.
Определение 13.9. Хордовая диаграмма называется хребтовой, если она
содержит хорду, пересекающуюся со всеми остальными хордами.
Теорема 13.6. Множество всех хребтовых диаграмм линейно порождает
пространство Ап.
Доказательство этой теоремы мы разобьем на шаги; каждый из этих
шагов остается читателю в качестве упражнения. Основной идеей доказательства
является индукция по многим параметрам.
Определение 13.10. Пусть дана хордовая диаграмма D и хорда d в ней.
Порядком хорды d называется количество хорд, ее пересекающих. Порядком
диаграммы D называется максимальный из порядков ее хорд.
Обозначения: deg(d), deg(D).
Рассмотрим некоторую хордовую диаграмму D. Из определения следует,
что если D имеет η хорд и deg(D) = η— 1, то D является хребтовой диаграммой.
Будем использовать индукцию по порядку диаграммы D и доказывать, что
если deg(Z}) < η — 1, то диаграмма D может быть представлена как линейная
комбинация хордовых диаграмм больших порядков.
Предположим, что deg(Z}) = /. Выберем хорду d такую, что deg(cf) = f <
η — 1. После поворота диаграммы можно считать, что хорда d вертикальная,
а правая часть диаграммы D (относительно d) содержит больше концов хорд,
чем левая часть.
228
Глава 13
Тогда существует хорда d!, оба конца которой лежат в правой части.
Верхний конец ее лежит на некотором расстоянии от верхнего конца хорды d.
Обозначим количество концов хорд между ними через к. Предположим, что мы
нашли минимальное возможное к.
Упражнение 13.1. Если к > 0; то диаграмма D может быть представлена
как линейная комбинация диаграмм большего порядка и хордовых диаграмм
того же порядка, но с меньшим к.
Следовательно, можно предполагать, что к = 0.
Рассмотрим теперь нижний конец хорды d!.
Определение 13.11. Нижний конец любой хорды, которая пересекает dl и не
пересекает хорду d, называется граничным. Конец хорды, который лежит на
нижней дуге между d и d! и не является граничным, называется свободным.
Пусть / — количество свободных точек в хордовой диаграмме, а Ъ —
количество граничных точек между нижним концом хорды d! и первой свободной
точкой. Индексом хордовой диаграммы называется пара (/,6). Индекс будет
использован в качестве параметра индукции относительно следующего
лексикографического упорядочения: (7ι, Ь\) > (/2, ^2) тогда и только тогда, когда или
1\ > Ϊ2 ИЛИ 1\ = 12,Ъ\ > Ъ2-
Теперь мы собираемся доказать, что всякая диаграмма ненулевой степени
может быть представлена линейной комбинацией диаграмм меньших степеней.
Доказательство состоит из двух шагов, которые предоставляются читателю
в качестве упражнения. Каждый из этих шагов заключается в
непосредственном использовании четырехчленного соотношения.
Первый шаг.
Упражнение 13.2. Если I > 0,6 = 0; то диаграмма может быть
представлена линейной комбинацией диаграмм большего порядка и диаграмм того же
порядка (к = 0) с меньшим I.
Второй шаг.
Упражнение 13.3. Если I > 0, Ъ > 0, то диаграмма может быть
представлена линейной комбинацией хордовых диаграмм большего порядка и диаграмм
того же порядка (к = 0) с меньшим индексом.
Итак, если I = 0, Ъ Φ 0, то каждая хорда, пересекающая хорду <i, пересекает
также и хорду d!, и существуют хорды пересекающие d!, но не пересекающие d.
Таким образом, порядок всей диаграммы больше, чем степень хорды <i, что
противоречит предположению.
Если / = 0, Ъ = 0, то мы имеем две "параллельные хорды" и следующее
4Т-соотношение, которое (вместе 1Т-соотношением не указанным на рисунке)
завершает доказательство теоремы см. рис. 13.14.
13.5.3. Нижняя граница
Мы собираемся описать нижнюю границу для размерности Лп следуя [CD2].
По словам авторов "история нижней границы для инвариантов Васильева
является более загадочной (по сравнению с историей верхней границы)".
13.5. Оценки размерностей
229
Рис. 13.14. Линейная комбинация диаграмм меньшей степени
Первая оценка, данная Бар-Натаном в [BN1], такова: dim Vn > еСл^, η —>· ос.
Эта оценка происходит из связи между инвариантами Васильева и
алгебрами Ли.
Определение 13.12. Диаграммой Якоби называется диаграмма Фейнманабез
ориентированной окружности; именно, граф, все вершины которого имеют
валентность один или три; при этом для каждой вершины указан циклический
порядок выходящих из нее ребер. Порядком диаграммы Якоби называется
половина общего числа ее вершин.
Рассмотрим соотношения антисимметрии и соотношения ШХ для диаграмм
Якоби. Очевидно, что они оба однородные по отношению к вышеописанной
градуировке. Как и диаграммы Фейнмана, диаграммы Якоби обладают
структурами умножения и коумножения, которые задаются даже проще, чем для
диаграмм Якоби: у нас нет ориентированной окружности, и умножение
представляет собой несвязную сумму, а коумножение определено с помощью
разбиения на связные компоненты.
Следовательно, мы знаем, какие диаграммы Якоби являются
примитивными: это просто связные графы, вершины которых имеют валентность один и
три, у которых каждая трехвалентная вершина снабжена циклическим
порядком исходящих ребер.
Дадим несколько определений. Рассмотрим пространство примитивных
диаграмм Якоби. Каждая примитивная диаграмма Якоби имеет четное число
вершин. Обозначим половину этого числа через d. Соотношения ШХ и
антисимметрии являются однородными по отношению к d. Пространство С является
таким образом биградуированным: С = фС^;П, где С^,п — подпространство
пространства С, порожденное примитивными диаграммами Якоби с общим числом
вершин, равным 2d, из которых в точности η являются одновалентными.
Определение 13.13. Диаграммой-батоном ВП1 ,...,nfc называется диаграмма
Якоби, имеющая вид, указанный на рис. 13.15.
У диаграммы -Bnij...jnfe имеется 2(ηι + · · · + η& + /с — 1) вершин, из которых
πι -\- · · · -\- rik имеют валентность один.
Теорема 13.7 (Основная теорема, [CD2]). Пусть η = п\ Л Ьп&? и пусть
d = п-\-к— 1. Элементы ВП1.„Пк, определенные выше, являются линейно
независимыми в Cd,n β случае всех четных ηι,... ,п&? удовлетворяющих
следующим условиям:
230
Глава 13
η вершин η вершин
Рис. 13.15. Диаграмма ВП1ушшшуПк
П\ < П2
П\ + П2 < П3
Πι + П2 + П3 < П4
П1-\-П2-\ h Пк-2 < Пк-1
п
П\ + П2 -\ h Пк-2 + Пк-1 < -
Доказательство этой теоремы использует технику, предлолсенную
Бар-Натаном. А именно, вместо хордовых диаграмм (диаграмм Фейнмана) молено
рассмотреть соответствующие свертки тензоров, происходящие из простейшего
представления алгебры Ли SL(n). Результат будет полиномом от N.
Полиномы, соответствующие батонам являются линейно независимыми,
следовательно, линейно независимыми являются и сами диаграммы. Далее, диаграммы
Якоби естественным образом замыкаются и образуют диаграммы Фейнмана,
более подробно см. [CDBook].
13.5.4. Таблица размерностей
Первое точное вычисление размерностей dim^n было проделано
Бар-Натаном для η ^ 9.
Внизу мы приводим таблицу размерностей вплоть до η = 12.
η
dim Vn
dim Λη
dim Vn
0
0
1
1
1
0
0
1
2
1
1
2
3
1
1
3
4
2
3
6
5
3
4
10
6
5
9
19
7
8
14
33
8
12
27
60
9
18
44
104
10
27
80
184
11
39
132
316
12
55
232
548
Ответ для п = 10,11,12 был получен с использованием специальной
структуры на множестве примитивных диаграмм.
Глава 14
Интеграл Концевича
и формулы для инвариантов
Васильева
В 1992 году Максим Львович Концевич предложил замечательную
конструкцию, описывающую комбинаторную структуру инвариантов Васильева,
впоследствии известную как интеграл Концевича. Этот интеграл основан на
конструкции мультипликативного интеграла, более известной как конструкция
Чена или формула итерационного интегрирования. Концевич использовал этот
метод в форме, предложенном Книжником и Замолодчиковым [KZ]. Интеграл
Концевича является универсальным инвариантом для инвариантов Васильева,
т. е. все инварианты Васильева выажаются через него. Более того, интеграл
Концевича определяется всеми инвариантами Васильева. Как оказалось, см.
[Кае, LM], он также является универсальным и для квантовых инвариантов.,
из чего следует, что инварианты Васильева слабее квантовых инвариантов,
подробнее см. в [Oht].
После оригинальной работы Концевича появились разнообразные (в
основном комбинаторные) конструкции, описывающие тот же самый инвариант, см.
работы Пьера Картье и Сергея Пиунихина [Car93, Piu93]. В работе Тхонга Ле
и Джун Мураками [LM] предложен явный комбинаторный метод вычисления
интеграла Концевича. Мы также рекомендуем книги [Oht, CDBook] и статьи
[La, ДЧ].
Пусть дан инвариант Васильева V порядка п. Его (п + 1)-я производная
тождественно равна нулю. Тогда его гг-я производная инварианта V (его
символ) зависит только от порядка обхода двойных точек, т. е. является корректно
определенной на хордовых диаграммах. Более того, символ представляет собой
систему весов, т. е. удовлетворяет одночленному и четырехчленному
соотношениям.
Теорема 14.1. 1. (В. А. Васильев) Каждый символ инварианта Васильева
порядка η происходит из некоторой функции на хордовых диаграммах,
удовлетворяющей одночленному и четырехчленному соотношениям, т. е. из
некоторого элемента из Ап.
2. (М. Л. Концевич) Каждый элемент из Ап является символом
некоторого инварианта Васильева порядка п.
232
Глава 14
Первая часть (которая следует из работ Васильева [Vas, Vas2]) уже была
доказана в предыдущей главе.
Целью настоящей главы является доказательство второй части этой
теоремы.
14.1. Предварительный интеграл Концевича
Определение 14.1. Пополнение Δ пространства Δ = 0^=οΔ7η — это
пространство всех формальных рядов J2mcmam, где ст Ε С — числовые
коэффициенты а ат Ε Ат — элементы базиса линейного пространства хордовых
диаграмм порядка га.
Рассмотрим пространство R3 как декартово произведение комплексной
прямой С1 с координатой ζ и вещественной прямой R1 с координатой t.
Пусть дан ориентированный узел К в R3 = Gz x Rt. Небольшим
шевелением в R3 (не меняющим изотопического класса данного узла) молено сделать
координату t простой функцией Морса на узле К, т. е. такой, что критические
точки функции t на узле К являются невырожденными и имеют попарно
различные критические значения.
Замечание 14.1. В дальнейшем такие вложения будут называться морсов-
скими узлами.
Определение 14.2. Предварительным интегралом Концевича узла К
называется следующий элемент пространства Δ:
~ 1 /■ „ , ? dZj - dz.
n \ΔΊΧΙ) / cmin<t1 <---<trri<cmax _ χ- — Z-
m=0 v ; tjнекритические p—uz z \\ 3 = 1 -J
По определению полагаем, что коэффициент при хордовой диаграмме без хорд
равен единице.
Опишем формулу (14.1) более подробно.
Вещественные числа ст\п и стах — минимальное и максимальное значения
функции t на узле К.
Областью интегрирования является га-мерный симплекс ст[п < t\ < · · · <
tm < cmax, точнее, связные компоненты, на которые он разбивается (с учетом
того, что все значения ti некритические). Здесь под Zi и dzi мы подразумеваем
соответствующие функции и дифференциалы от переменных ti (для
некритических значений они определены корректно). Так например, для тривиального
узла, изображенного на рис. 14.1, при га = 2 область интегрирования состоит
из шести компонент, которые выглядят так, как показано на рис. 14.1.
Количество слагаемых постоянно внутри каждой связной компоненты, но
оно может изменяться при переходе от одной компоненты к другой. Часть
узла, лежащая внутри полосы между двумя соседними критическими точками,
представляет собой набор кривых; каждая из этих кривых однозначно
параметризуется параметром t.
14.1. Предварительный интеграл Концевича
233
Л
Стах
С2
т\
С2
С\
t2
Cl
С2
Рис. 14.1. Область интегрирования для интеграла Концевича
Фиксируем число га и выберем га горизонтальных плоскостей {t = ti,
г = 1,..., га}, каждая из которых не содержит критических точек и лежит
между максимальным и минимальным уровнями. Далее мы будем брать сумму по
всем га от 0 до ос. Для каждой плоскости {t = ti} С R3 выберем
неупорядоченную пару (zi,ti), (z^U) точек, лежащих в пересечении узла К с этой
плоскостью. Обозначим через Ρ = {(ζϊ, ^)} выбор таких пар для каждой
плоскости. Зафиксируем спаривание Р. Если рассматривать узел как
ориентированную окружность, на которой пары точек Zi, z[ соединены хордами, мы получим
хордовую диаграмму. Обозначим ее через Dp.
Под интегралом в формуле (14.1) мы имеем сумму таких диаграмм по всем
спариваниям Р. Коэффициенты при этих диаграммах получаются следующим
образом. Фиксируем произвольную связную компоненту области
интегрирования и спаривание Р. Мы определили хордовую диаграмму Dp; далее мы можем
"вынести за скобку" эту хордовую диаграмму; коэффициент, который нам
нужен, получается интегрированием формы (—1)^Л^1 —3_ , °. Таким образом мы
J z3 z^
получим коэффициент при Dp, после чего нужно привести подобные члены.
Символ I для заданного спаривания Ρ означает число точек видов (z,ti) и
(zf,ti) в спаривании Р, в которых координата t убывает при движении вдоль
по ориентации узла.
В примере, приведенном выше, связной компоненте {cmin < t\ < c\, с2 <
t2 < Стах} соответствует пара точек на уровне t\ и пара точек на уровне t2,
следовательно, там возможно только одно спаривание. Для связной
компоненты {cmin < t\ < ci,ci < t2 < c2} мы имеем единственный выбор на уровне
{t = t\\ (две точки из двух), в то время, как плоскость {t = t2} пересекает
узел в четырех точках; таким образом мы имеем С\ = б возможных
спариваний (z2, ^2), следовательно, общее количество слагаемых равно шести. В случае
компоненты {с\ < t\,t2 < с2} мы имеем тридцать шесть слагаемых, это са-
234
Глава 14
мый интересный случай, в котором появляется нетривиальная диаграмма (/О·
В каждой части рисунка мы приводим ровно одно спаривание и
соответствующую ему хордовую диаграмму.
Во всех случаях, кроме {с\ < t\ < £2 < £2}, мы получаем тривиальную
хордовую диаграмму (] Q, равную нулю по модулю четырехчленного
соотношения. Поэтому в данном случае интегрирование сводится к симплексу {с\ <
ti<t2< с2}.
На рис. 14.2, показаны диаграммы, соответствующие разным областям
интегрирования.
Рис. 14.2. Области интегрирования и хордовые диаграммы
Возникают следующие естественные вопросы.
1. Имеет ли смысл формула (14.1), т.е. сходятся ли соответствующие
интегралы?
2. Является ли полученный элемент инвариантом узла?
3. Как он связан с инвариантами Васильева?
4. Как считать этот интеграл?
Теорема 14.2 ([Коп], см. также [BN1]). Все коэффициенты ряда (Ц.1)
конечны.
Определение 14.3. Под горизонтальной деформацией мы понимаем
изотопию морсовского вложения узла в R3, которое не меняет взаимного
расположения критических точек соответствующей функции Морса.
Очевидно, что горизонтальная деформация не меняет изотопического
класса узла. Любая горизонтальная деформация представима в виде композиции
простейших преобразований, показанных на рис. 14.3.
14.1. Предварительный интеграл Концевича
235
Рис. 14.3. Горизонтальная деформация
Теорема 14.3 ([BN1]). Функция Ζ (К) является инвариантной
относительно горизонтальных деформаций узла и относительно преобразования
(изотопии), указанного на рис. Ц.4, ко не инвариантна при преобразовании (*),
изображенном на рис. Ц.5.
Рис. 14.4. Перемещение критических точек
Рис. 14.5. "Запрещенное" преобразование
Обозначим тривиальный узел, представляющий собой простое замыкание
дуги, изображенной на рис. 14.5, (т. е. узел с двумя минимумами и с двумя
максимумами) через А.
Мы можем рассмотреть простейшую диаграмму тривиального узла (с
одним минимумом и одним максимумом) и реализацию, похожую на символ ос
(в дальнейшем мы этот тривиальный морсовский узел и будем обозначать
через ос), см. рис. 14.6. Легко видеть, что значение Ζ (К) для простейшей
реализации равно единице (т. е. весь ряд состоит из одной диаграммы без хорд,
так как остальные диаграммы обращаются в нуль в силу одночленного
соотношения). С другой стороны, Ζ (ос) не равно единице (в данном случае роль
единичного элемента играет О)·
Следовательно, Ζ не является инвариантом узлов.
Тем не менее имеет место следующая теорема.
236
Глава 14
Рис. 14.6. Узел "ос"
Теорема 14.4. Если узел К' получается из узла К преобразованием (*), то
Ζ(Κ') = Ζ(Κ)·Ζ(οο).
Доказательство. Заметим сначала, что ос получается из узла А
горизонтальной деформацией Ζ (ос) = Ζ (А).
Рассмотрим теперь связную сумму узла К с "маленьким" узлом ос, т. е.
узел, полученный из К добавлением пары критических точек — одного
максимума и одного минимума на некоторый малый отрезок узла К, не содержащий
критических точек до того, см рис. 14.7.
В силу теоремы 14.4, значение функции Ζ при таком преобразовании
умножатся на Ζ {об), т..е Ζ {Κ') = Ζ {К) · Ζ {об). D
Кфоо
Рис. 14.7. Добавление ос
14.2. Значение Ζ{οο) и нормализация
Мы видим, что изменение интеграла Ζ{·) при преобразовании (*) можно
проследить: его значение просто умножается на Ζ{οο). Пусть теперь К — мор-
совское вложение окружности S1 в R3, и пусть с — количество критических
точек функции t на узле К.
Рассмотрим теперь предварительный интеграл Концевича как формальный
ряд. Этот ряд состоит из элементов градуированной алгебры и его младший
коэффициент является единицей в этой алгебре. Следовательно, мы можем
формально обращать ряды по формуле
(1 + а)-1 = 1-а + а2-а3 + ...,
где а1 — формальная сумма, соответствующая градуировке г в ряде для а.
Кроме того, мы можем формально умножать такие ряды.
14.2. Значение Ζ (об) и нормализация
237
Определение 14.4. Под универсальным инвариантом Васильева-Концевича
для узла К мы понимаем следующий элемент пополнения алгебры хордовых
диаграмм:
1(К) = -£W . (14.2)
Ζ(ос)2
Замечание 14.2. Здесь мы взяли степень (| — 1) по следующим причинам.
В случае простейшей диаграммы Q тривиального узла мы имеем /(О) — 1>
таким образом, для одного максимума и одного минимума | — 1 = 0.
Замечание 14.3. Очевидно, что если ряд (Ц.1) сходится, то (Ц.2) имеет
смысл, как формальное частное двух рядов.
Таким образом мы получаем следующую теорему.
Теорема 14.5. Интеграл Концевича /(·) является инвариантом узлов.
Доказательство. Действительно, в силу теоремы 14.4 мы видим, что Ζ (К) для
заданного изотопического типа узла зависит не от расположения критических
точек, а лишь от их количества.
Легко проверить, что два морсовских вложения представляют один и тот лее
узел в том и только в том случае, когда одно из них может быть
трансформировано в другое посредством движений, не меняющих расположения критических
точек, а так лее движений, показанных на рис. 14.4 и рис. 14.5.
Принимая во внимание инвариантность Ζ относительно всех движений,
кроме последнего и поведения Ζ при добавлении пары критических точек, мы
получаем утверждение теоремы. D
Инвариант /(·) называется универсальным инвариантом
Васильева-Концевича.
Докажем теперь самую важную теорему.
Пусть W — система весов порядка га. Положим по определению W(d) = 0
для всех хордовых диаграмм d с количеством хорд, не равным га.
Теорема 14.6 (Концевич, см. также [BN1]). Инвариант W(I(·)) является
инвариантом Васильева порядка га с символом W, т. е. инвариант Васильева
V(W), имеющий символ W, задается по формуле
V(W)(K) = W(I(K))
для каждого узла К.
Из этой теоремы следует вторая (сложная) часть теоремы
Васильева-Концевича о существовании инварианта Васильева, соответствующего заданной
системе весов.
Нам осталось доказать теоремы 14.2, 14.3 и 14.6.
238
Глава 14
14.3. Инвариантность интеграла Концевича
Замечание 14.4. Под Zm(K) и 1т(К) мы понимаем слагаемое градуировки
πι в Ζ {К) и 1{К) соответственно.
Докажем сначала теорему 14.2, утверждающую, что интеграл (14.1)
сходится.
Доказательство. Рассмотрим морсовский узел К в R3. Фиксируем т Ε Ν и
выберем т плоскостей, не проходящих через критические точки узла К.
Рассмотрим некоторую хордовую диаграмму D. Коэффициент в
(предварительном) интеграле Концевича Ζ [К) при этой диаграмме получается
интегрированием формы
dz'Atj) - dzj(tj)
Λ
j=1 ζ№ά) ~ Фэ)
по части симплекса {ст\п < t\ < · · · < tm < cmax}, соответствующей этой
диаграмме D.
Рассмотрим множество сингулярных точек, в которых Zj = z'a имеет место
при некотором j. Интеграл от рассматриваемой формы может расходиться в
этой точке. Рассмотрим пару точек Zj, z'a, в которой Zj и z'A близки между собой.
Имеем две возможности:
1. Дуга между Zj и z'a содержит другие концы (как показано на рис. 14.8).
Тогда область интегрирования (по которой мы интегрируем форму —f^—-)
з 3
имеет малость порядка более высокого, чем z'A — Zj поскольку сингулярная
точка невырождена. Следовательно, эта часть интеграла (14.2) не
приведет к расходимости.
Рис. 14.8. Конец хорды ζ&, z'k находится в окрестности максимума
2. Дуга между Zj и z'a не содержит других концов хорд. см.рис. 14.9. тогда
хорда Zjz'a диаграммы D изолирована; поэтому диаграмма D равна нулю
по модулю 1Т-соотношения.
Этим завершается доказательство теоремы 14.2.
D
14.3. Инвариантность интеграла Концевича
239
Рис. 14.9. Случай отдельно стоящей хорды
14.3.1. Интегрирование голономии
Для доказательства двух оставшихся теорем нам придется интегрировать
голономии и ввести так называемую связность Книжника-Замолодчикова.
Сначала напомним некоторые конструкции.
Определение 14.5. Пусть X — гладкое многообразие, а Ы — ассоциативная
топологическая алгебра с единицей (рассмотренная над R или С).
Тогда U-связностью на многообразии X называется 1-форма Ω на X с
коэффициентами из U. Кривизной связности Ω называется 2-форма
Fn = аП + Ω Λ Ω.
Связность называется плоской если ее кривизна равна нулю.
Определение 14.6. Пусть В : / —>· X гладкое отображение интервала [а, Ь] в
пространство X. Пусть Ω является ΖΥ-связностью на X.
Назовем голономией Нв,п формы Ω вдоль пути В решение
дифференциального уравнения -^hB,n(t) = Ω(Β'(Ϊ)) · hB,n(t),t Ε /, с начальным условием
hBMa) = !■
Замечание 14.5. Легко показать, что если связность Ω плоская, то голо-
номия зависит только от концов пути и гомотопического типа пути.
В этом состоит обобщение формулы Гаусса-Остроградского на
некоммутативный случай. В коммутативном случае мультипликативный интеграл
равен экспоненте риманова интеграла для логарифмической функции. В
некоммутативном случае это не так из за дополнительных членов вида Ω Λ Ω.
Мультипликативный интеграл
Решение уравнения (голономия), как правило, существует. Оно называется
мультипликативным интегралом формы Ω. Во многих случаях голономия
может быть вычислена по итерационной формуле:
^β,Ω
(ί) = 1 + ί Ω(Β(*ι)) + ί Ω(Β(ίι)) ί Ω(Β(ί2)) + ... (14.3)
240
Глава 14
Подставляя в форму Ω путь B(ti), мы превращаем ее в обычную
дифференциальную форму от одной переменной, которую и рассматриваем на отрезке
интегрирования.
Для прояснения ситуации рассмотри следующую простую конструкцию.
Пример 14.1. Пусть Y' = AY — дифференциальное уравнение с начальным
условием Y(0) = 1, рассматриваемое, скажем в пространстве матриц размера
η χ п. 1 Очевидно, его решение Y(t) является произведением "бесконечно
большого" числа элементов "бесконечно близких" к единице. Естественно назвать
это мультипликативным интегралом от А и обозначить через
χ
Y(x) = [(E + A(t)dt). (14.4)
о
Заметим, что для вычисления Y(x) молено воспользоваться формулой
X X t\
Υ [χ) = Е+ f A(ii)dii + / Α(ίι) / A(t2)dt2dt1 + · · · (14.5)
0 0 0
если ряд (14.5) сходится.
Замечание 14.6. Во всех "нормальных" случаях этот ряд сходится.
Заметим, что при интегрировании ряда каждый следующий член
оказывается равным интегралу от предыдущего, помноженного на А.
Каждый член итерационного интеграла (14.5) можно рассматривать как
интеграл по некоторому симплексу.
Формула (14.3) полностью аналогична формуле (14.5).
Теория мультипликативного интеграла хорошо изложена в [DF, Мант1,
МанМар].
Замечание 14.7. В нормальном случае {случае сходимости) очевидно, что
эта формула дает решение нашего дифференциального уравнения. Начальные
условия также выполнены.
Связность Книжника— Замолодчикова
Обозначим через T>^Z множество всех диаграмм, состоящих из η
направленных вверх бесконечных стрелок (на рис. 14.10 они показаны толстыми
линиями) и конечного числа ребер таких, что:
1. Каждый конец каждого ребра лежит на стрелке или является
трехвалентной вершиной (с двумя другими концами ребер);
2. Каждая внутренняя точка на стрелке является концом не более, чем
одного отрезка.
1Или в любой другой топологической алгебре: все, что нам нужно это линейность операций
над избранным полем, умножение и естественная топология (для того, чтобы рассматривать
пределы последовательностей).
14.3. Инвариантность интеграла Концевича
241
Отметим, что все вершины графов на рис. 14.10 являются трехвалентными;
точка валентности четыре представляет собой "дефект изображения" —
пересечение двух ребер графа, и не является вершиной.
Такие диаграммы рассматриваются с точностью до комбинаторной
эквивалентности.
А Л
А
Рис. 14.10. Элемент Λκζ
Пусть С — основное поле. Рассмотрим множество A^Z= span(V^z)/{STU—
соотношения}. STU-соотношением называется то же, что и в случае фейнманов-
ских диаграмм , где мы рассматриваем часть стрелки вместо части
ориентированной окружности. Заметим, что STU- соотношение является локальным.
Когда мы в конечном итоге замыкаем стрелки для получения фейнмановской
диаграммы мы получаем STU-соотношения, см. рис. 13.4, стр. 219.
При фиксированном η множество Λ^ζ обладает алгебраической
структурой: произведением двух диаграмм является диаграмма, полученная
расположением одной из них над другой; далее это умножение продолжается по
линейности.
Пример умножения при η = 3 в Λ^ζ показан на рис. 14.11.
А
А
Рис. 14.11. Умножение в Λκζ
При фиксированном гг, Алгебра Λ^ζ является градуированной: порядок
элемента равен половине общего количества вершин.
Для 1 < i,j < гг, обозначим через Ω^ G Λ^Ζ элемент, у которого только
одно ребро, и это ребро соединяет стрелки с номерами г и j.
Замечание 14.8. Легко видеть, что если {hj}f]{^^}
мутируют.
то Vtij и Vtki ком-
242
Глава 14
J
1
Рис. 14.12. Элемент Ω;
Пусть Хп — конфигурационное пространство неориентированных наборов
из η попарно различных точек в С1. Пусть изц означает следующую 1-форму
на Хп:
ωιά = d(]n(zi - Zj)) = —l——-.
Z% Zj
Определим формально связность Книжника-Замолодчикова Ωη с
коэффициентами в A*z как Ωη = J2i<:i<j<:n ^ij^ij на Хп.
Теорема 14.7. Эта связность плоская. Более точно, Ωη Λ Ωη = О, а также
dVtn = 0.
Доказательство. Последнее утверждение очевидно. Действительно, аыц =
= d2(ln(zi — Zj)); последнее выражение обращается в нуль по определению d.
Докажем первое утверждение. Рассмотрим элемент
Ωη Λ Ωη = 2_^ QijQkiUijLdki
i<j;k<l
(14.6)
и множество {i,j,k,l}. Если это множество состоит из двух или четырех
элементов, то соответствующий член суммы равен нулю (это случай
коммутативности). Следовательно, искомая сумма равна сумме по всем i,j,k,l, где
множество {г, j, к, 1} состоит из трех различных элементов. Рассмотрим, например,
множество {г, j, к, 1} = {1, 2, 3} и все соответствующие ему члены в сумме (14.6).
В этом случае мы имеем:
/ j QijQki^ijOuki = (Ω12Ω23 — Ω23Ωΐ2)<^ΐ2 A CJ23 + (цикл, перестановки).
{i,j,k,l} = {l,2,3}
Применяя STU-соотношения, мы видим, что искомая сумма равна
Ωΐ23(^ΐ2 Λ ω23 + ^23 Α ω3ι + ω3ι Λ ω12),
где Ω123 элемент, показанный на рис. 14.13.
Упражнение 14.1 (Тождество В.И.Арнольда.). Покажите, что ω\2 А
^23 + ^23 A cj3i + ^31 Α ω\2 = 0.
Замечание 14.9. Это тождество появилось в [Арн2]; где автор изучал ко-
гомологии группы крашеных кос.
14.3. Инвариантность интеграла Концевича
243
Рис. 14.13. Элемент Ω123
Таким образом, если некоторое множество {z,j,/с,/} состоит в точности из
трех различных членов, то оно не добавляет ничего в сумму. Мы рассмотрели
все возможные случаи. Причем всегда Ωη Λ Ωη = 0. D
Замечание 14.10. Связность Ωη можно слегка модифицировать для случая
алгебры А^п · Эта алгебра порождена диаграммами с 2п стрелками (первые
η из них ориентированы вверх, а последние η стрелок ориентированы вниз).
STU-соотношения для таких диаграмм зависят от направления хорды, к
которому соотношения применяются, см. рис. Ц.Ц·
Рис. 14.14. STU-соотношение для положительных и отрицательных стрелок
Пусть Ωηη = J2i<:i<j<:n SiSj^ijUij, где Si равно 1 при г < η и -1 при г > п.
Упражнение 14.2. Покажите, что связность Ωηη плоская.
Здесь нужно пояснить схожесть 5Т{7-соотношения элементов алгебры Л^
и STU-соотношения для алгебры диаграмм Фейнмана (или, что эквивалентно,
четырехчленного соотношения для алгебры хордовых диаграмм).
Мы собираемся ввести интеграл Концевича от танглов. Мы будем разрезать
морсовский узел горизонтальными плоскостями на кусочки, и рассматривать
те из них, которые не содержат максимумов и минимумов. На каждом таком
кусочке мы имеем некоторое количество (/с) восходящих линий столько лее
нисходящих линий. При рассмотрении интеграла Концевича Ζ (К) узла К мы
сечем весь узел, при этом некоторые плоскости попадают в рассматриваемые
кусочки. При выборе пары точек на каждой плоскости, мы получаем некоторую
диаграмму, которую можно рассматривать элемент из A^jf. Все такие
диаграммы из A^jf затем соединяются в одну хордовую диаграмму, соответствующую
всему узлу К, см.рис. 14.15.
244
Глава 14
Рис. 14.15. Замыкание диаграмм Л22 в хордовую диаграмму
Если один из элементов из А^ заменить на 5Т {/-эквивалентный ему
элемент, то и вся хордовая диаграмма заменится на эквивалентный ей элемент
алгебры хордовых (фейнмановских) диаграмм.
Четырехчленное соотношение для хордовых диаграмм (или, эквивалентно,
5Т{7-соотношение для диаграмм Фейнмана, которые здесь не появляются) нам
понадобится в дальнейшем.
Докажем теперь теорему об инвариантности. (Теорема 14.3).
Доказательство. Сначала докажем, что предварительный интеграл Концеви-
ча Ζ [К) инвариантен относительно преобразований, сохраняющих
критические точки.
Дело в том, что интеграл Концевича по всему узлу может быть
разложен в произведение интегралов по частям этого узла; каждая из этих частей
представляет собой некоторый элемент алгебры Книжника-Замолодчикова со
стрелками вверх и вниз. Соединенные вместе, они образуют обычную
хордовую диаграмму. Под произведением элементов в некоторой Ακζ понимают
элемент Δ.
Пусть cmin
стах- Определим Z(K,\a,,b\) так же, как это
было сделано в (14.1), но взяв в качестве области интегрирования {а < t\ <
• · · < tn < &}, и заменив хордовые диаграммы элементами алгебры Книжника-
Замолодчикова.
Хотя Z(K,[a,b]) не принадлежит Дс, соответствующий ряд (со
значениями в Λκζ) сходится по той лее причине, что и Ζ. Так как интервал (а, Ъ) не
имеет критических точек, то пересечение узла с границей множества С χ (α, Ъ)
является множеством ориентированных кривых без горизонтальных
касательных. Допустим, что количество таких кривых равно 2гг. Очевидно, что η из них
возрастают и другие η убывают. Фиксируем нижние точки а\,..., <22п и
соответствующие верхние точки &ι,..., &2П, гДе первые η координат соответствуют
возрастающим кривым, а остальные убывающим кривым. Сходимость
интеграла может быть доказана так как и в замкнутом случае (для узла). Однако,
придется ввести аналог одночленного соотношения, положив все диаграммы с
14.3. Инвариантность интеграла Концевича
245
изолированной хордой (один конец хорды на возрастающей, а другой конец на
убывающей кривой) равными нулю.
Теперь интеграл Z(K[a,b]) может быть представлен как голономия
связности Ωηη вдоль пути от (αϊ,..., <22η) κ (&ι,. - -, Ъ2п) с помощью итерационной
формулы (14.3).
Действительно, га-й член итерационной формулы Ωηη соответствует га-у
члену интеграла Концевича (14.1) поскольку в обоих случаях мы интегрируем
форму
ρ={(ζ„ζ',)} i=i j j
где (—1)^ соответствует знаку произведения SjSj.
Напомним, что STU-соотношения для диаграмм Фейнмана это "то лее
самое", что 4Т-соотношения для хордовых диаграмм. Здесь как раз то место, где
мы используем 4Т-соотношение (в виде 5Т£/-соотношения).
Поскольку кривизна связности Ωηη равна нулю, то интеграл (14.7)
инвариантен относительно гомотопий пути интегрирования с фиксированными
концами, т. е. относительно горизонтальных изотопии части узла , лежащей внутри
интервала (а, Ь).
Нетрудно показать, что для произвольных точек а < b < с (возможно,
критических), мы имеем Z(K, [а, с]) = Z(K, [a,b]) · Z(K, [b,c]). Отсюда делаем
вывод о том, что интеграл Ζ (К), являющийся произведением Z(K, [q,q+i]),
где q,q+i все пары точек "регулирующих"критические точки, инвариантен
относительно горизонтальных деформаций в интервалах, не содержащих
критических точек.
Рассмотрим теперь случай, когда критические точки не остаются
неподвижными при изотопии узлов.
1. Критические точки двигаются, но взаиморасположение критических
значений не меняется, см. рис. 14.16.
Рис. 14.16. Перемещение максимума
2. Два критических значения меняются местами, см. рис. 14.17.
Как показано на рис. 14.16 и 14.17, можно сначала применить
преобразование, которое не меняет значения Ζ (К) и образует "иглу", а затем убрать эту
иглу. Покажем, что удаление иглы изменяет элемент градуировки т в
интеграле Концевича на некоторое малое ε, зависящее от толщины иглы.
Действительно, пусть К — узел и пусть К' — узел, полученный из узла К
добавлением вертикальной иглы около некоторого максимума (минимума).
246
Глава 14
Рис. 14.17. Изменение расположения критических значений
Очевидно, что разница Ζ (К) — Ζ {К') содержит лишь члены, содержащие
диаграммы, хотя бы один конец которых лежит на игле. Пусть ширина иглы
равна ε. Покажем, что Zm(K) — Zm{K') = О (ε).
Действительно, рассмотрим все хорды, концы которых лежат на игле. Если
самая верхняя из них имеет оба конца на игле, то соответствующая диаграмма
равна нулю по модулю одночленного соотношения. Если нет ни одной хорды,
оба конца которых лежат на игле, ситуация также простая: все коэффициенты
при хордовых диаграммах, соответствующие рис. 14.18, имеют малость
порядка ε: при интегрировании диаграмм, соответствующих левой и правой частям
рисунка, мы имеем значения |, отличающиеся на единицу, таким образом, мы
получаем сокращение с точностью до малых порядка ε, см. рис. 14.18.
Рис. 14.18. Сокращение двух членов
Остается рассмотреть случай, когда самая верхняя хорда (^,^), имеющая
один конец на игле, имеет другой конец не на игле, при этом под ней лежат
к хорд, оба конца каждой из которых принадлежат игле. Предположим, что
самая нижняя из них имеет координаты (zj1 , z'j ), а самая верхняя — (zjk, ζ', ),
см. рис. 14.19.
Можно считать, что (ζϊ,ζ^) — единственная хорда, один конец которой
лежит на этой игле, а другой — нет, Если таких хорд много, то соответствующий
коэффициент получается умножением изначального на некоторый
коэффициент, отделенный от нуля и от бесконечности.
Пусть δ а = \zja — Zj' |. Тогда разница Ζ {К') — Ζ {К) ограничена по модулю
14.3. Инвариантность интеграла Концевича
247
Зк
Л
Рис. 14.19. Расположение концов хорд на игле
некоторой константой, умноженной на
ε 5л бк-
ГИ
02
d6k
$к
dzj — dz[
(14.8)
Как и в формуле (14.1), интегрирование здесь ведется по переменным t^ от
которых ζι и z\ являются функциями.
Интеграл (14.8) имеет малость порядка е. Действительно, последний
интеграл J Зк
dzl — dz[
имеет малость порядка 6k — такую же, как область
интегрирования, так как подынтегральное выражение ограничено сверху и снизу.
Следовательно, член Sk сокращается в предпоследнем интеграле, поэтому
предпоследний интеграл имеет малость порядка Sk-i- Далее, малость порядка Sk-i
сокращается, и следующий интеграл имеет порядок 6^-2- В итоге мы получаем,
что интеграл (14.8) имеет малость порядка е.
Произвольность выбора ε влечет требуемую инвариантность. D
Таким образом показано, что /(·) является инвариантом узла.
Докажем теперь теорему 14.6 о том, что для каждой системы весов W
функция W(/(·)) задает инвариант Васильева с системой весов W.
Доказательство. Без ограничения общности можно считать, что
рассматриваемые узлы являются морсовскими и, кроме того, их проекции на некоторую
вертикальную плоскость (скажем, О χ ζ) являются плоскими диаграммами
узлов общего положения. Пусть W — система весов порядка га. Как и для любого
инварианта узлов, для интеграла Концевича можно определить (по Васильеву)
все его производные на сингулярных узлах соответствующих порядков.
Для доказательства теоремы нам нужно показать, что если D является
хордовой диаграммой порядка га, a Kjj — сингулярный узел, соответствующий
морсовскому погружению окружности в Gz x Rt (сингулярный узел
соответствует диаграмме D), то имеет место
Вт\Ко) = D + (члены порядка ^ га),
где D означает класс эквивалентности хордовой диаграммы D, a I^m\K]j)
определен как альтернированная сумма значений / на 2т узлах, полученных
разрешением узла Кв·
248
Глава 14
Пусть два морсовских узла Κι и Къ в Cz x Rt совпадают везде, кроме
малого участка, на котором ветви узла Κι образуют отрицательный перекресток
\У\ (при проекции на рассматриваемую вертикальную плоскость), а ветви
узла i^2 образуют положительный перекресток /\- Тогда значения Ζ(Κ<ι) и
Ζ (Κι) имеют различные коэффициенты только на тех хордовых диаграммах,
у которых концевые точки лежат на этих ветвях.
Согласно соотношению Васильева, значение га-й производной любого
инварианта на сингулярном узле Kjj представляет собой альтернированную сумму
значений этого инварианта на 2т узлах, отличающихся друг от друга в малых
окрестностях га точек (вершин соответствующего сингулярного узла).
Заметим, что знак этой альтернированной суммы регулируется сомножителем (—1)^
в (14.1).
Рассуждая как и прежде, мы видим, что Ζ (К в) имеет ненулевые
коэффициенты только при тех хордовых диаграммах, которые получаются спариванием
точек в окрестности каждой сингулярной вершины. Таким образом, хордовые
диаграммы, коэффициенты при которых ненулевые, должны иметь по крайней
мере га хорд.
Из хордовых диаграмм порядка га этот коэффициент не равен нулю только
при диаграмме К р.
Вычислим этот коэффициент.
Для каждого из га сомножителей интегрирование разницы дает сомножи-
dzl — dz[
тель ——Н1.
Эта разница равна интегралу от — вдоль пути на комплексной плоскости,
обходящего один раз вокруг нуля. По теореме Коши этот интеграл равен 2πί.
Так как количество таких обходов равно га (по одному в каждой точке), мы
получаем коэффициент (27гг)т, который сокращается с соответствующим
знаменателем в формуле (14.1). Это означает, что
Ζ (Ко) = D + (члены порядка ^ га).
Принимая во внимание 1(К) = ^ £_1; мы получаем
I(Kd) = D + (члены порядка ^ га).
Следовательно, W(I(Kd)) = W(D), таким образом, инвариант Васильева
W(/(·)) порядка га имеет W в качестве символа, что завершает доказательство.
D
Вычисление интеграла Концевича, является, однако, задачей технически
сложной. Например, в самом начале было проблемой вычисление
(предварительного) интеграла Концевича от тривиального узла ос. Вид этого
интеграла был предсказан Бар-Натаном, Розанским, Гаруфалидисом и Терстоном в
[BGRT] и окончательно установлен в [BLT].
Соответствующая формула (выписанная в терминах диаграмм Фейнмана)
выглядит так:
сю /со \ 1 / со \
/((Χ)) = βχρ Σ Ь2п^2п = 1 + Ι Σ ^2η^2η Ι + ο ( Σ ^2η^2η Ι + · · · ·
η=0 \η=0 / \η=0 /
14.3. Инвариантность интеграла Концевича
249
Здесь &2η — обобщенные числа Бернулли, т. е. коэффициенты следующего ряда
Тейлора:
5>2пХ2П = -1п
1. W2
-ж/2
71 = 0
ж/2
a W2n — так называемые колеса, т. е. фейнмановские диаграммы, описанные
ниже.
Каждое колесо W2n является умноженной на /2 ч, суммой (2п!) фейнманов-
ских диаграмм. Каждая такая диаграмма состоит из одной внешней
окружности (выделенной, как ориентированный цикл), одной внутренней окружности
(рассматриваемой как замкнутое циклическим образом множество внутренних
ребер) и 2п хорд, соединяющих фиксированные 2п точек на первой
окружности с фиксированными 2п точками на второй. Эти точки могут быть соединены
в любом порядке, в соответствии с любой перестановкой из S2n- Так что мы
рассматриваем (2п)! слагаемых и берем от них среднее арифметическое.
Например, если рассмотреть w^, то получим те восемь слагаемых,
представляющих диаграмму Di, показанную в левой части рис. 14.20 и другие
шестнадцать слагаемых, представляющих диаграмму D2, см. правую часть рис. 14.20.
Рис. 14.20. Элементы Ό\ и D2
В терминах хордовых диаграмм W4 может быть представлен следующим
образом:
W4
Аналогично (на самом деле еще более просто) можно найти выражение для w2
И Wn.
Первые члены окончательного результата имеют вид:
1
1
48 4608 2
1
5760
W4 +
/(ос) = 1
или, в терминах ходовых диаграмм
/(ос) = 1 ^ ' - ' ' 1
Кроме того, Ли и Мураками [LM] построили обобщение интеграла
Концевича для случая так называемых танглов — одномерных многообразий в
трехмерном пространстве, лежащих между двумя горизонтальными плоскостями и
250
Глава 14
имеющими с этими плоскостями лишь конечное число общих точек. Тангл
является обобщением одновременно узлов и кос, а вычисление интеграла Концевича
для случая кос много легче, чем в общем случае. В действительности, танглы
появились косвенным образом при вычислении авторами Ζ [α, b] на некотором
интервале [а, Ь]. Используя собственную технику, они вычислили Z(oo). Позлее
С.Д.Тюрина вычислила такие интегралы для различных узлов, см.[Тю1, Тю2].
14.4. Модуль Васильева
Неизвестно, различают ли инварианты Васильева изотопические классы
узлов и зацеплений. Предположение о том, что инварианты конечного порядка
различают неизотопные узлы сделано Васильевым и известно, как гипотеза
Васильева.
Введем в рассмотрение модуль Васильева, в котором два узла считаются
различными, если их различают инварианты Васильева порядка не выше, чем
некоторый фиксированный порядок. При этом каждый узел может быть
разложен в конечную сумму образующих модуля.
Дадим теперь точные определение.
Определение 14.7. Модулем Васильева порядка η называется модуль над Ζ
(или Q), порожденный классами изотопии ориентированных узлов и
сингулярных узлов по модулю следующих соотношений:
1. О = 0? гДе О тривиальный узел;
2. Соотношения Васильева;
3. Кт = 0 для т > гг, где Кт произвольный сингулярный узел порядка га.
Справедлива следующая теорема:
Теорема 14.8 (Теорема о разложении). В модуле Васильева порядка η
каждый узел К представим в следующем виде:
r-\-s
K = ^2vi(K)Ki,
г=1
где г размерность модуля инвариантов Васильева, имеющих порядок
меньший или равный (п—1), as — размерность весовой системы порядка п; все Vi
являются инвариантами Васильева порядка, меньшего или равного η, α Κι —
некоторые фиксированные базисные узлы, не зависящие от узла К.
Эта теорема вытекает непосредственно из определений.
Простейшее разложение в модуле Васильева [La] порядка два таково:
K = V2{K)
где V<2 является вторым коэффициентом полинома Конвея.
Подробности см.,например, в [CDBook, Тю1, Тю2].
&
14.5. Теорема Гусарова
251
14.5. Теорема Гусарова
14.5.1. Диаграммы Гаусса
Ориентированные плоские диаграммы узлов характеризуются их
диаграммами Гаусса. Диаграмма Гаусса состоит из окружности (образ замкнутой
кривой, представляющей собой узел) и набора хорд, соединяющих точки узла с
одинаковыми проекциями на плоскость диаграммы узла.
Для отражения информации о проходах и переходах хорды
ориентированы от верхней ветви к нижней ветви. Далее, каждая хорда снабжена знаком
соответствующего перекрестка. Пример показан на рис. 14.21.
Рис. 14.21. Диаграмма восьмерки и соответствующая ей гауссова диаграмма
Аналогичным образом, длинным узлам соответствуют диаграммы Гаусса,
у которых вместо окружности мы имеем ориентированную прямую линию, а
вместо хорд — дуги, соединяющие точки, лежащие на этой прямой линии.
Каждая дуга ориентирована от прообраза прохода к прообразу перехода и снабжена
знаком соответствующего перекрестка.
В дальнейшем в настоящей главе мы будем иметь дело только с длинными
узлами и соответствующими гауссовыми диаграммами.
Обозначим множество гауссовых диаграмм через Т>.
Одним из самых важных достижений в комбинаторной теории инвариантов
Васильева является теорема Гусарова, см. [GPV].
Обозначим множество всех гауссовых диаграмм через Т>.
Пусть D - гауссова диаграмма. Определим отображение / : V —>· Q[D] как
1(D) = ^2D\ где сумма берется по множеству всех поддиаграммам D'
диаграммы D. Далее это отображение продолжается на множество Q[D] по линейности.
Упражнение 14.3. Докажите, что I : Q[D] —> Q[D] является
изоморфизмом, обратное отображение к которому 1~х : Q[D] —> Qp}]) задается
следующей формулой:
Σ
D'CD
где D — гауссова диаграмма, сумма берется по всем поддиаграммам D'
диаграммы D, и \D — D'\ означает количество хорд, принадлежащих
диаграмме D, но не диаграмме D'
252
Глава 14
Введем в Q[D] скалярное произведение (·,·). Для любой пары гауссовых
диаграмм Όχ^Ό^ положим [Όχ^Ό^) равным единице если Ό\ = D^, и равным
нулю в противном случае; затем распространим его билинейно на все
множество Q[£>].
Это позволяет нам определить спаривание (·, ·} : Q[D] x Q[D] —>· Q
следующим образом. Для каждой пары A,D Ε Q[D] полагаем:
(A,D) = (A,I(D)) = (A, £ D').
D'dD
Теорема 14.9 (Теорема Гусарова). Пусть ν — инвариант классических
(длинных) узлов порядка η со значениями в Q. Тогда существует функция
π : Q[D] —> Q такая, что ν = π ο / и такая, что π равна нулю на каждой
гауссовой диаграмме с более, чем η стрелками.
Следствие 14.1. Всякий целочисленный инвариант конечного типа степени
η может быть представлен как (А, ·), где А — линейная комбинация
гауссовых диаграмм на прямой с η хордами.
Отметим, что важную роль в теореме Гусарова играет тот факт, что
классификация классических длинных узлов совпадает с классификацией
классических компактных узлов.
Главной идеей теоремы Гусарова является следующая. Обычный метод
вычисления инварианта Васильева ν таков, см. [Vas]. Можно рассмотреть базис
множества сингулярных узлов, на который натягивается модуль Васильева.
Инвариант ν (и его производные ) могут быть определены по таблице
актуальности, т. е. по значениям на этом множестве. Данную диаграмму узла можно
превратить в диаграмму тривиального узла, последовательно заменяя тип
перекрестков. При каждом таком изменении значение инварианта скачкообразно
изменяется. Согласно соотношению Васильева величина такого скачка равна
значению ν на соответствующем сингулярном узле.
При этом каждый сингулярный узел порядка один превращается в
сингулярный узел порядка один из таблицы актуальности с помощью изотопии и
последовательности изменений типов перекрестков. Скачок значений ν
соответствует узлам с двумя двойными точками. Они снова деформируются в
узлы из актуальной таблицы. Процесс продолжается до тех пор пока количество
двойных точек не превзойдет степени v.
Часть IV
Атомы и d-диаграммы
Глава 15
Атомы, высотные атомы
и узлы
В настоящей главе мы обсудим альтернативный способ кодирования узлов
и зацеплений (отличный от плоских диаграмм и замыканий кос). Речь пойдет
о том, что любой узел или зацепление могут быть закодированы с помощью
так называемых атомов и d-диаграмм.
Атомы являются комбинаторным объектом, введенным несколько лет назад
(см. [F]) с целью классифицировать гамильтоновы системы дифференциальных
уравнений малой сложности. Как оказалось, атомы играют важную роль в
разных задачах теории узлов, виртуальных узлов и других разделов маломерной
топологии, d-Диаграммы представляют собой хордовые диаграммы
специального вида; они тесно связаны с атомами.
Используя этот подход, мы собираемся доказать несколько теорем об узлах и
кривых: теорему Кауфмана-Мурасуги об альтернированных зацеплениях,
критерий вложимости некоторых графов и др. Мы опишем также способ
кодирования узлов и зацеплений словами в конечном алфавите посредством d-диаграмм
("скобочное исчисление"). Обозрению скобочного исчисления посвящена работа
[МаЗ]. Как оказывается, подход, рассматриваемый в настоящей главе, приводит
к построению новых бесконечных серий инвариантов Васильева.
15.1. Атомы и высотные атомы
Начнем с введения понятий и определений.
Определение 15.1. Атомом называется пара: компактное связное 2-много-
образие М2 без края и граф Г с М2 валентности четыре в каждой вершине
такой, что М2\Т является несвязным объединением клеток, допускающих
раскраску в белые и черные цвета так, что клетки, соседствующие по ребру
графа Г, имеют разные цвета. Граф Г называется остовом атома. Родом
(соответственно, эйлеровой характеристикой) атома называется род (эйлерова
характеристика) его первой компоненты.
Сложностью атома называется количество вершин в его остове.
Атомы рассматриваются с точностью до естественного изоморфизма: два
атома называются изоморфными, если существует взаимно однозначное
соответствие их первых компонент, переводящее остов в остов, черные клетки -
в черные клетки, а белые — в белые.
256
Глава 15
Атомы могут порождаться функциями Морса на компактных 2-поверхно-
стях, у которых все критические точки, кроме максимумов и минимумов, лежат
на одном уровне: в этом случае критический уровень является остовом атома, а
критические точки — вершинами. Докритический уровень состоит из
нескольких отдельно стоящих окружностей; из отдельно стоящих окружностей состоит
и послекритический уровень.
Определение 15.2. Атом называется высотным, если он изоморфен атому,
полученному при вложении некоторого 2-многообразия в R3 при условии, что
в качестве функции Морса выбрана аппликата (третья координата) точки
многообразия.
Каждый атом (более точно, его класс эквивалентности) может быть
полностью восстановлен по следующим комбинаторным данным:
1. Остов (четырехвалентный граф);
2. Α-структура (делящая четыре полуребра, исходящие из каждой вершины,
на две пары, называемые противоположными; отношение
противоположности определяется в соответствии с расположением ребер на
поверхности) и
3. В- структура (в каждой вершине выделены две пары соседних полу ребер
(или двух углов), которые образуют границы черных клеток).
В [Ман1] установлен следующий критерий.
Теорема 15.1. Атом V является высотным тогда и только тогда, когда
его остов Г вложим в R2 с сохранением Α-структуры (т. е. его собственная
Α-структура совпадает со структурой противоположных ребер,
индуцированной вложением остова в плоскость).
Оказывается, что высотные атомы тесно связаны с узлами в отличие от
невысотных (которые связаны с виртуальными узлами, см. главы 19 и 20). Имея
высотный атом У, можно построить диаграмму узла следующим образом.
Рассмотрим остов Г атома V и вложим Г в плоскость с сохранением А-структуры
атома V. Так как противоположные ребра при такой проекции переходят в
противоположные, то соседние ребра переходят в соседние. Следовательно, мы
можем описать 5-структуру атома, разбив четыре ребра на две пары соседних
(на плоскости) ребер, в которые перешли ребра, образующие границы черных
клеток на атоме.
Таким образом, мы имеем четырехвалентный граф на плоскости,
снабженный В-структурой. Эта £>-структура позволяет построить зацепление, как
показано на рис. 15.1.
Замечание 15.1. На рис. 15.1 углы послекритического уровня (в левой части)
изображены жирными линиями.
В каждой вершине А мы определяем тип перекрестка таким образом, чтобы
при повороте по часовой стрелке внутри угла послекритического уровня мы
двигались от ребра прохода к ребру перехода.
Таким образом, имея вложение остова атома, согласованное с А-структурой,
мы можем построить диаграмму узла (зацепления).
15.2. Теорема об атомах и узлах
257
Ψ
Рис. 15.1. Часть диаграммы узла (зацепления), соотвествующая окрестности
вершины
15.2. Теорема об атомах и узлах
Оказывается, что все узлы могут быть закодированы (неоднозначно)
высотными атомами.
Имеет место следующая теорема.
Теорема 15.2 (Теорема об атомах и узлах, [Ман1]). Пусть V — атом.
Тогда плоские диаграммы зацеплений, соответствующие разным вложениям
остова атома V (с сохранением А-структуры), задают зацепления одного и
того же изотопического типа.
Таким образом, молено сказать, что атом порождает узел (зацепление).
Доказательство теоремы об атомах и узлах следует из известной теоремы:
Теорема 15.3. Если два планарных графа изоморфны, то любые два их
вложения в R2 являются изотопными в R3.
Эта теорема позволяет восстановить изотопию узлов в объемлющем
пространстве по вложению остова атома. Более подробно см в [Ман1].
15.3. Задание узлов d-диаграммами
Начнем с важной теоремы из [МанЗ].
Теорема 15.4. Для каждого изотопического класса зацеплений L
существует высотный атом V, кодирующий зацепление из этого класса и имеющий
ровно одну послекритическую окружность.
Доказательство. Рассмотрим произвольную диаграмму зацепления L и
соответствующий ей высотный атом V\. Предположим, что атом V\ имеет к после-
критических окружностей. Если к = 1, то доказывать нечего.
Если к > 1, то существует вершина А атома V\, в малой окрестности которой
проходят две различные послекритические окружности.
Применим к этой диаграмме движение Ω2, как показано на рис. 15.2.
Легко видеть, что после такого преобразования две окружности,
показанные на рис. 15.2, переходят в одну окружность: послекритические окружности
258
Глава 15
к
Перестройка послекритического уровня
Рис. 15.2. Диаграмма зацепления (сверху)
и послекритические окружности (снизу)
изображены на рис. 15.2 тонкими линиями, а их поведение вне области
перестройки — пунктирной линией. Таким образом, мы уменьшаем число послекри-
тических окружностей на единицу, не изменяя при этом изотопического класса
зацепления. Повторяя эту операцию многократно, мы получим диаграмму
ровно с одной послекритической окружностью. D
Напомним, что d-диаграмма — это хордовая диаграмма, хорды которой
могут быть разбиты на два семейства так, что хорды из одного семейства не
пересекаются между собой.
Обход можно представить себе как отображение окружности в остов
атома, лежащий на плоскости. Малым шевелением (разведением) можно добиться
того, чтобы окружность была вложена в плоскость, при этом в окрестности
каждой вершины (через которую обход проходил дважды) мы поставим
маленькую хорду, соединяющую две разведенные ветви окружности.
Таким образом, мы получим окружность с набором хорд, соединяющих
некоторые пары точек на ней. Согласно теореме Жордана, окружность делит
плоскость на внешнюю и внутреннюю области. Таким образом, хорды
делятся на два семейства: внешние и внутренние. Полученная хордовая диаграмма
является d-диаграммой.
Следовательно, d-диаграммы кодируют все изотопические классы узлов и
зацеплений.
Приведем несколько примеров. Рассмотрим простейшую диаграмму левого
трилистника. Соответствующий высотный атом имеет две послекритические
окружности. Применяя один раз движение Ω2, мы получаем диаграмму того
15.3. Задание узлов ^-диаграммами
259
же трилистника с одной послекритической окру леностью. Соответствующая d-
диаграмма показана на рис. 15.3.
Рис. 15.3. d-Диаграмма левого трилистника
Упражнение 15.1. Покажите, что d-диаграммы, изображенные на
рисунках 15.4-а и 15.4-6 задают правый трилистник и восьмерку.
Рис. 15.4. d-Диаграммы правого трилистника и восьмерки
Из рассуждений, приведенных выше, мы видим, что если зацепление L
имеет плоскую диаграмму с η перекрестками такую, что соответствующий атом
V(L) имеет к послекритических окружностей, то зацепление L может быть
задано d-диаграммой с η -\- 2(к — 1) хордами.
Легко видеть, что общее число докритических и послекритических
окружностей атома V(L) равно x(V) — η + 2η, что не превосходит η + 2, где x(V) —
эйлерова характеристика атома V(L). Так как V имеет по крайней мере одну
докритическую окружность, то к не превосходит (п + 1). Таким образом, мы
получаем верхнюю оценку для минимального числа хорд d-диаграммы,
соответствующей данному узлу: она не превосходит Згг.
Упражнение 15.2. Покажите, что хордовая диаграмма является d-dua-
граммой тогда и только тогда, когда она не содержит поддиаграмм вида,
показанного на рис. 15.5 (2гг + 1 -угольников).
Мы построим отображение из множества всех d-диаграмм в множество всех
изотопических классов зацеплений. Это отображение не является инъективным
(так, например, добавление отдельно стоящей хорды к d-диаграмме не меняет
изотопический класс соответствующего зацепления). Кроме того, d-диаграммы
кодируют не все плоские диаграммы зацеплений, а лишь те, которые
соответствуют атомам с одной послекритической окружностью. Для прояснения
ситуации обобщим понятие d-диаграммы следующим образом.
260
Глава 15
Рис. 15.5. Хордовые диаграммы, не являющиеся d-диаграммами
Определение 15.3. Меченой d-диаграммой называется d-диаграмма, каждой
хорде которой сопоставлена метка "+" или "—". В случае отсутствия меток на
хордах d-диаграммы будем считать все метки положительными.
По имеющейся d-диаграмме С можно построить диаграмму зацепления
следующим образом. Разделим хорды d-диаграммы С на два семейства
непересекающихся между собой хорд. Вложим С в плоскость: окружность вложим
стандартным образом (как евклидову окружность радиуса единица), хорды первого
семейства расположим внутри окружности; хорды второго семейства поместим
вне окружности. Удалим хорды вместе с малыми дугами в окрестностях их
концов и поставим вместо них классические перекрестки так, как показано на
рис. 15.6.
Рис. 15.6. Перекрестки, соответствующие хордам
Легко видеть, что это определение совпадает со старым определением в
случае немеченых d-диаграмм.
Упражнение 15.3. Докажите, что построенный изотопический класс не
зависит от способа разбиения хорд диаграммы на два семейства
непересекающихся между собой хорд.
Теорема 15.5 ([МанО]). Каждая плоская диаграмма зацепления может быть
получена из некоторой меченой d-диаграммы вышеуказанным способом.
15.3. Задание узлов ^-диаграммами
261
Доказательство. Пусть L — плоская диаграмма некоторого зацепления.
Выберем обход этой диаграммы следующим образом. Выберем вершину V
диаграммы и ребро е, исходящее из этой вершины. Затем будем двигаться вдоль
е. Когда встретится вершина, поворачиваем направо или налево (но не в
направлении, продолжающем ребро е). Затем, дойдя до следующей вершины, —
опять поворачиваем направо или налево, и так далее.
Упражнение 15.4. Покажите, что можно так выбрать повороты налево
или направо, чтобы вернуться в исходную точку V, побывав в каждой
вершине ровно два раза.
Рис. 15.7. Обход диаграммы трилистника
Такой обход задает хордовую диаграмму. Действительно, он
представляет собой отображение окружности с указанием правила отождествления точек
на ней: мы отождествляем прообразы одной вершины. Обозначим полученную
хордовую диаграмму через С. Очевидно, что С является d-диаграммой, так как
множества ее хорд естественным образом разбиваются на внутренние и
внешние по отношению к окружности. Каждой хорде С соответствует перекресток
зацепления L.
Если в окрестности некоторого перекрестка окружность обхода локально
выглядит так, как показано в левой части рис. 15.6, мы устанавливаем
положительную метку; в противном случае мы устанавливаем отрицательную метку.
Полученная меченая d-диаграмма задает диаграмму зацепления L. D
Определение 15.4. Хорда а называется переполюсованной, если к ней
добавлена "маленькая" хорда а, перескающая только ее.
Переполюсованной дважды называется хорда, переполюсованная с двух
концов.
Упражнение 15.5. Если мы заменим отрицательную хорду на
положительную дважды переполюсованную (см. рис. 15.8), то мы получим d-dua-
грамму, представляющую тот же изотопический тип.
Укажем еще один способ построения d-диаграммы без меток, задающей
данное зацепление. А именно, рассмотрим зацепление L и произвольную его
плоскую диаграмму Р. Рассмотрим произвольную меченую d-диаграмму Dm,
соответствующую плоской диаграмме Р. Заменяя каждую отрицательную
хорду из Dm дважды переполюсованной положительной хордой, мы получим d-
диаграмму, представляющую зацепление, изотопное зацеплению L.
262
Глава 15
+
+
+
Рис. 15.8. Отрицательная и дважды переполюсованная положительная хорды
15.4. d-Диаграммы и хордовые диаграммы.
Критерий вложимости графа
в терминах хордовых диаграмм
Метод построения зацеплений по d-диаграммам может быть рассмотрен для
более простых объектов, а именно, для гладких замкнутых кривых —
пересекающихся окружностей на плоскости R2 в общем положении. Мы строим по
d-диаграмме кривую так лее, как в случае построения узла, но не обращаем
внимания на типы перекрестков (т. е. рассматриваем тень узла).
Помимо кодирования узлов (и плоских кривых) d-диаграммами можно
также описывать их гауссовыми диаграммами; гауссова диаграмма также
является хордовой диаграммой, при этом в отличие от описанного выше
способа кодирования (d-диаграммами) гауссовы диаграммы задаются посредством
уникурсального обхода диаграммы узла, т. е. каждый раз переходим с ребра на
противоположное.
В терминах d-диаграмм можно легко решить проблему реализуемости
гауссовых диаграмм. Одно такое решение приведено в работе [Бур].
Основная идея этого метода состоит в следующем. Мы рассматриваем
диаграмму кривой (взаимное расположение ее перекрестков) с двух точек зрения:
как гауссову диаграмму (когда мы проходим через перекрестки трансверсаль-
но) и как d-диаграмму (когда при обходе мы поворачиваем в каждом
перекрестке направо или налево). Во втором случае реализуемыми являются как
раз d-диаграммы (им соответствует окружность на плоскости и два семейства
хорд — внутренние и внешние). Таким образом, нам нужно уметь переводить
кодировку кривой посредством гауссовых диаграмм на язык d-диаграмм.
Решение этой задачи легко обобщается на случай узлов (т.е когда
гауссовы диаграммы имеют дополнительную информацию о перекрестках). Решим
сначала задачу для кривых. В этом случае каждая d-диаграмма задает одну
или несколько погруженных окружностей. Вместо гауссовых диаграмм будем
иметь дело лишь с хордовыми диаграммами.
Определение 15.5. Хордовые диаграммы, соответствующие погружениям
общего положения, называются реализуемыми.
Пусть G — хордовая диаграмма погруженной кривой общего положения.
Построим обход этой диаграммы (фактически — обход кривой) согласно "пра-
15.4. Критерий реализуемости
263
вилам d-диаграмм." А именно, выберем дугу а диаграммы G и начнем
движение вдоль по этой дуге в произвольном направлении. Когда мы попадем в
некоторую вершину V диаграммы G, повернем направо или налево (в
терминах плоских диаграмм). На языке гауссовых диаграмм это означает следующее.
Предположим, что некоторая вершина V инцидентна хорде X диаграммы G,
а две дуги, инцидентные вершине V, — это а и 6; с другого конца хорды X
мы имеем две дуги cud. Таким образом, нужно выбрать одну из двух дуг —
с или d — для продолжения нашего обхода. Продолжая обход, мы придем в
некоторую вершину, после которой мы должны повторить эту операцию
(перейти на противоположный конец хорды и продолжить движение по одной из
дуг). Очевидно, что обход может быть выбран таким образом, чтобы все хорды
и все дуги диаграммы G были пройдены по одному разу, и чтобы в конце мы
вернулись в ту точку, с которой стартовали.
Таким образом мы получаем хордовую диаграмму (которая в реализуемом
случае должна быть d-диаграммой). А именно, мы просто задаем другую
перенумерацию ребер плоской диаграммы (и соответствующую нумерацию дуг
хордовой диаграммы) согласно нашему обходу. Если четверка дуг p,q,r,s
соответствовала некоторой хорде изначальной диаграммы (например, р, q
инцидентны одному концу этой хорды, а г, s инцидентны другому ее концу), то
та же четверка будет соответствовать паре точек, соединяемых хордой в новой
хордовой диаграмме (скажем, р, г и q, s). Тем самым мы построили
неоднозначную функцию на хордовых диаграммах со значениями в хордовых диаграммах.
Обозначим эту функцию через А.
Таким образом, мы построили (многозначную) функцию, позволяющую
проинтерпретировать хордовую диаграмму на "языке d-диаграмм." Из этого мы
получаем следующее утверждение.
Утверждение 15.1. Если G — реализуемая хордовая диаграмма, то любая
диаграмма A(G) является d-диаграммой.
Приведенное выше условие, однако, не является достаточным. А именно,
для диаграммы СдО оно выполняется, хотя диаграмма не является
реализуемой.
А именно, одно из значений А(Гдп) равно диаграмме LXJ· Она является d-
диаграммой, но не является реализуемой гауссовой диаграммой по очевидной
причине.
Определение 15.6. Хорда d хордовой диаграммы D называется четной, если
число концов хорд, лежащих с одной стороны (любой из двух) между ее
концами, четно, и нечетной в противном случае. Хордовая диаграмма называется
четной, если каждая ее хорда является четной.
Упражнение 15.6. Докажите, что любая реализуемая хордовая диаграмма
является четной.
Замечание 15.2. Условие четности в данном случае совпадает с условием
источник-сток, см. главу 20.
Оказывается, условие четности является единственным дополнительным
условием. А именно, имеет место следующая теорема.
264
Глава 15
Теорема 15.6. Пусть G — хордовая диаграмма. Пусть D — произвольная
диаграмма вида A(G). Тогда G является реализуемой в том и только том
случае, если G является четной, a D является d-диаграммой.
Перед тем как доказывать эту теорему, сформулируем следствие из нее.
Следствие 15.1. Если G — четная хордовая диаграмма, то либо все
диаграммы вида A(G) являются d-диаграммами, либо ни одна из них не является
таковой.
Для доказательства теоремы 15.6 нужно построить функцию, обратную к
многозначной функции А (т. е. указать алгоритм, как восстанавливать
хордовую диаграмму кривой по d-диаграмме).
Пусть D — d-диаграмма. Она порождает некоторую замкнутую кривую К,
погруженную в R2. Для построения хордовой диаграммы, соответствующей К,
нам нужно обозначить уникурсальный обход для D (как и в случае построения
функции А). Фиксируем некоторую вершину V\ диаграммы Ό и некоторое
ребро а, исходящее из этой вершины (скажем, в направлении по часовой стрелке).
Приведем алгоритм построения некоторой хордовой диаграммы по
диаграмме D. На хордовой диаграмме, которую мы строим, мы не будем фиксировать
ориентацию окружности. Как будет видно в дальнейшем, выбор вершины V\ и
ориентированного ребра, из нее исходящего, не повлияет на конечный
результат.
Отметим, что свойство реализуемости не зависит от ориентации окружности
хордовой диаграммы.
Выходя из вершины V\ вдоль ребра а, мы попадем в некоторую другую
вершину V<2. После этого наш алгоритм определен (однозначно) следующим
образом. Мы обходим диаграмму, идя каждый раз вперед (а не налево и не направо).
Это означает, что, пройдя по хорде с, инцидентной вершине V2, мы переходим
на противоположную сторону, а затем продолжаем движение по окружности
согласно правилу: если мы двигались по часовой стрелке, то мы продолжаем
движение против часовой стрелки, а если двигались против часовой стрелки,
то продолжаем движение по часовой стрелке. При переходе в следующую
вершину, мы перешагиваем на противоположный конец хорды и продолжаем
движение в противоположном направлении. Если изначальная d-диаграмма
соответствовала одной кривой (а не нескольким), то в конце мы придем в ту точку,
из которой вышли, пройдя все дуги окружности и все хорды по одному разу.
Такое "хождение по хордовой диаграмме" можно представить отображением
окружности в нее, которое становится непрерывным, если отождествить
точки изначальной диаграммы, соединенные хордами. Отображение окружности
задает хордовую диаграмму.
Назовем построенный алгоритм алгоритмом В.
Пусть С — реализуемая хордовая диаграмма (рассматриваемая с точностью
до ориентации окружности). Тогда, применяя алгоритм В к А(С), мы получим
диаграмму С. Однако для некоторых нереализуемых хордовых диаграмм это
не так. Например, если мы рассмотрим диаграмму СхГ), то одно из значений
функции А(Гдп) равно СдО· Если затем применить алгоритм В, примененный
к "новой диаграмме ЫСТ, мы получим диаграмму
15.4. Критерий реализуемости
265
Единственное, что нам остается проверить, — то, что так не может быть,
если изначальная хордовая диаграмма была четной.
Причина состоит в следующем. Рассмотрим хордовую диаграмму С и
некоторую ее вершину V. Вершине V и вершине, противоположной ей (по хорде)
соответствуют четыре дуги. Обозначим их через a,b,c, d. Предположим, что
а противоположна с на плоской диаграмме (т. е. эти две дуги соседствуют на
диаграмме С). Далее, для d- диаграммы D = А (С) дуга а будет соседствовать
либо с 6, либо с d. Без ограничения общности предположим, что а соседствует
с Ъ. Тогда имеются две априорные возможности для алгоритма £>, чтобы
"восстановить" дугу, противоположную дуге а: это будет либо с (как это должно
быть), либо d, см. рис. 15.9.
Рис. 15.9. "Плохой" случай
Алгоритм В определен однозначно. Таким образом, нам нужно найти
достаточное условие на изначальную диаграмму С, чтобы алгоритм В правильно
восстанавливал исходную диаграмму (в нашем случае правильно определял,
что дуга с противоположна дуге а).
Предположим теперь, что С — четная хордовая диаграмма. Тогда для
любого обхода диаграммы С (согласно построению функции А, т. е. с поворотом
в каждом перекрестке направо или налево) мы ориентируем все дуги нашей
диаграммы некоторым образом. Вершину диаграммы С назовем хорошей,
если она является либо источником (т.е. обе дуги исходят из нее), либо стоком
(т.е. обе дуги, инцидентные ей, направлены в ее сторону). Если диаграмма С
является четной, то все ее вершины являются хорошими.
Случай, когда все вершины хорошие, — как раз то, что нам нужно: в этом
случае алгоритм В восстановит изначальную диаграмму С по диаграмме А(С).
Опишем это более подробно.
Пусть С, V, а, 6, с, d определены как сказано выше. Рассмотрим любую из d-
диаграмм А(С). Без ограничения общности предположим, что на диаграмме
С дуга с следует после а, а дуга d следует за дугой Ъ. Предположим, что мы
выбрали значение функции А таким образом, чтобы на диаграмме А(С) дуга Ъ
соседствовала с дугой а, а дуга d соседствовала с дугой с. Более того,
предположим, что дуга Ъ следует за α в нашем обходе (т. е. на d-диаграмме D). Таким
образом, вершина V является стоком. Вершина V', соединенная с V хордой
(в хордовой диаграмме С) является, таким образом, источником.
Следовательно, дуга d следует за дугой с. При этом, когда мы изображаем d-диаграмму
D на плоскости, мы получаем одну из картинок, изображенных на рис. 15.10
(в правой или в левой его части).
266
Глава 15
d , ., с с -,,.. d
α Χ" \J) by """-■ а
Рис. 15.10. Локальная структура ребер и дуг
Это означает, что дуга с является противоположной дуге а (и аналогичная
"правильная" ситуация имеет место для всех вершин хордовой диаграммы),
и, после применения алгоритма £>, мы правильно восстанавливаем исходную
диаграмму С. Это завершает доказательство теоремы.
Этот алгоритм распознавания реализуемости легко обобщается на случай
гауссовых узлов, что остается читателю в качестве упражнения.
15.5. Доказательство теоремы Кауфмана-My расу ги
Напомним, что теорема Кауфмана-Мурасуги (теорема 7.5) состоит в
следующем.
Теорема 15.7. Длина полинома Джонса для зацеплений со связной тенью
и η перекрестками меньше или равна п. Равенство достигается только для
альтернированных диаграмм без точек распадения или для связных сумм
таких диаграмм.
Для доказательства теоремы Кауфмана-Мурасуги нам нужно уметь
оценивать длину полинома Джонса, которая, очевидно, равна длине скобки
Кауфмана, разделенной на четыре.
Рассмотрим формулы (6.5) и (6.6), определяющие полином
Джонса-Кауфмана. Нас интересуют состояния, дающие максимальную и минимальную
возможные степени в сумме (6.5).
Определение 15.7. Назовем минимальным состоянием диаграммы L
состояние, в котором все перекрестки разрешены положительно, а минимальным
состоянием состояние диаграммы L, в котором все перекрестки разрешены
отрицательно.
Для оценки длин полиномов будем использовать атомы. А именно,
рассмотрим (связную) диаграмму L зацепления. Она имеет внутреннюю А-структуру,
как и любой четырехвалентный граф, вложенный в плоскость. Она имеет
также £>-структуру атома, который может быть восстановлен по зацеплению.
Будем считать, что диаграмма L проста (не разлагается в связную сумму).
Случай непростой диаграммы будет рассмотрен отдельно.
Легко видеть, что максимальная возможная степень монома в формуле (6.5)
соответствует максимальному состоянию, а минимальная возможная степень
этого монома соответствует минимальному состоянию. Эти несложные факты
оставляются читателю для проверки в качестве упражнения.
15.5. Доказательство теоремы Кауфмана-Мурасуги 267
Обозначим эти состояния через smax и sm^n, а количества окружностей в
этих состояниях — через 7таж и 7тгп соответственно.
Вычислим степени искомых максимального и минимального мономов.
Имеем: η + 2(jmax — 1) и —η — 2(jmin — 1). Здесь "2" и "минус 2" происходят
из мономов a±2(7(s)_1).
Разность (верхняя граница) равна
2n + 2(7mm+7maz) ~ 4.
Теперь вернемся к атому У, соответствующему зацеплению L. Его эйлерова
характеристика равна, — η + 7mm + Imax- Принимая во внимание, что она не
превосходит двух, мы делаем вывод о том, что верхняя граница не
превосходит 4гг.
Таким образом, нами доказана первая часть теоремы Кауфмана-Мурасуги,
т. е. что длина полинома Джонса-Кауфмана не превосходит 4гг.
Теперь остается вопрос: когда достигается верхняя граница? Во-первых,
должен достигаться максимум эйлеровой характеристики, т. е. атом должен
быть сферическим.
Для того чтобы получить сферический атом, мы должны задать
В-структуру сферического атома по имеющейся Α-структуре тени диаграммы L. Имеется
две такие структуры, соответствующие двум альтернированным диаграммам с
заданной тенью.
Но поскольку диаграмма L проста, то у нее нет других £>-структур,
порождающих сферический атом, кроме двух заданных. Это связано с тем, что
разбиение хорд на два семейства однозначно для d-диаграмм, не представимых
в виде связной суммы. Таким образом, диаграмма L альтернирована.
Покажем теперь, что единственным препятствием к тому, чтобы для
альтернированной диаграммы L полином X(L) имел длину 4гг является
существование точек распадения. Очевидно, что если диаграмма имеет точку
распадения, то она может быть представлена как связная сумма диаграмм, суммарно
имеющих меньшее количество перекрестков. Таким образом, длина скобки
Кауфмана для такой диаграммы не может быть равна 4гг.
Если длина скобки Кауфмана некоторой альтернированной диаграммы
зацепления с η перекрестками строго меньше, чем 4гг, то при разложении по
состояниям либо старший коэффициент (соответствующий smax), либо
младший (соответствующий smin) сокращается с коэффициентом, происходящим из
некоторого другого состояния. Без ограничения общности предположим, что
имеет место первый случай. Тогда существует состояние, отличное от smax,
дающее ту же степень переменной а: эта степень равна п-\- 2(7max — 1)·
Предположим, что оно отличается от состояния smax в нескольких перекрестках.
Выберем один из них и обозначим его через X. Очевидно, что в состоянии sfmax,
которое отличается от smax только в перекрестке X, мы также получим степень
η + 2(7max — 1)· Следовательно, 7(smax) = 7(smax) + 1· Это означает, что, когда
мы изменяем состояние smax в вершине X, одна окружность переходит в две
окружности. Учитывая, что изначальная диаграмма была альтернированной,
мы видим, что X является точкой распадения.
Наконец, если диаграмма L не является простой, мы можем разложить ее
на простые компоненты. Принимая во внимание мультипликативность поли-
268
Глава 15
нома Джонса-Кауфмана, мы видим, что все эти компоненты будут
альтернированными без точек распадения. Этим завершается доказательство теоремы
Кауфмана-Мурасуги.
15.6. Примеры инвариантов Васильева
В предыдущих главах мы показали, что полиномиальные инварианты
зацеплений выражаются через инварианты Васильева. Приведем еще один
пример такой связи.
Рассмотрим полином Джонса-Кауфмана. Вычислим его младший
коэффициент. Как было показано при доказательстве теоремы Мурасуги, в случае
альтернированных диаграмм зацеплений (без точек распадения) он равен единице
по причине того, что у соответствующего атома (лежащего на сфере) послекри-
тическая окружность не может подходить сама к себе. В случае неальтерни-
рованной диаграммы мы получим высотный атом, который уже не
обязательно будет сферическим. В этом случае некоторая послекритическая окружность
уже может подходить сама к себе, не образуя при этом точек распадения на
атоме. Способ подхода окружности самой к себе естественно описывать хордовой
диаграммой, которая в данном случае будет d-диаграммой. Если мы имеем
ровно одну послекритическую окружность, то младший коэффициент полинома
Джонса-Кауфмана описывается некоторой функцией на таких d-диаграммах,
которая, будучи естественным образом продолжена на произвольные хордовые
диаграммы, задает символы некоторых инвариантов Васильева.
Описание этой функции приведено в [ВаМо] и [Mnch]. Тот факт, что она
удовлетворяет четырехчленному соотношению, был обнаружен автором
настоящей книги.
Пусть К — диаграмма зацепления, V — соответствующий ей высотный атом
с η перекрестками. Рассмотрим послекритические окружности ci, C2,..., с&
атома V. Пусть эти окружности соответствуют минимальному состоянию smin
атома V. В этом состоянии формула для скобки Кауфмана дает младшую степень,
равную (—1)к~1а~п~2к+2. Вычислим коэффициент при этой степени в (К).
Замечание 15.3. Этот коэффициент, вообще говоря, не является
инвариантом узла. Дело в том, что, говоря "младший" коэффициент полинома, мы
обычно имеем в виду его младший ненулевой коэффициент. Однако может
оказаться, что вычисляемый по явной формуле (6.5) "младший коэффициент"
для скобки Кауфмана равен нулю, в то время как для некоторой другой
диаграммы (например, с меньшим числом перекрестков) аналогичное разложение
даст "настоящий", т. е. ненулевой, младший коэффициент.
Состояние s' (в котором / перекрестков разведены способом А) задает
минимальную возможную степень монома, если и только если в этом состоянии
количество окружностей равно к -\-1. Это значит, что при переходе от
состояния smin к состоянию sf мы должны все время делать преобразования,
разбивающие одну окружность на две. Соединим в состоянии s перемычками дуги
окружностей, проходящие в окрестностях классических перекрестков (вершин
атома). Получится нечто вроде хордовой диаграммы, в которой вместо одной
окружности имеется несколько, при этом некоторые пары точек (возможно, на
15.6. Примеры инвариантов Васильева
269
разных окружностях) соединены хордами. Рассмотрим перекрестки, в которых
состояние sf отличается от состояния sm^n, и соответствующие им хорды.
Ясно, что каждая такая хорда соединяет точки на одной и той лее окружности,
иначе, изменив разведение в соответствующем перекрестке, мы на первом шаге
получили бы к — 1 окружность, откуда следует, что на Z-м шаге мы не можем
получить больше, чем к -\-1 — 2 окружностей.
Рассмотрим одну окружность С и одну хорду с, соединяющую пару точек на
окружности С. Если мы перестроим состояние smin по хорде с, мы получим две
окружности. Далее, оба конца каждой последующей хорды d в диаграмме С
должны лежать по одну сторону от хорды с, так как иначе, изменив
состояние s' по хордам end, мы получим не к + 2 окружности, а к окружностей,
следовательно, любое изменение по I хордам, среди которых есть cud, даст
не более к + I — 2 окружности. Продолжая рассуждать аналогичным образом,
мы приходим к следующему. Каждой из окружностей состояния smin
соответствует хордовая диаграмма. Допустимым, т. е. приводящим к минимальной
степени монома, набором хорд является набор хорд, в котором любые две
хорды, соответствующие одной и той же окружности (хордовой диаграмме) не
пересекаются. Имея допустимый набор хорд, состоящий из а\ хорд на первой
окружности, а2 хорд на второй окружности, и т.д., dk хорд на к-й окружности,
мы получим состояние, которое дает вклад в младший коэффициент а~п~2 +2,
равный (—1)Σ* α*(—l)fe_1. Вынося (—l)fc_1 за скобку (в дальнейшем мы
позабудем про этот коэффициент), мы получим, что старший коэффициент равен
сумме X}/Lo(—-О^Ь гДе Νι — количество допустимых наборов из I хорд. Таким
образом, для вычисления младшего коэффициента скобки Кауфмана хорды,
соединяющие разные окружности, не играют роли, и задача сводится к
рассмотрению набора не связанных друг с другом хордовых диаграмм. Очевидно,
что этот коэффициент равен произведению коэффициентов по всем хордовым
диаграммам, где для каждой хордовой диаграммы D он равен
η
M\{D) = y^(—1)г(количество наборов г непересекающихся хорд) (15.1)
г=0
Эта формула в точности описывает младший (быть может, нулевой)
коэффициент скобки Кауфмана на зацеплении, соответствующем d-диаграмме.
Эту функцию можно рассматривать на произвольных хордовых
диаграммах.
Как оказывается, значение этой функции на хордовых диаграммах, не
являющихся d-диаграммами, относится к виртуальным узлам.
Предложение 15.1. Функция М\, определенная на хордовых диаграммах с
произвольным количеством хорд, удовлетворяет одночленному и
четырехчленному соотношениям.
Доказательство. Одночленное соотношение очевидно. Действительно,
сопоставим каждому набору непересекающихся хорд, не содержащему отдельно
стоящую хорду I набор, содержащий эту хорду; так как количество хорд у них
отличается на единицу, то соответствующие коэффициенты сокращаются.
270
Глава 15
Рассмотрим четырехчленное соотношение. Оно состоит из четверки хорд,
из которых две хорды являются подвижными. В первом слагаемом А\
имеются две пересекающиеся хорды а, 6, концы которых соседствуют, во втором
слагаемом А^ те лее две хорды не пересекаются, в третьем слагаемом А% мы
имеем две пересекающиеся хорды а, с, а в четвертом слагаемом А^ — две
непересекающиеся хорды а, с, см. рис. 15.11.
Рис. 15.11. Хорда, не пересекающая хорды а, 6, не пересекает также и с
Заметим теперь, что в разницу Μι (Α2)—Μι (Αι) дают вклад ровно те наборы
попарно непересекающихся хорд из Μι, в которые входят хорды а и Ъ. Точно так
же, в Μ\(Α±) — Μι (Аз) входят наборы хорд, содержащие хорды α и с. Осталось
заметить, что если некоторая неподвижная хорда не пересекает хорды а, 6, то
она не пересекает и хорду с и наоборот: если неподвижная хорда не пересекает
хорд а, с, то она не пересекает и хорду Ъ. D
Таким образом, для каждого натурального η функция Μι задает весовую
систему Μιη и, следовательно, некоторый инвариант Васильева узлов.
Очень интересной и важной является задача описания возможных
значений функции Μι на хордовых диаграммах с η хордами в зависимости от
рода соответствующих атомов (атомы, соответствующие d-диаграммам являются
высотными, но могут иметь произвольный род).
Помимо функции Μι можно построить скобку Кауфмана полностью по d-
диаграмме узла. В этом случае состояния скобки Кауфмана задаются
подмножествами хорд d-диаграммы, и мы можем подсчитать количество окружностей
в каждом состоянии. Этот формализм позволяет построить полином Джонса-
Кауфмана для любой хордовой диаграммы, (в том числе и тех, которые не
являются d-диаграммами): мы формально сопоставляем наборам хорд
состояния скобки Кауфмана.
На самом деле здесь есть еще промежуточное звено — виртуальное
зацепление.
Деля скобку Кауфмана на α_η, мы получаем функцию Д, которая каждой
хордовой диаграмме сопоставляет полином от переменной а2, с младшим по а
коэффициентом (свободным членом), равным М\.
Теорема 15.8. Функция Д удовлетворяет четырехчленному соотношению.
Замечание 15.4. У этой конструкции есть два обобщения: в случае
рассмотрения атома с количеством окружностей большим, чем одна, мы
получаем отображение
хордовая диаграмма с „ ^ г. f
ь^ виртуальный узел \-^ скобка Кауфмана,
несколькими окружностями
15.6. Примеры инвариантов Васильева
271
Это отображение также удовлетворяет четырехчленному соотношению,
следовательно, задает трехпараметрическую серию инвариантов Васильева
{оснащенных) зацеплений: один параметр — количество окружностей —
компонент зацепления, второй — количество хорд, а третий — коэффициент в
полиноме Джонса-Кауфмана.
Заметим также, что аналогичным образом можно рассматривать и
"оснащенные" хордовые диаграммы, т. е. хордовые диаграммы, хорды которых
разделены на "обычные" и "пунктирные". Эта теория связана с теорией J-
инвариантов кривых, см. [Arnl, Арн2, Gor, Лан].
Более подробное освещение затронутых вопросов мы осуществим в
отдельной публикации.
Глава 16
Скобочная полугруппа узлов
16.1. Представление длинных зацеплений
словами в конечном алфавите
Все зацепления могут быть закодированы d-диаграммами. Молено
интерпретировать d-диаграмму следующим образом. Зафиксируем сначала разбиение
хорд d-диаграммы на два семейства. Выберем "начальную" точку на
окружности d-диаграммы, не являющуюся концом хорды, d-Диаграммы с отмеченной
точкой допускают простое комбинаторное описание словами в четырехскобоч-
ном алфавите. Это описание таково. При обходе хордовой диаграммы начиная
с отмеченной точки против часовой стрелки будем выписывать круглую
скобку, если мы встречаем хорду из первого семейства и квадратную скобку, если
мы встречаем хорду из второго семейства, при этом мы пишем
открывающуюся скобку, если мы встретили хорду первый раз и закрывающуюся скобку, если
мы встретили хорду второй раз. Таким образом мы получим то, что называется
правильной двухскобочной структурой.
Определение 16.1. Правильной двухскобочной структурой называется слово
в алфавите из четырех букв-скобок ( , ) , [ , ] такое, что:
1. В каждом начальном под слове а' слова а количество скобок ")" не
превышает количества скобок "(", а количество скобок "]" не превышает
количества скобок " [";
2. В самом слове а количество скобок "(" равно количеству скобок ")", а
количество скобок "[" равно количеству скобок "]".
Очевидно, что d-диаграмма с выбранной начальной точкой и разбиением
хорд на два семейства однозначно восстанавливается по соответствующей
правильной двухскобочной структуре.
d-Диаграммы кодируют зацепления, следовательно, d-диаграммы с
отмеченной точкой кодируют зацепления с отмеченной точкой на выделенной
ориентированной компоненте или (что то лее самое) длинные зацепления.
Определение 16.2. Под длинным зацеплением мы понимаем гладкое
компактное 1-многообразие, вложенное в R3, совпадающее с осью Ох вне
некоторого шара с центром в начале координат, изотопное несвязной сумме одной
16.1. Задание словами в конечном алфавите
273
прямой линии и некоторого конечного (возможно пустого) множества
окружностей.
Длинное зацепление с одной связной компонентой называется длинным
узлом.
Длинные узлы рассматриваются с точностью до изотопии, которые
предполагаются тождественными вне некоторого достаточно большого шара с центром
в нуле.
Определим теперь полугруппу К длинных зацеплений следующим образом.
1. Элементами К являются классы изотопии длинных зацеплений.
2. Единицей в К является класс эквивалентности многообразия, заданного
как {у = 0, ζ = 0}. Этот класс эквивалентности называется тривиальным
длинным узлом.
3. Произведение двух элементов Lj_,L2 G G определяется следующим
образом. Сначала выберем представителей этих классов: некоторые длинные
зацепления Κι и i^2· Они совпадают с осью Ох вне шаров с центрами
в нуле и некоторыми радиусами R\ и i?2· Мы строим длинное
зацепление, состоящее из следующих трех частей. Одна часть лежит в {х > 2R2}
и {х < —2Ri} и совпадает там с осью Ох. Другая часть лежит внутри
шара Br2 (i?2,0,0) и совпадает там со сдвигом К^ Π Br2 (0,0,0) на вектор
(i?2,0,0). Третья часть лежит внутри шара Brx (—R\, 0,0) и совпадает там
со сдвигом К\ Π Влг (0, 0, 0) на вектор (—Ri, 0, 0); пример взятия связной
суммы длинных узлов изображен на рис. 16.1. Определим теперь L\ · L2
как изотопический класс описанного выше зацепления. Очевидно, что он
не зависит от произвола в выборе радиусов R\ и i?2·
Рис. 16.1. Произведение длинных зацеплений
Очевидно, что конкатенация правильных двухскобочных структур
соответствует операции взятия связной суммы соответствующих длинных зацеплений;
эта операция ассоциативна.
Таким образом, можно сказать, что полугруппа длинных зацеплений может
быть закодирована правильными двухскобочными структурами. Такая
кодировка носит название скобочного исчисления.
274
Глава 16
Все правильные двухскобочные структуры образуют полугруппу, в которой
роль единичного элемента играет пустое слово, а в качестве умножения
выступает конкатенация слов. Обозначим эту полугруппу через G.
Основной задачей скобочного исчисления является описание
эквивалентности (изотопии) длинных зацеплений в терминах правильных двухскобочных
структур. Это было сделано в [МанЗ].
Приведем основную идею нахождения этих соотношений.
Простейшими эквивалентностями d-диаграмм (и, соответственно,
правильных двухскобочных структур) являются движения Рейдемейстера и "замена
обхода".
Полугруппа G правильных двухскобочных структур, профакторизованная
по этим соотношениям, изоморфна полугруппе К.
Каждое из таких соотношений имеет вид А = В, где А, В — некоторые
(возможно, неправильные) слова в алфавите из четырех скобок. Такое соотношение
означает, что для любой правильной двухскобочной структуры вида хАу, где
хну — некоторые слова в четырехскобочном алфавите (возможно,
неправильные), слово хВу также является правильной двухскобочной структурой, и
представляет тот же изотопический класс зацепления. (Вместе с этим
соотношением постулируется также и соотношение в обратном порядке: хВу => хАу).
Профакторизуем полугруппу G по всем таким соотношениям хАу = хВу для
всех ж, у таких, что хАу является правильной двухскобочной структурой, где
соотношения А = В взяты из списка, который мы приводим ниже.
Выпишем некоторые такие соотношения. Первое движение Рейдемейстера:
( ) = пустое слово
[ ] = пустое слово
[ (] [) ] = пустое слово
([)(])= пустое слово.
Второе движение Рейдемейстера:
(КМШ) =а
ШМ)[)] =а,
В каждом из этих двух случаев А — произвольное слово, имеющее правильную
структуру круглых скобок.
К[М(])] =А
([)[А](]) =А.
Здесь А — произвольное слово с правильной структурой квадратных скобок.
Третье движение Рейдемейстера:
(([)[(]([)([)[)])(]) = ([(]([)[)][(]([)[)])
([)(([)([(](])(])[)] = [([)((])[(]]·
16.2. Представление зацеплений квазиторическими косами 275
Для замены обходов мы используем следующие соотношения:
[Л(]С) = [(]С([)[)М(]),
([М((])С) = (С([))А(]),
[А[(]]С[)] = [(}С[[)}А\,
([)А[(](])С[)] = (С[)А].
В каждом из них слово А должно иметь правильную структуру квадратных
скобок, а слово С — правильную структуру круглых скобок.
Необходимость таких соотношений проверяется непосредственно.
Теорема 16.1. ([МаЗ]) Эти соотношения являются достаточными, т. е. две
правильные двухскобочные структуры задают изотопные длинные
зацепления тогда и только тогда, когда одна из них получается из другой конечной
последовательностью применений таких соотношений.
16.2. Представление зацеплений
квазиторическими косами
В настоящем разделе мы опишем, как узлы могут быть представлены
некоторым небольшим классом кос, соответствующим некоторому небольшому
классу d-диаграмм, см. [Ма4].
16.2.1. Определение квазиторических кос
Напомним, что торические косы (зависящие от двух параметров ρ и q, где
ρ — количество нитей) задаются следующей формулой:
Т(р, g) = (<7i...<7„_i)«
и имеют интуитивное толкование см. рис. 16.2.а.
Определение 16.3. Коса β называется квазиторической типа (p,q), если она
может быть представлена в виде β\ ..., Pq, где для каждого Pj = σλ31 ... σ !ΐ^_1,
каждое e^h равно или 1 или — 1. Другими словами, квазиторическая коса типа
(р, q) это коса, полученная из стандартной диаграммы торической косы (р, q)
путем произвольного изменения типов перекрестков, см. рис. 16.2.6.
Легко видеть, что произведение квазиторических кос из η нитей
представляет собой квазиторическую косу из η нитей.
На самом деле справедливо более точное утверждение.
Предложение 16.1. Для каждого ρ Ε Ν квазиторические косы из ρ нитей
задают подгруппу в группе Вр.
Для доказательства этого утверждения достаточно доказать следующую
лемму.
Лемма 16.1. Для всякого натурального ρ обратный элемент к
квазиторической косе является квазиторической косой.
276
Глава 16
Рис. 16.2. Торическая и квазиторическая косы
Доказательство. Мы должны доказать, что для косы δ = σ\λ ... σρρ_Γι , где
каждый элемент е^ равен 1 или —1, коса δ-1 является квазиторической косой.
При этом доказательство леммы вытекает непосредственно из определений,
поскольку каждая квазиторическая коса есть произведение элементов, равных
положительным степеням таких кос.
Другими словами, мы должны доказать, что существует квазиторическая
коса η, такая, что коса η · δ тривиальна.
Мы хотим показать, что существует коса 5ι,... Sp-i, где Si = σ^Λ ... crJ^1,
такая, что для η = Si,..., Sp_i коса ηS — тривиальна.
Рассмотрим тень S диаграммы стандартной торической косы типа (р,р); эта
тень совпадает с тенью рассматриваемой диаграммы Si ... Sp-iS. Нижняя часть
этой диаграммы имеет типы перекрестков, происходящие из S. Так что нам
остается подобрать типы оставшихся перекрестков (т.е определить Si...Sp-i
так, чтобы получить тривиальную косу в произведении Si .. .Sp-iS). Нижняя
часть тени S состоит из п нитей ; одна из них (обозначим ее через х) пересекает
все другие нити по одному разу; все остальные нити не пересекают друг друга.
Если мы установим типы всех перекрестков в нижней части S так как в
косе 5, то увидим, что некоторые нити проходят над ж,и другие под ж, см.
рис. 16.3.а.
Обозначим нити первого множества через у ι,... ур, а нити второго мнжества
через zi,.. .zq.
Скажем, что для крашеной косы βι из г нитей с нитями α,ί,ί = 1... г,
установлен порядок нитей αϊ > а^ > · · · > аг если при каждом перекрестке X,
в котором пересекаются нити α^, α^·, г < j, нить а^ идет над нитью a,j. Очевидно,
что в этом случае коса βι тривиальна.
Теперь мы легко установим типы всех перекрестков для верхней части S ,
полагая для косы Si <Ь ... Sp-iS следующий порядок нитей yi > У2 > Уз · · -Ур >
χ > ζι > · · · > zq, см. рис. 16.3.6. При этом коса η5 тривиальна, что завершает
доказательство леммы. D
16.2. Представление зацеплений квазиторическими косами 277
21 У Ζ2 Χ Ζ\ У Ζ2 Χ
а б
Рис. 16.3. Обращение квазиторической косы
Итак, мы имеем группу квазиторических кос. Перейдем теперь к
доказательству основной теоремы этого раздела.
Теорема 16.2. Каждый изотопический класс зацеплений может быть
получен замыканием квазиторической косы.
16.2.2. Крашеные косы являются квазиторическими
Согласно теореме Александера, для каждого зацепления К существует
коса /3, замыканию которой этот узел изотопен. Нашей целью является
перестроить эту косу подходящим образом, чтобы она стала квазиторической (и,
конечно, осталась изотопной исходной косе).
Марковская эквивалентность была определена в 11.5, см. стр. 183.
Докажем следующую лемму.
Лемма 16.2. Для каждой косы β существует натуральное г такое, что β
марковски эквивалентна некоторой косе β' из г нитей, перестановка которой
равна некоторой степени циклической перестановки (1 —> 2 —> · · · —> г) для
некоторого г.
Доказательство. Обозначим число нитей косы β через п. Рассмотрим
перестановку се, соответствующую косе /3, и орбиты действия перестановки а на
множестве (1,..., п).
Эти орбиты могут содержать различные количества элементов. Применим
движения Маркова для преобразования этих орбит. Первое движение
Маркова сопрягает косы, следовательно, сопрягает соответствующие орбиты. Поэтому
количества элементов в орбитах не изменяются. Второе движение Маркова
увеличивает количество нитей косы на единицу, добавляя элемент (п-\-1) к орбите,
содержащей элемент гг, не изменяя при этом остальные орбиты. Можно
перенумеровать элементы таким образом, чтобы самая короткая по числу элементов
орбита содержала элемент гг, и, согласно второму движению Маркова,
увеличивалась на один элемент. Применяя указанную операцию много раз, можно
достичь того, что все орбиты будут иметь одинаковое количество элементов.
Предположим, что полученная таким образом коса β из km нитей действует
278
Глава 16
на множестве из km элементов таким образом, что каждая из к орбит
содержит ровно га элементов. После подходящего сопряжения можно считать, что
сопряженная коса есть m-ая степень циклической перестановки (12 ... /era),
fc,raeN. D
Обозначим построенную косу через 7· Как показано в лемме 16.2, коса 7
марковски эквивалентна косе β.
Следующим шагом будет доказательство того, что коса 7 является квази-
торической.
Будем теперь преобразовывать диаграмму косы 7 без изменения ее
изотопического типа. Для завершения доказательства теоремы 16.2 осталось доказать
следующую лемму.
Лемма 16.3. Коса из г нитей, перестановка которой представляет собой
степень циклической перестановки, является квазиторической.
Доказательство. Пусть 7 — коса из г нитей, которой соответствует
перестановка (12 ... r)s. Рассмотрим косу 77 = 7 * Τ (г, l)~s.
Коса 77 является крашеной. Если мы докажем, что коса jf является
квазиторической, то мы докажем, что квазиторической является и коса 7·
Таким образом, осталось доказать следующую лемму.
Лемма 16.4. Каждая крашеная коса является квазиторической.
Напомним, что в группе крашеных кос из г нитей можно выбрать в качестве
образующих косы bij, 1 ^ г < j ^ г, см. рис. 16.4.
i 3
V
г
ь»
Л
1J
Рис. 16.4. Образующая 6^ группы крашеных кос
Теперь нам достаточно показать, что все образующие Ьц являются квази-
торическими косами.
В самом деле, для каждых i и] между 1 и гг, г < j, коса Ьц является
произведением двух кос bjj · bfj (они показаны на рис. 16.4 сверху и снизу от
горизонтальной линии), где первая коса bjj = σ~ .. .aJ_2(Tj-i имеет
возрастающий порядок образующих, а вторая коса 6? = σ7_ισ7_2 ---(?% — убывающий
порядок образующих, см. рис. 16.4.
Определение 16.4. Для 1 ^ г < j' ^ η коса ζ из η нитей называется (г, j)-
квазиторической если она имеет диаграмму, в которой все нити, за
исключением нитей с номерами от г до j, вертикальны и не пересекаются с другими
нитями, а нити с номерами от г до j образуют квазиторическую косу в (обычном
16.2. Представление зацеплений квазиторическими косами 279
смысле этого слова). Такая диаграмма называется стандартной диаграммой
(г,^-квазиторической косы.
Для завершения доказательства леммы 16.4 и главной теоремы достаточно
доказать следующую лемму.
Лемма 16.5. Пусть 1 < г < j < г. Тогда каждая (г^)-квазиторическая
крашеная коса из г нитей является квазиторической.
Доказательство. Мы воспользуемся индукцией по числу г — (j — г + 1) (т. е.
разнице между общим количеством нитей и количеством нитей, на которые
натянута квазиторическая коса). Нам нужно показать, что добавляя отдельно
стоящую вертикальную нить к диаграмме квазиторической косы, мы получаем
квазиторическую косу.
Рассмотрим стандартную диаграмму квазиторической косы из q нитей и
добавим одну вертикальную нить справа от всех остальных (случай добавления
слева может быть рассмотрен аналогичным образом). Допустим, что
первоначальная диаграмма получена из торической диаграммы (q + 1, (q + 1)/)
изменением типов перекрестков.
Рассмотрим стандартную диаграмму крашеной торической косы типа (q + 1,
(q + 1)/) и ее первые q нитей. Очевидно, что они образуют диаграмму
торической косы типа (q,ql). Установим типы перекрестков на этих нитях так же,
как в случае диаграммы р, и упорядочим добавленную нить вместе со всеми.
Очевидно, что мы получим диаграмму косы, эквивалентную диаграмме,
получаемой из ρ добавлением отдельной нити справа, см. рис. 16.5. D
Рис. 16.5. Добавление "тонкой" нити к квазиторической косе
Таким образом, стандартные образующие группы крашеных кос Рп для
произвольного η являются квазиторическими косами. Следовательно, в силу
предложения 16.1, таковыми же будут и все крашеные косы. Используя движения
Маркова и изотопию диаграммы косы к начальной диаграмме, мы получили
квазиторическую косу С, замыкание которой изотопно зацеплению К. Тем
самым главная теорема доказана. D
280
Глава 16
16.2.3. d-Диаграммы квазиторических кос
Торические (и квазиторические) косы в своем естественном истолковании
позволяют легко кодировать себя двумя способами: косами и d-диаграммами,
причем эти кодировки оказываются тесно связанными между собой.
Пусть D — меченая d-диаграмма, K(D) — соответствующая ей диаграмма
зацепления. В каком случае диаграмму K(D) молено естественным образом
представить в виде замыкания косы?
Для ответа на этот вопрос нам потребуется сделать несколько оговорок, по
поводу того, как точно мы строим плоскую диаграмму K(D) no d-диаграмме D.
Более точно, мы предполагаем, что окружность стандартно вложена в R2 :
х2 + у2 = 1, и что концы хорд равномерно распределены вдоль окружности.
Хорды одного (внутреннего) семейства d-диаграммы считаются отрезками
прямых линий, а хорды другого семейства считаются образами отрезков при
преобразовании инверсии в рассматриваемой окружности. При этом естественно
наложить следующее ограничение на d-диаграмму: для каждой хорды с
количество концов хорд, лежащих с одной стороны, не равно количеству хорд,
лежащих с другой стороны. Благодаря этому, ни одна из хорд не проходит
через центр окружности (или бесконечную точку).
При таком подходе возникает явное препятствие к тому, чтобы полученная
диаграмма K(D) завивалась как коса вокруг центра окружности
d-диаграммы D.
Именно, пусть D — d-диаграмма, и пусть а и Ъ — некоторые пересекающиеся
хорды диаграммы D, принадлежащие различным семействам такие, что конец
а\ хорды а и конец Ъ\ хорды Ъ являются соседними вершинами. Тогда одна из
компонент зацепления K(D) ведет себя так, как показано на рис. 16.6 слева
снизу. А именно, имеется дуга окружности χ между концами а\ и &ι, которая
ориентирована противоположна смежным с ней ветвям диаграммы Ό {К).
Рис. 16.6. Два способа построения зацепления по d-диаграмме
Этого факта можно легко избежать, если слегка изменить правило
построения диаграммы зацепления K(D) no d-диаграмме D. А именно, нужно просто
считать, что дуга χ пуста, т. е. ветвь узла, соответствующая хорде а\ следу-
16.2. Представление зацеплений квазиторическими косами 281
ет непосредственно после ветви узла, соответствующей хорде &ι, см. рис. 16.6
справа снизу.
Справедливо следующее утверждение:
Утверждение 16.1. Пусть зацепление K(D) получается из некоторой d-
диаграммы D с положительными и отрицательными хордами описанным
выше способом и при этом обвивается вокруг центра этой диаграммы как
коса. Тогда это зацепление представляет собой стандартное замыкание ква-
зиторической косы.
Доказательство этого утверждения состоит в следующем. Для того,
чтобы диаграмма K(D) заплеталась вокруг центра окружности диаграммы D как
коса, нужно, чтобы каждый радиус этой окружности пересекал одно и то лее
количество хорд. В случае, если это количество хорд равно к мы будем иметь
замыкание косы из 2к + 1 нити. Для этого нужно, чтобы окончание одной
хорды совпадало с началом следующей хорды. Совпадение в буквальном смысле
невозможно, но, так как мы удаляем малые дуги окружности между
(некоторыми) соседними концами хорд, это становится возможным при следующих
обстоятельствах. Концу каждой хорды из первого семейства предшествует
начало хорды из второго семейства, а концу каждой хорды из второго семейства
предшествует начало хорды из первого семейства. Понятия "начало" и конец
определяются при движении против часовой стрелки; так как никакая хорда
не проходит через центр окружности, начало и конец корректно определены.
Далее из этого условия легко следует, что d-диаграмма задает торическую
косу, если все хорды d-диаграммы являются положительными.
d-Диаграмма, соответствующая торической косе Т(р,д), устроена
следующим образом. Пусть ρ = 2m +1. Отметим 4mq точек на окружности и разобьем
их на 2q группы, каждая из которых состоит из 2т соседних точек.
Перенумеруем точки в каждой группе номерами от 1 до 2т; в "четных группах" мы
нумеруем по часовой стрелке, а в нечетных группах — против часовой стрелки.
©оо...
Рис. 16.7. Квазиторические d-диаграммы при ρ = 3
Каждая отмеченная точка соединена с точкой из соседней группы с тем лее
номером. Соседняя группа выбирается согласно следующим правилам:
1. Соседняя группа одна и та лее для точек с одинаковой четностью в
данной группе; для точек с другой четностью выбирается другая соседняя
группа.
2. Никакая точка не соединяется непосредственно с соседней (по
окружности) точкой.
282
Глава 16
Рис. 16.8. Квазиторические d-диаграммы при ρ = 5
Примеры таких d-диаграмм показаны на рис. 16.7 при ρ = 3 и на рис. 16.8
при ρ = 5.
Очевидно, что квазиторические d-диаграммы с нечетным ρ получаются из
представленных таким образом "торических" диаграмм, если пометить
некоторые хорды как отрицательные.
Часть V
Виртуальные узлы
Глава 17
Виртуальные узлы.
Основные определения
и мотивация
Теория виртуальных узлов была предложена Кауфманом [Каи7] в 1996 году
Формальное определение виртуального узла (зацепления) задается как класс
эквивалентности виртуальных диаграмм по виртуальным движениям Рейде-
мейстера. Под виртуальной диаграммой понимается четырехвалентный граф
на плоскости, у которого помимо классических перекрестков имеются
виртуальные перекрестки. Виртуальный перекресток не является ни проходом, ни
переходом; его нужно понимать так, как будто две линии, его образующие,
не должны пересекаться вообще, но по размерностным соображениям они не
могут разойтись на плоскости. С геометрической точки зрения виртуальные
узлы происходят из узлов в "утолщенных поверхностях", исследованных Франсуа
Жижером, Луисом Кауфманом и Юбером Салером [JKS]. При проектировании
поверхности Sg на плоскость R2 утолщенная поверхность SgxR проектируется
на R3, при этом классические перекрестки задают классические перекрестки,
а виртуальные перекрестки возникают как дефекты проекции (когда разные
точки диаграммы кривой на Sg проектируются в одну точку диаграммы на
плоскости). Таких пересечений "как бы нет", и линия, содержащая такие
пересечения, может быть перенесена в другое место, что дает возможность
формального подхода к виртуальным узлам с помощью абстрактных гауссовых
диаграмм. Классическими узлами в таком случае являются узлы, диаграммы
которых лежат на сфере. Это согласуется с тем фактом, что диаграммы
зацеплений на S2, профакторизованные по классическим движениям Рейдемейстера,
задают классические зацепления так же, как и диаграммы на R2. Имея
виртуальную диаграмму на плоскости, можно построить диаграмму на поверхности
с ручками, однако количество этих ручек не является фиксированным. Таким
образом, добавляя и убирая "пустые" ручки, не пересекающиеся с
диаграммой, мы будем задавать тот лее виртуальный узел. Важная теорема состоит
в том, что виртуальные узлы — это в точности узлы в утолщенных
поверхностях, рассматриваемые с точностью до изотопии, а также гомеоморфизмов
утолщенных поверхностей Sg x Rt, сохраняющих координату t и
стабилизации/дестабилизации поверхностей. Ключевой является теорема Грега Купер-
286
Глава 17
берга [Кир] о том, что минимальный (по количеству ручек) поверхности
представитель заданного класса виртуального узла единственен. Из этого следует,
что классическая теория узлов является частью виртуальной теории узлов, т. е.
если два классических узла эквивалентны как виртуальные узлы, то они
эквивалентными как классические узлы.
Виртуальные узлы (и зацепления), как и классические узлы, являются
алгоритмически распознаваемыми, [Ма7]. Доказательство этого факта будет дано в
приложении В. Однако алгоритм, существование которого следует из этого
доказательства, вряд ли молено считать явным практическим руководством для
распознавания виртуальных узлов (скажем, в виде компьютерной программы),
как, впрочем, и известные к настоящему моменту алгоритмы распознавания
классических узлов.
В самом начале развития этой теории были предложены обобщения
основных инвариантов узлов: дистрибутивный группоид, фундаментальная
группа, полином Джонса-Кауфмана [КаиЗ]. Дальнейшее развитие см. в работах
[Kau8, Kau9, Kup, Ma2, Ma5, Маб]. В работе [GPV] виртуальные узлы впервые
появились как нереализуемые гауссовы диаграммы: при попытке реализовать
их на плоскости нужно использовать погружения, где виртуальные
перекрестки возникают как дефекты погружения. Расположение этих виртуальных
перекрестков не имеет значения: виртуальный узел можно трактовать как набор
классических перекрестков и указание, какие пары из них должны быть
соединены между собой (где проходят соединяющие линии и какие виртуальные
перекрестки образуют — неважно с точки зрения класса эквивалентности
виртуального узла). Напомним, что один из критериев реализуемости гауссовых
диаграмм был приведен в главе 15.
Особенно мы рекомендуем читателю готовящуюся фундаментальную
монографию Кауфмана и автора [КМО].
Переходим к точным определениям.
17.1. Комбинаторное определение
Начнем с основных определений и введения обозначений.
Определение 17.1. Диаграммой виртуального зацепления (виртуальной
диаграммой) называется плоский (вложенный на плоскость) граф валентности
четыре, снабженной следующей структурой: каждый перекресток либо имеет
структуру прохода/перехода (т.е. является классическим перекрестком), либо
обозначен кружочком (является виртуальным перекрестком, см. рис. 17.1).
Две виртуальные диаграммы называются эквивалентными, если
существует последовательность плоских изотопии обобщенных движений
Рейдемейстера, переводящая одну диаграмму в другую.
Как и ранее, в списке движений приводится преобразование части
диаграммы, изображенной на рисунке; оставшаяся (не показанная на рисунке) часть
диаграммы остается неизменной.
Определение 17.2. Список обобщенных движений Рейдемейстера таков:
1. Классические движения Рейдемейстера.
17.1. Комбинаторное определение
287
Рис. 17.1. Виртуальный перекресток
2. Виртуальные версии Ω^,Ω^,Ω^ классических движений Рейдемейстера,
в которых все классические перекрестки заменены на виртуальные, см.
рис. 17.2.
\
Рис. 17.2. Движения Ω^,Ω^,Ω^
3. "Полувиртуальная" версия Ω37 третьего движения Рейдемейстера, см.
рис. 17.3.
Рис. 17.3. Полу виртуальная версия Ω3
Замечание 17.1. Вместо виртуальных движений и полувиртуального
движения мы можем использовать одно {эквивалентное им всем) движение,
288
Глава 17
называемое объездом, состоящее в том, что если некоторая ветвь
виртуальной диаграммы содержит последовательно несколько виртуальных
перекрестков (и не содержит классических), то, зафиксировав концы, можно
перенести эту ветвь в другое место, поставив в новых местах пересечения
виртуальные перекрестки, см. рис. 17.4-
^ч
)-
ч <Ь '
т~~
Рис. 17.4. Объезд
Эквивалентность объезда набору из четырех движений {трех
виртуальных и одного полу виртуального) остается читателю в качестве
упражнения.
Определение 17.3. Виртуальным зацеплением называется класс
эквивалентности виртуальных диаграмм по виртуальным движениям Рейдемейстера.
Уникурсальный обход диаграммы виртуального зацепления определяет ее
компоненты. Виртуальным узлом называется виртуальное зацепление с одной
компонентой.
Замечание 17.2. Два варианта третьего движения Рейдемейстера,
похожие на полувиртуальное движение, см. рис. 17.5, являются запрещенными,
т. е. они не входят в список обобщенных движений Рейдемейстера и не
являются следствиями из них.
Более того, если мы будем наравне с обобщенными движениями Рейдме-
мейстера использовать оба запрещенных движения, любой виртуальный узел
(не зацепление!) может быть сведен к тривиальному. Впервые это свойство
было отмечено в работе [GPV]. Также оно было доказано Сэмуэлом
Нельсоном с использованием гауссовых диаграмм, см. [Nel]; а также Каненобу [Кап].
Идея Нельсона состоит в том, что несложным способом в каждой гауссовой
диаграмме можно уменьшить число пересечений хорд, применяя обобщенные
движения Рейдемейстера и запрещенные движения.
Если добавить только одно из них ("верхнее"), получится интересная
теория трубных узлов, см. работу Шина Сато, [Satoh].
Виртуальные узлы и зацепления, как и классические, бывают
ориентированные и неориентированные.
Замечание 17.3. Для классических диаграмм существуют два вида
эквивалентности: обычная классическая эквивалентность и виртуальная
эквивалентность. Оказывается, что они совпадают, следовательно, классические
17.2. Проекции из поверхностей с ручками
289
^
Рис. 17.5. Запрещенные движения
зацепления образуют подмножество во множестве виртуальных
зацеплений. Мы докажем это утверждение позднее.
Определение 17.4. Зеркальным образом виртуальной диаграммы
называется виртуальная диаграмма, полученная из изначальной диаграммы заменой
каждого классического прохода на переход и наоборот.
В теории виртуальных узлов имеется много феноменов, которые не
появляются в случае классических узлов, и, тем самым, определяют, что тот или иной
узел не является классическим. Так, например, группа (определение будет
дано позже) виртуального узла может не совпадать с группой его зеркального
образа.
17.2. Проекции из поверхностей с ручками
Выбор обобщенных движений Рейдемейстера является вполне
естественным. А именно, это полный список движений, которые могут возникнуть при
проекции узлов, лежащих в Sg х /, на R х / (или, эквивалентно, R3), когда
"наверху" на Sg x / мы применяем движения Рейдемейстера. Очевидно, что
таким образом могут получиться все классические движения Рейдемейстера
(рассмотренные как движения Рейдемейстера для частей диаграмм,
расположенных на малой части Sg, которая проектируется на плоскость взаимно
однозначно). Остальные движения, т. е. полувиртуальное и чисто виртуальные
движения Рейдемейстера, получаются в виде проекции способами, показанным на
рис. 17.6.
Существует еще одна наглядная топологическая интерпретация
виртуальных узлов в терминах вложений зацеплений в утолщенные поверхности, см.
[Каи 10, Каи8]. Рассмотрим каждый виртуальный перекресток как пересечение
290
Глава 17
r2 R Рейдемейстера
Третье виртуальное движение Рейдемейстера
Рис. 17.6. Обобщенные движения Рейдемейстера и утолщенные поверхности
линии объезда с некоторой другой линией. Вместо этого пересечения молено
добавить ручку и поместить одну из этих линий внутрь ручки, см. рис. 17.7.
Так как мы рассматриваем абстрактную поверхность, нам неважно, выше или
ниже мы добавляем ручку.
Добавление/удаление ручек называется стабилизацией/дестабилизацией.
Такой подход был впервые озвучен в пионерской работе Кауфмана, точная
теория была построена Наоко Камадой и Сейичи Камадой [КК].
Отметим, что поверхность, в которой лежит виртуальное зацепление, может
быть несвязной с "пустыми" компонентами: можно сначала применить
несколько стабилизации, а затем одну дестабилизацию, оставляющую все зацепление
в одной компоненте, и выделяющую отдельно "пустую" компоненту.
Этого можно избежать, наложив некоторые ограничения на стабилизацию.
Так, например, Куперберг в своей теореме (см. ниже) требует, чтобы каждая
связная компонента Mi поверхности Μ была такова, чтобы в Mi x / лежала по
крайней мере одна компонента рассматриваемого зацепления, а вместо
дестабилизации, отделяющей "пустую" компоненту он рассматривает композицию этой
дестабилизации с удалением получающейся компоненты, подробнее см. [Кир].
Упражнение 17.1. Покажите, что с точки зрения абстрактной
поверхности и кривой на ней не важно, какую из двух кривых мы поднимаем на
ручку.
17.2. Проекции из поверхностей с ручками
291
На рис. 17.7 показано также, как объезд выражается через добавления ручек
и стабилизацию.
Рис. 17.7. Ручки, соответствующие виртуальным перекресткам и объезд
Из приведенных рассуждений легко вытекает следующая
Теорема 17.1. Две виртуальные диаграммы задают изотопные
{эквивалентные) зацепления тогда и только тогда когда их представления в утолщенных
поверхностях получаются одно из другого посредством изотопии,
гомеоморфизмов поверхностей и стабилизации/дестабилизации.
Отметим важное обстоятельство.
Определение 17.5. Задание виртуального зацепление зацеплением в
утолщенной поверхности называется минимальным, если невозможно производить
дестабилизацию (удалять ручки).
Назовем минимальной такую реализацию виртуального узла в утолщенной
поверхности, которая не может быть дестабилизирована.
Важная теорема Куперберга ([Кир]) утверждает следующее.
Теорема 17.2. Для виртуального узла К существует единственный (с
точностью до изотопии) минимальный представитель — узел в утолщенной
поверхности.
Доказательство проводится индукцией по роду поверхности Sg. А именно,
предполагается, что для некоторого представителя К Ε Sg x / существуют две
различные дестабилизации К' с Sg-\ χ / и К" с Sg-\ х /, приводящие к
разным минимальным представителям, причем для диаграмм К' и К"
минимальные представители уже определены однозначно. Если любые две такие
дестабилизации К —>· К' и К" независимы, т. е. соответствуют непересекающимся
кривым в Sg, то минимальный представитель для К единственен.
Действительно, К' и К" можно дестабилизировать к одному и тому лее представителю
К' С Sg-2 х /, из чего следует совпадение их минимальных представителей. В
противном случае рассматриваются дестабилизирующие поверхности К —>· К'
и К —>· К"', приводящие к различным минимальным диаграммам,
пересечение которых минимально. Это приводит к противоречию. Более подробно см.
оригинальную работу [Кир].
292
Глава 17
17.3. Гауссовы диаграммы
Определение 17.6. Гауссовой диаграммой, соответствующей плоской
диаграмме (виртуального) узла К называется диаграмма, состоящая из
ориентированной окружности (с фиксированной точкой), на которой прообразы прохода
и перехода (для каждого перекрестка) соединены хордами. Прообразы каждого
классического перекрестка соединены стрелкой, которая направлена от
прообраза перехода к прообразу прохода. Каждая хорда (стрелка) снабжена знаком,
который совпадает со знаком перекрестка, т. е. равен единице для /С и минус
единице для JX^ .
Заметим, что прообразы виртуальных перекрестков никак не обозначаются
на гауссовой диаграмме. Это согласуется с определением движения объезда.
Замечание 17.4. Для классических зацеплений это определение согласуется
с приведенным ранее.
Если заданная гауссова диаграмма с мечеными стрелками реализуема, то
она однозначно определяет некоторую классическую диаграмму узла.
Если имеется нереализуемая диаграмма, то мы не можем получить
вложения. С другой стороны, можно рассмотреть погружение диаграммы в R2.
Разумеется, мы имеем в виду только "хорошие" погружения без тройных точек
и касаний. Заданному погружению мы будем сопоставлять виртуальные
перекрестки пересечениям образов ребер, а классические перекрестки — образам
перекрестков, см. рис. 17.8.
Рис. 17.8. Виртуальный узел и его гауссова диаграмма
Таким образом, мы построили виртуальную диаграмму узла по гауссовой
диаграмме (возможно, неоднозначно).
Теорема 17.3 ([GPV]). Класс изотопии виртуального узла однозначно
определен его гауссовой диаграммой.
Упражнение 17.2. Докажите этот факт.
17.4. Простейшие инварианты
293
Указание 17.1. Покажите, что собственно виртуальные движения и
полувиртуальные движения не изменяют гауссовой диаграммы.
17.4. Виртуальные узлы и зацепления
и их простейшие инварианты
Имеется много различных простых комбинаторных способов
конструирования виртуальных узлов и их инвариантов.
Рассмотрим виртуальное зацепление показанное на рис. 17.9.
Рис. 17.9. Виртуальное зацепление Хопфа.
Интуитивно ясно, что это зацепление не может быть изотопно никакому
классическому зацеплению из-за "странного коэффициента зацепления".
Напомним, что в классическом случае коэффициент зацепления (см. стр. 33)
двух компонент А, В ориентированного классического зацепления L
определяется следующим образом: мы рассматриваем те перекрестки, в которых
компонента А проходит над компонентой В и берем их алгебраическую сумму:
перекрестки /С считаем со знаком +1, а перекрестки ΛνΓ считаем со знаком — 1.
Легко проверить, что это число молено посчитать иным способом: взять
алгебраическую сумму всех перекрестк, в которых встречаются компоненты А и
В и разделить ее пополам. Читатель легко проверит, что определенный таким
образом коэффициент зацепления lk(A,B) совпадает с "настоящим"
(определенным на стр. 33) в случае классических узлов.
Рассмотрим новое определение для виртуальных узлов. Легко
доказывается, что оно инвариантно относительно всех обобщенных движений Рейдемей-
стера, и потому является инвариантом двухкомпонентного виртуального
зацепления с упорядоченными компонентами. При этом в классическом случае
оно всегда является целым, а в виртуальном случае — нет. Так, например, для
виртуального зацепления Хопфа, см. рис. 17.9 он равен =Ь^ (в зависимости от
ориентации компонент).
Этот пример демонстрирует, что виртуальное двухкомпонентное
зацепление, у которого число виртуальных перекрестков, образованных обеими
компонентами, нечетно, не изотопно никакому классическому зацеплению. Этот
факт, впрочем, следует и явно из анализа обобщенных движений Рейдемейсте-
ра.
294
Глава 17
Следующий простейший инвариант есть инвариант раскрасок: в нашем
распоряжении три цвета. Нам нужно установить для каждой длинной дуги (т. е.
части диаграммы, идущей от прохода до прохода без учета виртуальных
перекрестков) цвет из числа трех имеющихся. Затем мы должны сосчитать
количество так называемых правильных раскрасок, т. е. таких раскрасок, для
которых три цвета в каждом классическом перекрестке удовлетворяют
соотношению группоида, т. е. либо все три цвета в данном перекрестке одинаковы,
либо все три различны, см. стр. 56. Этот инвариант будет рассмотрен ниже
вместе с понятием дистрибутивного группоида и фундаментальной группы.
Упражнение 17.3. Докажите инвариантность инварианта раскрасок.
17.5. Инварианты, порождаемые
виртуальным группоидом
В настоящем разделе мы обобщим понятие дистрибутивного группоида для
виртуальных узлов многими способами. Мы собираемся строить инварианты,
"порождаемые дистрибутивным группоидом".
17.5.1. Фундаментальные группы
Хотя виртуальные узлы не вложимы в R3, можно легко построить
обобщение понятия фундаментальной группы дополнения к узлу (или попросту
группы узла) для виртуальных узлов. Именно, можно модифицировать
представление Виртингера виртуальных диаграмм. Рассмотрим ориентированную
диаграмму L виртуального зацепления L. Удалим из нее все виртуальные
перекрестки. Получим (несвязное) множество L, которое состоит из дуг. Каждая
дуга является представляет собой либо окружность — компоненту зацепления,
не имеющую виртуальных перекрестков, и проходящую сверху в каждом
классическом перекрестке, либо интервал, начало и конец которого представляют
собой либо удаленный виртуальный перекресток, либо классический
перекресток — проход. Все внутренние перекрестки дуги являются переходами. Подряд
идущие дуги, разделяемые виртуальными перекрестками, образуют длинные
дуги.
Выберем длинные дуги в качестве образующих той группы, которую мы
собираемся построить. После этого выпишем все соотношения в классических
перекрестках в точности так же, как и в классическом случае: если две длинные
дуги а ж с разделяются длинной дугой 6, причем длинная дуга а лежит справа
по отношению к ориентации 6, то мы пишем: с = баб-1.
Инвариантность этой группы относительно движений Рейдемейстера может
быть проверена непосредственно исходя из определений: комбинаторное
доказательство этого факта одинаково пригодно как для классических, так и для
виртуальных узлов (см. упражнение 4.3). Инвариантность относительно
движения объезда очевидна: оно не меняет самого копредставления группы узла.
Однако наша инвариантность следует из более тонкой инвариантности
дистрибутивного группоида, которую мы обсудим ниже.
Определение 17.7. Группа, определенная выше, называется группой
(виртуального) зацепления L.
17.5. Дистрибутивный группоид
295
Очевидно, что лемма, аналогичная лемме 4.6 об инвариантности количества
раскрасок верна и для случая виртуальных узлов; ее формулировка и
доказательство дословно совпадают с формулировкой и доказательством леммы 4.6.
17.5.2. Странные свойства виртуальных зацеплений
Некоторые виртуальные зацепления (и их инварианты) могут обладать
свойствами, которые не имеют места в случае классических узлов. Например, как в
классическом, так и в виртуальном случае молено определить верхнюю и
нижнюю группы (в классическом случае — фундаментальные группы дополнения);
нижняя группа для виртуальных узлов определяется как группа
зеркального образа виртуального узла. Для классических узлов эти группы являются
изоморфными по геометрическим причинам. В виртуальном случае верхнее и
нижнее копредставления могут задавать неизоморфные группы. Первый такой
пример был приведен в [GPV].
Рассмотрим виртуальный узел /С, изображенный на рис 17.10. Его четыре
длинные дуги а, 6, с, <i, указанные на рис. 17.10, можно выбрать в качестве
образующих группы. Здесь длинная дуга идет от прохода до следующего прохода,
по ходу образуя переходы и виртуальные перекрестки. Мы получим следующие
соотношения:
Ъ = dadT1, а = bdb-1, d = bcb~1, c = dbd~1.
Таким образом, образующие α и с выражаются через образующие bud.
Следовательно, мы получаем представление (b,d\bdb = dbd), которое задает
группу, изоморфную группе трилистника (группе кос из трех нитей).
Рис. 17.10. Виртуальный узел с неизоморфными верхней и нижней группами
Упражнение 17.4. Покажите, что группа зеркального образа этого узла
изоморфна Z.
Этот пример показывает, что узел К, не является классическим узлом. Более
того, его зеркальный узел представляет пример нетривиального виртуального
узла с группой, изоморфной Ζ (такой же, как у тривиального узла). В случае
классических нетривиальных узлов это невозможно по теореме Дена.
296
Глава 17
Простейшим примером виртуального узла с группой Ζ является
виртуальный трилистник. Два виртуальных трилистника — левый и правый —
изображены на рис. 17.11.
Рис. 17.11. Левый и правый виртуальные трилистники
Нетривиальность каждого из них и их неэквивалентность будут доказаны
позже.
Кроме этого примера важным феноменом является следующий: если взять
связную сумму двух тривиальных виртуальных узлов, то она может и не быть
тривиальной, см. рис. 17.12. Из этого следует, что связная сумма для
виртуальных узлов не является корректно определенной, и это тесно связано с понятием
длинного виртуального узла. Длинные виртуальные узлы будут рассмотрены
в главе 21.
Рис. 17.12. Нетривиальная связная сумма тривиальных виртуальных узлов
Хорошо известно, что дополнение к классическим узлам является
пространством Эйленберга-МакЛейна К (π, 1), где π — группа узла. Кроме того, все
группы гомологии пространства дополнения к классическому узлу, кроме
первой, являются тривиальными. Это, однако, не так для виртуальных узлов: в
работе [Kim] приведены примеры виртуальных узлов, вторая группа гомологии
которых не является тривиальной. Следовательно, все эти узлы не являются
классическими.
Глава 18
Инвариантные полиномы
виртуальных узлов
Мы уже построили обобщения некоторых основных инвариантов узлов на
виртуальные узлы: инвариант раскрасок, фундаментальная группа, полином
Джонса-Кауфмана (в форме, предложенной в [KaulO]).
Все приведенные выше обобщения были основаны на следующем:
диаграмма виртуального зацепления рассматривалась как набор классических
перекрестков с указанием способа соединения последних. При этом не учитывалось,
что происходит в виртуальных перекрестках. С одной стороны, это создавало
упрощение в доказательствах: нужно было доказывать инвариантность только
относительно классических движений Рейдемейстера, в то время как
инвариантность относительно объезда имеет место по определению. С другой стороны,
инварианты получались не очень сильными, так, например, группа
виртуального трилистника является тривиальной.
В настоящей главе мы опишем некоторые инварианты, предложенные в
работах автора [Ма2, Ма5, Маб] (короткие варианты см. в [Ман4, Ман5]).
Заинтересованного читателя мы также отсылаем к работе Кауфмана [Каи8],
его совместным работам с автором [КМ] и с Дэвидом Рэдфордом [KR]; в
последних двух работах описывается идея "бигруппоидов" (biquandles). Построению
полиномиальных инвариантов виртуальных узлов посвящены работы [Saw, SW],
а также многие другие.
В настоящей главе мы опишем модификации этих инвариантов следующим
образом: мы изучим, какой вклад может давать виртуальный перекресток в
объект, который мы строим (например, в случае фундаментальной группы,
как он может изменять образующие) и подберем подходящие преобразования,
оставляющие наш объект инвариантным.
Большая часть приводимых в настоящей главе результатов относится к
работам автора [Ма2, Ма4, Ма5, Маб, Ман4, Ман5, Манб].
Идея основной конструкции настоящей главы заключается в следующем:
когда мы строим инвариант виртуальных зацеплений (или кос), мы
сопоставляем некоторые (образующие элементы) дугам диаграммы, при этом если
длинная дуга проходит через виртуальный перекресток (в этом случае правильнее
было бы говорить о двух дугах — до и после прохождения перекрестка),
соответствующий элемент претерпевает следующие изменения. В случае кос (это
298
Инвариантные полиномы
будет подробно описано в главе 22) элемент, соответствующей одной дуге
умножается на £, а элемент, соответствующий другой дуге, проходящей через тот
лее перекресток, умножается на £-1. Если мы рассматриваем группу
зацепления (фундаментальную группу заданную представлением Виртингера), то при
переходе через виртуальный перекресток можно применить сопряжения с
помощью новой абстрактной переменной.
Оказывается, что во многих случаях (как, например, в случае модуля Алек-
сандера) эта новая переменная играет важную роль и позволяет строить
инварианты виртуальных зацеплений, которые не являются прямыми
обобщениями инвариантов классических узлов. Например, получаемые инварианты могут
быть тривиальными в классическом случае, что позволяет нам устанавливать
то, что некоторые виртуальные узлы не являются классическими.
На протяжение настоящей главы все узлы и зацепления (виртуальные или
классические) предполагаются ориентированными, если не оговорено
противное.
Под гомоморфизмом двух объектов Οι and O2, снабженных некоторыми
операциями (οι,..., om), мы понимаем отображение из Οι to O2, которой
согласуется со всеми этими операциями.
18.1. Виртуальный группоид (квандл)
Начнем с напоминания понятия дистрибутивного группоида,
предложенного Матвеевым [Mat] и Джойсом [Joy]. Дистрибутивный группоид является
(почти) полным инвариантом классических узлов, подробнее см. главу 5.
Напомним, что под дистрибутивным группоидом понимается множество М,
снабженное бинарной операцией о, для которой выполняются следующие
свойства:
1. Идемпотентность: Va Ε Μ : а о а = а,
2. Правая самодистрибутивность:
Va, 6, с Ε Μ : (α о b) о с = (α о с) о (6 о с), (18.1)
и
3. Левая обратимость: Va, 6ΕΜ:3!χΕΜ:χοα = 6. В таком случае
элемент обозначается через Ъ/а.
Как было сказано в главе 5, эти условия соответствуют инвариантности
объекта, сопоставляемого зацеплению, относительно движений Рейдемейстера.
А именно, если для диаграммы зацепления построить соответствующий
дистрибутивный группоид, то при применении к диаграмме движений
Рейдемейстера он будет преобразовываться в изоморфный ему дистрибутивный
группоид. Эта конструкция прямо обобщается на случай виртуальных зацеплений.
Пусть L — виртуальная диаграмма.
Определение 18.1. Под длинной дугой диаграммы будем понимать
ориентированный отрезок (часть кривой) между двумя проходами (таким образом,
18.1. Виртуальный группоид (квандл)
299
длинная дуга от прохода до следующего прохода может иметь переходы и
виртуальные перекрестки).
Легко видеть, что это определение длинной дуги согласуется с обычным
определением дуги для классических диаграмм.
Далее мы делаем то лее, что и в случае классических зацеплений. Каждой
длинной дуге сц,г = 1,...,п мы сопоставляем образующую а^. Сначала мы
берем свободный дистрибутивный группоид, порожденный всеми элементами,
соответствующими дугам αι,...,αη. Далее, если три длинные дуги αι,<22,&3
инцидентны одному и тому же перекрестку, как показано на рис. 18.1, мы
выписываем соотношение
α*ι ° ai2 = агз
(18.2)
Рис. 18.1. Соотношение в перекрестке для дистрибутивного группоида
Определение 18.2. Дистрибутивным группоидом (по Кауфману) для
зацепления L называется формальный дистрибутивный группоид, порожденный
cti,i = 1,..., η, и профакторизованный по соотношениям (18.2) во всех
классических перекрестках.
Более точно, элементами этого группоида являются классы
эквивалентности слов, полученных их образующих {сц} посредством операций о и /, где
соотношения эквивалентности определяются перекрестками.
Инвариантность этого дистрибутивного группоида относительно объезда
очевидна: образующие и определяющие соотношения остаются теми же.
Замечание 18.1. Инвариантность дистрибутивного группоида
относительно классических движений Рейдемейстера доказывается точно так же, как
и в классическом случае.
Обозначим полученный дистрибутивный группоид через Qk(L).
По построению, для тривиального узла мы U мы имеем Qk(L) = {α}.
Таким образом, мы имеем инвариант виртуальных зацеплений, который
совпадает с дистрибутивным группоидом в случае классических зацеплений.
С помощью этого дистрибутивного группоида можно доказать важную
теорему.
300
Инвариантные полиномы
Теорема 18.1. [GPV] Если L и L' — две {ориентированные) классические
диаграммы зацеплений такие, что существует цепочка обобщенных движений
Рейдемейстера, преобразующая L в V', то диаграммы L и L' представляют
изотопные классические зацепления.
Доказательство. Заметим, что параллель (см. определение на стр. 30)
сохраняется при виртуальных движениях Рейдемейстера (добавление виртуального
перекрестка к диаграмме не изменяет записи для параллели). Таким образом,
изоморфизм для Qk(L) и Qk(L'), индуцированный тем или иным
движением Рейдемейстера, сохраняет параллель. Так как дистрибутивный группоид
вместе с набором параллелей полностью классифицируют классические
зацепления, диаграммы L и L' являются классически эквивалентными. D
Замечание 18.2. Так как дистрибутивный группоид является почти
полным (но не полным) инвариантом классических зацеплений (например, он не
различает двух трилистников), то для доказательства теоремы 18.1 нам
потребовалась использовать некоторый дополнительный инвариантный объект
(параллель), который также можно инвариантно обобщить на виртуальные
узлы.
Другое (геометрическое) доказательство этой теоремы вытекает из
теоремы Куперберга [Кир].
Однако, в отличие от случая классических зацеплений, в случае
виртуальных зацеплений дистрибутивный группоид (в смысле Кауфмана) не является
сильными инвариантом: например, он, как и фундаментальная группа, не
различает тривиальности виртуального трилистника.
Действительно, рассмотрим диаграмму узла К, показанную в левой части
рисунка 18.2. Дистрибутивный группоид Qk-> соответствующий этой
диаграмме, имеет две образующие (дуги) а, Ъ и два соотношения а об = Ъ и Ъ об = а.
Очевидно, что из этих соотношений следует, что а = Ъ. Поэтому этот
дистрибутивный группоид состоит из одного элемента {а}, как и дистрибутивный
группоид тривиального узла.
Рис. 18.2. Размеченный виртуальный трилистник
Далее мы введем обобщение дистрибутивного группоида, так называемый
"виртуальный группоид", который является гораздо более мощным
инвариантом, чем описанный выше дистрибутивный группоид; в частности,он
распознает нетривиальность виртуального трилистника.
18.1. Виртуальный группоид (квандл)
301
Кроме виртуальных группоидов существует еще одно обобщение
дистрибутивных группоидов для виртуальных узлов, так называемые бигруппоиды
(см. Кауфман и Рэдфорд, [KR]). В отличие от подхода виртуальных
группоидов, Кауфман и Рэдфорд не вводили никакой структуры в виртуальных
перекрестках, а модифицировали структуру в классических перекрестках: в каждом
классическом перекрестке (в зависимости от его ориентации) вводится
бинарный оператор: по двум входящим элементам по определенному правилу
строятся два исходящих элемента. Если рассмотреть обе идеи вместе, мы получим
инвариант, называемый виртуальным бигруппоидом, см. [КМ].
Перейдем к построению виртуального группоида (который будет обозначен
через Q в отличие от группоида по Кауфману, обозначаемого через Qk)·
Определение 18.3. Виртуальным группоидом называется дистрибутивный
группоид (М, о), снабженный одноместной операцией /, такой, что:
1. Операция / является обратимой; обратная операция обозначается
через /-1;
2. Операция о дистрибутивна по отношению к /:
Va,beM : f(a) о f(b) = f(a о b). (18.3)
Замечание 18.3. Из уравнения (18.3) следует, что для всех а, 6 Ε Μ имеют
место равенства:
f-1(a)of-\b) = r1(aob),
f(a)/f(b) = f(a/b),
и
Г\а)/Г\Ъ) = Г\а/Ъ).
Для заданного виртуального зацепления L построим соответствующий
виртуальный группоид Q(L) следующим образом.
Выберем сначала правильную диаграмму L7, т.е. диаграмму, не имеющую
циклических длинных дуг. Очевидно, что правильная диаграмма с т
классическими перекрестками имеет т длинных дуг.
Некоторые диаграммы не являются правильными, однако правильности
можно легко добиться применением первого классического движения Рейде-
мейстера, см. рис. 18.3.
Упражнение 18.1. Покажите, что эквивалентные {задающие одно и то
же зацепление) правильные виртуальные диаграммы могут быть
переведены друг в друга посредством обобщенных движений Рейдемейстера в классе
правильных диаграмм.
Замечание 18.4. В дальнейшем в настоящей главе все виртуальные
диаграммы будут считаться правильными, если не оговорено противное.
302
Инвариантные полиномы
циклическая
длинная дуга
правильная
диаграмма
Рис. 18.3. Построение правильной виртуальной диаграммы
Пусть V — виртуальная диаграмма; будем считать, ребра прохода
разрывными, как это обычно изображается на плоскости. Пусть L' — множество,
полученное из L' удалением всех виртуальных перекрестков (вершин).
Таким образом линии, проходящие через виртуальный перекресток,
становятся разрывными в этой точке.
Определение 18.4. Дугой диаграммы L' называется связная компонента
множества L'.
Длинные дуги очевидным образом разбиваются на подряд идущие дуги.
Упражнение 18.2. Виртуальный узел, показанный на рис. 18.4 имеет три
классических перекрестка, три длинные дуги (αϊ и <22/ Ъ\ и 62; с) и пять дуг
(ai,a2,bi,b2,c).
Замечание 18.5. Виртуальный узел, изображенный на рис. 18.2 имеет
четыре дуги {см. средний рисунок): каждая из длинных дуг а и Ъ разбивается
виртуальным перекрестком на две дуги.
Инвариант Q(L) строится следующим образом. Рассмотрим все дуги аг,
г = 1,..., гг, диаграммы V'. Пусть X(Lf) — множество слов, получаемых
индуктивно из слов аг с использованием операций о, /, /, /_1. Для построения Q(L')
нужно профакторизовать X(L') по следующим элементарным соотношениям
эквивалентности.
Сначала для каждых трех элементов а,Ъ,с Ε X(L') мы отождествляем
следующие пары слов:
(а о Ь)/Ь ~ а;
(α/b) о Ъ ~ а;
а~аоа;
(а о Ъ) о с ~ (а о с) о (6 о с);
/(аоЬ)~/(а)о/(Ь).
18.1. Виртуальный группоид (квандл)
303
Рис. 18.4. Виртуальная диаграмма и ее дуги
Таким образом, мы получаем свободный виртуальный группоид с
образующими αϊ,..., ап. Дальнейшая факторизация будет проведена с учетом
структуры диаграммы V.
В каждом классическом перекрестке мы факторизуем по соотношению (18.2)
так лее, как и в классическом случае. Для каждого виртуального перекрестка
V мы также производим факторизацию. Пусть ап, ап, ап, а34 — четыре дуги,
инцидентные виртуальному перекрестку V так, как показано на рис. 18.5.
aJ4 aJ2 = f(aoi)
ал <b3=/(aJ4)
Рис. 18.5. Соотношение для виртуального перекрестка
Мы факторизуем по соотношениям:
a32=f{a3l) (18.4)
И
а3з = /(<bJ· (18·5)
Таким образом, виртуальный группоид Q(Lf) порожден всеми дугами аг,
г = 1,... ,гг, соотношениями вида (18.2) в классических перекрестках и видов
(18.4), (18.5) в виртуальных перекрестках.
304
Инвариантные полиномы
Теорема 18.2. Виртуальный группоид Q(L) является инвариантом
виртуальных зацеплений.
Доказательство. Инвариантность относительно классических движений Рей-
демейстера доказывается так лее, как и для дистрибутивного группоида (см.
замечание 18.1).
Будем считать все диаграммы правильными (упражнение 18.1).
Нам нужно показать, что при применении движения Рейдемейстера к
виртуальной диаграмме мы получаем изоморфизм виртуальных группоидов.
Рассмотрим некоторое движение Рейдемейстера. Пусть L и U — две
виртуальные диаграммы, получающиеся одна из другой применением этого
движение. Движение является локальным, т. е. происходит внутри некоторого
маленького круга С. Следовательно, все дуги диаграмм L и L' могут быть
разбиты на три семейства: общее множество Ε внешних дуг, принадлежащих как
к L, так и к 17, общее множество S дуг, пересекающих окружность круга С
и множества /,/7 внутренних дуг, принадлежащих соответственно к L и к V.
Таким образом, виртуальный группоид Q(L) имеет следующие образующие и
соотношения.
Во-первых, мы имеем общие соотношения — дистрибутивность и
идемпотентность. Обозначим это множество соотношений через ε;
Соотношения (соответствующие перекресткам) для диаграмм L,Z7 также
подразбиваются на части: внешние соотношения Re являются общими для L
и 17, а внутренние соотношения Rj^R^ относятся соответственно к L и к L'.
Кроме них, каждый из двух виртуальных группоидов имеет общие для всех
виртуальных группоидов соотношения ε (идемпотентность и правая
самодистрибутивность). Далее в доказательстве под соотношением мы будем понимать
только соотношение в некотором перекрестке (а не идемпотентность и не
самодистрибутивность) .
Легко видеть, что для каждого конкретного движения Рейдемейстера
посредством соотношений Rj можно избавиться от образующих /, выразив их
через S. Это приведет к добавлению некоторых "внутренних" соотношений R$
для S. То же самое может быть сделано и для V. Обозначим эти соотношения
через R's. Таким образом, мы преобразуем оба виртуальных группоида Q(L)
и Q(Lf) к изоморфным им Q(L) и Q(Lf). Последние порождены образующими
Е, S (и ε). У них есть общее множество внешних соотношений Re.
Единственное, что надо доказать, это то, что соотношения R$ и R's
определяют одно и то же отношение эквивалентности на S (посредством ε).
Выполним это для конкретных типов движений Рейдемейстера; другие
случаи полностью аналогичны тем, которые будут описаны.
Инвариантность группоида Q относительно всех классических движений
может быть проверена тем лее способом, что и раньше (для обычного
дистрибутивного группоида).
Проверим теперь инвариантность Q при применении чисто виртуальных
движений Рейдемейстера.
Первое виртуальное движение Рейдемейстера изображено на рис. 18.6. На
левом рисунке мы имеем одну образующую а. Мы добавляем еще одну
образующую Ъ и два совпадающих соотношения Ъ = /-1(а). Новая образующая
выражается через имеющиеся ранее; на старые образующие не накладывается
18.1. Виртуальный группоид (квандл)
305
никаких новых соотношений; тем самым виртуальный группоид преобразуется
в изоморфный ему виртуальный группоид.
Г~°~Л
Рис. 18.6. Инвариантность Q относительно первого движения
Случай противоположной ориентации перекрестка дает Ъ = /(а), что не
меняет ситуации.
Для каждого из последующих соотношений мы будем проверять только
один случай (другие случаи отличаются от выбранного заменой ориентации
некоторых компонент).
Второе виртуальное движение Рейдемейстера (см. рис. 18.7) добавляет две
образующие с и d и четыре соотношения, из которых различными являются
только два: с = /(а), с? = /_1(6). Таким образом, виртуальный группоид Q
переходит в виртуальный группоид, ему изоморфный.
Рис. 18.7. Инвариантность Q относительно второго виртуального движения
В случае третьего виртуального движения Рейдемейстера мы имеем шесть
"внешних дуг": три входящих (а,Ь,с) и три исходящих (p,q,r), см. рис. 18.8.
В обоих случаях мы имеем ρ = f2(a),q = 6, г = f~2(c). Три внутренних дуги
выражены через а,Ь,с, при этом других соотношений нет.
Проверим теперь движение Ω3. Мы будем проверять только одну версию
этого движения см. рис. 18.9.
На обеих картинках мы имеем три входящие ребра а,Ь,с и три выходящие
ребра р, q, г. В первом случае имеем соотношение: ρ = f(a),q = 6, г = /_1 (с) о а.
Во втором случае мы имеем: ρ = f(a),q = 6, г = /-1(со /(a)).
Из соотношений дистрибутивности f(xoy) = f(x)°f(y) вытекает
соотношение /-1(с) ° а = /_1 (с о /(a)). Следовательно, два виртуальных группоида до
применения смешанного движения и после смешанного движения совпадают.
Другие случаи смешанного движения ведут к другим соотношениям, при
этом все они эквивалентны f(x о у) = f(x) о f(y).
Это завершает доказательство теоремы. D
306
Инвариантные полиномы
Рис. 18.8. Инвариантность Q относительно третьего виртуального движения
г q r q
be Ъ
Рис. 18.9. Инвариантность Q относительно смешанного движения
Замечание 18.6. Заметим, что для классических зацеплений группоид Qk
может быть восстановлен по виртуальному группоиду Q. В случае
виртуальных узлов Q оказывается более сильным: имея Q можно легко
получить Qk, положив Ух Ε Q : f(x)=x.
Пример 18.1. Рассмотрим виртуальный узел К, показанный на рис. 18.2.
У него четыре дуги (см. средний рисунок): а\ = а, Ь\ = f(b) (до виртуального
перекрестка) и а^, Ь^ (после виртуального перекрестка).
Соотношения в этом виртуальном группоиде таковы: а^ = f(ai),bi = /(62)?
α2 о 62 = 61 и &2 ° Ъ\ = а\. Переписывая последние два соотношения для двух
образующих αϊ, 62, получаем: /(αϊ) о 62 = /(Ьг) and 62 о /(62) = а\.
Понятно, что распознавать изоморфность дистрибутивных группоидов
сложно. Тем более сложной задачей является определение изоморфности
виртуальных группоидов. Сейчас мы не можем сразу увидеть, что Q(K) φ {α}. Однако
в дальнейшем мы опишем некоторые упрощения виртуальных группоидов,
которые легче сравнивать. Из их построения, в частности, будет следовать, что
Q(K) φ {α}, тем самым, мы увидим, что виртуальный трилистник К
нетривиален.
18.2. Полином Джонса-Кауфмана
В своей первой работе по виртуальным узлам [KaulO] Кауфмана прямо
обобщил конструкцию полинома Джонса на случай виртуальных узлов. Она
18.3. Представления виртуального группоида
307
работает следующим образом. Рассмотрим ориентированную виртуальную
диаграмму L и соответствующую ей неориентируемую диаграмму \L\. После этого
будем разводить классические перекрестки диаграммы \L\ так лее, как в
классическом случае, и получать тем самым состояния диаграммы. Каждое
состояние s имеет три важные характеристики: количество a(s) сглаживаний типа А,
количество /3(s) = n—a(s) сглаживаний типа В и число j(s) компонент
зацепления в этом состоянии. После этого мы определяем полином Джонса-Кауфмана
по той же формуле, что и в классическом случае:
ХЩ = (-a)-3w^ Σ αα^~β^ (-α2 - α"2)^"1, (18.6)
S
где w(L) — число закрученности ориентированной диаграммы L, a ce(s),/3(s)
определяются так же, как и в классическом случае.
Доказательство инвариантности полинома Джонса-Кауфмана
относительно классических движений Рейдемейстера такое же, как и в классическом
случае; при применении чисто виртуальных движений или полу виртуального
движения формула (18.6) почленно остается неизменной.
Отметим важное свойство этого полинома [KaulO]: его неизменность
относительно одного локального преобразования, не являющегося эквивалентностью.
Упражнение 18.3. Покажите, что полином X инвариантен относительно
следующего локального движения, называемого выворачиванием или
виртуализацией классического перекрестка, см. рис. 18.10.
Рис. 18.10. Два варианта выворачивания
18.3. Представления виртуального группоида
Виртуальный группоид (как и дистрибутивный группоид) допускает
некоторые представления, получающиеся морфизмом из категории виртуальных
группоидов в некоторые другие категории. Так, морфизм в категорию групп
задает (фундаментальную) группу, также можно получить полином Алексан-
дера, инвариант раскрасок. В настоящем разделе мы опишем категории, в
которых имеется структура виртуальных группоидов, а также инварианты узлов,
получающиеся таким образом.
308
Инвариантные полиномы
18.3.1. Фундаментальная группа
Напомним, что фундаментальная группа G дополнения к
ориентируемому зацеплению L получается из соответствующего дистрибутивного группоида
Qk(L) следующим образом. Вместо элементов аг дистрибутивного группоида
Qx мы выписываем образующие группы G, которую мы строим, а вместо
операции о мы выписываем соотношение сопряжения: χ о у переходит в уху-1.
Легко проверить, что такое представление сохраняет свойства
идемпотентности, левой обратимости и правой самодистрибутивности. Обратная операция
единственна и задается по правилу а/Ъ = 6_1а6.
Таким образом, выписав все соотношения для всех классических
перекрестков зацепления L, мы получаем группу G(L), называемую группой
зацепления L. В случае классических узлов эта группа имеет геометрическую
интерпретацию как фундаментальная группа дополнения к зацеплению.
Замечание 18.7. Отметим, что не все элементы группы являются
образами элементов группоида: в группоиде нет операции, соответствующей
умножению в группе. Так, например, группоиду из одного элемента
соответствует группа Ζ (фундаментальная группа дополнения к тривиальному узлу).
Очевидно, что то лее самое молено проделать и в случае с виртуальными
узлами. Если мы будем исходить из дистрибутивного группоида Qk и работать
с длинными дугами, мы получим инвариант виртуальных зацеплений — группу
виртуального узла по Кауфману.
Как было сказано ранее, этот инвариант является не очень сильным,
например, он не распознает нетривиальности виртуального трилистника.
Построим теперь представление для Q в категорию групп исходя из
диаграммы зацепления и ее дуг (а не длинных дуг).
В качестве группового аналога операции о мы, как и раньше, можем взять
сопряжение. Таким образом, нашей задачей является выбор подходящей
операции /(·). Это может быть сделано следующим образом: мы фиксируем
(дополнительную) образующую q в группе и полагаем f(a) = gag-1.
Любая группа является виртуальным группоидом относительно таких двух
операций.
Более точно, имеет место следующая лемма.
Лемма 18.1. Для каждой группы G группа G * {q} (свободное произведение
группы G с бесконечной циклической группой, имеющей образующую q) с двумя
операциями о,/(·), определенными как а о Ъ = баб-1, f(c) = gcg-1 для всех
a,b,c G G * {q}, является виртуальным группоидом.
Доказательство. Действительно, нам нужно показать лишь, что f(a о Ь) =
f(a)of(b). В самом деле, f(aob) = f(bab~1)= qbab~1q~1 = g6g_1(qaq~1)qb~1q~x =
f(b)f(a)f(b-1)=f(a)of(b). D
Построим теперь фундаментальную группу G(L) виртуальной диаграммы L.
Обозначим все дуги диаграммы L через аг, г = 1,..., п. Группа G — это
группа, порожденная образующими αϊ,..., αη, q с определяющими соотношениями
видов (18.2), (18.4), (18.5), в которых мы полагаем f(x) = qxq~x,у о ζ = zyz~x.
Из сказанного выше следует
18.3. Представления виртуального группоида
309
Теорема 18.3. Пара: (группа G(L), элемент q Ε G(L)) является
инвариантом виртуальных зацеплений. Другими словами, если диаграммы L и V
задают эквивалентные виртуальные зацепления, то существует изоморфизм
h : G(L) —> G(L') такой, что h(qi) = qu ·
Доказательство следует непосредственно из теоремы 18.2 и леммы 18.1.
Очевидно, что для тривиального узла U мы имеем G(U) = (a,q\)] это —
свободная группа с двумя образующими.
Упражнение 18.4. С помощью построенного выше инварианта (G,q)
покажите, что виртуальный трилистник нетривиален.
Кроме фундаментальной группы, существует еще представление
виртуального группоида в группах, порожденное следующими соотношениями:
χ о у = урху~р, f(x) = qxq'1,
где ρ — фиксированное целое число, a q — фиксированный элемент группы.
Доказательство инвариантности такое лее, как в предыдущем случае.
Кроме того, для получения инвариантов молено воспользоваться одним из
следующих представлений:
χ о у = ух~гу, f(x) = qxq'1
или
χ о у = ух~ху, f(x) = qx~xq.
18.3.2. Инвариант раскрасок
Идея построения инварианта раскрасок (элементами некоторого
виртуального группоида) очень проста. Инвариант раскрасок равен количеству
гомоморфизмов виртуального группоида рассматриваемого зацепления в
некоторый конечный виртуальный группоид. Более точно, имеет место следующая
лемма.
Лемма 18.2. Пусть Q' — виртуальный группоид. Тогда множество
гомоморфизмов Q(L) —> Q' является инвариантом зацепления L. В частности, если
мощность множества Q' конечна, то количество гомоморфизмов Q(L) —> Q'
также конечно, и это количество является инвариантным.
Доказательство. Первое утверждение очевидно по построению.
Для доказательства второго утверждения рассмотрим виртуальное
зацепление L и его правильную диаграмму L. Для построения гомоморфизма h :
Q(L) —>· Q' нам нужно определить лишь Н(аг) образы элементов виртуального
группоида Q(L), соответствующего дугам диаграммы L, т.е. образующим. Так
как количество дуг у диаграммы конечно, искомое количество гомоморфизмов
также конечно. D
310
Инвариантные полиномы
Таким образом, для конечного виртуального группоида Q' мы имеем
целочисленный инвариант зацеплений, определяемый как число гомоморфизмов
Q(L) -* Q'.
Смысл этого инварианта очень прост: он представляет собой число
раскрасок дуг диаграммы L элементами виртуального группоида Q'\ раскраска
называется правильной, если она удовлетворяет соотношениям виртуального
группоида в классических и виртуальных перекрестках.
Важным является вопрос о том, где брать (конечные) виртуальные
группоиды. Приведем обобщения конструкций дистрибутивных группоидов,
предложенных в [Mat], на виртуальный случай. Вот некоторые примеры.
Пусть G — конечная группа, д Ε G — конечный элемент в этой группе, а
η — фиксированное целое число. Тогда множество всех элементов группы G,
снабженное операциями χ о у = упху~п, f(x) = gxg-1, является виртуальным
группоидом.
Иначе можно строить виртуальные группоиды следующим образом: для
(конечной) группы G с фиксированным элементом д Ε G мы полагаем χ о у =
yx~1y,f{x) = дхд-1.
В случае коммутативных колец с единицей можно использовать операцию
χ о у = tx + (1 — t)y,f(x) = sx, где t,s — некоторые обратимые элементы.
Список дистрибутивных группоидов малой сложности приведен в
монографии Скотта Картера, Сейичи Камады и Масахико Сайто [CKS2].
Эти примеры дают две серии целочисленных инвариантов виртуальных
зацеплений.
18.4. Полином VА
В настоящем разделе мы приведем обобщение модуля Александера.
Построенный модуль ведет к так называемому VA-полиному — инварианту, не
имеющему аналога в классическом случае и обращающемуся в нуль на всех
классических зацеплениях.
Рассмотрим кольцо R полиномов Лорана от одной переменной t над Q.
Замечание 18.8. Здесь мы рассматриваем поле Q {вместо кольца Ζ как в
случае классического модуля Александера) для того, чтобы получать
евклидово кольцо полиномов.
Для каждых двух элементов кольца полиномов Лорана определим операцию
о по следующему правилу:
aob = ta + (l-t)b. (18.7)
Эта операция, очевидно, является обратимой слева. Обратная операция /
задается по следующей формуле:
а/Ь= -α+ ίΐ- - J Ъ. (18.8)
Очевидно, что а о а = а. Самодистрибутивность операции (18.7) может быть
легко проверена.
18.4. Полином VA
311
Таким образом, имея диаграмму классического зацепления молено
определить модуль над этим кольцом по следующему правилу: система образующих
модуля состоит из элементов аг, соответствующих дугам диаграммы; в каждом
классическом перекрестке мы выписываем соотношение (18.2), где операция о
имеет вид (18.7).
Замечание 18.9. В дальнейшем в настоящей главе мы будем считать все
модули право-левыми модулями; умножение элемента модуля на элемент
кольца справа и слева дает один и тот же результат; все модули
рассматриваются только над коммутативными кольцами.
Итак, модуль, определенный выше, является инвариантом зацеплений. Этот
модуль позволяет построить более наглядный инвариант, называемый
полиномом Александера. Это молено сделать следующим образом.
Диаграмма классического узла задает систему соотношений, которые
представляют собой систему из η уравнений с η переменными аг, г = 1,..., п.
Получается матрица соотношений размера η χ η . Она называется матрицей
Александера M(L). Поскольку в каждом уравнении сумма коэффициентов рана
нулю, матрица является вырожденной и ее определитель равен нулю.
Нетрудно доказать, что все миноры этой матрицы порядка η — 1 равны
между собой с точностью до умножения на ±tk. Полное доказательство
инвариантности полинома Александера можно прочесть, например, [МанО].
Замечание 18.10. Заметим, что мономы ±tk представляют собой полный
список всех обратимых элементов в кольце полиномов Лорана.
Попробуем теперь обобщить подход Александера на случай виртуальных
узлов. Мы будем использовать то лее кольцо полиномов Лорана от
переменной t. Для определения виртуального модуля Александера, нам нужно найти
"хорошую" интерпретацию функции /, т. е. такую, что
/(αοδ) = /(ίο+(1-ί)6) = ί/(ο) + (1-ί)/(δ). (18.9)
Здесь мы можем положить f(a) = а + ε, где ε — новый вектор
(фиксированный элемент в новом модуле). Более точно, рассмотрим кольцо полиномов
от of t, t~x (скажем, с рациональными коэффициентами). Для любых а,Ъ,с Ε R
положим
Va, Ъ : а о Ъ = ta + (1 - t) 6, f(c) = с + ε. (18.10)
В этом случае условие (18.9) вытекает непосредственно из определений.
Таким образом, по имеющейся диаграмме зацеплений L мы можем
построить модуль Александера виртуальной диаграммы M(L) над R, выбрав дуги
диаграммы в качестве образующих и (18.2), (18.4), (18.5) в качестве
соотношений (в форме (18.10)). В этом модуле имеется фиксированный элемент,
обозначенный через ε.
Из этого определения и теоремы 18.2 мы получаем следующую теорему.
Теорема 18.4. Пара (Μ(£),ε)? состоящая из виртуального модуля
Александера и фиксированного элемента ε в нем является инвариантом виртуальных
зацеплений.
312
Инвариантные полиномы
Посмотрим, что происходит с полиномом Александера.
Замечание 18.11. Для простоты мы рассматриваем дуги как элементы
модуля Александера (т. е. не вводим новых букв для обозначения элементов
модуля).
Пусть L — правильная виртуальная диаграмма зацепления с га
перекрестками. Так что она имеет в точности га длинных дуг: каждая длинная дуга
(возможно) разделяется на (короткие) дуги. Согласно определению операции
/(·), имеет место утверждение: если две дуги ρ и q принадлежат одной и той
же длинной дуге, то они удовлетворяют соотношению
ρ = q + re.
Для каждой длинной дуги фиксируем некоторую принадлежащую ей дугу.
Поскольку длинных дуг имеется ровно га, обозначим выбранные дуги через
bi, 62, · · ·, Ьш и остальные дуги через Ъг -\- ρυε, где ρ Ε Ζ.
Выпишем соотношения полинома Александера. Для каждого классического
ν напишем соотношение (18.2) в форме (18.7). Получим η χ гг-матрицу, в
которой строки соответствуют классическим перекресткам, а столбцы
соответствуют длинным дугам. Так что элемент j-ro столбца и г-й строки имеет вид
P(t) · (Ь3 -\-рзге), где P(t) полином от переменной t.
Перенесем все члены, содержащие ε, в правую часть равенства. Получим
уравнение
АЪ = сг, (18.11)
где b — столбец (6ι,..., 6m)*, с — столбец (ci,... cm)*, состоящий из
коэффициентов при ε ж А матрица системы (здесь * означает транспонирование).
Система (18.11) полностью определяет виртуальный модуль Александера Μ
вместе с элементом ε Ε Μ.
Как и в классическом случае, А называется матрицей Александера
диаграммы L. Легко видеть, что в обоих случаях — классическом и виртуальном —
А вырождена: для вектора ж=(1,...,1)* имеем:
Ах = 0.
Однако в отличие от классического случая в виртуальном мы имеем
неоднородную систему уравнений (18.11).
Матрица А вырождена, следовательно, ее ранг не превышает га— 1. Так что
уравнение (18.11) накладывает некоторые ограничения на ε: поскольку строки
матрицы А линейно зависимы, то это порождает некоторое линейное
соотношение на βίε,..., cm£. Это значит, что наш модуль Александера может иметь
соотношения ν(ί)ε = 0. Здесь мы говорим "может иметь" потому, что может
случиться, что из V(t)e = 0 вытекает V(t) = 0.
Замечание 18.12. Эту конструкцию можно обобщить, на случай
многокомпонентного (крашеного) зацепления, вводя разные переменные ετ для разных
компонент.
18.4. Полином V А
313
Множество всех г Ε R таких, что is = 0, образует идеал I С R. Кольцо R
является евклидовым, следовательно, идеал / является главным. Он
характеризуется своим минимальным полиномом VΑ Ε /, который определен с
точностью до обратимого элемента в R.
Определение 18.5. Назовем минимальный полином VA(t) Ε R идеала / V А-
полиномом диаграммы L виртуального зацепления. В случае, если R = {0}
положим VА = 0.
Замечание 18.13. Очевидно, что VА определен с точностью до обратимого
элемента в R, т. е. с точностью до ±tk.
Полином VA(L) зависит только от модуля M(L) с выделенным элементом ε.
Таким образом, получаем следующую теорему.
Теорема 18.5. Полином VА (определенный с точностью до обратимого
элемента в R) является инвариантом виртуальных зацеплений.
Вычислим теперь значения УА-полинома на некоторых виртуальных узлах.
Упражнение 18.5. Рассмотрим виртуальный трилистник и вычислим его
виртуальный группоид. На рис. 18.2 справа, мы имеем два классических
перекрестка: lull. Они задают систему из двух соотношений:
I : (α + ε)ί + 6(1 - t) = 6 +ε
II:bt+(b + e)(l-t) = α,
или, что эквивалентно:
at-bt = ε(1 - t)
b-a = e(t- 1).
Умножая второе уравнение на t и прибавляя его к первому, мы получаем:
0 = e(t - 1)(1 - t). Таким образом, VA(K) = (1 - t)2.
Имея два ориентированных виртуальных узла Κι и К^·, можно определить
их связную сумму следующим образом. Мы берем их диаграммы, разрываем
каждую из них в некоторой точке, а затем соединяем их согласно ориентации
(предполагается, что внутри некоторого круга, содержащего точки разрыва,
находятся лишь два фрагмента дуг, содержащие эти точки и никаких
перекрестков). В классическом случае эта операция хорошо известна и корректно
определена (т.е. не зависит от диаграмм узлов и точек разрыва).
Посмотрим, что происходит в случае виртуальных узлов. Например,
рассмотрим два экземпляра одного и того же узла К (виртуального трилистника,
показанного на рис. 18.2) и соединим его с собой двумя способами, как показано
на рис. 18.11 и рис. 18.12.
Вычислим УА-полином для этих связных сумм. Мы имеем две системы
уравнений.
В случае первой связной суммы (рис. 18.11) получаем:
/ : а — Ъ = te
II : — ta + tc = ε
III : -tc + td=(l -2t)e
IV : tb+(l-i)c-d= -te.
314
Инвариантные полиномы
d + ε
Рис. 18.11. Одна связная сумма КфК
Рис. 18.12. Другой способ построения связной суммы К^К
Нулевая линейная комбинация имеет вид t2(I) + t(II) + (III) + t(IV) = 0.
Таким образом, УА-полином равен t2(t) + ί(1) + (1 - 2t) + t(-t) = (t - l)2(t + 1).
Для второй связной суммы (рис. 18.12) мы имеем:
II
III
IV
а — Ъ = te
-ta + tc=(l- t)e
tb + (1 — t)c — d = 0
(l-t)b-c + db= -te.
Мы имеем нулевую линейную комбинацию (t3 — t2-\- t)(I) + (t2 — t + l)(-f-0 +
t2(III) + t(IV) = 0, из которой следует, что VΑ-полином равен (t — l)2(t2 + 1).
Эти два полинома не являются пропорциональными с коэффициентом \tk,
обратимым в основном кольце. Таким образом, две рассмотренные связные
суммы представляют собой различные виртуальные узлы.
Определение 18.6. Под (ориентированной) диаграммой длинного
виртуального узла мы понимаем иммерсию общего положения ориентированной прямой
R1 в R2, каждый перекресток которой (двойной и трансверсальный) помечен
либо как классический, либо как виртуальный; в первом случае указано,
какая ветвь идет сверху (образует переход), а какая — снизу (образует проход);
виртуальные перекрестки помечаются кружочком. Кроме того, мы требуем,
чтобы погружение совпадало с тождественным вложением оси Ох вне
некоторой окружности достаточно большого радиуса.
18.4. Полином VA
315
Диаграммы длинных виртуальных узлов имеют естественную ориентацию
слева направо (согласно ориентации R1). Мы всегда будем предполагать
ориентацию таковой, не указывая ее на рисунках.
Замечание 18.14. Говоря "длинный виртуальный узел" мы всегда имеем в
виду узел, а не зацепление.
Определение 18.7. Под (ориентированным) длинным виртуальным узлом
мы понимаем класс эквивалентности ориентированных диаграмм длинных
виртуальных узлов по обобщенным движениям Рейдемейстера.
Из ориентированной диаграммы обычного (компактного) виртуального
узла молено легко получить диаграмму длинного виртуального узла, разрывая
изначальную диаграмму в некоторой точке и вытягивания концы на
бесконечность (—ос и +ОС на оси Ох) согласно ориентации узла так, чтобы при
вытягивании не образовывалось новых перекрестков. Известно, что классификация
классических компактных (ориентированных) узлов совпадает с
классификацией классических длинных узлов, т. е. изотопические классы длинных узлов
совпадают тогда и только тогда, когда совпадают классические узлы, из
которых они получаются.
Обратную операцию (замыкание), сопоставляющую длинному
виртуальному К узлу компактный, получаемый соединением концов, будем обозначать
через С1 : К ^ С1(К).
Два примера, приведенные выше показывают, что существуют два
неизотопных длинных виртуальных узла Κι, i^2, изображенные на рис. 18.13,
получающиеся разрыванием одного и того же виртуального узла Κι. Это еще один
феномен теории виртуальных узлов, он был впервые упомянут в [GPV].
Рис. 18.13. Два различных длинных виртуальных узла, происходящие из
одного и того же компактного виртуального узла
Действительно, если бы Κι и К2 были изотопны (эквивалентны), то
виртуальный узел, указанный на рис. 18.11 был бы изотопен виртуальному узлу,
316
Инвариантные полиномы
изображенному на рис. 18.12 (изотопия длинных узлов позволяет изотопиро-
вать слагаемое в связной сумме, оставляя его концы фиксированными).
Последнее невозможно, следовательно длинные узлы Κι и К2 не являются
эквивалентными.
Таким образом, теория длинных виртуальных узлов отличается от
теории компактных виртуальных узлов.
Более того, имеет место следующая теорема.
Теорема 18.6. Для каждого изотопического класса узла К множество
длинных узлов к таких, что Cl(k) = К счетно.
Эта теорема была доказана Д. Сильвером и С. Уильяме и (независимо)
автором настоящей книги. Ее доказательство будет приведено в главе 21.
18.4.1. Свойства VA-полинома
Теорема 18.7. Для каждого виртуального узла {не зацепления!) К полином
VA(K) делится (t - I)2.
Доказательство. Пусть К — виртуальная диаграмма, задающая
ориентированный узел К. Выберем классический перекресток V\ на этой диаграмме.
Пусть X — длинная дуга, исходящая из Vi, и пусть χ — первая (короткая)
дуга дуги X, инцидентная перекрестку V\. Обозначим метку,
соответствующую дуге ж, через а\. По определению, всем дугам, принадлежащим длинной
дуге X, сопоставлены элементы модуля вида ai~\-ks,k Ε N. Рассмотрим
последнюю дугу длинной дуги X; ей сопоставлен элемент а\ -\-k\e. Эта дуга упирается
в классический перекресток; обозначим его через V^- Выберем теперь первую
дугу, исходящую из V<2, и сопоставим ей <22 + к\е. Расставим далее все метки
CL2 + ке, соответствующие другим дугам этой длинной дуги. Пусть последней
из них соответствует α 2 + &2£? и пусть эта дуга заканчивается в перекрестке Vs.
Сопоставим аз + &2 первой дуге, исходящей из Уз, и так далее.
В конце мы вернемся в перекресток V\. Действуя по нашему правилу, мы
должны сопоставить некоторый элемент дуге, с которой мы начинали.
Покажем, что процесс сходится, т.е. дуге, исходящей из V\ соответствует а\ + 0 · е.
Действительно, будем следить за ε-частью меток при движении вдоль
ориентации узла от V\ к V\. В самом начале она равна нулю по построению. Далее,
при проходе через каждый виртуальный перекресток, она либо увеличивается
на ε, либо уменьшается ε в зависимости от того, в каком направлении мы этот
перекресток проходим, а при проходе через классический перекресток она не
меняется по построению. Но так как каждый виртуальный перекресток
проходится дважды, -\-е и —ε сокращаются. Таким образом, мы возвращается в V\
с 0· ε.
Заметим, что процесс сошелся бы, если бы мы начинали с любой дуги и
любого целого числа в качестве коэффициента при ε.
Таким образом, каждое соотношение в виртуальном модуле Александера
имеет правую часть, кратную e(t — 1): соотношение
(а,г +ps)t+ (clj + <?ε)(1 — t) = (afe +ρε)
18.4. Полином VA
317
эквивалентно соотношению
а^ + aj(l -t)-ak = (t- l)(q - ρ)ε. (18.12)
Из этого следует, что VA(K) делится на (t — 1).
Обозначим слагаемые (бывшие q и р), соответствующие г-у перекрестку в
правой части (18.12) через qi и ρ ι соответственно.
Найдем соотношения, которым удовлетворяют строки виртуальной
матрицы Александера. Каждое соотношение должно выполняться при любом t,
следовательно, и при t = 1.
Обозначим строки матрицы Μ через М^. Если для матрицы Μ имеет место
ΣΓ=ι с{М{ = 0, то ΕΓ=ι Ci\t=iMi\t=i = 0.
Матрица M(K)\t=i очень проста. Каждая ее строка (также как и каждый
столбец) состоит из элементов 1 и —1 и нулей. Соотношения между строками
этой матрицы очевидны: сумма всех строк с единичным коэффициентом равна
нулю. Таким образом мы имеем Уг, j = 1...,η : c^|t=i = cj\t=i·
Каждое соотношение на коэффициенты при ε имеет вид (Σ™=1 Ci(qi-pi)) x
x(t- 1) = 0.
Поскольку мы интересуемся тем, делится ли это выражение на (t— 1)2,
можно заменить q на Q|t=i- Таким образом, осталось доказать, что для заданной
диаграммы К имеет место Y^=1(qi — Pi) = 0.
Докажем это индукцией по числу η классических перекрестков.
Для η = 0 нечего доказывать.
Пусть К — диаграмма с η классическими перекрестками, а К' — диаграмма
полученная из К заменой классического перекрестка на виртуальный.
Рассмотрим случай положительного классического перекрестка X
("отрицательный" случай полностью аналогичен рассматриваемому положительному,
изображенному на. рис. 18.14).
Рис. 18.14. Метки для К и К'
Обозначим дугу, расположенную в левом нижнем углу обеих диаграмм
через а, а другие дуги — через Ъ и с, d (для К имеем а = d), см.рис. 18.14. пометим
меткой 0 дуги а обеих диаграмм. Вычислим ^2{q% — р%) для К' и К. Согласно
предположению индукции для К' эта сумма равна 0.
Пометим дугу Ъ первой диаграммы меткой Ζ&ι·
Перекресток X диаграммы К имеет q = 1ы,р = 0, так что его вклад
равен 1ы.
Все другие перекрестки диаграммы К (классические или виртуальные)
находятся во взаимно однозначном соответствии с перекрестками диаграммы К'.
318
Инвариантные полиномы
Подсчитаем разность между числами ридв этих диаграммах. Разница
порождается классическими перекрестками. В этих перекрестках метки отличаются
в той части, идущей от дуги d к дуге Ъ. Действительно, при прохождении с дуги
а на дугу d в диаграмме К'', мы не меняем метку, в то время как на диаграмме
К метка меняется. Таким образом, после d метки для диаграмм К и К'
отличаются на единицу во всех вершинах до дуги Ъ. После перехода с дуги Ъ на дугу
с метки в К и К' снова становятся одинаковыми.
Мы вычислим количество классических и виртуальных перекрестков по
пути от d до Ъ. Общее число перекрестков с учетом знаков равно нулю. Сумма
количеств виртуальных перекрестков с учетом знаков равна —q. Поэтому
алгебраическое число классических перекрестков равно q. Каждый из них дает
вклад —1 в разницу между К и К''. Таким образом, q — q = 0, что завершает
шаг индукции и, следовательно, доказательства теоремы. D
Следующая теорема может быть выведена непосредственно из определений.
Теорема 18.8. Инвариант VА аддитивен. Более точно, для каждой
связной суммы К = К1ФК2 двух зацеплений К\ и К2 существуют обратимые
элементы λ, μ е R : VA(K) = \VA(Ki) + μνΑ(Κι).
Следует заметить, что УА-полином может быть определен с большей
точностью (до ±tfc), если мы рассмотрим кольцо Q[£, £-1]. Однако, такой подход
работает для узлов, в то время как соответствующий идеал над Z[t,t-1]
является главным идеалом.
18.5. Мультипликативный подход
В настоящем разделе мы используем конструкцию аналогичную
предыдущей; однако, вместо дополнительного "аддитивного" элемента ε добавим к
модулю некоторые "мультипликативные" элементы.
Всюду в этом разделе мы будем иметь дело только с ориентированными
зацеплениями и только с правильными диаграммами.
18.5.1. Полином от двух переменных
Ниже мы построим два инвариантных полинома виртуальных зацеплений
([Ма5, КМ], краткую версию см. в [Ман5]). В настоящем подразделе будет
построен первый из них (от двух переменных). Второй, который описывается
в подразделе 18.5.2, связан с крашеными зацеплениями: каждому крашеному
зацеплению из гг-компонент мы сопоставим инвариантный полином от 2гг
переменных. Первый инвариант получается из второго заменой переменных.
Пусть L — диаграмма виртуального зацепления L с η классическими
перекрестками.
Построим матрицу M(L) размера (η χ ή) с элементами из Z[£, £-1,s,s-1]
следующим образом.
Сначала перенумеруем все классические перекрестки диаграммы L
натуральными числами от единицы до η и сопоставим каждому перекрестку
выходящую из него длинную дугу. Каждая длинная дуга начинается с (короткой)
дуги. Сопоставим такой дуге метку, равную единице. Все другие дуги длинной
18.5. Мультипликативный подход
319
дуги будут помечены степенями s , к Ε Ζ, следующим образом см. рис. 18.15.
Проходя через виртуальный перекресток, мы умножаем метку на s если
движемся слева направо (предполагая что дуга, по которой движемся,
ориентирована вверх) или на s_1 в противном случае.
Рис. 18.15. Символы sk на дугах
Поскольку диаграмма правильная, разметка определена корректно.
Рассмотрим классический перекресток Vi с номером г. Он инцидентен трем
дугам р, д, г, принадлежащим длинным дугам с номерами г, J, /с; при этом номер j
принадлежит дуге, проходящей сквозь перекресток V^. Обозначим степень
переменной s метки, соответствующей дуге q, через а^/, & степень метки,
соответствующей дуге г, через а^ь см.рис. 18.16.
Рис. 18.16. Дуги инцидентные классическим перекресткам
Определим г-ю строку матрицы M(L) как сумму следующих трех строк
У\-,У2·, Уз длины п. Каждая из этих строк имеет только один ненулевой элемент.
Элемент с номером г строки у\ равен единице. Если перекресток положителен,
мы полагаем
У2к = sa'H, y3j = (t- l)sa"; (18.13)
в противном случае полагаем
y2k = -sa'kt-\ y3j = (t-1-l)sa". (18.14)
Положим C(L) = detM(L). Очевидно, что C(L) не зависит от нумерации
строк матрицы.
320
Инвариантные полиномы
Теорема 18.9. Для любых двух диаграмм L и L' одного и того же
виртуального зацепления L имеем ((L) = tl((Lf) для некоторого Ι Ε Ζ.
Доказательство. Заметим, что чисто виртуальные движения Рейдемейстера
Ω^,Ω^,Ω^ не изменяют матрицы M(L) и, следовательно, полином ζ.
При применении полувиртуального третьего движения Рейдемейстера мы
умножаем одну строку матрицы на s и один столбец матрицы на s^1. В самом
деле, пусть г количество классических перекрестков, к которым применяется
полу виртуальное движение. Тогда мы получаем следующие две диаграммы:
L и L7, см. рис. 18.17.
Рис. 18.17. Инвариантность относительно полу виртуального движения
Для простоты предположим, что дуги, помеченные метками sz,sJ и s
соответствуют длинным дугам с номерами 2,3, и 4.
Для сравнения элементов матриц M(L) и M(Lf) в р-й строке и q-м столбце,
нужно рассмотреть метки (коротких) дуг на q-й длинной дуге инцидентной
перекрестку с номером р. При ρ φ 1 и q φ 1 метки двух дуг одинаковы. Если ρ = 1
и g = 1, то метки двух диаграмм совпадают по определению: они обе равны s°.
Первая строка ρ = 1, q Φ 1 может быть рассмотрена непосредственно: у нас не
более трех ненулевых элементов в этой строке. Наконец, если q = Ι,ρ φ 1, то
мы имеем дело с длинной дугой, выходящей из первого перекрестка.
Рассмотрим область D, в которой действует полувиртуальное движение Рейдемейстера,
показанную на рис. 18.17. Первая длинная дуга диаграммы L покидает эту
область с меткой s-1, соответствующей некоторой (короткой) дуге, а в случае
V — с меткой s°. Таким образом, все дальнейшие метки на данной длинной
дуге (т. е. все, кроме самой начальной) будут различаться. А именно, метка в
случае U будет равна соответствующей метке для L, умноженной на s.
Таким образом, мы получаем следующее:
Обе матрицы M(L) и M(Lf) имеют 1 на месте (1,1) и одни и те же элементы
везде, кроме позиций (1,р) и (д, 1) при ρ φ 1 и q φ 1.
При ρ φ 1 мы имеем M{L')pi = s-M(L)pi, а при q φ 1 имеет место M(L')iq =
s-l-M(L)lq.
Таким образом, полу виртуальное движение также не меняет определителя.
Приступим к рассмотрению классических движений Рейдемейстера.
Начнем с Ωι. Предположим, что мы добавляем петлю, которая разбивает некото-
18.5. Мультипликативный подход
321
рую дугу из первой длинной дуги, которая имеет метку sz, тем самым разбивая
нашу дугу (и длинную дугу) на две; одна из них лежит "до" добавленного
перекрестка, а вторая — после. Эти две части соответствуют некоторым столбцам
матрицы Μ. Обозначим их через А и В соответственно.
После применения такого движения количество строк матрицы также
увеличилось на единицу: новая строка будет соответствовать добавленному
перекрестку. Перенумеруем теперь перекрестки по следующему правилу: всякому
старому перекрестку с номером j сопоставим номер j' +1, а новому перекрестку
сопоставим номер один. Соответствующая строка будет иметь ненулевые
элементы только на первом и втором местах. Кроме этого, вместо столбцов А и В
(в сумму которых раскладывался изначальный рассматриваемый столбец), мы
получим столбцы А ж s~l · В так как, согласно правилам, часть длинной дуги,
соответствующей В, начинается не с s% но с s° = 1.
Таким образом, в каждом из четырех случаев первого движения Рейдемей-
стера, преобразование будет иметь вид:
(-*+* ")~{^ *! Ι)-
Здесь χ и у — некоторые функции, зависящие только от t. Действительно,
рассмотрим две дуги диаграммы после применения движения Рейдемейстера.
Если первая дуга инцидентна первому перекрестку лишь однажды, то χ равен
единице, а у равен минус единице, т. е. сумме — t и (t— 1), либо сумме — j и (| —1).
В случае, если первая дуга инцидентна перекрестку дважды, мы можем иметь
две возможности: χ = t,y = —t, или χ = |, у = — j. Здесь и далее W обозначает
некоторую фиксированную прямоугольную матрицу, которая не меняется при
применении конкретного движения Рейдемейстера к конкретной диаграмме.
Теперь можно непосредственно проверить, что в каждом из четырех
вышеуказанных случаев определитель либо не изменяется, либо умножается на t^1.
Перейдем теперь к движению Ω2. Мы будем выполнять все вычисления
лишь для случая, указанного на рис. 18.18.
|2
Рис. 18.18. Второе движение Рейдемейстера
Это движение добавляет два новых перекрестка (они получают номера один
и два, а все остальные перекрестки увеличивают свои номера на два).
Посмотрим, что произойдет с матрицей.
Допустим, что начальная диаграмма имела η перекрестков. Обозначим
первые два столбца матрицы через А и В + С, где В и С имеют следующий гео-
4/ \3
322
Инвариантные полиномы
метрический смысл. Столбец В + С соответствует длинной дуге, т. е. всем
перекресткам дуги. После второго движения Рейдемейстера эта длинная дуга
прервется некоторым интервалом, и все перекрестки этой дуги разделятся на
две части: перекрестки до и перекрестки после. Соответственно и столбец будет
разбит на два столбца, которые обозначены через В и С.
Таким образом, первая матрица имеет вид:
(А В + С W).
В правой части рис. 18.18 мы имеем диаграмму, которой соответствует
матрица размера (п + 2) χ (η + 2). Она имеет вид:
1
0
Cs-i
-t
1
0
(t- l)sz
(ί -1) **
A
0
t
в
0...0
0...0
w
Отметим, что второй столбец последней матрицы не имеет ненулевых
элементов, за исключением элементов (—t) и 1 в первой и второй строках.
Нам теперь нужно лишь показать, что начальная и преобразованная
матрицы имеют одинаковые определители.
Мы сделаем это, преобразуя вторую матрицу следующим образом. Сначала
мы прибавим второй столбец, умноженный на sl (^—), к третьему столбцу. Мы
получим:
1 -tO 0 0...0
О 1 0 -f 0...0
Cs-i О А В W
Теперь прибавим первый столбец, умноженный на sJ, к четвертому столбцу.
Получим:
1
0
Cs~j
-t
1
0
0
0
А
sJ 0... 0
-f 0...0
В + С W
Наконец, прибавим второй столбец, умноженный на ^-, к четвертому
столбцу. Мы получим матрицу
1
0
Cs-'
-t
1
0
0
0
А
0 0...0
0 0...0
В + С W
Определитель этой матрицы, очевидно, совпадает с определителем исходной
матрицы.
Теперь осталось доказать инвариантность ζ относительно Ω3. Как и прежде,
мы рассмотрим только одну возможность. Выполним все вычисления в случае,
изображенном на рис. 18.19.
Три перекрестка, помечены римскими цифрами 1,11, Ш, так что можно
однозначно восстановить номера выходящих дуг и их метки. Остальные
длинные дуги, изображенные на рисунке, имеют номера 4,5 и 6 с метками sl, sJ, s
на их последней дуге.
18.5. Мультипликативный подход
323
Рис. 18.19. Третье движение Рейдемейстера
Мы имеем две матрицы Μι и М2:
/
Μι
1
0
_1
(i-i) 0
1 0
0 1
S
0
0
4t-
ι)
-1)
к
0...0 \
0...0
-ts
О 0...0
V о
1
о
м2
о
о
W
W
-1)
1)
-tsK
J
0...0 \
0...0
0...0
V о /
Для того, чтобы показать, что эти две матрицы имеют одинаковые
определители, мы произведем следующие операции над строками и столбцами
(используя только первые три строки, имеющие нули на местах ^ 7) и только
шесть столбцов (первый из них имеет нули на местах ^ 4).
Преобразуем сначала первую матрицу следующим образом. Прибавим
первый столбец, умноженный на sJ(l - t), к пятому столбцу, а затем прибавим
первый столбец, умноженный на s (t — 1), к шестому столбцу. Получим
матрицу
/
М[
1
0
_1
(i-i)
1
0
0
0
1
S
0
0
sj (1
si(t-
-t)
1)
°(ί-ΐ)
-tsK
W
V 0
..0\
.0
.0
/
Мы видим, что все элементы матриц М[ и М2, за исключением тех, которые
принадлежат первой строке, совпадают. Если мы прибавим вторую строку
матрицы М2, умноженную на (l — j), к первой строке матрицы М2, то получим в
324
Инвариантные полиномы
точности первую строку матрицы М[. Таким образом, detM\ = detM[ = detM^^
что завершает доказательство. D
Пусть т, Μ — степени переменной t старшего и младшего мономов в ((L).
Положим ξ(Σ) = г(Е^)(Щ. По построению, ξ является инвариантом
виртуального зацепления.
Имеют место следующие свойства полинома ζ.
Теорема 18.10. Для виртуального зацепления L, изотопного классическому,
t(L) = 0.
Доказательство. Для диаграммы L зацепления L, не имеющей виртуальных
перекрестков, дуги совпадают с длинными дугами, следовательно все метки
равны s° = 1. Поэтому матрица Μ совпадает с обычной матрицей Алексан-
дера, которая вырождена, ибо имеет собственный вектор (1,..., 1) с нулевым
η
собственным значением. D
Теорема 18.11. Для каждой тройки Конвея L+,L-,Lq существуют ρ, q Ε Ζ
такие, что ίρξ(Σ+) - tqC(L_) = (1 - i)C(L0).
Доказательство. Имея в виду теорему 18.9, мы можем слегка модифицировать
тройку Конвея, выполнив первое движение Рейдемейстера и затем проверить
условия теоремы для троек диаграмм, имеющих (локально) вид, показанный
на рис. 18.20.
Рис. 18.20. Модифицированная тройка Конвея
Здесь мы нумеруем перекрестки римскими цифрами. Дуги, не выходящие из
выбранных перекрестков, помечаются метками и натуральными числами.
Такая "согласованная" нумерация возможна всегда, когда все дуги,
представленные на рисунке, различны. Главным случаем является тот, в котором каждый
диагональный элемент матрицы равен единице. В других случаях разметка,
показанная на рис. 18.20, возможно, не имеет места, но утверждение все-таки
остается верным.
Обозначим матрицы, соответствующие трем диаграммам на рис. 18.20 через
М_|_, М_, Mq. Как и прежде, мы ограничиваем наши вычисления малой частью
матриц. В этом случае эти матрицы отличаются только в первой и второй
строках. В этих строках все элементы, за исключением элементов с номерами 1,2,3
18.5. Мультипликативный подход
325
и 4, равны нулю. Так что мы выполним вычисления, относящиеся к
подматрицам размера 2x4 матриц М+, М_, Mq .
Изначально эти части таковы:
М+
м_
1 t - 1 0 -ts*
О 1 -si О
М0
1 0 0-^
-ι ι -т °
1 0 -sl 0
0 1 0 -sj
Прибавим вторую строку матрицы М+ к первой ее строке. В матрице М_
выполним следующее. Умножим первую строку на t и затем прибавим вторую
строку, умноженную на t, к (уже видоизмененной) первой строке. В матрице
Mq прибавим вторую строку, умноженную на t, к первой строке.
После выполнения этих операций, мы получим три матрицы М^, Mi, Mq,
имеющие одинаковую первую строку. Их подматрицы размера 2 χ 4, с которыми
нам предстоит работать, выглядят следующим образом:
М'+
м'_
Щ
1 t -sl -tsJ
0 1 -si 0
1 t -si -tsJ
-1 1 -£ 0
1 t -sl -tsJ
0 1 0 -si
Очевидно, что, det(M^) = det(M+), det(M^) = det(M0), det(Mi) = t · det(M_).
В матрице М'_ прибавим первую строку, умноженную на (1 — ^), ко
второй строке. Мы получим матрицу М" такую, что det M'J_ = detM'_. Матрицы
M^,M^,Mq отличаются только второй строкой. Их вторые строки выглядят
следующим образом:
р= (0,1,-^,0,0,...,0),
q= (0,i,-sz,(l-i)^',0,...,0),
г = (0,l,0,-sJ,0,...,0).
Принимая во внимание, что p — q= (1 — £)г, мы получаем утверждение теоремы.
D
Полином ξ позволяет различать некоторые виртуальные зацепления,
которые не могут быть распознаны полиномом Джонса-Кауфмана У,
предложенным в [КаиЗ] (например, тривиальное двухкомпонентое зацепление и
зацепление, показанное на рис. 18.21).
326
Инвариантные полиномы
С
Рис. 18.21. Зацепление с тривиальным полиномом Джонса-Кауфмана
18.5.2. Полином многих переменных
В настоящем разделе мы построим предложенной автором обобщение
полинома ξ на случай многокомпонентых зацеплений. Основная идея построения
полинома от η + 1 переменной появились в работе [Ма5]; приводимый ниже
полином от 2п переменных (для зацеплений из η компонент) впервые был
опубликован в [КМ].
Рассмотрим гг-компонентное зацепление L с нумерованными компонентами.
Фиксируем η образующих £]_,..., tn и η образующих si,..., sn. Мы будем
сопоставлять дугам диаграммы L зацепления L элементы модуля над кольцом
Z[si,..., sn, ίι,..., tn]] сам модуль при этом будет инвариантным. Занумеруем
классические перекрестки этого зацепления натуральными числами 1,..., га.
Перекрестки диаграммы (классические и виртуальные) соответствуют
соотношениям из этого модуля.
Соотношение в виртуальном перекрестке выглядит следующим образом:
при прохождении через г-ю компоненту зацепления слева направо
(относительно ориентации компоненты, через которую мы переходим), элемент "после"
получается умножением элемента, соответствующего дуге "до" на Si. В случае,
когда мы переходим с правой стороны на левую, элемент "после" получается
умножением элемента "до" на s~ , где j — номер компоненты, через которую
мы проходим.
В классических перекрестках мы делаем следующее. Рассмотрим
перекресток, в котором г-я компонента проходит над (образует переход), а j-я
компонента проходит под (образует проход). Предположим, что дуге перехода
соответствует метка 6, дуге, лежащей справа от нее (согласно ориентации) — метка
а, а дуге, лежащей слева от нее — метка с, см. рис. 18.22.
Тогда соотношение в модуле выглядит следующим образом tid-\-(l — tj)b = с.
Обозначим полученный модуль через Μ (Li).
Инвариантность самого модуля относительно движений доказывается теми
же методами, что и инвариантность произвольных виртуальных группоидов,
нужно лишь аккуратно проверить движения, в которых участвуют зацепления
из разных компонент. Оказывается, что этот модуль приводит к
полиномиальному инварианту, являющемуся обобщением инварианта, предложенного в
предыдущем разделе).
Сначала сопоставим каждой дуге диаграммы L моном от переменных si,...,
sn (он будет соответствовать операциям в виртуальных перекрестках) следу-
18.5. Мультипликативный подход
327
Рис. 18.22. Перекресток крашеного зацепления
ющим образом. Каждому классическому перекрестку соответствует длинная
дуга (так как диаграмма является правильной). Сопоставим начальной (по
ходу ориентации зацепления) дуге каждой длинной дуги метку 1. После этого
мы будем сопоставлять мономы от переменных Si всем дугам, относящимся к
данной длинной дуге так, как описано раньше, см. рис. 18.23.
2 компонента
1 компонента
Рис. 18.23. Размеченное двухкомпонентное зацепление
Построим теперь матрицу, исходя из соотношений в перекрестках. Каждая
строка этой матрицы соответствует перекрестку, а каждый столбец матрицы —
длинной дуге. Элемент матрицы выражает "инциденцию" перекрестка и
длинной дуги в следующем смысле. Предположим, что имеется положительный
перекресток /С под номером г (таковым же будет и номер исходящей длинной
дуги), в который входит длинная дуга номер j, имеющая метку Ρ (эта дуга
лежит на компоненте с номером р), при этом ребро перехода имеет номер к и
метку Q (это ребро лежит на компоненте с номером q). Тогда г-я строка
нашей матрицы будет состоять не более, чем из трех элементов, более точно, она
представляет собой сумму трех строк, в каждой из которых ровно один элемент
ненулевой. Одна из этих строк имеет г-ж элемент, равный единице, другая
имеет элемент с номером j, равный —tqP, а третья строка имеет элемент, равный
328
Инвариантные полиномы
(tp — 1)Q, на месте к. В случае отрицательного перекрестка JX^ мы также
имеем строку, являющуюся суммой трех строк: одна из них имеет tq на г-м месте,
у другой j-й элемент равен — Р, а у третьей /с-й элемент равен (1 — tp)Q.
Определитель этой матрицы не меняется при перенумеровке строк и
соответствующей ей перенумерации столбцов.
Таким образом, определитель корректно определен для правильных
диаграмм. Обозначим этот определитель через п.
Проверка инвариантности этого определителя относительно всех
обобщенных движений Рейдемейстера (кроме первого классического, при котором он
может умножиться на ti проходит так лее, как и в предыдущем разделе).
Продемонстрируем инвариантность относительно самого сложного движения,
а именно, третьего классического движения Рейдемейстера.
Рассмотрим две диаграммы, изображенные на рис. 18.24.
Номера перекрестков на этом рисунке помечены римскими цифрами,
номера дуг — арабскими цифрами, номера компонент — обведены в кружочек,
а мономы, соответствующие входящим дугам, обозначены буквами Р, Q, R, см.
рис. 18.24.
Рис. 18.24. Разметка дуг для Ω3
Рассмотрим матрицы, соответствующие диаграмме до применения
движения и диаграмме после применения движения. Первой диаграмме соответствует
матрица
/
1
0
-и
0 0 0 (tk-l)Q
1 0 (tj-l)P -UQ
0 1 (tk-l)P 0
-tjR 0.
0 0.
0 0.
.0\
.0
.0
V 0
w
(18.15)
18.5. Мультипликативный подход
329
Матрица, соответствующая второй диаграмме, выглядит следующим
образом:
/ 1 0 0 (ife-l)P
0 1 0 (tj - ΐ)Ρ
-tj (ife-1) 1 0
о
0
UQ
0
-UR 0.
0 0.
0 0.
.0 \
.0
.0
w
\ о
(18.16)
/
Вторые строки этих матриц совпадают. Рассмотрим их третьи строки. В
первой матрице прибавим первую строку, умноженную на ti, к третьей строке. Во
второй матрице прибавим первую строку, умноженную на tj, а также вторую
строку, умноженную на (1 — £&), к третьей строке. Мы получим две матрицы,
у которых совпадают третьи строки. Их общая третья строка имеет вид
(o,o,i,(^-i)p,^-i)q,
-^•Д,0,...,0).
Первые столбцы новых двух матриц совпадают и имеют ровно один
ненулевой элемент, а именно, единицу на первом месте. Таким образом, посредством
прибавления этого столбца можно сделать первые строки двух матриц
равными. По этой причине определители этих матриц, а следовательно, и
изначальных двух матриц, совпадают.
Что касается первого движения Рейдемейстера, после его применения
определитель матрицы может умножиться на ti , где г — номер компоненты, к
которой применяется первое движение Рейдемейстера.
Таким образом, мы получаем теорему.
Теорема 18.12. Полином к инвариантен относительно движений
Рейдемейстера с точностью до умножения на мономы от переменных ti.
Полином к можно нормировать по степеням ti подобно тому, как
нормируется полином ζ (для получения полностью инвариантного полинома ξ). Мы
этого делать не будем.
Следующее утверждение очевидно по построению.
Утверждение 18.1. Для зацепления из k-компонент L мы имеем
K(L)\s=Sl=...=Sk^=t1=-=tk = (Щ.
Из этого следует, что полином k(L), по крайней мере, не слабее, чем полином
ζ (или ξ). На самом деле к, строго сильнее.
Рассмотрим двухкомпонентное зацепление L, показанное на рис. 18.25.
Рис. 18.25. Зацепление, на котором ξ(Σ) = 0.
330
Инвариантные полиномы
Нетрудно подсчитать, что на зацеплении L полином k(L) не равен нулю,
а полином £(L) равен нулю, поэтому k(L) строго сильнее, чем £(L).
Полином к может служить и для распознавания узлов (а не только для
зацеплений из многих компонент). Для этого нужно рассматривать операции
удвоение (утроение, и т.д.) узла.
Глава 19
Обобщения полинома
Джонса-Кауфмана
В настоящей главе мы опишем обобщение полинома Джонса-Кауфмана для
виртуальных зацеплений, в котором учитывается некоторая "дополнительная
информация", а именно, некоторые геометрические объекты, связанные с
кривыми на двумерных поверхностях (см. [Маб, Ман7]). Во втором разделе
настоящей главы мы рассмотрим вопросы минимальности в теории виртуальных
узлов и предложим различные обобщения теоремы Кауфмана-Myрасуги
(некоторые из приводимых здесь результатов были опубликованы в [Манб]).
19.1. Введение. Основные опеределния.
Как было показано ранее (посредством дистрибутивного группоида и
посредством теоремы Куперберга), обычная эквивалентность на классических
узлах совпадает с эквивалентностью, происходящей из виртуальных узлов.
Поэтому важным является вопрос: какие инварианты классических узлов могут
быть естественным образом обобщены до инвариантов виртуальных узлов?
Мы будем строить инвариант (который мы будем называть полиномом, хотя
его значения на виртуальных зацеплениях являются не полиномами, а
некоторыми элементом модуля над кольцом полиномов Лорана) виртуальных
зацеплений, который совпадает с полиномом Джонса-Кауфмана на классических
узлах. Один такой полином уже имеется — полином, предложенный Кауфманом
[КаиЗ]; поэтому мы начнем с напоминания основных его свойств и путей его
модернизации посредством внесения "геометрии" виртуальных узлов. Пусть L —
ориентированная виртуальная диаграмма с η классическими перекрестками.
Как обычно, обозначим через \L\ неориентированную диаграмму, получаемую
из диаграммы L забыванием ориентации.
Напомним, что полином Джонса-Кауфмана виртуальных зацеплений имеет
вид
ХЩ = (-a)-3w^^aa^-^s\-a2 - α"2)^)"1, (19.1)
s
где сумма берется по всем состояниям диаграммы |L|, w(s) означает число
закрученности ориентированной диаграммы L.
332
Глава 19
В [КаиЗ] Кауфман показал инвариантность полинома X относительно
обобщенных движений Рейдемейстера. Он также указал на его инвариантность
относительно движения, не являющегося изотопией, см. рис. 18.10. Этот
замечательный факт служит для доказательства многих теорем о полиноме Джонса-
Кауфмана и некоторых других инвариантах.
По причине инвариантности относительно виртуализации полином Джонса-
Кауфмана не отличает тривиального двухкомпонентного зацепления от
виртуального зацепления Λ, изображенного на рис. 18.25 в предыдущей главе.
Перейдем к построению обобщения нашего инварианта. Пусть S —
множество всех пар (Μ, δ), где Μ — гладкая ориентированная замкнутая двумерная
поверхность без края (возможно несвязная, но с конечным числом связных
компонент), а δ — неупорядоченное конечное семейство простых замкнутых
кривых, погруженных в М.
Определим классы эквивалентности на множестве S посредством
следующих элементарных отношений эквивалентности:
1. Две пары (Μ, δ), (Μ7, δ') эквивалентны, если существует гомеоморфизм
Μ —>· Μ7, отождествляющий наборы δ и δ'.
2. Для фиксированного многообразия Μ если набор кривых δ свободно
гомотопен набору кривых δ' в М, то пары (Μ, δ) и (М, δ') эквивалентны.
3. Две пары (Μ, δ) и (М, δ') являются элементарно эквивалентными в
случае, если δ' получается из δ добавлением простой кривой,
ограничивающей диск и не пересекающей других кривых из множества δ'.
4. Пары (Μ, δ) и (7V, δ) эквивалентны, если N является многообразием,
полученным из Μ удалением двух дисков, не пересекающих кривых из δ,
и вклеиванием ручки на их место (стабилизация).
5. Для каждого компактного замкнутого ориентированного 2-многообразия
N пары (Μ, δ) и (М U Ν, δ) являются эквивалентными.
Здесь U означает несвязную сумму многообразия Μ (со всеми кривыми из
набора δ на этом многообразии) и многообразия N (с пустым набором кривых).
Замечание 19.1. Отметим, что последняя (пятая) эквивалентность
является частным случаем четырех предыдущих; мы оставляем ее для
дальнейшего удобства изложения.
Обозначим множество получающихся таким образом на S классов
эквивалентности через Θ. Вопрос о том, представляют ли два элемента из S один и
тот же класс эквивалентности в Θ, легко распознается алгоритмически [Rein].
Идея состоит в том, что (в общем положении) элемент из S является
минимальным по количеству перекрестков тогда и только тогда, когда он является
минимальным по роду. Рассмотрим элемент (Μ, δ) G S. Назовем двуугольником
два отрезка 1\, 1^ кривых (или одной кривой) из δ, такие, что 1\ Π1^ = dl\ = dl^
состоит из двух точек, при этом объединение 1\ U /2 ограничивает диск на М.
Под петлей будем понимать отрезок кривой из набора 5, конечные точки
которого совпадают, при этом отрезок не имеет других точек самопересечения,
кроме концевых, а получившаяся замкнутая кривая ограничивает диск на М.
19.1. Введение. Основные опеределния.
333
Таким образом, алгоритм сводится к поиску возможности
дестабилизировать поверхность (применить к ней четвертую эквивалентность,
уменьшающую род) либо к уменьшению ее посредством разведения двуугольника или
удаления петли, см. рис. 19.1, либо к удалению отдельно стоящей тривиальной
окружности, которая не имеет пересечений с другими кривыми. В случае,
когда ничего из вышеперечисленного сделать невозможно, диаграмма является
минимальной.
Рис. 19.1. Удаление петли и разведение двуугольника
Минимальные диаграммы отличаются друг от друга применением
третьего движения Рейдемейстера, которое не меняет ни поверхности, ни количества
перекрестков. Поэтому распознавание двух эквивалентных минимальных
диаграмм представляет собой простую комбинаторную задачу.
Основная идея построения нашего инварианта состоит в следующем. Мы
строим функцию на ориентированных виртуальных зацеплениях со
значениями в модуле Θ Ζ [α, а-1]; значения этой функции представляют собой линейные
комбинации элементов из Θ с коэффициентами из Ζ [α, α-1], при этом
коэффициенты строятся так же, как слагаемые в разложении полинома Джонса-
Кауфмана, а элементы из Θ представляют собой некоторую геометрию
виртуальных узлов.
Пусть L — виртуальная диаграмма. Рассмотрим реализацию
соответствующего виртуального узла (зацепления) в многообразии М. А именно, построим
по диаграмме Μ двумерное многообразие М' с краем следующим образом.
В каждом классическом перекрестке диаграммы зацепления мы располагаем
крест (верхняя часть рис. 19.2), а в каждом виртуальном перекрестке — пару
непересекающихся лент (нижняя картинка), ср. [КК]. Соединяя эти кресты и
ленты лентами (не перекрученными), идущими вдоль дуг зацепления, мы
получаем ориентируемое двумерное многообразие с краем, которое мы и обозначим
через М.
Естественным образом проекция диаграммы зацепления L проектируется
на М' таким образом, что дуги диаграммы отображаются в средние линии
лент, а классические перекрестки соответствуют перекресткам внутри крестов.
Следовательно, мы получаем набор кривых δ С М'. Заклеивая дисками гранич-
334
Глава 19
Рис. 19.2. Локальная структура поверхности М'
ные компоненты многообразия М7, мы получаем ориентируемое многообразие
Μ = Μ (Li) без края с набором кривых 5, погруженных в него.
Каждое состояние диаграммы L можно рассматривать непосредственно на
многообразии М, так как малая окрестность каждого классического
перекрестка диаграммы L гомеоморфно отображается на малую окрестность перекрестка
в М, порожденного двумя отрезками кривой (или двух кривых) из δ.
Следовательно, каждому состоянию s диаграммы L соответствует множество δ(β)
"сглаженных" непересекающихся кривых на М. Многообразие Μ со всеми
кривыми, принадлежащими множеству δ U 5(s), образует элемент из p(s) Ε Θ.
Определим теперь Ξ(£) следующим образом:
E(L) = (-a)-3wW ^p(s)aQW-^W(_a2 - α-2)7(*)-ι. (19.2)
s
Теорема 19.1. Функция Ξ(£) инвариантна относительно обобщенных
движений Рейдемейстера; таким образом, она является инвариантом
виртуальных зацеплений.
Доказательство. Очевидно, что как чисто виртуальные движения
Рейдемейстера, так и полувиртуальное движение, примененное к L, не меняют значения
S(L): по построению все члены в сумме 19.2 остаются неизменными.
Доказательства инвариантности функции Ξ(Ζ>) при первом и третьем
классических движениях Рейдемейстера полностью аналогичны соответствующим
доказательствам для классического полинома Джонса-Кауфмана; нужно лишь
аккуратно заметить, что сокращающиеся в обычном полиноме
Джонса-Кауфмана слагаемые играют роль коэффициентов при одном и том же элементе из
Θ и, следовательно, сокращаются и в Ξ(£).
Действительно, если L и L' — две виртуальные диаграммы, полученные
одна из другой применением первого или третьего движения Рейдемейстера, то
поверхности с краем M'(L) и M7(L7), соответствующие \L\ и |Z/|, гомеоморфны,
при этом поведение системы кривых δ для M(L) и для M(L') отличается только
внутри малой области, относящейся к движению Рейдемейстера.
19.1. Введение. Основные опеределния.
335
При движении Ω ι оба случая Пир (соответствующие локальным
числам закрученности +1 и —1) рассматриваются полностью аналогично. Пусть
L — виртуальная диаграмма, и пусть V — виртуальная диаграмма,
полученная из L добавлением петли. Каждому состоянию s диаграммы \L\ естественно
соответствуют два состояния диаграммы \L'\. Фиксируем одно из них и
обозначим его через sf. Пусть L' = L U О — несвязная сумма диаграммы L и малой
окружности. Тогда p(s) = p(s').
Действительно, поверхности, соответствующие \L\ и \L'\ гомеоморфны,
а единственная разница между соответствующими системами кривых состоит в
добавлении окружности (элементарная эквивалентность номер 3, см. стр. 332).
Таким образом, нам нужно сравнивать коэффициенты при одних и тех лее
элементах из Θ. Это делается точно так лее, как и в случае обычного полинома
Джонса-Кауфмана.
Пусть теперь зацепления L и V получаются друг из друга применением
третьего классического движения Рейдемейстера. В этом случае соответствующие
поверхности Μ также совпадают. Выберем три перекрестка P,Q,R
диаграммы L и три перекрестка P',Q',R' диаграммы Z/, к которым относится третье
движение Рейдемейстера, см. рис. 19.3.
Χ Υ Ζ
Рис. 19.3. Диаграммы и линии кривых после сглаживания
Таким образом, диаграммы L, L' отличаются лишь внутри малого диска D
на плоскости, а соответствующие им диаграммы M(L) и M(Lf) также
отличаются внутри некоторого малого диска Dm в М. Следовательно, можно указать
шесть точек на крае dD таких, что диаграммы сглаживаний (в М) для L,L7
проходили через эти и только эти точки на dD.
Рассмотрим три возможности X, У, Ζ соединения этих точек, как показано
на рис. 19.3. Можно соединить эти точки и другими способами, но именно
упомянутые выше способы будут возникать в разложении (19.2).
336
Глава 19
Пусть \Lx\, \Ly\, \Lz\ — три плоские диаграммы неориентированных
зацеплений, совпадающие с \L\ вне D и совпадающие с X, У и Ζ внутри D
соответственно.
Нам понадобятся три элемента из Θ, представимые элементами К χ, Κγ и
Κζ в S, см. рис. 19.4. Элемент Κχ содержит три линии, соответствующие
третьему движению Рейдемейстера (имеющие концами шесть выделенных точек)
внутри Dm-> sl также содержит X. Аналогично, система кривых Κγ содержит
те же три линии и У, а К ζ содержит те же три линии и Ζ. Единственное, что
нам нужно знать о поведении Κχ,Κγ и К ζ вне диска Όμ·> ~ эт0 т0> чт0 эти
диаграммы совпадают.
Κχ ΚΥ Κζ
Рис. 19.4. Части диаграмм Κχ,Κγ,Κζ
Нам нужно доказать, что S(L) = Ξ (Ζ/). С очевидностью мы имеем w(L) =
w(Lf). Нам нужно сравнить члены в разложении (19.2) для диаграмм \L\ и \L'\.
Каждому состоянию диаграммы L мож:но естественным образом сопоставить
состояние диаграммы L': мы сопоставляем перекресткам P,Q,L перекрестки
P',Q',Rf и естественным образом отождествляем все остальные перекрестки
диаграмм L и V'. Каждому состоянию диаграммы |L|, у которого перекресток
Ρ находится в положении А, соответствующее состояние диаграммы \L'\ вносит
тот же вклад в разложение (19.2), что и состояние для диаграммы |L|, так как
диаграммы \L\ и \L'\ после разведения в перекрестке Ρ (соответственно, Р')
способом А совпадают.
Таким образом, нам достаточно сравнивать члены в разложении (19.2),
соответствующие разведению вершины Ρ в состоянии В. Будем группировать
эти члены (для \L\ и для \L'\) в четверки; члены в одной четверке
различаются только разведением в перекрестках Яж S. Фиксируем теперь разведения
для диаграмм \L\ и \L'\ вне диска D одинаковым образом и будем сравнивать
соответствующие четверки. Если мы удалим части кривых внутри диска D и
заменим их на X, У, или Z, мы получим систему кривых на плоскости.
Обозначим количества кривых в соответствующих трех системах через ν χ, νγ и ν ζ
соответственно.
Четыре члена, соответствующие диаграмме |L|, в сумме дают следующее:
аКх(-а2 - а"2)^"1) + α-\Κζ(-α2 - α'^Ϋ^^Λ-
+Кх(-а2 - а'2)»*) + α-3Κχ(-α2 - а'2)^^ =
= α-\-α2-α-ψζ-^Κζ.
19.1. Введение. Основные опеределния.
337
Аналогичным образом для \L'\ мы имеем похожую формулу с К ζ и Κγ.
Коэффициенты при К γ сократятся, следовательно, мы получим то лее самое
выражение:
α-ι{-α2-α-2){νζ-^Κζ.
Проверим теперь инвариантность полинома Ξ при втором классическом
движении Рейдемейстера. Пусть L' — диаграмма, получаемая из L
применением второго классического движения Рейдемейстера, добавляющего два
перекрестка. Мы имеем w(L) = w(Lf).
Рассмотрим многообразие M(L). Образ зацепления L разбивает его на
связные компоненты. Имеются две принципиально различные возможности. В
одном случае движение Рейдемейстера применяется к одной и той же компоненте.
Тогда M(L') гомеоморфно многообразию M(L), а кривые из множеств S(L) и
S(L') представляют один и тот лее гомотопический тип, но при применении
движения появляются два новых перекрестка. В этом случае доказательство
равенства S(L) = Ξ (Ζ/) проходит точно так же, как и в классическом случае
(сокращение относится здесь к полиномиальным коэффициентам при
элементах из Θ). Кроме того, доказательство в этом случае даже проще, чем
доказательство инвариантности при Ω3: нам нужно рассматривать лишь четыре
слагаемых для |Ζ/|, соответствующих одному слагаемому для \L\. В каждом
случае три из них совместно сокращаются, а оставшееся слагаемое для \L'\
совпадает с соответствующим слагаемым для L. Принимая во внимание равенства
w(L) = w(L'), мы получаем требуемое.
Рассмотрим теперь сложный случай движения Ω2, при котором
многообразие M(U) получается из M(L) добавлением ручки. На этой ручке мы имеем
две новые точки Ри Q, см. рис. 19.5.
φ φ
Рис. 19.5. Добавление ручки при применении Ω2
Рассмотрим все состояния диаграммы \L'\. Они могут быть разбиты на
четыре типа в зависимости от способа разведения перекрестков Ρ и Q.
Таким образом, каждое состояние s диаграммы \L\ порождает четыре состояния
s++,s__,s |_ и S-\ диаграммы \L'\. Заметим, что p(s) = p(s.\ ) (а именно,
представитель p(s) в S получается из представителя элемента p(s') в S
удалением ручки 19.5), а также p(s++) = p(s__) = p(s_+).
338
Глава 19
Кроме того, для каждого s мы имеем следующие равенства:
a(s) - p(s) = a(s+_) - /3(s+_),7(s) = 7(s+-),
7(5++) = 7(5—) = 7(5-+) - 1.
Таким образом, все члены разложения (19.2) для Z/, соответствующие
состояниям s__, s++ и s |-, сократятся по причине тождества α2+α_2+(—α2—а_2)=0.
Члены, соответствующие s^ , дадут как раз то же самое, что и (19.2) для
диаграммы L. D
19.2. Пример
Пусть Ρ G Θ — элемент, представимый сферой с пустым множеством
кривых на ней. Очевидно, что для каждого классического зацепления К мы имеем
Ξ(Κ) = Ρ · V(K). Таким образом, для тривиального зацепления из двух
компонент L мы имеем Ξ(£) = Ρ · (—α2 — а~2).
Известно, что тривиальное зацепление L из двух компонент и зацепление Λ,
изображенное на рис. 18.21, имеют один и тот же полином Джонса.
Рассмотрим следующие элементы из Θ (на рисунках мы будем изображать
представляющие их элементы из S), см. рис. 19.6. Двумерным многообразием
Μ в этих случаях является тор, изображенный в виде квадрата с
отождествленными противоположными сторонами.
Рис. 19.6. Два элемента из S
Элемент Q е Θ представлен диаграммой, изображенной на рис. 19.6; две
дополнительные окружности могут быть удалены с помощью элементарной
эквивалентности номер 3, см. стр. 332.
Покажем, что Q / Р, й / Р, а так лее что Q ^ R в Θ. Действительно, Q ^ Р,
так как Q имеет две кривые с ненулевым алгебраическим пересечением (+2 или
—2 в зависимости от того, как мы ориентируем эти кривые); таким образом,
ни одна из этих кривых не может быть удалена, если мы будем применять
преобразования эквивалентности для S. Далее, мы также видим, что R Φ Ρ'.
Кроме того, R Φ Q, так как R содержит три негомотопные кривые на торе
(в координатах на рис. 19.6 они имеют вид (0,1), (1,0), и (2, —1)); каждые две
из них имеют ненулевое алгебраическое пересечение, значит, ни одна из них
19.3. Проблемы минимальности и атомы
339
не может быть удалена. Поэтому, простейшая диаграмма, представляющая [R]
в S не может состоять менее, чем из трех кривых.
Далее, для зацепления Λ мы имеем
Ξ(Λ) = Qa2 + 2R(-a2 - а~2) + Qa~2 = (2R - Q)(-a2 - a~2).
Таким образом, Ξ (Λ) φ S(L).
19.3. Атомы и виртуальные узлы.
Проблемы минимальности
В настоящем разделе мы не будем различать виртуальные диаграммы,
получающиеся друг из друга последовательным применением объезда. Такие
диаграммы мы будем называть сильно эквивалентными] кроме того,
эквивалентные диаграммы будут считаться различными, если для установления из
эквивалентности требуется применение классических движений Рейдемейстера.
Назовем сложностью виртуальной диаграммы количество классических
перекрестков. Очевидно, что диаграммы сложности нуль задают тривиальные
зацепления. Мы будем исследовать вопрос минимальности (в смысле
отсутствия диаграмм меньшей сложности) диаграммы, задающей данное
виртуальное зацепление.
В главе 7 мы сформулировали знаменитую теорему Кауфмана-My расу ги,
которая была доказана в главе 15. В настоящей главе мы обобщим этот
результат на случай виртуальных зацеплений и приведем несколько серий
минимальных диаграмм виртуальных зацеплений и оснащенных виртуальных
зацеплений. Нам понадобятся понятия простоты и точки распадения. Они хорошо
известны в случае классических диаграмм. В случае виртуальных диаграмм они
будут определены позднее.
Для доказательства теоремы 7.5 Кунио Мурасуги использовал некоторые
свойства полинома Джонса-Кауфмана. Пусть К — виртуальная диаграмма, и
пусть X — перекресток диаграммы К. Пусть теперь ρ χ {К) — диаграмма,
получающаяся из К применением виртуализации к перекрестку X, см. рис. 18.10.
Как было сказано ранее, это преобразование не меняет значения полинома
Джонса-Кауфмана. Кроме того, если применить это преобразование дважды
к одному и тому же перекрестку, мы получим изначальную диаграмму К
(точнее, диаграмму, сильно эквивалентную ей). Обозначим множество всех
виртуальных диаграмм, получаемых из диаграммы К применением преобразования
ρ к некоторым классическим перекресткам, через [К].
Определение 19.1. Под точкой распадения виртуальной диаграммы L
будем понимать классический перекресток X этой диаграммы такой, что для
некоторой диаграммы L7, сильно эквивалентной диаграмме L, удаление этого
перекрестка приводит к распаданию диаграммы.
Определение 19.2. Виртуальная диаграмма L называется составной, если
для некоторой диаграммы L7, сильно эквивалентной ей, существует простая
замкнутая кривая на плоскости диаграммы, пересекающая L' ровно в двух
точках и разделяющая множество классических перекрестков диаграммы V
на два непустых подмножества.
340 Атомы и виртуальные узлы. Проблемы минимальности
В этом случае диаграмма L' является связной суммой двух виртуальных
диаграмм.
Аналогичным образом, назовем виртуальную диаграмму L несвязной, если
существует сильно эквивалентная ей диаграмма L7, тень которой несвязна.
В дальнейшем все диаграммы, с которыми мы имеем дело на протяжении
настоящей главы, предполагаются связными.
Существуют в точности два (с точностью до комбинаторной
эквивалентности) способа вложения тени простой нераспадающейся диаграммы
классического зацепления в ориентированную сферу, которые сохраняют соотношения
противоположности исходящих вершин в каждом перекрестке. Эти два
вложения получаются друг из друга заменой ориентации сферы.
Диаграмма V виртуального зацепления называется квазиальтернирован-
ной, если существует классическая альтернированная диаграмма L такая, что
V е [L].
Докажем следующую теорему.
Теорема 19.2. Любая квазиалътернированная диаграмма без точек
распадения является минимальной.
Аналогичная теорема минимальности для зацеплений в RP была доказана
в [Дро].
Докажем сначала аналог теоремы My расу ги для виртуальных зацеплений.
В доказательстве мы будем использовать связь между атомами и
зацеплениями, описанную в главе 15.
Теорема 19.3. Пусть L — связная виртуальная диаграмма сложности η без
точек распадения. Тогда span(V(L)) < п. Более того, равенство span(V(L)) =
η имеет место только для виртуальных диаграмм, сильно эквивалентных
связной сумме квазиальтернированных диаграмм без точек распадения.
Рассмотрим формулу (19.1). Нас интересуют состояния диаграммы,
содержащие мономы максимальной и минимальной степени в разложении по этой
форме. Легко видеть, что никакое состояние не может содержать монома
степени выше, чем старшая степень монома в максимальном (а = гг, β = 0)
состоянии, и никакое состояние не может содержать монома степени меньшей, чем
младшая степень монома в минимальном состоянии (противоположное
максимальному во всех перекрестках).
Для оценки степеней мономов в этих состояниях нам понадобятся атомы и
d-диаграммы. Напомним, что атом — это двумерное замкнутое многообразие с
вложенным в него четырехвалентным графом (остовом), делящим его на
клетки таким образом, чтобы это клеточное подразбиение допускало шахматную
раскраску; атомы рассматриваются с точностью до естественной
эквивалентности. Атом (точнее, его класс эквивалентности) может быть задан
следующей комбинаторной структурой: его остов (граф валентности четыре в каждой
вершине), структура А (разбиение множества исходящих полуребер на пары
противоположных, происходящее из вложения остова в плоскость) и
структура В (в каждой вершине мы указываем две пары соседних полуребер, которые
Атомы и виртуальные узлы. Проблемы минимальности 341
локально соответствуют границам клеток черного цвета). Напомним, что
высотным атомом называется атом, остов которого вложим в R2 с сохранением
А- структуры.
В случае произвольного атома нужно заменить вложения регулярными
погружениями общего положения. Может существовать много комбинаторно
различных погружений данного остова. Каждой из них соответствует некоторая
диаграмма виртуального зацепления. Имея некоторую А-структуру (1, 3), (2,4)
в некоторой вершине атома, мы можем погрузить остов двумя локально
различными способами: 1, 2, 3, 4 или 1, 4, 3, 2 (имеется в виду циклический порядок
исходящих ребер на плоскости в направлении против часовой стрелки).
Определение 19.3. Назовем диаграмму L диаграммой, соответствующей
атому V и погружению р.
Лемма 19.1. Класс эквивалентности виртуального зацепления L определен
с точностью до виртуализации.
Доказательство. При погружении графа в плоскость учитывается только
структура противоположных ребер в каждом перекрестке. Допустим, что в
некоторой вершине А рассматриваемого атома сходятся четыре ребра а, 6, с, <i,
причем ребро с противоположно ребру а, а ребро d противоположно ребру Ъ.
При погружении на плоскость циклический порядок ребер (против часовой
стрелки) может быть либо a,b,c,d либо a,d,c, Ъ. Легко видеть, что виртуальные
зацепления, соответствующие таким погружениям, отличаются друг от друга
виртуализацией в соответствующем перекрестке (и объездами). D
Получаемые таким образом диаграммы виртуальных узлов отличаются друг
от друга виртуализацией.
Вернемся к доказательству теоремы 19.3. Рассмотрим сначала случай
простых диаграмм. Рассмотрим максимальное и минимальное состояния
диаграммы L зацепления L. Обозначим количества окружностей в этих состояниях
через jmax и 7mm соответственно. Из рассуждений, аналогичных
приведенным выше следует, что длина скобки Кауфмана (L) не превосходит А = 2п +
2(7таж + 7тт — 2). Диаграмма L имеет собственную Α-структуру. По ней
можно построить атом с jmax черными клетками, 7mm белыми клетками,
вершины которого соответствуют классическим перекресткам диаграммы, а
клетки приклеены вдоль ребер. Эйлерова характеристика этого атома равна χ =
η — 2п + 7mm + Ίπιαχ· Так как χ ^ 2, мы имеем А ^ 4гг.
При этом равенство может иметь место только в том случае, когда χ = 2, т. е.
атом является сферическим. В этом случае £>-структура диаграммы L задает
некоторый плоский атом.
Такие (плоские) структуры соответствуют вложениям остова атома в
сферу S2, согласованным с Α-структурой. Таких вложений существует ровно два.
Они соответствуют двум альтернированным диаграммам. Следовательно,
диаграмма L имеет одну из этих £>-структур. Таким образом, она может
отличаться от альтернированной диаграммы только виртуализациями. Поэтому она
является квазиальтернированной.
Наличие точек распадения приводит к существованию диаграммы с
меньшим числом перекрестков, поэтому для таких диаграмм А < 4гг. В противном
342 Атомы и виртуальные узлы. Проблемы минимальности
случае диаграмма зацепления, соответствующая плоскому атому, имеет
максимальную длину скобки Кауфмана (доказательство такое лее, как и в 15).
Если диаграмма не является простой, нужно разложить ее на простые и
воспользоваться мультипликативностью полинома Джонса-Кауфмана.
Таким образом мы доказали теорему 19.3. Теорема 19.2 является простым
следствием из нее.
Из приведенных выше рассуждений следует
Теорема 19.4. Пусть L — редуцированная диаграмма виртуального
зацепления с η классическими перекрестками. Тогда span(L) < 4п + 2(χ — 2), где χ —
эйлерова характеристика соответствующего атома.
Аналогично минимальности альтернированных диаграмм доказывается
следующая
Теорема 19.5. Пусть L — диаграмма виртуального зацепления с η
классическими перекрестками, такая что выполнено одно из двух условий:
1. span(L) = 4п;
2. span(L) ^ 4п — 4, при этом в (L) входят мономы степеней не сравнимых
по модулю четыре. Тогда диаграмма L является минимальной.
Доказательство. Предположим противное. Тогда существует диаграмма V
того же зацепления, количество перекрестков которой равно т ^ (п — 1).
Рассмотрим атом, соответствующий диаграмме V'. Так как диаграмма V
является связной, соответствующий ей атом является связным и имеет
эйлерову характеристику, не превышающую двух. Из теоремы 19.4 получаем, что
span(L) = span(L7} ^ 4(гг — 1). Противоречие.
Во втором случае скобка (L) = (Lf) имеет мономы, степени которых не
сравнимы по модулю четыре, атом, соответствующий диаграмме L, является
неориентируемым. Следовательно, его эйлерова характеристика χ не
превышает единицы. Значит, согласно теореме 19.4, span(L) = span(L7} ^ 4(гг — 1) — 2.
Противоречие. D
Кроме оценки для количества перекрестков для диаграмм виртуальных
зацеплений мы также можем получить оценку для количества перекрестков
диаграмм оснащенных виртуальных зацеплений. Под оснащенным виртуальным
зацеплением мы понимаем класс эквивалентности виртуальных диаграмм по
движению объезда и движениям Ω^, Ω2, Ω3. Здесь движение Ω^ — это удвоенное
первое движение Рейдемейстера, см. рис. 19.7, которое не меняет числа закру-
ченности компоненты зацепления. Иными словами, в качестве эквивалентности
мы рассматриваем те и только те комбинации движений Рейдемейстера,
которые не меняют числа закрученности (оснащения) компонент.
Движение Ω^ обладает тем свойством, что при применении его к диаграмме
L некоторого зацепления (классического или виртуального) диаграмма Dn(L)
(состоящая из η параллельных копий диаграммы L) преобразуется в
эквивалентную ей. Это свойство является важным, и оно присуще всем обобщенным
движениям Рейдемейстера, за исключением первого классического.
Атомы и виртуальные узлы. Проблемы минимальности 343
<-Ч>
Рис. 19.7. Движение Ω[
Теорема 19.6. Пусть диаграмма L оснащенного виртуального зацепления L
такова, что на атоме V, соответствующем диаграмме L, никакая точка
не является с двух сторон инцидентной одной и той же клетке. Тогда у
оснащенного зацепления L нет диаграмм с числом классических перекрестков
меньшим, чем у диаграммы L.
Для доказательства мы будем использовать следующее утверждение.
Лемма 19.2. Пусть виртуальная диаграмма L с η классическими
перекрестками такова, что на атоме V, ей соответствующем, никакая вершина не
является с двух сторон инцидентной одной и той же клетке, тогда для
каждого натурального т имеет место равенство
span(Dm(L)} = 4m2n + 2(Хт - 2),
(19.3)
где хт — эйлерова характеристика атома, соответствующего
диаграмме Dm(L).
Доказательство этой леммы состоит в следующем. Из приведенных выше
рассуждений мы получаем неравенство span(Dm(L)) < 4га2η + 2(%m — 2),
причем для достижения равенства нам достаточно, чтобы для каждого га в
разложении скобки Кауфмана (Dm(L)) по формуле (6.5) коэффициенты при старшей
и младшей степенях не сокращались. Для этого нам нужно, чтобы в
состояниях smax и smin для Dm(L) никакая окружность не подходила дважды к одному
и тому лее перекрестку. Это следует из того, что аналогичное условие
выполняется для диаграммы L по предположению теоремы.
Доказательство теоремы 19.6. Рассмотрим диаграммы ^(Ь), Ds(L),...,
Dm(L). Им соответствуют оснащенные зацепления, соответствующие
удвоению, утроению, взятию га параллельных копий оснащенного зацепления L.
Мы будем изучать длину span(Dm(L)), которая является инвариантом
зацепления L.
Пусть атом, соответствующий диаграмме L, имеет эйлерову
характеристику χ. Это значит, что количество Г клеток атома равно Г = χ + п. Рассмотрим
344 Атомы и виртуальные узлы. Проблемы минимальности
атом, соответствующий диаграмме Dm(L). Мы имеем т2п вершин, 2т2п ребер
и тТ клеток. Таким образом, эйлерова характеристика этого атома равна
χη = —т2п + тп + πιχ. (19.4)
Из леммы 19.2 следует, что старшая и младшая степени скобки
Кауфмана для диаграмм Dm не сокращаются. Поэтому, согласно теореме 19.4, длина
скобки Кауфмана диаграммы Dm равна
span(L>m(L)} = 4m2n + 2(χη - 2) = 2(m2 + m)n + 2τηχ - 4. (19.5)
Предположим, что у оснащенного зацепления L имеется диаграмма L7,
имеющая п', причем чп! < п. Обозначим эйлерову характеристику атома,
соответствующего диаграмме L7, через χ'.
Тогда, согласно теореме 19.4 и приведенным выше рассуждениям, мы
получаем:
span(L>m(L/)} < 2(m2 + m)nf + 2τηχ' - 4. (19.6)
Таким образом,
2(m2 + т)п + 2πιχ - 4 < 2(m2 + m)nf + 2rax' - 4. (19.7)
Сокращая, приводя подобные члены и учитывая, что т + 1 > 0, мы
получаем:
(х' - х) ^ (т + 1)(п - п') ^ (га + 1). (19.8)
Из этого следует, что эйлерова характеристика χ' больше сколь угодно
большого наперед заданного числа. Противоречие завершает доказательство
теоремы. D
Для того чтобы достигалась максимальная длина полинома
Джонса-Кауфмана для зацепления с η классическими перекрестками, а именно, 4п + 2(χ — 2)
важно, чтобы не сокращались старший и младший члены в разложении
Кауфмана. Вместо полинома Джонса-Кауфмана можно взять его обобщение Ξ.
При этом бывает так, что у полинома Джонса-Кауфмана сокращается старший
(младший) коэффициент, а у полинома Ξ — не сокращается (так как мы
имеем различные элементы из Θ с некоторыми коэффициентами). Для этих целей
также можно применять комплекс Хованова. Важной задачей является
вычисление старшего (младшего) коэффициента разложения полинома Джонса-
Кауфмана (который, вообще говоря, может быть равен нулю). В настоящей
книге этому посвящено приложение Д, написанное Романом Сергеевичем
Авдеевым.
Глава 20
Комплекс Хованова для
виртуальных узлов
В настоящей главе мы опишем три способа построения комплекса
Хованова для виртуальных узлов. В первом из них мы построим комплекс Хованова
для произвольных виртуальных зацеплений с коэффициентами в поле Ζ2, во
втором разделе мы покажем, как молено построить комплекс Хованова для
оснащенных виртуальных зацеплений (посредством удвоения виртуальных
зацеплений), а в третьем разделе — комплекс Хованова двулистных накрытий
над виртуальными узлами (в смысле атомов). Приводимые здесь результаты
принадлежат автору настоящей книги.
20.1. Комплекс Хованова виртуальных узлов
с коэффициентами в поле Ζ2
В настоящем разделе приводится результат, впервые опубликованный
в [Ман9].
Пусть L — ориентированная виртуальная диаграмма, \L\ —
соответствующая неориентированная виртуальная диаграмма, гг+ и гг_ — количества
положительных и отрицательных классических перекрестков, η — общее число
классических перекрестков. Таким образом η = п+-\-П-. Рассмотрим куб
состояний диаграммы \L\. Под кубом состояний мы понимаем куб {0,1}п, в каждой
вершине которого указано количество окружностей в соответствующем
состоянии, а на каждом ребре — какие окружности перестраиваются при переходе
от состояния к соседнему согласно этому ребру (см. главу 7, стр. 93).
Сопоставим каждой окружности линейное пространство V над полем Z2, порожденное
двумя векторами v+ и г>_, где вектора v± имеют градуировку =Ы. Каждой
вершине куба s = {αϊ,... ,αη} соответствует некоторое количество окружностей,
которое мы обозначим через 7(s)· Сопоставим каждой такой вершине векторное
пространство V®1^ · {Σ™=() сц}, получающееся из тензорной степени
пространства V сдвигом градуировки: здесь {·} означает операцию сдвига градуировки,
см. стр. 94. Сумма Σ™=0 сц называется высотой вершины куба. Определим
пространство цепей высоты к как тензорную сумму пространств, относящихся ко
всем вершинам куба высоты к. Дифференциал в комплексе будет согласован с
высотой, а именно, он будет повышать высоту на единицу.
346
Комплекс Хованова mod Z2
Определим частичные дифференциалы на цепях, действующие вдоль
ребер куба, следующим образом. Пусть ребро а соответствует переходу из
состояния s в состояние s7, при этом / окружностей не претерпевают изменений.
В перекрестке диаграммы |L|, соответствующем ребру а, происходит
перестройка либо одной окружности в две, либо двух окружностей в одну, либо одной
окружности в одну. В первых двух случаях мы определим дифференциал как
и раньше, а именно, Δ ® Id®1 · {1} или т ® Id®1 · {1}, определения отображений
т и Δ см. на стр. 96. В случае перестройки типа (1 —> 1) мы определим
частичный дифференциал на ребре как отображение, переводящее все пространство в
нуль. Обозначим получившийся куб через Q(L). Отметим, что в данном случае
(для поля Z2) антикоммутативность равносильна коммутативности.
Лемма 20.1. Куб Q(L) коммутативен.
Это утверждение доказывается рутинной проверкой, аналогичной той,
которую проделал Бар-Натан в работе [BN3]. А именно, проверяется, что имеет
место (анти)коммутативность на каждой двумерной грани двумерного куба.
Мы приведем лишь один пример такой проверки (самый интересный), см.
рис. 20.1.
Рис. 20.1. Проверка коммутативности двумерной грани куба
В настоящем случае нужно проверить, что отображение т о Δ : V —>· V
переводит все пространство V в ноль. Действительно, при таком отображении
V- ι—» V- (8) V- ι—>· 0, г;+ \-^ ν+ (8) V- + V- (8) ν+ ι—>· 2v- = 0 над полем Z2.
Отметим, что это — единственный существенный неклассический случай, в
котором встречается перестройка типа 1 —> 1. Действительно, из соображений
Комплекс Хованова mod Z2
347
четности следует, на каждой двумерной грани число таких перестроек не менее
двух. Если их нет, то дело сводится к одному из классических случаев (все
такие случаи были рассмотрены Бар-Натаном).
В случае, если таких перестроек две или четыре, то на двумерной грани
рассматриваемого куба
y®a{i} _А^ V®b{2}
г] U (20.1)
у®с Ρ > y®dr-n
либо каждая из композиций q о ρ и s о г содержит нулевое отображение вида
1 —> 1 (например, в случае а = 6, с = d отображения ρ и s — нулевые), либо
имеет место случай, разобранный выше.
Определим, как и ранее (см. стр. 94), C(L) = Q/(|L|){n+ — 2n_}[n_]. В этом
случае C(L) является корректно определенным комплексом. Обозначим
линейное пространство гомологии комплекса C(L) через Kh(L) (или Khz2(L) в
случае, если нужно подчеркнуть, что комплекс Хованова рассматривается именно
над полем Z2).
Теорема 20.1. Kh(L) является инвариантом зацепления L.
Доказательство этой теоремы полностью повторяет доказательство
инвариантности гомологии Хованова для случая классических зацеплений,
приведенное в главе 7.
Отметим, что комплекс C(L) распадается на два комплекса: четной
градуировки и нечетной градуировки (напомним, что дифференциал сохраняет
градуировку).
Мы получаем два типа гомологии Хованова: четный Khe и нечетный Kh°'.
Они соответствуют мономам полинома Джонса, имеющим степени, дающие
остаток два при делении на четыре (Khe) и мономам, степени которых делятся
на четыре без остатка (Kh°). У классического зацепления встречаются
гомологии только одного из этих двух типов, более точно, имеет место следующая
Теорема 20.2. Для классического зацепления с четным числом компонент
Kh0= 0, для классического зацепления с нечетным числом компонент Khe= 0.
Эта теорема полностью аналогична теореме 7.4 о степенях мономов,
входящих в полином Джонса.
Отметим, что построенный нами комплекс Хованова с коэффициентами в
поле Z2 полностью определяется структурой куба состояний и числами п+,П-.
Таким образом, гомологии Хованова не меняются при виртуализациях
исходной диаграммы.
В следующем разделе мы приведем другой подход к построению комплекса
Хованова (для оснащенных зацеплений), который чувствителен к
виртуализациям. Приведенный здесь комплекс Хованова в классическом случае совпадает
с обычным комплексом Хованова с коэффициентами в Z2; в этом случае
легко преодолевается трудность с перестройками вида 1 —>· 1. В двух следующих
разделах мы будем строить комплекс Хованова не для всех узлов, а лишь для
"хороших" — тех, у которых на кубе не возникает перестроек (локальных
дифференциалов) типа 1 —> 1. Далее мы будем каждое виртуальное зацепление
348
Комплекс Хованова mod Z2
(диаграмму виртуального зацепления) сводить к хорошей диаграмме и
смотреть, как преобразуются гомологии Хованова соответствующей хорошей
диаграммы при применении обобщенных движений Рейдемейстера к изначальной
диаграмме. Так, в следующей секции будет построен комплекс Хованова для
оснащенных зацеплений, где в качестве хорошей диаграммы будет выступать
диаграмма удвоения.
Рассмотрим узел Κι, см. рис. 20.2.
Рис. 20.2. Виртуальный узел, сводимый к тривиальному виртуализациями
и обобщенными движениями Рейдемейстера
Этот узел можно свести к тривиальному узлу виртуализациями и
обобщенными движениями Рейдемейстера, см. рис. 20.3.
На рисунке 20.3 преобразованием В' мы называем движение, применяемое к
одному классическому и одному виртуальному перекрестку; оно представляет
собой композицию виртуализации и второго виртуального движения
Рейдемейстера, см. рис. 20.4. Для каждого из преобразований, указанных на рис. 20.3
мы выделяем на рисунке область, к которому оно применяется.
Таким образом, гомологии Хованова узла, изображенного на рис. 20.2
совпадают с гомологиями Хованова тривиального узла.
20.2. Комплекс Хованова удвоений узлов
В оставшейся части настоящей главы мы будем использовать конструкцию,
связывающую атомы с виртуальными узлами. Напомним что конструкцию,
сопоставляющая высотному атому классическое зацепление, приведенную в
главе 15. Она состоит в том, что остов атома V вкладывается в плоскость с
сохранением его А-структуры, а далее каждый перекресток снабжается структурой
проход-переход согласно 5-структуре атома.
Пусть дан произвольный атом V. Рассмотрим погружение ρ его остова в
плоскость общего положения с сохранением Α-структуры. Мы получим
четырехвалентный граф на плоскости с двумя типами вершин: образами вершин
атома и "дефектами погружения" — пересечениями образов ребер атома. В
первом случае мы расставим классические перекрестки так же, как и в случае
вложения остова высотного атома; во втором случае мы расставим виртуальные
перекрестки. В итоге мы получим диаграмму L виртуального зацепления.
Как показано в лемме 19.1, класс эквивалентности виртуального зацепления
L определен с точностью до виртуализации.
20.2. Комплекс Хованова удвоений узлов
349
Рис. 20.3. Сведение к тривиальному виртуализациями
и обобщенными движениями Рейдемейстера
Отметим следующую важную лемму.
Лемма 20.2. Пусть L,Lf — две диаграммы, которым соответствуют
ориентируемые атомы, при этом L' отличается от L применением объезда или
одного из трех классических движений Рейдемейстера. Тогда Kh(L) = Kh(Lf).
При объезде структура классических перекрестков не меняется, таким
образом, не меняется куб состояний, и, следовательно, не меняется и весь комплекс.
В случае классических движений Рейдемейстера имеется доказательство
Бар-Натана инвариантности гомологии Хованова. Оно локальное, т. е. исполь-
350
Комплекс Хованова mod Z2
Рис. 20.4. Преобразование В' выражается через виртуализацию
зует только локальную структуру движения Рейдемейстера (вне зависимости
от того, как выглядит неподвижная часть зацепления). Следовательно, оно
проходит и для виртуальных узлов.
Предложение 20.1. Пусть L — произвольная диаграмма виртуального
зацепления. Тогда атом, соответствующий удвоению U2(L), является
ориентируемым.
Для доказательства нам понадобится еще одно вспомогательное
предложение.
Пусть дан некоторый атом V. Предположим, что Α-структура атома такова,
что существует ориентация всех ребер атома V такая, что в каждой вершине по
два противоположных ребра являются исходящим, а два других — входящими.
Назовем такую структуру структурой источник-сток.
Предложение 20.2. Если остов атома допускает структуру источник-сток,
то атом является ориентируемым.
Доказательство предложения 20.1 выводится из предложения 20.2
следующим образом.
Пусть L — виртуальная диаграмма. Ориентируем диаграмму U2(L) так,
чтобы для каждой точки А на диаграмме зацепления репер (OLa, та), задавал
положительную ориентацию плоскости, см. рис. 20.5.
Здесь dL — касательный вектор к зацеплению, ат^ — перпендикулярный
вектору dL вектор от точки А к близкой точке на соседней компоненте.
Искомая структура источник-сток получается так: все ребра (т. е. образы
ребер соответствующего атома) диаграммы D2(L) делятся на "длинные" (которые
происходят из ребер диаграммы L) и "короткие" (четыре коротких ребра
соответствуют каждой вершине диаграммы L, см. рис. 20.5). Сменим ориентацию
всех коротких ребер, оставив ориентацию длинных неизменной. Полученная
ориентация задает структуру источник-сток.
Докажем теперь предложение 20.2.
20.2. Комплекс Хованова удвоений узлов
351
Рис. 20.5. Локальная ориентация для удвоенной диаграммы
Доказательство. Действительно, пусть Α-структура атома обладает
структурой источник-сток. Рассмотрим его черные (послекритические) клетки. Мы
зададим ориентацию всех черных клеток таким образом, чтобы она была
согласована во всех вершинах атома. Легко видеть, что из этого следует
ориентируемость атома.
Граница каждой послекритической клетки атома представляет собой цикл,
состоящий из подряд идущих ребер, при этом каждое следующее ребро не
является противоположным предыдущему. Так как в каждой вершине
выполнено условие источник-сток, то цикл является ориентированным, т. е. таким,
что может быть представлен как отображение ориентированной окружности:
при этом ориентация ребер согласована с ориентацией окружности.
Ориентация границы клетки задает ориентацию и на внутренность этой клетки: для
этого достаточно выбрать репер, первый вектор которой ориентирован по
одному из ребер границы, а второй смотрит внутрь клетки. Проделаем это для
каждой черной клетки. Наличие структуры источник-сток в каждой вершине
означает, что ориентации клеток, соседствующих по вершине, согласованы. D
Учитывая сказанное в начале настоящей главы, мы приходим к выводу о
том, что комплекс Хованова для D2n(L) корректно определен над любым
кольцом коэффициентов. Отображение L ι—» D2n(L) является почти инвариантным
(оно инвариантно относительно всех комбинаций преобразований Рейдемейсте-
ра, которые не меняют числа закрученности w). По этой причине естественно
ожидать, что гомологии комплекса Хованова для удвоенного1 узла
являются инвариантами оснащенных зацеплений. А именно, имеет место следующая
лемма.
1 Удвоение, утроение и, более общо, операция взятия к параллельных копий диаграммы
К —► D}~ (К) было определено на стр. 34. Она является корректно определенной на
оснащенных зацеплениях.
352
Комплекс Хованова mod Z2
Лемма 20.3. Пусть L,U — две диаграммы эквивалентных оснащенных
виртуальных зацеплений. Тогда для любого η существует набор диаграмм D2(L) =
Lo, Li,..., Ln = D2(L') такой, что:
1. Все атомы, соответствующие диаграммам Li, ориентируемы.
2. Для каждого г = 0,..., η — 1 диаграмма Ζ^+ι получается из диаграммы
Li применением одного из обобщенных движений Рейдемейстера.
!^~D$C>5gC
Рис. 20.6. Удвоенные движения Рейдемейстера
Доказательство леммы 20.3. Воспользуемся предложением 20.1. Для
каждого удвоенного Рейдемейстера из цепочки от U2(L) к D2(Lf) укажем, как
изменяется структура источник-сток. Это сделано на рис. 20.6.
В некоторых очевидных случаях стрелки на рис. 20.6 означают не одно,
а два "симметричных" классических движения Рейдемейстера или лее
несколько движений, последовательность применения которых очевидна. Их можно
проделать одно за другим, и при этом в случае любого из изображенных на
рис. 20.6 преобразований легко видеть, что такое последовательное
перестраивание влечет и однозначное перестраивание структуры источник-сток. D
20.2. Комплекс Хованова удвоений узлов
353
Заметим следующее.
Имеет смысл рассматривать лишь классические движения Рейдемейстера,
так как движение объезда не меняет атома. Ориентации компонент при этом
меняться не будут.
Итак, рассмотрим все классические движения Рейдемейстера.
Если диаграммы К и К' отличаются применением первого или третьего
движения Рейдемейстера, то локальная структура источник-сток для К
однозначно соответствует локальной структуре источник-сток для К' таким образом,
что вне области применения движения Рейдемейстера эти диаграммы
совпадают. Здесь на линиях, изображенных пунктиром, ориентация источник-сток
задается как противоположная к примыкающим к ним сплошным" линиям. Это
видно из рисунка 20.7.
^^х s&L
Рис. 20.7. Разметка для удвоенных движений Ω ι и Ω3
У второго движения Рейдемейстера есть два принципиально разных случая,
приведенные на рис. 20.8.
Н-
ГТ™Т
Допустимый вариант второго движения Рейдемейстера
+-
+-
Недопустимый вариант второго движения Рейдемейстера
Рис. 20.8. Разметка для удвоенных движений Ω2
В первом из них (верхняя картинка) мы имеем две противонаправленные
дуги (согласно ориентации источник-сток), а во втором случае — две сонаправ-
ленные.
354
Атомы и комплекс Хованова
В первом случае указано, как перестраивается локальная разметка ребер
диаграммы.
Второй случай не допустим, т. е. может привести к тому, что при применении
второго движения Рейдемейстера атом перестанет быть ориентируемым.
Таким образом, из классических движений Рейдемейстера только второе
может нарушить ориентируемость атома. При преобразованиях, описываемых
в доказательстве леммы 20.3, оно не встречается.
Теорема 20.3. Пусть η — натуральное число. Тогда образ отображения L ι—>
Kh(D2n(L)) является инвариантом оснащенных виртуальных зацеплений.
Доказательство. Согласно предложению 20.1, C(D2n(L)) является корректно
определенным комплексом. Пусть теперь L,Z7 — две эквивалентные
диаграммы оснащенных виртуальных зацеплений. Тогда в силу леммы 20.3 существует
набор виртуальных диаграмм, D2n(L) = L$,...,Ln = D2n(L'),
соответствующих ориентируемым атомам, при этом L^+i получается из Li применением
обобщенных движений Рейдемейстера. Таким образом, в силу леммы 20.2, мы
имеем Kh(D2n(L)) = Kh(Li) = ■ ■ ■ = Kh(D2n(L'). Теорема доказана. D
Отметим, что удвоение диаграммы L и удвоение диаграммы L7, полученной
из L виртуализацией одного из перекрестков диаграммы L, имеют различные
кубы состояний. Так что построенный в настоящем разделе комплекс может
a priori различать оснащенные виртуальные диаграммы, полученные друг из
друга виртуализацией.
Однако построенный в настоящем разделе "удвоенный" комплекс Хованова
существенно отличается от "обычного" комплекса Хованова классических
узлов: как в классическом, так и в виртуальном случае нам нужно брать удвоение,
и после этого считать гомологии Хованова.
Естественным является вопрос о том, инвариантны ли "обычные"
гомологии Хованова Kh(L) в случае диаграмм, которым отвечают ориентированные
атомы. Положительный ответ на этот вопрос дается в следующем разделе.
20.3. Атомы и комплекс Хованова
двулистных накрытий
Основной целью настоящего раздела является доказательство следующей
теоремы.
Теорема 20.4. Пусть F — поле. Пусть L, V — две эквивалентные
виртуальные диаграммы, которым отвечают ориентируемые атомы. Тогда Khp(L) =
KhF(U).
Основная идея доказательства состоит в следующем. Для каждой
виртуальной диаграммы L можно рассмотреть соответствующий ей атом V(L). Далее
будем использовать технику ориентирующего накрытия. А именно, если атом
V(L) — ориентируем, рассмотрим две копии атома V(L), если нет, то
рассмотрим атом V(L) — ориентирующее двулистное накрытие над атомом V(L). Оно
определяется как двулистное накрытие над соответствующей поверхностью,
при этом прообразом остова является граф, который мы берем за остов,
прообразом черных клеток — черные клетки, а прообразом белых клеток — белые
Атомы и комплекс Хованова
355
клетки. Полученный атом может быть либо двухкомпонентным, либо одноком-
понентным, в зависимости от того, является исходный атом ориентированным
или нет.
Обозначим полученный атом через V2(L), а узел, ему соответствующий,
через K(V2(L)).
Эту конструкцию молено трактовать так: мы рассматриваем два набора
перекрестков атома с Α-структурой в них и соединяем перекрестки ребрами.
Таким образом, для каждого виртуального узла можно рассмотреть его
"накрытую версию":
L -> V(L) -> V2(L) -> KhF(K(V2(L))) (20.2)
Исходя из диаграмм узлов эта конструкция описывается так. Пусть дано
виртуальное зацепление L, у которого имеется η классических перекрестков
Χι,...,Хп. Эти перекрестки как-то соединяются между собой. Таким образом,
мы имеем граф Г, погруженный на плоскость. У каждого из перекрестков Χι
четыре конца Хц, Хг25 ^гз? XiA перенумерованные, скажем, по часовой стрелке,
при этом перекрестки соединяются ветвями узла, которым соответствуют ребра
атома. Пусть ребро lj соединяет концы Xjlj2 и Xj3j4, где j2, J4 £ {1,2,3,4}.
Диаграмма K(V2(L)) строится следующим образом. Она содержит 2п
перекрестков Х{,..., Х'п, X",..., X", которые соединяются ветвями. У каждой
ветви lj исходной диаграммы появляются два образа: Zj и I2. Каждое из двух
ребер Ц соединяет конец Xjlj2 или X"lj2 с концом Xj3j4 или Xj3j4· Для каждого
ребра I}· нам нужно указать, какие именно концы оно соединяет (X7 или X").
Здесь у нас имеется произвол в описании. Дело в том, что до того, как мы
начали описывать ребра, мы не имели естественного упорядочивания вершин:
какая из вершин Х[ или Х[' — "первая", а какая — "вторая". Для преодоления
этой трудности рассмотрим максимальное дерево Δ в графе Г и скажем, что
все ребра /j, соответствующие ребрам этого дерева, соединяют концы Xjlj2 с
Xj3j4 (тем самым, ребра I2 соединяют концы X'Lj2 и X" ·).
Выбор другого дерева будет соответствовать смене обозначений: в
некоторых парах X' и X" поменяются местами. После этого правило соединения
оставшихся концов ребрами lj и I2 таково. Мы опять позволим себе небольшой
произвол: указывая, какие пары концов нужно соединить ребром 1\, мы не
будем указывать, соединяем мы их ребром lj или ребром I2: соответствующая им
"симметричная" пара концов, получающаяся заменой X' <—> X" будет так лее
соединена ребром, при этом для диаграммы узла не важно, как эти два ребра
обозначаются.
Также мы не будем следить за тем, как именно на плоскости расположены
ребра If: результирующий класс виртуального зацепления от этого зависеть не
будет.
Итак, мы фиксировали максимальное дерево Δ с Г. Каждое ребро lj, не
принадлежащее этому дереву, задает минимальный цикл на подграфе AUljCT.
В случае, если этот цикл — хороший (см. далее), соединим ребром I1- концы
Xj1j2 и Xj3j4, а ребром I2 концы Xj7lj2 и Xj3j4· В случае плохого цикла
соединим ребром lj концы Xjlj2 и Xj3j4, а ребром I2 концы Xj7lj2 и Xj3j4·
Понятие хорошего и плохого ребра восходят к ориентирующим и неориентирующим
циклам на атоме. При накрытии атома ориентирующие циклы переходят в
356
Атомы и комплекс Хованова
циклы, а неориентирующие — в незамкнутые пути (с некоторыми
различными концами Х'к,Х'£. Определим теперь понятие хорошего ребра (для ребер, не
входящих в Г), а также понятие ориентирующего цикла, исходя из
диаграммы виртуального зацепления. Для этого рассмотрим все ребра данного цикла
hi, ij2 5 - - - 5 Ijk' hk+i = hi ? гДе Ребра lj%, ljt+1 сходятся в вершине ХПг (индексы г
берутся по модулю /с) и попробуем вдоль них локально определить структуру
источник-сток. Ориентируем некоторым образом ребро lj±. Далее, если ребро
lj2 противоположно ребру Цг в вершине ХП1, то мы ориентируем lj2 так, чтобы
либо оба ребра ljx и lj2 стали входящими в вершину ХП1, либо чтобы оба стали
исходящими из нее; в случае, если ребра не являются противоположными, мы
сделаем так, чтобы одно из них было входящим в данную вершину, а другое —
исходящим. Далее поступим точно так же при ориентации ребер /J3,/J4,....
Если процесс сойдется, т. е. мы определим на ребре ljt+1 = ljx ориентацию,
совпадающую с исходной, назовем цикл хорошим, в противном случае назовем его
плохим. Иными словами, цикл называется хорошим, если количество
его трансверсальных прохождений через вершины четно.
Легко проверить, что такое определение хорошего цикла совпадает с
определением ориентирующего цикла на атоме, заданного Α-структурой: задавая
последовательно ориентацию ребер согласно правилу источник-сток, мы
задаем ориентацию примыкающих к этим ребрам клеток (локально), и, если мы
возвращаемся в исходное ребро с той же ориентацией, то это означает, что мы
прошли по ориентирующему пути, а если с противоположной, — то по
неориентир ующему.
Итак, мы определили понятие ориентирующего цикла и хорошего ребра (для
ребер, не входящих в дерево Δ). Следовательно, мы полностью построили
диаграмму виртуального узла K(V2(L)). Отметим, что это определение не зависит
(с точностью до объезда) от выбора графа Г.
Более того, по атому V2(L) этот узел восстанавливается с точностью до
виртуализаций (что, впрочем, не меняет гомологии Хованова); мы же указали
явный способ построения диаграммы K(V2(L)) по диаграмме L; он соответствует
некоторому погружению остова атома V2(L) (с сохранением А-структуры).
Легко видеть, что при применении объезда к исходной диаграмме
зацепления L к K(V2(L)) также применяется некоторая комбинация объездов. Кроме
того, имеет место следующая лемма.
Лемма 20.4. При применении одного из классических движений Рейдемей-
стера к диаграмме L диаграмма K(V2(L)) будет изменяться следующим
образом: к ней будет применяться то же самое движение Рейдемейстера в
двух местах.
Доказательство. Мы будем обозначать зацепления до и после применения
движения Рейдемейстера через L^L', остовы соответствующих атомов через
Г, Г7, а соответствующие диаграммы накрытий — через L, V
Каждое движение Рейдемейстера представляет собой перестройку
диаграммы узла внутри некоторой области; диаграмма L имеет некоторый вид Р, а
диаграмма U — некоторый вид Q. При этом мы имеем некоторый вид "хвостиков"
ίι,..., tn, соединяющих поддиаграмму Ρ (диаграммы L) или поддиаграмму Q
(диаграммы L') с оставшейся (неподвижной) частью диаграммы. В случае пер-
Атомы и комплекс Хованова
357
вого движения Рейдемейстера η = 2, в случае второго — четырем, в случае
третьего — шести. На диаграммах L и L' каждый хвостик ti поднимается до двух
хвостиков t7, t'(. В случае, если поддиаграмма Ρ или поддиаграмма Q не
содержит неориентирующих циклов, на L мы получаем две копии поддиаграмм Р,
а на U — две копии диаграммы Q. Суть теоремы состоит в том, что эти копии
согласованным образом подсоединены к "хвостикам". Пример согласованного и
несогласованного соединений приведен на рис. 20.9.
Рис. 20.9. Согласованное и несогласованное соединения
В согласованном случае все вершины ti, t\ соединяются одинаковым
способом в случае поднятия диаграммы L и в случае поднятия L7, а именно, все £'·
соединяются между собой, a t'l — между собой. В несогласованном случае на
рис. 20.9 соединение при поднятии L такое же, а соединение при поднятии L' —
другое: одна копия Q соединяется с вершинами t^^t^t^t^t^t^ а вторая —
с t7/, ^2? ^з? ^4? t'l·) ^6· Нам нужно показать, что второй случай не имеет места.
В случае применения первого движения Рейдемейстера, добавляющего
петлю возникает петля, состоящая из одного ребра lj, начальная (она лее конечная)
точка которого разбивает некоторое ребро Z&. Очевидно, что ребро lj,
рассмотренное как цикл, является хорошим. Кроме того, ребро Ik разбивается на два
ребра 1кг и Ζ&2, которые не являются противоположными в вершине разбиения.
Рассмотрим цикл с на графе Г7, содержащий ребро Ζ&. Ему естественным
образом соответствует цикл с7, содержащий 1^ и Ζ&2 на графе Г7. Если цикл с
ориентируем, то ориентируем и цикл с' и наоборот. Это следует из того, что
если ребра 1^г и Ζ&2 не являются противоположными, следовательно, при
определении цикла, на них можно задать последовательную ориентацию,
происходящую из ориентации ребра Ζ&. Поэтому если на диаграмме K(V2(L)) ребро 1\
соединяет, скажем концы X'pq с X"s> то пара ребер Zj^Zj^ будет соединять
соответствующие им концы (с теми же обозначениями) X' и X'r's. Это и означает
согласованность соединения.
Аналогично обстоит дело и с двумя оставшимися движениями Рейдемейсте-
358
Атомы и комплекс Хованова
ра. Каждое из этих движений представляет собой перестройку некоторой
области на плоскости; из этой области выходит несколько ветвей (в случае второго
движения Рейдемейстера их четыре, а в случае третьего — шесть). Рассмотрим
набор концов {Xij} этих ветвей.
Рассмотрим сначала второе движения Рейдемейстера. У диаграммы V
имеется двуугольник cd и исходящих ребра а, 6, е, /, см. рис. 20.10.
Μ [в
Рис. 20.10. Случай второго движения Рейдемейстера
Этот двуугольник является хорошим, ибо как цикл не имеет трансверсаль-
ных прохождений через вершины. Таким образом, весь набор ребер однозначно
поднимается на диаграмму K{y2(L')). В итоге мы получим два набора ветвей
af,bf,cf,df,ef,ff и а", 6", с", d", е". Ветви с7, d! образуют двуугольник, к
которому можно применить уменьшающее движение Рейдемейстера. То же можно
сказать и о двуугольнике с7/, d". Применяя к ним уменьшающие движения
вторые движения Рейдемейстера, мы получим диаграмму K(V2(L)). Для этого
достаточно заметить, что после такого уменьшающего движения
Рейдемейстера ребро о! соединится с ребром е7, а ребро Ъ' — с ребром е' (при этом а"
соединяется с е7/, а Ь" — се"). Последнее вытекает из того соображения, любой
цикл на L, проходящий последовательно через а^с^е имеет столько лее транс-
версальных прохождений через вершины, сколько и соответствующий ему цикл
на L7, проходящий через ребро А.
В случае третьего движения Рейдемейстера как на диаграмме L, так и на
диаграмме L· мы имеем по треугольнику и шесть внешних ветвей.
Оба треугольника представляют собой хорошие циклы, так как не
содержат трансверсальных прохождений. Следовательно, соответствующие области
Ρ и Q поднимаются до двойных копий областей Ρ и Q. Осталось проверить,
что они поднимаются согласованно.
Для этого нужно показать, что любые два пути 7 £ L и jf Ε L\
соединяющие концы ti,tj "одинаково", поднимаются на и L,L. Например, если один из
двух прообразов η пути 7 поднимается до пути, соединяющего точки t^t', и
проходящего внутри Р, то у каждого пути η1', имеющего те лее концы, что и 7?
один из прообразов η' соединяет те же точки t'^tj (а не t^t"). На рис. 20.11
показан пример двух таких путей.
А именно, рассмотрим два пути между точками X и У на диаграммах L
и V'. Мы утверждаем, что они поднимаются одинаковым образом на L и V
соответственно. Это следует из того, что количество точек трансверсального
прохождения на этих путях одинаково (равно нулю). Аналогично
доказывается одинаковость поднятия любых двух путей на рис. 20.11 с одинаковыми
концами. D
Атомы и комплекс Хованова
359
Рис. 20.11. Случай третьего движения Рейдемейстера
Следовательно, по лемме 20.2 гомологии Хованова "удвоенного узла" не
меняется при применении движений Рейдемейстера к исходному. Отсюда
получаем теорему.
Теорема 20.5. Отображение L —> Kh(K(V2(L))) является корректно
определенным инвариантом зацеплений.
Замечание 20.1. Отметим, что движение Рейдемейстера может
изменить тип соответствующего атома (т. е. превратить неориентируемый
атом в ориентируемый и наоборот). Так например, если мы имели
ориентированный атом V(K) и две компоненты атома V2(K), то применение
второго движения Рейдемейстера к К может "соединить" эти компоненты в
одну (что соответствует тому, что после применения второго движения
Рейдемейстера атом может перестать быть ориентируемым).
Пусть теперь атом, соответствующий зацеплению L, ориентируем. Тогда
K(V2(L)) состоит из двух копий атома L. Поскольку F является полем, мы
имеем KhF(K(V2(L))) = KhF(L)m.
Следовательно, гомологии Kh(L) получаются из инвариантных гомологии
Kh(K(V2(L))) извлечением тензорного квадратного корня. В случае, когда
кольцо коэффициентов является полем, мы имеем полином Пуанкаре от двух
переменных со всеми целыми положительными коэффициентами. Из него
нужно взять "квадратный корень", чтобы получить полином с целыми
положительными коэффициентами. Так как эта операция однозначна, если определена, мы
получаем утверждение теоремы 20.4.
Кроме того, из этих рассуждений мы получаем следующую теорему.
Теорема 20.6. Пусть F — поле и пусть зацепление L таково, что
K}iy(K(V2(L))) не представимо в виде тензорного квадрата. Тогда L не
имеет диаграммы, которой соответствовал бы ориентируемый атом. В
частности, зацепление L не является классическим.
Естественно, что комплекс Хованова, построенный в настоящем разделе,
не может определить нетривиальность виртуального узла, изображенного на
рис. 20.2, поскольку этот узел получается из тривиального узла обобщенными
движениями Рейдемейстера и виртуализацией.
360
Атомы и комплекс Хованова
Важной и интересной гипотезой является вопрос о том, могут ли два
неизотопных классических зацепления L, V быть получены друг из друга
последовательностью обобщенных движений Рейдемейстера и виртуализаций. Комплекс
Хованова дает частичный ответ на этот вопрос.
Из теоремы 20.4 и инвариантности гомологии Хованова относительно
виртуализаций вытекает следующая
Теорема 20.7. Если классическое зацепление U получается из классического
зацепления L применением обобщенных движений Рейдемейстера и
виртуализаций, то L и L' имеют одинаковые гомологии Хованова с коэффициентами
в любом наперед заданном поле.
Глава 21
Длинные виртуальные узлы
и их инварианты
21.1. Введение
Длинные виртуальные узлы и их инварианты были впервые рассмотрены
в [GPV]. Настоящая глава содержит результаты автора [Ма9, Мал 10]. Мы
приводим некоторые инварианты длинных виртуальных узлов, с помощью которых
демонстрируем различные феномены теории длинных виртуальных узлов,
которые не имеют места в теории классических узлов: некоммутируемость
длинных узлов, наличие для каждого виртуального узла К бесконечного числа не
эквивалентных друг другу длинных виртуальных узлов, имеющих замыкание,
эквивалентное узлу К.
Инварианты длинных виртуальных узлов (скажем, в виде дистрибутивных
или виртуальных группоидов) можно строить так же, как и инварианты
компактных виртуальных узлов. Кроме той структуры, которую мы
рассматриваем в случае компактных узлов, мы также располагаем следующими сведениями:
1. Можно указать начальную и конечную (некомпактные) дуги длинного
виртуального узла; они по построению будут являться инвариантными
элементами в (дистрибутивном или виртуальном) группоиде, так как
элементы, им соответствующие, будут инвариантными относительно
обобщенных движений Рейдемейстера.
2. Классические перекерестки диаграммы длинного виртуального узла
можно разбить на два типа: те, в которых переход предшествует проходу
(согласно ориентации узла) и те, где проход предшествует переходу, см.
рис. 21.1. Можно рассмотреть две различные "группоидные" операции,
соответствующие этим ситуациям.
Как было сказано ранее, процедура разрывания виртуального узла
существенно зависит от точки, в которой мы его разрываем: в результате могут
получиться неизотопные длинные узлы. Более того, виртуальная диаграмма
тривиального узла после такого разрывания может привести к нетривиальной
диаграмме длинного виртуального узла. В настоящей главе мы с разных сторон
рассмотрим вопрос о существенности выбора такой "точки разрыва".
362
Глава 21
Рис. 21.1. Ранний переход и ранний проход
Замечание 21.1. На протяжении настоящей главы мы имеем дело только
с узлами, а не с зацеплениями.
Далее R будет обозначать поле рациональных функций от одной
(вещественной) переменной t: R = Q(£).
Напомним определение длинного виртуального узла.
Определение 21.1. Под длинной виртуальной диаграммой будем понимать
гладкую иммерсию / (равно как и образ этой иммерсии) ориентированной
прямой Их,х G (—ос, +оо) в R2 такую, что:
1. Вне некоторого достаточно большого круга на плоскости с центром в нуле
образы точек прямой лежат на прямой Ох, кроме того, мы имеем f(t) =
(ί,Ο);
2. Каждая точка самопересечения образа прямой R является двойной и
трансверсальной;
3. В каждой точке пересечения задана структура классического или
виртуального перекрестка.
Определение 21.2. Длинный виртуальный узел — это класс эквивалентности
длинных виртуальных диаграмм по обобщенным движениям Рейдемейстера.
Естественно определена операция замыкания для длинных виртуальных
узлов: каждому длинному виртуальных узлу К соответствует компактный
виртуальный узел С1(К), получаемый из него соединением "концов" , см. рис. 21.2.
Как будет показано в дальнейшем, обратная операция "разрывания" не
является корректно определенной.
Известно, что в классическом случае результат (т. е. класс эквивалентности
получающегося длинного узла) не зависит от выбора точки разрыва. Как мы
видели в главе 17, в случае виртуальных узлов это не так.
В настоящей главе будет приведено еще одно доказательство этого факта,
используя инварианты длинных виртуальных узлов.
21.2. Рациональная функция %3
363
Рис. 21.2. Замыкание длинного виртуального узла
Если две диаграммы Κι, Κ2 длинных виртуальных узлов, не имеющие
классических перекрестков, эквивалентны (в виртуальном смысле), то они задают
изотопные длинные классические узлы. Доказательство легко следует из
теоремы 18.1. Действительно, если К\,К2 эквивалентны как длинные виртуальные
узлы, то компактные узлы С1(К\),С1(К2) эквивалентны как виртуальные, из
чего следует их эквивалентность как классических. Учитывая, что в
классическом случае классификации в длинном и компактном случае совпадают, мы
получаем классическую эквивалентность длинных узлов К\,К2-
Для длинных виртуальных узлов корректно определена операция
конкатенации: в качестве К\^К^ мы рассматриваем диаграмму, в которой
поддиаграмма, задающая узел К?,, лежит справа от поддиаграммы, задающей узел К\.
Таким образом, можно определить полугруппу 2U длинных виртуальных узлов,
в которой тривиальный длинный узел (узел, имеющий диаграмму без
перекрестков) играет роль единичного элемента.
Дуга и длинная дуга длинной виртуальной диаграммой определяются так
же, как и в обычном (компактном виртуальном случае; единственное различие
состоит в том, что, помимо компактных дуг, для длинных виртуальных узлов
мы имеем две некомпактные длинные дуги, у каждой из которых один конец
уходит на бесконечность; для диаграммы без перекрестков имеется ровно одна
длинная дуга с обоими концами на бесконечности.
На рис. 21.3 показана процедура разрывания диаграммы виртуального узла
в некоторой точке и получения длинной виртуальной диаграммы.
21.2. Рациональная функция 2J
В каждой диаграмме длинного виртуального узла есть две особенные дуги:
начальная и конечная.
Рассмотрим диаграмму К длинного виртуального узла К. Будем строить
виртуальный модуль Александера для этой диаграммы. Будем использовать
те же обозначения, что и ранее, см. 18.4, стр. 310. Модуль (который теперь
будет рассматриваться уже как линейное пространство над R) будем обозначать
через М.
364
Глава 21
Рис. 21.3. Получение длинной виртуальной диаграммы разрыванием
Предположим, что у рассматриваемой диаграммы η + 1 длинная дуга (что
соответствует η длинным дугам в компактном случае). Без ограничения
общности молено считать, что начальная длинная дуга не совпадает с конечной, т. е.
диаграмма имеет по крайней мере один классический перекресток. Каждая из
двух некомпактных длинных дуг содержит одну некомпактную дугу.
Обозначим дугу, исходящую из —ос, через αϊ, а дугу, уходящую в +ос, через αη+ι·
Для каждой из оставшихся η — 1 длинных дуг выберем по короткой
дуге. Обозначим выбранные дуги через а2, · · ·, &п (в данном случае нумерация и
произвол выбора дуги на длинной дуге не имеют значения).
Будем теперь строить линейное пространство над R. Рассмотрим сначала
(п + 2)-мерное пространств S, порожденное элементами αϊ,..., ап+ъε·> гДе ε —
формальная новая образующая.
Определим теперь ΛΊ как факторпространство, полученное из S
факторизацией по тем лее соотношениям, что и в случае обычных (не длинных) узлов.
По причине того, что Μ построено по правилам длинного группоида, тройка
(ΛΊ, αϊ, αη+ι) является инвариантом длинного виртуального узла
относительно обобщенных движений Рейдемейстера. Очевидно, что в этом случае имеет
место αη+ι — αϊ = к · ε для некоторого к. По определению этот элемент к
(принадлежащий кольцу К) является инвариантом длинного узла. Обозначим его
через ЩК).
Очевидно, что ЯЗ удовлетворяет следующим свойствам.
Теорема 21.1. Для каждого длинного классического узла L имеет место
9J(L) = 0.
Теорема 21.2. Инвариант 9J аддитивен: Щ{К1фК2)) = 9J(ifi) + %J(K2).
Рассмотрим следующий пример, показывающий, что разрывание одного и
того же виртуального узла (виртуального трилистника) в различных точках
может привести к различным длинным виртуальным узлам, см. рис. 21.3. Мы
показали это с использованием инвариантов компактных виртуальных узлов.
Покажем теперь это с использованием инварианта ЯЗ. Обозначим длинный
виртуальный узел в правом верхнем углу рис. 21.3 через Κι, а узел в правом
нижнем углу — через К2.
21.3. Длинный группоид
365
Для длинного узла Κι мы имеем:
t · а\ + (1 - t)a3 — а>2 = (t— ΐ)ε
t · CL2 — t · as = (1 — t)e.
Умножая первое уравнение на t и прибавляя его ко второму, мы получаем:
(t- I)2
ЩК1) = а3-а1 = -^^-.
Для узла К2 мы имеем:
t · ci2 + (1 — t)a\ — as = (1 — 2t)e
t · a\ + (1 — t)as — a2 = te
Умножая второе уравнение на t и прибавляя его к первому, мы получаем
(t-lf
Щк2)
t2-t+l'
Таким образом, мы видим, что ЯЗ может различать длинные виртуальные
узлы, замыкания которых представляют собой изотопные виртуальные узлы.
21.3. Длинный группоид
Определение 21.3. Длинным группоидом назовем множество Q,
снабженное четырьмя бинарными операциями о, *,/,// и одной унарной операцией /(·)
такими, что (Q, о, /) является виртуальным группоидом, (Q, *, /) является
виртуальным группоидом, при этом выполняются следующие соотношения:
\/a,beQ: (а о Ъ)/Ъ = (а/Ъ) о Ъ = (а * Ъ)//Ъ = (а//Ъ) * Ъ = а (21.1)
\/а,Ъ,се Q,Va,pe {о, *,/,//}: (ααο)βο = (αβο)α(ϋβο), (21.2)
Va, 6, с G Q : (a * 6) о с = (а о с) * (6 о с) (21-3)
(новые соотношения дистрибутивности, см. рис. 21.4) и
Vx, a, b G Q : £<^(a о 6) = xce(a * 6) (21-4)
Vx,a,6GQ: x/3(a/6) = xp(a//b), (21.5)
где a vl β — некоторые операции из списка о,*,/,// (странные соотношения,
см. рис. 21.5).
Из рис. 21.5 мы имеем соотношение (а о 6) о с = (аос)о(6*с), которое вместе с
соотношением дистрибутивности (а о 6) о с = (аос)о(бос) приводит к странному
соотношению χ о (Ъ о с) = χ о (6 * с).
Замечание 21.2. Может показаться, что выполнение странных
соотношений может иметь место только в случае, когда операция о совпадает с
операцией *. Однако уравнение (а о Ь) = с имеет единственное соотношение
по а, но может иметь много различных решений относительно Ъ при
фиксированных а и с!
366
Глава 21
Рис. 21.4. Соотношения дистрибутивности
Рис. 21.5. Странное соотношение
Рассмотрим длинную виртуальную диаграмму К и ее дуги. Фиксируем
начальную дугу а и конечную дугу Ъ.
Будем строить длинный группоид, соответствующий диаграмме К
следующим образом. Рассмотрим сначала все дуги, включая а и 6, и построим
свободный длинный группоид, т. е. длинный группоид, формально порожденный
операциями о, *,/,//,/ и профакторизованный только по соотношениям
длинного группоида (21.1-21.5).
После этого профакторизуем свободный длинный группоид по следующим
соотношениям в перекрестках. В каждом виртуальном перекрестке
соотношение выглядит так же, как и в случае обычного виртуального группоида. В
каждом классическом перекрестке мы факторизуем по соотношению, в котором
участвует о или *, а именно, если переход предшествует проходу (согласно
ориентации длинного узла), мы факторизуем в точности по такому лее
соотношению, как и в случае виртуального группоида (с операцией о); в противном
случае вместо операции о мы используем операцию *.
После такой факторизации мы получаем алгебраический объект М,
снабженный пятью операциями о,/,*,// и /, в котором выделены два элемента
а и 6, соответствующие начальной и конечной дугам.
21.3. Длинный группоид
367
Определение 21.4. Обозначим полученный объект через Ql(K).
Теорема 21.3. Длинный группоид Ql вместе с элементами а, Ъ является
инвариантом длинных виртуальных узлов, т. е. для двух диаграмм К и К'
одного и того же длинного виртуального узла К существует изоморфизм
h : Ql(K) —> Ql{K'), переводящий элемент а в а, а элемент Ъ — в Ь.
Пусть К — диаграмма длинного виртуального узла К. Будем называть
Ql(K) длинным группоидом узла К.
Очевидно, что для длинного тривиального узла U мы имеем для начальных
дуг а,6 G Ql(U) :a = b.
Доказательство теоремы 21.3. Доказательство полностью аналогично
доказательству инвариантности виртуального группоида. Мы приведем здесь лишь
набросок, оставляя детали читателю. Инвариантность относительно объезда
доказывается так лее, как и в обычном (компактном) случае: мы имеем дело
только с операцией / и лишь с одной из операций о или *. Далее, только одна
из двух операций *, о может возникнуть при рассмотрении первого или второго
классического движения Рейдемейстера.
Самым интересным является здесь третье классическое движение
Рейдемейстера. Достаточным является рассмотрение его случаев, указанных
на рис. 21.6 (а, б, в, г).
Рис. 21.6. Проверка инвариантности относительно Ω3
В каждом из четырех вышеупомянутых случаев мы имеем три входящие
дуги и три исходящие дуги. Одна из дуг (которой соответствует метка р)
проходит выше в обоих перекрестках, так что метка на ней не меняется. Другая
дуга (которой соответствует метка q) подвергается действию дуги с меткой р\
это действие одинаково в обоих случаях, соответствующих конкретной версии
движения Ω3. Таким образом, нам остается исследовать исследовать, что
происходит с дугой, которой соответствует метка г.
368
Глава 21
На каждой из картинок в каждом перекрестке мы ставим некоторую
операцию се, /3 и 7 из множества операций {°, *, /, //}· Эта операция будет применена
к дуге снизу, образующей проход, для получения соответствующей дуги сверху.
Рассмотрим случай а. Каждая из операций се, /3,7 является "умножением",
т.е. о или * (операции / и // будем называть "делениями").
Таким образом, в левом верхнем углу мы получим: (r/yq)ap на левой
картинке и (rap)j(qPp) на правой картинке. Но по определению (rjq)ap = (rap)j(qap).
Последнее выражение равно (ναρ)^(ςβρ) согласно соотношению
дистрибутивности или странному соотношению (так как обе операции β и а являются
умножениями) .
Рассмотрим теперь случай б. Здесь η является умножением, а се, β —
делениями. Таким образом, мы имеем то же самое соотношение: (rjq)ap =
= (rap)j(qap) = (ναρ)^(ςβρ).
То же соотношение имеет место и для картинок виг: единственное, что
нужно заметить, это то, что либо обе операции а и β являются умножениями
(случай в), либо обе являются делениями (случай г). Оставшаяся часть
доказательства очевидна. D
21.4. Инвариант раскрасок
Длинные группоиды, как и дистрибутивные группоиды и как виртуальные
группоиды, имеют реализацию в виде инвариантов раскрасок. А именно, пусть
Ql(K, αϊ, (22) — длинный группоид длинного виртуального узла К с
операциями /, о, *, /, //, где а\ и CL2 — элементы длинного группоида Ql,
соответствующие начальной и конечной дугам узла К соответственно.
Пусть G — конечный длинный группоид с выделенными элементами д\, д2 ·
Тогда по построению имеет место следующая теорема.
Теорема 21.4. Количество гомоморфизмов из Ql(K) в G, при которых а\
переходит в gi, а а2 переходит в д2, конечно и является инвариантом
длинного узла К.
Эта теорема позволяет сделать следующее замечание: в отличие от
инварианта раскрасок (как в случае компактных узлов), каждый длинный группоид
G порождает матрицу раскрасок. А именно, занумеруем элементы из G
натуральными числами 1,..., п и определим М^ как общее число всех правильных
раскрасок диаграммы узла таких, что начальная дуга покрашена элементом
длинного группоида с номером г, а конечная дуга покрашена элементом с
номером j. Обозначим получившуюся таким образом для длинного виртуального
узла К матрицу через Μ (К).
Следующая теорема очевидна по построению.
Теорема 21.5. Для любых двух длинных виртуальных узлов К\,К2 имеет
место М(К1#К2) = М(Кг) · М(К2).
Это означает, что каждый конечный длинный группоид определяет
представление полугруппы 2U длинных виртуальных узлов.
С помощью такого матричного представления можно исследовать длинные
виртуальные узлы на коммутируемость. Некоммутируемость некоторых пар
21.5. Виртуальные узлы и длинные виртуальные узлы 369
виртуальных узлов будет показана в дальнейшем с использованием длинных
группоидов.
21.5. Виртуальные узлы
и длинные виртуальные узлы
Мы уже привели некоторые примеры, показывающие то, что операция
разрывания виртуального узла не является корректно определенной. Интересным
является пример нетривиального компактного узла, представляющего собой
связную сумму двух тривиальных узлов. Причина состоит в том, что эти
тривиальные узлы, рассмотренные как длинные, уже не являются тривиальными,
см. рис. 21.7. Нетривиальность каждого из них можно легко показать с
помощью длинного группоида.
/ \
—?*' г~
Q
а) б)
Рис. 21.7. Два длинных узла, получающиеся из тривиального узла
У каждого из длинных виртуальных узлов, изображенных в нижней части
рис. 21.7, обозначим начальную дугу через а, а конечную — через 6. Покажем,
что ни один из них не является тривиальным. Для этого мы будем использовать
следующее представление длинного группоида в категорию Ζιβ по формуле:
а о 6 = Ъа — 46, а * 6 = 9а — 86
f(x) = 3 · χ.
Проверка аксиом длинного группоида остается читателю в качестве
упражнения.
Можно считать, что мы просто исследуем множество гомоморфизмов
длинного группоида некоторого узла в длинный группоид, определенный на
множестве Ζ16 по формулам, описанным выше.
?3
370
Глава 21
Покажем теперь, что ни для одного из этих длинных виртуальных узлов
не имеет места равенство а = 6. Действительно, для первого узла (рис. 21.7.а),
обозначим через с дугу, следующую за дугой а. Мы получаем:
9а-8· (Зс) = с, 56 - 4 · (Зс) = с => 6 = 9а.
Для второго узла (рис. 21.7.6), обозначим через с верхнюю (короткую) дугу.
Мы имеем:
5 · (36) - Аа = с, 9 · (За) - 86 = с => 6 = 9а.
Как мы видим, ни в одном из этих случаев не имеет место равенство α = 6.
Таким образом, ни один из длинных узлов, изображенных на рис. 21.7.а и рис.
21.7.6, не является тривиальным. Далее мы покажем, что они неэквивалентны.
21.6. Коммутируемость длинных узлов
Как известно, классические длинные узлы коммутируют. Более того, верна
следующая теорема.
Теорема 21.6. Пусть длинный узел L не имеет виртуальных перекрестков.
Тогда для любого длинного виртуального узла V имеет место
коммутативность L#L' = Z/#L.
Доказательство. Действительно, сделаем сначала диаграмму узла L очень
маленькой и начнем протягивать ее сквозь диаграмму узла U. При протаскивании
ее через виртуальные перекрестки мы будем пользоваться движением объезда,
см. рис. 21.8, а при протаскивании через классические перекрестки —
классическими движениями Рейдемейстера.
В итоге мы получим желаемую изотопию. D
Замечание 21.3. Это доказательство не проходит в том случае, если узел
L имеет виртуальные перекрестки, так как в этом случае нельзя будет
протягивать L сквозь дуги диаграммы V', состоящие из классических
перекрестков. В этом случае нам пришлось бы воспользоваться запрещенным
движением, см. рис. 17.5.
Имеет место и более общая линейная модель длинных группоидов, в которой
f(a) = ka,
а о 6 = ра + (1 — р)6,
а * 6 = qa + (1 — q)b,
в которой длинный группоид Μ является модулем над некоторым
коммутативным кольцом, где p,k,q — обратимые элементы, при этом (р — 1)(р — q) =
(ί-1)(ρ-<ζ) = 0.
Оказывается, что с помощью конструкции длинного группоида можно
доказывать и более сильные утверждения, например, некоммутируемость тех
же двух узлов. А именно, рассмотрим кольцо Z112.1g2 и операции а * 6 =
20а - 196, α о 6 = (20 + 121 · 19)а - (122 · 19)6 и /(а) = 70а. Можно заметить,
21.6. Коммутируемость длинных узлов
371
Рис. 21.8. Классический длинный узел коммутирует с любым длинным узлом
что в модуле Μ для узла К\фК^ начальная дуга обязательно должна делиться
на 121, в то время как для модуля, соответствующего узлу К2ФК1,
существует гомоморфизм в кольцо Ζ υ 2. ]_ 92, при котором начальная дуга переходит в
11 · 192. Следовательно, эти узлы не коммутируют, что еще раз подтверждает
их различность, нетривиальность и не эквивалентность никакому
классическому каждого из них.
Имеют место два очевидных случая коммутирования длинных виртуальных
узлов: когда они совпадают либо когда один из них является классическим. Мы
предполагаем, что по существу других причин коммутирования быть не можем,
т. е. мы выдвигаем следующую гипотезу.
Гипотеза 21.1. Если два длинных виртуальных узла К, К' коммутируют,
то существует такой длинный виртуальный узел L, такие
неотрицательные целые числа т,п и классические длинные узлы Μ, Μ', что
К = ЬтфМ, К' = ЬпфМ',
где степень понимается в смысле многократного взятия связной суммы.
372
Глава 21
Отметим, что с помощью нетривиального узла Кишино, который
распадается на два нетривиальных длинных узла, каждый из которых имеет тривиальное
замыкание (см. рис. 21.7) молено доказать следующую теорему:
Теорема 21.7. Для каждого изотопического класса узла К множество
длинных узлов к, таких что Cl(k) = К, счетно.
Доказательство. Рассмотрим компактный виртуальный узел и произвольный
длинный узел Κι, полученный некоторым разрыванием узла К. Таким образом
мы имеем Cl(Ki) = К.
По каждому длинному узлу Μ мы можем построить новый длинный узел
М' так как показано на рис. 21.9.
Очевидным образом мы имеем Cl(M') = С1(М).
Μ
Рис. 21.9. Операция '
Пусть теперь Къ = {Κι)' ,Κ·^ = (-Кг)' и так далее: для каждого
натурального г положим Ki = (Ki-i)' для г = 2,3,.... Очевидно, что для каждого
натурального г мы имеем Cl(Ki) = CI (К ι) = Κ.
Мы утверждаем, что среди узлов Κι найдется бесконечно много различных.
Для этого нам достаточно заметить, что различны их замыкания Кишино,
которые определены так, как показано на рис. 21.10.
м
,1X2
Μ
Рис. 21.10. Замыкание Кишино
Легко проверить, что операция замыкания Кишино корректно определена:
для эквивалентных длинных узлов мы получаем эквивалентные компактные
21.6. Коммутируемость длинных узлов 373
узлы при таком замыкании. То, что среди замыканий Кишино узлов К ι
встречается бесконечно много различных узлов, следует из того, что эти замыкания
могут иметь любой сколь угодно большой наперед заданный род. Более того,
соответствующие виртуальные узлы имеют сколь угодно большой наперед
заданный род в плоской категории, т. е. если мы разрешим помимо обобщенных
движений Рейдемейстера применять замену типов классических перекрестков. D
Глава 22
Виртуальные косы
Аналогично тому, как классические зацепления могут быть получены в
виде замыкания классических кос, виртуальные зацепления пред ставимы в виде
замыкания виртуальных кос. Виртуальные косы были впервые упомянуты
Кауфманом в его первом докладе о виртуальных узлах, [KaulO]. Первые работы
о виртуальных косах принадлежат Сейичи Камаде [Кат] и Владимиру
Валентиновичу Вершинину, [Ver].
22.1. Определения виртуальных кос
Как и виртуальные узлы, виртуальные косы имеют чисто комбинаторное
определение. Они определяются как классы эквивалентности диаграмм
виртуальных кос по виртуальным движениям Рейдемейстера (допускаются все
движения Рейдемейстера, кроме первого классического и первого виртуального).
Тот факт, что мы запрещаем первое виртуальное движение Рейдемейстера,
ведет к замечательной (и простой) конструкции обобщения всех квантовых
инвариантов классических узлов на случай "виртуальных узлов" с некоторой
оговоркой. Здесь нужно рассматривать теорию, в которой виртуальные
диаграммы факторизуются по всем обобщенным движениям, кроме первого
виртуального. В этом случае говорят о теории жестких виртуальных узлов. Более
подробно об этой теории см. в [Каи7] и в монографии [КМО].
Определение 22.1. Диаграмма виртуальной косы из η нитей — это набор η
гладких кривых общего положения, соединяющих точки (г, 1) с точками (1, α^)>
монотонных относительно ординаты (где (αϊ,..., ап) — некоторая перестановка
чисел (1,... ,п), при этом некоторые перекрестки помечены как виртуальные,
а в других (классических) перекрестках указано, какая ветвь задает проход, а
какая — переход.
Определение 22.2. Виртуальной косой называется класс эквивалентности
диаграмм виртуальных кос по плоским изотопиям — деформациям плоскости,
оставляющим неподвижными все ее концевые точки и преобразующим
диаграмму косы в диаграмму косы, а также по всем движениям Рейдемейстера,
кроме первого классического и первого виртуального.
Замечание 22.1. Первое классическое и первое виртуальное движения
Рейдемейстера невозможны по той причине, что нить косы, имеющая петлю,
не может быть восходящей.
22.2. Представление Бурау и его обобщения 375
Как и классические косы, виртуальные косы обладают естественной
групповой структурой (умножение — расположение одной косы над другой, а взятие
обратной — зеркальное отражение диаграммы относительно горизонтальной
оси). Образующими группы виртуальных кос из η нитей являются: σ\,..., ση_ι
(для классических перекрестков) и ζι,..., Cn-i (для виртуальных перекрестков,
см. рис. 22.1).
I I Vм I I
/Л
Рис. 22.1. Образующая Сг
Обратные элементы для образующих вида σ определены так же, как и в
классическом случае. Очевидно, что для каждого г = 1,... ,п — 1 мы имеем
(f = е (это соответствует второму виртуальному движению Рейдемейстера).
Можно показать, что следующий набор соотношений [Ver] является
порождающим для группы виртуальных кос:
1. (Соотношения группы кос:) σ^σ:/=σ:/σ^ для \г—j\ ^ 2; σ^+ισ^=σ^+ισ^+ι;
2. (Соотношения группы перестановок:) (^Cj — Cjd Для \^~ j\ ^ 2; СгСг+iCi —
Сг+lCiCi+i; С = е5
3. (Смешанные соотношения:) σ^+ιΟ — Сг-ыСг^г-ы;
aiCj = Cj°i Для \i-j\ ^2.
Доказательство остается читателю в качестве упражнения.
Группы виртуальных кос из η нитей обозначаются как VB(n). Если
рассмотреть подгруппу группы кос из η нитей, состоящую из кос, в записи которых не
встречаются образующие ση и (п, мы получим группу, изоморфную VB(n— 1).
Поэтому имеют место вложения VB{1) С VВ(2) С · · · С VB(n) С ...
Таким образом можно говорить о стабильной группе виртуальных кос
VB{oo) как о прямом пределе групп виртуальных кос по вложению.
22.2. Представление Бурау и его обобщения
В [Ver] было предложено следующее обобщение *В представления Бурау
для группы виртуальных кос. Группа виртуальных кос VB(n)
представляется матрицами пхщ образующие σ^, d представляются блочно-диагональными
матрицами с единицами на диагонали и единственным нетривиальным
блоком размера два на два в строках и столбцах (η,η + 1). Блочная матрица для
образующей σι такая лее, как и в главе 8. Для ζι мы используем матрицы
транспозиций, а именно,
(Го)-
376
Глава 22
Доказательство того, что это действительно представление, остается
читателю в качестве упражнения.
Замечание 22.2. Отметим, что тривиальное обобщение инвариантов кос
на виртуальные косы, при котором виртуальной образующей соответствует
транспозиция, приводит к обобщению на случай виртуальных кос всех
квантовых инвариантов, см. [Каи7].
У этого представления имеется ядро далее в случае двух нитей. Легко
проверить, что для нетривиальной косы Ъ = (ο^ζι^ΐ (ισΓ Ci)2 мы имеем 53(6) =
53(e) = ( 1, где е — единичная коса. Действительно, легко видеть, что
матрица 53(σι) имеет следующие собственные значения: 1 и 1 — t. Более точно,
О
СЩа^С-1 = ( J г
t
где
В этом случае мы имеем
1 1
О -1
Будем писать просто ζ вместо C53(Ci)C_1 и σ вместо C53(ai)C_1.
Положим H(k,l,m) = ak(al(am( является верхне-треугольной матрицей с
1 и —1 на главной диагонали если k-\-l-\-m = 0. Положим к = 2, / = — 1, m = —1.
Тогда53(Я(2,-1,-1)2) = е.
Далее будет показано, что виртуальная коса Ъ = {σ\ζ\σϊ ζι&ϊ Ci)2
нетривиальна.
Имеет место следующее обобщение этого представления Бурау [Ма8]: мы
рассматриваем полиномиальные матрицы от двух переменных t и q (и их
обратных), берем тот же самый образ элементов σ^, что и раньше, и матрицу
0 q
q-1 0
в качестве блока для выражения образов элементов (^. Мы получим
отображение, заданное на образующих группы виртуальных кос. Обозначим его через R.
Теорема 22.1. Отображение R задает представление группы виртуальных
кос.
Доказательство. Для матрицы R(d) мы имеем (R((i))2 = е.
Далее, соотношения группы кос для образующих σ верны как и в случае
представления Бурау.
Таким образом, нам нужно лишь проверить следующие соотношения:
R{CiCi+lCi) = ^(Сг+lCiCi+l) И #(СгСг+10"г) = R{& ί+ΐζίζί+ΐ) ·
Они проверяются непосредственно прямым вычислением для матриц
размера 3x3. D
22.3. Инварианты виртуальных кос
377
Имеет место следующая теорема.
Теорема 22.2. Группа Вг(3) является естественно вложенной в
группу VB(3).
Доказательство. Действительно, пусть βχ,βι — некоторые слова-косы,
записанные в алфавите из букв σι, σ2, cr^ , σ^ · Предположим, что они
представляют одну и ту лее косу в VB(n). Тогда их матрицы Бурау совпадают. Так как
представление Бурау для классических кос является точным для кос из трех
нитей (это показано в главе 8), мы видим, что β\ и /?2 задают одну и ту же косу
в Бг(3). D
Вопрос о существовании точного представления группы виртуальных кос
из произвольного числа нитей до настоящего времени остается открытым.
22.3. Инварианты виртуальных кос
В настоящем разделе мы приведем обобщение Τ инварианта / классических
кос, описанного в главе 10; описываемый в настоящей главе инвариант был
предложен автором в [Ман8]; с его помощью доказывается, что классическая
группа кос является подгруппой виртуальной группы кос из того лее числа
нитей. Более точно, так как мы имеем инвариант виртуальных кос, являющийся
полным инвариантом для классических кос, то для любых двух классических
кос, которые эквивалентны как элементы группы виртуальных кос, значения
этого инварианта равны; в силу полноты мы заключаем, что эти классические
косы представляют один и тот лее элемент в соответствующей группе
классических кос. До сих пор не известно, является ли этот инвариант полным или
нет.
Назовем диаграмму виртуальной косы регулярной, если любые два ее
перекрестка имеют различные ординаты.
Замечание 22.3. В дальнейшем в настоящем разделе количество нитей косы
будет обозначаться через η (считаться равным п), если не оговорено
противное.
Замечание 22.4. В дальнейшем (регулярные) диаграммы виртуальных кос и
соответствующие слова-косы будут обозначаться греческими буквами
(возможно с индексами). Виртуальные косы будут обозначаться латинскими
буквами (возможно с индексами).
Замечание 22.5. Мы также будем употреблять слово "нить"
относительно слова-косы (записи косы по образующим), подразумевая под этим нить
соответствующей косы.
Опишем построение слова по заданной регулярной диаграмме виртуальной
косы. Будем двигаться вдоль оси Оу от уровня {у = 1} вниз до уровня {у = 0}
и следить за теми уровнями {y = t£[0,l]}, на которых имеются перекрестки.
Каждый такой перекресток переставляет нити с (локальными) номерами г и
(г +1) для некоторого г = 1,..., п— 1. Если перекресток является виртуальным,
мы будем писать (^; если он является классическим, мы выписываем σι в случае,
378
Глава 22
если переход соответствует направлению "северо-запад — юго-восток" и σ~ в
противном случае.
Таким образом мы получаем слово по заданной регулярной диаграмме
виртуальной косы, см. рис. 22.2.
(2σισ2σι
Рис. 22.2. Виртуальная коса и соответствующее ей слово
Основным вопросом теории виртуальных кос является вопрос
распознавания: Как распознать, задают ли две (собственные) диаграммы β\ и β2
виртуальных кос одну и ту же косу Ъ или нет1.
Частичный ответ на такой вопрос дает инвариант, который мы собираемся
описать.
22.3.1. Построение основного инварианта
Мы построим обобщение J- инварианта /, приведенного в главе 8, на случай
виртуальных кос.
Пусть G — свободная группа с образующими а\ ..., αη, t. Пусть Ei —
фактор- множество правых смежных классов {cti}\G при г = 1,..., п.
Замечание 22.6. В главе 10 той же буквой G обозначалась свободная группа,
порожденная образующими а\... ,an,t (без t), при этом буквами Ei
назывались аналогичные классы смежности группы G (без t) no элементами а^.
Определение 22.3. Виртуальной п-системой назовем множество элементов
{ei G Еъе2 е Е2,..., епе Еп}.
Нашей ближайшей целью является построение инвариантного отображения
(не гомоморфного) из множества всех виртуальных кос из η нитей во
множество виртуальных гг-систем.
1 Насколько известно автору, такой алгоритм (явный и удобный, не использующий теорию
Хакена нормальных поверхностей) до сих пор еще не найден.
22.3. Инварианты виртуальных кос
379
Пусть β — слово-коса. Будем строить соответствующую виртуальную п-
систему J-(P) шаг за шагом. А именно, мы будем получать значение Τ{βφ) по
значению J-'(P), где φ является одной из букв: σ^, σ~ или ζΐ ·
Рассмотрим сначала η классов смежности единичного элемента G: (е,е,... ,е).
Положим
Τ {г) = (е,е, ...,е).
Будем теперь читать слово β. Если его первой буквой является (^, то на
первом шаге все слова в виртуальной гг-системе, кроме слов e^e^+i, остаются
теми же, е^ становится равным t, a e^+i становится равным t_1 (здесь и далее
мы, естественно, имеем в виду классы смежности, т.е. [t] и [£-1], но пишем для
простоты t и ί-1)·
Если первой буквой в слове является σ^, то все классы, кроме e^+i, не
изменяются, при этом e^+i становится равным а~ . Если же первой буквой
была σ~ , то единственное изменение относится к е^: этот элемент становится
равным <2г+1·
Процедура для каждой следующей образующей такова. Пусть образующая
имеет индекс (номер) г. Предположим, что левая нить, подходящая к
перекрестку, выходит из точки (р, 1), а правая нить выходит из точки (</, 1). Пусть
до перекрестка мы имеем ер = Р, eq = Q, где P,Q — некоторые элементы из
Ер, Eq. После этого все классы смежности, кроме ер, eq, не изменяются.
Если рассматриваемой буквой является (^, то слово ер становится равным
P-t, а слово eq становится равным Q-t~x. Если мы имеем σ^, то ер не изменяется,
a eq переходит в QP~1a~1P. Наконец, в случае буквы σ~ класс смежности eq
остается тем же, в то время как ер становится равным PQ~1aqQ. Эти операции
корректно определены, т. е. не зависят от выбора представителей
соответствующих классов смежности. Проверка этого факта остается читателю.
Таким образом, мы определили отображение Τ из множества виртуальных
диаграмм кос из η нитей в множество виртуальных гг-систем.
Теорема 22.3. Функция Τ является инвариантом виртуальных кос. А
именно, если βι и β2 представляют одну и ту же виртуальную косу β, то
Ρ(β1)=Ρ(β2).
Доказательство. Нам нужно доказать, что функция Τ инвариантна при
применении соотношений группы виртуальных кос. Для этого достаточно
показать, что для слов βι = /?7ι и /?2 = /$72 > где 7ι — 72 — соотношение, мы имеем
3~(βι) = Τ{β<ι). Будем называть это утверждение утверждением А.
Доказав утверждение А, мы имеем также Τ{β\δ) = Ρ(β2$) в случае J-φι) =
Τ{β2) для произвольного слова δ, так как наш алгоритм является
пошаговым, т.е. 3-(βιδ) (как и JF(/32#)) определяется перестраиванием виртуальной
гг-системы 3-(βι) = Τ^β?) посредством косы δ. Таким образом, для слов /3, δ и
для любого соотношения группы кос 7ι — 72 мы имеем Τ(β^(\$) = Τ(^β^δ\ что
завершает доказательство теоремы.
Вернемся теперь к доказательству утверждения А.
Рассмотрим соотношения группы виртуальных кос. Случай соотношения
GiGj = GjGi для \i—i\ ^ 2 очевиден: порядок перестройки гг-системы по далеким
образующим не отражается на конечном результате. То же самое имеет место
380
Глава 22
и в случае коммутирования с одной образующей σ и одной образующей ζ или
с двумя образующими ζ.
Рассмотрим теперь соотношение ζ2 = е.
Рассмотрим слово-косу /3, и пусть слово β\ равно β ζ? для некоторого г. Пусть
Τ {β) = (Pi,..., Ρη),Τ(βι) = (Ρ[,..., Ρ^). Пусть ρ и ς — номера нитей (точнее,
абсциссы верхних концов нитей), подходящих к рассматриваемому перекрестку
слева и справа. Очевидно, что при j φ p,q мы имеем Pj = Pj. Кроме того,
ρ; = (рр ■ t) · ί-1 = pp,pq = (pq ■ ί-1) -t = pq.
Рассмотрим теперь случай β\ = β·σι·σ~ (очевидно, что случай Ь\ = βσ~ σι
полностью ему аналогичен).
Обозначим Τ {β) через (... Pi...), а Τ{β\) через (... Ρ/ ...), а номера нитей,
подходящие к перекрестку слева и справа обозначим через ρ и q. При j φ p,q
мы имеем Ρ'- = Р^. Более того, Рр = Р^ по построению отображения Τ (так как
р-я нить дважды образует переход, при этом P'q = (РдР~га~хРр)Р~гарРр = Pq.
Проверим теперь инвариантность относительно третьего виртуального
движения Рейдемейстера. Пусть β — слово-коса, β\ = /З^Сг+iCb а βι — /?Сг-ыСгСг-ы·
Пусть p,q,r — номера нитей (считая сверху), соответствующие положениям
п,п-\- 1, η + 2 внизу косы 6.
Обозначим .F(/3) через (Pi,..., Pn), a ^(/3i) через (Pj1,..., Р^). Обозначим
также Τ{βϊ) через Рр,..., Pp. Очевидно, что Уг φ p,q,r мы имеем Р^ = Р/ =
Pp. Из явных вычислений следует, что Рр = Рр = Рр · t2, Р^1 = Р2 = Рд, а также
Рассмотрим теперь смешанное соотношение (мы будем пользоваться теми
же соотношениями). Мы имеем: β\ = /ЗСгСг-ы°"г? /?2 — /?^"г-ыСгСг-ы· Как и
ранее, Р1 = Р2 = Pj для всех j φ p,q,r. Из явных вычислений следует, что
Pi = Ppt\Pl = Pqt-\PXr = Prt-^Pqt-1)-1^1^-1) = PrP^Pqt-1 И
p2 _ ρ f2 p2 _ ρ f-l p2 _ ρ p-\ -1 ρ
Рассмотрим, наконец, третье классическое движение Рейдемейстера β\ =
/3σ^σ^+ισ^, /?2 — βν%+\ν%ν%+\\ обозначения остаются прежними. Мы имеем: \/j φ
p,q,r : Pj = Ρ2 = Pj. Кроме того, так как р-я коса (в обоих случаях)
образует два перехода, то Р^ = Рр = Рр. Следовательно, Pq = PqP~1a~1Pp^P} =
(PrP-'a-'Pp) · (PgP-^Pp)-1^1 (Ρ,Ρ-1^^) = Ρ^α'^Ρ^α^Ρ^ по
построению имеют место равенства Pq=PqPp гар гРр, P2=PrPq xaq xPqPp гар гРр.
Совпадение окончательных результатов завершает доказательство теоремы.
D
Таким образом мы доказали, что Τ является инвариантом виртуальных кос,
т. е. для заданной косы значение отображения Τ не зависит от диаграммы,
представляющей Ъ. Таким образом мы можем писать просто 3~(Ъ).
Замечание 22.7. На самом деле функцию Τ можно рассматривать не как
функцию, принимающую значения (Ρι,...,Ρη); а как функцию,
принимающую значения в η экземплярах группы G: доказательство инвариантности
проходило как раз для (G,..., G).
22.3. Инварианты виртуальных кос
381
22.3.2. Первые следствия
Как и классические узлы, классические косы (т. е. косы без виртуальных
перекрестков) допускают два соотношения эквивалентности: классическое
(посредством обычных движений Рейдемейстера) и виртуальное (посредством
обобщенных движений Рейдемейстера). С помощью инварианта Τ покажем, что на
самом деле эти два соотношения эквивалентности совпадают. Впервые это
было доказано Роджером Фенном, Ричардом Риманьи и Колином Рурком, см.
[FRR].
Полагая t = 1 в инварианте Τ и возвращаясь к "старым" Ει (определенным
в главе 10), мы получаем обобщение полного инварианта / классических кос
на случай виртуальных кос.
Теорема 22.4. Две эквивалентные виртуальные слова-косы Ъ\ иЪ2, в записи
которых нет образующих ζ, задают эквивалентные классические косы.
Доказательство. Так как Ъ\ виртуально эквивалентна 62, мы имеем f{b\) =
/(62). Принимая во внимание полноту инварианта / для классических кос, мы
имеем Ъ\ = 62 (в классическом смысле). D
Запрещенное движение для виртуальных кос (соответствующее
запрещенному движению для виртуальных узлов) выглядит так: (Τί^ί+ιζί ~^ 0+ισζ^+ι·
Покажем, в общем случае оно не может быть представлено как композиция
соотношений в группе виртуальных кос.
Теорема 22.5. Запрещенное движение (соотношение) для виртуальных кос
не является соотношением эквивалентности.
Доказательство. Действительно, вычислим значения ^(σ^^ζι) и Τ^ζ^ι^Ί)·
В первом случае мы имеем:
(е, е, е) —>· (e,aj~ , е) —>· (e,aj~ , а± ) —>· (e,aj~ t,a^ t~x).
Во втором случае мы имеем:
(е, е, е) —>· (e,t,t_1) —>· (e,t,t~1a^ ) —>· (e,ta^ , t_1aj~ ).
Эти результаты (виртуальные η-системы) не совпадают; таким образом,
запрещенное движение изменяет виртуальную косу. D
Замечание 22.8. Если мы положим t = 1, то мы получим f(X) = f(Y)·
Следовательно, переменная t существенна в построении инварианта Τ.
Определение 22.4. Для заданной диаграммы виртуальной косы β из η нитей
и двух чисел 1 ^ г < j ^ η определим коэффициент зацепления h,j(P)
следующим образом. Рассмотрим перекрестки, в которых г-я нить косы (т. е. нить,
у которой верхний конец имеет номер г) образует проход, а j-я нить образует
переход, и положим hj(b) равным алгебраической сумме перекрестков (—1
соответствует образующей σ&, а 1 — обратному элементу af при некоторых /с, I).
382
Глава 22
Покажем, что эта функция выражается через 3~(β) и, следовательно,
является инвариантом виртуальных кос.
Рассмотрим косу Ъ и значение Т(Ъ). Оно состоит из η членов (ei,..., еп). При
1 ^ Ρ Φ Q ^ п пусть fpq — алгебраическое (с учетом знаков) число вхождений
aq в ер. Все числа fpq корректно определены по JF, так как каждый элемент е^
определен с точностью до умножения слева на αι; это умножение не меняет Д^·
при j φ г.
Следовательно, для любой пары неравных чисел р, q от единицы до гг,
функция fpq является инвариантом виртуальных кос.
Теорема 22.6. Инвариант fpq совпадает с —lpq.
Доказательство. Действительно, рассмотрим слово-косу β и будем пошагово
вычислять значение 3~(β)· Заметим, что fpq представляет собой коммутати-
визацию инварианта J-: вместо умножения образующих мы складываем
соответствующие коэффициенты. Будем доказывать это утверждение индукцией
по длине слова — косы β. В случае пустого слова (пустого множества
перекрестков) доказывать нечего. Добавим один перекресток и посмотрим, как это
отразится на рассматриваемых инвариантах.
В случае виртуального перекрестка коэффициенты зацепления не
изменяются по определению. Не меняется и алгебраическая сумма вхождений букв:
элементы е^, ej умножаются на t , а число вхождений а&, к = 1..., η
остается тем же. В случае, когда мы приписываем σ^, мы изменяем Д/,Ζ = 1,... ,гг
следующим образом. Пусть ρ — номер нити, приходящей в добавляемый
перекресток справа сверху, a q — номер нити, приходящей слева сверху. Тогда
единственное, что изменится, это eq. Этот элемент умножается на е~1р~1ер.
При подсчете алгебраического числа вхождения какой либо буквы, вхождения
в ер сокращаются се"1. Таким образом, fqp становится равным fqp — l,lqp
становится равным lqp-\-l, а все остальные коэффициенты lxy, fxy не изменяются.
Именно так изменяется коэффициент lpq.
Случай образующей σ~ рассматривается аналогично.
Тем самым мы выполнили шаг индукции. Теорема доказана. D
Приведем еще два примера, показывающих преимущества инварианта Τ.
Рассмотрим косу из трех нитей Ь = ζ^,σ^ C2Cri^2CicriCicr2^ σϊ ·
Компьютерные вычисления показывают, что для этой косы J~{b) φ 3~(β)· Однако, эта коса
не различается виртуальным полиномом Джонса-Кауфмана, предложенным в
[KaulO]. Более точно, рассмотрим зацепление Cl(b), полученное замыканием
косы Ъ и полином Джонса-Кауфмана V(CI(b)) этого зацепления. Известно, что
полином Джонса-Кауфмана не различает зацепления, отличающиеся друг от
друга виртуализацией, см. рис. 22.3.
Таким образом, легко видеть, что если для некоторой косы мы сделаем
замену σϊ на ζισϊ (^, то замыкание обеих кос будут иметь одинаковые полиномы
Джонса-Кауфмана.
В самом деле,
V(Cl(b)) = ν(01(σ^1σ1σ2σ1σ^1σ^1)).
Преобразованная коса тривиальна, поэтому V(С1 (6)) = V(С 1(e)).
22.3. Инварианты виртуальных кос
383
Рис. 22.3. Пары диаграмм, не различаемые полиномом Джонса-Кауфмана
Приведем второй пример, показывающий силу инварианта Т. Мы показали,
что коса Ъ = (σ^ζια^1 ζισ^1 ζι)2 лежит в ядре представления Бурау *В. Легко
видеть, что инвариант Τ распознает нетривиальность этой косы.
22.3.3. Насколько силен инвариант Т1
Как было показано выше, новый инвариант сильнее, чем коэффициент
зацепления, иногда он различает виртуальные узлы, которые не различаются
полиномами Джонса-Кауфмана или представлением Бурау.
Кроме того, ограничение инварианта Τ на случай классических кос (при
факторизации t = 1 и возвращении к обозначениям главы 10) совпадает с
полным инвариантом / классических кос.
Инвариант Τ дает нам пример отображения из одного алгебраического
объекта (группа кос) в другой алгебраический объект (п копий свободной группы
или η копий классов вычетов свободных групп). Однако это отображение не
является гомоморфизмом.
Для того, чтобы оценить силу инварианта JF, установим некоторые его
свойства.
Имеются, однако, некоторые свойства, которые делают Τ похожим на
гомоморфизм. Именно, справедлива следующая лемма.
Лемма 22.1. Если ^(bi) = Ffo) для некоторых кос 6ι, 62; то для любой пары
кос а и с мы имеем Р(аЬ\с) = T{ca)2C) (все косы предполагаются с одним и
тем же количеством нитей).
Доказательство. Докажем эту лемму в два шага. Первый шаг состоит в
доказательстве того, что J-(abi) = J-(ab2). На втором шаге нужно показать, что
если J-(ai) = JF(a2) то Т{а\с) = Т{ачс). Если будут доказаны оба утверждения,
то, подставляя ab\ вместо а\ и а&2 вместо <22> мы получим первое утверждение
теоремы.
Второе утверждение уже было доказано при доказательстве теоремы 22.3
как утверждение А.
Докажем теперь, что если Т{Ь\) = ^(Ьг)? то T{ab\) = Т{аЪъ). Рассмотрим
некоторые слова α,βι, и /?2, задающие косы α,6ι, и Ь^ соответственно. Будем
применять индукцию по длине слова а. Если слово а имеет длину нуль, т. е.
а = е, то J-(abi) = J-(ab2) в силу основного индукционного предположения.
Рассмотрим теперь случай, когда а имеет длину один, т. е. является буквой.
384
Глава 22
Пусть а = ζΐ. Тогда вместо набора образующих (αϊ,..., αη, t) группы G
рассмотрим набор образующих αϊ,..., α^-ι, ία^+ιί-1, ί_1α^, &г+2,..., αη. Очевидно,
что эти п элементов вместе с элементом t действительно порождают всю
группу G. Обозначим P(Pj) через Р/,..., Р^ при j = 1,2 (Ρ без верхнего индекса
соответствует β без нижнего индекса).
Каждый элемент Pj выражается некоторым образом через старые
образующие: Рг = Ρ? (αϊ,..., αη, £). Определим теперь по заданному выражению
Χ(αι,..., αη) новое выражение Χ'=Χ(αι,..., α^-ι, ία^+ιί-1, ί_1α^, &г+2, · · ·, &η)·
Покажем теперь, что для всех /3 имеет место Τ(αβ) = (Р[,... ,Ρ/_ΐ5 ίΡ/,
у--1р/ ρ/λ
Это проверяется индукцией по длине слова /3, но здесь набор Р· зависит
лишь от набора Pj и может быть по нему однозначно восстановлен (проверка
корректности, т.е. что при умножении Pj слева на аг·, все классы смежности
элементов Р'к остаются теми же, не представляет труда). Из этого следует, что
отображение T{fi) —> J-(αβ) корректно определено и инъективно.
Следовательно, если 3-(βι) = ^(Дг)? то Τ{αβ\) = Τ{αβ2).
Те же самые рассуждения остаются верными в случае, когда а = σί . Здесь
нужно лишь указать, каким способом мы перестраиваем набор из Pj.
В случае а = σι в качестве образующих мы выбираем: αϊ,..., α^-ι, α^+ια~ ,
a,i, ai+2,..., αη, Ρ(αβ) = (Ρ{,..., Ρ/_ι, Ρ/, аг_1Р/+1,..., Ρ^) (здесь и далее под Р/
мы понимаем результат подстановки новых образующих вместо старых).
В случае а = σ~ мы берем следующие образующие: αϊ,... , α^-ι,α^+ι,
αί+1α^+ι, α^+2,βζ+3, · · · ,^η? Τ{μβ) = (Ρ/,..., Ρ/_ΐ5 α^+ιΡ/, Ρ/+1,... , Ρ^)·
Таким образом, в каждом из трех вышеописанных случаев слово 3-(αβ)
однозначно восстанавливается по се и 3~(β). Следовательно, мы имеем Τ(αβ\) =
H<*fo).
Тем самым мы установили базу индукции. Предположим, что утверждение
леммы является верным для слов длины к при некотором к ^ 1. Пусть а —
слово длины к. Тогда имеет место разложение а = α'ψ, где ψ — последняя буква
слова а ж а' имеет длину к — 1. Пусть β[ = ψβι, β'2 = ψβ2· По предположению
индукции 3-(β[) = J-(β'2)' Применяя предположение индукции еще раз, мы
получаем Τ(αβι) = Т(а*'β[) = Τ {а!'β'2) = Τ[μβ^).
Этим завершается доказательство первого шага леммы. Учитывая, что
второй шаг уже доказан, мы получаем требуемое утверждение. D
Следствие 22.1. Если для некоторой косы а мы имеем JF(a)=JF(e) = (e,..., е),
то для любой косы Ъ с тем же количеством нитей имеет место JF(6_1a6) =
Не)·
Важной характеристикой инварианта является множество его значений.
Задача описания этого множества, однако, является очень сложной и нам
неизвестно ее решение даже для трех нитей. В качестве упражнения мы опишем
множество значений для случая виртуальных кос из двух нитей и, тем самым,
классифицируем эти косы. Впрочем, группа виртуальных кос из двух нитей
устроена очень просто: она изоморфна группе Ζ * Ζ2.
Смена обозначений: вместо образующих αι,α2 виртуальных 2-систем мы
будем писать а, 6; вместо образующих σι, Ci группы кос мы будем писать σ, ζ.
22.3. Инварианты виртуальных кос
385
Напомним / — инвариант, получаемый из Τ приравниванием t = 1.
Обозначим свободную группу с образующими а, Ъ через G'. Пусть Е[ = {a}\G',E2 =
{b}\G>.
В случае двух нитей / отображает множество VB(2) в (Е[, Е2), или, проще,
(С,С).
Для заданной косы а из двух нитей обозначим f(a) через (P(a),Q(a)).
Рассмотрим сначала простейшие виртуальные косы из двух нитей и
значения функции / на них:
1. Для тривиальной косы мы имеем (е, е);
2. Для σ мы имеем (Ι,α-1);
3. Для косы σ_1 мы имеем (6,1);
4. Для ζ получаем (1,1).
Несложно доказывается следующая теорема.
Теорема 22.7. Пусть β — слово-коса (виртуальная коса из двух нитей).
Тогда P(P)Q(P)~1 = akbl для некоторых k,l.
Доказательство. Мы будем использовать индукцию по количеству букв в
записи косы. В случае пустого слова нечего доказывать. Пусть теперь β — слово-
коса из η букв, β' = βα, где а — одна из букв ζ, σ или σ_1. Пусть Ρ(β)(^(β)~ =
апЪт.
Для α=ζ мы имеем Ρ(β')=Ρ, Q(/3')=Q(/3). Таким образом Ρ(β^(β')~1 =
апЪт.
При α=σ если коса β является четной, мы получаем: Рь^Р, Q\-^QP~1a~1P,
PQ-1 ^ a-ipQ-1-, для нечетной косы β: Q ^ Q,P ^ PQ^b^Q^PQ'1 ^
PQ^b-1.
В случае а = σ_1 и четной косы β: Q ι—> Q,P ι—> PQ~1bQ,PQ~1 \-^ PQ~1b,
для нечетной косы β: Ρ \-^ Р, Q \-^ QP~1aP, PQ~X \-^ aPQ~x.
Таким образом, мы осуществили шаг индукции и тем самым доказали
теорему. D
Условие на PQ~X является вполне естественным. Оно означает, что
существует элемент g Ε G' такой, что g Ε [Ρ] Ε Ε[ и g Ε [Q] Ε ϋ^· Очевидно,
что такой элемент g единственен. Таким образом, этот элемент g представляет
собой инвариант группы VB(2).
Очевидно, что для каждой виртуальной косы Ъ из двух нитей мы имеем
f(b) = f(b(). Кроме того, все косы естественным образом делятся на пары:
каждой четной виртуальной косе Ъ в VВ(2) можно сопоставить ровно одну
нечетную косу Ь(. Таким образом, нам достаточно рассмотреть подгруппу
четных кос EVB(2) группы VB(2).
Теорема 22.8. Инвариант g (так же, как и инвариант f) группы
виртуальных кос EVB(2) является полным.
Нам достаточно доказать полноту инварианта д. Для этого нам понадобится
вспомогательная лемма.
386
Глава 22
Лемма 22.2. Для каждых двух виртуальных слов-кос π, ρ Ε VB(2) из двух
нитей мы имеем: д(тгр) = д(р)д(тг) и д(п)~г = #(π_1). Таким образом,
отображение д антизомоморфно на VB(2).
Доказательство. Группа VВ(2) является свободной группой двумя
образующими а = ζσ и что β = ζσ_1-
Далее, что #(е) = е, 0(a) = Ь_1,^(/3) = α_1,0(α_1) = 6, #(/3_1) = α.
Утверждение об антигомоморфности отображения д явно проверяется на
образующих а и β. D
Доказательство теоремы 22.8. Из леммы 22.2 следует, что отображение д ан-
тигомоморфно и отображает группу EVB{2) в свободную группу с
образующими а, Ъ. Это отображение переводит α, β в образующие α, 6-1. Следовательно,
оно не имеет ядра. Таким образом, д является полным инвариантом группы
EVB{2), поэтому полным является и инвариант /. D
Итак, отображение Τ также является полным инвариантом для EVB(2).
Учитывая, что этот инвариант чувствителен к умножению на ζ справа, мы
видим, что Τ распознает все элементы из VB(2). Чтобы распознать, является
ли пара элементов (βι Ε Ει,βι Ε Ει) значением инварианта Т на некоторой
косе, нам нужно лишь профакторизовать их по t = 1, взять прообраз Ъ (если
таковой имеется) полученной пары (β^,β^) при отображении /, и определить,
верно ли F(b) = (βι,β2) или Т(Ь() = (βι,β2).
Простейшим примером пары (βι Ε Ει,β2 Ε Ε2), не являющейся
значением инварианта Τ на виртуальных косах, является пара (6, а). В этом случае
PQ~X = 6α_1, что не равно afc6^ ни для каких целых чисел k,l.
22.4. Виртуальные зацепления
как замыкания виртуальных кос
Аналогично случаю классических кос виртуальны косы имеют замыкания,
см. рис. 22.4. По аналогии с классическим случаем, получаемую замыканием
виртуальной косы мы назовем заплетающейся по отношению к некоторой
точке А.
Очевидно, что эквивалентные виртуальные косы задают изотопные
виртуальные зацепления. Кроме того, все классы эквивалентности виртуальных
зацеплений могут быть представлены как замыкания виртуальных кос.
Упражнение 22.1. Сформулируйте и докажите аналоги теорем Александе-
ра и Вожеля для построения виртуальных кос по виртуальным зацеплениям.
22.5. Аналог теоремы Маркова
В работе [Кат] Сейичи Камада доказал аналог теоремы Маркова об
эквивалентности виртуальных зацеплений, заданных замыканиями виртуальных кос
в следующей формулировке.
22.5. Аналог теоремы Маркова
387
Рис. 22.4. Замыкание виртуальной косы
Теорема 22.9. Замыкания двух виртуальных кос задают изотопные
виртуальные зацепления тогда и только тогда, когда эти две виртуальные
косы связаны конечной последовательностью соотношений из списка (VM0)-
{VM3).
VM0) Эквивалентность кос.
VM1) Сопряженность (в группе виртуальных кос).
VM2) Правая стабилизация {добавление справа нити, которая образует с
последней нитью внизу новый перекресток — положительный
классический, отрицательный классический или виртуальный), а также
дестабилизация {преобразование, обратное стабилизации);
VM3) Правое и левое виртуальные перебрасывания, см. рис. 22.5.
1 m m+l 1 m m+1 1 2 m+1 1 2 m+1
Χ—Π Π~Κ
Рис. 22.5. Виртуальные перебрасывания
Движения (VM0)-(VM2) полностью аналогичны классическим
преобразованиям Маркова с той лишь разницей, что в качестве сопрягающей косы
(движение (VM1)) можно брать произвольную виртуальную косу, имеющую то же
388
Глава 22
количество нитей, что и сопрягаемая коса. Новое движение (VM3) имеет два
варианта: правый и левый. Каждое из виртуальных перебрасываний состоит
в замене двух классических перекрестков, между которыми проходит нить
косы, не имеющая перекрестков, виртуальными. Эти преобразования не меняют
класса эквивалентности замыканий кос, так как соответствующие замыкания
получаются друг из друга применением второго классического движения Рей-
демейстера и второго виртуального движения Рейдемейстера.
Читателю оставляется в качестве упражнения проверить, что все эти
преобразования не меняют класса эквивалентности виртуального зацепления. За
доказательством достаточности мы отсылаем читателя к оригинальной
работе [Кат].
Часть VI
Другие теории
Глава 23
Трехмерные многообразия
и узлы в трехмерных
многообразиях
Настоящая глава является введением в теорию трехмерных многообразий,
инвариантов трехмерных многообразий и инвариантов узлов в трехмерных
многообразиях. Нашей целью является демонстрация того, как различные
ветви маломерной топологии могут взаимодействовать между собой и приводить к
весьма сильным результатам. В первой части настоящей главы в качестве
примера мы опишем некоторые аспекты теории узлов в RP3. Вторая (основная)
часть главы будет посвящена введению в замечательную теорию инвариантов
Решетихина-Тураева (называемых также инвариантами Виттена-Решетихина-
Тураева) трехмерных многообразий. Для этого нам потребуется описать
многие фундаментальные конструкции трехмерной топологии, такие как
разбиения Хегора, движения Кирби и Фенна-Рурка. С одной стороны они
необходимы для построения теории Виттена-Решетихина-Тураева, с другой стороны
они представляют собственный интерес, так как на их базе можно строить и
многие другие инварианты трехмерных многообразий, в частности, квантовые
инварианты, которые получаются из квантовых инвариантов узлов адаптацией
их к движениям Кирби (или Фенна-Рурка). Инварианты Виттена-Решетихина-
Тураева могут быть изящно описаны с помощью скобки Кауфмана. Это
описание принадлежит Решетихину, Тураеву [RT1, RT2] и Ликоришу [Licl]. Мы не
претендуем на полный обзор всех основных направлений теории трехмерных
многообразий. Так, мы совсем не коснемся алгоритмических вопросов (в том
числе алгоритмического распознавания классических узлов и
алгоритмического распознавания трехмерной сферы, [Rub, Th]) Мы также не будем работать с
теорией сложности трехмерных многообразий, предложенной Матвеевым. Эти
аспекты теории трехмерных многообразий освящены в в замечательной
монографии [Matv4].
23.1. Узлы в RP3
В настоящем разделе мы предложим метод кодирования узлов в RP3 и
обсудим обобщение полинома Джонса-Кауфмана, предложенное Юлией Дро-
ботухиной, см. [Дро].
392
Глава 23
Проективное пространство RP3 представляет собой сферу S3, у которой
противоположные точки отождествлены. Сфера S3 состоит из двух полусфер;
каждая полусфера топологически представляет собой шар D3. Таким образом,
проективное пространство RP3 может быть получено из трехмерного диска
отождествлением противоположных точек на его границе S2 = 3D3.
Следовательно, любое зацепление в RP3 может быть определено как набор
замкнутых кривых и дуг в D3; множество концов дуг лежит на границе 3D3 и
является симметричным относительно центра шара D3. Без ограничения
общности, можно считать, что все эти концы дуг лежат на экваторе шара. Поэтому
зацепления в RP3 можно кодировать диаграммами в круге D2; эти
диаграммы имеют перекрестки, которые являются двойными и трансверсальными (со
структурой проход-переход в каждом из них), и концевые точки на S1 = сШ2,
которые образуют множество, симметричное относительно центра круга.
Пример такой диаграммы показан на рис. 23.1.
Рис. 23.1. Диаграмма зацепления в RP3
Упражнение 23.1. Рассмотрим произвольную диаграмму зацепления в RP3.
Опишите прообраз этой диаграммы при естественном двулистном
накрытии ρ : S3 —> RP3.
Мы рассматриваем только диаграммы общего положения. Это значит, что
все ребра являются гладкими, все перекрестки двойные и трансверсальные,
никакой перекресток не лежит на граничной окружности и никакая кривая не
касается этой окружности.
Нарушение условий регулярности кривой в случае диаграмм классических
узлов приводит к движениям Рейдемейстера Ωι, Ω2, Ω3. Аналогичным образом
для диаграмм зацеплений в RP3 помимо обычных движений Рейдемейстера
мы получаем два новых движения, обозначаемые через Ω4 и Ω5, см. рис. 23.2.
Теорема 23.1. Две диаграммы задают изотопные зацепления в RP3 если
и только если одна из них может быть переведена в другую посредством
движений Рейдемейстера Ωι,Ω2,Ω3 и движений Ω4 и Ω5.
Доказательство этой теоремы полностью аналогично доказательству
теоремы Рейдемейстера. Оно остается читателю в качестве упражнения.
Теперь мы готовы определить аналог полинома Джонса-Кауфмана для
ориентированных зацеплений в RP3.
Сначала для заданной диаграммы неориентируемого зацепления L в RP3
23.1. Узлы в RP3
393
Рис. 23.2. Движения Ω4,Ωδ
определим аналог скобки Кауфмана, удовлетворяющий следующим аксиомам:
(i^>=a(QxO)+a_1OP); (1)
(LuO) = (-a2-a-2)(L); (2)
(О) = 1, (3)
где О обозначает отдельно стоящую незаузленную кривую.
Доказательство существования и единственности (L) полностью аналогично
доказательству существования и единственности скобки Кауфмана,
определенной на зацеплениях в R3 (или S3).
Инвариантность (L) относительно Ω2, Ω3 может быть тоже доказана по
аналогии.
Для доказательства инвариантности (L) относительно Ω4 воспользуемся
следующей формулой
(D) = ^аа^-^\-а2 - а~2у^-\ (4),
S
где j(s) количество окружностей диаграммы L в состоянии s.
Если диаграммы L,Lf отличаются друг от друга применением движения
Ω4, то существует очевидное взаимное однозначное соответствие между их
перекрестками. При этом в числа a(s),P(s) и ^(s) для L совпадают с
соответствующими числами для V.
Инвариантность скобки (L) относительно Ω5 следует из равенств,
показанных на рис. 23.3.
Как и в случае скобки Кауфмана зацеплений в R3 скобка (L) не
является инвариантной относительно Ωι; это движение умножает значение скобки
(-«)±3·
Пусть теперь дана ориентированная диаграмма L зацепления в RP3. Пусть
w(L) — число закрученности этой диаграммы.
394
Глава 23
Рис. 23.3. Инвариантность скобки относительно Ω5
Определение 23.1. Полипомом Дроботухиной ориентированного зацепления
L в RP3 называется полином Лорана
X(L) = (-a)-3^L\\L\),
где \L\ получается из L забыванием ориентации.
Теорема 23.2. Полином X(L) является инвариантом зацеплений в ИР3.
Доказательство. Доказательство полностью аналогично доказательству
инвариантности полинома Джонса-Кауфмана для зацеплений в R3. Оно следует из
теоремы 23.1, определения скобки, инвариантности скобки (·} при
преобразованиях Ω2 — Ω 5 и того, что ее изменение при Ω ι компенсируется изменением
значения w(-). D
Используя инвариантность этого полинома Ю.В. Дроботухина
классифицировала с точностью до изотопии все зацепления в RP3, имеющие диаграммы
с не более, чем шестью перекрестками и доказала аналог теоремы Кауфмана-
Мурасуги для зацеплений в RP3. Последнее приводит к результатам,
аналогичным тем, которые мы приводим в главах 15,19.
23.2. Введение в исчисление Кирби
Исчисление Кирби представляет собой весьма интересный способ
кодирования трехмерных многообразий. В настоящей книге мы приведем краткое
введение в теорию инвариантов Виттена-Решетихина-Тураева посредством
исчисления Кирби. Заметим, однако, что область применения теории Кирби много
23.2. Введение в исчисление Кирби
395
шире, и служит отправной точкой для построения, например, квантовых
инвариантов (Э.Виттен, О.Я. Виро, Н.Ю.Решетихин, В.Г.Тураев и другие), см.,
напр., [Oht] или теории виртуальных трехмерных многообразий, см. [DK1].
23.2.1. Теорема Хегора
Мы будем пользоваться результатом Мойза [Moi] о том, что всякое
трехмерное многообразие триангулируемо.
Мы будем иметь дело только с ориентируемыми трехмерными
многообразиями.
Определение 23.2. Разбиением Хегора ориентируемого замкнутого
компактного многообразия М3 без края называется разбиение М3 в объединение двух
тел с ручками, склеенных по их общей границе — сфере с д ручками Sg.
Существует много различных способов приклеивать одно тело с ручками к
другому (или, что то лее самое, к его границе — сфере с ручками). При этом
могут получаться, вообще говоря, различные (негомеоморфные) трехмерные
многообразия. Тем не менее топологический тип получающегося многообразия
полностью определяется набором из д независимых (в смысле первой группы
гомологии края) стягиваемых кривых (меридианов) в каждом теле с ручками.
Таким образом, чтобы получить трехмерное многообразие, молено взять два
тела с ручками М\ и М^ (гомеоморфные друг другу, или, что то лее самое,
имеющие одинаковое количество д ручек) и некоторое абстрактное двумерное
многообразие N, гомеоморфное дМ\ (и, следовательно дМ^). На многообразии
N нужно указать некоторую стандартную систему меридианов mi,...,mg
(например, считать N стандартно вложенным в R3 и понимать слово "меридиан"
в обычном смысле), см. рис. 23.4.
После этого мы фиксируем две системы меридианов (т. е.
непересекающихся кривых, стягиваемых внутри соответствующих сфер с ручками, разрезание
вдоль которых превращает трехмерное многообразие в шар): щ,..., ид для М\
и vi,..., vg для М.2 и два отображения j\ : М\ —> TV, j^ · М^ —> N.
Определение 23.3. Система из двух наборов кривых {fi(ui)} и {/г^)}
называется диаграммой Хегора склейки.
Склейка определена диаграммой Хегора неоднозначно. При этом имеет
место следующая
Теорема 23.3. Если два трехмерных многообразия Μ и М' получены
склейкой гомеоморфных тел с ручками согласно одной и той же диаграмме Хегора,
то они гомеоморфны.
Доказательство. Без ограничения общности будем считать, что Μ
получается склейкой гомеоморфных тел М\ и М2, a M' получается склейкой М[ и
М'2 = М2.
Пусть fi : dMi —>· TV, г = 1,2, — гомеоморфизмы склейки для многообразия
М; пусть многообразие М' задается отображениями /г7, г = 1,2.
Пусть Μ и М' имеют одну и ту же диаграмму Хегора. Тогда
отображения / и f являются гомеоморфизмами из дМ и дМ' в N такими, что
образы меридианов щ и и[ совпадают при всех г = 1,... ,д. Покажем, что в этом
396
Глава 23
Рис. 23.4. Диаграмма Хегора
случае тождественный гомеоморфизм hi : М2 —> М'2 может быть продолжен
до гомеоморфизма h : Μ —> Μ'. Гомеоморфизм (Л)-1 о Д : $Μι —> $Μ{
отображает каждый меридиан многообразия М\ в соответствующий меридиан
многообразия М[. Так как каждый гомеоморфизм окружности на окружность
может быть продолжен до гомемоморфизма затягивающих дисков (вдоль по
радиусам), то гомеоморфизмы меридианов могут быть продолжены до
гомеоморфизмов дисков, затягивающих эти меридианы в Μι и М[. После разрезания
Μι и М[ по этим дискам мы получим многообразия Ό\ и D[, гомеоморфные
трехмерному шару каждое.
Так как любой гомеоморфизм двумерных сфер продолжается (по
радиусам) до гомеоморфизмов шаров, ограничиваемых этими сферами, то
отображение между границами дисков Ό\ и D[ продолжается вовнутрь, тем самым
порождая гомеоморфизм многообразий Μ и Μ', что завершает доказательство
теоремы. D
Докажем теорему Хегора.
Теорема 23.4. Каждое ориентируемое трехмерное многообразие Μ без края
допускает разбиение Хегора.
Доказательство. Основная идея состоит в следующем. Каждое трехмерное
многообразие допускает триангуляцию. Фиксируем многообразие Μ и его
триангуляцию Т. Будем строить многообразия М\ и М.2 из частей тертраэдров
данной триангуляции. На внутренности каждого двумерного симплекса
триангуляции фиксируем круг. Разобьем каждый тетраэдр Τι триангуляции Τ на две
части Τ^ι и Тг;2 так, как показано на рис. 23.5, причем сделаем это так, чтобы
внутренняя часть Т^д была гомеоморфна трехмерному шару, а ее пересечение
с двумерным остовом тетраэдра Τι состояло из четырех выделенных кругов на
соответствующих симплексах.
23.2. Введение в исчисление Кирби
397
Рис. 23.5. Подразбиение тетраэдра
Пусть многообразие Μι является объединением всех (внутренних)
тетраэдров вида Т^д, а многообразие М^ — объединением всех тетраэдров вида Т^·
Легко видеть, что каждое из этих многообразий является телом с ручками
(ориентируемость следует из ориентируемости многообразия М). Количества ручек
у Μι и М.2 совпадают, так как эти многообразия имеют общую границу. D
Имеет место следующая теорема о представлениях многообразий
диаграммами Хегора, принадлежащая Зингеру, [Sin].
Теорема 23.5. Две диаграммы Хегора {Σ,α^,/^} и {Σ',α^,/^·} задают одно и
то же трехмерное ориентируемое многообразие если и только если одна из
них может быть получена из другой посредством цепочки следующих
преобразований:
1. изотопии: мы изотопируем кривую щ так, чтобы она не пересекала
других кривых а^ в процессе изотопии; то же для кривой β у,
2. замен кривой щ на кривую щ + а^ так, что три кривые ai,ak,&i + oik
вырезают из Σ сферу с тремя дырками, не содержащую других кривых
из семейства а; то же для кривых β.
3. стабилизации и дестабилизации: стабилизация заменяет поверхность
Σ {рода д) на связную сумму Σ#Τ2 и заменяет семейства {αι,..., а9},
{/?ι,...,/З^} Ηα{α1,...,α9,α9+1},{β1,...,β9,β9+1}, гдеа9+1 и β9+ι
-кривые, лежащие в торе Т2 и пересекающиеся там ровно в одной точке.
Очевидно, что единственное многообразие, которое можно получить
склеиванием двух шаров (в случае рода ноль количество кривых в диаграмме Хегора
398
Глава 23
равно нулю) — это сфера S3. Пространства, которые молено получить
склейкой двух полноторий — это сфера 5*3, проективное пространство RP3 и
линзовые пространства. На описании последних мы останавливаться не будем, см.,
напр., [BZ].
23.2.2. Построение многообразий по оснащенным зацеплениям
В настоящем разделе мы опишем основные понятия и конструкции теории
Кирби. Главная конструкция состоит в том, что все трехмерные многообразия
молено закодировать зацеплениями (точнее, оснащенными зацеплениями).
Определение 23.4. Зацепление в R3 называется оснащенным, если каждой
его компоненте сопоставлено целое число.
Замечание 23.1. Вообще говоря, можно рассматривать рационалиные
оснащения и перестройки. Нам понадобятся лишь целочисленные перестройки;
поэтому мы ограничились лишь целочисленными оснащениями.
Оснащенное зацепление молено представить себе в виде ленты S1 χ I: для
каждой компоненты рассматриваемого зацепления мы строим параллельную
ей компоненту, так что вместе они представляют собой края перекрученной
ленты. В качестве оснащения выступает коэффициент зацепления двух краев
ленты.
Определение 23.5. Два оснащенных зацепления называются изотопными,
если соответствующие ленты изотопны.
Имея оснащенное зацепления L, можно построить трехмерное
многообразие следующим образом. Для каждой компоненты К зацепления L
рассмотрим соответствующее оснащение п(К). Рассмотрим теперь полноторие D2 x S1,
средней линией * χ S1 которого является узел К. Можно считать, что
соответствующая оснащению лента имеет вторую компоненту края К'', лежащую на
торе dD2 χ S1 — границе полнотория. Таким образом, мы имеем набор
полноторий в окрестности каждой компоненты; на крае каждого полнотория лежит
по кривой.
После этого мы вырезаем из сферы все полнотория и вклеиваем вместо них
новые полнотория. Для описания результирующего полнотория посредством
приклейки полноторий достаточно указать, в какие кривые на торе
переходят меридианы (стягиваемые кривые) полноторий. Приклеим меридианы
краям лент (кривым вида К').
Таким образом, мы получаем трехмерное многообразие Μ.
В этом случае говорят, что трехмерное многообразие Μ получено из
трехмерной сферы перестройкой Дена вдоль по оснащенному зацеплению L.
Заметим, что то лее самое можно проделывать и для произвольного
многообразия: выбирать внутри него полноторие, вырезать его и вклеить новое
полноторие по гомеоморфизму края, если указано, в какую кривую должен
отображаться меридиан приклеиваемого полнотория. При этом если мы
производим перестройки по непересекающимся (но, быть может, заузленным или
зацепленным между собой) полноториям, то результат не зависит от порядка
перестройки.
Имеет место следующая теорема (Ликориш).
23.2. Введение в исчисление Кирби
399
Теорема 23.6. Для каждого ориентируемого трехмерного многообразия Μ
существует гомеоморфное ему трехмерное многообразие Μ', которое
получается перестройкой трехмерной сферы по оснащенному зацеплению.
Идея доказательства состоит в следующем. Рассмотрим многообразие Μ и
его разбиение Хегора М\ U М2, где дМ\ = дМ^ = Sg. Без ограничения
общности молено считать, что между Μι и М.2 вклеено еще многообразие Sg х /,
которое служит "буфером" между многообразиями Μι и М2. На одном краю
этого многообразия изображены кривые (меридианы), стягиваемые в Μι, на
другом — кривые, стягиваемые в М^· Это буферное многообразие
соответствует гомеоморфизму, переводящему одни меридианы в другие. Оказывается, что
если два гомеоморфизма /ιι, /ι2 : дМ\ —>· дМ2 отличаются друг из друга одним
скручиванием Дена (см. стр. 115), то многообразие, соответствующее
диаграмме Хегора /ι 2 получается из многообразия, соответствующего диаграмме
Хегора h 1 одной перестройкой Дена (докажите это!). Таким образом, нам осталось
разбить гомеоморфизм, соответствующий изначальной диаграмме Хегора на
простейшие.
Это обеспечивает теорема 8.5. Напомним ее формулировку.
Теорема 23.7 (Ден-Ликориш). Каждый гомеоморфизм сферы с ручками
Sg на себя, сохраняющий ориентацию, разложим в композицию скручиваний
Дена и гомеоморфизмов, гомотопных тождественному.
Первое доказательство этой теоремы (с некоторыми лакунами)
принадлежит Дену, см. [Dehn2]. Первое безупречное доказательство привел Ликориш
в [Lic2].
23.2.3. Изображение оснащенных зацеплений
Оснащенные зацепления могут быть закодированы плоскими диаграммами
неориентированных зацеплений. В качестве оснащения мы берем число закру-
ченности каждой компоненты (т. е. ориентируем ее и считаем число
перекрестен ч> \/
ков этой компоненты с ней самой вида У( минус число перекрестков X. ;
результат не зависит от выбора ориентации). Так определенное оснащение
выдерживает применение второго и третьего движений Рейдемейстера, но не
инвариантно относительно движения Ω ι, а именно, при применении первого движения
Рейдемейстера оно изменяется на единицу. Таким образом, добавляя нужное
количество петель, мы можем устроить произвольное целочисленное оснащение
для произвольного изотопического типа зацепления. Список движений,
которые не меняют оснащенного зацепления, таков: в него входят движения Ω2, Ω3,
и двойное перекручивание Ω^, см. рис. 23.6.
В качестве упражнения читателю остается доказательство того факта, что
любые две изотопные диаграммы зацеплений с одинаковыми оснащениями
могут быть переведены друг в друга последовательным применением таких
движений (и плоской изотопии).
23.2.4. Движения Кирби
Очевидно, что различные зацепления могут задавать гомеоморфные
трехмерные многообразия. Оказывается, что существуют два важных
преобразования — движения Кирби — которые не меняют многообразия.
400
Глава 23
<^Ч>
Рис. 23.6. Двойная петля
Первое движение Кирби состоит в добавлении (удалении) отдельно стоящей
(т.е. незаузленной и ни с чем не зацепленной) компоненты с оснащением ±1,
см. рис. 23.7.
±1
Рис. 23.7. Первое движение Кирби
Второе преобразование Кирби состоит в следующем. Рассмотрим две
компоненты L\ и L2 зацепления L из η компонент. Построим новое гг-компонентное
зацепление L7, в котором все компоненты, кроме Li, и их оснащения такие лее,
как у зацепления L, а компонента L\ переходит в связную сумму Li и
(несуществующей) компоненты L2, "параллельной" компоненте L2. В этом случае
если L\ имеет оснащение /с, a L2 имеет оснащение Z, то новая компонента L[
будет иметь оснащение к -\- I. На языке плоских диаграмм это выглядит так,
как показано на рис. 23.8.
Замечание 23.2. Компоненты L\ и L^ могли изначально быть как
зацепленными, так и незацепленными.
Этот подход с использованием плоских диаграмм позволяет нам не
загромождать изображения метками, задающими оснащения.
Теорема 23.8 (Теорема Кирби). Два оснащенных зацепления задают одно
и то же трехмерное многообразие (с точностью до гомеоморфизма), когда
23.2. Введение в исчисление Кирби
401
Рис. 23.8. Второе преобразование Кирби
одно из них может бить получено из другого последовательностью изотопии
и движений Кирби.
Эта теорема утверждает, что два движения являются необходимыми и
достаточными для преобразования друг в друга зацеплений, перестройки по
которым задают гомеоморфные многообразия. Необходимость первого движения
очевидна. Действительно, рассмотрим меридианы первого (вырезанного) и
второго (вклеенного) полноторий. Легко заметить, что существует непрерывная
деформация дополнения к полноторию, переводящая один меридиан в другой.
Необходимость второго преобразования Кирби устанавливается так. Пусть
К\ и i^2 — компоненты оснащенного зацепления до применения
преобразования Кирби, и пусть после преобразования Кирби первая из них переходит в
компоненту, которую мы условно назовем К ι + i^2· Нам нужно доказать, что
перестройка сферы по К ι и по К2 дает то лее многообразие, что перестройка
по К ι + Κ<ι и по К^. Сделаем сначала перестройку вдоль К^. После этого в
полученном многообразии образ узла К\ изотопен образу узла К\ + К^
(вместе с образами узлов изотопны и образы лент, задающих оснащения). Поэтому
результирующие трехмерные многообразия будут гомеоморфны.
Иногда (например, при построении квантовых инвариантов трехмерных
многообразий) вместо движений Кирби удобно использовать другое движение
(точнее, одну бесконечную серию движений), которое носит название движения
Фенна-Рурка, см. 23.9.
Теорема Фенна-Рурка утверждает, что два трехмерных многообразия,
заданные перестройками Дена вдоль оснащенных зацеплений гомеоморфны
тогда и только тогда, когда одно оснащенное зацепление перестраивается в другое
последовательным применением изотопии и движений Фенна-Рурка.
Доказательство необходимости и достаточности движений Фенна-Рурка мож-
402
Глава 23
П ЛИНИЙ П ЛИНИИ
Рис. 23.9. Движение Фенна-Рурка
но свести к доказательству необходимости и достаточности движений Кирби.
Доказательство этого факта можно найти в [Oht].
Пожалуй, самое простое доказательство теоремы Кирби (достаточность
движений Фенна-Рурка, не опирающаяся на достаточность движений Кирби),
приведено в работе [Lu].
23.3. Инварианты Виттена-Решетихина-Тураева
Настоящий раздел посвящен введению в теорию инвариантов Решетихина-
Тураева. Первая работа Виттена на эту тему [Wit2] была посвящена
построению инвариантов зацеплений в трехмерных многообразий исходя из некоторых
физических моделей, у которых Виттен обнаружил интересные топологические
инварианты. Однако эта работа была долгое время непонятна для
математиков. Математические основы теории Виттена были заложены Тураевым и Ре-
шетихиным. В настоящей книге мы следуем подходу Ликориша [Licl], который
упростил описание, предложенное первыми тремя авторами.
Отправной точкой построения инвариантов Виттена-Решетихина-Тураева
является скобка Кауфмана. Она является объектом, инвариантным
относительно Ω2, Ω3, Ω?, но не инвариантным относительно преобразований Кирби. С
другой стороны, из скобки Кауфмана можно получить много других функций,
инвариантных относительно Ω2, Ω3, Ω^: для этого нужно взять несколько копий
каждой из компонент зацепления (эта операция определена корректно) и для
получившегося (более сложного) зацепления взять скобку Кауфмана. Далее
можно подобрать комбинации обычной, удвоенной, утроенной, и т.д. скобок
Кауфмана, чтобы полученная функция была инвариантна не только относительно
движений Ω2, Ω3, Ω^, но и относительно второго преобразования Кирби.
Инвариантность относительно первого преобразования Кирби получить несложно:
она достигается нормировкой аналогично тому, как мы нормируем скобку
Кауфмана относительно Ω ι для получения инварианта Джонса-Кауфмана. В
итоге мы получим инварианты трехмерных многообразий; они и есть инварианты
Виттена-Решетихина-Тураева.
Подробные конструкции изложены ниже.
23.3. Инварианты Виттена-Решетихина-Тураева 403
23.3.1. Алгебра Темперли-Либа
Алгебра Темперли-Либа является классическим объектом в операторной
алгебре. У нее много общего с алгеброй Гекке. В настоящем разделе мы будем
определять алгебру Темперли-Либа как скейн-алгебру (название происходит
от скейн-соотношений). Она является необходимым инструментом для того,
чтобы строить инварианты Виттена-Решетихина-Тураева посредством скобки
Кауфмана.
Пусть М3 — многообразие, полученное из трехмерной сферы перестройкой
Дена по оснащенному зацеплению. Мы будем использовать ленты (точнее, их
плоские диаграммы) для задания оснащения. Напомним, что эквивалентные
диаграммы получаются друг из друга движениями Ω2,Ωβ и Ω2, см. рис. 23.6.
Алгебра Темперли-Либа является частным случаем так называемых скейн-
пространств. Приведем несколько примеров, которые понадобятся нам в
дальнейшем.
Фиксируем комплексное число ао. Пусть V — формальной линейное
пространство над С, состоящее из конечных линейных комбинаций различных
диаграмм Di (для начала это будут диаграммы зацеплений на плоскости
(рассматриваемые с точностью до изотопии), затем мы перейдем к большей общности).
В пространстве V рассмотрим подпространство Vb, порожденное векторами
({СК;-аоС^-а^00' (23.1)
{ "duo +К"2+ «§)£}/
Положим S = V/Vq. Множество S называется скейн-пространством для R2.
Обозначение: ^(R2).
При естественной проекции ρ : V —>· V/Vo = S элемент D отображается в
λβι, где λ — значение полинома (D) в точке ао, а е\ Ε S — образ диаграммы,
состоящей из одной окружности.
Пусть Ег — диаграмма, состоящая из г попарно непересекающихся окружностей.
Из существования и единственности скобки Кауфмана {D) следует, что D = ^ Аг-Ег +
wii а Σ ^iEi = \Е\ + u>2, где wi,W2 E Vb, а А равно значению скобки (D) при ао.
Положим с = /(О) — (~ао — ао"2)·
Пусть теперь е — ненулевой элемент из S. Тогда ρ(D) = f(D)e, где f(D) E С,
где в качестве е удобно выбрать элемент во, соответствующий пустой
диаграмме. Нормализация в данном случае выбрана так, чтобы функция / была
мультипликативной относительно несвязной суммы диаграмм.
Следовательно,
/(Di U D2) = 5>')λ· х (cTJ
= Dc<)A*x ΣΗ"' = /(^)/№)'
г 3
что завершает доказательство.
Построение пространства S допускает следующее обобщение. Пусть D —
ориентированная двумерная поверхность с краем dF (возможно, пустым).
Зафиксируем 2п точек на крае dF (в случае пустого края dF, η = 0).
404
Глава 23
Под диаграммой на F мы понимаем набор G (возможно, пустой несвязный,
но обязательно конечный) окружностей и дуг на F такой, что G Π dF состоит
в точности из 2п выбранных точек. Все точки пересечения и самопересечения
окружностей и кривых просты и трансверсальны. Конечные точки дуг
совпадают с GC\dF\ они являются точками кратности один; все остальные вершины
(перекрестки) имеют кратность четыре. Они снабжены структурой проходов
и переходов. Эти диаграммы рассматриваются с точностью до комбинаторной
эквивалентности (учитывающей структуру проход-переход).
Выберем а0 £ С и рассмотрим векторное пространство V(F, 2п) над С,
состоящее из конечных линейных комбинаций классов диаграмм
эквивалентности. Пусть Vo(F, 2п) — подмножество множества V(F, 2n), порожденное
векторами вида
{'X ■ " ao(rV " αο'0 О' D U ° + (°о 2 + ао)^}·
Положим 5(F, 2п) = F(F, 2n)/Vb(F, 2n). Для простоты будем обозначать S(F, 0)
через S(F).
Замечание 23.3. Существенным является то, что мы рассматриваем
ориентированные поверхности; в противном случае мы не могли бы различать
перекрестки \ζ и ^.? поэтому не могли бы точно выписать соотношения.
Теорема 23.9. Образ p(D) диаграммы D при естественной проекции на S(F, 2n)
является инвариантным относительно Ω^,Ω2,Ω3.
Доказательство этой теоремы полностью повторяет доказательство
инвариантности скобки Кауфмана.
Теорема 23.10. В качестве базиса пространства S(F,2n) можно взять
образы всех диаграмм Ό ι, не содержащих ни перекрестков, ни стягиваемых
кривых.
Это следует непосредственно из факторизации: перекресток \? мы
заменяем на яо,/~ч + ао 0 ( ' а отДельно стоящую окружность удаляем, заменяя ее
коэффициентом (—а^2 — Oq).
Следующее утверждение очевидно.
Предложение 23.1. S(S2) ^ S(R2) ^ С.
Предложение 23.2. Пространство S(I x S1) имеет естественную
алгебраическую структуру над С. Эта алгебра изоморфна С[а] — алгебре многочленов
с комплексными коэффициентами от переменного а.
Доказательство. По теореме 23.10, любой элемент из S(I x S1) можно
представить линейной комбинацией диаграмм, каждая из которых состоит из
некоторого (возможно, пустого) набора окружностей, параллельных основанию
цилиндра Ι χ S1. Умножение в S(I x S1) определим посредством составления
двух цилиндров вместе так, чтобы верхнее основание нижнего соединялось с
23.3. Инварианты Виттена-Решетихина-Тураева
405
нижним основанием верхнего. Пусть а — образ (при естественной проекции)
диаграммы, состоящей из одной окружности, параллельной основанию
цилиндра. Тогда, очевидно, что все элементы пространства S(I x S1) находятся во
взаимно однозначном соответствии с полиномами от переменной a. D
Этот результат нам понадобится для определения операции многоместной
скобки, получаемой как линейная комбинация скобок Кауфмана, которая была
бы инвариантны относительно преобразований Кирби.
Рассмотрим теперь пространство S(D2,2n). По теореме 23.10 базис этого
пространства состоит из сп наборов попарно непересекающихся дуг с концами
в dD. Количество элементов в базисе равно п-у числу Каталана.
Число Каталана сп обладает следующими свойствами:
-L· Сп+1 — / jj—Q Ci^n — j'-)
9 η — 1 Пп
Ζ· С™ - η+1°2η·
Пространство S(D2,2n) имеет структуру алгебры; эта структура, однако,
не является канонической. Для ее определения нужно представить диск D2
с фиксированными 2гг точками на крае как квадрат, у которого η точек рас-
пол ожены на левой стороне, а остальные η точек — на правой. После этого
умножение определяется склейкой квадратов по стороне (таким образом,
чтобы точки на левой границе правого квадрата совпадали с точками на правой
границе левого квадрата) и сжатием полученного прямоугольника в два раза
так, чтобы получился квадрат, см. рис. 23.10.
Рис. 23.10. Умножение в алгебре Темперли-Либа
Определение 23.6. Алгебра, определенная выше, называется алгеброй Тем-
перли-Либа.
Обозначение: TLn.
406
Глава 23
Алгебра Темперли-Либа, очевидно, является ассоциативной.
Пусть ei — элемент алгебры Темперли-Либа TLn, изображенный на рис. 23.11.
i-Ι линий I
D α
η-i-l линий
Рис. 23.11. Элемент а
Пусть теперь 1п означает элемент алгебры Темперли-Либа TLn,
соответствующий диаграмме, состоящей из η параллельных горизонтальных дуг.
Теорема 23.11. Элемент 1п является единицей в алгебре TLn. Элементы
ei,..., en_i представляют мультипликативный базис алгебры TLn.
Доказательство очевидно.
В алгебре Темперли-Либа TLn имеют место следующие соотношения:
1. е? = е*(-а§ - %2),г = 1,..., (п - 1);
2. β^+ιβ^ = ei, г = 1,..., η — 2 и e^-ie^ = е^, г = 2,..., η — 1.
Доказательство предоставляется читателю.
23.3.2. Идемпотент Джонса—Венцля
Для дальнейших построений нам понадобится идемпотентный элемент f^
алгебры Темперли-Либа TLn, называемый идемпотентом Джонса-Венцля.
Пусть Ап — подалгебра алгебры TLn, порожденная элементами ei,..., en_i
(без 1п). Тогда элемент /^ определяется следующими уравнениями:
/(n)4 = Λ»/(η) = 0; (23.2)
1„ - /(n) G А„. (23.3)
Такой элемент существует в случае, если мы наложим некоторые
ограничения на ао £ С.
Теорема 23.12. Пусть для каждого /с = 1,..., п — 1, α^ 7^ 1· Тогда
существует единственный элемент /("> € TL„, для которого имеют место {23.2,23.3).
Этот элемент является идемпотентом: f^ · f^ = f(n\
23.3. Инварианты Виттена-Решетихина-Тураева
407
Упражнение 23.2. Вычислите явно f(2\
Заметим, что существование элемента f(n' влечет его единственность и
идемпотентность. А именно, единственность следует из того, что 1п — /^
является единичным элементом алгебры Ап. Более того, так как ln — f(n) играет
роль единичного элемента для Ап, мы имеем (1 — /(п))(1 — f^) = (1 — f^).
Из этого уравнения легко следует идемпотентность элемента f^n\
Построение элемента f(n> ведется индукцией по п. Мы приводим лишь
краткое описание построения. Детали молено прочесть, например, в [Oht].
Нам понадобится еще одна вспомогательная конструкция. Пусть Δη £ ^(R2)
— замыкание элемента f^n\ см. рис. 23.12. Более точно, f^ представляет собой
линейную комбинацию некоторых диаграмм (танглов типа η — η с η концами
справа и η концами слева). Тогда молено соединить соответствующие правые
и левые концы так, как показано на рис. 23.12 для каждого слагаемого
линейной комбинации, происходящей из f^nK В итоге мы получаем линейную
комбинацию плоских диаграмм. Аналогичным образом определяется элемент
Sn(a) G S(S1 x /): этот элемент представляет собой замыкание для f^ в
цилиндре, или, что то лее самое, в кольце, см. рис. 23.13. Здесь а обозначает
образующую кольца полиномов, изоморфного Si^S1 x /). Очевидно, что Δη получается
из Sn естественной проекцией Si^S1 χ /) —>· ^(R2) (состоящей в заклеивании
основания цилиндра диском).
Рис. 23.12. Замыкание элемента /^
Элементы Δη определяются индуктивно по формуле Δη+ι = (—а0 —α$)Δη-
Δη_ι, причем Δι = — α2, — %2- Кроме того, если а$ φ 1, то Δη φ 0; более
точно, Δ^
(zMn+1)-o2Kl))
α2-α02
Приведем индуктивную формулу для получения j^n>\
f(n+i) _ An) _ Δη_ι An) An)
«7 — «71 д «71 ^n«7l j
где f[n) обозначает элемент из Ап, полученный из f(n^ (всех слагаемых с
коэффициентами) добавлением одной горизонтальной линии снизу.
Аналогичным образом элементы Sn(a) строятся индуктивно по следующей
формуле:
Sn+i(oi) = aSn ~ Sn-χ.
408
Глава 23
Рис. 23.13. Элемент Sn(a)
23.3.3. Основная конструкция
Теперь мы готовы определить инварианты Виттена-Решетихина-Тураева
трехмерных многообразий. Сопоставим каждой диаграмме D зацепления из
компонент Κι,..., Кп полилинейное отображение (многоместную скобку)
(.,..· ,.)D:SlX...xSn^S(R2),
где Si ^ S(I х S1).
Для этого мы сначала определяем {а\,..., ο^)ο £ 5(К2), где щ обозначает
стандартную образующую алгебры Si (подобно тому, как а является
образующей алгебры S(I x S1)).
Иными словами, "замыкание" идемпотент Джонса-Венцля в кольце,
состоящее из линейной комбинации набора окружностей, можно представить в виде
полинома. Затем, обратно, мы этот полином используем для описания того,
сколько копий компонент зацепления в каком порядке нужно брать.
Мы имеем дело с плоскими диаграммами неориентированных зацеплений.
Для получения диаграммы (и, наконец, числа), соответствующей элементу
(ск11,... ,θίηη)ο, рассмотрим узлы Bi, соответствующие К^ а вместо каждого
Bi мы берем ki его параллельных копий Dkt(Ki), определение см. на стр. 34).
Предположим, что оснащенные диаграммы D и D' эквивалентны с помощью
движений Ω2, Ω2, Ω3. Тогда диаграммы (а^1,..., о^)в и (а^1,..., ο^)ό' также
могут быть получены одна из другой посредством преобразований Ω2 и Ω2, Ω3.
Следовательно, образы этих диаграмм в £(К2) совпадают.
Таким образом, построенное нами полилинейное отображение является
инвариантом оснащенных зацеплений с нумерованными компонентами. Если мы
хотим получить инвариант оснащенных зацеплений с ненумерованными
компонентами, мы можем брать многоместную скобку, в которой все аргументы
(полиномы) равны друг другу.
Для того, чтобы получить с помощью полилинейного отображения (·,··· , ·}
инвариант трехмерных многообразий, нам нужно построить функцию,
инвариантную относительно преобразований Кирби.
23.3. Инварианты Виттена-Решетихина-Тураева 409
Пусть г ^ 3 — натуральное число. Для получения инвариантности
относительно второго преобразования Кирби мы будем использовать элемент
г-2
n=0
Теорема 23.13. Предположим, что ао таково, что а$ является
первообразным корнем из единицы степени г. Предположим, что диаграммы D и D'
получаются одна из другой применением второго движения Кирби. Тогда мы
имеем:
Основная идея доказательства состоит в следующем: при применении
второго движения Кирби разница между соответствующими скобками состоит из
линейной комбинации только тех членов из S(S1 χ /), которые содержат /(r_1)
в качестве поддиаграмм. Так как а^г = 1, мы имеем ΔΓ_ι = 0. При взятии
разницы (ω,ω,... ,ω)η — (ω,ω,... ,uj)d'· слагаемые, соответствующие всем
"промежуточным" произведениям AnSn, сокращаются между собой, а оставшийся
член сокращается по причине равенства ΔΓ_ι = 0.
Рассмотрим теперь первое движение Кирби. Для получения
инвариантности относительно этого движения нам понадобится нормализация, для которой
нужно определить матрицу коэффициентов зацеплений.
По диаграмме L гг-компонентного оснащенного зацепления построим
симметрическую матрицу размера (η χ η), состоящую из коэффициентов
зацеплений (предварительно можно ориентировать компоненты зацепления
произвольным образом, как будет видно в дальнейшем, от этого не будут зависеть
нужные нам инварианты для нормировки). В качестве диагональных
элементов мы возьмем коэффициенты самозацепления соответствующих компонент.
Обозначим полученную матрицу через В. Матрица В инвариантна
относительно движений Ω2,Ω3,Ω^. Так как матрица В является симметрической и
целочисленной, то все собственные значения этой матрицы вещественны. Пусть 6+
— число положительных собственных значений матрицы В, a L — число ее
отрицательных собственных значений. Для дальнейших построений нам
понадобится не сама матрица В, а лишь числа 6+, 6_.
Легко видеть, что замена ориентации некоторой компоненты зацепления L
приводит к преобразованию В —>· В' = ХТВХ, где X — некоторая
ортогональная матрица. Таким образом коэффициенты 6+ и 6_ не зависят от ориентации.
Покажем теперь, что числа 6+ и 6_ являются инвариантными относительно
второго движения Кирби. Для этого достаточно доказать следующую теорему.
Теорема 23.14. При втором преобразовании Кирби матрица В переходит
в матрицу В' = ХТВХ, где X — некоторая невырожденная вещественная
матрица.
Доказательство этой теоремы остается читателю в качестве упражнения.
410
Глава 23
Рассмотрим три стандартные оснащенные диаграммы [7+, U-, Щ,
показанные на рис. 23.14. Они представляют собой тривиальный узел с оснащениями
1, —1 и 0 соответственно. В случае, когда (uj)u+{^)u- φ 0, для каждой
диаграммы D молено рассмотреть следующее комплексное число:
1(D) = (u;,...,u;)D(u;)~b++(u;)~b_-.
и+ и и_
Рис. 23.14. Диаграммы С7+, Щ, U-
Предложение 23.3. Комплексное число 1(D) является инвариантом
многообразия, определенного перестройкой Дена вдоль диаграммы D при условии,
что (ω)υ+(ω)υ_ φ 0.
Чтобы это условие предложения 23.3 выполнялось, нужно наложить
некоторые ограничения на ао. А именно, нам нужно, чтобы ао было первообразным
корнем из единицы степени 4г или степени 2г в случае нечетного г. В обоих
случаях <2q является первообразным корнем из единицы степени г (и, таким
образом, удовлетворяет условиям теоремы 23.13).
Доказательство теоремы 23.3 весьма сложно и состоит из многих шагов.
Здесь мы опишем лишь главный шаг в доказательстве теоремы.
Лемма 23.1. Предположим, что ао удовлетворяет свойствам, описанным
выше. Тогда мы имеем:
1. При 1 < η < г — 3 каждая диаграмма, содержащая диаграмму Dn (см.
рис. 23.15), обращается в нуль;
2. При η = г — 2 в случае, если ао является первообразным корнем
порядка 4г, каждая диаграмма, содержащая Dn, также обращается в нуль,
а в другом случае (порядок 2г для нечетных τ) диаграмма Dn мож^ет
быть заменена (ω)υϊ^·
(Здесь под "диаграммами" мы понимаем их образы в ^(R2).)
Собирая воедино результаты теорем 23.13 и 23.14 и предложения 23.3, мы
приходим к основной теореме.
Теорема 23.15. Пусть г ^ 3 — натуральное число. Если ао G С — либо
первообразный корень из единицы порядка 4г, либо первообразный корень из
единицы порядка 2г при нечетном г, то
W(M3) = 1(D) = <",.· .,со)п(со)-Ь++(со)-Ь_- (23.4)
23.4. Инварианты зацеплений в трехмерных многообразиях 411
f(n)
г
U
Со
Рис. 23.15. Диаграмма Dn
является топологическим инвариантом ориентированных компактных
трехмерных многообразий без края. (Многообразие М3 является результатом
применения к трехмерной сфере перестройки Дена вдоль зацепления D).
Получаемые инварианты называются инвариантами Решетихина-Тураева
или Виттена-Решетихина-Тураева трехмерных многообразий.
Примеры 23.1. Сфера S3 представима пустой диаграммой; таким образом,
I(S3) = 1.
Многообразие S1 x S2 представимо диаграммой Щ. Матрица
коэффициентов зацепления для Uq имеет вид В = (6ц), где 6ц = 0. Таким образом,
6+ = 6_ = 0. Поэтому IiS1 χ S2) = (ω)υο.
Последнее выражение равно
(w)
2г
Uo
(α§ - % 2)2 '
если <2о — первообразный корень из единицы степени 4г.
23.4. Инварианты зацеплений
в трехмерных многообразиях
Предложенный выше способ построения инвариантов трехмерных
многообразий может быть обобщен на случай зацеплений в трехмерных
многообразиях. Основная идея — та же: мы берем скобку Кауфмана от некоторой
линейной комбинации зацеплений, только на этот раз часть компонент зацепления
представляют собой оснащенное зацепление, по которому строится трехмерное
многообразие, в то время как остальные компоненты зацепления образуют
зацепление в этом трехмерном многообразии. В основном мы придерживаемся
книги [ПС].
Рассмотрим компактное ориентированное трехмерное многообразие М3 с
краем и (оснащенное) зацепление L в нем. Многообразие М3 получается
перестройкой Дена трехмерной сферы S3 по оснащенному зацеплению. Это
означает, что существует гомеоморфизм
/ : S3\LM -+ M3\L
м,
где Lm — зацепление в Μ3. Без ограничения общности можно предполагать,
что зацепление Lm не пересекает зацепления L. Пусть Ll = /-1(Х) есть
прообраз зацепления L с М3 в сфере S3. Если L имеет оснащение, то это оснащение
412
Зацепления в трехмерных многообразиях
автоматически переносится и на Ll (мы имеем тор и в нем выбранную
параллель). Таким образом, оснащенное зацепление L в многообразии М3 задается
парой оснащенных зацеплений (Ll->Lm) b сфере S3; количество компонент
зацепления Ll равно количеству компонент зацепления L.
Зададимся следующим вопросом: когда две пары (Ll, Lm) и (Ll·) -^m) заДа~
ют одно и то лее (с точностью до изотопии) зацепление L в трехмерном
многообразии М3? Во-первых, перестройки сферы вдоль оснащенных зацеплений
Lm и L'm должны задавать одно и то лее многообразие М3; следовательно, L'M
может быть получено из Lm изотопиями и преобразованиеями Кирби. Кроме
того, в процессе изотопии зацепление Lm не должно пересекать зацепления Ll-
Дело в том, что изотопия, отображающая Lm в L'm индуцирует гомеоморфизм
/ : S3\LM -> M3\LM.
Ясно, что в общем положении преобразования Кирби не затрагивают малой
окрестности зацепления Ll- После того, как мы применим необходимые
преобразования Кирби и изотопии, мы можем считать, что L'M = Lm- После этого,
мы можем применять движения Кирби и изотопии уже к Ll U Lm, в то
время как зацепление Ll может быть только изотопируемо. Таким образом, нам
нужно выяснить связь между Ll и L'l в случае, когда Lm = L'M. В этом
случае, после перестройки сферы S3 по зацеплению Lm, мы получаем трехмерное
многообразие М3, в котором образы зацеплений Ll и L'l являются
изотопными. При этой изотопии образы зацеплений Ll и L'l могут пересекать образ
зацепления Lm- Таким образом, искомая перестройка не редуцируется к
изотопии зацеплений Ll и Lm в сфере S3. Более точно, если в М3 компонента К к
образа Kl пересекает компоненту Км образа Lm, to сфера S3 претерпевает
второе преобразование Кирби, а именно, лента, соответствующая зацеплению
Км добавляется к ленте, соответствующей зацеплению Kl·
Отметим два важных обстоятельства:
1. Количества компонент зацеплений Ll и L'l равны;
2. При втором преобразовании Кирби зацепления из Ll не участвуют в
качестве "второй неподвижной компоненты".
Оснащенному зацеплению L^ULm мы можем сопоставить оснащенную
диаграмму Dl U Dm- Для зацепления Lm рассмотрим матрицу В коэффициентов
зацепления и соответствующие числа 6+ и 6_ положительных и
отрицательных собственных значений этой матрицы; пусть η — число компонент
зацепления Ll- Фиксируем элементы
ρι(α),... ,рп(а) е S(I x S1) ^ C[a]
(здесь мы используем предыдущие обозначения).
Теорема 23.16. Пусть г ^ 3 — натуральное число, а — комплексное число,
ао — комплексное число такое, что: либо а$ является первообразным корнем
из единицы порядка 4г, либо ао является первообразным корнем из единицы
порядка 2г, причем г — нечетно.
23.5. Виртуальные трехмерные многообразия и их инварианты 413
Тогда комплексное число
W(M3,L) = (ρι(α),... ,рт(<х),и>,. ..u>)DLuDM(u)ub+- И^" (23.5)
является инвариантом пары (M3,L); где L — оснащенное зацепление в
многообразии М, а
г-2
п=0
Доказательство. Заметим сначала, что η инвариантно: оно равно количеству
компонент зацепления L. Доказательство инвариантности числа,
определяемого по формуле (23.5) при допустимых преобразованиях пары LlULm почти
такое лее, как доказательство инвариантности инварианта Решетихина-Тураева.
Единственным новшеством является следующее. При применении второго
преобразования Кирби мы не можем добавлять ленты, параллельные компонентам
зацепления Ll. Это позволяет нам использовать различные обозначения для
Ll (в отличие от Lm)'· мы выбираем произвольные ρ ι (а),.. .ρη(θί) Ε S(I x S1),
а не только ω. D
Замечание 23.4. Формула (23.5) определяет не один инвариант, а
бесконечную серию инвариантов, которые зависят от следующих параметров: с*о,
Ρι,Ρ2, · · · ,Ρηϊ при этом число ао должно удовлетворять приведенным выше
условиям при построении инвариантов трехмерных многообразиях.
23.5. Виртуальные трехмерные многообразия и их
инварианты
Недавно Луис Кауфман и его аспирантка Хизер Дай [DK1, Каи5], см.
также [Dye], обобщили теорию Кирби на случай виртуальных узлов и
построили теорию "виртуальных многообразий", для которых обобщили инварианты
Виттена-Решетихина-Тураева.
Все конструкции обобщаются непосредственно.
Для построения виртуальных трехмерных многообразий нужно
рассмотреть диаграммы виртуальных зацеплений. Две виртуальных диаграммы
считаются Кирби-эквивалентными, если одна из них может быть получена из
другой последовательным применением объезда, преобразований Ω2,Ω3,Ω^ и
двух движений Кирби.
Первое движение Кирби представляет собой то же самое, что и в
классическом случае: добавление отдельно стоящей окружности с оснащением ±1.
Что касается второго преобразования Кирби, следует заметить, что
компонента, вдоль которой перестраивается другая компонента, может иметь
виртуальные перекрестки. Виртуальная версия второго преобразования Кирби
показана на рис. 23.16. В ней на месте виртуального перекрестка возникают четыре
виртуальных перекрестка.
Классы Кирби-эквивалентности называются виртуальными трехмерными
многообразиями.
414
Зацепления в трехмерных многообразиях
Рис. 23.16. Виртуальная версия второго преобразования Кирби
До сих пор остается открытым следующий вопрос (поставленный автором
настоящей книги): пусть даны две Кирби-эквивалентные классические
диаграммы. Задают ли они гомеоморфные трехмерные многообразия?
Как показал Кауфман, в категории виртуальных трехмерных многообразий
неверна гипотеза Пуанкаре.
Инварианты Решетихина-Тураева виртуальных трехмерных
многообразий определяются так лее, как и инварианты обычных трехмерных
многообразий, с помощью скобки Кауфмана и идемпотента Джонса-Венцля, см.
теорему 23.15 и формулу 23.4. При этом коэффициент зацепления в
виртуальном случае вычисляется "полуцелым" способом, см. стр. 293. Полное описание
см. в оригинальной работе [Dye].
Глава 24
Лежандровы узлы
и их инварианты
Теория лежандровых узлов относится к контактной топологии малых
размерностей. Первое систематическое изучение лежандровых узлов как объекта
теории узлов принадлежит Дмитрию Борисовичу Фуксу и Сергею
Леонидовичу Табачникову [FT]. Эта теория сочетает в себе теорию узлов, теорию
волновых фронтов и контактную геометрию. Как и теория виртуальных узлов,
она богаче, чем обычная (классическая) теория узлов; в ней дело обстоит так:
некоторые (топологические) узлы в трехмерном пространстве являются лежан-
дровыми, и для них задается новый вид изотопии: лежандрова изотопия.
Каждый изотопический класс узла имеет своего лежандрова представителя, но при
этом для каждого такого класса существует бесконечное множество лежандро-
во неизотопных между собой узлов. Важнейшей задачей теории лежандровых
узлов является изучение связи между лежандровой и топологической
классификациями.
В конце настоящей главы мы приведем самые мощные известные на данный
момент инварианты, принадлежащие Юрию Витальевичу Чеканову и Петру
Евгеньевичу Пушкарю.
Лежандровы узлы в R3 представляют собой одномерный случай
лежандровых многообразий (в общем случае лежандрово многообразие является к-
мерным подмногообразием в (2к + 1)-мерном многообразии, удовлетворяющим
некоторым геометрическим условиям), см. стр.416.
24.1. Лежандровы многообразия и лежандровы кривые
Важнейшей задачей теории обыкновенных дифференциальных уравнений
(одной переменной) является нахождение огибающей кривой для семейства
прямых на плоскости. Хорошо известно, что в гладком случае эта задача всегда
имеет решение согласно теореме существования и единственности.
Если мы рассмотрим семейство плоскостей в R3 или, более общо, семейство
гиперплоскостей в нечетномерном пространстве R2n+1, то огибающая
поверхность полной размерности (т. е. размерности 2гг) будет существовать уже не
всегда.
416 Лежандровы многообразия и лежандровы кривые
В общем случае, который носит название максимально неинтегрируемого,
максимальная размерность поверхности, касающейся этого семейства
гиперплоскостей в каждой своей точке, равна п.
В случае η = 1 (при подходящем семействе плоскостей) мы получаем кривые
в трехмерном пространстве; если эти кривые являются замкнутыми, то они
представляют собой узлы.
Для дальнейшего изложения нам нужно ввести также понятие контактной
структуры.
24.1.1. Контактные структуры
Определение 24.1. Контактной структурой на нечетномерном
многообразии Μ2η+1 называется гладкая 1-форма ω на Μ такая, что форма
ω Λ άω Λ · · · Λ άω
ν
η
является невырожденной в каждой точке.
Имея контактную структуру, мы получаем семейство плоскостей: в каждой
точке X плоскость состоит из векторов ν, таких что ω\(ν) = 0.
Рассмотрим пространство R3 и стандартную контактную структуру,
заданную формой ω = — xdy + dz. Очевидно, что в каждой точке (ж, у, ζ)
соответствующее поле плоскостей порождено двумя векторами (1,0,0) и (0,1, ж).
Обозначим это поле через т.
Определение 24.2. Леэюандровым зацеплением называется множество
непересекающихся несамопересекающихся ориентированных замкнутых кривых в R3,
таких что каждая кривая в каждой своей точке имеет касательный вектор,
принадлежащий семейству т.
Имеет смысл рассматривать плоские диаграммы лежандровых зацеплений.
Оказывается, что такие диаграммы при проекциях на разные плоскости
обладают весьма интересными свойствами.
24.1.2. Плоские диаграммы лежандровых зацеплений
Пусть дано лежандрово зацепление L. Рассмотрим его проекцию на
плоскость Oyz. Эта проекция называется фронтальной проекцией. Пусть 7 —
проекция одной компоненты зацепления L. Рассмотрим касательный вектор к этой
кривой: 7 = (0, у, ζ). По определению мы имеем ху = i, таким образом,
координата χ лежандровой кривой L равна ^, или, иными словами, абсцисса равна
тангенсу угла наклона в проекции на Oyz.
Из этого следует важный факт: проекция на плоскость Oyz не может быть
гладкой.
Действительно, если бы проекция была гладкой, она не могла бы иметь
касательных, параллельных оси Ог, так как из у = 0 следует, что χ = ос. Так
как проекция замкнута, то из предположения гладкости следовало бы наличие
касательных в любом наперед заданном направлении.
Поскольку кривая является замкнутой, то у не может всегда иметь один и
тот же знак. Следовательно, у обращается в нуль, и кривая теряет гладкость.
Лежандровы многообразия и лежандровы кривые 417
Замечание 24.1. Этого эффекта можно было бы избежать, если
рассматривать узлы в R2 χ S1 вместо узлов в R3. В этом случае (как и на любом
многообразии с заданной контактной структурой) имеется замечательная
теория лежандровых узлов. Существует естественный способ задания
контактной структуры на многообразии, являющемся расслоением единичных
касательных векторов над двумерным многообразием.
Однако в данном случае мы рассматриваем узлы и зацепления в R3,
следовательно, мы должны считать, что у φ 0.
Это означает, что на плоскости Oyz наша кривая не имеет вертикальных
касательных. Единственной возможностью изменения знака производной у
является прохождение через точку, где у = ζ = 0, что приводит к наличию клюва,
см. рис. 24.1.
Рис. 24.1. Клюв на фронтальной проекции
Клюв имеет форму полукубической параболы: кривая (γ,ί2,ί3) является
типичным примером такой кривой (ее клюв находится в начале координат).
Имея кусочно-гладкую ориентированную кривую (гладкую везде, кроме
точек, где у меняет знак), мы можем построит лежандрову кривую в R3, полагая
ζ
χ = -.
У
Выбирая в качестве 7 кривую в общем положении (имеющую лишь двойные
трансверсальные точки самопересечения), мы получаем зацепление L с
проекцией 7· Таким образом, для получения тени зацепления того же изотопического
типа, что и L, нам нужно просто сгладить все клювы.
Кроме этого, трансверсальные точки пересечения однозначно определяют
структуру перекрестков зацепления. А именно, значение координаты χ больше
на той ветви, на которой больше тангенс угла наклона касательной 4.
Продеформируем слегка кривую проекции 7 (без изменения лежандрова
изотопического типа) так, чтобы две пересекающиеся ветви измененной
кривой 7 имели направления северо-запад — юго-восток и северо-восток — юго-
запад, см. рис. 24.2.
В этом случае направление северо-восток — юго запад будет образовывать
переход.
Таким образом, определен способ построеия плоских диаграмм обычных
(гладких) узлов по проекциям лежандровых узлов на плоскость Oyz.
Обратная процедура описана в доказательстве следующей теоремы.
418 Лежандровы многообразия и лежандровы кривые
Рис. 24.2. Восстановление перекрестков по фронтальной проекции
Теорема 24.1. В каждом изотопическом классе L зацеплений существует
лежандрово зацепление.
Доказательство приведено на стр. 419.
Посмотрим, как выглядит проекция лежандрова узла (зацепления) на
плоскость Оху.
В этом случае удобно рассмотреть каждую компоненту по отдельности.
Пусть 7 — кривая на проекции. Если мы возьмем отрезок этой кривой,
начинающийся в некоторой точке А и заканчивающийся в некоторой точке £>,
мы получим из ζ = ху, что ζ а — ζ в = Jв xdy. Рассмотрим интеграл вдоль 7
(от А до А).
xdy = О,
(24.1)
или, по теореме Гаусса-Остроградского,
S(M7) = О,
где S означает (ориентированную) площадь, а М7 — область, ограниченную
кривой 7 (если 7 имеет самопересечения и обходит много разных областей,
то нужно считать площади со знаками и с кратностями — положительными и
отрицательными).
Уравнение (24.1) является единственным необходимым и достаточным
условием, для того, чтобы лежандрова кривая была замкнутой.
Если мы хотим определить структуру проходов-переходов для лежандрова
узла, нам нужно рассмотреть перекресток Ρ и замкнутую кривую 7?
концами которой является два раза точка Р, лежащая на разных концах кривой 7·
Проинтегрируем форму xdy вдоль по этой кривой. Если значение интеграла
положительно, то интеграл J dz положителен, следовательно, точка на лежан-
дровом узле прообраз точки 7(0) лежит ниже прообраза точки 7(1)·
При рассмотрении гг-компонентного зацепления мы можем легко расставить
проходы-переходы, которые возникают при пересечении некоторой его
компоненты с самой собой. Далее у нас есть некоторая свобода в расположении
компонент (так как, зная координату ζ всех точек на одной из них, мы ничего не
можем сказать про координату ζ какой-либо точки на второй компоненте).
Таким образом, в случае зацеплений структура перекрестков однозначно не
восстанавливается по лагранжевой проекции.
24.2. Определения, основные понятия и теоремы 419
24.2. Определения, основные понятия и теоремы
Будем использовать обозначения из [Che2]. Будем строить основные
инварианты только для узлов; случай инвариантов зацеплений рассматривается
аналогично.
Рассмотрим гладкий узел в контактном пространстве R3 = {д,р, и} со
стандартной контактной формой а = du — pdq (мы вводим новые координаты д,р, и
вместо старых y,x,z).
Определение 24.3. Гладкий узел в R3 называется лежандровым, если в
каждой точке узла форма а обращается в нуль на касательном векторе к узлу в
этой точке.
Определение 24.4. Два лежандровых зацепления называются лежандрово
изотопными, если один из них может быть гладко продеформирован в другой
в классе лежандровых узлов.
Есть два удобных способа представления лежандровых зацеплений их
плоскими проекциями. Проекция π : R3 —>· R2, (q,p,u) —>· (q,p) называется лагран-
жевой проекцией (проекция Оху), а проекция σ : (p,q,u) —> (q,u) называется
фронтальной проекцией (проекция Oyz).
Фронтальная проекция
Фронтальная проекция лежандрова узла не может быть гладкой; как было
сказано выше, она должна содержать клювы.
По фронтальной проекции лежандров узел (лежандрово зацепление)
восстанавливается следующим образом. Мы сглаживаем все клювы и
устанавливаем проходы-переходы по следующему правилу: ветвь, образующая переход
должна иметь больший тангенс угла наклона. Так как проекция не имеет
вертикальных касательных, этот тангенс корректно определен, см. рис. 24.3.
Рис. 24.3. Восстановление диаграммы по фронтальной проекции
Фронтальная проекция называется σ-общей , если все перекрестки
соответствуют различным значениям координаты q.
Процедура построения лежан дрова зацепления, лежащего в заданном
изотопическом классе, выглядит следующим образом. Рассмотрим гладкую плоскую
диаграмму зацепления. Сначала расставим клювы в окрестностях всех точек, в
которых имело место вертикальное касание. Рассмотрим перекрестки
диаграммы. Во всех "хороших" перекрестках (в которых проход и переход согласуются
с правилом фронтальной проекции) мы оставим просто точку пересечения двух
ветвей узла. В случае плохого перекрестка нам нужно видоизменить
диаграмму, добавив к ней два клюва так, как показано на рис. 24.4.
420 Лежандровы многообразия и лежандровы кривые
Рис. 24.4. Построение фронта по диаграмме
Таким образом, мы показали, что в каждом изотопическом классе
зацеплений есть лежандрово зацепление, что утверждает теорема 24.1.
На рис. 24.5 мы приводим фронтальные диаграммы двух лежандровых
трилистников.
Рис. 24.5. Левый трилистник и правый трилистник
Непохожесть этих двух диаграмм происходит из "несимметричного"
соглашения о "хороших" и плохих перекрестках. Подобно этому простейшие
d-диаграммы правого и левого трилистников различаются.
Отметим, что формальное построение диаграммы длинного узла
(зацепления) по d-диаграмме приводит к "длинному" лежандрову узлу в его
фронтальной проекции: правило для расстановки перекрестков согласно d-диаграмме
противоположно правилу расстановки перекрестков на фронтальной
проекции проекции. При этом при построении зацепления по d-диаграмме
возникают места потери гладкости около концов хорд, см. рис. 24.6.
Интересным является вопрос о классификации преобразований
лежандровых узлов в терминах d-диаграмм; важно также понять, какие (все ли)
лежандровы узлы (зацепления) могут быть получены из d-диаграмм. Напомним,
что в главе 15 показано, что все изотопические классы зацеплений могут быть
заданы d-диаграммами.
Лагранжева проекция
Лагранжева проекция, в отличие от фронтальной, является гладкой.
Действительно, если бы в некоторой точке имело место q = ρ = 0, то мы имели бы
й = 0. Если наша параметризация регулярная, то это невозможно. Как и по
фронтальной проекции, по лагранжевой проекции можно восстановить
структуру перекрестков и, следовательно, изотопический тип узла.
24.3. Движения Фукса-Табачникова
421
Рис. 24.6. Построение длинного лежандрова узла по d-диаграмме
Лагранжева проекция называется π-общей если все ее пересечения
(перекрестки) являются двойными и трансверсальными.
Пусть дана плоская диаграмма L узла. Фиксируем точку Ρ на ней,
отличную от перекрестка. Будем считать, что и(Р) = 0. Покажем, как восстановить
координату и для всех точек проекции L. Принимая во внимание, что вдоль
кривой выполняется du = pdq, мы видим, что разница и а — ив равна
ориентированной площади области, ограничиваемой кривой, между точками А и В,
если А и В проектируются в одну точку. Тогда мы можем точно определить,
какая из двух ветвей (содержащая А или содержащая В) образует переход,
исходя из знака соответствующей площади. Таким образом, мы получаем набор
неравенств, соответствующих типам перекрестков. Кроме того, для того, чтобы
кривая проекции происходила из замкнутой кривой (узла), нам нужно, чтобы
ориентированная площадь, ограничиваемая всей кривой, равнялась нулю.
Из этого следует, что не каждая плоская диаграмма узла реализуется его
лагранжевой проекцией.
Например, имея диаграмму замыкания косы (см. рис. 24.7), мы видим, что
она не может быть реализована как лагранжева проекция лежандрова узла,
потому что каждая из площадей, ограничиваемых этой кривой, входит в общую
ориентированную площадь с положительным коэффициентом, следовательно,
ориентированная площадь, ограничиваемая этой кривой, не может быть равна
нулю.
В этом смысле понятие лагранжевой диаграммы противоположно
замыканию косы.
Замечание 24.2. Третья проекция (p,q,u) —> (ρ, и) не так интересна, как
первые две.
24.3. Движения Фукса-Табачникова
Лежандровы узлы и зацепления и их фронтальные проекции допускают
комбинаторное описание, как и обычные узлы и зацепления. А именно,
существует набор элементарных движений, такой, что любые две фронтальные
422 Лежандровы многообразия и лежандровы кривые
A+B+C+D+E+2F=0
при положительных
A,B,C,D,E,F
Рис. 24.7. Заплетающаяся диаграмма не является лагранжевой
АР
оо
А
>
Рис. 24.8. Лагранжева проекция и фронтальная проекция
проекции представляют лежандрово изотопные лежандровы зацепления тогда
и только тогда, когда одна из них может быть перестроена во вторую
посредством цепочки таких преобразований.
А именно, имеет место следующая теорема.
Теорема 24.2 (Фукс, Табачников [FT]). Две фронтальные проекции
задают лежандрово эквивалентные зацепления тогда и только тогда, когда одна
из них может быть перестроен в другую посредством движений 1)-3),
показанных на рис. 24-9.
24.3. Движения Фукса-Табачникова
423
Допуская движение, изображенное на рис. 24-9.4), мы получаем
топологическую эквивалентность зацеплений.
Рис. 24.9. Движения Фукса-Табачникова
Эта теорема, как и теорема Рейдемейстера, следует из соображений общего
положения.
Заметим, что преобразование фронтальной проекции, когда проекции двух
ветвей проходят друг через друга, по ходу образуя точку касания, не
представляет собой далее топологической изотопии, так как точка касания на
фронтальной проекции означает наличие точки пересечения в трехмерном пространстве.
Обратим внимание на последние два движения, отвечающие за
классическую изотопию, но меняющие лежандров изотопический тип. Они состоят в
добавлении к диаграмме в произвольном месте зига (см. рис. 24.10.а) или за-
га (см. рис. 24.10.а). Будем формально записывать это так: K^zig и K^zag.
Можно нарисовать кривую, состоящую из к зигов и η загов, см. рис. 24.10.в.
Будем ее обозначать через ((к, п). Стандартным зигзагом мы будем называть
кривую С = С(М)·
Выбрав горизонтальный отрезок фронтальной проекции лежандрова узла,
можно добавить к нему произвольный набор зигов и загов ((к,п).
Через ζρ будем обозначать "связную сумму" ρ экземпляров зигзага, т. е.
С(р>р)·
Имеет место важная
Лемма 24.1. Операция добавления зига (зага) К ι—> If #£(1,0) (или К ι—>
К#С(0,1)) является корректно определенной операцией на лежандровых
узлах, т. е. лежандров тип получающегося узла не зависит от выбора места
добавления зига (зага), а также от исходной диаграммы, представляющий
данный лежандров тип.
424 Лежандровы многообразия и лежандровы кривые
а* Зиг б. Заг
Зигзаг
Рис. 24.10. Зиги и заги
Доказательство состоит в аккуратной проверке того, что "прохождение" зига
или зага через перекресток или клюв является изотопией (выражается через
движения Фукса-Табачникова 1)-3)), а также того, что все движения 1)-3).
можно проводить при наличии дополнительного зига или зага.
Таким образом, к диаграмме можно добавлять зиги и заги в произвольном
порядке, тем самым для каждого типа лежандрова узла К и натуральных
чисел /с, η корректно определен лежандров узел к#((к,п). Оказывается, что при
таком добавлении неизотопные узлы могут стать изотопными. А именно имеет
место
Теорема 24.3. Пусть К, К' — два лежандровых узла, имеющие один и тот
же топологический тип. Тогда существуют числа р, q, r, s такие, что узлы
Κ#ζ(ρ, q) и K7#C(r, s) являются лежандрово изотопными.
Доказательство. Отметим, что искомое свойство является отношением
эквивалентности между узлами К, К'.
Разложим топологическую изотопию лежандровых узлов К и К' по
движениям 1)-4). Нас интересуют те ее моменты, когда мы применяем четвертое
движение Фукса-Табачникова, т. е. добавляем (убираем) зиги или заги. Мы имеем:
К = Ко —>· Κι —>· · · · —>· Кп = К1', где узлы Κι и i^Q+i отличаются одним зигом
(загом). Следовательно, они эквивалентны, из чего вытекает эквивалентность
К ж К'. D
24.4. Числа Маслова и Беннекина
Инварианты, поименованные в названии этого раздела, определяются
следующим образом. Рассмотрим поле плоскостей du = pdq; в каждой точке
выберем нормальный вектор ν = (—ρ, 0,1) в координатах (u,p,q)
24.4. Числа Маслова и Беннекина
425
Число Беннекина (также называемое числом Тер стона-Беннекина) P(L) ле-
жандрова узла L — это коэффициент зацепления между узлами L и s(L), где
s - малый сдвиг узла L в направлении вектора и в пространстве R(up g).
Число Маслова m(L) — это число вращения проекции диаграммы L на
плоскость (q,p), т.е. число, показывающее, сколько раз (в алгебраическом смысле)
единичный касательный вектор проекции проходит единичную окружность по
часовой стрелке.
Замена ориентации лежандрова узла L изменяет знак числа m(L) и
сохраняет P(L).
Оба эти инварианта определяются комбинаторно, исходя из фронтальной
проекции лежандрова узла. А именно, число Маслова представляет собой
разность между количеством отрицательных клювов и количеством
положительных клювов, см. рис. 24.11.
Упражнение 24.1. Докажите эквивалентность двух определений числа
Маслова.
Рис. 24.11. Положительные клювы Отрицательные клювы
Определение 24.5. Перекресток фронтальной проекции лежандровы узла
называется отрицательным, если обе ветви ориентированы вправо или обе влево
и положительным в противном случае, см. рис. 24.12.
Рис. 24.12. Положительные перекрестки и отрицательные перекрестки
Число Беннекена определяется как — ^(# клювы)+ (# отриц. перекр.)-
(# полож. перекр.).
Упражнение 24.2. Докажите эквивалентность двух определений числа
Беннекина.
Заметим, что добавление зигзага не меняет числа Маслова, но уменьшает
на единицу число Терстона-Беннекина.
Оказывается, что для некоторых топологических типов узлов (в частности,
для тривиального) числа Маслова и Беннекина являются полными
инвариантами. Первая теорема в этом направлении принадлежит Элиашбергу [Eli].
426 Лежандровы многообразия и лежандровы кривые
Теорема 24.4. Два топологически тривиальных узла К\ иК^, имеющие
одинаковые числа Маслова и Беннекина, являются лежандрово-изотопными.
Оригинальное доказательство этой теоремы [ЕН] очень сложное. Основные
идеи более простого доказательства (принадлежащие Джону Этнайр и Ко
Хонде, [ЕН]), состоят в следующем.
1. Число Беннекина тривиального лежандрова узла всегда не превосходит
— 1. Оно равно минус единице только на лежандровом узле, имеющем
диаграмму с двумя клювами и без перекрестков (и узлах, ему лежандрово
эквивалентных).
2. Для каждого фиксированного числа Маслова т существует ровно один
топологически тривиальный лежандров узел, имеющий число Маслова т
и максимально возможное число Беннекина.
3. Если число Беннекина некоторого топологически тривиального узла К
меньше (—1), то существует узел К' такой, что Κ'φζ(1,1) лежандрово
эквивалентен узлу К.
Пусть теперь К, К' — два тривиальных узла с одинаковыми числами
Маслова и Беннекина. Пусть число Маслова каждого из этих узлов равно га. Пусть
К — тривиальный узел, имеющий максимально возможное число Беннекина.
Тогда К и К' получаются из К прибавлением зигзагов. Так как их числа
Беннекина совпадают, то число зигзагов — одно и то же. Следовательно, К и К' —
лежандрово эквивалентны.
В замечательном обзоре по теории лежандровых узлов [ЕН] эта теорема
доказана и для некоторых других топологических классов узлов. К таковым
относятся, например, торические узлы. Как мы убедимся впоследствии, в общем
случае это не так (т. е. существуют топологически изотопные, но лежандрово не
изотопные, лежандровы узлы с совпадающими числами Маслова и Терстона-
Беннекина). Для ознакомления с теорией лежандровых узлов мы также
рекомендуем статью Эмануэля Жиру [Gir].
С очевидностью теорема 24.3 верна в предположении ρ = q. Добавление
зигов и загов изменяет числа Маслова и Беннекина. Таким образом, из
теоремы 24.3 получаем следствие.
Следствие 24.1. Пусть К, К' — два топологически эквивалентных узла с
одинаковыми числами Маслова и Беннекина. Тогда существует натуральное
ρ такое, что Κ#ζρ = Κ'#ζρ.
24.5. Инварианты лежандровых узлов конечного порядка
Лежандровы узлы являются узлами в трехмерном пространстве.
Аналогично общему случаю топологических узлов, определим сингулярные узлы порядка
η как лежандровы кривые имеющие ровно η точек простого трансверсального
пересечения.
24.5. Инварианты лежандровых узлов конечного порядка 427
Рассмотрим линейное (над Q) пространство всех (лежандровых)
изотопических классов сингулярных узлов и профакторизуем его по соотношению
Васильева, т. е. положим *Х* = %Л — у\ · Мы имеем вложенную систему
подпространств · · · С L2 С Li С Lo, где Li — пространство сигулярных лежандровых
узлов порядка не больше г. Каждый инвариант лежандровых узлов
продолжается по линейности на сингулярные узлы произвольных порядков. Инвариант
называется инвариантом Васильева порядка не больше гг, если он обращается
в нуль на пространстве Ln+i- Инвариант Васильева порядка η — это инвариант
Васильева порядка не больше, чем гг, не являющийся инвариантом Васильева
порядка не больше, чем η — 1.
Инварианты Васильева классических узлов, с очевидностью, являются
инвариантами Васильева лежандровых узлов тех же порядков.
Кроме того, как нетрудно заметить (это остается читателю в качестве
упражнения), что числа Маслова и Беннекина также являются инвариантами
Васильева лежандровых узлов порядков ноль и один соответственно. Оказывается,
что этим исчерпываются все принципиально новые (не топологические)
инварианты конечного порядка лежандровых зацеплений.
Более точно, имеет место следующая теорема.
Теорема 24.5 (Фукс, Табачников). Пусть К, К' — два топологически
эквивалентных лежандровых узла, имеющие одинаковые числа Маслова и
Беннекина. Тогда они не различимы инвариантами Васильева лежандровых узлов.
Доказательство. Фиксируем натуральное га. Покажем, что К и К' не
различимы инвариантами Васильева порядков не больше га.
В силу следствия 24.1 существует ρ такое, что Κφζρ = Κ'φζρ.
Отождествим формальную сумму лежандрова узла и зигзага с их "связной суммой".
В этом смысле будем понимать формальные линейные комбинации зигзагов,
в частности, (1 — ζ). Далее в доказательстве теоремы мы любые комбинации
лежандровых узлов будем называть узлами.
Так, например, для каждого узла L узел Ь#(1 — С) представляет собой
разницу двух узлов, которая, как легко видеть, лежит в Li. Далее, для каждого
узла L мы имеем Ьф(1 — ()т Ε Lm+i. Рассмотрим теперь формальную
линейную комбинацию
ι - (1 - Qm+1
Wm = τ ·
Она имеет смысл, так как в числителе единица сокращается, а
оставшиеся слагаемые можно формально поделить на ζ. Рассмотрим теперь узлы L =
Κφζρφνορη и U = Κ'φζρφνορη. Они лежандрово изотопны, так как
получаются добавлением w^ к лежандрово изотопным узлам Κφζρ и Κ'φζρ. С другой
стороны, узел L' лежандрово изотопен Кф{1 — (1 — ζ)7η+1)ί?. Все слагаемые,
содержащие (1 — С)т+1> лежат в Lm+i, таким образом, на данном узле все
инварианты порядка не больше га принимают те лее значения, что и на узле К.
Аналогично, все инварианты порядка не больше га принимают одно и то лее
значение на L и К'. Следовательно, К и К' не различимы инвариантами
любого наперед заданного порядка.
Теорема доказана. D
428 Лежандровы многообразия и лежандровы кривые
Из этого следует, что теория инвариантов конечного порядка лежандровых
узлов не является очень мощной, что побуждает к поиску новых инвариантов,
не вьфажающихся через инварианты конечного порядка.
24.6. Дифференциальная градуированная
алгебра лежандровых узлов
Описываемые в настоящем разделе инварианты узлов происходят из теории
гомологии Флура (или Хегора-Флура), см. [Floer]. Отметим, что в последние
годы сильно возрос интерес к этой теории в связи с инвариантами Петера Ожвача
и Золтана Сабо [OSz], связывающими многие разделы маломерной топологии.
В настоящем разделе мы опишем замечательную конструкцию
дифференциальной градуированной алгебры лежандровых узлов (DGA),
принадлежащую Юрию Витальевичу Чеканову, [Che]. Эта алгебра является свободной
ассоциативной некоммутативной алгеброй с единицей, которая сопоставляется
каждой лагранжевой проекции лежандрова узла. Все когомологии этой
алгебры являются инвариантами лежандровых узлов.
Каждой π-общей лагранжевой проекции лежандрова узла К мы сопоставим
дифференциальную градуированную алгебру (А, д) над полем Z2 следующим
образом.
Замечание 24.3. Аналогичная конструкция принадлежит Элиашбергу, Ги-
венталю и Хоферу, см. [EGH].
Пусть L — лагранжева диаграмма лежандрова узла. Пусть Υ — тень
диаграммы L. Обозначим перекрестки этой диаграммы через {αϊ,..., ап}.
Мы будем строить тензорную алгебру Т(а\,..., ап) с образующими а\,..., ап
и Zm(£)-градуировкой, где m(L) — число Маслова. Эта алгебра будет свободной
ассоциативной алгеброй с единицей.
Определим сначала градуировку элементов этой алгебры. Пусть a,j —
перекресток диаграммы L. Пусть ζ+, Ζ- — два прообраза перекрестка a,j в R3 при
лагранжевой проекции; здесь z+ имеет большую координату и, чем точка Z-.
Без ограничения общности предположим, что две ветви лагранжевой
проекции перпендикулярны в точке a,j.
Две точки ζ+, Ζ- делят диаграмму L на две части. Обозначим их через 71
и 72 и ориентируем каждую из них от ζ+ κζ_.
Пусть теперь для ε Ε {1,2} число вращения кривой π (7ε) имеет вид -γ + \
для некоторого Νε Ε Ζ. По определению разница Νι — N2 равна ±m(L). Таким
образом, Νι и N2 представляют один и тот же элемент в группе Zm(£). Мы
возьмем этот элемент в качестве градуировки для a,j.
Определим теперь дифференциал д. Для каждого натурального к
фиксируем криволинейный выпуклый /с-угольник Щ С R2, вершины которого
Жо,..., х\_х перенумеруем по порядку против часовой стрелки.
Форма dqAdp определяет ориентацию плоскости R2. Обозначим через Wk(Y)
набор гладких сохраняющих ориентацию погружений / : Щ —>· R2, таких
что f(dHk) С Υ. Заметим, что из условия / Ε Wk(Y) следует, что f(x^) E
{αι,...,αη}.
24.7. Инварианты Чеканова-Пушкаря
429
Будем рассматривать такие иммерсии с точностью до комбинаторной
эквивалентности (перепараметризации). Обозначим пространство классов экви-
валентностей погружений через Wk(Y). Диаграмма Υ разбивает окрестность
каждого перекрестка этой диаграммы на четыре сектора. Два из них
обозначены как положительные (так как показано на рис. 24.8), а оставшиеся два
угла обозначим как отрицательные. Для каждой вершины х\ многоугольника
Щ гладкая иммерсия / £ Wk (Y) отображает окрестность этой вершины либо в
положительный, либо в отрицательный сектор. В этих случаях будем называть
вершину х\ положительной или отрицательной соответственно.
Определим W^(Y) как множество, состоящее из погружений / Ε Wk(Y),
для которых вершина х§ является единственной положительной, а все
остальные — отрицательными. Пусть W^(Y,cij) = {/ Ε W^{Y)\f{x^} = cij}. Пусть
Αι = {αϊ,..., αη} ® Ζ2 С А, Ак = Afk. Тогда мы имеем А = Θ^0^ζ·
Пусть д = Σ^ο ^Ь где дк(Аг) Ε Ai+fc_i и
дк(а0)= Σ f(xi)'-f(xk).
f£W++1(Y,a3)
Далее отображение д продолжается на всю алгебру А по линейности и по
формуле Лейбница.
Теорема 24.6. Дифференциал д корректно определен. Имеют место
равенства deg(d) = — 1 и д2 = 0.
Основная теорема об инварианте Чеканова [Che], полное доказательство см.
в [Che2], утверждает следующее:
Теорема 24.7. Пусть (А,д), (Af,df) — дифференциальные градуированные
алгебры (π-общих) лагранжевых диаграмм L,Lf. Если L и L' лежандрово
изотопны, то алгебры (А, д) и (А\ д') являются стабильно изоморфными. В
частности, кольца гомологии Н(А,д) и Н(А',д') являются изоморфными.
24.7. Инварианты Чеканова-Пушкаря
Инварианты, предлагаемые в настоящем разделе, являются
комбинаторными. Тем не менее они, как и дифференциальная градуированная алгебра
Чеканова, происходят из теории гомологии Флура [Floer] и контактной геометрии.
Их инвариантность легко проверяется на движениях Фукса-Табачникова.
Будем рассматривать фронтальные диаграммы лежандровых узлов.
Рассмотрим σ-общую фронтальную диаграмму лежандрова узла L.
Обозначим через C(L) множество ее клювов. Определим индекс Масловад : L\C(L) —>·
Г = Zm как локально постоянную функцию по следующему правилу: значение
функции μ в клюве совершает скачок на =Ы, как показано на рис. 24.13.
Очевидно, что такая функция определена с точностью до прибавления постоянной.
Перекресток называется масловским, если μ принимает одинаковые значения
на его ветвях.
Предположим, что Σ = cr(L) представляет собой объединение замкнутых
кривых Χι,..., Хп, которые имеют конечное число трансверсальных
пересечений. Назовем неупорядоченный набор {Χι,..., Хп} разбиением диаграммы Σ.
430 Лежандровы многообразия и лежандровы кривые
Рис. 24.13. Скачки индекса Маслова на клювах
Рассмотрим следующие четыре условия.
1. Каждая кривая Χι ограничивает топологически вложенный диск £>^, т. е.
Хг = dBi.
2. Каждый диск В ι имеет ровно два клюва; таким образом, общее
количество клювов равно 2гг.
3. Если точка (до, и) принадлежит пересечению XiC\Xj при некотором г φ j,
то для каждого значения q φ qo достаточно близкого к до множество Bi{q) Π
Bj(q) либо пусто, либо совпадает с Bi(q), либо совпадает с Bj(q).
4. Каждый перекресток, имеющий вид, изображенный на рис. 24.14.6),
является масловским.
Определение 24.6. Разбиение называется допустимым, если оно
удовлетворяет условиям 1-3 и размерностно допустимым, если оно также удовлетворяет
условию 4.
Рассмотрим три типа "разведений", приведенные на рис. 24.14
Рис. 24.14. Три типа разведений
Первый тип разведений, показанный на рис. 24.14.а, не допустим в силу
условий 1, 2.
Второй тип (см. рис. 24.14.6) называется переключающим разведением.
Третий тип (рис. 24.14.в) называется не переключающим разведением.
Обозначим через Αάτη(Έ) (соответственно через Adm+(T,)) множество всех
допустимых (соответственно размерностно допустимых) разведений для Σ.
Пусть D G Adm(E), обозначим через Sw(D) набор ее точек переключения.
Определим Θ(Ό) = #(£>) - #Sw(D).
24.8. Основные примеры
431
Теорема 24.8 (Чеканов—Пушкарь). Если σ-общие лежандровы узлы
L,L'cR3 лежандрово изотопны, то существует взаимно однозначное
отображение
g : Adm(a(L)) -► Adm(a(L'))
такое, что
g(Adm+(a(L))) = Adm+(a(L'))
и S(g(D)) = Θ(Ό) для каждого D G Adm(a(L)).
В частности, числа #(Adm(a(L))) и #(Adm+(a(L))) инвариантны при
лежандровой изотопии.
24.8. Основные примеры
Ни дифференциальная градуированная алгебра, ни инвариант Чеканова-
Пушкаря не могут быть выражены в терминах инвариантов конечного
порядка. Дело в том, что они различают топологически эквивалентные (изотопные)
лежандровы узлы, имеющие одинаковые числа Маслова и Бенекина.
Пример таких узлов (в их фронтальной проекции) пара Чеканова приведен
на рис. 24.15.
Рис. 24.15. Пара Чеканова
Приложение А
Независимость преобразований
Рейдемейстера
В настоящем приложении мы имеем дело лишь с классическими узлами и
классическими преобразованиями Рейдемейстера.
Покажем, что каждое из движений Ωι,Ω2,Ω3 является необходимым для
установления изотопии узлов, т. е. для каждых двух из этих движений
существует пара диаграмм одного и того лее классического узла, которые не могут
быть переведены друг в друга применением только двух выбранных движений
Рейдемейстера (и плоской изотопии).
Первое движение Рейдемейстера — единственное, которое меняет четность
количества перекрестков, поэтому оно не выразимо через Ω2,Ω3· Более того,
имеется скобка Кауфмана, инвариантная относительно всех движений
Рейдемейстера, кроме первого классического.
Для построения примера диаграмм изотопных зацеплений, которые не
могут быть получены друг из друга применением только первого и третьего
движений Рейдемейстера и плоской изотопии, рассмотрим четыре плоские
диаграммы Κι, Κ2ι К%, К4 различных нетривиальных простых узлов. Рассмотрим
теперь диаграммы L = Κι#Κ2#Κ3#Κ4 и Μ = ΚιφΚ^φΚ2φΚ^^ показанные
на рис. A.l.a, б. Так как классические узлы коммутируют, узлы L и Μ
являются изотопными.
Покажем, что не существует цепочки преобразований, состоящей только из
Ωι,Ωβ, переводящей L в М. Действительно, рассмотрим поддиаграммы К^
г = 1,2,3,4 внутри диаграммы L. Их порядок таков, что между узлами Κι и
К% находятся нетривиальные узлы с двух сторон. Покажем, что это свойство
сохраняется при преобразованиях Ωι, Ω3. Действительно, применяя к
диаграмме L только эти преобразования, мы всегда можем разбить получающуюся
диаграмму на четыре части, соответствующие исходным узлам, потому что
узлы Ki,Kj не взаимодействуют (т.е. каждое из движений Ωι,Ωβ относится
не более чем к одному из этих двух узлов). Однако в узле Μ узлы Κι и К%
являются соседними, следовательно, Μ нельзя получить из L применением
лишь Ωι,Ωβ и плоской изотопии. Таким образом, движение Ω2 не выразимо
через Ωι,Ωβ. Отметим здесь связь с теорией плоских кривых (без структуры
проходов-переходов), которые можно рассматривать с точностью до
применения некоторого набора движений Рейдемейстера (например, только третьего).
Подробнее см. [Лан].
Независимость преобразований Рейдемейстера
433
Кл
к.
кл
к*
Рис. А.1. Контрпример к Ωι,Ωβ
Ω2
Рассмотрим теперь тень стандартной диаграммы колец Борромео и
диаграмму тривиального зацепления с этой тенью, показанную на А.2.а.
Обозначим эту диаграмму через L\.
Рис. А.2. Контрпример к Ωι,Ω2
Ω,
Рассмотрим диаграмму L2 тривиального трехкомпонентного зацепления,
изображенную на рис. А.2.б.
Покажем, что диаграмма L\ не может быть преобразована в диаграмму
Li посредством движений Ωι, Ω2 и плоской изотопии. Действительно, каждой
произвольной плоской диаграмме трехкомпонентного зацепления сопоставим
неупорядоченную тройку элементов из Ζ2 следующим образом. Определим
область U, "ограниченную" тенью компоненты I. Эта компонента разбивает
плоскость (точнее, сферу — одноточечную компактификацию плоскости) на клетки;
полученное разбиение допускает шахматную раскраску. Выберем раскраску,
у которой бесконечная точка является белой. Обозначим через U(l) множество
всех черных клеток, см. рис. А.З.
Рассмотрим перекрестки, образуемые двумя оставшимися компонентами,
отличными от Z, и выберем только те из них, которые лежат внутри U(l).
Рассмотрим четность числа таких перекрестков. Рассмотрим также четности
остальных чисел, соответствующих другим двух компонентам.
434
Приложение А
Рис. А.З. Область U(l) заштрихована
Получим неупорядоченную тройку элементов из Z2. Для зацепления L\ все
эти три числа равны единице, а для L2 они все равны нулю.
Покажем, что эта тройка инвариантна при движениях Ωι, Ω2.
При движении Ω ι инвариантность очевидна. Движение Ω2 может
применяться либо к двум разным компонентам, либо к двум ветвям одной
компоненты. Во втором случае утверждение очевидно. В первом случае нужно лишь
заметить, что либо оба перекрестка, участвующие в движении Ω2, лежат
внутри U(l), либо оба — вне U(l), где I — третья компонента. Таким образом, все
три четности не меняются.
Следовательно, диаграмма L\ не может быть продеформирована в L2
только посредством движений Ωι, Ω2.
Аналогичные рассуждения применимы к теории орнаментов, см. гл. 6
книги [Ва], а также [Bj, BW].
В работе [Hag] Тобиаш Хагге показал, что для каждого изотопического
класса узла К существует пара плоских диаграмм Κι, Κ^, представляющих этот
класс, таких, что для установления изотопии К\ и К2 требуются все три
движения Рейдемейстера.
Приложение Б
Инварианты Васильева
виртуальных зацеплений
Есть два подхода к построению инвариантов конечного порядка для
виртуальных узлов. Один из них был предложен Гусаровым, Поляком и Виро,
см. [GPV], а второй — Кауфманом. [Каи7]. Оба эти подхода являются с
некоторой точки зрения естественными, так как они обобщают комбинаторное
определение инварианта Васильева. Однако инварианты, предложенные в [GPV] не
являются столь сильными, как инварианты конечного порядка в смысле
работы [Каи7].
В настоящем приложении мы приведем основные определения и примеры.
Б.1. Подход Гусарова-Поляка-Виро
Введем некоторые вспомогательные определения. Под полу виртуальным
перекрестком будем понимать формальную метку для перекрестка, в котором
указывается, какая ветвь идет выше, а какая — ниже, при этом сам перекресток
обведен кружочком. Диаграмма с виртуальным перекрестком определяется как
формальная разница двух диаграмм, одна из которых имеет классический
перекресток, а другая — виртуальный.
х=х-х
Пусть D — диаграмма виртуального зацепления и пусть {с?1,с?2? · · · ?^п}
— некоторый набор классических перекрестков этой диаграммы. Для
набора {σι,..., σι} из единиц и нулей определим Όσ как диаграмму, получаемую
из Ό преобразованием всех перекрестков di, для которых σι = 1, в
виртуальные перекрестки. Обозначим через |σ| число единиц в наборе σ. Формальная
альтернированная сумма
Σ(-ΐ)|σ|^
σ
называется диаграммой с η полу виртуальными перекрестками.
Обозначим через /С множество всех виртуальных узлов. Пусть ν : /С —>· G —
некоторый инвариант виртуальных узлов со значениями в абелевой группе G.
Продолжим этот инвариант по линейности на Ζ [К] — множество формальных
436
Подход Гусарова-Поляка-Виро
линейных комбинаций виртуальных узлов. Скажем, что ν является
инвариантом конечного порядка, если для некоторого натурального η инварианта ν
обращается в нуль на каждом виртуальном узле К с более чем η
полувиртуальными перекрестками. Минимальное гг, для которого это выполнимо, называется
порядком инварианта v.
Формальное соотношение Васильева /С = /С ~ У\ вместе с
соотношением, определяющим виртуальный перекресток, влечет соотношение
Замечание Б.1. Отметим, что сингулярные узлы не рассматриваются здесь
не как независимые объекты, а лишь как линейные комбинации более простых
объектов.
Очевидно, что для всякого инварианта ν порядка η в смысле, описанном
выше, его ограничение на случай классических узлов является инвариантом
конечного порядка в обычном смысле. Обратное, однако, неверно. Так,
например, согласно приведенному выше определению, не существует инвариантов
второго порядка для (компактных) виртуальных узлов.
Исходя из формального соотношения, определяющего виртуальный
перекресток, и соотношения Васильева, Поляк построил так называемую алгебру
Поляка, см. [GPV], дающую полное комбинаторное описание всех виртуальных
узлов. Кроме того, в работе [GPV] приведены комбинаторные формулы для
вычисления инвариантов конечного порядка для длинных виртуальных узлов.
Б.2. Подход Кауфмана
Подход Кауфмана связан с обобщением понятия сингулярного узла
(зацепления) на виртуальный случай.
Определение В.1. Сингулярная диаграмма виртуального зацепления —
это четырехвалентный граф на плоскости, снабженный ориентацией уникур-
сальных компонент, а также структурой в перекрестках: каждый перекресток
этого графа является либо классическим (проход-переход), либо виртуальным,
либо сингулярным.
Определение В.2. Сингулярное виртуальное зацепление (узел) — это класс
эквивалентности диаграмм сингулярных виртуальных зацеплений (узлов) по
обобщенным движениям Рейдемейстера и жестким изотопиям, см. рис. Б.1
Определение В.З. Порядком сингулярного виртуального зацепления
называется количество его сингулярных перекрестков.
После этого определение инварианта Васильева для виртуальных узлов
(зацеплений) дословно совпадает с определением в классическом случае. А
именно, для каждого инварианта / виртуальных зацеплений можно определить его
формальные производные f, f",..., согласно соотношению Васильева:
/W( У^·) = /(п_1)( У^.) -/(п-1)( Λχ^■), а затем сказать, что инвариант / имеет
порядок меньший или равный гг, если j(n+1) = 0.
Б.З. Инварианты Васильева виртуальных зацеплений 437
Рис. Б.1. Жесткая изотопия
Б.2.1. Некоторые наблюдения
Пространство инвариантов конечного порядка виртуальных узлов
(определенное Кауфманом) является гораздо более сложным, чем в случае
классических узлов. Например, пространство инвариантов нулевого порядка для
виртуальных узлов является бесконечномерным, так как существует бесконечно
много классов виртуальных узлов, которые не могут быть получены друг из
друга изотопией и заменой типа классических перекрестков. Они
описываются свободными гомотопическими классами кривых в двумерных поверхностях,
рассматриваемых с точностью до стабилизации (см. главу 19). Естественно, что
структура инвариантов старших порядков является еще более сложной.
Полином Джонса-Кауфмана для виртуальных узлов может быть выражен в
видел линейной комбинации инвариантов конечного порядка; доказательство в
точности повторяет доказательство, приведенное в главе 12. Легко видеть, что
многие инварианты, которые имеют конечный порядок согласно Кауфману, не
являются инвариантами конечного порядка в смысле [GPV]. Это наблюдение
принадлежит Кауфману [KaulO].
Б.З. Инварианты конечного порядка
виртуальных зацеплений
Очевидным образом значение п-й производной инварианта виртуальных
узлов представляет собой альтернированную сумму значений этого инварианта
на 2П узлах, которые получаются из исходного всевозможными разведениями
исходного сингулярного узла в η рассматриваемых перекрестках.
В своей первой работе по виртуальным узла [Каи4] Кауфман показал, что
полином Джонса-Кауфмана в его простейшем обобщении на виртуальные узлы
может быть выражен через инварианты конечного порядка виртуальных узлов
(в смысле Кауфмана).
Мы докажем обобщение этого факта, а именно, что полином Ξ, приведенный
в главе 19 настоящей книги может быть выражен через инварианты Васильева
виртуальных зацеплений.
438
Подход Гусарова-Поляка-Виро
Б.4. Инварианты Васильева, происходящие от Ξ
Инвариант Ξ, предложенный в главе 19 (коэффициенты которого при
элементах из S являются полиномами Лорана от переменной а), молено
преобразовать в формальный ряд заменой переменной а = ех и разложением экспоненты
по формуле Тейлора. Для удобства мы будем использовать ту же букву Ξ для
обозначения полученного ряда от переменной х.
Пусть L — виртуальное зацепление. Пусть Em(L) — коэффициент в ряде
Ξ(£) при хш. Он представляет собой линейную комбинацию элементов из S с
рациональными коэффициентами.
Докажем следующую теорему.
Теорема Б.1. Для каждого т Ε Ν+ инвариант Ет является инвариантом
Васильева виртуальных узлов порядка не более га.
Эта теорема показывает, что инвариант Ξ в действительности слабее
инвариантов Васильева виртуальных зацеплений: для каждого элемента W Ε S
коэффициент при W в Ξ может быть представлен как формальный ряд из
инвариантов Васильева. С другой стороны, эта теорема явно описывает
бесконечные серии инвариантов Васильева виртуальных зацеплений произвольных
порядков.
Замечание Б.2. Для удобства мы будем обозначать ориентированную и
соответствующую неориентированную диаграмму виртуального зацепления
одной и той же буквой. Так, мы будем писать L вместо \L\.
Перейдем к доказательству теоремы Б.1. Для этого рассмотрим 2П
виртуальных диаграмм, которые отличаются ровно в η выбранных перекрестках: они
представляют собой все возможные комбинации положительных и
отрицательных перекрестков. Обозначим эти диаграммы через Lv где η Ε {0,1} ; пусть
L — одна из этих диаграмм. Пусть m(rj) — количество единиц в η (они
соответствуют отрицательным перекресткам -уС , в то время как нули соответствуют
положительным перекресткам /\)-
Нам нужно доказать, что
^(-1)™^Ξ„_1(^) = 0 (Б.1)
η
Первое наблюдение состоит в том, что многообразие М, соответствующее
всем этим многообразиям Lv по правилу построения инварианта Ξ (см. стр. 333)
— одно и то же. Более того, по построению, для каждого Lv набор кривых S(LV)
не зависит от η. Кроме того, множество всех возможных Sf(s) взятых при всех
различных s (и, соответственно, множество всех p(s)) одно и то же для всех
диаграмм Lv. Единственная разница в формуле (19.2) для определения Ξ(Ση)
состоит в том, что коэффициенты при p(s) различны.
Покажем теперь, что эта разница коэффициентов обращается в нуль в
формуле (Б.1). Для этого нужно доказать, что соответствующие коэффициенты
Б.4. Инварианты Васильева, происходящие от Ξ 439
(при фиксированном p(s)) в формуле
£(-l)"»M3(L4) = 0. (Б.2)
η
делятся на (α — 1)п (из чего следует делимость на хп).
Пусть L+ — та из диаграмм Σ,η, у которой все п перекрестков положительны.
Фиксируем некоторое состояние s диаграммы L+. Рассмотрим элемент p(s).
Для каждого η существует состояние s(ry) для диаграммы Lv с тем лее самым
p(s). Вообще говоря, может быть и более одного такого состояния, скажем,
может существовать s такое, что p(s) эквивалентно p(s) в S. Но мы будем
работать лишь с "естественными" состояниями, полученными посредством "того
же самого" сглаживания, что и сглаживание s для диаграммы L+.
Нам нужно сосчитать коэффициент при p(s) (альтернированную сумму 2П
коэффициентов, соответствующих диаграммам Lv). Предположим, что для
состояния s диаграммы L+ мы имеем т перекрестков, разведенных способом
А : ^χΛ —>· .)('·, остальные п — т перекрестков разведены способом В : ^χΛ —>
^^^ . Остальные классические перекрестки (не из числа выбранных п) имеют
одно и то же разведение для каждой диаграммы. Предположим, что сумма
знаков оставшихся классических перекрестков (одна и та же для всех 77)
равна w, количество перекрестков в состоянии А (не из числа выбранных) равно
се, а количество перекрестков в состоянии В равно β. Обозначим количество
окружностей (уникурсальных компонент) в состоянии s диаграммы L+ через Г.
Тогда искомый коэффициент равен
(-a)-3wa(a-P\-a2-a-2)F-iy>x
χ (-α"2 + а2)т(-а~4 + а4)п~т.
Последнее выражение делится на (а — 1)п. Таковы и все другие
коэффициенты, соответствующие различным p(s). Этим завершается доказательство
теоремы Б.1.
Приложение В
Алгоритмическое распознавание
классических и виртуальных
зацеплений
Классические зацепления являются алгоритмически распознаваемыми/ Это
следует из трех теорем. Первая из них (теорема Гордона-Л юкке) утверждает,
что классическое зацепление определяется своим дополнением в трехмерном
пространстве. Вторая теорема утверждает, что дополнение к каждому
классическому зацеплению (не являющемуся несвязной суммой тривиального узла
с некоторым зацеплением) является так называемым многообразием Хакена
(определение см. далее). Третьим фактом является алгоритмическая
распознаваемость многообразий Хакена. Последнее утверждение является
результатом трудов многих математиков, из которых следует выделить Хакена [На],
Хемиона [Нет] и Матвеева. В книге последнего [Matv4] дано безупречное
доказательство всех основных теорем теории Хакена.
В настоящем приложении мы приведем некоторые положения теории
Хакена и на основании их докажем следующую теорему
Теорема В.1. Существует алгоритм, определяющий по двум заданным
виртуальным зацеплениям L\ и L^ (заданным, например, плоскими
диаграммами), являются они эквивалентными или нет.
Эта теорема принадлежит автору настоящей книги, см. [Ма7].
Нам понадобится результат Мойза [Moi] о том, что все трехмерные
многообразия триангулируемы. В дальнейшем мы будем считать всякое
рассматриваемое трехмерное многообразие снабженным некоторой триангуляцией.
Мы будем иметь дело с трехмерными многообразиями (возможно, с
краем) и двумерными поверхностями в них. Компактная поверхность F в
многообразии Μ называется собственной, если F Π дМ = OF. В дальнейшем все
поверхности предполагаются собственными. Собственное двумерное
подмногообразие в трехмерном многообразии называется существенным, если оно не
высекает шар. Для нас будут важны собственные сферы, собственные диски и
собственные кольца S1 χ /.
Напомним, что трехмерное многообразие Μ называется неприводимым,
если каждая вложенная двумерная сфера в Μ ограничивает шар, вложенный
в М.
Алгоритмическое распознавание виртуальных зацеплений 441
Мы будем использовать определение виртуального зацепления как
зацепления в утолщенной поверхности ΛΊ х / с точностью до стабилизации/
дестабилизации. Здесь ΛΊ — компактная двумерная поверхность, не обязательно
связная. При этом мы требуем, чтобы для каждой связной компоненты Λίί
трехмерное многообразие Aii x I содержало по крайней мере одну компоненту
зацепления L.
Таким образом, каждое виртуальное зацепление имеет множество разных
представителей в многообразиях ЛЛ χ Ι для разных Μ, которые получаются
друг из друга в результате стабилизации/ дестабилизации. Напомним, что
представитель виртуального зацепления называется минимальным, если к нему не
может быть применена дальнейшая дестабилизация.
Нам понадобится теорема Куперберга 17.2 (стр. 17.2) утверждающая, что
минимальный представитель (ΛΊ х /, L) определен однозначно с точностью до
изотопии.
Таким образом, чтобы сравнивать виртуальные зацепления, нам
достаточно найти их минимальных представителей и сравнить их. Приводимый ни лее
алгоритм распознавания виртуальных зацеплений будет опираться на
распознавание трехмерных многообразий с узорами на крае (см. ниже), связанных
с виртуальными зацеплениями.
Мы будем использовать следующие положения из теории Хакена
нормальных поверхностей, см. [Matv4].
Пусть дано трехмерное многообразие с краем. Узором (понятие,
предложенное К. Иоганнсоном, см. [Joh]) называется фиксированный 1-полиэдр (граф) на
крае трехмерного многообразия, не имеющий изолированных вершин (мы
будем считать, что он является подполиэдром триангуляции нашего трехмерного
многообразия).
Наличие узора на крае многообразия не меняет определений несжимаемой
поверхности и неприводимого многообразия. Определения гранично
несжимаемой поверхности и гранично неприводимого многообразия дословно те же, что
и раньше с той лишь разницей, что все поверхности F с краем dF
предполагаются чистыми, т. е. такими, что dF Π Γ = 0. В дальнейшем будем считать все
поверхности с краем чистыми.
Напомним, что ориентируемое трехмерное многообразие Μ называется
достаточно большим, если оно содержит собственную несжимаемую гранично
несжимаемую поверхность, отличную от сферы и диска.
Трехмерное многообразие без края (и, следовательно, без узора)
называется многообразием Хакена, если оно неприводимо, гранично неприводимо и
достаточно велико. Неприводимое, гранично неприводимое трехмерное
многообразие (М, Г) с узором Г на крае называется многообразием Хакена либо если
оно достаточно велико, либо если узор Г непуст (и, следовательно, край дМ
непуст), и при этом Μ является телом с ручками, но не шаром.
Имеет место следующее утверждение [Матв]:
Предложение В.1. Неприводимое гранично неприводимое трехмерное
многообразие с непустым краем либо достаточно велико, либо является телом с
ручками.
В дальнейшем мы будем иметь дело с многообразиями с непустым узором на
442
Приложение В
крае. Для того, чтобы такое многообразие было многообразием Хакена,
достаточно проверить, что оно является неприводимым и гранично неприводимым,
но не является шаром.
Лемма В.1. ([Матв]) Существует алгоритм, распознающий, является ли
многообразие Μ приводимым; если оно является таковым, то алгоритм
приводит построение двумерной сферы S С М, не ограничивающей шара в М.
Лемма В.2. ([Матв]) Классические зацепления алгоритмически
распознаваемы.
Эта лемма следует из теории Хакена нормальных поверхностей и
доказывается исходя из следующих соображений: для каждого нетривиального
нераспадающегося классического зацепления дополнение в S3 к его трубчатой
окрестности является многообразием Хакена. Задав узор на его крае, мы сможем
восстановить исходное зацепление. Далее дело сводится к распознаванию
многообразий Хакена. Подробнее см. [Матв].
Лемма В.З. ([Матв]) Существует алгоритм, распознающий, имеет ли
многообразие Хакена Μ с узором Г на крае дМ собственное чистое существенное
кольцо. В случае, если таковое имеется, оно может быть построено
алгоритмически.
Эта лемма нам нужна для того, чтобы определить, возможно ли к
некоторому представителю виртуального зацепления применить дестабилизацию.
Лемма В.4. ([Матв]) Существует алгоритм, распознающий, являются ли
два многообразия Хакена (М, Г) и (Μ',Γ7) с узорами на крае гомеоморфными
посредством гомеоморфизма, отображающего узор Г в V.
Рассмотрим произвольный представитель виртуального зацепления L (см.
главу 17), т. е. пару (М, L), где Μ = Μ χ Ι для замкнутой двумерной
поверхности М, a L — зацепление в Μ (мы используем ту же букву L для обозначения
как исходного зацепления, так и зацепления в М). Пусть N — малая открытая
трубчатая окрестность зацепления L. Вырежем N из М. Мы получим
многообразие с краем, которое обозначим через Ml- Его край состоит из компонент
края многообразия Μ (двух в случае, если Μ связно) и нескольких торов;
количество торов равно количеству компонент зацепления L. Снабдим каждый
такой тор узором Г^,, представляющим собой меридиан соответствующей
компоненты (добавив к меридиану-ребру точку-вершину в произвольном месте).
Мы получим многообразие (Μ^,ΙΥ) с узором на крае.
Очевидно, что виртуальное зацепление L (и пара (М, L)) может быть
восстановлено по (Ml, Tl), поскольку известно, как восстановить многообразие Μ
приклейкой полноторий к компонентам края многообразия Ml, по известным
меридианам этих полноторий.
Лемма В.5. Пусть зацепление L не является несвязной суммой
(непустого) классического зацепления и виртуального зацепления. Тогда многообразие
(Ml^l) является многообразием Хакена.
Алгоритмическое распознавание виртуальных зацеплений 443
Доказательство. В силу предложения В.1, нам достаточно доказать, что это
многообразие является неприводимым и гранично неприводимым: оно не может
являться телом с ручками.
Пусть д = 0. Тогда для каждой связной ориентируемой двумерной
поверхности Sg многообразие Sg χ Ι является неприводимым. При д = 0 зацепление
является классическим. Таким образом, если зацепление L не является
классическим, то для его окрестности N(L) множество {Sg x I)\N{L) может быть
приводимым лишь в случае, если оно содержит сферу S, ограничивающую шар
в Sg х {0,1}, который содержит некоторые компоненты зацепления L. Это
означает, что эти компоненты составляют классическое зацепление, отделенное от
оставшейся части зацепления L.
Далее, так как зацепление L не является несвязной суммой тривиального
узла с некоторым виртуальным зацеплением, многообразие Ml является
гранично неприводимым.
Действительно, любая кривая на Sg x {0} или на Sg x {1}, которая может
служить границей диска, стягиваема по краю. Следовательно, граничная
приводимость могла бы иметь место только при наличии диска, край которого
лежит на некотором торе — границе вырезанного полнотория. Это означало
бы, что вырезанное полноторие соответствует отдельно стоящему
тривиальному узлу.
Следовательно, рассматриваемое многообразие является неприводимым,
гранично неприводимым и, следовательно (согласно предложению В.1),
многообразием Хакена. D
Из приведенного выше доказательства вытекает следующая
Лемма В.6. Пусть L — виртуальное зацепление, которое не может быть
представлено как несвязная сумма К U V классического зацепления К и
виртуального зацепления V'. Тогда многообразие Ml является неприводимым.
Перейдем теперь к доказательству основной теоремы. Пусть L, V —
виртуальные зацепления.
Шаг 1. Рассмотрим представителей (М, L), (М7, V) этих зацеплений.
Построим соответствующие многообразия с узорами на краях так, как
указано выше, и обозначим их через {Ml·,Г), (М^,,Г7).
Шаг 2. Определим, является ли хотя бы одно из многообразий Ml или M'l,
приводимым. Если оно является таковым, то, по лемме В.1 мы
можем найти сферу, не ограничивающую шара, и таким образом,
отделить некоторые классические зацепления рассматриваемых
зацеплений (т. е. классические зацепления, которые входят в
рассматриваемые зацепления в виде несвязной суммы).
Шаг 3. Определим (по лемме В.З), возможно ли применить дестабилизацию
к одной из поверхностей (Μχ,,Γ) или (Μ^,,Γ7). Если дестабилизация
возможна, применим ее. Возвратимся к шагу 2.
Будем выполнять шаги 2 и 3 до тех пор, пока это возможно. Очевидно,
что этот процесс остановится за конечное время.
444
Приложение В
Классические зацепления распознаются алгоритмически. Таким
образом, мы можем сравнить отдельно стоящие классические компоненты
для зацеплений L и L''. Если они представляют собой неизотопные
зацепления, мы останавливаемся: изначальные зацепления
неэквивалентны. В противном случае мы продолжаем.
Выполнив шаги 1 и 2 и 3, мы свели нашу проблему к случаю,
когда ни одно из рассматриваемых зацеплений не имеет отдельно
стоящих классических компонент. С настоящего момента
рассматриваемые многообразия являются многообразиями Хакена по лемме В.6.
Шаг 4. Каждая связная компонента многообразий (Μ/,,Γ) и (Μ^,,Γ7)
является многообразием Хакена с узором на крае. Таким образом, мы
можем алгоритмически разрешить вопрос о том, существует ли
гомеоморфизм / : Ml —> ML,, переводящий Г в Г7 (по лемме В.4). Если
такой гомеоморфизм существует, то виртуальные зацепления L, V
эквивалентны, если не существует, то виртуальные зацепления L,Z7 не
эквивалентны.
Выполняя шаги, описанные выше, мы решаем проблему распознавания.
Теорема В.1 доказана.
Замечание В.1. Доказательство, приведенное выше, проходит также для
случая ориентированных виртуальных зацеплений и оснащенных
виртуальных зацеплений.
Приложение Г
Энергия узла
Существует интересный подход к изучению узлов, связанный с понятием
энергии узла. Впервые энергия узла была рассмотрена Моффатом, см. [Mof].
Мы будем использовать подход, предложенный Джун О'Харой. В работе [ОН]
(см. также [ОН2, ОНЗ])) была определена энергия узла. Сначала это было
воспринято как однокомпонентный аналог электромагнитной формулы Гаусса для
зацеплений, но на самом деле энергия узла и энергия зацепления имеют совсем
разные свойства.
В частности, энергия узла, заданная на геометрических узлах в R3
является инвариантной относительно некоторых преобразований (но не является
корректно определенной функцией на изотопических классах узлов) и
обладает некоторыми свойствами. Эти свойства полезны для понимания каждого
отдельного класса изотопии узлов; энергия помогает лучше понять структуру
(бесконечномерного) пространства узлов.
В настоящем приложении мы сформулируем некоторые теоремы и
эвристические гипотезы по поводу энергии узлов, точнее, основной и самой известной
на данной момент энергии — энергии Мебиуса.
Пусть К — узел в трехмерном пространстве, параметризованный
натуральным параметром г : S1 —>· R3, где S1 — стандартная единичная окружность
в R2. Тогда энергия Мебиуса для узла г задается по формуле:
Ef(K)= [ [ f(\r(t1)-r(t2)lD(tut2))dt1dt2, (Г.1)
J Js1xS1
где /(·,·) — некоторая функция на плоскости (можно выбирать различные
функции для изучения различных свойств пространства узлов), D(·,·) —
функция на торе S1 x S1, представляющая собой расстояние между двумя точками
на окружности (берется длина минимальной из двух дуг, соединяющих эти
точки). Интегрирование ведется по декартову произведению узла на себя; это
декартово произведение параметризовано переменными ίι,^2·
По физическим причинам (например, если мы рассматриваем равномерно
заряженный узел) имеет смысл рассматривать энергию с функцией
f(x,y) = -. Однако такая энергия (т.е. соответствующий интеграл) не всегда
сходится. Поэтому стоит рассматривать энергии с другими функциями /.
Один из способов определения энергии Мебиуса такой:
ВД = // U.)-r(fa)l' " W^)) ■ |i,WI' feWI**-
446
Энергия узла
Соответствующий интеграл всегда сходится в случае гладких узлов.
Далее мы имеем:
1. Энергия Мебиуса является инвариантной при гомотетиях,
горизонтальных сдвигах и поворотах.
2. Энергия Мебиуса стремится к бесконечности если узел стремится к
сингулярному узлу.
3. Энергия Мебиуса строго положительна.
4. Энергия Мебиуса инвариантна относительно преобразований Мебиуса,
а именно, относительно инверсий с центром в некоторой точке
трехмерного пространства, не лежащей на узле. Если мы произведем инверсию
в точке, лежащей на узле К, мы получим некоторый длинный узел К'\
в этом случае энергия Мебиуса определяется таким же способом и мы
имеем Е(К) = Е{К') + 4.
5. Абсолютный минимум энергии Мебиуса реализуется на стандартной
окружности.
6. Энергия Мебиуса гладко изменяется при гладких деформациях узла.
Опишем эти свойства более подробно и докажем некоторые из них.
Первое свойство легко следует из вида энергии Мебиуса: при гомотетии
коэффициент, возникающий при двойном интегрировании, сокращается второй
степенью в знаменателе. Инвариантность относительно параллельных сдвигов
и ортогональных преобразований очевидна.
Второе свойство очевидно: мы имеем знаменатель, стремящийся к нулю,
в то время как область интегрирования и коэффициенты в числителе
ограничены снизу.
Третье свойство следует из того факта, что расстояние между точками в
трехмерном пространстве не превосходит расстояния между этими точками
вдоль дуги некоторой окружности (в случае натуральной параметризации).
Четвертое и шестое свойства проверяются непосредственно.
Рассмотрим теперь пятое свойство более подробно; мы также установим
некоторые новые свойства энергии Мебиуса. Докажем сначала "свойство
длинных узлов": если К — узел в трехмерном пространстве, а X — точка на узле К,
то для любой сферы с центром в точке X, мы получаем длинный узел К'',
полученный из К применением инверсии относительно этой сферы, для которого
Ε (К) = Е(К')+4.
Вместо того, чтобы доказывать этот факт явно, мы покажем, что энергия
окружности равна четырем. Далее нужное нам свойство будет легко следовать
из некоторых общих соображений.
Действительно, для окружности в натуральной параметризации длина вдоль
окружности равна (t\ — £2) если 0 ^ (t\ — £2) ^ тг- Расстояние в евклидовом
пространстве равно 2 sin (tl~t2).
После подходящей замены переменной и = t\ — £2 интеграл приводится к
виду однократного интеграла, умноженного на 2π. Кроме того, по причинам
Энергия узла
447
симметрии, достаточно рассмотреть лишь значения переменной и от нуля до
π, а затем удвоить получившийся результат. Таким образом мы получаем:
7Г
^ I ( ΤΤ~7Τ - Λ I du- (Г·2)
J V4sin2 ω/2 и2) ν '
о
Последнее выражение равно
lim^(-ictg(U/2)+4|J, (Г.З)
что, очевидно, равно четырем.
Слегка изменяя узел (так, чтобы его изотопический тип остался тем лее,
а энергия изменилась сколь угодно мало), молено считать, что малый отрезок
узла представляет собой отрезок прямой. В этом случае после инверсии мы
получим длинный узел
Принимая во внимание, что для любого длинного узла, отличающегося от
прямой линии, энергия Мебиуса строго положительна, мы получаем, что
единственный узел (не длинный), энергия которого равна четырем, это
геометрическая окружность. Этим завершается доказательство пятого свойства.
Это свойство является очень важным. Мы можем строить теорию Морса
узлов, выбирая в качестве функции Морса разные виды энергии Мебиуса на
пространстве всех узлов. Для каждого изотопического типа узла существуют
минимумы, максимумы и седла этой функции. По взаимному расположению
таких точек можно судить об узле. В частности, мы убедились, что тривиальный
узел имеет ровно один (с точностью до движений, гомотетий и
преобразований Мебиуса) абсолютный минимум; он же является абсолютным минимумом
среди всех узлов.
Таким образом, пространство всех узлов имеет смысл рассматривать с
точностью до движений, которые не меняют энергию Мебиуса, т. е. гомотетий и
изометрий.
В этом смысле можно говорить о том, что окружность — канонический
представитель тривиального узла.
Естественным является вопрос о том, насколько точно можно определить
канонический представитель того или иного (изотопического типа) узла. В
качестве кандидатов выступают узлы с минимальной энергией в данном
изотопическом классе (всегда можно профакторизовать пространство таких узлов
по соответствующим симметриям, не меняющим энергии).
Естественными являются следующим гипотезы:
1. Существует ли каноническая форма (реализующая абсолютный
минимум) для данного изотопического типа узла?
2. Единственна ли она?
Оба эти вопроса были впервые рассмотрены Фридманом, и к настоящему
моменту ни на один из них нет удовлетворительного ответа (за
исключением случая тривиального узла). Более того, эти гипотезы далее не являются
448
Энергия узла
корректно сформулированными: нужно еще сказать, какие узлы считать
одинаковыми (как минимум те, которые получаются друг из друга композициями
гомотетий, преобразований Мебиуса и сдвигов).
Однако множество минимумов и максимумов энергии для заданного
изотопического класса узла в некотором смысле может быть рассмотрено как
инвариант узла. Так как мы можем рассматривать различные энергии (для разных
функций /), эти инварианты, рассмотренные вместе, являются очень
сильными, возможно, даже полными в случае неориентированных узлов (нужно,
правда, сделать оговорку относительно зеркальных узлов). Это также является
гипотезой.
Единственное, что можно сказать определенно, это то, что для каждого
изотопического класса узла существует не более чем счетное число минимумов
энергии.
Абсолютный минимум не подсчитан ни для какого нетривиального узла,
при этом имеет место теорема.
Теорема Г.1 (Фридман, [FHW]). Если Ε (Κ) < 6π + 4; то узел К —
тривиальный.
Стоит отметить еще один важный результат (теорему существования):
Теорема Г.2. Пусть К — изотопический класс простого узла. Тогда
существует минимальный представитель ΚΊ класса К такой, что для любого
другого представителя К' имеет место Е(К') ^ Е(К9).
Отметим, что аналогичное утверждение про составные узлы не доказано и
не опровергнуто.
Приложение Д
Максимумы критических
коэффициентов полинома
Джонса-Кауфмана
Р. С. Авдеев
В настоящем приложении будут вычислены максимальные значения
функций Μι и М.2 на хордовых диаграммах, которые соответствуют экстремальным
коэффициентам значения полинома Кауфмана на виртуальных узлах —
младшему и следующему после него, см. главу IV: если М\ является коэффициентом
при a~N, то М.2 представляет собой коэффициент при a2~N. Очевидно, что те
лее оценки справедливы и для двух старших коэффициентов. Коэффициент
Μι впервые изучался Й.Баэ и Х.Мортоном, см. [ВаМо], а также П.Манчоном
[Mnch].
Д.1. Коэффициент Мг
Пусть Dn — множество хордовых диаграмм с η хордами, и пусть
сю
D = (J Г>„.
71 = 0
При этом мы будем рассматривать также и пустую хордовую диаграмму, не
содержащую хорд.
Замечание Д.1. Для удобства часто вместо словосочетания "хордовая
диаграмма" в дальнейшем мы будем писать просто "диаграмма".
На множестве D определим функцию Μι следующим образом. Пусть S —
произвольная хордовая диаграмма, и пусть количество ее хорд равно п. При г =
0,1,..., η рассмотрим величину Ki(S) — количество различных подмножеств из
г попарно непересекающихся хорд этой диаграммы. По определению положим
η
Μι(5) = ^(-lYKiiS).
450 Максимумы критических коэффициентов полинома Джонса
В этой формуле мы предполагаем, что Ko(S) = 1 и Ki(S) = п. Нашей задачей
является нахождение максимума модуля функции Μι на множестве Dn при
каждом п:
FAn) = max |Mi(5)|.
seDn ' v n
Отметим некоторые свойства функции М\. Во-первых, если мы рассмотрим
произведение (связную сумму) двух хордовых диаграмм А, В Ε D, то
значение функции Μι на диаграмме АВ не зависит от точек разрыва окружностей,
ограничивающих А и В. В самом деле, отношение пересечения или
непересечения двух хорд в диаграмме АВ остается неизменным при различных способах
перемножения диаграмм А и В. Таким образом, величина Μι(ΑΒ) определена
корректно. Во-вторых, имеет место еще одно свойство функции Μι, связанное
с рассмотренной операцией произведения хордовых диаграмм:
Лемма Д.1. Функция Μι мультипликативна, т. е. Μι(ΑΒ) = Μι(Α)Μι(Β)
для любых диаграмм А, В Ε D.
Доказательство этой леммы мы дадим позднее в более общем случае при
исследовании графов, см. теорему Д.5.
Посчитав значение функции Μι на единственной хордовой диаграмме с
одной хордой (-—-), найдем, что это значение равно 1 — 1, т. е. нулю. Отсюда следует,
что если какая-то хордовая диаграмма S содержит хорду, не пересекающуюся
с остальными хордами, то эта диаграмма представляется в виде произведения
некоторых диаграмм, среди которых есть диаграмма с одной хордой, откуда
по лемме Д.1 вытекает равенство Mi(S) = 0. Следовательно, справедлива
Теорема Д.1. Функция Μι удовлетворяет IT-соотношению.
Имеет место еще одно важное свойство функции Μι (теорема 15.1):
Теорема Д.2. Функция Μι удовлетворяет 4Т-соотношению.
Ключевую роль в дальнейших рассуждениях будет играть множество
диаграмм вида {^4-п}, где Ап — диаграмма с η попарно пересекающимися хордами.
Очевидно, что М\(Ап) = 1 — п. Теперь сформулируем результат касательно
функции Μι.
Теорема Д.З. Существует хордовая диаграмма Sn E Dn, такая что:
l)\M1(Sn)\=F1(n);
2) Sn = АГ1 ·ΑΤ2·.. .-АГк при некоторых ненулевых г ι, Г2,..., rk, для которых
т\ + г2 + ... + rk = п.
При этом Fi(n) = |(1 - г ι) · (1 - r2) · ... · (1 - г^)|.
К доказательству этой теоремы мы придем в конце раздела. Для этого
вначале нам потребуется совершить переход от хордовых диаграмм к графам.
Замечание Д.2. В дальнейшем все графы предполагаются конечными, без
петель и кратных ребер.
Д.1. Коэффициент М\
451
Нетрудно видеть [Mnch], что значение функции М\ на хордовой
диаграмме зависит только от структуры пересечений хорд в этой диаграмме. Более
удобным оказывается представление этой структуры в виде графа. А именно,
каждой хорде поставим в соответствие вершину графа и две вершины соединим
ребром в том и только в том случае, когда соответствующие этим вершинам
хорды пересекаются. Таким образом, мы имеем отображение /ι, которое каждой
диаграмме с η хордами ставит в соответствие некоторый граф с η вершинами.
Граф h(S) называется графом пересечения хордовой диаграммы S или графом
Чмутова-Дужина-Ландо ([CDL],[Mnch]). Следует отметить, что не для
каждого графа существует хордовая диаграмма, реализуемая этим графом (т. е.
образ отображения h составляет не все множество графов). Полный ответ на
вопрос реализуемости приведен в [Вой]. Пример графа, не реализуемого
никакой хордовой диаграммой, изображен на рис. Д.1.
О
Рис. Д.1. Граф, не реализуемый хордовой диаграммой
Аналогично определим множества Г всех графов и Гп всех графов с η
вершинами (п = 0,1, 2,...). Перенося определение функции Μι на графы, получим
следующее:
Пусть Τ — граф с η вершинами. Положим Li(T) (г = 0,1,..., п) —
количество подграфов графа Тег вершинами, не имеющих ни одного ребра. Такие
графы для краткости будем называть свободными графами. Тогда
η
Μ1(Τ) = Σ(-1)%(Τ).
г=0
Здесь снова полагаем Lo(T) = 1 и L\(T) = п. Аналогично функции F\
введем функцию G\(n):
0,(71) = max |M!(T)|.
Пусть, далее, Вп = h(An). Ясно, что Вп — полный граф на η вершинах.
Наконец, произведению хордовых диаграмм А и В будет соответствовать
произведение графов h(А) и h(B), представляющее собой их несвязную сумму
[CDL].
Все дальнейшие рассуждения этого раздела будут направлены на
доказательство следующей теоремы, формулировка которой почти дословно
повторяет формулировку теоремы Д.З:
Теорема Д.4. Пусть Gi(n) = gn. Тогда существует граф Тп Ε Γη; такой
что:
1) \М1(Тп)\=дп;
452 Максимумы критических коэффициентов полинома Джонса
2) Тп = ВГ1 -ВГ2·.. .-ВГк при некоторых ненулевыхτ*ι, Г2,..., г&? для которых
Т\ + г2 + ... + rk = п.
При этом дп = |(1 - п) · (1 - г2) · ... · (1 - гк)\.
Покажем, как из теоремы Д.4 следует теорема Д.З. Так как отображение
h сохраняет функцию Μι, то при любом η справедливо неравенство Fi(n) ^
Gi(n). По теореме Д.4, Gi(n) = \Mi(Bri -ВГ2 ·.. .-ВГк)\, но так как ВГг = h(ArJ,
то M1(BrJ = Mi(ArJ, поэтому
Gi(n) = |Mi(Sri.....Srfc)| =
= |M1(Ari)-...-M1(Arfc)| =
= \М1(АГ1 -...-АГк)\ <Fi(n),
где АГ1 · ... · АГк G Dn. Мы получили цепочку
Fi(n) < Gi(n) = |Μι(ΑΓι · ... · Arfc)| < Ή (η),
откуда Fx(n) = Gi(n) = |(l-ri).(l-r2)·.. .-(1-^)1 и ^lW = |Μι(ΑΓι ·.. ,АГк)\.
Для завершения доказательства теоремы Д.З осталось доказать теорему Д.4.
Сначала сформулируем и докажем несколько свойств функции М\ на
графах.
Теорема Д.5 (Мультипликативность). Для любых А, В G Г выполняется
равенство М1(АВ) = М1(А)М1(В).
Доказательство. Пусть A G Тр, В G Tq. Рассмотрим величину Li(AB). В
каждом свободном подграфе Ε с АВ с г вершинами всякая вершина лежит
либо в А, либо в В, поэтому Ε есть объединение двух свободных подграфов
из А и В. При каждом га = 0,1,..., г в графе А существует Lm(A) свободных
подграфов с га вершинами, и каждый из них может быть дополнен свободным
подграфом из графа В до свободного подграфа с г вершинами в графе АВ
ровно Li-m(B) способами, поэтому
г
Li(AB) = Σ Lm(A)Li-m(B).
m=0
Следовательно,
P+q
M1(AB) = Y/(-l)iLi(AB) =
г=0
P+q г
= Е("!)г Σ Lm(A)Lt.m(B) =
г=0 m=0
p+q г
= YJY,{-l)iLm{A)Li.m{B)-
г=0 m=0
Заметим, что в последней сумме каждое слагаемое вида (—l)r+sLr(A)Ls(£>),
где 0^r^p,0^s^<2, встречается ровно один раз, потому что по индексам
Д.1. Коэффициент М\
453
г и s однозначно определяются индексы т = гиг = г + 5,а все остальные
слагаемые равны нулю (так как Lr(A) = 0 при г > ρ и LS(B) = 0 при s > q).
Отсюда заключаем, что
Ρ q
r=0 s=0
Ρ
Мг(АВ) = ^2^2(-l)r+sLr(A)Ls(B) =
J2(-lYLr(A)J2(-l)sLs(B) =
r=0 s=0
= (^(-1)^Г(А))(^(-1)^,(Б)) = M1(A)M1(B),
r=0 s=0
что и требовалось доказать. D
Теорема Д.6 ([Mnch]). Пусть Τ — граф, ах — его произвольная вершина.
Пусть Тх — подграф, получающийся из графа Τ выбрасыванием вершины х,
иТх — подграф, образованный вершинами, с которыми вершина χ не
соединена. Тогда имеет место следующее соотношение:
Μι(Τ) = Мг(Тх) - MiCT,). (Д.1)
Это равенство будем называть разложением графа по вершине х.
Доказательство. Найдем величину Li(T). Количество свободных подграфов
графа Тег вершинами (г ^ 1) складывается из количества свободных
подграфов с г вершинами, не содержащих вершину ж, и из количества свободных
подграфов с г вершинами, содержащих эту вершину. Для первого случая искомое
количество равно Li(Tx). Во втором случае все вершины свободного подграфа
кроме χ лежат в подграфе Тх, поэтому число таких подграфов равно Li-i(Tx).
Отсюда имеем Li(T) = Li(Tx) + Li-i(Tx), и
г=1
Μι (Τ) = 1 + ^2(-1)гЬг(Т) = 1 + ^2(-lY(Lt(Tx) + Li-iCf*)) =
г=1
η η
Σ(-ΐ)%(τχ) + Σ(-ι)%-ι№,) =
г=0 г=1
η-1 t
= ^(-1)%(ТШ) - ^(-1)%(ТШ) = Μχ(Τχ) - MX{TX).
г=0 г=0
Здесь η — 1 и t — количества вершин в подграфах Тх и Тх соответственно.
Теорема доказана. D
Замечание Д.З. Соотношение (Д.1) является рекуррентным и позволяет
вычислять значения функции Μι косвенным путем без использования ее
определения.
Осталось рассмотреть последнюю группу свойств.
454 Максимумы критических коэффициентов полинома Джонса
Теорема Д.7. Для любого графа Τ Ε Γη,η = 1, 2,..., существует граф Т' Ε
Гп+Ь такой что Μι (Γ) = Μι(Τ').
Доказательство. Предъявим требуемый граф Т'. Для этого добавим к Τ еще
одну вершину χ и соединим ее со всеми вершинами графа Τ кроме одной. Тогда
в терминах теоремы Д.6 имеем Тх = Т, а Тх — граф с одной вершиной. Поэтому
Μι(Τ') = Μι (Τ) - 0 = Μι (Τ). D
Замечание Д.4. Проведенное рассуждение не проходит при η = 0; так как
после добавления новой вершины χ в полученном графе должна существовать
вершина, с которой χ не соединена, а при η = 0 такой вершины не
оказывается.
Следствие Д.1. При η ^ 1 функция G\{n) монотонно не убывает, т.е.
d(n) < <?i(ra + l).
Это утверждение прямо вытекает из теоремы Д.7.
Следствие Д.2. При η ^ 2 и для любого к = 0,1,...,η — 1 выполняется
неравенство Gi(n) ^ G\(k).
Доказательство. В силу следствия Д.1 осталось рассмотреть случай к = 0. Но
Gi(0) = 1 и, как нетрудно проверить, Gi(2) = 1, поэтому требуемое неравенство
имеет место и в этом случае. D
Теперь перейдем непосредственно к доказательству теоремы Д.4.
Воспользуемся индукцией по п. Несложный перебор показывает, что теорема верна при
η = 0,1, 2. Предположим, что η ^ 3 и утверждение теоремы доказано для всех
значений, меньших п. Установим его справедливость и для п. Рассмотрим граф
Теп вершинами, на котором достигается значение G\(n). Пусть ρ —
наименьшая из валентностей вершин в этом графе. Если ρ = 0, то граф Τ
представляется в виде несвязной суммы двух графов, один из которых является графом
с одной вершиной. Тогда Μι(Τ) = 0, что не так из соображений монотонности
функции G\(n). Значит, ρ > 0. Если ρ = η — 1, то граф Τ является полным и
справедливость теоремы установлена. Итак, считаем 0 < ρ < η — 1.
Выберем какую-нибудь вершину χ валентности ρ и вершины,
соединенные с вершиной χ ребрами, перенумеруем χι,Χ2, · · · ,хР, а подграф,
образованный оставшимися вершинами (их η — ρ — 1 штук), обозначим через П.
Пусть также Нх^Хъ+1^ш^Хр (г = 1,2,... ,р) — подграф, образованный
вершинами Xi, Жг+ъ · · ·, £р и вершинами подграфа П. Раскладывая граф по вершине ж,
получим
МХ(Т) = Mi(HI1>l2>...i!El>) - Мг(Н).
Так как ρ — минимальная из валентностей вершин в графе Т, то для любой
вершины t графа Τ и для любого подграфа, ее содержащего, в этом подграфе
имеется не более п — р—1 вершин, не связанных ребром с вершиной t.
Последовательно применяя рекуррентное соотношение, раскладывая на г-м шаге граф
Д.2. Коэффициент М2
455
^жг,жг+1,...,жр п0 вершине х^ получим:
М^Т) = Μ!(ΗΧι,Χ:ι,...,Χρ) - Μι (Я) =
= М^Я^,...^,) - Mi (Hi) - Μι (Я) =
= МЦЯяз,..,*,) - Mi(ff2) - Mi(ffi) - Μι (Я)
= Mi(ffIp) - Mi(ffp_i) - Mi(tfp_2) - ... - Mi(ffi) - Mi (Я) =
= Mi (Я) - Mi (Яр) - Mi(ffp_i) - ... - Mi (Я1) - Mi (Я) =
= -Mi(ffi) - Mi(Я2) - ... - Mi(Яр).
Далее,
ρ
|Μι(Τ)| = |Mi(ffi) + Mi(tf2) + ... + Mi(Яр)I < ^ |Mi(tf,)|.
г=1
Из сделанного выше замечания следует, что при любом г = 1,..., ρ
образующийся на г-м шаге граф Hi содержит не более п—р—1 вершин. Если п—р—1 = 1,
то Mi(Hi) ^ 1 при всех г = 1,... ,р, поэтому \М\{Т)\ ^ ρ = η — 2. Это
противоречит максимальности выбранного графа Т, потому что G\(n) ^ |Μι(£>η)| =
η — 1 > η — 2. Значит, η — ρ — 1 ^ 2. Тогда
<?ι(η) = |Μι(Τ)| < Σ ΙΜι№)Ι < Ρσι(" - Ρ - !)·
г=1
Так как гг — ρ — 1 < гг, то по предположению индукции существуют числа
ri,r2,... ,Гк, такие что т\ + r2 + ... + ги = η -ρ - 1 и Gi(n -ρ - 1) = |Μι(5Γι ·
£>Г2 ·... · £>rfc) I. Теперь рассмотрим граф ВГ1 · ВГ2 ·... · ВГк · Βρ+ι. На нем модуль
функции Μι равен
|Mi(Bri.....Brfc.Bp+i)| =
= |Mi(Bri-...-Brfc)|-|Mi(Bp+i)| =
= Gi(n - ρ - 1) · |1 - (ρ + 1)| = pGi(n - ρ - 1) ^ |Μι(Τ)| = <?ι(η).
Отсюда Gi(n) = |Mi(Bri · ... · £>rfc · Βρ+ι)\, что и требовалось доказать.
Теорема Д.4 и, тем самым, теорема Д.З доказана.
Д.2. Коэффициент М2
Теперь перейдем к рассмотрению функции М2. Эта функция определена на
множестве хордовых диаграмм с двумя различными типами хорд. Хорды мы
будем называть положительными и отрицательными, а диаграммы такого
вида — оснащенными.
Замечание Д. 5. Мы будем отождествлять положительные хорды и хорды
"обычных" диаграмм из предыдущего раздела.
456 Максимумы критических коэффициентов полинома Джонса
Подобно обычным хордовым диаграммам, рассмотренным в предыдущем
разделе, введем обозначение Еп для множества оснащенных диаграмм с η
хордами. Теперь определим функцию М.2. Пусть S Ε Еп — произвольная
оснащенная диаграмма. Введем величину Zi(S) как количество поддиаграмм
диаграммы S с г хордами, обладающих следующими свойствами:
1) по крайней мере одна хорда (в каждой из рассматриваемых поддиаграмм)
является отрицательной;
2) все отрицательные хорды попарно пересекаются;
3) каждая положительная хорда не пересекается ни с одной из оставшихся
хорд.
Тогда
М2(5) = £(-1)г+1ВД.
г=1
Так же как и в случае функции Μι, нам требуется найти максимум модуля
функции М.2 на множестве Еп. Обозначим этот максимум через Q(n).
Теорема Д.8. Справедливо равенство Q(n) = Fi(n + 1).
Доказательство проведем в два этапа.
1) По исходной оснащенной диаграмме S Ε Еп построим граф Τ Ε Γη+ι,
такой что |М2(5)| = |Μι(Γ)|.
Из этого сразу будет следовать неравенство Q(n) < i*i(n + 1).
2) Покажем, что значение F\(n + 1) достигается. Это и даст нам требуемое
равенство.
Приступим к доказательству.
1) Рассмотрим произвольную оснащенную диаграмму S Ε Εη. Пусть P(S)
и N(S) — соответственно количество положительных и отрицательных хорд в
этой диаграмме. Построим по диаграмме S граф Τ с гг+1 вершиной следующим
образом.
Сначала рассмотрим свободный граф с η + 1 вершиной. Разобьем
множество его вершин на три попарно непересекающихся подмножества, состоящих
из 1, P(S) и N(S) вершин соответственно. Вершину, входящую в первое
множество, обозначим через ж, а второе и третье множества обозначим через Р' и
Nf соответственно. Установим взаимно однозначное соответствие между
множеством Р' и множеством положительных хорд диаграммы S, а также между
множеством Nf и множеством отрицательных хорд диаграммы S.
Теперь будем соединять некоторые пары вершин ребрами. Прежде всего,
вершину χ соединим с теми и только теми вершинами, которые лежат в
множестве N'. Далее, пару вершин, обе из которых лежат лежат в Р' или одна
из них лежит в Р7, а другая — в TV7, соединим ребром тогда и только тогда,
когда соответствующие им хорды в диаграмме S пересекаются. Наконец, пару
вершин из множества N' соединим ребром в том и только в том случае, когда
соответствующие им хорды в диаграмме S не пересекаются. Построение графа
Τ завершено.
Нетрудно убедиться, что величина Zi(S) равна количеству свободных
подграфов в графе Т, удовлетворяющих следующим условиям:
а) множество вершин каждого из этих подграфов не содержит вершины ж;
Д.2. Коэффициент М2
457
б) в множестве вершин каждого из этих подграфов содержится хотя бы одна
вершина из множества Nf.
Теперь найдем значение функции Μι на графе Т. Раскладывая граф Τ по
вершине ж, получим
Μι (Γ) = Μι(Τ7) - Μι(Γρ/).
Здесь Τ' — подграф графа Т, образованный всеми вершинами графа Τ
кроме χ, а Τρι — подграф графа Т, образованный вершинами из множества Р'.
Воспользовавшись определением функции М\, получим
η P(S)
МЛТ) = Σ(-ιγκτ(τ>) - £(-№№») =
г=0 г=0
= ]Г(-1)Чкг(т')-кг(тР-)) =
г=0
η
= Σ(-ιγ(κι(τ')-κι(τΡ,)).
г=1
Здесь мы предполагаем, что Ki(Tp>) = 0 при г > P(S), и учитываем, что
Ко(Т') = Ко(Тр') = 1. Величина Ki(T') есть количество свободных подграфов
графа Т' с г вершинами, а величина Ki(Tp/) есть количество свободных
подграфов графа Т' с г вершинами, среди которых нет вершин из множества N'.
Таким образом, разность Κι(Τ') — Κι(Τρ>) представляет собой количество
свободных подграфов графа Т' с г вершинами, содержащих хотя бы одну вершину
из множества Nf. Поскольку любой подграф графа Т' не содержит вершины ж,
а любой подграф графа Т, не содержащий вершины ж, является подграфом
графа Т7, то величина Ki(T') — Ki(Tp>) в точности равна величине Zi(S).
Значит,
M.iT) = ]Г(-1)гВД = (-1)£(-1)<+1ад = -M2(S),
г=1 г=1
откуда \М\(Т)\ = \M2(S)\. Первая часть доказательства завершена.
2) Поскольку 0 < Q(0) < Fi(l) = 0, то Q(0) = Fi(l) = 0 и требуемое
равенство имеет место. Теперь пусть η ^ 1. Тогда η + 1 ^ 2 и по теореме Д.4
существуют такие натуральные числа τ*ι,..., г&, что:
a) ri + ... + Г& = η + 1;
6)Fi(n+l) = |Mi(Sri.....Srfc)|.
Так как η + 1 ^ 2, то Fi (гг + 1) > 0, поэтому при любом г = 1,..., /с
справедливо неравенство r^ ^ 2. Пусть А'Г1_1 — оснащенная диаграмма, состоящая из
т\ — 1 попарно непересекающихся отрицательных хорд. Из неравенства т\ ^ 2
следует, что эта диаграмма содержит по крайней мере одну хорду.
Лемма Д.2. Имеет место равенство \М2(А'Г1_1 · АГ2 · ... · АГк)\ = |Mi(£ri ·
БГ2 · ... · ВГк)\.
Замечание Д.6. В этой формуле все диаграммы АГ2,..., АГк предполагаются
состоящими только из положительных хорд.
458 Максимумы критических коэффициентов полинома Джонса
Доказательство. Рассмотрим граф Τ Ε Γη+ι, соответствующий диаграмме
S = A'ri_1 · АГ2 ·... · АГк, S Ε Еп. Подграф графа Τ с вершинами из множества
Р' представляется в виде ВГ2·.. .-ВГк. Вершина χ соединена со всеми вершинами
из множества TV7, поэтому подграф, образованный вершиной χ и вершинами из
множества TV7, является полным подграфом с г\ вершинами. Этот подграф по
определению равен подграфу ВГ1, следовательно, Τ = ВГ1 · ВГ2 ·... · ВГк, что и
завершает доказательство леммы Д.2, а вместе с тем и теоремы Д.8. D
Д.З. Вычисление значений функции i<\
В этом разделе мы вычислим точные значения функции F\(n) при
каждом п. Для этого будем использовать метод, даваемый теоремой Д.З. При
фиксированном η нужно рассмотреть всевозможные представления числа η в
виде суммы натуральных слагаемых
n = ril +ri2 +... + rifc, (Д.2)
где к — количество слагаемых в г -м представлении. После этого для каждого
представления нужно посчитать произведение
Pi = (ni-l)(ri2-l)...(rik-l) (Д.З)
и выбрать максимум среди р^.
Замечание Д.7. Представление натурального числа в виде (Д.2) будем
называть разбиением.
Замечание Д.8. Любое разбиение числа п, на котором достигается значение
Fi(n), будем называть максимальным разбиением.
Замечание Д.9. Для фиксированного разбиения вида (Д.2) числа η
произведением будем называть соответствующее произведение вида (Д.З).
Замечание Д. 10. Разбиение будем называть нетривиальным, если оно
содержит не менее двух слагаемых.
Число 1 нетривиальных разбиений не допускает, поэтому F\(l) = 0. Число 2
можно предствить в виде суммы двумя способами: 2 и 1+1. Посчитав в обоих
случаях соответствующее произведение, найдем, что F\{2) = 1. В силу
монотонности функции F\(n) при η ^ 3 имеем F\(n) ^ 1. Отсюда следует, что далее
нет смысла рассматривать разбиения числа гг, содержащие единицу в качестве
одного из слагаемых, так как в подобных случаях произведение будет равно
нулю и не даст максимума. Число 3 не имеет таких нетривиальных разбиений,
поэтому Fi(3) = 2. Далее, для η = 4 получаем два разбиения: 4 и 2+2, отсюда
Fi(4) = 3. Для η = 5 имеем тоже два разбиения: 5 и 2+3, что дает i*i(5) = 4.
Наконец, при η = б возможны четыре разбиения: 6, 2+4, 3+3, 2+2+2, поэтому
Fi(6) = 5.
Теперь будем рассматривать случай η ^ 7. Сначала приведем несколько
наблюдений.
Д.З. Вычисление значений функции F\
459
1. В разбиении числа гг, соответствующем значению Fi(n), никакие два
слагаемых не отличаются больше, чем на 1. В самом деле, пусть гиг + /с(/с^2) —
два таких слагаемых. Тогда мы их можем заменить на другую пару слагаемых
(г + 1)и(г + /с — 1), так что произведение увеличится:
(г - 1)(г + к - 1) < г(г + к - 2) при к > 1.
Мы пришли к противоречию с максимальностью исходного разбиения.
2. Существует максимальное разбиение, не содержащее слагаемых,
больших 6. Действительно, каждое такое нечетное слагаемое вида (2s + 1) можно
разбить на два меньших слагаемых s и (s + 1), так что произведение не
уменьшится:
2s < s(s — 1) при s ^ 3,
а каждое четное слагаемое вида (2s) можно разбить на два слагаемых s и s,
при этом произведение увеличится:
2s - 1 < (s - I)2 при О 4.
С этого момента считаем, что в максимальном разбиении каждое слагаемое не
превосходит 6.
Теперь покажем, что максимальное разбиение не содержит двоек. Если это
не так, то в рассматриваемом разбиении содержатся только двойки и тройки,
при этом количество слагаемых в разбиении не меньше двух (так как η ^ 7).
Значит, помимо двойки в разбиении есть еще одна двойка либо тройка. В
первом случае пару двоек можно заменить на четверку, а во втором — пару 2 и 3
можно заменить на 5. В обоих случаях произведение увеличивается, поэтому
исходное разбиение не может быть максимальным.
На данный момент мы получили, что при каждом η ^ 7 существует
максимальное разбиение одного из трех следующих видов:
1) среди слагаемых встречаются только числа 3 и 4;
2) каждое слагаемое равно либо 4, либо 5;
3) среди слагаемых нет других чисел, кроме 5 и 6.
Воспользовавшись этим, вычислим значения F\(n) еще для нескольких п.
η = 7. В этом случае нет разбиений вида 2) и 3), а единственное разбиение
вида 1) есть 3+4, поэтому i*i(7) = 6.
η = 8. В максимальное разбиение не могут входить числа 5 и 6, а также 3,
поэтому значение i*i(8) достигается на разбиении 4+4 и равно 9.
η = 9. Число 6 не может входить в максимальное разбиение, а числа 5 и 4
только в одном случае — 5+4. Остается еще одно разбиение 3+3+3, но на нем
произведение меньше, чем в первом случае. Отсюда Fi(9) = Fi{5 + 4) = 12.
гг = 10. Шестерка снова не входит в максимальное разбиение, пятерка
только в случае 5+5, а разбиение вида 1) одно: 3+3+4. Поэтому Fi(10)=Fi(5+5) = 16.
гг = 11. Разбиение вида 3) одно: 5+6, вида 2) нет, вида 1) тоже одно: 4+4+3.
Значит, Fi(ll) = Fi(5 + 6) = 20.
Все вычисленные на данный момент значения функции F\ (n) сведем в
таблицу:
гг
ад
0
1
1
0
2
1
3
2
4
3
5
4
6
5
7
6
8
9
9
12
10
16
11
20
460 Максимумы критических коэффициентов полинома Джонса
Теперь считаем η ^ 12. Покажем, что в этом случае максимальное разбиение
не содержит чисел 3 и 6 в качестве слагаемых и таким образом имеет вид 2).
Пусть максимальное разбиение содержит слагаемое 3. Тогда оно имеет вид 1).
Если в этом разбиении есть еще одно слагаемое, равное 3, то пару 3+3 можно
заменить на 6, при этом произведение увеличится, следовательно, такое
невозможно, и тройка встречается ровно один раз. Но η ^ 12, поэтому в разбиении
встречаются еще по меньшей мере две четверки, тогда сумму 3+4+4 можно
заменить на сумму 5+6, при этом произведение увеличится. Снова противоречие,
поэтому максимальное разбиение не содержит числа 3.
Теперь предположим, что максимальное разбиение содержит слагаемое 6.
Если это слагаемое встречается более одного раза, то сумму 6^6 можно
заменить на сумму 4+4+4 с увеличением произведения. Поэтому считаем, что
число 6 встречается в разбиении ровно один раз. Так как η ^ 12, то число 5
встречается в разбиении не менее двух раз. Но сумму 6+5+5 можно заменить
на сумму 4+4+4+4 с увеличением произведения: в первом случае оно равно
5 · 4 · 4 = 80, а во втором 3 · 3 · 3 · 3 = 81. Оба случая приводят к противоречию.
Мы показали, что максимальное разбиение содержит только слагаемые 4 и 5.
Осталось заметить, что число 4 встречается в разбиении не более четырех раз,
так как сумму 4+4+4+4+4 с произведением З5 = 243 можно заменить на сумму
5+5+5+5, для которой произведение равно 44 = 256 > 243.
Но разное количество четверок в разбиении соответствует различным
остаткам от деления числа η на 5, поэтому максимальное разбиение определено
однозначно.
Итак, при η ^ 12
ίι(η)
[27
36
48
64
I81
4к
4к
4к
4к
4к
если η = 5/с + 12:
если η = 5/с + 13:
если η = 5/с + 14:
если η = 5/с + 15:
если η = 5/с + 16.
(fc^O)
Приложение Е
Нерешенные проблемы
в теории узлов
В настоящем приложении мы обсуждаем некоторые важные проблемы в
теории классических и виртуальных узлов. Одним из главных критериев при
составлении была ясность формулировки. При составлении среди прочих
источников мы пользовались домашней страницей Робиона Кирби [KirHP] (его
книга о нерешенных задачах в маломерной топологии); конечно, лишь малая
часть проблем, приведенных в этой книге отражена здесь. Кроме того, мы
оставили некоторое количество "старых" проблем, сформулированных еще в книге
Кроуэлла и Фокса [КФ], которые остаются нерешенными и по сей день. Еще
одним из источников была обзорная статья Дужина и Чмутова [ДЧ].
Особенное место в этом списке занимают проблемы по теории виртуальных узлов.
Некоторые из них, как мы надеемся, могут пролить свет на давно стоящие
задачи классической теории узлов (как, например, задача о полноте полинома
Джонса-Кауфмана). Многое из приведенного здесь содержится в совместной
статье автора с Роджером Фенном и Луисом Кауфманом [FKM].
Как правило, мы указываем автора той или иной проблемы. Те из проблем,
которые были сформулированы автором настоящей книги, помечены (В.О.М).
1. Как распознать обратимость узла?
Естественно, имеется в виду более или менее прямой алгоритм
распознавания, не ссылающийся на известные алгоритмы распознавания узлов,
например, [Matv4]. To же для виртуальных узлов.
2. Пусть С(п) — число простых неориентированных классических узлов в
S3 с минимальным числом перекрестков, равным п. Описать поведение
функции С (ή) при η стремящимся к бесконечности ос.
Первые значения функции С (ή) (начиная с гг=3) таковы: 1,1, 2, 3, 7, 21,49,
165,552,2167,9988.
3. Пусть U(n) — число простых узлов, число заузленности которых равно
п. Каково асимптотическое поведение функции U(n)l Каково поведение
функции С (ή)/U (ή)?
4. Может ли классический узел, для которого минимальная классическая
диаграмма имеет η перекрестков, иметь виртуальную диаграмму с:
462
Нерешенные проблемы в теории узлов
общим количеством перекрестков, меньшим, чем п?
количеством классических перекрестков, меньшим, чем п?
5. Верно ли, что минимальное число перекрестков для классических узлов
аддитивно относительно связной суммы: с(К\фК^) = c(Ki) + c(i^2)?
6. (де Соуза) Верно ли, что связная сумма η нетривиальных узлов имеет
число заузленности не меньше гг?
Положительный ответ на этот вопрос следует из положительного ответа
на следующий вопрос:
7. Является ли число заузленности аддитивным относительно взятия
связной суммы: u{K\j^K2) = и{К\) + (i^)?
8. Для каждого ли четного η существуют (простые и альтернированные)
зеркальные узлы с минимальным числом перекрестков, равным п?
9. (Джонс) Существует ли нетривиальный узел, полином Джонса которого
равен единице?
Луис Кауфман предложил следующий подход к изучению этого
вопроса. Существует много способов построения виртуальных узлов с
единичным полиномом Джонса. Например, виртуализация и флипы (Tait flyping
moves) Есть ли классические узлы среди них?
Мы предлагаем следующие две гипотезы:
• Любой ориентируемый (т. е. имеющий диаграмму, которой соответствует
ориентируемый атом, см. главу 20) виртуальный узел, имеющий
тривиальный полином Джонса, сводится к тривиальному посредством
виртуализации.
• Любые два классических узла, эквивалентных посредством обобщенных
движений Рейдемейстера и виртуализации, изотопны.
Из положительного ответа на оба эти вопроса следует, что полином
Джонса распознает тривиальный узел.
10. Распознают ли гомологии Хованова тривиальный узел (в классе
классических узлов)?
11. Можно ли найти бесконечно много разных классических узлов, имеющих
один и тот же полином Кауфмана двух переменных?
Как было показано в [DH], если такой пример существует, то количество
перекрестков у него должно быть не меньше 18.
12. Найти верхнюю оценку на число движений Рейдемейстера, необходимых,
для того, чтобы продеформировать друг в друга две диаграммы одного
и того же классического (виртуального) узла, имеющие га и η
перекрестков соответственно. В виртуальном случае имеет смысл рассматривать
количество классических перекрестков и общее количество перекрестков.
13. Найти критерий простоты узла в терминах его плоской диаграммы (или
d- диаграммы).
14. Точно ли представление Бурау для группы кос из четырех нитей?
Нерешенные проблемы в теории узлов
463
15. (В.А.Васильев) Полна ли система инвариантов Васильева?
16. (Частный случай предыдущей задачи) Верно ли, что инварианты
Васильева всегда различают обратимость? Иными словами, верно ли, что для
любого необратимого узла К существует инвариант Васильева ν (К),
принимающий различные значения на узле К и на узле, полученном из К
обращением ориентации? В частности, к настоящему времени не найдено
инварианта Васильева, который различал бы узлы 8ιγ и узел, получаемый
из него обращением ориентации (см. таблицу узлов в конце книги).
17. Существует ли точное (конечномерное) представление виртуальной
группы кос VB(n) для произвольных значений п?
18. Два узла, заданные отображениями /ι,/2 · S1 —>· #3, называются кон-
кордантными если отображения Д52 могут быть расширены до вложения
F : S1 χ / -> S3.
Проблема (С. Акбулут и Р. Кирби) Пусть перестройки Дена по узлам Κι
и i^2 с нулевым оснащением задают гомеоморфные трехмерные
многообразия. Являются ли эти узлы конкордантными?
19. (И. Пржитицкий) Скажем, что ориентированная диаграмма D
(классического узла) является согласованной, если существует разбиение
перекрестков диаграммы D на пары такое, что каждая пара выглядит так,
как показано на рис. Е.1 (отметим, что ориентации выбраны
противоположными) .
Рис. Е.1.
Гипотеза. Существуют ориентированные узлы, не допускающие
согласованных диаграмм.
20. (В. Джонс и И. Пржитицкий) Узлом Лиссаэюу называется узел в R3,
заданный параметрически следующим образом:
χ = ο,ο$(ηχί + фх)
у = cos(%£ + фу)
χ = οοδ(ηζί)
для некоторых целых чисел τ]Χιηυιηζ. Какие узлы являются узлами Лис-
сажу?
21. (В.О.М) Построить аналог теории инвариантов Васильева для узлов и
зацеплений в терминах d-диаграмм, т. е. привести аналог теоремы
Гусарова и явные комбинаторные формулы типа Виро-Поляка, основанные на
кодировании узлов d-диаграммами.
Аналогичная задача для произвольных хордовых диаграмм и
виртуальных зацеплений.
464
Нерешенные проблемы в теории узлов
22. Назовем следующее свойство свойством Р: любая нетривиальная
перестройка Дена вдоль узла К задает неодносвязное многообразие. Верно
ли, что каждый классический узел К обладает свойством Р?
К настоящему моменту многие частные случаи этой задачи были решены
положите льно.
23. (Кауфман) Найти чисто комбинаторное доказательство (т. е. отличное от
доказательств, предложенных в [GPV] и [Кир]) того, что виртуально
эквивалентные классические диаграммы зацеплений задают изотопные
зацепления.
24. (В.О.М) Может ли запрещенное движение (одно или оба) быть
отправным пунктом для построения системы аксиом, определяющих
инварианты виртуальных зацеплений (подобно тому, как замена перекрестка и
приводит к алгебрам Конвея)?
25. Существует ли алгоритм, решающий проблему слов в виртуальной
группе кос? В частности, является ли инвариант, предложенный в главе 22
настоящей книги, полным?
26. Существует ли алгоритм, определяющий, является ли заданный
виртуальный узел (виртуальное зацепление) эквивалентным некоторому
классическому? Имеется в виду явный алгоритм, не опирающийся на алгоритм
распознавания виртуальных зацеплений, предложенный в приложении В.
27. Проблемы о количестве перекрестков (Р. Фенн, Л. Кауфман, В.О. М).
Для каждого виртуального зацепления L существуют три важных
характеристики: минимальное количество С классических перекрестков,
минимальное количество V виртуальных перекрестков и минимальное общее
число перекрестков Τ среди всех виртуальных диаграмм, задающих L.
1) Какова связь между минимальным числом виртуальных перекрестков
и родом виртуального узла?
2) Верно ли, что Τ = V + С?
28. (С.-С. Линь) Предположим, что ориентированные диаграммы
классических узлов К+ и К- отличаются ровно в одном перекрестке, в котором
К+ имеет вид '/\:, а К- имеет вид у\- Если К+ = К_, следует ли, что
К+ имеет вид
где одна из диаграмм К\ или К2 представляет тривиальный узел?
29. (В.О.М.) Построить теорию, аналогичную скобочному исчислению, для
лежандровых узлов и d-диаграмм.
Приложение Ж
Таблица узлов
В настоящем приложении мы приводим таблицу всех простых узлов (с
точностью до зеркального образа) с не более, чем десятью перекрестками.
Так как разложение каждого узла на простые сомножители единственно, то
имеет смысл составлять таблицы лишь простых узлов.
Простые узлы перечисляются в таком порядке. Сначала мы перечисляем все
узлы с не более, чем тремя перекрестками, затем с четырьмя, пятью, шестью
и т. д. При заданном количестве перекрестков узлы перечисляются в
произвольном порядке. Мы используем нумерацию, предложенную Дэйлом Рольфсеном
[Rol].
Однако таблица Рольфсена [Rol] содержит одно повторение, а именно,
знаменитую пару Перко диаграмм с десятью перекрестками, имеющих нумерацию
10i6i и 10i62 по Рольфсену. Эти узлы считались различными в течение более
семидесяти пяти лет. Их эквивалентность была установлена Перко [Per] в 1973.
В таблицах, приводимых ниже, мы удаляем "старый узел" с номером 10i62
и уменьшаем на единицу нумерацию всех последующих узлов с десятью
перекрестками.
466
Приложение Ж
<s>
3!
<2
4ι
|Й..
Ш1
φ
s
®
<РЧ>
5£
£
β?
©
®
74
Φ
О»·
©'
®··
18·.
®·-
©-
С?
S-
©·.
§ ·■■
Ш'-
Таблиц
ш·-
& -
Ш"
@,„
ζ^) 9»
φ'"
©9"
®-
^
Ф·-
^
@9"
<@ 9"
(ft>9z4
ΊΚ
€&'..
{^.о
<§ь
узлов 467
1©·.
7?9 9
fea 9"
ύΏ 9=s
@9"
®9-
§ 9«
kg)-
|@9з
С§Ь9"
®9"
ф\.
Ш9"
ъ&
<®9,<
ЙЬ
Ш9-
468
Приложение Ж
О1
Ж1
Ж ю.
*€©£
10.
®10s
IP7
$»-
^10,
§5? юи
Jo
Oo^f
ίο
21
P«LPf 10
ш
10
25
(3)
10
ь
11/ ю.
'Ч/ 10
10
«h
S3
10
12
я».
®"
16
ш "■
©"
20
а·
24
яри?ιυ"
<β&1 *'
Ш
f27
g> "is
10
31
й
10
зз
S
ю
35
/=*0
L0
37
Х9Я] ю39
<^10"
«S 10
43
©10«
ί&) 10"
<£
οσ^
49
(ш 10"
«Г
Q> io
28
®
ю30
1032
$
10
34
ш^
10
38
Щ"'
сЙ^10,г
^£10
44
■W<?\) io
ΰο^
46
φ10
43
^>4l0
^ 50
^
ю.
Stf
52
Таблица узлов
469
ш"
@>
10
55
Ок
10
57
-W
&·
10
59
623
10
61
i?Q-)10
63
йй10
65
Ω>. к
Ш
67
<@Р10"
®10'1
&fopi<
73
В10
54
*
10
56
PQ, ю
ш
62
10
ш
(@10"
СРй
Ш£
10
68
■<Ш/ 10та
ss
S& 10"
10
74
&
10
75
SO 1077
А
10,
79
J
10
81
10
89
«Ρ"
91
®»
93
Ж* К
δί
76
0^) 1080
&«
32
^э.
10
84
® 10"
10
33
^ 1 ίο
δ&
90
^>"
92
<^μ10
94
470
Приложение Ж
10
95
ш
ю
97
Йй
„ _, 10
^0 "
<@10»'
W
10
103
W
10
105
^
107
ΰ®Αιίΐ 10
^S>
109
10
s#
Ш "s
i)1
117
10
119
3§?v°.
©
10
98
^10
102
10
104
w1?0i
A1
0
юе
έχ
Ш10
10
112
® 10~
Ш
10
@ 10"°
6*
10
125
@10'
δ
10
)θάΟ
лгМ ю
V
10
133
10
135
©2
10
Г/ib
@-
10
β
23i io
ч/ 13°
8? l0
134
Щ^
136
10
'^V 13 8 1
@>"
Таблица узлов
471
L43
10
L45
$5
10
147
£V ю
149
<#
151
10
ЕУ
153
10
142
10
144
@в
10
14 6
10
143
10
150
10
152
10
£*10
155
10
157
Воч
10,
159
#
10
161
163
10
156
10
153 I
10
160
162
10
164
Литература
[Ada] Adams С. (1994), The knot book (New York: Freeman & Co.).
[AF] Artin, E., Fox, R. (1948), Some wild cells and spheres in three-dimensional
space, Ann. Math., 49, pp. 979-990.
[AH] Appel, K. I. and Haken, W. (1989), Every planar map is four colorable.
Contemp. Math., 98, AMS, Providence.
[Alel] Alexander, J. W. (1923), Topological invariants of knots and links. Trans.
AMS., 20, pp. 257-306.
[Ale2] Alexander, J.W. (1933), A matrix knot invariant. Proc. Nat. Acad. Sci.
USA, 19, pp. 222-275.
[Ale3] Alexander, J.W. (1923), A lemma on systems of knotted curves, Proc. Nat.
Acad. Sci. USA, 19, pp. 93-95.
[Arnl] Arnold, V.I. (1994), Topological invariants of plane curves and caustics,
Univ. Lect. Series, 5, Amer. Math. Soc, Providence RI.
[Arn2] Arnold. V.I. (1994), Plane curves, their invariants, perestroikas and
classifications, in: Singularities and Bifurcations, Advances in Soviet Math.,
21, Amer. Math. Soc, Providence RI, 33-91 (1994).
[Artl] Artin, E. (1925), Theorie der Zopfe. Abh. Math. Sem. Univ. Hamburg, 4,
pp. 27-72.
[Art2] Artin, E. (1947), Theory of braids, Annals of Mathematics (2) 48, pp. 101-
126.
[Ash] Ashley, С W. (1947), The Ashley book of knots (London: Coles Publ. Co.
Ltd).
[Ati] Atiyah M. (1989-90), The Jones-Witten invariants of knots, Seminaire
Bourbaki, 715.
[BaMo] Bae, Y. and Morton, H.R. (2003) The spread and extreme terms of the
Jones polynomial, Journal of Knot Theory and Its Ramifications, 12, (3),
pp. 359-373.
[Ber] Berger, M. (1994), Minimum crossing number for 3-braids. Journal of Physics.
A: Math. Com., 27, pp. 6205-6213.
[BF] Bartholomew, A. and Fenn R. (2003), Quaternionic invariants of virtual
knots and links, www.maths.sussex.ac.uk/Staff/RAF/Maths/Current/Andy/
equivalent.ps
Литература
473
[BGRT] Bar-Natan, D., Garoufalidis, S., Rozansky, L., Thurston, D. (2000),
Wheels, wheeling, and the Kontsevich integral of the unknot. Israel J.
Math., 119, pp. 217-237.
[BGRT1] Bar-Natan, D., Garoufalidis, S., Rozansky, L. and Thurston, D. (2002),
The Aarhus integral of rational homology 3-spheres.
i" : A highly non trivial flat connection on S3, Selecta Mathematica, 8 (3),
pp. 315-339;
II : Invariance and universality, Selecta Mathematica, 8 (3), pp. 341-372;
III : The relation with the Le-Murakami-Ohtsuki invariant, Preprint.
[Bigl] Bigelow, S. (2001). Braid groups are linear J. Amer. Math. Soc, 14, pp. 471-
486.
[Big2] Bigelow, S. (2002). Does the Jones polynomial detect the unknot, Journal of
Knot Theory and Its Ramifications 11, pp 493-505.
[Birl] Birman, J.S. (1994). Studying links via closed braids, In: Lecture Notes on
the Ninth Kaist Mathematical Workshop, 1, pp. 1-67.
[Bir2] Birman, J.S. (1974), Braids, links and mapping class groups. Princeton, NJ:
Princeton Univ. Press, 1974 (Ann. Math. Stud., 1982).
[Bir3] Birman, J.S. (1993), New points of view in knot and link theory, Bull. Amer.
Math. Soc. 28, pp. 253-287.
[Bj] Bjorner, A. (1993), Subspace arrangements. In: Proceedings of the First
European Congress of Mathematicians (Paris 1992). (Boston: Birkhauser)
pp. 321-370.
[BL] Birman, J.S. and Lin X.-S. (1993), Knot polynomials and Vassiliev's
invariants, Inventiones Mathematicae, 111, pp. 225-270.
[Bl] Bleiler, S. (1984), A note on the unknotting number, Math. Proc. Camb. Phil.
Soc, 96, pp. 469-471.
[BM] Birman, J.S. and Menasco W. (2002), On Markov's theorem, Journal of Knot
Theory and its Ramifications, 11, (3), pp. 295-310.
[BM2] Birman, J.S. and Menasco W. (1991), Studying links via closed braids II:
On a theorem of Bennequin, Topology and Its Applications, 40, pp. 71-82.
[BM3] Birman, J.S. and Menasco, W. (1993), Studying links via closed braids III:
Classifying links which are closed 3-braids, Pacific Journal of Mathematics
161, pp. 25-113.
[BM4] Birman, J.S. and Menasco, W. (1990), Studying links via closed braids IV:
Composite links and split links, Inventiones Mathematicae 102, pp. 115-139.
[BM5] Birman, J.S. and Menasco, W. (1992), Studying links via closed braids V:
The unlink, Transactions of the AMS, 329, pp. 585-606.
474
Литература
[ВМ6] Birman, J.S. and Menasco, W. (1992), Studying links via closed braids VI:
A non-finiteness theorem, Pacific Journal of Mathematics. 156, pp. 265-285.
[BN1] Bar-Natan, D. (1995), On the Vassiliev knot invariants, Topology 34,
pp. 423-475.
[BLT] Bar-Natan, D., T. Le and Thurston, D. (2003), Two applications of
elementary knot theory to Lie algebras and Vassiliev invariants, Geometry
and Topology, 7 pp. 1-31.
[BN2] Bar-Natan, D. (1995), Vassiliev homotopy string link invariants, Journal of
Knot Theory and its Ramifications 4 (1), pp. 13-32.
[BN3] Bar-Natan, D. (2002), On Khovanov's categorification of the Jones
polynomial, Algebraic and Geometric Topology, 2(16), pp. 337-370.
[BN4] Bar-Natan, D. (1997), Lie algebras and the four color theorem,
Combinatorica, 17 (1), pp. 43-52.
[BN5] Bar-Natan, D. (2004), Khovanov's homology for tangles and cobordisms,
arXiv:mat.GT/0410495.
[BNh] D. Bar-Natan. Homepage http://www.math.toronto.edu/^ drorbn
[Bou] Bouchet, A. (1994), Circle graph obstructions, J. Combinatorial Theory B,
60, pp. 107-144.
[Bourb] Bourbaki, N. (1982), Groupes et Algebres de Lie, IV,V,VI, (Paris: Masson).
[BPW] Bollobas В., Pebody, L. and Weinreich D. (2002), A state space definition
of the HOMFLY invariant, In: Contemporary Combinatorics, Budapest,
pp. 139-184.
[BR] Bollobas, В., Riordan O. (2000), Linearized chord diagrmas and an upper
bound for Vassiliev invariants, Journal of Knot Theory and its Ramifications,
9 (7), pp. 847-852.
[Br] Brunn, H., Uber verknotete Kurven, In: Mathematiker-Kongress Zurich 1897,
ss. 256-259, (Leipzig, 1898).
[Bril] Brieskorn, E.V. (1971), Die Fundamentalgruppe des Raumes der regularen
Orbits einer endlichen komplexen Spiegelsgruppe, Inventiones Mathematicae,
12 (1), pp. 57-61.
[Bri2] Brieskorn E.V. (1973), Sur les groupes des tresses (d'apres V.I.Arnol'd).
In: Seminaire Bourbaki, 1971-72 (401) (Berlin: Springer, 21-44, Lect. Notes
Math., 317).
[Bur] Burau, W. (1936) Uber Zopfgruppen und gleichzeitig verdrillte Verkettungen,
Abh. Math. Sem. Univ. Hamburg, 11, pp. 179-186.
[BW] Bjorner Α., Welker V. (1995), The homology of "k-equal" manifolds and
related partition lattices, Adv. Math., 110 (2), pp. 277-313.
Литература
475
[ВΖ] Burde, G. and Zieschang, H. (2003), Knots (Berlin: Walter de Gruyter).
[Car93] Cartier, P. (1993), Construction combinatoire des invariants de Vassiliev-
Kontsevich des noeuds, C.R.Acad. Sci. Paris, Ser. I, Math., 316, pp. 1205-
1210.
[CD1] Chmutov, S. and Duzhin, S. (1994), An upper bound for the number of
Vassiliev knot invariants, Journal of Knot Theory and its Ramifications, 2
(2), pp. 141-151.
[CD2] Chmutov, S. and Duzhin, S. (1999), A lower bound for the number of
Vassiliev knot invariants, Topology and its Applications, 92, pp. 201-223.
[CDBook] Chmutov, S. and Duzhin, S., CDBook. Book about chord diagrams.
Introduction to Vassiliev Knot Invariants, http://www.pdmi.ras.ru/
^duzhin/ papers/cdbook.ps.gz
[CDL] Chmutov, S.V., Duzhin, S.V. and Lando, S.K. (1994), Vassiliev knot
invariants i" — III, Advances in Soviet Mathematics, 21, pp. 117-147.
[CES] Carter, J. S., Elhamdadi M., Saito M. (2002), Homology theory for the set-
theoretic Yang-Baxter equation and knot invariants from generalizations of
quandles on sun, math.GT/0206255
[CKS] Carter, J.S., Kamada, S., Saito, M. (2002), Stable equivalence of knots on
surfaces, Journal of Knot Theory and Its Ramifications, 11, pp. 311-322.
[CKS2] Carter, J.S., Kamada, S., Saito, M. (2004), Surfaces in 4-space, (N.Y:
Springer Verlag).
[CM] Cromwell, P.R., Morton, H.R (1996)., Distinguishing mutants by knot
polynomials, Journal of Knot Theory and Its Ramifications, 5, pp. 225-236.
[Che] Chekanov, Yu. (2002), Differential algebras of Legendrian links, Inventiones
Mathematicae, 150(3), pp. 441-483.
[Che2] Chekanov, Yu. V. (2002), Invariants of Legendrian knots, In: Proceedings
of the International Congress of Mathematicians, Beijing, 2, pp. 385-394.,
(Beijing: Higher Education Press).
[Con] Conway, J.H, (1970), An enumeration of knots and links and some of their
algebraic properties, In: Computational Problems in Abstract Algebra (New
York, Pergamon Press), pp. 329-358.
[COT] Cochran, T.D., Orr, K.E. and Teichner, P. (2003), Knot concordance,
Whitney towers and L2-signatures, arXiv:math. GT/9908117, 22 Aug. 1999,
Annals of Mathematics,2 (157), pp. 433-519.
[Cr] Crowell, R. H. (1964), The derived group of a permutation representation,
Advances in Mathematics, 53, pp. 88-124.
[CV] Chmutov, S.V. and Varchenko A.N. (1997), Remarks on the Vassiliev knot
invariants coming from sh, Topology, 36, pp. 153-178.
476
Литература
[Da] Dasbach, О. (2000), On the combinatorial structure of primitive Vassiliev
invariants III — A lower bound, Communications in Contemporary
Mathematics, 2,(4), pp. 579-590.
[Deh] Dehornoy, P. (2002), Braids and self-distributivity, Progress in Mathematics,
vol. 192, Birkhauser.
[Dehl] Dehornoy, P. (1995), From large cardinals to braids via distributive algebra,
Journal of Knot Theory and its Ramifications, 4, pp. 33-79.
[Dehn] Dehn, M. (1914), Die beiden Kleeblattschlingen, Mathematische Annalen,
102, ss. 402-413.
[Dehn2] Dehn, M. (1910), Uber die Topologie des dreidimensionalen Raumes,
Mathematische Annalen, 69, ss. 137-168.
[DF] Dollard, J. D., Friedman, Ch. N. (1979), Product integration with applications
to differential equations (London: Addison-Wesley Publishing Company).
[DFN] Dubrovin, B.A., Fomenko A.T and Novikov, S.P. (1984,1985,1990), Modern
Geometry-Methods and Applications, Parts I—III (New York: Springer-
Verlag).
[DH] Dasbach O.T. and Hougardy, S. (1997), Does the Jones polynomial detect
unknottedness?, Journal of Experimental Mathematics, 6 (1), pp. 51-56.
[DK1] Dye, H.A. and Kauffman, L.H. (2003), Virtual knot diagrams and the
Witten-Reshetikhin-Turaev Invariants, Journal of Knot Theory and Its
Ramifications, to appear,arXiν:math. GT/0407407
[DK2] Dye, H.A., Kauffman, L.H. (2004), Minimal Surface Representation of
Virtual Knots and Links, arXiv:math. GT/0401035 vl, to appear.
[Dri2] Drinfeld, V.G. (1986), Quantum Group, Proc. Intl. Congress Math.,
Berkeley, USA, pp. 789-820.
[Dul] Duzhin, S. (1996), A quadratic lower bound for the number of primitive
Vassiliev invariants. Extended abstract, KNOT'96 Conference/Workshop
report, Waseda University, Tokyo, pp. 52-54.
[Dye] Dye, H.A. (2003), Detection and Characterization of Virtual Knot Diagrams,
Ph.D. Thesis, University of Illinois at Chicago.
[ECH...] Epstein D., Cannon J. W, Holt D. F, Levy, S.V.S, Paterson M. S. and
Thurston W.P.(1992), Word Processing in Groups, Jones and Barlett Publ.
[EGH] Eliashberg, Ya., Givental, A. and Hofer, H. (2002), An introduction to
symplectic field theory, Geom Funct. Anal., Special Volume, Part II, pp. 560-
673.
[EH] Etnyre, J., Honda, K. (2000), Knots and Contact Geometry, Part I, Part
II, arXiv:mat.GT/0006112. Part i": Torus knots and the figure eight knot,
Journal of symplectic geometry, (2001), 1, pp. 63-120.
Литература
477
[Eli] Eliashberg, Ya. (1993), Legendrian and transversal knot invariants in tight
contact 3-manifolds Topological methods in modern mathematics Houston:
Publish of Perish, pp. 171-193.
[EKT] Eliahou, Sh., Kauffman, L.H., Thistletwaite, M. (2003). Infinite families of
links with trivial Jones polynomial, Topology, 42, pp. 155-169.
[Erie] Erie, D. (1969), Die quadratische Form eines Knotens und ein Satz iiber
Knotenmannigfaltingkeiten, J. Reine Angewandte Math.,236 ss. 174-212.
[F] Fomenko A. T. (1991), The theory of multidimensional integrable hamiltonian
systems (with arbitrary many degrees of freedom). Molecular table of all
integrable systems with two degrees of freedom, Adv. Sov. Math, 6, pp. 1-35.
[FHW] Freedman, M.H., He, Z.-X., Wang, Z. (1994), Mobius energy for knots and
unknots, Annals of Mathematics, 139(2), pp. 1-50.
[FJK] Fenn, R., Jordan-Santana, M. and Kauffman, L.H., Biracks and virtual
links www.maths.sussex.ac.uk/Reports/TAGG/TAGG02-01.ps, Topology &
Appl,
[FKM] Fenn, R.A, Kauffman, L.H, and Manturov, V.O. (2004), Virtual Knots:
Unsolved Problems, Fundamenta Mathematical Proceedings of the Conference
"Knots in Poland-2003", to appear.
[Floer] Floer, A.,(1988), Morse theory for Lagrangian intersections, J. Differential
Geometry, 28, pp. 513-547.
[FMT] Tensor and vector analysis. Geometry, mechanics and physics (1998), edited
by A. T. Fomenko, O. V. Manturov, and V.V. Trofimov, (London: Gordon
and Breach Science Publishers).
[FRR] Fenn, R, Rimanyi, P. and Rourke, C.P. (1997), The braid-permutation
Group, Topology, 36(1), pp. 123-135.
[FT] Fuchs, D. and Tabachnikov, S. (1997), Invariants of Legendrian and
transverse knots in the standard contact space, Topology, 36, pp. 1025-1053.
[Gar] Garoufalidis, S. (2001), A conjecture on Khovanov's invariants, Fundamenta
Mathematicae, to appear.
[Gar] Garity, D.J. (2001), Unknotting numbers are not realized in minimal
projections for a class of rational knots, Rend. Inst. Mat. Univ. Trieste, Suppl.
2., Vol. XXXII, pp. 59-72.
[Gau] Gauss, C.F. (1877), Zur Mathematischen Theorie der electrodynamischen
Wirkungen, Werke Koningl. Gesell. Wiss. Gottingen 5 (1877), s. 605.
[Gir] Giroux, Ε (1999). Structures de contact en dimention trois et bifurcations de
feuilletages de surfaces, preprint.
[GL] Gordon., C. McA, and Luecke, J. (1989), Knots are determined by their
complements, J. Amer. Math. Soc, , pp. 371-415.
478
Литература
[GM] Gaifullin, Α.Α., Manturov V.O. (2002), On the recognition of braids, Journal
of Knot Theory and Its Ramifications, 11 (8), pp. 1193-1209.
[Gor] Goryunov, V. Vassiliev type invariants in Arnold's J+ -theory of plane curves
without direct self-tang encies, Topology, 37, 603-620 (1998).
[GPV] Goussarov M., Polyak M., and Viro 0.(2000), Finite type invariants of
classical and virtual knots, Topology 39, pp. 1045-1068.
[H] Hrencecin, D., On Filamentations and Virtual Knot Invariant, Thesis
www.math.uic.edu/ ^dhren/FINALCOPY.ps.
[Ha] Haken, W. (1961), Theorie der Normalflachen, Acta Mathematicae 105,
pp. 245-375.
[Hag] Hagge, T. J. (2004), Every Reidemeister move is needed for each knot type,
ArXivMath:/GT. 0404145
[Haz] Hazewinkel, M. (1995), Multiparameter quantum groups and multiparameter
i?-matrices, Acta Applicandae Mathematicae, 47, pp. 51-98.
[HK] Hrencecin, D. and Kauffman, L.H. (2003), On Filamentations and Virtual
Knots, Topology and its Applications, 134, pp. 23-52.
[Hem] Hemion, G. (1992), The classification of knots and 3-dimensional spaces,
(Oxford: Oxford Univ. Press).
[HM] Hirzebruch, F., Mayer, K.H. (1968), 0(n)-Mannigfaltigkeiten, exotische
Spharen und Singularitaten, Lecture Notes in Mathematics, 57, (New-York,
Springer).
[HOMFLY] Freyd, P., Yetter, D., Hoste, J., Lickorish, W.B.R, Millett, K.C. and
Ocneanu A. (1985), A new polynomial invariant of knots and links, Bull.
Amer. Math. Soc. 12, pp. 239-246.
[HTW] Hoste, J., Thistletwaite, M., and Weeks, J. Table of knots and
the KnotScape program, http://www.math.utk.edu/^morwen (Morwen
Thistletwaite's homepage).
[HTW2] Hoste, J., Thistletwaite, M. and Weeks, J. (1998), The first 1,701,936
knots, Mathematical Intelligencer, 20, pp. 33-48.
[Jac] Jacobsson, M. (2002), An invariant of link cobordisms from Khovanov's
homology theory, arXiv:mat.GT/0206303 vl.
[JJP] Myeong-Ju Jeong, Chan-Young Park (2002), The Critical Properties for
Fractional Chromatic Vassiliev invariants and knot polynomials. Topology
and Its Applications, 124, pp. 505-521.
[JKS] Jaeger, F., Kauffman, L.H., and H. Saleur (1994), The Conway Polynomial
in S3 and Thickened Surfaces: A new Determinant Formulation, J. Combin.
Theory. Ser. В., 61, pp. 237-259.
Литература
479
[Joh] Johansson, К.(1979), Homotopy equivalences of 3-manifolds with boundaries,
Lecture Notes in Mathematics, 761, (Berlin: Springer-Verlag).
[Jonl] Jones, V. F. R. (1985), A polynomial invariant for links via Neumann
algebras, Bull. Amer. Math. Soc, 129, pp. 103-112.
[Jon2] Jones, V. F. R. (1987), Hecke algebra representations of braid groups and
link polynomials, Annals of Mathematics, 126, pp. 335-388.
[Jon3] Jones, V. F. R. (1989), On knot invariants related to some statistical
mechanical models, Pacific Journal of Mathematics, 137 (2), pp. 311-334.
[Jon4] Jones, V. F. R. (2000), Ten Problems, In: Mathematics: frontiers and
perspectives, AMS, Providence, RI, pp. 79-91.
[Joy] Joyce D. (1982), A classifying invariant of knots, the knot quandle, Journal
of Pure and Applied Algebra, 23 (1), pp. 37-65
[Kaul] Kauffman, L.H. (1987), On Knots, (Annals of Math Studies, Princeton
University Press).
[Kau2] Kauffman, L.H. (1991), Knots and Physics, (Singapore: World Scientific).
[Kau3] Kauffman, L.H. (1987), State Models and the Jones Polynomial, Topology,
26 (1987), pp. 395-407.
[Kau4] Kauffman, L.H. (1983), Combinatorics and knot theory, Contemporary
Mathematics, 20, pp. 181-200.
[Kau5] Kauffman, L.H. (2003), e-mail to the author, May, 2003.
[Kau6] Kauffman, L.H. (1973), Link manifolds and periodicity, Bull. Amer. Math.
Soc, 79, pp. 570-573.
[Kau7] Kauffman, L. H. (1999), Virtual knot theory, European Journal of
Combinatorics 20(7), pp. 662-690.
[Kau8] Kauffman, L.H. (2001), Detecting virtual knots, Atti. Sem. Math. Fis.,
Univ. Modena, Supplemento al vol. IL, pp. 241-282.
[Kau9] Kauffman, L.H.., Diagrammatic Knot Theory, in preparation.
[KaulO] Kauffman, L. H. (1997), Virtual Knots , talks at MSRI Meeting, January
1997 and AMS meeting at University of Maryland, College Park, March 1997.
[Kam] Kamada, S. (2000), Braid presentation of virtual knots and welded knots,
arXiv:math. GT/0008092 vl, 2000.
[Kan] Kanenobu, T. (2001), Forbidden moves unknot a virtual knot, Journal of
Knot Theory and Its Ramifications, 10 (1), pp. 89-96.
[Kaw+] Kawauchi, A. et al. (1996), A survey of Knot theory, (Basel: Birkhauser).
480
Литература
[Kel] Thomson, W. (Lord Kelvin) (1867), Hydrodynamics, Proc. Royal. Soc.
Edinburgh, 41, pp. 94-105.
[Kfg] Kalfagianni, E. (1998), Finite type invariants of knots in 3-manifolds,
Topology, 37,(3), pp. 673-707.
[Khl] Khovanov, M. (1997), A categorification of the Jones polynomial, Duke Math.
J,101 (3), pp. 359-426.
[Kh2] Khovanov M., A functor-valued invariant of tangles, arXiv:
math.QA/0103190
[Kh3] Khovanov, Μ (2003), Patterns in knot homology, J. Experimental Math, 3,
pp. 365-375.
[Kim] Kim, S.G. (1999), Virtual Knot Groups, arXiv:math.GT/9907172, 1.
[KirHP] Kirby, R. Homepage www.math.berkeley.edu/ ^kirby
[KK] Kamada, N. and Kamada, S. (2000), Abstract link diagrams and virtual knots,
Journal of Knot Theory and Its Ramifications, 9 (1), pp. 93-109.
[КМ0] Kauffman, L. H and Manturov, V.O, Virtual Knot Theory, in preparation.
[KM] Kauffman, L. H. and Manturov, V.O., Virtual Biquandles, to appear
in Fundamenta Mathematica. (Proceedings of "Knots in Poland-2003"
Conference.)
[Kne] Kneissler, J. (1997), The number of primitive Vassiliev invariants up to
degree twelve. Preprint.
[Kon] Kontsevich, M. (1993), Vassiliev's knot invariants, Adv. in Soviet Math.,
16(2) (1993), pp. 137-150.
[Kon2] Kontsevich, M. (1992), Feynman diagrams and low-dimensional topology,
Preprint.
[KR] Kauffman, L.H. and Radford, D. (2002), Bi-Oriented Quantum Algebras and
a Generalized Alexander Polynomial for Virtual Links, A MS Contemp. Math,
318, pp. 113-140.
[Krai] Krammer, D. (1999), The braid group В4 is linear, Preprint, Basel.
[Kra2] Krammer, D. (2002), Braid groups are linear, Ann. of Math., 2 (155),
pp. 131-156.
[Kup] Kuperberg, G. (2002), What is a Virtual Link?, www.arXiv.org, math-GT/
0208039, Algebraic and Geometric Topology, 2003, 3, 587-591.
[KPT] Кассел, К., Pocco, Μ., Тураев, В.Г. (2002), Квантовые группы и
инварианты узлов (М.: Институт компьютерных исследований).
[KS] Kishino, Т., Satoh.S. (2004), A note on non-classical virtual knots, Journal
of Knot Theory and Its Ramifications, 13 (7), pp. 845-856.
Литература 481
[KZ] Knizhnik, V.G. and Zamolodchikov (1984), А.В., Current algebra and Wess-
Zumino model in two dimensions, Nucl. Phys., B247, pp. 83-103.
[La] Lando, S.K., Vassiliev knot invariants, Main constructions, In: Lando, S.,
Zvonkine, Α., Embedded graphs (Springer Verlag).
[Law] Lawrence, R. (1990), Homological representations of the Hecke algebra,
Comm. Math. Phys., 135, pp. 141-191.
[Leel] Lee, E. S. (2002) The support of the Khovanov's invariants for alternating
knots, arXiv: math.GT/0201105.
[Lee2] Lee, E.S. (2003) On Khovanov invariant for alternating links, arXiv:
math.GT/0210213.
[LH] Lagarias, J., Hass, J. (2001), The number of Reidemeister moves needed for
unknotting, J. Amer. Math. Soc, 14, pp. 399-428.
[Licl] Lickorish, W. B. R. (1993), The skein method for three-manifold invariants,
Journal of Knot Theory and Its Ramifications, 2, (2), pp. 171-194.
[Lic2] Lickorish, W. B. R. (1962), A representation of orientable combinatorial 3-
manifolds, Annals of Mathematics, 76, pp. 531-540.
[Lin] Lin, X.-S. (1992), Milnor link invariants are all of finite type, Columbia Univ.,
Preprint.
[Lin2] Lin, X.-S. (1994), Finite type link invariants of 3-manifolds, Topology, 33,
pp. 45-71.
[LM] Le, T.Q.T and Murakami, J. (1995), Representations of the category of tangles
by Kontsevich's iterated integral, Comm. Math. Phys., 168, pp. 535-562.
[LM2] Le, T.Q.T and Murakami, J. (1996), Representations of the category of
tangles by Kontsevich's iterated integral, Comm. Math. Phys., 168, pp. 535-
562.
[LR] Lambropoulou, S., Rourke, C. (1997), Markov's Theorem in Three-Manifolds,
Topology and Its Applications. 78, pp. 95-122.
[Lu] Lu, N. (1992), A simple proof of the fundamental theorem of Kirby calculus on
links, Transactions of the American Mathematical Society, 331, pp. 143-156.
[Mai] Manturov, V.O. (1999), d-Diagrams, Chord Diagrams, and Knots, Записки
научных семинаров ПОМИ 267, Геометрия и топология. 5, pp. 170-194.
[Ма2] Manturov, V.O. (2002), On Invariants of Virtual Links, Acta Applicandae
Mathematicae, . 72 (3), pp. 295-309.
[Ma3] Manturov, V.O.(2002), Knots and the Bracket Calculus, Acta Applicandae
Mathematicae, 74 (3), pp. 293-336.
[Ma4] Manturov, V.O. (2002) A combinatorial representation of links by quasitoric
braids, European Journal of Combinatorics, 23, pp. 203-212.
482
Литература
[Ма5] Manturov, V.O. (2003), Multivariable polynomial invariants for virtual knots
and links, Journal of Knot Theory and Its Ramifications, 12 (8), pp. 1131-
1144.
[Ma6] Manturov V.O. (2003), Kauffman-like polynomial and curves in 2-surfaces,
Journal of Knot Theory and Its Ramifications, 12 (8), pp. 1145-1153.
[Ma7] Manturov, V.O. (2004), Virtual knots are algorithmically recognisable,
arXiv:math. GT/0408255 vl.
[Ma8] Manturov, V.O. (2004), Knot Theory, (Boca Raton: Chapman & Hall: CRC-
Press), 516 pp.
[Ma9] Manturov, V.O. (2004), Long virtual knots and their invariants, Journal of
Knot Theory and Its Ramifications, 13 (8), pp. 1029-1039.
[Мак] Makanin, G.S. (1989), On an analogue of the Alexander-Markov theorem,
Izvestiya Acad. Nauk SSSR, 53 (1), pp. 200-210.
[Мака] Makanina, G.A.(1992), Defining relation in the pure braid group, Moscow
Univ. Math. Bull., 3, pp. 14-19.
[Man] Manturov, O. V. (2000), Polynomial invariants of knots and links, Записки
научных семинаров ПОМИ, 267, Геометрия и топология (5), pp. 195-206.
[Mar] Markoff, Α. Α. (1936), Uber die freie Aquivalenz der geschlossenen Zopfe,
Mat. Sbornik, 1, pp. 73-78.
[Mat] Matveev, S.V. (1981), Construction of a complete algebraic knot invariant,
Chelyabinsk Univ., p. 14.
[Matv4] Matveev, S.V. (2003), Algorithmic topology and classification of 3-
manifolds (Springer Verlag).
[MeM] Melvin, P. M. and Morton, H.R. (1995), The coloured Jones function,
Comm. Math. Physics, 169, pp. 501-520.
[Mi] Milnor, J. (1954), Link groups, Annals of Mathematics, 59, pp. 177-195.
[MM] Milnor, J., Moore, J. (1965), On the structure of Hopf algebras, Annals of
Mathematics, 81, pp. 211-264.
[Mnch] Manchon, P.M. (2004), Extreme coefficients of the Jones polynomial and
the graph theory, Journal of Knot Theory and Its Ramifications,lS, N. 2,
pp. 277-296.
[Mof] Moffat, H.K. (1985), Magnetostatic Equilibria and Analogous Euler Flows
of Arbitrary Complex Topology. Part 1. Fundamentals, Journal of Fluid
Mechanics, 35, pp. 117-129.
[Moi] Moise, E.E. (1952), Affine structures in 3-manifolds. V. The triangulation
theorem and Hauptvermutung, Annals of Mathematics, 57, pp. 547-560.
Литература
483
[Моо91] Moody, J.A.(1991), The Burau representation of the braid group Bn is
unfaithful for large n, Bull. Amer. Math. Soc, 25, pp. 379-284.
[Мог] Morton, H.R. (1986), Threading knot diagrams, Math. Proc. Cambridge Phil.
Soc, 99, pp. 247-260.
[Mor2] Morton, H.R. (1988), Problems, In: Braids (Birman, J.S. and A.Libgober,
eds), 78, Contemporary Math., pp. 557-574.
[Mos] Mostovoy, J. (2002), Short ropes and long knots, Topology, 41 (3), pp. 435-
450.
[MS] Mostovoy, J. and Stanford, T. (2003), On a map from pure braids to knots,
Journal of knot theory and its ramifications, 12 (3), pp. 417-425.
[MT] Menasco, W. and Thistlethwaite, M. (1993), A classification of alternating
links, Annals of Mathematics, 138, pp. 113-171.
[Murl] Murasugi, K. (1987), The Jones polynomial and classical conjectures in knot
theory, Topology 26, pp. 187-194.
[Mur2] Murasugi, K. (1987), Jones polynomial and classical conjectures in knot
theory 77, Math Proc. Cambridge Phil. Soc, 102, pp. 317-318.
[Nak] Nakanishi, Y. (1983), Unknotting numbers and knot diagrams with the
minimum crossings, Math. Sem. Notes, Kobe Univ., 11 (1983), pp. 257-258.
[Nel] Nelson, S. (2001), Unknotting virtual knots with Gauss diagram forbidden
moves, Journal of Knot Theory and Its Ramifications, 10 (6), pp. 931-935.
[Ng] Ng, Κ. Υ. (1998), Groups of Ribbon Knots, Topology, 37, pp. 441-458.
[OH] O'Hara, J. (1991), Energy of a Knot, Topology, 30 (2), pp. 241-247.
[OH2] O'Hara, J. (1992), Family of energy functionals on knots, Topology and Its
Applications, 48 (2), pp. 147-161.
[OH3] O'Hara, J. (1994), Energy functionals on knots, Topology and Its
Applications, 56 (1), pp. 45-61.
[OH4] O'Hara, J.(2003), Energy of knots and conformal geometry, World Scientific
(Singapore).
[Oht] Ohtsuki, T. (2002), Quantum Invariants. A Study of Knots, 3-Manifolds, and
Their Sets (Singapore: World Scientific).
[OSz] Oszvath, P, Szabo,Z. (2005), Knot Floer homology, genus bounds, and
mutations, arXiv:mat.GT/0303225.
[Per] Perko, K.A. (1973), On the classification of knots, Notices Amer. Math. Soc,
20, pp. 453-454.
[Piu93] Piunikhin, S. (1995) Combinatorial expression for universal Vassiliev link
invariant, Comm. Mat. Phys., 168, pp. 1-22.
484
Литература
[РР] Paoluzzi, L and Paris, L. (2002), A note on the Lawrence-Krammer-Bigelow
representation, Algebraaic and Geometric Topology, 2, pp. 499-518.
[PT] Przytycky, J. H. and Traczyk, P. (1987), Invariants of Conway type, Kobe J.
Math., 4, pp. 117-139.
[PV] Polyak, M. and Viro, 0. (1994), Gauss diagram formulae for Vassiliev
invariants, Int. Math Research Notices, 11, pp. 445-453.
[Ras] Rasmussen, J. A. (2004), Khovanov Homology and the slice
genus,ArXivMath:/GT. 0402131.
[Rei] Reidemeister, K. (1932) нем.: Knotentheorie, (Berlin: Springer)
англ: Knot Theory, (New York: Chelsea Publ. & Co.).
[Rein] Reinhart, B.L. (1962), Algorithms for Jordan Curves on Compact Surfaces,
Annals of Mathematics, 75, No. 2, pp. 209-222.
[Rob] Robertello, R.A. (1965), An invariant of knot cobordisms, Comm. Pure. Appl.
Math.,18, pp. 543-555.
[Rol] Rolfsen, D. (1976), Knots and Links, Mathematics Lecture Series, 7,
(Berkeley: Publish of Perish).
[RT1] Reshetikhin, N. and Turaev, V. (1990), Ribbon graphs and their invariants
derived from quantum groups, Comm. Math. Phys., 127, pp. 1-26.
[RT2] Reshetikhin, N. and Turaev, V. (1991), Invariants of three-manifolds via link
polynomials and quantum groups, Inventiones Mathematicae, 103, pp. 547-
597.
[Rub] Rubinstein, J.H. (1992), The solution to the recognition problem for S3,
Lectures, Haifa, Israel.
[Satoh] Satoh, S. (2000), Virtual knot presentation of ribbon torus-knots, J. Knot
Theory Ramifications, 9 (4), pp. 531-542.
[Saw] Sawollek, J. (2001), On Alexander-Conway Polynomial for Virtual Knots
and Links, arXiV: math. GT/9912173, 6 Jan. 2001.
[Scha] Scharein, KnotPlot — a program to visualize, manipulate, and physically
stimulate mathematical knots http://www.pims.ma.ca./knotplot
[Seil] Seifert, H. (1934), Uber das Geschlecht von Knoten, Mathematische Annalen,
110, ss. 571-592.
[Sei2] Seifert, H. (1935), Die Verschlingunginvarianten der zyklischen
knotenuberlagerungen, Abh. Math. Sem. Hansischen Univ., 11, ss. 84-
101.
[Sin] Singer, J. (1933) Three-dimensional manifolds and their Heegaard diagrams,
Trans. AMS, 35 (1), pp. 88-111.
Литература
485
[St] Stoimenow, A. (1998), Enumeration of chord diagrams and an upper bound
for Vassiliev invariants, Journal of Knot Theory and Its Ramifications, 7 (1),
pp. 94-114.
[Sta] Staic, M.D. (2004), Pure-Braided Hopf Algebras and Knot Invariants, J. Knot
Theory Ramifications, 13, No.3, pp. 385-401.
[SW] Silver, D.S, Williams, S.G. (2001), Alexander Groups and Virtual Links,
Journal of Knot Theory and Its Ramifications, 10 (1), to appear.
[Tait] Tait, P.G. (1898), On Knots, In: Scientific paper I, pp. 273-274, (London:
Cambridge University Press).
[Tei] Teichner, P. (2002), Knots, von Neumann Signatures, and Grope Cobordisms,
In: Proceedings of the International Congress of Mathematicians, Beijing, 2,
pp. 437-446. (Beijing: Higher Education Press).
[Th] Thistletwaite, M. (1987), A spanning tree expansion for the Jones polynonial,
Topology, 26, pp. 297-309.
[Tho] Thompson, A. (1994), Thin position and the recognition problem for S3,
Math. Res. Letters, 1 (5), pp. 613-630.
[Thu] Thurston, W.P. (1997), Three-Dimensional Geometry and Topology (New-
Jersey: Princeton University Press).
[Tor] Torres, G. (1953), On the Alexander polynomial, Annals of Mathematics, 57
(1), pp. 57-89.
[Tra] Traczyk, P. (1998), A new proof of Markov's braid theorem, In: Knot
theory (Warsaw,1995), (Warsaw: Banach Center Publ., 42, Polish Acad. Sci.),
pp. 409-419.
[Tro] Trotter, H.F. (1964), Non-invertible knots exist, Topology, 2, pp. 275-280.
[Turl] Turaev V.G. (1992), The Yang-Baxter equation and invariants of links,
Inventiones Mathematicae, 3, pp. 527-553.
[Tur2] Turaev, V.G. (1999-2000), Faithful linear representations of the braid group,
Seminaire Bourbaki, n. 878.
[Tur3] Turaev, V.G. (1994), Quantum invariants of knots and 3-manifolds, de
Gruyter Studies in Mathematics 18 (Berlin: de Gruyter, 1994).
[Vas] Vassiliev, V. A. (1990), Cohomology of knot spaces, in Theory of Singularities
and its applications, Advances in Soviet Mathematics, 1, pp. 23-70.
[Vas2] Vassiliev, V. A. (1994), Complements of Discriminants of Smooth maps:
Topology and Applications, Revised Edition, Amer. Math. Soc, Providence,
R.I.
[Ver] Vershinin, V. (2001), On Homology of Virtual Braids and Burau
Representation, Journal of Knot Theory and Its Ramifications, 18 (5),
pp. 795-812.
486
Литература
[Viro] Viro, 0. (2002), Remarcs on definition of Khovanov Homology, arXiv: math.
GT/0202199 vl.
[Vogel] Vogel, P. (1990), Representations of links by braids: A new algorithm,
Comm. Math. Helvetia, 65, pp. 104-113.
[Vogel2] Vogel, P. (1995), Algebraic structures on modules of diagrams, Institut de
Mathematiques de Juissieu, Prepublication, 32.
[Vogel3] Vogel, P. (1999), The Universal Lie Algebra, Preprint.
[Wal] Waldhausen, F. (1967), On irreducible 3-manifolds which are sufficiently
large, Annals of Mathematics, 87 (1), pp. 56-88.
[Wei] Weinberg, N.M. (1939), Sur l'equivalence libre des tresses fermees, Доклады
Академии Наук СССР, 23 (1939), pp. 215-216.
[Witl] Witten, Ε. (1986), Physics and geometry, In: Proc. Intl. Congress Math.,
Berkeley, USA, pp. 267-303.
[Wit2] Witten E. (1989), Quantum field theory and the Jones Polynomial, Comm.
Math. Phys., 121 (1989), pp. 351-399.
[Wit3] Witten E. (1990), Gauge theory, vertex models, and quantum groups, Nucl.
Phys. В., 330, pp. 225-246.
[Zag] Zagier, D. (2001), Vassiliev invariants and a strange identity related to the
Dedekind eta-function, Topology, 40 (5), pp. 945-960.
[Арн] Арнольд, В.И (1996), Особенности каустик и волновых фронтов) (М.,
Фазис).
[Арн2] Арнольд, В.И. (1969), Кольцо когомологий групп крашеных кос. Мат.
Заметки, 5 (2), с. 227-231.
[Атья] Атья, М. (1996), Геометрия и Физика узлов (М.: Мир).
[Бур] Бурман, Ю. М. (1999), Длинные кривые, гауссовы диаграммы и
инварианты Мат. Просвещение, 3, с. 94-115.
[Ва] Васильев, В.А. (1997), Топология дополнений к дискриминантам (М.:
Фазис).
[Ва2] Васильев, В.А. (1997), Введение в топологию (М.: Фазис).
[Гай] Гайфуллин, А.А. (2001), Проекции узлов с единственной точкой
многократного трансверсального пересечения, Труды конференции молодых
ученых - 2001, (М.: Изд-во МГУ).
[Гус] Гусаров, М.Н. (1991), Новая форма полинома Джонса-Конвея для
ориентированных зацеплений. Зап. научных семинаров ЛОМИ, 193, Геометрия
и топология, 1, с. 4-9, 161.
Литература
487
[Дри] Дринфельд, В.Г. (1985) Алгебры Хопфа и квантовые уравнения Янга-
Бакстера, ДАН СССР 32, 1.
[Дро] Дроботухина, Ю.В.. (1991), Аналог полинома Джоунса-Кауфмана для
зацеплений в RP3 и обобщение теоремы Кауфмана-Мурасуги, Алгебра и
анализ, 2 (3), с. 613-630.
[ДЧ] Дужин, СВ., Чмутов, СВ. (1999), Узлы и их инварианты, Мат.
просвещение, 3, pp. 59-93.
[Кае] Кассель, К. (1998), Квантовые группы (М.: Фазис).
[КФ] Кроуэлл, Р., Фокс, Р. (1967), Введение в теорию узлов (М.: Мир).
[Лан] Ландо, С.К., J-инварианты орнаментов и оснащенные хордовые
диаграммы, Функц. анализ и его приложения, в печати.
[МанО] Мантуров, В.О. (2001), Лекции по теории узлов и их инвариантов (М.:
УРСС).
[Ман1] Мантуров, В.О. (2000), Бифуркации, атомы и узлы, Вестник МГУ. Сер.
Матем., 1, с. 3-8.
[Ман2] Мантуров, В.О. (1998), Атомы, высотные атомы, хордовые диаграммы
и узлы. Перечисление атомов малой сложности с использованием языка
Mathematica 3.0, Топологические методы в теории гамильтоновых
систем (М.: Факториал), с. 203-212.
[МанЗ] Мантуров, В.О. (2000), Скобочная полугруппа узлов, Мат. Заметки,
67, (4), с. 449-462.
[Ман4] Мантуров, В.О. (2002), Инварианты виртуальных зацеплений, Доклады
РАН, 384 (1), с. 11-13.
[Ман5] Мантуров, В.О. (2003), Кривые на поверхнотях, виртуальные узлы и
полином Джонса-Кауфмана, Доклады РАН, 390 (1), с. 155-157.
[Манб] Мантуров, В.О. (2003), Атомы и минимальные диаграммы виртуальных
зацеплений, Доклады РАН, 391 (2), с. 166-168.
[Ман7] Мантуров, В.О. (2002), Инвариантный полином двух переменных для
виртуальных зацеплений, Успехи мат. наук, No.???, ее.???
[Ман8] Manturov, V.0 (2003), О распознавании виртуальных кос, Записки
научных семинаров ПОМИ, 299. Геометрия и топология, 8, с. 267-286.
[Ман9] Мантуров, В.О. (2004), Полином Хованова для виртуальных узлов,
Доклады РАН, 398 (2).
[МанЮ] Мантуров, В.О. (2005), О длинных виртуальных узлах, Доклады РАН,
401.
[Мант1] Manturov, О. V. (1986), Мультипликативный интеграл, Итоги науки,
22, с. 167-215 (in Russian).
488
Литература
[Мант2] Мантуров, О.В. (1992), Элементы тензорного исчисления (М.:
Просвещение) .
[МантЗ] Мантуров, О.В. (1991), Курс высшей математики (М.: Высшая школа).
[Мант4] Мантуров, О.В. (1986), Однородные пространства и инвариантные
тензоры, Итоги науки. Проблемы геометрии, 18, с. 105-142.
[Мант5] Мантуров, О.В., Алгебры с неприводимой группой автоморфизмов,
Доклады РАН, 281, (5), с. 1048-1051.
[МанМар] Мантуров, О.В., Мартынюк А.Н., Об одном алгоритме в теории
мультипликативного интеграла, Известия ВУЗов. Математика, 5, с. 26-
33.
[Map] Марков, Α.Α.. (1945), Основы алгебраической теории кос, Труды МИАН,
16, pp. 1-54.
[Матв] Matveev, S.V. (1997), Классификация достаточно больших трехмерных
многообразий, Успехи математических наук, 52 (5), с. 147-174.
[Матв1] Матвеев, СВ.. (1988), Преобразования специальных спайнов и
гипотеза Зимана, Известил АН СССР, 31(2), р. 423-434.
[Матв2] Matveev, S.V. (1982), Дистрибутивные группоиды в теории узлов,
Мат. Сборник, 119 1, pp. 78-88.
[МКС] Магнус, В., Каррас, Α., Солитеэр, Д. (1974), Комбинаторная теория
групп (М.: Наука).
[МФ] Матвеев, СВ., Фоменко, А.Т. (1991), Алгоритмические и компьютерные
методы в трехмерной топологии (М.: Изд-во МГУ).
[Нов] Новиков, СП. (2002), Топология, Регулярная и хаотическая динамика,
М.-Ижевск.
[О] Онищик, А.Л. (1985), Хопфа Алгебра, Математическая энциклопедия, 5
(М.: СЭ).
[Пап] Папакирьякопулос, С .Д. (1958), О лемме Дена и асферичности узлов,
Математика, 2 (4), с. 32-49.
[Пр] Прасолов, В.В. (1999), Поверхность Зейферта, Мат. Просвешение, 3,
pp. 116-126.
[Пр2] Прасолов, В.В. (1995), Наглядная топология, (М.: МЦНМО).
[ПС] Прасолов, В.В., Сосинский, А.Б. (1997), Узлы, зацепления, косы и
трехмерные многообразия, (М.: МЦНМО).
[Сем] Семенов-Тян-Шанский, М.А. (1983), Что такое классическая R-
матрица?, Функц. Анализ и его приложения, 17 (4), с. 17-33.
Литература 489
[Тю1] Тюрина, С.Д. (1999), О комбинаторных формулах типа Ланна и Виро-
Поляка для инвариантов конечного порядка узлов, Мат. Заметки, 64
(6).
[Тю2] Тюрина, С.Д. (1999), Диаграммные формулы типа Виро-Поляка для
инвариантов конечного порядка, Успехи мат. наук., 54 (3), pp. 187-188.
[Fr] Франсис Дж. (1991), Книжка с картинками по топологии, (М.: Мир).
[ФФ] Фукс, Д.Б., Фоменко, А.Т. (1989), Курс гомотопической топологии (М.:
Наука).
[ФЧ] Фарбер М.Ш., Чернавский А.В. (1985), Узлов теория, Мат.
Энциклопедия, 5 (М.: Наука).
[Ч] Чернавский, А.В.. (1963), Геометрическая топология многообразий, В:
Алгебраическая топология. 1962 (Итоги науки и техники. ВИНИТИ АН
СССР), с. 161-187.
[Шу] Шуберт, X. (1966), Алгоритм для разложения зацеплений на простые
слагаемые, Математика, 10 (4), с. 57-104.
Предметный указатель
L^D-Квазигруппа 157
L^D-Система 154
^-матрица 194
d-Диаграмма 10, 225, 258
— меченая 260
г-Ручка 162
/-Движение 143
Абсолютное значение слова-косы 165
Алгебра Гекке 119
— Темперли-Либа 405
Алгоритм Вожеля 137
Арифметика узлов 13
Артина соотношения 107
Атом 255
— высотный 256
Бигруппоид 301
Вилка 126
Виртуализация перекрестка 307
Виртуальная диаграмма 286
Виртуальный узел сингулярный 436
Восходящая диаграмма 6
Выбор переходов 178
Гамильтонов цикл 225
Гауссова диаграмма 262, 292
— реализуемая 262
Гипотеза Васильева 250
Гнездо 137, 164
Голономия 239
Горизонтальная деформация 234
Градуированная размерность 94
Градуированная эйлерова
характеристика 94
Граф Кэли 165
— пересечения 451
Группа виртуального узла 294
— кос стабильная 111
— узла 46
Группоид длинный 365
Гурвица действие 152
Движение Фенна-Рурка 401
— запрещенное 288
Движения Рейдемейстера 16
— Ω4,5 392
— обобщенные 286
Дестабилизация 290
Диаграмма Гаусса 251
— Фейнмана 218
— Хегора 395
— Якоби 229
— альтернированная 18
— виртуальной косы 374
— заплетающаяся 137
— косы 109
— согласованная 463
Дистрибутивный группоид 55, 56
Дифференциальная градуированная
алгебра 428
Дуга 39, 302
Замена бесконечности 44
Замыкание косы 117
— виртуальной 386
Заплетающаяся диаграмма
виртуальная 386
Зацепление 6
— Уайтхеда 7
— Хопфа 7
— виртуальное 288
— длинное 272
- — заплетающееся вокруг точки 135
— лежандрово 416
— тривиальное 7
Зацепление Хопфа виртуальное 293
Зацепление-коса 178
Зеркальное отражение 5
Предметный указатель
491
Зеркальный образ 289
Зигзаг 423
Идемпотент Джонса-Венцля 406
Изотопия зацеплений 6
— кос 106
— лежандрова 419
— узлов 4
Инвариант Арф 35
— Васильева 200
— Решетихина-Тураева 411
виртуальных трехмерных
многообразий 414
— конечного порядка 200
— раскрасок 40
— узлов 4
Индекс Маслова 429
Интеграл Концевича 231
— предварительный 232
Итерационная формула 239
Кольца Борромео 7
Компонента зацепления 6
Конкордантность 37
Контактная структура 416
— стандартная 416
Конфигурационное пространство 107
— упорядоченное 107
Копредставление Виртингера 53
Копроизведение диаграмм Фейнмана
222
Коса 105
— 1-нейтральная 153
— 1-отрицательная 153
— 1-положительная 153
— виртуальная 374
— квазиторическая 275
— крашеная 107
— унарная 191
— утолщенная 114
Коэффициент зацепления 33
— виртуальный 293
Коэффициент самозацепления 34
Кривизна связности 239
Лагранжева проекция π-общая 421
— простая 183
Матрица Александера 75
— раскрасок 368
Меридиан 30
Многообразие Хакена 441
Модуль Васильева 250
Моноид неотрицательных кос 156
Мультипликативный интеграл 239
Неупорядоченная грань 138
Обобщенные числа Бернулли 249
Окружности Зейферта 23
Ось косы 178
Пара Перко 465
— Чеканова 431
Параллель 30
Пасс-эквивалентность 36
Переворачивание слова 165
Перекресток 5
— пол у виртуальный 435
Переполюсованная хорда 261
Плоская диаграмма косы 109
Плоская диаграмма узла 5
Плоская изотопия 16
Поверхность Зейферта 23
Подмногообразие существенное 440
Полином Джонса 81
— Джонса-Кауфмана 80
— Дроботухиной 394
— Кауфмана 82
Дубровник 83
— Кауфмана двух переменных 82
— Конвея 76
— почти альтернированный 102
Правильная двухскобочная структура
272
Правильная раскраска 39
Представление Бурау. 125
— Крамера-Бигелова 131
Примитивный элемент 218
Проекция лагранжева 419
— фронтальная 416, 419
Произведение кос 106
Прошивание 178
Марковская эквивалентность 183
Разбиение Хегора 395
492
Предметный указатель
Расширение на сингулярные узлы 200
Редукция ручки 162
— собственная 164
Род узла 25
Свойство Ρ 464
Связная сумма 19
Связность 239
— плоская 239
Сглаживание 137
Сдвиг высоты 94
Сдвиг градуировки 94
Сжимаемая поверхность 62
Система весов 214
Скейн-пространства 403
Скобка Кауфмана 80
Скручивание Дена 115
Слово свободно редуцированное 159
Слово-коса 108
Сложность узла 5
Собственная поверхность 440
Соотношение Васильева 200
— одночленное 212
Состояние 79
Стабилизация 290
Стебель 127, 133
Сферическая диаграмма 44
Тангл 249
Тень 5
Теорема Ван-Кампена 50
— Гордона-Люкке 46
— Дена 48
— Маркова 182
— о четырех красках 224
Тоннельное число 21
Трехмерное многообразие
виртуальное 413
— гранично неприводимое 62
— достаточно большое 49, 63, 441
— неприводимое 62
Трилистник виртуальный левый 296
— правый 296
Тройка Конвея 66
Трюк Александера 136
Удвоение узла 34
Узел 4
— Лиссажу 463
— виртуальный 288
— восьмерка 5
— дикий 14
— длинный 6, 20, 273
тривиальный 273
— зеркальный 5
— лежандров 419
— морсовский 232
— обратимый 18
— ориентированный 6
— особый 199
— полигональный 13
— простой 22
— ручной 14
— сингулярный 199
— тривиальный 5
— трилистник 5
левый 6
правый 6
Узлы конкордантные 463
Узор 441
Универсальный инвариант Васильева-
Концевича 237
Уравнение Янга-Бакстера квантовое
194
Уравнения Янга-Бакстера 194
Формула Лейбница 208
Фронтальная проекция σ-общая 419
Фундаментальная группа 46
Число Беннекина 425
— Каталана 405
— Маслова 425
— закрученности 80
— заузленности 21, 210
Электромагнитная формула Гаусса 34
Энергия Мебиуса 445
Интересующие Вас книги нашего издательства можно заказать почтой или
электронной почтой:
subscribe@rcd.ru
Внимание: дешевле и быстрее всего книги можно приобрести через наш
Интернет-магазин:
http://shop.rcd.ru
Книги также можно приобрести:
1. Москва, ФТИАН, Нахимовский проспект, д. 36/1, к. 307,
тел.: 332-48-92 (почтовый адрес: Нахимовский проспект, д. 34)
2. Москва, ИМАШ, ул. Бардина, д. 4, корп. 3, к. 414, тел. 135-54-37
3. МГУ им. Ломоносова (ГЗ, 1 этаж)
4. Магазины:
Москва: «Дом научно-технической книги» (Ленинский пр., 40)
«Московский дом книги» (ул. Новый Арбат, 8)
«Библиоглобус» (м. Лубянка, ул. Мясницкая, 6)
Книжный магазин «ФИЗМАТКНИГА» (г.Долгопрудный,
Новый корпус МФТИ, 1 этаж, тел. 409-93-28)
С.-Пб.: «С.-Пб. дом книги» (Невский пр., 28)
Научное издание
Мантуров Василий Олегович
Теория узлов
Авторская редакция
Дизайнер М. В. Ботя
Технический редактор А. В. Широбоков
Корректор 3. Ю. Соболева
Подписано в печать 09.02.2005. Формат 60 χ 84%6.
Печать офсетная. Усл.печ.л. 41,6. Уч. изд. л. 40,32.
Гарнитура Computer Modern Roman. Бумага офсетная №1. Заказ №
АНО «Институт компьютерных исследований»
426034, г. Ижевск, ул. Университетская, 1.
Лицензия на издательскую деятельность Л У №084 от 03.04.00.
http://rcd.ru E-mail: borisov@rcd.ru