ri'taox® яядя«г«
ГЛАВА 4
ПРЕДЕЛ ФУНКЦИИ.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
§ 1. Предел функции
Теория пределов выясняет точный смысл таких понятий,
как «/ (х) приближается к А, если х приближается к а», «/(х)
приближается к А, если х неограниченно возрастает» и др.
Рассмотрим, например, функцию у=х2. Значения этой
функции будут близки к 4, если значения аргумента будут
близки к 2, значения функции будут близки к 25, если значе-
ния аргумента будут близки к 5, и т. д. В этом случае при-
нято говорить соответственно, что значения этой функции при-
ближаются к 4, если х приближается к 2, значения х2 прибли-
жаются к 25, если х приближается к 5, и т. д. Факт, что х2
приближаются к 9 при значении х, приближающемся к 3, озна-
чает, что величина ] х2—9 | может быть сделана как угодно ма-
лой, если брать значения х из соответствующей малой окрест-
ности точки х—3.
Рассмотрим функцию f(x)==x/x. Эта функция определена
при всех х, отличных от 0, и равна 1 для каждого х из обла-
сти существования, и в частности, для всех х, близких к точке
х=0. Поэтому естественно считать, что данная функция стре-
мится к 1 при х, стремящемся к 0, несмотря на то, что функ-
ция не определена в точке x=Q.
Если существует такое число Л, что для любого 8 > 0 най-
дется такая окрестность (а—6; а+6) с центром в точке х = а,
что для каждого х # а из этой окрестности значение функции
f (х) будет принадлежать окрестности (4—-8; А 4-е), то принято
говорить, что (х) приближается к Л, если х стремится к а»,
и записывать это так: «f(x) —> Л, если х —> а» или lim /(х) = Л,
х-+а
В этом случае говорят, что число Л является пределом функции
f(x) в точке х==а.
Для каждогб х, принадлежащего окрестности (а—6; «4-6),
справедливы неравенства
а-*б<х<«4-^ или ^б<х***а<6.
Последнее неравенство записывается так:
|х—а| < 6.
Заметим, что по свойству абсолютной величины |х—а	0 для
каждого х, причем
| х а ]=0, если х=а,
|х«*а[>Ол если х&а.
$ 1. ПРЕДЕЛ ФУНКЦИИ
293
Поэтому все значения х, принадлежащие окрестности (а—б;
#4-6), но не равные а, можно записать следующим образом:
О < | лг—а | < 6;
множество (а—а)Ц(а; «4-6) принято называть проколотой б-
окрестностью точки, а. Для любого значения /(х), принадле-
жащего окрестности (Л—<8; А + &), справедливы неравенства
Л — е < f (х) < Л4-е или — & </(х) — А < в.
Последнее неравенство можно записать так:
Л| < е.
Следовательно, данное выше определение того, что «/(х) —► А,
если х —> аъ> можно сформулировать в другой форме:
число Л называется пределом функции f(x) при х —> а,
если для любого положительного числа е существует число
6(e) > 0 такое, что для каждого х, удовлетворяющего условию
О < | х—а | <6, выполняется неравенство
|/(X) —Л | < 8.
Из определения предела функций в точке х—а следует,
что если функции f(x) и g(x) таковы, что f(x) — g(x) в некото-
рой окрестности точки х==а, кроме, быть может, точки х=а,
и lim f (х)~ Л, то Пто(х) = Л.
х->а	х-*а'
Геометрически тот факт, что А является пределом функции
f(x) при х —> а можно проиллюстрировать следующим обра-
зом (рис, 4.1, а):
для произвольного положительного в можно найти такое
положительное 6, что все точки (х; f (х)) графика функции у =
= f(x) при xg(a—6; a)(J(«; п + б) будут лежать внутри поло-
сы Л—«8 < у < Л4-8, при этом, если f (х) определена при х = а,
точка (a; f (а)) не обязательно принадлежит этой полосе
(рцс. 4.1, б).
Опишем, как, пользуясь геометрическими соображениями,
по любому положительному 8 можно найти число 6(e).
Рассмотрим произвольное положительное число е. На оси
OY отметим точки с ординат?ми Л, Л —8 и Л + е. Через точки
с ординатами Л—>8 и Л+8 проведем прямые, параллельные
оси ОХ, В горизонтальной полосе между прямыми у~А—е и
у=^А-}-ъ лежат все те точки (х; f (х)) графика функции у = /(х),
для каждой из которых справедливо неравенство | / (х) — Л| < 8.
Отметим на оси ОХ точку х—а. На оси ОХ найдем все точки
х около точки х = а, для каждой из которых соответствующие
точки графика функции y=f(x), т. е. точки (х; f(x)), х^а,
лежат в полосе Л—е < у < Л^-е. На рис. 4.1,в видно, что для
каждого х (х yfe а) из промежутка (а; р) точка (х; f (х)) лежит
в указанной полосе. Длину меньшего из двух промежутков
(а; а) и (а; Р) обозначим через 6. Тогда для каждого х^а,.
удовлетворяющего неравенству a—6<x<a-f-6, справедливо
неравенство А—8 < f (х) < Л + 8. Ясно, что в качестве 6 можно
также взять любое положительное число, меньшее найденного.
294 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Пример 1. Доказать, что
lim (Зх+2) = 8.
х->2
Решение. Надо доказать, что для любого 8 > 0 найдется
6>0 такое, что для каждого х, удовлетворяющего условию 0 <
< |х«*2| < б, справедливо неравенство | (Зх+2) -*81 < 8. Тан
как
| (3x4-2)^81 == | Зх-*61=31 х—21,
то для 6=8/3 и каждого х, удовлетворяющего условию
О < |х«**2| < 6=8/3, имеем
|(Зх4-2)—8| = 3|х—2| < 36яя34=«8.
О
Поскольку приведенные рассуждения верну для любого 8 > О,
’о тем самым доказано, что Пщ (3x4-2)=8.
2
Пример 2. Доказать, что
Решение. В определении предела функции при х —>
аргумент х не может принимать значение, равное at Тан как
§1. ПРЕДЕЛ ФУНКЦИИ
295
х2—9
при х # 3 имеем ^^jr—x+S, то предел данной функции при
х—>3 совпадает с пределом функции f(x) — х-|-3 при х —> 3.
Возьмем произвольное е > 0 и по нему подберем 6 такое, что
для каждого х, удовлетворяющего условию 0< |х—3| < 6,
справедливо неравенство | (х + 3)—6| < 8. Так как | (х+3)—61 =
= |х—3|, то, например, для 6 = 8/3 имеем, что для каждого х,
удовлетворяющего условию 0 < |х—3| < 6, справедливо нера-
венство
| (х+3)—61 = | х—31 < 6=е/3 < е.
хч__9
Тем самым lim (х+3) = 6, а следовательно, Нт ----5~=6.
у ->• 3	3 Х’—о
Пример 3. Доказать, что функция f (х) = | х |/х при х —* О
предела не имеет.
Решение. Доказательство проведем от противного. Пред-
положим, что при х —> О функция /‘(х) = |х|/х имеет предел,
равный А. Это означает, что для любого 8 > 0 существует та-
кое 6(e), что |/(х)— Д| <8 для каждого х, удовлетворяющего
условию 0 < | х | < 6. Тогда, в частности, и для 8 = 1 сущест-
вует 61 такое, что для каждого х, удовлетворяющего условию
О < | х| < 6i, имеем
\	\f (х) — А\< 1.
Так как при х > О имеем f (х) = |х|/х = 1, а при х < 0 /(х) =
= |х]/х=-4, то при 0 < х <61
|1—Л|<1,	(1)
а при 6f < х < О
|-1-/1| = |1 + Л| < I.	(2)
Из неравенства (1) имеем 0 < А < 2, а из неравенства (2) име-
ем —2 < А < 0. Итак, если число А является пределом данной
функции, то, с одной стороны, А должно быть положительным,
а с другой—отрицательным, что невозможно.
Из полученного противоречия вытекает, что предположение
о существовании предела функции f(x) = |x|/x при х —> 0 не-
верно.
Пример 4. Доказать, что
a)	lim sinx=sinx0; б) lim cosx = cosx0.
X Xq	к —•> Xq
Решение, а) Возьмем произвольное 8 > 0 и по нему под-
берем 6 (е) > 0 такое, что для каждого х, удовлетворяющего
условию 0<| х—х0| <6, справедливо неравенство | sin х—sinx0| <
<8. Используя неравенство | sin х |	| х |, справедливое дл-
каждого х, получаем
| sin х— sin х01 = 2 cos
х + %о
2
. X — х0
sin—2^
, X Хо I .	
sin——- <|x—x0|
296 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Если, например, взять 6 = е/10, то для каждого х, удовлетво-
ряющего условию 0 < | х—х0 | < 6, выполняется неравенство
|slnx—sin х0 |<|ж—• аг0 | < 6 = 8/10 < е.
Тем самым доказано, что lim sinx=sinx0. В	частности $
lim sinx=0;
%-> о
б)	аналогично предыдущему, если для любого положитель-
ного числа е взять, например, 6 = 8/4, то для каждого х, удов-
летворяющего условию 0 < ]х—х0| < 6, имеем
|о . Х4-Хо . х —Хо
2 sin —sin —<
&	I
< 21 sin -	<|х—х0| < 6=~ <в,
а это означает, что lim cosx = cosx0. В
Пример 5. Доказать, что
КяЧП— 1
частности, lim cosx=l.
О
0 X
Решение. При х 0
1	1)(К^+7+0 x2+i-i _
*	х(Г^П + 1)	x(j/F+T+i)~
_____X___
“ /х*+Т+ 1 '
Так как при каждом х справедливо неравенство Ух2+14-1 > 1,
то при каждом х # 0 имеем
I х I . ,
Возьмем произвольное в > 0 и положим, например, 6=8/2.
Тогда для каждого х, удовлетворяющего условию 0 < | х | < 6,
справедливо неравенство
. х
К^+1+i
О <|х|<б=|<8.
Это по определению означает, что lim	----==0, а зна-
х~> о у х2+ 1 + 1
ЧИТ| и
lim
х->0
У х2+1 —1
X
х~>0 }<х2+ 1 + 1
=0.
Для функций* имеющих предел, имеют место следующие
утверждения:
§ L ПРЕДЕЛ ФУНКЦИИ	297
1.	Если предел функции ^ = /(х) при х—+а существует, то
он единствен.
2.	Если функция y~f(x) при х —> а имеет предел, то у
точки х = а существует окрестность (a—d; a)(J(a; а+6), на ко-
торой функция f (х) ограничена.
3.	Если lim f(x) = A и А > О (Л < 0), то существует окре-
х -> а
стность точки х — а такая, что для каждого х из этой окрест-
ности, кроме, быть может, х=а, имеем f (х) > A (f (х) < Л).
4.	Если функция f (х) тождественно равна постоянной С,
то lim f(x)^=C.
х-+ а
5.	Если lim f (х) = Л, то существует предел функции у =з
г-> а
= |/(х)| при х—>а, и он равен | Л |, т. е.
lim | f (х) | = | Л |.
х -> а
6.	Если точка х=а вместе с некоторой окрестностью при-
надлежит области существования элементарной функции f(x)t
то существует предел функции f (х) при х —и он равен f (а),
т. е.
Um =
х-+а
7.	Если lim /(х) = Л, и lim g(x) = B, то
х-+ а	х-*а
а)	существует предел функции f(x)+g(x) при х —> а, и он
равен Л + В, т. е.
lim (f(x)+g(x))=^ lim Дх) + lim g(x) = A + B;
x-+ a	x ~>a	x-> a
б)	существует предел функции f(x)—g(x) при x—±at и он
равен Л—В, т. е.
lim (/ (х) — g(x))^ lim f (х) — lim £(х) = Л—В;
х-+ а	х-> а х-+а
в)	существует предел функции f (х) g (х) при х —* а, и он
равен ЛВ, т. е.
lim (/(x)g(x)) = lim /(х) lim £(х) = ЛВ;
х-+ а	х-+ а х-+а
в частности, если С—константа, то существует предел функции
С/(х) при х—и он равен СЛ, т. е.
lim Cf(x) = С lim /(х) = СЛ;
х —>а	х—> а
г)	при В 0 существует предел функции f{x)lg{x} при
х—и он равен Л/В, т. е.

lim
х-+а
lim f(x)
x-> a
Um g(x)
x-*a
A
В *
298 гл. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
8.	Если lim f(x) = A, lim g(x) = B и существует окрест-
а	а
ность точки х = а, для каждого х из которой, кроме, быть мо-
&ет, х = а, справедливо неравенство f (x)^g (х), то 4<:В, т. е.
lim f (х) «с lim g (х).
х -> а	х-+а
Отметим, что если вместо неравенства f (х) «С g (х) выпол-
нено неравенство f(x) <g(x), то все равно можно утверждать
только, что
lim f(xX lim g(x).
xa	xa
Например, для функции f (x) = | sign x | и функции g(x) = l+x2
имеем f(x) < g(x), однако
lim (1 + x2) = lim |signx| = 1.
x-> о	о
9.	Если lim /(x)= lim g(x)—A и существует окрестность
x-> a x-+a
точки x=a, для каждого x из которой, кроме, быть может,
х = а, справедливо неравенство /(х)	(х) «Cg (х), то сущест- '
вует предел функции h (х) при х —> а, и он равен 4.
Пример 6. Найти
lim (10 sin2 х+3 cos3 х+^=^
х-> О \	Х + 2
Решение, Так как
lim sin2 х—[ lim sin х]2 = 0,
0	х-> 0
lim cos3 х = [ lim cos x]3 «= 1,
-?Лх+2 lim (x+2)	2’
x -> 0
то на основании утверждений 6 и 7 имеем
(у 1 \
10 sin2 х+3 cos3 хЧ ) =
Х + 2/
= lim 10sin2x+ lim 3cos3x+ lim	0 + 3—-=-5..
Пример 7, Найти
x2 —1
hm -Г| g-£•.
x-^1 x2+5x—6
Решение. Так как x2 + 5x—6 = (x—1) (x + 6) и для лю-
бого x Ф 1
х2—1	_(х— 1)(х+1)_х+1
х2+5х—6 (х—1) (х+6)“"х+6’
§ 1. ПРЕДЕЛ ФУНКЦИИ
299
то
„ ,	. , lim (х+1)	„ '
..	х2—1	__.	х+1___х-»1	__2
/*”1 х2+5х—6“	Н6“ Um («+6)— 7*
I
поскольку lim (х+6)=7^0и lim (х4-1)=2,
ЛС-> 1	1
Пример 8. Доказать, что
lim -i—!—:-------------------=m,
к->0 X
где т—некоторое натуральное число.
Решение. По формуле бинома Ньютона имеем при х О
X	X	~~
=/714-----L х+ *., +**»**•
Так как для любого натурального числа k имеем 11шял=я0, то
х-* о
.. П+дгР—-1	, т (т—1) .	, m .Д
lim *-  	----- lim । /п-|-Цг—-х+.>. + хт~* )=з
X	х -> о \	&	/
= lim т 4- lim —~ х-|- *.. 4- lim
х->о х -*о	2
Приведем следующие часто встречающиеся пределы:
т sinx ,
I. lim-----=1.
х->0 х
II.	Нт (14-х)1/ж=в.
О
III,	Um !н£±*)=1.
х-> X
IV.	Ita,	о^О.
жно х
У. lim	in а, а > 0, а L
X ->0 X
Пример 9. Найти
.. sin ах
lim 3 -л-,
о sin рх
а(3 О»
Решение, Заметим, что теорему о пределе частного
применить нельзя, таи каи limsinpx»=o. Вычисляем предел
90Q гл. *. предал функции, непрерывность функции
следующим образом:
lim	Ит _Д-----------
к -*) ita рх к «* о staft*
sin ах	.. sin ах
......... -	lim —
lim а а* __а ах	У
** ***° Р sin fix Т Цт sin рх р *
ffx	₽Х
Здесь использован следующий факт: если х —► О, то и ах —► 0.
Поэтому
UmMU lim ^=lim =1.
х«*о ах ах«*о	и и
Пример 10. Найти
Ит ?.+с”.Ч
Х-ф-Л/2 COSX
Решение»
.. J4-cos2x „ 2cos2x
lim	—-я- Пт ---------------
Х-ф—Л/2 COS X	Х->—Л/2 cos X
Um 2cosx=0.
Я-ф-Л/2
Пусть функция f (х) определена внутри некоторого интер-
вала, содержащего точку а, за исключением, возможно, самой
точки Говорят, что функция f(x) при х—>а стремится
к +оо, и при этом пишут
lim f(x)=+oo,
х+а
если для любого числа Е > 0 существует такое число 6 > 0,
что для каждого х, удовлетворяющего условию 0 < |х—а| '< 6,
выполнено неравенство
f(x)>E.
Пусть функция f (х) определена внутри некоторого интервала,
содержащего точку а, за исключением, возможно, самой точки
х=а. Говорят, что функция f(x) при х—>а стремится к — оо,
и при этом пишут
lim /(х)=—оо,
х->а
если для любого числа Е > 0 существует такое число 6 > 0, что
для каждого х, удовлетворяющего условию 0 < | х —«а | < б,
выполнено неравенство
/(х) <*—Е.
Пусть функция f (х) определена внутри некоторого интер-
вала, содержащего точку а, за исключением, возможно, самой
точки х-с, Говорят, что функция / (х) при х—у а бесконечно
§ i. йрёдел Функции r ’ 30Р
большая или стремящаяся к оо, и при этом пишут
lim f (х) «= оо,
х->а
если
lim | f(x) |=4-oo.
X-+O
На рис. 4.2, а изображен график функции, которая при
х—>а стремится к +оо; на рис. 4.2, б—-график функции,
которая при х—>а стремится к —оо; на рис. 4.2, в—графим
функции, которая при х—стремится к оо.
Рис. 4.2
Из определений следует, что если при х—► а функция f(x)
стремится +оо или к — оо, то она является бесконечно боль-
шой. Однако если функция f (х) при х—бесконечно боль-
шая, то при х—>а она не обязательно стремится к 4-оо или
к —оо (рис. 4.3).
Пример 11. Доказать, что для функции
f W “ (л—1)«(х—2)(х—3)3
имеют место следующие соотношения:
a), lim f (х)=—оо;
Х-* 1
б) lim /(x) = 4-ooj
х*>3
в) limf(x) = oo.
2
Решение, а) Так как в этом случае рассматривается
предел функции при х, стремящемся к 1, то достаточно рас-
сматривать функцию при значениях аргумента, близких к еди-
нице, например для х, удовлетворяющих неравенствам 0 <
302 гл. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
< |х-*1 | < 1/2. При всех таких х имеем неравенство
f 1 __ 8 1
’5<«-
Возьмем произвольное положительное число Е. Для доказа-
тельства соотношения а) нужно подобрать такое б, 0 < б < 1/2,
Рив< 4.3
чтобы для каждого х, удовлетворяющего условию 0 < | х— 11< б,
выполнялось неравенство
(3)
Так как
75(X_ip
при 0 < ] х—11 < 1/2, то подберем число 0 < б < 1/2 таким,
чтобы для каждого х, удовлетворяющего неравенству 0 < I х-*-11 <
< б, и для числа Е выполнялось неравенство
г 8 I— £
75 (х— 1)? <	’
или
..1_> т/Ж,
|х—1 | V 8
Это неравенство при условии 0 < |х—11 < б равносильно не-
равенству
 v-lKl/"-2^2	1
1	11 < V 75 Е~ /75
fl. ПРЕДЕЛ ФУНКЦИИ
303
Отсюда следует, что если в качестве 6 взять наименьшее из
2/2 11	.
чисел—~=--т= и-х-, то неравенство (3) будет выполнено!
5 У 3 V Е
тем самым соотношение а) доказано.
б) Доказательство соотношения б) можно провести анало-
гично тому, как это делалось в п. а). Для этого заметим, что
при 0 < | х—31 < 1/2 имеем неравенство
1 I 1	__8	1
/ W^i7/2_2 (7/2— 1>а (х—З)2 ~~75 (х—З)2*
в) Так как при 0 < | х—2 | < 1/2 имеет место неравенство
х-2|(|-Зу=
2| < 6|х—2|,
то на множестве 0 < |х—2| < 1/2 имеем
HWI > 6|Jt—2|‘
Возьмем произвольное положительное число Е. Если в качестве
числа б выбрать такое число, чтобы были одновременно выпол-
нены неравенства 0<6<~-Hgg>£, т. е. неравенства 0 <
<б<-~иб<^,то тогда из (4) получим, что для выбран-
ного числа Е существует число б, например, число б == min
> 0, такое, что справедливо неравенство | f (х) | > Е для
каждого х, удовлетворяющего неравенству 0 < | х—2 [ < б. Тем
самым доказано соотношение в).
График функции /(х) приведен на рис. 4.4,
|х— 1 р | х—2 11 х
(4)
Рио, 4,4
304 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Для бесконечно больших функций справедливы следующие
утвер жден и я:
Пусть каждая из функций f(x) к g(X) определена в неко-
торой окрестности точки х=а, кроме, быть может, самой точки
х — а (проколотой окрестности точки х=а), тогда:
I. Если Нт /(*) = + 00 и Ит 8 (*)=+*»
 х-*а	х-+а
а) UnHfW+g(*))==+»»
6)*lim(f(x)g W)=+oo.
II, Если lim f(x)=+oo и lim g(x)=—’оо, to
x+a	x-+a
a)	Hm (/(*)—g(x))=4-oo;
x-+a
6)	lim (/W g(x))=—oo.
x~+a
III.	Если lim /(*)=+оо и lim g(x) = At to
x-+a	x-+a
a)	Hm (f(x)g(x))=+oo, если A > 0;
6)	lim (f (x) g (x)) =—оо, если A < 0.
x-+a
IV.	Если lim f(x)=—oo, to
x-+a
a)	lim f2»(x)=+oo, ngN;
x~ta
6)	lim рп+Цх) = —ъ, ngN.
x-+a
V.	Если lim f(x)=+oo, T0
x-+a
lim f(x) = 4-oo, n^2, ngN.
x-+a
VI.	Пусть lim f (x)==+00 > т°гда:
x-t-a
а)	если g(x)^m> 0 в некоторой проколотой окрестности
точки х=а (т. е. всех х таких, что 0<|х—а]<6), то
lim (f (x)g(x)) =+oo;
б)	если g(x)<M <0 в некоторой проколотой окрестности
точки то
lim
х-+а
VII,	Если lim /(х) = 4-оо, то
&-*а
$1, ПРВДЕЛ ФУНКЦИИ	- 305
УЩгЕсли lim /ф)=О и f (х) & 0 в некоторой проколотой
х-*а
окрестности точки х=а, то
Иш-77-7 = 00,
х-*а f (х)
Например,так как для функции из примера И
„	1	1	I
lim т-tvs=+©о и lim ------------575=—,
x-+i(x— 1)а	*->i(x—2)(х—3)*	4'
то по утверждению III. б) имеем, что
(х-1)Чх-2)(х-3)г==~°°-
Пример 12. Доказать, что
Решение. Так как
lim -т—-=4-оо
1 х |	1
и в некоторой окрестности точки х=0 имеем cosx ^51/2, то
по утверждению VI. а) заключаем, что
.. cos х ,
lim п—г=4-оо.
х-01*1
Пример 13. Доказать утверждение VI. б)
Решение. Поскольку g(x)^M < 0 в некоторой проко-
лотой окрестности точки х=а, то это значит, что существует
6i > 0 такое, что для каждого х, удовлетворяющего условию
О < | х—а | < 6i, справедливо неравенство g (х)^М. Возьмем
произвольное положительное число Е. Так как Jim f (х) = 4-00,
то для числа £7| М | существует такое число 62 > 0, что для
каждого х, удовлетворяющего условию 0 < | х*-а | < 62, имеет
место неравенство
> риг
Если взять 6=min (6Х; 62), тогда для каждого х, удовлетво-
ряющего условию 0 < |х—а \ < 6, справедливо неравенство
/И8И<^<г4|*< — В.
Тем самым утверждение VI. б) доказано.
Пусть промежуток [а; +<эо) входит в область определения
функции /(х). Число А называется пределом функции f(x) при
х—если для любого положительного числа е найдется
такое положительное число А, что для каждого х, удовлетво-
306 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
ряющего условию х > А, справедливо неравенство | f (%) — А | < 8J
при этом пишут
lim f(x)~A.
Х-* +00
Пусть промежуток (—оо; а] входит в область определения
функции f(x). Число А называется пределом функции f(x) при
х—> — оо, если для любого положительного числа 8 найдется
такое положительное число Д, что для каждого х, удовлетво-
ряющего условию я < — Д, справедливо неравенство |/ (х)-~А |<в;
при этом пишут
lim /(х) = 4.
Пример 14. Доказать, что
Ura ^тт=0-
X -* + оо X* -j- 1
Решение. Возьмем произвольное положительное число 8.
Требуется доказать, что существует Д такое, что для каждого х,
удовлетворяющего условию х > Д, выполняется неравенство
ьЬ-<8’	__
Действительно, если взять, например, число Д==^ 1/е, то
для каждого х, удовлетворяющего условию х > Д (Д > 0), имеем
1 1 1 — 1 _
ТП5* < х* < Д** (У' цф
Пусть каждый из промежутков (— ©с; а] и [&; + ©о), а,
входит в область определения функции f (х). Число А называется
пределом функции f (х) при х—>©о, если для любого положи-
тельного числа 8 найдется такое положительное число Д, что
для каждого х, удовлетворяющего условию | х | > А, справед-
ливо неравенство \f (х)«*~Л| < в; при этом пишут
Um f(x) = A
оо
Пример 16. Доказать, что
lim ~т;®=0, п > 0«
Х-»>оо X
Решение. Возьмем произвольное положительное число 8.
Требуется доказать, что существует А такое, что для каждого х,
удовлетворяющего условию (х | > А, выполняется неравенство
11/х» | < 8«
Действительно, если взять, например, число А «= 1/8 то для
каждого х, удовлетворяющего условию | х | > А, имеем
§1. ПРЕДЕЛ ФУНКЦИИ
307
Отметим, что утверждения, приведенные на с. 297—298, спра-
ведливы и для пределов функции при х—>+оо (х—оо или
х—> оо). Например, если lim f(x)~A и lim g(x) = B, то
Х-+ +<Ю	Г-+ +00
lim (/(х) + §(х)) = Л+В, Um (f (х) g (х)) = Л5;
+ 00	х-+ + оо
если В 0, то
lim
д^+оо g(X)
А
В
и т. д<
Пример 16. Найти
.	1-	4х—1	х34-1
a	) lim --т; б) lim --------.
' х-> + оо х—2	' х_>-оох8+х2Ч-х+1
Решение. Так как при х#0
то, применяя соответствующие утверждения, получаем
a) lim
4—L
lim ---
X—”*£	£-* + <*> ।
X
lim (4—4— lim
jy-»4-oo \	X /______X—X
Вт (1------)	1— hm —
JC-> + oo \	X/	Х->+<» X
1J- —
яЗД.1	v3
б	) lim	—о-:---г-7= Hm ----------:-г-г—=Н.
7	А34“Х2 + Х-}-1	х-*-°° 11^-t j I *
^'х*х*"ГхЪ
Пример 17, Найти
lim (К я-+#****)•
+ да
308 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Решение,
lim	Ит	=,
Х-* + ”°	х-*+оо	у хг-\-Х-\-Х
= 11Ш —7=====------= lim    '7 	----S3»
х->+<»	х->+оо х(К1+ 1/^+0
« 1	1
х->+« Kl+l/x+l	2
Пример 18. Найти
4	V~9x*+l — Ух* + 1 .
a)	hm ------.1..—, £--LX ।
Х->+<Ю	j/ £3_|_2
Кэ^+Г-УТ+Т
б) 1Ш1 ------ .
Х-Э--00	i/x* + 2
Решение.
a)
,.m K9x2 + 1- У^ + l
lim ------yt===2==-----’=»
*->+<»	x3 +2
$ !. ПРЕДЕЛ ФУНКЦИИ
309
Пусть промежуток [а; + оо) входит в область определения
функции f(x). Если для любого положительного числа М су-
ществует число N такое, что для каждого х, удовлетворяющего
условию x>N, справедливо неравенство f(x) > М, то говорят,
что функция f(x) при х, стремящемся к + оо, имеет предел, рав-
ный + ПРИ этом пишут
lim /(%)==+оо.
Например,, lim х2 = + оо, так как для любого положи-
X -*+СО	__
тельного числа М существует число AZ = )/"Л4 + 1 такое, что
при каждом х > /V справедливо неравенство
х2 > № = (//И + 1)2 > (У"М)^=М.
Аналогично определяются пределы при х> — оо их—> оо.
Приведем некоторые часто встречающиеся пределы:
С	С
1.	lim -5-=ss-|-oo, lim -о—г==оо, С=const, С > 0, ngN.
X -> о X2n	х _>ox2n*	» ч.
2.	lim Cx2« = +oo, lim Cx2«-“x = —00,
X + 00	X ->-00
lim Cx2n~i = + 00, C=const, C > 0, ngN.
QO
3.	lim -2-=0, C—const, n£N.
x -> «> xn
4.	um	=
x -*+<*> bmxmx+».,+&0
О, если
-~L если
bm
00, если
— оо, если
n < tn\ tn, ngN, bm Ф 0,
n^=tn\ ngN, bm 0,
n > tn', tn, rcgN, anbm >0,
n > m; n, mgN, anbm < 0.
310 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
5.	a) lim аАГ = + со, если 0 < а < 1;
Х->-оо
б)	lim я* —0, если 0 < а < 1.
Х->+оо
6. a) lim	=-[-оо, если а > 1;
X ->+ а>
б) lim ах = 0, если а > 1.
#-►-00
ах	хп
7. а) Ит -—=4-оо, Ит —=0, если а>1, ngN;
' х"	*-+«> ах
пХ	х^
б) lim —'=0, lim —«оо, если а > 1, ngN.
8) a) lim -2--=0, lim -~г-= + оо, если 0 < а < 1, wgN;
X ->.4-00 X"	х -> + оо а*
б) lim -^--sssoo, lim -^--=0, если 0<а<1, ngN.
' Х^оо Хп	х->-^ <*х
Иногда полезно пользоваться понятиями односторонних
пределов функции f(x) при х —► а—понятиями предела справа
Рио* 4*5
и предела слева, которые определяются соответственно следу-
ющим образом:
предел функции /(х) справа при х—+а
lim	Hm/(а+1И);	(5)
х->а+0	f->0
предел функции f(x)	слева	при х—>а
lim f(x)« lim	(6)
Отличие в определениях односторонних пределов функции
в точке х=а от определения предела функции в точке х=а
состоит в том, что на способ стремления переменной х к числу
а в определениях односторонних пределов накладываются огра-
ничения: при определении предела справа переменная х долж-
на быть больше а, а при определении предела слева перемен-
ная х должна быть меньше а (это и выражают правые части в
равенствах (5), (6)).
§1. ПРЕДЕЛ ФУНКЦИИ
311
Так, например, для функции /(х), график которой приве-
ден на рис. 4.5, а, имеем равенство lim f(x)~ А, а для
_________________	х->а + 0	_
функции у~У х (рис. 4.5,6)—равенство	lim Ух =0.
х -> 0 + 0
Имеет место следующее утверждение: для того чтобы функ-
ция f (х) при х—имела пределом число Л, необходимо и
достаточно, чтобы выполнялось равенство
lim f(x)~ lim f(x) — A.
x -> a + 0	x -> a-0
Пример 19. Найти lim f(x), если
x-+ 1
*2 + 3x+4, x > 1,
| 7x2+l, x<l.
Решен ие. Так как
lim f(x)=lim f(l+P|) = lim ((1+P |)2 + 3 (1+p |)+4) =
1+0	t-+ 0	0
= Kmo (8+5 PH-1 N2) = 8,
lim f(x)=lim /(I—J H)= Um (7(1—1/1)^ + !) =
x-> 1—0 Z *-> 0	/->0
= limo (8—14 p |+7 Pl2) =8
и lim /(x) = lim /(x), to lim f (x)=8.
x -> 1 + о	x -> i - о	x -> 1
Пример 20. Выяснить, имеет
ли функция

sin x
x 9
1
у COS Xt
предел при х 0.
<Г	г Sin|/| .	..	1 Ijtl 1
Решение. Так как lim —cos р = — и
|q / о 2	11	2
lim f(x) = l#4-= lim f(x}, то данная функция не имеет
х •+ о+	* X о—
предела при х —> 0.
Отметим также, что определения предела функции f (х) при
х—> + оо, х—>— оо и х—> оо могут быть даны соответственно
следующим образом:
lira /(*)== lim f (т-тА lim f (х)= lim f f— +
X -> + «>	t Q \ I* I / X ->-00	I -f 0 \ PI
lim f(x)= lim f (Д-\
X •* «>	о \ * /
312 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
По
аналогии с предыдущим считается, что
a)	lim /(л) = 4-00, если lim f(a+|/|) =+oo;
*->а+о	/->0
б)	lim f(x) =+oo, если lim / («—I /
X-*a~Q	/ —> О
Так, например, для функции /(*) =
1
(х-1)2 (х-2) (х-3)2
имеем
lim /(х)=—00,
х-* 1-0
lim /(х)=— 00,
*-> 2-0
lim f(x) = -|-oo,
*->3-0
lim f(x)=O,
X ->-00
lim /(*)=—ooj
*-> 1+0
lim /(*) = +00;
*-> 2+0
lim /(%) —+00;
x-> 3 + 0
lim f(x)~O.
*->+<»
Приведем следующие часто встречающиеся пределы:
I. a) lim logax=— со, если а> 1;
*->о+о
б) lim loga х== + оо, если а > 1.
х ->+ 00
II.	a) lim logax=+ со, если 0 < а < 1;
х~>0 + 0
б) lim logax=— 00, если 0 < а < 1.
*->+<»
III.	lim хп logtf х=0, а > 0, a^l, n^N.
*->о+о
f 1 \*	/ IV
IV.	lim (1+— =* lim ( 1I =<?.
x ->+<» \ x J x ->-«> \	% )
ЗАДАНИЕ 1
1.	Какие из функций, графики которых приведены на
рис. 4.6, имеют предел в точке х=1?
2.	Для функции f(x)=x2 и заданного числа 8> 0 указать
число 6 такое, что для каждого х, удовлетворяющего условию
0 < | х—“21 < б, справедливо неравенство | х2—41 < 8, если:
1)8 = 1; 2) 8 = 1/2; 3) 8 = 1/4; 4) е = 80.
3.	Пользуясь определением предела функции в точке, до-
казать, что:
1) lim (2х—1)=3; 2) lim (х24-2) = 6; 3) lim *3=1;
х-> 2	х-> 2	х-> 1
4)	lim cosx=cosx0; 5) lim	х0 # 0;
*->*о	X^XqX X(j
6) lim
*->*o
4. Доказать, что если lim f(x)=A и функция y~f(x)
*->*o
определена в точке х=хо, то в некоторой окрестности этой
точки функция является ограниченной.
§1. ПРЕДЕЛ ФУНКЦИИ
31Э
ЗАДАНИЕ 2
1.	Привести пример функции # = /(*)> удовлетворяющей
условию:
1)	lim /(х) = 3;
х -> 2
2)	функция у ~ f (х) не имеет предела в точке я = 2$
Рис. 4.6
3)	функция y~f(x) определена на всей числовой прямой и
не имеет предела ни в одной точке этой прямой.
2.	Для функции /(х) = 2х+3 и заданного числа е > О ука-
зать число о такое, что для каждого х, удовлетворяющего
314 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
условию 0 < | х—31 < 6, справедливо неравенство | (2х+3) — 91 <
< 8, если:
1)е = 1; 2) 8 = 1/2; 3)8 = 0,001; 4) е = 80.
3.	Пользуясь определением предела в точке, доказать, что:
1)	lim (Зх — 7) =2; 2) lim х* = 1;
3	х-> I
3)	lim sinx = sinx0;	4) lim К х = /”хо, х0 > 0.
X *0	х х0
4.	Доказать, что если lim /(х) = Л, А > 0, функция у =
Х-*Х0
= / (х) определена в точке х = х0 и f(xo)>O, то в некоторой
окрестности этой точки функция у=/(х) принимает только по-
ложительные значения.
ЗАДАНИЕ 3
1. Известно, что lim /’ (х) == Л и lim g(x) = B. Найти:
1) lim /«(х), ngN; °2) lim (/1 2 (x) + g(x));
X х0	х -> х0
3) lim (fW+l)teW-2); 4) Пт
5) lim (х/ (х) + x2g (х));	6) lim g (х) sin f (х).
X Хо	х х$
2. Найти:
1) lim f2x2 +—4-3x— 1); 2) lim (x3+2cosx);
X 1 \	X	/	X -► Л/4
3) lim (sin x) (4x2+l); 4) lim	;
5) lim (2—x)10;	6) Um	.
3. Доказать, что если lim f (x)=0, to lim sinf(x) = O.
x X0	X -> Xo
4. Привести пример функций y — f(x) и у — g(x)t каждая
из которых не имеет предела в точке х = 0 и таких, что их
1) сумма; 2) произведение
имеет предел в точке х=0.
ЗАДАНИЕ 4
1. Известно, что lim f(x) — A и lim g(x) — B. Найти:
х -> х0	х -> х0
1) lim (PW-^U)+2); 2) lim
X ->x0	X -> Xo ё W 4
3) lim cos/(x); 4) lim j/"/2 (x).
X ->• Xo	X -> x0
2.	Найти:
1) lim (x3—3x2-f-2x-f-l); 2) lim xsinx; 3) lim — b * .
X->2	X-*2	X-f-2
§1. ПРЕДЕЛ ФУНКЦИИ
315
4) !.(.'+
6) lim
X + 1
К х2-рЗх—х3
/J+2-7 ’
3.	Привести пример функции у—f (х), определенной на всей
числовой прямой, принимающей только отрицательные значе-
ния и такой, что
lim f (х) = 0, lim / (х) =—1.
х-* о	х~> 1
4.	Привести пример функций # = / (х) и у~g(x), каждая из
которых не имеет предела в точке х = 0 и таких, что их
1) разность; 2) частное
имеет предел в точке х = 0.
ЗАДАНИЕ 5
Найти:
x2—4 .
x—-2 ;
x—2
1.
lim
X -» Й
2) Um ; 3) Hm *+**+*3±**-4-
x-—i X-J- 1
х—1
4)
lim
lim
Ух— v2 ’
x2—1
3/~ f »
l/ X — 1
5)
lim
7)
lim
8)
Вт	;
^x—1
I A\ „	/	3
x—1	’
-3.1,	____________,
x i \ 1— x3	x -> Ц. 1«-1^-p/x /
Сформулировать, что означает утверждение:
число А не является пределом функции y = f(x) при
2)’функция ^==f(x) не имеет предела при х->Хб«
3» Доказать, что число 1 не является пределом функции
/у = /(х) при х~*0, если:
1} f (x)=signx;
9)
2.
1)
X ”> X0J
1, X&sO,
0, x < 0,
О
. 6)
ЗАДАНИЕ 6
!• Найти:
у2 О
1) Um ^г-4-; 2)
Xя*» о
.. х^Зх+2
3> ?”,.гат+3'
Ч1д,£«Е=1
Bn. <|+?-<1+^,
х->о х24-х§
х-**2
4) lim Х.д^..г;
к х-**4
3/~	4/—
u F Х***у X
1
316 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
4”1fer> m’n€Ni 8) lim^^g-^fi;
9>Ыт^-Г^)- «• *€*
10)	(г^+х^-к+г)'
2. Доказать, что число 0 не является пределом функции
gmf(x) при х-*0, если:
х<о’ 2П<*)=1
3. Доказать, что функция
. . ( sin—
«(«)=< а
I о,
не имеет предела
точке 0.
в
х#0,
№0,
ЗАДАНИЕ 7
1.
1)
4)
Найти:
sin2x
lim------- ;
Х-+0 X
1 cos 5х
7)
9)
m .. sin 5x
2) lim ——
' x->o sin 3x
Um —; 5) lim
x->o x sin 7x #-►()
stox . 8)
V" 1 COS X8
1—cosx *
.. sin22x
sin2 ix *
; 6) Mm
tg 2x %->o x
„ cos x-** cos a
Um------ь——•
x-+a x*»a
3)
2.
1)
4)
6)
9)
Ilin
l-/o sin6x«*sin 7x
lim------; IO) lim
X	x->0
Найти:
lira (!4-2x)1/x; 2) lim	3) lim (I —
X->0	X->0 \1***X/	X-*<X>
lim (x/(x-|-3))*+3; 5) lim x (in (x+1)—In x);
x->ao
2*—I _ .. 3s,nx—I	(l-|-2x)V» —i
lim-------; 7) lim-----x-----; 8) lim -2—-1—I----------;
x->o x x->o 2x	x->o x
; 10) B„ «1
lim
Х->0
х—* 1
х
X
ЗАДАНИЕ 8
1.
1)
4)
Найти:
.. sin 3x
sin 7x *
llm^;
X-*0 X
sin3 ax o , л
^ЙЧР afM0:
5) lim	6)
z arosifi3x 9	1
3)
lim
„ 1 — cos 4х
lim —r—x—
х+о sin 3x
tg x—-sinx
x3 *
11. ПРЕДЕЛ ФУНКЦИИ
317
7) lim
x-t-a
9) lim
X->1
sin x—sine
x—a	’
sin лха .
sin лх3 *	'
m • cosmx—cosnx
8)Kl——1
lim ...S?!*
Х->Л/2 Х-*-Л/2
2. Найти:
1) lim (l+3x)I/(2x>; 2) lim (I—x)l/JC;
A»0	A»0
3)
5)
7)
9)
lim
x-»o
lim
X->0
lim
X->0
lim
2x\i/sin*;	x [in (2x4-1) —ln2x];
24“ Xj	X->+oo
&X.-.&X
X *
In COS X
In cos 3x ’
In x—In 7
’ x—7
?/14-2x—[/1 +
6) lim У..........
x~>0	x
O4 v 2*2—In cos x—1
8) lim —;------r-s-----
x_>o	sin2 x
1	(vX vd
10) lim ----—, a >
x-*a X—a
J
ЗАДАНИЕ 9
1.	Найти односторонние пределы функции y~f (х) в точке
х = а, если:
«/ ч Г 2—х, х > 0, л -
1)	f(x) = < о !	а=0, а=1;
' v 9	(х3—4, хСО,
ох *. . f sinx/x, х^О, л
2)	г(х) = <	1 J а = 0;
v '	( cos х, х < 0,
3)	f(x)=х[1/х], а —0, а=1;
4)	f (x) = signx2, а = 0, а = 2.
2.	Доказать, что функция y — f(x) не имеет предела при
х->а, если:
14 £ 7 4	( х, х > 0, л
» 'м-1 1+>, ,«;0, “=0;
2) t И-{ «+’’+«+ ’ '^1.
ЗАДАНИЕ 10
1. Найти односторонние пределы функции	в точке
х = а, если:
14 £ / 4	( 14~*> X > 0, л J
,)ZW = {l-x.x<0, «=<>>«=»?
2)/WJ<8?*’’ хх°:
3) Н*) = иЬ « = 0> « = 2. а==5/2;
2. Доказать, что функция (х) не имеет предела при
х->а, если;
318 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
IX х / ч f %2> Х^О, л
,)/(z) = V. х<0, ° = 0;
2)	f(x) = {x}, а = 0, а —2.
ЗАДАНИЕ 11
1.	Привести пример функции ^==/(х), для которой!
1)	lim f (х) =+оо; 2) lim /(х)=—оо; 3) lim / (х) = оо.
х->1	х->1	х->1
2.	Доказать, что:
1) lim (—1/х2)= —со; 2) lim 1/(х2~ 1)= ©о;
х->0	л»1
3)	Um 1/(1—х)« =+<Ю.
х->1
3.	Доказать, что для функции
f (ж) = (х—2)« (х—3)3(*—4)1
имеют место следующие соотношения:
lim /(х)——оо, limf(x)==oo, lim f(x)==+oo.
х->2	х->3	х->4
4.	Найти:
1)	lira ; 2) Um ; 3) Um т *	; 4) Um
Х->0 х	х-*0 Ха	х->0 1—ЙСО8 х	x->oSinx
5.	Доказать, что если lim /(х) = 4-оо и lim g(x) = — оо, то
х->а	х->а
lim f (x)g(x)= —оо.
ЗАДАНИЕ 12
1.	Привести пример функции y — f(x}, для которой:
1)	lim /(%)—+оо, lim f(x)=—-оо;
х->1	х->2
2)	lim /(х) = оо, lim f(x) = 4-oo; lim /(х) ——оо;
x->0	х-И	x->2
3)	lim f(x) = oo, lim f(x) = oo.
Й»!	X->~1
2.	Доказать, что:
'	9	1 -L у2	1
1)	lim -r =+oo; 2) lim —----=—oo; 3) lim—------==oo.
X» О X4	‘	x3 sin x	sin x
3.	Найти:
« *+l	nx «	cosx o. .. cosx
1)	I’™ -7-; 2) Um —3-; 3) Um -г-™-;
x->o x	x->o | X J
4. Доказать, что если lim /(x) =+oo и lim g(x) = B, В > 0,
x-*a
TO Um /ИйИ=4-°о«
x**a
§ I. ПРЕДЕЛ ФУНКЦИИ
819
ЗАДАНИЕ 13
1. Привести пример функции y=f(x)t для которой!
1) lim f(x) = l; 2) lim f(x) = 2;
X->4-00
3) lim /(x)=0; 4)
2.	Доказать, что:
з)
Х*>оо «ул
3.	Найти:
•х v	*2+*
Л+- 2х*4-х4-1
3) Ига (/х*+2-х); 4) Ига (/*«+2+х);
*-++00	*-*•-«
lim /(х) —1.
х-+®
4)
2) lim
Х-> —ОО X
„	1+х«
Пт -5—
Х~>оо X
1.
* у- *2+4*+7
2) Д™ Зх2—2х+3
5)
]/ х+/7+/х
lim —----7=----
Х-> + оо	у х+ 1
т Нт +2~	+1
8) lim----Г7===-----*
р/^+8
4. Найти наклонные асимптоты графика функции
если:
J) t (*)=; 2) / (x)=-§ig-;
3)/(x)=/i5+T~2x; 4)f(x)=^2x« + l-l.
ЗАДАНИЕ 14
1. Доказать, что если lim f(x)~A и lim	то|
1) lim	2) lim Hx)g(x)«*ABt
X-+ + O)
3> “1.7Й-Т'
2. Доказать, что:
1) Ит -j-jedja) Um-2—=0;3) Um	1 „i,
X**»+oo Л“Г •	X*	X
8. Найти:
r	(x—-l)(x + 2) o. r x24-x+l
1) lim	 ; 2) hm -д-.Х. \ g
4320 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
5) Bra (х+(KF+8); 6) lim (V~х*4-2х—ОТВ;
х->®	Х-+®
7) lim (j/^х8+3х2--У"х*~-2х); 8) lim
Х"* + 00	4С->®
9) Um
«->+»	|/ х& _|_2
w, „т Z2^±^±L.
**-<» ух*+2
4. Найти наклонные асимптоты графика функции У»"/(х),
если:
2)f(X)^-^;
3) f (x)»x~K^"-|«x-|-l; 4) / (*)=== я-j-arctg x,
ЗАДАНИЕ 15
1.	Привести пример функции y=f(x), для которой:
1) lim f(x)==+oo; 2) lim f(x) ——оо;
х->0 + 0	л»0+0
3) lim /W = »; 4) lim f(x) —oo.
x->0 + 0	x->0-0
2» Привести пример функции, для которой:
1)	lim f(x)»l, lim f(x) = oo, lim f(x) = oo;
x->®	1	x-*l
2)	lim f(x)~lt lim f(x)=+oo, lim f(x) =—00J
X-*a>	X->-1	й»1
3)	lim f(x)==l, lim fW=“"l> lim fW =+00»
x->+®	x->-co	я»—1
lim f(x) = —oo,
x->l
3.	Сформулировать с помощью неравенств, что означает:
1)	lim f(x)~+<x>-t 2) lim f(x)=—oo;
x->-l-ao	x->-®
3) lim f(x) = oo.
x->ao
Привести примеры»
4. Доказать, что:
1} lim х?=+°о; 2) lim (л^+х^+х) —+оо;
X-*+<n	Х->— СО
3) lim (х-*х8)=оо; 4) lim (]/гх^4-1+2х) =—оо»
х-+а>	х->-во
ЗАДАНИЕ 16
!• Привести пример функции y—f(x), для которой;
1) lim f(x) =—оо; 2) lim f (х)«+ оо;
х-*0+0	£->-2-0
3)	Ит f(x)=oo;
х-М + О
§1. ПРЕДЕЛ ФУНКЦИИ
821
4)	11m f(x) =+oo,	11m f(x) = -—оо;
x->0 + О	x->0 - 0
5)	lim /(x) =+oo,	lim f(x) = oo;
x->0 + 0	x->0-0
6)	Um f(x)=3 0o, lim f(x) = oo.
x~*0 + 0	x->0~0
2.	Привести пример функции, для которой!
1)	lim f(x)==O, lim /(x) = -j-oo, lim f(x) =+ooj
x-> + оо	x->0	+ 0	x->l
2)	lim f(x)«=l,	lim f(x) = -|-oo,	lim /s(x)=—oo;
X->~00	Х-И	+0	Х-И-0
3)	lim/(x)=—4,	Um f W==+°o,	lim f(x) =—oo.
x->a>	x->0	+ 0	x->0-0
3.	Сформулировать с помощью неравенств, что означает!
1)	lim f(x) =+oo; 2) lim j(x) = oo.
X-* - oo	X-> + ®
Привести примеры.
4.	Доказать, что:
1)	Hm	2) lim (—x2+x+l)=—00.
x->®	x->-oo
Упражнения
1.	Пользуясь определением предела функции в точке, дока-
зать, что:
1) lim(2x—1)=3; 2) limx2=9; 3) Um ----------i-=2)
Х-»2	Хч-3.	Х-*1 X—1
4)	lim xcos~=0; 5) lim —=-3-; 6) lim х3 = х3;
X->0 X	x-*2 X 2	x->x0
rJl
7)	lim tgx = tgx0, Xo	k&Z',
, ’ X-*XQ	*
8)	lim ctgx=ctgx0, Хб Ф m, n^Z.
x->x0
2. Доказать, что число Л = 1 не является пределом функ-
ции y=f(x) при х-*0, если:
2»
3. Доказать, что функция y~f(x) не имеет предела в точке
х=»а, если:
1) /(*) =	f 0 у Г) 1—2,’ x<(X a==0’ 2) H^)=signal, «==0j	
3) fW=	J t ^—2,	„_n. x < 0,
4) f(x) =	J xa —1, I x+2,	X^! 1,	, a = l; x < 1,
5)f(x)=-	| x2 —41 x—2	•, a=2; 6) /(x)==cos-i-, a=0<
4. Найти односторонние пределы функции y—f(x) в задан-
ной точке х=а и выяснить существование предела функции
в каждой точке ее области существования, если:
И Задачи по математике. Начала анализа
322 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
1) | (я) == sign (sin х)9 а = 0, а=л/2;
2)fW-{2«+1’	»— 1:
оч я / ч ( X sin -1-, X & 0, л 1
3) |(х) = < х	а=0, а= —;
I 2,	х=0,	П
( Х2^9	> о
4) f(x)=< ]*+31 ’	’ а=0, а=—3;
v 0,	хг==*~~3,
«‘«-O+t4'	“-1' -°'
( СОЗ™ | X I < 1,
6)	f(x)=|	2	a=l,a=-lt
( |х-11. |х| > 1,
.	( dx+t>, х > О,
7)	f(x)—< „	„ а==0;
I 2—сх, х < О,
8)	f(x)=arctg(tgx), а—0, а = я/2, a—ni
( ех -** 1 л
я 1 \	>	111 ' о X т2^ О, л
9)	/(х) = < х 9	» л = 0|
к 1, х = 0,
_ П, х-* рациональное число,
Ю) f(x) = xD(x), где £>(х) = <
(О, х—иррациональное число;
Г 1/п, если х—т/п, где т и п—взаимно простые
Ц)/(л:) = <[	числа,
( 0, если х—иррациональное число.
5. Найти:
3)
-*+3^ ; 2) lim (x Kx+2—x2-—x);
\ &	/	Jf->2
?i±l. 4)	»'+!%+4- ; 5) lira —1-;
1	x+2	' x^.i x—1
x2^-+g- 7)limx3'~1‘
lim 5-----г,
ж-»1 Зх— 1
6) lim
^а2Х3-Зх+2’ ''““Jx2-!’
8) lim * к> ^€N, n^2; 9) lim
x->U~i	X1>V"2
х4—4х2 + 4
х3—2х 5
x—V3x—2
hm ---я--7—;
x->2	x4—4	’
1Л\ lim X— 1—*2 e ... „ j/*5—'X — 2#
10) lim 	'	, 11) lim
X-.S x—5	у2—x— 1
i/l—x—l/'14-x	у x—1
13) hm  ------------1—; 14) hm  -----;
x-0	X	x-»l x —1
16) lim log^-~1; 17) hm ?-'“3X-; 18) lim ———— 5
X-.5 x—5	’ х^.ч x	x^&x + lx — 2
19) lim10-1”* ; 20) lim (14-2x)1/(3x); 21) Um (1—x)1/<2X)s
X—e	£->0	x->o
15) liml^l+2-);
Л-0 x
3*—5*
§1. ПРЕДЕЛ ФУНКЦИИ
323
22) lim Kl+^H-2* ; 23) lim	•
24) lim (x4-e*)Vx.
x-*0
6, Найти:
х
1) lim (sin x+2 cos x); 2) lim ; 3) lim — 	;
x—x~> i x x-*-0 sin 3x
4) Um tg x ctg x; 5) Um -v*"*2';	6) lim —-A ?to 1;
X-*Q	x~>2 xa—- 4	X-+-1	x+1
cos 2x—cos 4	ctg x—ctg 5 л	tgx—tg7
7> rew •_“> а Л-Л • ’> J“ >
x-+v"3 sin V 3-*sinx	sln44-sin4x
12) Um £=±-, 13) Um	14) Um ltg4xl
х-и sin лх х-*л/з tga 6x x-*o l**-*cos4x ’
15\ lim	. 16x нт 14~2sinx .
' x^ni 4 cos (x+л/4) * х->л/б sin (r+л/6) ’
1^74	sin(x—-Л/6) 1O4 v 8cos3x—1
17)Л“ч 1 — 4sin2x ; 18) J*®;i x/2—Л/6 5
19)	Um ^±i; 20) Um	;
л/S OX-f-Jl	1 «"-о COS3 X
lim (1sin x) tg2 x; 22) lim sin^~~tg~;
Х->Л/л	X-*~5	3 it)
sin K~x—sin К 7 . 24) ym ctgx—1 .
2x*— 14	х->л/4 З/’ адд 2X
К sin 2x— 1 #	 l-“y sin3x
►j/tgx-1	у tg^—1
21)
23)
lim
25)
lim
Х->Л/ 4
Ktgx—v"tg 1
27) lim
;X->1
7. Найти:
v sin3/nx , л пч
1) lim t-s—, mn # 0; 2)
' X^Q sin3 nx
arctgfx—3) л.
----2-1----L ; 4) 11П1
v x—sin 2x
lim ---7-=-;
л^ох-— sin 5x
3) lim ------5—
f x-3 x—3
5) Iimtg x-Sta x
x-*0
sin3 2х
Y COS X— у cos X .
sin2x
14-x sin x—cos 2x л
sin2 x *
7) lim
8)
sin nx
6) lim
x-*o
, X
In—	, n
e m .. In cos 3x
lim -----; 9) lim 7---------=-
x~*e x~-e x^.q In cos 5x
11*
324 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
«л\ lim Sta (Sln . in lim ' l + 2x— V l-bsinx
10) “fjlta&r ; 11 ’ b”0---ind + sinxj----
12) Um(l + x+sin *)V*; 13) lim	•
их к t£3 x-*“3 tg x 1Г-Ч ..
жДадз cos (x-j-л/б) ’	1-»	2—ctgx
16) 11m . -*~S* ; 17) lim (tg*)'®8*;
1 K+oSiax—-sin2x x-*w,i
sin ха *
l~-ctg3x
ctg3x
. ax
.ct8~
18) Um (cos x)®*»2*-, 19) Um (2—4)
#->o	х~>з \ о /
20)
22)
24)
1/
21) Iim f э-~л_;
j/14-xa—xa	'r^°	* + sinx
lim fт~Зз+“7^ i 23)	(——2x’>
X-+1 \1	1 X***1J	Х-+Я1И к COS X	J
11 cos x cos 2x cos 3x
lim ----г-т--------;
л	* + COS X
25) Um1".!!4^?/4.); 26)Ump£±iy/xa.
X->O x	X^\xn +^J
8. Привести пример функции y — f(x), определенной на всей
числовой прямой, не имеющей предела ни в одной ^точке и та-
кой, что функция y*saf2(x) имеет предел в каждой точке.
9. Функция ycsf(x) определена и ограничена в некоторой
окрестности точки х=2 и не имеет предела при х—>2. Дока-
вать, что функция #==(х«»2) f (х) имеет предел в точке х==2, и
он равен 0. Показать, что требование ограниченности функции
f(x) существенно.
10« Доказать, что если функция y = f (х) имеет предел, рав-
ный А при х—► «, и функция y=g(x) совпадает с функцией
ycaf (x) всюду, кроме конечного множества точек, то предел
функции y=g(x) существует при х—и также равен А.
11< Привести пример функций ye=f(x) и y=g(x) таких, что
каждая из них не имеет предела в точке х=0, однако:
1) Um (/W+gWM; 2) Um (f (x)g(x))=l;
3) lim (x/(x))==0; 4) lim (xf(x)) не существует.
x->0
12* Известно, что lim (J (x}g (лс))«О. Следует ли отсюда, что
л»0
lim f (х)=0 или limg(x)=0?
jc->0	я» 0
13. Известно, что lim (f lx)g(x))^0 и функция y<=f (х) не
лмеет предела в точке х== 0* Следует ли отсюда, что lim g (x)~(ft
х-^-0
14< Привести пример функций yx=f(x' и y^g(x) таких, что
f (х)>§ М в некоторой окрестности точки х=0 и lim f (*)=limg (х),
х->0	я->0
§1. ПРЕДЕЛ ФУНКЦИИ
325
15. Доказать, что если Пт/(х) = Л и функция y=sf(x) опре-
делена в точке х=а, то в некоторой окрестности точки х~а
функция y~f(x) ограничена. Верно ли обратное утверждение?
16. Известно, что lim f (х) — limg(x)==0. Привести примеры
х->0	х->0
функций y=f(x) и ^=g(x) таких, что:
1) Um i^=l; i2) lim Ш=0; 3) lim Ш-=₽ + <»;
x^og(x) ’ ‘	»-og(x)	x-og(x)
4)	Um Д^=—oo; 5) Um Д4=09: 6) Ит XUl,= l.
x-og(x)	x-»og(x) \v^ox“g(x)
17.	Доказать, что если функции y~f(x) и y=»g(x) опре-
делены в некоторой окрестности точки х=%$ и такие, что функ-
ция y~f(x) ограничена в этой окрестности, а Дп^£(х)=>0, то
И® |f (x)g(x)|=0.
х-+а
18.	Доказать, что:
1)	lim —5=—оо; 2) lim -г-—г==оо;
х->ох4—х2 ’	1
V Я2 .	V Х**1
3) 1,га <v__9V.i=+00'’ 4) llmn~r2~“—00!
Х~>2 (X—-’2)	Х-*0 X
5) lim	--у=-[~оо; 6) lim —L-asoo,
Х->-Э у Х24“Х4	x-*Jt/2 cosx
19., Найти
Um f (х), Um f (x), Um f (x),
x->l X->0	X->2
если:
!) f	= (x—l)?x(x—2)S; 2) f“(x—1) J(x—Й)4s
3)	^x) = (x— l)3x2(x—2)’
20.	Найти:
1)	lim cos^~T: 2) Ига(х*-1п I x|); 3) Um
X-+Q COS X —— I	X-*2 X
4)	Um	5) limpi; 6) lim-r^—I
’ x_.l (X— I)3	’ xh.0 X2	’ x-^9 81П"» X
3 у .....
rrv V V 1+<XX—1 O4 v In COSX
7)	hm —^—3,-----; 8) hm------g—.
X-*0	x	X->0 vP
21.	Доказать, что если limf(x)=—-оо и limg (х)==—-оо, то:
х-*а
1)	lira (/(x)+g(x))=—оо; 2) lim (f (х) g (х)) =+оо;
х-+а	х-^а
3)	Um (If(x)|g(x))=—оо.
22.	Доказать, что если lim/(x) = —оо и limg(x) = 4, то:
х-+а	х-^а
I)	Um(f(x)+g(x))=—оо;	2) Um(f(x)g(x)) = +oo,	4<0.
x-*a	x^a
Зйб ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕИРЕРЫВОСТЬ ФУНКЦИИ
23.	Доказать, что е;сл«и lim/(«)=== А (Л # 0), то:
х-*о
.Г) lim -^=00, &g>N; 2) ,lim{j»V'W) = 0, kfiN.
Jt->0 XK	x-*o
24.	Привести пример функций y~f(x) и y = g(x) таких,
что llmf(x) =+oo, lim £{&)=<, ню:
1)	lim <Hx) g2) ta (f W 1;
A»0	x->0
3)	4> liml/(x)g.(x)) = — oo,
x->0	ж-^0
25.	Привести «фиадер функции $=f (х) и y—gW таких,
что Im f (^)=4“оо,	—*ю, но:
1)	lim (/ (л>)+g (х)) =+оо; 2) lim (f (х)+g (х)) =—оо.;
х~*а	х-+а
3)	Нт Ш.=-оо; 4) Нт ^=г=0;
t-agW	x->af(x)
5)	lim — /(x) = oo; 6) Нт Ц±Ц1^=0.
x-*a g W	x-*a A — a
26.	Показать, что функция # = —cos — не является огра-
ниченной в любой окрестности точки х=0‘(х^0) и в то же
время не является бесконечно большой при х —> 0.
27.	Привести пример функции, для которой lim f (х) ==4~оо,
х->0
но которая не является монотонной ни на каком интервале
(0;б).
28.	Доказать, что если Hm f(x) — A, lim f(x) = B, то:
1)	lira (f(x)+g(x)) = ^ + B; 2) Km (/ (x) |g (x) |) = 4 |В |;
X-*+QO	X->+«>
3)	Um	4^0; 4) Цщ Ж=А B * °’
,t-> + co	x~> + oog{%)	D
29.	Доказать, что для того, чтобы lim f(x) — A, необходимо
1 и достаточно, чтобы
lim f (х) == A, Um / <х) == А.
Х-> + '<50	00
30.	Доказать, что:
1-	2х о пч х*2+1	1
1)	hm —г-5—2; 2) hm —L__=—1;
X-*“i-xxi 'X tJ—’3	,x -* — *» x — -X
3)	Km	4) Km (/^+2-У^П) = 0.
Х» + эо 1фХй
31.	Найти:
1Ч .. 2x+3+sinx пч 2х2 —3x4-4+2*
1J hm —!—— ; 2) hm	..;
х-*+™ 1—-x4-x24-2x
У^(х+2) .
х2—4
х—2
0. „	Ух^хч-г)
3) Вт -——т-J—4) ,iim
X^-t-oo ха + 4
§L ПР ЕЖ Л Ф УН КДда
327
5> Ил> |1 + *)И+2«)...<1 + 10»)
х->+<>»
(2х-1)» (Зх-1)» .	]
(х2+13х + 4)® ’ "Л?/
6) lim
Х'-><х
8) lim
оо у 2х-М
10) lim (х— Ух3 + х-Ь2);
Я»~С»
11) lim х1/3[(х4-1)2/3-(х-1)2/3]>,
;	9) lim (х—/*л®’+х4-2);'
12)
13)
lim	К^+г-р/8x*+x .
х -* +<»	x®-f-5	’
—У Зх’+х
1ТПТ ......... .---!—> ?
х -* -<ю у х2 +5
lim К*2+2—
# оо У"х2 -J-5
15) lim <У х2,+ Уха+ У х2 — Ух2-.
х-> <ю
IS) Um (:4И’",; 14 Нёт1У”!
X -> оо \X-\-4 /	X оо \ £Х ТО/
18) lim 2x[ln(l^-x) —In (2+х).];
х-^- +®
im г Г^ + Зх2 \ от 2*+3»
19)х^Д_т+^“л7; 2Q)2l®„w^J
21) lim	22) lim
X» + oo In (х4 + е2лг)	7 x + - oo In (x*+eW)
32. Найти наклонные асимптоты графика функции y^f (л),
если:
I) р=Ух2+Зх+2{ 2)	;
3) j^x+y^^H; 4), ys==x+arcct<gx;
5) y=ln(x« + e^); 6) y=x j-pg ,
83.	Найти числа а и b из условия:
(y2 1_ 1	\
*-Н_____ /
2) lim (Кх2 Н“Х+1 —ах+$ = 0;
Х-> - СО
3) lim (Ух2+х+1+ах— &)=0.
+®
328 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
34. Сформулировать с помощью неравенств, что значит?
1)	lim	f(x)=4-oo;	2)	lim	/(х)=4-°°’>
3)	lim	f(x) =—оо;	4)	lim	f(x)==oo;
л->л+0	x*+a—0
6)	lim	f;(x)e=—oo;	6)	lim	f(x) = oo;
H- + «	x *> + <ю
7) Urn /(x)==oo; 8) lim /(x)=-~oo;
я*->а+©	x^+a-O
9)	lim f(x)=—oo; 10) lim f(x) = oo.
X^ »	X«+ -“00
35.	Найти односторонние пределы функции #==/(х) в точ-
ках х = 0, х=1 и х = 2, если:
n f /дл в- I *1 (х4~2)	.	2) f (х\ х 1)	•
х(х^1)а(х— 2)2*	)f{X)	(х—1)2(% + 2) ’
х2 «**> 4	1	1
3) f (#) « ।	| ха (/*» IP ’	(sin х) (х -* I)31 х**21’
36.	Доказать, что:
1)	lim (хг*»х-*2)== 4"	2) lim V^+sin *= + оо;
*£►’+ со	А'-> +00
3) lim	х+2«—оо; 4) lim J^x2 4-х 4- 1 = 4-оо;
-оо	х-+ +с©
5) Mm —АА «=а 4- оо; 6) lim х"^--с=а «~оо;
X *> + оо X	X -»• — оо X
7) Мт (1^х24-х-*K^ld-14-х)«о®.
»
37. Привести примеры функций rg^f (х) и #=g(x), для
которых:
1)	Мт ЛИВВ + ОО> Нт ^W^-00)
Х&> +00	+оо
Мт (/(л)+^;(х))«0;
Х«=+ +со
2)	Мт /(х) = 4-оо, Мт g(x) = — oo,
х + со	х=^ +»
lim (f(x)+g (х))=Б;
+оо
3)	lim /(я)==4-оо* Мт ^(х)«**оо,
№->+«	Х^ +<ю
Мт (/(х)+§(х))«4-оо;
X +00
4) Нт fWes4“°°>
X +00
Нт
X -> + оо
Мт
X +-00
fWe + «>,
lim £(*)==+«>»
Л-> +00
Um g(x) = 4-oo,
+«
lim
X •+ + оо
^4=0;
sW
$ 2. НЕПРЕРЫВНОСТЬ ФУНКЦИИ	329
6)	Mm /(«) = +00, Um g(x)== + o»,
X-> +00	+00
x" + cog(x)
7)	lim f(x) = + 00, lim g(x)~0,
X —► + 00	x —► + 00
Mm (f (x)g(x))=0;
x-+ +<x>
8)	I'm ~Ла'== + 00> lim g!(*)= + «>,
X -> + «>/ W	x •+ +00
Um (f (x) — g(x))=0;
X -> +00
9)	Um (x/(x))=+oo, Hm f/W+-r7-r') = + Л>2;
X -> + ~	X -» + 00 \	lW/
10)	Um (f (x)~g(x))=0, Um (f (x)+xg(x)) = l.
X~> + 00	X~> + 00
38. Доказать, что если lim f(x) = + oo и функция y=g(xj
X -> + CO
ограничена на [a; + oo), то
Um (f(x)+g(x))=+oo, Um (f (x)— g(x))= + oo.
X-+ +00	#-++<»
§ 2. Непрерывность функций
Напомним, что в определении предела функции в данной
точке значение функции в этой точке не учитывается.
Особый интерес представляет случай, когда предел функции
y = f(x)t xg(a; b), в точке xog(a; b) равен значению f(x0).
Пусть функция f (х) определена на интервале (а; Ь) и х0 —
точка из этого интервала. Функция называется непрерывной
в точке х0, если
lim f(x)=f(x0).
х —> х0
Например,
а)	функция у = х3 непрерывна в точке х = 2, так как
lim х?=8, #(2) =8, т. е. lim х3=8=23;
2	х -> 2
б)	функция у = sig Их в точке хо = О не является непрерыв-
ной, так как не существует lim sign х:
о
lim signx==l, lim signx=—1,
я->0+	x->0~
т. e.
lim signx?& lim signx;
o+	o~
в) функция
{(sin x)/x, x 0,
2,	x=0,
3^0 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ.. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
в точке хо = 0 не является непрерывной,, так как, хотя и суще-
ствует
.. sin х .	1ч
lim ------ (он равен
: о X
не совпадает со значением функции в точке
Выяснить, является ли непрерывной в каж-
но этот предел
х = 0: у (0) = 2.
Припер t
дой точке Xq^R функция
( 1—. COSX	, А .
I --------- хг#О;
X2
V Л,	х — 0.
Решение. Пусть х0~* любое действительное число, отлич-
ное от нуля. Тогда, так как lim х2«==хо	0 и Mm (1—cos х) =
Х-*Х0
== 1*»со8Хо, то по утверждению о пределе частного имеем
, х 1—cosx 1—cosx0 . х
lim у\х)*~ hm ------1=у(х0).
х->х6	х-*х» х	хь
Следовательно, данная функция непрерывна в точке х0,
если х0 0.
Пусть Хо==О. Так как
п , п х / , х \2
2 sin2 -тг - / sin -г \
1 —cosx_________L-—_________2 I
ха	х2 2 \ х/2 / 9
то
f . X \2
,	,	/ БШ-тт \	,
.. l«cosx 1	2 )	1
lim---------=-— hm \—тх- =-?г.
х -> о я 2 х -> о v х/2 /	2
Поэтому, если j/(0) = l/2, данная функция непрерывна в точке
х=0, а если у(0) = Л й 1/2, функция не является непрерывной
в точке х=0.
Итак, при А=1/2 данная функция непрерывна в каждой
точке xgT?, а при Л й 1/2 непрерывна в каждой точке x^R,
кроме х==0.
Основные теоремы о непрерывных функциях
в точке.
I.	Пусть функции р = #(х), xg(a; и ^=g(x), xg(a; b)t
непрерывны в точке xog(«; ty, тогда:
1)	у точки х0 существует окрестность (х0 — 6; х0 + 6), 6 > 0,
на которой функция y^fix) ограничена;
2)	если f (х0) > 0- (/ Оо) < ОК то у точки х0 существует
окрестность (х0-~б; х0+б), б > 0, такая, что для каждого х из
этой окрестности /(х) > 0 (/ (х) < 0);
3)	функции y=f (x) + g (х) и y~f (х)—g (х) непрерывны
в точке х0;
4)	функция y==^f{x)g (x) непрерывна в точке х0;
§2. НЕПРЕРЫВНОСТЬ ФУНКЦИИ	33J
5)	если функция у = £(х) в точке не обращается в нуль,
то функция y — f(x)Jg(x) непрерывна в точке х0;
6)	если функция y = f(x) монотонно возрастает (убывает) на
(a; b)t тогда обратная ей функция x—f-Цу) непрерывна
в точке f (xq).
II.	Если функция /(х) [непрерывна в точке х$, а функция
g(u) непрерывна в точке UQ=f (xiQ), то сложная функция g(f (я))
непрерывна в точке х0, т. е.
lim g(f(x))=g( lim f(x)\~g(fM).
X-+XQ	\X-+X9 J
Более того,, для сложной функции g (f (х)) верно также сле-
дующее утверждение: если функция gfeij непрерывна в точке
п= А и lim / ,(х}) = Д, то
^->х0
lim gtf(x))=g( lim f№\~g(A).
x x°	V^?» J
Отсюда следует, что каждая элементарная функция непре-
рывна в любой внутренней точке своей области существования.
Так, например, поскольку функции f (x)&C и g(x)~x
непрерывны в любой точке числовой прямой, то
а)	многочлен Рп (х) =	. + я/хп~^ +...
... +an-ix + an есть функция, непрерывная в каждой точке
числовой прямой;
б)	рациональная функция	где й
Qz» W — многочлены, есть функция, непрерывная в каждой
точке числовой прямой, в которой она определена.
Пусть функция y~f(x) определена на некотором интервале
(а; 6). Функция y~f(x) называется непрерывной справа {слева)
в точке xog(a; b)t если
lim f(x) = lim /(x)=./(x0) / lim f(x)=* Hm f(x)=7(*d)\ •
x-+x0 X->Xo + O	I X-*X9	1
X>X9	\x<x9	7
Например,
а) функция # = x2 непрерывна справа и непрерывна слевд
в любой точке xogR, так как
lim х2 = х2 = lim х2;
x->xo--O	х->хо+О
б) функция
/ х, х^О,
I 1+х, х < О,
непрерывна справа в точке х=0, так как
lim у(х)~ lim у{х)~ lim х—0 = у(0),
#->0 + 0	х->ч0
х > 0 х > ;0
и не является непрерывной слева в точке :х~§> так как
lim у(х)= lim у {х)~ Нт Щ-х)— 1
х-> 0-0	0	х-><0
х < 0	х < 0
332 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
в)	функция y==signx не является непрерывной слева
в точке х=0и не является непрерывной справа в точке я=0,
так как
lim у(х) = Пт у(х)^ Пт (1) = 1,
х->0+0	х->0	х-»0
х > 0	х > 0
Пт у(х) = Нт 0(х) = Пт (— !)=—!,
х —> 0— 0	0	0
х<0	х<0
а у(0) = 0.
Функция y—f(x},	b), непрерывна в точке xog(a; b)
тогда и только «тогда, когда y^f {x) непрерывна слева и не-
прерывна справа в точке х$.
Функция y~f(x), непрерывная в каждой точке интервала
(а; Ь) (числовой прямой), называется непрерывной на этом ин-
тервале (прямой).
Функция y~f(x) называется непрерывной на отрезке[а;ЭД,
если она непрерывна на интервале [(а\ ЭД и в точке а непре-
рывна справа, а в точке b непрерывна слева.
П ример 2. Исследовать на непрерывность функцию
_____________________sin х
9=х«—5x4-6’
Решение. Данная функция существует всюду, кроме
точек х=2 и хе=3. Докажем, что она непрерывна в каждой
точке своей области существования. Действительно, функции
0~slnx и у=х^-*»бх+6 непрерывны в каждой точке числовой
прямой, и функция у=х2—5x4-6 всюду отлична от нуля, кроме
точек х = 2 и х=3. Поэтому по теореме о непрерывности част-
ного данная функция непрерывна в каждой точке числовой
прямой, кроме точек х —2 и х = 3; следовательно, она непре-
рывна на множестве (— оо; 2)U (2; 3)U(3; оо).
График непрерывной на некотором промежутке функции
представляет собой сплошную линию, т. е. линию, которую
можно нарисовать, «не отрывая карандаша от бумаги».
Свойства функции непрерывной на отрезке.
Пусть функция y—f(x) непрерывна на отрезке [а; ЭД, тогда:
Г. Функция y—f(x) ограничена на этом отрезке.
2°. Функция 0=f(x) достигает своего наибольшего и наи-
меньшего значений, т. е. если т—наименьшее значение, а /И—
наибольшее значение функции y=f(x) на отрезке [а; ЭД, то
существуют такие х± и х2 из отрезка (a; Ь]> что
f(Xi) = m, 1(хъ)=*М.
3°. Если f(a)f(b) < 0, то существует точка х^(а; ЭД такая,
что f(xo) = O. Это утверждение означает, что график функции
gz=f(x), непрерывной на отрезке [а; ЭД, хотя бы в одной точке
пересекает ось {ОХ, если точки (a; ((a)) и (b*t f (ЭД) лежат по
разные стороны от оси ОХ (рис. 4.7).
4°. Если т—наименьшее значение, а М *- наибольшее зна-
чение непрерывной функции y~f(x) на отрезке [а; ЭД, то для
§ 2. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
333
любого М] существует хотя бы одно х^ (S|a; b\ такое,
что f(x0)=c<
5°. Если функция У—f (х) обращается в нуль в точках х — а
и x—b (f (a)—f (4=0) и не обращается в нуль нив каких дру-
гих точках отрезка [а; &], то на всем интервале (а; Ь) функция
y~f(x) либо отрицательна, либо положительна.
Пример 3. Решить неравенство
(1—х2) arcsin х > 0.
' Решение. Рассмотрим функцию #=(1 ^х2) arcsin х, обла-
стью существования которой является отрезок [—1; 1]. Заметим,
что данная функция непрерывна на этом отрезке и Обращается
в нуль только в точках х=—1, х=0 и х = 1. Следовательно,
по свойству 5° функция # = (1—*х2) arcsin х на интервалах (—1; 0)
и Г(0; 1) сохраняет постоянный знак. Так как	=
—	arcsin у > 0, то на интервале (0; 1) функция у =
== (1 — х2) arcsin х положительна. Так как f
= 1 — ~arcsin < 0, то на интервале (—1; 0) функция
отрицательна. Итак, каждое х из интервала (0; 1) является
решением данного неравенства.
Пример 4. Доказать, что уравнение
(1+х)-2*2+*+2^уТ+х2 sin2x=0
имеет хотя бы один действительный корень.
Решение. Рассмотрим непрерывную на всей числовой
прямой функцию г/ = (1 + х)*2х2+Л?+§ — У 1 +х2sin2х. Так как
у(0) = 4> 0 и ^(—1)=— К 2 sin2 1 < 0, то по свойству 4° су-
ществует точка Xog(—1; 0) такая, что £/ (х0) =0; тем самым
доказано существование корня у данного уравнения.
Пусть функция y~f(x) определена на интервале (а; 6),
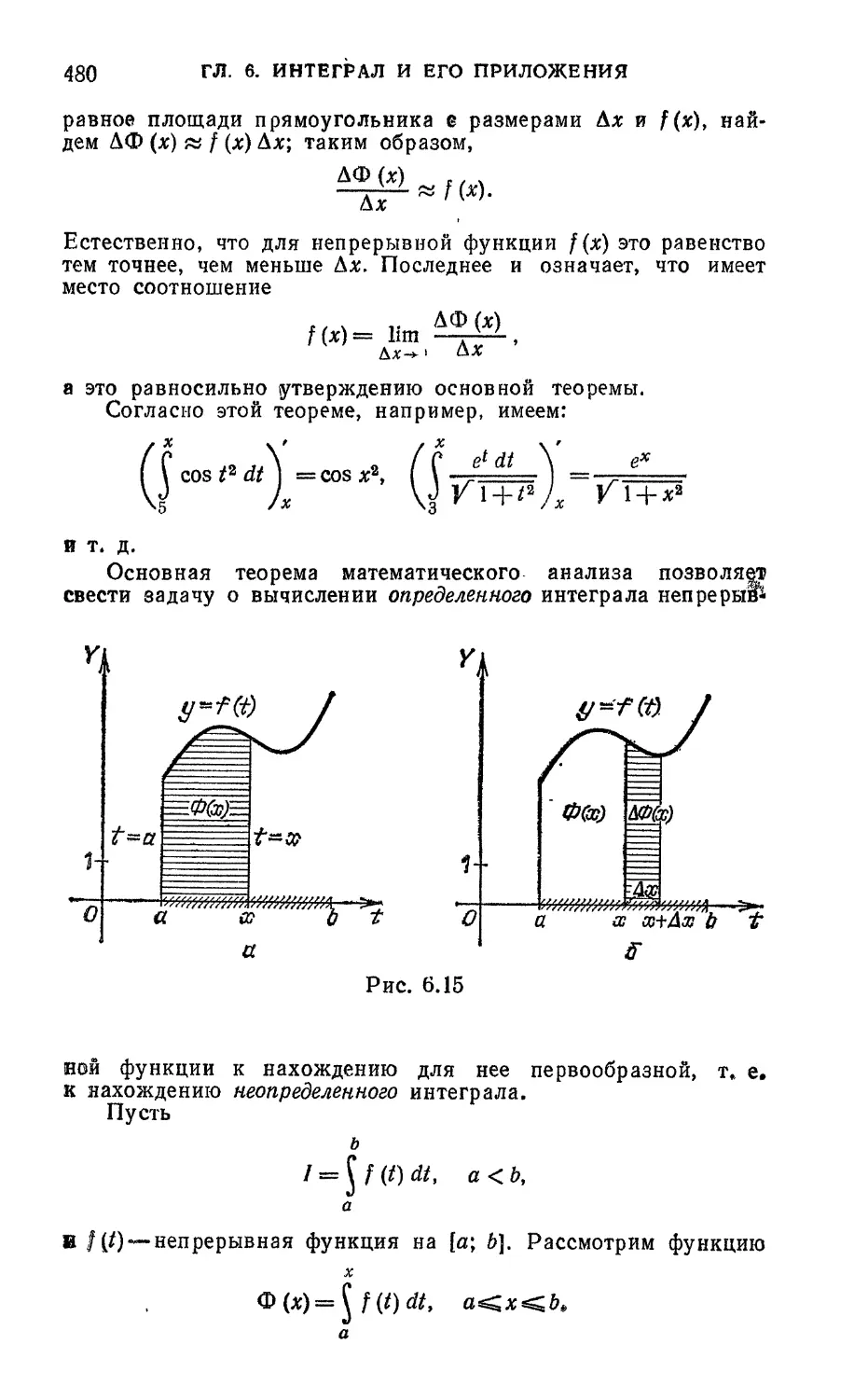
кроме, быть может, точки Xq—•точки этого интервала.
334 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Если в точке х# равенство lim t(x)t=f(x^) не выполняется,
X х0
то точка х0 называется точкой разрыва функции
На рис» 4.6 приведены графики функций, у которых точка
я© является точкой разрыва,
ЗАДАНИЕ I
1. Является ли функция	непрерывной в точке *0>
если:
1) у = х2+2, х0 = 3; 2) у =	*о==О;
1 —~*х2
3j у= ।	, х0 = 1;
(	1	х^2
4)	у^\	х-2’	Х^’	х0=2;
V	5,	х=2,
( sinx / о
5)	</={	х	’	х '	хо=О;
V	2,	х=0э
(	я2—'4	„
6)у={ х—2 ’	’ х0=2;
(	4,	лг»=2э
§2. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
335
(	- * % 1
7) у=\ 1-х3 ’ ь х0 = 1;
V 2, х= 1,
( 1, х —рациональное число,
8) ^ = 4	хй = 0?
(О, х—иррациональное число,
2. Найти точки разрыва следующей функции:
1) #=signx; 2) у~{х}, х02; 8]; 3) #=»tgx$
лч х + 2 кч х2+х+1 4	cos х в
) х—1 ’	х2—х—2 ’	х3—8 5
у2 ..... f Л
7) j/=ctgxsin2x; 8) #= |xsl_4t •
3. При каком значении А следующая функция является не-
прерывной в точке х=0:
1) «/={
(
2)j/={
к
tgx/x, xg(— л/4; 0)U(0; я/4),
А, х=0;
. «ё(-1; О.
Л,	х=0?
4. Привести пример двух функций, каждая из которых не
является непрерывной в точке х0, но их сумма есть функция,
непрерывная в точке Xq.
5. Доказать, что следующее уравнение имеет хотя бы один
действительный корень:
1) 1пх+* = 0; 2) 8*-~3-2* —16 = 0;
3)	х5—6х2+3х—7 = 0; 4) х3—|х| + 2 = 0.
6. Решить неравенство:
1) log2 (х+5) logn(3—-х) /(х+5)(3-х) < 0;
2) (х*-1) /Чб—x2logiZ2(10-x)SsO.
ЗАДАНИЕ 2
I.	Является ли непрерывной в точке х$ следующая функция!
1) #=|*+2|, Хо=1;	2) # = 2*+sinx-f-3, хо=0|
3)	y^\sign х |, хо = О;
4)	У = < х+2 ’ Х ’ х0=—2;
I _4,	х==—2,
(	1
I cos —, х О, п
5)	у=1	х	хо = О;
I 1,	х=0,
_( 0, х—рациональное число, —о?
' х, х-* иррациональное число, Хб
2.	Найти точки разрыва функции:
1)	#=signx; 2) £=ctgx; 3) ^=-^1===-;
У 1—«х2
336 гл. 4. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
4)	у —----—;
7 * arcsin х
5)0=1 7^7’ х*7>	6)0=1 SiDT’ Х540’
15,	х = 7; I 2,	х =
3.	При каком значении А следующая функция является не-
прерывной в точке х=0:
n о= /	х&О,	*€[0j 10];
,У I А, х = 0;	lV \ А,	х = 0?
4.	Привести пример двух функций, каждая из которых не
является непрерывной в ^очке xQ> а их произведение есть функ-
ция, непрерывная в точке х§.
5.	Доказать, что следующее уравнение имеет хотя бы один
действительный корень:
1) х§+х +17«0; 2) 3sin3х**5sinx+1 «=0;
3) sin х***х+1 =0; 4) х3«»Зх+1=0г
6. Решить неравенство:
1) (1 +*)* V4*»х? cos х > 0; 2) V4—х (logs х) sin х < 0.
Упражнения
1. Исследовать на непрерывность следующую функццн^
1) 0=К*+5;
3) г,=(1 — х)«?
2) ^=2x^1+A:^4-sInx?;
( xsin-^, х#0,
4)	х
10,	х=0;
r\ — J sinjtx, рациональное число,
'	0,	х**иррациональное число;
г пх , . _ 1	( fl х |
6)J/=Jcos-r> НК1’ 7)0=1 ЙЙ5’
I |х— 11, |х|>1;	11/2,
х = 0;
8) y=e’,nx(l+x+xa+5x?);
j xOH- cos *)
9) у = < x+sinx
I 0,	х==0;
— / Зх«**2, х—рациональное число,
x2t х—иррациональное число)
и) 9=M+W; i2)^=i«tgxtg(y+x).
2. Найти точки разрыва следующей функции:
( 1ж+2|	, „	(	1
1)0=4 «4-2 ’ *54“-2’	2)0=1	Х*1г
I 1,	х==—2;	к 3,	|вв1;
§2. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
337
f COS "А”» х °, ,ч 1
3)У = < X*	4)^ = ——;
I 1, х—0; х l*J
I 21/х, х £ 0,	_ х2 + |х|Н-х
х = 0;	6) у~х*—|х|+3х
х2«*|х| QX Х«* 1 Н-] X—1 ]
7)	9=’гаГ; 8) -----------га—;
оч	2 (х—х3) +1 х х31	1	(	1.11
9)	я=к“7--«rra-----чт ‘» 10) #=(х+1)ехр <---Ьт~тг
**	2(Х-*Х§)-*|Х-~Х3|	х I ]х| J
(	х2, х«** рациональное число,
'	—х2, х-** иррациональное число;
12^ =/ ^“т/Л*в*несокРатимая Дробь,
’	0,	х*«» иррациональное число.
3.	Пусть функция y«f(x) определена на интервале (а; Ь)
и непрерывна в точке х0(£(а; Ь). Доказать, что функция y~f (х)
ограничена в некоторой окрестности точки Хо.
4.	Пусть функция y=f(x) определена на интервале (а; Ь)
и непрерывна в точке xQ£(a\ b). Доказать, что если /(х0) > О,
то f (х) > 0 в некоторой окрестности точки х0.
5,	Пусть функция #=/(х) определена и ограничена на интер-
вале (а; Ь) и точка х^(а\ Ь) является ее точкой разрыва. При-
вести пример функции (х), определенной на интервале (а\Ь)
и такой, что функция y = f(x)g(x) непрерывна в точке х0.
6.	Пусть функции y = f(x) и y~g(x) определены на отрезке
[а; £] и известно, что их сумма и разность являются функциями,
йепрерывными в точке. х$(£(а; Ь). Доказать, что тогда функции
у==/(х)и y=g(x) являются непрерывными в точке х0.
7.	Пусть функции y~f(x) и y~g(x) определены на интер-
вале (а; Ь) и известно, что их сумма есть функция, непрерывная
в точке х0(£(а; Ь). Являются ли функции y~f(x) и y~g(x)
непрерывными в точке х$
8.	Доказать, что если функция y~f(x) непрерывна в точ-
ке Хо, то функция р«=|/(х)| также непрерывна в точке х0.
9.	Привести пример рациональной функции, определенной
на отрезке [2; 5] и непрерывной на множестве [2; 3)0(3; 4) U (4; 5].
10.	Привести пример функции, определенной на интервале
(0, 1), разрывной в каждой точке этого интервала и такой, что
функция у~\ f (х)I непрерывна на интервале (0; 1).
11.	Являются ли непрерывными на всей числовой прямой
функции y—f(g(x)) и y==g(f (х)), если
f (х) = sign х, g ® 1+х** [xl?
12.	Является ли непрерывной на всей числовой прямой
функция
где
{х, х«-рациональное число,
— х, х**иррациональное число?
338 ГЛ. 4. ПРЕДЕЛ ФУНКЦИИ НЕПРЕРЫВНОСТЬ ФУНКЦИИ
13.	Является ли непрерывной на всей числовой прямой
функция
f(u) = cos ut
где
{х, х — рациональное число,
— х2, х—иррациональное число?
14.	Функция	задана следующим образом:
2)>
' w (х—4)*4~6, xg[2; 4].
Существует ли точка х0 такая, что хо^[О; 4] и f(x0) = l? Суще-
ствует ли точка х0 такая, что xog(O; 4] и /(х0) = 7?
15.	Функция y~f(x) задана следующим образом:
УбЯЛ. *€1-1; 1].
Существует ли точка ха такая, что f(x0) <	15?
16.	Пусть функции y=f(x) и y~g(x) непрерывны на отрез-
ке [а; &], причем f(a) < g (а) и f (b) > g(b). Доказать, что суще-
ствует точка с из интервала (a; b)t для которой f(c)~g(c).
17.	Доказать, что множеством значений непрерывной на
отрезке функции является отрезок.
18.	Доказать, что уравнение х3+рх>+1 ==0, где р—некото-
рое действительное число, имеет по крайней мере один действи-
тельный корень.
19.	Пусть для функции y—f(x), непрерывной на отрезке
(0; 1], область значений есть отрезок [0; 1}. Доказать, что суще-
ствует точка xo£[O; 1] такая, что f(x0)=x0.
20.	Пусть функция y—f(x) непрерывна на промежутке
[а\ 4-со) и lim f(x) = A. Доказать, что функция f (х) ограничена
00
на {а; 4- °0)-
21.	Функция y~f(x) определена и непрерывна на (2; 5].
Известно, что для любого х, принадлежащего отрезку [2; 5],
функция у=/(х) принимает только рациональные значения.
Найти f (е) и /(л), если f(4)=7/9.
22.	Доказать, что следующее уравнение имеет хотя бы один
действительный корень:
1) х3+12х—-8 = 0;	2) х4-«*х3+2х2+х—3 = 0;
3)	6х3—х2—20x4-12 = 0;
4)	5х4—14х3—79х2 4-84x4-180 = 0;
5)	27х34-8—(х— I)3—(2х4-3)3 = 0;
6)	х! —6х4—9х3—6х24-8х4-8 = 0.
23. Доказать, что следующее уравнение имеет более одного
действительного корня:
1) х3—19х—30=0;	2) 9х2—27х44-4 — 14х = 0;
3)	ЗОх4— 17х?—228х24- 17x4-30=0;
4)	(х6—1)4-2(х4—1)4-1=0;
§2. НЕПРЕРЫВНОСТЬ ФУНКЦИИ	339
5)	2 к2х2—х+1 — х— 3=0;
6)	|х| —|х—2[—|х+2|+3=0.
24. Решить неравенство:
1) (Xе—1) (х— 1X0;	2) (х«—I) (Xе—1) < 0^
3)	(х«—1) logs (х+у) >0;
4)	(х2—2х—>35) arcctg х < 0;
5)	(х4—2х2) arotg х 0;
6)	f х2	Varctg х 0.
ГЛАВА 5
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
§ 1. Производная
Пусть функция y — f(x) определена на интервале (а; &),
х0(£(а; Ь), и величина Ах такова, что х0 +Ах также принадлежит
интервалу (а\ Ь). Разность
f (хо + Ах)—f (х0)
называется приращением функции в точке х0, а прираще-
нием аргумента в точке х0. Приращение функции у — f (х) в точ-
ке х0 принято обозначать А/ (х0) или А// (х0), т. е. по определению
Д/ (х0)	— f (х0 + д*)—f (ХО).
Если через х обозначить х0+Д*, тогда Дх=х—х0> и прираще-
ние функции в точке х0 можно записать в виде f (х)—f (х0).
Производной функции y~f(x) в точке х0 называется предел
отношения Af(x0)/Ax при Ах—>0 (если предел существует).
Производная функции y~f(x) в точке х0 обозначается через
у' (х0), или f' (х0)> или ~	.
ах |х=х0
Итак, по определению
f' (*о) =
=» iim	цт
Дх -> о Ах Дх о
f(x)-*-f(x^
X — Xf)
f(xl> + &x)^f(xo)_ hm
Д-V	X -+ Ха
Функция, имеющая производную в точке Хо, называется
дифференцируемой в точке х0.
Если функция y=f(x) дифференцируема в каждой точке
интервала (а\ Ь), то говорят, что функция y — f(x) дифференци-
руема на этом интервале.
Пример 1. Найти производную функции у = х2 в точке
Хо=2.
Решение. Найдем приращение функции f (х) = х2 в точке
х0 = 2:
Д#=f (2+Ах)	(2) = (2+Дх)2 -*»22 = 4Дх+(Ах)2.
Имеем
Д/(х0)	4Ах+(Дх)2	/л 1 л \ л
hm	hm ------Р—hm (4+Дх)=4.
Дх -> 0 Дх Дл: -> о Дх дх -> о
Таким образом, производная функции в точке Хб=2
равна 4, т. е. ^'(2)—4*
§1. ПРОИЗВОДНАЯ
341
Если производная данной функции вычисляется при каждом
допустимом значении аргумента, то его обозначают той же бук-
вой, что и аргумент, без каких-либо индексов при нем.
Пример 2, Доказать, что
(х2)' = 2х, xgR.
Решение. Найдем приращение функции f (х) — х2 в точке х:
А/ (х) == f (х+Ах) f (х) = (х+А*)2 **х2 = 2х Ах+(Ах)2<
Таким образом, А/(х)/Ах=2х+Ах, и, следовательно,
lim	lim (2х+Ах)=2х«
Дх -* о Ах Дх. -<0
Итак, (х2)' = 2х в каждой точке х.
Пример 3. Найти производную функции f (х) ® 1/х8 в про-
извольной точке х, х 0.
Решение. Так как при х ?£ 0 и х+Ах £ 0,
Л f (1_____________L —	(2х + Ах)
' W ~ _|_ дХ)2 , Х2	Х2 (л. + ДХ)2 ’
.. W>__ г	л“".(2,,+ад г
дх-? о Ах	х2(х+Ах)2 lim х2 (х~(-Ах)2
дх-> о
Таким образом,
(1/х2)'=—2/хЗ, х^О.
Пример 4. Доказать, что
(xn)f ~пхп~\ ngN, xgR.
Решение. Придадим аргументу х приращение Ах; тогда
приращением функции f(x) —х" будет величина
f (х+Ах) — f (х) = (х+Ах)"—х" =
= (х"+сйх’,-1д*+с^'’-з (Дх)а+ ... +Crt(Ax)n)—х” =
=пх”-1 Дх +C£x”~s (Дх)а+(Дх)».
Таким образом,
-^^-=Ях«-1+СпХ«-? Дх+,,, 4-СЙ (Дх)”"*.
Так как при Ах —> 0 все слагаемые, кроме первого, стремятся
к нулю, то
f' (х)« lim =пхп ” \
Дх о ДХ
что и требовалось доказать.
Пример 5. Доказать, что
a) (cosx)' — — sinx, xgRj
б) (sinx)?s= cosx, xgR.
342
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Р е ш е н и е. а) Для отношения приращения функции / (х)=
= cos х к приращению аргумента в точке х имеем
А/ (х)__ cos (х-|-Ах)—« воз х_
Ах	Ах
Ax
Sin~ (
==•— lim —т--- lim sin(x4
Дх -* ° Ax Дх -> о \
2
Итак, (cosx)' =—sinx в каждой точке x.
б) Для отношения приращения функции f (x) = sinx к при-
ращению аргумента в точке х имеем
А/ (х)sin (х-|-Ах) —sinх
Ах	Ах
п , Ах / , Ах
2 sin-ту- cos I х-|—~
—
. Ах
sin —
—-----cos
Ах
2
Следовательно,
.. А/ (х)	.. I 2
iim —lim I —-—
x -> о Ax Дх -> о I Ах
. &х
sm~2~	/
= lim —i------ lim cos ( x
&x ° “lL Дх -> °	\
2
Итак, (sinx)' = cosx в каждой точке x.
При вычислении
cos (х+Ах)— cos x	sin (х+Ах) — sin х
hm ------—J-T-2----- и lim -----*—-----------
Ах -> о	Ах	£х -> о	Ах
были использованы следующие утверждения:
1) lim 1; 2) lim sin f х+Д^-У—sin х;
и -> о и	дх->о \	2 /
§1 ПРОИЗВОДНАЯ
343
3} lim cos f x-F — ) — cos х; 4> теорема о произведении
&х -> о \	* /
пределов.
Пример 6. Доказать,, что
(е*У xgEL
Решение. Пусть f (х) = е*; имеем
Д/ (х)._ех+Дх— ех	1
Дх Дх	Дх *
Так как
дл? -> о Дх *
ТО
Вт	Bm
Дх -> и Дя Дх -► о &Х &Х -*• о* Дх
и тем самым утверждение доказано.
Пример 7. Доказать,, что если х л/2-рлп, zi(SZ, то
^t.gx)7 ——is—.
v z cos2x
Решение. Так как tgx=sinx/cosx, то при указанны»
значениях переменной и при достаточно малых значения^ j Arf |
имеем
, . , А х	. sin (х + Дх)	sinx
tg (х4-Дх)—tg X  ---; »ТЦ-----------
v 1	1	to соя(х + Дх)	cosx
 Fs in; (x+Ax) cos x—cos (x 4~ Ax) sin X
~~	cos (x-j-Дх) COS XJ
— sin (x+ Ax —'x) _ sin Дx
COS Сх + Дх) COS x ~~ COS X COS (x + Дх)*
Поскольку константу можно выносить за знак предела и
lim cos (х+Дх) = cos х, то при х # ~ + ля, жё Z, получаем
Дх -+ о	А
lim tg^ + ^)-tgx= Jim /steAr......	1 -----\
дх -♦ о Дх	дх-> А Дх cos(x+Дх), cos х/
Г 1Г sinAx ..	1	1
s==——-— lim —т——- lim ——~......5= —~ ,,
COS X Дх -> 0 Дх Дх -> О COS (х +Дх)	cos2 X
т. е. утверждение доказано.
Основные правила нахождения производ-
ных:
Г. (с)'=0, где с—постоянная величина.
2°. Если функция f(x) имеет производную в точке х и с —
постоянная величина, то функция cf (х) также имеет производ-
ную в точке х, и

344
ГЛ. 5. ПРОИЗВОДНА^ И ЕЕ ПРИМЕНЕНИЕ
3°. Если каждая из функций f (х) ng (х) имеет производную
в точке х, то функция f(x)+g(x) также имеет производную
в точке х, и
(Кх)+ё(х)У^Г(х)+§Чх).
4°. Если каждая из функций f(x) и g(x) имеет производную
в точке х, то функция f(x) — g(x) также имеет производную
в точке х, и
(f (х) — S (X))' = f (х) —g' (х).
5°. Если каждая из функций f(x) и g(x) имеет производную
в точке х, то функция f(x)g(x) также имеет производную
в точке х, и
(f (X) g (х))' = f' (х) g(x)+f (х) g’ (х).
6°. Если каждая из функций f(x) и g(x) имеет произвол-
ную в точке х и g(x)#0, то функция f(x)/g(x) также имеет
производную в точке х, и
/7 (*) У  f' W g(x)~f (х) g' (х) .
7°. Если функция x=g(y) дифференцируема в точке у,
g' (у)	0, и имеет обратную функцию y = f(x), непрерывную
в точке х, то функция y~f(x) имеет производную в точке х, и
g'(Hx)) •
8°. Если функция g(y) имеет производную в точке у, где
y=f(x)t причем функция f (х) имеет производную в точке х,
то сложная функция h~g(f(x)) также имеет производную
в точке х, и
hx^gyfx-
Пример 8. Доказать, что если в точке х каждая из
функций f(x) и g(x) имеет производную, то
(f (X) g (х))' = f (x) g (X)+f (x) g' (X).
Решение. По условию имеем
Дх->о Дх
Г (х),
цт g(x+&x)-»g(x)_
дя-,.0 Дх
g'(х).
Отсюда, например, получаем, что
e(,+A^-g(>Uf,,w+cb
где а —» 0, если Дх —► 0. Следовательно, g (х+Дх) =g (х) +
+ Ax(g* (х)4-а), где Дх(£* (х)+а) —> 0, если Дх-—>0, а это
значит, Зто
Пт g(x<4-Ax)=g(x).
$1. ПРОИЗВОДНАЯ
345
Поскольку
f (х+A х) g (x 4- Дх)—f (x) g (x) .
=f (x+Дх) g (x+Дх) — f (x) g (x 4- Дх) 4- f (x) g (x4- Дх)—f (x) g (x)=
= (/ (x4- Дх)—f (x)) g(x4-Ax)4-f (x) (g (х4-Дх)—g(x)),
TO
lim f(x+^x)g(x+^x)-^f(x)g(x) __
Дя~*о	Ax
^№+Ag-;wg(>+aj()+,w,(«+^-ew\
Дл-*0 \	&X	ISX /
H /(x4»Ax) — f (x) .. z , A x , f/ s g(x4-Ax)-*g(x)
= ifm xA—1—Z—LLZ hm g(x+Ax) + f (x) lim SA-J—/—
Дх»о Ax	Дл»о Ax
= f' (x)g(x) + f(x) £'(*)>
что и требовалось доказать. Подобным образом обосновываются
остальные правила нахождения производных.
Пример 9. Найти производную многочлена
Pn(x) = anxw + an^ix»-l+ ... +aix+a$.
Решение. По правилу 3°, а затем 2° имеем
Рп (х) - (апх*У + (ап-1хП~1У +... + (а&У+(а0)' =
= ад (x*/4-a»-f (х«~хГ+♦ н +аде+(«бГ.
Используя теперь правило Г и формулу из примера 4, получаем
Р'п(х) — папхп-*+(п — 1) а»«1Х"-^+ ♦. * +2a2x+af*
Пример 10. Найти f' (х), если:
a)	f (х) = (х?—5x4-6) sin х; б) f
Решение, а) По п равилу 5°
f' (х) = (ха 5х 4- 6)' sin х 4~ (х?—5х 4- 6) sin' х.
Так как (х?—5x4-6/ = 2х*~5, sin'x = cosx, то отсюда нахо-
дим, что
(х) = (2х**5) sin х4-(х2~*5%4-6) cos х.
б)	Так как
f +	_ 2-Зх
zw х?4-х4-1	1'гд:24-Х4-1’
то
1 < 2-»3x tv । ( 2«**»3х V / 2-*-Зх
ZW (14-xa+x+J =J) +^2+x+jj —^x»+x+J«
34G ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
и, согласно правилу 6°, имеем
и	_ (2—Зх)' (хг + + 1) — (2 — Зх) . х2 + к + 1)' _
w	(x2H~x+ip	—
_ __ 3*^+ х+ ту— (2—Эх) (2х+ 1)
(x^-x-MF	—
— Зх2—Зх—3 — 4х + 6х2—2 + Зх Зх2 — 4х—5
(ха + х+1)2	(х2 + х+1)2 •
Пример 11. Доказать, чт&
х^пп, ngz.
Решение. Так как ctgж = cosx/sinх при указанных
значениях переменной и (cosx)' — —sin х, (sinxy = cos х., то,
согласно правилу 6?’, имеем
~	, ( соз х \\'	(cos х)' sin х — (sin х)' cos х
(ctgx) “te; =—1—ж------------------------=
__—sin2x — cos2;x  — 1
sin2 x sin2’ x *
что и требовалось доказать.
Подобным образом можно обосновать, что
(tg*),==Eir x*n/2+nk> k<&
Пример 12. Найти f' (х), если:
. f . . sin4 х—cos4х , ,	,
я> f	. х # лй„ k g Z;
6) ^(x),=tg2x—cig2jf„ х#л>6Д, &£Z;
ct£|-ta|
----7^---Г-Д----. ***№, *€Z.
(ctg|_tg|) —4
Решение, а} Поскольку
sin4x-—cos4x__(sin2 x + cos2 x) (sin12 x>^ cos2 x)i
isin2x “	sin2 x	~~
TO
f (x) = (1 —ctg2 X)'	(ct^2 x)/ = — 2ctg,X (Ctg x)/ «X
n 1 f 1 \
==!—2ctg X-----Г-7Г- I
& \ sin? x /
б) Так как
. ft . Л sin 2^ cos 2x	sin2 2r— cos2 2x
g x«*»c g x— COS2X sin 2x cos2xsin2x
__ 2 ctg x
sin2x *
—2 cos 4x n . .
-----—-----=± — 2 ctg 4x,
sin 4x-----&
§1. ПРОИЗВОДНАЯ
347
то
(1	\	о
в) Поскольку (см. пример б))
. X . X
ctgy-tgy _	,
/ . X . X V л . X х >х А / f. X . X \~х
(ctgy-tg_j -4 ctgT-tgy_4^gу-tg-gj
_____ 1	__	1 _tg2x
S-cig х—2tg X 4dtg2x 4 ’
TO
Пр-и мер 13, Доказать, что
1
а) (1пгс)'=—, х>@;
в) (arctg X)' = j-^5-, х € R.
Решение. Применяя правило 7° для дифференцирования
обратных функций и формулы
(ех) ' — ех, (sin х)' = cos х, (tg х)' = -	,
находим, что
а)	(1п*)'=тк=4;
б)	(arcsin х) ----------t
cos (arcsin х) У 1 — sin2 (arcsin х)
1
УТ^Х* 5
в)	(arQtgx)'==!--j------=cos2 {arctg х) =
cos2 (arctg x)
1 1
1 + (arctg x)	14- x- *
Подобным образом доказывается, что
...
(arccosx)'=«7==, | х ,| < 1,
У 1 — х2
(arcctgx)'=Y^5-, xgR.
848
ГЛ. б. ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
Пример 14. Найти f' (х), если
a} f (х) ® In8 х8, х > 0;
б) f (х) = arcsin4-^-, | х I > 1;
в) f (x)==arccos ]/"1 **X8, 0 < | х| < L
Решение, а) Так как
In8 х8=(3 In х)8=27 In8 х,
то
f(x) = (271n’x)?=27(lnSx)'=81 ln2x(lnx)'=^-^-.
б) f' (X) = 4 arcsin3 -V ( arcsin ДЛ ==a
v '	x8 \ x8 j
«= 4 arcsin3 Д-
x2
*-*8 arcsin3 X
x2
в) Поскольку (}^ 1—x2)z =— .1—.- (—2x) s= /~“X —, to
2/ 1-х2	К 1-x2
f (x)=-r=^L== (Г b^)'=—
Пример 15. Доказать, что
a)	(a*)'= a* Ina, xgR, a > 0, a & 1;
<5) (log® *)'в7БГ7;’ * > °* a > °« a * !•
x in a
Решение, а) Поскольку
ax _ й1п a* _gX In а,
то, согласно правилу 8°, а затем правилу 2°, имеем
(ах)' = (ех ln а)' = ех ln а (х In a)' = ах In а (х') = ах In а.
б)	Так как
то, согласно правилу 2°, имеем
Z1 ZlnxV 1 /1 w 1
(logtf x)' = 1-- =-; (In x) =—i .
\	/ \lna/ Ina v ' xlna
Пример 16. Найти ff (x), если
a) f (x) - loge УТх-, 6) f (x) = V2.52*+i;
7
в)	/(x)=5cos3— logs у.
§1. ПРОИЗВОДНАЯ
349
= / 10.5?x/21пб(^-
Решение, а) Поскольку
logs У= -i- (log6 7 + log6 х) = j log6 7+-|- log5 x,
TO
/ 1 i V/1	V/1 V
( у loge7+y log6xl =f—log67) 4- f j log6 x ] =
1 ,1	ч,_	1	1
=y (logBx) »Ж=ПП25'
б) Поскольку V 2>5ax+l= V 10*5?Лг^а, то
(Ki0.5?x/2)'= Kio (58*/8)'=
в) Поскольку
7
logs —«a logs 7 *• logs Xt
X
TO
(5 cos 3 + logs 7 •*» logs x)!=
I
= (5 cos 3+logs 7)^ (logs xY*=—YTn3 *
Приведем основные формулы для нахождения производны»!
(0*8x0, где С*»постоянная!
(*)М;
(хаУ^аха^
цу_______1_,
\ х J х% *
(ex)f,^=eXef
(аху^ах In aj
(1пя)г=-|;
<log«*)'=nk-5
(Sin %)' == COS х;
(arcsin х)’«у==- 5
(arctg	J
330 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
(cos х)'=—зйах;
(arccos -??=== ;
К 1-Х*
(ct«x)'=^7;
ш* I
(arcctgx)'«y-p^-.
Используя таблицу производных и правило дифференциро-
вания сложной функции, получаем следующие формулы, спра-
ведливее для дифференцируемой функции f (х):
irW-FjW''W'
(hit) =“7Пч,'М;
(«/<*>)'=е/<х) f' (x);
(lna)f'(x);
(lnf(x))'®-^ Г(х);
<10^(x))'=7w1K7rW:
(sin f (x))' = cos f (x) /' (x);
(arcsinH^-pU^Nx);
(tgfW),=OTxTfW;
(arctg f (x))'=y-A-^ f (x);
(cos f (x))' = (— sin f (x)) /' (x);
(arccos/(x))'-^-L — ftx);
(ctg/(x))'-
(arcctg f (x))' = — i	f' (*)•
Пример 17. Найти производную функции:
a) y=5xs+V~x-Y-^; б) ₽=log2x+log3x+2*;
ех f---------------------------------
в) z/=sin Зх-*-х cos2 х; г) у=== ।	х2-±х\
§1. ПРОИЗВОДНАЯ	351
Решение. Применяя таблицу производных и правила
дифференцирования, имеем:
a)	j/=10x+—2х-3;
2 К х
б)	у’= —1—-X.—L---U2* 1п2;
' х In 2 • х In 3 * 1
в)	r/'=3 cos Зх—(cos2 * х+2х cosх(— sinx));
. , г*(1 + х2)—е**2х	1
—(!+?>•----------?тщ7‘2«+»'
д) у' = 3 cos2 (In 2х) (— sin (In 2x)) -X«2-Ц- (— -X) ।
cos?— '	'
x
e) #'=
1па(х+/ГТВ)
Пример 18. Найти производную функции
0=(l + 4x)ct8*.
Решение. Первый способ. Так как ^==ect8*ln(1+4*b
то
./ — z>cts X In (1 + 4Х) /	(1~Ь4х) . ctgX л \
у-~е	\	sin2х ‘1 + 4х )
_Л4. A^tzx( -Ип(1+4х) . 4ctgx\
\ sin2 х ^т+й;в
Второй способ. Рассмотрим логарифм данной функции^
In y~ctgx In (1 + 4х).
Дифференцируя обе части этого равенства по х и считая, что
функция In у (х) является сложной функцией, получаем
1	1	4
7’'“-№^'"'1+4 * * *>’+№”Гн7-
и, следовательно,
„/ _ (I . 4ж)«8х (_ 1п(1+4х) , 4ctgx\
я-и+ад)	sin2x ф—
Применение предварительного логарифмирования функций
иногда упрощает нахождение производной.
Пример 19. Найти производную функции
V=	jzpj (х2+2х)8 при х > 1.
Решение. Рассмотрим логарифм данной функции
In	In х+4In (* — О—Т In (*+1)4-3 In (x®+2x).
352 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Дифференцируя обе части этого равенства, получаем
1” '	__1_________!__| 3 (2x4-2)
‘ я?4-2х *
Отсюда
/ =	j/’ —. (х2-|-2х)з^—4-	4-
, 3 (2x4-2) \
’г х24-2х /'
Пример 20, Доказать, что
(_______________1 У- Г(х) t
cos f (х) J cos f (x) B' w*
Решение. Используя правило 6° для дифференцирования
частного двух функций, найдем, что
1
cos f (х)
у_ (<x>sf(x)Y
} cos? / (х)
Так как (cos f (х))'==— (sin f (х)) /' (х), то
1	\_ (sinf(x))f (х)^ f (х)
cos f (х) / cos2 f (х) cos f (x)

Пример 21, Доказать, что если функция f(x) имеет про-
изводную f' (х), то
(f (sin t)y «= f' (sin t) cos t.
Решение. Отметим, что в этой формуле символ /'(.,.)
означает производную по аргументу sin t9 от которого зависит
функция.
Функция y=/(sin/) является сложной функцией, для ко-
торой, если x=sin/, имеем у=/(х). Тогда по правилу 8°
(f (sin t)Y == f' (x)j^a= fl (х) cos t = f • (sin t) cos t.
Чтобы найти производную этой функции в точке х0, при-
надлежащей (а; Ь)> поступают следующим образом: находят про-
изводную этой функции в произвольной точке xg(a; Ъ)9 если
это возможно, а затем в выражение для у' (х) вместо х под-
ставляют х0; в противном случае вычисляют производную
в точке х0, исходя из ее определения.
Пример 22. Найти производную функции f (х)==х?4*
в точках:
а) х=1; б) х=— 1/2; в) х=0.
Решение, Так как ff (х)«2x4-1, то
a) /f(l)=3j б) Г(-1/2)=0} в) Г (0) = 1.
§1. ПРОИЗВОДНАЯ
353
Пример 23. Найти производную функции
...	( х2 sin —, х # О,
/(*)={ х
к О,	х = 0,
в точках х = 2 и х = 0.
Решение. Для каждого х, х О, используя правила и
формулы для нахождения производной, получаем
/'(х) = (х2 sin — = 2х sin — 4-х2 cos — (----=
\ х J ' x 1	x \	x* J
— 2х sin J--—cos 45
X X
поэтому f' (2) = 4 sin --— cos
Производную данной функции в точке х = 0 найдем непо-
средственно из определения производной в точке:
Р(0)_ й,	lta
Ах о Дх	Дх -> о
Дх
Дх
Так как Дх—*0, a	то
lim (Дх sin -4^ =
Дхо \ Дх/
Итак, Г(0) = 0.
Пусть функция f(x) определена на интервале (a; Ь) и
х£(а; Рассмотрим односторонние пределы
lim
Дх -> о-о
А/(х)
Дх
lim
Дх •* о+о
А/(х)
Дх *
Если эти пределы существуют и конечны, то они соответственно
называются левой и правой производной функции g=f(x)n точке х
и обозначаются через f'_ (х) и f'+ (х).
Для существования производной f' (х) в точке х необходимо
и достаточно, чтобы обе односторонние производные (х) и /1(х)
существовали в точке х и были равны, т. е. f'+ (х)=£ (х).
Заметим, что если функция g=f(x) определена на интер-
вале (а; Ь) и дифференцируема в точке xg(a; b), то она непре-
рывна в этой точке.
Обратное утверждение, как показывает следующий пример,
неверно.
Пример 24, Доказать, что функция р=1 х| не дифферен-
цируема в точке х=0,
12 Задачи по математике. Начала анализа
854
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Решение. Приращение функции f(x) = |х| в точке х=«=0
равно
&f (0) = /(0+Дх)—/(0) = |0+Дх| —0 = |Дх|.
По определению находим, что
I Дх I v —Дх	.
f' (0) = ]im J——L= lim —т—=—1,
~ Дх -> о—с	Дх -> о-о Дх
£, /ЛЧ	V	|ДХ|	1-	А*	1
fl (0) =	hm	1 д— =	hm	-д— =	1.
+ Дх -► о+о Дх дх -> о+о Дх
Так как f'+ (0) Ф f'_ (0), то функция у— 1х| в точке х = 0 не
дифференцируема (хотя она является непрерывной в этой точке).
Пример 25. Доказать, что функция у~ | (х— 1) (х—2) |
не дифференцируема в точках х= 1 и х = 2.
Решение. Найдем /1(1),	(1) и f'_ (2), f'+ (2). Прираще-
ния функции f(x) в точках х=1 и х = 2 соответственно равны
Д/(1) = /(1 + Дх)—•/(1) = | Дх (Дх—1) |,
Д/ (2) = f (2 + Дх) (2) = [ Дх (1 + Дх) |.
Следовательно,
£/ /1Ч v |Дх(Дх —1)|	Дх(Дх—1)
Г (1)= lim J-----4-----^-= lim ------4-----1J
• Дх -> о—о Дх Дх -> о—о Дх
/1Ч	.. |Дх(Дх—1)1	,.	— Дх(Дх—1)	,
f' (1) = hm J----4-----— = hm --------------=1;
+ Дх 0+0 Дх Дх -> о+о Дх
.. I Дх (1 + Дх)] v — Дх(1 + Дх)
f (2)= lim  ----4г------— ~ hm --------------=—И
“ Дх -> 0-0 Дх Дх -> 0-0 Дх
Л(2) = lim 1А*(1+А*М.= Иш +
Так как f'_ (1) # f'+ (1) и f'_ (2) f'+ (2), то функция f(x) =
= | (х—1) (х—2) | не является дифференцируемой в точках
Л = 1 и х=2.
Пример 26. Доказать, что функция f (х) = х | х |
дифференцируема в точке х=0, и найти ее производную в этой
точке.
Решение. Имеем
f (0)= lim Д*1Д*1 „ lim (—Дх) = 0!
'	Дх-0-0 Дх Дх -> о-о '
/Л\	1*	ДХ | ДХ |	«.	j л \ гх
fl (0)== hm —{--------~=	lim (Дх) = 0.
+	Дх-^04-0 Дх Дх->о+о'
Таким образом, f(0) = f(0) = 0, и, следовательно, функция
gr=f(x) дифференцируема в точке х=0 и ff (0) = 0.
Заметим, что, например, в теореме о производной суммы
двух функций предположение о дифференцируемости слагае-
мых существенно. Так, если f(x)= х| и g (х)= 1 —| х |, то
f(x)+g(x)=l. Каждая из функций (х) и g(x) в точке х = 0
не является дифференцируемой, в то время как функция
§ 1. ПРОИЗВОДНАЯ
355
f(x)^-g(x) в точке х = 0 дифференцируема. Поэтому высказы-
вание «производная суммы равна сумме производных» без
предположения о существовании производной у каждого из
слагаемых, вообще говоря, неверно.
Аналогичные замечания справедливы и для других правил
дифференцирования.
ЗАДАНИЕ 1
1. Найти приращение функции г/ = х2+2 в точке х=1 при:
1) Ах = 0,01; 2) Ах = —0,5.
2. Пользуясь определением производной, найти производ-
ную функции:
1) »=х+3; 2)	3) ?=у+1
в точке х= 1.
3» Пользуясь определением производной, найти производ-
ную функции в каждой точке ее области существования, если:
1) g=x3; 2) ^=cos2x; 3) #=1^ х, х > 0.
4.	Найти Л0)> Г (2), Г (—2), если f(x) = 3х2 + х4-1.
5.	Пользуясь правилом о производной частного, найти
производную функции y = tgX.
6.	Найти производную функции:
1)	у =	2)	у ж;
3) 0=(1-х)*; 4)
5)	y=2» + 3x4-4~*+2*.3*;
6)	y=log2 %4-2 log4 х—Inx;
7)	— sin x —>3 cos x—8) ^=3 tg x-f-0,1 ctg x;
9)	g = arcsin x—ex cos x; 10) g = у * 2 + 22* + x3- sin x;
I rT” X
sinx—cos x 1Oi .r— 2~x
} V~ sin x+ cos x ’	K arctg x ‘
ЗАДАНИЕ 2
1.	Найш приращение функции £=х-—х? в точкех=0 при:
1) Ах = 0,01; 2) Дх =—1/10.
2.	Пользуясь определением производной, найти производ-
ную функции:
1) y=2xd~l; 2) 0=х2 + х; 3) у=^/х
в точке х= 1.
3.	Пользуясь определением производной, найти производ-
ную функции в каждой точке ее области существования, если:
1) y=sin3x; 2) у=х§4»х§; 3) ^=1/х2.
4.	Найти Г (1), Г(—1)> Г (0), если f (х) = (1—х)3.
5.	Пользуясь теоремой о производной частного, найти
производную функции ^=ctgxft
12*
356 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
6» Вывести правило нахождения производной произведе-
ния
и (х) v (х) w (х),
7. Найти производную функции:
1)	2) г/=1—±+_^_5
5 Z~“
3) £=3**—logr/;,2х; 4) у~у x*^cosл-j-ctgх;
9*	1
б) »=33г4*1п*+—5 6) j/=exsinx;
7) z/=x?arcctgx; 8)	9) ^==—
10)	in »=а+х+х8)«?
tgj л •*!* vig л
ч».	1	1OS arctg х ... \^~xsinx
12) ^-^arccosx; 13) p=	14) y=	i
ЗАДАНИЕ 8
1. Найти производную функции:
1) y=cos5x: 2) у=(1 + «)ж; 3) p=K27^Is
4) t/=tg8 3xj 5) y=2*a+«+*? 6) p==e* ,n(*+2>s
7) p=sin3 4 (x—x*)-l-ctg l^T/x; 8) y=Kl + Ksi+log^Sj
9) p<=sin«(cosUx); 10) y=--a— 1 2 , 9 ;
11) y~Varcsin (14- 2x); 12) у ==x*.
2. Доказать, что каждая из следующих функций является
дифференцируемой в каждой точке:
1)
3)
2) sign х;
х > 0,
х^О;
4)
0,
х\
х^09
х < 0.
*/«=*8l*h
3, Привести пример функции, областью определения кото-
рой является вся числовая прямая и которая не имеет произ*
водной ровно в двух точках.
4. Привести пример двух функций, каждая из которых не
имеет производной в точке л®»1 и таких, что:
1) их сумма имеет производную в точке х=1;
2) их произведение имеет производную в точке л=Ь
357
§1. ПРОИЗВОДНАЯ
5. Найти производную функции
, .	( х1 sin X, я # О,
= { х
V 0,	х = 0,
в точках х = 2 и х = 0.
ЗАДАНИЕ 4
1. Найти производную функции:
1) У = Ctg (2х + 3); 2) # = sin3x2;
3) у=arcctg4 —J-5 ; 4) у=х2*?-1'*;
X а»
5) у== агссозНп хГ; б) г,= 10g2 (logs (log4 Х)):
alvCUo ^111 Л)
7) У= j/^sin^cos-^J ; 8) y=tg*^ctg
9) у= 10g^+*2l; 10) logx. 4+log_x 2;
У x
11) #=(sin x)cos12) g = У~x* ( iij у' ’ (x+х«)в.
2. Доказать, что каждая из следующих функций является
дифференцируемой в каждой точке:
1) у = | х | sin xi 2) y=x4signx; 3) ^=x|sinx|;
л fl, х^О,
4)	х4+1, *> 0.
3.	Привести пример функции, областью определения кото-
рой является вся числовая прямая и которая не имеет произ-
водной в четырех точках.
4.	Привести пример двух функций, каждая из которых не
имеет производной в точке х=2 и таких, что:
1)	их разность имеет производную в точке х==2|
2)	их частное имеет производную в точке х = 2#
5.	Найти производную функции
( 1 — COS X
*5*0»
х=0,
в точках 1 и х = 0.
Упражнения
1. Пользуясь определением, найти производную функции
в заданной точке
1) ^г=2—х, *о=1;	2) г/“-х2—4, хо=О^
3)	х0=1; 4) 0=sin2x, х0==л/4|
5) cos2x, я0=я/4; 6) 0»2*в *a=ij
, 858	ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
хо=о;
(	X2, XSsO,
)У“{ — X*, х<0,
8) y=ctg х, ж0=л/4.
2. Пользуясь определением, найти производную функции
в каждой точке ее области существования:
1) у~х2+х+1;
3) у=х8+2; 4)
6) #=cos7x; 7)
9)Н !-а
2) y=Vх+1, х>-15
г/=ТТ2’’ 5) #=sln5*;
y=logi/2x; 8) у =(1/3)*;
х 0,	( ех, х^О,
х < 0;	I *+ 1, х < 0.
3. Найти производную функции:
(1 + 2х)2 оч / f 1 O1/“V
1) у=--	; 2) # = х+--2П ;
ух	\ х /
3) г/=sin2 ^-4-cos2А; 4)	)ае-х*;
5)	у=(1п /Т=^)/Т+^; 6) j/=logx2-logA.3-logjc4j
7)	у=arcsin х + arccos х;
8)	^=1п(/Г+^-х)+1п(КТ+Т24-х);
9)	z/ —2log2 *+х2+х;	10)	;
их	sinx + cosx 1ft4 1 . х
11) t/ = arctg—————; 12) y=lntg —— cosxlntg*;
o111 Л CUu л»
13) y = log2 У igrcg ; 14) у=агСс12трр^=;
15) j/=ln(e^Ki + e2x); 16) y = eJC4-eeX+e^;
3 Z~ d ' — ..'..л."'
17)	0=y x+i/x+ j/14-ж2 ;
18>	У= -arcctgx6;
19)	j/=arctg(x+/'bFx2);
20)	'y= In2 (arccos -J=A + e~xtexi
X V */
21)	y=A*arcsin KI+ x2c^sjc ;
22)	^In^+ln^l+lnl))-,
23)	</=logx2 + logA2(x24-l);
24)	^=210S4^+*+i); 25) y = x+x*-,
26)	y=xW; 27) »=xcot*S 28) y^xX}.
§1. ПРОИЗВОДНАЯ
359
4. Доказать, что каждая из следующих функций является
дифференцируемой при любом значении х:
1)	y=x2|sinx|; 2) r/ = |x|sin2x;
(х4 sin ~, х # О, л. о .
3)	х	4) iy = x3signx.
( 0, х = 0;
5.	Построить график производной функции:
1)	у = х2+2х + 3; 2) j/=|x+2|;
3)	г/ = |х| + |х+11; 4) f/ = tgxctgx;
(	х2, х О,	.Illi
5)0=j_x6, х < 0; 6) 0=11*1--Ч-
6.	Привести пример двух функций, каждая из которых не
имеет производной в точке х = х0 и таких, что:
1)	их сумма является функцией, дифференцируемой в
точке х0;
2)	их произведение является функцией, дифференцируемой
в точке х0.
7.	Привести пример двух функций, каждая из которых не
имеет производной в точках х0 и Xf, х0 #: хх, и таких, что:
1)	их сумма является функцией, дифференцируемой в точ-
ках Х)0 И X1J
2' их сумма является функцией, дифференцируемой в точ-
ках Хо и Xi, но не имеет производной в точке х3, х3 # Xi, х3 Ф х0;
3)	их произведение является функцией, дифференцируемой
в точках х0 и Xi.
8.	Привести пример функции, областью определения кото-
рой является вся числовая прямая и которая имеет производную:
1)	ровно в одной точке;
2)	ровно в двух точках;
3)	ровно в п точках.
0. Найти f' (а), если f (х) = (х—• а) <р (х), где функция <р(х)
имеет производную в точке х = а.
10. Найти f (0), если f (х) = х (х+ 1) (х+2). * .(x+n), ngN.
11. Найти правую и левую производные функции в точке х0:
1)$/ = |х+1|, х0 = —1;	2) ^=х2«-1, х0 = 2;
OV f X, X 0, Л
3)г/-\5х, х < 0, *0-°!
4) у — | sin х |, х0 —л;
( ех> х^О, Л
'	( cos х, х < 0, и
6)	| х ] — |х4-11, хо = 0;	7) Г/=|Х2—х], ха=!|
8)	j/^sin2 х—sin х, х0==л;
9)	f/=tgxctgx, х0 = л/4;
10)	у = arcsin (sin х), х0=л/2,
12.	Пусть

(
I ах + &,
Х<Хб,
* > ХО.
Подобрать коэффициенты а и b так, чтобы функция Цх) была
непрерывной и дифференцируемой в точке х = х0<
360	ГЛ, б. ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
13,	Пусть
Г/Н /«**+&*+!> *^0,
''	х < 0,
Подобрать коэффициенты аиЬ так, чтобы функция f(x) была
непрерывной и дифференцируемой в точке х=0.
14,	Доказать, что производная дифференцируемой четной
(нечетной) функции есть нечетная (четная) функция.
15.	Привести пример дифференцируемой функции, которая
не является нечетной, но ее производная есть четная функция.
16.	Доказать, что если производная дифференцируемой
функции f (х) есть нечетная функция, то функция f (х) является
четной.
17.	Доказать, что производная дифференцируемой периоди-
ческой функции есть функция, периодическая с тем же периодом»
18.	Вывести формулы для суммы:
1)	l+2x + 3^+...+nx"~i;
2)	Р+22х + 32ха+... + п*х”-\
рассмотрев производную функции х-f-x2 + x3
19.	Пользуясь тождеством
. п +1	. пх
sin——xsin -у-
sin х+sin 2х	»*+ sin пх =*-----------—,
Sin у
вывести формулу для суммы
cos х4-2 cos 2х+ ... + п cos х.
§ 2, Производная и касательная
Касательная к окружности в геометрии определяется как
прямая, имеющая с окружностью лишь одну общую точку.
Это определение имеет частный характер и не раскрывает су-
щества дела. Если применить его к параболе у=х2 (рис. 5.1),
то з начале координат обе координатные оси подошли бы под
это определение; между тем интуитивно ясно, что касательной
является лишь ось абсцисс»
Пусть точка Л10(х0; у0) принадлежит графику функции
gz^Kx), определенной на интервале (а\ 6). Рассмотрим кроме
точки точку М {х\ у), также принадлежащую графику функ-
ции y*=*f(x)t и проведем прямую называемую секущей.
При перемещении точки М (х; у) по графику функции секущая
будет менять свое положение. Если точка М приближается
к точке Л40, то может случиться так, что секущая будет стре-
миться занять некоторое предельное положение, не зависящее
от того, как точка М приближается к точке (рис. 5.2).
Карательной к графику функции y=f(x) в точке Л40 = (х0;
называется предельное положение секущей MQM (если
он® существует), когда точка М (х; f (х)) стремится к точке /Щ.
Подчеркнем, что в данном определении содержится допу*
щение о тем, что предельное положение секущей существует;
$ 2. ПРОИЗВОДНАЯ И КАСАТЕЛЬНАЯ
361
Рис, 5,4
Рис. 5»5
362
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
не всякая функция y—f(x) обладает касательной в каждой
точке своего графика. На рис. 5.3 показаны графики функций,
которые не имеют касательных в точках х0, 0, и х2, так как,
если бы предельное положение секущей в каждой из этих точек
существовало, то оно не должно зависеть/ например, от того,
«слева» или «справа» точка М стремится к точке Л40.
Отметим также, что в данном определении не требуется,
чтобы касательная к графику функции имела только одну об-
щую точку; так, на рис. 5.4 касательная к графику функции
у=х$ с точкой касания Мо пересекает его еще в точке A4lt
Уравнение секущей (рис. 5.5), т. е. прямой, проходящей
через две точки Л40 (х0; f (х0)) и М (х04-Дх; f(*o + ^*))» сле-
дующее:
»-/<«.>- (м>).
Если функция y~f(x) дифференцируема в точке % —х0, то пре-
дельное положение секущей MQM при стремлении точки М
к точке (при Дх ~>0) существует, и ее уравнение (уравне-
ние касательной к графику функции y=f(x) в точке (х0, f (х0))
следующее:
У — f' (*о) (я*~*о) + М*о)«
Если прямая пересекает ось ОХ в точке А (рис. 5.6), то
наименьший угол, на который надо повернуть против часовой
стрелки относительно точки А ось ОХ, чтобы она совпала
с данной прямой, называется углом между данной прямой и
положительным направлением оси ОХ, Если прямая парал-
лельна оси ОХ, то этот угол считается равным нулю.
Из уравнения касательной получаем следующую геометри-
ческую интерпретацию производной функции у=/(х) в точке
х~х& значение f' (х0) есть тангенс угла между положительным
направлением оси ОХ и касательной к графику функции у=/\х)
в точке (х0; f (х0)). Коротко говорят, что производная /' (х0)
есть тангенс угла наклона касательной к графику функции
y=f(x) в точке х=Хо.
Если прямая ij~kx-\-b пересекает ось абсцисс и является
касательной к графику функции у~[(х) в точке х==х0> то ве-
личина угла ф между этой прямой и положительным наврав-
§2. ПРОИЗВОДНАЯ И КАСАТЕЛЬНАЯ
лением оси абсцисс удовлетворяет соотношению &=tg cp = f' (х0).
Отсюда находим, что
( arctg f' (х0), если f' (х0) > О,
( л+arctg /' (х0)> если /' (х0) < 0.
Пример 1. Найти уравнение касательной к графику функ-
ции у = х2—х в точке х0—1.
Решение. Так как у'(х)~2х—1, то у' (1)=1, и урав-
нение касательной следующее: у~у‘ (1) (х-— 1) + у (1). Таким
образом, у = х—1 — искомое уравнение касательной.
Пример 2. Найти уравнение касательной к графику
функции:
а)	у = х2; б) </ = х3
в точке х —х0.
Решение, а) Так как (х2)'=2х, то уравнение касатель-
ной к графику функции у — х2 в точке х = х0 следующее:
у=2х0 (х—хо) + хо,
или
^ = 2х0х —хо.
б)	Так как (х3)' = 3х2, то уравнение касательной к графику
функции у = х8 в точке х=х0 следующее:
у=3хо (х—хо)+хо,
или
у — Зхох—2хо.
Анализ полученных уравнений показывает, в частности, что
касательные к графику функций у = х2 и у=х3 в точке х = х0
пересекают ось абсцисс соответственно в точках х0/2 и 2х0/3.
Отсюда следует простой геометрический способ построения
касательной к каждому из этих графиков. Для того чтобы
построить касательную к графику функции # = х2 (у = х3), нужно
разделить отрезок [0, х0] на две (три) равные части и провести
прямую через точку (х0; f (х0)) графика функции у—х2 (функ-
ции у=х3) и точку (х0/2; 0) (точку (2х0/3; 0)) — рис. 5.7.
Пример 3. Найти угол между положительным направле-
нием оси абсцисс и касательной к параболе у = х2—4х—17
в точке с абсциссой Хо = 2,5.
Решение. Так как у' = 2х—4, то у' (2,5)= 1. Поэтому для
искомого угла <р имеем tg<p= 1, откуда находим ф=л/4.
Угол между положительным направлением оси ОХ и каса-
тельной к графику функции y~f(x) в точке х=х0 такой, что
f(xo) = O, называется углом между, графиком и осью абсцисс
в точке хо.
Пример 4. Под каким углом график функции y=sinx
пересекает ось абсцисс в точке х=0?
Решение. Так как (sinx)' = cosx и cos 0=1, то график
функции у = sinx пересекает ось ОХ в точке х=0 под углом ф,
§ля которого tg ф= 1. Таким образом, ф=45°«
364 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Пример 5. Найти все точки графика функции У—§
в каждой из которой касательная, проведенная к этому гра-
фику, образует угол 135° с положительным направлением оси ОХ.
Решение. Пусть (х0; f(x0))~точка графика функции

х + 2
х—2
в которой касательная к ее графику образует
с положительным направлением оси ОХ угол в 135°, а у =
==	6*-уравнение этой касательной. Тогда k = f' (х0) =
==tg 135°=—1.
Так как
и- 4 У-_________4—
Т W \х^2/	~	(х^-2)2’
то для х0 имеем уравнение — 4/(х0—2)2 =—1; отсюда хо^О
и хо2) = 4. Проверкой убеждаемся, что обе точки (0; — 1) и (4; 3)
графика данной функции удовлетворяют условию задачи.
Углом между двумя пересекающимися прямыми называется
наименьший из углов, возникающих при пересечении этих пря-
мых. Угол между параллельными прямыми считается равным
нулю. Таким образом, величина угла между прямыми равна
наименьшему из чисел | Ф1“—ф21 и л—| Ф1~-ф21> где фх и ф2 —
величины углов наклона каждой из данных прямых к поло-
жительному направлению оси ОХ.
Пример 6. Найти угол между касательными к графику
функции /(х)™х3—х в точках с абсциссами — 1 и 0.
Решение. Так как f' (х)=3х?~- 1, то f' (—1) = 2 и f' (0) =
= — 1. Таким образом, нужно найти угол между прямой
0==2(л>,4-1) и прямой у = —х. Имеем tg ф1=а2 и tg<p2 = —-1,
Отсюда находим
<РХ=arctg 2, ф2 = Зл/4*
§ 2. ПРОИЗВОДНАЯ И КАСАТЕЛЬНАЯ	365
Так как arctg2 < л/2 < Зл/4, то величина искомого угла равнз
наименьшему из чисел (р2***ф1 и я—(ф2~-Ф1)> т. е. из чисел
-|-л—arctg2 и-~4-arctg2.
Так как arctg2 >arctgl=^~, то -j4"arctS2 > и, сле*
довательно, величина искомого угла между касательными
равна -л — arctg2.
Если заданы две прямые y~kix-\-bt и g — k^x-^-bz {k± О,
&2 5^ 0),|то величина угла <р, О^ф’С л/2, между этими прямыми
находится из соотношений
tg4> I l+feli I’
если ^1^2 # —1,
ф = л/2, если ^2=—1«
Углом между графиками
функций g~f(x) и g=g(x) в
точке их пересечения называ-
ется угол между касательными
к их графикам в этой точке
(рис. 5.8).
В случае, когда этот угол
равен нулю, графики функций
касаются друг друга.
Рис. 5.8
При_мер 7. Найти угол между графиками функций
и g(x) = x2/2 в точке их пересечения (с положи-
тельной абсциссой).
Решение. Абсциссы точек пересечения данных графиков
удовлетворяют уравнению
У" 2х = х2/2
и тем самым следующей системе;
( х^О,
( 2х = х4/4.
Отсюда находим, что графики функций пересекаются в двух
точках, абсциссы которых равны 0 и 2. Найдем тангенсы углов
наклона касательных к обоим графикам функций в точке
абсциссой, равной 2< Имеем
f*>(#)=-! - -7~*2=-Д=-э g*(x)>=4-*2x==xe
2 /2х О*	2
Отсюда ^(2) = 1/2 и gfj (2) = 2. Так как f(2)=g(2) = 2, то урав-
нения касательных к графикам функций #=/(4 и #«=£(4
ГЛ 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
В точке (2; 2) соответственно имеют вид
^ = 2. (х—2)4-2 и //=2 (х*—2)4-2,
t»e.
У=у*+1 и $r=2x—2.
Следовательно, величина угла а между касательными удовлет-
воряет уравнению
в тем самым графики функций f(x) и g(x) в точке с абсциссой
х—2 пересекаются под углом, равным arctg-—-.
Пример 8. Найти величину угла, под которым пересе-
каются окружности
^4-^2—>4х =3 1,
х2+у2—2^=9.
(1)
(2)
Решение. Координаты точек пересечения данных окруж-
ностей удовлетворяют системе уравнений
f x2 + j/2*—4х — 1,
( л2 + ^2—2^ = 9.
Вычитая из первого уравнения системы второе, получим
—4х-|-2#= — 8, т. е. 0 = 2х-—4. Подставляя 2х —4 вместо у в
первое уравнение системы, найдем, что числа 3 и 1 будут корня-
РИСе 5«9
ми полученного уравнения.
Таким образом, решениями
системы являются пары чи-
сел (3; 2) и (1; —2). Так
как углы между окруж-
ностями в точках А и В
(рис. 5.9) равны (в силу
симметрии окружностей от-
носительно прямой Oj О2,
проходящей через их цент-
ры), то достаточно найти
угол между касательными
к этим окружностям, про-
ходящим через точку (3; 2).
В окрестности точки х~3
уравнения (1) и (2) опреде-
ляют соответственно функ-
ции yt (х) = 4-4х—«х2 и
^2 (х) = 14*	Так
§ 2. ПРОИЗВОДНАЯ И КАСАТЕЛЬНАЯ
как
/	— 2x4-4	—х+2
2К1+4х-х»
' { ч	—2х	—х
УЪ (х) =-;?======- =	_ ..-,
2К10-Х2 V 10-х2
то #i(3) =—1/2 и #2(3)=—3. Таким образом, искомый угол о$
находится из соотношения
—
откуда а = л/4.
Пример 9. Найти на графике функции f(х) = х2—7х+3
такую точку, касательная в которой параллельна прямой
Решение. Прямые	y^k2x-\-b2 параллельны
(в том числе совпадают) тогда и только тогда, когда —
Так как уравнение касательной к графику функции y~f(x)
в точке с абсциссой х0 имеет вид
j/=(2xo—7) (х-хп) + (х?-7х0 + 3),
то эта прямая параллельна прямой #=5х+2 при условии, что
2х0—7 = 5. Отсюда находим ха = 6. Таким образом, касательная
к графику функции y=f(x) параллельна прямой # = 5х+$
только в точке (6; —3).
Пример 10. Найти точку, в которой касательная к гра-
фику функции # = х2 перпендикулярна прямой 2х—#+1=0.
Решение. Прямые y — k1x+b1 и yz — k^x+bz
k2 Ф 0) взаимно перпендикулярны тогда и только тогда, когда
^2 =—1. Уравнение касательной к графику функции #=х*
в точке (х0; Хо) следующее:
# = 2х0 (х—х0)+хо = 2х0х—хо.
Для того чтобы эта прямая была перпендикулярна прямой
#=2х+1, необходимо и достаточно, чтобы выполнялось равен-
ство 4х0=—1. Отсюда находим, что касательная, проведенная
к графику функции # = х2, перпендикулярна данной прямой
только в точке (—1/4; 1/16).
Пример 11. Найти все значения параметров b и с, при
которых прямая #=2х+26 касается графика параболы /(х) =
= х2 + ^х+с в точке (2; 0).
Решение. Переформулируем задачу следующим образом:
найти все значения параметров b и с, при которых уравнение
касательной к графику функции #=х2+Ьх+<? в точке (2; 0)
имеет вид #=2х+26. Отсюда получаем два условия:
1) точка (2; 0) принадлежит графику функции f (х)=х2+&х+с,
т. е. 4 + 2д+<? = 0;
2) /'(2) = 2, т. е. тангенс угла наклона касательной в точке
(2; 0) с положительным направлением оси ОХ равен 2 (угло-
вому коэффициенту прямой #=2х+26).
Зб8 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Отсюда с учетом формулы f' (х)—2х-[-Ь имеем систему
( 4 + 2*-f-c = 0,
\4+&=х2,
из которой получаем & =—2, с = 0.
Пример 12. Найти все значения параметра at а > 1, для
каждого из которых график функции у~а* касается прямой
Решение. Условия касания графиков данных функций
в точке с абсциссой х0 можно сформулировать следующим
образом:
1) значения функций в точке х = х0 равны;
2) значения производных функций в точке я = х0 равны^
Таким образом, для нахождения искомых значений а
(а также х0) имеем систему уравнений
(а*о = х0,
( ахо In а = 1.
Из второго уравнения имеем а*о=1/1па. Подставляя в первом
уравнении системы 1/1п а вместо а*о, получаем уравнение
я0== 1/1па.
Подставляя во втором уравнении системы 1/1па вместо х0, по-
лучаем уравнение
а1/1па1па=1,
после логарифмирования которого, получаем уравнение
-г-—Ina-Pin 1па = 0,
Ina 1
Таким образом,
In Ina——1,
и тем самым Ina— 1/е, т. е. a=e1/e. Проверкой убеждаемся,
что значение а—е1^ является искомым.
Пример 13. На графике функции у(х) = х3—Зх2—7х+6
найти все точки, касательная в каждой из которых к этому
графику отсекает от положительной полуоси ОХ вдвое мень-
ший отрезок, чем от отрицательной полуоси OY. Определить
длины отсекаемых отрезков.
Решение. Уравнение касательной к графику функции
у(х} в точке с координатами (я0; у(*о)) следующее;
y=kx-\-bt
где&=у'(я0), Ь^у (х0) *б- Эта прямая пересекаетесь
ОХ в точке с координатами (—b/k\ 0) и ось OY в точке с ко-
ординатами (0; Ь)ь Таким образом, из условия задачи получаем
систему условий, которым должны удовлетворять координаты
искомых точек:
«-*/£> о, &<о, 2(—
Учитывая, что b < 0, последнее условие можно переписать в
виде /г=2, а всю систему условий—в виде £ = 2, b < 0.
§ 2. ПРОИЗВОДНАЯ И КАСАТЕЛЬНАЯ	369
Таким образом, имеем систему
Г /W = 2,
\у(*о)—у' (Шо < 0.
Так как у' (х) = 3хI 2—6х—7, то абсциссы искомых. точек удо-
влетворяют уравнению Зх2—6х—9 = 0. Его корни равны xt = 3
и х2== —1. Проверим для найденных значений х выполне-
ние неравенства системы. Имеем у (3)-~у' (3)*3 =—15—2«3=
= — 21 < 0,
у(-1)-у' (—1) (—1) = 9 > 0.
Таким образом, есть только одна точка, удовлетворяющая ус-
ловию задачи. Ее координаты равны х0 = 3, yQ = у (3) = —15.
Длины отрезков, отсекаемых касательной в точке (3; —15) на
осях OY и OXt равны соответственно значениям —b и —blk,
Где —6 = / (х0)х0--У (*о) и —х0; отсюда находим,
что они равны соответственно 21 и 21/2,
Пример 14. Найти уравнение прямой, проходящей через
х2
точку (1/2; 2), касающейся графика функции у=----g"+2 и
пересекающей в двух различных точках график функции у =
scj/' 4—х2.
Решение. Обозначим через (а; (3) координаты точки,
в которой искомая прямая касается графика функции f (х) =
—[-2. Тогда угловой коэффициент этой прямой равен
/'(«)==—-а, и тем самым ее уравнение принимает вид
а(х—а).
Прямая по условию проходит через точку (1/2; 2); поэтому
должно выполняться равенство 2 = 0 —а (1/2—а), т. е. р-[-а2 —
— а/2 = 2, Так как точка (а; 0) лежит на графике функции f (х),
то найдем еще одно условие: 0 = — а2/2 + 2. Решая систему
уравнений
J 04-а2 — а/2 = 2,
\ 0=-^а2/2 + 2,
находим две точки касания: (0; 2), (1; 3/2). Уравнения каса-
тельных к графику функции y=f(x) в этих точках следующие:
у=2 и у ——х4-5/2. Найдем число точек, в которых каждая
из найденных прямых пересекает график функции ^=1^4—х2.
Система
I У~Ъ
имеет единственное решение (0; 2). Значит, касательная у=2
имеет только одну общую точку с графиком функции К4—х2.
370 ГЛ. б. ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
Решим систему
I £= —*4-5/2.
5
Подставив в первом уравнении — х+у вместо у, получим
систему
( — *4-5/2= У 4^,
I у=—*4-5/2,
равносильную исходной системе. Множество решений первого
уравнения этой системы содержится в промежутке —2 «сх=С2.
На этом промежутке обе части этого уравнения неотрицательны,
и поэтому оно равносильно на этом промежутке уравнению
(— х4-5/2)а = 4—х2.
Полученное уравнение имеет два корня:
5 — VI	54-К7
*1=----5---- й «2=—14------->
принадлежащих промежутку —2 «С* «С 2. Поэтому рассматри-
ваемая система имеет два решения:
/5-/7. 54-К7\ /54-К7. 5 — К 7 \
\	4	’	4	/’ \	4	’	4	/'
Следовательно, прямая # = — х+5/2 пересекает график функции
^=уг4—х2 ровно в двух различных точках и тем самым яв-
ляется искомой.
Пример 15. Найти геометрическое место вершин прямых
углов, обе стороны которых касаются графика функции у=-^х2.
Решение. Пусть (а; Ь) — вершина искомого прямого угла,
a Xi и х2—абсциссы точек касания сторон этого угла с гра-
фиком функции ^=~х2 (рис. 5.10).
Заметим, что
1)	касательная к графику функции У~-^ х2 в точке
(1	2 \	. х
— Xi I должна проходить через точку (а; Ь);
2)	касательная к графику функции у=:~х2 в точке
•— xl'j должна проходить через точку (а; &);
3)	обе эти касательные должны быть взаимно перпендику-
лярными.
Уравнения	касательных к графику	функции	у=-^-х2,	про-
/	1 2\	(	1 2\
ходящие через	точки	I х±;	-г- Xi )	и	( х2; -г х2 I >	соответственно
\	4 ]	\	4 /
§ г. ПРОИЗВОДНАЯ и касательная
следующие:
1	1 2
У=^Х1Х—у хн
1	1 -
Х2Х--J-X2.
Из условий 1)—3) получаем следующую систему уравнений!
к	1	12
6 =	хь
и	1	1 2
’ *2’
1	1	1
yx1.1-x2=-L
Вычитая из первого уравнения системы второе, найдем, что
О=у («f—х2) — Y (X!—Х2) (Xi+Хг),
т, е.
(%1 — х2) (2а — (xj + х2))« 0.
Таким образом, Xi + %2 —2а. Складывая теперь первые два
уравнения системы, получаем
2Ь=у (%1+Ха) — ’j- (*i+
т. е»
26==у (xi + x2)-~	2х1ха)\
^2 гл. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Отсюда, учитывая, что «iX2=—4 и х£-|-х2=2а, имеем
2*=-|-.2а—1(4^+8),
т. е. 6 =—1. Так как 6 =—1, то вершина угла, удовлетворяю-
щего условию задачи, может лежать только на прямой #==—L
Проверкой убеждаемся, что точка (а; —-1), где а—любо®
действительное число, удовлетворяет условию задачи.
Понятие «касательная к графику функции» позволяет дать
важную характеристику свойства выпуклости функции. Имеет
место следующее утверждение:
Пусть функция y — f(x) непрерывна иа интервале (а; Ь) и
имеет в каждой точке этого интервала производную. Для вы-
пуклости вниз (вверх) функции f (х) на (а; Ь) необходимо и доста-
точно, чтобы ее график всеми точками лежал не ниже (не выше}
&*4aib)
-I
&	0 i х
4^0 Q £
Риа« 5Д1
любой своей касательной, m, e. для функции, выпуклой вниз,
f (X) f! (х0) (X **Х0) + f (х0)
для любых х и х$ из интервала (а; Ь) (рис. 5,11, а), а для функ-
ции, выпуклой вверх,
f (х) < f' (хо) (х—х0) + f (х0)
для любых х и хо из интервала (а\ Ь) (рис. 5.11, б}9
Пример 16. Доказать, что
еь еа+еа (Ь•**«)
для любых действительных чисел а и Ь.
Решение. Так как функция у~ех выпукла вниз, то ее
график расположен не ниже касательной к нему, проведенной
в точке (а; еЛ), и, следовательно, для любого числа b имеем
еа (Ь *•*»#) 4“
что и требовалось доказать.
В частности, если а«==0, то из доказанного неравенства
следует, что еь'£* 1-J-& при любом
§2. ПРОИЗВОДНАЯ И КАСАТЕЛЬНАЯ
Пример 17. Доказать, что
In п <	. +*^Z7f » л^2.
Решение. Докажем неравенство более общего характера,
имеющее и другие приложения.
Пусть y=f(x) имеет производную и выпукла вверх
на некотором интервале (a; Ь), а числа Xf, х2) .хп из этого
интервала являются членами арифметической прогрессии с раз-
ностью rf. Тогда
f (хп) «С f (xt) + d (Г (Х1) + Г (х2) + ... +Г (х^)).	(3)
Действительно, так как функция у—f (х) выпукла вверх, то ее
график лежит не ниже касательной, проведенной в любой точке
(х*; f(xk)) графика функции y=f (х); в частности,
f(xA+iX/:(xA) + f'(Xft) (х^+1 —xfe), 6=1, 2, ..., n —1,
т. е.
f(xk+iXf (xk} + df (xk)> 6=1, 2, n—1.
Сложив все полученные для £—1, 2, ,,,, п—1 неравенства,
найдем, что
f	(хО + Г (x2) + ,,.+f (x^i)).
Если теперь f(x)=lnx, x^ — k (£=1, 2,	n), то из (3) сле-
дует, что
(1) + Г (XxJ+r (x2)+	(xn^i),
t. e.
lnn<C	n^2.
ЗАДАНИЕ 1
1. Найти уравнение касательной к графику функции y=f(xj
в точке с абсциссой х0:
1)	х0 = 2;
2) /(x) = cosx, х0 = л/4.
2.	Найти уравнение касательной к графику функции у=/(х),
проходящей через заданную точку Л4:
1)	f (х) = х\ М = (1; —1);
2)	f (x)=Vx—l, М = (5;3).
3.	Найти все точки графика функции	в каждой
из которых касательная к этому графику образует угол 45°
с положительным направлением оси ОХ.
4.	Найти угол между касательными к графику функции
у=4(х) в точках с абсциссами х = —1 и
1) f W=«2—1; 2) /1*) -
374
ГЛ. б. ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
ЗАДАНИЕ 2
1. Найти уравнение касательной к графику функции в точке
с абсциссой х0:
1) f(x)~e*, х0==1; 1 2) f(x) = x2 + x+h хо = О.
2. Найти уравнение касательной к графику функции y—f(x),
проходящей через точку М:
1)	f(X^i/Xf М(—1; 1);
2)	f (х) =	М (0; 2).
3.	Найти все точки графика функции
х+2
в каждой
из которых касательная к этому графику образует угол 135°
с положительным направлением оси ОХ.
4.	Найти угол между касательными к графику функции
y~f(x) в точках с абсциссами хо = О и хх = 1/2:
1) /(х) = К 4-х*; 2) f (х) = log, (х-|-2).
ЗАДАНИЕ 3
1. Под каким углом график функции y=f(x) пересекает
ось абсцисс в точке х = х0:
1)	f (х) = cos 2х, х0 — л/4;
2)	/(х) = х4 —х2, х0=—1?
2.	Найти угол между графиками функций y~f(x) и y=g(x)
в точках их пересечения:
1) f (х) = 1/х, g(x) = x; 2) f(x) = x*, g(x) = v~x.
3.	На графике функции y=f (х) найти точку, касательная
в которой параллельна прямой у+2х—3 = 0:
1) f(x) = e~x; 2) f(x)=l — f/ х.
4.	На графике функции y—f(x) найти точку, касательная
в которой перпендикулярна прямой у—2x4-1 = 0:
1) /(х) = х3—х+1; 2) /(х) = — /2х+т.
5.	Найти все значения параметра а, при каждом из которых
касательные, проведенные к графику функции # = х3—а2х
в точках пересечения этого графика с осью абсцисс, пересе-
каются под углом л/4.
ЗАДАНИЕ 4
1. Под каким углом график функции y~f(x) пересекает
ось абсцисс в точке х = х0:
1) /(x) = tg2x, хо = 0;
2) f(x)=l-^x, х0=1?
2.	Найти угол между графиками функций y—j{x} и y~g(x)
в точках их пересечения:
1) f(*) = Ki—*2; g W = К
2) f( x) = x?—x, g (X) = 12/X.
§2. ПРОИЗВОДНАЯ И КАСАТЕЛЬНАЯ	375
3.	На графике функции y—f(x) найти точку, касательная
в которой параллельна прямой 2у—х 4-2 = 0:
1)	/(х) = ^; 2) у = х3—Зх24-1.
4.	На графике функции y — f(x) найти точку, касательная
в которой перпендикулярна прямой х4-2у+1 =0:
1)	/(х) = х2; 2) f (х) = log2 х.
5.	Доказать, что при любом значении а существует каса-
тельная к графику функции 0=х3~-а2х, перпендикулярная
прямой 0=—х.
Упражнения
1. Найти уравнение касательной к графику функции y=f(x)
в точке с абсциссой х = х0:
1) /(х) = х2—2х, хо = О,5;
*0=1;
3)/(х)=К^+1> *о = 2)
4) f (х) = х In х, х0 = е;
5) f(x)=-~sin2 (4х—л/3), х0 = п/6.
2.	Найти уравнение касательной к графику функции
0=7 (х), проходящей через заданную точку М:
1)	f(x) = —х2+1, 2И = (1; 1);
2)	f(x) = x3, М = (2; 4);
3)	/(х) = х2—х, /И = (—1; — 1);
4)	/(х) = К*> /И = (1/4; 1/2);
5)	f (х) = 1/х, М = (-1; 1).
3.	Найти координаты точки пересечения касательных
к графику функции y — cosx в точках с абсциссами х =—л/3
и х=л/3.
4.	Найти уравнение касательной к графику функции
y=f(x) в точке пересечения этого графика с заданной прямой:
1)	f (х) = х2 — 4х + 5, х=0;
2)	f(x) = 4—х2, 0=0;
3)	f (x) = tg х, 0 = 0.
5.	Найти уравнение горизонтальной касательной к графику
ФУНКЦИИ 0 = 0х4-£~*.
6.	Найти координаты точек пересечения с осью ОХ каса-
тельных к графику функции	которые образуют
угол 135° с положительным направлением оси ОХ.
7.	На графике функции y = f(x) найти все такие точки,
в которых касательная, проведенная к графику, параллельна
данной прямой:
1)	f(x) = x3 — Зх24-2 0 = 3>с;
2)	/ (х) = х2««7х4”3,	=
376 ГЛ- 5- ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
3)	f(x)==-~-sin 2х—sin х„ 1/.-^- х— 1 ~0;
4)	f (x) = ln (4х— I), г/ = х;
1	У 3
5)	f (х)=-~ sin 3x4—cos Зх, у~—х<
о	о
8.	На графике функции y—f(x) найти все такие точки,
в каждой из которых касательная, проведенная к графику,
перпендикулярна заданной прямой:
1)	f (х) = х3+2х— 1, х+у=0;
2)	f(x) = x?+x+l, ^+5 = 0;
3)	f(x) = sinx, х—10 = 0;
4)	f(x)~tgx, #4-х = 0;
5)	/ (х) = In х, 2^+х+1 = 0.
9.	Найти координаты точки пересечения двух касательных,
j^2 I |
проведенных к графику функции у=-----5- в точках с абсцис-
X о
сами х = 4 и х=—2.
10.	Найти координаты точки пересечения двух касательных,
проведенных к графику функции y = sin3x в точках с абсцис-
сами х=л/18 и х = 5л/18.
11.	Найти на графике функции /(х)=4> х3—-2Х? — 22х—28
о
все такие точки, касательная в каждой из которых к графику
пересекает положительные полуоси и отсекает от них равные
по длине отрезки.
12.	Найти на графике функции /(х) = х3—Зх2—7x4-6 все
такие точки, касательная в каждой из которых к графику
отсекает от положительной полуоси ОХ по длине вдвое меньший
отрезок, чем от отрицательной полуоси OY, Определить длины
отсекаемых отрезков.
13.	Найти уравнение параболы у~х2 + Ьх+в, касающейся
прямой у=х в точке (1; 1).
14.	Найти уравнение прямой, проходящей через точку
(1/2; 2), касающуюся графика функции у=—х?/24-2 и пере-
секающую в двух различных точках окружность (х—2)2+^= 1.
15.	Найти на графике функции f (х)=-ух3—х2 —х4~
все такие точки, касательная в каждой из которых к графику
перпендикулярна прямой 5х—3z/4~2 —0.
16.	Какой угол образует с осью абсцисс касательная к па-
раболе z/=х2-—4х —-17-, проведенная в точке с абсциссой
Хо-5/2?
17.	На графике функции f (х) = Зх?«-»4х24-7 найти все такие
точки, касательная в каждой из которых образует с осью ОХ
угол л/4.	___
18.	В какой точке графика функции у = —]/"2х3 касатель-
ная к нему перпендикулярна прямой 4х«—3^ 4-2 = 0?
19.	Найти уравнения касательных к графикам функций
/(X)=s=j/"2x и /(х)=х2/2, проведенных в точке пересечения
этих кривых»
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ 377
20.	Найти угол между касательными к графику функции
f (х) = 3х3—7х2т|-Зх+5, проведенными в точках с абсциссами
0 и 1.
33
21.	Известно, что прямая у=— Тх~“32 является касатель-
ной к графику функции f (х)=~ х*-х. Найти координаты
точки касания.
22.	Найти величину угла между двумя касательными, про-
веденными из точки М (0; —1) к графику функции у—х2.
23.	Доказать, что для любых действительных чисел х и у
имеет место неравенство
хп^ yn + tiyn~i (х — у), ngN
24.	Доказать, что для любых положительных чисел х и у
имеет место неравенство
(*—£)•
. л У \ У /
25.	Доказать, что для любых х и у из промежутка [0; я]
имеет место неравенство
sin х—sin у < (х—у) cos у,
26.	Доказать, что для любых положительных чисел х и у
имеет место неравенство
у\п—<х—у.
27.	Доказать, что:
1)	/г*> 14-й(1й-14-2*-1+.,. + (п— 1)»-*), п^2, «,
2)	K»<4+4(y^-+yj+>«-+y=Y)> «^3,
п g N;
3)	пп > en~l	n^2, ngN.
§	3. Исследование функций и построение графиков
Общая схема исследования функции и построение ее графика
включает в себя такие элементы, как нахождение участков
возрастания и убывания, точек экстремума, участков выпук-
лости функции и т. д< Применение производной позволяет
упростить исследование функции. Справедливы следующие
утверждения:
1.	Пусть функция f(x) дифференцируема на интервале
(а; Ь), Функция f(x) является постоянной на (а; Ь) тогда и
только тогда, когда f(x)=0 при любом х из интервала (а; Ь).
Если для дифференцируемых на интервале (а; Ь) функций
/(х) и g(%) при любом х из интервала (а; Ъ) справедливо ра-
венство	(х)а то	Ь)9 где С «-неко-
торая постоянная»
878
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
2.	Если дифференцируемая функция f(x) возрастает (убы-
вает) на интервале (a; Ь), то f' (х)^0 (/' (х)<:0) при х£(а; Ь).
3.	Достаточный признак возрастания (убы-
вания) функции:
а)	если функция f (х) дифференцируема на интервале (а; Ь)
и f' (х) > 0 (f (х) < 0), х£(а; Ь), то функция f(x) возрастает
(убывает) на этом интервале;
б)	если функция /(х) непрерывна на отрезке [а; Ь]} диффе-
ренцируема на интервале (а; Ь) и f' (х) > 0 (f (х) < 0), х£(а; Ь),
то функция f(x) возрастает (убывает) на отрезке [а; 6].
Отметим, что утверждения а) и б) остаются в силе, если
производная f (х) положительна (отрицательна) во всех точках
интервала (а; д), кроме конечного числа точек этого интер-
вала, в которых /'(х) равна нулю. Так, например, для функции
y = x+sinx на интервале (—100; 100) имеем f' (х) = 1 + cos х^0,
причем f (х) = 0 лишь в конечном числе точек этого интервала;
поэтому функция /(x) = x+sinx возрастает на интервале
(—100; 100).
4.	Теорема Ферма. Пусть функция f (х) определена
на интервале (а; Ь) и точка х0 этого интервала является точкой
локального максимума или минимума. Тогда, если функция f (х)
дифференцируема в точке х0, то f' ^х0) = 0.
Таким образом, касательная, проведенная к графику диф-
ференцируемой функции в точке (х0; f(x0)), где х0—точка
экстремума функции, параллельна оси абсцисс (рис. 5.12).
Теорема Ферма дает необходимое условие того, что внут-
ренняя точка области определения дифференцируемой функции
является точкой локального максимума или минимума. То,
что условие f' (хо) = О не является достаточным, показывает
пример функции #=х3, у которой производная равна нулю
при х = однако точка х = 0 не является ни точкой макси-
мума, ни точкой минимума этой функции.
Отметим, что функция f (х), xg(a; Ь)> у которой х(£ Ь)
есть точка локального экстремума, может оказаться недиффе-
ренцируемой в этой точке. Например, точка х=0 является
точкой локального минимума функции #=|х|, х g(—1; 1),
однако эта функция не является дифференцируемой в этой точке.
Из теоремы Ферма следует, что точки экстремума функ-
ции f (x) находятся среди ее критических точек, т. е. тех точек
области определения функции, в которых производная равна
нулю или не существует.
§ 3, ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ 379
5.	Достаточные условия экстремума:
а)	Пусть функция f(x) определена на интервале (а; Ь)
и непрерывна в точке xog(a; b). Если f' (х) < 0 на интервале
(а; х0) и f' (х) > 0 на интервале (х0; Ь), то точка х0 является
точкой минимума функции f (х) на интервале (а; Ь).
б)	Пусть функция f (х) определена на интервале (а; Ь)
и непрерывна в точке х0^(а; Ь\ Если f' (х) > 0 на интервале
(а; х0) и f' (х) < 0 на интервале (х0; &), то точка х0 является
точкой максимума функции f (х) на интервале (а; Ь).
Таким образом, то, что точка х = х0 является точкой ло-
кального экстремума непрерывной функции, характеризуется
следующей таблицей:
Знак производной		Вывод
х <хй	X > х0	Хо
+	4-	Не является точкой экстремума
+	—•	Точка максимума
	+	Точка минимума
—’	—	Не является точкой экстремума
Иллюстрация для каждого из приведенных в таблице слу-
чаев приведена соответственно на рис. 5.13.
6.	Критерий выпуклости функции. Пусть
функция /(х) определена и дифференцируема на интервале
(а; Ь), Для того чтобы функция /(х) была выпуклой вниз (вверх)
на интервале (а; 6), необходимо и достаточно, чтобы ее произ-
водная f (х) была неубывающей (невозрастающей) функцией
на интервале (а; Ь).
Пример 1, Найти промежутки возрастания и убывания
функции
Решение. Область определения функции есть объедине-
ние промежутков (— оо; 0) и (0; -f-oo). Так как функция /(х)
380 ГЛ. 6. ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
дифференцируема в каждом из промежутков {— оо; 0) и (0; 4- оо) и
то /'(х) = 0 при х0==р/< 2. Точка x0=j/^ 2 разбивает область
определения данной функции на три промежутка: (—со; 0),
(0;^2)и(^;+оо) . В каж-
дом из этих промежутков про-
изводная f'(x) сохраняет посто-
...янный знак; знак производной
X в каждом из них отмечен на
рис. 5.14. Следовательно, данная
рис 5	функция возрастает на проме-
жутках (— оо; 0) и 2; +оо) .
Поскольку f (х) непрерывна в точке р/* 2, то эту точку можно
присоединить к промежутку, на котором функция f (х) возра-
стает. Окончательно получаем, что функция f (х) возрастает на
промежутках (— оо; 0) и [f/ 2; + оо). Так как /'(х) <0 при
хё(о; У 2) и так как функция непрерывна на полуинтервале
(б; I/ 2], то данная функция убывает на (б;	2]. График
данной функции изображен на рис. 5.15.
Пример 2. Найти точки экстремума функции
fW = (x-~l)2U+l)8.
Решение. Функция f (х) определена, непрерывна и диф-
ференцируема при всех х. Так как
Г (х) = 2 (х- 1) (х+1)*+3 (х- 1)*(х+1)2 »= (х- 1)Кх +1)2 (5х-1),
то Пх) = 0 при Xi= 1, х2 =—1, Хз=1/5. Отсюда методом ин-
тервалов получаем, что /' (х) > 0 при xg(—• 00; 1/5) и xg(l; + 00)
и /'(х) < 0 при xg(l/5; 1). Следовательно, так как функция
непрерывна при всех х, то она возрастает на промежутках
(—оо; 1/5] и [1; + <») и убывает на отрезке [1/5; 1]. Таким
образом, точка х= 1/5 является точкой локального максимума,
а точка х=1—-точкой локального минимума.
Отметим, что, хотя f' (—1) = 0, точка х2==—1 не является
точкой локального экстремума функции f (х). График данной
функции изображен на рис. 5.16.
Пример 3. Найти участки возрастания, убывания и
точки локальных экстремумов функции
f (х) = (1 + cos х) sin х<
Решение. Данная функция является непрерывной и
дифференцируемой при всех х, и
f' (X) = — SinS х+ (1 + cos х) COS X == 2 COS5* х+ COS X —> 1.
Критические точки функции находяхся из уравнения /\л)=0,
или
2 cosax+ cos х—1 s= О*
§3. ИССЛЕДОВАНИЕ ФУНКЦИЙ ^ПОСТРОЕНИЕ ГРАФИКОВ 3$|
Решениями этого уравнения являются числа
х== £ л/3-|-2лп, х=л+2£л, k, ngN.
Функция / (х) является периодической и имеет период 2л»
поэтому при исследовании свойств функции можно ограни-
читься только значениями х из промежутка 0«Сх*С2л.
Из тех точек, где /' (х)==0, отрезку [0; 2л] принадле-
жат точки Х1 = л/3, х2 = л и х8 = 5л/3. Так как /• (х) =
= 2 ^cosx —(cosx+1), то /'(х) < 0 при х£(л/3; л) и
xg (л; 5л/3), a f( (х) > 0 при xg(0; л/3) и х£(5л/3; 2л).
Таким образом, на отрезке [0; л/3] и на отрезке [5л/3;2л]
функция f (х) возрастает, а на отрезке [л/3; 5л/3] убывает, Сле-
довательно, точка х = л/3 является точкой локального макси-
мума (f (л/3) = 3/3/4), а точка х = 5л/3 является точкой ло-
кального минимума (/(5л/3) = —3 У 3/4). Точка х —л не яв-
ляется ни точкой максимума, ни точкой минимума данной
функции.
Так как f (0) == f (2л) = 0, то из периодичности функции
следует, что все точки х = л/3+2лп, ngZ, являются точками
локальных максимумов, а точки х==—л/3-|-2л&,	точ-
ками локальных минимумов данной фуйкции.
Кроме того, на всех отрезках [—л/3-|-2лп; л/32 л/г],
ngZ, функция убывает, а на всех отрезках [л/3 + 2ли; 5л/3+2лп|*
n§Z, функция возрастает.
График данной функции на промежутке [0; 2л] изображен
на рис, 5Л7Л
Пример 4. Найти точки экстремума функции
f (х) =	(х** 1)?*
Решение, Функция /(х) непрерывна при всех значе-
ниях х. Заметим, что для того, чтобы найти точки экстремума
функции /(х), достаточно найти точки экстремума функции
gW=^z(«—о8.
ГЛ. б. ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
Для всех х 1 имеем
,, ч 2 ,	1Ч_1/3	2	1
Так как g' (х) > 0 при х > 1 и g' (х) < 0 при х < 1 и функция
•f(x) непрерывна в точке х=1, то точка х=1 есть точка мини-
мума функции, причем значение
„Ук	функции g(x) в этой точке есть
2(1)-°.
Таким образом (рис. 5.18),
функция f (х) имеет одну точку
экстремума, а именно х=1 есть
* ее точка максимума, причем
/(!)== 1.
Пример 5. Найти проме-
жутки выпуклости функции
l4 \,
y«(1+cas4?)$ln^
Рис. 5.17	f(x) = 3x4—4х3+1.
Решение. Функция f (х) дифференцируема в каждой
«очке числовой прямой, и
Г (х) = 12х8—12х2.
Для того чтобы найти промежутки [выпуклости функции f (х),
яужно исследовать на возрастание и убывание функцию
g (х) = f' (х) = 12х8 — 12х2
Для этого воспользуемся достаточным признаком монотон-
ности функции.
/ о \
g' (х) = 36х2—24х = 36х ( х—5- ).
Так как g'(x) = 0 при х = 0 и х=2/3, g' (х) > 0 при xg(—оо;0)
и xg(2/3; +°°)>	(* *) < 0 ПРИ 2/3), то функция g(x) на
у л
промежутках (—* оо; 0] и £2/3; + оо) возрастает, а на промежутке
[0; 2/3] убывает. Следовательно на промежутках (—оо; 0] и
[0; 2/3J {функция f (х) является выпуклой вниз, а на проме-
жутке (0; 2/3] выпукла вверх. График данной функции изобра-
жен на рис. 5.19.
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ
Пример 6. Найти промежутки
выпуклости функции
f(x) = 2+i/~4.
Решение. Функция f (х) не-
прерывна в любой точке числовой
прямой и дифференцируема для лю-
бого х # 4. Имеем
jZ (х—4)а
Найдем участки возрастания и убы-
вания функции:
S W = f' (*) =—3/I—--, X & 4.
3 V (х- 4)2
Так как функция (х—4)2 возрастает при х > 4, а функция
у— у/ х возрастает на всей числовой прямой, то сложная функ-
ция y=V (X— 4)2 является возрастающей при х > 4; следова-
тельно, функция g (х) = —x—zx..	является убывающей на
3 gZ (х _4)2
промежутке (4; + оо). Аналогично доказывается, что функция
g (х) возрастает на промежутке (-—оо; 4). Таким образом, учи-
тывая непрерывность функции f(x) в точке х=4, получаем
что функция f (х) является выпуклой вверх на промежутке
J4; —jP оо) и выпуклой вниз на промежутке (—оо; 4]. График
данной функции изображен на рис. 5.20.
Пример 7. Исследовать функцию
f (х) = х3—9х2+24х— 1
и построить ее график.
Решение, Исследование свойств данной функции прово-
дится по схеме, которая была описана в § 1 гл. 3, однако для
нахождения промежутков монотонности функции, ее экстрему-
мов, а также промежутков выпуклости применим производную.
Функция f(x) является непрерывной и дифференцируемой
на всей числовой прямой.
-384 ГЛ. Б. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Так как f (1)= 15 и f (— 1) = —35, то функция f (х) не является
ни четной, ни нечетной. Кроме того, так как функция f(x)
принимает значение 0 не более чем в трех точках, то она не
является периодической.
Из соотношений
lim	оо, hm -L-^-=+ oo
X ->• + oo X	x —oo X
следует, что ни горизонтальных, ни наклонных асимптот гра-
фик функции y~f(x) не имеет.
Найдем промежутки, на которых функция f (х) монотонная.
Так как /' (х) = 3х2 — 18х+24=3 (х—2) (х—4), то a) f' (x)==Q
при х — 2 и х = 4, б) /' (х) > 0 при х < 2 или х > 4, в) f (х)<0
при 2 < х < 4. Следовательно, функция f(x) возрастает на
промежутках (—оо; 2) и [4; 4-оо) и убывает на промежутке
[2; 4]. Точка х = 2 является точкой локального максимуму
функции f(x)(f (2)= 19), а точка х = 4—-точкой ее локального
минимума (/ (4) = 15).
Для того чтобы найти промежутки выпуклости данной
функции, нужно найти участки возрастания и убывания
функции
g (х) f' (х) = Зх2 — 18х+24.
Так как функция g (х) — квадратный трехчлен с положитель-
ным коэффициентом при х2, то она убывает на промежутке
оо; 3] и возрастает на промежутке (3; 4-оо). Отсюда заклю-
чаем, что функция /(х) является выпуклой вверх на проме-
жутке оо; 3] и выпуклой вниз на промежутке [3; + оо).
Результаты проведенного исследования функции /(х) при-
ведены в табл. 5,1, а график изображен на рис. 5.21,
Пример 8. Исследовать функцию
и построить ее график»
§3. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ 385
Решение. Функция f (х) непрерывна во всех точках чис-
ловой оси. Так как
/(— х) — jZk— х)2 — у/ (—х)2 —1 = р/	х2 —l~f(x\
то функция f(x) является четной. Поскольку f(x) = l только
в трех точках: х = 0, х—1 и х =—1, то функция f(x) не яв-
ляется периодической. Так как
lim	х2—у/" х2—1)= lim (j/^ х2 —*1/” х2 —1) =
-> -СО	Х-* +00
lim	x2—f/х2 —1)(^ х^+i/ х2 (х2 — 1)+^(х2—!)2)^
Х +о°	I/+ l/х2 (Х2—1) + У(Х2—I)2
= lim  "А 1	.—_________-=0,
х‘>+°° у х4Н-^х2(х2—1) + р/(X2—I)2
то прямая 0 = 0 (с учетом четности функции) является гори-
зонтальной асимптотой графика функции y = f(x) как при
х —> — оо, так и при х оо.
Функция f (х) принимает только положительные значения,
так как неравенство х2 > х2 — 1 имеет место при любом
действительном х.
Для любого х, отличного от 0, —1 и 1, имеем
Г (х) =1X-V3--1 (Ж»_ 1)-2/з.2х=
о	о
_2 (X2— 1)2/3 — *4/8 _2 I/(х2—I)2 — ^7
-3 Х1/З(х2-1)3/3 -3	'
Исследуя знаки "числителя и знаменателя, получим
(рис. 5.22), что Г (х) > 0 на промежутках
(-оо; -1), (-1; -1/V 2), (0; 1/V 2)
и У (х) < 0 на промежутках
(-1// 2; 0), (1// 2; 1), (1; + оо).
С учетом того, что функция^/ (х) непре-
рывна в точках х — —1/У 2, х = 0 £
х~ \[У 2,^получаем, что точки х = —1/}/~ 2
и х= 1/]/*2 являются точками локальных
максимумов, а точка х = 0—точкой локаль-
ного минимума.
Можно показать, что функция f (х)
на промежутках (—оо; —1] и [1; +00)
является выпуклой вниз, а на проме-
жутках [—1; 0] и [0; 1]—выпуклой вверх.
13 Задачи по математике. Начала анализа
386
ГЛ 5 ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Так, например, на промежутке [0; 1}
г .	3 Z ‘ Л 3	7	3 / а | 3 /"7“	2
f (X) = V X2 — у X2 «— 1 = у X2 4“ И I — *2,
т» е* функция / (х) есть сумма двух выпуклых вверх функций,
а именно If х2 и 1 — х2.
Рис. 5.22
Результаты исследования функции Цх) приведены в
табл. 5.2, а ее график изображен на рис. 5.23.
Таблица 5.2
X	(—«>; —О	— i			-	। W	(-*")		0
Г(х) g‘(x) = f(x) Их)	+ +	ОО не су- щест. экст- рем. нет	1 +		0 max				00 не су- щест. min
X	(”'тт)	1		( 1 \		I		0:	; +оо)
f'(x) g* (х) = /"(Х) /(*)	>	1 +	0 оо шах		1 1 /*" 	;			00 не су- ще ст.		+1	
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ 387
ЗАДАНИЕ I
1.	Найти промежутки возрастания и убывания функции:
1) f (х) = 2х2 —8х+ 11; 2) f(x) = x3—2х2;
3)	/(х) = х/3— ]/ х\ 4) f(x) — x\nx.
2.	Найти точки экстремумов функции:
1)	f(x)=4-x2; 2)
3)	f (х) = хе~х\ 4) f (х) — х sin х.
Рис. 5.23
3.	Найти промежутки выпуклости функции:
1)	f(x) = x+l/2x; 2) f(x) = (l+2x2)^;
3) f (X) = V~х (14-Х); 4) f (х) = Iх 1/(1 +*)
4.	Исследовать функцию и построить ее график:
1)	=	1л?; 2)
3) f(x) = x2«-*; 4) f(x) = x(l/~x+l).
ЗАДАНИЕ 2
1.	Найти промежутки возрастания и убывания функции:
1)	f (X) = | ^+-1 х2; (2) f (х) =	;
3)	f(x) = x2e«; 4) Цх) = х(У~х— 1).
2.	Найти точки экстремумов функции:
1)	/(х) = х2(1—х); 2)/(х) = j/?—х;
3)	f(x) = -l^i-; 4) f (х) = х + cos х.
3.	Найти промежутки выпуклости функции:
1)	f(x) = 2x3-x2; 2)/(х) = ^±у;
3)	f(x) = x2lnx; 4) f(x) = j!/ x—p^x+L
13*
388 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
4.	Исследовать функцию и построить ее график:
1)	f (х) = (л-4- 1) (х—2)2; 2) f (х) = х8—Зх— 1;
3)	4) Н*)=УлП—*)•
ЗАДАНИЕ 3
1. Найти промежутки возрастания и убывания и точки
экстремумов функции:
1) f(x) = x?-5x4+5x3+l; 2) /(x)=^~2Hlzi^;
3) f (x)==sin x+cos 2x, xg[0; л/2];'
4) П*)=У(2х-1)У(x-1)’.
2* Найти промежутки выпуклости функций:
1) f (х) = х2е“*2; 2) f (x) = sin x + sin2x;
3) f(x)=g/i^; 4)/(x)=-y+^->
3. Исследовать функцию и построить ее график:
1) f(*)=4-+4; 2н (*)=«-*’;
3) f(x) = 2sinx4-cos2x; 4) Цх)~у^ x+l.
ЗАДАНИЕ 4
L Найти промежутки возрастания и убывания и точки
экстремумов функции:
1) М*)=д£2х ; 2) fW=U+V'’(»*5)’!
3) f (x) = sin 2х—-х, xg[—jt/2; л/2);
4) f(x)==2e*+3e-*.
2, Найти промежутки выпуклости функции:
1)	2) f(x)=2+y(7Z^;
3) f (х)—sin8 x4~cos? х; 4) f (x) = x/lnx.
3. Исследовать функцию и построить ее график:
1) f (х)=ха +1 + 1/х; 2) f (х) = х2г*2;
3) (х) = sin х sin 2х; 4) f (х)= К*2 (1 + х).
У пражнения
1. Найти промежутки возрастания и убывания функции:
1) f(x) = 3x4—8х3+6х2+1; 2) f (х) = 2х8—Зх2;
3) Н*)=-*3-«2-7х-л к 3; 4) f (х) = х+^-Ь ;
5) f(x)=x«—ах; 6) f<x) = axs—x; 7) f (x) = -^zL_ ;
(Хл "Я* 1)л
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ 389
1 Оу	,_________
8) f (*) =-+]f±i • 9> f w = К 2х3+9х2,’;
10) /(х) =
12) f(x) = 24x-
15) f(x) = x*e~x;
11) f(x) = xe~6x;
14) f (x) — ext/x’,
13) f(x) = x2lnx;
16) f(x) = (x—2)3 У x2; 17) f (x) = x—sin2x;
18) f (x) = (x +1)	19) f (x) = In2 x/V x;
20) f(x) = x«; 21) / (x) = x2 —In x2;
22) f (x) = n/2x—x arctg x; 23) f (x) = arctg x— In xj
24) f (x) =arcsln У 1—!4x2—2 У1— 4x2.
2.	Найти точки экстремумов функции:
1)	f(x) = x34-6x2—Зх + З, xg(—5; 1/5);
2)	/ (х) = 2х3 4-Зх2—12x4-5;
3)	f (х) = (х-2)2 (х+4)/4; 4) f (х) = | х-5 | (х-3)?|
5)	/(х) = х2е~^, xg[0; 4-оо);	_
6)	f(x) = x4-/^; 7) f(x)=i/ х2 (| x-J-1 Di
8)	/(x) = x4-l/x2; 9) f(x) — xex~xt;
10)	f (x) = x-|-sin2x; 11) f (x) = xe_^*4~2;
12)	f (x) = V2x2—x-l-2; 13) f (x) = (2x— 1) e«*j
14)	f (x) = x24-l/x2; 15) f (x) = | x3-—x |;
16)	f(x) = sinx—cos2x—1; 17) f(x) = sin-»Д—т;
X - -f- 1
18)	f(x)=^^sin2x4--j-cos2x4-^^;
19)	f(x) = V 3cos у 4-sin
20)	f(x)=(x— l)2Kx2—2x4-3, x^[0; 3];
21)	f (x) = In cos x—cos x; 22) f (x) = In (x2 +1)«2 aretg
23) f(x) = f/(l-x)(x-2)2.
3. Найти промежутки возрастания и убывания и точки
экстремумов функции:
1) f(x) = (x-l)e3*;	2) /(х) = -^-у-;
3)/М = -^Йр-; 4) f(x)=|x2—5x4-61;
5) f(х) = х3—2х|х—2|, xg[0; 3];
6) f (х)=— 5х34-х|х— 11, х$[0; 2];
7) f(x) = /8^=^;	8)f(x)=-nJ7;	9)/(х) = и|т»
Ю) Цх)=хУ 2-х2;
11) f (х) = 21п(х-2)-х24-4х4-1; 12) f(x)=
390
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
4. Исследовать функцию и построить ее график:
г3	х24-1
1) f (х) = (х—1) х2; 2) f (х) =	; 3) f (х) = x'4'T+i •>
4)	5) f(x) = -j^y; 6)f(x)= |Л
7) /(*)=]/; 8) /(x)=
9) f (x) = (x—6)e-VX;	10) f (x) = ^ (x— 2)2 — f/(x + 2)2 ;
11) f W = уЛ£+ 2)2+ V(x-2)2 ;	12) f (x) = j/x(x-3)2;
13) \f (x) = К x2 (2 + x); 14) / (x) = cos x cos 2x;
15) f (x) = 2 sin x •*- cos 2x; 16) f (x) = x2 In2 x;
17) f (*);== К * In x; 18) f (x) = ln2/*x/x;
19)	f (x) = 2x+4arcctgx; 20) f (x) = 2+ у .
5.	Найти все значения параметра а, при каждом из кото-
рых функция
ys=2x6 + 5ax4+10x3
является всюду возрастающей.
6.	Найти всё значения параметра а, при каждом из кото-
рых функция
у~аsin 4х— 10x+sin 7x-j-4ax
всюду убывает и не имеет критических точек.
7.	Найти все значения параметра а, при каждом из кото-
рых функция
уе=0,5е2* + (1**-а) е*—ax+sin2
имеет критические точки, и найти эти точки,
8.	Найти все значения параметра а, при каждом из кото-
рых функция
y = sin2x—8 (a-f- 1) sin х+(4а2^|-8а-* 14) х
является всюду возрастающей и при этом не имеет критиче-
ских точек.
9.	Найти все значения параметра а, при каждом из кото-
рых функция
у — 16 (a-f-1) sin х—sin 2х—(16а? + 32а*-10) х
является всюду убывающей и при этом не имеет критических
точек.
10.	Найти все значения параметра а, при каждом из кото-
рых уравнение
х3—ах~- 1 = 0
имеет единственное решение.
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 391
11.	При каждом значении а найти наименьшее значение
функции
1 а2
*£[2; зь
12.	Найти все значения а из промежутка [3/4; +оо), при
каждом из которых наименьшее значение кубического трех-
члена
^ = х3-^2ах2 + 1
достигается на правом конце отрезка [0; 1].
13.	Найти число корней уравнения
f(x)—af' (х) = 0,
где f(x) = (x—хх)(х—х2)(х-~х3)(х--.х4) и а, хь х2, х$, х<
(*i < х2 < х3 < х4)—заданные действительные числа.
14.	В зависимости от значений Р найти те значения а, при
каждом из которых уравнение
х3 + 2рх2 + Р = а
имеет три различных корня.
§ 4. Наибольшее и наименьшее значения функции
Многие задачи на отыскание наибольшего и наименьшего
значений функции сводятся к исследованию непрерывных функ-
ций на различных промежутках (отрезке, полуинтервале, пря-
мой и т. п.).
Наибольшее (наименьшее1) значение на отрезке [а; Ь] не-
прерывной функции f (х) достигается либо в критической точке
этой функции (т. е. в точке, где функция fr (х) или равна нулю,
или не существует), либо в одной из граничных точек данного
отрезка.
Таким образом, чтобы найти наибольшее и наименьшее зна-
чения непрерывной функции на отрезке [а; Ъ\, имеющей на ин-
тервале (а; Ь) конечное число критических точек, достаточно
вычислить значения функции во всех критических точках функ-
ции, принадлежащих интервалу (а; &), и на концах отрезка и из
полученных чисел выбрать наибольшее и наименьшее.
Если функция f (х) исследуется на интервале, на всей пря-
мой и на промежутках [а; Ь), [а; +<»), (—со; b], (a*t 4~оо),
(—оо; Ь), (а; о], то на таких промежутках непрерывная функ-
ция может и не иметь наибольшего (наименьшего) значения.
Так, например, функция у — х не имеет на промежутке
[0; 1) наибольшего значения, на промежутке (0; 1] наимень-
шего значения и на промежутке (0; 1) ни наибольшего, ни
наименьшего значения. Функция t/==x2 на всей прямой не
имеет наибольшего значения, a # = arctgx не имеет ни наиболь-
шего, ни наименьшего значения.
Напомним, что квадратичная функция у — ах2 + Ьх+с при
4ас—Ь2
а>0 имеет наименьшее значение, равное—^—, которое
392
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
достигается в точке х ——	, а при а<0 имеет наибольшее
4ас—b2	Ъ
значение, равное ——— , которое достигается в точке х=—.
Если непрерывная функция f (х) на промежутке [а; Ь)
([а; +оо)) возрастает (убывает), то на этом промежутке она
имеет наименьшее (наибольшее) значение, которое достигается
в точке х — а.
Аналогичные утверждения имеют место для функции, за-
данной на промежутке (а; 6] ((—оо; &]).
Если непрерывная функция f (х) на промежутке (а; Ь) имеет
критическую точку х0, принадлежащую рассматриваемому про-
межутку, и возрастает (убывает) на промежутке (а; х0] и убы-
вает (возрастает) на промежутке [х0; &)» то на рассматриваемом
промежутке функция f (х) имеет наибольшее (наименьшее) зна-
чение в точке xQ.
Если непрерывная функция f (х) на промежутке (а; Ь) имеет
конечное число критических точек а < х0 < Xi <... < хп < b и
возрастает (убывает) на промежутке (а; х0] и убывает (возрас-
тает) на промежутке [хп; Ь), то на промежутке (а; Ь) функция
f(x) имеет наибольшее (наименьшее) значение, которое дости-
гается в одной из критических точек этого промежутка.
Если непрерывная функция f(x) рассматривается на про-
межутке (—оо; +оо) ([а; &)) и имеет пределы (конечные или
бесконечные) при х->—оо и х->+°° (х->Ь—0), то можно
заключить, имеет ли эта функция f (х) наибольшее или наи-
меньшее значение на рассматриваемом промежутке, сравнив
значения функции в критических точках с предельными зна-
чениями на бесконечности (предельным значением при х О
и точке х — а) (рис. 5.24).
Пример 1. Найти значение х, при котором функция
f (х) = (х—aj)2 + (х—а2)8 +... + (х—а„)2,
где «х, а2,	ап—заданные числа, принимает наименьшее
значение.
Решение. Так как
f (х)~пх2—2 («i+a2+ • • • +#») x+(ai+a2+ ... +«п)
есть квадратный трехчлен относительно х, то наименьшее зна-
чение функция f(x) принимает в точке	,
Ч- #2 ап
т. е. при х=———=-~----—
Пример 2. Найти наименьшее значение функции
f (x) = 4x4-^--|-sinx
на промежутке (0; -f-oo).
Решение. Запишем данную функцию в виде
/ (х) — —---^1)—12 л-J-sinx.
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 393
При всех х > 0 справедливо неравенство
f (х)^ 0 + 12л— 1 — 12л— 1,
г. е. значение функции f (х) в любой точке промежутка (0; 4“°°)
не меньше числа 12л—1. Заметим, что при х = Зл/2 имеем
f (Зл/2) = 12л— 1. Значит, наименьшее значение данной функ-
ции на промежутке (0; 4-оо) равно 12л—1.
ПримерЗ. Найти наибольшее и наименьшее значения
функции
f(x) = x3 + 3x2—72х + 90
на отрезке [—5; 5].
Решение. Для того чтобы найти наибольшее и наимень-
шее значения данной непрерывной функции на отрезке [—5; 5J,
достаточно вычислить значение функции в критических точках,
принадлежащих интервалу (—5; 5), а также на концах отрезка.
Среди полученных чисел нужно выбрать наибольшее и наи-
меньшее.
Поскольку функция f (х) = х34~Зх2 — 72x 4-90 дифференци-
руема на всей числовой прямой, то критические точки данной
функции найдем, решая уравнение f' (х) = 0, т. е. уравнение
Зх24-6х—72 — 0. Корни этого квадратного уравнения есть xi — 4
и х2=—6. Из этих корней только хх = 4 принадлежит интер-
валу (—5; 5). Вычислим значение функции в точкак х=4,
394
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
х = 5 и х =—5:
/(4) = —86, /(5) = -—70, /(-5) = 400.
Следовательно, наибольшее значение данной функции равно 400.
а наименьшее значение равно —86.
Пример 4. Найти наибольшее и наименьшее значения
функции
f (x) = sin2x-f-cosx — у.
Первое решение. Данная непрерывная функция имеет
период 2л, поэтому ее наибольшее и наименьшее значения
совпадают соответственно с наибольшим и наименьшим значе-
ниями f (х) на отрезке [—л; л]. Найдем критические точки f (х)
на интервале (—л; л). Так как ff (х) = 2 sin х cos х—sin х, то
для нахождения этих точек имеем уравнение
2 sin х cos х —sin х = 0.
Это уравнение равносильно совокупности двух уравнений:
sinx = 0 и cos х = 1/2.
Первое уравнение на интервале (—л; л) имеет единственный
корень хх = 0, Второе уравнение на этом промежутке имеет
два корня: х2 =— л/3 и х3 = л/3. Вычислим значения функции
f (х) в этих точках и на концах отрезка [—л; л]:
/ (0) = 1/2, f (- л/3) = 3/4, f (л/3) = 3/4, f (—л) = f (л) = -3/2.
Значит, наибольшее значение f (х) равно 3/4, а наименьшее
значение равно —3/2.
В орое решение. Пользуясь основным тригонометри-
ческим тождеством sin2x + cos2 х= 1, можно написать, что
f (х) = sin2 х-|~ cos х—-= 1 — cos2 x + cos X —
3	(	1 V
= T-(cosx-Y 1 .
Теперь очевидно, что при всех х функция / (х) не превосходит
3/4 и принимает значение 3/4, например, при х=л/3 I cos—=— );
следовательно, наибольшее значение / (х) равно 3/4. Функция
(1 \ 2
cos х*—g- 1 принимает наибольшее значение (3/2)2, например,
при х = л (соэл=—1); следовательно, наименьшее значение
о / о X 2
/(х) равно —J
Пример 5. Найти наибольшее значение функции
3_
2 *
f(x) = x3—2х|х—2|
на отрезке [0; 3].
Решение. Рассмотрим функцию / (х) отдельно на мно-
жествах 0«СЖ2 и 2 < х^З.
§ 4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 395
а)	Пусть х принадлежит промежутку [0; 2]. Тогда [х-**2| =
= — х4~2, и данная функция может быть записана в виде
f (х) = х3—- 2х (—х+2) = х3Ц-2х2 —4х.
Отсюда следует, что она дифференцируема в каждой точке
интервала (0; 2) и f' (х) = Зх2 + 4х—4. Квадратное уравнение
Зх24-4х—4 = 0 имеет корни х3 =—2 и х2 = 2/35 первый из ко-
торых не содержится в интервале (0; 2), а второй содержится.
Имеем f' (2/3) = 0 и /' (х) < 0 при 0 < х < 2/3 и f' (х) > 0 при
2/3 < х < 2. Отсюда следует, что на интервале (0; 2) имеется
единственная точка минимума х = 2/3.
б)	Пусть х принадлежит промежутку (2; 3]. Тогда | х—*2| =
= х—2, и данная функция может быть записана в виде
f (х) = х3«—2х (х—2) = х3—2х2 + 4х.
Отсюда следует, что она дифференцируема в каждой точке
интервала (2; 3' и /' (х) = 3х2— 4x4-4. Дискриминант квадрат-
ного трехчлена Зх2—4x4-4 равен —32, и, значит, уравнение
(х) = 0 не имеет корней. Следовательно, на всем интервале
(2; 3) производная положительная; тем самым функция f(x)
не имеет точек максимума и минимума на этом интервале.
Функция f (х) задается на отрезке [0; 2] многочленом
х34~2х2—4х поэтому она непрерывна на отрезке 10; 2] и диф-
ференцируема на интервале (0; 2), причем /' (2/3) = 0. Значит,
ее наибольшее значение на отрезке (0; 2] равно большему из
чисел / (0), f(2/3), f№.
Аналогично наибольшее значение f (х) на отрезке [2; 3]
равно большему из чисел f (2) и f (3). Поэтому наибольшее зна-
чение f (х) на всем отрезке [0; 3] равно большему из чисел f (0),
f (2/3), f(2), f(3). Следовательно, наибольшее значение данной
функции на отрезке [0; 3J равно 21.
Пример 6. Доказать, что для функции f (х) = cos х sin 2х
справедливо неравенство
min f (х) >—7/9.
к € [ - Л; л]
Решение. Найдем наименьшее значение непрерывной
функции f (х) на отрезке [—л; л]. Для этого сначала преобра-
зуем функцию к более удобному виду:
f (х) = 2 sin х cos2 х = 2 sin х (1 —sin3 х) = 2 sin х—2 sin^x.
Найдем теперь критические точки /(х). Поскольку f (х) диф-
ференцируема в любой точке числовой прямой, то критические
точки f(x) есть решения уравнения f (х) = 0. Найдем /' (х):
f (х) = 2 cos х—6 sin2 х cos х = 2 cos х (1 — 3 sin2 x).
Решая на отрезке [—л; л] уравнения cosx = 0 и 1—3sin2x = 0,
получаем критические точки
хг = л/2, х2 = —л/2, х3 = arcsin—Д=-
х4 = — arcsin	, х5 = л—arcsin , хб = — л 4- arcsin -4=-,
396	ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
принадлежащие этому отрезку* Вычислим значения f (х) в кри-
тических точках и на концах промежутка [—л; л]:
fta)-f(x2) = 0;
(1	/ 1 \3\	4
ТтГД/з) / “з/Т:
f(x4)=f(xe)=2(-pU-^-pU)
Дя)«/(-л) = 0.
Наименьшим значением функции f (х) на отрезке [— л; л] будет
наименьшее из этих чисел. Таким образом,
4
min /(х) = Нх4)=— 777=--
ле [-л; л]	Зу 3
Осталось проверить справедливость неравенства —4/3]^ 3>
> —7/9. Ясно, что это неравенство будет выполнено, если будет
выполнено неравенство К 3 < 7/4. Справедливость последнего
неравенства вытекает из справедливости очевидного неравенства
3 < 49/16. Значит, действительно, справедливо неравенство
min /(х)>—7/9.
х€[~л; л]
Пример 7. Найти наименьшее из значений, принимаемое
функцией
4
у(х)=х + ^^2)?
на отрезке [0; 5|.
Решение. Данная функция дифференцируема в каждой
точке интервала (0; 5), за исключением точки х== 2, и для этих
х получаем
ZZ X 1	8
у W-1	(х—2)3 •
Из этого выражения следует, что при 0 < х < 2 выполнено не-
равенство у' (х) > 0. Таким образом, данная функция монотонно
возрастает на множестве 0 < х < 2. Следовательно, в силу не-
прерывности наименьшее ее значение на множестве [0; 2) равно
Уравнение д' (х) = 0 или 1—--5^=0 имеет единственный
(X — А)
корень х = 4. В области 2<х<4 справедливо неравенство
у* (х) < 0 в области 4 < х < 5 — неравенство у' (х) > 0. Так как
функция у(х) непрерывна в точке х = 4, то отсюда заключаем
что
1)	в области 2 < х<;4 функция у(х) монотонно убывает;
2)	в области 4=Сх^5 функция у (х) монотонно возрастает;
3)	точка х —4 является точкой минимума.
Доказанные факты означают, что наименьшее значение у (х)
в области х>2 равно у (4) = 5. Поскольку точка х=4 содер-
жится в множестве (2; 5), то у (4) будет также и наименьшим
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 397
значением функции у (х) в области (2; 5). Таким образом, наи-
меньшее значение функции у (х) на отрезке (0; 5] равняется
меньшему из чисел ^/(0), ^(4), т. е. равно f/(0) = l.
Пример 8. Найти наименьшее значение функции
х
у~ 1+х2
на промежутке [—1; +оо).
Решение. При любом х > —1 данная функция дифферен-
цируема, и ее производная равна
1 —*2
У ~(1 + х2)2'
Отсюда видно, что производная данной функции при — 1 < х < 1
больше нуля; при х > 1 меньше нуля и при х=1 равна нулю*
Следовательно, на проме-
жутке [—1; 1] функция
возрастает, а на проме-
жутке [1; +<ю) убывает.
Так как наименьшее зна-
чение функции на отрезке
1;	1] равно —1/2 и
lim / (х) — 0, то наименьшее
Х-+ + а>
значение данной функции
на промежутке [1; +<эо)
равно —1/2 (рис. 5.25).
Пример 9. Найти наибольшее и наименьшее значения
функции
Q
У (*) = I х2+2х—314-у In х
на отрезке [1/2; 4].
Решение. Квадратный трехчлен ха + 2х—3 имеет корни
х1 = —3, х2=1. Из них только х2 = 1 лежит на отрезке [1/2; 4j.
Найдем наибольшее и наименьшее значения у(х) на отрезках
[1/2; 1] и [1; 4]. На множестве 1/2*Сх^1 справедливо нера-
венство х2 + 2х-—ЗС0. Значит,
Q
I х2 + 2х —31 = — X2 —2х+3, у (X) = — х2—2x4-3+In х.
Функция f (х) —— х2—-2х+3+у In х определена на множестве
х > 0 и имеет производную в каждой точке этого множества,
причем
2.^^ 4ха + 4х —3^ (2х— 1) (2х+3)
‘ 2х	2х	2х *
Отсюда следует, что на множестве 1/2 < х < 1 справедливо
неравенство f' (х) < 0, т. е. на этом множестве f (х) монотонно
убывает. Так как f (х) непрерывна при х= 1/2 и х=1, то ока
убывает на отрезке [1/2; 1]. Поскольку на этом отрезке функ-
398 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
ции у(х) и f (х) совпадают, то данная функция у(х) монотонно
убывает на отрезке [1/2; 1]. Поэтому
min y(x) — y(\) = 0, max у (х) = у (!') =4—у in 2.
хе[1/2; 1J	хе[1/2; I]	\2 )	4	2
На множестве 1 <Сх«с4 справедливо неравенство х2+2х — 3^0.
Значит,
|х2+'2х—3|=х24~2х—3, у(х) = х2+2х—3+у 1пх.
з
Функция g(x) = x2 + 2x**3+-g-lnx определена на множестве
х > 0 и имеет производную в каждой точке этого множества,
причем
г/ч о foi 3	4х2 + 4х+3	(2х +1)2 + 2
g'(x)=2x+2+§j=-Xr^=A—.
Отсюда следует, что на множестве х > 0 справедливо нера-
венство g' (я) > 0. Следовательно, функция g (х) возрастает на
множестве х > 0, и в частности на отрезке [1; 4]. Так как на
этом отрезке функции у(х) и g(x) совпадают, то данная функ-
ция у(х) монотонно возрастает на отрезке [1; 4]. Поэтому
min у M = i/(l)~0, max у (х) — у (4) = 214-3 In 2.
лге[1;4]	лге[1;4]
Итак, наибольшее значение функции у(х) на отрезке [1/2; 4]
равно большему из чисел у (1/2) и у (4), т. е. у (4) = 21 + 3 In 2.
Наименьшее значение функции у(х) на отрезке [1/2; 4] равно
р(1) = 0.
Пример 10. Найти все значения а из промежутка [1; +©о),
при каждом из которых больший из корней уравнения
%2*—6х + 2ая+а—13 = 0
принимает наибольшее значение.
Решение. Найдем дискриминант D данного уравнения:
D = (2а—6)2—4 (а —13) = 4а2—28а + 88 = (2а—7)2+39.
Поскольку теперь очевидно, что дискриминант D положителен
для любого значения а, то исходное уравнение имеет два дей-
ствительных корня:
Xi = (3—а) — К»2—7а+22, х2 = (3—а) + /а2—7а+22.
Задачу теперь можно переформулировать следующим об-
разом: найти все значения параметра а из промежутка [1; +оо),
при каждом из которых выражение (3—а) + р^а2—7« + 22 при-
нимает наибольшее значение, т. е. надо найти наибольшее зна-
чение функции f(a) — (3—aJ + J^a2—7а+22 на промежутке
П; +оо). Рассмотрим эту функцию на промежутке (1; +оо).
В каждой точке этого промежутка функция f (а) имеет про-
изводную
.	, ,	2а—7	2а—7—2J<а2—7а-|-22
f (а) =—1Н--...	—_=--------7  ... _J----,
2/а2 — 7а 4-22	2/а2—7а+22
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 399
Так как
2Ка2 —7а + 22= К(2а—7)2 + 39 > |2а—7|^2а—7,
то для любого а из промежутка 1 < а <+оо выполнено нера-
венство f' (а) < 0, т. е. на этом промежутке функция f (а) убы-
вает. Поскольку функция f (а) непрерывна при а=1, то функ-
ция f (а) убывает и на промежутке [1; +оо). Следовательно,
наибольшее значение функция f (а) принимает при
Пример 11. Найти наименьшее из расстояний от точки
М с координатами (0; —2) до точек (я; у) таких, что
—2, я > 0.
Решение. Квадрат расстояния от точки М с коорди-
натами (0; —2) до точки А с координатами (я; у) вычисляется
так: AM 2 = (я—0)2 + (#4-2)2. Так как по условию коорди-
наты х и у точки А связаны равенством
"16
//=—------2, то
АМ2 = х2 +
256
Зя® *
Теперь ясно, что квадрат искомой величины равен наименьше-
му значению функции
2	256
на множестве 0 < х < + ©о. Функция f (х) в каждой точке этого
множества имеет производную. Найдем ее:
г (х) = (х«4-^-)'=2х-512х-г=^=^.
Отсюда следует, что на промежутке 0 < х < 2 производная /' (я)
отрицательна, а на промежутке 2 < х < + оо производная f  (х)
положительна. Значит, функция f (x) убывает на промежутке
0 < х < 2 и возрастает на промежутке 2 < х<-|-оо; кроме того,
функция f (х) непрерывна в точке я = 2. Следовательно, наи-
меньшее значение f (я) на множестве 0 < я < + оо равно f (2) =
= 5а искомое наименьшее расстояние равно 4/|/~3.
Пример 12. Найти наибольший член последовательности
ап = пУп, ngN.
Решение. Рассмотрим функцию f(x) — x1/x, я^1, и най-
дем ее наибольшее значение на промежутке (1; +00)- Так как
1 .
— In X
f[x)~ex , то при я > 1 имеем
— In х /	in я
Г(х)=е*	(--jr
—-^еХ 1ПЯ (1 —1пх),
400
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
откуда
f(x)=:0 При
f' (х) > 0 при
f' (х) < О при
х = е\
1 < х < е;
х > е.
Так как функция f (х) непрерывна на отрезке [1; е] и f' (х) > 0
на интервале (1; е), то функция f (х) возрастает на отрезке
[1; е]; так как функция f (х) непрерывна на промежутке [е; -j-oo)
и /' (х) < 0 при х > е, то функция f (х) убывает на промежутке
[е; +оо). Следовательно, наибольшее значение данной функции
на промежутке [1; + ©о) достигается в точке х = е и равно е11е.
Принимая во внимание тот факт, что 2 < е < 3, и доказан-
ное выше свойство монотонности функции f (х) для нахождения
наибольшего члена последовательности ап = п^п, достаточно
сравнить по величине только два ее члена—-второ^й и третий,
т. е. числа К2 и ^3. Так как очевидно, что V 3 > /2 , то
искомым членом последовательности является «3=1/3.
Пример 13. Найти наименьшее значение а, при котором
уравнение
4 ,	1
-----L--------
sinx 1 1—sinx
на интервале (0; л/2) имеет хотя бы одно решение.
Решение. Так как функция у=sinx монотонно возраста-
ет на интервале (0; п/2) и принимает все значения из интер-
вала (0; 1), то для решения задачи нужно найти наименьшее
значение «, при котором уравнение
имеет хотя бы одно решение из интервала (0; 1).
Найдем наименьшее значение функции
4	1
^)=7+т^
на интервале (0; 1). Так как при 0 < у < 1
(и.___4 ,	1	У*—4(1—у)*_____Зу^-8у+4
' w	уг(1-у)2 ~
3(у—2) (у—g-)
= *
то f' (2/3) = 0, /' (у) > 0 при 2/3 < у < 1 и /' (у) < 0 при 0 < у <
< 2/3. Таким образом,
min /(у) = /(2/3) = 9.
хб(0; 1)
Следовательно, если «=9, то уравнение (1) имеет ровно один
корень у=2/3 из интервала (0; 1), а если а < 9, то уравнение
(1) на интервале (0; 1) корней не имеет»
§ 4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 401
Таким образом, а = 9 является наименьшим значением, при
котором данное уравнение имеет хотя бы одно решение из ин-
тервала (0; л/2).
Пример 14. Дан равносторонний треугольник с длиной
стороны а. Найти длину наименьшего отрезка, соединяющего
Рис. 5.27
точки двух сторон этого треугольника и делящего треугольник
на две равновеликие части.
Решение. Пусть точки М (на стороне ВС) и W (на сто-
роне АС) (рис. 5.26) таковы, что площадь треугольника CMN
равна половине площади треугольника АВС. Тогда имеем
— (1. с A- CBsin 60° ) =4- СМ • CN sin 60°,
Z \ 2#	J £
1	аа
и, следовательно, CM* CN=-^ СА-СВ ==—. Так как
)СМ то существует число х, 0 < х=С1, такое, что CM =
— ах. Тогда CN Так как CN^.а и СМ^а, то от-
сюда находим, что 1/2 <; ж 1.
Из треугольника CMN по теореме косинусов находим, что
NM СМ *+ CN 2 CM-CN cos 60°,
или
#М2 = а«(х2+	1	2.
\	‘ 4х2 J 2
Таким образом, для решения задачи нужно найти наимень-
шее значение функции
/(Х) = Х2+ 1
'	4х2
на отрезке [1/2; 1].
Так как при 1/2 < х < 1
f (х) = 2х —«пЦ-,
1	' 1	2х^
402
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
то уравнение f'(х) = 0 имеет единственный корень х=1/рг2 из
интервала (1/2; 1). Функция f (х) непрерывна на [1/2; 1], и
f (1/2) == 1/4 +1 == 5/4, f (1) = 1 +1/4 = 5/4,
f (1/><2)=1/2+1/2= L
Поэтому
min f (x)= f (1//2)= 1.
хв [1/2; 1]
Отсюда заключаем, что квадрат длины искомого отрезка равен
2
а2/2, и тем самым его длина равна	—а.
Пример 15. От канала шириной а под прямым углом к
нему отходит канал шириной b (рис. 5.27). Найти наибольшую
длину бревна, которое при сплаве из одного канала в другой
не застрянет на повороте.
Решение. На рис. 5.27 отрезком АВ схематично изобра-
жено бревно в одном из возможных его положений при сплаве
из одного канала в другой. Ясно, что концы бревна А и В
упираются в берега канала и бревно касается точки С—точки
излома берегов каналов при наибольшей длине бревна.
Длина отрезка АВ равна
где а—-возможный угол наклона бревна к одному из берегов
канала.
Наименьшее значение величины d и будет наибольшей дли-
ной бревна, которое можно сплавить из одного канала в другой.
Угол а изменяется в интервале (0; л/2). Так как d > 0, то наи-
меньшее значение величины d будет достигаться одновременно
с наименьшим значением da; имеем
=	—I----— Y=(a+Mga)2 (14-—l-Y
\sina ‘ cos a /	v*1	’ \ *tg2a/
Положим tga=£, где 0 < х < + оо. Тогда задача сводится к
отысканию наименьшего значения функции
f(x) = (a+H2(l+^r)
на промежутке (0; + оо). Имеем
Г(х)=[(а+*х)а (^Тг)] =
—2b(a-}-bx)
= 2(a+&x)[&(l+^-)-^±^]=2(a+M
Отсюда находим, что f (х)=0 при x—i/'a/b, f (х) > 0 при х >
> У а/Ь, Г (х) < 0 при 0 < х < If а/Ь-
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 403
Так как
lim f (х) = + оо и lira f (х) = + оо,
Я->0+	Х->+со
то проведенный выше анализ показывает, что min f(x) =
х6(0; + со)
тем самым величина d2 достигает своего наимень-
шего значения, если tgao—j/a/b. Так как aog(O; л/2), то
,	tg «о	1
sin а0 =  г -—г-, cos а0=— —- ,
У H-tg2a0	к l + tg2a(j
и, следовательно,
sin а0 =
cos а0 =
Таким образом, обозначив через d0 наибольшую длину бревна,
имеем
do=_^+_^_
sina0 cosa0
(а2/ 4-^2/3)3/2е
ЗАДАНИЕ 1
1. Найти наибольшее и наименьшее значения функции / (х)
на заданном отрезке, если:
1) f (x) = x3--3x2 + 3x4-2, xg[—2; 2];
2)/W = y+4-
3)/(*) = |Щ|. хё!-2;0];
4)	Н*) = |х2 + х-2|-1п1 xg[l;2j.
2.	Представить число а в виде суммы двух положительных
чисел так, чтобы их произведение было наибольшим.
3.	Найти расстояние между графиками функций у = х2 и
у — Х — 1.
4.	Найти длины сторон прямоугольника наибольшего пери-
метра, вписанного в полуокружность радиуса так, что одна
из его сторон лежит на диаметре окружности.
ЗАДАНИЕ 2
1. Найти наибольшее и наименьшее значения функции f (х)
на заданном отрезке, если:
1) f (х) = Зх* + 4х3+1, xg| — 2; Ц;
2)/W = y+y. *€1—5; -1];
404
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
3) f(x) = /'l — 2х-|-х2J-K14- 2x4-х2 xg[—2; 0];
4) f (х) = 4х3—х| х — 2 |, xg|0; 3].
2,	Доказать, что
9—^85	—2x 4-3	9+^85
2	< х2 + 6х4 10 <	2
3.	Найти расстояние между графиками функций у — —х и
У =
4.	Найти длину высоты прямого кругового конуса наимень-
шего объема, описанного около шара радиуса R.
ЗАДАНИЕ 3
1.	Найти наибольшее и наименьшее значения функции f (х)
на заданном промежутке, если:
/ 2 -f- cos х \2
\ sin х /
2)	f (х) = tg x-j-ctg 2х, х£[л/6; зт/3];
3)	f (X) = /х(10—х), х(Ц0; 10];
X —• 1
4)	/ W=x>_3x+3-’ *€(- оо; 4- оо).
2.	Найти наименьшее значение функции f(x) =
на интервале (0; л).
3.	Найти все значения а, при каждом из которых сумма
квадратов корней уравнения
х2 —(л —2) х—а— 1 = 0
принимает наименьшее значение.
4.	На графике функции у—Ух, х£[1; 9] найти такую
точку М, для которой имеет наибольшее значение площадь тре-
угольника АМВ, где А и В — точки графика с абсциссами 1 й
9 соответственно.
5,	Каким должен быть угол при вершине равнобедренного
треугольника заданной площади S, чтобы радиус вписанного в
этот треугольник круга был наибольшим?
ЗАДАНИЕ 4
L Найти наибольшее и наименьшее значения функции f (х)
на заданном промежутке, если:
!)/(*)= К2ГГТ’
У х2
2)	/(х) = 2|/ х , х(Ц—8; -1];
3)	f (х) = (х— 1)2Кх2—2x4-3, х^10; 3];
4)	/(x) = sin2x—х, xg[—л/2; л/2].
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 405
2.	Найти наименьшее значение функции
"€N’
у 14-х у 1—X
на интервале (—1; 1).
3.	Доказать, что если [0; зт/3), то
___J______+-1__________
slnf4r4"4 sin f —4	3
4.	При каком значении х функция
f (x) = I х— 1 l + l x—2 14-, ,, 4-1 x«- 19861
принимает наименьшее значение?
5.	В данный круговой сектор радиуса R вписать прямо-
угольник наибольшей площади (угол сектора равен а). Вычис-
лить значение этой площади.
Упражнения
1. Найти наибольшее и наименьшее значения функции на
заданном промежутке:
1)	z/ = x3—х> xg[0; 4];
4
2)	^=ух3 — 4х, xg[0; 2];
3)	</=х4—8ха—9, xg [— 1; 3];
4)	у=2х3—9х2 J-12x4-1, xg[0; 2];
5)	у=х — 2 In х, xg[l; е];
6)	^=iqrr- *€I-С 0];
7)	у=2 In8 х—9 In2 *4-12 In x, xg[e3^4; e3];
8)	y=x2 —41 x Ц-4, xg[—3; 3];
9)	y=\(x+ 1) (2x-5)2|, x^-5; 4];
10)	«/=sin2x—x, xg[0; л];
12)	^ = e2A?~;l4-2^-2A?4-7x—3, xg[0,14; 1J;
13)	^=2.23*--9.22* 4-12‘2*, xg[—1; 1];
14)	2sin 2x4-cos 4x, xg[0; зт/3];
15)	y=|logi2x—log28x|, xg[l/2; 2 V2];
16^=1Л^=й’ ж4т:2];
17)	y=|x3+6x24-9x+l|, xg[—3; 1];
18)	0=—|2x34-15x2 + 36x—30|, xg[—3; 2];
19)	0=cos?4sinA:’ nJ;
406
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
20)	y=3x2+2*-1, xg[—2; 0|;
21)	p==-g-X In х—х In 2, xg[l; 4];
22)	gr=2x In х*—х In 49, xg[l; 7];
23)y=|x2+x-2|-lnl> хё[у;2];
24)	y=— у Inx—|x2—2x—3|, xg^y;4p
25)	jr=(x—3)e**+1l, xg[—2; 4];
26)	j/=(x—3)2е|л|, xg[—1; 4];
27)	y=x+V(x2+6x+9)(x2 + 2x4-l)t xg[—4; —5/4];
28)	у == —2x + К(x2—10x4-25) (x2—4x4-4), x£[9/4; 6].
2. Найти наибольшее значение функции на заданном про*
межутке:
1)г/=1пх—х, я(Е(О; + °°);
2)# = 2tgx—tg2x, xg(—л/2; л/2);
о. Х2-|“ Х-f" 1	<- /	х
3>	’ х€(— 00; «о);
4) у~—f/х2—х, х£[1; ЧЬ оо);
5) у=4-*1пх—~ х 1п9, xg(l; 3];
о	о
6)у=Чтг- ж<=1“5= °)’
3. Найти наименьшее значение функции на заданном про-
межутке:
1) iy=3x + 2ctgx, xg(0; л/2);
2) z/== х In х—х In 5, xg(l; 5];
^(0; i);
x24-l
4)	-r, "~t~7 , *€(-<»; +<»);
X2 +x+ 1	4-
еч /2+cosx\2	.
Ь}у=х\Г^Т-)  *€(0;«);
6) j/=2x84-3x2 —120x4-100, x£(—4; 5];
7)JZ='Ип^+х10, x€[!;+“)-
4.	Доказать, что max f (x) < 0,77, если f (x) = sin xsin 2x.
хе[-л; 3Tj
5.	Доказать, что min f (x) > —7/18, если f (x)=cos2xsinx.
x 6 [ - л; л}
Х.ГТ	л	2	_ ( л Л \
6.	Доказать, что sin 2а < -х, если ag ( 0;	)«
§4. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ 407
7.	Найти наибольшее значение функции:
2х
1)	f (*) = 2 arctg х + arcsin j_|_y2 ;
2)	f (х) = 74-2х In 25—5»-1—52~*;
3)	f (x) = io'+4xln9—З*-1— З3-*;
4)	/W=x8+X+4i+cosx;
4
5)	f	~ х* + Злх + 2з+Sin Х-
8.	Найти наименьшее значение функции:
1)	f (%) = cos2 х + cos2 (л/3 + х)—cos х (л/3+х);
2)	f (х) = 2*2-1+—---;
2^+2
3)	f (х)=3* + 2-33~«—xln27—9;
4)	f (х) = 2х-|- 18ji2/x+cos х, 0<х<ео.
9.	Решить уравнение:
9г
1)	==х2-2x4-2; 2) 1пх—х = —14-(*~I)2!
3)	^2 4-11^ (14-sin2(x—2)) = 14-7 cos2 (х2—4x4-4);
4)	к^+^4-	И--^- = К^+3;
5)	(х34~4) (х2 —4х-|-5) = 3х2.
10.	Определить кратчайшее расстояние от точки М до гра-
фика функции f(x) = f(x), если:
1)	f(x) = 2x4-3, 44(3; 2);
2)	f (х) = Vх24-6х4-10, М (1; 0);
3)	/(х) = 2-х24-у, М (2; 0);
4)	f(x) = ex, М(2; —1); 5) f(x) = sinx, 2И(—1; I).
11.	Найти минимум квадрата расстояния от точки М до
точек графика функции y = f(x), если:
1)/(х)=1+ТгЬ^’ М(0:1);
27
2)/(х) = -~==-----, xg(—1; 4-оо), М(— 1; 0).
7 К 2(х4-1)2
12.	На интервале (0; л) задана функция у= 1— cosjf.
Найти наибольшее значение абсциссы точек пересечения каса-
тельных к графику данной функции с осью ОХ.
13.	Найти координаты точки Mt лежащей на графике
функции ^=l-]-cosx при О^х^л и наименее удаленной от
прямой х/ ЗЧ-2//-]-4 = 0.
14.	Найти координаты точки Му лежащей на графике
функции у~ 1—sinx при л/2^х^Зл/2 и наименее удаленной
от прямой х-»К 2 у—5 = 0,
408 ГЛ. 5. ПРОИЗВОДНАЯ Й ЕЕ ПРИМЕНЕНИЕ
15.	Найти координаты точки М, лежащей на графике
функции у —24-cosx при О^х^зт и наименее удаленной от
прямой х + 2^4-3 = 0.
16.	Найти координаты точки А4, лежащей на графике
функции y==cos2x при 0^х«Сзт и наименее удаленной от
прямой х 3 —2г/—7 = 0.
17.	Даны точки А (0; 3) и В (4; 5). Найти на оси ОХ точку М
такую что сумма расстояний от этой точки до точек А и В
наименьшая.
18.	Из всех прямоугольников, у которых две вершины
лежат на интервале (—2; 2) оси абсцисс, а две другие —на
графике функции у = 4—х2, найти прямоугольник наибольшей
площади и вычислить эту площадь.
19.	В фигуру, ограниченную линиями у — х2, у = 2х2, х~6,
вписан параллелограмм наибольшей площади так, что две его
вершины лежат на прямой х = 6, а две другие — на параболах
у — х* и у~2х2. Найти эту площадь.
20.	В фигуру, ограниченную линиями у = 3х и у = х2, впи-
сан прямоугольник наибольшей площади так, что две его вер-
шины лежат на прямой, а две другие — на параболе. Найти
эту площадь.
21.	Криволинейная трапеция ограничена параболой
у = х2+1и отрезками прямых у = 0, х= 1, х = 2. В какой точке
М данной кривой ^ = х2+1, xg[l; 2], следует провести каса-
тельную, чтобы она отсекала от криволинейной трапеции обыч-
ную трапецию наибольшей площади.
22.	Из всех прямоугольников данной площади S найти тот,
периметр которого наименьший.
23.	Определить размеры открытого бассейна с квадратным
дном, объем которого равен V, чтобы на облицовку его стен
и дна пошло наименьшее количество материала.
24.	Сумма длин диагоналей параллелограмма равна 8.
Найти минимум суммы квадратов длин всех сторон паралле-
лограмма.
25.	Сумма двух сторон треугольника равна а, а угол между
ними равен 30°. Каковы должны быть длины сторон этого
треугольника, чтобы его площадь была наибольшей?
26.	В равнобедренной трапеции меньшее основание и боко-
вая сторона равны а. Найти большее основание, чтобы пло-
щадь трапеции была наибольшей.
27.	Найти высоту конуса наибольшего объема, образующая
которого имеет заданную длину I.
28.	В шар радиуса R вписан цилиндр наибольшего объема.
Найти его радиус, высоту и объем.
29.	Среди всех конусов, периметр осевого сечения которых
равен 8, найти конус с наибольшим объемом и вычислить этот
объем.
30.	Сумма длин всех ребер правильной шестиугольной
призмы равна 36. Найти длину стороны основания призмы,
при которой объем призмы будет наибольшим.
31.	Дан шар радиуса 10. Найти радиус основания и длину
образующей вписанного цилиндра, имеющего наибольшую пло-
щадь боковой поверхности.
32.	В конус, радиус основания которого 6 и высота 12;
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	409
вписан цилиндр наибольшего объема (основание цилиндра
лежит на основании конуса). Найти радиус основания и высоту
цилиндра.
33.	В основании пирамиды МАВС лежит прямоугольный
равнобедренный треугольник АВС, в котором С = 90°, МА — вы-
сота пирамиды, —	3, где О —середина АВ. Найти длину
высоты пирамиды, при которой ее объем будет наибольшим.
34.	В основании пирамиды- MABCD лежит прямоуголь-
ник ABCD, в котором АВ—ЗВС, MD—высота пирамиды
и MD-A-BC— 12. Найти длину отрезка ВС, при которой объем
пирамиды будет наибольшим.
35.	Боковое ребро правильной треугольной пирамиды имеет
постоянную длину и составляет с плоскостью основания угол,
величина которого равна а. Найти значение а, при котором
объем пирамиды будет наибольшим.
§ 5.	Применение производной
Область применения производной при решении задач эле-
ментарной математики очень широка. Это, например, использо-
вание производной при преобразовании алгебраических выра-
жений, разложении на множители, доказательстве тождеств,
вычислении сумм, решении уравнений, неравенств и систем,
доказательстве неравенств, решении задач с параметрами,
исследований функции и т. д. В основе таких приложений
лежит ряд основных теорем, которые приводятся ниже.
1.	Если функции f (х) и g (х) дифференцируемы на интер-
вале (а; Ь) и f(x)^sg(x), xg(a; b), то f(x)^g'(x), xg(a; b).
2.	Если функции f(x) и g(x) дифференцируемы на интервале
(а; b) и (х) g'(х), х^(а; Ь), то f(x) = g(x) + c, где с—неко-
торая постоянная.
В частности, если функция f (х) дифференцируема на интер-
вале (а; Ь) и ff (х) = 0, xg(a; b), то функция f (х) на интервале
(а; Ь) тождественно равна постоянной, т. е. f (х)^с.
3.	Если функция f (х) дифференцируема в точке Хо£(а; Ь),
то она является непрерывной функцией в точке х = х0.
4.	Если функция f (х) дифференцируема на интервале (а\ Ь)
и f (х) > 0 (/' (х) < 0), х£(а\ Ь), то функция f (х) возрастает
(убывает) на интервале (а; Ь).
5.	Если функция f (х) непрерывна на промежутке [а;/»)
([а; b], (а\ д]) и убывает (возрастает) на интервале (а; Ь), то
функция f (х) убывает (возрастает) на промежутке [а; Ь)
([а;	(а; &]).
6.	Если функции f (х), g (х) непрерывны на промежутке
[а; и дифференцируемы на интервале (а; Ь), причем f' (х) <
< g'W, *(&', Ь), и f(a)^g(a), то f (х) < g (х), xg(a; b).
7.	Теорема Ролля. Если функция f (х) непрерывна на
отрезке [я; 6], дифференцируема на интервале (я; Ь) и f (a) ~f(b),
то существует по крайней мере одно значение с£(а\ Ь) такое,
что Г (с) = 0.
Геометрическая интерпретация теоремы Ролля состоит в том,
что у графика непрерывной на отрезке и дифференцируемой
внутри его функции, принимающей на концах этого отрезка
410 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
одинаковые значения, существует хотя бы одна точка (с; /(c)),
через которую проходит касательная, тангенс угла наклона
которой равен нулю, т. е. ff (с) — 0. Другими словами, сущест-
вует касательная (с точкой касания (с; f (с)) графика функции),
которая параллельна оси ОХ (рис. 5.28).
8.	Теорема Лагранжа. Если функция f (х) непре-
рывна на отрезке [а; Ъ] и дифференцируема на интервале (а\ Ь),
то найдется по крайней мере одно значение eg (а; Ь) такое, что
(Ъ—а).
Геометрический смысл теоремы Лагранжа состоит в сле-
дующем. Пусть АВ — хорда, соединяющая точки A (a; f (а))
ъ В (b; f (&)) (рис. 5.29). Тогда отношение	равно
§5 ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	4Ц
тангенсу угла наклона к оси ОХ прямой, проходящей через
точки Л и В, а производная ff (с) равна тангенсу угла наклона
касательной к графику функции у= f (х) в точке касания
(с; Другими словами, у графика непрерывной на отрезке
[а-, 6] и дифференцируемой на интервале (а; Ь) функции суще-
ствует хотя бы одна точка (с; f (с)), через которую проходит
касательная, параллельная хорде АВ.
Пример 1. Разложить на множители выражение
ху (х—у) 4- У* (у—z)+ xz (z *-х).
Решение. Считая х переменной величиной, рассмотрим
функцию f(x) = xy (х — y)+yz(y-*z)4-xz(z**-x). Имеем
f' W = 2ху—у2 + z2—2xz = (y—z) (2x^y*-z)<
Так как
(х2—(y4-z) х)' = 2х—у—z,
((у—г) (х2 —(у4~г) х))' = (у—z);(2x*-y—z),
то отсюда заключаем, что
Г (*) = ((У** г) (х2 — (у+г) х)\
По теореме 2 получаем
f (x)==(y--z} (x2—(y4-z) x)+G,
где С не зависит от х, но зависит, вообще говоря, от у и 2*
Так как последнее равенство верно при любом х, то, по-
лагая, например, в нем х —О и учитывая, что f (0) = yz(y*-z),
найдем C = yz(y—z).
Таким образом,
IW == (У—г) (х2 —— (у + z) х) + yz (у— г) =
~(У~-2) (х2—(y+z)x+yz) =
== (у—г) (х (х—у)—z (х—у)) = (х—у) (у—г) (х-* г>.
Итак,
ху (х—у) + у г (у—г) + xz (z—х) = (х—у) (х — z) (у—г).
Пример 2. Разложить на множители выражение
(у—2) (у+г)3+(2—x)(z+x)3+(x—у) (x-f-y)3.
Решение. Считая х переменной величиной, рассмотрим
функцию f (x) = (y—z) (y+2)3+(z—х) (г+х)3 + (х—у) (х+уЯ.
Найдем ее производную:
? (x) = —(z+x)3+3(z+x)2 (z—х)+(х + у)3 + 3(х + у)2 (х—у)==
= (z+x)2 (3z-3x-(z+x)) + (x+y)2 (х + у+3х-3у) =
=2 (г 4-х)2 (г-2х)+2 (х4~у)2 (2х—у).
Отсюда после алгебраических преобразований получаем
Г (x) = 2(z3^y34-3(y^z)x2).
412 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Так как
((г8—у3) %+((/ — г) x8)' = z3-“j/34-3(z/—z) ха,
ТО
г (х) = (2 (^-y^x+iy-^x*))',
и, следовательно, по теореме 2 заключаем, что
f (х) = 2 ((г3-^ х+(у-г) х3) + С,
где С не зависит от х, но, возможно, зависит от у и г. Пола-
гая в этом равенстве, например, х = 0 и учитывая, что f(0) =
= (y^z)	+ найдем
С=(у—г) (у+г)3+г4—у*.
Итак,
f (*)==2 ((г3—f/З) —Z) Х3) + (у^г) (^ + z)3 + z4—I/4,
или
f (*) == 2 (У г) (— У*х — xyz—z2x+х3 + y*z + уг*).
Для того чтобы разложить на множители выражение в по-
следних скобках, применим тот же самый прием. Считая
у переменной величиной, рассмотрим функцию
g (у)» — у*х—Xyz — г2х+х3+у*г уг*;
тогда
g' (#) = —2ху—хг+2уг+г2 = 2у (z—x) + z(z-*x) = (z—х) (2^+г).
Отсюда получаем
g(#) = (z—x) (y2 + zy)+Cit
где Ct зависит от х и г и не зависит от у. Полагая, например,
#=0 и учитывая, что g (0) =—z2x + x3, из последнего равенства
найдем Cf = x(x2—г2). Таким образом,
g (У) = (г—х) (у2 + гу) + х (х2 — г2) = (х—z) (х2 + xz—$/2 — гу) =
==(х—z) ((x-Г/) (х+^) + г(х—^)) = (х—г) (х—у) (х+^+г).
Итак, окончательно имеем
f (х) = 2 (х—0 (х-*г) (у—z) (х+^+г).
Пример 3. Упростить выражения
а)	(* + #+г)3 — (х + «/ —г)3—(у+г—х)? —(г + х—г/)3;
б)	sin3x(14-ctgx) + cos3x(l + tgx).
Решение, а) Считая х переменной величиной, рассмот-
рим функцию
f (х) = (х + г/+г)3-~(х+у~г)*~(у+2^х)*~(г+х--уУ.
Тогда, дифференцируя ее, имеем
г (х)=3(х+г/+г)2- 3 {x+y^z^+3(y+z^x)^3(z+x^y)^2^yz.
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	413
Отсюда находим, что f (x)~24xyz-]~Ct где С не зависит от х,
но может зависеть от у и г. Полагая, например, х==0, полу-
чаем
C^f^^(y + z)^(y^zY^(y+z)^{z^y)\
Поскольку (^/4-г)3 —(f/—г)3-—*(^/+г)3*—t/)3==0, то С=0.
Следовательно,
f (x) = 24xyz.
б)	Для функции /(x) = sin3x (1 + ctg x) + cos3 х (1 +tg х) на
ее естественной области существования имеем
f (х) == 3 sin2 х cos х (1 + ctg х) — sin3 х gj-g— ~~
-*3 cos2 х sin х (1 + tg х) + cos3 х =
= 3 sin2 х cos х—3 cos2 x sin x—-sin x+cos x +
4-3 sin x cos2 x—3 cos x sin2 x= cos x—sin xt
Таким образом, из тождества (sin x-|-cos x)' = cos х—sin х сле-
дует, что
f (х) = cos х + sin x,+C,
где С—‘Некоторая постоянная. Полагая"в последнем тождестве,
например, х = л/4, найдем, что С = 0. Следовательно, f (х) =»
= sinx+cosx при всех действительных значениях х таких,
что х 7^ fat/2, k£N.
Пример 4. Доказать тождества
2х
a)	2arctgx+arcsin-jq--^==jT, x^sl;
б)	1 + Зх?+5х4+... + (2п—1)х2«~2 =
(2п — 1) х2”~2—(2n4- 1) х2” + х2+ 1	. > t
Решение, а) Рассмотрим функцию
2х
f (x) = 2arctg х4 arcsin-p-j-p-, x^l.
При х= 1 имеем f (l) = 2arctg 14-arcsin 1 = 2-~-4-~-=jt. Пусть
2
x> 1; тогда (2arctg х)'=т-.- и
i —x
(	. 2x V'	1	/ 2x V
\	1+*2/	1/1	/ 2x \2 \1 + *2/
V \T+xV
i+x2 2(1—x2) _2 1—X2 1 _	2
K(l—x2)2 (1 + x2)2	|l-x2| l+xa“" H-x3'
Поэтому
/'(x) sO, X > 1,
414	ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Следовательно, функция f(x) при х> 1 является тождественно
равной постоянной. Чтобы найти эту постоянную, вычислим,
например, f(]^ 3); имеем:
f (V”3)=2arctg'K 34-arcsin J^-=2
о о
Таким образом, данное тождество доказано для всех х^\.
б) Так как
1+Зх2 + 5я4+ ... + (2л— 1) х2«-2= (x + x3-J- ...
то, используя формулу для суммы первых п членов геометри-
ческой прогрессии при | х [ #1, найдем
Поскольку
/х—х2"*1 у_ (1 —(2ге+1)х2«)(1—х2)+2х(х—х2л+1) _
\	1—х2 )	(1—х2)2
1—(2n +1) х2«—х2+(2 га +1) х2«+2 4- 2х2—2х2в+2 _
₽	(1 —х2)2	~
_ 1 +х2 — (2га + 1) х2«+ (2га —1) х2в+2
~	(1—х2)2
то требуемое тождество доказано.
Отметим, что из доказанного в п. б) тождества можно
получить некоторые числовые равенства. Так, например, по-
лагая в нем х —2. а затем х=1/У~ 2, соответственно найдем
1) 1+3.4+5.4Ч-...+99.4-=!”-2“,-'901-2“,+5 =
=4(1+592io“);
У
2) 1+4+^+... 4-^=4. (101.^5-103.^+1+1) =
/101	1	105
\ 2	103 J ’ 2«16 — 6	260 '
Пример 5. Найти сумму
Sn (х)=Ь2+2.3^ + 3«4х2+...+(л— l)n*«-24-M"+l)*“~x>
х Ф 1.
Решение. Пусть
fn (x)=1 + x+x2+4..+x" + x"+1.
Так как
gn (ж) = fn (X) = 1 +2х+ Зх2+... +«х«-1+(»+1) х»
g„ (х)= Ь2+2.3х+3.4х2+... +га (га—1) хл-?+(га+1) гах”-1,
то
Sn(x) = gn(x).
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
415
Поскольку fn (х) есть сумма первых п+1 членов геометри-
ческой прогрессии со знаменателем х, х й 1> то
Так как gn (x)~fn (х), то
,	1— хл+2 V — (п+2)х« + 1(1— х) + (1 — х«+2)
SnW \ 1—х )	(1— X)2	“
_ (n+l)x”+2—(п+2)хп+*+)
-	(1-х)2
е ,г\_( (n+Dx'»+2-(n + 2)x'’ + »+l V
S„(x)-^-----------——г----------J =
_((л-Н) (« + 2)х»+1—(п+2)(п-|-1)х»)(1—х)8
(1—х)4	"Г
, 2(1 — х) ((n+1) хп+2—(n+2) хп+1+1)_
+	(1— х)4	—
__ —-n (n + I) xw*2+2n (n+2) xn+1—>(п+1) (n+2)x”+g
~~	(1-х)з
Пример 6. Найти сумму
Se==2>. Ь2+22.2.3+23<3‘4+... +2йп (п+1).
Решение. Рассмотрим функцию
f (х) = х2+ха+... + х"+х.
Имеем
g W - г (х)=2х+Зх2 +...+(п +1) х«,
g' (х) х = 2х+2*3х2+.,. + (п+1) пх".
и поэтому Sn=2g'(2). С другой стороны,
Хп + 2^,х2
X—1
fM
как сумма первых п членов геометрической прогрессии е пер-
вым членом х» и знаменателем х, х Ф I. Поэтому
/ х« + 2—х2 V	((л+2)х»+1—2х) (х— 1)—(х«+2—х2)
1	) —	(х— 1)2
__(n+ I) хл+2-~(п + 2) хп+1—х2+2х
“	(X— I)2	5
((»+1) (я+2) х«+4-(п+2) («4-1) х«-2х+2) (х-1)2
g (XJ---------------------
2 (х— 1) ((«+ 1) хп+2—(п+2) х”+*—х2+2х)
(х-1)4
Таким образом,
Sn=2 ((п+ 1) (п+2).2«+4-(п+2) (п+1).2»-4+2)-
—2((п + 1)-2«+2—(п + 2)-2л+1) = 2'1+1(2(п + 1)(п+2) —
—(л + 2) (п+1)—4кп + 1)+2п + 4) —4 = 2«+1(п2—п+2)—4.
416
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Пример 7. Найти сумму
s„=cS+2cU-3c£+...+(» + !)ей, п^1,
где число сочетаний из п элементов по k элементов.
Решение. Рассмотрим многочлен
Рп (*) = Сп+2СпХ+ЗСпХ2 +... + (л +1) СЙХ«.
Значение этого многочлена при х=1 дает искомое значение
суммы, т. е. Sn = pn(l).
Рассмотрим функцию
?„+1 (х)==С^4-САх2+С^»+ ... +СЙх»+*.
производная которой равна prt(x).
Используя теперь формулу бинома Ньютона, получаем
<7п+1 (х) = х (С^4-С^4-С^+... +О) = х (1 +хр.
Тогда
Рп (х) = ^+1 (х) = (х (1 +х)«)' = (1 +х)« + пх (14-х)”-»,
и, таким образом, получаем
Sn = pn(l) = 2” + n*2«-i = (n + 2)*2«-a.
Пример 8. Найти все пары чисел (a; Ь), где а > 0, 6^0,
такие, что справедливо тождество
a In х+& = 1п (ах+&), х > 0.
Решение. Пусть пара (а0; Ьо) такова, что
«о 1пх+&о = 1п (аох+&о)
при каждом х > 0.
После дифференцирования при всех х > 0 получаем тож-
дество
ffd ао
х a0*+fy)*
На рассматриваемом множестве пар (а; &), а > 0, послед-
нее тождество справедливо только для пары (1; 0). Непосред-
ственной проверкой убеждаемся, что найденная пара чйсел
(1; 0) является решением исходной задачи.
Пример 9. Найти все функции f(x), каждая из которых
имеет непрерывную производную при всех xgR и удовлетво-
ряет тождеству f (2x) = 2f (х), xgR.
Решение. Пусть f (х) — искомая функция. Тогда из тож-
дества f (2x) = 2f (х) имеем f(0) = 0 и 2/' (2х) = 2f- (х), откуда
находим
Г(2х) = Г (х).
Так как х—произвольное число, то получаем
^(2х) = Г(х)=Г	=	xgR.
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	417
Так как х/2п —>0 при п —> оо и по условию y~fr (^ — непре-
рывная функция на 7?, то
Г(*) = lim f' (х)= lim f	( lim £}=Г (0), xgR.
Таким образом, функция f' (x), xgR, есть константа, откуда
f (x)~ax-\-bt где a = f' (0). Положив, например, x — 0, из по-
следнего тождества с учетом равенства f(0)=0 получим, что
£ = 0. Следовательно, искомыми функциями могут быть только
функции вида f(x) = ax. Проверкой убеждаемся, что любая
функция вида f(x)=ax удовлетворяет условию задачи.
Применение производной к решению уравнений, неравенств
и систем, а также к доказательству неравенств основано на связи
между возрастанием или убыванием функции на некотором
промежутке и знаком ее производной.
Пример 10. Решить неравенство
2х9 —х^+х > 2.
Решение. Найдем участки возрастания и убывания функ-
ции f(x) — 2x9—х5-4~х—2. Производная f' этой функции равна
18х8—5х4+Ь Так как дискриминант квадратного трехчлена
18z/2—является отрицательным числом и коэффициент
при у2 этого квадратного трехчлена больше нуля, то для каж-
дого действительного х имеем неравенство (х) > 0.
Таким образом, функция y = f(x) является непрерывной и
возрастающей на всей числовой прямой; поэтому ее график мо-
жет пересекать ось ОХ только в одной точке. Учитывая, что
/(1)=0, заключаем, что решениями данного неравенства являются
все числа х из промежутка (1; +оо).
Пример И. Решить неравенство
х2+^<й‘	(1)
Решение. Корнями уравнения
ж2 4-1/х=з/У1	(2)
являются абсциссы точек пересечения или касания графика
функции f (х)=х2+1/х и прямой	4. Найдем участки
возрастания и убывания функции г/ = /(х), а также ее точки
экстремумов.
Так как
f' (х) =2х*-Л/х2,
то
f' (х) > 0 при х > ill/ 2;
при х~1Ц/ 2;
f' (х) < 0 при х < 0 и при 0 < х < 1/^/ 2,
Таким образом, функция y=f(x) убывает на промежутках
(— оо; 0) и (б; l/i/ 2) и возрастает на промежутке {ill/2;
14 Задача до математике. Начала анализа
418 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
+ оо). Так как f (л) непрерывна в точке x=l/^Z 2, то в точке
2 она имеет локальный минимум, равный
Отсюда ваключаем, что число х—1/р/ 2 является корнем урав-
нения (2) (рис. 5.30), и, следовательно, при х > 0 данное нера-
венство решения не имеет.
Так как функция / (х) = ха + ™' непрерывна и убывает на
(—оо; 0), то при условии, что f(x0)=3/j/ 4, где xog(— оо; 0),
решением исходного неравенства
будет интервал (х0; 0),
Таким образом, если точка
xog(—оо; 0) существует, то она
является корнем уравнения (2).
Так как x—l/p/ 2 является од-
ним из корней уравнения (2), то
это число является корнем и
равносильного ему уравнения
т^х+1 = 0-	(3)
|/4
Для нахождения остальных кор-
ней уравнения (3) воспользуемся
теоремой Безу. По теореме Безу
многочлен X3--—— х4-1 делит-
V 4
лен	Найдем частное от
деления:
0
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
419
Таким образом, уравнение (3) можно переписать в виде
и поскольку
то уравнение (3) равносильно уравнению
Из (4) получаем х0=—2/j/^ 2.
Таким образом, решениями неравенства (1) являются все
числа х из промежутка (-2/^2; о).
пр и мер 12. Решить уравнение
х2— х 4-2 = 2 У2х—1.
Решение. Переписав данное уравнение в виде
х2—2х4-2 = 2 р^2х—1—х,	(5)
заметим, что его корнями являются абсциссы точек пересечения
или касания графиков функций f (х) = х2 —2х+2 и g(x) =
= 2]/2х—1—х. Для выяснения взаимного расположения гра-
фиков этих функций найдем их точки экстремумов.
Так как f (х) = (х—1)24-1, то эта функция достигает своего
наименьшего значения, равного 1, в точке х = 1. Область суще-
ствования функции g (х) = 2 2х— 1 —х состоит из всех х таких,
что х^ 1/2. Так как
ТО
g' (*) > о	при	1/2 < х < 1.
g' W=o	при	«= 1>
g' W < 0	при	х > 1. §
Так как функция y = g(x) непрерывна на [1/2; -р оо), то отсюда
заключаем, что функция g(x) возрастает на промежутке [1/2; 1]
и убывает на промежутке [1; 4“ °0)- Следовательно, точка х = 1
является наибольшим значением функции g(x) на ее области
существования.
Таким образом, при любом xg[l/2; 4-°°)/
х2 — 2x4-2	1,
2	2х в®9 & •«* X
14*
420
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Следовательно, уравнение (5) и, значит, исходное уравнение
имеют единственный корень х=1.
Взаимное расположение графиков функций у = f (х) и у —g (х)
показано на рис. 5.31.
Пример 13. Опреде-
лить число действительных
корней уравнения
12х4—14х3 — 3х2—5 = 0. (6)
Решение. Найдем
промежутки возрастания и
убывания непрерывной
фу н кци и f (х) = 12х4 —
•— 14х3—Зх2—5.
Так как
f (х)~ 48х3 — 42х2 —• 6х =
Рис. 5.32
Рис. 5.31
то отсюда заключаем, что на промежутках (— оо; —1/8] и [0; 1]
функция f(x) убывает, а на промежутках [—1/8; 0] и [1; Ч-оо)
возрастает.
Таким образом, точки х = —1/8 и х=1 являются точками
локальных минимумов функции f (х), а точка х = 0—точкой
локального максимума функции / (х) (рис. 5.32). Имеем
/(0)=-5; /(!>=—10.
и, следовательно, /(—1/8) < /(0).
Отметим также, что /(—Г) = 18 и /(2) = 63. Так как функция
/(х) возрастает на промежутке [1; +оо), то она возрастает и
на отрезке |1; 2J. Поскольку на концах отрезка [1; 2] вепре*
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	421
рывная функция f(x) принимает значения разных знаков, то по
теореме о промежуточном значении непрерывной функции за-
ключаем, что функция f(x) принимает на промежутке [1; +00)
значение, равное нулю в единственной точке х — х± такой, что
1 < Xi < 2, Аналогично находим, что существует еще ровно одна
точка х2, —1 < х2 < —1/8, в которой график функции y~f(x)
пересекает ось абсцисс.
Таким образом, уравнение (6) имеет только два действитель-
ных корня.
Пример 14. Для каждого значения а найти число кор-
ней уравнения
х3—Зх2—а — 0.	(7)
Решение. Найдем участки возрастания и убывания функ-
ции f (х) = х3—Зх2.	Так как f' (х) = 3х2 — 6х = 3х (х—2), то
f'	(х) < 0	при	0 < х < 2;
f'	(х) = 0	при	х —0 и х—2;
f'	(х) > 0	при	х < 0 и х > 2.
Таким образом, непрерывная функция y = f(x) в точке х —2
имеет локальный минимум, а в точке х = 0—локальный мак-
симум, причем /(0) = 0, Д(2) = —4. Кроме того, функция y~f(x)
убывает на промежутке * [0; 2] и возрастает на промежутках
(—оо; 0] и [2; + оо). При этом lim f (х)=+оо и lim f(x)~—оо.
+ оо	х-> - 00
Отсюда следует, что для выяснения зависимое!и числа кор-
ней уравнения (7) от возможных значений а нужно выяснить
взаимное расположение графика функции y = f(x) и прямой у —а,
когда а изменяется в промежутке (—оо; + оо). Из доказанных
выше свойств функции f (х) и того, что функция f (х) непре-
рывна в каждой точке своей области существования и является
многочленом третьей степени, а значит, имеет или один дей-
ствительный корень, или три действительных корня, заклю-
чаем (рис. 5.33), что
при а > 0 уравнение имеет один корень;
при а = 0 уравнение имеет три корня (xi = x2 = 0; х3=*=3),
среди которых два совпадающих;
при —4 < а < 0 уравнение имеет три различных корня;
при а = —4 уравнение имеет три корня (xi = x2 = 2, х3=—1),
среди которых два совпадающих;
при а < —4 уравнение имеет один корень.
Если хх, х2, ...» xrt—-корни алгебраического уравнения
f (x) = anac« + a„_1x«-I4-...+ao = O, аа £ 0,	(8)
то многочлен, стоящий в левой части этого уравнения, может
быть представлен в виде
апхп+ап-IX» ~14- ... + а0=ап (х—х,) (х—х2),. . (х—хй).
Если'среди корней х/, х2/ ..., хп имеются корни, равные между
собой, то говорят, что уравнение (8) имеет кратные корни,
при' этом, если xi = x2 = ... =5=Х£ = я и среди других корней нет
равного числу а, говорят, что число х=а является корнем
422	ГЛ. 5. ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
кратности k. Например, так как
х4»—7х3 + 9х2-|-27х—54= (х—З)3 (x-J-2),
то корень х = 3 имеет кратность 3, а корень х ——2 является
корнем кратности 1 (или простым корнем).
Применение производной позволяет, не решая уравне-
ния (о), не только убедиться в существовании кратных корней
(если они есть), но и дать способ отобрать все кратные корни,
отделив их от простых корней. Имеет место следующее утверж-
дение:
Наибольший общий делитель многочленов f (х) и f' (х)
имеет своими корнями лишь корни многочлена f (х), причем
только те из них, которые имеют кратность не менее 2. Каж-
дый из этих кратных корней многочлена f (х) является корнем
наибольшего общего делителя кратности на единицу ниже.
Простые корни многочлена f (х) не являются корнями наиболь-
шего общего делителя многочленов f (х) и f (х).
Отсюда вытекает следующее правило для нахождения
кратных,корней уравнения (8):
1.	Находим f' (х).
2.	Находим наибольший общий делитель многочленов f(x)
и f (х).
3.	Находим корни наибольшего общего делителя много-
членов f (х) И f' (X).
Каждый из найденных корней наибольшего общего дели-
теля многочленов /(х) и /' (х) является корнем многочлена
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	423
f (х), причем кратность этого корня на единицу больше его
кратности в наибольшем общем делителе.
Отметим, что если наибольший общий делитель многочле-
нов / (х) и f' (х) есть константа, то уравнение f (х) = 0 не имеет
кратных корней.
Пример 15. Решить уравнение
хз_8х24-13х—6 = 0.
Решение. Рассмотрим многочлен
/ (х) =	8х2+ 13х—6,
производная которого равна
Г (х) = Зх2—16x4-13.
Найдем наибольший общий делитель многочленов f(x) и f* (х)<
Имеем
x3__8x2-|-13x—6 Зх2—16x4-13
8 а , 128х 104
--3*8+—--9-
—50 , 50	50~ Т"
—	-----д (х—1).
^Зх2—16x4-13 1 х—1
Зх2—Зх |3х-«13
__ — 13x4-13
— 13x4-13
0.
Таким образом, наибольший общий делитель многочленов
/(х) и f' (х) равен х—1 (с точностью до постоянного множи-
теля).
Так как х= 1 является простым корнем наибольшего об-
щего делителя, то число х=1 будет двукратным корнем дан-
ного уравнения, и, значит, многочлен / (х) делится без остатка
йа (х—I)2. Разделив f (х) на (х—I)2, находим, что f (х) =
= (х— I)2 (х—6). Следовательно, корни исходного уравнения —
это числа Х1 = х2=1 и х=6 и только они.
Пример 16. Решить систему уравнений
х2^+2х^«+^==9,
х*у—р*=7.
Решение. Перепишем данную систему в виде
у{х + у)2 = 9,
(Ю)
424 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Из первого уравнения этой системы следует, что ее решениями
могут быть такие пары чисел (х, у), для каждой из которых
у > 0. Тогда эти пары чисел должны удовлетворять неравен-
ству х > у > 0, что следует из второго уравнения системы (10).
Пусть / = у\ тогда из первого уравнения системы находим,
что х — 3/t—t2. Подставляя во втором уравнении системы
3//— /2 вместо хи/2 вместо у, получаем
((3/Z —Z2)3—/6) = 7,
или
(3—/3)3—/9—7^ = 0.	(11)
Так как
((3 —/3)3 —/9 — 7/)' =— 9 (3_/2)2 /2 — 9/8 —7=:=
=— (9 (3 — /2)2 Z2 + 9/8-f-7) < 0,
то уравнение (11) имеет не более одного корня. Нетрудно за-
метить, что число / = 1 является корнем. Отсюда находим, что
решением данной системы может быть только пара чисел х = 2
и у~\. Проверкой убеждаемся, что эта пара чисел действи-
тельно является решением системы (9).
Пример 17. Доказать, что при х^О имеет место нера-
венство
х2—х3 < 1/6.	(12)
Решение. Найдем участки возрастания и убывания
функции
/(х) = х2 — х3 = х2 (1 — х), Х^О.
Так как /' (х) = 2х—- Зх2 = х (2—Зх), то
Г (х) > 0 при 0 < х < 2/3;
f(x) = 0 при х = 2/3;
/' (х) < 0 при х > 2/3.
Функция f(x) непрерывна на [0; 4-оо); поэтому она возрастает
на отрезке [0; 2/3] и убывает на промежутке [2/3; +©о). Отсюда
заключаем, что точка х = 2/3 является точкой локального мак-
симума функции / (х) (рис. 5.34).
Так как f (2/3) = (2/3)2 — (2/3)3 = 4/27 и 4/27 < 1/6, то нера-
венство (12) доказано.
Ри«. 5.34
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	425
Пример 18. Доказать, что при х^О имеют место не-
равенства
х—х3/& «С sin х <; х,	(13)
1—-х2/2 «с cos х=< 1.	(14)
Решение. Sin х «С х справедливо для хл/2, поскольку
для таких х имеем sin х^ 1 < л/2. Рассмотрим функцию Л(х)=
= sin х— х, х0О; л/2). Так как функция h (х) непрерывна на
промежутке [0; л/2), Л(0) = 0 и h' (х) = cos х — 1 < 0 на (0; л/2),
то, согласно утверждению 6, заключаем, что h (х) < 0 на
(0; л/2), т. е. sin х < х при xg(0; л/2). Так как sinx — x при
х = 0, то неравенство sinx^x при х^О доказано.
Для доказательства неравенства
cosx^sl—- х2/2	(15)
при х^О рассмотрим функцию
f (х) = cos х + х2/2 — 1.
Так как f(0) = 0 и функция / (х) непрерывна, то для доказа-
тельства неравенства (15) достаточно доказать, что функция
f (х) возрастает на промежутке (0; +оо), т. е. достаточно дока-
зать, что
Гх) = — sin х+х > 0
при х > 0.
Справедливость последнего неравенства sin х < х при х > 0
уже установлена, тем самым доказана и справедливость нера-
венства (15).
Для доказательства неравенства
sinx — x—х3/6, х^0,	(16)
рассмотрим функцию
gr’(x) = sin х—х+x3/6t х 0.
Так как g(0) = 0 и функция g (х) непрерывна на [0;
то для доказательства неравенства (16) достаточно доказать,
что функция g(x) возрастает на промежутке (0; + оо), т, е.} что
g' (х) = cos х-— 1 + х2/2 > 0
при х > 0.
Справедливость последнего неравенства уже установлена.
Тем самым доказана справедливость неравенства (16)» Графи-
ческая иллюстрация неравенств (13) и (14) показана соответ-
ственно на рис. 5.35, а, б.
Пример 19. Доказать, что
1 + х/2
при х^0.
Решение, Рассмотрим функцию
/(х)==— У l+x+x/2-f-l
при х^0<
426	ГЛ Ь ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Так как f (0) = О и функция f (х) непрерывна при х^О, то
для доказательства данного неравенства достаточно доказать,
что функция f (х) возрастает на промежутке (0; + оо), т. е.,
что
f' (х) =______ -к—- =	1 Х > 0
'	2/ 1 + х+ 2	2/1-^х
при х > 0.	___
Заметим, что V 1 + х > 1 при х > 0. Отсюда следует спра-
ведливость последнего неравенства, а тем самым и исходного
неравенства. Взаимное расположение графиков функций
и р=1 + у показано на рис. 5.36.
Пример 20. Доказать неравенство
In2л > In 1) In («+ 1), п > 2.
Решение, Перепишем данное неравенство в виде
In п In (п+ 1)
In 1) > Inn
Рассмотрим функцию
In y
- хё(2; +оо)’
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
427
и найдем ев производную. Имеем
1п(х—1) 1пх . х—1 . , 1Ч
----------------V-----------L----------- х 1п-In (X — 1)
Г (Г\ - х-------------------------------------1— х-_<
1 w~ ln2(x—1)	х(х— 1)1п2(х— 1) -•
Так как f' (х) < 0 при х > 2, то функция y~f(x) убывает на
промежутке (2; 4-оо), и, следовательно,	п > 2»
т. е.
In п In (и +1)
In (п— 1) Inn ’
откуда следует нужное неравенство.
Пример 21. Пусть a, bt с, d —произвольные положитель-
ные числа. Доказать, что
Решение. Рассмотрим непрерывную функцию
(1 \ь л л~/\а+ь
i+y) -------------
при t > 0.
Дифференцируя fit), получаем
/ (0— ——	—
(1+0<г+ь-1а^—|-
Отсюда заключаем, что
f' (0 > 0 при t > bfa\
при t~b/a\
f' (0 < 0 при 0 < t < b/a>
428 ГЛ. б. ПРОИЗВОДЙАЯ Й ЕЕ ПРИМЕНЕНИЕ
Таким образом, функция f (t) в точке t — b/a достигает своего
наименьшего значения на множестве (0; + оо), и, следовательно,
7 (£-)</(О, ОО,	(18)
причем знак равенства достигается лишь при t-b/a. Полагая
t~d[c в (18), получаем
(Я \ а /	с	/	h \а /	/7 \ь
1+-) (J+4) >( 1+-) (1+4) .
с J \	d J	\	a J \	b }
откуда и следует неравенство (17).
Отметим, что равенство в (17) дос игается только тогда,
когда a/c — bld.
Замечание. Из неравенства (17) в качестве его след-
ствий можно получить некоторые классические неравенства:
о среднем арифметическом и среднем геометрическом, нера-
венство Гёльдера, Коши — Буняковского и др.
Действительно, переписав неравенство (17) в виде
/ Х± Х2	/ Х± / X2\^«
\ Ui+Уг ) *\~yij кК/
и заменив в нем х2 на х2+х3, а z/2 на г/г+^з, получим
(Xi -|--Х2 -J~ Х3 \ATi+X2+X8^ / Х£\х1 f Х2 Xg
i/1 + ^2 + ^8 /	\У1/ \Уз + Уз)
( ** V1 ( *2 Vя ( ХзУ8
\ W \ Уз J \ Уз J .
Отсюда, используя метод математической индукции, легко дока-
зать, что, каковы бы ни были положительные числа хь х2, ...
..., хп и yt, у* .уп, имеет место неравенство
/ *1+ *2+.  •+xnyi+*g+-•V2 ( хп\Уп
(19)
в котором	равенство достигается	только	в	том	случае,	когда
Xi Х2	хп
У1 Уз	Уп	'
Теперь,	подставляя	в (19) х/ = р/	и	yi—ptai	(i==l,	2,	nh
получаем
ap*api ,,,ар»<.(.^+^+ .. +р»ап• • • +₽»	(20
12 п \	Р1+Рз+»..+Рп J	'
если в (20) pi = p2 = ,.. =рп==1, то получаем неравенство между
средним арифметическим и средним геометрическим чисел
#3»
а.а« а /’а* + а2+ • • • +а»
«1«2 •••	।	----------- 1 е
(21)
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
429
Выбирая в (20) числа р/ так, чтобы выполнялось равенство
Р1+Р2+ • •. +р«— получаем неравенство
• ••«„”< Piai + р2а2 + •.. + Рпвп-	(22)
Во всех трех неравенствах (20) —(22) равенство достигается
только в том случае, когда aj = a2 = ... ~ап.
Из неравенства (22) следует неравенство
+ • • • + dfibn =С (Д1 + • • • + ап)а (bi + *»»+ Ьп)$, (23)
где а > 0, р > 0 и а+Р= 1.
Действительно, из (22) следует, что
_____afbi -|- -р •»•	___г=з,
(^1 + а2 + ... + ап)а 01 + ^2 + • • • + Ьп)$
__/_____Ctj___\а /bj\|3 .
\ ai + a2+ • • • Ч~^п/ \ 61 + &2+ • • • ЧгЬп /
ап \<Ч Ьп \В	at
” * ‘ \«1+^2+-•-+ап/ \&i4-Ai+» • «+^п/	^1+^2+’ • »4"а/»
I ft_________J____________I I а ип
Ь1 Ч~ 62+ • ’ • 4"^П	а1 + #2+ • • • 4"ЛЛ
I ft________2?_______—а (_______________________I
^1“Ь^2"Ь • • •	\ cii #2 4“ • • • ~h ап ***
к..-----—\=а+Р=1.
^14“^г+ • • • -pbn /
Полагая а—1/р и Р=1/^ и сц — х1} и Ъ^ — у^ (f=l, 2, ,tM n)
в (23), получаем неравенство Гёльдера
^1У14" х2#2 4“ • • • + хпУп
< (*? 4- X? + •.. + хй)1/р {yl + yl + ... +^)1/9. (24)
Из (24) при р = 7=2 получим неравенство Коша—Буняковского
(Х1У1+хъУъ 4- • • • + хпУп)2	4- *2 +... 4“ Хп) (у! 4-^2 4- • • • 4-^п)*
(25)
При этом равенства (24) и (25) справедливы только тогда, когда
Xityi=Хъ1Уъ =. ♦. = хп!уп.
Пример 22. Доказать, что неравенство
0^4-^+^^: Заде
имеет место для любых положительных значений а, b и
Решение. Без ограничения общности можно считать,
например, что Q <а^Ь^с. Рассмотрим функцию
/ (х} = 4- 4- « ЗхЬо9
430 ГЛ. б- ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
Так как
f (х) = Зх2 =3 (х2—be),
то
f' (х) < 0 при 0 < х < Ь^с.
Отсюда следует, что функция f (х) убывает на отрезке [0; £].
Таким образом, f(x)^f (b), т. е.
х3+ь9+с9—ЗхЬс 263+с3—ЗА.
Рассмотрим теперь функцию
g (х) == 2х3+с3—Зх2с,
где с—фиксированное число и 0 < х < с.
Имеем
g' (х) = 6х2—•бхе = 6х (х — с).
Отсюда g' (х) < 0 при 0 < х < с, и, следовательно, функция g(x)
убывает на отрезке (0; с]. Заключаем, что g(b)^g(c), т. е.
2Ь9+с3—ЗЬ2с 2с3+с3—ЗА = 0.
Это завершает доказательство требуемого неравенства.
Пример 23. Доказать, что если х^О, и ngN, то
/х+у\и хп+у”
2~‘
Решение. Рассмотрим функцию
считая у фиксированным положительным числом. (Если у=0,
то очевидно, что неравенство имеет место.)
Так как
то неравенство f'(х)^0 имеет место при	т. е. при
х^у. Таким образом, функция f(x) является возрастающей
функцией на промежутке [у\ оо). Следовательно,
если х^у.
Если х^у, то	и поэтому f (х)«с0. Следова-
тельно, функция f (х) является убывающей на промежутке [0; у].
Таким образом, если х^у, то f (х) f (у) 0.
Итак, f (х)^0 при х^0, и требуемое неравенство доказано.
При доказательстве числовых неравенств или для сравне-
ния двух чисел часто бывает полезно перейти к более общему
функциональному неравенству.
Пример 24. Какое из чисел больше: cos 1988 или
14-соэ 1989?
§3. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
Решение. Рассмотрим функцию f(х) —x-]-cosx. Так как
f (х) = 1—sinx^O и f' (х)=0 при х=-~+2лп, ngZ, то функ-
ция y~f(x) возрастает на множестве всех действительных
чисел. Поэтому / (1988) < / (1989}, т. е. cos 1988 < 1+cos 1989.
Пример 25. Доказать, что
4 tg 5° tg 9° < 3 tg 6° tg 10°.
Решение. Рассмотрим функцию
f (х) == tg x/xt 0 < х < л/4.
Так как
. х—sinxcosх л
f W== ’ 0<
x—sinx cos x=~- (2x—sin 2x) > 0,
то функция f(x) возрастает на
Таким образом,
tg—
ё 180
5л
180
. 6л
tg 180
6л ’
180
4 ’
интервале (0; л/4).
tgJi taJ^L
g180 g 180
9л	Юл
180	180
л
4 ’
и, следовательно,
4 tg 5° tg 9° < 3 tg 6° tg 10°.
Пример 26. Какое из чисел больше: (sirin/6)s,tlrt^ или
(sin JT/3)sin
Решение.
Рассмотрим функцию
ч 1пх
/(х)=—, х>
Так как
-. , .	1 — In х
Г (*)
х2
то
f'(x)>® при
f' (х) = 0 при
f'(x)<0 при
х > е.
Таким образом, функция f(x) возрастает на промежутке (0| е\
и убывает на промежутке |ie; -J-oo).
Следовательно, если 0 < х < у < е> то
In х In#
X < у 9
т, е»	1	-
< у* при 0 < х < у <
432
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
Аналогично, если е<х < у, то
In х In j/
Т“ У ’
т* е.
ху > ух при е^х<у.
Отсюда с учетом неравенства
sin л/6 = ~ < sin л/3 = jA~3/2
ваключаем, что
(sin Ji/6)sin я/- < (sin n/3)sin я/6.
Отметим, что из установленных выше функциональных нера-
венств, например, имеем
lOOOxool> 1001100% еп>я*,
(V"2)v~*- < (Кз)’/_*-	5)” <3'g6-
Пример 27. Найти все значения а>0, при каждом из
которых неравенство
In (1 + х)^х—ах2
выполняется при всех неотрицательных значениях х.
Решение. Рассмотрим на интервале (—1; + 00) непре-
рывную функцию
f (x) = ln (1+х)+ах2—х
и ее производную
''W~iT7+
2а х—1
_2ах24-(2а— 1)х
x-f-1	'
Если 2а—1^0, то
f (х) > 0 при х > 0.
Поэтому функция f (х) будет возрастающей на промежутке
[0, 4-оо); следовательно, в этом случае
f(x) > f(0) = 0 при любом х>0.
Пусть 2а— 1 < 0 и а > 0; f' (х) обращается в нуль в точках
1 2а
Xi=0 и ^2=—2^—> причем в точке х=0 функция f' (x) меняет
зна$ с плюса на минус. Следовательно, точка х = 0 является
точкой локального максимума функции f (х). Кроме того, при
достаточно малых положительных значениях х выполняется -
неравенство f (х) < f (0) = 0.
Таким образом, условию задачи удовлетворяют все числа
а 1/2.
Пример 28. Является ли периодической функция
f (х)=cos х sin (х Y 2)?
§б. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
433
Решение. Воспользуемся следующим утверждением:
если дифференцируемая в каждой точке числовой прямой функ-
ция имеет период Т, то ее производная также имеет период Т.
Предположим, что данная функция f (х) является периоди-
ческой с периодом Т. Применяя формулу
cos a sin b =	(sin (a + &) + sin (Ь—а)),
f(x)-l(sinx(K 2+0+
получаем
sinx (К 2—l)^=-~(sin ах + sin (Зх),
где а—р/'~2+1, ₽=К"2~1-
Имеем
у (х) = — (а cos ах+Р cos [Зх),
й—а2	62
Г (х) = (У (х))' = -у- sin ах—sin рх.
Поскольку по предположению функция f (х) имеет период Т,
то функция У (х), а следовательно, и функция g (х) = f" (х) ==
а2	р2
==—sin ах——sin^x также имеют период Т,
Значит, и функция
g (X)+0V (X)=-	sin ах
также имеет период Т. Отсюда следует, что существует число kt
fcgZ, k Ф 0, такое, что T = 2fort/a. Аналогично показывается,
что существует число n, ngZ, п Ф 0, такое, что Т = 2пл/р.
Но тогда
k__а___J^"2+1
~И~	’
O+i
т. е. число  - является рациональным, что неверно. Сле.
довательно, данная функция не является периодической.
Пример 29. Доказать, что все корни производной мно-
гочлена
Р (х) = х(х—1) (х—2) (х—3) (х-~4)
различны.
Решение. Применим теорему Ролля к функции у=Р (х)
на отрезке [0; 1]. Так как Р (0)==Р (1) = 0 и функция £/ = Р(х)
является непрерывной на отрезке {0; 1] и дифференцируемой
на интервале (0; 1), то по теореме Ролля существует хотя бы
одно число Xf из интервала (0; 1) такое, что Р' (xj) = O. Анало-
гично, применяя теорему Ролля к функции у = Р(х) на каждом
из отрезков (1; 2J, [2; 3] и [3; 4], убеждаемся, что внутри
каждого из них имеется корень уравнения Р' (х) = 0. Так как
степень многочлена Р' (х) равна 4, то он имеет не более четы-
рех действительных корней. Поэтому все корни хх, х2, х8, х4
434 ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
многочлена Р( (х) действительны, причем 0<хх<1<х2<2<
< х3 < 3 < х4 < 4.
Пример 30. Доказать, что для любых положительных
чисел а и & таких, что b > а, и любого натурального числа
имеет место неравенство
п (&—а) а”"1 < Ьп—ап < п (6—а) Ьп~*.
Решение. Рассмотрим функцию f (х) — хп, х > 0. Имеем
— __bn—an
b—а	b—а
Так как функция /(х) = хп непрерывна на отрезке [а; &] и диф-
ференцируема на интервале (a; b)t то по теореме Лагранжа
существует точка g из интервала (а; Ь) такая, что
hfl — лП
Учитывая неравенство < gw”x < bn~\ Имеем
Ьп—ап
па””1 < —т----< nbn~\
Ь~-а
Отсюда следует доказываемое неравенство.
Пример 31, Доказать, что
ех > 1 + х при х > 0.
Решение. Пусть b—любое положительное число. Рас-
смотрим функцию f(x)~ex на промежутке [0; £]. По теореме
Лагранжа имеем
ёё(0.6),
т. е.
b
где g(£(0; 6). Так как 1 при любом g>0, то отсюда полу-
чаем
т. е, eb> 1+& для любого положительного числа Ь,
Заметим, что установленное неравенство может быть дока-
зано способом, аналогичным доказательству неравенства (12}.
Вообще неравенство ех > 1 + х верно при любом х #= 0, так как
функция у~ех выпукла вниз на всей числовой оси, и поэтому
ее график при х =4 0 лежит выше прямой у=1 + х, которая
является касательной к графику у~ех в точке (0; 1).
Замечание. Из неравенства
а*~х^х,
справедливого при любом значении^, в качестве простого след-
ствия можно получить, например, классическое неравенство
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	435
между средним арифметическим и средним геометрическим
положительных чисел х2, ..., хп (а также и другие класси-
ческие неравенства). Пусть xt, х2, .хп*—положительные числа
и Sn = ^(xi + x2+‘•♦+*«)• Так как по доказанному
х —
то, перемножая эти неравенства, получаем неравенство
*1*2 --- хп
xt + x9+ . . . +Хп
<е sn "=1,
т. е. неравенство
или
...
?/—-----—^.Xi+Xi+...+Хп
У Х1Х2 . . . Хп^л-------- .
Пример 32. Решить уравнение
(^0Ч(^-Йа=1/2.
Решение. Заметим, что левая часть данного уравнения
представляет собой квадрат расстояния между точкой А (х; ех),
графика функции у~ех и точкой В (у; у), лежащей на биссект-
рисе первого и третьего координатных углов.
Так как ех^1-{-х и прямые #=1-|-х и у=х параллельны
друг другу, то из треугольника О АВ (рис. 5.37) следует, что
расстояние между любой точкой М графика функции у~ех и
любой точкой W прямой # = х не меньше 1/"/*2. Равенство ех =
= 1+х имеет место только при х = 0. Поэтому расстояние меж-
ду точками на графике функции у=е*_и точками на прямой
у~х будет наименьшим и равным 1/1^2 при х = 0. Соответст-
вующее значение у удовлетворяет уравнению #24~(1>—#)2= 1/2,
откуда находим #=1/2. Итак, пара чисел (х0; #0), где хо = О и
#0=1/2, является единственным решением исходного уравнения.
Пример 33. Доказать, что
1 . 5? ±
52 < 1П 51 < 5Г
Решен и е. Рассмотрим функцию f (х) = In х на отрезке
[51; 52]. Имеем
/(52) —^(51) . ,о . К|
=3 In 52 In 5 Е
436	ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
По теореме Лагранжа заключаем, что существует такая точка
а, 51 < а < 52, что
In 52 — In 51 — f' (а) (52 — 51) = 1/а.
Так как 51 < а < 52, то отсюда следует, что ,
1/52 < 1п 52 — In 51 < 1/51,
т. е.
1 I 5? 1
52 П 51 < 5Г
Пример 34. Доказать, что уравнение
3*+2_26х = 29
имеет не более двух различных действительных корней.
Р е ш е н и е. Пусть данное уравнение имеет не менее трех
различных корней и хх, х2, х3*~ некоторые его корни такие,
что Xi < х2 < Применяя теорему Ролля к функции f (х) =
= зх+2__26х — 29 на отрезках [хх; х2] и [х2; х3], получаем, что
существуют числа ^1^(хг; х2) и |а^(х2; х3) такие, что /' (ti) =
= Г (Ь) = 0. Однако уравнение f (х) = 3*+з in 3—26 = 0 имеет
только одно решение.
Полученное противоречие доказывает, что данное уравнение
имеет не более двух различных корней.
Отметим, что корнями данного уравнения являются числа
Xi =—1 и х2 = 2.
ЗАДАНИЕ 1
1« Разложить на множители выражение:
1) х(#2—z2) + ^(za—х3, + г(х2—у*)%
2)	г)+^(г—^4-г4(х—у\.
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	437
2. Упростить выражение:
и х~~у ! y~z\ г~~х-
? х+у'гг/+г"гг+*’
о\ (У~г)2 I (z—x)2	.	(х—у)*
; (г—х) (х—yV(x—у) (у—г) ' (</—г) (г—х)’
3. Доказать тождество:
1	3
2) sin® x + cos6 х = -Г4-"Т‘ (cos2 х—-sin2 х)2;
4	4
3) cos2 а + cos2 р + cos2 у = 1 —2 cos а cos Р cos 7, где а -|~ Р +
+ у = Л.
ЗАДАНИЕ 2
1. Упростить выражение:
1) cos2 x-j- cos2 (х+z/)—-2 cos x cos у cos (x+y)\
1	1	1	I	1
’ x(x—y) (X—Z^yiy—X) (y—z)'z(z—x) (x—y)!
3j______!________1______!______1_______!_____
’ x* (x—yMx—z)^у* (y—x) (у—г)тхг(г-x) (x—y)'
2. Доказать тождество:
Зх	x
1) arctg x+arctg Зх = arccos -j^=== 4- arccos у j
2) 1 — (sin6 x+cos6 x) = 3 sin2x cos2 x;
1	15
3) cos4 x —g- cos 4x = 2 cos2 x —cos 2x—g-;
41 „ (x—b)(x—c)	(x—c)(x—a) .	(x—a)(x—b)
’	(a—b)(a—c)''r (b—cjlb—a)^ (c—a)(c—b)	1
5) 2 (sin6 x+cos6 x) — 3 (sin4 x+cos4 x) 4-1 = 0;
6) sin 2a 4- sin 2P 4- sin 2y = 4 sin a sin p sin у, где a 4- р4-у==л1
n	1	n	n
k-1	fe=l	fe=l
ЗАДАНИЕ 3
1.	Доказать, что если 0 < х < у < л/2, то
sin х sin у
2.	Доказать, что
х—х2/2 < In (14-х) < х
при х > 0.
3.	Найти все значения а, при каждом из которых уравнение
Зх44-4х3—6х-«* 12х4-я==0
имеет два различных корня.
438	ГЛ. 5.- ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
4.	При каждом значении а определить число корней урав-
нения
х In х = а.
5.	Доказать, что уравнение
х9+9х2 + 2х—48 == О
не имеет кратных корней.
6.	Решить уравнение
Л;24-Ж-|_12 /7+1 = 36.
ЗАДАНИЕ 4
1.	Доказать, что если 0 < х < у < л/2, то
tg* < tgy
х У
2.	Доказать, что
X9
< tgx
при 0 < х < л/2.
3.	Найти все значения а, при каждом из которых уравне-
ние
Зх4 — 14л;3 — 45х2+а = 0
имеет четыре различных корня.
4.	При каждом значении а определить число корней урав-
нения
аех = х9.
5.	Доказать, что уравнение
х4	15х2 — 10х + 24 = О
не имеет кратных корней.
6.	Решить уравнение
VЗх—2 _ 1
х2	Г
ЗАДАНИЕ 5
1.	Решить неравенство
х»+хб+448 <0,
2.	Доказать неравенство
2	1
k/ ГТ । к/ 7 >
fl у|- 1 у fl >—» 1 у п
при п^2,	n,
3.	Решить уравнение’
зр 7х9 4~ 9л;2 27 х «« 54 = 0.
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
439
4.	Доказать, что если а > О, b > 0, с > 0, то
_L4._l_4._2_>—9.. .
a-\-b ’ b~t~c с + а a-^b-j-c
5.	Решить систему
( x-j-ex = y-j-eyt
1 x24-xfz+fz2= 12.
6.	Доказать, что
У3+1/"з +УЗ — 1/з <2|/з.
ЗАДАНИЕ 6
1.	Решить неравенство
logs ( 1 + К* ) > logfe X.
2.	Доказать неравенство
—1—< In fl4-l^ <1, n£N.
п-у 1	\	«/	«
3.	Решить уравнение
х4 _5хз _ 9х2 + 81 х—108=0.
4.	Доказать, что если а > 0, b > 0, с > 0, то
/а2 + Ь2 + с2 у+Ъ+с
—ааЬьсс.
\ я—j-b-j-c j
5.	Решить систему
J tg* — tg г/ = №у,
( sin x-j-sin 0= ]/”2 #
где xg(— л/2; л/2),	л/2; л/2).
6.	Доказать, чю
cos 200 < 1 4-cos 201.
ЗАДАНИЕ 7
1.	Решить уравнение
е*—e~* = 2 In (х+ КТ+х2)-
2.	Найти сумму
х + 2х2 + 3х3 + ...	х # 1.
3.	Доказать, что при | х | «с 1 /2 имеет место тождество
3 arcsin х«— arccos (Зх—4х^) = л.
4.	Найти все значения а, при которых уравнение
х8-|~ ах,+ 2=0
имеет два совпадающих корня.
440
ГЛ. 5. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
5.	Доказать, что функция
f (х) = sin х+ sin х К2 + sin^ КЗ +,,, + sin х
п^2, n£N,
не является периодической.
6.	Доказать, что
sin 3 р/cos 2—sin 2-	cos 3 > I/cos 2• cos 3.
ЗАДАНИЕ 8
1.	Решить уравнение
10gl2 (/х + Vхx)=2-logex.
2.	Найти сумму:
1)	х + 22х2 + 32х3 + 42х44“ ... +«2хп, х Ф 1;
9\ 2’1 к3-2Д_4‘3Х5*4^ Д- "(п-Ц
} 1 "* 2	22 "• 23	‘
3.	Найти все значения а, для каждого из которых урав-
нение
х3+«х2+2 = 0
имеет три корня, причем два из них совпадающие.
4.	Доказать, что функция
f (х) = cos x+cos х KS’+cosx Кз" +,,, -f-cos х
n 2, rcgN,
не является периодической.
5.	Доказать, что
ееля> е2я.
Упражнения
1. Решить уравнение:
В_____£=________1==А;
X-f-J^X^ + X	X — Кх2 + х	х
2) хе-*+«-*+у х2—1 =0;
3) KW2S4- 1+^2 =/27+3;
4) logs (2«+l) + log5 (4n+l) + log7(6n+l) = 3n, ngN;
5) (4*+2) (2—x) = 6; 6) x+K3+/x =3;
7) logf2 (/2x+ У 2x)=4 iogs 2x;
8) l/4x+3=l/ 27— У2x; 9) xJC+xi“*=«+1;
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ	441
10) |6x-5| = 4sin — ; 11) 1+2/7 = 3^(1-In у);
О	X
12) l-l=ecos8'; 13) 4*+l = 2*+1sinp.
2.	Разложить на множители выражение:
1)	(а — Ь) (а^Ь-~с)* с-\-(Ь~-с) (&4~с—а)2 а;
2)	(1+х2) у2 + 2(х^у)(\ + ху)+\-
3)	(x*-l)* + (y+l)(4x-y-l).
3.	Найти число решений системы уравнений
х2 = +,
*+/+ }/ х*у=26.
4.	Найти число действительных корней уравнения;
1) /7=1 +/7+4+/зТ+Т=9; 2) x6+x«+l = 0j
3) /47ГТ+ /7=2=1; 4) /зТ+2—/77=1=4,
5.	Решить неравенство:
1)	х8+4х—16 > 0; 2)	(1-х) <| j/l ;
3) х—1 < loge (х*Ч-3), xgZ;
4) log5 (1 + /4х) > logi, 4х; 5) х2?+х*«+448 < 0;
6) /37+5+ /Зх+12 > 4; 7) 2х+3 < In (х?+9), xgZ;
6	l + log2(2+x). m 6-3*+*	10 .
8)ТТП>--------X-----’ 9)—77=1’
9 l + logs (х+6)
? Зх+2 > х
6.	Доказать, что если 0 < х < л/2, то:
•	2х2 пч 1	п Л
1) sin х > х-— ; 2) x+cosx > у^1—
3) 1 tg х + — sin x > x; 4) /cos x < /2 cos j
О	о	<&
кч . n 2	sinx 1 х2
5) sin2x< ; 6)— >1—T-,
2
7)	sin 2x < 3jf_xa I
8)	tg”x + ctg"x^2+n?cos2x, ngN;
9)	ptg!/₽x+<?ctg’«х^ 1, где 1+1=1, p > 0, q>0;
Г 4
X*	2	1
10)	x 4—“<tgx; 11) sin x >—x; 12)tgx—s-tg§x<x;
О	л r	о
13)	X < tgx—ltg3x + ltg5xj
о о
442	ГЛ. 5. ПРОИЗВОДНАЯ и ЕЕ ПРИМЕНЕНИЕ
14)	tgx—Ltgsx_|l tg^x— 1 tgv x < x-,
О	О	/
1СГЧ ( sin х X3
15)	I—— j ^cosx.
7.	Доказать неравенство:
пг— п/-~ п/
1)	/ х — у а < у х—а при х > а > 0;
2)	(1 + *)а + (1—“*)а^2 при |х|> 1 и 0^а^С1;
3)	2ab In у < &2—а2 при b > а > 0;
4)	е2х < у—— при 0 < х < 1;
5)	е~х > 1—-х при х < 0;
6)	2х4—4х3+Зх2+4х+1 > 0 при х > 0;
у2 оХ
7)	ех 1+х+~у- при х^&0;
8)	2sin~4*sin^-— > 0 при п^2, ngNj
/ £Z 4- bx X X+х
при « > 0, 6 > 0, х > 0;
\ 1т* /
.<l)Дi,v^<(»+2t+3c+ц)1^
при а > О, b > 0, о > 0, d > 0;
11)	(sin2 x)8ln2 * (cos2 x)cos2* у при x Ф у п9 п g Z;
х3
12)	х--у < arctg х < х при х > 0;
13)	ех > ех при х > 1;
i лч /1 ч	, In*а X _ а2— 1	_ ,
14)	(Inа) 2-|*——)<------ при а^\\
\
Оу
15)	In (1 + х) >24^ п₽и xSs0;
X2
16)	ех^ 1+х+у- при х0;
17)	а4+^^а3/?+а/?8;
18)	(а + &+02<3(а2 + ^+с?);
(1 X2 / IX2 25
] +( &-|*у j ^"2"’ если « + L л > О, b > 0;
20) (а + Ь)р^ар+Ьр9 если а > О, b > 0, 0«Ср«С1;
2!)-4т+;4—h—г-^—ГГТ— ’ а>0. &>0. в>0;
' а-}-Ь 1 Ь-}-$ * с-{-a a-j-b-j-o	9
22)	cos (sin х) > sin (cos x);
23)	2x > 5 при 0 < x < -i- j
24)	х* + (1~хГ^1/16, xgR;
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
4П
25)	2х4—4х3+3х24~4х+1 > 0 при х > 0;
26)	1п(1 + х)<х при х > 0.
8.	Доказать, что:
1986 корней
3)	sin3 1° + sin8 4° > sin3 2° + sin3 3°; 4) In 2 < 0,72.
9.	Решить уравнение:
1)	x3—7x24-16x—12 = 0; 2) x4—6x2—8x—3 = 0;
3)	x4 + 6x3+x2—24x+16 = 0;
4)	x4—9x34-23x2—3x—36 = 0;
5)	x4—6x3+10x2—8 = 0;
6)	x6—x4—5x8+x2+8x+4 = 0;
7)	x6—15x3+10x2+60x—72 = 0.
10.	Для каждого значения а найти число действительный
решений уравнения:
1) х4—4ах3—2 = 0; 2) 2х3—Зах2+1=0; 3) 1пх = ах;
4) е* = ях2; 5) cos3xsinx=a, xg[0; л];
6) х3—Зх = а; 7) Зх5—-50х3 + 135х=а;
8)	хМ = а; 9) ах = logtf х; 10) 6*=ах;
И) Зх4+4хЗ— 36х2 = а; 12) -^=а.
11.	Определить все значения а, при каждом из которым
уравнение имеет заданное число корней:
1)	2х3— 13х2 — 20х+а = 0,
один корень;
2)	2х8 —4х2 —30х+а = 0,
два совпадающих корня и один простой;
3)	х2 — х—1пх-|-а = 0;
ни одного корня;
4)	10х = ах,
два корня.
5)	ах = х, один корень.
6)	6 arctg х—х34-а = 0, три корня.
12.	Доказать, что уравнение
V 2—2 cos х+ V10—6 cos х =	16—6 cos 2х
не имеет корней на отрезке [л/2;л].
13.	Доказать, что уравнение
4х3—5х2—6х+3 = 0
не имеет корней на промежутке [2; 4-оо).
14.	Доказать, что уравнение
х*— зх3—6х? + 14х +12 = 0
не имеет кратных корней.
444 ГЛ. б. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
15», Доказать, что если 4^34~г-==0, то уравнение
х3 з^х 4" г=== о
имеет корень кратности два.
16.	Доказать, что если г (4р34~г) = 0, то-уравнение
х3+Зрх24-г = 0
имеет корень кратности два.
17.	Доказать, что уравнение
х34-рх4-0 = О
имеет только один действительный корень при 4р34-27<?2 > 0 и
три действительных корня при 4р34-27#2 < 0.
18.	Доказать, что сумма значений второй производной мно-
гочлена третьей степени в корнях многочлена, являющегося
производной данного многочлена, равна нулю.
19.	Привести пример функции вида
_____________________ах2 + с
У~~ px* + qx^r’
которая имеет локальный максимум, равный Л, и локальный
минимум, равный В, но Л < В.
20.	Найти многочлен наименьшей степени, для которого
соответственно точки х = 0 и х=1 являются точками локаль-
ного минимума и локального максимума, а значения в этих
точках соответственно равны 0 и 1.
21.	Многочлен Рп (х) степени п имеет п действительных
корней. Доказать, что уравнение Рп (х)+аР'п (х) = 0, где а # 0,
имеет также п действительных корней (с учетом кратности).
22.	Найти сумму:
1)	1.2.3+2.3«44-3-4-54-...4-(п—2) (п—1)и;
2)	х4-х2(1 + х)4-х3(14-х4-х2)4-...
а а . +х« (1 4-Х4-Х24- . * *	X ф 1.
23.	Среди квадратных трехчленов со старшим коэффициен-
том 1 найти трехчлен / (х), для которого наибольшее значение
|/ (х) | на отрезке [—1; 1] имеет наименьшее значение.
24.	Доказать, что при увеличении числа сторон периметр
правильного многоугольника, вписанного в данную окруж-
ность, возрастает, а периметр описанного многоугольника убывает.
25.	Доказать, что если рп и qn—соответственно периметры
правильного многоугольника, вписанного в окружность радиу-
са R и описанного вокруг этой окружности, то при любом д^З
имеет место неравенство
2	1
ри <2л/г < ^рп+у7п.
26.	Найти наименьшее расстояние между:
1)	точками прямой р==—х и гиперболой р=1/х;
2)	графиками функций у—х* и z/=x—1;
3)	графиками функций у=х? и	2х—4.
27.	Доказать, что уравнение Inх=sinx на отрезке (Зл/2;
7л/2] имеет единственный корень»
§5. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
445
28.	Доказать, что неравенство
Зх — tgx> 1,75
на отрезке [0; л/2] не имеет решений.
29.	Найти все значения а, при каждом из которых урав-
нение
К х—2+ К 8—2х = а
имеет хотя бы одно решение.
30.	Найти все значения а, при каждом из которых нера-
венство
V 2х— 1	х+а
имеет хотя бы одно решение.
31.	Найти все значения а, при каждом из которых из не-
равенства
х > а
следует неравенство
3*—1 > 2а.
32.	Доказать, что:
1)	| a sin а —р sin р |	2 | а — р |, если	0«Ср«с1;
2)	^<tg₽-tga<fey если °<«<₽<у-
33.	Найти все пары значений (а; Ь), для каждой из кото-
рых равенство:
1)	aex-]-b — eax+b,t 2) a sin х+6 — sin (ах+&)
является тождеством на множестве всех действительных чисел х.
34.	Пусть f (х) — (х3—Зх2 + 2) In (х2—2х+3). Доказать, что
система
( Г(*)+ГШ = 0,
I х2 + у2==«
имеет по крайней мере одно решение при любом значении
а 2.
35.	Найти все дифференцируемые функции /: R—> R, для
которых:
/ (1)= 1,	+	(Х)+Ш + Х0
при любых действительных х и у.
36.	На некотором интервале (а; Ь) функция
j [х) = A sin х + В sin 2х+ С sin Зх
тождественно равна нулю. Найти А, В и С.
37.	Функция, отличная от константы, определена на от-
резке 10; 1] и дифференцируема на интервале (0; 1), f(0) = 0.
Доказать, чю существует такое число а, 0 < а < 1, что f(a)<f'(а).
38.	Пусть функция / (х) непрерывна на отрезке (0; 1] и
дифференцируема на интервале (0; 1) /'(х) $£ 0 при х£(0; 1).
Доказать что существует такое число а4 0 < а < 1, что
1/(а)1 < !/'(«)!.
ГЛАВА 6
ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
6.1. Пусть функция f(x) непрерывна на отрезке [a; &J.
Разобьем этот отрезок произвольным образом на п частей и
обозначим последовательно точки деления через х0, хь ..xn_f,
т. е.
а = х0 < Xi < х2 <« ..< xn~i < xn — b.
Обозначим через Ах^ длину отрезка to-ijx^]; тогда Дх^ =
~ хь—*Хк~ч. Диаметром данного разбиения, который обозначим
через dw назовем длину наибольшего из отрезков [х^-х; х^],
т. е.
dn~ max Дх£.
k
В каждом из отрезков [х^-ь х^], 6=1, 2, ...» п, выберем
произвольную точку значение f (g$) функции f (х) в точке
умножим на Дх^ для 6=1, 2, ..., пи составим сумму всех
таких произведений, которую обозначим Sn и назовем интег-
ральной суммой функции f (х) для данного разбиения, т. е.
Sn—f (£1) to~*o)+/ (Ы to-Xi) +... +/ (gw) (х„ —x„_t) =
п
= 2 f(h)(xn-xn-i).
fc=l
Таким образом, при каждом ngN интегральная сумма
п
Sn= 2 t Ufc) зависит от выбора точек деления отрезка
/е=1
[а; и выбора точек
Для функции f (х), непрерывной на отрезке [а; Ь], справедли-
во следующее утверждение: если с неограниченным увеличением
числа п частей, на которые разбивается отрезок [а; Ь], диаметр
разбиения dn стремится к нулю, то последовательность интег-
ральных сумм Sn имеет предел, который не зависит от способа
разбиения отрезка [«;/>] на п частей при каждом ngN и вы-
бора точек gg, fn-
Число, равное этому пределу, называют определен
нным интегралом функции f (х) от а до b и обозначают
ь
J f (х) dx; b и а соответственно называют верхним и нижним
а
пределом интегрирования, a f (х) — подынтегральной функцией.
Итак,
ь	н
С f (X) dx = lim 2 > (U)
j	d«-*0 "i
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	447
Понятие «определенный интеграл» возникло из практи-
ческих задач, решение которых стало возможным или упрос-
тилось благодаря введению над функцией действия, содержа-
ние которого составляет рассмотренный выше предельный
переход. Одна из таких задач — вычисление площадей плоско
фигур.

Рис. 6.1
Q. 3>д 32?	322	&
Рассмотрим фигуру, ограниченную графиком непрерывной
функции y=f(x) на отрезке [а; Ь}, принимающей только неот-
рицательные значения, двумя вертикальными прямыми х = а и
х==Ь и осью ОХ (рис. 6.1, а). Такая фигура называется кри-
волинейной трапецией. (Криволинейные трапеции могут быть
и такими, как показано на рис. 6.2.)
Придерживаясь тех же обозначений, что и раньше, соста-
вим интегральную сумму
п
8а~ 2
В этом случае Лг-е слагаемое интегральной суммы Sn можно
рассматривать как величину площади прямоугольника шириной
и высотой f (Hfc), где &=1, 2, ..., п; тогда интеграль-
ная сумма Sn выражает собой величину площади ступенча-
той фигуры, составленной из п прямоугольников (рис. 6.1, б,
где п=5). Ясно, что, чем больше число частей разбиения
отрезка [о; б] и меньше диаметр разбиения dni тем меньше
интегральная сумма Sn отличается от величины площади дан-
ной криволинейной трапеции.
Эти геометрические рассмотрения вместе со сформулиро-
ванным выше утверждением позволяют не только ввести поня-
Ъ
тие определенного интеграла	но и вычислить
<48	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
величину площади криволинейной трапеции S, так как эти
ь
числа совпадают, т. е. S = J f (%) dx. Одним из первых нетри-
а
виальных примеров на вычисление величин площадей криво-
линейных трапеций и тем самым на вычисление определенных
интегралов является пример, который рассмотрел Архимед,
вычисливший величину площади между параболой у = х2 на
отрезке La; Z?] и осью ОХ.
Пример 1, Вычислить
J хт dxt tn «а 0, 1,2, b > 0.
Решение. Так как в каждом из этих случаев функция
у—хт на отрезке [0; 6] принимает только неотрицательные^
ъ
значения, то число J xmdx совпадает о величиной площади
о
соответствующей криволинейной трапеции.
а)	При /п = 0 криволинейная трапеция представляет собой
прямоугольник (рис. 6.3, а), ширина и высота которого соот-
ветственно равны Ь и 1, Поэтому величина его площади равна Ь,
РЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	449
ь
Вычислим число 1 -dx согласно его определению. Вне за-
о
висимости от способа разбиения отрезка (0; Ъ} на п частей и
Рис. 6.3
выбора точек gf, |2, •»», In (рис. 6.3,6, где п = 6), для интег-
ральной суммы Sn имеем
п	п
$п= 2	2	1	=	+
*=1	6=1
-Н~(Х2—Х1)+ . . +(Х«—xn-i) = х„—х6=&—0=6.
Таким образом, при каждом ngN интегральная сумма равна
ь
Sn=b, поэтому \ ldx = lim = lim b~b*
"	drr+0 п-><ю
b
Итак, 1 dx — b.
6
б)	При m—\ криволинейная трапеция представляет собой
прямоугольный равнобедренный треугольник, каждый катет
которого равен b (рис. 6.4, а). Поэтому величина его площади
равна 62/2.
ъ
Вычислим число ^xdx согласно его определению. По-
о
скольку предел интегральных сумм Sn не зависит от способа
разбиения отрезка [0; на пчастей и выбора точек £2, ...,
то в этом случае при каждом ngN разобьем отрезок [0; Ь] на
п равных частей (рис. 6.4, где п = 4); тогда кх^-Ь/п и х#=кЬ1п*
Положим = тогда f (^ki—kb/n, и для интегральной
15 Задачи по математике. Начала анализа
450	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
суммы Sn получим
и	п
sn= £иЫА^=11“ = 7а(1 + 24-...+«).
k=\	/е=1
Так как 1 + 2-}- • . • + я~ - ^—11, то
поэтому, согласно определению определенного интеграла j xdx,
о
имеем
ь
С . ГС Г	I & \	*2 I *2 V 1
\ xdx — lim S„ = hm Г —— \=—hm -=y.
v	dn-> co	n->ao	z * n->oo n л
b
ы C
Итак, \ xdx=-y.
о
в)	При m = 2 криволинейная трапеция представляет собой
фигуру, ограниченную параболой у = х2, осью ОХ и прямой
х = Ь (рис. 6.5, а). Формулы для вычисления величины площади
этой фигуры в геометрии нет. Вычислив, согласно определе-
ь
яию, определенный интеграл	тем самым найдем вели-
о
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
451
а
Рис. 6.5
15*
452	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
чину площади этой фигуры. Для этого разобьем отрезок [0;
на п равных частей (рие. 6.5,6, где п = 5). Тогда' Ая^ — б/п и
xk~kbln. Полагая	= получаем f (^k) — k2b2/n2.
Тогда для интегральной суммы Sn имеем
п	п
Sn==^f (b)	5~=5 <12+22+• ’ ’+n2)-
Так как
p_|_22 + , , . + B2 —Я<Я+1Н2П+1) >
TO
Q	Az(n+I)(2n+I)^3(rt+I)(2n+I)_z>3/<1 t 1Voi Ц
^-n3	6	IT	6 n ) V + n J •
Следовательно,
ъ
fx2dx = lim S„= lim [t (1+tX2+4)1=4’
J rf„-.O n^o> L 6 V n J\ «/J	3
b
Итак, Jx2dx==68/3; поэтому величина площади фигуры между
о
параболой у=к2 и осью ОХ на отрезке |0;6] равна Ь3/3.
Рассмотрим криволинейную трапецию, т. е. фигуру, огра-
ниченную графиком непрерывной функции y—f(x)t хg[а\ Ь],
принимающей только неположительные значения, двумя верти-
кальными прямыми х = а и х~Ь и осью ОХ (рис. 6.6, а). При-
держиваясь тех же обозначений, что и прежде, составим интег-
ральную сумму
п
Ь=1
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
453
В этом случае /г-е слагаемое f (£$) Дх^ интегральной суммы Sn
представляет собой величину площади прямоугольника шириной
xk—и высотой —f (Ы> где £ = 1, 2, п, и n(JZ. Поэ-
тому интегральная сумма Sn> взятая со знаком минус, выра-
жает собой величину площади соответствующей ступенчатой
фигуры (рис. 6.6, б, где	следовательно, число, равное
— у f (х) dx, совпадает с величиной площади криволинейной
трапеции S. Таким образом, если /(х)«сО на отрезке [а; Ь], то
число, равное \ f (х) dx, представляет собой величину площади
S между графиком функции у = /(х)
OXt взятую со знаком минус, т. е.
а
на отрезке [а;&] и осью
f (х) dx = — S.
Рис. 6.7
Рассмотрим фигуру, ограниченную непрерывной функцией
у==/(х), х^[а\Ь], принимающей как отрицательные, так и по-
ложительные значения. Пусть, например (рис. 6.7, а), а<с<
<d<b,	f(d)—O- на множестве [а\ с} (J (d; b] функция
f (к) принимает только положительные значения, а на интер-
вале (с; d) — только отрицательные значения. Составим интег-
ральную сумму
п
s»= 2
/г=1
Согласно сформулированному выше утверждению, предел интег-
ральных сумм Sn не зависит от выбора точек деления отрезка
[а; Ь] при составлении интегральных сумм Поэтому при
n£N и «>3 точки деления отрезка [а\ /?] будем выбирать
так, чтобы среди них содержались точки с и d. Тогда в интег-
ральной сумме сгруппировав слагаемые, соответствующие
разбиению на отрезках [а; с], [с; d] и [d*, Z>], обозначим соот-
454	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
ветствующие им суммы через S«\ S^. В этом случае диа-
метр разбиения на каждом из трех отрезков не превосходит
диаметра dn разбиения на отрезке [я; Ь]. Поэтому, если с не-
ограниченным увеличением числа п частей, на которое разби-
вается отрезок [а; Ь], диаметр разбиения dn стремится к нулю,
то тем более диаметр разбиения на каждом из трех указанных
отрезков также стремится к нулю. Если обозначить через Si(S2,
S8) величины площадей между графиком функции y = f(x)\
xg[a;c] (соответственно y = f(x), xg[c;d]; y = f(x)> xg[d; b])
и осью OX (рис. 6.7,6, где n=9), то
lim S^ = Si, lim S^ = —S2, lim S^ = S,.
n->CO	/2->00	rt~>O0
Так как S„ = S#y + S®y + S«3> и предел каждого слагаемого этой
суммы существует, то
ь
f (х) dx = St —S2 -|-S8.
а
Таким образом, если функция г/ = /(х), xg[a; Ъ], принимает
как положительные, так и отрицательные значения, то число,
ь
равное определенному интегралу ^f(x)dx, совпадает евеличи-
а
ной, равной сумме площадей фигур между графиком функции
0 = f (*),	dj, и осью ОХ, лежащих выше оси ОХ, минус
сумма площадей фигур между графиком функции y=f(x),
xg[a;Z>J, и осью ОХ, лежащих ниже оси ОХ.
Например, для функции y~f(x), непрерывной на [а; ЭД,
график которой изображен на рис. 6.8, имеем
ь
р (х) dx = (Ss+S4) - (Si + S3 + S6) •
a
Так как для всякой четной функции y=f(x), непрерывной на
отрезке [—а; а], график ее симметрично расположен относи-
тельно оси ОУ, то
а	а
J /(х) dx = 2 J f (x)dx.
-а	О
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	455
Например, для функции г/—/(х), непрерывной на отрезке
f—a;a]t которая является четной и график которой изображен
на рис. 6.9, а, имеем
J f (х) dx - (Si+Si) - (S,+S2) = 2 (Si —S2) = 2 J f (x) dx.
-a	0
Так как для всякой нечетной функции	непрерывной
на отрезке [—а; а], график ее симметрично расположен отно-
сительно начала координат, то
J f(x)dx = 0.
-а
Например, для функции #=f(x), непрерывной на отрез-
ке [—а\ а], которая является нечетной и график которой
Рис. 6.9
изображен на рис. 6.9, б, имеем
J / (х) d« = (Si vf-Sa)—(S2 + Si) = 0.
-а
Так как для всякой периодической функции y — f(x)> непре-
рывной на множестве всех действительных чисел с главным
периодом Т, при любом а из фигуры, расположенной между
графиком функции ^=f(x), xg[a;a4-7,b и осью ОХ, при
помощи параллельного переноса можно получить фигуру,
456	гл. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
расположенную между графиком функции y — f (х), хg[0; Т], то
а + Т	Т
J f (х) dx — J f (х) dx.
а	О
Например, для периодической функции y~f(x) G главным
периодом Т, график которой изображен на рис. 6.9, в, имеем
а + Т
J f (х) dx — (S5+S2) — (54-|-5б + 51 + 5з) =
а
т
= б + 5г)— (51 + S3 + S4 + So) = J f (х) dx.
о
ь
При введении выше определенного интеграла J / (х) dx
а
предполагалось, что b > а. Положим по определению
b	а
J / (х) dx — -— / (х) dx, если а > Ь\
а	Ь
b	а
f (х) dx—^ f (x)dx — 0, если a — b.
а	а
Основные свойства определенных интег-
ралов непрерывных функций (доказательства сле-
дуют непосредственно из определения):
Г, Если а < b < с, то (рис. 6.10)
с	Ь	с
J f (х) dx = f(x)dx+^f (х) dx.
а	а	ь
Ь	Ь
2Q.	kf (х) dx= k р (х) dx,
а	а
где k константа.
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	457
3°« Если f (x) = g (х), то
b	ь
J f (х) dx = J g (х) dx+ J ft (х) dx»
а	а	а
b	b	b
4’. р(х) dx=p(^) djr=p(z)dz,
а	а	а
т. е. определенный интеграл не зависит от обозначения неза-
висимой переменной.
5°. Если f (х)^0, xg[a; ft], и a < b, то
ft]
J f (x) dx 0.
a
Более того, если Z(x)«Cg(x), x£ [a; 6], и a < b, to
b	b
J f (x) dx < J g (x) dx.
a	a
6°. Если f (x) > 0, xgla; b], n a < bt to
b
J f (x) dx > 0.
a
Более того, если f (x) < g(x), xg[a; ft], и a < ft, to
b	b
^f(x)dx<^g (x) dx.
a	a
7®. Если a < ft, то
ft	b
^f(x)dx < J | f (x) I dx.
a	a
Пример 2. Вычислить
xm dx,
m—3, 4, 5,
где а и ft—произвольные
и m—натуральное число.
Первое решение.
действительные числа, ft > а > 0,
Сначала вычислим интеграл
хт dx9
458
ГЛ 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Согласно определению, отрезок [0; а] разобьем на п равных
частей. Точками деления будут
„ а n a	/ а
*6 = 0, Xi=— , х2=2—........xn-i=(n— 1) —, хп=а;
Гъ	Tv	Tv
положим —	(&=1, 2,	и). В этом случае диаметр раз-
биения dn~aln стремится к нулю при п—> оо.
Интегральная сумма Sn для рассматриваемого разбиения
и выбора точек принимает вид
п
о < k Лт 1^4-2^ + 3^+.
п \ п ) п	пт + 1
k -1
Так как (см. гл. 1, § 4)
\т + 2т + Зт+...+пт ___ 1
Лтоо	”т+Г
то
а
. \xmdx= lim Sn ——
g	п т+1
ь
хт dx=—V~r bm+х.
m+ 1
о
Отсюда и свойства Iе теперь заключаем, что
b	b	а
р	р	^ + l_awz + X
хт dx = \ хт dx — \ хт dx~--—---.
J J	т+1
а	0	0
Аналогично находим j
Второе решение. Разделим отрезок [а; Ь] при по-
мощи точек вида
х0 = а, Xi = a<7n, х2 = а^, ..., хп^1 = а^й“1, xn = aq%=b,
где дп=^Ь/а>\ и положим	т. е. lk = a^~l
(k— 1, 2,	п). В этом случае диаметр разбиения dn — aqn —
— aqn^ — bil — у/a/b) при п—>Ц-оо стремится к нулю. Иско-
мый интеграл является пределом при п—*4-оо следующей
суммы:
$„= 2 (^)и
6=1
= ат (aqn—a)+(aqn)m (aq2n—aqn)+ ... +(aq"~1)m (aq„—aqR~1) =
(qn^ 1) (1 +9Г1 + -7Гт+1,+ • • • +?ГП W+1>).
Используя формулу для суммы первых п членов геометри-
ческой прогрессии со знаменателем получаем
AW2 + 1_am + 1
Sn = a^ (qa- 1)	—L= (qn-1)	..—
qn	—’ i	qn —1
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	459
Таким образом,
ь
хт dx=(bm+1~-am+l) lim ............'•
п 00 Qn — 1
а
На основании формулы для суммы первых п, членов гео-
метрической прогрессии со знаменателем qn имеем
9„-1	1________.
Яп71— 1	1 +	• • • ~lrQn
поэтому, учитывая теперь, что qn —* 1 при п—>оо (см. гл. 1,
§ 4), окончательно получаем
ь
хт dx ——(bm+1-— am+1).
m-\- 1
a
Пример 3. Найти
ъ
C — dx. 0 < a < b.
J x
a
Решение. Как и в примере 2, разобьем отрезок [а; 6]
точками
*о = а, Xi = a?rt, x2 = aqn,	=	xn = aq% = bt
где qn=yf b/a> 1. В этом случае диаметр разбиения dn =
= aqn —ш/п"1 — b (1 —	a/b) при п—> + оо стремится к нулю.
Рассмотрим интегральную сумму Sn (положив ^ = хд-_1):
/2—1	П-1
S- = Z* (i) («<7й+1-«Л =Ц (<7п-1) =
£ = 0 4 4 '	fe=0
= п(Яп— 1) = п^|Л4 -1) •
Имеем
ь	___
Г 1 ,	..	/'}/' b	,
| —dx— hm п\ I/------1
J X и->оо\г а
а
Отсюда с учетом равенства (см. гл. 1, § 4)
г	Л 1 и 1	1 ь
hm I/---------1 )—In b—In а —In —
п -> оо \ г а /	а
заключаем, что
ь
С 1 А . ь
\ — dx— In—.
J х а
а
460	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Замечание 1. Подобным образом, используя соотно-
шение
х—1	_ 1
х/л*1'1-—1 ”т4-1’
устанавливается, что
ъ
CJ-</x=---L—(б-и+1—а-»+1), zn=2, 3, ...
J хт	—m+1 v
а
Замечание 2. Аналогично доказятельству формул
в примерах 2 и 3 доказывается более общая формула (Ь > а > 0,
agR)
b	/1
Р	« ——	если а 5^—1;
\ x^dx={ а+1
а	\ In b — Ina,	если а = — 1,
Пример 4. Вычислить
2
J (5х + 2) dx.
-з
Решение. Используя сначала свойство 3®, а затем
свойство 2°, получаем
2	2	2	2	2
J (5x4-2)dx — J 5xdx+ J 2dx=5 J xdx4-2 j dx,
-3	-3	-3	-3	-3
Так как
2
pi	i
J xdx=y(22^(-3)2)=±(4~9)=-|e
-3
2
J dx = 2 — (—3) = 5,
-3
wo
2
P	1
J (5x + 2)dx = -^+10 = -|—2±,
-3
Пример 5. Вычислить
Cx3 + x + x2 + l
J	1 + ^
-2
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	461
Решение. Имеем
г3 + х + х24-1_/(г2+1) + (г2+1)
14-Х2	Г+х2 —х+1.
Поэтому
2	2	2
/= V (x+l)dx= Cxdx + С dx=4-(22—(—2)2)4-(2—(—2))=4.
-2	-2	-2
Пример 6. Решить уравнение
х +1
J (^ + 4)dy=H.
X
Решение. Так как
х+1	я+1	х+1
J (f/3+4)rfy= J уЩ+ § 4^=-|((х+П4-г«) +
X	XX
+4 (х +1 -х) =1 ((х +	+ 4,
то получаем уравнение
(х+1)4—jr4+5 = 0.
Положим / —^4-1/2; имеем
(*+1/2)4-*(/-* 1/2)4 = —5,
[(/ + 1/2)2_1/2)2] [(/ + 1/2)2 +	1/2)2] = _5>
2/ (2/2 4-1/2) = — 5,
4/з + /+5==о.
Последнее уравнение имеет единственный корень / =—1, таи
как 4/$+^+5 = (/;+-1) (4/2—4/4-5). Поэтому данное уравне*
ние имеет единственный корень х =—3/2.
Пример 7. Вычислить площадь, ограниченную парабо-
лой у = 2х24-*4-1, прямыми х — 1, х = 3 и осью абсцисс.
Решение. Так как функция у = 2х24-х4"1 принимает
только положительные значения на [1; 3], то величина ис-
комой площади S равна интегралу
з
J (2х24~*4-1) d*.
1
Применяя сначала свойство 3°, а затем свойство 2е, найдем
3	3	3	-зз
S=^ 2x2dx4>^ xdx-j- J 1 dx = 2 J x2dx-\- J xdx + J Idx.
1	11	ill
462
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Так как
з
*Мх=4(33-13)=?- f хЛ=1(3«-1)=4,
о	о J
3
J 1 dx = 3— 1 = 2,
1
то
5=®+4+2_®+«=™_24.
Пример 8. Найти площадь фигуры, ограниченной пара-
болой #=-^х2.+ 1 и прямой ^ = х+3.
Решение. Требуется найти площадь S фигуры, изобра-
женной на рис. 6.11. Из уравнения уХ24-1=х-|-3 находим
абсциссы точек пересечения графиков данных функций: 1 — ^5
и 1 + К 5. Следовательно,
1+V“5
<S=S1— У (±-x2+l^dx,
l-V~5
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	463
где Si —площадь трапеции ABCD. Имеем (см. свойства 3° и 2°)
3=у(1 + Кб+3+1-Кб+3)(1 + К5-(1-К 5))-
1+V"5	1+У"б	1+1/"5
— У ухМх- J 1 dx — 4-2 Кб —i У хМх—
1-V“5	l-VT	1-V5
-(1 + К‘5-1 + К5) = бК5—|((1 + К'5)3-(1-К5)8) =
= 6 Кб—К 3=^ К 5=у Кб •
Пример 9. Через точку Р (х0; yQ), расположенную внутри
параболы у — х2, провести прямую, отсекающую от этой пара-
болы сегмент наименьшей площади.
Решение. Уравнение прямой, проходящей через точку Р,
имеет вид у = k (х — х0) 4-Уо> и поэтому координаты точек пере-
сечения этой прямой и параболы у — х2 удовлетворяют системе
уравнений
( y = k(x —х0) + ув,
I У = х2.
Таким образом, абсциссы х± и х2 этих точек являются корнями
уравнения х2—kx-\-kxQ—Уо~® (рис. 6.12). Это уравнение при
любом k имеет два различных корня, так как для его дискри-
минанта имеем:
^2 —4(^х0 —уо) = ^2'—4^о + 4уо = (^—2xo)2 + 4(z/o--^) > 0;
точка Р (х0; Уо) лежит по условию внутри параболы у=ха,
и тем самым > х§.
Площадь сегмента (рис. 6.12) найдем по формуле
Xi
S = Si— J x2dx,
Xi
где Si — площадь трапеции ABCD. Имеем
5=4 (*1+^) (Х8-Х1)-у (х!-х?)=у (Х2-Х1)3.
Так как
х2 _ Xi=1 {k + К fe2-4fex0+4j/0) -1 (й - K^-4Axo+4{/o) =
= К fe2-4ftx0+4W>
ТО
$=-§- ( КА2-4йхо+4^о)з.
Таким образом, площадь S будет иметь наименьшее значение
при угловом коэффициенте & = 2xq, при котором квадратный
464	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
трехчлен £2«—4&х04-4#0 достигает своего минимального значе-
ния; при этом
^rtiin 27 V У®	) 3-
Отметим, что прямая с угловым коэффициентом & = 2х0,
проходящая через точку Р х0; «/о), параллельна касательной
к параболе $г=х2 в точке (х0; Хо).
Пример 10. Доказать формулу Ньютона для натураль-
ной степени бинома, т. е. формулу
(«+ b)n^an + C1nan^b+C2nan^b2‘+ . *. + Cn~1abn~i-j-bn. (1)
Решение. Доказательство проведем методом математи-
ческой индукции.
При л = 2 нужное равенство справедливо. Выберем теперь
любое натуральное число k > 2 и докажем, что из равенства
(1) при n^=k— 1 следует равенство (1) при Действи-
тельно, так как
ь
J k	dx— (а-}-Ь)Ь**»аЬ,
0
то
ь
J k dx,
а
По предположению индукции
(a+x)»-i=a»-i+C*_iaft~?x+... +d zW~2 + xft-J.
Поэтому (ем. свойства 3®, 2° и пример 2)
ь
(«+&)*= a^+k J (aft-i+cLiaft-M-.  .+Cfe=W"?+xft-i) dx=
a
=	—jr—1~ t,. *ф- kCtk—id^,'a'm —— -ф- t, -ф-^.
tn
Так как при O^m^k имеет место равенство
k (k— 1) (fe—2)...	1)
ml	k f
то отсюда заключаем, что
(a + ^=a^+C^"^ +. s. +Cka*~"*bm~[--... + ^,
Следовательно, по принципу полной математической индук-
ции равенство (1) верно для любого натурального значения д.
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
465
Пример 11. Доказать, что если 0 < а < Ь, то
2ab In — < 62-—а2.
а
Решение. Так как (х — 1)2 = х2 — 2х+ 1 > 0 при х > 1,
то 2х2 < х8+ х, и поэтому
1	*2+*
х 2х2
при х > 1.
Из этого неравенства и свойства 6° следует, что при с > 1
имеет место интегральное неравенство
Отсюда при с<=Ь/а получаем нужное неравенство.
Пример 12. Пусть функция f (х) непрерывна на отрезке
la; b], а <Ь< Доказать неравенство (см. свойство 7°)
ь
f (х) dx
а
I f (*) I dx.
Решение. Так как
-1Нх)|</(x)<|f(x)|, х£[а; Ь],
то отсюда и по свойству 5° заключаем, что
b	b	ь	ъ
— J I f (х) I dx — J (— |/ (х) I) dx^ J f (х) dx< I/ (х) \dx*
а	а	а	а
Таким образом,
ь	ь
f(x)dx < j | f (x) | dx9
a	a
что и требовалось доказать.
466	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
6.2.	В гл. 5 было введено действие дифференцирования
функции. Обратное ему действие называется интегрированием
и заключается в том, чтобы найти все такие функции, произ-
водная каждой из которых равна данной функции.
Функция F (х) называется первообразной для непрерывной
функции f (х) на заданном промежутке, если для каждого зна-
чения х из этого промежутка имеет место равенство
F' (х) = /(х).
При этом, если промежуток содержит, например, свой левый
конец а, то в этом равенстве требуется, чтобы правая произ-
водная функции F (х) в точке х=а была равна f (а); аналогич-
но, если правый конец b принадлежит промежутку, то левая
производная функции F (х) в точке х = Ь должна быть равна
f(b)-
Зная таблицу производных (см. гл. 5, § 1), нетрудно при-
вести примеры первообразных. Так, функция F (х) = х2 явля-
ется первообразной для функции f(x) = 2x на промежутке
(—оо;-|-оо), а функция F (х) = —cosx — первообразной для
функции f(x) = sinx на промежутке (—оо;-|-оо).
Пример 13. Найти первообразную для функции f (х) =
= l/j/x на промежутке (0; +оо).
Решение. Пусть F (х) = -^- х2^3. Учитывая формулу
(х05)'»»*06-1, при х > 0 имеем
F'<x>=4"3x3 =х 3=yj-
Поэтому функция F (х)—'~-х2/? является первообразной для
функции f(x)~l/iSх при х > 0.
Легко заметить, что функции
А^+1, 4x^+7. 4х*/?.+ К2
4	4	4
также являются первообразными для функции f(x)=ll\/r^
при х > 0. Вообще при любом фиксированном значении в
функция ~-х2/3 + С является первообразной для функции
Пример 14. Найти первообразную для функции f (х) m
= Ух на промежутке [0; + <эо).
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	467
2
Решение. Пусть F(x)=—х3/2. Так как при х> 0 имеем
<5
F' (х) = (4 х8/2 У=4 • 4 *1/2 = Кх,
У О j D Z
то функция F (х) является первообразной для функции f (х)
на промежутке (0;+оо). Чтобы доказать, что F (х) является
первообразной для функции f (х) на промежутке [0; +оо),
осталось проверить, что правая производная F'+ (х) функции
F (х) в точке х = 0 равна /(0)==0. Имеем
4(0) = lim 4*) —4°) = lim 2 j/--	2 Иш y--=0
x -> 0	x	x -> 0	x 0
x> 0	x > 0	% > 0
Пример 15. Доказать, что функция F(x) = 5 —ctgx яв-
ляется первообразной для функции f (x) = l/sin2x на интервале
(0; л). •
Решение. При xg(0; л) имеем
F' (х) = (5—ctg х)' = (5)' — (ctg х)' =
Подчеркнем, что задача интегрирования состоит не только
в том, чтобы найти для данной функции f (х) лишь некоторую
первообразную, а в том, чтобы найти все ее первообразные.
Основное свойство первообразных:
Пусть функция F (х) является первообразной для функции
f(x) на промежутке I. Тогда
1°. При любом значении постоянной С функция
F(x)+C
является первообразной для функции f (х) на промежутке 7.
2°. Любая первообразная G (х) для функции f (х) на про-
межутке / может быть записана в виде
G(x) = F(x) + C,
где С — некоторая постоянная.
Другими словами, если для заданной функции f (х) на
Промежутке^/ найдена некоторая первообразная F (х), то ре-
шением задачи интегрирования для функции f (х) является
множество всех ее первообразных вида F(x)4~C, где С—про-
извольная постоянная.
Z Основному свойству первообразных можно придать про-
стой геометрический смысл: графики любых двух первообраз-
ных для функции y — f(x) получаются один из другого парал-
лельным переносом вдоль оси Оу (рис. 6.13).
Пример 16. Для функции f (х) = ]/"х , х 0, найти пер-
вообразную, график которой проходит через точку (9; 7).
Решение. Из основного свойства первообразной и при-
мера 14 следует, что любая первообразная для функции У~1с
468
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
записывается в виде
9	_
F(x} = ^xVx+C,
О
где С—произвольная постоянная.
Эскизы графиков некоторых из этих первообразных изобра-
жены на рис. 6.14. Чтобы найти ту функцию, график которой
проходит через точку (9; 7), надо решить уравнение
о ______
-T.9Fr9+C=7.
О
Откуда находим С=—11. Следовательно, искомая первообраз-
ная имеет вид F (х) = -|-х/Т —И.
о
Пример 17. Для функции f (х) = sin х найти первообраз-
ную F (х) такую, что^(1) = 3.
Решение. Так как (cosx)' =—sinx, то при каждом С
функция F (х) = —cosx + C является первообразной для функ-
ции f(x) = sinx. Из равенства Г(1) = 3 следует, что 3 =
= — cos 1 + С. Таким образом, при C=3-|-cos 1 получаем иско-
мую первообразную, т. е. функцию F(x) = 3+cosl— cos х.
Замечание. Часто при нахождении первообразной для
функции f (х) промежуток, на котором задана функция f (х),
не указывается; в этом случае считают, что первообразную на-
ходят на всей естественной области существования функции f (х).
Пусть F (х) — какая-либо первообразная для функции f (х);
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
469
тогда F (х)-]-С, где С—произвольная постоянная, часто назы-
вают общим видом первообразных для функции Цх). Напри-
мер, -$ х3-)-С является общим видом первообразных для функ-
о
ции х2.
Множество всех первообразных для функции f (х) называ-
ется неопределенным интегралом функции f (х) и обозначается
символом
f (х) dx,
т. е, по определению
$ f {x)dx = F (х) + С
Таким образом, неопределенный интеграл функции пред-
ставляет собой общий вид первообразных для этой функции*
Величина С, входящая в определе-
ние неопределенного интеграла,
называется произвольной постоянной.
Придавая ей то или иное значение,
можно получить из неопределенно-
го интеграла любую первообразную.
В неопределенном интеграле^ f (х) dx
функция f (х) называется подынте-
гральной функцией.
Из определения неопределенно-
го интеграла следует основное
равенство
(J f (х) dx'j =f(x),
т. е. производная любой перво-
образной подынтегральной функции
равна ей самой.
В основе всех методов нахож-
дения неопределенных интегралов,
или, как принято говорить, инте-
грирования функций, лежат инте-
гралы от простых функций.
Ниже приводится таблица нео-
пределенных интегралов некоторых
функций:
Рис. 6.14
а # —1;
4) \ ах dx = т--------1-
' J In а 1
С, а > 0, а 1;
470
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
5) ех dx — ex-J-C; 6) cos xdx==sin х-|-С;
7) sin х dx — — cos х + С;
8,jisfc=,|!'+c'	‘«z:
р dx
9)	y-^F7s~ctg*+c- x^nk,k^Z;
10)	C—	— =a resin — -!-<?, a > 0, |x| < a;
J /fl2-x2	a
11)	V -Л-5=- arctg—-J-C, а * 0;
J x2 +a2 a a 1
12)	C_^_=’ln |ir^|-{-C, a^O, |x|^]a|.
J x2— a2 2a |x-|-6Z | 1	1 1	1 1
Проверка правильности каждой из этих формул состоит
в проверке того, чю производная функции в правой части
равна подынтегральной функции в ее левой части.
Проверим, например, формулу 3). При х > 0 имеем 1п|х| =
= In X и
(In | х |-|-С), = (In х-\-С)' — \/х.
При х<0 имеем In | х | — In (— х) и
(1п|х| + С)' = (1п (-х) + С)' = —L(_1)=1.
Таг им образом, при х Ф 0 получаем
(In |х| + С)'= 1/х,
т. е. формула 3) верна.
Интегралы от функций, не входящих в таблицу, при их
нахождении стараются свести к приведенным «табличным»
интегралам. Два основных и простых правила нахождения
неопределенных интегралов (первообразных) состоят в следу-
ющем:
1	. Интеграл от суммы двух функций равен сумме интег-
ралов слагаемых, т. е.
$ (/ to+g to) d*= J f to dx+ $ g to dx-
2	, Постоянный множитель k, k # 0, можно вынести за
знак гнтеграла, т. е.
J kf (х) dx — k J f (x) dx.
3	амечание. Отметим, что, например, равенство
J (f(x)+g(x))dx= J f (x)dx+^g(x)dx
понимается в следующем смысле. Для любой первообразной
Т (х) для функции f(x)+g(x) найдется такая пара первооб-
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	471
разных F (х) и G (х) для функций f (х) и g (х) соответственно,
что Т (х) = F (x) + G (х). И обратно, для любой пары каких-
либо первообразных F (х) и G (х) для функций f (х) и g(x) со-
ответственно найдется такая первообразная Т (х) для функции
f (*)+#(*)> T(x) — F (x) + G (х). Значит, справедливы сле-
дующие равенства:
J (/ W + g W) dx = F (х)+ J g (х) dx,
f (х) dx-]- g (х) dx = F (х)+ J g(x) dx,
где F (x) — некоторая первообразная для функции f(x).
Отметим также, что в этих равенствах нельзя взаимно
уничтожить в левой и правой частях g (х) dx, так как это
может привести к ошибкам. Например,
J xdx = (x-|-0)dx= J xdx-f- Odx = J xdx+C,
где С—произвольная постоянная. Поэтому, например, имеют
место равенства
Jxdx=^xdx+5, xdx= хdx+7.
Взаимное уничтожение интегралов, стоящих в левой и правой
частях, приводит к неверным числовым равенствам 0 = 5, 0 = 7.
Аналогичные замечания справедливы и для формулы
f kf (х) dx = k f f (x) dx, k # 0;
в частности, имеет место равенство
kf (х) dx — k J f (х) dx~kF (х)4-С,
где С—«произвольная постоянная, a F (х)-*некоторая перво-
образная для функций f(x).
Пример 18. Найти
С —4sinx) dx.
Первое решение. Используя правила 1 и 2 (с уче-
том сделанного выше замечания), находим
J -----4 sin dx = § ~dx-±~ J (—4 sin x) dx —
1 C	1 C
\ (—4 sin x) ^x~—~—4 \ sinx dx —
= —-4 (— cos x)-|-C = — -~+4cosx+C,
где С—произвольная постоянная.
472
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Второе решение. Первообразными для функций
f(x)=l/x2 и g(x) = —-4sinx являются, например, функции
F (х) =— 1/х и G(x) = 4cosx. Поэтому функция F (х) 4~G (х) =
=	4 cos х является первообразной для функции -
— 4sinx. Следовательно,
( х^—4 Sin	dx~---Г" 4 cos х + С,
где С — произвольная постоянная.
Пример 19. Найти:
1) У (*2 + рх+<7) dx; 2) J 2x^7 dx‘
Решение. 1) Используя правила 1 и 2, получаем
(х2 + рх + q) dx = J х2 dx + J px dx+ J q dx =
= J x2 dx-\-p x dx 4~q dx.
Затем, согласно формуле 2) таблицы интегралов, находим
У (x2+px-H)dx = y х3+-£-Ха + <?х+С,
где С—произвольная постоянная.
2) Имеем
Р 5	, __5 С dx ____5 С dx
bx2+7 ^^2+7-2j^yry-
Отсюда по формуле 11) из таблицы интегралов находим
с 5	.	5 V2 „ КТх , „
\ q 2 , ~dx=—-r=- arctg J-——j-С,
J 2х2 +7	2 К7	/7
где С—-произвольная постоянная.
Пример 20. Найти F (х), если:
1) F' (х) = 6х + 3 и F(—2) = 4;
2) Г(х) = 9х24-4х—10 и F(—1)=10.
Решение. 1) Так как искомая функция F (х) содержится
в множестве функций
F' (х) dx = J (6х+3) dx==3x24-3x4-C
то найдется такое Со, что F (х) = Зх24-3x4-Со. Для нахожде-
ния Со воспользуемся условием F(—2) = 4; имеем 4 = б4-С0*
Отсюда Со = —2. Итак, F (х) =3х24-3х—2.
2) Имеем
f F' (x)dx= f (9х24~4х—10) dx = 3x34~2x2—10x4-0»
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	473
Пусть Cq таково, что
F (х) = Зх8+2х2 — 1 Ох+
Так как
F (—1) = 3 (—1)3+2 (—1)2—1О(—1)Ч-Со = 9 + Со,
то из условия F (—1) = 10 найдем Со=1. Таким образом,
F (х) = 3х3+2х2—10х+1.
Полезным методом приведения интеграла к табличной
форме является метод замены переменной.
Первое правило. Чтобы вычислить интеграл вида
$ /(<₽(•*))<₽' (*Мх,
запишем его в форме
р (<р (х)) d<p (х),
заменим здесь ср (х) на у и вычислим (по у) полученный интег-
рал; в полученном результате произведем замену переменной у
на <р(х). При этом по определению dtp (х) = <р' (х) dx.
Так, например,
и С —С л у dx ________Cdlnx_ Cdy__
Jxln2x~-J( } ln2x J ln2x-~J t/2”"
=_1_|-C=--/-+C;
у ‘ Inx 1
P cos x dx _ P (sin x)' dx_ P dsinx __
' J l + sin2x~J 1 -J-sin2 x ~~ J 14-sin2x~"
=J	2 “ arctg у+c = arct g (sin x) тЬ C.
Второе правило. Чтобы вычислить интеграл
J f (х) dx,
положим х = <р(/), где ср (/) —дифференцируемая функция,
имеющая обратную функцию / = ф(х). Вычислив полученный
интеграл (по /), в найденном результате заменим t на ф(х).
Пример 21. Найти
Р dx
J 1+К*’
Решение. Положим t=V х; тогда х=/? и dx — 2tdt.
Отсюда
ЬтЫтр-2^1-ТТ7?'^'-2 '"I1,+'|+е-
= 2 К х-21п(1 + К х)+С.
474	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Пример 22. Найти:
1) Jcos4xdx; 2) J (Зх4-2)Мх.
Первое решение. Имеем:
1) у cos 4xdx=-^- у cos 4xd (4х)=-~ у cos ydy~
=-|- sin r/4-C= ~ sin 4x+C;
2) J (3x + 2)Mx==l J(3x4-2)3d(3x+2)=l
=-^+С=1(Зх+2)*+С.
Второе решение. 1) Положим / = 4х; тогда x=//4 и
dx — d (t/4). Отсюда
J cos 4xdx = § cos t d ^~.)=-l.y cos t dt =
=-|- sin	sin 4x+C;
t__2
2) Положим / = 3x4-2; тогда я=—x— и
о
(3x+2)3rfx= f t3d( -1-/— 2^=4- C Z3d/=~/4+C=
J \ V /	□ J 12
=l(3x+2)*+C.
Для усвоения методов интегрирования заменой переменной
предлагаем проверить правильность приведенных ниже выкла-
док, в которых специального обозначения для замены не вво-
дится и соответствующие действия проделываются устно:
Jdx 0 d(lnx) ...	. ,
---= \	in Inх 4-С;
х In х J In x
2)	у sin" x cosxrfx = y sin" xd(sin x)==—~j-sin"+1 x-J-C;
3)	У sin mx dx-~- у sin mx d (mx) cos mx4-C;
4)	f x<^x ____ 1 f d _________1 Cd(l—x2)
5)	J(ax+d)Mx = lJ (ax+j)»d(M+6)=M^+C;
6)	У sin (ax+&) dx=4 J sin (ax-]-b) d (ax-|-b) =
=— — cos (ax 4- b) 4- C;
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
475
~С dx 1 Cd(ax+b) 1 t ,	. . , . _
7)	\-гт=- \	In ax+b +С;
p dx _p dx ______p dx _____
J Sinx J2sin|cos~ J2tg-|cos2y
=f^=taHI+c-
ё 2
Приведем несколько примеров на применение неопределен-
ных интегралов.
Пример 23, Упростить выражение
F (х) ~ sin Зх cos3 х + cos Зх sin3 х.
Решение. Найдем производную данной функции; имеем
F' (%) = 3 cos Зх cos3 х—3 sin Зх cos2 х sin х —
—3 sin Зх sin3 х+3 cos Зх sin2 х cos х —
= 3 (cos Зх cos х—sin Зх sin х) = 3 cos 4х.
Так как функция F (х) является одной из первообразных
для функции 3 cos 4х, то она содержится в множестве функций
J3cos4xdx, т. е. среди функций ~sin4x+C. Надо опреде-
лить постоянную С так, чтобы для каждого х выполнялось
равенство
3
-у sin 4х+С = sin Зх cos3 х+cos Зх sin3 х.
Полагая, например, х=0, находим, что С=0. Следовательно,
,	3
sin Зх cos8 х+ cos Зх sin3 x = -j- sin 4х.
Пример 24. Упростить выражение
F(x) = (x + a+^)3—(х+а—й)3—(х.-а+&)8—(—х + а+&)3.
Решение. Имеем
f(x) = F' (х) =
= 3(х+а+6)2—3(*+а—6)2—3(х—а+&)2+3(—х+а+6)«,
f* (х) = 6(х + а + ^)— 6 (хa-—Z?) — 6(х—а+&) — 6(—х-]-о4-Ч^0.
Так как Jodx = C и f (х) содержится среди всех этих
первообразных, то найдется такое Со, что при каждом х верно
равенство f (х) = С0. В частности, при х = 0 получаем 24а6=Со*
Итак, f(x) = 24ad.
476
ГЛ 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Поскольку 24ab dx = 24abx-\-C, то существует такое Ct,
что при каждом х справедливо равенство
F (x)~24abx~}~Ci.
В частности, F (0) = 0; отсюда следует, что Ci — Q,
Таким образом, F (x)—24abx, т. е.
(х-|-а + £)3—(* + а—Ь)3-—(х—я4~Ь)3-—(— x-[-a-\-b)2 — 24abx.
Пример 25. Доказать тождество
tgx +2 tg 2х4~4 tg 4x4-8 tg 8x = ctg x— 16 ctg 16xt
Решение. Положим
f (x) = tg x4-2 tg 2x4-4 tg 4x4-8 tg 8x
и найдем неопределенный интеграл
f (х) dx =
== ^ tg х dx+ J tg 2x d (2x) + J tg 4x d (4x) 4- tg 8x d (8x).
Из табличной формулы 3) получаем
j / (х) с/х~ —ln| cos х| —In | cos 2x | — In | cos 4x | — In | cos 8x |4-C=
= — In | cos x cos 2x cos 4x cos 8x 14~ £ =
____1| Sin 2x sin 4x sin 8x sin 16x I .
I 2 sin x 2 sin 2x 2 sin 4x 2 sin 8x | ‘ ~~
= — ln |	= — 1° I sin 16x|4-ln | sin x 14~ In 164~С»
Отсюда, используя формулу 3), находим
f (х) = (J f (x) dx) = —16 ctg 16x4-ctg x.
Довольно общим приемом преобразования неопределенных
интегралов является правило интегрирования по частям.
Пусть /(х) и g(x)—две дифференцируемые функции, опре-
деленные на одном и том же интервале. Тогда
(7 (х) g (х))' = Г (х) g (х) 4- f (х) g' (х),
и из определения неопределенного интеграла получаем
$ (/' (х) g (х) 4- f (х) g' (х)) dx = f(x)g (x) 4- C,
t. e.
S (x) /' (x) dx+^f (x) gf (x) dx = f (x) g (x)+C,
где C—произвольная постоянная. Так как f' (х) dx~df (х) и
gf (х) dx — dg (х), то, согласно сделанному выше замечанию,
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
477
имеем
J f М dg (х) = f (х) g (х) — ^g (х) df (х).
Полученная формула называв!ся формулой интегрирования по
частям} она представляет собой некоторое тождественное пре-
образование одного интеграла в другой.
Пример 26а. Найти
J х In х dx.
Решение. Пусть /(х)«1пх и xdx = dg(x). Тогда df(x)~
— dxfx и g(x) = x2/2. Из формулы интегрирования по частям
находим
I х Inxdx— \ In xd (J=-y Inx— \ -у d In x =
x2 * P x . x* %2 i
=_. in _ dxs=— In Х-Т+С.
Следовательно,
Г	xa ( IX
\ x In x dx==-g- ( In x-—J 4*C,
где С—-произвольная постоянная.
Пример 266. Вычислить
eaxsin bxdx.
Решение. С помощью двукратного интегрирования по
частям получаем (f(x)~eax9 g (х) = — cos bx)
Р	1	а С
1 еах sin bx dx=—еах cos bx+-у \ еах cos bx dx «=
=—еах cos	р- еах sin 6х-—~ J еах sin bx dx.
Определяя из полученного уравнения нужный интеграл,
находим
J еах sin bx ^==^2q_p‘ е°х (а sin bx—b cos bx) -f-C*
Пример 26в. Найти
С У a^—x^dx.
473	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Решение. По формуле интегрирования по частям имеем
(/ (х) = Кл2—х2, g(x)~x)
S	______ р ______2л
И а2 — x2dx — x У а2 — х2 — | х - -^=^=^-dx =
J 2/а2—х2
5---х- Г х2 .	---X , Р х2—а2 + а2 ,
==хУ а2—х2 + I .... ^dx — x у а2— х2 + | —г. - .--dx =
jKa2 —х2	J /а2—х2
Из полученного равенства следует, что
У а2—х2 dx~x У а2—х2+«2 arcsin
—— \ У a2—x2dx.
a J
Отсюда находим
С У аъ — х2 dx~-~ У а2 — х2-|—arcsin ~+С.
Чтобы освоить метод интегрирования по частям, предла-
гаем проверить правильность приведенных ниже вычислений:
1)	J х3 Inxdx = J In xd ===‘^"л'4 I*1
—г? хМ1пх=4-х4 1пх—~х4 + С;
4 J	4	16
2)	arctg х dx — х arctg х— J х d (arctg x) =
, P x ,	,	1 P d (x2)
=x arctg x-dx = x arctg x—у j
= x arctg x—у J	x arctg xIn (1 + x2) + C;
3)	x2 sin x dx = J x2 d (— cos x) =
—x2cosx—(—cosx)dx2 = —x2 cos x+2 xcosxdx =
=—x2 cosx + 2 J xd (sin x) — — x2 cos x + 2 (x sin x— J sin x dx) =
= — x2 cos x + 2x sin x + 2 cos x+C;
4)	J x2ex dx = x2d (ex) = x2ex — ex dx2 = x2ex—2 J ex x dx =
s=x2ex—2 J x d(ex) — x2ex—2 (^xex— ex dx^ =
= x2ex—2xex + 2ex+C == (x2—2x + 2) ex + C.
Аналогично с неоднократным применением метода интегри-
рования по частям вычисляются неопределенные интегралы
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
479
вида
хп lnw х dx, хп sinw х dx, J хп cos'® х dx,
\ хп ех dx, \ епх cos mx dx, \ епх sin пх dx.
6.	3. Пусть функция f(t) непрерывна на отрезке [а; 6],
а < 6; тогда для каждого xg[a; b] она непрерывна на отрезке
[а; х]. Рассмотрим определенный интеграл
X
f (t)dt,	b,
а
как функцию аргумента х и тем самым определенную на от-
резке [а; 6].
Имеет место теорема, устанавливающая связь между опера-
циями дифференцирования и интегрирования, которую назы-
вают основной теоремой математического анализа: справедливо
равенство
(^f(t)dt^~f(x), a^x^b.
Смысл этой теоремы состоит в том, что она отвечает на глав-
ный вопрос интегрального исчисления—-вопрос о существова-
нии первообразной для данной непрерывной функции.
Приведем здесь наглядное рассуждение, поясняющее основ-
ную идею доказательства этой теоремы. Для простоты будем
считать, что функция f непрерывна на отрезке |а; Ь] и прини-
мает на нем только неотрицательные значения.
Пусть
X
ф (x) = Jf (/) dt, a^x^b.
а
Тогда Ф (я)—-площадь криволинейной трапеции, ограниченной
графиком функции	и прямыми линиями у —0, t = a,
t=x (рис. 6.15, а).
Дадим аргументу х приращение Дх (на рис. 6.15 Дх > 0);
тогда для соответствующего приращения функции Ф (х) имеем:
х+Дх	х
Дф (х) = Ф (х-(-Дх) — Ф (х) = J	— ^f(t)dt =
а	а
х + Дх
= J
X
Величина ДФ (х) представляет собой площадь достаточно узкой
криволинейной трапеции, заштрихованной на рис. 6.15, б.
Приняв приблизительно за площадь этой трапеции число,
480
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
равное площади прямоугольника е размерами Ах и f(x), най-
дем АФ (х) « f (х) Ах; таким образом,
АФ (х)
Ах
«Их).
Естественно, что для непрерывной функции /(х) это равенство
тем точнее, чем меньше Ах. Последнее и означает, что имеет
место соотношение
f(x)= lim
Ах-*
АФ (х)
Ах
а это равносильно утверждению основной теоремы.
Согласно этой теореме, например, имеем:
и т, д.
Основная теорема математического анализа позволяет
свести задачу о вычислении определенного интеграла непрерьпЬ
Рис. 6.15
ной функции к нахождению для нее первообразной, т, е.
к нахождению неопределенного интеграла.
Пусть
ь
I = р (/) dt,
а
а <Ь,
н /(/) —непрерывная функция на [а; />]. Рассмотрим функцию
X
Ф (х) = f (t) dt, a^x<b*
а
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	481
Имеем /=Ф(£). Таким образом, если функция Ф(х) найдена,
to легко вычисляется и число /=Ф(6).
Согласно основной теореме, имеет место соотношение
ФМ*)=/(*),
и тем самым функция Ф (х) является одной из первообразных
для функции f(x) на [а; 6]. Следовательно, если г(х)—какая-
либо первообразная для функции f (х), то -
Ф(х)=Г(х)+Св,
где Сб—некоторая постоянная. Так как Ф(а)==0, то отсюда
заключаем, что Со =—F (а); поэтому
Ф(х) = Г(х)-~Г(а).
В частности, при х*=Ь получаем
ъ
/=p(O<W=F(&)—Г (aj.
а
Полученная формула называется формулой Ньютона—Лейб-
ница.
При выводе формулы Ньютона***Лейбница предполагалось,
что а<Ь. Однако это несущественно. Действительно, при а«=6
эта формула справедлива:
а
.0= р (0 dt =F (a)—F (а) = 0.
а
Случай же а > b приводится к а < Ъ при помощи перемены
знаков в обоих частях формулы: если а > Ь, то
Ь	а
J f(t)di=— ^f(t)dt = — (F(a)—F(6))==F(fr)— F (a),
a	b
и формула доказана.
Формулу Ньютона—Лейбница принято записывать иначе,
используя для разности F(b)^F(a) удобное обозначение
F(x)\*~F(b)~F(a).
В этих обозначениях имеем
ь
$ f(x)dx=*F(x)\b.
а
Замечание. Разные обозначения переменной интегриро-
вания в определенном интеграле ничего не меняют, таи как
интегралы
t b	b	b	ь
^f(x)dx, ^f(t)dt,	^f(y}dy9^&
a	a	a	a
16 Задачи до математике. Начала анализа
482	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
обозначают одно и то же число. Однако это не так для обо*
вкачения переменной в неопределенных интегралах. Например,
лМх = 4-х«4-С,
О
z«dz=4-«3+C.
О
f(x)dxt fe==const.
Вычисляя интеграл
J sin3 х cos xdx,
при помощи замены z = sinx приходим к интегралу
J в* dz.
Последний интеграл не равен х3/3-]-С, а равен именно выра-
жению г8/34~С, в котором z==sinx> т. е.
С sin2 х cos
V	**
Основные правила вычисления определен-
ных интегралов:
ъ	ъ
1.	J kf (х) dx~k
а	а
b	b	Ь
2.	W+e W1 <&==р (x)	(x)dx.
a	a	a
b	b
3.	J /(*)<*£(*)=/(*)?(*)£— $ g(x)df(x).
a	a
4.	Пусть функция ф (0 и ее производная ф' (/) непрерывна
на отрезке Ja; ₽], а=ф(а), £=ф(₽) и множество значений
функции ф(О совпадает о отрезком {а; ЭД. Тогда для любой
непрерывной на отрезке {а; ЭД функции у=/(х) имеет место
равенство
Ъ	Р
J / (х)	р (ф (0) <f‘ (/) dt.
а	а
6 чаетноети,
f (йх+е) dae-i J f(x)dx,
a	ka+a
где k и е<*»п0сйянные, k & 0,
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	483
Пример 27. Доказать, что при любом натуральном л
имеют место следующие равенства:	>
у2	уЗ	уП
а)	1п(1 + х)=я-±-4-А_- ,,.+(_1)П-а£.+
Z	О	п
X
+*)?
о *
уЗ уб	*”
б)
X
Jjridy' *€R-
У ”T 1
о
Решение* Так как
а)	1 —Х-]-х2—.. + (—	 х^— 1;
* i х
б)	i_x«+^-...+(-l)»-»x«<»-i)=15fc^-", xgR,
1 *|* л
то
а) ~=1-»+х2-...+(-1)и-1хп-14-(-1)'‘
х^—1;
1 “Г’ л	1 л
xgR.
Из этих двух тождеств почленным интегрированием с приме-
нением правил 1 и 2 находим
X
ч С dy . Z1 . . х2 . х9 . .	.
а)	]т+у= n(i+*i=*—2”*"з—
о
х
+(—1)вУНг/
о
.ч Г dy .	х9 х%	x9n^i
б)	JTf^=aretgxx=x-T+T-....+(-!)» *2^+
О
х
Р 1/2п
+(-1)" i rf+l*
о
и тем самым требуемые равенства установлены.
Пример 28. Найти
К?	\
t +p2dz\dt.
о J
16*
484	гл. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Решение. Имеем
Поэтому
Ф(х) = С (<+-§<*)
о	о о -
Ч-^+п*1г4*‘+15л
Основные свойства определенных инте-
гралов:
1°. Если а < с < Ь, то
bob
J f(x)dx=>^f (х) dx-j- J f (x) dx.
a	a	c
2°. Если функции y=f[x) и y~g{x) непрерывны на от-
резке [а; Ь] и при каждом х£[а; 6] выполняется неравенство
f(x)^g(x), то
b	ь
^f(x)dxs* ^g(x)dx.
а	а
В частности, если f (х)^0 при каждом х^[а; $], то
ь
Jf(x)dx^O.
а
3°. Если функции у 5= fix) и y~g(x) непрерывны на отрезке
[а; 6], при каждом х из отрезка [а; 6] выполняется неравен-
ство f(x)^g(x) и, кроме того, существует по крайней мере
одна такая точка х0€[а; для которой f (х0) > g(x0), то
£	ь
^f(x)dx> J g (х) dx.
а	а
Отсюда, в частности, следует, что если функция y~f(x)
непрерывна на отрезке xg[a; fc], f(x)^O, при каждом xg[a; b]
и существует по крайней мере одйа такая точка 6], для
которой /(Хо) > 0, то
ь
f (х) dx > 0.
а
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
485
ъ
4°. J f (х) dx < J | f (х) 1 dx.
а	а
5°. Еели функция / непрерывна на отрезке (а; 6] и
min f(x), Mx= max f(x), то
хе [a; ft]	хе [a; ft]
ft
т (b—a) <,^f(x)dx^M (b—*a).
a
6°, Если f (x)—непрерывная и периодическая функция
е главным периодом Г, то для любого чи&ла а имеет место
равенство
а+г,	Т
J f(x}dx= J f(x)dx.
a	0
7°. Если функция f (x) определена и непрерывна на отрезке
[— а; а], а > 0, и являетея^четной функцией, т. е. /(—#) = /(%),
xg[—а; а], то
а	а
J f (х) dx =2 J f (x) dx.
-a	0
8°. Если функция f (x) определена и непрерывна на отрезке
{—а; а], а > 0, и является нечётной функцией» т, е, f (— х) =
«—f(*)»	—а* аЬ то
а
J f(x)dx = 0.
-а
9°. Если функции f и g непрерывны на отрезке |а; &], то
имеет место неравенство Коши^Буняковского
“ ft	"la ft	ft
j f (X) g (*) dx < J P (*) dx J g® (x) dx.
J a a
Пример 29. Вычислить:
2	зт
a)	J x4 dx; 6) sin x dx.
1	°
Решение, а) Поскольку для функции	одной.
из первообразных является функция	то по формуле
о
Ньютона—Лейбница получаем
j xMx = yX8|2_i = y(32+l)=S.
— 1
486	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
б)	Пользуясь формулой Ньютона—Лейбница и тем, что
{— cos х)1 = sin х, получаем
л
С	I31
\ sin xdx~(—cos ж) I ==— cos л+cos 0=2,
Пример 30, Вычислить
лм
г dx
J cos2 др *
о
Решение. Так как иа рассматриваемом промежутке од-
ной из первообразных для функции У^-^г^ является функ-
ция //—tgx, то
Л/4
Р dx ,	]Л/4	. л . л t
Пример 31, Вычислить
4 л
J КТ** cos 2xdx,
о
Решение, Так хак КТ** <&s 2ж«= К 2eln* *= ]/”2 | sin х |,
то
4л	4л
J КГ** соз 2х с?х= К 2 J I sin х | dx»
о	о
Воспользуемся теперь свойством 1°; имеем
4л	л	2л	Зл	4л
J | sin х | dx~ Jsin х dx ** J sin x dx + sin x dx — sin x dx==*
0	0	л	2л	3л
/	. |Л .	\ 12л . t . |3л	,	. 14л
=(— cos x) — (— cos x) +(— COS X) — (— COS X) I =
|v	|7l	{ZJi	1иЛ
= 24-2+2+2=8.
Поэтому искомый интеграл равен 8К~2*
Пример 32, Вычислить
2
J | 1**5х |dx.
I
Решение, Так как
11	— 1 1*ж5х,' х 1/5,
5х-1, х > 1/5,
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	487
то по свойству 1° получаем
2	1/5	2
J 11«**5х| dx= J (1—5х) dx-J- § (5х~- l)dx=
О	О	1/5
1/5	2	2
с-А—5 J xdx+5 J x,dx— § dx=s
о	1/5	1/5
1 ч 1 и-5*4 54 JL—10—5Н~50°—5-90—410_±L
Т 25-2*** 2	2-25 5 ~~	2-25	50f~ 5 *
Пример 33. Вычислить
1
-1
Решение. Так как	х|^3 и функция ^/==|
является четной функцией, то по свойству 8® получим
1 ____ 1 1
С У"х%/з dx~ С |*11/3 dx~2 С х1^ dx=
•*1	-1	о
Пример 34. Вычислить
2
С e*dx
Решение. Пусть
fgle-B; а2), и по правилу
t—e*; тогда если xgf—1} 2]» то
4° имеем
2	2	е*	е*
f exdx _ f _ С _ f d(* + l)_
J i+ex~- J 1+e*	/+1 ~
-1	-1	e-J
=s In {t + IXГ I = In (UH2) —In (1 +<3-i) = In
Jg—*
14-e8
1
.	1 / sin2nx\ |л
nxdx^lx-----
(-Л
488	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Пример 35. Вычислить
л	л
a)	J sin2 пх dx; б) J sin пх sin тх dx» п т,
-л	-л
Решение, а) Так как
JL	•— к—- ) ==i cos2/rx) = sina пх»
то по формуле Ньютона—Лейбница получим
л
sin2
-л
б)	Имеем
sin пх sin /их =-g- [cos (n,rj-zn) х—cos (m—n) x].
Поэтому, если n # m, to
л	л	Л
p	1 C	1 p
\ sin nx sin mx dx~-~- i cos (m+n) xdx—g- \ cos (zn—zi)xdx=
-Л	— Л	-Л
Л
cos (m+n)xd(m+n)x-—
-л
Л
cos xd (tn—ri) x—
-л
~2(^H0 Sb <т+я) X|-«“2(^ij SIn	x I” „= °-
Замечание. Вычисляя определенные интегралы при
помощи формулы Ньютона—Лейбница, следует обращать вни-
мание на выполнение условий, при которых она имеет место,
В частности, эта формула справедлива лишь тогда, когда
для непрерывной на отрезке [а; 6] функции y=f(x) равенство
f(x) = F'(x) имеет место для каждого xig[a; ЭД, Так как, на-
пример,
barctgl)^-^. x^q,
то для любых чисел а» Ъ таких, что ab > 0, справедливо ра-
венство
ь
С 1	.	( i 1 \ р
J bRdJK~arctg TJI?
2
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	489
нельзя,
1
—5Г лишено
в то же время для любых чисел а и Ъ таких, что ab < О, инте-
ъ
f 1	.
грал j	заменить выражением
а
так как при х=0 равенство —arctj
смысла.
Или, например, равенство
b
а
верно при любых значениях а и Ъ таких, что отрезок (а; не
содержит точки х=3, в то же время для чисел а и о таких,
что а < 3 < Ъ> запись
ъ
С dx
J (х—3)<
а
лишена смысла, так как в точке х=3 подынтегральная? фу нк*
ция не определена.
П р и м е р 36. Найти все значения а, а > 0, для каждого
из которых
а
а)	С е* dx > Л:
J	£
-а
2
б)	(4—4a)x4-4x3)dx<12.
1
Р е ш е н и е. а) Так как
а
f ех dx=ех |а =
-а
то исходное неравенство равносильно неравенству
ea—e~a > 3/2,
Если г/=еа, то у > 0, и последнее неравенство можно записать
следующим образом:
1	3
у“7> 2
Полученное неравенство на промежутке (0; 4~ оо) равносильно
неравенству у > 2; поэтому исходное неравенство .равносильно
неравенству еа > 2. Отсюда получаем, что условию задачи
удовлетворяют все а > In 2»
490
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
б) Имеем
2	2	2	2
f (а2 — (4*— 4а) х + 4х8)dx — a? J dx—(4—4а) xdx + 4 J x3dx =
1	ill
X2 12	1
c=a2_(4_4a)i-|i+4.±x<
2
1 =а2—(4—4а)-2+(2—2а)+16—1=
= «2—8 + 8а+2—2а+15=а2+6а+9 = (а+3)2.
Таким образом, все искомые значения а, а > 0, удовлет-
воряют неравенству (а-|-3)2<С 12. Так как
J а> 0,	( а> 0,	( a > 0,
\ (a+3)»<12^\ а+3<2/3^ j a<2/3—3^
ОО < а<2/’3—3,
то все искомые значения а принадлежат промежутку (0; 2рл3—3].
Пример 37. Найти числа А и В такие, чтобы функция
з
/(х) = Д« 2* + В удовлетворяла условиям f( (1) = 2 и J f(x)dx — 7,
о
Р е ш е н и ё. Поскольку fr (х) = А>2Х In 2, то из равенства
f (1)=2 найдем, что 2 А In 2=2, поэтому	. Таким обра-
1П Ал
зом, f (х)“ ^7]^) *2л + ^. Кроме того, функция F(x) =
является одной из первообразных для функ-
ции f (%); следовательно, по условию
3
рИ•“-(ьЙ  2'+в«) |«-и+3«-и“’-
7 (1—L.A
~	D \	1п22/	7	.24
Отсюда находим В =—-—5-----—=-^- Q1 — log^e).
о	о
Итак, Д —log2e и (1 —logsk).
о
Пример 38. Вычислить
Л/4
а)	/|= J ctg*2x dx;
п/8
3
б)	/2=| (-44 Г)
Решение, а) Так как для х$[л/8; л/4] имеет место тож-
дество
t 29 — cos22x -4—sin22x„_ 1	1
g sin22x ~ sin22x ~ sin22x
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
491
ТО
Л/4	Л/4
, С ( 1	, \ . f dx |л/4
i=J \sin22x / Х~ J sin22.» Х|л/8 =
л/8	л/8
Л/4
1 р d(2x) st 1 А о |л/4 'л
= 2 J 8-ОТ-Т=—2 Ctg2x
Л/8
1 / . Л . Л \ л 1 л
==-y^tgT-ctgl-J-T=y-T.
б) Так как
31-х4.(1/3)2х-1==3.3-^+3.3~2л:=аЗ(3~л;^з-2^>
то
3	3	3
/2=3 С (3~*+3-3*)dx=3 Г 3~*dx+3 (* 3“^^»=
О	0	0
3	3
P	3 P	3~* 13	3 3~2*I3
= тну(—3,3~,+3~2"3",'}"2‘)“Тпт(~1г“18^+т)=
-ЖЭТП^'+^-^ЯТ-
Пример 39. Вычислить
1
/== J х K l +
о
Решение. Так как х /^+*==(*4-1** 1)У"Т+* ==
===(х+1)?/2-(1+х)1/а и
J (х +!)«/«dx^2^4^-—4-С.
J («+1)1/2 dx == 2(*+2^-4-С,
то
/=(j (,+и-»-! <«+d«) |>4.2«2-4.2«-|+4=
вК2 4^2,4	4/2 ,4_4(О+1)
“ Т~ 3	15“ 15	15—	15
Пример 40, Вычислить
/«=f /a2—x«dx, а>0.
492	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Решение. Используем правило 4 замены перемени^)
положим x=asin/, где 0=С/<^л/2. Легко проверить, что вс£
необходимые условия для такой замены выполнены. Так как
dx—асоз t dt, то
Л/ 2
/»а« J a&tdt~-
Замечание. При вычислении интеграла по формуле
Ь.	3
р (х) dx = р (ф (0) ф- (0 dt,
&	а
т. ё. при помощи замены переменной вида х—ф (/), где ф(/)~~
дифференцируемая функция, новые пределы интегрирования
а и р определяются из системы уравнений
а==ф (а),
* = Ф(Р).
Если функция х=ф(/) не является монотонной, то может
случится так, что эта система будет иметь несколько различ-
ных решений* В этом случае следует взять любое из трех ре-
шений системы, которое определяет отрезок [а; р] и на кото*
ром функция х=ф(О является монотонной. Покажем это на
примере.
Пример 41. Вычислить
0/2
Решение. Положим х =?sin t; тогда dx = cos t dt. Новые
пределы интегрирования аир определяем из системы
1/2 = sin а,
/"5/2 = sin р.
Множеством всех ее решений является множество пар
(а; Р), где а = (—•!)* ~4-л&, &gZ, и-р ==(—-1)^—--\-пт>
Возьмем из них, например, пару (а; Р), где а = л/6 ир — л/3;
тогда на отрезке [л/6; л/3] функция # = sin/ является моно-
тонной. Следовательно, а = л/6 и р = л/3 можно взять за новые
пределу интегрирования.
Если а = л/6 и Р = л/3, то на отрезке [л/6; л/3] cos / > О,
и поэтому У1—sin21 — cos/. Следовательно, имеем
л/з	л/3
/—С CQS___________с
*’’’ J sin / cos / “ J sin /
л/6	Л/6
t |л/3	2 + У 3
Intg-n =ln—-4--------------.
2 л/6	3
ГЛ. 6. ИНТЕГРАЛ И ЕГО. ПРИЛОЖЕНИЯ г, 493 !
Можно взять некоторую другую Пару, например пару (a; g),
где а=бл/6, ₽=2я/3» Так как при изменении t от 5л/6 до
2я/3 функция x=sin/ является возрастающей, то в этом слу-
чае cos/ < 0; следовательно, У1—sina/ = — cos/ и /
2л/3
/== —
dt
Sint
12л/3
|5л/6
=bl±p.
□
В то же время, например, пара (а; Р), где а=л/6 и 0 =»
= 2л/3, такова, что на отрезке [л/6; 2я/3] функция x = sin/ не
является монотонной. Поэтому а=л/3 и р = 2л/3 не могут быгь
новыми пределами ,интегрирования.
Замечание, При вычислении интеграла
ь
/== J / (х) dx
а
с помощью замены переменной вида /==ф(х), где <р (*)— диф-
ференцируемая функция на (а; Ь), монотонная на отрезке (a; bit
новые пределы интегрирования определяются из соотношений:
а=ф(а) и р==ф(£), где ф(ф(х))=х» Если функция / = ф(х) на
отрезке [а; />] не является монотонной, то он разбивается на
отрезки монотонности функции / = ф(х) и интеграл / на отрезке
[а; 6] заменяется суммой интегралов на полученных отрезках»
Покажем это на примере вычисления интеграла J x2dx
« в"1
с помощью замены t~x2.
Так как функция /=х2 на отрезке [—1; 2] не является
монотонной, то разобьем его на отрезки монотонности функции
1-1; 0] и (0; 2J.
Тогда
2	0	2
J х2#х = J х2dx+ С х*dx,
-1	-1	о
Если
1
то yt на отрезке {—-1; 0] и dx=
-----—dt. а на отрезке [0; 21 имеем х=1^7 ndx~—
2У t	2/ t
Тогда получим
о	о
с X»dx~—L (vidi—44^2Ii =4«
dj	J	* О	|1 О
2	4
494
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
и, следовательно,
2
С хМх=4-+4=3.
J	О О
-1
В то же время ясно, что
Пример 42. Вычислить
/=?-----.
J х у 14-In *
Решение. Положим /=14-1пх. Функция у= 14-In* на
отрезке [1; е] монотонно возрастает, непрерывна и дифференци-
руема. Поэтому, когда х возрастает, изменяясь от 1 до е, пе-
ременная t пробегает отрезок [1; 2]. Так как dt—dx/x, то
2
I — С ________1	д -1/2 I2 о (if*2 1)
“ 1 — 1/2	|1 и '•
Пример 43. Вычислить
л/3
/== j sin 3x4-cosdx.
-Л/3
Решение. Так как функции
i/=x10 sin Зх и #=tg1* х
являются нечетными функциями и промежуток интегрирования
симметричен относительно начала координат, то
л/3	z л/3
J х10 sin Зх dx = 0, j tg1-1- х dx = 0.
-л/3	-л/3
Следовательно,
л/3	л/3
/==	С cos-^dx==3 С cos 4-^4“•
V	J	О	О
-л/з	—л/3
Отсюда имеем
J Q х l31^3 о f . л . { я \ \
Z = 3 SM у 1-^ = 3 Sin-д—sin ( - у J J =6 sin у.
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	495
Пример 44. Доказать» что для любой непрерывной на
отрезке [0; 1] функции имеет место равенство
л/2	л/2
J f(sinx)dx= J /(cosx)dx.
о	о
Решение. Положим х=-~-—/; тогда dx——di. При уве-
личении х от 0 до л/2 значение i изменяется от л до 0. Поэтому
rt/2	0
С / (cos х) — — J f^cos	=
0	Л/2
0	л/2
s=— С /(з1п0<# = J f{tint)dt9
п/2	0
что и требовалось доказать»
Пример 45» Доказать равенство
1	1
J хт (l~-x)ndx= J хп (1— х)т dx.
о	о
Решение. Пусть 1—тогда di——dx. Имеем
1	о	1
Сх®(1— x)ndx—~ ( (1—о® tndt = f <»(1 —
о	1	о
что и требовалось доказать.
Пример 46. Вычислить
2
/=J xlnxdx.
Решение, Для вычисления интеграла применим формулу
интегрирования по частям для определенного интеграла, поло-
жив f (х) = 1пх и g(x)=x2/2. Имеем
2	2
/=2jlnxd(4)=2(4)lnx|^2^1dx=
2
=41n2-« J xrfx = 41n2—|^=41п_2— ^2—==41п2—
I
Пример 47» Вычислить
л
I» \ х sin х dx9
о
ГЛ- в. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Реш1нив. Воспользуемся формулой интегрирования по
частям, положив f(x)=x, g(x)=—cosx. Тогда
л
Zc=— X COS J COS X d* = л + sln
Пример 48, Вычислить
л
/=з J e* sin2xdx.
о
Решен ие. Пусть f (я)«= sin2х, #(*)=»а*. Тогда по пра-
вилу 3 интегрирования по частям найдем, что
л	л
/«в* sin 2я	2 J ех cos 2х dx=—2 § ех cos 2х dx.
Для вычисления этого интеграла снова воспользуемся форму-
лой интегрирования по частям (f(x) = e*, ^(я)=соз2я):
л	л
Г ех cos 2xdx=e* cos 2хГ-|-2 J sin 2яех^х=вя -*-1+2/,
о	° о
Таким образом, имеем
Z«—2e”-f-2«**4Zt
Откуда
Z=-|-(l*<*e!n').
Пример 49. Какое из чисел больше:*
Л/2	л/2
cos2xdx или J cos10 х di?
о	о
Решение. Так как cos2хcos40х при х£[0; л/2] и для
всех х из интервала (0; л/2) имеет место знак строгого не-
равенства, то из свойства 3° заключаем, что
л/2	л/2
cos2 х dx > J cos10 x dx.
о	о
Пример 50. Доказать, что
%2 ___________ к
у < J Kl+cosajfdjs <
о
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
497
Решение. Воспользуемся тем, что (см. гл. б, § 5)
1</Т+7< 1+уЛ t>o.
Для подынтегральной функции f (х) = К1 + cos2 х из этого не-
равенства следует двойное неравенство:
1 < f (х) < 1+у cos2 х, 0 < х < «р
Поэтому (см. свойство 3°)
л/2	я/2	Л/2
К1 + cos2 х dx < j 1 -|-у cos2 х^ dxt
Имеем
л/2	л/2	л/2
С (1+4- COS2X^ dx« C d* + 4 \
J \	/	•/	" t/	**
л/2	oi/2
С (1-|“ cos 2x) rfx=-^-у cosSxdx»»
о	о
Л/2
=•^•4--§• j cos2«i(2x)=-^.+-g.(sin2x)|”/2sa^4
что и требовалось доказать.
Пример 51. Доказать, что
1
1	С xndx I
(п+1) К 2	J F1+* «4-1	'с
Решение. Так как при 0 < х < 1 имеет место неравенство
1 < КТ+* < V 2,
т. е*
FT < кг+* < *’
то по свойству 3° находим, что
1	i	1
1 С	С	хп	Р
-тг=- \ хп dx < \	-7====- dx <\ хп dx.
К 2 J	J	F 1 + х	J
о	о	’	о
1 !
Так как хп	+ 1	Т° отсю,аа полУчаем
о
нужное неравенство.
498
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Пример 52. Доказать неравенство Коши—БуняковскогоВ
если f и g—непрерывные на отрезке [а; £>] функции, то
0 f (x)g (х) dx} Р (ж) <*ж^^ gi (*) dx}.
Решение. Так как при любом действительном Л имеет
место неравенство
то отсюда по свойству 3° получаем, что
ъ
J (/ W—(ж))’ dx О,
а
т, е.
ъ
J (/? «-2М(x)g W+1V(ж)) dxSsO,
а
ИЛИ	4
g* (ж) dx}—2A.Q f (ж) g (ж) Л»^4- J Р (ж)	0.
Таким образом, квадратный трехчлен относительно %, стоя-
щий в левой части этого неравенства, принимает только неот-
рицательные значения. Поэтому его дискриминант не превос-
ходит 0, т. е.
^2 J f (ж) g (x)dx} —4^ J р (ж)	J g* (ж) dxJ<0,
что и требовалось доказать.
Пример 53, Доказать, что
1
о
Решение. Положим
1
о
и воспользуемся неравенством Коши—Бу ня ко веко го. Имеем
',iaG
хо
\ dx 1=у • у \ e^xd (2х) =
о ' о
=4е8*|*=Т(е2-П=£Т^Се-”1) <«-1.
откуда и следует нужное неравенство.
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	49$
Пример 54. Доказать неравенство:
a)	cos х 1—, х 0;
у2 у4
б)	COS X<1--гг + "НГ»
'	2 1 24
Решение, а) Воспользуемся известным неравенством:
sin/^Z,
Отсюда, проинтегрировав его в пределах от 0 до х, х^О, по
свойству 2° получаем
х	х
J sin / dt dt,
о	о
или
(-cosn|* <(/2/2)|*.
т. е*
—cos х+1 *Сх2/2,
что и требовалось доказать.
б) Воспользуемся неравенством
t*
cosZ^l— -g-, /^0,
установленным в п. а). Снова проинтегрируем его в пределах
от 0 до х; по свойству 2° найдем, что
хх	хх
Jcos^Ssj ^1—у)л = Сл —-i-Cz24tt.
о	О	0	0
или
IX
т. е.
%з.
sin х^х-—-т-. х^0«
о
Проинтегрируем теперь в тех же пределах обе части по-
следнего неравенства; имеем
X	X	XX
CsinZd/SsC (i—	di—L-C^dt,
о	о V	о о
т, е.
(-c°sZ)|^±x2-l^.
500	INI. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Таким образом,
**COSx+l^y X*—^Х4, Х^О,
откуда следует нужное неравенство.
Замечание. Другое доказательство неравенств в
пп. а) и б) содержится в гл, 5, § 5.
Пример 55. Доказать, что если 0<х<л/2, то
tgx+sinx^2x.
Решение. Производные функций, стоящих в левой и
правой частях неравенства, соответственно равны	х
и 2. Так как при 0<х < несправедливы неравенства
—L-+cos х —U-+cos3 х 2,
cosaxr	cos^x’	*
то
-£-4-008X^2, 0<ж<|.
Проинтегрируем это неравенство в пределах от 0 до л,
< х < л/2; тогда по свойству 2° получим
( (z^n+cos/^ dtes С2<Й==2я
или
tgx-J-sinx^2x, 0<x < n/2,
что и требовалось доказать.
Пример 56. Доказать, что если функция f и ее произ-
водная непрерывны на отрезке [а; 6], то
ь	ъ
a) lim \ /(х) sin nxdx—O*, б) lim \ f (х) cos nxdx~0.
CO V	П-> CO *>
a	a
Решение, а) Воспользуемся формулой интегрирования
по частям; имеем:
ь	ь
§ f (х) sin nxdxJ / (*) d (cos пх) =
а	а
г
I cos nxf* (x)dx аз
а	,1

/ (b) cos nb (а) cos па
b
J cos nxf' (x) dx
a
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
501
Так как функции f (х) и f' (х) непрерывны на отрезке 1а; Ь],
то они ограничены на этом отрезке; положим
7И==тах |/(х)|, М' = тад | f  (ж) |.
(а; 6]	[а; Ь]
Тогда по свойству 4° имеем
/ (х) sin пх dx
( £
2М 4-1 M'dx
а

откуда и следует нужное утверждение
б) Доказывается аналогично.
6.4. Одним из важных приложений определенного инте-
грала является его использование при нахождении площадей
плоских фигур.
Пусть функция y~f(x) непрерывна и неотрицательна на
отрезке [а; 6]. Площадь S фигуры Ф, являющейся криволи-
нейной трапецией (рио. 6,16), ограниченной графиком функции
Рис. 6.17
y=*f(x), осью абсцисс и прямыми х=а и х~Ь> находится,
как было отмечено выше в п. 6.1, по формуле
8 = f (х) dx.
а
Отсюда следует, что если на отрезке [а; Ь] заданы две непре-
рывные функции f(x) и причем f (х) g (х) при лг^[а; 6],
то площадь (рис. 6.17) фигуры Ф, ограниченной графиками
функций y = f(x)t y — g(x} и прямыми х = а и x = bt вычисля-
ется по формуле
ь
s = \ (f(x)—g(x))dx.
а
502.
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Пример 57. Используя геометрический смысл интеграла,
вычислить:
а
а)	J У а2--» х2 dxf
~а
2
б)	Za = J |[ х | — 1 \dx.
— 1
а > 0;
Решение, а) График функции у= Уа2—%2 представляет
собой полуокружность радиуса а (рис. 6.18). Так как искомый
-а
Рис. 6.18

Рис. 6.19

определенный интеграл представляет собой площадь полукруга
с тем же радиусом, то 1^ла2/2.
б)	График функции у=| | х |—1|,	—1, 2] показан на
рис. 6.19. Следовательно, величина искомого интеграла равна
сумме площадей двух треугольников. Таким образом,
4=4-2-1Ч-4-Ы = 1+1-11.
Пример 58. Используя геометрический смысл интеграла,
вычислить:
1	8
а)	/1= J arccos xdx*t б) Z2= J 1п(1+КН~*)<&-
-1	з
Решение, а) Определенный интеграл /< численно равен
площади криволинейной трапеции, показанной на рис. 6.20.
Если дополнить эту криволинейную, трапецию до прямоуголь-
ника, стороны которого определены уравнениями —1, я=1,
у=0, уе=л и площадь которого равна 2л, то из свойства сим-
метрии графика функции у = arccos х и этого прямоугольника
относительно точки (0; л/2) следует, что число /< представ-
ляет собой половину площади прямоугольника; поэтому /=л.
б)	Заметим, что функция у®=1п (1 + К1+*) является воз-
растающей функцией на отрезке [3; 8]. Поэтому при вычисле-
нии определенного интеграла Z2, который численно равен пло-
щади криволинейной трапеции, показанной на рис. 6.21, вос-
пользуемся тем, что интеграл /2 равен также площади фигу-
ры EGBF* получающейся из рассматриваемой криволинейной
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	503
трапеции после преобразования симметрии относительно пря-
мой у=х, Площадь этой фигуры, как видно из рис. 6.21, мо-
жет быть вычислена, если известна площадь криволинейной
трапеции ABCD. Действительно
Seckf—Sofcd~Sofba*--Sabcd~8 4“~3 1п 3 —S^bCD.
Из равенства у = In (1 4 К1+Д х^ — 1, следует, что х =
= е2у—2еу. Таким образом, функция, обратная к функции у=г
У.
Рис. 6.20	Рис. 6.21
== In (1 +1^14“*)» х^—1, задается формулой у~е2х—2evt
х^О.
Точки В и С имеют абсциссы х^ и х2, соответственно рав-
ные ординатам точек графика функции ^=1п (14-	14-х) при
х = 3 и х = 8, т. е. Xi = ln 3, х2 = 1п4. Поэтому для искомого
интеграла 72 получаем	-	.—
in 4
Р	48
/2 = 81п4—• 3 1п3— \ (е2х—2ех) dx= 1п~-
1пЗ
-(|^-2^)|11пПз=>п^-(1е2’"4-2е’»<) +
4-(4e21n3-2e'n3) = ln ^—84-8+1-6=,
216	3	. /216 _3/2\
п 27	2 П ( З3 е )’
Пример 59. Вычислить площадь фигуры, ограниченной
параболами #=х2—-2x4-2 и ^=24-4х—-х2.
Решение. Нарисуем графики данных функций (рис. 6.22)
и найдем абсциссы точек их пересечения из уравнения х2—
— 2x4-2=24-4х—х2, Решая это уравнение, имеем х==0 и
564:	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
х—3. Искомая площадь равна
з
S = j <(2 + 4х—х2) —(x2—2x4-2)) dx=
з • '	3
«= J (24-4х—х2—х24-2х—2)dx== j (6х—2х2)с?х=
3	3
Г	Р	13 2 13
=6 \ xdx—2 \ хМх=Зх2 -4х8 =27^18=9,'
J	J	ООО
О	о
Пример 60. Найти площадь фигуры, ограниченной гра-
фиками следующих функций и указанными прямыми:
а)	у*= Sinx, y==cosx, х = 0,х=2л;
б)	у = ха, Jp=x1/a, х=0, х= 1 (а > 1);
в)	д®In(х4-6), ^=31пх, х==0, у=0;
2	Г	л \
г)	у — tg*.	#=-5-COSX,	Xg 0{	— ),	х = 0;
о	L	z 1
д)	у—6х2—5x4"L	у==со8лх,	х=0,	х=1.
Решение, а) Искомая площадь (рис. 6.23) равна
Л/4	5 л/4	2 л
J (cos х—sin х) dx 4-	(sin х—cos х) dx + J (cos x—sin x)dx~
0	Л/4	5л/4
= (sin X4- cos X) |“/4 4- (— cos X—sin X) |^4 4- (sin X4- cos X) |^/4=
( V2 , J<2	, ( /2 , V2 , ^2 , ^2^ ,
~\j-2~+-2-1;+\-2-4“2-+-2-+-^-;+
+(K2 »1 +2 K2 +1 + K2 = 4 /2 .
\	**	•* в
ГЛ. 6, ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Ж
И
Рис. 6.23
б)	Искомая площадь (рис. 6.24) равна
J ха) dx= J	ха dx —
о	оо
1 xi/.a+1 I1 * v«+111_ а
|о а-Н |о~ а-Н
1 ___
а-]-1	1
506
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
в)	Уравнение 1п (*4-6) = 3 1п х, как нетрудно убедиться,
имеет единственный корень х=2. Поэтому площадь фигуры,
которая показана на рис. 6.25, равна
2	2	2	2
1п (64-*) dx—3 lnxdx= J In (64-х) d (64-х)—3 J In х dx—
CIO	1
= ((* + 6) In (%4-6) — (х4-6)) |о — 3 (х In X —х) |2 в
=8 In 8—8—6 In 64-6—6 In 24-3= 12 In 2—6 In 34-1.
2
г)	Уравнение tg x=-x-cosx, т. e. уравнение 2 sin2 х4-3 sin х —
о
— 2 = 0, равносильно уравнению sin х= 1/2. Отсюда, учитывая
условие Xg[0, л/2), находим, что х = л/6. Поэтому искомая
площадь равна (рис. 6.26)
л/6
J cosxdx=
о
л/6
2	\	С
-тг-cos х—tg х ) dx =— \
О”	/v
о	о
fft/6
(* d (cos x) , 2 t -.J*/6 , ,	4 W6 2	1
= \	slnx) z==ln(cosx) --------------о -TF
J cos x 1 3 '	' |o	|o 3 2
о
. Кз 1
д)	Уравнение 6x2—5x4~ 1 “ cos лх, как нетрудно доказать,
используя монотонность функций, имеет два корня: х==0 и
х—1/2. Поэтому искомая площадь равна (рис. 6.27)
1/2	1
f (cos лх—6х24~5х— 1) dx4-	(6х2—5x4-1 — cos лх) dx =
О	1/2
1 ,	]1/2 O.J1'2 < 5 J1/2	1 , п J1 5 211 .
№-*-81йЛХ1	— 2x4	4*ТГ*2	—-о-+2л:3-----5-Х2	+
rt |о |о 1 2 |о 21	|1/2	2	|1/2 ’
,1	1 4 I1 1	2 , 5 . о Л 1 \ 5 / ,	1 \ .
+ ~2-A sin пх |i/2=”'8	1 ""в ) - 2 {*“Т) +
.1	2.1
Пример 61. Прямая касается параболы ^=х2 в точке
Д, хорда ВС параболы параллельна этой касательной. Дока-
зать, что площадь параболического сегмента, ограниченного
кордой ВС и дугой ВАС параболы, равна 4/3 площади тре-
угольника АВС.
Решение. Уравнение касательной (рио. 6,28) к параболе
в точке А (а; а2) имеет вид
у=2а (х—я)4~Л
ГЛ. & ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
507
Следовательно,
является уравнением прямой, параллельной этой карательной
и проходящей через точки параболы В и С,
Абсциссы точек В и С находятся из уравнения
508	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
обозначим его корни через х± и ха, х± < х$. Тогда площадь
параболического сегмента ВО АС равна
$DBCE	X2 &Х®=у	X* I*
Xi
= у (xi + *2) (Xz — Xi) — у (xl — Xi) =S
да(Х2**Х1) ^y (xl + xi) g-(xi + XiX2 4-Xa))=s
==y (x2«-xi) (xt+xl*~2xixa)«=y (xa—xi) (xa —xi)a«
«у (Xa—Xi)«.
Найдем теперь площадь S^bc треугольника ABC. Имеем
(рис» 6.28)
ЗдВС « SdrcB'^DBAF-^Sface^
« у (xi+xi) (х2—Х1) —у (xi+аа) (а — xi) — у (ха+а?) (х2—а)»
дау (xix2+Х2—xi xtxl — ах!—aft + xi+xta2 л$
—x^dft +<ш+ а?)=у ((xix2^XiX2)4-a? (xi*-X2)+«(xl—х?)) да
==у (Х£—х2) (Х1х2+а3-«а (хх+ха))»
Так как Xf й х^корни ^уравнения х2—^==0, то 2а =»
= Xi+x2. Следовательно,
&АВС = у (*1 ~~*2) (xix2	(*f + хг)2 "~*у (Xi + Х2)а J да
да X (Х1 ^а) (4xixa + xi+2x1 х2 -* 2x1 *- 2x2 — 4х£Х2) =
о
(Х2-~Xi)8 = -g- (Xft— XjJ3.
Поскольку у=у (*а—Х1Я=-|-• ^.(х2—*1)? •то нуж-
ное утверждение доказано.
Пример 62, Доказать, что
1+4+4+-+п=т>1пя’ ra^N’
Реше н ие» Сумма
1+|+у+--’4-^т
ГЛ. в. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
509
представляет собой сумму площадей всех n—1 четырехуголь-
ников, показанных на рис. 6.29, Так как эта сумма постав-
ляет собой площадь всей ступенчатой фигуры (рио. 6.29), то
п
С dx
она строго больше, чем t Таким образом,
п
i+4+у+...+—?> jv=,nn’
что и требовалось доказать»
Пример 63. Доказать, что
V2 —, т1, п N, tn N,
~ « V п у т
П~ J
Решение. Рассмотрим функцию
f(x)=---L., XSsi.
х Y х
Так как на рассматриваемом промежутке функция f(x) явля-
ется убывающей, то имеют место следующие неравенства:
"р" 1<л<2'
П|,н 2<'<3'
—^=7^—~7^=- ори
S10	гл. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Интегрируя эти неравенства, получаем
2
L С—
2К2	J xV х
з
___1	С---1 А
..........7?^"	\ 	-^=- dx,
З/З Jxfx
»««•••*•••••
т
--7=г < С  7=- dx>
тут J хух
т-1
Складывая полученные неравенсгва, найдем
2
TVT+3ibr+• • • +7гЙг S ТУ? dx+
3	т
+ ? —^=-dx+...+ С	у—	dx==
J хУх	2, xfx
т
с 1	.	—2	|т	2
J xfx	Vx	|i	т
откуда следует доказываемое неравенство.
Пример 64. Доказать неравенство
n! < nw+vag-n+i^ flgN.
Решение. Пусть Ль Л2, ЛЛ*— точки на числовой
оси ОХ, абсциссы которых равны соответственно 1, 2, ..., п,
и В±, В$,	Вп—точки графика функции ^=1пх с этими
же абсциссами (рис. 6.30). Тогда площадь криволинейной тра-
п
пеции AfBnAnt т. е. J Inxdx, больше суммы площадей тре-
1
угольника Л^В2Ла и трапеций AzB2BaA3t ...» An~iBn~iBnAn.
Таким образом,
1п2 , !п2 + !пЗ f
2 +	2 "Г
, In (я— 1) + 1пп
+	2
I
In xdx.
Интегрируя по частям, получаем
п	п	п
lnxdx—xln — ^xdlnx = nlnn— J dx = n In л—л-f-L
l	1
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
511
Следовательно,
In 1+1п2+...4-1п(п*-*1)+у 1пя < п1пл—«+1,
откуда
или
Inn! < (л+1/2) Inп«*«+1,
In nJ < In
и тем самым неравенство
п! <
доказано.
ЗАДАНИЕ 1
1, Вычислить определенные интегралы как пределы интег
ральных сумм:
Л/2
1) j sinxdx; 2)
о
2	2
J 2*dx; 3) x*dx;
1	2	е
4)	5)	6) J Inxdx,
о	X 1
2, Вычислить определенный интеграл
з
е
512
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
п
как предел интегральной суммы 2 f (Ы	следую-
ЬО
щим способом:
1)	разбивая отрезок [0; 3] на равные части и выбирая в
качестве g* левые концы этих частей, fc = 0, 1, 2, ...» я,
2)	разбивая отрезок (0; 3) на равные части и выбирая в
качестве g* правые концы этих частей, &=0, 1, 2, .я;
3)	разбивая отрезок [0; 3] на равные части я выбирая в
качестве g* середины этих частей, 6=0, 1, 2, я; ~
4)	разбивая отрезок [0; 3] на части точками	3,
в выбирая в качестве g* левые концы этих частей, k^6t 1,2,«»я;
5)	разбивая отрезок [0; 3] на части, как в п, 4), и выби-
рая в качестве g* правые концы этих частей, й=»0,1,2, , .,,я|
6)	разбивая отрезок [0; 3] на части, как в п, 4), и выбирая в
качестве g& средние геометрические значения Яёвых и правый
концов этих частей, £==0, 1, 2, • >», я.
ЗАДАНИЕ 2
1. Вычислить определенные интегралы как пределы инте-
гральных сумм:
ъ	х	ь	а
1) ( екх dx\ 2) J cos х dx; 3) J xn dx; 4) J xe* dx;
a	о	a	0
b	b
0< a < 6; 6)	0 < a < b.
J X	v X
a	a
2, Вычислить определенный интеграл
4
J я4 dx
2
n
как предел интегральной суммы 2 / (£л)	следую-
I	/г=0
щим способом:
1)	разбивая отрезок [2; 4] на равные части и выбирая в
качестве g# левые концы этих, частей, ^=0, 1, 2, 4S., я;
2)	разбивая отрезок {2$ 4] на равные части и выбирая в
качестве g& правые концы этих частей, 1, 2, я;
3)	разбивая отрезок [2; 4J на равные части и выбирая в
качестве gA середины этих частей, &=0, 1, 2, IMJ я;
^разбивая отрезок [2; 4] на части точками ^=2^, q =
== / 2, и выбирая в качестве g& левые концы этих частей,
& ~з0, 1, 2, ««nj
5) разбивая отрезок [2; 4] на части, как в п* 4), и выби-
рая в качестве g^ правые концы этих частей, ^=0, 1, 2, ...,я;
6) разбивая отрезок (2; 4] на части, как в п. 4), и выбирая
в качестве g& средние геометрические значения левых и пра-
вых концов этих частей, й==0, 1, 2, <««, я»
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
513
ЗАДАНИЕ 3
1. Исходя из геометрического смысла интеграла, вычислить:
1	2
arccos xdx\ 2) \ | х1 ] dx\
о '	-з
dx.
-1	V 2/2
3) — J к Ь^х3 х dx-, 4) V
I	о
2« Какое из чисел больше:
3) arccos xdx или j arcsin
-1 -1
1 1
4) \ In х dx или \ In2 х dx?
1	1
2) \ V\+x*d% или xdx\
О	О
xdx\
1/2	1/2
3. Доказать, что последовательность {а„}, ngN, имеет
предел^ и найти его, если:
1 ( . л , . |2 п .	। . п — 1 \
I) a„=— ^sinT-|-sm*—+••• +8Ш—
2) апг=^Г:
4)	а„= ‘/1+	\
V п \ V 2	V П /
4. Доказать, что
ЗАДАНИЕ 4
1. Исходя из геометрического смысла интеграла, вычислить?
У“2/2	4
1) j arcsin xdx; 2)	11 х—21—-1 |dx;
О	-2
О	Q
3)	( VT^dx; 4) J (КГЛ2—X— l)dx,
-2	-I
47 Задачи по математике. Начала анализа
514
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
2. Какое из чисел больше:
1/2	2
П С —-* или 4* > 2) \	dx или 2е;
м J К1 -*2 -	2	%
о	о
л	Л/2
3) f dx или 9; 4) С e~sta х dx или л/2?
•J X "t* £	J
О	О
3. Доказать, что последовательность {«„}, ngN, имеет
предел, и найти его:
° °"=4’(	у<1+4+-”+ у *+^):
,п
2) «»=£(l+-^sin^;
. . \ п ) п*
/?=1 4 '
о\ 1 । 2 	। 2n—1
з) ап=^+^4----+-^з-;
4. Доказать, что
Иш
й»0
ЗАДАНИЕ 6
1.	При каких значениях х справедливы формулы?
1)	J^=lnx+C; 2) j V"x d%=y x/x+C?
2.	Найти:
1)	$ (/' (X)+£'(*)) dx; 2) J (f (x) g (x) +se (x) f (x)) dx.
3.	Найти производную функции:
л
1)	I In t dt9 x > 0; 2) C cos /2 di, x > О*
1	i/x
4.	Найти наименьшее значение функции
с С **—16 ,
f W — J 1 t di*
о
5.	Доказать тождество:
1)	cos2 (jx/4~x)—sin2 (л/4—x) = sin 2я$
113
2)	cos*x=-s-cos 4х+-з-cos 2х+—,
О	£	О
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
515
6.	Найти сумму
с"—у с'’+у С"~Т с"+• • ’ +(—!)“	с«-
ЗАДАНИЕ 6
1.	При каких значениях х справедливы формулы:
2.	Найти:
1)	j dx-, 2) ^t(x)f (x) dx.
3.	Найти производную функции:
V~x	х2
1)	С s-toldt, х>0; 2) J
2	Г
4.	Найти наименьшее значение функции
X
f (х) = J (/ —1) (^—2)2 ей.
о
5.	Доказать тождество:
1)	tgx4~2tg 2x4-4 tg 4x4-8 ctg 8x = ctgx;
1	13
2)	sin4x = -o-cos 4x—x-cos 2x4—q-.
о	Z	о
6.	Найти сумму
Cfl+v Cfl+y ^n+ • • • + r 1 cS*
£t	О	lb I
ЗАДАНИЕ 7
1.	Доказать тождество:
1)	arcsin x=arccos У1 — *2 == arctg 	=!
V 1—x2
l/-! — x2
=arcctg-—-- , 0 < x < 1;
2)	arccos x == arcsin К1 — x2 = arctg  К I—*.=
X
* X
=arcctg7rCT'’ 0<x<1:
3)	2 arcsin x = arccos (1 —2x2), t 0 x «С 1; ’
4)	2arccosx=arccos (2x2 —1), O^x^l?
5) уarccosx=arccos j/ , 0<x<l;
17*
516
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
х+1^	( —arccos х+л/4, х^1/У^ 2,
6)	arccos----тг=----==/
г 2	( arccos х *— л/4, х^ 1/У 2.
2.	Доказать неравенство:
1)	х*~- sin х «с 1 — cos х «С *У 2 — sin х, О «С л «С л/2;
2)	sin х^х (п — х), 0«Сх<л/2;
3)	cos х + In cos х < 1 «~ха, 0 < х < л/2;
4)	x+cos х > л/2 (1— л2/24)	0 < х< л/2;
х^
5)	sin х > х—, 0 < х < л/2.
ЗАДАНИЕ 8
1.	Доказать тождество:
I	х	1
1)	arctg x=-arcctg—=arcsin- r_^=_^--== arccos 7===^, x>0;
7 s s x К1 +*2 К1 4-X2
x л
arccos , x>0;
К l + x«
2)	arcctgx=arctg~=arcsiny====
1 1ГТ1 X2
3)	2 arctg x= arcctg—75— , x > 0;
.. I
4)	2 arcctg x~ arcctg —, x > 0;
б)	у arcsinx = arccos -iClii+lCl——, 0 < x < 1 j
..	.	.	. 1 —x /л/4, x >—I,
6)	arctgx + arctg
2.	Доказать неравенство:
1)	In(2sinx) > yx(n-x)—-2-<x<y;
1	Л
2)	In (COS x) <— у xa, 0<x < -g-;
3)	2 sin x	л/2 + (x —* л/2) cos x, 0 < x л/2;
4/ sin x > х**2х2/л, 0 < x < л/2;
5) sKT+x^l + x/? —№/8,	|x| < 1.
ЗАДАНИЕ 9
Проверить вычисления:
1)	J (Зх4-4х!!—Зх3+2)!1х=Зхг/2+4х8/3—Зх4/4 + 2х+С;
2)	J (x4-2)2xdx= J (x?-f"4x + 4) xdx= J (jr34-4xa4-4x) dx=
= x‘/4+4x3/3+2x2+C;
3)	j(K'x+3)8urfx = j(*4-6 К x+9)dx = ^4-4x/x+9x+C;
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
517
^Р+2,44Г)л=-^+й+ж+С;
6)	=	—124-6/ x—x^dx =
= 16 /7—12хЦ-4х/х—у4-С;
Х3+1 — 1
х2 + 1
dx=
dx _____f cos2 x+sin2 x
sin2 x cos2* J sin2 x cos2 x
9) СВх+Зсоз^
J X COS3 X
= х—arctg х+С;
“ J ( sin2 х*^ cos2 х) ^х=я
= — ctg x+tg x+Ci
dx = 2tg x+3 in | x|+C;
x==J(~,+^sk)dx==”x+tgx+C; \
-X2 — x2 + x4
I--2—!--dx
1—x2
— х2
1—X2 x2(l—x2\ , ___
)x2
dx~ arcsin x«»y+C,
ЗАДАНИЕ 10
Проверить вычисления:
1) J (x—4)3dx = J (x—4)3d(x—4)=+%—4)44-C;
2) $ x(x4-l)Mx= J (x+1 — 1)(х4-1)Чх =
= J (x + D«dx—
- j (x+1)8 d (x+1) el (x+Ф- -g- (*+!)• +Q
518	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
3) С (4—Зх)’ dx = — у С(4—Зх)’ d (4—Зх)==—± (4—Зх)8 + С;
—3/17 —2xV , „
+С:
5)	J х (х2 + 3)» dx=1J (х2+3)М (х2+3) = 1 (х2 + 3)’+С;
6)	J sin (4x4-3) dx = -l У sin(4x4-3)d(4x4-3)=^cos(4x4-3)4-Ci
_ С , /5—7х\ .	-3 f , /5—7х\ ./5—7х\
7)	\ sin ( —g— j dx=-y \ sin (—g— ld(—— ) =
3	/5—7x\ । л
«yc°s^—— J+C;
8)	У cos (4—5#) d#=^~ J cos (4—5#) d (4—5#) =
=—p— sin (4—5#) -p Cj
О
9)	J cos (?£d^L2) dx==| у cos
e|sta(^HV12)+C|
i0> 5 Sin2(3—2x)“~ *2* J sin2 (3—2x)“"2 ctg (3“2x)+C;
“> f	УsWx^+V-2ctg(x/2+4)+C}
19. C dx	4 C rf(5-3#/4) _
’ J cos* (5—3#/4)	3 J cos2 (5—3#/4)““
—4
=— tg(5-3#/4)+C;
lox C dx .0 d(x/4-^l)	.. . t. л
13) J cos2(X/4-1)-4 J ^r(y/4-tg(*/4-1)4-0.
ЗАДАНИЕ 11
Проверить вычисления:
*> J 1^“пГпЙ^-Пь1м’-31+С;
2-	^=^F4^“-4i"i<-2-''=i+ci
3)	f eS-8*dx=^ Ce$-8*d(5—3x)=—l-e8-?*4-C!
J	О J	d
A 3 + 0	к _ 3 + 4X	, x - 3+4X
4)	Ce 8 dx=-^-Ce 8	e 8 4-Cj
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
519
2’*+’dx=y C27*+M(7x4-3) = ^L..2’*+s+C;
«> J5 ..	••	.. +С;
ov Г dx If d(5x-H)	1	.	, ,4 , „
8) J l+(5x+4)2“ 5 J l + (5>:+4)2‘_ 5 arctg<5x+4)+C>
_ Г dx — 1 Г d(5—7x) __
J V1— (б-7ж)»	7 J jG-fg—7x)8
1 Г dx2_________
У 1 _(X2_ 1)2 - 2 J у 1 _ (X2_	“
1 f d(x*—l)
2 J
=s arcsin (x*—1) + C.
ЗАДАНИЕ 12
Проверить вычисления:
n C dx _ 1 C dx . 1 C d(x/a)
J x*+&~~ a2 J (х/аЯ+l ~ a J (x/a)*+1
=4arctg7+C;
520
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
2)
3)
4)
dx 1 f dx . C d(x/a)
/a2—x2	l«l jV l-(x/a)2 J/l-fx/a)2
f . * \ I
= sign a I arcsin — j -f
dx ___f dx ________ 1	, x
X2 + ]°—j Ж2+(/П))2~К1о arcg/To ’
dx ___ if dx If dx
ll + 7x2“7 J 11
x + 7
7
= arctg.........7-=.-— 4-С;
/77 V 11/7
dx_____С dx__________f* d(x4~2)___________
х?Ч-4*+9 J (x + 2)2+5~J (х4-2)г + (K'S)2—
1	4 x-j-2 1
—	arctg ~-Л=г + С;
S)
6)
7)
8)
9)
10)
dx f dx
+ П J (	3 \ 2 « 35 —
+4
.(	3 \	3
P	d (*-t)	9	X~T
== I-----i--; /	=_^__ arctg -y-4- 4-C;
J /	3\2.//35\2 /35	/35/2
\X~'2J + \~2~)
dx f dx _P d(x—3)	_
xs_6x+ 19=J (x-3)2+10“ J (x-3)2+ (/io)2 ”
__ C dx______
/ЗСТ “J /(^3)2_X2:
dx If dx
=-=-arctg x 4-C;
/10	/10T
=arcsin x—+C;
1	f_____dx____
2	J/(/Т/г)2—Xs
=_arCSIn 4
dx __ C dx___________
/3—2x—№ J /4—(x+l)a“
f d(*+l)
J /22— (x-H)2
____dx______f dx_________
V15+4X—x2 “J/il — (X—2)2 “
_C_____d (x — 2)_
V (/II)2—(x-2)2
arcsin
arcsin
/11
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	521
-1 Г_______dx__________1__ f_____dx_______
J /11-6^3». ~ /3 .! у-
“ з J y'n_(x+1)2 ~ W J Г (Г177з)2-(х+1)«“
= * arcsin -|-C.
Г з	к 17/3
ЗАДАНИЕ 13
Проверить вычисления:
1)	у sin2 xdx = §	2* dx==-^- dx—~ J cos2xd(2x) =
= y—i-sin^+Cj
nx C 9 j C 1 + cos 2x j 1 С . , 1 C n j /о x
2)	\ cos2 xdx—\ —!—75--dx=-~- \ dx+~ \ cos 2x d (2x) =»
V	V	«	" V	* t)
=|+^sin2x+C}
3)	J sin4 xdx = ~ J (2 sin2x)2 dx=-i- J (l-*-cos 2x)2 dx=»
=~ J (1 —2 cos 2x+ cos2 2x) dx~
==y J ^1—2 cos2x+y+y cos 4л dx—
=-|- j* dx—-i- J cos 2x d (2*) +J cos 4x d (4x) ==
e= 3x/8—sin 2x/4+sin 4x/32 +C|
4)	J sin® jr dx = -g-j* (2sin2x)8dtf=~« J (1 — cos 2x)3 dx^
=-~ J (1 —3 cos 2^+3 cos2 2л-—cos3 2x) dx =
===4’У^’~’1’ J cos2x J (1 +cos 4x) dx—
—— У (1 —sin2 2x) cos 2x d (2x) = x/8—3 sin 2x/16+3x/16+
+ 3 sin 4x/64—sin 2х/16 +sin8 2x/48+C=5x/16 —sin 2x/4+
+ sin8 2x/48+3 sin 4л/64 +C|
5)	J cos4 x dx=J- J (2 cos2 x)*dx= J(l + cos 2x)2dx=
==~ C(l+2 cos 2*+cos2 2x) dx=Y Ju+2 cos 2x+l/2+cos 4x/2)dx^»
3 p 1 P	ip
= y \ dx-^-^ j cos 2x d (2л) + gg \ cos 4x d (4x) == 3x/3 +
+ cos 2x/4+cos 4x/32+<J|'
522	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
6)	Ceos6 х dx = Д- С (2 cos2 %У3 dx—Д- Г (1 + cos 2*)8 dx =
J	о J	о J
=4* С (1 +3 cos 2x4- 3 cos2 2х+ cos3 2х} dx~
о V
1 Р 3 Р	3 Р
s=y \ dx4~ jg J cos %* d (2x)4-yg \ О + cos 4х) dx^
4~ jg J О —sin2 2x) cos 2x d (2x) ==
r , 3 3x , 3 sin 4x . sin 2x sin3 2x . ~
=“+16 Sln 2л + 16+“-64-+-16---------48~+C=
___5x j sin 2x sin8 2x t 3 sin 4x
~~ lir 4	48 ‘	64
7)	J cos 5л cos 3x dx = -~ J (cos 8x4- cos 2x) dx-=?
s=y J cos 8л dx4-y У cos 2x dx =
» Jg I cos 8л d (8x) 4- J \ cos 2x d (2x) =——|---h C;
8)	J sin 4x sin lx dx = ~ J (cos 3x—cos llx) dx =
s=y J coS 3x dx—J cos llxdx =
If	1 C .. .4 sin3x sin I lx . ~
=— \ cos3xd(3x)-~я* \ cos llx d (Hr) =—%—.----------|~C;
9)	У cos 8x sin 5x dx « ~ J (sin I lx—sin 3x) dx »
==-— J sin llx dx—J sin 3xdx =
= -gl sin llxd(llx) — sin 3xrf(3x) =------1-------g-|-C;
10)	J cos 2x sin 3x cos 4x dx=y J (sin 5x4-sin x) c°s ^x dx=
=4* J (sin 5x cos 4x4“ 81° A cos M dx =
s=-l J (Sin 9x4- sin x4- sin 5x—sin 3x) 4x=®
__— cos 9x cos x cos 5x t cos 3x .
“~	36	4	20	12
11)	J cos3 x sin2 x dx = J cos2 x sin2 x cos x dx~
(1 —sin2 x) sin2 x d sin x==
= C sin2 rd sin x— Csin4 xdsinx=-2li-i—^i-i.4-C;
J	J	do’
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
523
12)	j sin3 х cos4 х dx = cos4 х sin2 х sin х dx =
= — J cos4 x (1 — cos2 x) d cos x=
P	R'	C 4 J cos7x cos5x , ~
= \ cos6 x d cos x— \ cos4 x d cos x=—=--—=---1- C;
13)	J cos x5 sin3 x dx = cos5 x sin2 x sin x dx =»
= — J cos5 x (1 — cos2 x) d cos x =
P _	p _	cos8 X COS6 X . л
= \ cos7xdcosx — \ cos5xdcosx =-----------%---
J	J	8	6	‘
14)	J cos5 x sin3 x dx = J (sin x cos x)3 cos2 x dx =
= ~ f sin32x (14-cos 2x) dx~
IO J
1 p	Ip
s=7£ \ sin3 2x dx4-7£ \ sin3 2x cos 2x dx ==
lo J	lb J
s=X C sin22xsin2xd(2x)4-4> C sin32xdsin 2x =
оЛ j	J
=— 35 J (1 — COS2 2x) d cos 2x+- ~^2--=
cos 2x , cos3 2x । sin4 2x . r
~~	32 “* 96	1 128~+ ’
icx С д 3 a л p/14-cos2x\2 1 —cos2x,
15)	\ cos4 x sin2 x dx= \ ( —5—-J  ---------dx =
=-g- J (14-cos 2x—cos22x—cos3 2x) dx =
“=4 Ji^ Jcos %x d $x)—£T
IP	X	1
~7H \ cos2 2x cos 2x d (2x) = -3“4"7Z sin 2x —
10 J	О	10
11	IP
—1 -jg- x — -gj- sin 4x-* -j-g- \ (1 — sin2 2x) d (sin 2x) =
x sin 4x . sin3 x . r
~~16	64 + 48 + *
ЗАДАНИЕ 14
Проверить вычисления:
С xdx — 1 с^+о
' J 14-^а— 2 t
2) Cxe*2"3dx=
j-^+T-4-l"^+n+C;
>1 Je^-M(x2-3)=ye^-s+C;
524
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
3) x cos (2 —x2) dx —
~~2~ sin (2—x2) + C;
xdx 1 P dx2 1	.	9 , ~
1 +xs ~"2J 1-H*2)2- 2 arctgX +C:
arctg3 x , C x ч j *	1 t
dx=j arctg3 x d arctg x—— arctg4 x-\-C\
dx	P d In x	. .,	. .
---— \ ------= ln In x 4-C;
X n X J Inx 1	‘ ‘
sin (In х) d In x — —~ cos (In x)4-C;
. P sin x dx 0 d cos x . . _ . , n
gxdx= \--------— — \---------==— In cos x H-C;
J COS X J cos X	1	’ ‘
, , P cos x dx P d sin x < . . . , „
tgxdx— \ —: = \  ==ln sinx +C;
s J sm x	J sin x 1	11
dx P dx C dtg x . . .	. . _
-------~= i ------- = i =in tg x 4-C;
sm x cos x J tg x cos2 x J tg x
d
dx _ 1 f dx __P	2	_
sinx 2 J . x x J. x 9 x ~~
sin у COS у tg у COS2 у
K
io\ C __ C dx _____________1 C____________a*_________~~
' J cos x J sin (л/‘/ — x) 2 J sin (л/4—x/2) cos {я/4—x/2)~“
_ P ^(n/4—x/2)	___ P d tg (л/4 —x/2) ___
“~J tg (л/4 — x/2) cos2 (л/4—x/2)J tg (л/4 —x/2)
==— In | tg (л/4 —x/2) ] 4-C;
13)	J sin3 x dx = J sin2 x sin x dx — — J (1 — cos2 x) d cos x ==
, cos3x ,
= — cos x4--------pC;
u
14)	J cos3 x dx = J cos2 x cos x dx — (1 — sin2 x) d sin x =
= sin x — (sin3 x)/3 4- C;
15)	J cos5 x dx = J cos4 x cos x dx = (1 — sin2 x)2 d sin x ==
P	2	1
: \ (1 — 2 sin? x+sin4 x)d sin x = sin sin3 x4~-g- sin6 x4~C<
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
525
ЗАДАНИЕ 15
Проверить вычисления:
1)	f хех dx — f xdex — xex— t ех dx — xex—ex-\-C\
2)	\ x2exdx — \ х2 dex—x2ex— \ exdx2 — х2ех — 2 \ хех dx —
— х2ех — 2 J х dex — х2ех—2 хех — J ех dx ) = х2ех — 2хех-\-2ех-\-С\
3)	J х cos х dx = J х d sin x — x sin x — sin x dx—
— x sin % + cos х+Ф
4)	J xa cos x dx — J x2 d sin x = x2 sin x — J sin x dx2 =
— x2 sin x—2 J x sin x dx — x2 sin x-|-2 x d cos x —
= x2 sinx-f-2 ^x cos x— ^cos x dx^—x2 sin x-j-2x cos x—2sinx-НФ
5)	J x sin x dx — — x d cos x—— ^x cos x— cos x dx^ —
— — X cos X-f-Sin х+Ф
6)	J x2 sin x dx — — Jx2 d cos x = — (x2 cos x— J cos x dx2) =»
==— x2 cos x+2 J x cos x dx=s —x2 cosx-J-2 J x d sinx^
=— x2 cos x+2 ^x sin x— J sin x dx) =
ee— X2 COS x4*2x sinx + 2 cosx + C;
7)	Jin xdx=x In x—Jx d In x = x In x —Jx-i-dx=»xlnx—х+Ф
8)	J x lnxdx«y J lnxdx2==y ^x2 In x—J x2 dln x)=®
=yX2 In x —J x2idx==yx2 In x —-^-Jx dx=-~-x2lnx—-|-х2+Ф
9)	J arctgxdx==xarctgx—- J xdarctgx==
= X arotg X—§ x	dx=x arctg *—у	"
= x arctg x—у In (xa4- 1)4-C;
10)	J x arctg x dx = у J arctg x dx* =
arctgx — J x*Y^x?dx} ~T x2arctg* —	14-^Г1
=y X* arctg X—У J	—[7^) dz=y *2 arctS x-"4
4-y arctgx+C;
526
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
11)	arcsinxdx=xarcsinх—^xdarcsinx =
s Г 1	: I 1 Cd(l—X2)
= x arcsin x — | x.?---- dx = x arcsin x -Ьтг I.
J / 1 —x2	2 J К 1—x3
= xarcsin x-f-у (1—x2)~*/2d(l—x2) =
— x arcsin x + (l — x2)1/2 + C = x arcsin x+K 1 — x2-|-C.
ЗАДАНИЕ 16
Доказать, используя метод интегрирования по частям, фор-
мулу (а > 0)
С	х/'а2—х2 а2 , х . п
| У а2 — х2 dx=—-—тг-----и- arcsin-kC
J r	2	2 a 1
и проверить вычисления:
1) j V~4—^dx=X	2 arcsin -g-+C;
nx Г ----s , xfll—x2 11	. x lz>
2) J у 11—x2dx==—------yarcsinp=4-C;
-5j	x/13—x2 13	, x
x2dx= ——й--------7Г- arcsin -7г—-
2	2	j/-13
—5 x Ktg22-x2 tg2 2
*— X UX —
X
arcsin j^+C;
2
log2z7 5—-x2dx=
2
Iog2V75 . x
"^“arCSine 7 8
6) J Vsin2 11— x^dx
x Y sin2 11—x2
2
sin2 11	x
------— arcsin —n-
2	sin 11
18—6x—x2rfx=
7) J Y3-x-^dx
:J=Jr27-(x+3)2 dx =y=-f/(3 К 3)2-(x+3)2d(x+3)=
_(x4-3)/(3/l)a-(x+3)2	27	x+3
2 К 6	2/6 3K 3
8) j Кб —(x+4)2dx = J /5—(x4-4)2 d(x+4) =
_(x+4) Гб-(x+4)2 5
P=------g--------у arcsin 4-C;
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
527
9)	$ V11— (х—5)adx== j V11— (х—5)ad(x—5) =
(х—5) КП—(х—5)а	11	, х—5 .'
2	2	К П
10)	J К10—6х—xadx=J К19—(x+3)ad(x+3) =
= (x + 3)K193xW	Ю	х±3
2	2	К19
11)	J К11 + 4Х—xadx=K15—(х—2)М(х—2) =
(х—2) К15—(х—2)а	15	, х—2 , „
—---—------------77- arcsin -т=4-С*
2	к 15
2
ЗАДАНИЕ 17
Найти:
1) J (2x4-3) dx; 2) J (х2—3x4-5) dx;
d) j (i—x)‘xax; 4) j ^-1-^8—J“x;
5) f(V*+—)dx; 6) И--~2*Г-Лх; 7) f(4—e*)dx;
8) J(2*+28*+28*)dx; 9) J — dx;
10) § (2 sin x—3 cos x) dx; 11) J cos8 dx;
191 C dx	131 C	in С й
1 ' J sinaxcos8x: ’ J 5xa+7’	' J 3xa—4’
15) f - **	; 16) f ...4*.17)
J К2x8+1	J КЗх8—4	J К2—5xa
f x4 .	(*xa+3 ,	(* dx
18) J T+^dx‘ 19) J 1— x*dX< 20) J x*4-2xa—3-
ЗАДАНИЕ 18
Найти:
1) J (2x3—3x8+6x—6) dx; 2) J (1 — x) (1 — 2x) dx;
3)	C fla-21^x; 4) C *)!ах-
f J \*2	J X 5 * 7
5) C	dx; 6) f (e8*-
J у x	J
P	P / O^X \
7) I 2*.3*<5*dx; 8) I 2—)dx;
2-3*) die;
528
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
ч
sin2 х—4 cos2 х
sin х— 2 cos x
dx\ 10)
sin2 dx\
P cos 2x . . 1оч C d* , P
11) \ . о о dX) 12) \ n q . o , 13) \
f J sin2 x cos2 x zJ2x2+3 J
dx
5x2—7 ’
14) f z.....- ; 15) f
J / l+3x2 J К1—Зх2
18>)т=т^ l9>
20)
<1 f 1 *’’** X^
; 16) f /-if?.......
J / 2x2—5
Jdx
x4+x2—6’
ЗАДАНИЕ 19
Найти:
i) J 2^’з * %) §sin $X dXf 3) J (1—*)7
4)	Cx(l—2x)Bdx; 5) f	6)	,
J	J V x —1	J x4-t-x-|-l
7\ C dx • Я1 C dx • 01 C (£±_Ll^ •
’ J 2x2 + 4x—7 ’ 1 J Ц-2х-х2 ’ ’ J x2+1 ’
J9r*—\	Г	___
^3^411) JxKl-xMx;
P	Pl dx	C dx
12) I cos3xdx; 13) I sin—22; 14) 1
t)	X X	J X 1 "
sin X ,
—----5— dx\
1 + COS2 X
dx
(l+x)K x’
19)
X	f
J^L-. 22)
(x4 + l)7’
4x—ldx' 24)
dx (
; 20) *
X in X 7 J
* dx t
sin x *
C dx
ЗАДАНИЕ 20
Найти:
1) j 1 %) j cos7xdx; 3) \ (x + 3)udx;
4) Г x (2x—3)8dx; 5) Cx2Kl— xdx; 6) C u ;
J	J	J Хл -“* X -f- 1
7) [--Aa—
J K2X2—x+6
10) jx/TT*5^; 11) jsln«xdxi 12) f cos X (
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
529
Г x2dx .. f dx 1С. Г .
13) * -г-"."" A-; 14 |	; 15) I ctg xdx;
J»‘ + 4 J	J
,Сч Г C0S * dX  171 CKlnxdx. |S, f dx
lb> J 4 + sin2X ’	’ J ----x--’	’ J x In x In (In x) *
19) fx^’dx; 20) C **£*  ; 21) C ;
J	J (x3 + 2)3 J cos x
ЗАДАНИЕ 21
Применяя формулу интегрирования по частям, найтщ
1) Jln(x+l)dx; 2) ^х In xdx; 3) ^A~*dx;
4) i x sin x dx; 5) \ x cos2 x dx; 6) \ . — dx*
J	J	J srn^x
7) J ex cos x dx; 8)	К x2— 4 dx;
9) C V^—x2dx\ 10) f arccos xdx.
ЗАДАНИЕ 22
Применяя формулу интегрирования по частям, найти*!
1) Jlnxdx; 2) J х In (х + 1) dx-, 3) хЗх dx\
4) ^xcosxdx; 5) yxsin2xdx; 6) J
7) § ex sin x dx; 8)	К x2 4- 3 dx;
9) C y~5 ~x*dx; 10) ( arcsin xdx.
ЗАДАНИЕ 23
Найти:
x2 x dx; 2) cos x Ksin x dx; 3)
dx; 8) j -
ГЧЧ C
e^«l
530
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
ЗАДАНИЕ 24
Найти:
х2 £
sin2 х cos6 х
dx
2ех — 1 ,
3e*+ldx:
х2
dx
-х2)8/2 ’
С cos2x -
3) \ ...... dx\
' J sin4 х
dx
ЗАДАНИЕ 25
Применяя формулу Ньютона—Лейбница, найти:
2	0	л
1) J (2х—x^dx; 2) С (2i/'x—\)dx-, 3) fsinaydjc|
1-1	о
1/2	3
f dx r\ Г dx
J : J l~*4 5
-1/2	2
Л/2
J cos^xdx;
о
0
4
9) b(x)dx, где fW = K’ £
J	I Z, X > UJ
0
10) Г | 1 — x \ dx.
о
ЗАДАНИЕ 26
Применяя формулу Ньютона «-Лейбница, найти!
1	2	_	_
0	f(*4-2x*)dx;	2)	J	х—	x)dx;
о	-1
л/2	У"з
3)	j	cos^dxi	4)	j
0	i/Vs
Iogs3	2
5) $ (5»4-5-*)?d*; 6) ^(КТ+4х)Чя}
log! 2	1
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	531
О
7) J х(1 + х)1(Чх;
— I
5
9) J f (х) dx, где
2
3
10)	2 — x\dx.
о
л/3
8) J sin3 х dx;
о
( 0, х<0,
f (х) = { *+1, 0 < х<3,
2х, 3 < х;
ЗАДАНИЕ 27
Применяя формулу интегрирования по частям, найти:
2	л/2	1
1) J In xdx; 2) J х cos xdx; 3) хе~*х dx;
10	о
Л/4	1
4) J arctg х dx; 5) J ex cos x dx;
о	о
1	2
6) J arccos x dx; 7) J x3 In x dx.
о	1
ЗАДАНИЕ 28
Применяя формулу интегрирования по частям, найти:
1	л	1
1) J In (1 + х) dx; 2) ^х sin xdx; 3) J arcsin xdx;
о	oo
In 5	л/4
4) J xe~x dx; 5) J xarctg xdx;
о	о
2	л/4
6) J x2 In x dx; 7) J arcctg x dx,
1	о
ЗАДАНИЕ 29
Применяя указанную замену переменной, найти:
У“з	2
11	'-=,; Чтйт'
1	1
3/2
3) С ,4x+X dx, z-2 = /;
' J (х—2)3
1
532
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
4)
5)
6)
л/2
J sin2 х cos х dx, sin x —
о
Л/2
cos5 x sin x dx, cos2 x —1\
о
1
f x2 dx
i ..-a ... ,	x = 2 sin t; 7)
J K4-x«
0
л/4
1/2
dx
х — iQ-
8)
9)
C ______dx
J 3 sin x + cos x ’	2	’
0
in 8
f dx x .
I —7^==r, ex=xt\
J /14-е*
1/2 r_______
Г к 1 -x2 .
1 Xs ^X-
1
1/з
ЗАДАНИЕ 30
Применяя указанную замену
1/2	1
1) \ xts=ti 2) (
переменной, найти:
x dx
/5^1%
5 —4я = /;
3)
л/2
\ cos4 х sin х dx, cos x = t\
4)
5)
7)
л/2
J sin3 x cos x dx, sin x»i\
о
In 5	2
J eX=t> 6)
In 3	0
3	•	л/4
\ x2 К9—x2 dx, x=3sin/; 8)
dx . x _____
6-3 cos я’ ь
9)
з
С dx
2
/==T: l0) f r-d^T7=- ’ x=i*-
x J x+v x
ЗАДАНИЕ 31
Найти площадь фигуры, ограниченной графиком функции
и прямыми:
1)
х=1, х —4, #=0;
X
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
533
2)	у = 2х2--|-1, г/“О, х =—1, х=1;
3)	^=2 1^ х, 6—’£/ = 0, х = 0;
4)	у~ \(х, у~х, х = 2;
5)	у — 3х, х ——1, х = 3, $ = 0;
х
6)	г/=sin-у, х = — л, х —2л, # = 0;
о
7)	0=—L_( y==Qt х = 0, х=Д;
* cos2 х *	4
8)	y=V^+-i=, х = 2, х=3, y=0't
Г х
9)	у = х*—2х2+5, у=1, х=0, х=1;
,П1	— х2-|-Зх—1	, о _
Ю) у=-----------, х= 1, х = 2, 0=0.
ЗАДАНИЕ 32
Найти площадь фигуры, ограниченной графиком функция
прямыми:
1)
2)
3)
4)
5)
6)
#=xs 6 7, r/ —8, x = 0;
^ = 4x —x2, r/ = 0, T x==2;
y=/"x, 0=2—X, 0=0;
£ = 9/x,	x = 9, y~Q\
у = ех; y~®, x = 2;
(X	X \ %
stoy+cosyj , x = 0,
7)	0=(x—2) КЗх^Л, x=l/3, ;
1
8)	{/==-5-7-7лТ» X = 0, Х = ЗЛ,
1 *	cos2(x/9)	’
9)	f/ = x4*—10x2+9, x = 0, r/ = 0;
10)	^=l/x, r/ = 0, x = 0,5, x==2,5.
Л>
x=-g-» f/==0j
№=5/3, r/ = Oj
, //=0;
ЗАДАНИЕ 33
Найти площадь фигуры, ограниченной графиками функций
1)
2)
3)
4)
^=x2 и y=x+2;
^~x2—*2x + 3 и y=Зх—1;
y=x2 и ^=14-~x2;
y^2/x и y^—x/2—^-;
6x2*~x4	-
---g--и ^=1;
5)
6) 0 = Х3 И y=V"x-,
7) y=sin-^- и 0=х3;
534	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
8)	^ = Jcos2 х (l-|-sina х), xg[0; 2л], и # = 0;
9)	У= * 4~^Х । и 0=7—| х |;
10)	у=4-^-.р-|- и 0=1—*+21.
ЗАДАНИЕ 34
Найти площадь фигуры, ограниченной графиками функций:
1)	у—х2-—х и #=3х;
2)	#=~х2—2х+4 и #==10—-х;
3)	#=х2 и #=2х—х2;
4)	#=3/х и #=4—х;
5)	#=х2 и у=2 Y2х;
.6) #=х2 и #=jZ х;
7)	#=cosx, х£[—л; л/4], и #=1-|-2х/л;
8)	# = 4sln? х (1 + cos2 х), х(£[—л; л], и #=0;
9)	#=2 —|2—х| и #=3/| хI;
Ю) #=6/|х+Ц и #=3-|3-х|.
ЗАДАНИЕ 35
1.	Найти площадь фигуры, заданной неравенством:
1)	|0|4-у<КТ+ГЙ; 2) |^+х2-2|<2(х+(/).
2.	Найти площадь фигуры, ограниченной графиком функции:
1)	# = о,5х2—2х+2 и касательными к графику этой функ-
ции в точках (1; 1/2) и (4; 2);
2)	# = х2—х+2 и касательной к графику функции # =
= 1пх4-3 в точке (1; 3).
3.	Найти площадь фигуры, ограниченной графиками функ-
ций # = tgx, # = sinx и прямыми х = — л/3, х = л/4.
4.	Фигура ограничена графиком функции #=(х+3)2 и
прямыми х = 0, #~0. Под какими углами к оси ОХ надо про-
вести две прямые через точку (0; 9), чтобы они разбили фигуру
на три равновеликие части?
ЗАДАНИЕ 36
1. Найти площадь фигуры, заданной неравенством;
1) 10|4-4<е-,хЬ 2) я«4-0а<2(|х|+|0|).
2. Найти площадь фигуры, ограниченной графиком функции
1)	#== —16—х2 и Касательными к этой параболе, прове-
денными из начала координат;
2)	#=cosx, xg[0; л/2], касательной к графику этой функ-
ции в точке (л/4;	2/2) и прямыми х = 0, # = 0.
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	535
3.	Найти площадь фигуры, ограниченной графиками функ-
ций ^=cosx, fz=ctgx и прямыми х=л/6, х=Зл/4.
4.	Фигура ограничена графиком функции ^=|sin-~-|
и прямыми #=0, х=—1. Под какими углами к оси ОХ надо
провести прямые через точку (0; 0), чтобы они разбили фигуру
на три равновеликие части?
У пражнения
1. Вычислить определенные интегралы как пределы интег-
ральных сумм:
Ъ	6	1	л/2
1) J sin х dx; 2) J xk dx; 3) J e* dx; 4) J cos x dx;
а	а	о	о
1	Л/2
6)	C(x3+x)dx; 6) j f sinx—dx,
о	о
2. Доказать, что последовательность {an},
предел, и найти его, если:
n(~N, имеет
о
2)
_____1_._____1_,	j_________1_.
«+1 ' я4-2 ‘ *** ‘ п^п *
I3 , 23 .____, (4д—I)3
a* п* /г4	+	/г4	’
ап~~ я2+1-	п2 + 22
п .
/г2 + /г2 ’
4)
б)
6)
7)
8)
9)
10)	“»==^гг(’а+2“+«>• + «“). а>-1.
536	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
3.	Найти сумму:
2> 4-^+ус«+4с',+-,-+7Т2 с";
С) с’-|си-~С3п-...+(-1)'’-^СЙ;
л . 2л ,	, - тл
4)	cos— cos —+ ••• + cos	•
4.	Доказать, что:
I
1)	J(2/ —1)9е'-‘2Л = 0;
О
3)
5)
7)
8)
9)
л/8	1	1
j x6sin7xdx = 0; 4) J ecosxdx==2 eCQSX dx’t
-л/8	-1	0
2л	Л
J sin3 x dx— 0;	6) \ cos6 x dx » 0;
о	0
1/2
I cosx In|i^dx==0|
J 1*—x
-1/2
4	1
C (1 —x)m x” dx	x” (1 —X)” dx=
о	0
л/2
\ cos* xcos (n+2)xdx»=0, ngN;
Я/2
tl *“ 1	(*
10)	/„=—при n>2, вели /„= \ sinnxdx|
П)
13)
15)
16)
1	__ Л
J yf x2sin6xdx==0; 12) J arctg (cos x)dx=0j
2	io
C x2—l	. л	(*	Inx . л
J VtW ' 1 > J T+^dx ;
1/2 Г	0,1
1
-1
C	17) {^Ш-dx ="ln2.
J l + cosax	4	' J IH-x3 8
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	537
5» Доказать, что:
1
8) C / 1 + x2 К x3+ ldx<4
Л/2	2
1)	< j sin10 х dx < -2-; 2) 2 < J 2*s dx < 16?
л/4	I
e	3
3) g < C dx <e • -i)	1 < f dx < ъ
1 3 J lnx+2 2 ’	'	6 J 1 + x—2x2	13’
2
1	2
P	sin x	,	2	3	f 4*	,	AQ
j	7+TodJC<9 ; 6)T<	J 7djc<48;
-I	1/2
_ < I dx___________< 2.
25 J (x2-~4x + 8)2	16*
1
1
; 9)j	j/yi
0
л
P -________ 9тг5
10)	i x2 К sin x dx<—g- ;
3
2 P
11)	J K(14-x3)sinxdx<2n+-2^-;
0
12> 1 < f	13) | <^-**^<11
о	0
1	20
14)	sin 1 < J< 2sin 1; 15) J	1
-1	10	,
1
1 Г xpx	2
!6) -g- < J yr==== dx < 3	;
0
2H	Л/2
17)	J sta(xs)dx>0; 18) 0,7 < I sin(x2)dx < 1,8)
0	0
«/3 _
19)	f _______dx _ > K3.
J cos2 x К 3+sin x 2
20)	-i ln22 < Г dx < 4ln2*
**	v * *T* **
0
538
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
5
21)
t)	О	I и
О
6.	Какое из чисел больше:
1)
2)
3)
4)
6)
7)
9)
1 1
J е~х sin xdx или J е~х* sin х dx}
Q	О
1 1
J х2 sin2 х dx или х sin2 х dx;
о	о '
л
J е“*2 cos2 х dx
л
С sin х .
I	•" dx
J i/x2 + 2
о
2л
или J е~** cos2 dx;
л
1
л _ч С cosx .	1
или ; 5) J 2jp-a- dx или У 2;
I
р рХ dx	1
j(7+W^-nT(e-l);
О
1 1
~ или С ---------; 8) f х2а~*2 dx или ~ ;
6 J 4_Х2_%8 J	3
о	о
3	2
J arotg х dx или J arcctg х dx?
-2	-з
7.	Упростить выражение:
1)	sin Зх cos8 х + cos Зх sin3 х;
2)	tgx-Mg (х—~)+tg	;
\ О /	\ о /
3
3)	sin Зх sin8 х+cos Зх cos3 х — - j- cos 2х;
4)	1 **3 (sin4 х + cos4 х)+2 (sin6 х+cos6 х);
5)	tgx+ tg(x+^)+tg (x+^)+tg	;
S)	-4-+.....r+..........-Л-У
sin2 x’ 19/ , л \ ‘ 19/ я \
sin2 x+-^- sin2 I x~-y ]
\	3 /	\ о /
8.	Доказать тождество:
arccos	, x 0,
V1 + X*
1)	arctg x=<	.
arccos

ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	539
2) arctg х=<
4 1
arcctg у
х > О,
х < 0;
3) arcsin у—
х
arccos -7==- = 0,
4)	4arctg	— 2arcsin х = л, |x| < 1;
2х
5)	arcsin --~-j--2-s=2 arctg x, | x | «С1;
6)	2arctgx+arcsin-j-q~^-==n;, x> 1
9. Найти:

И x У xdx\
X2 )
4) J К*А+д~А+£_	5) J(5^—2^)2 dxt
6) J —7) J --s^ -dx;
8) J Кl-sin2xrfx, *g(O; л/2); 9)
10) C sta2 ; П) Casiri fx+-dx-, 12) ? -? . dxf
7 J 1—cosx 7 J- \ 1 4/	7 J x2—4
13) J tg4 x dx-, 14) J ctg2 X dx-, 15) J ;^2_щх2_3)~ =
1C. P dx	P l+2x2 .	1O4 PKl— x*
16) \ 7 I Л a I о ; I7) \ "a7i—i-57 dx'> I8) \	.™z.d*.
7 J x4+4x2 + 3 J x3(l + *2) J KP?
10. Найти:
n C (x + 3)dx .
J(x+2)(x-l)‘
f (2 + x)dx
—5x
3) J (3*4-5)ndx;
; 6) C x У1—3xdx;
O4 P2x —3 ,
xdx> 8> |jqT4^;
x2rfx;
x+2
~5-1--7^dx\
x2—4x+7
f—Д=г; 1
J X у In X
sin2 x cos 3xdx;
2x—3
, —.„dx;
' x2+4
f xdx .
} J 1+x4 ’
P dx
|x(2+lnx);
640	ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
18) (* sin х sin 4х dx; 19) f —sin Y x dx; 20) fsin2xdx;
J	J V x	J
21) J (sin я4-3 cos x)2 dx; 22) ex sin ex dx;
23)	24) C—l-K-dx;
J sin2 7x J cos 3x
25) C —--; 26) C —----------dx.
J ;sin x 4- cos x J 14- cos к
И. Найти:
1) Cx2 У 2— xdx; 2) C—.......... dx; 3) C sin3 x ?/cos x dx;
J	J к1—x2 J	и
il j	<-v	С 1	.	C	sin2 x .
---т— dx;	5)	\ -—7— dx;	6)	\	—s- dx;
cos4x	f	J sin4x	J	cos6x
7) f —; 8) f *-.r ;
J e*/2 + e* J V 1+e^
«) p(2-w>,/,*i W) j	____
11) C	; 12) C ^l~~--dx; 13) f ** dx-.
J /4-x2 J *	J *
'=>ЧтгйтГ
9ГГЧ f ^X	104 C ^X	1m C l~“X7	,
17) |	; 18) i —т-о~7-пг * l9) | —77—;—dx;
J l + f/l + x J x (*3+ 2) J
f* y2 - | I	p	y2 „ I, t
J л^Н-l dx’ 21) J х^х2 + 1 dxi
(Xa+1)2 ; 23) J (1 4-х2)3/3,
12. Найти:
n J	In2 x dx; 2) p	:2 In (14-x) dx; 3) \	arci g xd x;
4) J	. arcctg x dx; 5)	У x In	6) J x arctg x dx;
D j	1 x arcsin x dx; 8) \ sin (In x) dx; 9)		J x2 sin 2x dx;
10)	P arosinx . \		— dx; J x2	11) J x2arccosxdx;	
12)	J arctg VHdx;	13) e2x sin2 x dx;	14) x2e^2x dx;
15)	^x3e^x2dx; 16)	fxln^i^dx; 17 J	1 —x	) X ^x»
18)	J x sin У~х dx;	19) J x arccos — dx;	P x^ 20) J (14-x2)2 dx'
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
541
х* In^-idjc+C,
/n£Nj
13.	Доказать, что:
1)	С xk 1п/л х dx^7-^—r х^+х 1п^ Х—7~~~г
J	&+1	&+1
fcgR, 1,
оч Р _	. , dsin bx-\-a cos bx „„ , ~
2)	\ е* * cos bx dx —-, , 9-----еах 4- С;
а2~^Ь2
a sin bx — aeosbx „v , „
eax + о >
*ах sin bx dx =
а2 -|- b2
х
' dx
(х2 -]- а2)п+1 2па2 (х2 + а2)п
. 2п — 1 1 Р dx
"* 2п "о2" J (х2 +а2)«

 = — —	I— x24-
/1— X*	M
m — l f xm~2 ,	„
-4----I —dx-\-C, m^2,
m J
и/rv , / т MZZV<2Sin6x—bzosbx
xneax sin bx dx == xneax-r r ---
a2-{-b2
.9^r9 C xn^leax cos bx dx+O.
a2+b2J
mgN;
па
a* + b*
4л
8) J x sign (sin x) dxi
0
x < 0,
0<x<l,
1 < x;
14. Найти:
2	9 * * * * 14	/— «
1	4
Л/3	1/2	$
3) J stay cos-J dx; 4) j Kb=2idx; 5) С урД
л/6	0	x
2л	л/2
6) J sin3 x dx\ 7) J cos6 * * x dx;
о	о
C	( *•
9) \ f(x)dx, где — i 2x,
-2	( 5,
3	100л
1°) J 11*1 — •И-*"* И) J Г 1—cos2xdxj
-1/2	0
Л	1
12)fsta4 *xdx; 13) f
J	J	x24-x+l
о	-i
14) Jt/2
\ sin x sin 2x sin 3x dx;
0
542
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
2
15)	J [ex]dx, где [а] — целая часть числа а.
о
15.	Найти:
1
1)	J х (1 + #)5 dx, 1Н-х —/;
О
л/2
2)	sin5 х cos4 х dx, cos x = t\
о
Л/2
3)	J sin2 x cos3 x dx, sinx = /;
о
Уз"
C dx . .
4)	\ ———— , tg/ = x;
j Kd+xa)«
a
5)	|Gz2—x2 dx, x~as\nt\
a
6)	J x2 К a2 —x2 dx, x — a cos t\
о
ln2
7)	J yT^Adx, ex —1=42;
o
3/4
8)	C -----^=-, —гт=«5
J (x4-1)	1	*+l
2л
9)	C	igjL — t
}J3 + cosx' S2"r‘
0
16.	Доказать, что если функция f(x) непрерывна на от
резке интегрирования, то:
Л/2	л/2
1)	\ f (sin х) dx= \ f (cos х) dx;
о	о
Л	л	л/2
2)	\ xf (sin х) dx= \ f (sin х) dx = я \ f (sin х) dx;
о	оо
1 1 1
3)	С f (х) dx= j f(l—x) dx== J f(l + ^) dx;
оо	о
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
543
1 1
4)	J х3/ (х1 2) 4.x=— J xf (х) dx;
о	о
1 1
5)	J cos f (х2) dx » 2 J cos xf (x2) dx;
-i	о
i
6)	J sinx/(cos x)dx==0;
— 1
л/2	'	л/2
7)	J f (sin 2x) cos x dx= J f (cos2 x) cos x dx*
о	о
17	» Доказать, что если функция /(х) непрерывна на всей
числовой прямой и является нечетной функцией, то для лю-
бого числа а, а > 0, имеет место равенство
%	— X
р (t) dt = р (/) dt.
а	—а
18.	Доказать, что если функция / (х) непрерывна, возрас-
тает и выпукла вниз на отрезке [а; Ь], то
ь
(Ь— а)	< р (Х) ах <	/ (6).
а
19.	Найти:
в	2л	е
1)	J х2 In2 х dx; 2) J х2 cos x dx; 3) J | In x | dx;
I	о	i/e
1	1	e2
4) p arctg2 x dx; 5) J arcsin2 x dx; 6) J cos (In x) dxj
о	-1	e
л/3	л	л
7) \	8) f (xsin x)2dx; 9) CT dx;
1 J sin2 x ' J f	J 1 + cos2 x
Л/4	0	0
C	/—~
10) \ arcsin 1/ т-J— dx.
J	Г I ~r X
0
20.	Доказать справедливость равенства (m,
л/2	л/2
1) C sin^ xdx=^^—^ Г sin^-2xdx;
J	mJ
0	0
Л/2	Л/2
2) C cos®dx=--™-"- C cos®xdx;
а	о
544
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Я/2
3) f
(2л — 1) (2п—3)...3«1 я
2п (2п—2) . . 4	"2 ;
4)
о
Л/2
С * 2п+1 j	2п (2л —2).. .4-2
\ sin2"+1 dx—-^—гтт7п—Нт---гг5
J	(2п4-1)(2л — ]).. .3-1
О
Л/2	Л/2	1
5)	\ cos" х sin пх dx = — —[- I cos"”1- x sin xdx ;
J	2 n * J
0	(o	)
Л/2
АЧ V n * A 1	/2 , 22, 28	t 2"
6)	j cos" x sin nx dx =	( y4—g—|—y + --H—~
о
Л/2
7)	J cos" x cos nx dx = 7^73-;
0
Л/2
8)	\ cos'" x cos (m 4-2) x dx = 0;
b
л/2
9)	\ cos"2 xsin (m4-2)xdx=—r-r
J	tn 4-1
0
Л/2
10)	\ sin'" x cos (m + 2) x dx =
О
. ntn
Sin -g-
m-\- 1
cos
11)	J sinxsin(m4-2)xdx	.
0
21.	Найти площадь фигуры, ограниченной графиками функ-
ций и прямыми:
1)	# = 3x4-18-—х2, у = 0;
2)	у — х2, у~^, х^З;
х2
3)	У^-2---*+2, У==Х9 Х==0;
4)	# = 2(1—х), 0=1—х2, х = 0;
5)	0 = х2, 0=2—х, 0 = 0;
6)	0 = 4(х—2), 0 = (х —I)2, 0 = 0;
7)	^~х24-1, 0=4—2х, 0 = 0, х = 0;
8)	0 = 2—х2, 0=1—х, 0 = 0, х = 0;
9)	0 = х24-2, 0=1—х2, х=0, х=1;
10)	0=х8—Зх2-«-9х4-1> ^ё[°1+00)> У — fy
11)	0 = cosx, 0=0, х=Зл/4, х=—л/4;
12)	0=—х\ y=^2ext х = 0, х=«1;
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
645
13)	р = 4/х2, х=1, у~х—\\
14)	£/=1/х, х=1, х = 2, £/ = 0;
15)	£/ = 5/х, £/ = 6 —х, х — 6;
л ..
17)	у=У 4 — Зх, //=0;
18)	^/ = sinx, xg[0; я], £/ = 0;
19)	y = sin6x, у—®, x = 0, х==л;
20)	у = 8 sin4 x + 4 cos 2x, xg[0; л], // = 0.
22.	Найти площадь фигуры, ограниченной графиками
функций:
1)	^==14-х2, z/=2;	2) £/ = —х24-2, £/ = х~|-2;
3) £/==х, £/==2х—х2;	4) £/ = 7х—2х2, £/ = 7/2—х;
5) у = х2—2x-j-2, £/=2 + 4х —х2;
6) /у=х2, £/ = Зх + 4;	7) £/=х2/4, £/ = 3—х;
8) £/ = х2—2х + 3, у~4—2х;
9) £/ = х4, у^Ух\ 10) £/ = 5—х, р = 6/х.
23.	Найти площадь фигуры, задаваемой неравенствами:
1)	4^х2 + ^<2(|х| + |г/|); 2) \у | + 2 | х | <х2 +1.
24.	Найти площадь фигуры, ограниченной графиком функ-
ции:
1)	£/ = 2х2 — 8х, касательной к этому графику в точке (2;—8)
и осью ординат;
2)	£/ = х2 + 10 и касательными к этому графику, проведен-
ными из точки (0; 1);
3)	^==х2—2х + 2> касательной к этому графику в точке
(0; 2) и прямой х=1;
4)	£/=1/х, касательной к этому графику в точке (2; 1/2) и
прямой х = 1;
5)	у^езх касательной к этому графику в точке (0; 1) и
прямой х = 3;
6)	£/=arcsinx и прямыми t/=9, х = 0, х=1/2;
7)	у = 1п (1Н-х) и прямыми у = х, х = 2;
8)	^=^, £/=1пх и прямыми £/ =—1, х = 0, х=1.	<
25.	Прямая, проходящая через точку (1/2; 1), образует с
положительными полуосями координат треугольник. Найти
минимальное значение площади треугольника.
26.	В какой точке графика функции £/ = х24-1 надо про-
вести касательную, чтобы она отсекала от фигуры, образуемой
графиком этой функции и прямыми £/ = 0, х = 0, х=1, трапе-
цию наибольшей площади?
27.	В какой точке графика функции #=1/х надо провести
касательную, чтобы она отсекала от фигура, образуемой гра-
фиком этой функции и прямыми £/ = 0, х=И, х = 2, трапецию
наибольшей площади?
28.	Найти значение р, р < 0, при котором площадь фигу-
ры, образуемой параболой г/ = (1+р2)2 я2 + Р и прямой у — $,
была бы наибольшей.
29.	Найти наименьшее значение площади фигуры, ограни-
ченной параболой £/ = х2 + 2х—3 и прямой y =
18 Задачи по математике. Начала анализа
546
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
30.	Найти площадь
венств:
фигуры, задаваемой системой нера-
1)
3)
у<х4>1,
х sin (пу),
х «С 2;
у < 14-х2,
1—X2,
<	р<х4-1,
р>—1+*.
к— 1 <х< 1;
у arccos х,
< р^О,
у arcsin х,
1;
4) farcctgx^p,
«J arctg х < у,
V х^ 1.
31.	Найти площадь криволинейной трапеции, ограничен
ной параболой у — х?~{-Ьх-\-с и касательными р=4х—13, у~
=—4x4-3, проведенными к этой параболе.
32.	Через данную точку (х0; у$), лежащую внутри пара-
болы р=х2, провести прямую, отсекающую от внутренности
параболы сегмент наименьшей площади, и найти эту площадь.
33.	Пусть f(х) = х24-рх4-^ и f(x)>0, a^x^b, Дока-
зать, что
ъ
p(x)dx=l(ft-a)(/(«)+H&)+4f (^)).
а
34.	Две прямые, пересекающиеся в точке А, касаются па-
раболы р —х2 в точках В и С. Доказать, что площадь криво-
линейного треугольника АВС, ограниченного дугой, параболы
ВС и отрезками АВ и АС, равна АВ • AC-sin ВАС),
35.	Доказать, что если функция f(x) имеет непрерывную
вторую производную /" (х) на отрезке [а; Ь], то
ъ
J xf” (х) dx = (&/' (&) — /(&)) —(а/' (а) — f (а)).
а
36.	Доказать, что функции
X	X
. 1) J sin6 х dx; 2) J cos1A x dx
0	0
являются периодическими.
37.	Доказать, что если функция f(x) непрерывна на про-
межутке [0;4-°°) и /(») = «> то
Х->+00
1
lim \f(nx)dx=a.
"-**» о
38.	Доказать, что отношение площадей подобных криво-
линейных трапеций равно квадрату коэффициента подобия.
ГЛ. 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ	547
39.	Доказать, что площадь эллипса с полуосями а и b
равна nab.
40.	Доказать, что если функции f (х) и g{x) непрерывны
и обе являются или возрастающими, или убывающими на
отрезке [а; 6] то
ь
р (X) g (х) dx SS
а
/ b
J /(x) dx
\a
41.	Доказать, что:
2) lim
X	\2
J et2 dt
2_____L
^e^di
0
x
3)	lim e-x2\e&dt = ^
X -> co J
0
Г
4)	lim *- ? sin (ax) sin(ftx) dx = 0, |a|^|ft|.
T J
42.	Доказать, что если функция f(x) непрерывна
ется возрастающей на отрезке [а; Ь], то
и явля-
ft
(b—a)f(a) < f(x}dx < (ft—a) f (b).
а
43.	Пусть функция f (х) непрерывна на отрезке [a; ft] и
ft]. Доказать, что если
ft
J f (x)dx = 0, то f(x)^Q.
а
44.	Доказать, что если функция f(x) непрерывна на
[0; +оо) и lim f (х) = 1, то
а
lim —{f(t)dt = O.
а ->+ с» а J
0
45.	Пусть функция f (х) дифференцируема на отрезке [<2;ft],
f' (х) является непрерывной функцией на [a; ft] и, кроме того,
/(1)—/(0) = 1. Доказать, что
1
С (/' (х))2 dx 1.
о
18*
548
ГЛ, 6. ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
46. Доказать, что если функция f(x) непрерывна на от-
резке [а; 6], то:
1) lim
я -> <ю
2) lim
<ю
3) lim
п -> со
\0	/
f(x)>0, х£[а\ &J.
47* Доказать, что если р (.х) —* многочлен степени п и
ь
J х&р (х) dx«= 0, & = (), 1, 4.., /г —1,
а
то все его корни простые и принадлежат отрезку [а; &).
48. Доказать, что если для непрерывной на (—оо; 4~оо)
функции / (0 имеет место тождество
х+1
J /(Z)J/a»0, х(£(—со; + оо),
х
то функция /(х) периодическая*
ОТВЕТЫ И УКАЗАНИЯ
ГЛАВА 1 •
§ i
ЗАДАНИЕ 1
1. 2, 5, 8, И, 14, 17, 20. 2. —И, —9, —7, —5, —3. 3. #3 = 0.
4,	. 5s #4=5, #6 = 7, #i0=ll,
ЗАДАНИЕ 2
L —3, — 1, 1, 3, 5, 7. 2« — 13, —10, —7, —4, —1. 3. #4 = 0.
4.	5. а5 = 7, а2 = 4; а9=11. 6. 4.
О
ЗАДАНИЕ 3
1. #5=11. 2. CL§ — #2 + 3d, #lo = #2*4~3^> #100 = #2 ~Ь ^8^. 3« 450.
4. 332. 5. #г = 29, #17=30,6. 6. #х=1, ^=0,5.
ЗАДАНИЕ 4
1. clq = #3-f-3d, #2оо—#зЧ- 197<i. 2. #g = —4. 3. 45. 4. 199.
5. #1 = 1,1, #21 = 3,1. 6. #х=1, d = 0,5.
ЗАДАНИЕ 5
1	2	2
1. #2 — 3 у , #з — 3 у , #6 = 4-у . 2. #А = — 1, d=%, 3. #i = 3,
J = 3 или #i = — 9, d — 3. 4. Нет. 5. 1665.
ЗАДАНИЕ 6
1	3
1. ад—] — , #4—.	#б = 2. 2. #1= — 2, d = 3. 3. #i = 3,
d = —1,5 или #i=— 1,5, d=l,5. 4, Нет. 5. 55 350.
Упражнения
1. 1) #n = 5—10(n—1); 2) #rt = —3 + 3(n —1); 3) #„ = 6 +
-J-3(#— 1). 2. 1) #i =— 23, rf = 3; 2) #1з=34i 3) #io=lj 4) #13 = 3;
5) #1+#20-50; 6) #i=10; 7) n = 18; 8) d = —1; 9) #i = —70,
d=5; 10) aS4o = 324O; 11) S2O = 320; 12) #t = 14, rf = —3 или
#i = 2, d = 3; 13) #i = 2, d = 2 или #i = 22, rf = —2; 14) n = 6;
15) #ь =—й; 16) Sao=lOO; 17) #л = —1 — (fi—* 1);> 18)	—
= l+2(n—1); 19) Si2=129 или $i2 = — 69; 20) $ю=100;
21) S8=100; 22) $ie=1488; 23) #i = 4, d=6; 24) #1=—1, d = 4;
25) #i0 = 55; 26) #i = 4, d = 8; 27) #i = 2, rf = 4; 28) #7=13.
3. 1) ”	2) n(«+l); 3) na; 4) *lre+6 ; 5) 494 550;
An	A
550
ОТВЕТЫ И УКАЗАНИЯ
6) 165 150; 7) 329 400; 8) 1620; 9) 25 100; 10) 5050. 4. 1) нет;
2) нет; 3) нет; 4) да. 5. 9, И, 13. 6. 9, 11, 13, 15. 7. ^ = 5, <1 = 4.
8. 135, 630, 765. 9. ai = 0,5, d=0,5. 10. <1=7. 11. 0,1, 0,2, 0,3,
0,4 или 0,4, 0,3, 0,2, 0,1. 12. 20, 18, 16, 14, 12, 10, 8, 6, 4, 2,
0, —2, —4, —6, —8, —10, —12. 13. а„=—2,5 + («—1).
14. с—рациональное число. 15. 1) Не могут; 2) 4567.
16.	1) х = 7; 2) х = 55; 3)	х=1.	17. 25. 18.	—А, —ЦрС-L
It.	4ра = 25?. 20^ Да:	За,	4а, 5а.	21. 3:5:7.	22. 2(f6—1) см,
2 V 6 см, 2(/6+1)	см.	23. 3,	5, 7, или 4,	5, 6, или 5, 5, 5.
24.	а„=1+2(й —1).	25.	1) 0,	1, 161-72	V 5; 2) у(2* + 1),
(- 1)*+*эт/6+лЛ, k&Z; 3) log25; 4) n/2+nk, — 1)*л/6+лА,
5) 10, 2. 26. 1) Да; 2) да; 3) не всегда, например ап =
~Ьп~п, 4) не всегда, например ап~ — 6 + п— 1; 5) не всегда,
например an~nt Z?rt = n+1. 27. 3, 9, 15. 28. Числа, содержащие
16^4-4 троек, где & = 0, 1, 2, ... 29. -*1, 0, 1, 2. 30. (p-q)a-{-
+	*р)<з = 0. 31. 6, 6, 6, 6 или 10, 14, 18, 22 или
14, 70, 126, 182 или 0, 144, 288, 432. 32. $„ = —1. 33. ап =
~ at (2п—1), где произвольное число. 49. 2rt~;L («1 + ап+1).
50. Указание. Использовать равенство 2Сп = Сп~
§ 2
ЗАДАНИЕ 1
1. 2, 1, 1/2, 1/4, 1/8, 1/16. 2. 2, 3, 9, 27. 3. 1024. 4. *4=6,
*5=3, *9 = 3/16 ИЛИ *4 = —6, *в = 3, *9 = 3/16. 5.*4 = 62^,*,=*29в,
*25 = Ы28> ьк—ь*<г~*.
ЗАДАНИЕ 2
1. 1/2, 1, 2, 4. 2. 1, 2, 4, 8, 16. 3. 8. 4. *$=4, *в=1, *8 = 1/8
ИЛИ *й —— 4, *6 = —1, *9=1/8. 5. *В = *87~, *17 = *з714» *37=*37*+
**=*зГ~9-
ЗАДАНИЕ 3
1. 1) 1/128; 2) *£=*17==—1; 3) *1=1, <7 = 2 или *,=— 1,
?=—2. 2. *а=1/2, &з=1/4, *6=1/16, *5=1/32. 3. *1 = 2, ?=2.
4. Нет.
ЗАДАНИЕ 4
1. 1) 1/48; 2) *1=2, *9 = 2; 3) *1=1, 7=3 или *1=1, 7=—3.
2. *2=1/18, *а= 1/12, *4=1/8, *5=3/16, *в=9/32 или *2=— 1/18,
*=1/12, *=—1/8,| *5=3/16, *в=—9/32. 3. *i=l, 7=3. 4. Нет.
ЗАДАНИЕ 6
1. 93. 2. —21. 8. 1. 4. 5.
ЗАДАНИЕ 6
1. 3g. 2. 21 j. 3. 65. 4. 6.
ОТВЕТЫ И УКАЗАНИЯ
551
Упражнения
1. 1) д2==2; 2) <7=3/2; 3) &б=72; 4) 67 = 1/1458; 5)	= 405;
6) bi — 2,5; 7) ^8 = 21,87; 8) q — 2 или fl —-—3; 9) fl—2; 10)_&6— 1;
11) 6i3 = 100; 12) 632 = 32; 13). 67=5/3; 14) Ьц= У12/144;
15) S4 = 468; 16) Se = 31,5; 17) 6f = l/75; 18) n = 4; 19) S12=15;
20) 6t = 2, 7=5 или 61=50, ?=l/5; 21) Se=—728; 22) q=V 2;
23) 6i = 2; 24) 67=8/~2; 25) n=7; 26) q=V"2; 27) « = 6;
28) 6„ = 9; 29) 6t = 128; 30) n=5; 31) 7=1/3 или q=—4/3;
32) 6s = 3/"2 или 63 = 4К'2+2Кб; 33) 6, = 2 или 6i = 32;
34) 7=3 или <7=—3/4; 35) 6,= l/3; 36) S, = 80; 37) 6i = 2,
A==3; 38) Z>f=10, fl —2 или bi — 40, fl—1/2; 39) Sn —
—Ь	; 40> &i=1’ Ч=5 или &i = 25 <7=1/5;
у b— у a
41) &f=2, fl —2 или —8, fl—1/2; 42) 6f=l, fl—3; 43) Z?i = l,
7=2, n=6; 44) 62=6; 45) 626s = 8; 46) /626a= 4 V"2; 47) 6Х = 5,
6g=640; 48) ra=10; 49) 68=729; 50) 6f=3, 7=2 или61=12,
m~n Г nP~n
q<=l/2; 51) 62 = 45 или 62=— 175; 52) 6p = 1/	;
53) *2 = 36; 54) n = 6; 55) S5 = 31/96; 56) S6=121 или S6=ll
2. Sn =	7”2- 4* Указание. > У aYa3.
5. *6 = 243 или &6 = —243. 6. 18 446 744 073 709 551 615 зерен,
т. е. 18 квинтиллионов 446 квадриллионов 744 триллиона 73 мил-
лиарда (биллиона) 709 миллионов 551 тысяча 615 зерен. 7. 1) Не
всегда, например, {2п+2п} и {2П+3П}; 2) не всегда, например,
{2П—2^~х} и {3rt—’2й); 3) да; 4) да; 5) да. 8. а± — а2 — а3 0.
10. 1) Нет; 2) могут, например, bi — 18, fl=2/3, 62 = 8, ^ = 64/27;
14-1^*5
3) могут: fl— у 4~5* ’ 4) нет. 11. Могут: q— у —.
12. я/6, л/4, л/3. 13. 1) %——1; 2) {± У (— I)™*1 л/64-л/п,
ы ^2-^п+2 b^b^	t
 '(в—*)(!—«) (а—6)(1—6)’ ' ха«(ха—1)	+
4-2/1. 15.	= г —2. 16. 1) {л$; л/124-л£; 5л/124-л&, k£7}\
2) x = log25. 17. Неизвестные являются членами геометрической
. Q	1 -о lx 2(Ю^1—10)-9л
прогрессии с Xi — 8 и fl —y* 8*	------81— -----’
2) 7(10”+t~~!.9).z2”, 19, 66... 67. 23. а = 2, 6= 32. 38. 931.
о!	---,т-п.'
п-1 цифра
39. 6, = 4, 6а = 8, 6, = 16 или 6,=4/25, 62=—16/25, 63=64/25.
40. 1) 7=2/5; 2) <7=3/2; 3) 7=3/2; 4) 7=3/2; 5) 7=3; 6) 7=3,
d=4; 7) 7 + <1=6; 8) 64 = 3/2 или 6, = 24; 9) 6в= 128; 10) 6,+64=
= 130; 11) в!+бв=2060; 12) 6*+&8= 109-|-; 13) 68-)-а8=0;
552
ОТВЕТЫ И УКАЗАНИЯ
14)п=10; 15) п = 4; 16) я = 20; 17) п = 8 илип=11; 18) Slo=200;
19) Sis=135; 20) 64=1; 21) ав=105, 68 = 256; 22) &, = 27;
23)М+«з9=288; 24) as+&8= 118; 43. Л„+1В„+1=2-«(64-а)—а;
44. ,а„=1 + 3.2«-1.
§ з
ЗАДАНИЕ 1
1. 1) 1, 8, 27, 64, 125, 216; 2) 1, 0, —1, 0, 1, 0;
3. 4, 5, 6; 4) 1, 2, 1/3, 4, 1/5, 6; 5) 1, 3/2, 16/9, 125/64,
16 807/7776; 6) 1, 3, 6, 10, 15, 21. 2. 1) 1, 1, 1, 1, 1; 2)
(—Пи+1
1, 1/2; 3) 1, 1, 2, 4, 8. 3. 1) п2/«1; 2)	; 3)
4)
Л. sin (2лп/3—л/3); Б)
3) 1, 2,
1296/64,
1, 2, 2,
пЧ-1
п
ЗАДАНИЕ 2
1. 1) 1/3, 1/4, 1/5, 1/6, 1/7; 2) —1, —1, 1, 1, —1; 3) 0, 0,
0, 0, 0; 4) 1/2, 2/3, 3/4, 4/5, 5/6;. 5) 1, 1/2, 1/6, 1/24, 1/120;
6) 2/3, 8/15, 16/35, 128/315, 256/653. 2. 1) 1, 2, 3, 4, 5, 6; 2) 2,
_б 41 3281 21523361	926 510094 425921	2в_х
4 ’ 40 ’ 3280 ’ 21523360 ’ 926510094 425 920 ‘	4	’
2) 3tL r~; 3) (- 1)""х	: 4) 3(- 1)и+1; 5) (- l)«+M-«n.
п~г 1	У п
ЗАДАНИЕ 3
4. 1) Не является монотонной; 2) возрастает; 3) не является
монотонной; 4) убывает.
ЗАДАНИЕ 4
4. 1) Не является монотонной; 2) убывает; 3) не является
монотонной.
ЗАДАНИЕ 5
5. Например: 1) ад = 3п-—л2; 2)	; 3) ап~пcos^~.
ЗАДАНИЕ b
4. 1) Ограниченная; 2) не является ограниченной (ограни-
чена снизу); 3) не является ограниченной (ограничена снизу);
4) не является ограниченной (ограничена снизу). 5. Может быть
любой. Например, если —я, Ьп~— 2п, то ап-}-Ьп~—п не
является ограниченной; если ад = л, Ьп — 2—п, то ап^-Ьп = 2
ограниченная.
ЗАДАНИЕ 7
/	1 \
1. 1)	; 2)	3) 2-2»-». 2. 1) «в = 3;
\	6=1	/
2) а.» 1/6. 3. 1) а4=—9; 2) аа = 4,5. 5. 1) Sa=-^- ; 2) S„ =
ОТВЕТЫ И УКАЗАНИЯ
553
ЗАДАНИЕ 8
1. 1) аа^+2^	..; 2)	; 3) -!((«+*) <2«~Ч>
+ (6—2а) (—!)«). 2. 1) «3 = 5/64; 2) «3 = 9/8. 3. 1) a5 = logh —
-3 logs5; 2) «8=1,48/3. 5. 1) 3„=|	) ; 2) 3„-
_ 1 / 1 1 \
8 \3-7 (4л + 3)(4л+7) ) ’
Упражнения
1. 1)	2)(«-»)/«. 2) «+(-!)«; 3)
х(_	4)	5) 3” + (—1)«;
” х
Зп—1 Х
6> >
Х(_1)л<«+1)/2. 2. 1) ап = -~; 2) ап= 17-3”-1-10-2"
3 ' .	_	2-5»-1	_з.2«-1-2
о) «л— 2.4п-1_1 • 4) °’’- 8-3'1-1—7-5n-i ’	an~~3-2n-i —I *
6) а„=2-2*-«; 7) а„ = 2«-2-(- 1)«; 8) ая=Рп~1+(~	;
У
9w + X  11" 3
9) ап —--------О-------- • 8* «37 = 1, «1967 = V2. 4. «90 =— L
О
«885=1- 5. 1) 1/1224; 2) 1226. 7, 1) Возрастающая; 2) возрас-
тающая; 3) убывающая; 4) не является монотонной; 5) невозрас-
тающая; 6) возрастающая; 7) не является монотонной; 8) не
является монотонной. 14. 1) «2 = 7/2; 2) «2==1б; 3) «1 = 5/4; 4) та-
кого нет; 5) «хо=1/2О; 6) «3 = 9/8; 7) «7 = 48/11; 8) а1 = ]/' 2-~1.
15. 1) «2= «з =— 5; 2) «1о = 2О; 3) «3=—2; 4) «1 = 2 У 2;
9	9	8
5) такого нет; 6) «6 = — 3^; 7) «4=— 1	; 8) «3 = -§-.
16. Указание. Рассмотреть последовательности: 1) ап — п
и 6д = «4-2, «„ = « и 6„ = 2—п, «„ = «+— и Ьп~ —ап~п
1	(___пк
И Ьп~ — 2п----, ап = п+~--— и 6» = —-п; 2) «Л = 2л и 6п=п,
ti	а
ап~2п и Ьп = 3п, ап = — п и Ьп = — 2«, «Л = 3л и bn = 3nf
ап~}/п и Ьп = п, ап~п и 6Л=1/п, ап — п и bn~n— 1, ап =
(________п»
—	и бд==п2. з) ад==Л и bn=nt ап~п и Ьп=1/п,
,	. , «	о . К ( 2nt n — 2kt
ап^п и ^= 1/«а, «П = п—3 и &Л = п—5, а„=< 2n—1, я=2£-~1,
и У//ом~?12Г2Ь 4) вге = П и /’»=1/п> а« = п и
1 if	ib —— Лгь 1 }
аЛ = 1/« и &П=1/У п, ап = п и =	«„ = <	—Jt пж=2^«1,
_ J —1, « = 2^,
и а~\ 2п, в=й«1.
554
ОТВЕТЫ И УКАЗАНИЯ
17. Указание. Рассмотреть последовательности: 1) ап=п
и *„=(—1)и/п, я„ = /г и Ьп—-^ (— 1)и+х, ап—п и &„ = — « +
+ (—1)й+»; 2) а„=л и &„ = (—1)«+*/п.	« и	l)n+1,
J —Зп/2, п = 2/г,
оя=п и 6n=« + (—1) , ап — п и Ьп — | _зп/2+2, n = 2k— 1;
3) а„=л и &„=1 + (-!)»/«. а„=(3+(-1)«)/2 и &„ =
j 2+4(2<п-2>/2-1), n=2k,	4) а =и и йи==(3+(—1)»у/2,
I !+4(2(м)/2-1),л = 2^-1;
«.-»»».-{;Л"ц°--" ° '’•>=<’зд- >
1, 8/7» 1» 12/11, 1, 17/16, 1, ...}. 21. 1) Нет (ограничена снизу);
2) нет; 3) да; 4) да; 5) да; 6) да; 7) да; 8) нет (ограничена
снизу); 9) да; 10) да; И) да; 12) да; 13) нет; 14) да; 15) да;
16) нет. 24. Например, ап = п+1/п и 6п = п. 25. Например,
ап ---п + 1/п и =— л. 26. Рассмотреть последовательности:
а^^Л/п п bn — n; ап~1/п* и Z>w==l/n. 28. Например, аЛ = п(~1)П.
чл n h (п +1) (п + 2) t	п (п+1) (п + 2) (п + 3) л
30. 1) Ьп-----, 2)	-------Ь27з1	9
3) 6й==п2; 4) Ьп^п2 (п+1); 5) Ьп = п3; 6) Ьп~п+ 7) Z>w =
„»("+‘)<»уН» + 3> (» + <>. 8) „п==2.„,; 9)
1*а*О*тс*О	П “р* 1
1	окййГ 1
«® »"-тя+т: п> ‘--зтя+зГ 12>
,3) Z'“°="2(n+l)(n+2) ’ 14) &п== 8(4п+3)(4п+7) ’ 15) Ьа~
-1	. 161 ft -	-1
“3(п+1)(»+2)(л+3) ’	' п 4(n+l)(n4-2)(n+3)(n + 4)’
17) «>„=(«+ 1)1
32. Указание. Рассматривая разность
(m+l)k^^mk+l^Ck+imk+Ck+ifnk^+Ck+itn^2+.+ 1
и полагая т=0г 1, п, получаем равенства
l^+^l,
3*+1—2й+1=Сд+12*+С^+124-*+... -j-1,
(n+ l)k+l-»4ik+l^Ck+1nll+Cl+ink-1+... +1.
Складывая почленно эти равенства, имеем
(л-f-l)^+is»C^+iS^-JrCl+iS^ 1-J~... 4-Gfe+i$? -)-яН-1.
Эта рекуррентная формула позволяет вычислить сумму Sn, если
известны предыдущие суммы Sht	Положив в ней
ОТВЕТЫ И УКАЗАНИЯ
555
Ы1, получим (п+1)2 = 25п+п + 1, откуда Sh =	.
Затем, положив в ней k = 2, найдем Sn и т. д.
§4
ЗАДАНИЕ 1
1. Например: 1) яЛ = 5,1 + W, Ъп — 5,1 4- 1/п2; 2) лй = 0,1 +
4-0,1» ^ = 0,099...9. 2. Например: 1) М = 9; 2) W=24; 3) /V=999.
3. Например: 1) A/ = [l/3e] 4-1; 2) N = [2/814-1; 3) A = [1/8]+!;
4) Af = [l/8]+5; 5) A/ = [l/e]+ 1.
ЗАДАНИЕ 2
3	(_3	/_пя
L 1) Например, 47ff=y+v — и ^„=xy+-A_£—> 2) Ha’
. (л—3,14)(—1)"	,
пример, ап = л+—------------- и bn есть последовательность,
ДЛЯ которой: &£=1, &2 = 2> ^ + 1 = ^2/г + Ь ^ + 2 = ^ + 2,
2, .... где Pzk+i равно половине периметра вписанного в ок-
ружность радиуса /? = 1 правильного (26 + 1)-угольника, a Pzk+z
равно половине периметра описанного вокруг-окружности ра-
диуса #=1 правильного (2/? +2)-угольника. 2. Например:
1) W=5; 2) Л/ == 100; 3) W = 200. 3. Например: 1) W = [l/8] + l;
2) W = [l/e]-|-l; 3) JV = [l/e]4-l; 4) ^ = [2//”ё] +1; 5) W=
= [5/«]+1.
ЗАДАНИЕ 3
2 П3 | 2_.2)П~'2 -3) L -1)77 1 7^
‘ 1 2 +у з ’ ’у з+2 ’ 7 (/3+1) ’ 2^ + 4/з )•
3. 1) 2; 2) —2; 3) 0; 4) 1/2; 5) 0; 6) 0; 7) 0; 8) 1/7, 4. Да, на-
пример «п=-^рр.
ЗАДАНИЕ 4
2. 1) 1/2; 2) 5/6; 3) —1/4; 4) 3-1. 3. 1) /1; 2) —3/2; 3) 0;
4) 1/3;5) 0; 6) 0; 7) 0; 8) 2. 4. Нет, например ап~—1/п, Ьп—\/п.
ЗАДАНИЕ 5
2. Существует такое 8 > 0, что для любого N найдется
«б > N такое, что | аПоА |	8. 4. Например, «„ = (•—l)n + 1.
6. 1) Нет, например ап=1/п> Ьп = п2\ 2) нет, например, ап =
= (—1)”/П, б„ = п. 6. 0.
ЗАДАНИЕ 6
2. Какое бы число А не взять, существует 8 > 0 такое, что
для любого N найдется /ц > N, что 1аПо — А | ^8. 3. Например:
1) ап = (— 1)п/п2; 2) ап — 2-(— 1)”. 4. 1) Нет, например ай=1/п,
^д=1/п2; 2) нет» например = (—!)"/«» ^д=1/п, 5. 0.
656
ОТВЕТЫ И УКАЗАНИЯ
ЗАДАНИЕ 7
2. 1) 0; 2) 0; 3) 0; 4) 0; 5) 0; 6) 0; 7) 0; 8) 1/2. 4. 1) 1;
8) 1/3; 3) 1/5; 4) 0; 5) .0; 6) 0.
ЗАДАНИЕ 8
1. 1) 0; 2) 0; 3) 0; 4) 0; 5) 0; 6) 0. 3. 1) 1/5; 2) 0; 3) 0; 4) 0;
5) 0; 6) 1/2; 7) 0; 8) 1.
ЗАДАНИЕ 9
1. 1) —6; 2) 28. 2. 1) 4/9; 2) 37/30; 3) 1907/4500. 3. Напри-
мер: 1) ап — п3/2; 2) ап~-—п? —	3) ап — n cos ли.
ЗАДАНИЕ 10
L 1) 8/9; 2) —4/3. 2. 1) 109/90; 2) —647/900; 3) 23/99.
3. Например: I) ап—]^п-1~2; 2) ап -=— log2 л; 3) ап—п sin (л/2-|-лп).
6. 1) Да; 2) нет, например ап ~	1^?z.
ЗАДАНИЕ 12
2. 1) 1; 2)	; 3) 1;з. /‘а, 1,732. 4. 1) е3/2; 2) е~2;
3) е; 4) е~2/6; 5) 0; 6) 1.
ЗАДАНИЕ 13
2. 1) 1/2; 2) 1; 3) 2. 3. 2,080. 4. 1) в2; 2)	3) 1; 4) е~™\
5) 16; 6) е2.
Упражнения
5. 1) 1/2; 2) 3; 3) /г; 4) 5/2; 5) 3; 6) 1/2; 7) 32; 8) 3. 7. 1) 2/3;
2) 0; 3) 0; 4) 1/2; 5) —5/9; 6) —1/4, 7) 0; 8) 1; 9) 1/5; 10) 1;
И) 3/5; 12) 1/2; 13) 1; 14) —1; 15) —1/2; 16) /"§; 17) 0; 18) 1/2;
19) 2/3; 20) —1; 21) 1; 22) 0; 23) 0; 24) 5; 25) (2/3)5; 26) —16/25;
27) 1/3; 28) 0. 9. 1) 1; 2) 1/2; 3) —2/5; 4) 16/21; 5) 0; 6) 1/5;
7) —1; 8) 0; 9) 0; 10) 1; 11) 0; 12) 1; 13) 3; 14) 1; 15) log2 9/4/log212;
16) 0. 10. 1) 0; 2) 9; 3) 1; 4) 1/2; 5) 2; 6) 1/5; 7) 3/4; 8) 0; 9) 1/2;
10) 1; 11) 2/3; 12) 3/2; 13) 1/4. 11. 1) Да; 2) да; 3) нет. 15. Нет,
например, = (—4)". 16. Нет, например, ап = (--1)п. 20. 1) Нет;
2) нет. 21. 1) нет; 2) да; 3) нет. 22. Нет, например, ап—\/п\
Ьп~ц(— 1)и. 23.Нет,например,	—.
24. Например: I) ап=; 2) а„ =
- -W-O-.	:	3) п,_2±Ь1)1, Р._
=	.	27. Нет, например ага=И-|-------, a^V п.
*	ti
28. 1) 2; 2) 0; 3) 2; 4) 1; 5) J+^13 . 29. 1) 2,236; 2) 1,59; 3) 1,97.
30. 1) в2; 2) е"1/3; 3) 0; 4) е; 5) е~\ 6) а"3; 7) е-1; 8) 0.
31. 1) 8/3J 2) 9/4; 3) -5/2; 4) -27/8.	32. 1) 1 ^; 2)^;
loU ои
ОТВЕТЫ И УКАЗАНИЯ
557
5 *	7
3) —то; 4) 21-7=-. 35. 1) Да, например а„=1/п2, Ьп~п\ 2) да,
1о	тЮ
например а„ = (—1)"/п;	=	3) да, например ай=1/п,	=
4) да, например art = 2/n; Ьп~п. 36. 1) Нет, например ап ==
/_____(_______________________________1)п4-1
=   —— п\ 2) нет, например, ап—±—/г2. 37. Напри-
мер: 1) а„ = л2, Ьп — п\ 2) ал = п2,	=	38. Например: 1) а„=
= 1/п, Ьп~ 1/п2*, 2) ал=1/п2, 6л=1/я. 39. 1) Нет; 2) нет; 3) нет.
ГЛАВА 2
§ 1
ЗАДАНИЕ I
1. 1) у——5х; 2) у=±х-, 3)	4; 4) z/ = —-g-x-f-2.
2. 1) j/ = -4-x2; 2) y=>3x\ 3) у = 2х24-1; у =
6) 0 = 1х24-3х—2; 6) £/=—Зх2 —2x4-10. 3. 1) (3/2; 4]; 2) (—3;
□
-2/31; 3) (-7; 4); 4) /о; —^=.1(1 [8; 4-оо).
\ 4^2 J
ЗАДАНИЕ 2
1. I)j=-jx; 2) у=3х-, 3) у = 2x4-3; 4)^=-2х-1.
2. 1) у—^-х*-, 2) д=— 2х2; 3)	х«—5; 4) у=>— 4х2-|-2;
5) 0 = 2х24-х4-3; 6) у=х2—3x4-2.
U ---j4—; +«); 2) (0; 1);
U 2‘V а; -g-)u(l; 2V 2].
3. 1)
3) (-2; 2)!	4)(0;1)и
о и
ЗАДАНИЕ 3
1. У (0) = 1, у(1) = 1/2, //(—3) == 1/10. 2. 1) X3; 2) х2—2х4-1|
3) 1/х2; 4) cos2x; 5) 2х2; 6) х4; 7) | х |; 8) х4; 9)-^—.
3. 1) —оо < х < + °о> ®^У <+°°*> 2) 0«Сх <-J-oo, 0	< 4-°°;
3) —оо < х < + оо, —* оо < # < + оо; 4) —оо <х <0, 0 < х < - - оо,
—оо < z/< 0,	0<i/<4-oo; 5) —оо < х < 4-оо,	0<^<4-оо;
6) —оо < х <4-оо, —7)	—оо< х < +°°, —
8) — n/2 + kn	< х < л/24-&гс? fcgZ,	«-*оо< у < + °°; 9)	<	х	<
<	«—оо < у < 4- оо; 10) —1 ^Х*С 1, —л/2^г/^л/2;
П) — 1 х	I, 0=С^ < я; 12) — оо	< х < 4~ оо> —л/2 < у	< л/2.
4. Например:	1) ^=угх«^14“К	2)	|/^х2-^х4	—	;
658
ОТВЕТЫ И УКАЗАНИЯ
3) y=V(х-1)(2-х); 4) |/=5; 5) jf=sign(x«); 6) £_=[|*1+П-
5. 1) f (7)=—3, f(0)=l, f (2)=5; 2) у=х\ xg(l; V 2]; 3) у=-х\
xg(—оо; 0); 4) у — 2n4*arcsinxg[—1; 0].
ЗАДАНИЕ 4
1. Н-2)=1/4, у (0)=5, Н1)=3, И3)=5. 2. 1)	—х/(1 —х),
2) 14-1/х;	3) 2х/(1 +2х);	4) 2х+ 1/(х+1);	5) 2x/(x-f-l);
6) (1 х)/(2—х). 3. 1) —оо < х < 0, —оо < у < + 00 J 2) x — 2nk,
k СЕ У:=^	3) —2 х <С + > —1 У 1»	4) 0 х 1,
2;	5) —оо<х<2,	2 < х < 3,	3<х<4-оо,
— 00<^/еС—4, 0<#< + °О;	6) —оо < х < 1,	1 < х < + 00 >
—оо<г/<—1, —1 < у < + оо; 7) —оо < х < О, 0<x<-j~oo,
1 < У <+<», —оо < у <— 1; 8) 0 < х< + оо, 0<^< + oo;9)xgR,
л / -—• /г, у — 1; 10) —оо < х <+°о, —2<^»С2; 11) —оо <х<+оо,
//={—2; 1;3}; 12) —оо < х <+оо, —K# <+оо. 4. 1) f(g(x)) =
=2*2, f(Hx)) = 25 g(f(x)) = 24 g(g(x)) = x*; 2) f(g(x)) = \,
x&O; f(f(x))=x4, x#0; g(f (x)) = l, x 0; g (g(x)) =sign x.
4 z-----------------
5. Например: 1) g== у —x2 (x— I)2 (x — 2)2; 2) g=log2 (x—x2);
3) f/==signx^; 4) g=(x].	6. 1) y=2 при x=5;	2) у —
= (-l + VT+4^/2, x6[3/4; 6];	3) {/=(-1-/ThS)/2,
xg[—1/4; 6]; 4) y=2n—arccosx, xg[cos4; cos5].
Упражнения
1. f(—1/3) =1/9,	/(0)=l,	f(l/2) = 0,	f (4/5) = cos 4я/5.
2. 1) f(l)=l, f(2)=16, f(3) = 1, f (4) = 25;_2) / (1) = 49, / (2)=1,
f (3) = 64, f (4)=4. 3. 1) — oo < x < (—3—/53)/2, (—3—/53)/2<
< x<—5, 4<Cx«Coo;2) —3 < x<0; 3) x=2;4) log67 < x <log23;
5) 1/4 < x«C 1; 6) —4<x <—?r/2, —л/2 < x < я/2, jt/2 < x«c4;
7) xg/?> x 23tk, k^Z; 8) 2/3 < x < 2; 9) 2nk < x < si/2-^2nkt
k^Z\ 10) x=0, x—1, 3Cx<+oo. 4. 1) 0<gsC3/2;
2) (—}<2-1)/2<£<(О-1)/2;3)-оо<0<1;4) 0<y<2;
5)—к_у<1; 6) — 7<y<—1; 7)0<i/<l/4; 8) —/'13<
<y<K13; 9) l<y<2;	10) 1/2<J/<1;	11) 0 < у <+oo;
12) 0 < y< 1; 13) —240<{/<1/4; 14) y=Q. 5. 1) Да; 2) да;
3) да; 4) да; 5) да; 6) да; 7) нет; 8) да; 9) да; 10) да. 6. х2+х+1.
_ тт	n	1	(х—1)(2—х)(2—х),
7. Например: 1) у—	; 2)	—-----У----i
/(х-1)(2-х)	2-х
3) y=Vrl — \x\-, 4) у=У(х—2У(х—х^.	8. 1) f (Х)=Х2+1;
2) f(x)=№—2; 3) f(x)=x; 4) f(x) = 3x2.	11. 1) 0 < х < 1;
2) 0 < х < 1/2; 3) 1 < х < е; 4) 0 < х < я/4. 12. 1) f (f (х)) = f (я);
/ 1	\	Г9
г),(7чч)-1: 3>г(/и>=Ш?<°;
5)	’<0; ®>	1. В. 1>»W-
=/’ь7х2, xg[0; 1]; 2) у’(х)=х2-2х-Ь_2, х£(— оо; +оо).
ОТВЕТЫ И УКАЗАНИЯ
659
14. Да, например
fo(X)*=
V1—х2,
—У^Т^х2,
/1— х2,
*€1-1; 0),
хёЮ; П;
*ё[-1; -1/2],
*€(-1/2; 0],
*€(0; 1];
( У 1—х2, х—рациональное число, xg[—1; 1],
Ге (•«) = <	-----
( —У 1—х2, х—иррациональное число, xg[—1; Ц.
у2_. 1
15. Например: 1) ф(х) = х8; 2) ф(х) = х3р ; 3) <р(х)=»
= (х—1)2+1. 16. Например: 1) f = 2*; 2) / = 2х; 3) f(x)=xj
4) ffx) = lnx. 17. l)/-i(l)=l, f-i(2)=3,/-И(3)=2;2)/-« = 1г7,
xg]l;+oo); 3)/-1=-/x, xg[0; +oo); 4)	+

6)f-x
( 1]< i — 4x2
= <	2x
I	0,
g)	arccos x,
10)
x€(-co; -/ 3).
4)
4x-f?5
3—3x *
7)	xg[l; 6|;
x=0;
|x|<l;	9) f-* = logax, xg[l/4; 16];
xg[l/16; 1/2];	11) f-i = arctgx+«,
«о 2 x	1	.	3	2 »
,8‘ * 3x 3 ‘	2) 1 —x ’ 3) 5x2 ~ 5 X ;
§ 2
ЗАДАНИЕ 1
1. 1) Четная; 2) четная; 3) четная; 4) нечетная; 5) нечетная;
6) нечетная; 7) четная; 8) нечетная; 9) не является ни четной,
ни нечетной; 10) нечетная; 11) четная; 12) не является ни чет-
' ной, ни нечетной. 2. 1) f (x)+g(x) является четной, если сумма
имеет смысл; 2) f(x)—g(x) является четной, если разность имеет
смысл; 3) f(x)g(x) является четной, если произведение имеет
смысл; 4) f(x)g(x) является нечетной, если произведение имеет
о 1ч /ч (1/2)-*+(1/2)*	(1/2)*—(1/2)-*
смысл. 3. 1) ф(х)=^-^—% \ ., -ф(х)=^-^—  f—;
2) <р (х) — 1, г|) (х) — х; 3) ф (х) = х2, ip (х) = 2х;
Ух + З+^З-х t(T) Ух + З-УЗ-х .
4) <р(х) =
2
ЗАДАНИЕ 2
1. 1) f (x)-f-g(x) является нечетной, если сумма имеет смысл;
2) fix) ^g(x) является нечетной, если разность имеет смысл;
3) нет; 4) нечетнаяЛ если произведение имеет смысл, 2. Напри-
560
ОТВЕТЫ И УКАЗАНИЯ
X,
’ 3. 1) Нечетная; 2) четная; 3) нечет-
. ная; 4) нечетная; 6) не является ни четной, ни нечетной; 6) не-
четная; 7) четная; 8) четная; 9) не является ни четной, ни не-
четной; 10) не является ни четной, ни нечетной. 4. 1) <р(х) = х2,
W) = —х\ 2) <р(ж) = -^-у, 1|>(х) = 0; 3) <р(х)=3, ф(х) = 2х;
4) ч
Упражнения
L 1) Четная; 2) не является ни четной, ни нечетной; 3) чет-
ная; 4) четная; 5) нечетная; 6) не является ни четной, ни не-
четной; 8) не является ни четной, ни нечетной; 9) четная; 10) не
является ни четной, ни нечетной; 11) нечетная; 12) четная;
13) нечетная; 14) является четной и нечетной; 15) четная; 16) не
является ни четной, ни нечетной. 2. 1) Мечетная; 2) четная;
3) четная. 4. 1) Да, например, ^(х)—х3; 2) да, например, f (х) =
=—х; 3) нет; 4) да, например, /Дх) = 5.
Г 3 х =6 о	( х
6. 1) Ф(*)-К*	Ф(*) = < 0, х = 0,	2)ф(х)=ш
V *’ X~U’ I 1, х < 0;
1 । ,	# о\ / \ I Х-— 1 I —1~ | X—|— 1 I . .
=-—2-1*1. •ф(*)=у;	3) <p(x)=J---- «у—	- '!’(*) =
-II —|х+1|	..	, . А . , ч , -X	.
=------'2	4) q>(x) = 0, ф(х)=-1—;	5)<р(х) =
= -g : ф(х)=0{ 6)<р(х)=х2, ф(х) = 2х.	7. Например,
/м={_2:
|х|<1,
|х|> I.
12. 1) 1/(х) =
1-Ь
1—»х ’
*е[о; 4-)и(1; +оо),
*€(—оо; 0);
О’
— lgi/з (х + V1 + х*), х < 0,
lgi/г (х 4- V 1-|-х2), х > 0.
§3
задание 1
1.	1) Да; 2) да; 3) нет; 2. 1)' Нет; 2) нет; 3) да. 3. 1) Да;
2)	нет; 3) нет. 4. Например: 1) {/ = — Ух—х2; 2) Vх—х2';
3)	*-• в» 1) Да; 2) да; 3) да; 4) да; 5) нет; 6) нет.
ОТВЕТЫ И УКАЗАНИЯ
561
ЗАДАНИЕ 2
1.	1) Нет; 2) да; 3) нет» 2. 1) Нет; 2) да; 3) цет. 3. 1) Нет;
2) да; 3) нет. 4. Например: 1) i/~|log2x|; 2) у=1—е*; 3) у
«= arctg--. 6. 1) Не является ограниченной, но ограничена
снизу; 2) ограничена; 3) ограничена; 4) ограничена; 5) ограни-
чена; 6) ограничена.
ЗАДАНИЕ 3
1. Для любого положительного числа А существует х0^Х
такое, что |/(х)| > А; 2) для любого числа Л существует xogX
такое, что f (х) > Л; 3) для любого числа Л существует х0^Х
такое, что f (х) < Л. 3. 1) Ограничена снизу, не является огра-
ниченной сверху; 2) ограничена снизу, не является ограничен-
ной сверху; 3) ограничена; 4) ограничена; 5) ограничена;
6) ограничена.
ЗАДАНИЕ 4
1. Необязательно, например, у = х2. 3. 1) Не является огра-
ниченной снизу, ограничена сверху; 2) ограничена; 3) не яв-
ляется ограниченной как сверху, так и снизу; 4) не является
ограниченной как сверху, так и снизу; 5) ограничена; 6) огра-
ничена.
Упражнения
1. 1) Ограничена; 2) ограничена снизу, не является огра-
ниченной сверху; 3) ограничена; 4) ограничена снизу, не яв-
ляется ограниченной сверху; 5) ограничена снизу, не является
ограниченной сверху; 6) ограничена; 7) ограничена; 8) ограни-
чена; 9) ограничена; 10) ограничена; 11) ограничена; 12) огра-
ничена. 3. Например: 1) уж	; 2)y=zl/
у X2	F	I —-X
3) «/=logi/2(x — l) + 10g2x. 4. Например: 1) yi~l/x, y2(x)=xt
xg(0; 1); 2) ^ = 1/х2, z/2(x)==x, xg(0; 1); 3) yt^l/x, y2(x)^x,
y%(x)lyt(x)^x\ xg(0; 1); 4) yi=*l/x, y2 (x)==x, (x)/y2 (x)== 1/x2,
xg(0; 1). 5. Да, например, z/i—x2, y2==x24-1, xg(0; -f-oo). 6. Да,
например, У1=х, y2==l-~x, xg(0; + oo). 8. 1) Нет, например,
/(x) = x, g(x)=—x2, flg^\/x\ 2) нет, например, /(x)=x,
f (x)=x8, flg~\lx\ 3) нет,-например, / (x)=x, g (x)==x4, flg~\jx\
0. Например, f (x) = | x sin x|.
§4
ЗАДАНИЕ 1
1.	1) Да; 2) да; 3) да; 4) нет; 5) нет: 6) нет. 3. 1) На
(—оо; 2] убывает, на [2; -]-оо) убывает; 2) на (—оо; 0) воз-
растает, на (0; + оо) убывает; 3) на [—Зл/8-|-л^; л/84-лй],
&£Z, возрастает, на [л/8 + л&; 5л/8 + ^], k^Zt убывает; 4) на
(ля; л/2+л&], fegZ, убывает, на [л/2+лй; л+зй), k^Zt воз-
растает. 4. Существуют Xi и х2, 0«СХ£<х2«С1, такие, что
я \	\ и	ж	Г *’» *€[0; I], х й 1/2,
/(^i)^/№). Например, функция £/=<0
не является возрастающей на [0; Ц«
562
ОТВЕТЫ И УКАЗАНИЯ
ЗАДАНИЕ 2
2.	1) Нет; 2) да; 3) нет; 4) нет» 4. 1) На (— оо; —1/2) воз*
растает, на (—1/2; 4-оо) убывает; 2) на £л&; -^--{"Л^^, &gZ,
возрастает; 3) на (—оо; —1] убывает, на [— 1; + °0) возрастает;
4) на arccos-pLg-; л/2+у arccos —L=-+ л^^|, &gZ,
убывает, на Г л/2-|-i arccos —^=-+л&; л+4"агосоз —лй! »
|_	2 У 5	2 У 5 J
fcgZ, возрастает; 5) на [2л£-*л/2; 2л& + л/2], fcgZ, возрастает,
на [2л&4-л/2; 2л& + Зл/2], &gZ, убывает; 6) на (—оо; —2]
убывает, на [—2; -|-оо) возрастает» 5. Существуют Xi и х2, хь
x2gM такие, что из неравенства х± < х2 следует неравенство
/(XiXf (х2).
У пражнения
1. Да, например, / (х)— х—х2, g(x) = x-\-x\ 2. Да, напри-
мер, #=sinx можно представить в виде разности двух функций
yi=x+sinx и у%~х.
3.	Например,
. f 4х,	xg[0; 2),	/ ч f Зх,	xg[0; 2),
^~\4х4-4, xg[2; 4],	3x4-3, xg[2; 4],
У (*)=fW -~g(x).
5. 1) На (•—оо; 1/2] убывает, на [1/2, 4~оо) возрастает;
2) на (—оо; —1/2) и на (—1/2; +оо) возрастает; 3) на (— оо;0)
возрастает, на (0; 4~оо) убывает; 4) на (—оо; 0) и на (0; 1]
убывает, на [1; +00) возрастает; 5) на (—оо, —1/4] убывает,
на [—1/4; + оо) возрастает; 6) на (—оо; —5/2] убывает, на
[—5/2; 0] возрастает, на [0; 5/2] убывает, на [5/2; +00) возра-
стает; 7) на (—оо; —1), (—1; 1) и (1; 4~оо) возрастает; 8) на
[—2; + оо) возрастает; У) на [—л/24-л&/2; л/4 + л&/2], #gZ,
[3	3
arcsin	— я/2+> а rcsin р=-- +
4- л/2 + 2л& j J, k g Z, возрастает, на Гarcsin yr— + л/2+2л&;
3	1
arcsin-+Зл/24-2лИ, ^gZ, убывает; 11) на [Зл&; Зл + Злй],
£gZ, убывает; 12) на у (^ + l)j » функция посто-
янная; 13) на [—л/2 + 2л£; л/24-2л&], fcgZ, функция постоян-
ная, на [л/2-р2л/; л-|-2л/], ZgZ, возрастает, на [л-(-2лт;
Зл/24-2л/п], mgZ, убывает; 14) на (—оо; —1) и [0; 1) убывает,
на (—1; 0] и (1; +00) возрастает; 15)на(—оо;—1/2]возрастает,
на [—1/2; + оо) убывает; 16) на [— л/16лАг/2; Зл/16 + л£/2],
fcgZ, убывает, на [—5л/16 + л/п/2; — л/16 + лт/2], mgZ, воз-
растает; 17) на (—оо; — 1] и [1; + оо) возрастает, на [—1; 1]
убывает; 18) на (—оо; 1) и [1; + оо) убывает»
ОТВЕТЫ И УКАЗАНИЯ
563
§ 5
ЗАДАНИЕ 1
1. 1) х =—1/2—локальный максимум; 2) х = 0 и х — 2 — ло-
кальные минимумы; 3) х— 1—нестрогий локальный минимум,
х = 2—нестрогий локальный максимум, на множествах (—оо; 1)
и (2; -j—оо) функция постоянная; 4) х = 0— локальный минимум.
2. 1) */гоах = 9/4 при х—1/2; 2) ymin =—1 прих = 1; 3)j/mx=/2
R	R	R
при х=лД 6gZ, r/min=l при x = n/2-\-nk‘t &gZ; 4) ymsiX~ 1
R	__ R
при х=0; 5) £/т1ц = 0 при х = —1; 6) утах = 2//'3 прих =
_ R	_	R
= (-! + / 3)/2,	2/К 3 при х = (—1—1<“з)/2; 7) г/тах=
R	R
1
arccos ~2=^=
= /’26+1 при х=2л&/3 +------.26, k£Z, — /26
6	R
1
arccos -7=
я . 2nk .	/ 26	49
при X=j-| g—|---------g-----. ^Z; 8) f/max=-g при x =
Q	«Т
= (—1)* arcsin -т~+л&, fcgZ, ymin = 0 при х=-у+2л&, &gZ;
9) #min = 2 при x=0; 10) f/max = l при x=^-, 6gZ, r/min=l/4
R	R	2_______ R
при х = л/4 + л£/2, ZjgZ. 3. Например, y — Vx+l/x. 4. Напри-
мер, #f = x+sin x, г/2 — — x.
ЗАДАНИЕ 2
1. х = 0,— локальный минимум, х ——1 и х= 1—локальные
максимумы; 2) х — — 1—локальный максимум, х = 0 —локаль-
ный минимум; 3) х = 0—локальный минимум, х = — 1/У~2 и
х = 1// 2—локальные максимумы; 4) х = 0 — локальный мини-
— / ”2
мум. 2. 1) Ып = 3/4 при х =—1/2; 2) утЫ = ~——^ ПрИ х =
R	__	R 4+2У 2
= -1~К2,	при х=-1 + Л; 3) уш>п=-4
R 4—2/ 2	R
при х=—л/2 + 2л&, Утах = 0 прих=л/2 + 2л£; 4) у min = 0 при
R	[1; 3]
х=1, у щах — 1прих=3;о'у min =0 при х=л/2+2л/г,
[1; 3]	{(2л£; я+2л/е, 6eZ}
1	3
&£Z; 6) #тш—— 5 при х=—Зл/14+2л&/7 —— arccos , 6gZ,
R	з 
arccos -g-
*/max = 5 при х=л/14+2лй/7—-------, 6gZ; 7) #гаах=2при
R	*	R
x = 2nk, ^gZ, ^min=V2 при x = —л + 2л£, 6gZ; 8) ymin=l
R	R
при 2^x^3; функция не ограничена сверху; 9) у тах =7
564
ОТВЕТЫ И УКАЗАНИЯ
при х=0, у mifl =3 при х=1 и х=—1;
[-1; Ц
х=л&/2, &gZ, #га1п=1/2 при ^=л/44-д^/2,
R
мер, р==х». 4. Например, yt (x) = log2
Уз (х) = log, -j—£j—г.
|«*w»X I Xf
10) Утах**! при
R
6gZ. 3. Напри-
2x
-sin — log2 x(l— x),
ЗАДАНИЕ 3
1. 1) 2^13-, 2) 1/2; 3) 2; 4) 2 4-log, 3; 5) Зл2/4; 6) -5.
2. 1)0; 2) 1/32; 3) —Зл/2; 4)—9/8; 5) 2; 6) arctg (—1). 3. 4 =—19
при x =—5 и y=3. 4. Квадрат.
ЗАДАНИЕ 4
1. 1) Кб(1 + Kt3); 2) 8/4^ 3) —9/4; 4) 24; 5) 2/3;
6) 7 </(5/6)». 2. 1) 7+К13б; 2) 243; 3) 4; 4) 12; 5) 16; 6) л».
3. 4 = 4 при х=2 и у=—3. 4. Квадрат.
Упражнения
1. 1) х = —1/4—локальный минимум; 2) х= 1/2—локальный
максимум; 3) х= —1/2—локальный максимум; 4) х=0—нестро-
гий минимум, х=1—нестрогий максимум, на множествах
(— оо; 0) и (1; 4-оо) функция постоянная; 5) х = 2 и х = 3 —
локальные минимумы, х=5/2—локальный максимум; 6) х = —1
и х = 1—локальные минимумы; 7) х = 0, х=— 6их = 6—локаль-
ные минимумы; ж»—2 и х=2—локальные максимумы; 8)х=1
и х=2 — нестрогие локальные минимумы, на множестве (1; 2)
функция постоянная; 9) х = я/2-[-2л&, л gZ,—локальные макси-
мумы; 10) х = л/2-|-2л^—arccos, &gZ,— локальные
максимумы, х =—л/2 + 2лfe—arccos	> kQZ,— локальные
минимумы; 11) х=л/^*й»локальные нестрогие минимумы, (2л&;
л+2л&), ^gZ,—функция постоянная, Зл/24-2л&, &gZ,— ло-
кальные максимумы; 12) х=0 —локальный максимум, х =
= -1/К2 и х=1//"2 —локальные минимумы; 13) х=л/2 + 2л&,
^gZ,—локальные максимумы, х=—л/2-[-2л&, 6gZ, — ло-
кальные минимумы; 14) х=л/44-л&, &gZ,—локальные макси-
мумы, л/2-|-л&, &gZ,— локальные минимумы; 15) х = 0—ло-
кальные максимумы, х = — 1/У 2 и х— MV" 2—локальные мини-
мумы; 16) х = 0—локальный минимум, х = —1 и х=1—локаль-
ный максимум; 17) точек локального экстремума нет; 18)х=0—
точка локального минимума; 19) х = 0—локальный максимум;
20) точек локального экстремума нет; 21) х=—1—нестрогий
локалньый максимум, х=1— нестрогий локальный минимум;
22) х = 2 и х = 3—локальные мунимумы, х = 5/2—локальный
максимум; 23) при а < 1/2 х=1/2— локальный минимум, при
2 > а 1/2 экстремумов нет; 24) указание: у—--s
У 2 cos
ОТВЕТЫ И УКАЗАНИЯ
565
при х = 4э
= 62+Н-1
то У шах =
(й; Ь]
локальных экстремумов нет. 2. 1) у max = 27
[-2’4]
у m:n =2 при х= —1; 2) если a^s—1/2, то у max
[-2; 4]	[а; Ь]
при х = Ь, у min = а24-^+1 при л: = а; если 1/2,
[а; д]
=а24-а4-1 при х = а, у min =624-^+-1 прих = 6; у min = 3/4 при
[а; Ь]	•	[а; Ь]
х=х— 1/2; у max ==а24-а+1, если а< —1/2 < b и &+а + 1 < 0;
[а; Ь]
У max“Ь24~1» если а <	1/2 b и /> + а + 1 > 0; 3) ^max =
[а;д] _	jR
=2/К 3 при х~—1/2, утах = 1/2 при х = 1 и х—~ 1, 4)0min=O
_ R	R _
при х==0; 5) ymax — V 2/4 при х — ~ 1 + V 2, </min = — V 2/4
R	_	Л
/—	V	з—1	г-
при х =—1 — V 2; 6) ymar,~——7= при	х = —2 + У 3,
R	6—2 V 3
__।	i/’	~g	___
^т5п==: -- при ^ = -2--к 3; 7)#тах=1при — 00 <ж—4,
Я 6+2 УЗ	R
^min = ~~l ПРИ —1	< + оо; 8) у Шах =4/ min = 1»
Я	Е-1;0]	Ы;0]
9) у т1п =2 при х— 1, функция не является ограниченной
^тах=6 при х=л/2+2л^ —arccos 4",
R	4	5
х = Зл/2+2л£—arccos у , &gZ; 11) ух
1
сверху; 10)
► k£Z,
289
'Т“32
ymin = —* ПРИ
R
при х = (—1)^+1 arcsin ^+л/г, 6gZ, ^min = 0 при я=Зл/2+2л£,
Z?gZ; 12) у max =4 при х = 0, х = л и х = 2л, у rain =1 при
[0; 2зх]	[0; 2л]
х = л/2 и х = Зл/2; 13) у max — при * —3, у min —4 при
[1; 3]	*	[1;3]
Х=1, 14) ^/max^l при Х = Л/2 + яЛ, 6gZ, #min =—1 при х = stk,
D	‘ я
У шах =16 при Х = 2л,
[3; 10]
если а==0, то у тах = 4
[2; 3]
__	, „	.	а > 0, то у max = 9а-f“4
(2; 3]	[2; 3]
при х = 3, у min = 4а + 3 при х = 2; если а <—1/4, то у тах =
[2; 3]	[2; 3]
= 4а4-3 при х = 2, г/min =9а-|-4 при х = 3; если 0 > а^—1/6,
[2; 3]
то	у max =9а4-4	при х = 3,	у	rain	=4«+3	при	х = 2;	если
[2;3]	[2^3]	1
—1/4 <—1/5,	то	{/max	тт ПРИ	Xs=2	st»	У min =9а+4
[2; 3]	4а	га	[2.3J
при х=3; если -у < а < у, то ^=1-^ при х= -1,
У min =4а4-3 при х=2;	18) Ьах =Д= при
£2; 3]	Я О V о
16
Я
15) у min =2 при
(0; л/2)
У min = 1/4 При Х = я и
[3;10]
при х = 3; у min =3 при
х = л/4; 16)
х = 3л; 17)
х = 2, если
566
ОТВЕТЫ И УКАЗАНИЯ
= ± arccos-р=^4-2л;£, kgZ, tfmin =
= ± arccos f—р1^Л + 2л;&,	19)
4
---7r= ПОИ X =
ЗУ 3
К 2
^х==тпри хж
V 2
г/Г="л<зпри х=
== £ arccos -рк=-4-2л£, k^Z,
1	л
= ± arccos -уг= -}-2л&, &gZ; 20) Утах = 1 при x^==-^--\-nkf
У 6	R	2
1 при х = л&, ££Z; 21) у max =2 при
Я	Я\{л + 2л/г | kQ Z}
х = 2л&,	&(£Z, функция не является ограниченной снизу;
22) z/mln=3 при х=~3+^ и х= — ~	5 - Функция не
R	*	*
является ограниченной сверху; 23) Указание: максимальные
значения данной функции и функции 4у2(х) достигаются в одной
и той же точке х0; поскольку 4х2 + (1—4х2)si, го наибольшее
значение функции 4х2(1 — 4х2) будет при таком х0) что 4хо =
= 1—4хо, т. е. при х$=—и хо = — —; у тах =
2 У 2	2 У 2	[—1/2; 1/2]
1 1 1
==-- -~=- при Х=-------, у т1п =-----------------7=- при Х==
4/2	2/2	[-i“;i/2]	4/2
= — --47--Я ; 24) если а=0, то у тах =2 при х=1, у min =—2
2 У 2	Я\{а}	Я\{а}
при х=—1; если а & 0, то у тах =2 + « при х=1+а,
Я\{«}
у tnin =—2+« при х=-14-«; 25) у ть = 2а2 при х==|а1
Л\{а}	Я\{0}
и x=-|al;	26)	+ при
3. 1) (0; 0); 2)_(0; л/2-|-2лй), k&Z-, 3) (2лЛ; / 2), (2лй; — /li),
(л+-2л£; / 2), (л+2яА; —/2), k£Z-, 4ji (0; 1); (0; -I);
5) (3; n/4+nk), fcgZ; 6) (io’'*5; 1), (lO"1' 3; 1); 7) (0; 0);
8) (л/£+лй/2; л/2+2л/), AgZ, ZgZ. 4. 100 =50 + 50. 5. 20 =
= /20-/20. 6. Точка пересечения медиан треугольника ABC,
7. Зха—36х+96. 8. 2х’+8х+15,. 9. а=1. 10. —4х«+4х+24.
§ 6
ЗАДАНИЕ 1
2. 1) л; 2) 2л; 3) 2л; 4) л. 3. Существует точка х0€-^ такая,
что Хо + Т или х0**Г не принадлежит X либо не выполняется
равенство f (х0 + Т)=/(х0)-
ЗАДАНИЕ 2
2. 1) 4л; 2) зг> 3) 2л; 4) 2л. 3. Для любого числа Т 0 най-
дется точка х^Х такая, что х0 + ^ или х0 — Т не принадле-
жит X либо не выполняется равенство f(xo + T)=f(xo)- 5. 1) Нет;
2) да, 6. Да; главный период равен 2л, 7. Например, Т^л/Уз.
ОТВЕТЫ И УКАЗАНИЯ
567
Упражнения
4. 1) л; 2) 4л; 3) л; 4) л; 5) л/т; 6) 2л; 7) 2л; 8) 1/2; 9) л;
~	л тт	( U х*~ рациональное число,
10) 2л/у 2. 8. Например, «/==< л
* миг “	и	| 0, х~-иррациональное число,
9.	Нет. 10. f(x) = cosx; g(x) = sinx.
13.	1) f (x) = x + sinx, g(x)= — x+sin x;
m Hrf-J siax’ x*n/2,	(sinx, х^л/2,
2)	t(x) — i/2> x=n/2, S(x> \ 2,	х = л/2.
14.	1) /(x)=ctgx, g(x)=4 *’ Xx^q’
ft \__/ sinx, х(Е12л6; л + 2л/г],	/egZ,
\ 0,	х£(л-|-2л£; 2л + 2л/г), /egZ,
( sinx, х£[2л&; л4~2л£], &gZ,
х£(л + 2лт; 2л + 2л/п), mgZ.
15.	^(2) = 0:/(4)m(14-4)=/(4)=-4^(-257) =
==/_24y) =ff-23y) =... -y ) =/(1 ~4) (t)=
_/3\2	3	12
“ \ 7 )	7 — 49 '
19.	1) -i-arcsin ( sin л	•
{0,	xg[ — t+2«; 4-+2nl, n£Z,
1	/1	3	\ J
|x—2n—1 |—y, хЦу+2/г; y+2nj, n^Z;
3
3) ^=—arccos (cosx) — 1.
§ 7
ЗАДАНИЕ 3
1. 1) Выпуклая вниз на всей числовой прямой; 2) выпук-
лая вниз на (0; +<ю), выпуклая вверх на (—оо; 0); 3) на
£л&; -^+л&^ ,	выпуклая вниз, на — ~-4-л^; л&^,
fcgZ, выпуклая вверх; 4) на [0; +оо) выпуклая вверх, на (— оо; 0)
выпуклая вниз. 3. Правильный п-угольник.
ЗАДАНИЕ 4
1. 1) На оо; 0) и (0; 4~оо) выпуклая вверх; 2) на
(—оо; —2/ выпуклая вниз, на (—2; +оо) выпуклая вверх;
3) на “~|-2л&; ~-|-2л6^, ^gZ, выпуклая вверх, на
£ —~Ь-|-2л^; —~рН~2л£^	выпуклая вниз; 4) на
/	1 1 Г 1 .X
оо;	_-__j и	4-00J выпуклая вниз, на
(— UY 3; 1/К 3) выпуклая вверх, 3. Равнобедренный®
568
ОТВЕТЫ И УКАЗАНИЯ
Упражнения
1. 1) На (—оо; 2) выпуклая вниз, на (2; +00) выпуклая
вверх; 2) на [—л/2-[-2л&; л/2 + 2л&], 6gZ, выпуклая вверх,
на [л/2+2л&; Зл/2-|-2л&], &gZ, выпуклая вниз; 3) на (—- оо; —2)
выпуклая вниз, на (—2; 4>оо) выпуклая вверх; 4) на (—оо; 0]
и [0; 4-оо) выпуклая вверх; 5) на (0; 1] выпуклая вниз, на
[1; +оо) выпуклая вверх; 6) на (—оо; —1J и [0; 4-оо) выпук-
лая вниз, на [—1; 0] выпуклая вверх; 7) на (0; + °0) выпуклая
вниз, на (— оо; 0) выпуклая вверх; 8) на (—- оо; —1] выпуклая
вниз, на [—1: Ч~оо) выпуклая вверх; 9) выпуклая вниз на всей
числовой прямой; 10) на ^0;	[Зл/4; 5л/4] и [7л/4; 2л]
выпуклая вверх; на [л/4; Зл/4], [5л/4; 7л/4] выпуклая вниз;
11) выпуклая вниз на всей числовой прямой; 12) выпуклая
вниз на всей числовой прямой; 13) выпуклая вверх; 14) выпук-
лая вверх на (0; 4~оо); 15) выпуклая вниз ^указание:
5х+12	2 . 3 \ л
: 16) выпуклая вниз*
ГЛАВА 8
§ 1
ЗАДАНИЕ 1
2. 1) д); 2) в); 3) в); 4) б); 5) а); 6) а).
ЗАДАНИЕ 2
2. 1) а); 2) б); 3) а)\ 4) в); 5) б); 6) а).
ЗАДАНИЕ 3
2. Например: __
1)	х-ЬУ^^-х; 2) «/=log2 (—х2+2х);
3) V ; 4) Ig(3х~л2)+177т=и==Т ’
Г	у (l—x) (2—х)
5) у=Пх+2)2(*-^); 6)	]/
7)	/(х+2)2 (х+ 1)а х; 8) у = log2 | х |.
8. Например, (/=	.
ЗАДАНИЕ 4
2. Например:
i/Th-----ГТ--ЕГ дч ]/"(* +5)2 (2х—X2)
б) У = V х- (1 —х) (х—5); 6) yss' -----о-------
Л А

ОТВЕТЫ И УКАЗАНИЯ
669
7) у = К(х-Ь2)а ха (ж_ 1); 8) у= уж2__ж{
9/ у=У— (х-2)2 (х—3)а (х- 4)2 (х—5)2.
3. Например, #=l/log2x.
ЗАДАНИЕ 5
2. Например:
i/ZZT±
Г 1 + X2 X ’
1) #=1/х2; 2) # = log2 (Зх—х2—2); 3) #«
ЗАДАНИЕ 6
2. Например:
1)	VА-1; 2){/=/(x+2)2(x-x2)±iX|
Л	Г | Л I	Л X*""* 1
__ , /	4.3.2.4.5.6.x2	"
6}У~~ V х* (6-х) (х—5) (х-4) (х+2) (х+3) (х + 4) ‘
Упражнения
2. Например:	____
1)9=/2+1; 2)у= ^+2 ; 3) 9-)<(9-1) (4-х)|
Л “““* х	Л " 1
6)	: 7) НЙ5 8)^ = l°g2(x~2){
9) у =/7^2; 10) у = К=^+Т; Н) y = log6(-1-х);
1О.	* * * * * 4	V 2х—х2	У 2х—х2
,2> v~ х (х—2)(х— 1) ; 13>	х— 1	’
14)	(х-0 й-2) 1 15) V= ^-<x-3)2^-5)ai
16) ^ = /F^24-K2^; 17)	К(х4-1)2 х;
18) s=±i±i>L£;” и, 9=Х--7.|*+2>-<4-» .
20) у=У (х4-3)2(х-2)(3-х);
9П ... _К(^+1)2(х-2)2(х-х2) .
21) у--------ж(ж-1)	•
22) у^(У(,г4-1)(3~х) + К(х-1)(х-2)) 1/(х2~1);
23) у=У—sin2пх4-1/1^ х; 24) y=V^—sin2mx;
25) y—V — sin2 ях--; 26) у—1/У sinitx;
COS-T
27) у = j/"sin лх 4- 1/V'"x— 1;
_ / (x 4- 2) (x - 2) (x - 3) (x - 4) (x - 5) (6 - x) .
1 y	(x?-4)(x-3)(x-4)(x^5)
В70
ОТВЕТЫ И УКАЗАНИЯ
от У (х4-2)(х-2)(х-3)2 .
29) у----------,
30) у — V х (х— 1) (х—2)2 (х—3) (х—4) (х—5)а (х—6) (7—х).
3. Например:
1) j/ = —(х4-2)(х + 3); 2) f/=(x4-3)(x4-2)x(l—х);
3) У = V(х + 3)(-х-2); 4) у = Их4-3) (-х-2) £±|;
У(х4-3)(-Х~2) .
1 У~	(х + 3)(х+2)	’
К (Х4-3) (-х-2)
х ф —2,5,
х= — 2,5; _______
х2)хг^+(х+1)
f х—х2 ‘ 4 1 '
6) у—
У =
«4-2,5
. 5.
/(х+3)(-х-2).
Т>У----(х4-3)(х+2)	’ 8)
9) У— V (5 —-2х).
4. Например: 1) ^ = 2-—3x4-2“ 1*1; 2) ^==|х|—* 2“1*1;
_v .	1 1 I п лч I X	Зх-j-l	X2
3) £/ = 1 х~ 1 14-2; 4)^ = х4--у-р^; 5)	; 6)	_ ;
х3 оч 2х2 т	। х2 —1	1Ч
7)^7a7ZT: 8) ^=T2ZT‘> 9) ?=sinx4--5—т. 5.1)0 =
У^ТхЬг1 2)	3) у=-^;
4) 0=3^ sign х. в. 1; д; 2) а); 3) в); 4) а); 5) ас); 6) б); 7) л)-
8) в); 9) л); 10) а); 11) «); 12) лг); 7. 1) ж); 2) д); 3) к); 4) б);
Б) з); 6) ж)\ 7) и)\ 8) е); 9) а); 10) в); 11) л); 12) а).
§2
ЗАДАНИЕ 27
1) #==(14-cos х)/2;	2) ^==2 cos (х4-л/3);	3) ^=~sin2x;
4) г/==х, х^О; 5) y=|slnx|; 6) y=xt х > 0; 7)#=х2, х?£0;
8) ^=2 log21 х |; 9) х & •у4“"Т’>	10) f/ = sin2x==
тг <4
» (l**cos 2х)/2; 11) #s=-j-sin2 2х=(1 —cos 4х)/8;	12) ^=1/2,
4gZ; is) s_k+ii«+i)_{	’>=;;
14) 0=х24-1, х > 0, xj4 1} 15) 0=44-]- cos 4х; 16) 0 =
Ж 4
( X, xfe 1,
~\Цх, 0<х<1.
ОТВЕТЫ И УКАЗАНИЯ
571
ЗАДАНИЕ 28
1) 4' = |-»1; 2) y=]/"2jsin-j |; 3) у=х—\, x^l;
4) 0 = cos2x, л/4 + л&Сх«сЗл/4 + л&, £gZ;
б) y=21oga|x-l|; 6) £«1, х^уА, fegZ;
7) yg=cos8x=^~^~^>S —, — п/2-|-лй < x < Л/2-4-ЛЙ, k(£Zf
8) у — \ cos 2х|; 9) 0=1—ха, xg(0; 1);
Ю)
H)
13)
14)
I 101/10)	/	(*+2)2>	х^—2,
у-\х+2\(х+2) — j _(х+2)2> х<_2.
. it > 1	( l/Я, 0 < X
J,=|x—1[, х?Ы; 12) j/=< x5a)
#=sinx, x 56 л/2+лй, &£Z;
^=| sin x | + | cos x| =
К 2 sin (х+л/4),
К”2 sin (x—л/4),
— К"2 sin (х+л/4),
k — j<2sin (х<**л/4),
15) у = ]/*l cos (x+л/4),
16)jr=KCtgX’ Х>Л
1 y 10, x < 0,
х$(2лх; л/2+ 2л/г],
xg [л/2-|-2лх; л + 2л&],
xg[n+2;ri/?; Зл/2 + 2л&],
xg[3H/2-)~2n/?; 2л+2л^],
Х56—4+^» k^Z.
х $£ л/24~л&, £ = 0э 1, 2.
&gN;
&£Z,
fegZ,
k£Z,
k^Z;
17)	1; 18)
х—— 1 ’
X*- 1
y = \
ЗАДАНИЕ 31
.	_( x—2лй, xg[—я/24~2л&; jt/24-2h&], ^gZ,
)У <—х+л+2л^; xg[ я/2+2л^; Зл/2-]-2эт&1, k£Z\
2)	z/=x, xCl-l; 1];
3)	уs= arcsinsin (л/2—x) = —arcsinsin^x—=
__f — x+W2 + 2flA xg[2n£; л + 2л&], &gZ;
\ x—Зл/2-—2л^, х£[л4-2л/г, 2л + 2л&]» k£Z\
4)	y = V 1—x2; 5) y^n/2, xg[—1; 1];
6)	r/ = л/2-—2arcsin x;	____
7)	0 = 2 sin arcsin x cos arcsinx=2x К1 —x2;
8)	0 = 2x2 — 1, xg[—1; 1]; 9)0=2xj/T^x^
10) 0=4x3—3x, xgb-1; 1].
2. 1) 3л—10; 2) 7 —2л; 3) 37— Юл—Зл/2,
ЗАДАНИЕ 32
1 п ( х—2л^,
— —х+2л^,
2)	0«х, xgl-l; lh
xg[2n&; л + 2л&], k^Zt
xg[—-л-]-2л£; 2л&], &gZ;
Б72
ОТВЕТЫ И УКАЗАНИЯ
3)	у = arccos cos (л/2—я) = arccos cos ^х—% } =
( х—л/2—2л&, xg[ л/24-2л/г; Зл/2 + 2л&], k g Z,
—-х +л/24-2л&, х g [—згс/2-|-2л&; л/24~2л&],	k g Z;
4)	z/= У 1 ~—x2; 5) # = л/2 —2 arccos x;
6) y=l—2x2, xg[—1; 1]; 7) у = 2х^Т^;
8) y=l, xgl—1; 1]; 9) «/=-1—2x2; 10) y—3x—4x3.
2. 1) 10—7л/2; 2) 25—8л; 3) —11-|-9л/2.
ЗАДАНИЕ 33
1. 1)	= л/г, xg(—л/2-|-л/г; л/24-л/г), /egZ; 2) r/ = x,
x(~R; 3) у =—х + л/2 + л/г, x^(—л/2-j-л/г; л/2-|~л&), &(~Z;
Ъ 1 га	/О га	%x Г7\	X2~~ 1 m	—2x
4)^=--y; 5) у=я/2; 6) y^-—^-, 7)y=-—-.- s) y=-^—-p
,0> i-
2. 1) 5 —2л; 2) —17 + Зл/2; 3) 5л/2 —8.
ЗАДАН И Е 34
1. 1) у--х—л/г, х^(л&; л-|-л&), k^Z\ 2) z/=l/x; 3) г/=х,
л
x^R; 4) у—-^—х-\-як, x£(nk; л-|-лй), £gZ;5) у=я/2—2arcctgx;
в) ^ = (1-х2)/2х; 7) у = 2хЦх2-1)-, 8) // = -!; ?) ^=(1-ха)/2х;
Ю) (/=1/1 — х. 2. 1) 23—7л; 2) 13л/2—19; 3) 9л/2—11.
ЗАДАНИЕ 35
1) у — 2х~1-1; 2) у——У х, х(£(0; -{- оо); 3) у — х2, xg(0; 1);
4) у=arcsin х;
xg(-l; 4-оо);
Х0Л/2; Зл/2].
5) у = л—arcsin х, xg[0; 1];
7) у—— Кlog2x, xg(l; 4-оо);
6>
8) # = sinx,
ЗАДАНИЕ 36
1) у = {\— Зх)/2; 2)	хё(0;4-оо); 3) у = ха,х€(1;2);
4) f/=arccos х; 5) #~2л—arccos х, xg[—1; 0]; 6) #=(1+2х)/(х—1),
xg(-oo; 1); 7) </=-(1/7)^; 8) у=-1-/-х-2, х^-оо; ^2).
5) 0; 6) х=1; 7) 0; 8) Х! = 7; 9) х==0, х = 4; 10) х = 0, х =
х—L 2. 1) х = 24-а, xs=2—а при а > 0; х~2 при а = С
НИЙ
при
ЗАДАНИЕ 37
1. 1) х=2, х=—6; 2) х«С1; 3) —5^х^3; 4) х^—1/2;
:--1,
!=0; реше-
нет при а < 0; 2) х = 2 + а, х=а—2 при agR; 3) х~а/2
а > 0; х > 0 при «=0; решений нет при а < 0; 4) х = —-
1
1	< + оо; х=—-т—7, х=----- при 0<а < 1; х = 0 при
CL “т~ 1	1 *~“tZ
а=0; *=--т-7 при — оо < а <—1; решений нет при — 1<а <0.
й’Т" 1
при
ОТВЕТЫ И УКАЗАНИЯ
573
ЗАДАНИЕ 38
1. 1) х=4, х=~1; 2) х==—5/2; 3)—2<х<1; 4) х=1;
5) х = 0, х= 1, х=2, х=3; 6) х=—2; 7) х=1; 8) №=0, х=1,
х=2; 9) х=0; 10) х==—1, х=1. 2. 1) х=а— 1, х — — а—1 при
а < 0; х=—1 при а = 0; решений нет при а>0;2)х=-Ц^,
х=	при agR; 3) х=^_1 при —1 < а; х^—1 при
а =—1; решений нет при а <—1; 4) х=0, х=1/а, х =—1/а
при а > 0; х=0 при а<0.
ЗАДАНИЕ 39
1. 1) х£(—оо;_j-l)U(5;+oo); 2)_х£(—3; 1);3)xg(-l/2; +оо);
4) хе(-со;-К 5)U(-1; 1)U(K 5; +«); 5) х £ (-оо;-3/4);
6) х£(— 1; —1/3); 7) xg[2; 4-оо); 8) х=—1, х£[1; 4-оо)}
9) х£(—1; 2); 10) х€(—00; — 2]Щ1; +00). 2. 1) xg(a4-2; 4-oo)(J
(J(—оо; 2—а) при а > 0; x$RX{2} при й=0; xgR при а < 0;
2) а—2<х<а4-2; 3) х£(а/2; 4~°°) при а > 0; решений нет
при .асО; 4) xg (jqrj'	ПРИ ° < а <	*€0/2; 4*®)
при а= 1; xg f— оо; -~т—г) при — оо < а < —1; решений нет
у	d 1 J
ЗАДАНИЕ 4Q
1. 1) xg(—1; 3); 2) х€(—<*>; —1)U(O; 4-со); 3) х£(-1/2; + оо»
4) хв~2; 2)\{0}; 5)xg(-oo; —1)U(O; +оо); 6) xg(- оо; —1/2>j
7). Л € (— оо 5 — 1]; 8) л € (— 1; 0) и (2; + оо); 9) х € (— оо; 0) и (0; +оо);
10) х^(—5; —2)U(—2; — 1). 2. 1) x£R при а > 0; х^Ноо; — 1)Ц
и<—1; 4-оо) при а = 0; xg(— со; — 1-H)U(— 1 —а; + оо) при
л п. - / — !—*«	1—**а\ о. - /а-*1	\
а < 0; 2) xg [—; —гр ) 5 3)	( —?р; +00 ) приа>—1;
решений нет при а^**1; 4) х^(—1/я; 0)U1/я) при а > 0;
xg(— оо; 0)U(0; 4-оо) при а<0.
ЗАДАНИЕ 43
1, 1) 2 корня при а > 1/4 и а = 0; 3 корня при а= 1/4;
4 корня при 0 < а < 1/4; нет корней при а < 0; 2) 2 корня при
а> 2 и а < —2; 1 корень при а=2 и а=—2; нет корней при
—2 < а < 2; 3) 1 корень при любом а; 4) 1 корень при а=—1/4
и а > 0; 2 корня при —1/4 <а<0; нет корней при а <**1/4;
5) 2 корня при а < (—3— 8)/2,J-3 + К 8)/2 < а <0 и а > 0;
1 корень при а = 0, а_=(—8)/2 и а==(-~3-[-8)/2; кор-
ней нет при (—3***К 8)/2 < а < (—3-}-]/" 8)/2; 6) 2 корня при
а = 9/4 и а < 2; 3 корня при а = 2; 4 корня при 2 < а < 9/4;
нет корней при а > 9/4. 2. 1) 4 решения при а=1 и а =1/2;
8 решений при 1/2 < а < 1£ решений нет при а > 1 и а < 1/2;
2) 1 решение при а=|/~2 и а = —1^2; 2 решения при
— "2 < а < К 2; решений нет при а >	и а <
574
ОТВЕТЫ И УКАЗАНИЯ
ЗАДАНИЕ 44
1. 1) 2 корня при а —0 и а < —1/4; 3 корня при а = —1/4;
4 корня при —1/4 < а < 0; нет корней при а > 0; 2) 2 корня
при а < 0 и а = 1; 3 корня при а = 0; 4 корня при 0 < а < 1;
2	2
нет корней при а > 1; 3 1 корень при а <-%—=иа >   -  ;
3/3	3/3
2	2
2 корня при а =--------и а = —-	3 корня при
зу 3 зу 3
2	2
----< а <.......-а—— ; 4) 2 корня при любом значении а;
3^3	Зр/з
5) 2 корня при а <— 4—2 К 3> —4+2 Y 3 < а < 0_и а > 0;
1 корень при а — 0, а = —4—2}^ 3_и а=—4+2 У 3; корней
нет при —4—2 Y 3 <а < — 4+2 ]/" 3; 6) 1 корень при а < 0
и а—1/4; нет корней при а> 1/4; 2 корня при 0«Са < 1/4.
2. 1) 4 решения при а—1 и а = 1/~~2; 8 решений при 1 <а <j/~2;
решений нет при а < 1 и а >	2; 2)_ 2 решения при
— У 8 <а < V~ 8; 1 решение при а =— У 8 и а =	8; реше-
ний нет при а < — К 8 и а > у 8.
Упражнения
5. 1) у = (4х—1)/3, xg[-1/2; 7/4];	2) у = (х-3)/2,
3;+сю); 3)//=—2+рЛ3—х, xg(3; —00); 4)	1—4,
хё(4;+оо);	5)	* € [0; + оо); 6) 0=+1
_________________________________________ X-f~ 1
х€(-«>; -1); 7) у=24-2*; 8) $f=- У~1. «€(0; Ц;
9) # = — >/'1— х2, xg[0; 1]; 10) ^=arcctg2x» xg(l/2; + оо);
И) ^=arcsin (х—1); 12) i/—я—arcsin (х—1); 13) у=2л+агссоз х,
xg[0; 1]; 14) z/=n+arctgx, xg[0; +<»); 15) ^=2^ + arctgx,
xg(-oo; 0]; 16) r/= 10Л-1—4; 17) y=log8I+, xg(0; 1);
18) y^logs^+^^+J?; 19)j/=2^,xgR\{0};20)g=^2f(
xg(-oo; 0);	21)	* +	**, xg[-l; 0);	22) /?=
f1"-*^ 1 — X* n / ( r I <	1 I V 1 —.v2
= j	X ’ 0 < 1 X| <T’ 23) уЛН±-£_ , x € (0; U;
( 0,	_ x=0;
24) у=arcsin	x; 25) «/ = In (x-f-	x2)> x g [1; +00);
26) ff = l/1—Xs; 27) y={x}+2, xg(0; 1); 28) y=x—
xg[l; +_oo);	29)	y=—	xg[0; +«>);	30) y =
= ( К x,	xg[0;+oo),	31)у/ 2-/T=2, xg[2; +»),
\ У x, x€(— oo; 0];	I 4—x,	xg(—co; 2J;
ОТВЕТЫ И УКАЗАНИЯ
575
32) г/ = хН-4л, х£[—л/2; л/2]; 33) г/=7л—х, xg{—л/2; л/2];
. х
___	л—arcsin-у
34) у=	, xg]0; 1); 35)у= /1 х | signх; 36) у=-=---
У 1—х2	6
37) у=3 sin 4 > * € ]—Зл/2; Зл/2]; 38) у=— cos х, xg [0; л/2];
О
х
F5
39) у = arcsin
л/4;
4°)	х € (0; +оо);
41) р=
1—У 1—х, х<(—оо; 0],
-14-К14-х([[0; 4-<ю);
42Н =
ха4- 1
2х
xg(—со; —I].
6. 1) х=—1, х=2; 2) х^2; 3) —3<х<2; 4) х=—5, х=0,
х=2, х=6; 5) х=0, х=3; 6) х=1; 7) х=—2; 8) х——1,х=0,
х=1; 9) х=—1; 10) х£(— со; —2]Щ6; 4-®)1 П) х=0, х=1;
12} х=1; 13) х=1; 14) х = 0, х=3; 15) х=0, х = 1; 16) х=—1,
х=0, х=1; 17) —1<х<0; 18) х=—8, х=0, х=8; 19) х=4;
20) х= 1, х=4;	21) х=0;	22)х=1; 23) х= 1/2, х= 1/4,
х = а, где х—единственный корень уравнения (1/16)* = х.
7. 1) xg(—со; — 1)U(3; 4-®)1 2) х£(-5; 1); 3) х€(—1/3; 1);
4) х€(—со; —2,5); 5) 0; 6) х€(-оо; —O,5)U(1.5; 4-®);
7) х€(—со; 0); 8) х^(—оо; —2/3]Щ0; 4-оо); 9)_х=—1, х = 0,
х=1; 10) х^]-2; 2); И) х g (- со; - К 5)и(/5; -f-oo);
12) х£(—оо; — 1](J(1; 4-®);	13) х£(—8; 4-оо);	14) x£R;
15) хё[1; 4]; 16) xg(—со; 0]; 17) х£[— 1; 0]; 18) х£(— оо; 7);
19) х€(1; 4-со); 20) х£(0; 1/8). 8. 1) x=«4-3, х=—а-]-3 при
а > 0; х=3 при а — 0; решений нет при а < 0; 2) х—а— 1,
х ——а—3 при а > — 1; х±~—2 при а =—1; решений нет при
а <—1; 3) х=(1-Н)/2, х = (п —1)/2; 4) х —{— а—1)/2 приа < 1;
х^—1 при а = 1; решений нет при а > 1; 5) x — O-j-lK 1+4а)/2,
х = (! — ]< 14-4а)/2 при а > 1/4; х = (14- К 2)/2, х = (1 — У 2)/2,
х=1/2 при а =1/4; х = (1-|-Vе 1 +4а)/2, х=(1 — /"14-4а)/2,'
х=(14-Уг 1—4а)/2, х=(1 —К1 —4а)/2 при 0 < а < 1/4; х=0-
п I 2
х—1 при а==0; решений нет при а < 0; 6) х~—~ при а > 2;
х^—2 при а = 2; решений нет при а < 2; 7) х = (14-а)/(а — 1)
при а > 1; решений нет при0<а<;1; х ——1 при д=0;
х = (1+а)/(а—1) при 1; х = (1+а)/(а—1), х==(а—1)/(а+1)
при — 1 < а < 0; 8) х=24-л, х=—2— а при —2 < а < 2; х=0
при а=—2; решений нет при а <—2; х=2+«» х——2—а,
х=0 при а —2; х=2+«, х==—2—а, х-а—2, х=2—при
а > 2; 9) xg(0; 1] при а=1; х—, х==2^-^при—1 <а<1;
xg[—1; 0] при «=—1; решений нет при а^(—«о; —1)U(H +00);
Ю) х=0, х=1 при а = 0; х = (1-f	при а < 0;
х=(1-|- V	х=(1 — Y 1*“*4а)/2 при 0 < а < 1/4; х=1/2
при 1/4; решений нет при а > 1/4; 11) х= (а-|-КЯ2-8)/2,
Х=(а—Yx=(a-f- Vа24- 8)/2 при а <—2/ 2; х=/2,
х=24- V 2 при в=—2 У 2; х=(— а-^Уа2+ 8)/2 при а >—2У 2;
676
ОТВЕТЫ И УКАЗАНИЯ
—14“ К 14-4$	— i -j- j/* 1 -j-46z л
12) х =	, х = — у —  —!----при а > 0;
-| - "У~ мша
х=0 при а — 0; решений нет при а < 0; 13) х —	,
х	при а < 0 и а > 8; х — ~ при а = 8; решений
„р.	0<а<8;	14) ,= :±ЩЛ5М!,
^^(а+[)^Ка3+14а + 1 при „	_Р Г/'У <о<0
и а > 0;	х===3 при «=~0; х = (б —4 КЗ)/8 К~3—14 при
а^—7 + 4 у' з; х = (б + 4 КЗ)/—8 КЗ—14_при а = — 7—4/3;
решений нет при —7—4 V 3<а<~7 + 4К 3; 15) х=а/(1—2а)
при а 1/2; решений нет при а— 1/2; 16) х=(3-|-2а)/(а—2) при
а>2 и 2; х =—3/2 при а = 0; х = (3 4-2я)/(а— 2),
х~(2а—3)/(а4~2) при —2 < а < 0; 17) х=1 при а — 1/2; х~6
при а = 0; х = (14~К 1 —4а2)/2а, х = (1 — К1 — 4а3)/2а при
0 < а < 1/2 и —1/2 < а < 0; х =—1 при а = —1/2; решений нет
при а > 1/2 и а < — 1/2; 18) х<—1 при а=1; х = —(14~а)/2
при — 1 < а < 1; х^О при а =—1; решений нет при а > 1 и
а < —1; 19) х —	4~4а2 д х~ — у 1 + К1 + 4а“ ПрИ
а > 0; х=—1, х = 0, х=1 при а = 0; решений нет при а < 0;
(—14.Kl + 4а V
-----------!——5----J при а^0; решений нет при а < О,
9. 1) xg(—оо; 1—a)(J(l+«; +оо) при а^эО; xgR при а < 0;
2) xg(2—а; а-}-4) при а>—1; решений нет при 1;
3) xgf^^; 4~оо^ при а > — 4; решений нет при а «С—4;
4) xg[—Ц-; 4~оо^ при 1 < а <+оо; xgf—оо; —ЦЛ при
\ а ***** 1 у------\ а 1 j
—оо < a<-l; xg^ —	при — 1 < а < 0; решений
/2	\
нет при 0«са^1; 5) х < —2 при a = 0; xg ( у; 4-°° ) U
/	2 \	(	___2 \
U —оо;	) при а > 1; xg(—оо; --pj 1 при 0<а<1и
—1 .< а < 0; 6) л:€((1-~/Т+4а)/2; (1 + У Г+4П)/2) при —1/4 <
< а<0;	—а; (1 + 1^ 1+4а)/2) при а > 0; решений нет при
—1/4;	7) xg(—оо; —1**а]иП+а; +00) при а > 1;
xg(—оо; —2](J[2; +<»)U{0} при а = 1; xg(—оо; —1— а]Н
Ul—1+а; 1 — a]Ull+^+.°°) ПРИ 0 < # <1> ПРИ
8) xg(— оо; (—1 **К 1—4а)/2а) U (—14“К1 ~-^4д)/2а; + °0) при
О <а<1/4; xgR при а > 1/4;	xg((— 1 + К1 -*4а)12а\
(—1 —/1 — 4а)/2а:) при а < 0; 9) xg(—оо; (1 — К1+4а)/2а) U
U ((—1 + К 1 + 4а)/2а; + оо) при а > 0; xg(— оо; — 1)U(U + <»)
ОТВЕТЫ И УКАЗАНИЯ
577
при а = 0;	х^((14-1^1+4а)/2а;	(1 —/1 + 4а)/2а) U
U((—1 + К 1 + 4а)/2а; (—1 — / 1+4а)/2а) при —1/4 < а < 0;
решений нет при —1/4;	10) xg((a— j/"aa— 4)/2;
(а4-^^+4)/2) U ((— а— Ка2 + 4)/2; (— а+ /а2 — 4)/2) при
а > 2; решений нет при а ^2,
ГЛАВА 4
§ 1
ЗАДАНИЕ 1
1. а); в); г) значение предела функции совпадает со значе-
ниями функции в точке х=1; е). _	____
2. Например: 1) 0<б<]/5-2; 2) 0 < 6</9/2—2;
3)	0 <	17/4—2; 4) 0 < S<min{1; е0/3}.
ЗАДАНИЕ 2
1.	Например:
1)Ш=5х-7; 2Н(х)={
ft	рациональное число,
' /{ ) — \ —2f х—иррациональное число.
2.	Например: 1) 0< о^1/2; 2) 0 <б<:1/4; 3) 0 < 6^
< 1/200; 4) 0 < б<е0/2.
ЗАДАНИЕ 3
1. 1) Л"; 2) Л2—В; 3) (Л + 1)(В-2); 4)	5) х0А +
4-хоВ; 6) В sin Л. 2. 1) 5; 2) -gj+/2; 13) 17 sin 2; 4) 0; 5) 1;
6) (^13+0/4.
4. Например:
/ х+2, х < 0,	( хН-1, х < О,
О fW=< b	х=0, g(x) 1 х+3, х > 0, 2HW = (x, х^О, 8^\ ЗАДАНИЕ 4 1. 1) Л2-В2+2; 2)	; 2) 2 sin 2; 3) 13/4; 4) 8/3; 5) 2; 6) —	==<	2,	/=0, 1	х,	х <	0; х,	х	<	0, 1,	х	>	0. 3) cos А; 4) | А |. 2. 1) 1; =т=	. 3. Например, f(x) =
= -|х-1|-1. 4. Например: ( х* 1) fW = { 2, 1 1—X,	х > 0, х=0,	^(х)=1 + /(х); х<0
49 Задачи по математике. Начала анализа
578
ОТВЕТЫ № УКАЗАНИЙ
( х, х > О,
.2) /(*)=£« = 5, х-0,
11, х < 0.
ЗАДАНИЕ 5
1. 1) 4; 2) 5; 3) 10; 4) 2^2; 5) 4/3; 6) 6; 7) —44/3; 8) я//#,'
9) 1; 10) 1/2. 2. 1) Существует положительное е такое, что для.
любого положительного б найдется х0 такое, что для любого х:
0 < | х—х01 < 6 выполняется неравенство | f (х) — А |	8; 2) для
любого числа А найдется положительное число 8 такое, что для
любого положительного числа 6 найдется х0 такое, что для
любого х: 0<| х—х0 |<б выполняется неравенство | f (х) — А |^>е.
ЗАДАНИЕ 6
1. 1) 6; 2) 3; 3) 1; 4) 1/4; 5) 12/5; 6) 1/24; 7) т/п; 8) 13;
9) (п—£)/2; 10) —1/2.
ЗАДАНИЕ 7
1. 1) 2; 22 5/3; 3) 4/9; 4) 25/14; 5) 1/2; 6) 1; 7) 1; 8) cos а;
9) 0; 10) /2. 2. 1) е2; 2) в4; 3) е“2; 4) е~3; 5) 1; 6) In 2;
7) In 3/2; 8) 2/3; 9) In 5-1/2; 10)
ЗАДАНИЕ 8
1. 1) ‘3/7; 2) а3/р; 3) 0; 4) 1; 5) 2/3; 6) 1/2; 7) cos а;
8) (я2 —m2)/2; 9) 2/3; 10) —1. S. 1) e3/2; 2) e"1; 3) e~\ 4) 1/2;
5) —1; 6) 11/21; 7) 1/9; 8) In2; 9) 1/7; 10) aalny.
ЗАДАНИЕ 9
1. 1) /+ (0)=2, /_ (0) = — 4, f+ (1)=1, /_ (1)=1; 2) f+ (0) =
*=/- (0) = 1; 3) f+ (0)= 1. f+ (l) = 0, f_ (1) = 1; 4) f+ (0)=
= /_(0)=l, + 2)=f_(2)=l.
ЗАДАНИЕ 10
1. l)f+(0) = l f_(0)=l, f+ (!) = /_ (l)=2j 2) f+(0)=l.
/- (0)=—1 f+ (n)=f (л)=0; 3) + (0)=0, (0)=—1, f+ (2)=2.
f_(2)=l, f+(5/2) = f_(5/2) = 2; 4) /_ (0) = f+ (0)= 1 при 6=1;
/_(0)=1, f+(0) = 6 при 5*1; /_(!) = /+(!)=*+!.
ЗАДАНИЕ 11
1. Например: 1) f (x) = l/(x—I)2; 2) f(x)=—l/(x—I)2;
3) f(x) — l/(x— 1). 4. 1) oo; 2) — oo; 3) +oo; 4) 1.
ЗАДАНИЕ 12
3
2 X
1. Например: 1)	2) /(x) =
3
~2~~x	x
= x(x— I)2(2—x)2 : 3)	3- o °0’ 2) 00’ 3) +°°;
4) 4/3; 5) oo; 6) oo.
ОТВЕТЫ И УКАЗАНИЯ
579
ЗАДАНИЕ 13
1. Например: 1) f(x) = e~*+l; 2) f (х) = 2-|-—; 3) f(x) =
X
х	9
= jqTr 4) f W = { I arctgх|. 3. 1) 1/2; 2) 1/3; 3) 0; 4) 0; 5) i;
6) 0; 7) 2; 8) не существует. 4. 1) r/=x;_2) y = x; 3) y=—x при
x—> oo; z/ = —Зх при x—> oo; 4) 2x—1.
l.7 ЗАДАНИЕ 14
3- 1) 1; 2) 1/2; 3) 216/335; 4) 1/2; 5) 0; 6) 1; 7) 2; 8) 0; 9) 3;
10) —3. 4. 1) y—x—«1; 2) y=— x; 3) y~—1/2 при x—>4-oo;
л . 1	.v	> «пс	.	я»
r/=2x+-y при x —> —oo; 4) у—x4--^ при x —> +oo; </=x*«-—
Z	2»	Z
при X	—oo.
ЗАДАНИЕ 15
!♦ Например:
1) f(x) = l/x\ 2) f (x)= —1/sinx;
3)	=
4) fM =
t]- t€"’
x *
£
x ’
£
x ’
n TT	(x4-4)(x—2)	P x(x2+l) (x—2)
2. Например: 1) f (x) =	; 2) f (x) = ^3—Z-ZJ__2.
3. 1) Для любого положительного числа М существует х9
такое, что для каждого х, х > х0, выполняется неравенство
f (х) > М\ 2) для любого отрицательного числа М существует х9
такое, что для каждого х, х < х0, выполняете# неравенство
f(x) < М; 3) для любого положительного числа М существует
Хо такое, что для каждого х, |х| >|х0|, выполняется неравен-
ство |/(х) | > М. Например: 1) /(х)~х2; 2) f(x) = x3;
< п, 2п—1 < |х|2n, ngN,
3) f(x) = < —n, 2n < | х| ^2/i-f-l, ngN,
I 0, |x|<l.
ЗАДАНИЕ 1G
1.	Например:
1) f(x)=-ctgx; 2) /(x)=2=^;
' —Ц, xg[ 4 —; 1H — 1, fegN,
Л f	X— 1	1 92Й-1	1 O2fc-2 I
3)/W = <	.	Lz j	i 4J
T2_, xg(i^,_L; 1 +	fcgN;
V 1—x	1 22A	/
19*
580
ОТВЕТЫ И УКАЗАНИЯ
х£[1/22*-1; 1/23*-?], 5gN, .
x€(l/2?*; 1/22*~*), AgN;
4) /(х)=1/х?;
(	1/х\
5) /(*) = <	1/х.
I —1/х,
6) f(x) =
(	1/х, x€[1/22A-j, l/22*-2]UI—1/22»"2, —1/22*-*], AgN,
I —1/х, x€(l/22* l/22*-J)U(—1/22*-1, —1/22*), fcgN.
2.	Например: 1)	' 2>
= —l+—.
1 X
3.	1) Для любого положительного числа М существует
такое, что для каждого х, х < х0> выполняется неравенство
2) для любого положительного числа М существует число
такое, что для каждого х, х > Хо, выполняется неравенство
^(*Йапрямер: 1)/(х) = 2"^;
х€12л— 1, 2л), ngN,
xg(2n, 2n+l), ngN.
Упражнения
4.	1) /_ (0)=—1, f+ (0) = 1, /_ (л/2)=/+ (л/2) = 1; 2)'/_ (0) =
= f+ (0)=1, /_ (-1) = /+ (—1)=0; 3) / (0)=/+ (0)=0, /_ (1/л)=
= /+(1/л) = 0; 4) /_ (0) = /+(0) = —3, /_(—3) = 6, /+(3)=—6;
5) /_ (l)=f+ (l)=Z>4-c,	(0) = 2; f+ (0) = 5; при 5 = 2 и любом
с функция имеет предел в точке х=0; 6) /_ (1) = /+(1) = 0,
/_(—1)=2, /+(—1) = 0; 7)/_(0) = 2, /+(0)=5 при 5 = 2 и
любых с и d функция имеет предел в точке х=0;
«)	f_(0) = /+(0) = 0, /_(л/2) = я/2, f+ (л/2) = -л/2,
/_ (л)=/+ (л) = 0; 9) /_ (0)=-1, /+ (0)=1; 10) /_ (0)=/+ (0)=0;
Н) f_ (ty — f+ (0) = 0. 5. 1) 5/2; 2) —2; 3) 3/2; 4) 2; 5) 2; 6) —1;
7) 3/2; 8) л/2; 9) 0; 10) 1/4; 11) 1/2; 12) 1/16; 13) —2/3; 14) 1/6;
15) £2; 16),^; 17) 1п-|; 18) In-g-/ln 42; 19) 1/е; 20) е*я;
21) е~№; 22) —7/75; 23) 1; 24) е2. 6. 1) 2; 2) sin 1; 3) 10/3;
4) 1; 5) 1/4; 6) cos 1; 7) sin 4/7; 8)	; 9) sec2 7; 10) tg /З;
11) tg 4; 12) —1/л; 13) 0; 14) /2; 15)2; 16) 1/2; 17)' /3;
18) —б/З; 19) /3/2; 20) —l/З/З; 21) 1/2; 22)	; 23) -SXJ;
4 у 7
бу
24) 0; 25) 0; 26) 0; 27)	. 7. ц тз/пз. 2) 1/4;
z cos21 у cos 1
3) 1; 4) —1/12; 5) 1/16; 6) 3; 7) —8 In 2/л; 8) 1/е; 9) 9/25; 10) 1/5;
11) 6/7; 12) ё*', 13) -1/2; 14) -24; 15) 3/4; 16) 1п-|; 17)
18) е"*/2; 19) в-1/я; 20) 0; 21) 1/6; 22) 1; 23) 2; 24) 6; 25) 8;
26)
ОТВЕТЫ ’И УКАЗАНИЯ	581
х—рациональное число,
х—иррациональное число.
х=2,
sin —J-д, х # 2,
х—2
8. Например, f(x) = ^ _
( 5»
9. Например, f(x) —
' И. Например:
1) / (х)=—g(x)=signx; 2) f (х) =g(x) = sign х\
(	1,	х = 0,
3) f(x)=signx;	4)	f(x)=J	1	J_	0
к	X*	X
12. Нет. Рассмотреть примеры функций
.	/О,	х^О,	.	. (	5,	х^О,
х < о, g(x)=to. *<<>•
13< Нет. Рассмотреть примеры функций
g(x)=x2;
2, х^О,
О, х < 0.
х=0,
15. Нет. Например, функция
f(x)=J 2,
V 1—*>
/(x)=sini,
Л
...	/О, xSsO,
j х<0>
{Х^
1’
gi W =
х —О,
х < О
ограничена в окрестности точки х=0, но она не имеет предела
при х —> 0.
16. Например: 1) f (х)=^(х)=х; 2) /(х)=х2, g(x)—x;
3) f (x) ==x, g (x) = x3; 4) f (x) =x, g (x) =—x3; 5) f (x) =x, g (x) = x2;
6) f(x)=xa+1, g — x, если a > 0; f(x)—x, g(x) — x1-a, если a^O.
19.1) lim f(x)==—oo, lim /(x) = oo, lim f(x) = oo;2) lim f(x)—
x-> 1	x -> 0	x -> 2	X -> 1
= oo, lim f(x) =—oo, lim /(x) = oo;3) lim /=—oo, lim f(x) —
x~>0	x —>• 2	x->l	x->0
=t«—oo, lim f(x)=oo. 20. 1) oo; 2) + oo; 3) op; 4) + oo; 5) oo;
x-> 2
6) + oo, если tn четное; — oo, если tn нечетное; 7) oo; 8) 0, если
f = l; — 1/2, если p = 2; — oo, если $ — k g N; oo, если P =
= 2£4-l, k £ N. 24. Например: 1) f (x) = l/x2, g(x)=x3; 2) f (x) =
= 1/X2, g (x) =x2; 3) f (x) = 1/x4, g (x) =x2; 4) f (x) = 1/x4, g (x) =—x2.
25.	Например: 1)	;2)/(x)== J ,
s W“-2 (r^)9; 3) f • 8{x}=~ (i)2; 4) f(x}=
(1	\2	/1\4	/1\2
—) ; 5) fw==(—) .	; 6) /W =
’V' 11 яП 1
-(x-ajV^W- (x—a)V
ОТВЕТЫ И УКАЗАНИЯ
582
27. Например, f (х)=Н'Н'еСЛИ Х~ Рациональное число,
r г | 2/|х|, если х—иррациональное число.
31. 1) 2; 2) 1; 3) 1; 4) —1; 5) 101; 6) 2Ч-331; 7) 1; 8) 1//2;
9) —1/2; 10) — оо; 11) 4/3; 12) —1; 13) 3; 14) не существует, так
как lim f(x)^ lim / (х); 15)1/2; 16) е~*; 17) е8;. J8) — 2;
х + <х>	х - со
19) 3; 20) не существует, так как lim /(х)=0, lim f(x) =
«-{-оо; 21) 1/2; 22) 1/4. 32. 1) #=х4~3/2 при х—-> + оо;
=— х*-3/2 при х —> —оо; 2) r/= 1 при х —> + °°;	при
х —3) //—Зх при х —> + °°;	—х при х —> — оо; 4) г/— х
при х—> + оо; £/=х-|-л при х —> — оо; 5) у—х при х—> + °°*,
6) г/=х—5/2. 33. 1) а = 1, & = —1; 2) а=—1,6= 1/2; 3) а =—1,
6 = 1/2. 34. 1) Для любого положительного числа М существует
6 > 0 такое, что для каждого х, 0 < х—а < б, выполняется не-
равенство /(х)>Л4; 2) для любого положительного числа М
существует о > 0 такое, что для каждого х, —б < х—а < О,
выполняется неравенство /(х) > М; 3) для любого положитель-
ного числа /И существует б > 0 такое, что для каждого х, 0 <
< х**а < б, выполняется неравенство f (х) < —/И; 4) для любого
положительного числа М существует б > 0 такое, что для каж-
дого х, — б < х—а < 0, выполняется неравенство | f (х) | > М\
5) для любого положительного числа М существует х0 такое,
что для каждого х, х > х0, выполняется неравенство / (х) <—/И;
6) для любого положительного числа М существует х0 такое, что
для каждого х, х > х0, выполняется неравенство |/(х) | >/И;
7) для любого положительного числа М существует положитель-
ное число б такое, что для каждого х, 0 < х—а < б, выполняется
неравенство I f (х) | > М; 8) для любого положительного числа М
существует о>0 такое, что для каждого х, —б<х«—а<0,
выполняется неравенство /(х) < — М; 9) для любого положитель-
ного числа М существует х0 такое, что для каждого х, J х | >
> | х01, выполняется неравенство f (х) < —/И; 10) для любого
положительного числа М существует х0 такое, что для каждого х,
х < х0» выполняется неравенство |f(x)| > М. 35. 1) f+ (0) = 1/2,
(0)=— 1/2; /+(1) = +оо, (1)=— оо; f+ (2)=/L (2) = + оо;
2) /+(0)=/_(0)=0; /+(!)=/_ (!) = +«; f+ (2)=/_ (2)=3/2;
3) /+ (0)=/_ (0)=— оо при а четном; /+ (0) =— оо, /_ (0) = 4-оо
при а нечетном; f+(l)=f_ (1)=—оо;/+(2) = 4/2“,/_(2)==—4/2“;
4) К (0)=—оо, /_ (0)=+оо; f+ (1)=+«, f_ (1)-----оо; f+ (2)=
==/_ {2)=+оо. 37. Например: 1) f(x)=x, g(x)=— х; 2) f (x)==
= х-|-5, g(x)=— х-, 3) f(x)=2x,g(x)=—x; 4) f(x)=2x,_g(x)—x;
5) /(x)=x, g(x)=x2; 6) f (x)=A g(x)=x; 7) f(x) = ^/ x, g(x) =
= 1//x; 8) /(x)=gW=/7; 9) /(x)=2; 10) f (x) = 0, g(x)=l/x.
§2
задание 1
1. 1) Да; 2) да; 3) да; 4) нет; 5) нет; 6) да; 7) нет; 8) нет,
2. 1) х = 0; 2) х=2, х=3, х = 4, х=5, х = 6, х=7, х=8; 3) х=
=	k € Z; 4) х=1; 5) х=-1, х=2; 6) х=2; 7) x=ak,
k £ Z; 8) х=2, х=—2. 3. 1) Л= 1; 2) Л= 1/2.
ОТВЕТЫ И УКАЗАНИЯ
( I, Х<0,
4. Например, f(x) = -| 2, х=0,
V 3, х>0,
6. 1) — 5 < х <— 4, 2 < х < 3; 2) —1 <х*Ск
{3, х < О,
2, х=0,
1, х>0.
ЗАДАНИЕ 2
1. 1) Да; 2) да; 3) нет; 4) да; 5) нет; 6) да. 2. 1) х = — 1;
2)	х = яп, п g Z; 3) х=1, х=—1; 4) х = 0; 5) х=7; 6) х=0.
3.	1) Л = 0; 2) Л=е"1/4.
. „	П . f 1,	Х^О, t . fl, Х^О,
4.	Например, f(x) = j 1/2> х=0>	g(x) = j 2> х==0
6. 1) — л/2 <х< — I, —1 < х < л/2; 2) О < х < 1, л < х < 4.
Упражнения
1. 1) xSs—5; 2) х € R; 3) х ё (— оо; 1) Ц (1; + оо); 4) хё R;
5) х=й, AgZ; 6) xg(—оо; — 1)(J(— 1; +<»); 7) xg(—оо; —1) (J
U (—1; 0) U (0; + оо); 8) х ё R; 9) х g (— оо; 0) (J (0; + оо);
10) х = 2, х=1; И) x£R; 12) х £ R\{n/2+nft/2}, k f Z.
2. 1) x = —2; 2) x=l; 3) x=0; 4) x=k, k ё Z; 5) x=0; 6) x=0,
x=—4; 7) x=0, x=—1; 8) x—l, x=—1; 9) x=0, x=—1, x=l;
10) x=0, x=l; 11) x ё R\{0}; 12) во всех рациональных числах.
5. Например, g(x)=x—х0. 7. Не обязательно; например,
к*)={ 2,’ xij г(ж)аа{1’ Uia 9- НапР”меР- /W’
К (2-х) (5-х)
(х—3) (х—4) •
-Л _т	х. ч (	1, х—рациональное число,
10.	Например, /(х) = < ' г
г г» \	। —j, х—ИррацИоНальНое число.
11.	Да. 12. Да. 13. Непрерывна при х = 0. 14. 1) Нет; 2) да;
например, х0 = 3. 15. Нет. 21. f (e) — f (л) = 7/9. 24. 1) х=1;
2) х < —1; 3) —1/2 < х < 1/2, х > 1; 4) — 5 < х < 7; 5) — V 2<
<х<0, х^1; 6) xSsl/2.
ГЛАВА 5
§ 1
ЗАДАНИЕ 1
1. 1) 0,0201; 2)—0,75. 2. 1) 1;2) 1;3)—1. 3. 1)Зх3; 2)—2sta2x;
3) —4. /'(О =7, Г (2) = 13, Г (-2) =-11. 5. -J-.
2 У х	cosax
6. 1) х2— х34-2х; 2) —L=--|-J—_ j-А_ ; 3) —2 (1 —х);
' Т 2fx 3 j/x* 4 у х3 ’ '	1
4) 3(х+ /х)2^1+ 2^—у, 5) 2* 1п2+3* In3—4-* In4 +
+ 6* In 6;
<	12	1	1
ж+ил-т:	cos х+3 siD х+^ 5
584
ОТВЕТЫ И УКАЗАНИЯ
8) ...Л _ ~ Jb-L ; 9)	1 gx cos x4-g^ sinx;
cos2x sin2 я у 1 — x2
10) (1 + ^)2+2»22jc In 24-Зх2 sin х+х3 cos х;
' (sinx+cosx)2 ’
1	2~*	-2-*ln2arctgx-2-^—Lj
12) —t= —------1-/ x---------------------1±£_
2 И x arctg x	arctg2 x
2)
6.
ЗАДАНИЕ 2
1. 1) 0,0099; 2) —0,101. 2. 1) 2; 2) 3; 3) 1/3. 3. 1) 3cos3x;
Зх24-2х; 3) —2/л®. 4. f'(l) = 0. /'(—!) =—12, /'(0)=—3.
----4— . 6. u'vw+uv'w+uvw'.
sin2x
7. 1) 20*»-d_; 2)------------3) 3*ln3J----— •
’	/2x	x® x*	xln3
л 1	। .	1	-4 /2\*	2 , 1	1
4) —r-7="+sinx-------; 5) i — ) In—-----;
5$/x*	sin2 x \3j	3 x x2
X2
6) ex (sinx+cos x); 7) 2xarcctgx—rj—5;
lnx-)-l	2x2 In x . 9) 6x—5x4'» ln3
' 1+x2	(1+x2)2’ ' 3(1-®/x)2 3*+*
10) 2sin2x;
о
11) 2 (1+x+x2) (2x4-1); 12)-~arccosx
x3
13>
M)
j-j-bg (2* 4-x2)—arctg x (2* In 2+2x)
(2*+x2)2	;
V xcosx——^=^sinx— K^sin x In 6
2y x
x6*
15) 9* In 9 —~У + 1 ц.9*	; 16) —-fd-L,
V x	2xK X	x«
ЗАДАНИЕ 3
1. 1) — 5sln5x; 2) 100(14-x)M; 3) l/]<2x^l;
4) ; 5) 2**+*+1 (2jc+ ° In 2:
6)	ex In »+2> (In (x4-2)«|.-^5^ ;
\	X 4 “ /
7)	3 sin2 (x — x2) cos (x ** x2) (1 — 2x)	(---X
\ sin2 У 1/х /
ОТВЕТЫ й 'указания
585
8)	1________________In 2 _
2/2x(l + /S) xln2x’
9)	—6 sin (2 cos3 4x) (sin 8x) (cos 4x); 10) —	>
11)		==•	1	—; 12) x* (14- In x).
/arcsin (l+2x) /1 —(l + 2x)2	7
3.	Например, f(x) = { °’	либо f(x) = |x2—x|.
4.	Например:
'>'«={?: ‘it:
2)/(*)=«(*)={ £
,;2, j;1,;
fl/<*)=₽<*)=! i’
5.	y' (2)=32 sin -y—4 cos	, y'(0) = 0.
ЗАДАНИЕ 4
h Sta42T+3j ’ 2) 3xsin(2x2)smx2;
3) -{rwarcctgS(d^T+(7w); 4) e”1,*<2*+D>
5) ---!------7=1=-!-.
arccos2 In x Y 1 —ln2x x
1	1__£ J___1	1 .
' logs (Iog4X)log4x x In 2 ln3 ln4 *
7)	1	00,(005^-) (-Sin-^)^2 ;
2 у (Sincos-^j-
8)2tg(ctg
2x+l
(x+x«)lnl
9) ----,---1
^y^log1/2(x+x3)
X
im In4 1	"r«	2	1 •
WJ	'rin«(—X) —X 1
586
ОТВЕТЫ И УКАЗАНИЯ
11) (sin x)cos* (— sin х In sin x+ctg x cos x);
5/~Z f*4-2V/7	, 248 / 4	18	,8(l+2x)
l2) У* J (*+*) ^5x (x+2)(x—1)+ x+xi
3. Например, f(x) = | x(x+1)l(* + 2) (x-]-3) |.
4. Например:
г / v	f 1> x # 2,	z 4	j' 0, x # 2,
О fW-j 2> x=2,	£(*)-{ 1, x = 2;
£ / x	f 2, x Ф 2,	. 4 fl, x # 2,
2) /(*)-j 3> x==2, ffW-j 3/2, x=2.
6./(l) = sinl + cosl —1, у'(0) = 1/2.
Упражнения
1. 1) —1; 2) 0; 3) 2; 4) 0; 5) —2; 6) 2 In 2; 7) 0; 8) —2.
2. 1) 2*4-1; 2) 2|?=; 3) Зх2; 4)	I 5) 5cos5x;
6) —7sin7x; 7)	8) -(y)*ln3; 9) j,'=/	£
X	\ О J	I ^Л, X v,
10)	0' = / f’	3.	1)	_lx-3/24-2x-l/2+6xV*;
I 19 X U •	A
2) з(х4-у-2К7у(1—3) 0 при x # 0;
4)
X ,
УТ+х2
In к 1—x2; 6)
31n21n31n4
xln4x
7) 0 при xg(—1; 1);
4	л
8) 0; 9) 2(х-Н) при х > 0; 10) (^+е-^8; И) —1 прих#=-£--|-
+ nkt
12)
1
лх X
2tg^-
l-sindntgx)^^;

9	la*
13) _	J.-_; 14)-7==-; 15) -  -— ; 16) e« +
' In 2 cos 2x 2)^1 —x2 J^l-l-e2*
+«^6*4-/^^;	17) у (x4-|/'*4-|/14-*2)-2/3X
x(l 4-y ^Х+У1 + *2) 2/3)(1 +y (’+x2)-2/32x); 18)
19) 2(14-x2) 1 20)
. 1
In arocos —7г=-
К X
1
arccos" ___
Vx
1
/x«=T2
px-x* (1 —2x);
21)
3x2 arcsin У x
x3_____ 2xcos x—x2 sinx .
2УхУь=х X*cos»x
ОТВЕТЫ И УКАЗАНИЯ
587
22)
23)
25)
1 f 1 । I (
1 . т f 1 । 1 1 \ X2 + 1 , , И
•— 4-1п —-~|-1п— ) I	—I* 1п—
X '	\ X 1 X J (	X ' X
In 2	( 2х , 2	2	( 2	\	1	14-2х
—и .....7 In х2--In (х2— 1) т-г-5 ; 24) —ь=г—-.
х!п2х \х2 + 1 х	1п2х2	7 2J^x2+x4-1
(-^Inx+A-); 27) xC0S*X
—-sinx In x+^3 Y 28) x*x (x* (1 + Inx) lnx-f-—Y
5. 1) /=2(*4-1); 2)	= {	Хх^2.
x > 0,
-1<х<0, 4) / = 0,	k£Z;
1+х* (1 +1п х); 26) х1}*
j______i_
х2	х
3) / = <
2,
О,
—2,
(	2x,
< ~6x6,
I 0,
x<0 6) «'-I bxgC-l.OJUd^oo),
x < 0, b) у	х€(_да._1)и(0.1}
6* Например:
1) f(x) = {
2) /(*) = {
g(*) = j
0, x—рациональное число,
1/2, x—иррациональное число,
0,	х—рациональное число,
—1/2,	х-* иррациональное число,
0,	х—рациональное число,
—1/2,	х—иррациональное число;
1, х — рациональное число,
0, х—иррациональное число.
7. Например:
п /<х)=/ °’ *€(-1; 1).
4 'W 11, *ё(—оо;—null; 4-00),
1, хё(-1; 1),
g(*) =
О, *ё(-2; 11UU; 2),
5, xg(-oo; —2) и [2; +«);
2)
3>
Нх) =
gW=
/w=
g(*) =
О, х—рациональное число,
1, х — иррациональное число,
—-/(х), х#х3,
2,	x=s=x3;
1, х—рациональное число,
2, х—иррациональное число,
1,	х—рациональное число,
1/2„ х—иррациональное число.
8. Например:
( х2, х — рациональное число,
'	0, х—иррациональное число;
588
ОТВЕТЫ И УКАЗАНИЯ
m г J х2 (х—I)2, х—рациональное число,
'	0,	х—иррациональное число;
г/ \	/х2(х—1)2...(х—п + 1)2,х—рациональное число,
(	0,	х—иррациональное число.
9. <р(а). 10. я!. 11. 1) 4 = 1, 4=—1; 2) 4 =4 = 4; 3) 4 =
= 1,4=5; 4) 4=+1. 4=~fi 5) 4 = 1, 4=0; 6) 4=0,
4=-2; 7)4 = 1, 4=-1; 8) 4=2, 4 = 0; 9) 4 = 4='0;
10) 4=—1, 4 = 1- 12. я=2х0, b——xt 13.я= 1, &= 1/2.-15. На-
пример, f=x®+2.
1Я\ п 1 — («+1)*п+пх"+х .
18) 0 -------’
2) 1 + 2х - (я +1)* х” + (2п*.+ 2п — 1) хп+1 + ях»+2 j 3 а.
'	(1—-х)3 *
н и е: данная сумма равна xf"-\-f't где f (х) = х+х2 + ♦.. +х").
§ 2
ЗАДАНИЕ 1
: 1. 1)у=12х—16; 2) у=—&x+-^-i±^. 2. 1)у =
= (2+2}<2)х—3—2/Y, у=(2—2/Т)х-3+2/Г; 2) у =
1	, о	5	1
= —	..х+3............, у==—	.- — х+
2Y 14+6 У 5	2К14 + 6]<5	' 2И14—6/5
+ 3--- 5	г-^. 3. (1; 0), (-1; -~).4. l)2arctgl;
2г 14 — 6/5	X 6	*4	*
2) 0,
ЗАДАНИЕ 2
1	2
1. 1) у~ех\ 2) z/==x+l. 2. 1) z/=-^г=х + ---^=г,
:	*	3 + 2/ 2	1 + / 2
3-2/2-‘,+747 * *Т; 2>	»=/^+2-
3. (0; 2), (-2; 0). 1. » arctg 2) »rMg	'
ЗАДАНИЕ 3
1. 1) arotg2; 2) arotg (—2). 2. 1) л/2; 2) ai = jt/2, а2 = л/4.
4> / 1 о ох пх f ( 1 \3/? 1 1 \ / ( 1 \3/з t , 1 \
з-1)(-1«2;2К2>^+ . 1—jT»). (- +) ; Чу=).
D С  ; !_ 5 \ Л_ 2 ; 1+ S \ 2) (3 _Л
<Кв 61^6 } \ К6 6/6/ Ч2’ J
с —1 1
5» Л —11	> а —— “"“/К—-" •	‘к*
У 2	У 2	  < ’
ОТВЕТЫ И УКАЗАНИЯ
589
ЗАДАНИЕ 4
L 1) arctg2; 2) arctg. 2. 1) arctg У5~; 2) arctg-—.
3. I) 4); J>
4(1— V*Т’ "1'1 7Г /в)’ 4‘ 11	|;; 2* (зна’|оу-2TFT2<
Упражнения
1. \)у=-Х-1- 2) у=-4х+7; 3) у=»+-}-,
*	У 5 У 5
4) у = 2х—е; 5) у— УЗх-}--—	. 2. 1) у— 1, у——4х+5;
2) у=3х—2, у=3(44-2Кз)х— 12/3"—20, у=3(4—2/3 )х+
+ 12/Г— 20;3)//=(—3+2/3)х—4+2/3, у={—3—2/з)х—
-4-2/З"; 4) 0=л;4-1; 5) у=-(3+2 /2 )х+2+2 /2,
0=(2/2—3)х—2/2+2. 3. (0; 1/2+л/з7б). 4. 1) у =
= — 4x4-5; 2) У~~ 4х+8, «/ = 4x4-8; 3) y-x—kn, k^Z.
5. у=2. 6. (8;0), (0;0). 7. 1) (1+/2; — /Г), (1 —/Г; /2);
2) (1; —3); 3) (2лп; 0), n£Z, (л/3+2лт; —/3/4), m£Z,
(—л/3+2л/; /3/4), /gZ; 4) (5/4; 1п4); 5) (л/9+2лй/3; 1//3),
ftgZ; (—л/3+2л//3; —1//з), l^Z. 8. 1) Таких точек не су-
ществует; 2) (—1/2; 3/4); 3) (2лЛ; 0), fegZ; 4) _(лт; 0), mgZ;
5) (1/2; — In 2).». (11/2; 7/2). 10. (л/6; 1/2+л/2/3). 11. (—3; И).
12. (3; —15). 13. у=хг—х+1. 14. у= —х+5/2. 15. (—1; 76/15),
(3; —8). 16. л/4. 17. (1; 6), (—18. (1/8; -1/16).
19. у=±х+1, у=2х—2. 20. л/4. 21. (1/2; —15/32). 22. arctg-l.
аЬ	О
§3
ЗАДАНИЕ 1
1.	1) На [2; 4-о°)	возрастает,	на	(—оо; 2]	убывает;	2)	на
(—оо; 0)U[4/3; 4-оо)	возрастает,	на	[0; 4/3]	убывает;	3)	на
j—оо; —1]U[1; 4-оо)	возрастает,	на	[—1; 1]	убывает;	4)	на
(0; 1/е] убывает, на [1/е; +00) возрастает. 2. 1) х = 0—точка
локального максимума, х—У2 и х=— У2"—точки локаль-
ного минимума; 2) х=0—точка локального минимума; 3) х=1—
точка локального максимума; 4) экстремальных точек нет.
3. 1) На (0; 4-оо) выпуклая вниз, на (— со; 0) выпуклая вверх;
/	_4 —i/lfl	Г— 44-/6	\
2)	на ( — оо;--------- I и I ----; 4~ 00 ) выпуклая вниЭ|
\	I I	Z
590
ОТВЕТЫ И УКАЗАНИЯ
на
—4 — /6 . —4+ /6
4	2	;	2
выпуклая вверх; 3) на (—оо; 0]
и [1/2; + оо) выпуклая вниз, на [0; 1/2] выпуклая вверх; 4) на
(—оо; —1) и [0; +оо) выпуклая вверх, на (—1; 0] выпуклая
вниз.
ЗАДАНИЕ 2
1. 1) На (—оо; —1] и [1; + оо) возрастает, на [—1; 1] убы-
вает; 2) на (— оо; —1), (—1; 1) и (1; + оо) убывает; 3) на (—оо;0]
и [2; +00) убывает, на [0; 2] возрастает; 4) на (—оо; —27/64]
убывает, на [—27/64; + оо) возрастает. 2. 1) х=0—точка локаль-
ного минимума, х= 2/3—точка локального максимума; 2) х=0—
точка локального минимума, х=8/27—точка локального мак-
симума; 3) х=е—точка локального максимума; 4) экстремаль-
ных точек нет. 3. 1) На (— оо; 1/6] выпуклая вверх, на [1/6; + оо)
выпуклая вниз; 2) на (—оо; 0] и [0; + оо) выпуклая вверх;
3) на (0; выпуклая вверх, на [е~3^2; +оо) выпуклая
вниз; 4) на (—оо; —1] и [0; +<х>) выпуклая вверх, на [—1; 0]
выпуклая вниз.
ЗАДАНИЕ 3
1. 1) На (—оо; 1] и [3; +оо) возрастает, на [I; 3] убывает,
х=1—точка локального максимума, х=3—точка локального
минимума; 2) на (— оо; 0) и [4/3;+оо) убывает, на (0; 4/3]
возрастает, х=4/3—точка локального максимума; 3) на
[Л -М	Г , 1 л 1 л
0; arcsin 1 возрастает, на | arosln-р ;-g-1 убывает, х =
1
= arcsin—точка локального максимума; 4) на (—оо; 2/3] и
[1; Ч-оо) возрастает, на [2/3; 1] убывает, х=2/3—точка локаль-
ного максимума, х= 1 —точка локального минимума, 2. 1) На
вверх; 2) на [2л£; 2л/3+2л£], &gZ, и [л+2л&; 4л/3+2л&],
&gZ, выпуклая вниз, на [2л/3+2л&; л+2л&], и [4л/3-[-2л&;
2л4-2л£], £gZ, выпуклая вверх; 3) на (— оо; —1] и [1; 4-оо)
выпуклая вниз, на [—1; 1] выпуклая вверх; 4) на (— оо; 0) и
(0; + оо) выпуклая вниз.
ЗАДАНИЕ 4
1. 1) На (0; 1/2) и (1/2; 1] возрастает, на (— оо;0) и [1; 4-оо)
убывает, х=0—точка минимума, х=1—точка максимума;
2) на (—оо; —1] и [1/2; 5] убывает, на [—1; 1/2] и [5;+оо)
возрастает, х=—1—точка минимума, х= 1/2—точка максиму-
ма, х—5—точка минимума; 3) на [—л/2; —л/3] и [л/3; л/2]
ОТВЕТЫ Й УКАЗАНИЯ
501
на
убывает, на [—л/3; л/3] возрастает, я=— л/3—точка миниму-
(1	31
— оо; — 1и-д- г убывает,
J
возрастает, х—-^-In——точка минимума.
2. 1) На (—оо; —2] и [2;-(-оо) выпуклая вверх, на [—2\ 2]
выпуклая вниз; 2) на (—оо; 1] и [Г,+оо) выпуклая вверх;
;$) на [2&л; (2&+1) л], 6gZ, выпуклая вверх, на [(2&-J-1)зт;
(26+ 2) л], 6gZ, выпуклая вниз; 4) на (0; 1) и [а2; + °0) вы-
пуклая вверх, на (1; е2] выпуклая вниз.
Упражнения
1.	1) На [0;
(— оо; 0] и П
(	1 —/2!
-оо;-----5—
оо) возрастает, на (—оо; 01 убывает; 2) на
оо) возрастает, на [0; 1] убывает; 3) на
Г 1 + К22	. \ х Г1—у 22
и —L—-------; оо I убывает, на I --~;
  !-I возрастает; 4) на (— оо; 0] и [2; 4-оо) возрастает,
о I
на [0; 1) и (1; 2] убывает; 5) при а <10 возрастает на всей чис-
ловой прямой; при а > 0 возрастает на (—оо; —У а/3] и
[Ка/3; +00), убывает на [—У а/3; У а/3]; 6) при убы-
вает на всей числовой прямой; при а > О возрастает на (— оо;
— К1/ (За)] и [К 1/(За); + оо), убывает на [—У l/(3a); У1/ (За)];
7) на (—оо; 0) и (0; 1/2] убывает, на [1/2; +оо) возрастает;
8) на (— оо; —1), (—1; 1) и (1; + оо) возрастает; 9) на [—9/2; —3]
и [0; +°о) возрастает, на [—3; Of убывает; 10) на (— оо; —2) и
(—2; 2] возрастает, на [2; Н-оо) убывает; И) на (—со; 1/5] воз-
растает, на [1/5; +<») убывает; 12) на (— оо; 0) и (0; +00) убы- .
вает; 13) на (0; 1/У е ) убывает, на [1/Уе ; возрастает;
14} на (— оо; —1/У 2*] и [l/J^2 ; + оо) возрастает, на[—l/J^2 ;0)
и (0; 1/УТ] убывает; 15) на (—оо; 0] и [2; +оо) убывает, на
[0; 2] возрастает; 16) на (—оо; 0] и [4/11; +оо) возрастает, на
[0; 4/11J убывает; 17) на [л/б4-л&; 5л/64-л&], &gZ, возрастает
на [— л/6 + лй; л/6+л£], убывает; 18) на (—оо; —1] и
[1; + оо) возрастает; 19) на (0; 1] и [е4; + оо) убывает, на [1 ;e*J
возрастает; 20) на (0; 1/ё\ убывает, на [1/е; -f-oo) возрастает;
21) на (—оо; —1] и (0; 1] убывает, на [—1; 0) и [1; +со) воз-
растает; 22) на (— оо; —1), (—1; 0), (0; 1) и (1; + оо) убывает;
23) на (0; Ц-оо) убывает; 24) на (—оо; —1] и [1; -f-oo) убывает,
на [—1; 1] возрастает. 2. 1) х——2—У5—точка максимума;
2) х==1—точка минимума, х = —2—точка максимума; 3) х =
= —2—точка максимума, х = 2— точка минимума; 4) х=9/2—
точка максимума, х — 5—точка минимума; 5) х=1—точка мак-
симума; 6) х~ 19/4—точка максимума; 7) х ——1/2—точка мак-
симума, х ——1 и х = 0—точки минимума; 8) х=^2—точка
минимума; 9) %—1—точка максимума, х =—1/2—точка мини-
мума; 10) х=-^-|-л/г, /egZ, — точки максимума, х —
ftgZ,—точки минимума; 11)	1/5—точка максимума; 12) х=ж
592	ОТВЕТЫ И УКАЗАНИЯ
= 1/4—точка минимума; 13) х— 1/6—точка минимума; 14) х=1
их——1—точки минимума; 15) х =—1, х = 0 и х=1—точки
минимума, х=—1/^3" и х= 1/1^3—точки максимума; 16) х —
= ~-|-2л&, k£Zt—точки максимума, (—1)й+1 -2—|~nk, k£Zf—
2	и	к
точки минимума; 17) х=0—точки минимума, х= 1 и х=—1 —
точки максимума; 18) х=-^4-ля, я gZ,—точки максимума, х~
=—|-л/, /gZ,—точки минимума; 19) х ———--|-4л£, k£Z, —
точки минимума, х=4л/п, mgZ,—точки максимума; 20) х=1 —
точка минимума; 21) х=2л&, kgZ,—точки максимума; 22)х=1—
точка минимума; 23) х=4/3—точка минимума, х = 2—точка
максимума. 3. 1) На (—оо; 2/3] убывает, на [2/3; + оо) воз-
растает, а —2/3—точка минимума; 2) на (—оо; —3] и [—Г, 4-оо)
убывает, на [—3; —2) и (—2; —1] возрастает, х = —3—точка
минимума, х——1—точка максимума; 3) на (— оо; 0] и (1; +оо)
убывает, на [0; 1) возрастает, х=0—точка минимума; 4) на
(— оо; 2] и [5/2; 3] убывает, на [2; 5/2] и 13;Н~оо) возрастает,
х = 5/2—точка максимума, х = 2 и х=3—точки минимума;
5) на [0; 2/3] убывает, на [2/3; 3] возрастает, х = 2/3—точка
минимума; 6) на [0; 1/5] возрастает, на J. 1/5; 2] убывает, х =
= 1/5—точка максимума; 7)_на [—2)^2;—2] и [0; 2] воз-
растает, на [—2; 0] и [2; 2 ]/"2] убывает, х=0—точка миниму-
ма, х=—2 и х = 2—точки максимума; 8) на (0; 1) и [е2; + оо)
возрастает, на (1; е2] убывает, х=е2—точка минимума; 9) на
(0; 1/е] возрастает, на [1/е; 1) и (1; +оо) убывает, х=1/е —
точка максимума; 10) на [—1^2;—1] и [1; ]^2] убывает, на
1—Г, 1] возрастает, х =—1—точка минимума, х=1—точка
максимума; 11) на (2; 3) возрастает, на (3; + оо) убывает, х — 3—
точка максимума; 12) на (—2; 0] убывает, на (0, + оо) возра-
стает, х = 0—точка минимума. 5. а^[—У 3; У 3]. 6. а < 3/8.
7. ag(0; +оо), х=1пя. 8. ag(—оо; — 2 — У 5) U (/* 5; + оо).
9., ag(-co; -у (0+3)) (J (-§-(/ 7-1); + «). 10. ag
(—оо; з/р/ 4). 11. *~fl при | a|g[O; 1), (1+а)2/6 при
|а|€[1; 2), (2+а2)/4 при | а | £ [2; + оо). 12. ag[3/4;+oo).
(( 32	\
р; — Р3+Р ),
27	J
32	\
2уР®+₽; ₽)•
§ 4
ЗАДАНИЕ 1
1. 1) 4. —24; 2)2, 125, 1; 3) 1Д); 4) 21 +31п2, 0, 2.«=*+«,
;<=г,=а/2 3, 3 К 2/8. 4. 4R V 5/5, R / 5/5.
ОТВЕТЫ И УКАЗАНИЯ
593
ЗАДАНИЕ 2
1. 1) 17, 0; 2) —2, —10/3; 3) 4, 2; 4) 105, 1/3. 3. /2. 4. 4S.
ЗАДАНИЕ 3
1. 1) 1, 0,8; 2) 2 V 3/3, 1; 3) 5, 0; 4) 1, —1/3. 2. 3. 3. а = 1.
4. М (4; 2). 5. ос —л/З.
ЗАДАНИЕ 4
1. 1) ^/9/2; 2) 16, 2; 3) 4 У 6, 0; 4) я/2, — я/2. 2. 2.
4. 993,5 5. R«tgy.
Упражнения
1. 1) 60, —2 У 3/9; 2) 8/3, —8/3; 3) 0, —25; 4) 6, 1; 5) 1,
2—In 4; 6) 0, —1/4; 7) 9, 4; 8) 4, 0; 9) 900, 0; 10)	,
3 У"3—5л	17	2	е«+4е+2	10—?1п2
6	: 4 In 16’ In 2* l )	2_	’	2	5
13) 5, 4; 14) 3/2, 1; 15)_7/4, —9/4; 16) р/Зб/з, 1; 17) 17, 0;
18) —57, —118; 19) 3 К 3/8, 0; 20) 1/3, 1/9; 21) 0, —2/е; 22) О,
—14/е; 23) 4+In 2, 0; 24) 0, —3(7+In 2); 25) е6, — е»; 26)_е\ 0;
27) —3/4, —3; 28) —15/4, —10. 2. 1) —1; 2) 1; 3) XZ±£:
4) —2; 5)0; 6) 1! 7) ХД. 3. 1) 3 arcsin ХД+Г'"2;
£i	О
2) -у; 3) 64; 4)	5) 3; 6) —204; 7) —-%* 	7. 1) л;
2)l+81n5;3)241n3; 4)1+^^; 5) 1+д^. 8. 1)3/4;
2) 2/3; 3) 6(1 —1пЗ); 4) 12л—1. 9. 1) х=1; 2) х=1; 3) х==2;
4) х~—1 (указание: возвести обе части уравнения в квад-
рат); 5) х = 2 (указание: переписать уравнение в виде
a f • 10- 0 ЦР-; 2)3; 3) /”2; 4)2 /2-
5) /2. 11. 1) А ; 2)	. 12.	13. М (0; 2). 14. М (Al;
) • 15. М	, 16. М (л; 1). 17. /И (3/2; 0).
18. 32_У”з/9. 19. 32. 20. 3 К"3/2. 21. М (3/2; 13/4). 22. а = Ь = .
= У s. 23. Высота бассейна вдвое меньше стороны квадрата
основания^ 24. 32. 25. а/2^а/2, аУ2—з/2. 26. 2а. 27. /р^З/З.
28. г=Кб/?/3, Н=2 У 3R/3,_V = 4yinR/9. 29. 64 У 3,2л/75.
30. 2. 31. Х=5У 2, /=5К 2. 32. R=4, Н=4. 33. Я = 4,
т/"?
34» ВС=8. 35. a = arctg
А
594
ОТВЕТЫ и УкАзанйя
§s
ЗАДАНИЕ 1
1. 1) (Z-у) (х-у) (х-2); 2) (ir-2)(2-X)(jr-x)(x2+J/2 +
+2.1)	> *> з.
ЗАДАНИЕ 2	' 1,1
1. 1) sin2 г/; 2) —; 3)
' xyz 1 (xyz)2
задание 3
3. ag(— оо; 11). 4. Два корня при а£(—\/е; 0), один корень
при а =—1/е и а^[0; -)-оо). 6. х = 3.
ЗАДАНИЕ 4
3. ag(O; 621/16). 4. Два корня при ag(O; 27/е3), один корень
при со; 0] и а=27/е3. 6* х=2 ^указание: рассмотреть
г_________________ х2 \
функции	Зх—2 и #=—-jja
ЗАДАНИЕ б
1. *(£(— оо; —2). 3. xi=*2=*a = 3» *4=— 2. 5/xi=2, #f = 2;
х2=—2, #а=—2.
ЗАДАНИЕ 6
1. О < х < 16. 3. хг = х2 = хз =3/х4=—4. 5. *=л/4, #=л/4*
ЗАДАНИЕ 7
„а 2.	4.	3,.
ЗАДАНИЕ 8
I. х=81.
„ ,v	хп2хп+2—(2и24-2п— l)xn+i4-(rt+l)2xn—х— |
'	(х—1)?	*
2) 16-?ЦЗ»+ . 3. а=-К27/2.
Упражнения
1.	П х=—1; 2) х = 0; 3) х=—1/2; 4) л= 1; 5) xf = 0,
*2=1/2, х3 = 1; 6) х = 1; 7) х = 40,5; 8) *= 16; 9) х= 1; 10) *1 = 1/2,
*2 = 3/2; 11) *1 = 1, r/= 1; 12) х — е, у~ — л4-2л&,	13) х=0,
у=-у4-2л&, k£L. 2. 1) 6(a-c)(a+c-Z>)2; 2) (х^-^+1)х
Х(*^+2*—#+1); 3) (*2 + 2х—у) (х2—2*+^+2). 3. Два.
4. 1) Один; 2) один; 3) решений нет; 4) один. 5. 1) * > 2;
2) ОС* < 3/5, 3/5 < х < 4-оо; 3) х±=—1, х2=0, *3=1, х4=2;
4) 0 < х< 4; 5) х< —	6) х>—1; 7) Xf=—2, х2=—1}
8) — 1/2 < х < 0; 9) 0 < х < 1/2; 10) (—2/3; 0). 9. 1) xf=х2=2,
х3==3; 2) Х1 = х2=1, х3 = —1, х4 = 3; 3) xi=x2 = —4, х3=х4=1;
ОТВЕТЫ И УКАЗАНИЯ
595
4)	Х£=—1, х2 = х3 = 3, я4 = 4; 5) xi = x2=2, х3 = 1 + К 3, х4 = 1—
—К 3; 6) Xi—х2 = *з=1, х4—л5 —2; 7) х1=х2=х3=2, x4=xs = —2.
10. 1) При любом а решения; 2) при а < 1 одно решение,
при а> 1 три решения, при а=1 два решения (Х£, х2 = х3);
3) одно решение при а^О и а=1/е, два решения при 0 <а <
< 1/е, при а > \/е решений нет; 4) нет решений при а<:0, одно
решение при 0 < а < е2/4, два решения при а=е2/4, три корня
при а > е2/4; 5) нет решений при |а| > 3 Y 3/16, одно_решение
при | а| = 3 У' 3/16, два решения при 0 < | а| < 3 V 3/16, три
решения при а = 0; 6) при |а|<2три решения, при |а|=2
два решения, при |а| > 2 одно решение; 7) при |aj > 216 одно
решение, при |а|=216 два решения, при 88 < | а | < 216 три
решения, при | а | = 88 четыре решения, при |а| <88 пять ре-
шений; 8) при а<0 решений нет, при а = 0 и а > 4/е2 одно
решение, при 0 < а < 4/е2 три решения, при а = 4/е2 два реше-
ния; 9) при а<0 и а > е1,е нет решений, при 0<а< \/ее
три решения, при 1/ее< 1 и а=е1/е одно решение, при
1 < а < е1^ два решения; 10) при а < 0 и а = е одно решение,
при а > е два решения, при Ъ^а<е решений нет; 11) при
а < —189 не. решений, при а——189 одно решение, при —189<
< а <—64 и а > 0 два решения, при а~—64 и а=0 три реше-
ния, при —64 < а < 0 четыре решения; 12) при а < 0 и а — е
одно решение, при а > е два решения, при 0<:я < е нет реше-
ний. 11. 1) а <—188/27, а >175; 2) ^=122, а2=—800/27;
3) а > 0; 4) а > eln 10; 5) 0 < а < 1, а=в1/е; 6) f аf <	1.
1	( я+ 1 п+ 1	. пх . X .
19.		 —2— cos —— х sin -jr- sm 77 4-
, о X \	2	2	2	2 1
sln2 т
. П . п + 1 ПХ л X 1 Я 4 1	* пх х\
+ у sm—5г- * cos	sln 2~ Y sin ~2“ х sin Т C0S Т ) ‘
20.	/(«)=—2х»+3х«.	22. 1)	~-Р ”	;
2)	• 23‘ /W=x2-y- *
2) -4=-; 3) -Д=-. 29.	30. а<0. 31. о<0,
'	Кб
а>1. 33. 1)я= 1,6=0; 2) а= 1,6=0; а=—1, 6=0. 35. ^±4
30. Л=Й=С=О.
ГЛАВА в
ЗАДАНИЕ 1
1. 1) 1; 2) 2/1п2; 3) 15/4; 4) 1/4; 5) 1п 2; 6) 1. 2. 81/4.
ЗАДАНИЕ 2
1. 1)	е»«);	2) sinx; 3) —р-(6»+i_e»+i);
4) ае“—е«+1; 5) у In ab In; 6) -1—1. 2. 992/5.
596
ОТВЕТЫ И УКАЗАНИЯ
ЗАДАНИЕ 3
1. 1) 1; 2) 0; 3) 4; 4) л/8. 2. 1) Первое число больше; 2) вто-
рое число больше; 3) первое число больше; 4) второе число
больше. 3. 1) 2/л; 2) \/е (указание: рассмотреть 1пап);
3) е—1; 4) 2.
ЗАДАНИЕ 4
*• °	2)4,5; 3) НИ 4)4(1Н)-
2. 1) Первое число больше; 2) второе число больше; 3) первое
число больше; 4) первое число больше. 3. 1) -^-(2 К 2-—1);
2)	у я; 3) 2; 4) у.
ЗАДАНИЕ 5
1.	1) х> 0; 2)
2.	1) f W+^W+C; 2) f (x)g(x)+C.
COS X , 1	1
3.	1) In*; 2) ^y=-+^cos -s .
4.	1/3—15 In 3. 8. l/(«4-l).
ЗАДАНИЕ 6
1. 1) x 0; 2) *#n/2-f-nn, ngZ. 2. 1) In |/(*) Ц-С;
2) -Lp(x)-^C.	3. 1) sin V~x/x-, 2) 2*/(l+*e).
4.	3. (2»+«-!)/(»+!).
ЗАДАНИЕ 17
3	jc3
1) x*+3x+C-, 2) x3/3—4xa+5x+C; 3) 4—X^^.X^C;
z	о
4) _ 1/*—l/*24-l/*34-C; 5) 4-*8/a + ln|*|+C; 6) —3x~lla —
О
— 6*a/s+-^*6/8+C;	7) 4*—e*+C;	8) 2*/ln 2 + 2^/ln 4 +
О
4-2’*/ln8+C; 9) 3*—2(3/2)^lny4-C; 10) — 2 cos *—3sin*+C;
1 1
y*4-sin*/24-C; 12) tg*—ctg*+C; 13) arctg
—Ur In
H)
14)
16)
2 — V 3*
2+УЪ
4-C; 15) In | V~2x+V2*«+l |+C;
y=-ln|K3i+/3^4|+C; 17) -y=- arcsin -yy+«l
ОТВЕТЫ И УКАЗАНИЯ
597
18) *+arctg*+C;	19) In ||^-^|+arctg *+С;
о	11 """"Л I
20) -I In 1I--------7=- arctg
8 I 1+-Ч 4/3	/3^
ЗАДАНИЕ 18
• I) х*/2—х8+3х2—6х+С; 2) ^-х?—Л-^+^+С; 3) — 1/х+
<5	£»
+ 1/х2+С;	4) in |х|+4 /х+х+С;	5)	tx*/» _
-|««»+С; в)^-т?т.з«+с; 7) ^+с; 6) 2^-2Г;+С;
9) — cosx+2sinx+C; 10) |х-8-у+С; 11) — ctgx—tgx+C;
12)
14)
1 arctg '	< г. iq\ 1 in У7—и 5я. । £«
/ 6 arCtg /3 +С’	13) т1Т/7+/5х +С‘
’ ln|/3x+/iWI+C; 15) -4=rarcsin/Зх+С;
16) 4=ln|K 2х+/2х3-5|+С; 17)-£-x4--i-ln|M+C;
1/2	о л j 1—х ।
18) arctg х+ In ||у4|+С;
---7=r arctg -4=-+С;
/3	/3
19) ----1— In	_
10 / 2 I / 2+х
20) arcsin х + In | х + У' 1+ х214- С.
ЗАДАНИЕ 19
1) ±1п|2х+3|+С; 2) -4-cos5x+C; 3) — 1(1-х)8+С;
Z	О	о
4) ^(1^2х)’.~(1-2х)’+С;	5) 1 (х-1)5/2+4 (х-1)3'2+
2	, 2х+ 1
7=- arctg  '
г3 /3
8) —4^ In -
+С; 2VTX
К 2+x-l I
' I *Т* >
4
10) In (х2 +3x4-4)--1_х
9) A In (х2+1) +arctg х+С;
X arctg ?^^+С; 11) —(1 — х2)3/2+С; 12) sin х—sin8 х/З+С;
13). cos —+С; 14) —L_ln
; х '	8 /2
10$ — 1п| cosx|+C; 17) — arctg (cos л)+6;
+ С; 15) 2arctg/х+<?;
1п^ X
18) ^4-с;
598
ответы' и укйания
19) In I tax|+C; 20)	21)
22) In | tgy|+C; 23)Хх4-у1»|4х-7Ц-С; 24) X(i+x)3/2+
+ 4(x-1)s/2+C.
О
ЗАДАНИЕ 20
1)	‘ ln|l-3x|4-C;	2) ^2i-|-C;	3)
4) ^(2>-3)1<>4-1 (2x-3)’+C; 5) -1(1-хУ'^±-(1-хГ^-
-4 (l-«)"+C; e> arctg ^+C; 7) ^resm^g+C;
8) ln|x2 —4| —|ln| — |4-C; 9) -2/ | x2-2x+41 4-~x
V 1	1
Xarctg^+C; 10) -i-(1 +x2)3'2+C; 11)
уз	d
I	1	X3
12) -slny4-C; 13) -g-arctgi-4-С;	14)
15) In|sinxf4-C; 16) X arctg ХГГ-f-C;
4	&
18) In fin lnx|-|-C;	19) X^’-f-C; 20)
О
cos3 к
~T~
cos *+<?;
ln|1 + ^.f 4-C;
1-K x
О
17) 4 (In x)3*2 + C;
<5
--1(^+2Г24-С;
21) lnltg(^4-i')Uc; 22) Ax-g inf 5x4-3
I V "	“ ✓ I	v zv
23) In |14- lA+ik^ 24) 2Г1+е*+С.
I л T	Л I
ЗАДАНИЕ 21
1) (14-x)ln(x4-l)-x-f-C;2)y (lnx-X)4-C;3)—e-*(24-
у2 у
4-2x4-x2)4-C; 4) — xcosx-f-sin x-f-C; 5)	sin2x-f-
4-X cos 2x4-C; 6) —x ctg x+ In | sin x | -f-C; 7)-X- (cos ^+sin -f-Cj
8)	ln|x4-}/'x5=4 |+C;9) ±/2^x24-arcsinp=4-Cj
10) xarccosx—j/'l—x2+C.
ЗАДАНИЕ 22
1) x (In x— 1)4-C; 2) y21n/x+^—1 (x—1)8—1”.I0'H|C}
3*	x2 1
3) 1^23(xIn3— 1) + C; 4) xsinx-|-cosx-|-C; 5) ——^-xsin2x^-
ОТВЕТЫ И УКАЗАНИЯ
599
—|-cos2x+C; 6) xtgx+ln|cosx|fC; 7) **(sin*
o	2
8) £/-jq3+-|-in|x+K^q^3|+C;	9)	+
5	jc	г..
+y arcsin	—|-C; 10) x arcsin x+y 1 я24~С.
ЗАДАНИЕ 23
1)^(1-x)7'2 +4(1— х)Ч*-~1(1—x)8/2+C; 2)|sit№x+C;
/DO	О
3) ‘Д^+С; 4) ±К?+4+21п|х+К^5+4|+С; 5)
6 __ л	—	У з
X^^Q^K^^+arcsin )+С; 6) 2/'1-21п(1+/х)+
+С;7)х+4У^+4 ^х*+2 К х+3 ^7+6 In |1—£/х|-Н?;
D	2
v	1
8)	.- —arcsin х + С;9) In (г*—I)2—х+С\ 10) arcsin—।-|-С.
ЗАДАНИЕ 24
1) ^(1-х)<«+у(1-х)7«—^(1-х)Ю'8+С; 2)
-y-sta^+ySin’x+C; 3) ~^3*4-С;	4) у/+=’7Е +
+ -g-arcsin -^=- +С; 5) ^±1х--|--^1п|У 2х+К5+2^|+С;
6) —2/х—2 In | 1—КЯ+С; 7) 2К х—4^7+4 In |1 + Ух 4-С;
8)	+С; 9) 11п|е* + 11-х+С; 10) -1п|Ш^!±11+ с.
у 1 + X2 6 I 61	I х
ЗАДАНИЕ 25
19	1
1) 2/3; 2) —1/2; 3) л/2; 4) я/3; 5) ±1п4+л/2—?rarctg~;
4 о	2	/
6) 2/3; 7) 4/3—5К2/6; 8) 23/8; 9) 7; 10) 1.
ЗАДАНИЕ 26
1) 5/3; 2) у ^2-у 1/7+1/12; 3) л/4 + 1/2; 4) л/6;
5)ЗбТГ25+21°§64: 6) ^(38-25/5); 7) -1/132; 8) 5/24;
.9) 19,5; 10) 2,5.
600
ОТВЕТЫ И УКАЗАНИЯ
ЗАДАНИЕ 27
1)	2) я/2—1; 3) 1/4—|-е-2; 4) л/4—^-Х
X In (^4-1); 5) cosl + sin 1 g—1/2; 6) 1; 7) 4 In 2-15/16.
ЗАДАНИЕ 28
1) In-i; 2) л; 3) л/2—1; 4) 1—Цр; 5) 1/2+л2/32—л/8;"’
6) 1 (Щ 2-1/3) +1/3; 7) л2/8—я/4+4 In (ла/16+1).
<5	х
ЗАДАНИЕ 29
1) 4>п2; 2) 3/4—К 7/12; 3) -12,5; 4) 1/3; 5) 1/6; 6)л/3—
- / 3/2; 7)3-3«/2+6arctgl; 8)	ln
+ -Д=- In
jf 10
tg-£-3-/10
—л-----7^ +
tg-2—з+К ю
о
; 9> 4 : 10) - К 3-л/6+2К2+агс81п1.
ЗАДАНИЕ 30
l)lln-i; 2)1/6; 3) 1/5; 4) 1/4; 5) 1 In ; 6) Г 7 +
+ -| In 1 7) 81Л/16; 8) 1 arctg	;	9) л/3-
- arccos 4; 10) 2/”2—4^/2+4 In l±^C?+2.
О	£,
ЗАДАНИЕ 31
1) 4 (8 К 2—l)/7; 2) 10/3;_3) 18; 4) 3/2—In 2; 5) 80/ln27;
6)3; 7)1; 8) 2(6 ]Z 3—5 V 2)/3; 9) 53/15; 10) 3/2—ln'2.,
. ЗАДАНИЕ 32
1) 12; 2) 16/3; 3) 7/6; 4) 9(l/2+ln3); 5) e2—1; 6) л/2+l;
7) 9 / 3; 8) 1/3; 9) 88/15; 10) 8/5.
ЗАДАНИЕ 33
1)9/2; 2)9/2; 3) 8/3; 4) (15—16 In 2)/4; 5) 16 V 3/15;
6) .1/3; 7) i 8) бл/2; 9) 16; 10)11—6 In 3.	?ss
OJl
ОТВЕТЫ И УКАЗАНИЯ
601
ЗАДАНИЕ 34
1) 32/3; 2) 81/2; 3) 1/3; 4) 4—3 In 3; 5) 8/3; 6) 5/12;
7) (Зл-4)/4; 8) 5л; 9) (4-1п 27)/2; 10) 90,5-6 In 2.
ЗАДАНИЕ 35	_
1. 1) 5/6; 2) 2л+4. 2. 1) 9/8; 2) 4/3. 3.-|(1п 2-1)+!^.
4. arctg (27/2) и arctg (27/4).
ЗАДАНИЕ 36
1.1)2(1 — 1п2);2)4л+8.2.1) 128/3; 2) (4 ]/”2+л/2-1б)/16.
8. y(ln2-l)+i-^-. 4. л-arctg А и л-arctg^.
Упражнения
1. 1) cos a-cos 6; 2) Д-Г0*+»-а*+>); 3) е-1; 4) 1; 5)4;
6) 1-4. 2. 1) In 2; 2) 16; 3) -J; 4) %; 5) 2; 6) 1; 7) ±;
л ’ ' 2 , } 1-+>а*	4 (n + l)(n+2)’ (п + 1)(п42)’
3)	Где 2п!1 = 2*4«6..,2 (п—1)«2п и-(2п +1)!! = 135.-
'(2п4-1)!!
(/п+ \ \ . ( т \
cos { —я j sin I — л 1
...(2n—1) (2п+1); 4) --------------k±LJ.. 6. 1) Первое
sin#-
2п
число меньше; 2) первое число меньше; 3) первое число боль-
ше; 4) первое число меньше; 5) первое число меньше; 6) первое
число меньше; 7) первое число меньше; 8) первое число меньше;
3	1
9) первое число меньше. 7. 1) -j- sin 4х; 2) 3 tg Зх; 3)	cos блг; 4) 0;
5) —4ctg4x; 6)	9. 1) у+^+х+С; 2) 2Г*+2л«/« +
+ 4*6/a+yX’/2+C; 3) £л’/*+^-1/«+С;4)1п|х|—1-х_4+С;
сч 25х	2 .лг >	4* I Г> ЙЧ 1	( 1 V I 27
5)	1п25 In 10° + 1п4 +С’	6)	+1п4Х
(1 \лс .	/32\*	1
т) +С’’ 7) Т	—5¥+С;	8)	— cos х—sinx-j-C;
Ч /	\О /	1 OZ
,П5
1	3 1/” 9
9) — yctg2x-f-C; 10) x+sinx4-C; 11)—(-—cos x+sinx)+C>
12 v I
i-i-iH-C; 13) tgx—x+C; 14) — ctgx—x+Cj
602
ОТВЕТЫ И УКАЗАНИЯ
15) —1=-1п
4‘”|Ы1+С; 161 Tarct"-jHx
Xarctg^=4-C; 17) —l-^-arctg *+<?; 18) In | x-f- П+? | +<?.
Ю. 1) _^.1п|х + 2|+±1п|х-1|+С;2)1х—}ln|14-2x|+(?;
3)	^(Зх+5)«+С;	4)	^(i_5x)»/»-§(l-5x)^+C;
5) g(l+4x)MA’+C;	6) ^(l-3x)*«-l(l-3x)2124-C;
7) 2 (l + x)7;2_.2(1+x)3/2+C;	8)	ln(x«4-4)-
/	0	О
-4arctg 4-FC;	9) гКхЧ^-З!!! |x+/F+4|+C;
10) —-U1— x2)8'2+C; 11) 4(1+x2)3'2+C; 12) i-arctg xs +C;
О	и	Z
13) 4-ln|^-4x+7|+-4=-arctg^+C;	14) 2КЙП+С;
z	у з уз
15) ln|24-lnx|+C; 16) —21n| 1—e*|—x+C; 17) уcosx —
—-j^cosSx+C; 18)-g-sln 3x—^sin5x+C; 19) —2 cos К x+C;
О
20)	x/2—sin2x/44-C;	21)	5x4-2 sin 2#—~cos2x+^;
22) — cos<?*-{-C; 23) —-i-ctg 7x+C; 24) A-In | tg(3x/2+n/4)| +<?;
/	О
25)	| tg (х/24-я/8) Ц-С; 26) tg^^C. 11.1) -^-x)7^
4-g-(2—x)5'2—|-(2—x)8/2+C; 2) 2-(i_x2)3/2 _
3) Л cos1»/3 x—4 cos4/8 x-FC; 4) tgx-F-|-tg8x-FC; 5) — ctgx —
— 4-ctg?x+C; 6) 4-tg3x+4-tgsx+C; 7)	—x—2e~*/2 +
О	dO
+21n(l+^'2)+C; 8) x-ln|l + VTT^I+C; 9)-^g?x
1	3tg|+l
X(2—5x3)6/3+C; 10) pA=-arctg - - y--—FC; 11) 2arcstay —
—±У"4^+С; 12) — 1-~— -arcsin x+C; 13) — —о-ф——
2	' x	7	2x2
1. 11 +/*14-x2l	1J|4 tg4x tg^x .
— -g- In j-----1 4~£»	14) —------g---In j cos x | -J- C;
ОТВЕТЫ Й УКАЗАНИЯ
603
15) x-tgl-f-C; 16) 2Kl + x-2ta(l + Kl+x)+C;
17) -|-(1+х)2^~3(1+х)^»+31п|1+|/Г+^1+С;	18) ~-х
191 7,п<1Т??+е; м>Йагс,87Й+е'
»'* 1	1	v2__1	х	I
2,) Frrctg7rs+C; 22) iRTW+2arct^+C;
23) .. , х  —UC. 12. 1) х 1п2х+2х1пх+2х+С; 2)
V1—х2	3
Xln(l+x)-j+J—J+C;	3) * arctg х~1 In (1+х2)+С;
4) xarcctgx-]-l In (1 4-х2)4-С;	5)	у In (14-1 'j	i- х —
— 11п| 1-)-х|4-С; 6) — у4""ф*’ arctgх4-С; 7) yarcsinx —
—1arcsinх4~ф V1 — хг;	8)	y(sinlnx—coslnx)4-C;
9) 1=^ cos2x4-4 sin 2X4-C; 10)	11+fEg 4-
4-C; 11) —2~^* Kl-x24-yarccosx4-C; 12) (14-x) arctg V"x—
a2X	_z>~2x
— / x+C', 13) -g-(2—sin2x—cos2x)4-C;	14) —-—x
x(x24-x+4)+C: 15) -^-е‘хг+с;16)^-^1пЩ+С;
17) 2(K~x—l)ev~+C-, 18) 2(6-x) Kxcos Kx-6(2-x)x
Xsin/74-С; l^^arcsin^-yK^Tsign x+C; 20)-уф-^ +
4-1 arctg x+C. 14. l)2,5-ln2; 2)^; 3) ^|=1; 4) 1;
5) Ц; 6) 0; 7) 1; 8) -2л2; 9) 14; 10)2.1; 11) 200/ 2^
О	Ю	о
12) Зл/8; 13) 11пЗ—л/2КЗ; 14) 1/6;	15)	14-1п(7!).
15. 1) (27—1)/7—(2е—1)/6; 2) 8/315; 3) 2/15; 4) (]/~ 3— /"2)/2;
5) ла2/4; 6) л2а4/16; 7) 2—л/2; 8) у=-1п —; 9) л//2?
19. 1)1(5е»-2); 2) 4л; 3) 2(1-1/е); 4) =р(4-л)-|-11п2;
5) л2/2—4; 6) у (sin 24-cos 2) —(sin 1 + cos 1)]; 7) л/4 —
-gy=-4-llnl; 8) л2/6-л/4; 9) л2/4;	10) 4л/3-/3.
604
ОТВЕТЫ И УКАЗАНИЯ
21. 1) 121,5; 2) 9; 3) 4/3;	4) 1/3; 5) 4,5;	6) 2/3;	7) 7/3;
8) (8 V 2 —3)/6; 9) 5/3; 10) 7/4; И) 2; 12) (бе—5)/3; 13) 3/2;
14) In 2; 15) 5 In (6/5)—0,5; 16) 14,5-J-ln 16; 17)8/9; 18)2; 19)1/3;
20) Зл. 22. 1) 4/3; 2) 1/6; 3) 1/6; 4) 9; 5) 9; 6) 125/6; 7) 64/3; 8) 4/3;
9) 7/15; 10) 2,5—6 In (3/2). 23. 1) 4/3; 2) 8. 24. 1) 16/3; [2) 18;
3) 1/3; 4) In 2—5/8; 5) (2e9 —101 )/6. 6) -+-Ц^. К7)4—In 3;
8) e—e-K 25. S=l. 26. (1/2; 5/4). 27J3/2; 2/3). 28. p=—1.
29.-S (2) = 32/3. 30. 1) 4—2/л; 2) л—^(1—л/8); 3) 11/3; 4)л.
31. y = xa—4x-{-3, 5 = б4-. 32. $ = -1-(x2 —Xi)8, гдехх, x2—кор-
о	о
ни уравнения	«уо = О.
h Oil
Дополнение
НЕКОТОРЫЕ ЗАДАЧИ
ИЗ ВАРИАНТОВ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ
ПО МАТЕМАТИКЕ В МГУ ИМ. М. В. ЛОМОНОСОВА
1. Найти область определения функции у = р/Л	(Зх2—2х).
1	2
Отв. —тг<х < 0,
о	о
3
2,	Найти координаты точки графика функций у-х2—-^,
ближайшей к точке (2; — 1).
Отв. ^1; —
3.	Найти координаты точки графика функции у=2 —х2,
(1	3 \
“Т » “о* ) •
4	" /
Л { 1	7\
ow. (д;
4.	Найти такое значение х из промежутка — 1^х«с2, что
точка с абсциссой х и ординатой
£==	2х—
удалена на наименьшее расстояние от начала координат.
Отв. xmin=l.
5. Найти такое значение х из промежутка 1<;х<;3, что
точка с абсциссой х и ординатой
12-2x4-1
удалена на наибольшее расстояние от начала координат.
Отв. Ходах =2.
6.	Найти наибольшее значение функции
__ 1
У~ —2х»+15х2—36x4-34
на отрезке 1	4.
°тв-
7.	Найти наибольшее значение функции
__ 1
у~ — 2х34-Зх24-12х4-8
на отрезке — 3^х«с3.
Отв. ушах=1.
ДОПОЛНЕНИЕ
606
8.	Найти наименьшее значение функции
___________________________1______
х3—6х2 4- 9х+20
на отрезке — 1 «С х «с 5.
Отв, ^miu=40«
9.	Найти наибольшее значение функции
4
У=хз__| х|
на отрезке —l,l*cx«cl, 1.
Отв.
10.	Найти наименьшее значение функции
3 ]	| о
j/ = _|x| — X3
на отрезке — 0,7 ^х^ 0,7.
Отв. упнп = 0.
11.	Решить неравенство
(х2 —4x4-3) log^— ^cos2 Ji*4-cos*4-2sin2-~^ ^=2.
Отв. х = 2.
12.	Решить неравенство
(6х—10—х2) logy— 1 + cos2 x-|-sin2 л*4-4 sin2 ~ cos2	^=—2.
Отв. х —3*
13.	Решить уравнение
(2х 4-1) (2 4- Y (2х 4- 1 )2 4- 3) + Зх (2 + К9х24-3) == 0.
Отв. хг = 2К2+)/“2, x2=2Ks—2 V~2-
14.	Решить уравнение
(2х+1) (1 + К (2х + 1)’4-7)+х (14- V^+7)=0.
- 1
Отв. х~——.
о
15.^Решить неравенство
9	14-log3(*4-6)
х4-2 л х
„	2
Отв. — -у < х < 0.
16.	Доказать, что при всех х > 0 выполняется неравенство
15
x24-Jtx4~y rcsinx > 0.
17.	Доказать, что при всех х > 0 выполняется неравенство
х24~л;х+4л cos х > 0.
Г 1	11
I 5 ’ 3 Г
/ИГГСЙЙЕНЙЕ	607
18.	Найти площадь фигуры, заданной на координатной пло-
скости соотношением
2 (2 —х)>] у-х* | + | ^+%2|.
Отв, 15.
19.	Найти площадь фигуры, заданной на координатной пло-
скости соотношением
w р—+2|4+++2|<(*+2)-
Отв. -у.
20.	Найти все значения параметра а, при каждом из кото-
рых область значений функции
а—cos х
^“~2a+sin2x— 1
содержит отрезок
Отв, ng [—-2; 0]U(0; 4/3).
21.	Найти все значения параметра а, при каждом из
рых неравенство
| sin2 х—2 (а— 1) sin х cos х+5 cos2x+2 — а | «С 6
выполняется при любых значениях х.
Отв, ag £1;
22.	Найти все значения параметра а, при каждом из
рых неравенство
15 sin2 x-j-2a sinx cos x+cos2x+«+11^6
выполняется при любых значениях х,
[24	।
—	L
23.	Найти наибольшее значение величины а, при котором
неравенство
а Y ~а (^-2х+1)+»^— < «/^51 sin " х I
имеет хотя бы одно решение.
Л	<
Отв,
10
кото-
291
5 Г
кото-
Справочное издание
ВАВИЛОВ Валерий Васильевич
МЕЛЬНИКОВ Иван Иванович
ОЛЕХНИК Слав Николаевич
ПАСИЧЕНКО Петр Иванович
ЗАДАЧИ ПО МАТЕМАТИКЕ
Начала анализа
Заведующий редакцией Е. Ю. Ходан
Редактор А. Т, Цветков
Художественный редактор Т. Н. Кольченко
Технический редактор Л, В. Лихачева
Корректоры: М. А. Смирнов, Н. Б._ Румянцева
ИБ № 32844
Сдано в набор 15.04.89. Подписано к печати 10.11.89.
Формат 84ХЮ8/з2. Бумага тип. №	2.	Гарнитура	лите-
ратурная. Печать высокая. Усл. печ.	л.	31,92.	Усл. кр.-отт.
31,92. Уч.-изд. л. 39,28. Тираж 150	000 экз.	(1-й	завод
1—75 000 экз.). Заказ № 670. Цена 2	р.	40 к.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва В-71, Ленинский проспект, 15.
Ордена Октябрьской Революции и ордена Трудового Крас-
ного Знамени МПО «Первая Образцовая типография»
Государственного комитета СССР по печати.
113054, Москва, Валовая, 28.
Отпечатано в типографии № 2 Госкомиздата РСФСР.
152901, г. Рыбинск, ул. Чкалова, 10.