Вариационные принципы теории упругости и теории оболочек - Абовский Н.П., Андреев Н.П., Деруга А.П.

Author: Абовский Н.П. Андреев Н.П. Деруга А.П.
Tags: общая механика механика твердых и жидких тел строительство конструкции машиностроение теория упругости теория оболочек
Year: 1978
Similar
Пространственные деревянные конструкции
Вариационные методы в теории упругости и пластичности
Прикладная механика твердого деформированного тела
Метод конечных элементов в статике и динамике тонкостенных конструкций
Text
                    Н. П. Абовский
Н. П. Андреев
А. П. Деруга
ВАРИАЦИОННЫЕ
ПРИНЦИПЫ
ТЕОРИИ УПРУГОСТИ
И ТЕОРИИ ОБОЛОЧЕК
Под редакцией
Н. П. АБОВСКОГО
и ygfu МОСКВА «НАУКА»
V/7 ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1978

22.25
A 15
УДК 531
Абовский Н. П., Андреев Н. П., Деруга А. П., Ва-
Вариационные принципы теории упругости и теории оболочек. — М.:
Наука. Главная редакция физико-математической литературы,
1978. —288 с.
В книге в справочной форме впервые приведены результаты
систематического исследования вариационных принципов теории
упругости и оболочек в соответствии с теорией преобразования
вариационных проблем Куранта и Гильберта.
Наряду с систематизацией известных вариационных принци-
принципов, книга содержит новые результаты и обобщения. Получена
система полных и частных функционалов, в том числе смешан-
смешанных. Изучены свойства функционалов не только с позиций ста-
стационарности, ио н экстремальности. Выявлены экстремальные и
минимаксные свойства ряда известных и новых функционалов.
Установлена вариационная форма статико-геометрнческой анало-
аналогии в теории оболочек. Результаты обобщены на ребристые, мно-
многосвязные, многослойные и другие конструктивно-анизотропные
оболочки и применены для анализа и решения ряда сложных
задач.
Книга рассчитана на научных работников, аспирантов, инже-
инженеров, студентов университетов и втузов, применяющих вариа-
вариационные и вариационно-разностные методы расчета авиационных,
судостроительных, строительных, гидротехнических, машинострои-
машиностроительных и других конструкций.
Табл. 30, илл. 44, библ. 80.
. 20302—171 1О„„О © Главная редакция
А псо/гк» 7е '<>""'О физико-математической литературы
иоо(Ш)-10 издательства сНаука», 1978

ОГЛАВЛЕНИЕ
Предисловие 7
Глава 1
Основные положения вариацвоиного исчисление
§ I. Формулировка вариационной задачи 13
§ 2. Метод Эйлера — Лагранжа решения вариационных за-
задач. Условия стационарности 15
§ 3. Некоторые достаточные условия экстремума 25
Глава 2
Общие и частные вариационные принципы и теоремы.
Основы теории преобразования вариационных проблем
§ 1. Общие и частные вариационные принципы и теоремы 27
§ 2. Преобразование задач о стационарном значении ... 33
§ 3. Исследование экстремальных свойств полных и частных
функционалов 41
§ 4. Заключение 47
Глава 3
Вариационные принципы теории упругости
для неоднородных анизотропных тел
§ 1. Вводные замечания . ....... 50
§ 2. Различные варианты принципов Лагранжа и Кастилья-
чо — исходные пункты для преобразования вариацион-
вариационных принципов 54
§ 3. Полные функционалы 63
§ 4. Частные функционалы. Их взаимосвязь с полными функ-
функционалами 70
§ 5. Экстремальные свойства полных и частных функциона-
функционалов теории упругости 84
§ 6. Вариационные принципы и экстремальные свойства
функционалов теории упругости при разрывных переме-
перемещениях, деформациях, напряжениях и функциях напря-
напряжений г . 89
I*

ОГЛАВЛЕНИЕ
§ 7. Развернутая форма записи некоторых функционалов в
различных системах координат 94
Глава 4
Вариационные принципы теории упругих тонких
неоднородных анизотропных оболочек переменной толщины
§ 1. Ьводные замечания 99
§ 2. Различные варианты принципов Лагранжа и Кастилья-
но — исходные пункты для преобразования вариацион-
вариационных принципов - . . 110
§ 3. Полные функционалы 119
§ 4. Частные функционалы. Их- взаимосвязь с полными
функционалами 125
§ 5. Экстремальные свойства полных и частных функциона-
функционалов теории оболочек 130
§ 6. О вариационных принципах и экстремальных свойствах
функционалов теории оболочек при разрывных переме-
перемещениях, деформациях, усилиях и функциях напряжений.
О контактных задачах в теории оболочек 131
§ 7. Вариационная форма статико-геометрической аналогии 133
§ 8. Развернутая форма записи функционалов в различных
системах координат 136
§ 9. О вариационных функционалах для некоторых нелиней-
нелинейных задач теории оболочек 141
Глава 5
Использование вариационных принципов
для анализа и решения задач теории упругости
и теории оболочек
§ 1. Различные формы вариационных уравнений теории упру-
упругости и теории оболочек 142
§ 2. Особенности вариационных формулировок при сложных
граничных условиях, в том числе для многосвязных об-
областей 146
§ 3. О классификации прямых вариационных методов рас-
расчета 169
§ 4. Формирование алгебраических уравнений прямых мето-
методов на основе вариации функционала 177
§ 5. Использование экстремальных свойств функционалов прв
решении конечномерных (дискретизованных) задач . . 180
§ 6. Примеры построения алгоритмов расчета пологих анизо-
анизотропных оболочек вариационно-разностным методом . . 182
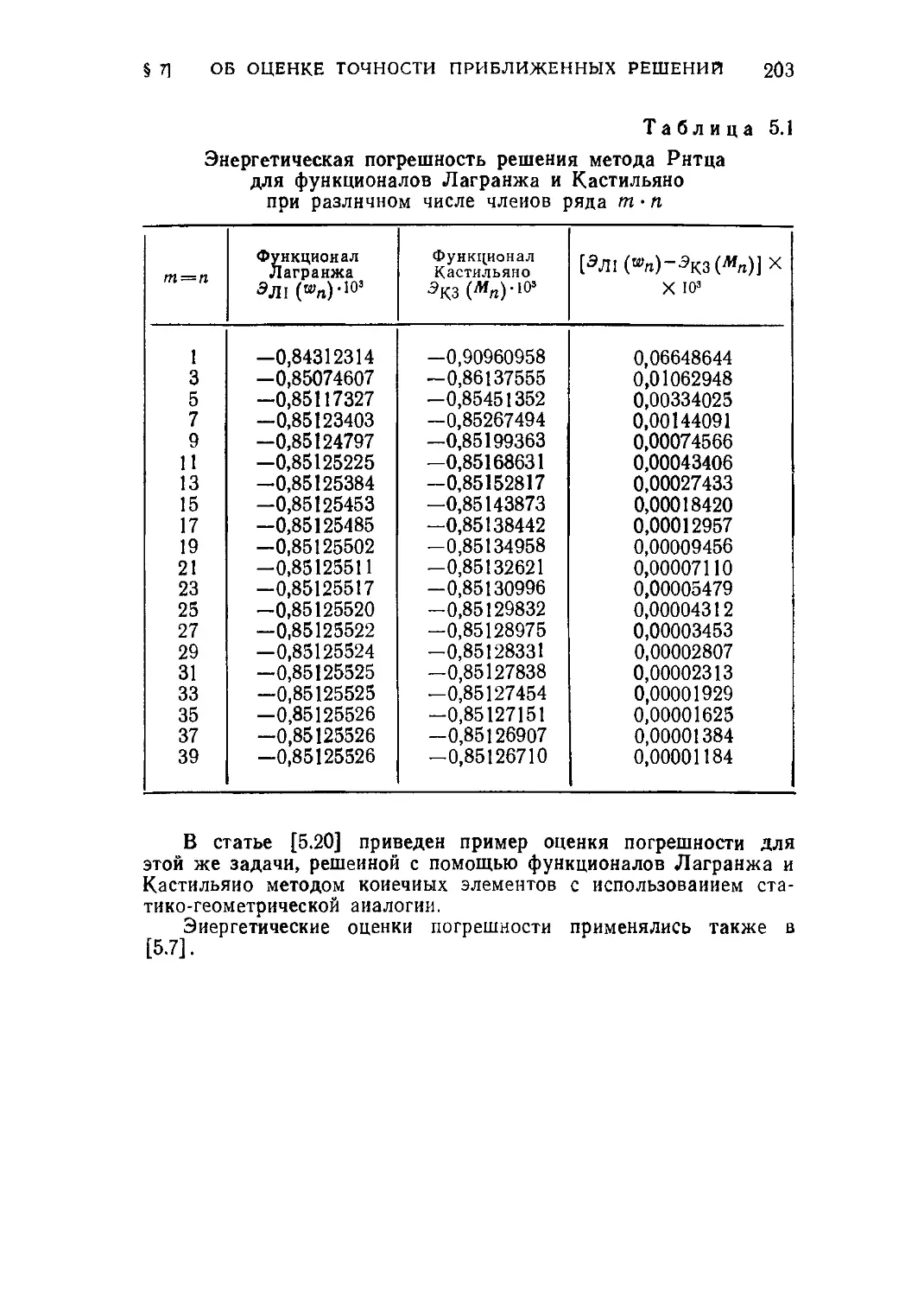
§ 7. О применении различных функционалов для оценки точ-
точности приближенных решений 192
Приложение 1
Понятия функционального и выпуклого анализа
в вариационной теории упругости и теории оболочек 204

ОГЛАВЛЕНИЕ 5
Приложение 2
Некоторые сведения из векторного
и тензорного анализа 208
Приложение 3
Обобщение теории неоднородных анизотропных оболочек
иа конструктивную и приобретенную анизотропию 217
Таблицы 220
3.1. Различные варианты функционала Лагранжа для не-
неоднородного анизотропного упругого тела B21). 3.2. Раз-
Различные варианты функционала Кастильяно для неоднородно-
неоднородного анизотропного упругого тела B23). 3.3. Лагранжева се-
серия полных функционалов для неоднородного анизотропного
упругого тела B25). 3.4. Кастильянова серия полных функ-
функционалов для неоднородного анизотропного упругого тела
B29). 3.5. Некоторые частные функционалы для неоднород-
неоднородного анизотропного упругого тела B31). 3.6. Экстремальные
свойства вариационных функционалов теории упругости
B37). 3.7. Различные варианты функционала Лагранжа при
разрывных перемещениях, деформациях и напряжениях B38).
3.8. Различные варианты функционала Кастильяно при раз-
разрывных функциях напряжений, напряжениях и деформаци-
деформациях B38). 3.9. Лагранжева серия полных функционалов при
разрывных перемещениях, деформациях, напряжениях и функ-
функциях напряжений B39). 3.10. Некоторые системы коор-
координат в трехмерном пространстве B41). 3.11. Функционал
Рейсспера в криволинейных ортогональных координатах
B44). 3.12. Полный функционал в симметризованном
основном пространстве состояний в криволинейных ортого-
ортогональных координатах B45). 3.13. Полный функционал в
симметризованном квазиосновиом пространстве состояний в
криволинейных ортогональных координатах B45).
4.1. Различные варианты функционала Лагранжа для
неоднородной анизотропной оболочки B47). 4.2. Различные
варианты функционала Кастильяно для неоднородной анизо-
анизотропной оболочки B49). 4.3. Лагранжева серия полных функ-
функционалов для неоднородной анизотропной оболочки B51).
4.4. Кастильянова серия полных функционалов для неодно-
неоднородной анизотропной оболочки B55). 4.5. Некоторые част-
частные функционалы для неоднородной анизотропной оболочки
B59). 4.6. Экстремальные свойства вариационных функцио-
функционалов теории оболочек. Вариационная форма статнко-геомет-
рической аналогии B64). 4.7. Некоторые системы коорди-
координат, используемые в теории оболочек B66). 4.8. Функцио-
Функционал Рейсскера в криволинейных ортогональных координатах
B69). 4.9. Полный функционал в симметризованном основ-
основном пространстве состояний в криволинейных ортогональных
координатах B69). 4.10. Полный функционал в симметризо-
симметризованном квазиосновном пространстве состояний в криволи-
криволинейных ортогональных координатах B70).

6 ОГЛАВЛЕНИЕ
П. 1. Элементы матрицы соотношений упругости для обо-
оболочки, подкрепленной произвольно ориентированными узкими
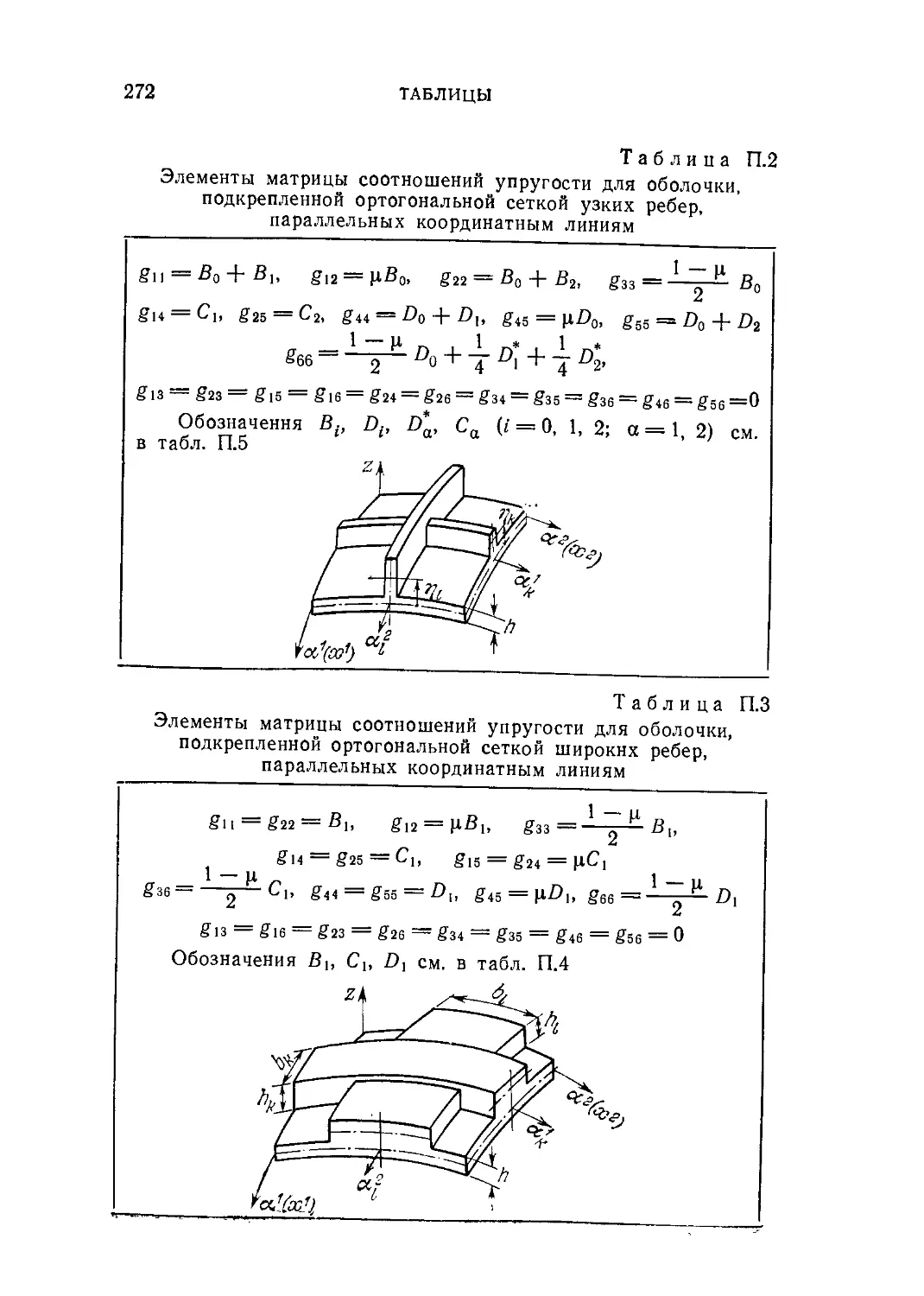
ребрами B71). П. 2. Элементы матрицы соотношений упру-
упругости для оболочки, подкрепленной ортогональной сеткой уз-
узких ребер, параллельных координатным линиям B72).
П. 3. Элементы матрицы соотношений упругости для оболоч-
оболочки, подкрепленной ортогональной сеткой широких ребер, па-
параллельных координатным линиям B72). П. 4. Элементы
матрицы соотношений упругости для оболочки, подкреплен-
подкрепленной косоугольной сеткой широких ребер, параллельных коор-
координатным линиям B73). П. 5. Элементы матрицы соотноше-
соотношений упругости для оболочки, подкрепленной косоугольной
сеткой узких ребер, параллельных координатным линиям
B74). Г1.6. Элементы матрицы соотношений упругости для
многослойной оболочки B75).
Основные обозначения 276
Литература 279
Предметный указатель 285

*...ё Науке есть своя эстетика, и красота
логической стройности вариационных прин-
принципов механики не может ие восхищать
математиков, физиков, механиков.»
Л. С. Полак
(Из предисловия к книге К. Лаицоша
«Вариационные принципы механики»)
ПРЕДИСЛОВИЕ
Хотя история создания вариационных принципов
механики сплошных сред насчитывает более ста лет,
а вариационное исчисление является одним из клас-
классических разделов математики, развитие вариацион-
вариационных принципов механики деформируемых тел, в част-
частности теории упругости, теории оболочек и пластин,
еще далеко от завершения. Отсутствует систематиче-
систематический анализ (и синтез) вариационных проблем теории
упругости и теории оболочек, включающий исследо-
исследования как условий стационарности вариационных
функционалов, так и их экстремальных свойств.
В данной книге представлены результаты система-
систематического исследования вариационных принципов ста-
статической теории упругости и оболочек с позиций ста-
стационарности и экстремальности функционалов. Бла-
Благодаря общему подходу выявлены некоторые новые,
не менее интересные, но еще не исследованные
вариационные формулировки для анизотропного не-
неоднородного тела и анизотропной неоднородной обо-
оболочки.
В качестве инструмента систематического исследо-
исследования взята теория преобразования вариационных
проблем, разработанная Д. Гильбертом и Р. Куран-
Курантом [0.9], которая позволяет не только эквивалентным
образом преобразовать одну задачу и другую, но и

8 ПРЕДИСЛОВИЕ
дает возможность во многих случаях проследить за
изменением экстремальных свойств функционалов.
Эта теория создана уже около половины века тому
назад, но в литературе известны лишь немногие при-
примеры применения ее к задачам механики деформируе-
деформируемых тел. Первые работы принадлежат Р. Куранту
[0.9] и Э. Рейсснеру [0.13]. Р. Курант впервые при-
применил преобразование Фридрихса для установления
связи между принципами Лагранжа и Кастильяно.
Э.Рейсснер [0.13].оценивая результаты своих четырех
работ, посвященных вариационным принципам теории
упругости, характеризует новизну использования тео-
теории [0.9] и полученную в итоге полную формулировку
вариационной теоремы как вклад в теорию упру-
упругости. В отечественной литературе теория [0.9] впер-
впервые применена в работах [0.4], а впоследствии в
[0.15, 0.6, 0.1] и др. Однако все эти исследования, как
правило, не имеют общего характера и относятся
к вариационным формулировкам в терминах ста-
стационарности функционалов. К анализу экстремаль-
экстремальных свойств функционалов эта теория не приме-
применялась.
Используемые в книге сведения из вариационного
исчисления приведены в гл. 1. В гл. 2 изложены
основы теории преобразования вариационных проб-
проблем, которая рассмотрена в несколько более общей
форме, чем в [0.9], с применением выпуклого анализа
для изучения экстремальных свойств функционалов.
Для построения и систематического исследования си-
систем функционалов оказалось целесообразным выде-
выделить полные функционалы (без каких-либо допол-
дополнительных условий) в качестве узловых пунктов
вариационной теории упругости или оболочек и сово-
совокупность частных функционалов, имеющих дополни-

ПРЕДИСЛОВИЕ 9
тельные условия, и дать общие формулировки общего
и частных вариационных принципов.
В соответствии с изложенной в гл. 2 теорией, в
гл. 3 и 4 построены системы полных и частных функ-
функционалов для формулировки вариационных принци-
принципов теории упругости и теории оболочек. В книге
принят вариант теории тонких оболочек, выбранный
в [4.12] в качестве «наилучшего»; показана возмож-
возможность перехода к вариационным принципам для дру-
других вариантов.
Наряду с известными полными функционалами
Ху — Вашицу [0.17, 0.18], Рейсснера [0.13] и полным
функционалом в перемещениях [3.11, 0.12] построен
ряд новых полных функционалов, среди которых пол-
полный функционал в «квазиосновном» пространстве со-
состояний, подобный функционалу Ху — Вашицу, И дру-
другие полные функционалы, не зависящие от перемеще-
перемещений, но содержащие функции напряжений, некоторые
функционалы в основном и квазиосновном симметри-
зованных пространствах, в неполных пространствах
перемещений, деформаций, напряжений и функций
напряжений и другие. Выявлены экстремальные свой-
свойства всех рассмотренных функционалов. Установ-
Установлено, что большинство полных функционалов, в том
числе известные функционалы Ху—Вашицу, Рейс-
Рейсснера и другие, имеют в качестве точки стационар-
стационарности седловую точку, а среди некоторых новых функ-
функционалов обнаружены такие, которые не имеют ни
экстремумов, ни минимаксов.
Впервые получены функционалы относительно фи-
физических соотношений упругости, ряд функционалов
граничных условий, функционал Лагранжа, не содер-
содержащий перемещений, функционалы физико-геометри-
физико-геометрического и физико-статического характера и другие. Эти

Ю ПРЕДИСЛОВИЕ
новые функционалы по своим свойствам теоретиче-
теоретического и вычислительного характера не уступают ранее
известным.
Показано несоответствие некоторых общих реше-
решений уравнений равновесия вариационному принципу
Кастильяно и выводимым из него определенным ви-
видам уравнений неразрывности. В этом плане следует
подчеркнуть целесообразность проверки новых и из-
известных старых дифференциальных формулировок на
соответствие вариационным принципам.
Построена и изучена с точки зрения стационар-
стационарности и экстремальности система полных и частных
функционалов в случае разрывных полей перемеще-
перемещений, деформаций, напряжений и функций напряже-
напряжений; некоторые вариационные принципы для таких
полей впервые рассматривались В. Прагером [0.12].
Аналогичные вопросы рассмотрены и в теории оболо-
оболочек. Необходимость рассматривать разрывные поля
в качестве возможных состояний упругого тела возни-
возникает иногда при численном решении задач, в частно-
частности при использовании метода конечных элементов.
Установлена вариационная форма статико-геомет-
рической аналогии в теории непологих неоднородных
анизотропных оболочек, которая выражается в соот-
соответствии между функционалами, их дополнительными
и естественными условиями и экстремальными свой-
свойствами.
Пятая глава посвящена некоторым приложениям,
показывающим, что вариационные методы являются
мощным орудием качественного анализа и средством
численного решения задач. Рассмотрены различные
формы вариационных уравнений. Предложена клас-
классификация прямых вариационных методов расчета,
основанная на идеях главы 2. Разработан универсаль-

ПРЕДИСЛОВИЕ И
ный метод вычисления коэффициентов алгебраиче-
алгебраических уравнений прямых методов, удобный для реали-
реализации машинных алгоритмов расчета. Дана общая
методика решения и рассмотрены на примерах осо-
особенности задач со сложными граничными условиями
для многосвязных упругих тел и оболочек и др. На
основе этой методики получены как условия стацио-
стационарности функционалов уравнения неразрывности
контура отверстия в одних задачах и равновесия кон-
контура в других. Показаны некоторые возможности ис-
использования экстремальных свойств вариационных
функционалов для получения двусторонней оценки
точности решений.
Небольшой объем книги не позволил уделить до-
достаточное внимание обширным историческим аспектам
теории вариационных принципов. В связи с этим отме-
отметим, что за последние десятилетия в развитие и при-
применение вариационных принципов теории упругости,
оболочек, пластинок и стержней внесли свой вклад
такие ученые, как Л. Я. Айнола, Н. А. Алумяэ,
Л. И. Балабух, В . В. Болотин, К- Вашицу, А. С. Воль-
мир, К- 3. Галимов, И. И. Гольденблат, Р. Зелигер,
Л. М. Качанов, Л. С. Лейбензон, А. И. Лурье,
С. Г. Михлин, В. В. Новожилов, В. Прагер, Э. Рейс-
снер, Л. И. Седов, И. Н. Слезингер, И. Г. Терегулов,
Э. Тонти, К. Ф. Черных и др.
С целью облегчить использование книги в каче-
качестве справочника по вариационным принципам теории
упругости и теории оболочек большинство результа-
результатов представлено в табличной легко обозримой форме.
В Приложении 1 приведены краткие сведения из функ-
функционального и выпуклого анализа, в Приложении 2 —
из векторного и тензорного анализа. В Приложении 3
вариационная теория гладких анизотропных оболочек

12 ПРЕДИСЛОВИЕ
обобщается на различные конструктивно-анизотроп-
конструктивно-анизотропные (ребристые, многослойные и др.) оболочки, а
также и на случай приобретенной в процессе дефор-
деформирования анизотропии (например, возникновение
упруго-пластических зон).
Данная книга является некоторым обобщением ра-
работ авторов. Ей предшествовало учебное пособие
[0.2], которое можно рассматривать как первое изда-
издание данной книги.
Проведенные исследования, основанные на при-
применении теории преобразования вариационных проб-
проблем, могут служить методологическим примером для
целого ряда других задач механики деформируемого
тела и родственных задач математической физики.
Систематическое изучение вариационных принци-
принципов с позиций стационарности и экстремальности обо-
обогащает как постановку, так и аппарат математиче-
математического исследования задач.
Авторы искренне благодарны коллегам и друзьям,
чье внимание, замечания, пожелания и советы спо-
способствовали появлению этой книги.

Глава 1
ОСНОВНЫЕ ПОЛОЖЕНИЯ ВАРИАЦИОННОГО
ИСЧИСЛЕНИЯ
В данной главе приведены необходимые для чтения
книги сведения из вариационного исчисления. Подроб-
Подробное изложение с доказательствами можно найти в
[1.3], а также в [1.6, 1.7].
§ 1. Формулировка вариационной задачи
Классическое вариационное исчисление имеет дело
с отысканием максимумов или минимумов функцио-
функционалов, имеющих вид определенных интегралов:
F{u)=\f(u{x))dQ. A.1)
Q
Область определения функционала A)—множество
непрерывных или непрерывно-дифференцируемых
функции и(х) (возможно, векторных или тензорных),
определенных в области Q n-мерного (чаще всего
одно-, двух- или трехмерного) евклидова простран-
пространства. Функция / может зависеть не только от функции
и, но и от ее частных производных.
Множество функции и(х) можно считать линей-
линейным пространством (см. Приложение 1), если опре-
определить на нем обычным образом операции сложения
и умножения на число. Это линейное пространство
можно превратить в (бесконечномерное) евклидово
пространство Е, если ввести скалярное произведение
с помощью равенства
«I ° и2 = \ щ (х) и2 (х) du. A.2)
Пополнение евклидова пространства является гиль-
гильбертовым пространством Н.

14 ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. I
На функции и{х) могут быть наложены дополни-
дополнительные условия в форме равенств
Ф(и) = 0. A.3)
В этом случае вариационная задача — задача об ус-
условном экстремуме — формулируется следующим об-
образом: среди всех функции и(х), удовлетворяющих
условию C), найти такую, для которой функционал
A) имеет экстремум. Условие C) обычно имеет вид
системы дифференциальных (а иногда и алгебраиче-
алгебраических) уравнений.
Вариационную задачу без дополнительных усло-
условий называют свободной, а задачу об условном экс-
экстремуме — несвободной.
Вариационная задача является обобщением задачи
об отыскании экстремума функции нескольких пере-
переменных. Решение последней задачи есть конечный на-
набор значений аргументов, реализующий экстремум
данной функции. Решением вариационной задачи яв-
является неизвестная функция, реализующая экстре-
экстремум функционала. Связь между этими задачами
можно увидеть, рассматривая функцию и(х) как
бесконечный набор аргументов. Аргументов в этом
наборе столько же, сколько точек х в множестве Q:
каждой точке х е Q поставлен в соответствие аргу-
аргумент и(х) функционала F.
Если в обычной экстремальной задаче необходимое
условие экстремума представляет собой систему ко-
конечного числа уравнений (алгебраических или транс-
трансцендентных), то условия экстремума (или стационар-
стационарности, см. § 2) вариационной задачи выражаются бес-
бесконечной системой подобных уравнений — дифферен-
дифференциальными уравнениями (уравнениями Эйлера, см.
§§ 2, 3).
Вариационная задача отличается от обычной эк-
экстремальной не только количеством неизвестных, но
и характером наложенных на них связей: значения
и(х) функции и, являющиеся аргументами функцио-
функционала A), обычно связаны между собой условиями
непрерывности или дифференцируемости. Именно это
приводит к различиям в методах решения.

§2] МЕТОД ЭЙЛЕРА —ЛАГРАНЖА 15
В вариационном исчислении различают классиче-
классические задачи, имеющие ограничения в форме равенств,
и неклассические задачи, ограничения в которых мо-
могут быть в виде неравенств и в других формах. В дан-
данной книге рассматриваются классические вариацион-
вариационные задачи, с помощью которых формулируются
вариационные принципы механики твердого деформи-
деформируемого тела.
§ 2. Метод Эйлера — Лагранжа решения
вариационных задач. Условия стационарности
Для отыскания экстремумов в вариационном ис-
исчислении используют обобщение основного понятия
анализа бесконечно малых — дифференциала. Диффе-
Дифференциал
в« = «'(*) —и (ж) B.1)
функции и, рассматриваемой как аргумент функцио-
функционала F, называется вариацией функции и. Здесь и и
и' — две разные функции, принадлежащие области
определения функционала F. Следует отличать вариа-
вариацию бы от дифференциала
du = u(x + dx) — u (х), B.2;
который является приращением одной функции и, вы-
вызванным изменением ее аргумента х.
Дифференциал 6F, т. е. главную линейную часть
приращения функционала F(u), вызванного вариа-
вариацией бы, называют вариацией функционала F(u).
Естественный и наиболее распространенный способ
решения задачи об отыскании экстремума функцио-
функционала вида A.1) при условии A.3) состоит в исполь-
использовании необходимого условия: в точке экстремума и°
выполняется уравнение A.3) и вариация 8F равна
нулю при любых допустимых вариациях б« неизвест-
неизвестной функции и:
б^ = |^б« = О, B.3)
где dF/du — производная (градиент) функционала F
(см. Приложение 1). Допустимыми считаются такие

16 ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ ГГЛ. I
бы, для которых и° + бы принадлежит области опре-
определения функционала и удовлетворяет дополнитель-
дополнительному условию A3)
Ф (ы° + бы) = 0. B.4)
Необходимое условие C) является обобщением ана-
аналогичного условия для экстремума функции конечного
числа переменных и выводится с помощью аналогич-
аналогичных рассуждении. Так как ф(нс) = 0, то D) можно
преобразовать:
Ф (ы° + бы) = ф (ы° + бы) — ф (ы°) = |J- бы + о (бы) = 0.
Отсюда следует, что допустимыми можно считать та-
такие бы, для которых
|> = 0, B.5)
так как условие D) эквивалентно E) с точностью до
бесконечно малых более высокого порядка чем бы
[1.2].
Если и° удовлетворяет ограничению A.3) и при
и = и° функционал A.1) удовлетворяет условию C)
при всех бы, удовлетворяющих E), то говорят, что
F(u) имеет в точке и = и° условное стационарное
значение, а и° есть его точка стационарности. При от-
отсутствии условия A.3) стационарное значение назы-
называют безусловным.
Необходимым условием наличия экстремума функ-
функционала F в точке и° является его стационарность в
этой точке. Следовательно, стационарность — более
общее свойство функционала в данной точке, чем
экстремальность. Функционал может иметь стацио-
стационарное значение в точке перегиба, минимакса, макси-
мина, в седловой точке (см. гл. 2, § 2). Задачи об
отыскании точек стационарности функционалов вида
A.1) тоже называют вариационными.
Таким образом, вариационная задача может быть
сформулирована как задача об экстремуме функцио-
функционала A.1):
F {и) -> max (tnin), B.6)

§ 2] МЕТОД ЭПЛЕРА - ЛЛГРАНЖА 17
или как более общая задача о стационарном значе-
значении C):
6F («) = 0. B.7)
2.1. Условия стационарности для свободной вариа-
вариационной задачи. Вообще говоря, поставленная-вариа-
поставленная-вариационная задача для функционала F(u) может не
иметь решения. Не останавливаясь на вопросе о су-
существовании решения, предположим, что точка ста-
стационарности функционала F существует.
Для дифференцируемых функционалов при отсут-
отсутствии дополнительных условии, т. е. когда вариации
бы независимы, равенство C) эквивалентно уравнению
которое означает, что в точке стационарности произ-
производная функционала F есть нулевой элемент соответ-
соответствующего линейного пространства (пространства Е*,
сопряженного с Е), и называется условием стационар-
стационарности функционала F. Если ? — гильбертово про-
пространство, то Е и Е* изоморфны [1.2], и поэтому ли-
линейный оператор -^— е Е" можно считать элементом
из Е, а -з— Ьи — скалярным произведением [1.2].
Чтобы воспользоваться условием C) или (8),
нужно выяснить конкретный вид вариации 8F и
производной dF/du, соответствующих функционалу
A.1).
а) Условия стационарности для функционала, за-
зависящего от одной функции и ее первых частных про-
производных
F{)f{u, иЛ, ы.2, ..., uJdQ.
Здесь индекс i после запятой обозначает производную
функции и по переменной xt. Для того чтобы найти
дифференциал 6F, рассмотрим разность
I- (и 4 6и) - F (и) = J [/ (и + ви) - / (и)) rfQ. B.9)

18 ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. 1
При отыскании главной линейной части выраже-
выражения (9) по бы (этого требует определение дифферен-
дифференциала и производной) трудность состоит в том, что
подынтегральная функция f зависит не только от
функции ы, но и от ее производных и,\, ..., ы,„ по пе-
переменным Хи ..., х„. Поэтому здесь нельзя применить
правило дифференцирования сложной функции, так
как неизвестно, что такое <3(ы,,)/<3ы.
Разложим разность f (и-\-8и) — f (и) в ряд Тей-
Тейлора по бы и по 6(m,i), ..., б(ы,„) в каждой точке
множества Q, считая временно функцию и и ее произ-
производные «,,• независимыми. Получим
F (и + бы) - F («) =
B.10)
с точностью до бесконечно малых более высокого по-
порядка, чем бы, 6(m,i), ..., б(ы,„).
Теперь учтем зависимость производных ы,,- от функ-
функции и, которая приводит к равенству б(ы,,) = (бы),,-.
Так как производные (би),,- — линейные функции от
бы, то главная линейная часть разности (9) есть
B.11)
Преобразуем слагаемые с производными от бы сле-
следующим образом. Представим эти слагаемые с по-
помощью формулы дифференцирования произведения
в виде
Затем с помощью формулы Грина, Стокса или Остро-
Остроградского (см. Приложение 2) преобразуем интегралы
по области Q от слагаемых вида я; . бы 1 в ин-
\-"\и.и J. i
тегралы по ее границе dQ (для одномерных интегра-

МЕТОД ЭЙЛЕРА-ЛАГРАНЖА 19
лов используется основная теорема интегрального ис-
исчисления). В результате получим
L д (и i) J, i L д (u, n) l.n
<2ЛЗ>
где Vj, •••, vn — компоненты вектора нормали к гра-
границе 6Q.
Если на границе dQ заданы значения функции и,
то второе слагаемое в A3) равно нулю, так как
бы = 0. В этом случае дЬ'/ди есть линейный функцио-
функционал, который каждой функции бы ставит в соответ-
соответствие число по закону
B.14)
Следовательно, выражение в фигурных скобках в A4)
можно рассматривать как dF/du. Равенство (8) при-
принимает вид
] \=0- BЛ5)
Оно является условием стационарности функционала
A.1) и называется уравнением Эйлера данной вариа-
вариационной задачи.
При отсутствии граничного условия для функции
и на всей границе dQ или на ее части б« ф 0; чтобы
было 6F = 0 при любом бы, необходимо выполнение
уравнения Эйлера A5) и равенства
которое называется естественным граничным усло-
условием данной вариационной задачи.
б) Функционалы, зависящие от производных бо-
более высокого порядка. Если подынтегральная функция
в функционале A.1) зависит не только от первых, но

20 ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. 1
и от вторых производных и (или) от производных бо-
более высокого порядка функции и, то вывод условий
стационарности (уравнений Эйлера и естественных
граничных условий) сводится к повторному примене-
применению формулы интегрирования по частям, или Грина,
или Остроградского. Во многих случаях приходится,
кроме того, преобразовывать интеграл по границе в
выражении вида A3), так как этот интеграл должен
содержать независимые вариации функции и и ее
производных по нормали к границе. Для этого исполь-
используется формула интегрирования по частям, если гра-
граница— контур, и формула Стокса или Грина (см.
Приложение 2), если граница является поверхностью.
в) Функционалы, зависящие от нескольких функ-
функций, можно записать в виде A.1), если считать функ-
функцию и векторной. В этом случае вариация би также
является вектором, и вывод условий стационарности
сводится к преобразованию каждой его компоненты.
Подробнее о выводе условий стационарности раз-
различных конкретных функционалов см. в гл. 3 и 4.
2.2. Приведение вариационной задачи с ограниче-
ограничениями к свободной задаче: два пути учета ограниче-
ограничений. Для задач с ограничениями вида A.3) необходи-
необходимое условие экстремума C) означает, что в точке ус-
условного экстремума (или стационарности) и0 линейный
функционал dF/du (не обязательно нулевой) отобра-
отображает в нуль те функции би, которые удовлетворяют
уравнению E). Условие C) здесь не приводит к усло-
условию стационарности (8), так как функция и, для кото-
которой справедливо (8), может не удовлетворять ограни-
ограничениям A.3). Поэтому прямое использование условия
C) для вывода условий стационарности, как правило,
невозможно.
Для вывода условий стационарности в задачах с
ограничениями эти задачи преобразуют в эквивалент-
эквивалентные им свободные. Существует два способа учета
ограничений A.3) в форме равенств: использование
общих решений уравнений A.3) и метод неопределен-
неопределенных множителей Лагранжа.
Использование первого способа практически воз-
возможно лишь при достаточно простых уравнениях

$ 2) МЕТОД ЭЙЛЕРА - ЛАГРАнЖА 21
A.3), имеющих общее решение. Этот путь обычно
приводит к уменьшению количества неизвестных за
счет усложнения выражения для функционала и усло-
условий стационарности.
При использовании второго способа за счет увели-
увеличения количества неизвестных достигается „общность
и универсальность метода и простота записи разре-
разрешающих уравнений.
Оба способа учета дополнительных условий ис-
используются в теории преобразования вариационных
проблем (см. гл. 2, §§ 2 и 3).
а) Использование общих решений. Уравнение A.3)
является недоопределенным и имеет бесконечное мно-
множество решений (в противном случае задача об эк-
экстремуме была бы тривиальной).
В некоторых случаях уравнение A.3) удается раз-
разрешить относительно части компонентов щ векторной
переменной и, т. е. выразить их через остальные ком-
компоненты и2:
щ = и1(и2). B.17)
Если любое решение уравнения A.3) представимо в
виде A7), то выражение A7) называется общим ре-
решением уравнения A.3). Множество элементов и2
образует подпространство Е2 в данном простран-
пространстве Е.
Подставив A7) в функционал A.1), получим но-
новый функционал
FMu2), u2]. B.18)
Задачу об условной стационарности функционала F
теперь можно заменить задачей о безусловной ста-
стационарности: среди всех элементов и2 пространства
?2 найти такой, что функционал A8) имеет стацио-
стационарное значение. Условия стационарности этой задачи
выводятся так же, как в § 2.1.
Уравнение A.3) может не иметь общего решения
вида A7), особенно если оно дифференциальное, но
иметь параметрическое решение
и = «(/), B.19)

UU, ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ ГГЛ. I
где t — параметр (возможно, векторный или функцио-
функциональный). Если любое решение уравнения A.3) мож-
можно представить в виде A9), то A9) тоже называется
общим решением уравнения A.3).
Подставив A9) в A.1), получим свободную ва-
вариационную задачу для функционала F[u(t)], кото-
которую можно решать в соответствии с § 2.1.
Заметим, что при использовании общих решений
задача на условный экстремум заменяется вспомога-
вспомогательной задачей на безусловный экстремум, в отличие
от метода множителей Лагранжа, в котором, вообще
говоря, можно утверждать лишь наличие точки ста-
стационарности у вспомогательного функционала (см.
гл. 2, § 3).
В гл. 3 и 4 будут использоваться, например, сле-
следующие общие решения: решение а'7 = аГ]Меы вида
A7) системы физических уравнений а'7 — aiikleki = 0;
параметрические общие решения уравнений равнове-
равновесия в функциях напряжений, уравнений неразрывно-
неразрывности (параметры — перемещения), статических гранич-
граничных условий в функциях напряжений и деформацион-
деформационных граничных условий для оболочек и др.
б) Метод неопределенных множителей Лагранжа.
Для облегчения дальнейшего изложения целесооб-
целесообразно уточнить, что функция ф в ограничении A.3)
представляет собой отображение Е—»Ф данного ев-
евклидова пространства Е в евклидово пространство Ф,
которое может быть множеством действительных чи-
чисел, конечномерным евклидовым пространством или
(чаще всего) функциональным пространством со ска-
скалярным произведением вида A.2). Например, Ф мо-
может быть множеством функций, определенных на гра-
границе дО, области Q, со скалярным произведением
да
таково, например, геометрическое граничное условие
и — и* = 0 в гл. 3 и 4. Пространство Ф может пред-
представлять собой также прямое произведение несколь-
нескольких евклидовых пространств различного строения, из

§ 2] МЕТОД ЭЙЛЕРА — ЛАГРАНЖА 23
которых одни могут быть конечномерными, а дру-
другие— функциональными; сюда включаются случаи,
когда дополнительное условие A.3) состоит из урав-
уравнений в области и на границе.
В бесконечномерном случае пространство Ф можно
считать гильбертовым; если Ф не гильбертово, то
может быть рассмотрено его пополнение (см. Прило-
Приложение 1).
Метод множителей Лагранжа является обобще-
обобщением правила множителей Лагранжа для функций
нескольких переменных и состоит в том, что для оты-
отыскания точки условной стационарности функционала
A.1) используется другой, вспомогательный функ-
функционал
Fn(u, Л) = F (и)+ М<Р («И. B-20)
где Я, — линейный функционал на Ф. Так как Ф —
гильбертово пространство, то можно считать [1.2],
что 1еФ, а Я,(ф) есть скалярное произведение в Ф,
и писать вместо B0)
Fa(u, l) = F(u) + Ko<p(u). B.21)
Применение функционала B1) основано на тео-
теореме: существует такой элемент Я° е Ф*, что решение
и° задачи на условный экстремум функционала A.1)
при ограничениях A.3) (или, в более общем случае,
точка «° условной стационарности) совпадает с без-
безусловной точкой стационарности по и функционала
Fn(u, K°). Значения и° и Я° определяются уравнениями
^2. = 0 и -^- = 0. Доказательство см. в [1.21.
ди
Подчеркнем, что вариационные задачи для функ-
функционалов F(u) и Fn(u,%°) эквивалентны с точки зре-
зрения стационарности по и, но не экстремальности:
Fa(u,h°) может не иметь экстремума в точке стацио-
стационарности (см. пример в гл. 2, § 3.26).
Справедлива и обратная теорема: все точки ста-
стационарности (и°, К°) функционала B1) соответствуют
точкам условной стационарности функционала A.1).
Действительно, в точке (ы°Д°) уравнение A.3)

24 ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. I
выполняется, так как оно совпадает с-^- = 0. Второе
условие стационарности
т?«« = ?*< + *&«« = 0 B-22)
показывает, что при любом К, для которого Х~Ьи = О,
выполняется C). Тем более C) выполняется, если
¦Ц-бы = 0. Таким образом, при ¦^• = 0, ^-=0
все пункты определения условной стационарности вы-
выполнены, так что любая точка стационарности функ-
функционала B1) соответствует точке условной стацио-
стационарности функционала A.1).
Приведем пример построения функционала B1).
Функционал Лагранжа и дополнительные условия
для задачи изгиба плиты (см. гл. 4) в пространстве Е
функций, определенных в плоской области S и при-
принимающих любые значения на границе, имеют вид
)]%4(w) - qw] dS -
- \[Q?W - M* ЩйС; B.23)
^._fl.« = 0, w-w* = 0 на Си.
Пространство Ф состоит из функций, определенных
на части Си контура плиты С. Скалярное произведе-
произведение в Ф определяется равенством
Ф1°фг= \ Ф1Ф2 dC> B.24)
а функционал B1) данной задачи имеет вид
B.25)
где —Q иМ — множители Лагранжа.

§ 3] Достаточные условия экстремума 25
Заметим, что понятия свободной и несвободной ва-
вариационной задачи относительны. Например, сформу-
сформулированную выше несвободную вариационную за-
задачу для функционала Э(ш) в пространстве Е, мож-
можно рассматривать как свободную в пространстве Е\
функций, определенных в области Q и принимающих
на ее границе заданные значения:
§ 3. Некоторые достаточные условия экстремума
Необходимое условие экстремума B.8) является
прямым обобщением такого же условия для функций
конечного числа переменных и имеет аналогичный
вид. Иначе обстоит дело с достаточным условием.
Для того чтобы функция f(xi х„) конечного
числа переменных имела в точке х°, .... х°п локаль-
локальный минимум, достаточно, чтобы при любых ненуле-
ненулевых приращениях независимых переменных ее первый
дифференциал был равен нулю, а второй дифферен-
дифференциал был положительным:
i, k=\
Для функционалов в бесконечномерных простран-
пространствах второй дифференциал (вторая вариация) опре-
определяется как
F"{6u, бы), C.2)
т. е. как квадратичное выражение, отвечающее ото-
отображению (функционалу) F" пространства ЕХ.Е на
¦вещественную ось R. Как показывает контрпример,
приведенный в [1.2], условие вида A): 62F > 0 в точ-
точке стационарности — недостаточно для минимума
функционала F, определенного в пространстве беско-
бесконечного числа измерений.

26 ОСНОВЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ [ГЛ. J
Достаточным условием локального минимума
функционала F(u) является его выпуклость вниз в
некоторой окрестности точки стационарности [1.1, 1.5].
Функционал F(u) является выпуклым вниз в не-
некоторой выпуклой области Р евклидова пространства
Е, если его вторая вариация неотрицательна при лю-
любых 6ц в каждой точке области Р.
Все, что написано выше о достаточных условиях
минимума, переносится на максимум с заменой нера-
неравенства 62F >0 на б2/7 <0 и выпуклости вниз на
выпуклость вверх.
Условие выпуклости позволяет иногда решить воп-
вопрос и о глобальном экстремуме: выпуклый вниз функ-
функционал имеет на выпуклом множестве не более одного
минимума, а выпуклый вверх — не более одного мак-
максимума.

Глав а 2
ОБЩИЕ И ЧАСТНЫЕ ВАРИАЦИОННЫЕ
ПРИНЦИПЫ И ТЕОРЕМЫ.
ОСНОВЫ ТЕОРИИ ПРЕОБРАЗОВАНИЯ
ВАРИАЦИОННЫХ ПРОБЛЕМ
В данной главе изложены общие вопросы теории
преобразования вариационных проблем, которая по-
позволяет выделить общие и частные вариационные
принципы и теоремы и установить между ними экви-
эквивалентную взаимосвязь. Эта глава служит теорети-
теоретической основой для исследования вариационных прин-
принципов теорий упругости и оболочек в гл. 3 и 4.
§ 1. Общие и частные вариационные
принципы и теоремы
Основные положения механики могут быть сфор-
сформулированы в трех эквивалентных формах: в виде
дифференциальных уравнений, или интегральных
уравнений, или вариационных принципов.
За всем комплексом зависимостей и уравнений
теории упругости скрывается общий вариационный
принцип, заключающий в себе смысл всей совокуп-
совокупности уравнений и граничных условий данной теории.
Аналогичное утверждение справедливо и для теории
оболочек, пластин, стержней, а также для систем, со-
составленных из них.
Выявление этого общего принципа может быть
основано на теории преобразования вариационных
проблем, разработанной Р. Курантом и Д. Гильбер-
Гильбертом [0.9]. Эта теория позволяет поставить в соответ-
соответствие друг другу различные функционалы с дополни-
дополнительными условиями и построить полный функционал
без каких-либо дополнительных условий, из которого
как частные случаи могут быть получены все возмож-
возможные функционалы с дополнительными условиями и
сформулированы частные вариационные принципы.

28 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. 2
1.1. Выбор пространства состояний упругой си-
системы. Прежде чем сформулировать систему аксиом,
описывающую упругую систему, нужно выделить со-
совокупность независимых элементов, характеризующих
ее состояние, например поля напряжений, деформа-
деформаций, перемещений. Эти элементы удобно рассматри-
рассматривать как координаты изображающей точки в некото-
некотором пространстве, которое мы назовем пространством
состояний. Это пространство можно считать линейным
или евклидовым со скалярным умножением вида A.2)
гл. 1. Оно может состоять из различных комбинаций
полей перемещений, деформаций и других, обладаю-
обладающих необходимыми свойствами непрерывности и диф-
ференцируемости.
Совокупность полей перемещений, деформаций и
напряжений (усилий) назовем основным простран-
пространством состояний. Его можно представить как прямую
сумму линейных пространств перемещений, деформа-
деформаций и напряжений, т. е. как множество точек (и, е, а)
с покомпонентными операциями сложения и умноже-
умножения на число.
Можно также выделить квазиосновное простран-
пространство состояний {ф, о, е}, представляющее собой со-
совокупность полей функций напряжений, напряжений и
деформаций. Квазиосновное пространство в некотором
смысле симметрично основному.
Могут быть рассмотрены усеченные (частные) про-
пространства, являющиеся некоторой частью основного
пространства (подпространством). Усеченные про-
пространства могут быть смешанными, т. е. содержать
только некоторые компоненты вектора перемещений
и тензоров напряжений и (или) деформаций, функ-
функций напряжений.
Подпространство (усеченное пространство) часто
бывает определено системой уравнений. При этом осо-
особую роль в теории Куранта — Гильберта играют урав-
уравнения, являющиеся дополнительными условиями к
функционалам.
Расширенное пространство состояний может быть
получено как из основного, так и из его подпро-
подпространств за счет введения вспомогательных элементов,

S I] ОБЩИЕ И ЧАСТНЫЕ ПРИНЦИПЫ И ТЕОРЕМЫ 29
не содержащихся в них. Пространство расширяют,
например, за счет введения общих решений уравнений
равновесия в функциях напряжений, а также при ис-
использовании множителей Лагранжа (см. § 2 и
гл. 3, 4).
Пространство состояний может быть, кроме того,
преобразовано линейной заменой переменных в ряд
других, изоморфных ему. При этом преобразуются и
функционалы, и дополнительные условия (если они
имеются), так что получаются разные эквивалентные
формулировки одной и той же задачи в одинаковых
(изоморфных) пространствах. Такие преобразования
показаны на примере функционалов Эп2 и Э„4а
(гл. 3 и 4).
1.2. Полные и частные функционалы. В каждом из
пространств состояний системы может быть опреде-
определено бесконечное множество различных функциона-
функционалов. Среди них нас интересуют лишь некоторые, осо-
особые, с помощью которых могут быть сформулированы
вариационные принципы для данной системы (см.
§§ 1.3 и 1.4).
Все вариационные принципы и соответствующие
функционалы, рассматриваемые в гл. 1—4, представ-
представляется целесообразным разделить на два класса: пол-
полные и частные.
Функционалы, для которых вариационная задача
формулируется без дополнительных условий, охваты-
охватывая все компоненты полей выбранного пространства
состояний, будем называть полными функционалами.
Полный функционал является наиболее общей энерге-
энергетической характеристикой данной системы, выражен-
выраженной через все компоненты выбранного пространства
состояний. Общность состоит, во-первых, в том, что
из полного функционала могут быть получены все
возможные частные функционалы в данном простран-
пространстве и, во-вторых, в том, что его достаточно для
определения всех компонентов полей, т. е. для пол-
полного решения задачи в данном пространстве со-
состояний.
Например, в основном пространстве состояний пол-
полный функционал характеризует состояние системы

30 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. 2
всеми компонентами полей перемещений, деформаций
и напряжений.
Функционалы, для которых вариационная задача
формулируется с дополнительными условиями (опре-
(определяющими подпространство в выбранном простран-
пространстве состояний), назовем частными функционалами.
Частные функционалы получаются из полных пу-
путем наложения дополнительных условий на некото-
некоторые компоненты данного пространства состояний (см.
§ 2). Они являются некоторыми энергетическими ха-
характеристиками системы в усеченных пространствах.
Таким образом, в выбранном пространстве состоя-
состояний понятия полного и частного функционалов строго
определены и имеют абсолютный характер. При пере-
переходе от одного пространства к другому эти понятия
становятся относительными. Полный функционал,
определенный в некотором пространстве, можно рас-
рассматривать как частный в расширенном пространстве;
он является частным (менее общим) по отношению
к полному функционалу в расширенном пространстве.
Например, функционал Рейсснера (гл. 3) является
полным в пространстве перемещений и напряжений
и частным в пространстве перемещений, деформаций
и напряжений (по отношению, например, к полному
функционалу Ху — Вашицу). Функционал Лагранжа
Эл>(и> е)—частный в любом пространстве, содержа-
содержащем поля перемещений и деформаций.
1.3. Общий вариационный принцип и общая ва-
вариационная теорема.
Общий вариационный принцип. Истинные поля
параметров напряженно-деформированного состояния
системы отличаются от всех других полей в данном
пространстве состояний тем, что полный функционал
имеет стационарное значение.
Например, применительно к основному простран-
пространству состояний общий вариационный принцип чи-
читается так: истинные поля перемещений, деформаций,
напряжений (усилий) системы таковы, что полный
функционал имеет стационарное значение.
Стационарному значению полного функционала
непосредственно соответствуют истинные поля тех па-

S 1] ОБЩИЕ И ЧАСТНЫЕ ПРИНЦИПЫ И ТЕОРЕМЫ Si
раметров напряженно-деформированного состояния
системы, от которых он зависит (которые входят в
соответствующее пространство состояний). Например,
полный функционал в основном пространстве опре-
определяет все компоненты истинных полей перемещений,
деформаций и напряжений.
Если полный функционал определен в усеченном
пространстве (например, функционал Рейсснера — в
пространстве перемещений и напряжений), то истин-
истинные значения недостающих параметров напряженно-
деформированного состояния (в данном примере —
поля деформаций) в случае необходимости могут быть
определены с помощью зависимостей, связывающих
полный функционал в усеченном пространстве с ка-
каким-либо полным функционалом в основном простран-
пространстве. Эта часть расчета является вторичным этапом
(обработкой).
В случае расширенного пространства состояний
стационарному значению полного функционала в этом
пространстве соответствуют, кроме истинных полей
перемещений, напряжений и деформаций, еще неко-
некоторые поля вспомогательных величин, которые допол-
дополняют основное пространство до расширенного. При-
Примером здесь служит функционал Эгц(и, е, а,Х, ц)
(гл.З, § 3.1), зависящий не только от и, е, а, но и от
вспомогательных величин X, ц.
Общая вариационная теорема. Полный функцио-
функционал имеет в качестве уравнений Эйлера и естествен-
естественных граничных условий полный комплекс уравнений
и граничных условий данной теории, выраженных че-
через компоненты соответствующего пространства со-
состояний.
Иными словами, полный функционал содержит в
необходимой и достаточной мере всю информацию о
данной теории и классе задач в используемом про-
пространстве состояний, так что для их решения не тре-
требуется каких-либо дополнительных условий.
Так как уравнения Эйлера и естественные гранич-
граничные условия являются необходимыми и достаточными
условиями стационарности (гл. 1), то общую вариа-
вариационную теорему можно сформулировать и как

32 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. 2
утверждение об эквивалентности вариационного прин-
принципа и системы дифференциальных уравнений: в дан-
данном пространстве состояний математические модели
упругой системы, построенные на основе системы диф-
дифференциальных уравнений и общего вариационного
принципа, совпадают.
Как правило, может быть дана более сильная фор-
формулировка общего вариационного принципа: истин-
истинному напряженно-деформированному состоянию си-
системы соответствует не просто стационарное значе-
значение, а минимакс (или максимин, или седловая точка)
полного функционала. Исключение составляют функ-
функционалы, не имеющие ни экстремумов, ни минимак-
сов, ни максиминов, например 5П4а (гл. 3).
1.4. Частный вариационный принцип и частная ва-
вариационная теорема.
Частный вариационный принцип. От всех возмож-
возможных, т. е. удовлетворяющих данным ограничениям (до-
(дополнительным условиям), состояний упругой системы
истинное состояние отличается тем, что частный функ-
функционал имеет стационарное значение при данных до-
дополнительных условиях, т. е. в подпространстве дан-
данного пространства состояний.
Как правило, справедлива более сильная форму-
формулировка: частный функционал имеет не просто стацио-
стационарное значение, а условный экстремум, или мини-
минимакс, или максимин, или седловую точку.
Частная вариационная теорема. Уравнения Эйлера
и естественные граничные условия задачи на услов-
условное стационарное значение частного функционала со-
составляют вместе с дополнительными условиями пол-
полный комплекс уравнений и граничных условий данной
теории.
Отсюда следует тождественность постановки ва-
вариационных задач на основе полных и частных функ-
функционалов.
Доказательство вариационных теорем основано на
выводе условий стационарности функционалов (см.
гл. 1).
Примерами частных вариационных принципов слу-
служат различные варианты принципа минимума потен-

§ 2] ЗАДАЧИ О СТАЦИОНАРНОМ ЗНАЧЕНИИ 33
циальной энергии (принципа Лагранжа), принципа
максимума дополнительной энергии (принципа Ка-
стильяно) и др. (гл. 3 и 4).
§ 2. Преобразование задач
о стационарном значении
В данном параграфе изложены основные положе-
положения теории преобразования вариационных проблем
Р. Куранта и Д. Гильберта [0.9] с точки зрения ста-
стационарности функционалов. Вопросы исследования
экстремальных свойств функционалов, полученных в
соответствии с этой теорией, обсуждаются в § 3. Рас-
Рассматриваемая в §§ 2 и 3 область преобразований не-
несколько шире, чем это предусмотрено в [0.9]. В эту
область включены и преобразования функционалов с
исключенными множителями Лагранжа. Эти функ-
функционалы обладают интересными свойствами (см.
гл. 3 и 4).
2.1. Основные определения. Пусть требуется найти
точку стационарности функционала F(u), определен-
определенного в евклидовом пространстве Е:
6F(u) = 0, B.1)
при дополнительных условиях в форме равенств
Ф(«) = О. B.2)
Функция ф определена на Е и принимает значения в
гильбертовом пространстве Ф (см. гл. 1). Уравнение
B) включает в себя дифференциальные уравнения и
граничные условия.
Условия стационарности данной вариационной за-
задачи A), B) (уравнения Эйлера и естественные гра-
граничные условия) будем называть естественными усло-
условиями, в отличие от дополнительных условий B).
Теория Куранта—Гильберта построена на основе
двух общих положений. Первое положение очевидно и
состоит в том, что любое из условий стационарности
функционала (полного или частного) можно вклю-
включить в список дополнительных условий, причем полу-
полученная вариационная задача эквивалентна исходной.
2 Н, П. Абовский и др,

34 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. 2
Второе заключается в использовании метода множите-
множителей Лагранжа для учета дополнительных условий;
эквивалентность получающейся при этом вариацион-
вариационной задачи с исходной доказана в гл. 1.
Во многих задачах, например для выпуклых функ-
функционалов, использование этих двух положений позво-
позволяет проследить и за изменением экстремальных
свойств функционалов (см. § 3). В ряде задач без
ограничений можно искусственно ввести дополнитель-
дополнительные условия, чтобы затем внести их в функционал с
множителями Лагранжа и производить дальнейшие
преобразования. Эта идея оказалась очень плодотвор-
плодотворной. Она позволяет получить множество различных
формулировок одной и той же вариационной задачи с
различными переменными и, в частности, осущест-
осуществлять важное преобразование Фридрихса (см.
§2.4).
2.2. Вывод полных функционалов. Как показано в
гл. 1, существует два способа преобразовать частный
функционал F(u), участвующий в формулировке ва-
вариационной задачи A) с дополнительным условием
B), в полный функционал (не имеющий дополнитель-
дополнительных условий): использование общих решений и метод
множителей Лагранжа. Кроме того, ниже рассмот-
рассмотрены две часто используемых в гл. 3 и 4 усложнен-
усложненные схемы, содержащие в себе в качестве промежу-
промежуточных этапов эти два способа и переход от полных
функционалов к частным.
а) Преобразование частного функционала в пол-
полный в усеченном пространстве состояний с помощью
общих решений уравнения B). В тех случаях, когда
уравнение B) имеет общее решение
u = u(t), B.3)
задачу A) с ограничением B) можно заменить зада-
задачей об отыскании точки стационарности полного
функционала
F, (/) = f («(/)) B.4)
в усеченном пространстве Т параметров /. Параметр
t обычно векторный или функциональный; в частности,
он может иметь вид t = и2 (см. гл. 1).

§ 2] ЗАДАЧИ О СТАЦИОНАРНОМ ЗНАЧЕНИИ 35
Пространство Т усеченное, так как оно определяет
с помощью C) подпространство в Е. Хотя все рас-
рассматриваемые функциональные пространства имеют
одну и ту же—счетную — размерность [1.2], Т обыч-
обычно содержит меньше параметров, чем Е. Например,
три уравнения равновесия в теории обрлочек связы-
связывают шесть функциональных неизвестных — усилий, а
их общее решение выражает эти неизвестные через
три функции напряжений (см. гл. 4).
Для одного и того же уравнения B) может суще-
существовать несколько различных форм общих решений
C) (см., например, гл. 3, § 2).
Вообще говоря, задача
e/f,@ = -^LW = 0 B.5)
о стационарности функционала D) не эквивалентна
задаче A), B). Это подтверждается простым приме-
примером [5.3]. Пусть F— функция двух переменных х и у.
F(x, у) = х -f- у, а ограничение B) имеет вид
ф(х, у) = х — у = 0. Ясно, что данная задача об
условной стационарности решения не имеет. Если же
использовать общее решение х = t3, у = t3 уравнения
х — у = 0, то функционал F\ (/) = t3 -f- t3 = 2t3 имеет
точку стационарности t = 0, которой соответствуют
значения х = 0, у = 0. «Ложная» точка стационарно-
стационарности появилась потому, что при / = 0 обращаются в
нуль обе производные dx/dt и dy/dt, а значит, и диф-
дифференциалы dx= -тг dt и dy = -jj- dt\ это не дает воз-
возможности проверить условие B.5) гл. 1 в определе-
определении условной стационарности.
Чтобы обеспечить эквивалентность задач A), B)
и E), необходимо потребовать, чтобы общее решение
C) удовлетворяло еще одному условию: при всех t,
при которых —^- = 0, выражение
Ьи = Щ-Ы B.6)
должно быть общим решением уравнения
!> = 0, B.7)

36 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. 2
т. е. должно содержать все решения этого уравнения
(неизвестным является бы). Действительно, если при
i = f выполнено E) и последнее условие, то при
всех б«, удовлетворяющих G), вариация 8F имеет
вид
дг, dF ди л, dFt a/ n
6f 6/6/ 0
и все условия, содержащиеся в определении условной
стационарности (гл. 1, § 2), выполнены.
Обычно на общее решение C) накладывают более
сильное требование невырожденности: требуют, что-
чтобы производная -ду была невырожденным линейным
оператором при всех значениях t, т. е. чтобы равен-
равенство -гт-6/ = 0 выполнялось только при 6^ = 0. Для
наших целей невырожденность —слишком сильное
ограничение, так как ему не удовлетворяют общие
решения дифференциальных уравнений равновесия,
неразрывности и другие (гл. 3 и 4).
б) Вывод полного функционала в расширенном
пространстве состояний из частного с помощью мно-
множителей Лагранжа. Метод множителей Лагранжа для
учета дополнительных условий B) (см. гл. 1) приво-
приводит к построению нового функционала
Ftt(u, A) = F(«) + Aoq>(u). B.8)
В литературе функционал (8) часто называют функ-
функционалом Лагранжа вариационной задачи A), B).
Мы не будем пользоваться этим термином, оставив
его для функционала, участвующего в формулировке
принципа Лагранжа (принцип минимума потенциаль-
потенциальной энергии) в теории упругости и теории оболочек.
Функционал (8), как и все функционалы без дополни-
дополнительных условий, полный.
Вариационная задача A), B) при этом переходит
в следующую:
6Fn(u, A) = 0. B.9)
Здесь превращение частного функционала в полный
достигается ценой увеличения количества пеизвест-

$ 2] ЭАДАЧИ О СТАЦИОНАРНОМ ЗНАЧЕНИИ 37
ных: нужно искать стационарное значение Fn не толь-
только по и, но и по Я.
Условия стационарности функционала (8) имеют
вид
Ц^ = А(и, Л) = 0._ B.10)
¦Ж—Ф(и) = 0. B.11)
Уравнение A1) есть дополнительное условие B)
к функционалу A), а A0)—условие стационарности
для задачи A), B), содержащее вспомогательную пе-
переменную Я. Исключая Я из A0), можно получить
условие стационарности для задачиA),B), выражен-
выраженное только через и:
А {и, Я (и)) = В (и) = 0. B.12)
В гл. I показано, что существует взаимно одно-
однозначное соответствие между точками условной ста-
стационарности и° для задачи A), B) и компонентами
и° точек (м°, Я0) безусловной стационарности функцио-
функционала (8). Задачи A), B) и (9) в этом смысле экви-
эквивалентны.
Значение Я°, соответствующее точке условной ста-
стационарности и°, может быть не единственным. Чтобы
обеспечить единственность Я°, обычно накладывают
требование независимости на уравнения, содержа-
содержащиеся в дополнительном условии B); это требование
выражается в том, что матрица Якоби множества
функций, сокращенно записанных ф(«), должна иметь
соответствующий ранг (см., например, [0.9, 1.6]).
В данной книге нет необходимости заботиться об един-
единственности множителей Лагрянжа. В гл. 3 и 4 будут
часто встречаться случаи, когда существует бесконеч-
бесконечное множество Х° (например, функционал Эпз (е, ф),
где тензор функций напряжений ф является множи-
множителем Лагранжа, гл. 3). В этих случаях нас устраи-
устраивает любое из бесконечного множества значений %°,
так как все они определяют одно и то же решение и°
Исходной задачи A), B).

38 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. г
в) Вывод полного функционала в усеченном про-
пространстве состояний из полного функционала в рас-
расширенном пространстве. Пусть Fn{u\, u2)—полный
функционал. Во многих случаях среди его условий
стационарности есть уравнение i|)(ui, «2)— О, которое
можно разрешить относительно щ, т. е. выразить и\
через и2, и использовать для исключения и\ из
'Fn(u\, u2). В результате получится полный функ-
функционал
= M«i («г), «*). B-13)
эквивалентный Fn в том смысле, что компонент
й°2точки стационарности (u°, u°) функционалаРп(и1, и2)
является точкой стационарности Fn\{u2).
Действительно, это преобразование можно разбить
на два этапа. Сначала, в соответствии с первым об-
общим положением теории преобразования вариацион-
вариационных проблем (§ 2.1), наложим условие стационар-
стационарности ty(uu и2) — О и получим частный функционал,
эквивалентный Fn (см. также § 2.3). Затем исклю-
исключим и\ в соответствии с § 2.2а; общее решение вида
щ = щ (иг) удовлетворяет всем наложенным там тре-
требованиям, необходимым для эквивалентности преоб-
преобразования. Таким образом, функционалы Fn\ и Fn
эквивалентны.
г) Вывод полного функционала с исключенными
множителями Лагранжа. Пусть полный функционал
Fa (u,X) построен из F(u) в соответствии в § 2.26.
Иногда оказывается возможным исключить из Fn
множители Лагранжа % с помощью § 2.2в и получить
полный функционал в том же пространстве состоя-
состояний, в котором был определен F(u). Таким путем
построены, например, функционалы Эп4а (и, е, а) и
Э'паА<(> а> <?)(гл.З).
Заметим, что схема г) вывода полного функцио-
функционала является усложненным вариантом схемы в), а
схема в)—усложненным вариантом схемы а).
2.3. Вывод частных функционалов из полного. Вы-
Вывод осуществляется на основе общего положения о
том, что любое из условий стационарности можно на-
наложить в качестве дополнительного условия (см. §2.1).

§ 2] ЗАДАЧИ О СТАЦИОНАРНОМ ЗНАЧЕНИИ 39
При этом выражение для функционала обычно упро-
упрощается, так как некоторые слагаемые обращаются в
нуль (см. гл. 3 и 4). Преобразования можно продол-
продолжить, используя § 2.2.
2.3.1. Условия стационарности полных функциона-
функционалов в качестве дополнительных условий к частным
функционалам и возможные схемы их-классификации.
Переход от полных функционалов к частным оказы-
оказывается гораздо богаче, чем переход от исходного част-
частного функционала к полному. Здесь может быть по-
получен не только исходный частный функционал, но и
множество других в соответствии с множеством ва-
вариантов условий стационарности, каждый из которых
может быть принят в качестве дополнительных усло-
условий.
Условия стационарности полного функционала мож-
можно разделить на группы в соответствии с двумя раз:
личными схемами классификации: а) по физическому
смыслу уравнений — геометрические, статические, фи-
физические; б) по геометрическому расположению —
уравнения в области и граничные условия. Эти груп-
группы могут быть разбиты на еще более мелкие под-
подгруппы, если рассмотреть компоненты векторных
уравнений. В качестве дополнительных условий могут
быть приняты различные комбинации из этих групп
и подгрупп (здесь должна быть использована теоре-
теоретико-множественная операция объединения множеств
уравнений). Число таких комбинаций для большин-
большинства полных функционалов в теории упругости и обо-
оболочек велико. В гл. 3, 4 будут рассмотрены только
некоторые, наиболее интересные из них.
2.3.2. Особенности вывода частных функционалов
из полных функционалов с неисключенными множи-
множителями Лагранжа. Вывод частных функционалов из
полного функционала (8), полученного из A), B)
с помощью множителей Лагранжа, имеет некоторые
особенности, которые будут использованы при иссле-
исследовании экстремальных свойств (см. § 3).
а) Уравнение -^- = 0 в качестве дополнительг
ного условия. Нетрудно видеть, что это уравнение

40 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. 2
совпадает с B), так что при условии ~gf-= 0 множи-
множитель при к в функционале (8) обращается в нуль, и
вариационная задача (9) переходит в исходную за-
Дачу A), B).
б) Дополнительное условие -^- = 0. При этом
ограничении задача о стационарности полного функ-
функционала Fn переходит в задачу об условной стацио-
стационарности частного функционала F\: bFi(u,k) = 0,
ди v ' '
л/г ?/¦
в) Дополнительные условия -j-5- = 0, -щ-?- = 0.
Переменные и, Я обычно векторные. Их можно разде-
разделить различным образом на две группы и = («ь «г)
и ^ = (А,1Дг)- Накладывая на функционал (8) допол-
дополнительные условия
Ul П (\ У1 П Л /О П\
можно при различном выборе щ, к\ получать различ-
различные частные функционалы.
г) Дальнейшие преобразования. Преобразования,
проведенные с помощью способов, описанных в
§ 2.3.2а, б, можно продолжить, исключая некоторые
переменные с помощью общих решений по аналогии
с § 2.2а. Новые частные функционалы можно исполь-
использовать для вывода новых полных в соответствии
с § 2.2, и т. д. Среди всего этого множества взаимных
переходов функционалов особое место занимает пре-
преобразование Фридрихса.
2.4. Преобразование Фридрихса. Преобразование
F(u)^Fa(u, K)-*Fi{u, к),
выполненное в соответствии с § 2.26 и 2.3.26, можно
продолжить, если уравнение -г-2- = А (и, Я) = 0 при
каждом к имеет единственное решение и. В этом слу-
случае можно и выразить через к (явным или неявным
образом) и перейти к частному функционалу F2(k).

ИССЛЕДОВАНИЕ ЭКСТРЕМАЛЬНЫХ СВОЙСТВ 41
Дополнительные условия к /^(Я.) представляют
собой уравнения В(Х) = 0, полученные из А(и,К) = 0
после исключения и. Условия стационарности / (Д.) —
уравнения B), выраженные через X. Таким образом,
дополнительные условия функционала /^(Я.) яв"
ляются уравнениями, эквивалентными условиям ста-
стационарности функционала F(u), которые получаются
из Л(иД)=0 исключением Я, (см. § 2.26); условия
стационарности F2(X) являются преобразованными
дополнительными условиями к F(u). Преобразование
функционала A) в F2(A.) называют преобразованием
Фридрихса. Оно инволютивно: применив к /^(Я,) пре-
преобразование Фридрихса, получим вариационную за-
Дачу A), B).
Примеры преобразования Фридрихса и дополни-
дополнительные разъяснения приведены в гл. 3, §§ 2.2 и
3.2в, г; гл. 4 §§ 2.2 и 3.2в, г; гл. 5, §§ 7.4в и 7.5а.
§ 3. Исследование экстремальных свойств полных
и частных функционалов
Теория Куранта — Гильберта во многих случаях
позволяет проследить за изменением экстремальных
свойств вариационных функционалов при преобразо-
преобразованиях, рассмотренных в § 2. Эта теория — не един-
единственный способ исследования экстремальных свойств
функционалов. Можно было бы, например, для каж-
каждого из функционалов исследовать вторую вариацию.
Теория Куранта имеет то преимущество, что она поз-
позволяет подойти с единых позиций к исследованию их
свойств. Другое ее преимущество в том, что все по-
полученные функционалы имеют одно и то же стацио-
стационарное значение, это важно для оценки точности при-
приближенных решений (см. гл. 5).
В данном параграфе, в отличие от [0.9], прн ис-
исследовании вопросов преобразования экстремальных
задач использованы некоторые результаты из выпук-
выпуклого анализа, которые помогают глубже понять суть
дела и дают достаточные условия применимости опи-
описанных процедур.

42 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. 2
3.1. Определение минимакса, максимина, седловой
точки. Пусть функционал F зависит от двух перемен-
переменных (возможно, векторных или функциональных) щ
и «2. Другими словами, функционал F определен на
прямом произведении Е = Е\ X ?г евклидовых про-
пространств Е\ и Е2. Каждому фиксированному значе-
значению щ можно поставить в соответствие число
(u,, и2) C.1)
и тем самым определить функционал F\ на множестве
тех элементов щ пространства Е\, для которых суще-
существует указанный максимум. Точно так же можно
определить функционал
(ub u2). C.2)
Запись
F(u\, u°2) = minmax F(uv и2) C.3)
(минимум по и\ максимумов по и2 функционала F)
означает, что при «, = и° функционал A) имеет ми-
минимум, причем указанный в A) максимум дости-
достигается при uz = u\. При этом говорят, что функционал
F(u\, и2) имеет в точке (ы°, aj) минимакс. Другими
словами, выражение C) означает, что сначала для
каждого фиксированного и\ находится максимум
функционала F по и2, а затем из всех найденных
значений F выбирается минимальное.
Аналогично с помощью равенства B) опреде-
определяется максимин:
F (u\, «2) = max xn'mF (uv и2). C.4)
U? tl\
Если в точке (ы°, ы°) функционал F(uu u2) имеет
одновременно и минимакс C) и максимин D), то го-
говорят, что (и°, ы2) является его седловой точкой.
Часто используют другое, эквивалентное определение
[1.1, 1.5]: точка (и°, и^) называется седловой точкой
функционала F{u\,Ui), если при любых и\, и2
F („;, «2)<F («;, u])^F (И„ и2).

§ 3] ИССЛЕДОВАНИЕ ЭКСТРЕМАЛЬНЫХ СВОЙСТВ 43
3.2. Изменение экстремальных свойств при выводе
полного функционала из частного.
а) Использование общих решений для учета до-
дополнительных условий (§ 2.2а). Задача на минимум,
очевидно, переходит в задачу на минимум,_ а макси-
максимум — в максимум. Для минимаксных задач в каж-
каждом конкретном случае необходимо дополнительное
исследование.
б) Метод множителей Лагранжа. Пусть требуется
найти экстремум (для определенности минимум)
функционала F(u)
F(u)-*min C.5)
при дополнительных условиях
<р(и) = 0. C.6)
Полный функционал, построенный с помощью множи-
множителей Лагранжа, имеет вид (§ 2.26)
Fn{u, Я,) = Р(и) + Я,оФ(и). C.7)
Пусть и" — решение задачи E), F), а (ы°Д°) —
точка стационарности полного функционала G).
Тогда F(u°)= РП(«°Д°), так как ф(и°) = 0, т. е.
значения функционалов F и Fn в точке стационарно-
стационарности совпадают. Для функционала F(u) всегда выпол-
выполняется равенство
F {и0) = Fa {и°, Я0) = min max Fn (и, Я), C.8)
и X
которое показывает, что точка стационарности пол-
полного функционала G) есть точка минимакса. Дей-
Действительно, рассмотрим любой фиксированный век-
вектор и. Если он не удовлетворяет условиям F), то
maxFn(«, X) = oo. Если же условия F) выполнены,
А
то Fn (и, X) = F(u) < оо, Fn не зависит от Я, и поэтому
max Fa(u, Я) = F (и). Таким образом, минимальное
значение (по и) функционала maxFn(«, Я) совпадает
А.
с условным минимумом F(u) при условиях F).

44 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ [ГЛ. 7
С другой стороны, справедливо неравенство
F (и0) > max min Fn (и, А), C.9)
К и
для доказательства которого нужно при каждом фик-
фиксированном К взять и" в качестве одного из испытуе-
испытуемых значений и при отыскании минимума [0.3] (при
этом Fn(u°,X)=F(u0)).
Неравенство (9) показывает, что точка стационар-
стационарности полного функционала может быть точкой мак-
симина, а может и не быть — это зависит от вида
функционала F и функции <р.
В тех случаях, когда (9) есть равенство
F(u°)=*Fn(u°, k°)=*maxminFn(u, Л), C.10)
Л и
точка стационарности полного ¦ функционала Fn яв-
является одновременно точкой максимина и минимакса
(так как равенство (8) всегда справедливо), т. е. по
определению седловой точкой.
Достаточным условием того, чтобы в (9) выполня-
выполнялось равенство, или, что то же самое, точка стацио-
стационарности полного функционала была седловой точ-
точкой, является выпуклость вниз функционала F и вы-
выпуклость множества, определяемого ограничением F)
[1.1, 1.5]. Очевидно, ограничение-равенство тогда и
только тогда определяет выпуклое множество, когда
оно является линейным уравнением. Поэтому выше-
вышеуказанное условие можно сформулировать следующим
образом: для выполнения равенств (8) и A0) доста-
достаточно, чтобы функционал F(u) был выпуклым вниз, а
равенство <р(и) = 0 — линейным уравнением.
Таким образом, если функционал F(u) выпуклый
вниз, а условия F) — линейные уравнения, то для
полного функционала G) вариационная задача фор-
формулируется следующим образом: найти седловую
точку функционала Fn{u,"k), или
Fn (и, X)-*- max min == min max. C.1!)
k и и К
В противном случае можно лишь утверждать, что
справедливо равенство (8).

§ 3] ИССЛЕДОВАНИЕ ЭКСТРЕМАЛЬНЫХ СВОЙСТВ 45
Следующий пример показывает, что указанное до-
достаточное условие не необходимо:
Fix, У) = х + у
Fn(x, у, Л) = х + «,
Здесь функция <р определяет невыпуклое множество
(эллипс) на плоскости (х,у), а точка стационарности
х = У2/3 , г/=д/1/6, Я- = д/3/8 функционала Fs,
есть его седловая точка.
в) При выводе полного функционала в усеченном
пространстве из полного функционала в расширенном
пространстве (§ 2.2в) и полного функционала с ис-
исключенными множителями Лагранжа (§ 2.2г) не
представляется возможным установить общие зако-
закономерности изменения их экстремальных свойств.
В этих случаях при наличии минимакса и максимина
у исходного полного функционала полученные функ-
функционалы могут не иметь ни экстремума, ни седловой
точки, ни минимакса, ни максимина: см., например,
полные функционалы Эпи, Эпц& в гл. 3 и 4.
Полученные в гл. 3 и 4 полные функционалы тео-
теорий упругости и оболочек имеют в точке стационар-
стационарности минимакс или максимин, или то и другое (сед-
ловую точку), или не имеют ни экстремумов, ни
минимаксов. Среди них не обнаружено полных функ-
функционалов, имеющих минимум или максимум.
3.3. Изменение экстремальных свойств при выводе
частных функционалов из полного. Ограничимся слу-
случаем, когда полный функционал имеет седловую
точку; вариационная задача примет вид A1).
При наложении некоторых условий стационарно-
стационарности в качестве дополнительных условий экстремаль-
экстремальное свойство A1) полного функционала G) может
сохраниться, а может теряться. Пусть векторную пе-
переменную и можно разделить на две группы и =
= («ь и?) и то же самое для X: Я, = (Д,1, А,2). Воз-
Возможны следующие случаи при наложении условий
стационарности в качестве дополнительных условий.
а) Дополнительное условие
dFn(u,k) =0- (ЗЛ2)

46 ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ (ГЛ 2
Уравнение A2) есть необходимое условие минимума
по и функционала Fn при фиксированном Я, см. A1).
Если Fn имеет единственный минимум при каждом
фиксированном Я (например, если функционал Fn
выпуклый по и), то при дополнительном условии A2)
символ min в равенстве A0) теряет смысл (так как
и
минимум уже найден) и оно переходит в
Fn(u°, Я0) = max/Мы, Я) C.13)
А-
при условии A2). Равенства A3, 12) означают сле-
следующее: чтобы найти Я0, и°, нужно при каждом фик-
фиксированном Я выбирать значение и, удовлетворяющее
уравнению A2), и из полученных пар (и, Я) выбрать
ту, которая доставляет максимум функционалу Fi.
В тех случаях, когда равенство A2) таково, что
его можно разрешить относительно и, т. е. выразить и
через Я, преобразование можно продолжить: подста-
подставить выражение для и в A3) и перейти к равенству
Fn(«°. Я°) = тах^2(Я), C.14)
А-
т. е. выполнить преобразование Фридрихса F(u)—*
-^^(Я), см. § 2.4. Таким образом, преобразование
Фридрихса для выпуклого функционала принимает
вид
min F (и) -»• max min Fn (и, Я) -»• max F2 (Я).
и X и К
б) Дополнительное условие
дРАиЛ) =0 (ЗЛ5)
При этом ограничении символ max в равенстве (8) те-
теряет смысл и оно переходит в
Fu(u°, X°)=minFn(M, Я). C.16)
и
Если уравнение A5) разрешить относительно Я, то
A6) можно преобразовать в
). C.17)

§ 4] ЗАКЛЮЧЕНИЕ 47
в) Дополнительное условие
дК(*1.игЛиЬ) ^ (ЗЛ8)
есть одно из двух необходимых условий минимума по
и функционала Fn при фиксированном X.
Левая часть равенства A8) означает производную
функционала Fn на подпространстве {«i} при фикси-
фиксированных «2, X. Так как в A0) отыскивается минимум
по и при фиксированном К, то при дополнительном
условии A8) равенство A0) сохраняется. В равен-
• стве (8) минимакс по данным переменным может
быть нарушен, так как при отыскании максимума
по X при фиксированном и A8) накладывает ограни-
ограничения на К, и минимакс может быть найден неверно.
Равенство (8) сохраняется, если A8) не содержит К:
тогда в (8) просто сужается область поиска мини-
минимума по и.
г) Дополнительное условие
ж ° ^ЛУ)
ж, — ° ^ЛУ)
может быть рассмотрено аналогично A8).
Если Я,1 и %2— множители Лагранжа, то при усло-
условии A9) функционал Fn не зависит от переменной Х\
и равенства (8) и A0) переходят в
Fn{u°, a,°) = maxminFn(u, Я,) = minmax Fn (и, X). C.20)
Лг ill, Щ lit, и, к,
§ 4. Заключение
Теория преобразования вариационных проблем
представляет собой непрерывный многообразный про-
процесс, охватывающий все возможные формы функцио-
функционалов в различных пространствах состояний.
На рис. 2.1 множество функционалов данной тео-
теории изображено в виде сферы. На полюсах располо-
расположены функционалы, имеющие максимум и минимум;
полные функционалы тяготеют к экватору и имеют
минимакс и максимин, а у некоторых из них от-
отсутствуют какие-либо экстремальные свойства.

48
ПРЕОБРАЗОВАНИЯ ВАРИАЦИОННЫХ ПРОБЛЕМ
[ГЛ. 2
Многообразные частные функционалы занимают про-
промежуточное положение.
Сферическая модель отражает систематизацию и
богатство многообразий преобразования вариационных
Рис. 2.1. Схема многообразия преобразований вариационных
проблем линейной теории упругости (теории оболочек).
проблем, взаимосвязь всех функционалов, которые
могут быть построены на основе теории, изложенной
в гл. 2.
В каждом пространстве состояний есть полный
функционал, который занимает в этом пространстве
центральное положение и из которого могут быть из-
извлечены всевозможные частные функционалы, опре-

ЗАКЛЮЧЕНИЕ
49
деленные в данном пространстве, с различными до-
дополнительными условиями. Эта взаимосвязь полного
и частных функционалов отражена на круговой схеме
(рис. 2.2), которая относится к основному простран-
пространству состояний. Аналогичные схемы могут быть по-
построены для других пространств. Характерно, что
классификация дополнительных условий (§ 2.3.1) поз-
позволяет выделить три группы частных функционалов,
Физический
принцип
функционяп
физичЕСких
соотндшЕ~
ний,) ;
Обш,ий
принцип
(полный
ункционял
Рис. 2.2. Взаимосвязь полного и частных функционалов в основ-
основном пространстве состояний.
выражающих статический, геометрический и физиче-
физический принципы наряду с многообразием смешанных
принципов (относительно различных комбинаций ста-
статических, геометрических и физических уравнений).
Из приведенных в конце книги таблиц к гл. 3 и 4
видно, что используемые в литературе функционалы
составляют лишь малую часть того множества, кото-
которое содержится в схемах на рис. 2.1 и 2.2. Отсюда
ясно, какое большое число различных функционалов
еще может быть привлечено с помощью теории пре-
преобразования вариационных проблем в активную об-
область анализа и расчета.

Глава 3
ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ
УПРУГОСТИ ДЛЯ НЕОДНОРОДНЫХ
АНИЗОТРОПНЫХ ТЕЛ
В этой главе рассматриваются полные и частные
функционалы, участвующие в формулировке вариа-
вариационных принципов трехмерной теории упругости.
Соответствующие общие и частные вариационные
принципы в различных пространствах состояний со-
содержатся в обобщенных формулировках, приведенных
в гл. 2, § 1, и могут быть получены путем конкрети-
конкретизации параметров пространства состояний и допол-
дополнительных условий (если они имеются). Функцио-
Функционалы, рассмотренные в данной главе, помещены
в таблицах 3.1—3.13 в конце книги.
§ 1. Вводные замечания
1.1. Рассматриваемое неоднородное анизотропное упругое
тело занимает объем V, ограниченный поверхностью S с внешней
нормалью п. Всюду в объеме V задан вектор объемных сил F,
а на поверхности S заданы некоторые компоненты вектора по-
поверхностных сил (напряжений) /* и дополнительные компоненты
вектора перемещений и*. Будем различать статические и геомет-
геометрические граничные условия, смотря по тому, будут ли они ка-
касаться поверхностных сил или перемещений. Краткие сведения и
пояснения по используемой тензорной форме записи уравнений
и функционалов см. в Приложении 2.
Полное решение краевой задачи теории упругости включает
построение трех взаимосвязанных полей. Поле деформаций е
представляв собой симметричную часть тензорного поля градиен-
градиентов перемещений и
e = i-(Vu + uV) A.1)
и связано с полем напряжений а законом Гука в прямой A.2)
или обратной A.3) форме
а — е- а = 0, A.2)
е — а- ¦ Ь = 0. A.3)

§ I) ВВОДНЫЕ ЗАМЕЧАНИЯ 51
Поля перемещений н напряжений подчиняются статическим D)
и геометрическим E) граничным условиям
(О-«-Г)' = 0. A.4)
(ц-ц*)" = 0, A.5)
где штрих н двойной штрих соответственно показывают, что ра-
равенство относится только к заданным компонентам поверхност-
поверхностных снл и перемещений, так что скалярное произведение
(an)' и" равно нулю.
Выражения (паи)' и (л-о-и)" означают, что скалярное
умножение ограничено теми компонентами поверхностных сил
или перемещений, которые входят в статические или геометриче-
геометрические граничные условия соответственно.
Поле напряжений должно удовлетворять уравнениям равно-
равновесия
у.а + Г = 0. A.6)
Уравнения равновесия F) имеют общее решение
o = or° + VX<PXV, A.7)
где о0 — частное решение неоднородного уравнения, а <р — произ-
произвольный симметричный двухвалентный тензор (тензор функций
напряжений) с шестью независимыми компонентами [3.10, 3.3,
3.5]. Существуют другие разновидности общего решения (см.
§ 2.2в).
Зависимости Коши A) между перемещениями и деформа-
деформациями являются общим решением уравнений совместности дефор-
деформаций
VXeXV = 0. A.8)
Уравнения A) и (8) эквивалентны в том смысле, что из су-
существования для данного е вектора и такого, что выполняется
A), следует справедливость (8), а (8) влечет за собой существо-
существование вектора и такого, что выполняется A). Точно так же за-
зависимости G) и F) эквивалентны*).
Геометрические граничные условия E) могут быть заданы
в дифференциальной форме — в виде деформационных граничных
условий [0.3, 3.8], а статические уравнения на поверхности D) —
в интегральной форме, в функциях напряжений. В этом случае
могут быть заданы некоторые компоненты тензоров тангенциаль-
тангенциальной и иэгибной деформаций поверхности S и дополнительные
компоненты тензора функций напряжений.
*) Строго говоря, утверждение об эквивалентности A) и (8)
справедливо, когда функция и трижды непрерывно дифференци-
дифференцируема, в противном случае уравнение неразрывности (8) услож-
усложняется.

62 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
Деформационные граничные условия имеют вид
0аВ-еавГ = 0, Ке(«)-<зГ = 0 («, Э = 1,2), A.9)
еа&) > V^aS/ — заданные компоненты тангенциальных и из
гибных деформаций поверхности S в системе координат, нор-
нормально связанных с этой поверхностью (см. § 7); здесь
Деформации е , к (е) поверхности S упругого тела выра-
выражаются через ее перемещения иа, «з точно так же, как дефор-
деформации е , Р базисной поверхности оболочки (см. гл. 4, § I) —
через ее перемещения иа, w. Это нетрудно проверить, если вы-
выразить в е (и), у. . (е) трехмерные ковариантные производные
Up Up
через поверхностные.
Деформации еа^, ха$ следует задапать так, чтобы выполня-
выполнялись условия неразрывности поверхности, аналогичные уравне-
уравнениям неразрывности для оболочек.
Уравнения (9) являются условиями стационарности функцио-
функционала Кастильяно; выражения для е , к возникают также при
выводе функционала Лагранжа в форме Элз (е) [0.3] (см. §§ 2.2
и 2.1 в).
Статические граничные условия в функциях напряжений
имеют вид
(<Pa0-<P*ae)' = O, (У«_^)' = 0, A.10)
где(<рар) —заданные компоненты тензора функций напряжений
в системе координат, связанной с поверхностью S, а (tyj ) —
заданные производные по нормали к 5 от этих компонентов (см.
табл. 3.2).
Величины <pap, ij)J связаны с заданными поверхностными /*
и объемными F силами равенством
(VX<P*XV)-n = f* + oe.n, A.10а)
где о"—частное решение уравнений равновесия F). Таким обра-
образом, для отыскания <р* по заданным /* и F необходимо сначала
найти частное решение системы трехмерных уравнений с част-
частными производными F), а затем — частное решение системы дву-
двумерных уравнений A0а).
Следует иметь в виду, что эквивалентность E) и (9), а
также D) и A0), соблюдается с точностью до постоянных инте-
интегрирования. Если условия E) заданы на одной связной части
поверхности о, то E) и (9) эквивалентны с точностью до жест-
жесткого смещения. В этом случае заданные тангенциальные и изгь'б-

§ I] ВВОДНЫЕ ЗАМЕЧАНИЯ 53
пые деформации еаC и иаC поверхности S связаны с заданными
перемещениями и{ равенствами
где \а — поверхностная ковариантная производная от поверх-
поверхностного вектора (см. Приложение 2, а также гл. 4). В случае,
когда условия (9) охватывают несколько различных связных ча-
частей поверхности S, необходимо учитывать уравнения, согласую-
согласующие взаимные смещения различных связных частей:
в
0.12)
U dr ¦ [е + (V<o) X (rB ~ r)] = «* (В) - и* (A),
A
где и*, ш. — перемещения и углы поворота в точках А и В,
принадлежащих различным связным участкам поверхности S.
Уравнения A2) могут быть получены с помощью формул Чезаро
(см., например, '"
1.2. Все функционалы обозначены буквой Э с ин-
индексом, которым, как правило, служит первая буква
названия; например, Эл — функционал Лагранжа,
•Эк — функционал Кастильяно, Э*п, Эп — полные функ-
функционалы. Наиболее важные, с нашей точки зрения,
функционалы и их дополнительные и естественные
условия размещены в табл. 3.1—3.5. Между их ар-
аргументами установлено соответствие
и ^ ф; е «_* а; е*^, <0 *^ Г; «* ++ Ф*аВ. 1?в. О -13)
которое приводит к тому, что функционалы Лагранжа
(табл. 3.1) и Кастильяно (табл. 3.2), полные функ-
функционалы лагранжевой серии (табл. 3.3) и кастилья-
новой серии (табл. 3.4) с одинаковыми номерами
имеют соответствующие наборы независимых пере-

54 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
менных, т. е. соответствующие пространства состоя-
состояний. При этом дополнительные условия и условия ста-
стационарности также оказываются соотнесенными друг
с другом: геометрические уравнения со статическими,
физические в прямой форме с физическими в обрат-
обратной форме.
§ 2. Различные варианты принципов Лагранжа
и Кастильяно — исходные пункты
для преобразования вариационных принципов
Вариационные принципы Лагранжа и Кастильяно
изучены в литературе с точки зрения как стационар-
стационарности, так и экстремальности соответствующих функ-
функционалов. Поэтому их целесообразно использовать
как исходные пункты для построения и исследования
системы полных и частных вариационных функциона-
функционалов теории упругости. В соответствии с § 2 гл. 2 здесь
рассмотрены различные варианты принципов Лагран-
Лагранжа и Кастильяно. Экстремальные свойства соответ-
соответствующих им функционалов будут использованы
в §6.
2.1. Различные варианты функционала Лагранжа
(табл. 3.1).
а) Функционал Лагранжа Эт (и) в перемеще-
перемещениях, наиболее распространенный в литературе, рас-
рассматривается здесь как частный функционал в про-
пространстве перемещений при дополнительных усло-
условиях A.5).
Данный функционал может быть преобразован
путем расширения пространства состояний за счет
замены переменных е(м) = е, в(е)=в и искусствен-
искусственного введения соответствующих дополнительных усло-
условий в другие разновидности, имеющие различные
особенности. Некоторые из полученных таким путем
вариантов функционала Лагранжа (наиболее инте-
интересные с точки зрения авторов) представлены
в табл. 3.1.
Как видно из табл. 3.1, условия стационарности
различных вариантов функционала Лагранжа — урав-
уравнения равновесия, но в различной форме, выражен-

§ 2] ПРИНЦИПЫ ЛАГРАНЖА И КАСТИЛЬЯНО 55
¦ные через компоненты того пространства состояний,
в котором сформулирован данный функционал.
б) Функционал Лагранжа Элъ{и,е) в перемеще-
перемещениях и деформациях. Пространство перемещений
расширено за счет введения тензора деформаций по
формуле A.1) и дополнительного условия е — -^(
+ ttV) = 0. Искусственное расширение "пространства
состояний сделано с целью увеличения возможностей
для преобразований функционалов. В частности,
Эл2{и,е) может быть преобразован в функционалы
Ху — Вашицу Эп2{и,е,а) (табл. 3.3) и Кастильяно
«Экз(ог) (табл. 3.2), которые нельзя получить из Эд\(и).
в) Функционал Лагранжа Элз(е) в деформациях.
В этой формулировке ни функционал, ни дополни-
дополнительные условия не содержат варьируемых перемеще-
перемещений (а значит, и условия стационарности включают
только деформации). Функционал ЭЛз(е) в усеченном
пространстве состояний е получим, исключая переме-
перемещения из Эт{и,е) и из дополнительных условий
к нему.
Исключение перемещений из геометрических урав-
уравнений в объеме A.1) и на поверхности A.5) рассмот-
рассмотрено в § 1: зависимости Коши A.1) переходят в урав-
уравнения неразрывности деформаций A.8), а граничные
условия в перемещениях A.5)—в деформационные
граничные условия A.9).
В табл. 3.1 приведен наиболее простой частный
случай, когда на части Su поверхности тела S заданы
все компоненты вектора перемещений, а на остальной
части Sf — все компоненты вектора усилий, причем
Su — связное множество (т. е. состоит из одного це-
целого куска любой формы). Если граничные условия
A.5) охватывают несколько связных участков по-
поверхности S, то в список дополнительных условий
должны быть включены уравнения вида A.12).
Рассмотрим преобразование ЭЛ2 в Элз в указанном частном
случае. В функционале ЭЛ2 перемещения содержатся в слагаемом
F-udV B.1)

66 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
объемного интеграла и в поверхностном интеграле, который в
рассматриваемом частном случае граничных условий S=Su+St
имеет вид
\\f*u dSf. B.2)
Чтобы избавиться от перемещений в слагаемом A), предста-
представим вектор F в форме
J? = _\7.a°, B.3)
где тензор а" можно рассматривать как частное решение уравне-
уравнения равновесия A.6), которое обычно легко найтн. Используя C),
преобразуем F-u:
F. и = (- V ¦ о°) ¦ и = - V ¦ (а° ¦ в) + а° • • (Vb). B.4)
В силу симметрии тензора напряжений а0 справедливо равенство
так что выражение D) можно представить в виде
F. и = — V • (о0 • и) + а° • • y (Vb + «V). B.5)
Подставив E) в A) и преобразовав интеграл от первого слагае-
слагаемого по формуле Остроградского (см. Приложение 2), получим
\\\F-udV=\\\o°. .±¦(Vu + uV)dV-
\\ B.6)
Поверхностный интеграл в преобразованном функционале
Э д2 имеет нид
- \\ ив° -ndSu -\\ и ¦ (f* + в° • п) dSf.
Так как на Su должно выполняться граничное условие в — в* = 0,
то в первом интеграле можно заменить в на в* н переписать по-
последнее выраженне следующим образом:
*-a°.rtrfSu- \[ и ¦ (f* + 0° • я) dSf. B.7)
В первое слагаемое входят известные, неварьируемые величины;
оно не нуждается в дальнейших преобразованиях. Чтобы изба-
избавиться от перемещений во втором слагаемом, выразим вектор на-
напряжений f*-\-oa-n через компоненты тензора функций на-
напряжений Ф^ и некоторые функции ф"^ (а, Р= 1, 2) от их нор-
нормальных производных в системе координат, связанной с поверх-

§ 2] ПРИНЦИПЫ ЛАГРАНЖА И КАСТИЛЬЯНО 57
ностью S; (см. гл. 4, § 1.1). Для этого предположим, что в
окрестности S/ найден тензор <р*, удовлетворяющий уравнениям
f + eo-n = (VX<P'1XV)-n, B.8)
т. е. что известно частное решение ф* системы дифференциальных
уравнений с частными производными (8) (способы нахождения
частных решений здесь не обсуждаются). Для "дальнейших пре-
преобразований используем равенство
«•(VX<P*XV)-n =
= - {V X [и ¦ (V X Ф*Ш • п - еЧ*б""Р GЛ) G/Ф;,) пр. B.9)
В системе координат, связанной с поверхностью Sj(e3 = я—век-
я—вектор нормали к Sf, rii = п.2 = 0, п3 = 1), второе слагаемое имеет
вид
) + .ив Gв
(^вп)Ф3*а}, B.10)
где е"* — дискриминантный тензор.
Подставим (8) 'с учетом (9) и A0) в G) и преобрчэуем по-
поверхностные интегралы от производных вида V| [...] в контур-
контурные по формуле Грина (см. Приложение 2); получим
- J \ и ¦ (f + о°. п) dsf = - \ \ в«^«з [(Ve) GзФ;а) _
dSf + § U* ¦ G X Ф*) dCuf +
а + GY«*B) фз*а] t* dCuf. B.11)
Заменяя в формулах (б) и A1) — (Va«g + 7р«а) на еац и
р на хав; =V(ea3 —Vpea, — 7ae;p и подставляя их
вЭЛ2(«,е), перейдем к функционалу Эт (е) (табл. 3.1).
Заметим, что хотя в принципе преобразование 5Л2 в Элз
всегда возможно, его практическое выполнение при конкретных
нагрузках F /* может натолкнуться на значительные трудности,
связанные с отысканием частного решения ф* системы уравые-

58 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
ний (8). Такое частное решение легко найти, например, когда
/* + а"-п — 0: в этом случае можно принять <р* = 0.
В вычислительном отношении функционалы
Эл2(и, е) и Элз(е) имеют несколько различные обла-
области применения с точки зрения учета граничных усло-
условий. Функционал Эдз(е) удобнее применять в случае
деформационных граничных условий.
Функционал Злз(в) легко преобразуется в полный
функционал Эпз(е, <р) и функционал Кастильяно
ЭК1(ф) в функциях напряжений, которые можно по-
получить и из Эл2 или Эли но окольным путем.
г) Функционал Лагранжа Эти{и, е, а) в основном
пространстве состояний (и, е, а) получается из
Зл2 (н, е) за счет расширения пространства состояний.
Вводятся новые неизвестные — компоненты тензора
напряжений а и соответствующие дополнительные ус-
условия— закон Гука A.2). Эта форма функционала
удобна для дальнейших преобразований.
Функционалы Эли Эл2 и Эл* имеют отличия по
форме и дополнительным условиям к ним. Различия
в вычислительном аспекте между ними несуществен-
несущественны. Однако разнообразие форм исходного пункта пре-
преобразований приводит к важным особенностям полу-
полученных из них функционалов не только по форме, но
и в вычислительных, и, в частности, экстремальных
свойствах (см. §§ 3, 5 и 6).
д) Функционалы Лагранжа с неполными полями
и, е, а. Функционалы Эль Зла выражены через все
компоненты используемых тензоров и представлены
в тензорной форме. Вводя в качестве новых пере-
переменных некоторые компоненты тензоров деформаций
и напряжений или исключая отдельные компоненты
вектора перемещений из функционала Эл2 или Злз
и дополнительных условий, в некоторых системах ко-
координат можно получить формулировки принципа
Лагранжа в пространствах состояний, содержащих
лишь часть компонентов полей напряжений, деформа-
деформаций и перемещений. Это возможно, например, в де-
декартовой координатной системе.
В табл. 3.1 приведено лишь два примера функцио-
функционалов такого рода —Эл5(«<, взд и Элб(«ь «аг), из ко-

§ 2] ПРИНЦИПЫ ЛАГРАНЖА И КАСТИЛЬЯНО 59
торых могут быть получены полные и частные функ-
функционалы с неполными полями.
2.2. Различные варианты принципа Кастильяно
(табл. 3.2).
а) Функционал Кастильяно в напряжениях Экз(о)
получен из функционала Лагранжа Эл2{и,е) по сле-
следующей схеме (преобразование Фридрихса, см. гл. 2,
§2.4):
множители
5Л2 ("- «) Лагранжа> 5п2 («, в, в) - 3К3 (в), B.12)
где Эп2(и,е,а)—полный функционал Ху — Вашицу
(табл. 3.3). Это позволяет утверждать, что функцио-
функционалы Элг(и.^) и Экз(о) имеют одно и то же стацио-
стационарное значение.
При преобразовании Фридрихса A2) дополнитель-
дополнительные условия (геометрические уравнения) и условия
стационарности (статические уравнения) функционала
Лагранжа переходят соответственно в условия ста-
стационарности и дополнительные условия функционала
Кастильяно. См. также § 3.2г, в котором схема A2)
дополнена обратным преобразованием Фридрихса,
и § 3.2в, где дана аналогичная схема для функциона-
функционалов Лагранжа в деформациях и Кастильяно в функ-
функциях напряжений.
Другие разновидности функционала Кастильяно
могут быть получены из Экз(а) с помощью общего
решения A.7) уравнения равновесия A.6) и замены
переменных е(о) = е либо преобразованием Фрид-
Фридрихса из функционалов Лагранжа (табл. 3.1). Как
видно из табл. 3.2, условия стационарности различных
вариантов функционала Кастильяно — уравнения не-
неразрывности в объеме и деформационные граничные
условия на поверхности. В табл. 3.2 приведены усло-
условия стационарности лишь для простого случая, когда
компоненты перемещений заданы на связной части
поверхности 5. В гл. 5 показано, как из этих функ-
функционалов извлечь условия стационарности в некото-
некоторых более сложных случаях.
б) Функционал Кастильяно ЭК2(<р, а) в напряже-
напряжениях и функциях напряжений. Этот функционал полу-

60 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
чен из Экз(о) путем замены дополнительных условий
в форме уравнений равновесия A.6) на эквивалент-
эквивалентные им зависимости между напряжениями и функ-
функциями напряжений A.7), в связи с чем Эц2 зависит
не только от а, но и от ф. Поверхностный интеграл
в Экз путем замены а-п на (о°+ \ ХфХ V) -я и при-
применения формулы Стокса записан в функциях напря-
напряжений (см. аналогичные преобразования в § 2.1в),
с тем чтобы функционал Экг(ф, о) имел вид, анало-
аналогичный функционалу Элг (и, е) (тензор функций на-
напряжений ф соответствует вектору перемещений и,
а тензор напряжений а — тензору деформаций е,
см. § 1).
Функционал Экг(ф, о) связан преобразованием
Фридрихса с функционалом Лагранжа Эд3(е).
Функционал ЭК2 является промежуточной сту-
ступенью при преобразовании Зкз(о) в Зк1(ф). В то же
время ЭК2 имеет большие возможности, чем Эщ, как
исходный пункт для преобразований, подобно анало-
аналогичному ему функционалу Лагранжа Эд2(и,е). Из
•Эк2(ф. а) можно получить полный функционал
Э*? (ф, о, е) и функционал Лагранжа Эт{е).
в) Функционал Кастильяно Эк\ (ф) в функциях
напряжений получен из Экг(ф, а) путем исключения
тензора напряжений а с помощью A.7). Дополнитель-
Дополнительное условие A.6) в объеме V оказывается выпол-
выполненным, остается лишь граничное условие для ф
A.10).
Переход от ЭКз к 3Ki означает учет дополнитель-
дополнительного условия A.6) с помощью общего решения
A.7).
Уравнение равновесия A.6) имеет и другие общие
решения [3.3, 3.9], которые могут служить основой
для других разновидностей функционала Кастильяно
в функциях напряжений. В частности, ряд разновид-
разновидностей общего решения A.7) можно получить, пола-
полагая некоторые компоненты тензора функций напря-
напряжений ф равными нулю [3.3]. В декартовой системе
координат существует пять, а в криволинейной си-
системе — больше различных общих решений, в кото-
которых напряжения выражены через три компонента

§ 2] ПРИНЦИПЫ ЛАГРАНЖА И КАСТИЛЬЯНО 61
тензора ф. Среди них известные решения Максвелла
°11 === Ф22, 33 Ч~ ФЗЗ, 22! °22 = фзз, II Ч~ ф] 1, 33!
О33 = ф11.22 + Ф22, П'> ^23= ~ Фп.23". B-13)
°31 = — Ф22, 13; ^12 = — ФЗЗ, 12
и Морера
°i 1 = — 2ф23,2з; <% = — 2ф13,13; (Тзз = —2ф12, [2;
°23 = (— Ф23, I + Ф13, 2 + Ф12, з).1;
°13 = (ф23. I — Ф13, 2 + Ф12. з), 2, B.1 4)
О|2 = (ф23, 1 + Фп. 2 — Ф12, з), 3-
Используя общее решение A.7), легко доказать,
что условиями стационарности функционала Кас-
тильяно являются уравнения неразрывности A.8) (в
отличие от длинного доказательства Саусвелла, при-
приведенного в [3.6]).
Действительно, вариационное уравнение для функ-
функционала Кастильяно 5к[(ф) (табл. 3.2) имеет вид
5ЭК1 (tf) = - \ \ \ [V X е (Ф) X V] • • 6Т dV +
B.15)
Отсюда следуют уравнения неразрывности A.8).
Кроме того, из вариационного уравнения A5) сле-
следуют деформационные граничные условия A.11).
Саусвелл первоначально дал вывод уравнений не-
неразрывности, основанный на применении общих ре-
решений Максвелла и Морера, т. е. фактически исполь-
использовал тензор функций напряжений ф. По-видимому,
появление нового длинного и запутанного доказатель-
доказательства объясняется тем, что этот вывод его не удовле-
удовлетворил по следующей причине.
Равенство A.8) содержит шесть уравнений. При
использовании общих решений A3) и A4), в кото-
которых участвуют по три компонента тензора функций
напряжений, т. е. по три варьируемых функции, ва-
вариационное уравнение Кастильяно принимает вид

62 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ 1Гл. 3
соответственно A6) и A7):
6ЭК1 (фц. Ф22. Фзз) = — J J J ^33' 22 ~^~ в<П- 33 ~ в2Ъ' ^ 6(Pl' ~^~
+ («II. 33 + «33. 11 — «13. 13) 6Ф22 +
+ («22. u+ «11,22 — «12,12) &Рзз1 <*У + у\ {. . .}dS= О,
BЛ6)
где ец — ЬцЫа (<рм, ф^, Фзз);
(ф2з, Ф13. Ф12> =
~ ~ \\ \ ^~ 2е"'23 + ^~ б23'' + е'3> 2 + е'2> 3^ '^бф23 +
+ [— 2^22. 13 + («23. 1 — «13, 2 + «12, з), г] бф13 +
+ [ —2«33. 12 + («23, 1 + «13. 2 — «12, з). з] бф12> ^ +
...}dS = O, B.17)
где etl = bilkiakl((f23, ф13, ф,2).
Равенства A6) и A7) показывают, что при ис-
использовании каждого из общих решений Максвелла
или Морера условиями стационарности функционала
Кастильяно являются различные системы из трех
уравнений неразрывности и соответствующих дефор-
деформационных граничных условий. Из функционала
3ki(<p) (табл. 3.2), в котором используется общее ре-
решение A.7) с шестью функциями напряжений (оно
имеет вид «Максвелл + Морера»), следует шесть
уравнений неразрывности с соответствующими гра-
граничными условиями [5.3]. Использование других об-
общих решений приводит к несоответствию между ва-
вариационной и дифференциальной формулировками
задачи [5.3]; этот вопрос нуждается в дальнейшем
исследовании.
г) Функционал Кастильяно ЭК4 (<р, о,«) в квазиос-
квазиосновном пространстве состояний (ф, а, е) получен из
•Экг(ф,о) путем расширения пространства (ф,а) за
счет искусственного введения новой переменной —
тензора деформаций е—и дополнительного условия
A.3) (закон Гука в обратной форме). Он соответ-
соответствует функционалу Лагранжа 3ju(u, е,в) и служит

§ 3] ПОЛНЫЕ ФУНКЦИОНАЛЫ 63
для преобразований и построения новых вариацион-
вариационных принципов, в частности полного функционала
3*п4а (ф, о, е) (табл. 3.4).
д) Функционалы Кастильяно с неполными полями
Ф, а, е. Функционалы Эки ЭК4 выражены через все
компоненты используемых тензоров ф,лт, ей представ-
представлены в тензорной форме. В декартовой и некоторых
других системах координат существуют разновидно-
разновидности функционала Кастильяно, в которых аргументами
являются не все, а лишь часть компонентов тензоров
функций напряжений, напряжений и деформаций. Та-
Такие разновидности можно вывести, например, из
•Экз(о) (табл. 3.2), вводя некоторые компоненты функ-
функций напряжений в качестве параметров общего реше-
решения части уравнений равновесия, или из 3Ki((p), вводя
в качестве новых переменных некоторые компоненты
напряжений и деформаций и исключая часть компо-
компонентов функций напряжений.
В табл. 3.2 приведено лишь два примера функцио-
функционалов такого'рода, Эк5(ф(/, а'3) и 5к6(ф,7, ст'а), из ко-
которых могут быть получены полные функционалы
с неполными полями.
§ 3. Полные функционалы
В соответствии с теорией преобразования вариа-
вариационных проблем (см. гл. 2, § 2), различные варианты
исходной вариационной задачи приводят к различным
полным функционалам и соответствующим общим
вариационным принципам в различных пространствах
состояний.
Из функционалов Эщ (табл. 3.1) построены пол*
ные функционалы Эп1 (табл. 3.3), которые мы будем
называть лагранжевой серией полных функционалов.
Соответственно кастильянова серия 3*ni полных функ-
функционалов (табл. 3.4) получена из Эщ (табл. 3.2). Пол-
Полные функционалы имеют, как правило, те же номера,
что и частные, из которых они получены.
Каждый полный функционал позволяет сформули-
сформулировать вариационную задачу без каких-либо допол-
дополнительных условий. Здесь независимо варьируются

64 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
асе параметры, указанные а скобках: например, у
•Эп2(и, е, в) независимо варьируются поля и, е и а.
Между многими полными функционалами может
быть установлена взаимосвязь посредством преобра-
преобразований одного пространства состояний в другое: усе-
усеченное, расширенное или эквивалентное (см. гл. 2,
§ 2.2).
Из полных функционалов получаются частные,
в том числе функционалы Лагранжа (табл. 3.1) и
Кастильяно (табл. 3.2) в различной форме.
3.1. Лагранжева серия полных функционалов
(табл. 3.3).
а) Полный функционал 9m(u,f) в перемещениях
и поверхностных реактивных напряжениях. Построен
путем внесения дополнительных условий (граничных
условий в перемещениях) в функционал Эц\(ц)
(табл. 3.1) с множителями Лагранжа /. Величины f
являются, как показывают условия стационарности,
компонентами напряжений, соответствующими задан-
заданным компонентам перемещений (и*)", т.е. реакциями.
Условия стационарности Эп1(и, f) — уравнения рав-
равновесия, статические и геометрические граничные ус-
условия в перемещениях плюс уравнения для вычисле-
вычисления реакций / по известным перемещениям.
б) Полный функционал в перемещениях Эп1а(и).
Если выражения для реакций f через перемещения
подставить в 9ni(u,f) (т. е., с точки зрения теории
преобразования вариационных проблем, наложить не-
некоторые из условий стационарности в качестве допол-
дополнительных условий и с их помощью исключить /), то
3ni перейдет в полный функционал в перемещениях
3nia(«), который обсуждался Д. Рюдигером [3.11],
а для разрывных полей перемещений — В. Прагером
[0.12] (см. также § 6).
в) Полный функционал Ху — Вашицу Эп2(и,е,а)
[0.17, 0.18] в основном пространстве состояний полу-
получен из Эл-2(и,е) с помощью множителей Лагранжа а
при геометрических соотношениях. Как видно из ус-
условий стационарности о — е-а = 0 (физических со-
соотношений), множители Лагранжа являются напря-
напряжениями.

§ 3] ПОЛНЫЕ ФУНКЦИОНАЛЫ 65
Условия стационарности функционала Ху — Ва-
шицу имеют классическую, наиболее употребительную
в теории упругости форму: геометрические соотноше-
соотношения A.1), статические уравнения A.6) и физические
уравнения A.2) в объеме V; геометрические A.5)
и статические A.4) граничные условия на поверх-
поверхности S.
Исключение множителей Лагранжа о из функцио-
функционала Ху — Вашицу в соответствии с § 2.2г гл. 2 при-
приводит к полному функционалу в пространстве (и, е),
который оказывается одной из форм функционала
Рейсснера [0.2]:
(и, е) =
- J J (/* • и)' dS - JJ (и - и*)" -(е- -a)-ndS. C.1)
Можно исключить из Эп2(и,е,а) деформации е (в со-
соответствии с § 2.2 в гл. 2) и прийти к другой форме
функционала Рейсснера Э*п3(а, и) (табл. 3.4) в про-
пространстве (а, и).
г) Полный функционал Эпз(е,<р) в деформациях
и функциях напряжений получен из Злз(е) (табл. 3.1)
с множителями Лагранжа ф.
Условия стационарности функционала Эп3 — гео-
геометрические уравнения в деформациях в объеме и на
поверхности и зависимости между деформациями
и функциями напряжений, которые одновременно иг-
играют роль статических и физических уравнений. От-
Отсюда следует, что множители Лагранжа совпадают
с компонентами тензора функций напряжений в форме
Финци — Блоха — Круткова (см. § 1).
Заметим, что использование Эпз(е,<р) можно рас-
рассматривать как инструмент для установления зави-
зависимости между напряжениями и функциями напря-
напряжений, т. е. для получения общего решения уравнений
равновесия. Иными словами, преобразование функ-
функционала Лагранжа Эд3(е) в Эп3(е,ф) фактически при-
привело к преобразованию условий стационарности Э
3 И. П. АбивскиЛ и др.

C6
ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
(статических уравнений) к форме, являющейся их об-
общим решением. Этот пример раскрывает то богатство
возможностей, которое заключено в вариационных
формулировках и их преобразованиях.
д) Полный функционал Эп4 (и, е, а, X,, ц) в расши-
расширенном основном пространстве состояний получается
из ЭЛ4(и,е,а) (табл. 3.1) с помощью множителей
Лагранжа X, и (л. Как видно из условий стационарно-
стационарности, ц имеет смысл уе, а к = (у а + уе • • а).
Функционал Эп4(и, е,оД, ц) является промежуточ-
промежуточным звеном преобразования Эм{и,е,а) в Эп4а(и, е, о).
е) Полный функционал Эп4а (и, е, а) в симметри-
зованном основном пространстве состояний [0.1] по-
получен из 5П4 путем исключения множителей Лагран-
Лагранжа X, и ц в соответствии с § 2.2г гл. 2.
Функционал 9nia(u,e,а)— линейный (неоднород-
(неоднородный) относительно каждого из параметров и, е, а при
фиксированных остальных. Отсюда следует его осо-
особенность, заключающаяся в том, что каждое условие
стационарности содержит два параметра и не содер-
содержит третий, по которому варьировался функционал
(см. схему на рис. 3.1).
3n/ia(u,e,6)
ди
Рис. 3.1. Симметричный характер условий стационарности полного
функционала Эп4а (табл. 3.3).
Линейное преобразование пространства состояний
(и, е, а) в (и', е', а') по формулам
„ = «', е = е', ет = у(е'. -а + о') C.2)
переводит функционал Эп2(и, е,а) в Э„4а(и',е',а'). Об-
Обратное преобразование определяется формулами
и' = И) е' = е, а' = 2о — е'-а. C.3)

§ 3] ПОЛНЫЕ ФУНКЦИОНАЛЫ 67
По свойствам, связанным со стационарностью,
функционалы Эпг и Эп^ эквивалентны, но имеют раз-
различные экстремальные свойства (см. § 5).
ж) Полные функционалы с неполными полями пе-
перемещений, деформаций, напряжений и функций на-
напряжений могут быть построены с помощью множите-
множителей Лагранжа из соответствующих разновидностей
функционала Лагранжа в декартовой и некоторых
других системах координат. В табл. 3.3 представлено
лишь два таких функционала, Эп5(и{, e3i, a'3, fa) и
Эп6(и{, eai, о'а, /3), полученных из Эл; {щ, е3{) и
Элб(«(. еа1) (табл. 3.1).
Условия стационарности этих функционалов —
уравнения смешанного метода в теории упруго-
упругости [3.2].
3.2. Кастильянова серия полных функционалов
(табл. 3.4).
а) Полный функционал Э*п1 (ц>, ?аВ, хаВ) в функ-
функциях напряжений и деформациях поверхности тела
получен из 3Ki(q>) (табл. 3.2) путем внесения в функ-
функционал дополнительных условий (статических гра-
граничных условий в функциях напряжений) с множите-
множителями Лагранжа. Множители Лагранжа при(сраВ — ф^)
целесообразно записать в виде сас&6кУ6, а при
(¦фу5 — ipj6) — в виде eyls, с тем чтобы оба поверхно-
поверхностных интеграла в Э*п1 имели одинаковую форму.
Условия стационарности Э*а1 — уравнения нераз-
неразрывности и деформационные граничные условия и ста-
статические граничные условия в функциях напряжений,
а также равенства, раскрывающие смысл множителей
Лагранжа: выражение незаданных деформаций по-
поверхности S через функции напряжений.
б) Полный функционал Э*п1а (<р) в функциях напря-
напряжений получен из функционала Э*п1 путем исключе-
исключения множителей Лагранжа еа$, иар в соответствии
с § 2.2г гл. 2. Функционал Э*п1я (<р) — аналог полного
функционала в перемещениях Э„\а(и), см. § 3.16.
в) Полный функционал 5*?(ff, о, е) в квазиоснов-
квазиосновном пространстве состояний получен из Зкг (q>, °) ПУ'

68 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
тем внесения дополнительных условий (общих реше-
решений уравнений равновесия в объеме V и граничных
условий в функциях напряжений на поверхности 5)
в функционал с множителями Лагранжа. Множители
Лагранжа являются деформациями в объеме и на по-
поверхности. Условия стационарности —полный набор
уравнений и граничных условий теории упругости
в функциях <р, а, е.
Функционал 5*2 (ф, о, е) является промежуточным
звеном преобразования Фридрихса (см. гл. 2, § 2.4)
5к2(ф, а) в Элз(е). Обратное преобразование Элз
в Эк.2 производится через полный функционал Эпз(е, Ц>)
(табл. 3.3), так что эти четыре функционала связаны
между собой по схеме, изображенной на рис. 3.2.
Рис. 3.2. Взаимосвязь функционалов Кастильяно ЭК2 и Лагранжа
Эд3с полными функционалами: прямое и обратное преобразова-
преобразование Фридрихса.
г) Полный функционал Э*п3 (о, н) в напряжениях
и перемещениях (функционал Рейсснера [0.13]) по-
получен внесением в Экз(а) (табл. 3.2) статических до-
дополнительных условий с множителями Лагранжа и,
которые можно считать, как видно из условий стацио-
стационарности, перемещениями.
Функционал Рейсснера Э*п3(а, и) является проме-
промежуточным звеном преобразования Фридрихса
(см. гл. 2, § 2.4) Экз(с) в Эл2(и,е). Промежуточным
звеном обратного преобразования Эд> в Экз служит
функционал Ху — Вашицу Э„2(и,е,о) (табл. 3.3), так
что эти четыре функционала связаны между собой по
схеме, аналогичной рис. 3.2..

§ 31 ПОЛНЫЕ ФУНКЦИОНАЛЫ 69
Используя линейное преобразование пространства
состояний
« = «', о — в'-а, C.4)
можно Э*п3(а, и) преобразовать в функционал Рейс-
снера A) в деформациях и перемещениях (см. § ЗЛв).
д) Полный функционал Э*4 (ф, а, е, |, ц) в рас-
расширенном квазиосновном пространстве состояний.
Получен из 5К4(<р,о,е). Множители Лагранжа— тен-
тензоры |, г\. Их физический смысл определен вторым
и третьим условиями стационарности.
Функционал 5П4 имеет вид, аналогичный 3П4
(табл. 3.3) и является промежуточным звеном для
перехода к Э*4а(<р, а, е) (сравните с § 3.1д).
е) Полный функционал Э*4а (<р, а, е) в квазиос-
квазиосновном симметризованном пространстве выведен" из
Э*4 путем исключения множителей Лагранжа |, т). .
Между 5*4а и 5*2 существует связь, аналогичная
связи между 5п4а (и, е, а) и 5п2(и, е, о): Э*2 перехо-
переходит в Э*Мя при замене E); обратное преобразование
дается формулами F):
<р = <р', в = о', «=!(/ +У. -Ь), C.5)
ф' ==ф, а' = а, е' = 2е — о-<Ь. C.6)
По свойствам, связанным со стационарностью, функ-
функционалы 5*2 и Э*4а эквивалентны, но имеют различ-
различные экстремальные свойства (см. § 5).
Функционал 5*1а (<р, а, е), подобно 5п4а (и, е, а),
линейный (неоднородный) относительно каждой из
трех переменных <р, о, е и имеет в этом смысле ана-
аналогичные свойства: связь 5*4а с его условиями ста-
стационарности имеет симметричный вид, аналогично
схеме на рис. 3.1.
ж) Полные функционалы с неполными полями
функций напряжений, деформаций и перемещений мо-
могут быть построены с помощью множителей Ларранжа
из соответствующих разновидностей функционала

70 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
Кастильяно в декартовой и некоторых других систе-
системах координат по аналогии с Эпь и 3П6 (табл. 3.3
и § 3.1ж).
§ 4. Частные функционалы. Их взаимосвязь
с полными функционалами
Согласно § 2 гл. 2 частные функционалы полу-
получаются из полных при наложении некоторых условий
стационарности в качестве дополнительных условий.
При этом выражение для функционала обычно упро-
упрощается, так как некоторые слагаемые обращаются
в нуль.
Из приведенной в § 2.3.1 гл. 2 классификации до-
дополнительных условий, которые можно наложить на
полный функционал, видно, что количество возможно-
возможностей для получения различных частных функционалов
очень велико. В частности, легко осуществляется пе-
переход к функционалам Лагранжа и Кастильяно. Не-
Некоторые другие, наиболее характерные, на наш
взгляд, частные функционалы, приведены в табл. 3.5.
4.1. Различные варианты частных функционалов
Лагранжа и Кастильяно (табл. 3.1 и 3.2).
а) Получение функционалов Лагранжа из лагран-
жевой серии полных функционалов и Кастильяно —
из кастильяновой серии представляет собой обрат-
обратный переход от полных функционалов к частным, из
которых они получены. Для этого перехода в качестве
дополнительных условий принимают те уравнения,
которые были внесены в функционал с множителями
Лагранжа; при этом слагаемые в функционале, со-
содержащие множители Лагранжа, обращаются в нуль.
б) Преобразование некоторых полных функциона-
функционалов лагранжевой серии (табл. 3.3) в различные ва-
варианты функционала Кастильяно (табл. 3.2). Нало-
Наложение в качестве дополнительных условий тех усло-
условий стационарности полных функционалов, которые
не были дополнительными условиями исходных функ-
функционалов Лагранжа (табл. 3.1), и исключение с по-
помощью этих уравнений переменных, входящих в ис-
исходные функционалы Лагранжа, приводит (см. гл. 2,

§ 41 ЧАСТНЫЕ ФУНКЦИОНАЛЫ 71
§ 2.4) к различным вариантам функционала
Кастильяно, зависящим от статических величин, кото-
которые при построении полных функционалов были мно-
множителями Лагранжа. Это преобразование является од-
одним из этапов преобразования Фридрихса Эм —*ЭК1.
Так, например, Э„2(и,е,а) (табл. 3.3) после нало-
наложения в качестве дополнительных условий статиче-
статических уравнений в объеме и на поверхности тела те-
теряет переменную и. Это становится очевидным, если
с помощью формул
о • • -i-(V« + «V) = V • (о • и) — (V • о) • и
и формулы Остроградского (см. Приложение 2) пре-
преобразовать функционал Эп2 к виду
Эа2(и, е, а) =
= \\\[je' a- -e-o-e-(V-o + F)-
55 (иУ'-a-ndS.
Действительно, если о удовлетворяет статическим
уравнениям в объеме и на поверхности, то коэффи-
коэффициенты при и в объемном и поверхностном интегралах
равны нулю, и Э„2 не зависит от и. Продолжая пре-
преобразование, наложим в качестве дополнительных ус-
условий еще и физические уравнения A.2), выразим е
через о и подставим е=а-Ь в функционал A); по-
получим функционал Кастильяно ЭКз(с).
Подобным образом, накладывая статические до-
дополнительные условия и исключая переменную е из
полного функционала Эпз(е, <р) (табл. 3.3), перейдем
к другой разновидности функционала Кастильяно
3Ki(tp) (табл. 3.2).
Функционал 9ni(u,f) нельзя указанным путем пре-
преобразовать ни в какую разновидность функционала
Кастильяно, так как он не содержит статических пе-
переменных в объеме V.
Функционал 9nii(u,e,a) переходит, как и
Эп2{и, е, а), в 5кз(о), если наложить статические

72 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
Дополнительные условия
V-у(а + е- -a) + F = 0 в V,
Г1(о + в- .а)-гТ=0 на S
L ^ J
и исключить е с помощью уравнений
а - 1 (Vh + hV) • • а = 0, е-j(Vw + «V) = O в К.
в) Преобразование некоторых полных функциона-
функционалов кастильяновой серии (табл. 3.4) в функционалы
Лагранжа (табл. 3.1). Переход от 5*, к Эл- — один
из этапов преобразования Фридрихса Э^\-^Эщ
(см. гл. 2 § 2.4)—осуществляется по аналогии с пре-
преобразованием ЭП[ в 5Kj (см. § 4.16).
Функционал 5П2(ф, а, е) после наложения допол-
дополнительных условии A.8) и A.2) в объеме тела и де-
деформационных граничных условий на поверхности
(которые являются его условиями стационарности)
и исключения переменной а переходит в 5лз(е), так
как преобразование объемного интеграла с использо-
использованием формулы Остроградского (см. Приложение 2)
приводит Э*а2 к виду
= $$$[-уа- -Ь- -а + е- -а-е- • а°-
+ J J IW)' еуь - спУс"& (ф'-е)' *« (еIdS
\ J {(^-<б)" %Ь (Ф)
+ const,
откуда ясно, что при условиях
VXeXv = 0B V;
Кб - <в)" = °> [^v6(е) - V]" = 0 «a S
коэффициенты при q> обращаются в нуль.
Подобным образом преобразуется Э*п2 (а, и)
в 5Л1(и).

§ 4] ЧАСТНЫЕ ФУНКЦИОНАЛЫ 73
Нельзя указанным путем преобразовать 5*, (f,
еа~, хар) в функционал Лагранжа, так как он не содер-
содержит геометрических переменных в объеме.
Функционал Э*4(ф, а, е, 1, ц) переходит в одну из
форм функционала Лагранжа
\ \ №
toe)' \б (*»] dS + const
с дополнительными условиями
VXnXV = 0, 4-26- -6 = 0 в V,
(\& - <6)" = 0. К« W - *;«]" = 0 на 5.
Функционал 5*4а (<р, а, е) переходит, как и 5*2 (ф,
а, е), в Злз(е), если налол<ить геометрические допол-
дополнительные условия
+ <r- -6)XV = 0 в V,
и исключить о с помощъю уравнений
e-(o° + VXfpXV)- -6 = 0,
<T-(<r° + vXq>XV) = o B у.
4.2. Вывод частных функционалов из полных пу-
путем наложения различных комбинаций геометриче-
геометрических, статических и физических уравнений в качестве
дополнительных условий (схема а) классификации в
гл. 2, § 2.3.1). Разберем на примерах полных функ-
функционалов в основном и квазиосновном пространствах
состояний различные возможности, возникающие при
наложении указанных дополнительных условий.
а) Использование одной группы из множества гео-
геометрических, статических и физических уравнений
в качестве дополнительных условий, накладываемых
на полный функционал Э„2{и,е,а) приводит к преоб-

74 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ (ГЛ. 3
разованиям, показанным на схеме (рис. 3.3). Эта
схема показывает некоторую неравноправность усло-
условий стационарности функционала Эп2 с точки зрения
их использования для получения частных функцио-
функционалов. Неравноправность геометрических уравнений
по отношению к статическим и физическим состоит
в том, что они приводят к функционалу Лагранжа
Эпг(и,е,6)
Условия стационарности:
геометрические, статические, физические
уравнения
/ Т \
Дппол нигпельные условия
t Ч
[геометрические (статические^ Г
^И^»^ ^rf*<
11
условия стационарности
t I Y
[геометрические,
[ *? )
Рис. 3.3. Использование геометрических, или статических, или фи-
физических уравнений в качестве дополнительных условий для вы-
вывода частных функционалов из полного в основном пространстве
состояний.
Эл2(и,е), условия стационарности которого состоят
из одной группы уравнений — статических, а физиче-
физические оказываются ненужными, так как ни частный
функционал 5Л2> ни его дополнительные условия не
содержат переменную а. Это, конечно, не значит, что
физические уравнения оказываются нарушенными,
так как они выполнены заранее, и поэтому уравнения
равновесия как условия стационарности Эт запи-
записаны в деформациях.
При наложении в качестве дополнительных усло-
условий статических уравнений 5П2(и.*. о) переходит
в функционал для физических и геометрических соот-

S 4J
ЧАСТНЫЕ ФУНКЦИОНАЛЫ
75
ношений ЗфГ(е,<т) (табл. 3.5). Этот функционал яв-
является промежуточным звеном преобразования 3„2
в 5Кз(о) (см. § 4.16). ЭфГ преобразуется в полный
функционал 5пз(е, ф) (табл. 3.3), если для удовлетво-
удовлетворения дополнительных условий к нему использовать
общее решение A.7) уравнений равновесия.
Эпг(и,е,б)
Условия стационарности:
геометрические, статические, физи-
физические уравнения
Доп ол н и тел ьн ые условия
± » JL
{геометрические {геометрические), [сто
I физические J 1 статические 1 1 фи
Г статические,]
физические J
1
1/
Условия
I Г
cm аци онар но с ти
{статические \ ( физические} {геометрически}.
Рис. 3.4. Использование двух групп нз множества геометрических,
статических и физических уравнений в качестве дополнительных
условий для вывода частных функционалов из полного в основ-
основном пространстве состояний.
При наложении физических уравнений 5П2 пере-
переходит в функционал ЭГс(и,е,а) для геометрических
и статических уравнений (табл. 3.5). Исключив из
него в соответствии с гл. 2, § 2.2в деформации, полу-
получим полный функционал Рейсснера Э*п3(о, и), а ис-
исключив напряжения, получим другую разновидность
функционала Рейсснера — 5Pi(h, е) (см. § 3.1в).
б) Использование двух групп из множества гео-
геометрических, статических и физических уравнений для
получения частных функционалов из 5пг(«, в, о) по-
показано на схеме рис. 3.4.
Неравноправие геометрических дополнительных
условий с другими по отношению к функционалу 5„2

76 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
(§ 4.2а) может привести к тому, что при наложении
геометрических и физических или геометрических
и статических дополнительных условий Э„2 перейдет
в функционал Лагранжа Эд?(и, е), который не содер-
содержит напряжений. Тогда мы получим в качестве усло-
условий стационарности статические уравнения с учетом
физических, как и в схеме на рис. 3.3. Но так как
цель состоит в том, чтобы принять два дополнитель-
дополнительных условия, должно получиться, что при этих до-
дополнительных условиях из Эп2 следуют частные функ-
функционалы в соответствии со схемой на рис. 3.4. Дей-
Действительно, принимая вначале не геометрические,
а физические или статические уравнения, приходим
к результату на схеме рис. 3.4. Заметим, что этот же
результат получается, если к частным функционалам
на рис. 3.3 принять соответствующее второе дополни-
дополнительное условие, как на рис. 3.4.
При геометрических и статических дополнитель-
дополнительных условиях ЭП2 переходит в функционал Эф\(е, а)
(табл. 3.5), условиями стационарности которого яв-
являются физические соотношения в форме V-(<j —
— е--а)=0.
При наложении статических и физических условий
Эп2 переходит в одну из разновидностей функционала
Кастильяно
ЭК7(е, а)= JJJ ( - ic • в) dV-\\(uy -a-ndS
с дополнительными условиями
\.a-\-F = 0, а —е- • а = 0 в V;
(а • п - f)' = 0 HaS.
Этот функционал легко преобразуется в 5кз(о).
в) Использование одной группы из множества ста-
статических, геометрических и физических уравнений
в качестве дополнительных условий, накладываемых
на полный функционалЭ*п2 (ф, а, е), можно проиллю-
проиллюстрировать схемой, аналогичной рис. 3.3, заменив на
нем и на ф, е на а и а на е и поменяв местами гео-
геометрические и статические уравнения. Здесь, анало-
аналогично § 4.2а, обнаруживается неравноправность ста-

$ 4] ЧАСТНЫЕ ФУНКЦИОНАЛЫ 7?
тических условий функционала 5*2 по отношению
к остальным. При статических дополнительных усло-
условиях 5*2 переходит в функционал Кастильяно
•Эк2(<р, о) (§ 4.1а), который не содержит деформаций
и условия стационарности которого состоят из одной
группы уравнений — геометрических, а физические
уравнения оказываются выполненными.
При наложении в качестве дополнительных усло-
условий геометрических уравнений 5*2((f, о, е) переходит
в функционал для физических и статических соотно-
соотношений 5фс(<1, е) (табл. 3.5). Этот функционал яв-
является промежуточным звеном преобразования 5*2
в Злз(е) (см. § 4.1в). Функционал 5фс преобразуется
в 5*3 (а, и) (табл. 3.4), если для удовлетворения до-
дополнительных условий к нему использовать общее
решение A.1) уравнений неразрывности.
При наложении физических условий 5*2(ф, а, е)
переходит в функционалы 5сг(ф,а,е) для статических
и геометрических уравнений.
г) Использование двух групп из множества стати-
статических, геометрических и физических уравнений для
получения частных функционалов из 5*2(ф, сг, е)
можно проиллюстрировать схемой, аналогичной
рис. 3.4 (см. § 4.26).
При статических и геометрических дополнитель-
дополнительных условиях 5*2 переходит в функционал 5ф2(о, е)
(табл. 3.5), условиями стационарности которого яв-
являются физические соотношения в форме
VX(e-o. -6)XV = 0.
При наложении геометрических и физических
уравнений 5*2 переходит в одну из разновидностей
функционала Лагранжа
, e)=\\](ja' e-a°- -e)dV+\\l...]dS
с дополнительными условиями
VXeXV = 0, е-о- -Ь = 0 в V,

78 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ (ГЛ. 3
Этот функционал легко преобразуется в Эдз(е)
(табл. 3.1).
4.3. Функционал физических соотношений. Усло-
Условиями стационарности функционала
Эф(а, е) =
D.1)
являются физические соотношения в прямой и обрат-
обратной формах. Хотя он и не входит в систему преобра-
преобразованных функционалов Лагранжа и Кастильяно,
но близко к ней примыкает и обладает интересными
свойствами с точки зрения стационарности и экстре-
экстремальности (см. также § 5).
Функционал A) можно получить из функционалов
рассматриваемой системы следующим образом. Из
Эфг(е, о) (табл. 3.5) вычтем функционал Кастильяно
Экз(о) (табл. 3.2) и положим
Эф (о, е) = Зфг (е, о) - Экз (о). D.2)
Так как 5фГ и 5кз имеют одни и те же дополнитель-
дополнительные условия — статические уравнения, то естественно
считать, что Эф также имеет в качестве дополнитель-
дополнительных условий статические уравнения, а в качестве ус-
условий стационарности — геометрические и физические.
Этот вывод показывает, что стационарное значение
Эф(а, е) равно нулю, так как Эф равен разности двух
функционалов с одним и тем же стационарным значе-
значением, достигающимся в одной и той же точке.
Другой вывод Эф(а,е) состоит в использовании
функционала Лагранжа Эдз(е) (табл. 3.1) и функ-
функционала для физических и статических соотношений
ЭфС(а, е) (табл. 3.5):
Эф (о, е) = Злз (в) - % (о, в). D.3)
Отсюда видно, что дополнительными условиями к Эф
можно считать геометрические уравнения, и тогда
условия стационарности суть статические и физиче-
физические соотношения.

§ 4] ЧАСТНЫЕ ФУНКЦИОНАЛЫ 79
Если в качестве дополнительных условий к Эф(а,е)
принять и геометрические, и статические уравнения,
то он превратится в разность функционалов Лагранжа
и Кастильяно; его условиями стационарности будут
и геометрические, и статические уравнения с учетом
физических, как это наглядно показано в примере,
разобранном в статье [4.3].
Третий путь вывода функционала A) становится
очевидным, если его преобразовать к виду
Эф (о, е) = \\\ 1 (а - е ¦ ¦ а) • • (Ь ¦ -a-e)dV. D.4)
Эквивалентная запись равенства D)
показывает, что использование функционала A) сво-
сводится к одному из вариантов метода наименьших
квадратов для решения физических уравнений, так
как подынтегральное выражение в E) является не-
неотрицательно определенной квадратичной формой,
принимающей нулевое значение для тех деформаций
и напряжений, которые удовлетворяют физическим
уравнениям.
Равенство D) или E) (см. замечание 1 в конце
данного пункта) показывает, что функционал A)
можно считать не имеющим дополнительных усло-
условий; в этом случае его условия стационарности — фи-
физические зависимости, задача о его минимуме имеет
бесконечное множество решений (о, е), а для пол-
полного решения краевой задачи теории упругости нужно
привлекать еще геометрические и статические урав-
уравнения в объеме и на поверхности.
Так как функционал A) неотрицательно опреде-
определен, а его стационарное значение равно нулю, то это
стационарное значение является минимумом. Этот
факт может быть полезен для оценки точности при-
приближенных решений (см. гл.5); при этом функционал
A) имеет некоторые преимущества по сравнению
с функционалами Лагранжа и Кастильяно,

80 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
Замечание 1. Функционалы Эф, Эф\, 5ф2 обла-
обладают любопытным свойством: варьирование по неко-
некоторым переменным (Эф по о и е, Эф] по е, Э$2 по о)
без выполнения дополнительных условий приводит
к физическим уравнениям в прямой A.2) или обрат-
обратной A.3) форме в качестве условий стационарности,
т. е. независимое варьирование некоторых перемен-
переменных не приводит к ошибке.
Замечание 2. В гл. 2, § 2, было показано, как
с помощью усечения пространства состояний преобра-
преобразуются . частные функционалы в полные. Здесь за
счет определенного выбора подпространства преобра-
преобразуются условия стационарности.
Рассмотрим функционал F{us, u2) с дополнитель-
дополнительными условиями ф(«ь«2) = 0, условиями стационар-
стационарности которого являются уравнения ф] («ь и2) = 0,
*M"i,) = 0. Выберем подпространство, в котором
выполняются, например, условия стационарности
^2 = 0 данного функционала.
Так как известно (см. гл. 2, § 2), что точка ста-
стационарности функционала F на всем пространстве сов-
совпадает с его точкой стационарности, отыскиваемой на
этом подпространстве, то для идентификации точки
стационарности на подпространстве можно исполь-
использовать уравнение dFldu = 0, где производная берется
ня всем пространстве. Раз мы взяли подпространство,
то количество неизвестных уменьшается, соответ-
соответственно уменьшается количество уравнений в выра-
выражении dF/du = 0: на данном подпространстве урав-
уравнение фг = 0 является тождеством.
Рассмотрим, например, полный функционал
•Эпз(в, ф) (табл. 3.3). Отыскивая точку его стационар-
стационарности на подпространстве, состоящем из всех <р и тех
е, которые удовлетворяют уравнению VXeX ^ = 0
и применяя для идентификации точки стационарности
условия дЭ/де = 0, дЗ/дф = 0, получаем уравнение
(a° + VX<PXV)-e- -a = 0; D.6)
второе условие стационарности VXeX^ = 0 на
данном подпространстве выполняется тождественно.
Если для выделения этого подпространства использо-

ЧАСТНЫЕ ФУНКЦИОНАЛЫ 81
вано общее решениеe=-^iyu-\-uV) уравнения
X V = 0, то уравнение F) принимает вид
Эта форма физических зависимостей представляется
интересной для класса задач, в которых решения
статических и геометрических уравнений известны,
а все отличия заключены в физических уравне-
уравнениях A.2).
4.4. Функционалы граничиых условий. Рассмотрим
второй вариант классификации дополнительных ус-
условий, накладываемых на полные функционалы для
перехода к частным (гл. 2 § 2.3.1): разделение их на
уравнения в объеме н на поверхности.
Использование в качестве дополнительных усло-
условий уравнений на поверхности тела не приводит к су-
существенным изменениям в структуре функционала.
Один из поверхностных интегралов обращается
в нуль, а условиями стационарности являются все
уравнения в объеме.
Как с точки зрения структуры, так и в вычисли-
вычислительном аспекте (см. гл. 5) представляют интерес
функционалы граничных условий, которые полу-
получаются из полных, если в список дополнительных ус-
условий включить все уравнения в объеме. Условиями
стационарности полученных таким путем функциона-
функционалов являются граничные условия — статические, или
геометрические, или и те и другие. В табл. 3.5 пред-
представлено шесть наиболее характерных представителей
обширного семейства функционалов граничных ус-
условий.
а) Функционал граничных условий Эт(и,а) в пе-
перемещениях и напряжениях. Может быть выведен из
5*з(и. о) (табл. 3.4), или из Эп2(и,е,а), или из
5п4а(м, е,а) (табл. 3.3) путем наложения всех усло-
условий стационарности в объеме V в качестве допол-
дополнительных условий и исключения (из Эп2 и ЭП4а) пе-
переменной е. Условия стационарности ЭГ—геометри-

82 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
ческие граничные условия в перемещениях и статиче-
статические— в деформациях.
б) Функционал Эп (и) для статических граничных
условий в перемещениях. Этот функционал можно
вывести из 9ni(u,f), Эп2(и,е,а), Эп4а(и,е,а) (табл.3.3)
или из 5*3 (а, и) (табл. 3.4), наложив все уравнения
в объеме V и геометрические граничные условия в пе-
перемещениях на поверхности 5 в качестве дополни-
дополнительных условий и исключив все переменные, кроме и.
Условия стационарности — статические граничные ус-
условия в перемещениях.
в) Функционал 9ri(a) для геометрических (дефор-
(деформационных) граничных условий. Выводится из
5*з (а, и) и других полных функционалов путем на-
наложения в качестве дополнительных условий всех ус-
условий стационарности в объеме V и статических гра-
граничных условий на поверхности 5 и исключения из
функционала и дополнительных условий всех пере-
переменных, кроме а. Условия стационарности ЭГ2 — де-
деформационные граничные условия, выраженные в на-
напряжениях.
г) Функционал граничных условий Э* (у, е)
в функциях напряжений и деформациях. Может быть
получен из полных функционалов, зависящих от пе-
переменных ф и е: 5пз(е,ф) (табл. 3.3),. 3*2(q>, а, е)
(табл. 3.4) и др. Дополнительные условия — уравне-
уравнения неразрывности в деформациях и зависимости
между деформациями и функциями напряжений
(в качестве статических и физических уравнений)
в объеме V. Условия стационарности—статические
граничные условия, выраженные в функциях напря-
напряжений, и деформационные граничные условия.
д) Функционал Э*т1 (ф) для геометрических (де-
(деформационных) граничных условий в функциях на-
напряжений. Может быть выведен из 3*, (ф, еаВ, хаВ)
(табл. 3.4) и других полных функционалов, содержа-
содержащих переменную ф. Дополнительные условия: урав-
уравнения неразрывности и статические граничные усло-
условия в функциях напряжений. Условия стационарно-

§ 41 ЧАСТНЫЕ ФУНКЦИОНАЛЫ 83
сти — деформационные граничные условия в функциях
напряжений.
е) Функционал Э*2 (в) для статических граничных
условий в деформациях. Его можно вывести из
Эп2(и,е,а) и других полных функционалов, содержа-
содержащих переменную е. Дополнительные .условия: урав-
уравнения неразрывности и равновесия в деформациях
в объеме тела и деформационные граничные условия
на его поверхности. Условия стационарности — стати-
статические граничные условия, выраженные в дефор-
деформациях.
Используя функционалы для деформационных
граничных условий, следует иметь в виду ограничения
на поверхностные условия при наличии нескольких
связных участков поверхности с заданными переме-
перемещениями или напряжениями, см. § 1.
4.5. Смешанные функционалы с неполными полями
перемещений и функций напряжений могут быть вы-
выведены из соответствующих полных функционалов
в декартовой и некоторых других системах координат.
В табл. 3.5 представлено два таких функционала:
5,н («у. Фа) и 3„2(из, Фа. ф)> полученных из полных
функционалов ЭП5 и Эа& с использованием общих ре-
решений G) и (8) уравнения равновесия У(-о/з + ^з = О
и системы двух уравнений ViOia-\-Fa = 0 соответ-
соответственно:
°аз = <з ~ V.A- °эт = а°зз + V,4>, + V2*2; D.7)
оп - а°, + V2V2<p - V3a|v а22 = o°n -f V.V.q)-?,*,,
°12 = а°2-У.У2Ф> "l^^ + 'l*!- °23 — °й + V2*2-
Дополнительными условиями к этим функционалам
служат геометрические граничные условия для тех
компонентов перемещений и статические — для тех
компонентов функций напряжений, которые являются
их аргументами. Условия стационарности — уравне-
уравнения смешанного метода теории упругости [3.2] и со-
соответствующие граничные условия.

84 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ (ГЛ. 3
§ 5. Экстремальные свойства полных
и частных функционалов теории упругости
В соответствии с теорией (гл. 2, § 3) здесь приве-
приведено исследование экстремальных свойств для неко-
некоторых характерных функционалов. С этой целью ис-
используются свойства выпуклости (см. Приложение 1)
одних функционалов Лагранжа и Кастильяно и не-
невыпуклости других. Результаты для этих и других
полученных в §§ 2, 3, 4 функционалов представлены
в табл. 3.6.
5.1. Выпуклость различных вариантов функцио-
функционала Лагранжа и их экстремальность. В качестве ха-
характерного примера докажем, что функционал
Эд2(и,е) (табл. 3.1)—выпуклый вниз. На основании
определения выпуклости (Приложение 1) нужно по-
показать, что для любого числа а такого, что 0 <; а ^ 1,
и любых щ, е\, и2, е2 неотрицательна разность
R (щ, еи и2, е2) = аЭл2 (и,, ег) + A — а) Эт (и2, е2) —
— Зл2[аи, + A — а)и2, аех + A — <*)е2]. E.1)
Учитывая, что
[ае, + A — а) е2] • • а • • [ае, + A — а) е2] =
= а% • • а • • е, + 2а A — а) е, • • а • • е2 +
+ A - аJ е2 • • а • • е2, E.2)
эту разность можно преобразовать:
-а- .«, + A—<х)е2- .а- • е2-
- [ае, + A - а) е2] • -а- • [ае, + A - а)е2)} dV =
= SS5a(l-a)[(ei-e2)- -a- • (е, - е2)} dV. E.3)
Так как е--а-е—положительно определенная квад-
квадратичная форма и0^а^1,то/?^0и функционал
•Элг(и, е)— выпуклый вниз.
Аналогично можно доказать, что функционалы
Эл1{и), Злз(е), 5Л5, Эпв (табл. 3.1) выпуклы вниз.
Функционал 5л4 (и, е, а) не выпуклый ни вниз, ни
вверх. Для доказательства этого утверждения доста-

5 б] ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНКЦИОНАЛОВ 85
точно взять любые щ, и2 и —е\ = е2, —tri = сг2 =»
= ei--a. В этом случае разность A) равна
R = S S S
• «1 + A — «) о2 • • е2 —
- [ас, + A - а)о2] • • [ае, + A -а)
= S S S аA ~ а) (<Т' ~ °2) * * (е' ~ «*> dV==
= — 4а (I — а) J J J е, • • а • ¦ е, dV < 0, E.4)
а при «1 = е2, <ii = <i2 = в\- -а разность A) положи-
положительна, R > 0. Дополнительные условия ко всем
функционалам Лагранжа являются линейными урав-
уравнениями и определяют выпуклые подмножества
в пространстве переменных (см. гл. 2, § 3).
Из выпуклости функционалов Эт — Злз, Эд$, Зле
и линейности их дополнительных условий следует тот
хорошо известный факт, что они в точке стационар-
стационарности имеют минимум. Минимальность 3Л4 следует
из того, что он получен из Эщ просто заменой пе-
переменных.
5.2. Выпуклость различных вариантов функцио-
функционала Кастильяно и их экстремальность. Все функцио-
функционалы в табл. 3.2 выпуклы вверх, кроме Зк4, который
не выпуклый ни вверх, ни вниз.
Докажем выпуклость вверх, например, функцио-
функционала Экз(сг). Для этого, как и в § 5.1, вычислим раз-
разность
R — «Зкз (о,) + A — а) Зю (»s) — 5Кз [ас, + A - а) о2] =
= -$$$аA-а)(О1-о2). -Ь- -(щ-oddV. E.5)
Так как а--Ь--а — положительно определенная
квадратичная форма и O^cc^l, то R < 0 при лю-
любых о,, о2, и Зкз — выпуклый верх.
Для доказательства невыпуклости 5К4(ф, о, е) до-
достаточно, как и в § 5.1 для Эщ(и,е,а), проверить,
что R > 0 при —С| = о2 и —е\ = е2 = с,-** и R < 0
при в\ = е2 = oi • • Ь = о2 • • Ь.
Все дополнительные условия к функционалам
(табл. 3.2)—линейные уравнения и опре-

86 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
деляют выпуклые множества в соответствующих
пространствах состояний (см. гл. 2, § 3).
В литературе встречаются два утверждения об
экстремальных свойствах функционала Кастильяно:
о том, что он в точке стационарности имеет максимум
[4.11] и минимум [0.9, 3.7, 4.10]. Оба утверждения,
конечно, правильные, но относятся к разным функ-
функционалам: первое — к Экз (табл. 3.2), а второе —
к (—Зкз)- Здесь функционалами Кастильяно названы
разновидности 5Ki—Зкв, связанные с функционалами
Лагранжа преобразованием Фридрихса и имеющие
то же стационарное значение: max Эк; = ттЭл,-.
Максимальность функционалов ЭК1 — Экз, Зк5, 3К6
в точке стационарности следует из их выпуклости
вверх и линейности дополнительных условий (см. При-
Приложение 1), а максимальность «9К4 — из того, что он
получен из 3К2 заменой переменных.
5.3. Экстремальные свойства полных функциона-
функционалов лагранжевой серии (табл. 3.3). На основании § 3
гл. 2 задачам минимизации выпуклых функционалов
Эл\ — Элз, Эл5, Элб (табл. 3.1) соответствуют задачи
отыскания седловых точек (т. е. одновременно мини-
макса и максимина) полных функционалов 3ai — Эп3,
ЭП5, 5П6 (табл. 3.3) (см. табл. 3.6). Невыпуклому
функционалу Эл4 соответствует задача отыскания ми-
нимакса, но не максимина полного функционала ЭП4
(см. § 3.26 гл. 2). Функционал Эп4а получен из Эп4
путем исключения множителей Лагранжа. Для опре-
определения его экстремальных свойств необходимо до-
дополнительное исследование (см. гл. 2, § 3.3), которое
показывает, что этот функционал не имеет ни седло-
вой точки, ни минимакса, ни максимина. Действи-
Действительно, при каждом фиксированном наборе части пе-
переменных он линейно зависит от остальных перемен-
переменных и, следовательно, принимает все значения от
—оо до +оо, т. е. не имеет ни конечного максимума,
ни конечного минимума.
5.4. Экстремальные свойства полных функционалов
кастильяновой серии (табл. 3.4). Полные функционалы
э*п\ — 5пз- 5п5, 5пб (табл- 3-4)- выведенные с по-
помощью множителей Лагранжа из выпуклых функ-

§ 5] ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНКЦИОНАЛОВ 87
ционалов Кастильяно ЭК1 — Зкз, ЭКь, 3К6 на основа-
основании § 3 гл. 2, имеют в точке стационарности одновре-
одновременно минимакс и максимин, т. е. седловую точку
(см. табл. 3.6). Функционал Э*м, полученный из не-
невыпуклого варианта функционала Кастильяно 3К4,
имеет в точке стационарности максимин, но не мини-
минимакс, что соответствует § 3 гл. 2. Дальнейшее преоб-
преобразование 3*4 приводит к полному функционалу 3*4а,
вовсе не имеющему экстремумов (сравните с 3П4а.
§ 5.3).
5.5. Экстремальные свойства частных функциона-
функционалов (табл. 3.5). Если известны экстремальные свой-
свойства полных функционалов, то можно во многих слу-
случаях выявить свойства полученных из них частных
функционалов с помощью гл. 2, § 3.
а) Функционал граничных условий ЭГ(и,а)
(табл. 3.5). С одной стороны, его проще всего полу-
получить из полного функционала Рейсснера Э*, (о, и)
(табл. 3.4), наложив все условия стационарности
в объеме V в качестве дополнительных условий. Так
как уравнение дЭ*п3/ди = 0 не содержит неизвестных
и, то на основании гл. 2 § З.Зв можно сделать вывод,
что ЭГ(и, а) имеет в точке стационарности max min.
о и
С другой стороны, можно вывести Эг из функцио-
функционала Ху — Вашицу (табл. 3.3), также наложив все
условия стационарности в объеме V в качестве до-
дополнительных условий. Уравнение дЭп2/да = 0 не со-
содержит неизвестных а, и поэтому на основании гл. 2
§ З.Зв функционал ЭГ имеет min max.
U О
Таким образом, точка стационарности функцио-
функционала граничных условий Э. Рейсснера Эг(и,а) есть
его седловая точка.
б) Функционал для статических граничных усло-
условий Эг\(и) имеет в точке стационарности минимум,
так как его можно вывести из функционала Лагранжа
Эл\, имеющего минимум.
в) Функционал для статических граничных усло-
условий Э,2(а) в точке стационарности имеет максимум,
так как промежуточным звеном при выводе его из

88 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
Э*3(о, и) (табл. 3.4) служит функционал Кастильяно
Зкз(а).
г) Функционал 5* (ф, е), условиями стационарно-
стационарности которого являются статические граничные усло-
условия в функциях напряжений и деформационные гра-
граничные условия, в некотором смысле аналогичен
функционалу граничных условий Э. Рейсснера
Эт(и, а). Для доказательства того, что 5* имеет сед-
ловую точку, нужно, по аналогии с § 5.5а, получить
его из Эп3(е,ф) (табл. 3.3) и из 5*2(ф, а, е) (табл. 3.4).
д) Промежуточным звеном при получении функ-
функционала для статических граничных условий в функ-
функциях напряжений 5*, (ф) из 5*, (ф, еар, каР) (табл. 3.4)
служит функционал Кастильяно 5К1(ф), а при по-
получении функционала для деформационных гранич-
граничных условий 5*2(е) из 5п3(е, ф) (табл. 3.3)—функ-
3.3)—функционал Лагранжа 5лз(е). Поэтому 5*, (ф) в точке
стационарности имеет максимум, а 5*2 (е)— минимум
е) Частный функционал ЭфГ(е,а) получен из
ЭП2(и,е,а) (табл. 3.3) при использовании в качестве
дополнительных условий уравнений, не содержащих
переменную и, и части уравнений дЭп21ди = 0, не со-
содержащих переменную а. На основании гл. 2, § З.Зв
ЭфТ(е, а) имеет седловую точку.
Точно так же можно проверить, что частный функ-
функционал Эфе (о, е) имеет седловую точку.
ж) Функционал для геометрических и статических
уравнений ЭГС(и,е,о) имеет седловую точку:
•9ГС—> minmax = max min. E.6)
и е, о е, а и
Для доказательства можно использовать уже изве-
известное экстремальное свойство функционала Рейсснера
5*з (о, и). Функционал Эгс можно получить из Э*3,
введя новую переменную и и дополнительное усло-
условие а — е--а=0. Так как это уравнение связывает
новую переменную е лишь с переменной а, по кото-
которой 5*3 имеет максимум, то имеет место E.6).

§ 61 РАЗРЫВНЫЕ СМЕЩЕНИЯ И НАПРЯЖЕНИЯ 89
Аналогично, используя уже известное экстремаль-
экстремальное свойство полного функционала Эп3(е,а), можно
доказать, что
з) функционал Эсг(ф, а, е) имеет седловую точку.
и) Функционалы для физических уравнений Эф\
и 5ф2 имеют седловые точки в соответствии с гл. 2,
§ З.Зв, так как дополнительные условия к каждому
из них можно разделить на две части, одна из кото-
которых содержит только переменную е, а другая —
только <т-
§ 6. Вариационные принципы и экстремальные
свойства функционалов теории упругости
при разрывных перемещениях, деформациях,
напряжениях и функциях напряжений
В контактных задачах, а также при численном ре-
решении задач теории упругости, в частности при ис-
использовании метода Ритца и метода конечных элемен-
элементов, иногда возникает необходимость рассматривать
в качестве варьируемых переменных разрывные поля
параметров напряженно-деформированного состояния.
Теория Куранта —Гильберта позволяет построить
для этого случая систему полных и частных функцио-
функционалов и исследовать их экстремальные свойства.
6.1. Определение разрывов. Следуя [0.12], предпо-
предположим, что область V разделена на конечное число
смежных подобластей, в каждой из которых поля пе-
перемещений, деформаций и напряжений обладают
свойствами непрерывности и дифференцируемости,
принятыми в основных уравнениях теории упругости.
Эти смежные области регулярности разделены по-
поверхностями разрывов, на которых некоторые ком-
компоненты усилий и дополнительные компоненты пере-
перемещений изменяются не обязательно непрерывным
образом. Будем использовать термины «статические»
и «кинематические», чтобы различать разрывы соот-
соответственно в компонентах усилий и перемещений.
Для определения разрыва тензора напряжений а
в точке Р на поверхности разрыва D введен единич-
единичный вектор нормали п к поверхности D в точке Р.

90 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
Таким образом, указывается направление внешней
нормали для одной из смежных областей регулярности
и направление внутренней нормали для другой обла-
области. Скачок {<?} параметра поля q в точке Р опре-
определим как разность значений q во второй и первой
областях (точнее, как предел разности значений q
в точках второй и первой областей при стремлении
этих точек к Р).
Ниже будут часто встречаться разрывы скаляр-
скалярных величин паи. Обозначим
{„. а ¦ и} = {п • а}' • и + п ¦ а • {и}", F.1)
где штрих и двойной штрих соответственно указы-
указывают, что скалярное умножение вектора усилий па
на вектор перемещений и выполняется в подпростран-
подпространстве трехмерного пространства, в котором задан ста-
статический или кинематический разрыв.
6.2. Различные варианты функционала Лагранжа
с разрывными полями. Говоря о функционале Лагран-
Лагранжа 3ju(u), обычно требуют непрерывности переме-
перемещений и вместе со своими частными производными,
т. е. вместе с деформациями и напряжениями. Эти
требования непрерывности можно ослабить. А именно,
напряжения ог[е(и)] могут быть лишь кусочно-не-
кусочно-непрерывными; их непрерывность, как и все условия
равновесия, является условием стационарности функ-
функционала Зл1 («)•
Действительно, пусть тензор напряжений а[е(и)]
может иметь разрывы на поверхности G, которая раз-
разбивает объем V на конечное число частей. Вариация
функционала Лагранжа имеет вид
6(V + uV)F6
F.2)
Чтобы получить условия стационарности, нужно B)
преобразовать с помощью формулы Остроградского
(см. Приложение 2), учитывая, что
о • • 6 у (VH + «V) = V • (о • 6н) — (V • а) ¦ бы.

§ 6] РАЗРЫВНЫЕ СМЕЩЕНИЯ И НАПРЯЖЕНИЯ 91
Так как формула Остроградского применима только
к непрерывной функции а-би, то объем V следует
разбить на подобъемы, в которых тензор а непреры-
непрерывен, выполнить преобразование и сложить получен-
полученные интегралы. В результате B) примет вид
= J J J [- (V • а + F) • бн] dV +
(о • л - Г)' • бн dS + ^ {а • п}' • бн dO. F.3)
Равенство C) показывает, что одно из условий ста-
стационарности функционала Эл\ — равенство нулю ста-
статических разрывов {an}', т. е. непрерывность тен-
тензора а.
Это справедливо и для остальных разновидностей
функционала Лагранжа (табл. 3.1): отсутствие ста-
статических разрывов является их условием стацио-
стационарности.
Так как в качестве G можно взять любую поверх-
поверхность, разделяющую объем V на конечное число час-
частей, то можно рассматривать, вообще говоря, любые
кусочно-непрерывные поля напряжений. Мы ограни-
ограничимся рассмотрением полей, которые могут иметь раз-
разрывы лишь на заданной поверхности D.
При необходимости рассматривать разрывные
поля перемещений принцип минимума потенциальной
энергии можно сформулировать следующим образом.
Рассмотрим поля перемещений, непрерывные
и дифференцируемые в каждой области регулярности
и, возможно, имеющие разрывы на поверхности D.
Чтобы среди них найти поле перемещений, соответ-
соответствующее состоянию равновесия упругого тела, нужно
выполнить следующие действия: а) выбрать из за-
заданного множества кусочно-непрерывных полей пе-
перемещений непрерывные, т. е. удовлетворяющие усло-
условию A.5) и уравнению
{н}" = 0 на D. F.4)
Другими словами, область V разделяется на подобла-
подобласти с разрывами, которые затем ликвидируются с по-
помощью D); б) из всех полученных непрерывных по-

92 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
лей выбрать такое, которое доставляет минимум
функционалу Зл| (и) (табл. 3.1). Нетрудно проверить,
что условие D) определяет выпуклое множество.
Таким образом, если при отыскании состояния
равновесия рассматриваются кусочно-непрерывные
поля перемещений (область поиска расширена), то со-
состояние равновесия характеризуется системой усло-
условий 3Л1-»-тт, A.5), D). Действия а) и б) отражают
ход решения задачи теории упругости, например, ме-
методом конечных элементов.
Само по себе равенство D) ничего не добавляет
к условиям непрерывности, которые участвуют в фор-
формулировке вариационной задачи для Эщ (табл. 3.1)
и не помогает при решении задачи, если решение вы-
выполняется с помощью принципа минимума потен-
потенциальной энергии. Однако это равенство позволяет
переходить к другим функционалам, использование
которых может упростить решение.
Как и в § 2, с помощью замены переменных
е(и)=е, а(е) = а и частного решения V-a° + /;i = 0
уравнения равновесия A.6) можно получить ряд дру-
других разновидностей функционала Лагранжа для раз-
разрывных полей перемещений и деформаций; они пред-
представлены в табл. 3.7. Одно из условий стационарно-
стационарности для всех этих функционалов — непрерывность на-
напряжений на D.
Так как функционал Элз зависит только от де-
деформаций и не зависит от перемещений, то условия
непрерывности перемещений на поверхности D заме-
заменены условиями непрерывности деформаций; для не-
непрерывности перемещений необходимо, чтобы танген-
тангенциальные и изгибные деформации поверхности D как
границы одной области регулярности были равны со-
соответствующим деформациям D как границы смеж-
смежной области регулярности.
6.3. Полные функционалы лагранжевой серии с
разрывными полями. Вводя в функционал Лагранжа
•Элг— Эпв (табл. 3.7) с множителями Лагранжа все
дополнительные условия, в том числе и условие от-
отсутствия кинематических разрывов на поверхности D,

§ 6] РАЗРЫВНЫЕ СМЕЩЕНИЯ И НАПРЯЖЕНИЯ 93
можно получить полные функционалы (табл. 3.9),
аналогичные табл. 3.3. Их условием стационарности,
кроме обычных уравнений теории упругости, приве-
приведенных в табл. 3.3, служат условия отсутствия стати-
статических и кинематических разрывов на D. Разрывы
тензора функций напряжений ф и его нормальных
производных также будем называть" статическими
разрывами.
6.4. Различные варианты функционала Кастильяио
с разрывными полями. Часть условий стационарно-
стационарности— физические и статические уравнения, в том
числе и условия отсутствия статических разрывов на
D, — можно наложить в качестве дополнительных ус-
условий и, исключив кинематические переменные, пе-
перейти к различным вариантам . функционала Кас-
Кастильяно (табл. 3.8). Их условия стационарности — все
геометрические уравнения, в том числе и условия
отсутствия кинематических разрывов на D.
6.5. Полные функционалы кастильяиовой серии с
разрывными полями. Из различных вариантов функ-
функционалов Кастильяно можно получить полные функ-
функционалы, аналогичные табл. 3.4, условия стационар-
стационарности которых включают отсутствие статических
и кинематических разрывов на поверхности D и кото-
которые здесь не приводятся.
6.6. Частные функционалы для разрывных полей
отличаются от функционалов, представленных в
табл. 3.5, наличием интегралов по поверхности и до-
дополнительных условий на этой поверхности. Они мо-
могут быть получены из соответствующих полных функ-
функционалов и в данной книге не приводятся.
6.7. Экстремальные свойства функционалов для
разрывных полей исследуются точно так же, как в §6.
Функционалы Зл1 — Злз, Зда, Зле — выпуклые вниз,
3Ki - ЭЬ, Э15, 3?6 - выпуклые вверх, 3Л4 и 3К4 -
иевыпуклые.
Все функционалы Лагранжа в точке стационар-
стационарности имеют минимум, функционалы Кастильяно —
максимум. Экстремальные свойства всех функциона-
функционалов с разрывными полями перемещений, деформаций,

94 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ. 3
напряжений и функций напряжений такие же, как
овойства функционалов с непрерывными полями, свод-
сводка которых дана в табл. 3.6.
Замечание. Некоторые вариационные прин-
принципы теории упругости при разрывных полях переме-
перемещений, деформаций и напряжений впервые были рас-
рассмотрены без исследования экстремальных свойств
в [0.12]. Функционалы с разрывными функциями
напряжений и экстремальные свойства получены ав-
авторами.
§ 7. Развернутая форма записи некоторых
функционалов в различных системах координат
В данном параграфе приведены характеристики некоторых
наиболее употребительных систем координат (метрические тен-
тензоры, символы Кристоффеля) и рассмотрен переход от тензорной
формы записи функционалов к развернутой. Приведен ряд пол-
полных н частных функционалов в развернутой форме в криволи-
криволинейных координатах.
7.1. Различные системы координат, их метрические тензоры и
символы Кристоффеля.
7.1.1. Ортогональные (прямоугольные) координаты различно-
различного вида используются чаще всего. В любых ортогональных коор-
координатах трн компонента метрического тензора равны нулю:
gn = 0 прн 1 ф /. Остальные трн компонента обычно заменяют
тремя величинами Я; — параметрами Ляме — по формулам
Н\ = g{l (не суммировать). G.!)
Другие формулы для вычисления параметров Ляме:
да1) \да1) \да'
где х, у, г — декартовы координаты;
H2i = elel (не суммировать). G.3)
Параметры Ляме имеют ясный геометрический смысл: онн явля-
являются масштабными факторами, связывающими приращения длин
дуг координатных линий с приращениями соответствующих им
криволинейных координат:
ds{ = H{ da1. G.4)
В табл. 3.10 приведены компоненты метрического тензора и сим-
символы Кристоффеля для некоторых наиболее распространенных

РАЗВЕРНУТАЯ ФОРМА ЗАПИСИ ФУНКЦИОНАЛОВ 95
ортогональных систем координат. Эти величины дают возмож-
возможность легко записать все формулы из §§ 2—6 в развернутой
форме.
В некоторых системах ортогональных координат часть пара-
параметров Ляме — константы; поэтому часть символов Кристоффеля
обращается в нуль, и слагаемые, содержащие производные, еще
более упрощаются Например, в цилиндрической системе коор-
координат tfi = Н3 = I, Нг = R, а в сферической — Н\ = R,
ff tfie Я 1
Наиболее простой вид все функционалы и их дополнительные
и естественные условия имеют в прямоугольной декартовой си-
системе координат, в которой все параметры Ляме равны единице,
а все символы Кристоффеля равны нулю.
7.1.2. Прямолинейные косоугольные (аффинные) координаты
(табл. 3.10)— важный частный вид координатной системы. Эти
координаты удобны, например, прн расчете кристаллов и других
тел, имеющих форму наклонного параллелепипеда, призмы или
пирамиды.
7.1.3. Особо должна быть рассмотрена система координат,
нормально связанных с поверхностью S. Такие координаты ис-
используются в теории оболочек. В этих координатах компоненты
метрического и дискрнминантного тензоров н символы Крнстоф-
феля выражаются через коэффициенты первой и второй квадра-
квадратичных форм поверхности S (табл. ЗЛО).
7.2 Развернутая форма записи функционалов в криволиней-
криволинейных ортогональных координатах. Чтобы представить функциона-
функционалы в развернутой форме, нужно использовать формулы и пра-
правила из Приложения 2. Определенную трудность представляет
развертывание выражений, содержащих производные.
7.2.1. Развернутая форма записи выражений вида (V-a-y-F),
Vu + uV, VX eXV, e а использована в табл. 3.11—3.13. Ниже
подробно описан переход к развернутой форме первого выраже-
выражения н сокращенно — для остальных.
а) Преобразуем запись выражения
В (а) = V • or + F, G.5)
которое в индексной форме имеет вид
В> (a) =Vpa"' + F>; G.6)
1) придадим свободному индексу / значение I: В1 (а) =
2) развернем сумму по р: В1 (а) = Via" -f ^or21 + 73а31 + f1;
3) выполним ковариантиое дифференцирование:
S1 (о) = а]\ + Г>" + Г>" -f a2I2 + г»аа" +

96 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ [ГЛ 3
4) раскроем суммирование по р и подставим выражения
символов Кристоффеля:
ЙГ *"•3aS1" W^g33-ia33+
5, 6) выразим компоненты метрического тензора gu через
параметры Ляме Я2; выразим a'7, F1 через физические компонен-
компоненты <Т(г/>, f(i) по формулам Приложения 2; приведем подобные
члены:
BW (a) = Я,Я2Я3 [(^2^A1)), 1 + (Я1ЯзаA2)), г +
(!3)). 3 + Я3Я1, 2аA2) + Я2Я1, 3ffA3) ~ Я3Я2, 1аB2) ~
~ ^2^3, 1аC3) + РЩН\Н2Иъ\ G>7)
Выражение в квадратных скобках совпадает с левой частью
уравнения равновесия в криволинейных ортогональных координа-
координатах [II.9]. Аналогично получаются 5<2)(сг) и В(з;(а).
В дальнейшем, чтобы не загромождать запись, скобки при
индексах в развернутых выражениях, где это ие вызывает дву-
двусмысленности, будем опускать.
б) Рассмотрим выражение
К(е, «) = e-y(V« + «V). G.8)
В индексной форме:
Выполнение коаариантного дифференцирования и развертывание
сумм даег
Ки (е, и) = ец - 1 («л i + ии f) + Г}/В, + Г^и, + ^и,.
Придавая I, } значения 1, I и 1, 2, после замены компонентов
метрического тензора gy па параметры Ляме Н\ и компонентов

§ 7] РАЗВЕРНУТАЯ ФОРМА ЗАПИСИ ФУНКЦИОНАЛОВ 97
/, «,- через физические составляющие ец», «(i> получим
—
К, i (е, и) = й11 — — и, , + н н Ни 2и2 + н И Я,, 3«3;
Скобки у индексов физических компонентов опущены. Приравни-
Приравнивая Ki<(e,u) и Кч(е,и) нулю, можно получить выражения для
компонентов деформаций ?<н) и ?<i2). Точно так же для других
значений индексов i и /.
в) Поступая аналогичным образом, можно получить развер-
развернутую форму записи выражений
G.11)
или
Cnk (е) = elmnel!k4mV\e/г G.12)
R силу симметрии различными будут только шесть выражений.
Например, при п = 1, k = 2 получим до выполнения ковариант-
ного дифференцирования
С12 (в) = 727,е3з - Vs (V,e23 + V2e3i - Vse,*).
В прямоугольных декартовых координатах, когда ковариаитиые и
обычные производные совпадают, получается
Cij (е) = езз, и — («23, i + ?31,2 — ?12, з), з- G.13)
Приравняв С12(е) нулю, приходим к одному из известных урав-
уравнений совместности деформаций.
г) Легко получить развернутую форму записи дли
ф(о, е) = а — е- -о. G.14)
В индексной форме
ф*/(о, e) = ai] -epqaP. G.15)
Переход к физическим компонентам и раскрытие сумм дает
). G.16)
Придавая «, / значения 1, 2, 3 и приравнивая Фу(о, е) нулю, по-
получим уравнения закона Гука. Аналогичным образом можно по-
лучигь обратные зависимости е через а, рассмотрев
Ф(е, (г) = е — о- Ь. G.17)
7.2.2. Развернутая форма записи некоторых функционалов.
На примере функционала Рейссиера ЭПЗ (о, и) (табл. 3.4) пока-
покажем, как преобразуются функционалы. Преобразование выраже-
выражений, содержащих E) или F), ясно из вышерассмотреииого
примера. В остальных членах, содержащихся в объемном и
4 Н, П, Абовский в др,

98 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИЙ УПРУГОСТИ [ГЛ. 4
поверхностных интегралах, нужно только перейти к физическим
компонентам (Приложение 2). Например,
В результате приходим к развернутой форме функционала
(табл. 3.11).
В табл. 3.12 представлен полный функционал Эща (и, е, о)
в развернутой форме. Из него можно получить частные функцио-
функционалы, используя преобразования Куранта — Гильберта, не прибе-
прибегая к развертыванию тензорной записи соответствующих частных
функционалов.
В табл. 3.13 приведев функционал ЭпАа (<р. о, е}, в котором
не выполнено ковариантное дифференцирование. Чтобы получить
окончательную развернутую форму, которая представляет в об-
общем случае криволинейных ортогональных координат громоздкое
выражение, необходимо воспользоваться формулами дифференци-
дифференцирования (Приложение 2) и выразить ф</ через физические компо-
компоненты.
Некоторые другие функционалы в развернутой форме при-
приведены в [0.2].

Глава 4
ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ
УПРУГИХ ТОНКИХ НЕОДНОРОДНЫХ
АНИЗОТРОПНЫХ ОБОЛОЧЕК
ПЕРЕМЕННОЙ ТОЛЩИНЫ
В данной главе рассматриваются полные и част-
частные функционалы, участвующие в формулировке ва-
вариационных принципов линейной технической теории
тонких оболочек. Соответствующие общие и частные
вариационные принципы в различных пространствах
состояний могут быть сформулированы на основе об-
общих определений (гл. 2, § 1).
Существует несколько эквивалентных разновидно-
разновидностей теории тонких оболочек, отличающихся выбором
деформаций и усилий. В этой книге использован ва-
вариант [4.12], который признан авторами работы
[4.12] «наилучшим»; он обладает статико-геометри-
ческой аналогией, тензорной формой и построен на
основе симметричных деформаций, усилий и момен-
моментов. О связи этого варианта теории с другими, на-
например [П. 10], [4.11], см. §§ 1 и 8. Функционалы,
рассматриваемые в данной главе, помещены
в табл. 4.1—4.10 в конце книги.
§ 1. Вводные замечания
1.1. Система координат. Рассматриваемая тонкая иепологая
анизотропная оболочка переменной толщины имеет срединную (а
точнее, базисную) поверхность S с нормалью я, ограниченную
контуром С. Конт>р С имеет единичный вектор касательной t и
единичный вектор тангенциальной нормали v (т. е. нормали, рас-
расположенной в касательной плоскости к поверхности S), рис. 4.1.
Поверхность S может быть определена векторным параметриче-
параметрическим уравнением
r = r(aI, a2),
где г—радиус-вектор точки, лежащей на S, и характеризуется
коэффициентами aYa первой квадратичной формы и 6Ув вто-
второй квадратичной формы (у, 6=1,2); через cvj обозначены
4*

100
ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
const
компоненты дискриминантного тензора первой квадратичной фор-
формы (см. Приложение 2).
Уравнения теории оболочек записывают в специальной кри-
криволинейной системе координат, нормально связанной с поверх-
поверхностью S (pfic. 4.1). В ней радиус-вектор точки равен
R = г (а1, а2) + гп.
Векторы локального базиса в точках, лежащих на S, равны:
d = ог/да*, <?2 = drjda2, вз = п. При этом используют понятия
поверхностного вектора и
тензора. Компоненты по-
поверхностных векторов имеют
индексы, обозначенные гре-
греческими буквами и прини-
принимающие значения 1, 2. Сим-
Символ Va в данной главе обо-
обозначает ковариантную про-
производную на поверхности от
компонентов поверхностного
тензора (см. Приложение 2).
Оболочка занимает часть
трехмерного пространства,
ограниченную двумя поверх-
поверхностями S, и S2, точки ко-
которых имеют координаты
2 = Л,(а1 а2) и z = /i2(aI,
a2), h2 > fti, и (если обо-
оболочка не замкнутая) третьей
поверхностью, образованной движением нормали гп вдоль кон-
контура С. Величина ft = ft2 — ft, есть толщина оболочки.
1.2. Перемещения и деформации в оболочке. Геометрические
уравнения. Перемещения точек базисной поверхности S характе-
характеризуются вектором
и = иаеа + wn, A.1)
где иа — компоненты поверхностного вектора тангенциальных пе-
перемещений, а w — перемещение по нормали к S (прогиб).
Гипотезы Кирхгофа — Лява позволяют приближенно выра-
выразить перемещения о, и деформации ец (i, j = 1, 2, 3) в оболочке
как трехмерном теле через перемещения и деформации базисной
поверхности S. Гипотеза о прямолинейном нормальном элементе
(гипотеза прямых нормалей) сводится к равенствам
»а = «а + **а. »з = W, A.2)
где ©а — углы поворота поверхности S,
*>а - - (?oe + 6a»6> A-3)
= 0, по-
Рис. 4.1. Криволинейные координа-
координаты, нормально связанные с базис-
базисной поверхностью оболочки.
Гипотеза о ненадавливании волокон, т. е. равенство а33
зволиет выразить деформацию езз через еа[:
A.4)

§ 1]
ВВОДНЫЕ ЗАМЕЧАНИЯ
101
Деформации eat можно выразить через иа, w, вычислив
компоненты трехмерного метрического тензора g { в недеформи-
рованном состоянии и gai в деформированнодм с учетом B) и
сохранив в выражении eai=giii — gai лишь слагаемые, линей-
линейные относительно перемещений:
р ^ 0 о о <yft JU
где е и ($ — симметричные поверхностные тензоры соответ-
соответственно тангенциальных и изгибных деформаций базисной по-
поверхности, зависящие от ее перемещений:
V«> (V« + V)V (L6)
Величины е , Ва имеют ясный геометрический смысл: е
трехмерного тензора деформации
совпадают с компонентами е
в точках поверхности
S, а
Pag = Ьа s — bai представляют
собой разность кривизны обо-
оболочки до и после деформиро-
деформирования. Однако эти деформации
имеют недостаток: между ними
и соответствующими им (в
энергетическом смысле) компо-
компонентами усилий S и момен.
тов //а(:!нет статико-геометриче-
ской аналогии [4.12] (см. § 7).
Чтобы ее обеспечить, для
запнсн уравнений теории обо-
оболочек используют другие де-
деформации, связанные с е, р ли-
линейными зависимостями, и соот-
соответствующие им усилия. Например, в [4.11] наряду с $ рассмат-
рассматривается несимметричный теизор изгибиой деформации AИС:
Рнс. 4.2. Усилия и моменты в
оболочке.
и несимметричный тензор усилий 7\,с (рис. 4.2). Несимметрич-
Несимметричность цкс и Тис приводит к тому, что они, кроме дифференциальных

102 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
уравнений неразрывности и равновесия, должны быть подчинены
условиям
&бЧа) = 0. са& (Tfc + ftgAfV») = 0, A.9)
выражающим симметрию трехмерных тензоров деформаций и на-
напряжений.
В дайной книге в качестве меры изгибной деформации ис-
используется симметричный тензор [4.12]
*а* = \ (Kl + Uga) = " Pali + J №V» + bM' (L1°>
Деформациям е, ц. соответствуют симметричные тензоры усилий
и моментов
Г5 (Tf + Г»»)
J (Tfc + Г), М = | (Mfc + M%). A.11)
Из F), G), A0) следуют выражения ц. через перемещения
Пае («) = J (V>U + ?а) ~ Т F«VP"V + ftFa«V) +
+
Шесть компонентов деформации: en, ei2 = 82i, е2з и ц.,,,
(Ai2 = Ц21, Ц22 связаны между собой уравнениями неразрывности
базисной поверхности
?(е,ц) = 0, A.13)
где
8, И)
L (8, p) = - VJ6 (с<*с«\^ + Kb 0aYc64s>
Геометрические граничные условия теории оболочек, согла-
согласующиеся с гипотезами B), D), имеют вид
(и-«*)" = 0, (va0a - О*)" = 0. A.15)
Здесь, как и в гл. 3, штрих и двойной штрих соответственно
означают, что равенство относится к тем компонентам усилий
(перемещений), для которых заданы статические или геометриче-
геометрические граничные условия; звездочкой обозначены заданные на кон-
контуре величины.

1] ВВОДНЫЕ ЗАМЕЧАНИЯ 103
Соотношения F), A2), A5), а также A3) являются геомет-
геометрическими уравнениями теории оболочек в области S и на кон-
контуре С.
1.3. Усилия и моменты, физические зависимости. Энергетиче-
Энергетические компоненты усилий и моментов, соответствующие выбран-
выбранным компонентам деформаций (т.е. работающие на этих дефор-
деформациях), удобнее всего ввести вариационным путем на основе
функционала Лагранжа.
После того, как перемещения и деформации в оболочке как
трехмерном теле выражены через перемещения и деформации и,
в, \i ее базисной поверхности, а геометрические граничные усло-
условия для v—через контурные условия для u, ftv. трехмерный
функционал Лагранжа для оболочки становится квадратичной
функцией от u, e, \i:
ft,
. .¦ 1 ,p 1
ЭЛ2 («, е, ц) = J J J { -i [еар + 2 ( Ца6 - 1 6|
S А,
X [eve + г (
- Fa (ыа + zba) - F3w J д/-|-
ft.
J [fa («a + Zba) + ГМ д/4 rf2 rfC, A.16)
C" ft,
Т. е. функционалом Лагранжа для двумерной краевой задачи
расчета оболочки, Дополнительными условиями к нему являются
геометрические уравнения F), A2), A5).
Полученная двумерная вариационная задача отличаетси от
трехмерной тем, что минимум функционала отыскивается не по
всем трехмерным полям перемещений и деформаций, а только по
тем, которые совместимы с гипотезами Кирхгофа — Лява.
Квадратичная часть функционала A6) представляет собой
интеграл от квадратичной формы П(е, ц), зависящей от шести
Деформаций еор = 8ра, цар = цр0, которые можно считать об-
обобщенными перемещениями.
Квадратичная форма П имеет 21 различный коэффициент,
которые однозначно определяются выражением A6); ее можно

104 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
записать в виде
6
П(е, Ц)=2" Y, dPixPx4 (dPi = dqp)> A-17)
P. 7=1
где (xi, X2, хз, xt, x>,, j:e) = (en, ?22, e,2, Цн, Ц22, Щг). Для обес-
обеспечения тензорной формы записи в качестве аргументов П рас-
рассматривают восемь переменных еар, Aар, связанных двумя усло-
условиями симметрии 8i2 = 821, р.12 = p.2i| при этом
П (е, ») = ±(8^\ьеу6 + Ча/У
В A8), вообще говоря, 48 различных коэффициентов g" , они
связаны с dpq из A7) 21 уравнением, которые можно получить,
если в A7) и A8) приравнять коэффициенты при одинаковых
произведениях деформаций с учетом симметрии г, \i. Таким обра-
образом, коэффициенты gf^y определяются выражением A8) не-
неоднозначно. Целесообразно их выбрать симметричными, положив
VSY6= y66v 1212 2121 П22 2211.
f J (y ф б. . = 1( 2> 3. . = u 3) A 19)
В A9) содержится 27 равенств, которые вместе с 21 уравнением,
указанными выше, составляют систему из 48 уравнений, одно-
однозначно определяющих 48 коэффициентов в A8), среди которых
не более 21 различных.
Обобщенные усилия Т и моменты Ма® можно ввести
формально как производные от A6) по обобщенным перемеще-
перемещениям eag, (xag; условия A9) обеспечивают симметрию тензоров
Т, М:
Га6 (8, ц) = Т&а = <ЗЭЛ2/«Зеа3 = g^\& + gfy\6,
Ма0 (е, ц) = М*а = дЭт/дЦа& = gf У\& + (L20)
Равенства B0) являются физическими зависимостями теории обо-
оболочек и позволяют записать функционал A6) в форме, пред-
представленной в табл. 4.1. Физические константы g™ v совпадают
с коэффициентами квадратичной формы A8). Из A6) следует,
что они зависят от кривизн 6ар. Однако обычно их упрощают,
пренебрегая (в соответствии с точностью уравнений теории обо-
оболочек) величинами такого же порядка малости, как hba^, по
сравнению с единицей в E). Выражения для упрощенных таким
образом физических коэффициентов не содержат кривизн Ьа$;
из A6)—A9) следует:
h,
г1-\ (a«M _ aa033a33V6/a3333) ^ A 2{)

5 И
ВВОДНЫЕ ЗАМЕЧАНИЯ
105
Исходя из трехмерного функционала Лаграпжа и учитывая,
что е, ц ие зависят от г, можно A6) записать в виде:
9т (и, е, ц) =
dS+
A.22)
Отсюда следует физический смысл величин Т, М как1 интеграль-
интегральных характеристик напряженного состояния оболочки и тот факт,
что введенные, согласно B0), Т, М
совпадают с построенными в [4.12]
на основе A1).
Физические зависимости B0) мо-
могут быть представлены в обратной
форме:
Рис. 4.З. Усилия и момеит
на контуре оболочки.
A.24)
A.23)
1.4. Статические уравнения. Сим-
Симметричные усилия и моменты B0)
должны удовлетворять уравнениям
равновесия [4.12], которые можно
вывести, например, из функционала Лагранжа A6) в качестве
условий стационарности:
B(Af, Т)=0,
где
В (М, Т) = Ва (М, Т)еа + В (М. Т) п,
Ва (Af, Т) = 70Г6а - ЬрьМт - Vu (б^Л1бе - 6^Ва) + qa, A.25)
В (Af, Т) = VaV6M6a + ЬаAТа6 + q,
q — qaea + ?я — вектор нагрузки на поверхности S. Кроме того
Т и М должны удовлетворять статическим граничным усло-
условиям (рис. 4.3)
[<?(Af, Г) — QJ' == 0,
(Af) - Лу •' = 0 на С, A.26)

106 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
где
Q = Qaea + Qn, A.27)
Qa (М, Т) = v0 [гВа +1 {Ь*№а - U°M0V)] - t4%v6tyM&4,
Q (Af) = vavpM0a + /а7а {tyvuMy% (J.28)
Mvv (M)
Здесь штрих обозначает, что равенства B6) относятся к тем
компонентам усилий и моментов, для которых заданы статиче-
статические граничные условия.
Уравнения равновесия B4) имеют параметрическое общее
решение
A.29)
F^*+ 6«7А) + т Fv
Т
где параметры i|)a, <p — компоненты вектора функций напряжений
Ч> = Фа*0 + <рп, A.30)
1\й — «углы напряжений»
Af°^, Г™^ — какое-либо частное решение неоднородных уравиений
равновесия.
Соотношения B4) и B6), а также B9), являются статиче-
статическими уравнениями теории оболочек в области S и на контуре С.
1.5. О взаимосвязи различных форм геометрических и стати-
статических граничных условий. Геометрические граничные условия во
многих случаях могут быть поставлены в деформациях. В част-
частности, уравнения A5) могут быть преобразованы к деформа-
деформационным граничным условиям следующим образом.
Производную по контуру от трехмерного вектора перемеще-
перемещений контурных точек можно выразить через тензоры трехмерных
деформаций е и углов поворота и в окрестности данной точки:
A.32)

$ 1] 6ВОДНЫЕ ЗАМЕЧАНИЯ 107
Как известно, три ненулевых компонента кососимметричного теи-
зора й) можно выразить через компоненты вектора углов пово-
поворота Q: й)(/ = e,;*Q*, откуда
t ¦ <о = Л»//ге* = elkit'ulek = e[]kQitlek = Я X t A-33)
На основе гипотезы прямых нормалей компоненты Q в системе
координат, связанной с базисной поверхностью, равны
Qa = cav^ Qn==^c^^ A34)
Вектор /ев системе координат (v, /, n), связанной с контуром,
можно представить в виде
t ¦ е = (tl0ei}) t + (Melf) v + A1п'е{1) п. A.35)
В силу гипотезы прямых нормалей третье слагаемое равно нулю,
а первые два представляют собой деформации базисной поверх-
поверхности
e«-<aAsaB, e,v = /avfieaE. A.36)
Вектор v можно представить в виде v = —я X t, и тогда равен-
равенство C2) с учетом C5) примет внд
Производная по контуру от вектора
dQt__ __ a
dc —*¦ — *¦
где Qt = Q—ely/n. A.37)
т A.38)
представляет собой вектор искривлений граничного элемента, ко-
который с помощью гипотезы прямых нормалей может быть выра-
выражен через деформации базисной поверхности:
С помощью F), A2) нетрудно проверить, что величины ха, х, ett
являются функциями перемещений иа, w и угла поворота
Gv = va0a на контуре С и их производных t'lVa по С:

108 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
Компоненты вектора х вместе с е« составляют набоо деформа-
деформаций контура, которые определяют перемещения и углы поворота
на контуре с точностью до шести констант, определяющих жест-
жесткое смещение. Действительно, интегрируя равенства C8) и C7),
можно по известным х и е» и начальным значениям Ua, (CIi)a
векторов и и Qi в точке А иайти перемещения и углы поворота
в точке В контура:
в
A.41)
А
Деформационные граничные условия имеют вид
[&tt (f) — е^]" = 0, [к (г, \i) — х*]" = 0 на С. A.42)
Уравнения D2) являются условиями стационарности функцио-
функционала Кастильяно в функциях напряжений [5.3], см. § 2.2. Заме-
Заметим, что деформационные граничные условия получены в [4.11]
невариационным путем в координатах (v, t, n) и выражены через
компоненты деформаций е, (х"с; их можно преобразовать к D2),
используя (8) и правило преобразования компонентов векторов
при замене координат (см. Приложение 2).
Статические граничные условия в функциях напряжений
(* — Ч»Т = 0, (vaTH — т)У = 0 A.43)
могут быть поставлены взамен граничных условий в усилиях
B6), например в тех случаях, когда B6) заданы на одной связ-
связной части контура С. Для этого граничные усилия B8) должны
быть выражены через граничные значения функций напряжений
\|>а, ф и нормальной производной va 70ф, которую можно заме-
заменить «углом напряжений» var|0, см. C1):
Qa (ф) = Qa (М , Т )-Л7„ ГЛ
\ О О/ TL
t (Ч„% - ftveq>). ^
QW) = Q (Mo) + taVa [y<
Mvv (¦) = vovBAff - № (Va% - 6а0ф).
Граничные значения t|:* вектора функций напряжений можно по-
получить, интегрируя, по рмалогии с D1), вектор Q, и момент М„

5 I] ВВОДНЫЕ ЗАМЕЧАНИЯ 109
в соответствии с равенствами
в
\ IQ Ш. t)-q (Мо, то)\ dc,
А
w W - Mvv (Mo))
/ - о-45)
А
где в — вспомогательный вектор, который, пользуясь аналогией
с О/, можно назвать вектором «углов напряжений» элемента кон-
контура оболочки.
Граничные условия A5) и D2) эквивалентны с точностью до
постоянных интегрирования. Если уравнения A5) заданы на од-
одной связной части контура С, то A5) и D2) эквивалентны с точ-
точностью до жесткого смещения контура. В данной главе, как пра-
правило, рассмотрены функционалы для задач с этими простыми
граничными условиями. В случаях, когда условия A5) охваты-
охватывают несколько различных связных частей контура С (в част-
частности, при многосвязной области S), необходимо учитывать урав-
уравнения, согласующие взаимные смешения различных связных ча-
частей. Некоторые из этих случаев рассмотрены в гл. 5. Данное
замечание относится и к статическим граничным условиям D3)
и B6).
1.6. Некоторые соотношения теории пологих оболочек. Теория
пологих оболочек является частным случаем общей теории обо-
оболочек при дополнительных к основным гипотезам допущениях.
Геометрическая гипотеза
а| » а22- 1, а1г~ a? « 0, A.46)
т. е. внутреннюю геометрию оболочки можно приближенно счи-
считать совпадающей с геометрией плоскости ее проекции. Это озна-
означает также, что в исходных уравнениях приближенно прини-
принимается равной нулю гауссова кривязна поверхности
Статическая гипотеза. В уравнениях равновесия можно пре-
пренебречь моментными членами, содержащими в качестве коэффи-
коэффициентов выражения кривизн 6ар и их производных.
При этих допущениях уравнения теории оболочек упрощают-
упрощаются и принимают следующую форму.
Геометрические уравнения:
8()(V + vL ^vV <Ы8>

ПО ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛг 4
Vе*+ «а «О, VaVeMaB + 6ap7'aB + «7 = 0. A.49)
Статические уравнения:
V
Соответственно упрощаются уравнения неразрывности A3)
и общее решение уравнений равновесия B9)
Упрощаются также зависимости D0) между деформациями гра-
граничного элемента и перемещениями
к (и) = taVa [vY/B (Ve«v - &„,»)} A.52)
и выражения D4) для граничных усилий через функции напря-
напряжении
Q» (Ф) = Та (Мо, Го) - Wv (_ /%Вуеф + va
[YB ] A.53)
Так как метрика базисной поверхности пологой оболочки
считается совпадающей с метрикой плоскости, то пологие обо-
оболочки можно рассчитывать в декартовых координатах. В этом
случае во всех уравнениях надо положить
§ 2. Различные варианты принципов Лагранжа
и Кастильяно — исходные пункты
для преобразования вариационных принципов
В качестве исходных пунктов для применения тео-
теории преобразования вариационных проблем исполь-
использованы принцип минимума потенциальной энергии

§ 2) ПРИНЦИПЫ ЛАГРАНЖА И КАСТИЛЬЯНО Щ
(принцип Лагранжа) и принцип максимума допол-
дополнительной энергии (принцип Кастильяно), как и
в гл. 3.
2.1. Различные варианты функционала Лагранжа
(табл. 4.1).
а) Функционал Лагранжа в перемещениях и де-
деформациях Эj\i(u,z,\i) рассмотрен в-§ 1.
Этот функционал может быть преобразован в дру-
другие разновидности функционала Лагранжа, имеющие
различные особенности: путем расширения простран-
пространства состояний за счет замены переменных
ГаР (е, ц) = ГаР, Ма& (г, ц) = Ма& и искусственного вве-
введения соответствующих дополнительных условий; пу-
путем усечения пространства состояний за счет исклю-
исключения некоторых переменных. Некоторые из получен-
полученных таким путем вариантов функционала Лагранжа
(наиболее интересные с точки зрения авторов) пред-
представлены в табл. 4.1. Условия стационарности различ-
различных вариантов функционала Лагранжа — уравнения
равновесия, но в различной форме.
б) Функционал Лагранжа в перемещениях Эл\ Ы)
(табл. 4.1) получен из ЭЛ2(и, е, ц) путем исключения
деформаций еар, цар, с помощью дополнительных ус-
условий A.6), A.12). Это наиболее распространенная
форма функционала Лагранжа, чаще всего при-
применяющаяся в приложениях как при численном,
так и при аналитическом решении задач теории
оболочек.
Дополнительными условиями являются геометри-
геометрические граничные условия, а условиями стационарно-
стационарности— уравнения равновесия и статические граничные
условия в перемещениях.
в) Функционал Лагранжа в деформациях
Зл:(е,ц). В теории оболочек, как и в теории упруго-
упругости (гл. 3, § 2.1в), возможна формулировка принципа
Лагранжа в деформациях, в которой ни функционал,
ни дополнительные условия (а значит, и условия ста-
стационарности) не содержат перемещений.
В тех случаях, когда геометрические граничные ус-
условия заданы на одном связном участке контура С,
функционал •9лз(е, ц) может быть получен из

112 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ..
(и, е, ц). Чтобы преобразовать Эт в Элз, нужно
исключить перемещения иа, w из 5Л2 и из дополни-
дополнительных условий к нему. Рассмотрим это преобра-
преобразование в случаях, когда контур оболочки С состоит
из двух связных частей Си и Ст, на которых заданы
геометрические и статические граничные условия со-
соответственно.
После исключения перемещений из дополнительных условий
A.6), A.12) они переходят в уравнения неразрывности A.13);
граничные условия в перемещениях A.15) переходят в деформа-
деформационные граничные условия A.42).
В функционале ЭЛ2(и, е, fi) перемещения содержатся в сла-
слагаемом
jjjj (qaua + qw) dS B.1)
поверхностного интеграла и в контурном интеграле, который в
рассматриваемом частном случае граничных условий С = Си + Ст
имеет вид
\ [Q% + Qw + Mb («)] dC. B.2)
Чтобы избавиться от перемещений в слагаемом A), пред-
представим нагрузку <7а, q в форме
B.3)
)
где Г , Ма® — какое-либо частное решение неоднородных урав-
уравнений равновесия A.24). Используя C) н правило дифференци-
дифференцирования произведения, преобразуем qaua и qw:
{24)
+ [if -1 (ым?- бJjwota)] v,ua - м1\ (ь%иа),

§2] ПРИНЦИПЫ ЛАГРАНЖА И КАСТИЛЬЯНО
Подставив D) в A), после простых преобразованнй получим
as =
(
0F" + *Z V) +
т (*)( V«
Отсюда видно, что множителем при Г"в является еар (и) A.6),
а множитель при М*а есть цва (и) A.12). Поверхностный интеграл
от остальных слагаемых нужно преобразовать по формуле Грииа
(см Приложение 2) в контурный интеграл. В результате
\ \ 04
dC. B.5)
Последнее слагаемое в контурном интеграле можно с помощью
равенства
veva + Ve~6ff B.6)
реобразовать к виду
- M^V6w = - \&Mf\aVaw - t6MftaVaw. B.7)
Второй член в G) содержит производную taVaw от w по каса-
касательной к контуру С. Интегрируя по частям, получим
dC =
vuveywoa8vv7va) + /VVy (va/eMf) ^] rfC. B.8)
Чтобы множителем при vaVgMa был угол поворота
= vv * = — vv Gш + b6
= vv *v =
vv Gуш + b6yыв), см. A.3), преобразуем с по-
поE)
мощью (G) еще один член в E):
< fv^e«0 B.9)

114 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
С помощью (8) н (9) н равенство E) можно представить в виде
?% + qw) dS = J J [Т«\& (и) + M«Va[S («)] rfS -
o\ + Q.w + Mav4y) dC, B.10)
где Qos= Q0 (АГо> Го), Qo = Q (MJ, Mo = Afvv (JJfJ, см. A.28).
После этих преобразований контурный интеграл в ЭЛ2(и,e,fi)
примет вид
% + Qw + MovVdY)rfCu. B 11)
Так как на Си перемещения иа, w и угол поворота vvfrv известны
уап=иа, w = w , v*'O1Y = '0i )n не варьируются, то второй инте-
интеграл в A1)—постоянная, неварьируемая величина и не нужда-
нуждается в дальнейших преобразованиях.
Чтобы исключить перемещения из первого интеграла в A1),
воспользуемся общим решением A.29) уравнений равновесия.
Пусть ф* — какая-либо функция напряжений, для которой
усилия и моменты, вычисленные по A.29), удовлетворяют гра-
граничным условиям A.26). Тогда, согласно A.44),
Q« - Q« = /Yy^y + v»^ (VB<p* + 6jVe)] -
в^Ч^*) B.12)
Таким образом, величины Qa — Qa, Q* — Q , M — M выраже-
выражены через четыре функции ф[, \|J> ф > ¦>)*> заданные на части
контура Ст, и их производные по касательной к контуру. Подста-
вив A2) в A1) и проинтегрировав по частям, получим
- «О "а + (<?о - Q,) W + (М„ - М*) VV*Y] dCT =
= J [>a (u) ^ + и (и) <р* + вы (н) г)*] rfCr -f A t, B.13)
B.14)

$ 2) ПРИНЦИПЫ ЛАГРАНЖА И КАСТИЛЬЯНО Ц5
где 8| и В2 — начало и конец части Ст контура С. В точках Bi
и Вг иа = u*, w = w*, Ф (и) = Ф , так как эти точки принадлежат
одновременно и Су и Си.
Заменив в равенствах A0) и A3) еа$(и), Hag (й), иа («),
¦л (и), гн (и) на еаВ, ца0, иа (е, ц.), х (е), е„ (е) соответственно,
получим, с учетом A1), функционал Лаграижа в деформа-
деформациях Элз (е, И) (табл. 4.1), где
А = А, + J (Q«u*a + Q^* + Afo0*) dCu, B.15)
константа v4j определена в A4).
Функционал 5ЛЗ (е, (г) имеет некоторые особенно-
особенности по сравнению с Эл\ (и) и Элг(и, е, (г) в вычисли-
вычислительном отношении, с точки зрения учета граничных
условий. Его удобнее применять в случае деформа-
деформационных граничных условий.
Преобразование Фридрихса (см. гл. 2, § 2.4) пе-
переводит Элз(е, ц) в функционал Кастильяно 3Ki(\j))
(табл. 4.2) в функциях напряжений (см. § 2.2в).
г) Функционал Лагранжа в основном пространстве
состояний 5л4 (и, е, ц, Т, М) получается из Эд2 (и, е, \i)
за счет расширения пространства состояний. Вводятся
новые неизвестные — усилия ГаР и моменты Ма$, и со-
соответствующие дополнительные условия — закон Гука
A.20)
Та* - Та6 (е, ц) = 0, Ма6 - Ма6 (г, ц) = 0. B.16)
Эта форма представления функционала Лагранжа
в расширенном пространстве удобна для дальнейших
преобразований по теории Куранта — Гильберта.
Функционалы ЭЯ\, Эт и Эт имеют отличие по
форме и дополнительным условиям к ним. Различия
в вычислительном аспекте между ними несуществен-
несущественные. Однако разнообразие форм исходного пункта
преобразований приводит к важным особенностям
преобразованных функционалов не только по форме,
но и в вычислительном отношении и, в частности,
в экстремальных свойствах (см. § 5.1).
д) Функционал Лагранжа с неполными полями
перемещений и деформаций ЭЛь{ю,г) может быть

116 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ.4
получен для пологих оболочек из Эт(и). Для этого
нужно в ЭЛ|(й) заменить выражения еа0(и) A-48)
новыми переменными еаE и ввести соответствующие
дополнительные условия, а затем исключить танген-
тангенциальные перемещения иа из функционала и из до-
дополнительных условий таким же путем, как это было
сделано при выводе Эт(г, ц). Исключение иа воз-
возможно для пологих оболочек, для которых выраже-
выражения цав(ы) A.48) содержат только перемещения w,
а два уравнения равновесия A.49), в правых частях
которых стоят нагрузки qa, не зависят от третьего
уравнения.
Функционал Эль(хю,г) может служить исходным
пунктом для получения смешанного функционала тео-
теории пологих оболочек 9c(w,ср) (см. § 4).
е) Другие разновидности функционала Лагранжа,
не представленные в табл. 4.1, можно получить из
Эл\ — Эл5, заменяя часть переменных е, ц, Т, М вы-
выражениями е(и), ц(и), Г(е, ц), М(г, ц) или наоборот;
например, функционал вида
+ (ХаВ (и) МаВ (е, ц)] - д\ - Ц dS -
- J [(<?)' «а + (Q.)' ш + (Л1.)' д (и)] rfC
с дополнительными условиями A.G), A.12), A.15).
2.2. Различные варианты функционала Кастпльяно.
а) Функционал Кастильяно в усилиях. Принцип
Кастильяно и функционал Экз(Л1, Т) (табл. 4.2) в тео-
теории оболочек хорошо известны. Этот функционал мо-
может быть выведен из функционала Лагранжа
Эл2 (и, е, ц) (табл. 4.1) по следующей схеме (преоб-
(преобразование Фридрихса, см. гл. 2, § 2.4):
.множители /»#т\ /О 1-74
-•Эп2(и,е,(х,7\М)->Экз(М,7'). B-17)
где ЭП2 — полный функционал Ху—Вашицу
(табл. 4.3). Это позволяет утверждать, что функцио-

§2] ПРИНЦИПЫ ЛАГРАНЖА И КАСТИЛЬЯНО Ц7
налы Элг и Эк.з имеют одно и то же стационарное
значение.
Другие разновидности функционала Кастильяно
(табл. 4.2) могут быть получены из Экъ(М, Т) с по-
помощью общего решения A.29) уравнений равновесия
A.24) и замены переменных е(М, Т) — е, ц(М, Г) =
= ц либо преобразованием Фридрихса из функцио-
функционалов Лагранжа (таб.1 4.1).
б) Функционал Касш.!ьяно в усилиях и функциях
напряжений ЭК2(Ч>, М, Т) получен из Эк3(М, Т) путем
замены дополнительных условий в форме уравнений
равновесия A.24) на эквивалентные им зависимости
между усилиями и функциями напряжений A.29).
После этой замены ЭК2 зависит не только от М, Т,
но и от г|з. Поверхностный интеграл в 5Кз(А1, Т) пу-
путем замены Qa(Af, Т), Q(M), MVV(M) на Qa(\|>), Q(\|>),
Mvv(\|)) A.44) и интегрирования по частям записан
в функциях напряжений (см. аналогичное преобразо-
преобразование в § 2.1в), с тем чтобы функционал ЭКг(г|5, М, Т)
имел вид, аналогичный функционалу Элг (", е, ц)
(см. § 7).
Функционал Эк2(^, М, Т) связан преобразованием
Фридрихса (см. гл. 2, § 2.4) с функционалом Лагран-
Лагранжа 3Лз(е,ц).
Функционал 5К2(¦, М, Т) является промежуточной
ступенью при преобразовании ЭКз(Л1. Т) в 3Ki(^),
который имеет преимущества в вычислительном от-
отношении, заключающиеся в уменьшении количества
неизвестных и отсутствии дополнительных условий.
В то же время Экг имеет большие возможности, чем
5ki, как исходный пункт для преобразований по тео-
теории Куранта — Гильберта, аналогично функционалу
Лагранжа Эл2 (и, е, ц).
в) Функционал Кастильяно в функциях напряже-
напряжений 3Ki(\|>)—наиболее удобная для расчетов форма.
Этот функционал может быть получен из ЭК2(^, М, Т)
путем исключения усилий М, Т: для этого нужно
всюду заменить М, Т на их выражения через г|з A.29).
Дополнительные условия в области S оказываются
выполненными, остается лишь граничное условие
для ф.

118 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ.4
Переход от Эк,з к Эщ означает учет дополнитель-
дополнительных условий A.24) с помощью общего решения A.29)
(см. гл. 1, § 2.2).
г) Функционал Кастильяно в квазиосновном про-
пространстве состояний ЭК4(^>, М, Т, ц, е). Функционал
3К4(Ч>,М, Т, |и, е) получен из ЭЯ2(^,М,Т) путем рас-
расширения пространства (\р, М, Т) за счет искусствен-
искусственного введения новых переменных — деформаций е, ц—
и дополнительных условий
вв„-ваВ(Л1,Т) = 0, цаВ-цар(Л1,Т) = 0 B.18)
(закон Гуна A-23) в обратной форме). В соответствии
с замечанием в гл. 2, § 2.1 введение новых перемен-
переменных и дополнительных условий расширяет возмож-
возможности для преобразований функционалов Кастильяно
в другие полные и частные функционалы.
д) Функционал Кастильяно с неполными полями
функций напряжений и усилий Эц5(<р,М) может быть
получен для пологих оболочек из 9xi(ty). Для этого
нужно в 3ki(i|>) заменить выражения Ма$($) A.51)
новыми переменными Ма$ и ввести соответствующие
дополнительные условия, а затем исключить функции
напряжений г|)а из функционала и из дополнительных
условий. Исключение г|)а возможно для пологих обо-
оболочек, для которых выражения Та^(^>) не содер-
содержат 1|>а.
Функционал ЭК5(ф, Щ, как и Элъ(®, е) (см.
§ 2.1д), может служить исходным пунктом для полу-
получения смешанного функционала теории пологих обо-
оболочек 9c(w, ф) (см. § 4).
е) Другие разновидности функционала Кастилья-
Кастильяно, не представленные в табл. 4.2, можно получить из
Экл — Эк.5, заменяя часть переменных М, Т, (г, е выра-
выражениями Л!(ф), Т($), ц(М,Т), г(М,Т) или наоборот,
например, функционал вида
Зкза (М. Г, ц, в) - $$ (-•IеарГв -1К,Ма6) dS +
+ \ [Qa (М, Т) («;)" + Q (М) (af) + Mvv (М) ОТ] dC
с дополнительными условиями A8), A.24), A.26).

ПОЛНЫЕ ФУНКЦИОНАЛЫ 119
§ 3. Полные функционалы
Различные варианты исходной вариационной за-
задачи (§ 2) приводят, в соответствии с теорией преоб-
преобразования вариационных проблем (см. гл. 2, § 2), к
различным полным функционалам и" соответствую-
соответствующим общим вариационным принципам в различных
пространствах состояний.
Из разных видов функционала Лагранжа Эт
(табл. 4.1) построен ряд полных функционалов ЭП1
(табл. 4.3), который, как и в гл. 3, § 3, назван лагран-
жевой серией полных функционалов. Соответственно
кастильянова серия полных функционалов Эа\
(табл. 4.4) получена из функционала Кастильяно 3ki
(табл. 4.2). Полные функционалы имеют те же но-
номера, что и частные, из которых они получены с по-
помощью множителей Лагранжа.
Каждый полный функционал позволяет сформули-
сформулировать вариационную задачу без каких-либо допол-
дополнительных условий. При этом независимо варьируют-
варьируются все параметры, указанные в скобках. Например,
у ЭП2 (и, е, ц, Т, М) независимо варьируются поля пе-
перемещений, тангенциальных и изгибных деформаций
н усилий-моментов.
Из полных функционалов могут быть получены
разнообразные частные, в том числе функционалы
Лагранжа (табл. 4.1) и Кастильяно (табл. 4.2) в раз-
различных формах.
3.1. «Пагранжева серия полных функционалов.
а) Полный функционал Эи\(и, Q, Mv) в переме-
перемещениях и контурных реактивных усилиях построен из
3Л|(и) (табл. 4.1) путем учета ограничений (гранич-
(граничных условий в перемещениях) с помощью множителей
Лагранжа Q, Mv; они являются, как показывают усло-
условия стационарности, компонентами вектора усилий
Q = Qaea + Qn и изгибающим моментом Mvv, соответ-
соответствующими заданным компонентам (и*)", (w*)", (О*)",
т. е. реакциями.
Условия стационарности — уравнения равновесия
и статические и геометрические граничные условия в

120 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. *
перемещениях плюс уравнения для вычисления реак-
реакций по известным перемещениям.
б) Полный функционал в перемещениях Эща(и)
получается, если выражения для реакций (Q)", (Mv)"
через перемещения подставить в Э„\{и, Q, Mv), т. е.
с точки зрения теории преобразования вариационных
проблем наложить некоторые из условий стационар-
стационарности в качестве дополнительных условий и с их по-
помощью исключить Q, Mv (см. гл. 2, § 2).
в) Полный функционал в основном пространстве
состояний Э„2(и, е, ц, Т, М) (функционал Ху — Ваши-
цу) получен из ЭЛ2 (и, е, ц.) с помощью множителей
Лагранжа Т, М при геометрических соотношениях.
Как видно из условий стационарности B.16) (физи-
(физических соотношений), множители Лагранжа являются
усилиями и моментами.
Условиями стационарности функционала Эпг яв-
являются уравнения и граничные условия теории обо-
оболочек в классической, наиболее распространенной
форме: геометрические уравнения в области S A.6),
A.12) и на контуре С A.15), физические соотношения
B.16), статические уравнения в области A.24) и ста-
статические граничные условия A.26).
Исключение множителей Лагранжа Т, М из функ-
функционала 5п2(н, е, ц., Т, М) в соответствии с гл. 2, § 2.2г
приводит к полному функционалу в пространстве
(и, е, ц.), который является одной из форм функцио-
функционала Рейсснера [0.2]:
Эр, (и, е, ц) =
+ Май (е, и) ЦаВ («) - q\ - qw] dS -
X + Q.w + ММ")У dC - \ (Qa(e, н)(ца - иа) +
+ Q (г, ») (w - of) + Mvv (8, ,1) [О (и) - V}}" dC. C.1)
Можно исключить из Э„2 деформации е, ц (в соответ-
соответствии с гл. 2, § 2.2в) и перейти к другой форме функ-

§ 31 ПОЛНЫЕ ФУНКЦИОНАЛЫ 121
ционала Рейсснера Э*иг(М.,Т, и) (табл. 4.4) в про-
пространстве (М, Т, и).
г) Полный функционал в деформациях и функ-
функциях напряжений Зпз(е, ц, tj)) построен путем учета
с помощью множителей Лагранжа дополнительных
условий функционала 5Лз(е, ц). Условия стационар-
стационарности Э„з — геометрические уравнения в деформациях
в области и на контуре и зависимости между дефор-
деформациями и множителями Лагранжа tya, ф, которые
одновременно играют роль статических и физических
уравнений. Последние зависимости показывают, что
множители Лагранжа совпадают с компонентами век-
вектора функций напряжений.
Отсюда видно, что использование полного функ-
функционала Э„3(е, ii, ф) можно рассматривать как инстру-
инструмент для получения общего решения уравнений
равновесия, более универсальный, чем статико-геомет-
рическая аналогия. Преобразование функционала Ла-
Лагранжа 5лз (г, ц) в Эп3(е, ц, tj)) привело к преобразо-
преобразованию условий стационарности 3Лч (уравнений рав-
равновесия в деформациях) к форме, являющейся их
общим решением. Этот пример показывает, какое бо-
богатство возможностей заключено в вариационных фор-
формулировках и их преобразованиях.
д) Полный функционал в расширенном основном
пространстве состояний 9ni(u, г, ц, Т, М, ki, %% К3, №)
получается из Эщ(и, е, ц, Т, М) (табл. 4.1) с помо-
помощью множителей Лагранжа ki, fa, №, АЛ
Функционал 5„4 является промежуточным звеном
преобразования 5л4 (и, е, ц, Т, М) в Зп4а(и, е, ц., Т, М).
е) Полный функционал в симметризованном основ-
основном пространстве состояний Э„^ (и, е, ц, Т, М) полу-
получен из Эп4 путем исключения множителей Лагранжа
к с помощью условий стационарности в соответствии
с гл. 2, § 2.2 г.
Функционал Э„4а(и, е, ц, Т, М) линейный (неодно-
(неоднородный) относительно каждой группы переменных
и; е, (i; T, M при фиксированных двух других группах.
Отсюда следует его особенность, заключающаяся в
том, что каждое условие стационарности связывает
две группы переменных из вышеуказанного списка и

ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК (ГЛ. 4
не содержит третью группу параметров, по которым
варьировался функционал (см. схему на рис. 4.4).
Рис. 4.4. Симметричный характер условий стациоиариости полиого
функционала 9W.
Линейное преобразование пространства состояний
(и, е, ц, Т, М) в (и', е', ц', Т, ЛГ) по формулам
Т = 1 [Г
Г],
М']
переводит функционал Эп2(и, е, ц., Т, М) в 5П4а(и', е',
ц', Г', М'). Обратное преобразование определяется
формулами
и'— и; в' = 8, ц' = ц,
Г = 2Г-Г(в,ц), М' = 2М-
По свойствам, связанным со стационарностью,
функционалы 5П4а и Э„2 эквивалентны. Они имеют
различные экстремальные свойства (см. § 5).
ж) Полный функционал с неполными полями пе-
перемещений, деформаций и функций напряжений
5П5(ш, е, ф, Q, Му) для пологих оболочек построен
с помощью множителя Лагранжа tp из Эл5 (а>, е)
(табл. 4.1). Его условия стационарности — уравнения
для пологих оболочек в смешанной форме, которые
показывают, что ф — функция напряжений Эри для
решения двух уравнений равновесия A.49).
Исключение я в соответствии с гл. 2, § 2.2 в, пере-
переводит Э Л5 в смешанный функционал 9c(w,q>) (см. § 4).

S 3J ПОЛНЫЕ ФУНКЦИОНАЛЫ 123
3.2. Кастильянова серия полных функционалов.
а) Полный функционал в функциях напряжений
и деформациях граничных элементов Э*п1 (i|-, x, еЛ мо-
может быть получен из 5Ki(t|)) (табл. 4.2) путем внесе-
внесения дополнительных условий (статических граничных
условий в функциях напряжений) в "функционал с
множителями Лагранжа.
Условия стационарности Э*п1 — уравнения нераз-
неразрывности, деформационные граничные условия и ста-
статические граничные условия в функциях напряжений
и равенства, раскрывающие смысл множителей Ла-
Лагранжа: выражение незаданных деформаций на кон-
контуре С через функции напряжений.
б) Полный функционал в функциях напряжений
3*Ia (if) выведен из 5*, в соответствии с § 2.2г гл. 2,
т. е. путем исключения множителей Лагранжа и, е<.
Функционал Э*1а является аналогом полного функ-
функционала в перемещениях 5nia(«) (см. § 3.16).
в) Полный функционал Э*а2($, М, Т, \х, Е) в квази-
квазиосновном пространстве состояний, получен из
5к2(^. М, Т) путем внесения дополнительных условий
(общих решений уравнений равновесия в области S
и граничных условий в функциях напряжений на кон-
контуре С) в функционал с множителями Лагранжа ц, 8.
Смысл величин ц, 8 раскрывается условиями стацио-
стационарности: множители Лагранжа ц, г являются дефор-
деформациями в области и на контуре.
Условия стационарности — полный набор уравне-
уравнений и граничных условий теории оболочек в функциях
Т|), М, Т, Ц, 8.
Функционал 3*2(i|\ M, Т, ц, е) является промежу-
промежуточным звеном преобразования Фридрихса (см. гл. 2,
§ 2.4) ЭК2(Ч), М, Т) в 5л (е, ц). Обратное преобразо-
преобразование Элз в 5кг производится через полный функцио-
функционал Эпз(е, ц, ф), так что эти четыре функционала свя-
связаны между собой по схеме, изображенной на рис. 4.5.
г) Полный функционал в усилиях и перемеще-
перемещениях Э*п3(М,Т, и) (функционал Рейсснера [0.13]) по-
получен внесением в ЭкзЩ, Т) (табл. 4.2) статических

124
ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
дополнительных условий с множителями Лагранжа
и, которые следует считать, как показывают условия
стационарности, перемещениями.
Функционал 5*з является промежуточным звеном
преобразования Фридрихса (см. гл. 2, § 2.4) ЭКЗ{М, Т)
в ЭП2 (и, е, ц). Промежуточным звеном обратного
преобразования Элг в 5Кз служит функционал Ху —
Вашицу Эп2(и, е, ц, Т, М) (табл. 4.3), так что эти
четыре функционала связаны между собой по схеме,
аналогичной рис. 4.5,
Рис. 4.5. Взаимоспязь функционалов Кастильяно ЭК2 и Лаграижа
Элз с полными функционалами: прямое и обратное преобразова-
преобразование Фридрихса.
Используя линейное преобразование пространства
состояний
и = и, Т = Т (г, р), М = М(г, ц),
можно 5*3 (M, Т, и) преобразовать в функционал
Рейсснера A) в деформациях и перемещениях (см.
§ 3.1в).
д) Полный функционал в расширенном квазиос-
квазиосновном пространстве состояний 5*4 (if1, М, Т, ц, е, I1,
I2,1з> %д получен из 5K4<i|5, М, Т, ц,, г) с помощью мно-
множителей Лагранжа %\ %2, %3, %*¦
Функционал Э*пА имеет вид, аналогичный 9ni
(табл. 4.3), и является промежуточным звеном для
перехода к 5*п4а (>|-, М, Т, и, е) (ср. § 3.1 д).
Условия стационарности — уравнения теории обо-
оболочек, записанные с помощью вспомогательных пере-
переменных |.

§ 4] ЧАСТНЫЕ ФУНКЦИОНАЛЫ 125
е) Полный функционал Э*та (i|\ М, Т, и, е) в квази-
квазиосновном симметризованном пространстве выведен из
Э*пА путем исключения множителей Лагранжа % в со-
соответствии с гл. 2, § 2.2г.
Между 3*4а и Э*п2 (§ 3.2 в) существует связь, ана-
аналогичная связи между Эп4а и Эа2 (§ 3.1 е): Э*2 пере-
переходит в Э*4а при замене переменных
Обратное преобразование дается формулами
Ч-/ = г|-, М' = М, Т = Т,
?1' = 2м - м (М, Г), е' == 2е - 8 (М, Г).
По свойствам, связанным со стационарностью,
функционалы Э\Л н Э*4а эквивалентны. Они имеют
различные экстремальные свойства (см. § 5).
ж) Полный функционал с неполными полями
функций напряжений, усилий-моментов и перемеще-
перемещений 5*5(ф, М, w, х, е() для пологих оболочек построен
с помощью множителя Лагранжа w из функционала
Кастильяно Зке(ф, М) (табл. 4.2). Условия стацио-
стационарности 5*- — уравнения теории пологих оболочек
в функциях ср, М, w. Исключив М в соответствии с
гл. 2, § 2.3.2в, нетрудно преобразовать Э*иЬ в смешан-
смешанный функционал 5с(да,ф) (см. § 4).
§ 4. Частные функционалы. Их взаимосвязь
с полными функционалами
Согласно гл. 2 § 2, частные функционалы полу-
получаются из полных при наложении некоторых условий
стационарности в качестве дополнительных условий.
При этом выражение для функционала обычно упро-
упрощается, так как некоторые слагаемые обращаются в
нуль. В частности, легко осуществляется переход к

12б ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
функционалам Лагранжа и Кастильяно. Некоторые
другие частные функционалы, представляющие, на
наш взгляд, наибольший интерес, приведены в
табл. 4.5.
4.1. Вывод различных вариантов частных функ-
функционалов Лагранжа и Кастильяно из полных функ-
функционалов (табл. 4.3 и 4.4) не имеет существенных от-
отличий от преобразований, описанных в гл. 3, § 4.1, и
поэтому здесь подробно не описан.
4.2. Вывод частных функционалов из полных пу-
путем наложения различных комбинаций геометриче-
геометрических, статических и физических уравнений в качестве
дополнительных условий (в соответствии с классифи-
классификацией в гл. 2, § 2.3.1) можно проиллюстрировать
схемами на рис. 3.3, 3.4 гл. 3, заменив на них дефор-
деформации трехмерного тела е деформациями базисной
поверхности оболочки е, ц, а напряжения о — уси-
усилиями и моментами Т, М Для оболочек справедливы
сделанные в гл 3, § 4.2 выводы о неравноправии не-
некоторых из перечисленных выше групп уравнений с
точки зрения их использования в качестве дополни-
дополнительных условий при выводе частных функционалов
из полных.
Разберем в качестве двух характерных примеров
вывод частных функционалов из полных в основном
и квазиосновном пространствах состояний.
Принимая в качестве дополнительных условий к
полному функционалу Эп2{и, е, ц, Т, М) в основном
пространстве состояний или к полному функционалу
Э*п2 (if, М, Т, м, р) в квазиосновном пространстве одну
или две из указанных групп уравнений, можно полу-
получить следующие частные функционалы, отличные от
функционалов Лаграижа и Кастильяно (см. табл. 4.5).
а) Функционал для физических и геометрических
соотношений ЭфГ(е, ц, Т, М) получен из Э„2(и, е, ц,
Т, М) (табл. 4.3) при наложении в качестве дополни-
дополнительных условий статических уравнений.
Условия стационарности 5фГ — физические и гео-
геометрические уравнения. Этот функционал является
промежуточным звеном преобразования Эаг в функ-
функционал Кастильяно 5кз(-М. Т) (табл. 4.2).

$ 4J ЧАСТНЫЕ ФУНКЦИОНАЛЫ 12?
б) Функционал для геометрических и статических
уравнений ЭГС(и, е, ц., Т, М) получается из Эп2(и, е,
li, T, М) (табл. 4.3) при наложении физических урав-
уравнений в качестве дополнительных условий. Исключив
из него деформации или усилия в соответствии с гл. 2,
§ 2.2в, можно получить полный функционал Рейсснера
в форме Эпз (М, Т, и) (табл. 4.4) или 3pi(m, e, ц.) (см.
§ 3.1в).
в) Функционал для физических и статических со-
соотношений ЭфС(М, Т, ii, е) выведен из Э\а (if, M, Т, и, е)
(табл. 4.4) путем наложения в качестве дополнитель-
дополнительных условий геометрических уравнений в области
(уравнения неразрывности) и на контуре (деформа-
(деформационные граничные условия).
Условия стационарности ЭфС— физические и ста-
статические уравнения. Этот функционал является про-
промежуточным звеном преобразования Эп% в функ-
функционал Лагранжа Элз (е, м.) (табл. 4.1).
г) Функционал для статических и геометрических
уравнений ЭСт($, М, Т, ц,, е) получается из Эпч (o|), M,
Т, ц, е) при наложении в качестве дополнительных
условий физических уравнений. Его условия стацио-
стационарности— статические уравнения в форме зависи-
зависимостей между усилиями и функциями напряжений,
геометрические уравнения (уравнения неразрывности)
в области и граничные условия: статические в функг
циях напряжений и геометрические в деформациях.
Исключив из Эсг усилия в соответствии с гл. 2,
§ 2.2в, можно получить полный функционал Э„3 (е, Ш
¦ф) (табл. 4.3).
д) Функционалы для физических уравнений Эф\ (&,
М, Т, М) и Эф2{М, Т, ii, е) получены соответственно из
полных функционалов Э1Г2(и, е, ц,, Т, М) (табл. 4.3) и
Э„2 (\|i, М, Т, ,и, 8) (табл. 4.4) при наложении геомет-
геометрических и статических уравнений в области S и на
контуре С в качестве дополнительных условий. Усло-
Условиями стационарности Эф\ и Э^ч служат уравнения, со-
содержащие дифференциальные операторы от левых
частей физических уравнений в прямой и, соответ-
соответственно, обратной формах (см. табл. 4.5).

128 Вариационные принципы теории оболочек [гл. 4
4.3. Функционал физических соотношений для обо-
оболочки Эф(г, ц, Т, М) имеет вид
эф (в, ц, т, м) = ^ [ъЫ
Этот функционал можно получить всеми способами,
которыми выведен в гл. 3, § 4.3 функционал физиче-
физических соотношений для трехмерного тела; он обладает
всеми свойствами, описанными в § 4.3 гл. 3.
Замечание. Функционалы Эф, Эфь Эф2, обла-
обладают свойством, аналогичным гому, которое имеют
функционалы с этими же названиями для трехмерного
тела: в них можно независимо варьировать некоторые
аргументы (е, ц, Т, М в функционале Эф; е, ц —
в Эфь Т, М—в Эф2; сравните с замечаниями к § 4.3
гл. 3).
Таким путем можно прийти к физическим урав-
уравнениям вида
Т ft) - Т [г (и), ц (и)] = О, М ft) - М [е (и), р (и)] = О,
которые могут служить разрешающими дифферен-
дифференциальными уравнениями данной краевой задачи.
4.4. Функционалы граничных условий соответству-
соответствуют второму варианту классификации дополнительных
условий, накладываемых на полные функционалы для
перехода к частным (гл. 2, § 2.3.1): разделению их на
уравнения в области и на контуре.
Включение в список дополнительных условий урав-
уравнений на контуре оболочки не приводит к существен-
существенным изменениям в структуре функционала. Как с
точки зрения структуры, так и в вычислительном
аспекте (см. гл. 5) представляют интерес функциона-
функционалы граничных условий, которые получаются из пол-
полных, если в список дополнительных условий включить
все уравнения в области. Условиями стационарности
полученных функционалов являются граничные уело-

§ 4] ЧАСТНЫЕ ФУНКЦИОНАЛЫ 129
еня: статические, или геометрические, или и те и
другие. В табл. 4.5 представлено шесть наиболее
характерных вариантов функционалов граничных
условий.
а) Функционал граничных условий в перемеще-
перемещениях и усилиях ЭГ(и, Т, М) может быть выведен из
Э„з(М, Т, и) или из других полных функционалов, со-
содержащих перемещения и усилия. Дополнительные
условия — уравнения теории оболочек в перемеще-
перемещениях и усилиях в области S. Условия стационарно-
стационарности— геометрические граничные условия в перемеще-
перемещениях и статические — в усилиях.
б) Функционал для статических граничных ус-
условий в перемещениях ЭГ\ (и) можно вывести из
ЭП\(и, Q, Mv) и из других полных функционалов, со-
содержащих перемещения. Дополнительные условия —
уравнения теории оболочек и геометрические гра-
граничные условия в перемещениях. Условия стацио-
стационарности— статические граничные условия в переме-
перемещениях.
в) Функционал для геометрических (деформацион-
(деформационных) граничных условий в усилиях Эг2(М, Т) выво-
выводится из любого полного функционала (табл. 4.3 и
4.4), содержащего усилия. Условия стационарности —
деформационные граничные условия, выраженные че-
через усилия.
г) Функционал граничных условий в функциях на-
напряжений и деформациях ЭГ(^, м> Е) может быть по-
получен из 5пз(е, ц, ^) и других полных функционалов,
зависящих от переменных е, ц, if. Дополнительные ус-
условия— уравнения неразрывности в деформациях и
зависимости между деформациями и функциями на-
напряжений (в качестве статических и физических урав-
уравнений) в области S. Условия стационарности —стати-
—статические граничные условия, выраженные в функциях
напряжений, и деформационные граничные условия.
д) Функционал для геометрических (деформацион-
(деформационных) граничных условий в функциях напряжений
ЭГ[ (if) может быть выведен из 5ni («!", х, е*) (табл. 4.4)
и других полных функционалов. Дополнительные
5 Н, И, Абовский и др,

130 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК (ГЛ. 4
условия — уравнения неразрывности и статические
граничные условия в функциях напряжений, условия
стационарности — деформационные граничные усло-
условия в функциях напряжений.
е) Функционал Э\% (е, м) для статических гранич-
граничных условий в деформациях. Его можно вывести из
•9П2(и, е, ц, Т, М) и других полных функционалов, со-
содержащих переменные в, ц. Дополнительные усло-
условия— уравнения неразрывности и равновесия в де-
деформациях в области и деформационные граничные
условия на контуре. Условия стационарности — стати-
статические граничные условия, выраженные в деформа-
деформациях.
4.5. Смешанный функционал в функциях w, <p для
пологих оболочек 9c(w,<p). Этот функционал можно
вывести из 9n5(w, e, ф, Q, Mv) (табл. 4.3) или из
Э*п5 (ф, М, да, х, е() (табл. 4.4), исключая переменную
в или М в соответствии с гл. 2, § 2.3.2в. Дополни-
Дополнительными условиями к 5с служат некоторые из геомет-
геометрических и статических граничных условий. Условия
стационарности — уравнения теории пологих оболочек
в функциях ф,фи остальные статические и геометри-
геометрические граничные условия.
§ 5. Экстремальные свойства полных
и частных функционалов теории оболочек
Для исследования экстремальных свойств функ-
функционалов, участвующих в формулировке вариацион-
вариационных принципов теории оболочек, так же как и для
функционалов теории упругости, может быть исполь-
использовано свойство выпуклости (см. Приложение 1) од-
одних функционалов Лагранжа и Кастильяно (исход-
(исходных пунктов преобразований) и невыпуклости дру-
других. Экстремальные свойства различных полных и
частных функционалов можно выяснить, используя
§ 3 гл. 2. Результаты представлены в табл. 4.6; в этой
таблице стрелки ** обозначают, что знаки min и max
можно поменять местами, так что данный функционал
имеет седловую точку.

§ 6] РАЗРЫВНЫЕ СМЕЩЕНИЯ И УСИЛИЯ 131
5.1. Выпуклость различных вариантов функциона-
функционалов Лагранжа и Кастильяно и их экстремальность.
Исследование выпуклости функционалов Лагранжа и
Кастильяно в теории оболочек ничем не отличается
от аналогичного исследования в теории упругости
(см. гл. 3, § 5).
Используя тот факт, что энергия деформирования
срединной поверхности оболочки
является положительно определенной квадратичной
формой, и исследуя знак разности вида E.1) в гл. 3,
нетрудно установить, что все приведенные в табл. 4.1
разновидности функционала Лагранжа, кроме ЭЛ4(и,
в, ц, Т, М), выпуклые вниз, а все разновидности функ-
функционала Кастильяно (табл. 4.2), кроме Зк4(*С М, Т,
ц, в) выпуклые вверх, функционалы Э ni и Зк4 не вы-
выпуклые ни вниз, ни вверх.
Отсюда следует, что все варианты функционала
Лагранжа в точке стационарности имеют условный
минимум, а все варианты функционала Кастильяно —
условный максимум. Условная экстремальность функ-
функционалов Зл4 и Зк4 следует, из того, что они получены
соответственно из Эпг и из Зк2 заменой переменных.
5.2. Экстремальные свойства полных функциона-
функционалов лагранжевой и кастильяновой серий и частных
функционалов представлены в табл. 4.6. Они выво-
выводятся точно так же, как свойства аналогичных функ-
функционалов теории упругости (см. гл. 3, § 5).
§ 6. О вариационных принципах и экстремальных
свойствах функционалов теории оболочек
при разрывных перемещениях, деформациях,
усилиях и функциях напряжений.
О контактных задачах в теории оболочек
В § 1—5 рассматривались вариационные принципы
теории сплошных оболочек, в которых варьируемыми
были непрерывные поля параметров напряженно-де-
формнрованного состояния.
5»

132 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
Формулировку вариационных принципов этой тео-
теории, так же как и теории упругости для сплошного
тела (см. гл. 3, § 6), можно обобщить, рассматривая
в качестве варьируемых переменных разрывные поля
перемещений, деформаций, усилий и функций напря-
напряжений. Вариационные принципы при разрывных по-
полях параметров напряженно-деформированного со-
состояния могут служить для построения алгоритмов
расчета оболочек, в частности при использовании ме-
метода Ритца и метода конечных элементов, а также
для решения некоторых контактных задач.
6.1. Всю систему вариационных функционалов для
разрывных полей можно построить из исходных функ-
функционалов Лагранжа и Кастильяно для непрерывных
полей, рассматривая, по аналогии с§ 6 гл. 3, эти функ-
функционалы на пространствах разрывных перемещений
(деформаций) и функций напряжений (усилий), но
с соответствующими дополнительными условиями,
обеспечивающими их непрерывность. Этот прием не
меняет существа формулировок принципов Лагранжа
и Кастильяно, но позволяет построить ряд полных и
частных функционалов, одним из условий стационар-
стационарности которых является непрерывность некоторых
варьируемых полей (или условия контакта).
Не останавливаясь подробно на выводе функцио-
функционалов теории оболочек для разрывных полей, укажем
на некоторые особенности этой задачи по сравнению
с аналогичными вопросами в случае трехмерного тела.
Особенность задач теории оболочек состоит в том,
что в них нужно требовать непрерывность не только
перемещений иа, w, но и углов поворота Ьа, которые
являются функциями частных производных Vaw; не
только функций напряжений фа, <р, но и «углов напря-
напряжений» т^а (или частных производных от ср); не только
усилий Т, М, но и поперечных сил (или производных
от М) и т. д. При этом дополнительными компонен-
компонентами к геометрическим величинам иа, w, bv = vaba,
ка, х, ett на линии разрыва базисной поверхности обо-
оболочки с тангенциальной нормалью v являются соот-
соответственно статические величины 0х, Q, Mvv, tya, ф,
Tiv = V*Tla.

§ 71 СТАТИКО- ГЕОМЕТРИЧЕСКАЯ АНАЛОГИЯ 133
6.2. Аналогичным путем можно построить полную
систему вариационных функционалов для контактных
задач теории оболочек. При рассмотрении контактных
задач для оболочек, соединенных под углом, необхо-
необходимо учитывать, что разные части оболочки рассчи-
рассчитываются в различных системах координат.
Вариационные принципы для контактных задач
теории оболочек подробно рассмотрены в работах
[0.1, 4.1], в которых разобраны случаи контакта обо-
оболочек под углом, контакта оболочек с ребрами и
Другие.
§ 7. Вариационная форма статико-геометрической
аналогии
Между однородными уравнениями равновесия в
усилиях A.24) и уравнениями неразрывности в де-
деформациях A.13) существует статико-геометрическая
аналогия [4.7, П.9, П. 10], которая заключается в том,
что соотношения A.24) переходят в A.13) при замене
-евВ). {7Л)
Этот факт облегчил построение общего решения урав-
уравнений равновесия в форме A.29) по аналогии с общим
решением A.6), A.12) уравнений неразрывности.
Наличие аналогии между геометрическими и ста-
статическими уравнениями теории оболочек наводит на
мысль о существовании аналогии между статическим
вариационным принципом Лаграпжа, в формулировке
которого участвуют геометрические переменные и, е,
in, и геометрическим принципом Кастильяно со стати-
статическими переменными tp, M, Т. И действительно, такая
аналогия имеет место между функционалами Лагран-
жа и Кастильяно, записанными в форме табл. 4.1 и
4.2, и их дополнительными и естественными усло-
условиями. Например, функционал Лагранжа Э.п\ (и) пе-
переходит в 5Ki(if) после замены вар(и) на
Veu^'fo), ГвР[е(«). ii(u)] на Л%

134 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ, 4
и т. д. по схеме G.1) с учетом A.6), A.12), A.23) и
A.29). При этом аналогия в вариационной форме
имеет место между квадратичными частями двумер-
двумерных интегралов, подобно тому как аналогия в диф-
дифференциальной форме существует между однородны-
однородными частями дифференциальных уравнений. Входящие
в функционалы Лагранжа и Кастильяно контурные
интегралы оказываются полностью аналогичными,
если между статическими и геометрическими гранич-
граничными величинами установить соответствие
а о
x°^>Q°, х «*-»¦<?, e^^Mvv. G.3)
Нетрудно проверить, что соответствие G.3) яв-
является следствием G.1): при замене G.1) ха(е, ц) пе-
переходит в Qa(M, Т), х(е) в Q(M), ett(e) в MVV(M) и
обратно, см. A.39), A.28); для проверки можно ис-
использовать равенства
va = c°%, ta = c*\, vV-/V = A G.4)
Статико-геометрическая аналогия в вариационной
форме распространяется на все функционалы, полу-
полученные из исходных пунктов — функционалов Лагран-
Лагранжа и Кастильяно. Таким образом, каждому полному
или частному функционалу теории оболочек, пред-
представленному или не представленному в табл. 4.1 —
4.5, можно поставить в соответствие его статико-гео-
метрический аналог, который можно построить с по-
помощью G.1) — G.3) и который имеет аналогичные
дополнительные условия и условия стационарности.
Смешанный функционал 9c(w, <р) теории пологих обо-
оболочек является своим собственным аналогом.
Важная черта статико-геометрической аналогии в
вариационной форме состоит в том, что она распро-
распространяется на экстремальные свойства вариационных
функционалов теории оболочек. При этом минимуму
функционала по какой-либо группе переменных соот-
соответствует максимум его аналога по соответствующей
группе переменных; минимаксу соответствует макси-

5 1\ СТАТИКО-ГЕОМЕТРИЧЕСКАЯ АНАЛОГИЯ 135
мин, седловой точке — седловая точка, а отсутствию
каких-либо экстремумов — отсутствие экстремумов.
Поэтому табл. 4.6, в которой приведена сводка экстре-
экстремальных свойств функционалов, служит одновремен-
одновременно для иллюстрации статико-геометрической анало-
аналогии в вариационной форме.
Следует иметь в виду, что любой данный функ-
функционал и его статико-геометрический аналог отно-
относятся, вообще говоря, к разным задачам.
Например, для задачи расчета оболочки с чисто
статическими граничными условиями функционал
Лагранжа Эп\ (и), представленный в табл. 4.1, не
имеет дополнительных условий; для этой же задачи
функционал Кастильяно Зк^яр) не имеет контурного
интеграла, но имеет дополнительные условия, ука-
указанные в табл. 4.2; а статико-геометрический аналог
данного функционала Лагранжа, который имеет кон-
контурный интеграл и не имеет дополнительных условий,
относится к задаче расчета оболочки с чисто геомет-
геометрическими граничными условиями.
Другой пример дают задачи расчета многосвяз-
многосвязных оболочек, разобранные в гл. 5. Функционал Ка-
Кастильяно для многосвязной оболочки при статических
граничных условиях имеет в качестве одного из усло-
условий стационарности уравнения неразрывности конту-
контура отверстия; его аналог — функционал Лагранжа —
имеет в качестве условий стационарности уравнения
равновесия контура отверстия, но для задачи с де-
деформационными граничными условиями. Этот пример
показывает, что вариационная форма статико-геомет-
статико-геометрической аналогии позволяет глубже увидеть связь
уравнений и найти ее между соотношениями, которые
раньше казались несвязанными.
Таким образом, статико-геометрическая аналогия
в вариационной форме проявляется по всем четырем
взаимосвязанным каналам: 1) между функционалами;
2) между дополнительными условиями; 3) между есте-
естественными условиями в области и на контуре; 4) меж-
между экстремальными свойствами функционалов. Она
имеет место как для односвязных, так и для много-
связных областей.

136 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
При расчете оболочек по линейной теории всегда
решаются две задачи: исходная и ее аналог. Напри-
Например, алгоритм или программа, предназначенная для
решения задач теории оболочек в перемещениях, бу-
будет давать решение сразу двух задач: данной — в пе-
перемещениях и ее аналога — в функциях напряжений.
Существование аналогии облегчает вывод вариацион-
вариационных формулировок многих задач теории оболочек.
При использовании статико-геометрической анало-
аналогии в вариационной форме проявляется преимущество
вариационных формулировок, охватывающих все сто-
стороны задачи и согласующих дифференциальные урав-
уравнения и граничные условия. В частности, эта форма
содержит в себе аналогию между статическими и гео-
геометрическими граничными величинами, между геомет-
геометрическими граничными условиями в перемещениях
или деформациях и статическими — в функциях на-
напряжений или усилиях, а также между сложными
граничными условиями для односвязных и многосвяз-
пых областей.
Замечание. Из табл. 4.1—4.6 можно получить
статико-геометрическую аналогию в вариационной
форме для различных вариантов теории оболочек,
обладающих ею в дифференциальной форме и отли-
отличающихся от использованного в данной книге ва-
варианта [4.12] выбором деформаций и усилий, напри-
например, [П. 10, 4.7, 4.11]. Для этого нужно использовать
связь деформаций и усилий рассматриваемой теории
с [4.12] (см., например, §§ 1 и 8).
§ 8. Развернутая форма записи функционалов
в различных системах координат
В данном параграфе приведены характеристики некоторых
наиболее употребительных систем координат (метрические тензо-
тензоры, символы Кристоффеля) и рассмотрен переход от тензорной
формы записи функционалов к развернутой. Приведен ряд пол-
полных и частных функционалов в развернутой форме в криволи-
криволинейных ортогональных координатах.
8.1. Различные системы координат и их метрические теи-
зоры и символы Кристоффеля.
8.1.1. Ортогональные (прямоугольные) координаты. В любых
ортогональных координатах компонент an метрического тензора

5 8] РАЗВЕРНУТАЯ ФОРМА ЗАПИСИ ФУНКЦИОНАЛОВ 137
равен нулю. Остальные два компонента обычно заменяют величи-
величинами At — параметрами Л яме базисной поверхности — по форму-
формулам
^а~ааа (не суммировать). (8.1)
Если, кроме того, координатные линии совпадают с линиями кри-
кривизны, то некоторые коэффициенты второй квадратичной формы
равны нулю (б12 = Ь12 = bl2 = b'f = 0), что приводит к допол-
дополнительным упрощениям.
В табл. 4.7 приведены коэффициенты первой и второй квад-
квадратичных форм и символы Кристоффеля для некоторых наиболее
распространенных систем координат. Эти величины дают возмож-
возможность легко записать все формулы из §§ 1—7 в развернутой
форме. В некоторых системах ортогональных координат (напри-
(например, в круговых цилиндрических) метрические коэффициенты
а?»3~ константы, поэтому символы Кристоффеля обращаются п
нуль, и выражения для ковариантпых производных упрощаются.
Различные частные виды ортогональных координат исполь-
используют при расчете оболочек, имеющих соответствующую форму:
цилиндрические координаты — для расчета цилиндрических обо-
оболочек, сферические — для сферических оболочек и т. д.
8.1.2. Прямолинейные косоугольные координаты на плоскости
(табл. 4.7) — важный частный вид координатной системы. Эти
координаты удобны, например, при расчете параллелограммных
пластинок с ребрами. Система функционалов для параллело-
граммиых ребристых пластинок в развернутой форме приведена
в [0.21.
8.2. Развернутая форма записи функционалов в криволиней-
криволинейных ортогональных координатах. Чтобы представить функциона-
функционалы в развернутой форме, нужно использовать, аналогично § 7
гл. 3, формулы и правила из Приложения 2. Ниже будем рас-
рассматривать координатные сетки, образованные линиями главных
кривизн, т. е. сопряженные координаты, в которых
612 = 612 = 0. (8.2)
8.2.1. Развернутая форма записи некоторых выражений, при-
приведенных ниже, использована в § 8.2.2.
а) Уравнения равновесия. Левая часть момеитного уравнения
равновесия A.25)
В (М, Т) = V0VpMpa + Ьо0Тар + q (8.3)
в физических компонентах имеет вид
В (М, Т) = t (%РыМт + bmTm) +? = 0. (8.4)
<т, р» 1

138 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
Преобразуем члены, содержащие производные, воспользовавшись
формулами для физических компонентов ковариантных производ-
производных (Приложение 2):
2
г — Т7 | > V М \ I V I \
(оа) 1 ?_i (р) <pl) I 21 Z-/
V р / V р
\\V(P)M(I
a, r-1
(Z v<») 2+як л>- ¦ (Z 7<л
Z 7<а»] +[^Z 7л>] J
та {[ ] [
k {[ ( ^ +
-}- (а5)
Перейдем к усилиям и моментам [П. 10], которые определены в
сопряженных координатах и связаны с Т, М равенствами
Т(Н) — Tl< 7"B2) = T2' SA2) = 5B1) = S> -g „
Af(U) = М{, М&2) = М2, М A2) = МB1) = Я;
при этом
Tm-Tm^S + ^(±- + -^-), (8.7)
где
В этих усилиях и моментах выражение D) принимает вид
в ш, Т) = - Ii - ? + ^
^ (^я)д - лt> 2м,
= 0. (8.9)
Преобразуем к развернутой форме левые части тангенциальных
уравнений равновесия A.25)
Ва (М, Т) = Vproa - b^VpM00 + qa. (8.10)
Первый физический компонент выражения A0) имеет вид
% <«• Г) = Z [V(P)^(PU - Z 6(.a) V(po)] + <?,„. (8.11)

РАЗВЕРНУТАЯ ФОРМА ЗАПИСИ ФУНКЦИОНАЛОВ 139
Используя формулы для физических компонентов ковариантных
производных (Приложение 2) и переходя к усилиям F), получим
0. (8.12)
Аналогично получается развернутое выражение В2{М,Т), к ко-
которому можно перейти от A2), выполнив замену индексов
Aч* 2). Соотношения (9) и A2) дают развернутую форму
записи уравнений равновесия для оболочек в криволинейных ор-
ортогональных координатах.
б) Геометрические уравнения. Зависимости между тангенци-
тангенциальными деформациями и перемещениями
ЯаВ (8, и) = 8аВ -1 (VaH3 + Va) - ba&w = 0 (8.13)
в физических составляющих имеют вид
*taB) (е- ») = е(«В) ~ Т (V(«)"(S) + V(8)"(a)) - *(оВ)* = °- (8Л4>
где V(aj — физические компоненты коварнантной производной
(см. Приложение 2). Через компоненты деформации [П. 10]
со
8(Щ — el> еA2) — у- еB2) = Е2, ^gl5j
величины ?((,3) могут быть выражены в сопряженных коорди-
координатах следующим образом:
№16)
ЯA2) (е, „) =?B1) (е, „) = 4-[» ~ 4Hl7) . ~
Физические компоненты зависимостей между изгибными дефор-
деформациями и перемещениями
О*.«) = р„в - т
&(ctp)V(B)"(p) + 6(8p)V(a)"(p) -

НО ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ ОБОЛОЧЕК [ГЛ. 4
в компонентах деформации A5) имеют вид
*,„,(*, в) = *,--!. О, .1-^^1.2*» = ° A^2), (8.19)
Я A2) (*> «) = *<21) (*> «) =
где
в) Уравнения неразрывности деформаций A.13) преобра-
преобразуются аналогичным образом и в компонентах деформации A5)
имеют вид
L ( ) {(А\ (Л) Л
), 2
г) Развернутая форма записи физических зависимостей A.20)
в компонентах деформаций A5) и усилий F) очевидна.
д) Развернутая форма записи статических граничных усло-
условий A.26)
Q, (Л, Г) = v,
A
AIvv(iM) = -
где
За2 '
/. (8.25)

§ 9] О ФУНКЦИОНАЛАХ ДЛЯ НЕЛИНЕЙНЫХ ЗАДАЧ 141
При этом
Vi = cos y, V2 = sin v> 11 = — sin Y> h = cos y. (8.26)
где y — угол между направлением а1 н нормалью v к контуру С.
Круглые скобки у индексов физических компонентов всюду
опущены.
е) Развернутая форма записи деформаций граничного эле-
элемента A.36), A.39):
ХЦ (е, х) = ;2х2 + t, (т - ^) + A. 8(v (I ^>2),
где
8/v = 'iv,8i + '2V282 + (tiVi + hvi) -у . (8.28)
8.2.2. Развернутая форма записи функционалов приведена в
табл. 4.8—4.10 и в [0.2]. Их вывод аналогичен § 7 гл. 3 н осно-
основывается на формулах § 8.2.1.
§ 9. О вариационных функционалах
для некоторых нелинейных задач теории оболочек
Теория преобразования вариационных проблем [0.9] приме-
применима, конечно, не только к квадратичным функционалам, которым
соответствуют линейные краевые задачи: известны примеры ее
применения для исследования вариационных принципов в некото-
некоторых нелинейных задачах теории оболочек, но без исследования
выпуклости и экстремальных свойств функционалов.
а) Гибкие пологие оболочки. Исследование системы функцио-
функционалов геометрически нелинейной теории оболочек с точки зрения
стационарности, вообще говоря, не встречает затруднений; оно
выполняется аналогично данной главе и связано лишь с учетом
в геометрических соотношениях нелинейных членов. Система ва-
вариационных принципов теории гибких пологих оболочек (глад-
(гладких) (т. е. геометрически нелинейной теории пологих оболочек)
на основе теории [0.9] была исследована в [0.4]. Для ребристых
гибких пологих оболочек система вариационных уравнений н
функционалов была построена и изучена в [0.2, 4.1].
Исследование экстремальных свойств функционалов геометри-
геометрически нелинейной теории связано с определенными трудностями
(невыпуклость, наличие нескольких локальных экстремумов) и
еще не выполнено.
б) Вариационные принципы для линеаризованных задач рас-
расчета ребристых оболочек в упруго-пластической стадии исследо-
исследовались в [4.5, 4.9].

Глава 5
ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ
ПРИНЦИПОВ ДЛЯ АНАЛИЗА И РЕШЕНИЯ
ЗАДАЧ ТЕОРИИ УПРУГОСТИ
И ТЕОРИИ ОБОЛОЧЕК
Все приведенные в предыдущих главах вариацион-
вариационные функционалы теорий упругости и оболочек
являются эффективным средством качественного ана-
анализа вариационных и дифференциальных формули-
формулировок и служат теоретической основой для построе-
построения прямых вариационных и вариационно-разностных
методов, получающих все большее развитие и приме-
применение благодаря возрастающим возможностям ЭЦВМ.
В этой главе показаны некоторые возможности тео-
теоретического анализа сложных задач теорий упругости
и оболочек и практического применения вариационных
формулировок для построения алгоритмов решения
этих задач и исследования их точности.
§ 1. Различные формы вариационных уравнений
теории упругости и теории оболочек
Вариационные уравнения, соответствующие функ-
функционалам, приведенным в гл. 3 и 4, можно вывести
обычным путем по правилам вариационного исчисле-
исчисления. Левые части их имеют энергетическую структуру
и выражают работу обобщенных сил на соответ-
соответствующих возможных обобщенных перемещениях
(для вариационного уравнения Лагранжа) или обоб-
обобщенных перемещений (деформаций) на возможных
обобщенных силах (для уравнения Кастильяно), или
их комбинаций в полных и различных смешанных
формах. При этом возможными называются обобщен-
обобщенные перемещения (силы), которые удовлетворяют до-
дополнительным условиям, наложенным на них, следую-
следующим из дополнительных условий данного функцио-

$ 1] РАЗЛИЧНЫЕ ФОРМЫ ВАРИАЦИОННЫХ УРАВНЕНИЙ 143
нала. В вариационных уравнениях для полных функ-
функционалов все обобщенные силы и обобщенные переме-
перемещения возможны.
В этом смысле вариационному уравнению Ла-
гранжа соответствует принцип возможных перемеще-
перемещений, уравнению Кастильяно — принцип возможных
напряженных состояний, а полным и другим част-
частным— различные общие и частные вариационные
принципы (см. гл. 1, § 2).
Интегрирование по частям с применением фор-
формулы Грина, Стокса или Остроградского позволяет
получить несколько форм одного и того же вариа-
вариационного уравнения.
Для полного функционала Э существует следую-
следующая форма:
где би« — вариации независимых аргументов «,• функ-
функционала, fi(iij), (fi(Uj) — левые части уравнений, вы-
выражающих равенства дЭ/dui = 0 соответственно в об-
области Q и на ее границе дп и приведенных в табли-
таблицах функционалов, Q = V, dQ = S для трехмерного
тела, Q = S, dQ = С для оболочки, at, Р» — постоянные
множители, которые с целью упрощения были отбро-
отброшены в записи условий стационарности, приведенных
в таблицах функционалов, гл. 3 и 4. Равенство A)
может служить для контроля правильности вариа-
вариационного уравнения полного функционала. Таким об-
образом, имеющиеся в таблицах функционалов сведе-
сведения, а именно: условия стационарности, позволяют
для полных функционалов упростить процедуру вы-
вывода вариационных уравнений и составить их по
форме A).
Для частных функционалов такая непосредствен-
непосредственная взаимосвязь между условиями стационарности
и вариационным уравнением отсутствует. Дополни-
Дополнительные условия, наложенные на аргументы щ функ-
функционала, влекут за собой (см. гл. 1) дополнительные
условия для вариаций биг, которые необходимо

144 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
учитывать при выводе условий стационарности. В гл. 1
было указано два способа получения условий стацио-
стационарности частного функционала: а) из вариационного
уравнения для соответствующего полного функцио-
функционала путем наложения дополнительных условий;
б) с помощью общих решений для дополнительных
условий или выбора допустимого подпространства для
варьируемых функций.
Приведем несколько примеров получения вариа-
вариационных уравнений полных и частных функционалов.
Пример 1. Вариационное уравнение полного
функционала Эп2{и, е, а) в основном пространстве
состояний (табл. 3.3) имеет вид
63п2 = JJJ {(е- а - а) ¦ -бе - 6а- [е - I (Vu + «V)] +
-f а- -6 j(Vu + «V) -F • 6u} dV - [[ (f)' -6udS-
-0-ndS = O, A.2)
где все вариации ба, бе, 8а независимы. Выражение
о--бу (Vm + mV), которое в силу симметрии тензора
а равно 0--S(Vu), с помощью формулы дифферен-
дифференцирования произведения и равенства 8(Tu) = V(8u)
можно представить в виде V- (о-би)— (У-а) -8и. Объ-
Объемный интеграл от первого слагаемого можно преоб-
преобразовать в поверхностный по формуле Остроград-
Остроградского (см. Приложение 2) и получить другую форму
вариационного уравнения B):
- [е - j (У и + mV)] ¦ • ба} d V + J J (о • п - f)' -6udS-
-\\(и — «*)" • ба• иdS = 0. A.3)
Вариационное уравнение в форме C) используется
для вывода условий стационарности, а также в ме-
методе Бубнова — Галеркина, в форме B)—в методе

§ 1] РАЗЛИЧНЫЕ ФОРМЫ ВАРИАЦИОННЫХ УРАВНЕНИЙ 145
Ритца и при выводе вариационно-разностных схем
(см. §§ 3 и 4).
Пример 2. Вариационное уравнение полного
функционала Эп3(е, ц, ф) в деформациях и функциях
напряжений в теории оболочек (табл. 4.3) может
быть получено таким же путем, как B), с заменой
объемных интегралов поверхностными, а поверхност-
поверхностных контурными, и преобразовано к нескольким раз-
различным формам; приведем две из них:
[МаР (г, м) - Моа3] 6цаВ - o|;aLa (бе, 8ц) - cpL (бе, 6ц) -
- 6t|>aL« (г, ц) - 6cpL (г, ц)} dS + J [<иа (бе, 6м) +
Ф*% (ве) + ЛЧ* (б8)]'dC + J {Ч, [«" (с> I») - х^] +
+ 6Ф [х (в) - хJ + г, Fv|-) [в„ (е) - е;,]}" dC +
[фах« Fе, 6,.) + Фх (бе) + Л (*) е„ (ве)Г dC = 0; A.4)
= J \ {[Г6 (в, ,а) - ГаВ (if)] 6еар + [Ма6 (г, fx) -
- La (8, ц) 6фа - L (e, |i) 6ф} d5 -
а) Ий (бБ- 6.») + (Ф - Ф*) X F8) +
+ (П - V) в„ (ве)]' t?C + ^ {[ха (в, М) - *а.] 6^а +
+ [х (в) - хJ 6Ф + [е„ (8) - Б^] л(в*)>" <*С = 0. A.5)
Пример 3. Вариационное уравнение Кастилья-
но теории оболочек в усилиях может быть получе-
получено из частного функционала Кастильяно ЭКЗ(М, Т)
(табл. 4.2):
6-9кз = \ \ [- йав (М, Т) 6МаВ - еар (М, Т) бГаВ] dS -
^0. A.6)

146 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
Здесь вариации 6М, 6Т связаны однородными урав-
уравнениями равновесия и однородными граничными усло-
условиями, так как и М, Т, и М -f 6М, и Т -f 6Т должны
удовлетворять дополнительным условиям функцио-
функционала. Поэтому из F) нельзя непосредственно сделать
никаких выводов об условиях стационарности.
Пример 4. Смешанное вариационное уравнение
теории пологих оболочек для прямоугольной в плане
изотропной оболочки в декартовых координатах мо-
может быть получено, например, из смешанного функ-
функционала 5c(ay,tp) (табл. 4.5):
{[Q (w, ф) - Q.] бш + [Af (да, ф) - М,]G(ого)}' dC +
{[% (ш, Ф) - х,] бФ + [е(г (а,, Ф) - г](] г, (бф)}" dC. A.7)
В силу дополнительных условий к функционалу 6w
и бф должны удовлетворять однородным граничным
условиям Fш)" = 0, [Q«(Sf)]' = 0 на С.
§ 2. Особенности вариационных формулировок
при сложных граничных условиях, в том числе
для многосвязных областей
В гл. 3 и 4 приведены вариационные функционалы
теорий упругости и оболочек для случая простых гра-
граничных условий, когда геометрические величины за-
заданы на одном связном участке границы так же, как
и статические (сюда включены и смешанные гра-
граничные условия — эти участки могут пересекаться).
В более сложных случаях необходимо учитывать связь
между перемещениями и усилиями на различных связ-
связных участках границы, влияющую либо на функцио-
функционал, либо на дополнительные условия к нему. В этих

§ 2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 147
случаях есть особенности и в методике вывода усло-
условий стационарности. Например, для многосвязных
оболочек со статическими граничными условиями не-
необходимо учитывать уравнения неразрывности кон-
контура, которые являются условиями-стационарности
функционала Кастильяно и дополнительными усло-
условиями— для функционала Лагранжа.
При вариационной формулировке любой сложной
задачи нужно уделять особое внимание обеспечению
полного набора независимых вариаций разрешающих
функций. Тогда совокупность условий стационарности
вместе с дополнительными условиями для используе-
используемого функционала представляют все уравнения, не-
необходимые для правильной формулировки задачи, в
том числе и граничных условий.
В ряде случаев при решении задач со сложными
граничными условиями можно использовать пред-
представление их как контактных задач, проводя искус-
искусственную линию контакта или поверхность контакта,
при достаточно простых граничных условиях для каж-
каждой части. При этом дополнительными условиями к
функционалам являются статические и (или) геометри-
геометрические условия контакта.
Ниже для функционалов Лагранжа и Кастильяно
разобрано несколько характерных примеров, которые
дают представление об общей методике учета слож-
сложных граничных условий при вариационной постановке
задач теории упругости и теории оболочек. Для дру-
других функционалов можно использовать эту методику,
а также теорию преобразования вариационных проб-
проблем с функционалами Лагранжа и Кастильяно в ка-
качестве исходных пунктов, а для теории оболочек —
статико-геометрическую аналогию в вариационной
форме (гл. 4, § 7).
2.1. Некоторые дополнительные сведения о связи перемеще-
перемещений с деформациями и напряжений с функциями напряжений
понадобятся при обсуждении примеров со сложными граничными
условиями.
а) Векторы перемещений и и углов поворота (о в любой точ-
точке В трехмерного тела можно определить по известным началь-
начальным значениям «л, а>л в точке А н известным деформациям с

148 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
помощью формул Чезаро (см., например, [3.3])
в
B.1)
А
,-rA)+ \dr-[e + (Vco) X {rB - г)].
А
Вектор углов поворота в данной точке связан с вектором переме-
перемещений в ее окрестности:
Чтобы перемещения определялись формулами A) однозначно
(независимо от пути интегрирования), необходимо чтобы равен-
равенства
' B.3)
(Sj> dr ¦ [е + (Va) X (rB - г)] = О
i
выполнялись для любого замкнутого контура /. Отсюда, исполь-
используя формулу Стокса, можно вывести дифференциальные уравне-
уравнения неразрывности Сен-Венана (см., например, [5.13]).
б) Перемещения и и углы поворота Qt в точке В базисной
поверхности S оболочки при известных нх значениях ua, (й()л
в начальной точке А и известных деформациях поверхности i>
определяются формулами A.41) гл. 4.
Из этих формул следуют уравнения, которым должны удо-
удовлетворять деформации, чтобы вычисленные по ним перемещения
были однозначными:
К = & х dC = О, Е = & [(г - г0) X х + ettt] dC = 0 B.4)
l i
для любого замкнутого контура / на поверхности S (выражение ?
получается из A.41) гл. 4 интегрированием по частям). Из D)
могут быть с помощью формулы Грипа выведены уравнения не-
неразрывности A.13) гл. 4. Векторы К и Е по аналогии с в) назо-
назовем главным вектором и «глаоным моментом» деформаций эле-
элементов контура /.
в) Функции напряжений \|з и «углы напряжений» 0/ в обо-
оболочке при известных усилиях можно определить с точностью до
начальных значений ifu, (вг)л в точке А по формулам A.45)
гл. 4.

§ 2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 149
Уравнения равновесия любой части Si оболочки, ограничен-
ограниченном замкнутым контуром /, представляют собой условия равен-
равенства кулю главного вектора F и главного момента G внешних и
внутренних сил, приложенных к этой части:
B-5)
г X <? (М, Т)] dC = 0
(которые получаются с помощью A.45), гл. 4 и интегрирования
по частям). Отсюда можно вывести дифференциальные уравнения
равновесия с помощью формулы Грииа. Если вектор нагрузки q
выразить через Мо, Го, то поверхностные интегралы можно пре-
преобразовать в контурные; получим уразнения равновесия E) в
виде
F = &[Q(M,T)-Q (Мо, Г„)] dC = О,
I
с B 6)
+ г X [<? (М, Т) - Q (Мо, Г.)]} dC - О,
где контур / может состоять из нескольких замкнутых кривых.
В случае односвязной оболочки эти уравнения представляют со-
собой условия однозначности функций напряжений (иезавнсимости
от пути интегрирования). В многосвлзной оболочке интегралы F)
по контуру, охватывающему отверстие, зависят от главного век-
вектора и главного момента внешних сил, приложенных к контуру от-
отверстия; поэтому они могут быть любыми наперед заданными
величинами и определяют «статические дисторсии» (сравните
с д)). Следовательно, если в многосвязной оболочке к контуру
отверстия приложена несамоуравновешелмая нагрузка, то функ-
функции напряжений могут быть многозначными с многозначностями
типа днсторсий.
г) Функции напряжений в трехмерном теле определяются на-
напряжениями с точностью не до шести констант, как перемеще-
перемещения— деформациями, а с точностью до произвольных функций,
дающих нулевые напряжения и эквивалентных бесконечному мно-
множеству констант. Вероятно, поэтому для определения функций
напряжений нет формул, аналогичных A).
При рассмотрении сложных граничных условий в теории
упругости могут быть полезны равенства, выражающие главный
вектор Р и главный момент G поверхностных сил (относительно

150 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 6
начала координат) через функции напряжении [3.3]:
р = С С а ¦ п dS = [[ а" • п dS + & dl • (q> X V),
s '
Х'°-яй+ B.7)
Кроме того, нужно иметь в виду, что уравнения равновесия лю-
любой части тела представляют собой условия равенства нулю
главного вектора и главного момента приложенных к ней сил:
Bl8)
V
Отсюда с помощью формулы Остроградского можно вывести
дифференциальные уравнения равновесия (см., например, [3.3]).
д) Дисторсии в теории упругости и теории оболочек. На
основании теоремы единственности теории упругости в односвяз-
ном теле при отсутствии внешних сил напряжения и деформации
равны нулю. В поверхностно-многосвязном теле и при отсутствии
нагрузок может существовать ненулевое напряженно-деформиро-
напряженно-деформированное состояние, которое может быть получено следующим об-
образом.
Превратим миогосвязное тело в одиосвязное путем необхо-
необходимого числа разрезов, сдвинем обе стороны сечеиий друг отно-
относительно друга и соединим сечения, убирая нли добавляя мате-
материал там, где это необходимо, и снова получая миогосвязное
тело. При этом векторы взаимных смещении Аи и углов пово-
поворота До соединяемых сечений выражаются формулами (см., на-
например, [3.3, 5.131)
До = const, Аи = Аи0 + Дю X г,. B.9)
которые показывают, что Ди представляет собой жесткое смеще-
смещение, так что края склеиваемых сечений должны иметь одинако-
одинаковую форму. Этот способ получения напряжений в поверхностно-
многосвязиом теле (типа тора) называется дисторсиями (или
дислокациями) Вольтерра, которые характеризуются векторами
Д«о и До.
Аналогичным образом вводятся дисторенн в многосвязной
оболочке. Для оболочек существует лишь одно понятие миого-
связиостн, так что иеодносвязиая оболочка обладает свойствами,
аналогичными тем, которые имеют пространственно-неодносвяз-

§ 2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 151
ные тела, и тем, которые имеют поверхностно-неодносвязпые
трехмерные тела. Ниже мы увидим, что особые свойства про--
странственно-многосвязных тел связаны с уравнениями равнове-
равновесия н условиями стационарности функционала Лаграижа, а по-
поверхностно-многосвязных — с уравнениями неразрывности и усло-
условиями стационарности функционала Кастильяно.
2.2. Учет сложных граничных условий при исполь-
использовании различных вариантов функционала Лагран-
жа в теории оболочек.
а) Несколько связных участков контура с задан-
заданными перемещениями и*, О* (рис. 5.1,а, б). В этом
Рис. 5.1. Два связных участка контура оболочки с заданными
перемещениями, а) Края АС и BD жестко закреплены; б) контур
оболочки и контур отверстия жестко закреплены.
случае функционалы Лагранжа ЭЛ1, Эл2, Эл4 и их до-
дополнительные условия и условия стационарности не
имеют никаких особенностей по сравнению с табл. 4.1.
При переходе от Эщ к Эт(е) требования непрерыв-
непрерывности перемещений должны быть сформулированы в
деформациях; в рассматриваемом случае граничных
условий при этом появляются специфические уравне-
уравнения, отличные от приведенных в табл. 4.1.
Для функционала Элз (г, ц) дополнительные усло-
условия A.42) гл. 4 (деформационные граничные условия)
содержат не всю информацию о взаимных переме-
перемещениях различных участков контура, поэтому, кроме
них, должны быть поставлены дополнительные условия
в деформациях, задающие взаимные перемещения
и углы поворота различных связных участков части
Си контура С, на которой поставлены геометрические
граничные условия. Эти дополнительные условия с

152
ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ.5
помощью формул A.41) гл. 4 могут быть записаны
в виде
А
В
Х(гв-гА)] = 0, B.10)
где и*А> и*в — заданные векторы перемещений в точ-
точках А и В, принадлежащих различным связным уча-
участкам части Си контура С; (Ф)л> (Ф)д ~~ заданные
векторы углов поворота в точках А и В.
Эти уравнения являются условиями стационарно-
стационарности функционала Кастильяно (см. § 2.3а).
Для функционала 3Лз (w, г) из шести условий A0)
нужно ставить лишь три, связывающие перемещения
а) б)
Рис. 5.2. Деформационные граничные условия для оболочки.
а) Участок контура CD подкреплен абсолютно жестким телом;
б) отверстие подкреплено абсолютно жесткой шайбой D.
w и углы поворота (Qt)A, (tit)в различных связных
участков Си-
б) Несколько связных участков контура с задан-
заданными деформациями х, е« (например, рис. 5.2:
а) часть контура подкреплена незакрепленным абсо-
абсолютно жестким телом; б) отверстие, подкрепленное аб-
абсолютно жесткой шайбой). Здесь фактически смешан-
смешанные граничные условия: на подкрепленных участках
контура Си известны как деформации, так и главный

§ 2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ lg1?
вектор и главный момент нагрузки. В этом случае функ-
функционалы Э;и — Эда отличаются от представленных в
табл. 4.1 тем, что содержат слагаемые неинтеграль-
неинтегрального вида, представляющие собой работу внешних
сил на соответствующих им перемещениях:
F°ua + F.w + O*Qa + GtQ, B.11)
где F", /%,— компоненты главного вектора, G", G* —
компоненты главного момента нагрузки на жесткое
подкрепление относительно какой-либо точки D, рас-
расположенной в жестком подкрепляющем элементе,
иа, w, Qa, Q — компоненты вектора перемещений и
вектора углов поворота в этой точке. Заменить в этих
слагаемых векторы перемещений и углов поворота на
деформации невозможно, так что функционал
5>лз (s, (л) зависит не только от деформаций, но и от
перемещений и углов поворота (по шесть параметров
на каждый подкрепленный участок).
Условия стационарности функционалов Эщ — Эле
в данном случае содержат, кроме равенств, приведен-
приведенных в табл. 4.1, еще уравнения интегрального вида
(см. ниже A4)), по шесть на каждый участок. Эти
условия легче всего вывести из функционала Лагран-
жа Эл1 (и), который в данном случае имеет вид
= Эл1 (я) + F>« + /> + G^Q" + G\ B.12)
где слагаемое Эл1 (и) представлено в табл. 4.1. Де-
Деформационные граничные условия (условия недефор-
недеформируемости подкрепленных частей контура), записан-
записанные в перемещениях, представляют собой дифферен-
дифференциальные уравнения относительно перемещений; их
общее решение можно представить в виде
в = в' + <*, + <*2Хг, B.13)
где и* — какое-либо частное решение, d\, d2 — неиз-
неизвестные векторы (произвольные постоянные), для
определения которых нет геометрических условий. Эти
константы можно выразить через векторы перемеще-
перемещений и углов поворота и, Qt подкрепленного участка,
участвующие в A1). Варьируя и, Q, найдем, что среди

154 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
условий стационарности функционала Лагранжа есть
уравнения вида
в
в
которые уместно назвать уравнениями равновесия под-
подкрепленных частей контура. Они являются дополни-
дополнительными условиями к функционалу Кастильяно для
данной задачи (см. § 2.36) и аналогичны уравнениям
неразрывности контура (см. § 2.2а, в и § 2.3а).
В частности, в случае многосвязной базисной по-
поверхности оболочки, имеющей подкрепленные абсо-
абсолютно жесткой шайбой отверстия (как на рис. 5.2,6),
о) 6)
Рис. Б.З. Два связных участка контура со статическими гранич-
граничными условиями.
из функционала Лагранжа следуют уравнения равно-
равновесия контура отверстия вида A4), где интегралы
берутся по замкнутому контуру.
Если подкрепленные участки контура не нагру-
нагружены (величины F, G равны нулю), то функционал
A2) не отличается от Эл1 (и) (табл. 4.1), а среди его
условий стационарности есть однородные уравнения
вида A4).
в) Статические граничные условия в усилиях при
многосвязной базисной поверхности оболочки (рис.
5.3,6). В этом случае отличие от табл. 4.1 имеют до-

5 2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 155
полнительные условия функционала Элз (е, ц): кроме
уравнений неразрывности в области S, для него долж-
должны быть поставлены еще дополнительные условия
интегрального вида, которые уместно назвать уравне-
уравнениями неразрывности контура отверстия:
}dC = 0. B.15)
Этот факт легко обнаружить при выводе функционала
Элз (г, ix) из Эд2 (и, е, ц). При этом условие непрерыв-
непрерывности перемещений, которое для Эл2 выполняется ав-
автоматически за счет выбора пространства состояний,
переходит в систему уравнений неразрывности, среди
которых в данной задаче есть A5). Ниже дан вывод
условий A5).
Уравнения неразрывности представляют собой
условия однозначности перемещений, определяемых
по данным деформациям; эти условия можно запи-
записать в виде D), где / — любой замкнутый контур. Для
односвязной области условия однозначности переме-
перемещений D) следуют из уравнений неразрывности в
области; для многосвязной области дифференциаль-
дифференциальных уравнений неразрывности недостаточно для D),
если замкнутый контур охватывает отверстие. По-
Поэтому при переходе от D) к уравнениям неразрыв-
неразрывности в области необходимо сохранить для каждого
отверстия по одному набору уравнений A5) вида
D). В случае геометрических граничных условий они
выполняются автоматически.
Проведенное рассуждение позволяет поставить для
функционала Эля (е) задачу с дисторсиями (см.
§ 2.1д). В этом случае уравнения A5) неоднородные;
в правых частях их стоят заданные взаимные пере-
перемещения и углы поворота двух краев разреза.
Уравнения неразрывности контура A51 являются
условиями стационарности функционала Кастильяно
(см. § 2.3а) и связаны статико-геометрической ана-
аналогией с уравнениями равновесия контура (§§ 2.26,
2.36).

156 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
2.3. Учет сложных граничных условий в теории
оболочек при использовании различных вариантов
функционала Кастильяно. Разберем три примера гра-
граничных условий, аналогичных приведенным в § 2.2,
и еще несколько интересных примеров, встречавшихся
авторам в расчетной практике. При этом будем ис-
использовать статико-геометрическую аналогию и тео-
теорию преобразования вариационных проблем, в част-
частности преобразование Фридрихса.
а) Несколько связных участков контура с задан-
заданными усилиями Q*, М* (рис. 5.3, а, б). Этот случай
можно рассмотреть так же, как в § 2.26, пользуясь
вариационной формой статико-геометрической анало-
аналогии. Функционалы 3Ki — ЭКь при этих' граничных усло-
условиях отличаются от представленных в табл. 4.2 сла-
слагаемыми неинтегрального вида, см. D), E):
КаЖ + К^ + Е*ава + Е*в. B.16)
При выводе условий стационарности функционала
Кастильяно при данных граничных условиях с исполь-
использованием функций напряжений необходимо учитывать,
что граничные значения функций напряжений опре-
определяются граничными условиями не однозначно, а с
точностью до постоянных (шесть констант для каж-
каждого связного нагруженного участка). Выразив эти
константы через величины if, Qt и варьируя послед-
последние, можно обнаружить, что среди условий стационар-
стационарности функционала Кастильяно есть уравнения не-
неразрывности контура вида A5), где деформации
должны быть выражены через усилия или функции
напряжений.
В случае многосвязной оболочки (рис. 5.3,6),
когда оба конца нагруженного участка совпадают,
К* и Е* представляют собой заданные дисторсии. При
отсутствии дисторсии К* = 0, Е* = 0, и функционал
Кастильяно не отличается по виду от табл. 4.2. Но
приведенное рассуждение показывает, что величины
if, в( все равно нужно варьировать, и в результате
получаются однородные уравнения неразрывности
контура.

§ 2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 157
Замечание. Уравнения неразрывности контура
отверстия были выведены авторами [5.3] в качестве
условий стационарности функционала Кастильяно.
Преобразование Фридрихса ЭКз($, М, Т)^-Элз(г, ц)
показало, что эти условия являются дополнительными
для функционала Лагранжа Эт (г, ц), после чего они
были получены путем рассуждений, приведенных в
§ 2.2в. При этом получение уравнений A5), а также
a) 6)
Рис. 5.4. Граничные условия для оболочки, при которых на участ-
участках с заданными усилиями могут быть определены функции на-
напряжений, а) Разность функций напряжений в точках Л и В опре-
определяется главным вектором и главным моментом внешних сил,
приложенных к подкрепленному участку АВ; б) разность функций
напряжений в точках А и В определяется из условий равновесия
и симметрии.
A4) и др., как естественных и дополнительных усло-
условий различных функционалов, позволяет правильно
учесть граничные условия и лучше понять физический
смысл уравнений. Теория преобразований и расчет-
расчетная практика позволяют рекомендовать такую взаим-
взаимную проверку при решении сложных задач. Одни
условия или стороны задачи легче и яснее формули-
формулируются в связи с одними функционалами, другие —
с другими. Теория преобразования вариационных
проблем служит инструментом для исследования всех
сторон задачи и взаимной проверки различных вариа-
вариационных (и дифференциальных) формулировок.
б) Несколько участков контура с заданными функ-
функциями напряжений (рис. 5.4, а, б). Вообще говоря,

158 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
задать функции напряжений из физических сообра-
соображений в соответствии с условиями задачи нельзя:
всегда задают усилия.
Однако в случае одного связного участка контура
со статическими граничными условиями легко по за-
заданным усилиям Q*, М* определить удовлетворяющие
этим условиям функции напряжений t|)*, r|* и, наобо-
наоборот, по функциям напряжений ij?*, ri* определить уси-
усилия Q*, М„ (см. § 2.1в). В этом случае годятся любые
i|)*, ц* из всех, отличающихся друг от друга на слагае-
слагаемые типа «жесткого смещения».
В случае нескольких связных участков со статиче-
статическими граничными условиями, описанном в § 2.3а,
функции напряжений на каждом связном участке
определяются с точностью до шести констант, кото-
которые нужно варьировать.
В случаях, изображенных на рис. 5.4, задав
функции напряжений на одном участке, на другом их
можно определить однозначно. Действительно, при
наличии абсолютно жесткого подкрепления (рис. 5.4,а)
разность «углов напряжений» и функций напряжений
в точках А а В определяется главным вектором и
главным моментом внешних сил, приложенных к
участку АВ (см. E), F)), которые в данном случае
известны. Для многосвязных оболочек иногда можно
из некоторых соображений (например, из симметрии)
определить главный вектор и главный момент усилий,
действующих в сечении АВ (рис. 5.4,6), а следова-
следовательно, и разность «углов напряжений» и функций на-
напряжений в точках А и В; при нагрузках, указанных
на рис. 5.4,6, они равны нулю. Эту задачу можно
решать как способом, описанным в § 2.3а, так и опи-
описанным ниже способом, в котором константы ij), St
уже найдены из соображений симметрии и не варьи-
варьируются. В любом случае необходимо использовать
разрывные функции напряжений (см. § 2.1в).
По аналогии с § 2.2а можно заключить, что при
рассматриваемых граничных условиях имеет особен-
особенности функционал ЭщзШ. Т). Статические граничные
условия в усилиях A.26), гл. 4, содержат не всю ин-
информацию о нагрузке на различных участках контура;

2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 159
кроме них должны быть поставлены уравнения рав-
равновесия участков АВ (рис. 5.4) или, что то же самое,
уравнения, согласующие значения функций напряже-
напряжений и «углов напряжений» в точках А и В:
в
\ [q (м, т) - q (мо) г„)] dc = (е;)в - (е;)л = f\
А
(M) - Mvv (М „)] + (г - гв) X [Q (М, Т) -
-Q[Mo,To]}dC =
=-фа - t|U - (в;)л X (гв - гА) = G*. B.17)
Для функционала ЭК5(ц>, М) из шести условий A7)
нужно ставить лишь три (сравните с § 2.2а).
в) Деформационные граничные условия при много-
многосвязной базисной поверхности (рис. 5.2,6). В этом
случае отличие от табл. 4.2
имеют дополнительные усло-
условия функционала 3Кз(М, Т):
кроме уравнений равновесия в
области S, для него должны
быть поставлены дополнитель-
дополнительные условия интегрального ви-
вида A4) (уравнения равновесия
контура отверстия), по шесть
на каждое отверстие в поверх-
поверхности S. Эти дополнительные
условия функционала Экз мож-
можно получить тремя путями:
1) формально по статико-гео-
метрической аналогии с уравнениями неразрывности
контура (§ 2.2в); 2) при преобразовании Фридрихса
функционала Лагранжа (см. § 2.26); 3) с помощью
рассуждений, аналогичных проведенным в § 2.2в, ис-
используя вывод уравнений равновесия из условий E).
г) Расчет жестко защемленной по боковым сторо-
сторонам балки-стенки (плоская задача теории упругости)
в функциях напряжений (рис. 5.5). Для решения пло-
плоской задачи теории упругости можно использовать
Рис. 5.5. Балка-стенка
(плоская задача теории
упругости): коитур имеет
два связных участка с
заданными перемещения-
перемещениями и два — с заданными
усилиями.

160 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. S
функционалы теории оболочек, исключив члены, учи-
учитывающие кривизну и изгиб базисной поверхности.
Функционал Кастильяно в декартовых координатах
имеет вид
$ $ VЛ ) **
(контурный интеграл отсутствует, так как «i = «2 =
= 0). Дополнительные условия к нему — уравнения
равновесия в области
Т —1— Т = П Т Л- Т = П
1 11,1 Г х 12,2 и> ' 12,1 "Г 22,2 U
и статические граничные условия.
Общее решение уравнений равновесия имеет вид
Гп == ~ Ф.22. ri2 = Ф.12» ^г^-ф.и- С2-19)
На стороне CD можно выбрать функцию напряжений
Ф и ее нормальную производную в виде
нагрузке на стороне АВ соответствуют любые из ве-
величин вида
ц=-а.2х + Ь2, q>i2 = c2. B.20)
Из шести констант а.\, b\, c\, a2, b2, с2 три можно
выбрать произвольно и не варьировать, так как изме-
изменение трех констант соответствует прибавлению к
функции ф полинома первой степени ах -\- су -\- b, a
это не влияет на напряжения и, следовательно, на
значения функционала. Например, выберем ai = 6i =
= ci == 0; тогда а% Ь%, Сг нужно находить из условий
стационарности функционала A8), среди которых
есть уравнения
в
дЭк
B-21)
дЭк Г дЭк
^0 d

21 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 161
где х =2 ei2,i — ец,2 (см. гл. 4, § 1), а ец, е2г должны
быть выражены через Гар(ср).
д) Использование смешанного функционала
Эс(ш, ф) (табл. 4.5) для расчета пологой изотропной
х
г
b
L
-a -
6)
в)
Рис. 5.6. Оболочка типа гиперболического параболоида.
оболочки типа гиперболического параболоида (рис.
5.6, а) с граничными условиями вида
B.22)
при y =
Учет граничных условий для w не связан с какими-
либо затруднениями. Статические граничные условия
должны быть представлены через функцию напря-
напряжений <р:
<?2Ф т* »
ду2 — У"~ и>
при х = 0, а
при у — О,Ь
Q Н, П. Абэвский и др,
B.23)

162 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ (ГЛ. 5
Отсюда следует линейный закон распределения функ-
функции напряжений вдоль контурных кромок, который
может быть представлен с помощью четырех пара-
параметров— значений фл, фв, фс, фв функции напряже-
напряжений в углах. Три из этих параметров можно зафик-
зафиксировать, так как функции напряжений, отличаю-
отличающиеся друг от друга на полином первой степени
а + Ьх -\- су, дают одни и те же усилия Та$, а значит,
одно и то же значение функционала 9c(w,<р). Дру-
Другими словами, стационарное значение функционала
Эс(х0, ф) достигается на любом элементе из множе-
множества функций напряжений, отличающихся друг от
друга слагаемыми вида а -\- Ьх -\- су, и поэтому, что-
чтобы найти один какой-либо представитель этого мно-
множества, параметры а, Ь, с следует зафиксировать.
Например, можно выбрать Ча~\1&) == {~д) ===^
и получить распределение функции напряжении по
контуру с одним неизвестным параметром фс
(рис. 5.6,6). Тогда на кромках ВС и АВ <р = 0, а на
кромках ВС и CD соответственно ф = — фс и ф =
«= —- фс. Таким образом, варьируемыми параметрами
на контуре являются функция ду/dv и число фс.
При этих граничных условиях, кроме уравнений в
области и деформационных граничных условий:
при # = 0, а
1 (д\ д2<р\__(ди2 Л
~Ш \~Ш ~~ V- -Jf) = \-gf + kyw ) = 0;
при у = 0, b B.24)
из вариационного уравнения A.7) для смешанно-
смешанного функционала следует уравнение B5) — условие

§ 2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 163
обращения е
ху
j
У-Ь
Ь
'А 1дх
+ 2k*v дх
i нуль
1 .
b 1
кх
множителя
х — а
0
dw 1
при бф
¦ &
с"
X —
до
V)-
Eh
а
0
Э^2 дуJ
р.) 52ф
3^ ду
г!
B
-rr'
-6
25)
Здесь kxy — кривизна кручения, Е — модуль упругости,
ц — коэффициент Пуассона материала, h — толщина
оболочки. Выражение B5) представляет собой инте-
интегральную зависимость, связывающую функцию напря-
напряжений ф с заданной деформацией перекоса (рис. 5.6, в),
выраженной в левой части B5) через смещения угло-
угловых точек. При граничных условиях B2) левая часть
B5) равна нулю.
Таким образом, мембранная часть граничных
условий B2) реализуется линейным характером
распределения функции напряжений вдоль кромок
(рис. 5.6,6) и уравнениями B4), B5). Действитель-
Действительно, выполнение условий B4), т. е. ъп = 0 на контуре,
еще недостаточно для реализации условий отсутствия
тангенциальных смещений. Остается возможность де-
деформации перекоса (рис. 5.6,в), которая и фикси-
фиксируется условием B5).
В оболочках рассматриваемого вида условие B5)
является весьма существенным, так как учитывает
основную особенность их деформации, вызываемую
их формой (две оси антисимметрии), — стремление к
перекосу в плане даже при симметричной нагрузке.
2.4. Учет сложных граничных условий в теории
упругости. В отличие от теории оболочек, в которой
существует одно понятие многосвязной области, в
6*

164
ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
трехмерной теории упругости необходимо в одних за-
задачах учитывать пространственную многосвязность
объема, занятого телом (например, полый шар), а в
других—поверхностную мно-
многосвязность (например, тор).
а) Несколько связных уча-
участков поверхности с заданны-
заданными перемещениями (рис. 5.7).
Сюда относятся в принципе
и пространственно-неодносвяз-
ные тела.
.„ „ В этом случае функционалы
Рис. 5.7. Два связных п о q я q
участка поверхности с за- -^агранжа am, -УЛ2, ^Л4 — Оле
данными перемещениями: не отличаются от представ-
А — упругое тело, В— ленных в табл. 3.1, а Элз(е)
абсолютно жесткое тело, имеет те же особенности, что
и функционал Элз(?, ») в тео-
теории оболочек (§ 2.2а) с той разницей, что взаимные
перемещения и углы поворота различных связных
участков части Su поверхности S могут быть выра-
выражены через деформации с помощью формул Чезаро
A) и задаются уравнениями
B.26)
UD ~ «С
X (Го ~ ГС),
которые следует включить в список дополнительных
условий функционала Злз(е).
С помощью преобразования Фридрихса функцио-
функционала Элз(е) для данной задачи можно выяснить, что
уравнения B6) являются условиями стационарно-
стационарности функционала Кастильяно и что для правильного
решения ее с помощью функционала Кастильяно сле-
следует рассматривать не только непрерывные функции
напряжений, но и имеющие разрывы на линиях, сое-
соединяющих различные участки Su (сравните с § 2.4г).

% 21 ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 165
б) Несколько связных участков поверхности с за-
заданными деформациями. Примерами таких граничных
условий могут служить: контактная задача для жест-
жесткого штампа, вдавливаемого в упругое тело силой Р;
резиновый поршень, подкрепленный стальной пласти-
пластиной; упругое тело с жесткими включениями (прост-
(пространственно-многосвязное тело) (рис. 5.8,а, б, в).
о)
Рис. 5.8. Деформационные граничные условия в теории упругости.
а) Вдавливание абсолютно жесткого штампа В в упругое тело А;
б) упругое тело А между абсолютно жесткими телами В и С;
в) упругое тело с жестким включением.
В этом случае, как н в аналогичных задачах теории
оболочек (§ 2.26), все разновидности функционала
Лагранжа, приведенные в табл. 3.1, должны быть до-
дополнены слагаемыми неинтегрального вида
B.27)
где Р*, G; —главный вектор и главный момент на-
нагрузки на t-й подкрепленный участок (или на штамп).
Условия стационарности функционалов Лагранжа
5л1 — Эле, содержат, кроме равенств, приведенных в
табл. 3.1, уравнения равновесия подкрепленных участ-
участков поверхности интегрального вида, по шесть на каж-
каждый участок (в соответствии с числом варьируемых
параметров: по три компонента векторов и,- и аи):
o-ndS — G*~0. B.28)

166
ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ, 5
Эти уравнения можно получить такими же различ-
различными способами, как подобные уравнения в § 2.26.
Функционал Кастильяно при рассматриваемых
граничных условиях имеет дополнительные условия
вида B8). Этот факт можно обнаружить непосред-
непосредственно либо при преобразовании Фридрихса функ-
функционала Лагранжа Элз. С помощью формул G) эти
условия можно записать в функциях напряжений.
в) Несколько связных участков поверхности с за-
заданными напряжениями (в юм числе пространствен-
пространственно-многосвязные тела) (рис. 5 9). На каждом из этих
6)
Рис. 5.9. Несколько связных участков поверхности со статическими
граничными условиями, а) Односвязное упругое тело А (иа верх-
верхней и нижней гранях заданы напряжения, боковые грани состав-
составляют связный участок поверхности с заданными перемещениями,
В — абсолютно жесткое тело); б) пространственно-многосвязное
упругое тело (тело с полостью).
участков функции напряжений определяются задан-
заданиями напряжениями не однозначно, а с точностью до
некоторых произвольных функций. Казалось бы, функ-
функционал Кастильяно должен иметь, как и в аналогич-
аналогичной задаче теории оболочек (§ 2.3а), специфические
условия стационарности, которые согласовывали бы
значения произвольных функций на разных участках.
Но ни один вариант функционала Лагранжа, оче-
очевидно, не имеет в данной задаче никаких особых до-
дополнительных условий, так как Su — связное множе-
множество; преобразование Фридрихса показывает, что и
функционал Кастильяно не имеет никаких особых
условий стационарности по сравнению с табл. 3.2. От-
Отсутствие в данном случае специальных уравнений
Следует и из физических соображений: так как пере-

I 2] ВАРИАЦИОННЫЕ ПРИНЦИПЫ ПРИ СЛОЖНОЙ ГРАНИЦЕ 167
мещения заданы на одном связном участке, то их не
надо согласовывать, в отличие от аналогичной задачи
теории оболочек, в которой наличие нескольких связ-
связных участков Sf обязательно связано с существова-
существованием нескольких связных участков Su либо с много-
связностью базисной поверхности.
Из отсутствия в данной задаче каких-либо специ-
специфических условий стационарности функционала Ка-
стильяно можно сделать вывод, что выбор упомяну-
упомянутых выше произвольных функций не влияет на напря-
напряженное состояние тела; другими словами, отсюда
следует, что для данного поля напряжений а, удов-
удовлетворяющего уравнениям равновесия в объеме тела
и статическим граничным условиям на поверхности,
можно найти поле функций напряжений, которое на
каждом связном участке с заданными напряжениями
имеет любые наперед заданные значения ф* и if*,
лишь бы эти значения удовлетворяли условию
(с-п)(ф*, *•) = /•.
г) Статические граничные условия в напряже-
напряжениях для поверхностно-многосвязного тела (например,
Рис. 5.10. Поверхностно-многосвязное тело — тор.
тор) (рис. 5.10). В данном случае имеются особенно*
сти в дополнительных условиях функционала Лагран-
жа Элз (е) по сравнению с табл. 3.1: в список его до-
дополнительных условий следует включить уравнения
интегрального вида C), по шесть уравнений для каж-
каждой степени неодносвязносги. Эти уравнения можно
вывести путем таких же рассуждений, как в § 2.2 для
оболочек, с использованием вывода уравнений нераз*
рывности из справедливости равенств C) для каж«
дого замкнутого контура.

168 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
Поверхностно-многосвязные тела (типа тора) мо-
могут иметь днеторсии, см. § 2.1 д. Для решения задач
с дисторсиями в перемещениях необходимо делать
разрезы, превращающие область в односвязную, и за-
затем решать контактную задачу, склеивая эти разрезы.
Функционал Лагранжа в деформациях Элз {е) позво-
позволяет решать эту задачу, не делая разрезов; допол-
дополнительные условия C) в этом случае неоднородные:
в правых частях их стоят заданные величины ди-
сторсий.
Преобразование Фридрихса позволяет определить,
что при данных граничных условиях уравнения вида
C) являются условиями стационарности функционала
Кастильяно, несмотря на то, что вся поверхность 5/
представляет собой единственный связный участок
с заданными напряжениями (в отличие от соответ-
соответствующей задачи теории оболочек, в которой есть
два различных участка со статическими граничными
условиями).
Преобразование Фридрихса показывает также, ка-
каким образом из функционала Кастильяно следуют
уравнения неразрывности контура C). Построим из
Элз(е) полный функционал Эпч (е, q, h, \.ч), внеся в
него все дополнительные условия, в том числе и C),
с множителями Лагранжа; получим
>/е<* - V/,) d*?e, - До
ц, Г§ dr ¦ [е + (?©) X (гв - г)] XdC- Аи 1|.
Смысл h. |li,- можно выяснить, если предположить, что
функции ср„- могут иметь разрывы вдоль контура U;
тогда из вариационного уравнения 65П! = 0 следует,
что Я,», \ii представляют собой постоянные величины
разрывов некоторых комбинаций компонентов ср,у на
контуре /.

§ 3] О КЛАССИФИКАЦИИ ПРЯМЫХ МЕТОДОВ ]69
Выходит, чтобы правильно решить задачу теории
упругости для поверхностно-многосвязиой области V
с помощью функционала Кастильяно, необходимо рас-
рассматривать в качестве варьируемых параметров не
только непрерывные функции напряжений, но и имею-
имеющие разрывы на некотором контуре /. Условия ста-
стационарности вида C) получаются при варьировании
величии разрывов.
Очевидно, разрывные функции напряжений можно
рассматривать и для односвязных тел, но получаю-
получающиеся при варьировании разрывов уравнения вида
C) являются в этом случае следствием уравнений не-
неразрывности Сен-Венана.
§ 3. О классификации прямых вариационных
методов расчета
Теория преобразования вариационных проблем
дает в наше распоряжение все множество вариацион-
вариационных функционалов, точки стационарности которых
являются решением задачи теории упругости или
теории оболочек; наиболее интересные из них приве-
приведены в гл. 3 и 4. В каждой вариационной формули-
формулировке задачи принципиально можно применить любой
из прямых методов решения: вариационные методы
в аналитической, численной и комбинированной
форме.
Расчет упругой системы вариационным методом
можно разделить на две взаимосвязанные составные
части. Первая состоит в выборе наиболее подходя-
подходящего функционала, вторая—-в решении вариационной
задачи для выбранного функционала.
С этими двумя частями расчета связаны два ос-
основания для классификации вариационных методов
расчета: по используемому функционалу и по методу
решения вариационной задачи. Этот подход отражен
на рис. 5.11, на котором радиусы разделяют методы,
связанные с выбором функционала, а окружности —
методы решения вариационной задачи (методы ди-
дискретизации). Выбор метода расчета приводи- к од-
одному из криволинейных прямоугольников !..i этой

170
ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ, 5
схеме. Для трудных задач выбор вариационного ме-
метода может оказаться сложным процессом поиска
оптимального криволинейного прямоугольника на
рис. 5.11.
Рис. 5.11. Схема классификации прямых вариационных методов
расчета: множество методов делится радиусами на подмножества
в соответствии с выбором функционала н окружностями в соот-
соответствии со способом дискретизации.
3.1. О выборе вариационного функционала для
расчета упругой системы. Как в теоретическом отно-
отношении, так и с точки зрения вычислительных свойств,
совокупность вариационных функционалов изучена
еще недостаточно; рациональные области применения
многих из них еще не определены. Можно высказать
лишь некоторые соображения по этому вопросу.
При выборе функционала учитывают, какие и
сколько разрешающих функций являются его аргу-
аргументами. Количество аргументов обычно стремятся

§ 3] О КЛАССИФИКАЦИИ ПРЯМЫХ МЕТОДОВ 171
уменьшить: это связано с объемом информации, ко-
которую нужно хранить при вычислениях. Но уменьше-
уменьшение количества функций достигается обычно за счет
введения дополнительных условий.
Сложность выполнения дополнительных условий —
второй фактор, который необходимо иметь в виду при
выборе функционала. В частности, при сложной форме
области возникают трудности в выполнении гранич-
граничных условий, а при наличии анизотропии и неодно-
неоднородности— в выполнении физических уравнений.
Третий фактор — экстремальные свойства функ-
функционала. Для функционала, имеющего экстремум или
минимакс, в отдельных случаях могут быть приме-
применены континуальные варианты методов математиче-
математического программирования (оптимизация в гильберто-
гильбертовых пространствах [1.1, 1.5]). Чаще же всего при-
применяются различные методы дискретизации; при этом
экстремальные свойства выбранного функционала
переносятся на дискретный функционал, и это помо-
помогает при решении задачи (см. § 5). Исторически сло-
сложилось так, что экстремальные функционалы появи-
появились раньше и больше разрабатывались. Однако есть
примеры, показывающие, что минимаксные функцио-
функционалы используются и дают хорошие результаты.
Выбор метода дискретизации тесно связан с вы-
выбором функционала. В частности, вариационно-раз-
вариационно-разностные схемы могут быть построены на основе об-
общей идеи расчленения сложной системы на элементы.
При этом возникает понятие метода конечных элемен-
элементов (МКЭ). С математической точки зрения расчле-
расчленение означает выбор определенного частного функ-
функционала и дополнительных условий к нему, т. е. рас-
расчленение всей разрешающей системы уравнений на
две части, одна из которых (дополнительные условия)
должна выполняться предварительно, до использова-
использования другой. Расчленение обычно сопровождается
механической трактовкой, которая выражается в вы-
выборе так называемой основной системы (для кото-
которой дополнительные условия выполнены) и неиз-
неизвестных (отыскиваются с помощью частного функ-
функционала).

172 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
Для построения расчетных схем, основанных на
МК.Э, могут быть использованы различные функцио-
функционалы для разрывных полей перемещений, напряжений
и т. д. (см. гл. 3 § 6 и гл. 4 § 6), а в более сложных
случаях —комплекс полных и частных функционалов
для многоконтактных задач [4.1]. Особый интерес
представляют функционалы граничных условий, кото-
которые могут быть использованы как в варианте МКЗ,
основанном на методе Ритца, так и в варианте, осно-
основанном на аппроксимации функционала. Первый пред-
представляет интерес для энергетических оценок погреш-
погрешности; он может быть реализован при достаточно
простых законах распределения упругих констант и
нагрузок в области, таких, что все уравнения (гео-
(геометрические, физические, статические) внутри конеч-
конечного элемента могут быть выполнены за счет выбора
аппроксимирующих функций; это возможно, напри-
например, для однородного анизотропного тела при отсут-
отсутствии объемных сил. Задача о стационарном значении
функционала граничных условий служит для прибли-
приближенного выполнения граничных условий и условий
контакта между элементами.
Можно показать, что классические методы строи-
строительной механики (методы сил, перемещений, сме-
смешанные), система функционалов для строительной
механики стержневых систем, предложенная И.И. Голь-
денблатом [5.8], как и некоторые варианты метода ко-
конечных элементов [5.11], исходят из функционала гра-
граничных условий многоконтактной задачи.
Различные схемы МК.Э систематизируются на ос-
основе вариационных принципов в [5.16].
3.2. Методы дискретизации. Вариационная задача
состоит в отыскании точки стационарности функцио-
функционала, определенного в бесконечномерном евклидовом
пространстве (см. гл.1). Для отыскания бесконечного
множества координат точки стационарности в подав-
подавляющем большинстве случаев требуется бесконечное
количество вычислений, а значит, и бесконечное время
счета. Поэтому задачи расчета континуальных систем
решают приближенно, ограничиваясь конечным чис-
числом вычислений, выполняемых в ограниченное время.

§ 3] О КЛАССИФИКАЦИИ ПРЯМЫХ МЕТОДОВ 173
Возможность приближенного решения вариацион-
вариационной задачи определяется тем, что существует после-
последовательность конечномерных задач на стационарное
значение, размерность которых стремится к бесконеч-
бесконечности и решения которых сходятся к решению исход-
исходной задачи. Существование такой последовательности
связано с сепарабельностью (см. Приложение 1) про-
пространства или, что эквивалентно, с наличием в нем
счетной базы.
Все пространства состояний, на которых определе-
определены функционалы, рассмотренные в гл. 3 и 4, сепара-
бельны.
Существуют различные способы сведения беско-
бесконечномерной вариационной задачи к последователь-
последовательности конечномерных, которые объединены общим
названием «Прямые вариационные методы». Все эти
способы можно разделить на два пересекающихся
класса, которые условно можно назвать «аналитиче-
«аналитическими» и «численными» (вариационно-разностными)
методами. Теория преобразования вариационных
проблем помогает прояснить некоторые вопросы клас-
классификации прямых вариационных методов, в частно-
частности указать в ней место метода Трефтца и методов,
основанных на сложных конечных элементах (супер-
(суперэлементах).
3.2.1. «Аналитические» методы состоят в построе-
построении последовательности конечномерных подпро-
подпространств данного пространства состояний и отыскании
стационарных значений данного функционала на этих
подпространствах и соответствующих точек стационар-
стационарности в качестве приближенных решений.
Метод Ритца — наиболее распространенный пред-
представитель «аналитических» методов приведения бес-
бесконечномерной вариационной задачи к конечномерной.
Суть его в том, что приближенное решение (п-е при-
приближение) отыскивается в виде линейной комбинации
я
un— Z я/ф/. • C-1)
где координатные элементы ср; берутся из последова-
последовательности фь фг, ..., фл, ..., которая удовлетворяет

174 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. В
следующим трем условиям: 1) все элементы ф„ при-
принадлежат области определения функционала и удов-
удовлетворяют всем его дополнительным условиям; 2) при
любом п элементы фь фг, .... фи линейно независимы;
3) последовательность фЬ ф2, ..., фи, ... полна в про-
пространстве состояний, т. е. этой последовательностью
может быть как угодно точно аппроксимирован (в со-
соответствующей метрике) любой элемент пространства.
Замена в функционале неизвестной функции и сум-
суммой A) приводит к задаче определения точки ста-
стационарности функции конечного числа переменных.
Обоснование метода Ритца для экстремальных функ-
функционалов, а также вопросы его сходимости и устой-
устойчивости подробно рассмотрены в книгах [0.11]. Для
неэкстремальных функционалов (минимаксных и не
имеющих экстремумов) эти вопросы еще не решены;
тем не менее метод Ритца в ряде случаев успешно
применяется.
Метод Трефтца (см., например, [0.11]) отличается
тем, что координатные функции в A) выбирают та-
таким образом, чтобы они удовлетворяли всем уравне-
уравнениям данной задачи в области; задача о стационар-
стационарном значении функционала используется для прибли-
приближенного выполнения граничных условий. Другими
словами, этот способ заключается в использовании
функционала граничных условий, так что с точки зре-
зрения системы функционалов, представленной в гл. 3
и 4, метод Трефтца можно трактовать как метод Рит-
Ритца по отношению к функционалу граничных условий.
Метод Бубнова — Галеркина (см. исторический
очерк в [0.11]) возник как видоизменение метода
Ритца, связанное с вычислением коэффициентов си-
системы алгебраических уравнений Ритца на основе
вариационного уравнения. Позднее было замечено, а
затем и доказано, что аналогичным образом можно
приближенно решать также и некоторые дифферен-
дифференциальные уравнения, не являющиеся условиями ста-
стационарности никакого функционала (краевые задачи
для несамосопряженных операторов), т. е. что метод
Бубнова — Галеркина является более общим, чем ме-

§ 3] О КЛАССИФИКАЦИИ ПРЯМЫХ МЕТОДОВ 175
тод Ритца. По отношению к вариационным задачам,
приведенным в данной книге (гл. 3 и 4), метод Буб-
Бубнова — Галеркина следует рассматривать как один из
вариантов метода Ритца, отличающийся способом вы-
вычисления коэффициентов алгебраических уравнений.
Метод Л. В. Канторовича приведения к обыкновен-
обыкновенным дифференциальным уравнениям существенно от-
отличается от метода Ритца. Приближенное решение
ищут в виде
п
«* (х,«/) = ? ф6 (х, у) fk (х), C.2)
6 1
6-> 1
где <р/г(х, у) — известные функции такие, что сумма B)
удовлетворяет всем дополнительным условиям исполь-
используемого функционала F(u), а функции fk(x) одной
переменной х отыскивают из условия стационарности.
Таким образом, вариационная задача, в которой не-
неизвестный параметр — функция и нескольких пере-
переменных, сводится к вариационной задаче с п неизвест-
неизвестными функциями одной переменной fk(x). Условием
стационарности полученной задачи является краевая
задача для системы обыкновенных дифференциаль-
дифференциальных уравнений, которая обычно проще исходной за-
задачи с частными производными, но дает лишь при-
приближенное решение.
К методу Л. В. Канторовича близко примыкают
некоторые способы сведения задачи расчета оболочки
как трехмерного тела к последовательности двумер-
двумерных задач. Например, упомянутый в гл. 4 способ вы-
вывода функционала Лагранжа для оболочки из трех-
трехмерного функционала Лагранжа на основе гипотез
Кирхгофа — Лява можно рассматривать как получе-
получение первого члена такой последовательности.
3.2.2. Вариационно-разностные методы дискрети-
дискретизации отличаются большей универсальностью, чем
«аналитические». Они заключаются в том, что иско-
искомая функция и, доставляющая стационарное значение
используемому функционалу F(u), приближенно за-
задается своими значениями в конечном числе точек
области интегрирования, а значения в промежуточных

176 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
точках определяются с помощью того или иного спо-
способа интерполяции; при этом производные заменяются
конечными разностями. Интеграл может быть вычис-
вычислен либо точно, либо с помощью кубатурнои формулы
той или иной точности. В первом случае переход к
конечномерной (разностной) задаче можно тракто-
трактовать как метод Ритца со специальным выбором коор-
координатных функций, он связан с аппроксимацией про-
пространства состояний Е конечномерными подпростран-
подпространствами Еп; этот подкласс является общей частью
(пересечением) классов вариационно-разностных и
«аналитических» методов. Второй случай связан с ап-
аппроксимацией функционала [5.17].
Метод конечных разностей (МКР), или метод сеток
целесообразно рассматривать как вариационно-раз-
вариационно-разностный метод, основанный на аппроксимации функ-
функционала. Он удобен тем, что для вычисления инте-
интеграла нужно знать значе-
значения подынтегральной
функции только в узлах
сетки, так что для вычис-
вычисления производных в раз-
различных узлах можно при-
применять разные интерпо-
Рис. 5.12. Неоднозначная интер- ляционные формулы, не
поляция функции / в точке А: ТГ J п«..гпм
кривая /, связана с вычисле- С,ВЯЗа"Н.Ь'е, ДРуГ С ДРУГОМ
ннем производной в точке С, а (рис. o.lz).
/2 — с вычислением произвол- Метод локальных ва-
ваши, в точке D. риаций [5.19] с точки зре-
зрения классификации ва-
вариационных методов является методом конечных раз-
разностей. Особенность его заключается в способе реше-
решения дискретизованной задачи, который является
одним из вариантов метода координатного спуска
(см. § 5).
3.2.3. Комбинированные методы. Методы дискре-
дискретизации, основанные на совместном применении «ана-
«аналитических» и «численных» методов, будем называть
комбинированными. Одним из примеров может слу-
служить метод прямых для задач с частными производ-
производными, в котором используется разностная аппрокси-

§ 41 ФОРМИРОВАНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИИ 177
мация производных по одному направлению и анали-
аналитическое решение—по другому.
К классу комбинированных методов относится ис-
использование некоторых сложных конечных элементов
(суперэлементов), которые можно определить [5.1]
как элементы, внутри области которых выполняются
все уравнения данной теории; следовательно, примене-
применение сложных конечных элементов связано с функцио-
функционалом граничных условий. Эти уравнения могут быть
выполнены точно (в этом случае получаем метод
Ритца для функционала граничных условий) или при-
приближенно— с помощью аналитических или численных
методов. Здесь заключена возможность и удобство
комбинированного применения МКЭ с другими мето-
методами, в том числе с МКР и разными вариантами МКЭ.
§ 4. Формирование алгебраических уравнений
прямых методов на основе вариации функционала
Пусть требуется решить вариационную задачу
бЭ(и) = 0, где Э(и)—квадратичный функционал, ко-
который зависит от функции и (возможно, векторной)
и от ее частных производных:
Э'\и,
) er(u)]dU, DЛ)
где еь е2)..., ег — дифференциальные операторы.
Вариация функционала Э имеет вид
где 6еь бе2, ..., бег — дифференциальные операторы
от Ьи. Ее можно преобразовать интегрированием по
частям к форме
63= \F[u, e(u)]6udQ+ ^(...)d{dQ). D.3)

178 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
Пусть выбран какой-либо метод дискретизации для
приближенного решения поставленной задачи; тогда
функционал Э зависит от п переменных «ь «г, .... «п
и может быть представлен в виде
3i(«b «2 «„) =
= э/[«1, щ, ...,вл,в*(в„ ...,«„),...,«;(«,, ...,«„)],
D.4)
где 8р е*, ..., е* — дискретные аналоги дифференци-
дифференциальных оператов е1( е2, ..., ег. Задача о стационар-
стационарности функционала Э\
ЬЭг (и*, би,) = J] U tat = 0 D.5)
эквивалентна системе линейных алгебраических урав"
нений
f-0 (/-1,2,..., п), D.6)
которая может быть записана в виде
п
?( atlu, + Ь, = 0 (/ = 1, 2 ft). D.7)
Вариация 8Э в виде E) может быть выведена спо-
способом, подобным применяемому в вариационном ис-
исчислении (суммированием по частям), из промежуточ-
промежуточного звена
б^ = t ? Ч + ? ? К (Щ. «,..... %)¦ D-8)
i-i ' fe-i *
Если представить вариационное уравнение E)
в виде
63, (и* Ьщ) = t Z («//«/ + 6/) S«; = 0, D.9)
¦1 / 1
то нетрудно видеть, что коэффициенты системы G)

§ 4] ФОРМИРОВАНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 1?9
можно вычислить по формуле
fl« = йЭ, (му =1, &/,«!), D.10)
где все остальные неизвестные ик и бш, а также сво-
свободные члены b равны нулю (k Ф j, I Ф i).
При использовании метода Ритца или Бубнова —
Галеркина так и поступают: коэффициенты ац вычис-
вычисляют по формуле A0), в которой ЬЭ\ берут в виде
C). В некоторых случаях в методе Ритца удобнее
использовать 65i в виде B); в этом случае можно
брать менее гладкие координатные функции, так как
в B) стоят производные от и менее высокого порядка.
При решении задачи вариационно-разностным ме-
методом применяют несколько способов вычисления
коэффициентов ац. По первому способу получают вы-
выражение для функционала D), заменяя производные
в 8i, 8г, ..., ът конечными разностями, дифферен-
дифференцируют его, чтобы получить выражения для коэффи-
коэффициентов ац через исходные данные (физические кон-
константы, шаг сетки и др.), и эти выражения используют
для составления программ формирования систем
уравнений. Второй способ состоит в использовании
формулы A0) совместно с C); при этом коэффи-
коэффициенты ац могут отличаться от вычисленных по пер-
первому способу, т. е. соответствовать другой разностной
схеме.
Третий способ заключается в применении A0) сов-
совместно с B) или, что то же самое, с (8) и имеет то
преимущество, что он очень прост и удобен для про-
программирования, хотя и связан с довольно большим
объемом вычислений, что сказывается на затратах
машинного времени: большая часть вычислений вы-
выполняется вычислительной машиной. На основе фор-
формулы A0) совместно с (8) могут быть легко состав-
составлены программы для решения вариационно-разност-
вариационно-разностным методом сложных задач расчета неоднородных
анизотропных упругих тел и оболочек; можно исполь-
использовать сетку с переменным шагом и покрывать расчет-
расчетную область сетками разных видов.
Вариация функционала в виде (8) может быть
использована и для решения вариационных задач

18Э ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
методами спуска и другими методами нелинейного
программирования без вычисления коэффициентов
алгебраических уравнений. Данный способ составле-
составления системы уравнений был использован авторами для
составления универсальной программы расчета неод-
неоднородных анизотропных оболочек, в том числе ребри-
ребристых (см. § 6).
§ 5. Использование экстремальных свойств
функционалов при решении конечномерных
(дискретизованных) задач
При применении прямых методов получение до-
достаточно точных решений связано с решением боль-
больших систем уравнений, решение которых затруднено
из-за ограниченных возможностей вычислительных
машин (память, быстродействие, ошибки округления).
Поэтому при составлении программ решения боль-
больших систем линейных алгебраических уравнений, по-
полученных при дискретизации вариационных задач,
стремятся учесть особый вид матриц таких систем;
например, их малую заполненность, ленточную струк-
структуру и т. д. Такие системы можно решать на ЭВМ
«точными» методами (Гаусса, Жордана), если исполь-
использовать внешние запоминающие устройства и приме-
применять специальные приемы, направленные на экономию
памяти и времени счета, например блочный метод
Гаусса.
Системы вариационно-разностных уравнений хоро-
хорошо приспособлены для решения итерационными мето-
методами. Это становится очевидным, если учесть, что
большинство итерационных методов можно тракто-
трактовать как различные методы спуска из выпуклого про-
программирования (см., например, [5.14]). При этом ста-
становятся ясными вопросы их сходимости. Важное до-
достоинство итерационных методов в том, что они
являются самоисправляющимися, т. е. не только не
накапливают, но и исправляют ошибки округления.
В частности, наиболее распространенный метод
Гаусса — Зейделя является методом циклического ко-
координатного спуска и состоит в том, что каждая неиз-

§ 5] ИСПОЛЬЗОВАНИЕ ЭКСТРЕМАЛЬНЫХ СВОЙСТВ IS 1
вестная по очереди изменяется таким образом (при
фиксированных остальных), чтобы функционал при-
принял экстремальное значение по этой неизвестной. От-
Отсюда ясно, что метод Зейделя всегда сходится для
функционалов, имеющих экстремум (минимум или
максимум); его сходимость для минимаксных и дру-
других неэкстремальных функционалов нуждается в изу-
изучении в каждом конкретном случае.
С точки зрения экстремума функционала легко
объяснить, в чем заключаются некоторые приемы
ускорения сходимости итерационных методов. Напри-
Например, одним из лучших способов ускорения сходимости
метода Зейделя (который называют также методом
релаксации) является метод неполной релаксации.
С позиций поиска экстремума он заключается в том,
что, найдя минимум функционала по /-Й переменной
Ui, в качестве нового значения (и?+|У берут промежу-
промежуточное значение между предыдущим значением и? и
точкой минимума н™+1: («™+1)' = «" + <а(м?+1 —
— и?) (ш < 1—«нижняя» релаксация) или продви-
продвигаются несколько дальше минимума (оа > 1 — «верх-
«верхняя» релаксация). Из рис. 5.13 ясно видно, что «верх-
«верхняя» релаксация представляет собой метод борьбы с
«оврагами» функционала и что метод неполной релак-
релаксации всегда сходится при значениях коэффициента
релаксации 0 < ш < 2.
Имеются и другие примеры использования свойств
функционалов для поиска коэффициента релакса-
релаксации и ускорения сходимости метода Зейделя [5.2,
5.5].
В некоторых задачах, особенно с ограничениями
в форме неравенств (например, односторонние связи)
может оказаться эффективным метод локальных ва-
вариаций [5.19], который представляет собой один из
вариантов метода координатного спуска без вычисле-
вычисления производных.
Решение систем алгебраических уравнений, соот-
соответствующих неэкстремальным функционалам (ка-
(какими являются все полные функционалы), сложнее
как для «точных», так и для итерационных методов.

182 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. S
Для отыскания седловой точки дискретизованных ми-
минимаксных функционалов (Рейсснера, Ху — Вашицу
X,
Метод Зейделй (координатного спуснй)
¦ Метод'неполной релаксации
Рис. 5.13. Два способа поиска экстремума функционала в ко-
конечномерном пространстве, I — линии уровня выпуклого функцио-
функционала, имеющего экстремум в точке А.
и др.) могут быть использованы методы поиска мпни-
макса из нелинейного программирования и теории
игр, например [5.6, 5.9, 5.10, 5.15].
§ 6. Примеры построения алгоритмов
расчета пологих анизотропных оболочек
вариационно-разностным методом
В данном параграфе описаны вариационно-разно-
вариационно-разностные схемы и приведены некоторые другие данные
об алгоритмах, на основе которых составлен комплекс
программ для расчета пологих оболочек, имеющих
ребра различной ориентации, отверстия, вырезы и
другие особенности [5.2, 5.4].
6.1. Разностные схемы построены на основе ап-
аппроксимации функционала. Функционал Лагранжа

ПРИМЕРЫ
183
записан в перемещениях, деформациях и усилиях
[П.10] (см. гл. 4, § 8) в декартовых координатах:
(и) = ^[~
где
d2w
ал;2
т = —
ди{ ,
d2w
дх ду
¦(I,*-
F.1)
F.2)
JV = G-e. F.3)
Контур оболочки — любая ломаная линия, состоящая
из отрезков, параллельных осям координат; могут
б).
-и.
1*1
-4-
+-+-Н-
m-f
m
-А/
¦у-/
Рис. 5.14. Два вида прямоугольной сетки для вариационио-разно-
стиых методов расчета оболочек, а) Деформации и усилия вычис-
вычисляются в узлах lj основной сетки; б) деформации и усилия вы-
вычисляются как в узлах Ц основной сетки, так и в узлах тп, in,
mj дополнительной сетки.
быть отверстия и вырезы, ограниченные такими лома-
ломаными. Наличие ребер и других особенностей конструк-
конструктивной, приобретенной и естественной анизотропии
учитывается матрицей G согласно Приложению 3.
Значения неизвестных функций мь "г, w отыски-
отыскиваются в узлах ij прямоугольной сетки с шагом X по
направлению оси х и |Я, по оси у (рис. 5.14,а).
Разностные схемы имеют погрешность <?(Я2) та-
такого же порядка малости, как Я,2, и при этом оказы-
оказываются ненамного сложнее, чем менее точные схемы

184 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
с погрешностью О ("к). Увеличение порядка погреш-
погрешности до О(Xs) и далее требует значительного услож-
усложнения разностного метода. Практически проще увели-
увеличить точность расчета путем сгущения сетки.
Схема 1 применена в [5.2] для расчета пологих
оболочек из изотропного материала, подкрепленных
ортогональной сеткой ребер, параллельных осям ко-
координат. Для таких оболочек матрица G в C) упро-
упрощается, и функционал A) можно представить в виде
d2w , д-w
wgk
/ d2w у d2w д'-w , gn Г/ dm
Us- j + ё45 дх- ду- "•" 2 LV дх )
ж йл: J ' bu y дх sl4 дх
d2w
дх2
ди-
d2w , _. <9mi duo
с)г/2 + gl2 ЫГду + ^331*7 дх
> F.4)
где gtj — элементы матрицы G, в которой для данной
задачи
gl3 = §15 — §16 = §23 = §24 = §26 = §34 = §35 =
= §36 = §46 =§56 = 0-
Вычисление производных. Первые производные в
D) вычисляются в виде dujdx = (н'41' — и'!')/Х, но их
значения приписываются точкам между узлами (это
затем учитывается при приближенном вычислении ин-
интеграла). Для этого вводится дополнительная сетка
(рис. 5.14), узлами которой являются промежуточные
точки. Остальные производные вычисляются в узлах

S 6] ПРИМЕРЫ 185
основной или дополнительной сетки по формулам
\ дх /т/ Я \ ду /in ty
fd2w\ _
\dx4il~
dxdy
ду2 Jit
и = ^— ~wl w~W''' +W' • F-5)
Для того чтобы в произведениях вида (ди2/дх) {dujdy)
в функционале D) оба сомножителя соответствовали
одной и той же точке, кроме E) применяются еще
разностные формулы
дх )шп 2 W дх Jmj+i \ дх Jmjr
и т. д., которые можно получить из E) интерполиро-
интерполированием. Для вычисления значений w в узлах допол-
дополнительной сетки также применяется интерполяция:
wml — _L (щ;'+1. / -j- ХЮЦ), Wln = — (W'- /+1 + Wli),
2 , F.7)
wmn-= _Цш/+1, /+1 _|_ш1+1, / -j-щ;", /+1 -f-tj)'/).
Вместо неизвестных производных dw/dv в контурных
точках используются прогибы в законтурных точках;
угловая законтурная точка не вводится.
Разностные и интерполяционные формулы E) —
G) имеют погрешность порядка О{%2), т. е. такого же
порядка малости, как I2 (см., например, [5.17]).
Вычисление интеграла производится приближенно
с помощью кубатурных формул таким образом, чтобы
погрешность имела порядок малости (У(Х2). Это со-
согласуется с погрешностью вычисления производных:
при менее точных кубатурных формулах теряется точ-
точность, достигнутая в E) — G), а применять более

1S6 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ, 8
точные (а значит, и более сложные) кубатурные фор-
формулы нет смысла, так как из-за E) — G) общая погреш-
погрешность все равно будет порядка О (К2). Функционал A)
заменяется суммой вида
i I
d2w . g44 (d2w
г 2 \ду2 J ^S45 дх2 ду2
3«i
дх
ml
ди, д2ш
~gu~dx~~bT>
w
I n
dtl2 du2 d2W
W8
ду
-?{...}&*, F.8)
где fi/, Fm/, Fm, Fmn — весовые множители, которые
равны отношению площади занимаемой оболочкой
части площадки размерами А.Х!^> в центре которой
находится узел ц, mj, in или тп, к площади всей пло-
площадки. Таким образом, интеграл от первой группы
слагаемых в D) заменяется суммой по площадкам с

§ 6] ПРИМЕРЫ 187
центрами в точках ij, от второй—по площадкам mj
и т. д.
Для внутренней точки ij замена интеграла по пло-
площадке ij произведением fij\%2Fij, где /;/ — значение
подынтегральной функции, вносит погрешность по-
порядка к*. Действительно, разложим подынтегральную
функцию / в ряд в окрестности точки ij:
f (*. У) = fi, + ax + by + 0 (К7), F.9)
где 0(№)— бесконечно малая величина такого же по-
порядка, как К2, и вычислим интеграл:
V2 |
-Л/2 -
. (ело)
Здесь интеграл от ах-\-Ьу равен нулю благодаря
особому положению точки ц — в центре площадки ин-
интегрирования. Для контурных точек, которые нахо-
находятся не в центре площадки интегрирования, погреш-
погрешность вычисления интеграла по каждой площадке
имеет порядок малости 0(к3).
Так как количество внутренних точек пропорцио-
пропорционально 1Д2, то сумма по всем внутренним точкам в
(8) отличается от соответствующего интеграла на ве-
величину порядка малости 0(К2). Количество контурных
и угловых точек пропорционально 1/Я, поэтому сумма
по контурным и угловым точкам в (8) тоже имеет
погрешность порядка 0(к2).
Аналогичным образом можно показать, что по-
погрешность замены интегралов по площадкам Fm/, Fin,
Fmn конечными суммами имеет порядок 0{%2).
Таким образом, разностная схема 1 аппроксима-
аппроксимации функционала имеет погрешность 0(А.2).
Схема 2. Производные, входящие в B), вычисля-
вычисляются в узлах // основной сетки: вторые по формулам
E) с погрешностью 0(№), а первые и смешанные вто-
вторые с помощью нецентральных разностей (погреш-
(погрешность 0(к)).

188 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
При этом деформации B) имеют аппроксимации
четырех видов:
 2
CO1' (ft, l) = l Г7 (- fi
ЬЛ Л
т'' (ft, /) = kl — %2 » F-11)
где k = 1 (/=1) соответствует нецентральным разно-
разностям, взятым в направлении оси х(у), a ft — —1
(/= —1)—в противоположном направлении; щ, х2
не зависят от k, l, так что можно считать
(a='l,2).
Для определения углов поворота О = dw/dv рас-
рассматривается ряд законтурных точек.
Функционал A) заменяется усредненной суммой
(Mfe, 0 е, (?
i
+ T2(k,l)e2(k, l)+ ...
... +2H(k,l)t (k, I) - qlUl - qM2 -
+ %{...}*•+!!{..-ПК FЛЗ)
•••}. X {•••} заменяют контурные интегралы.
При этом в.угловых и контурных точках выражение в
квадратных скобках в A3) считается равным нулю,
если для вычисления хотя бы одной из входящих в
него деформаций требуются перемещения щ или Пъ
в законтурных точках (так как за границей оболочки
нет Ы], м2).
Рассуждая так же, как при рассмотрении схе-
схемы 1, можно для погрешности е аппроксимации A3)

§ 6) ПРИМЕРЫ 189
функционала A) получить лишь оценку
в = О(к), F.14)
так как деформации A1) вычисляются с погрешно-
погрешностью С (Я).
Дискретизация функционала A) в форме A3)
(схема 2) имеет более универсальный характер, чем
в форме (8), которая соответствует одной конкретной
матрице физических зависимостей G. Представление
A3) пригодно для любой неоднородной анизотроп-
анизотропной оболочки.
Расчетный опыт показывает, что схема 2 имеет
хорошую точность для тех задач, в которых направле-
направления анизотропии совпадают с направлениями коорди-
координатных осей. Для задач с «косой» анизотропией, осо-
особенно дискретного характера (например, для оболо-
оболочек с ребрами произвольного направления) схему 2
лучше модифицировать, добавив к A1), A2) форму-
формулы вычисления деформаций по направлениям диагона-
диагоналей сетки и включив в функционал A3) соответ-
соответствующие слагаемые (т. е. «усреднять» значения
функционала не по четырем, а по восьми направле-
направлениям вычисления нецентральных разностей).
Применительно к схеме 1 идея совмещения на-
направления анизотропии с направлением дифференци-
дифференцирования реализована в программе расчета оболочек
с ребрами произвольного направления [5.4] путем
введения дополнительной системы координат, связан-
связанной с направлением ребер.
6.2. Алгоритм расчета. Разностная схема E) — (8)
была использована для составления программ расчета
пологих ребристых оболочек с узкими и широкими
ребрами, параллельными контуру или наклонными
[5.2, 5.4]. Дифференцированием функционала (8) с
учетом E) — G) были выведены формулы для коэф-
коэффициентов разностных уравнений, которые затем про-
программировались.
Например, для оболочки с ортогональной сеткой
параллельных контуру ребер три рязностнь^ урав-
уравнения в каждой точке содержат 62 различных не-
ненулевых коэффициента. На рис. 5.15 изображены

190
ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ, Б
шаблоны для трех уравнений, записанных в точке Ц:
шаблон для уравнения дЭ/дщц получается из шаб-
шаблона а), если его повернуть на 90 градусов и поме-
поменять местами и\ и щ. В квадратиках записаны
a)
1
ш
1
-
-
i
Ul
1
1
-
-
-
1
1
1
-
-
-
.1
1
1
-
—
I
w
1
-
-
us
\
w
1
U)
1
-
-
-
-
-
w
1
I
Ul
III
\
w
1
w
1
w
1
w
1
-
-
Ul
Of
1
"/
to
1
1
Ul
1
1
-
-
o,
lit
\
Ш
1
Ш
1
-
—
—
IV
\
w
1
Ш
1
Рис. 5.15. Шаблоны сеточных уравнений вариационно-разностного
метода расчета оболочек с ребрами, параллельными контуру.
а) дЭ/дищ = 0; б) дЭ/ди>ц = 0.
неизвестные, коэффициенты при которых, вообще го-
говоря, отличны от нуля. Весовые множители позволяют
использовать эти шаблоны для составления уравне-
уравнений как для внутренних, так и для контурных и за-
законтурных точек.
Коэффициенты уравнений вычисляются подпро-
подпрограммой вычисления коэффициентов и записываются
на магнитный барабан. Тот факт, что коэффициенты
уравнений, записанных в различных точках, могут
быть одинаковыми, используется для экономии места
на барабане и для экономии времени счета за счет
уменьшения количества обменов информацией между
оперативной памятью и барабаном: на барабане хра-
хранятся только различные строки коэффициентов и ин-
информация об их соответствии точкам сетки. Про-
Программа для ЭВМ типа М-20 с оперативной памятью
4096 ячеек может решать задачи с сеткой более
800 узлов.

ПРИМЕРЮ
191
Разностная схема A1)—A3) была использована
для составления программы расчета пологих неодно-
неоднородных анизотропных оболочек переменной толщины
и кривизны. Шаблоны разностных уравнений пока-
показаны на рис. 5.16; в них содержится Г09 ненулевых
1
10
1
-
-
-
Л)
I
ш
\
и>
\
и„иг
ш
1 •
-
—
1
10
1
ш"
1
u/tt/,
ш
1
и„а
ш
X
ш
1
-
I
ш
1
и,,иг
10
\
и„иг
10
1
-
1
IV
\
i
-
- -
-
1
ш
\
и,,иг
10
1
10
1
-
-
-
-
-
1
ш
1
и„иг
ш
1
ш
\
и,,иг
ш
1
ш
1
-
-
1-
-
-
1
"Л
ш
1
ш
1
иЛ
ш
1
и„иг
ш
1
W
1
-
-
-
-
1
i6»
1
1
1
ш
1
1
—
-
-
-
-
ш
1
и„ие
ю
1
ш
\
Рис. 5.16. Шаблоны сеточных уравнений вариационно-разностного
метода расчета неоднородных анизотропных оболочек (в том
числе ребристых), а) дЭ/дищ — 0; б) дЭ/dw,/ = 0.
коэффициентов. Коэффициенты разностных уравне-
уравнений вычисляются подпрограммой вычисления коэф-
коэффициентов способом, описанным в § 4; при этом вся
информация (физические константы и кривизны
в каждом узле сетки и информация о форме области
и граничных условиях) не помещается в оперативной
памяти и хранится на барабане.
Решение системы уравнений выполняется итера*
ционным методом релаксации (методом Гаусса — Зей-
деля) с использованием различных приемов ускоре-
ускорения сходимости (см. § 5). Для метода неполной
релаксации применялся автоматический поиск «опти-
«оптимального» коэффициента релаксации, обеспечиваю-
обеспечивающего самое быстрое убывание невязок уравнений, т, е.
градиента функционала,

192 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ 1ГЛ. 5
§ 7. О применении различных функционалов
для оценки точности приближенных решений
Одним из наиболее эффективных способов опре-
определения меры погрешности и ее вычисления или
оценки является применение энергетических оценок,
основанных на том или ином вариационном функцио-
функционале; при этом используются его экстремальные
свойства.
7.1. Различные критерии точности решения и меры
погрешности. При расчете конструкции инженер мо-
может использовать различные критерии точности ре-
решения в зависимости от смысла и практического на-
назначения задачи. В соответствии с этим в каждом
конкретном случае может быть выбрана наиболее
подходящая мера погрешности.
Оценка погрешности приближенного решения свя-
связана с определением расстояния р(ип,и°) между при-
приближенным решением ип и точным решением и0. Как
известно, в одном и том же линейном пространстве U
могут быть введены различные меры расстояния, или
метрики (см. Приложение 1). Например, при реше-
решении задачи теории упругости в перемещениях мерами
расстояния между точками пространства состояний
могут служить:
а) равномерная метрика для перемещений
9l(u,v) = max{[u(r)-v(r)]-[u(r)-v(r)]}\ G.1)
в которой расстояние р(м, v) определяется как мак-
максимальное отклонение к от в в объеме V, занятом
упругим телом;
б) равномерная метрика для напряжений
р2(и, v) =
= тах{[о (и (г)) - о (v (г))] • • [о (и (г)) - о (v (r))}}1!', G.2)
rs V
где о (и (г)), o(v(r))—напряжения, вычисленные по
перемещениям и и v соответственно. Расстояние B)
связано с разностью производных от перемещений
и и v;

5 7] ОБ OUEHKE ТОЧНОСТИ ПРИБЛИЖЕННЫХ РЕШЕНИЙ 193
в) энергетическая метрика
Рз («> v) = {Э (и - v + и0) - Э (u°)}S G.3)
где 5 (и) —какой-либо функционал в перемещениях,
имеющий минимум (см. § 7.4), м° —его точка мини-
минимума. Другие варианты энергетической метрики мо-
могут быть построены на основе других функционалов,
имеющих экстремум (минимум или максимум); ми-
минимаксные функционалы не определяют метрику, так
как расстояние между различными точками простран-
пространства состояний должно быть положительным;
г) среднеквадратичная метрика для перемещений
G.4)
д) среднеквадратичная метрика для невязок раз-
разрешающих уравнений
G.5)
где и° — решение краевой задачи теории упругости.
Можно определить и ряд других мер расстояния.
Таким же образом определяются метрики в теории
оболочек.
Вообще говоря, метрики A) — E) не эквива-
эквивалентны: последовательность приближенных решений
ип может сходиться к точному при одном способе
определения расстояния между ними и не сходиться —
при другом. Но во многих задачах различные метрики
оказываются взаимосвязанными. Взаимосвязь между
различными метриками дают теоремы вложения
С. Л. Соболева [5.18]. В [0.11] показано, если опера-
оператор V-а[е(и)] положительно определенный (это за-
зависит от формы области и физических зависимостей),
а элементы и, v принадлежат его области определе-
определения, т. е. являются достаточно гладкими функциями,
7 Н. П. Абовский и др.

194 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
то метрики C), D) и E) связаны между собой не-
неравенствами
Р4(«.*)<|рз («.*)< у Ре («.*). G.6)
где у, К — некоторые положительные числа. В [0.11]
приведены также примеры получения равномерных
оценок погрешности A) на основе энергетической
оценки с метрикой C).
Метрики C), D) и E) имеют, вообще говоря, раз-
различную область применимости. Например, E) может
не иметь смысла на элементах и", выбираемых в ка-
качестве приближенного решения; это относится ко мно-
многим разновидностям вариационно-разностного метода.
Наиболее универсальна энергетическая метрика C).
7.2. Априорные оценки дают возможность оценить
погрешность еще до того, как приближенное решение
построено [0.11]. Как правило, априорные оценки
суть оценки асимптотические — они дают лишь поря-
порядок убывания погрешности при бесконечном возра-
возрастании числа параметров, используемых при дискре-
дискретизации: координатных элементов в методе Ритца или
числа узлов сетки в вариационно-разностном методе.
Другими словами, большинство априорных оценок не
дает возможности указать заранее, какое число чле-
членов ряда в методе Ритца или число узлов сетки
следует взять, чтобы обеспечить нужную точность ре-
решения; они только говорят: «чтобы уменьшить по-
погрешность в k раз, достаточно увеличить число варьи-
варьируемых параметров в / раз».
Априорные оценки для метода Ритца рассмотрены
в [0.11]. Основой для получения как среднеквадра-
среднеквадратичных оценок, так и равномерной в [0.11] служит
энергетическая оценка вида C). Эти результаты при-
применимы для вариационно-разностных схем, построен-
построенных на основе метода Ритца (см. § 3).
Пример априорной оценки погрешности вариаци-
вариационно-разностных схем, основанных на аппроксимации
функционала (см. § 3), приведен в § 6. Сделанный
там вывод о порядке убывания погрешности вычисле-
вычисления функционала Лагранжа 0{%.2) означает, с одной

§ 71 ОБ ОЦЕНКЕ ТОЧНОСТИ ПРИБЛИЖЕННЫХ РЕШЕНИЙ 195
стороны, что минимальное значение 5Л1(и^) дискре-
тизованного функционала F.8) отличается от мини-
минимума Эд\ (и0) исходного функционала F.1) на вели-
величину порядка малости
так как различные значения F.8) можно рассматри-
рассматривать как приближенные значения F.1) при всевоз-
всевозможных функциях mi, м2, w, удовлетворяющих допол-
дополнительным условиям. С другой стороны, Эд\ (и°;) яв-
является приближенным значением Эд\(и1) для любой
гладкой функции и\, имеющей в узлах сетки значе-
значения и?/ и поэтому
1(;/) и) G.8)
Из G) и (8) следует, что
G.9)
Соотношение (9) является энергетической оценкой
C) погрешности, которую дает замена истинных
функций мь Иг, w функциями м^, м?, wl, полученными
из решения сеточной задачи с помощью любого спо-
способа интерполяции, для которого погрешность вы-
вычисления всех производных, входящих в функционал,
не больше чем 0(№). Используя [0.11], можно на
основании (9) получить другие оценки сеточного ре-
решения, в частности равномерную.
Для погрешности схемы 2 из § 6 удается получить
с помощью аналогичных рассуждений и формулы
F.14) лишь оценку О(Х). Однако полученные на ее
основе решения, как показывают выполненные авто-
авторами расчеты, имеют такую же точность, как и на
основе схемы 1, что, по-видимому, связано с усред-
усреднением в F.13).
7.3. Апостериорная оценка — это оценка погреш-
погрешности уже построенного приближенного решения.
Для некоторых решений можно вычислить меру
погрешности E), если эти решения принадлежат

196 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
области определения оператора А =-=—. т. е. имеют
соответствующее число производных. Этой области не
принадлежат многие функции, используемые для по-
построения вариационно-разностных схем, например
кусочно-линейные функции, применяемые в методе
конечных элементов. Невозможно вычислить значе-
значение дифференциального оператора А и для функции,
определенной лишь в узлах сетки, при решении за-
задачи вариационно-разностными методами, основан-
основанными на аппроксимации функционала.
Погрешность более широкого класса решений под-
поддается оценке в энергетической метрике C). Для
этого требуется использовать экстремальные функ-
функционалы: расстояние C) между точным и прибли-
приближенным решениями определяется разностью точного
и приближенного значений функционала.
Для вычисления апостериорной энергетической
оценки решения, полученного, например, на основе
минимального функционала, необходимо знать либо
его минимальное значение Э(и0), либо оценку снизу
для этого значения, см. далее A5) — A7). В гл. 3 и 4
есть по одному функционалу, минимальные значения
которых известны: это функционалы физических со-
соотношений Эф(е,а) и Зф(е,ц,Т,М), минимум которых
равен нулю. Минимальные значения остальных функ-
функционалов, имеющих минимум, заранее неизвестны
и поэтому нуждаются в оценке снизу. Соответственно,
чтобы вычислить энергетическую оценку погрешности
решения, полученного на основе максимального функ-
функционала, необходимо оценить его стационарное зна-
значение сверху.
Оценку снизу для минимального значения функ-
функционала можно получить, если приближенно решить
данную задачу с помощью какого-либо максималь-
максимального функционала, приведенного в гл. 3 или 4, так
как все функционалы в гл. 3 или 4, кроме Зф, имеют
одно и то же стационарное значение; минимальные
функционалы дают оценку сверху для этого значения,
а максимальные —оценку снизу.

«71 ОБ ОЦЕНКЕ ТОЧНОСТИ ПРИБЛИЖЕННЫХ РЕШЕНИЙ 197
7.4. Экстремальные функционалы в теории упруго-
упругости и теории оболочек.
а) Минимум имеют всевозможные разновидности
функционала Лагранжа (табл. 3.1, 4.1) и другие част-
частные функционалы, которые могут быть из них полу-
получены путем включения в список дополнительных ус-
условий некоторых условий стационарности. Сюда отно-
относятся функционалы Эт\ и Э*г2, а также, например, функ-
функционал Лагранжа, имеющий в списке дополнитель-
дополнительных условий не только геометрические граничные ус-
условия, но и статические.
б) Максимум имеют всевозможные разновидности
функционала Кастильяно (табл. 3.2, 4.2) и другие
частные функционалы, которые могут быть из них
получены путем включения в список дополнительных
условий некоторых условий стационарности: функцио-
функционалы для геометрических граничных условий и др.
в) Экстремальные функционалы для некоторых
частных задач, отсутствующие в гл. 3 и 4, могут быть
получены с помощью преобразований Фридрихса из
рассмотренных выше. Приведем два примера.
Для плоской задачи теории упругости (анизотроп-
(анизотропное однородное тело) при нулевых статических гра-
граничных условиях функционал, имеющий минимум,
может быть получен с помощью преобразования
Фридрихса из функционала Кастильяно ЭК1(ф)
в функциях напряжений, который для этой задачи
можно преобразовать к виду
ЭК1 (Ф) = - \ \ [j (АФJ - fф] dS, G.10)
д2 , д2 тт
где А =-T-J-+-г-! оператор Лапласа, с дополни-
дополнительными условиями ф|с = 0, <Эф/ду|с = О. Условие
стационарности его — бигармоническое уравнение. За-
Запись A0) показывает, что можно следующим образом
ввести новую переменную v и соответствующие до-
дополнительные условия:
Л Л ¦- л -.
S, G.11)
G.12)

198 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
Внесем дополнительные условия A2) в функционал
A1) с множителями Лагранжа р, выведем условия
стационарности и исключим с их помощью перемен-
переменные ф, v из функционала и из дополнительных усло-
условий; получим задачу о минимуме функционала
P2dS G.13)
с дополнительными условиями Др — / = 0, эквива-
эквивалентную A0), а значит, и всем рассматриваемым ва-
вариационным постановкам плоской задачи теории
упругости.
Для задачи изгиба однородной изотропной плас-
пластинки при однородных геометрических граничных ус-
условиях с помощью преобразования Фридрихса из
функционала Лагранжа в перемещениях может быть
выведен еще один функционал, имеющий максимум
и аналогичный A3):
с дополнительными условиями Д| = q, где q—попе-
q—поперечная нагрузка.
Функционалы A3) и A4) соответствуют методу
негармонического остатка получения энергетических
оценок (см. ниже).
7.5. Различные методы получения энергетических
оценок погрешности и их трактовка с точки зрения
теории преобразования вариационных проблем. Будем
считать, что имеется приближенное решение вариа-
вариационной задачи на основе одного из экстремальных
(для определенности — минимальных) функционалов.
Для энергетической оценки погрешности нужно [0.11]
построить максимальный функционал Э*(р), имею-
имеющий то же стационарное значение, что и данный Э(и),
решить приближенно вариационную задачу для по-
построенного функционала и вычислить его значение.
Разность
Э(ип)-ЭЧрт) G.15)

§7] ОБ ОЦЕНКЕ ТОЧНОСТИ ПРИБЛИЖЕННЫХ РЕШЕНИЙ 199
и будет служить оценкой погрешности для обоих
приближенных решений ип и рт, так как, очевидно,
Э (и") - Э (ы°) < Э (ип) - Э* (рт), G.16)
Э* {р°) - Э* (рп) < Э (ип) - Э* {рт). G.17)
Принципиальное звено здесь — построение макси-
максимального функционала. В {0.11] приведено несколько
способов построения максимального функционала,
предложенных различными авторами. Покажем, что
все эти способы можно свести к преобразованиям
функционалов по Куранту—Гильберту [0.9].
Нетрудно проверить, что все рассмотренные ниже
минимальные функционалы выпуклы вниз, откуда
следует, что преобразованные функционалы имеют
максимум.
а) Метод ортогональных проекций для задачи Ди-
Дирихле сводится к тому, что для данного функционала
3(")=$$[]-(gradиJ -/и]dS, G.18)
условием стационарности которого является краевая
задача Дирихле для уравнения Пуассона
A« + f = divgradw + f = O, «L = 0, G.19)
строят новый функционал (двойственный), имеющий
максимум:
$$[j]S, G.20)
где вектор р подчинен дополнительному условию
G.21)
Функционал B0) легко получить из A8) с по-
помощью преобразования Фридрихса (так же, как
функционал Кастильяно из Лагранжа, гл. 3 и 4),
если, согласно общей методике преобразований
(гл. 2), искусственно ввести новый переменный век-
гор v и дополнительное условие
V — grad« = 0. G.22)

200 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. 5
Функционал A8) примет вид
)S. G.23)
Построив с помощью множителей Лагранжа р пол-
полный функционал Эп(и,v,p) и исключив из него с по-
помощью условий стационарности переменные и, v, по-
получим функционал B0) с дополнительным условием
B1), который эквивалентен A8).
Точно так же легко свести к преобразованию
Фридрихса приведенную в [0.11] общую формули-
формулировку метода ортогональных проекций. В свете этого
преобразования можно естественным образом сфор-
сформулировать указанные в [0.11] условия применимо-
применимости метода ортогональных проекций, которые заклю-
заключаются в выполнении дополнительных условий функ-
функционала B0).
Теория преобразования вариационных проблем
позволяет получить множество других минимальных
и максимальных функционалов для решения задачи
Дирихле, в частности функционал метода Трефтца.
б) Метод Трефтца оценки погрешности решения
задачи Дирихле для уравнения Лапласа B4) при
граничном условии B5)
Ли = div grad и = 0, G.24)
u\c = f G.25)
заключается в том, что вместе с минимумом функ-
функционала
Э (и) =\\j(grad "J dS G-26)
при условии B5) отыскивают максимум функционала
-dC G.27)
с дополнительным условием div grad w = 0, который
является функционалом граничного условия B5) для
данной задачи и может быть выведен таким же пу-
путем, как функционалы граничных условий в теории
упругости и теории оболочек (гл. 3 и 4).

§71 ОБ ОЦЕНКЕ ТОЧНОСТИ ПРИБЛИЖЕННЫХ РЕШЕНИЙ 201
Таким образом, метод Трефтца и различные его
обобщения сводятся к применению функционалов
граничных условий.
в) Метод негармонического остатка для оценки
погрешности решений бигармонического уравнения
заключается в том, что вместе с задачей максимиза-
максимизации функционала A0) решают задачу минимизации
функционала A3). Отсюда видно, что этот метод
укладывается в рамки теории преобразования вариа-
вариационных проблем.
Таким образом, теория преобразования вариаци-
вариационных проблем дает общий алгоритм построения ми-
минимальных и максимальных функционалов для
оценки точности решения. Среди всех минимальных
и максимальных функционалов данной теории можно
выбрать наиболее подходящую пару и использовать
ее для решения задачи с одновременным получением
оценки погрешности.
7.6. Пример. Оценка погрешности решения Навье для шар-
нирно опертой пластинки с равномерно распределенной нагруз-
нагрузкой с помощью функционалов Лаграижа и Кастильяно. Решение
Навье соответствует применению метода Ритца к функционалу
Лагранжа в перемещениях и имеет вид
«¦-I /=.1
где a, b — размеры пластинки, D — цилиндрическая жесткость,
16?
Функционал Кастильяно при данной нагрузке и граничных
условиях можно представить следующим образом:
LV
Л
9
2ДAц)
X J J [М2Х + М\ - 2рМхМу + 2(l + |i) M2xy] dS G.29)
с дополнительным условием
дгМх дгМу дгМхи
ду2 дх ду ч

202 ИСПОЛЬЗОВАНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ [ГЛ. б
Моменты Мх, My, Mxy должны удовлетворять граничным усло-
условиям
Мх\хш0 = Мх\Хша~0, Му\и=0 = Му)и=ь=0. G.31)
Выберем в качестве координатных функций метода Ритца триго-
тригонометрические полиномы и представим функции Мх, Му, Mxjl в
виде сумм
m n
тп_\-\-И -:- 1ПХ -:- 1ЯУ
my
Р2У + Р3— у qxy.
которые удовлетворяют уравнению равновесия C0) и граничным
условиям C1), а также и геометрическим (деформационным)
граничным условиям. Максимуму функционала B9) соответствуют
значения коэффициентов C2)
"W+W m
,
Для квадратной пластинки с а = b =¦ \, D = 1 значения
функционалов Лагранжа и Кастпльяно при различном числе чле-
членов ряда представлены в табл. 5.1 и иллюстрируют сходимость
метода Рнтца при выбранных координатных функциях.
Приведенные в табл. 5.1 разности Ь.Эп = Э'д — Э? значений
функционалов Лагранжа и Кастильяно показывают, что энергия
системы в состоянии, соответствующем решению с данным числом
членов ряда п2, отличается от энергии, соответствующей истинным
значениям параметров напряженно-деформированного состояния,
не больше чем на Д5".

ОБ ОЦЕНКЕ ТОЧНОСТИ ПРИБЛИЖЕННЫХ РЕШЕНИЙ 203
Таблица
Энергетическая погрешность решения метода Рнтца
для функционалов Лагранжа и Кастильяно
при различном числе членов ряда т ¦ п
5.1
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
Функционал
Лагранжа
ЭЛ1 («>„)• Ю'
—0,84312314
-0,85074607
—0,85117327
—0,85123403
—0,85124797
-0,85125225
-0,85125384
—0,85125453
—0,85125485
-0,85125502
-0,85125511
-0,85125517
-0,85125520
—0,85125522
—0,85125524
—0,85125525
—0,85125525
—0,85125526
—0,85125526
-0,85125526
Функционал
Кастильяно
*кз (*»)•">•
-0,90960958
—0,86137555
-0,85451352
-0,85267494
—0,85199363
—0,85168631
—0,85152817
—0,85143873
—0,85138442
-0,85134958
—0,85132621
—0,85130996
-0,85129832
-0,85128975
-0,85128331
-0,85127838
-0,85127454
-0,85127151
-0,85126907
-0,85126710
9
I Jll \ п) КЗ \ п}\
X Ю3
0,06648644
0,01062948
0,00334025
0,00144091
0,00074566
0,00043406
0,00027433
0,00018420
0,00012957
0,00009456
0,00007110
0,00005479
0,00004312
0,00003453
0,00002807
0,00002313
0,00001929
0,00001625
0,00001384
0,00001184
В статье [5.20] приведен пример оценкя погрешности для
этой же задачи, решенной с помощью функционалов Лагранжа и
Кастильяио методом конечных элементов с использованием ста-
тико-геометрической аналогии.
Энергетические оценки погрешности применялись также в
[5.7].

Приложение 1
понятия функционального
ИВЫПУКЛОГО АНАЛИЗА В ВАРИАЦИОННОЙ
ТЕОРИИ УПРУГОСТИ И ТЕОРИИ ОБОЛОЧЕК
«Вариационное нечисление фактически стало
одним из разделов функционального анализа
и занимает в нем такое же место, как теория
максимумов и минимумов в обычном анализе.*
Л. Янг
Цель данного приложения — очертить круг понятий функцио-
функционального и выпуклого анализа, которые применяются в вариа-
вариационных формулировках теории упругости и теории оболочек.
Их использование является перспективным для развития данной
теории и, в частности, позволило рассмотреть в данной книге
полные и частные вариационные принципы и теоремы, сделать
ряд выводов об экстремальных свойствах функционалов и т. д.
Основные определения, теоремы и обозначения функциональ-
функционального и выпуклого анализа см. в [1.2].
1. Пространства состояний упругой системы как линейные и
аффиииые пространства. Совокупность возможных состояний
упругой системы (т. е. полей перемещений, усилий, деформаций,
функций напряжений), среди которых отыскивается истинное со-
состояние, целесообразно рассматризать как линейное (векторное)
пространство (пространство состояний, см. гл. 2). Iiro элементами
являются трехмерные (или двумерные) векторные или тензорные
функции и(г), с (г) и т. д. положения точки в области V, зани-
занимаемой упругим телом (или в области S, занимаемой базисной
поверхностью оболочки); здесь г—радиус-вектор точки в какой-
либо декартовой системе координат. Таким образом, различные
пространства состояний упругой системы являются пространства-
пространствами функций, определенных на V или S (функциональными про-
пространствами) н имеют бесконечную размерность.
Линейное пространство — частный случай аффинного про-
пространства, т. е. пространства, которое вместе с любыми двумя
точками х, у содержит всю проходящую через них прямую линию
(множество ах-\-(\—a)j/, a — любое вещественное число). Ли-
Линейное пространство отличается тем, что всегда содержит нулевой
элемент. В книге встречаются пространства состояний, являю-
являющиеся лишь аффинными, например множество полей перемеще-
перемещений, удовлетворяющих неоднородным геометрическим гранич-
граничным условиям (пространство, связанное с функционалом Лагран-
жа), или пространство напряжений, удовлетворяющих неоднород-
неоднородным уравнениям равновесия (на котором определен функционал
Кастильяно).
Иногда удобно от аффинного пространства А перейти к ли-
линейному пространству L, представив все элементы a s А в виде
а = а°+Ь, (П

ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ 205
где а° — какой-либо фиксированный элемент из А; в этом случае
элементы b составляют линейное пространство. Например, по-
построив какое-либо поле перемещений к", удовлетворяющее не-
неоднородным граничным условиям данной задачи, можно любое
допустимое поле перемещений представить в виде
и = «° + «'. B)
где поля и' удовлетворяют однородным граничным условиям и,
следовательно, составляют линейное пространство.
Рассматриваемые в книге подпространства пространств со-
состояний определяются, как правило, теми или иными линейными
уравнениями. Линейное однородно» уравнение определяет в ли-
линейном пространстве линейное подпространство (в аффинном —
аффинное), линейное неоднородное уравнение определяет аффин-
аффинное подпространство. Например, поля напряжений, удовлетворяю-
удовлетворяющие неоднородному уравнению разновесия V-O + F = 0, состав-
составляют аффинное подпространство в линейном пространстве напря-
напряжений.
Пространства состояний вида («, а) илн (ф, а, е) удобно
рассматривать как прямые (декартовы) суммы 1/©2 или
Ф © 2 © Е пространств перемещений U, напряжений 2, дефор-
деформаций Е и функций напряжений Ф.
2. Функции и функционалы в теории упругости и теории обо-
оболочек. В книге рассматриваются главным образом линейные и
аффинные функции (отображения, операторы) в функциональных
пространствах. Например, выражение -~- (Vя + и\7) определяет
линейное отображение пространства перемещений U в простран-
пространство деформаций Е (линейный оператор); V-a + F—аффинное
отображение пространства напряжений 2 в пространство объем-
объемных сил (аффинный оператор). Соответственно равенство
е — -~-(Чи + UV) =0 есть линейное однородное уравнение, а
V-a + f = 0 —линейное неоднородное уравнение (здесь 0 сле-
следует рассматривать как нулевой элемент пространства).
Функции, отображающие какое-либо линейное пространство
в множество действительных чисел, называются функционалами.
Различные виды энергии упругого тела (полная потенциальная,
дополнительная, смешанная и т. д.) представляют собой функ-
функционалы, определенные на пространствах состояний. В линейной
теории упругости и оболочек этн функционалы квадратичные.
3. Выпуклые множества и выпуклые функционалы в аффин-
аффинных пространствах. В книге выпуклые множества представляют
собой, как правило, линейные или аффинные подпространства.
В частности, все решения линейного уравнения (однородного или
неоднородного) образуют выпуклое множество.
Выпуклые вниз функционалы иногда сокращенно называют
просто выпуклыми. Функционал Э(а, Ь), определенный на прямой
сумме двух аффинных пространств А и В, называется выпукло-
вогнутым, если он является выпуклым вниз на А при каждом

206 ПРИЛОЖЕНИЕ I
фиксированном b s В и выпуклым вверх (вогнутым) на В при
каждом фиксированном а е А.
4. Скалярное произведение, норма, метрика в пространствах
состояний упругой системы. Если в линейном пространстве опре-
определить скалярное произведение, то оно становится евклидовым
пространством. Например, в пространстве перемещений U ска-
скалярное произведение и ° v(u,veU) можно определить равен-
равенством
u°v=\\[uividV- C)
В пространстве напряжений 2 рассматривают скалярное произ-
произведение вида
г г г .,
D)
Для вариационной теории особый интерес представляет энер-
энергетическое скалярное произведение. Оно может быть определено
в тех пространствах состояний, в которых вариационные прин-
принципы формулируются на основе выпуклых (вверх или вниз)
функционалов; это соответствует положительной определенности
[0.11] операторов, являющихся нх градиентами. Например, в про-
пространстве U* перемещений, удовлетворяющих геометрическим
однородным граничным условиям, энергетическое скалярное про-
произведение имеет вид
[и, v] = [[ [ е (и) ¦ ¦ а ¦ ¦ е (v) dV (и, v e= U*). E)
В пространстве 2* напряжений, удовлетворяющих всем однород-
однородным уравнениям равновесия, можно рассматривать скалярное про-
произведение
\ И''ь ¦ ¦р dV {a> p e 2*)- (б)
В пространстве U" перемещений, удовлетворяющих всем урав-
уравнениям теории упругости в области и однородным геометриче-
геометрическим граничным условиям, скалярное произведение можно опре-
определить на основе функционала граничных условий
[и, v] = V V я ¦ о (и) ¦ vdS (u,vz=U**). G)
Энергетическое скалярное произведение порождает энергетиче-
энергетическую норму [0.11]
| и | = Vl«. и] , | а | = VI», а]. (8)
На основе норм, соответствующих различным скалярным произ-
произведениям, можно определить различные метрики р(н, i>), харак-

ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ 207
теризугощне «расстояние» между двумя элементами и, v рассма-
рассматриваемого пространства:
р(«, v) = \u — v\. (9)
С помощью метрики оценивают близость прнблил<енного решения
задачи к точному. В энергетической метрике-расстояние между
любыми двумя полями перемещений, отличающимися на смеще-
смещение твердого тела, равно нулю, т. е. эти поля не различаются
и их отождествляют.
С метрикой связаны понятия полноты и сепарабельности про-
пространств, имеющие важное значение в вопросах существования
решений и применимости приближенных методов; эти вопросы,
однако, выходят за рамки данной книги.
5. Дифференцирование вариационных функционалов. Норми-
Нормирование пространства состояний позволяет при исследовании ва-
вариационных формулировок применять понятия производной и
дифференциала. Дифференциал функционала энергии в нормиро-
нормированном пространстве (дифференциал Фреше) в вариационном ис-
исчислении называют вариацией. Производная функционала энергии
(производное отображение) является дифференциальным опера-
оператором соответствующей краевой задачи. Этот оператор получают,
преобразуя вариацию функционала методами вариационного
исчисления (см гл. 1). Производную функционала иногда назы-
называют его градиентом. Точкой стационарности функционала назы-
называется такое значение его аргумента, при котором его градиент
равен нулю, т. е. соответствующие дифференциальные операторы
обращаются в нуль.
Если пространство состояний представляет собой прямую
сумму нескольких пространств, то можно рассматривать частные
производные отображения. Например, выражение
ди
(Ю)
обозначает производную в подпространстве U при фиксирован-
фиксированных е, а.
Заметим, что в [0.11] на основе функционального анализа
рассмотрены вопросы построения вариационных формулировок,
соответствующих данным краевым задачам, и применения их для
приближенного решения.

Приложение 2
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО
И ТЕНЗОРНОГО АНАЛИЗА
сТензорная алгебра и тензорный анализ яв-
являются естественным аппаратом механики (и
физики вообще) сплошных сред. Они выде-
выделяют то существенное, что относится к самим
изучаемым явлениям, отбрасывая то, что
привнесено выбором конкретных координатных
осей.»
В. Л. Фомин
Механика континуума для инженеров.
Приводятся обозначения и некоторые соотношения вектор-
векторного и тензорного анализа, используемые в гл. 3—5 для записи
функционалов и их преобразований и вывода условий стационар-
стационарности. При составлении этого приложения были использованы
книги [П. 7, П.12. 3.3, 3.7, 4.11].
1. Метрический тензор; ковариантиые и контравариантные
компоненты векторов и тензоров. Пусть Еп — л-мерное (в данной
книге л = 2 или л = 3) евклидово пространство, ei, е2, ..., е„ —
элементы базиса (базисные векторы); скалярное произведение в
Е" обозначим а-Ь. Базнс характеризуется числами
которые определяют длины базисных векторов (||е,||2 = ei-ei =
= gu) и углы между ними (е,-е, = || е,- || • || е/ ll-cosy*/), <\ / =
= 1, 2, ..., л, и называются ковариантными компонентами мет-
метрического тензора данной системы координат. Кроме данного
основного базиса е,-, в тензорном исчислении вводят взаимный
базис е1, связанный с основным соотношением
B)
где g4 — элементы матрицы, обратной к gi/. Здесь и во всей
книге используется обычное в тензорном исчислении соглашение
о суммировании по повторяющимся индексам от 1 до п.
Нетрудно проверить, что gil = е'-е', так что величины t;''
являются компонентами метрического тензора, но связанного с
взаимным базисом: они называются контравариантными компо-
компонентами. Из B) следует также, что е • е^ = 6j, где 6', — символ
Кронекера, определяемый равенствами 6(. = 1, 6j = 0 при i =^= j.
Любой элемент (вектор) а пространства Е" можно предста-
представить в виде лииейиой комбинации векторов осиовиого или взаим-
взаимного базиса:

ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ 209
Величины а' называются контравариантными, а ai — ковариант-
ными компонентами вектора а; они связаны между собой соот-
соотношениями
a'=*gilaf; а{=чИа*. D)
Их можно вычислить по формулам
al = a-el, al = a-ei. ' E)
Пусть d{ (i = 1, 2, ..., «)—какой-либо другой набор базис-
базисных векторов, ad' — взаимный базнс к d{. Векторы d< можно
разложить по базисным векторам ее.
dl = c>ler F)
где с\ — элементы матрицы преобразования координат, которые
на основании E) равны с[ = dt • еК Взаимные векторы d' свя-
связаны с е' соотношениями
d'^b'je1, G)
где bj — матрица, обратная к с\: bjC'k = 6^. Отсюда следует, что
при переходе от базиса е< к базису di контраварнантные н коза-
риантные компоненты вектора а преобразуются по закону
т. е. соответственно как векторы взаимного и основного базиса.
Равенства (8) являются необходимыми и достаточными усло-
условиями того, чтобы набор величин <ц, ..., ап (а1, ..., ап) можно
было рассматривать как ковариантные (контравариантные) ком-
компоненты вектора, т. е элемента пространства Еп. Другими сло-
словами, эти равенства могут рассматриваться как аналитическое
определение вектора.
Это определение позволяет обобщить понятие вектора. Пусть
какой-либо объект а в каждой системе координат характеризует-
характеризуется nr+s величинами а,1 " Л Такой объект называют экстенси-
I, ... ir
вом (r-fs)-ft валентности (по числу индексов). Экстенсив а на-
называется тензором, если его компоненты при линейном преобра-
преобразовании координат F), G) меняются по закону
В частности, вектор есть тензор первой валентности, а скалир—
тензор нулевой валентности. Компоненты (9) тензора а назы-
называются г раз ковариантными и s раз контравариантными. С по-
помощью метрического тензора g можно по формулам, аналогич-
аналогичным D), поднять или опустить любой индекс у компонентов
тензора а и получить контравариаитные или ковариаитные по
этим индексам компоненты.

210 ПРИЛОЖЕНИЕ 2
Коварнантные компоненты дискриминантного тензора е
(в пространстве Е„) определяются условиями: €(- ,• = 0, если
среди индексов i'i, ..., in есть хотя бы два одинаковых; если все
числа i'i In различны, то (, . / — VF" или — Vg в за-
1 *' * п
висимостн от того, является четной или нечетной перестановка,
переводящая индексы it in в 1, 2, .. , п; здесь g — опреде-
определитель матрицы gii. Контравариантные компоненты тензора ( оп-
определяются теми же условиями с заменой V# на /Vi
2. Операции иад тензорами. Тензоры одной и той же валент-
валентности образуют линейное пространство по отношению к сложе-
сложению и умножению на число, которые в любой системе координат
выполняются покомпонентно, причем складываться могут лишь
одинаковое число раз ковариаитиые (коигравариантные) компо-
компоненты.
Если а и b — два тензора, то величины вида
cii lit ip = aii i bii i p A°)
являются r + p раз контравариантными и s + q раз ковариант-
пыми компонентами (г + s + Р + Q) -валентного тензора с, кото-
который называется диадным, или тензорным произведением тензоров
а и b и обозначается с = ab.
Суммы вида
I. ... k ... I I t ... m ... t
в/| ... k. ..irt = bm*t\. ..i...!sr D)
являются s—1 раз ковариантными иг—1 раз кочтраварнант-
ными компонентами нового (г + s — 2)-валентного тензора с, ко-
который называется сверткой тензора а по индексам m и /. Напри-
Например, свертка двухвалентного тензора с = а\ = g'*a{j = g^a'1 есть
скаляр.
Векторным произведением тензоров а и b валентности г и s
соответственно в трехмерном пространстве называется
(г + s — 1) -валентный тензор с = аХЬ с компонентами вида
с, , , , =<? 'г''а, , , Ь, , , , A2)
где ? — дискриминантиый тензор.
Скалярным произведением а-b тензоров а и Ь называется
свертка тензора ab по последнему индексу а и первому индек-
индексу о. Двойное скалярное произведение а- Ъ есть двойная свертка:
последний индекс а с первым индексом Ь, предпоследний — со
вторым.
3. Криволинейные координаты, локальный базис, тензорное
поле. Положение точки в евклидовом пространстве может быть
задано с помощью криволинейных координат а', которые связаны
с декартовыми координатами х1 нелинейными соотношениями
г = г(а') пли х! = х!{а\ A3)

ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ 211
где г— радиус-вектор точки, х'(а1) — непрерывяо-дифференцируе-
мые функции. Чтобы в криволинейных координатах использовать
понятия производной и тензора, в определении которых суще-
существенную роль играет линейность, в каждой точке пространства
вводят локальный базис, векторы которого определены форму-
формулами
.,-fr- <»>
да
Любые непрерывно-дифференцируемые преобразования криволи-
криволинейных координат а' = а'(Р') определяют (согласно правилу
дифференцирования сложной функции) линейные преобразования
локального базиса
, дг дг да да1 „„
d{ = —г = —г= г«,- A5)
д$' да' д$ др
Определение тензора в криволинейных координатах рассматри-
рассматривается по отношению к этим линейным преобразованиям: матри-
матрицей преобразования их служит матрица Якоби с\ =—г; обрат-
,i д$
пая матрица есть Ь,=——г.
да'
Заметим, что не всякий объект, являющийся тензором по от-
отношению к линейным преобразованиям декартовых координат,
есть тензор по отношению к преобразованиям криволинейных
координат; например, большие перемещения, рассматриваемые в
геометрически нелинейной теории упругости, при нелинейных пре-
преобразованиях A3) преобразуются по нелинейному закону, а не
по векторному. В данной книге используются только бесконечно
малые перемещения и деформации, являющиеся векторами и тен-
тензорами.
Векторную (тензорную) функцию, заданную в области V ев-
евклидова пространства, называют также векторным (тензорным)
полем.
4. Дифференцирование векторов и тензоров. Т1ри отыскании
производных от векторных и тензорных полей в криволинейных
координатах приходится учитывать то обстоятельство, что коор-
координатные векторы являются переменными величинами. Различие
координатных систем в точках а' и а' + da1 приводит к тому,
что компоненты Vjai производной —- вектора а не совпадают
да
да1
с частными производными —г, а вычисляются по формулам
да
^f> v/ = ^- + lV\ A6)

212 ПРИЛОЖЕНИЕ 2
где Г^—величины (вообще говоря, нетензорные), называемые
символами Кристоффеля второго рода. Для вычислений приме-
применяют символы Кристоффеля первого рода
2 V да да' да
связанные с Т\] соотношениями
Величины V/a;(V/a') называются ковариантными производными от
ковариантных (контравариантных) компонентов вектора а. Ана-
Аналогично ковариантные производные от компонентов тензора вы-
вычисляются по формулам вида
да
(<4) + TmlaTk Tfia^ T^a\m. A9)
Совокупность величин Cj[k = va^ образует тензор с = Va
на единицу большей валентности, чем а, который называется
градиентом тензора а. В частности, градиент скаляра — вектор.
Для ковариантной производной справедливы те же правила
дифференцирования суммы, произведения и т. д., что и для обыч-
обычной производной. Ковариантные производные от компонентов
метрического и днскриминантиого тензоров равны нулю, так что
эти компоненты при ковариантном дифференцировании должны
рассматриваться как постоянные.
В трехмерных задачах часто используется символический
набла-оператор Гамильтона V, который рассматривается как век-
вектор, компоненты которого представляют собой дифференциальные
операторы V*. Диадное произведение Va есть градиент тензо-
тензора а; рассматривают также произведение aV, отличное от Ve;
например, если a — вектор, то набор компонентов aV представ-
представляет собой транспонированную матрицу по отношению к Va, а
сумма с = — (уа-f-eV) представляет собой симметричную часть
тензоров Va и aV и имеет компоненты Сц = — (v;a + Vy^)-
Векторное пронзведенне V X о. называется ротором (вихрем) тен-
тензора а, скалярное произведение V-а — дивергенцией тензора а.
В книге часто встречается выражение c = VXeXv, где а
и с — двухвалентные симметричные тензоры; приведем его коор-
координатную запись:
И 11 М1 B0)
5. Поверхность в трехмерном пространстве обычно задают
с помощью параметрического уравнения
r = r (g1, |2) нли *f = *4ia), B1)

ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ 213
где I = 1, 2, 3; а = 1, 2. Параметры *а представляют собой кри-
криволинейные координаты на поверхности. Поверхность S пред-
представляет собой двумерное пространство, которое, вообще говоря,
не является евклидовым, так как для большинства поверхностей
не существует системы координат, в которой компоненты метри-
метрического тензора были бы постоянными, т. е. все системы коорди-
координат на них — криволинейные.
На поверхности задают локальный базис еа и метрический
тензор а с помощью соотношений
при этом поверхность становится римановыч пространством. Ком-
Компоненты метрического тензора а называют также коэффициен-
коэффициентами первой квадратичной формы поверхности S; онн опреде-
определяют внутреннюю геометрию поверхности. В полученном римано-
вом пространстве вводят тензоры и ковариантные производные
по отношению к преобразованням двумерного локального базиса,
которые называют поверхностными тензорами и поверхностными
ковариантными производными. Заметим, что в рнмановом про-
пространстве ковариантные производные V, и Vj не перестановочны:
Положение поверхности в трехмерном пространстве характе-
характеризуется двухвалентным тензором Ь , компоненты которого на
зывают коэффициентами второй квадратичной формы поверхно-
поверхности. Коэффициенты Ь определяют кривизну поверхности и свя-
связаны с поведением единичного вектора нормали п-
6. Интегрирование тензорных величин. Элемент объема (по-
(поверхности) в евклидовом или римановом пространстве опреде-
определяется выражением
dV = VF da> da2 da3 (dS = л/Т d|' d|2). B4)
Для тензорных функций, удовлетворяющих известным усло-
условиям непрерывности и дифференцируемое™, справедливы форму-
формулы преобразования интеграла по области в интеграл по ее гра-
границе. Эти формулы в книге применяются для интегрирования по
частям при преобразованиях функционалов.
Формула Грина связывает ннтеграл от векторной функции / по
границе (контуру) С двумерной области S с интегралом от V/
по S:
JadC, B5)

214 ПРИЛОЖЕНИЕ 2
где va — компоненты вектора тангенциальной нормали к конту-
контуру С (т.е. нормали, лежащей в касательной плоскости к 5).
Формула Остроградского — аналог формулы Грина для трех-
трехмерного пространства — связывает интеграл от функции F по по-
поверхности 5, ограничивающей область V в трехмерном простран-
пространстве, с интегралом по V:
ш
= О я • F dS. B6)
Формула Стокса является обобщением формулы Грина:
B7)
где t — единичный вектор касательной к контуру С.
7. Физические компоненты тензоров и векторов. В криволи-
криволинейных координатах векторы локального базиса A4) не норми-
нормированы, и компоненты векторов и тензоров в этом базисе «изме-
«измерены» в каждой точке в своих единицах, которыми служат
длины базисных векторов. Но для практики представляют инте-
интерес компоненты, «измеренные» в одних и тех же единицах, не
зависящих от системы координат, т. е. в нормированных базисах.
Рассмотрим ортогональную систему координат с единичными
векторами—, е Взаимные векторы —г= е1 в силу орто-
тональности будут совпадать с —; е. Составляющие векто
ров и тензоров в этом базисе называют физическими компонен-
компонентами и обозначают скобками, в которые заключают индексы.
Физические и обычные компоненты связаны соотношениями вида
Обратная связь дается формулами
a'=vg"a"" a = vTa<0' ац
1
= <»<>)• aii"*WSii81ja{lj),
B9)
a;
В B8) и B9) не нужно суммировать по повторяющимся индек-
индексам.

векторный и тензорный анализ 215
Физические компоненты для неортогональной системы коор-
координат введены, например, в [4.11].
Для физических составляющих поверхностных ковариантных
производных в ортогональных координатах справедливы формулы
[4.11]
v _ 1 1
v(l)"(D — "л7 "A)> ' ~А~М '• 2"B)>
V(l)"B)— Ax "B), I дхАг Л\, 2"A)>
) =— «"A2), 1 + ^47 ^1. 2
^A)^22, - 17 Ш<22>- ' ~ ~АЖА'• 2 (Ш<12> + ^f2'))
где Ль Лг — параметры Л яме, <4i = Vaib Лг = Va22
8. Переход от тензорной формы записи к развернутой. В за-
задачах теории упругости и теории оболочек физические компо-
компоненты векторов и тензоров (представляющие практический инте-
интерес) можно получить двумя путями: 1) решить соответствующую
краевую или вариационную задачу в обычных компонентах и за-
затем по формлам B8) перейти к физическим; 2) записать в фи-
физических компонентах все необходимые уравнения и функцио-
функционалы и получить решение. Ниже приведены правила, которые
можно использовать при реализации второго пути.
Чтобы записать какое-либо тензорное выражение из теории
упругости в развернутой форме в физических компонентах,
нужно:
1) придать свободным индексам значения 1, 2, 3;
2) развернуть сокращенную запись сумм;
3) выполнить ковариантное дифференцирование по формулам
A6) или A9);
4) подставить выражения символов Крнстоффеля;
5) выразить компоненты метрического тензора gu через па-
параметры Ляме At;
6) заменить соответствующие величины через физические
компоненты.
В результате получаются развернутые формулы рассматри-
рассматриваемых выражений. В некоторых более простых случаях отдель-
отдельные этапы выпадают.
9. Односвязные и многосвязные области (см., например:
Ф и х т е и г о л ь и Г. М. Курс дифференциального и интеграль-
интегрального исчисления, т. I, III—M.: Наука, 1966, 1969). Область Q
евклидова или риманова пространства ? называется связной, если

216 ПРИЛОЖЕНИЕ 2
любые две точки х, у е Q можно соединить кривой, целиком
лежащей в Q.
Связная область S в двумерном римановом пространстве на-
называется односвязной, если, каков бы ни был простой замкнутый
контур, лежащий в S, ограниченная этим контуром область це-
целиком принадлежит S; в противном случае область S называется
неодносвязной или многосвязной. Если речь идет о конечной об-
области 5, то понятие односвязности можно сформулировать проще:
область S должна быть ограничена единственным связным замк-
замкнутым контуром; многосвязная область имеет границу, состоя-
состоящую из нескольких связных участков, т. е. имеет отверстия.
Связная область V в трехмерном евклидовом пространстве
называется поверхностно-односвязной, если, каков бы ни был
простой замкнутый кусочно-гладкий контур I в области V, суще-
существует кусочно-гладкая самонепересекающаяся поверхность S, ог-
ограниченная контуром / и целиком лежащая в V, в противном слу-
случае V называется поверхностно-чеодносвязной или поверхностно-
многосвязной. Пример поверхностно-многосвязной области — тор.
Область V называется пространственно-односвязной, если, ка-
какова бы ии была принадлежащая V простая замкнутая поверх-
поверхность S, области V целиком принадлежит тело Т, ограниченное
(извне) поверхностью S; в протизном случае область V назы-
называется пространственно неодносвязной или пространственно-мно-
пространственно-многосвязной. По отношению к конечной области V определение про-
пространственной односвязности сводится к тому, что V должна
быть ограничена единственной связной замкнутой поверхностью.
Пример простраиственно-многосзязной области — полый шар.

Приложение 3
ОБОБЩЕНИЕ ТЕОРИИ НЕОДНОРОДНЫХ
АНИЗОТРОПНЫХ ОБОЛОЧЕК
НА КОНСТРУКТИВНУЮ И ПРИОБРЕТЕННУЮ
АНИЗОТРОПИЮ
На основе вариационного подхода рассмотрен способ приве-
приведения конструктивно-анизотропных, в частности ребристых, обо-
оболочек, к задачам теории неоднородных анизотропных оболочек
[0.2, П.1, П.2]. Обобщение распространено и на учет приобре-
приобретенной анизотропии, которая создается даже в изотропных обо-
оболочках при работе в упруго-пластической стадии [П.З]. Благо-
Благодаря такому обобщению формулировки гл. 4 распространяются
на оболочки с конструктивной и приобретенной анизотропией.
1. Приведение конструктивно-анизотропной оболочки к анизо-
анизотропной. Представим некоторую конструктивно-анизотропную обо-
оболочку в виде многоконтактной задачи собственно оболочки с ба-
базисной поверхностью S и подкрепляющих ее элементов (напри-
(например, узких и широких ребер, подкрепляющих слоев и др.), зани-
занимающих подобласти S* иа этой поверхности. Контакт S* с S
осуществляется по точкам, по линиям или поверхностям. Обозна-
Обозначим через и, е, N матрицы-столбцы перемещений, деформаций и
усилий-моментов. Данная несвободная вариационная задача
(варьируются е и и)
6Э = 6Э° (и0, е°, JV0) + ? ЬЭк {uk, e\ Nk) =
k
= \ 6W (и°, ?°, iV°) dS + ]Г \ 6И7* (uk, efe, iVfe) dSk = 0, A)
S k Sk
кроме дополнительных условий в области и в каждой из подоб-
подобластей, имеет геометрические условия контакта S с S*
ft {u°, uk, е°, efe) = 0. B)
Индекс о относится к оболочке, k — к подкрепляющим элемен-
элементам; область S — двумерная, а подобласти S* могут быть дву-
двумерными (для слоистых оболочек или широких ребер) и одно-
одномерными (для узких ребер).
Распространим интегрирование по подобласти S* на об-
область S, введя специальные функции Г*. Для узких ребер Г* —
импульсные функции, для широких ребер — ступенчатые функ-
функции, для слоистых оболочек — Tft = 1 Тогда
ЬЭ = \ б [W (и0, г°, №) + Wk (и*, е*. Nk) Tfe] dS. C)

218 ПРИЛОЖЕНИЕ 3
Пусть условия контакта B) такие, что можно выразить дефор-
деформации элементов через деформации оболочки:
efe = g(e°). D)
Подстановка D) в C) позволяет выделить обобщенные усилия
N = № + ? I\JV4, E)
k
которые работают на деформациях бе°.
Тогда вариационные уравнения для всех рассматриваемых
конструктивно-анизотропных оболочек в качестве условий ста-
стационарности имеют одинаковые дифференциальные уравнения
равновесия, выраженные в обобщенных усилиях (производные
понимаются в обобщенном смысле), и геометрические соотноше-
соотношения такие же, как для гладкой оболочки. Все различия содер-
содержатся в физических уравнениях, которые в общем случае по
форме совпадают с уравнениями для анизотропных оболочек, но
имеют различные параметры упругости, отражающие все особен-
особенности конструктивной анизотропии. Таким образом, приведение
конструктивно-анизотропных оболочек к анизотропным состоит в
определении физических параметров.
2. Проиллюстрируем приведенные рассуждения на примере
оболочки, подкрепленной узкими ребрами произвольной ориента-
ориентации. Оболочка описывается уравнениями в развернутой форме
(гл. 4, § 8), а ребра — теорией стержней Кирхгофа — Клебша.
Для данного случая в вариационном уравнении C)
V* (и*, ш\ /) =
где qk, q — тангенциальная и вертикальная нагрузки, U — длина,
i)k — эксцентриситет /г-го ребра, B==EFk, ?/?, Glk — жесткости
ребра при продольной деформации, изгибе и кручении; ф — угол
закручивания ребра. Условия B) контакта й-го ребра с оболочкой
ff = и0 - ик + ть (dwkldx\) = О, % = w° - wk = 0,
k ° 2 к B'}
Специальная функция Tfe в C), E) равна
г* = б [(*2 - *о*) - (*' - *i») tg D. ^'I [г (*' - Х1) -
- Г (ж1 - *;ft)] cos (ж', х1) + б [(х1 - ^) -

КОНСТРУКТИВНАЯ, ПРИОБРЕТЕННАЯ АНИЗОТРОПИЯ 219
причем Г (х) — ступенчатая функция:
Г(*) = {0 при лг < 0; 0,5 при лг = 0; 1 при х > 0}, (8)
б (х) — симметричная единичная импульсная функция, или функ-
функция Днрака, определяемая условием
* /0 при х < а или х > Ь, \
^ { (I) б (I - х) d% = ) о,5/ (*) прн х = а или х = Ь, I
{ f (х) прн а < х < Ь )
(а<Ь)
для произвольной функции f(l), непрерывной в точке 1 = х.
С учетом B') перейдем от деформаций в ребре е*, и*, т*
к компонентам деформации в оболочке по направлению й-го реб-
ребра. Используя G) и формулы преобразования компонентов де-
деформаций при переходе от координат х\, х\ (см. рис. в табл. П. I)
к координатам х1, хг, получим соотношения упругости, связы-
связывающие обобщенные усилия с деформациями [0.2]. Параметры
этих соотношений представлены в табл. П, 1.
3. Элементы матриц соотношений упругости для оболочек с
широкими и узкими ребрами, параллельными координатным ли-
линиям, и многослойных оболочек приведены в табл. П. 2 — П. 6.
Возможно обобщение н иа другие конструктивио-аиизотропные
оболочки, например частоперфорированные [П. 5], сетчатые
[П. 11], некоторые пространственные системы.
4. Линеаризованные физически нелинейные задачи для глад-
гладких и ребристых оболочек. Учет приобретенной анизотропии на
примере линеаризации физически нелинейных задач теории малых
упруго-пластическнх деформаций при использовании метода пере-
переменных параметров упругости рассмотрен в [П. 3]. В этом случае
связь между компонентами усилий и деформаций для гладких и
ребристых оболочек можно представить в форме A 20) гл. 4
для неоднородных анизотропных оболочек. В этих уравнениях
коэффициенты упругости являются функциями напряженио-де-
формированного состояния. При решении данной нелинейной за-
задачи методом переменных параметров упругости физические со-
соотношения на каждом шаге линеаризации сохраняют форму A.20)
с постоянными коэффициентами упругости. Часть коэффициентов
в этих соотношениях обращается в нуль, а вид других зависит
от интегральных физических характеристик сечения (например,
[П. 6]). Уравнения равновесия и геометрические завнсимостн,
естественно, остаются одинаковыми для теории малых упруго-
пластических деформаций н линейной теории неоднородных ани-
анизотропных оболочек.
Таким образом, задачи расчета однородных и неоднородных
оболочек с учетом физической нелинейности приводятся к после-
последовательности линеаризованных задач для неоднородных анизо-
анизотропных оболочек.

ТАБЛИЦЫ
Различные варианты функционала Лагранжа
Функционал Лагранжа
3Л1 (и) = J J 5 [j е (и) • • а ¦ ¦ е (и) - F ¦ и] dV - JJ (f* ¦ и)'
dS
- f- ¦) ^ ~ \\ (Г • ")'
ф^O] rfS + С (ff°, и*, <р*) (см. табл. 3.2)
3Л4(«. •• ff)=
в декартовых координатах
-F'u.^dV - [[(}*'и.YdS
где еар = у (Vau,3 + V3ua) a, P = I, 2
в декартовых координатах
где е33 = V3U3

ТАБЛИЦЫ
221
Таблица 3.1
для неоднородного анизотропного упругого тела
Дополнительные условия
(а — а*)" = 0 на S
e-l(Va + aV) = 0 в V;
(„ _ иу = 0 на S
V Х«Х V = 0 в V;
e--i-(Va + aV)=0,
О— е •• а = 0 в V;
(и - и*)" = 0 на S
е31-уGз«,- + ^«з) = 0 bV<
(Ui-u*)" = 0 на S
(«,- — «*)" = 0 на S
Условия стационарности
V-ff[e(a)]+F = 0 в V;
{a[e(u)]-n-f*V = 0 на S
V-ff(e)+F = 0 в V;
[а(е)-я-П' = 0 на S
V -о(е) + Р = 0 в V;
[а(е)-я-П' = 0 ка S
V-a+F = 0 в V;
(ff-n-f)' = 0 на S
V/ff'y (e) + F' = 0 в V;
\р1' (в) Л/ - /*']' = 0 на S
V,a" (e) + F' = 0bV;
[а'/(е)я/-Г']' = 0 на S

222 ТАБЛИЦЫ
5K1
где
где
где
фУб=саус13бГ_
(Ф. ff) = \ \ \
+ [саус$
(ф, О, е) = \ \
в декартовых
/ C\ 1
1 ф . о 1 =^ 1
в декартовых
/ ш\ V
1 ф^ it G 1 ^— 1
Различные варианты
функционала
Функционал Кастильяно
[~2^пФчйЧ~^ вФ^З ) —
о • •b••о\dV— \
Л 2 " " )
координатах
координатах
::Z
\ •! саус®6(е*
-SS-—¦-
dy + \ X («/0
JJ v '
Y, 6=1,2
Кастильяно
у/ ^ФаВ
,33}rfs + c
а3] dS + C
"я,)" rfS,

ТАБЛИЦЫ
для неоднородного аннзотропного упругого тела
223
Таблица 3.2
Дополнительные условия
(ФаЗ - Фаз)' = °>
(ф^6 - фу6)' = 0 на 5
V дп 1ар/
V • а + F = 0 в V;
(а.п- f*)' = 0 на S
6 — О • • b = 0 В V',
(фУ« _ фу«у = 0(
(фа0 - Ф*аз)' = ° Ha S
в V;
(ФаЗ - Фаз)' = 0.
(ty^ —Ф ) =0 на S
в V;
(ф«3 - Фаз)' = °
Условия стационарности
VXe[o((f)]XV=0 в V;
\ уЬ ^ ^Ф/J \б) == ^^
VXeHXV=0 в V,
< V Г/» (П\"\ V \ П и а ^
V VO *¦ \ ft уЬ) '
V Хе WX V=0 в V;
\еу6 (а) - ev6 (a*)]" = 0,
VX«XV = 0 в V;
[~v ('p'l V T7 0 на 9
|_Луб \e/ y^-I —
[eY5 (ff)-ev5 («*)]" = 0,
emHeklny у e (ff) _ g B y.
{xYj [e (a)] — xYs (a*)}" = 0 на 5

224 ТАБЛИЦЫ
Лагранжева серия полных функционалов
Полные функционалы
(«¦ f) = J J J [у е (и) ¦ ¦ а ¦ ¦ е (и) - Р ¦ и] dV -
Зп,а (в) = J J J [-у е (в) ¦ • а • • е (в) - P • в] rfH -
- ^ (ГУ ¦ и dS - J J (и - и*)" ¦ а [е (и)] • п
dS
Функционал Ху — Вашицу
(и, е, <т) =
-\\ (f*)' ¦ и dS - \ \ (и - и*)" a ndS
3„з (е. q>) = J J J [у е • ¦ а ¦ ¦ е - а" ¦ • е - <р -. (V X в X V)] dV +
+ J S K^6)' ev6 - С°^В6 (ф'ар)' Ne (•)] dS + C (a°, „*, „*) +
Г Г
-L. V \ -fibv6 Ги — л* У га^г^а> - fv . (р\ — v* 1"\ rf<J
J J
где ^ves=^v»(q)) (см. табл. 3.2)

ТАБЛИЦЫ
для неоднородного анизотропного упругого тела
225
Таблица 3.3
Условия стационарности
~ди~~°
дЭ — о
ди ~
17 = 0
дЭ
-т— = 0
да
дЭ
де
дЭ
{а
{"
(«
(а
o(e(e)J + F = 0 в V,
е(и)\-п-П' = 0,
в(в)].я-/}* = 0 на S;
- и")" = 0 на S
е («)] • п - П' = 0, (d - и*)" = 0 на S
V.a + F = 0 в V, (а-п —/*)' = 0 на S,
a — е • • a = 0 в F;
(« — «*)" = 0 на S
е ¦• а — (о°+ V Х<РХ V)=0 в V,
(у>У& _ ,|)Y6y _ 0>
(Фар - «Ров)' = ° на S;
У^в^У=^0 в V
[ху& (е) — к*6]" = 0 на S
Множители
Лагранжа
—
о
ч\
8 II. П Лбоискмй и др.

226 ТАБЛИЦЫ
Полные функционалы
_Ч
ЭП4 (и, е, а, к, ц) =
- ц • • (а — е ¦ ¦ а) }dV — \ \ (Г)' • и rfS — \ \ (и - и*)" -X-ndS
Эа4а {и, е, а)
-у11 • •е + \(ff +е¦ ¦«) • • тг (v« + «v)-'•«]dV-
- J J (ГУ ¦ и dS - jj jj (а - и*)" • 1 (о + в .. а) •
- 2аа3 [е3а - j (V3"« + V««,)] - а33 (е33 -
где еар = -|- (Va«p + Vp«a) (a, P = l, 2)
- ^Ч ~
- аРа [вар- j (Va«p +Vp«a)]-2a3a [вв3- y (Va«3+ Vs«a)] } ^
- \ \ № («a - «:Г + ^ («3 - «D'l -« " J J (Г')' «I
где взз = V3«3

ТАБЛИЦЫ 227
Продолжение табл. 3.3
Условия стационарности
Множители
Лагранжа
дЭ
ди
дЭ
де
дЭ
да
дЭ
дк
дЭ
= 0 в V, (k-n- f*Y = 0 на S;
в V;
1«-ц=0 в V;
е- j (Vu+uV) = 0 в V, (и-и*)" =0 на S;
а — е ¦ • а = 0 в F
--a) + jP = 0 в V,
а)-п-г]'=0 на S.
ЗЭ
де
дЭ_
да
a _l(Va-+«V) --а = 0 в F;
е-4- (V«+«V) = 0 в V, («—«*)" = 0 на S
ЗЭ
дЭ
да'3
дЭ
i = 0 в V,
- /")" = 0 «a S;
0 на S;
° «а S
/a
дЭ
ди.
дЭ
deai
дЭ
daia
дЭ
Д/3
в V,
о, (а/зЛ/
0 в V;
на S;
= ° B V'
S;
aia, f3

228 ТАБЛГЩЫ
Кастильянова серия полных функционалов
Полные функционалы
(«Р, *аР. "ар) = \ \ \ [- у* («Р) • • Ь • ¦ О (<р)] dV -
\ \
где ,р* =
Э*п2 («р, а, е) = J J J [- 1 а . • 6 • • о+в •. (a-a°-VX4>XV)] dF-
Функционал Ренсснера
Э*п3(о, и) = ^[- -Lo ¦ ¦ Ь ¦ ¦ о - и ¦ (V -а + F)]dV +
+ \ \ (и*)" .ff-«rfS + \\«-(<*•«- f)' dS

ТАБЛИЦЫ
для неоднородного анизотропного упругого тела
229
Таблица 3.4
дЭ
d(f
дЭ
двуь
дЭ
д*у&
дЭ _
дЭ
<5<р
дЭ
да
дЭ _
дЭ
W
о
и
= 0
-п
= 0
= 0
V
[«
[е
Условия стационарности
Хе
v5-
["Y5~
V
A
V
(е
е
а
«
а
(и
Xe
Xe
Y6-
-a
-a"
b
— и
¦<H
[a (»p)] x V = 0 в 7,
P) - еубТ = °> ["y8 D
-"Y5D>)]' = 0 на S;
- ,|)Y8y = о, (фар - ф*
H<PIXV = O в 7,
?)-<v]" = 0- [jcve(q;
- ^vey = о, (фаВ - ф*
(a) X V = 0 в 7,
• 6 = 0 в 7;
-VX4>XV=0 в
_l(V« + «V)=0
*)" = 0 на S;
-jP = 0b7, (ff-n —
')-"Y
p)' =
7i
7,
ib) =
в V,
D' =
о]" = °-
0 на S
6]" = o,
= 0 на S;
OHaS
= 0 на S
Множители
Лагранжа
еар> "ар
—»
е
и

230 ТАБЛИЦЫ
Полные функционалы
5*4 («Р. о, е, I, Ц) =
= \\ \ [~Ja ¦ ¦ е+
- \ \
- J J
С -
Некоторые частные функционалы для
Частные функционалы
Эгс(и, е, ст) = ЗЗз[-7е ¦•о-Р.и

ТАБЛИЦЫ
231
Продолжение табл 3.4
Условия стацнонарностн
<Э<р
до
?-«
?-
дц~°
?._ 0
dq>
да ~и
де
?X4XV=0bF,
[eY6 (Л) - е*в]" = 0,
[«Ye (Л) - '«Ye]" = 0 на S;
4- ^ + ? • • 6 — Т) = 0 в V;
La —1 = 0 в F;
е _ а ¦ ¦ Ь — 0 в V;
а~ (<г°+ V Х<Р X V) = 0 в F,
(*ve_^vey_Oi (фаВ-Ф;р)' = 0 „aS
VX(e + CT..6)xV = 0 в V;
[j(e+<>--b)yS-e*ySY =0,
OY6 ~~ Vsl" = ° Ha S;
|e-|(a4VX<PXV)-'J = 0 в V,
(^6-^6)' = 0, (фаВ-Ф;в)' = Она5;
а-(а°+ VX4>XV) = 0 в V,
(*^-*:в)/=*°'(ч'ар-ф*ар)/ = Оиа S
Множители
Лагранжа
1, п
—
Таблица 3.5
неоднородного анизотропного упругого тела
Дополнительные условия
Условия стационарности
а— е •• а =0
e-Y(V« + «V) ==0,
?.0 + ^ = 0 в V;
(и—и*)" = 0, (а-я—/*)' =
на S

232 ТАБЛИЦЫ
Частные функционалы
3СГ(Ч>, <г, е)== Jj J [^"СТ • е — е • (ст°+
~ J J O
va
¦Эф. (в, а) = ^Ц1 е • • а ¦ • е - а ¦ • в) dV + ^ (и*)" -a-ndS
ЭФ2 (о, е) = ^ (- 1а • • 6 • • а + е ¦ ¦ а - е
Зфс К в) = ^ Ц- 1а • • 6 • • а + е • • а

ТАБЛИЦЫ 233
Продолжение табл. 3.5
e -
V
[x
V)
(
0
(a
V
(a
V
(•
0
V
a -
Дополнительные условия
- a • • 6
a+P =
¦п-П
*
уб(')-
<eXV =
HE
Y6 («) ~
¦п-П
ff+ F =
¦ я - Г)
x«xv
*<<)-
a + P--
= 0
= 0, VxeX^ =
' = 0,
)" = o,
vJ =° на
= 0, V .a+P =
) -°>
xy6] =0,
' = 0 на S
= 0 в F;
' = 0 на S
' = 0 в F;
Г-0,
хУ/ = 0 на
= 0,
t + ttV) •• a —
0
S
0
S
0
в
в
в
F;
V;
V
a -
V
(Ф
(•
[x
V
V
a -
V
{-
e -
V
[«
(a
("
Условия стационарности
- (a° + V X <P X V) =
X«XV = 0 в F;
аЗ-ф'аз)^0' (Ф^-Ф
У6-<М) =0'
Y6 («) - Цв]" = ° на
(а - е • • а) + Р = 0
X (е - о ¦ ¦ Ь) X V = С
- е • • а = 0,
X«XV = 0 в F;
_ а • • 6 = 0,
(а-а°)=0 в F;
¦«- f (*Г. ч»^)Т-
.„-f*)' = 0,
_«*)" = 0 на S
0,
ГГ=о,
S
на S
0 на S
1

234 ТАБЛИЦЫ
Частные функционалы
= J J J [т е {и)'' а '' е (и) ~ F' u]dV~ j j {u*]"
2(ff)== JJJ (~Ta"b "
где T|,vfl = T|)Vfl (ф) (см. табл. 3.2)
+ J J Ova (O' ~ c
dv+
4 ()'] ^ + С
у «63 («у) <
- ,36 [...] авз (*а) - 1*331- • ¦] a33 (O - F6u&} dV -
(в декартовых координатах)
н, («3' V Ф) = JJ J { - J^ [«33 («з). ff'V (%' Ф)] ffP6 (*a. ф)~
(в декартовых координатах)

ТАБЛИЦЫ 235
Продолжение табл. 3.5
Дополнительные условия
V -a[e(u)] + F = 0 в V;
(я - и*)" = 0 на S
Va + F = 0,
V X (ff • ¦ b) X V = 0 в V;
(a-n —f)' = 0 на 5
V X в X V = 0,
е - @° + V X <Р X V) = 0 в V
VXe[ff(<P)]XV=O в V;
(фаВ - Ф*ар)' = °.
(^6-^6)' = 0 на S
V X е X V = 0,
V • (е ¦ ¦ а) + F = 0 в V;
[ку& (е) - х*6]" = 0 на S
[«^(чО + Л'-о.
(«v-«*v)" = 0 на S
[»|а«(*в,Ф)-ГВу-О.
(ug — Ug)" = 0 на 5
Условия стационарности
{<г[е(и)]-п-П' = 0 на 5
[вав (») - евр («•)]" = 0,
[xa0(ff)-xa6(u*)]" = O на S
[¦Хуб (в) - и*б]" = 0,
(ф«Р ~ Фар)' = ° на 5
К6[^(Ф)]-е^Г=°.
{ху6[е@(Ф))]-х;б}" = Она5
[0(е).п-/(^«, 9;p)]' = 0HaS
Уравнения теории упругости
В фуНКЦИЯХ Uy, T))a
и соответствующие граничные
условия
Уравнения теории упругости
в функциях «з> i|)a> Ф
и соответствующие граничные
условия

236
ТАБЛИЦЫ
Экстремальные свойства вариационных
Полные
функционалы
Экстремальные свойства
в точке стационарности
Лагранжева серия
3„| (и, f)
max mm = mm max
•Эта (и)
нет экстремумов
5п2 (и, е, а)
max mm = mm max
a a, e a, e a
Эпз (е, Ф)
maxmin = minmax
Эт(и, е, а, к,
mm max
a, e, a x, p.
(«, e, a)
нет экстремумов
max mm
oi3tfa ut, eu
mm max
max mm = mm max
o'a, f3 ui< eai uv
'°. f3
Кастильянова серия
ea0>
min max = max mm
(Ф)
нет экстремумов
mm max = maxmm
е <р, о ip, о е
mm max
U (I
max min
0 U
, w, e, l, Ц)
max mm
<p, a, e i, ч
нет экстремумов
Функционалы с неполными
полями ф, а, е
mm max = max mm

ТАБЛИЦЫ
функционалов теории упругости
237
Таблица 3.6
Частные
функционалы
Частные
функционалы
Экстремальные свойства
в точке стацнонарностн
Функционал
Лагранжа
-> min
Функционал
Кастильяно
-> max
(Ф)
Р, а)
¦ЭК4 (Ф, а, е)
а'а)
Эг (и, с)
5Л1 («)
3Л2 (и,
а Се1
ЛЗ ^ '
5Л4 (">
^лзК
*)
е,
> е
, е
а)
3*)
at)
Эп(и)
Зг2 (а)
Эг (ф, в)
5г1 (Ф)
5фг (в, в)
•Эфе («I, в)
•Эф (в, а)
Н2 («з, фа. Ф)
max min = min max
аи и а
min
и
max
а
mm max = max mm
e <p <p e
max
min
e
max min= mm max
о е е а
min max = max mm
e а о е
min = 0
e, a
max mm = mm max
max min = min max
Ч'а'Ч» "з "з V1

238
ТАБЛИЦЫ
Таблица 3.7
Различные варианты функционала Лагранжа при разрывных
перемещениях, деформациях и напряжениях
Функционал
Лагранжа
(см. табл. 3.1)
ЗрЛ!(и) = Эт(и)
5Л2 (и, е) =
= Эт (и, е)
ЭРт(е) = Эт(е)
5Л4 (и, е, а) =
= Эм (и, е, а)
•ЭЛ5(«,-. е«) =
= 5л5К>е,-з)
5Л6 ("«' е«а) =
= 5Л6 ("/- е<а)
Дополнительные
условия:
как в табл. 3.1
и. кроме того,
{ц}" = 0 на D
(ц}" = 0 на D
{еа0 (е)}" = 0,
{«ар (в)}" = 0 на ?>
{ц}" = 0 на О
{^}" = 0 на D
{ы.}" = 0 на D
Условия стационарности:
как в табл. 3.1
и, кроме того,
{О (и) ¦/!}' = 0 на D
{<г(е)-п}' = 0 на D
l<f(e)-n}' = 0 на D
{ff.n}' = 0 на D
(ог'Щ^О на Д
тто11 = а4шек1,
е«0 = Y (V« + V0"a)
{a'ynJ' = 0 на Д
где a" = «'/%,
е3з = V3U3
Таблица 3.8
Различные варианты функцнонала Кастильяно при разрывных
функциях напряжений, напряжениях и деформациях
Функционал
Кастильяно
(см. табл. 3.2)
5Р,(ф) = 5к,(ф)
э\2 (ф, *) =
= ЭК2 (Ф> ff)
5K3(ff)=5K3W
Дополнительные
условия:
как в табл. 3.2
и, кроме того,
{фа0}' = О,
{i|)vS}' = 0 на D
{Ф(/}' = 0,
{а-п}' = 0 на D
Условия
стационарности:
как в табл. 3.2
и, кроме того.
{еае(Ф)}" = 0,
{ха0 (Ф)}" = 0 на D
{Sag (*)}" = 0,
{хар(»)Г = 0 на D
{ea0 («)}* = 0,
{xa0 ИГ = 0 на D

ТАБЛИЦЫ
239
Таблица 3.9
Лагранжева серия полных функционалов
i ри разрывных перемещениях, деформациях, напряжениях
и функциях напряжений
Полные функционалы
(см. табл. 3.3)
ЭР, (в, f) = 3n, (и. f)+\\{u}»-fdD
9lia (и)=Эп[в(и)+^\и}"-о (и) -ndD
ЗР2 (и, е, о) =
= Эп, (а, е, а) + [[ {и}" o-ndD
Э13(е, Ф) = Эп3(е, Ф) +
+ \\ №&{еуь}"-саус%а^{куь (e))"]dD
ЗР4 (в, е, а, X,, ц) =
3Pn4a(U,e, a)=5n4a(a,e, а) +
+ JJ {u}"-±(o + e--a)-ndD
ЭРп5(и(,ез(,а'3,/а) =
= 5п5(^,е3^'3.Г) +
Условия стационарности:
как в табл. 3.3
и, кроме того,
{о(в)-п}'=0, (а}"=0,
{a(u).n—f}"=0 на D
{a(u).n}' = 0,
{ц}" = о на D
{с.п}' = 0,
{ц}" = 0 на D
{еуь}" = 0,
{xY5(e)}" = 0 на D
{Х-п}' =0,
{и}" = 0 на D
|l(a+e-fl)-n|=0,
{u}" = 0 на D
{<?%}'= 0,
{иг}" = 0 на О,
где aaB = aaB''e(y,
{а"Я/Г-0.
{И/}" = 0 на О,
где ^-Л,,,
е33 = ^з"з

240
ТАБЛИЦЫ
Некоторые системы координат
Название,
координатные линии,
локальный базис
Связь с прямоугольными
декартовыми координатами
Прямолинейные косоугольные
(аффинные) координаты &
У — a2!l'
Криволинейные ортогональные
координаты общего вида о^
х — х (а')
У = У (а1)
Цилиндрические координяты р, ф,
У
ЛГ = р COS ф
у = р sin ф
Z ш= Z

ТАБЛИЦЫ
241
Таблица 3.10
в трехмерном пространстве
Компоненты метрического
тензора
Символы Кристоффеля
(компоненты, не приведенные в таблице, тождественно равны нулю)
eij = aikajk
?рр=1
1?ФФ = Р
gzz= 1
2 3afe
г г ' д8"
Т"> ' Г/'' ' 2 ^
Р .-.
фф, р — г
Грф, ф = Р

242
ТАБЛИЦЫ
Название,
координатные линии,
локальный базис
Связь с прямоугольными
декартовыми координатами
Сферические координаты г, 6,
х = г sin 6 cos ф
у = г sin 6 sin ф
z — — г cos 6
Тороидальные координаты г, ф, 6
х = (а + г sin 6) cos ф
у = (а + г sin 6) sin ф
z = г cos 6
¦х
Координаты, нормально связанные
с поверхностью ?', |2, ?
У =

ТАБЛИЦЫ 243
Продолжение табл. 3.10
Компоненты метрического
тензора
Символы Кристоффеля
(компоненты, ие приведенные в таблице, тождественно равны нулю)
gw = r2sin2e
gap = (• — 12К) a<t$ ~
— 2J A — ?#) Ьаа
(а, Р=1, 2),
где
р Р г
гв, е ее. г ~ г
• ф» ф фф> ^ Oill W
6ф» ф фф* 6
Гге, е = гее, г~г
ггф, ф = -Гфф, г = (а + rsine) sin 6
р р
Эф. ф ~ фф. е —
= (а + г sin 6) г cos 6
¦^ ар, з * рз, а ~~1

244 ТАБЛИЦЫ
Таблица 3.11
Функциоиал Рейсснера
в криволинейных ортогоиальных координатах
Э*3 (*,«) =
+ 0^22 (.ЬззцОц
+ «i [(//2Я3ОГ1
+ "з@Г31 +
+ JJ[-K
+ И2 (ff21nl +
Н%Нъ [о"п (Ьц цСц + 6 11220*22+ • ¦ • +26lll2O'l2) +
+ 62222С22 + •.. + 262212G12) + •••
l), l + (#I#3Cl2), 2 + (^1^2С)з), 3+^зЯ], 2Of|2+
-«,,,.„-»*,* + '*»*] +
^«г + о'ззЯз)]" rfs +
о'гг^ + ff23n3 ~ Q' +
+ «3 (ff31nl + ff32n2 + ^"З "~ ^з) ] dS
Примечание. Множители [...] при и2 и и3 полу-
получаются циклической перестановкой индексов из соответствую-
соответствующего множителя при и\.

ТАБЛИЦЫ 245
Таблица 3.12
Полный функционал
в симметризованном основном пространстве состояний
в криволинейных ортогональных координатах
(«, е, ог) = \\\ | — —
Г«1,1 #1,2«2 Н\, 3«3 с Г«2, 2 #2, 3«3 #2, l"l]
1.777+~^я7+"^яГ]+°22\ЛП +17Ж+~fTJU J
Здесь обозначено:
( - 4)" [ff2l"l + СТ22«2
( - "з)'ТСТ31«1 + ff32«2 + ^ЗЗ^з] } dS
Таблица 3.13
Полный функционал
в снмметризованном квазиосновном пространстве состояний
в криволинейных ортогональных координатах
~ <22,
е)
[
[
>
0
~ ["B2)
Здесь
J J J \ л
7/' 2VV
W2
о 
+ 2(ТA2)е<12)]-
7ЗФ22)] -
7зФп)]----
п m \\ 11 ^т/
j J {(е(*11)^A1) + 2e(*12)tA2) + e(*22)tB2))" ~
22)(ГA1) ~ 2иA2)ФA2) + Х(П)ФB2)) } ^
E(II>-"**il>)'r+2ef12> D5A2) —"**i2))'+ef22
е ' (фA1) "" Ф(П)) — 2хA2) 'е / (фA2)
, + X(inie )(ФB
обозначено: ( ' v K
(«/) "f" ^(llij)a{U) "Ь *B2i/)(TB2) + • ¦ •
((, /= 1, 2, 3)
J + C-
VtB2)~^B2)J —
-ФA2Ь) +
2)-фB2))]}^
+ 2&A2«7)(ТA2))

246 ТАБЛИЦЫ
Различные варианты фуикционала Лагранжа
Функционал Лагранжа
эт («) = J $ {
+ у Пар («) МаВ [е («). И («)] - Аа - <7«>>} <« -
- \ [Qya + Qw + МЪ (и)]' dC
Эт (и, г, ц) = J J [1 еаВГаВ (е, ц) +1 царМаВ (е, ц) -
- <7а«а - <7ш] rfS - J [Qya + Qw + М« (и)]' dC
, ц) = J J [т еаВГа» (8, ц) +1 ЦиВМаВ (8, ц) -
<ча (е, ц)+Ф*х
Эт (и, г, v,T,M)=^ A еа0ГаЧ 1
для пологих оболочек
f
p*x (8) + rfett (e) - Qtw - Mfi (w)]> dC + A2

ТАБЛИЦЫ
247
Таблица 4.1
для
(и
[ft
неоднородной
анизотропной оболочки
Дополнительные условия
- и*)" = 0,
(и) - $*]" = 0
на С
г—г (и) = 0, ц—ц (и) = 0 в S;
(и
[ft
L
[X
[•
е -
Т
М
(«
[ft
L
[х
[е
(да
[ft
- и*)" = 0,
(u)-ftT = o
(е, ц) = 0 в S
(е, и) - х,]" =
н (?) - е^]" =
- Е (и) = 0, (Д. -
- Г (е, ц) = 0,
- М(г, ц)=0
- и*)" = 0,
(u)-ft*]" = 0
[е, (А(да)] = 0 Е
(е) - х*]" = 0,
„ (е) - z*tiJ =
- да*)" = 0,
(а>)-0Ч" = О
на С
0,
0 на С
- ц (а) = 0,
в S;
на С
i S;
0.
на С
Условия стационарности
В {М [г (а)
Т[г
{<?{...}-
{Afvv{...}
B[iM(8,H)
{<?[...]-
{Mvv[...]
В [Л! (е, ц)
{<?[...]-
lAfvvl...]
В (Л1, Г) =
[Q (М, Т) -
[Mw Ш) -
В til [в, М
т
{Q{...t-
{Afvv {...}"
(^ (")],
(«). И («)]}
QJ' = o,
Т (г, ц)] «
<?»}' = 0,
Г (е, ц)] =
Q «*)>' = (
-«„(*•)
0 в S;
-QJ' = o,
-Af,]' = O
[е. И («»)]}
Э,}' = 0,
- M.Y = 0
= 0
на
= 0
на
= 0
),
' _
на
= 0
на
в
С
в
С
в
S;
S;
S;
0 на С
С
в
С
S;

248 ТАБЛИЦЫ
Экз (М, Т)
Различные варианты функционала Кастильяно
Функционал Кастильяно
Г Г ( 1
- у 7"*3 W еар [М (t), Г №)] ] dS -
Т) = \\\~Т мп&^^ (М, Г)- 4- ^аВеа
J J L л Z
— \ \ Г L ддар ,u Т1_ ' тавр
+ J [Qa (Л1 Г) иа + Q (М) да* + /И
_ Г г а
J *
для пологих оболочек
ЭК5 (Ф, Л!) = \ J { - у МаВц„р [Л, Г (Ф)] -
- у га3 (ф) «ар [-М, Г (ф)] | rfS +
(- \ [да*(Э (М) + ft*Mvv (М) - хф - е",т)
3 (Л. Г)] а
f л,
(М, Г)] rfS +
vv(*)#']
(t)]"rfC-
"rfC
ьл,

ТАБЛИЦЫ
для неоднородной анизотропной оболочки
249
Таблица 4.2
_
Дополнительные условия
(Ф - ГУ = о,
[П(Ф)-П*]' = 0 на С
Т — Т(г|)) = 0 в S;
[T)H>)-riT = 0 на С
В (Л|, Г) = 0 в S;
[Q(M, T) -(?,]' = 0,
[Mvv (M) - М.]' = 0 на С
М-М(г|)) = 0, Г — Г (г|з) = 0,
Ц-ц(Л1, Л=0,
е — е (М, Т) = 0 в S;
(ф - ^)' = 0,
[tl№-iT = 0 на С
В [М, Т (ф)] = 0 в S;
[Q (М) - Q,]' = 0,
[Alvv (Л) - Mt]' = 0,
(Ф - Ф')' = 0,
[П(ф)-П*]' = 0 на С
Условия стационарности
LiB[MW,TW].
Ц[Л1(г|>), Т(г|))]} = 0 в S;
{х{...}-х,Г = 0,
{8<<{...}-e;i}" = 0 на С
?[8(М, Г), р(М, Т)] = 0 в S;
{х[...]-х,Г = 0,
{еи{...}-г%}" = 0 на С
L [8 (М, Г), ц (Л1, Г)] = 0 в S;
{х [...]-х (и*)}" = 0,
{е„ [...]-е„ («*)}" = 0 на С
? (е, ц) = 0 в S;
[X (Е, (i) — Xj" = 0,
[ett(B)-e*tJ = 0 на С
L {е [Л, Г (Ф)], (i [М, Т (Ф)]} =
= 0 в S;
{х {...}-и,}" =0,
(е<< {...}_ 4}" = 0 на С

250 ТАБЛИЦЫ
э„
3П2
—
Зпз
+S
(«
.о
—
(«, 8
~\[
(8, И
1
Т
Лагранжева
серия
Полные функционалы
+ 1цар(«)МаВ
г
J {Qa {Л* [е (в), 1
+ Q{...
<tl,T,M) = ^.
... Т^Р Го
Qaua + Q^ + M
бар (в) ГаВ [е
[е(в),ц(в)]-
+ Q.. + Af,«
^ a) + Q (да —
)^[.(.).ц
[8 (В), Ц(В)]-
i (в)], Г [е (в
} (да — да*) +
' ' е Га» (г
- еар («)] -
t«(B)]'dC-
(«). И
-Аа
>(.)J
WH
-Аа
><«)]'
полных функционалов
(«)] +
— qw\ dS —
dC-
Mv [О (в) — ft*]}" dC
— qw | dS —
dC-
, И («)И (иа - и*а) +
Mvv{
(^) +
\{Q«
+ Q (M) (да - да*) + Mvv
[«^)-«Я4
ГаВ (8, |1) + -
ф — i|)aLa (8,
..}[*(e)-**]}"dC
1,^(8,11)-
tap — Hap(«)]} rfS —
(Л,Г)(аа-а;) +
(Л1) [Ф (в) - Г]}" dC
HttP (E, Ц) -
<¦"•">]¦* +

ТАБЛИЦЫ
251
Таблица 4.3
для неоднородной анизотропной оболочки
Условия стационарности
ди
дЭ дЭ
дЭ
-=— = 0
ди
Се C(i
сТ=0'с1Й=0
СЭ_ дЭ
= 0
В {М [е (и), ц (и)], Т [е (и), ц (а)]} = 0 в S,
{Q {...}- ЯЛ' = о, {Mvv {...} - мл' = о,
{MV~MVV {...}}" = 0 на С;
(а-и*)" = 0. [Ф(и)-Ф*]" = 0 иа С
В {М[е (и), ц (и)], Г [8 (и), ц (и)]} = 0 в S,
(и - и*)" = 0, [& (и) — f>*]" = 0 иа С
В (М, Т) = 0 в S,
[Q(M,T)-QJ=0,
[Mvv (M) — МJ' = 0 иа С;
Г — Г (е, ц) = 0, Л! — Л! (е, ц) = 0;
е _ е (и) = 0, ц - ц (и) = 0 в S,
(и — и*)" = 0, [t> (и) — #*]" = 0 иа С
Т (г, ц) — Г (г|)) = 0,
Л* (е, ц) - Л4 (г|)) = 0 в S,
(.ф _ уу = о, [т) (г|)) — т)*]' =0 на С;
L (е, ц) = 0 в S,
[х(е, ц)—х»]" = 0, [ef( (e)—e*<]" = 0 иа С
Множи-
Множители Ла-
гранжа
Г, .М

252 ТАБЛИЦЫ
Эт (и, г, ц, Т, М, 1) =
лаЗ г„ „ /,,\i
Л1 1еаЗ~еаз("М~
- л4а3 [лГ6 - ма6 (е,
-${<га(Ь)(«в-«:)
Эп43 (а, е, ц, Г, Л*) =
- $ [Q.4 + Q.«> +
+
5„5 (t». е, ф, Q, iMv) =
+ lna3(K-)AIae[e, |i
+ J [ф*Х (8) + П
+ J {ф [я (e) - и
Полные функционалы
ц)] } rfS -
+ Q (>-) (w
уЦар^а3
13 (е, ц)] ЦС
уМ^ (в)]'
Э (М) (w -
т-
(да)] - Га
•е„ (е) - С
] + ч(ф)[
(для пологих оболочек)
: -
5Га0 +
-да*)
+ |1
•р («) -
,С->
да*) +
рГа» [8
еа3
е« (е) -
-, лЗ Гга3 гаЗ/Р ,.\1
J~ла3 1-" У ' ' f*H —
ia + Qtw + Mb(u)JdC-
+ Mvv (Ц [* (в)-**]}" rfC
ГаР + 7-аР (е> ^ 8ар (ц) +
- qaua — qw \ dS —
\{Q№(M,T)(ua-u*a) +
Mvv (M) [в (и) - ¦&*]}" dC
. 1* («»)] +
</0) — ф! [г, ц (да)] | dS +
VJ> (да)]' dC + A2 +
~ e*tt\ —Q{w — w*) —
-Mv[b(w)-ff*}}" dC

ТАБЛИЦЫ 253
Продолжение табл. 4.3
Условия стационарности
Множи-
Множители Ла
гранжа
дЭ
ди
55 =
де
дЭ
дТ '
дЭ
= 0
дЭ
5^7- =0
д_9_
дМ
= 0
В (*,,, 12) = 0 в S,
[<? (>-)-<?*]' = 0, [Mvv М-М.]' == 0 иа С;
уГ-3., + Г(ЗЛ 3.4) = о,
1е-^ = о, -1ц-).4 = 0;
е — е (и) = 0, ц — ц (и) = О
Т - Г (ё, ц) = О, М - М (е, ц) = 0 в S,
(и - и,)" = О, [Ф (и) - Г]" = 0 иа С
3l3, 3.4
В
д.9
За
= 0
{1 [Л* +М (е, ц)], -1 [Т+Т (е, ц)]} = О
в S,
{} <?}'0
иа С;
—
Eц
Г-Г[е(в),
дТ °' дМ ~°
е — ? (а) = 0, ц — ц (о) = 0 в S,
(а-а*)" = 0, [Ф (а)-#*]" = 0 иа С
<5Э
= 0
Eе
= 0
__.Q Jl^_,_-Q
В{М [г, ц(ш)], Т(ф)} = 0 в S,
{Q {¦¦¦}-<?*}' = О, {Mvv{..->-'M»}' = 0,
{Q-Q {...}}" = О,
{Mv — Mvv {...}}" = О на С;
Г [ё, ц (а))] — Т (ф) = 0 в S,
(Ф-ФГ = О, [п(ф)-П*]/ = О иа С;
L [ё, ц (да)] = 0 в S,
[к(е)-л*]" = 0, [е„(е)-е*г]" = О иа С;
(да — да*)" = О, [Ф (да) - ¦»*]" = 0 на С
Q,

254 ТАБЛИЦЫ
Кастильянова серия полных функционалов
3*„,а <*
L 7"а
—
-и
Кз (М,
+ Q
-л,
) =
in,
+ м
*у
т,
-«с
(Af
-)-!${¦
) еаР [Л* (¦)
-${«Ч<
))еаз [AT(i|)
ха {е [М (ф
Г, л е) = [
")== Ш~
1Ва (Д1, Г)
ш* + Mvv
+
Полные
Ра ~~
«"»
и-
<(е)
~ Y
-
w}
¦Э
«,
1
~ 2
(Ф-
функционалы
(t) naC [Af (if), Г (r|))] -
«-$[«М.в+«.Ф+й
+ x (ф — ф*) + e( [т] (if
rfS—X [х°'Фа+Х!йФ+е^
д*аЗ / jtf т^ таЗ
м Пар v-™!-";—"о"* '
ф*) + е^ (8) [л (ф) — т]
i IM Т\ 7"аРс
*ag vJKIi l) 9 aP
- ш5 (AT, ГI rfS + \ [Qa (M, Г
(Af)
w[Q
(Af)
rfC + 5 К [Qa (Af, Г)
- Q J+ « («) [MVv (Af)
)-ч ]}
5ap (Af, Г
Af, Г)-
"a +
-«Л +
-Af.]}'
:+
dC
Ax
) +
Л,
rfC

ТАБЛИЦЫ
для неоднородной анизотропной оболочки
255
Таблица 4.4
Условия стационарности
(Эф
<Эф ~"
|f = 0
(Эф
(Эц <Эе
?-=<>
ди
L {г [ЛГ(ф), Г (ф)], ц [Д1(ф), Г (ф)]}=0 в S,
{x{...}-xjv = o, {8„{...}-е;,}" = 0,
{Х-х{...}}' = 0, {8(-8^{...}}' = 0 на С;
(Ф - Ф*)'= 0, [т)(ф)-Т1]*]' = 0 на С
? {е [JH (ф), Г (ф)], ц [Д1(ф), Г (ф)]}=0 в S,
{*{...}-*/' = <), К,{...}-е;,}" = 0,
(Ф-Ф*)' = О, [т,(ф)-т,*]' = О на С
L (г, ц) = 0 в S,
[И(8, A)-Х,]" = 0,
[e«(e)-e«]" = 0 на С;
ц - Ц (Л*, Т) = 0, е - е (М, Г) = 0;
Д1 — Д1 (ф) = 0, Г - Г (ф) = 0 в S,
(Ф-^)' = О- [Г1(Ф)-Т1*]' = О на С
ц (М, Т)-ц («)=0, е (Д1, Г)-е (и)=0 в S,
(и-«*)'' = ". [© («) - 0*]''= 0 на С;
В (М, Т) = 0 в S,
[Q(iM,r)-QJ' = 0,
[Afvv (iW) — AiJ' = 0 на С
Множи-
Множители Ла-
гранжа
1
—
и

256 ТАБЛИЦЫ
'Sag LJ
-$<„
*;.. <¦
l
— \
Э в (а>,
П5 \т>
ИаC
¦«
М
— ¦
, Т, ц
¦Нар С
*о + »
W, X,
• гаР
2 Y
Полные функционалы
в> ^ J J I IF
1
+ X (8) (ф - ф*) -
(ф) 8ag [М, Т (ф)] -
(Д1) + Ь Mvv (M) -
(для пологих оболочек)
") + ги A) [ц (Ф)-ч*
i Л- 7"аР»
^ар > о аР
[8ар+8ар (Л*, Г)] ГаР
' " J {«" С 1») (Фа "
f 8t< (Е) [л (Ф) — Л*]]
^ца3 [Л1, Г (ф)] -
- «>В[Л1, Г(ф)] \dS
— х^ф — е^т) (ф)] dC
- в, [л (Ф) - Л*]}
f
Ф)]
(¦)}
-С
+
'rfC
r,]+
rfs-

таблицы 257
Продолжение табл. 4.4
Условия стацнонарностн
Множи-
Множители Ла-
гранжа
дЭ
<Эг|>
= 0
и-*я-
(Эц дг
дЭ
= 0
L(t2, 10 = 0 в S,
[х (|) -xj" = 0, [е„ (|) -еУ = 0 на С;
1 е - |2 + е (|3, |4) = 0;
iH - iH (ф) = О, Г —Г(ф) = О,
ц - Ц (Л*, Г) = 0, е - е (М, Т) = 0 в S,
(*-**)' = 0, [л (-ф) — п*]'=-0 на С
б1. I2
|3, &4
L {у [е+е (Д1, Г)], у [ц + ц (М, Г)]} =0
= 0
дМ ' дТ
— =0 — =0
<Эц ' дг
{и {...}-«,}"=• О,
ц-ц[Л* (Ф), Т
в S,
на С;
-О,
М — М (г|>) = 0, Г —Г (г))) = О в S,
(г|) — г|)*)' = 0, [rj (ф) — т)*]'^0 на С
дЭ_
(Эф
дЭ
дМ
дЭ
dw
= 0
21=0 — =0
(Эй ' (Эе(
Z. {е [М, Г(ф)], Ц (да)! =0 в S,
{«{...}-xj"=о, {e,,{...}-e;j"-o,
{х-х {...}}' = О,
{е^-е^ {...}}' = О на С;
ц[Л1, Г(ф)]-ц(ш)=0 в S,
(да — а>*)" = 0, [0(ш) — д*]" = 0 на С;
В [Д1, Г (ф)] = 0 в S,
[Q (iM)-QJ"=O, [Mvv (JM)-Af J'=0 на С;
(Ф-Ф*)' = О, [т)(ф)-т)*]' = О на С
, и,
8.
9 Н, П. Абовскнй н др.

258 tAБЛИЦЫ
Некоторые частные функционалы для
Частные функционалы
Зфг (е, ii, Т, М) = ^ [1 еарГоР (е, ц) +
МаР (8, р) - ГаРеар - Л1а
Qa (iH, Г) «; + Q (М)
2 (Д1, Г, fi, 8) = J J [- 1 ЛГаРЦар (Л*. D - у 7"аРеаЭ (iM. Г)
- Tf)] dS +
[ха (8, ц) ^ + к (8) <р* + гн (8) t|']'d
Згс («, 8, fi, Г, М) = ^ [- у еар^Р - 1 цар^аР - qaua-qw +
+ ГаВеар (в) + Ma&ixa& (и)] rfS-J [Q% + Qw + Mb (в)]' rfC -
Q-1 (Д1, Г) (ua-u*a)+Q (M) (w-w*)+Mv
3cr (t, in, Г, fi, 8) =
dS -
- J К (8, (i) Oa - О + x (8) (ф - Ф*) + ен (8) [т, (*) - т,*]}'
Зф, (8, Ц, Г, Д1) = Зфг (8, Ц, Г, М)

ТАБЛИЦЫ
неоднородной анизотропной оболочки
269
Таблица 4.5
Дополнительные условия
В(М,Т) = 0 в S;
[Q(M, T)-Q,]' = 0,
[Mvv (M) — МJ' = 0 на С
L (8, ц) = 0 в ' S;
[И (8, A)-Х,]" = 0
[б« (е) - 4]" = 0 на С
Г — Г (е, ц) = 0,
JH - Л1 (е, ц) = 0
ц - ц (JH, Г) = 0,
е — е (JH, Г) = 0
В (Д1, Г) = 0, Ь(г, ц)=0 в S;
Ю(М,Г)-«.]' = 0,
[Mvv(Al)-AfJ' = O,
[Х(Е, Ц)- X («*)]" = 0,
[е^(е)-е^ («*)]" = 0 на С
Условия стационариости
Г — Т (8, ц) == 0,
Д1 - Д1 (е, ц) = 0,
?(е, ц)=0 в S;
[и(е, ц) — и («*)]" = 0,
[в„ (е)-е„ (и*)]* = 0 на С
ц—Ц (Л*, Г) = 0, е-е (Л*, Г) = 0,
В(М, Г) = 0 в S;
[<?(Л1, Г)-Q (¦•)]'= 0,
[Mvv (ЛГ) — Mvv (¦**)]' = 0 на С
г — е(и)=0, ц —ц(и)=0,
В (Д1, Г) = 0 в S;
(и - и*)" = 0, [0 («) - 0*]" = 0,
[<?(in, r]-<?j' = o,
[Мvv (М) — ЛГ.]' = 0 на С
М-М($) = 0, Т - Т ("Щ = 0,
?(8, ц) = 0 в S;
(ф - if»)' = 0, [Т1(г|))-т1*]/ = О,
[И(Е, Ц) -Xj" = 0,
[8^(e)-e*J' = 0 на С
В [М-М (8, Ц), Г-Г (8, Ц)] = 0
9*

260 ТАБЛИЦЫ
Частные функционалы
ЭФ2 (М, Т, ц, е) = Зфс (JH, Г, ц, е)
Зг (в, Г, М) = ^ (- 1 <?% -
1 <?% - у
q" <*•Г) - Q»]и» + [у q (Л|) ~
1 Mvv (JM) - M.] d (и) }' dC - J { Qa (Д1, Г) A ua - <
+ Q (JM) A a, _ a,*^ + Afvv (JM) [1 d (a) - Г] }"
jQ («) - Q.] * + [4 ^w («) - Af.]<> (и) }' dC
[Qa (a) «*a + Q (и) да* + Mvv (u) **]" dC,
где Afvv (u) = Afvv {Л1 [e (u), ц (а)]},
<?(«) = <? {Д1 [е (и), |i (и)], Г [в (и), ц (и)]}
3r2 (M, Г) - J J [- 1 Af «Рйвр (Д1, Г) - 1 ГаРЕар (in, Г)] dS +
[Qa (M, T) «; + Q (M) w* + Mvv (M) О*]" rf

ТАБЛИЦЫ 261
Продолжение табл. 4.5
Дополнительные условия
L (е, ц) = 0, В (М, Т) = 0 в 5;
[и(е,ц)-и,]" = о,
Ьи <е) -««]" = о.
W(iM, Г)-«(*•)]' = 0,
[Mvv (М) - Mvv (t*)]' = 0 на С
Г-Г[е(«), ц(«)] = 0,
Д1-Д1[г(и), ц(«)]=0,
В (М, Т) = 0 в 5
В {М [е (и), ц («)], Г[е(и),
ц(«)]} = 0 в 5;
(« - «*)" = 0,
[d(«)-OT = 0 на С
В(М, Г)=0,
? [е (JH, Г), ц (Л*, Г)] = 0 в S;
[Q(M, r)-QJ'-O,
[Mvv (Af) — Af J' = 0 на С
Условия стационарности
L [е-е (М, Г), ц—ц (М, Г)] =0
[<?(iH,r)-<?J'=0,
[Afvv(iM)-AlJ' = O,
(u - и*)" = 0,
[О(и)-в*Г = 0 на С
[<?(«) -<?J' = o,
[Afvv («) - М,]' = 0 на С
{х [е(Д1, Г), ц(М.Т)]-х («*)}"=а
{е„[в(Д|, Г)]-8<< («*)}" = 0
на С

262 ТАБЛИЦЫ
Частные функционалы
, Ц, 8) :
+ [1 х (е) - х.] ф + [1 гп (е) - e;J л (*) }" rfC -
1 т т~ т м=ец«р [jm(*)> t
dC, где и (*) =
(8, ц) = ^ [1 еаЭГаР (8, » +1 ЦарМ^ (8, ц) -
>а (8, (i) + Ф*х (е) + т)'в„ (8)]'
, ф) = J J | - 1 еар [ц (да), Г (ф)] ГаР (Ф) +
+ 1 цар (в) Мае [ц (Ш), Г (ф)] - qw J dS -
]' rfC - ^ [\<p + е^т) (ф)]"
dC

ТАБЛИЦЫ 263
Продолжение табл. 4.5
Дополнительные условия
ц-ц[Д1(ф), Г«)]=0,
е - е [JH (ф), Т (*)] = 0,
L (8, ц) = 0 в 5
L {е [jM fl>), Г (*)],
H[iH(t), T(t)]} = 0 в S;
[Ч(*)-ЧТ=»О на С
?,(е,ц)=0,
В [JH (ё, ц), Г (8, ц)] = 0 в S;
[х(в,ц)-и.Г = 0,
[е„(е)-е^-0 на С
(да-а>Т = 0, [« (да)-**]" = 0,
(Ф-Ф*)' = О, [T,(<p)-Tf]' = O
на С
Условия стационарности
[X (8, Ц) - X,]" = 0,
[%(е)-4]" = 0>
h(t)-T,*]' = O на С
[xA>)-Kj* = 0,
[е„ (¦) - eJJ'7 - 0 на С
{<?[Л1(е, ц), Г(е, ц)]-<? (**)}'=0,
{^vv[iH(e, (i)]-Alvv (**»'-0
на С
В {iH [ц (w), T (ф)], Г (Ф)} = 0,
М<ММк>)> Г (Ф)], Ц (а>)} =0 в S;
{Q {Af [ц {«>), Т (у)]} - Q.V = 0,
{Mvv{...}-Mty = o,
{%{г[ц(ш), Г(ф)]}-х,}" = 0,
{еи{...}-г*и}" = 0 на С

Таблица 4.6
Экстремальные свойства вариационных функционалов теории оболочек.
Вариационная форма статико-геометрической аналогии
Полные функционалы
лагранжева серия
max min
0, Mv и
->
Эп2 {и, г, ц, Т, М)
max min
Г, Л1 и, с, |t
-^-
Зп3 (е, |1, Ц>)
max min
М> г, |l
->
<—
кастильянова серия
5п1 (*¦ «• е()
min max
Э*п2 (+, М, Г, ц, е)
min max
ц, с -ф, Д1, Г
min max
и Л1, Г
Полные функционалы
лагранжева серия
Эп4 (и, е, цТ, М, 1)
min max
и, е, ц, Г, Л1 X
Эпб(ю, е, Ф, Q, Mv)
max min
ф, Q, Afv И), е
—>
<—
3„,а(«)
нет экстремумов
Зп4а(н, е, |1. Г, М)
нет экстремумов
кастильянова серия
Э*п4 (it, М, Г, и, г, 1)
max min
*¦ М, Т, |i, е |
Э*5 (Ф, Л1, да, и, е()
min max
rw, и, е^ ф, Л1
—>
з;,а(+)
нет экстремумов
Э*п4а (ф, iM, Г, М-, ?)
нет экстремумов
Е

Продолжение табл. 4.6
Частные функционалы
Лагранжа -*min
Зщ («)
ЭЛ2 (а, е, |i)
злз (?. 1*)
3Л4 (и, е, ц, Т, М)
ЭЛ5(а>, е)
Эфг (е, ц, Г, ill)
max min
Т,М г, р
->
<—
Эг„ (и, е, ц, Т, М)
max min
е, |i, Г, Л1 а
<—
Кастильяно ->тах
3К1 (¦)
3К2 (гр, iM, Г)
Экз (М, Г)
ЭК4 (¦*, М, Т, М-, 8)
ЭК5 (ф, iM)
Эфе (iM, T, ]i, е)
min max
|1,г Л1, Г
->
<—
ЭСГ СФ, ЛГ, Г, ц, е)
min max
М, Т. |1, г *
<—
Частные функционалы
Эф1 (8, Ц, Г, ill)
max min
Т,М t, |i
->
Эг (а, Г, М)
max min
Г, Л1 и
<—
Эг1 (и)
min
Эг2 (ill, Т)
max
Эс (да, ф)
max min
ф Ш
Зф2 (М, Т, |1, 8)
min max
<—
3* (*, |1, 8)
min max
|t,E If
<—
Э*! (¦)
max
3;2 (e, |i)
min
Эс (да, ф)
min max
W ф
<—

Некоторые системы координат, используемые в теории оболочек
Таблица 4.7
to
СП
СП
Название, координатные лнннн,
локальный базнс
Коэффициенты пер-
первой квадратичной
фор мы
Коэффициенты второй
квадратичной формы
(физические компоненты)
Символы Кристоффеля
(компоненты, не приведенные в таблице, равны нулю)
Цилиндрические координаты
общего вида s, a
•s=censt
022=
-- const
Круговые координаты
общего вида s, <р
Оц=1
022 = Г2 (S)
'B2) =

Сферические координаты 6, ф
a22 = R2 sin2 6
и(П):
JB2) :
R
~R
— sin e cos e
Круговые цилиндрические
координаты s, ф
a22 = R2
const
6B2) ¦^-

Продолжение табл. 4.7
Название, координатные линии,
локальный базис
Коэффициенты пер-
первой квадратичной
формы
Коэффициенты второй
квадратичной формы
(физические компоненты)
Символы Кристоффеля
(компоненты, не приведенные в таблице, равны нулю)
Круговые конические
координаты «. Ф
а„=
агг =
¦¦ s2 sin2
6B2) = -
Г'2 = — s sin2
А,-
Прямолинейные косоугольные
>РД1
координаты на плоскости а1, а2
вц= 1
022 = 1
Ol2 = COS %

ТАБЛИЦЫ 269
Таблица 4.8
Функционал Рейсснера
в криволинейных ортогональных координатах
3*пз (*.
= — \
+ $[Q,
+
Т, и)
»
=
[Г,е,(А1, Г) + Г2е2 (Af, Г) +
1 (М, Т)
(Af, Г) u\+Q
Приме
..., t(Af, Г)
через Та, S,
[Q,(Af
+ w
ч а н и е
Ма, И
+ а2В2 (Af, Г) + wB
2(Af, r)«2+Q(Af) w
, Т)-Я]] + и2[я2A
[Q (Af) - Q*] + ft (u)
Выражения для е,
T), Q (Af), Mvv (Af),
см. в § 8.2.1.
(Af,
+ A
+ 2Ят (Af, T)]
T)) dS +
Ivv (Af) ft*]" dC
И, Г) - Q2] +
(Af,
Ba
v (Af) - M*]}'
T), e2 (Af, Г),
(Af, Г), В (Af,
+
dC
rj
Таблица 4.9
Полный функционал в симметризованном основном пространстве
состояний в криволинейных ортогональных координатах
Зп1а(«, 8, x, Г, Af)
-qxux-q2u2
+ M*[v,ft|(a) +
- qw | dS - \ {С
v2ft2 (u)]}' dC - [
+Q2 (Af, Г) (u2-u2)+Q(M)(w-w*)-
Здесь обозначено:
Г" = — (Г. -1- с,p., 4- o,,f..
1
2
Примечание. Выражения для
через 7\, Тг, .... Я, а е,(и), е2(и),
через перемещения см. в § 8.2.1
-f-
-1-
Qa
1, + и2Л12 + 2тЯ) +
+ Q*2u2 + Q*w +
, (Af, D о, -«;) +
vv(Af)[ft(U)-ft*]}"dC.
¦ • +2g26T),
(Af, Г), Q (Af), Mvv (Af)
, т (u), fta (и), ft (u) —

270 ТАБЛИЦЫ
Таблица 4.10
Полный функционал
в симметризоваином квазиосиовном пространстве состояний
в криволинейных ортогоиальиых координатах
Э;4а (ifc M, Г, х, е) = JJ { 1 (ri8l + 7>2
I f * 1 *KI * *
~~ 1 1^/1*1 t X/2ipn "т~ X ф "т~ 8//Т] (
— \ {x^ (e, x) (t|)j — t|)*) — xi2 (e, x)
+ я (8) (ф — Ф*) + 8^ (e) [t] (
Здесь обозначено:
ef =I(8l + /Iiri+fl2r2 +
с 1
2
Примечание. 8[ (t|)), 82 (if), ..., т
гичны компонентам деформации 8i, e2, .
рота ft, но построены не по перемещениям
циям напряжений t|)a> Ф; [Т1 + х2 (if)], ...
это другая запись выражений A.29), гл. 4.
+ •
Sis
+ 1
^)}
(¦фг"
(+)
• , т
«а.
[«•
-со
АГ
аС
«Л
И 1
и
да,
+
+ 2Ят) -
т (if
(+)]
г *
ч(+)
углу
а по
] —
анало-
пово-
функ-
(+)]-

ТАБЛИЦЫ
271
Таблица П.1
Элементы матрицы соотношений упругости для оболочки,
подкрепленной произвольно ориентированными узкими ребрами
СО
rx'(x')
v. = Bo +
= цВо +
8l6
= E B
S25 = E
=Е
8,5=
Обозначения
xk, x ), q — cos \хк, x*),
г = cos (л;2,, л;1), s = cos (л|, *2)
G°= ?/[2 A + ц)], G°/j — жесткость ребра при кручении.

272
ТАБЛИЦЫ
Таблица П.2
Элементы матрицы соотношений упругости для оболочки,
подкрепленной ортогональной сеткой узких ребер,
параллельных координатным линиям
§п = Bo + В,, §12
§14 = Cl> §25 :
§22 = В0 + В2, g33=L-± Во
§25 = С2, §44 = -Do + Db gi5 = [iZH, g55 = Do + Z>2
_ 1 — (I 1 * 1 *
§66 2 ° T ' T 2>
§13 = §23 = §15 = §16 = §24 = §26 = §34 = §35 = §36 = §46 = §56 =0
Обозначения B(., Dt, D*a, Ca 0 = 0, 1, 2; a=l, 2) см.
в табл. П.5
z,
Ш1(со1) Kl
Таблица П.З
Элементы матрицы соотношений упругости для оболочки,
подкрепленной ортогональной сеткой широких ребер,
параллельных координатным линиям
§11 =
e 1-
§36 2
§13 =
Обозна
§14 = §25
= §16 = §23 =
1ения В,, С
г,
— С[
= §26
, ?».
= |Я/
= §34
СМ. В
/
5 = §
§45
= §35
табл
_4
IP
т
П 1 ц ^
^D\, §66 „ /)i
= §46 = §56 = 0
П.4

ТАБЛИЦЫ 273
Таблица П.4
Элементы матрицы соотношений упругости для оболочки,
подкрепленной косоугольной сеткой широких ребер,
параллельных координатным линиям
g!3= ?-
= 0, #33
-Cctg* ,зе=^=^,
Обозиачення
D, = Do + Z (Dk + Bk4) Го* (а") + Z (D, + Btnf) Г*, (а?)
R -
0 —
0 — 1 _ ц2 . efc(«-fZ^T. "О" 12A -
uk(D-
k(D- 12 A — ц») ' n*(')-
прн A; > Aft Г* (a') = Го (a'), Г* (a?) = Го (а?); при А, < Aft
ro(aft) = Го(aft)> Го (aD = ro (a?)> 6 —Угол между коорди-
координатными линиями

274 ТАБЛИЦЫ
Таблица П.5
Элементы матрицы соотношений упругости для оболочки,
подкрепленной косоугольной сеткой узких ребер,
параллельных координатным линиям
2~^ Во cose, gH = Cisin9,
g33 = y^f (' + cos2 e - » si e> 8u = Ci ctg Э,
c2 ctg e, g44 = -^ + dx sin2 e + d\ cos2 e
c2 ctg e, g44 = -^ + dx sin e + d\
= ш(cos2 e + ^sin2 e)> fe = i&e + D*si e + D*cos2 e
Й46 = — Do A - ц) ctg e + D{ cos Э — D* cos e
g56 = -jDoO -n)ctge + d2cose-d\cose,
gl5 = g24 = g34 = g35 = g36 = 0
g66=т [2 ~шA - ^ +(Z)»+ Л2) ctg2 e + D*+ ^
Обозначения
— |x' 2A+11)' ° 12 A — jx2) '
2 -
I
6(*2-*2),
'-xf) A,2, /?2, 1, *);
G°/j (г) — жесткость ребра при кручении, 6 ¦- угол между
координатными линиями

ТАБЛИЦЫ
275
Таблица П.6
Элементы матрицы соотношений упругости
для многослойной оболочки
§23
=gis=E S
Здесь всюду суммирование выполнено по i от 1 до п,
а интегрирование — в пределах от F,-_i —А) до F,-— Д).
/ l
рр р
DKL = Ak;l ~ АкзАзь/Азз <-
циенты упругости г-го слоя.
= Ь 2,6), где AlMN - коэффи-

коэффиОСНОВНЫЕ ОБОЗНАЧЕНИЯ
К главам 1, 2
-^- производная (производное отображение) функции f (и).
-= производная (градиент) функционала F (и).
6F, б/, би — вариации (дифференциалы) функционала F.
функции f, переменной (функциональной) и.
и" — точка стационарности функционала.
u°v— скалярное произведение в евклидовом пространстве.
u-v — скалярное произведение в трехмерном евклидовом про-
пространстве.
u,i — частная производная функции u(Xi, Хг, ..., хп) по ('-и пе-
переменной Xi.
Fn — полный функционал, полученный из частного функцио-
функционала F с помощью множителей Лаграижа.
К главе 3
I, /, k, I, p, r, s — индексы, принимающие значения 1, 2, 3.
о, Р, у. 6. 1> Ч< ? — индексы, принимающие значения 1, 2.
V — объем, занятый упругим телом.
S — поверхность, ограничивающая объем V.
я — внешняя нормаль к S.
F — заданный вектор объемных сил.
/* — заданный вектор поверхностных сил.
и — вектор перемещений.
е — тензор деформаций.
{ }" или { }'¦—рассматриваются компоненты заключенных в
скобки величин, соответствующие геометрическим или статиче-
статическим граничным условиям (или разрывам).
Su, Si — части поверхности S с заданными перемещениями,
усилиями.
а —тензор напряжений,
а° — частное решение уравнений равновесия.
<р — тензор функций напряжений.

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ 277
а, Ь — тензоры физических констант для физических уравне-
уравнений в прямой и обратной форме.
V — набла-оператор Гамильтона, Va. V,- ¦— ковариантные про-
производные в двух- и трехмерном пространстве.
ху — диадное (тензорное) произведение.
х X у — векторное произведение.
х-у — скалярное произведение.
х--у — двойное скалярное произведение.
е , к — поверхностные тензоры тангенциальной и изгиб-
ной деформации поверхности S.
eiIk — компоненты днскриминантного тензора.
Э — функционал (энергия), Э„ — полный функционал, Эл —
функционал Лагранжа, Эк — функционал Кастильяно.
и*, ф*, ... — заданные значения величины и, ф н т. д. на по-
поверхности.
К главе 4
a, р, v> °> ?> 1> Л — индексы, принимающие значения 1, 2.
S — базисная поверхность оболочки.
С — контур, ограничивающий поверхность S.
я — единичный вектор нормали к S.
t — единичный вектор касательной к С.
v — единичный вектор тангенциальной нормали к С.
а ., Ъ . — коэффициенты первой и второй квадратичной фор-
формы поверхности S.
с . — компоненты днскрнмннантного тензора первой квадра-
квадратичной формы.
Va — поверхностная коварнантная производная.
еа — базисные векторы па поверхности S.
и = иаеа + wn— трехмерный вектор перемещений базисной
поверхности.
w — прогиб.
®а — углы поворота базисной поверхности.
еар — компоненты тензора тангенциальной деформации.
р , ц — компоненты двух различных тензоров нзгибнин
деформации.
L = Laea + Ln— левая часть векторного уравнении нераз-
неразрывности базисной поверхности.
х = хаеа + %п — вектор изгнбной деформации граничного
элемента.
ей — тангенциальная деформация граничного элемента.
g.aPv8) f*pv8 (k=\, 2, 3) — тензоры физических констант для
физических уравнений в прямой н обратной форме.
7"afl, д|ар — компоненты тензоров усилий и моментов.
q = qaea + qn — вектор нагрузки на базисной поверхности.

278 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
В = Ваеа + Вп — вектор левых частей уравнений равновесия.
Q = Qaea + Qn — вектор усилий на контуре.
Mvv — изгибающий момент на контуре.
¦ф = 'Фа*0 + фя — вектор функций напряжений.
¦Па — «углы напряжений».
7 , Ма^ — частное решение уравнений равновесия.
{ }" или { }' — рассматриваются компоненты заключенных
в скобки величин, соответствующие геометрическим или стати-
статическим граничным условиям.
Сц, Ст — участки контура с заданными перемещениями, уси-
усилиями.
еь е2, о, хь %2> т, Тъ Г2, S, Мь М2, Я —деформации и уси-
усилия по В. В. Новожилову.
и*, Qt, ... — заданные значения величин и, Q и т. д. на
контуре.
Э — функционал (энергия), Эа — полный функционал, Эл —
функционал Лагранжа, Эк — функционал Кастильяно.
К главе 5
Используются обозначения, принятые в гл. 1—4 и, кроме того:
г — радиус-вектор точки в трехмерном пространстве.
о — вектор углов поворота в точке трехмерного тела.
Qt — вектор углов поворота нормального элемента оболочки,
связанного с линией на базисной поверхности.
G/ — вектор «углов напряжений», аналогичный Q/.
"к — шаг сетки.
Э — приближенное значение функционала Э, вычисленное по
методу сеток, для сетки с шагом X.
kx, ky, kxy — кривизны пологой оболочки.
Е—модуль упругости материала.
\i — коэффициент Пуассона материала.
h — толщина оболочки или пластинки.
D — цилиндрическая жесткость оболочки или пластинки.

ЛИТЕРАТУРА
Ко всей книге
0.1. Абовский Н. П. Вариационные уравнения для многоконтакт-
многоконтактных задач теории гибких пологих ребристых оболочек. —
В кн.: Пространственные конструкции в Красноярском крае,
вып. IV. Красноярск: Красноярский политех, нн-т, 1969; Ва-
Вариационные принципы теории упругости. — В кн.: Справоч-
Справочник по теории упругости. Киев: Буд!вельник, 1971.
0.2. Абовский Н. П., Андреев Н. П. Вариационные принципы
теории упругости и теории оболочек. — Красноярск: Красно-
Красноярский политех, ин-т, 1973.
0.3. Абовский Н. П., Деруга А. П. Экстремальные свойства ва-
вариационных функционалов теории оболочек. — Тр. X Все-
Всесоюзной конференции по теории оболочек и пластин. Тбилиси:
Мецннереба, 1975; Экстремальные свойства вариационных
функционалов линейной теории упругости. — В сб.: Про-
Пространственные конструкции, вып. VII. Красноярск: Красно-
Красноярский политех, ин-т, 1975.
0.4. Айнола Л. Я. О возможностях формулировки вариационной
задачи в нелинейной теории упругих оболочек. — Тр. Тал-
Таллинского политехнического института, сер. А, № 104. Тал-
Таллин, 1957; Вариационные задачи в нелинейной теории упру-
упругих оболочек. — ПММ, 1957, т. 21, вып. 3.
0.5. Алумяэ Н. А. Теория упругих оболочек и пластинок.— В кн.:
Механика в СССР за 50 лет, т. 3. М.: Наука, 1972.
0.6. Болотин В. В. Вопросы общей теории упругой устойчиво-
устойчивости.—ПММ, 1965, т. 20, № 5.
0.7. Вариационные принципы механики/ Под ред. Л. С. Пола-
ка. — М.: Физматгнз, 1959.
0.8. Вольмир А. С. Гибкие пластины и оболочки. — М.: Гостех-
нздат, 1956.
0.9. Курант Р., Гильберт Д. Методы математической физики, т. 1,
М. — Л.: Гостехиздат, 1951.
0.10. Ланцош К. Вариационные принципы механики. — М.: Мир,
1965.
0.11. Михлин С Г. Вариационные методы в математической фи-
физике.— М.: Наука, 1970; Численная реализация варнациоН'
ных методов. — М-: Наука, 1966,

280 ЛИТЕРАТУРА
0.12. Прагер В. Вариационные принципы линейной статической
теории упругости при разрывных смещениях, деформациях,
и напряжениях. — Сб. переводов «Механика», 1969, № 5.
0.13. Рейсснер Э. О некоторых вариационных теоремах теории
упругости. — В кн.: Проблемы механики сплошной среды
(к 70-летию акад. Н. И. Мусхелишвили). — М.: Изд-во АН
СССР, 1961.
0.14. Седов Л. И. Механика сплошной среды, т. 1, 2.— М.: Наука,
1973.
0.15. Слезингер И Н. О вариационных теоремах нелинейной тео-
теории упругости. — Бюллетень Ясского политехнического ин-
института, 1959, т. V (IX).
0.16. Тонти Э. Вариационные принципы в теории упругости. — Сб.
переводов «Механика», 1969, № 5.
0.17. Ни Hay-Chang. On some variational principles in the theory
of elasticity and the theory of plasticity. — Acta sei. sinica,
1955, v. 4, No. 1.
0.18. Washizu K. Variational methods in elasticity and plasticity.—
Oxford: Pergamon Press, 1968.
К главам 1, 2
1.1. Балакришнан А. Введение в теорию оптимизации в гильбер-
гильбертовом пространстве. — М.: Мир, 1974.
1.2. Колмогоров А. Н., Фомин С. В. Элементы теории функций
и функционального анализа. — М.: Наука, 1976.
1.3. Лаврентьев М. Л., Люстерник Л. А. Курс вариационного ис-
исчисления.— М. — Л.: Гостехиздат, 1950.
1.4. Рокафеллар Р. Выпуклый анализ. — М.: Мир, 1973.
1.5. Хоменюк В. В. Методы оптимизации.— Л.: Изд-во ЛГУ, 1973.
1.6. Цлаф Л. Я. Вариационное исчисление и интегральные урав-
уравнения. — М.: Наука, 1970.
1.7. Янг Л. Лекции по вариационному исчислению и теории опти-
оптимального управления. — М.: Мир, 1974.
К главе 3
3.1. Абовский Н. П., Андреев Н. П. Функционал физических со-
соотношений. — В кн.: Пространственные конструкции в Крас-
Красноярском крае, вып. VI. Красноярск: Красноярский политех,
ин-т, 1973.
3.2. Вениаминов Д. М. Уравнения смешанного метода в теории
упругости. — Строительная механика и расчет сооружений,
1975, № 5.
3.3. Блох В. И. Теория упругости. — Харьков: Изд-во ХГУ, 1964.
3.4. Власов Б. Ф. Об уравнениях неразрывности деформаций. —
Прикладная механика, 1970, т. 6, № 11.
3.5. Крутков Ю. А. Тензор функций напряжений и общие реше-
решения в статике теории упругости. — М.: Изд-во АН СССР,
1949.

ЛИТЕРАТУРА 281
3.6. Лейбензон Л. С. Собрание трудов, т. 1, —М.: Изд-во АН
СССР, 1951.
3.7. Лурье А. И. Теория упругости. — М.: Наука, 1970.
3.8. Розин Л. А. Деформационные граничные условия в теории
упругости. — Изв. АН СССР, Механика и машиностроение,
1964, № 4.
3.9. Филоненко-Бородич М. М. Теория упругости. — М.: Физмат-
гиз, 1959.
3.10. Finzi В. Integrazione della equazioni indefinite delta mecca-"
nica del sistemi continui. — Rend. Lincei, 1934, v. 19, ser. 4.
3.11. Rildlger D. Eine Verallgemeinerung des Prinzips vom Mini-
Minimum der Potentiellen Energie Elastischer Korper. — Inge-
neuer-Archiv, 1960, B. 27.
К главе 4
4.1. Абовский Н. П. Вариационные уравнения для многоконтакт-
многоконтактных задач теории гибких пологих оболочек, в том числе
ребристых. — Тр. VII Всесоюзной конференции по теории
оболочек и пластинок. М.: Наука, 1970; О вариационных
уравнениях для гибких ребристых и других конструктивно-
анизотропных оболочек. — В кн.: Теория пластин и оболо-
оболочек.— М.: Наука, 1971.
4.2. Абовский Н. П. Смешанное вариационное уравнение для
пологой ребристой оболочки.—Строительная механика и
расчет сооружений, 1969, № 4.
4.3. Абовский Н. П., Андреев Н. П. Использование функционала
физических соотношений для расчета оболочек и пласти-
пластинок.— В кн.: Пространственные конструкции в Краснояр-
Красноярском крае, вып. VIII. Красноярск: Красноярский политех,
ин-т, 1976.
4.4. Абовский Н. П., Деруга А. П. Исследование экстремальных
свойств вариационных функционалов теории оболочек. —
В кн.: Пространственные конструкции в Красноярском крае,
вып. VIII. Красноярск: Красноярский политех, ин-т, 1976.
4.5. Абовский Н. П., Енджиевский Л. В., Петухова И. Я. Упруго-
пластические деформации гибких ребристых пологих оболо-
оболочек.— Прикладная механика, 1977, т. 13, № 1.
4.6. Алумяэ Н. А. Одна вариационная формула для исследова-
исследования тонкостенных оболочек в послекритической стадии.—
ПММ, 1950, т. 14, вып. 2.
4.7. Гольденвейзер А. Л. Теория упругих тонких оболочек. М.:
Наука, 1976.
4.8. Енджиевский Л. В , Абовский Н. П. Вариационные уравне-
уравнения для конструктивно-анизотропных плит. — Прикладная
механика, 1973, т. 9, вып. 5.
4.9. Енджиевский Л. В., Абовский Н. П. К расчету пологих реб-
ребристых оболочек и их систем в упруго-пластической ста-
стадии.— В кн.: Метод конечных элементов в строительной
механике. — Горький: ГГУ 1975.

282 ЛИТЕРАТУРА
4.10. Огибалов П. М., Колтунов М. А. Оболочки и пластины.—
М.: Изд-во МГУ, 1969.
4 11. Черных К Ф- Линейная теория оболочек, ч. 1, II. — Л.:
Изд-во ЛГУ, 1962, 1964.
4.12. Budianski В., Sanders J. L. On the «best» first order linear
shell theory. — Progress in applied mechanics (The Prager
Anniversary Volume), Macmillan Co., 1963.
К главе 5
5.1. Абовский Н. П. О применении МКЭ совместно с другими
методами. — В кн.: Пространственные конструкции в Крас-
Красноярском крае, вып. VIII. Красноярск: Красноярский поли-
политех, ин-т, 1975.
5.2. Абовский Н. П., Азархин А. М., Шестопал Б. М., Кирилло-
Кириллова Л. И. Программа расчета пологих ребристых оболочек
для ЭЦВМ. — Красноярск: Красноярский политех, ин-т,
1969.
.5.3. Абовский Н. П., Андреев Н. П., Деруга А. П. Условия ста-
стационарности функционала Кастильяно для некоторых задач
механики деформируемых тел. — В кн.: Пространственные
конструкции в Красноярском крае, вып. VI. Красноярск:
Красноярский политех, ин-т, 1973.
5.4. Абовский Н. П., Гетц И. И. Расчет пологих оболочек с на-
наклонными ребрами. — Красноярск: Красноярский политех,
ии-т, 1971; Пологие оболочки, подкрепленные ребрами про-
произвольной ориентации. — Красноярск: Красноярский поли-
политех, ин-т, 1973.
5.5. Азархин А. М., Андреев Н. П. Два приема ускорения схо-
сходимости решения конечно-разностных уравнений для плит и
оболочек методом неполной релаксации. — В кн.: Вопросы
оптимального использования ЭЦВМ в расчете сложных кон-
конструкций.— Казань: Изд-во КГУ, 1973.
5.6. Беленький В. 3. и др. Итеративные методы в теории игр и
программировании. — М.: Наука, 1974.
5.7. Власов Б. Ф. Построение двусторонних приближений по
энергии в задачах изгиба тонких плит для произвольной
ортогональной системы координат. — Докл. VII научио-тех.
конф. инж. факультета УДН. —М.: Ун-т Дружбы народов
нм. П. Лумумбы, 1971.
5.8. Гольденблат И. И. Экстремальные и вариационные принци-
принципы в теории сооружений. — В кн.: Строительные материалы
в СССР A917—1957). —М.: Госстройиздат, 1957.
5.9. Демьянов В. Ф., Певный А. Б. Численные методы разыска-
разыскания седловых точек. — Ж. выч. матем. и матем. физ. 1972,
т. 12, № 5.
5 10. Евтушенко Ю. Г. Итеративные методы решения минимакс-
минимаксных задач. —Ж. выч. матем. и матем. физ., 1974, т. 14, № 5.
5|1. Зенкевич О. Метод конечных элементов в технике. — М.:
Наука, 1975.

ЛИТЕРАТУРА 283
5.12. Канторович Л. В., Крылов В. И. Приближенные методы
высшего анализа —М.: Гостехиздат, 1949.
5.13. Новацкий В. Теория упругости. — М.: Мир, 1975.
5.14. Полак Э. Численные методы оптимизации. Единый подход.—
М.: Мир, 1974.
5.15. Поляк Б. Т. Итерационные методы, использующие множите-
множители Лагранжа для решения экстремальных задач с ограниче-
ограничениями типа равенств. — Ж. выч. матем. и матем. фнз.-; 1970,
т. 10, № 5.
5.16. Розин Л. А. Систематизация схем метода конечных элемен-
элементов в теории упругости на основе вариационных принци-
принципов.—В кн.: Метод конечных элементов в строительной
механике.— Горький: Горьковский гос. ун-т, 1975.
5.17. Самарский А. А., Андреев В. Б. Разностные методы для эл-
эллиптических уравнений. — М.: Наука, 1976.
5.18. Соболев С. Л. Некоторые применения функционального ана-
анализа в математической физике. — Л.: Изд-во ЛГУ, 1950.
5.19. Черноусько Ф. Л. Метод локальных вариаций для числен-
численного решения вариационных задач. —Ж. выч. матем. н ма-
матем. физ., 1965, т. 5. № 4.
5.20. Elias Z. M. Duality in finite element method. — Proc. ASCE,
v. 94, No. EM 4.
К приложениям
П. 1. Абовский Н. П. О взаимосвязи вариационных уравнений
для гибких анизотропных и различных ребристых оболо-
оболочек.— Тр. VIII Всесоюзной конференции по теории оболо-
оболочек и пластинок. — М.: Наука, 1973.
П. 2. Абовский Н. П., Андреев Н. П., Полный функционал упру-
упругой анизотропной оболочки переменной толщины. — В кн.:
Пространственные конструкции в Красноярском крае, вып. V.
Красноярск: Красноярский политех, нн-т, 1972.
П. 3. Абовский Н. П., Андреев Н. П. К расчету оболочек в упру-
упруго-пластической стадии. — В кн.: Пространственные кон-
конструкции в Красноярском крае, вып. VIII, Красноярск:
Красноярский политех, ин-т, 1976.
П. 4. Амбарцумян С. А. Общая теория анизотропных оболочек.—
М.: Наука, 1974; Некоторые вопросы развития теории ани-
анизотропных слоистых оболочек. — Изв. АН Арм. ССР, сер.
фнз.-мат. наук, 1964, т. 17, № 3.
П. 5. Григолюк Э. И., Филыитинский Л. А. Перфорированные
пластины и оболочки. — М.: Наука, 1970.
П. 6. Енджиевский Л. В., Ларионов А. А. Уравнения МКР для
ребристых оболочек при упруго-пластических деформа-
деформациях.— В кн.: Пространственные конструкции в Краснояр-
Красноярском крае, вып. VI, Красноярск: Красноярский политех,
нн-т, 1973.
П. 7. Кочин Н. Е. Векторные исчисления и начала тензорного
исчисления. — М.: Наука, 1965.

284 ЛИТЕРАТУРА
П. 8. Лехницкий С. Г. Анизотропные пластинки. — М.: Гостехиз-
дат, 1957.
П. 9. Лурье А. И. Общая теория упругих тонких оболочек. —
ПММ, 1940, т. 4, вып. 2.
П. 10. Новожилов В. В Теория упругости. — Л.: Судпромгиз,
1958; Теория тонких оболочек. — Л.: Судпромгиз, 1-е изд.
1951, 2-е изд. 1962.
П. 11. Пшеничное Г. И. Расчет сетчатых оболочек. — В кн.: Ис-
Исследования по теории сооружений, вып. XXII. М.: Строй-
издат, 1976.
П. 12. Рашевский П. /(. Риманова геометрия и тензорный ана-
анализ. — М.: Наука, 1967.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аналогия статико-геометрическая
101, 133—136
Анизотропия конструктивная 217
— приобретенная 217, 219
Аппроксимация пространства со-
состояний 176
— функционала 176, 182—189
— —, погрешность 187—189
Базис взаимный 208
— локальный 100, 211
— основной 208
Валентность тензора 209
Вариационная задача 13, 16
— — классическая 15
минимаксная 44
— — некласснческая 15
— — несвободная 14
об экстремуме 16, 43
о стационарном значении 17, 33
, решение 14, 169
— •— свободная 14
— теорема общая 31
частная 32
Вариационное уравнение 142—146
Вариационный принцип геометриче-
геометрический 49
Кастильяно (максимума допол-
дополнительной энергии) 33, 54, 111
Лаграижа (минимума потен-
потенциальной энергии) 33, 54, 111
общий 30, 63, 119
при разрывных полях 89, 131
при сложных граничных усло-
условиях 146—169
статический 49
физический 49
частный 32
Вариация функции 15
— — допустимая 15
— функционала 15. 177, 207
Вектор базисный 208
— поверхностный 100, 213
— функций напряжений 106
Возможные перемещения, силы 142
Гипотезы Кирхгофа — Лява 100
— пологих оболочек 109
Градиент тензора 212
— функционала 207
Граничные условия геометрические.
51, 102, 151, 164, 165
— — деформационные 52, 108, 151.
159, 165
— — естественные 19, 32
¦ смешанные 152
— — статические 51, 105, 156, 158,
166, 167
в функциях напряжений 52,
108
Гука закон 50, 97
Деформации 50, 97
— оболочки 101, 102, 139
— поверхности тела 52
Дивергенция тензора 212
Дирака функция 219
Дисторсии (дислокации) Вольтерра
150
— статические 149
Дифференциал 15
— Фреше функционала 15, 207
Дифференцирование векторов и тен-
тензоров 211
Интегрирование приближенное 185—
187
— тензорных величин 213
Интерполирование 185
Компоненты тензора (вектора) ко*
вариантные 208
— — (—) контравариантные 208
(—) физические 96, 137, 214
Контактные задачи 133
Координаты аффинные (прямолч-
нейные косоугольные) 95, 240, 258
— декартовы 210
— конические 268
— криволинейные 210
— круговые 266
— на поверхности 213

286
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Координаты нормально связанные с
поверхностью 95, 100, 242
— ортогональные 94, 240
— сферические 242, 267
— тороидальные 242
— цилиндрические 240, 266, 267
Кристоффеля символы 212, 240—2-13,
266—268
Кронекера символ 208
Ляме параметры 94, 137, 215
Мера погрешности 192
Метод Бубнова — Галеркина 174
— вариационно-разностный 175, 182
— Канторовича 175
•— конечных разностей 176
элементов 171, 172
— локальных вариаций 176
— множителей Лагранжа 22, 36, 43
— негармонического остатка 198, 201
— ортогональных проекций 199
— прямых 176
— Рнтца 172, 173
— сеток 176
— Трефтца 174, 200
— Эйлера — Лагранжа 15
Методы дискретизации 172
— прямые вариационные «аналити-
«аналитические» 173
¦ — комбинированные 176
«численные» 176
¦— релаксации 181
Метрика 192, 206, 207
— равномерная 192
—¦ среднеквадратичная 193
— энергетическая 193
Мннимакс, максимин 42
Множества выпуклые 85, 86, 205
Множители Лагранжа 22 36 39—41
64-69, 119-125
Набла-оператор Гамильтона 212
Норма 206
— энергетическая 206
Область многосвязная (неодносвяз-
ная) 146—169, 216
— односвязная 216
— поверхностно-многосвязная 167, 216
— пространственно-многосвязная 166,
216
— связная 146—169. 215
Общее решение 21, 22, 153
уравнений неразрывности 51
равновесия 51, 106
Оценка погрешности 192
— — апостериорная 195, 201
априорная 188, 194
энергетическая 198
Перемещения обобщенные 104
Поверхность базисная (срединная)
оболочки 99
Поверхность многосвязная (см,
область многосвязная)
— трехмерного тела 50
— в трехмерном пространстве 212
Погрешность 183—189, 192—203
Подпространство 28, 205
— аффинное 205
— линейное 13, 205
Поле векторное (тензорное) 30, 50,
100, 211
Поля разрывные 96, 132
Произведение векторное 210
— диадное (тензорное) 210
— скалярное 13, 206, 210
двойное 210
энергетическое 206
Производная (градиент) функциона-
функционала 15, 207
— ковариантная 212
¦ поверхностная 100, 213
Производное отображение 207
частное 207
Пространство аффинное 204
— гильбертово 13
— евклидово 206
— линейное 204
— риманово 213
— состояний упругой системы 28,
204
— — — — квазиосновное 28
основное 28
— — — •— расширенное 28
• симметризованное квази-
квазиосновное 69, 125
основное 66, 120
¦ — усеченное 28 .
— функциональное 204
Радиус-вектор 211
Разностные схемы 182—191
Разрывы кинематические, статиче-
статические 89
Ротор (вихрь) тензора 212
Свертка тензора 210
Седловая точка 42
Стационарное значение (условное,
безусловное) 16, 17
Сумма прямая (декартова) 28, 205
Тело многосвязное (см. область мио-
госвязная)
Тензор 50, 52, 101, 102, 104, 209
— днскримииантный 57, 100, 210
— метрический 101. 208. 209, 240—243
— поверхностный 101, 213
— функций напряжений 51
Теория преобразования вариацион-
вариационных проблем 33—49
— тонкнх оболочек «наилучшая» 99
Точка седловая 42
— стационарности 16. 207

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
287
сУглы напряжений» 106, 109, 148
Уравнения вариационные 142—146
— неразрывности базисной поверх-
поверхности 102, ПО, 140
контура отверстия 155, 156
— равновесия 51, 96, 105, ПО
подкрепленных частей контура
154, 165
— совместности деформаций 51
Усилия и моменты 101, 102, 104, 138
обобщенные 104, 218
Условия дополнительные 14, 73, 126
— естественные 33
— контакта 217
— однозначности перемещений 155
¦ функций напряжений 149
— стационарности 17, 20
-»- экстремума необходимые 14, 15
достаточные 25
Физически нелинейные линеаризо-
линеаризованные задачи 219
Физические соотношения для анизо-
анизотропных оболочек 104, 105
ребристых оболочек 217—
219, 271—274
— — — слоистых оболочек 217—219,
275
Формула Грина 213
— Остроградского 214
— Стокса 214
— Чезаро 148
Фрндрихса преобразование 40, 59,
116, 199 -
Функции (отображения, операторы)
аффинные 14, 205
— линейные 205
Функционал 205
— выпукло-вогнутый 205
— выпуклый (вверх или вниз) 84,
85, 131, 205, 206
— граничных условий 81—83, 128—
130, 232—234, 260—262
многокоитактной задачи 172
— для геометрических и статиче-
статических уравнений 74, 127, 230, 232,
258
физических и геометрических
уравнений 74, 126, 232, 258
и статических уравнений 74,-
77, 127, 232, 258
— Кастнльяно 59, 70, 76, 85, 93, 116,
156, 222, 248
— Лагранжа 54, 70, 77, 90, 103, 111,
151, 220, 246
— полный 29, 245, 269, 270
— Рейсснера 68, 75, 97, 228, 244, 269
— смешанный для пологих оболочек
130, 161, 262
— — с неполными полями 83, 234
— физических соотношений 76, 78,
80, 127, 128, 232, 258
— Ху — Вашицу 64. 244
— частный 29, 70, 93, 125, 230, 258
Функционалы полные, кастильяно-
ва серия 63, 67, 93, 123, 228, 254
, лагранжева серия 63, 64, 92.
119, 224, 239, 250
Шаблоны сеточных уравнений 190
Экстремальные свойства функциона-
функционалов 43, 84, 93, 130, 197, 236, 264
Экстремум условный 13

Наум Петрович Абовский
Николай Петрович А н д р е е в
Анатолий Петрович Д е р у г а
ВАРИАЦИОННЫЕ ПРИНЦИПЫ ТЕОРИИ УПРУГОСТИ
И ТЕОРИИ ОБОЛОЧЕК
М., 1978 г., 288 стр. с илл.
Редактор А. Г. Мордвинцев, В А. Романов
Техн редактор Е. В. Морозова
Корректор А. Л, Ипатова
ИБ N» 2312
Сдаио в набор 23.05.78. Подписано к печати 20.11.78. T-20I53.
Бумага 84Х108'/и, тип. № 1. Литературная гарнитура. Высо-
Высокая печать. Услови. печ. л. 15,12. Уч.-изд. л. 14,30. Тираж
5 800 экз. Заказ № 1121 Цеиа книги 90 коп.
Издательство «Наука»
Главная редакция фнзико математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типогра-
типография № 2 имени Евгении Соколовой «Союзполиграфпрома» при
Государственном комитете СССР по делам издательств, по-
полиграфии н кинжной торговли. 198052, Ленинград, Л-52, Из-
Измайловский проспект, 29