РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО ХОЗЯЙСТВА
И ГОСУДАРСТВЕННОЙ СЛУЖБЫ
ПРИ ПРЕЗИДЕНТЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
СЕРИЯ «АКАДЕМИЧЕСКИЙ УЧЕБНИК»
В.П. Носко
Эконометрика
Книга первая
Часть 1
Основные понятия, элементарные методы
Часть 2
Регрессионный анализ временных рядов
Рекомендовано
федеральным государственным бюджетным угреждением
высшего профессионального образования
«Российская академия народного хозяйства и государственной службы
при Президенте Российской федерации»
в кагестве угебника для студентов высших угебных заведений,
обугающихся по экономигеским специальностям
МОСКВА
ИЗДАТЕЛЬСКИЙ ДОМ «ДЕЛО»
2011

УДК 330.43@75.8)
ББК 65в6я73
Н84
Рецензент:
И.И. Елисеева, доктор экономических наук,
профессор, член-корреспондент РАН, заслуженный деятель науки РФ,
зав. кафедрой статистики и эконометрики Санкт-Петербургского
государственного университета экономики и финансов
АВТОР:
Носко Владимир Петрович,
кандидат физико-математических наук,
старший научный сотрудник механико-математического факультета
МГУ им. М.В. Ломоносова, зав. кафедрой эконометрики
и математической экономики РАНХиГС.
Преподает эконометрику с 1994 г., читает курсы лекций
в МГУ им. М.В. Ломоносова, в Российской академии
народного хозяйства и государственной службы при Президенте РФ
и в Институте экономической политики им. Е.Т. Гайдара.
Автор более 60 научных работ
Носко В.П.
Н84 Эконометрика. Кн. 1.4. 1,2: учебник / В.П. Носко. — М.:
Издательский дом «Дело» РАНХиГС, 2011. — 672 с. (Сер.
«Академический учебник».)
ISBN 978-5-7749-0654-3
В учебнике излагаются методы эконометрического анализа — от самых простых
до весьма продвинутых. В основе учебника — курсы лекций, прочитанные автором
в Институте экономической политики им. Е.Т. Гайдара, на механико-математическом
факультете Московского государственного университета им. М.В. Ломоносова и на
экономическом факультете РАНХиГС.
Учебник состоит из двух книг (четырех частей): в кн. 1 рассматриваются линейные
модели регрессии; модели стационарных и нестационарных временных рядов, особенности
регрессионного анализа для стационарных и нестационарных переменных; в кн. 2 — модели
одновременных уравнений, модели с дискретными и цензурированными объясняемыми
переменными, модели для анализа панельных данных; модель стохастической границы
производственных возможностей, а также содержится дополнительный материал по
анализу временных рядов (прогнозирование, методология векторных авторегрессий и др.).
В каждой части учебника имеется словарь употребляемых в ней терминов.
Для студентов, аспирантов, преподавателей, а также для специалистов по
прикладной экономике.
УДК 330.43@75.8)
ББК 65в6я73
ISBN 978-5-7749-0654-3 О ФГБОУ ВПО «Российская академия народного
хозяйства и государственной службы
при Президенте Российской Федерации», 2011

Содержание
Предисловие 6
Предисловие к первой книге 8
Часть 1
ОСНОВНЫЕ ПОНЯТИЯ, ЭЛЕМЕНТАРНЫЕ МЕТОДЫ
Раздел 1. ЭКОНОМЕТРИКА И ЕЕ СВЯЗЬ С ЭКОНОМИЧЕСКОЙ ТЕОРИЕЙ.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 11
Тема 1.1. Модели связи и модели наблюдений;
эконометрическая модель, подобранная модель 11
Тема 1.2. Метод наименьших квадратов. Прямолинейный характер
связи между двумя экономическими факторами 26
Тема 1.3. Примеры подбора линейных моделей связи
между двумя факторами. Ложная линейная связь 45
Тема 1.4. Нелинейная связь между экономическими факторами 51
Раздел 2. ЛИНЕЙНАЯ МОДЕЛЬ НАБЛЮДЕНИЙ.
РЕГРЕССИОННЫЙ АНАЛИЗ 74
Тема 2.1. Линейные модели с несколькими объясняющими
переменными. Оценивание и интерпретация
коэффициентов 74
Тема 2.2. Свойства оценок коэффициентов при стандартных
предположениях о вероятностной структуре ошибок.
Доверительные интервалы для коэффициентов 90
Приложение П-2а. Случайные векторы и их характеристики 109
Приложение П-26. Многомерное нормальное распределение 111
Раздел 3. ПРОВЕРКА ГИПОТЕЗ, ВЫБОР «НАИЛУЧШЕЙ» МОДЕЛИ
И ПРОГНОЗИРОВАНИЕ ПО ОЦЕНЕННОЙ МОДЕЛИ 113
Тема 3.1. Проверка статистических гипотез о значениях
отдельных коэффициентов и общей линейной гипотезы 113

4 Содержание
Тема 3.2. Использование F-статистики для редукции
исходной эконометрической модели. Проверка
односторонних гипотез 127
Тема 3.3. Сравнение альтернативных моделей.
Мультиколлинеарность. Прогнозирование
по оцененной модели 149
Раздел 4. ПРОВЕРКА ВЫПОЛНЕНИЯ СТАНДАРТНЫХ
ПРЕДПОЛОЖЕНИЙ О МОДЕЛИ НАБЛЮДЕНИЙ 170
Тема 4.1. Графические методы 170
Тема 4.2. Формальные статистические критерии 184
Раздел 5. УЧЕТ НАРУШЕНИЙ СТАНДАРТНЫХ ПРЕДПОЛОЖЕНИЙ
О МОДЕЛИ 203
Тема 5.1. Включение в модель фиктивных переменных 203
Тема 5.2. Учет гетероскедастичности 215
Тема 5.3. Учет автокоррелированности ошибок 224
Раздел 6. ОСОБЕННОСТИ РЕГРЕССИОННОГО АНАЛИЗА
ДЛЯ СТОХАСТИЧЕСКИХ ОБЪЯСНЯЮЩИХ
ПЕРЕМЕННЫХ 234
Тема 6.1. Линейные регрессионные модели со стохастическими
объясняющими переменными 234
Тема 6.2. Метод инструментальных переменных 243
Задания для семинарских занятий, работы в компьютерном классе
и для самостоятельной работы 261
Приложение. Таблицы статистических данных к заданиям 287
Литература 291
Глоссарий 292
Ч асть 2
РЕГРЕССИОННЫЙ АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
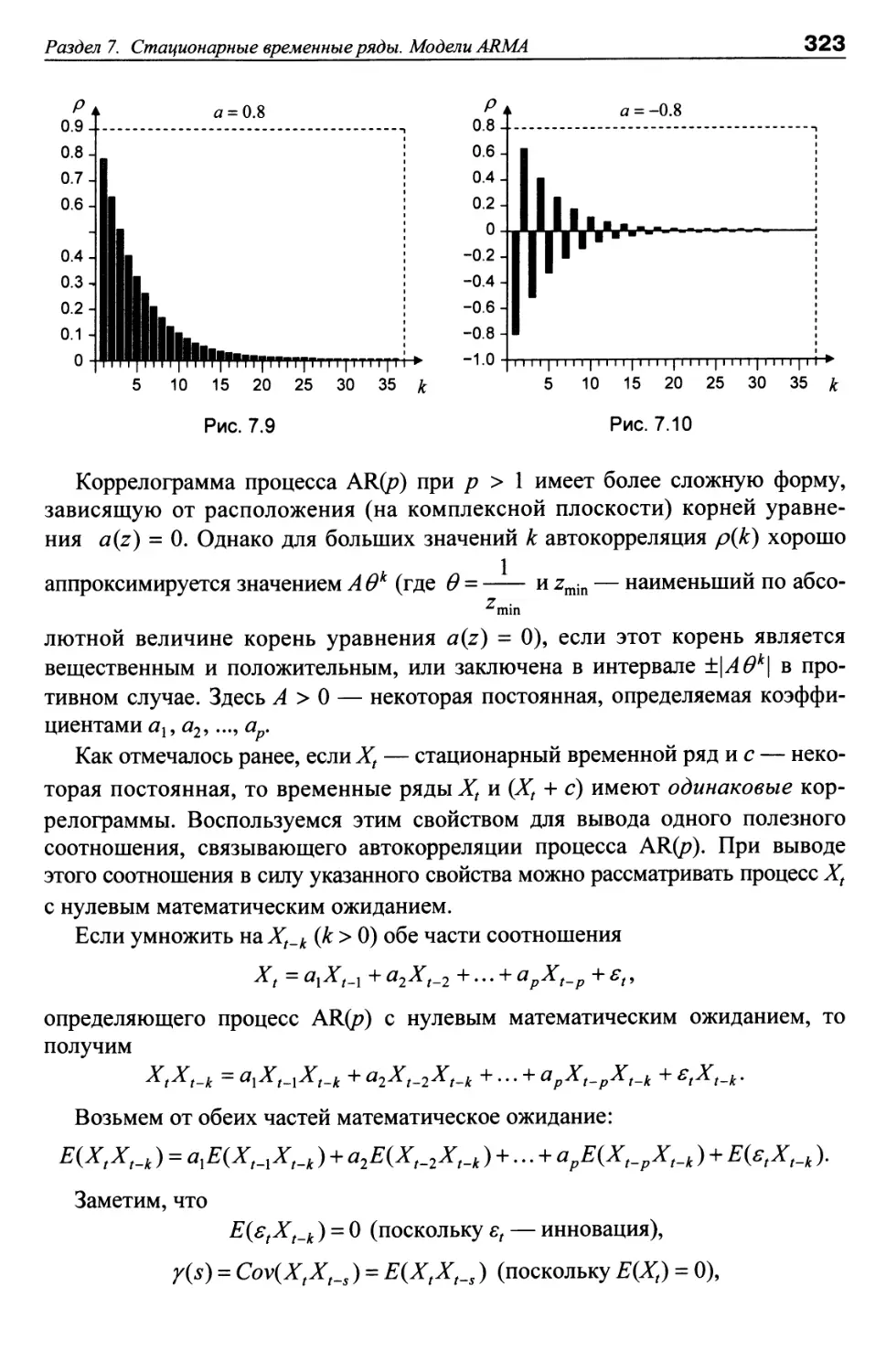
Раздел 7. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ.
МОДЕЛИ ARMA 307
Тема 7.1. Стационарные модели ARMA 307
Тема 7.2. Подбор стационарной модели ARMA для ряда
наблюдений 340
Приложение П-7. Проверка гипотезы случайности 369

Содержание 5
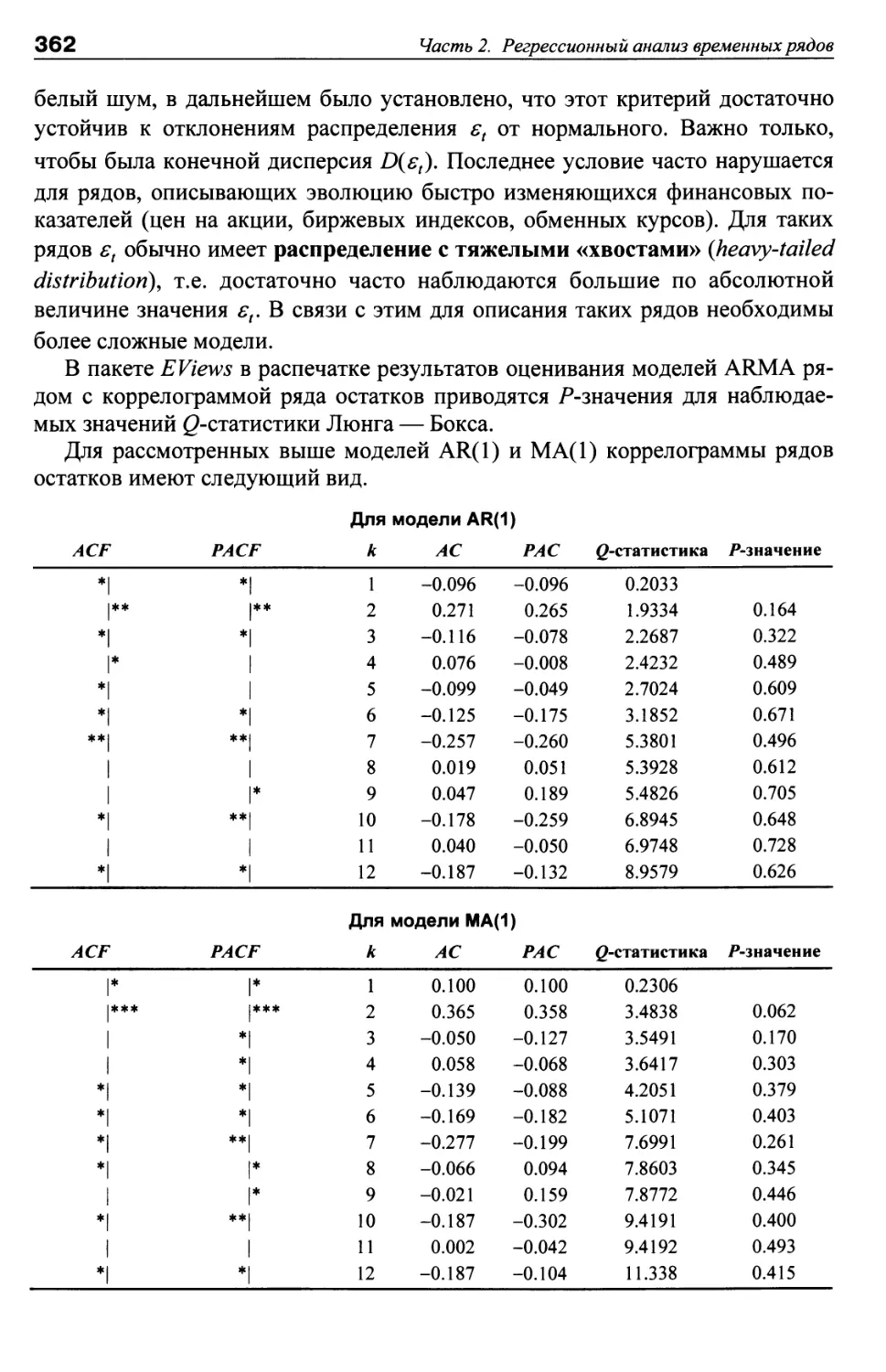
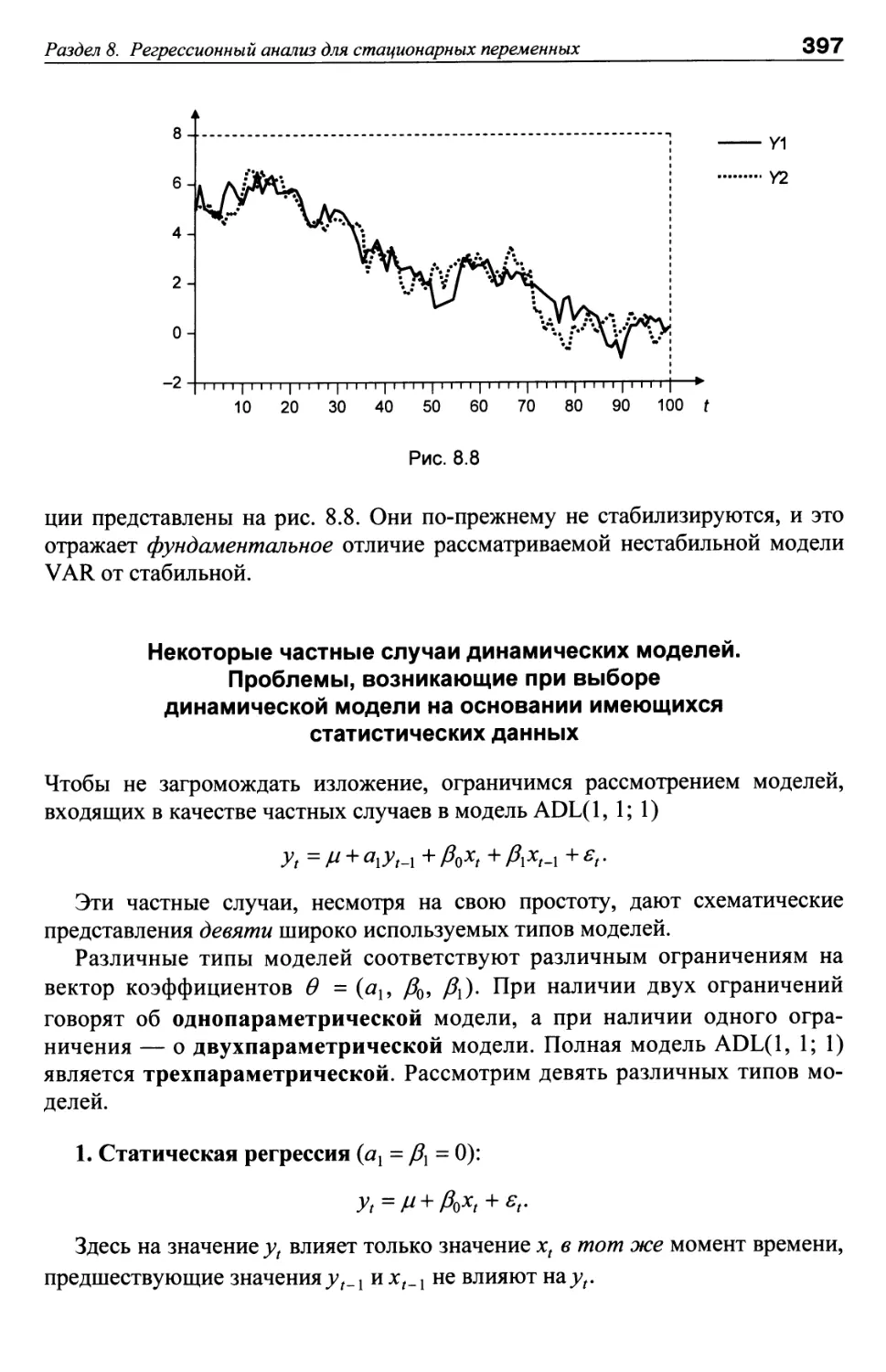
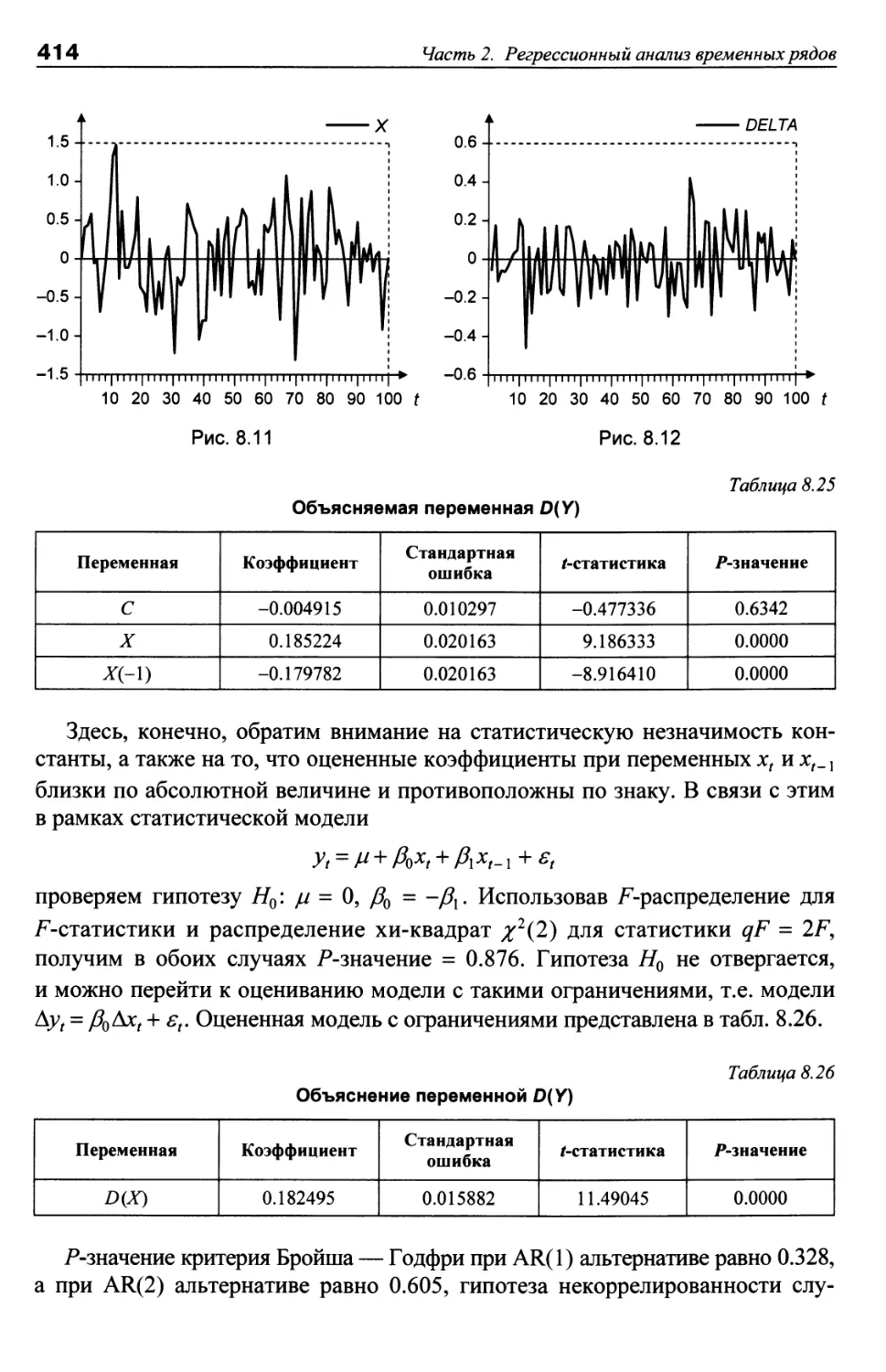
Раздел 8. РЕГРЕССИОННЫЙ АНАЛИЗ ДЛЯ СТАЦИОНАРНЫХ
ПЕРЕМЕННЫХ 377
Тема 8.1. Асимптотическая обоснованность стандартных процедур 377
Тема 8.2. Динамические модели. Векторная авторегрессия 383
Раздел 9. НЕСТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ.
МОДЕЛИ ARIMA 423
Тема 9.1. Нестационарные ARMA модели 423
Тема 9.2. Проблема различения TS- и AS-рядов. Гипотеза
единичного корня 448
Раздел 10. ПРОЦЕДУРЫ ДЛЯ РАЗЛИЧЕНИЯ TS- И DS-РЯДОВ 454
Тема 10.1. Критерии Дики—Фуллера. Многовариантные процедуры
проверки гипотезы единичного корня 454
Тема 10.2. Обзор некоторых других процедур 489
Раздел 11. РЕГРЕССИОННЫЙ АНАЛИЗ ДЛЯ НЕСТАЦИОНАРНЫХ
ПЕРЕМЕННЫХ. КОИНТЕГРИРОВАННЫЕ ВРЕМЕННЫЕ РЯДЫ.
МОДЕЛИ КОРРЕКЦИИ ОШИБОК 520
Тема 11.1. Проблема ложной регрессии. Коинтегрированные
временные ряды. Модели коррекции ошибок 520
Тема 11.2. Оценивание коинтегрированных систем
временных рядов 558
Тема 11.3. Оценивание ранга коинтеграции и модели коррекции
ошибок методом Йохансена 579
Задания для семинарских занятий, работы в компьютерном классе
и для самостоятельной работы 605
Приложение. Таблицы статистических данных к заданиям 637
Литература 647
Глоссарий 651
Предметный указатель 665

Предисловие
Учебник содержит изложение основ эконометрики и написан на базе
курсов лекций, прочитанных автором в Институте экономической политики
им. Е.Т. Гайдара, на механико-математическом факультете Московского
государственного университета им. М.В. Ломоносова и на отделении экономики
экономического факультета Российской академии народного хозяйства и
государственной службы при Президенте РФ.
Учебник состоит из четырех частей, объединенных в две книги. В первой
части изучаются линейные модели регрессии, методы статистического
анализа таких моделей, методы выявления нарушений стандартных
предположений, лежащих в основе статистического анализа линейных моделей, и методы
коррекции статистических выводов при выявлении таких нарушений. Во
второй части рассматриваются модели стационарных и нестационарных
временных рядов, особенности регрессионного анализа для стационарных и
нестационарных переменных, в третьей — модели одновременных уравнений,
модели, объясняющие наличие или отсутствие у субъекта некоторого признака
значениями тех или иных характеристик субъекта, модели с цензурирован-
ными данными, модели, служащие для описания панельных данных. Четвертая
часть содержит дополнительный материал по анализу временных рядов
(прогнозирование, методология векторных авторегрессий и др.), в ней также
рассматривается модель стохастической границы производственных возможностей.
Материал каждой части рассчитан на изучение его в течение одного семестра
B часа лекций и 2 часа практических занятий в неделю).
Каждая часть учебника состоит из разделов, объединяющих несколько
тем. В конце темы приводятся контрольные вопросы, позволяющие закрепить
усвоенный материал. В каждой части имеется набор заданий для
самостоятельной работы и работы в компьютерном классе под руководством
преподавателя. Методические указания по выполнению практических заданий
на компьютере ориентированы в основном на использование пакета эконо-
метрического анализа Econometric Views, а для некоторых разделов курса —
на использование пакета Stata. В конце каждой части приведен словарь
употребляемых в ней терминов.
Для удобства читателя при первом упоминании в тексте основные
термины выделяются жирным шрифтом, а в скобках приводятся их англоязычные

Предисловие
7
эквиваленты. Некоторые слова или целые предложения, требующие
привлечения внимания читателя, выделены светлым курсивом.
Автор считает своим приятным долгом выразить признательность
академику РАН Револьду Михайловичу Энтову и доктору экономических наук
Сергею Германовичу Синельникову-Мурылеву, которые инициировали работу
по написанию данного учебника и поддерживали автора на всех этапах этой
продолжительной работы. В значительной мере на изложение материала
повлияли заинтересованные обсуждения лекций автора по различным
аспектам эконометрических исследований в коллективе Института экономики
переходного периода (в настоящее время - Институт экономической
политики им. Е.Т. Гайдара). Автор благодарен Марине Юрьевне Турунцевой
и Илье Борисовичу Воскобойникову, которые внимательно прочитали
материал, вошедший во вторую часть учебника, и сделали ряд замечаний,
способствовавших улучшению изложения. Автор весьма признателен Ирине
Михайловне Промахиной, апробировавшей все задания, содержащиеся в учебнике,
на занятиях со студентами отделения экономики экономического факультета
Академии народного хозяйства при Правительстве РФ, что позволило
устранить имевшиеся неточности в формулировках заданий и в методических
указаниях по их выполнению. Автор благодарен Надежде Викторовне
Андриановой за тщательную правку текста при подготовке учебника к изданию.

Предисловие к первой книге
Первая книга объединяет две первые части учебника.
Первая часть состоит из 6 разделов и предназначена для
ознакомления студентов с местом эконометрики в системе
экономических дисциплин, основными задачами эконометриче-
ского анализа данных экономической статистики,
элементарными эконометрическими методами, практической реализацией
этих методов с использованием специализированных пакетов
программ эконометрического анализа, для подготовки
студентов к последующему изучению более сложных моделей и более
продвинутых методов исследования, специфических для
различных типов статистических данных. Включенный в нее
материал в основном соответствует первым пяти главам ранее
изданной книги автора1.
Изучение материала этой части не требует от читателя
серьезной математической подготовки. Для его усвоения достаточно
минимальных знаний из теории вероятностей и
математической статистики: необходимые дополнительные сведения
приводятся в процессе изложения. Что касается математического
анализа и линейной алгебры, читатель должен иметь некоторое
представление о дифференциальном и интегральном
исчислении функций нескольких переменных, а также о матрицах и
операциях над ними. Акценты в изложении смещены в сторону
разъяснения базовых понятий и основных процедур
статистического анализа данных с привлечением большого количества
иллюстративных примеров. Строгие доказательства
некоторых утверждений читатель может найти в других
руководствах, на которые даются соответствующие ссылки2.
Носко В.П. Эконометрика. Элементарные методы и введение в регрессионный анализ
временных рядов. М: ИЭПП, 2004.
В основном автор ссылается н
кийА.А. Эконометрика. Начальный курс. 7-е изд., испр. М.: Дело, 2005.
2
В основном автор ссылается на известный учебник: Магнус Я.Р., Катышев П.К, Пересец-

Предисловие к первой книге
9
В первом разделе обсуждается связь эконометрики с
экономической теорией, излагается метод наименьших квадратов
для оценивания параметров модели линейной связи между
двумя переменными. Второй и третий разделы посвящены
построению и статистическому анализу линейных регрессионных
моделей при классических предположениях о модели
наблюдений. В четвертом разделе рассматриваются графические
и формальные статистические методы выявления ряда
нарушений классических предположений, а в пятом - методы
коррекции статистических выводов при обнаружении таких
нарушений. В шестом разделе рассматривается особый тип нарушений
стандартных предположений: нарушение предположения о том,
что объясняющие переменные — детерминированные величины
(т.е. что единственным источником случайности значений
объясняемой переменной являются случайные ошибки в правой
части модели наблюдений), излагается метод
инструментальных переменных, используемый в случае коррелированности
объясняющих переменных с ошибками.
Вторая часть учебника содержит краткое введение в
современные методы анализа статистических данных,
представленных в виде временных рядов, которые учитывают возможное
наличие в динамике ряда стохастического тренда. Изучаются
различные модели стационарных рядов, методика подбора
таких моделей для ряда наблюдений и регрессионный анализ
для стационарных переменных; модели рядов, стационарных
относительно детерминированного тренда (ГЗ-ряды), и
нестационарных рядов, приводящихся к стационарным путем
дифференцирования (DS-ряды). Анализируются процедуры
различения таких рядов и проблемы, возникающие при их
применении. Рассматривается задача регрессионного анализа для
DS-рядов. Обсуждается понятие коинтегрированности
нескольких рядов, излагаются методы оценивания коинтеграцион-
ных соотношений и построения модели коррекции ошибок для
коинтегрированных рядов, порождаемых моделью векторной
авторегрессии. Освоив материал второй части, читатель может
получить дополнительные сведения, касающиеся методов
статистического анализа временных рядов, в четвертой части
учебника.
Включенный во вторую часть учебника материал в основном
соответствует главам 6—12 цитированной выше книги автора
и содержанию другой ранее изданной публикации автора3.
Носко В.П. Эконометрика: введение в регрессионный анализ временных рядов. М.:
Логос, 2004.

10
Предисловие к первой книге
Как и в первой части, основные акценты здесь смещены в
сторону разъяснения базовых понятий и основных процедур
статистического анализа данных с привлечением большого
количества иллюстративных примеров. Вместе с тем от читателя
требуется несколько большая осведомленность в отношении
вероятностно-статистических методов исследования и
владение методами регрессионного анализа в рамках начального
курса эконометрики (достаточно владения материалом
первой части учебника). Кроме того, читатель должен иметь
представление о комплексных числах и комплексных корнях
полиномов.

ЧАСТЬ 1
ОСНОВНЫЕ ПОНЯТИЯ,
ЭЛЕМЕНТАРНЫЕ МЕТОДЫ
Раздел 1
ЭКОНОМЕТРИКА
И ЕЕ СВЯЗЬ С ЭКОНОМИЧЕСКОЙ ТЕОРИЕЙ.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Тема 1.1
МОДЕЛИ СВЯЗИ И МОДЕЛИ НАБЛЮДЕНИЙ;
ЭКОНОМЕТРИЧЕСКАЯ МОДЕЛЬ, ПОДОБРАННАЯ МОДЕЛЬ
Эконометрика {Econometrics) — совокупность методов анализа связей между
различными экономическими показателями (факторами) на основе
реальных статистических данных с использованием аппарата теории вероятностей
и математической статистики. При помощи этих методов можно уточнять
или отвергать различные гипотезы о существовании определенных связей
между экономическими показателями, предлагаемые экономической теорией,
выявлять новые, ранее неизвестные связи, производить прогнозирование
будущих значений экономических показателей.
Наряду с микроэкономикой и макроэкономикой эконометрика является
одним из базовых предметов современного экономического образования. Для
анализа статистических данных эконометрика использует методы теории
вероятностей и математической статистики. При этом одни модели и методы
чаще применяются к исследованиям на микроуровне, тогда как другие —
к исследованиям на макроуровне. В связи с этим иногда говорят о
подразделении эконометрики на микроэконометрику и макроэконометрику (в этом
отношении можно сослаться, например, на монографии {Favero, 2001) и {Cameron,
Trivedi, 2005)). В течение многих лет основной задачей эконометрики
являлось по возможности наиболее эффективное оценивание параметров
математических моделей, предлагаемых экономической теорией. При этом было
принято исходить из предположения о правильности спецификации модели,
предлагаемой экономистами. В соответствии с таким подходом эконометрист
только оценивал модель на основании статистических данных, не пытаясь ее
изменить, и по результатам оценивания делай! выводы о подтверждении или
неподтверждении заявленных теоретических связей между экономическими

12
Часть 1. Основные понятия, элементарные методы
факторами, а также априорных значений некоторых параметров теоретических
моделей. В этом отношении можно сослаться на определение эконометрики,
приведенное в работе {Samuelson, Koopmans, Stone, 1954): «The application of
mathematical statistics to economic data to lend empirical support to models
constructed by mathematical economics and to obtain numerical estimates»1.
С течением времени в прикладных эконометрических исследованиях
значительное место стал занимать так называемый разведочный анализ (data
mining), при котором исследователь в первую очередь обращается именно
к имеющимся статистическим данным и пытается подобрать к ним несколько
альтернативных моделей, прежде чем остановиться на какой-то одной из них
и принять результаты, полученные для этой предпочтительной модели.
Анализируя характер имеющихся статистических данных, исследователь делает
определенные заключения о возможной форме теоретической модели, что
помогает при построении окончательной модели. Более того, если в процессе
такого анализа предложенная теоретическая модель отвергается, сами данные
могут указать на то, в каком направлении следует изменить спецификацию
исходной теоретической модели.
В настоящее время построение окончательной модели производится с
учетом как представлений экономической теории, так и информации,
содержащейся в эмпирических данных. Последняя может, например, указать на
необходимость включения в модель, предлагаемую экономической теорией,
дополнительных переменных или на исключение из модели тех или иных
«лишних» переменных, на необходимость изменения функциональной формы
связи между рассматриваемыми переменными и т.п. В процессе построения
модели естественно учитывать и результаты предшествующих
эконометрических исследований. Заметим только, что в основе всякого эконометриче-
ского исследования лежит представление о существовании некоторого
«истинного» механизма порождения эмпирических данных, о котором мы будем
говорить в дальнейшем как о процессе порождения данных (ППД, или DGP —
data generating process).
Рассмотрим, например, связь между располагаемым доходом домашнего
хозяйства (disposable personal income) DPI и расходами домашнего
хозяйства на личное потребление (personal consumption expenditures) CONS. Кейнс
в своей знаменитой книге (Keynes, 1936) отметил как фундаментальный закон
психологии склонность людей (как правило, и в среднем) увеличивать расходы
на личное потребление по мере возрастания своих доходов, но не в той
степени, в какой возрастает их доход. Это означает, что если расходы на личное
потребление связаны с располагаемым доходом соотношением
CONS = f (DPI),
где обе переменные измерены в одних единицах, то:
Применение математической статистики к экономическим данным для эмпирической
поддержки построенных экономико-математических моделей и получения числовых оценок
(англ.). — Пер. автора.

Раздел 1. Эконометрика и ее связь с экономической теорией...
13
• функция f(DPl) должна быть возрастающей;
• скорость изменения этой функции, т.е. предельная склонность к
потреблению (предельная норма потребления), должна быть меньше 1.
Вместе с тем Кейнс не указал явную форму такой функциональной связи,
справедливо замечая, что она должна соответствовать реальным
статистическим данным.
Простейшей моделью функциональной связи между DPI и CONS
удовлетворяющей указанным требованиям, является линейная модель связи (linear
relation) — модель линейной зависимости CONS от DPI:
CONS = a + /3DPI,
где Р — постоянная величина, 0 < /? < 1, характеризующая в данном круге
домашних хозяйств их склонность к потреблению (propensity to
consume), связанную с традициями и привычками;
а — автономное потребление (autonomy consumption).
Для подтверждения правильности выбора такой теоретической модели
и для проверки гипотез о ее параметрах (например, о том, что для некоторой
совокупности домашних хозяйств в определенный период склонность к
потреблению не превышала значения 0.9) надо обратиться к статистическим
данным.
Пусть имеем данные о размерах располагаемого дохода и о расходах на
личное потребление для п домашних хозяйств, так что DPIt и CONS; —
соответственно располагаемый доход и расходы на личное потребление /-го
домашнего хозяйства. (Заметим, что получение подобных статистических данных
само по себе является далеко не простой задачей, поскольку требует от всех
выбранных домохозяйств ежедневного учета их доходов и расходов и
сообщения итоговых результатов без искажения).
Если на плоскости в прямоугольной системе координат разместить точки
[DPI,, CONS;) с абсциссами DPI; и ординатами CONS; (такое построение
называется диаграммой рассеяния — scatter plot, scatter diagram, scatter
graph), то, как правило, эти точки не будут лежать на одной прямой вида
CONS = а + Р • DPI, соответствующей линейной модели связи. Они будут
образовывать облако рассеяния (scatter cloud), вытянутое вдоль
гипотетической прямой CONS = а + /3 • DPI.
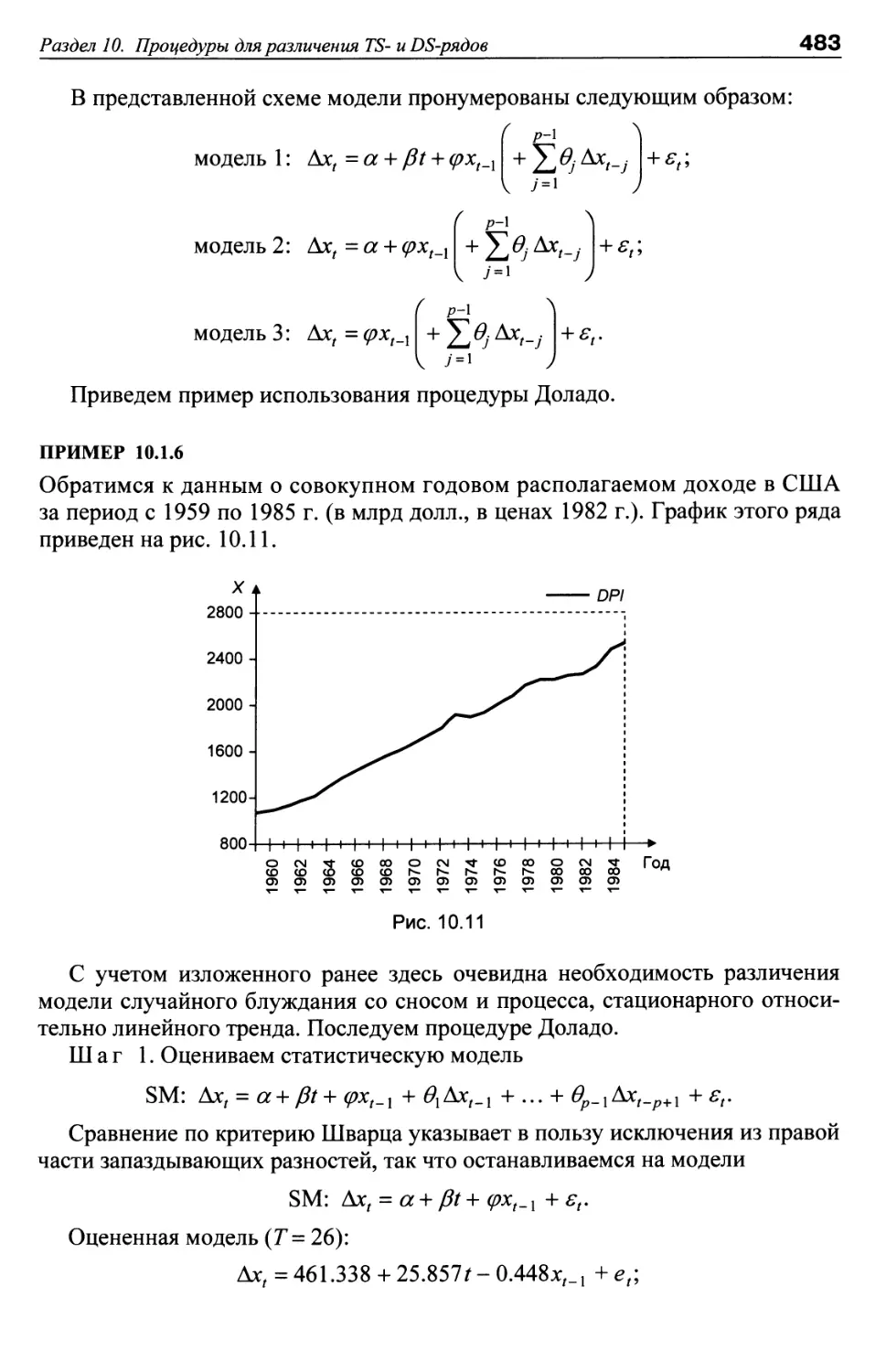
Подобная форма облака приведена на диаграмме рассеяния (рис. 1.1),
соответствующей смоделированным данным о годовых располагаемом доходе
и расходах на личное потребление (в 1999 г., в условных единицах) 20
домашних хозяйств Российской Федерации (табл. 1.1).
Значение
е, = CONSj-(a + /3DPI!)
является отклонением реально наблюдаемых расходов на потребление CONS;
от значения а + {3 • DPI;, предсказываемого гипотетической линейной моделью

14
Часть 1. Основные понятия, элементарные методы
связи для /-го домашнего хозяйства, имеющего располагаемый доход DPIt.
Это отклонение отражает совокупное влияние на конкретные значения CONSt
множества дополнительных факторов, не учитываемых принятой моделью
связи, так что реальное соотношение между DPIt и CONSt принимает форму
модели наблюдений {observation model):
CONS^ia + p-DPI^ + e^ =1, ...,я.
Соответственно о величине st = CONSt - {а + J3 • DPIt) говорят как об ошибке
наблюдений {observation error, disturbance), точнее, как об ошибке в i-м
наблюдении.
Особенность эконометрического
подхода состоит в том, что отклонения
£{ рассматриваются как случайные
величины (реализации случайных величин),
так что связь между переменными,
в данном случае между DPIt и CONSi9
является не детерминированной, а
стохастической. При этом несколько
расплывчатые рассуждения о теоретической
(усредненной) функции связи
становятся более формализованными, если
предположить, что процесс порождения
данных имеет вид:
СОЛУ, =/(/№/,) + *,, i = l,..., л,
., £п— случайные величины, условные математические ожидания
которых при фиксированных значениях располагаемого дохода равны 0:
E(si\DPIi) = 09 i = l,..., я.
Таблица 1.1
Смоделированные данные для 20 домашних хозяйств
2200
2400 2600
Рис. 1.1
2800 DPI
где е19
i
1
2
3
4
5
6
7
8
9
10
DPI
2508
2572
2408
2522
2700
2531
2390
2595
2524
2685
CONS
2406
2464
2336
2281
2641
2385
2297
2416
2460
2549
#
11
12
13
14
15
16
17
18
19
20
DPI
2435
2354
2404
2381
2581
2529
2562
2624
2407
2448
CONS
2311
2278
2240
2183
2408
2379
2378
2554
2232
2356

Раздел I. Эконометрика и ее связь с экономической теорией...
15
При таком предположении имеем:
E(CONS,\DPIl) = f(DPI,)9 z = l,...,w,
так что f (DPI f) можно трактовать как ожидаемую величину расходов на
личное потребление домохозяйства, имеющего располагаемый доход DPIr
Пусть процесс порождения данных имеет вид:
CONS ,.=(« + /?■ DPI ,.) + *,-, / = 1, • •., п,
где DPI{, ..., DPIn— заданные (фиксированные) величины;
£и...,£п—случайные величины, для которых E(£j\DPIl) = 0, так
что E(CONSi \DPIt ) = a + /3- DPI};
J3 — коэффициент, выражающий изменение ожидаемой
величины расходов домохозяйства на личное потребление
при увеличении располагаемого дохода домохозяйства
на единицу.
В реальных условиях эконометрист имеет в своем распоряжении только
статистические данные и не знает вида функции f(DPI). Выбирая ту или
иную функцию f(DPI\ он формирует соответствующую статистическую
модель (statistical model)
CONS, = f (DPI,) + у,., / = 1, ...,w,
где Vj, ..., vn — случайные величины.
Такую модель часто называют также эконометрической моделью
(econometric model), имея в виду два обстоятельства:
• она не является детерминированной (усредненной) моделью связи и
предусматривает возможные отклонения реально наблюдаемых
значений CONS; от значений f(DPf), предсказываемых детерминированной
моделью связи;
• она выбирается эконометристом, и ее вид может отличаться от
истинного процесса порождения данных, который эконометристу неизвестен.
Определение эконометрической модели в явном виде (т.е. задание ее в виде
уравнения, с указанием задействованных переменных и функциональной
формы связи между переменными, задание априорных ограничений на параметры
и вероятностного описания последовательности vl9 ..., vn) называется
спецификацией эконометрической модели (specification of an econometric model).
В рассмотренных условиях
vi = CONS,. - f{DPlt ) = (« + /?• DPI, ) + e,- /(DPI,),
так что E(v,\DPIi) = (a + fi-DPIi)-f(DPIi). При этом значение E(v,\DPI,)
может быть не равным нулю, и тогда E^CONS^DPI^* /(DP/.), т.е./(DPI)

16
Часть 1. Основные понятия, элементарные методы
уже нельзя трактовать как ожидаемую величину расходов на личное
потребление домохозяйства, имеющего располагаемый доход DPIt. При подобном
неправильном выборе формы функции связи говорят, что статистическая
модель неправильно специфицирована (misspecified model).
Представим теперь, что выбранная статистическая модель все же
специфицирована правильно и, как и процесс порождения данных, имеет линейную форму:
CONSi={a + pDPIi)+si, i = l, ...,п.
Однако при этом эконометрист все равно не знает значений параметров а
и р процесса порождения данных. Поэтому он должен оценить эти параметры,
используя имеющиеся статистические данные, т.е. наблюдаемые пары
значений (DPIi9 CONS;), i = 1,..., п. При этом интерес могут представлять не только
точечные оценки этих параметров, но и доверительные интервалы для них.
Если модель специфицирована правильно и оценки а для а и Ъ для /?
каким-то образом получены, то подобранная модель (fitted model)
CONS = a + bDPI
может использоваться для прогнозирования объема расходов на личное
потребление для домохозяйства, имеющего располагаемый доход DPI. Разумеется,
такой прогноз может иметь смысл:
• если полученные оценки достаточно близки к истинным значениям
параметров а и /?;
• для домохозяйств, имеющих ту же (или хотя бы близкую к ней)
склонность к потреблению, что и у домохозяйств, по которым производилось
оценивание параметров модели.
После оценивания эконометрической модели обычно проверяют
адекватность модели имеющимся статистическим данным, а также те или иные
гипотезы о значениях параметров модели.
Может оказаться, например, что наблюдаемое облако рассеяния больше
соответствует модели, в которой «теоретическая» (усредненная) функция
связи CONS =f(DPI) имеет вид CONS = y+ SlnDPI, y>0,S>0. Заметим, что
в такой модели предельная склонность к потреблению уже не является посто-
dCONS 8
яннои величиной, а зависит от уровня располагаемого дохода: = ,
убывая с возрастанием располагаемого дохода. (При этом условие DPI > 5
обеспечивает выполнение предположения о том, что предельная склонность
к потреблению положительна и принимает значения меньше единицы.)
Подобные ситуации более характерны для описания связи между располагаемым
личным доходом и расходами на потребление отдельных продуктов или
группы продуктов (например, молочных продуктов).
Подобранная модель, прошедшая проверку на адекватность имеющимся
статистическим данным, может использоваться как для прогнозирования, так
и для управления (для проведения определенной экономической политики).

Раздел 1. Эконометрика и ее связь с экономической теорией...
17
Таким образом, эконометрический анализ представляет собой
совокупность следующих действий:
• получение на основе экономической теории исходных представлений
о существовании связей между определенными экономическими
факторами (экономическая гипотеза);
• выражение этих представлений в математической форме в виде
соответствующих уравнений или систем уравнений (математическая модель);
• сбор необходимых (и доступных) статистических данных;
• согласование выбранной математической модели с имеющимися в
распоряжении статистическими данными (модель наблюдений),
спецификация статистической (эконометрической) модели;
• оценивание статистической (эконометрической) модели;
• проверка гипотезы о правильности выбранной спецификации
статистической (эконометрической) модели (проверка адекватности подобранной
модели имеющимся статистическим данным); сохранение или изменение
этой спецификации по результатам проверки гипотезы адекватности;
• уточнение математической модели связи путем проверки тех или иных
гипотез о значениях параметров выбранной модели (с учетом
результатов проверки эконометрической модели на адекватность имеющимся
данным); проверка возможности упрощения модели; проверка
экономических гипотез (единичная эластичность и т.п.);
• использование подобранной модели для прогнозирования или управления.
В процессе эконометрического анализа исследователи часто
придерживаются принципа парсимонии (экономичности, простоты - parsimony
principle): модель должна быть простой, насколько это возможно, пока не доказана
ее неадекватность имеющимся статистическим данным. Исследователи
используют также принцип охвата {encompassing principle): модель должна
быть в определенном смысле «неулучшаемой» и объяснять результаты,
получаемые по конкурирующим с ней моделям (в конкурирующих моделях не
должно содержаться информации, которая позволила бы улучшить
выбранную модель). При проведении исследования рекомендуется также
придерживаться метода «от общего к частному» {general-to-specific approach), т.е.
в качестве первоначальной брать более полную модель, а затем пробовать
редуцировать ее к более простой модели.
Две переменные: меры изменчивости и связи
В табл. 1.2 приведены уровни безработицы среди белого {BEL) и цветного
{ZVET) населения США с марта 1968 г. по июль 1969 г. (месячные данные).
Рассмотрим графики изменения уровней безработицы в обеих группах
в течение указанного периода (рис. 1.2). Первое впечатление: уровень
безработицы среди цветного населения существенно выше и изменяется со временем
со значительными колебаниями, уровень безработицы среди белого
населения изменяется плавно и в довольно узком диапазоне.

18
Часть 1. Основные понятия, элементарные методы
Таблица 1.2
Уровни безработицы среди белого (BEL) и цветного (ZVET) населения США, %
I
Период
BEL
ZVET
1968 г.
1
2
3
4
5
6
7
8
9
10
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
3.2
3.1
3.2
3.3
3.3
3.2
3.2
3.1
3.0
3.0
6.9
6.7
6.5
7.1
6.8
6.4
6.6
7.3
6.5
6.5
#
Период
BEL
ZVET
1969 г.
11
12
13
14
15
16
17
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
3.0
2.9
3.1
3.1
3.1
3.0
3.2
6.0
5.7
6.0
6.9
6.5
7.0
6.4
Обозначим через xl9..., х17 последовательно наблюдаемые уровни
безработицы среди цветного населения, а через yl9 ..., у17 — соответствующие им
уровни безработицы среди белого населения США. Таким образом, можно говорить
о наблюдаемых значениях двух переменных: х - уровня безработицы среди
цветного населения, и у — уровня безработицы среди белого населения. Всего
имеем п = 17 наблюдаемых пар значений переменных х и у: (х19ух)9..., (хп9уп).
о.
СО
2
о.
>s
@
2
л
I
V
S
JD
ц,
9
S
h
о
Г
00
<
л
о.
ю
Сентя
Л
о.
ю
Октя
Л
о.
ю
Ноя
Л
а.
Ю
Дека
Л
а.
со
Янв
Л
Ц
га
Февр
£
о.
га
:>
л
q
<D
Апр
>s
@
s.
Л
X
9
S
Л
ц
9
S
Рис. 1.2

Раздел 1. Эконометрика и ее связь с экономической теорией... 19
Наиболее простыми показателями, характеризующими
последовательности х19..., хп иуь ...,уп9 являются их средние значения (means)
_ 1А х{+... + х„ - 1Л Ух+ — + У„
X = -Z.xi=z > У = -£,У1=- ~>
п м п п /=1 п
а также выборочные дисперсии (sample variances)
1 " 1 "
Var(x) = £ (х,. - хJ , ИяггОО = ]Г (^ - уJ ,
характеризующие степень разброса значений х{, ..., хп (у,, ...,>>„) вокруг своего
среднего J (или j7 соответственно), или вариабельность (изменчивость —
variability) этих переменных на множестве наблюдений. Отсюда обозначение
Var (variance). Впрочем, более естественным было бы измерение степени
разброса значений переменных в тех же единицах, в которых измеряется и сама
переменная. Эту задачу решает показатель, называемый стандартным
отклонением1 (Std.Dev. — standard deviation) переменной х (переменной у),
который определяется соотношением
Std.Dev.(x) = yjVar(x) (Std.Dev.(y) - ^Var(y) соответственно).
Определяя выборочную дисперсию, сумму квадратов отклонений
наблюдаемых значений переменной от их среднего значения делим не на
количество наблюдений п, а на п - 1. Именно такое определение используется в
математической статистике по следующей причине. Если предполагать, что
хь ..., хп — случайная выборка из распределения с математическим
ожиданием ju и дисперсией а1, то, как известно из курса математической статистики,
1 " 1 "
х=-Ух;. является несмещенной оценкой для ju, a Var(x) = У](хг -хJ
является несмещенной оценкой для а1. Задания для практических занятий
ориентированы на применение специализированного пакета прикладных
программ Econometric Views (Е Views), и в этом пакете принято именно такое
определение выборочной дисперсии.
Вычисления по указанным выше формулам приводят в нашем примере
к значениям: х = 6.576, StdDev.(x) = 0.416, у = 3.118, Std.Dev.iy) = 0.113.
Иными словами, средний уровень безработицы среди цветного населения
более чем в 2 раза превышает средний уровень безработицы среди белого
населения. Стандартные отклонения соответственно относятся
приблизительно как 4:1, что указывает на гораздо более сильную изменчивость
(вариабельность) уровня безработицы среди цветного населения. Размах колебаний
уровней соответственно равен: 7.3 - 5.7 = 1.6 и 3.3 - 2.9 = 0.4.
Здесь мы следуем терминологии словаря статистических терминов (The Oxford dictionary
of statistical terms, 2003).

20
Часть 1. Основные понятия, элементарные методы
Удобным графическим средством
анализа данных является, как
говорилось ранее, диаграмма рассеяния, на
которой в прямоугольной системе
координат располагаются точки xi9 yi9 i - 1,..., п,
где п — количество наблюдаемых пар
значений переменных х и у (иногда эту
диаграмму называют корреляционным
полем — correlation diagram). Диа-
5,5 6,0 6,5 7,0 7,5 zvet грамма рассеяния для нашего примера
приведена на рис. 1.3.
Рис-1-3 Вытянутость облака точек на
диаграмме рассеяния вдоль наклонной
прямой позволяет сделать предположение о том, что существует некоторая
объективная1 тенденция линейной связи между значениями переменных х и у9
определяемая соотношением
y=a + fix, /3*0.
В то же время такое соотношение выражает всего лишь тенденцию: реально
наблюдаемые значения у. отличаются от значений а + /Зх( на величину
так что
yi=(a + Pxi) + si, / = 1,..., л.
Последнее соотношение определяет линейную модель наблюдений (linear
observation model), тогда как соотношение
у = а + fix
определяет линейную модель связи (linear relation) между рассматриваемыми
переменными (математическая модель — mathematical model, dependence
model), в которой у — зависимая (dependent) переменная, ах —
независимая (independent) переменная.
Заметим, однако, что видимая степень проявления вытянутости облака
точек на диаграмме рассеяния существенно зависит от выбора единиц
измерения переменных х и у.
Поэтому, во-первых, желательно при построении диаграммы выбирать
масштаб и интервалы изменения переменных таким образом, чтобы окно
диаграммы имело вид квадрата и чтобы на диаграмме имелись точки,
достаточно близко расположенные к каждой из 4 границ этого квадрата (как на
рис. 1.3). Это автоматически реализуется при построении диаграмм рассеяния
в пакете Econometric Views.
Впрочем, достаточно хорошо выраженная вытянутость облака точек вдоль наклонной
прямой может возникать и в случае так называемой ложной (паразитной) линейной связи,
не имеющей содержательной экономической интерпретации (см. пример 1.3.4, тема 1.3).

Раздел 1. Эконометрика и ее связь с экономической теорией...
21
BEL
3,4 +--
3,2
3,0 +
2,8
♦ ♦
♦♦!♦ ♦
♦ ♦
5,5
6,0 6,5 7,0
Рис. 1.4
-Ч ►
7,5 ZVET
Во-вторых, желательно иметь какие-то числовые характеристики, которые
отражали бы действительное наличие вытянутое™ облака точек вдоль
некоторой наклонной прямой и не зависели от шкал, в которых представлены
значения переменных.
Одна из возможных характеристик такого рода связана с разбиением
диаграммы рассеяния горизонтальной и вертикальной прямыми на 4
прямоугольника (рис. 1.4).
Разбивающие диаграмму прямые
(секущие) проводятся через точку
(ху у) так что если точка (х7, yt) лежит
правее вертикальной секущей, то
отклонение xt - х имеет знак «плюс»,
а если левее — то знак «минус».
Аналогично, если точка (х,, j;,) лежит выше
горизонтальной секущей, то
отклонение у; -у имеет знак «плюс», а если
она расположена ниже этой секущей —
знак «минус».
В нашем примере т++ = 4, т+_ - 4,
т_+ = 3 (точки, соответствующие
наблюдениям с номерами 6 и 17, имеют совпадающие координаты), т__ - 6
(точки, соответствующие наблюдениям с номерами 9 и 10, имеют
совпадающие координаты), так что количество точек с совпадающими знаками
отклонений xt -xwyt -у равно т++ + т__ = 10, а количество точек, у которых знаки
отклонений различны, равно т+_ + т_+ = 7.
Количество точек с совпадающими знаками отклонений от средних
значений (для таких точек произведение (х, - х)(у; -у) положительно) составляет
10/17 = 0.59, т.е. около 59% общего числа точек, и это служит некоторым
указанием на наличие вытянутости облака точек в направлении прямой,
имеющей положительный угловой коэффициент. Если бы большинство
составляли точки с противоположными знаками отклонений от средних
значений (для таких точек произведение (х, - х){\\ - у) отрицательно), то это
служило бы некоторым указанием на наличие вытянутости облака точек
в направлении прямой, имеющей отрицательный угловой коэффициент.
Последняя ситуация часто наблюдается при рассмотрении зависимости спроса
на товар от его цены.
В качестве примера приведем диаграмму рассеяния (рис. 1.5) для
статистических данных о еженедельных закупках куриных яиц 7 домохозяйст-
вами у одного и того же розничного продавца в течение 15 недель при
общем снижении цен на этот продукт в течение этого времени
(статистические данные приведены в табл. 1.4; спрос измерялся в дюжинах, цена —
в долларах).

22
Часть 1. Основные понятия, элементарные методы
Спрос ,
15 "
9 -
0,
i
35
♦
^ ♦
0,55
Рис. 1.5
Цена
Более распространенным является
определение степени выраженности
линейной связи между произвольными
переменными х и у, принимающими
значения xt nyi9 i = 1, ..., п, посредством
выборочного коэффициента
корреляции {sample correlation coefficient)
Cov(x,y)
?xy ^Var(x) JVar(y) '
учитывающего не только знаки
произведений (х, - x)(yt - у), но и
абсолютную величину этих произведений. Величина Cov(x, у) определяется
соотношением
1 п _ _
Cov(x,y) = ]Г (х. - х)(у( - у)
и называется выборочной ковариацией (sample covariance) переменных хиу.
Так что формально
Cov(x, х) = Var(x), Cov(y, у) = Var(y).
Заметим также, что Cov(x,у) = Cov(y, х)игху = гух.
Свойства выборочной ковариации, выборочной дисперсии
и выборочного коэффициента корреляции
Пусть а — некоторая постоянная, х, у, z — переменные, принимающие в /-м
наблюдении значения xi9 yi9 zi9 i = 1, ..., n (n — количество наблюдений).
Тогда а можно рассматривать как переменную, значение которой в i-м
наблюдении равно а{ = я, и
1 п 1 п
Cov(x9а) = £(xt - x)(at -а) = £(х, - х)(а - а),
п-Ц.
i=\
п-\
так что Cov(x,a) = 0. Далее очевидно, что
Cov(x, a) = Cov(a, x) и Cov(x, x) = Var(x).
1 ^
1
Кроме того,
Cov(ax9y) = -^—y£(axi-ax)(yi -y) = a-^—^(xi -*)CV/ ~У)>
Cov(ax, y) = a Cov(x, y).
так что

Раздел 1. Эконометрика и ее связь с экономической теорией...
23
Наконец,
1 п
Cov(x,y + z) = X(*/ ~ *Х(У1 + */)" E> + z)) =
= -^1(^/-^)((л-50 + (^-г)) =
1 " 1 "
n~\tt п-\ i=x
так что
Cov(x, jy + z) = Cov(x, у) + Co v(x, z).
Исходя из этих свойств находим, в частности, что
Var(a) = 0, Var(ax) = a2Var(x\ Std.Dev.(ax) =| a | Std.Dev.(x)
(при изменении единицы измерения переменной в я > 0 раз во столько снсе
раз изменяется и величина стандартного отклонения этой переменной),
Var(x + a) = Var(x)
(сдвиг начала отсчета не влияет на изменчивость переменной).
Наконец,
Var(x + y) = Cov(x + у, х + у) = Cov(x, х) + Cov(x, у) + Cov(y, х) + Cov(y, у),
т.е.
Var (x + y) = Var(x) + Var(y) + 2Cov(x, у)
(дисперсия суммы двух переменных отличается от суммы дисперсий этих
переменных на величину, равную удвоенному значению ковариации между
этими переменными).
Что касается выборочного коэффициента корреляции г^,, то если
изменяются начало отсчета и единица измерения, скажем, переменной х, так что
вместо значений хх, ..., х„ получаем значения
Xi=a + bxi9 / = 1,..., я, (Ь>0)
переменной х = а + Ъх, тогда
_ Cov(x,y) _ Cov(a + bx,y) _ bCov(x,y) _
ху yjVar(x) ^Var(y) ^Var(a + bx) yjVar(y) ^b2Var(x) ^jVar(y) **
Иными словами, выборочный коэффициент корреляции г инвариантен
относительно выбора единиц измерения и начала отсчета переменных хиу.
Значения выборочного коэффициента корреляции не могут быть больше 1
по абсолютной величине, что непосредственно вытекает из применения
известного неравенства Коши — Буняковского в виде:

24
Часть 1. Основные понятия, элементарные методы
£(*,.-*)(>>,.->>)
/=1
<2>,-*J •]►>,■->о2.
;=i
/=1
Если линейная тенденция выражена на диаграмме рассеяния довольно
ясно, то значения г^ будут по абсолютной величине близки к 1 (значения г^
близки к +1, если облако существенно вытянуто вдоль прямой, имеющей
положительный угловой коэффициент, или к -1, если облако существенно
вытянуто вдоль прямой, имеющей отрицательный угловой коэффициент).
Значение г^ равно +1 тогда и только тогда, когда все точки (хх, ух),..., (х„, уп)
лежат на прямой, имеющей положительный угловой коэффициент.
Значение г^ равно -1 тогда и только тогда, когда все точки (х19 yY)9 ..., (хп9 уп)
лежат на прямой, имеющей отрицательный угловой коэффициент.
В нашем примере Var(x) = 0.1732, Variy) = 0.0128, Cov(x, у) = 0.0217,
откуда находим:
00217 =0.4608,
Гху V0.1732V0.0128
т.е. получаем положительное значение г^9 расположенное приблизительно
посередине между 0 и 1.
В примере с закупками куриных яиц получаем отрицательное значение
выборочного коэффициента корреляции: г^ = -0.717. Соответственно в
первом случае говорят о положительной корреляционной связи (positive
correlation), а во втором — об отрицательной корреляционной связи (negative
correlation) между переменными.
Однако не следует считать, что
большое положительное или большое
отрицательное значение коэффициента
корреляции обязательно
свидетельствует именно о линейном характере связи
между переменными. Даже при
достаточно большом по абсолютной
величине значении выборочного
коэффициента корреляции построенная по
конкретным статистическим данным
диаграмма рассеяния может указывать
скорее на нелинейную связь между
переменными. Обратимся, например, к
статистическим данным об уровне безработицы UNJOB и темпах инфляции INF
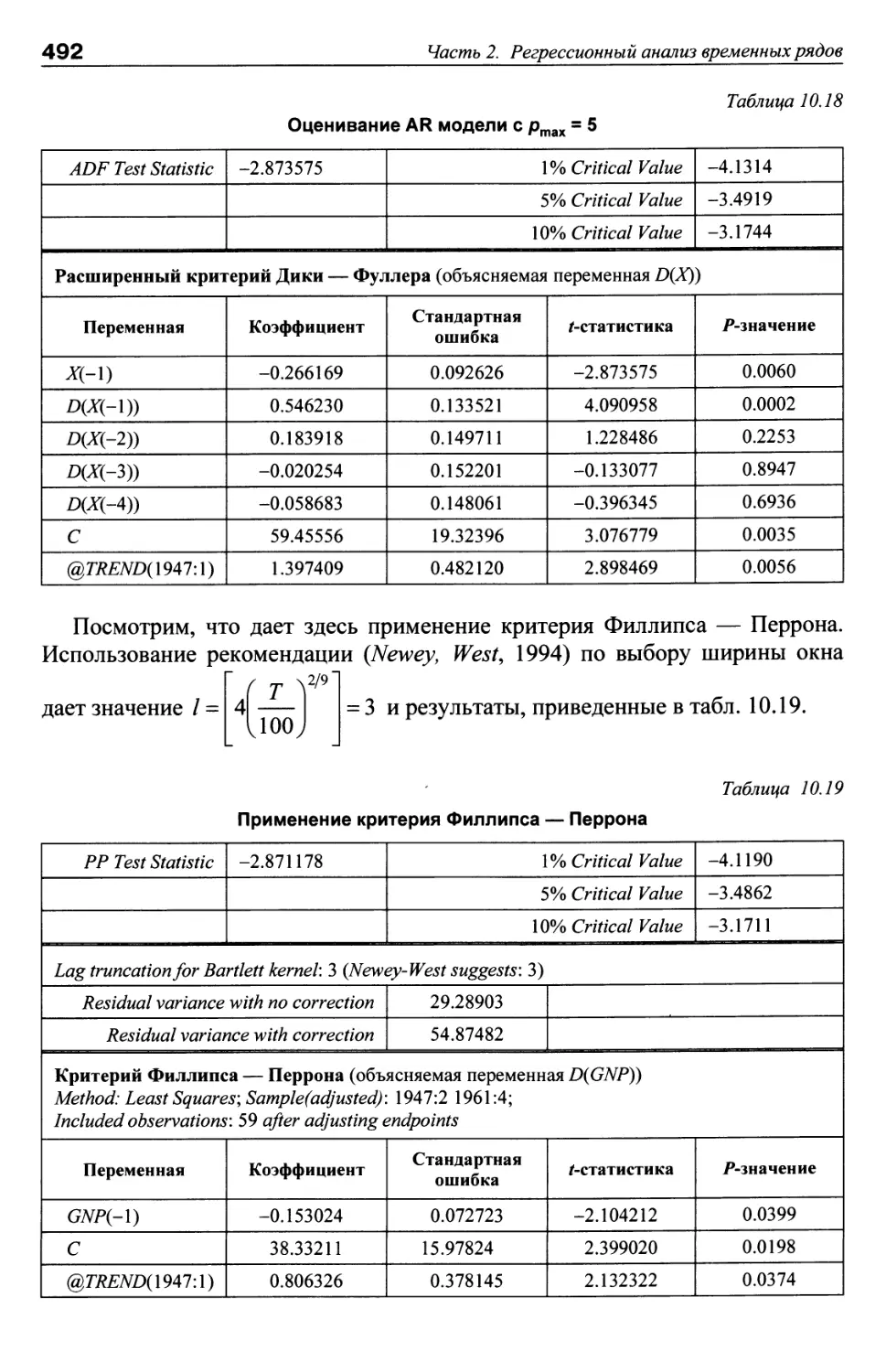
в США за период с 1961 по 1969 г. (эти данные приведены в табл. 1.23 и
подробно анализируются при рассмотрении темы 1.4). Значение выборочного
коэффициента корреляции между этими переменными равно -0.848.
Соответствующая статистическим данным диаграмма рассеяния (рис. 1.6) имеет
UNJOB

Раздел 1. Эконометрика и ее связь с экономической теорией...
25
вид, который вряд ли может указывать на линейный характер связи между
этими переменными.
В то же время близость выборочного коэффициента корреляции к нулю
вовсе не означает отсутствия какой-либо другой — отличной от линейной —
зависимости между данными переменными. Рассмотрите самостоятельно
пример, в котором переменные у и х связаны квадратичной зависимостью
у = х2, но значения у наблюдаются только при х = -2, -1,0, 1,2. Постройте
для этих данных диаграмму рассеяния и определите выборочный
коэффициент корреляции.
V Замечание 1.1.1. Мы определили Var и Cov путем деления
соответствующих сумм квадратов на п - 1. Вместе с тем, например, в
учебнике {Доугерти, 2004) соответствующие суммы квадратов делятся
не на п - 1, а на я. К счастью, Var и Cov у нас играют лишь
вспомогательную роль, а величина более существенного для нас
коэффициента корреляции г^ не зависит от того, каким из двух способов
определяют Var и Cov, лишь бы только при определении обеих этих
характеристик использовался один и тот же способ.
V Замечание 1.1.2. Выборочный коэффициент корреляции,
определенный указанным выше способом, более точно называется
выборочным коэффициентом парной линейной корреляции Пирсона.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Почему наряду с теоретическими моделями связи между переменными
приходится рассматривать модели наблюдений? Чем различаются эти типы моделей?
В чем состоит особенность эконометрического подхода к исследованию связей
между экономическими переменными?
2. Что понимается под процессом порождения данных? Что понимается под эконо-
метрической (статистической) моделью? Чем отличается эконометрическая модель
от процесса порождения данных?
3. Каковы основные элементы эконометрического анализа?
4. В чем состоит принцип экономичности, используемый при подборе модели?
5. В чем состоит принцип охвата, используемый при подборе модели?
6. В чем заключается метод «от общего к частному», используемый при подборе
модели?
7. Может ли совпадать подобранная модель связи с теоретической?
8. Какое графическое средство полезно использовать для выяснения характера
теоретической (усредненной) связи между двумя экономическими показателями?
9. Какая числовая характеристика измеряет степень выраженности линейной связи
между двумя экономическими показателями в имеющихся наблюдениях?
10. В каких случаях говорят о положительной (отрицательной) корреляционной связи
между экономическими переменными?
11. Инвариантна ли выборочная ковариация Cov(x, у) относительно выбора единиц
измерения и начала отсчета переменных х и yl

26
Часть 1. Основные понятия, элементарные методы
12. Инвариантен ли выборочный коэффициент корреляции г относительно выбора
единиц измерения и начала отсчета переменных х и yl
13. Всегда ли высокое значение коэффициента корреляции указывает на линейный
характер связи между экономическими переменными?
Тема 1.2
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.
ПРЯМОЛИНЕЙНЫЙ ХАРАКТЕР СВЯЗИ МЕЖДУ ДВУМЯ
ЭКОНОМИЧЕСКИМИ ФАКТОРАМИ
Обсудим вопрос о том, каким образом по имеющимся наблюдениям можно
(хотя бы приблизительно) восстановить гипотетическую линейную связь
между переменными, если таковая действительно существует. Как было сказано,
проблема состоит в том, что даже при действительном существовании
линейной связи между двумя переменными истинные значения параметров a yl P
такой связи обычно остаются неизвестными, и судить об этих истинных
значениях можно лишь приближенно, оценивая a yl /5 на основании
ограниченного количества имеющихся в распоряжении данных наблюдений
(статистических таблиц).
Ранее отмечалось, что если между переменными х и у существует
теоретическая (усредненная) линейная связь в виде
у= а + fix,
то наблюдаемые значения xi9yi9 i = 1, ..., п, этих переменных связаны
линейной моделью наблюдений
У;=(а + 0Х;) + еп 1 = 1,...., л.
Если а и /3 — истинные значения параметров линейной модели связи, то
*,=>>,-(« + £*,■)
представляет собой ошибку (error, или disturbance) в /-м наблюдении. Заметим,
что в англоязычной литературе параметру а соответствует термин intercept,
а параметру /3 — slope.
Если в качестве эконометрической модели выбрана линейная модель, то
поиск подходящих оценок для а и /? можно осуществлять, например, путем
нахождения на диаграмме рассеяния прямой, проходящей через точку (х, у) -
«центр» системы точек (хх,ух), ..., (хп,уп) yl наилучшим образом выражающей
направление вытянутости этой системы (облака) точек.
Пусть прямая
у = а* + J3*x
рассматривается в числе прочих в процессе такого поиска (так что а* + J3*x=y).
Тогда для /-го наблюдения будем иметь расхождение

Раздел 1. Эконометрика и ее связь с экономической теорией...
27
причем значения е* могут быть как положительными, так и отрицательными.
При изменении значений а* и /Г будут изменяться и расхождения £*, ..., £*.
Конечно, хотелось бы подобрать а* и /3* таким образом, чтобы s\ - ... = е*п - 0.
Однако это невозможно, если точки (д^, ух),..., (хп9у„) не лежат на одной
прямой. Поэтому приходится останавливать свой выбор на значениях а* и /Г,
минимизирующих некий подходящий показатель, характеризующий
совокупность расхождений в целом.
В качестве такого показателя можно взять, например, сумму квадратов
п
расхождений ^(£*J и тогда остановить свой выбор на прямой у = а* + Р*х,
для которой эта сумма минимальна1. Соответствующие этой прямой значения
а* и Р* обозначим символами а и /?.
Поскольку прямая у = а*+ /3*х проходит через точку (х, у), то
у = а* + р*х . Отсюда
* - п*—
а -у-р х,
и для поиска «наилучшей» прямой у = а + /3х достаточно определить ее утло-
вой коэффициент /?, при этом а-у-^х. Изменяя значения /? и следя за
п Л
изменением значений ^(£*J, можно, в принципе, найти искомое р с любой
/=i
наперед заданной точностью. Заметим, однако, что если во всех наблюдениях
переменная х принимает одно и то лее значение, то хх = ... =х„=х9
s* =yi-(a*+p*x) = yi-y9
ЖJ=£и->о2.
/=i /=1
п
В этом случае сумма ^(s*J одинакова для любой прямой у = а + Р х, про-
i=i
ходящей через точку (х, у).
Соотношение y = d + J3x представляет подобранную модель линейной
связи, которая служит аппроксимацией для «истинной» модели у = а + /?х
линейной связи между переменными х и у. В подобранной модели наблюдае-
Такой выбор удобен с точки зрения простоты вычислений и простоты математических
выводов. Однака можно использовать и другие показатели, характеризующие совокупность
расхождений в целом, — например, сумму абсолютных величин расхождений.

28
Часть I. Основные понятия, элементарные методы
У А
• у наблюдаемое
• у прогнозное
Теоретическая
прямая
Подобранная
прямая
Рис. 1.7
мому значению xt переменной х сопоставляется прогнозное значение (fitted
value) у. =ai+pxi переменной^. Последнее обычно отличается от
наблюдаемого значения^. Разность
ei=yi-yi=yi-(a + ^xi)
называется остатком (residual) в z'-м наблюдении. Для реальных данных, как
правило, все остатки отличны от нуля, одни из них имеют положительный
знак, а другие — отрицательный.
Для наблюдаемых значений объясняемой переменной имеем, таким
образом, два представления:
yt = (а + pxt) + si (из процесса порождения данных);
yt = (а + pxt) + et (из определения остатков).
Поскольку оценки для а и /3 отличаются от истинных значений этих
параметров (за исключением тривиальных ситуаций), в общем случае
а + рх^а + Рхг Отсюда вытекает, что ег Ф ei9 т.е. в /-м наблюдении
значение остатка отличается от значения ошибки et. На рис. 1.7 остатки и ошибки
имеют одинаковые знаки в первом, втором и четвертом наблюдениях и
противоположные знаки — в третьем наблюдении.
Если не все xl9 ..., хп одинаковы, то ту же самую «наилучшую» прямую
у = а + Cх можно получить, исходя из общего принципа наименьших
квадратов (least squares principle). Согласно этому принципу среди всех воз-

Раздел 1. Эконометрика и ее связь с экономической теорией...
29
можных значений а*9 /Г, претендующих на роль оценок параметров а и Д
следует выбирать такую пару а**, /3**, для которой
5>, -сГ -/Г*,.J = min £(у,-а -/?ЧJ.
Иначе говоря, выбирается такая пара а**, /Г*, для которой сулша
квадратов расхоэюдений оказывается наименьшей. Получаемые при этом оценки
называются оценками наименьших квадратов (НК-оценками) или
/^-оценками {least squares estimates). Можно показать, что они совпадают с ранее
определенными оценками а и /?:
** л о** h
а =#, р -р.
Заметим, что при построении оценок наименьших квадратов заранее
не требуется, чтобы соответствующая прямая проходила через точку (х, У);
этот факт является свойством оценок наименьших квадратов. Наличие такого
свойства докажем чуть позднее (см. Приложение П-1.2а в конце темы), а
сейчас рассмотрим, как практически найти указанные оценки а и /3.
Идеально, если бы существовала возможность прямого вычисления
значений а и Р по какой-нибудь формуле на основе известных значений xi9 yi9
i - 1,..., п. В связи с этим заметим, что функция
е(«;я=2>,-«*-/?ЧJ
как функция двух переменных описывает поверхность z = Q(a*9 J3 ) в
трехмерном пространстве с прямоугольной системой координат а , /? , z, так что
поиск пары а9 /? сводится к известной математической задаче —
определению точки минимума функции двух переменных.
Соответствующие выкладки приводятся в Приложении П-1.2а, здесь же
укажем только конечное решение:
п
Р = ^, >
2>,-*J
/ = 1
а = у- fix.
Разумеется, такое решение может существовать и быть единственным
только при выполнении условия

30
Часть I. Основные понятия, элементарные методы
£(*,-*J*о.
/ = 1
которое называется условием идентифицируемости. Оно означает, что
не все значения xl9..., хп совпадают между собой1. При невыполнении
этого условия все точки (xi9y()9 i = 1,..., п, лежат на одной вертикальной
прямой х = х.
Обратим еще раз внимание на полученное выражение для J3. Нетрудно
заметить, что в это выражение входят уже знакомые нам суммы квадратов
2>,-хJ
из определений выборочной дисперсии Var(x) = — и выборочной
п
Х(*/-*)Су/->0
ковариации Cov(x,y) = — .
Так что в этих терминах
-Cov(x,y)
Var(x)
Отсюда, в частности, видно, что знак /? совпадает со знаком ковариации
Cov(x, у), поскольку Var(x) > 0, и что значения /? близки к нулю, если кова-
риация между наблюдаемыми значениями переменных х и у близка к нулю.
Однако близость /? к нулю здесь следует понимать как относительную,
с учетом реальных значений выборочной дисперсии Var(x).
В качестве одного из примеров проанализируем в дальнейшем
статистические данные о годовом потреблении свинины у на душу населения в США
(в фунтах) и оптовых ценах на свинину х (в долларах за фунт) за период
с 1948 по 1961 г. (табл. 1.3). Если использовать для этих данных линейную
модель связи, то коэффициент /3 оценивается по этим данным как /3 = -24.925.
Если же оптовую цену на свинину указать не в долларах, а в центах, то
получим значение /? = -0.24925.
Таким образом, изменяя единицу измерения переменной х (или
переменной у), можно получать существенно различные значения /? — от сколь
угодно малых до сколь угодно больших. Близость значений /? к нулю всегда
должна интерпретироваться с оглядкой на используемые единицы измерения
переменных х и у.
В дальнейшем всегда будем предполагать, что это условие выполнено.

Раздел 1. Эконометрика и ее связь с экономической теорией...
31
Таблица 1.3
Годовое потребление свинины на душу населения в США с 1948 по 1961 г.
Год
1948
1949
1950
1951
1952
1953
1954
Потребление,
фунт
67.8
67.7
69.2
71.9
72.4
63.5
60.0
Цена,
долл. за фунт
0.5370
0.4726
0.4556
0.4655
0.4735
0.5047
0.5165
Год
1955
1956
1957
1958
1959
1960
1961
Потребление,
фунт
66.6
67.4
61.5
60.2
67.6
65.2
62.2
Цена,
долл. за фунт
0.4256
0.4111
0.4523
0.4996
0.4183
0.4433
0.4448
Отметим в связи с вышесказанным полезное представление ft в виде
Р = г3
хул
Уаг(у)
Var(x)
Действительно,
* = Cov(x,y) = r^Varjx) ^Уаг(у)
Var(x) Var(x)
откуда и вытекает указанное представление.
На основе последнего соотношения иногда оценивают модели со
стандартизованными переменными (standardized variables).
Стандартизованная переменная — это безразмерная переменная, которая получается
из исходной переменной делением всех значений последней на ее
стандартное отклонение. Если хст и уСТ — стандартизованные варианты
переменных х и у9 то
( \ ( \
Var(xCT) = Var\
^Var(x)
= 1, Var(yCT) = Var
yjVariy)
= 1,
и при оценивании модели для стандартизованных переменных
получаем:
>.. .. уаы.г_
хст > .Уст '
Var{x„)
В модели со стандартизованными переменными значение J3 показывает,
на сколько стандартных отклонений изменяется в среднем переменная у при
изменении переменной х на одно стандартное отклонение.

32
Часть 1. Основные понятия, элементарные методы
В нашем примере с уровнями безработицы переменная х представляет
уровень безработицы среди цветного населения, а переменная у - уровень
безработицы среди белого населения. Применим метод наименьших
квадратов для оценивания параметров модели линейной связи между этими
переменными, исходя из модели наблюдений
у{ =(а + /3х;) + £п i = l,...,п.
Вычисление а и /? по приведенным выше формулам дает значения
/? = 0.020415/0.162976 = 0.125,
a = y-fix = 3.118 -0.125 -6.576 = 2.294.
Таким образом, «наилучшая» прямая имеет вид
j/ = 2.294+ 0.125*.
Примем ее в качестве аппроксимации для истинной модели линейной связи
между переменными х и у. Эта аппроксимация указывает на то, что при
изменении переменной х на 1 единицу (измерения х) переменная у изменяется
в среднем на 0.125 единицы (измерения у). Если в этом же примере перейти
к стандартизованным переменным, то получим: /? = 0.461, а = 20.280. Это
указывает на то, что при изменении переменной х на одно стандартное
отклонение переменная у изменяется «в среднем» на 0.461 ее стандартного
отклонения.
Факт горизонтальности прямой у = а + fix при /? = 0 (Cov(x,у) = 0) и
наличие у этой прямой наклона при Р * 0 (Cov(x, у) * 0) позволяют произвести
некоторую детализацию структуры
остатков et =yt-a + j3xr Нанесем на
диаграмму рассеяния на рис. 1.3 график
прямой у = 2.294 + 0.125* и отметим
на этой диаграмме точку А = GЛ, 3.3),
соответствующую данным о
безработице в США в июне 1968 г. (рис. 1.8).
Опустим из этой точки перпендикуляр
на ось абсцисс. Он пересекает прямую
у = у в точке В = G.1, 3.118) и
прямую у = а + /3х в точке С =G.1, 3.183),
так что расстояние по вертикали от
точки А до прямой у = у, равное АВ = 3.3 - 3.118 = 0.182, раскладывается
в сумму
АВ = АС+СВ.
7,5 ZVET

Раздел 1. Эконометрика и ее связь с экономической теорией... 33
Отсюда находим, что расстояние по вертикали от точки А до прямой
у = а + fix равно
АС = АВ -СВ = 0.182 -C.183 -3.118) = 0.117.
Вообще, для любой точки (xi9 У;) на диаграмме рассеяния можно записать:
где yt = a + P xt — ордината точки «наилучшей» прямой, имеющей абсциссу xt.
Возведем обе части последнего представления в квадрат и просуммируем
левые и правые части полученных для каждого / равенств:
1>, -УJ =1G,- - У? +2>, -hf +2ICP, -ПУ, -Уд-
/=1 /=1 /=1 /=1
Можно показать (см. Приложение П-1.26), что в полученном
представлении третья сумма в правой части равна нулю, так что
tiy^yf^ih-yy+tiy^yd2- A.1)
/=1 /=1 /=1
При этом существенно, что оценивали здесь модель наблюдений с
включением в нее константы а:
yi={a + Pxi) + si, i = l,..„и.
Если вместо такой модели оценивать модель наблюдений без константы
(модель пропорциональной связи —proportional relation)
У(=Рх(+8^ / = 1,...,Л,
то соотношение A.1) не выполняется. Подробнее этот случай обсуждается
при изложении темы 1.3.
Сумму квадратов, стоящую в левой части соотношения A.1), будем
называть полной суммой квадратов {total sum of squares) и обозначать TSS.
Таким образом,
TSS = £,&,-уJ.
i = \
Первую сумму квадратов в правой части выражения A.1) будем называть
суммой квадратов, объясненной моделью {explained sum of squares), и
обозначать ESS, так что
ESS^i^-yf.
i = \
Вторая входящая в правую часть выражения A.1) сумма

34
Часть 1. Основные понятия, элементарные методы
чаще всего называется остаточной суммой квадратов {residual sum of squares)
и обозначается RSS1.
Иначе говоря, равенство A.1) представляет собой разложение полной
суммы квадратов на сумму квадратов, объясненную моделью, и остаточную
сумму квадратов:
TSS = ESS + RSS.
Заметим, что если /? = 0, то а = у и у. = у . Следовательно, при (i - О
1=1 /=1
t.q.RSS=TSShESS = 0.
При р ф О, по самому определению прямой у - а + fix, имеем
2>,-ЛJ<1>,-я2,
/=i /=i
T.e.RSS<TSSuESS*0.
Если считать, что тенденция линейной связи между переменными х и у
выражена в тем большей степени, чем меньшую долю составляет RSS по
отношению к TSS, либо, иначе, чем большую долю составляет ESS по
отношению к TSS, то естественно предложить в качестве показателя,
характеризующего степень выраженности линейной связи между переменными х и у,
отношение ESS/TSS. Этот показатель называется коэффициентом
детерминации (coefficient of determination) и обозначается R2, так что
^2 _ ESS / = i
1(А-уJ
TSS А _
2Jyt-y)
i = \
или в силу равенства A.1)
R2 = l_RSS_ = l_lll
TSS 5>,-уJ
i = \
Коэффициент детерминации возрастает с уменьшением доли RSS в TSS.
Минимальное значение коэффициента детерминации равно 0 и достигается
Такая аббревиатура используется, например, в учебнике (Доугерти, 2004). Однако в
литературе по эконометрике можно встретить и другие варианты: SSR, ESS {error sum of squares),
{Магнус, Катышев, Пересецкий, 2005), SSE. Поэтому при чтении различных руководств
по эконометрике следует обращать внимание на то, какие именно термины и обозначения
используют авторы.

Раздел 1. Эконометрика и ее связь с экономической теорией...
35
при RSS = TSS. В этом случае тенденция линейной связи между переменными
х и у не обнаруживается, ^ = 0 и ESS = 0 (подобранная модель не объясняет
изменчивость переменной^).
Максимальное значение коэффициента детерминации равно 1 и
достигается при RSS = 0. В этом случае тенденция линейной связи между переменными
х и у выражена в наибольшей степени: все точки (xh yt), i = 1, ..., п,
располагаются на одной прямой y = d + fix. При этом ESS = TSS (подобранная
модель в полной мере объясняет изменчивость переменной у).
Таким образом, для коэффициента детерминации справедливо соотношение
0<Л2<1.
Рассмотрим термины «полная сумма квадратов» и «сумма квадратов,
объясненная моделью». Полная сумма квадратов соответствует значению RSS
в ситуации, когда ^ = 0 и «наилучшая» прямая имеет вид у = у,
отрицающий наличие линейной зависимости у от х. Вследствие этого информация
о значениях переменной х не дает ничего нового для объяснения изменений
значений у от наблюдения к наблюдению. Степень этой изменчивости была
охарактеризована нами значением выборочной дисперсии
Гаг(у) = -±-£(у,-у)>=Щ;
при этом TSS = RSS и ESS = 0.
При /?* 0 имеем нетривиальное представление TSS = ESS + RSS с ESS * 0,
поэтому можно записать:
ТЛ , ч TSS ESS RSS
Var(y) = - = - + -.
п-\ п-\ п-\
Однако
™ Ы-уJ Ы-~уJ
п-\ п-\ п-\
где у — переменная, принимающая в /-м наблюдении значение j>,.
/=i
Здесь использовано доказываемое далее1 соотношение ^£,=0, так что
п п п _
Х*>/-й) = 0> &"=ХЛ и 7 = .р.Ктомуже
/=i /=i /=i
См. Приложение П-1.2а в конце темы 1.2.

36
Часть 1. Основные понятия, элементарные методы
2>,-АJ 2>? 2>,-ю2
где е — переменная, принимающая в /-м наблюдении значение е(.
п
Здесь использован тот факт, что е = —— = 0.
п
В итоге получаем разложение
Var(y) = Var(y) + Var(e),
показывающее, что изменчивость переменной у (степень которой
характеризуется значением Var(y)) частично объясняется изменчивостью переменной
у (степень которой характеризуется значением Var(y)). He объясненная
переменной у часть изменчивости переменной у соответствует изменчивости
переменной е (степень которой характеризуется значением Var{e)).
Последнее разложение для Var(y) часто называют дисперсионным анализом
{analysis of variance — ANOVA).
Таким образом, вспомогательная переменная у берет на себя объяснение
некоторой части изменчивости значений переменной у. И эта объясненная
часть будет тем большей, чем выше значение коэффициента детерминации
R2, который теперь можно записать также в виде
Var(y) Var(y)
Поскольку переменная у получается линейным преобразованием
переменной х, то изменчивость у однозначно связана с изменчивостью х, так что,
в конечном счете, построенная модель объясняет часть изменчивости
переменной у изменчивостью переменной х. В таком контексте о переменной у
говорят как об объясняемой переменной (explained variable), а о
переменной х — как об объясняющей переменной (explanatory variable). При этом
неявно подразумевается, что в действительности между этими
переменными имеется определенная (нестрогая) причинная связь, направленная в
сторону объясняемой переменной. Однако отсутствие причинной связи между
переменными вовсе не исключает получения высоких значений
коэффициента детерминации при подборе модели линейной связи между этими
переменными1.
Вернемся опять к нашему примеру. Мы оценили параметры модели
линейной связи, исходя из модели наблюдений
yi=(a + j3xi) + ei, 1 = 1,..., л,
См. ниже пример 1.3.4 (тема 1.3).

Раздел 1. Эконометрика и ее связь с экономической теорией...
37
так что объясняемой переменной здесь является уровень безработицы среди
белого населения у9 а объясняющей переменной — уровень безработицы
среди цветного населения х. При этом
ESS = 0.043474
+ RSS = 0.161231
TSS = 0.204705 ,
так что
Variy) = 0.043474/16 = 0.002717
+ Varje) = 0.161231/16 = 0.010077
Variy) = 0.012794,
Л2 =0.043474/0.204705 = 0.212374.
Значение коэффициента детерминации оказалось достаточно малым.
Далее имеет смысл выяснить, сколь близким к нулю должно быть значение R2,
чтобы можно было говорить о практическом отсутствии линейной связи
между переменными.
Рассмотрим коэффициент корреляции г^ между переменными у и у, где
у = а + /?х, а а и /? — оценки наименьших квадратов параметров а и /5
гипотетической линейной связи между переменными хну. Заметим, что
у = у + е (так как et = у. - yt по определению), тогда:
r Covjy, у) = Covjy + е, у) _ Covjy, у) + Covje, у)
* JVar{y) JVar(y) ^Var(y) JVar{y) yjVar{y) JVar(y)
Но выше при выводе разложения для TSS приводилось соотношение
1СР,->00',-Л) = о,
п
которое с учетом ^(yt -yf) = 0 приводит к равенству
1 п
левая часть которого есть не что иное, как Cov(e, у). Следовательно,
r = Var{y) ^jVar(y)
* JVariy) JVariy) ivar(y)'

38
Часть 1. Основные понятия, элементарные методы
так что
* Var(y)
Последнее соотношение показывает, что коэффициент детерминации равен
квадрату коэффициента корреляции между переменными у и у. Таким
образом при достаточно сильно выраженной линейной связи между х и у, что
соответствует значению R2, близкому к 1, оказывается близким к 1 и коэффициент
корреляции между переменными у и у.
По причинам, которые будут указаны в теме 2.1, г^ называют
множественным коэффициентом корреляции (multiple-R, множественный-/?).
Отметим также, что переменная у измеряется в тех же единицах, что и у,
и при изменении масштаба измерения переменной у значение г^ не
изменяется. Отсюда вытекает, что коэффициент детерминации R2 инвариантен
относительно изменения масштаба и начала отсчета переменных х и у.
Заметим, наконец, что
Cov(y,y) _ Cov(y,d + /3x)
jVar(y) ^Var(y) ^Var(y) yjvar(d + J3x)
pCov(y,x) _sign(fi)Cov(y,x)
JVar(y) yjfi2 Var(x) <JVar(y) J Var{x)
Здесь sign(z) = -1 для z < 0, sign(z) = 0 для z = 0, sign(z) = 1 для z > 0.
Поскольку
-Cov(x,y)
Var(x) '
то sign(fi) = sign(Cov(x,y)) и r^ =s\gn(Cov{x,y))rxy, так что
r2xy=r2yy=R2.
Из этого соотношения вытекает, что:
• вычислить значение R2 можно еще до непосредственного оценивания
модели линейной связи (для этого достаточно определить значение
коэффициента г и возвести его в квадрат);
• значение коэффициента детерминации R2 указывает на степень
выраженности линейной связи между переменными х и у {тесноту
линейной связи между х и у), на качество линейной аппроксимации
действительной модели связи между х и у в рассматриваемом
диапазоне изменения переменной х, а значение коэффициента г^ указы-

Раздел 1. Эконометрика и ее связь с экономической теорией...
39
вает на тесноту линейной связи между этими переменными (в
рассматриваемом диапазоне изменения переменной х) и на направление
этой связи.
V Замечание 1.2. Если г < О, то sign(Cov(y, х)) = -1 и г^ >0; если
г^ = О, то sign(Cov(y, х)) = 0 и /^ = 0; если г^ > 0, то sign(Cbv(y, х)) = 1
и г^ > 0, так что всегда г^ > 0 .
Приложение П-1.2а
Согласно принципу наименьших квадратов оценки а и /? находятся путем
минимизации суммы квадратов
^а,/?) = 2>,-а-/?*,J
по всем возможным значениям а и /5при заданных (наблюдаемых) значениях хх,..., хп,
у19 ..., уп. Точка минимума этой функции двух переменных находится путем
приравнивания нулю частных производных функции z = Q(a, /3) по переменным а и Д
т.е. приравниванием нулю производной функции 0(ог, р) как функции только от а
при фиксированном /?:
ag(a,/7)_0^
да
и производной функции £?(а, /3) как функции только от /? при фиксированном а:
др
■=о.
Это приводит к так называемой системе нормальных уравнений (normal
equations)
dQ(a,J)=0
да
dQ(a,p)
= 0,
dp
решением которой и является пара а, р. Остается заметить, что согласно правилам
вычисления производных
dQ(a,P)
да ,=1
- = 22>,-«-/?*,)(-!),
Можно проверить, что при найденной паре значений указанная сумма квадратов
действительно достигает минимума.

40
Часть I. Основные понятия, элементарные методы
др
= 25>,-а-/?х,)(-х,),
так что искомые значения а и J3 удовлетворяют паре соотношений
2>,-а-£х,) = 0, ]|>,.-«-/?*,)*,. =0,
/ = 1 i=l
первое из которых можно записать в виде
5>,-Л)=о,
или
5>, = о.
Таким образом, алгебраическая сумма остатков равна 0.
Соотношения системы нормальных уравнений можно записать также в виде
Г г, Л
па
2>« /*=2>,
i=i ) i=i
) (п V п
£>,. р+ Xх'2 £ = E>W-
Данная система является системой двух линейных уравнений с двумя
неизвестными а, р, она может быть легко решена, например, методом подстановки.
Из первого уравнения системы находим:
Iя 1 а "
nlt\ =1
так что точка (х, у) действительно лежит на прямой у = а + р х. Подстановка
полученного выражения для а во второе уравнение системы дает
\( п Л
1 Nr
( п \
1л ЕчЧЬгЬ'гЬ^
\\~\ Д/=1 ; >4/=i ; ^=1 ; /=i
откуда
( „ V „ Л
E>w-dE>4 2>/ 2>л-
WJ^X
/? = -
у/ = 1 УУ> = 1 у _ / = 1
1
^]jc2 -их2
Заметим еще, что
]Г(х, -хJ = £х,2 -2х£х;. + их2 = £х,2 -«х2,
/=1 ;=1 /=1 /=1
я я я п и
/=1 /=1 i=l i=l i=l

Раздел 1. Эконометрика и ее связь с экономической теорией...
41
Последние соотношения позволяют получить более употребительную форму записи
выражения для /5 (в отклонениях от средних значений):
Р = -
I
которая в паре с выражением
а-у-рх
дает явное и простое решение задачи отыскания оценок d, J5 на основе принципа
наименьших квадратов в ситуации, когда не все значения хр ..., хп одинаковы.
Приложение П-1.26
Имеем:
Но
£(Л -АХЛ -У) = £(Л -Уду, "?2>/ = Zto " AXa + M)-JZe/ =
/=i i=i /=i /=i i=i
/7 Л И /7
= a^e/+yff^(^/-j),.)x,.-J^ej.
/=1 1=1
(см. первое уравнение из системы нормальных уравнений). К тому же
/=1 /=1
(см. второе уравнение из системы нормальных уравнений). Таким образом,
2>,-Л)(й->о=о.
Геометрическая интерпретация основных соотношений
метода наименьших квадратов
Основные соотношения метода наименьших квадратов имеют наглядную
геометрическую интерпретацию.
Введем в рассмотрение следующие «-мерные векторы:
У-
(V
Uj
» У =
'V
UJ
, i=
ri>
bj
, х =
V
\Хп)
, 6 =
V
Vе" У

42
Часть 1. Основные понятия, элементарные методы
Тогда
j) = a-l + /?x, e = y-y,
так что
у = у + е.
Полученные в Приложении П-1.2а соотношения
2>,-<М*,) = о, !>,-«-£*,)*,= о
1=1 /=1
можно записать теперь в виде
п п
£(е,-1) = 0, £е,х,. =0, или /1 = 0, егх=0.
/=1 i=i
Но последние соотношения означают, что вектор остатков е ортогонален
единичному вектору 1 и вектору х значений объясняющей переменной х. А это,
в свою очередь, означает, что он ортогонален порожденному векторами 1 их
двумерному линейному подпространству Z2(l, x) «-мерного векторного
пространства, в котором расположены все введенные в рассмотрение векторы1.
Вектор у является линейной комбинацией векторов 1 и х, а потому он
принадлежит 2,2A, х). Поскольку же вектор е ортогонален Z,2(l, jc), он ортогонален
любому вектору, принадлежащему Z,2(l, х), а значит, ортогонален и вектору у.
Таким образом, в представлении у = у + е векторы-слагаемые ортогональны,
поэтому изображенный на рис. 1.9 треугольник ABC — прямоугольный. При
этом вектор у является ортогональной проекцией вектора у на£2A, х).
Предположим, что среднее арифметическое у значений yl9 ...9у„ отлично
от нуля. Отложим от точки А вектор у =у- 1, который получен
растяжением вектора 1 в у раз. Этот вектор принадлежит 12A, х), начинается в точке
А и заканчивается в некоторой точке D. Рассмотрим треугольник BCD.
Вектор DC является разностью векторов у и у - 1, а потому также
принадлежит Z2(l, x). Но тогда ВС LCD (так как вектор е ортогонален Z2(l, x)), и
треугольник BCD — прямоугольный. По теореме Пифагора получаем:
\ВЦ2 = \СЩ2 + \ВС\\т.е.
\у-у\2=\у-у\2+\у-у\2,
или в координатной форме
2>, - У? =1(Л - УJ +2>, -Уд2- A.2)
1=1 1=1 1=1
Подпространство L2(l, х) состоит из всех векторов, являющихся линейными
комбинациями векторов 1 и х. Условие идентифицируемости обеспечивает неколлинеарность
векторов 1 их.

Раздел 1. Эконометрика и ее связь с экономической теорией...
43
Рис. 1.9
Это и есть указанное ранее разложение полной суммы квадратов
TSS = ESS + RSS.
Отсюда находим, что коэффициент детерминации равен:
Ш-уJ ,.
= \У-У\
-|2
Ri = ESS
TSS
1 = 1
2 «у-зр
5>,-Я2 \у~у\
у-у
- cos2 ZBDC.
i = i
Заметим также, что соотношение ВС ± CD означает, что (у-у) -L (у-у),
или в координатной форме
$,(у,-уКу,-у,) = 0-
1 = 1
Это именно то соотношение, которое выведено в Приложении П-1.26.
Заметим теперь, что при у = 0 равенство A.2) остается в силе, поскольку
оно принимает в этом случае вид
iyf=iyf+t(y,-*J>
i=\ i=\ i=l
а последнее соотношение есть результат применения теоремы Пифагора
к прямоугольному треугольнику ABC,
Отметим, наконец, что расположение точки С на рис. 1.9 соответствует
случаю, когда а Ф 0 и J3 Ф 0. Ситуация, в которой а - 0, но C * 0, отлича-

44
Часть 1. Основные понятия, элементарные методы
ется только тем, что точка С располагается на той же прямой, что и вектор х;
все приведенные выше рассуждения остаются в силе. Если /3 - 0, но а ф 0, то
точка С располагается на той же прямой, что и вектор 1. Но, как установлено
выше, в этой ситуации а - у и ух. = у, так что вектор у совпадает с вектором
у = у-1. Если при этом у ф 0, то точка С совпадает с точкой Д но не
совпадает с точкой А, Соотношение A.2) опять выполняется, сводясь к тождеству
п п
^{Уг ~УJ =Х(^« ~УJ- Наконец, если еще и у = 0, так что и а = 0
/=1 /=1
и р = 0, то точки С и Z) совпадают с точкой ^, вектор j; ортогонален
подпространству Z2(l, л:), j) = 0 и вектор е совпадает с вектором^. Соотношение A.2)
и п
сводится в этом случае к тождеству ^у? =^у?-
i=i /=1
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как ставится задача поиска «наилучшей» прямой для аппроксимации линейной
модели связи между двумя экономическими переменными?
2. В чем состоит метод наименьших квадратов? Как он реализуется при оценивании
параметров линейной модели наблюдений? Что такое система нормальных
уравнений, каков ее геометрический смысл?
3. Чему равна алгебраическая сумма остатков, полученных при оценивании
параметров линейной модели наблюдений?
4. В каком соотношении находятся знак оценки наименьших квадратов углового
коэффициента модели прямолинейной связи у = а + /Зх и знак выборочной кова-
риации Cov(x, y)l
5. Зависит ли значение оценки наименьших квадратов углового коэффициента модели
прямолинейной связи у = а + рх от выбора единиц измерения переменных х и yl
6. Каково соотношение между полной, объясненной моделью и остаточной
суммами квадратов, получаемыми в результате оценивания методом наименьших
квадратов линейной модели наблюдений? Каков геометрический смысл этого
соотношения?
7. Что такое коэффициент детерминации? Для какой цели он предназначен? В каких
границах он изменяется и когда достигает своих граничных значений? Каков
геометрический смысл коэффициента детерминации?
8. Какие переменные называются объясняющими, а какие — объясняемыми?
9. Как связаны значения коэффициента детерминации, получаемого при
оценивании линейной модели наблюдений yi = (а + /Ц) + е/? / = 1, ..., и, со значениями
множественного коэффициента корреляции и коэффициента корреляции между
переменными х и yl
10. Что можно сказать о корреляционной связи между остатками и прогнозными
значениями объясняемой переменной?
11. Как располагаются точки на диаграмме рассеяния, на которой по оси абсцисс
откладываются прогнозные значения объясняемой переменной, а по оси ординат —
наблюдаемые значения объясняемой переменной?

Раздел 1. Эконометрика и ее связь с экономической теорией...
45
12. Как располагаются точки на диаграмме рассеяния, на которой по оси абсцисс
откладываются наблюдаемые значения объясняемой переменной, а по оси
ординат — прогнозные значения объясняемой переменной?
Тема 1.3
ПРИМЕРЫ ПОДБОРА ЛИНЕЙНЫХ МОДЕЛЕЙ СВЯЗИ
МЕЖДУ ДВУМЯ ФАКТОРАМИ. ЛОЖНАЯ ЛИНЕЙНАЯ СВЯЗЬ
ПРИМЕР 1.3.1
В табл. 1.4 приведены данные об изменении потребительского спроса на
куриные яйца семи домашних хозяйств в зависимости от цены на этот продукт
в течение 15 недель (спрос измерялся в дюжинах, цена — в долларах).
Таблица 1.4
Изменение потребительского спроса на куриные яйца в течение 15 недель
I
1
2
3
4
5
6
7
8
Спрос, дюжин
12
10
13
11.5
12
13
12
12
Цена, долл.
0.54
0.51
0.49
0.49
0.48
0.48
0.48
0.47
/
9
10
И
12
13
14
15
Спрос, дюжин
12
13
13.5
14
13.5
14.5
13
Цена, долл.
0.44
0.44
0.43
0.42
0.41
0.40
0.39
Диаграмма рассеяния для этих
данных приведена на рис. 1.10.
Предполагая, что модель наблюдений
имеет вид у. = а + /?лг, + ei9 i = 1, ..., я,
где yi спрос в |-ю неделю, х( — цена
в |-ю неделю, получим следующие
оценки для неизвестных параметров а
и Р модели линейной связи между
ценой и спросом: а = 21.100, Р = -18.559.
Таким образом, подобранная модель
линейной связи имеет вид у = 21.100 -
- 18.559х. При этом
7SS=17.6, Я55=8.562, £55=9.038,
0,35 0,55 Цена
Рис. 1.10

46
Часть 1. Основные понятия, элементарные методы
так что коэффициент детерминации R2 = 0.514, т.е. изменчивость цен
объясняет 51.4% изменчивости спроса на куриные яйца. На диаграмме
рассеяния изображена прямая линия, соответствующая подобранной модели
линейной связи. ■
ПРИМЕР 1.3.2
В табл. 1.5 указаны данные о годовом потреблении свинины >> на душу
населения в США (в фунтах) и оптовых ценах на свинину х (в долларах за фунт)
за период с 1948 по 1961 г.
Таблица 1.5
Годовое потребление свинины на душу населения в США с 1948 по 1961 г.
Год
1948
1949
1950
1951
1952
1953
1954
Потребление,
фунт
67.8
67.7
69.2
71.9
72.4
63.5
60.0
Цена,
долл. за фунт
0.5370
0.4726
0.4556
0.4655
0.4735
0.5047
0.5165
Год
1955
1956
1957
1958
1959
1960
1961
Потребление,
фунт
66.6
67.4
61.5
60.2
67.6
65.2
62.2
Цена,
долл. за фунт
0.4256
0.4111
0.4523
0.4996
0.4183
0.4433
0.4448
Диаграмма рассеяния для этих данных
приведена на рис. 1.11.
Оценивая модельyt = а + /?+ si9i=l9..., и,
где yt — потребление свинины в /-й год
рассматриваемого периода, xt — оптовая
цена на свинину в /-м году, получим
следующие оценки для неизвестных
параметров а и р модели линейной связи между
оптовой ценой и потреблением: а = 77.552,
Р = -24.925. Таким образом,
подобранная модель линейной связи имеет вид у =
= 77.552 - 24.925л;. При этом
7X5 = 208.194, Ш=196Ш, ESS =11А93,
так что коэффициент детерминации R2 = 0.055. В данном случае
изменчивость оптовой цены объясняет лишь 5.5% изменчивости потребления
свинины.1
Потребление
74

Раздел 1. Эконометрика и ее связь с экономической теорией...
47
ПРИМЕР 1.3.3
Рассмотрим данные о размерах совокупного располагаемого дохода и
совокупных расходах на личное потребление в США в период с 1970 по 1979 г.
(табл. 1.6). Обе величины выражены в текущих ценах (в млрд долл. США).
Таблица 1.6
Совокупный располагаемый доход и расходы на личное потребление
в США с 1970 по 1979 г., млрд долл.
Год
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
Располагаемый доход
695.2
751.9
810.3
914.0
998.1
1096.2
1194.3
1313.5
1474.3
1650.5
Расходы на потребление
621.7
672.4
737.1
811.7
887.9
976.6
1084.0
1204.0
1346.7
1506.4
Этим данным соответствует диаграмма рассеяния, приведенная на рис. 1.12.
Предполагая, что модель наблюдений
имеет вид у. = а + /?*, + ei9 i = 1, ..., и,
где yi — совокупные расходы на личное
потребление в /-й год рассматриваемого
периода, xt — совокупный
располагаемый доход в этом году, получим
следующие оценки для неизвестных
параметров а и р модели линейной связи
между совокупным располагаемым
доходом и совокупными расходами на личное
потребление: а = -30.534, р = 0.932.
Таким образом, подобранная модель имеет
вид у = -30.534 + 0.932*. При этом
600
1700 Доход
Рис. 1.12
7X5=791138.545, RSS= 740.320, ESS= 790398.225,
коэффициент детерминации R2 = 0.9995. Изменчивость совокупного
располагаемого дохода объясняет в данном случае 99.95% изменчивости совокупных
расходов на личное потребление. ■

48
Часть 1. Основные понятия, элементарные методы
Впрочем, не следует слишком оптимистически интерпретировать близкие
к 1 значения коэффициента детерминации R2 как указание на то, что
изменения значений объясняемой переменной практически полностью определяются
именно изменениями значений используемой объясняющей переменной.
В связи с этим рассмотрим поучительный пример.
ПРИМЕР 1.3.4
Рассмотрим динамику изменений в период с 1957 по 1966 г. трех совершенно
различных по природе показателей: Е — суммарного производства
электроэнергии в США (в млрд. кВт/ч), С — совокупных потребительских
расходов в Таиланде (в млрд бат) и Я — мирового рекорда на конец года в
прыжках в высоту с шестом среди мужчин (в см). Значения указанных
показателей приведены в табл. 1.7, а динамика изменения этих показателей показана
на рис. 1.13.
Таблица 1.7
Данные для иллюстрации ложной линейной связи между переменными
Год
1957
1958
1959
1960
1961
1962
1963
1964
1965
1966
Потребительские
расходы, млрд бат
34.9
35.9
37.9
41.1
43.5
46.7
48.9
52.0
56.1
62.6
Электроэнергия,
млрд кВт/ч
716
724
797
844
881
946
1011
1083
1157
1249
Мировой рекорд,
см
478
478
478
481
483
493
520
528
528
534
По этим данным можно формально, используя метод наименьших
квадратов, подобрать модели линейной зависимости каждого из трех показателей
от каждого из остальных показателей. Это приводит, например, к моделям
Е = -2625.5 + 7.131Я, R2 = 0.900;
С = -129.30 + 0.350Я, R2 = 0.871;
Е= 23.90+19.950С, Л2 = 0.993;
С = -0.860 + 0.0498£, R2 = 0.993.
Заметим, несколько забегая вперед, что произведение угловых
коэффициентов двух последних прямых, соответствующих моделям линейной связи,

Раздел 1. Эконометрика и ее связь с экономической теорией...
49
ELECTRO USA
CONS TAILAND
WORLD RECORD
i
1400 -
1200 -
1000 -
800 -
600 -
i
♦♦
♦♦
♦
к
1956 1967
Год
▲
70 -
60-
50 -
40 -
30-
♦
^Ф
♦
♦ ♦
♦
♦
к
1956 1967
Год
J
540 -
520 -
500-
480 -
460 -
i
♦ ♦♦
♦ ♦
♦
♦ ♦
г-
1956 1967
Год
Рис. 1.13
в которых объясняемая и объясняющая переменные меняются местами,
равно: 19.950 • 0.0498 = 0.993 и совпадает со значением R2 в этих двух
подобранных моделях.
Во всех подобранных моделях значения коэффициента детерминации
весьма высоки. Это формально означает, что изменчивость «объясняющих»
переменных в этих моделях составляет значительный процент от
изменчивости «объясняемой» переменной в левой части уравнения. Однако вряд ли
можно всерьез полагать, что динамика роста суммарного производства
электроэнергии в США действительно объясняется динамикой роста мирового
рекорда по прыжкам в высоту с шестом, несмотря на высокое значение @.9)
коэффициента детерминации в первом из четырех уравнений. ■
В ситуациях, подобных последнему примеру, принято говорить о ложной
(фиктивной, паразитной — spurious) линейной связи, не имеющей
содержательной экономической интерпретации. Такие ситуации часто
встречаются при рассмотрении показателей, динамика изменений которых
обнаруживает заметный тренд (убывание или возрастание), именно такой характер
имеют исследуемые показатели в примере 1.3.4.
Чтобы понять, почему это происходит, используем полученное ранее
равенство R2 =г£х. Из него вытекает, что близкие к 1 значения коэффициента
детерминации соответствуют близким по абсолютной величине к 1
значениям коэффициента корреляции между переменными у и х. Но этот
коэффициент корреляции равен
Cov(y,x)
ГУ* =
JVar(y)^Var(x) '
1
где Cov(y,x) = ^ (у,. - y)(x,. - х).

50
Часть 1. Основные понятия, элементарные методы
При фиксированных Var{x) и Var(y) значение г^ будет тем ближе к 1, чем
большим будет значение Cov(y, x) > 0. Последнее обеспечивается
совпадением знаков разностей (у, - у) и (л:7 - х) для максимально возможной доли
наблюдений переменных j/их, что как раз и имеет место, когда в процессе
наблюдения обе переменные возрастают или обе переменные убывают по
величине. (В этом случае превышение одной из переменных своего среднего
значения сопровождается, как правило, и превышением второй переменной
своего среднего значения. Напротив, если одна из переменных принимает
значение, меньшее среднего значения этой переменной, то и вторая переменная,
как правило, принимает значение, меньшее своего среднего.)
Аналогичным образом значение г^ будет тем ближе к -1, чем меньшим
будет значение Coviy, x) < 0. Последнее обеспечивается несовпадением знаков
разностей (у, - у) и (х, - х) для максимально возможной доли наблюдений
переменных у и х, что имеет место, когда в процессе наблюдения одна из
переменных возрастает, а вторая убывает. (В этом случае если одна из переменных
принимает значение, меньшее среднего значения этой переменной, то вторая
переменная, как правило, принимает значение, большее своего среднего.)
Из сказанного следует, что близость к 1 наблюдаемого значения
коэффициента детерминации не обязательно означает наличие причинной связи
между двумя рассматриваемыми переменными, а может являться лишь
следствием тренда значений обеих переменных.
Последнее обстоятельство часто наблюдается при анализе различных
экономических показателей, вычисленных без поправки на инфляцию (недефли-
рованные данные). Проиллюстрируем это следующим примером.
ПРИМЕР 1.3.5
Обратимся к данным о совокупном располагаемом доходе и личных расходах
на местный транспорт в США за период с 1970 по 1983 г. (табл. 1.8). Данные
представлены как в текущих ценах, так и в ценах 1972 г.; пересчет к
последним выполнен с учетом динамики индекса потребительских цен в указанном
периоде. (Уровень цен в 1972 г. принят за 100%.)
Диаграмма рассеяния для недефлированных (номинальных) величин
приведена на рис. 1.14. Соответствующая модель линейной связи: у = 1.743 + 0.0023х.
Коэффициент детерминации R2 = 0.9398.
Диаграмме рассеяния дефлированных величин (рис. 1.15) соответствует
модель линейной связи у - 3.758 - О.ОООЗх. Коэффициент детерминации на
этот раз всего лишь R2 = 0.0353.■
В связи с последним примером вернемся к примеру 1.3.3 и выясним, не
является ли обнаруженная там сильная линейная связь между совокупным
располагаемым доходом и совокупными расходами на личное потребление
лишь следствием использования недефлированных величин.

Раздел 1. Эконометрика и ее связь с экономической теорией...
51
Таблица 1.8
Совокупный располагаемый доход и личные расходы
на местный транспорт в США с 1970 по 1983 г., млрд долл.
Год
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
1980
1981
1982
1983
Располагаемый
доход
номинальный
695.2
751.9
810.3
914.0
998.1
1096.2
1194.3
1313.5
1474.3
1650.5
1828.7
2040.9
2180.1
2333.2
Расходы
номинальные
3.1
3.3
3.4
3.6
4.0
4.4
4.7
5.0
5.5
6.2
6.3
6.2
6.6
6.6
Индекс
потребительских
цен
92.0
96.5
100.0
105.7
116.4
125.3
131.7
139.3
149.1
162.5
179.0
194.5
206.0
213.0
Располагаемый
доход
дефлированный
751.6
779.2
810.3
864.7
857.5
874.5
906.4
942.9
988.8
1015.7
1021.6
1049.3
1058.3
1095.4
Расходы
дефлнрованные
3.4
3.4
3.4
3.4
3.5
3.5
3.6
3.6
3.7
3.8
3.5
3.2
3.2
3.1
Номинальные величины
600 2400 Доход
Рис. 1.14
Дефлнрованные величины
Расходы
4 +--
700 1200 Доход
Рис. 1.15
Для этого рассмотрим дефлнрованные значения данных показателей
(табл. 1.9).
Соответствующая диаграмма рассеяния приведена на рис. 1.16.
Подобранная модель линейной связи у = -67.655 + 0.979*. Коэффициент
детерминации при переходе от номинальных величин к дефлированным
остается очень высоким: Л2 = 0.9918. Следовательно, наличие сильной линей-

52
Часть 1. Основные понятия, элементарные методы
Таблица 1.9
Дефлированные данные таблицы 1.6
Год
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
Д еф л нро ванный
доход
751.6
779.2
810.3
864.7
857.5
874.5
906.4
942.9
988.8
1015.7
Дефлированное
потребление
672.1
696.8
737.1
767.9
762.8
779.4
823.1
864.3
903.2
927.6
Индекс
потребительских цен
92.0
96.5
100.0
105.7
116.4
125.3
131.7
139.3
149.1
162.5
Дефлированные величины
Расходы
950
700 900 1100 Доход
Рис. 1.16
нои связи между совокупным располагаемым доходом и совокупными
расходами на личное потребление не является только лишь следствием
инфляционных процессов.
V Замечание 1.3.1. Использование линейных моделей связи для
описания зависимости спроса на продукт от цены этого продукта в
примерах 1.3.1 и 1.3.2 (спрос на куриные яйца и на свинину
соответственно) представляется на первый взгляд совершенно абсурдным.
Действительно, вряд ли можно серьезно полагать, что увеличение
цены на 1 долл. приводит к снижению спроса в среднем на одну
и ту же величину независимо от того, какова была первоначальная
цена соответствующего продукта. Дело, однако, в том, что во многих
ситуациях при работе в определенном диапазоне изменения
экономических показателей нелинейные зависимости достаточно хорошо

Раздел 1. Эконометрика и ее связь с экономической теорией...
53
аппроксимируются линейными (линеаризуются), что подтверждается
расположением точек на диаграмме рассеяния — видимой вытяну-
тостью облака рассеяния вдоль некоторой наклонной прямой. Более
подробно нелинейные функции связи рассмотрим в теме 1.4.
Частный коэффициент корреляции
Возникновение паразитной линейной связи между двумя переменными часто
можно объяснить тем, что, хотя эти переменные не имеют причинной связи,
изменение каждой из них достаточно хорошо объясняется изменением
значений некоторой третьей переменной, «координирующей» динамику изменения
первых двух переменных. Проиллюстрируем это на данных примера 1.3.4.
В этом примере была подобрана модель линейной связи между суммарным
производством электроэнергии в США (Е) и мировым рекордом на конец
года в прыжках в высоту с шестом среди мужчин (Я). Коэффициент
детерминации для этой модели оказался весьма высоким: R2 = 0.900.
Поскольку динамика изменения этих двух показателей на периоде
наблюдений обнаруживает видимый положительный тренд, попытаемся
аппроксимировать каждый из них линейной функцией от времени. Подбор методом
наименьших квадратов приводит к моделям:
£ = 613.333 + 59.539/, Н= 459.067 + 7.461/,
где t — t-й год на периоде наблюдений.
При этом в первом случае коэффициент детерминации равен 0.9812,
а во втором — 0.8705. Иначе говоря, наблюдаемая изменчивость переменных
Е и Я достаточно хорошо «объясняется» изменением переменной /,
фактически являющейся здесь выразителем технического и спортивного прогресса.
Чтобы найти «объективную» связь между показателями Е и Я,
«очищенную» от влияния на эти показатели фактора времени, поступим следующим
образом.
Возьмем ряд остатков
eE(t) = Et -F13.333 + 59.5390,
получаемых при подборе первой модели, и ряд остатков
ея(*) = Я,-D59.067+ 7.46If),
получаемых при подборе второй модели. Тогда переменные еЕ и ен,
принимающие значения eE(t) и eH(t) соответственно, t = 1, ..., 10, можно
интерпретировать как результат «очистки» переменных Е и Н от линейного тренда
во времени. Соответственно «истинная» линейная связь между переменными
Е и Я, если таковая имеется, должна, скорее всего, измеряться
коэффициентом корреляции re e между «очищенными» переменными еЕ и ен.

54
Часть 1. Основные понятия, элементарные методы
Подобранная линейная связь между еЕ и ен имеет вид
еЕ = 0.0000 + 1А20ен.
При этом получаем значение R2 = 0.2454 против 0.900 в модели с
«неочищенными» переменными. Коэффициент корреляции между «очищенными»
переменными еЕ и ен
г в =V0.2454 =0.4954,
еЕ*еН
т.е. почти вдвое меньше коэффициента корреляции гЕ н = л/0.900 = 0.9487
между «неочищенными» переменными ЕиН.
Коэффициент корреляции re e между «очищенными» переменными еЕ и ен
называется частным коэффициентом корреляции {partial correlation
coefficient) между переменными Е иНпри исключении влияния на них переменной t.
В дальнейшем будет показано, что при «стандартных предположениях»
значение ге е = 0.4954 при п = 10 «слишком мало» для того, чтобы можно
было отвергнуть гипотезу о том, что коэффициент при ен в линейной модели
связи еЕ = у+ 8ен действительно равен 0.
Обратная модель линейной связи
В рассмотренном в начале раздела примере с уровнями безработицы среди
белого и цветного населения США уровень безработицы среди белого
населения был использован в качестве объясняемой переменной, а уровень
безработицы среди цветного населения - в качестве объясняющей переменной.
Если, однако, отсутствует экономическое обоснование такого направления
причинной связи, то с тем же успехом можно было бы поменять эти
переменные местами.
Пусть наша задача состоит в оценивании модели линейной связи между
некоторыми переменными х и у на основе наблюдений п пар (xi9 >>,), / = 1,..., п,
значений этих переменных. Мы уже рассмотрели вопрос об оценивании
параметров такой связи исходя из модели наблюдений у{ = а + /?х, + $, / = 1,..., п.
Что изменится, если будем исходить из обратной модели
х: = а + 0у: + £!9 /= 1 л?
Пусть аух9 /3' — оценки параметров в прямой модели наблюдений yt =
= а + /Зх{ + ei9 i = 1, ..., п, а а^.р^ — оценки параметров а и /? в обратной
модели наблюдений xt = а + Ру{ + ei9 i = 1,..., п. Тогда
\2
п п ^Cov(x,y) Cov(y,x)
р*уРу* Var{y) ' Var(x)
Cov(y,x)
^Var{y)^Var{x)

Раздел 1. Эконометрика и ее связь с экономической теорией...
55
(так как Cov(y, х) = Cov(x, у)), т.е. Д^ Рух=г^яс, или, поскольку R2 = г£,
В обратной модели наблюдений в качестве «наилучшей» получаем прямую
Х = К+Р*уУ>
а в прямой модели — прямую
Формально если выборочная ковариация Cov(x, у) точно равна 0 (что
маловероятно для реальных статистических данных, но может получаться
в специально подобранных искусственных примерах), то р - /3^ = 0, и тогда
«наилучшие» прямые имеют вид: х = аху — в обратной модели, у = ссух —
в прямой модели.
Если же Cov(x, у) * 0, то первую прямую можно записать:
у = —^-+-х— х.
Р* Р*у
Сравнив коэффициенты при х в этом уравнении и в уравнении
j> = a + РухХ, приходим к выводу, что эти коэффициенты равны в том и
только в том случае, когда выполнено соотношение
Рху
или, с учетом предыдущего, когда R2 = 1.
Отрезки на осях будут совпадать тогда и только тогда, когда
аУ*=~~ТГ* ИЛИ аухРху=~ахУ
Рху
Но аух=у-рухх, так что
При R2 = 1 получаем
&ухК=уК-х-
В то же время у

56
Часть 1. Основные понятия, элементарные методы
ZVET а
7,5 4-
6,5+ ♦ ♦ |
♦ ♦
5,5 J | 1
2,8 3,0 3,2 3,
Рис. 1.17 Рис. 1.18
так что при R2 = 1 совпадают и отрезки на осях. Таким образом,
«наилучшая» прямая одна и та эюе при обеих моделях наблюдений, это прямая, на
которой расположены все наблюдаемые точки (jc,., yf)9 i = 1,..., п.
Иными словами, «наилучшие» прямые, построенные по двум
альтернативным моделям, совпадают в том и только в том случае, когда все точки
(xi9 У;), i = 1,..., п, расположены на одной прямой (так что ех - ... = еп - 0), при
этом R2 =1. В противном случае R2 *1, и подобранные «наилучшие»
прямые имеют разные угловые коэффициенты. Поскольку обе эти прямые
проходят через точку (х, j7), то при R2 Ф1 они образуют раскрытые «ножницы».
В случае R2 = 0 «ножницы» раскрыты под прямым углом.
Кстати, в примере с уровнями безработицы диаграмма рассеяния с
переставленными осями (соответствующими модели наблюдений xt - а + fiyt + st,
i = 1,..., п) имеет вид, приведенный на рис. 1.17.
«Наилучшая» прямая в данном случае имеет вид
х = 1.291 + 1.695.у,
коэффициент детерминации равен
R2 =0.212374.
Произведение угловых коэффициентов 0.125265 и 1.695402 «наилучших»
прямых в прямой и обратной моделях наблюдений равно 0.212374 и
совпадает со значением R2.
Несовпадение «наилучших» прямых в альтернативных моделях связано
с тем, что в них минимизируются разные суммы квадратов: в прямой
модели минимизируется сумма квадратов отклонений точек от подбираемой
прямой в направлении, параллельном оси .у, а в обратной — в направлении,
параллельном оси х. Подобранные прямые для альтернативных моделей
показаны на рис. 1.18 (пунктирная линия — прямая, подобранная для
обратной модели).
4 BEL
5,5 6,0 6,5 7,0 7,5 ZVET

Раздел 1. Эконометрика и ее связь с экономической теорией...
57
Пропорциональная связь между переменными
В некоторых случаях экономическая теория описывает связь между двумя
экономическими факторами хиу как пропорциональную, т.е.
так что в этом случае возникает необходимость подбора прямой, проходящей
через начало координат.
В этой связи можно вспомнить, например, известную модель оценки
финансовых активов САРМ {capital asset pricing model). В простейшей форме
модель наблюдений, соответствующая САРМ, имеет следующий вид:
rji-rfi=Pj(rmi-rfi) + Sji> / = 1,.-,Л,
где гч — доходность за /-й период ценной бумагиу'-го вида;
rmi— доходность за /-й период рыночного портфеля;
rfi — доходность безрисковой бумаги;
pj — (коэффициент бета, или просто бета) — мера систематического
(рыночного) риска бумаги у'-го вида.
Пусть имеем наблюдения (x„ yt), i = 1, ..., п, и предполагаем, что
гипотетическая линейная связь между переменными хиу имеет вид
(пропорциональная связь между переменными), так что ей соответствует
модель наблюдений
>>,=/?*,+£,., / = 1,...,л.
Применение метода наименьших квадратов в данном случае сводится
к минимизации суммы квадратов расхождений
Ш?) = 1>,-МJ
1 = 1
по всем возможным значениям /?. Последняя сумма квадратов является
функцией единственной переменной /? (при известных значениях (xi9 yt)9 i = 1,..., w),
и точка минимума этой функции легко находится. Для этого приравниваем
нулю производную Q(JS) по /?:
п
2^(;л - PxtX-Xi) = О (нормальное уравнение).
i=i
Откуда получаем:
±УЛ=Р±х1
1=1 1=1

58
Часть 1. Основные понятия, элементарные методы
или
1>Л
= \
п
2>,2
1 = 1
Отсюда видно, что при таком подборе Cф и точка (х, у) уже
Var(x)
не лежит, как правило, на подобранной прямой у = fix.
п
При этом здесь не выполняется и равенство ^et = 0, которое имеет место
/=1
в модели с включением в правую часть постоянной составляющей (см.
замечание 1.3.4 в конце этого раздела.)
Более того, в такой ситуации
1(л-Я2*1(А-502+1(л-АJ.
i=l i=l i=l
где yt = рх(, т.е.
TSS*RSS + ESS,
поэтому теряют силу соображения, приводившие к определению
коэффициента детерминации R2 как доли полной суммы квадратов, объясненной
подобранной моделью.
При этом отношения и могут принимать значения больше 1.
TSS TSS
ESS
Таким образом, при определении коэффициента детерминации как R2 =
1 *j*3
его значения могут превышать 1, а при определении коэффициента детерми-
RSS
нации как R2 = 1 могут оказаться отрицательными.
1 оо
ПРИМЕР 1.3.6
Пусть переменные х и у принимают в четырех наблюдениях значения,
приведенные в табл. 1.10.
Соответствующая диаграмма рассеяния приведена на рис. 1.19.
Будем предполагать пропорциональную связь между этими переменными, что
соответствует модели наблюденийу{ - /Зх( + ei9 i= l, 2, 3, 4. Для этих данных
/3 = — = 0.7217.
X*2

Раздел 1. Эконометрика и ее связь с экономической теорией...
59
Результаты наблюдений
Таблица 1.10
I
*/
Уг
1
0
0.5
2
0.2
0.8
3
0.4
1.2
4
3
2
При этом RSS = 1.5377, Ж = 1.2675,
ESS = 4.0088. Вычисление R2 по формуле
ESS
R2 = дает значение R2 = 3.1627 > 1,
TSS
а по формуле R2 = 1 -
RSS
TSS

отрицательное значение R2 = -0.213138.
Заметим также, что сумма остатков здесь
равна J^. =1.9017.
i = i
Возникающие затруднения можно преодолеть, если в модели наблюдений
без постоянной составляющей использовать так называемый нецентриро-
ванный коэффициент детерминации {uncenteredR2):
RSS
Ex2
/=i
где в знаменателе дроби — сумма квадратов нецентрированных значений
переменной у (отклонений значений переменной у от «нулевого уровня»).
Неотрицательность коэффициента R2U гарантируется наличием соотношения
Irf-Itf+IO',-*J.
A.3)
/ = 1
/ = 1
i = l
отражающего геометрическую сущность метода наименьших квадратов,
которое выполняется как для модели без постоянной составляющей, так и для
модели с постоянной составляющей в правой части модели наблюдений. Раз-
делив обе части последнего равенства на ^у?, получим
/=1
1 =
;=1
/=1
2>,2 Ту?
i = l
i = l

60
Часть 1. Основные понятия, элементарные методы
Из этого соотношения непосредственно следует, что
Л 2
1(и-АJ L#
Л2=1- — -'='
п
2
Ту? 5>;
i=i /=i
так что
0<ЛМ2<1.
Доказать соотношение A.3) несложно. Действительно,
tyf = 2>i -У, +У,J=£(У, -У,J + I# +2Z(yi -УдУг
i=i i=i i=i i=i i=i
Но
i = i / = i / = 1
(см. нормальное уравнение), что и приводит к искомому результату.
В примере 1.3.6 при использовании нецентрированного коэффициента
1 5377
детерминации получаем R2 = 1 —: = 0.7571.
6.33
v Замечание 1.3.2. Поскольку соотношение
1л2=1А2+1(и-АJ
j=l i=l i=l
выполняется и для моделей с постоянной составляющей, нецентри-
рованный коэффициент детерминации остается в пределах от 0 до 1
и для таких моделей. Однако R2U обладает следующим
нежелательным для таких моделей свойством: значение коэффициента R2U
изменяется, если все значения объясняемой переменной у увеличить
(уменьшить) на одну и ту же величину.
Замечание 1.3.3. В обозначениях, введенных в конце темы 1.2,
соотношение
принимает вид у-ул-е.
В данной ситуации имеем только одно нормальное уравнение
22>,-ax-*i)=o,
1=1

Раздел 1. Эконометрика и ее связь с экономической теорией... 61
которое просто означает, что е _L х. При наличии в модели
постоянной составляющей возникает еще одно нормальное уравнение,
отражающее соотношение е _L 1. Отсутствие этого дополнительного
уравнения как раз и приводит к тому, что здесь не выполняется ра-
п
венство ^#/=0, которое имеет место в модели с постоянной со-
ставляющей.
Невыполнение в модели без постоянной составляющей
соотношения TSS = ESS + RSS связано с тем, что в данном случае вектор у
имеет вид у = fix и является проекцией вектора у на одномерное
линейное подпространство Lx(x\ порожденное вектором х, а не на
двумерное линейное подпространство L2(l9 x\ порожденное
векторами 1 и х, как это было в случае модели с постоянной
составляющей. Изображенный на рис. 1.9 треугольник BCD на сей раз не
является прямоугольным.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что понимается под фиктивной линейной связью между двумя переменными?
Каковы причины ее возникновения?
2. Что выражает частный коэффициент корреляции?
3. Как соотносятся между собой оценки угловых коэффициентов подобранных
прямых, полученных при оценивании прямой и обратной моделей?
4. Каковы особенности оценивания методом наименьших квадратов модели
пропорциональной связи? Почему для интерпретации результатов такого оценивания
нельзя использовать коэффициент детерминации, определенный для случая модели
прямолинейной связи? Как можно выйти из этого положения?
Тема 1.4
НЕЛИНЕЙНАЯ СВЯЗЬ
МЕЖДУ ЭКОНОМИЧЕСКИМИ ФАКТОРАМИ
Связь между уровнями экономических факторов вовсе не обязательно
должна быть линейной. Например, если рассмотреть зависимость от
располагаемого дохода DPI не всех затрат на личное потребление, а лишь затрат С на
некоторый продукт питания или группу продуктов питания (например, на
молочные продукты), то уже по чисто физиологическим причинам функция
связи
С = /(£>/>/),
скорее всего, должна замедлять свой рост при возрастании DPI. Возможный
график этой функции приведен на рис. 1.20.

62
Часть 1. Основные понятия, элементарные методы
DPI
Рис. 1.20
В такой ситуации нельзя говорить о
склонности к потреблению данного
продукта как о постоянной величине. Вместо
этого в рассмотрение вводят понятие
предельной склонности к потреблению
{marginal propensity to consume — MPC)
(или предельной нормы потребления),
которая для заданной величины
располагаемого дохода DPI0 определяется
соотношением:
/(ди.+дпяО-Адрг.)
0/ adpi-*o M)pi
Иначе говоря,
dC
MPC(DPI0) =
dDPI
= f\DPI0).
DPI=DPI0
Замедление скорости роста функции f(DPI) соответствует убыванию
MPC{DPI) при возрастании DPI. Уточняя предположения о поведении МРС,
можно получить ту или иную форму связи между переменными DPI и С.
Среди возможных форм связи между DPI и С отметим степенную связь
(power relationship):
C = f(DPI) = a(DPiy,
в которой а > 0, 0 < Р < 1. Для такой связи
MPC(DPI) = ap(DPI)p~\
так что предельная склонность к потреблению монотонно убывает с
ростом DPI.
Степенную форму связи можно привести к линейной, если вместо уровней
дохода и расходов на потребление рассмотреть логарифмы уровней по какому-
нибудь (но по одному и тому же!) основанию (например, натуральные или
десятичные логарифмы). Действительно, переходя к логарифмам уровней,
получаем:
logC = loga + /?log£>P/,
или, обозначая logC= С*, loga= a*, logDPI = DPI*,
С* =а +PDPI*.
Линейной модели связи в логарифмах соответствует линейная модель
наблюдений:
C*=a+j3DPI*+si9 / = 1,...,л,
которую мы уже умеем оценивать методом наименьших квадратов.

Раздел 1. Эконометрика и ее связь с экономической теорией...
63
Напомним: если имеется связь между какими-то переменными
экономическими факторами X и Y в виде
Y = f(X),
то функция
MPY(X) = ^ = f(X)
ал
определяется как предельная склонность 7 по отношению кХ.
В экономической теории существенную роль играет функция
эластичности (elasticity function) tj(X), значение которой при X = Х0 определяется как
предел отношения процентного изменения Y = f(X) к процентному
изменению X, когда последнее стремится к 0:
f(X0+AX)-f(X0) 1(W
Ti(X0)= lim ^^
^•100
Если т](Х0) > 1 или rj(X0) < -1 (так что | ^7(АГ0)| > 1), то говорят, что фактор Y
эластичен (elastic) по отношению к фактору X при Х=Х0. Если же |/7№I - Ь
то говорят, что фактор Y неэластичен (non-elastic) по отношению к фактору X
при Х= Х0. Отдельно выделяют пограничные случаи tj(X0) = 1 и rj(X0) = -1
(единичная эластичность (unit elasticity)).
Правую часть соотношения, определяющего функцию эластичности,
можно записать в виде:
У dY X
rj(X) = —— = — MPY(X).
/V ' Y dX Y
Заметим также, что
dlnf(X) _
dlnX
dX
d\xvX
_X dY
~~ Y dX
dX
так что
,(Х) = ^ = ±МРУ(Х) = ^:^.
dlnX Y Y X
Значение MPY(X0) равно угловому коэффициенту касательной к графику
функции Y=f(X) приХ = Х0, тогда как значение rj(X0) равно угловому
коэффициенту касательной к графику зависимости In 7 от lnA" при X = Х0. Как
следствие, условие постоянства MPY(X), т.е. MPY(X) = Д означает линейную
связь между уровнями факторов:
Y = a + pX,

64
Часть 1. Основные понятия, элементарные методы
а условие постоянства эластичности rj(X) = /? означает линейную связь между
логарифмами уровней
lnY = a + pinX,
соответствующую степенной связи между уровнями
Y = ехр(а + /ЗЫХ) = Const-Х^
которая выражает степенное возрастание (при /?> 0) или убывание (при /?< 0)
уровней фактора Y при возрастании уровней фактора X.
Заметим: если rj(X) = Д то постоянную /3 можно в определенной мере
трактовать как процентное изменение уровня фактора Y при изменении
фактора X на 1%. Пусть, например, Y = у/Х, так что /? - 0.5, и пусть значение
фактора Х= 4 возрастает на 1% , т.е. до значения Х= 4.04. Тогда значение
фактора Г изменяется от 7= 2 до 7=л/4.04, т.е. на 0.498%, что очень близко к 0.5%.
Если р > 1 или /?< -1 (так что |/?| > 1), то фактор Y эластичен по
отношению к фактору X. Если же |/?| < 1, то фактор Y неэластичен по отношению
к фактору X. Пограничные случаи /? = 1 и /? = -1 соответствуют единичной
эластичности.
Отметим также, что в модели Y= а + РХ функция эластичности имеет вид
Y а + рХ а ; х
рх
и при ар > 0 возрастает от 0 до 1 с возрастанием значений X от 0 до оо. Если
а= 0, то rj(X) = 1. При аР<0 функция эластичности rj(X) убывает от +оо до 1,
когда X изменяется от до +со.
н
Заметим, наконец, что степенную форму связи С =f(DPI) = a (DPI)^ можно
линеаризовать переходом к логарифмам по любому основанию:
logC = loga + piogDPI.
При этом величина р = не зависит от выбора основания логариф-
dbg DPI
мов (так что
„ dlnC
dXnDPI
, когда используются натуральные логарифмы,
Р = , когда используются десятичные логарифмы)
dig DPI
и представляет собой эластичность расходов на потребление
соответствующего продукта (группы продуктов) по располагаемому доходу.

Раздел 1. Эконометрика и ее связь с экономической теорией...
65
ПРИМЕР 1.4.1
Вернемся к примеру с совокупным располагаемым доходом (DPI) и
совокупными расходами на личное потребление (Q в США. Будем использовать де-
флированные данные, принимая за базовый 1972 г. (табл. 1.9).
По таким данным за период 1970—1979 гг. была подобрана модель
линейной связи
С = -67.66 + 0.98£>Р/
(значения оценок, полученные ранее, округлены здесь до сотых долей).
Величина 0.98 оценивает склонность к потреблению по отношению к
располагаемому доходу, которая в этой модели постоянна. Оцененная эластичность
расходов на личное потребление по отношению к располагаемому доходу
изменяется на периоде с 1970 по 1979 г. от значения
0.98-751.6 _ = ио
-67.66 + 0.98-751.6
до значения
0.98-1015.7
= 1.07.
-67.66 + 0.98-1015.7
Таким образом формально расходы на личное потребление оказываются
эластичными по располагаемому доходу на всем этом периоде. В дальнейшем
мы подробно обсудим вопрос о том, насколько надежны такие выводы, имея
в виду, что при вычислениях эластичностеи в данном случае используются
не «истинные» значения параметров а и Д а их оценки. ■
К линейной форме связи можно привести и некоторые другие виды
зависимости, характерные для экономических моделей.
Так, если Y - объем плановых инвестиций, a Z - норма банковского
процента, то между ними существует связь, которая иногда может быть
выражена следующим образом:
Y = a + ^-, a>0, Д>0,
и имеет графическое представление, приведенное на рис. 1.21.
Заменой переменной X = — приводим указанную связь к линейной
форме Y = а + J3X. В этой модели эластичность Y по Z отрицательна и меньше 1
по абсолютной величине:
dZY У Z2)a + l P + aZ
Z
(объем плановых инвестиций неэластичен по отношению к норме процента).

66
Часть 1. Основные понятия, элементарные методы
Z
Рис. 1.21
Рис. 1.22
В моделях «доход — потребление», относящихся к потреблению
продуктов питания, линейная модель в логарифмах уровней, выражающая
уменьшение MPC{DPI) с возрастанием DPI, все же не всегда удовлетворительна,
поскольку эластичность в такой модели постоянна. Опять же по
физиологическим причинам более подходящей будет, скорее, модель связи с
убывающей (в конечном счете) эластичностью. Такого рода связь между факторами
Y и Z может иметь вид
Y = a + /3lnZ, a>0, /?>0
(см. график на рис. 1.22, построенный при а= 5, /?= 10).
Действительно,
Г7Л dY Z
' dZY
Z) a + p\nZ
->0.
Однако здесь возникают проблемы с отрицательными значениями Y при
малых значениях Z.
Последнего недостатка нет в модели
0 (
\nY = a-£-, /?>0, т.е. У = ехр|
а-1.
Z
Здесь
«*>-!
(закон Энгеля (убывание эластичности потребления продуктов питания по
доходу)). Заметим также, что значения Y в этой модели ограничены сверху
значением ехр(а).
f ^
Приведенный на рис. 1.23 график кривой 7 = ехр|
значениям а = 3, E = 10.
а- —
соответствует

Раздел 1. Эконометрика и ее связь с экономической теорией...
67
При этом ехр(З) = 20.09, так что
прямая Y = 20.09 является
горизонтальной асимптотой для кривой
Обе последние модели
приводятся к линейной форме связи путем
перехода от уровней переменных
к их логарифмам или к обратным
величинам.
Y А
20
15 -
10 -
5-
U 
/ |
Г 1
20
1 |
i i
40 60
Рис. 1.23
I
i
80
-
100 2
У
Замечание 1.4.1. Пусть X и Y— уровни двух экономических
переменных, тогда
• уравнение Y = а + рх называют level-level уравнением.
Коэффициент Р в таком уравнении равен изменению значения
переменной Г при увеличении значения переменной Хна 1;
• уравнение 1п7 = а + pinX называют log-log уравнением.
Коэффициент Р в таком уравнении является эластичностью
переменной Y по отношению к переменной X и приблизительно
равен процентному изменению значения Y при увеличении
значения переменной Хна 1%;
• уравнение 1п7= а + РХ называют log-level уравнением.
Коэффициент Р в таком уравнении называют
полуэластичностью {semi-elasticity). При увеличении значения
переменной X на 1 значение переменной Y изменяется приблизительно
на 100/?%;
• уравнение Y = а + pinX называют level-log уравнением. При
увеличении значения переменной Хна 1% значение
переменной Y изменяется приблизительно на единиц.
100
Если исследователь принимает модель наблюдений
\nYt=a +p\nXi+ei,
значит, он соглашается с тем, что
Y^e^Xfe81, или Y(=aXfvt,
т.е. допускает мультипликативное вхождение ошибок v,- в нелинейное
уравнение для Yt.
В то же время не исключено, что, по существу, модель должна иметь вид
Yt=aXf + vi9

68
Часть 1. Основные понятия, элементарные методы
т.е. содержит аддитивные ошибки. Преобразование X —> Х& не является
доступным, если значение /? — неизвестный параметр, подлежащий
оцениванию. Соответственно в последней модели Х& не является объясняющей
переменной, поскольку значения Xf недоступны наблюдению. Взятие
логарифмов от обеих частей не приводит здесь к линейной модели наблюдений, и мы
имеем дело с существенно нелинейной моделью наблюдений.
В такой ситуации оценки параметров а и /? можно опять определить как
значения а и Ъ, минимизирующие сумму квадратов
Q(a,b) = fj(Yi-aXbI.
i = \
Однако нормальные уравнения в данном случае становятся нелинейными,
и решения этих уравнений не выражаются в явном виде. Здесь приходится
прибегать к нелинейному методу наименьших квадратов {nonlinear least
squares — NLLS). Сумму квадратов отклонений минимизируют с помощью
итерационных методов, в которых сначала задаются некоторые стартовые
значения оцениваемых параметров, а затем производится последовательное
приближение значений а и Ъ к значениям, минимизирущим Q{a, b). При этом
возникает проблема поиска именно глобального, а не локального максимума
функции Q{a, b). Более того, результаты, касающиеся вероятностных свойств
получаемых оценок (что и представляет основной интерес в эконометрике),
в нелинейных моделях только асимптотические, т.е. предполагают наличие
большого количества наблюдений. В то же время в линейной модели:
а) оценки параметров вычисляются по явной формуле и гарантируют
обеспечение глобального минимума суммы квадратов;
б) результаты, касающиеся вероятностных свойств получаемых оценок,
являются точными и при небольшом количестве наблюдений.
Поэтому так важна возможность сведения модели нелинейной связи к
линейной модели наблюдений.
Пример подбора моделей нелинейной связи,
сводящихся к линейной модели преобразованием
переменных
Если в нашем распоряжении нет теоретической модели связи между
переменными, приходится исходить из характера расположения точек на
диаграмме рассеяния и на этой основе подбирать подходящую модель.
Рассмотрим следующий пример.
Суть политики Кеннеди — Джонсона1 состояла в сокращении налогов,
увеличении расходов на оборону и в ускорении роста количества денег в об-
Джон Кеннеди — президент США с 1961 по 1963 г., Линдон Джонсон — президент США
с 1963 по 1969 г.

Раздел 1. Эконометрика и ее связь с экономической теорией...
69
ращении. Предполагалось, что это вызовет оживление экономики США и
будет способствовать снижению нормы безработицы (т.е. доли безработных
в общей численности рабочей силы). Ожидалось также, что возрастание темпов
инфляции будет при этом не очень сильным. Обратимся, однако, к реальным
статистическим данным за период с 1961 по 1969 г. (табл. 1.11).
Таблица 1.11
Темп инфляции и безработица в США с 1961 по 1969 г., %
о/*
Год
INF
UNJOB
1961
1.0
6.5
1962
1.1
5.4
1963
1.2
5.5
1964
1.3
5.0
1965
1.7
4.4
1966
2.9
3.7
1967
2.9
3.7
1968
4.2
3.5
1969
5.4
3.4
* UNJOB — доля безработных в общей численности рабочей силы; INF— темп инфляции.
На рис. 1.24 приведены диаграмма рассеяния для переменных UNJOB
и INF, построенная по указанным данным, и прямая, подобранная методом
наименьших квадратов исходя из предположения о линейном характере связи
между этими переменными, т.е. исходя из модели наблюдений
INF^a + pUNJOBj+Cj, / = 1,...,я.
Достаточно высокое значение
коэффициента детерминации — R2 = 0.7184,
соответствующее полученной прямой,
могло бы говорить о хорошем
приближении истинной модели связи
линейной моделью1. Однако характер
расположения точек на диаграмме рассеяния
явно указывает на наличие нелинейной
связи между рассматриваемыми
переменными в период с 1961 по 1969 г.
(кривая Филлипса).
В связи с этим при подборе моделей
к реальным статистическим данным
следует обращать внимание не только
на коэффициент детерминации, но и на соответствие подобранной модели
характеру статистических данных. Позднее мы специально обсудим эту
проблему, известную как проблема адекватности полученной модели
имеющимся статистическим данным.
Поскольку на первый взгляд расположение точек на рис. 1.24 напоминает
график обратно пропорциональной зависимости, можно рассмотреть модель
наблюдений
UNJOB
Позднее мы сможем более квалифицированно говорить о том, действительно ли
получаемое при подборе модели значение коэффициента детерминации достаточно велико.

70
Часть 1. Основные понятия, элементарные методы
INFt -а + В + £., / = 1,...,и,
Н UNJOB, l
соответствующую линейной связи между переменными INF и UNJOBINV =
. Подбор такой связи приводит к модели
UNJOB
1
INF = -3.90 + 27.47 -
UNJOB
с еще более высоким значением коэффициента детерминации: R2 = 0.8307.
Однако характер диаграммы рассеяния переменных INF и UNJOBINV (рис. 1.25)
указывает на нелинейную связь и между этими переменными.
Обратившись еще раз к диаграмме рассеяния исходных переменных INF и
UNJOB для данных за 1961 —1969 гг. (рис. 1.24), можно заметить, что кривая
зависимости INF от UNJOB, по-видимому, имеет вертикальную асимптоту
INF= 3. Последнее обстоятельство можно учесть в рамках модели
Михаэлilea — Ментон (Michaelis-Menton model):
в2+UNJOB'
которую можно преобразовать к виду
Вг-в,
INF = 9X- ' ?
в2+UNJOB
предусматривающему наличие вертикальной и горизонтальной асимптот.
Такая модель связи линеаризуется переходом к обратным величинам
Y = , X = . Действительно, тогда
INF UNJOB
в2 §г_
Y^ 1 J2+UNJOB l + WJd~B 1 , 3 -Д| ffy
INF 9Х- UNJOB 9Х вх UNJOB '
1 а 92
Тта=^р=тх-
Диаграмма рассеяния для обратных величин Y = , X =
приведена на рис. 1.26.
Теперь уже точки на диаграмме рассеяния весьма хорошо следуют прямой
линии, подобранной методом наименьших квадратов:
Y= 1.947 - 5.952JT, R2 = 0.9914.

Раздел 1. Эконометрика и ее связь с экономической теорией...
71
0,15 0,20 0,25 0,30 UNJOBINV 0,15 0,20 0,25 0,30 UNJOBINV
Рис. 1.25 Рис. 1.26
Здесь а = 1.947, /? = -5.952, так что ^ = — = 0.514, в2 =^ = -3.057,
и оцененная модель Михаэлиса -
INF = -
а
Ментон имеет вид:
0.514 UNJOB
- 3.057 + UNJOB'
Модель Михаэлиса — Ментон хороша тем, что учитывает наличие
асимптот и линеаризуется. В то же время она является лишь частным случаем
более общей нелинейной модели связи
INF = a+-
ft
02+UNJOB
с тремя свободно изменяющимися параметрами.
Действительно, в модели Михаэлиса — Ментон
въ = -вх • в2,
и она только двухпараметрическая, так что модель с тремя свободными
параметрами является более гибкой. Однако указанная трехпараметрическая
модель уже не линеаризуется, и параметры вх в2 въ приходится оценивать,
используя итерационную процедуру последовательного уменьшения суммы
квадратов
Q@iAA) = 1L
г
1=1
iNFt-a--
о,
V
в2 + UNJOB.у
(конечно, в предположении аддитивности ошибок €t). Стартовые значения
параметров в19 62 в этой процедуре можно взять близкими к оценкам 0l9 в2,
полученным при оценивании предыдущей модели (например, вх = 0.5 в2 = -3.0),
а стартовое значение въ можно положить равным 1.

72
Часть 1. Основные понятия, элементарные методы
INF -
6-
4-
2-
0 -
i
□
$
п°
1
i
5
Рис
Р П
1
1.27
П INFmodel
О /AFfrue
fc
r UNJOB
INF
15
10
5
о
7 12 IWJOB
Рис. 1.28
Реализация итерационной процедуры приводит к следующим оценкам
параметров:
3 =0.581, в2 =-3.117, 6>3 =1.370;
оцененная модель имеет вид
INF = 0.5Sl + -
1.370
UNJOB-3M7
На рис. 1.27 показаны диаграммы наблюдаемых значений переменной INF
(INFtrue) и значений (INFmodel), получаемых по оцененной модели.
Подобранная модель показывает, что экспансионистские экономические
мероприятия сначала обеспечивают снижение нормы безработицы и
реальный экономический рост при умеренной инфляции. Однако удержать норму
безработицы ниже ее естественного уровня в течение продолжительного
времени можно лишь за счет постоянно ускоряющегося темпа инфляции.
К окончанию срока пребывания у власти Линдона Джонсона темп инфляции
стал стремительно расти, в связи с этим потребовалась смена экономической
политики.
V Замечание 1.4.2. Формально можно получать все большее
соответствие модели имеющимся статистическим данным, усложняя
функцию связи и вводя в нее все большее количество параметров. Однако
при этом становится все труднее содержательно интерпретировать
параметры модели и проверять гипотезы о значениях этих
параметров.
Более того, детальная модель, построенная по статистическим
данным за некоторый период времени, может оказаться совершенно
бесполезной для описания связи между рассматриваемыми
переменными на другом временном промежутке.
Так, если рассмотреть данные о значениях переменных UNJOB
и INF на более широком периоде — с 1958 по 1984 г., то для такого
набора данных диаграмма рассеяния имеет вид, представленный
на рис. 1.28.

Раздел 1. Эконометрика и ее связь с экономической теорией...
73
На сей раз облако рассеяния довольно округло, и это согласуется
с весьма низким значением коэффициента детерминации R2 = 0.0864,
полученным при подборе модели линейной зависимости INF от UNJOB.
Диаграмма рассеяния не указывает и на какой-либо другой тип
зависимости между этими двумя переменными на расширенном периоде
наблюдений.
v Замечание 1.4.3. Рассматривая альтернативные модели зависимости
темпа инфляции от доли безработных в общей численности рабочей
силы, всякий раз мы приводили значение коэффициента
детерминации, соответствующее оцененной модели. При этом использовались
как модели, в которых объясняемой являлась переменная INF, так
и модель, в которой объясняемой являлась переменная Y = .
Однако следует иметь в виду, что сравнение значений коэффициента
детерминации, полученных при оценивании моделей, в которых
объясняемые переменные различны, не имеет смысла, поскольку при
этом оказываются различными и полные суммы квадратов.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как ведет себя предельная склонность к потреблению при возрастании DPI в модели
степенной связи между DPI и расходами на потребление?
2. Как ведет себя эластичность расходов на потребление при возрастании DPI в модели
степенной связи между DPI и расходами на потребление?
3. Как ведет себя эластичность расходов на потребление при возрастании DPI в модели
линейной связи между DPI и расходами на потребление?
4. Какие две различные эконометрические модели можно выбрать для эконометри-
ческого анализа исходя из одной и той же модели степенной связи между
переменными? Как влияет при этом выбор модели на процедуру, реализующую метод
наименьших квадратов?
5. Что дает возможность сведения модели нелинейной связи к линейной модели
наблюдений?
6. Каковы достоинства модели Михаэлиса — Ментон? Каким образом она
линеаризуется?
7. Частным случаем какой трехпараметрической модели является модель
Михаэлиса — Ментон? Как реализуется метод наименьших квадратов в этих двух
моделях?
8. Почему нельзя сравнивать между собой значения коэффициента детерминации,
полученные при оценивании альтернативных моделей связи, в которых
объясняемые переменные различны? Как можно поступать в таких случаях?

Раздел 2
ЛИНЕЙНАЯ МОДЕЛЬ НАБЛЮДЕНИЙ.
РЕГРЕССИОННЫЙ АНАЛИЗ
Тема 2.1
ЛИНЕЙНЫЕ МОДЕЛИ С НЕСКОЛЬКИМИ
ОБЪЯСНЯЮЩИМИ ПЕРЕМЕННЫМИ.
ОЦЕНИВАНИЕ И ИНТЕРПРЕТАЦИЯ КОЭФФИЦИЕНТОВ
Говоря о линейных эконометрических моделях с несколькими
объясняющими переменными, мы фактически исходим из предположения о
существовании усредненного (теоретического) соотношения
у = в1х1+... + врхр
между переменными у и х{9 ..., хр9 которые являются или непосредственно
уровнями тех либо иных экономических факторов, или функциями от уровней
этих факторов (например, степенями или логарифмами уровней этих
факторов). Иными словами, «в среднем» значения переменной у являются
линейной комбинацией значений переменных х19 ..., хр9 а в19 ..., в суть
коэффициенты этой линейной комбинации. Если в правую часть такого соотношения
включается константа — постоянная составляющая (intercept), то в
качестве хх берется «переменная», тождественно равная 1, тогда соответствующая
константа равна вх.
Рассмотрим, например, модель производственной функции Кобба — Дугласа
Q{K9L)=AKaLfi9
где Q — объем выпуска;
К — затраты капитала;
L — затраты рабочей силы,
которая линеаризуется переходом к логарифмам уровней:
\ogQ = \ogA + a\ogK + p\ogL.

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
75
Заметим, что в этой модели параметр а выражает эластичность выпуска
по капиталу, а параметр /?— эластичность выпуска по затратам труда.
Такую модель связи можно записать следующим образом:
где .у = logg, хх = 1, х2 = logAT, х3 = logL, вх = logA,#> = «,#,=/?.
Обращенная к статистическим данным линейная эконометрическая
модель с р объясняющими переменными (модель наблюдений),
соответствующая модели связи;; = вххх + ... + врхр9 имеет вид
yi=e[xil+... + 0pxip + £i9 / = 1,...,л, п>р,
где yt — значение объясняемой переменной в /-м наблюдении;
6j — коэффициент приу-й объясняющей переменной;
Xfj — значениеу-й объясняющей переменной в j-м наблюдении;
st — случайная составляющая (ошибка) в /*-м наблюдении;
п — количество наблюдений.
Значения >>,, хп, ..., xip, i = 1,..., и, наблюдаются — это и есть
статистические данные (statistical data), или наблюдения (observations). На основании
этих данных производится оценивание неизвестных параметров ви ..., 6р.
Заметим: поскольку эти коэффициенты ненаблюдаемы, ненаблюдаемы и
значения sl9„ .,£■„.
Следует особо остановиться на интерпретации коэффициентов. Выше уже
говорилось о том, что интерпретация усредненных моделей связи становится
более определенной, если предполагается, что условные математические
ожидания случайных ошибок при известных значениях объясняющих
переменных в эконометрической модели равны 0. Будем предполагать, что это
так, т.е. что
Е(£{\хп,...,х{р) = 09 / = 1,..., и.
Если имеем дело с эконометрической моделью парной линейной связи
yt = а + /3xt + e,, то при указанном условии
E(yi\xi) = a + fixi9
и тогда коэффициент /3 равен изменению ожидаемого значения у( при
увеличении xt на 1.
Пусть, однако, в линейную эконометрическую модель помимо постоянной
составляющей (которой, впрочем, может и не быть) включается более одной
объясняющей переменной. В этом случае увеличение значения переменной дс-
на 1 уже не обязательно приводит к изменению ожидаемого значения пере-

76
Часть 1. Основные понятия, элементарные методы
менной у на величину 6j. Дело в том, что переменная Xj может быть связана
с другими объясняющими переменными, включенными в модель, так что
при ее изменении одновременно изменяются и значения других
объясняющих переменных. Соответственно ^ представляет ожидаемое изменение у
при увеличении Xj на 1, только если значения всех других объясняющих
переменных остаются неизменными (правило «при прочих равных» —
ceteris paribus).
Вернемся к примеру с производственной функцией Кобба — Дугласа и
используем модель наблюдений в логарифмах уровней:
logg. = log A + alogKj +p\ogLt +s(, i = 1,..., и,
предполагая, что E{st \Kt, L{) = О, i = 1,..., п. Тогда
£(loga|^,A) = log^ + alog^.+ /?logL/?
при этом:
• коэффициент а равен изменению ожидаемого значения log Qt при
увеличении log^ на 1 при неизменном значении logL, и интерпретируется
как эластичность выпуска по затратам капитала при сохранении затрат
труда на постоянном уровне;
• коэффициент /? равен изменению ожидаемого значения logg, при
увеличении logZ,, на 1 при неизменном значении log^ и интерпретируется
как эластичность выпуска по затратам труда при сохранении затрат
капитала на постоянном уровне.
Оценивание неизвестных коэффициентов модели методом наименьших
квадратов {least squares) состоит в минимизации по всем возможным
значениям в19..., вп суммы квадратов
Q(ex,...,9p) = fJ(yi-e,xn-...-9pxipJ.
/ = 1
Минимум этой суммы достигается при некотором наборе значений
коэффициентов
вх =в19...,вр =вр,
так что
0ФХ,...,0Р)= min QXffy,...,9p).
в\,...,вр
Это минимальное значение опять обозначим RSS, так что
RSS = ft(yl-elxn-...-0pxlpJ,
и назовем остаточной суммой квадратов.

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
77
Коэффициент детерминации R2 определяется как
TSS
где
/ = 1
Обозначив
У!=01Хп+... + врх,р9 z = l,...,w,
(подобранные —fitted, или прогнозные значения объясняющей
переменной по оцененной линейной модели связи) и определив остаток (residual)
в |-м наблюдении как
получим:
RSS = ±(yi-yiJ=±ef.
/ = 1 1=1
Обозначив
ESS^in-yJ
1 = 1
— сумму квадратов, объясненную моделью (explained sum of squares), как
и в случае линейной модели ср = 29 имеем разложение
TSS = RSS + ESS,
так что
R2 = ESS
TSS '
Опять же это разложение справедливо только при наличии постоянной
составляющей в модели линейной связи. При этом
R2=r2yy9
т.е. коэффициент детерминации равен квадрату выборочного коэффициента
корреляции гуу между переменными у и у. Последний называется
множественным коэффициентом корреляции (multiple-R), поскольку является
выборочным коэффициентом корреляции между переменной у и переменной^,
являющейся, так сказать, «представителем» всего множества объясняющих
переменных, включенных в правую часть оцениваемой модели.
Для поиска значений вх,..., в , минимизирующих сумму
Q(el9...9ep) = fi(yt-elxa-...-epx¥J9
1=1

78
Часть 1. Основные понятия, элементарные методы
следует приравнять нулю частные производные этой суммы (как функции
от вХ9..., в) по каждому из аргументов 0l9..., 6р.
В результате получаем систему нормальных уравнений:
fd2(yi-eixil-...-epxip)(-xn) = 0,
i = \
£2(yi-exxn-...-epxip)(-xi2) = 0,
1 = 1
fd2(yi-eixn-...-0pxip)(-xip) = O
; = i
или
в2+...+
Л
V = 1 ) v=1 ) V/ = 1 ) ,=1
\ . ( П \ ( n \
Y.xnxiP \9р=11У1хп
\l-\. J
Z*,2x,, #,+ £>;
a2+...+
V, = i у
^•=1 ; .=1
1=1
i = l
62+...+
( n \
v = i J
-//?•
Это системар линейных уравнений ср неизвестными в19..., вр. Ее можно
решать или методом подстановки, или по правилу Крамера с использованием
соответствующих определителей. В векторно-матричной форме эта система
имеет вид
ХТХв = ХТу,
где X — матрица значений р объясняющих переменных в п наблюдениях
Х =
хп хп
Х2\ *22
Хп\ Хп2
Хт — транспонированная матрица
хт =
хп х2\
х\2 ^22
\Х\р Х2р
к\р
К2р
пр J
кп2
"Р J

Раздел 2. Линейная модель наблюдений. Регрессионный анализ 79
у и в — соответственно вектор-столбец значений объясняемой
переменной в п наблюдениях и вектор-столбец оценок р неизвестных
коэффициентов
(уА
Уг
КУп)
, в =
\ёЛ
02
UJ
Система нормальных уравнений имеет единственное решение (которое
указывает именно точку минимума), если выполнено условие:
матрица А^Х невырожденна, т.е. ее определитель отличен от 0:
detXrX*0,
которое можно заменить условием:
столбцы матрицы X линейно независимы.
При выполнении этого условия матрица ХТХ (размера р х р) имеет
обратную к ней матрицу (ХТХ)~1. Умножая в таком случае обе части уравнения
X7Хв' = X1у слева на матрицу (ХТХ)~\ находим искомое решение системы
нормальных уравнений:
е=(хтху1хту.
Введем дополнительные обозначения:
(*}
вг
UJ
, е =
hi
£2
\£п )
» У =
Г1]
Уг
J»J
, е =
(еЛ
е2
\еп)
Тогда модель наблюдений
У{=вхХп+... + врХ¥+£,9 / = 1,...,/1,
можно представить в матрично-векторной форме
у = Хв + е.
Вектор подобранных значений имеет вид
У = Х9,
вектор остатков равен
е = у-у = у-Х6.

80
Часть 1. Основные понятия, элементарные методы
Как и для модели линейной связи между двумя переменными, указанные
выше алгебраические соотношения имеют простую геометрическую
интерпретацию.
Система нормальных уравнений попросту выражает тот факт, что вектор
остатков е ортогонален векторам значений объясняющих переменных
Х2\
\Хп1 )
5
х2 =
fx }
л12
х22
\Хп2 )
• • • X =
9 ? Лр
fx Л
Х2р
кх»р )
т.е. ортогонален линейному подпространству L(X) = L(xl9x2,..., хр) евклидова
пространства R", содержащему векторы х19 х29 ..., хр и все их линейные
комбинации.
Вектор у = Хв можно записать следующим образом:
у = вххх+--- + врхр,
т.е. этот вектор является линейной комбинацией векторов xl9 х2, ..., хр9 а
значит, принадлежит подпространству L(X) и ортогонален вектору остатков е.
Поскольку же из соотношения е = у-у следует, что
у = у + е,
это означает, что:
• вектор у является ортогональной проекцией вектора ушЬ (X);
• вектор е является ортогональной проекцией вектора у на
подпространство, являющееся ортогональным дополнением к
подпространству L(X) в R".
Заметив, что
у = Хв = Х(ХТХу1ХТу, е = у-у = у-Хв = Aп-Х(ХтХу1Хт)у,
и обозначив Н = Х(ХТХ)~1ХТ, получим:
у = Ну, е = Aп-Н)у,
так что Н = Х{ХТХ)~ХХТ — матрица ортогонального проектирования из R"
на L(X); (/n - Н) — матрица ортогонального проектирования из Rn на LL(X) —
ортогональное дополнение к L(X).
При этом для остаточной суммы квадратов получаем:
RSS = \e\2=eTe = (y-y)T(y-y) = (y-x3)T(y-Xe) =
= УТУ - ОтХту - утХв + втХтХв.

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
81
Поскольку здесьутХв — скаляр, то у1Хв - (утХ6)т = вт Хту, так что
RSS = уту - втХту + втХтХв - втХту = уту - вт Хт у + вт (ХтХв - X т у).
Но из соотношения XтХв = Хту (система нормальных уравнений) вытекает
тогда, что
RSS = yTy-6TXTXe,
что можно записать также в виде:
RSS = \y\2-\X0\2.
Это равносильно соотношению | у |2 = | у |2 + \е |2, выражающему теорему
Пифагора в R".
Рассмотрим статистические данные о потреблении текстиля (текстильных
изделий) в Голландии в период между двумя мировыми войнами с 1923 по
1939 г., приведенные в табл. 2.1. В этой таблице Т— реальное потребление
текстиля на душу населения; DPI — реальный располагаемый доход на душу
населения; Р — относительная цена текстиля. Все показатели выражены
в индексной форме.
Таблица 2.1
Потребление текстиля в Голландии с 1923 по 1939 г., % к 1925 г.
Год
1923
1924
1925
1926
1927
1928
1929
1930
1931
Т
99.2
99.0
100.0
111.6
122.2
117.6
121.1
136.0
154.2
DPI
96.7
98.1
100.0
104.9
104.9
109.5
110.8
112.3
109.3
Р
101.0
100.1
100.0
90.6
86.5
89.7
90.6
82.8
70.1
Год
1932
1933
1934
1935
1936
1937
1938
1939
Т
153.6
158.5
140.6
136.2
168.0
154.3
149.0
165.5
DPI
105.3
101.7
95.4
96.4
97.6
102.4
101.6
103.8
Р
65.4
61.3
62.5
63.6
52.6
59.7
59.5
61.3
Для объяснения изменчивости потребления текстиля в указанном периоде
в качестве объясняющей переменной можно привлечь как располагаемый
доход DPI, так и относительную цену на текстильные изделия Р. Если
исходить из предположения о постоянстве эластичностей потребления текстиля
по доходу и цене, следует подбирать линейные модели для логарифмов
индексов, а не для самих индексов.
Рассмотрим сначала модели парной связи между логарифмами
рассматриваемых переменных
IgT = ах + Д lgDP/, lgr = а2 + /32 lgP.

82
Часть 1. Основные понятия, элементарные методы
Здесь для разнообразия использованы десятичные логарифмы, хотя можно
использовать логарифмы по любому другому основанию (обычно применяют
натуральные логарифмы) — при переходе в обеих частях уравнения к
логарифмам по другому (но одинаковому) основанию значения интересующих
нас в первую очередь коэффициентов Д и /?2 не изменяются.
Пусть Ti9 DPIt, Pt — значения переменных Г, DPI, P в i-м по порядку году
на периоде наблюдений, так что i = 1, ..., 17 и, например, / = 3 соответствует
базовому 1925 г.
Сначала рассмотрим эконометрические модели парной линейной связи
между логарифмами переменных:
IgT^ai+ftlgDPIt+eu, lgT) =a2 +/?2lg/> +e2i9 i = l,...,17.
Оценивание этих моделей методом наименьших квадратов приводит к
следующим результатам:
для первой модели: ах - 1.442, Д = 0.348, что соответствует оцененной
модели связи lg7"= 1.442 + 0.348 IgDPI, при этом
£55 = 0.000959, RSS = 0.099185, 755=0.100144, Л2 = 0.0096;
для второй модели: а2 = 3.564, Д = -0.770, что соответствует оцененной
модели связи \gT = 3.564 - 0.7701gP, при этом
£55=0.087729, RSS = 0.012415, 755 = 0.100144, Л2 = 0.8760.
Вторая модель имеет более высокую объясняющую способность. Однако,
естественно, возникают вопросы: нельзя ли для объяснения изменчивости
переменной Т использовать одновременно и располагаемый доход, и
относительную цену текстиля? Улучшит ли это объяснение изменчивости
потребления текстиля?
Чтобы привлечь для объяснения изменчивости потребления текстиля обе
переменные — DPI и Г, рассмотрим расширенную модель связи:
lgr = a + p\gDPI + y\gP.
Коэффициент р интерпретируется здесь как эластичность спроса на
текстиль по доходу при неизменном значении относительной цены Р на
текстиль, а коэффициент у— как эластичность спроса на текстиль по цене при
неизменном уровне располагаемого дохода.
Расширенной модели связи соответствует расширенная эконометрическая
модель
lg7;.=a + /?lgD/>//+^lg/>+£/, / = 1,...,л.
Оценивание методом наименьших квадратов расширенной модели
приводит к следующим результатам:
а = 1.374, J3 = 1.143, f =-0.829,

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
83
что соответствует оцененной модели связи
lgr = 1.374 + 1.1431gD/Y- 0.829 lg/>,
при этом
ESS =0.097577, RSS= 0.02567, Л2 = 0.9744.
Заметим: полная сумма квадратов TSS = 0.100144 одна и та же во всех трех
случаях, поскольку во всех трех моделях объясняемая переменная была
одной и той же.
Как видим, в результате привлечения для объяснения изменчивости
потребления текстиля сразу двух показателей — DPI и Р произошло заметное
увеличение коэффициента детерминации по сравнению с лучшей из двух
моделей, использовавших только один показатель — от значения 0.8760 до
значения 0.97441. Заметим для дальнейшего, что значение коэффициента
детерминации в расширенной модели 0.9744 не равно сумме коэффициентов
детерминации 0.8760 и 0.0096 в моделях с включением только одного из двух
показателей — DPI или Р.
Коэффициент 1.143 в подобранной модели связи интерпретируется как
оценка эластичности спроса на текстиль по доходу при неизменном значении
относительной цены Р на текстиль, а коэффициент -0.829 — как оценка
эластичности спроса на текстиль по относительным ценам при неизменном уровне
располагаемого дохода. Такие значения оцененных коэффициентов формально
говорят в пользу того, что спрос на текстиль эластичен по доходам и
неэластичен по ценам. Вопрос о том, в какой степени можно доверять подобным
заключениям, будет рассмотрен далее в контексте вероятностных моделей.
Еще одну интерпретацию оценок коэффициентов линейных моделей
с несколькими объясняющими переменными дает теорема Фриша—Во—
Ловелла (Frisch-Waugh-Lovell theorem). На нее часто ссылаются как на FWL-
теорему. (Один из вариантов доказательства этой теоремы приведен в книге
{Davidson, MacKinnon, 1993).)
Пусть в модели у = Хв + е ср объясняющими переменными и п
наблюдениями объясняющие переменные разбиты на две группы, так что
х = [ххх2\ *=(£].
где Хх — матрица размера п х (р - 1);
Х2 — (пх 1)-вектор;
J3X — (р - 1) х 1-вектор;
/?2 — число (скаляр);
Как увидим в дальнейшем, при введении в правую часть модели дополнительных
объясняющих переменных коэффициент детерминации практически всегда возрастает. Однако это
еще не означает, что надо обязательно использовать более полную модель. Этот вопрос будет
рассмотрен в разд. 3.

84
Часть 1. Основные понятия, элементарные методы
y = Xxj3x+X2j32+e, B.1)
где Х2 — вектор значений выделенной объясняющей переменной.
Поскольку нумерация переменных, включаемых в модель, произвольна,
пусть выделенной переменной будет хр.
Пусть Рх — оператор проектирования из R" на линейное подпространство
L(XX), порожденное векторами-столбцами матрицы Хь а Мх — оператор
проектирования из R" на ортогональное дополнение к L(XX). Оценивание
линейной модели регрессии переменной у на первую группу переменных, т.е. на
переменные хх,..., хр_х, приводит к представлению
у = Рху + Мху9
при этом вектор остатков Мху - у - Рху является результатом очистки
переменной у от влияния переменных хх,..., хр_ х.
Аналогично оценивание линейной модели регрессии переменной хр на
переменные xl9..., хр_ х приводит к представлению
Хр=Р1Хр+М1Хр9
при этом вектор остатков Мххр = хр- Рххр является результатом очистки
объясняющей переменной хр от влияния переменных хх,..., хр_ х.
Рассмотрим теперь модель наблюдений, в которой объясняемой
переменной является очищенная переменная у, а объясняющей — очищенная
переменная хр:
Мху = /32Мххр+£. B.2)
ТЕОРЕМА Фриша — Во — Ловелла. Оценки наименьших квадратов
коэффициентов /?2 в моделях B.1) и B.2) численно совпадают.
v Замечание 2.1.1. Очистка переменных у и хр от влияния остальных
переменных является, по существу, удалением оцененных линейных
составляющих связей у и хр с остальными переменными.
Вернемся к примеру со спросом на текстильные изделия, где оценивалась
эконометрическая модель lgTf = а + p\gDPIt + у\%Р{ + €i9 i = 1, ..., 17 и были
получены оценки наименьших квадратов а = 1.374, Д = 1.143, у = -0.829.
В качестве переменной, выделяемой в FPTL-теореме, возьмем
переменную 1пР.
Для очистки объясняемой переменной IgT следует оценить модель lgT{ =
= ах + j3x\gDPIi + €li9 i = 1, ..., 17, что уже сделано выше и получены оценки

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
85
ах = 1.442, Д = 0.348. Следовательно, полученная в результате очистки
переменная Мх\%Тпринимает значения: Mx\gT = lg7; - A.442 + 0.348 lgDP/,).
Для очистки объясняющей переменной IgP оцениваем модель lgPt = а3 +
+ P3\gDPIt + £3i, i = 1, ..., 17. При этом получаем оценки а3 = -0.0586,
Д = 0.960, и полученная в результате очистки переменная Mx\gP принимает
значения: M^gP,- = \gPt - (-0.0586 + 0.960\gDPIf).
Остается оценить модель M{\gTt = yMxlgPf + s4i9 i = 1, ..., 17. Оценка
наименьших квадратов для коэффициента у принимает значение у = -0.829.
Таким образом, оценка наименьших квадратов коэффициента при IgP в
расширенной модели численно совпадает с оценкой наименьших квадратов
в модели наблюдений, соответствующей модели пропорциональной связи
между переменными IgTn IgP, очищенными от влияния переменной IgDPI.
Рассмотрим теперь квадратичную модель связи между факторами у и z:
у = а + Pz + yz2.
Ей соответствует модель наблюдений:
ух =a + j3zf+yz? +£., / = 1,..., п.
Перейдя к переменным х2 =z,x3 = z2, получим линейную модель наблюдений:
yt=a + J3xi2 + yxi3 + €i9 / = 1,..., п.
Следуя правилу «при прочих равных», в данном случае следовало бы
интерпретировать коэффициент Р как ожидаемое изменение у{ при увеличении
значения хп на 1 при сохранении неизменным значения xi3. Но последнее
невозможно, так как xi3 - хJ. Увеличение значения хп на А приводит здесь
к изменению ожидаемого значения объясняемой переменной в /-м
наблюдении от значения yt = а + /?х/2 + yx2i2 до значения
У;=а + Р(ха+А) + у(ха+АJ=(а + Рх12+ух?2) + рА + 2ух12А + уА2,
так что ожидаемое изменение yt при увеличении значения х/2на А равно
У?А + 2^х/2А + ^А2.
Если А мало (близко к 0), то
PA + 2yxi2A + yA2 *(p + 2yxi2)A,
так что предельный эффект переменной xi2 равен /? + 2yxi29 а не /?.
Хотя правило «при прочих равных» оказывается здесь неприменимым, это
никак не препятствует обращению к теореме Фриша — Во — Ловелла, в
которой можно использовать поочередно в качестве выделенной переменной
переменную х3 = z2 и переменную x2=z.

86
Часть 1. Основные понятия, элементарные методы
Пусть в качестве выделенной берется переменная х2 = z. Тогда методом
наименьших квадратов оцениваем две модели наблюдений:
yi = ах+ух xi3 + еа — используется для очистки переменной у,
хп - а2 + А х/з + £п — используется для очистки переменной х2.
Получаем значения у. =ах+ухxi3, xi2 = d2+ /32xi3 и находим значения
очищенных переменных yt = yt - yt, xi2 = xi2 - xi2, т.е. остатки, полученные в
результате оценивания этих двух моделей. Согласно F^L-теореме оценка
наименьших квадратов коэффициента J3 в исходной модели численно равна оценке
наименьших квадратов в модели наблюдений, соответствующей
пропорциональной связи между очищенными переменными у- = yi - у. и xi2 = xi2 - xi2.
Модель наблюдений с ортогональной структурой матрицы X
Вернемся к модели наблюдений^ = вххп + ... + 6pxip + ei9 i = 1,..., п. Как
правило, оценка наименьших квадратов коэффициента вр в этом уравнении
отличается от оценки наименьших квадратов коэффициента вр в модели,
содержащей в правой части помимохр лишь часть из переменныххх,..., хр_х.
Однако в некоторых моделях такое совпадение гарантируется, и это связано
со специальными свойствами объясняющих переменных, включаемых в модель.
Рассмотрим случай, когда все столбцы Xl9 ..., Хр матрицы X попарно
ортогональны, так что XTjXk = О для k*j\ к J = 1,...,/?.
Тогда оценка наименьших квадратов вектора в в полной модели равна:
в = (ХТХу1ХТу.
гх\хх
о
о
о
2 2
о
о
о
Л ЧУ
XPXPJ
Х\у
Ку.
(хтхххухх1у
(Хт2Х2ГХт2у
(ХтрХр)Хтру
где О — матрица, все элементы которой равны нулю.
Но {XTjXj)~xХ*у есть оценка наименьших квадратов коэффициента ^
в модели
v Замечание 2.1.2. Если в правую часть модели включается также
постоянная составляющая, так что хп = 1, то соотношения Х\Хк = О,
., и, означают, что ^xik = 0 и хк = 0, т.е. в этом случае
/=1
к = 2,
переменные х2, ..., хр центрированы (centered variables). При этом

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
87
условия XjXk = 0 для к *j, к, j = 2, ..., р, можно записать в виде
п п
]ГxtJxik = ^Г(xtJ -Xj)(xik -xk) = 0. Но последнее означает, что
/=1 i=i
Cov(Xj, хк) = 0. Поскольку хп = 1, то хх = 1 и Cov(xl9 xk) = 0 для всех
к = 2,...9п.
Иными словами, при попарной ортогональности всех столбцов
матрицы X и наличии постоянной составляющей в правой части
модели наблюдений переменные х19 х2, ..., хр (выборочно)
некоррелированны. При этом коэффициент детерминации R2, получаемый при
оценивании модели, равен сумме квадратов выборочных
коэффициентов корреляции между объясняемой переменной и каждой из
объясняющих переменных. Но это означает, что этот коэффициент
детерминации равен сумме коэффициентов детерминации, получаемых
в моделях парной регрессии переменной у на константу и одну
из остальных объясняющих переменных. Соответственно в такой
ситуации каждый из суммируемых коэффициентов детерминации
определяет вклад, который вносит соответствующая объясняющая
переменная в объяснение изменчивости переменной у.
Выведем указанное свойство, полагая для простоты р = 3, т.е. рассмотрим
три модели
М: у. =6Х+ в2ха + въх{Ъ + ег-9 / = 1,..., л (полная модель),
М2: yi=ei+e2xi2+£i,
М3: yi=ei+e3xi3+ei9 / = 1,...,л.
Остаточная сумма квадратов в полной модели равна:
RSS = \e\2=eTe = (y-y)T(y-y) = (y-X0)T(y-Xe) =
= УТУ ~ вТХту - утХв + втХтХв.
На основании этого представления ранее было получено выражение
RSS = yTy-eTXTxe.
Теперь будет полезным другое выражение для RSS, которое выводится
с учетом того, что ХтХв = Хту (нормальное уравнение):
RSS=yTy-eTXTy-yTxe + eTXTy = yTy-yTXe = yTy-(XTy)Te =
= yTy-^xnyi-02^xi2yi -ё3^х13у( =
i=i i=i i=i
= (yTy-ny2)-eiYjxi2yi-e,fjxnyi = TSS-e2Ydxnyi-e£xayi.
1=1 /=1 /=1

88
Часть 1. Основные понятия, элементарные методы
Следует установить, что R2 = R\ + R\, где R\ — коэффициент
детерминации в модели М*, т.е.
х RSS
TSS
RSS2
TSS
TSS
J
где RSSk — остаточная сумма квадратов, получаемая при оценивании
модели М*.
Это равносильно соотношению
(RSS2 +RSS3)-RSS = TSS.
Проверим выполнение этого соотношения в модели с х2 _1_ хх, х3 J. хх, х3 J. х2.
Имеем:
RSS = TSS - в2 £ xi2yt - 9Ъ £ xByt,
1=1 1=1
RSS2 =TSS-e2£xi3yi, Ш3=Ш-ё£х13у,
/=1 1=1
(значения оценок вк при оценивании полной модели и модели Мк совпадают
при сделанных предположениях об ортогональности переменных), откуда и
вытекает выполнение указанного соотношения.
Нормальная линейная модель
с несколькими объясняющими переменными.
Стандартные предположения о модели
Начиная с этого момента будем предполагать следующее:
1) модель наблюдений имеет вид
где yt — значение объясняемой переменной в /-м наблюдении;
xtj — известное фиксированное значение у-й объясняющей
переменной в |-м наблюдении;
Oj — неизвестный коэффициент приу-й объясняющей переменной;
е{ — случайная составляющая (ошибка) в /-м наблюдении.
В матрично-векторной форме модель соответственно имеет вид:
у = Хв + £.
2) £и ..., еп — случайные величины, независимые в совокупности,
имеющие одинаковое нормальное распределение 7V@, а2) с нулевым мате-

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
89
матическим ожиданием и дисперсией а2 > 0. Для краткости обозначим
это следующим образом:
€l9...9e„~Uxl.N@9a2),
где lid. —независимые, одинаково распределенные (аббревиатура
от independent, identically distributed).
Иначе говоря, случайный вектор е = (sl9 ..., sn)T имеет «-мерное
нормальное распределение1 с нулевым математическим ожиданием
(точнее, с математическим ожиданием, равным нулевому вектору @,..., ОO)
и диагональной ковариационной матрицей Cov(s) - а11п9 где 1п —
единичная матрица размера п х п\
3) если не оговорено противное, то в число объясняющих переменных
включается переменная, тождественно равная 1, которая объявляется
первой (по порядку) объясняющей переменной:
хп si, i = l9...9n;
4) Определитель матрицы ХТХ отличен от нуля:
tetXTX*09
что можно заменить условием: столбцы матрицы Xлинейно независимы.
Для краткости будем ссылаться далее на предположения B), как на
стандартные предположения об ошибках в линейной модели наблюдений.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что понимается под линейной эконометрической моделью с несколькими
объясняющими переменными?
2. В чем состоит правило «при прочих равных», используемое для интерпретации
коэффициентов линейной эконометрической моделью с несколькими
объясняющими переменными?
3. Что такое множественный коэффициент корреляции и почему он так называется?
Какова его связь с коэффициентом детерминации?
4. Какова геометрическая интерпретация системы нормальных уравнений,
используемых для нахождения оценок наименьших квадратов? При каком условии эти
система имеет единственное решение?
5. Как интерпретируются оценки наименьших квадратов коэффициентов линейных
моделей с несколькими объясняющими переменными? Какие проблемы
возникают при интерпретации таких оценок?
6. Какие преимущества дает ортогональная структура матрицы значений
объясняющих переменных?
7. Что понимается под нормальной линейной моделью с несколькими объясняющими
переменными? В чем состоят стандартные предположения о такой модели?
Об определении многомерного нормального распределения и о некоторых его свойствах
см. Приложение П-2а в конце раздела.

90
Часть 1. Основные понятия, элементарные методы
Тема 2.2
СВОЙСТВА ОЦЕНОК КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ МОДЕЛИ
ПРИ СТАНДАРТНЫХ ПРЕДПОЛОЖЕНИЯХ
О ВЕРОЯТНОСТНОЙ СТРУКТУРЕ ОШИБОК.
ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ КОЭФФИЦИЕНТОВ
При сделанных выше предположениях о модели наблюдений у{9 ..., уп
являются наблюдаемыми значениями нормально распределенных случайных
величин Yl9 ..., Yn9 которые независимы в совокупности и для которых
математические ожидания и дисперсии равны соответственно:
E(Yi) = 9lxn+... + epxip, D{Yt) = a\
так что
^~М(вхха+... + 6рх1р9ст2)9 / = l,...,w.
Случайные величины Yl9..., Yn в отличие от е19 ..., еп имеют неодинаковые
математические ожидания. В совокупности случайные величины Yl9 ..., Yn
образуют случайный вектор Y- (Yl9 ..., Yn)T с независимыми компонентами,
имеющий «-мерное нормальное распределение1. При этом
Y = Хв + s9 E(Y) = Хв + Е(е) = Хв9 Cov(y) = a2In.
Определяющим для всего последующего является то обстоятельство, что в
нормальной линейной модели с несколькими объясняющими переменными
оценки в19...9в коэффициентов в19...9в как случайные величины имеют
нормальные распределения (хотя эти случайные величины уже не являются
независимыми в совокупности).
Действительно, случайный вектор в = (Х7X)~lXTY можно представить
в виде e = CY9 где С = (ХТХ)~1ХТ — неслучайная матрица размера р х п9
так что в является линейным преобразованием нормально
распределенного случайного вектора Y и, следовательно, имеет нормальное
распределение.
Математическое ожидание этого случайного вектора равно:
ЕF) = Е((ХТХУ1 XTY) = (ХТХУ1 XTE(Y) = (ХтХу1 Хт Е(Хв + е) =
= (хтху1хтхв = в9
так что в является несмещенной оценкой вектора коэффициентов в.
См. Приложение П-2а в конце данного раздела.

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
91
Для случайных величин вХ9 ..., вр — компонент вектора в получаем
соответственно:
так что Oj является несмещенной оценкой коэффициента ^ приу-й
объясняющей переменной.
Найдем ковариационную матрицу случайного вектора в9 используя
формулу для вычисления ковариационной матрицы случайного вектора,
полученного линейным преобразованием другого случайного вектора с
неслучайной матрицей преобразования:
Cov0) = Cov(CY) = CCov(Y)CT = ((XTXylXT)cov(Y) ((XTXyl XTJ =
= ((ХТХУ1 XT)a2In ((ХТХУ1 XTJ = a2 (XT X)~x XTX(XTXyl =
= or2(XTXyl.
Здесь использованы правило транспонирования произведения матриц
(АВ)Т = ВТАТ и тот факт, что матрица (ХТХ)~1 симметрична, как и матрица
(ХТХ). Отсюда получаем, в частности, выражение для дисперсии Oj:
D(ej) = cr2(XTXyJ,
где (X7Х)~} —у-й диагональный элемент матрицы (ХТХ)~1.
Рассматриваемая нами модель относится к классу так называемых
регрессионных моделей (regression models), имеющих вид:
Г,=ДХП9...9Хф) + е19 / = 1,..., л,
где Хп,..., Xip9 i = 1,..., п9 как и Yx,..., Yn9 могут быть случайными величинами,
и при этом условное математическое ожидание случайной величины Yt при
заданных значениях Хп = хП9 ..., Xip=xip равно:
Е(Г1\хп=хП9...9Хф=хф) = ДХП9...9Хф)9 / = 1 «.
Последнее соотношение можно интерпретировать следующим образом:
если мы наблюдаем (или, если это возможно, задаем) значения Хп =хП9...,
Xip = xip9 то ожидаемым значением для Yt является значение f(Xn,..., Xip). Если
имеется возможность многократно наблюдать значения Yt при одном и том
же наборе значений Хп =хП9..., Xip =xip9 но с разными (независимыми)
реализациями случайного вектора £ = (£Х9...9£п)т9 то среднее значение
наблюдаемых при этом значений У, будет близким к f(Xil9..., Xip).

92
Часть 1. Основные понятия, элементарные методы
Заметим, что, поскольку €t = У) -f{Xn, ..., Xip)9 i = 1, ..., п9 условие
^О^л =xi\9--->Xip =xiP) = f(xn,...,xipx / = i,...,«,
равносильно условию
Е(е,\хп=хП9...,Хф=хф) = 0.
В разд. 2—5 предполагается, чгоХП9 ..., Xip9 i = 1, ..., п9 являются
неслучайными величинами, а в разд. 6 обсуждаются проблемы, возникающие при
рассмотрении моделей, в которых такое предположение не является
оправданным.
Совокупность вероятностно-статистических методов исследования
регрессионных моделей называется регрессионным анализом {regression analysis).
О регрессионной модели У, = f{Xil9 ..., Xip) + et с E{Y\Xn = xil9 ..., Xip = xip) =
=f{Xil9 ..., Xip)9 i = 1, ..., n9 часто говорят как о модели регрессии
переменной Yt на переменные Х19 ...9Хр.
Соотношение Yt =f{Xil9..., Xip) + et в модели регрессии называют
уравнением регрессии {regression equation), объясняющие переменные ХХ9 ..., Хр —
регрессорами {regressors).
Функция /в этом контексте называется функцией регрессии {regression
function). Эта функция может быть полностью произвольной (и тогда говорят
о непараметрической регрессии — nonparametric regression) или
параметрической, заданной с точностью до конечного числа неизвестных параметров
(и тогда говорят о параметрической регрессии — parametric regression).
В последнем случае различают линейные {linear) и нелинейные {nonlinear)
регрессионные модели.
В линейной регрессионной модели функция регрессии линейна
относительно неизвестных параметров, производные функции регрессии по
неизвестным параметрам не зависят от этих параметров. В нелинейной модели
хотя бы одна из таких производных зависит от неизвестных параметров.
Например, в регрессионной модели
Q^AKfL'+ei, i = l л,
функция регрессии параметрическая: f{K9 L) =f{K9 L; A9 a9 /?) = AKaL^\ она
задана с точностью до неизвестных параметров А, а, Д При этом
df{K9L\A9a9P) =KaLp df{K9 L; A9 a9 fi) = AaKa-\Lfi
дА ' да
df{K9 L\ A9 a9 P) = iKagL0-i
dp p
так что производные функции регрессии по неизвестным параметрам зависят
от неизвестных параметров. Следовательно, рассматриваемая регрессионная
модель нелинейна.

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
93
Рассмотрим регрессионную модель для натуральных логарифмов уровней
в виде:
In б,- = 1пА + а\пК; +р\пЦ + е..
Для нее функция регрессии имеет вид: ДАТ, L) = \пА + alnK + fllnL.
Если опять считать неизвестными параметрами А, а и Д то производная
функции регрессии по параметру А зависит от этого параметра:
df(K9L;A9afi)_A_x
8А
так что регрессионная модель нелинейна.
Если же считать неизвестными параметрами \пА9 а и Д то производная
функции регрессии по параметру ХпА не зависит от этого параметра:
df(KMA9a9P)_x
д\пА
и регрессионная модель становится линейной.
Модель, удовлетворяющую предположениям A) и B) в конце темы 2.1,
можно называть нормальной линейной моделью множественной
регрессии переменной j на переменные л,,..., хр. Термин «множественная»
(multiple) указывает на использование в правой части модели наблюдений двух
и более объясняющих переменных, отличных от постоянной. Термин
«нормальная» (normal) — на предположение о нормальности распределения
случайных ошибок. Если такое предположение отсутствует (т.е. допускаются
и другие вероятностные распределения ошибок), то говорят просто о
линейной модели множественной регрессии (или о множественной линейной
регрессии — multiple linear regression). Термин «регрессия» (regression) имеет
определенные исторические корни и используется лишь в силу традиции. Тем
не менее приведем пример, в какой-то мере поясняющий это название.
ПРИМЕР 2.2.1
Некоторая дисциплина изучается в течение года. Пусть значения
переменной х представляют оценки студентов на экзамене по этой дисциплине в
первом семестре, а значения переменной у — оценки, полученные теми же
студентами на экзамене во втором семестре (используется 100-балльная система
оценок). По данным, относящимся к 38 студентам, методом наименьших
квадратов была получена оцененная модель линейной связи между этими
переменными в виде
;; = 17.5+ 0.789*
с достаточно высоким коэффициентом детерминации R2 = 0.823.
Прямая _у = 17.5 н- 0.789х пересекает прямую у = х при х = 82.94 и имеет
меньший угловой коэффициент, чем прямая у = х. Следовательно, если
студент получил на экзамене за первый семестр более 82 баллов, то ожидаемая
для него оценка на экзамене за второй семестр будет меньшей, чем оценка,

94
Часть 1. Основные понятия, элементарные методы
полученная им за первый семестр. В этом смысле можно говорить о «регрессе»
студентов, имеющих достаточно высокие оценки. В то же время если студент
получил на экзамене за первый семестр менее 83 баллов, то ожидаемая для
него оценка на экзамене за второй семестр будет большей, чем оценка,
полученная им за первый семестр. Но тогда следовало бы говорить о «прогрессе»
студентов, имеющих достаточно низкие оценки. Поэтому термины «регрессия»,
«регрессионный» надо воспринимать просто как исторически укоренившиеся,
не придавая им особой смысловой окраски. ■
Модель простой линейной регрессии {simple linear regression)
у^а + Рх^е^ / = 1,...,л, с E{£t) = 0, / = 1,...,л,
вкладывается в модель множественной линейной регрессии ср = 2:
Уг
\ynJ
Х =
1 х,
1 х,
0=\
nj
9
8-
\еЛ
£2
Такую модель называют иначе парной линейной регрессией {two-variable
linear regression), а также моделью прямолинейной регрессии {straight-line
regression).
Матрица {ХТХ)~Х здесь имеет вид:
{хтху1=-
лХхНХх/
1 = 1
,/=1
( п п
I*,2 -2>,
1=1 1=1
п
-Xх/ п
1 = 1
Учитывая, что
п I п \ п
"Xх*2- Xх/ =лХ(х»-"хJ»
1 = 1
,/=1
1=1
находим:
D{a) = \o\XTXy\x= n "
г:\2
; = 1
2
DiP) = \r\XTxr]n =-r-Z
£(*,-*J
/ = 1

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
95
Заметим еще, что
Cov(aJ) = [or\XTXyl]l2 = ^
1 = 1
п
откуда следует, что Cov(d,/3) = 0, только если ]Tx,. =0. Иначе говоря, при
/=i
п
^х;. ^ 0 случайные величины а и /? коррелированы.
i=i
Использование метода наименьших квадратов для оценивания линейных
эконометрических моделей оправдывается следующим важным результатом.
ТЕОРЕМА Гаусса — Маркова {Gauss-Markov theorem). Пусть модель
наблюдений имеет вид:
у1=вххп+... + врх1р+£1, 1 = 1,..., л, п>р9
где xtj — фиксированные значения;
9и ..., вр— неизвестные коэффициенты;
£l9 ...9£п — случайные ошибки, имеющие нулевые математические
ожидания, одинаковые дисперсии а1 и попарно некоррелированные;
в матрично-векторной записи: Y- X6+ £, Е{£) = 0, Cov{£) = <J2In.
Предполагается также, что столбцы матрицы X линейно независимы, так
что эта матрица имеет полный столбцовый ранг, а определитель матрицы
ХТХ отличен от 0.
Тогда оценка наименьших квадратов в = (ХтХ)~1Хту неизвестного вектора
коэффициентов в является наилучшей линейной несмещенной оценкой
{BLUE — best linear unbiased estimate) этого вектора в том смысле, что если
в — любая несмещенная оценка вектора в, имеющая вид в = Су {С —
матрица размера р х л), то разность Cov{6) - Cov{6) является неотрицательно
определенной (положительно полуопределенной) матрицей.
Заметим, чтоу'-й диагональный элемент матрицы Cov{0) - Cov{0) равен
разности D{0j) - D{0j)9 так что при выполнении условий Гаусса — Маркова имеем:
Таким образом, оценка наименьших квадратов 0j коэффициента ^ имеет
наименьшую возмоэюную дисперсию в классе всех линейных несмещенных
оценок этого коэффициента, т.е. является эффективной оценкой, и в этом
смысле она является оптимальной оценкой этого коэффициента.

96
Часть 1. Основные понятия, элементарные методы
Доказательство теоремы Гаусса — Маркова. Если в = Су —
несмещенная оценка вектора в, т.е. Е(в) = в, то
в= Е(в) = Е{Су) = СЕ{у) = СХв.
Соотношение в= СХв должно выполняться при всех #, поэтому СХ= 1р.
Обозначив В = С- (ХТХ)~1ХТ (матрица размерар х и), получим:
CovF)-CovF) = Cov(Cy-(XTXylXTy) =Cov(By) =
= BCov(y)BT = ст2ВВт = a2 A,
где A=BBT — симметричная матрица размера р х р.
Для любого ненулевого вектора z размерар х 1 имеем:
zTAz = zTBBTz = (BTz)TBTz = wTw > О,
где w = BTz — вектор размера/?xl, так что разность Соу(в) - Cov{6)
является неотрицательно определенной матрицей, что и
требовалось доказать.
Условия, накладываемые на эконометрическую модель в теореме Гаусса —
Маркова, называют условиями Гаусса — Маркова {Gauss-Markov conditions).
Заметим, что эти условия отличаются от стандартных предположений о
нормальной линейной модели с несколькими объясняющими переменными
отсутствием предположения о нормальном распределении случайных ошибок.
Если к условиям Гаусса — Маркова добавить предположение о
нормальном распределении случайных ошибок, то оценка в - (ХТХ)~1ХТу является
наилучшей (в том же смысле) в классе всех несмещенных оценок, а не только
в классе линейных несмещенных оценок. (Доказательство этого утверждения
можно найти в монографии (Рао, 1968).)
Итак, при выполнении условий Гаусса — Маркова оценка наименьших
квадратов #7 коэффициента ^ является несмещенной и эффективной оценкой
коэффициента ffj. Однако, как известно из курса математической статистики,
помимо свойств несмещенности и эффективности, желательно, чтобы оценка
неизвестного параметра обладала еще и свойством состоятельности, т.е.
чтобы при неограниченном увеличении количества наблюдений эта оценка
сходилась по вероятности к истинному значению оцениваемого параметра.
Пусть Х(п) — матрица значений объясняющих переменных в п
наблюдениях, так что Y = Х(п)в + £, и в(п) — оценка наименьших квадратов вектора в
по п наблюдениям.
Утверждение. Пусть для модели Y = Х(п)в + е выполнены условия Гаусса —
Маркова. Если tr \Х{п) Х{п)\ -> 0 при п -> оо (здесь trA — след матрицы А),
то #(w) является состоятельной оценкой вектора в.

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
97
Доказательство. Поскольку матрица Х(п) Х(п) по предположению
является невырожденной, то таковой же является и матрица \Х(п) Х{п)] .
Поэтому р х/7-матрица \Х^п) Xin)J положительно определена. Но тогда все ее
диагональные элементы положительны, и если их сумма, т.е. tr^X(w) Х(п)) ,
стремится к 0, то и каждый из этих элементов стремится к 0 при п -> оо.
В то же время для оценки #jw) коэффициента ^ имеем:
v-l
► ОО
Щв(/п)) = а2(х(п)ТХ{п)) ->0, п-
при каждом j = 1, ..., р. Поскольку при выполнении условий Гаусса —
Маркова EF{jl)) = 6j, можно использовать неравенство Чебышева, из которого
вытекает, что (#jw) -0j)—^—>0, или #jw)—^~—*0j Для всех у = 1, ...,/?. А это
и означает, что #(w) ——>в, т.е. в(п) является состоятельной оценкой вектора в.
Заметим в связи с доказанным утверждением, что для состоятельности #(w)
отнюдь не достаточно, чтобы все диагональные элементы матрицы Xin) X^n)
стремились к бесконечности (см. монографию {Amemiya, 1985)).
Нормальная линейная множественная регрессия:
доверительные интервалы для коэффициентов
Рассматривая нормальную линейную модель множественной регрессии
yi=eiXil+... + 0pXip+£i9 1 = 1,..., Л,
с е{ ~ i.i.d. 7V@, <j2)9 мы установили, что оценка наименьших квадратов Oj
неизвестного истинного значения 6j коэффициента приу-й объясняющей
переменной имеет нормальное распределение, причем
£@,) = 0у, D(ej) = c72(XTX)-j;, у = 1,...,л.
Рассмотрим теперь случайную величину
в*-о,
получаемую путем вычитания из случайной величины 0^ ее математического
ожидания и деления полученной разности на корень из дисперсии в- (т.е. путем
центрирования и нормирования случайной величины 0.). При совершении

98
Часть 1. Основные понятия, элементарные методы
этих двух действии мы не выходим за рамки семейства нормальных
случайных величин и получаем опять нормальную случайную величину, но только
уже с другими математическим ожиданием и дисперсией. Используя
известные свойства математического ожидания и дисперсии, находим:
(
Oj-Oj
1
Щ)) Щ)
(вф-е}-
о,
D
Щ)
d(^.-^.)=i,
так что
~N@,1)9 j = l9...,p.
(Здесь и далее будем употреблять знак «~» для обозначения того, что
случайная величина, стоящая слева от него, имеет распределение, указанное справа.)
Иными словами, в результате центрирования и нормирования случайной
величины 6j получена случайная величина, которая имеет стандартное
нормальное распределение, т.е. нормальное распределение с нулевым
математическим ожиданием и единичной дисперсией. Функцию распределения
и функцию плотности распределения такой случайной величины обозначим
соответственно Ф(г) и cp{z):
<P(z) =
l **• «о-Ыг
72
dt.
Для каждого значения q, 0 < q < 1, определим символом zq число, для
которого 0(z) = q, так что если случайная величина Z имеет стандартное
нормальное распределение, то
?{z<zq\=q.
Как известно, такое число называется квантылью уровня q стандартного
нормального распределения.
Заштрихованная на рис. 2.1 площадь под графиком плотности
стандартного нормального распределения находится правее квантили zq уровня q = 0.95;
эта квантиль равна z095 = 1.645. Поэтому площадь под кривой, лежащая левее
точки z = 1.645, равна 0.95, а заштрихованная площадь равна: 1 - # = 1 - 0.95 =
= 0.05. Последняя величина есть вероятность того, что случайная величина Z,
имеющая стандартное нормальное распределение, примет значение,
превышающее 1.645.

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
99
з z
3 Z
Рис. 2.1
Рис. 2.2
Если взять какое-нибудь число а в пределах от 0.5 до 1 @.5 < а < 1) и вы-
, получится картина, изображенная на рис. 2.2.
делить интервал
2хл> ZXJL ;
V 2 2 J
Из симметрии функции плотности нормального распределения вытекает
равенство площадей областей, заштрихованных на рис. 2.2. Но площадь
правой заштрихованной области равна 1 -
а \ а
1 = —, следовательно, такова же
2) 2
и площадь левой заштрихованной области. Это, в частности, означает, что
вероятность того, что случайная величина Z примет значение, не превышаю-
( \
щее
-z
1— .
2У
а
, равна —, так что
в пределах центрального интервала
2 2
Часть площади под кривой стандартной нормальной плотности, лежащая
г \
-z a9 z „ , меньше 1 на сумму пло-
1— 1—
V 2 2)
щадей заштрихованных областей («хвостов»), т.е. равна:
1 (а аЛ 1
I- —+ — \ = \-а.
[2 2)
Эта величина есть вероятность того, что случайная величина Z, имеющая
стандартное нормальное распределение, примет значение в пределах
указанного интервала1:
Заметим, что в этом и других подобных выражениях знак < можно свободно заменять
знаком < , а знак > знаком > (и обратно), если распределение рассматриваемой случайной
величины имеет плотность.

100
Часть I. Основные понятия, элементарные методы
Pi-z ZZZz
I 2 2 j
= 1-а.
Однако ранее было установлено, что стандартное нормальное
распределение имеет случайная величина
ej-Oj
поэтому для этой случайной величины справедливо соотношение
в, -в:
-Z <
1-2-~
1 у[щё~)
L<z
= \-а.
Таким образом с вероятностью, равной 1 - а, выполняется двойное неравенство
в,-в,
-Z „< / ' <2 „,
Т ^Щ)
т.е.
2 2
Иными словами, с вероятностью, равной 1 - а, случайный интервал
ej-z JE^Jj+z JE0J)
2 2
накрывает истинное значение коэффициента в-. Такой интервал называется
доверительным интервалом для в/ с уровнем доверия (доверительной
вероятностью) 1 - а, или A - а)-доверительным интервалом, или
100A - а)%-м доверительным интервалом для ^ в случае, когда истинное
значение а2 дисперсии случайных ошибок el9..., еп известно.
Последний рисунок был получен при значении а - 0.05. Поэтому площади
а
заштрихованных областей («хвосты») равны — = 0.025, сумма этих
площадей равна 0.05, и площадь области под кривой в пределах интервала
( \
Zx_cr> Z, a
2
2 J
равна 1 - 0.05 = 0.95.
Остается заметить, что z0 975 = 1.960, так что случайный интервал
0j-1.96 Jd0j)9 Oj+1.96 fi{ej)

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
101
является 95%-м доверительным интервалом для 0j. Его ширина
2Л.96JD@j) пропорциональна JDCj) — среднеквадратической ошибке
(среднеквадратическому отклонению) оценки коэффициента Oj.
Хотелось бы, конечно, прямо сейчас построить доверительные интервалы
для коэффициентов линейной модели по каким-нибудь реальным
статистическим данным. Однако этому препятствует то обстоятельство, что в
выражение для дисперсий
D(ej) = <T2(XTX)-jj9 j = l9...9n9
входит неизвестное нам значение а2.
Доверительные интервалы для коэффициентов:
реальные статистические данные
Итак, практическому построению доверительных интервалов для
коэффициентов Oj нормальной линейной множественной регрессии
yi=e\Xi\+ — + epXtp + et> * = !,—,*,
с st ~ lid. 7V@, а2) препятствует вхождение в выражение для дисперсий
D(ej) = (j\xTxy^ j = \,...,n,
неизвестного значения а2.
Единственный выход из этого положения — заменить неизвестное
значение а2 какой-нибудь подходящей его оценкой, которую можно было бы
вычислить на основании имеющихся статистических данных. Такого рода
оценки принято называть статистиками (statistics).
В данной ситуации такой подходящей оценкой для неизвестного значения
<т2 является статистика
2 RSS
Sz =
п- р
п
Это объясняется следующим образом. Поскольку сумма RSS=^(yt-ytJ —
/=i
квадратичная функция от случайных величин е19 ..., £„, она является
случайной величиной, а следовательно, случайной величиной является и
статистика S2. При выполнении стандартных предположений о модели наблюдений
с р объясняющими переменными, включающих нормальность распределения
ошибок, отношение
(n-p)S2 RSS
а2 " а2

102
Часть 1. Основные понятия, элементарные методы
(как случайная величина) имеет такое же распределение, как и сумма
квадратов (п -р) случайных величин, независимых в совокупности и имеющих
одинаковое стандартное нормальное распределение (доказательство можно найти,
например, в учебнике (Магнус,
Катышев, Пересецкий, 2005)).
Распределение такой суммы относится к
стандартным распределениям и
называется распределением хи-квад-
рат с (n-р) степенями свободы.
График функции плотности p(z) этого
распределения при п-р = 15 имеет
вид, изображенный на рис. 2.3.
Для обозначения распределения
хи-квадрат с К степенями свободы
используют символ Z2(K)-
Итак, при сделанных предполо-
(n-p)S2 RSS
£у— = —— имеет распределение хи-квад-
40 z
жениях случайная величина
рат с (n-р) степенями свободы, т.е.
(n~p)S2
~Z2(n~p).
Поскольку у такого распределения математическое ожидание равно (п -р), то
E(S2) = a\
т.е. S2 — несмещенная оценка для а2.
v Замечание 2.2.1. В частном случае р = 1 модель наблюдений
принимает вид:
у(=вх+€19 1 = 1,..., л,
при этомух,..., уп — случайная выборка из распределения N@X, а2).
Несмещенной оценкой для <т2 служит
s2 =
RSS
n-l
Оценкой наименьших квадратов для параметра вх является вх =у,
п
так что RSS = ^(у, - уJ = TSS , и
/=i
Х<и-уJ
S2=^ = Var(y).
n-l

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
103
Таким образом, выборочная дисперсия Variy) переменной у,
получаемая делением TSS именно на (п - 1) (а не на /?), является
несмещенной оценкой для <т2 в модели случайной выборки из
нормального распределения, имеющего дисперсию а2.
Итак, не зная истинного значения а2 и желая построить доверительный
интервал для в., необходимо заменить неизвестное значение
D(ej) = CT2(XTX^
на его несмещенную оценку
i=s2(xTx)z;.
Соответственно вместо отношения
в,-в,
fi>0j)
приходится использовать отношение
%
Однако последнее отношение как случайная величина уже не имеет
стандартного нормального распределения, поскольку в знаменателе теперь не
постоянная, а случайная величина.
Тем не менее распределение последнего отношения совпадает со
стандартным распределением, известным как /-распределение Стьюдента с
(п-р) степенями свободы (доказательство можно найти, например, в
учебнике (Магнус, Катышев, Пересецкий, 2005)).
Для распределения Стьюдента с К степенями свободы принято
обозначение t(K). Квантиль уровня q такого распределения будем обозначать tq(K).
График функции плотности распределения Стьюдента симметричен
относительно 0 и похож на график функции плотности нормального распределения.
Например, при К = 10 он имеет вид, изображенный на рис. 2.4.
Для сравнения на рис. 2.5 приведен график функции стандартного
нормального распределения. Отличие графиков столь невелико, что они почти
неразличимы. Однако квантили этих двух распределений различаются более
ощутимо:
za95 = 1.645, /0Л5A0)= 1.812;
Zo.975= 1.960, /а975A0) = 2.228;
z0.99 = 2.326, t099(l0) = 2-764;
za995 =2.576, /0>995A0) = 3.169;

104
Часть 1. Основные понятия, элементарные методы
Распределение Стьюдента имеет более тяжелые «хвосты». Из
приведенных значений квантилей следует, например, что случайная величина,
имеющая стандартное нормальное распределение, может превысить значение
1.645 лишь с вероятностью 0.05. В то же время с такой же вероятностью 0.05
случайная величина, имеющая распределение Стьюдента с 10 степенями
свободы, принимает значения большие, чем 1.812.
Впрочем, для К>30 используемые обычно квантили распределения
Стьюдента t{K) практически совпадают с соответствующими квантилями
стандартного нормального распределения N@, 1).
Итак,
ё,-е,
^ J-~t{n-p).
Поэтому для этой случайной величины выполняется соотношение
■ = \-а,
9-в-
-t а(п-Р)^~ L^t С(П-Р)
*i,
1-—
2
так что с вероятностью, равной 1 - а, выполняется двойное неравенство
Й — в
-t а{п-р)<-1 L<t (n-p),
Х~2 S6i '
т.е.
0j -t {n-p)se < 0j <9j +/ a {n-p)se
1—
2
Иными словами, с вероятностью, равной I - а, случайный интервал

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
105
Oj-t а(П~Р)^., Oj+t a{n-P)Se
2 2
накрывает истинное значение коэффициента dj9 т.е. является 100A - а)%-м
доверительным интервалом для в; в случае, когда истинное значение а2
дисперсии случайных ошибок еи ..., еп неизвестно. В среднем ширина такого
интервала больше, чем ширина доверительного интервала с тем же уровнем
доверия, построенного при известном значении а2.
V Замечание 2.2.2. Выбор конкретного значения а определяет
компромисс между желанием получить более узкий доверительный
интервал и желанием обеспечить более высокий уровень доверия.
Попытка увеличить уровень доверия 1 - а, выраженная в выборе
меньшего значения а, приводит к квантили t ^{п- р) с более высо-
2
ОС
ким значением 1 , т.е. к большему значению /._«(и - р) • Но шири-
2 2
на доверительного интервала пропорциональна f «(л - р)- Следова-
2
тельно, повышение уровня доверия сопровождается увеличением
ширины доверительного интервала (при тех же статистических данных).
Для (п-р)> 30 можно приближенно считать, что
1 2 2
где zq — квантиль уровня q стандартного нормального распределения.
Соответственно, выбирая уровень доверия 1 - а равным 0.9, 0.95
или 0.99, получаем для t\_An~P) значения, приблизительно рав-
2
ные: z095 = 1.64, z0975 = 1.96, z0995 = 2.58. Это означает, что
повышение уровня доверия от 0.9 до 0.95 сопровождается увеличением
ширины доверительного интервала приблизительно в 1.2 раза, а
дополнительное повышение уровня доверия до 0.99 увеличивает ширину
доверительного интервала еще примерно в 1.3 раза.
Теперь можно перейти к построению интервальных оценок параметров
моделей линейной регрессии для различного рода социально-экономических
факторов на основе соответствующих статистических данных.
ПРИМЕР 2.2.2
Вернемся к модели зависимости уровня безработицы среди белого населения
США от уровня безработицы среди цветного населения. Оценим линейную
эконометрическую модель

106
Часть 1. Основные понятия, элементарные методы
ВЕЦ = 6Х + 61ZVETi + ei9 i = l,..., n.
RSS 0 161231
В результате получим: S2 = = — = 0.010749. Коэффициент 62
/?-2 17-2
оценивается величиной 62 = 0.125265, дисперсия D@2) — величиной
sj =@.062286J. Для построения 95%-го доверительного интервала для в2
остается найти квантиль уровня 1—:— = 0.975 распределения Стьюдента
с 15 (п -р=П - 2) степенями свободы: /0.975A5) = 2.131. Соответственно
получаем 95%-й доверительный интервал для 62\
ё2 -Wi5)^2 <е2 <4 +/0.975(i5)^2,
т.е.
-0.0075 <в2< 0.2580.
Для Эх имеем вх =2.293843, s^ =0.410396. 95%-й доверительный
интервал для вх:
т.е.
ex - wi5)^ <ex <ех +/0<975A5)^,
1.4193 <вх<Ъ. 1684.
В связи с этим примером отметим два обстоятельства.
1. Полученный доверительный интервал для коэффициента 62
допускает как положительные, так и отрицательные значения этого
коэффициента.
2. Каждый из двух построенных интервалов имеет уровень доверия 0.95,
однако это не означает, что с той же вероятностью 0.95 сразу оба
интервала накрывают истинные значения параметров 0l9 Q2.
Разрешить первое затруднение в данном примере можно, например,
понизив уровень доверия до 0.90. В этом случае в выражении для доверительного
интервала квантиль /0.975A5) = 2.131 заменяется на квантиль /095A5) = 1.753,
так что левая граница доверительного интервала для 62 становится
положительной и равной 0.0164. Однако это достигается ценой того, что новый
доверительный интервал будет накрывать истинное значение параметра 62
в среднем только в 90, а не в 95 случаях из 100.
Что касается второго затруднения, то наиболее простой путь взятия под
контроль вероятности одновременного накрытия доверительными
интервалами для 6Х, 92 истинных значений этих параметров связан с тем, что

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
107
Р {оба интервала накрывают вх и в2, соответственно} =
= 1 -Р {хотя бы один из них не накрывает соответствующее 6? =
= 1 - [Р {доверительный интервал для вх не накрывает вх} +
+ Р {доверительный интервал для в2 не накрывает в2} -
- Р {оба интервала не накрывают свои 6?}] =
= 1 - [а + а - Р {оба интервала не накрывают свои в}}] > 1 - а - а =
= 1-2а.
Следовательно, если построить доверительные интервалы для вх и в2
с уровнями доверия I - а*, а* = — для каждого, то правая часть полученной
цепочки соотношений будет равна 1 - 2а - 1 - а.
Это означает, что в нашем примере можно гарантировать, что вероятность
одновременного накрытия истинных значений вх, в2 соответствующими
доверительными интервалами будет не менее 0.95, если возьмем а* = 0.025. Но
тогда при построении этих интервалов вместо значения
/_£a5) = /0.975A5) = 2.131
2
придется использовать
' ,/A5) = ' 0.025 A5) = /0.9875A5) = 2.49,
■-г 1~—
2.49
так что каждый из исходных интервалов увеличится в = 1.17 раза. Это,
конечно, приводит к еще более неопределенным выводам относительно
истинных значений параметров 0l9 в2.
v Замечание 2.2.3. В последующем изложении (в разд. 3) обсуждается
среди прочего вопрос о выборе «наилучшей» модели из нескольких
возможных вариантов. В рамках линейных моделей это может быть
выбор между моделями с большим или с меньшим количеством
объясняющих переменных в правой части. Введение в модель
«лишних» переменных может приводить к неоправданному
возрастанию ширины доверительных интервалов для коэффициентов
при остальных переменных. В то же время использование модели,
в которой пропущены существенные объясняющие переменные, ведет
к смещению оценок, что может перекрывать положительный эффект
от уменьшения их дисперсий.

108
Часть 1. Основные понятия, элементарные методы
ПРИМЕР 2.2.3
Обратимся опять к дефлированным (приведенным к ценам 1972 г.) данным
о совокупном располагаемом доходе (DPI) и совокупных расходах на
потребление (С) в США за период с 1970 по 1979 г. (см. тему 1.3). Оцененная там
линейная модель имеет вид: С = -67.555 + 0.979DPI.
При этом
sp =0.031454, /0975A0-2) = /0975(8) = 2.306,
так что 95%-й доверительный интервал для коэффициента при DPI
0.907 <J3 < 1.052
имеет ширину / = 1.052 - 0.907 = 0.145.
Если исходить не из модели С, = а + j3DPIt + ei9 а из модели С, = PDPIt + st
(соответствующей нулевому автономному потреблению в усредненной
модели связи), то при ее оценивании получим
У? = 0.903, ^ =0.033633, /0975A0-1) = /0975(9) = 2.262,
так что 95%-й доверительный интервал для коэффициента при DPI теперь
имеет вид:
0.895 <р <0.911,
и ширина этого интервала равна: / = 0.911 - 0.895 = 0.016.
Во втором случае ширина доверительного интервала меньше
приблизительно в 9 раз. Однако если в действительности (усредненное) автономное
потребление отлично от 0, то, используя модель пропорциональной связи,
можно сделать неправильные статистические выводы, основываясь на этом
неоправданно узком доверительном интервале. (Заметим в связи с этим, что
гипотеза о том, что в истинной модели порождения данных автономное
потребление равно 0, отвергается при уровне значимости 0.05 — см. пример
3.1.5 в теме 3.1.)
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое регрессионная модель и что понимается под регрессионным анализом?
Что такое уравнение регрессии?
2. Что такое линейная модель множественной регрессии?
3. Что представляет собой нормальная линейная модель множественной регрессии?
Что означают в этом названии термины «линейная», «множественная», «регрессия»?
4. Что называется парной (простой) линейной регрессией? Как такая модель
вкладывается в модель множественной регрессии?
5. В чем заключаются условия Гаусса — Маркова? Чем они отличаются от
стандартных предположений линейной нормальной модели?
6. Что утверждает теорема Гаусса — Маркова?
7. Что следует из теоремы Гаусса — Маркова в отношении оценок отдельных
коэффициентов линейной модели множественной регрессии?

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
109
8. Как строятся доверительные интервалы для коэффициентов нормальной
линейной множественной регрессии? Из каких соображений выбирается уровень
доверия при построении доверительного интервала?
9. Как можно построить доверительные интервалы для нескольких коэффициентов
нормальной линейной множественной регрессии, гарантирующие одновременное
накрытие этими интервалами истинных значений указанных коэффициентов с
вероятностью, не меньшей заданной?
Приложение П-2а
СЛУЧАЙНЫЕ ВЕКТОРЫ И ИХ ХАРАКТЕРИСТИКИ
Под случайным вектором размерности п понимается упорядоченный набор (Х19Х29
..., Xn) n одномерных случайных величин Х19 Х2, ..., Хп9 имеющих некоторое
совместное распределение вероятностей, задаваемое функцией распределения
F(vl9v29...9vn) = P{Xl<vl9X2<v29...9Xn<vn}9 -co<vl9v29...,vn<co.
В первой части учебника рассматриваются в основном случайные векторы, у
которых совместное распределение случайных величин ХХ9Х29 ..., Хп имеет совместную
плотность распределения р(х19..., хп), так что
F{vl9v29...9vn)= J J... Ip(xl9x2,...9x„)dxldx2—dx„.
—00-00 —00
EcnHF{vl9v29...9vJ=P{Xl<vl}.p{X2<v2}.-.p{Xn<vn} = f\F(vj)9
7 = 1
n
p(xl9...9xn) = Y[p(Xj),
7=1
то набор (Xl9 X29 ..., Xn) представляет случайную выборку из распределения F9
имеющего функцию плотности р(х).
Пусть функция распределения F(vl9 v2,..., v„) известна (задана). Тогда:
• для каждогоу,у = 1, ..., п9 становится известной одномерная функция
распределения Fjiyj) = P{Xj <Vj}'9 например, F,(v,) = F(vl9 oo,..., oo). Последней
соответствует/7! (jc, ) — одномерная плотность распределения случайной величины Хх;
• для каждой пары индексов у, к9 1 <j <к<п9 становится известной двумерная
функция распределения Fjk(yj9 vk) = Р{Х; < vj9 Хк < vk}'9 например, Fx 2(vp v2) =
F(vj, v2, oo,..., oo). Последней соответствуетpU2(xx, x2) — совместная плотность
распределения пары случайных величин^ иХ2.
При выводе формул и формулировании результатов часто удобно представлять
случайный вектор как вектор-столбец
х =
1
X,
\XnJ
— \ХХ, X2, ..., Xп )

110
Часть 1. Основные понятия, элементарные методы
Математическое ожидание случайного вектора Х= (Хх, Х2, ..., Хп)Т
определяется как вектор, состоящий из математических ожиданий случайных величин, его
составляющих (конечно, если таковые существуют):
Е(Х)=
Е(Х2)
Математическое ожидание случайного вектора обладает свойствами,
аналогичными свойствам математического ожидания одномерной случайной величины:
• математическое ожидание вектора, компонентами которого являются
неслучайные величины (константы), есть этот же самый вектор;
• математическое ожидание линейной комбинации случайных векторов равно
линейной комбинации математических ожиданий этих случайных векторов
(с теми же коэффициентами). В частности, математическое ожидание суммы
случайных векторов равно сумме их математических ожиданий, а
математическое ожидание произведения случайного вектора X на число равно
произведению этого числа на математическое ожидание вектора Х\
• если случайный вектор Y получен линейным преобразованием другого
случайного вектораХ, так что Y = СХ, где С — матрица с неслучайными элементами, то
E(Y) = CE{X) (постоянную можно выносить за знак математического ожидания).
Важными характеристиками случайного вектораXявляются дисперсии D(XX\ ...,
D(Xn) и ковариации его компонент
CoV(Xj, Хк) = E{Xj -E(Xj) )(Xk -Е(Хк)),
а также коэффициенты корреляции
Cov{Xj,Xk)
rXj,Xk=Corr{Xj,Xk) =
^/z^Vw*)'
\<j,k<n.
Совокупность ковариации Cov(Xj, Хк), 1 <j, к < п, обычно представляют в виде
матрицы
^Cov{X„X,) - Сох{ХиХ„)Л
Cov(X) =
Cov{Xn,X0 - Cov(X„,X„)
которую чаще называют ковариационной матрицей случайного вектора Х9 но
иногда — дисперсионной матрицей вектора X и дисперсионно-ковариационной
матрицей вектораХ, имея в виду, что Cov(Xj9 Xj) = D(Xj), так что на диагонали этой
матрицы расположены дисперсии компонент случайного вектора:
Cov(X) =
D(X{)
Cov(Xn9Xx)
Cov(Xl9Xn)

Раздел 2. Линейная модель наблюдений. Регрессионный анализ
111
Заметим также, что Cov(XJ9 Хк) = Cov(Xk9 Xj), таким образом ковариационная
матрица симметрична. Более того, если ни одна из компонент случайного вектора X не
является линейной комбинацией остальных компонент этого вектора (в которой хотя бы
один из коэффициентов отличен от 0), то ковариационная матрица этого случайного
вектора положительно определена. Последнее означает, что для любого «-мерного
вектора-столбца Z, не все компоненты которого равны нулю, выполняется соотношение
ZTCov(X)Z>0.
Ковариационные матрицы имеют свойства, аналогичные свойствам обычных ко-
вариаций:
• ковариационная матрица вектора, состоящего из постоянных элементов, состоит
из одних нулей;
• ковариационная матрица вектора, являющегося линейной комбинацией
случайных векторов, равна линейной комбинации ковариационных матриц этих
случайных величин (с теми же коэффициентами).
Кроме того, при выводе различных утверждений используется следующее свойство:
• если случайный вектор Y получен линейным преобразованием другого
случайного вектора Jf, так что Y= СХ9 где С— матрица с неслучайными элементами, то
т
Cov(Y)= Cov(CX) = CCov{X)C
Заметим также, что если компоненты случайного вектора X попарно не коррели-
рованы, то в этом случае Cov(X) — диагональная матрица. Если в такой ситуации все
компоненты имеют еще и одинаковую дисперсию D(Xj) = <j29j = 1,..., п9 то
Cov(X) = a2In9
где 1п — единичная матрица размера п х п.
Приложение П-26
МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
По аналогии с плотностью одномерного нормального распределения
1
/
Ж*) = -7==ехР|
л/2;г<72
т.е.
1
2*2<Х~М) ''
р(х) = \1па2) 2ехр
1(х-/1)Т(<Т2Г\х-/4)\,
2
определяется плотность и-мерного нормального распределения
р(х19х2,...9х„) = к 2ехр --(x-//)rL \х-ц) , -оо <х19х29...9хИ <оо , B.3)
где х= (х19х29...9хп)т;
1Л = (//j, //3,..., /лп)т— вектор с постоянными элементами;
X —положительно определенная матрица размера п х п.

112
Часть 1. Основные понятия, элементарные методы
Если Х- (Х}, Х29..., Хп)Т— случайный вектор с функцией плотности B.3), то
£ = B;rydetX;
E(X) = {i, Cov(X) = Z.
При этом говорят, что векторе имеет «-мерное нормальное распределение Nn(/u, Е)
с математическим ожиданием // и ковариационной матрицей Е. Обозначим этот факт
следующим образом:
X~N„(m,I).
Заметим, что если вектор X имеет «-мерное нормальное распределение Nn{fi, Е),
то его компоненты имеют обычное (одномерное) нормальное распределение:
где Еу. — у-й диагональный элемент матрицы Е.
Среди свойств многомерного нормального распределения отметим лишь
наиболее полезные для нашего изложения (ознакомление с другими свойствами
нормального и связанных с ним распределений предусмотрено в заданиях для
самостоятельной работы):
• если Х~ Nn{fu, Е), то Y= Х- /л ~ N„@, Е) (центрирование вектора X);
• если компоненты вектора X, имеющего «-мерное нормальное распределение
Nn{fu, E), являются взаимно независимыми случайными величинами, то в этом
случае ковариационная матрица Е диагональна, если при этом все компоненты
имеют одинаковые дисперсии D(Xj) = Е;у = a2 J = 1,..., и, то
X~N„(fi, аЧп).
В частности, если все компоненты вектора X имеют нулевые математические
ожидания, то
Х~МИ@,<тЧя).
• Если Х~ Nn{/u, Е), а матрица С размера^ х п имеет ранг jp, то
Y=CX~Np(C{i,CI,CT).
(сохранение нормальности при линейных преобразованиях).

Раздел 3
ПРОВЕРКА ГИПОТЕЗ,
ВЫБОР «НАИЛУЧШЕЙ» МОДЕЛИ
И ПРОГНОЗИРОВАНИЕ ПО ОЦЕНЕННОЙ МОДЕЛИ
Тема 3.1
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
О ЗНАЧЕНИЯХ ОТДЕЛЬНЫХ КОЭФФИЦИЕНТОВ
И ОБЩЕЙ ЛИНЕЙНОЙ ГИПОТЕЗЫ
В примере 2.2.2 был построен 95%-й доверительный интервал для
параметра в2 в виде:
в2 - W15)^2 <в2<в2 +/а975A5M4,
т.е.
-0.0075 <в2< 0.2580.
Полученный результат следует интерпретировать следующим образом:
при любом истинном значении параметра в2 вероятность накрытия этого
значения построенным доверительным интервалом равна 0.95.
Рассмотрим значение в2 = 1, построенный интервал его не накрывает.
Однако если в2 действительно равняется 1, то вероятность такого ненакрытия
равна: 1 - 0.95 = 0.05. Таким образом, факт ненакрытия значения в2 = 1
построенным интервалом представляет (в случае, когда в2 = 1) осуществление
довольно редкого события, имеющего малую вероятность 0.05. И это дает
основания сомневаться в том, что в действительности в2 = 1.
То же самое относится и к любому другому фиксированному значению в°2,
не принадлежащему указанному 95%-му доверительному интервалу:
предположение о том, что в действительности в2 - в°2, представляется маловероятным.
Априорные предположения о значениях параметров модели называют
в этом контексте статистическими гипотезами (statistical hypothesis). О базо-

114
Часть 1. Основные понятия, элементарные методы
вой проверяемой гипотезе говорят как об исходной — нулевой (null), ее
обозначают Н0. Таким образом в последнем случае имеем дело с гипотезой
Н0:в2=в2.
В соответствии со сказанным выше такую гипотезу естественно отвергать
(отклонять), если значение в\ не принадлежит 95%-му доверительному
интервалу для #2, т.е. интервалу [-0.0075, 0.2580].
Вспомнив, как этот интервал строился, заметим, что в\ не принадлежит
этому интервалу тогда и только тогда, когда
В 2 ~~ 92
-в2
>/.
0.975
A5),
т.е. когда наблюдаемое значение отношения
и~> — и~>
Ог
«слишком велико» по
абсолютной величине. Последнее означает «слишком большое» отклонение
оценки в2 от гипотетического значения в \ параметра в2 по сравнению
с оценкой Sq2 значения ^D@2) — корня из дисперсии оценки этого параметра.
Итак, будем отвергать гипотезу Н0 : в2 = 6\, если выполнено неравенство
С7л — Uгу
02
>/0>975A5).
C.1)
Однако это неравенство может выполняться и тогда, когда гипотеза Я0
верна, т.е. когда в2 = б\. Вероятность такого события равна: 1 - 0.95 = 0.05.
Следовательно, если в действительности в2 = в°2, но неравенство C.1)
выполняется, то в соответствии с принятым соглашением отвергаем гипотезу Н0
и совершаем при этом ошибку 1-го рода (error of the first kind). Вероятность
ошибки 1-го рода равна здесь 0.05, т.е. такая ошибка происходит в среднем
в 5 случаях из 100.
Если бы мы выбрали произвольный доверительный уровень 1 - а, то
отвергали бы гипотезу Н0 : в2 = в\ при выполнении неравенства
#>-02
%
>', аA5),
и ошибка 1-го рода допускалась в среднем в 100а случаев из 100. Точнее,
вероятность ошибки 1-го рода была бы равна а:
Р{Я0 отвергается | Я0 верна} = а.

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 115
Правило решения вопроса об отклонении или неотклонении статистической
гипотезы Н0 называется статистическим критерием проверки гипотезы
(statistical test of hypothesis) Я0, а выбранное при формулировании этого правила
значение а называется уровнем значимости критерия (significance level),
В практических исследованиях по умолчанию обычно используют уровень
значимости а = 0.05, хотя иногда используют и другие уровни значимости
(например, а = 0.01 или а = 0.10). Выбор большего или меньшего значения а
определяется степенью значимости для исследователя исходной гипотезы
Н0. Скажем, выбор между а = 0.05 и а = 0.01 в пользу а = 0.01 означает, что
исследователь заранее настроен в пользу гипотезы //0, и ему требуются очень
весомые аргументы против этой гипотезы, чтобы отказаться от нее. Выбор же
в пользу уровня значимости а = 0.05 означает, что исследователь не столь
сильно отстаивает гипотезу Н0 и готов отказаться от нее и при менее
убедительной аргументации против этой гипотезы.
Заметим только: если в рассматриваемой ситуации выбираем меньшее
значение а и тем самым уменьшаем вероятность ошибки 1-го рода, то
уменьшаем также и вероятность отвергнуть гипотезу Я0 : в2 = в°2, когда в
действительности в2 = в\ * в°2. Последнюю вероятность называют мощностью (power)
рассматриваемого критерия при альтернативе в2 - в\.
В реальных ситуациях статистические критерии часто имеют довольно
низкую мощность, так что рассматриваемая нулевая гипотеза отвергается
соответствующим критерием довольно редко и в случаях, когда она неверна.
Поэтому если некоторая гипотеза Н0 оказалась не отвергнутой
статистическим критерием, правильнее говорить именно о неотвержении этой гипотезы,
а не о ее принятии.
Всякий статистический критерий основывается на использовании той или
иной статистики (статистики критерия, тестовой статистики — test
statistics), т.е. случайной величины, значения которой могут быть вычислены
(по крайней мере, теоретически) на основе имеющихся статистических
данных и распределение которой известно (хотя бы приближенно).
В нашем примере критерий для проверки гипотезы Н0 : в2 = в\
основывался на использовании /-статистики (t statistic)
02 — в2
se2
значение которой можно вычислить по данным наблюдений, поскольку в\ —
заданное число, а в2 и s$ вычисляются по данным наблюдений. Критерии,
основанные на использовании /-статистик, называют /-критериями (t tests).
Каждому статистическому критерию соответствует критическое
множество (critical region) R значений статистики критерия, при которых гипо-

116
Часть 1. Основные понятия, элементарные методы
теза Я0 отвергается в соответствии с принятым правилом. В нашем примере
таковым является множество значений указанной /-статистики,
превышающих по абсолютной величине значение / „A5).
1 1
Итак, статистический критерий определяется заданием:
а) статистической гипотезы Я0;
б) уровня значимости а;
в) статистики критерия;
г) критического множества R.
Можно подумать, что пункты б) и г) дублируют друг друга, поскольку
в нашем примере критическое множество R однозначно определяется по
заданному уровню значимости а. Однако одному и тому же уровню
значимости можно сопоставлять различные критические множества, что дает
возможность выбирать множество R наиболее рациональным образом — в
зависимости от выбора гипотезы Я0 (выбор наиболее мощного критерия).
В компьютерных пакетах программ статистического анализа данных
первоочередное внимание уделяется проверке гипотезы
Я0: д. = 0
в рамках нормальной линейной модели множественной регрессии
У1=в1Хп+... + врХ(р+£{9 1 = 1 Л,
с et ~ i.i.d. N@, сг2). Эта гипотеза соответствует предположению
исследователя о том, чтоу-я объясняющая переменная не имеет существенного значения
с точки зрения объяснения изменчивости значений объясняемой переменной
у, так что она может быть исключена из модели.
Для соответствующего критерия:
а) Я0: 0у = О;
б) уровень значимости а по умолчанию обычно выбирается равным 0.05;
в) статистика критерия имеет вид:
/ч Л /ч
Ч %'
если гипотеза Я0 : ^ = 0 верна, то эта статистика имеет ^-распределение
Стьюдента с(п-р) степенями свободы:
%
в связи с чем ее обычно называют /-статистикой (t statistic) или
/-отношением (t ratio);

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 117
г) критическое множество имеет вид:
>', М-р)-
2
При этом в распечатках результатов регрессионного анализа (т.е.
статистического анализа модели линейной регрессии) сообщаются:
• значение оценки в} параметра 9j в графе «Коэффициенты» {Coefficients)',
• значение s* знаменателя /-статистики в графе «Стандартная ошиб-
ка» (Std. Error);
п
• значение отношения —— в графе «/-статистика» (t statistic).
Сообщается также Р-значение (P-value), т.е. вероятность того, что
случайная величина, имеющая распределение Стьюдента с (п - р) степенями
свободы, примет значение, не меньшее по абсолютной величине, чем
наблюденное значение
в,
в графе «Р-значение» {P-value или Probability).
В отношении полученного Р-значения возможны следующие варианты.
1. Если Р-значение меньше выбранного уровня значимости а, это
равному
сильно тому, что значение /-статистики -J- попало в область
отвержено
ния гипотезы Я0 : Oj, = О, т.е.
Н0 отвергается.
в.-
> t а (п ~ Р) • В этом случае гипотеза
2. Если Р-значение больше выбранного уровня значимости а, это равно-
сильно тому, что значение /-статистики —— не попало в область от-
вержения гипотезы Н0 : 0j> = 0, т.е.
потеза Н0 не отвергается.
в.-
<t а (п - р). В этом случае ги-
1—
2

118
Часть 1. Основные понятия, элементарные методы
3. Если (в пределах округления) Р-значение равно выбранному уровню
значимости а, то в отношении гипотезы Н0 : в}■- 0 можно принять
любое из двух возможных решений.
В случае, когда гипотеза Я0 : Oj, = 0 отвергается (вариант 1), говорят, что
оценка #у параметра ^ статистически значима или статистически значимо
отличается от нуля (statistically significant estimate). Это соответствует
признанию того, что наличие у-й объясняющей переменной в правой части
модели существенно для объяснения наблюдаемой изменчивости объясняемой
переменной.
Напротив, если гипотеза Я0 : ^ = 0 не отвергается (вариант 2), говорят,
что оценка 0. параметра в} статистически незначима или статистически
незначимо отличается от нуля (statistically non-significant estimate). В этом
случае в рамках используемого статистического критерия мы не получаем
убедительных аргументов против предположения о том, что ^ = 0. Это
соответствует признанию того, что наличиеу-й объясняющей переменной в
правой части модели несущественно для объяснения наблюдаемой изменчивости
объясняемой переменной, следовательно, можно обойтись и без включения
этой переменной в модель регрессии.
В соответствии с вышесказанным гипотезу Н0 : 6^, = 0 часто называют
гипотезой значимости для коэффициента 0j (hypothesis of the statistical
significance of the coefficient 6^ hypothesis that the coefficient 6j is equal to zero).
Впрочем, выводы о статистической значимости (или незначимости)
оценок того или иного параметра модели зависят от выбранного уровня
значимости а. Так, решение в пользу статистической значимости оценки может
измениться на противоположное при уменьшении а, а решение в пользу
статистической незначимости оценки может измениться на противоположное
при увеличении а. Заметим только: выбор уровня значимости следует
производить до обращения к самим статистическим данным, используя
соображения, высказанные выше.
ПРИМЕР 3.1.1
В рассмотренном выше примере с уровнями безработицы в США имеем в
распечатке R2 = 0.212375 и таблицу, полученную на основе протокола
применения метода наименьших квадратов в пакете Econometric Views (табл. 3.1).
Таблица 3.1
Объясняемая переменная BEL
Переменная
1
ZVET
Коэффициент
2.294
0.125
Стандартная
ошибка
0.410
0.062
/-статистика
5.589
2.011
Р-значение
0.0001
0.0626

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 119
В самом протоколе оценивания в пакете Econometric Views результаты
оценивания оформляются в следующем виде (табл. 3.2).
Таблица 3.2
Dependent Variable: BEL
Variable
С
ZVET
Coefficient
2.293843
0.125265
Std. Error
0.410396
0.062286
t-Statistic
5.589344
2.011120
Prob.
0.0001
0.0626
Соответственно при выборе уровня значимости а = 0.05 оценка
коэффициента при переменной ZVET признается статистически незначимой (Р-значе-
ние больше уровня значимости). Однако если выбрать а = 0.10, то Р-значение
меньше уровня значимости, и ту же оценку коэффициента при переменной
ZVET придется признать статистически значимой. ■
ПРИМЕР 3.1.2
При исследовании зависимости спроса на куриные яйца от цены (данные
в табл. 1.7) получаем R2 = 0.513548 и табл. 3.3.
Таблица 3.3
Объясняемая переменная SPROS
Переменная
1
CENA
Коэффициент
21.100
-18.559
Стандартная
ошибка
2.304
5.010
/-статистика
9.158
-3.705
Р-значение
0.0000
0.0026
Здесь оценка коэффициента при объясняющей переменной CENA
статистически значима даже при выборе а = 0.01, так что цена признается
существенной объясняющей переменной. ■
ПРИМЕР 3.1.3
При регрессионном анализе потребления свинины на душу населения США
в зависимости от оптовых цен на свинину (данные в табл. 1.8) получаем
R2 = 0.054483 и табл. 3.4.
Таблица 3.4
Объясняемая переменная CONS
Переменная
1
CENA
Коэффициент
77.484
-24.775
Стандартная
ошибка
13.921
29.794
/-статистика
5.566
-0.832
Р-значение
0.0001
0.4219

120
Часть 1. Основные понятия, элементарные методы
В этом примере оценка коэффициента при переменной CENA оказывается
статистически незначимой при любом разумном выборе уровня значимости
а(а = 0.0\, а = 0.05, а=0Л0).Ш
V Замечание 3.1.1. Ранее отмечалась возможность ложной линейной
связи между двумя переменными и соответственно возможность
ложного использования одной из переменных в качестве
объясняющей для описания изменчивости другой переменной.
Проиллюстрируем такую ситуацию на основе рассмотренных методов
регрессионного анализа.
ПРИМЕР 3.1.4
В числе прочих подобных примеров мы получили модель линейной связи
между мировым рекордом по прыжкам в высоту с шестом среди мужчин
(Я, см) и суммарным производством электроэнергии в США (Е, млрд кВтч).
Было указано на высокое значение коэффициента детерминации для этой
модели: R2 = 0.900. Теперь можно привести результаты регрессионного
анализа (табл. 3.5).
Таблица 3.5
Объясняемая переменная Е
Переменная
1
Я
Коэффициент
-2625.497
7.131
Стандартная
ошибка
420.840
0.841
/-статистика
-6.234
8.483
Р-значение
0.0000
0.0000
Формально переменная Н признается существенной для объяснения
изменчивости переменной Е, так что здесь сталкиваемся с ложной (паразитной)
регрессией переменной Е на переменную Я, обусловленной наличием
выраженного (линейного) тренда обеих переменных во времени. ■
ПРИМЕР 3.1.5
Исходя из примера 2.2.3, обратимся снова к дефлированным (к 1972 г.)
данным о совокупном располагаемом доходе (DPI) и совокупных расходах
на потребление (CONS) в США за период с 1970 по 1979 г. Результаты
регрессионного анализа приведены в табл. 3.6.
Таблица 3.6
Объясняемая переменная CONS
Переменная
1
DPI
Коэффициент
-67.65523
0.979441
Стандартная
ошибка
27.77342
0.031454
/-статистика
-2.435970
31.13836
Р-значение
0.0408
0.0000

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 121
Как и было указано при рассмотрении примера 2.2.3, гипотеза о том, что
постоянная составляющая в модели наблюдений равна нулю, отвергается на
5%-м уровне значимости.■
Проверка значимости параметров линейной регрессии
и уточнение спецификации модели
с использованием F-критериев
В табл. 3.7 приведены ежегодные данные о следующих показателях
экономики Франции за период с 1949 по 1960 г. (млрд франков, в ценах 1959 г.):
Y — объем импорта товаров и услуг во Францию;
Х2 — валовой национальный продукт;
Хъ — совокупное потребление домашних хозяйств.
Таблица 3.7
Показатели экономики Франции с 1949 по 1960 г., млрд франков
Год
1949
1950
1951
1952
1953
1954
Показатель
Y
15.9
16.4
19.0
19.1
18.8
20.4
*2
149.3
161.2
171.5
175.5
180.8
190.7
*з
108.1
114.8
123.2
126.9
132.1
137.7
Год
1955
1956
1957
1958
1959
1960
Показатель
Y
22.7
26.5
28.1
27.6
26.3
31.1
*2
202.1
212.4
226.1
231.9
239.0
258.0
*з
146.0
154.1
162.3
164.3
167.6
176.8
Выберем модель наблюдений в виде:
Уг = &1ХП + e2Xi2 + <V/3 + £/> / = 1,..., 12,
где xfj — значение показателя Xj в /-м наблюдении G-му наблюдению
соответствует A948 + 0-й год, хп = 1 (значения «переменной» Xl9
тождественно равной 1).
Предположим, что el9..., % ~ lid. N@, а2) и значение <т2 нам неизвестно.
При регрессионном анализе получим R2 = 0.9560 и результаты, приведенные
в табл. 3.8.
Обратим внимание на выделенные жирным шрифтом Р-значения. В
соответствии с ними проверка каждой отдельной гипотезы Н0 : 92 = 0, Н0 : въ - 0
(даже при уровне значимости 0.10) приводит к решению о ее
неотклонении. Соответственно при реализации каждой из этих двух процедур проверки

122
Часть J. Основные понятия, элементарные методы
Таблица 3.8
Объясняемая переменная У
Переменная
*
*г
*з
Коэффициент
-8.570
0.029
0.177
Стандартная
ошибка
2.869
0.110
0.166
/-статистика
-2.988
0.267
1.067
Р-значение
0.0153
0.7953
0.3136
оценка соответствующего параметра {в2 или в3) признается статистически
незначимой. И это выглядит противоречащим весьма высокому значению
коэффициента детерминации.
В связи с этим возникает необходимость построения статистической
процедуры для проверки совместной гипотезы
#0 : в2 = въ - 0,
конкретизирующей значения не одного, а сразу двух коэффициентов.
Эта задача вкладывается в общую задачу проверки линейных гипотез
{linear hypotheses) в нормальной линейной модели
M:yi = eixn+... + epxip+si9 i = l,..., л, п>р,
£{,...,£п~иЛЫ{0,ст2),
с целью уточнения спецификации модели. Линейные гипотезы имеют вид:
апвх+... + аХрвр=сх
[aql0l+... + aqpep=cq,
где akj иск(к=19..., q, j = 1,..., р) — заданные числа.
Предполагается, что линейные комбинации в левых частях не дублируют
друг друга, точнее, векторы (ап, ..., аХр)т, ..., (aql9 ..., aqp)T линейно
независимы. В этом случае говорят, что имеется q линейных ограничений {linear
restrictions) на коэффициенты вХ9..., вр (на вектор в- {вх,..., вр)т).
В матричной форме такая линейная гипотеза принимает вид:
где ,4
Н0:Ав=с,
матрица размера {q х р), имеющая полный строковый ранг, гяпкА = q,
А =
tfi
Кая1
4\р
а,
, с =
яру
KC*J

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 123
Если в — оценка наименьших квадратов вектора #, конечно, вряд ли
стоит ожидать, что если гипотеза Я0 : Ав- с верна, то будет выполнено и соот-
ношение Ав = с. Однако можно ожидать, что при этом разность Ав - с
не будет слишком сильно отклоняться от нулевого вектора, так что «слишком
большие» отклонения А в - с от нуля могут указывать на невыполнение
гипотезы Н0 \Ав- с. Для формализации этой идеи заметим: поскольку случайный
вектор в имеет р-мерное нормальное распределение Np(e, cr2(XTX)~x\
случайный вектор Ав - с, получаемый из него линейным преобразованием
и сдвигом, также имеет нормальное распределение, а поскольку rank^ = q,
это будет ^-мерное нормальное распределение. Найдем математическое
ожидание и ковариационную матрицу вектора А в - с:
Е(Ав-с) = АЕ(в)-с = Ав-с,
Соу(Ав-с) = Соу(Ав) = ACov0)AT = а2 А(ХТ X)~l AT.
Если гипотеза Я0 :Ав=с верна, то Е(А в - с) = 0, так что
Ae-c~Nq(o,cr2A(XTXylAT).
Обозначим для краткости V = А(ХТХ)~1АТ. Поскольку cr2V —
ковариационная матрица ^-мерного нормального распределения, матрица V
симметрична и положительно определена. Поскольку матрица V симметрична и
положительно определена, такой же будет и обратная к ней матрица V~\ Но тогда
существует такая невырожденная (п х и)-матрица Р9 что Vх = РТР. Используя
матрицу Р, преобразуем вектор А в - с к вектору
(Ав-с)*=Р(Ав-с).
При этом Е(Ав - с)* = 0 и ковариационная матрица вектора (Ав - с)*
Cov((Ae-cY) = Cov(P(Ae-c)) = PCov(Ae-c)PT =a2PVPT.
Но V= (V~Y = (РТРТ\ так что
Cov((A в-с)*) = а2Р(РтРу1 Рт = ст2РР-{ (Рт )-1 Рт = a2Iq,
(Ae-cy~Nq@9v2Iq).
Таким образом, компоненты вектора (Ав - с)* являются независимыми,
одинаково распределенными случайными величинами, имеющими нулевое
математическое ожидание и дисперсию <т2. Но тогда сумма квадратов этих
компонент, предварительно разделенных на <т, есть сумма квадратов q неза-

124
Часть L Основные понятия, элементарные методы
висимых нормальных величин, имеющих стандартное нормальное
распределение. А такая сумма по определению имеет распределение хи-квадрат
с q степенями свободы. Остается заметить, что указанная сумма квадратов
нормированных на а компонент вектора (А в - с)* равна
-2
|(Л0-с)*|2 =(Т-2\Р(Ав-с)\2 =ст-2[р(Ав-с)]Т [р(Ав-с)]=
-2/ л А „\Т пТ П/ а л „\ —-2/лл Л\Гт/-1/
= ст'\Ав-сУ Р1Р{Ав-с) = а~\Ав-суу-\Ав'-с) =
= (Т-2(Ав-с)т(А(ХтХу1АтУ(Ав-с).
Следовательно,
(Ав-с)т(А(ХтХу1АтУ(Ав-с)
х\чУ
с
При «слишком больших» отклонениях (А в - с) от нуля получаются
и «слишком большие» (положительные) значения последнего отношения.
Таким образом, гипотезу Я0 : Ав= с естественно отклонять, если значения
этого отношения превышают квантиль Х\-а(я) распределения х\яУ гДе а —
выбранный уровень значимости статистического критерия.
Проблема, однако, в том, что значение дисперсии а2 неизвестно
исследователю. Преодолевается это затруднение аналогично тому, как это было
сделано для получения ^-статистики: неизвестное значение а2 заменяется его
несмещенной оценкой S2.
Рассмотрим следующую статистику (F-отношение — F ratio, или F-ста-
тистика — F statistics):
S2
F_(A6-c)T(A(XTXyxATY{Ae-c)lq
Представим ее в виде:
F =
а-2 (Ав- с)т (а(ХтХУ1 Ат)\а6- c)/q
a-2RSS/(n-p)
Если гипотеза Н0 :Ав= с верна, то в числителе этой дроби стоит деленная
на q случайная величина, имеющая распределение х\я\ а в знаменателе —
деленная на (п - р) случайная величина, имеющая распределение х\п ~ Р)-
Можно доказать, что эти две случайные величины независимы
(подробнее см. (Магнус, Катышев, Пересецкий, 2005)). Но тогда по определению
последнее отношение имеет F-распределение Фишера с q и (п - р) степенями
свободы:
F~F(q, n-p).

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 125
На этой основе строится F-критерий (F test) для проверки гипотезы
Я0 : Ав= с в нормальной линейной модели с выполненными стандартными
предположениями:
• при заданном уровне значимости а гипотеза Н0 : Ав- с отвергается,
если наблюдаемое значение статистики F превышает критическое
значение, равное FKp=F{_ a(q, п -р\ т.е. если F>FX_ a(q, n -р).
С указанной F-статистикой связана статистика Вальда (Waid statistic)
w (Ав-с)Т(А(ХТХГ1АТУ(Ав-с)
S2
на основании которой строится критерий Вальда (Wald test) для проверки
гипотезы Н0 : Ав- с. При этом используется тот факт, что при п -> сю
случайная величина S2 сходится по вероятности к <т2. Из этого факта и известной
из курса теории вероятностей теоремы Слуцкого вытекает, что W имеет то же
предельное распределение, что и отношение
(Ав-с)т(А(ХтХ)-1АтУ(Ав-с)
а2
которое, как было сказано выше, имеет распределение х\я)-
При использовании критерия Вальда гипотеза Н0 : А в' = с отвергается,
если выполняется соотношение W > Х\-а(я) • Поскольку критическое значение
Х\-а(я) рассчитывается по предельному при п -> оо (асимптотическому)
распределению статистики W, использование его оправданно при больших
значениях п. Соответственно о критерии Вальда говорят как об асимптотическом
критерии (asymptotic test). В противовес этому F-критерий, рассмотренный
выше, является «точным», неасимптотическим критерием (non-asymptotic
test) — в том смысле, что распределение F-статистики при любом конечном
количестве наблюдений п > р имеет при сделанных предположениях F-pac-
пределение F(q, n -р), соответствующее этому количеству наблюдений.
Таким образом, если выполнена гипотеза Н0 : Ав= с (с q линейными
ограничениями), то статистика
F =
_ (Ав-с)т(А(ХтХу1АтУ(Ав-с)/д
S2
имеет распределение F(q, п - р\ а значит, с вероятностью \ - а выполняется
неравенство
F<Fx_a(q,n-p),
т.е.
(Ae-c)T(A(XTX)-lATY(A3-c)<qS2Fl_a(q9n-p).

126
Часть 1. Основные понятия, элементарные методы
Следовательно, если верна гипотеза
Н0:в1=в?,...,ер=в°р, т.е. Н0:в = в°,
так что q = р и А = 1р (единичная матрица), то тогда с вероятностью 1 - а
выполняется соотношение
(в-во)ТХТХ0-во) < pS2F{_a(p,n-p),
определяющее 100A - а)%-й доверительный эллипсоид для в0 (имеющий
уровень доверия /= 1 - а).
При р = 2 получаем доверительный эллипс для коэффициентов модели.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое статистический критерий? Опишите его структуру.
2. Как формулируется гипотеза значимости для отдельного коэффициента линейной
эконометрической модели? Каким образом проверяется эта гипотеза?
3. Что такое статистически значимая (статистически незначимая) оценка
коэффициента линейной эконометрической модели?
4. Как зависят выводы о статистической значимости (о статистической незначимости)
оценок коэффициентов от выбора уровня значимости статистического критерия?
Чем руководствуется исследователь при выборе уровня значимости
статистического критерия?
5. Какой из двух уровней значимости — а = 0.10 или а = 0.01 — является более
высоким? Как влияет выбор между уровнями значимости а = 0.10 и а - 0.01 на
мощность статистического критерия?
6. Опишите использование ^-критерия для проверки гипотезы о значении отдельного
коэффициента линейной эконометрической модели.
7. Какие основные результаты линейного регрессионного анализа приводятся в
протоколах оценивания?
8. Что такое Р-значение? Какие выводы делаются на основе этого значения при
проверке гипотезы значимости для отдельного коэффициента линейной
эконометрической модели?
9. Означает ли статистическая значимость оценки коэффициента при объясняющей
переменной в линейной эконометрической модели наличие причинной связи между
объясняющей и объясняемой переменными?
10. Какая гипотеза относительно коэффициентов линейной эконометрической модели
называется линейной? Как такая гипотеза представляется в матричной форме?
11. Как выглядит F-отношение (F-статистика) для проверки линейной гипотезы
относительно коэффициентов линейной эконометрической модели? Какое
вероятностное распределение имеет это отношение в случае, когда проверяемая линейная
гипотеза верна и выполнены стандартные предположения о модели?
12. Как выглядит статистика Вальда для проверки линейной гипотезы относительно
коэффициентов линейной эконометрической модели? Чем она отличается от
соответствующей F-статистики? Почему ее применение оправданно только при
большом количестве наблюдений?
13. Как определяется доверительный эллипсоид (доверительный эллипс) для
коэффициентов линейной модели?

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 127
Тема 3.2
ИСПОЛЬЗОВАНИЕ F-СТАТИСТИКИ
ДЛЯ РЕДУКЦИИ ИСХОДНОЙ ЭКОНОМЕТРИЧЕСКОЙ МОДЕЛИ.
ПРОВЕРКА ОДНОСТОРОННИХ ГИПОТЕЗ
Для рассмотренной выше F-статистики, используемой для проверки общей
линейной гипотезы с q линейными ограничениями на коэффициенты, имеется
и более простое выражение:
FJRSSHQ-RSS)/q
RSS/(n-p) '
где RSS — остаточная сумма квадратов в модели наблюдений
М:у, = вххп +... + врх1р + si9 i = 1,..., п
(модель без ограничений — unrestricted model), a RSSH — остаточная сумма
квадратов при оценивании модели, соответствующей гипотезе Я0, т.е.
учитывающей ограничения Ав= с.
Для установления возможности такого представления F-статистики
необходимо прежде всего получить явное выражение для оценки наименьших
квадратов в модели с указанными ограничениями — будем снабжать эту
оценку подстрочным индексом Н0, так что вн — оценка наименьших
квадратов вектора в в модели с линейными ограничениями, заданными
гипотезой Н0 (restricted least squared estimate). Такое выражение можно
получить, минимизируя сумму квадратов
по всем наборам в* = (в*,..., в*р)Т при линейном ограничении А в* = с,
используя метод множителей Лагранжа. В результате получается выражение,
которое можно записать в виде:
вНо =9-{ХтХУхАт(а(ХтХУхАтУ{А9-с) =
= (ХтХу1 Хту - (ХТХУ1 Ат (а(ХтХУх АтУ (а(Хт Хух Хту -с)=
= \{ХтХухХт -{ХТХУХ Ат(а(ХтХУх АтУ А(ХТХУХХт]у +
+(хтхухат(а(хтхухагУс.

128
Часть 1. Основные понятия, элементарные методы
Отсюда, во-первых, вытекает, что если выполнены стандартные
предположения без требования нормальности ошибок, т.е. выполнены условия
Гаусса — Маркова, и гипотеза Н0 :Ав=с верна, то
ЕфНо) = Еф)-{ХТХуит(А(ХТХуитУ{АЕф)-с)=
= в-(ХтХу1Ат(А(ХтХу1АтУ(Ав-с) = в,
так что вн — несмещенная оценка вектора в.
Во-вторых, эта оценка имеет форму:
где В — неслучайная матрица;
d — неслучайный вектор.
Оценка вн является наилучшей несмещенной оценкой такого вида, в
том смысле, что если в — какая-то другая несмещенная оценка вектора в,
имеющая вид в = By + d, то матрица, равная разности CovF) - CovFH ),
является неотрицательно определенной.
Поскольку оценка наименьших квадратов в модели без ограничений
является несмещенной и имеет вид в - (ХтХ)~1Хту = Су, то в принадлежит классу
несмещенных оценок вида в - By + d, в котором оценка вн является
наилучшей. Следовательно, матрица Cov(O) - Cov@H ) является неотрицательно
определенной, и дляу-х компонент векторов оценок в и вн выполняется
соотношение:
D(ej)>D(eHoJ), j = l,...,p.
Остаточная сумма квадратов в модели с ограничениями равна:
RSSHo =
У-ХвнА =(У-^нп)Т(У~ХвНп),
#о>
у#о>
тогда как остаточная сумма квадратов в модели без ограничений равна:
А|2
Q\T,
RSS = \y-Xe\ =(у-Хву(у-Хв).
Можно показать, что
RSSHo-RSS = \y-XeHo\2-\y-Xe\2=\x0-eHo)\2.
Еслид> = Хв и ун =Хвн , то последнее равенство записывается в виде:

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 129
I - I2 I ч2 I- - I2
\У-Ун0\ =\У-У\ + \У-УнЛ >
и это означает просто, что векторы j/ -у и у -ун взаимно ортогональны.
v Замечание 3.2.1. Можно было ожидать, что аналогично последнему
соотношению и соотношению \у\ =\у\ + \у-у\ справедливо и со-
1 I |2 | |2
отношение \у\ = \ун + \у-Ун \ • Однако если с Ф О, то это не так.
При этом отношение
\Уи
может принимать значения, большие 1.
В этом можно убедиться (задание для самостоятельной работы),
рассматривая гипотезу Я0 : вх + в2 = 1 в линейной модели
наблюдений у = Х9+е с р = 2, п = Ъ,
^2] [О 2Л
У =
кЬ
х =
1 3
v3 4y
Итак,
RSSHo -RSS
\Х0-0ноЦ =Ф~вНй)ТХТХ{в-вщ) =
(XTXyxAT{A(XTXyxAT)~\AQ-c)\ x
х ^ГгхГ(ХгХ)-' Ат(а(ХтХ)~1 Ат)'\Ав- сI =
= {Ав-с)т[а(ХтХУх АтУ А(ХтХ)~'ХТХ(ХТХ)~' х
х Ат(а(ХтХ)'1 Ат)'\Аё-с) = (Ав-с)т(А(ХтХу1 Ат)~\а9-с),
что приводит к соотношению
rJRSSHQ-RSS)/q
RSS/(n-p)
В пакетах программ эконометрического анализа среди прочих результатов
оценивания нормальной линейной модели множественной регрессии
с хп = 1 приводятся значения F-статистики, предназначенной для проверки
гипотезы
Я0 : в2 = въ =... = вр = О

130
Часть 1. Основные понятия, элементарные методы
(гипотеза значимости регрессии в целом — hypothesis of overall significance
of a regression, hypothesis that all of the slope coefficients, excluding the constant,
or intercept in a regression are zero).
Это частный случай общей линейной гипотезы, так что соответствующий
статистический критерий основывается на F-статистике
FJRSSHo-RSS)/(p-l)
RSS/(n-p)
где RSS — остаточная сумма квадратов, получаемая при оценивании полной
модели (с р объясняющими переменными, включая
тождественную единицу);
RSSH — остаточная сумма квадратов, получаемая при оценивании модели
с наложенными гипотезой Н0 ограничениями на параметры.
Но последняя (редуцированная) модель здесь имеет вид
yi=ex+ei9 / = 1,...,и,
и применение к ней метода наименьших квадратов приводит к оценке
так что
RSSHa =±{yt -ЛJ = IU -у,У=ш.
/=1 /=1
Следовательно,
р ^ (TSS - RSS)/(p -1) = ESS/(p ~ 1)
RSS/(n-p) RSS/(n-p)'
В некоторых пакетах статистического анализа (например, в Excel) в
распечатках результатов приводятся значения числителя и знаменателя этой
статистики (в графе «Средние квадраты» — mean squares).
Если sl9..., еп ~ i.i.d. N@, <т2), то указанная F-статистика, рассматриваемая
как случайная величина, имеет при гипотезе Н0 (т.е. когда действительно
в2- ...- вр- 0) распределение F(p - 1, п - р\ т.е. F-распределение Фишера
с(р - 1)и(п-р) степенями свободы.
Чем больше отношение ESS/RSS, тем больше есть оснований говорить
о том, что совокупность переменных^* —>Хр действительно помогает в
объяснении изменчивости объясняемой переменной Y.
В соответствии с этим гипотеза
Я0: в2 = въ =... = вр = О
отвергается при «слишком больших» значениях F-статистики, скорее,
указывающих на невыполнение этой гипотезы. Соответствующее пороговое значе-

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 131
ние определяется как квантиль уровня A - а) распределения F(p - 1, п - р),
обозначаемая символом Fx_a(p -\,n -р).
Итак, гипотеза Н0 отвергается, если выполняется неравенство
При этом вероятность ошибочного отвержения гипотезы Я0, когда она
верна (ошибка 1-го рода), равна а.
Статистические пакеты, выполняющие регрессионный анализ, приводят
помимо вычисленного значения F указанной F-статистики и
соответствующее ему Р-значение {P-value, observed level of significance), т.е. вероятность
Р-значение = P{F(p -1, n- p)> F).
Правило отвержения гипотезы Я0 при превышении F-статистикой
порогового уровня Fx_a(p - 1, п -р) соответствует отвержению этой гипотезы при
выполнении неравенства
Р-значение < а.
В частности, в рассмотренном выше примере с импортом товаров и услуг
во Францию вычисленное (наблюдаемое) значение F-статистики очень велико:
F= 97.75, в то время как критическое (пороговое) значение F095B, 9) = 4.26.
Соответственно Р-значение крайне мало — в распечатке результатов
приведено значение 0.000000. Значит, здесь есть весьма убедительные
основания отвергнуть совместную гипотезу Н0 : в2 = въ = 0, хотя каждая из
частных гипотез
Я02 :в2=0, Я03 :в3=0,
рассматриваемая сама по себе, в отрыве от второй, не отвергается.
Подобное положение встречается не так уж и редко и связано с проблемой
мультиколлинеарности данных. Определенное внимание этой проблеме
уделим при рассмотрении темы 3.3.
Для рассмотренных выше примеров результаты использования F-статис-
тики таковы.
ПРИМЕР 3.2.1
Анализ данных об уровнях безработицы среди белого и цветного населения
США приводит к следующим результатам:
R2 = 0.212, F = 4.0446, Р-значение = 0.0626,
так что при выборе а = 0.05 гипотеза Я0 не отвергается, а при выборе а = 0.10
отвергается. ■

132
Часть 1. Основные понятия, элементарные методы
ПРИМЕР 3.2.2
Анализ зависимости спроса на куриные яйца от их цены приводит к
следующим результатам:
R2 = 0.513, F = 13.7241, Р-значение =0.0026,
так что гипотеза Н0 отвергается, а регрессия признается статистически
значимой. ■
ПРИМЕР 3.2.3
При анализе зависимости производства электроэнергии в США от мирового
рекорда по прыжкам в высоту с шестом получены следующие результаты:
R2 = 0.900, F = 71.96, Р-значение =0.0000,
регрессия признается статистически значимой. ■
ПРИМЕР 3.2.4
Анализ потребления свинины в США в зависимости от оптовых цен
приводит к следующим результатам:
R2 = 0.054, F= 0.6915, Р-значение =0.4219,
так что гипотеза Я0 не отвергается даже при выборе а- 0.10.Н
Отметим, наконец, еще одно обстоятельство. Во всех 4 рассмотренных
примерах регрессионного анализа модели простой (парной) линейной
регрессии (р = 2) вычисленные Р-значения F-статистик совпадают с Р-значениями
^-статистик, используемых для проверки гипотезы 02 = 0. Объяснение такого
совпадения будет дано чуть позже.
ПРИМЕР 3.2.5
В табл. 3.9 приведены данные по следующим макроэкономическим
показателям США:
DPI — годовой совокупный располагаемый личный доход;
С — годовые совокупные потребительские расходы;
А — финансовые активы населения на начало календарного года.
Рассмотрим модель наблюдений:
Мг : Ct=ei+e2DPIt+e3At+04DPIt_l+£i, / = 1 11,
где индексу t соответствует A965 + t)-n год. Это модель с 4 объясняющими
переменными:

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 133
Таблица 3.9
Макроэкономические показатели США, млрд долл., в ценах 1982 г.
Год
1966
1967
1968
1969
1970
Показатель
С82
1300.5
1339.4
1405.9
1458.3
1491.8
DPIS2
1433.0
1494.9
1551.1
1601.7
1668.1
AS2
1641.6
1675.2
1772.6
1854.7
1862.2
Год
1971
1972
1973
1974
1975
1976
Показатель
С82
1540.3
1622.3
1687.9
1672.4
1710.8
1804.0
DPIS2
1730.1
1797.9
1914.9
1894.9
1930.4
2001.0
AS2
1902.8
2011.4
2190.6
2301.8
2279.6
2308.4
X,=l, X2=DPI, ХЪ=А, X4=DPI(-l),
где DPI{-\) — переменная, значения которой запаздывают на одну единицу
времени относительно значений переменной DPI, DPI0 = 1367.4.
Оценивание этой модели дает следующие результаты:
§2 = 0.904, Р-значение = 0.0028;
въ = -0.029, Р-значение = 0.8387;
<94 = -0.024, Р-значение = 0.9337;
DCC
RSS = 2095.3, 7SS = 268 835, R2 =\ = 0.9922.
TSS
F-статистика критерия проверки значимости регрессии в целом:
F = 297.04, Р-значение = 0.0000.
Регрессия имеет очень высокую статистическую значимость. Вместе с тем
оценки каждого коэффициента при двух последних переменных
статистически незначимы, так что, в частности, не следует придавать особого значения
отрицательности оценок этих коэффициентов.
Используя ^-критерий, можно попробовать удалить из модели одну из двух
последних переменных и, если оставшиеся переменные окажутся значимыми,
остановиться на модели с 3 объясняющими переменными. Если же и в новой
модели окажутся статистически незначимые переменные — произвести еще
одну редукцию модели.
Рассмотрим в связи с этим модель:
М2 : Ct=ei+e2DPIt+e3At+si, / = 1 11,

134
Часть 1. Основные понятия, элементарные методы
с удаленной переменной DPI(-l). Для нее получим:
в2 = 0.893, Р-значение = 0.0001;
03 = -0.039, Р-значение = 0.6486;
RSS = 2098.31, R2 = 0.9922.
F-статистика критерия проверки значимости регрессии в этой модели
F = 508.47, Р-значение = 0.0000.
Поскольку здесь остается статистически незначимой оценка
коэффициента при переменной Ап можно произвести дальнейшую редукцию, перейдя
к модели
М3 :Ct=el+02DPIt+ei9 / = 1,...,11.
Для этой модели
02 = 0.843, Р-значение = 0.0000;
RSS = 2143.57, R2 = 0.9920.
F-статистика критерия проверки значимости регрессии в этой модели
F = 1119.7, Р-значение = 0.0000,
и эту модель в данном контексте можно принять за окончательную.
Вместе с тем, обнаружив при анализе модели М{ (посредством
применения ^-критериев) статистическую незначимость оценок коэффициентов при
двух последних переменных, можно попробовать выяснить возможность
одновременного исключения из этой модели указанных объясняющих
переменных, используя соответствующий F-критерий.
Исключение двух последних переменных из модели М^ соответствует
гипотезе
Н0: в3 -9А =0,
при которой модель Mj редуцируется сразу к модели М3. Критерий проверки
гипотезы Я0 основывается на статистике
F_(RSSHo-RSS)/q
RSS/(n-p) '
где RSS — остаточная сумма квадратов в модели М,;
RSSH — остаточная сумма квадратов в модели М3;
q - 2 — количество зануляемых параметров;
п-р=\\-4 = 7.

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 135
Для наших данных получаем
F = B143.57 -2095.3)/2^00g
2095.3/7 ' '
это значение следует сравнить с критическим F095B, 7) = 4.74. Поскольку
F < F095B, 7), не отвергаем гипотезу Я0 : въ - в4 = 0 и можем сразу перейти
от модели Mj кМ3.1
v Замечание 3.2.2. В рассмотренном примере мы действовали двумя
способами:
• дважды использовали F-критерии (эквивалентные ^-критерию),
сначала не отвергнув гипотезу Н0 : в4 - 0 в рамках модели Mj,
а затем не отвергнув гипотезу Я0 : въ - 0 в рамках модели М2;
• однократно использовали F-критерий, не отвергнув гипотезу
Н0 : въ = в4 = 0 в рамках модели М{.
Выводы при этих двух альтернативных подходах оказались
одинаковыми. Однако в общем случае из выбора модели М3 в подобной
последовательной процедуре, вообще говоря, не следует, что такой
же выбор будет обязательно сделан и при применении F-критерия,
сравнивающего первую и последнюю модели1. Заметим в связи с этим,
что вероятность ошибочного отвержения гипотезы Н0 : въ - в4 = 0
в результате применения последовательной процедуры
тестирования с уровнями значимости а не равна а. В рамках
рассмотренной процедуры приходится, по крайней мере, сначала проверять
гипотезу Нх : в4 = 0 в рамках модели Мх, а затем, если она не
отвергается, проверять гипотезу Я2 : въ = 0 в рамках модели М2. Пусть
каждая из этих гипотез в отдельности проверяется на уровне
значимости а. Тогда:
Р {ошибочно отвергается Я0} =
= Р {ошибочно отвергается хотя бы одна из гипотез НиН2} > а
(происходит накопление вероятности ошибки первого рода),
Р {ошибочно отвергается Н0} =
= Р {ошибочно отвергается хотя бы одна из гипотез НиН2} <
<Р {ошибочно отвергаетсяНх) +Р {ошибочно отвергаетсяН2} =
= а + а-2а.
Вопрос о сравнении получаемых альтернативных моделей с точки зрения выбора среди
них «наилучшей» модели обсудим в теме 3.3.

136
Часть 1. Основные понятия, элементарные методы
Следовательно, если для такой последовательной процедуры
зададим результирующий уровень значимости а*, то можем обеспе-
а* ^
чить его, положив а - —. (Соответственно если последовательная
процедура проверок предполагает наличие К шагов, то уровень зна-
*
ее
чимости а* обеспечивается, если положить а-—.) Например,
К
если а* = 0.05, то в нашей потенциально двухшаговой процедуре
достаточно взять а= 0.025. Это гарантирует вероятность ошибочного
отвержения гипотезы Н0 в пределах от 0.025 до 0.05. Реальная
вероятность ошибочного отвержения гипотезы Н0 может быть ближе
к нижнему пределу, так что указанная процедура оказывается
консервативной: гипотеза Н0 отвергается при а = 0.025 с вероятностью
меньшей, чем заданный уровень значимости 0.05 («более редко»).
Остановимся отдельно на ситуации, когда q = 1, но линейная гипотеза
затрагивает более одного коэффициента, например, когда
Мы уже знаем представление
р = (RSSHq -RSS)/q = (Ав-с)Т[А {Хт Х)~х Ат у\Ав - с)
RSS/(n-p) qS2
Пусть линейная гипотеза имеет вид Я0 : Ав- с, где А = (яп, ..., а1р)9 т.е.
q-\. Тогда (Ав - с) и [^(ХГХ)_1^Г] — скалярные величины, поэтому
выражение для F-статистики можно записать в виде:
F_ (Ав-сJ
S2[A(XTXylAT]'
Иначе говоря, в рассматриваемом случае F-статистика равна квадрату
статистики:
,= (АО-с)
S[A(XTXylAT]l/2 '
Последняя же имеет при гипотезе Н0 : Ав- с, q = I (и при выполнении
стандартных предположений нормальной линейной модели), ^-распределение
Стьюдента с(п-р) степенями свободы.
Таким образом, в случае q = 1 для проверки линейных гипотез можно наряду
с F-критерием использовать ^-критерий, основанный на приведенной
^-статистике. Это обстоятельство оказывается важным в ситуациях, когда приходится
иметь дело с односторонними гипотезами. Об этом будет сказано в примере 3.2.7.

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 137
Теперь вернемся к наблюдавшимся совпадениям Р-значений при проверке
гипотезы значимости регрессии в модели парной регрессии. Там как раз
q = 19 так что если наблюдается некоторое значение t* ^-статистики,
используемой для проверки гипотезы /3 = 0, и этому значению соответствует Р-зна-
чение Р*9 вычисленное по распределению Стьюдента с (п - 2) степенями
свободы, то при этом будет наблюдаться значение F = f1 F-статистики,
используемой для проверки гипотезы значимости регрессии, и вычисленное для него
по распределению F(l, п - 2) Р-значение совпадает с Р*.
Проверка односторонних гипотез
о значениях коэффициентов:
односторонние критерии
Вспомним пример с потреблением текстиля. Мы подобрали линейную модель
в десятичных логарифмах (с постоянными эластичностямиI
lgT = 1.3739 -0.8289 lgP + 1.1432 lgDP/,
где Т — расходы на личное потребление текстиля;
Р — относительная цена текстиля;
DPI — располагаемый доход.
В рамках этой модели представляют, в частности, интерес гипотезы
Н0: в2 = -\ ^Н0\ въ = \ о единичной эластичности расходов на потребление
текстиля по доходу и по цене.
Построить критерии с уровнем значимости а для проверки этих гипотез
можно по той же схеме, по которой строятся критерии проверки гипотез
Я0: dj = 0. Только теперь для проверки гипотезы Я0: в2 = -1 следует
использовать ^-статистику
ег -(-1)_ 4+1
а для проверки гипотезы Я0: въ = 1 — ^-статистику
% '
Каждая из этих статистик в случае справедливости соответствующей
нулевой гипотезы (и, конечно, при выполнении стандартных
предположений о модели) имеет распределение t{n-p) = t(\4). При использовании
обычного уровня значимости а - 0.05 нулевая гипотеза отвергается, если
значение ^-статистики превышает по абсолютной величине критическое значе-
Здесь оставляем у оценок 4 десятичных знака, а не 3 (как ранее).

138
Часть 1. Основные понятия, элементарные методы
ние t «_A4) = t0975 A4) = 2.145 . Если нулевая гипотеза верна, то, исполь-
2
зуя это правило, можно ошибочно отвергнуть ее с вероятностью 0.05,
допустив ошибку 1-го рода.
В нашем примере:
4+1 -0.8289 + 1 АПЛЛ ^,АС
-^ = = 4.740 > 2.145,
S* 0.0361
iz! = i!«2zi = o.9,8<2.,45.
S. 0.1560
Таким образом, отклонение значения 02 от гипотетического значения в2--\
статистически значимо — гипотеза Н0 : в2 = -1 отвергается. В то же время
отклонение значения въ от гипотетического значения в3 = 1 не является
статистически значимым, и гипотеза Н0 : 0Ъ - 1 не отвергается.
Замечание 3.2.3. Как видим, важны не только абсолютные значения
отклонений оценок 6j от гипотетических значений параметров в., но
и точности оценок в., измеряемые их дисперсиями D@j) и
оцениваемые величинами s§.. Действительно, абсолютные величины
отклонений в рассмотренном примере равны:
1-0.8289 + 1| = 0.1711 и |1.1432 - 1| = 0.1432
соответственно, т.е. отличаются не очень существенно. Однако s§2
примерно в 4.3 раза меньше, чем s§ , и именно такое большое
отличие s§ от s§ и приводит, в конечном счете, к противоположным
решениям в отношении гипотез Я0 : в2 = -1 и Я0 : въ = 1.
Итак, на основании построенной процедуры гипотеза Я0 : в2 = -1
отвергается. А что же тогда принимается?
Формально альтернативой для Н0 : в2 = -1 в построенном критерии
является гипотеза Н0 : в2 Ф -1, поскольку критическое множество содержит в
равной степени как большие положительные, так и большие (по абсолютной
величине) отрицательные значения ^-статистики —— . В то же время значе-
%
П , 1
ние — = 4.740, соответствующее отклонению в2 - (-1) = 0.1711, скорее,
говорит в пользу того, что в действительности в2>-\.

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 139
В связи с этим естественным представляется более определенный выбор
альтернативной гипотезы, а именно сопоставление нулевой гипотезе Я0 : в2 - -1
односторонней альтернативы НА : в2 > -1 (односторонняя альтернатива —
в отличие от двусторонней альтернативы Я0 : в2 Ф -1). При такой постановке
задачи отвержение нулевой гипотезы Я0 : в2 = -1 в пользу альтернативы
НА : в2 > -1 производится только при больших положительных
отклонениях в2 - (-1), т.е. при больших положительных значениях ^-статистики. Если
к последним отнесем значения, превышающие ^_аA4) = t095(l4) = 1.761,
получим статистический критерий, у которого ошибка 1-го рода (уровень
значимости) равна 0.05. Его критическое множество определяется соотноше-
в +1
нием —— > 1.761; справа теперь — значение 1.761, а не 2.145, как было при
в +1
двусторонней альтернативе. Поскольку у нас — = 4.740, отвергаем гипо-
%
тезу Я0 : в2 - -1 в пользу гипотезы НА : в2>-\.
Построим аналогичную процедуру для параметра в2. А именно построим
критерий уровня 0.05 для проверки гипотезы Я0 : въ - 1 против
односторонней альтернативы Я0 : въ > 1. Критическое множество такого критерия
должно состоять из значений ^-статистики, превышающих t095(l4) = 1.761. У нас
3—1
значение — = 0.918 < 1.761 опять меньше порогового, так что гипотеза
%
Я0 : #з = 1 не отвергается в пользу Я0 : въ > 1.
Обратим внимание на то, что при рассмотрении пары конкурирующих
гипотез
Яо:03=1, НА:в3>1
в гипотезу Я0 выделяется только одно частное значение въ = 1, хотя, по
существу, проблема состоит, скорее, в выборе между гипотезами
Я0 :0<в3<\, НА:въ>\.
Последняя ситуация коренным образом отличается от предыдущей: Я0
оказывается сложной гипотезой {composite hypothesis), т.е. гипотезой,
допускающей более одного значения параметра, в данном случае — даже
бесконечно много значений параметра в3. В противоположность этому в
предыдущей ситуации гипотеза Я0 была простой (simple hypothesis).
Какие трудности возникают при использовании сложной нулевой
гипотезы?

140
Часть 1. Основные понятия, элементарные методы
Возьмем для примера частную гипотезу Н0 : в3 = 0.5. Мы отвергли бы ее
в пользу НА : въ > 1 при
t^>,095A4) = 1.761.
%
В то же время частную гипотезу Н0 : въ = 1 отвергаем в пользу той же
НА : #, > 1 при
tl>,095A4) = 1.761.
%
Иначе говоря, при различных частных гипотезах, входящих в состав
сложной нулевой гипотезы Я0 : 0 < въ < 1, получаем различные критические
множества, обеспечивающие заданный уровень значимости (ошибку 1-го рода)
0.05. При построении каждого такого множества непосредственно
используется конкретное гипотетическое значение въ = #3°> Т0ГДа как в рамках
гипотезы Н0 : 0 < въ < 1 отдельное гипотетическое значение параметра въ не
конкретизируется.
Возникающее затруднение можно преодолеть следующим образом. Так как
нельзя построить единое для всех 0 < въ < 1 критическое множество,
вероятность попадания в которое равна а = 0.05 при справедливости каждой
отдельной частной гипотезы, следует попытаться построить единое для всех 0 < въ < 1
критическое множество, вероятность попадания в которое при выполнении
каждой отдельной частной гипотезы была бы не больше а = 0.05. Такая задача
решается путем использования критического множества, соответствующего
граничному значению односторонней гипотезы, в данном случае в3 = 1.
в —1
Действительно, пусть выбрано критическое множество —— > 1.761, соот-
%
ветствующее граничной частной гипотезе въ = 1, так что
pJ^—U 1.7611 = 0.05.
К J
Тогда если в действительности верна частная гипотеза въ - 0.5, то
А-0.5 0.5
^—->1.761|А=0.5
= РГ3 """М.761 + —1&=0.51-<
e-i
Sh
<Р
^±1> 1.7611 ^з=0.5
= 0.05.

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 141
Вообще, какая бы частная гипотеза 0Ъ - #3° @ < 03° - 1) ни была верна,
вероятность отвергнуть ее в рамках указанной процедуры не превысит 0.05.
В этом контексте а = 0.05 по-прежнему называется уровнем значимости
критерия, тогда как понятие ошибки 1-го рода уже теряет смысл для
критерия в целом. Уровень значимости ограничивает сверху ошибки 1-го рода,
соответствующие частным гипотезам, входящим в состав сложной нулевой
гипотезы.
Из сказанного можно сделать основной вывод: при указанном подходе
к построению критериев проверки сложных нулевых гипотез вида
Я0 : 0j < -1 (гипотеза эластичности при 0j < 0),
Я0 : -1 < 0j < 0 (гипотеза неэластичности при 0j < 0),
Я0 : 0 < 0j < 1 (гипотеза неэластичности при 6? > 0),
Я0 : 0j > 1 (гипотеза эластичности при 0j > 0)
против соответствующих односторонних альтернатив можно пользоваться
критериями уровня а, построенными для работы с теми же альтернативами,
но при простых гипотезах 0. = -\9 0}, = -1, 0.. = 1, 0}г = 1 соответственно.
V Замечание 3.2.4. То же относится и к другим аналогичным парам
гипотез, в которых вместо значений 1 или -1 берутся иные
фиксированные граничные значения.
Некоторые проблемы, связанные с проверкой гипотез
о значениях коэффициентов
Итак, фактически уже построен критерий для проверки гипотезы
Я0: 02<-\
против альтернативы
НА : -1 < 02 < 0.
Это тот же критерий с уровнем значимости 0.05, который был
предназначен для проверки гипотезы Я0 : 02 = -1 против альтернативы НА : 02 > -1. Такой
критерий отвергает гипотезу Я0 при
А±!>1.761,
что и имеет место в нашем примере. Соответственно нулевая гипотеза
эластичности потребления текстиля по цене отвергается.
Также фактически построен критерий для проверки гипотезы
Яп : 0 < А < 1

142
Часть 1. Основные понятия, элементарные методы
против альтернативы
НА:в3>1.
Это тот же критерий с уровнем значимости 0.05, который был
предназначен для проверки гипотезы Я0 : в3 - 1 против альтернативы НА : в3 > 1. Такой
критерий отвергает гипотезу Я0 при
&Z!> 1.761,
что не выполняется в нашем примере. Соответственно нулевая гипотеза
неэластичности потребления текстиля по доходу не отвергается.
Представляет, однако, интерес то, какие решения будут приняты, если
поменять местами нулевую и альтернативную гипотезы.
В отношении эластичности по цене возьмем теперь пару гипотез
Я0:-1<#2<0, НА:в2<-\.
При построении соответствующего критерия достаточно обратиться к
критерию для пары
Но '• вг = _Ь НЛ : в2 < -1,
который отвергает гипотезу Я0 при
^±1<,аA4) = /а05A4) = -1.761
(на левом «хвосте» распределения 7A4)). Но у нас
А±1»о.
так что гипотеза Я0 : в2 = -1, а значит, и Я0 : -1 < в2 < 0, не отвергаются
в пользу НА : в2 < -1.
Итак, здесь нулевая гипотеза о неэластичности потребления по цене не
отвергается, и это решение согласуется с отклонением нулевой гипотезы об
эластичности потребления по цене.
Рассмотрим, наконец, пару гипотез
Н0:в3>\, НА:0<в3<1.
Здесь исходим из критерия, предназначенного для пары
Щ : #з = Ь Нл : ^з < Ь
и отвергаем гипотезу Н0 : в3> I при
^£/вA4) = Г0Ю5A4) = -1.761.
5*3

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 143
В нашем случае
^—- = 0.918 > -1.761,
%
так что гипотеза Н0 : в3 > 1 не отвергается.
Итак, здесь нулевая гипотеза об эластичности потребления по доходу не
отвергается. Однако ранее было установлено, что и нулевая гипотеза о
неэластичности потребления по доходу также не отвергается. Таким образом,
имеем конфликт критериев (conflict among testing procedures).
Из рассмотренного примера можно сделать важнейший вывод.
Решения об отклонении или неотклонении одной из двух соперничающих гипотез
могут быть различными в зависимости от того, какая из двух гипотез принимается
за основную (нулевую).
При решении вопроса о характере зависимости потребления текстиля от его
относительной цены оба варианта выбора нулевой гипотезы дали
согласованные результаты: нулевая гипотеза неэластичности не отвергается, а
нулевая гипотеза эластичности отвергается.
Однако при решении вопроса о характере зависимости потребления
текстиля от располагаемого дохода не отвергаются ни нулевая гипотеза
эластичности, ни нулевая гипотеза неэластичности. В такой ситуации каждый из
исследователей, придерживающихся противоположных априорных позиций
относительно эластичности или неэластичности потребления текстиля по
доходу, может считать, что имеющиеся статистические данные «подтверждают»
именно его гипотезу, хотя правильнее заключить, что имеющиеся
статистические данные «не противоречат» его гипотезе в рамках соответствующего
статистического критерия.
Необходимо сделать еще одно важнейшее замечание. Пусть
Н0: 0j< #0, HA: 6j> в0.
Тогда ^-статистика критерия равна:
%
Гипотеза Н0 отвергается в пользу НА, если
в,-в0
-J—L>ti-ain-p).
Но tx_a(n -р)>0 при а < 0.5, и это означает, что если 6j < #0, то гипотеза
#0 не может быть отвергнута в пользу НА.

144
Часть 1. Основные понятия, элементарные методы
Следовательно, если сначала оценить по имеющимся статистическим
данным коэффициент 6j и только после этого выбрать указанную пару гипотез
для некоторого значения в0 > #у, то в такой ситуации построенный по тем же
данным указанный ^-критерий никогда не отвергнет гипотезу Я0 в пользу НА.
Аналогично если, оценив 0J9 формулируем пару гипотез
Я0 : dj > в0, НА: fy < в0.
для некоторого в0 < 6j9 то соответствующий односторонний ^-критерий,
построенный по тем же данным, никогда не отвергнет гипотезу Я0 в пользу НА.
В случае двустороннего ^-критерия
*/-<%
Ч
>Ч-а(П~Р)
формулирование гипотезы Я0 : 9}• - 0О с в0 = #у, где #у — оцененное
значение параметра 0J9 приводит к тому, что эта гипотеза заведомо не будет
отвергнута (^-статистика принимает нулевое значение).
Логическая ошибка в последних трех случаях состоит в том, что теория
статистических критериев строится в предположении, что гипотезы Я0 и НА
фиксируются до обращения к статистической обработке данных.
При таком предположении нельзя абсолютно точно сказать априори, будет
значение #у больше или меньше заранее выбранного гипотетического
значения в0.
ПРИМЕР 3.2.6
Пусть С — совокупные расходы на личное потребление в США, Y —
совокупный располагаемый доход A970—1979 гг., млрд долл. в ценах 1972 г.).
Ранее для этих данных получена модель
С = -67.655 + 0.9797.
Уже зная, что в2 = 0.979, бессмысленно (или нечестно) ставить задачу
проверки гипотезы Я0 : в2 < 1 против альтернативы НА : в2 > 1, поскольку
на основании имеющихся наблюдений гипотеза Я0 заведомо не будет
отвергнута. Она отвергается лишь при больших положительных значениях 7-ста-
4-1
тистики ——, а у нас числитель последнего отношения принимает отрица-
тельное значение. Другое дело, что сформулировать такую гипотезу еще до
анализа статистических данных вполне разумно. Впрочем, последнее вовсе
не означает, что в2 будет всегда меньше 1, даже если истинное в2 < 1.

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 145
Проверим теперь гипотезу Я0 : в2 = 0.9 против односторонней
альтернативы Я0 : в2 > 0.9 в той же ситуации, но на основании данных за период с 1970
по 1981 г., п= 12 лет.
В этом случае в2 = 0.952, s§ = 0.0261, так что /-статистика
0,-0.9 0.052
/ = -
о2
0.0261
= 1.99.
Если для проверки гипотезы Я0 использовать двусторонний /-критерий
с уровнем значимости а = 0.05, то будем отвергать Я0, когда
M>U=WW) = 2.228.
Если же использовать односторонний /-критерий с уровнем значимости
а = 0.05, то будем отвергать Я0, когда
t>tcrit=t095(lO) = lM2.
В обоих случаях вероятность ошибочного отклонения гипотезы Я0 равна 0.05.
Представим теперь, что в действительности в2 - 0.95. Тогда
распределение Стьюдента /A0) имеет статистика
4-0.95
Какова вероятность того, что гипотеза Я0 будет отвергнута?
При использовании двустороннего критерия:
Р{| t\ > 2.228 \в2 =0.95} =Р
в2-0.9
%
> 2.228 |02=О.95
= Р\\02 -0.9 |> 2.228*^ | в2 =0.95} = Р\в2 -0.9 <-2.228s^
или в2 -0.9 > 2.228s^ \ в2 = 0.95} = р{в2 -0.95 + 0.05 < -2.228s^
или в2 - 0.95 + 0.05 > 2.2285^ | в2 = 0.95} = Р\
^о^<_2.228_о^
вг
<h
или
0, -0.95
в2
> 2.228-
0.05
h
02=О.95 \ =
= Р{((Щ<-4Л4

146
Часть 1. Основные понятия, элементарные методы
или fA0) > 0.312} = P{fA0) < -4.14} + Р{^A0) > 0.312} =
= 0.001006 + A-0.619276) = 0.3817.
А при использовании одностороннего критерия эта вероятность будет
равна:
/>{f>1.812|02=O.95}=pi
^—^ > 1.812 \в2 =0.95
= pKz2^>L8i2-Ml|el=o.95 =P{KlO)>-0.104} =
I 'к % \
= 1 -P{t(l 0) < -0.104} = 1 -0.4596 = 0.5404.
Таким образом, вероятность отвергнуть ошибочную гипотезу Н0 : в2 = 0.9
в случае, когда в действительности в2 - 0.95, равна:
0.3817 — при использовании двустороннего критерия,
0.5404 — при использовании одностороннего критерия.
Две последние величины представляют собой мощности соответствующих
критериев при частной альтернативе в2 = 0.95.
Односторонний критерий имеет более высокую мощность @.5404 против
0.3817 у двустороннего критерия) при той же вероятности ошибочного
отклонения нулевой гипотезы, равной 0.05. Такое же положение будет, если в
действительности в2 = в\ и значение в\ входит в множество значений
параметра #2, составляющих альтернативную гипотезу НА : в2 > 0.9 (т.е. в\ > 0.9).
Это говорит о предпочтительности одностороннего критерия по сравнению
с двусторонним при использовании в качестве альтернативной гипотезы
НА:в2> 0.9.И
Рассмотренные выше односторонние гипотезы были связаны со
значениями только одного из коэффициентов. Между тем в ряде случаев
возникает задача проверки односторонних гипотез, связанных сразу с несколькими
коэффициентами.
Мы уже обращались к производственной функции Кобба — Дугласа
Y = AKaLfi9
где а — эластичность выпуска по капиталу;
Р — эластичность выпуска по труду.

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 147
Если а + E > 1, то имеется эффект масштаба, выражающийся в наличии
дополнительной отдачи от возрастания масштабов производства. Для
выяснения наличия такого эффекта приходится иметь дело с парой односторонних
гипотез
#0 :а + /3<1, НА :а + 0>\,
затрагивающих пару параметров аиДис двойственной к ней парой
#0 :« + /?> 1, НА : а + Р<\.
Пусть модель наблюдений имеет вид:
у(=в{хп+... + врхф+£19 / = 1,..„л, ь-иЛ #@,сг2),
есть только одно линейное ограничение на коэффициенты (q = 1), но
линейная гипотеза затрагивает более одного коэффициента, например:
Hq : в2 + $з = 1 •
Пусть эта линейная гипотеза имеет вид Н0:Ав = с, где >4 = (ахх,..., аХр).
Ранее уже говорилось, что в таком случае статистика
(Ав-с)
* = —г
s[i(XTXylAT]2
имеет при гипотезе Н0: А в = с, q = 1 (и при выполнении стандартных
предположений нормальной линейной модели), ^-распределение Стьюдента с (п - р)
степенями свободы. Но тогда можно обычным образом использовать эту
статистику для проверки односторонних гипотез в парах
Н0:Ав<с, НА:Ав>с,
или
Н0:Ав>с, НА :Ав<с,
ПРИМЕР 3.2.7
Рассмотрим данные о производстве продукции сельского хозяйства в Тайване
в период с 1960 по 1972 г. (табл. 3.10). Здесь Y— объем произведенной
продукции (млн новых тайваньских долл.); К — затраты капитала; L —
количество отработанных человеко-дней (млн).
Используем производственную функцию Кобба — Дугласа и перейдем к
логарифмам задействованных в ней переменных, получим модель
наблюдений в виде:
1п^.=1пЛ + а1п^/+/Ип1/+£/, i = l,..., 13.
Оценивание этой модели приводит к следующим результатам (табл. 3.11).

148
Часть 1. Основные понятия, элементарные методы
Таблица 3.10
Производство продукции сельского хозяйства в Тайване с 1960 по 1972 г.
Год
1960
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
1972
Y
20171.2
20932.9
20406.0
20831.6
24806.3
26465.8
27403.0
28628.7
29904.5
27508.2
29035.5
29281.5
31535.8
К
269.7
267.0
267.8
275.0
283.0
300.7
307.5
303.7
304.7
298.6
295.5
299.0
288.1
L
18271.8
19167.3
19647.6
20803.5
22076.6
23445.2
24939.0
26713.7
29957.8
31585.9
33474.5
34821.8
41794.3
Таблица 3.11
Объясняемая переменная Ln У
Переменная
С
LnAT
LnL
R-squared
Коэффициент
-2.026556
0.372618
1.481073
Стандартная
ошибка
1.195492
0.052261
0.259434
/-статистика
-1.695165
7.129920
5.708868
Р-значение
0.1209
0.0000
0.0002
0.959293
В пакете Econometric Views можно получить значение F-статистики для
проверки гипотезы Н0 : а + /? = 1, оно равно F = 13.90. Это означает, что
абсолютная величина ^-статистики для проверки этой же гипотезы равна
л/13.90 =3.728. Поскольку а + E - 1 > 0, то и значение самой ^-статистики
равно t - 3.728. Это значение существенно превышает квантиль уровня 0.95
^-распределения с A3 - 3) = 10 степенями свободы — 7095A0) = 1.812 и квантиль
уровня 0.99 этого распределения — ^о^ОО) = 2.764, так что нулевая гипотеза
Я0 : а + Р< 1 отвергается в пользу альтернативной гипотезы Н0 : а + fl> I
даже на 1%-м уровне значимости. Тем самым приходим к выводу о наличии
эффекта масштаба в сельском хозяйстве Тайваня (по крайней мере, на
рассматриваемом периоде). ■

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 149
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какова формула для оценки наименьших квадратов вектора коэффициентов
линейной эконометрической модели при наличии линейных ограничений на эти
коэффициенты? Какими свойствами обладает эта оценка?
2. Как выражается F-статистика для проверки линейной гипотезы о коэффициентах
линейной эконометрической модели через остаточные суммы квадратов в
исходной модели и в модели, учитывающей ограничения, накладываемые линейной
гипотезой?
3. Как формулируется гипотеза о значимости регрессии в целом? Как проверяется
такая гипотеза?
4. Чему равна оценка наименьших квадратов постоянной составляющей
эконометрической модели при отсутствии в модели других объясняющих переменных?
5. Как применяется F-критерий для редукции исходной эконометрической
модели?
6. Как связаны между собой F- и /-критерии для проверки гипотезы о выполнении
единственного линейного ограничения на коэффициенты линейной
эконометрической модели?
7. Какие проблемы возникают при установлении уровня значимости
последовательной процедуры проверки гипотезы о равенстве нулю нескольких коэффициентов
модели?
8. Как формулируются и как проверяются односторонние гипотезы о значении
отдельного коэффициента линейной эконометрической модели?
9. В чем может состоять конфликт критериев при проверке односторонних гипотез
против односторонних альтернатив?
10. Почему статистическая гипотеза о значениях коэффициентов эконометрической
модели должна формулироваться до оценивания этих коэффициентов?
11. Как проверяются односторонние гипотезы, затрагивающие значения сразу
нескольких коэффициентов линейной эконометрической модели?
Тема 3.3
СРАВНЕНИЕ АЛЬТЕРНАТИВНЫХ МОДЕЛЕЙ.
МУЛЬТИКОЛЛИНЕАРНОСТЬ. ПРОГНОЗИРОВАНИЕ
ПО ОЦЕНЕННОЙ МОДЕЛИ
Мы неоднократно задавались вопросом: как следует интерпретировать
значения коэффициента детерминации R2 с точки зрения их близости к 0 или,
напротив, их близости к 1?
Естественным было бы построение статистической процедуры проверки
значимости линейной связи между переменными, основанной на значениях
коэффициента детерминации /?2, ведь R2 является статистикой, поскольку
значения этой случайной величины вычисляются по данным наблюдений.
Теперь можно построить такую статистическую процедуру.
Представим F-статистику критерия проверки значимости регрессии в
целом в виде

150
Часть 1. Основные понятия, элементарные методы
= ESS/(p -1) = ESS/TSS (n-p)= R2 (я - р)
~ RSS/(n-p)~ RSS/TSS (p-l)~l-R2 (р-1)'
Отсюда находим:
{p-\)F(\-R2) = {n-p)R2, (p-\)F = ((p-l)F + (n-p))R2,
(p-l)F + (n-p) u n-p
(p-\)F
Большим значениям статистики F соответствуют и большие значения
статистики Л2, так что гипотеза Я0 : в2 = 9Ъ = ... = в = 0, отвергаемая при
F > Fcrit = Fx_a(p - I, п-р), должна отвергаться при выполнении неравенства
R2 > R2crin где
Rcrit = "
1
1 + -
п- р
При этом вероятность ошибочного отклонения гипотезы Я0 по-прежнему
равна а.
Интересно вычислить критические значения R2crit при а = 0.05 для
различного количества наблюдений.
Ограничимся здесь парной линейной регрессией (р = 2), так что
2 _ 1
crit ~ „_9 ' ^crit ~ ^0.95 0» П ~ 2).
1 + ^-^
В зависимости от количества наблюдений п получаем следующие
критические значения R2crit (табл. 3.12).
Таблица 3.12
Критические значения
п
Rcrit
3
0.910
4
0.720
10
0.383
20
0.200
30
0.130
40
0.097
60
0.065
120
0.032
500
0.008
Иначе говоря, при большом количестве наблюдений даже весьма малые
отклонения наблюдаемого значения R2 от 0 оказываются достаточными для
того, чтобы признать значимость регрессии, т.е. статистическую значимость
оценки коэффициента при содержательной объясняющей переменной.
Поскольку же значение R2 при р = 2 равно квадрату выборочного
коэффициента корреляции между объясняемой и (нетривиальной) объясняющей
переменными, аналогичный вывод справедлив и в отношении величины этого
коэффициента корреляции (табл. 3.13).

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 151
п
^xy\crit
3
0.953
4
0.848
Критические значения
10
0.618
20
0.447
30
0.360
40
0.311
60
0.254
Таблица 3.13
120
0.179
500
0.089
В конце разд. 2 мы обещали уделить некоторое внимание вопросу о выборе
«наилучшей» модели из нескольких возможных вариантов. В рамках
линейных моделей это может быть выбор между моделями с большим или с
меньшим количеством объясняющих переменных в правой части.
Пусть имеются К переменных, которые, по нашему мнению, могут
объяснять изменчивость переменной Y в рамках линейной модели наблюдений, а
в действительности п наблюдений порождаются линейной моделью, в
которую входят только р < К из этих К переменных. Пусть это будут переменные
Хи ..., Хр9 где, как обычно, Хх = \. Соответственно процесс порождения
данных имеет вид:
DGP:y = Xe + s,
где матрицаXимеет размер п х р9 £ ~ N@9 сг21п).
Не зная этого, (ошибочно) оцениваем линейную статистическую (эконо-
метрическую) модель с К переменными, в которую в качестве объясняющих
в дополнение к Xl9 ..., Хр включены еще и «лишние» переменные Zl9 ..., Zq9
q = K-p:
SM: у = Wp + v = Xe + Zy + v,
здесь матрица W имеет размер пхК, матрица Z — размер п х q,
W = [XZ], /3 =
г)
и предполагается, что матрица W имеет полный столбцовый ранг К.
В действительности в рассматриваемой статистической модели у = 0, так
что v = е, а значит, v ~ JV@, <у21„). Оценивая статистическую модель методом
наименьших квадратов, получаем оценку для /3 в виде:
р = (WTWyx WTy = {WTWyx WT{Wp + e).
При этом имеем:
E(J3) = J3, т.е. Е
У)
так что Е@) =в,и в — несмещенная оценка для в. Полученная при
оценивании статистической модели статистика S\ = RSSK/(n - К) (здесь индекс К

152
Часть 1. Основные понятия, элементарные методы
указывает на модель с К объясняющими переменными) является
несмещенной оценкой для <т2. Однако
D0j)><T\XTXrj, j = l,...,p.
Доказательство этих фактов можно найти в учебнике (Магнус, Катышев,
Пересецкий, 2005).
Рассмотрим теперь обратную ситуацию:
DGP: у = Wp + s = Xe + Zy + s, у±0, s ~ N@,a2In),
SM : у = Хв + 7 («пропуск существенных переменных»).
Оценив статистическую модель, получим только оценку для в:
в = (ХТХУ1 Хту = (ХТХУХ Хт (Хв + ц) = в + (ХТХУ1 Хтг].
Поскольку в такой ситуации rj = Zy+£, Cov(rf) = cr2In9 E(rj) = Zy то
E0) = e + (XTXylXTZy.
Последнее означает, что оценка для #, полученная по указанной
статистической модели, оказывается смещенной, за исключением случая, когда
выполнено условие:
XTZ= 0 (столбцы матрицы Xортогональны столбцам матрицы Z).
При выполнении последнего условия справедливо также следующее (см.
(Магнус, Катышев, Пересецкий, 2005)): оценки для 0, полученные по
указанной статистической модели и по статистической модели у - Хв + Zy + s,
совпадают между собой.
Что касается дисперсий оценок коэффициентов и статистики S2 в обратной
ситуации, то (см. (Магнус, Катышев, Пересецкий, 2005)):
• дисперсии оценок коэффициентов ди ..., вр, полученных по
статистической модели у = Хв + rj, не больше дисперсий оценок тех же
коэффициентов, полученных по статистической модели у = Хв + Zy + s;
• полученная при оценивании статистической модели у = Хв + rj
статистика S2p = RSSpl(n - р) является, вообще говоря, смещенной оценкой
для g2 : E(S2p) > a2.
Таким образом, введение в модель «лишних» переменных не приводит
к смещению оценок коэффициентов, но может приводить к неоправданному
возрастанию длин доверительных интервалов для коэффициентов при
остальных переменных. В то же время использование модели, в которой пропущены
существенные объясняющие переменные, ведет к смещению оценок
коэффициентов, что может перекрывать положительный эффект от уменьшения их
дисперсий. Поскольку при анализе реальных статистических данных обычно
нет никаких гарантий того, что верна именно полная или именно редуциро-

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 153
ванная модель, встает задача выбора «наилучшей» модели, обеспечивающей
определенный компромисс между двумя указанными опасностями.
Если сравнивать модели по величине коэффициента детерминации R29 то
с этой точки зрения полная модель всегда лучше (точнее, не хуже)
редуцированной — значение R2 в полной модели всегда не меньше, чем в
редуцированной, просто потому, что в полной модели остаточная сумма квадратов
не может быть большей, чем в редуцированной.
Действительно, в полной модели с р объясняющими переменными
минимизируется сумма
2>,
■вххп -.
■<W
J
; = 1
по всем возможным значениям коэффициентов вХ9 ..., 0р. В случае
редуцированной модели, например, без /7-й объясняющей переменной,
минимизируется сумма
2>,-*Л1
•-0p-\xi,P-\)
по всем возможным значениям коэффициентов вХ9 ..., вр_Х9 что равносильно
минимизации первой суммы по всем возможным значениям #,, ..., вр_х при
фиксированном значении вр = 0. Но получаемый при этом минимум не может
быть меньше, чем минимум, получаемый при минимизации первой суммы по
всем возможным значениям вХ9 ..., вр9 включая все возможные значения вр.
Последнее означает, что RSS в полной модели не может быть большей, чем
в редуцированной модели. Из того, что полная сумма квадратов в обеих
моделях одна и та же, вытекает заявленное выше свойство коэффициента R2.
Чтобы сделать процедуру выбора «наилучшей» модели более приемлемой,
было предложено использовать вместо R2 скорректированный вариант —
скорректированный/?2 (adjustedR-squared, adjustedR2):
RSS/(n-p)
Ke=i-
TSS/(n-\) '
в котором, по существу, вводится штраф (penalty) за увеличение количества
объясняющих переменных. При этом
^=ь
RSS
TSS
= R2_RSS
TSS
так что при п >р и р > 1
и-1
п-р)
(п-\
п-р
= 1-
RSS\
TSS)
RSS RSS
■1 =R2-
TSS TSS
4
p-\ RSS
n-p TSS'
n-\
n-p)
\\
J
KdJ<R2

154
Часть 1. Основные понятия, элементарные методы
Заметим, что в отличие от самого R2 скорректированный коэффициент
может принимать и отрицательные значения. Это происходит, когда
RSS
TSS
п-\
п- р
>1,
а для выполнения последнего неравенства достаточно, например, чтобы
D2 1 и + 1
R <— и р> .
2 2
При использовании коэффициента R2adj для выбора между
конкурирующими моделями «налучшей» признается та, для которой этот коэффициент
принимает максимальное значение.
v Замечание 3.3.1. Если при сравнении полной и редуцированных
моделей оценивание каждой из альтернативных моделей производится
с использованием одного и того же количества наблюдений, то, как
следует из формулы, определяющей R2adj9 сравнение моделей по
величине R2adj равносильно сравнению их по величине S2 = RSS/(n - р)
или по величине S = yjRSS/{n - p). Только в последних двух случаях
выбирается модель с минимальным значением S2 (или S).
ПРИМЕР 3.3.1
Продолжая пример 3.2.5, находим значения коэффициента R2adj при подборе
моделей Ml9 М2, М3:
Щ о R2adj =0.9889,
М2 о R2adj =0.9902,
М3 оЛ^=0.9911.
По максимуму R2adj из этих трех моделей выберем именно модель М3,
к которой уже пришли до этого, пользуясь t- и F-критериями.И
Информационные критерии
Для выбора между альтернативными моделями наряду со скорректированным
коэффициентом детерминации часто используют так называемые
информационные критерии {information criteria), также штрафующие за увеличение
количества объясняющих переменных в модели, но несколько отличными
способами.
Критерий Акаике {Akaike 's information criterion — AIC). При
использовании этого критерия нормальной линейной модели с р объясняющими
переменными, оцененной по п наблюдениям, сопоставляется значение

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 155
Л/С = In
(RSS„
J
+ — + 1 + 1п2л",
п
где RSSp — остаточная сумма квадратов, полученная при оценивании
коэффициентов модели методом наименьших квадратов.
При увеличении количества объясняющих переменных первое слагаемое
в правой части уменьшается, а второе — увеличивается. Среди нескольких
альтернативных моделей (полной и редуцированных) предпочтение отдается
модели с наименьшим значением AIC, в которой достигается определенный
компромисс между величиной остаточной суммы квадратов и количеством
объясняющих переменных.
Критерий Шварца (Schwarz's information criterion — SC, SIC). При
использовании этого критерия нормальной линейной модели с р объясняющими
переменными, оцененной по п наблюдениям, сопоставляется значение
SC = In
(RSSr
plnn
+ - + 1 + 1п2я\
И здесь при увеличении количества объясняющих переменных первое
слагаемое в правой части уменьшается, а второе — увеличивается. Среди
нескольких альтернативных моделей (полной и редуцированных) предпочтение
отдается модели с наименьшим значением SC
ПРИМЕР 3.3.2
В последнем примере для полной модели М, и редуцированных моделей М2
и М3 получаем следующие значения AIC и SC (табл. 3.14).
Таблица 3.14
Сравнение моделей
м,
м2
М3
AIC
8.8147
8.6343
8.4738
SC
8.9594
8.7428
8.5462
Предпочтительной по обоим критериям опять оказывается модель М3.И
v Замечание 3.3.2. В рассмотренном примере все три критерия —
R2adj, AIC и SC — выбирают одну и ту же модель. В общем случае
подобное совпадение результатов выбора вовсе не обязательно.
Критерий Шварца является состоятельным в следующем смысле:
если среди альтернативных моделей есть модель, соответствующая
истинному процессу порождения данных, то при неограниченном
увеличении количества наблюдений использование критерия Шварца

156
Часть 1. Основные понятия, элементарные методы
выводит именно на эту модель. Критерий Акаике в такой ситуации
может с положительной вероятностью вывести на более полную
модель. Исходя из принципа экономичности (парсимонии),
предпочтительнее использовать критерий Шварца. Однако в некоторых
ситуациях, когда критерий Акаике останавливается на более полной
модели по сравнению с моделью, выбранной критерием Шварца,
исследователи все же оставляют для дальнейшего рассмотрения и модель,
выбранную критерием Акаике.
V Замечание 3.3.3. Существует одна очень серьезная проблема,
связанная с предварительным отбором модели. Когда в результате
такого отбора останавливаются на некоторой модели, то далее
действуют так, как будто этого отбора не было вовсе, сосредоточившись
на интерпретации результатов оценивания отобранной модели и на
получении на ее основе стандартных статистических выводов. Дело,
однако, в том, что эти выводы, вообще говоря, являются условными
и связаны именно с тем, как прошел отбор модели. Наличие
предварительного тестирования влияет на свойства получаемых в
результате оценок коэффициентов отобранной модели. Мы лишь
обозначим здесь существование такой проблемы (более подробно с ней
можно ознакомиться, например, в учебнике (Магнус, Катышев,
Пересецкий, 2005), гл. 14, с. 351—382).
Проблема мультиколлинеарности
Важность выбора среди нескольких альтернативных моделей «наиболее
подходящей», в которой правая часть уравнения не перегружена «лишними»
переменными, объясняется, в частности, тем, что включение в модель большого
количества объясняющих переменных часто приводит к ситуации, которую
называют мультиколлинеарностью.
Мы обещали ранее коснуться проблемы мультиколлинеарности и сейчас
выполним это обещание. Прежде всего напомним наше предположение:
4) определитель матрицы ХТХ отличен от 0:
detXrX*0,
которое можно заменить условием: столбцы матрицы X линейно независимы.
Полная мультиколлинеарность соответствует случаю, когда это
предположение нарушается, т.е. когда столбцы матрицы X линейно зависимы,
например:
Xip ~Y\Xi\ + • • • + Yp-\Xi,p-\ •> J = 1, ..., W,
(р-й столбец является линейной комбинацией остальных столбцов
матрицы X). При наличии полной мультиколлинеарности оценка наименьших

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 157
квадратов для вектора параметров (коэффициентов) не определена
однозначным образом.
Простейшей иллюстрацией такого положения является ситуация, когда
в модели
yt =a + j3xf+£i9 / = l,...,w,
все п наблюдений значений переменной у произведены при одном и том же
значении xt = х*. В этом случае оценкой для параметра а является а = у,
и в качестве подобранной может быть взята любая (кроме вертикальной)
прямая, проходящая через точку (х*9у).
На практике, говоря о наличии мультиколлинеарности (multicollinearity),
обычно имеют в виду осложнения со статистическими выводами в ситуациях,
когда формально условие 4 выполняется, но при этом определитель матрицы
ХТХ близок к 0, так что существует высокая степень линейной корреляции
между двумя или более объясняющими переменными. На наличие
мультиколлинеарности указывают:
• большие изменения оценок коэффициентов при удалении или
добавлении объясняющих переменных;
• большие изменения оценок коэффициентов при изменении или
удалении наблюдения;
• несоответствие знаков оцененных коэффициентов априорным
ожиданиям, вытекающим из экономической теории;
• большие стандартные ошибки оценок коэффициентов при переменных,
которые априори ожидались существенными для объяснения.
Указанием на то, что р-я объясняющая переменная «почти является»
линейной комбинацией остальных объясняющих переменных, может служить
большое значение коэффициента возрастания дисперсии (variance inflation factor)
оценки коэффициента при этой переменной
вследствие наличия такой «почти линейной» зависимости между этой и
остальными объясняющими переменными. Здесь R2p — коэффициент детерминации
при оценивании методом наименьших квадратов модели
Если R2p = О, то (VIF)p = 1, это соответствует некоррелированностир-й
переменной с остальными переменными. Если же R2p Ф О, то (VIF)p > 1, и чем
больше корреляция р-й переменной с остальными переменными, тем в
большей мере возрастает дисперсия оценки коэффициента при р-й переменной
по сравнению с минимально возможной величиной этой оценки.

158
Часть 1. Основные понятия, элементарные методы
Аналогично можно определить коэффициент возрастания дисперсии
(VIF)j оценки коэффициента приу-й объясняющей переменной для каждого
7=1, ...9р:
здесь Rj — коэффициент детерминации при оценивании методом
наименьших квадратов модели линейной регрессии у'-й объясняющей переменной на
остальные объясняющие переменные.
Слишком большие значения коэффициентов возрастания дисперсии
указывают на то, что статистические выводы для соответствующих объясняющих
переменных могут быть весьма неопределенными: доверительные интервалы
для коэффициентов могут быть слишком широкими и включать как
положительные, так и отрицательные значения, что ведет, в конечном счете,
к признанию коэффициентов при этих переменных статистически
незначимыми при использовании ^-критериев. (Однако это вовсе не обязательно —
см. пример 3.3.5.)
ПРИМЕР 3.3.3
Обратившись опять к данным об импорте товаров и услуг во Францию, найдем:
(VIFJ = (VIFK = = 109.89.
п /3 1-0.9909
(Коэффициенты возрастания дисперсии для переменных Х2 и Х3 совпадают
вследствие совпадения коэффициентов детерминации при оценивании
регрессии переменнойХ2 на переменные 1} и!3 и регрессии переменнойХ3 на
переменныеХх иХ2.)
Полученные значения коэффициентов возрастания дисперсий отражают
очень сильную коррелированность переменных Х2 и Х3 (выборочный
коэффициент корреляции между этими переменными равен Согг(Хъ Х3) = 0.995).И
При наличии мультиколлинеарности может оказаться невозможным
разделение влияния отдельных объясняющих переменных, включенных в
модель согласно соответствующей экономической теории.
Удаление одной из переменных может привести к хорошо оцениваемой
модели. Однако оставшиеся переменные примут на себя дополнительную
нагрузку, так что коэффициент при каждой из этих переменных не измеряет
уже собственно влияние одной этой переменной на объясняемую
переменную, а учитывает также часть влияния исключенных переменных,
коррелированных с данной переменной. Возникает смещение, связанное с пропуском
существенной объясняющей переменной.
Конечно, согласно экономической теории можно говорить о том, что
некоторые объясняющие переменные могут заменять друг друга в соот-

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 159
ветствующем уравнении, но тогда включение сразу двух таких переменных
в уравнение в качестве объясняющих приводит фактически к избыточной
модели.
ПРИМЕР 3.3.4
Продолжая пример с импортом товаров и услуг во Францию, рассмотрим
редуцированные модели, получаемые исключением из числа объясняющих
переменных переменной Х2 или Х3. Оценивание этих моделей приводит
к следующим результатам:
У= -6.507+ 0.146Х,
с R2 = 0.9504 и Р-значение = 0.0000 для коэффициента приХ2\
У = -9.030 + 0.222Х3
с R2 = 0.9556 и Р-значение = 0.0000 для коэффициента при Х3.
В каждой из этих двух моделей коэффициенты при Х2 и Х3 имеют очень
высокую статистическую значимость. В первой модели изменчивость
переменной Х2 объясняет 95.04% изменчивости переменной У, во второй модели
изменчивость переменной Х3 объясняет 95.56% изменчивости переменной Y.
С этой точки зрения переменные Х2 и Х3 вполне заменяют друг друга, так что
дополнение каждой из редуцированных моделей недостающей объясняющей
переменной, практически ничего не добавляя к объяснению изменчивости Y
(в полной модели объясняется 95.60% изменчивости переменной У),
приводит к неопределенности в оценивании коэффициентов при Х2 и Х3.
Но коэффициент при Х2 в полной модели соответствует связи между
переменными Х2 и У, очищенными от влияния переменной Х3, тогда как
коэффициент при Х3 в полной модели соответствует связи между переменными
Х3 и У, очищенными от влияния переменной Х2. Поэтому неопределенность
в оценивании коэффициентов при Х2 и Х3 в полной модели, по существу,
означает невозможность разделения эффектов влияния переменных Х2 и Х3
на переменную У.
В табл. 3.15 приведены значения R2adj, S, AIC и SC для всех трех моделей.
Таблица 3.15
Сравнение моделей
i Полная
i
БезХ3
Без Х2
Radj
0.9462
0.9454
0.9512
S
1.1788
1.1870
1.1228
AIC
3.379
3.332
3.220
SC
3.500
3.413
3.301
Все четыре критерия выбирают в качестве наилучшей модель без
переменной Х2М

160
Часть 1. Основные понятия, элементарные методы
200 J
i i | i i i i | i i i i | i i i i | i i i i |
100 150 200 250 300 350 400 450 500
Рис. 3.1
Не будем далее углубляться в проблему мультиколлинеарности,
обсуждать другие ее последствия и возможные способы преодоления
затруднений, связанных с мультиколлинеарностью (использование гребневых оценок,
ортогонализация используемого набора объясняющих переменных и
оценивание модели, в которой объясняющими являются лишь наиболее
существенные из полученных переменных, — регрессия на главные компоненты
и другие методы). По этому вопросу можно обратиться к соответствующей
литературе. Некоторые примеры рассматриваются на практических занятиях,
а здесь приведем только один пример, показывающий, что большая
величина коэффициента возрастания дисперсии вовсе не обязательно приводит
к большим значениям оцененной дисперсии оценки соответствующего
коэффициента.
ПРИМЕР 3.3.5
На рис. 3.1 показаны графики изменений в 500 наблюдениях,переменных
У, Х29 Х3, Х4. Истинная модель порождения данных имеет вид:
yt = 1 + 5 xi2 + xi3 + 0.5 xi4 + et,
где jca = 1+0.1/+ 0.1^д, xB =2+ 0.5/+ 0.1%, xi4=3+ t + 0Asi4,
si9 ей9 €Q9 8i49 ~ i.i.d. N@9 1), i = 1,..., 500.
Здесь значения коэффициентов возрастания дисперсии чрезвычайно высоки:
(VIFJ = 21 747.73, (VIFK = 441 819.28, (VIFL = 444 750.88. Однако результаты
регрессионного анализа показывают, что в данном случае это не так страшно
(табл. 3.16).

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 161
Таблица 3.16
Объясняемая переменная У
Переменная
С
х2
Ъ
X,
Коэффициент
0.888304
5.355627
0.905120
0.511572
Стандартная
ошибка
0.373803
0.464932
0.419226
0.210310
/-статистика
2.376393
11.51916
2.159026
2.432463
Р-значение
0.0179
0.0000
0.0313
0.0153
Оцененные значения коэффициентов достаточно близки к их истинным
значениям, а оцененные стандартные ошибки достаточно малы.
Для объяснения этих результатов обратимся к формуле для дисперсии
оценки коэффициента приу-й объясняющей переменной, которую можно
представить в виде (см. (Gujarati, 2003)):
(доказательство приведено, например, в (Wooldridge, 2000)).
Из этой формулы вытекает, что большое значение (VIF)j может
компенсироваться:
• малым значением а2\
п
• большим значением суммы ^(*,-,• - ЗсуJ.
/=1
В нашем примере как раз имеет место последнее обстоятельство.
Заметим, наконец: тот факт, что здесь значение /-статистики для
коэффициента при переменной Х2 более чем в 5 раз превосходит значение
/-статистики для коэффициента при переменной Хъ, объясняется тем, что в истинной
модели в2 - ЪвъШ
Использование статистических критериев
для выбора между двумя негнездовыми моделями
До сих пор мы применяли F-критерии в ситуациях, когда проверяемая
гипотеза Н0 представляла собой линейную гипотезу относительно коэффициентов
исходной линейной эконометрической модели М. В таких случаях
получаемая при выполнении гипотезы Н0 модель М0 «вложена» в модель М (nested
within model M) — говорят, что это случай проверки гипотез для гнездовых
моделей (nested models). При этом сама исходная модель М «охватывает»
модель М0 (encompasses model M0).

162
Часть 1. Основные понятия, элементарные методы
Рассмотрим две конкурирующие модели М! и М2 с одной и той же
объясняемой переменной у, но с разными наборами объясняющих переменных —
такими, что в каждой модели хотя бы одна из объясняющих переменных
не является объясняющей переменной в конкурирующей модели. Для
простоты пусть это будут модели парной регрессии:
Mj : yi=ax+px xt +ei9 / = 1,...,и,
M2 : yi=a1+p1zi+vi9 i = l,..„л,
и при этом xt Ф zt хотя бы для одного наблюдения. В этом случае модели М х
и М2 не являются гнездовыми — это негнездовые модели {nonnested models):
ни одна из них не «вложена» в другую, не является частным случаем другой
модели. Для выбора между такими моделями мы использовали
скорректированный коэффициент детерминации и информационные критерии. Но можно
поступить иначе — свести дело к проверке некоторой гипотезы с помощью
статистического критерия.
В качестве исходной можно взять гибридную модель М\ в которой набор
объясняющих переменных исчерпывает все объясняющие переменные,
задействованные в конкурирующих моделях. Если М{ и М2 — модели парной
регрессии, то это будет модель
М*: у. =вх+в2 Х;+в3г( + *., i = 1,..., п.
Гибридная модель М* охватывает обе модели М{ и М2: они являются
частными случаями гибридной модели.
Если наблюдения порождаются моделью М {, то въ = О, если же
наблюдения порождаются моделью М2, то 92 = 0. Отсюда напрашивается простое
решение проблемы выбора между моделями Мх и М2: поочередно проверить
в рамках гибридной модели гипотезы значимости для коэффициентов в2 и въ,
применяя ^-критерий. Если Мх и М2 являются моделями не парной, а
множественной регрессии, то в соответствующей гибридной модели может быть
использован F-критерий (такой подход называется использованием
негнездовых F-критериев (nonnested F-tests)).
Однако не все так просто. Рассмотрим возможные результаты применения
изложенного подхода к указанным выше моделям парной регрессии,
предполагая, что в каждой из этих регрессий оцененные коэффициенты
статистически значимы (табл. 3.17).
Таблица 3.17
Возможные результаты
Гипотеза Я0 : въ = 0
Не отвергается
Отвергается
Гипотеза : Я0 : в2 = 0
Не отвергается
А
С
Отвергается
В
D

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 163
В случае исхода А решить, какую из двух конкурирующих моделей
считать правильной, не представляется возможным. Но такой исход вполне
возможен, если векторы значений переменных х( и zt близки к коллинеарным.
Тогда при оценивании гибридной модели оцененные коэффициенты при обеих
этих переменных оказываются статистически незначимыми, хотя тест на
одновременное зануление коэффициентов при этих переменных отклоняет
соответствующую гипотезу.
Исход В приводит к выводу о правильности модели М х, исход С — к
выводу о правильности модели М2. Но здесь возникает уже известная нам
ситуация конфликта критериев: вывод зависит от того, какая гипотеза
выбрана в качестве нулевой гипотезы. Наконец, в случае исхода D ни одна из
моделей Mj и М2 не годится для описания изменчивости переменной^.
Выбор между моделью связи,
линейной в уровнях переменных, и моделью связи,
линейной в логарифмах уровней
Выбор между двумя негнездовыми моделями приходится делать, в частности,
в ситуации, когда решается вопрос о том, какая из двух моделей связи верна:
модель, линейная в уровнях переменных, или модель, линейная в логарифмах
уровней {log-log model). Снова обратимся для простоты к моделям парной
регрессии и рассмотрим задачу выбора между моделями:
М j : yi = ах + Д xi + et, / = 1,..., п, (линейная в уровнях переменных)
М2 : In у. = а2 + /?2 lnx, + v,-, / = 1,..., л, (линейная в логарифмах уровней).
Простая процедура, опять же основанная на идее построения охватывающей
модели, была предложена МакКинноном, Уайтом и Дэвидсоном {MacKinnon,
White, Davidson, 1983) и состоит в следующем.
Методом наименьших квадратов оцениваем Мх и М2, при этом для
объясняющих переменных получаем прогнозные значения yt и liry,- соответственно.
Если за основную берется модель, линейная в уровнях, a log-log модель
рассматривается как альтернативная, то производится проверка гипотезы yLIN = О
в рамках расширенной модели:
М|:д;|.=а1+Дх/+у^Aп5>|.-1пУ/) + ^, / = 1,...,л.
Если же за основную берется log-log модель, то производится проверка
гипотезы yLOG = 0 в рамках расширенной модели:
М2*: М2'Лпу{=а2+^2\пх^ГюсI A-expOiry,)J + v/f / = 1,...,л.
В обоих случаях используются критерии, основанные на /-статистиках,
имеющих при нулевых гипотезах распределение, которое при достаточно

164
Часть 1. Основные понятия, элементарные методы
большом количестве наблюдений близко к стандартному нормальному.
И опять здесь возможны 4 исхода с интерпретацией, аналогичной ситуации
с применением негнездовых F-критериев (табл. 3.18). Примеры
использования этого подхода оставляем для практических занятий.
Таблица 3.18
Возможные исходы
Гипотеза Я0 : yLOG = 0
Не отвергается
Отвергается
Гипотеза Я0 : yLIN = 0
Не отвергается
А
С
Отвергается
В
D
Заметим, что существуют и другие статистические критерии для
различения моделей, линейных в уровнях или в логарифмах уровней, — например,
критерий Бокса—Кокса (Айвазян, 2001), критерий Зарембки (Доугерти, 2004).
Использование оцененной модели
для прогнозирования
Пусть имеем нормальную линейную модель наблюдений у = Хв + £ с р
объясняющими переменными, Е(е) = 0, Cov(s) = cr2In9 известны значения
объясняемой и объясняющих переменных в п наблюдениях и необходимо дать
прогноз, каким будет значение объясняемой переменной^ в (п + 1)-м
наблюдении при условии, что вектор (вектор-строка) значений объясняющих
переменных хп+1 задан. Будем считать при этом, что коэффициенты модели не
изменяются при переходе к (п + 1)-му наблюдению и модель для п + 1
наблюдений удовлетворяет всем стандартным предположениям, так что
Р 2
yi = L°jxij +si> * = 1,...,л + 1, el9...9en+l-UdN@9cr ).
7 = 1
Р
Обозначим для краткости: g(i,0) = Х^Л' такчто
7 = 1
Р
7 = 1
8(п + 1,&) = £еухя+и=Е<уя + 1).
7 = 1
Можно оценить коэффициенты модели по имеющимся п наблюдениям,
получить для них оценки наименьших квадратов вХ9 ..., вр и предложить
в качестве прогнозного значения для g(n + 1, в):

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 165
g(n + \,e) = g{n + \,9) = fjejxn+lJ=xn+l9.
7 = 1
При этом
E{g{n + \,e)) = x„+xe = g{n + \,e),
р л
так что g(n +1, в) = ]Г 0jXn+l9 . является несмещенной оценкой для Е{уп+ Х), и
7=1
D(g(n +1, 0)) = Cov(g(n +1, 0)) = Cov(xw+1 0) = xw+1 Cov@) xTn+l =
где обозначено:
= a\+l(XTXylxTn+l=*2v,
v = xw+1 (XrX) l xTn+x (v — скалярная величина).
Заметим, что J] ^yxw+j . является несмещенной оценкой и для самого уп+1.
Рассмотрим теперь разность уп+х -g(n + \,6). Поскольку предполагается,
что ошибки распределены нормально, то эта разность — ошибка прогноза
(forecast error) имеет нормальное распределение. При этом имеем:
E(yn+1-g(rt + \,e)) = E(yn+1)-E(g(n + l,e)) = g{n + l,e)-g(n + l,e) = 0,
D{yn+x-g(n + \,9)) = D{{g{n + \,e) + en+x)-g{n + \,e)) =
= D(sn+i -g{n +1, в)) = D{sn+X) + D(g(n +1,0)) = a2 + a2v = a2v ,
где обозначено:
v'=l + v = \ + xn+l(XTXylxTn+l.
Отсюда вытекает
yH+l-g(n + l,0)~N(O,<T2v),
Уп+х-ё{п + \,в)
~N@,l).
(TVV*
Замена неизвестного значения а2 на S2 = RSS/(n -p) приводит к статистике
~t(n-p),
на основе которой можно построить доверительный интервал для j>„+1 с
заданным уровнем доверия у. Если у = 1- а, то 100^%-й доверительный интервал
для >>„+1 (интервальный прогноз —forecast interval) имеет вид:

166
Часть J. Основные понятия, элементарные методы
g(n + l,0)-t „(n-p)sJ7<yn+i <g{n + \,9) + t SL{n-p)sJ7.
2 2
Средняя точка этого интервала g(n + 1, в) = хп+1 в соответствует точечному
прогнозу (forecast) значения уп+1.
В некоторых экономических задачах более интересно не само значение
уп+1, соответствующее фиксированному набору значений объясняющих
переменных xn+l9 а математическое ожидание этого значения Е(уп+1\хп+1). В этом
случае точечный прогноз для Е(уп+1 \хп+1) определяется по той же формуле
Е(уп+{ | xn+l ) = g(n +1, в) = хп+1в,
но дисперсия прогноза равна не cr2v*, a a2v. Соответственно интервальный
прогноз для Е(уп+1\хп+1) с уровнем доверия A - а) имеет вид:
g(n + l,ff)-t An-p)S^<E(yn+l\xn+l)<g(n + ie) + t K(n-p)S^.
2 2
Для модели парной регрессии (р = 2):
у{=а + 0х{+£;9 / = 1,...,и,
в качестве точечного прогнозауп+1 при заданном хп+1 берется значение
Л + 1= <* + /?** + !>
где а и J3 — оценки наименьших квадратов, полученные по имеющимся
п наблюдениям.
Это же значение служит точечным прогнозом и для Е(уп+1\хп+1).
Интервальные прогнозы для^„+1 и для Е(уп+Х\хп+Х) можно построить,
используя ранее полученные выражения для соответствующих доверительных
интервалов. При этом формула для вычисления значения v принимает вид:
v= 1 , (**+i-*J
П Z^-ЗсJ
/=1
п
где, как обычно, х = .
п
Заметим, что при заданных значениях (yi9 xt)9 i = 1, ..., п, (по которым
строится прогноз) доверительный интервал для уп+1 будет тем шире, чем
больше v*. Последнее же равно
i+i
при хп+1 = х и возрастает с ростом

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 167
(хп+1 - хJ. Это означает, что ширина доверительного интервала возрастает
при удалении значения хп+1 = х*9 при котором строится прогноз, от среднего
арифметического значений х{,..., хп.
Таким образом, прогнозы для значений хп+1 = х*9 далеко отстоящих от х,
становятся менее определенными, поскольку ширина соответствующих
доверительных интервалов для значений объясняемой переменной возрастает.
ПРИМЕР 3.3.6
Для данных о размерах совокупного располагаемого дохода и совокупных
расходах на личное потребление в США в период с 1970 по 1979 г. (млрд долл.,
в ценах 1972 г.) оцененная модель линейной связи имеет вид:
С = -67.555 +0.979DPI.
Представим, что мы находимся в 1979 г. и ожидаем увеличения в 1980 г.
совокупного располагаемого дохода (в тех же ценах) до DPI* = 1030 млрд
долл. Тогда прогнозируемый по подобранной модели объем совокупных
расходов на личное потребление в 1980 г. равен:
С*980=-67.555+ 0.979-1030 = 940.815.
При этом
S2 =66.46, ~DPI = 879.16, J(x,. -xf =68015.18,
SV =95.340, S<J7 = 9.7642.
Если выбрать уровень доверия 0.95, то
', <uk("-2) = W8) = 2.306,
2
и доверительный интервал для соответствующего DPI* = 1030 значения С*1980
имеет вид:
940.815 - 2.306 • 9.7642 < С\ш < 940.815 + 2.306 • 9.7642,
т.е.
940.815-22.516 < С\ш < 940.815+ 22.516,
или
918.299 < С;980 < 963.331.
Заметим, что этот интервал достаточно широк и его нижняя граница
допускает даже возможность некоторого снижения уровня потребления по
сравнению с предыдущим годом.
В действительности, в 1980 г. совокупный располагаемый доход достиг
1021 млрд долл., а совокупное потребление — 931.8 млрд долл. Тем самым
ошибка прогноза составила

168
Часть 1. Основные понятия, элементарные методы
|940.815-931.8|
931.8
•100 = 0.97%.
Если бы исходили при прогнозе из действительного значения DPImo = 1021,
а не из DPI* = 1030, то прогнозируемое значение для С1980 равнялось бы 932.0
и ошибка прогноза составила всего лишь
1932.0-931.81
931.8
•100 = 0.021%.
Проиллюстрируем, как
изменяется в этом примере ширина
95%-х доверительных интервалов
в интервале наблюдаемых
значений объясняющей переменной
DPI. На рис. 3.2 приведены
отклонения нижней и верхней
границ таких интервалов от центра
интервала.
Заметим, что .374, та-
750 800 850 900 900 юоо dpi ким образом, 95%-й доверительный
Рис. 3.2 интервал для E(C*9S0\DPI* = IQ30)
имеет вид:
940.815 -2.306- 5.374 <Е(С*ХШ ЬрГ =1030) < 940.815 + 2.306 -5.374,
т.е.
или
940.815-12.392<£(C*980p/V*=1030)<940.815 + 12.392,
928.423 <Е(Сто \DPI* =1030) < 953.207.
Конечно, этот интервал существенно уже доверительного интервала,
полученного ранее для С*980.И
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как можно проверить гипотезу значимости регрессии в целом на основе одного
только коэффициента детерминации?
2. Каковы последствия неправильной спецификации линейной эконометрическои
модели в отношении выбора объясняющих переменных: включения в модель
переменных, которые не участвуют в процессе порождения данных; невключения
в модель переменных, которые участвуют в процессе порождения данных?
3. В чем заключается задача выбора «наилучшей» модели среди некоторого
количества конкурирующих моделей?

Раздел 3. Проверка гипотез, выбор «наилучшей» модели и прогнозирование... 169
4. Почему не имеет смысла выбор «наилучшей» модели на основании коэффициента
детерминации?
5. Как определяется скорректированный коэффициент детерминации? Какова цель
его введения?
6. Какова суть критерия Акаике для выбора между конкурирующими моделями?
7. Какова суть критерия Шварца для выбора между конкурирующими моделями?
8. Какой из двух информационных критериев — Шварца или Акаике —
предпочтительнее?
9. В чем состоит проблема мультиколлинеарности? Какие признаки могут указывать
на наличие мультиколлинеарности? Каковы последствия мультиколлинеарности?
10. Как определяется коэффициент возрастания дисперсии?
11. Всегда ли большая величина коэффициента возрастания дисперсии приводит к
большим значениям оценки дисперсии оценки соответствующего коэффициента?
12. Что такое гнездовые и негнездовые модели? Какие статистические критерии
используются для выбора между двумя негнездовыми моделями?
13. Как используются результаты оценивания линейной эконометрической модели
для целей прогнозирования? Что такое точечный прогноз?
14. Что такое интервальный прогноз? Каким образом он строится?

Раздел 4
ПРОВЕРКА ВЫПОЛНЕНИЯ
СТАНДАРТНЫХ ПРЕДПОЛОЖЕНИЙ
О МОДЕЛИ НАБЛЮДЕНИЙ
Тема 4.1
ГРАФИЧЕСКИЕ МЕТОДЫ
Рассмотренный комплекс процедур получения статистических выводов для
моделей простой или множественной регрессии опирается на вполне
определенные стандартные предположения о модели наблюдений (линейная модель,
независимые нормально распределенные ошибки с нулевыми
математическими ожиданиями и одинаковыми дисперсиями).
В связи с этим большие значения коэффициента детерминации R2
(близкие к 1) или статистическая значимость всех коэффициентов вовсе не
обязательно говорят о том, что подобранная модель вполне соответствует
характеру имеющихся статистических данных, воспроизводит глобальные
особенности имеющихся статистических данных — адекватна статистическим
данным {adequate model) — и для нее можно использовать указанный
комплекс статистических процедур.
В этом отношении весьма поучителен искусственный пример с 4
различными множествами данных (табл. 4.1), которые имеют качественно
различные диаграммы рассеяния и в то же время приводят при использовании
модели наблюдений
yt =а + /3х; +*,., i = l,..„л,
к одним и тем же (в пределах двух знаков после запятой) оценкам
параметров, значениям коэффициента R2 и ^-статистик.
Для всех 4 множеств:
• подобранная модель линейной связи имеет вид^ = 6.00 + 0.50х;
• а имеет (оцененную) стандартную ошибку s^ = 1.12;
• Р имеет (оцененную) стандартную ошибку si = 0.12;

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 171
• ^-статистика для проверки нулевой гипотезы Н0 : а= О равна 2.67, что
соответствует Р-значению 0.026;
• ^-статистика для проверки нулевой гипотезы Н0 : /? = 0 равна 4.24, что
соответствует Р-значению 0.002;
• R2 = 0.67.
Таблица. 4.1
Пример статистических данных D множества)
I
i 1
2
3
4
5
6
7
8
9
10
11
Множество 1
X
20
16
26
18
22
28
12
8
24
14
10
У
16.06
13.90
15.16
17.62
16.66
19.92
14.48
8.52
21.68
9.64
11.36
Множество 2
X
20
16
26
18
22
28
12
8
24
14
10
У
18.28
16.28
17.48
17.54
18.52
16.20
12.26
6.20
18.26
14.52
9.48
Множество 3
X
20
16
26
18
22
28
12
8
24
14
10
У
14.92
13.54
25.48
14.22
15.62
17.68
12.16
10.78
16.30
12.84
11.46
Множество 4
X
16
16
16
16
16
16
16
38
16
16
16
У
13.16
11.52
15.42
17.68
17.94
14.08
10.50
25.00
11.12
15.82
17.98
Однако диаграммы рассеяния различаются коренным образом (рис. 4.1—4.4).
Уже чисто визуальный анализ 4 диаграмм рассеяния показывает, что
только первое множество данных (рис. 4.1) можно признать удовлетворительно
описываемым линейной моделью наблюдений
yi = a + fixi+ei, i = l,...,и.
Для второго множества (рис. 4.2) более подходящей представляется модель
yi =а + рх(+ух* +ei9 i = l,..„л.
В третьем множестве (рис. 4.3) явно выделяется одна точка C-е
наблюдение), которая существенно влияет на наклон и положение подбираемой
прямой.
Четвертое множество (рис. 4.4) совершенно непригодно для подбора
линейной зависимости, поскольку наклон подобранной прямой фактически
определяется наличием одного выпадающего наблюдения.
Метод наименьших квадратов достаточно устойчив к малым отклонениям
от стандартных предположений в том смысле, что при таких малых
отклонениях статистические выводы на основе статистического анализа модели

172
Часть 1. Основные понятия, элементарные методы
У1&Х1
Y2&X2
УЗ А
25-
15 -
5-
Y3&X3
i
♦
' ^^«^*
1 1 1
ь-*
У4&Х4
15
Рис. 4.3
25
ХЗ
в основном сохраняются. Однако существенные отклонения от стандартных
предположений могут серьезно исказить статистические выводы. Возможные
последствия таких отклонений:
• оценки в19..., в коэффициентов линейной модели, построенные на базе
стандартных предположений, оказываются смещенными;
• оценки дисперсий случайных величин в19 ..., вр (оценок коэффициентов
линейной модели), построенные на базе стандартных предположений,
оказываются смещенными;
• построенные на базе стандартных предположений доверительные
интервалы для в19 ..., вр не соответствуют заявленным уровням значимости;
• вычисленные значения t- и F-отношений нельзя рассматривать как
наблюдаемые значения случайных величин, имеющих t- и F-распределе-
ния. Поэтому при сравнении вычисленных значений t- и F-отношений
с квантилями указанных t- и ^-распределений можно прийти к
ошибочным статистическим выводам о гипотезах о значениях коэффициентов
линейной модели;
• прогнозы, построенные по подобранной модели, оказываются
смещенными.

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 173
В связи с этим, необходимо иметь инструментарий:
• для обнаружения отклонений от стандартных предположений, или,
говоря иначе, для проведения диагностики подобранной модели
{diagnostic for model mis specification)',
• для коррекции выявленных отклонений от стандартных предположений,
позволяющий проводить строгий и информативный анализ статистических
данных.
В конечном счете, диагностические процедуры предназначены для
проверки гипотезы о том, что выполнены все стандартные предположения о
модели. В то же время они помогают выявить характер нарушений этих
предположений, если таковые обнаружены, а это позволяет изменить в правильном
направлении спецификацию модели или соответствующим образом
скорректировать статистические выводы. Специализированные диагностические
процедуры, рассмотренные ниже, направлены на выявление следующих
типов нарушений стандартных предположений:
• отличие распределения ошибок от нормального;
• неодинаковые дисперсии ошибок;
• статистическая зависимость ошибок в наблюдениях, производимых
в последовательные моменты времени;
• неправильный выбор функциональной формы модели;
• непостоянство коэффициентов модели на периоде наблюдений.
При выявлении некоторых типов нарушений стандартных предположений
можно, в принципе, не изменяя спецификации модели, ограничиться лишь
коррекцией статистических выводов в отношении подобранной модели
(например, соответствующим образом корректируя значения используемых
^-статистик, о чем будет сказано ниже). Однако методология эконометрических
исследований, известная как методология Лондонской школы экономики
(LSE approach; LSE — London School of Economics), предлагает другой
подход. При обнаружении нарушений стандартных предположений следует
изменить спецификацию модели таким образом, чтобы при оценивании модели
с измененной спецификацией нарушения стандартных предположений уже
не выявлялись, по крайней мере, теми диагностическими процедурами,
которые имеются в распоряжении исследователя. Таких процедур в распоряжении
исследователя должно быть достаточно много для того, чтобы выявлять
различные типы нарушений, и эти процедуры должны быть по возможности
достаточно эффективными, чтобы можно было обнаруживать нарушения
стандартных предположений и при не очень большом количестве наблюдений.
Основатель и пропагандист этого подхода Девид Хендри указывает в связи
с этим на «три золотых правила эконометрики»: проверка, проверка и
проверка (test, test and test) (см. (Hendry, 2003), с. 27—28).
Согласно методологии Лондонской школы экономики модели, которые
претендуют на научность, должны:

174
Часть 1. Основные понятия, элементарные методы
• успешно проходить диагностические процедуры;
• объяснять результаты предыдущих исследований;
• быть обоснованными с точки зрения экономической теории.
Эффективным средством обнаружения отклонений от стандартных
предположений о линейной модели наблюдений
yi=0ixn+ — + epxip+ei> * = 1,...,л,
т.е.
является анализ остатков {residual analysis), т.е. анализ разностей
ег=У1-Уг> * = 1,...,Л.
Наблюдаемые разности yt - yt в силу случайности значений st в модели
наблюдений можно рассматривать как значения соответствующих случайных
величин Yj - Yi9 за которыми сохраним те же обозначения et. Соответственно
вектор остатков
е = у-Хв = у- Х(ХТХУХ Хту = A- Х(ХТХ)~1 Хт )у = A- Н)у
можно рассматривать как реализацию случайного вектора, за которым
сохраним то же обозначение е.
Если выполнены наши стандартные предположения о модели
наблюдений, то случайный вектор е имеет математическое ожидание
Е(е) = Е(у-Хв) = Е(Хв + е-Хв) = Хв-Хв = 0
и ковариационную матрицу
Cov(e) = Cov((I - Н)у) = (/ - H)Cov(y)(I - Н)т =
= a2(I-H)(I-Hf =<т2A-Н).
Это означает, что для компонент этого случайного вектора, т.е. для
остатков ei9 имеем:
Е(е() = 0, / = 1,...,и,
D{ei) = <j\\-hii), / = 1,...,л,
где hu — /-й диагональный элемент квадратной (п х я)-матрицы
н = х(хтху1хт.
Таким образом, несмотря на то что дисперсии ошибок е{ равны между
собой при наших предположениях (все они равны <т2), дисперсии остатков,
вообще говоря, различны.

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 175
Для выравнивания дисперсий можно перейти к рассмотрению
нормированных остатков
ei в:
Щ£) ст^/гй:9
/ = !,...,«,
т.е. остатков, деленных на их стандартные отклонения. Для таких остатков
D\
4Щ)
= 1, 1 = 1,...,И.
Поскольку значение а2 опять неизвестно, вместо нормированных
остатков приходится использовать стьюдентизированные остатки (studentized
residuals)
ds=—J. , i = l,..., л,
где, как обычно, S2 =•
п- р
Во многих пакетах программ величины hti в знаменателе правой части
выражения для dt игнорируются, что приводит к так называемым
стандартизованным остаткам (standardized residuals)
(так сделано, например, в пакетах Excel и Econometric Views).
Практический анализ показывает, что графики остатков dt и с, обычно
(но отнюдь не всегда!) несущественно различаются по характеру поведения.
Поэтому для предварительного графического анализа адекватности (graphical
diagnostic analysis) часто можно удовлетвориться и значениями ci9 i = 1, ..., п.
К тому же поскольку Н = Х(ХТХ)~ХХТ — проекционная матрица, ранг этой
матрицы равен ее следу. Так как проектирование производится на линейное
подпространство размерности р (р — количество объясняющих переменных),
ранг матрицы Н равен р,
п
1 = 1
так что если/? «п(р намного меньше п\ то «в среднем» значения hu
достаточно малы.
Графики стандартизованных (стьюдентизированных) остатков позволяют
выявлять типичные отклонения от стандартных предположений о модели
наблюдений по характеру поведения остатков. При этом имеется в виду, что,

176
Часть I. Основные понятия, элементарные методы
по крайней мере, при большом количестве наблюдений поведение
остатков ei9 i = 1, ..., п9 должно в той или иной степени имитировать поведение
ошибок si9 i = 1, ..., п. Иначе говоря, поскольку предполагается, что ошибки
ei9 i = 1,..., п9 — независимые в совокупности случайные величины, имеющие
одинаковое нормальное распределение N@, <т2), ожидается, что поведение
последовательности остатков ei9 i = 1, ..., п9 должно имитировать поведение
последовательности независимых в совокупности случайных величин, имеющих
одинаковое нормальное распределение N@9 <т2). Соответственно от
стандартизованных остатков можно было бы ожидать поведения, похожего на
поведение последовательности независимых в совокупности случайных величин,
имеющих одинаковое стандартное нормальное распределение N@, 1).
Строго говоря, последнее ожидание не вполне оправданно. Хотя
стандартизованные остатки и имеют распределения, близкие (хотя бы при
больших п) к стандартному нормальному, они не являются взаимно
независимыми случайными величинами. Это можно понять хотя бы из того, что (как
мы помним) при использовании оценок наименьших квадратов
алгебраическая сумма остатков равна нулю, так что каждый остаток линейно
выражается через остальные остатки. Тем не менее при большом количестве
наблюдений наличие такого соотношения между остатками практически
не делает картину поведения стандартизованных остатков сколь-нибудь
существенно отличной от поведения последовательности независимых в
совокупности случайных величин, имеющих одинаковое стандартное нормальное
распределение N@9 1).
Наиболее часто для диагностики (для проверки на наличие) типичных
отклонений используют графики зависимости стандартизованных остатков
(как ординат) от:
• оцененных значений yt = вххп + ... + 0pxip\
• отдельных объясняющих переменных;
• номера наблюдения, если наблюдения производятся в
последовательные моменты времени с равными интервалами.
График зависимости с, от yi = 0xxlX + ... + 6pxip позволяет выявлять
3 довольно распространенных нарушения стандартных предположений
классической модели.
Выделяющиеся наблюдения {outliers) — наличие наблюдений, для
которых либо математическое ожидание ошибки E(st) существенно отличается
от 0, либо дисперсия ошибки D{st) существенно превышает величину <т2
дисперсий остальных ошибок. Подобные наблюдения могут выявляться на
графике как наблюдения со «слишком большими» по абсолютной величине
остатками. Такая ситуация возникает, например, при подборе прямой по третьему
(из 4 рассмотренных выше) множеству данных (рис. 4.5).

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 177
Standard Residuals & Y3F
Resid Stand
24 V3F
Standard Residuals & YF
Resid Stand
Неоднородность дисперсий, или гетероскедастичность {heteroskedasticity\
которая выражается, например, в форме той или иной функциональной
зависимости D(sf) от величины вхха + ... + 0pxip. Так, если график зависимости
с,- от^г = вхха + ... + 6pxip имеет вид, как на рис. 4.6, то это, скорее всего,
отражает возрастание дисперсий ошибок с ростом значений вххп + ... + 6pxip.
Неправильная спецификация модели в отношении множества
объясняющих переменных {regression error specification) приводит к нарушению
условия E(sf) = 0, так что E(Yt) Ф вххп + ... + 9pxip. Такая ситуация возникает,
например, при оценивании второго множества данных из 4 рассмотренных
выше (рис. 4.7).
Standard Residuals & Y2F
Resid Stand
Standard Residuals & X2
Resid Stand
10 20 30 X2
Рис. 4.8
График зависимости ci9 от значений х^ j-й объясняющей переменной
полезен для выявления нелинейной зависимости^ оту'-й объясняющей
переменной. Например, график для второго из 4 искусственных множеств
приведен на рис. 4.8.

178
Часть 1. Основные понятия, элементарные методы
е а
Рис. 4.9
Рис. 4.10
График зависимости остатков от номера наблюдения полезен в том
случае, когда наблюдения производятся последовательно во времени (через
равные интервалы времени). По такому графику можно обнаружить:
• изменение дисперсии ошибок с течением времени (рис. 4.9);
• невключение в модель (пропуск) переменных, зависящих от времени
и существенно влияющих на объясняемую переменную (рис. 4.10);
• невыполнение условия независимости в совокупности случайных
ошибок si9 i = 1, ..., п, в форме их автокоррелированности. Более подробно
о такой форме статистической зависимости между случайными
ошибками поговорим позднее, здесь продемонстрируем, как выглядят
графики остатков в случае положительной автокоррелированности (рис. 4.11)
и в случае отрицательной автокоррелированности (рис. 4.12).
Рис. 4.11
Рис. 4.12
В первом случае проявляется тенденция сохранения знака остатка при
переходе к следующему наблюдению (за положительным остатком, скорее,
следует также положительный остаток, а за отрицательным — отрицательный).
Во втором случае проявляется тенденция смены знака остатка при переходе

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 179
к следующему наблюдению (за положительным остатком, скорее, следует
отрицательный остаток, а за отрицательным — положительный).
Отдельную группу составляют графические методы проверки
предположения о нормальности распределения случайных составляющих si9
i= l,...,«.
Диаграмма «квантиль-квантиль» (Q-Q plot). Для построения этой
диаграммы значения стандартизованных остатков ci9 / = 1, ..., п, упорядочивают
в порядке возрастания. Упорядоченные значения образуют ряд
СA) < СB) < '
<Ct
(я)'
Если теперь для каждого к = 1, ..., п нанести в прямоугольной системе
координат на плоскости точку с абсциссой Сщ и ординатой
й=ф
2
п
к —
где£?*
квантиль уровня
стандартного нормального распределения;
0(z)— функция стандартного нормального распределения,
то полученные п точек (с{к), Qk\ к = 1, ..., я, в случае нормального
распределения ошибок должны располагаться вдоль прямой, имеющей угловой
коэффициент, близкий к 1. Подобное расположение имеют точки на диаграмме,
построенной указанным способом по первому из 4 множеств искусственных
данных (рис. 4.13).
v Замечание 4.4.1. Если в последней процедуре не проводить
стандартизацию остатков, а использовать непосредственно остатки ei9
/ = 1, ..., я, то полученные точки (е{к), Qk\ к - 1, ..., я, также будут
располагаться (при нормальном распределении ошибок) вдоль
некоторой прямой, но уже имеющей угловой коэффициент, не
обязательно близкий к 1.
Указанное свойство диаграммы «квантиль-квантиль» основано
на том, что при больших значениях п имеет место приближенное
равенство
С(*)*Ф"
2

180
Часть 1. Основные понятия, элементарные методы
Normal Quantile
2-
1 -
0
-1 -
о _
■ ♦
♦
2
♦
Q-Q Plot
♦♦
♦
I
I
0
Рис.
♦
2
4.13
. *.
Resid_Stand
DP A
0.5-
0.4-
0.3-
0.2-
0.1 -
n
и i
3
i
r
-2
л
♦ ♦
♦
i i i i
I I I I
-10 12 2
Рис. 4.14
»
\ C_k
которому соответствует приближенное соотношение, используемое
для проверки нормальности ошибок в пакете Excel.
Ф(%>)
2
п
Диаграмма плотности (DP-plot, DPP) отличается от диаграммы
«квантиль-квантиль» тем, что по оси ординат вместо значений квантилей Qk
откладываются значения функции плотности стандартного нормального
распределения (р(х) при значениях аргумента, равных Qk9 т.е. значения <p(Qk).
По такой диаграмме при достаточном количестве наблюдений можно не только
проверить предположение о нормальном распределении ошибок, но и выявить
характер альтернативного распределения в случае отклонения распределения
ошибок от нормального. В качестве примера приведем диаграмму плотности,
построенную по остаткам, полученным в результате подбора модели
линейной зависимости совокупных расходов (CONS) на личное потребление от
совокупного располагаемого личного дохода (DPI) (данные по США в млрд долл.
1982 г., за период с 1959 по 1985 г.) (рис. 4.14).
На этой диаграмме обнаруживается определенная асимметрия, что
представляется не вполне согласующимся с предположением о нормальности
ошибок. Однако не следует на этом основании сразу делать вывод о
нарушении такого предположения. Дело в том, что при небольшом количестве
наблюдений структура подобной диаграммы весьма неустойчива. Поэтому
даже при заведомо нормальном распределении ошибок редко можно увидеть
вполне симметричную картину расположения точек на диаграмме при малом
количестве наблюдений.
Ядерные оценки плотности (kernel density estimates) — метод
оценивания функции плотности, позволяющий получать график в виде
непрерывной кривой. Существует много вариантов таких оценок, в детали которых
вдаваться не будем, отметим только, что в пакете EViews предлагается на

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 181
Kernel Density
(Epanechnikov, h = 0.5025)
выбор 8 вариантов, в рамках
которых можно еще и варьировать
параметры. Вариант, применяемый
по умолчанию, дает для
рассмотренных данных следующую оценку
плотности распределения ошибок
(рис. 4.15).
Как видим, и при таком подходе
получается график, не очень
похожий на график функции плотности
стандартного нормального
распределения, но это опять может быть
вызвано малым количеством
наблюдений (п = 27).
Выявить определенную
нестабильность модели (instability) для данных, развернутых во времени, можно
путем наблюдения за изменением значений оценок коэффициентов в
процессе последовательного добавления данных (график рекурсивных
коэффициентов — recursive coefficients). Для тех же данных по США такой график для
оценки коэффициента при DPI имеет вид, приведенный на рис. 4.16, он
указывает на явную нестабильность оценок коэффициента при DPI на
рассматриваемом периоде.
1 2
RESID STAND
Рис. 4.15
■ Recursive CB)
Estimates
• ±2 S.E.
1966 1968 1970 1972 1974 1976 1978 1980 1982 1984 Год
РИС. 4.16
В пакете Е Views наряду с наблюдением за рекурсивными коэффициентами
можно наблюдать и за рекурсивными остатками (recursive residuals),
которые представляют собой последовательность нормированных ошибок
прогнозов на один шаг для значений объясняемой переменной линейной эконо-
метрической модели в процессе последовательного добавления данных. Если
в модели р объясняющих переменных, то при добавлении данных впервые

182
Часть 1. Основные понятия, элементарные методы
модель можно оценить, взяв первые р наблюдений. Нормированная ошибка
прогноза по оцененной модели на (р + 1)-е наблюдение представляет
рекурсивный остаток w + j. Взяв теперь первые (р + 1) наблюдений, оценим модель
по этим наблюдениям и найдем нормированную ошибку прогноза по
оцененной модели на (р + 2)-е наблюдение. Это будет рекурсивный остаток wp + 2-
Продолжив этот процесс, получим последовательность нормированных
рекурсивных остатков.
Заметим, что дисперсия ошибки прогноза на (t + l)-e наблюдение,
сделанного по модели, оцененной по первым t наблюдениям, равна:
<г2A + х,+1(*,7Х)~1(*,+,)Г),
где Xt —матрица значений объясняющих переменных в первых t
наблюдениях;
xt+x —вектор-строка значений объясняющих переменных в (t + 1)-м
наблюдении.
Нормировка ошибки прогноза на (t + l)-e наблюдение производится
делением этой ошибки на величину A + xt+l(X?Xt)~l (X+i)r)- При выполнении
стандартных предположений, включая нормальность ошибок, рекурсивные
остатки wp+l9 ..., wn являются одинаково распределенными, взаимно
независимыми нормальными случайными величинами, имеющими нулевое среднее
и дисперсию а2. Это дает возможность построить доверительные интервалы
для рекурсивных остатков, и тогда выход рекурсивных остатков за эти
доверительные интервалы говорит не в пользу стабильности модели.
Проблема, однако, в том, что для построения доверительных интервалов
необходимо знать дисперсию а1 случайных ошибок в модели. Так как она
неизвестна, ее приходится оценивать, и оценки оказываются разными для
моделей, использующих разное количество наблюдений. Поэтому реально
построенные доверительные интервалы для рекурсивных остатков имеют
различную ширину.
Поведение рекурсивных остатков для тех же данных по США показано
на рис. 4.17.
В пакете ЕViews можно также отслеживать поведение кумулятивных
сумм нормированных рекурсивных остатков (CUSUM— cumulative sums),
которые определяются по формуле Wk = V — , где S = I , a RSS —
t=P+i S \п-р
остаточная сумма квадратов при оценивании модели по всем п наблюдениям.
При выполнении стандартных предположений о модели (включая
нормальность ошибок) график Wk как функции от к должен оставаться в пределах
коридора, ограниченного прямыми, соединяющими точки (/?,±0.948-Jn-p)
с точками (и, ±3-0.948^-/?), с вероятностью 0.95.

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 183
Recursive
Residuals
±2 S.E.
3
со
CD
О
^ CD CO О
|v. |v. |v. да
О) О) О) О)
Рис. 4.17
В рассматриваемом примере такой график (рис. 4.18) не выявляет
нестабильность коэффициентов модели.
■cusum
• ±2 S.E.
I I I I I I I I I
сч ^t «о со о см <«■
CD CD CD CD h- h-
<J> <J> О) G) G) О)
Год
Рис. 4.18
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как влияют нарушения стандартных предположений о модели на результаты,
полученные методами, предполагающими выполнение всех этих предположений?
2. Каковы основные типы нарушений стандартных предположений?
3. В чем состоит методология Лондонской школы экономики?
4. На чем основывается использование графических процедур обнаружения
нарушений стандартных предположений о модели?
5. Какие графические процедуры используются для обнаружения:
• выделяющихся наблюдений;
• неоднородности дисперсий ошибок (гетероскедастичности);
• неправильной спецификации модели в отношении множества объясняющих
переменных;

184
Часть 1. Основные понятия, элементарные методы
•
изменения дисперсии ошибок с течением времени;
невыполнения условия независимости в совокупности случайных ошибок;
нарушения предположения о нормальности распределения случайных ошибок;
нестабильности коэффициентов модели на периоде наблюдений?
Тема 4.2.
ФОРМАЛЬНЫЕ СТАТИСТИЧЕСКИЕ КРИТЕРИИ
Помимо графических существует довольно много процедур, предназначенных
для проверки выполнения стандартных предположений о линейной модели
наблюдений, использующих статистические критерии проверки гипотез.
Остановимся только на нескольких таких процедурах. В каждой из них в качестве
нулевой фактически берется гипотеза
#0: *!,..., еп ~ lid. N@, о-2).
Однако соответствующие критерии приспособлены для выявления
специфических нарушений стандартных предположений, что делает каждый
из критериев особо чувствительным именно к тем нарушениям, на которые
он «настроен».
Критерий Голдфелда — Квандта {Goldfeld-Quandt test). Если
графический анализ остатков указывает на возможную неоднородность дисперсий
ошибок £>(£,), т.е. на наличие гетероскедастичности, то:
• сначала наблюдения, насколько это возможно, упорядочивают по
предполагаемому возрастанию дисперсий случайных ошибок;
• затем отбрасывают г центральных наблюдений (для более надежного
разделения групп с малыми и большими дисперсиями случайных
ошибок), так что для дальнейшего анализа остается (п - г) наблюдений;
• производят оценивание выбранной модели раздельно по первым {п - г)/2
и по последним (п - г)/2 наблюдениям;
• вычисляют отношение F = RSS2/RSSX остаточных сумм квадратов,
полученных при подборе модели по последним (п - г)/2 (остаточная
сумма квадратов RSS2) и по первым {п - г)/2 (остаточная сумма
квадратов RSS{) наблюдениям.
При принятии решения учитывают, что если все же D{st) - <т2,
i = 1, ..., п, (дисперсии однородны) и выполнены остальные
стандартные предположения о модели наблюдений, включая предположение
о нормальности ошибок, то отношение F = RSS2/RSS{ имеет F-pacnpe-
деление Фишера F\
степенями свободы;
гп-г п-г Л (п-г Л (п-r л
— /?,— р\ с — р\ и \——-р

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 185
• гипотеза Я0 : D{st) = <т2, / = 1, ..., п, (гомоскедастичность,
однородность дисперсий ошибок — homoscedasticity) отвергается, если
вычисленное значение F-отношения «слишком велико», т.е. превышает
Л
критический уровень Fx_ax
бранному уровню значимости а.
п-г п-
V
, соответствующий вы-
Критерий Дарбина — Уотсона (Durbin-Watson test) применяется, когда
наблюдения производятся последовательно во времени, с равными
интервалами, и график изменения остатков во времени указывает на наличие
автокоррелированности (зависимости во времени) случайных составляющих Et
модели наблюдений. Предполагается, что структура автокоррелированности
определяется соотношением
£,. =/ягм + £,., / = 1,...,и,
где \р\ < 1, a Si9 i = 1, ..., и, — независимые в совокупности случайные
величины, имеющие одинаковое нормальное распределение N@, <т|), причем St
не зависит статистически от 8t_s для s > 0.
Статистика Дарбина — Уотсона {Durbin-Watson statistic) определяется
соотношением
К*,-*,-,J
DW = —
Те?
г2
1 = 1
где el9..., еп— остатки, получаемые при оценивании линейной модели
наблюдений.
В качестве нулевой здесь берется гипотеза
Я0:/7=0,
соответствующая (при нашем предположении о нормальности распределения
случайных ошибок) независимости в совокупности случайных величин sl9 ..., sn.
В качестве альтернативной при анализе экономических данных чаще всего
используют гипотезу
#0:/?>0,
соответствующую положительной автокоррелированности случайных
величин е19..., £п (т.е. тенденции преимущественного сохранения знака случайной
ошибки при переходе от /-го к (i + 1)-му наблюдению).
Статистика DW принимает значения в интервале от 0 до 4.
Рассматриваемая как случайная величина, она имеет при гипотезе Я0 : р = 0 (т.е. если эта

186
Часть 1. Основные понятия, элементарные методы
гипотеза верна) функцию плотности р(х\ симметричную относительно точки
х = 2 — середины этого интервала. Если в действительности р = р* > О, то
значения статистики DОтяготеют к левой границе интервала. Поэтому в
соответствии с общим подходом к построению односторонних статистических
критериев необходимо было бы для выбранного нами уровня значимости а
найти соответствующее ему критическое значение da (О < da < 2) и отвергать
гипотезу Я0 : р = 0 в пользу Я0 : р > О при выполнении неравенства DW <da.
Однако распределение статистики Дарбина — Уотсона зависит не только
от п и/?, но и от конкретных значений xij9j - 1,...,/?, i = 1,..., и, объясняющих
переменных, что делает неосуществимым построение таблиц критических
значений этого распределения. Дарбин и Уотсон преодолели это затруднение
следующим образом. Предполагая, что в правой части модели наблюдений
присутствует постоянная составляющая и отсутствуют запаздывающие
значения объясняемой переменной, они нашли (при различных значениях пир)
нижнюю dLa и верхнюю dUa границы интервала, в котором только и могут
находиться критические значения da статистики Дарбина — Уотсона,
независимо от того, каковы конкретные значения xij9j = 1, ..., р9 i= 1, ..., п. Иными
словами,
°<dLa<da<dUa<29
где dLa и dUa не зависят от конкретных значений xij9j = 1, ..., р, i = 1, ..., п,
а определяются только количеством наблюдений, количеством объясняющих
переменных и установленным уровнем значимости критерия.
Гипотеза Я0 : р=0:
• отвергается в пользу гипотезы НА : р > 0, если DW< dLa;
• не отвергается, если D W > dUa.
Если же dLa <DW< dUa, то никакого вывода относительно справедливости
или несправедливости гипотезы Я0 : р= 0 не делается.
При соблюдении этих правил вероятность ошибочного отвержения
гипотезы Я0 : р = 0 не превосходит заданного уровня значимости а.
Критерий Харке — Бера {Jarque-Bera test) используется в ряде пакетов
статистического анализа данных (например, в ЕViews) для проверки гипотезы
Я0 нормальности ошибок в модели наблюдений, точнее,
Я0: £l9...,e„~uxl.N@9(r2)
(значение а1 не конкретизируется). Если эта гипотеза верна, то при большом
количестве наблюдений п статистика
(sample skewnessJ (sample kurtosis-3J
6 24
JB = n

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 187
имеет распределение, близкое к распределению хи-квадрат с 2 степенями
свободы ^2B), функция плотности которого имеет вид:
1 --
р(х) = — е 2,х>0.
Здесь:
• sample skewness — выборочный коэффициент асимметрии
т^
sample skewness =-
f3
з
ч J
sample kurtosis — выборочный куртозис
m4
ml
(т2У
sample kurtosis =—j;
1 n
• eu ..., en — остатки, полученные при оценивании модели методом
наименьших квадратов.
Если распределение ошибок действительно является нормальным, то
значения выборочного коэффициента асимметрии близки к 0, а значения
выборочного куртозиса — к 3. Существенное отличие выборочного коэффициента
асимметрии от 0 указывает на несимметричность (относительно 0) графика
функции плотности распределения ошибок («скошенность» распределения).
При нарушении условия нормальности распределения ошибок значения
статистики JB имеют тенденцию к возрастанию. Поэтому гипотеза
нормальности ошибок отвергается, если значения этой статистики «слишком велики»,
а именно если
JB >zlaB),
где х\-аО)— квантиль распределения ^2B), соответствующая уровню 1 - а.
v Замечание 4.2.1. Критерии Дарбина — Уотсона и Голдфелда —
Квандта являются точными (неасимптотическими — non-
asymptotic tests) в том смысле, что они непосредственно учитывают
количество наблюдений п. В противоположность этому, критерий
Харке — Бера является асимптотическим {asymptotic test):
распределение статистики JB хорошо приближается распределением ^2B)
только при большом количестве наблюдений. Поэтому вполне
полагаться на результаты применения критерия Харке — Бера можно
только в таких ситуациях. Помимо критерия Харке — Бера, в
специализированные пакеты программ статистического анализа дан-

188
Часть 1. Основные понятия, элементарные методы
ных часто встраиваются и другие асимптотические критерии
(например, критерии Уайта и Бройша — Годфри, которые
рассматриваются ниже).
Критерий Бройша — Годфри {Breusch-Godfrey test) используется в ряде
пакетов статистического анализа данных (например, в Е Views) для проверки
гипотезы некоррелированности ошибок в модели наблюдений
У!=в1Хп+... + врХ,р+£,9 1 = 1,..., Л.
При наших предположениях (включающих нормальность распределения
ошибок) это соответствует гипотезе независимости в совокупности
случайных величин si9 i = 1,..., п. Напомним, что критерий Дарбина — Уотсона
основан на рассмотрении модели наблюдений, в которой случайные
составляющие £{ связаны соотношением
£,=/?£;_!+ £;, 1=1,..., Л,
где \р\ < 1, a Si9 i = 1, ..., л, — независимые в совокупности случайные
величины, имеющие одинаковое нормальное распределение N@9 a2s), причем S(
не зависит статистически от st_s для s > 0.
В такой модели наблюдений случайные составляющие si9 разделенные
двумя или более периодами времени и очищенные от влияния
промежуточных £J9 оказываются независимыми.
Критерий Бройша — Годфри допускает зависимость случайных
составляющих ei9 разделенных К периодами времени и очищенных от влияния
промежуточных £.. Соответствующая модель зависимости имеет вид
процесса авторегрессии порядка К:
£i=al£i_l+... + aKei_K+Si9 / = 1,...,л,
где опять Si9 i = 1,..., л, — независимые в совокупности случайные величины,
имеющие одинаковое нормальное распределение N@9 <j2s)9 причем 8t не
зависит статистически от e._s для s > 0, а условие \р\ < 1 заменяется следующим
условием:
все корни многочлена 1 - atz - ... - aKzK = 0, в том числе
и комплексные, по модулю больше 1.
Статистика этого критерия равна nR29 где R2 — коэффициент
детерминации, получаемый при оценивании вспомогательной модели
где еХ9..., еп — остатки, полученные при оценивании основной модели
наблюдений

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 189
У1=ОхХй+... + врХ1р+£^ 1 = 1,..„Л.
Недостающие значения е0,..., ех_к заменяются нулями.
В рамках вспомогательной модели проверяется гипотеза
Н0:ах= ... = ак = 0.
Если эта гипотеза верна, то при большом количестве наблюдений п
статистика критерия имеет распределение, близкое к распределению хи-квадрат
с К степенями свободы. Гипотеза Н0 отвергается при заданном уровне
значимости а, если вычисленное значение nR2 превышает критическое значение,
равное квантили уровня A - а) указанного распределения, т.е. если
nR2>(nR2)crit=xla{K).
Конечно, при интерпретации результатов применения критерия Бройша —
Годфри следует помнить, что этот критерий асимптотический, тогда как
критерий Дарбина — Уотсона точный. Однако, в свою очередь, возможность
применения критерия Дарбина — Уотсона ограничивается тем, что он
• допускает зависимость «очищенных» случайных ошибок только на
один шаг, т.е. К = 1;
• неприменим в ситуациях, когда в число объясняющих переменных
включаются запаздывающие значения объясняемой переменной.
Критерий Бройша — Годфри свободен от этих ограничений.
Критерий Уайта (White test) используется в ряде пакетов статистического
анализа данных (например, в Е Views) для проверки однородности дисперсий
ошибок в модели наблюдений
У1=01Хп+... + ерХф+£19 1 = 1,..., И.
Критерий имеет два варианта.
Вариант I. В рамках вспомогательной модели
р р
e?=al+Y<aJxiJ+Ydj3jxl-+vi, / = l,...,w,
у=2 j=2
где е!,..., еп — остатки, полученные при оценивании основной модели
наблюдений,
проверяется гипотеза
H0:aj =fij =0, у = 2,...,/?.
Статистика критерия равна nR2, где R2 — коэффициент детерминации,
получаемый при оценивании последней модели. Если указанная гипотеза верна,
то при большом количестве наблюдений п статистика критерия имеет
распределение, близкое к распределению хи-квадрат с Bр -2) степенями свободы.
Гипотеза Н0 отвергается при заданном уровне значимости а, если вычислен-

190
Часть 1. Основные понятия, элементарные методы
ное значение nR2 превышает критическое значение, равное квантили уровня
A -а) указанного распределения, т.е. если
nR2>(nR2)crit=XlaBp-2).
Вариант И. В рамках вспомогательной модели
р р р
е? =ai+Iv? + ZZ^¥*+v/» / = 1,...,и,
у=2 j=2 k=j
где е!,..., еп — остатки, полученные при оценивании основной модели
наблюдений,
проверяется гипотеза
н .14 =0' 7 = 2,...,р,
0'[/?д=0, 2<j<k<p.
Статистика критерия равна nR2, где R2 — коэффициент детерминации,
получаемый при оценивании последней модели. Если указанная гипотеза верна,
то при большом количестве наблюдений п статистика критерия имеет рас-
_ р2+р-2
пределение, близкое к распределению хи-квадрат с степенями
свободы. Гипотеза Н0 отвергается при заданном уровне значимости а, если
вычисленное значение nR2 превышает критическое значение, равное
квантили уровня A - а) указанного распределения, т.е. если
nR2>(nR2)crit=xla
Гр2+р-2
Как и в случае критерия Бройша — Годфри, при интерпретации
результатов применения обоих вариантов критерия Уайта следует помнить, что этот
критерий асимптотический.
V Замечание 4.2.2. При описании критерия Уайта неявно
предполагалось, что хп = 1. Если постоянная не включена в исходную модель
наблюдений, то в моделях, оцениваемых на втором шаге обоих
вариантов критерия Уайта, суммирование в первой сумме следует
начинать с j = 1.
Критерий Рэмси RESET (Ramsey's Regression Specification Error Test)
используется для проверки в рамках нормальной линейной модели
У г = в\хп + — + OpXip + ei9 i = l,..., n.
предположения
£(£,.) = (), / = 1,..., и,
из-за невыполнения которого возникает смещение оценок коэффициентов.

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 191
При помощи этого критерия можно выявить:
• наличие «пропущенных» переменных (т.е. невключение в правую часть
уравнения некоторых существенных переменных);
• неправильную функциональную форму представления некоторых (или
всех) переменных (например, неправильное использование логарифмов
переменных вместо уровней этих переменных);
• наличие корреляции между объясняющими переменными и ошибкой
в уравнении регрессии (которая может быть вызвана, например,
наличием ошибок измерения объясняющей переменной — об этом см.
разд. 6).
Есть несколько вариантов критерия Рэмси. Рассмотрим вариант,
используемый в пакете ЕViews. В этом варианте сначала оценивается заявленная
модель наблюдений, и по результатам ее оценивания вычисляются значения
Затем оценивается вспомогательная модель
У1=вххп+... + Орх¥+у$ +... + уг_ху\9 / = 1,...,л,
и в рамках этой модели проверяется гипотеза
Н0:ух=... = уг_х=0.
Если эта гипотеза верна, то при большом количестве наблюдений п
статистика критерия имеет распределение, близкое к распределению хи-квадрат
с (г - 1) степенями свободы. Гипотеза Н0 отвергается при заданном уровне
значимости а, если вычисленное значение nR2 превышает критическое
значение, равное квантили уровня A - а) указанного распределения, т.е. если
nR2>(nR2)crit=xla(r-\).
По поводу выбора значения г нет общих рекомендаций. Рэмси
рассматривал возможность включения в правую часть вспомогательного уравнения
второй, третьей и четвертой степеней j>;. Однако в более поздних работах
другие авторы рекомендуют использовать только вторую степеньjp,.
Критерии Чоу {Chow tests). Чоу предложил два критерия для проверки
стабильности модели на всем периоде наблюдений. Один из них — Chow
breakpoint test — основан на проверке гипотезы о сохранении значений всех
коэффициентов при переходе от одного подпериода полного периода
наблюдений к другому и будет рассматриваться в рамках приводимого ниже
примера. Другой — критерий Чоу на качество прогноза {Chow forecast test) —
сравнивает качество прогнозов, сделанных на основе оценивания модели
на одной части периода для значений объясняемой переменной на другой

192
Часть 1. Основные понятия, элементарные методы
части периода, с качеством «прогнозов», сделанных на основе оценивания
модели на всем периоде наблюдений. Более точно, возьмем на периоде
наблюдений два отрезка:
/=1,..., п0 и / = и0 + 1,..., и.
Оценив коэффициенты модели
Л=01*/1+-" + 0р**,+*/> / = 1,...,л,
по всем п наблюдениям, получим прогнозные значения
j>,.(w), / = w0+l,...,w.
Наряду с этим оценим коэффициенты модели только по первым п0
наблюдениям. При этом получим прогнозные значения будущих значений
объясняемой переменной
й(и0), 1 = л0+1,...,и.
Если модель стабильна, то значения у{(п0) не должны слишком сильно
отличаться от значенийyt(n\ i = n0 + l,..., п.
Степень различия измеряет статистика
г (RSS„-RSSno)/(n-n0)
RSSnJ(n0-p) '
где RSS„ — остаточная сумма квадратов при оценивании модели на всем
периоде наблюдений;
RSS„o— остаточная сумма квадратов при оценивании модели по первым
п0 наблюдениям.
Если модель стабильна (и выполнены другие стандартные предположения),
то указанная статистика имеет F-распределение, F{n - п0, п0 - р). Гипотеза
о стабильности модели отвергается, если вычисленное значение этой
статистики превышает значение Fx_a{n - п0, п0 -р).
ПРИМЕР 4.2.1
Рассмотрим статистические данные по США за период с 1960 по 1985 г. о
следующих макроэкономических показателях:
DPI — годовой совокупный располагаемый личный доход;
CONS — годовые совокупные потребительские расходы;
ASSETS — финансовые активы населения на начало календарного года.
(все показатели в млрд долл., в ценах 1982 г.). Данные приведены в табл. 4.2.
Характер изменения этих макроэкономических показателей демонстрирует
график на рис. 4.19.

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 193
Таблица 4.2
Статистические данные по США с 1960 по 1985 г. (в ценах 1982 г., млрд долл.)
Год
1960
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
1972
DPI
1090.9
1122.5
1168.7
1208.7
1289.7
1367.4
1433.0
1494.9
1551.1
1601.7
1668.1
1730.1
1797.9
CONS
1005.2
1024.3
1067.6
1109.6
1169.4
1237.9
1300.5
1339.4
1405.9
1458.3
1491.8
1540.3
1622.3
ASSETS
1203.1
1226.7
1293.7
1374.9
1464.5
1544.0
1641.6
1675.2
1772.6
1854.7
1862.2
1902.8
2011.4
Год
1973
1974
1975
1976
1977
1978
1979
1980
1981
1982
1983
1984
1985
DPI
1914.9
1894.9
1930.4
2001.0
2067.9
2166.5
2211.4
2214.8
2249.0
2261.4
2332.5
2470.5
2527.3
CONS
1687.9
1672.4
1710.8
1804.0
1884.9
1960.2
2003.6
2000.7
2024.4
2050.7
2146.5
2246.3
2323.9
ASSETS
2190.6
2301.8
2279.6
2308.4
2421.6
2554.9
2666.2
2704.3
2682.8
2741.8
2850.1
3038.1
3267.7
млрд долл. ^
3500
Рис. 4.19
Рассмотрим модель наблюдений
CONSt =вх+ 62DPIt + 03ASSETSt +sn / = 1 26,
где индексу t соответствует A959 + t)-n год. Это модель с 3 объясняющими
переменными:
Хх =1, Х2= DPI, X3 = ASSETS.
Оценивание этой модели дает следующие результаты: R2 = 0.9981,

194
Часть 1. Основные понятия, элементарные методы
в2 = 0.672, Р-значение = 0.0000;
въ = 0.174, Р-значение = 0.0069;
так что оценки коэффициентов при объясняющих переменных Х2 = DPI,
Хъ - ASSETS имеют высокую статистическую значимость.
Ниже представлены диаграмма рассеяния для предсказанных (CONSF)
и наблюдаемых (CONS) значений переменной CONS (рис. 4.20), а также гра-
фик зависимости стандартизованных остатков ct = — (RESJSTAND) от пред-
сказанных (CONSF) значений переменной CONS (рис. 4.21).
2500
CONSF
2500
CONSF
График на рис. 4.20 отражает высокое значение коэффициента
детерминации. На графике на рис. 4.21 заметно возрастание разброса точек относительно
нулевого уровня при значениях CONSF > 1600.
Поскольку первый из приведенных в этом примере графиков указывает
на возрастание годовых потребительских расходов с течением времени, для
реализации процедуры Голдфелда — Квандта естественно воспользоваться
уже имеющимся упорядочением наблюдений во времени (это и будет
направлением ожидаемого возрастания дисперсий случайных ошибок). Выделим
из 26 наблюдений две группы, состоящие из первых 10 и последних 10
наборов значений (хп, xt29 хв)9 соответствующие периодам с 1960 по 1969 г. и
с 1976 по 1985 г. (так что отброшены г = 6 центральных наблюдений). При
раздельном подборе линейных моделей по этим группам наблюдений
получаем остаточные суммы квадратов RSSX = 208.68 и RSS2 = 1299.66
соответственно, так что наблюдаемое значение F-статистики критерия Голдфелда —
Квандта равно:

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 195
^ = 1^66=6.228.
RSSl 208.68
Если стандартные предположения о случайных ошибках в модели
наблюдений выполнены, то тогда отношение указанных остаточных сумм
квадратов как случайных величин имеет F-распределение Фишера
( 'Л/Г /Г Л/Г /Г \
F 3, 3 = FG,7). Если, как обычно, зададим уровень
значимости а - 0.05, то соответствующее этому уровню значимости критическое
значение F-статистики равно F095G, 7) = 3.79.
Наблюдаемое значение этой статистики 6.228 превышает критическое,
поэтому гипотеза о выполнении стандартных предположений об ошибках
отклоняется в пользу гипотезы о возрастании дисперсий D{st) с ростом
значений вх + 92DPI + d3ASSETS. Заметим, наконец, что вероятность превышения
случайной величиной с распределением FG, 7) значения 6.228 (Р-значение)
равна 0.0138.
Сравним результаты применения критерия Голдфелда — Квандта с
результатами, полученными при использовании двух вариантов критерия Уайта.
Для первого варианта наблюдаемое значение статистики критерия равно
nR2 = 8.884. Поскольку р = 3, число степеней свободы соответствующего
распределения хи-квадрат равно 2р - 2 = 4. Вероятность того, что случайная
величина, имеющая такое распределение, превысит значение 8.884, равна
0.0641, так что значение nR2 = 8.884 меньше критического, а значит, гипотеза
об однородности дисперсий этим вариантом критерия Уайта не отвергается.
При использовании второго варианта наблюдаемое значение статистики
критерия равно nR2 = 9.699. Число степеней свободы соответствующего рас-
Р2+Р~2 с о
пределения хи-квадрат равно — = 5 . Вероятность того, что случайная
величина, имеющая такое распределение, превысит 9.699, равна 0.0842, так
что значение nR2 = 9.699 меньше критического, а значит, гипотеза об
однородности дисперсий не отвергается и этим вариантом критерия Уайта.
Таким образом, статистические выводы относительно однородности
дисперсий случайных составляющих в рассматриваемой модели наблюдений
оказались противоречивыми: гипотеза об однородности дисперсий
отвергается критерием Голдфелда — Квандта, но не отвергается обоими вариантами
критерия Уайта. Как можно объяснить такое противоречие?
• Оба варианта критерия Уайта асимптотические, тогда как критерий
Голдфелда — Квандта учитывает реально имеющееся количество
наблюдений.
• Оба варианта критерия Уайта являются критериями согласия, не
настроенными на какой-то специфический класс альтернатив гипотезе

196
Часть 1. Основные понятия, элементарные методы
об однородности дисперсий, тогда как использование критерия Голд-
фелда — Квандта непосредственно связано с альтернативой,
выраженной в форме возрастания дисперсий ошибок для соответствующего
упорядочения наблюдений. И здесь проявляется общее положение:
критерии, построенные с расчетом на некоторый узкий класс альтернатив,
оказываются более мощными в отношении этих альтернатив по
сравнению с критериями, рассчитанными на более широкий класс
альтернатив (т.е. они чаще отвергают нулевую гипотезу, когда верна не она,
а гипотеза из указанного узкого класса альтернатив).
Рассмотрим график зависимости стандартизованных остатков ct=— от
номера наблюдений (рис. 4.22) и его вариант в виде зависимости от года
наблюдения (рис. 4.23).
RESID_STAND
2 +
RESID STAND
i
z -
1 -
П -
и
-1 -
-2-
-3-
i
Iiii . .1 1
1
i i I i i i i | i i i i | i i i
ill. .In
1 '"
1
i I i i i i I i i i i I
—►
Рис. 4.22
1960 1965 1970 1975 1980 1985 Год
Рис. 4.23
В данном случае обращает на себя внимание наличие серий остатков
одинакового знака, что сигнализирует о том, что ошибки в модели наблюдений,
скорее всего, имеют полоэюительную автокорреляцию. Для 26 наблюдений
и р = 3 объясняющих переменных границы для критического значения
статистики Дарбина — Уотсона при а = 0.05 (односторонний критерий) равны:
,о.о5 = 1-22, dU005 = 1.55.
В то же время вычисленное по остаткам от оцененной модели значение
статистики Дарбина — Уотсона равно DW - 1.01, что меньше нижней
границы я^о.05 = 1.22. Следовательно, нулевая гипотеза о выполнении стандартных
предположений отклоняется в пользу гипотезы о положительной автокорре-
лированности ошибок.
Сравним результаты применения критерия Дарбина — Уотсона с
полученными при использовании критерия Бройша — Годфри.
Если исходить из допущения зависимости очищенных случайных ошибок
только на один шаг (К= 1), как это делается при использовании критерия

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 197
Norm Quantile
DP
3 С k
i
u.o -
0.4-
0.3-
0.2-
0.1 -
<
0-
к
,1
♦ ♦
♦ ♦
♦ ♦
♦ ♦
► ♦
—I—I—I—I—I—I
—►
-3-2-1 0 1 2 3 C_k
Рис. 4.25
Дарбина — Уотсона, то в этом случае вычисленное значение статистики
критерия Бройша — Годфри равно nR2 = 6.068, что соответствует Р-значе-
нию, равному 0.014. Гипотеза независимости ошибок отвергается, что
согласуется с результатом, полученным при использовании критерия Дарбина —
Уотсона.
В то же время если взять К = 5, то nR2 = 10.331, что соответствует Р-зна-
чению, равному 0.066. Гипотеза о независимости ошибок в этом случае не
отвергается при установленном уровне значимости а = 0.05, что расходится
с результатом, полученным при использовании критерия Дарбина —
Уотсона. Эта гипотеза не отвергается также при выборе К = 6 (nR2 = 0.095), К = 7
(nR2 = 0.127) и т.д. Это вполне объяснимо: выбор К= 5, К =6, К-1
соответствует выбору все более широкого
Kernel Density
(Epanechnikov, h = 025)
класса альтернатив по сравнению
с К = 1, что приводит к
уменьшению вероятности отвергнуть
гипотезу независимости ошибок в
случае, когда она неверна.
Проверим, наконец,
предположение о нормальном
распределении ошибок. Для этого сначала
рассмотрим диаграмму «квантиль-
квантиль» (Q-Q plot) (рис. 4.24),
диаграмму плотности (DP-ploi)
(рис. 4.25) и ядерную оценку
плотности (рис. 4.26).
Первая диаграмма не выглядит
удовлетворительной, вторая
обнаруживает определенную асимметрию, как и ядерная оценка плотности.
Выборочный коэффициент асимметрии здесь равен -1.285, выборочный куртозис
1 2
RESID STAND
Рис. 4.26

198
Часть 1. Основные понятия, элементарные методы
равен 5.321. Оба эти значения говорят отнюдь не в пользу нормальности
ошибок. Статистика критерия Харке — Бера принимает значение 12.997, что
соответствует Р-значению 0.0015. Следовательно, и этот критерий не
подтверждает гипотезу о выполнении стандартных предположений об ошибках.
Результаты применения критерия RESET приведены в табл. 4.3.
Таблица. 4.3
Результаты применения критерия RESET
Включенные степени у /
2
2, 3
2, 3, 4
Р-значение
0.0015
0.0046
0.0032
Они говорят о нарушении предположения
E(st) = 0, f = l,...,w.
Что касается критерия Чоу, сравнивающего прогнозные значения (Chow
Forecast Test), полагая в нем л0 = 13, получим значение F-статистики
F = 11.037, что соответствует Р-значению 0.0003 и говорит о нестабильности
модели.
Итак, обнаружили, что модель линейной связи
CONSt = вх +e2DPIt+03ASSETS,+£t, t = 1,..., 26,
оказалась неудовлетворительной, поскольку анализ остатков от оцененной
модели выявил гетероскедастичность и автокоррелированность ошибок,
отличие распределения ошибок от нормального, нарушение условия E(st) = 0,
t = 1,..., и, и нестабильность модели.
График зависимости стандартизованных остатков ct= — от номера
наблюдений и его вариант в виде зависимости от года наблюдения
указывают на заметную разницу в поведении остатков в первой части периода
наблюдений (до 1972 г.) и во второй его части A973—1985 гг.). Такое
различие в поведении остатков объясняется тем, что в 1973 г. произошел
структурный сдвиг в экономике, связанный с мировым
топливно-энергетическим кризисом, который изменил характер связи между рассматриваемыми
макроэкономическими факторами. Последнее могло, например, выразиться
в изменении значений параметров в19 в2> &з ПРИ переходе ко второй части
периода наблюдений. Возможность такого изменения учитывает
расширенная модель

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 199
CONS, = yl(Dl),+y2(D2),+y3(DPIl),+y4(DPI2), +
+y5(ASSETS\),+y6(ASSETS2),+sn r = l 26,
где (D\), — фиктивная переменная, равная 1 для t = 1, ..., 13 (что
соответствует периоду с 1960 по 1972 г.) и равная 0 для t = 14, ..., 26 (что
соответствует периоду с 1973 по 1985 г.);
(D2)t = 1 - (D\), — фиктивная переменная, равная 0 для t = 1,..., 13 и
равная 1 для t= 14,..., 26;
(DPIl), = DPI, • (Dl), — переменная, равная (DPI)t для t = 1, ..., 13 и
равная 0 для t = 14,..., 26;
(DPI2), = DPI, • (D2)t — переменная, равная 0 для t = 1, ..., 13 и равная
(DPI), для t= 14, ...,26;
(ASSETSl), = ASSETS, • (Dl), — переменная, равная ASSETS, для t = 1,..., 13
и равная 0 для t - 14,..., 26;
(ASSETS2), = ASSETS, • (D2), — переменная, равная 0 для t = 1, ..., 13
и равная ASSETS, для t = 14,..., 26.
Заметим, что при этом
(DPIl),+(DPI2),=DPI„ r = l 26,
(ASSETSl) t + (ASSETS!)t = ASSETS,, t = 1,..., 26.
В рамках расширенной модели проверим гипотезу
Н0'.ух=у2, Уз=Г4> Г5=Г6-
Это линейная гипотеза с q = 3 линейными ограничениями, которые можно
записать в виде
#о: Ух -Г2=°> Уъ -Уа =°> Уз -Ув=°-
Будем проверять эту гипотезу, используя F-критерий. В такой постановке
F-критерий известен как критерий Чоу на структурный сдвиг (Chow
breakpoint test). Значению F-статистики 10.490 соответствует F-значение 0.0002,
так что гипотеза Н0 отвергается, и это говорит об изменении хотя бы одного
из параметров в19 #2, въ при переходе ко второй части периода наблюдений.
Поскольку оценки параметров у5 и у6 статистически незначимы (им
соответствуют F-значения 0.1157 и 0.5599), проверим линейную гипотезу о
равенстве нулю обоих этих параметров (q = 2), используя F-критерий. Получаемое
Р-значение 0.2412 свидетельствует о том, что последняя гипотеза не
отвергается, так что, допуская изменение параметров модели при переходе ко второй
части периода наблюдений, можно вообще отказаться от включения в модель
переменной ASSETS и ограничиться моделью
CONS,=yl(D\),+y2(D2),+y3(DPIl),+y4(DPI2),+s„ * = !,..., 26.

200
Часть 1. Основные понятия, элементарные методы
Оценивание этой модели дает следующие результаты: R2 = 0.9992,
ух = 58.786, Р-значение = 0.0119;
у2 = -234.836, Р-значение = 0.0000;
у3 = 0.864, Р-значение = 0.0000;
ft = 1.012, Р-значение = 0.0000.
Гипотеза Н0 : у3 = ft (q = 1) здесь отвергается (Р-значение = 0.0000), как
и гипотеза Н0 : ух = у29 так что структурный сдвиг затрагивает и постоянную,
и коэффициент при DPI.
Значение статистики Дарбина — Уотсона равно DW - 2.06 и не выявляет
автокоррелированности ошибок. К тому же результату приводит и
применение критерия Бройша — Годфри с Я" = 1, К = 2, К= 3. Критерий Уайта дает
Р-значение = 0.508, не выявляя гетероскедастичности, а критерий Харке —
Бера дает Р-значение = 0.469, не выявляя существенных отклонений
распределения ошибок от нормального.
Вспомним, однако, про критерий Голдфелда — Квандта. Опять выделив
периоды с 1960 по 1969 г. и с 1976 по 1985 г., получим значение F-статистики
3.354, соответствующее Р-значению = 0.0832, так что на сей раз и этот
критерий не обнаруживает существенной гетероскедастичности.
Результаты использования критерия RESET приведены в табл. 4.4.
Таблица. 4.4
Результаты применения критерия RESET
Включенные степени у /
2
2, 3
2, 3, 4
Р-значение
0.3080
0.4132
0.3659
В данном случае не обнаруживается и нарушения предположения
£(£,) = 0, f = 1,..., л.
В связи с этим есть основания принять в качестве возможной модели
наблюдений, объясняющей изменение объема совокупного потребления на периоде
с 1960 по 1985 г., оцененную модель
CONS, = 58.786(D1), -234.836(D2), +
+ 0.864(Z)/Yl),+1.012(D/Y2),+£,, r = l 26.
Эту модель можно также записать в виде
Г58.786 + 0.864ф/>/),+£,, г = 1 13
CONSt=<
•234.S36 + \M2(DPI)t+st, r = 14,...,26.

Раздел 4. Проверка выполнения стандартных предположений о модели наблюдений 201
Исходя из последней формы записи такая модель называется двухфазной
линейной регрессией {two-phase linear regression model) или линейной
моделью с переключением {switching regression model). Заметим, наконец,
что, допустив возможность изменения постоянной и коэффициента при DPI
при переходе ко второй части периода наблюдений, можно допустить при этом
и изменение дисперсии ошибок, т.е. полагать, что D{st) = а\ для t - 1, ..., 13
и D{st) = <j\ для t = 14, ..., 26. Оценки для ах и <т2 в этом случае равны
соответственно 8.887 и 14.886.
v Замечание 4.2.3. Следуя идеологии «тест, тест, тест»,
останавливаемся на модели, которая успешно проходит целый ряд тестов,
проверяющих гипотезу о выполнении всех стандартных предположений
и направленных на выявление специфических нарушений основных
предположений. Между тем при таком подходе возникает проблема,
связанная с потерей контроля над уровнем значимости
используемой процедуры.
Предположим, что для проверки нулевой гипотезы (в данном
случае — гипотезы о выполнении всех стандартных
предположений) используются К тестов (статистических критериев),
основанных на К различных статистиках Tl9 Г2, ..., Тк и имеющих
критические множества Rl9..., RK, соответствующие одинаковому для всех к
уровню значимости а, так что Р{ТК е RK} = a, k = 1, ..., К. Обычно
при использовании совокупности К тестов нулевая гипотеза
отвергается, если ТК е RK хотя бы для одного к, к- 1, ..., К. При
использовании такого правила результирующая ошибка 1-го рода а*, т.е.
вероятность отвергнуть в итоге нулевую гипотезу, когда она верна,
не совпадает с уровнем значимости а каждого отдельного
критерия. Значение а* больше, чем а, но его невозможно вычислить, если
неизвестно совместное распределение вероятностей указанных К
статистик. В связи с этим возникает необходимость в получении
верхней границы для а*. Наиболее простым способом является
использование для этой цели неравенства Бонферрони:
а* = Р{ТК е RK хотя бы для одного к, к = 1,..., К} <
<^Р{ТкеЛК} = Ка.
Отсюда вытекает, что если мы хотим обеспечить для процедуры
в целом уровень значимости а, то для каждого отдельного критерия
достаточно взять уровень значимости а/К. При этом
результирующая ошибка 1-го рода не превысит а. Такая процедура весьма
проста, но в случае сильной коррелированности статистик Tl9 Г2, ..., Тк

202
Часть 1. Основные понятия, элементарные методы
реальная ошибка 1-го рода этой процедуры может оказаться
существенно меньше заявленного уровня значимости а. Исследование этого
вопроса проведено в работе {Godfrey, 2005).
у/ Замечание 4.2.4. Вообще говоря, при построении моделей
регрессии для переменных, значения которых развернуты во времени, т.е.
являются временными рядами, возникает целый ряд проблем,
которые рассматриваются в соответствующем разделе эконометрики —
анализе временных рядов (time series analysis). Эти проблемы будут
изучены во второй части данного учебника.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие статистические критерии используются для выявления гетероскедастично-
сти? Чем принципиально различаются критерии Голдфелда — Квандта и Уайта?
2. Какие критерии используются для выявления автокоррелированности ошибок? Чем
принципиально различаются критерии Дарбина — Уотсона и Бройша — Годфри?
3. Какие критерии используются для выявления нарушения предположения о
нормальном распределении ошибок?
4. Какие критерии используются для выявления неправильной спецификации модели
(неправильная функциональная форма, нестабильность коэффициентов модели)?

Раздел 5
УЧЕТ НАРУШЕНИЙ
СТАНДАРТНЫХ ПРЕДПОЛОЖЕНИЙ
О МОДЕЛИ
Тема 5.1
ВКЛЮЧЕНИЕ В МОДЕЛЬ
ФИКТИВНЫХ ПЕРЕМЕННЫХ
В разд. 4 для выявления наличия структурного сдвига к данным по США
за период с 1960 по 1985 г. был применен критерий Чоу. Мы пришли к
выводу, что вследствие мирового топливно-энергетического кризиса 1973 г.
в модели
CONSt = вх + e2DPIt + 03ASSETSt +st, t = 1,..., 26,
выявляется наличие структурного сдвига (изменяются значения
коэффициентов). Для того чтобы примененить этот критерий, была допущена
возможность изменения всех трех коэффициентов при переходе от периода с 1960
по 1972 г. к периоду с 1973 по 1985 г. и соответственно изменена
спецификация модели с переходом к расширенной модели:
CONSt = 7x(D\)t+Y2(D2)t+Y,(DPI\)t +yA(DPI2)t +
+ ys(ASSETS\)t+y6{ASSETS2)t+en t = l,..„ 26,
использующей искусственно построенные переменные (Z)l), и (ZJ)„ при этом
(ZJ), = 1 - (Dl)n (Dl)t = 1 для t = 1,..., 13 (что соответствует периоду с 1960 по
1972 г.) и (D1), = 0 для t = 14,..., 26 (что соответствует периоду с 1973 по 1985 г.).
Переменные такого типа принято называть фиктивными переменными
(dummy variables — дамми-переменные, или просто dummies — дамми),
поскольку они не являются собственно макроэкономическими (или
микроэкономическими) показателями, а указывают просто на какие-то временные
промежутки, группы стран или отдельные страны, группы регионов или
отдельные регионы, служат для обозначения принадлежности субъекта той

204
Часть 1. Основные понятия, элементарные методы
или иной социальной или этнической группе и т.п. Введение таких
переменных позволяет выявлять наличие эффектов, специфических для отдельных
стран, групп стран, социальных групп, регионов и т.п.
В отличие от исходной модели с 3 объясняющими переменными, в модели
с 6 переменными использованные статистические критерии не выявили
нарушений стандартных предположений. Поэтому в рамках расширенной модели
уже можно было пользоваться стандартными статистическими выводами
в отношении коэффициентов модели, и это привело нас к редуцированной
модели с 4 объясняющими переменными, которая, по сути, является
двухфазной линейной моделью.
Расширение модели наблюдений за счет включения в нее дамми-пере-
менных весьма типично при анализе факторов, имеющих сезонный характер
(сезонную динамику). Рассмотрим в связи с этим следующий пример.
ПРИМЕР 5.1.1
Приведенный на рис. 5.1 график показывает динамику изменения совокупного
располагаемого дохода DPI и объемов продаж SALES лыжного инвентаря
в США (квартальные данные за период с 1964 по 1972 г.; DPI— в млрд долл.,
SALES— в млн долл., в ценах 1972 г., см. табл. 5.1).
Оценивание линейной модели
SALES t = a + j3 DPIt +sn t = 1,..., 3 6,
дает результаты, приведенные в табл. 5.2.
DPI
SALES
РИС. 5.1
Оценка коэффициента при переменной DPI статистически значима.
Однако график стандартизованных остатков (приведенный для удобства в двух
формах — рис. 5.2 и рис. 5.3) обнаруживает явную неадекватность
построенной модели имеющимся наблюдениям.
Характер этой неадекватности таков, что он не улавливается критерием Дар-
бина — Уотсона: значение 1.966 статистики Дарбина — Уотсона близко к 2.

Раздел 5. Учет нарушений стандартных предположений о модели 205
Таблица 5.1
Совокупный располагаемый доход DPI и объемы продаж SALES
лыжного инвентаря в США (в ценах 1972 г.)
Год,
квартал
| 1964:1
1 1964:2
1 1964:3
| 1964:4
1965:1
1965:2
1965:3
1965:4
1966:1
1966:2
1966:3
1966:4
1967:1
1967:2
1967:3
1967:4
1968:1
1968:2
DPI1972,
млрд долл.
157.4034
165.5068
161.5369
165.2709
166.4503
168.7129
170.4000
172.0651
172.5916
173.6561
175.2532
175.7250
175.9565
178.6025
181.4444
181.8293
182.3892
185.2722
SALES1972,
млн долл.
53.43051
48.21284
44.02953
53.99799
52.75629
44.42772
47.48852
52.86840
54.79100
47.48408
47.04873
53.51625
55.43292
45.90745
51.01481
56.75671
56.37485
50.91834
Год,
квартал
1968:3
1968:4
1969:1
1969:2
1969:3
1969:4
1970:1
1970:2
1970:3
1970:4
1971:1
1971:2
1971:3
1971:4
1972:1
1972:2
1972:3
1972:4
DPI1972
млрд долл.
184.8915
185.3775
185.6923
186.6742
188.8089
189.7213
190.0968
192.7143
195.0632
193.6364
196.1125
196.9447
197.6725
197.3382
197.0121
197.6394
196.3040
196.0000
SALES1972,
млн долл.
47.97185
55.73602
54.49402
49.77978
51.92244
55.98525
56.91452
49.47460
46.63579
56.43117
56.65473
49.45025
49.78809 1
55.02500 1
53.84310
48.12981 1
48.36770 1
52.80000 1
Таблица 5.2
Объясняемая переменная SALES
(Method: Least Squares; Sample: 1964Q1 1972Q4; Included observations: 36)
I
I Переменная
I
! с
DPI
■ R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
F-statistic
Prob. (F-statistic)
Коэффициент
27.99904
0.119943
0.208644
0.185369
3.583419
436.5904
-96.00037
8.964254
0.005103
Стандартная
ошибка
6.954436
0.040061
/-статистика
4.026069
2.994036
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter
Durbin-Watson stat
Р-значение
0.0003
0.0051
48.74395
3.970245
5.444465
5.532438
5.475170
1.965655

206
Часть 1. Основные понятия, элементарные методы
о т- см
h- h- h-
О G) О)
Год
Рис. 5.2
i
2.0-
0.5-
1.0-
1.5-
П -
■0.5-
■1.0-
1.5-
2.0-
11. J il II li ll III,
И1
i м I i
1 1 1 М 1 1 1 1 1 | 1 1 1 | 1 II | 1 1 1 | 1 1 1 | М | ►
со
ю
со
со
со
со
СО
со
со
о
CN
Год
Рис. 5.3
RES01
8
Это неудивительно: за положительными остатками с равным успехом следуют
как положительные, так и отрицательные остатки, что соответствует
практическому отсутствию корреляции между соседними ошибками и
подтверждается диаграммой рассеяния (рис. 5.4).
На рис. 5.4 RES01 — переменная,
образованная остатками от подобранной
модели линейной связи, a RES0l(-l) —
переменная, образованная
запаздывающими на один квартал значениями
переменной RES01.
В то же время налицо отрицательная
коррелированность остатков для
наблюдений, отстоящих на два квартала
(рис. 5.5), и положительная — для
наблюдений, отстоящих на четыре квартала
(рис. 5.6).
В отличие от критерия Дарбина —
Уотсона, критерий Бройша — Годфри
«замечает» такую коррелированность:
допустив коррелированность очищенных
ошибок для наблюдений, разделенных
двумя кварталами, получим Р-значение = 0.000009, что ведет к безусловному
отклонению гипотезы о независимости ошибок.
Обратим теперь внимание на весьма специфическое поведение остатков.
Все остатки, соответствующие I и IV кварталам, положительны, а все остатки,
соответствующие II и III кварталам, отрицательны. Такое положение, конечно,
просто отражает тот факт, что спрос на зимний спортивный инвентарь
возрастает в осенне-зимний период и снижается в весенне-летний период года,
т.е. имеет сезонный характер.
6 7
4 Т
2 4-
°|
-2 +
-4
-6
-8
-8
4 8
RES01(-1)
Рис. 5.4

Раздел 5. Учет нарушений стандартных предположений о модели
207
RES01
▲
8+- ;
el А
4 + . &
о+ :
-2 + ' ■ :
-6 -L' ■ ■
-8 -| 1 1 1 }-+
-8-4 0 4 8
RES01(-4)
Рис. 5.5 Рис. 5.6
Построенная модель не учитывает фактора сезонности спроса и потому
оказывается неадекватной. Вследствие этого такая модель не может, в
частности, быть использована для прогнозирования объема спроса в зависимости
от величины совокупного располагаемого дохода.
Дополним модель переменной DUMMY, значение которой равно 1 для
I и IV кварталов и равно 0 для II и III кварталов. Добавление такой
переменной в качестве объясняющей позволяет учесть сезонные колебания спроса.
Оценивание расширенной модели
SALESt=a + pDPIt+yDUMMYt+st, / = 1,...,36,
дает результаты, приведенные в табл. 5.3.
Таблица 5.3
Объясняемая переменная SALES 1972
(Method: Least Squares; Sample: 1964Q1 1972Q4; Included observations: 36)
Переменная
С
DPI1972
DUMMY
Коэффициент
23.93338
0.124919
6.410030
Стандартная
ошибка
2.781524
0.015933
0.475062
/-статистика
8.604413
7.840376
13.49303
Р-значение
0.0000
0.0000
0.0000
Оцененное значение 6.410 коэффициента при переменной DUMMY
фактически свидетельствует о том, что спрос на лыжный инвентарь в I и IV
кварталах возрастает по сравнению со спросом во II и III кварталах в среднем
примерно на 6.41 млн долл. (в ценах 1972 г.). График на рис. 5.7 иллюстрирует
качество подобранной расширенной модели.
На сей раз Р-значение для статистики критерия Бройша — Годфри (с
включением в правую часть запаздываний на 1 и 2 шага) равно 0.4389 против
RES01
4 8
RES01(-2)

208
Часть 1. Основные понятия, элементарные методы
▲
4-
2-
п
и
■2-
■4-
:..!...!_
"V Л/
1 1 1 1 1 1
^•7 м
-У- -| "
1 | 1 1 1 | 1 1 1 | 1 1 1 | 1
.< •••*
V
i i I i i i I i i
i
*••* ~
н-Ин-
к
-55.0
-52.5
-50.0
-47.5
-45.0
-42.5
-40.0
►
1964 1965 1966 1967 1968 1969 1970 1971 1972
Год
5 Residual
• Actual
■ Fitted
Рис. 5.7
прежнего 0.000009, так что теперь этот критерий не отвергает гипотезу
независимости случайных ошибок sl9..., £п.
По существу, мы подобрали две различные модели линейной связи между
DPI и SALES:
модель SALES = 23.93338 + 0.124919DP/
для весенне-летнего периода;
модель SALES = B3.93338 + 6.410030) + 0.124919 DPI
для осенне-зимнего периода.
При этом (одинаковая для обеих моделей) предельная склонность к
закупке лыжного инвентаря оценивается величиной 0.124919.
Вообще говоря, в подобных задачах возможны ситуации, когда и угловой
коэффициент не остается постоянным для различных наблюдений, как это
было показано при рассмотрении зависимости расходов на потребление от
располагаемого дохода по данным для США за период с 1960 по 1985 г. Поэтому
в текущем примере следовало бы предусмотреть и такую возможность. Для
этого рассмотрим расширенную модель:
SALES, =а + pDPIt+y DUMMY, + 8{DUMMYrDPIt) + et9 f = l,...,36.
В такой модели предельная склонность к потреблению имеет вид:
d SALES t
dDPIt
т.е. зависит от значения DUMMYt\
d SALES, \fi9
L = j3 + SDUMMYt,
если DUMMY =0
dDPIt {J3 + S9 если DUMMY, =1.

Раздел 5. Учет нарушений стандартных предположений о модели
209
Иначе говоря, переменная DPI взаимодействует с переменной DUMMY
(фактически с климатическими условиями), и в этом контексте входящую
в правую часть уравнения переменную DUMMY, • DPIt называют
взаимодействием {interaction) переменных DPI и DUMMY.
Вопрос о действительном наличии такого взаимодействия в
рассматриваемом примере оставляем для практических занятий. ■
v Замечание 5.1.1. Вместо модели SALESt = a + pDPIt + yDUMMYt + е„
t = 1, ..., 36, можно было бы рассмотреть модель с двумя дамми-
переменными — той же переменной DUMMY, значение которой
равно 1 для I и IV кварталов и равно 0 для II и III кварталов, и
переменной DUMMY* = 1 - DUMMY, значение которой равно 0 для I
и IV кварталов и равно 1 для II и III кварталов:
SALES, = j3DPIt + у DUMMY, +S DUMMY* +et9 t = 1,..., 36.
При такой спецификации оцененные значения коэффициентов у
и 8 представляют собой постоянные составляющие в подобранных
моделях связи для весенне-летнего и осенне-зимнего периодов,
тогда как в первой спецификации оцененное значение
коэффициента у представляет дифференциальный эффект {differential effect)
осенне-зимнего периода.
V Замечание 5.1.2. При спецификации моделей с дамми-переменными
следует помнить о существовании так называемой дамми-ловушки
{dummy trap). В уравнение, рассмотренное в Замечании 5.1.1, мы
намеренно не включили постоянную составляющую, чтобы не попасть
в такую ловушку. Если бы в правую часть уравнения помимо двух
использованных дамми-переменных включили еще и постоянную,
т.е. оценивали модель
SALES, = a + j8DPI,+ уDUMMY,+SDUMMY* +£,, f = l,...,36,
то матрица значений объясняющих переменных приняла бы вид:
Х =
'1
1
1
1
1
1
1
1
DPf
DPI2
DPI3
DPL
DPI
DPL
DPI
33
34
35
DPL
36
1
0
0
1
1
0
0
1
°)
1
1
0
0
1
1
о

210
Часть 1. Основные понятия, элементарные методы
Но в этой матрице 1-й столбец равен сумме 3-го и 4-го столбцов,
т.е. столбцы матрицы X линейно зависимы, столбцовый ранг этой
матрицы меньше 4, матрица XТХ вырождена (det XТХ = 0) и не имеет
обратной, так что выражение (XтХ)~хХту попросту не определено.
В пакете Econometric Views при возникновении подобных
ситуаций программа отказывается от вычисления оценки наименьших
квадратов вектора коэффициентов и выдает следующее сообщение
об ошибке (Error Message): Near singular matrix (матрица близка
к вырожденной).
V Замечание 5.1.3. Вместо подбора отдельных моделей для осенне-
зимнего и весенне-летнего периодов можно было бы заняться
подбором отдельных моделей для каждого из четырех кварталов года.
С этой целью в качестве дополнительных объясняющих переменных
можно взять, например, переменные DUMMYX, DUMMY2, DUMMY4,
принимающие значение 1 соответственно в I, II и IV кварталах
и равные 0 в остальных кварталах. При оценивании такой
расширенной модели для наших данных оказывается незначимым
коэффициент при DUMMY!, что означает близость в среднем уровней
продаж во II и в III кварталах. Более того, оказываются близкими
оценки коэффициентов при переменных DUMMY4 и DUMMYX.
Гипотеза о совпадении двух последних коэффициентов не отвергается,
и в итоге возвращаемся к модели с одной фиктивной переменной
DUMMY, которую мы уже оценили ранее.
Использование фиктивных переменных полезно при анализе
агрегированных (объединенных) данных, полученных при объединении
наблюдений, относящихся к различным полам (мужчины и женщины), к различным
возрастным, языковым и социальным группам, к разным периодам времени.
В таких ситуациях модели, построенные по отдельным группам, могут
существенно различаться, и тогда модель, построенная по объединенным данным,
не учитывает этого различия. При привлечении фиктивных переменных
становится возможным оценить значимость такого различия и в зависимости
от результата остановиться на модели с агрегированными данными или на
модели, в которой учитывается различие параметров связи для разных групп,
на модели с едиными коэффициентами связи для всех наблюдений или на
модели, в которой учитывается различие параметров связи на разных
периодах времени. Достаточно подробно модели с дамми-переменными
рассматриваются в учебнике (Доугерти, 2004).
v Замечание 5.1.4. Если дамми-переменные используются для
разбиения множества наблюдений по некоторому признаку на К
категорий и в модель включена постоянная составляющая, то для
непопадания в дамми-ловушку, о которой говорилось в Замечании 5.1.2,

Раздел 5. Учет нарушений стандартных предположений о модели 211
в правую часть уравнения следует включать только (К - 1) дамми-
переменных. Это связано с тем, что сумма всех К дамми-перемен-
ных дает переменную, равную 1 во всех наблюдениях.
V Замечание 5.1.5. Если множество наблюдений разбивается на две
части с использованием соответствующей дамми-переменной и при
этом оказывается, что имеется лишь одно наблюдение, для которого
эта дамми-переменная равна 1, то это наблюдение фактически не
участвует в формировании оценок наименьших квадратов
коэффициентов при остальных объясняющих переменных.
Использование дамми-переменных оказывает практическую пользу при
анализе панельных данных {panel data), т.е. данных об экономических
показателях нескольких предприятий (регионов, стран) за несколько месяцев
(кварталов, лет). В этом контексте данные по нескольким предприятиям
(регионам, странам) за один промежуток времени (месяц, квартал, год) называют
одномоментными или перекрестными данными {cross-section data), тогда
как данные по отдельным предприятиям (регионам, странам) за несколько
месяцев (кварталов, лет) — временными рядами {time-series data).
ПРИМЕР 5.1.2
Рассмотрим приведенные в табл. 5.4 ежегодные данные об объемах
инвестиций у и прибыли х 3 предприятий (N = 3) за десятилетний период {Т = 10)
(см. {Greene, 1993), с. 481). Столбцы Yt, Xt содержат данные по /-му
предприятию, /= 1, 2, 3.
Таблица 5.4
Данные об объемах инвестиций и прибыли 3 предприятий в течение 10 лет
1
Предпр
У1
иятие 1
XI
Предпр
Y2
иятие 2
XI
Предпр
1 У3
ият
иятие 1
1
2
3
4
5
6
7
8
9
10
13.32
26.30
2.62
14.94
15.80
12.20
14.93
29.82
20.32
4.77
12.85
25.69
5.48
13.79
15.41
12.59
16.64
26.45
19.64
5.43
20.30
17.47
9.31
18.01
7.63
19.84
13.76
10.00
19.51
18.32
22.93
17.96
9.160
18.73
11.31
21.15
16.13
11.61
19.55
17.06
8.85
19.60
3.87
24.19
3.99
5.73
26.68
11.49
18.49
20.84
гиеЗ
ХЪ
8.65
16.55
1.47
24.91
5.01
8.34
22.70
8.36
15.44
17.87

212
Часть 1. Основные понятия, элементарные методы
Раздельное оценивание (в пакете Econometric Views) парных моделей
регрессии
yXt=(Z\+PiXit+€\n t = l,...9W9
y2t = a2+/32x2t +s2n t = 1,..., 10,
y3t = a3 + fi3x3t +s3n t = 1,..., 10,
дает следующие результаты:
для 1-го предприятия (табл. 5.5):
Таблица 5.5
Объясняемая переменная УЛ
Переменная
С
Х\
R-squared
Коэффициент
-2.468913
1.167170
0.9805
Стандартная
ошибка
0.980426
0.058250
/-статистика
-2.518205
20.03737
Р-значение
0.0359
0.0000
для 2-го предприятия (табл. 5.6):
Таблица 5.6
Объясняемая переменная У2
Переменная
С
XI
R-squared
Коэффициент
-1.384797
1.014542
0.9063
Стандартная
ошибка
1.972680
0.115314
/-статистика
-0.701988
8.798102
Р-значение
0.5026
0.0000
для 3-го предприятия (табл. 5.7):
Таблица 5.7
Объясняемая переменная УЗ
Переменная
С
хз
R-squared
Коэффициент
0.455479
1.076374
0.9350
Стандартная
ошибка
1.491604
0.100360
/-статистика
0.305362
10.72516
Р-значение
0.7679
0.0000
Различие между оценками коэффициентов при переменных хи х29 х3
довольно невелико, так что возникает вопрос о проверке гипотезы совпадения
этих коэффициентов:
Проверить эту гипотезу можно в рамках расширенной модели,
обращенной ко всем 30 наблюдениям и допускающей различие постоянных состав-

Раздел 5. Учет нарушений стандартных предположений о модели
213
ляющих и угловых коэффициентов для разных предприятий (модель
ковариационного анализа). Определим дамми-переменные D\, D2, D3
следующим образом:
fl, если/ = 1, fl, если/= 2, fl, если г = 3,
Dh=\ D2it=\ D3U=\
[О, еслиг'^1; [0, еслиi*2; [0, если/^3.
Тогда указанная расширенная модель принимает вид:
М0 : Уи = or,Dlu+a2D2it+a,D3it+fr{D\itxit)+p2{D2uxit)+рг(D3itxu) + su,
/=1,...,3, t=l,..., 10,
и ее можно записать в матрично-векторной форме следующим образом:
У\,\0
■У2,10
Уъ\
или
где
1 хи 0 0 0 0
1 хмо 0 0 0 0
0 0 1 jc21 0 0
0 0 1 jc210 0 0
0 0 0 0 1 х31
0 0 0 0 1 х3,юу
у = Хв + е,
\
f ~ Л
\а\
\\fil
а2
\Рг
а3
UJ
+
(г Л
611
•
^1,10
S2\
^2,10
4^3,10 J
У =
ГУпЛ
У\,ю
Ун
У2Л0
Уз\
V-^3,10 у
, X
ого
А
а->
\nj
611
'1,10
8 =
'21
'2,10
V *3,Ю J
Эта запись соответствует модели линейной множественной регрессии, и ее
можно оценивать обычным образом: в = (XТХ)~хХТу.

214
Часть 1. Основные понятия, элементарные методы
Если предположить, что все случайные ошибки независимы в
совокупности и имеют одинаковое нормальное распределение, то проверить
интересующую нас гипотезу Я0 : Д = J32 = J33 можно с помощью F-критерия. При
этом получаются следующие результаты (табл. 5.8).
Таблица 5.8
Объясняемая переменная Y
Переменная
т
D2
D3
D\ X
D2X
ЭЪХ
R-squared
Коэффициент
-2.468913
-1.384797
0.455479
1.167170
1.014542
1.076374
0.950532
Стандартная
ошибка
1.388033
2.233064
1.137109
0.082467
0.130535
0.076508
/-статистика
-1.778714
-0.620133
0.400559
14.15324
7.772208
14.06874
F-statistic
Probability
Р-значение
0.0880
0.5410
0.6923
0.0000
0.0000
0.0000
0.592788
0.560676
Таким образом, гипотеза Н0 : Д = /?2 = /?3 не отвергается, а при этой
гипотезе расширенная модель сводится к модели с общим угловым коэффициентом:
М1 : yit = axDlit + a2D2it + a3D3it + /3 xit + sin / = 1,...,3, ^ = 1,...,10.
В рамках модели М{, опять записывая ее как модель линейной
множественной регрессии, можно проверить гипотезу о совпадении коэффициентов при
дамми-переменных. Кроме того, можно проверить гипотезу Н'0 : ах = а2 = а3,
Р\-Рг-Ръъ рамках модели М0. На основе полученных результатов
выбирается окончательная модель. Эти исследования оставляем для
самостоятельной работы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Для каких целей в эконометрическую модель вводятся дамми-переменные и как
они определяются?
2. Что представляет собой дамми-ловушка? Как надо специфицировать модель с дамми-
переменными, чтобы не попасть в такую ловушку?
3. Как используются дамми-переменные для коррекции нестабильности модели,
выраженной в наличии структурного сдвига на периоде наблюдений?
4. Как используются дамми-переменные для коррекции нестабильности модели,
выраженной в наличии сезонного фактора?
5. Как используются дамми-переменные для коррекции модели, построенной по
агрегированным данным?
6. Что понимается под панельными, перекрестными и продольными данными? Как
используются дамми-переменные при анализе панельных данных?

Раздел 5. Учет нарушений стандартных предположений о модели
215
Тема 5.2
УЧЕТ ГЕТЕРОСКЕДАСТИЧНОСТИ
Такой вид нарушений стандартных предположений, как неоднородность
дисперсий ошибок (гетероскедастичность, heteroscedasticity), характерен
для статистических данных, относящихся к одному моменту времени, но
собранных по различным регионам, предприятиям, социальным группам
(перекрестные данные). Неоднородность дисперсий возникает также как результат
тех или иных структурных изменений в экономике (например, связанных
с мировыми экономическими кризисами). Пример 4.2.1 как раз иллюстрирует
подобную ситуацию: в нем резкое возрастание абсолютных величин остатков
относится к периоду глобального нефтяного кризиса.
Последствия неоднородности дисперсий ошибок (гетероскедастич-
ности):
• оценки дисперсий случайных величин ви ..., вр (оценок
коэффициентов линейной модели), построенные на базе стандартных
предположений, оказываются смещенными;
• построенные на базе стандартных предположений доверительные
интервалы для в19 ..., вр не соответствуют заявленным уровням
значимости;
• вычисленные значения t- и F-отношений уже нельзя рассматривать как
наблюдаемые значения случайных величин, имеющих t- и F-pacnpe-
деления, соответствующие стандартным предположениям. Поэтому
сравнение вычисленных значений t- и F-отношений с квантилями
указанных t~ и F-распределений может приводить к ошибочным
статистическим выводам по поводу гипотез о значениях коэффициентов
линейной модели.
ПРИМЕР 5.2.1
Для исследования вопроса о зависимости количества руководящих
работников от размера предприятия были собраны статистические данные по 27
промышленным предприятиям (табл. 5.9). Обозначим:
xt — численность персонала на j'-m предприятии,
у{ — количество руководителей на /-м предприятии.
Оценим линейную модель наблюдений
у{=а + 0х{+еп / = 1,..., 27.
В ходе регрессионного анализа получим R2 = 0.776 и результаты,
приведенные в табл. 5.10.

216
Часть 1. Основные понятия, элементарные методы
Таблица 5.9
Данные о численности персонала X
и количестве руководителей Уна 27 предприятиях
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
X
294
247
267
358
423
311
450
534
438
697
688
630
709
627
Y
30
32
37
44
47
49
56
62
68
78
80
84
88
97
i
15
16
17
18
19
20
21
22
23
24
25
26
27
X
615
999
1022
1015
700
850
980
1025
1021
1200
1250
1500
1650
Y
100
109
114
117
106
128
130
160
97
180
112
210
135
Таблица 5.10
Объясняемая переменная Y
Переменная
1
X
Коэффициент
14.448
0.105
Стандартная
ошибка
9.562
0.011
/-статистика
1.511
9.303
Р-значение
0.1433
0.0000
На рис. 5.8 приведена диаграмма рассеяния с подобранной прямой
у = 14.448 + 0.105х, на рис. 5.9 — график зависимости стандартизованных
е
остатков ct = — от значений yt = 14.448 + 0.105*,.
Похоже, что имеет место тенденция линейного возрастания
абсолютных величин остатков с ростом j), соответствующая наличию
приближенной зависимости вида D(et) = of = <j2xf для дисперсий ошибок. Чтобы
погасить такую неоднородность дисперсий, разделим обе части соотношения
угг = а + рх{ + et наxt\
X; Xt Xt

Раздел 5. Учет нарушений стандартных предположений о модели
217
Y А
250-
200-
150-
100-
50-
0 -
С
i
♦
♦ У
I
I
) 1000
Рис. 5.8
♦
♦
i
2000
X
RES_STAND a
3-к
-3
* *
т.е. перейдем к модели наблюдений
у*=Р + ах]+е],
где
* у{ * 1 * st
У1=—> xt=— > st= — •
xi Xj xt
Если действительно выполняется соотношение D(st) = а? = cr2x?, то
в преобразованной модели
£(*,*) = 0, D(e*) = \D{si) = a\
xt
т.е. неоднородность дисперсий ошибок преодолевается.
Результаты оценивания преобразованной модели приведены в табл. 5.11.
Объясняемая переменная Y/X
Таблица 5.11
Переменная
1
\/х
Коэффициент
0.121
3.803
Стандартная
ошибка
0.009
4.570
/-статистика
13.445
0.832
Р-значение
0.0000
0.4131
В исходных переменных это соответствует модели линейной связи
у = 3.803 + 0.121 х.
Отметим уменьшение оцененных стандартных ошибок оценок обоих
параметров а и Д Именно на эти значения следует опираться при построении
доверительных интервалов для параметров. Средними точками этих
интервалов будут соответственно а = 3.803 и J3 = 0.121. График на рис. 5.10 показы-

218
Часть 1. Основные понятия, элементарные методы
Рис. 5.10
вает характер зависимости
стандартизованных остатков в преобразованной
модели от у*. На этот раз
неоднородности дисперсий остатков (по крайней
мере, явной) не обнаруживается.■
Проанализируем наши действия
при оценивании преобразованной
модели. Оценки коэффициентов,
приведенные в табл. 5.11, получены
применением метода наименьших квадратов
к модели наблюдений^* = /?+ ах* + £*,
т.е. путем минимизации суммы
квадратов
^{у*-р-ахУ,
/ = 1
которую (зная, что обозначают переменные со звездочками) можно записать
в виде:
1V 1 ^ ^ 1 1
/=1 xi
/=i
хи
Обозначив теперь wtr = —, заметим, что задача минимизации суммы квад-
ратов отклонений в преобразованной модели равносильна задаче
минимизации взвешенной суммы квадратов отклонений в исходной (непреобразован-
ной) модели. Величина wt интерпретируется в этом контексте как вес,
приписываемый квадрату отклонения в /-м наблюдении. Этот вес будет тем
меньше, чем больше значение х?, которое в силу наших предположений
пропорционально дисперсии случайной ошибки D(st) = а2 = а2 х ? в /-м
наблюдении. Следовательно, чем больше дисперсия случайной ошибки ei9 тем
меньше вес, с которым входит квадрат отклонения в /-м наблюдении в
минимизируемую сумму.
С учетом того что оценивание преобразованной модели наблюдений
сводится к минимизации суммы
п
рассмотренный метод оценивания обычно называют взвешенным методом
наименьших квадратов, хотя точнее его следовало бы называть методом
наименьших взвешенных квадратов. В учебнике {Магнус, Катышев, Пере-
сецкий, 2005) он называется методом взвешенных наименьших квадратов, что

Раздел 5. Учет нарушений стандартных предположений о модели
219
ближе к англоязычному варианту: WLS — weighted least squares в отличие
от OLS — ordinary least squares.
v Замечание 5.2.1. В некоторых руководствах по эконометрике и
пакетах статистического анализа данных (например, в пакете
Econometric Views) используется несколько иное равносильное
представление минимизируемой суммы квадратов в преобразованной модели
наблюдений:
X(w,.G,.-«-^,.)J.
В этом случае вес приписывается не квадрату отклонения, а
самому отклонению (yt - а - J3 xt). Разумеется, в рассмотренном
примере при таком определении веса последний будет равен: wt= —.
Об этом следует помнить при спецификации весов в процедурах,
реализующих взвешенный метод наименьших квадратов.
Обратим теперь внимание на то, в каком виде выдается информация о
результатах применения взвешенного метода наименьших квадратов на
примере пакета Econometric Views. При этом используем данные примера 5.2.1
о зависимости количества руководящих работников от размера предприятия.
Согласно только что сделанному замечанию, при обращении к процедуре
оценивания взвешенным методом наименьших квадратов в условиях нашего
примера специфицируем веса как w = — .
х
Протокол оценивания приведен в табл. 5.12. В этом протоколе приводятся
значения двух видов статистик:
• взвешенные статистики {weighted statistics) — статистики,
основанные на остатках, получаемых по взвешенным данным, т.е. на остатках
е* =у* - р - ах) в преобразованной модели;
• невзвешенные статистики {unweighted statistics) — статистики,
основанные на остатках и{ - у{ - aWLS - j3WLSxi9 т.е. на отклонениях
наблюдаемых значений объясняемой переменной у от значений,
предсказываемых линейной моделью связи, в качестве параметров которой
берутся их оценки, aWLS9 pWLS-> полученные в преобразованной модели.
Отметим весьма низкое @.02696) значение коэффициента детерминации
в преобразованной модели. Однако это обстоятельство не должно нас
волновать — линейная связь в преобразованной модели значима, о чем говорят
весьма высокое значение F-статистики, равное 180.7789, и соответствующее
ему Р-значение 0.0000 (см. Weighted statistics). В конечном счете нас инте-

220 Часть 1. Основные понятия, элементарные методы
Таблица 5.12
Объясняемая переменная Y
(Method: Least Squares; Sample: 1 27; Included observations: 27; Weighting series: 1/X)
Переменная
С
X
Коэффициент
3.803296
0.120990
Стандартная
ошибка
4.569745
0.008999
/-статистика
0.832277
13.44540
Р-значение
0.4131
0.0000
Взвешенные статистики {Weightedstatistics)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.026960
-0.011961
13.15902
4328.998
-106.8543
2.272111
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob (F-statistic)
74.04946
13.08103
8.063280
8.159268
180.7789
0.000000
Невзвешенные статистики {Unweightedstatistics)
R-squared
Adjusted R-squared
S.E. of regression
Durbin-Watson stat
0.758034
0.748355
22.57746
2.444541
Mean dependent var
S. D. dependent var
Sum squared resid
94.44444
45.00712
12743.54
ресует значение R2, находящееся в части протокола, соответствующей не-
взвешенным статистикам, а это значение достаточно велико @.758).
Отметим также, что приведенные в начале табл. 5.12 значения оценок
параметров, их стандартных ошибок и ^-статистик, а также Р-значения
соответствуют величинам, полученным на стадии оценивания преобразованной модели.
Заметим, наконец, что значение R2 = 0.758, указанное в числе невзвешенных
статистик, отличается от значения R2 = 0.776, полученного при оценивании
исходной (непреобразованной) модели наблюдений. Причина этого,
разумеется, в том, что при вычислении значения R2 = 0.776 использовались остатки
где а,/3—оценки наименьших квадратов параметров исходной модели,
полученные без использования взвешивания отклонений.
Взвешенный метод наименьших квадратов предполагает известной
форму зависимости дисперсий случайных ошибок от объясняющих
переменных. В примере 5.2.1 мы предположили, что такая зависимость имела вид:
D(st) = а2 = а2х29 ориентируясь лишь на график зависимости стандартизо-

Раздел 5. Учет нарушений стандартных предположений о модели
221
ванных остатков ci = — от прогнозных значений j),. Некоторым подспорьем
при определении формы зависимости здесь может стать применение
критерия Глейзера {Glejser test). Этот критерий, не вполне оправданный с
теоретической точки зрения и предполагающий наличие большого количества
наблюдений, состоит в следующем. После оценивания методом
наименьших квадратов основной модели производится оценивание вспомогательной
модели, объясняющей изменчивость абсолютных величин полученных на
первом этапе остатков изменчивостью значений одной из объясняющих
переменных. Если X— такая объясняющая переменная, то более или менее
оправданным является рассмотрение моделей следующего вида:
hl = ri+r2—+^>
В рамках каждой из этих моделей проверяется гипотеза о равенстве 0
коэффициента у2. Если эта гипотеза не отклоняется, то гетероскедастичнось
соответствующей формы не обнаруживается. При отклонении этой гипотезы
можно с определенными оговорками ориентироваться на соответствующую
функциональную форму зависимости а отХ
Как отмечалось выше, результатом неоднородности дисперсий случайных
ошибок в модели наблюдений является смещение оценок дисперсий
случайных величин 0j,..., 0р. В то же время наличие такого нарушения
стандартных предположений оставляет сами оценки 0l9 ..., 0р несмещенными.
(Доказательство оставляем для самостоятельной работы, см. также разд. 6.) В связи
с этим один из методов коррекции статистических выводов при
неоднородности дисперсий ошибок состоит в использовании обычных оценок
наименьших квадратов (OLS-оценок, ordinary least squares estimates) 0l9 ..., 0p
коэффициентов 0l9 ..., 0p вместе со скорректированными на гетероскедас-
тичность оценками стандартных ошибок s§. Один из вариантов получения
скорректированных на гетероскедастичность значений s§. был предложен
Уайтом и реализован в ряде пакетов статистического анализа данных, в том
числе в пакете ЕViews. При этом удовлетворительные свойства оценки
Уайта {White estimator) гарантируются только при большом количестве
наблюдений.

222
Часть 1. Основные понятия, элементарные методы
Оценка Уайта строится на базе явного выражения для ковариационной
матрицы вектора в оценок коэффициентов линейной эконометрической
модели, в которой ошибки хотя и имеют нулевые математические ожидания,
но не являются одинаково распределенными и/или взаимно независимыми
случайными величинами, так что
Cov(s) = V,
где V — симметричная, положительно определенная матрица, Уф а21п.
В такой ситуации имеем:
Cov0)= Cov((XTXylXTy) = (XTXylXTCov(y)X(XTXyl =
= {XTX)'\XTVX)(XTXy\
Если имеет место чистая гетероскедастичность, то
о, • • • U
V = dmg(a?,...,CT2) =
О .- а2
" J
и матрица Cov(O) содержит п неизвестных параметров — столько же,
сколько имеется наблюдений. Тем не менее можно получить состоятельную
оценку матрицы Cov@), а значит, и состоятельные оценки для дисперсий оценок
коэффициентов и стандартных ошибок оценок коэффициентов s#.9 если
заменить в матрице V неизвестные значения дисперсий ошибок of, ..., а2 на
квадраты остатков, полученных в результате оценивания модели обычным
методом наименьших квадратов, т.е. на е2, ..., е2. Это приводит к оценке
Уайта.
ПРИМЕР 5.2.2
Используем данные из предыдущего примера, но применим для их анализа
последнюю процедуру, воспользовавшись пакетом EViews.
Согласно этой процедуре оцениваем коэффициенты а и /? обычным
методом наименьших квадратов, так что в качестве оценок берутся а = 14.448
и Р = 0.105. В качестве оценок стандартных ошибок sd и Sp вместо sa = 9.562
и Sp = 0.011, полученных выше при оценивании модели обычным методом
наименьших квадратов, берем значения оценок Уайтаsd = 10.633 и^ = 0.018.
Бросающееся в глаза значительное различие оценок для параметра а при
применении двух рассмотренных методов C.803 и 14.448) в
действительности не столь уж удивительно, поскольку оценки стандартной ошибки для а,
полученные каждым из двух методов, довольно высоки (sd = 4.570 и^ =
10.633 соответственно).■

Раздел 5. Учет нарушений стандартных предположений о модели
223
Избавиться от неоднородности дисперсий ошибок в ряде случаев позволяет
переход к логарифмам объясняемой переменной.
ПРИМЕР 5.2.3
По данным, использованным в примерах 5.2.1 и 5.2.2, оценим модель наблюдений
ln^. =a + /3xt +*,., / = 1,..., 27.
График зависимости стандартизованных остатков, полученных при оцени-
л
вании этой модели, от предсказанных значений In у. приведен на рис. 5.11.
RESID_STAND
3
RESID_STAND
2 4-
3,5 4 4.51 5 5.5 6 LnYF
Рис. 5.11
5.5 LnYF
Он указывает на неправильную спецификацию модели, связанную с
возможным пропуском квадратичной составляющей х?. Оценивание
расширенной модели наблюдений, включающей дополнительную объясняющую
переменную х2, приводит к остаткам, обнаруживающим существенно более
удовлетворительное поведение (рис. 5.12). Результаты оценивания расширенной
модели приведены в табл. 5.13.
Таблица 5.13
Объясняемая переменная 1_пУ
Переменная
1
X
X2
Коэффициент
2.851
0.003
-1.10£-06
Стандартная
ошибка
0.157
0.000399
2.24Я-07
^-статистика
18.205
7.803
-4.925
Р-значение
0.0000
0.0000
0.0001
Таким образом, использовав разные преобразования переменных,
получили две альтернативные оцененные модели связи между переменными хну:
7 = 3.803 + 0.121х и 1п>; = 2.851 + 0.003х-1.Ы(Г6х2.
Первую из этих двух моделей можно предпочесть из соображений простоты
интерпретации. ■

224
Часть 1. Основные понятия, элементарные методы
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. К каким последствиям приводит наличие неоднородности дисперсий ошибок (гете-
роскедастичность) в линейной эконометрической модели?
2. Какими способами можно получить корректные статистические выводы при
наличии гетероскедастичности?
3. В чем состоит взвешенный метод наименьших квадратов? Каким образом
выбираются веса? Как еще можно трансформировать модель для преодоления
последствий гетероскедастичности?
4. Можно ли при наличии гетероскедастичности получить корректные
статистические выводы, не прибегая к преобразованию переменных?
Тема 5.3.
УЧЕТ АВТОКОРРЕЛИРОВАННОСТИ ОШИБОК
Такой вид нарушений стандартных предположений, как
автокоррелированность (сериальная корреляция) ошибок {autocorrelation, serial correlation),
характерен для статистических данных, развернутых во времени (временные
ряды). Автокоррелированность ошибок обычно возникает вследствие
неправильной спецификации модели, например, при невключении в модель
существенной объясняющей переменной с выраженной автокорреляцией.
Последствия автокоррелированности ошибок:
• стандартная оценка S2 = дисперсии случайных ошибок смещена
п-р
вниз в случае положительной автокоррелированности ошибок и
смещена вверх в случае отрицательной автокоррелированности ошибок;
• стандартные оценки дисперсий случайных величин ви ..., вр (оценок
коэффициентов линейной модели) оказываются заниженными в случае
положительной и завышенными в случае отрицательной
автокоррелированности ошибок;
• построенные доверительные интервалы для ви ..., вр не соответствуют
заявленным уровням значимости: в случае положительной
автокоррелированности ошибок построенные интервалы неоправданно узки, а в
случае отрицательной автокоррелированности ошибок — неоправданно
широки;
• вычисленные значения t- и F-отношений нельзя рассматривать как
наблюдаемые значения случайных величин, имеющих t- и F-распреде-
ления, соответствующие стандартным предположениям. Поэтому
сравнение вычисленных значений t- и F-отношений с квантилями
указанных t- и F-распределений может приводить к ошибочным
статистическим выводам по поводу гипотез о значениях коэффициентов линейной

Раздел 5. Учет нарушений стандартных предположений о модели
225
модели. Вычисленные значения t- и F-отношений завышены в случае
положительной и занижены в случае отрицательной автокоррелирован-
ности ошибок.
Коррекция статистических выводов
при автокоррелированности ошибок
Пусть имеем дело с наблюдениями, производимыми последовательно через
равные промежутки времени (ежедневные, еженедельные, ежеквартальные,
ежегодные статистические данные), и выявляем по графику зависимости
станку
дартизованных остатков с. = — от / тенденцию сохранения знака соседних
наблюдений. В таком случае можно подозревать нарушение условия
независимости случайных ошибок el9..., sn в принятой нами модели наблюдений
yi=0lXil+... + epXip+£i9 1 = 1,..., Л,
в форме положительной автокоррелированности ряда ошибок.
Предположим, что ошибки образуют процесс авторегрессии первого
порядка (first order autoregressive process):
ei =pei_l+Si9 / = 2,...,л,
где 0 < p< 1, a Si9 i = 2, ..., n9 — независимые в совокупности случайные
величины, имеющие одинаковое нормальное распределение N@9 а2), причем St
не зависит статистически от st_s для s > 0. Тогда для получения правильных
статистических выводов относительно коэффициентов модели необходима
соответствующая коррекция.
Итерационная процедура Кохрейна — Оркатта (Cochrane-Orcuti).
Умножим обе части уравнения для (/ - 1)-го наблюдения на р9 так что
РУг-Х = OlPXi-i, 1 + • • • + 8pPXi-X, р + РЬ-i,
и вычтем обе части полученного выражения из соответствующих частей
выражения для z-го наблюдения:
yt - pyt.x = 9Х (хп - pxt_u j) +... + вр (xip - pxt_lp) + {et - р8,_х)
(авторегрессионное преобразование — autoregressive transformation). Таким
образом приходим к преобразованной модели наблюдений
у\ = вхх'а+... + врх',р+е\9 i = 2,...,n,
где
y'i=yi-pyi-i>
Xi\ = Xj\ — PXi-\,\ >--">Xip=Xip~ PXi~Up'
е1 = Ь~РЬ-1-

226 Часть L Основные понятия, элементарные методы
Поскольку в принятой модели ошибок
*,--/>£,■_, =Si9 i = 29...9n9
это означает, что ошибки ef29..., е'п в преобразованной модели — независимые
в совокупности случайные величины, имеющие одинаковое нормальное
распределение N@9 а2).
Иными словами, случайные ошибки в преобразованной модели
удовлетворяют стандартным предположениям. Следовательно, в рамках
преобразованной модели никакой дополнительной коррекции обычных статистических
выводов о коэффициентах модели не требуется. Проблема только в том, что
используемое в процессе преобразования модели значение коэффициента р
нам неизвестно. Поэтому реально провести указанное преобразование
невозможно. Вместо этого можно пытаться заменить указанное преобразование
какой-либо его аппроксимацией с заменой неизвестного значения р на его
оценку по данным наблюдений. Конечно, при использовании такой
аппроксимации уже нельзя гарантировать, что s'29 ..., е'п в преобразованной модели
будут независимыми в совокупности случайными величинами, однако есть
надежда на то, что эти ошибки все же будут обнаруживать меньшую авто-
коррелированность по сравнению с ошибками в исходной модели.
Процедура Кохрейна — Оркатта использует для получения
аппроксимации теоретического преобразования оценку для р в виде
п
i = 2
Г=— ♦
/ = 2
где е]9..., еп — остатки, получаемые при оценивании исходной модели
наблюдений. Аппроксимирующее преобразование определяется
соотношениями
* *
хп = ха — rxi-\, и • • • ? xiP = xiP~ rxi-\, p •>
которые приводят к преобразованной модели
у]=вхх]х+... + врх]р+£]9 / = 2,..., л.
Если в последней модели автокоррелированность используемыми тестами
не выявляется, то полученные в рамках этой модели оценки параметров
в19 ..., вр можно принять в качестве уточненных оценок параметров вХ9 ..., вр.
Если же в преобразованной модели еще остается выраженная автокоррелиро-

Раздел 5. Учет нарушений стандартных предположений о модели
227
ванность, то процесс преобразования применяют уже к преобразованной
модели и еще раз уточняют значения параметров и т.д., пока последовательно
уточняемые значения параметров не перестанут изменяться в пределах
заданной точности.
Заметим, наконец, что обычно предполагаем хп = 1. Соответственно для
первой объясняющей переменной получим
* — _ — 1 —
Xi\ ~ Xil ~ rXi-\,l ~ A Г'
так что фактически имеем преобразованную модель
у] =а* +в2х*2+... + врх*р+£*, / = 2,..., л,
с а* = в{A - г). Получив в этой модели оценку а* для а*, можно оценить
параметр вх исходной модели, просто полагая вх .
\-г
ПРИМЕР 5.3.1
Проанализируем статистические данные о совокупных потребительских
расходах (CONS) и денежной массе (MONEY) в США за 1952—1956 гг. (табл. 5.14).
Таблица 5.14
Данные о совокупных потребительских расходах (CONS)
и денежной массе (MONEY) в США за 1952—1956 гг., млрд долл.
Год, квартал
1952:1
1952:2
1952:3
1952:4
1953:1
1953:2
1953:3
1953:4
1954:1
1954:2
MONEY
159.3
161.2
162.8
164.6
165.9
167.9
168.3
169.7
170.5
171.6
CONS
214.6
217.7
219.6
227.2
230.9
233.3
234.1
232.3
233.7
236.5
Год, квартал
1954:3
1954:4
1955:1
1955:2
1955:3
1955:4
1956:1
1956:2
1956:3
1956:4
MONEY
173.9
176.1
178.0
179.1
180.2
181.2
181.6
182.5
183.3
184.3
CONS
238.7
243.2
249.4
254.3
260.9
263.3
265.6
268.2
270.4
275.6
Результаты оценивания линейной модели наблюдений
yi =а + 0Х;+£п / = 1, ..., 20,
где yt — значения объясняемой переменной CONS;
xt — значения объясняющей переменной MONEY, приведены в табл. 5.15.

228
Часть 1. Основные понятия, элементарные методы
Объясняемая переменная Y
Таблица 5.15
Переменная
1
X
R-squared
Коэффициент
-154.719
2.300
0.957
Стандартная
ошибка
19.850
0.114
^-статистика
-7.794
20.080
Durbin-Watson stat
Р-значение
0.0000
0.0000
0.328
Хотя коэффициент детерминации весьма близок к 1, значение статистики
Дарбина — Уотсона достаточно мало, и это дает основание подозревать
наличие положительной автокоррелированности ошибок в принятой
модели наблюдений. График на рис. 5.13 дает представление о рассеянии
значений переменных, а на рис. 5.14 — о поведении остатков. Здесь
наблюдаются серии остатков, имеющих одинаковые знаки, что как раз
характерно для моделей, в которых имеется положительная автокоррелирован-
ность ошибок.
CONS
RESIDOI
i
280-
270-
260-
250-
240-
230-
220-
210-
200-
i
P
у
V
Н 1
J
/£
Л*
¥
h
s
f
1
b-*
150 160 125
180 190
MONEY
52:1 52:3 52:3 53:1 53:3 54:3 55:1 55:3 56:1 56:3
Год, квартал
Рис. 5.13
Рис. 5.14
Для подтверждения положительной автокоррелированности ошибок
используем критерий Дарбина — Уотсона. Из табл. А.5, приведенной в
учебнике (Доугерти, 2004, с. 403), находим нижнюю границу для критического
значения d005 при п = 20: dL 005 = 1.20. Полученное при оценивании модели
значение DW= 0.328 существенно меньше этой нижней границы, так что
гипотеза Я0 : р = 0 отвергается в пользу альтернативной гипотезы НА : р > 0.
Для коррекции статистических выводов используем процедуру Кохрейна —
Оркатта.

Раздел 5. Учет нарушений стандартных предположений о модели
229
Прежде всего, найдем оценку для неизвестного значения коэффициента р\
п
г = — = 0.874.
П
Основываясь на этой оценке, перейдем к преобразованной модели,
результаты оценивания которой приведены в табл. 5.16.
Таблица 5.16
Объясняемая переменная У*
Переменная
1
X*
R-squared
Коэффициент
-30.777
2.795
0.554
Стандартная
ошибка
14.043
0.609
/-статистика
-2.192
4.593
Durbin-Watson stat
Р-значение
0.0426
0.0003
1.667
Хотя в преобразованной модели коэффициент детерминации существенно
ниже, чем в непреобразованной модели, значение статистики Дарбина —
Уотсона теперь превышает верхнюю границу dv 0 05 = 1.40 для критического
значения d0m059 соответствующего п = 19. (В преобразованной модели
наблюдений на единицу меньше, чем в исходной, так как при преобразовании
используются запаздывающие значения переменных.) Поэтому гипотеза о
независимости в совокупности ошибок в преобразованной модели не отвергается
(в пользу гипотезы об их положительной автокоррелированности). График
на рис. 5.15 дает представление о рассеянии значений преобразованных
переменных, а на рис. 5.16 — о поведении остатков в преобразованной модели.
Обратим внимание на существенно более нерегулярное поведение остатков
по сравнению с исходной моделью.
Обратившись к результатам оценивания коэффициентов в
преобразованной модели, отметим значительное (более чем в 5 раз!) возрастание оценки
стандартной ошибки Sp, что подтверждает сделанное ранее замечание о
занижении стандартных ошибок при неучете имеющейся в действительности
положительной автокорреляции случайных ошибок в модели наблюдений.
Столь существенное возрастание значения Sp приводит к возрастанию более
чем в 5 раз и ширины доверительного интервала для мультипликатора Д.
Если при оценивании исходной линейной модели 95%-й доверительный
интервал для этого параметра имел вид 2.058 < Д < 2.542, то при оценивании
преобразованной модели получим интервал 1.516 < Д< 4.074.И

230
Часть 1. Основные понятия, элементарные методы
CONS_ TRANSFORMED
41 J--
RESID02
22 23 24 25
MONEY_ TRANSFORMED
Рис. 5.15
52:1 52:3 53:1 53:3 54:1 54:3 55:1 55:3 56:1 56:3
Год, квартал
Рис. 5.16
Рассмотренный пример ясно демонстрирует опасность пренебрежения
возможной неадекватностью построенной модели в отношении
стандартных предположений об ошибках и необходимость обязательного проведения
в процессе подбора подходящей модели связи между теми или иными
экономическими факторами анализа остатков, полученных при оценивании
выбранной модели.
Более того, используя преобразованную модель, можно получить
улучшенную модель для прогнозирования объемов расходов на потребление при
планируемых объемах денежной массы. Поясним это на примере простой
линейной модели
У;=а + /3х;+€п / = 1,...,л.
Предполагая, что st - psi_l = Si9 i = 2, ..., я, и используя оценку г для
коэффициента р9 перейдем к преобразованной модели
у* =а* +J3x*+s*, i = 2,..., л,
У* = Уг-гУг-м А = (Xi-rxt-\)> ' = 2,..., л, а = аA-г).
В рамках этой модели получим оценки а и Д параметров а и Д. Тогда
оцененная модель линейной связи между преобразованными переменными
имеет вид:
yt =a +Дх/5 i = 2,..., п.
В исходных переменных последние соотношения принимают вид:
Уг-гУы =aQ-r) + P(xi-rxi_l), i = 2,..., л,
где а = -
а
1^7
, откуда получаем:

Раздел 5. Учет нарушений стандартных предположений о модели
231
yt =d + J3xi+r(yi_l-d-/3xi_l), / = 2,...,л.
Если прогнозировать будущее значение уп+х, соответствующее плановому
значению хп+1 объясняющей переменной, то естественно воспользоваться
полученным соотношением и предложить в качестве прогнозного для уп+х
значение
yn+x=a + J3xn+x+r(yn-a-f3xn).
При таком способе вычисления прогнозного значения для^„+1
учитывается тенденция сохранения знака остатков: если в последнем наблюдении
значение уп больше а + /Зх„, предсказываемого линейной моделью связи
у = а + /?х, то и последующее значение уп+1 прогнозируется с превышением
значения а + Рхп+{9 предсказываемого этой линейной моделью связи при
г > 0. Если же значение уп меньше, чем а + (Зхп, то будущее значение у„+х
прогнозируется значением, меньшим, чем а + fixn+l.
Рассмотрим еще одно важное следствие автокоррелированности ошибок
в линейной модели
yt=a + рх(+б^ / = 1,...,/!,
£i-p£i_x =Si9 i = 2,...,n.
Преобразование
У1=У1-РУ{-1> х\ = хг-Рхг-\
приводит к модели наблюдений
у\ = а' + Рх\ + 819 / = 2,...,и,
на основании которой получаем
yt = а{\ -р) + pyt_x + fi(xt -pxt_x) + Si9 i = 2,..., п.
Вспомним теперь о нашем предположении, что 0 < р < 1, и преобразуем
последнее соотношение следующим образом:
yt = a(\-p) + yt_x -(\-p)yt_x + /?(*,- -*M +(\-p)xi_x) + 8i =
= yt_x + A - p)(a + fi xt_x - yt_x) + P (xf - xt_x ) + Si9
или
Ay^PAXi+ip-lXy^-a-px^ + S;,
здесь Ayt =yt -yt_X9 AXi=xt - xt_x и -1 < (p- 1) < 0.
Второе слагаемое в правой части, по существу, поддерживает
«долговременную» линейную связь (тенденцию)
у = а + Рх.

232
Часть 1. Основные понятия, элементарные методы
Если в момент (/ - 1) отклонение yt_ х от а + /?х,_ х положительно (yt_х > а +
+ /3xt_x), то второе слагаемое будет отрицательным и действовать в сторону
уменьшения приращения Ayf = yf -j^-i- Если же отклонениеyt_x от а + Pxt_x
отрицательно (yf_x < а + /3xf_x), то второе слагаемое будет положительным
и действовать в сторону увеличения приращения Ayt =yt ->V-i-
Указанная модель коррекции приращений переменной у использует
истинные значения параметров а, /?, /?. Поскольку эти значения неизвестны,
можно построить только аппроксимацию такой модели, использующую
оценки параметров. При этом естественно воспользоваться оценкой г и
уточненными оценками а, /?, полученными на базе преобразованной модели.
В рассмотренном примере аппроксимирующая модель коррекции
приращений принимает вид:
Ду, =2.975Дх, -0.126(.ум -244.262-2.795хм).
Как и в случае неоднородности дисперсий случайных ошибок, при
наличии автокоррелированности ошибок в модели наблюдений возникает
смещение оценок дисперсий случайных величин в{9 ..., вр9 хотя наличие и такого
нарушения стандартных предположений оставляет сами оценки в19 ..., вр
несмещенными. В связи с этим один из методов коррекции статистических
выводов при автокоррелированности ошибок состоит в использовании
обычных оценок наименьших квадратов в19..., вр коэффициентов #lv.., вр вместе
со скорректированными на автокоррелированность оценками стандартных
ОШИбоК Sq..
Один из вариантов получения скорректированных на
автокоррелированность значений s§. был предложен Ньюи и Вестом (Newey, West) и реализован
в ряде пакетов статистического анализа данных, в том числе в пакете EViews.
При этом удовлетворительные свойства оценки Ньюи — Веста (Newey-
West estimate) гарантируются только при большом количестве наблюдений.
Не будем приводить здесь детали получения оценки Ньюи — Веста (вид этой
оценки указан, например, в книге {Магнус, Катышев, Пересецкий, 2005),
а просто воспользуемся пакетом EViews для анализа данных из только что
рассмотренного примера.
Напомним результаты оценивания исходной линейной модели без учета
автокоррелированности ошибок (табл. 5.17).
Таблица 5.17
Объясняемая переменная Y
Переменная
1
X
Коэффициент
-154.719
2.300
Стандартная
ошибка
19.850
0.114
/-статистика
-7.794
20.080
Р-значение
0.0000
0.0000

Раздел 5. Учет нарушений стандартных предположений о модели
233
Результаты использования оценки Ньюи — Веста приведены в табл. 5.18.
Таблица 5.18
Объясняемая переменная У
Переменная
1
X
Коэффициент
-154.719
2.300
Стандартная
ошибка
32.729
0.139
Г-статистика
-6.520
16.449
Р-значение
0.0000
0.0000
Как и ожидалось, во втором случае обнаруживаем возрастание оценок
стандартных ошибок для оценок обоих коэффициентов.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каковы причины автокоррелированности ошибок в линейной эконометрической
модели?
2. Каковы последствия автокоррелированности ошибок в линейной
эконометрической модели?
3. Как можно скорректировать модель с автокоррелированными ошибками, чтобы
получить корректные статистические выводы?
4. Как можно получить корректные статистические выводы без преобразования
модели с автокоррелированными ошибками?
5. Как можно использовать автокоррелированность ошибок в линейной
эконометрической модели для улучшения качества прогнозов, строящихся на основе
оцененной модели?

Раздел 6
ОСОБЕННОСТИ РЕГРЕССИОННОГО АНАЛИЗА
ДЛЯ СТОХАСТИЧЕСКИХ
ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ
Тема 6.1
ЛИНЕЙНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ
СО СТОХАСТИЧЕСКИМИ ОБЪЯСНЯЮЩИМИ
ПЕРЕМЕННЫМИ
В предыдущих разделах главное внимание было уделено статистическим
выводам в рамках классической нормальной линейной модели наблюдений
(модели нормальной линейной множественной регрессии)
yi=GiXil+e2xi2+... + epxip+ei9 / = 1,...,л,
в которой предполагается, что значения объясняющих переменных хП9 хй9 ...,
xip9 i = 1,..., п фиксированы, а случайные составляющие sl9 el9..., sn (ошибки)
являются независимыми случайными величинами, имеющими одинаковое
нормальное распределение с нулевым математическим ожиданием и
конечной дисперсией (такие предположения об ошибках называются
стандартными). Далее были проанализированы последствия различного типа нарушений
таких предположений об ошибках и рассмотрены некоторые методы
коррекции статистических выводов о коэффициентах модели при наличии
соответствующих нарушений стандартных предположений.
В матрично-векторной форме классическая нормальная линейная модель
наблюдений имеет вид:
У = Хв + £9
где;/ = (у\9У2> —>Уп)Т —вектор-столбец значений объясняемой переменной
в п наблюдениях;
X — («х /?)-матрица значений объясняющих переменных
в п наблюдениях, п >р;

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 235
в- (в19 #2, ..., вр)Т — вектор-столбец коэффициентов;
8- (е{, %, ..., sn)T — вектор-столбец случайных ошибок (возмущений)
в п наблюдениях.
Предполагается, что случайный вектор е имеет л-мерное нормальное
распределение с нулевым вектором математических ожиданий
Я(^) = (£(^),^(^2) £(^я))г = @,0 0)г
(в краткой записи: E{s) = 0)
и ковариационной матрицей
Cov(s) = (Cov(snSj)) = a2In9
где /„ — единичная матрица (размера п х п).
Здесь
Cov(ei,sj) = E{si-E(si))(sj -Е{е,))
— ковариация случайных величин st и Sj.
Предположение о фиксированности значений объясняющих переменных
в совокупности со стандартными предположениями об ошибках удобно с чисто
математической точки зрения: при таких предположениях оценки
параметров, получаемые методом наименьших квадратов, имеют нормальное
распределение. Это, в свою очередь, дает возможность:
• строить доверительные интервалы для коэффициентов линейной
модели, используя квантили ^-распределения Стьюдента;
• проверять гипотезы о значениях отдельных коэффициентов, используя
квантили ^-распределения Стьюдента;
• проверять гипотезы о выполнении тех или иных линейных
ограничений на коэффициенты модели, используя квантили F-распределения
Фишера;
• строить интервальные прогнозы для будущих значений объясняемой
переменной, соответствующих заданным будущим значениям
объясняющих переменных.
Вместе с тем используемое в классической модели предположение о
фиксированности значений объясняющих переменных в п наблюдениях
фактически означает, что можно повторить наблюдения значений объясняемой
переменной при том же наборе значений объясняющих переменных хп, хй9 ..., xip,
i = 1, ..., п. При этом получим другую реализацию (другой набор значений)
случайных составляющих sl9 ^ ..., £„, что приведет к значениям объясняемой
переменной, отличающимся от значенийУ\9у19 ---9у„9 наблюдавшихся ранее.
С точки зрения моделирования реальных экономических явлений
предположение о фиксированности значений объясняющих переменных можно счи-

236
Часть 1. Основные понятия, элементарные методы
тать реалистичным лишь в отдельных ситуациях, связанных с проведением
контролируемого эксперимента. Между тем в реальных ситуациях по
большей части нет возможности сохранять неизменными значения объясняющих
переменных. Более того, и сами наблюдаемые значения объясняющих
переменных (как и ошибки) часто интерпретируются как реализации некоторых
случайных величин. В таких ситуациях становится проблематичным
использование техники статистических выводов, разработанной для классической
нормальной линейной модели.
Поясним последнее, обратившись к матрично-векторной форме
классической линейной модели с р объясняющими переменными
y = X6 + s
и не требуя нормальности распределения вектора s.
Если матрица X имеет полный ранг р9 то матрица ХТХ является
невырожденной, для нее существует обратная матрица (ХТХ)~\ и оценка наименьших
квадратов для вектора в неизвестных коэффициентов имеет вид:
в = {ХтХухХту.
Математическое ожидание вектора оценок коэффициентов равно:
Е{в) = Е((ХтХухХт{Хв+е)) =
= Е({ХтХухХтХв)+Е({ХтХ)'хХте) = в+Е((Хт Х)~х Хте).
Если матрица X фиксирована, то
E((XTXyxXTs) = {XTXyxXTE(s) = О,
так что ЕF) = #, т.е. в — несмещенная оценка для в.
Пусть, однако, мы имеем дело со стохастическими {stochastic)
объясняющими переменными, т.е. столбцы матрицы X рассматриваются как
случайные векторы, а сама матрица Xобразует систему/? случайных векторов и
является случайной матрицей. Элементы этой матрицы xij9 i = 1, ..., и, j = 1, ...,/?,
являются случайными величинами, имеющими некоторое совместное
распределение вероятностей. Тогда в общем случае Е{{ХТХ)~ХХТs)) Ф 0, так что
Е@) * 0, и в — смещенная оценка для 6. Кроме того, эта оценка уже не
имеет нормального распределения, даже если вектор е имеет нормальное
распределение.
Если объясняющие переменные стохастические, то в некоторых случаях
все же остается возможным использовать стандартную технику
статистических выводов, предназначенную для классической нормальной линейной
модели, по крайней мере, в асимптотическом плане (при большом количестве
наблюдений).
Рассмотрим несколько таких ситуаций.

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 237
Ситуация А (наиболееблагоприятная)
• случайная величина sk не зависит (статистически) от хП9 ха, ..., xip при
всех i и к;
• sl9 62, ..., еп являются независимыми случайными величинами,
имеющими одинаковое нормальное распределение с нулевым
математическим ожиданием и конечной дисперсией а2 > 0. Как и ранее, кратко
обозначим это как st ~ lid. N@9 a2).
При выполнении таких условий имеем:
Е{{ХТХУ1ХТ8) = E((XTXylXT)E(s) = 0,
так что оценка наименьших квадратов для в является несмещенной.
Распределение статистик критериев (тестовых статистик) можно найти с помощью
двухшаговой процедуры. На первом шаге находим условное распределение
при фиксированном значении матрицы Х\ при этом значения объясняющих
переменных рассматриваются как детерминированные (как в классической
модели). На втором шаге получаем безусловное распределение
соответствующей статистики, путем умножения условного распределения на
плотность X и интегрирования по всем возможным значениям X.
Если применить такую процедуру для получения безусловного
распределения оценки наименьших квадратов в, то на первом шаге найдем:
6\Х~Щв,G2{ХтХух).
Интегрирование на втором шаге приводит к распределению, являющемуся
смесью нормальных распределений jV@, a2(XTX)~l) по X. Это распределение
в отличие от классического случая не является нормальным.
В то же время для оценкиу'-го коэффициента имеем:
ej\x-N{eJ9^{xTxr^
где (ХТХ)~~ —у-й диагональный элемент матрицы (ХТХ)~\ так что
A-ft
J J |jr~tf@,l).
^{xTxyl
v (n-p)S2 e2 RSS _ce
Условным распределением для £г , где S = , RSS — остаточ-
сг п- р
ная сумма квадратов, является распределение хи-квадрат с (п-р) степенями
свободы:
(У

238
Часть 1. Основные понятия, элементарные методы
Заметим, что /-статистика для проверки гипотезы Н0 : в; = в* определяется
соотношением
Из предыдущего вытекает, что если гипотеза Н0 верна, то условное
распределение этой /-статистики имеет /-распределение Стьюдента с (п -р)
степенями свободы
t\X~t(n-p).
Это условное распределение одно и то же для всех X. Поэтому независимо
от того, какое именно распределение имеет Х9 безусловным распределением
/-статистики для Н0 : в; = в* при выполнении этой гипотезы будет все то же
распределение t(n -p).
Аналогичные рассуждения показывают возможность использования
стандартных F-критериев для проверки линейных гипотез о значениях
коэффициентов.
Те же самые выводы остаются в силе при замене предположений ситуации
А следующим предположением.
Ситуация Аг
• £ | Х- N@, <J2I„)9 где 1п — единичная матрица размера (п х п).
Для краткости будем далее обозначать:
Х; = (хП9хй9 ...9xip)T—вектор-столбец значений/? объясняющих
переменных в /-м наблюдении;
Хп — матрица значений объясняющих переменных для
п наблюдений.
Ситуация В
• случайная величина ек не зависит (статистически) от xil9 xil9 ..., xip при
всех i и к\
• распределение случайной величины st не является нормальным, но
е( ~ НА, Е(£г) = О, D(st) = а2 > О и E(ef) - ju4 < оо;
• E{xtxJ) = Qt — положительно определенная матрица, (l/n)(Q{ + ... +
+ Qn)^> Q ПРИ п ~~> °°> гДе Q — положительно определенная матрица;
• E{xtj xik xn xis) < оо для всех i9j9 k9l9s\
• (l//i)(jc1jc1r + ... +xnxf) = (l/ri)X*X„ -> Q при n —► оо по вероятности.
В силу первого предположения оценка наименьших квадратов вектора
коэффициентов в остается несмещенной, как и в ситуации А. Однако при
конечном количестве наблюдений п из-за негауссовости (ненормальности)

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 239
распределения st распределения статистики S29 а также t- и F-статистик будут
отличаться от стандартных, получаемых в предположении нормальности.
Чтобы продолжать пользоваться обычной техникой регрессионного анализа,
необходимо сослаться на следующие асимптотические результаты, строгий
вывод которых можно найти, например, в книге (Hamilton, 1994).
Пусть
6(п) — оценка наименьших квадратов вектора в поп наблюдениям;
S29 tn9Fn — статистики S29t9 F9 вычисляемые по п наблюдениям.
Если выполнены предположения, перечисленные при описании ситуации
В9 то при л —► оо:
• yfc(Sn2-a2)-+N@,M4-G4y,
• *я->ад1);
• qFn —► х\ч)-> гДе Ч — количество линейных ограничений на
компоненты вектора ft
Здесь везде имеются в виду сходимости по распределению, т.е. функции
распределения случайных величин, стоящих слева от стрелки, поточечно
сходятся при п —► оо к функциям распределения, стоящим справа от стрелки.
При этом имеют место приближенные соотношения:
• в(п) *И(в9 cr2Q~l/n\ или в(п) * N@9 а\ХтпХУ) (последнее аналогично
точному соотношению в гауссовской модели);
• SZ*N{<y\(iiA-o*)lny9
• '„«WD;
• qFn~x\q)-
Если в ситуации В при имеющемся количестве наблюдений п
использовать не асимптотические распределения, а распределение Стьюдента t{n -p)
для ^-статистики (вместо N@9 1)) и распределение Фишера F(q9 п-р) для
F-статистики (вместо х\ч) Для Ч^п\ то это приводит к более широким
доверительным интервалам (по сравнению с интервалами, построенными по
асимптотическим распределениям). Многие исследователи предпочитают
поступать именно таким образом, учитывая это обстоятельство и то, что при
конечных п распределения Стьюдента и Фишера могут давать лучшую
аппроксимацию истинных распределений статистик tnnF„.
Ситуация С
В рассмотренных выше ситуациях, как и в классической модели,
предполагалось, что ех \Х~ lid. Откажемся теперь от этого предположения и
предположим, что:

240
Часть 1. Основные понятия, элементарные методы
• условное распределение случайного вектора е относительно матрицы X
является «-мерным нормальным распределением N@9 a2V)\
• V — известная положительно определенная симметричная матрица
размера (п х п).
Поскольку матрица V симметрична и положительно определена, такой же
будет и обратная к ней матрица V~\ Но тогда существует такая
невырожденная (п х я)-матрица Р, что V~l =РТР. Используя матрицу Р9 преобразуем
вектор £ к вектору
s*=Ps.
При этом E(s*) = О и условная (относительно X) ковариационная матрица
вектора s*
Cov{s*\X) = E(s*£*T\X) = E(Ps(Ps)T\X) = PE(esT\X)PT = Pa2VPT.
UoV = {V~xyx = (PTP)~\ так что
Cov(s* \X) = Pa2VPT = a2P(PTPylPT = a2I„.
Преобразуя с помощью матрицы Р обе части основного уравнения
у = Хв+£9
получим:
Ру = РХв+Ре9 или у* = Х*в+е\
щеу* = Ру9 Х* = РХ9 е=Ре.
В преобразованном уравнении
e'\X~N@9(T2IH)9
так что преобразованная модель удовлетворяет условиям, характеризующим
ситуацию А\ Это означает, что все результаты, полученные в ситуации А,
применимы к модели
у* = Гв+8*.
В частности, оценка наименьших квадратов
0* =(X*TX*ylX*Ty* =(XTPTPXylXTPTPY = (XTV-lXylXTV-ly
является несмещенной, т.е. Е(в*) = в, ее условное распределение
(относительно X) нормально и имеет ковариационную матрицу
CovF* \Х) = а2(Х*тХ*у1 = <T2(XTV-lXyl.
Получение этой оценки равносильно минимизации по в суммы
п п
Z Z w&(yi - в\хп - - - ОрХфКУк ~ в\хк\ - - - врхир)>
i=\k=\
где wik = v^_1) —элементы матрицы V~l.

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 241
Отсюда название описанного метода оценивания — обобщенный метод
наименьших квадратов (GLS — generalized least squares). Сама оценка в*
называется обобщенной оценкой наименьших квадратов (GLS estimator),
для ее обозначения обычно используется подстрочный индекс GLS:
e'=eGLS=(xTv-lxylxTv-ly.
Заметим, что в рамках модели;;* = Х*в+ е можно использовать обычные
статистические процедуры, основанные на t- и F-статистиках.
v Замечание 6.1.1. Если матрица V диагональная, V- diag(Af, ..., /*„2),
hl9 ..., hn > О, и не все hk одинаковы (так что sl9 ..., еп — условно
независимые случайные величины с неодинаковыми дисперсиями),
то Vх = diagA /Лj2, ..., l//zw2), и в качестве подходящей матрицы Р
естественно взять Р = diag(l//zl9 ..., \/hn). При этом в
преобразованном уравнении
y*=yi/hi> xl=xv/hi> J = U—,P, * = 1,...,л,
так что обобщенная оценка наименьших квадратов вектора в
получается как результат минимизации по в суммы
f yi-exxiX—-epxi^1
/=l
h,
Р V_
J
п 1
= ZT70'/-0i*/i ffpxiPJ>
/=i Л,-
т.е. суммы квадратов взвешенных отклонений, или взвешенной
суммы квадратов отклонений. Соответственно в подобных случаях
обобщенный метод наименьших квадратов называют взвешенным
методом наименьших квадратов.
Подобная ситуация уже встречалась в примере 5.2.1. Там имели
р = 2 и предполагали, что значения ха, i = 1, ..., я, фиксированы
и/zj2 =х22.
V Замечание 6.1.2. При рассмотрении темы 5.3 предполагалось
наличие автокоррелированности ряда ошибок в форме процесса
авторегрессии 1-го порядка:
et =pet-i+St9 t = 29...,n,
где \р\ < 1, St91 = 29..., п, — независимые в совокупности случайные
величины, имеющие одинаковое нормальное распределение
N@9 а2)9 и 8t не зависит от st_s9 s > 0. Если предположить еще, что
ех имеет такое же распределение, как и ^ ..., еп9 то Е(ех) = 0,
D{sx) a2
1-Р2

242
Часть 1. Основные понятия, элементарные методы
V =
Р
1
Р
Р
1
лА7-1 лЛ-2 ЛА7-3
\Р Р Р
-И "Л
и-2
^л-3
Соответственно
V-- 1
1-р*
1
->с
О
-р A + р2) -р
О
-р A+р2)
о
о
о
(О
о
о
0 0 0 ... A + р2) -р
ч 0 0 0 ... -/? 1
(«трехполосная» матрица), и в качестве Р можно взять
«двухполосную» матрицу
Ul-P2 О О
1 О
-р 1 ..
р =
\-р-
-р
о
о
о
о
о
о
о
.. 0
.. 0
.. 0
.. 1
.. -р
0
0
0
0
и
При этом в преобразованном уравнении получаем:
у\=*\\-р2 .yl9 x*Xj=^\-p2 -xlJ9 7 = 1,...,/?,
У* = Уг -РУх-\, xtj = xtj -Pxt-\J> j = l9...,P, t = 2,...,n.
Это преобразование называют преобразованием Прайса —
Уинстена (Prais-Winsten transformation). Заметим: если
использовать для оценивания преобразованные уравнения, начиная со
второго (игнорируя первое уравнение), то это точно соответствует
преобразованию, использованному при изложении темы 5.3 в связи
с итерационной процедурой Кохрейна — Оркатта.
Если матрица V не известна априори, то часто ограничиваются моделями,
в которых она параметризована, так что V= V(/3), где /3— векторный параметр,
который приходится оценивать по имеющимся наблюдениям. При этом
достаточно часто можно использовать стандартные выводы в асимптотическом
плане, заменяя в выражении для GLS-оцеяш в* = (XTV~lX)~lXTV~ly неиз-

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 243
вестную матрицу V= V(/30) (<J2V(/30) — истинная ковариационная матрица
вектора е) матрицей V(j3„), где /?„ — любая состоятельная оценка для Д. В таких
случаях говорят о «доступном» обобщенном методе наименьших квадратов
(feasible GLS). Так, для реализации преобразования Прайса — Уинстена
достаточно получить состоятельную оценку для параметра /?, и такая оценка уже
использовалась в разд. 4.5 при рассмотрении процедуры Кохрейна — Оркатта:
п
р=Ч—.
где el9..., еп — остатки, получаемые при оценивании обычным методом
наименьших квадратов исходной модели наблюдений.
Рассмотренные выше ситуации не охватывают, однако, многие важные для
приложений модели временных рядов. Для их изучения необходимо освоить
основные понятия и факты, касающиеся временных рядов, рассмотреть
особенности регрессионного анализа временных рядов, что предусмотрено в
следующей части учебника.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие преимущества дают стандартные предположения о линейной нормальной модели?
2. К каким нежелательным последствиям может приводить отказ от предположения
о детерминированности объясняющих переменных?
3. Какое дополнительное условие на случайные ошибки достаточно добавить к
стандартным предположениям об ошибках в нормальной линейной модели, чтобы
можно было на законных основаниях использовать стандартные /- и F-критерии?
4. Как следует поступать в случае, когда условное распределение случайного
вектора s относительно матрицы X является «-мерным нормальным распределением
N@9 a2V)c ковариационной матрицей V, отличающейся от единичной матрицы?
5. В чем состоит обобщенный метод наименьших квадратов? Как он реализуется на
практике? •
6. Чем отличается оценка Прайса — Уинстена в модели с автокоррелированными
ошибками от оценки, получаемой путем авторегрессионного преобразования
переменных, используемого в процедуре Кохрейна — Оркатта?
Тема 6.2
МЕТОД ИНСТРУМЕНТАЛЬНЫХ ПЕРЕМЕННЫХ
Заметим, что в ситуациях А, А' к С, рассмотренных в теме 6.1, общим
является условие
E(es\X) = 09 / = l,...,л,
так что
E(si\xQ) = Q для у = 1, ...,/? при всех ink.

244
Часть 1. Основные понятия, элементарные методы
Но тогда
И
Cov(si9xkJ) = E((st -E{st)\xkj -E(xkj))) = E{st{xkj - E(xkj)) = E(st xkj) = 0
(конечно, при этом предполагаем, что математические ожидания E(xkJ)
существуют и конечны).
Таким образом, если ошибка в i-u уравнении коррелирована хотя бы
с одной из случайных величин xkj9 то ни одно из условий А9А\ С не
выполняется. Например, эти условия не выполняются, если в /-м уравнении какая-
либо из объясняющих переменных коррелирована с ошибкой в этом уравнении.
Последнее характерно для моделей с ошибками в измерении объясняющих
переменных и моделей одновременных уравнений, о которых поговорим
ниже. Пока же приведем пример, показывающий, к каким последствиям
приводит нарушение условия некоррелированности объясняющих переменных
с ошибками.
ПРИМЕР 6.2.1
Смоделированные данные соответствуют следующему процессу порождения
данных:
DGPrj;. =a + Pxi+ei9 s^iLd. 7V@,1), / = 1,...,100,
a=10, /?=2,
jcz =^ -0.9^_l9 / = 2,...,100,
при этом Corr(xi9 st) = 0.743.
Предположим, что имеем в распоряжении значения yi9 xi9 i - 2, ..., 100,
но ничего не знаем о процессе порождения данных. Оценим на основе этих
данных статистическую модель уг■- а + J3x{ + st методом наименьших
квадратов. Получим результаты, приведенные в табл. 6.1
Таблица 6.1
Объясняющая переменная Y_FIXED
(Method: Least Squares; Sample (adjusted): 2 100
Переменная
1
X
Коэффициент
10.13984
2.553515
Стандартная
ошибка
0.069148
0.054971
/-статистика
146.6398
46.45184
Р-значение
0.0000
0.0000
Для параметра /3 получаем оценку J3 = 2.553, имеющую весьма сильное
смещение.

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 245
Зафиксировав полученную реализацию х2, ..., £100, смоделируем еще 499
последовательностей {si**,...,*^}, k = 2, ..., 500, имитирующих реализации
независимых случайных величин, имеющих стандартное нормальное
распределение, и для каждой такой последовательности построим
последовательность \у{к),..., у[кH) по формуле:
y\k)=a + Pxt+£\k\ / = 2 100.
Для каждого к = 2,..., 500, по «данным»^, xi9 i = 2,..., 100, оценим
статистическую модель yf^ = a + J3xt + sf^ и получим оценки коэффициентов а(к\ Р(к\
В результате имеем последовательности оценок аB\ ..., с?E00) и Д2),..., Д500).
На рис. 6.1 приведены статистические характеристики полученной
последовательности /?B),..., /3{500\
Series: SLOPE
Sample 2 500
Observations 499
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
Jarque-Bera
Probability
1.999663
1.994058
2.238951
1.740510
0.083992
0.161028
2.895625
2.383013
0.303763
Рис. 6.1
Среднее значение практически совпадает с истинным значением
параметра Д гипотеза нормальности распределения оценки /? не отвергается.
Поступим теперь другим образом. Для каждой из смоделированных
последовательностей j^,...,^}, к = 2, ..., 500, сначала построим
последовательность |xf),...,jc1(o0)|, а затем — последовательность {^^---^юо)
по формуле:
у\к)=а + 0х\к)+е\к\ i = 2,...,НЮ.
В отличие от предыдущего способа здесь для различных значений к
используются различные последовательности {х^,...,*^}, определяемые
последовательностью \е^,..., еЩ).

246
Часть 1. Основные понятия, элементарные методы
После получения последовательностей {*2^--->-xioo) и {>2*)>--->>;i(ooj
при каждом к = 2, ..., 500 произведем оценивание статистической модели
у{к) = а + fixf} + £{к) и получим оценки коэффициентов а*(к\ р(к). В итоге
имеем последовательности оценок а*{2\ ..., сГE00) и р{2\ ..., /ГE00).
На рис. 6.2 приведены статистические характеристики последовательности
80
60
40
20 -\
2.53
li
i I II
2.54
2.55
III..
2.56 2.57
Series: SLOPE RANDOM
Sample 2500
Observations 499
/Wean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
2.552114
2.551333
2.588107
2.530200
0.007346
0.754039
4.608878
Jarque-Bera 101.1054
Probability 0.000000
'rrrri i i г i _
2.57 2.58 2.59 fi*
Рис. 6.2
На этот раз среднее значение полученных значений р(к\ равное 2.552114,
весьма сильно отличается от истинного значения параметра /3=2, а
наблюдаемое значение статистики Харке — Бера говорит о том, что
распределение оценки наименьших квадратов параметра /3 = 2 не является
нормальным.
Заметим также: положительная коррелированность х{ и £( означает, что
значениям xi9 превышающим их среднее значение в выборке, по большей части
соответствуют и значения остатков, превышающие их среднее значение в
выборке. Но последнее равно 0 при использовании метода наименьших
квадратов, так что значения остатков, превышающие их среднее значение в выборке,
суть просто положительные значения остатков. В итоге для первоначально
смоделированных данных у., xi9 i = 2,..., 100, это приводит к картине,
изображенной на рис. 6.3. Здесь Linear (Y) — прямая, подобранная по этим данным
методом наименьших квадратов, т.е. прямая у = 10.13984 + 2.553515х,
a YTHEOR — теоретическая прямая >> = 10 +2х. Как видно на рис. 6.3, первая
прямая повернута относительно второй прямой в направлении против
часовой стрелки, так что для больших значений х, наблюдаемые значения у.
смещены вверх по отношению к прямой>> = 10 +2х.Ш

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 247
♦ У
-+— Y_THEOR
Linear {У)
Рис. 6.3
Модели, в которых есть объясняющие переменные,
коррелированные с ошибкой
Модели с пропущенными переменными (missing variables). В разд. 3
говорилось о возможности смещения оценок в множественной линейной модели
регрессии при невключении в правую часть уравнения некоторых
существенных переменных. Рассмотрим модель порождения данных
DGP:^ =a + /3z( + ух( +ei9 / = 1,...,я,
со стохастическими объясняющими переменными z и х, в которой £{ ~ иЛ9
Е(ег) = О, D(st) = <j29 Cov(xi9 st) = Cov(zi9 et) = 0. Предположим, что между
переменными z и х имеется сильная корреляционная связь, которая проявляется
при оценивании коэффициентов модели в форме опасной мультиколлинеар-
ности, так что при применении /-критерия каждый из оцененных
коэффициентов при этих переменных объявляется статистически незначимым, хотя
гипотеза незначимости регрессии в целом отвергается.
Как говорилось в разд. 3, в качестве одного из возможных выходов из такой
ситуации часто используют исключение одной из сильно коррелированных
между собой переменных из правой части уравнения. Если поступить таким
образом и исключить из правой части оцененного уравнения переменную х,
то оценивать станем статистическую модель
SM:^- =a + /3zf+ui9
а в этой модели и( = yxt + st. Но тогда

248
Часть 1. Основные понятия, элементарные методы
Cov(z( ,ut) = Cov(zt ,yxi+si) = y Cov(zt, xt) * 0,
что приводит к смещению оценки коэффициента при переменной z.
Модели с ошибками в измерении объясняющих переменных
(errors-invar iables models). Рассмотрим модель порождения данных
DGP: у. = a + fizt+Uj, i = 1,..., 100,
со стохастической объясняющей переменной z, для которой выполнены
предположения:
E(u() = 0, D(Ui) = a2, £(«/|z/) = 0,
так что
E(yi\zt) = a + pzi.
Предположим, что значение zt невозможно измерить точно, и в результате
измерения вместо истинного значения zt наблюдается
х{=ъ+уп
где V, — ошибка измерения. Пусть при этом выполнены следующие условия:
. £(v,.) = 0,Z)(v,.) = <7v2;
• случайные величины ut и vz независимы:
• случайная величина vt не зависит от истинного значения z{.
Выразим zt через xt и подставим xt - vt вместо zt в исходное уравнение.
Получим:
У1=а + Ръ+е19
где et = ut - pv{ и
Covix^) = Cov(z,. + v,.,!/,. -^v,.) = -Pa].
Если р > 0, то xt и s( имеют отрицательную корреляцию; если Р < 0, то xt и
е{ имеют положительную корреляцию.
Покажем, что оценка наименьших квадратов /? не только имеет смещение
при конечных п, но и несостоятельна, т.е. даже при неограниченном
увеличении количества наблюдений не сходится к истинному значению /? по
вероятности. С этой целью в формулу для /?:
п
Zta-.yX*/-*)
р=—п
/ = 1
подставим выражение для yt. Получим:

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 249
£(/?х, - J3x + е, - еХх, -х) £(*, -е)(*,. -х)
Р = ~ = = Р + —„
1=1 1=1
так что
Таким образом, /? не стремитсА по вероятности к Д за исключением
случая, когда crv2 = 0, т.е. когда ошибки измерения z, отсутствуют. Если
отношение дисперсий <уЦ<у22 мало, то мало и асимптотическое смещение оценки
наименьших квадратов. В противном случае асимптотическое смещение
оказывается значительным.
Системы одновременных уравнений {simultaneous equations).
Рассмотрим кейнсианскую модель потребления
С, =a + fiYt+et9
где С, — реальное потребление на душу населения;
Yt — реальный доход на душу населения;
/3 — параметр @ < /3 < 1), интерпретируется как склонность к
потреблению (норма потребления).
Можно было бы на законных основаниях использовать для оценивания этого
параметра метод наименьших квадратов, если бы не одно осложняющее
обстоятельство. В случае модели замкнутой экономики без правительства в
дополнение к указанному уравнению в этой модели имеется еще и соотношение
Yt=Ct+It,
где 7, — реальные инвестиции на душу населения.
Таким образом имеем систему уравнений
[С, =a + pYt+et
U=Ct+I,
О такой системе уравнений говорят как о структурной форме
одновременных уравнений {structural form of simultaneous equations), подразумевая
под этим, что такая форма представляет в явном виде взаимные связи между
входящими в модель переменными, показывает, как эти переменные
взаимодействуют друг с другом (в данном случае Yt воздействует на С„ а С, — на Yt).
В структурной форме модели одновременных уравнений переменная,
являющаяся объясняемой переменной в одном из уравнений, может входить в
другое уравнение в качестве объясняющей переменной.

250
Часть 1. Основные понятия, элементарные методы
Выразив из этой системы С, и Yt через /„ получим приведенную форму
(reducedform of simultaneous equations) модели в виде:
1-Д 1-Д ' 1-Д
v а 1 1
1-Д 1-Д ' 1-Д '
В такой форме взаимодействие между С, и Yt уже не представлено в явном
виде, однако коэффициенты приведенной формы отражают итог
взаимодействия этих переменных.
Действительно, предположим, что в указанной системе значение
переменной It увеличивается на 1. Это приведет к увеличению значения Yt также на 1.
Но тогда согласно первому уравнению системы значение С, должно
увеличиться на р. Это изменение приведет, в свою очередь, к увеличению значения
Yt на Д а последнее — к увеличению значения С, на Д2, и т.д. В итоге
получим последовательное возрастание значений Yt на 1, Д Д2, Д3, ... и
последовательное возрастание значений С, на Д Д2, Д3, ... Просуммировав эти
приращения, получим в результате возрастание значения Yt на
1 + Д + Д2+Д3 + 1
и возрастание значения С, на
Но именно такие выражения имеют коэффициенты при переменной It
в уравнениях приведенной формы.
Предположим теперь, что £( ~ i.i.d., E(st) = О,0(е{) = а2 > 0 и для каждого /
случайные величины It и et независимы. Тогда из второго уравнения
приведенной формы находим:
Cov(Ynst) = ^-Cov(snst) = ^-^09
так что в исходном уравнении для С, объясняющая переменная Yt коррели-
рована с ошибкой. При этом для оценки Д коэффициента Д получаемой
(по п наблюдениям) применением метода наименьших квадратов к
исходному уравнению, имеем:
r h Q Cov(Ynst)
phmp = p+ ' ' ,
и-»00 D(Yt)
где
1-Д
P

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 251
D(Yt) = -^-^(D(It) + *2e),
plimfi = fiHl-P)°' 2*
Поскольку а] > О и в модели Кейнса О < /? < 1, то /? переоценивает
значение нормы потребления.
v Замечание 6.2.1. Приведенное выражение для plim/3 подразумевает,
п-+ао
что значение D(It) не зависит от t и конечно. Однако такое
предположение обычно не выполняется на практике.
В данном случае получить оценки параметров а и /? можно, минуя
исходное уравнение и обращаясь только к уравнениям приведенной формы. В
каждом из этих двух уравнений объясняющие переменные не коррелированы
с ошибкой.
Первое уравнение приведенной формы можно записать в виде:
С, = a + plt +sn
где
а = а/A-/3), Р = РЦ\-Р), st=stl(\-P), E&) = 0,
D(Zt) = *t=*2J(l-PJ.
Применив метод наименьших квадратов к данному уравнению, найдем
оценки коэффициентов а и /? и оценку дисперсии а\. После этого можно
найти оценки для параметров исходного уравнения из соотношений:
Р = р/A + Р), а = а/A + Д), *2£=*У(\ + РJ.
Таким образом, структурная форма восстанавливается по первому
уравнению приведенной формы. Второе уравнение оказывается в этом плане
избыточным. Но, используя одно это уравнение, можно также восстановить
структурную форму.
Действительно, это уравнение можно записать в виде:
Yt=y+SIt+sn
где y=a=a/(l-P), S=l/(l~P).
Применив метод наименьших квадратов к этому уравнению, найдем
оценки коэффициентов у и 8 и оценку дисперсии о\. После этого можно найти
оценки для параметров исходного уравнения из соотношений:
/3 = (S-1)/S, a = y/S, a] = al/s2.

252
Часть 1. Основные понятия, элементарные методы
Возникает вопрос: будут ли совпадать результаты восстановления
параметров структурной формы, полученные по двум различным уравнениям
приведенной формы?
Если обратиться к выражениям для сг,Ди^2 через параметры этих
уравнений, то нетрудно заметить, что
Г/S =3/A + 0), (S-Y)/S=p/A + P), al/S2=al/(l + PJ.
Таким образом, зная истинные значения параметров уравнений приведенной
формы, однозначно восстанавливаем по ним значения параметров
структурной формы. Однако в данном случае истинные значения параметров
уравнений приведенной формы нам не известны, и их приходится оценивать по
имеющимся статистическим данным. При этом оценки параметров
структурной формы, полученные с использованием оценок коэффициентов для
разных уравнений приведенной формы, могут в общем случае отличаться друг
от друга. Это связано с тем, что количество параметров приведенной формы
больше минимально необходимого для восстановления значений параметров
структурной формы.
Метод инструментальных переменных
Прежде чем перейти к описанию метода инструментальных переменных,
обратимся к обычному методу наименьших квадратов, который применяется к
простейшей линейной модели
у{ = а + J3xt + ei9 $~иЛ9 E(£t) = 09 D{si) = a29 /=1,...,«.
В этом случае оценка наименьших квадратов для коэффициента /?
удовлетворяет системе нормальных уравнений
К>,.-а-/?х,.) = 0
1 = 1
I
[/=i
выражающей ортогональность вектора остатков е = (еи ..., еп)Т9 где е{ = у{ -
- а - Eх{ — остаток в /-м наблюдении, векторам 1 = A,..., 1)г и х = (хх,..., хп)т.
Эти условия ортогональности, записанные в равносильных формах
л п 1 п
являются выборочными аналогами теоретических соотношений
Cov(st, 1) = 0, Cov(£t 9xt) = 0.
Первое из двух последних соотношений выполняется автоматически,
а второе в силу предположения E{st) = 0 можно записать в виде E(st xt) = 0.

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 253
1
1 п 1 п
Если Cov(si9xt) * О, то plim — Уед *0 и соотношение — TV-*. =0
»-*** 7=t пы\
не является эмпирическим аналогом теоретического соотношения E(sf х() = 0.
Можно было бы попытаться найти какую-то другую переменную zi9 для
которой выполняется соотношение Cov(sh zt) = Е($г^ = 0, и заменить второе
уравнение нормальной системы выборочным аналогом последнего
соотношения, т.е. уравнением
2>,--«-/?*,)*, =0.
1 = 1
Конечно, решение новой системы отличается от решения исходной
системы, поэтому временно обозначим получаемые оценки коэффициентов как
а* и /?*. Эти оценки удовлетворяют соотношениям
!>,-«* - А/) = 0, 2>, -а -fx,)z, =0,
1 = 1 1=1
из которых находим явное выражение для /?*:
п
* /
/?* =
= 1
/ = 1
которое можно также записать в виде:
П 1 П
X (у?х, -J3X + S,- ёХг, - z) - ^ (г,- - J)(z,- - 2)
/Г=Ь] = /? + ^ .
_w. 1 J1
£ О, - *)(*/ - z) - X (*/ " *)(*,- " *)
£i =1
Здесь
;? lim - У (et - e)(zt -z) = Соу(е(,г{) = 0,
1 w
p lim - £(*,. -x)(zt -z) = Covix^Zj),
так что, чтобы /? lim/?*=/?, необходимо выполнение еще одного условия:
п—>оо
CovC*;,, zf) * 0.
Если для переменной zt выполнены оба условия:
Cov(£t, zt) = 0, Cov(xi9 zt) * 0,

254
Часть 1. Основные понятия, элементарные методы
то ее называют инструментальной переменной или просто инструментом
(instrumental variable, instrument). Наличие такой переменной позволяет
получить состоятельную оценку коэффициента /? при переменной xt в ситуации,
когда х, коррелирована с st. Инструментальная переменная является
экзогенной переменной (exogenous variable) — в том смысле, что она определяется
вне связи с рассматриваемым уравнением у. = а + J3xt + st. Переменная xt
в рассматриваемом контексте является эндогенной переменной (endogenous
variable) — она связана (коррелирована) с ошибкой в этом уравнении, так что
значения xt устанавливаются совместно (одновременно) с st. Следуя обычной
практике, будем снабжать оценки коэффициентов, полученные с
использованием инструментальных переменных, подстрочным (или надстрочным)
индексом IV: dIV, J3rv (или dIV, J3IV), где IV — аббревиатура от Instrumental
Variables (инструментальные переменные). Метод получения таких оценок
называют методом инструментальных переменных (IV method —
instrumental variables method).
Возвратимся к системе, включающей кейнсианскую функцию потребления:
1г,=с,+/,.
При сделанных ранее предположениях относительно этой модели имеем:
Cov(Ynst) = —— *0, так что У, — эндогенная переменная. В то же время
Cov(In st) - О (в силу предположения о независимости этих случайных
величин), так что It — экзогенная переменная. Используя второе уравнение
приведенной формы, найдем:
Cov(YnIt) = Cov\-^- + ——/,+——*„/,] = ——£>(/,)* О,
так что переменную It можно применять в качестве инструмента для
получения состоятельной оценки коэффициента Д Это приводит к оценке
£(С,-С)(/,-/)
Piv~ = •
£(Г,-Г)(/,-7)
Это же выражение для /F-оценки коэффициента /? можно получить
следующим формальным образом. Возьмем ковариации обеих частей
структурного уравнения С, = а + fiYt + et с /,. Это приведет к соотношению:
Cov(CnIt) = Cov(atJt) + /lCov(YnIt) + Cov(£nIt).

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 255
При сделанных предположениях оно сводится к равенству
Cov(C„lt) = l3Cov(Yt,It),
откуда находим:
Cov{C„I,)
Cov{Y„I,Y
Чтобы получить оценку для /? по п имеющимся наблюдениям, заменим
теоретические ковариации в правой части их выборочными аналогами:
1
Х(С,-С)(/,-7) £(С,-С)(/,-7)
t = \
t = \
'IV
1 ^
2(Г,-Г)(/,-7) ^{Yt-Y)(It-I)
t = \
t=\
ПРИМЕР 6.2.2
В табл. 6.2 приведены взятые из (Economic Report of the President, 2000,
Appendix В) статистические данные (тыс. долл. 1996 г., в расчете на
душу населения) о следующих макроэкономических показателях
экономики США:
CONS — расходы на личное потребление (personal consumption
expenditures);
Y — располагаемый личный доход (disposable personal income),
а также вычисленные на их основе значения переменной
I=Y-CONS.
Таблица 6.2
Статистические данные макроэкономических показателей США
в расчете на душу населения, тыс. долл. 1996 г.
Год
1959
1960
1961
1962
1963
1964
1965
1966
1967
Y
9.068
9.111
9.260
9.561
9.779
10.342
10.842
11.288
11.641
CONS
8.213
8.267
8.298
8.574
8.799
9.197
9.655
10.088
10.278
/
0.855
0.844
0.962
0.987
0.980
1.145
1.187
1.200
1.363
Год
1979
1980
1981
1982
1983
1984
1985
1986
1987
Y
15.942
15.944
16.154
16.250
16.564
17.687
18.120
18.536
18.790
CONS
14.073
13.918
13.973
14.038
14.644
15.303
15.924
16.448
16.867
/
1.869
2.026
2.181
2.212
1.920
2.384
2.196
2.088
1.923

256
Часть 1. Основные понятия, элементарные методы
Окончание табл. 6.2
Год
1968
1969
1970
1971
1972
1973
1974
1975
1976
1977
1978
Y
12.055
12.322
12.688
13.044
13.492
14.269
14.099
14.236
14.653
15.010
15.627
CONS
10.755
11.055
11.180
11.429
11.972
12.428
12.259
12.414
12.960
13.364
13.842
/
1.300
1.267
1.508
1.615
1.520
1.841
1.840
1.822
1.693
1.646
1.785
Год
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
Y
19.448
19.746
19.967
19.892
20.359
20.354
20.675
21.032
21.385
21.954
22.636
CONS
17.397
17.682
17.818
17.653
18.025
18.372
18.878
19.272
19.727
20.272
21.060
/
2.051
2.064
2.149
2.239
2.334
1.982
1.797
1.760
1.658
1.682
1.576
При оценивании по этим данным методом наименьших квадратов уравнения
CONSt=a + CYt+st
получим график остатков, приведенный на рис. 6.4. Он говорит о наличии
двух фаз в модели связи. Переломным здесь можно считать 1986 г. — год
одного из глобальных нефтяных кризисов, выразившегося в обвальном
снижении мировой цены нефти до 10 долл. за баррель. Чтобы не заниматься
двухфазной моделью, ограничимся далее рассмотрением докризисного периода
с 1959 по 1985 г. При оценивании на этом периоде того же уравнения
получим график остатков, приведенный на рис. 6.5. Он уже не обнаруживает смены
режима связи. Результаты оценивания даны в табл. 6.3.
800 4
600 4
400 J
200 4
юо-4
O(NTf(D»O(Mt(DC0O(M^
(D(D(D(D(DSSNSS0OCO0O
RESID
Год
RESID
Год
РИС. 6.4
Рис. 6.5

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 257
Таблица 6.3
Объясняющая переменная CONS
(Method: Least Squares; Sample: 1959 1985; Included observations: 27)
Переменная
С
Y
Коэффициент
546.7669
0.841496
Стандартная
ошибка
105.9135
0.007803
/-статистика
5.162389
107.8374
Р-значение
0.0000
0.0000
Оценив уравнения приведенной формы, получим:
CONSt =4012.195 + 4.949/,+*,,
Yt =4012.195 + 5.949/,+*,,
так что в принятых ранее обозначениях:
S = у = 4012.195, р = 4.949, д = 5.949.
При использовании оценок коэффициентов первого уравнения получим
следующие оценки для а и /?:
Р = -^ = 0.832, £=-Аг = 674.5;
\ + Р 1 + Д
при сохранении в вычислениях большего количества десятичных знаков
Р - 0.831891 и а - 674.4849 соответственно.
Если использовать оценки коэффициентов второго уравнения, получим
те же самые значения оценок:
J3 = -^У- = 0.831891, а = 4 = 674.4849.
S 8
Это вовсе не случайно и означает, что ситуация весьма благоприятная,
когда, оценив коэффициенты уравнений приведенной формы, по ним можно
однозначно находить оценки коэффициентов структурной формы. Тем самым
реализуется косвенный метод наименьших квадратов (ILS — indirect least
squares).
Заметим: если коэффициенты некоторого уравнения структурной формы
однозначно восстанавливаются по оценкам коэффициентов приведенной
формы, то говорят, что соответствующее уравнение структурной формы
идентифицируемо точно.
Вычислив оценку коэффициента р с привлечением в качестве
инструмента переменной/, найдем: С = 1737.04, Т = 1561.04, F= 13298.07,

258
Часть 1. Основные понятия, элементарные методы
£(С,-сх/,-/)
Лк=1Т = 0.831891. ■
£(У,-7)(/,-/)
/ = 1
Ту же самую оценку для /? можно получить, используя двухшаговую
процедуру, ее идея состоит в построении искусственной инструментальной
переменной У,, которой можно подменить эндогенную объясняющую
переменную Yt в структурном уравнении.
На первом шаге обычным методом наименьших квадратов оценивается
модель линейной зависимости эндогенной объясняющей переменной У,
от инструментальной переменной It (она соответствует второму уравнению
приведенной системы). Используя полученные оценки у и 8, строим
новую переменную
Yt=y + SIt9
которая интерпретируется как результат очистки переменной Yt от линейной
корреляционной связи с ег Фактически при этом производится
«расщепление» переменной У, на две составляющие:
Y,=Y,+(Yt-Yt),
одна из которых затем отбрасывается.
На втором шаге обычным методом наименьших квадратов оценивается
модель
CONSt=a + pit+st,
в которой прежняя объясняющая переменная Yt заменяется ее очищенным
вариантом.
Такой метод оценивания параметров структурного уравнения CONSt =
= а + /3Yt + st называется двухшаговым методом наименьших квадратов
BSLS — two-stage least squares). Оценки cc2Sls и P2sls-> получаемые этим
методом, удовлетворяют соотношениям
ZiCONS, -d2SLS - P2SLSYt) = 0, £(СО№,-а2Я£ - fi2SLSYt)It = 0,
t=l t=\
т.е. являются /F-оценками.
При использовании метода инструментальных переменных в форме 2SLS
в примере 6.2.2 на втором шаге получим результаты, приведенные в табл. 6.4.
В пакете Е Views предусмотрена специальная процедура, реализующая
двухшаговыи метод наименьших квадратов. Часть протокола применения
этой процедуры для примера 6.2.2 приведена в табл. 6.5.

Раздел 6. Особенности регрессионного анализа для стохастических... переменных 259
Таблица 6.4
Объясняющая переменная CONS
(Method: Least Squares; Sample: 1959 1985; Included observations: 27)
Переменная
С
YF
Коэффициент
674.4849
0.831891
Стандартная
ошибка
667.4401
0.049231
/-статистика
1.010555
16.89762
Р-значение
0.3219
0.0000
Таблица 6.5
Протокол процедуры двухшагового метода наименьших квадратов
(Estimation Method: Two-Stage Least Squares; Sample: 1959 1985; Included observations: 27;
Total system (balanced) observations 27; Instruments: I C)
Переменная
0A)
CB)
Коэффициент
674.4849
0.831891
Стандартная
ошибка
112.2025
0.008276
/-статистика
6.011319
100.5160
Р-значение
0.0000
0.0000
Замечание 6.2.2. В рассмотренном примере оценки параметров
модели CONSt = а + j5Yt + st при использовании обычного метода
наименьших квадратов оказались равными:
а = 546.7669 и /? = 0.841496,
соответственно. В то же время оценки, полученные косвенным
методом наименьших квадратов, инструментальные оценки и оценки,
полученные двухшаговым методом наименьших квадратов
(совпавшие для всех этих методов из-за точной идентифицируемости
структурного уравнения), несколько отличаются от них и равны
а = 674.4849 и /? = 0.831891,
соответственно.
Замечание 6.2.3. При использовании метода инструментальных
переменных в случае наличия коррелированности некоторых
объясняющих переменных с ошибками возникают определенные проблемы:
• этот метод может обеспечить только состоятельность
получаемых оценок и при определенных условиях асимптотическую
нормальность этих оценок, но не обеспечивает несмещенность
оценок при небольшом количестве наблюдений;
• для применения метода при наличии нескольких эндогенных
переменных требуется достаточное количество
инструментальных переменных, с помощью которых можно было бы очистить
эндогенные объясняющие переменные; найти такие переменные
удается далеко не всегда.

260
Часть 1. Основные понятия, элементарные методы
Первое обстоятельство означает, что ориентироваться на оценки,
полученные методом инструментальных переменных, можно только
при достаточно большом количестве имеющихся наблюдений, так
что приведенный пример можно рассматривать только как
иллюстрацию. Если наблюдений мало, то /F-оценки могут иметь даже
большее смещение, чем О/^-оценки.
Второе обстоятельство значительно затрудняет практическое
использование метода инструментальных переменных. Из-за этого,
например, на практике обычно игнорируется тот факт, что
используемые статистические данные содержат ошибки измерений.
Кроме того, исследования показывают, что если выбранные
инструментальные переменные являются «слабыми инструментами»
{weak instruments), т.е. слабо коррелированы с эндогенными
объясняющими переменными, то качество /F-оценок с такими
инструментами может быть хуже, чем у О/.З'-оценок.
Обстоятельное рассмотрение методов оценивания систем одновременных
уравнений и проблем, связанных с возможностью идентификации уравнений
структурной системы, будет продолжено в третьей части учебника.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие нежелательные последствия имеет наличие коррелированное™ между
случайными ошибками в правых частях регрессионных уравнений и некоторыми
объясняющими переменными?
2. Как отражается на оценках наименьших квадратов коэффициентов линейной модели
наличие пропущенных переменных?
3. Как отражается на оценках наименьших квадратов коэффициентов линейной модели
тот факт, что значения объясняющих переменных, включенных в уравнение
регрессии, измерены неточно?
4. Чем отличается приведенная форма одновременных уравнений от структурной
формы и как она получается на основании заданной структурной формы?
5. Что такое инструментальная переменная, какие на нее накладываются требования?
Что дает использование инструментальных переменных?
6. Как можно получить оценки коэффициентов структурного уравнения методом
инструментальных переменных?
7. В чем состоит двухшаговый метод наименьших квадратов?

Задания для семинарских занятий,
работы в компьютерном классе
и для самостоятельной работы
К разделу 1
А. Задания для семинарских занятий и работы в компьютерном классе
Задание 1. Оценка наименьших квадратов
п
Проверьте, что E = ,=1 .
2>;-*J
1 = 1
Задание 2. Диаграмма рассеяния и коэффициент корреляции
Наблюдались следующие пары значений переменных хиу:
a) @,1), A,3), C,3), D,1);
b) (-2, 4), (-1,1), @,0), A,1), B, 4);
c) @,1), A,0), C,4), D,3);
d) @,3), A,4), C,0), D,1);
ё) A,1), B,3), C,2), D, 4);
В каждом из вариантов самостоятельно («вручную») постройте диаграмму
рассеяния и вычислите выборочный коэффициент корреляции между
переменными хиу. Проинтерпретируйте полученные значения этого коэффициента
и сопоставьте их с формой облака точек на диаграммах рассеяния. Измените
масштаб по одной из переменной и вычислите коэффициент корреляции в новой
ситуации. Изменилось ли значение коэффициента корреляции?
Задание 3. Прогнозные значения, коэффициент детерминации
Для тех же наблюдений вычислите ЯЛТ-оценки коэффициентов линейной модели
зависимости у от х, а также значения TSS, ESS, RSS и R2. Нанесите на диаграмму
рассеяния прогнозные значения переменной у. Сопоставьте значения R2, г2 , rjy.

262
Часть 1. Основные понятия, элементарные методы
Задание 4. Влияние масштабов измерений
Докажите, что /3 = г'—.
Задание 5. Свойства выборочных характеристик
Выведите свойства выборочных средних, выборочных дисперсий и выборочных
ковариаций, аналогичные свойствам их теоретических аналогов.
Задание 6. Оценки наименьших квадратов в агрегированной модели
Пусть ^ =У\ +Уг- Пусть методом наименьших квадратов оцениваются модели:
уи = al+/3lxi + eli9 y2i = cc2 + p2xi + sli, yt = a + fixt +si9 /=1,...,л.
Покажите, что а = ax + d29 ft = fix+ fi2.
Задание 7. Связь коэффициента детерминации с коэффициентами корреляции
7 7 7 7 7 7 7
Докажите: r~y = R , г^у - гху , так что R = г~у = гху , и, следовательно, можно
найти значение R2, не вычисляя «иД
Задание 8. Минимизация суммы квадратов отклонений
Докажите, что пара а, E действительно минимизирует сумму квадратов
отклонений наблюдаемых значений у от подбираемой прямой.
Задание 9. Оценивание прямой и обратной моделей
Для модели у. = а + fixt + si9 i = 1,..., 4, вычислите оценки коэффициентов и
коэффициент детерминации по наблюдениям A, 1), B, 3), C, 2), D, 4). (Это было
сделано ранее.)
Используя результаты этих вычислений, найдите оценки коэффициентов
обратной модели х{- ул- 8у{ + ut.
«Вручную» постройте график, в котором по оси абсцисс откладываются
значения xi9 а по оси ординат — значения yi9 yt и значения у*, вычисляемые для
значений X, с использованием подобранной обратной модели.
Задание 10. Использование пакета Eviews
Возвратитесь к заданию 2 и используйте для анализа тех же данных средства
пакета EViews.
Создайте рабочий файл.
Для каждого набора данных:
• сгенерируйте ряды значений хиу;
• образуйте группу, состоящую из рядов хиу;
• постройте диаграмму рассеяния;
• найдите коэффициент корреляции между рядами х и у;

Задания для семинарских занятий... и для самостоятельной работы
263
• оцените модель у. = а + J3x{ + st и получите ряд прогнозных значений у.
(используя Forecast)',
• создайте группу из рядов х, у и у. Постройте график зависимости у и у от х
(диаграмма рассеяния с подобранной прямой). Проверьте, что тот же
график получается при использовании scatter with regression в группе,
состоящей из рядов х и у;
• вычислите коэффициенты обратной модели и на их основе получите
значения^*, вычисляемые для значений х( с использованием подобранной
обратной модели;
• создайте группу из рядов х, у, у и у*;
• постройте график зависимости у, у и у* от х. Обратите внимание на
раскрытые «ножницы».
Выполните задание двумя способами: используя экранное меню и используя
командную строку.
Задание 11. Пакет ЕViews: использование экранного меню
и командной строки
Создайте рабочий файл tabl_l с данными об уровнях безработицы среди белого
и цветного населения США за период с марта 1968 г. по июль 1969 г.,
приведенными в табл. 1.1 (разд. 1).
• Найдите средние значения, стандартные отклонения и выборочные
дисперсии для обеих переменных.
• Выполните действия, перечисленные в задании 10.
• Постройте диаграмму рассеяния, в которой по оси ординат откладываются
значения переменной BEL, а по оси абсцисс — прогнозные значения этой
переменной. Вдоль какой прямой вытянуто облако точек? (Для объяснения
результата оцените уравнение BELi = у+ 8BELt + щ.)
• Постройте ряд остатков, вычислите RSS. Вычислите TSS, ESS, R2.
ill
• Убедитесь в том, что R = г^у - г^.
Выполните задание двумя способами: используя экранное меню и используя
командную строку.
Задание 12. Итерационный подбор аппроксимирующей прямой
Используя те же данные, что и в задании 11, произведите итерационный подбор
аппроксимирующей прямой. Для этой цели:
• перейдите к рядам отклонений от средних и постройте для них диаграмму
рассеяния;
• посмотрите на построенную диаграмму рассеяния, выберите начальное
значение /?0 коэффициента /? и нанесите на диаграмму рассеяния точки,
соответствующие модели связи у - а + /?0х. Вычислите RSS0 — сумму
квадратов (вертикальных) отклонений точек диаграммы рассеяния от этих
точек;

264
Часть 1. Основные понятия, элементарные методы
• измените немного значение /?0, получая значение /?15 которое
представляется более подходящим к облаку точек. Повторите проделанное выше при
значении /?0, используя теперь f3x вместо /?0, получая при этом значение
RSSX. Сравните значение RSSX с RSS0;
• если RSSX < RSS0, to выберите новое значение /?2, двигаясь в том же
направлении (в смысле его увеличения или уменьшения), и повторите
проделанное выше, заменив J3X на /?2. В противном случае выберите значение /?2,
двигаясь в обратном направлении и переходя через значение /?0;
• далее поступайте аналогичным образом до получения
удовлетворительного результата.
Выполните задание как с использованием экранного меню, так и с помощью
самостоятельно написанной программы, в которой последовательно задаются
значения углового коэффициента подбираемой прямой.
Задание 13. Оценивание моделей наблюдений по реальным статистическим
данным
Оцените модели наблюдений, рассмотренные в примерах 1.3.1 —1.3.5. Данные
к этим примерам поместите в рабочие файлы: tabl_2, tabl_7, tabl_8, tabl_9,
tabl_10.
Постройте диаграммы рассеяния с подобранными прямыми для номинальных
и дефлированных данных.
Задание 14. Очистка переменных
Используя пакет EViews и привлекая статистические данные, использованные в
примере 1.3.4 (tabl_9)
• проанализируйте:
связь между переменными ЕиС (зависимая переменная Е);
связь между переменными С и Я (зависимая переменная С);
• оцените соответствующие модели наблюдений, вычислите для них
коэффициенты детерминации и коэффициенты корреляции между входящими
в модель переменными;
• произведите очистку переменных от линейного тренда;
• оцените модели связи между очищенными переменными, найдите значения
коэффициентов детерминации для оцененных моделей и значения
коэффициентов корреляции между очищенными переменными;
• сравните результаты, полученные в моделях до и после очистки переменных.
Задание 15. Модель пропорциональной связи
Произведите оценивание моделей наблюдений, соответствующих модели САРМ,
описанной в теме 1.3, для статистических данных, содержащихся в файле
capm.wfl на сайте: http://www.econ.kuleuven.be/gme/. Создайте рабочий файл
camp с этими данными. Вычислите суммы квадратов TSS, ESS, RSS, используя

Задания для семинарских занятий... и для самостоятельной работы
265
определения этих сумм, введенные для линейной модели связи. Проверьте,
выполняется ли для них соотношение TSS = ESS + RSS. Вычислите обычный и нецен-
трированный коэффициенты детерминации для оцененной модели.
При работе с объектом Equation в спецификацию модели не включайте
константу. Обратите внимание на то, какое значение коэффициента детерминации
указывается в протоколе оценивания.
Оцените линейную модель с константой, сравните полученные результаты.
Задание 16. Сравнение альтернативных моделей связи с различными
объясняемыми переменными
Используя пакет EViews, по данным примера 1.3.1 (файл tabl_7), подберите
модель зависимости спроса на куриные яйца от цены, линейную в логарифмах
переменных (log-log модель). На основе этой модели постройте прогнозные
значения для уровня спроса и вычислите соответствующее значение коэффициента
детерминации (найдите TSS по результатам оценивания модели в уровнях).
Сравните это значение со значением R2, полученным при оценивании модели,
линейной в уровнях переменных.
Задание 17. Оценивание нелинейных зависимостей
Повторите исследование, проведенное при рассмотрении темы 1.4 для данных об
уровнях безработицы и темпах инфляции в США (данные возьмите из табл. 1.5).
Б. Задания для самостоятельной работы
Задание С-1. Применение метода наименьших квадратов
для оценивания параметров модели линейной связи
между двумя переменными (вычисления «вручную»)
Ниже приведены результаты 4 наблюдений значений пары переменных X и Y.
X 1 2 3 4
Г 1 3 2 4
Не прибегая ни к каким вычислительным средствам («вручную»):
• постройте диаграмму рассеяния;
• вычислите выборочный коэффициент корреляции между переменными
1и7;
• подберите модель линейной связи между переменными X и У, используя
метод наименьших квадратов;
• найдите коэффициент детерминации R2, используя 3 способа его
вычисления; убедитесь в том, что все 3 способа приводят к одному и тому же
результату.
Методические указания. Используя метод наименьших квадратов, оцените
коэффициенты аи J3 предполагаемой линейной связи. Убедитесь в том, что
сумма остатков равна 0. Найдите полную, объясненную и остаточную суммы
квадратов. Убедитесь в том, что полная сумма квадратов равна сумме двух осталь-

266
Часть 1. Основные понятия, элементарные методы
ных. Используя полученные суммы, вычислите коэффициент детерминации.
Вычислите коэффициент детерминации двумя другими методами:
а) используя выборочный коэффициент корреляции между переменными X и Y;
б) используя выборочный коэффициент корреляции между переменными Y и Y.
Задание С-2. Оценка наименьших квадратов для постоянной составляющей
в линейной модели с одним параметром
Покажите, что применение метода наименьших квадратов к модели
yi = 0i + ei9 /=1, ...,и,
приводит к оценке 9х-у.
Методические указания. Получите и решите нормальное уравнение для этого
случая.
Задание С-3. Ложная линейная связь между переменными
В табл. П-1 приведены статистические данные о годовом объеме потребления
пива (на душу населения в возрасте старше 18 лет, в галлонах — американский
галлон равен 3.7854118 л) и об уровне детской смертности в США (количество
умерших детей, имевших возраст менее года, на 1000 рожденных живыми) в
период с 1935 по 1945 г. Можно ли по этим данным сделать вывод о влиянии объема
потребления пива на уровень детской смертности?
Методические указания. Постройте диаграмму рассеяния, оцените
подходящую модель и проанализируйте динамику изменения указанных показателей на
рассматриваемом периоде.
Задание С-4. Нелинейные модели связи между переменными
Вычислите прогнозные значения для переменной INF, полученные на основе
оцененной модели Michaelis-Menton
0.514 UN JOB
INF = ,
- 3.057 + UNJOB
и по обычной формуле вычислите коэффициент детерминации R2. Сравните это
значение с коэффициентом детерминации, полученным при оценивании модели
Y = а + J&X, где Y= l/INF, Х= 1/UNJOB.
К разделу 2
А. Задания для семинарских занятий и работы в компьютерном классе
Задание 18. Оценивание модели наблюдений с несколькими объясняющими
переменными
Используя приведенные в табл. 2.1 (разд. 2) статистические данные о
потреблении текстиля (текстильных изделий) в Голландии в период между двумя
мировыми войнами с 1923 по 1939 г., создайте в пакете EViews рабочий файл tab2_l
и повторите анализ, проведенный в теме 2.1.

Задания для семинарских занятий... и для самостоятельной работы
267
Для иллюстрации результата Фриша — Во — Ловелла рассмотрите также
случай, когда в качестве выделенной переменной берется не lgP, a \gDPL
Обратите внимание на то, что в примере, рассмотренном в теме 2.1,
использованы десятичные логарифмы (модуль перехода от натуральных логарифмов
к десятичным равен 0.434294). Оцените модель также в натуральных
логарифмах, сравните оценки эластичностей в двух оцененных моделях.
Задание 19. Иллюстрация теоремы Фриша — Во — Ловелла
Используя пакет EViews, проиллюстрируйте теорему Фриша — Во — Ловелла,
оценив по смоделированным самостоятельно статистическим данным модель,
соответствующую квадратичной модели связи между факторами у и z.
Имеется в виду модель связи
у= а + J3z + yz2;
ей соответствует модель наблюдений
у( = а + ^ + гг) + ^9 /=1,..., и.
Оцените эту модель методом наименьших квадратов. Сравните полученные
оценки коэффициентов с оценками, получаемыми для коэффициентов парных
моделей связи между очищенными переменными.
Задание 20. Ортогональная структура матрицы значений объясняющих
переменных
По приведенным в табл. П-2 статистическим данным о поступлении
растительного масла на 5 оптовых рынков США создайте в пакете EViews рабочий файл
tabc_4 и проведите статистический анализ этих данных.
Оцените модель наблюдений, в которую включаются постоянная
составляющая и переменные cos at, smat. Выберите параметр а таким образом, чтобы
учесть характер наблюдаемой периодичности статистических данных и получить
ортогональную структуру матрицы X. Сравните результаты оценивания указанной
модели с результатами оценивания моделей, в правые части которых включены
постоянная составляющая и только одна из двух тригонометрических функций.
Методические указания. После выбора параметра а убедитесь в том, что
матрица X действительно имеет ортогональную структуру и переменные cosatf, smat
имеют в выборке нулевые средние, так что выборочные коэффициенты
корреляции между объясняющими переменными равны 0.
Задание 21. Свойства оценок наименьших квадратов коэффициентов
линейной эконометрической модели
Используя моделирование с применением пакета EViews, убедитесь, что оценки
наименьших квадратов параметров а и /3 в модели yt = а + /?х, + si9 E(sf) =0,
D{st)= a2, i= 1,..., п:
1) являются несмещенными оценками этих параметров;
п
2) отрицательно коррелированы, если ^£jxi >0.

268
Часть 1. Основные понятия, элементарные методы
Методические указания:
а) задайте значения параметров а и /?;
б) зафиксируйте некоторую последовательность xl5..., хп\
в) сгенерируйте реализацию последовательности dp, i = 1, ..., и, независимых
случайных величин, имеющих стандартное нормальное распределение,
образуйте последовательность у\1\ / = 1, ..., п, по формуле: у^ = а + /?хг + s^P
и на основании значений xi9 y\l\ i = 1, ..., и, получите оценки наименьших
квадратов а({) и /Т^;
г) повторите шаг в) с новой последовательностью sf\ i = 1, ..., и, постройте
последовательность^, / = 1,..., и, по формуле: у\2) - ал- {5х{ + sf^ и
получите оценки наименьших квадратов аB) и /^2);
д) продолжите указанный алгоритм и получите в итоге последовательности
оценок аA\ ..., а(/° и frx\ ..., /^
е) найдите средние значения каждой из последовательностей а^1\ ..., а^
и /Т^, ..., 0^. Вычислите коэффициент корреляции между этими
последовательностями.
Задание 22. Построение доверительных интервалов для параметров модели
линейной связи между двумя переменными
Используя пакет EViews, постройте 90%-й, 95%-й и 99%-й доверительные
интервалы для параметров линейных эконометрических моделей, которые были оценены
методом наименьших квадратов для данных, содержащихся в файлах tabl_7 (спрос
на яйца), tabl_8 (спрос на свинину) и tabl_10 (расходы на местный транспорт).
Методические указания. Получив протокол оценивания в объекте Equation,
извлеките из него необходимые для построения доверительных интервалов
элементы: оценки коэффициентов и оценки их стандартных ошибок. Необходимые
квантили распределения Стьюдента найдите, используя соответствующую
функцию в EViews (см. Function Reference в Help).
Задание 23. Построение доверительных интервалов для параметра модели
пропорциональной связи
Используя пакет EViews, постройте доверительные интервалы с уровнями
доверия 0.90, 0.95 и 0.99 для коэффициента бета в модели САРМ по данным,
содержащимся в файле сарт, образованном ранее.
Методические указания. Действуйте, как и в предыдущем задании, но в
спецификацию уравнения не включайте постоянную.
Задание 24. Построение доверительных интервалов для коэффициентов
нормальной линейной множественной регрессии
1. Используя пакеты EViews и Excel, постройте 95%-е доверительные
интервалы для эластичностей спроса на текстиль по цене и по располагаемому
доходу в модели линейной множественной регрессии, описывающей
статистические данные в файле tab2_l.

Задания для семинарских занятий... и для самостоятельной работы
269
2. Постройте доверительные интервалы для эластичностей спроса на текстиль
по цене и по располагаемому доходу, обеспечивающие вероятность
одновременного накрытия истинных значений этих эластичностей не ниже 0.95.
Методические указания. Используйте формулы для вероятности
противоположного события и для вероятности суммы двух событий.
Б. Задания для самостоятельной работы
Задание С-5. Формулы в модели парной линейной регрессии
Выведите формулы для оценок наименьших квадратов коэффициентов модели
парной линейной регрессии, для ковариационной матрицы и дисперсий этих
оценок на основании соответствующих формул для модели множественной линейной
регрессии.
Задание С-6. Ортогональная структура матрицы значений
объясняющих переменных
Постройте примеры, показывающие, что если Rf9 R2 и R\2 — коэффициенты
детерминации, получаемые при оценивании методом наименьших квадратов моделей
yt^a + fiXi + Su, i= 1, ...,и,
y^a + yz^^ i= 1,..., и,
у( = а + Pxt + yzt + % i9 i = 1,..., n,
соответственно, то:
• если переменные х и z имеют нулевые выборочные средние и выборочно
некоррелированы, то R2{2 = R\ + R-h
• в противном случае R2l2 может быть как больше, так и меньше суммы Rx + R2.
Методические указания. Воспользуйтесь пакетом EViews для построения
соответствующих примеров:
а) сгенерируйте 3 последовательности независимых случайных величин,
имеющих равномерное распределение в интервале @, 1): хх, х2, zx\
б) сгенерируйте 4 последовательности независимых случайных величин,
имеющих равномерное распределение в интервале @, 1): еХ9 £2, s39 sA.
в) создайте последовательностьz2 = zl+0Asl;
г) создайте выборочно некоррелированные переменные с нулевыми
средними: v{ и v2;
д) создайте последовательности^ = х{ + х2 + s2, w = zx + z2 + еъ, v = vx + v2 + eA;
е) сравните коэффициент детерминации в линейной модели регрессии
переменной у на константу и переменные хх и х2 с суммой коэффициентов
детерминации в линейной модели регрессии переменной у на константу
и переменную хх и в линейной модели регрессии переменной >> на константу
и переменную х2 (можно ожидать, что в этом случае коэффициент
детерминации в расширенной модели будет больше суммы коэффициентов
детерминации в частных моделях);

270
Часть 1. Основные понятия, элементарные методы
ж) сравните коэффициент детерминации в линейной модели регрессии
переменной w на константу и переменные zx и z2 с суммой коэффициентов
детерминации в линейной модели регрессии переменной w на константу
и переменную zx и в линейной модели регрессии переменной w на константу
и переменную z2 (можно ожидать, что в этом случае коэффициент
детерминации в расширенной модели будет меньше суммы коэффициентов
детерминации в частных моделях);
з) сравните коэффициент детерминации в линейной модели регрессии
переменной v на константу и переменные vx и v2 с суммой коэффициентов
детерминации в линейной модели регрессии переменной v на константу
и переменную vx и в линейной модели регрессии переменной v на константу
и переменную v2 (можно ожидать, что в этом случае коэффициент
детерминации в расширенной модели будет равен сумме коэффициентов
детерминации в частных моделях).
Проинтерпретируйте полученные результаты, обратив внимание на
корреляционную связь между объясняющими переменными в каждом случае.
Задание С-7. Нормальная линейная модель с несколькими объясняющими
переменными. Стандартные предположения
1. Покажите, что при выполнении стандартных предположений в нормальной
линейной модели с несколькими объясняющими переменными оценка
максимального правдоподобия для вектора коэффициентов совпадает с
оценкой этого вектора, получаемой методом наименьших квадратов.
2. Найдите оценку максимального правдоподобия для неизвестного значения
дисперсии случайных ошибок.
Методические указания. Выпишите в явном виде совместную плотность
вероятности для наблюдаемых значений объясняемой и объясняющих переменных,
рассмотрите ее как функцию правдоподобия для вектора параметров,
содержащего неизвестные коэффициенты модели и неизвестную дисперсию случайных
ошибок, при известных значениях объясняемой и объясняющих переменных
и максимизируйте эту функцию по всем возможным значениям этого вектора
параметров. Используйте тот факт, что максимизация этой функции равносильна
максимизации ее логарифма.
Задание С-8. Изучение доказательства теоремы Гаусса — Маркова
Методические указания. Ознакомьтесь с доказательством теоремы Гаусса —
Маркова, приведенным в книге {Магнус, Катышев, Пересецкий, 2005, с. 63—64).
Задание С-9. Изучение распределения остаточной суммы квадратов
при выполнении стандартных предположений о модели
Докажите, что при выполнении стандартных предположений о модели
наблюдений с р объясняющими переменными, включающих нормальность распределения
ошибок, отношение

Задания для семинарских занятий... и для самостоятельной работы
271
(n-p)S2 _ RSS
(как случайная величина) имеет такое же распределение, как и сумма квадратов
(п - р) случайных величин, независимых в совокупности и имеющих одинаковое
стандартное нормальное распределение.
Методические указания. См. {Магнус, Катышев, Пересецкий, 2005, с. 66).
Задание С-10. Изучение распределения центрированной и нормированной
оценки наименьших квадратов коэффициентов
линейной эконометрической модели при выполнении
стандартных предположений о модели
Докажите, что при выполнении стандартных предположений о модели
наблюдений с р объясняющими переменными, включающих нормальность распределения
ошибок, отношение
имеет /-распределение Стьюдента с(п-р) степенями свободы.
Методические указания. См. (Магнус, Катышев, Пересецкий, 2005, с. 70—71).
К разделу 3
А. Задания для семинарских занятий и работы в компьютерном классе
Задание 25. Проверка значимости оценок коэффициентов
парной линейной регрессии с использованием t-критерия
Проверьте значимость оценок отдельных коэффициентов, полученных при
оценивании линейных моделей регрессии по данным, приведенным в файлах tabl_l,
tabl_2, tabl_7, tabl_8, tabl_10, используя пакеты EViews и Excel.
Методические указания:
• в пакете EViews используйте объект Equation',
• в пакете Excel в главном меню выберите: Сервис —> Анализ данных —>
Регрессия. В меню Регрессия укажите расположение значений объясняемой
и объясняющей переменных.
Задание 26. Проверка значимости оценок коэффициентов множественной
линейной регрессии с использованием t-критерия
Проверьте значимость оценок отдельных коэффициентов, полученных при
оценивании log-log модели регрессии по статистическим данным о потреблении
текстиля (текстильных изделий) в Голландии, приведенным в файле tab2_l,
используя пакеты EViews и Excel.

272
Часть 1. Основные понятия, элементарные методы
Методические указания:
• в пакете EViews используйте объект Equation',
• в пакете Excel в главном меню выберите: Сервис —» Анализ данных —»
Регрессия. В меню Регрессия укажите расположение значений объясняемой
и объясняющих переменных.
Задание 27. Сравнение двусторонних и односторонних t-критериев
Оцените норму потребления в США в период с 1959 по 1980 г. по данным о
совокупном располагаемом доходе и совокупных расходах на личное потребление
(дефлированные данные с базой 1982 г.), содержащимся в табл. 4.4 разд. 4. Для
этого создайте рабочий файл tab4_4.
Используя протокол оценивания:
• проверьте гипотезу о том, что указанная норма потребления была равна
0.9, против двусторонней альтернативы;
• проверьте гипотезу о том, что указанная норма потребления была меньше
0.9, против альтернативной гипотезы о том, что указанная норма
потребления была не менее 0.9.
Методические указания. Необходимые критические значения получите,
используя функцию @qtdist(p, v). В первом случае 5%-е критическое значение равно
-2.074, а во втором 5%-е критическое значение равно -1.717.
Задание 28. Односторонние гипотезы, односторонние t-критерии,
конфликт критериев
Используя односторонние /-критерии, рассмотрите вопрос об
эластичности/неэластичности спроса на текстиль в Голландии по цене и по располагаемому доходу
по статистическим данным, приведенным в файле tab2_l.
Методические указания. Обратите внимание на выбор областей отклонения
нулевых гипотез и на возможность конфликта критериев, использующих взаимно
дополнительные нулевые односторонние гипотезы.
Задание 29. Гипотеза значимости регрессии
В табл. П-7 содержатся ежегодные данные о следующих показателях экономики
Франции за период с 1949 по 1966 г. (млрд франков, в ценах 1959 г.):
Y — объем импорта товаров и услуг во Францию;
Х2 — валовой национальный продукт;
Х3 — изменение запасов;
ХА — совокупное потребление домашних хозяйств.
По данным за период с 1949 по 1959 г. оцените линейную эконометрическую
модель
yi=Olxn +в2хп+6ъхп+вАхи +ei9 i = l,...,11, гдехп = 1.
Оцените модель линейной регрессии переменной у на константу и
переменные х2,х3 их4.

Задания для семинарских занятий... и для самостоятельной работы
273
Проверьте значимость оценок параметров с использованием /-критерия.
Проверьте гипотезу значимости регрессии.
Методические указания. Создайте рабочий файл tab3_7. Запишите гипотезу
значимости регрессии в форме общей линейной гипотезы. Сколько ограничений
накладывает эта гипотеза?
Для проверки указанной гипотезы используйте F-критерий в форме,
использующей сравнение остаточных сумм квадратов в полной и редуцированной
моделях. Необходимые значения остаточных сумм квадратов получите, оценивая
полную и редуцированную модели.
Сравните полученное значение F-статистики со значением, приведенным
в правом нижнем углу протокола Е Views, содержащего результаты оценивания
полной модели.
Задание 30. Гипотеза значимости регрессии. Редукция модели
с использованием F-критерия
Используя приведенные в табл. П-3 данные о продажной цене 24 домов в городе
Эри {Erie, штат Пенсильвания, США), оцените линейную эконометрическую
модель, объясняющую зависимость продажной цены дома (PRICE) от
следующих факторов:
TAXES
BATH
LOTSIZE
LIVSP
GAR
ROOMS
BED
AGE
FIRE
— размер уплачиваемых налогов (местные + школьные + окружные);
— количество ванных комнат;
— площадь земельного участка;
— жилая площадь;
— количество гаражных мест;
— количество комнат;
— количество спален;
— возраст дома;
— количество каминов.
На основании результатов этого оценивания произведите уточнение
спецификации модели.
Используя F-критерий, проверьте гипотезу значимости линейной регрессии
продажной цены на константу и остальные переменные.
Используя F-критерии, исключите из модели часть объясняющих переменных
и получите модель со статистически значимыми коэффициентами.
Методические указания. Создайте рабочий файл tab c_5.
Оценив полную модель с использованием объекта Equation, в меню этого
объекта выберите: View —» Coefficient Tests —» Wald— Coefficient Restrictions.
В открывшемся окне специфицируйте ограничения на коэффициенты,
накладываемые соответствующими гипотезами, и нажмите кнопку ОК.
Рассмотрите возможность редукции полной модели к следующим вариантам:
• к модели, объясняющей продажную цену дома только величиной налогов,
количеством комнат и возрастом дома;
• к модели, объясняющей продажную цену дома только величиной налогов.
Используйте для этой цели соответствующие F-критерии.

274
Часть 1. Основные понятия, элементарные методы
Задание 31. Гипотеза значимости регрессии. Редукция модели
с использованием F-критерия
По данным опроса сотрудников 30 структурных подразделений крупной
финансовой организации (см. табл. П-4) выявите факторы, значимо влиющие на
рейтинг руководителя подразделения. Список переменных:
у — рейтинг руководителя;
Z1 — отношение руководителя к жалобам сотрудников;
Z2 — недопущение особых привилегий для отдельных сотрудников;
Z3 — возможность приобретения новых профессиональных знаний;
Z4 — повышение заработной платы по результатам деятельности;
Z5 — чрезмерная критичность к низкой эффективности работы;
Z6 — скорость продвижения к более высокой должности.
Данные были получены на основе индивидуальных ответов сотрудников на
соответствующие вопросы. Ответ на каждый вопрос предполагал выставление от 1 до
5 баллов, причем 1 считалась наилучшим баллом, а 5 — наихудшим. Полученные
ответы с баллами 1 и 2 классифицировались как благоприятные для руководителя,
а ответы с баллами 3, 4, 5 — как неблагоприятные. Для каждого подразделения
были вычислены проценты благоприятных ответов по каждому из 7 вопросов.
Методические указания. Действуйте, как и в предыдущем задании.
Задание 32. Построение доверительного эллипса
1. Используя статистические данные о поступлении растительного масла на
оптовые рынки США (табл. П-2), оцените линейную модель наблюдений
с константой и косинусоидой (с периодом 12) в правой части, на основе
результатов оценивания постройте 95%-й доверительный эллипс для
коэффициентов модели. Сравните площадь этого эллипса с площадью прямоугольника,
сторонами которого служат доверительные интервалы для коэффициентов,
обеспечивающие вероятность одновременного накрытия не менее 0.95.
2. Рассмотрите задачу построения доверительного эллипса для пары
коэффициентов при косинусоиде и синусоиде (с периодом 12) в модели наблюдений
с константой, косинусоидой и синусоидой (с периодом 12) в правой части.
3. Рассмотрите задачу построения доверительного эллипса для значений эла-
стичностей спроса на текстиль в Голландии по цене и по располагаемому
доходу, используя статистические данные, приведенные в файле tab2_l.
Задание 33. Использование F-критерия и односторонних t-критериев
при проверке гипотезы о выполнении
единственного неисключающего ограничения
Проанализируйте данные о производстве продукции сельского хозяйства в
Тайване в период с 1960 по 1972 г., приведенные в табл. 3.10 (разд. 3). Используемые
переменные:
Y — объем произведенной продукции (млн новых тайваньских долларов);
К — затраты капитала;
L — количество отработанных человеко-дней (млн).

Задания для семинарских занятий... и для самостоятельной работы
275
Проверьте гипотезу о существовании в сельскохозяйственном производстве
Тайваня эффекта масштаба, выражающегося в наличии дополнительной отдачи
от возрастания масштабов производства.
Методические указания. Используя производственную функцию Кобба —
Дугласа и перейдя к логарифмам задействованных в ней переменных, получим
модель связи в виде:
lnY=lnA + alnK + j3lnL.
Наличие эффекта масштаба соответствует гипотезе Н0: а + J3 > 1.
Создайте рабочий файл с указанными данными. В меню объекта Equation
выберите: View —> Coefficient Tests —> Wald — Coefficient Restrictions.
Специфицируйте заданные ограничения и получите результаты проверки выполнения этих
ограничений. Выберите из этих результатов значение F-статистики и извлеките
из него квадратный корень — это будет значение ^-статистики, с помощью
которой проверяется указанная гипотеза. Критическое значение этой статистики
можно получить обычным образом, а соответствующее ей (одностороннее) Р-зна-
чение равно половине Р-значения, указанного для F-статистики. Это Р-значение
можно вычислить, используя функцию @ctdist(/, п -р).
Задание 34. Проверка значимости регрессии с использованием
коэффициента детерминации
Используя связь между коэффициентом детерминации и F-статистикой критерия
для проверки значимости регрессии, вычислите 5%-е критические значения
коэффициента детерминации в модели парной линейной регрессии при различном
количестве наблюдений:
п = 3, 4, 10, 20, 30, 40, 60, 120, 500.
Методические указания. Необходимые квантили F-распределения получите
двумя способами:
• обратившись к соответствующим таблицам;
• используя функцию @qfdist(x, vl, v2) пакета Е Views.
Задание 35. Свойства оценок наименьших квадратов
при линейных ограничениях на коэффициенты линейной
эконометрической модели
По условиям задания 31 (рейтинг руководителя):
• специфицируйте модель наблюдений без ограничений на коэффициенты,
оцените эту модель;
• проверьте гипотезу о том, что в модели, порождающей наблюдения,
коэффициент при переменной Z1 вдвое больше коэффициента при переменной
Z3. Специфицируйте модель наблюдений, соответствующую этому
ограничению;
• не оценивая модель с ограничениями, ответьте на следующие вопросы:
а) в каком соотношении находятся коэффициенты детерминации в модели
с ограничениями и в модели без ограничений (больше, меньше, равны)?

276
Часть 1. Основные понятия, элементарные методы
б) в каком соотношении находятся дисперсии оценок коэффициентов при
переменных Z2, Z4, Z5 и Z6 в модели с ограничениями и в модели без
ограничений (больше, меньше, равны)?
• оцените модель с ограничениями и проверьте правильность ответов на
вопросы пп. а) и б).
Задание 36. Проблема мулыпиколлинеарности
По условиям задания 29 (импорт товаров и услуг во Францию) установите,
указывают ли результаты оценивания полной модели на периоде 1949—1959 гг. на
возможное наличие мультиколлинеарности данных? Имеются ли другие признаки
наличия мультиколлинеарности указанных данных?
Методические указания. Обратите внимание на оценку коэффициента при
переменной Х2.
Произведите оценивание наряду с исходной эконометрической моделью
различных ее редуцированных вариантов и сравните результаты их оценивания.
Указывают ли эти результаты на возможное наличие мультиколлинеарности?
Для установления причины мультиколлинеарности найдите коэффициенты
корреляции между объясняющими переменными и вычислите значения
коэффициентов возрастания дисперсии для переменныхХ2,Х3,Х4.
Задание 37. Проблема мультиколлинеарности
Используя пакет EViews, постройте пример, аналогичный примеру 3.3.5.
Исследуйте влияние количества имеющихся наблюдений на результаты
оценивания.
Исследуйте влияние соотношения между величинами коэффициентов в
модели порождения данных на результаты оценивания.
Методические указания. Реализуйте модель порождения данных
yt = 1 + 5ха + хв + 0.5xr4 + £t> гДе xt2= I +0At + 0.\£t2, хв = 2 + 0.5/ + 0.1%,
х,4 = 3 + / + 0.1%, % %, %, stA -lid. N@, 1), t= 1,..., 500.
Оцените соответствующую эконометрическую модель при разном количестве
используемых наблюдений: 500, 100, 50,25.
При тех же значениях объясняющих переменных и случайных ошибок
измените коэффициенты в модели порождения данных, полагая коэффициенты при
переменных, отличных от постоянной, равными 4.
Задание 38. Выбор между альтернативными моделями с одной и той же
объясняемой переменной, отбор объясняющих переменных
Сравните модели с различными наборами объясняющих переменных в заданиях
29, 30 и 31, используя:
• скорректированный коэффициент детерминации;
• критерий Акаике;
• критерий Шварца.

Задания для семинарских занятий... и для самостоятельной работы
277
Методические указания. Значения всех указанных характеристик приведены
в протоколе оценивания объекта Equation. Используйте метод последовательного
включения переменных, метод последовательного исключения переменных,
пошаговую регрессию, метод сравнения всех регрессий.
Задание 39. Выбор между моделью связи, линейной в уровнях, и моделью связи,
линейной в логарифмах уровней
Рассмотрите вопрос о предпочтительности одной из двух указанных в заголовке
моделей для описания:
• статистических данных о спросе на куриные яйца, использованных в
примере 1.3.1;
• статистических данных о потреблении текстиля в Голландии,
использованных при изложении темы 2.1.
Задание 40. Построение точечных и интервальных прогнозов
по оцененной эконометрической модели
В ситуации, описанной в примере 3.3.6, произведите построение точечного и
интервального прогнозов, используя процедуру прогнозирования, встроенную в пакет
EViews. Сравните результаты, полученные при применении этой процедуры,
с результатами, полученными в примере 3.3.6.
Б. Задания для самостоятельной работы
Задание С-11. Линейные гипотезы в линейной модели наблюдений
Пусть в линейной модели наблюдений р = 6. Выясните, являются ли линейными
указанные ниже гипотезы, и если являются, то запишите соответствующую
гипотезу в матричной форме с матрицей, имеющей полный строковый ранг.
1)^=0; 2)^ = 0,3=0; 3K = 1,3=0; 4K = 1,3=-!; 5K = 3 = 0;
6K = 3; 7K + 3 = 1; 8)з = 3 = 3> = о; 9K = 3 = ^ = 1;
ю) 3 = 3 = ft; пK-04 = 3; 12K-ft = 4.
Методические указания. Используйте определение общей линейной гипотезы
в линейной модели наблюдений.
Задание С-12. Вычисление оценок наименьших квадратов
при линейных ограничениях на коэффициенты линейной
эконометрической модели
В результате оценивания методом наименьших квадратов линейной модели
у = Хв+ s ср = 3 были получены следующие результаты:
ГЪ\ C 0 О
0 = 1 0 L S2(XTXyl=\
0
V2y
0 1 0
1 0 1

278
Часть 1. Основные понятия, элементарные методы
Как будет выглядеть оценка наименьших квадратов для вектора в при
гипотезе Я0: вх = 02 + 6ъ1
Методические указания. Используйте формулу для оценки наименьших
квадратов при линейных ограничениях вида,40= с.
Задание С-13. Оценка наименьших квадратов для постоянной составляющей
в линейной модели с одним параметром
Покажите, что применение метода наименьших квадратов к модели yi - вх + si9
i = 1,..., п, приводит к оценке вх = у.
Методические указания. Получите и решите нормальное уравнение для этого
случая.
Задание С-14. Проверка гипотезы значимости регрессии на основании
значения коэффициента детерминации
Каждая из двух моделей нормальной линейной регрессии включала 4
объясняющие переменные. Первая модель оценивалась по 24, а вторая — по 44
наблюдениям. Для первой модели коэффициент детерминации оказался равным 0.25, для
второй модели — равным 0.20. Являются ли соответствующие регрессии
статистически значимыми?
Методические указания. Воспользуйтесь формулой F = j и тем
фактом, что при выполнении стандартных предположений о модели и равенстве
0 истинных значений коэффициентов при всех переменных, отличных от
константы, статистика F имеет F-распределение Фишера с (р - \)и(п-р) степенями
свободы.
Задание С-15. Преодоление затруднений, связанных с наличием
мультиколлинеарности
Ознакомьтесь самостоятельно со способами преодоления затруднений,
связанных с наличием мультиколлинеарности.
Методические указания. См. {Айвазян С. А., 2001, гл. 2, разд. 2.4.)
Задание С-16. Информационные критерии, штрафное правдоподобие
Покажите, что при оценивании методом максимального правдоподобия модели
У{ ~ &\хп + в&п + *•• + OpxiP + ei9 i = Ь ••• 9 п> гдехп = 1 и ех, ~ НА N@, <т2),
выполняется соотношение:
-2\nL(el9...,ep9az)
= ln
V п J
+ 1 + 1п2;г,
п
используемое при построении информационных критериев для сравнения моделей.

Задания для семинарских занятий... и для самостоятельной работы
279
Методические указания. Здесь L@{, ..., вр, а2) — значение функции
правдоподобия для параметров вг, в2, ..., в ь а2, соответствующее оценке
максимального правдоподобия.
К разделу 4
А. Задания для семинарских занятий и работы в компьютерном классе
Задание 41. Проблема соответствия выбранной спецификации
эконометрической модели имеющимся статистическим данным,
графический анализ
Используя пакет EViews, оцените парные линейные модели для 4 множеств
данных, приведенных в табл. 4.3 разд. 4.
Методические указания. Выполните оценивание парных линейных моделей,
используя объект Equation. Сравните результаты оценивания этих моделей.
Рассмотрите диаграммы рассеяния с нанесенными на них подобранными прямыми.
Задание 42. Проблема соответствия выбранной спецификации
эконометрической модели имеющимся статистическим данным,
графический анализ.
Для данных о продажной цене 24 домов (табл. П-3), проведите графический анализ
модели, выбранной в качестве наилучшей, на адекватность статистическим данным.
Методические указания. Постройте диаграмму рассеяния для величины
налогов и стандартизованных остатков, полученных при оценивании наилучшей
модели. Используя объект Series, постройте график квантиль-квантиль и получите
ядерную оценку плотности распределения стандартизованных остатков.
Задание 43. Проблема соответствия выбранной спецификации
эконометрической модели имеющимся статистическим данным,
графический анализ
Используя данные о рейтинге руководителей (табл. П-4), проведите графический
анализ модели, выбранной в качестве наилучшей, на адекватность
статистическим данным.
Методические указания. Проанализируйте диаграмму рассеяния для
переменной Z1 и стандартизованных остатков, полученных при оценивании наилучшей
модели. Постройте график квантиль-квантиль и получите ядерную оценку
плотности распределения стандартизованных остатков.
Задание 44. Проблема соответствия выбранной спецификации
эконометрической модели имеющимся статистическим данным,
графический анализ
Проведите графический анализ на адекватность подобранных моделей для
следующих данных:
• об уровнях безработицы среди цветного и белого населения США (tabl_l);
• о спросе на куриные яйца (файл tabl_7);

280
Часть 1. Основные понятия, элементарные методы
• о спросе на свинину (файл tabl_8);
• о доходности акций и рыночного портфеля (файл сарт);
• о потреблении текстиля (файл tab2_l);
• о поступлении растительного масла (файл tab c_4);
• об импорте во Францию на периоде с 1949 по 1966 г. (табл. П-7);
• о совокупном располагаемом личном доходе и совокупных расходах на
личное потребление в США в период с 1959 по 1985 г. (файл tab4_4);
• о количестве сотрудников на 27 предприятиях, приведенных в табл. 5.17
разд. 5 (для этой цели создайте рабочий файл tab5_17);
• о потребительских расходах и денежной массе в США, приведенных в таб-
л. 5.18 разд. 5 (создайте файл tab5__18).
Методические указания. Обратите внимание: если наблюдения произведены
последовательно во времени, то это требует дополнительной диагностики.
Задание 45. Проблема соответствия выбранной спецификации
эконометрической модели имеющимся статистическим данным,
применение статистических критериев
По условиям задания 42 проведите анализ модели, выбранной в качестве
наилучшей, на адекватность статистическим данным, применяя соответствующие
статистические критерии.
Методические указания. Используйте критерии Голдфелда — Квандта, Уайта
и Харке — Бера. Почему здесь нельзя полностью доверять результатам
применения двух последних критериев?
Задание 46. Проблема соответствия выбранной спецификации
эконометрической модели имеющимся статистическим данным,
применение статистических критериев
По условиям задания 43 проведите анализ модели, выбранной в качестве
наилучшей, на адекватность статистическим данным, применяя соответствующие
статистические критерии.
Методические указания. См. задание 45.
Задание 47. Проблема соответствия выбранной спецификации
эконометрической модели имеющимся статистическим данным,
применение статистических критериев
По условиям задания 44 проведите анализ моделей на адекватность, применяя
соответствующие статистические критерии.
Методические указания. Используйте критерии, указанные в задании 45, а
также критерии Дарбина — Уотсона и Бройша — Годфри.
Задание 48. Проблема стабильности коэффициентов модели:
графический анализ, применение статистических критериев
Используя пакет EViews, проведите для данных об импорте во Францию на периоде
с 1949 по 1966 г. (табл. П-7) графический и статистический анализ на
стабильность коэффициентов модели.

Задания для семинарских занятий... и для самостоятельной работы
281
Методические указания. Выполните оценивание модели регрессии Y на
константу и переменные XI, ХЗ, Х4 на указанном периоде. Обратите внимание на
поведение ряда остатков. Проанализируйте графики рекурсивных коэффициентов,
рекурсивных остатков и CUSUM. Примените критерий Рэмси, а также
встроенные критерии Чоу, ориентируясь на дату начала фактического
функционирования Общего рынка в Европе A960 г.).
Сгенерируйте дамми-переменную D\, равную 1 на периоде с 1949 по 1959 г.,
и дамми-переменную D2, равную 1 на периоде с 1960 по 1966 г. Расщепите
с помощью этих дамми-переменных постоянную составляющую и переменные
XI, ХЗ, Х4. Продиагностируйте расширенную модель. Оцените эквивалентную
модель, включающую константу и переменные D2, XI, ХЪ, Х4, D2 • Х2, D2 • ХЗ,
D2 • Х4. Изменения каких коэффициентов статистически значимы? Исключите
из последней модели переменные со статистически незначимыми оценками
коэффициентов. Запишите полученную модель.
Задание 49. Проблема стабильности коэффициентов модели:
графический анализ, применение статистических критериев
Используя пакет EViews, проведите для данных о совокупном располагаемом
личном доходе и совокупных расходах на личное потребление в США в период с 1959
по 1985 г. (файл tab4_4) графический и статистический анализ на стабильность
коэффициентов модели. Постройте подходящую модель, описывающую эти данные.
Методические указания. Действуйте по аналогии с предыдущим заданием.
Б. Задания для самостоятельной работы.
Задание С-17. Проблема соответствия выбранной спецификации
эконометрической модели имеющимся статистическим данным
Исходя из условия задания С-3 (данные о потреблении пива и детской
смертности в США — табл. П-1) рассмотрите вопрос об адекватности модели парной
линейной регрессии, в которой уровень детской смертности — объясняемая
переменная, а объем потребления пива — объясняющая переменная.
Методические указания. Используйте графические процедуры и
статистические критерии.
К разделу 5
А. Задания для семинарских занятий и работы в компьютерном классе
Задание 50. Сезонные дамми
Используя пакет EViews, проведите анализ статистических данных о спросе на
лыжный инвентарь в США (табл. 5.16), привлекая сезонные дамми.
Методические указания. Оцените и продиагностируйте модель парной
регрессии. Сравните результаты применения критериев Дарбина — Уотсона и Брой-
ша — Годфри. Объясните расхождение в выводах, полученных на основании
этих критериев.

282
Часть 1. Основные понятия, элементарные методы
Расщепите константу и переменную DPI, используя 4 сезонных дамми.
Оцените расширенную модель, проверьте ее на адекватность. Проверьте гипотезу об
отсутствии сезонного изменения коэффициента при DPI.
Перейдите к редуцированной модели (с единым коэффициентом при DPI).
Проверьте возможность использования единой константы для всех кварталов.
Проверьте возможность использования одинаковых коэффициентов в паре II—III
кварталы и в паре I—IV кварталы. Постройте окончательную модель.
Задание 51. Использование дамми-переменных для эконометрического анализа
данных, относящихся к различным периодам времени
В 15 наблюдениях, произведенных последовательно во времени, переменные Z
и X приняли значения, приведенные в табл. П-5. Постройте модель связи между
переменными Z и X, считая X объясняющей переменной.
Методические указания. Постройте диаграмму рассеяния для указанных
наблюдений и проанализируйте ее на предмет возможного представления эконо-
метрической модели в виде модели трехфазной парной линейной регрессии.
Оцените модель простой линейной регрессии по всем 15 наблюдениям и
рассмотрите график остатков от подобранной модели связи.
Специфицируйте эконометрическую модель с дамми-переменными,
учитывающими наблюдаемую форму диаграммы рассеяния и наблюдаемую форму
графика остатков.
Оцените модель с дамми-переменными и проанализируйте полученные результаты.
Задание 52. Дамми-переменные, дамми-ловушка
В задании 51 проверьте утверждение, содержащееся в Замечании 5.1.2.
Методические указания. Используйте объект Equation пакета Е Views.
Задание 53. Использование дамми-переменных для проверки гипотез
о совпадении коэффициентов линейных эконометрических моделей
для разных субъектов исследования (ковариационный анализ)
Обратитесь к примеру 5.1.2 (файл tab5__3) и, используя объект Equation пакета
Е Views:
• оцените модели М0 и Ml9 найдите остаточные суммы квадратов,
получаемые при оценивании этих моделей, и с их помощью вычислите значение
статистики F-критерия для проверки гипотезы Н0 : J3х = /?2 = fi3 - Сравните
полученное значение с критическим значением F-статистики,
соответствующим уровню значимости 0.05;
• в рамках модели Ых проверьте гипотезу Н'0: ах - а2 - аъ\
• в рамках модели М0 проверьте гипотезу Н$ : ах - а2 = ос3, J3{ = /?2 = /?з-
На основании полученных результатов выберите окончательную модель.
Методические указания. Прежде всего следует образовать рабочий файл,
рассчитанный на 30 наблюдений, и образовать переменную у, значения которой
составляют вектору, определенный в примере 5.1.2, а также 6 переменных,
значения которых составляют столбцы матрицы X, определенной там же. Затем в объ-

Задания для семинарских занятий... и для самостоятельной работы
283
екте Equation следует специфицировать уравнение линейной множественной
регрессии, соответствующее модели М0, в котором переменная у будет объясняемой
переменной, а остальные 6 переменных — объясняющими переменными (регрес-
сорами), и оценить это уравнение. После этого надо специфицировать и оценить
уравнение линейной множественной регрессии, соответствующее модели Мх, в
котором объясняемой переменной будет опять у, а объясняющими переменными
(регрессорами) — 3 дамми-переменные и переменная х, значения которой
составляют вектор, являющийся суммой 3 столбцов матрицы X: 2-го, 4-го и 6-го.
Для проверки гипотез Н'0 и Hq используйте в меню объекта Equation опцию
Views, а в ней — опцию Coefficient Tests.
Задание 54. Коррекция модели при наличии гетероскедастичности:
метод взвешенных наименьших квадратов, изменение
функциональной формы модели
Используя пакет EViews, произведите необходимую коррекцию модели,
оцененной по статистическим данным о количестве сотрудников на 27 предприятиях
(файл tab5_17).
Методические указания. Выполните оценивание модели регрессии Y на
константу и X, сформируйте ряд остатков. Ориентируясь на график зависимости
остатков от X и другие графики, а также используя критерии Бройша—Пагана
и Глейзера, подберите подходящую форму зависимости дисперсии ошибок от X.
Сравнивайте качество моделей с одинаковой левой частью, используя критерий
Шварца. Запишите преобразованное уравнение, в котором гетероскедастичность
не должна наблюдаться вовсе или быть достаточно слабо выраженной. Оцените
это уравнение. Протестируйте оцененную модель.
Оцените модель регрессии Y на константу и Х9 используя встроенную в
ЕViews процедуру взвешенного метода наименьших квадратов (WLS). В
соответствующем окне укажите весовую функцию (с которой взвешиваются отклонения).
Сравните оценки коэффициентов с оценками, полученными при
непосредственном оценивании преобразованного уравнения.
Обратите внимание на особенности протокола оценивания WLS (взвешенные
и невзвешенные статистики). Сравните значения R2 для взвешенных и для невзве-
шенных статистик. Какое из двух значений больше и почему?
Рассмотрите возможность использования log-level модели. Оцените такую
модель, продиагностируйте остатки. При необходимости расширьте
спецификацию правой части уравнения. Убедитесь в оправданности такого расширения.
Задание 55. Коррекция модели при наличии автокоррелированности:
авторегрессионное преобразование переменных
Используя пакет Е Views, произведите необходимую коррекцию модели,
оцененной по квартальным данным о совокупных расходах на личное потребление и об
объеме денежной массы в США в 1952—1956 гг. (табл. 5.18).
Методические указания. Оцените линейную модель зависимости совокупных
расходов на личное потребление от объема денежной массы. Продиагностируйте
оцененную модель. Предполагая модель AR(\) для ряда ошибок, оцените эту мо-

284
Часть 1. Основные понятия, элементарные методы
дель, привлекая полученный ряд остатков. Выполните авторегрессионное
преобразование переменных, оцените преобразованную модель и проведите
диагностику. Если необходимо, продолжите итерационный процесс.
Оцените линейную модель зависимости совокупных расходов на личное
потребление от объема денежной массы, дополнив спецификацию слагаемым AR(\).
Сопоставьте полученные при этом результаты с результатами, полученными ранее.
Используя оцененную модель, постройте модель коррекции ошибок.
Переоцените исходную модель и модель с ARA) на периоде 1952—1955 гг.
и постройте прогнозы совокупных расходов на потребление по оцененным
моделям на 1956 г. (считая объемы денежной массы в 1956 г. плановыми). Сравните
на одном графике полученные прогнозы с истинными значениями ряда в 1956 г.
Задание 56. Использование моделей с сезонными дамми для принятия
бизнес-решения об объеме производства сезонного товара
на последующий период
В табл. П-6 приведены данные по США о потреблении мороженого на душу
населения (в пинтах) за период с марта 1951 г. по июнь 1953 г.
Представьте, что вы имеете в своем распоряжении статистические данные за
период с марта 1951 г. по март 1953 г. включительно. Вам необходимо принять
бизнес-решение о плановых объемах производства мороженого на апрель, май,
июнь 1953 г. Такое решение должно основываться на прогнозе спроса на
мороженое в эти три месяца. Постройте соответствующий бизнес-прогноз.
Методические указания. Рассмотрите динамику изменения спроса на
мороженое на периоде с марта 1951 г. по март 1953 г. Основываясь на анализе
графика изменений, предложите и оцените эконометрическую модель, подходящую
для описания этой динамики; привлеките для этой цели сезонные дамми-пере-
менные. Оцененную модель используйте для прогноза спроса на мороженое на
апрель, май и июнь 1953 г. Сравните полученный прогноз с реальными данными
о спросе на мороженое в эти три месяца.
Задание 57. Коррекция статистических выводов при наличии
гетероскедастичности
В задании 54 скорректируйте статистические выводы, используя оценку Уайта.
Задание 58. Коррекция статистических выводов при наличии
автокоррелированности.
В задании 55 скорректируйте статистические выводы, используя оценку Ньюи —
Веста.
Б. Задания для самостоятельной работы
Задание С-18. Матрично-векторная форма записи уравнений с фиктивными
переменными
Запишите в векторно-матричной форме (с явным указанием всех элементов
матриц и векторов) линейные модели, использованные в примере 4.2.1 (на периоде
1960—1985 гг.).

Задания для семинарских занятий... и для самостоятельной работы
285
Методические указания. Имеются в виду исходная модель наблюдений с 3
объясняющими переменными, расширенная модель наблюдений с 6 объясняющими
переменными и редуцированная модель наблюдений с 4 объясняющими переменными.
Задание С-19. Сезонные дамми
Запишите в векторно-матричной форме (явно укажите все элементы матриц и
векторов) линейные модели, использованные в примере 5.1.1 (спрос на лыжный инвентарь).
Методические указания. Имеются в виду исходная модель парной линейной
регрессии и расширенная модель наблюдений с 3 объясняющими переменными.
Задание С-20. Дамми на одно наблюдение
Докажите утверждение, сформулированное в Замечании 5.1.5. Выясните, чему
в этом случае равен оцененный коэффициент при указанной дамми-переменной.
Проиллюстрируйте указанное утверждение на конкретном примере.
Методические указания. Проследите, как в этом случае происходит
минимизация суммы квадратов отклонений.
Обратитесь, например, к примеру с уровнями безработицы в США. Сравните
результаты оценивания модели^ = а + /3xt + et по первым 16 наблюдениям с
результатами оценивания по всем 17 наблюдениям модели^ - а л- J3xf + yD\li + si9
где DM — дамми-переменная, равная 1 для 17-го наблюдения и равная 0 для
остальных 16 наблюдений.
Задание С-21. Процедура Кохрейна — Оркатта
Как можно преобразовать к модели с выполненными стандартными
предположениями линейную эконометрическую модель с р объясняющими переменными
в случае, когда ошибки образуют процесс авторегрессии второго порядка?
Методические указания. Действуйте по аналогии со случаем, когда ошибки
образуют процесс авторегрессии первого порядка.
Задание С-22. Преобразование модели в связи с результатами анализа
ее адекватности статистическим данным
Еще раз обратитесь к данным о потреблении пива и уровне детской смертности
(табл. П-1) и, если это необходимо, преобразуйте модель, оцененную ранее.
Методические указания. Используйте результаты анализа указанной модели
на адекватность.
К разделу 6
А. Задания для семинарских занятий и работы в компьютерном классе
Задание 59. Применение доступного обобщенного метода наименьших квадратов
В задании 55 примените доступный обобщенный метод наименьших квадратов.
Методические указания. Используйте преобразование Прайса — Уинстена.
Сравните результаты с полученными при использовании авторегрессионного
преобразования.

286
Часть 1. Основные понятия, элементарные методы
Задание 60. Модели с ошибками в переменных
1. Проведите исследование модели с ошибками в измерении объясняющих
переменных, используя смоделированные данные.
DGP: д;,. = 10 +2z/ + 2^/,
z=10 + 10*@rnd,
xi=zi + 2$ci9
exi9 eyi~ lid N@9l)9i=\9...9 100.
Сравните результаты оценивания, полученные по истинным данным и по
измеренным данным. Сравните диаграммы рассеяния (xi9yt) и (zi9yt).
2. Проверьте, можно ли здесь обнаружить нарушение стандартных
предположений, используя критерий RESET Рэмси?
Б. Задания для самостоятельной работы
Задание С-23. Применение доступного обобщенного метода наименьших
квадратов
1. Сгенерируйте данные, порождаемые моделью
DGP: # = 10+ 2xt + 2ei9 x = 10*@rnd,
ех = 0, et = O.S€i_l + vi9 vt ~ lid. N@9 1), / = 2,..., 100.
2. Используя сгенерированные данные как статистические данные, проведите
OLS оценивание статистической модели у. = а + Pxt + ei9 выполните
диагностику подобранной модели.
3. Учитывая результаты диагностики, произведите необходимую коррекцию
статистических выводов относительно значений коэффициентов. Сравните
полученные статистические выводы в отношении коэффициента J3 при
использовании OLS оценки, оценки Ньюи — Веста, оценки, получаемой
в ЕViews с AR(\) составляющей, оценки Прайса — Уинстена и оценки Кох-
рейна — Оркатта.
4. Можно ли сравнивать соответствующие оцененные модели между собой,
используя информационные критерии? (Если не все, то какие можно?)
Методические указания. В п. 4 обратите внимание на объясняющие
переменные в соответствующих моделях.
• Преобразование Прайса — Уинстена:
1* =yjl-p29 у* =yjl-p2 -yl9 X* =^1-P2 'Xl9
l*=l-p, y*=yt-pyt-\9 x*=xt-pxt_l9 t = 29...9n.
• Для оценивания коэффициента р оцените линейную модель у{ = а + J3xf +
ei9 а затем — линейную модель для остатков: et = pet_x + v,-.
• Преобразование Кохрейна — Оркатта отличается игнорированием первого
наблюдения в преобразованном уравнении.

Задания для семинарских занятий... и для самостоятельной работы
287
Задание С-24. Смещение оценок вследствие коррелированности объясняющей
переменной с ошибкой
Проведите исследование, аналогичное рассмотренному в примере 6.2.1.
DGP: yt = a + pxt + $, st ~ Lid N@9 1), i = 1,..., 100,
a =10, /? = 2,
*,- = £;. -0.9^.!, / = 2,..., 100.
Задание С-25. Метод инструментальных переменных и 2SLS
Повторите исследование, описанное в примере 6.2.2.
Приложение
ТАБЛИЦЫ СТАТИСТИЧЕСКИХ ДАННЫХ К ЗАДАНИЯМ
ТаблицаП-1
Потребление пива и уровень детской смертности
Год
1935
1936
1937
1938
1939
PIVO
10.3
11.8
13.3
12.9
12.3
DET
55.7
57.1
54.4
51.0
48.0
Год
1940
1941
1942
1943
1944
1945
PIVO
12.4
12.3
14.1
15.8
18.0
18.6
DET
47.0
45.3
40.4
40.4
39.8
38.3
Таблица 17-2
Поступление растительного масла, по месяцам
Год, месяц
1935:01
1935:02
1935:03
1935:04
1935:05
1935:06
1935:07
1935:08
1935:09
1935:10
1935:11
1935:12
Объем
48.9
43.4
43.8
50.8
67.6
83.7
82.7
60.8
55.4
48.4
37.4
41.0
Год, месяц
1936:01
1936:02
1936:03
1936:04
1936:05
1936:06
1936:07
1936:08
1936:09
1936:10
1936:11
1936:12
Объем
48.3
47.1
52.4
55.3
64.7
79.5
62.6
51.3
51.0
54.0
45.2
44.9
Год, месяц
1937:01
1937:02
1937:03
1937:04
1937:05
1937:06
1937:07
1937:08
1937:09
1937:10
1937:11
1937:12
Объем
42.4
41.4
49.0
50.8
65.8
85.9
70.6
55.8
49.1
45.7
43.8
46.7

288
Часть 1. Основные понятия, элементарные методы
Таблица П-3
Данные о продажной цене домов
AGE
1 42
1 62
1 40
54
42
56
51
32
32
30
30
32
46
50
22
17
23
40
22
50
44
48
3
31
BATH
1.5
1.5
1.5
1
1
1
1
1.5
1.5
1
1
BED
4
4
3
3
3
3
3
3
3
3
2
3
2
4
3
3
3
3
3
4
3
4
3
4
FIRE
0
0
0
0
0
0
1
0
0
0
0
0
1
0
1
0
0
1
0
1
0
1
0
0
GAR
1
2
1
1
1
1
1
0
2
1
1
2
0
2
1.5
1
1.5
2
1
2
1
2
2
1.5
LIVSP
0.998
1.500
1.175
1.232
1.121
0.988
1.240
1.501
1.225
1.552
0.975
1.121
1.020
1.664
1.488
1.376
1.500
1.256
1.690
1.820
1.652
1.777
1.504
1.831
LOTSIZE
3.472
3.531
2.275
4.050
4.455
4.455
5.850
9.520
6.435
4.988
5.520
6.666
5.000
5.150
6.902
7.102
7.800
5.520
5.000
9.890
6.727
9.150
8.000
7.326
ROOMS
1
1
6
6
6
6
1
6
6
6
5
6
5
8
7
6
7
6
6
8
6
8
7
8
PRICE
25.9
29.5
27.9
25.90
29.9
29.9
30.9
28.9
35.9
31.5
31.0
30.9
30.0
36.9
41.9
40.5
43.9
37.9
37.9
44.5
37.9
38.9
36.9
45.8
TAXES
4.918
5.021
4.543
4.557
5.060
3.891
5.898
5.604
5.828
5.300
6.271
5.959
5.050
8.246
6.697
7.784
9.038
5.989
7.542
8.795
6.083
8.361
8.140
9.142
Таблица П-4
Рейтинг руководителей
Y
43
63
71
61
81
43
58
Z\
51
64
70
63
78
55
67
Zl
30
51
68
45
56
49
42
ZЪ
39
54
69
47
66
44
56
Z4
61
63
76
54
71
54
66
ZS
92
73
86
84
83
49
68
Z6
45
47
48
35
47
34
35

Задания для семинарских занятий... и для самостоятельной работы
289
Окончание табл. П-4
Y
1 71
72
67
64
1 67
69
68
77
81
74
65
65
50
50
64
53
40
63
66
78
48
85
82
Z1
75
82
61
53
60
62
83
77
90
85
60
70
58
40
61
66
37
54
77
75
57
85
82
Z2
50
72
45
53
47
57
83
54
50
64
65
46
68
33
52
52
42
42
66
58
44
71
39
Z3
55
67
47
58
39
42
45
72
72
69
75
57
54
34
62
50
58
48
63
74
45
71
59
Z4
70
71
62
58
59
55
59
79
60
79
55
75
64
43
66
63
50
66
88
80
51
77
64
Z5
66
83
80
67
74
63
77
77
54
79
80
85
78
64
80
80
57
75
76
78
83
74
78
Z6
41
31
41
34
41
25
35
46
36
63
60
46
52
33
41 1
37 1
49
33
72 1
49
38
55 |
39 1
Таблица П-5
Данные 15 наблюдений двух переменных
I
1
2
3
4
5
6
7
8
X
1.000000
2.000000
3.000000
4.000000
5.000000
6.000000
7.000000
8.000000
Z
1.257072
1.811984
3.641244
4.401497
5.561015
0.865034
1.929552
2.944438
i
9
10
И
12
13
14
15
X
9.000000
10.00000
11.00000
12.00000
13.00000
14.00000
15.00000
Z
4.316424
5.322512
1.804023
1.956286
3.134308
4.648561
4.559242

290
Часть 1. Основные понятия, элементарные методы
Таблица П-в
Потребление мороженого, по месяцам
Год, месяц
1951:03
1951:04
1951:05
1951:06
1951:07
1951:08
1951:09
1951:10
1951:11
1951:12
1952:01
1952:02
1952:03
1952:04
Объем
0.386
0.374
0.393
0.425
0.406
0.344
0.327
0.288
0.269
0.256
0.286
0.298
0.329
0.318
Год, месяц
1952:05
1952:06
1952:07
1952:08
1952:09
1952:10
1952:11
1952:12
1953:01
1953:02
1953:03
1953:04
1953:05
1953:06
Объем
0.381
0.381
0.470
0.443
0.386
0.342
0.319
0.307
0.284
0.326
0.309
0.359
0.376
0.416
Таблица П-7
Импорт товаров и услуг во Францию
Год
1949
1950
1951
1952
1953
1954
1955
1956
1957
Y
15.9
16.4
19.0
19.1
18.8
20.4
22.7
26.5
28.1
XI
149.3
161.2
171.5
175.5
180.8
190.7
202.1
212.4
226.1
ХЪ
4.2
4.1
3.1
3.1
1.1
2.2
2.1
5.6
5.0
Х4
108.1
114.8
123.2
126.9
132.1
137.7
146.0
154.1
162.3
Год
1958
1959
1960
1961
1962
1963
1964
1965
1966
Y
27.6
26.3
31.1
33.3
37.0
43.3
49.0
50.3
56.6
XI
231.9
239.0
258.0
269.8
288.4
304.5
323.4
336.8
353.9
ХЪ
5.1
0.7
5.6
3.9
3.1
4.6
7.0
1.2
4.5
Х4
164.3
167.6
176.8
186.6
199.7
213.9
223.8
232.0
242.9

Литература
1. Айвазян С.А. B001). Прикладная статистика. Основы эконометрики. Т. 2. М.:
ЮНИТИ.
2. Вербик М. B008). Путеводитель по современной эконометрике. М.: Научная книга.
3. Доугерти К. B004). Введение в эконометрику. 2-е изд. М.: ИНФРА-М.
4. Магнус Я.Р., Катышев П.К., Пересецкий А.А. B005). Эконометрика. Начальный
курс. 7-е изд., испр. М.: Дело.
5. Носко В.П. B004). Эконометрика. Элементарные методы и введение в
регрессионный анализ временных рядов. М.: ИЭПП.
6. Носко В.П. B004). Эконометрика: введение в регрессионный анализ временных
рядов. М.: Логос.
7. Рао СР. A968). Линейные статистические методы и их применения. М.: Наука.
8. Amemiya Т. A985). Advanced Econometrics. Oxford: Basil Blackwell.
9. Cameron A.C, Trivedi P.K B005). Microeconometrics: Methods and Applications.
New York: Cambridge University Press.
10. Davidson R., MacKinnon J.G. A993). Estimation and inference in econometrics. New
York: Oxford University Press.
11. Favero С A. B001). Applied Macroeconometrics. Oxford University Press.
12. Godfrey L.G B005). Controlling the overall significance level of a battery of least squares
diagnostic tests // Oxford Bulletin of Economics and Statistics. Vol. 67. P. 263—279.
13. Greene W.H B003). Econometric analysis. 5th ed. Upper Saddle River, Prentice Hall.
14. Gujarati D.N. B003). Basic econometrics. 4th ed. Boston: McGraw Hill.
15. Hamilton J.D. A994). Time series analysis. Princeton: Princeton University Press.
16. Hendry D.F. B003). Econometrics: Alchemy or Science? Essays in Econometric
Methodology. Oxford: Blackwell Publishers.
17. Keynes J.M. A936). The General Theory of Employment, Interest and Money. London:
Macmillan.
18. MacKinnon J.G., White H, Davidson R. A983). Tests for model specification in the
presence of alternative hypotheses: some further results // J. of Econometrics. Vol. 21.
P. 53—70.
19. Samuelson P.A., Koopmans T.C., Stone J.R. A954). Report of the Evaluation
Committee for Econometrics, Econometrica. Vol. 22. P. 141 —146.
20. The Oxford dictionary of statistical terms. B003). New York: Oxford University Press.
21. Wooldridge J.M. B000). Introductory econometrics: a modern approach. Cincinnati, OH:
South-Western College.

Глоссарий
К разделу 1
Аддитивные ошибки {additive errors) — ошибки, входящие в правую часть
уравнения в виде отдельного слагаемого.
Вариабельность {variability) — изменчивость переменной на множестве
наблюдений.
Выборочная дисперсия {sample variance) — деленная на {п - 1) сумма квадратов
отклонений наблюдаемых значений xl9 ..., хп переменной х от их
арифметического среднего. Характеризует степень разброса значений хх, ..., хп
вокруг своего среднего х, или вариабельность (изменчивость) этой
переменной на множестве наблюдений.
Выборочная ковариация {sample covariance) — деленная на {п - 1) сумма
произведений отклонений наблюдаемых значений xl9 ..., хп переменной х от их
арифметического среднего на отклонения наблюдаемых значений yl9 ...,yn
переменной у от их арифметического среднего.
Выборочный коэффициент корреляции {sample correlation coefficient) —
показатель степени выраженности линейной связи между произвольными
переменными х и у на множестве наблюдений, в которых эти переменные
принимают значения хх nyi9 i = 1,..., п.
Диаграмма рассеяния {scatter plot, scatter diagram, scatter graph) — способ
представления связи между результатами измерений двух переменных.
Диаграмма, на которой в прямоугольной системе координат располагаются
точки (xi9 yt)9 i = 1, ..., п9 где п — количество наблюдаемых пар значений
переменных х и у.
Дисперсионный анализ {analysis of variance) — разложение выборочной
дисперсии объясняемой переменной на две компоненты.
Зависимая переменная {dependent variable) — переменная в математической
модели связи, значения которой определяются значениями независимых
переменных.
Корреляционное поле {correlation diagram) — См. Диаграмма рассеяния.

Глоссарий
293
Коэффициент детерминации {coefficient of determination) — отношение суммы
квадратов, объясненной моделью, к полной сумме квадратов.
Линейная модель наблюдений {linear observation model) — модель,
согласующая принятую линейную математическую модель связи с наблюдаемыми
данными.
Линейная модель связи {linear relation) — математическое выражение
линейной зависимости между переменными.
Ложная (фиктивная, паразитная — spurious) линейная связь — подобранная
линейная связь между переменными, не имеющая содержательной
экономической интерпретации.
Математическая модель связи {mathematical model, dependence model) —
модель, выраженная в форме функциональной зависимости значений одной
переменной от значений других переменных и отражающая усредненную
зависимость одной переменной (зависимая переменная) от других
переменных (независимые переменные).
Метод «от общего к частному» {general-to-specific approach) — в качестве
первоначальной выбирается более полная модель, которая затем, если это
возможно, редуцируется к более простой модели.
Множественный коэффициент корреляции {multiple-R) — коэффициент
корреляции между наблюдаемыми значениями объясняемой переменной и
прогнозными значениями этой переменной.
Модель Михаэлиса - Ментон {Michaelis-Menton model) — модель нелинейной
связи между двумя переменными, предусматривающая наличие
вертикальной и горизонтальной асимптот графика зависимости.
Модель наблюдений {observation model) — модель, согласующая принятую
математическую модель связи с наблюдаемыми данными, учитывающая
совокупное влияние на конкретные значения зависимой переменной множества
дополнительных факторов, не учитываемых принятой моделью связи.
Модель пропорциональной связи {proportional relation) — модель, в которой
зависимая переменная имеет с независимой переменной
пропорциональную связь.
Мультипликативные ошибки {multiplicative errors) — ошибки, входящие в
правую часть уравнения в виде сомножителя.
Независимая переменная {independent variable) — переменная в математической
модели связи, от значений которой зависят значения зависимой переменной.
Нелинейный метод наименьших квадратов {nonlinear least squares — NLLS) —
реализация принципа наименьших квадратов для нелинейных моделей
наблюдений. Поиск значений оценок наименьших квадратов
осуществляется с использованием процедур последовательной минимизации целевой
суммы квадратов.
Нецентрированный коэффициент детерминации {uncentered R2) — вариант
коэффициента детерминации, который используют при оценивании
линейной эконометрической модели без постоянной составляющей.

294
Часть 1. Основные понятия, элементарные методы
Облако рассеяния (scatter cloud) — совокупность точек на диаграмме рассеяния.
Обратная (inverse) модель линейной связи — модель линейной связи между
двумя переменными, в которой зависимая и независимая переменные
исходной (прямой) модели меняются местами.
Объясняемая переменная (explained variable) — переменная, уединенная в левой
части уравнения эконометрической модели.
Объясняющая переменная (explanatory variable) — переменная, входящая в
правую часть уравнения эконометрической модели.
Остаток в 1-м наблюдении (residual) — разность между значением зависимой
переменной в z'-м наблюдении и прогнозным значением этой переменной,
вычисленным для значения независимой переменной в /-м наблюдении
по формуле, соответствующей подобранной модели связи.
Остаточная сумма квадратов (residual sum of squares — RSS) — сумма квадратов
отклонений наблюдаемых значений зависимой переменной от прогнозных
значений, полученных в результате оценивания эконометрической модели.
Отрицательная (negative) корреляционная связь между переменными —
связь между переменными х и у, при которой значение выборочного
коэффициента корреляции, вычисленного на основе имеющихся наблюдений,
отрицательно.
Оценки наименьших квадратов (least squares estimates), или 1,5-оценки —
оценки параметров эконометрической модели, полученные из условия
минимизации суммы квадратов расхождений между наблюдаемыми
значениями зависимой переменной и значениями этой переменной,
вычисленными для наблюдаемых значений независимой переменной по
оцененной модели связи.
Ошибка в 1-м наблюдении (error, disturbance) — разность между значением
зависимой переменной в /-м наблюдении и значением этой переменной,
вычисленным для значения независимой переменной в /-м наблюдении
по формуле, соответствующей теоретической модели связи.
Подобранная модель (fitted model) — модель связи между переменными,
построенная в результате оценивания выбранной эконометрической модели.
Полная сумма квадратов (total sum of squares — TSS) — сумма квадратов
отклонений наблюдаемых значений зависимой переменной от их
среднеарифметического.
Положительная (positive) корреляционная связь между переменными —
связь между переменными х и у, при которой значение выборочного
коэффициента корреляции, вычисленного на основании имеющихся
наблюдений, положительно.
Принцип наименьших квадратов (least squares principle) — принцип, согласно
которому находятся оценки наименьших квадратов.
Принцип охвата (encompassing principle) — модель должна быть в
определенном смысле «неулучшаемой», должна объяснять результаты, получаемые
по конкурирующим с ней моделям.

Глоссарий
295
Принцип парсимонии, экономичности, простоты {parsimony principle) —
модель должна быть простой, насколько это возможно, пока не доказана ее
неадекватность имеющимся статистическим данным.
Прогнозное значение зависимой переменной в #-м наблюдении {fitted value) —
значение зависимой переменной, вычисленное для значения независимой
переменной в /-м наблюдении по формуле, соответствующей подобранной
модели связи.
Процесс порождения данных (ППД, или DGP — data generating process) —
«истинный» механизм порождения эмпирических данных.
Система нормальных уравнений {normal equations) — система уравнений, из
которой находятся оценки наименьших квадратов.
Спецификация эконометрической модели (specification of an econometric model) —
задание эконометрической модели в виде уравнения с указанием
задействованных переменных и функциональной формы связи между
переменными, задание априорных ограничений на параметры и вероятностного
описания последовательности случайных ошибок.
Среднее значение (mean, mean value) — среднеарифметическое наблюдаемых
значений хи..., хп переменной х.
Стандартизованная переменная (standardized variable) — переменная,
получаемая в результате стандартизации исходной переменной, т.е. деления
значений исходной переменной на ее стандартное отклонение.
Стандартное отклонение переменной (standard deviation) — квадратный
корень из выборочной дисперсии переменной. Имеет ту же размерность, что
и сама переменная.
Статистическая модель (statistic model) — См. Эконометрическая модель.
Сумма квадратов, объясненная моделью (explained sum of squares — ESS) —
сумма квадратов отклонений прогнозных значений зависимой переменной
от среднеарифметического наблюдаемых значений зависимой переменной.
Частный коэффициент корреляции (partial correlation coefficient) —
коэффициент корреляции между двумя переменными, очищенными от линейных
связей с другими переменными.
Эконометрика (econometrics) — совокупность методов анализа связей между
различными экономическими показателями (факторами) на основе реальных
статистических данных с использованием аппарата теории вероятностей
и математической статистики.
Эконометрическая модель (econometric model) — модель, выбираемая эконо-
метристом для описания статистических данных на основании модели связи,
указываемой экономической теорией, и ранее проведенных исследований,
структура которой по возможности наиболее приближена к «истинному»
процессу порождения статистических данных. Отклонения наблюдаемых
значений зависимой переменной от значений, вычисленных по принятой
математической модели связи, рассматриваются как случайные величины
(реализации случайных величин).

296
Часть 1. Основные понятия, элементарные методы
К разделу 2
Ковариационная матрица {covariance matrix) случайного вектора —
квадратная матрица, элементами которой являются ковариации пар случайных
величин, составляющих случайный вектор.
Математическое ожидание {expectation) случайного вектора — вектор,
состоящий из математических ожиданий случайных величин, его составляющих.
Метод наименьших квадратов {least squares) — метод оценивания параметров
эконометрической модели, состоящий в минимизации суммы квадратов
расхождений между наблюдаемыми значениями зависимой переменной
и значениями этой переменной, вычисленными для наблюдаемых значений
независимых переменных по оцененной модели связи.
Многомерное нормальное распределение {multivariate normal distribution) —
совместное распределение компонент случайного вектора, обобщающее
понятие одномерного нормального распределения.
Множественная линейная регрессия {multiple linear regression) — модель
множественной регрессии, в которой функция регрессии является линейной
функцией неизвестных параметров.
Множественная регрессия {multiple regression) — регрессионная модель,
содержащая более двух объясняющих переменных, не считая постоянной
составляющей.
Наилучшая линейная несмещенная оценка {BLUE — best linear unbiased
estimate) — оптимальная оценка в классе несмещенных линейных оценок
вектора коэффициентов линейной эконометрической модели.
Непараметрическая регрессия {nonparametric regression) — регрессионная модель,
в которой функция регрессии полностью произвольна (непараметризована).
Нормальная линейная модель регрессии {normal linear regression) — модель
линейной регрессии, в которой ошибки имеют нормальное (гауссовское)
распределение.
Ортогональная структура матрицы наблюдаемых значений объясняющих
переменных — ситуация, в которой векторы наблюдаемых значений
переменных, являющихся объясняющими переменными в линейной
эконометрической модели, попарно ортогональны.
Параметрическая регрессия {parametric regression) — регрессионная модель,
в которой функция регрессии задана с точностью до некоторого числа
неизвестных параметров, подлежащих оцениванию.
Правило «при прочих равных» {ceteris paribus) — предположение о том, что
при изменении значения одной из объясняющих переменных значения
остальных объясняющих переменных остаются неизменными.
Простая {simple) линейная регрессия (то же что, Парная {two-variable)
линейная регрессия, то же, что Прямолинейная {straight-line) регрессия) —
регрессионная модель, в которой функция регрессии является линейной
функцией единственной объясняющей переменной, отличной от константы.

Глоссарий
297
Регрессионная модель, уравнение регрессии {regression model, regression
equation) — эконометрическая модель, в которой условное математическое
ожидание аддитивной ошибки в i-м наблюдении при фиксированных
значениях объясняющих переменных в этом наблюдении равно нулю.
Регрессионная сумма квадратов {regression sum of squares) — См. Сумма
квадратов, объясненная моделью.
Регрессионный анализ {regression analysis) — совокупность
вероятностно-статистических методов исследования регрессионных моделей.
Регрессоры {regressors) — объясняющие переменные в модели регрессии.
Случайный вектор размерности п {n-dimensional random vector) —
упорядоченный набор п одномерных случайных величин, имеющих некоторое
совместное распределение вероятностей.
Статистика 52 {S2 statistic) — статистика, являющаяся несмещенной оценкой
дисперсии случайных ошибок в нормальной линейной модели регрессии.
Статистические данные {statistical data), или наблюдения {observations) —
наблюдаемые значения переменных, включенных в эконометрическую модель.
Теорема Гаусса — Маркова {Gauss-Markov theorem) — теорема об оптимальности
оценки наименьших квадратов вектора коэффициентов линейной эконо-
метрической модели в классе несмещенных линейных оценок этого вектора.
Теорема Фриша — Во — Ловелла {Frisch-Waugh-Lovell theorem) — теорема,
дающая интерпретацию оценок коэффициентов линейных моделей с
несколькими объясняющими переменным.
Условия Гаусса — Маркова {Gauss-Markov conditions) — условия,
накладываемые на эконометрическую модель в теореме Гаусса — Маркова.
Функция регрессии {regression function) — функция, выражающая зависимость
условного математического ожидания значения объясняемой переменной
в /-м наблюдении (при фиксированных значениях объясняющих переменных
в /-м наблюдении) от значений объясняющих переменных в i-м наблюдении.
Центрирование переменной {centering) — вычитание из всех наблюдаемых
значений переменной их среднего значения. Центрированная переменная
имет среднее значение, равное нулю.
Центрирование случайного вектора {centering) — вычитание из случайного
вектора его математического ожидания. Центрированный случайный
вектор имеет нулевой вектор математических ожиданий.
К разделу 3
Асимптотический критерий {asymptotic test) — критерий, рассчитываемый на
основании асимптотического распределения тестовой статистики
(статистики критерия).
Гипотеза значимости для отдельного коэффициента {hypothesis of the
statistical significance of a coefficient, hypothesis that a coefficient is equal to zero) —
гипотеза, предполагающая равенство нулю коэффициента при
определенной объясняющей переменной.

298
Часть 1. Основные понятия, элементарные методы
Гипотеза значимости регрессии в целом {hypothesis of overall significance of
a regression; hypothesis that all of the slope coefficients, excluding the constant,
or intercept in a regression are zero) — гипотеза о равенстве нулю всех
коэффициентов линейной модели регрессии, не затрагивающая только
постоянную составляющую.
Гнездовые модели {nested models) — пара линейных эконометрических моделей
с одной и той же объясняемой переменной, одна из которых вложена
в другую, являясь ее частным случаем.
Интервальный прогноз {forecast interval) — доверительный интервал для
наблюдаемого значения (или для математического ожидания наблюдаемого
значения) объясняемой переменной, получаемого при заданном наборе
значений объясняющих переменных.
Информационные критерии {information criteria) — полученные на основе
теории информации критерии для выбора между несколькими альтернативными
эконометрическими моделями с одной и той же объясняемой переменной;
все эти критерии предусматривают «штраф» за увеличение количества
объясняющих переменных в модели, но несколько отличными способами.
Конфликт критериев {conflict among testing procedures) при рассмотрении
альтернативных гипотез — ситуация, когда при рассмотрении пары
альтернативных статистических гипотез ни одна из них не отвергается, будучи
взятой в качестве нулевой гипотезы.
Коэффициент возрастания дисперсии {variance inflation factor) — показатель,
характеризующий степень возрастания дисперсии оценки коэффициента
при некоторой объясняющей переменной вследствие коррелированности
этой переменной с другими объясняющими переменными, включенными
в эконометрическую модель.
Критерий Акаике {Akaike 's information criterion — AIQ — один из
информационных критериев, в котором штрафная составляющая равна —, где р —
п
количество объясняющих переменных, п — количество наблюдений.
Критерий Вальда (Waid statistic) — основанный на использовании статистики
Вальда критерий для проверки линейной гипотезы в нормальной линейной
модели со стандартными предположениями.
Критерий Шварца {Schwarz's information criterion — SC, SIC) — один из
информационных критериев, в котором штрафная составляющая равна
р\пп г
, где р — количество объясняющих переменных, п — количество
п
наблюдений.
Линейная гипотеза (linear hypothesis) — гипотеза, накладывающая одно или
несколько линейных ограничений на коэффициенты линейной экономет-
рической модели.
Модель без ограничений {unrestricted model) — эконометрическая модель, в
которой на значения коэффициентов не накладывается никаких ограничений.

Глоссарий
299
Модель с ограничениями {restricted model) — эконометрическая модель, в
которой на значения коэффициентов накладываются определенные ограничения.
Мультиколлинеарность {multicollinearity) — наличие высокой степени
линейной корреляции между двумя или более объясняющими переменными.
Негнездовые F-критерии {nonnested F-tests) — F-критерии, используемые для
выбора между двумя негнездовыми эконометрическими моделями.
Оценка наименьших квадратов в модели с ограничениями {restricted least
squared estimate) — оценка наименьших квадратов вектора параметров
в модели с ограничениями, заданными гипотезой Я0.
Ошибка прогноза {forecast error) — разность между значением объясняемой
переменной, наблюдаемым для заданного набора значений объясняющих
переменных, и прогнозным значением объясняемой переменной для этого
набора значений объясняющих переменных.
Полная мультиколлинеарность {exact collinearity) — ситуация, в которой
столбцы матрицы значений объясняющих переменных линейно зависимы.
Редуцированная модель {reduced model) — модель, получаемая на основании
исходной эконометрической модели и включающая в результате
наложения на коэффициенты исходной модели определенных ограничений
меньшее количество объясняющих переменных.
Скорректированный коэффициент детерминации, скорректированный R2
{adjusted R-squared, adjusted R2) — показатель, используемый для выбора
между несколькими альтернативными эконометрическими моделями с одной
и той же объясняемой переменной. Получается путем коррекции обычного
коэффициента детерминации, учитывающей количество объясняющих
переменных в модели и количество наблюдений.
Статистика Вальда {Wald statistic) — используемая для проверки линейной
гипотезы в нормальной линейной модели со стандартными
предположениями статистика, имеющая при нулевой гипотезе асимптотическое
распределение хи-квадрат с соответствующим числом степеней свободы.
Статистика критерия {test statistics) — используемая для проверки нулевой
гипотезы случайная величина, значения которой могут быть вычислены
(по крайней мере, теоретически) на основании имеющихся статистических
данных и распределение которой известно (хотя бы приближенно).
Статистическая гипотеза {statistical hypothesis) — априорное предположение,
уточняющее спецификацию эконометрической модели.
Статистически значимая оценка {statistically significant estimate) — значение
оценки коэффициента при некоторой объясняющей переменной,
попадающее в критическое множество статистического критерия для проверки
гипотезы о равенстве этого коэффициента нулю.
Статистически незначимая оценка {statistically non-significant estimate) —
значение оценки коэффициента при некоторой объясняющей переменной,
не попадающее в критическое множество статистического критерия для
проверки гипотезы о равенстве этого коэффициента нулю.

300
Часть 1. Основные понятия, элементарные методы
Точечный прогноз, прогнозное значение (forecast) — значение объясняемой
переменной, вычисленное для заданного набора значений объясняющих
переменных на основании подобранной модели связи.
Точный, неасимптотический критерий (non-asymptotic test) — критерий,
рассчитываемый на основании неасимптотического распределения тестовой
статистики, соответствующего имеющемуся количеству наблюдений.
F-критерий для проверки линейной гипотезы (F-test) — основанный на
использовании F-статистики критерий для проверки линейной гипотезы
в нормальной линейной модели со стандартными предположениями.
F-статистика (F-statistic) — статистика, имеющая при нулевой гипотезе F-pac-
пределение Фишера
Р-значение (P-value), наблюденный уровень значимости (observed level of
significance) при применении /-критерия — вероятность того, что случайная
величина, имеющая ^-распределение Стьюдента с соответствующим числом
степеней свободы, примет значение, большее по абсолютной величине,
чем наблюдаемое значение ^-статистики критерия.
Р-значение (Р-value), наблюденный уровень значимости (observed level of
significance) при применении F-критерия — вероятность того, что
случайная величина, имеющая F-распределение Фишера с соответствующим
числом степеней свободы, примет значение, большее, чем наблюдаемое
значение F-статистики критерия.
/-критерии (t-tests) — статистические критерии, основанные на использовании
^-статистик.
/-отношение (t-ratio) — форма ^-статистики, предназначенная для проверки
гипотезы равенства нулю определенного коэффициента линейной эконо-
метрической модели.
/-статистика (t-statistic) — статистика, имеющая при нулевой гипотезе
^-распределение Стьюдента.
К разделу 4
Автокоррелированность ошибок (autocorrelated errors) — невыполнение
условия независимости случайных ошибок в эконометрической модели для
данных, развернутых во времени.
Адекватная статистическим данным модель (adequate model) — модель,
соответствующая характеру статистических данных, воспроизводящая
глобальные особенности имеющихся статистических данных. В более узком
смысле: эконометрическая модель, в которой выполнены стандартные
предположения об ошибках.
Анализ остатков (residual analysis) — совокупность методов обнаружения
отклонений от стандартных предположений о модели наблюдений,
использующих остатки от подобранной модели.
Асимптотические критерии (large sample tests) — статистические критерии для
проверки нулевой гипотезы, у которых критическая область (критические

Глоссарий
301
значения) рассчитывается на основании асимптотического (предельного)
распределения статистики критерия, получаемого при неограниченном
увеличении количества наблюдений.
Выделяющиеся наблюдения (outliers) — наблюдения, для которых либо
математическое ожидание ошибки существенно отличается от нуля, либо
дисперсия ошибки существенно превышает величину дисперсий остальных
ошибок.
Гетероскедастичность (heteroscedasticity, heteroskedasticity) — неодинаковость
(неоднородность) дисперсий случайных ошибок в линейной эконометри-
ческой модели.
Гомоскедастичность, однородность дисперсий ошибок (homoscedasticity) —
одинаковость (однородность) дисперсий случайных ошибок в линейной
эконометрической модели.
Графический анализ адекватности (graphical diagnostic analysis) —
совокупность графических методов обнаружения отклонений от стандартных
предположений об эконометрической модели.
Двухфазная линейная регрессия (two-phase linear regression model) — линейная
регрессионная модель, параметры которой скачкообразно изменяются при
переходе от одного подпериода наблюдений к последующему.
Диагностика подобранной модели (diagnostic for model misspecificatiori) —
анализ подобранной модели с целью проверки возможного нарушения
стандартных предположений об эконометрической модели.
Диаграмма «квантиль-квантиль» (Q-Q plot) — одно из графических средств
выявления нарушения предположения о распределении ошибок в принятой
эконометрической модели.
Диаграмма плотности (DP-ploty DPP) — одно из графических средств
выявления нарушения предположения о распределении ошибок в принятой
эконометрической модели.
Критерии согласия (goodness-of-fit tests) — статистические критерии для
проверки нулевой гипотезы, не настроенные на какой-то определенный класс
альтернатив нулевой гипотезе.
Критерии Чоу (Chow tests) — два статистических критерия, предназначенных
для проверки стабильности модели на всем периоде наблюдений. Один
из них — критерий Чоу на структурный сдвиг (Chow breakpoint test) —
проверяет гипотезу о сохранении значений всех коэффициентов при
переходе от одного подпериода полного периода наблюдений к другому,
другой — критерий Чоу на качество прогноза (Chow forecast test) -
сравнивает качество прогнозов, сделанных на основании оценивания модели
на одной части периода для значений объясняемой переменной на другой
части периода, с качеством «прогнозов», сделанных на основании
оценивания модели на всем периоде наблюдений.
Критерий Бройша — Годфри (Breusch-Godfrey test) — статистический
критерий, предназначенный для проверки гипотезы некоррелированности
ошибок в нормальной линейной модели регрессии.

302
Часть 1. Основные понятия, элементарные методы
Критерий Голдфелда — Квандта {Goldfeld-Quandt test) — статистический
критерий, предназначенный для выявления неоднородности дисперсий
случайных ошибок в нормальной линейной модели регрессии.
Критерий Дарбина — Уотсона {Durbin-Watson test) — статистический
критерий, предназначенный для выявления автокоррелированности случайных
ошибок в нормальной линейной модели регрессии.
Критерий Рэмси {regression specification error test — RESET) — статистический
критерий, предназначенный для проверки в рамках нормальной линейной
модели предположения о равенстве нулю математических ожиданий
случайных ошибок. Может использоваться для обнаружения наличия
пропущенных переменных, неправильной функциональной формы представления
некоторых переменных, наличия корреляции между объясняющими
переменными и ошибкой в уравнении регрессии.
Критерий Уайта {White test) — статистический критерий, предназначенный для
проверки гипотезы однородности дисперсий ошибок в нормальной
линейной модели регрессии.
Критерий Харке — Бера {Jarque-Bera test) — статистический критерий,
предназначенный для выявления отклонений от нормальности случайных ошибок
в линейной модели регрессии.
Кумулятивные суммы нормированных рекурсивных остатков {CUSUM -
cumulative sums) — суммы рекурсивных остатков, получаемые в процессе
последовательного добавления данных.
Линейная модель с переключением {switching regression model) — См.
Двухфазная линейная регрессия.
Методология Лондонской школы экономики {LSE approach) — методология
эконометрических исследований, согласно которой при обнаружении
нарушений стандартных предположений следует изменить спецификацию
модели таким образом, чтобы при оценивании модели с измененной
спецификацией нарушения стандартных предположений уже не выявлялись,
по крайней мере, теми диагностическими процедурами, которые имеются
в распоряжении исследователя.
Нестабильность модели {instability) — непостоянство коэффициентов модели на
периоде наблюдений.
Ошибка прогноза {forecast error) — разность между значением объясняемой
переменной, наблюдаемым для заданного набора значений объясняющих
переменных, и прогнозным значением объясняемой переменной для этого
набора значений объясняющих переменных.
Рекурсивные коэффициенты {recursive coefficients) — последовательность
значений оценок коэффициентов линейной эконометрической модели в
процессе последовательного добавления данных.
Рекурсивные остатки {recursive residuals) — последовательность
нормированных ошибок прогнозов на один шаг для значений объясняемой переменной
линейной эконометрической модели в процессе последовательного
добавления данных.

Глоссарий
303
Стандартизованные остатки (standardized residuals) — остатки от подобранной
модели, деленные на квадратный корень из несмещенной оценки
дисперсии ошибок в эконометрической модели.
Статистика Дарбина — Уотсона (Durbin-Watson statistic) — статистика, на
которой основан критерий Дарбина — Уотсона.
Стьюдентизированные остатки (studentized residuals) — остатки от
подобранной модели, деленные на оценки их стандартных отклонений.
Точный, неасимптотический критерий (non-asymptotic test) — критерий,
критические значения которого учитывают количество имеющихся наблюдений.
Ядерные оценки плотности (kernel density estimates) — метод получения
суждений о форме функции плотности распределения ошибок в эконометрической
модели, позволяющий получать график в виде непрерывной кривой.
К разделу 5
Автокоррелированность, сериальная корреляция ошибок (autocorrelation,
serial correlation) — нарушение стандартного предположения о
независимости случайных ошибок в эконометрической модели, характерное для
статистических данных, развернутых во времени (продольных данных).
Авторегрессионное преобразование (autoregressive transformation) —
преобразование исходных статистических данных в итерационной процедуре Кох-
рейна — Оркатта, в результате которого случайные ошибки в
преобразованной модели удовлетворяют стандартным предположениям.
Взаимодействие (interaction) — искусственная переменная, являющаяся
произведением одной из объясняющих переменных на дамми-переменную.
Взвешенные статистики (weighted statistics) — при использовании взвешенного
метода наименьших квадратов: статистики, основанные на остатках,
получаемых по взвешенным данным.
Взвешенный метод наименьших квадратов (WLS — weighted least squares) —
процедура, состоящая в минимизации определенным образом взвешенной
суммы квадратов отклонений наблюдаемых значений зависимой
переменной от значений, вычисляемых по подбираемой модели связи.
Дамми-ловушка (dummy trap) — полная мультиколлинеарность данных,
возникающая при включении в эконометрическую модель с дамми-перемен-
ными «лишних» переменных.
Дамми-переменные (dummy variables, dummies) — переменные, указывающие
на принадлежность наблюдения тому или иному промежутку времени,
группе стран или отдельным странам, группам регионов или отдельным
регионам, служащие для обозначения принадлежности субъекта той или
иной социальной или этнической группе и т.п. Введение таких переменных
позволяет выявлять наличие эффектов, специфических для определенных
периодов времени, для определенных групп стран, социальных групп,
регионов и т.п.

304
Часть 1. Основные понятия, элементарные методы
Итерационная процедура Кохрейна — Оркатта (Cochrane-Orcuti) —
процедура коррекции статистических выводов при наличии автокоррелированно-
сти ошибок в линейной эконометрической модели.
Критерий Глейзера (Glejser test) — критерий для выявления определенного
вида зависимостей дисперсий случайных ошибок от значений объясняющей
переменной.
Невзвешенные статистики (unweighted statistics) — при использовании
взвешенного метода наименьших квадратов: статистики, основанные на
остатках, получаемых по невзвешенным, оригинальным данным.
Обычные оценки наименьших квадратов (ordinary least squares estimates, OLS
estimates) — оценки, получаемые применением принципа наименьших
квадратов непосредственно к исходной эконометрической модели.
Обычный метод наименьших квадратов (OLS — ordinary least squares) —
метод наименьших квадратов, применяемый непосредственно к исходной
эконометрической модели; противопоставляется взвешенному методу
наименьших квадратов и другим обобщениям обычного метода
наименьших квадратов.
Оценка Ньюи — Веста (Newey-West estimator) — скорректированная на авто-
коррелированность ошибок в линейной эконометрической модели оценка
стандартных ошибок оценок коэффициентов модели.
Оценка Уайта (White estimator) — скорректированная на неоднородность
дисперсий ошибок в линейной эконометрической модели оценка стандартных
ошибок оценок коэффициентов модели.
Панельные данные (panel data) — данные об экономических показателях
нескольких предприятий (регионов, стран) за несколько месяцев (кварталов, лет).
Перекрестные, одномоментные данные (cross-section data) — данные по
нескольким предприятиям (регионам, странам) за один промежуток времени
(месяц, квартал, год).
Процесс авторегрессии первого порядка (first order autoregressive process) —
динамическая модель, в правой части которой присутствуют только
запаздывающие на один шаг значения объясняемой переменной.
К разделу 6
Двухшаговый метод наименьших квадратов (two-stage least squares — TSLS,
2SLS) — метод оценивания коэффициентов уравнения структурной формы,
состоящий в предварительной очистке стохастической объясняющей
переменной от коррелированности с ошибкой в этом уравнении с
использованием инструментальных переменных и в последующем оценивании
уравнения, в котором исходная объясняющая переменная заменяется ее
очищенным вариантом.
Доступный обобщенный метод наименьших квадратов (FGLS—feasible GLS) —
практически реализуемая процедура оценивания коэффициентов линейной

Глоссарий
305
модели регрессии в ситуации, когда случайные ошибки имеют разные
дисперсии и коррелированы между собой, повторяющая процедуру
обобщенного метода наименьших квадратов, но использующая оцененную
ковариационную матрицу вектора ошибок.
Инструментальная переменная, инструмент {instrumental variable, instrument) —
переменная, коррелированная со стохастической объясняющей
переменной, включенной в уравнение регрессии, но не коррелированная со
случайной ошибкой в этом уравнении.
Метод инструментальных переменных {IV method — instrumental variables
method) — метод получения оценок коэффициентов уравнения регрессии в
ситуации, когда некоторые стохастические объясняющие переменные
коррелированы со случайными ошибками в этом уравнении.
Модели с ошибками в измерении объясняющих переменных {errors-in-
variables models) — эконометрические модели, в которых значения
некоторых объясняющих переменных измерены с ошибками и отклонения
измеренных значений от истинных (ошибки измерений) трактуются как
случайные величины.
Обобщенная оценка наименьших квадратов, GLS оценка {GLS estimator) —
оценка вектора коэффициентов линейной модели регрессии, полученная в
результате применения обобщенного метода наименьших квадратов.
Обобщенный метод наименьших квадратов {GLS — generalized least squares) —
теоретическая процедура оценивания коэффициентов линейной модели
регрессии в ситуации, когда случайные ошибки имеют разные
дисперсии и коррелированы между собой, при этом предполагается, что
ковариационная матрица вектора ошибок невырожденна и все ее элементы
известны.
Преобразование Прайса — Уинстена {Prais-Winsten transformation) —
преобразование, приводящее к получению GLS оценки в ситуации, когда ошибки в
линейной эконометрической модели образуют процесс авторегрессии
первого порядка.
Приведенная форма системы одновременных уравнений {reduced form of
simultaneous equations) — полученная на основе структурной формы
системы одновременных уравнений система уравнений, в которой переменные,
являющиеся объясняемыми в одних уравнениях, не используются в
качестве объясняющих в других уравнениях.
Система одновременных уравнений, одновременные уравнения {simultaneous
equations) — система из нескольких регрессионных уравнений, в
которых переменные могут одновременно быть объясняемыми
переменными в одних уравнениях и объясняющими переменными в других
уравнениях.
Слабые инструменты {weak instruments) — инструментальные переменные,
слабо коррелированные с эндогенными объясняющими переменными.
Стохастические {stochastic) объясняющие переменные — объясняющие
переменные, значения которых трактуются как реализации случайных величин,

306
Часть 1. Основные понятия, элементарные методы
возможно, связанных статистической зависимостью со случайными
ошибками в модели наблюдений.
Структурная форма системы одновременных уравнений {structural form of
simultaneous equations) — система из нескольких регрессионных
уравнений, представляющая в явном виде взаимные связи между входящими в
модель переменными, показывающая, как эти переменные
взаимодействуют друг с другом. В структурной форме модели одновременных уравнений
переменная, являющаяся объясняемой переменной в одном из уравнений,
может входить в другое уравнение в качестве объясняющей переменной.
Экзогенная переменная {exogenous variable) — переменная, значения которой
определяются вне рассматриваемого уравнения регрессии. В более узком
смысле: переменная, не коррелированная с ошибкой в рассматриваемом
уравнении регрессии.
Эндогенная переменная {endogenous variable) — переменная, значения которой
определяются в рамках рассматриваемой системы уравнений регрессии. В
более узком смысле: переменная, коррелированная с ошибкой в уравнении
регрессии.

ЧАСТЬ 2
РЕГРЕССИОННЫЙ АНАЛИЗ
ВРЕМЕННЫХ РЯДОВ
Раздел 7
СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ.
МОДЕЛИ ARMA
Тема 7.1
СТАЦИОНАРНЫЕ МОДЕЛИ ARMA
Общие понятия
Под временным рядом (time series) в экономике понимается ряд значений
некоторой переменной, измеренных в последовательные моменты времени.
Для многих рядов измерения производятся через равные промежутки
времени (годовые, квартальные, недельные, дневные данные). Если принять
длину такого промежутка за единицу времени (год, квартал, неделя, день), то
можно считать, что последовательные наблюдения xl9 ..., хп переменной х
произведены в моменты t = 1, ..., п. Впрочем, для некоторых экономических
и финансовых показателей производить измерения через равные промежутки
времени не удается. Например, значения биржевых индексов на момент
закрытия фиксируются только в те дни, когда биржа работает. В последнем
случае наблюдения хХ9 ..., хп соответствуют п последовательным рабочим
дням биржи.
В начальном курсе математической статистики базовым понятием
является случайная выборка (random sample). Мы имеем п наблюдений значений
некоторого признака (фактора, характеристики) X и предполагаем, что эти
значения х19 х29 ..., хп случайным образом выбраны из некоторой
(теоретически бесконечной) совокупности, называемой генеральной совокупностью
(generalpopulation), так что х19 х2, ..., хп являются реализациями независимых
(в совокупности) случайных величин Xl9 Xl9 ...9Xn9 которые имеют
одинаковое распределение вероятностей (одинаковый закон распределения),
характеризующееся функцией распределения F(x) = Р(Х < х)9 -оо < х < оо. При этом
говорят о случайной выборке из распределения F (точнее, из
распределения, имеющего функцию распределения F).

308
Часть 2. Регрессионный анализ временных рядов
Если F — непрерывное распределение, то для него определена функция
X
плотности вероятности р(х)9 F(x) - \p{x)dx. В этом случае для любых а и Ь,
-00
-оо < a, b < go, P(a <X<b) = F(b) - F(a)9 причем знаки неравенств могут быть
здесь как строгими, так и нестрогими.
Основная отличительная особенность статистического анализа временных
рядов состоит в том, что наблюдаемая последовательность наблюдений хХ9 ...9хп
рассматривается как реализация последовательности, вообще говоря,
статистически зависимых случайных величин ХХ9 ..., Хп9 имеющих некоторое
совместное распределение с функцией распределения
F(vl9v29...9v„) = P{xx<vl9X2<v29...9X„<v„}.
Будем рассматривать в основном временные ряды, у которых совместное
распределение случайных величин ХХ9 ..., Хп имеет совместную плотность
распределения р{хх,..., хп)9 так что
F(vl9v29...9v„)= J J... jp(xX9 x29...9x„) dxxdx2—dxn.
-00 -00 -00
Пусть функция распределения F(vl9 v2,..., vn) известна (задана). Тогда
• для каждого момента t9t-\9..., п9 становится известной одномерная
функция распределения
Ft(yt) = P{Xt<vt}9
например, Fx(yx) = F(yX9 оо,..., оо);
• для каждой пары моментов tl9 tl9 1 < tx < t2 < n9 становится известной
двумерная функция распределения
Ftut2{vh9vt2)9 = P{Xh<vh9Xt2<vt2}9
например, Fl2(vl9 v2) = F(vl9 v2, oo,..., оо);
• для каждого набора моментов tX9 tl9 ..., tm9m <n9\ <tx <t2< ... <tm<n9
становится известной w-мерная функция распределения
Fh, t2,...,<m (vv v,2,..., vtJ = P{Xh <vh9Xh<vh9 ...,Xtm < vtJ9
например,Fu>..^(v^ v2,.., vm) = P{X{ <vl9X2< v2, ...9Xm < vm, oo,..., oo}.
Если совместное распределение случайных величин ХХ9 ..., Хп имеет
совместную плотность распределения р(х{9 ..., хп)9 то соответственно для
каждого набора моментов tX9 tl9 ..., tm9 m <n9 \ <tx <t2 < ... <tm <n9 становится
известной pt ^ t (xt 9xt 9 ..-9xt) — совместная плотность распределения
случайных величин X,, X,,..., X, .

Раздел 7. Стационарные временные ряды. Модели ARMA
309
Последовательность случайных величин Xl9 ..., Хп образует случайный
процесс Xt с дискретным временем {discrete-time stochastic process, discrete-
time random process) в качестве альтернативы случайному процессу с
непрерывным временем. Поскольку в данном учебнике будут рассматриваться
только такие случайные процессы, о последовательности случайных величин
Xl9 ...9Хп будем говорить просто как о случайном процессе.
Если
F{vl,v1,...,vn) = P{Xl<vx}p{X2<v2}-P{X„<vn} = f[F{vt),
п
p{xl9...,xn) = Y[p{xt),
t=\
то ряд Xl9 ..., Хп представляет случайную выборку (random sample) из
распределения, имеющего функцию распределения F{x) и функцию плотности
р{х). В связи с этим одним из элементов предварительного анализа
случайных рядов является проверка гипотезы случайности (гипотезы случайной
выборки) {randomness test):
Н0 : наблюдаемая последовательность xl9 х29 ..., хп является реализацией
случайной выборки из некоторого распределения.
Если эта гипотеза не отвергается, то для статистического анализа такой
последовательности не требуется каких-либо специальных методов,
предназначенных для последовательностей со статистически зависимыми между
собой элементами. Описание некоторых статистических критериев для
проверки гипотезы случайности приводится в Приложении П-7.
Чтобы сделать задачу статистического анализа временных рядов
доступной для практического решения, приходится так или иначе ограничивать
класс рассматриваемых моделей временных рядов, вводя те или иные
предположения относительно структуры случайного процесса Xt9 порождающего
наблюдаемый временной ряд, и структуры его вероятностных характеристик.
Одно из таких ограничений предполагает стационарность случайного
процесса Х„ порождающего наблюдаемый временной ряд.
Случайный процесс Xt9 порождающий наблюдаемый временной ряд xt9
t=l9 ..., п9 называется строго стационарным {strictly stationary) или
стационарным в узком смысле {strict-sense stationary), если для любого т {т < п)
совместное распределение вероятностей случайных величин Xt, ..., Xt такое
же, как и дляXt +Т9 ..., Xt +т9 при любых tx <t2 < ... < tm и г, таких, что 1 < tl9
tl9...9tm<n и 1 <t{ + r9...,tm + T<n;
Другими словами, свойства строго стационарного случайного процесса
не изменяются при изменении начала отсчета времени. В частности, при т-\
из предположения о строгой стационарности случайного процесса Xt следует,

310
Часть 2. Регрессионный анализ временных рядов
что закон распределения вероятностей случайной величины Xt не зависит
от t, а значит, не зависят от t и все его основные числовые характеристики
(если, конечно, они существуют), в том числе математическое ожидание
E(Xt) = ju и дисперсия D(Xt) = a2.
Значение // определяет постоянный уровень, относительно которого
колеблется анализируемый временной ряд xt9 а постоянная а характеризует размах
этих колебаний.
При проведении теоретического анализа процессов, порождающих
временные ряды, удобно предполагать (и мы будем это делать), что значение п
может быть сколь угодно большим, так что случайные величины Xt определены
для всех t- 1,2,..., и что для любого т и любого набора 1 < tx < t2 < ... < tm < оо
задано совместное распределение вероятностей случайных величин Xt, ..., Xtm,
что определяет случайный процесс Xt как бесконечную случайную
последовательность Хх, Х2,...
Более того, часто удобно предполагать, что процесс Xt может начинаться
в «бесконечном прошлом», так что t - 0, ±1, ±2, ..., и тогда должны быть
заданы совместные распределения вероятностей случайных величин Xtl, ..., Xtm
для любого т и любого набора моментов -оо < tx < t2 < ... < tm < оо.
Как уже говорилось, одно из главных отличий последовательности
наблюдений, образующих временной ряд, заключается в том, что
порождающие этот ряд случайные величины являются, вообще говоря, статистически
взаимозависимыми. Степень тесноты статистической связи между
случайными величинами Xt и Xt + T может быть измерена парным коэффициентом
корреляции
Corr(XnXt+T)= C°<X<f^ ,
где
Cov(XnXt+T) = E[(Xt -E{Xt))(Xt+T -E(Xt+T))].
Заметим, что ковариация Cov(XnXt+T) случайных величин^ nXt+T
полностью определяется совместным (двумерным) распределением этих случайных
величин. В случае строгой стационарности случайного процесса Xt это
распределение не зависит от t и является функцией только от г. Соответственно
если случайный процесс^ строго стационарный, то значение Cov(Xt,Xt+T) не
зависит от t и является функцией только от г. Будем использовать для него
обозначение у(т):
r(r) = Cov(Xt,Xt+T).
В частности,
D(Xt) = Cov(Xt,Xl) = y@).

Раздел 7. Стационарные временные ряды. Модели ARMA
311
Соответственно для стационарного случайного процесса и значение
коэффициента корреляции Corr{Xn Xt+T) зависит только от г. Будем использовать
для него обозначение р{т):
p{T) = Corr{XnXt+T) = ^.
у{0)
В частности, р{0) = 1.
Практическая проверка строгой стационарности процесса Xt на основании
наблюдения значений хХ9 ..., хп затруднительна. В связи с этим под
стационарным случайным процессом на практике часто подразумевают случайный
процесс Хп у которого
E(Xt) = fi;
D{Xt) = cr2;
Cov(Xt, Xt+T) = у{т) для любых /иг.
Случайный процесс, для которого выполнены эти три условия, называют
стационарным в широком смысле {wide-sense stationary), слабо
стационарным {weak-sense stationary, weakly stationary), стационарным второго
порядка {second-order stationary) или ковариационно стационарным {co-
variance-stationary).
Если случайный процесс является стационарным в широком смысле, то он
необязательно является строго стационарным. Возможны ситуации, когда
указанные три условия выполняются, но, например, Е{Х?) зависит от t.
В то же время и строго стационарный случайный процесс может не быть
стационарным в широком смысле просто потому, что у него могут не
существовать математическое ожидание и/или дисперсия. Примером служит
случайная выборка из распределения Коши, являющегося частным случаем
распределения Стьюдента, а именно распределением Стьюдента с одной
степенью свободы. Функция плотности этого распределения имеет вид:
р{х) = г-, -оо<х<оо.
7Г{1 + Х2)
У случайной величины Х9 имеющей такое распределение, математическое
ожидание не существует. Это вытекает из расходимости интеграла
\\x\p{x)dx = — \ —2-fdx.
i л Ц + х
В дальнейшем часто будем говорить о тех или иных свойствах
наблюдаемого временного ряда хп подразумевая под этим свойства случайного
процесса Хп порождающего наблюдаемый ряд. В частности, говоря о
стационарности рядах,, будем иметь в виду стационарность случайного процессаХг

312
Часть 2. Регрессионный анализ временных рядов
Ряд xt называется гауссовским (соответственно порождающий этот ряд
случайный процесс Xt называется гауссовским — Gaussian process), если для
каждого т и для каждого набора tl9 tl9 ..., tm совместное распределение
случайных величин Xt 9 —,Xt является w-мерным нормальным распределением.
Для гауссовского процесса понятия стационарности в узком и в широком
смыслах совпадают.
В дальнейшем, говоря о стационарности некоторого ряда хп если не
оговаривается противное, будем иметь в виду, что этот ряд (точнее,
порождающий его случайный процесс X,) стационарен в широком смысле.
Итак, пусть xt — стационарный ряд с
E(Xt) = M,D(Xt)=a2HP(T) = Corr(XnXt+T).
Поскольку в данном случае коэффициент р(т) измеряет корреляцию между
членами одного и того лее временного ряда (внутри этого ряда), его принято
называть коэффициентом автокорреляции (или просто автокорреляцией —
autocorrelation). По той же причине о ковариации y(f) = Cov(Xn Xt+T)
говорят как об автоковариации (autocovariance). При анализе изменения
величины р(т) в зависимости от значения г принято говорить об
автокорреляционной функции р(т) (autocorrelation function — ACF). Автокорреляционная
функция безразмерна, т.е. не зависит от масштаба измерения
анализируемого временного ряда. Ее значения могут изменяться в пределах от -1 до +1,
при этом р@) = 1. Кроме того, из стационарности ряда xt следует, что
р(т) = р(-т). Поэтому при анализе поведения автокорреляционных
функций обычно ограничиваются рассмотрением только неотрицательных
значений г.
График зависимости р(т) от т = 1,2, ... часто называют коррелограммой
(correlogram). Его можно использовать для характеризации некоторых
свойств механизма, порождающего временной ряд. Для дальнейшего
заметим: если xt — стационарный временной ряд и с — некоторая постоянная, то
временные ряды xt и (xt + с) имеют одинаковые коррелограммы.
Если предположить, что временной ряд описывается моделью
стационарного гауссовского процесса, то полное описание совместного распределения
случайных величин Xl9 ..., Хп требует задания (п + 1) параметров: //, /@),
у{\)9..., у(п - 1) (или //, /@), /?A),..., р(п - 1)). Это намного меньше, чем без
требования стационарности, но все же больше, чем количество наблюдений.
В связи с этим даже для стационарных гауссовских временных рядов
приходится производить дальнейшее упрощение модели с тем, чтобы ограничить
количество параметров, подлежащих оцениванию по имеющимся
наблюдениям. Рассмотрим некоторые простые по структуре модели временных рядов,
которые в то же время полезны для описания эволюции во времени многих
реальных экономических показателей.

Раздел 7. Стационарные временные ряды. Модели ARMA
313
Процесс белого шума
Процессом белого шума {white noise process) или просто белым шумом
{white noise) называют стационарный случайный процесс Хп t - О, ±1, ±2, ...,
для которого
E{Xt) = 0,D{Xt)=a2>0
и
р{т) = 0 при г^О.
Последнее означает, что при t Ф s случайные величины Xt nXs,
соответствующие наблюдениям процесса белого шума в моменты t и s,
некоррелированны. Если ряд xt гауссовский, отсюда вытекает независимость
случайных величин Xt и Xs при t Ф s, при этом для каждого m и для каждого набора
tu t2, ..., tm случайные величины Xt, ..., Xt взаимно независимы и имеют
одинаковое нормальное распределение 7V@, сг2), образуя случайную выборку
из этого распределения. Такой ряд называют гауссовским белым шумом
{Gaussian white noise process).
В общем случае даже если для каждого m и для каждого набора tl9t2, ...9tm
случайные величины Xt, ..., Xt взаимно независимы и имеют одинаковое
распределение, это еще не означает, что Xt — процесс белого шума, так как
случайная величина Xt может просто не иметь математического ожидания
и/или дисперсии (в качестве примера опять можно указать на распределение
Коши).
Временной ряд, соответствующий процессу белого шума, ведет себя
крайне нерегулярным образом из-за некоррелированности при t Ф s случайных
величин Xt иХ8. Это иллюстрирует график смоделированной реализации гаус-
совского процесса белого шума {NOISE) с D{Xt) = 0.04 (рис. 7.1I.
В связи с этим процесс белого шума не годится для непосредственного
моделирования эволюции большинства временных рядов, встречающихся
в экономике. В то же время, как увидим ниже, такой процесс является базой
для построения реалистичных моделей временных рядов, порождающих более
гладкие траектории ряда. В связи с частым использованием процесса белого
шума в дальнейшем изложении будем отличать этот процесс от других
моделей временных рядов, употребляя для него обозначение sr
В качестве примера ряда, траектория которого похожа на реализацию
процесса белого шума, можно привести ряд, образованный значениями темпов
изменения (прироста) индекса Доу — Джонса в течение 1984 г. (дневные
данные). График этого ряда показан на рис. 7.2.
Здесь и далее для моделирования и статистического анализа реализаций временных рядов
используется пакет программ статистического анализа EViews {Econometric Views).

314
Часть 2. Регрессионный анализ временных рядов
X
0.8-
0.6-
0.4
0.2
-0.2
-0.4
-0.6
NOISE
i м i I i i ) i I i i i i | i i i i | i i ) i | i i i i | i i i i | i i i i | i i i i | i i i i |—►
50 100 150 200 250 300 350 400 450 *
Рис. 7.1
DOW JONES TEMP
11111111111111111111111111111111111111111111111111
50 100 150 200 250 *
Рис. 7.2
Заметим, однако, что здесь наблюдается некоторая асимметрия
распределения вероятностей значений xt (скошенность этого распределения в сторону
положительных значений), что исключает описание модели этого ряда как
гауссовского белого шума.
Процесс авторегрессии
Одной из широко используемых моделей временных рядов является процесс
авторегрессии {autoregressive process), В простейшей форме модель
авторегрессии описывает механизм порождения ряда следующим образом (процесс
авторегрессии первого порядка —first-order autoregressive process, ARA)):
Xt=aXt_x+et9 t = l,...,n9
где sx — процесс белого шума, имеющий нулевое математическое
ожидание и дисперсию &1;
Х0 — некоторая случайная величина;
а Ф 0— некоторый постоянный коэффициент.

Раздел 7. Стационарные временные ряды. Модели ARMA
315
При этом
E(Xt) = aE(Xt_x),
так что рассматриваемый процесс может быть стационарным только при
E{Xt) = О для всех t = О, 1,..., я.
Далее,
Xt -aXt_x +et =a(aXt_2 +et_x) + et =a2Xt_2 + a£t_x + et =...=
= a'X0 + af~l£x + af~2£2 + ... + £,,
Xt_x = aXt_2 + st_x = af~lX0 + a'~2£x + a'~3£2 +... + £t_x,
X,_2 = aXt_3 + £,_2 = a1'1 X0 + аг~ъех + a'~4£2 +... + £,_2,
Л^ = aX0 + £x.
Если случайная величина Х0 не коррелирована со случайными величинами
&\9 ^2' •"» ^«' ТО
и
D(Xt) = D(aXt_x+£t) = a2D(Xt_x) + D(£t), t = l,...,n.
Предполагая, наконец, что
D{Xt) = ах для всех t - О, 1,..., и,
находим:
2 2 2 2
ах=а (Тх+сг£.
Последнее может выполняться только при условии а2 < 1, т.е. \а\ < 1. При
этом получаем выражение для ах :
гт1 - U*
Что касается автоковариаций и автокорреляций, то
Cov{X„Xt+I) =
= Cov(a'X0 + a'-xsx + а'~2£2 + ... + *„ а,+тХ0 + a'+I^ex + a'+T-2s2 + ... + st+r) =
= a2,+TD(X0)+aT(l + a2+...+a2(t-l))cr2=aT
(„1t„2 п „2Г-. 2^\
к\-а2 \-а2 j
а ^
\-а2 е
Corr(Xt,Xt+I) = ar,

316
Часть 2. Регрессионный анализ временных рядов
т.е. при сделанных предположениях автоковариации и автокорреляции
зависят только от того, насколько разнесены по времени соответствующие
наблюдения.
Таким образом, механизм порождения последовательных наблюдений,
заданный соотношениями
Xt = aXt_x +et9 f = 1,...,и,
порождает стационарный временной ряд, если
• |я| < 1;
• случайная величина Х0 не коррелирована со случайными величинами
^1? £*2? —9 sn\
. D(X0) = -^T.
\ — а
При этом Corr(Xt9 Xt+T) = р(т) = ат.
Рассмотренная модель порождает (при указанных условиях)
стационарный ряд, имеющий нулевое математическое ожидание. Однако ее можно
легко распространить и на временные ряды yt с ненулевым математическим
ожиданием E(Yt) = /и, полагая, что указанная модель относится к
центрированному ряду Xt = Yt-ju:
Yt-ju = a(Yt_x-ju) + sn f = l,...,w,
так что
Yt =aYt_x +S + sn f = 1,..., w,
где S= ju(l -a).
Поэтому без ограничения общности в текущем рассмотрении можно
обойтись моделями авторегрессии, порождающими стационарный процесс с
нулевым средним.
Продолжая рассмотрение ранее определенного процесса Xt (с нулевым
математическим ожиданием), заметим, что для него
r(l) = E(XtXl_l) = E[(aXt_,+£l)Xl_l] = ar@),
так что
Г@)
и при значениях а > О, близких к 1, между соседними наблюдениями имеется
сильная положительная корреляция, что обеспечивает более гладкий
характер поведения траекторий ряда по сравнению с процессом белого шума. При
а < О процесс авторегрессии, напротив, имеет менее гладкие реализации,
поскольку в этом случае проявляется тенденция чередования знаков последова-

Раздел 7. Стационарные временные ряды. Модели ARMA
317
а = -0.8
50 100 150 200 250 250 350 400 450 t
РИС. 7.3
50 100 150 200 250 250 350 400 450 t
РИС. 7.4
тельных наблюдений. Приведенные графики демонстрируют поведение
смоделированных реализаций временных рядов, порожденных моделями
авторегрессии Xt = aXt_x + st с а2 = 0.2 при а = 0.8 (рис. 7.3) и а = -0.8 (рис. 7.4).
Теперь необходимо обратить внимание на следующее важное
обстоятельство. На практике стартовое значение Х0 = х0, на основе которого в
соответствии с соотношением Xt = aXt_x + st получаются последующие значения
ряда хп может относиться к концу предыдущего периода, на котором — просто
в силу других экономических условий — эволюция соответствующего
экономического показателя следует иной модели, например, модели Xt = aXt_ x + st
с другими значениями а и а2. Более того, статистические данные о
поведении ряда до момента t = 0 могут отсутствовать вовсе, так что значение х0
является просто некоторой наблюдаемой числовой величиной. В обоих
случаях ряд Xt уже не будет стационарным даже при \а\ < 1. Рассмотрим
подробнее характеристики и поведение ряда в таких ситуациях.
Если не конкретизировать модель, в соответствии с которой порождались
наблюдения до момента t = 1, то значение х0 можно рассматривать как
фиксированное. При этом имеем:
Xt =а*Х0+а'~Х£х +а'~2£2 +... + £,,
E(Xt) = а'х0 + а'-хЕ{£{) + at~1E{s1) + ...+ E{st ) = a'x0,
D(^) = (fl2(M)+fl2(r-2)+... + l)^2 =
\-а2
*!=-
\-aL ' 1-я2
Cov(XnXt+T) = Cov(Xt -afx0, Xt+T -at+Tx0) =
1-я
_2
2 °в>
\-a2

318
Часть 2. Регрессионный анализ временных рядов
так что и математическое ожидание, и дисперсия случайной величины Хп
а также ковариации Cov(Xn Xt+T) зависят от t.
Будем считать, что указанный механизм порождения случайных величин Xt
действует для всех /=1,2,...
Если \а\ < 1, то при t -> оо получим
ВД)^0, ВД)-*-^, Cov(XnXt+T) = aT-^,
\—а \—а
т.е. при t —> оо значения математического ожидания и дисперсии случайной
величины Хп а также автоковариации Cov(Xn Xt + T) стабилизируются,
приближаясь к своим предельным значениям.
С этой точки зрения условие \а\ < 1 можно трактовать как условие
стабильности ряда, порождаемого моделью Xt = aXt_x + et при фиксированном
значении Х0 = х0. Наряду с только что исследованным случайным процессом Хп
Xt = а*х0 + ^ak£t-k, M<1>
к = 0
рассмотрим случайный процесс^, определяемый соотношением
^, = Z-*> ' = 1,2,...
к = 0
Имеем:
при t -> оо
V^=A + ZA^;
k=t
afxn —> 0 и Е\
2>Ч-*
k=t
= *lY,a*^0.
k = t
Таким образом, случайный процесс Xt является предельным для Xt\
процесс Xt «выходит на режим» Xt при t -> оо. При этом «выход на режим» Xt
происходит тем быстрее, чем ближе Х0 и а к 0.
Проиллюстрируем сказанное с помощью смоделированных реализаций
ряда хп порожденных моделью Xt = aXt_ { + et с ое = 0.2 и разными значениями
коэффициента а и стартового значения х0 (рис. 7.5—7.8).
Для процесса Xt имеем
E(Xt) = E
i>4-J=ix^-*)=o'
к = 0
к = 0

Раздел 7. Стационарные временные ряды. Модели ARMA
319
0.5
0
-0.5
х0 = 2; а = 0.5
2.5 4
2.0
1.5
1.0
0.5
11111111111 м 11111111 м | м м 111111111111111111111 ^
10 20 30 40 50 60 70 80 90 100 t
РИС. 7.5
х0 = 0; а = 0.5
о МЧ^\/\>/\а>*^
11111 111111111111111111111111111111II11 11111111111 ^
10 20 30 40 50 60 70 80 90 100 t
РИС. 7.6
х0 = 2; а = 0.9
X
2.5 4
2.0-|
1.5
1.0
0.5
111111111|i111рiм11111111111111111111|iш111111 ► ~0.5
10 20 30 40 50 60 70 80 90 100 t
РИС. 7.7
х0 = 0; а = 0.9
"r^WT'-^Vi
I i|iii || м м |1111|1111|1111|1111|1М I |i I м | in i| ►
10 20 30 40 50 60 70 80 90 100 t
РИС. 7.8
(
D(Xt) = D\
\
к = 0
5>V* |=1«"^^)=^1«2'=7^г
к = 0
Cov(XnXt+T) = E\
( оо у оо Л
U = 0 Ак = 0
к = 0
Г* . Л а2
-а
^агкЕ{е1к) =а<
\к = 0
1-я2
таким образом Xt — стационарный случайный процесс (в широком смысле).
Кроме того,
1
^,-1=-2>Ч-*>
к=\
так что
^м+*г = £*Ч-*=^
к = 0
т.е. Xt удовлетворяет соотношению
Xt = aXt_x + st.

320
Часть 2. Регрессионный анализ временных рядов
Поскольку st не входит в правую часть выражений для Xt_x, Xt_2, ... ,
случайная величина st не коррелирована с Xt_x, Xt_2, ... В итоге получаем, что
Xt — стационарный процесс авторегрессии первого порядка, и фактически
именно этот процесс имеется в виду, когда речь идет о стационарном
процессе авторегрессии первого порядка.
Таким образом, говоря, что процесс Xt является стационарным процессом
авторегрессии первого порядка, подразумеваем, что процесс Xt начинается
в «бесконечном» прошлом, так что соотношение Xt = aXt_x + et (с \а\ < 1)
выполняется не только для t = 1, 2,..., но и для t = 0, -1, -2,... Но тогда из этого
соотношения получаем
Xt -aXt_x +st =a(aXt_2 + £t_x) + £t =...=
= a'X0 + af~lsx + ах~2е2 +... + st = et + aet_x +... + af~2s2 + af~lsx + a'X0 =
= et+ ast_x +... + af~2s2 + al~X£x + a* {a X_x + s0) =
00
= et+ aet_x +... + af~2s2 + af~xsx + a*£0 + at+lX_x =... = £ ak£t-k >
k = 0
именно так и определялся процесс Xt, оказавшийся стационарным.
Рассмотренную модель Xt = aXt_ x + et называют процессом авторегрессии
первого порядка. Процесс авторегрессии порядка р (pth-order autoregressive
process — AR(/?)) определяется соотношениями
Xt = axXt,x + a2Xt_2 +... + apXt_p + st, ap*0,
где st — процесс белого шума с D(st) = a*.
При этом будем предполагать, что Cov(Xt_s, st) = О для всех s > 0. В таком
случае говорят, что случайные величины et образуют инновационную
(обновляющую) последовательность {innovation sequence), а случайная величина st
называется инновацией (innovation) для наблюдения в момент t. Такая
терминология объясняется тем, что наблюдаемое значение ряда в момент t
получается здесь как линейная комбинация р предшествующих значений этого
ряда плюс не коррелированная с этими предшествующими значениями
случайная составляющая et, отражающая обновленную информацию (скажем, о
состоянии экономики) на момент t, влияющую на наблюдаемое значение Хг
При рассмотрении процессов авторегрессии и некоторых других моделей
удобно использовать оператор запаздывания L (lag operator), который
воздействует на временной ряд и определяется соотношением
LXt =Xt_x.
В некоторых руководствах его называют оператором обратного сдвига
(backshift operator).

Раздел 7. Стационарные временные ряды. Модели ARMA
321
Нетрудно проверить, что оператор запаздывания обладает теми же
алгебраическими свойствами, что и оператор умножения. Поэтому для
простоты можно говорить не о применении оператора L к последовательности Хп
t = 0, ±1, ±2, а об умножении L тХг Соответственно если оператор
запаздывания применяется к раз, это обозначается Lk. В результате получаем
L Xt -Xt_k.
Единичный оператор будет выражен при этом как Z,0, так что
JL Л. * =L'JLf = Ji j,
а обратный к L оператор — как Vх:
L Xt =Xt+l.
Более подробно о свойствах оператора запаздывания говорится, например,
в работе (Канторович, 2002).
Используя оператор Lk, выражение
a\Xt-\+aixt-2+- + apXt-P
можно записать в виде:
alLXt+a2L2Xt+^^apLpXt=(alL + a2L2+... + apLp)Xn
а соотношение, определяющее процесс авторегрессии р-го порядка, в виде:
a(L)Xt=sn
где
a(L) = l-(alL + a2L2 +... + apLp).
Условие стационарности
процесса авторегрессии р-го порядка
Для того чтобы процесс авторегрессии р-го порядка a(L)Xt = et был
стационарным, необходимо1 и достаточно, чтобы все (вещественные и комплексные) корни
алгебраического уравнения a(z) = 0 (обратное характеристическое уравнение)
лежали вне единичного круга \z\ < 1 на комплексной плоскости.
В частности, для процесса ARA) имеем a(z) = 1 - az, уравнение a(z) = 0
имеет корень z = 1/а, и условие стационарности \z\ > 1 равносильно уже
знакомому нам условию | а \ < 1.
Если et не являются инновациями, то это условие не является необходимым для
стационарности процесса, определяемого соотношением a(L) Xt - et (см. задание 9 к разд. 7).

322
Часть 2. Регрессионный анализ временных рядов
При выполнении условия стационарности решение уравнения a(L)Xt - st
можно представить (см., например, {Hamilton, 1994, р. 58—59)) в виде:
1 °°
Xt=—T7£t=Y<bJ£t-j>
00
где Ь0 = 1, Xl671<0°*
7 = 0
Отсюда, в частности, следует
E(Xt) = E
U = ° J 7=0
Стационарный процесс AR(p) с ненулевым математическим ожиданием /и
удовлетворяет соотношению
a(L)(Xt-ju)=en или a(L)Xt = S + st,
где
S = a(L)jU = jU(l-al-a2-...-ap) = Jua(l).
При этом решение уравнения a{L){Xt - //) = et имеет вид:
ауь) J=0
Таким образом, если стационарный процесс AR(p) задан в виде a(L)Xt = S+ еп
то надо помнить о том, что математическое ожидание этого процесса равно не S9 a
д
A-^- а2-...~ ар)
Конечно, если S = 0, то и /и = 0. Заметим, что сумма коэффициентов здесь
не может равняться 1, иначе процесс будет нестационарным.
Для процесса ARA) имеем а{Ь) = 1 - аЬ, и если \а\ < 1, то
Xt-ju = et - A + ah + a2L2 +...)et=st+ ast_x + a2st_2 +...
1-aL
Из последнего выражения видно, что
p(k) = Corr(XnXt+k) = ak, к = 0,1,2,...
При 0 < а < 1 коррелограмма (график функции р(к) для к = 1,2, ...)
отражает показательное убывание корреляций с возрастанием интервала между
наблюдениями, при -1 < а < 0 коррелограмма имеет характер затухающей
косинусоиды.
Коррелограммы стационарного процесса ARA) при а = 0.8 и а = -0.8
приведены соответственно на рис. 7.9 и 7.10.

Раздел 7. Стационарные временные ряды. Модели ARMA
323
10 15
TTfTTTTTTI »
20 25 30 35 £
Рис. 7.9
I I I I I I I I I I I I I I I I I I I [ I I I I I I I I I I I I I I I I I ►
5 10 15 20 25 30 35 к
РИС. 7.10
Коррелограмма процесса AR(p) при р > 1 имеет более сложную форму,
зависящую от расположения (на комплексной плоскости) корней
уравнения a{z) = 0. Однако для больших значений к автокорреляция р(к) хорошо
аппроксимируется значением А вк (где в = —
nz„
наименьший по
абсолютной величине корень уравнения a(z) = 0), если этот корень является
вещественным и положительным, или заключена в интервале ±|Л0*| в
противном случае. Здесь А > 0 — некоторая постоянная, определяемая
коэффициентами ах, <я2,..., а .
Как отмечалось ранее, если Xt — стационарный временной ряд и с —
некоторая постоянная, то временные ряды Xt и {Xt + с) имеют одинаковые кор-
релограммы. Воспользуемся этим свойством для вывода одного полезного
соотношения, связывающего автокорреляции процесса AR(p). При выводе
этого соотношения в силу указанного свойства можно рассматривать процесс Xt
с нулевым математическим ожиданием.
Если умножить наХ,.* (к > 0) обе части соотношения
Xt = axXt_x + a2Xt_2 +... + apXt_p + et,
определяющего процесс AR(p) с нулевым математическим ожиданием, то
получим
XfXt-k = a\Xt-\Xt_k + a2Xt_2Xt_k +... + apXt_pXt_k + £tXt_k.
Возьмем от обеих частей математическое ожидание:
E{XtXt_k) = axE(Xt_xXt_k) + a2E(Xt_2Xt_k) + ... + apE{Xt_pXt_k) + E{stXt_k).
Заметим, что
E{stXt_k) = 0 (поскольку et — инновация),
r(s) = Cov(XtXt_s) = E(XtXt_s) (поскольку E(Xt) = 0),

324 Часть 2. Регрессионный анализ временных рядов
тогда имеем
Y(k) = alY(k-\) + a2y{k-2) + ... + apy(k-p)9 к>0.
Разделив обе части последнего выражения на у@), придем к системе
уравнений Юла—Уокера (Yule-Walker equations):
р(к) = ахр(к -1) + а2р(к - 2) +... + арр(к - р), к> 0.
Эта система позволяет последовательно находить значения
автокорреляций и дает возможность, используя первые р уравнений, выразить
коэффициенты я • через значения первых р автокорреляций, что можно непосредственно
использовать при подборе модели авторегрессии к реальным статистическим
данным (об этом см. ниже).
ПРИМЕР 7.1.1
Рассмотрим процесс авторегрессии ARB):
Xt = 4.375 +0.25 *м -0.125Х,_2 +*,.
Уравнение a(z) = 0 принимает в этом случае вид:
l-0.25z + 0.125z2=0, или z2-2z + 8 = 0,
и имеет корни zl2=l±i Оба корня по абсолютной величине больше 1,
так что процесс стационарный. Математическое ожидание этого процесса
равно:
8 4.375
М~1-ах-а2 " 1-0.25 + 0.125" '
так что траектории этого процесса флуктуируют вокруг уровня 5.
Для построения коррелограммы воспользуемся уравнениями Юла — Уокера.
В нашем случае/? = 2, так что
р(к) = 0.25р(к-1)-0Л25р(к-2\ к>0.
По определению р@) = 1. Для р(\) имеем
р(\) = 0.25р@) - 0.125/К-1) = 0.25 - 0.125рA),
откуда находим
рA)= °25 =- = 0.222.
1 + 0.125 9
Далее последовательно находим
рB) = 0.25рA) -0.125 /КО) = 0.25 • 0.222 -0.125 = -0.069,
рC) = -0.045, рD) = -0.003, рE) =-0.005 и т.д.

Раздел 7. Стационарные временные ряды. Модели ARMA
325
р<
0.24-
0.20-
0.16-
0.12-
0.08-
0.04-
П -
-0.04 -
-П ПЯ -
i
I
1
I
1
1
1
1
El
г-
2
i
i i i i i
3 4 5 6 7
Рис. 7.11
i
8
i i
9 10
к
х *
10-
8-
6-
' ARB)
IfffffflrnRNm
^"fTflTPffff
2-
0-
w
I I 1 I I I I I 1 I 1 1 1 I I 1 I 1 1 I I I 1 I 1 1 1 1 1 1 1 1 1 1 1 1 М 1 | 1 1 1 1 1 1 1 1 1 ' *■
50 100 150 200 250 250 350 400 450 t
Рис. 7.12
Корреляции даже между соседними наблюдениями очень малы, поэтому
можно ожидать, что поведение траекторий такого ряда не очень существенно
отличается от поведения реализаций процесса белого шума. Теоретическая
коррелограмма рассматриваемого процесса и смоделированная реализация
этого процесса показаны на рис. 7.11 и 7.12 соответственно.■
Процесс скользящего среднего
Еще одной простой моделью порождения временного ряда является процесс
скользящего среднего порядка q (qth-order moving average process — MA(q)).
Согласно этой модели
Xt=et+ bxet.x + b2st_2 +... + bqst_q, bq Ф 0,
где et — процесс белого шума с D(st) = сте2.
Такой процесс имеет нулевое математическое ожидание. Модель можно
обобщить до процесса, имеющего ненулевое математическое ожидание //,
полагая
xt ~ М = et + b\£t-\ + b2£t-i + • • • + bq£t-q *
т.е.
Xt=j£ + et+ bxst_x + b2st_2 +... + bqst_q.
При q = 0 и ju = 0 получим процесс белого шума. Если q = 0, то
Xt= ju + st+ bst_x — скользящее среднее первого порядка (МАA)).
В последнем случае
D(Xt) = (l + b2)*2£, E[(Xt-M)(Xt_x-ju)] = ba2£,

326
Часть 2. Регрессионный анализ временных рядов
Е[(Х,-МХ,_к-М)] = 0, к>\,
так что процесс Xt является стационарным с
Е(Х,) = М, D(Xt) = (l + b2)a2E,
№ =
Автокорреляции этого процесса равны
fl,
р(к) = <
(l + b:
bcrl
0,
W2
к--
к--
= 0,
= 1,
к>1.
\ + Ь2
о ,
к = 0,
к = 1,
к>\,
т.е. коррелограмма процесса имеет весьма специфический вид.
Коррелированными оказываются только соседние наблюдения. Корреляция между ними
положительна, если Ъ > 0, и отрицательна при Ъ < 0. Соответственно процесс
МАA) с Ь > 0 имеет более гладкие по сравнению с белым шумом реализации,
а процесс МАA) с Ь < 0 — менее гладкие по сравнению с белым шумом
реализации. Заметим, что для любого процесса МАA)
|рAI<0.5,
т.е. корреляционная связь между соседними наблюдениями довольно слабая,
тогда как у процесса ARA) такая связь может быть сколь угодно сильной
(при значениях \а\9 близких к 1).
Модель МА(д) кратко можно записать в виде:
где b{L)=\+bxL + ... + bqLq.
Для нее
Г(к)^Е[(Х,-М)(Х,_к-М)] =
0,
0<k<q,
k>q.
Таким образом, МА(#) является стационарным процессом с математическим
ожиданием //, дисперсией
<т2х=(\ + Ь?+... + Ь2я)<т2в
и автокорреляциями

Раздел 7. Стационарные временные ряды. Модели ARMA
327
q-k
2>А+*
7 = 0
Я
z*;
7=0
0,
к = 0, \,...,q,
k-q + l,q + 2,..
р(к)=
Здесь статистическая связь между наблюдениями сохраняется в течение
q единиц времени (т.е. «длительность памяти» процесса равна q).
ПРИМЕР 7.1.2
Рассмотрим три процесса:
а) процесс МАA) с Ь = 0.8 и E(Xt) = 6, т.е. Xt=6 + et +0.8*м ;
для него р(Х) = -
0.8
= 0.488;
1 + 0.82
б) процесс МАA) с Ь - -0.8 и E{Xt) = 6 — для него имеем
-0.8
РA) =
1 + 0.82
= -0.488.
Коррелограммы этих двух процессов приведены на рис. 7.13 и 7.14.
Смоделированные реализации этих двух процессов с а* = 1
показаны на рис. 7.15 и 7.16;
6 = 0.8
Рис. 7.13
12 456789 10 k
РИС. 7.14
в) процесс MA{2)Xt = 5 + et- 0.75£,_, + 0A25st_2 — для него имеем
,(,). АЦ*Л_ . -0.75-0.750.125 _
hl+tf+b\ l + 0.752+0.1252

328
Часть 2. Регрессионный анализ временных рядов
50 100 150 200 250 250 350 400 450 t
Рис. 7.15
0 1111111111111111111111111111111111111111 |м м| 1111' ►
50 100 150 200 250 250 350 400 450 t
РИС. 7.16
р \
10-
0.8-
0.6-
0.4-
0.2-
0 -
0.2-
0.4-
0 6-
i
ш
I
1
■
i i i i i i i i i i *■
123456789 10 к
Рис. 7.17
пG\ =
0.125
U I II I I I М I I I I I I I | I I II I I I I I 1 I I I I I I М I | I I М | I II I | I I I I
50 100 150 200 250 250 350 400 450 t
Рис. 7.18
= 0.079.
1.578
Коррелограмма и смоделированная реализация этого процесса
приведены на рис. 7.17 и 7.18.И
Если влияние прошлых событий ослабевает с течением времени
показательным образом, так что bj = aJ, 0 < а < 1, то искусственное предположение
о том, что ряд st начинается в «бесконечном прошлом», приводит к модели
скользящего среднего бесконечного порядка МА(оо):
где
у = о
оо оо
b(L) = l + ^bjLJ и 2>у1<«>-
У=1 7=0

Раздел 7. Стационарные временные ряды. Модели ARMA
329
Ранее было показано, что такое же представление допускает
стационарный процесс авторегрессии первого порядка ARA):
Xt -aXt_x +en |я|<1,
т.е. в рассматриваемом случае процесс МА(оо) эквивалентен процессу ARA).
Вообще, всякий стационарный процесс AR(p), задаваемый соотношением
a(L)(Xt-ju) = sn a(L) = l-(a{L + a2L2 + ... + apLp),
где st — инновации, можно представить в форме процесса МА(оо):
Xt=ju + c(L)st,
где
00 1 00
c(L)=ZcjlJ=-t; и 2>,1<0°-
(См., например, {Hamilton, 1994, section 3.4)).
В связи с последним обстоятельством, естественно, возникает следующий
вопрос. Если оказывается возможным обратить авторегрессионное
представление a(L)(Xt - ju) = st стационарного процесса Хп получая
представление этого процесса в виде скользящего среднего бесконечного порядка, то
можно ли аналогичным образом обратить МА-представление Xt - ju= b{L)st
стационарного процесса Хп получая при этом его авторегрессионное
представление?
Если процесс Xt имеет МА(д)-представление
ч
Xt-/u = b(L)£t = Y.bj£t-j> 6о=1>
7=0
то положительный ответ на поставленный вопрос будет в случае, когда
выполнено условие обратимости (invertibility condition):
все корни алгебраического уравнения h(z) = 0 лежат
вне единичного круга \z\ < 1 на комплексной плоскости.
При выполнении этого условия для процесса Xt существует
авторегрессионное представление
d(L)(Xt-<u) = e„
где
j = 1 0\Ь) j = i
так что
( «
(Xt-M) = e»

330
Часть 2. Регрессионный анализ временных рядов
т.е.
(Xt -ft) = dl(Xt_l -ju) + d2(Xt_2 -м)+...+е,.
(По поводу абсолютной суммируемости коэффициентов dj см., например,
{Pollock, 1999).)
Для процесса скользящего среднего первого порядка X, = ju + s, + bst_x
условие обратимости принимает вид: \Ъ\ < 1, поэтому рассмотренные в
пунктах а) и б) примера 7.1.2 МАA)-представления обратимы. Для процесса
скользящего среднего второго порядка, рассмотренного в пункте в) того же
примера, уравнение b(z) = 0 принимает вид:
l-0.75z + 0.125z2=0.
Корни этого уравнения B и 4) находятся за пределами единичного круга, так
что рассмотренное МАB)-представление также обратимо.
Соответственно, например, в первом случае на основании МА(
^-представления X, = 6 + st + 0.&£,_\ получаем
b{L) = 1 + 0.81, X, -6 = A + 0.81)*,,
1
1 + 0.81
(l-0.SL + 0.S2L2 --■)(Х,-6)=€„
(Х,-6) = 0.8(Х,_,-6)-0.82(Х,_2-6) + --- + £,
(Х,-6) = е„
X, =6A-0.8 + 0.82----) + 0.8Хм-0.82Х,_2+--- + ^ =
6
1 + 0.8
+ 0.8Х,_,-0.82Х,_2 +■■■ + £,.
Что получается, если в МА( 1 ^представлении Xt = /л + е, + Ъ е,_, имеем | Ъ \ > 1 ?
В такой ситуации
x,+i -М = *,+\ +Ье,=Ъ\е, + -*,+1 \=b\£t +JFe'
= b\l + -F
b
£t>
где F = LX — оператор прямого сдвига, FXt =Xt+l, так что
If. 1
s,=-\l + -F
' b{ b
(xt+l -//)=!
!_IF+1F2_ 1F3+.
(*t+i-M) =
if 1 1 1 л
b b b
(X,+\~ ») = T<<x,+2- »)—72<<х,+г- ») + Тг(х,+4- V) — - + be,,
bob

Раздел 7. Стационарные временные ряды. Модели ARMA
331
хм=А
j_ j i_
b*b2 b3 J b f~ b2 m b5
1"'T + 7T■•TГ + •,, + TX'+2 ~UX'+i +TTXt+*"" + b£t>
Иначе говоря, в данном случае значение Xt определяется не через
прошлые, а через будущие значения Xt+k9 Л = 1, 2,...
Смешанный процесс авторегрессии —
скользящего среднего (процесс авторегрессии
с остатками в виде скользящего среднего)
Процесс Xt с нулевым математическим ожиданием, принадлежащий классу
смешанных процессов авторегрессии — скользящего среднего,
характеризуется порядками р и q его AR и МА составляющих и обозначается как процесс
ARMA(p, q) {autoregressive moving average, mixed autoregressive moving
average). Более точно, процесс Xt с нулевым математическим ожиданием
принадлежит классу ARMA(p, q\ если
р я
xt = Y<aJxt-j + llbJ£t-j> aP*°> ья*°>
у=1 у=0
где st— инновации, образующие процесс белого шума с D{st) = <rf2, и b0 = 1.
В операторной форме последнее соотношение имеет вид:
a{L)Xt=b{L)sn
где a{L) и b(L) имеют тот же вид, что и в определенных ранее моделях AR(p)
и MA{q). При этом для определенности обычно предполагается, что
многочлены а{Ь) и b{L) не имеют общих корней (см. Замечания 7.1.2—7.1.4).
Если процесс имеет постоянное математическое ожидание /и, то он
принадлежит классу ARMA(p, q) при следующем условии:
р я
у=1 у=0
Отметим следующие свойства ARMA(p, q) процесса Xt с E{Xt) = /л (см.,
например, {Hamilton, 1994, р. 59—61)):
• если все корни алгебраического уравнения a{z) = 0 лежат вне
единичного круга \z\ < 1 на комплексной плоскости, то Xt — стационарный
процесс и существует эквивалентный ему процесс МА(оо)

332
Часть 2. Регрессионный анализ временных рядов
Xt=ft+^Cjet_j9 с0=1, ]Г|су1<00' или Xt=ii + c(L)en
у=0 7=0
где
• если все корни уравнения b(z) = 0 лежат вне единичного круга \z\ < 1
(условие обратимости), то существует эквивалентное
представление процесса Xt в виде процесса авторегрессии бесконечного
порядка AR(oo)
00
Х,-р = %^(Х,ч-р) + еп или d(L)(Xt-n) = sn
7 = 1
где
у = 1 b\Z)
Отсюда вытекает, что стационарный процесс ARMA(p, q) можно
аппроксимировать процессом скользящего среднего достаточно высокого порядка,
а при выполнении условия обратимости его можно также аппроксимировать
процессом авторегрессии достаточно высокого порядка.
Специфику формы коррелограммы процесса ARMA(p, q) в общем случае
указать труднее, чем для моделей AR(p) и MA(q). Отметим только, что для
значений к > р коррелограмма процесса a(L)Xt = b{L)st выглядит так же, как
и коррелограмма процесса авторегрессии a(L)Xt = sr Так, для процесса
ARMAA, 1)
р(к) = ах р(к -1) для к = 2, 3,...,
как и у процессаX, = aXt_x + sr При этом, однако, р(Х) Ф ах.
Предпосылкой для обоснования использования моделей ARMA является
следующий факт. Если ARMA(p1? qx) ряд Xt и ARMA(p2, q2) ряд Yt
статистически независимы между собой и Z, = Xt + Yt9 то типичным является
положение, когда Z, является ARMA(p, q) рядом, у которого
р=Р\+Рг,
q=P\+qi, если/?! + q2 >p2 + q\ 9
q=Pi + q\, если/?2 + q\ >Р\ + qi.
Возможны также ситуации, когда значения pnq оказываются меньше
указанных значений. (Такие ситуации возникают в случаях, когда многочлены
ax{z) и aY(z)9 соответствующие авторегрессионным частям процессов^ и Yt9
имеют общие корни.)

Раздел 7. Стационарные временные ряды. Модели ARMA
333
В частном случае, когда оба ряда имеют тип ARA), но с различными
параметрами, их сумма имеет тип ARMAB, 1).
В экономике многие временные ряды являются агрегированными. Из
указанного выше факта следует, что если каждая из компонент отвечает простой
модели AR, то при независимости этих компонент их сумма будет ARMA
процессом. Такого же рода процесс получим, если часть компонент имеет
тип AR, а остальные компоненты — тип МА. Единственным исключением
является случай, когда все компоненты являются МА процессами — здесь
получаем МА процесс.
Предположим, наконец, что истинный экономический ряд отвечает АК(р)
модели, но значения этого ряда измеряются со случайными ошибками,
образующими процесс белого шума, т.е. МА@). Тогда наблюдаемый ряд имеет
тип АЮАА(р,р).
v Замечание 7.1.1. Как было сказано выше, стационарный ARMA(/>, q)
процесс Xt можно представить в виде процесса скользящего
среднего бесконечного порядка, а если этот процесс удовлетворяет условию
обратимости, то его можно представить и в виде процесса
авторегрессии бесконечного порядка. Соответственно такой процесс можно
аппроксимировать как стационарным процессом AR(p) достаточно
высокого порядка, так и процессом скользящего среднего MA(q)
достаточно высокого порядка.
Таким образом, в практических задачах можно было бы и вовсе
обойтись без использования моделей ARMA, ограничиваясь либо
AR, либо МА моделями. При этом, однако, количество
коэффициентов, подлежащих оцениванию, может оказаться слишком большим
(что снижает точность оценивания) и даже превосходить количество
имеющихся наблюдений. В этом смысле модели ARMA могут быть
более экономными (more parsimonious models).
v Замечание 7.1.2. С вопросом о выборе более экономной модели
связана и так называемая проблема общих множителей (common factor
problem). Поясним, что при этом имеется в виду, на следующем
примере. Рассмотрим модель ARMAB, 2):
Xt = 13Xt_x - 0AXt_2 +st- 0.3£M - 0.4^_2.
С использованием оператора запаздывания эта модель
записывается в виде:
a(L)Xt=b(L)sn
где
a(L) = l-l.3L + 0AL2 =A-0.8L)A-0.5L),
b(L) = l-03L-0AL = (l-0.8L)(l + 0.5L).

334
Часть 2. Регрессионный анализ временных рядов
Таким образом, многочлены a(L) и b(L) имеют общий множитель
A-0.81)и
A - 0.81)A - 0.5ВД = A - 0.8L)A + 0.5L)sr
Сократив обе части последнего уравнения на этот общий
множитель, получим
(l-0.5L)Xt = (l+0.5L)sn
т.е.
Xt = 0.5Xt_x + st + 0.5et_1.
Для процесса X, получается представление в виде модели ARMAA, 1),
которая более экономна по сравнению с моделью ARMAB, 2).
Наличие общих множителей у многочленов a(L) и b(L) в представлении
a(L)Xt = b(L)st модели ARM А значительно затрудняет оценивание
коэффициентов такой модели. Несколько забегая вперед, проиллюстрируем (табл. 7.1)
это результатами оценивания коэффициентов модели
Xt = axXt_x + a2Xt_2 + st + bxst_x + b2st_2
по смоделированной реализации (длины 100) модели
Xt =\3Xt_x -QAXt_2 +st -0.3^M -0.4^_2.
Таблица 7.1
Объясняемая переменная X
Method: Least Squares; Sample (adjusted): 3 100; Included observations: 98 after adjusting endpoints;
Convergence achieved after 16 iterations; Backcast: 1 2
Переменная
ARA)
ARB)
MAA)
MAB)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Inverted AR Roots
Inverted MA Roots
Коэффициент
0.188566
0.088017
0.809562
0.183854
0.544602
0.530068
0.892383
74.85665
-125.8557
0.41
-0.40-0.14/
Стандартная
ошибка
0.732636
0.364477
0.726516
0.392497
/-статистика
0.257381
0.241489
1.114307
0.468421
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Durbin-Watson stat
-0.22
-0.40 + 0.14/
Р-значение
0.7974
0.8097
0.2680
0.6406
-0.142850
1.301768
2.650117
2.755626
1.989028

Раздел 7. Стационарные временные ряды. Модели ARMA
335
Полученные оценки всех 4 коэффициентов не имеют ничего общего с
коэффициентами модели, порождавшей наблюдения. Все эти оценки
статистически незначимы. В то же время если оценивать не модель ARMAB, 2),
а модель ARMAA, 1), то результаты получаются другими (табл. 7.2).
Таблица 7.2
Объясняемая переменная X
Method: Least Squares; Sample (adjusted): 2 100; Included observations: 99 after adjusting endpoints;
Convergence achieved after 6 iterations; Backcast: 1
Переменная
ARA)
MAA)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Inverted AR Roots
Inverted MA Roots
Коэффициент
0.458982
0.529106
0.542302
0.537583
0.880745
75.24399
-126.8929
0.46
-0.53
Стандартная
ошибка
0.115096
0.108628
/-статистика
3.987819
4.870793
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Durbin-Watson stat
Р-значение
0.0001
0.0000
-0.141407
1.295189
2.603897
2.656324
1.969688
Полученные оценки коэффициентов имеют высокую статистическую
значимость и весьма близки к значениям коэффициентов ARMAA,
^-представления модели, порождавшей данные.
v Замечание 7.1.3. Пусть Xt — процесс типа ARMA(p, q), a(L)Xt =
- b(L)sr Выше отмечалось, что если все корни алгебраического
уравнения a(z) = 0 лежат вне единичного круга \z\ < 1 на комплексной
плоскости, то Xt — стационарный процесс. Но такой процесс может
быть стационарным и в случае, когда уравнение a(z) = 0 имеет корень
z с \z\ = 1. Поясним это следующим простым примером.
Пусть Xt - sr Этот процесс стационарный. Рассмотрим разность:
Xt =Xt_x:
Xt -Xt_x - st- st_v
Последнее выражение записывается в виде:
(l-L)Xt = (\-L)en
т.е. a(L)Xt = b{L)st, где a{L) = 1 - L и b(L) = 1 - L. Иными словами,
для процесса X, получили ARMAA, 1) представление

336
Часть 2. Регрессионный анализ временных рядов
Xt -Xt_x + £t - £t_l9
для которого уравнение a(z) = О имеет корень z = 1.
v Замечание 7.1.4. В общем случае, если у ARMA(p, q) процесса Хп
a(L)Xt - b(L)sn многочлены a(z) и b(z) не имеют общих корней,
условие нахождения всех корней уравнения a(z) = О вне единичного
круга \z\ < 1 является необходимым и достаточным для
стационарности процесса Хг
v Замечание 7.1.5. Представить в виде процесса скользящего среднего
бесконечного порядка можно не только стационарный процесс Xt
типа ARMA(p, q), но фактически и любой стационарный процесс,
встречающийся на практике. Это вытекает из так называемого
разложения Вольда (Wold's decomposition). Вольд в работе (Wold, 1938)
показал, что любой стационарный в широком смысле процесс Xt с
нулевым математическим ожиданием может быть представлен в виде:
00
xi = TicJet-j+zf
7=0
00
гдес0= 1и J^cj <oo,
7 = 0
st — процесс белого шума;
Z, — стационарный случайный процесс с нулевым математическим
ожиданием, Cov(Zn et_j) = 0 для всех у, и значение Z,
можно сколь угодно точно предсказать на основании линейной
функции от прошлых значений процесса^ : Xt_l9Xt_2,...
Тем самым стационарный процесс Xt представляется в виде суммы
двух компонент: линейно недетерминированной (linearly indeter-
00
ministic) компоненты Xе/^-у и линейно детерминированной (/ше-
7 = 0
arly deterministic) компоненты Zt. Если вторая компонента в
разложении Вольда отсутствует, т.е. Z, = 0, то процессе, называется чисто
линейно недетерминированным (purely linearly indeter-ministic).
Таким образом, если стационарный случайный процесс с нулевым
математическим ожиданием является чисто линейно недетерминированным, то
он представим в виде процесса скользящего среднего бесконечного порядка
00 00
Xt = Zc7 st-j> где со = ! и Zcj < °° •
у=о ;=о

Раздел 7. Стационарные временные ряды. Модели ARMA
337
В качестве тривиального примера линейно детерминированного
стационарного процесса с нулевым средним можно указать на модель случайного
уровня:
Xt = Х0, t = 1,2,...,
где Х0 — случайная величина, имеющая нулевое математическое ожидание
и конечную дисперсию.
В практических исследованиях обычно сразу предполагают отсутствие
линейно детерминированной компоненты.
Модели ARMA, учитывающие
наличие сезонности
Если наблюдаемый временной ряд обладает выраженной сезонностью, то
модель ARMA, соответствующая этому ряду, должна содержать составляющие,
обеспечивающие проявление сезонности в порождаемой этой моделью
последовательности наблюдений.
Для квартальных данных чисто сезонными являются стационарные
модели сезонной авторегрессии первого порядка (SAR(l) —first order seasonal
autor egress ion)
Xt=a4Xt_A+st, |д4|<1,
и сезонного скользящего среднего первого порядка (SMA(l) —first order
seasonal moving average)
Xt=et+b4£t_4.
В первой модели
p(k) = akJA для к - Am, m = 0, 1,2,...,
p(k) = 0 для остальных к > 0.
Во второй модели
р@) = 1, рD) = Ь49
р(к) - 0 для остальных к > 0.
Смоделированные реализации модели SAR(l) с а4 = 0.8 и модели SMA(l)
с Ь4 = 0.8 приведены соответственно на рис. 7.19 и 7.20.
Комбинации несезонных и сезонных изменений реализуются, например,
в моделях ARMA(A, 4), 1):
Xt = axXt_x + aAXt_A +st+bx st_x
hARMAA,A,4)):
Xt = axXt_x +st+bx st_x + b4st_4.

338
Часть 2. Регрессионный анализ временных рядов
~4 ||||||ц||||||||i||||||ц||||||щ|||м||мц|мм| ►
10 20 30 40 50 60 70 80 90 100 t
РИС. 7.19
10 20 30 40 50 60 70 80 90 100 t
Рис. 7.20
Следующие два графика показывают поведение смоделированных
реализаций таких рядов при ах = —, а4 = , Ь4 =— в первой модели (рис. 7.21)
и при ах = 0.4, Ьх = 0.3, Ь4 = 0.8 во второй модели (рис. 7.22).
ARMA(A,4),1)
ARMAA,A,4))
~4 ||||||1М1|||1 i|i|||||щ||||i|iii11м 11|1И1|мм| ►
10 20 30 40 50 60 70 80 90 100 t
РИС. 7.21
10 20 30 40 50 60 70 80 90 100 t
Рис. 7.22
Заметим, что для первой модели уравнение a(z) = 0 принимает вид:
l--z +—z4=0, т.е. z4-32z + 48 = 0;
3 48
корни этого уравнения z{ = 2, z2 = 2, z3 =- 2 + / V8, z4 = -2 - i V8 лежат вне
единичного круга, что обеспечивает стационарность рассматриваемого процесса.
Во второй модели уравнение a{z) = 0 принимает вид:
l-0.4z = 0;
корень этого уравнения z = 2.5 > 1, так что и эта модель стационарна.

Раздел 7. Стационарные временные ряды. Модели ARMA
339
Кроме рассмотренных примеров аддитивных сезонных моделей,
употребляются также мультипликативные спецификации, например:
(l-axL)Xt=(l + bxL)(l + b4L4)£,
(\-axL)(\-a4LA)Xt=(\ + bxL)et.
Первая дает
Xt = axXt_x + st + bxst_x + b4st_4 + bxb4et_5,
а вторая —
Xt = axXt_x + a4Xt_4 - axa4Xt_5 +et+ bxst_x.
В первой модели допускается взаимодействие составляющих скользящего
среднего на лагах 1 и 4 (т.е. значений st_x и st_4\ а во второй —
взаимодействие авторегрессионных составляющих на лагах 1 и 4 (т.е. значенийXt_x nXt_4).
Конечно, эти две модели являются частными случаями аддитивных моделей
Xt = axXt_x + St +ЬХ£,_Х + V,-4 + V,-5 >
Xt = axXt_x + a4Xt_4 + a5Xt_5 +st+ bxst_x
с b5 = bxb4, a5 - -axa4. При приближенном выполнении последних
соотношений (по крайней мере, если гипотезы о наличии таких соотношений не
отвергаются), естественно перейти от оценивания аддитивной модели к оцениванию
мультипликативной модели, опять следуя принципу экономности модели
(parsimony model). Впрочем, каких-либо теоретических оснований для
предпочтения одной формы сезонности перед другой (мультипликативной или
аддитивной) не существует.
Более подробно с сезонными ARMA моделями можно ознакомиться,
например, в {Ghysels, Osborn, 1991).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется временным рядом? Какова отличительная особенность анализа
временных рядов?
2. Какой временной ряд называется строго стационарным (в узком смысле)?
3. Какой временной ряд называется слабо стационарным (в широком смысле)?
4. Как соотносятся между собой свойства строгой и слабой стационарности
временного ряда?
5. Какой временной ряд называется гауссовским? Как соотносятся между собой
свойства строгой и слабой стационарности в случае гауссовости временного ряда?
6. Что представляет собой автокорреляционная функция стационарного временного
ряда? Что такое коррелограмма?
7. Почему приходится упрощать модель даже в классе стационарных гауссовских
временных рядов?
8. Что представляет собой процесс белого шума? Как выглядят реализации процесса
белого шума?
9. Что представляет собой процесс авторегрессии первого порядка? Как выглядят
реализации этого процесса при разных значениях его параметров?

340
Часть 2. Регрессионный анализ временных рядов
10. В каком случае процесс авторегрессии первого порядка является слабо
стационарным? Как вычисляются дисперсия и корреляционная функция стационарного
процесса авторегрессии первого порядка?
11. Как ведут себя реализации процесса авторегрессии первого порядка при
фиксированном стартовом значении ряда?
12. От каких факторов зависит скорость выхода процесса авторегрессии первого
порядка, удовлетворяющего условию стабильности, на стационарный режим?
13. Что представляет собой процесс авторегрессии порядка/7? Как записывается
уравнение, определяющее такой процесс, с помощью оператора запаздывания?
14. Каково условие стационарности процесса авторегрессии порядка/7?
15. В каком виде можно представить стационарный процесс авторегрессии порядка/7?
Как выглядит это представление для стационарного процесса первого порядка?
16. Как выглядит коррелограмма стационарного процесса авторегрессии порядкар!
17. Что представляет собой система уравнений Юла — Уокера? Для каких целей
используется эта система уравнений?
18. Что представляет собой процесс скользящего среднего порядка ql Как
записывается уравнение, определяющее такой процесс, с помощью оператора запаздывания?
19. Когда процесс скользящего среднего порядка q является стационарным?
20. Чему равна дисперсия процесса скользящего среднего порядка ql Чему равны
автокорреляции этого процесса?
21. Чему равны автокорреляции процесса скользящего среднего первого порядка?
Как это отражается на поведении реализаций такого процесса?
22. Что представляет собой модель ARMA(p, q)l Как записывается такая модель
с использованием оператора запаздывания? Какие представления допускает такая
модель в случае выполнения условия стационарности? В случае выполнения
условия обратимости?
23. Каковы предпосылки использования ARMA моделей?
24. В чем состоит (применительно к моделям ARMA) проблема общих множителей?
25. Что понимается под экономностью модели ARMA?
26. Как моделируется сезонность в рамках моделей ARMA?
Тема 7.2
ПОДБОР СТАЦИОНАРНОЙ МОДЕЛИ ARMA
ДЛЯ РЯДА НАБЛЮДЕНИЙ
Если предположить, что некоторый наблюдаемый временной ряд хи ..., хп
порождается моделью ARMA, то при этом возникает проблема подбора
конкретной модели из этого класса. Решение этой проблемы предусматривает
три этапа:
1) идентификация модели (identification stage);
2) оценивание модели (estimation stage);
3) диагностика модели (diagnostic checking stage).
На этапе идентификации производится выбор некоторой частной модели
из всего класса ARMA, т.е. выбор значений р и q. Используемые при этом
процедуры являются не вполне точными, что при последующем анализе мо-

Раздел 7. Стационарные временные ряды. Модели ARMA
341
жет привести к выводу о непригодности идентифицированной модели и
необходимости замены ее альтернативной моделью. На этом же этапе делаются
предварительные грубые оценки коэффициентов al9 а29 ..., ар9 bl9 Ъ29 ..., bq
идентифицированной модели.
На втором этапе производится уточнение оценок коэффициентов модели
с использованием эффективных статистических методов. Для оцененных
коэффициентов вычисляются приближенные стандартные ошибки, которые
при дополнительных предположениях о распределениях случайных
величин Х{9 Х29 ... дают возможность строить доверительные интервалы для этих
коэффициентов и проверять гипотезы об их истинных значениях с целью
уточнения спецификации модели.
На третьем этапе применяются различные диагностические процедуры
проверки адекватности выбранной модели имеющимся данным.
Неадекватности, обнаруженные в ходе такой проверки, могут указать на необходимую
корректировку модели, после чего производится новый цикл подбора, и т.д.
до тех пор, пока не будет получена удовлетворительная модель.
Разумеется, если уже имеется достаточно отработанная и разумно
интерпретируемая модель эволюции того или иного показателя, можно обойтись и
без этапа идентификации.
Если ряд порождается моделью ARMA(p, q)9 то в дальнейшем для
краткости будем обозначать это как Xt ~ ARMA(p, q). Соответственно если ряд
порождается моделью AR(p), то Xt ~ AR(/j), и если ряд порождается моделью
МА(я),тоЯ;~МА(я).
Идентификация стационарной модели ARMA
Основной отправной точкой для идентификации стационарной модели
ARMA является наличие различий в поведении автокорреляционных и
частных автокорреляционных функций (ACF — autocorrelation function,
PACF— partial autocorrelation function) рядов, соответствующих различным
моделям ARMA.
О поведении автокорреляционных функций для различных моделей
ARMA было сказано выше. Однако по поведению только автокорреляционной
функции трудно идентифицировать даже порядок чистого (без МА
составляющей) процесса авторегрессии. Решению этого вопроса помогает
рассмотрение поведения частной автокорреляционной функции (PACF)
стационарного процесса Хг Ее значение Ppart(k) на лаге к — частная автокорреляция
{partial autocorrelation) — определяется как значение коэффициента
корреляции между случайными величинами Xt и Xt+k9 очищенными от влияния
промежуточных случайных величин Xt+ х,..., Xt+k_ x.
Это соответствует тому, что ppart(k) является коэффициентом при Xt_k
в линейной комбинации случайных величин Xt_l9 ..., Xt_k9 наилучшим
образом приближающей случайную величину Хг Исходя из последнего, можно

342
Часть 2. Регрессионный анализ временных рядов
показать (см., например, {Hamilton, 1994, р. 111)), что рраг,(к) определяется
как решение относительно ак системы первых к уравнений Юла — Уокера
p(s) = alp(s-l) + a2p(s-2) + ... + akp(s-k), s = l,2,...,k,
которую в этом случае удобнее записать в виде:
p(s - \)ах + p(s - 2)а2 + ... + p(s - к)ак = p(s), s = l,2,...,k,
подчеркивая, что неизвестными здесь являются ах, а2, ..., ак, а /?A - к), ...,
р(к - 1) — известные коэффициенты. Исходя из этого и применяя правило
Крамера решения системы к линейных уравнений с к неизвестными, находим,
что вычисление PACF можно производить по формулам:
РраЛ0) = и
Рраг,$) = р(У),
' 1 Р(Щ
Рраг,B) =
P(S) РB)
1 Р(Ц
рB)-р\1)
\-р2(\) '
Рраг,C) =
1 1
Ui)
\РB)
1 1
но
\РB)
р(\)
1
/*У)
РA)
1
/>0)
/>0)
рЦ
р(Ц
РB)\
Р(П
1 1
'part
1
/>0)
РB)
РA) РB)
1 />0)
РA) 1
р{к-\) р(к-2) р(к-3)
р{к-\)
р(к-2)\
р(к-З)
1

Раздел 7. Стационарные временные ряды. Модели ARMA
343
Здесь определитель в числителе выражения для ppart{k) отличается от
определителя в знаменателе этого выражения только заменой последнего столбца
столбцом, состоящим из значений р{1)9 /?B),..., р{к).
Замечательным является тот факт, что если Xt — процесс типа AR(p),
тогда
/V,(/?)*o,
РрагЛк) = ° ДДЯ Ь>р.
Это позволяет по графику PACF определять порядок процесса
авторегрессии и отличать процесс авторегрессии от процессов скользящего среднего
и ARMA(p, q) с q > 0.
Напомним, что зануление ACF после лага q соответствует процессу МА(#).
Теперь же видно, что зануление PACF после лага р соответствует процессу
AR(p). Поэтому идентификация этих моделей по ACF и PACF более
определенна по сравнению с идентификацией моделей ARMA(p, q)cp*0,q*0.
В то же время вместо неизвестных истинных последовательностей
автокорреляций р{к) и частных автокорреляций ppart{k) приходится
довольствоваться только их оценками — выборочной ACF {sample ACF — SACF),
образованной выборочными автокорреляциями {sample autocorrelations)
1 Т~к
К*) = -^Н = ^> * = 1,..,г-1,
1 t=\
1 т
где ju = x = —^xt —оценка для ju = E{Xt);
1 т~к
у {к) = —— ]Г (х, - И){х1+к - /л) — оценка для у {к),
и выборочной PACF {sample PACF — SPACF), образованной
выборочными частными автокорреляциями r^^k) {sample partial autocorrelations).
Получить последние можно, заменив входящие в выражения для ppart{k)
автокорреляции p{s) их оценками r{s). Однако проще поступить иначе. Исходя
из того, что ppart{k) является коэффициентом при {Xt_k - ju) в линейной
комбинации случайных величин Xt_x -//, ..., Xt_k- ju9 наилучшим образом
приближающей случайную величину Xt - ju, можно просто методом наименьших
квадратов оценить коэффициенты в модели
Xt = а + axXt_x + a2Xt_2 +... + akXt_k + ut

344
Часть 2. Регрессионный анализ временных рядов
(в которой составляющая ut получается как разность
ut=Xt-(a + axXt_x+a2Xt_2+... + akXt_k),
так что на нее не накладывается никаких предварительных ограничений).
Полученная в результате оценка коэффициента ак и есть rpart(k).
Если у ARMA(/?, q) процесса a{L)Xt = b(L)et все корни алгебраических
уравнений a(L) = О и b(L) = О лежат за пределами единичного круга на
комплексной плоскости, е19 ..., sT ~ Lid. и Е(е}) < оо, то указанные оценки /2,
/(к), г(к) и rpart(k) являются состоятельными оценками для //, у{к), р(к)
и ppart(k) соответственно (см. {Hamilton, 1994, р. 199)). Но поскольку г(к)
и rpart{k) всего лишь оценки для р(к) и ppart{k), то их наблюдаемые значения
могут значительно отличаться от р(к) и ppart(k). В частности, если при
некоторых к = кх и к = А:2 в модели, порождающей наблюдения, /?(&!) = 0 и ppart(k2) = О,
то, как правило, г(кх) * 0 и rpart{k2) Ф 0, что вносит дополнительную
неопределенность в задачу идентификации. Более того, характер изменения
теоретической автокорреляционной функции вовсе не обязательно будет
воспроизводиться в ее выборочном аналоге — в выборочной
автокорреляционной функции.
Тем не менее во многих случаях поведение теоретических ACF и PACF
в какой-то мере отражается и на поведении их выборочных аналогов.
Поэтому представление о поведении теоретических ACF и PACF может помочь
в решении задачи идентификации соответствующих моделей в рамках
общего класса моделей ARMA. Имея это в виду, сведем в табл. 7.3
свойства ACF и PACF для некоторых популярных моделей стационарных
временных рядов.
Исходя из возможности идентификации моделей AR(p) и МА(#) по
графикам функций г {к) и грап(к) желательно иметь статистические критерии для
проверки гипотез о равенстве нулю тех или иных значений р{к) и ppart(k)
на основе наблюдаемых значений г(к) и г^^к). Вопрос этот весьма сложный,
ограничимся только двумя приближенными рецептами, которые предполагают
гауссовостъ инноваций (т.е. что st — гауссовский белый шум).
1. Если Xt — процесс типа МА(д), то
и при больших Т
ton E(r(k)) = p(k),
Г->оо
ДК*))*- 1 + 22>2(у)
1 \ У=1
для k > q,
так что чем длиннее ряд наблюдений, тем надежнее выявляются
нулевые значения р(к), k>q.

Раздел 7. Стационарные временные ряды. Модели ARMA
345
Таблица 7.3
Свойства ACF и PACF для некоторых моделей
стационарных временных рядов
Модель
Белый шум,
МА@)
ARA),
\ а\>0
ARA),
\ а\<0
AR(p)
1 МАA),
\ Ь\>0
1 МАA),
1 МА(?)
1 ARMAA, 1),
\ ах>0
ARMAA, 1),
ах<0
ARMA(p,?)
SAR(l)
SMA(l)
ACF
p(k) = 0 для к * 0
Экспоненциальное убывание
Осциллирующее затухание
Затухание с возможной осцилляцией
Положительный пик при к - 1;
зануление при к > 1
Отрицательный пик при к = 1;
зануление при к > 1
Зануление при к > q
Экспоненциальное затухание с лага 1;
знак р(\) совпадает со знаком (ах + Ьх)
Осциллирующее затухание с лага 1;
знак р(\) совпадает со знаком (я, + Ь{)
Осциллирующее или прямое
затухание, начинающееся с лага q
Затухание на лагах, кратных периоду
сезонности;
зануление на остальных лагах
Пик на лаге, равном периоду
сезонности;
зануление на остальных лагах
PACF
Рраг((к) = 0ддяк*0
\Ppart(l) = ai
\ppart(k) = 0,k>2
Ppart(l) = ai
PparAk) = ^k>2
Зануление при к >р
Осциллирующее затухание;
Убывание по абсолютной
величине; ppart(k) < 0 при к > 1
—
Осциллирующее (при Ьх > 0)
или экспоненциальное (при Ьх < 0)
затухание с лага 1
Экспоненциальное (при Ъх < 0)
или осциллирующее (при Ьх > 0)
затухание с лага 1
Осциллирующее или прямое
затухание, начинающееся с лагар
Пик на лаге, равном периоду
сезонности;
зануление на остальных лагах
Затухание на лагах, кратных
периоду сезонности;
зануление на остальных лагах
Более того, при больших Тик> q распределение случайной
величины г{к) близко к нормальному. Отсюда вытекает, что естественный
приближенный критерий проверки гипотезы Н0 : «Xt — процесс типа
МА(#)» состоит в том, чтобы отвергать эту гипотезу, если
|r(*)|>-jLl + 2£r2G0
1
для k>q.

346
Часть 2. Регрессионный анализ временных рядов
Уровень значимости такого критерия приближенно равен 0.05.
В частности, если q = 0, то Xt ~ МА@) — белый шум, и гипотеза
Я0: «Xt — белый шум» отвергается указанным приближенным
критерием при
|r(*)|>-jL, *>0.
2. Если Xt — процесс типа AR(p), то при больших Тик>р распределение
rpart(k) можно аппроксимировать нормальным распределением
г^ (*)«#(<>, Г), так что D(rpart{k))*T-\
Следовательно, если гипотезу Я0 : Xt ~ AR(p) отвергать при
2
ГраЛк)\>-Ш> к>Р,
то получим критерий, уровень значимости которого приближенно
равен 0.05.
С учетом двух указанных приближенных критериев в процедурах анализа
временных рядов обычно предусмотрена распечатка графиков выборочных
2
ACF и PACF, на которые нанесены границы полосы ±-т=. В этих границах
с вероятностью, близкой к 0.95, должно заключаться при к > 0 значение г(к\
если Xt — белый шум, и при к >р значение rpart{k), если Xt ~ AR(p). Здесь
следует сделать одно важное предупреждение: оба построенных критерия имеют
уровень значимости, близкий к 0.05, только в том случае, когда гипотеза Н0
проверяется при некотором фиксированном к.
Что, однако, обычно происходит на практике? Рассмотрим это на примере
смоделированного белого шума, график которого уже приводился ранее.
Всего там было получено Т= 499 наблюдений хи х2, ..., х499. В табл. 7.4
приведены значения выборочных автокорреляционной и частной
автокорреляционной функций для значений (лагов) к= 1,2, ...,36.
2
В значениях ACF замечаем, что из полосы ±-j= = ±0.0895 выбивается
значение гA3) = 0.102. Означает ли это, что нужно отвергнуть гипотезу
Я0: Xt — белый шум? В значениях PACF также обнаруживаем данные,
выходящие за пределы этой полосы, что приводит к тому же вопросу.
Поскольку количество наблюдений у нас весьма велико (Г = 499), можно
воспользоваться утверждением об асимптотической независимости rpart(k),
£=1,2,...

Раздел 7. Стационарные временные ряды. Модели ARMA
347
Таблица 7.4
Значения выборочных автокорреляционной и частной
автокорреляционной функций (к= 1,..., 36)
к
1
2
3
4
5
6
7
8
9
10
11
12
ACF
-0.019
-0.013
-0.083
0.038
-0.047
0.017
-0.024
0.062
0.061
0.074
0.079
0.021
PACF
-0.019
-0.014
-0.083
0.035
-0.049
0.009
-0.019
0.053
0.069
0.073
0.099
0.034
к
13
14
15
16
17
18
19
20
21
22
23
24
ACF
0.102
-0.071
-0.044
0.017
-0.083
0.035
-0.049
0.069
0.041
-0.014
-0.035
0.034
PACF
0.126
-0.051
-0.036
0.034
-0.115
0.028
-0.085
0.032
0.022
-0.057
-0.018
0.012
к
25
26
27
28
29
30
31
32
33
34
35
36
ACF
-0.053
-0.015
-0.064
0.032
-0.057
-0.053
0.011
0.034
0.029
-0.042
0.013
0.046
PACF
-0.031
-0.018
-0.035
0.042
-0.075
-0.044
-0.006
0.021
0.034
-0.057
0.064
0.055
Пусть Вк — событие, состоящее в том, что rpart(k) выходит за пределы по-
2
лосы ±—7=-. Вероятность этого события приближенно равна 0.05. Тогда веро-
ятность выхода за пределы полосы ровно двух (из 36) rpart(k\ к = 1,2, ..., 36,
приближенно равна:
Р2 = С326 0.052A -0.05K6 = ^^ 0.052 • 0.9534,
и
№) = lgF30) + 21g@.05) + 341g@.95) = - 0.560.
Отсюда находим: Р2 - 0.275, так что вероятность двух выходов из полосы
графика выборочной PACF при рассмотрении 36 лагов вовсе не мала.
Что касается вероятности единственного выхода из полосы выборочной
ACF, то здесь можно воспользоваться утверждением об асимптотической
независимости г(к), к = 1,2, ..., при условии, что Xt — белый шум (в случае
МА(#) процесса с q > 1 это не так). При этом вероятность наличия
единственного выхода выборочной ACF из все той же полосы приближенно равна:
Р2=С\6 0.05A-0.05K5,
так что lgCP,) = -0.780, откуда находим: Рх = 0.166.

348
Часть 2. Регрессионный анализ временных рядов
Рассмотренный пример показывает, что к интерпретации графиков
выборочных ACF и PACF следует подходить достаточно осторожно1. Сюда же
относится и то обстоятельство, что выражение, используемое при
вычислении значений г{к) в пакете EViews, отличается от приведенного выше: в
формуле для у (к) деление производится не на (Т- к), а на Г. Последнее приводит
к тому, что вычисляемая таким образом оценка для р(к) имеет смещение в
направлении нуля.
В распечатках анализа временных рядов вместе с графиками выборочных
ACF и PACF обычно указаны значения (^-статистики (Q-statistics),
относящиеся к критерию для проверки гипотезы о том, что наблюдаемые данные
являются реализацией процесса белого шума.
Существует несколько вариантов g-статистик. Одна из таких статистик —
статистика Бокса — Пирса (Box-Pierce Q-statistic) была предложена Боксом
и Пирсом в работе (Box, Pierce, 1970) и имеет вид:
м
е=г£г2(*).
к = \
Вспомним приведенные ранее результаты об асимптотической
независимости гA), гB),..., г(М) в случае, когда Xt — белый шум, и отметим, что при
больших Т в этом случае г (к) «N@,1), так что Tr2(k) « [N@, I)]2 = J2(l)
(заметим, что в этой ситуации не требуется гауссовость Xt — см. (Хеннан,
1974)). Отсюда вытекает, что при больших Г приближенно имеем
Против гипотезы Н0 говорят, скорее, большие значения этой статистики.
Поэтому если выбрать уровень значимости равным 0.05, то естественно
отвергать эту гипотезу при выполнении неравенства
Q>Z2o.9s(M),
где z$m9S(M) — квантиль уровня 0.95 распределения хи-квадрат с
Мстепенями свободы.
В распечатках коррелограмм приводятся Р-значения (наблюдаемые
уровни значимости) статистики Q для последовательных значений М- 1, 2,... При
конкретном значении М гипотеза Н0 отвергается, когда соответствующее
Р-значение меньше 0.05.
Впрочем, исследования показали, что статистика Бокса—Пирса плохо
приближается распределением Х2(№) ПРИ умеренных значениях Г. Вместо нее
По этой причине в распечатках коррелограмм не будем давать графическое изображение
границ полосы ± -j=r.

Раздел 7. Стационарные временные ряды. Модели ARMA 349
в таких случаях предпочтительнее использовать статистику Люнга — Бокса
(Ljung-Box Q-statistic), предложенную в работе (Ljung, Box, 1979):
которая (при Т —>оо) также имеет асимптотическое распределение J2(^0, но
ближе к этому распределению при умеренных значениях Г, чем статистика
Бокса — Пирса. В пакете Е Views значения статистики Люнга—Бокса
распечатываются вместе с приближенными Р-значениями, соответствующими
распределениям z2(M)-
При практическом использовании g-статистик возникают определенные
трудности. Посмотрим на таблицу Р-значений g-статистики Люнга — Бокса
для рассмотренного выше примера с реализацией процесса белого шума
(табл. 7.5).
Таблица 7.5
Q-статистика Люнга — Бокса для процесса белого шума
м
1
2
3
4
5
6
7
8
9
/^значение
0.670
0.873
0.292
0.348
0.349
0.455
0.539
0.438
0.360
_____
М
10
11
12
13
14
15
16
17
18
Р-значение
0.243
0.146
0.187
0.064
0.045
0.049
0.066
0.037
0.044
М
19
20
21
22
23
24
25
26
27
Р-значение
0.044
0.033
0.037
0.049
0.056
0.064
0.061
0.077
0.063
м
28
29
30
31
32
33
34
35
36
Р-значение
0.072
0.065
0.061
0.076
0.084
0.096
0.099
0.119
0.119 j
Здесь Р-значения, соответствующие М- 14, 15, 17—22, меньше 0.05, так
что формально при использовании статистики Люнга — Бокса с любым из этих
значений М гипотеза Н0 : «Xt — белый шум» должна отвергаться. При
остальных значениях М соответствующие Р-значения больше, чем 0.05, и
гипотеза Н0 в этом случае не отвергается.
Какого-либо определенного рецепта, указывающего, как поступать в
подобных ситуациях, на какое значение М следует ориентироваться, до сих пор
не существует. Среди многочисленных исследований в этом направлении
можно отметить работы (Kwan, 1996) и (Kwan, Sim, 1996).
Уже из рассмотренного примера ясно, что на этапе выбора подходящей
модели среди множества ARMA моделей используемые процедуры являются
не вполне точными и часто приводят к довольно неопределенным выводам.
В результате этого этапа возможно оставление для дальнейшего исследова-

350
Часть 2. Регрессионный анализ временных рядов
ния не одной, а нескольких потенциальных моделей. Более определенные
выводы при выборе модели на первом этапе можно получить, применяя
информационные критерии отбора моделей.
Использование информационных критериев. Если заранее
ограничиться рассмотрением только AR моделей, т.е. полагать, что процесс Xt следует
модели AR(£)
к
Xt-V = Ysakj(Xt-j-H) + £t
с неизвестным истинным порядком к, то для определения к в таких ситуациях
долгое время использовался информационный критерий Акаике {Akaike
information criterion —AIC) (см. Akaike, 1973). Согласно этому критерию среди
альтернативных значений к выбирается такое, которое минимизирует величину
21с
А1ОД = 1п<7,2+ —,
где Т — количество наблюдений;
ак — оценка дисперсии инноваций st в AR модели А:-го порядка1.
Для вычисления <тк производится подбор модели А:-го порядка с
использованием уравнений Юла—Уокера
к
Ps=T,akjPs-j>
У = 1
полученные оценки коэффициентов a^9j = 1, ..., к, подставляются вместо akj
в уравнение модели, /и заменяется на х9 так что получаются оценки для st
к
st = (xt-x)-^akj(xt_j -3c),
7 = 1
после чего ак определяется как
1 т
1 t=\
Впоследствии было выяснено, что оценка Акаике несостоятельна и
асимптотически переоценивает (завышает) истинное значение к0 с ненулевой
вероятностью. В связи с этим были предложены состоятельные критерии,
основанные на минимизации суммы
Приведенное выражение несколько отличается от предложенного в работе Акаике и
используемого в пакете EViews. В нем опущено слагаемое, которое не зависит от порядка модели,
а потому не влияет на результат выбора среди альтернативных значений к. Это замечание
относится и к другим информационным критериям, рассмотренным ниже.

Раздел 7. Стационарные временные ряды. Модели ARMA
351
\п&1 + ксТ,
где ст = 0(Т~х\пТ) (т.е. ст при Т -» оо имеет тот же порядок малости, что
и Г ^пГ).
Одним из таких критериев является часто используемый в настоящее
время информационный критерий Шварца (Schwarz information criterion —
SIC) (см. (Schwarz, 1978)):
SIC = ln<r*+A:—.
Несколько позднее был предложен критерий Хеннана — Куинна (Нап-
nan-Quinn information criterion — HQC) (см. (Наппап, Quinn, 1979)), в
котором сТ = 2скГ1ШпТ9 о 1,
и_ .2l7 2с1п1пГ
HQ = ln0^ +к ,
обладающий более быстрой сходимостью к истинному значению к0 при Т —> оо.
Однако при небольших значениях Т этот критерий недооценивает порядок
авторегрессии.
ПРИМЕР 7.2.1
Рассмотрим модель процесса ARB)
Xt=\2Xt_x-Q36Xt_2+er
Уравнение a(z) = 0 принимает в этом случае вид
l-1.2z + 0.36z2=0
и имеет двойной корень z1?2 = —>1, так что процесс, порождаемый такой
моделью, стационарен.
Смоделированная реализация этого процесса для /=1,2,..., 500
изображена на рис. 7.23.
111111111111111111111111111111111111111111111111111—►
50 100 150 200 250 300 350 400 450 500 '
Рис. 7.23

352
Часть 2. Регрессионный анализ временных рядов
Построенная по этой реализации выборочная коррелограмма имеет
следующий вид:
ACF PACF к АС РАС g-статистика Р-значение
1*******
1****** ***
1****
1***
1**
1*
1*
******* j
2
3
4
5
6
* 7
8
9
10
11
12
0.899
0.732
0.561
0.409
0.277
0.167
0.095
0.045
0.014
-0.001
0.003
0.019
0.899
-0.396
-0.005
-0.027
-0.048
-0.015
0.071
-0.045
0.011
0.020
0.055
0.001
406.25
675.97
834.98
919.59
958.40
972.59
977.15
978.19
978.29
978.29
978.30
978.49
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
Здесь из полосы ± —1= - ±0.089 выходят только значения выборочной PACF,
л/Г
соответствующие лагам к = 1, 2. В соответствии с приближенным критерием,
указанным ранее, это приводит к неотвержению гипотезы Н0 : Xt ~ ARB).
Для подтверждения этой гипотезы сравним значения информационных
критериев Акаике и Шварца, получаемые при оценивании AR моделей 4-го,
3-го, 2-го и 1-го порядков, допускающих ненулевое математическое
ожидание соответствующих AR процессов (табл. 7.6). Оба критерия выбирают
модель ARB).B
Таблица 7.6
Выбор порядка модели
AIC
SIC
/>=1
3.083264
3.100148
/> = 2
2.91800
2.94336
/> = з
2.919244
2.953116
/, = 4
2.924441
2.966846
Если не будем ограничивать себя моделями AR и допустим, что модель,
порождающая данные, имеет вид ARMA(p0, q0) (с неизвестнымир0, q0)
a(L)Xt=b(L)sn
то для этого случая имеется несколько процедур оценивания пары (р0, q0)9
одну из которых сейчас рассмотрим {Kavalieris, 1991).
На первом шаге этой процедуры уже известными нам методами
производится подбор модели авторегрессии AR(&):
к
Xt = YaakjXt-j+£t>
7 = 1

Раздел 7. Стационарные временные ряды. Модели ARMA
353
вычисляются оценки коэффициентов а^, 7=1, ..., &, и на их основе
получаются оценки инноваций
к
7 = 1
Порядок к авторегрессионной модели на этом шаге должен быть
достаточно высоким. Его можно выбрать путем сравнения значений критерия
Акаике для оцененных моделей авторегрессии различных порядков.
(Вспомним, что критерий Акаике склонен завышать порядок модели, а это в данном
случае как раз и устраивает нас.)
На втором шаге берутся регрессии Jf, на ^_у, j = 1,...,/?, и регрессии Л", на
ек (t -j), У=1, ..., q. По первым из них получаем начальные оценки
наименьших квадратов для параметров aj9 т.е. а7, j = 1,...,/?, а по вторым — оценки bj
для bj, 7 = 1> •••> Я- Соответственно оценками полиномов a(z), b(z) служат
a(z) = l-£a,z>, b(z)=j^bjz\
7=1 7=0
и с помощью оцененных полиномов получаем оценку для инноваций
st=yl(L)a(L)xn
на основании которой строим уточненную оценку для дисперсии инноваций
1 Т
1 t=\
При этом предполагается, что сами инновации, если известны точно
коэффициенты ARMA модели, можно найти по формуле st = b~l(L)a(L)xt9 что
соответствует обратимости этой модели.
В качестве оценок для р0, q0 берется пара значений (р9 q\ при которой
минимизируется величина
Существенно, что SIC E^) — возрастающая функция от р и q9 когда
p>p09q>q0, что ведет к состоятельности оценок (р9 q).
Оценивание коэффициентов модели
После того как произведена идентификация (стационарной) модели ARMA,
т.е. на основании имеющихся наблюдений принято решение о значениях
параметров р9 q модели ARMA(p, q), порождающей данные, переходят к этапу
оценивания коэффициентов модели. На этом этапе обычно используется метод

354
Часть 2. Регрессионный анализ временных рядов
максимального правдоподобия, который в случае нормальности инноваций
сводится к методу наименьших квадратов. За исключением некоторых
наиболее простых случаев (например, модели ARA)), эта задача решается
итерационными методами, требующими задания некоторых начальных
(стартовых) значений параметров, которые затем последовательно уточняются.
В качестве таких начальных значений можно использовать
предварительные оценки, полученные на первом этапе. Начальные значения можно найти,
приравнивая неизвестные истинные значения автокорреляций р{к) значениям
г(к) выборочной автокорреляционной функции и используя функциональную
связь между значениями р(к) и значениями коэффициентов модели.
Например, если оценивается модель АЩр)9 то коэффициенты а{9 а29 ..., ар
определяются из системы первых р уравнений Юла — Уокера
р
P(k) = YsajP(k-J)> к = 19...9р9
7 = 1
в которые вместо неизвестных значений р{\)9..., р(р) автокорреляций
подставляются наблюдаемые (вычисляемые по реализации ряда) значения гA),..., г(р)
выборочных автокорреляций.
При оценивании моделей с MA(q) составляющей (q > 0) существенным
оказывается условие обратимости, сформулированное выше. Покажем это
на примере МАA) модели
Xt-jU = £t+bl£t_l, / = 1,...,Г.
Имея наблюдаемые значения х{9 ..., хТ9 последовательно выразим sl9 ..., ет
через эти значения и (ненаблюдаемое) значение s0:
sx =Xl-Ju-bs09
£2=Х2- ju-b£l=X2- ju- b(X{ - /и- bs0) = (Х2 - /и)- b(Xx - /и) + b2s09
sT = Хт - ju - bsT_x = (X{ - /и)- b(XT_x - /и) + b2(XT_2 - /и)-.. .+
+ (-l)^bT-\X^M) + (-l)TbTs0.
Максимизация (по b) условной функции правдоподобия, соответствующей
наблюдаемым значениям х{9 ..., хп при фиксированном значении s09
равносильна минимизации суммы квадратов
которая является нелинейной функцией от Ъ. Для поиска минимума этой
суммы квадратов приходится использовать численные итерационные методы
оптимизации, которые, в свою очередь, требуют задания начального
(стартового) значения параметра Ь. Как уже говорилось, такое стартовое значение
может быть получено на этапе идентификации модели. Однако полученное

Раздел 7. Стационарные временные ряды. Модели ARAM
355
в итоге итераций оптимальное значение Ь зависит от неизвестного
значения £0, что затрудняет интерпретацию результатов. Задача интерпретации
облегчается, если выполнено условие обратимости \Ь\ < 1, и при этом
значение \Ь\ существенно меньше 1.
Действительно, при выполнении этого условия можно просто положить
£0 = 0. Эффект от такой замены истинного значения s0 на нулевое быстро
убывает, так что сумма квадратов, получаемая в предположении s0 = 0,
может служить хорошей аппроксимацией для суммы, получаемой при
истинном значении £г0, при достаточно большом количестве наблюдений. Те же
аргументы пригодны и для модели MA(q) с q > 1: в этом случае можно
положить е0 = £_х = ... = £_ +1 = 0. Для получения более точной аппроксимации
в пакетах статистических программ (в том числе и в Е Views) предусмотрена
процедура backcasting, в которой процесс итераций включает также
оценивание значений £0 = s_x = ... = £ +1 путем построения для них обратного
прогноза.
Если в результате оценивания получена модель, в которой условие
обратимости не выполняется, рекомендуется повторить процедуру оценивания
с использованием другого набора начальных значений.
Более подробное изложение процедур оценивания стационарных ARMA
моделей методом максимального правдоподобия можно найти, например,
в {Hamilton, 1994, р. 117—151). Там же можно прочитать о том, каким
образом вычисляются приближения для стандартных ошибок оценок
коэффициентов этих моделей, которые можно использовать при большом количестве
наблюдений обычным образом.
В заключение сделаем одно важное замечание.
Пусть имеем стационарную АЩр) модель
a(L)Xt = S + er
Ранее говорилось о том, что в этом случае математическое ожидание /и
процесса Jf, связано с константой 8 соотношением
д
М= ,
\-ах- а2-...~ ар
При этом можно сначала оценить коэффициенты al9 a2, ..., ар и S,
применяя обычный метод наименьших квадратов к модели
Xt = 8 + axXt_x + a2Xt_2 +... + apXt_p + eg9
а затем, используя полученные оценки dl9 ..., dp и S, получить оценку для /и
в виде:
д

356
Часть 2. Регрессионный анализ временных рядов
Однако можно поступить иначе, как это предусмотрено, например, в пакете
EViews. Можно записать ту же модель в виде:
Xt=Ju(l-al-a2-...-ap) + alXt_l+a2Xt_2+... + apXt_p+£t
и одновременно оценивать и al9 a2, ..., ар, и /и. Такая процедура
теоретически более эффективна. Однако в такой форме модель оказывается
нелинейной по параметрам, и это обстоятельство, как и при оценивании МА
моделей, требует применения нелинейного метода наименьших квадратов
(NLLS — nonlinear least squares) и численных итерационных методов
оптимизации.
ПРИМЕР 7.2.2
Рассмотрим ряд данных о годовом потреблении рыбных продуктов в США
(на душу населения, в фунтах). Статистические данные приведены в табл. 7.7,
график ряда — на рис. 7.24.
Таблица 7.7
Годовое потреблении рыбных продуктов в США, на душу населения
Год
1946
1947
1948
1949
1950
Потребление,
фунт
10.8
10.3
11.1
10.9
11.8
Год
1951
1952
1953
1954
1955
Потребление,
фунт
11.2
11.2
11.4
11.2
10.5
Год
1956
1957
1958
1959
1960
Потребление,
фунт
10.4
10.2
10.6
10.9
10.3
Год
1961
1962
1963
1964
1965
Потребление,
фунт
10.7
10.6
10.7
10.5
10.9
со
ч-
СП
СО
3
о
ю
СП
см
ю
СП
S
СП
со
ю
СП
со
ш
о>
о
со
о>
см
со
СП
Рис. 7.24

Раздел 7. Стационарные временные ряды. Модели ARMA
357
Коррелограмма, построенная по этим данным, имеет следующий вид:
Autocorrelation Partial Correlation к АС РАС g-статистика Р-значение
4.2694
7.5350
7.6255
7.6324
8.3498
10.3930
13.8790
14.5230
0.039
0.023
0.054
0.106
0.138
0.109
0.053
0.069
Ориентируясь на указанные ранее приближенные критерии, прежде всего
2 2
найдем значение —= = -1= = 0.447. Из полосы ±0.447 не выходит ни одна
л/Г V20
из выборочных автокорреляций и частных автокорреляций. Поэтому исходя
из этих критериев не должна отвергаться гипотеза о том, что наблюдаемый
ряд порождается моделью МА@)
X0=JU + £r
В то же время если ориентироваться на критерий Люнга — Бокса, то пик
ACF на лаге 1 является статистически значимым. Это означает, что в качестве
потенциальных моделей порождения данных можно предварительно
рассматривать модели ARA) и МАA). Таким образом, здесь сталкиваемся
с конфликтной ситуацией: статистические выводы, получаемые при
использовании разных критериев, не соответствуют друг другу. Подобная ситуация
не является чем-то исключительным и достаточно часто встречается при
идентификации модели, порождающей наблюдаемый ряд, тем более что
используемые критерии — асимптотические, тогда как обычно в распоряжении
исследователя имеется не слишком большое количество наблюдений. ■
Последнее обстоятельство связано в значительной степени с тем, что для
многих экономических рядов периоды, на которых порождающая ряд модель
может считаться стационарной, обычно непродолжительны из-за изменения
общей экономической обстановки, в которой эволюционирует
рассматриваемый ряд. Это соображение можно легко проиллюстрировать на примере того
же самого ряда данных о потреблении рыбных продуктов в США, если
привлечь дополнительно статистические данные за период с 1940 по 1945 г. (годы
Второй мировой войны). Эволюция ряда на расширенном периоде с 1940 по
1965 г. представлена на рис. 7.25.
Провал траектории ряда в 1942—1944 гг. не позволяет трактовать этот ряд
как стационарный на всем периоде с 1940 по 1965 г. Поэтому продолжим далее
рассматривать значения ряда только на послевоенном периоде — с 1946 по 1965 г.
1
2
3
4
5
6
7
8
0.429
0.366
0.059
0.016
-0.156
-0.255
-0.321
-0.133
0.429
0.222
-0.204
-0.034
-0.129
-0.195
-0.123
0.175

358
Часть 2. Регрессионный анализ временных рядов
X
12 4
11
ЮЧ
о
гтттттттттттттттттттт
S<o оо о см ч- Год
1Л Ю ф ф (О М
5<OOOOCN"<r<OOOOCN
Рис. 7.25
Если остановиться на модели ARA), то для нее, как мы знаем, р{\) = ах.
Поэтому, приравняв неизвестное значение р{\) значению гA) = 0.429,
получим предварительную оценку для неизвестного значения ах. В то же время,
непосредственно оценив модель ARA) с ненулевым математическим
ожиданием нелинейным методом наименьших квадратов, получим следующие
результаты (табл. 7.8).
Таблица 7.8
Объясняемая переменная X
Method: Least Squares; Sample (adjusted): 1947 1965;
Included observations: 19 after adjusting endpoints; Convergence achieved after 3 iterations
Переменная
С
ARA)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Коэффициент
10.81451
0.430515
0.184864
0.136915
0.395238
2.655627
Стандартная
ошибка
0.159261
0.219257
/-статистика
67.904450
1.963522
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Р-значение
0.0000
0.0662
10.81053
0.425434
1.080645
1.180060
В данной ситуации уточненная оценка практически совпадает с
предварительной оценкой для ах.
Если остановиться на модели МАA), то в ней р(Х)
-__L
\+ъ:
-.
Приравнивание неизвестного значения рA) значению гA) = 0.429 приводит к уравнению
h
1
\+ъ:
0.429. Корни последнего уравнения равны 0.567 и 1.704. Первый

Раздел 7. Стационарные временные ряды. Модели ARMA
359
корень соответствует обратимой МАA) модели, второй корень —
необратимой МАA) модели. Уточненное оценивание МАA) модели с использованием
обратного прогноза (backcasting) дает следующие результаты (табл. 7.9).
Таблица 7.9
Объясняемая переменная X
Backcast: 1945
Переменная
С
МАA)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Коэффициент
10.81379
0.280610
0.117961
0.068959
0.399561
2.873684
Стандартная
ошибка
0.113355
0.228102
/-статистика
95.38726
1.230195
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Р-значение
0.0000
0.2345
10.81000
0.414094
1.097739
1.197313
В этом случае уточненное значение коэффициента Ьх существенно
отличается от предварительной оценки этого коэффициента. Отметим также
большое отличие Р-значений для t- и F-статистик в отношении значимости
коэффициента Ьх. Это можно объяснить тем, что величина стандартной ошибки
вычисляется согласно асимптотической процедуре, тогда как в нашем
распоряжении имеется лишь 20 наблюдений.
Если не производить обратного прогнозирования значения инновации для
1945 г., то результаты получаются близкими (табл. 7.10).
Таблица 7.10
Объясняемая переменная X
Method: Least Squares; Sample (adjusted): 1946 1965; Included observations:
20 after adjusting endpoints; Convergence achieved after 24 iterations; Backcast: OFF
Переменная
С
MAA)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
Коэффициент
10.81515
0.274024
0.116800
0.067734
0.399824
2.877464
-8.990543
1.778286
Стандартная
ошибка
0.112582
0.229231
/-статистика
96.06431
1.195405
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
Р-значение
0.0000
0.2474
10.81000
0.414094
1.099054
1.198628
2.380443
0.140261

360
Часть 2. Регрессионный анализ временных рядов
Диагностика оцененной модели
После выбора типа модели и оценивания ее коэффициентов производится
диагностика оцененной модели, т.е. выяснение того, насколько хорошо
модель соответствует данным наблюдений (адекватна данным наблюдений).
Это — третий этап процедуры подбора модели.
Для диагностики можно использовать целый ряд различных
статистических процедур, которые направлены в основном на проверку гипотезы Н0
о том, что в модели, порождающей наблюдения, последовательность st
действительно образует процесс белого шума.
Пусть на этапе идентификации остановили свой выбор на модели
ARMA(p, q)
a(L)Xt=b(L)sn
т.е.
Xt = axXt_x + a2Xt_2 +... + apXt_p +et+ bxst_x +... + bqst_q,
и на втором этапе оценили ее как
a(L)Xt=b(L)st,
где
a(L) = l-a1L-...-apLp,
b{L) = \ + i>xL + ... + bqLq.
Если MA составляющая модели ARMA(p, q) обратима, то
»(£)
и оценки для st теоретически можно получить заменой a(L) и b(L) на a(L)
и b(L) соответственно:
b(L)
На практике, конечно, эту формулу можно использовать лишь частично,
поскольку бесконечный ряд в правой части приходится обрывать из-за
наличия только конечного количества наблюдений.
При большом количестве наблюдений поведение st должно имитировать
поведение самих sr Следовательно, если ошибки st образуют процесс белого
шума, то остатки должны имитировать процесс белого шума.
Основываясь на этом соображении, Бартлетт (Bartlett, 1946) и Бокс и Пирс
(см. (Box, Pierce, 1970)) предложили исследовать статистическую значимость
выборочных автокорреляций для ряда инноваций st:

Раздел 7. Стационарные временные ряды. Модели ARMA
361
Т-к
и суммы их квадратов
м
Qbp = Т^Ге(к) ((^-статистика Бокса — Пирса).
к=\
Если модель правильно специфицирована, то QBP имеет распределение,
которое близко к распределению х2Щ~Р ~ Я) при условии, что Г и Мвелики, а
отношение М/Гмало. Гипотеза адекватности подобранной модели отвергается, если
Qbp>x1^m~P-4\
Однако впоследствии было замечено, что при конечных Т распределение
статистики QBP может существенно отличаться от распределения х2Щ- р - q).
Используя результаты Люнга и Бокса, можно показать, что
E{QBP)*{M-p-q) ^г^-
п М(М + 5)
Следовательно, если отношение — существенно, то использова-
27+ 2
ние х2Щ-р - q) приближения не является оправданным.
Люнг и Бокс предложили два способа преодоления проблемы смещения.
Первый — прямой метод — состоит в использовании приближения
Qbp*X2(E{Qbp)\
где для E(QBP) используется указанное выше выражение (модифицированный
критерий Бокса — Кокса).
Второй способ учитывает более точное выражение для D{rs{k)) — вме-
1 Т-к
сто — берется — . Это приводит к (^-статистике Люнга — Бокса
М „2
е
QLB=T(T + 2)Z-^
k-xT-k
которая имеет то же асимптотическое распределение х2Щ ~ Р ~ #)> что и
QBP, но зато при конечных Г распределение статистики QBP гораздо ближе
к х2Щ - р - q\ чем распределение статистики QBP. При этом качество
приближения ухудшается, если значения параметров находятся вблизи границы
стационарности или обратимости модели; особенно это заметно при малых М
Заметим: хотя первоначально вывод асимптотического распределения
статистики Люнга — Бокса производился в предположении, что st — гауссовский

*
*
ю
1
о
187
1
о
104
1.338
о
415
-
о
300
1
о
042
ЧО
4192
о
493
*
*
*
о
1
о
187
i
о
302
ЧО
4191
о
400
*
ЧО
1
О
021
о
159
^j
8772
о
446
*
*
оо
1
о
990
о
094
^j
8603
о
345
*
*
*
^j
1
о
277
1
о
199
^j
6991
о
ю
as
*
*
as
1
о
169
i
о
182
LH
1071
о
403
*
*
t-л
1
О
139
i
о
о
оо
оо
-^
2051
о
379
*
-^
о
058
i
о
068
U)
6417
о
303
*
U)
1
о
050
i
о
127
U)
5491
о
170
*
*
*
*
*
*
ю
о
365
о
358
U)
4838
о
390
*
*
-
о
100
о
100
о
2306
о
9
о
н
&»
н
*
*
ю
1
о
187
i
132
оо
9579
о
939
-
о
040
i
о
050
as
9748
о
728
*
*
*
о
1
о
178
i
о
653
as
8945
о
648
*
ЧО
О
047
о
189
t-л
4826
о
705
оо
о
019
о
о
t-л
3928
о
612
*
*
*
*
^j
i
о
257
i
о
093
t-л
3801
о
496
*
*
as
1
о
125
i
о
175
U)
1852
о
as
*
t-л
1
О
660
i
о
049
ю
7024
о
609
*
-^
о
076
i
о
008
ю
4232
о
489
*
*
U)
1
о
as
1
о
078
ю
2687
о
322
*
*
*
*
ю
о
271
о
593
9334
о
as
*
*
-
1
о
960
i
о
960
о
2033
о
>
7)
Ф

Раздел 7. Стационарные временные ряды. Модели ARMA
363
В обоих случаях все Р-значения для статистики QBP больше 0.05, так что
гипотеза о том, что в специфицированных моделях составляющие st
образуют процесс белого шума, не отвергается. Заметим также, что в обоих
случаях не отвергается гипотеза нормальности распределения et: Р-значения
критерия Харке — Бера равны соответственно 0.480 и 0.608. Об
оправданности применения последнего критерия при анализе временных рядов будет
сказано ниже.
Проверка предположения о нормальности. Многие статистические
процедуры, используемые при анализе временных рядов, опираются на
предположение гауссовости (нормальности) анализируемого ряда. Последнее
означает, что для любого набора tl9 ..., tn случайные величины Xt 9 ..., Xt
имеют совместное нормальное распределение.
Имея в распоряжении одну-единственную реализацию временного ряда,
невозможно проверить справедливость такого утверждения. В то же время
можно проверить гипотезу о нормальности одномерного (маргинального)
распределения стационарного временного ряда. Соответствующая процедура
предложена в работе Ломницкого (Lomnicki, 1961).
Пусть
В указанной работе было доказано, что если Xt — стационарный гауссов-
ский временной ряд, то при больших Т статистики Gx и G2 имеют
приближенно нормальные распределения с нулевыми математическими ожиданиями
и дисперсиями
* к=-<х> ■*■ к=-сс
Оценить эти дисперсии можно путем замены бесконечных сумм степеней
автокорреляций р(к) конечными суммами степеней выборочных
автокорреляций г (к). Используя такие оценки D(G{)9 D(G2)9 получим статистики
Г* - ^1 Г* - ^2
p(G{) 4D(G2)
которые при гипотезе нормальности имеют распределения,
аппроксимируемые стандартным нормальным распределением. Поскольку последние
статистики еще и асимптотически независимы, то при Т -> оо
(G;J+(G2*J*j2B).

364
Часть 2. Регрессионный анализ временных рядов
Моделирование показывает, однако, что при умеренных значениях Т
распределение статистики G2* плохо приближается нормальным
распределением. Более того, процедура проверки здесь весьма общая (структура
временного ряда не специфицируется). Поэтому критерий нормальности,
основанный на статистике (G*J +{G*2J, имеет довольно низкую мощность при
применении его к моделям AR и МА, т.е. слишком часто не отвергает гипотезу
нормальности ряда^, когда она неверна.
Более подходящей в этом отношении является аналогичная процедура,
применяемая не к самому ряду Хп а к остаткам еп полученным при
оценивании специфицированной модели ряда Хг В стационарных и обратимых
моделях ARM А остатки et состоятельно оценивают инновации еп которые
в предположении нормальности являются независимыми, одинаково
распределенными случайными величинами, имеющими распределение 7V@, a2).
Поэтому при применении метода Ломницкого для проверки предположения
о нормальности инноваций получаем
Щ7,) = |, D(G2) = y,
(так как для ряда инноваций p(k) = 0 при к * 0), причем при построении
статистик Gj и G2 вместо
используются
т,_ =
I т
Соответственно
так что
V6 V24
(G,J+(G2*J=r
24
v
Это есть статистика, используемая для проверки нормальности в популярном
критерии Харке — Бера (Jarque, Bera, 1980).
Таким образом, критерий Харке — Бера можно использовать не только
в рамках классической модели регрессии (с фиксированными значениями
объясняющих переменных), но и для проверки нормальности инноваций
в моделях временных рядов, помня, конечно, о том, что это всего лишь
асимптотический критерий. Для улучшения приближения статистики критерия

Раздел 7. Стационарные временные ряды. Модели ARMA
365
распределением хи-квадрат в пакете Е Views в статистике критерия вместо
множителя Т используется множитель (Г - К), где К — количество
коэффициентов, оцениваемых при построении модели исследуемого ряда.
Правда, здесь мы не заметили еще одного подводного камня. Мы
предполагали неявно, что остатки берутся как результат оценивания правильно
идентифицированной модели. Как будет влиять на свойства критерия
неправильное определение порядка модели?
При больших Т критерий Шварца достаточно надежно определяет порядок
(р, q) модели ARMA, так что проверка нормальности инноваций по модели,
выбранной критерием Шварца, асимптотически равносильна проверке
нормальности инноваций по правильно идентифицированной модели.
На третьем шаге производят также проверку выбранной модели на
оптимальность, при этом имеется в виду, что «более сложные» модели не
должны существенно отличаться от подобранной модели. Точнее говоря, при
увеличении порядка модели оценки коэффициентов при добавленных
составляющих должны быть статистически незначимыми, а оценки
коэффициентов при сохраняемых составляющих должны изменяться не очень
существенно.
V Замечание 7.2.1. При построении статистики Харке — Бера для
проверки нормальности инноваций в модели ARMA существенным
является центрирование остатков, полученных в результате
оценивания модели, т.е. вычитание из каждого остатка et среднего et всех
полученных остатков.
При оценивании модели линейной регрессии методом
наименьших квадратов сумма полученных остатков равна 0, так что остатки
автоматически являются центрированными. Поскольку же при
оценивании ARMA моделей приходится привлекать метод
максимального правдоподобия, получаемые остатки необязательно являются
центрированными, и надо позаботиться об их центрировании. В
противном случае статистика Харке — Бера уже не имеет
асимптотического распределения j2B) (см. (Yu, 2007)).
ПРИМЕР 7.2.3
Обратившись опять к результатам оценивания МАA) и ARA) моделей для
данных о потреблении рыбных продуктов в США, заметим, что гипотеза
#0 : ах = 0 в ARA) модели и гипотеза Н0 : Ь{ = 0 в МАA) модели не
отвергаются. Это означает, что обе эти модели могут быть редуцированы к модели МА@)
Xt=n + er
При оценивании последней получим результаты, приведенные в табл. 7.11.
Однако оцененная коррелограмма для этой модели уже была приведена
выше (в примере 7.1.2) и именно она дала повод рассматривать в качестве

366
Часть 2. Регрессионный анализ временных рядов
Таблица 7.11
Результаты оценивания модели МА@)
Переменная
С
R~squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Коэффициент
10.81000
0.000000
0.000000
0.414094
3.258000
-10.23258
Стандартная
ошибка
0.092594
^-статистика
116.7460
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Durbin-Watson stat
Р-значение
0.0000
10.81000
0.414094
1.123258
1.173045
1.138735
возможных кандидатур модели ARA) и МАA). При этом, решая вопрос
о статистической значимости р{\) и ppart(\), мы опирались на
асимптотические результаты, хотя имели в распоряжении лишь небольшое количество
наблюдений, и это может быть причиной несогласованности полученных
выводов.
Впрочем, можно воспользоваться и точным критерием, основанным на
статистике Дарбина — Уотсона. Поскольку в последней модели нет никаких
объясняющих переменных, кроме константы, можно получить таблицы
непосредственно для критических значений этой статистики, а не для границ,
между которыми заключены эти критические значения. Соответствующие
критические значения приведены в {Sargan, Bhargava, 1983). В частности, для
уровня значимости 0.05 и Т= 21 критическое значение равно 1.069.
Ориентируясь на него, мы не отвергаем гипотезу о том, что наблюдаемые данные
порождены процессом МА@).
Сравним оцененные модели МА@), МАA) и AR(l) по критериям Акаике и
Шварца (табл. 7.12).
Таблица 7.12
Сравнение моделей
Критерий
AIC
SIC
Модель
МА@)
1.123
1.173
МАA)
1.098
1.197
ARA)
1.081
1.180
Предпочтительной по критерию Акаике является модель ARA), тогда как
с точки зрения критерия Шварца более предпочтительна модель МА@). Такое
положение в практическом анализе временных рядов возникает достаточно
часто: если критерии Акаике и Шварца выбирают разные модели, то
критерий Акаике выбирает модель более высокого порядка. ■

Раздел 7. Стационарные временные ряды. Модели ARMA
367
ПРИМЕР 7.2.4
Обратимся к приведенной в примере 7.2.1 реализации процесса
авторегрессии второго порядка Jf, = \2Xt_x - 0.36^_2 + ег Используя выборочную кор-
релограмму, построенную по этой реализации, мы (правильно)
идентифицировали порядок этого процесса. Среди AR моделей порядков 4, 3, 2 и 1 оба
критерия — AIC и SIC — также выбрали модель второго порядка.
Оценивание модели с ненулевым математическим ожиданием нелинейным методом
наименьших квадратов приводит к следующим результатам (табл. 7.13).
Таблица 7.13
Объясняемая переменная X
Method: Least Squares; Sample (adjusted): 3 500;
Included observations: 498 after adjusting endpoints; Convergence achieved after 3 iterations
Переменная
С
ARA)
ARB)
Коэффициент
0.001015
1.256580
-0.397095
Стандартная
ошибка
0.330958
0.041257
0.041290
^-статистика
0.003067
30.45723
-9.617188
Р-значение
0.9976
0.0000
0.0000
Коррелограмма ряда остатков имеет следующий вид:
ACF PACF к АС РАС ^-статистика ^-значение
*| *
1
2
3
4
5
6
7
8
9
10
11
12
-0.003
-0.005
0.000
0.036
0.037
-0.086
0.005
-0.004
-0.002
-0.054
-0.014
0.019
-0.003
-0.005
0.000
0.036
0.037
-0.085
0.005
-0.006
-0.004
-0.050
-0.008
0.011
0.0042
0.0165
0.0165
0.6866
1.3675
5.0736
5.0882
5.0977
5.0993
6.5887
6.6897
6.8676
0.898
0.709
0.713
0.280
0.405
0.531
0.648
0.582
0.669
0.738
Все Р-значения для статистики QBP намного больше 0.05, так что гипотеза
о том, что в специфицированной модели составляющие st образуют процесс
белого шума, не отвергается. Не отвергается также и гипотеза нормальности st
(Р-значение в критерии Харке — Бера равно 0.616). Вместе с тем оценка
математического ожидания процесса Xt статистически незначима, что
позволяет не отвергать гипотезу о нулевом математическом ожидании ARB)
процесса. Оценив модель с нулевым математическим ожиданием, получим
результаты, приведенные в табл. 7.14.

368
Часть 2. Регрессионный анализ временных рядов
Таблица 7.14
Объясняемая переменная X
Method: Least Squares; Sample (adjusted): 3 500;
Included observations: 498 after adjusting endpoints; Convergence achieved after 2 iterations
Переменная
ARA)
ARB)
S.E. of regression
Sum squared resid
Inverted AR Roots
Коэффициент
1.256581
-0.397096
1.036707
533.0816
0.63 - 0.05/
Стандартная
ошибка
0.041215
0.041248
/-статистика
30.48807
-9.627056
Akaike info criterion
Schwarz criterion
Р-значение
0.0000
0.0000
2.91398
2.93089
0.63 + 0.05/
Исследуем последнюю модель на оптимальность в указанном выше смысле.
С этой целью приведем коэффициенты оцененных ARB), ARC) и ARD)
моделей и Р-значения для тех коэффициентов двух последних моделей,
которые являются «лишними» с точки зрения «оптимальной» модели ARB)
(табл. 7.15).
Таблица 7.15
Данные оцененных моделей AR
Модель
ARB)
ARC)
ARD)
*,-!
1.26
1.25
1.25
Коэффициенты при переменных
Xt_2
-0.40
-0.39
-0.40
*,-з
/> = 0.87
Р = 0.72
*,-4
Р = 0.56
Эта таблица показывает, что в моделях с неоправданно высоким порядком
«лишние» коэффициенты оказались статистически незначимыми, а
коэффициенты при переменных, включенных в «оптимальную» модель, практически
не изменяются при изменении порядка модели. Именно это и характеризует
подобранную модель ARB) как оптимальную.
Интересно, наконец, обратить внимание еще на одно обстоятельство. Как
было уже отмечено ранее, в теоретической модели ARB), по которой
строилась исследуемая реализация, уравнение a(z) = 0, т.е. 1 - \2z + 0.36z2 = 0,
имеет двойной корень z = —«1.67. Этот корень больше 1, что обеспечивает
стационарность процесса, порождаемого такой моделью. В то же время для
оптимальной модели, полученной в результате подбора, соответствующее

Раздел 7. Стационарные временные ряды. Модели ARMA
369
уравнение имеет корни, обратные величинам, указанным в последней строке
распечатки результатов оценивания этой модели. Указанные в этой строке
величины равны 0.63 ± 0.05/, так что сами корни равны z = 1.58 ± 0.125/. Хотя
эти корни, конечно, отличаются от (двойного) корня уравнения a{z) = 0 в
теоретической модели, тем не менее оба они больше 1 по абсолютной величине,
а значит, подобранная ARB) модель также является стационарной. ■
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие три этапа используются при подборе стационарной модели ARMA для
ряда наблюдений? В чем состоят эти этапы?
2. Что является отправной точкой для идентификации стационарной модели ARMA?
3. Как можно идентифицировать процесс авторегрессии и его порядок?
4. Как можно идентифицировать процесс скользящего среднего и его порядок?
5. Как можно идентифицировать сезонные процессы авторегрессии и скользящего
среднего?
6. Каким образом производится оценивание коэффициентов модели,
идентифицированной как AR{p)?
7. Каким образом производится оценивание коэффициентов модели,
идентифицированной как МА(#)?
8. Какие статистические процедуры применяются для диагностики подобранной
модели?
Приложение П-7
ПРОВЕРКА ГИПОТЕЗЫ СЛУЧАЙНОСТИ
В практических исследованиях реальных временных рядов, особенно на первом этапе
исследования, обычно нет никаких предварительных данных о вероятностной модели,
порождающей наблюдения. Поэтому естественным будет начать анализ с проверки
гипотезы о том, что наблюдаемый ряд следует модели случайной выборки —
простейшей модели временного ряда. Для краткости эту гипотезу будем называть
гипотезой случайности {randomness test), хотя более точно ее следовало бы именовать
гипотезой случайной выборки. В рамках этого приложения такую гипотезу сделаем
исходной (основной) и будем обозначать ее, следуя традиции, символом Я0 (нулевая
гипотеза) {null hypothesis).
На практике используется целый ряд критериев проверки этой гипотезы,
отличающихся мощностью при различных альтернативных гипотезах. Рассмотрим
некоторые из таких критериев, предполагая непрерывность распределения, из которого
извлекается выборка.
Критерий серий {runs test) основан на следующем соображении. Пусть М —
медиана распределения F , так что F{M) = Р{Х< М} = Р{Х> М) = 1 - F{M) = — .
Тогда последовательные значения дс,,..., хп не должны «слишком долго» задерживаться
по одну сторону от уровня М.

370
Часть 2. Регрессионный анализ временных рядов
Если не известно распределение F, то не известна и его медиана, поэтому
приходится использовать ее выборочный аналог — выборочную медиану. Для ее
вычисления расположим значения хх, ..., хп в порядке возрастания, т.е. образуем
вариационный ряд (ряд порядковых статистик): дсA),..., х{п). Выборочная медиана
вычисляется по формуле:
med = med(xl,...,xn) =
х, +1 ч, если п нечетно,
1
№) Ъ
+ */„
2 AJJ
если п четно.
По исходному временному ряду построим последовательность из плюсов и
минусов следующим образом: вместо xt ставится «+», если xt > med, и «-», если xt < med.
Под серией (run) понимается последовательность идущих подряд плюсов или
идущих подряд минусов.
Пусть в полученной последовательности имеется пх плюсов и п2 минусов, п{ + п2 = п,
и при этом имеется z, серий плюсов и z2 серий минусов — всего z = z, + z2 серий.
Значения zx и z2 можно рассматривать как реализации соответствующих случайных
величин Z, и Z2. Если гипотеза Н0 верна, то для случайной величины Z=ZX + Z2
E(Z) = ^h!h+h
П
В{2^^1п\пгAп\пг-п)
п2(п-\)
и если при этом числа «,и«2 велики, то для случайной величины
Z-E(Z)
Г =
V5(Z)
можно использовать нормальное приближение N@, 1), отвергая гипотезу Н0 при
«слишком больших» отклонениях наблюдаемого числа серий от ожидаемого.
Критерий поворотных точек (turning points test) особенно удобен при
графическом представлении данных, так как значение его тестовой статистики S
непосредственно определяется по графику ряда х( и представляет собой суммарное количество
«пиков» и «впадин» на этом графике.
«Пик» — это наблюдаемое значение, которое больше двух соседних, «впадина» —
наблюдаемое значение, которое меньше двух соседних. Каждое из таких наблюдений
называется поворотной точкой (turning point). Начальное jcj и конечное хп значения
не могут входить в число поворотных точек, так как у хх нет соседнего наблюдения
слева, а у хп нет соседнего наблюдения справа.
Для t - 1,2,..., п - 2 определим «считающую переменную»
[\ если xt < xt+l и xt+l > xt+2 или если xt > xt+l и xt+l < xt+2,
О — в противном случае.

Раздел 7. Стационарные временные ряды. Модели ARMA
371
При этом Z, = 1 тогда и только тогда, когда х„+1 — поворотная точка, и суммарное
п-2
число поворотных точек в ряду наблюдений равно S = ^Г Z,.
Математическое ожидание случайной величины S равно:
E(S) = "ftE(Z,) = "fdP{Z,=l}.
Если гипотеза Я0 верна, а распределение F непрерывно, то
/>{Z, =l} = |, / = 1,2,...,«-2,
так что
£(S) = (/j-2)|.
Дисперсия случайной величины S при гипотезе Я0 равна
90
При больших и стандартизованная случайная величина
5*=-
л/ад
имеет при гипотезе Н0 распределение, близкое kN(Q, 1).
Гипотеза Я0 отвергается, если наблюдаемое количество поворотных точек
значимо отличается от ожидаемого.
V Замечание П-7-1. При практическом применении критерия поворотных
точек, когда данные являются округленными, возникают трудности,
связанные с тем, что некоторые соседние значения оказываются совпадающими.
В таких ситуациях можно рекомендовать следующий подход. По
имеющимся данным анализируются последствия возможного (хотя бы и
гипотетически) уточнения совпадающих значений. Исследуются все
потенциальные возможности увеличения или уменьшения округленных значений
при их уточнении («разокруглении»). В результате можно найти верхнюю
и нижнюю границы для «истинного» количества поворотных точек,
соответствующего исходному «неокругленному» ряду. Для этих граничных
значений применяется критерий, указанный выше, и делаются
соответствующие выводы относительно гипотезы случайности.
Критерий Кендалла (Kendall test) основан на попарном сравнении всех
наблюдений. Для каждой пары индексов(/,Д 1 < / <j < n, положим
ГО если х, < х,,
J II если х. > Xj,

372
Часть 2. Регрессионный анализ временных рядов
т.е. Htj = 1 тогда и только тогда, когда значения xi9 Xj расположены в порядке,
обратном порядку их индексов, т.е. образуют инверсию.
Случайная величина
1</<У<и
равна суммарному количеству инверсий в ряду дс,,..., хп. Минимальное значение Q = 0
достигается при х, < ... < хп, а максимальное Q = С„ = — при х, > ... > хп.
Среднее значение Q = С2п = соответствует «наибольшему беспорядку» среди
значении ряда, при этом
46
= 1,
п(п-\)
Критерий Кендалла использует статистику
г = 1-
п(п-\)
в литературе ее часто называют «тау Кендалла». При гипотезе Я0 распределение
случайной величины г имеет симметричную относительно нуля плотность с нулевым
математическим ожиданием и дисперсией
2Bи + 5)
D(t) = -
9ф-\)
а стандартизованная величина
г =
<Щт)
имеет распределение, которое уже при п > 11 хорошо аппроксимируется
стандартным нормальным распределением. Гипотеза Н0 отвергается при значениях г*,
значимо отличающихся от нуля.
V Замечание П-7-2. Как и в случае критерия поворотных точек, при
применении критерия Кендалла возникают трудности, связанные с наличием
у ряда двух или нескольких совпадающих наблюдений. Обойти эти
трудности можно двумя способами:
• в первом производится прореживание ряда, в процессе которого
удаляются «дублирующие» значения. При этом ряд становится короче, но если
гипотеза Н0 верна для всего ряда, то она верна и для «укороченного»
ряда, а для последнего она проверяется без проблем;
• во втором сначала каждой паре совпадающих значений сопоставляется
нулевой вклад Htj = 0, при этом получается нижняя граница для
значения Q, соответствующего «истинному» (разокругленному) ряду. Затем
каждой паре совпадающих значений сопоставляется единичный вклад

Раздел 7. Стационарные временные ряды. Модели ARMA
373
Щ =1, при этом получается верхняя граница для Q. Полученные два
граничных значения используются для вычисления соответствующих им
значений г*, и на основании этих значений делается заключение
относительно справедливости гипотезы Н0.
Критерий Кендалла чувствительнее критерия поворотных точек при наличии
в данных линейного тренда. Однако в случае если исследуемая характеристика
подвержена сезонным изменениям, критерий Кендалла оказывается бесполезным,
поскольку он, как правило, не отвергает гипотезу случайности Н0 даже при
наличии выраженного периодического тренда. Напротив, критерий поворотных точек
может помочь в выявлении такого тренда, отвергая в такой ситуации гипотезу
случайности.
Общий принцип состоит в том, что каждый конкретный критерий наилучшим
образом работает при вполне определенных альтернативах, так что не существует одного
универсального критерия проверки гипотезы случайности, эффективно работающего
абсолютно во всех ситуациях. В связи с этим полезно иметь на вооружении арсенал
критериев проверки случайности, которые в совокупности помогают либо принять
модель случайной выборки либо отказаться от нее в пользу той или иной более
сложной модели временного ряда.
Критерии согласия (goodness of fit tests). В приложениях интерес представляет
проверка не только гипотезы о том, что наблюдаемый ряд значений следует модели
случайной выборки, но и гипотез о том, что это случайная выборка из вполне
определенного распределения F или что это случайная выборка из распределения,
принадлежащего некоторому параметрическому семейству распределений, без
уточнения параметров этого распределения.
В пакете EViews 6 для таких проверок предусмотрены встроенные процедуры,
реализующие критерии, основанные на сравнении эмпирической функции
распределения и специфицированной теоретической функции распределения и на
использовании той или иной меры расхождения между этими функциями.
Для случайной выборки Хх, ..., Хп эмпирическая функция распределения
определяется формулой
1 п
где 1Х < х — индикаторная функция, равная 1, если Xt < х, и равная 0 в противном
случае.
Критерий Колмогорова (критерий Колмогорова — Смирнова) (Kolmogorov
test, Kolmogorov-Smirnov test). Пусть эмпирическая функция распределения Fn(x)
построена по случайной выборке объема п из непрерывного распределения с функцией
распределения G(x). Пусть F(x) — заданная функция распределения. Проверяется
гипотеза Я0 : G(x) = F(x).
Статистика Колмогорова определяется соотношением
Dn=sup\Fn(x)-F(x)\.

374
Часть 2. Регрессионный анализ временных рядов
При гипотезе Н0 распределение случайной величины Dn не зависит от того,
каково истинное распределение выборки. При гипотезе Я0 и п -» оо статистика Dn -> О
с вероятностью 1. Поэтому чаще используют статистику v« Dn, распределение
которой имеет невырожденный предел. При гипотезе Я0 и п -> оо функция распределения
случайной величины yfn Dn сходится к функции некоторого специального
распределения, которое называется распределением Колмогорова. Если условие G(x) = F(x)
не выполняется, то при п —» оо
D„-*sup|G(x)-F(x)|>0,
X
так что v« Dn —» со. Отсюда вытекает правило: гипотезу Н0 следует отвергать, если
наблюдаемое значение Dn слишком велико.
Нулевая гипотеза о том, что набор хх, ..., хп соответствует случайной выборке
из заранее специфицированного распределения F, отвергается на уровне
значимости а, если
V^ А, >*,-„,
где Кх_а — квантиль уровня A - а) распределения Колмогорова.
При практическом вычислении значения статистики Dn можно воспользоваться
соотношением
(к к-\^
D„ = max I —F(x{k)), F(x{k))-
lSk<n\„ — **'' n
в котором хA), ..., x(n) — вариационный ряд для xl9 ..., xn, полученный путем
упорядочивания элементов рядах15..., хп по возрастанию.
Критерий Купера (Kuiper test). В отличие от статистики Колмогорова,
статистика критерия Купера определяется соотношением
fh \
■ max
к
п
г
-F(x{k)) +max F(x{k))-
\<к<п
jfc-П
Критерий Лиллиефорса {Lilliefors test) предназначен для проверки гипотезы
о том, что набор х15 ..., хп соответствует случайной выборке из нормального
распределения, но значения параметров этого распределения (математического ожидания
и дисперсии) не специфицируются заранее.
В данном случае сначала производится оценивание по имеющейся выборке
математического ожидания и дисперсии распределения, а затем производится сравнение
эмпирической функции распределения с функцией нормального распределения,
имеющего в качестве параметров оцененные значения математического ожидания
и дисперсии. Поскольку сравнение производится не с заранее заданной функцией
распределения, а с функцией, параметры которой оценены по выборке, максимальное
расхождение этих функций оказывается меньшим, и распределение статистики
критерия будет другим (распределение Лиллиефорса).

Раздел 7. Стационарные временные ряды. Модели ARMA
375
Критерий Крамера — фон Мизеса (критерий омега-квадрат) (Cramer-von Mises,
W -test). Здесь в качестве меры расхождения между эмпирическим
распределением Fn и теоретическим распределением F берется величина
W2=n^F„(x)-F(xfdF(x).
Можно показать, что
12л h
2к-\
2п
•F(*(k))
Критерий Андерсона — Дарлинга (Anderson-Darling test) является одним из
наиболее мощных критериев для проверки нормальности, его можно использовать при
малых выборках, п < 25. В качестве меры расхождения между эмпирическим
распределением Fn и теоретическим распределением F берется величина
А^п[
1
F(xXl-F(x))
\F„(x)-F(xfdF(x).
Пусть данные х,, ..., х„ упорядочены по возрастанию. Эти данные стандартизуются
на выборочное среднее и выборочную дисперсию:
Y = хг-х_
А2^_п_^^Л[1пф(ук) + ЫA-Ф(¥„+1_к))],
Статистика критерия вычисляется по формуле
^ 2*-1|
где Ф(х) — функция стандартного нормального распределения.
Статистика, скорректированная на размер выборки, имеет вид:
А*2=А2
f 0.75 2.25л
1 + -
п п
Уровню значимости 0.05 соответствует отвержение нулевой гипотезы при
А*2> 0.752.
Критерий Ватсона (Уотсона) (Watson test). В качестве меры расхождения
между эмпирическим распределением Fn и теоретическим распределением F берется
величина
00 Г 00 |
U2=n UF„(x)-F(x)- j[F„(x)-F(x)]dF(x)\ dF(x).
-00 ^ -00 J
При рассмотрении финансовых рядов отклонение от нормальности распределения
часто проявляется в наличии у распределения F тяжелых (длинных) «хвостов»,

376
Часть 2. Регрессионный анализ временных рядов
в более медленном убывании функции плотности при удалении от центра
распределения по сравнению с плотностью нормального распределения. Такие отклонения
улавливает статистика Харке — Бера:
6 24
где у — выборочный коэффициент асимметрии рассматриваемого рядах,,..., хп;
к — его выборочный эксцесс {к = выборочный куртозис - 3),
у = ~г, выборочный куртозис = —у, к = —j - 3,
(т2) Щ т2
1 " _
тк =—J](xi-x)k — выборочный центральный момент порядка к.
Пых

Раздел 8
РЕГРЕССИОННЫЙ АНАЛИЗ
ДЛЯ СТАЦИОНАРНЫХ ПЕРЕМЕННЫХ
Тема 8.1
АСИМПТОТИЧЕСКАЯ ОБОСНОВАННОСТЬ
СТАНДАРТНЫХ ПРОЦЕДУР
Прежде чем перейти к изложению материала данного раздела, отметим, что в
этом разделе не будем различать в обозначениях случайные величины и их
наблюдаемые значения — в обоих случаях будут использоваться строчные
буквы.
Асимптотическая обоснованность
стандартных процедур
В разд. 6 ч. 1 учебника было отмечено, что рассмотренные там случаи, в
которых можно использовать стандартные процедуры регрессионного анализа,
несмотря на то что объясняющие переменные являются стохастическими
(ситуации А, А\ В9 С), не охватывают наиболее интересные для нас модели
стационарных и нестационарных временных рядов. Это замечание
относится и к широко используемым на практике моделям авторегрессии, в том
числе к стационарным.
Рассмотрим модель авторегрессии AR(p)
yt=a + axyt_x+a2yt_2+... + apyt_p+£n / = 1,2,..., л,
где et — инновации, образующие процесс белого шума с D(et) = а*.
Эту модель можно представить в виде линейной модели регрессии
yt=xfe + et9
где

378
Часть 2. Регрессионный анализ временных рядов
Но для нее невозможно использовать результаты, полученные в ситуациях
А и В. Хотя es и х, статистически независимы при s > t9 они оказываются
зависимыми уже при s = t - 1, поскольку st_x участвует в формировании
случайной величиныyt_X9 входящей в состав х,. Это нарушает условие, входящее
в определения ситуаций А и В.
Невозможно использовать и результаты, полученные в ситуациях А' и С.
Там требовалось, чтобы условное распределение вектора s = {sX9 sl9 ..., sn)T
при фиксированной матрице X значений объясняющих переменных имело
вид N@9 a2V) с положительно определенной (невырожденной)
матрицей V (в ситуации А' — это единичная матрица). Однако если зафиксировать
х,+ 1 = (l,j>/,<y,_i, ...,yt-P+\)T и xt9 то значение st известно с полной
определенностью.
Тем не менее если AR(p) модель стационарна, то положение вполне
благополучно. Это подтверждается следующим фактом.
Ситуация D
• Процесс yt порождается моделью
yt=a + axyt_x + a2yt_2 +... + apyt_p + st {et — инновации);
• все корни полинома 1 - axz - a2z2 - ... - apzp = О лежат за пределами
единичного круга;
• et~ ild.9 E(st) = О, D{st) = а2 > О, E(ef) = ju4<co.
При выполнении перечисленных условий для оценки наименьших
квадратов вп вектора коэффициентов в= (а9 аХ9 а29..., ар)Т9 полученной по п
наблюдениям, выполняется соотношение
*V20n-ff)^>N(O9*2Q-l)9
где Q — положительно определенная матрица, элементы которой
выражаются в явной форме через математическое ожидание и
автокорреляции процесса yt\
cr2Q~x—ковариационная матрица асимптотического распределения, мо-
(хтх V1
жет быть оценена состоятельно посредством S2\ —-—- , и это
I п )
означает, что асимптотически обоснованны статистические
процедуры, трактующие распределение вп как NF9 S^(X^Xn)~l)
(здесь Хп — матрица значений объясняющих переменных в
п наблюдениях).
Иными словами, и в рассматриваемой ситуации можно пользоваться
стандартными методами регрессионного анализа, имея в виду их
асимптотическую обоснованность.

Раздел 8. Регрессионный анализ для стационарных переменных
379
Если перейти к процессам, стационарным относительно
детерминированного тренда, то следует отметить возникающую здесь особенность,
связанную со сходимостью распределения оценок наименьших квадратов
к асимптотическому распределению. Поясним эту особенность на
следующем примере.
Пусть ряд>>, порождается простой моделью временного тренда
где st ~ lid., E{st) = О, D{st) = а2 > О, Е(е?) = //4 < оо.
Если и здесь записать модель в стандартной форме:
у,=х]в + £и х, =(U)r, 0 = (a,/3),
то, для того чтобы получить невырожденное асимптотическое распределение
оценки наименьших квадратов вп = (ап, /?„), придется использовать различные
нормирующие множители; (ап - ап) умножается на п /2, а (/?„ - /?„) — на п ,2.
Однако это различие компенсируется тем, что аналогичным образом ведут
себя и стандартные ошибки для ап и /5п. Как результат, обычные
/-статистики имеют асимптотическое распределение 7V@, 1). Иными словами, можно
использовать стандартную технику регрессионного анализа, имея в виду ее
асимптотическую обоснованность.
Те же принципы можно использовать и для исследования процесса
авторегрессии произвольного порядка, стационарного относительно
детерминированного временного тренда.
Ситуация Е
• Процесс yt порождается моделью
yt=a + flt + axyt_x + a2yt_2 +... + apyt_p + et (et — инновации);
• все корни полинома 1 - axz - a2z2 - ... - apzp = 0 лежат за пределами
единичного круга;
• et~ Lid., E{st) = 0, D{st) = а2 > 0, Е(е?) = ju4 < оо.
При выполнении этих предположений обычные /-статистики и статистики
qF (где q — количество линейных ограничений на коэффициенты, a F —
обычная F-статистика критерия для проверки выполнения этих ограничений)
имеют асимптотические распределения N@, 1) и z2(<l)- Можно использовать
стандартную технику регрессионного анализа, имея в виду ее
асимптотическую обоснованность.
Если не ограничиваться процессами авторегрессии, но оставаться в классе
стационарных моделей, то и в этом случае все еще можно надеяться на
возможность использования стандартной техники регрессионного анализа, опять
имея в виду ее асимптотическую обоснованность.

380
Часть 2. Регрессионный анализ временных рядов
Рассмотрим линейную модель
у = хе+е9 х = хп9
или в эквивалентной форме:
yt=xje + et, Г = 1,2,...,я,
где xt = (xtl9 xtl9 ..., xtp)T — вектор значений р объясняющих переменных
в /-м наблюдении.
Пусть вп — оценка наименьших квадратов вектора коэффициентов
9- @Х9 в19 ..., вр)Т9 полученная по п наблюдениям. Следующие три условия
обеспечивают состоятельность и асимптотическую нормальность вп при п -> оо:
1) /?lim
(\ п \
= о
(в эквивалентной форме: р lim(w Хп s) = 0);
2) plim
(л п Л
2^xtxt
\" /=i
= Q
(в эквивалентной форме: p\\m{n xXTnXn)-Q)9 где Q — положительно
определенная матрица;
3)
1
г— 2^xtst
у1П t = \
N@,a2Q)
(в эквивалентной форме: (п x^XTns) ->N@9 <r2Q)).
Здесь plim — предел по вероятности; стрелка в последнем условии означает
сходимость по распределению.
Если эти условия выполнены, то при п -> оо, как и в ситуации Д
В работе {Mann, Wald9 1943) дана теорема Манна — Вальда: если
plim
(\ п \
2^xtxt
Vw*«i
= Q
(в эквивалентной форме: /?Нт(я хХтпХп) = 0, где £? — положительно
определенная матрица;
• et~U.d.9E(£t) = 0, D{st) = а2 > 0, £(|£,Г) < оо для всех m = 1, 2, ...;
• £(jt, £,) = 0, f = 1,2, ..., л,

Раздел 8. Регрессионный анализ для стационарных переменных
381
то тогда выполнены также первое и третье условия из предыдущей тройки
условий, обеспечивающих состоятельность и асимптотическую нормальность
вп при п -> оо.
Заметим, что условие E(xt et) = О, t = 1, 2, ..., п9 в сочетании с E(st) = О
означает, что
Cov(xtk9 £,) = 0, £= 1,2, ...,/?,
т.е. означает некоррелированность значений объясняющих переменных с et
в совпадающие моменты времени. Условие E(\et\m) < °° для всех т = 1, 2, ...
выполняется, в частности, для нормального распределения £г
Приведенные результаты теперь можно объединить.
Ситуация F
Пусть в линейной модели
у,=х?в + еп Г = 1,2,..., л,
где xt = (xri, х,2, ..., х/Л:)г — вектор значений А^ объясняющих переменных
в t-м наблюдении;
вп — оценка наименьших квадратов вектора коэффициентов в- (в{, въ ..., вк)Т9
полученная по п наблюдениям.
Пусть для этой модели выполнены следующие условия:
\=Q
J
plim -£x,x/
Vnt=x J
(в эквивалентной форме: p\\m(n ХпХп) = Q), где Q — положительно
определенная матрица;
• £t~U.d.9E(et) = 09 D(et) = a2>09 E(\st\m) <оо для всех rn = I, 2, ...;
• Cov(xtk9 st) = О, для k = 1, 2, ..., К.
Тогда при п -> оо
Предположим теперь, что х, — стационарный векторный (/Г-мерный)
ряд (K-dimensional stationary time series), так что
£*(*,) = /л = const, Cov(xt) = Q9 Cov(xtk, xt+sJ ) = yw (s)
при всех /, ^ для каждой пары k9 I = 1, 2, ..., А^. Здесь %7(s) — кросс-
ковариация (cross-covariance) значений k-й и /-й компонент векторного ряда х„
разнесенных на s единиц времени.

382
Часть 2. Регрессионный анализ временных рядов
Если рассматривать s как аргумент, ykl(s) — как функцию от s , то ykI(s) —
кросс-ковариационная функция (cross-covariance function) k-й и 1-й
компонент векторного ряда хг Тогда первое из трех условий для ситуации F
обеспечивает возможность оценивания неизвестной ковариационной матрицы
Cov(xt) = Q простым усреднением доступных наблюдению матриц xtxTt по
достаточно длинному интервалу t = 1,2, ...,«.
В рамки ситуации F помещается достаточно распространенный класс
ARX моделей:
Уг = а\Уг-\ + *2Л-2 + • • • + аРУг-р + *] Р + st >
где
z = (ztl9zt29...9ziM)T, /1 = (/319/32,...,J3M)T.
Подобная модель вписывается в ситуацию F, если положить
xt ~\Уг-\->Уг-2-> •••>>;/-p9Zl9Z2' •••'ZA/) 9
6> = (^1,^2,...,^,Д,у?2,...,^Л/)г.
Пусть для этой модели выполнены следующие условия:
• zt — стационарный векторный (М-мерный) ряд;
plim
-Е*аг
\", = 1
=&,
где Qz — положительно определенная матрица;
• et~i.i.d.,E(et) = 0, D(st) = a2 > О, E(\et\m) < °° для всех т = 1, 2, ...;
• Cbv(z,m, et) = О для m = 1, 2, ..., М;
• Cov(yt_j9et) = 0jw*j = 1,2, ...,р;
• все корни уравнения 1 - axz - a2z2 - ... - apzp = О лежат вне единичного
круга.
Тогда выполнено и первое условие ситуации F, и при п -> оо
Последнее из перечисленных условий, касающееся корней уравнения
я(z) = 0, обеспечивает стабильность модели ARX. Это означает, что по мере
продвижения в будущее (т.е. с ростом t) устанавливается определенная
долговременная {long-run) связь между переменнымиjy„ ztl9 ztl, ..., xtM9 no
отношению к которой происходят достаточно быстрые осцилляции.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие затруднения возникают при попытке оценивания коэффициентов
процесса авторегрессии и как они разрешаются в случае использования стационарного
процесса?

Раздел 8. Регрессионный анализ для стационарных переменных
383
2. Какие затруднения возникают при попытке оценивания параметров процесса
авторегрессии, стационарного относительно детерминированного линейного тренда,
и как они разрешаются?
3. В чем состоит условие стабильности модели ARX?
Тема 8.2
ДИНАМИЧЕСКИЕ МОДЕЛИ.
ВЕКТОРНАЯ АВТОРЕГРЕССИЯ
Модели с авторегрессионно распределенными
запаздываниями (динамические модели)
В эконометрических исследованиях среди различных ARX моделей широко
применяются динамические модели (модели с авторегрессионно
распределенными запаздываниями, autoregressive distributed lag models — ADL).
Для такой модели используют обозначение ADL(p, r; s):
yt = a0 + axyt_x + a2yt_2 +... + apyt_p +
+(Ао^/+Ал,н+- + АЛ/-г)+,,,+
где р — глубина запаздываний по переменной yt\
г —глубина запаздываний по переменным xXt, x2tt9 ..., xsn не
являющимся запаздываниями переменной jy,;
s — количество таких переменных.
При такой форме записи допускается, что некоторые из коэффициентов J3tj
равны нулю, так что глубина запаздываний может быть различной для
разных переменных хиг
Модель ADL(p, r; s) можно представить в компактном виде:
a(L)yt=ju + bl(L)xlt+... + bs(L)xst+€n
где
a(L) = l-alL-a2L2 ~...-apLp9
bi(L) = pib+paL + ... + CirL\ i = l9...,s.
Если выполнено условие стабильности, Toyt представляется в виде:
a(L) a(L) a(L) a(L)
или

384
Часть 2. Регрессионный анализ временных рядов
Уг =—77V + Cl(L)xu +... + Cs(L)xst + ——€п
a(L) a(L)
где
a(L)
Долговременную связь между переменными можно найти, полагая L = 1
и st = 0 в выражении для уг
При этом получим
yt=—^M^-cl(l)xlt^-... + cs(l)xsr
а(\)
Строго говоря, в последнем выражении указание на момент t следует
исключить:
У = -тгМ + с1A)х1+... + са(})ха.
a(l)
Коэффициенты сх(\)9 ..., с5A) в последнем соотношении называются
долгосрочными мультипликаторами (long-run multipliers, equilibrum
multipliers). Поясним это название на примере модели ADLA, 1; 1), которую
запишем в виде:
A - axL)yt = /i + /?0 х, + P\xt-\ + st •
При \ax\ < 1 получаем равносильное представление
(l-axL) (l-axL)
т.е.
yt = A + ax + ax +.. .)ju + A + axL + axL2 +...) (J30xt + J3xxt_x + et),
из которого последовательно находим:
oxt
&*_£«-_ Д+вЛ>
oxt oxt_x
OXt OXt_2
oxt oxt_3
и т.д. Правые части дают значения импульсных мультипликаторов {impact
multiplier, short-run multiplier), показывающих влияние единовременного

Раздел 8. Регрессионный анализ для стационарных переменных 385
(импульсного) изменения значения xt на текущее и последующие значения
переменной jyr Просуммировав полученные выражения, получим
fyt , & , & , ty , =
dxt dxt_x dxt_2 dxt_3
= fi0(l + ax +at +•-•) +Px(\ + ax+at +•••) =
= (l-a1)"Vo+A)-
Как легко заметить, правая часть этого соотношения представляет собой
долгосрочный мультипликатор рассматриваемой ADLA, 1; 1). В соответствии
с левой частью этот мультипликатор показывает изменение значения yt при
изменении на 1 текущего и всех предыдущих значений переменной хг
Прежде чем рассмотрим пример оценивания конкретной ADL модели,
заметим следующее.
При выполнении условий, обеспечивающих возможность использования
стандартной техники регрессионного анализа (имеется в виду ее
асимптотическая обоснованность — см. тему 2.1, ситуация F):
• обычная /-статистика имеет асимптотическое N@, 1) распределение;
• если F — обычная F-статистика для проверки гипотезы о выполнении
q линейных ограничений на коэффициенты модели, то статистика qF
имеет асимптотическое ^-распределение с q степенями свободы;
• при умеренном количестве наблюдений параллельно с
асимптотическими распределениями для t и qF можно для контроля использовать
и точные (стандартные) распределения (распределение Стьюдента для
/-статистики, распределение Фишера для F-статистики). Согласованность
получаемых при этом результатов подкрепляет уверенность в
правильности соответствующих статистических выводов;
• при наличии в правой части запаздывающих значений объясняемой
переменной проверку гипотезы об отсутствии автокоррелированности
у ряда st следует производить, используя критерий Бройша — Годфри.
Критерий Дарбина — Уотсона не годится для этой цели, поскольку
в данном случае значения статистики Дарбина — Уотсона d смещены
в направлении значения d - 2, так что использование таблиц Дарбина —
Уотсона приводит к неоправданно частому неотвержению указанной
гипотезы («презумпция некоррелированности £,»).
ПРИМЕР 8.2.1
Рассмотрим модель ADLC, 2; 1):
A - 0.5L - 0.1L2 - 0.05L3)^ = 0.7 + @.2 + 0.1L + 0.05L2)x, + et.
Для нахождения долговременной связи между переменными у и х
полагаем L = 1 и st = 0:

386
Часть 2. Регрессионный анализ временных рядов
A - 0.5 - 0.1 - 0.05);; = 0.7 + @.2 + 0.1 + 0.05)х,
т.е. 0.35.У = 0.7 + 0.35х, или у = 2 + х.
На рис. 8.1 представлены смоделированная реализация ряда xt = 0.1xt_x + ехп
sxt ~ Lid., N@, 1), и соответствующая ей реализация ряда jy„ порождаемого
указанной моделью ADLC, 2; 1), где et ~ u.d.9 N@, 1), причем ряд et
порождается независимо от ряда £хГ В качестве начальных значений при
моделировании были взяты: хх = 0,у{ =у2 -уъ - 0.
Если в распоряжении только эти две реализации, неизвестно, с какой
моделью имеем дело. Начнем с оценивания статической модели yt = /u + J3xt + st
методом наименьших квадратов, в результате получим оцененную модель
yt = 1.789 + 0.577х, + еп где et — ряд остатков. График ряда остатков показан
на рис. 8.2.
DELTA
-4 11in|м1111м 1 |м111м11|i11111111|iм111111111111 ►
10 20 30 40 50 60 70 80 90 100 t
Рис. 8.1
10 20 30 40 50 60 70 80 90 100 t
РИС. 8.2
Здесь обнаруживается явная автокоррелированность ряда остатков,
которая подтверждается построенной для него коррелограммой
ACF
PACF
АС
РАС g-статистика Р-значение
*****
I****
***
г
\*
I
I*****
I*
*|
1
2
3
4
5
6
0.696
0.536
0.364
0.227
0.130
0.057
0.696
0.099
-0.081
-0.056
-0.015
-0.020
49.981
79.868
93.801
99.279
101.100
101.460
0.000
0.000
0.000
0.000
0.000
0.000
а также критерием Бройша — Годфри с запаздыванием на один шаг, который
дает Р-значение 0.0000. Это означает, что мы имеем дело не со статической, а
с динамической моделью. Поэтому следует прежде всего рассмотреть
характер поведения обоих рядов и произвести их идентификацию.

Раздел 8. Регрессионный анализ для стационарных переменных
387
Для ряда xt коррелограмма имеет вид:
ACF PACF к АС РАС g-статистика Р-значение
48.468 0.000
67.594 0.000
71.527 0.000
71.591 0.000
71.958 0.000
74.090 0.000
По этой коррелограмме ряд xt идентифицируется как ARA).
Для ряда>>, коррелограмма имеет вид:
ACF PACF к АС РАС g-статистика Р-значение
60.58 0.000
101.75 0.000
127.37 0.000
144.32 0.000
155.21 0.000
162.38 0.000
Так что и этот ряд идентифицируется как ARA).
Такой предварительный анализ ограничивает рассмотрение моделью ADL
с глубиной запаздываний, равной 1:
yt=ju + axyt_x + 0oxt + P\xt-\ + £r
Результаты оценивая такой модели ADLA, 1; 1) приведены в табл. 8.1.
Анализ остатков не выявляет автокоррелированности (Р-значение
критерия Бройша — Годфри при ARA) альтернативе равно 0.164), не выявляет
значимых отклонений от нормальности распределения st (Р-значение
критерия Харке — Бера равно 0.267), не обнаруживает гетероскедастичности
(Р-значение критерия Уайта равно 0.159), так что можно, опираясь на
приведенные выше факты, использовать асимптотическую теорию статистических
выводов и на ее основе использовать результаты, получаемые при
применении t- и F-критериев.
Таблица 8.1
Объясняемая переменная У
Переменная
С
Г(-1)
X
Х{-\)
Коэффициент
0.558588
0.695204
0.208971
0.161690
Стандартная
ошибка
0.157276
0.066095
0.126135
0.132352
/-статистика
3.55163
10.51828
1.65673
1.22166
Р-значение
0.0006
0.0000
0.1009
0.2249
1
2
3
4
5
6
0.686
0.429
0.193
0.024
-0.058
-0.140
0.686
-0.079
-0.132
-0.066
0.003
-0.107
1
2
3
4
5
6
0.767
0.629
0.494
0.399
0.318
0.257
0.767
0.100
-0.042
0.019
-0.003
0.004

388
Часть 2. Регрессионный анализ временных рядов
При проверке гипотезы Н0: /?0 = рх = 0 получаем при использовании F-pac-
пределения Р-значение = 0.0032, при использовании асимптотического
распределения i?^2B) получаем Р-значение = 0.0022. В обоих случаях эта гипотеза
отвергается. Исключение из правой части модели запаздывающей
переменной xt_l9 коэффициент при которой статистически незначим и имеет большее
Р-значение, чем коэффициент при х„ дает результаты, приведенные в табл. 8.2.
Таблица 8.2
Объясняемая переменная У
Переменная
С
Г(-1)
X
Коэффициент
0.517868
0.719738
0.310343
Стандартная
ошибка
0.154098
0.063131
0.095241
/-статистика
3.360648
11.40064
3.258511
Schwarz criterion
Р-значение
0.0011
0.0000
0.0015
3.024602
Здесь все коэффициенты имеют высокую значимость, а остатки вполне
удовлетворительны.
Если из предыдущей модели исключить не x,_l9 ax„ то это приводит к
оцененной модели (табл. 8.3).
Таблица 8.3
Объясняемая переменная У
Переменная
С
У(-1)
Х(-1)
Коэффициент
0.567821
0.692523
0.305939
Стандартная
ошибка
0.158600
0.066673
0.100582
/-статистика
3.580215
10.38690
3.258511
Schwarz criterion
Р-значение
0.0005
0.0000
0.0030
3.037497
По критерию Шварца чуть более предпочтительной выглядит модель с
исключенной xt_l9 так что на ней можно и остановиться. Посмотрим, к какому
долговременному соотношению приводит такая модель.
Итак, останавливаемся на оцененной модели
A - 0.720L)yt = 0.518 + 0.310*, + ег
Заменяя здесь оператор L единичным оператором и полагая et = 0, получаем:
0.28у, = 0.518 н- 0.310х„ так что долговременное соотношение оценивается как
;у = 1.839+1.107х.
Это соотношение, конечно, несколько отличается от теоретического.
Посмотрим, однако, что дало бы оценивание динамической модели ADLC, 2; 1)
(табл. 8.4).

Раздел 8. Регрессионный анализ для стационарных переменных
389
Таблица 8.4
Объясняемая переменная У
Переменная
С
Д-1)
У(-2)
Ц-3)
X
■ц-1)
Х(-2)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
Коэффициент
0.539617
0.590293
0.153936
-0.031297
0.205570
0.191959
-0.024779
0.643818
0.620072
1.051648
99.536670
-138.8891
1.999213
Стандартная
ошибка
0.174057
0.105583
0.120517
0.099814
0.129483
0.153608
0.138389
/-статистика
3.100239
5.590795
1.277303
-0.313555
1.587626
1.249666
-0.179053
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob. (F-statistic)
Р-значение
0.0026
0.0000
0.2048
0.7546
0.1159
0.2147
0.8583
1.882787
1.706160
3.008022
3.193826
27.11327
0.000000
Если найти долговременное соотношение между у и х на основе такого
оцененного уравнения по той же схеме, что и прежде, получим
у= 1.882 + 1.300х,
и это соотношение отнюдь не ближе к теоретическому, чем то, которое было
получено по редуцированному уравнению. Впрочем, и по критерию Шварца
полная оцененная модель хуже редуцированной. ■
Векторная авторегрессия
Популярной моделью связи между временными рядами является векторная
авторегрессия (VAR — vector autoregressiori).
В своей простейшей форме такая модель связывает два ряда^, ny2t
следующим образом:
Ун -Иг + ^21.1 Уи-\ + ^22.1 Уи-\ + €2п
т.е. в отличие от простого процесса авторегрессии значение уи связывается
не только с запаздыванием уи ,_l9 но и с запаздыванием y2f /_1 второй
переменной у2г Случайные величины еи и elt являются инновациями:
• Cov(sjn sls) = 0 для t Ф s при любых у, /=1,2;
• Cov(ejn yu t_r) = 0 для г > 1 при любых у, /=1,2.

390
Часть 2. Регрессионный анализ временных рядов
В то же время для совпадающих моментов времени случайные величины
еи и e2t могут быть коррелированными.
Модель векторной авторегрессии для двух рядов допускает включение в
правые части уравнений для ^и ny2t и большего количества запаздываний этих
переменных. Наибольший порядок запаздываний, включаемых в правую часть,
называется порядком векторной авторегрессии. Если этот порядок равен р,
то для такой модели используют обозначение VAR(p) (pth-order VAR).
В общем случае рассматривается к временных рядов у1п у2п ..., УкГ
Модель векторной авторегрессии порядка р предполагает, что связь между этими
рядами имеет вид:
У и =М + *илДм +*п2Уи-2 +--- + Лп.РУи-Р +
+ я2л Дм + п\г.гУи-г + • • • + яп.РУи-Р +
+ ••• +
+ Я\клУк*-\+Я\к2Ук*-г+"- + Я\к.рУк*-р+е\п
y2t=Ml +^21.1 Дм +^21.2Д/-2 +--- + 7Г2\.рУи-р +
+ ^22.1 Дм + ^22.2 Д/-2 + • •' + ^22.р Д/-р +
+ ••• +
Л* =/** + л*илДм +^1.2Д/-2 +--- + xkLpyu_p +
+ Пк2.\Уи-\ + ^2.2 Д/-2 + • • • + Пк1.рУ1*-р +
+ ••• +
+ пкк.\Ук^-\ + пкк.гУк^-2 + • • • + пкк.РУк^-р + £**»
где я^г — коэффициент прид/.,_г в уравнении дляд,.
Здесь £и, £2р ..., £д., — случайные величины, для которых
• Cov(ejn els) = 0 для / * ^ при любых у, / = 1,..., А:;
• Cov{sjnyl t_r) = О для г > 1 при любых у, / = 1,..., £;
• Cov(£Jn slt) могут отличаться от нуля.
Случайные величины еи, s2n ..., ekt образуют случайный вектор st =
= (sln s2n ..., skt)T, компоненты которого не коррелированы по времени и не кор-
релированы с запаздывающими значениями переменных у1м у2п ..., j;^. Этот
вектор называют вектором инноваций (обновлений) относительно
информационного множества
У(-\ =(Л,м>Дя Д/-р»'"»Л,м» Д/-2»---' Ук,1-Р)-

Раздел 8. Регрессионный анализ для стационарных переменных
391
ПРИМЕР 8.2.2
Рассмотрим следующую модель VAR(l) для двух рядов {к = 2,р = 1):
уи = 0.6 + 0.7^,.! + 0.2.y2?,_i + eU9
У it = 0.4 + 0.2.yu_i + 0Jy2,t_{ + s2n
Поведение смоделированной пгфыуи,у2п порождаемой этой моделью для
t = 2, 3, ..., 100, показано на рис. 8.3. В качестве начальных значений были
взяты^ц -у2\ = 0; еи и e2t моделировались как независимые случайные
величины, имеющие одинаковое нормальное распределение N@9 0.12).
График на рис. 8.4 представляет поведение разности (уи -y2t).
Y1
У2
' i i i i I i i i i I i i i i I i i i i I i i i i I i i i i I i i i i | i i i i | i i i i | i i i i |—►
10 20 30 40 50 60 70 80 90 100 t
Рис. 8.3
10 20 30 40 50 60 70 80 90 100 t
РИС. 8.4
У1-У2
Как видно, с течением времени поведение рядов стабилизируется: они
осциллируют вокруг установившихся уровней. График на рис. 8.4
показывает, что установившийся уровень для ряда^^ превышает установившийся
уровень для ряда y2t приблизительно на 0.4 (среднее арифметическое
разности (уи -y2t) равно 0.403). Такой характер поведения пары^и,^2/ указывает
на стабильность данной модели VAR.B

392
Часть 2. Регрессионный анализ временных рядов
Предсказать стабильный характер поведения реализаций рядов, связанных
VAR моделью, можно, проанализировав коэффициенты модели. Для этого
удобно записать УАЩр) модель для к рядов в более компактной форме:
У U = Ml + U\yt-l + П2^-2 + • •. + Ц,У^р + £Г
Здесь
Л=(Лг^2/»—»^)Г> M = (Mi>M2>-->Juk)T> £t=(£\t>s2t>--->£kt)T >
Пг = (п^r) — матрица размера (к х к) коэффициентов приyh t_r9 y2f ,_,., ...,
yk t_r в к уравнениях.
Последнее представление можно записать как
yt ~ П^.! - П2у,_2 -... - Tlpyt_p = // + *„
(Ik-TllL-Tl2L2-...-TlpL!>)yt=M + £„
или
W)yt = м + £»
где
A(L)=Ik-nlL-n2L2-...-npL?.
Условие стабильности такой VAR модели состоит в следующем:
• все к корней уравнения
fe\{Ik-zT\x -z2n2 -...-zpTlp)=0 (T.e.det^(z) = 0)
лежат за пределами единичного круга на комплексной плоскости (т.е.
модули всех к корней больше 1).
Если это условие выполняется, то при продвижении вперед по оси
времени система постепенно «забывает» о том, при каких исходных значениях
У\->Уг-> —чУР она начала реализовываться. Стабильное состояние системы
находится путем приравнивания L = 1 и st = 0. При этом получим
так что стабильное состояние определяется как
yt=A-\\)M.
ПРИМЕР 8.2.3
Продолжим рассмотрение модели VAR(l) для двух рядов:
уи = 0.6 + 0.7;^,_! + 0.2j2>,_, + еи,
у21 = 0.4 + 0.2 yUl_x + 0.7;^,_, + £2„
В компактной форме эта система имеет вид:
Я = /* + П,я_, +е„

Раздел 8. Регрессионный анализ для стационарных переменных
393
где
или
где
У,=
У2.)
м =
0.6
0.4
ГТ,=
Г0.7 0.2")
0.2 0.7J
е,=
ML)y, = M + s„
A(L) = I2-YlxL =
0 1
так что
/
0.7L 0.2L
0.2L 0.71
А{\) =
0.3 -0.2
А~\\) =
ч-0.2 0.3,
Уравнение det A(z) = 0 принимает здесь вид:
1-0.71
4-0.2L
F 4^
4 6
\S2tJ
-0.2L}
1-0.71 J
det A(z) = \
'l-OJz -0.2z\
= 0,
v 0.2z l-0.7z,
т.е. A - 0.7zJ - @.2zJ = 0, или A - 0.9z)(l - 0.5z) = 0. Оба корня z = 1/0.9
и z = 1/0.5 больше 1, т.е. условие стабильности выполняется.
Долгосрочное (стабильное) состояние системы находим по формуле
'6 4Y0.6^l Г5.2Л
yt = A-l(l)M =
4 6
v0.4,
4.8
Таким образом, стабильное состояние системы определяется здесь как
уи = 5.2, у2, = 4Я,
так что стабильное состояние разности (уи -y2t) есть
У1-у2 = 0А.
Соответственно с течением времени независимо от начальных условий
ряд уи станет осциллировать вокруг уровня 5.2, а ряд y2t — вокруг
уровня 4.8; разность (уи -y2t) осциллирует вокруг уровня 0.4. Именно такое
поведение смоделированных реализаций рассматриваемой VAR(l) и наблюдалось
ранее.!
Векторные авторегрессии, определенные так, как было указано выше,
называют также замкнутыми VAR {closed VAR), отличая тем самым эти
модели от открытых VAR (open VAR), в правые части которых наряду с
запаздывающими значениями переменных, находящихся в левых частях уравнений
(эндогенные переменные — endogenous variables), входят некоторые другие
переменные и их запаздывания (экзогенные переменные — exogenous
variables).

394
Часть 2. Регрессионный анализ временных рядов
Проводя различие между эндогенными и экзогенными переменными, по
существу, предполагают, что значения экзогенных переменных формируются
вне рассматриваемой системы, а значения эндогенных переменных
порождаются в рамках этой системы. Фактически в этом случае система
рассматривается как условная по отношению к экзогенным переменным. Заметим,
что в замкнутой VAR экзогенные переменные отсутствуют.
Открытую VAR можно представить в виде:
A(L)yt=;u + B(L)xt+en
где A(L) и B(L) — матричные полиномы,
A(L) = I-n{L-Tl2L2 -...-TIpLp.
Если все решения уравнения detA(z) = 0 лежат за пределами единичного
круга на комплексной плоскости, что необходимо для обеспечения
стабильности системы, то справедливо также представление
yt=A-l(L)fi + C(L)xt+A-\L)et9
где C(L) = A~l(L)B(L) — передаточная функция (transfer function);
C(L) — матричная функция, она устанавливает влияние единичных
изменений в экзогенных переменных на эндогенные переменные.
Долговременную (долгосрочную, стабильную — long-run) связь между
экзогенными и эндогенными переменными можно найти, если в последнем
представлении положить L - 1 и et = 0. При этом получаем
у,=А-\\)» + С(\)хг
Матрица СA) называется матрицей долгосрочных мультипликаторов.
Ее (/, у)-й элемент ctj(\) представляет влияние единичного изменения
переменной xjt шуи в долгосрочном плане.
ПРИМЕР 8.2.4
На базе рассмотренной выше замкнутой модели VAR(l) для двух рядов
построим открытую VAR:
уи = 0.6 + 0.7^^! + 0.2^2,/-1 +0-l*i,f-i +0.2jc2>, + ^ip
y2t = 0.4 + 02yXt_x + 0.7y2ft_{ + 0.2* u + 0.4x2,,-i + eb9
Здесь ju и матричный полином A(L) — те же, что и ранее, а
B(L) = B0+BlL =
0 0.2
0.2 0
0.1 0
0 0.4
L =
0.1 L 0.2
0.2 0.4 L

Раздел 8. Регрессионный анализ для стационарных переменных
395
так что
ЯA) = Я0+Я,=
ГОЛ 0.2'
,0.2 0.4^
Матрица долгосрочных мультипликаторов равна
СA) = Л"A)ДA) =
6 4
4 6
0.1 0.2
0.2 0.4
(Л .4 2.8^1
1.6 3.2
1.4 2.8
1.6 3.2
так что стабильное решение есть
(УА=E2Л г
\Уг) 14-8У V1-" D^J\*U
т.е.
у{ =5.2 + 1.4*! + 2.8х2,
у2 =4.8 + 1.6^! +3.2х2.
Ниже приведены графики смоделированных реализаций этой открытой
системы в случае, когда хи и x2t — независимые друг от друга ARA) ряды:
хи = 0.1xht_l + vlt9 xlt = 0.5х2 ,_! + v2t\ vu и v2, - lid. N@, 1).
В качестве начальных значений при моделировании взяты
• вариант 1: хи = jc21 =0, уп -у1Х = 0 (рис. 8.5),
• вариант 2: jcu =x2l = 0, уи = 5.2, >>21 = 4.8 (рис. 8.6).
и Г| м 11111111111111111111111111111111111111111111111 *
10 20 30 40 50 60 70 80 90 100 t
Рис. 8.5
1 ||||||1111|1111[1111|иii|iщ|мирницм|щi| ►
10 20 30 40 50 60 70 80 90 100 t
Рис. 8.6
В первом случае из-за несоответствия начальных значений переменных
стабильным соотношениям системе требуется некоторое время, чтобы выйти
на стабильный режим. Во втором случае начальные значения переменных
согласованы с долговременными соотношениями между переменными. ■

396
Часть 2. Регрессионный анализ временных рядов
Рассмотрим следующую замкнутую VARA) для двух переменных:
y2, = 0.2yltt_l+0.Sy2<t_l + £2t.
Для этой системы
V
'0.81 0.2L)(yu
так что
При этом
\Уь)
A(L) =
0.2L 0.8Z,
Л (
)\y2tj
1-0.8Z, -0.21Л
\S2t,
А(\) =
-02L 1-0.8L
f 0.2 -0.2^
ч-0.2 0.2 ^
определитель этой матрицы равен нулю, и матрица A~\l) не определена.
Уравнение det A(z) = 0 имеет здесь вид A - 0.8zJ - @.2zJ = 0, т.е.
(l-z)(l-0.6z) = 0.
Корни этого уравнения равны — и 1. Наличие корня, равного 1, нарушает
0.6
условие стабильности системы. Как ведут себя в этом случае реализации
системы? Ответ на этот вопрос иллюстрирует рис. 8.7.
У1
У2
-6Н
-8 i i i i i |iii i | i i i i | i iii| i i i i | i i i I |iii i | i i i i | i iii| i i i i |
10 20 30 40 50 60 70 80 90 100 t
РИС. 8.7
Здесь стабилизация системы не наблюдается. Можно предположить, что
это происходит из-за неудачного выбора начальных значений уп = у1Х - 0.
Перемоделируем реализации, полагая начальные значения приблизительно
равными наблюдаемому «конечному» уровню: уи -у1х - 5. Новые реализа-

Раздел 8. Регрессионный анализ для стационарных переменных 397
84
6 1А /
4 I
2 I
0 I
-2 | i i i i | i i i i|iiii|iiii| i i i i | i i i i | i i i i | i i i i | i i i i|iiii |—►
10 20 30 40 50 60 70 80 90 100 t
Рис. 8.8
ции представлены на рис. 8.8. Они по-прежнему не стабилизируются, и это
отражает фундаментальное отличие рассматриваемой нестабильной модели
VAR от стабильной.
Некоторые частные случаи динамических моделей.
Проблемы, возникающие при выборе
динамической модели на основании имеющихся
статистических данных
Чтобы не загромождать изложение, ограничимся рассмотрением моделей,
входящих в качестве частных случаев в модель ADLA, 1; 1)
yt = м+я iJVi + Ал + Ал-1 + £t •
Эти частные случаи, несмотря на свою простоту, дают схематические
представления девяти широко используемых типов моделей.
Различные типы моделей соответствуют различным ограничениям на
вектор коэффициентов в = (аи /?0, Д). При наличии двух ограничений
говорят об однопараметрической модели, а при наличии одного
ограничения — о двухпараметрической модели. Полная модель ADLA, 1; 1)
является трехпараметрической. Рассмотрим девять различных типов
моделей.
1. Статическая регрессия (а{ = Д = 0):
yt=/u + p0xt + er
Здесь на значение yt влияет только значение xt в тот же момент времени,
предшествующие значенияyt_x их,.! не влияют на^г
У1
У2

398
Часть 2. Регрессионный анализ временных рядов
Эта модель обычно не характерна для данных, получаемых
последовательно во времени, поскольку в таких ситуациях, как правило, случайные
величины st автокоррелированы.
2. Процесс авторегрессии (Д = Д = 0):
Здесь значение^, зависит только от значенияyt_l9 значения переменной xt
в моменты t и (t - 1) не влияют на^г
Подобные ситуации затрудняют экономический анализ и проведение
соответствующей экономической политики из-за того, что в этом
случае нет «управляющей» переменной, значения которой можно было бы
устанавливать принудительно с целью «управления» значениями
переменной^,.
3. Модель опережающего показателя (ах - Д0 = 0):
yt=/u + pxxt_x + sr
Такие модели можно использовать для прогнозирования, если изменения
показателя у следуют с запаздыванием за изменениями показателя х с
достаточной надежностью. Однако при отсутствии серьезных теоретических
оснований коэффициент Д вовсе не обязан быть постоянным. В последнем случае
это может приводить к некачественным прогнозам, особенно в периоды
структурных изменений, когда хороший прогноз особенно необходим. Кроме
того, не видно каких-то особых причин для исключения из правой части
запаздывающих значений переменной у.
4. Модель скорости роста (al = \,fil= -Д0):
Ayt = ju + j30Axt+sr
Здесь А = 1 - L, так что Ay, =yt-yt_{, Axt=xt- xt_x. Эта модель
соответствует модели статической регрессии, но не для рядов в уровнях, а для рядов в
разностях (для продифференцированных данных). Однако переход к рядам
разностей оправдан только в том случае, если исходные ряды имеют
стохастический тренд и не коинтегрированы. Об этом подробно будем говорить
ниже, а пока укажем только на то, что при неоправданном переходе к рядам
разностей теряется информация о характере долговременной экономической
связи между рядами в уровнях.
5. Модель распределенных запаздываний (ах - 0):
yt = /u + p0xt + pxxt_x + et.
Эта модель не содержит в правой части запаздываний переменной у. Она
страдает теми же недостатками, что и статическая регрессия, но к ним может
добавиться также проблема мультиколлинеарности переменных xt nxt_x.

Раздел 8. Регрессионный анализ для стационарных переменных
399
6. Модель частичной корректировки (Д = 0):
yt = M + aiyt-i+A>Xt + £r
Она не содержит в правой части запаздывающих значений переменной х.
К такой модели приводят, например, следующие соображения.
Пусть у* = а + Дс, — целевой уровень переменной у, а фактически
приращение Ayt =yt-yt_{ описывается моделью
*-*-i = (l-W-*-i) + *r, 0<Л<1,
т.е.
yt = (l-X)y; + Ayt_l + en
так что с точностью до случайной ошибки st текущее значение yt равно
взвешенному среднему целевого у* и предыдущего значения переменной у.
(Например, yt — уровень запасов, xt — уровень продаж.) Тогда
yt=yt-i + 0 - Л)(а + fixt-yt_x) + et = A - A)a+Ayt_x + A - Л)Дх, + st9
или
J>, = // + *lJ>,-l+ $>*, + *,,
где// = A-Л)а, ^!=Я, Д0=A-А)Д
Во многих случаях вывод подобных уравнений приводит к
автокоррелированным ошибкам, а игнорирование xt_ х часто порождает оценку
коэффициента ах, существенно отличающуюся от оценки ах в полной модели.
7. Фальстарт, или приведенная форма (Д0 = 0):
К такой модели можно прийти, например, если xt = Xxt_x + ur Тогда
подстановка выражения для xt в полное уравнение ADLA, 1; 1) дает
yt = ju + alyt_l+0oxt + 0lxt_l + et = p + alyt_l + (fi>A + Д) xt_x + (et +fout\
или
л=^ + ед-1+Д\-1 + ^
По одному последнему уравнению (приведенная форма исходного
уравнения) невозможно восстановить значения Д0 и Д, не зная значения Я. Таким
образом, можно оценить коэффициенты приведенной формы, но не
коэффициенты структурной формы (исходного представления ADLA, 1; 1)).
8. Авторегрессионные ошибки (Д = -ахро):
yt = ;u + axyt_x + Д0х, - axp0xt_x + er
Запишем это уравнение в виде:
yt ~ tfiJV-i = A - Q\)(* + fiofa - axxt_x) + et.

400
Часть 2. Регрессионный анализ временных рядов
В последнем уравнении легко узнается преобразование Кохрейна — Ор-
катта, используемое для преодоления проблемы автокоррелированности
ошибок в модели парной регрессии:
yt- а + Д0х, + ип ut = axut_x + sn \а{\<1.
9. Модель коррекции ошибок {\ах\ < 1, Д0 + Д = Ь{\ - ах), Ъ Ф 0):
АУ/ = м + АД^/ - С1 - «1ХУ/-1 - 6**-i) + £»
или
Ду, = Д0Дх, - A - fl?i)(y,_i - л - fo,_i) + £„
где а- , & = ———.
1 - «! 1 - «!
Модели такого вида будут очень часто встречаться у нас при
рассмотрении связей между нестационарными временными рядами. В этих случаях
такая модель описывает механизм поддержания долговременной связи
у - а + Ъх
между переменными yt и xt в форме коррекций отклонений yt_x - а - bxt_x
от долговременной связи в предыдущий момент времени.
V Замечание 8.2.1. Исходную (полную) модель ADLA, 1; 1)
yt = M + а\Уг-\ + Дл + ДЛ-i + £»
всегда можно преобразовать к виду:
л-л-1=^-A-й1)л-1+А(^-^1) + (А+ДК-1 + ^
Если выполнено условие \а{\ < 1 (условие стабильности модели), то
и при Д0 + Д * 0 получаем модель коррекции ошибок.
Таким образом, модели с \ах\ < 1 и Д0 + Д * 0 могут быть
представлены в равносильной форме в виде модели коррекции ошибок.
Обратим теперь внимание на следующее. На практике мы имеем дело
только со статистическими данными и не можем знать точно, какая именно
модель лежала в основе процесса порождения данных {data generating
process — DGP). Можем только, привлекая какие-то теоретические
положения или результаты ранее проведенных исследований с другими
множествами данных, выбрать некоторую статистическую модель {statistical
model — SM), которую, по нашему мнению, можно использовать для
описания процесса порождения данных. Выбрав такую модель, производим ее оце-
У,~1 Х-а. '
t-\
+ s„

Раздел 8. Регрессионный анализ для стационарных переменных
401
нивание и затем по оцененной модели можем проверять различные гипотезы
о ее коэффициентах, строить доверительные интервалы для коэффициентов
и прогнозировать значения объясняемых переменных для нового набора
объясняющих переменных. Между тем здесь решающее значение имеет
соотношение между истинным процессом порождения данных и выбранной
статистической моделью.
Если статистическая модель SM оказывается более полной по сравнению с
DGP, то оценивание SM приводит к менее эффективным оценкам. В то же
время если процесс порождения данных оказывается полнее, чем выбранная
SM, то это приводит к более неприятным последствиям — к смещению
оценок. Вследствие этого обычно рекомендуется следовать принципу «от общего
к частному», т.е. первоначально выбирать в качестве статистической
достаточно полную модель, а затем, производя последовательное тестирование
статистической модели, редуцировать исходную статистическую модель
к более экономной форме.
ПРИМЕР 8.2.5
Статистические данные (п = 100) порождены стабильной моделью ADLA,1; 1)
yt = 0.5у,_{ + 0.2х, + 0.3 jc^ + et9 et ~ lid. N@, 0.12),
xt = 0.5jt,_! + v„ v, ~ lid N@, 0.52),
причем ряды st и vt порождаются независимо друг от друга.
Смоделированные реализации изображены на рис. 8.9.
•х
- у
-1-5 | i i i i | i i i i [ i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i |—►
10 20 30 40 50 60 70 80 90 100 f
Рис. 8.9
Оценивание по этим реализациям полной модели ADLA, 1; 1) в качестве
статистической модели дает следующие результаты (табл. 8.5).
Исключая из правой части статистической модели константу, получаем
результаты, приведенные в табл. 8.6.

402
Часть 2. Регрессионный анализ временных рядов
Таблица 8.5
Объясняемая переменная У
Sample (adjusted): 2 100
Переменная
С
П-1)
X
1 Х(-\)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Коэффициент
0.014122
0.555208
0.188567
0.258377
0.913395
0.910660
0.092824
0.818547
Стандартная
ошибка
0.009556
0.034143
0.018421
0.020673
^-статистика
1.477773
16.26107
10.23666
12.49808
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Р-значение
0.1428
0.0000
0.0000
0.0000
0.062869
0.310554
-1.876660
-1.771806
Таблица 8.6
Объясняемая переменная Y
Sample (adjusted): 2 100
Переменная
Г(-1)
X
Д-1)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Коэффициент
0.565569
0.190325
0.256578
0.911404
0.909558
0.093394
0.837363
95.76965
Стандартная
ошибка
0.033621
0.018495
0.020764
^-статистика
16.82186
10.29043
12.35668
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Durbin-Watson stat
Р-значение
0.0000
0.0000
0.0000
0.062869
0.310554
-1.874134
-1.795494
2.218619
Редуцированная модель признается лучшей по критерию Шварца.
Проверка ее на адекватность дает следующие результаты:
• коррелограмма ряда остатков соответствует процессу белого шума;
• критерий Бройша — Годфри указывает на отсутствие автокоррелиро-
ванности у ряда st (Р-значение = 0.375 при ARA) альтернативе и 0.165
при ARB) альтернативе);
• критерий Харке — Бера не обнаруживает значимых отклонений от
нормальности (Р-значение = 0.689);
• критерий Уайта не обнаруживает гетероскедастичности (Р-значение =
= 0.285).

Раздел 8. Регрессионный анализ для стационарных переменных
403
Иными словами, применение критериев адекватности к оцененной модели
дает удовлетворительные результаты.
Посмотрим теперь, что дает оценивание по тем же данным выбираемых
в качестве SM перечисленных ранее 8 редуцированных моделей.
SMj Статическая регрессия: yt = /и + J30xt + ег
Оцененная модель представлена в табл. 8.7.
Таблица 8.7
Объясняемая переменная Y
Переменная
X
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Коэффициент
0.271208
0.174472
0.174472
0.280794
7.805700
14.37805
Стандартная
ошибка
0.053356
/-статистика
5.082965
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Durbin-Watson stat
Р-значеиие
0.0000
0.062241
0.309046
0.307561
0.333613
0.839862
В правой части этой статистической модели нет запаздывающих значений
объясняемой переменной. Поэтому здесь можно ориентироваться на значения
статистики Дарбина — Уотсона. Низкое значение этой статистики указывает
на автокоррелированность ряда еп т.е. на неправильную спецификацию
выбранной статистической модели.
SM2 Процесс авторегрессии: yt = ju + axyt_x + sr
Оцененная модель представлена в табл. 8.8.
Таблица 8.8
Объясняемая переменная У
Переменная
С
Д-1)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Коэффициент
0.013941
0.764874
0.536633
0.531856
0.213344
4.415033
13.98284
Стандартная
ошибка
0.020679
0.065621
/-статистика
0.674149
11.65594
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Durbin-Watson stat
Р-значение
0.5018
0.0000
0.062869
0.310554
-0.228643
-0.176216
1.349170

404
Часть 2. Регрессионный анализ временных рядов
Поскольку в этой статистической модели правая часть содержит
запаздывающее значение объясняемой переменной, ориентироваться на статистику
Дарбина — Уотсона не следует. Проверку на отсутствие автокоррелированно-
сти для ряда st выполняем, используя критерий Бройша—Годфри. При ARA)
альтернативе Р-значение этого критерия равно 0.00003, так что гипотеза
некоррелированности случайных величин et отвергается. Следовательно,
выбранная статистическая модель специфицирована неправильно.
SM3 Модель опережающего показателя: yt = /и + J5Xxt_x + sr
Оцененная модель представлена в табл. 8.9.
Таблица 8.9
Объясняемая переменная У
Переменная
С
Х(-\)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Коэффициент
0.049508
0.455497
0.652012
0.648424
0.183939
3.281850
28.15718
Стандартная
ошибка
0.019722
0.037291
/-статистика
2.510238
12.21457
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Durbin-Watson stat
Р-значение
0.0137
0.0000
0.062869
0.310554
-0.525251
-0.472824
1.420075
При ARA) альтернативе Р-значение критерия Бройша — Годфри равно 0.0002,
гипотеза некоррелированности случайных величин et отвергается. Выбранная
статистическая модель специфицирована неправильно.
SM4 Модель скорости роста: Ду, = /л + Д,Axt + sv
Оцененная модель представлена в табл. 8.10.
Таблица 8 АО
Объясняемая переменная D(Y)
Sample (adjusted): 2 100
Переменная
С
D(X)
Log likelihood
Durbin-Watson stat
Коэффициент
-0.001126
0.040538
13.74152
1.574116
Стандартная
ошибка
0.021384
0.033362
/-статистика
-0.052674
1.215078
F-statistic
Prob(F-statistic)
Р-значение
0.9581
0.2273
1.476415
0.227286

Раздел 8. Регрессионный анализ для стационарных переменных
405
При ARA) альтернативе Р-значение критерия Бройша — Годфри равно 0.029,
гипотеза некоррелированности случайных величин et отвергается. Выбранная
статистическая модель специфицирована неправильно.
SM5 Модель распределенных запаздываний: yt = ju + J30xt + Д xt_x + er
Оцененная модель представлена в табл. 8.11.
Таблица 8.11
Объясняемая переменная Y
Sample (adjusted): 2 100
Переменная
С
X
Х{-\)
Коэффициент
0.046032
0.156214
0.414363
Стандартная
ошибка
0.018096
0.035435
0.035435
/-статистика
2.543741
4.408526
11.69370
Р-значение
0.0126
0.0000
0.0000
При ARA) альтернативе Р-значение критерия Бройша — Годфри равно 0.0000,
гипотеза некоррелированности случайных величин et отвергается. Выбранная
статистическая модель специфицирована неправильно.
SM6 Модель частичной корректировки: yt - ju + axyt_x + J30xt + er
Оцененная модель представлена в табл. 8.12.
Таблица 8.12
Объясняемая переменная У
Sample (adjusted): 2 100
Переменная
С
УН)
X
Коэффициент
0.007088
0.753212
0.253493
Стандартная
ошибка
0.015431
0.048925
0.028588
/-статистика
0.459354
15.39514
8.867013
Р-значение
0.6470
0.0000
0.0000
При ARA) альтернативе Р-значение критерия Бройша — Годфри равно 0.012,
гипотеза некоррелированности случайных величин et отвергается. Выбранная
статистическая модель специфицирована неправильно.
SM7 Приведенная форма: yt = /л + axyt_x + j3lxt_l + sr
Оцененная модель представлена в табл. 8.13.
Здесь Р-значение критерия Бройша — Годфри при ARA) альтернативе
равно 0.499, а при ARB) альтернативе равно 0.538. Гипотеза
некоррелированности случайных величин et не отвергается, и можно перейти к проверке
адекватности другими критериями. Критерий Харке — Бера не обнаруживает
значимых отклонений от нормальности (Р-значение = 0.937). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.348).

406
Часть 2. Регрессионный анализ временных рядов
Таблица 8.13
Объясняемая переменная Y
Sample (adjusted): 2 100
Переменная
С
7(-1)
Х(-\)
S.E. of regression
Sum squared resid
Коэффициент
0.020438
0.517457
0.318058
0.133909
1.721440
Стандартная
ошибка
0.013757
0.048968
0.028613
/-статистика
1.485648
10.56734
11.11579
Akaike info criterion
Schwarz criterion
Р-значение
0.1406
0.0000
0.0000
-1.153476
-1.074836
Иными словами, применение критериев адекватности к оцененной модели
дает удовлетворительные результаты. Поэтому можно осуществить редукцию
модели, основываясь на статистической незначимости константы в правой
части уравнения. Исключение константы из правой части дает (табл. 8.14).
Таблица 8.14
Объясняемая переменная У
Переменная
У(-1)
д-1)
S.E. of regression
Sum squared resid
Коэффициент
0.532005
0.316252
0.134740
1.761018
Стандартная
ошибка
0.048276
0.028765
/-статистика
11.02001
10.99445
Akaike info criterion
Schwarz criterion
Р-значение
0.0000
0.0000
-1.150947
-1.098520
Модель без константы предпочтительнее по критерию Шварца.
С точки зрения анализа остатков последняя модель вполне может быть
использована для описания процесса порождения данных. Однако если
сравнить результаты ее оценивания с полученными ранее результатами
оценивания модели yt - axyt_x + J30xt + j3xxt_x + en то обнаружим, что в модели
с включением xt в правую часть значения критериев Акаике (-1.874) и
Шварца (-1.795) гораздо предпочтительнее.
SM8 Авторегрессионные ошибки: yt = /л + axyt_x + /3Qxt - axjB0xt_x + sr
Использование нелинейного (итерационного) метода наименьших
квадратов для оценивания параметров этого уравнения дает результаты,
представленные в табл. 8.15.
При AR( 1) альтернативе Р-значение критерия Бройша — Годфри равно 0.0002,
гипотеза некоррелированности случайных величин st отвергается. Выбранная
статистическая модель специфицирована неправильно.

Раздел 8. Регрессионный анализ для стационарных переменных
407
Таблица 8.15
Результаты оценивания модели
У = СA) + СB)*У(-1) + СC)*Х- (СB)*СC))*Х(-1)
Переменная
СA)
СB)
СC)
Коэффициент
0.014489
0.749747
0.052577
Стандартная
ошибка
0.020617
0.070184
0.036535
/-статистика
0.702743
10.68267
1.439066
Schwarz criterion
Р-значение
0.4839
0.0000
0.1534
-0.269859
Рассмотрим также оценивание SM в форме модели коррекции ошибок (хотя
эта модель и не является редуцированной).
SM9 Модель коррекции ошибок: Ду, = /л + Д>Axt - A - ax)(yt_x - bxt_ x + ег
Оцененная модель (нелинейный метод наименьших квадратов)
представлена в табл. 8.16.
Таблица 8.16
Результаты оценивания модели
D(Y) = СA) + CB)*D(X) + (СC) - 1)*(У(-1) - СD)*Х(-1))
Переменная
СA)
СB)
СC)
СD)
Коэффициент
0.014122
0.188567
0.555208
1.004839
Стандартная
ошибка
0.009556
0.018421
0.034143
0.078119
/-статистика
1.477773
10.23666
16.26107
12.86299
Schwarz criterion
Р-значение
0.1428
0.0000
0.0000
0.0000
-1.771806
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.130,
а при ARB) альтернативе равно 0.318, гипотеза некоррелированности
случайных величин £t не отвергается. Критерий Харке — Бера не обнаруживает
значимых отклонений от нормальности (Р-значение = 0.711). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.380).
Иными словами, применение критериев адекватности к оцененной модели
дает удовлетворительные результаты. Опираясь на них, редуцируем модель,
исключая из правой части константу (табл. 8.17).
Таким образом:
Ayt = 0.190Д*,- 0A34(yt_{ - 1.029jc,_1) + er
Модель без константы предпочтительнее по критерию Шварца.

408
Часть 2. Регрессионный анализ временных рядов
Таблица 8.17
Объясняемая переменная D(Y)
Convergence achieved after 3 iterations; D(V) = CB)*D(X) + (CC) - 1)*(У(-1) - CD)*X(-1))
Переменная
CB)
CC)
CD)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Коэффициент
0.190325
0.565569
1.028710
0.812174
0.808261
0.093394
0.837363
95.76965
Стандартная
ошибка
0.018495
0.033621
0.080225
/-статистика
10.29043
16.82186
12.82279
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Durbin-Watson stat
Р-значение
0.0000
0.0000
0.0000
-0.001100
0.213288
-1.874134
-1.795494
2.218619
Уединяя yt в левой части уравнения, получаем
yt = 0.566^_! + 0.190х, + 0.253х,_! + ег
Сравним это уравнение с реально использованным для моделирования:
DGP: yt = 0.5y,_i + 0.2jc, + 03xt_Y + st
и с результатом оценивания соответствующей ему статистической модели:
yt = 0.565yt_l + 0.190*, + 0.257*,.! + sr
Найдем долговременное соотношение между переменными yt и хп
соответствующее теоретическому процессу порождения данных:
yt = 0.5yt + 0.2jc, + 0.3jc,_1 -+y = x.
В то же время долговременное соотношение, получаемое по оцененной
SM, соответствующей этому DGP:
yt = 0.565.У, + 0.190х, + 0.257*, -+у = 1.002jc.
Далее, долговременное соотношение, получаемое по оцененной SM9 (в
варианте без константы в правой части):
yt = 0.566^ + 0.190х, + 0.253х,->.у= 1.021*.
Наконец, если взять результаты оценивания модели SM7 (приведенная
форма) без включения константы, то для этого случая получим
yt = 0.532yt + 0.316х, -^у = 0.675х.
Эти результаты указывают на возможность серьезных последствий,
проистекающих из неправильной спецификации SM, когда эта спецификация
оказывается уэюе спецификации DGP. Заметим, что в рамках такой SM

Раздел 8. Регрессионный анализ для стационарных переменных
409
отнюдь не всегда удается обнаружить статистическими методами узость
выбранной спецификации. Мы смогли это сделать в рамках оцененных
статистических моделей SMj — SM6 и SM8, но не в модели SM7.B
Рассмотрим теперь обратную ситуацию, когда, напротив, выбранная для
оценивания статистическая модель SM оказывается полнее (шире) модели DGP,
так что модель, соответствующая DGP, является частным случаем
статистической модели, выбранной для оценивания.
В качестве DGP будем последовательно брать модели A) — (8), а в
качестве SM — полную модель ADLA, 1; 1) без ограничений на коэффициенты:
Уг =И+"\Уг-\ + Ръ*г + P\xt-\ + £г
Значения коэффициентов при переменных в моделях A) — (8) будем брать
такими же, как и в исходной модели ADLA, 1; 1)
yt = 0.5y,_i + 0.2xf + 0.3x,_! + et.
При моделировании DGP во всех случаях берется st ~ lid. N@, 0.12).
DGPj: Статическая регрессия
yt = 02xt + sr
Оцененная статистическая модель представлена в табл. 8.18.
Таблица 8.18
Объясняемая переменная У
Переменная
С
Y(-\)
X
Х(-\)
S.E. of regression
Sum squared resid
Коэффициент
-0.004647
0.102848
0.186813
0.000201
0.102190
0.992068
Стандартная
ошибка
0.010300
0.101833
0.020222
0.028272
/-статистика
-0.451175
1.009966
9.238033
0.007101
Akaike info criterion
Schwarz criterion
Р-значение
0.6529
0.3151
0.0000
0.9943
-1.684398
-1.579545
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.760,
а при ARB) альтернативе равно 0.951, гипотеза некоррелированности
случайных величин et не отвергается. Критерий Харке — Бера не обнаруживает
значимых отклонений от нормальности (Р-значение = 0.733). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.770).
Иными словами, применение критериев адекватности к оцененной
модели дает удовлетворительные результаты. Опираясь на них, можно перейти
к проверке гипотез о значениях коэффициентов. При проверке гипотезы

410
Часть 2. Регрессионный анализ временных рядов
о занулении константы и коэффициентов при yt_ { и xt_ { получаем значение
обычной F-статистики, равное F = 0.738, nqF = 2.214. Исходя из F-распреде-
ления для статистики F, получаем Р-значение = 0.532. Использование
асимптотического распределения ^2C) для qF приводит к Р-значению = 0.529.
При обоих вариантах гипотеза о занулении трех указанных коэффициентов
не отвергается. Тем самым можно перейти к оцениванию редуцированной
модели j;, = /?0jc, + st (табл. 8.19).
Таблица 8.19
Объясняемая переменная У
Sample: 1 100
Переменная
X
S.E. of regression
Sum squared resid
Коэффициент
0.190067
0.101512
1.020359
Стандартная
ошибка
0.019291
/-статистика
9.852604
Akaike info criterion
Schwarz criterion
Р-значение
0.0000
-1.727139
-1.701087
Редуцированная модель лучше полной и по критерию Акаике, и по
критерию Шварца. Остатки от оцененной редуцированной модели проходят тесты
на нормальность, отсутствие автокоррелированности и гетероскедастичности.
DGP2: Процесс авторегрессии
Оцененная статистическая модель представлена в табл. 8.20.
Таблица 8.20
Объясняемая переменная У
Переменная
С
УН)
X
Х(-\)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Коэффициент
-0.004519
0.576756
-0.013220
0.021476
0.338422
0.317530
0.102290
0.994011
Стандартная
ошибка
0.010315
0.084134
0.020253
0.020228
/-статистика
-0.438075
6.855173
-0.652774
1.061719
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Р-значение
0.6623
0.0000
0.5155
0.2911
-0.007891
0.123820
-1.682441
-1.577588
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.600,
а при ARB) альтернативе равно 0.773, гипотеза некоррелированности
случайных величин £t не отвергается. Критерий Харке — Бера не обнаруживает

Раздел 8. Регрессионный анализ для стационарных переменных
411
значимых отклонений от нормальности (Р-значение = 0.654). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.956).
При проверке гипотезы о занулении константы и коэффициентов при xt и
xt_{ получаем значение обычной F-статистики, равное F = 0.641, nqF = 1.283.
Исходя из F-распределения для статистики F, получаем Р-значение = 0.529.
Использование асимптотического распределения ^2C) для qF приводит
к Р-значению = 0.527. При обоих вариантах гипотеза о занулении трех
указанных коэффициентов не отвергается. Тем самым можно перейти к
оцениванию редуцированной модели yt = axyt_x + st (табл. 8.21).
Таблица 8.21
Объясняемая переменная У
Переменная
Г(-1)
S.E. of regression
Sum squared resid
Коэффициент
0.575922
0.101482
1.009258
Стандартная
ошибка
0.082705
/-статистика
6.963585
Akaike info criterion
Schwarz criterion
Р-значение
0.0000
-1.727825
-1.701612
Редуцированная модель предпочтительнее и по критерию Акаике, и по
критерию Шварца. Анализ остатков не выявляет значимых отклонений от
сделанных предположений в отношении ряда ег
DGP3: Модель опережающего показателя
yt=03Xt_x+St.
Оцененная модель представлена в табл. 8.22.
Таблица 8.22
Объясняемая переменная У
Переменная
С
П-1)
X
х{-\)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Коэффициент
-0.005202
0.052373
-0.012475
0.315962
0.736662
0.728346
0.102236
0.992959
Стандартная
ошибка
0.010305
0.054196
0.020310
0.020645
/-статистика
-0.504767
0.966363
-0.614213
15.304330
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Р-значение
0.6149
0.3363
0.5405
0.0000
0.004035
0.196154
-1.683501
-1.578647 1

412
Часть 2. Регрессионный анализ временных рядов
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.614,
а при ARB) альтернативе равно 0.868, гипотеза некоррелированности
случайных величин st не отвергается. Критерий Харке — Бера не обнаруживает
значимых отклонений от нормальности (Р-значение = 0.740). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.804).
При проверке гипотезы о занулении константы и коэффициентов при xt и
yt_x получаем значение обычной Р-статистики, равное F = 0.577, nqF = 1.730.
Исходя из Р-распределения для статистики Р, получаем Р-значение = 0.632.
Использование асимптотического распределения %\Ъ) для qF приводит
к Р-значению = 0.630. При обоих вариантах гипотеза о занулении трех
указанных коэффициентов не отвергается. Тем самым можно перейти к
оцениванию редуцированной модели yt = fixxt_x + st (табл. 8.23).
Таблица 8.23
Объясняемая переменная У
Переменная
*(-1)
S.E. of regression
Sum squared resid
Коэффициент
0.315777
0.101572
1.011044
Стандартная
ошибка
0.019302
/-статистика
16.35987
Akaike info criterion
Schwarz criterion
Р-значение
0.0000
-1.726058
-1.699844
Редуцированная модель предпочтительнее и по критерию Акаике, и по
критерию Шварца. Анализ остатков не выявляет значимых отклонений от
сделанных предположений в отношении ряда ег
DGP4: Модель скорости роста
Оцененная модель представлена в табл. 8.24.
Таблица 8.24
Объясняемая переменная У
Included observations: 99 after adjusting endpoints
Переменная
С
У(-1)
X
Х{-\)
Коэффициент
-0.029026
0.959750
0.184064
-0.173461
Стандартная
ошибка
0.017741
0.024228
0.019993
0.020340
/-статистика
-1.636049
39.613030
9.206520
-8.528162
Р-значение
0.1051
0.0000
0.0000
0.0000

Раздел 8. Регрессионный анализ для стационарных переменных
413
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.944972
0.943234
0.101277
0.974412
88.26661
1.745026
Окончание табл. 8.24
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
-0.599911
0.425076
-1.702356
-1.597502
543.7988
0.000000
Отметим близкое к 1 оцененное значение коэффициента при >>,_15 что может
говорить о том, что в DGP истинное значение коэффициента равно: ах = 1. Но
тогда нарушается условие стабильности системы. И действительно, график
ряда >>,, полученного в результате моделирования (рис. 8.10), имеет вид, явно
указывающий на нестационарность ряда.
10 20 30 40 50 60 70 80 90 100 t
Рис. 8.10
Вопрос о проверке гипотез типа Я0: ах = 1 требует специального
рассмотрения, обсудим его в последующих темах. Сейчас же, исходя из
наблюдаемого поведения ряда^ и близости оцененного значения коэффициента к 1,
займемся оцениванием модели
Мы можем использовать для нее стандартную (асимптотическую) технику
статистических выводов, поскольку реализация ряда xt имеет вид (рис. 8.11),
указывающий на стационарность этого ряда, и реализация ряда разностей Ду,
имеет вид (рис. 8.12), говорящий в пользу стационарности ряда Ду,.
В результате оценивания получим (табл. 8.25).

414
Часть 2. Регрессионный анализ временных рядов
пир!м||и||ми|||ii|11м|ми[мирщ|1111[ ► -0.6
10 20 30 40 50 60 70 80 90 100 t
РИС. 8.11
■ DELTA
i|мм11мi|iiм|iiii|мирт11in|iмi|in11 >
10 20 30 40 50 60 70 80 90 100 t
РИС. 8.12
Объясняемая переменная D(Y)
Таблица 8.25
Переменная
С
X
Х(-\)
Коэффициент
-0.004915
0.185224
-0.179782
Стандартная
ошибка
0.010297
0.020163
0.020163
/-статистика
-0.477336
9.186333
-8.916410
Р-значение
0.6342
0.0000
0.0000
Здесь, конечно, обратим внимание на статистическую незначимость
константы, а также на то, что оцененные коэффициенты при переменных xt и xt_ l
близки по абсолютной величине и противоположны по знаку. В связи с этим
в рамках статистической модели
yt = /U + P0Xt + PxXt_x + £t
проверяем гипотезу Н0: /и = 0, Д, = -Д. Использовав F-распределение для
F-статистики и распределение хи-квадрат ^2B) для статистики qF = 2F,
получим в обоих случаях Р-значение = 0.876. Гипотеза Я0 не отвергается,
и можно перейти к оцениванию модели с такими ограничениями, т.е. модели
Ду, = До Д** + £t- Оцененная модель с ограничениями представлена в табл. 8.26.
Объяснение переменной D(Y)
Таблица 8.26
Переменная
D(X)
Коэффициент
0.182495
Стандартная
ошибка
0.015882
/-статистика
11.49045
Р-значение
0.0000
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.328,
а при ARB) альтернативе равно 0.605, гипотеза некоррелированности слу-

Раздел 8. Регрессионный анализ для стационарных переменных
415
чайных величин et не отвергается. Критерий Харке -
значимых отклонений от нормальности (Р-значение =
не обнаруживает гетероскедастичности (Р-значение =
и в этом случае в результате тестирования вышли на
имеющую ту же спецификацию, что и DGP.
DGP5: Модель распределенных запаздываний
yt = ju + 0.2х, + 03xt_ i + er
Оцененная модель дана в табл. 8.27.
Таблица 8.27
Объясняемая переменная У
Переменная
С
Д-1)
X
Х{-\)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Коэффициент
-0.003282
0.000523
0.181735
0.289502
0.804020
0.797831
0.101218
0.973283
Стандартная
ошибка
0.010206
0.058294
0.019977
0.024922
/-статистика
-0.321584
0.008975
9.097166
11.61638
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Р-значение
0.7485
0.9929
0.0000
0.0000
0.010665
0.225113
-1.703515
-1.598661
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.972,
а при ARB) альтернативе равно 0.826, гипотеза некоррелированности
случайных величин st не отвергается. Критерий Харке — Бера не обнаруживает
значимых отклонений от нормальности (Р-значение = 0.689). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.433).
Проверяем гипотезу Я0: ju = 0, а{ = 0 . Использовав F-распределение для
F-статистики и распределение хи-квадрат ^2B) для статистики qF = 2F,
получим в обоих случаях Р-значение = 0.950. Гипотеза Я0 не отвергается, и можно
перейти к оцениванию модели с /и = 0, ах =0, т.е. модели^ = J30xt + Pxxt_x + st.
Оцененная модель с ограничениями дана в табл. 8.28.
Таблица 8.28
Объясняемая переменная Y
Переменная
X
Х{-\)
Коэффициент
0.181461
0.289367
Стандартная
ошибка
0.019754
0.019756
/-статистика
9.185972
14.64736
Р-значение
0.0000
0.0000
— Бера не обнаруживает
= 0.673). Критерий Уайта
= 0.988). Таким образом,
статистическую модель,

416
Часть 2. Регрессионный анализ временных рядов
DGP6: Модель частичной корректировки
<y, = // + 0.5y,_1+0.2x, + sr
Оцененная модель представлена в табл. 8.29.
Таблица 8.29
Объясняемая переменная У
Переменная
С
Y{-\)
X
Х{-\)
Коэффициент
-0.005099
0.592041
0.188766
0.000973
Стандартная
ошибка
0.010263
0.071296
0.020280
0.025019
/-статистика
-0.496869
8.304016
9.308077
0.038898
Р-значение
0.6204
0.0000
0.0000
0.9691
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.904,
а при ARB) альтернативе равно 0.723, гипотеза некоррелированности
случайных величин st не отвергается. Критерий Харке — Бера не обнаруживает
значимых отклонений от нормальности (Р-значение = 0.691). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.533).
Проверяем гипотезу Я0: // = 0, Д =0. Использовав F-распределение для
F-статистики и распределение хи-квадрат %\2) для статистики qF - 2F,
получим в обоих случаях Р-значение = 0.884. Гипотеза Я0 не отвергается, и можно
перейти к оцениванию модели с ju = 0, Д =0, т.е. модели >>, = alyt_l + J30xt + ev
Оцененная модель с ограничениями показана в табл. 8.30.
Таблица 8.30
Объясняемая переменная У
Переменная
УН)
X
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Коэффициент
0.592666
0.188468
0.690477
0.687286
0.100924
0.988000
Стандартная
ошибка
0.056702
0.019202
/-статистика
10.45233
9.814814
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Р-значение
0.0000
0.0000
0.004719
0.180476
-1.728911
-1.676484
DGP7: Приведенная форма
yt = 0.5yt_l + 03xt_l + st.
Оцененная модель дана в табл. 8.31.

Раздел 8. Регрессионный анализ для стационарных переменных
417
Таблица 8.31
Объясняемая переменная У
Переменная
С
Г(-1)
X
Х{-\)
Коэффициент
-0.005886
0.559497
-0.010318
0.316645
Стандартная
ошибка
0.010271
0.042762
0.020320
0.020229
/-статистика
-0.573100
13.08387
-0.507807
15.65291
Р-значение
0.5679
0.0000
0.6128
0.0000
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.701,
а при ARB) альтернативе равно 0.827, гипотеза некоррелированности
случайных величин st не отвергается. Критерий Харке — Бера не обнаруживает
значимых отклонений от нормальности (Р-значение = 0.740). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.586).
Проверяем гипотезу Н0: /и = 0, J30 = 0. Использовав F-распределение для
F-статистики и распределение хи-квадрат %2{2) для статистики qF = 2F ,
получим в обоих случаях Р-значение = 0.734. Гипотеза Н0 не отвергается,
и можно перейти к оцениванию модели с /и = 0, J30 = 0, т.е. к оцениванию
модели^, = alyt_l + pxxt_x + st. Оцененная модель с ограничениями
представлена в табл. 8.32.
Таблица 8.32
Объясняемая переменная У
Переменная
Г(-1)
Х(-\)
Коэффициент
0.561389
0.313207
Стандартная
ошибка
0.041849
0.019269
/-статистика
13.41452
16.25422
Р-значение
0.0000
0.0000
DGP8: Авторегрессионные ошибки
^ = 0.5^.! +0.2x,-0.1x,_! + ег
Оцененная модель представлена в табл. 8.33.
Таблица 8.33
Объясняемая переменная У
Переменная
С
У(-1)
X
Х{-\)
Коэффициент
-0.004519
0.576756
0.186780
-0.093875
Стандартная
ошибка
0.010315
0.084134
0.020253
0.025414
/-статистика
-0.438075
6.855173
9.222532
-3.693770
Р-значение
0.6623
0.0000
0.0000
0.0004

418
Часть 2. Регрессионный анализ временных рядов
Р-значение критерия Бройша — Годфри при ARA) альтернативе равно 0.600,
а при ARB) альтернативе равно 0.773, гипотеза некоррелированности
случайных величин st не отвергается. Критерий Харке — Бера не обнаруживает
значимых отклонений от нормальности (Р-значение = 0.654). Критерий Уайта
не обнаруживает гетероскедастичности (Р-значение = 0.682).
Исключим из статистической модели статистически незначимую
константу (табл. 8.34).
Таблица 8.34
Объясняемая переменная У
Переменная
У(-1)
X
Х{-\)
Коэффициент
0.578309
0.186426
-0.094531
Стандартная
ошибка
0.083705
0.020151
0.025263
/-статистика
6.908866
9.251413
-3.741827
Р-значение
0.0000
0.0000
0.0003
Заметим, что произведение оцененных коэффициентов при yt_ х и xt равно
0.108, т.е. близко по абсолютной величине и противоположно по знаку
коэффициенту при xt_x. В связи с этим наблюдением проверим гипотезу Я0: Д = -ах/30.
Здесь имеем дело с нелинейной гипотезой, и результаты проверки могут
зависеть от формы записи этого ограничения на коэффициенты. Поэтому
проверяем указанную гипотезу в трех формах:
я0:Д=-^0; #0:А>=-—; #o:„i=_A
<*х До
Соответствующие этим формам Р-значения ^2A)-критериев равны 0.515,
0.514 и 0.506, так что выводы в отношении гипотезы Н0 согласуются: эта
гипотеза не отвергается. Последнее означает, что можно перейти к
оцениванию модели с ограничением на коэффициенты в виде Д = -ах/30, т.е. к
модели^ = axyt_x + J30xt - axj30xt_x + st. В итоге получаем оцененную модель
(табл. 8.35).
Таблица 8.35
Объясняемая переменная У
Convergence achieved after 3 iterations; У = СA)*У(-1) + СB)*Х- (СA)*СB))*Х(-1)
Переменная
СA)
СB)
Коэффициент
0.575812
0.182370
Стандартная
ошибка
0.083369
0.019110
/-статистика
6.906747
9.543254
Р-значение
0.0000
0.0000

Раздел 8. Регрессионный анализ для стационарных переменных
419
Ее можно записать в виде
yt = 0.576у,_! + 0.182*, - 0A05xt_l + et.
Таким образом, во всех рассмотренных случаях, когда DGP являлся
частным случаем выбранной для оценивания статистической модели,
последовательное применение метода редукции модели «от общего к частному»
(с предварительной проверкой SM на адекватность) выводило нас на
редуцированные модели, спецификация которых соответствовала спецификации
DGP. В то же время, как было показано выше, при движении «от частного
к общему» возможны ситуации, когда остановка происходит на модели,
существенно отличающейся от DGP, хотя и проходящей стандартные тесты
на адекватность имеющимся статистическим данным.
Это еще раз подчеркивает предпочтительность использования при
подборе моделей по статистическим данным метода «от общего к частному», т.е.
к первоначальному выбору достаточно общей модели, проверке ее на
адекватность имеющимся статистическим данным и в случае признания выбранной
модели адекватной данным последующей редукции этой модели с
использованием стандартных критериев спецификации.
В связи с последними замечаниями обратимся еще раз к модели линейной
регрессии с автокоррелированными ошибками, образующими стационарный
процесс авторегрессии первого порядка. В учебной литературе по
эконометрике довольно часто делается упор на эту модель как на средство
преодоления проблемы автокоррелированности ошибок в рамках известных процедур
Кохрейна — Оркатта или Прайса — Уинстена. Однако, как ясно из
предыдущего изложения, такая модель (в нашей нумерации — модель 8) является
всего лишь весьма частным случаем общей динамической модели ADLA, 1; 1).
В рамках этой общей модели
yt=M + а\Уг-\ + Дл + P\xt-\ + Ь
модель, о которой идет речь, выделяется выполнением соотношения
A=-«iA-
В то же время при Д Ф 0 общую модель ADLA, 1; 1) можно представить
в виде:
( В ^
l + ^-L
А
A-<*,!)>,=#,
где
a{L) = \-axL, b(L) = j30
x,+st, или a(L)yt -b(L)xt+st,
( a \
v A j
(Для простоты полагаем /и = 0.)
Если ах = -—, то модель принимает вид:
Ро

420
Часть 2. Регрессионный анализ временных рядов
(\-axL)yt=P0{\-axL)xt+£n
и многочлены a{L) и b(L) имеют общий множитель A - axL). Разделив обе
части уравнения на этот общий множитель, получим
Уг = АЛ + и»
где
ut = ■—>
\-axL
так что A - axL) ut = st и ut = ахщ_х + st.
В связи с наличием общего множителя модель авторегрессионных ошибок
относят к классу моделей, называемому COMFAC {common factors).
Рассматриваемая модель обязана принадлежностью к этому классу именно из-за
наличия ограничения Д = -ах/30. Класс COMFAC является весьма частным
случаем моделей с авторегрессионно распределенными запаздываниями.
Поэтому применение обычной процедуры проверки автокоррелированности
ошибок в модели регрессии yt = J30xt + ut и коррекции обнаруженной
автокоррелированности посредством авторегрессионного преобразования
переменных, вообще говоря, некорректно. Правильный порядок действий должен
быть следующим:
• установление пригодности модели a(L)yt = b(L)xt + st с помощью
различных критериев адекватности; гипотеза о том, что ряд et является
гауссовским белым шумом, не должна отвергаться — в противном
случае следует говорить о непригодности уже этой общей модели;
• проверка гипотезы о том, что многочлены a(L) и b(L) имеют общие
корни;
• наконец, в случае подтверждения обеих гипотез следует проверить
гипотезу Н0: ах = 0 (она соответствует модели статической регрессии).
Заметим, что отвержение этой гипотезы непосредственно в модели
с автокоррелированными ошибками вовсе не доказывает наличия
указанных общих множителей.
Однако здесь имеются некоторые сложности.
На первом шаге гипотеза Н0: «st — белый шум» проверяется, в частности,
против альтернативы НА: et ~ AR(£) с к </?, т.е.
где v, ~ Lid. и хотя бы одно pj * 0.
Модель, соответствующая альтернативе, имеет вид:
Уг =a\yt-\ + АЛ + A*r-i + A^-i + - +РрЪ-р + v„

Раздел 8. Регрессионный анализ для стационарных переменных
421
и фактически речь идет о проверке гипотезы Н0: рх = ... = р£ = 0 против
НА: рх + ... + Рр ф 0. Такую проверку можно осуществить, используя
стандартный критерий Бройша — Годфри. В то же время не рекомендуется
использовать для этой цели критерии, основанные на статистиках Бокса — Пирса
и Люнга — Бокса (введенные в теме 1.2) и предназначенные для анализа
«сырых» рядов (см., например, (Kwan, Sim, 1996)).
Проблемы возникают и с применением стандартного критерия Вальда для
проверки гипотезы Нх\ J3X = -axj30 против альтернативы НА: J3X Ф -Я\/30. Дело
в том, что эта гипотеза не является линейной, а в таких случаях результаты
применения критерия Вальда зависят от того, в какой форме записано
ограничение: Д = -axfiQ, ах --^- или /?0 = -—, что может приводить к проти-
А) а\
воречивым выводам.
Отметим также проблему, связанную с последовательным использованием
нескольких критериев проверки гипотез. В рамках рассмотренной процедуры
приходится, по крайней мере, сначала проверять гипотезу Нх о наличии
общих множителей, а затем, если она не отвергается, проверять гипотезу
Н2: ах = 0 о некоррелированности ошибок в статической модели регрессии.
Пусть каждая из этих гипотез проверяется на уровне значимости а,
скажем, а = 0.05. Какова в такой ситуации вероятность ошибочного отвержения
модели статической регрессии? Имеем:
^{ошибочно отвергается хотя бы одна из гипотез НХ,Н2} <
< ^{ошибочно отвергается Нх} + ^{ошибочно отвергается Н2} =
= а + а = 2а.
Следовательно, если положить а = 0.025, то вероятность отвержения
модели статической регрессии в рамках двухступенчатой процедуры не будет
превышать 0.05. Заметим, что при этом еще не принимали в расчет ошибки,
связанные с возможностью неправильной диагностики общей модели.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что представляют собой модели с авторегрессионно распределенными
запаздываниями? Как можно найти долговременную связь между переменными в такой
модели?
2. Что представляют собой импульсные и долгосрочные мультипликаторы в
динамической модели?
3. Как производятся оценивание модели с авторегрессионно распределенными
запаздываниями и диагностика оцененной модели?
4. Что представляет собой модель векторной авторегрессии (VAR)? Какое условие
обеспечивает стабильность векторной авторегрессии?
5. Какое условие обеспечивает стабильность векторной авторегрессии? Как можно
найти долгосрочное (стабильное) состояние системы?

422
Часть 2. Регрессионный анализ временных рядов
6. Чем различаются замкнутые и открытые VAR?
7. Как находится передаточная функция стабильной открытой VAR? Как находится
долговременная связь между экзогенными и эндогенными переменными? Что
понимается под матрицей долгосрочных мультипликаторов?
8. Какие частные случаи можно получить, основываясь на динамической модели
первого порядка?
9. Какие проблемы возникают при оценивании динамических моделей (если
статистическая модель полнее процесса порождения данных, если процесс
порождения данных полнее статистической модели)?
10. Какие динамические модели называют моделями с общим множителем? Какие
проблемы возникают при проверке принадлежности динамической модели классу
моделей с общим множителем?

Раздел 9
НЕСТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ.
МОДЕЛИ ARIMA
Тема 9.1
НЕСТАЦИОНАРНЫЕ ARMA МОДЕЛИ
Нестационарные временные ряды
В данном разделе временно вернемся к прописным и строчным обозначениям
для случайных величин и их реализаций соответственно.
Начнем изложение с рассмотрения двух временных рядов.
Первый из них представляет статистические данные о величине валового
национального продукта (GNP — gross national product) в США за период
с I квартала 1947 г. по IV квартал 1961 г. (сезонно скорректированные
квартальные данные в пересчете на год — 60 наблюдений, млрд долл., в текущих
ценах). График этого ряда (рис. 9.1) имеет выраженный линейный тренд.
600
500 ^
400 А
300 А
200 111111111111111111111111111111111111111111111111111111111111 ►
1948 1950 1952 1954 1956 1958 1960
GNP
ГОД
Рис. 9.1
Второй ряд (NONDURABLE) представляет статистические данные об
объеме потребительских расходов на товары кратковременного пользования и
услуги в Великобритании за период с I квартала 1974 г. по IV квартал 1985 г.

424
Часть 2. Регрессионный анализ временных рядов
54 000
52 000
50 000
■ NONDURABLE
i i i I i i i | i м | i i i I i i i I i i i I i i i | i i i | i i i | i i i | i i i | i i I
4fr
N.
О)
(О
N.
О)
О)
N.
(Л
о
00
(Л
СМ
ОС
СО
оо
(Л
Год
Рис. 9.2
(сезонно скорректированные квартальные данные — 48 наблюдений, млн
фунтов стерлингов, в текущих ценах). Этот ряд также обнаруживает линейный
тренд (рис. 9.2).
Хотя выборочные автокорреляционные и частные автокорреляционные
функции определялись для стационарных рядов, посмотрим на коррелограм-
мы, построенные по представленным данным.
Для ряда GNP коррелограмма имеет вид:
Autocorrelation Partial Correlation
AC
РАС g-статистика Р-значение
1*******
1*******
1******
1******
******
*****
*****
1*****
1****
1****
1*** *
1***
1***
**
I**
1**
******* 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0.946
0.893
0.840
0.791
0.743
0.696
0.648
0.599
0.550
0.498
0.442
0.388
0.337
0.291
0.253
0.218
0.946
-0.021
-0.024
0.013
-0.021
-0.022
-0.030
-0.044
-0.033
-0.052
-0.073
-0.034
-0.002
0.007
0.041
-0.002
56.419
107.52
153.55
195.14
232.52
265.90
295.41
321.09
343.13
361.57
376.44
388.08
397.06
403.91
409.21
413.22
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000

Раздел 9. Нестационарные временные ряды. Модели ARIMA
425
А для ряда NONDURABLE:
ACF PACF к АС РАС g-статистика Р-значение
42.921
79.976
111.92
138.99
162.09
181.36
196.57
208.14
216.39
222.07
225.99
228.56
230.11
230.91
231.28
231.41
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
Если отвлечься от видимой нестационарности этих рядов, то поведение
выборочных ACF и PACF предполагает идентификацию обоих рядов как
рядов типа ARA). Имея в виду наличие у рядов выраженного линейного тренда,
произведем оценивание моделей
Xt = a + fit + a1Xt_l +ur
(Здесь используем обозначение ип а не sn поскольку ряд ut на этот раз может
и не быть белым шумом.)
Это приводит к следующим результатам1.
Для ряда GNP результаты приведены в табл. 9.1.
Остатки обнаруживают явную автокоррелированность: Р-значение
критерия Бройша — Годфри при альтернативе ARA) равно 0.0000. Переоценивание
с включением в модель запаздывания на два квартала дает результаты,
приведенные в табл. 9.2.
Модули комплексных чисел, обратных авторегрессионным корням, равны
0.7926, что говорит в пользу стационарности детрендированного ряда
X«=Xt-ti-yt.
Приводимые в таблицах оценки константы (Q и коэффициента при переменной t (Г)
соответствуют оценкам ju и у в представлении
{Xt-fi-yt) = al{Xt_l-fi-y{t-\)) + a2{Xt_2-ju-r{t-2)) + ut
(а2 - 0 для табл. 9.1). Эти оценки получаются применением нелинейного метода наименьших
квадратов. При этом обозначение ARA) указывает на оценку для ах, a ARB) — на оценку для а2.
I******* i*******
I******* j
I****** |
|***** |
I*** i
|*** * |
г* i
Г* I
I* I
Г I
I* I
I* I
I I
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0.917
0.843
0.774
0.704
0.643
0.581
0.510
0.439
0.366
0.300
0.246
0.196
0.150
0.106
0.072
0.041
0.917
0.014
-0.004
-0.040
0.013
-0.041
-0.090
-0.050
-0.066
-0.012
0.026
-0.006
-0.013
-0.025
0.036
-0.016

426
Часть 2. Регрессионный анализ временных рядов
Таблица 9.1
Объясняемая переменная GNP
Method: Least Squares; Sample (adjusted): 1947:2 1961:4;
Included observations: 59 after adjusting endpoints; Convergence achieved after 3 iterations
Переменная
С
T
ARA)
Inverted AR Roots
Коэффициент
216.0630
5.269279
0.846976
Стандартная
ошибка
11.30237
0.281754
0.072723
/-статистика
19.11661
18.70170
11.64665
Р-значение
0.0000
0.0000
0.0000
0.85
Таблица 9.2
Объясняемая переменная GNP
Method: Least Squares; Sample (adjusted): 1947:3 1961:4;
Included observations: 58 after adjusting endpoints; Convergence achieved after 3 iterations
Переменная
С
т
ARA)
ARB)
Inverted AR Roots
Коэффициент
217.7399
5.221538
1.380274
-0.630066
Стандартная
ошибка
5.054473
0.140436
0.109452
0.109453
/-статистика
43.07865
37.18089
12.61078
-5.756490
Р-значение
0.0000
0.0000
0.0000
0.0000
0.69 - 39/ 0.69 + 39/
К построению модели для ряда GNP можно подойти иначе. Сначала
произведем детрендирование ряда, оценивая модель
Xt = /j + yt + ur
Результаты приведены в табл. 9.3.
Таблица 9.3
Объясняемая переменная X
Переменная
С
Т
Durbin-Watson stat
Коэффициент
218.4825
5.181995
0.316211
Стандартная
ошибка
2.640153
0.075274
/-статистика
82.75373
68.84144
Prob(Fstatistic)
^-значение
0.0000
0.0000
0.000000

Раздел 9. Нестационарные временные ряды. Модели ARIMA
427
Остатки, полученные при оценивании этой модели, образуют оцененный
детрендированный ряд со следующей коррелограммой:
Autocorrelation Partial Correlation к АС РАС g-статистика /^значение
******
1****
1*
1
**|
***|
***
***|
**
**
**|
**|
1******
****!
**1
*1
*1
*1
*1
***1
1*
1
2
3
4
5
6
7
8
9
10
11
12
0.836
0.531
0.183
-0.100
-0.272
-0.339
-0.350
-0.332
-0.281
-0.234
-0.234
-0.226
0.836
-0.554
-0.210
0.044
-0.004
-0.082
-0.169
-0.072
0.058
-0.177
-0.321
0.103
44.028
62.115
64.294
64.960
69.949
77.846
86.446
94.332
100.070
104.160
108.320
112.260
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
Она позволяет идентифицировать этот ряд как ARB). После этого можно
строить ARB) модель (табл. 9.4) для (оцененного) детрендированного ряда
X, а^ш^Х, -218.4825-5.181995/.
Таблица 9.4
Объясняемая переменная Xdetrended
Переменная
ARA)
ARB)
Коэффициент
1.379966
-0.630426
Стандартная
ошибка
0.107605
0.107605
/-статистика
12.82435
5.858722
Р-значение
0.0000
0.0000
Объединив результаты последних двух оцениваний, получим оцененную
модель
X, -218.4825-5.181995? =
= 1.379966(Х,_, -218.4825-5.181995(^-1))-
-0.630426(Х,_2 -218.4825-5.181995G-2)),
или
X, =[A-1.379966+0.630426)-218.4825 +
+ 1.379966-5.181995-0.630426-5.181995-2] +
+ (l-1.379966 + 0.630426)-5.181995f + 1.379966X,_, -0.630426Z,_2 +е, =
= 55.338375 +1.297882/+ 1.379966Х,_, -0.630426Х,_2 +е,

428
Часть 2. Регрессионный анализ временных рядов
В то же время по приведенным результатам оценивания модели
Xt = а + fit + axXt_x + a2Xt_2 + ur
получаем
JT,-217.7399-5.221538* =
= 1.380274(JTM -217.7399-5.221538(/
-0.630066(X,_2-217.7399-5.221538(/
или
Z, = [A -1.3 80274 + 0.630066) • 217.7399 +
+ 1.380274-5.221538-0.630066-5.221538-2] +
+ (l-1.380274 + 0.630066)-5.22153& + 1.380274JTM -0.630066X,_2 +et =
= 55.17011 + 1.304298/ + 1.380274Лгм -0.630066X,_2 +et
Таким образом, результаты, полученные при использовании обоих
вариантов построения модели, практически совпадают. Поэтому можно
использовать смешанный вариант — применять детрендированный ряд для
идентификации порядка модели, а оценивать идентифицированную модель вместе
с включенным в нее трендом, в данном случае — оценивать модель Xt = а +
+ fit + axXt_x +a2Xt_2+ur
Заметим, что диагностика рядов остатков в обеих оцененных моделях
говорит в пользу их адекватности.
Перейдем теперь к ряду NONDURABLE. Коррелограмма детрендированного
ряда (ряда остатков от оцененной модели регрессии Xt на константу и /)
имеет вид:
Autocorrelation Partial Correlation к АС РАС g-статистика Р-значение
32.083
52.942
62.887
65.515
65.965
66.218
69.647
77.505
93.500
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
Она обнаруживает резко выделяющийся пик на лаге 1, так что можно
попробовать оценить модель Xt = а + fit + axXt_x + ur Это дает следующие
результаты (табл. 9.5).
-1))-
-2)),
-1
2
3
4
5
6
7
8
9
0.793
0.632
0.432
0.219
0.090
-0.067
-0.242
-0.362
-0.510
0.793
0.011
-0.195
-0.193
0.062
-0.152
-0.277
-0.084
-0.211

Раздел 9. Нестационарные временные ряды. Модели ARIMA
429
Таблица 9.5
Объясняемая переменная X
Переменная
С
Т
ARA)
Коэффициент
47962.75
315.1909
0.884803
Стандартная
ошибка
2862.678
76.44770
0.080824
/-статистика
16.75451
4.122961
10.94727
Р-значение
0.0000
0.0002
0.0000
Наблюдаемые Р-значения статистик Люнга — Бокса для ряда остатков
превышают 0.05 при всех выборах М от 1 до 20. Проверка на отсутствие
автокоррелированности по критерию Бройша — Годфри дает Р-значения,
большие 0.05, как при ARA) альтернативе, так и при альтернативах ARB),
ARC) и т.д. Наконец, при проверке нормальности Р-значение статистики
Харке — Бера равно 0.648 , так что по совокупности этих результатов можно
было бы говорить о пригодности оцененной модели
jrr-47962.75-315.1909r = 0.884803(JTM-47962.75-315.1909(/-l)) + er
Обратим, однако, внимание на следующее обстоятельство. Оцененное
значение 0.884803 коэффициента при Xt_x достаточно близко к 1, и если
ориентироваться на вычисленное значение 0.080824 стандартной ошибки для
этого коэффициента, то при допущении отклонений от оцененного
значения в пределах двух стандартных ошибок в интервал допустимых значений
0.884803 ± 2-0.080824 попадают и значения, большие или равные 1. Но
последние соответствуют нестационарному процессу авторегрессии.
Таким образом, несмотря на то что при полученной точечной оценке
0.884803 коэффициента при Xt_x построенная модель формально оказывается
стационарной относительно детерминированного линейного тренда (т.е. детрен-
дированный процесс следует стационарной ARA) модели), нельзя с
достаточной степенью уверенности гарантировать, что истинная модель порождения
наблюдений также стационарна относительно линейного тренда.
Между тем вопрос о стационарности или о нестационарности модели,
порождающей наблюдаемый ряд, привлекает к себе постоянное внимание уже
в течение нескольких десятков лет. Это внимание особенно усилилось после
серии работ 1980-х гг., в которых было введено понятие коинтеграции. С
помощью этого понятия была обоснована методика построения «моделей коррекции
ошибок», в рамках которых удается моделировать наличие долговременных
связей между переменными вместе с указанием краткосрочной динамики,
обеспечивающей поддержание этих долговременных связей.
Далее будут рассмотрены вопросы, связанные с методами различения
стационарных (стационарных относительно детерминированного тренда) и
нестационарных рядов в рамках ARMA моделей, а также вопросы построения
моделей связи между временными рядами.

430
Часть 2. Регрессионный анализ временных рядов
Поведение реализаций
процесса авторегрессии первого порядка
при различных значениях коэффициента
при запаздывающей переменной
Начнем с рассмотрения наиболее простой модели — процесса ARA)
Xt = axXt_x +er
Мы уже знаем, что такой процесс является стационарным при выполнении
условия -1 < ах < 1. А как проявляется нестационарность ряда Xt при
нарушении этого условия? Приведем смоделированные реализации такого ряда при
ах = 0.5 (рис. 9.3), ах = 0.7 (рис. 9.4), ах = 0.9 (рис. 9.5), ах = 1 (рис. 9.6), ах = 1.05
(рис. 9.7), ^ = 1.1 (рис. 9.8).
5 10 15 20 25 30 35 40 45 50 t
Рис. 9.3
X <
4-
2-
П -
-2-
4 -
i
А
\ к
Ц
1Щ|ШТ|Ш
а\
1
1
J
Г1
|1Ш]-!1
= 0.7
\ Л. . N
Л MAip
W Vl/i
V j
1|1111|1И1|1111|1МЦМП| ►
5 10 15 20 25 30 35 40 45 50 t
Рис. 9.4
ах = 0.9
5 10 15 20 25 30 35 40 45 50 t
Рис. 9.5
0 |i1111111111111|i11111111111111111111111р111111111 »
5 10 15 20 25 30 35 40 45 50 t
Рис. 9.6

Раздел 9. Нестационарные временные ряды. Модели AR1MA
431
Xf в, = 1.05
10-
П -
-10-
-20-
-30-
I 1 II I II I I I 1 I 1 I III II I II I I I I I II I I I I I I I I IIIIIIII II I I w
5 10 15 20 25 30 35 40 45 50
Рис. 9.7
t
*t fll = u
50-
0-
-50-
-100-
-150-
-200-
-250-
1111111111111111111111111111111111111111111111111 "
5 10 15 20 25 30 35 40 45 50 t
Рис. 9.8
NOISE
Во всех случаях в качестве начального значения Хх взято хх = 0 и
использовалась одна и та же последовательность значений еи ..., еТ9 имитирующая
гауссовский белый шум с дисперсией, равной 1 (график этой
последовательности приведен на рис. 9.9).
Однако поведение
смоделированных рядов оказалось
качественно различным. Полезно проследить
(табл. 9.6), как изменяется характер
траектории ряда с возрастанием
значений коэффициента ах от ах = 0.5
до ах = 1.1. Заметим при этом, что
в порождающих моделях
математические ожидания Xt равны 0. При
возрастании значения ах от ах = 0
(белый шум) до ах = 1 количество
пересечений нулевого уровня
уменьшается, все более длинными
становятся периоды, в течение которых
значения ряда находятся по одну сторону от нулевого уровня.
Расширенный график ряда при ах = 1, продленный до 500 наблюдений
(рис. 9.10), иллюстрирует характерное свойство реализаций процесса
Xt =Xt_x + £„
состоящее в том, что такой процесс, начавшись в момент t = 1 со значения
Xt = хх (в данном случае хх = 0), в дальнейшем очень редко пересекает
уровень хх («возвращается к уровню хх») и, находясь в течение длительного
времени по одну сторону от этого уровня (выше или ниже), может удаляться
от этого уровня на значительные расстояния.
i титр м i|i i м i мирт [in || им |i мним!»
5 10 15 20 25 30 35 40 45 50 t
Рис. 9.9

432
Часть 2. Регрессионный анализ временных рядов
Таблица 9.6
Поведение траектории ряда при изменении коэффициента аЛ
Модель
Noise (белый шум)
ARA) в! =0.5
ARA) я, =0.7
ARA) в, =0.9
ARA) fll = 1.0
ARA) ax = 1.05
ARA) в, =1.1
Количество пересечений
нулевого уровня
25
14
8
8
1
1
1
Среднее значение
-0.046
-0.097
-0.191
-0.649
-3.582
-13.511
-59.621
50 100 150 200 250 300 350 400 450 500 f
Рис. 9.10
«Повернутая вертикально», траектория ряда
напоминает траекторию движения сильно
нетрезвого человека, пытающегося продвигаться
вперед по прямой, но не имеющего
возможности успешно выдерживать нужное направление
(рис. 9.11). И это служит некоторым
оправданием термина, используемого для ARA)
процесса с ах - 1:
Xt =Xt_t + st — случайное блуждание
(процесс случайного блуждания —
random walk).
Далее рассмотрим этот процесс подробнее,
а сейчас обратим внимание на поведение
реализаций процесса
Рис. 9.11

Раздел 9. Нестационарные временные ряды. Модели ARIMA
433
Xt = axXt_x +et
при ах - 1.05 (рис. 9.7) и ах = 1.1 (рис. 9.8). Обе реализации иллюстрируют
«взрывной» (explosive) характер поведения ARA) процесса при ах > 1:
траектории процесса очень быстро удаляются от начального уровня на
всевозрастающие расстояния. В связи с этим «взрывные» модели непригодны для
описания поведения макроэкономических рядов на сколь-нибудь протяженных
интервалах времени.
Пониманию столь различного поведения реализаций ARA) процесса
помогает представление модели в виде:
Xt -Xt_x = axXt_x -Xt_x + et = (ax - \)Xt_x + et9
или
AXt=cpXt_x + £n
где AXt = Xt -Xt_x, cp -ax - 1.
При ax = 1 имеем cp - ax - 1 = 0, и приращения AXt ряда Xt образуют
процесс белого шума, так что условное математическое ожидание AXt при
фиксированном (наблюдаемом) значении Xt_ x =xt_x не зависит от xt_ x и равно 0.
Соответственно при фиксированном (наблюдаемом) значении Xt_x - xt_x
условное математическое ожидание случайной величины Xt - AXt + Xt_ x равно
xt_ x. Если распределение случайной величины et симметрично относительно
нуля (а именно таково гауссовское распределение, которое было использовано
при моделировании), то наблюдаемое значение Xt = xt может с равным
успехом оказаться как больше, так и меньше xt_x. Именно это и определяет
блуждающий характер траектории ряда.
При ах > 1 имеем ср - ах - 1 > 0, и условное математическое ожидание AXt
при фиксированном (наблюдаемом) значении Xt_x =xt_x, равное E(AXt\Xt_x =
= xt_x) = cpxt_x, имеет знак, совпадающий со знаком xt_x. Таким образом, если
xt_x > 0, то ожидаемое значение следующего наблюдения Xt = xt больше
значения х,_ х, а если xt_ х < 0, то ожидаемое значение следующего
наблюдения Xt = xt меньше значения xt_ x. Наличие такого механизма приводит
к быстрому и прогрессирующему удалению траектории процесса от
начального уровня, что и наблюдалось для реализаций ARA) модели при ах - 1.05
иах = 1.1.
Наконец, при 0 < ах < 1 имеем ср - ах - 1 < 0, и условное математическое
ожидание AXt при фиксированном (наблюдаемом) значении Xt_ x = xt_ x,
равное E(AXt\Xt_x = xt_x) = (pxt_x, имеет знак, противоположный знаку xt_x.
Таким образом, если xt_ х > 0, то ожидаемое значение следующего наблюдения
Xt =xt меньше значения xt_x, а если xt_x < 0, то ожидаемое значение еле-

434
Часть 2. Регрессионный анализ временных рядов
5 10 15 20 25 30 35 40 45 50 t
Рис. 9.12
0 |||||||||Ц||М||||||||||||||||1М1|| ||||11М| MM j »
5 10 15 20 25 30 35 40 45 50 t
РИС. 9.13
дующего наблюдения Xt = xt больше значения xt_ х. Наличие такого
механизма обеспечивает удержание траектории процесса в относительной близости
от уровня, равного безусловному математическому ожиданию E{Xt) = /и ряда
(в данном случае — ju = 0), и достаточно частое пересечение траекторией
ряда этого уровня.
Мы рассмотрели ситуации с ах > 0, поскольку они наиболее типичны для
экономических временных рядов. Для полноты приведем также
смоделированные реализации процесса Xt = axXt_x + st при ах = - 1 (рис. 9.12) и ах = - 1.1
(рис. 9.13).
Случайное блуждание
как модель стохастического тренда
Обратимся теперь к процессу случайного блуждания
Xt = Xt_x + sn t= 1, ..., 7,
со стартовым значением^ =х0. Можно представить^ в виде:
Xt = Xt_x +st= (Xt_2 + st_x) + st = Xt_2 + st_x +et= (Xt_3 + et_2) + st_x + et =
= Xt_3+et_2+£t_x+£t=... = X0+(ex+... + £t),
7 = 1
Отсюда получаем
E{Xt IX0 = x0) = x0,
D(Xt\X0=x0) = D(et+... + £t) = D(ex) + ... + D(£t) = tD(£x) = tcr2e.

Раздел 9. Нестационарные временные ряды. Модели ARIMA
435
Далее,
Cov(Xt, Х,_х | Х0 = х0) = Е[{Х, - х0 )(*,_, - х0) | Х0 = х0 ]
= £[(*, +... + et)(s,+... + et_l)] = (t-l)a2£
не зависит от значения х0, так что
^D(XtLD{Xt_x) Jaftilalit-l) V/
Отсюда находим
Г
1
2
3
4
5
CorrGT,,*,.,)
0
0.707
0.806
0.866
0.894
/
6
7
8
9
10
сои-с*;,*,.,)
0.913
0.925
0.935
0.943
0.949
т.е. соседние значения Xt и Xt_ г очень сильно коррелированы, притом
положительно и тем более сильно, чем больше t. Именно это приводит к траектории
случайного блуждания, которая наблюдалась выше. На первых нескольких
шагах траектория как бы «определяется», где она будет находиться в течение
довольно длительного периода — выше или ниже начального уровня х0. Так
что если после нескольких первых шагов траектория случайного блуждания
оказалась ниже уровня х0 (как это было у смоделированной нами
реализации), она может оставаться там в течение весьма продолжительного времени.
Если смоделировать очень длинную реализацию случайного блуждания, то
она будет состоять из чередующихся длинных участков, на которых функция
находится соответственно выше или ниже уровня х0.
При Х0 = 0 получаем
7=1
Рассматривая последний ряд сам по себе (не связывая его со стартовым
значением), имеем
E(Xt) = 09 D(Xt) = ta?,
следовательно, этот ряд — нестационарный.
Этот ряд является моделью стохастического тренда (stochastic trend),
который обнаруживается во многих экономических временных рядах и
должен обязательно приниматься во внимание при построении регрессионных
моделей связи между двумя или несколькими рядами, имеющими
стохастический тренд.
■Я-

436
Часть 2. Регрессионный анализ временных рядов
Фундаментальное различие между временными рядами,
имеющими только детерминированный тренд,
и рядами, которые (возможно, наряду с детерминированным)
имеют стохастический тренд
Поясним фундаментальное различие между временными рядами, имеющими
только детерминированный тренд, и рядами, которые (возможно, наряду
с детерминированным) имеют стохастический тренд. Для этого рассмотрим
следующие две простые модели нестационарных рядов.
В первой пусть
Xt = a + fit + £n t=l,...,T,
т.е. на детерминированный линейный тренд накладываются случайные
ошибки в виде белого шума.
А вторая модель пусть представляет случайное блуждание со сносом
(random walk with drift), т.е. процесс
Xt — а + Xt_ х + sn t = 1, ..., 7, X0 = x0,
приращения которого имеют ненулевое математическое ожидание
Процесс^ во второй модели можно представить в виде:
Xt = а + Xt_x +st=a + (a + Xt_2 + et_x ) + st-2a + Xt_2 + st_x +£t =
-Ъал- Xt_3 + £t_2 + £t_x + £t =... = x0 + at + {sx +... + £t),
t
Xt=x0+at + Y,£j,
так что ряд Xt имеет и детерминированный, и стохастический тренды.
Детрендирование первого ряда приводит к ряду
который является стационарным,
Детрендирование второго ряда приводит к ряду
X?=Xt-(x0+at) = j^£j,
7 = 1
который не является стационарным.
Пытаться остационарить ряд можно и другим способом. Можно для этого
перейти от ряда уровней Xt к ряду разностей
AXt=Xt-Xt_x.

Раздел 9. Нестационарные временные ряды. Модели ARIMA
437
Такой переход в теории временных рядов называют
дифференцированием {differencing), a A — оператором дифференцирования {difference
operator).
При таком переходе получаем для первого ряда:
AXt=Xt-Xt_{ ={a + fit + et)-{a + fi{t -\) + st_x) = Р + st - et_v
а для второго ряда:
AXt =Xt-Xt_x = a + £r
Оба продифференцированных ряда AXt стационарны. Первый
продифференцированный ряд относится к классу МАA) и имеет математическое
ожидание р. Второй продифференцированный ряд относится к классу МА@)
и имеет математическое ожидание а.
Таким образом, в отличие от детрендирования, операция
дифференцирования приводит к стационарному ряду в обоих случаях. Однако в результате
дифференцирования первого ряда получается процесс скользящего среднего,
который не является обратимым. Это имеет некоторые нежелательные
последствия при подборе модели по статистическим данным и
использовании подобранной модели для целей прогнозирования будущих значений ряда
(см., например, {Hamilton, 1994, р. 72—151)).
Обобщая описанную ситуацию, рассмотрим ряды
Xt=e0+e{t + e2t2+£t
И
Yt =a + pt + yt2 +Zn
где Zt — процесс, определяемый соотношениями
Z, =st + 2sM +3£,_2 + ... + t£l9 t = l,...,T.
Детрендирование первого ряда приводит к стационарному ряду
X?=Xt-{e0+e{t + e2t2) = £r
Детрендирование второго ряда приводит к ряду
Yt°=Yt-{a + pt + yt2) = Zn
у которого
D{Zt) = D{£t+2£t_l+3£t_2+... + t£l) = a2{\ + 2 + ... + t) = a2^t^ J ,
следовательно, детрендированный ряд не является стационарным.
Если вместо вычитания линейного тренда произвести дифференцирование
рядов, то для ряда Xt это приводит к ряду
AXt = вх-в2 + 202t + et- £t_u

438
Часть 2. Регрессионный анализ временных рядов
стационарному относительно линейного тренда: ряд
АХ, -FХ -в2 +262t) = st -et_x
является стационарным, но необратимым МАA) рядом.
Если же продифференцировать ряд Yn то в этом случае
продифференцированный ряд
AYt = (/3-y + 2yt) + Zt-Zt_x =
= j3-y + 2yt + {st + 2st_x + 3st_2 + ... + te1)-
- {st_x + 2st_2 + 3st_3 +... + (t-l)sx) =
= J3 - у + 2yt + (£x + S2 + ... + £t_x + £t)
уже не является стационарным относительно линейного тренда: ряд
AYt-(j3-y + 2yt) = (sx+£2+... + £t_x+st)
нестационарен и представляет собой стохастический тренд.
С другой стороны, осуществляя двукратное дифференцирование ряда Yn
т.е. переходя к ряду Д2У„ где А2 = A - LJ = 1 - 2L + Z,2, получаем
стационарный МА@) ряд
A2Yt = 2y + A2Zt = 2у+ Z, - 2Zt_x + Zt_2 =
= 2у + {st + 2et_x + 3et_2 +... + tsx) -
- 2{st_x + 2et_2 + 3st_3 +... + (t- l)sx) +
+ (et_2 + 2et_3 + 3et_A +... + (t - 2)ex) = 2y+ st.
При двукратном дифференцировании ряда Xt приходим к ряду
A2Xt = А(АХ,) = A{Xt -Xt_x) = (Xt -Xt_x)-(Xt_x -Xt_2) =
= **■ t t—\ ~^~ t-2 = ^2 ~^~ ^t — t-\ ~^~ ^t-2'
который представляет собой стационарный процесс скользящего среднего
МАB) с математическим ожиданием 2#2, не удовлетворяющий условию
обратимости. Действительно, уравнение b(z) = О здесь принимает вид:
l-2z + z2=0
и имеет двойной корень z = 1.
Таким образом, двукратное дифференцирование «остационаривает» и ряд
Хп и ряд Yt9 но в случае ряда Xt результирующий ряд не обладает свойством
обратимости.
Обобщение подобных примеров приводит к следующим понятиям.
Временной ряд Xt называется стационарным относительно
детерминированного тренда f{t), если ряд Xt - f{f) — стационарный. Если ряд Xt
стационарен относительно некоторого детерминированного тренда, то говорят,

Раздел 9. Нестационарные временные ряды. Модели ARIMA
439
что этот ряд принадлежит классу рядов, стационарных относительно
детерминированного тренда {trend-stationary time series), или что он является
Г£-рядом {TS — trend-stationary). В класс TS-рядов включаются также
стационарные ряды, не имеющие детерминированного тренда.
Временной ряд Xt называется интегрированным порядка к {integrated of
order к), к = 1, 2, ..., если:
• ряд Xt не является стационарным или стационарным относительно
детерминированного тренда, т.е. не является TS-рядом;
• ряд АкХп полученный в результате ^-кратного дифференцирования ряда
Хп является стационарным рядом;
• ряд Ak~lXt, полученный в результате {к - 1)-кратного
дифференцирования ряда^У,, не является TS-рядом.
Если полагать A°Xt = Хп то при к = 1 третье условие дублирует первое.
Для интегрированного ряда порядка к используют обозначение 1(к). Если
ряд Xt является интегрированным порядка к, будем обозначать это для
краткости как Xt ~ 1{к). В этой системе обозначений соотношение Xt ~ ДО)
соответствует ряду, который является стационарным и при этом не является
результатом дифференцирования Г£-ряда.
Пусть TS-ряд имеет вид Xt - а + fit + Yt9 где Yt — стационарный ряд,
имеющий нулевое математическое ожидание. Тогда Xt можно представить
в виде:
00 00
Xt=a + pt+Ypjet_J9 у/0=1 Х^у2<00'
7=0 j=0
где st — процесс белого шума.
(Мы не рассматриваем здесь теоретическую возможность наличия в
правой части еще и так называемой линейно детерминированной стохастической
компоненты.) Перейдя к ряду разностей, получим
АХ, = ДД0+ 2>,(£,_у -е,_хч) = Р^Ь1Е,_}=р + Ь{1)е„
у=о у=о
00
где b{L)=^bjLJ, 60=1, bj=y/j-y/j_x, y = l,2,...
7 = 0
Отсюда вытекает, что
6A)=|>у=0,
7 = 0
т.е. уравнение b{z) = О имеет единичный корень.

440
Часть 2. Регрессионный анализ временных рядов
Таким образом, если для некоторого стационарного ряда Z,
Zt=ju + b(L)sn
00
где b(L)=^TibjLJ\ b0=l, выполнено соотношение 6A) = 0, то последнее
7 = 0
указывает на «передифференцированность» (overdifferencing) ряда Z,: этот
Г£-ряд получен в результате дифференцирования некоторого Г£-ряда.
Совокупность интегрированных рядов различных порядков к = 1,2, ...
образует класс разностно стационарных, или ZW-рядов (DS — difference
stationary time series) . Если некоторый ряд Xt принадлежит этому классу, то
о нем говорят как о Л^-ряде.
Ряды типа ARIMA.
Последствия неправильного выбора метода
очистки ряда от тренда
Пусть ряд Xt — интегрированный порядка к. Подвергнем этот ряд ^-кратному
дифференцированию. Если в результате получается стационарный ряд типа
ARMA(p, q), то говорят, что исходный ряд Xt является рядом типа
ARIMA(p, к9 q\ или к раз проинтегрированным ARMA(p, q) рядом (ARIMA —
autoregressive integrated moving average). Если при этом р = 0 или q = 0, то
употребляют и более краткие обозначения:
АШМА(р, к, 0) = ARI(p, к), ARIMA@, к, q) = IMA(£, q\
ARIMA@, к, 0) = ARI@, к) = 1МА(к, 0).
Возвращаясь к рассмотренным примерам, получаем
1) Xt = a + pt + st — TS-ряд;
2) Xt = a + Xt_{ +£,~/(l), Xt— ряд типа ARIMA@, 1,0);
3) Xt = в0 + 6xt + 62t2 + st — TS-рящ
4) Xt = a + pt + yt2 + st + 2et_x + 3st_2 + ... + tex ~ 1B), Xt — ряд типа
ARIMA@, 2, 0).
Первый и третий ряды являются Г£-рядами, а второй и четвертый —
£)£-рядами.
Используя ту же имитацию белого шума, что и в предыдущих примерах,
получим смоделированные реализации для двух первых процессов:
TREND_\t = l+0.5f + s„ £,~N@, 1) (рис. 9.14),
WALKt = 0.5 + WALKt_ x + en £t ~ N@, 0.52), WALK0 = 0 (рис. 9.15).

Раздел 9. Нестационарные временные ряды. Модели ARIMA
441
Xf TRENDИ
60-
50-
40-
30-
20-
10-
П -
11111111111111111111111111111111111111111111111111 ►
10 20 30 40 50 60 70 80 90 100 t
Рис. 9.14
Xf WALK
50-
40-
30-
20-
10-
П -
1111111111111111111111111111111111111111111111111 r
10 20 30 40 50 60 70 80 90 100 t
Рис. 9.15
Оценим для каждой из этих реализаций модель прямолинейной
зависимости (табл. 9.7).
Полученные при этом детрендированные ряды ведут себя, как показано на
рис. 9.16 и 9.17.
Таблица 9.7
Оценивание модели прямолинейной зависимости
Переменная
Коэффициент
Стандартная
ошибка
/-статистика
Р-значение
Для TREND!
С
Т
0.796390
0.501522
0.208085
0.003577
3.827226
140.1946
0.0002
0.0000
Для WALK
С
Т
-0.930832
0.437818
0.249804
0.004295
-3.726248
101.9477
0.0003
0.0000
X DETRENDED
WALK DETRENDED
[1 I ll|ll ll[lll l|l 111 | II I l|llll| MM [III l|l I ll|ll II j ►
10 20 30 40 50 60 70 80 90 100 t
-3 liiii|iiii|iiii|iiii|iiii|iiii|ii i i|iii i|iiii | мм j ►
10 20 30 40 50 60 70 80 90 100 t
Рис. 9.16
РИС. 9.17

442
Часть 2. Регрессионный анализ временных рядов
График на рис. 9.16 характерен для стационарного ряда, а график на
рис. 9.17 —для стохастического тренда. Отметим наличие видимой
цикличности с длинным периодом у графика на рис. 9.17. На эту особенность было
указано в {Chan, Hayya, Ord, 1977): в результате очистки ряда от
детерминированного тренда могут возникать систематические колебания — длиннопе-
риодные циклы, которых не было у исходного ряда (ложная периодичность)
и которые могут быть ошибочно истолкованы как проявление некоторого
экономического цикла.
В то же время первые разности реализаций исходных рядов ведут себя,
как показано на рис. 9.18 и 9.19.
WALK DIF
"^ I I II I | I I I I | I I I I | I I I I | И I I | I I I I I I I I I I I I I I I I I I I I I I I I I ^
10 20 30 40 50 60 70 80 90 100 t
111111111111111111111111111111111111111111111111111
10 20 30 40 50 60 70 80 90 100 t
Рис. 9.18
Рис. 9.19
Коррелограммы рядов первых разностей имеют следующий вид.
Для первого ряда (XJTRENDDIF):
ACF
PACF
АС
РАС g-статистика Р-значение
***|
I*
*|
I*
**|
I*
*** I
** I
** I
** I
•I
** I
I*
*|
I
*|
1
2
3
4
5
6
7
8
9
10
-0.449
-0.045
-0.006
-0.052
0.078
-0.074
0.194
-0.216
0.079
-0.056
-0.449
-0.308
-0.236
-0.266
-0.157
-0.221
0.073
-0.120
-0.047
-0.143
20.527
20.736
20.740
21.021
21.676
22.258
26.358
31.473
32.159
32.513
0.000
0.000
0.000
0.000
0.001
0.001
0.000
0.000
0.000
0.000

Раздел 9. Нестационарные временные ряды. Модели ARIMA
443
Для второго ряда (WALKDIF):
ACF PACF к АС РАС g-статистика Р-значение
*
*
*
*
1
2
3
4
5
6
* 7
8
9
10
0.035
-0.044
-0.042
-0.025
0.065
-0.004
0.101
-0.173
-0.041
-0.057
0.035
-0.045
-0.039
-0.024
0.063
-0.012
0.107
-0.181
-0.013
-0.073
0.1271
0.3271
0.5099
0.5766
1.0215
1.0231
2.1405
5.4243
5.6087
5.9707
0.721
0.849
0.917
0.966
0.961
0.985
0.952
0.711
0.778
0.818
Вторая коррелограмма соответствует процессу белого шума. Что касается
первой коррелограммы, то наличие единственного значимого пика у
автокорреляционной функции говорит в пользу идентификации наблюдаемого ряда
разностей как реализации МАA) процесса. Подставив значение гA) = -0.449
А А
вместо р{\) в формулу р{\) = —1—, получим - 0.449 = —1— . Это уравнение
\ + bx l + b{
имеет два решения: -1.6036 и -0.6236. Первое соответствует необратимому,
а второе — обратимому МАA) процессу. Выбрав обратимую версию,
получим в качестве предварительной оценки коэффициента bx значение -0.6236.
Уточнение этой оценки в процессе оценивания модели МАA) приводит к
следующему результату: табл. 9.8 — при использовании процедуры обратного
прогноза (backcasting — см. разд. 7, тема 7.2) — и табл. 9.9 — без
использования процедуры обратного прогноза.
Таблица 9.8
Объясняемая переменная XJTRENDJDIF
Sample (adjusted): 2 100; Included observations: 99 after adjusting endpoints;
Convergence achieved after 10 iterations; Backcast 1
Переменная
С
MAA)
Коэффициент
0.501429
-0.977743
Стандартная
ошибка
0.004483
0.015377
/-статистика
111.8447
-63.58459
Р-значение
0.0000
0.0000
Для обоих вариантов оценивания в качестве оценок для коффициента Ьх
получили значения, очень близкие к 1, что отражает необратимость МАA)
модели, порождающей ряд. Обратим внимание, что в этом случае
продифференцированный ряд оказывается автокоррелированным, несмотря на то
что исходный ряд представляет собой сумму детерминированного линейного

444
Часть 2. Регрессионный анализ временных рядов
Таблица 9.9
Объясняемая переменнаяX_TREND_DIF
Method: Least Squares; Sample (adjusted): 2 100; Included observations: 99 after adjusting
endpoints; Convergence achieved after 18 iterations; Backcast: OFF
Переменная
С
MAA)
Коэффициент
0.518807
-1.062852
Стандартная
ошибка
0.007616
0.042816
/-статистика
68.12224
-24.82378
Р-значение
0.0000
0.0000
тренда и белого шума. Это явление известно как эффект Слуцкого (Slutsky
effect — см. (SlutzhU 1937)).
Смоделируем реализации двух оставшихся рядов:
Xt = 0.01/2 + еп €п ~ N@, 52) (рис. 9.20),
Yt = 0.04/2 + st + 2et_x + 3st_2 + ... + tel9 £t~N@, 0.12) (рис. 9.21).
10 20 30 40 50 60 70 80 90 100 t
РИС. 9.20
10 20 30 40 50 60 70 80 90 100 t
РИС. 9.21
Оценим для каждой из этих реализаций модель квадратичной зависимости
(для реализации X константа и линейная составляющая статистически
незначимы) (табл. 9.10).
Таблица 9Л0
Оценивание модели квадратичной зависимости
Переменная
Коэффициент
Стандартная
ошибка
/-статистика
Р-значение
ДляХ
Т2
0.009926
0.000114
86.93333
0.0000
ДляУ
С
Т
Т2
-2.273387
-0.119781
0.013087
0.621988
0.028427
0.000273
-3.655036
-4.213709
47.99344
0.0004
0.0001
0.0000

Раздел 9. Нестационарные временные ряды. Модели ARIMA
445
X DETRENDED
У DETRENDED
10 20 30 40 50 60 70 80 90 100 t
10 20 30 40 50 60 70 80 90 100 t
Рис. 9.22
Рис. 9.23
Детрендированные реализации приведены на рис. 9.22 и 9.23.
Коррелограмма v%jxdLX_DETRENDED соответствует процессу белого шума:
ACF
PACF
АС
РАС g-статистика Р-значение
I*
I*
1
2
3
4
5
6
7
8
9
10
0.030
-0.049
-0.042
-0.024
0.071
0.000
0.101
-0.171
-0.039
-0.050
0.030
-0.050
-0.039
-0.024
0.068
-0.008
0.107
-0.177
-0.011
-0.068
0.0936
0.3429
0.5278
0.5867
1.1208
1.1208
2.2429
5.4698
5.6366
5.9165
0.760
0.842
0.913
0.965
0.952
0.981
0.945
0.706
0.776
0.822
Коррелограмма ряда YDETRENDED характерна для нестационарного
ARB) процесса:
ACF
PACF
АС
РАС g-статистика Р-значение
1********
I*******
|#******
*******
I******
******
1*****
1****
1***
1***
****
**
**
*
*
*
Не******* |
2
3
4
5
6
7
8
9
10
0.985
0.956
0.912
0.857
0.791
0.716
0.635
0.549
0.458
0.365
0.985
-0.507
-0.314
-0.196
-0.136
-0.073
-0.044
-0.067
-0.043
-0.051
99.989
195.02
282.52
360.52
427.67
483.36
527.61
560.97
584.49
599.58
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000

446
Часть 2. Регрессионный анализ временных рядов
У DIF2
10 20 30 40 50 60 70 80 90 100 t
Рис. 9.24
111111111111 м 11111111111111111111111111111111111 j *
10 20 30 40 50 60 70 80 90 100 t
РИС. 9.25
Поведение вторых разностей рядов Xt и Yt показано на рис. 9.24 и 9.25.
Коррелограмма ряда X_DIF2 отражает свойство необратимости МА
модели:
ACF
PACF
АС
РАС g-статистика Р-значение
*****!
i*
i
*i
i*
*i
I**
**i
г
•I
*****
****
**
**
*
**
1
2
3
4
5
6
7
8
9
10
-0.635
0.128
0.038
-0.064
0.081
-0.137
0.243
-0.254
0.160
-0.099
-0.635
-0.463
-0.294
-0.273
-0.141
-0.292
0.037
-0.037
0.057
-0.056
40.777
42.440
42.586
43.014
43.710
45.710
52.065
59.064
61.891
62.976
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
0.000
В этом случае значение гA) = -0.635 даже выходит за пределы
интервала возможных значений р{\) процесса МАA), т.е. за пределы интервала
-0.5<рA)<0.5.
Подстановка значения -0.635 вместо р{\) в формулу
приводит к квадратному уравнению
0.6356?+ &! +0.635 = 0,
которое не имеет действительных решений.

Раздел 9. Нестационарные временные ряды. Модели ARIMA
447
Коррелограмма ряда Y_DIF2 соответствует процессу белого шума:
ACF
PACF
АС
РАС g-статистика Р-значение
1*
1*
*|
*|
I*
1*
* 1
* 1
1
2
3
4
5
6
7
8
9
10
0.031
-0.041
-0.038
-0.013
0.073
-0.006
0.104
-0.172
-0.031
-0.066
0.031
-0.042
-0.036
-0.013
0.071
-0.012
0.111
-0.178
-0.006
-0.084
0.0942
0.2636
0.4127
0.4313
0.9925
0.9958
2.1713
5.3769
5.4804
5.9673
0.759
0.877
0.938
0.980
0.963
0.986
0.950
0.717
0.791
0.818
Рассмотренные примеры отражают общую ситуацию:
• вычитание детерминированной составляющей Г5-ряда приводит к
стационарному ряду;
• вычитание детерминированной составляющей AS-ряда приводит к
.ОЯ-ряду;
• дифференцирование ГЯ-ряда приводит к ГЯ-ряду; если стохастическая
составляющая исходного ГЯ-ряда описывается стационарной моделью
ARMA, то дифференцирование приводит к ГЯ-ряду с необратимой МА
составляющей, имеющей единичный корень;
• ^-кратное дифференцирование ряда Xt ~ 1(к) приводит к стационарному
ряду; если стохастическая составляющая исходного 1(к) ряда
описывается моделью ARIMA, то ^-кратное дифференцирование приводит
к стационарному ряду ARMA.
Важным обстоятельством является также то, что в ГЯ-рядах влияние
предыдущих шоковых воздействий затухает с течением времени, а в DS-рядах
такое затухание отсутствует и каждый отдельный шок влияет с одинаковой
(или даже с возрастающей) силой на все последующие значения ряда.
Поясним это на примере простой ARA) моделиXt = aXt_x + snt= 1, ..., и.
Для нее (см. разд. 7, тема 7.1):
Xt = а'Х0+а* х€х +а* 2£2+..
Л е.
так что
Xt+h=a X0+a s{+a s2 +... + a st +... + €l
t+h-
Отсюда получаем значения импульсных мультипликаторов,
показывающих влияние единовременного (импульсного) изменения (шока)
инновации st {shock innovation) на текущее и последующие значения ряда:
dXt
де,
t _
=i,
ах,
t+\
де.
= a,
ах,
де.
^ = a\
ах,
де,
**- = «*,

448
Часть 2. Регрессионный анализ временных рядов
Таким образом, при h —> оо:
dxt+h
dst
dxt+h _
-»0 для \а\ < 1,
= 1 при а = 1.
dst
Попутно заметим, что если а > 1 (взрывной процесс), то
dXt+h
—->оо,
так что влияние прошлых шоков геометрически возрастает по мере удаления
в прошлое. Это обстоятельство служит определенным аргументом против
использования взрывных моделей для описания экономических временных
рядов.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как выглядят реализации процесса авторегрессии первого порядка при различных
значениях его параметров? При каких значениях коэффициента процесс имеет
взрывной характер? В чем состоит механизм удержания траектории стационарного
процесса авторегрессии первого порядка вблизи среднего уровня?
2. Каковы вероятностные характеристики процесса случайного блуждания? Является
ли этот процесс стационарным? Как ведут себя реализации процесса случайного
блуждания? Что обусловливает блуждающий характер траекторий такого процесса?
3. В чем состоит фундаментальное различие между временными рядами, имеющими
только детерминированный тренд, и рядами, которые (возможно, наряду с
детерминированным) имеют стохастический тренд?
4. Какие временные ряды составляют класс Г£-рядов?
5. Какие временные ряды составляют класс /ЭЗ-рядов?
6. В каком случае временной ряд называется рядом типа ARIMA?
7. Каковы последствия неправильного выбора метода очистки временного ряда
от тренда?
Тема 9.2.
ПРОБЛЕМА РАЗЛИЧЕНИЯ TS- И DS-РЯДОВ.
ГИПОТЕЗА ЕДИНИЧНОГО КОРНЯ
Постановка задачи
При построении моделей связей между временными рядами в долгосрочной
перспективе необходимо учитывать факт наличия или отсутствия у
анализируемых макроэкономических рядов стохастического (недетерминированного)
тренда. Иначе говоря, приходится решать вопрос об отнесении каждого из
рассматриваемых рядов к классу рядов, стационарных относительно детер-

Раздел 9. Нестационарные временные ряды. Модели ARIMA
449
минированного тренда (или просто стационарных), — это ГЯ-ряды, или
к классу рядов, имеющих стохастический (возможно, наряду с
детерминированным) тренд и приводимых к стационарному только путем однократного
или ^-кратного1 дифференцирования ряда, — это DS-ряды.
Принципиальное различие между этими двумя классами рядов выражается
в том, что в случае ГЯ-ряда вычитание из ряда соответствующего
детерминированного тренда приводит к стационарному ряду, тогда как в случае DS-ряда,
вычитание детерминированной составляющей ряда оставляет ряд
нестационарным из-за наличия у него стохастического тренда.
Проблема отнесения макроэкономических рядов динамики, имеющих
выраженный тренд, к одному из двух указанных классов активно обсуждалась
в последние два десятилетия в мировой эконометрической и экономической
литературе. Помимо того что траектории TS- и DS-рядов отличаются друг
от друга кардинальным образом, определение принадлежности рядов классам
TS или DS весьма важно для правильного построения долгосрочных
регрессионных моделей, в которых объясняемыми и объясняющими переменными
являются макроэкономические временные ряды (модели коинтеграции, модели
коррекции ощибок, векторные авторегрессии).
Если выявляется группа макроэкономических рядов, принадлежащих
классу DS-рядов, то между этими рядами возможна так называемая коинте-
грационная связь (cointegratiori) (см. ниже, разд. 11, тема 11.1), анализ
которой позволяет, например проверять:
• гипотезу эффективности финансовых рынков;
• выполнение на практике теории паритета покупательной способности;
• проверять выполнение в долгосрочной перспективе уравнения спроса
на деньги.
Более того, при наличии коинтеграционной связи между /ЭЯ-рядами
можно построить комбинацию краткосрочной и долгосрочной динамических
регрессионных моделей в форме так называемой модели коррекции
ошибок {error-correction model), что предоставляет возможность построения
на основании подобранной модели как краткосрочных, так и долгосрочных
прогнозов.
Литература по этому вопросу весьма обширна. В качестве обзорных работ
можно сослаться на монографии (Maddala, Kim, 1998), (Enders, 1995),
(Hamilton, 1994).
TS-рящл имеют линию тренда в качестве некоторой «центральной» линии,
которой следует траектория ряда, находясь то выше, то ниже этой линии, с
достаточно частой сменой положений выше-ниже. DS-ряды, помимо
детерминированного тренда (если таковой есть), имеют еще и стохастический
тренд, из-за присутствия которого траектория DS-ряда весьма долго
пребывает по одну сторону от линии детерминированного тренда (выше или ниже
Здесь не затрагиваем вопрос о возможной дробной интегрированности рядов.

450
Часть 2. Регрессионный анализ временных рядов
этой линии), удаляясь от нее на значительные расстояния, так что, по
существу, в этом случае линия детерминированного тренда перестает играть роль
«центральной», вокруг которой колеблется траектория процесса.
В ГЯ-рядах влияние предыдущих шоковых воздействий затухает с
течением времени, а в DS-рядах такое затухание отсутствует. Поэтому при наличии
стохастического тренда необходимо проведение определенной
экономической политики для возвращения макроэкономической переменной к ее
долговременной преспективе, тогда как при отсутствии стохастического тренда
серьезных усилий для достижения такой цели не требуется — в этом случае
макроэкономическая переменная «скользит» вдоль линии тренда как
направляющей, пересекая ее достаточно часто и не уклоняясь от нее сколь-нибудь
далеко.
В течение довольно долгого времени было принято при анализе рядов
с выраженным трендом производить оценивание и выделение
детерминированного тренда, после чего производить подбор динамической модели
(например, ARMA) к ряду, очищенному от тренда, т.е. к ряду остатков от
соответствующей оцененной регрессионной модели. После введения Боксом
и Дженкинсом в обиход моделей ARIMA стало модным остационаривание
рядов с выраженным трендом и медленным убыванием (оцененной)
автокорреляционной функции путем перехода к рядам первых или вторых разностей.
Однако, как показали дальнейшие исследования, произвольный выбор одного
из этих двух способов остационаривания ряда вовсе не так безобиден, как это
казалось поначалу.
Было показано, что остационаривание DS-рядов путем перехода к
очищенному ряду (детрендирование) изменяет спектр ряда, приводя к появлению
ложной периодичности (ложные длиннопериодные циклы), которая может
быть ошибочно истолкована как проявление некоторого экономического
цикла. В то же время дифференцирование ГЯ-ряда приводит к
«передифференцированному» ряду, который хотя и является стационарным, но обладает
некоторыми нежелательными свойствами, связанными с необратимостью его
МА составляющей, при этом возникает паразитная автокоррелированность
соседних значений продифференцированного ряда (в спектре доминируют
короткие циклы). Более того, в случае необратимости МА составляющей
продифференцированного ряда становится невозможным использование
обычных алгоритмов оценивания параметров и прогнозирования ряда (см.,
например, (Hamilton, 1994, гл. 4, 5)).
Итак, построение адекватной модели макроэкономического ряда, которую
можно использовать для описания динамики ряда и прогнозирования его
будущих значений, и адекватных моделей связей этого ряда с другими
макроэкономическими рядами невозможно без выяснения природы этого ряда
и природы рядов, с ним связываемых, т.е. без выяснения принадлежности ряда
к одному из двух указанных классов (TS или AS).
Как свидетельствуют многочисленные исследования, подробный обзор
которых можно найти, например, в (Maddala, Kim, 1998), проблема отнесения

Раздел 9. Нестационарные временные ряды. Модели ARIMA
451
ряда к одному из указанных двух классов на основании наблюдения
реализации ряда на некотором интервале времени оказалась весьма сложной. Было
предложено множество процедур такой классификации, но и по настоящее
время предлагаются все новые и новые процедуры, которые либо несколько
превосходят старые по статистической эффективности (по крайней мере,
теоретически), либо могут составить конкуренцию старым процедурам
и служить дополнительным средством подтверждения классификации,
произведенной другими методами. Описание многих таких процедур и ссылки
на статьи с подробным описанием и теоретическим обоснованием этих
процедур можно найти, например, в (Maddala, Kim, 1998), (Enders, 1995),
{Hamilton, 1994).
Здесь заметим только, что использование различных процедур может
приводить к противоположным выводам о принадлежности наблюдаемого ряда
классу Г£-рядов или классу DS-рядов. В этом отношении весьма
показательным является сопоставление выводов, полученных при анализе 14
макроэкономических рядов США в работе (Nelson, Plosser, 1982) и в более поздней
работе Перрона (Perron, 1989). Если в первой работе лишь один из 14
рассмотренных рядов был отнесен к классу TS, то во второй, напротив, к этому
классу было отнесено уже 11 из них. Правда, такое кардинальное изменение
результатов классификации было связано с расширением понятия TS-рядов.
В класс TiS-рядов стали включать и ряды, стационарные относительно
трендов, имеющих излом в известный момент времени. Отказ от
предположения об известной дате излома тренда, в свою очередь, привел к некоторому
изменению классификации, полученной Перроном (см. (Zivot, Andrews,
1992)). Допущение еще более гибких форм функции тренда изменило
и последнюю классификацию (см. (Bierens, 1997)). Наконец, работа (Nunes,
Newbold, Kuan, 1997) «замкнула круг»: изменение предположения о
характере процесса порождения данных по сравнению с (Zivot, Andrews, 1992)
привело к той же классификации 14 рядов, которая была получена в (Nelson,
Plosser, 1982).
В связи с такими результатами обычно при анализе конкретных
макроэкономических рядов применяют несколько разных статистических процедур,
что позволяет укрепить выводы, сделанные в пользу одной из двух (TS или
DS) конкурирующих гипотез.
Различение TS- и DS-рядов в классе моделей ARIMA.
Гипотеза единичного корня
Как было отмечено выше, для решения вопроса об отнесении исследуемого
ряда Xt к классу TS (стационарных или стационарных относительно тренда)
или DS (разностно стационарных) процессов имеется целый ряд различных
процедур. Однако все эти процедуры страдают теми или иными
недостатками. Процедуры, оформленные в виде формальных статистических критериев,
как правило, имеют достаточно низкую мощность, что ведет к весьма частому

452
Часть 2. Регрессионный анализ временных рядов
неотвержению исходной (нулевой) гипотезы, когда она в действительности
не выполняется. В то же время невыполнение теоретических предпосылок,
на которых основывается критерий, при применении его к реальным
данным приводит к тому, что реально наблюдаемый размер критерия отличается
от заявленного уровня значимости. Вследствие последнего обстоятельства
теряется контроль над вероятностью ошибки первого рода, это может
привести к слишком частому отвержению нулевой гипотезы, когда она в
действительности верна. Исходя из этого исследователи обычно при анализе рядов
на принадлежность их к классу TS или DS применяют не один, а несколько
критериев и подкрепляют выводы, полученные с использованием
формальных критериев (с установленными уровнями значимости), графическими
процедурами. Мы также будем использовать в нашем исследовании несколько
процедур различения TS- и DS-рядов и в следующем разделе кратко опишем
эти процедуры.
В большинстве критериев, предложенных для различения DS- и ^-гипотез,
эта задача решается в классе моделей ARMA (стационарных и нестационарных).
Если ряд Xt имеет тип ARIMAQ?, k, q), то в результате его ^-кратного
дифференцирования получим стационарный ряд AkXt типа ARMA(/?, q) —
скажем,
a\L)AkXt = b{L)sn
где a*(L) и b{L) — полиномы от оператора обратного сдвига Z, имеющие
степени р и q соответственно.
Заметим, что AXt = A - L)Xn так что
A% = {\-L)kXn
и
a\L)(l-L)% = b(L)en
или
a(L)Xt = b(L)et9
где a(L) = a*(L)(l - L)k — полином степени (р + к).
Поскольку ряд AkXt стационарный, все р корней полинома a*(z) находятся
за пределами единичного круга, так что полином a(z) имеет р корней за
пределами единичного круга и к корней на границе этого круга, точнее, корень
z = 1 кратности к.
Таким образом, ряд Xt представляется нестационарной моделью ARMA(p+к, q\
в которой авторегрессионный полином a(L) имеет роено к корней, равных 1,
а все остальные корни по модулю больше 1. Поэтому проверка нулевой
гипотезы Н0 о том, что некоторый ARMA ряд Xt является DiS-рядом (а не
стационарным рядом), может быть сведена к проверке гипотезы о том, что
авторегрессионный полином a(L) имеет хотя бы один корень, равный 1. Это
оправданно, если исходить из предположения, что a(z) не имеет корней внутри

Раздел 9. Нестационарные временные ряды. Модели ARIMA
453
единичного круга, т.е. исключить из рассмотрения взрывные модели. При
этом о гипотезе Я0 кратко говорят как о гипотезе единичного корня (UR —
unit root hypothesis), хотя точнее было бы говорить о гипотезе
авторегрессионного единичного корня. В качестве альтернативной тогда выступает
rS-гипотеза о том, что рассматриваемый ARMA ряд — стационарный.
Критерии, в которых за исходную (нулевую) берется гипотеза TS, служат,
скорее, для подтверждения результатов проверки /M-гипотезы. В этом случае
вместо проверки гипотезы единичного корня у полинома a(z) проверяется
гипотеза о наличии единичного корня z = 1 у уравнения b*(z) = 0, где b*(L) —
полином от оператора обратного сдвига L в представлении в виде процесса
скользящего среднего AXt = b*(z)et ряда разностей AXt = Xt - Xt_x исходного
процесса Xv
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие проблемы возникают при решении на основании статистических данных
вопроса об отнесении временного ряда к классу TS- или к классу DS-рядов?
2. Как формулируется соответствующая задача в классе моделей ARM А?

Раздел 10
ПРОЦЕДУРЫ ДЛЯ РАЗЛИЧЕНИЯ
7S- И /M-РЯДОВ
Тема 10.1
КРИТЕРИИ ДИКИ-ФУЛЛЕРА
Здесь и далее случайные величины и их реализации будем обозначать
строчными буквами.
Прежде чем двигаться дальше, обратим внимание на одно важное
обстоятельство, которое иногда является причиной недоразумений при
практическом толковании полученных результатов.
Рассмотрим TS-ряд
xt = а + fit + axXt_x +£п \ ах \ < 1.
Относительно какого именно линейного тренда этот ряд является
стационарным? Пусть у л- St — искомый тренд, a yt — детрендированный ряд, так
что>>, = xt - у- St, nyt является стационарным процессом авторегрессии
Подставив выражения для>>, иу(_х в последнее соотношение, найдем
xt-y-St = axxt_x -y-S(t-1)) + sn
xt=(y-axy + ax8) + £A - ах )t + axxt_x + et,
так что а= y-axy+axSn$ = S(l - ах\ откуда получаем
8 = _J_ a-ax{a + P)
\-ах A-ахJ
Таким образом, ряд xt является стационарным относительно линейного
тренда
а-ах{а + Р) | /3 f
{\-axf \-ax '

Раздел 10. Процедуры для различения TS- uDS-рядов
455
В частности, при /? = 0 и а ф О процесс стационарен и имеет
математическое ожидание
а
М =
\-ах
Если ах = 1, то последнее представление невозможно, и надо исходить
непосредственно из определения ряда хг В этом случае
xt =a + J3t + xt_x +£t =
= (a + j3t + £t) + (a + j3(t-l) + £t_l) + ... + (a + j3 + £l) + x0 =
= x0 +
a + —\t +—t2+(sx+£2+... + £t).
При a- f3- О имеем простое случайное блуждание
xt = xt_x +en xt=x0+(£l+e2+... + st).
При а Ф 0, /?= 0 имеем
jc, = a + xt_x +£n xt = x0 + at + {ex + £ 2 +... + st\
т.е. случайное блуждание вокруг детерминированного линейного тренда х0 + at.
Наконец, при а ф 0, /?* 0
я,,/?
х, =a + ^/ + jcM + £,, xt =x0 + a+— f+ — t + (sx +e2 + ... + £,),
V 2y 2
так что исходный ряд xt представляет случайное блуждание вокруг детерми-
н Ч +—Г.
2
нированного квадратичного тренда х0 + [ а +
Таким образом, в модели
xt =a + /3t + axxt_x + sn
если a* 0, /?=0, то:
• при \ах\ < 1 у ряда xt тренда нет;
t
• при ах = 1 ряд х, имеет стохастический тренд ^£у и линейный тренд
х0 + а/;
если/?* 0, то:
..I ~ - а-аЛа + Р) /? ^
• при | а х | < I ряд xt имеет линейный тренд —-^ 2— +~Л t»
0-в.Г i-«i

456
Часть 2. Регрессионный анализ временных рядов
• при ах = 1 ряд xt имеет стохастический тренд ^s- и квадратичный
У = 1
тренд х0 +
Р] Р 2
2 2
Ниже приводятся смоделированные реализации, порожденные моделью
xt = а + 0t + axxt_x + £,
при различных наборах значений параметров a, 0,ах:
ST_1: ^ = 0.8, а = 0, 0=0 (рис. 10.1).
ST_2: ^ = 0.8, а = 0.2, /?= 0 (рис. 10.2).
ST_3: ^ = 0.8, а = 0.16, £=0.04 (рис. 10.4).
WALKJ: ^ = 1, а = 0, /?=0 (рис. 10.3).
WALK_2: а1 = 1, « = 0.2, 0=0 (рис. 10.5).
WALKJ: ах = 1, а = 0.2, /?=0.1 (рис. 10.7).
Кроме того, приводится смоделированная реализация, порожденная моделью
xt=a + 0t + yt2+ axxt_x + et:
• ST_4: ^ = 0.8, a = 0.12, £=0.13, ^=0.01 (рис. 10.6).
10 20 30 40 50 60 70 80 90 100 t
Рис. 10.1
Сравнение графиков ST_1, ST2, WALKX между собой и сравнение
графиков в парах ST3 — WALK2, ST_4 — WALK3 показывает, сколь трудно
различить визуально реализации процессов с единичным корнем от
реализаций, соответствующих стационарным или стационарным относительно
детерминированного тренда процессам.
Перейдем теперь к формальным статистическим критериям наличия (или
отсутствия) единичного корня.

Раздел 10. Процедуры для различения TS- uDS-рядов
457
WALK 1
i mi I in i| i mi I м м |i м i|i щ| м м 11 in |i mi [in i|
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.2
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.3
WALK 2
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.4
-10 |мii|iiii|iiii|iiii|iiii|iiм|iмi|iмi|мii|iiм| >
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.5
WALK 3
10 20 30 40 50 60 70 80 90 100 t
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.6
РИС. 10.7

458
Часть 2. Регрессионный анализ временных рядов
Критерии Дики — Фуллера
Предположим, что истинная модель, порождающая данные (процесс
порождения данных, DGP — data generating process), имеет вид:
DGP: xt = axxt_x + st,
где st — гауссовский белый шум;
ах — неизвестный параметр A < ах < 1), который мы оцениваем в рамках
статистической модели
SM: xt = axxt_x + st, t=l,..., Г.
Поскольку при сделанных предположениях ряд xt стационарен, то, как
отмечалось в разд. 8 (тема 8.1), оценка наименьших квадратов для неизвестного
коэффициента ах является асимптотически нормальной, так что можно
пользоваться стандартными методами регрессионного анализа, имея в виду их
асимптотическую обоснованность. Естественно, возникает вопрос о том,
сохраняется ли такое положение и в нестационарном случае.
В 1958 г. Уайт опубликовал работу (White, 1958), которая привела
впоследствии к полному пересмотру методологии эконометрического анализа
статистических данных, представляемых в виде временных рядов. Уайт
впервые обнаружил, что если истинная модель, порождающая данные, имеет вид:
DGP:x, =jtM+£„ t = l,2,...,T, jc0=0,
(случайное блуждание, выходящее из нуля), т.е. ах = 1, то распределение
(центрированной и нормированной) оценки наименьших квадратов для ах
не сближается с нормальным даже при неограниченном возрастании
количества наблюдений. Иначе говоря, в такой ситуации оценка наименьших
квадратов ах не является асимптотически нормальной.
Последнее означает, в частности, что в рамках указанной статистической
модели нельзя проверить нулевую гипотезу
Н0:ах = 1,
основываясь, как обычно, на критических или Р-значениях /-статистики,
вычисляемых согласно распределению Стьюдента (даже в асимптотическом плане!).
В действительности имеет место следующий факт. Если ах = 1, то при Г-> <х>
U[W(\)]2-l\
Т{ах-\)^^ ,
j[W(r)fdr
о
где W(f) — стандартное броуновское движение {standard Brownian motion),
и сходимость понимается как сходимость распределения случай-

Раздел 10. Процедуры для различения TS- uDS-рядов
459
ной величины, стоящей слева, к распределению случайной
величины, стоящей справа.
Процесс W(r) является непрерывным аналогом дискретного случайного
блуждания
Это процесс, для которого:
• W@) = 0;
• приращения (W(r2) - W(rx)\ ..., (W(rk) - W(rk_x)) независимы в
совокупности, если 0 < гх < г2 < ... < rk; W(s) - W(r) ~ 7V@, s - г) при s > r\
• реализации W{f) непрерывны с вероятностью 1.
Из определения, в частности, следует, что W(X) - W{\) - W(Q) ~ 7V@, 1), так
что [ W(l)]2 ~ ^2A). Отсюда вытекает, что при больших Т
P{al<l} = P{al-l<0}np{[W(l)]2-l<o}=p{x2(l)<l}=0.6S.
Таким образом, если DGP — простое случайное блуждание (без сноса), DGP:
xt =xt_{ + €t9 то оценивание SM: xt = axxt_x + et дает значение ах < 1 примерно
в 2/з случаев.
Критические значения распределения статистики Т(ах - 1) при гипотезе
ах = 1 для конечных Г находятся методом статистических испытаний (Монте-
Карло), впервые это было сделано Фуллером (Fuller, 1976).
Соответствующие таблицы построены в предположении, что st - 7V@, <rff2), el9 ..., sT —
независимые случайные величины и х0 = 0. Однако следует заметить: хотя
значение х0 не влияет на асимптотическое распределение Т(ах - 1), оно влияет
на распределение Т(ах - 1) при малых выборках.
Критерий, основанный на статистике Т(ах - 1), отвергает гипотезу Я0: ах = 1
в пользу альтернативной гипотезы НА: ах < 1 на 5%-м уровне значимости при
значениях Т(ах - 1), меньших Т(ах - 1)крит, или при значениях ах, меньших
а1крит, указанных в табл. 10.1.
Таблица 10.1
Критические значения распределения статистики
т
25
50
100
250
500
00
Д«1-1)крит
-7.3
-7.7
-7.9
-8.0
-8.0
-8.1
1 крит
0.708
0.846
0.921
0.968
0.998

460
Часть 2. Регрессионный анализ временных рядов
Как видно из табл. 10.1, при небольших значениях Г гипотеза Я0
отвергается лишь для значений ах, намного меньших 1. Чувствительность критерия
возрастает только при весьма большом количестве наблюдений. Это
приводит к тому, что при небольших Г отвергнуть гипотезу Я0: ах = 1 в пользу
альтернативной гипотезы НА: ах < 1 довольно трудно, даже если ах существенно
меньше 1.
Более привычным было бы, конечно, использование для проверки
гипотезы Н0: ах = 1 противНА: ах < 1 отношения
А-1
t = -
s(ax)
(/-отношение, /-ratio, /-статистика),
где s(ax) — оцененная стандартная ошибка оценки ах.
Однако, поскольку при ах = 1 уже и сама оценка ах не имеет нормального
распределения, то и это отношение не имеет /-распределения Стьюдента.
Критические значения этой /-статистики при Т —> <х> и некоторых конечных
значениях Г также впервые были приведены в работе Фуллера {Fuller, 1976).
Гипотеза Я0: ах- 1 отвергается в пользу альтернативной гипотезы НА: ах < 1
при больших отрицательных значениях указанной статистики. Сравним 5%-е
критические значения, указанные Фуллером, с 5%-ми критическими
значениями обычного одностороннего /-критерия, вычисляемыми по
распределению Стьюдента /(Г- 1) с (Г- 1) степенями свободы (табл. 10.2).
Таблица 10.2
Критические значения f-статистики
Т
25
50
100
250
500
00
'крит (Фуллер)
-1.95
-1.95
-1.95
-1.95
-1.95
-1.95
'крит (Стьюдент)
-1.71
-1.68
-1.66
-1.65
-1.65
Таблица 10.2 иллюстрирует скошенность распределения отношения —
s(ax)
при ах = 1. Она показывает, что если использовать критические значения,
рассчитываемые по распределению Стьюдента, это будет приводить к
неоправданно частому отвержению гипотезы единичного корня, когда эта
гипотеза верна.

Раздел 10. Процедуры для различения TS- uDS-рядов
461
В числе прочего выше была приведена смоделированная реализация
процесса случайного блуждания без сноса xt = xt_x + st (WALKI). Оценим
по этой реализации статистическую модель xt = axxt_x + sn используя первые
50 наблюдений (табл. 10.3).
Объясняемая переменная WALKJ\
Sample (adjusted): 2 50; Included observations: 49 after adjusting endpoints
Таблица 10.3
Переменная
WALKJ{-\)
Коэффициент
0.970831
Стандартная
ошибка
0.035729
/-статистика
27.17224
Р-значение
0.0000
0.970831-1 noi_
Значение указанного выше /-отношения равно = -0.816 и пре-
0.035729
вышает критическое значение -1.95. Поэтому гипотеза о наличии единичного
корня не может быть отвергнута на 5%-м уровне значимости. Это согласуется
с полученной оценкой 0.970831 коэффициента а19 значительно превышающей
критический уровень 0.846.
В то же время если возьмем смоделированную реализацию STI
стационарного ряда xt = 0.Sxt_x + st (имеющего нулевое математическое ожидание)
и оценим по этой реализации статистическую модель xt = alxt_l + sn
используя первые 50 наблюдений, то получим результаты, приведенные в табл. 10.4.
Таблица 10.4
Объясняемая переменная S7_1
Method: Least Squares; Sample (adjusted): 2 50;
Included observations: 49 after adjusting endpoints; Convergence achieved after 2 iterations
Переменная
ARA)
Коэффициент
0.790557
Стандартная
ошибка
0.090501
/-статистика
8.735349
Р-значение
0.0003
Интересующее нас ^-отношение равно -2.314 < -1.95, что приводит к
отвержению гипотезы единичного корня. Это согласуется с тем, что оцененное
значение ах здесь равно 0.791 и значимо отличается от 1.
Обратимся теперь к смоделированной реализации ST_2 стационарного ARA)
процесса xt = 0.2 + 0.&xt_x + st (математическое ожидание которого равно 1).
Среднеарифметическое первых 50 значений ряда равно 0.596. Поэтому даже
если не знать, как этот ряд моделировался, все же можно сказать, что если
этот ряд стационарный, то он имеет, скорее, ненулевое математическое
ожидание. Но тогда альтернативой для гипотезы Н0: xt = xt_x + st (наличие
единичного корня) должна быть гипотеза НА: xt - а + axxt_х + £п ах < 1, а Ф 0.

462
Часть 2. Регрессионный анализ временных рядов
Поэтому в качестве статистической берем теперь модель
SM:x, = a + axxt_x + st.
Предельное распределение статистики Т(ах - 1) не только не является
нормальным, но и отличается от распределения этой же статистики при
оценивании SM с а = О, при Т = 25 Р{ах < 1} = 0.95. В табл. 10.5 приведены
критические значения для этого случая.
Таблица 10.5
Критические значения распределения статистик
т
25
50
100
250
500
00
Д«1-1)крит
-12.5
-13.3
-13.7
-14.0
-14.0
-14.1
1 крит
0.500
0.734
0.863
0.944
0.972
'крит (Фуллер)
-3.00
-2.92
-2.89
-2.88
-2.87
-2.86
Анализ в рамках статистической модели SM: xt = а + alxt_l + et ряда
WALK_\ (по первым 50 наблюдениям) дает значение:
^ = -2.143>/крит=-2.92,
так что гипотеза о том, что мы имеем дело с реализацией случайного
блуждания xt =xt_{ + £п не отвергается.
Анализ в рамках этой же статистической модели ряда STJ2 дает (при Т = 50)
значение t = -2.245, так что гипотеза единичного корня не отвергается,
несмотря на то что моделировалась реализация стационарного процесса.
Последнее связано, конечно, с тем, что оцененное значение ах = 0.794 выше
критического уровня 0.734.
v Замечание 10.1.1. Если проанализируем в рамках все той же SM:
xt = а + axxt_ j + st ряд ST_\ (с а = 0), то получим
ах = 0.785 > ах крит = 0.734, / = -2.298 > /крит = -2.92,
так что гипотеза единичного корня для STX не отвергается. В то же
время, как показано ранее, если ряд STX анализируется в рамках
статистической модели SM: xt = axxt_x + sn то гипотеза единичного
корня отвергается.
Этот пример иллюстрирует то обстоятельство, что при
добавлении в статистическую модель излишних объясняющих переменных
(в том числе константы) мощность критерия снижается, и отверг-

Раздел 10. Процедуры для различения TS- uDS-рядов
463
нуть гипотезу единичного корня становится трудно, даже если она
неверна. Поэтому важно выбирать статистическую модель «без
излишеств», включая в нее только такие составляющие, которые
соответствуют поведению наблюдаемого временного ряда.
Посмотрим теперь на реализацию ST_3 процесса
xt = 0.16 + 0.04/ + 0.8xt_x + еп
стационарного относительно линейного тренда 0.2/ (рис. 10.8). Эта
реализация похожа на реализацию WALKJ2 (рис. 10.9) случайного блуждания со
сносом 0.2
xt - 0.2 + xt_x + £г
х 4
WALK 2
10 20 30 40 50 60 70 80 90 100 t
Рис. 10.8
10 20 30 40 50 60 70 80 90 100 t
Рис. 10.9
Отсюда возникает проблема различения подобных процессов, и в связи с
этим рассматривается задача проверки гипотезы
Н0: xt = а + xt_х + £п а* 0, (случайное блуждание со сносом)
в рамках статистической модели
SM:x, = a + /3t + axxt_x + sv
Фуллер затабулировал процентные точки распределений оценки ах и
/-статистики для проверки гипотезы ах = 1 в такой ситуации.
Если DGP: xt = а + xt_x + st с а * 0, то 5%-е критические значения
статистики Т(ах - 1) и указанной /-статистики доя этого случая приведены в табл. 10.6.
Проанализируем в рамках статистической модели SM: xt - а + fit + axxt_ x + st
смоделированные реализации (опять берем Т= 50).
Для WALK_2 имеем ах = 0.858 > ахкрит = 0.604, / = -2.027 > t^m = -3.50, так
что гипотеза единичного корня не отвергается.

464
Часть 2. Регрессионный анализ временных рядов
Таблица 10.6
Критические значения распределения статистик
Т
25
50
100
250
500
00
Г(«1-1)кр„х
-17.9
-19.8
-20.7
-21.3
-21.5
-21.8
1 крит
0.284
0.604
0.793
0.914
0.957
'крит (Фуллер)
-3.60
-3.50
-3.45
-3.43
-3.42
-3.41
Для STJ имеем ах = 0.733 > аХкрш = 0.604, t = -2.687 > /крит = -3.50.
Здесь значения ах и t ближе к критическим, чем у WALKJ2, но все же
значительно их превышают, так что гипотеза единичного корня не отвергается
и в этом случае.
Строго говоря, при реализациях, подобных ST_3, не надо исключать
возможность того, что DGP — случайное блуждание без сноса. Так что следовало
бы знать также распределения ах и t в статистической модели
SM: xt = а + J3t + axxt_x + st
в предположении, что
DGP:x, = xt_x + sv
Исследование этих распределений показало, что они совпадают с
распределениями ах и /, полученными в предположении
DGP: xt = а + xt_x + sn аФ 0,
так что при использовании статистической модели
SM:x, = a + fit + axxt_x + st
одни и те лее таблицы распределений ах и t годятся и при DGP: xt = xt_x + sn
и при DGP: xt = а + xt_ x + еп а Ф 0.
Проанализируем в рамках статистической модели SM: xt = а + fit + axxt_ x + st
реализацию DGP: xt - xt_x + £n представленную рядом WALK_\. Оценивая
эту статистическую модель, получаем (как и при DGP: xt = 0.2 + xt_x + st)
ах = 0.858 > а1крит = 0.604, t = -2.027 > /крит = -3.50, так что гипотеза
единичного корня не отвергается.
Отметим, наконец, замечательный результат Маккиннона {MacKinnon,
1991), который нашел простую приближенную формулу для вычисления
критических значений ^-статистик в критериях Фуллера. Он показал, что если

Раздел 10. Процедуры для различения TS- uDS-рядов
465
'критС/7* Т) — критическое значение /-статистики по Фуллеру,
соответствующее уровню значимости р и количеству наблюдений Г, то
где До, Д, А — некоторые коэффициенты, зависящие от/? и от того, какое из
трех распределений Фуллера рассматривается.
Маккиннон привел таблицу этих коэффициентов для/? = 0.01, 0.05, 0.10.
ПРИМЕР 10.1.1
В разд. 9 (тема 9.1) были проанализированы статистические данные об объеме
потребительских расходов на товары кратковременного пользования и услуги
в Великобритании за период с I квартала 1974 г. по IV квартал 1985 г. Этот ряд
был идентифицирован как процесс авторегрессии первого порядка
относительно линейного тренда:
Xt- 47962.75 - 315.1909/ = 0.884803(ХГ_1 - 47962.75 - 315.1909(f- 1)) + еп
или
Xt = 5804.037 + 36.30898 t + 0.884803Jf,_ { + et.
Там же было отмечено, что, несмотря на то что при полученной точечной
оценке 0.884803 коэффициента при Xt_x построенная модель формально
оказывается стационарной относительно детерминированного линейного тренда
(т.е. детрендированный процесс следует стационарной ARA) модели), нельзя
с достаточной степенью уверенности гарантировать, что истинная модель
порождения наблюдений также стационарна относительно линейного тренда.
Рассмотрим эту проблему с точки зрения критериев единичного корня.
Поскольку исследуемый ряд обладает выраженным линейным трендом,
будем действовать в рамках статистической модели
SM:x, = a + J3t + alxt_l + sr
Проверим гипотезу Н0: xt - а + xt_x + en пользуясь статистическим
пакетом Е Views, в котором используется приведенная выше формула Маккиннона
(критические значения для отвержения гипотезы единичного корня,
вычислены по формулам Маккиннона):
Test Statistic -1.425277 1 % Critical Value -4.1630
5% Critical Value -3.5066
10% Critical Value -3.1828
В соответствии с этими результатами гипотеза Н0 не отвергается. Но если
считать, что она выполнена, тогда в конечном счете следует оценивать не
модель xt = а + pt + alxt_l + sn а модель xt - а + xt_x + sr Оценивание
последней в форме Ах, = а + et дает следующий результат (табл. 10.7).

466
Часть 2. Регрессионный анализ временных рядов
Таблица 10.7
Объясняемая переменная АХ
Переменная
а
Коэффициент
236.8958
Стандартная
ошибка
80.80998
/-статистика
2.931517
Р-значение
0.0052
Это соответствует модели случайного блуждания со сносом
xt = 236.8958 + xt_x +£tM
Все рассмотренные варианты проверки гипотезы о наличии единичного
корня в рамках статистических моделей:
SM:x, = axxt_x + st,
SM:x, = a + axxt_x + sn
SM:x, = a + J3t + axxt_x + st
основывались на распределениях оценки наименьших квадратов
коэффициента ах и /-статистики для проверки гипотезы ах = 1 при соответствующих
предположениях о процессе порождения данных:
DGP: xt -xt_x + st (случайное блуждание),
DGP: xt = a + xt_x + st (случайное блуждание со сносом).
В то же время, например, если SM: xt = а + axxt_ х + £п то гипотеза xt = xt_ x + st
равносильна гипотезе
Н0: а=0, ах = 1.
Если бы мы находились в рамках классической модели линейной
регрессии, то проверяли бы подобную гипотезу с использованием F-статистики
RSS0-RSS
ф1= 2
1 RSS '
(Г-1)-2
которая в классическом варианте имеет при гипотезе Н0 F-распределение
Фишера FB, Г- 3) с двумя и (Г- 3) степенями свободы. Поскольку, однако,
мы имеем дело при гипотезе Н0 с нестационарным процессом, то, вообще
говоря, не следует ожидать, что распределение статистики Фх при гипотезе
Н0 будет иметь (хотя бы асимптотически) распределение FB, T - 3). Этот
вопрос был исследован Дики и Фуллером (Dickey, Fuller, 1981). Они
построили таблицы распределения статистики Фх при гипотезе Я0: а = 0, ах = 1.
В табл. 10.8 приведены 5%-е критические значения статистики Ф1? рассчи-

Раздел 10. Процедуры для различения TS- и DS-рядов
467
Критические E%-е) значения распределения статистик
Таблица 10.8
т
25
50
100
250
500
00
ф,
1 крит
5.18
4.86
4.71
4.63
4.61
4.59
F
крит
3.44
3.20
3.10
3.00
3.00
3.00
тайные Дики и Фуллером, а также (для сравнения) 5%-е критические
значения FKpjIT, рассчитанные по распределению FB, п - 3) (см., также {Hamilton,
1994, табл. В.7 Case 2) и {Enders, 1995, табл. С)).
ПРИМЕР 10.1.2
Возьмем для примера опять ряды WALK_\ (случайное блуждание без сноса),
STJ2 (стационарный процесс ARA) с ненулевым математическим
ожиданием), ST_l (стационарный процесс ARA) с нулевым математическим
ожиданием) — по 50 наблюдений для каждого ряда.
Оценивая SM: xt = a + axxt_x + st для ряда WALKX, получаем ах = -0.579,
ах = 0.850, RSS = 48.0335. В модели с ограничениями а = 0, ах = 1 имеем
xt = xt_!, так что
ЛЯ50 = 5>,-*мJ =52.7939,
г = 2
52.7939-48.0335
*i=-
48.0335
- = 2.853 < 4.86 -> гипотеза Н0 не отвергается.
50-1-2
Для ST2 : а = 0.181, ах = 0.777, RSS = 52.6618. В модели с ограничениями
а = 0, ах = 1 имеем RSS0 = 59.0547,
59.0547-52.6618
Ф,=-
52.6618
= 2.853 < 4.86 -> гипотеза Я0 не отвергается.
50-1-2
Для STI : а = -0.042, ах = 0.785, RSS = 52.7007. В модели с
ограничениями а = 0, ах = 1 имеем RSS0 = 58.0671,
Ф} = 2.662 < 4.86 -> гипотеза Н0 не отвергается.

468
Часть 2. Регрессионный анализ временных рядов
Таким образом, для всех трех рядов статистические выводы, сделанные
на основании /-статистик для коэффициента аь совпали со статистическими
выводами, сделанными на основании F-статистики. ■
В рамках статистической модели
SM: xt - a + pt + axxt_x + st
гипотеза DGP: xt = xt_ x + st соответствует гипотезе
Я0: a= fi = 09al = 1,
а гипотеза DGP: xt = a + xt_ x + st — гипотезе
Я0:/?=0,а1 = 1.
F-статистика для первого случая имеет обозначение Ф2, 5%-е критические
значения приведены в табл. 10.9 (см. также (Enders, 1995, табл. С)).
Таблица 10.9
Критические E%-е) значения F-статистики
Т
25
50
100
250
500
00
^2 крит
5.68
5.13
4.88
4.75
4.71
4.68
F-статистика для второго случая имеет обозначение Ф3, 5%-е критические
значения приведены в табл. 10.10 (см. также {Hamilton, 1994, табл. В.7 Case 4)
и {Enders, 1995, табл. С)).
Таблица 10.10
Критические E%-е) значения F-статистики
т
25
50
100
250
500
00
^3 крит
7.24
6.73
6.49
6.34
6.30
6.25

Раздел 10. Процедуры для различения TS- uDS-рядов
469
ПРИМЕР 10.1.3
Рассмотрим ряды WALK_\ (случайное блуждание без сноса), WALK_2
(случайное блуждание со сносом), ST_3 (процесс ARA), стационарный
относительно линейного тренда). Оценим статистическую модель
SM: xt = а + /3t + axxt_x + st
для каждого из этих рядов и проверим для них
• гипотезу Я0: а - J3 = 0, ах = 1, опираясь на статистику Ф2;
• гипотезу Я0: J3 = 0, ах = 1, опираясь на статистику Ф3.
Гипотеза Я0: а = J3= 0, ах = 1
WALKJ: а = -0.854, 0 = 0.012, ах = 0.858, RSS = 46.7158. В модели с
ограничениями RSS0 = 52.7939,
Ф2 = 1.995 < 5.13 —> гипотеза Н0 не отвергается.
WALK_2: а = -0.711, $ = 0.040, ах = 0.858, RSS = 46.7158. В модели с
ограничениями RSS0 = 52.7939,
Ф2 опять равно 1.995 < 5.13 —> гипотеза Я0 не отвергается.
STJ: а = -0.345, C = 0.070, ах = 0.733, RSS = 50.3928,
Ф2 = 1.207 < 5.13 —> гипотеза Н0 не отвергается.
Гипотеза Н0: /3 = 0, ах = 1
WALKX: ДУЯ = 46.7158. В модели с ограничениями RSS0 = 52.7282,
Ф3 = 1.973 < 6.73 -> гипотеза Я0 не отвергается.
WALKJ2: Ф3 опять равно 1.973 -> гипотеза Я0 не отвергается.
5Т_3: /гЖУ = 50.3928, Ф3 = 0.711 -> гипотеза Я0 не отвергается.■
Рассмотренные примеры указывают на то, что и с помощью формальных
статистических критериев бывает практически невозможно при небольшом
количестве наблюдений отличить реализации процессов с единичным корнем
и без наличия такового. Это связано с весьма низкой мощностью
соответствующих критериев при умеренном количестве наблюдений и «близких»
альтернативах. Скажем, достаточная мощность критерия Ф} достигается только
при ах < 0.8, а также если а близко к 1 или а > 1. Мощности критериев Ф2
и Ф3 еще ниже. Эти замечания относятся и к критериям, основанным на
/-статистиках и на статистике Т(ах - 1).
Все это приводит к «презумпции наличия единичного корня» в случае, когда
в качестве нулевой берется именно гипотеза единичного корня.

470
Часть 2. Регрессионный анализ временных рядов
В связи с этим многие авторы уделили внимание задаче проверки нулевой
гипотезы стационарности (стационарности относительно
детерминированного тренда) против альтернативной гипотезы единичного корня. В дальнейшем
рассмотрим этот вопрос подробнее, а сейчас отметим только, что при таком
подходе наблюдается похожая картина. Критерии стационарности имеют
низкую мощность, вследствие этого возникает уже «презумпция отсутствия
единичного корня». Поэтому отложим пока знакомство с такими критериями
и вернемся к рассмотрению ситуации, когда основной (нулевой) является
гипотеза наличия единичного корня.
Полученные выше результаты проверки гипотезы единичного корня для
смоделированных реализаций стационарных процессов представляются
крайне пессимистическими — при использовании первых 50 наблюдений эта
гипотеза не отвергается:
• для STX и STJ2 в паре:
DGP: xt =xt_] + sn
SM: xt = a + alxt_l + st\
• для ST3 в паре:
DGP: xt = а + xt_x + st (или DGP: xt =xt_l + £,),
SM: xt = a + J3t + alxt_l + er
Проследим, что дает проверка гипотезы единичного корня в этих же
связках, но при использовании большего количества наблюдений. Для этого
возьмем теперь Т- 100. Сравним полученные результаты (в последней строке
табл. 10.11 использованы 10%-е критические значения). Последняя серия
результатов показывает, что при увеличении количества наблюдений мощность
критериев Дики — Фуллера возрастает.
Таблица 10.11
Сравнение результатов
STJ
ST_2
STJ
/i = 50
t = -2.298 >,крит= -2.92,
гипотеза единичного корня
не отвергается
t = -2.245 > ;крит=-2.92,
гипотеза единичного корня
не отвергается
/ = -2.687 > /крит=-3.18,
гипотеза единичного корня
не отвергается на 10%-м уровне
//=100
t = -3.238 < ^^=-2.89,
гипотеза единичного корня
отвергается
, = -3.217 < tvpm= -2.89,
гипотеза единичного корня
отвергается
t = -3.207 < Гкрит=-3.15,
гипотеза единичного корня
отвергается на 10%-м уровне

Раздел 10. Процедуры для различения TS- uDS-рядов
471
Расширенные критерии Дики — Фуллера
Обратимся опять к статистическим данным о величине валового
национального продукта (GNP) в США за период с I квартала 1947 г. по IV квартал
1961 г. В разд. 9 мы идентифицировали этот ряд как процесс авторегрессии
второго порядка:
Xt-2l7J40-5222t = l380(Xt_x-2n.l40-5.222(t-l))-
-0.630(ЛГ,_2-217.740-5.222(/-2)) + £„
или
jrr=55.017 + 1.304r + 1.380JTM-0.630Jrr_2+^.
Как проверить гипотезу о наличии единичного корня в модели
авторегрессии, порождающей этот ряд? Ведь в рассмотренных выше критериях Дики —
Фуллера проверка такой гипотезы велась в рамках моделей авторегрессии
первого порядка. Выход из этого положения оказался достаточно простым.
Рассмотрим статистическую модель
SM: xt = а + J3t + axxt_х + a2xt_2 + ... + apxt_p + sr
Путем чисто алгебраических преобразований ее можно преобразовать к
виду:
xt=a + /3t + pxt_x+FxAxt_x+... + 6p_xtet_p+x) + en A0.1)
где
р = ах+а2+... + ар9 0j=-(aJ+l+... + ap).
(В примере с GNP такое преобразование дает
Xt = 55.017 + 1.304*+ 1.380JrM -0.630JSTM +0.630JrM -0.630Jf,_2 +st =
= 55.017 + 1.304f + 0.750JrM+0.630A*M+s,.)
Если исходить из того, что уравнение a(z) = 0 может иметь только один
корень z = 1, а остальные (р - 1) корней лежат за пределами единичного
круга, то наличие единичного корня равносильно тому, что ах + а2 + ... + ар = 1,
т.е. р = 1 (см., например, (Hamilton, 1994, р. 517)). Таким образом, гипотеза
о существовании единичного корня у процесса AR(p) сводится в этом случае
к гипотезе Я0: р = 1 в преобразованном соотношении A0.1). Для проверки
этой гипотезы можно пользоваться теми же таблицами Фуллера, только на
этот раз используются значения статистики Т(рх - 1) и ^-отношения для
проверки гипотезы р- 1, полученные при оценивании расширенной (augmented)
статистической модели A0.1) (с /? и а, равными или не равными нулю).
Соответствующие ^-статистики обозначают обычно ADF (augmented Dickey-Fuller)
в отличие от статистики DF, получаемой для модели ARA).

472
Часть 2. Регрессионный анализ временных рядов
Для того чтобы не вычислять самим каждый раз значение ^-статистики для
гипотезы р = 1, можно преобразовать A0.1) к виду
Axt=a + 0t + <pxt_l+(eltet_l+... + e^ltet_^l) + €n (Ю.2)
где <р = р - 1, так что гипотеза Н0: р- 1 в выражении A0.1) равносильна
гипотезе Я0: (р- 0 в выражении A0.2).
В качестве альтернативной кЯ0: р- 1 в выражении A0.1) выступает
гипотеза НА: р < 1. При переходе от уравнения A0.1) к A0.2) она преобразуется
в гипотезу НА: (р < 0.
При этом значение ^-статистики для проверки гипотезы Н0: р= 1 в
выражении A0.1) численно равно значению ^-статистики для проверки гипотезы
Н0: <р = 0 в выражении A0.2).
ПРИМЕР 10.1.4
Для ряда GNP оценивание модели
Axt = а + fit + cpxt_x + #j Дх,_! + £г
(обычным методом наименьших квадратов) приводит к результатам,
приведенным в табл. 10.12 (критические значения для отвержения гипотезы
единичного корня вычислены по формулам Маккиннона).
Таблица 10.12
Оценивание обычным методом наименьших квадратов
ADF Test Statistic
-4.117782
\% Critical Value
5% Critical Value
10% Critical Value
4.1219
-3.4875
-3.11718
Расширенный критерий Дики — Фуллера (объясняемая переменная D(X))
Переменная
Д-1)
ДД-1))
с
@TREND(\947:\)
Коэффициент
-0.249792
0.630066
56.32136
1.304300
Стандартная
ошибка
0.060662
0.109453
13.18303
0.315357
/-статистика
-4.117782
5.756490
4.272264
4.135949
Р-значение
0.0001
0.0000
0.0001
0.0001
Гипотеза единичного корня отвергается: значение ^-статистики для
проверки гипотезы Н0: <р = 0 оказывается ниже 5%-го критического значения,
вычисленного по формуле Маккиннона, и близко к 1%-му критическому
значению. ■

Раздел 10. Процедуры для различения TS- и DS-рядов
473
В связи с последним примером следует особо отметить, что использование
расширенной модели предполагает, что количество запаздывающих
разностей, включенных в правую часть, исчерпывает временную зависимость, так
что st — независимые случайные величины. В то же время не следует
включать в правую часть излишних запаздывающих разностей, так как это
снижает мощность критериев из-за оценивания дополнительных параметров
и уменьшения используемого количества наблюдений.
Для определения надлежащей глубины запаздываний следует начать с
относительно большого порядка р =/?*, а затем опираться на то обстоятельство,
что хотя при наличии единичного корня распределения оценки ф и 7-ста-
тистики для проверки гипотезы ср = О нестандартны, распределения оценок
коэффициентов в19 ..., вр_х все же являются асимптотически нормальными.
Поэтому можно сначала проверить гипотезу о том, что вр*_х = 0, используя
обычную ^-статистику и критические точки соответствующего
^-распределения Стьюдента. Если эта гипотеза не отклоняется, то проверяем гипотезу
вр*_х = вр*_2 = 0, используя F-критерий и процентные точки F-распределения
Фишера, и т.д. После этого производится обычная диагностика адекватности
подобранной модели.
ПРИМЕР 10.1.5
Продолжим предыдущий пример. Если взять первоначально р* = 5, то
получим следующие результаты (табл. 10.13) (критические значения для
отвержения гипотезы единичного корня вычислены по формулам Маккиннона).
Таблица 10.13
Оценивание обычным методом наименьших квадратов при р* = 5
1 ADF Test Statistic
-2.873575
1% Critical Value
5% Critical Value
10% Critical Value
-4.1314
-3.4919
-3.1744
Расширенный критерий Дики — Фуллера (объясняемая переменная D(X))
Переменная
Д-1)
D(X(-\))
D(X(-2))
дд-з»
D(X(-4))
С
@TREND(\947:\)
Коэффициент
-0.266169
0.546230
0.183918
-0.020254
-0.058683
59.45556
1.397409
Стандартная
ошибка
0.092626
0.133521
0.149711
0.152201
0.148061
19.32396
0.482120
/-статистика
-2.873575
4.090958
1.228486
-0.133077
-0.396345
3.076779
2.898469
Р-значение
0.0060
0.0002
0.2253
0.8947
0.6936
0.0035
0.0056

474
Часть 2. Регрессионный анализ временных рядов
Поскольку здесь t = -2.873575 > -3.1744, то гипотеза единичного корня
не отвергается даже при выборе 10%-го уровня значимости. В то же время
статистически незначимыми оказываются коэффициенты при трех последних
запаздывающих разностях. Р-значение F-статистики критерия для гипотезы
о занулении этих трех коэффициентов равно 0.44. Поэтому можно обойтись
без трех последних запаздывающих разностей, а такую модель мы только что
оценивали, и в ней гипотеза единичного корня была отвергнута. ■
Критерии Дики — Фуллера фактически предполагают, что наблюдаемый ряд
описывается моделью авторегрессии конечного порядка (возможно, с
поправкой на детерминированный тренд). Как поступать в случае, когда ряд xt имеет
тип ARMA(p, q)cq>0?
Пусть xt ~ ARMA(p, q), так что a{L)xt = b(L)st, где a(L), b(L) — полиномы
порядков р и q, и пусть оператор b(L) обратим, так что процесс можно
представить в виде процесса авторегрессии бесконечного порядка
c{L)xt = st,
/гч a(L) Л Т т2
где c(L)x,:=—^-L = \ + c]L + c7L+ ...
' b(L) l 2
В этом случае представление A0.2) с конечным числом запаздываний в
правой части заменяется бесконечным представлением
Ах, = а + fit + (pxt_x +(#1Дх,_1 +d2Axt_2 +...) + *,. О 0.3)
Однако все коэффициенты последнего невозможно оценить по конечному
количеству наблюдений. Как выйти из этого положения?
В работе (Said, Dickey, 1984, p. 599—607) было показано, что процесс
ARIMA(p, l9q)c неизвестными р и q можно достаточно хорошо
аппроксимировать некоторым процессом ARI(p*, 1) с р* < у/Т . Это дает возможность
ограничиться в правой части выражения A0.3) конечным числом
запаздывающих разностей.
Краткий обзор критериев Дики — Фуллера
Под критерием Дики — Фуллера в действительности понимается группа
критериев, объединенных одной идеей, предложенных и изученных в работах
(Dickey, 1976), (Fuller, 1976), (Dickey, Fuller, 1979), (Dickey, Fuller, 1981).
В критериях Дики — Фуллера проверяемой (нулевой) является гипотеза о том,
что исследуемый ряд xt принадлежит классу DS (^^-гипотеза);
альтернативная гипотеза — исследуемый ряд принадлежит классу TS (Г^-гипотеза).
Критерий Дики — Фуллера фактически предполагает, что наблюдаемый ряд
описывается моделью авторегрессии первого порядка (возможно, с поправкой
на линейный тренд). Критические значения зависят от того, какая статисти-

Раздел 10. Процедуры для различения TS- uDS-рядов
475
ческая модель оценивается и какая вероятностная модель в действительности
порождает наблюдаемые значения. При этом рассматриваются следующие
три пары моделей.
1. Если ряд xt имеет детерминированный линейный тренд (наряду с
которым может иметь место и стохастический тренд), то в такой ситуации
берется пара
SM: Axt = a + pt+ (pxt_x + st, t = 2,...,T,
DGP: Axt = a+st, t = 2,...,T, a*0.
В обоих случаях st — независимые случайные величины, имеющие
одинаковое нормальное распределение с нулевым математическим
ожиданием.
Методом наименьших квадратов оцениваются параметры данной
SM и вычисляется значение обычной ^-статистики t9 для проверки
гипотезы Н0: <р= 0. Полученное значение сравнивается с критическим
уровнем f , рассчитанным в предположении, что наблюдаемый ряд
в действительности порождается данной моделью DGP (случайное
блуждание со сносом), /^-гипотеза отвергается, если t9 < t^^.
Критические уровни, соответствующие выбранным уровням значимости,
можно взять из таблиц, приведенных в (Fuller, 1976), (Fuller, 1996),
если ряд наблюдается на интервалах длины Т = 25, 50, 100, 250, 500.
Если количество наблюдений Т другое, можно вычислить
приближенные критические значения, используя формулы, приведенные в
(MacKinnon, 1991).
2. Если ряд xt не имеет детерминированного тренда (но моэюет иметь
стохастический тренд) и имеет ненулевое математическое ожидание,
то берется пара
SM: Axt = a+ (pxt_x + st, t = 2,...,T,
DGP: Axt = st, t = 2,...,T.
Методом наименьших квадратов оцениваются параметры данной
SM и вычисляется значение ^-статистики t9 для проверки гипотезы
Н0: ср - 0. Полученное значение сравнивается с критическим уровнем
tKpm, рассчитанным в предположении, что наблюдаемый ряд в
действительности порождается данной моделью DGP (случайное блуждание
без сноса), ^^-гипотеза отвергается, если t9 < tKpm. Критические
уровни, соответствующие выбранным уровням значимости, можно взять
из таблиц, приведенных в (Fuller, 1976), (Fuller, 1996), если ряд
наблюдается на интервалах длины Т= 25, 50, 100, 250, 500. Если количество
наблюдений Т другое, можно вычислить приближенные критические
значения, используя формулы, приведенные в (MacKinnon, 1991).

476
Часть 2. Регрессионный анализ временных рядов
3. Наконец, если ряд xt не имеет детерминированного тренда (но может
иметь стохастический тренд) и имеет нулевое математическое
ожидание, то берется пара
SM: Axt = <pxt_{ + st, t = 2,..., Г,
DGP: Axt = st, t = 2,...,T.
Методом наименьших квадратов оцениваются параметры данной SM
и вычисляется значение ^-статистики t для проверки гипотезы Н0: cp-Q.
Полученное значение сравнивается с критическим уровнем tKpm,
рассчитанным в предположении, что наблюдаемый ряд в
действительности порождается данной моделью DGP (случайное блуждание без сноса).
ZXS-гипотеза отвергается, если f < tKpm. Критические уровни,
соответствующие выбранным уровням значимости, можно взять из таблиц,
приведенных в {Fuller, 1976), {Fuller, 1996), если ряд наблюдается на
интервалах длины Т = 25, 50, 100, 250, 500. Если количество
наблюдений Т другое, можно вычислить приближенные критические значения,
используя формулы, приведенные в {MacKinnon, 1991).
Неправильный выбор оцениваемой статистической модели может
существенно отразиться на мощности критерия Дики — Фуллера. Например, если
наблюдаемый ряд порождается моделью случайного блуждания со сносом,
а статистические выводы производятся на основании результатов оценивания
статистической модели без включения в ее правую часть трендовой
составляющей, то тогда мощность критерия, основанная на статистике t9, стремится
к нулю с возрастанием количества наблюдений (см. {Perron, 1988)). В то же
время оцениваемая статистическая модель не должна быть избыточной,
поскольку это также ведет к уменьшению мощности критерия.
Формализованная процедура использования критериев Дики — Фуллера
с последовательной проверкой возможности редукции статистической модели
приведена в {Dolado, Jenkinson, Sosvilla-Rivero, 1990), см. также {Enders,
1995). Эта процедура (в изложении {Enders, 1995, р. 251—260)) будет
рассмотрена ниже. Если наблюдаемый ряд описывается моделью авторегрессии
a{L)xt = st более высокого (но конечного) порядка/?, уравнение a{z) = 0 имеет
не более одного единичного корня и не имеет корней внутри единичного
круга, то можно воспользоваться расширенным {augmented) критерием
Дики — Фуллера. В каждой из трех рассмотренных выше ситуаций
достаточно дополнить правые части оцениваемых статистических моделей
запаздывающими разностями Лхг_у,у = 1, ..., /7-1, так что оцениваются
расширенные статистические модели:
р-\
1) SM: Ах, = а + fit + q>xt_x + ^Ojkxt_j +en t = p + \,...,T\
7 = 1

Раздел 10. Процедуры для различения TS- и DS-рядов
477
Р-\
2) SM: Axt = а + (pxt_x + ^OjAxt_j + st, t = p +1,...,T;
y=i
p-\
3) SM: Axt -cpxt_x + ^jOjl±xt_j + st, t = p + \9...9T.
7 = 1
Полученные при оценивании расширенных статистических моделей
значения ^-статистик f для проверки гипотезы Н0: ^ = 0 сравниваются с теми же
критическими значениями /крит, что и для нерасширенных моделей,
/^-гипотеза отвергается, если ^ < tKpm.
Расширенный критерий Дики — Фуллера может применяться и тогда, когда
ряд xt описывается смешанной моделью авторегрессии — скользящего
среднего. Как было указано в (Said, Dickey, 1984), если ряд наблюдений хх, ..., хт
порождается моделью АШМА(р, 1, q) с q > О, то можно его
аппроксимировать моделью АШ(р*, 1) = ARIMA(p*, 1, 0) ср* < чГ и применять процедуру
Дики — Фуллера к этой модели.
Однако даже если ряд наблюдений хх, ..., хт действительно порождается
моделью авторегрессии AR(p) конечного порядка р, то значение р обычно
неизвестно, и его приходится оценивать на основании имеющихся
наблюдений, а такое предварительное оценивание влияет на характеристики
критерия. Поэтому при анализе данных приходится сначала выбирать значение
Р =Рт*к достаточно большим, чтобы оно было не меньше истинного
порядка р0 авторегрессионной модели, описывающей ряд, или порядка р*
аппроксимирующей авторегрессионной модели, а затем пытаться понизить
используемое значение р, апеллируя к наблюдениям.
Такое понижение может осуществляться, например, путем
последовательной редукции расширенной модели за счет исключения из нее незначимых
(на 10%-м уровне) запаздывающих разностей (С^-стратегия перехода от
общего к частному) или путем сравнения (оцененных) полной и
редуцированных моделей с различными р < /?тах по информационному критерию Шварца
(SIQ. В работах (Hall, 1994) и (Ng, Perron, 1995) показано, что если/?тах >р0,
то в пределе (при Т -> оо) SIC выбирает правильный порядок модели, а
стратегия GS выбирает модель с р>р0, при этом факт определения порядка
модели на основании имеющихся данных не влияет на асимптотическое
распределение статистики Дики — Фуллера. Таблицы критических значений для
конечных значений Т, учитывающие порядок модели, приведены в (Cheung,
Lay, 1995).
При практической реализации указанных двух подходов (GS и SIC), когда
есть лишь ограниченное количество наблюдений, эти две процедуры могут
приводить к совершенно разным выводам относительно необходимого
количества запаздываний в правой части статистической модели, оцениваемой

478
Часть 2. Регрессионный анализ временных рядов
в рамках расширенного критерия Дики — Фуллера. Так, при анализе
динамики валового внутреннего продукта (GDP) США по годовым данным на
периоде с 1870 по 1994 г. (см. (Murray, Nelson, 2000)), выбрав/?max = 8, авторы
получили при использовании С^-стратегии значение р - 6, тогда как по SIC
было выбрано значение р = 1. В подобных конфликтных ситуациях для
контроля можно ориентироваться также на достижение некоррелированности
по LM-критерию остатков от оцененной модели (см. (Holden, Perman, 1994)).
Заметим, однако, что в статье (Taylor, 2000) автор приходит к выводам,
отличающимся от выводов Ng и Perron: при конечных выборках расширенные
критерии Дики — Фуллера очень чувствительны и к форме детерминистских
переменных, и к принятой структуре запаздываний. Это, в свою очередь,
ведет к отклонениям от номинальных уровней значимости критериев Дики —
Фуллера.
Многовариантная процедура проверки
гипотезы единичного корня
Доладо и др. (Dolado, Jenkinson, Sosvilla-Rivero, 1990) предложили
многовариантную процедуру проверки гипотезы единичного корня с использованием
критерия Дики — Фуллера, при которой последовательно перебираются
различные комбинации оцениваемой статистической модели (SM) и процесса
порождения данных (DGP). Объясним суть этой процедуры (в изложении
(Enders, 1995)), считая для простоты, что рассматриваемый ряд порождается
моделью ARA), быть может, с поправкой на линейный тренд.
На шаге 1 многовариантной процедуры оценивается статистическая
модель, допускающая наличие тренда, содержащая в правой части уравнения
константу и трендовую составляющую:
SM: Axt = а + fit + (pxt_x +sn f = 2,...,7\
и при использовании таблицы критических значений предполагается, что
данные порождаются моделью
DGP: Axt=a + et9 t = 2,...,T.
Это естественная пара: реализация с видимым трендом (сносом).
Критерий принадлежности ряда классу DS формулируется как критерий
единичного корня (UR — Unit Root) в авторегрессионном представлении ряда.
Проверяемой в рамках данной статистической модели является гипотеза Н0: ср = 0,
альтернативная гипотеза НА: <р < 0. Получаемое в результате оценивания такой
расширенной модели значение /-статистики критерия Дики — Фуллера
сравнивается с критическим значением, соответствующим предположению, что
данные порождаются моделью случайного блуждания со сносом. Это
критическое значение не зависит от того, а = 0 или а * 0.

Раздел 10. Процедуры для различения TS- и DS-рядов
479
Если гипотеза Н0: ср = О отвергается этим критерием, то гипотеза о
наличии единичного корня тем самым отвергается окончательно. Дело в том, что
если Я0: р=0 отвергнута при
DGP: Лх, = а + st (с а = О или а * 0),
то она тем более будет отвергнута при
DGP: Axt = a + j3t+et, /?*0,
так как в последнем случае значение f выше (используется нормальное
приближение).
Шаг 2. Если на шаге 1 гипотеза Н0: ср = 0 не была отвергнута, то
возможны две причины:
• действительно, ср - 0;
• ср * 0, но гипотеза Н0: #> = 0 не была отвергнута из-за того, что исходили
из DGP с Р- 0, тогда как в действительности имел место
DGP: Axt = a + /3t + snP*0.
В связи с последней возможностью на шаге 2 производится проверка
гипотезы Н0: /В= 0 в рамках статистической модели
SM: Axt = а + fit + до,_ х + £„
но с
DGP: Axt = a + j3t+sn /?*0.
Критические значения соответствующей /-статистики (ТрТ — в
обозначениях Дики — Фуллера) указаны в {Dickey, Fuller, 1981). В табл. 10.14
приведены 5%-е критические значения для |/| в случае двустороннего критерия
и для t в случае одностороннего критерия.
Таблица 10.14
Критические E%-е) значения для t-статистики
п
25
50
100
250
500
оо
Двусторонний критерий
3.25
3.18
3.14
3.12
3.11
3.11
Односторонний критерий
(против fl>0)
2.85
2.81
2.79
2.79
2.78
2.78
Если гипотеза Н0: /3=0 здесь не отвергнута, то это означает, что на 1-м шаге
гипотеза ср = 0 не была отвергнута не из-за использования критических
значений, соответствующих DGP с /В= 0.

480
Часть 2. Регрессионный анализ временных рядов
Если же гипотеза Н0: /?= О оказалась отвергнутой, то следует повторить
проверку гипотезы <р = О в рамках статистической модели
SM: Axt = a + J3t + cpxt_ x + st,
но уже опираясь на
DGP: Axt = a + /3t+£nj3*0.
Соответствующая ^-статистика имеет (при /? * 0) асимптотически
нормальное N@, 1) распределение. Для конечных Г можно обратиться к
таблицам в {Kwiatkowski, Schmidt, 1990). И теперь уже, если гипотеза ср - 0 будет
отвергнута, то отвергнута окончательно. Если же она не отвергнута,
принимаем модель
Ах, = a + fit + et, /3*0.
Шаг 3. Попадаем на шаг 3, не отвергнув гипотезу единичного корня в
рамках статистической модели
SM: Axt = а + fit + <pxt_x+ st.
Возможно, что это связано с пониженной мощностью критериев из-за
включения в модель лишней объясняющей переменной t.
В связи с этим на шаге 3 переходим к модели
SM: Axt = a+ <pxt_x + st
без трендовой составляющей и проверяем гипотезу <р = 0 (против ср < 0) в
рамках этой SM. Критические значения соответствующей ^-статистики берем
опять у Фуллера (ситуация 2). Они получены в предположении, что
DGP: Дх, = sr
И опять если гипотеза Н0: ср = 0 отвергается, то отвергается
окончательно (по тем же причинам, что и на шаге 1).
Шаг 4. Если на шаге 3 гипотеза ср = 0 не отвергается, то выясняется
причастность к этому включения в SM сноса а. С этой целью производится
проверка гипотезы а = 0 в рамках статистической модели
SM: Axt = а+ <pxt_x + st,
но с
DGP: Дх, = €г
Критические значения соответствующей ^-статистики (т — в
обозначениях Дики — Фуллера) указаны в (Dickey, Fuller, 1981). В табл. 10.15
приведены 5%-е критические значения для 11 | в случае двустороннего критерия
и для t в случае одностороннего критерия.
Если при этом гипотеза а = 0 не отвергается, тогда не считаем, что
неотвержение ср - 0 на предыдущем этапе было связано с опорой на DGP с а = 0.

Раздел 10. Процедуры для различения TS- uDS-рядов
481
Таблица 10.15
Критические значения для t-статистики
п
25
50
100
250
500
00
Двусторонний критерий
2.97
2.89
2.86
2.84
2.83
2.83
Односторонний критерий
(против ог>0)
2.61
2.56
2.54
2.53
2.52
2.52
Если же гипотеза а = 0 оказалась отвергнутой, то производится
повторная проверка гипотезы Я0: <р = 0 в рамках
SM: Дх, = а+ <pxt_x + sn
но с опорой на
DGP: Axt = a+£t с а*0.
В этом случае /-статистика для а = 0 опять асимптотически нормальна,
и, опираясь на ее значение, либо отвергаем гипотезу Я0: <р = 0 окончательно,
либо принимаем модель
Дх, = а + st с а * 0.
Следует только помнить о том, что при конечных Т при значениях а,
близких к нулю, распределение этой статистики ближе к распределению,
указанному Фуллером для случая а = 0, чем к нормальному распределению.
Шаг 5. Наконец, если и на шаге 4 гипотеза Я0: ср - 0 не была отвергнута,
остается последняя возможность сделать это в рамках статистической модели
SM: Дх, = q>xt_i + sr
Критические значения /-статистики для Я0: (р = 0 находятся по таблицам
Фуллера (случай 1). И теперь уже каждое из двух возможных решений —
окончательное:
Н0: <р=0 отвергается —> единичного корня нет;
Я0: ср- 0 не отвергается —> Дх, = et
(точнее Дх, = Qxbxt_x + ... + вр_хДх,_р+1 + £,).
V Замечание 10.1.2. Построенный алгоритм отнюдь не лишен
недостатков. Помимо того что здесь не контролируется уровень
значимости критерия проверки гипотезы единичного корня, возникают
сложности и с интерпретацией результатов, что будет видно из
последующих примеров.

482
Часть 2. Регрессионный анализ временных рядов
Процедуру Доладо схематически можно представить в виде дерева
решений, приведенного на рис. 10.10.
Оценивается модель 1
l
Н0:<р=0
I
не отвергается
I
Я0: Р- 0 при условии (р- 0 ■
i
не отвергается
Оценивается модель 2
i
Н0:<р=0
i
не отвергается
l
Я0: а- 0 при условии <р= 0-
i
не отвергается
-*► отвергается
Axt = а + pt + cpxt_
I
+ I3-A-;
. >=1 )
+ e,
отвергается
t
отвергается
-► Я0: <p= 0 при условии /?* 0
l
не отвергается
Axt = a + /3t
+ X3AV;
V У-» )
г
+ е.
^OjAxt_j
-► отвергается ► Дх, = а + #>*,_!
I
отвергается
I
-► отвергается ► Я0: #>= 0 при условии а* 0
l
не отвергается
+ гг,
Оценивается модель 3
Ах, = а
I
Я0:?=0
I
ITB
I
k ;=1
+*/
/
-► отвергается ► Axt = #>*,_!
р-1
+ 13^-/
+£,
не отвергается
Дх,= £^-7
+ £,
Рис. 10.10

Раздел 10. Процедуры для различения TS- uDS-рядов
483
В представленной схеме модели пронумерованы следующим образом:
( Bzl ^
модель 1: Axt =a + /3t + cpxt_x
+ £,;
(
модель 2: Ах, = а + срх,А
-1
Л
+ et;
модель 3: Ах, = срх,
( р-\
\
■-1
+ ег
+ 2>уД*,_,
Приведем пример использования процедуры Доладо.
ПРИМЕР 10.1.6
Обратимся к данным о совокупном годовом располагаемом доходе в США
за период с 1959 по 1985 г. (в млрд долл., в ценах 1982 г.). График этого ряда
приведен на рис. 10.11.
2800-
2400-
2000-
1600-
1200-
800-
DPI
I i I ■ I ■ I i I i I i I < I i I i I ' I ■ I ' I I
I—►
OCN^CDOOOCslxrCDOOOCN^r ГОД
0HHHHHHHHHHHH)
Рис. 10.11
С учетом изложенного ранее здесь очевидна необходимость различения
модели случайного блуждания со сносом и процесса, стационарного
относительно линейного тренда. Последуем процедуре Доладо.
Шаг 1. Оцениваем статистическую модель
SM: Дх, = а + /3t+ (pxt_x + Oxkxt_x + ... + 0p_xAxt_p+x + sr
Сравнение по критерию Шварца указывает в пользу исключения из правой
части запаздывающих разностей, так что останавливаемся на модели
SM: Ах, = а + J3t + (pxt_x + sr
Оцененная модель (Т= 26):
Axt = 461.338 + 25.857/ - 0A4Sxt_x + et;

484
Часть 2. Регрессионный анализ временных рядов
/-статистика для проверки гипотезы Я0: ср- 0 равна t9 = -2.640. Критическое
E%-е) значение выбирается при
DGP: Ах, = а + еп а * 0,
и равно / = -3.59 (для Т= 26). Наблюдаемое значение /^ больше /крит —>
Гипотеза единичного корня не отвергается.
Шаг 2. Статистическая модель та же, но в качестве DGP рассматривается
DGP: Axt = a + /3t+sr
Проверяемая гипотеза
НО:0 = О.
Статистика критерия ТрТ = 2.680. Критическое E%-е) значение
одностороннего критерия {НА: /? > 0) равно 2.85 —> гипотеза Н0: /3 = 0 не
отвергается.
Шаг 3. Оцениваем модель
SM: Ах, = а+ q>xt_x + £,;
в качестве DGP рассматривается
DGP: Ах, = €г
Проверяется гипотеза Я0: ср - 0. Оцененная модель: Ах, = 47.069 +
+ 0.00522х,_! + et; /-статистика /^ = 0.335. Критическое E%-е) значение
tKpm = -2.98 —> гипотеза единичного корня не отвергается.
Шаг 4. Оцениваем модель
SM: Ах, = а+ <pxt_{ + £„
в качестве DGP рассматривается
DGP: Ах, = £„ Я0: а=0.
Оцененная модель: Ах, = 47.069 + 0.00522x/_1-h et\ /-статистика ta = 1.682 <
< /крит =2.61 —> гипотеза Я0: а = 0 не отвергается.
Шаг 5. Оцениваем модель
SM: Ах, = cpxt_x + €п
в качестве DGP рассматривается
DGP: kxt = £n Я0: <р=0.
Оцененная модель: Ах, = 0.03070х/_1 + et\ /-статистика t = 7.987 > tKpm =
= -1.95 —> гипотеза Я0: ср=0 не отвергается —> окончательная модель:
Х( — t— 1 ^ • ^^

Раздел 10. Процедуры для различения TS- uDS-рядов
485
Интерпретация. Если мы соглашаемся с несомненной тенденцией
возрастания совокупного располагаемого дохода с течением времени (по
крайней мере, в США), то принятую на последнем шаге модель вряд ли можно
считать удовлетворительной: случайное блуждание без сноса должно со
временем обнаружить убывание значений ряда.
Возможной причиной этого является неотклонение гипотезы Н0: C= О
на шаге 2 (заметим, что там разница между наблюдаемым и критическим
значениями /-статистики была довольно небольшой: г^г = 2.680, /крит = 2.85.)
Если возвратиться к шагу 2 и изменить решение в пользу отклонения гипотезы
Я0: /?= 0, так что тогда /?* 0, то гипотеза Я0: <р=0 проверяется в рамках пары
SM: Дх, = а + fit + <pxt_ { + st,
DGP: Axt = a + j3t + sn J3*0.
В таком случае статистика t9 имеет асимптотически нормальное 7V@, 1)
распределение, 5%-е критическое значение одностороннего критерия
приближенно равно: /крит = -1.645. У нас же наблюдаемое значение t9 - -2.640
(см. шаг 1), так что гипотеза единичного корня отвергается, и мы имеем дело
с процессом, стационарным относительно линейного тренда'.
Ах, = 461.338 + 25.857/- 0.448х,_! + ег
Некоторые другие сочетания DGP и SM
Рассмотрим следующий естественный вопрос: что будет, если оцениваем
SM: xt = a + axxt_x + sn
а процессом порождения данных является
DGP: xt = а + х,_ х + еп а ф 0 (случайное блуждание со сносом)?
В этом случае при больших t возникающий в DGP детерминированный
t
тренд «забивает» стохастическую составляющую ^£/9 и поведение пере-
/=i
менной х,_ j в SM похоже «в целом» на поведение детерминированной
переменной a(t - 1). Как результат, распределения оценок для а и ах оказываются
асимптотически нормальными. Но тогда, в принципе, можно было бы в
качестве приближения использовать стандартную технику статистического
анализа, т.е. использовать критические значения /-отношения, взятые из таблиц
распределения Стьюдента. Однако если а*0 близко к нулю, то при конечных Т
распределение /-отношения ближе к распределению, указанному Фуллером
для случая B=0, чем к нормальному распределению.

486
Часть 2. Регрессионный анализ временных рядов
ПРИМЕР 10.1.7
Для смоделированной реализации WALKJ2 случайного блуждания со
сносом 0.2 оценивание статистической модели SM: xt = а + axxt_x + st дает
результаты, приведенные в табл. 10.16.
Таблица 10.16
Объясняемая переменная WALK_2
Переменная
С
WALK_2{-\)
Коэффициент
0.173019
0.991851
Стандартная
ошибка
0.160495
0.045395
/-статистика
1.078031
21.84958
Р-значение
0.2865
0.0000
Таким образом, интересующая нас /-статистика принимает значение
t = _: = -0.180.5%-е критическое значение /-распределения Стью-
0.045395
дента с (п - р) = D9 - 2) = 47 степенями свободы равно -1.68, тогда как
5%-е критическое значение по Фуллеру, предназначенное для случая DGP:
xt = xt_{ + st {a = 0), равно -2.92, что приводит к более редкому отвержению
гипотезы единичного корня. Впрочем, гипотеза о наличии единичного корня
здесь не отвергается при использовании любого из двух критических
значений-1.68 и-2.92.
Оценивание смоделированной реализации ST_2 процесса х, = 0.2 + 0.8х,_ { + £t
(стационарный процесс с математическим ожиданием, равным 1) при Т= 50 дает
результаты, приведенные в табл. 10.17.
Таблица 10.17
Объясняемая переменная ST_2
Переменная
С
ST_2(-\)
Коэффициент
0.166899
0.793680
Стандартная
ошибка
0.159693
0.091904
/-статистика
1.045128
8.635959
Р-значение
0.3013
0.0000
Таким образом, интересующая нас /-статистика принимает значение
0.793680-1 „_с тж
t = = -2.245. Использование критического значения -1.68 приво-
0.091904
дит к отвержению гипотезы единичного корня, тогда как использование
критического значения -2.92 не дает возможности отвергнуть эту гипотезу.■
Отметим еще одно важное обстоятельство. Опять рассмотрим
смоделированную реализацию 5Т_1 ряда xt = 0.8х,_! + sr Если будем проверять для
ряда xt гипотезу единичного корня, то, как теперь ясно, можем исходить либо

Раздел 10. Процедуры для различения TS- uDS-рядов
487
из SM: xt = axxt_x + £п (подозревая, что DGP — простое случайное
блуждание), либо из SM: х, = а + axxt_x + st (подозревая, что DGP — случайное
блуждание со сносом).
В первом случае 5%-е критическое значение /-статистики (при Т = 50)
находим по таблицам Фуллера: оно равно -1.95. Во втором случае
критическое значение определяется либо в соответствии с нормальной теорией, тогда
^крит = -1-68 (в предположении, что снос — ненулевой), либо по Фуллеру —
тогда /крит= -2.92.
Оценивание SM в первом случае дает t = -2.314. Гипотеза единичного
корня отвергается.
Оценивание SM во втором случае дает t = -2.298. Если исходить из
предположения, что в DGP снос ненулевой, то t < /крит = -1.68, и гипотеза
единичного корня отвергается. Если же исходить из предположения, что в DGP
сноса нет, то t > tKpiiT = -2.92, и гипотеза единичного корня не отвергается.
Такой неожиданный результат объясняется тем, что пополнение
статистической модели (SM) дополнительными регрессорами требует их
оценивания, что снижает, в конечном счете, мощность критерия. Поэтому желательно
при проверке гипотезы единичного корня оценивать SM, выбираемую «без
запаса». Однако при отсутствии информации о том, равен нулю снос в DGP
или нет, при отклонении гипотезы единичного корня следует опираться
на консервативное значение, даваемое таблицами Фуллера. Иначе можно
ошибочно отвергать эту гипотезу более чем в 5% случаев, если в
действительности снос в DGP отсутствует.
Ряды с квадратичным трендом
Следует рассмотреть также случай, когда по поведению траектории ряда
можно подозревать наличие у него детерминированного квадратичного
тренда.
Здесь наличие единственного1 единичного корня может осуществляться
уже в форме трех различных DGP:
а) xt = xt_x + €п
б) х, = а + xt__ j + еп а * 0,
в) xt = a + J3t + xt_x + еп 0*0.
Последний случай гарантирует наличие квадратичного тренда, в двух
других — возможна имитация такого тренда на не очень продолжительном
периоде наблюдений.
Квадратичный тренд может возникать и в моделях с двумя единичными корнями. Эта
ситуация рассматривается ниже, при изложении темы 10.2.

488
Часть 2. Регрессионный анализ временных рядов
Если строить проверку гипотезы единичного корня в рамках
статистической модели
SM: xt = а + /3t + axxt_x + st, C*0,
то распределение /-статистики при гипотезе Н0: ах = 1 будет различным, в
зависимости от того, каким в действительности является DGP.
Как было отмечено ранее, распределение этой /-статистики одно и то лее
для случаев а) и б), т.е. не зависит от того, а = 0 или а * 0.
Если DGP имеет форму в) с /3 Ф 0, то указанная /-статистика имеет
распределение, близкое к /-распределению (точнее, асимптотически
нормальное N@, 1)). Для конечных Г можно обратиться к таблицам (Kwiatkowski,
Schmidt, 1990).
ПРИМЕР 10.1.8
Рассмотрим смоделированную реализацию WALK3 случайного блуждания
вокруг квадратичного тренда:
DGP: х, = 0.2 + 0.1/ + xt_x + sr
В качестве статистической модели берем SM: х, = а + /?/ + a{xt_{ + et,
ее оценивание дает: а = 0.989 и / = -0.775. Использование
/-распределения Стьюдента приводит к /крит = -1.68, так что гипотеза единичного корня
не отвергается. Использование критического значения Фуллера,
соответствующего DGP с /?= 0 , дает /крит = -3.50, так что гипотеза единичного корня
не отвергается тем более.
При анализе смоделированной траектории ST4 процесса
DGP: х, = 0.12 + 0.13/ + 0.01 /2 + 0.8х,_! + еп
стационарного относительно того же квадратичного тренда, получаем а = 0.990
и / = -0.577 . Гипотеза единичного корня не отвергается при использовании
как распределения Стьюдента, так и таблиц Фуллера. ■
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Относительно какого линейного тренда является стационарным TS-ряд xt= a + fit +
+ alxt_l + et9\al\<l'>
2. Почему для проверки гипотезы единичного корня не удается воспользоваться
обычным /-критерием?
3. Как соотносятся обычные критические значения /-статистики со значениями,
применяемыми при оценивании статистической модели в форме процесса
авторегрессии xt = alxt_l + et9t= l, ..., Г, в случае, когда модель, порождающая
данные, имеет вид: xt =xt_Y + sn где et — гауссовский белый шум?

Раздел 10. Процедуры для различения TS- uDS-рядов
489
4. Как добавление в статистическую модель лишних объясняющих переменных
влияет на мощность критериев единичного корня?
5. Как можно приближенно вычислять критические значения статистик критериев
Дики — Фуллера?
6. Можно ли использовать обычные критические значения F-статистик при
проверке гипотез о наличии единичного корня?
7. Почему с помощью формальных статистических критериев бывает практически
невозможно отличить реализации процессов с единичным корнем и без наличия
такового при небольшом количестве наблюдений?
8. В чем состоит «презумпция наличия единичного корня»?
9. В чем состоит «презумпция отсутствия единичного корня»?
10. Чем обусловлено привлечение к проверке гипотезы единичного корня
расширенных вариантов критериев Дики — Фуллера?
11. Как строятся расширенные критерии Дики — Фуллера? Какое количество
запаздываний следует использовать при построении этих критериев? Как можно
оценить это количество по имеющимся статистическим данным?
12. Можно ли воспользоваться критериями Дики — Фуллера в случае, когда ряд xt
имеет тип ARMA(/?, q)cq>0?
13. Какие три стандартных сочетания статистических моделей и процессов
порождения данных рассматриваются в рамках критериев Дики — Фуллера?
14. Как влияет на мощность критериев Дики — Фуллера неправильный выбор
оцениваемой статистической модели?
15. В чем состоит многовариантная процедура проверки гипотезы о наличии
единичного корня? Каковы ее достоинства и недостатки?
16. Какие процессы порождения данных используются при проверке гипотезы о
наличии (единственного) единичного корня в случае, когда подозревается наличие
у ряда детерминированного квадратичного тренда?
Тема 10.2
ОБЗОР НЕКОТОРЫХ ДРУГИХ ПРОЦЕДУР
Критерий Филлипса — Перрона
Этот критерий, предложенный в (Phillips, Perron, 1988), сводит проверку
гипотезы о принадлежности ряда xt классу DS к проверке гипотезы Н0: <р = 0
в рамках статистической модели
SM: Ах, = а + J3t + cpxt_x +un t = 2,...9T,
где, как и в критерии Дики — Фуллера, параметры а и /? могут быть взяты
равными нулю. Однако, в отличие от критерия Дики — Фуллера, случайные
составляющие ut с нулевыми математическими ожиданиями могут быть
автокоррелированными (с достаточно быстрым убыванием автокорреляционной
функции), иметь различные дисперсии (гетероскедастичность) и
необязательно нормальные распределения (но такие, что E\ut\6 < С < оо для некото-

490
Часть 2. Регрессионный анализ временных рядов
рого 8 > 2). Тем самым, в отличие от критерия Дики — Фуллера, к
рассмотрению допускается более широкий класс временных рядов.
Критерий Филлипса — Перрона основывается на /-статистике для
проверки гипотезы Н0: ср= 0 в рамках указанной статистической модели, но
использует вариант этой статистики Zt, скорректированный на возможную авто-
коррелированность и гетероскедастичность ряда иг При вычислении
статистики Z, приходится оценивать так называемую долговременную {long-run)
дисперсию ряда ut, которая определяется как
Я2 = МтТ-Уаг\
1щ +... + итЛ
7"->оо
Г-юо { Т
Если и* — остатки от оцененной (методом наименьших квадратов)
статистической модели Axt = а л- Ct + (pxt_x + ut, t- 2, ..., Т, то в качестве оценки
(Я2)* для А2 можно взять оценку Ньюи — Веста (Newey, West, 1994):
(Л2)'=Го'+2Х
j=\\
1-
J
/ + 1
Гр
где уjr = Т l ^u*tut_j —у-я выборочная автоковариация ряда иг
Если и /, и Т стремятся к бесконечности, но так, что
/
-1/4
->0, то(Л2)* —
состоятельная оценка для Я2 (см. (Phillips, 1987)) и асимптотические
распределения статистики Zt совпадают с соответствующими асимптотическими
распределениями статистики t^ в критерии Дики — Фуллера. Поскольку
реально имеем лишь конечное число наблюдений, встает вопрос о выборе
количества используемых лагов / в оценке Ньюи — Веста (параметр /
называют шириной окна — window size). Этот вопрос достаточно важен, так как
недостаточная ширина окна ведет к отклонениям от номинального размера
критерия (уровня значимости). В то же время увеличение ширины окна для
избежания отклонений от номинального размера критерия ведет к снижению
мощности критерия. Таким образом, выбор какой-то конкретной ширины
окна является компромиссом между этими двумя противоположными
тенденциями.
Несмотря на многочисленность исследований в этом направлении (сюда
относятся, например, работы (Phillips, Perron, 1988), (Schwert, 1989)), какое-
либо простое правило выбора значения / так и не было установлено.
Часто при выборе этого параметра пользуются рекомендациями (Schwert,
1989), полагая / =
К
т
100
1/4
, где выражение в квадратных скобках [а] — це-

Раздел 10. Процедуры для различения TS- uDS-рядов
491
лая часть числа а, а К полагается равным 4 для квартальных и 12 — для
месячных данных. Другое правило выбора значения /, реализованное, в част-
' Г т Л2/9'
ности, в пакете ЕViews, состоит в выборе значения 1-\1
100
(Newey,
West, 1994). Некоторые авторы рекомендуют не опираться только лишь
на длину ряда, а учитывать при выборе / количество значимых
автокорреляций ряда.
Критические значения для статистики Z, берутся из тех же таблиц (Fuller,
1976) или вычисляются по формулам (MacKinnon, 1991).
Заметим также: если ряд xt представляется моделью IMAA, q), то
значение q и следует использовать в качестве параметра / в оценке Ньюи — Веста.
Если при этом q = I, так что Axt = st + bxst_x, то при b{ > 0 критерий
Филлипса — Перрона имеет более высокую мощность, чем критерий Дики — Фул-
лера, при одновременном уменьшении вероятности ошибки первого рода.
В то же время при Ъх < 0 высокая мощность критерия Филлипса — Перрона
достигается за счет значительного возрастания ошибки первого рода, так что
этот критерий не рекомендуется применять при Ьх < 0 (он будет слишком
часто ошибочно отвергать гипотезу о принадлежности ряда классу DS).
ПРИМЕР 10.2.1
В рассмотренном ранее примере с GNP оценивание модели
Дх, = а + fit + <pxt_{ + вх Дх,_! + st
привело к следующему результату:
ADF Test Statistic -4.117782 1% Critical Value -4.1219
5% Critical Value -3.4875
10% Critical Value -3.1718
Гипотеза единичного корня отвергается: значение /-статистики для
проверки гипотезы Н0: ср - 0 оказывается ниже 5%-го критического значения,
вычисленного по формуле Маккиннона, и близко к 1%-му критическому
значению.
В то же время если взять первоначально AR модель с ртяк = 5, получим
(табл. 10.18).
Поскольку здесь / = -2.873575 > -3.1744, гипотеза единичного корня не
отвергается даже при выборе 10%-го уровня значимости. В то же время
статистически незначимыми оказываются коэффициенты при трех последних
запаздывающих разностях. Р-значение F-статистики критерия для гипотезы
о занулении этих трех коэффициентов равно 0.44. Поэтому можно обойтись
без трех последних запаздывающих разностей, а такая модель только что была
рассмотрена, и в ней гипотеза единичного корня была отвергнута.

492
Часть 2. Регрессионный анализ временных рядов
Таблица 10.18
Оценивание AR модели с ртах = 5
ADF Test Statistic
-2.873575
1% Critical Value
5% Critical Value
10% Critical Value
-4.1314
-3.4919
-3.1744
Расширенный критерий Дики — Фуллера (объясняемая переменная D(X))
Переменная
Д-1)
D(X(-\))
D(X(-2))
ДД-3))
ДАН»
С
@TREND(\941:l)
Коэффициент
-0.266169
0.546230
0.183918
-0.020254
-0.058683
59.45556
1.397409
Стандартная
ошибка
0.092626
0.133521
0.149711
0.152201
0.148061
19.32396
0.482120
/-статистика
-2.873575
4.090958
1.228486
-0.133077
-0.396345
3.076779
2.898469
Р-значение
0.0060
0.0002
0.2253
0.8947
0.6936
0.0035
0.0056
Посмотрим, что дает здесь применение критерия Филлипса — Перрона.
Использование рекомендации {Newey, West, 1994) по выбору ширины окна
дает значение / =
Л 2/9
100
= 3 и результаты, приведенные в табл. 10.19.
Таблица 10.19
Применение критерия Филлипса — Перрона
1 РР Test Statistic
-2.871178
\% Critical Value
5% Critical Value
10% Critical Value
-4.1190
-3.4862
-3.1711
Lag truncation for Bartlett kernel: 3 (Newey-West suggests: 3)
Residual variance with no correction
Residual variance with correction
29.28903
54.87482
Критерий Филлипса — Перрона (объясняемая переменная D(GNP))
Method: Least Squares; Sample(adjusted): 1947:2 1961:4;
Included observations: 59 after adjusting endpoints
Переменная
GNP(-l)
С
@TREND(\947:\)
Коэффициент
-0.153024
38.33211
0.806326
Стандартная
ошибка
0.072723
15.97824
0.378145
/-статистика
-2.104212
2.399020
2.132322
Р-значение
0.0399
0.0198
0.0374

Раздел 10. Процедуры для различения TS- uDS-рядов 493
Статистические выводы, полученные при применении критерия Филлипса —
Перрона с шириной окна, выбранной в соответствии с рекомендациями
{Newey, West, 1994), противоположны выводам, полученным при применении
расширенного критерия Дики — Фуллера с включением в правую часть одной
запаздывающей разности. ■
ПРИМЕР 10.2.2
Сравним результаты применения критериев Дики — Фуллера и Филлипса —
Перрона на реализациях ST_1, ST_2, ST3 (табл. 10.20).
Для ST_l и ST2 — в паре:
DGP: xt = xt_x + €t9
SM:x, = a + axxt_x + st\
для STJ5 — в паре:
DGP: xt = a + xt_x + et (или DGP: xt =xt_x + et\
SM: xt = a + /3t + axxt_x + sr
Для статистик этих критериев используем обозначения DF и РРA)
соответственно, где / — ширина окна, используемая при построении статистики
Филлипса — Перрона и выбираемая в соответствии с рекомендациями
(Newey, West, 1994).
Таблица 10.20
Результаты применения критериев Дики — Фуллера и Филлипса — Перрона
STJ
ST_2
STJ
/i = 50
DF= -2.298 > Гкрт10%=-2.60,
РДЗ) = -2.394>Гкрит10о/о=-2.60,
гипотеза единичного корня
не отвергается на 10%-м уровне
DF = -2.387 >Гкрит10%= -2.60,
РРC) = -2.322 >tKpmlm= -2.60,
гипотеза единичного корня
не отвергается на 10%-м уровне
DF= -2.687 > 'крит10о/0=-3.18,
РРC) = -2.755 > ГЧН1Г,«4=-3.18,
гипотеза единичного корня
не отвергается на 10%-м уровне
и = 100
DF= -3.238 < Гкрит5%=-2.89,
РРD) = -3.399 < Гкрит5%=-2.89,
гипотеза единичного корня
отвергается на 5%-м уровне
DF=-3.217 <Гкрит5„/о=-2.89,
РРD) = -3.364 <>крит5%= -2.89,
гипотеза единичного корня
отвергается на 5%-м уровне
OF =-3.207 < ?крит10%=-3.15,
PPD) = -336S <(щ>ИтШ<1=-ЗЛ5,
гипотеза единичного корня
отвергается на 10%-м уровне
Статистические выводы, полученные с применением статистик DF и РР,
здесь совпадают и указывают на возрастание мощности критериев при
увеличении количества наблюдений. ■

494
Часть 2. Регрессионный анализ временных рядов
Критерий Лейбурна
В работе (Leybourne, 1995) предлагается вычислять значения статистики
критерия Дики — Фуллера (DF) для исходного ряда х, и для ряда, получаемого
из исходного обращением времени (т.е. перестановкой наблюдений в
обратном порядке), затем взять максимум из двух полученных значений (DFmaJ.
Лейбурн изучил асимптотическое распределение статистики DFmax и построил
таблицы критических значений при Т = 25, 50, 100, 200, 400 для моделей
с (линейным) трендом и без тренда. Таблицы получены моделированием
в предположении независимости и одинаковой распределенности ошибок
(инноваций). Однако автор утверждает, что ими можно пользоваться и в
рамках расширенного варианта критерия Дики — Фуллера. Критерий Лейбурна
обладает несколько большей мощностью по сравнению с критерием Дики —
Фуллера.
ПРИМЕР 10.2.3
При анализе стационарного ряда STJ3 по 100 наблюдениям было получено
значение статистики Дики — Фуллера DF = -3.207. Для обращенного ряда
значение статистики Дики — Фуллера равно -3.352. Максимум из этих двух
значений, равный -3.207, остается выше 5%-го критического уровня -3.45,
рассчитываемого по таблицам Фуллера. Однако 5%-й критический уровень
для максимума приблизительно равен (по Лейбурну) -3.15, и это дает
возможность отвергнуть гипотезу единичного корня для ряда STJ3 уже на 5%-м
уровне. ■
Критерий Шмидта — Филлипса
В работе (Schmidt, Phillips, 1992) авторы строят критерий для проверки
гипотезы DS (в форме гипотезы единичного корня) в рамках модели
xt = у/+ %t + wn
где wt = J3wt_{ + sn t = 2,..., Т.
Это удобно тем, что здесь в любом случае (/? = 1 или /? Ф 1) параметр у/
представляет уровень, а параметр £ — тренд. При этом распределения
статистик критерия и при нулевой (DS), и при альтернативной (TS) гипотезах
не зависят от мешающих параметров щ % и ае. Асимптотические
распределения выводятся при тех же условиях, что и в критерии Филлипса — Перрона,
и при ширине окна / порядка Г1/2. Вместо линейного тренда в модели можно
использовать полиномиальный тренд. Более полное описание этого критерия
и таблицу критических значений можно найти в (Maddala, Kim, 1998, p. 85).
Здесь ограничимся рассмотрением примера его применения.

Раздел 10. Процедуры для различения TS- и DS-рядов
495
ПРИМЕР 10.2.4
Опять обратившись к анализу ряда ST3 по 100 наблюдениям, найдем
значение статистики критерия Шмидта — Филлипса, оно равно -3.12. В то же
время 5%-е критическое значение равно -3.06. Это дает возможность отвергнуть
гипотезу единичного корня на 5%-м уровне.■
Критерий DF-GLS
Этот критерий, асимптотически более мощный, чем критерий Дики — Фуллера,
был предложен в работе (Elliott, Rothenberg, Stock, 1996). Критерий DF-GLS
проверяет (см. (Maddala, Kim, 1998)) нулевую гипотезу а0 = 0 в модели
byf = aQy? + ax Ay ?_ { + ... + apAydt_p + error,
rj\eyf—«локально детрендированный» ряд (подробнее см. в указанной
работе).
ПРИМЕР 10.2.5
Продолжая предыдущий пример, вычислим статистику критерия DF-GLS. Ее
значение равно -3.246, что меньше 5%-го критического уровня -2.89.
Гипотеза единичного корня отвергается на 5%-м уровне, причем более уверенно,
чем в случаях критериев Лейбурна и Шмидта — Филлипса. ■
Критерий Квятковского — Филлипса — Шмидта — Шина
(KPSS)
Этот критерий, предложенный в работе (Kwiatkowski, Phillips, Schmidt, Shin,
1992), в качестве нулевой опирается на гипотезу TS. Рассмотрение
осуществляется в рамках модели:
р _ Детерминированный Стохастический Стационарная
~ тренд тренд ошибка
Стохастический тренд представляется случайным блужданием, и нулевая
гипотеза предполагает, что дисперсия инноваций, порождающих это
случайное блуждание, равна нулю. Альтернативная гипотеза соответствует
предположению о том, что эта дисперсия отлична от нуля, так что
анализируемый ряд принадлежит классу DS-рядов. В такой формулировке
предложенный критерии является LM-критерием для проверки указанной нулевой
гипотезы.
Как и в критерии Филлипса — Перрона, требования на ошибки здесь менее
строгие, чем в критерии Дики — Фуллера. Однако при применении данного
критерия возникает проблема выбора ширины окна / в оценке Ньюи — Веста,
поскольку значения статистики критерия довольно чувствительны к значе-

496
Часть 2. Регрессионный анализ временных рядов
нию /. Авторы в указанной статье рассматривают варианты выбора ширины
окна, следуя рекомендациям Шверта (Schwert, 1989).
Подробное описание критерия KPSS вместе с таблицей критических
значений можно найти в (Maddala, Kim, 1998, p. 120—122).
ПРИМЕР 10.2.6
При анализе ряда STJ5 по 100 наблюдениям значение статистики критерия
KPSS с / = 3 равно 0.157. В рамках этого критерия нулевая гипотеза о том, что
имеет место Г^-ряд, отвергается, если наблюдаемое значение статистики
критерия превышает критический уровень. По таблицам, предусматривающим
наличие линейного тренда, находим: 5%-й критический уровень равен 0.146,
так что ГЯ-гипотеза отвергается в пользу £>£-гипотезы. Такой вывод
противоречит статистическим выводам, полученным при применении критериев
Лейбурна, Шмидта — Филлипса и DF-GLS, он иллюстрирует трудности с
различением TS- и Л^-рядов, имеющих похожие реализации. ■
Процедура Кохрейна (отношение дисперсий)
Эта процедура, предложенная в работе (Cochrane, 1998), основана на
изучении характера поведения отношения дисперсий (VR — variance ratio):
vx
где Vk=TD(xt-xt_k).
к
Если xt — случайное блуждание, то VRk = 1, а если xt — процесс,
стационарный относительно линейного тренда (или просто стационарный), то VRk —» 0
при к —» оо.
При работе с реальными данными дисперсии заменяют их состоятельны-
Т
ми оценками, полученное отношение умножают еще на для
достижения несмещенности полученной оценки для VRk. Затем строят график
значений полученных оценок для VRk при различных к = 1, ..., К, и по
поведению этого графика делают выводы о принадлежности ряда классу TS или DS,
имея в виду различия графиков для этих двух классов временных рядов.
Другой вариант работы с реальными данными состоит в использовании
равносильного представления статистики отношения дисперсий VRk:
где г;- — значение на лаге j автокорреляционной функции ряда разностей

Раздел 10. Процедуры для различения TS- и DS-рядов
497
ПРИМЕР 10.2.7
Обратимся опять к реализации ST3 ряда, стационарного относительно
линейного тренда, по которой оказалось затруднительным вынести определенное
решение относительно принадлежности к классу TS или DS модели,
порождающей эту реализацию. Привлечем к решению этого вопроса процедуру
Кохрейна. Поведение отношения дисперсий показано на рис. 10.12 и говорит
в пользу Г^-гипотезы.
VARRATIO для ST_3
VARRATIO для WALK_2
11111111111111111 1111111 111 11111 111111 11—►
5 10 15 20 25 30 35 40 t
РИС. 10.12
0.8 1111111111111111111111111111111111111111—►
5 10 15 20 25 30 35 40 t
Рис. 10.13
Для сравнения приведем аналогичный график отношения дисперсий
для реализации WALKJ2 случайного блуждания со сносом (рис. 10.13).
Поведение отношения дисперсий указывает на то, что WALK2 порождается
DS моделью. ■
Коррекция сезонности
В рассмотренных процедурах не затрагивался вопрос о коррекции сезонного
поведения ряда, которое не снимается ни введением в модель линейного
тренда, ни путем дифференцирования ряда. Разумеется, данные,
поступающие в распоряжение исследователя, уже могли быть подвергнуты сезонной
коррекции соответствующими статистическими агентствами. Более того, во
многих странах сырые (не скорректированные на сезонность) данные просто
недоступны. В то же время при анализе данных, подвергшихся сезонному
сглаживанию с использованием фильтров или специфических методик
правительственных агентств, существенно больше шансов классифицировать
исследуемый ряд как DS (см., например, (Ghysels, Perron, 1992)), чем при
анализе сырых данных. Поэтому некоторые авторы {Davidson, MacKinnon,
1993) рекомендуют по возможности избегать использования сезонно-сгла-
женных данных. Более предпочтительным является использование сырых
данных и устранение из них сезонности путем оценивания регрессии сырого

498
Часть 2. Регрессионный анализ временных рядов
ряда на сезонные фиктивные {dummy) переменные Dl9 ..., D12 (если данные
месячные) или £>1, ..., D4 (если данные квартальные). Остатки от оцененной
регрессии образуют очищенный ряд, к которому можно применять
изложенные выше методы. Теоретическое оправдание такого подхода при
применении критерия Дики — Фуллера дано в (Dickey, Bell, Miller, 1986), где
показано, что асимптотическое распределение статистики t^ не изменяется при
исключении из ряда детерминированных сезонных компонент.
Протяженность ряда и мощность критерия
Следует иметь в виду, что мощность критериев единичного корня зависит
в первую очередь от фактической протяженности ряда во времени, а не от
частоты, с которой производятся наблюдения. Соответственно, если имеются
значения ряда за десятилетний период, мы не получаем выигрыша в
мощности, анализируя месячные данные, а не квартальные или годовые. Результаты
исследований в этом направлении можно найти, например, в (Shiller, Perron,
1985) и (Perron, 19896).
Проблема согласованности
статистических выводов при различении
TS- и DS-гипотез
При решении задачи отнесения рассматриваемого ряда к классу TS или DS
двумя статистическими критериями, один из которых в качестве нулевой
использует гипотезу TS, а другой — гипотезу DS, возможны 4 ситуации,
(табл. 10.21).
Таблица 10.21
Статистические выводы при различных критериях
#0: DS — не отвергается
Н0: DS — отвергается
#0: TS — не отвергается
Исход 1
Исход 3
Я0: TS — отвергается
Исход 2
Исход 4
Эти ситуации интерпретируются следующим образом:
• исход 2 — в пользу DS модели;
• исход 3 — в пользу TS модели;
• исход 1 — невозможность принять решение из-за низкой мощности
обоих критериев;
• исход 4 — процесс порождения данных (DGP) не сводится к
допускаемым используемыми критериями TS- и DS-моделям.

Раздел 10. Процедуры для различения TS- uDS-рядов
499
Наличие нескольких единичных корней
После появления работ (Fuller, 1976) и (Dickey, Fuller, 1981) было проведено
довольно много практических исследований экономических временных рядов
с целью решения вопроса о наличии или об отсутствии единичных корней
в моделях процессов, порождающих эти ряды.
При этом обычно сначала рассматривался сам временной ряд и
проводилась проверка его на нестационарность с использованием критериев Дики —
Фуллера. Если гипотеза единичного корня не отвергалась, то после этого
переходили к рассмотрению ряда разностей и проверяли гипотезу
единичного корня для этого ряда, применяя к ряду разностей процедуру Дики —
Фуллера.
Если при анализе ряда разностей гипотеза единичного корня отвергалась,
принималось решение о том, что исходный ряд — интегрированный порядка 1.
В противном случае переходили к рассмотрению ряда вторых разностей
и для него проверяли гипотезу единичного корня. Обычно на этом шаге
гипотеза единичного корня отвергалась и исходный ряд определялся как
интегрированный порядка 2.
Более поздние исследования показали, что такого рода последовательные
процедуры не обладают заявленными уровнями значимости, имеют
тенденцию к занижению действительного количества единичных корней. В таком
несоответствии нет ничего удивительного: критерии Дики — Фуллера
основаны на предположении, что если единичный корень и имеется, то он
единственный. Положение здесь похоже на другие ситуации, когда
последовательная проверка гипотез идет не от общего к частному, а от частного
к общему.
В связи с этим для ситуаций, когда предполагаемая модель авторегрессии
для анализируемого ряда может иметь порядок/> выше первого,;? > 1, в
работе (Dickey, Pantula, 1987) была предложена процедура последовательной
проверки гипотез о количестве единичных корней характеристического
уравнения, построенная по принципу «от общего к частному». Сначала проверяется
гипотеза о том, что все р корней характеристического многочлена
единичные, при ее отвержении проверяется гипотеза о наличии (р - 1) единичных
корней и т.д.
Поясним смысл этой процедуры на примере процесса авторегрессии ARB)
a(L)xt = st,
т.е.
A - axL - a2L2)xt = st, или A - aL)( 1 - bL)xt = st,
где a = —, b = — ,az,,z2 — корни уравнения a(z) = 0.
zx z2
При этом предполагаем, что процесс не носит взрывного характера, так что
\zx\ и \z2\ ^ 1, а значит, \а\ и \Ь\ < 1.

500
Часть 2. Регрессионный анализ временных рядов
Раскрывая скобки и перенося все составляющие, кроме х„ в правую часть
уравнения, получаем:
xt = (а + b)xt_x - abxt_2 + £r
Вычтем из обеих частей xt_ х:
Axt = (а + Ь - 1)х,_! - abxt_2 + sr
Из обеих частей полученного равенства вычтем Axt_ х:
A2xt = Axt - Axt_x = -Axt_x +{a + b - \)xt_x - abxt_2 + £t =
= {a + b - 2)xt_x + A - ab)xt_2 + sr
Выделим в правой части первую разность:
A2xt = (a + b- 2)xt_x + [-(ab - l)xt_2 + (ab - l)xt_x] - (ab - \)xt_x +€t =
= (a + b -ab - \)xt_x + {ab - l)Axr_j + et9
так что
A2xt = (a- 1)A -b)xt_x +{ab - l)Axt_{ + et.
Это базовое соотношение позволяет идентифицировать ситуации, когда
имеются 2 единичных корня, когда имеется 1 единичный корень и когда
единичных корней нет:
• если а = Ъ = 1 (два единичных корня), то A2xt = et\
• если а - 1, \Ъ\ < 1 (один единичный корень), то
A2xt = ф - \)Axt_x + sn или A2xt = <pAxt_x + et с q> < 0;
• если \а\ < 1 и |6| < 1 (нет единичных корней), то
A2xt = y/xt_x + g>Axt_x + st с q> < 0 и ^<0.
Соответственно процедура, предложенная Дики и Пантулой, такова.
Если допускаем наличие двух единичных корней, то сначала оцениваем
статистическую модель
A2xt = а + cpAxt_ х + ut
и сравниваем значение /-статистики для коэффициента ср с критическим
значением соответствующей статистики Дики — Фуллера (случай 1 или 2 —
в зависимости от того, будем исходить из а = 0 или а Ф 0). Здесь ut — либо
просто процесс белого шума, либо он включает еще и запаздывающие
значения второй разности A2xt_x,..., A2xt_p+X.
Если гипотеза о наличии двух единичных корней (<р = 0) отвергается, то
следует оценить статистическую модель
A2xt = y/xt_x + q>Axt_x + ut

Раздел 10. Процедуры для различения TS- uDS-рядов
501
и проверить гипотезу у/ = 0 против альтернативы у/ < 0. Отклонение этой
гипотезы означает признание того, что у ряда х, нет единичных корней, а ее
неотклонение — того, что х, ~ 1A).
ПРИМЕР 10.2.8
Рассмотрим смоделированные реализации трех моделей ARB) с различным
количеством единичных корней (рис. 10.14 — 10.16). Посмотрим, что дает
применение процедуры Дики — Пантулы в этой ситуации.
ROOT0
ROOT1
111111111111111111111111111111111111111111 м 111111
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.14
11111111111111111111 [ 111111111111111111111111111111—►
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.15
ROOT2
На первом шаге для каждого ряда оцениваем статистическую модель
SM: Д2х, = а + <pbxt_x + e,
и проверяем гипотезу q> = 0 против
альтернативы ср < 0. (Анализ рядов
остатков для обеих оцененных
моделей указывает на отсутствие
необходимости включать в правую
часть статистической модели
запаздывающих значений второй
разности.) Для ряда ROOT2 используем
критические значения Фуллера,
соответствующие случаю 2 (а * 0),
ориентируясь на наличие у
реализации видимого квадратичного
тренда. Для Т = 100 критическое
5%-е значение статистики Дики —
Фуллера равно -2.89. Вычисленное
значение /-статистики равно -1.64, гипотеза о наличии двух единичных
корней не отвергается. Для рядов ROOT0 и ROOT1 используем критические
11111N1111111 |i 1111 и 11111111111111111 |i 111111111—►
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.16

502
Часть 2. Регрессионный анализ временных рядов
значения Фуллера, соответствующие случаю 1 {а = 0), принимая во внимание
отсутствие у реализаций видимого квадратичного тренда. В этом случае для
Т- 100 критическое 5%-е значение статистики Дики — Фуллера равно -1.95.
Вычисленные значения /-статистик равны -7.83 для ряда ROOT0 и -5.50 для
ряда ROOT1, в обоих случаях гипотеза о наличии двух единичных корней
отвергается.
Исходя из этого следующий шаг процедуры выполняется только для рядов
ROOT0 и ROOT1. Для этих рядов оцениваем статистическую модель
SM: Д2х, = y/xt_x + (pAxt_Y + st
и проверяем гипотезу у/ = 0 против альтернативы у/ < 0. Значения
соответствующей /-статистики равны -3.89 для ряда ROOT0 и -1.63 для ряда ROOT1,
так что гипотеза у/ = 0 отвергается для ряда ROOT0 и не отвергается для ряда
ROOT1.
Заметим теперь, что в модели DGP для ряда ROOT2 действительно было
два единичных корня, в модели DGP для ряда ROOT1 — один единичный
корень, а в модели DGP для ряда ROOT0 не было ни одного единичного корня:
DGP для ROOT0: х, = \Axt_Y - 0.3х,_2 + еп
или A - 0.6Z)A - 0.5Z)x, = et\
DGP для ROOT1: xt = 1.5x,_! - 0.5x,_2 + et9
или A - Z)(l - 0.5L)xt = st\
DGP для ROOT2: xt = 2xt_x -xt_2 + sn
или A -LJxt = stM
Более подробно с проблемами, возникающими при проверке гипотез,
связанных с наличием нескольких единичных корней, можно ознакомиться,
например, в {Patterson, 2000).
Критерий Перрона
Предложенная в {Perron, 1989a) процедура проверки нулевой гипотезы о
принадлежности ряда классу DS обобщает процедуру Дики — Фуллера на
ситуации, когда на периоде наблюдений имеются структурные изменения модели
в некоторый момент времени Тв в форме либо сдвига уровня (модель «краха»),
либо изменения наклона тренда (модель «изменения роста»), либо сочетания
этих двух изменений. Важность такого обобщения связана со следующим
обстоятельством: если DS-критерий не допускает возможности изменения
структуры модели, тогда как такое изменение в действительности имеет место,
то он имеет очень низкую мощность, т.е. практически всегда не отвергает
DS-гипотезу (см., например, {Engle, Granger, 1991)).

Раздел 10. Процедуры для различения TS- uDS-рядов
503
Последнее можно лучше всего проиллюстрировать на примере работы
Нельсона и Плоссера (Nelson, Plosser, 1982), в которой был проведен
статистический анализ 13 основных макроэкономических рядов США по годовым
данным за достаточно длинные периоды (от 62 до 111 лет) и квартального
ряда GNP, относящегося к периоду после Второй мировой войны A948—
1987 гг.). Все ряды, за исключением ряда процентных ставок, были взяты
в логарифмах.
Для этих рядов гипотеза единичного корня проверялась в связке:
SM: Axt = а Л-fit + <pxt_x + ип
где ut — стационарный процесс AR(£),
DGP: Дх, = а + и, (с а = 0 или а Ф 0),
и использовались критические значения Фуллера для этой ситуации. При
этом Нельсон и Плоссер обнаружили, что для 13 из 14 рядов гипотеза
единичного корня не отвергается. Единственным исключением оказался ряд
логарифмов уровней занятости.
Полученные Нельсоном и Плоссером результаты сформировали
устойчивое мнение о том, что макроэкономические ряды, обнаруживающие тренд,
скорее всего, могут моделироваться как DS-ряды. В то же время, как было
показано на примерах, критерии Дики — Фуллера имеют не очень высокую
мощность, и последнее может являться причиной неотвержения гипотезы
единичного коршг^цля указанных 14 рядов. Вместе с тем надо учесть и
следующее обстоятельство, на которое обратил внимание Перрон (Perron,
1989а).
Рассмотрим для примера график ряда GNP для периода с I квартала 1958 г.
по IV квартал 1979 г. (рис. 10.17).
В качестве альтернативы процессу случайного блуждания (со сносом или
без сноса) критерий Дики — Фуллера предлагает процесс, стационарный
относительно линейного тренда. Однако при просмотре приведенного графика
возникает впечатление, что линейный тренд ряда имеет различный наклон на
подпериодах до 1974 г. и после 1974 г.
Если непосредственно оценивать линейный тренд на всем периоде
1958:1 —1979:4, то угловой коэффициент тренда оценивается как 19.086. При
оценивании на подпериоде 1958:1 —1973:4 угловой коэффициент тренда
оценивается как 19.852. В то же время при оценивании на подпериоде
1975:1 —1979:4 угловой коэффициент тренда оценивается как 31.995. Это
заставляет усомниться в адекватности выбора в качестве альтернативы
случайному блужданию процесса, стационарного относительно именно
линейного тренда. Скорее, надо было бы использовать в качестве альтернативы
процесс, стационарный относительно ломаной с узлом в районе 1975 г.
В связи с процедурами, допускающими излом траекторий, следует
обратить особое внимание на различие между моделями внезапного и
постепенного излома.

504
Часть 2. Регрессионный анализ временных рядов
GNP
ОООС\|ч£СООООС\1^СО
mcococococofv-i^-i^-i^-.
Рис. 10.17
В течение нескольких лет в этом вопросе была некоторая путаница, так
что даже сам автор первоначальной процедуры, допускающей изломы
разных видов (Perron, 1989a), ошибочно интерпретировал оцененные им
модели и критические значения, полученные путем статистического
моделирования.
Пусть z, — стационарный процесс авторегрессии первого порядка с
нулевым математическим ожиданием:
zt = a{zt_{ +en
и ряд>>, определяется как
yt=f(t)+zn
где ДО = 0 при t < Тв и ДО = ju ф 0 при / > Тв.
Поскольку E(zt) = 0, то E(yt) = 0 при / < Тв и E(yt) = /л при t > Тв. Таким
образом, при переходе через дату излома Тв ряд yt сразу начинает
осциллировать вокруг уровня ju (вместо осцилляции вокруг нулевого уровня до этого
перехода).
Рассмотрим теперь другую модель, в которой функция скачка «встроена»
в уравнение ARA) для^г Пусть
yt=At) + axyt_x +et, ax<l9
где ДО = 0 при / < Тв и ДО = ju(l - al)npnt> TB, ju^ 0.
До момента Тв ряд yt осциллирует вокруг нулевого уровня. Как будут
вести себя траектории такого ряда^, после перехода через дату излома Тв? Для
ответа на этот вопрос удобно записать:
Уг = а\Уг-\ + (Я0 + £t) = <*\Уг-\ + vr

Раздел 10. Процедуры для различения TS- uDS-рядов
505
Тогда для t=TB + h имеем:
Утв+и = У1В+" +1>>Ч-* -УТов+" +l>f (f(t-k) + st_k) =
ylB+h +
к = 0
TB+h-l
к = 0
Z a\£t-
к = 0
/7-1
+ 2>iV(i-*i).
* = 0
Первое слагаемое в правой части (выражение в квадратных скобках)
соответствует модели с E(yt) = 0. Вторая сумма при h —> сю имеет предел
/7-1
lim £^//A-^) = //.
h->co
к = 0
В этой модели после момента / = Г5 процесс yt лишь постепенно выходит
на новый уровень //, вокруг которого начинает происходить осцилляция
траектории ряда.
Поскольку во второй модели значения f(t) обрабатываются аналогично
инновациям st (влияние обоих здесь убывает геометрически), вторую модель
называют моделью инновационного выброса (innovation outlier), В то время как
первая модель называется моделью аддитивного выброса (additive outlier).
Аналогично можно рассматривать пары моделей (аддитивная —
инновационная), допускающие изменение наклона тренда без изменения уровня ряда
или допускающие и изменение наклона тренда, и изменение уровня ряда.
Ниже приводятся графики, иллюстрирующие подобные ситуации:
• сдвиг среднего уровня ряда — рис. 10.18;
• сдвиг реализации без изменения наклона тренда — рис. 10.19;
• сдвиг реализации с изменением наклона тренда — рис. 10.20;
• изменение наклона тренда без сдвига реализации (сегментированный
тренд) — рис. 10.21.
Y^_ADD
Y1 INNOV
10 20 30 40 50 60 70 80 90 100 t
РИС. 10.18

506
Часть 2. Регрессионный анализ временных рядов
100 4
Y2_ADD
У2 INNOV
0 р i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | ►
10 20 30 40 50 60 70 80 90 100 t
Рис. 10.19
Y3_ADD
УЗ INNOV
О pi i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | ►
10 20 30 40 50 60 70 80 90 100 t
Рис. 10.20
У4 ADD
10 20 30 40 50 60 70 80 90 100 t
Рис. 10.21

Раздел 10. Процедуры для различения TS- uDS-рядов
507
Трем различным формам изменения структуры модели Перрон (Perron,
1989а) сопоставляет три различные пары гипотез:
A) модель «краха»:
Я0 : х, = с + dDTBt + xt_x + st (Л!>-ряд),
НА: xt=c + 6DUt +pt + st (ГС-ряд);
B) модель «изменения роста»:
Я0: xt=c + eDUt+ xt_x + st (DS-щд),
НА: xt=c + fit + yDTSt + st (ГС-ряд);
C) модель, допускающая наличие обоих эффектов:
Я0: xt=c + 6DUt + dDTBt + xt_x + et (AS-ряд),
HA: xt=c + 0DUt +fit + SDTt + st (ГС-ряд).
Здесь
с — постоянная;
[\ для / = Гя+1,
D7B, =^ *
[О в противном случае;
fl для t>TR,
DUt=\ B
[О для t<TB\
[t-TR для t>TR,
DTSt=\ в в
[О для t<TB;
[t для t>TR,
DTt=\ B
[О для /<Г5;
st ~ ARMA(p, g) (значения pnq могут быть неизвестными).
Перрон предложил следующую процедуру проверки нулевых гипотез
в рамках моделей А, В и С. Пусть et — ряд остатков, полученных при
оценивании методом наименьших квадратов:
статистической модели
xt=c + 6DUt+ pt + £t —в ситуации А;
статистической модели
xt=c + jBt + yDTSt+st —в ситуации В;
статистической модели
xt=c + 0DUt+/3t + SDTt+£t —в ситуации С.

508
Часть 2. Регрессионный анализ временных рядов
На основании этого ряда остатков методом наименьших квадратов
оценивается коэффициент а в модели
et=aet_x+vt
или (если последовательность v, в этой модели автокоррелирована) в
расширенной модели
к
et=aet_Y + Y.cAet-j+vf
Значение к выбирается, как и в расширенном критерии Дики — Фуллера,
таким образом, чтобы в последовательности v, не обнаруживалась автокорре-
лированность. Пусть ta — /-статистика для проверки гипотезы а = 1 в соот-
Т
ветствующем уравнении; Т— длина ряда xt\ Л = —-, где Тв — момент (дата)
изменения структуры.
Перрон указал асимптотические (при Т —> об) распределения статистики ta
при нулевых гипотезах в моделях А, В и С, а также (полученные методом
статистического моделирования) критические уровни /крит для статистики ta,
соответствующие различным уровням значимости. Эти распределения и их
Т
процентные точки зависят от значения отношения Л = —-, т.е. от того, в ка-
Т
кой части периода наблюдений происходит изменение структуры. При этом
предполагается, что момент Тв определяется экзогенным образом — в том
смысле, что он не выбирается на основании визуального исследования
графика ряда, а связывается с моментом известного масштабного изменения
экономической обстановки, существенно отражающегося на поведении
рассматриваемого ряда.
Гипотеза единичного корня отвергается, если наблюдаемое значение
статистики ta оказывается ниже критического уровня, т.е. если ta < /крит.
Проблема, однако, в том, что Перрон неправильно интерпретировал свои
результаты. Действительно, получив ряды остатков еп Перрон, по существу,
предполагает, что тем самым он детрендирует ряд xt и что в качестве тренда
выступает:
функция
f{t) = c + 6DUt+ fit —в ситуации А,
функция
f{t) = c + pt + yDTSt — в ситуации В,
функция
fit) = c + 6DUt +fit + SDTt — в ситуации С.

Раздел 10. Процедуры для различения TS- uDS-рядов
509
Однако это может быть верным только в случае, когда st — белый шум.
Если же последовательность st автокоррелирована, так что st ~ АКМА(р, q),
р2 + q2 > О, мы имеем дело с инновационным выбросом, а в таком случае
указанные функции/(/) вовсе не являются трендами, относительно которых ста-
ционаре^^рассматриваемый ряд xt (если он является ТХ-рядом).
Итак, если р2 + q2 > О, то рассмотренные Перроном модели соответствуют
инновационным, а не аддитивным выбросам. Но если это так, то следует
ориентироваться на другую /-статистику ta, а именно на /-статистику для
проверки гипотезы а = 1
в модели
xt=c + 6DUt + pt + at_x+£t —в ситуации А,
в модели
xt=c + fit л-yDTSt + axt_x +st — в ситуации В,
в модели
xt = с + 6DUt + /3t + SDTt + axt_x + et — в ситуации С.
Если внимательно посмотреть на доказательство основного результата
статьи {Perron, 1989a), то можно заметить, что в действительности Перрон
в этом доказательстве опирается на статистики ta, полученные именно для
последних трех моделей. Таким образом, асимптотические распределения
и критические значения для статистик ta, приведенные Перроном, верны для
моделей с инновационными выбросами. На это обстоятельство было указано
позднее в работе {Perron, Vogelsang, 1993). В этой же работе описано, как
следует действовать в моделях с аддитивными выбросами.
В случаях А и С достаточно взять статистику ta для проверки гипотезы
а = 1 в модели
к к
y = o y = o
и использовать для нее те же критические значения f , которые указаны
в таблицах Перрона {Perron, 1989a).
Для случая В (сегментированный тренд) приведены новые таблицы
критических значений статистики ta для проверки гипотезы а = 1 в модели
к
et=aet_x + Y,cj^et-j+vt>
7 = 1
где et — ряд остатков, полученных при оценивании методом наименьших
квадратов статистической модели
xt =c + pt + yDTSt+et.

510
Часть 2. Регрессионный анализ временных рядов
Возвратимся теперь к обсуждению статьи {Perron, 1989a).
Проведя ревизию результатов Нельсона — Плоссера для 14 рядов с
допущением структурных изменений модели и экзогенным выбором даты излома,
Перрон получил совершенно другие результаты. Теперь уже гипотеза
единичного корня была отвергнута для 11 из 14 рядов, т.е. результаты
получились практически прямо противоположными результатам Нельсона —
Плоссера. Это обстоятельство обсудим чуть позже, а сейчас приведем пример
применения процедуры Перрона к одному из основных российских
макроэкономических рядов.
ПРИМЕР 10.2.9
В качестве примера использования процедуры Перрона с экзогенной датой
излома рассмотрим проверку гипотезы о наличии единичного корня в авто-
регрессионном представлении модели, порождающей ряд xt = Ml, где Ml —
денежный агрегат, представляющий все денежные средства в экономике
Российской Федерации, которые могут быть использованы как средство платежа.
Здесь используем месячные данные за период 1995:06—2000:07 в
номинальных величинах. График рядаД = Ml показан на рис. 10.22.
700 000 4 i М1
600 000-^ / |
500 ооо Н у :
400 000 Н [ \
300 000 \ д J \
200 000 \ ^_^_^/
100 000 Гм 1111111111111111111111111111111111111111111111111111111111 i—►
1996 1997 1998 1999 2000 Год
Рис. 10.22
При анализе этого ряда на наличие единичного корня с использованием
критериев Дики — Фуллера и Филлипса — Перрона (см. (Эконометрический
анализ динамических рядов.., 2001)) гипотеза единичного корня не была
отвергнута, что может быть связано с неудачным выбором альтернативных
гипотез. График ряда позволяет предположить, что более подходящей может
оказаться модель с изломом тренда в конце 1998 г. — начале 1999 г.,
связанным с финансово-экономическим кризисом 1998 г.

Раздел 10. Процедуры для различения TS- и DS-рядов
511
Если предполагать, что излом тренда выражается в изменении его наклона
после августа 1998 г., то можно обратиться к статистической процедуре
проверки гипотезы единичного корня, предложенной в упомянутой выше работе
Перрона и соответствующей одномоментному (внезапному) изменению наклона
тренда (АО модель — модель с аддитивным выбросом).
Согласно этой процедуре если Тв — момент скачка, то сначала следует
оценить статистическую модель
xt = /и + Ct+yDTSt + un
в которой переменная DTSt равна t - Тв для t>TBn равна 0 для всех других
значений t. В результате оценивания этой модели получаем ряд остатков ег
Затем оценивается модель регрессии et на et_x и запаздывающие разности
Aet_x,...,Aet_p:
р
et=aet_x+Y<cAet-j+£n
полученное при этом значение ^-статистики для проверки гипотезы Н0: а = 1
сравнивается с критическим значением из таблицы, приведенной в статье
(Perron, Vogelsang, 1993, p. 249). В правую часть оцениваемой
статистической модели следует включать достаточное количество запаздывающих
разностей, чтобы исключить автокоррелированность ошибок в расширенной
модели.
В нашем случае Тв = 42, что соответствует 1998:08. В правую часть
уравнения для остатков приходится дополнительно включать 12 запаздывающих
разностей, так как иначе (при 11 разностях) получаем Р-значение критерия
Бройша — Годфри (с ARA) альтернативой), равное 0.0002 и указывающее
на автокоррелированность остатков. Для повышения мощности критерия,
используя стратегию GS («от общего к частному») и критерий Шварца SIC,
осуществим редукцию модели, последовательно исключая из нее
запаздывающие разности со статистически незначимыми (на 10%-м уровне
значимости) коэффициентами. Результаты такой последовательной редукции
приведены в табл. 10.22.
В первой графе табл. 10.22 указаны порядки запаздывания разностей,
последовательно исключаемых из правой части оцениваемой статистической
модели. Запаздывающая разность исключается из уравнения, если
коэффициент при этой разности признается статистически незначимым на 10%-м
уровне значимости.
Во второй графе приведены значения информационного критерия Шварца
(SIC), соответствующие редуцированным моделям.
В третьей графе приведены Р-значения (P-values) LM-критерия автокор-
релированности ошибок Бройша — Годфри. Цифры, предваряющие эти Р-зна-
чения, указывают на допускаемый (при альтернативе) порядок
авторегрессионной модели для ошибок в редуцированном уравнении.

512
Часть 2. Регрессионный анализ временных рядов
Таблица 10.22
Результаты последовательной редукции статистической модели
Порядок
запаздывания
исключаемой
разности
- (полная модель
с 12 запаздывающими
разностями)
8
И
10
9*
4
5
3
Г* (выбор по GS)
1
6
2 (выбор по SIC)
SIC
22.236
22.157
22.089
22.018
21.986
21.974
21.935
21.898
21.837
21.834
21.793
21.782
Р-значение
/Ж-критерия
1 — 0.983
2 — 0.967
1 — 0.590
2 — 0.844
3 — 0.954
Р-значение
White
0.701
0.372
0.040
0.035
0.016
0.006
0.002
Р-значение
J-B
0.281
0.223
0.518
0.184
0.008
0.006
^-статистика
критерия
Перрона
-1.92
-2.27
-2.60
-2.90
-3.27
-2.78
-2.59
-2.22
-2.04
-1.37
-1.31
-0.92
В четвертой графе приведены Р-значения критерия Уайта {White) для
выявления гетероскедастичности ошибок.
В пятой графе приведены Р-значения критерия Харке — Бера для проверки
нормальности распределения ошибок.
В последней графе таблицы приведены значения ^-статистики
(расширенного) критерия Перрона, получаемой при оценивании соответствующей
редуцированной (или полной) модели.
При редукции модели методом «от общего к частному» (с 10%-м уровнем
значимости) из расширенной модели с 12 запаздывающими разностями
последовательно удаляются разности, запаздывающие на 8, 11, 10, 9 единиц
времени (месяцев). Это приводит к модели, содержащей в правой части
разности, запаздывающие на 1—7 и 12 месяцев; результаты оценивания этой
модели приведены в строке таблицы, отмеченной звездочкой. Если
продолжать редукцию, отбрасывая запаздывающие разности с коэффициентами,
статистически незначимыми на 10%-м уровне, то остановка происходит на
модели, результаты для которой находятся в строке, отмеченной двумя
звездочками. Критерий Шварца выбирает модель, результаты оценивания которой
приведены в последней графе таблицы.

Раздел 10. Процедуры для различения TS- uDS-рядов 513
Поскольку отклонения от нормальности, некоррелированности и гомоске-
дастичности могут отражаться на критических значениях статистики
критерия, в этом отношении предпочтительнее модель, результаты для которой
приведены в строке, отмеченной звездочкой.
Асимптотические критические значения статистики критерия Перрона
зависят от положения момента излома на интервале наблюдений через
параметр Я
Т
где Тв — момент, непосредственно после которого происходит излом тренда;
Т — количество наблюдений.
В нашем случае Я = 42/62 = 0.667. Соответствующее 5%-е критическое
значение (при сделанном предположении о внезапном изменении наклона
тренда) заключено между значениями -3.94 (для Я = 0.6) и -3.89 (для Я = 0.7).
Гипотеза единичного корня не отвергается ни в полной модели и ни в одной
из редуцированных моделей.
Отметим также, что момент излома тренда 1998:08 был выбран на
основании уже имеющейся информации об августовском кризисе 1998 г. и
визуального обращения к графику ряда Ml. Между тем выбор даты излома тренда на
основании анализа графика ряда влияет на критические значения
^-статистики критерия единичного корня. ■
Обобщенная процедура Перрона
Анализируя результаты Перрона в отношении 14 макроэкономических рядов
США, некоторые авторы задались вопросом о влиянии метода датировки на
критические значения соответствующих статистик. В работе Зивота и Эндрюса
(Zivot, Andrews, 1992), которая уже была процитирована в разд. 9 (тема 9.2),
обращается внимание на то, что при рассмотрении послевоенного GNP в
качестве даты структурного сдвига Перрон взял II квартал 1973 г. (что
соответствует мировому топливо-энергетическому кризису). И это можно было бы
считать экзогенным выбором, поскольку решение принималось
международной организацией (ОПЕК). Однако в послевоенный период имели место
и такие крупные события, как снижение налогов A964 г.), война во Вьетнаме
A965—1974 гг.), финансовое разрегулирование в 1980-е гг. Тем не менее
Перрон взял за точку сдвига именно 1973 г., обращаясь предварительно к
поведению ряда GNP. А если это так, то нарушается принцип, согласно которому
статистические гипотезы формулируются до любого (даже визуального)
анализа данных, на основании которых принимается решение об отклонении или
неотклонении нулевой гипотезы. С этой точки зрения, критерий Перрона,
предложенный в работе {Perron, 1989a), является условным, при условии, что
точка смены режима известна.

514
Часть 2. Регрессионный анализ временных рядов
Вместо условного критерия Перрона, в котором точка смены режима
известна, Зивот и Эндрюс предложили использовать безусловный критерий
(относящийся к инновационным выбросам), в котором датировка точки смены
режима производится в «автоматическом режиме», путем перебора всех
возможных вариантов датировки и вычисления для каждого варианта датировки
^-статистики ta для проверки гипотезы Я0: а = 1; в качестве оцененной даты
берется дата, для которой значение ta оказывается минимальным (tm[n). К чему
это приводит?
Возьмем для примера ряд, представляющий занятость A890—1970 гг.).
Этот ряд исследуется в {Zivot, Andrews, 1992) в рамках модели А (см. выше
модели А, В, С), но только без включения в правую часть переменной DTBt.
Перрон для всех рядов, кроме послевоенного GNP, определил в качестве
точки смены режима 1929 г. (Великая депрессия). Для ряда занятости значение ta
для этого года равно ta = -4.95, Тв = 40, Я = 40/81 = 0.49. При таком Я
критическое E%-е) значение для ta приближенно равно -3.76, так что гипотеза
единичного корня отвергается. В то же время, выполняя указанный перебор,
Зивот и Эндрюс получили ту же дату A929 г.), так что tm[n = -4.95. Значение
^-статистики не изменилось. Однако распределение статистики tmm
отличается от распределения статистики ta для фиксированного года: 5%-е
критическое значение для tm[n равно -5.26. Поскольку tmin = -4.95 > -5.26, гипотеза
единичного корня (Я0: а = 1) теперь не отвергается.
Аналогичный анализ для остальных рядов из работы Нельсона и Плоссера
приводит к следующим результатам. Гипотеза единичного корня не
отвергается для И из 14 рядов (исключение составляют реальный и номинальный
GNP (годовые данные) и промышленное производство A860—1970)). И это
объясняется консервативностью критических значений при эндогенной
датировке (путем перебора): при заданном значении Я последние существенно
ниже критических значений, соответствующих экзогенной датировке.
Следует, впрочем, заметить, что при оценивании уравнений для
номинального GNP, номинальной заработной платы и биржевого курса обыкновенных
акций ряды остатков имели слишком большие значения коэффициента пико-
образности — куртозиса (kurtosis): 5.68, 4.658, 4.324, говорящие не в пользу
предположения о нормальности инноваций, при котором были получены
критические значения статистики tmm. (Куртозис распределения определяется
как отношение четвертого центрального момента распределения к квадрату
дисперсии. Для нормального распределения значение куртозиса равно З1.)
В отечественной литературе в качестве характеристики пикообразности распределения
чаще используется коэффициент эксцесса к (к = куртозис - 3), равный 0 для нормального
распределения. Ориентируемся здесь на куртозис из-за того, что в распечатках результатов,
получаемых при применении пакета статистического анализа Econometric Views, приводятся
именно значения (оцененного) куртозиса.

Раздел 10. Процедуры для различения TS- uDS-рядов
515
При перемоделировании критических значений с использованием (вместо
нормального) распределения Стьюдента с подходящими числами степеней
свободы для этих трех рядов получены следующие 5%-е критические
значения: -5.86, -5.81 и -5.86 (против -5.38, -5.33 и -5.63 соответственно).
Значения статистики tm[n для этих рядов равны: -5.82, -5.30 и -5.61, что, в общем,
практически не изменяет статистических выводов.
Наконец, если предположить, что распределение инноваций имеет
настолько тяжелые «хвосты», что D(st) = оо, то критические значения
статистики f min уменьшаются столь значительно, что отвергнуть гипотезу
единичного корня на 5%-м уровне значимости становится невозможным ни для
одного ряда.
Перрон вернулся к проблеме проверки гипотезы единичного корня в работе
(Perron, 1997). Развивая результаты Зивота и Эндрюса, он исследовал
зависимость критических значений статистики fmin от выбора количества
запаздывающих разностей, включаемых в правые части оцениваемых уравнений.
При этом Перрон работал с моделями А и С, содерэюащими в правых частях
(в отличие от Зивота и Эндрюса) переменную DTBt. Напомним, что
fl для t = TR +1,
[0 для t*TB+\.
Методика, разработанная в (Perron, 1997), реализована в виде процедуры
PERRON97 в пакете статистического анализа RATS.
При этом рассматриваются модели:
101 — с инновационным выбросом, изменяющим постоянную;
102 — с инновационным выбросом, изменяющим и постоянную, и наклон
тренда;
АО — с аддитивным выбросом, изменяющим только наклон тренда.
Предусмотрены три метода оптимального выбора даты излома:
UR — по минимуму ^-статистики критерия для проверки гипотезы
а- 1;
STUDABS — по максимуму абсолютной величины /-статистики критерия
для проверки гипотезы о равенстве нулю коэффициента при
переменной, отвечающей за изменение константы (в модели
101) или за изменение наклона тренда (в модели 102);
STUD — по минимуму /-статистики критерия для проверки гипотезы
о равенстве нулю коэффициента при переменной,
отвечающей за изменение константы (в модели 101) или за
изменение наклона тренда (в модели 102).
При практической реализации критерия обычно несколько ограничивают
интервал возможных дат излома, чтобы исключить слишком ранние или
слишком поздние даты излома.

516
Часть 2. Регрессионный анализ временных рядов
ПРИМЕР 10.2.10 (продолжение примера 10.2.9 с рядом Ml)
Для учета влияния датировки при проверке гипотезы единичного корня
в моделях, допускающих структурное изменение, воспользуемся процедурой
PERRON97 из пакета статистического анализа RATS, реализующей методику,
приведенную в (Perron, 1997). Исходя из предыдущих результатов,
максимальное запаздывание разностей, включаемых в правую часть оцениваемых
уравнений, ограничим тринадцатью.
Сначала рассмотрим модель, допускающую сдвиг траектории и изменение
наклона тренда в форме инновационного выброса A0). Результаты
применения процедуры PERRON97 для этой модели приведены в табл. 10.23.
Таблица 10.23
Применение процедуры PERRON97 для модели с инновационным выбросом
break date TB = 1999:07; statistic ta (alpha = 1) = -3.34124
Critical values at
For 70 observations
1%
-6.32
Number of lag retained: 12
Explained variable: Ml
CONSTANT
DU
D(Tb)
TIME
DT
M1{1}
Coefficient
124786.79561
-2506239.31872
40455.79442
9769.03708
23866.02686
-0.91050
5%
-5.59
Student
3.33345
-3.77751
2.72347
3.44839
3.78217
-1.59235
10%
-5.29
Здесь
DUt = 1 для t > Тв и DUt = 0 для всех других значений t\
D(Tb)t = 1 для t = Тв + 1 и D{Tb)t = 0 для всех других значений t;
DT- t для t > Тв и DTt = 0 для всех других значений t,
(М1{1}), = М1,_,.
Заметим: при постулировании инновационного выброса оценивание
регрессионной модели при каждой испытываемой дате производится в один
этап — в правую часть регрессионной модели в качестве объясняющих
включаются сразу все 6 переменных: CONST, DU, D(Tb), TIME, DT и
запаздывающая на один шаг переменная Ml {1}.

Раздел 10. Процедуры для различения TS- uDS-рядов
517
Процедура PERRON97 определяет в этом случае дату излома как 1999:07,
если выбор даты излома осуществляется по минимуму /-статистики критерия
единичного корня tassl9 взятому по всем возможным моментам излома. При
этом ta=l = -3.341, что выше 5%-го критического уровня -5.59, и гипотеза
единичного корня не отвергается. Наибольшее запаздывание разностей,
включаемых в правую часть уравнений, выбирается равным 12 в рамках
применения процедуры GS для редукции модели с 10%-м уровнем значимости.
Если выбор даты излома осуществляется по максимуму абсолютной
величины /-статистики для коэффициента d при переменной DTn отвечающей за
изменение наклона тренда, то выбирается 1998:04. При этом ta=x = -0.547,
что выше 5%-го критического значения -5.33, гипотеза единичного корня
не отвергается. (Наибольшее запаздывание разностей здесь уменьшается
до 11.) Наконец, если выбор даты излома тренда осуществляется по
минимуму /-статистики критерия для проверки гипотезы о равенстве нулю
коэффициента при переменной DT, отвечающей за изменение наклона тренда,
то выбирается опять 1998:04 с тем же выводом о неотверэюении гипотезы
единичного корня (Ш-гипотезы).
Рассмотрим теперь модель, допускающую только изменение наклона
тренда (без сдвига траектории) в форме аддитивного выброса (АО).
Результаты применения процедуры PERRON97 для этой модели приведены
в табл. 10.24.
Таблица 10.24
Применение процедуры PERRON97 для модели с аддитивным выбросом
break date TB = 1999:02; statistic ta (alpha = 1) = -3.59417
Critical values at
For 100 observations
1%
-5.45
Number of lag retained: 12
Explained variable: Ml
CONSTANT
TIME
DT
M1{1}
Coefficient
104939.65455
4832.56930
14335.07564
-0.75752
5%
-4.83
Student
20.48279
26.73200
21.11189
-1.54915
10%
-4.48
Заметим: при постулировании аддитивного выброса оценивание
регрессионной модели при каждой испытываемой дате производится в два этапа.
На первом шаге в правую часть регрессионной модели в качестве
объясняющих включаются только переменные CONST, TIME, DT, в результате оцени-

518
Часть 2. Регрессионный анализ временных рядов
вания этой модели получаем ряд остатков ег На втором шаге оценивается
модель регресии et на et_{ и запаздывающие разности Aet_{,..., &et_p.
Датировка момента излома осуществляется по минимуму статистики ta=l
для проверки гипотезы о равенстве 1 коэффициента при et_ { в последней
модели. При этом дата излома определяется как 1999:02, ta=l = -3.594
(используются 12 запаздывающих разностей), 5%-е критическое значение равно -4.83,
так что [/Л-гипотеза не отвергается и в этом случае.
Заметим, что распределение ошибок в последней ситуации отличается
от нормального: оцененный коэффициент пикообразности распределения —
куртозис — превышает на 1.626 значение куртозиса нормального
распределения, равного 3. Как следует из {Zivot, Andrews, 1992) (это было отмечено
ранее), в таких ситуациях критические уровни сдвигаются в сторону
больших отрицательных значений, так что если использовать скорректированные
на ненормальность критические уровни, то £/Л-гипотеза тем более не будет
отвергнута.
Приведем для полноты итоги анализа ряда Ml на интервале с 1995:06
по 2000:07, проведенного в работе (Эконометрический анализ
динамических рядов.., 2001). Результаты применения различных процедур сведены
в табл. 10.25.
Таблица 10.25
Результаты анализа ряда М1 на интервале с 1995:06 по 2000:07
Используемая процедура
(критерий)
Критерий Дики — Фуллера (расширенный)
Критерий Филлипса — Перрона
Критерий DF-GLS
Критерий KPSS
Отношение дисперсий Кохрейна
Критерий Перрона
(экзогенный выбор даты излома тренда)
Обобщенный критерий Перрона
(эндогенный выбор даты излома тренда)
Исходная (нулевая) гипотеза
DS
Не отвергается
Не отвергается
Не отвергается
TS
Отвергается
В пользу DS
Не отвергается
Не отвергается
Статистические выводы, полученные при применении всех
перечисленных в таблице процедур, согласуются между собой: нулевая DS-гипотеза не
отвергается, тогда как нулевая TS-гипотеза отвергается', поведение
отношения дисперсий Кохрейна также говорит в пользу Л^-гипотезы.И

Раздел 10. Процедуры для различения TS- uDS-рядов
519
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие критерии, помимо критериев Дики — Фуллера, используются для
различения TS- и DS-рядов?
2. Как влияет на свойства критериев единичного корня наличие у ряда выраженной
сезонности?
3. Как влияет протяженность ряда на мощность критерия?
4. В чем состоит проблема согласованности статистических выводов при
различении TS и DS-гипотез?
5. Как проверяется гипотеза единичного корня в ситуации, когда ряд может иметь
несколько единичных корней?
6. Чем различаются модели с внезапным и постепенным изломом (аддитивным и
инновационным выбросом)?
7. Какие варианты поведения рядов при наличии структурного сдвига
рассматриваются при различении TS- и £>£-рядов?
8. Как производится датировка момента излома в критерии Перрона?
9. Как производится датировка момента излома в критерии Зивота — Эндрюса?

Раздел 11
РЕГРЕССИОННЫЙ АНАЛИЗ
ДЛЯ НЕСТАЦИОНАРНЫХ ПЕРЕМЕННЫХ.
КОИНТЕГРИРОВАННЫЕ ВРЕМЕННЫЕ РЯДЫ.
МОДЕЛИ КОРРЕКЦИИ ОШИБОК
Тема 11.1
ПРОБЛЕМА ЛОЖНОЙ РЕГРЕССИИ.
КОИНТЕГРИРОВАННЫЕ ВРЕМЕННЫЕ РЯДЫ.
МОДЕЛИ КОРРЕКЦИИ ОШИБОК
Проблема ложной регрессии
Начнем обсуждение с проблемы ложной (фиктивной, паразитной — spurious)
регрессии. О ней говорилось в первой части учебника (см. пример 1.3.4
в разд. 1) и при этом был сделан вывод о том, что близость к 1 абсолютной
величины наблюдаемого значения коэффициента детерминации необязательно
означает наличие причинной связи между двумя переменными, а может
являться лишь следствием наличия тренда значений обеих переменных.
ПРИМЕР 11.1.1
Смоделируем реализации двух статистически независимых между собой
последовательностей su и slt независимых, одинаково распределенных
случайных величин, имеющих стандартное нормальное распределение 7V@, 1).
Смоделированные реализации показаны на рис. 11.1 и 11.2.
На их основе построим реализацию линейной модели DGP
DGP: xt = l+0.2t+eln
yt = 2 + 0 At + €ln
в которой переменные х и у не связаны между собой причинными
отношениями.

Раздел 11. Регрессионный анализ для нестационарных переменных...
521
EPS 1
EPS 2
5 10 15 20 25 30 35 40 45 50 t
Рис. 11.1
 11111111111111111111111111111111111111111111111111 ►
5 10 15 20 25 30 35 40 45 50 t
РИС. 11.2
Рассмотрим, однако, результаты оценивания статистической модели
SM: yt = а + ]3xt + st
по смоделированной реализации. Графики рядов xt nyt приведены на рис. 11.3.
Оба ряда имеют выраженные линейные тренды.
j 1111111111111111111111111111111111111111111111—►
5 10 15 20 25 30 35 40 45 50 t
РИС. 11.3
Оцененная статистическая модель приведена в табл. 11.1.
Оцененные коэффициенты статистически значимы, коэффициент
детерминации высокий, проверка на адекватность не выявляет нарушений
стандартных предположений классической линейной модели регрессии.
Включим в правую часть статистической модели линейный тренд.
Оценивание расширенной модели дает следующий результат (табл. 11.2).
Остатки проходят тесты на адекватность, так что можно обратить
внимание на протокол оценивания расширенной статистической модели. В соот-

522
Часть 2. Регрессионный анализ временных рядов
Таблица 11.1
Объясняемая переменная У
Переменная
С
X
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
Коэффициент
1.553866
1.800255
0.864218
0.861389
2.206028
233.5948
-109.4860
2.150060
Стандартная
ошибка
0.685771
0.102997
^-статистика
2.265868
17.478780
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob. (F-statistic)
Р-значение
0.0280
0.0000
12.22809
5.953260
4.459442
4.535923
305.507600
0.000000
Таблица 11.2
Расширенная статистическая модель, объясняемая переменная У
Переменная
С
Т
X
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
Коэффициент
2.037450
0.412232
-0.054186
0.975727
0.974694
0.942598
41.75908
-66.44428
2.249075
Стандартная
ошибка
0.294861
0.028055
0.133658
^-статистика
6.909879
14.69394
0.405410
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob. (F-statistic)
Р-значение
0.0000
0.0000
0.6870
12.228090
5.925326
2.777771
2.892492
944.6386
0.000000
ветствии с этим протоколом коэффициент при переменной xt статистически
незначим, так что хп по существу, не проявляет себя в качестве переменной,
объясняющей изменчивость значений переменной^.
Исключение xt из правой части уравнения приводит к оцененной модели
(табл. 11.3), которая предпочтительнее расширенной модели и по критерию
Акаике, и по критерию Шварца.
Более того, по этим критериям последняя модель намного
предпочтительнее исходной модели jy, = а + /3xt + sr Это связано с тем, что при оценивании
исходной SM остаточная сумма квадратов равна 233.59, а при оценивании

Раздел 11. Регрессионный анализ для нестационарных переменных...
523
Таблица 11.3
Объясняемая переменная Y
Переменная
С
Т
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
Коэффициент
1.990020
0.401493
0.975642
0.975134
0.934357
41.90511
-66.53155
2.249658
Стандартная
ошибка
0.268291
0.009157
^-статистика
7.417403
43.84727
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob. (F-statistic)
Р-значение
0.0000
0.0000
12.228090
5.925326
2.741262
2.817743
1922.583
0.000000
последней модели — равна всего лишь 41.91. Это еще более убедительно
подтверждает, что изменчивость переменной yt в действительности не
объясняется изменчивостью переменной хгШ
В рассмотренном примере паразитная связь между переменными была
обусловлена тем, что в модели DGP обе переменные имеют в своем составе
детерминированный линейный тренд.
Однако ложная (паразитная) связь между переменными может возникать
не только в результате наличия у этих переменных детерминированного
тренда. Паразитная связь может возникать и между переменными,
имеющими не детерминированный, а стохастический тренд. Приведем
соответствующий пример.
ПРИМЕР 11.1.2
Возьмем процесс порождения данных в виде:
DGP: xt =x,_i + €U9
yt=yt-i +£m
где su и £2t — те же, что и в примере 11.1.1.
Графики рядов xt nyt показаны на рис. 11.4.
Предположим, что нам доступны статистические данные,
соответствующие последним 50 наблюдениям (с 51-го по 100-е). Оценивание по этим
наблюдениям статистической модели
SM: yt = а + /3xt + st
приводит к следующим результатам (табл. 11.4).

524
Часть 2. Регрессионный анализ временных рядов
А
10-
5-
0-
-5-
-10-
-15-
9П -
— ZU
♦••* ***
Ч- v-v *J4 /'"* V*
1 1 1 1 | 1 1 1 1 | 1 1 1 1 | 1 1 1 1 | 1 1 1 1 | 1 1 1 1 | 1 1 1 1 | 1 1 1 1 | 1
10 20 30 40 50 60 70 80
РИС. 11.4
..
.♦-.и'""""
1 I I I I I I I *"
90 100 t
— х
..... у
Объясняемая переменная Y
Sample: 51 100; Included observations: 50
Таблица 11.4
Переменная
С
X
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
Коэффициент
8.616496
0.597513
0.553120
0.543810
2.265356
246.3283
-110.8130
0.213611
Стандартная
ошибка
0.748277
0.077520
/-статистика
11.515120
7.707873
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob. (F-statistic)
Р-значение
0.0000
0.0000
3.404232
3.354003
4.512519
4.589000
59.41131
0.000000
Несмотря на то что в DGP ряды
yt и xt порождаются независимо друг
от друга и их модели не содержат
детерминированного тренда, здесь
также наблюдаем довольно высокое
значение коэффициента
детерминации: 0.553. Конечно, это связано
с тем, что на рассматриваемом
периоде реализации обоих рядов имеют
видимый тренд (рис. 11.5).
Если, однако, обратиться ко
всему периоду из 100 наблюдений, то
результаты оценивания будут совсем
другими (табл. 11.5).
55 60 65 70 75 80 85 90 95 100 t
РИС. 11.5

Раздел 11. Регрессионный анализ для нестационарных переменных...
525
Таблица 11.5
Объясняемая переменная Y
Sample: 1 100; Included observations: 100
Переменная
С
X
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
Коэффициент
1.490206
0.055097
0.004373
-0.005786
3.523613
1216.753
-266.8324
0.061638
Стандартная
ошибка
0.664538
0.083978
^-статистика
2.242470
0.656086
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob. (F-statistic)
Р-значение
0.0272
0.5133
1.120548
3.513463
5.376648
5.428752
0.430449
0.513306
В этом случае значение коэффициента детерминации близко к нулю,
а оцененный коэффициент при xt равен 0.0551 против 0.5975, полученного
при оценивании по наблюдениям с 51-го по 100-е. Это отражает
действительное отсутствие детерминированного тренда в DGP и в связи с этим
крайнюю нестабильность оценок коэффициента при хп полученных на различных
интервалах. Последнее сопровождается также крайне низкими значениями
статистики Дарбина — Уотсона @.214 на полном периоде наблюдений и 0.062
на второй половине этого интервала).■
Все указанные признаки являются характерными чертами, которые
присущи результатам оценивания линейной модели связи между переменными,
которые имеют стохастический (но не детерминированный!) тренд и
порождаются статистически независимыми моделями. Теоретическое исследование
подобной ситуации показывает следующее.
Пусть DGP: xt =xt_{ + eu, yt =yt_x + sln где х0 = 0, y0 = 0, a eu и slt —
статистически независимые между собой последовательности одинаково
распределенных случайных величин, еи ~ N@, <j{2\ slt ~ 7V@, сг22), так что
Cov(xn yt) = 0. Предположим, что по Т наблюдениям (хп yt)9 t - 1,2, ..., Г,
производится оценивание статистической модели
SM: yt = f3xt + un ut ~ lid. N@, сгм2), Cov(xn ut) = 0.
Стандартная оценка наименьших квадратов для коэффициента /? в этой
гипотетической модели имеет вид:
т
Т. У Л

526
Часть 2. Регрессионный анализ временных рядов
При сделанных предположениях относительно DGP оценка /?г не сходится
по вероятности при Т —> оо ни к какой константе и имеет предельное
распределение, отличное от нормального.
Вместе с тем при выбранной спецификации SM (статистической модели),
в предположениях этой модели (а не DGP!) имеем
Cov(xt, yt) = Cov(xt, f3xt +ut) = pCov(xt , x,) = /3D(xt),
т.е. оцениваемым параметром является
Cov(xnyt)
D(xt)
Поскольку в действительности (в DGP) Cov(xn yt) = О, то и это значение C
равно нулю, так что если бы гипотетическая модель (соответствующая SM)
была верна, то имело бы место J3T —> О по вероятности.
Далее, при Т-> оо значения /-статистики tp для проверки гипотезы Н0: /?= О
неограниченно возрастают по абсолютной величине, так что использование
таблиц /-распределения будет практически всегда приводить к отклонению
этой гипотезы, т.е. к выводу о том, что между переменными xt и yt существует
линейная регрессионная связь. В действительности нетривиальное предель-
1
ное распределение имеет не статистика tp, а статистика —f=tp, причем
предельное распределение последней является нестандартным.
Что касается статистики Дарбина — Уотсона (DW), то в рассматриваемой
ситуации DW —> 0 по вероятности при Т —» оо, и это позволяет распознавать
неправильную спецификацию статистической модели в форме паразитной
регрессии. Последнее обстоятельство проявляется в поведении остатков от
оцененной статистической модели, которое не соответствует поведению
стационарного процесса.
ПРИМЕР 11.1.3
В предыдущем примере было задано
DGP: xt =xt_x + eln
yt=y,-i +£2n
где su и slt — последовательности независимых, одинаково распределенных
случайных величин, имеющих стандартное нормальное
распределение 7V@, 1).
Мы оценивали статистическую модель
SM: yt = а + J3xt + st

Раздел 11. Регрессионный анализ для нестационарных переменных...
527
и по наблюдениям с 51-го по 100-е получили
Д. = 0.598, ^ = 7.708, DW= 0.214.
При этом график остатков (рис. 11.6) не похож на график стационарного
ряда.И
RESIDS
-20
Естественно было бы для
выявления такого «неподобающего»
поведения остатков не просто увидеть
график остатков, но и попытаться
использовать формальные
статистические критерии, тем более что
критерии проверки интегрированное™
временных рядов были
рассмотрены ранее (критерии Дики — Фул-
лера, Филлипса — Перрона и др.).
Проблема, однако, в том, что
теперь мы имеем дело не с «сырым»
рядом, а с рядом остатков, которые
вычисляются после
предварительного оценивания модели (коэффициентов а и /3 в последнем примере). Это
обстоятельство существенно влияет на распределения соответствующих
статистик и не дает возмоэюности пользоваться таблицами, которые были
использованы ранее при анализе на интегрированность «сырых» рядов. С
учетом этого были построены таблицы, позволяющие производить анализ
остатков в случае интегрированных объясняемой и объясняющих переменных, о чем
подробнее будет сказано в теме 11.2. Сейчас же только покажем, что дает
применение соответствующих таблиц к рассмотренному выше примеру.
11111111Ч111111111111111111111
55 60 65 70 75 80 85 90 95 100 t
РИС. 11.6
ПРИМЕР 11.1.4
При оценивании статистической модели SM: yt = а + Cxt + st по наблюдениям
с 51-го по 100-е получили оцененную модель
yt = 8.616 + 0.598х,+ е,.
С полученным рядом остатков поступим так же, как и в случае
применения критерия Дики — Фуллера к «сырому» ряду, т.е. оценим модель
Aet = (pet_ j + v,
и вычислим /-статистику t для проверки гипотезы Н0: (р- 0, интерпретируя
эту гипотезу как гипотезу единичного корня для ряда остатков.
Гипотеза Я0 отвергается в пользу НА: (р < 0 (интерпретируемой как
гипотеза стационарности ряда остатков), если f < /крит. Приближенные значения
/крит (в применении к ряду остатков) можно найти по формуле:

528
Часть 2. Регрессионный анализ временных рядов
где к^, кх, к2 зависят от выбранного уровня значимости и указаны в табл. П-9
в Приложении к заданиям для семинарских занятий... {MacKinnon, 1991). Для
5%-го уровня значимости
>крит * -3.3377 - 5.967Г - 8.98Г,
что при Т = 50 дает tKpm = -3.46. Последнее значение существенно меньше
5%-го критического значения статистики Дики — Фуллера (-2.92),
рассчитанного для случая «сырого» ряда.
В нашем примере оценивание тестового уравнения Дики — Фуллера дает
значение f = -2.01. Последнее существенно выше 5%-го критического
уровня, и гипотеза единичного корня не отвергается. ■
Вообще говоря, вопрос о ложной (паразитной) или неложной
(действительной) линейной регрессионной связи между двумя переменными xt и уп
представляющими интегрированные ряды первого порядка {xt, yt ~ 7A)),
более точно формулируется следующим образом: существует ли такое
значение Д при котором ряд jy, - f3xt стационарен?
Если ответ на этот вопрос положительный, то говорят, что ряды xt и yt
(переменные xt и yt) коинтегрированы {cointegrated time series). Если же
ответ оказывается отрицательным, то ряды xt и yt (переменные xt и yt)
не являются коинтегрированными.
В последнем случае непосредственное оценивание модели yt = а + fixt + ut
бессмысленно, так как получаемая оценка J3T, собственно говоря, не является
оценкой какого-либо теоретического параметра связи между переменными xt
nyt (см., впрочем, ниже замечание 11.1.6).
Напротив, если переменные xt и yt коинтегрированы, то /3Т является
оценкой того единственного значения Д при котором ряд yt - J3xt стационарен.
Заметим теперь, что если в
DGP: xt =xt_{ + sln
yt=yt-i +£it
допустить коррелированностъ значений su и slt в совпадающие моменты
времени, т.е. Cov{sXn s2t) * 0, то коррелированность еи и slt вовсе не
означает, что ряды xt и yt коинтегрированы. Предположим все же, что существует
некоторое значение Д при котором yt = Cxt + ut, где ut — стационарный ряд.
Тогдаyt_x = /3xt_x + ut_x, так что Ayt = Д\х, + Aut, а отсюда s2t = j3sXt + Aur
Последнее можно записать в виде ut -ut_x + rjt, где

Раздел 11. Регрессионный анализ для нестационарных переменных...
529
rit = £ъ ~ Р£и ~ i-i-d- N@9 rf).
Но это означает, что ut — нестационарный процесс.
В то же время если х0 - у0 = 0, то
Cov(xt9yt) = Cov(sxx + ... + sU9 e2l + ... + s2t) = tCov(en, s2x)9
так что xt и yt — коррелированные, но не коинтегрированные случайные блу-
ждания.
Существенно, что распределение статистики Дики — Фуллера в подобной
ситуации не зависит от конкретного вида матрицы ковариаций
I = (Cov(skl,esl))9 k9s=l92.
Тем же свойством обладает и распределение статистики Дарбина —
Уотсона, примененной к ряду остатков (CRDW — cointegrating
regression DW)\
При Т = 50 5%-е критическое значение последней статистики равно 0.78.
Гипотеза некоинтегрированности рядов отвергается, если наблюдаемое
значение этой статистики превышает критическое значение.
В примере 11.1.3 значение статистики Дарбина — Уотсона равно 0.214,
так что гипотеза некоинтегрированности не отвергается и этим критерием.
Что следует предпринять в случае обнаружения паразитной связи между
интегрированными порядка 1 переменными xt uyt? Имеются три возможных
пути обхода возникающих здесь трудностей.
1. Включить в правую часть уравнения запаздывающие значения обеих
переменных, точнее, рассмотреть статистическую модель
SM: yt = а+ yyt_x + Ext + Sxt_x + ип
где ut — стационарный ряд и переменная xt трактуется как экзогенная
переменная.
Последнее уравнение можно записать иначе в следующих двух формах:
а) yt = а+ yyt_x + j3Axt + (/? + S)xt_x + ип
б) yt = а+ yyt_x +(/3+ S)xt - SAxt + un
В обеих формах слева стоит интегрированная переменная^ ~/A).
В правой части уравнения а) параметр /? является коэффициентом
при стационарной переменной Ахп имеющей нулевое математическое
ожидание; yt_l9 xt_x ~ 7A), ut — стационарный ряд. Как было показано
в (Sims, Stock, Watson9 1990), в такой ситуации оценки наименьших
квадратов для всех коэффициентов SM состоятельны, оценка пара-

530
Часть 2. Регрессионный анализ временных рядов
метра Д асимптотически нормальна. Обычная /-статистика для
проверки гипотезы Я0: Д = О имеет асимптотически нормальное распределение
7V@, 1), если ut — белый шум.
Аналогично в правой части уравнения б) параметр -S является
коэффициентом при стационарной переменной Дх„ имеющей нулевое
математическое ожидание; yt_l9 xt ~ 7A), ut — стационарный ряд. Поэтому
оценка параметра S в рамках модели SM асимптотически нормальна,
и /-статистика для проверки гипотезы Н0: S = О имеет асимптотически
нормальное распределение N@, 1), если ut — белый шум.
Оценки для Д и S остаются асимптотически нормальными и в том
случае, если ut — стационарный ряд, не являющийся белым шумом.
Однако при этом асимптотическое распределение 7V@, 1) имеет
скорректированные варианты /-статистик, в знаменателях которых
стандартные оценки дисперсии ряда ut заменяются состоятельными оценками
долговременной дисперсии этого ряда, определенной в теме 10.2.
В то же время статистика qF - 2F для проверки гипотезы Н0: Д = S = О
не имеет асимптотического распределения %2{2), поскольку
рассматриваемую SM не удается линейно репараметризовать таким образом,
чтобы в правой части преобразованного уравнения и Д и S одновременно
стали коэффициентами при стационарных переменных, имеющих
нулевые математические ожидания (у нас они становятся таковыми при
разных репараметризациях).
2. Перед оцениванием модели связи продифференцировать ряды xt и уп
т.е. рассмотреть модель в разностях
SM: Ду, = а + ДДх, + ип
где ut — стационарный ряд.
В этой модели оценки наименьших квадратов и для а, и для Д
асимптотически нормальны. Обе /-статистики имеют асимптотически
нормальное распределение 7V@, 1), если ut — белый шум. Если ut —
стационарный ряд, не являющийся белым шумом, то необходимо
произвести коррекцию /-статистик, как в предыдущем пункте.
3. Использовать для оценивания модель регрессии с
автокоррелированными остатками:
SM: yt - а + Дх, + un ut = pxt_x + sn ut ~ /.Id. 7V@, crf2),
При этом предпочтительнее оценивать все три параметра а, Д р
одновременно, используя представление
Уг-рУг-\ = <*A -p) + j3(xt-pxt_x) + £r

Раздел 11. Регрессионный анализ для нестационарных переменных...
531
В случае ложной регрессии р —> 1 (по вероятности), так что при
больших Т этот метод фактически равносилен предварительному
дифференцированию рядов.
ПРИМЕР 11.1.5
Применим указанные три подхода к анализу реализаций, смоделированных
ранее в данном разделе в соответствии с
DGP: xt = xt_x + sln
где eu и s2t — последовательности независимых, одинаково распределенных
случайных величин, имеющих стандартное нормальное
распределение 7V@, 1).
Для анализа используем последние 50 наблюдений.
Применив первый подход, получим оцененную модель, приведенную
в табл. 11.6.
Таблица 11.6
Объясняемая переменная У
Переменная
С
X
Д-1)
Д-1)
Коэффициент
0.447271
-0.014458
0.970105
0.033532
Стандартная
ошибка
0.550358
0.123861
0.055989
0.120061
Г-статистика
0.812691
-0.116725
17.32664
0.279290
Р-значение
0.4206
0.9076
0.0000
0.7813
Наблюдаемые Р-значения для коэффициентов при переменных xt и xt_x
указывают на то, что переменная xt фактически не объясняет изменчивость
переменной^.
Применив второй подход, получим оцененную модель, приведенную
в табл. 11.7.
Оба коэффициента статистически незначимы, и это отражает
некоррелированность рядов £и и £2г
Таблица 11.7
Объясняемая переменная D(Y)
Переменная
С
D(X)
Коэффициент
0.184523
-0.033386
Стандартная
ошибка
0.117614
0.116361
Г-статистика
1.568884
-0.286915
Р-значение
0.1232
0.7754

532
Часть 2. Регрессионный анализ временных рядов
Применив третий подход, оценим модель
yt -pyt.x = а{\ -р) + J3(xt -pxt_x) + et9
т.е.
Уг = a* + pyt-\ +P(xt-pxt_x) + sr
При этом получим следующие результаты (табл. 11.8).
Таблица 11.8
Объясняемая переменная Y
Method: Least Squares; Convergence achieved after 7 iterations; Y=CA )+СB)*У(-1 )+СC)*(Х-СB)*Х(-1))
Переменная
0A)
0B)
0C)
R-squared
Коэффициент
0.217398
0.988791
-0.027306
0.940380
Стандартная
ошибка
0.159423
0.035801
0.119276
f-статистика
1.363650
27.61920
-0.228934
Mean dependent var
Р-значение
0.1792
0.0000
0.8199
3.404232
Как и ожидалось, коэффициент при >>,_! оказался очень близким к 1, а два
других коэффициента статистически незначимы. Проверка на одновременное
зануление этих двух коэффициентов дает Р-значение 0.367.■
ПРИМЕР 11.1.6
Изменим процесс порождения данных, оставляя те же формулы для xt и уп
т.е.
Xf — Xf_ j "г ojj,
yt=yt-x +£2r
Но теперь пусть:
s\t-> £it — последовательности независимых, одинаково распределенных
случайных величин, имеющих нормальное распределение N@, 1.25);
Cov(su, s2s) - 0 для t*s, Cov(su, s2t) = 1.
Отсюда, в частности, следует, что Corr(su, s2t) = 0.8.
Смоделированные реализации еи и slt изображены на рис. 11.7.
Траектории смоделированной пары рядов еи и slt ведут себя достаточно
согласованным образом, оцененный коэффициент корреляции между этими
рядами равен 0.789. Полученные при этом реализации рядов xt nyt ведут себя
так, как показано на рис. 11.8. Для сравнения на рис. 11.9 изображено
поведение реализаций рядов xt и yt при полной статистической независимости
рядов еи и slv

Раздел 11. Регрессионный анализ для нестационарных переменных...
533
10 20 30 40 50 60 70 80 90 100 t
Рис. 11.7
NOISE_X
NOISE Y
AJ 111111111111111111 м 1111111111111111111111111111111 ^
10 20 30 40 50 60 70 80 90 100 t
Рис. 11.8
10 20 30 40 50 60 70 80 90 100 t
Рис. 11.9
Для сопоставимости с ранее полученными результатами опять обратимся
ко второй части отрезка наблюдений; здесь оцененный коэффициент
корреляции между рядами еи и e2t равен 0.792.
Сначала оценим модель yt - а + J3xt + иг В результате получим для ряда
остатков значение статистики Дики — Фуллера, равное -2.112, которое выше
5%-го критического уровня -3.46. Соответственно гипотеза о ложности
регрессионной связи не отвергается.
Применив первый подход, получим оцененную модель, приведенную
в табл. 11.9.
По сравнению с ранее рассмотренным случаем, где ряды еи и s2t были
между собой статистически не связанными, теперь оказываются
статистически значимыми и коэффициенты при переменных xt nxt_x. Исключив из
правой части модели константу, получим табл. 11.10.

534
Часть 2. Регрессионный анализ временных рядов
Таблица 11.9
Объясняемая переменная У
Переменная
С
X
Д-1)
Х(-\)
R-squared
Коэффициент
0.548392
0.718479
0.913556
-0.641522
0.987574
Стандартная
ошибка
0.377080
0.079943
0.067811
0.088805
^-статистика
1.454312
8.987361
13.47210
-7.223976
Mean dependent var
Р-значение
0.1526
0.0000
0.0000
0.0000
-0.957402
Таблица 11.10
Объясняемая переменная У
Переменная
X
Y(-\)
Д-1)
R-squared
Коэффициент
0.695862
1.005257
-0.707002
0.987003
Стандартная
ошибка
0.079341
0.025245
0.077447
f-статистика
8.770553
39.82053
-9.128837
Mean dependent var
Р-значение
0.0000
0.0000
0.0000
-0.957402
То есть>>г = 1.005У,.! 4- 0.695л;, - 0.101 xt_x 4- et. Оценка коэффициента при^.!
близка к 1, оцененные коэффициенты при xt и xt_x близки по абсолютной
величине и противоположны по знаку, что вполне согласуется с
реализованной моделью DGP.
Применив второй подход, получим оцененную модель, приведенную
в табл. 11.11.
Таблица 11.11
Объясняемая переменная D(Y)
Переменная
С
D(X)
R-squared
Коэффициент
0.100915
0.694000
0.626921
Стандартная
ошибка
0.083851
0.077274
f-статистика
1.203508
8.981039
Mean dependent var
Р-значение
0.2347
0.0000
0.226857
И здесь в отличие от ранее использовавшегося DGP становится значимым
коэффициент при переменной Ахп что отражает коррелированность
случайных величин sXt и £2п т.е. коррелированность Ах, и Луг Исключив из правой
части уравнения статистически незначимую константу, получим результаты,
приведенные в табл. 11.12.

Раздел 11. Регрессионный анализ для нестационарных переменных...
535
Таблица 11.12
Объясняемая переменная D(Y)
Переменная
D(X)
Коэффициент
0.709553
Стандартная
ошибка
0.076533
f-статистика
9.271155
Р-значение
0.0000
То есть Ayt = 0.7ЮДх, 4- еп илиуг = yt_x + 0.710л;, - 0.710bcr_i 4- et.
Наконец, применив третий подход, оценим модель
yt = a+pyt_x + fi(xt -pxt_x) 4- er
При этом получим табл. 11.13.
Таблица 11.13
Объясняемая переменная Y
Convergence achieved after В iterations; У=СA)+СB)*У(-1)+СC)*(Х-СB)*Х(-1))
Переменная
СA)
СB)
СC)
R-squared
Коэффициент
0.329205
0.941984
0.723593
0.987410
Стандартная
ошибка
0.250398
0.056946
0.079341
/-статистика
1.314726
16.54170
9.119982
Mean dependent var
Р-значение
0.1950
0.0000
0.0000
-0.957402
Здесь становится статистически значимым коэффициент Д
Исключение из правой части константы дает табл. 11.14.
Таблица 11.14
Объясняемая переменная У
Convergence achieved after Л iterations; У=СB)*У(-1)+СC)*(Х-СB)*Х(-1))
Переменная
СB)
СC)
Коэффициент
1.014411
0.702102
Стандартная
ошибка
0.020750
0.078268
f-статистика
48.88608
8.970448
Р-значение
0.0000
0.0000
То есть
yt = 1.014yr_! +0.702(jc, - \№Axt_x) + en
или
yt = 1.014уг_! 4- 0.702jc, - 0.712jcr_! 4- er

536
Часть 2. Регрессионный анализ временных рядов
Отметим близость результатов, полученных тремя методами:
yt = 1.005^.! + 0.695jc, - 0.707х,_! + et (метод 1);
yt = yt-X + 0.71 Ox, - 0.7\0xt_x + e, (метод 2);
yt = 1.014^_! + 0.702jc, - 0.712jc,_! + e, (метод 3).
Фактически во всех трех случаях воспроизводится одна и та же линейная
модель связи между рядами разностей:
Ау, = 0.7 Ах, + ег
Эта регрессионная связь между продифференцированными рядами не
является лоэюной (в отличие от регрессионной связи между рядами уровней):
статистика Дарбина — Уотсона принимает значение 1.985, Р-значение критерия
Харке — Бера равно 0.344.■
V Замечание 11.1.1. В связи с результатами, полученными в
последних примерах, естественно возникает следующий вопрос, который
поднимался в свое время различными исследователями. Не будет ли
разумным, имея дело с рядами, траектории которых обнаруживают
выраженный тренд, сразу приступать к оцениванию связей между
рядами разностей (между продифференцированными рядами)?
Против некритичного использования такого подхода говорят два
обстоятельства:
• если ряды в действительности стационарны относительно
детерминированного тренда, то дифференцирование приводит
к передифференцированным рядам, имеющим необратимую
МА-составляющую;
• если ряды являются интегрированными порядка 1 и при этом
коинтегрированы, то при переходе к продифференцированным
рядам теряется информация о долговременной связи между
уровнями этих рядов.
Дифференцирование рядов оправданно и полезно, если ряды
являются интегрированными, но при этом между ними отсутствует
коинтеграционная связь.
Коинтегрированные временные ряды
Пусть yt ~ 1A), xt ~ 7@). Строить регрессию yt на xt в этом случае
бессмысленно, так как для любых аиЬв такой ситуации
yt - a- bxt ~/(l).
Пусть, наоборот, yt ~ 1@), xt ~ 7A). Для любых аиЬ^О здесь опять
yt - a- bxt ~/(l)

Раздел 11. Регрессионный анализ для нестационарных переменных...
537
и только при Ь = 0 получаем
yt-a-bxt -ДО),
так что и в таком сочетании строить регрессию одного ряда на другой не
имеет смысла.
Пусть теперь^ ~ 7A), xt ~Д1) — два интегрированных ряда.
Если для любого Ъ
yt-bxt ~Д1),
то регрессия yt на xt является фиктивной, и мы уже выяснили, как следует
действовать в такой ситуации.
Обратимся теперь к случаю, когда при некотором ЬфО
yt - bxt ~ ДО) — стационарный ряд.
Если это так, то ряды yt и xt называют коинтегрированными, а вектор
A, -Ь)Т— коинтегрирующим вектором (cointegrating vector).
Вообще, ряды^г ~ 1A), xt ~ 1A) называют коинтегрированными (в узком
смысле — детерминистская коинтеграция, deterministic cointegratiori), если
существует ненулевой (коинтегрирующий) вектор /?= (Д, Д)г * 0, для
которого
Д xt + /32yt ~ ДО) — стационарный ряд.
Заметим, что если вектор /? = (Д, Д)г является коинтегрирующим для
рядов xtnyt, то коинтегрирующим для этих рядов будет и любой вектор вида
cj3= (cj3{, cj32)T, где с * 0 — постоянная величина. Чтобы выделить какой-то
определенный вектор, приходится вводить условие нормировки
(normalization) — например, рассматривать только векторы вида A, -Ь)Т (или только
векторы (-а, \)т).
Поскольку предполагаем в данном случае, что xt,yt ~ Д1), то ряды
разностей Ах,, Ду, стационарны. Будем предполагать в дополнение, что
стационарен векторный ряд (Axt, Ayt)T и для него существует представление в виде
векторного скользящего среднего (УМА)
(Axt, Ayt)T = ju +B(L)st,
где ju = (juu ju2)T, ju{ = E(Axt), ju2 = E(Ayt),
st = (sXt, s2t)T — векторный белый шум,
т.е. sx, s2, ... — последовательность не коррелированных между собой,
одинаково распределенных случайных векторов, для которых
E(st) = (О, 0)Т, D(sXt) = <тх, D(s2t) = <j2, Cov(eu, s2t) = an— постоянные
величины;
v0 К
00
k = \
u(k) h(k)
\u2\ u22 J

538
Часть 2. Регрессионный анализ временных рядов
Таким образом, предполагается, что разложение Вольда центрированного
векторного ряда (Ах„ Ayt)T- /л не содержит линейно детерминированной компоненты.
Знаменитый результат Грейнджера (см. (Granger, 1983), а также (Engle,
Granger, 1987)), состоит в том, что в случае коинтегрированности 1A) рядов
х, и у, (в узком смысле):
(I) в представлении (Ах„ Ду,)г - /и+ B(L)et матрица 5A) имеет ранг 1;
(II) система рядов xt и yt допускает векторное ARMA представление
A(L)(x„yt)T = c + d(L)st,
где st — тот же векторный белый шум, что и в (I);
с = (сх, с2)Т, сх и с2 — постоянные;
A(L)— матричный полином от оператора запаздывания;
d(L) — скалярный полином от оператора запаздывания,
причем ДО) = 12 (единичная матрица размера B х 2)),
rank А(\) = 1 (ранг B х 2)-матрицы^A) равен 1),
значение d(\) конечно.
В связи с тем что в последнем представлении ранг B х 2)-матрицы А(\)
меньше двух, об этом представлении часто говорят как о векторной
авторегрессии пониженного ранга (reduced rank VAR).
В развернутой форме представление (II) имеет вид:
р я
К =с\ + ХКЛ-У +6iy^-y)+ X^*u-*'
7=1 к=0
Р Я
У{=С2 + ^Q2jXt-j +b2jyt-j)+Ysek£2,t-k-
7 = 1 fc = 0
При этом верхние пределы р и q у сумм в правых частях могут быть
бесконечными.
Если возможно векторное AR представление, то в нем d(L) = \,р < оо.
(III) Система рядов xt и yt допускает представление в форме модели
коррекции ошибок (error correction model — ЕСМ)
00 00
Дх, = /лх + axzt_x + ^(rij^Ct-j +eXJAyt_j)+ ^eksXt_k,
7=1 £=0
00 00
Ay, = //2 + a2zt_x + ^{Уу A*,-y + S2j Ay,.,) + £^2,,-*>
7=1 k=0
где z, =yt - J3xt - E(yt - J3xt) — стационарный ряд с нулевым математическим
ожиданием, z, ~ 1@);
а? + а} > 0.

Раздел П. Регрессионный анализ для нестационарных переменных...
539
Если в (II) возможно векторное AR(p) представление (р < оо), то ЕСМ
принимает вид:
р-\
Л** = М + a\zt-\ + Z^iy^-y + s\Ayt-j) + *i,n
Р-\
Ayt={l2+a2Zt-l + Z^27^r-y -*-^2уАУг-у) + ^2,Г-
7=1
Здесь важно отметить следующее.
• Если ряды хп yt ~ 1A) коинтегрированы, то все составляющие в ЕСМ
стационарны.
• Если векторный ряд (xt, yt)T ~ 1A) (так что векторный ряд (Ахп Ayt)T
стационарен) и порождается ЕСМ-моделью, то ряды xt и yt
коинтегрированы. (Действительно, в этом случае все составляющие ЕСМ,
отличные от zt_ х, стационарны, но тогда стационарна и zt_ x.)
• Если ряды xt, yt ~1A) коинтегрированы, то VAR в разностях не может
иметь конечный порядок (в отличие от случая, когда ряды xt и yt не
коинтегрированы) .
Абсолютную величину zt -yt - a-J3xn где а = E(yt - J3xt), можно
рассматривать как расстояние, отделяющее систему в момент t от равновесия
(equilibrium), задаваемого соотношением yt - a -fixt - 0. Величины и направления
изменений xt и yt принимают во внимание величину и знак предыдущего
отклонения от равновесия zt_x. Ряд zt, конечно, вовсе не обязательно убывает
по абсолютной величине при переходе от одного периода времени к другому,
но он является стационарным и поэтому расположен к движению по
направлению к своему среднему (mean-reversion).
v Замечание 11.1.2. Переменная xt не является причиной по Грейнд-
жеру для переменной уt, если неучет прошлых значений переменной
xt не приводит к ухудшению качества прогноза значения yt по
совокупности прошлых значений этих двух переменных. Переменная yt
не является причиной по Грейнджеру для переменной хп если неучет
прошлых значений переменной yt не приводит к ухудшению
качества прогноза значения xt по совокупности прошлых значений этих
двух переменных1. (Качество прогноза измеряется среднеквадрати-
ческой ошибкой прогноза.)
В четвертой части учебника рассмотрим более подробно вопросы, связанные с
определением причинности по Грейнджеру.

540
Часть 2. Регрессионный анализ временных рядов
Если xt, yt ~1A) и коинтегрированы, то должна иметь место
причинность по Грейнджеру (Granger causality), по крайней мере,
в одном направлении. Этот факт вытекает из представления такой
системы рядов в форме ЕСМ, в которой ах + а* > 0. Значение xt_x
через посредство zt_ х помогает в прогнозировании значения yt (т.е.
переменная xt является причиной по Грейнджеру для переменной yt),
если а2 ф 0. Значение yt_ х через посредство zt_ х помогает в
прогнозировании значения xt (т.е. переменная yt является причиной по
Грейнджеру для переменной xt), если ах Ф 0.
V Замечание 11.1.3. Пусть xt, yt ~ 1A) коинтегрированы и wt ~ 1@).
Тогда для любого к коинтегрированы ряды xt и yyt_k + wt, у Ф 0.
Если xt ~ 1A), то коинтегрированы ряды xt и xt_k. (Действительно,
тогда xt - xt_k = Axt + Axt_x 4- ... + Axt_k — сумма /(О)-переменных,
которая также является /(О)-переменной.)
Процедура Энгла — Грейнджера построения модели
коррекции ошибок
Итак, при коинтегрированности рядов xt,yt ~ 1A) имеем:
• модель долговременной (равновесной) связи уt = а + f5xt\
• модель краткосрочной динамики в форме ЕСМ,
и эти модели согласуются друг с другом.
Проблема, однако, состоит в том, что для построения ЕСМ по реальным
статистическим данным надо знать коинтегрирующий вектор (в данном
случае — знать значение /?). Хорошо, если этот вектор определяется
экономической теорией. К сожалению, чаще его приходится оценивать по имеющимся
данным.
Энгл и Грейнджер (Engle, Granger, 1987) предложили двухшаговую
процедуру построения ЕСМ для коинтегрированных рядов.
На первом шаге значения а и /3 оцениваются в рамках модели регрессии
yt на xt
yt - а + /3xt +ur
Получив методом наименьших квадратов оценки а и ft для параметров
этой модели (МНК-оценки), находим оцененные значения отклонений от
положения равновесия
zt=yt- а - fixt,
т.е. остатки от оцененной регрессии.

Раздел 11. Регрессионный анализ для нестационарных переменных...
541
На втором шаге методом наименьших квадратов раздельно (не как
система!) оцениваются уравнения:
Р-\
Axt=jux +axzt_x + XOiyA*,_y +<V^-y) + ^
7 = 1
p-\
7 = 1
т.е. предполагается модель VAR(p) для хп yr
Определяющим в этой процедуре является то обстоятельство, что (в
случае коинтегрированности рядов xt и yt) полученная на первом шаге оценка Д
быстрее обычного приближается (по вероятности) к истинному значению Д —
второй компоненте коинтегрирующего вектора A, Д)г (иначе говоря, Д
является суперсостоятельной оценкой для Д). Это, в конечном счете, приводит
к тому, что оценки в отдельном уравнении ЕСМ, использующие оцененные
значения zt_l9 имеют то же асимптотическое распределение, что и оценка
максимального правдоподобия, использующая истинные значения zt_ x
(обычно это асимптотически нормальное распределение). При этом МНК-
оценки стандартных ошибок всех коэффициентов являются состоятельными
оценками истинных стандартных ошибок.
Заметим, что последние результаты справедливы, несмотря на то что ряд
оцененных значений £, формально не является стационарным, поскольку
Отметим также, что если использовать другую нормировку
коинтегрирующего вектора в виде (Д, 1)г, то придется оценивать регрессию х, на
константу и yt, а это приведет к вектору, не пропорциональному вектору,
оцененному в первом случае.
/
v Замечание 11.1.4. Тот факт, что Д быстрее обычного сходится
(по вероятности) к Д, вовсе не означает, что на первом шаге
процедуры Энгла — Грейнджера можно использовать обычные
регрессионные критерии. Дело в том, что получаемые на первом шаге оценки
и статистики имеют, вообще говоря, нестандартные
асимптотические распределения. Кроме того, при небольших Т оценка Д может
иметь весьма значительное смещение.
Однако в данном контексте первый шаг является
вспомогательным, и на этом шаге нет необходимости обращать внимание на
сообщаемые в протоколах соответствующих пакетов программ значения
статистик. Напротив, на втором шаге можно использовать обычные
статистические процедуры (разумеется, если количество наблюдений
достаточно велико и ряды коинтегрированы).

542
Часть 2. Регрессионный анализ временных рядов
V Замечание 11.1.5. При практическом применении двухшаговой
процедуры Энгла — Грейнджера полученный на первом шаге ряд
остатков zt-yt - а - J5xt используют не только при оценивании модели
коррекции ошибок на втором шаге процедуры, но и для проверки
гипотезы о некоинтегрированности рядов xtnyr
Эту гипотезу можно проверять следующим образом. Для ряда £,
строится статистика Дики — Фуллера f , которая использовалась бы
для проверки гипотезы существования единичного корня у этого ряда,
если бы этот ряд был «сырым», а не являлся рядом остатков от
оцененной регрессии. Гипотеза некоинтегрированности рядов xt и yt
отвергается, если вычисленное значение t оказывается ниже
критического значения tKpm, соответствующего заданному уровню
значимости, т.е. если t < tKpm. Следует отметить только, что это tKpllT
отличается от критического значения статистики f , рассчитанного для
случая «сырого» ряда, так что здесь необходимы другие таблицы
критических значений. В связи с этим уже указывалась работа
(MacKinnon, 1991); среди других источников, содержащих необходимые
таблицы, упомянем монографии (Patterson, 2000) и (Hamilton, 1994).
Более подробно этот вопрос будет рассмотрен в теме 11.2.
ПРИМЕР 11.1.7
Расмотрим реализацию процесса порождения данных
DGP: xt =*,_! + st,
Уг = 2*, + V,,
где х{ = 0;
stYLvt — порождаемые независимо друг от друга последовательности
независимых, одинаково распределенных случайных величин,
имеющих стандартное нормальное распределение N@, 1).
Графики полученных реализаций рядов xt nyt изображены на рис. 11.10.
Пара (xt,yt) образует векторный процесс авторегрессии
Xf — Xf_ j тор
yt = 2xt_l + 7jt,
где rjt = vt + 2st ~ lid. N@, 5).
В форме ЕСМ пара уравнений принимает вид:
Дх, = st,
AV/ = -(V/-i -2x/-i) + 7/ = -Vi + 7/>
mezt=yt-2xt,

Раздел 11. Регрессионный анализ для нестационарных переменных...
543
10 20 30 40 50 60 70 80 90 100 t
Рис. 11.10
ИЛИ
Axt = axzt_x + sn
&yt = a2zt_l + 7]n
где ax = 0, a2 = -1, так что ax + a2 > 0.
На практике, приступая к анализу статистических данных, исследователь
не знает точно, какой порядок имеет VAR в DGP. Имея это в виду, выберем
для оценивания в качестве статистической модели ЕСМ в виде:
Axt = alzt_l +yuAxt_l +£11Ду,_1 +v„
Ay, = a2zt_x + r2\Axt-\ + ^iAVr-i + ™n
допуская, что данные порождаются моделью векторной авторегрессии второго
порядка (р = 2). Для анализа используем 100 наблюдений.
Шаг I. Исходим из модели yt - а + fixt + иг
Оцененная модель приведена в табл. 11.15.
Объясняемая переменная У
Таблица 11.15
Переменная
С
X
R-squared
Коэффициент
-0.006764
1.983373
0.989284
Стандартная
ошибка
0.165007
0.020852
/-статистика
-0.040992
95.11654
Durbin-Watson stat
Р-значение
0.9674
0.0000
2.217786
То есть у, = -0.006764 + 1.983373*, + й„ так что
f = й =yt + 0.006764 - 1.983373*,.

544
Часть 2. Регрессионный анализ временных рядов
Допустив, что VAR имеет порядок 2, при использовании критерия Дики —
Фуллера для проверки рядов yt и xt на коинтегрированность в правую часть
уравнения включаем одну запаздывающую разность:
Д£, = <pzt_x + 6xbzt_x + £r
Оценивив последнее уравнение, получим табл. 11.16.
Таблица 11.16
Объясняемая переменная D(Z)
Переменная
Z(-l)
D(Z(-\))
Коэффициент
-1.153515
0.038156
Стандартная
ошибка
0.151497
0.100190
/-статистика
-7.614088
0.380837
Р-значение
0.0000
0.7042
Значение тестовой статистики f = -7.614 ниже 5%-го критического
уровня -3.396 (см. {Patterson, 2000, табл. 8.7)). Гипотеза некоинтегрированности
рассматриваемых рядов уверенно отвергается. (Ввиду статистической
незначимости коэффициента при запаздывающей разности можно было бы
переоценить модель, не включая запаздывающую разность в правую часть
уравнения. Но это дало бы значение t - -11.423, при котором гипотеза
некоинтегрированности отвергается еще более уверенно.)
Таким образом, принимаем решение о коинтегрированности рядов yt и^и
переходим к построению модели коррекции ошибок.
Шаг П. Сначала отдельно оцениваем уравнение для Axt (табл. 11.17).
Таблица 11.17
Объясняемая переменная D(X)
Переменная
С
Z(-l)
D(X(-l))
ЩУ(-\))
Коэффициент
-0.028016
0.250942
0.639967
-0.258740
Стандартная
ошибка
0.100847
0.176613
0.257823
0.116654
/-статистика
-0.277810
1.420858
2.482201
-2.218019
Р-значение
0.7818
0.1587
0.0148
0.0290
Поочередное исключение из правой части уравнения переменных со
статистически незначимыми коэффициентами и наибольшим Р-значением
приводит к оцененной модели (табл. 11.18) и, в конечном счете, к модели
Ах, = v„
которая и была использована при порождении ряда хг

Раздел 11. Регрессионный анализ для нестационарных переменных... 545
Таблица 11.18
Объясняемая переменная D(X)
Переменная
ОД-1»
Коэффициент
0.115141
Стандартная
ошибка
0.100249
/-статистика
1.148554
Р-значение
0.2536
Оценивая теперь уравнение для Ду„ получаем табл. 11.19.
Таблица 11.19
Объясняемая переменная D{Y)
Переменная
С
Z(-l)
ОЩ-1))
D(Y(-l))
Коэффициент
-0.060101
-0.641060
1.313872
-0.482981
Стандартная
ошибка
0.211899
0.371097
0.541733
0.245111
/-статистика
-0.283630
-1.727472
2.425311
-1.970459
Р-значение
0.7773
0.0874
0.0172
0.0517
Исключая из правой части оцениваемого уравнения константу, получаем
табл. 11.20.
Таблица 11.20
Объясняемая переменная D{Y)
Переменная
Z(-l)
D(X(-l))
Д(Г(-1))
Коэффициент
-0.638888
1.317763
-0.483722
Стандартная
ошибка
0.369218
0.538932
0.243908
/-статистика
-1.730381
2.445138
-1.983217
Р-значение
0.0868
0.0163
0.0502
Хотя формально здесь следовало бы начать исключение статистически
незначимых переменных с zt_x, необходимо учитывать уже принятое решение о
коинтегрированности рядов yt и хг Но если эти ряды действительно коинтег-
рированы, то в ЕСМ должно выполняться соотношение ах + а22 > 0.
Поскольку переменная zt_x не вошла в правую часть уравнения для Лх„ она
должна оставаться в правой части уравнения для Ау,. Если начать
исключение с переменной Лу,_15 то в оцененном редуцированном уравнении (табл.
11.21) оказывается статистически незначимым коэффициент при Axt_u что
приводит нас к уравнению Ay, = a2zt_x + wr Оценивая последнее, получаем
табл. 11.22.
Проверка гипотезы Н0: а2--\ дает табл. 11.23.

546
Часть 2. Регрессионный анализ временных рядов
Таблица 11.21
Объясняемая переменная D(Y)
Переменная
Z(-l)
D(X(-\))
Коэффициент
-1.186411
0.331411
Стандартная
ошибка
0.248876
0.210732
/-статистика
-4.767072
1.572671
Р-значение
0.0000
0.1191
Таблица 11.22
Объясняемая переменная D(Y)
Переменная
Z(-l)
Коэффициент
-1.273584
Стандартная
ошибка
0.247887
/-статистика
-5.137760
Р-значение
0.0000
Таблица 11.23
Проверка гипотезы СA) = -1
F-statistic
Chi-square
1.218077
1.218077
Probability
Probability
0.272441
0.269738
Поскольку эта гипотеза не отвергается, можно остановиться на модели
ЕСМ
где £,м = yt_x +0.006764- 1.983373х,_1.
Подстановка последнего выражения для zt_ x в уравнение для Ду, приводит
к соотношению
yt = -0.0068 + 1.983*,.! + wn
которое близко к соотношению
yt = 2xt_x +7]п
соответствующему использованному DGP.
Заметим, наконец, что последовательность wt = Ду, + £,_ x
идентифицируется по наблюдаемой ее реализации как гауссовский белый шум с оцененной
дисперсией 4.62 (использованному DGP соответствует значение 5.00), а
последовательность et - Дх, идентифицируется как гауссовский белый шум с
оцененной дисперсией 1.04 (использованному DGP соответствует значение 1.00).
Остановившись на модели
Axt = sn Ayt = -zt_{ + wt,
тем самым получили, что коррекция производится только в отношении ряда jy„
а именно — при положительных zt_l9 т.е. при

Раздел 11. Регрессионный анализ для нестационарных переменных...
547
yt_x - (-0.0068 + 1.983х,_1)> 0,
в правой части уравнения для Ду, корректирующая составляющая £,_ х
отрицательна и действует в сторону уменьшения приращения переменной уг
Напротив, при отрицательных £,_ х корректирующая составляющая действует в сторону
увеличения приращения переменной^,.
Прошлые значения переменной xt через посредство zt_ х помогают в
прогнозировании значения уп т.е. переменная xt является причиной по Грейнд-
жеру для переменной уг В то же время прошлые значения переменной yt
никак не помогают прогнозированию значения х„ так что>>, не является
причиной по Грейнджеру для хгШ
Заметим далее, что даже если в ЕСМ Cov(v„ wt) Ф 0, оценивание пары
уравнений ЕСМ как системы не повышает эффективности оценок, поскольку
в правые части обоих уравнений входят одни и те же переменные.
Расмотренный в нашем примере процесс порождения данных
DGP: xt =xt_x + sn yt = 2xt + v,
является частным случаем модели, известной как треугольная система
Филлипса (Phillips's triangular system). В общем случае (для двух рядов) эта
система имеет вид:
Уг = P*t + V„
Xt — Xf_ x -г Cf9
где (sn vt)T ~ i.i.d. N2@, S) — последовательность независимых, одинаково
распределенных случайных векторов, имеющих двумерное
нормальное распределение с нулевым математическим ожиданием
и ковариационной матрицей £. Такая последовательность
называется двумерным гауссовским белым шумом (two-dimentional
Gaussian white noise).
Если матрица S диагональная, так что Cov(sn vt) = 0, то xt является
экзогенной переменной в первом уравнении, и никаких проблем с оцениванием
коэффициента J3 в этом случае не возникает.
Если же Cov(sn vt) Ф 0, то xt не является экзогенной переменной в первом
уравнении, так как при этом Cov(xn vt) = Cov(xt_x + st, vt) Ф 0. Поэтому
получаемая в первом уравнении оценка наименьших квадратов для /? не имеет
даже асимптотически нормального распределения.
В дальнейшем еще вернемся к проблеме оценивания коинтегрирующего
вектора, а сейчас обратимся к вопросу о коинтеграции нескольких
временных рядов.

548
Часть 2. Регрессионный анализ временных рядов
Коинтегрированная система нескольких
временных рядов. Проверка на коинтегрированность
нескольких временных рядов
Пусть имеем N временных рядов у1п ..., yNn каждый из которых является
интегрированным порядка 1. Если существует такой ненулевой вектор /? = (Д,..., PN)T,
для которого
Р\Уи + • • • + P^y^t ~ ДО) — стационарный ряд,
то говорят, что эти ряды коинтегрированы (в узком смысле), такой вектор
Р называется коинтегрирующим. Если при этом
c = E(Pxyu + ...+pNyNt\
то можно говорить о долговременном положении равновесия системы
{long-run equilibrium relation) в виде:
Pxyx + ...+PNyN = c.
В каждый конкретный момент времени t существует некоторое
отклонение {deviation) системы от этого положения равновесия, характеризующееся
величиной
Ъ = Р\Уи + — +РыУт-с-
В силу сделанных предположений ряд z, является стационарным,
имеющим нулевое математическое ожидание, так что он достаточно часто
пересекает нулевой уровень, т.е. система колеблется вокруг указанного выше
положения равновесия.
При проверке на коинтегрированность нескольких рядов надо различать
несколько случаев.
1. Коинтегрирующий вектор определяется экономической теорией.
В этом случае надо просто проверить на наличие единичного корня
соответствующую линейную комбинацию
РхУи + ...+PNyNr
При этом используются те же критические значения, которые
рассчитаны на применение к отдельно взятому «сырому» ряду. Эти
значения не зависят от количества задействованных рядов N.
Пусть возможный коинтегрирующий вектор не определен заранее.
Тогда отдельно рассматриваются следующие ситуации.
2. Ряды у1п ..., yNt не имеют детерминированного тренда (точнее,
E(Aykt) = О для всех к = 1, 2,..., N).
2а. В коинтеграционное соотношение (SM) константа не
включается. В этом случае оцениваем

Раздел 11. Регрессионный анализ для нестационарных переменных...
549
SM: ylt = y2y2t + ... + yNyNt + Щ>
получаем ряд остатков
Щ=Уи-(Г2У2г + '-- + ГмУт),
оцениваем модель регрессии
Дм, = <put_l + Ci&ut_i + ... + £KAiit_K + st
с достаточным количеством запаздывающих разностей и проверяем
гипотезу Н0: #? = 0 против альтернативы Н0: #>< 0.
На этот раз критические значения для ^-статистики f зависят от
количества задействованных рядов N. При большом количестве
наблюдений можно использовать критические значения, приведенные
в (Hamilton, 1994, табл. В.9, случай 1). Однако на практике в правую
часть оцениваемого уравнения константа обычно включается.
2Ь. В коинтеграционное соотношение (SM) константа включается.
В этом случае оцениваем
SM: yu = a+ y2y2t + ... + yNyNt + ut9
опять получаем ряд остатков — теперь это будет ряд
"/ =Уи ~ (« + УгУъ + ••• + ГмУт)>
оцениваем модель регрессии
Aw, = cput_x + ^lAut_l + ... + ^Kt±ut_K + st
с достаточным количеством запаздывающих разностей и проверяем
гипотезу Н0: ср - 0 против альтернативы Н0: (р<0.
Критические значения в этом случае отличаются от случая 2а.
При большом количестве наблюдений можно использовать
критические значения, приведенные в (Hamilton, 1994, табл. В.9, случай 2).
При небольших Т критические значения вычисляются по формуле,
приведенной в (MacKinnon, 1991, табл. 1 (вариант «по trend»)) (см.
также (Patterson, 2000)).
3. Хотя бы один из рядов у1п ..., yNt имеет линейный тренд, так что
E(Aykt) Ф 0 хотя бы для одного из регрессоров.
За. В коинтеграционное соотношение включается константа. В этом
случае оцениваем
SM: ylt = a+ y2y2t + ... + yNyNt + и,.
Действуем опять как в случае 2Ь, только критические значения
другие. При большом количестве наблюдений можно использовать
критические значения, приведенные в (Hamilton, 1994, табл. В.9,

550
Часть 2. Регрессионный анализ временных рядов
случай 3). При небольших Т критические значения вычисляются
по формуле, приведенной в работе (MacKinnon, 1991, табл. 1
(вариант «with trend»)) и воспроизведенной в (Patterson, 2000).
ЗЬ. В коинтеграционное соотношение включается линейный тренд.
В этом случае оцениваем
SM: уи = а+ St+y2y2t + ... + yNyNt + ur
Действуя так же, как и ранее, используем те же таблицы, что и
в случае За, но не для N, а для (N + 1) переменных.
Включение тренда в коинтеграционное соотношение приводит к
уменьшению мощности критерия из-за необходимости оценивания
«мешающего» параметра S. Однако такой подход вполне уместен
в тех случаях, когда нет полной уверенности в том, имеется ли
ненулевой тренд хотя бы у одного из рядовуи,у2п ...,>Vr
ПРИМЕР 11.1.8
Смоделируем реализации 4 рядов У\пУгпУъпУ*п следуя процессу порождения
данных
DGP: yu =y2it +y3it +y4ft + еи\
Ун ~Уи-\ + £2п
У At = Уа,г-\ + S4n
где £lt9 s2n £3n sAt— независимые друг от друга процессы гауссовского белого
шума с дисперсиями, равными 1 для s2n s3n sAt и 2 для еи.
Графики полученных реализаций для Т= 200 приведены на рис. 11.11.
Не зная точно процесс порождения данных, нужно было бы начать с
исследования отдельных рядов. У всех 4 рядов не обнаруживается
детерминированного тренда. Проверка по критерию Дики — Фуллера дает значения
^-статистик, равные -2.18, -1.78, -0.57, -1.70 соответственно. Все 4 ряда
признаются интегрированными. Продифференцированные ряды
идентифицируются как гауссовские белые шумы, так что ряды уи, у2п у3п y4t
идентифицируются как АЯA)-ряды с единичным корнем, т.е. как интегрированные ряды
порядка 1.
Теперь можно приступить к проверке этих 4 рядов на коинтегрированность.
1. Если предполагается теоретическое долговременное соотношение между
рассматриваемыми рядами в форме
Уи=Уи+Уэ,1+У4,»
то просто проверяем на интегрированность ряд
Уу-У2,г-Уз,г-Уа,г

Раздел 11. Регрессионный анализ для нестационарных переменных...
551
-60
i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i
20 40 60 80 100 120 140 160 180 200 t
РИС. 11.11
График этого ряда (рис. 11.12) вполне похож на график
стационарного ряда. Это подтверждается проверкой по критерию Дики — Фуллера
(вычисленное значение /-статистики критерия равно -15.07). Гипотеза
некоинтегрированности рядов отвергается.
COINT
i i i i I i i i i I Г| i i | i i i i | i i i i | i i i i | i i i i | i i i i
20 40 60 80 100 120 140 160 180 200 t
РИС. 11.12
Представим теперь, что теория не предлагает нам готового коинтегрирую-
щего вектора.
2а. Оценивание статистической модели без включения в нее константы
дает результаты, приведенные в табл. 11.24.
При оценивании тестового уравнения Дики — Фуллера для ряда
остатков получаем табл. 11.25.
Вычисленное значение /-статистики критерия равно -15.17, что
намного ниже 5%-го критического значения -3.74 (Hamilton, 1994,
табл. В.9, случай 1). Гипотеза некоинтегрированности отвергается.

552
Часть 2. Регрессионный анализ временных рядов
Таблица 11.24
Объясняемая переменная Y\
Переменная
72
Y3
74
Коэффициент
0.996084
0.992550
1.002305
Стандартная
ошибка
0.009973
0.009578
0.012393
^-статистика
99.88161
103.6296
80.87922
Р-значение
0.0000
0.0000
0.0000
Таблица 11.25
Оценивание тестового уравнения Дики — Фуллера для ряда остатков
Dependent Variable: D(RESID_2A)
Переменная
RESID_2A(-\)
Коэффициент
-1.075552
Стандартная
ошибка
0.070892
^-статистика
-15.17178
Р-значение
0.0000
2Ь. Оценивание статистической модели с включением константы дает
результаты, приведенные в табл. 11.26.
Таблица 11.26
Объясняемая переменная У1
Переменная
С
72
73
74
Коэффициент
0.332183
1.002583
0.987369
0.999022
Стандартная
ошибка
0.373542
0.012369
0.011215
0.012937
^-статистика
0.889279
81.05843
88.04048
77.22129
Р-значение
0.3749
0.0000
0.0000
0.0000
При оценивании тестового уравнения Дики — Фуллера для ряда
остатков получаем табл. 11.27.
Таблица 11.27
Оценивание тестового уравнения Дики — Фуллера для ряда остатков
Dependent Variable: D(RESID_2B)
Переменная
RESID_2B(-\)
Коэффициент
-1.079049
Стандартная
ошибка
0.070861
f-статистика
-15.22764
Р-значение
0.0000
Вычисленное значение /-статистики -15.23 опять намного ниже 5%-го
критического значения -4.11 (см. (Hamilton, 1994, табл. В.9, случай 2)). Гипотеза
некоинтегрированности отвергается.

Раздел 11. Регрессионный анализ для нестационарных переменных...
553
3. Модифицируем теперь ряд уи, переходя к ряду y\t =yu + 0.75/, график
которого в сравнении с графиком ряда^, приведен на рис. 11.13.
Картина изменения всех 4 рядов показана на рис. 11.14.
[ i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i I
20 40 60 80 100 120 140 160 180 200 t
РИС. 11.13
-50
i i i i I i i i i I i i i i I i i i i I i i i i I i i i i I i i i i I i i i i
20 40 60 80 100 120 140 160 180 200 t
Рис. 11.14
За. Оцениваем статистическую модель с константой в правой части
(табл. 11.28). В этом случае график остатков имеет несколько
отличный вид (рис. 11.15).
Таблица 11.28
Объясняемая переменная Y\_STAR
Переменная
С
72
73
74
Коэффициент
11.49053
-1.333762
2.856952
0.072630
Стандартная
ошибка
2.704802
0.089561
0.081207
0.093677
/-статистика
4.248195
-14.89224
35.18115
0.775323
Р-значение
0.0000
0.0000
0.0000
0.4391

554
Часть 2. Регрессионный анализ временных рядов
RESID-3A
-15 | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i [ i i i i | ►
20 40 60 80 100 120 140 160 180 200 t
Рис. 11.15
При оценивании уравнения Дики — Фуллера для ряда остатков
получаем результаты, приведенные в табл. 11.29.
Таблица 11.29
Оценивание тестового уравнения Дики — Фуллера для ряда остатков
Переменная
RESID_3A(-\)
Коэффициент
-0.119805
Стандартная
ошибка
0.033630
/-статистика
-3.562431
Р-значение
0.0005
Вычисленное значение /-статистики -3.56 выше 5%-го
критического значения, которое здесь равно -4.16 (см. (Hamilton, 1994,
табл. В.9, случай 3)). Гипотеза некоинтегрированности не
отвергается.
ЗЬ. Включаем в правую часть тренд (табл. 11.30).
График остатков (рис. 11.16) похож на график стационарного ряда.
Это подтверждается проверкой по Дики — Фуллеру (табл. 11.31).
Объясняемая переменная Y\_STAR
Таблица 11.30
Переменная
С
@ TREND
72
УЪ
74
Коэффициент
0.304068
0.751890
1.008470
0.982658
1.001356
Стандартная
ошибка
0.390739
0.007507
0.026468
0.021830
0.015942
/-статистика
0.778187
100.1621
38.10166
45.01453
62.81247
Р-значение
0.4374
0.0000
0.0000
0.0000
0.0000

Раздел 11. Регрессионный анализ для нестационарных переменных...
555
1 RESID-3B
I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I ►
20 40 60 80 100 120 140 160 180 200 t
Рис. 11.16
Таблица 11.31
Оценивание тестового уравнения Дики — Фуллера для ряда остатков
Dependent Variable: D(RESID_3B)
Переменная
RESIDJB{-\)
Коэффициент
-1.079492
Стандартная
ошибка
0.070859
/-статистика
-15.23448
Р-значение
0.0000
Вычисленное значение /-статистики -15.234 намного ниже 5%-го
критического значения, которое здесь равно -4.49 (см. {Hamilton, 1994, табл. В.9,
случай 3)). Гипотеза некоинтегрированности отвергается.И
Последние два результата весьма важны для уточнения того, что
понимается под коинтеграцией заданных рядов.
Фактически мы обнаружили следующее. Ряды у1п у1г,уъ„ y4t
коинтегрированы в том смысле, который был определен первоначально (коинтегрированы
в узком смысле). Именно в таком виде ввели в обиход понятие коинтеграции
Энгл и Грейнджер. Ряды у\п у2п у3п y4t не являются коинтегрированными
в узком смысле. В то же время включение в правую часть статистической
модели трендовой составляющей приводит к стационарным остаткам.
Вспомним в связи с этим, что при включении тренда в правую часть
линейного регрессионного уравнения коэффициенты при объясняющих переменных
интерпретируются как коэффициенты линейной связи между переменными,
очищенными от детерминированного тренда. Последние же действительно
были коинтегрированы по построению.
Наблюдаемая ситуация известна под названием «стохастическая коинте-
грация» (stochastic cointegratiori). Оно указывает на наличие коинтеграцион-

556 Часть 2. Регрессионный анализ временных рядов
ной связи между стохастическими трендами, входящими в состав
рассматриваемых рядов. Стохастическая коинтеграция не требует согласованности
детерминированных трендовых составляющих (если таковые имеются). В этом
случае коинтегрирующий вектор аннулирует стохастический тренд, но не
обязан одновременно аннулировать и детерминированный тренд. Другими
словами, существует линейная комбинация рассматриваемых рядов, которая
образует ряд, стационарный относительно детерминированного тренда, но
необязательно стационарный.
В противоположность стохастической коинтеграции, при наличии коинте-
грации в узком смысле коинтегрирующий вектор аннулирует и
стохастический, и детерминированный тренды, т.е. существует линейная комбинация
рассматриваемых рядов, образующая стационарный ряд. В связи с этим
о коинтеграции в узком смысле говорят также как о детерминистской
коинтеграции {deterministic cointegratiori).
v Замечание 11.1.6. Как уже говорилось, при отсутствии
коинтеграции между двумя интегрированными рядами непосредственное
оценивание модели
yt = а + J3xt + ut
бессмысленно, так как получаемая оценка /3Т не является оценкой
какого-либо теоретического параметра связи между переменными
xtnyr
Если оба ряда имеют, помимо стохастического,
детерминированный тренд, то оценка (Зт все же сходится к некоторой постоянной.
Соответствующее исследование, приведенное в работе (Entorf, 1992),
показало следующее.
Пусть
DGP: xt=Jux+xt_l +£u,
где еи и £2t — некоррелированные между собой процессы белого
шума, причем /лх Ф О, /л Ф 0.
Тогда при оценивании статистической модели
SM: yt = а + /3xt + ut
оценка ат для а, вычисляемая по Т наблюдениям, при Т -> оо
расходится, а оценка /3Т для /? сходится по вероятности при Т —> оо
My
к отношению -JL-.
Мх

Раздел 11. Регрессионный анализ для нестационарных переменных... 557
Если при тех же условиях оценивать статистическую модель
SM: yt - а + /?х, + yt + un
то (при Т -> оо) ут сходится по вероятности к /jy, a f3T сходится по
распределению к некоторой случайной величине, как и в случае
ложной регрессии для случайных блужданий без сносов.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В каких ситуациях говорят о ложной (паразитной) регрессионной связи между
переменными?
2. Каковы признаки ложной регрессионной связи между нестационарными
временными рядами?
3. Что понимается под коинтегрированностью нестационарных временных рядов?
Вытекает ли из коррелированности в совпадающие моменты времени двух
процессов белого шума коинтегрированность случайных блужданий, порождаемых
этими двумя процессами?
4. Можно ли для проверки ряда остатков на стационарность использовать критерии,
применяемые для различения TS- и AS-рядов?
5. Что следует предпринять в случае обнаружения паразитной связи между
интегрированными порядка 1 переменными*, иу(?
6. Что вытекает из коинтегрированности двух временных рядов?
7. Что можно сказать о составляющих модели коррекции ошибок в случае, когда
ряды хп yt ~ 7A) коинтегрированы? Как интерпретируется модель коррекции
ошибок в таком случае?
8. Может ли VAR в разностях иметь конечный порядок, если ряды jc,, yt ~ 7A)
коинтегрированы (не коинтегрированы)?
9. Пусть ряды jc,, yt ~ 7A) коинтегрированы и wt ~ ДО). Будут ли коинтегрирован-
ными ряды jc, и yyt_k + wn уф О?
10. Пусть jc, ~ 7A). Будут ли коинтегрированными ряды jc, и xt_kl
11. Пусть ряды jc,, yt ~ 7A) и коинтегрированы. Вытекает ли из этого наличие
причинности по Грейнджеру между этими рядами?
12. В чем состоит процедура Энгла — Грейнджера построения модели коррекции
ошибок?
13. Можно ли пользоваться на первом шаге процедуры Энгла — Грейнджера
обычными регрессионными критериями? Можно ли пользоваться на втором шаге
процедуры Энгла — Грейнджера обычными регрессионными критериями? Можно
ли для проверки гипотезы некоинтегрированности рядов хп yt ~ 7A) применить
критерий Дики — Фуллера к остаткам, полученным на первом шаге процедуры
Энгла — Грейнджера?
14. Какие случаи следует различать при проверке на коинтегрированность нескольких
временных рядов?
15. В чем состоит различие между детерминистской и стохастической коинтегра-
циями? Что можно сказать об оценке наименьших квадратов углового
коэффициента в простой линейной регрессии, когда объясняемая и объясняющая
переменные не коинтегрированы?

558
Часть 2. Регрессионный анализ временных рядов
Тема 11.2
ОЦЕНИВАНИЕ КОИНТЕГРИРОВАННЫХ СИСТЕМ
ВРЕМЕННЫХ РЯДОВ
Треугольная система Филлипса.
Свойства оценок
Пусть имеем N временных рядов уи, ..., yNn каждый из которых является
интегрированным порядка 1. Если существует такой вектор /? = (Д, ..., /3N)T,
отличный от нулевого, для которого
Рхуи + ... -f j3NyNt ~ 1@) — стационарный ряд,
то ряды коинтегрированы (в узком смысле); такой вектор /? называется коин-
тегрирующим вектором. Если при этом
c = E(CxyXt + ...+fiNyNt\
то можно говорить о долговременном положении равновесия системы в виде:
Рхух + ...+ j3NyN = c.
В каждый конкретный момент времени / существует отклонение системы
от этого положения равновесия, характеризующееся величиной
В силу сделанных предположений ряд zt является стационарным,
имеющим нулевое математическое ожидание, так что он достаточно часто
пересекает нулевой уровень, т.е. система колеблется вокруг указанного выше
положения равновесия.
Положение, однако, осложняется тем, что у коинтегрированной системы
7A) рядов может быть несколько линейно независимых коинтегрирующих
векторов. Если максимальное количество линейно независимых
коинтегрирующих векторов для заданных рядов у1п ..., yNt равно г, то это число г
называется рангом коинтеграции (cointegrating rank). Для коинтегрированной
системы, состоящей из N рядов, ранг коинтеграции может принимать
значения г = 1,..., N- 1. (Формально если ряды не коинтегрированы, то г = 0. Если
же имеется г линейно независимых коинтегрирующих векторов и г = N,
то все 7V рядов стационарны.) Совокупность всех возможных
коинтегрирующих векторов для коинтегрированной системы 1A) рядов образует г-мерное
линейное векторное пространство, которое называют коинтеграционным
пространством (cointegrating space). Любой набор г линейно независимых
коинтегрирующих векторов образует базис этого пространства, и если
зафиксировать этот набор в качестве базиса, то любой коинтегрирующий вектор
является линейной комбинацией векторов, составляющих базис.

Раздел 11. Регрессионный анализ для нестационарных переменных...
559
Пусть коинтегрированная система 1A) рядов уи, ..., yNt имеет ранг коинте-
грации г и может быть представлена в форме VAR(p) — векторной
авторегрессии порядка р:
A(L)yt=H + £n
meyt = (yu,...,yNt)T;
// = (//l5...,/^)r;
A(L) = A0-AlL-...-ApLp;
A0,Al9..., Ap — матрицы размера (Nx /V);
A0 = IN (единичная матрица),
т.е.
yt=M+Alyt_l + ... +Apyt_p + st.
Тогда ранг матрицы A(\) равен rank А(\) = ги (по аналогии со случаем N=2)
существует представление этой VAR в форме ЕСМ (модели коррекции
ошибок)
/7-1
У = 1
р-\
tyNt = MN + aNizu-i + --' + aNrzrt_l + ^(yNlJAylt_j + ...^
7 = 1
где zln ..., zrt — стационарные 1@) ряды, соответствующие г линейно
независимым коинтегрирующим векторам /?A),..., Дг);
(ап,..., aNl)T,..., (а1г,..., aNr)T—линейно независимые векторы
корректирующих коэффициентов.
Такую модель коррекции ошибок можно записать в компактном виде:
Ayt=ju + apTyt_x+£xAyt_x+... + £p_xAyt-p + x+en
где £j,..., £ х — матрицы размера N х N;
а и Р — (N х г)-матрицы полного ранга г.
При этом столбцы /?A),..., /?(г) матрицы /? являются линейно независимыми
коинтегрирующими векторами, а элементы аг^ матрицы а —
коэффициентами при стационарных линейных комбинациях
ZU-\ ~ Н(\)Уг-\ >•••> Zr,t-\ = Р(г)У^\
(представляющих отклонения в момент (/ - 1) от г долговременных
соотношений между рядами уХп ...,yNt) в правых частях уравнений для Ауи,..., AyNr

560
Часть 2. Регрессионный анализ временных рядов
Представление коинтегрированной VAR в форме модели коррекции
ошибок не единственно, поскольку в качестве набора /?A), ..., /?(г) можно взять
любой базис коинтеграционного пространства. Соответственно неоднозначность
имеется и в отношении матрицы а. Один из возможных вариантов выбора
базисных коинтегрирующих векторов дается следующим представлением
системы коинтегрированных 1A) рядов.
Если ранг коинтеграции равен г, 0 < г < N, то при соответствующей
перенумерации переменных система 7A) рядов уи, ..., yNt допускает
представление (треугольная система Филлипса):
( \
Уи
=
+с
Уг+и
1 У".')
+
JrtJ
/а >
-
E Л
+
Vr+\,,
где С = (ctj) — матрица размера rx(N- г);
vt = (vip •••? vNt)T—стационарный (в широком смысле) векторный
случайный процесс с E(vt) = 0;
ряды уг+1? „ ..., ук , не коинтегрированы.
Отсюда получаем
У и ~спУг+и - — -CitN-ryN,t=Mi +vir>
Уп -спУг+1{----Сг,м-гУм,г=Мг +vrt>
так что векторы
y5A)=(l,050,...,0,-cll5...,-c1JV_r)r,
РB) ~ (У> *■> V, ..., 0, — С2\,...,— С2 дг_г ) ?
^(r)-@50,0?...,l,-crl5...,-cr^_r)r
являются линейно независимыми коинтегрируюгцими. Им соответствуют
г стационарных линейных комбинаций рядов уи, ...,yNtt
Z\,t ~ Н{\)Уг = Уи ~С\\Уг+\,( ~---~c\,N-ryN,f>
Zr, t = Р(г)Уг = Уп ~ Сг\Уг+\, t~'-~Cr, N-гУы, t •

Раздел 11. Регрессионный анализ для нестационарных переменных...
561
Если ряды vlt9..., vrt не коррелированы с рядами vr+1>/, ..., vNn то
переменные yr+itt9 ..., yNj являются экзогенными в первой подсистеме, и ее можно
оценивать методом наименьших квадратов. Полученные оценки ctj элементов
матрицы С суперсостоятельны, хотя распределение T{ctj - ctj) не стремится
к нормальному при Т —> <х>.
В случае г = 1 имеем
yu=Hi+cny2t+... + c^N_xyN^+vlt,
условное распределение оценок наименьших квадратов для коэффициентов
(при фиксированных значениях у2%п ..., yNtt) является асимптотически
нормальным, и это обеспечивает возможность использования стандартных
процедур, основанных на t- и F-статистиках (конечно, в асимптотическом
плане), с коррекцией стандартных ошибок коэффициентов в случае, если
ряд vu не является белым шумом. Коррекция, как и в разд. 10, состоит в
замене стандартной оценки дисперсии ряда vu оценкой долговременной
дисперсии этого ряда.
Значения ctj можно использовать для построения г линейно независимых
(N х 1)-векторов — оценок коинтегрирующих векторов /?A),..., /?(г):
^A)=(l,0,0,...,0,-cn,...,-c1A,_r)r,
Дг)=@,0,0,...,1,-сг1,...,-сг^_г)г.
Используя построенные оценки коинтегрирующих векторов /?A), ..., /?(г),
получаем оценки искомых стационарных линейных комбинаций в виде:
Zl,t-\ =/'(l)>V-l» •••> Zr,t-l = У{г)У1-\'
Теперь можно вместо указанной выше истинной ЕСМ оценить систему
Ду, = // + azt_x + £ Ду,_, +... + CP-Ayt-P+i + £t >
в которой
ZU-1
zt-i=\ '• •
При этом оценки наименьших квадратов для коэффициентов последней
модели имеют те же асимптотические распределения, что и при
оценивании истинной ЕСМ.
Заметим: если имеем дело со стохастической (а не с детерминистской)
коинтеграцией, то для достижения стационарности рядов zln ..., zrt прихо-

562
Часть 2. Регрессионный анализ временных рядов
дится в «остационаривающую» линейную комбинацию рядов уш ..., yNt
включать еще и дополнительную трендовую составляющую, так что в этом
случае речь идет о существовании стационарных линейных комбинаций
(N + 1) переменных у1п ..., yNt и t9 в которых не все коэффициенты равны
нулю.
Если ранг матрицы ^4A) равен г, то существует г таких стационарных
линейных комбинаций, в которых не все коэффициенты равны нулю,
а именно
Рг\Уи+ — + РмУм+Рг,*+\*
с линейно независимыми ((N+ 1) х 1)-векторами
P(i) =(Mi> ••> Pin9 P\,n+\) »
P{r) ~\PrV •••» /v#> Pr,N+\) •
При этом последние векторы интерпретируются как линейно
независимые коинтегрирующие векторы в системе стохастически коинтегрирован-
ных рядов.
Возможность наличия нескольких линейно независимых коинтегрирую-
щих векторов значительно усложняет задачу построения модели коррекции
ошибок (ЕСМ), поскольку, как минимум, приходится по реальным
статистическим данным оценивать количество таких векторов. Само по себе решение
о коинтегрированности нескольких 1A) рядов в результате использования
рассмотренных выше процедур Дики — Фуллера отнюдь не дает нам
никакой информации о ранге коинтеграции г, для этого требуются другие
статистические процедуры.
Однако если не известен ранг коинтеграции, то теряется смысл
оценивания уравнения регрессии в уровнях
yu=c + y2y2t+... + yNyNt+ut
(или уи=с + y2y2t +... + yNyNt + yN+lt + щ).
Действительно, если г > 1, то вектор A, -уъ ..., -yN)T (или вектор A, -у2, ...,
-yN, -Ун+iO) является оценкой всего лишь одной из возможных линейных
комбинаций г линейно независимых коинтегрирующих векторов, которая
может и не иметь разумной экономической интерпретации.
Но даже если ранг коинтеграции г по каким-то причинам известен, при г > 1
возникает другая проблема. В рассмотренном выше представлении Филлипса
линейно независимые коинтегрирующие векторы имели вид:

Раздел П. Регрессионный анализ для нестационарных переменных...
563
Д1)=A,0,0,...,0,-с11,...,-с1>А,_г)г,
^r)=@,0,0,...,l,-crl,...,-crJV_r)r.
Любая линейная комбинация этих векторов (не все коэффициенты
которой равны нулю) также является коинтегрирующим вектором, а совокупность
всех возможных линейных комбинаций этих векторов образует линейное
векторное пространство размерности г. Любой вектор из этого пространства
(не все коэффициенты которого равны нулю) является коинтегрирующим
вектором для уи, ..., yNn а векторы /?A), ..., /?(г) образуют всего лишь один из
возможных базисов этого пространства. В практических задачах на первый
план (наряду с определением ранга коинтеграции) выходит идентификация
коинтегрирующих векторов {identification of the cointegrating vectors),
приводящих к долговременным соотношениям, имеющим разумную
экономическую интерпретацию.
В настоящее время наиболее распространенной является методика
определения ранга коинтеграции, предложенная Иохансеном в {Johansen, 1988).
Однако точное описание этой процедуры требует более детального
рассмотрения соответствующего математического аппарата. Мы рассмотрим эту
процедуру при изложении темы 11.4, а сейчас сосредоточимся на случае,
когда г = 1, т.е. (с точностью до пропорциональности) имеется всего один коин-
тегрирующий вектор.
Оценивание модели парной регрессии
для двух рядов, имеющих стохастический
и детерминированный тренды
Наиболее простой является ситуация, когда N = 2. В этом случае если
рассматриваемые ряды уи и y2t коинтегрированы, то ранг коинтеграции может
быть равным только 1. Как отмечалось ранее, при построении модели
коррекции ошибок на первом шаге процедуры Энгла — Грейнджера, вообще
говоря, нельзя пользоваться обычными регрессионными критериями (даже
в асимптотическом плане). И причина этого в том, что получаемые на первом
шаге оценки и статистики в общем случае имеют нестандартные
асимптотические распределения.
Об одном исключении из общего случая уже говорилось выше — это
треугольная система Филлипса
yt = Ext + v„
где stYLvt — не коррелированные между собой процессы белого шума.

564
Часть 2. Регрессионный анализ временных рядов
Вторым исключением является ситуация, исследованная в работе Веста
(West, 1988):
yt = a + jBxt + un
где xt ~ 7A), E(Axt) = /л * О (так что ряд xt содержит и стохастический, и
детерминированный тренды);
ut ~ ДО) — стационарный ряд с нулевым средним, необязательно
являющийся процессом белого шума.
В работе Веста доказывается асимптотическая нормальность
соответствующим образом нормированной оценки наименьших квадратов для вектора
(а, Р)Т. Если ряд ut не является процессом белого шума, то для применения
этого результата необходимо скорректировать значения /-статистик,
вычисляемых по стандартным формулам, соответствующим предположениям
классической линейной модели регрессии.
В знаменателях обычных /-статистик для параметров а и /? стоят оценки
стандартных ошибок оценок аТ и J3T этих параметров, а именно:
S^(XTXyx\ — дляаг, SJ(XTX)£ — для/?г,
где X — (Г х 2)-матрица значений объясняющих переменных A и х,) в Г
наблюдениях;
S2 — несмещенная оценка дисперсии ut в случае, когда ut ~ U.d,
1 т
Поскольку у нас не предполагается, что ut ~ U.d., для сохранения
/-распределения (точнее, распределения N@, 1)) /-статистик (хотя бы при больших
7), требуется замена S2 на другую подходящую величину.
Мы предположили, что ряд ut стационарный и имеет нулевое
математическое ожидание. Пусть yh = Cov(un ut+h). Вест показал, что подходящей
является замена S2 долговременной дисперсией ряда ип
Я2 = МтТ-Гаг
f щ +... + ит^
\\mTE
Г->оо
/ Л2
которая для стационарного ряда вычисляется по формуле
00
я2 = 2>„,
h = -oo
если ХЫ<0°-
h = -oo

Раздел 11. Регрессионный анализ для нестационарных переменных...
565
Проблема, однако, в том, что значение Л2 не известно, и его приходится
оценивать по имеющимся наблюдениям. Для этого, в свою очередь,
следовало бы оценить бесконечное множество автоковариаций yh9 h = О, ± 1, ± 2, ...,
что, конечно, невозможно. Из-за этого, в конечном счете, приходится так или
иначе делать более определенные предположения о характере автокоррели-
рованности ряда ип что дало бы возможность ограничиться при оценивании
Л2 оценкой лишь конечного числа автоковариаций yh = Cov(un ut+h). В
процессе такого оценивания приходится учитывать и то, что автоковариаций yh
с возрастанием h оцениваются все менее точно, поэтому желательно
регулировать (уменьшать) влияние yh на оценку долговременной дисперсии Л2 при
возрастании И.
Если исходить из того, что случайный процесс ut можно представить в виде
процесса МА(#) конечного порядка q, то тогда yh = О для | h \ > q, и можно
не получать оценок yh для таких h. Это вместе с предшествующими
соображениями приводит к оценке
Л2=у0+2^
1 Т
где yh=— X*W-i —оценки автоковариаций yh.
При этом можно показать (см., например, (Hamilton, 1994, р. 513), что
выбор q = 0(TV5) обеспечивает состоятельность такой оценки для Л2 (оценка
Ньюи — Веста).
В рамках пакета Е Views реализация такого метода производится без труда.
Следует просто при спецификации уравнения заказать опцию: «вычисление
стандартных ошибок методом Newey — West» (отметим, однако, что в этой
опции используется несколько отличающаяся от приведенной оценка,
реализующая еще и поправку на возможную гетероскедастичность ряда).
Если предположить, что динамика ряда ut хорошо аппроксимируется
моделью авторегрессии AR(p) с конечным/?,
ut = axut_x + a2ut_2 +... + aput_p + st,
где st — инновационный процесс белого шума с D(st) = а2, тогда
(\-ах-а2-...-арJ
Поэтому в такой ситуации в качестве оценки для Л2 естественно взять
величину
-ах-а2-...-ар)
а + \
П

566
Часть 2. Регрессионный анализ временных рядов
где о,, а2,..., ар — оценки наименьших квадратов для ау, а2,..., ар;
1 Т
61 =
1 -Р t = p + \
st — остатки при оценивании модели авторегрессии для ряда иг
В любом случае замена S2 на Я2 равносильна умножению значения
/-статистики, полученного обычным путем, на
Л
ПРИМЕР 11.2.1
Смоделируем систему
DGP: yt = 2xt + ип
xt = 1 + xt_x + v„
где ut = 0.4ut_x + 0.2ut_2 + £t — стационарный ARB) ряд;
€nvt — гауссовские процессы белого шума, коррелированные в
совпадающие моменты времени: Cov{sn vt) = 0.8.
Поведение смоделированных реализаций показано на рис. 11.17.
-50 |iiii|i i м | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | ►
10 20 30 40 50 60 70 80 90 100 t
РИС. 11.17
Оценивание статистической модели SM: yt - а + J3xt + ut обычным
методом наименьших квадратов дает результаты, представленные в табл. 11.32.
Если ориентироваться на приведенные значения статистик, то оба
параметра оказываются статистически значимыми, хотя в DGP константа
в уравнении для yt отсутствует. Ряд остатков (рис. 11.18)
идентифицируется по коррелограмме как ARB). Оцененная ARB) модель приведена
в табл. 11.33.

Раздел 11. Регрессионный анализ для нестационарных переменных...
567
Таблица 11.32
Объясняемая переменная У
Переменная
С
X
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
Коэффициент
-0.398071
2.031938
0.998757
0.998745
1.071308
112.4748
-147.7718
1.080957
Стандартная
ошибка
0.172093
0.007241
/-статистика
2.313111
280.6336
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob. (F-statistic)
Р-значение
0.0228
0.0000
37.39809
30.23477
2.995436
3.047539
78755.23
0.000000
RESIDS
10 20 30 40 50 60 70 80 90 100 t
Рис. 11.18
Объясняемая переменная RESIDS
Таблица 11.33
Переменная
1 RESIDS(-\)
1 RESIDS(-2)
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Коэффициент
0.363522
0.205074
0.240364
0.232451
0.941891
85.16727
Стандартная
ошибка
0.100494
0.100427
/-статистика
3.617344
2.042024
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
Р-значение
0.0005
0.0439
-0.008547
1.075097
2.738343
2.791098

568
Часть 2. Регрессионный анализ временных рядов
Отсюда находим оценку для Л:
Х= °-941891 =2183
1-0.363522-0.205074 ' '
S L071 ЛЛП1
так что -г = = 0.491.
Л 2.183
Это приводит к следующим скорректированным значениям /-статистик
и Р-значений:
ta\ -2.313111 (Р-значение = 0.0228) -> -1.135738 (Р-значение = 0.2588);
tp: 280.6336 (Р-значение = 0.0000) -> 137.791098 (Р-значение = 0.0000).
При использовании скорректированных значений постоянная в
оцениваемом уравнении становится статистически незначимой. ■
Снимем теперь ограничение N =2 и будем интересоваться существующей
и единственной (по предположению) долговременной связью между TV
нестационарными 7A) рядами уи, ...,yNr
Оценивание статистической модели
приводит в этом случае к суперсостоятельным оценкам независимо от того,
будут ли регрессоры иметь линейный тренд, если только в правую часть
уравнения не включается тренд. Однако, как было отмечено выше,
повышенная скорость сходимости по вероятности оценок коэффициентов к истинным
значениям этих коэффициентов вовсе не предотвращает смещения оценок
при небольшой длине ряда наблюдений. Многие авторы на основании
результатов моделирования отмечали весьма значительное смещение оценок
коэффициентов при небольших Т.
Как и в случае TV = 2, особое место в этом отношении занимает
треугольная система Филлипса
Ум=с + ГгУп+- + УкУт+£\п
У It ~ Уи-\ + 82t>
yNt = Уы,1-\ +£Nf>
где st = (sln €2t9 ..., sNt)T — TV-мерный гауссовский белый шум, т.е.
sl9 s2-> ... — последовательность независимых, одинаково
распределенных случайных векторов, имеющих TV-мерное нормальное рас-

Раздел 11. Регрессионный анализ для нестационарных переменных...
569
пределение с нулевым математическим ожиданием и
ковариационной матрицей I = (а^).
Случайные величины £2п ..., sNt могут быть коррелированными между собой,
но еи не коррелирована ни с одной из них (так что <7Xj = О для всех у = 2,..., N).
В этом случае регрессоры j/2„ ..., yNt не коинтегрированы, и /?= A, -у29..., -у^У—
единственный коинтегрирующий вектор. Условное распределение
(с-с, у2-у2,..., Ун-Гн)Т\{Уъ>—>Уш> t = l,...,T}
является ТУ-мерным нормальным, с нулевым средним, так что F-критерии для
проверки линейных гипотез о значениях коэффициентов с, у2, ..., yN имеют
точные F-распределения, а f-критерии — точные /-распределения.
В общей ситуации пусть
Уи=с + Г2У2г+--- + ГмУт+ии>
yNt ~yN,t-\ +UNf>
где ut = (uln u2t, ..., uNt)T — TV-мерный гауссовский стационарный векторный
ряд (теперь уже необязательно Л^-мерный гауссовский белый шум).
Ряды и2п ..., uNt могут быть коррелированнными между собой, но ряд ии
не коррелирован с остальными рядами, так что Cov(uln uks) = О при к * 1 для
всех /, s. Последнее условие обеспечивает экзогенность переменных в правой
части первого уравнения треугольной системы. (Гауссовость ряда ut означает,
что совместное распределение значений ряда в любые Г различных моментов
времени является ЛТ-мерным нормальным распределением.)
В такой ситуации для проверки линейных гипотез о коэффициентах
можно использовать скорректированные F- и /-статистики с асимптотически
оправданными F- и /-распределениями, предварительно заменив обычную
оценку S2 для дисперсии ии на состоятельную оценку Я2 «долговременной
дисперсии» Л2 ряда ии. Последнее соответствует умножению обычной F-
S2 S
статистики на -гг и умножению обычной /-статистики на —.
Я Я
Таким образом, проблема нестандартных распределений, по существу,
связана с возможным нарушением экзогенности регрессоров j/2„ ...9yNt в
первом уравнении треугольной системы.
Сток и Уотсон (Stock, Watson, 1993) и Сайконнен (Saikonnen, 1991)
предложили процедуру устранения нежелательной корреляции, которая состоит
в пополнении правой части первого уравнения треугольной системы
запаздывающими (lags) и опережающими (leads) значениями приращений per-

570
Часть 2. Регрессионный анализ временных рядов
рессоров. (Отсюда название метода — leads and lags .) Именно вместо
первого уравнения системы оценивается его расширенный вариант
р
Уи=с + Г2Уь+--- + ГмУт + Y,@2j АУ2,^+••• + %■ AyN,t-j) + ut •
J=-p
Если значение р выбрано правильно (достаточно велико), то
статистические выводы в отношении у2, ..., yN можно проводить обычным образом
(конечно, имея в виду асимптотическую оправданность соответствующих
статистических процедур), но опять с использованием скорректированных
значений обычных t- и F-статистик, если ut не является белым шумом.
Предложенная процедура остается асимптотически оправданной и в
случае, когда все или некоторые из рядов у2п ..., yNt имеют
детерминированный тренд.
Более того, дополнительных проблем не возникает и в случае, когда в
правую часть первого уравнения треугольной системы добавляется линейный
тренд и проверяется гипотеза о его значимости. Это позволяет проводить
раздельную проверку гипотез о том, что:
а) уи - y2y2t -... - yNyNt не имеет детерминированного тренда;
б) Уи ~УгУн -----ГмУмг ~ стационарный ряд.
Заметим, что а) может выполняться при невыполненном б), если
детерминированный тренд устраняется, а стохастический тренд остается.
ПРИМЕР 11.2.2
DGP: yt = 5+zt + un
где zx = 0;
ut = vt + 0.25v,_! + 0.25v,+ 1 +0.1v,_2 +0.1v,+2 +0.1^;
snvt — не коррелированные между собой гауссовские процессы белого
шума.
Здесь случайная величина ut коррелирована с v„ v,_l9 vf+1, v,_2, v/+2, так
что непосредственное использование стандартных статистических выводов
неоправданно.
Обратимся к смоделированной реализации этого DGP (рис. 11.19 — 100
наблюдений). Оба ряда^ и zt идентифицируются по 100 наблюдениям как
интегрированные ряды первого порядка. Рассмотрим эту пару в рамках
треугольной системы Филлипса. Оценивание методом наименьших квадратов
уравнения yt = a + fizt + rjt дает результат, представленный в табл. 11.34.
Этот метод известен также как DOLS (динамический OLS).

Раздел 11. Регрессионный анализ для нестационарных переменных...
571
12 4
-4 | i'i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | ►
10 20 30 40 50 60 70 80 90 100 t
Рис. 11.19
Объясняющая переменная Y
Таблица 11.34
Переменная
С
Z
Коэффициент
4.851262
1.088870
Стандартная
ошибка
0.133152
0.047570
/-статистика
36.43410
22.88977
Р-значение
0.0000
0.0000
Проверять гипотезу Я0: /? = 1, используя обычный /-критерий, нельзя, если
Согг(т]п Azs) Ф 0 хотя бы для одной пары значений /, s. Для выяснения
вопроса о наличии или об отсутствии такой коррелированности обратимся к кросс-
коррелограмме, построенной для пары рядов еп Azn где et — ряд остатков,
полученный при оценивании уравнения^, = а + /?z, + rjr
Included observations: 96
Correlations are asymptotically consistent approximations
e, AZ(-i)
e, AZ(+i)
lag
lead
*********
*********
0
1
2
3
4
5
6
7
8
9
0
0.9017
-0.0217
-0.0956
0.0064
-0.0510
-0.0824
-0.0171
-0.1858
-0.0292
0.0833
0.0125
0.9017
0.0830
-0.0413
0.0341
0.0118
-0.0228
0.0150
-0.1579
-0.0272
0.0701
0.0216

572
Часть 2. Регрессионный анализ временных рядов
Левый график показывает поведение кросс-корреляций Corr(en Azt_t) для
/ = 0, 1, 2, ...; значения этих кросс-корреляций приведены в графе «lag». Правый
график показывает поведение кросс-корреляций Corr(en Azt+i) для i = 0, 1,2,...;
значения этих кросс-корреляций приведены в графе «lead».
На основании этой кросс-коррелограммы можно предполагать наличие
ненулевых кросс-корреляций в DGP до 7-го порядка. В соответствии с этим
добавим в правую часть оцененного ранее уравнения запаздывающие и
опережающие разности переменной zt вплоть до 7-го порядка (табл. 11.35).
Таблица 11.35
Объясняемая переменная У
Переменная
С
1 Z
D(Z)
D(Z(-\))
D(Z(-2))
Z)(Z(-3))
£>(Z(-4))
D(Z(-5))
D(Z(-6))
D(Z(-7))
D(Z(\))
D(Z(T>)
Z)(ZC))
Z)(ZD))
Z)(ZE))
D(ZF))
D(Z(J))
Коэффициент
4.987362
1.000689
1.006216
0.237875
0.089302
-0.008934
-0.002997
-0.011646
-0.010012
-0.003586
0.262537
0.116863
-0.010921
0.003903
0.021536
-0.008452
0.002945
Стандартная
ошибка
0.020874
0.007818
0.013125
0.012764
0.012810
0.012368
0.012391
0.012179
0.011925
0.011634
0.013373
0.013365
0.013219
0.013276
0.013232
0.012699
0.012199
/-статистика
238.9236
127.9955
76.66298
18.63643
6.971105
-0.722323
-0.241901
-0.956245
-0.839615
-0.308269
19.63226
8.744236
-0.826184
0.294017
1.627644
-0.665583
0.241376
Р-значение
0.0000
0.0000
0.0000
0.0000
0.0000
0.4726
0.8096
0.3423
0.4041
0.7588
0.0000
0.0000
0.4116
0.7696
0.1082
0.5079
0.8100
Ряд остатков не обнаруживает автокоррелированности: Р-значения
критерия Бройша — Годфри равны 0.252 (при глубине запаздываний К = 1) и 0.427
(К = 2). Поэтому можно использовать для проверки гипотезы Н0: J3= 1
обычную /-статистику без коррекции стандартной ошибки; ее значение равно:
(.Ш06»-1
0.007818
так что гипотеза Я0: /?= 1 не отвергается. ■

Раздел 11. Регрессионный анализ для нестационарных переменных...
573
ПРИМЕР 11.2.2 (продолжение)
Изменим теперь DGP так, чтобы слева и справа в первом уравнении стояли
1A) ряды с линейным трендом.
DGP: yt = 5+xt +un
xt = 1 +xt_x + v„
где хх = О, а ип vt — те же, что и ранее.
Смоделированная реализация этого DGP приведена на рис. 11.20.
-20 Iiii i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i i i i | i I i i | ►
10 20 30 40 50 60 70 80 90 100 t
РИС. 11.20
Результаты оценивания уравнения регрессии yt = а + J3xt + t]t приведены
в табл. 11.36.
Таблица 11.36
Объясняемая переменная Y
Переменная
С
X
Коэффициент
5.172117
0.997147
Стандартная
ошибка
0.201812
0.003444
/-статистика
25.62837
289.5306
/'-значение
0.0000
0.0000
Кросс-коррелограмма ряда остатков от оцененного уравнения и
приращений ряда xt имеет вид, аналогичный предыдущей коррелограмме. Поэтому
опять переходим к оцениванию расширенного уравнения, дополненного
7 запаздывающими и 7 опережающими разностями. Результаты оценивания
приведены в табл. 11.37.

574
Часть 2. Регрессионный анализ временных рядов
Таблица 11.37
Объясняемая переменная У
Переменная
С
X
D(X)
D(X(-\))
D(X(-2))
ОЩ-3))
ОЩ-4))
D(X(-5))
D(X(-6))
D(X(-7))
ад1))
D(XB))
ОЩЗ))
D(XD))
D(XE))
D(XF))
D{XA))
Коэффициент
3.224675
1.000621
1.009585
0.241440
0.093472
-0.004479
0.001328
-0.007856
-0.006808
-0.001175
0.266271
0.120232
-0.007953
0.006576
0.023956
-0.007153
0.003367
Стандартная
ошибка
0.098061
0.000520
0.012922
0.012760
0.012938
0.012656
0.012648
0.012272
0.011934
0.011513
0.013016
0.012948
0.012873
0.012866
0.012814
0.012294
0.011821
/-статистика
32.88423
1923.269
78.12803
18.92225
7.224562
-0.353864
0.104986
-0.640121
-0.570501
-0.102067
20.45699
9.286042
-0.617748
0.511164
1.869580
-0.581813
0.284813
Р-значение
0.0000
0.0000
0.0000
0.0000
0.0000
0.7245
0.9167
0.5242
0.5702
0.9190
0.0000
0.0000
0.5388
0.6109
0.0658
0.5626
0.7767
В ряде остатков и здесь не обнаруживается автокоррелированности, так
что можно использовать для проверки гипотезы Н0: J3= 1 обычную
/-статистику без коррекции стандартной ошибки. Ее значение равно:
„Щ0Ю1-1
0.00520
гипотеза Н0: J3= 1 не отвергается.
Включим в правую часть оцениваемого уравнения еще и тренд (табл. 11.38).
Таблица 11.38
Объясняемая переменная У
Переменная
С
@TREND
X
Коэффициент
3.223725
-0.000317
1.000938
Стандартная
ошибка
0.101508
0.007802
0.007798
f-статистика
31.758480
-0.040686
128.3544
Р-значение
0.0000
0.9677
0.0000

Раздел 11. Регрессионный анализ для нестационарных переменных...
575
Окончание табл. 11.38
Переменная
D(X)
D(X(-\))
D(X(-2))
D(X(-3))
ОЩ-4))
D(X(-S))
D(X(-6))
D(X(rl))
D(X(\))
D(XB))
D(XQ))
D(XD))
D(XE))
D(XF))
D(XG))
Коэффициент
1.009461
0.241345
0.093380
-0.004552
0.001255
-0.007941
-0.006888
-0.001256
0.266438
0.120397
-0.007809
0.006723
0.024098
-0.007035
0.003469
Стандартная
ошибка
0.013372
0.013061
0.013231
0.012877
0.012867
0.012541
0.012181
0.011767
0.013736
0.013657
0.013441
0.013451
0.013370
0.012719
0.012172
/-статистика
75.49241
18.47841
7.057897
-0.353495
0.097531
-0.633231
-0.565473
-0.106726
19.397180
8.815884
-0.58098
0.499805
1.802394
-0.553156
0.285016
Р-значение
0.0000
0.0000
0.0000
0.7248
0.9226
0.5287
0.5736
0.9153
0.0000
0.0000
0.5632
0.6189
0.0760
0.5820
0.7765
Гипотеза Н0: /3= 1 не отвергается и для переменных, очищенных от
тренда. Коэффициент при трендовой переменной статистически незначим.
Полученные результаты указывают на то, что мы имеем дело с детерминистской
коинтеграцией. ■
ПРИМЕР 11.2.3
Рассмотрим следующий DGP:
Wt = 5 +1 + rwn
Vt = 1 +t + 0.5rwt + 0.ln2n
где rwt = rwt_x + 0.5иЗ, — случайное блуждание без сноса;
п2п riit — некоррелированные гауссовские процессы белого шума с
единичной дисперсией.
Смоделированная реализация показана на рис. 11.21.
Оцениваем статистическую модель Vt - a + j3Wt + r/t (табл. 11.39).
Ряд остатков (рис. 11.22) идентифицируется как интегрированный
(статистика Дики — Фуллера равна -2.22 при 5%-м критическом значении -3.46),
так что ряды Vt и Wt не являются детерминистски коинтегрированными.
Близость к 1 оценки коэффициента /3 соответствует равенству угловых коэф-

576
Часть 2. Регрессионный анализ временных рядов
Объясняемая переменная V
Таблица 11.39
Переменная
С
W
Durbin-Watson stat
Коэффициент
-2.657128
1.021898
0.290480
Стандартная
ошибка
0.325116
0.011165
^-статистика
-8.172855
91.52908
Prob(F-statistic)
Р-значение
0.0000
0.0000
0.000000
RESID V W
10 15 20 25 30 35 40 45 50 t
Рис. 11.22
фициентов детерминированных трендов, входящих в состав рядов Vt и Wt.
Ряд (Vt - Wt) не имеет выраженного детерминированного тренда, и его
график отличается от ломаной, представленной на рис. 11.22, практически
только сдвигом.
Добавим в правую часть оцениваемого уравнения трендовую
составляющую (табл. 11.40).

Раздел П. Регрессионный анализ для нестационарных переменных...
577
Таблица 11.40
Объясняемая переменная V
Переменная
С
@TREND
W
Durbin-Watson stat
Коэффициент
-1.493506
0.503277
0.496897
2.275079
Стандартная
ошибка
0.035792
0.007131
0.007519
^-статистика
-41.72787
70.57274
66.08810
Proh(F-statistic)
Р-значение
0.0000
0.0000
0.0000
0.000000
RESID V W TREND
0.2 4
0.1 -\
-0.1
-0.2
т-ггг
5
ч
10
1 I • ■ ' ' I
15 20
Т
25
i I i i i i I i i м I i i i i I i i i i | ►
30 35 40 45 50 t
Рис. 11.23
Теперь ряд остатков (рис. 11.23) идентифицируется как стационарный
(статистика Дики — Фуллера равна -7.09). Кросс-коррелограмма ряда
остатков и приращений ряда Wt имеет вид:
е, W_DIF(-i)
е, W_DIF(+i)
lag
lead
0
1
2
3
4
5
6
7
8
9
10
0.0353
-0.0237
-0.0846
0.0052
-0.0776
0.1352
0.1986
0.1093
-0.1751
-0.2456
0.1177
0.0353
0.1217
0.0115
-0.1083
0.1174
0.1018
0.0347
0.1669
0.0614
-0.3565
-0.0421
Она указывает на то, что здесь для пополнения оцениваемого уравнения
достаточно ограничиться включением в правую часть 9 запаздывающих и
опережающих разностей ряда Wt.

578
Часть 2. Регрессионный анализ временных рядов
Оценивая пополненное уравнение, получаем новые значения
коэффициентов при тренде и Wt (табл. 11.41).
При этом гипотеза гауссовского белого шума для ряда остатков не
отвергается. Это означает, что здесь имеем дело со стохастической коинтеграцией.
В рамках расширенной модели не отвергается гипотеза о равенстве 0.5
коэффициентов при тренде и Wt.
Объясняемая переменная V
Таблица 11.41
Переменная
@TREND
W
Коэффициент
0.497313
0.505495
Стандартная
ошибка
0.023984
0.025512
/-статистика
20.73533
19.81437
Р-значение
0.0000
0.0000
График ряда Vt - 0.5/ - 0.5Wt приведен на рис. 11.24, и этот ряд
идентифицируется как стационарный.
Подведем итог. Ряд Vt - Wt не имеет выраженного детерминированного
тренда, но имеет стохастический тренд. Ряд Vt - 0.5 Wt (график этого ряда
представлен на рис. 11.25) имеет выраженный линейный тренд, но не имеет
стохастического тренда.
-8 11111111111111111111111111111111111111111111111111 ►
5 10 15 20 25 30 35 40 45 50 t
РИС. 11.24
5 10 15 20 25 30 35 40 45 50 t
Рис. 11.25
Наконец, ряд Vt - 0.5/ - 0.5 JF, идентифицируется как стационарный, со
средним значением -1.493 и стандартным отклонением 0.104. И это находится
в полном соответствии с процессом порождения данных, который использовали
при моделировании реализаций. Действительно, в соответствии с этим DGP
Vt-0.5t-0Wt=(l + t + 0.5nvt+0An2t)-0.5t-0.5E + t + nvt) =
= -1.5 + 0.1л2,.И

Раздел П. Регрессионный анализ для нестационарных переменных...
579
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется рангом коинтеграции? Что называется коинтеграционным
пространством?
2. Пусть коинтегрированная система 1A) рядов уи, ..., yNt имеет ранг коинтеграции г
и может быть представлена в форме VAR(p). Как выглядит в этом случае модель
коррекции ошибок для этой системы? Единственно ли представление указанной
системы в форме модели коррекции ошибок?
3. Что представляет собой треугольная система Филлипса как представление коин-
тегрированной системы 1A) рядов? Как используется эта система для получения
оцененной модели коррекции ошибок?
4. Как производится оценивание статистической модели
Уи=с + Г2У2г+-- + ГмУм+иг
при наличии единственной долговременной связи между N нестационарными 1A)
рядами уи, ...,yNt (треугольная система Филлипса, метод leads and lags)?
Тема 11.3
ОЦЕНИВАНИЕ РАНГА КОИНТЕГРАЦИИ
И МОДЕЛИ КОРРЕКЦИИ ОШИБОК МЕТОДОМ ЙОХАНСЕНА
Оценивание ранга коинтеграции
Пусть 1A) ряды уи,..., yNt в совокупности образуют векторный ряд
У( = (Уш->УтУ>
который следует модели векторной авторегрессии VAR(p)
A(L)yt=ju + sn
meA(L) = A0-AlL-...-ApLP;
А0, Al9 ...,Ap — матрицы размера (Nx N);
А0 = IN (единичная матрица),
т.е.
yt = ju +Axyt_x + ... +Apyt_p + er
Путем алгебраических преобразований эту модель можно представить
также в виде:
ДУ, = М + СоУг-i + САУг-i +••• + Cp-iAyt-P+i + Ъ >
ще£0=А1 + ...+Ap-IN,
Ck = -(Ak+l + ...+Ap), £=1,2,...,/?-!.

580
Часть 2. Регрессионный анализ временных рядов
Заметим, что
&=Al+...+Ap-IN = A(l)9
так что rank <^0 = rank А{\).
Как было отмечено выше, если ряды ylt9 ..., yNt коинтегрированы, то
матрица А{\) имеет пониженный ранг (rank А{\) < N). Этот же пониженный ранг
в данном случае будет иметь и матрица <£>. В общем случае, ранг матрицы £,
может принимать значения г = rank <^0 = 0, 1,..., N:
• значения г = 1, ..., N - 1 соответствуют коинтегрированной VAR (ряды
Уи> ->Ут ~ ДО коинтегрированы);
• если г = 0, то ряды уи,..., jy^, we коинтегрированы;
• если г = N, то любой TV-мерный вектор является коинтегрирующим,
так что коинтегрирующими будут, например, векторы A, 0, ..., 0)г,
(О, 1, ..., 0)г, ..., (О, 0, ..., 1)Т. Но это означает, что все ряды уш ..., yNt
являются стационарными.
Ранг матрицы <£>, г = rank £J>, обычно называют рангом коинтеграции
рассматриваемой системы рядов уи,..., ^r независимо от того, имеет ли место
действительная коинтеграция этих рядов.
Выяснение ранга коинтеграции является ключевым моментом в
построении ЕСМ — модели коррекции ошибок по наблюдаемым статистическим
данным. Один из возможных путей решения этой задачи был предложен
Иохансеном (Johansen, 1988; 1991). Изложение этого метода требует перехода
к более высокому математическому уровню. Поэтому, не выходя слишком
далеко за принятую планку строгости и детальности изложения, дадим здесь
только самое общее представление об этом методе.
Как уже говорилось, если коинтегрированная система 7A) рядов yln -..9yNt
может быть представлена в форме VAR с rank ,4A) = г, то существует
соответствующее представление VAR в форме ЕСМ. Исходя из этого Иохансен
в качестве отправной точки берет представление1
Лу, = и + СоУг-х + & АУм + • • • + Cp-Ayt-p+i + £t
с матрицей
Со = (*Р\
где а и р — (N х г)-матрицы полного ранга г.
При этом столбцы /?A),..., /?(г) матрицы J3 являются линейно независимыми
коинтегрирующими векторами, а элементы матрицы а — коэффициентами
при стационарных линейных комбинациях
ZU-\ - РA)Л-1» '••' Zr,t-\= Р(г)У^\
В данном учебнике мы ограничимся системами 7A) рядов. Иохансен рассматривал также
системы, включающие ряды типа 1B).

Раздел 11. Регрессионный анализ для нестационарных переменных...
581
(представляющих отклонения от г долговременных соотношений между
рядами yU9 ...9yNt в правых частях уравнений для AyU9 ..., AyNt).
В процедуре Йохансена предполагается, что st — TV-мерный гауссовский
белый шум. Таким образом случайный вектор st = (sU9 ..., sNt)T имеет
TV-мерное нормальное распределение с нулевым средним и ковариационной
матрицей Cov(£t) = Q, и Cov(ekt9 sJS) = О при t * s для всех k9 j - 1,..., N.
Прежде чем применять процедуру Йохансена, следует определиться с
порядком р векторной авторегрессии, которой следует векторный ряд. Для этого
можно использовать стандартные t- и F-критерии (с асимптотическим 7V@, 1)
распределением для ^-статистик и асимптотическими х1 распределениями
для qF) и, применяя их к VAR в уровнях, порядок которой взят «с запасом»,
понизить по возможности порядок этой «избыточной» VAR. Заметим в связи
с этим, что процедура Йохансена достаточно чувствительна к выбору
порядка VAR, в рамках которой эта процедура реализуется.
Сама процедура начинается с того, что по имеющимся наблюдениям
значений ylt9 ...9yNt9 t=l9..., Г, вычисляются максимумы логарифмических
функций правдоподобия L(Q, ju, <^0, gl9 ..., £р_{) для неизвестных параметров Q, /л,
£09 £l9..., С,р_х при различных предположениях о ранге коинтеграции г. С
точностью до слагаемых, одинаковых при различных г, эти максимумы равны:
Lmax(r) = ~t\n(l-Xi), r = l,...,N,
1 1 = 1
некоторые величины, вычисляемые на основе одних только
статистических данных без всяких предположений о ранге
коинтеграции, 1 > Ях > ... > Ям > 0.
Сравнивая значения LmaK(f)9 полученные при различных г, можно отдать
предпочтение той или иной гипотезе об истинном ранге коинтеграции. Для
формализации соответствующего решения в виде некоторой статистической
процедуры можно использовать известный из математической статистики
критерий отношения правдоподобий.
Пусть в качестве исходной (нулевой) выступает гипотеза Н0: г = г*, а в
качестве альтернативной — гипотеза НА: г - г + 1. Для проверки гипотезы Н0
сравниваются значения:
1 1 = 1
и
1 1 = 1
где Л19..., Ядг —

582
Часть 2. Регрессионный анализ временных рядов
Критерий максимального собственного значения {maximum eigenvalue
test) основывается на статистике
Ятах(г*) = 2Aтах(/+1)-^тах(г*)) = -|1пA-А.+1).
Асимптотическое (при Т -> оо) распределение этой статистики при
гипотезе Н0 зависит от г* и N. Для него рассчитаны соответствующие таблицы
(см., например, (Patterson, 2000, табл. 14.3—14.7), (Enders, 1995, табл. В) или
(Hamilton, 1994, табл. В.11)).
Если гипотеза Я0: г = г верна, то значения Лг*+{, •••> ^n близки к нулю.
Если верна альтернативная гипотеза, то значение Яг*+1 отделено от нуля, и
значения статистики Ятах(г*) смещаются в сторону больших положительных
значений. Поэтому гипотезу Н0: г = г* следует отвергать в пользу гипотезы
НА: г = г* + 1 при больших положительных значениях статистики Лтах(г*),
превышающих соответствующий критический уровень.
Пусть теперь в качестве исходной (нулевой) опять выступает гипотеза
Н0: г = г*, но в качестве альтернативной берется гипотеза НА\ r> r'. Для
проверки гипотезы Н0 сравниваются значения:
*
z / = 1
и
^ / = 1
Критерий следа (trace test) основывается на статистике
Kace{r*) = 2{Lmm{N)-Lmm(r')) = -?- £ 1пA-Я,.).
^ i = r*+\
Асимптотическое (при Т —> оо) распределение этой статистики при
гипотезе Н0 зависит от г* и N. Для него также рассчитаны соответствующие
таблицы (см., например, (Patterson, 2000, табл. 14.3—14.7), (Enders, 1995, табл. В)
или (Hamilton, 1994, табл. В. 10)).
Если гипотеза Н0: г = г* верна, то значения Лг*+1, ..., Ям близки к нулю.
Если верна альтернативная гипотеза, то эти значения отделены от нуля, и
значения статистики Л^асе(г*) смещаются в сторону больших положительных
значений. Поэтому гипотезу Н0: г = г следует отвергать в пользу гипотезы
НА: г > г при больших положительных значениях статистики Л^асе(г*),
превышающих соответствующий критический уровень.

Раздел 11. Регрессионный анализ для нестационарных переменных...
583
Проблема, однако, в том, что заранее обычно не известно, на какое
значение г следует рассчитывать. В таком случае возникает множество
альтернативных пар гипотез, при проверке которых можно получить несогласующиеся
результаты. Йохансен предложил последовательную процедуру проверки
гипотез, с помощью которой можно получить состоятельную оценку
истинного ранга коинтеграции.
Зададимся некоторым уровнем значимости а — скажем, 0.05, и начнем
с проверки гипотезы Н0: г = 0 против альтернативы НА\ г > 0. Если эта
гипотеза не отвергается, то полагаем г = 0. В противном случае проверяем
гипотезу #0: г- 1 против альтернативыНА: г> 1. Если гипотезаН0: г = 1 не
отвергается, то полагаем г = 1, в противном случае проверяем гипотезу Н0: г = 2
против НА:г>2,и т.д.
Полученная оценка г состоятельна в следующем смысле. Если в
действительности г = г0, то при Т —» оо
Р{г = к} ->0, £ = 0,1,...,г0-1,
Р{г = г0} ->1-а.
Таким образом, оценить ранг коинтеграции можно, по крайней мере,
теоретически.
Однако есть еще одна серьезная проблема, возникающая при оценивании
истинного ранга коинтеграции. Дело в том, что критические значения
статистик критериев отношения правдоподобий зависят не только от г* и N, но и от
того, имеют ли ряды детерминированные тренды, включается ли константа
и/или тренд в коинтеграционное соотношение {коинтеграционное уравнение,
СЕ — cointegrating equation). В связи с этим при каждом значении г ранга
коинтеграции можно рассмотреть следующие 5 ситуаций (именно эти
ситуации учитываются, например, в пакете ЕViews):
• Н2(г): в данных нет детерминированных трендов,
в СЕ не включаются ни константа, ни тренд;
• Н*(г): в данных нет детерминированных трендов;
в СЕ включается константа, но не включается тренд.
• Нх (г): в данных есть детерминированный линейный тренд;
в СЕ включается константа, но не включается тренд.
• Н*(г): в данных есть детерминированный линейный тренд;
в СЕ включаются константа и линейный тренд.
• Н(г): в данных есть детерминированный квадратичный тренд;
в СЕ включаются константа и линейный тренд.
При фиксированном ранге г перечисленные 5 ситуаций образуют цепочку
вложенных гипотез:
H2(r)aHl(r)^Hx{r)ciH\r)czH{r).

584
Часть 2. Регрессионный анализ временных рядов
Это дает возможность, опять используя критерий отношения
правдоподобий, проверять выполнение гипотезы, стоящей левее в этой цепочке, в рамках
гипотезы, расположенной непосредственно справа. Во всех случаях
асимптотическое распределение статистики критерия является распределением хи-
квадрат (%2). Что касается степеней свободы у этого асимптотического
распределения, то оно равно
г — для пар Я2(г) еЯ;(г) и Нх{г)^Н\г\
(N-r) — для пар Hx\r)<zHx(r) и Н*(г)с:Н(г).
Заметим, что для каждой из 5 ситуаций, в свою очередь, образуются
цепочки вложенных гипотез:
Я@) с...с Н{г) с...с Я(Л0;
Я*@) с ... с H\r) с ... с Я*(Л0;
^@)e...e^(r)e...e^(AO;
я;@)с...ся;(г)с...ся;(л);
Я2@) с ... с Я2(г) с ... с Я2(Л0.
Критические значения статистик Ятах и Я1пке9 используемые при решении
вопроса о ранге коинтеграции, различны для этих 5 цепочек. Это осложняет
задачу оценивания ранга коинтеграции, поскольку приходится предварительно
выбирать цепочку, в рамках которой будет производиться оценивание.
Некоторым подспорьем в этом отношении является сводка значений
информационных критериев Акаике (AIC) и Шварца для всех указанных 5GV+ 1)
вариантов. Как обычно, наилучшая модель выбирается по минимуму значений
критерия Акаике или критерия Шварца. Впрочем, практика показывает, что
в этом отношении больше доверять стоит критерию Шварца. При анализе
смоделированных данных выбор по критерию Акаике часто приводит к
результатам, совершенно не соответствующим процессу порождения данных.
Рассмотрим 5 ситуаций, перечисленных выше, на простейшем примере
треугольной системы Филлипса для двух 7A) рядов.
VGVx:yt=/3xt + £n
Х,=*,-1 +V,.
На основе этих двух уравнений находим:
Уг ~ Уг~\ = ~yt-\ + Р <Л-1 + vt) = ,-1 " М-1) + ип
где ut=j3vt + £r
Так что получаем ЕСМ в виде
Axt = v„
где zt-yt- Pxt («константа и тренд не включаются в СЕ»).

Раздел 11. Регрессионный анализ для нестационарных переменных...
585
Поскольку ряды yt и xt не содержат детерминированного тренда («тренда
в данных нет»), то все это соответствует ситуации Я2(г).
DGP2: yt=Po + jBxt + €»
xt=xt_x +v,.
Эту систему можно записать в виде:
Ayt=-zt_{ +un
Axt = v„
где zt=yt - р0- (ixt («константа включается в СЕ»).
Поскольку ряды yt и xt не содержат детерминированного тренда («тренда
в данных нет»), все это соответствует ситуации Н*(г).
DGP3: yt=p0 + j3xt + sn
Xt = n+Xt-\ +v,.
В этом случае
У г ~Уг-\ = ~Уг-\ + Л) +Р(Го +xt-l + V,) + *, =
= -CVM - Д) - Pxt_x ) + fir0+ut9
так что получаем
Лх, = Го + v„
где zt=yt- p0- J3xt («константа включается в СЕ»).
Ряд xt содержит детерминированный линейный тренд («тренд в данных»).
Все это соответствует ситуации Нх(г).
DGP4: yt = p0 + pxt + J3xt + et9
xt = y0+xt_x +v,.
Здесь
Уг -Уг-\ = ~yt-\ +Ро+Р\* + Р(Го +xt-\ +Vt) + £t =
= -{yt-\ -Po-Pi*- pxt-i ) + 0Го+ип
или
Ayt = -zt_x +Руъ + и„
Ax, = y0 + v„
где z, =yt - p0 - pxt - pxt («константа и тренд включаются в СЕ»).

586
Часть 2. Регрессионный анализ временных рядов
Ряд xt содержит детерминированный линейный тренд («тренд в данных»).
Все это соответствует ситуации Н*(г).
DGP5: yt=p0 + Pit + /Sxt + £»
xt = yo + r\t + xt_l + v,.
В этом случае
= -(Л-i -р0- Pxt - /3xt_x ) + Pyq+ J3yxt + ut,
или
Ay, = -z,_! + J3y0 + j3yxt + un
&xt = y0 + yxt + v„
где zt=yt- p0- pxt - /3xt («константа и тренд включаются в СЕ»).
Ряд xt содержит квадратичный тренд («квадратичный тренд в данных»).
Все это соответствует ситуации Н{г).
ПРИМЕР 11.3.1
В качестве примера проведем анализ смоделированных данных,
реализующих рассмотренные 5 вариантов DGP. При этом были использованы
следующие значения параметров:
/? = 2, А) = 5, А = 0.2, /о = 0.2, к =0.01.
В качестве рядов st и v, были взяты имитации длины Т = 400 независимых
между собой гауссовских белых шумов, имеющих дисперсии, равные 4 и 1
соответственно.
DCPp yt = 2xt + st9
xt=xt_x +v,.
Смоделированная реализация приведена на рис. 11.26.
Сводка статистик для определения ранга коинтеграции по этим
смоделированным данным, получаемая в пакете Е Views (в предположении, что VAR в
уровнях имеет порядок 2), представлена в табл. 11.42.
В табл. 11.42 для каждой из 5 возможных ситуаций при 3 возможных
рангах коинтеграции (г = 0, 1,2) приведены:
• значение Lmax(r) максимума логарифма функции правдоподобия (Log
Likelihood), соответствующее выбранному сочетанию ситуация — ранг;
• значение информационного критерия Акаике (AIC — Akaike
Information Criteria), соответствующее выбранному сочетанию ситуация —
ранг;
• значение информационного критерия Шварца (Schwarz Criteria),
соответствующее выбранному сочетанию ситуация — ранг.

Раздел 11. Регрессионный анализ для нестационарных переменных...
587
-50 |i 111|1М1|11 м 11111111 м| мирт [мир! 11|м м|1 три! |мм| щ|| 11М|1М1| ►
50 100 150 200 250 300 350 400 t
Рис. 11.26
Таблица 11.42
Статистики для определения ранга коинтеграции
Sample: 1 400; Included observations: 398; Series: Y1 X1; Lags interval: 1 to 1
Data Trend:
Rank or
No. ofCEs
None
No Intercept
No Trend
None
Intercept
No Trend
Linear
Intercept
No Trend
Linear
Intercept
Trend
Quadratic
Intercept
Trend
Log Likelihood
0
1
2
-1526.582
-1434.108
-1434.100
-1526.582
-1433.925
-1432.926
-1526.015
-1433.357
-1432.926
-1526.015
-1433.324
-1430.264
-1525.928
-1433.242
-1430.264
AIC
0
1
2
7.691369
7.246775
7.266836
7.691369
7.250880
7.270985
7.698565
7.253051
7.270985
7.698565
7.257911
7.267658
7.708180
7.262521
7.267658
Schwarz Criteria
0
1
2
L.R.Tesf.
7.731434
732690$
7.387030
Rank = 1
7.731434
7.341026
7.411212
Rank = 1
7.758663
7.353213
7.411212
Rank = 1
7.758663
7.368089
7.427918
Rank = 1
7.788309
7.382716
7.427918
Rank = 2
В первой графе {Rank or No. of CEs) указывается «испытываемый» ранг
коинтеграции. Следующие 5 граф соответствуют 5 ситуациям, указанным
выше (в порядке слева направо — #2(г), Н*(г\ Нх{г\ Н*(г), Н{г)). Внизу
каждой графы приведен результат оценивания ранга коинтеграции в рамках

588
Часть 2. Регрессионный анализ временных рядов
цепочки, соответствующей данной графе. Таким образом, в рамках первых
4-х ситуаций ранг коинтеграции оценивается как г - 1, а в рамках 5-й
ситуации Н{г) ранг коинтеграции оценивается как г = 2.
Если ориентироваться на критерий Акаике, наилучшей следует признать
модель Н2(\) (нет тренда в данных, в СЕ не включаются ни константа, ни
тренд; ранг коинтеграции равен 1) — для нее значение критерия минимально
(равно 7.246775). Та же модель выбирается и критерием Шварца (для нее
значение критерия равно 7.326905).
Процесс получения оценки ранга коинтеграции в ситуации Н2(г\
соответствующей второй графе табл. 11.42, расшифровывает табл. 11.43.
Таблица 11.43
Оценивание ранга коинтеграции в ситуации Н2(г)
Sample: 1 400; Included observations: 398;
Test assumption: No deterministic trend in the data; Series: У1 X1; Lags interval: 1 to 1
Eigenvalue
0.371673
4.00E-05
Likelihood
Ratio
184.9642
0.015911
5%
Critical Value
12.53
3.84
Critical Value
16.31
6.51
Hypothesized
No. ofCE(s)
None**
At most 1
* Отвержение гипотезы на 5%-м уровне значимости.
** Отвержение гипотезы на 1%-м уровне значимости.
Критерий отношения правдоподобий указывает на одно коинтегрирующее уравнение на 5%-м
уровне значимости.
В первой графе {Eigenvalue) табл. 11.43 указаны значения Яи Л2,
используемые в критерии отношения правдоподобий. В первой строке 184.9642 —
наблюдаемое значение статистики Л^ДО), используемой при проверке
гипотезы Я0: г = 0 против альтернативы НА:г>0. Далее в строке приведены 5%-е
и 1%-е критические значения статистики Я(гасе@) в рассматриваемой
ситуации. Поскольку наблюдаемое значение существенно превосходит оба
критических значения, гипотеза Н0: г = 0 отвергается в пользу альтернативы НА:г>0.
Во второй строке 0.015911 — наблюдаемое значение статистики Я&асе{\\
используемой при проверке гипотезы Н0: г = 1 против альтернативы НА\г> 1.
Далее в строке приведены 5%-е и 1%-е критические значения статистики
Я(гасеA). Наблюдаемое значение статистики A,trace(l) намного меньше
критических, так что гипотеза Н0: г = 1 не отвергается. В итоге оцененное значение
ранга коинтеграции принимается равным 1, что соответствует истинному
положению вещей.
DGP2: yt = 5 + 2xt + st9
xt=xt_x +v,.

Раздел 11. Регрессионный анализ для нестационарных переменных...
589
-50 |м 11|1111|1111||1м|1111|||11|1111|м|1|1111|1111|11И|11[||1111|11М|1111|М1|| ►
50 100 150 200 250 300 350 400 t
Рис. 11.27
Смоделированная реализация приведена на рис. 11.27.
Сводка статистик для определения ранга коинтеграции по этим
смоделированным данным приведена в табл. 11.44.
Таблица 11.44
Статистики для определения ранга коинтеграции
Sample: 1 400; Included observations: 398; Sehes: V2 X2; Lags Interval: 1 to 1
Data Trend:
Rank or
No, ofCEs
None
No Intercept
No Trend
None
Intercept
No Trend
Linear
Intercept
No Trend
Linear
Intercept
Trend
Quadratic
Intercept
Trend
| Log Likelihood
I °
1
2
-1526.582
-1513.785
-1513.777
-1526.582
-1433.925
-1432.926
-1526.015
-1433.357
-1432.926
-1526.015
-1433.324
-1430.264
-1525.928
-1433.242
-1430.264
AIC
0
1
2
7.691369
7.247159
7.667223
7.691369
7Д5МНЮ
7.270985
7.698565
7.253051
7.270985
7.698565
7.257911
7.267658
7.708180
7.262521
7.267658
Schwarz Criteria
0
1
2
L.R.Test:
7.731434
7.727289
7.787417
Rank = 1
7.731434
7J4M26
7.411212
Rank = 1
7.758663
7.353213
7.411212
Rank = 1
7.758663
7.368089
7.427918
Rank = 1
7.788309 |
7.382716 1
7.427918 |
Rank = 2

590
Часть 2. Регрессионный анализ временных рядов
Если ориентироваться на критерий Акаике, наилучшей следует признать
модель Н*(\) (нет тренда в данных, в СЕ включается константа; ранг коинте-
грации равен 1) — для нее значение критерия минимально (равно 7.250880).
Та же модель выбирается и критерием Шварца (для нее значение критерия
равно 7.341026).
Процесс получения оценки ранга коинтеграции в ситуации Н{(г%
соответствующей третьей графе табл. 11.42, расшифровывает табл. 11.45.
Таблица 11.45
Оценивание ранга коинтеграции в ситуации Н^{г)
Test assumption: No deterministic trend in the data; Series: V2 X2; Lags interval: 1 to 1
Eigenvalue
0.372251
4.005008
Likelihood
Ratio
187.3130
1.998159
5%
Critical Value
19.96
9.24
1%
Critical Value
24.60
12.97
Hypothesized
No. ofCE(s)
None**
At most 1
* Отвержение гипотезы на 5%-м уровне значимости.
** Отвержение гипотезы на 1%-м уровне значимости.
Критерий отношения правдоподобий указывает на одно коинтегрирующее уравнение на 5%-м
уровне значимости.
Наблюдаемое значение 187.310 статистики Л(пке@)9 используемой при
проверке гипотезы Н0: г = 0 против альтернативы НА: г > 0, значительно
превосходит оба критических значения. Гипотеза Н0: г = 0 отвергается в пользу
альтернативы НА: г > 0. Наблюдаемое значение 1.998159 статистики Л^асе(\)^
используемой при проверке гипотезы Я0: г = 1 против альтернативы НА\г>\,
намного меньше критических значений. Гипотеза Н0: г = 1 не отвергается.
В итоге оцененное значение ранга коинтеграции принимается равным 1, что
соответствует истинному положению вещей.
DGP3: yt = 5 + 2xt + sn
xt - 0.2 +x,_! + v,.
Смоделированная реализация приведена на рис. 11.28.
Сводка статистик для определения ранга коинтеграции по этим
смоделированным данным приведена в табл. 11.46.
Если ориентироваться на критерий Акаике, наилучшей следует признать
модель Нх{\) (тренд в данных, в СЕ включается константа; ранг коинтеграции
равен 1) — для нее значение критерия минимально (равно 7.252889). Та же
модель выбирается и критерием Шварца (для нее значение критерия равно
7.353051).

Раздел 11. Регрессионный анализ для нестационарных переменных...
591
50 100 150 200 250 300 350 400 t
Рис. 11.28
Таблица 11.46
Статистики для определения ранга коинтеграции
Sample: 1 400; Included observations: 398; Series: УЗ ХЗ; Lags interval: 1 to 1
Data Trend:
Rank or
No. ofCEs
None
No Intercept
No Trend
None
Intercept
No Trend
Linear
Intercept
No Trend
Linear
Intercept
Trend
Quadratic
Intercept
Trend
Log Likelihood
I °
1
2
-1531.268
-1506.877
-1504.370
-1531.268
-1438.576
-1432.880
-1526.015
-1433.325
-1432.880
-1526.015
-1433.324
-1430.264
-1525.928
-1433.242
-1430.264
AIC
0
1
2
7.714915
7.612447
7.619950
7.714915
7.274253
7.270753
7.698565
7.252889
7.270753
7.698565
7.257911
7.267658
7.708180
7.262521
7.267658
Schwarz Criteria
0
1
2
L.R.Test:
7.754980
7.692577
7.740144
Rank = 2
7.754980
7.364399
7.410980
Rank = 2
7.758663
7353051
7.410980
Rank = 1
7.758663
7.368089
7.427918
Rank = 1
7.788309
7.382716
7.427918
Rank = 2
Процесс получения оценки ранга коинтеграции в ситуации Нх (г),
соответствующей четвертой графе табл. 11.42, расшифровывает табл. 11.47.
Гипотеза Н0: г = 0 отвергается в пользу альтернативы НА: г > 0. Гипотеза
Н0:г= 1 не отвергается в пользу альтернативы НА:г> 1. В итоге оцененное

592
Часть 2. Регрессионный анализ временных рядов
Таблица 11.47
Оценивание ранга коинтеграции в ситуации Н^(г)
Sample: 1 400; Included observations: 398;
Test assumption: Linear deterministic trend in the data; Series: УЗ ХЗ; Lags interval: 1 to 1
Eigenvalue
0.372353
0.002234
Likelihood
Ratio
186.2692
0.890114
5%
Critical Value
15.41
3.76
1%
Critical Value
20.04
6.65
Hypothesized
No. ofCE(s)
None**
At most 1
* Отвержение гипотезы на 5%-м уровне значимости.
** Отвержение гипотезы на 1%-м уровне значимости.
Критерий отношения правдоподобий указывает на одно коинтегрирующее уравнение на 5%-м
уровне значимости.
значение ранга коинтеграции принимается равным 1, что соответствует
истинному положению вещей.
DGP4: yt = 5 + 0.2t + 2xt + st9
xt = 0.2 +xt_x +vr
Смоделированная реализация приведена на рис. 11.29.
Сводка статистик для определения ранга коинтеграции по этим
смоделированным данным приведена в табл. 11.48.
50 100 150 200 250 300 350 400 t
РИС. 11.29
Если ориентироваться на критерий Акаике, наилучшей следует признать
модель Я*A) (тренд в данных, в СЕ включаются константа и линейный
тренд; ранг коинтеграции равен 1) — для нее значение критерия минимально
(равно 7.257911). Та же модель выбирается и критерием Шварца (для нее
значение критерия равно 7.368089).
Процесс получения оценки ранга коинтеграции в ситуации Я*(г),
соответствующей пятой графе табл. 11.42, расшифровывает табл. 11.49.

Раздел 11. Регрессионный анализ для нестационарных переменных...
593
Таблица 11.48
Статистики для определения ранга коинтеграции
Series: У4 Х4; Lags interval: 1 to 1
Data Trend:
Rank or
No. ofCEs
None
No Intercept
No Trend
None
Intercept
No Trend
Linear
Intercept
No Trend
Linear
Intercept
Trend
Quadratic
Intercept
Trend
Log Likelihood
0
1
2
-1533.049
-1525.311
-1521.201
-1533.049
-1525.279
-1518.005
-1526.015
-1518.361
-1518.005
-1526.015
-1433.324
-1430.264
-1525.928
-1433.242
-1430.264
AIC
0
1
2
7.723863
7.705079
7.704525
7.723863
7.709944
7.698520
7.698565
7.680208
7.698520
7.698565
izmn
7.267658
7.708180
7.262521
7.267658
Schwarz Criteria
0
1
2
L.R.Test:
7.763928
7.785208
7.824720
Rank = 2
7.763928
7.800090
7.838747
Rank = 2
7.758663
7.780370
7.838747
Rank = 1
7.758663
iMmw
7.427918
Rank = 1
7.788309
7.382716
7.427918 1
Rank = 2
Таблица 11.49
Оценивание ранга коинтеграции в ситуации Н*(г)
Test assumption: Linear deterministic trend in the data; Series: У4 X4; Lags interval: 1 to 1
Eigenvalue
0.372355
0.015260
Likelihood
Ratio
191.5010
6.120353
5%
Critical Value
25.32
12.25
1%
Critical Value
30.45
16.26
Hypothesized
No. ofCE(s)
None**
At most 1
* Отвержение гипотезы на 5%-м уровне значимости.
** Отвержение гипотезы на 1%-м уровне значимости.
Критерий отношения правдоподобий указывает на одно коинтегрирующее уравнение на 5%-м
уровне значимости.
Гипотеза H0: r = 0 отвергается в пользу альтернативы НА: г > 0. Гипотеза
Н0: г = 1 не отвергается в пользу альтернативы НА\г>\. Оцененное значение
ранга коинтеграции принимается равным 1, что соответствует истинному
положению вещей.

594
Часть 2. Регрессионный анализ временных рядов
DGP5: yt = 5 + 0.2t + 2xt + en
xt = 0.2 + 0.01/ + xt_x +vt.
Смоделированная реализация приведена на рис. 11.30.
Сводка статистик для определения ранга коинтеграции по этим
смоделированным данным указана в табл. 11.50.
2000 4
1500
1000
500
300 350 400 t
Рис. 11.30
Статистики для определения ранга коинтеграции
Series: У5 Х5; Lags interval: 1 to 1
Таблица 11.50
Data Trend:
Rank or
No. ofCEs
None
No Intercept
No Trend
None
Intercept
No Trend
Linear
Intercept
No Trend
Linear
Intercept
Trend
Quadratic
Intercept
Trend
Log Likelihood
0
1
2
-1672.222
-1527.340
-1527.280
-1672.222
-1527.331
-1520.795
-1630.634
-1525.738
-1520.795
-1630.634
-1525.724
-1432.659
-1525.928
-1432.667
-1432.659
AIC
0
1
2
8.423224
7.715279
7.735077
8.423224
7.720258
7.712538
8.224289
7.717274
7.712538
8.224289
7.722231
7.279694
7.708180
7,259633
7.279694
Schwarz Criteria
0
1
2
L.R.Test:
8.463289
7.795408
7.855272
Rank = 1
8.463289
7.810404
7.852765
Rank = 2
8.284386
7.817436
7.852765
Rank = 2
8.284386
7.832409
7.439953
Rank = 2
7.788309
73ПШ1
7.439953
Rank = 1

Раздел 11. Регрессионный анализ для нестационарных переменных...
595
Если ориентироваться на критерий Акаике, наилучшей следует признать
модель #A) (квадратичный тренд в данных, в СЕ включаются константа
и линейный тренд; ранг коинтеграции равен 1) — для нее значение критерия
минимально (равно 7.259633). Та же модель выбирается и критерием Шварца
(для нее значение критерия равно 7.379827).
Процесс получения оценки ранга коинтеграции в ситуации Я(г),
соответствующей шестой графе табл. 11.42, расшифровывает табл. 11.51.
Таблица 11.51
Оценивание ранга коинтеграции в ситуации Н(г)
Test assumption: Quadratic deterministic trend in the data] Series: У5 X5; Lags interval: 1 to 1
Eigenvalue
0.374152
3.97E-05
Likelihood
Ratio
186.5374
0.015819
5%
Critical Value
18.17
3.74
Critical Value
23.46
6.40
Hypothesized
No. ofCE(s)
None**
At most 1
* Отвержение гипотезы на 5%-м уровне значимости.
** Отвержение гипотезы на 1%-м уровне значимости.
Критерий отношения правдоподобий указывает на одно коинтегрирующее уравнение на 5%-м
уровне значимости.
Гипотеза H0: r = 0 отвергается в пользу альтернативы НА: г > 0. Гипотеза
Я0: г = 1 не отвергается в пользу альтернативы НА\г>\. Оцененное значение
ранга коинтеграции принимается равным 1, что соответствует истинному
положению вещей. ■
Следующий пример, в котором процесс порождения данных представляет
треугольную систему, иллюстрирует процедуру определения ранга
коинтеграции при большем количестве рядов.
ПРИМЕР 11.3.2
Рассмотрим процесс порождения данных, образующий треугольную систему
Филлипса.
DGP: 1234, = 0.5 Wlt + W3t + 2WAt + eln
L23t = W2t + 0.5W3t + s2n
^3f = ^3,f-l + €4t9
t = ,f-l + G5t>
где eln €2n s3t9 £4t, s5t— независимые между собой гауссовские процессы белого
шума, имеющие нулевые математические ожидания
и дисперсии, равные 0.04.

596
Часть 2. Регрессионный анализ временных рядов
Ряды W2n W3n W4t являются случайными блужданиями и
интерпретируются в рамках этой системы как общие тренды (common trends), в том смысле,
что вся (стохастическая) нестационарность системы управляется этими тремя
рядами. Нестационарное поведение ряда L23, регулируется рядами W2t и W3n
а нестационарное поведение ряда£234, —рядами W2n W3t и W4r
Смоделированные данные содержат 500 значений для каждого из 5
входящих в DGP рядов L234„ Z,23„ W2n W3t и W4t. На рис. 11.31 и 11.32 показано
поведение смоделированных реализаций.
-30 |IIII|IIII|IIII|IIII|IIII | I I I I | I I I I | I I I I | | I I I | I I I I | ►
50 100 150 200 250 300 350 400 450 500 t
Рис. 11.31
i i I i i i i I i i i i I i i i i I i i i i I i i i i I i i i i I i i i i I i i i i I i i i i I ►
50 100 150 200 250 300 350 400 450 500 t
Рис. 11.32
Оценивая по смоделированной реализации 5 рядов модель VAR(l) в
уровнях (без ограничений на ранг коинтеграции) и анализируя коррелограммы
полученных рядов остатков, не обнаруживаем автокоррелированности у всех

Раздел 11. Регрессионный анализ для нестационарных переменных...
597
5 рядов остатков. Например, коррелограмма ряда остатков от ряда L234t
имеет вид:
Autocorrelation Partial Correlation
AC
РАС g-статистика Р-значение
1
2
3
4
5
6
7
8
9
10
-0.044
-0.037
0.031
-0.020
0.031
0.036
0.008
0.039
0.003
0.001
-0.044
-0.039
0.028
-0.019
0.031
0.037
0.015
0.041
0.007
0.005
0.9530
1.6395
2.1276
2.3355
2.8073
3.4726
3.5055
4.2674
4.2734
4.2743
0.329
0.441
0.546
0.674
0.730
0.748
0.835
0.832
0.893
0.934
Поэтому можно остановиться на статистической модели в виде VAR(l)
для уровней. Соответствующая ей модель коррекции ошибок не содержит
в правых частях уравнений запаздывающих разностей, и это следует учитывать
при оценивании ранга коинтеграции.
Сводка статистик для определения ранга коинтеграции по
смоделированным данным приведена в табл. 11.52.
Таблица 11.52
Статистики для определения ранга коинтеграции
Series: /_234 /_23 WALK2 WALK3 WALK4; Lags interval: No lags
Data Trend:
Rank or
No. ofCEs
0
1 1
1 2
3
4
5
0
1
2
3
4
5
None
No Intercept
No Trend
99.73833
279.21780
457.04190
461.17540
464.54380
464.77990
-0.400556
-1.081960
-1.755188
-1.731628
-1.704995
-1.665783
None
Intercept
No Trend
Log Li
99.73833
279.4377
457.6821
463.9622
468.0578
470.6760
Ak
-0.400556
-1.078063
-1.749727
-1.730772
-1.703044
-1.669382
Linear
Intercept
No Trend
kelihood
103.2311
282.9301
461.1675
466.3818
469.2034
470.6760
aike
-0.394502
-1.076025
-1.751677
-1.732457
-1.703628
-1.669382
Linear
Intercept
Trend
103.2311
283.2575
462.6611
469.2587
472.1756
473.8191
-0.394502
-1.073323
-1.749643
-1.731963
-1.699501
-1.661924
Quadratic
Intercept
Trend
104.7734
284.7997
464.2006
470.4661
473.0952
473.8191
-0.380616
-1.063453 1
-1.743777
-1.728780 J
-1.699178
-1.661924 1

598
Часть 2. Регрессионный анализ временных рядов
Окончание табл. 11.52
Data Trend:
Rank or
No. ofCEs
None
No Intercept
No Trend
None
Intercept
No Trend
Linear
Intercept
No Trend
Linear
Intercept
Trend
Quadratic
Intercept
Trend
Schwarz
0
1
2
3
4
5
L.R.Test:
-0.400556
-0.996646
-*»5Mom
-1.477977
-1.366794
-1.243032
Rank = 2
-0.400556
-0.985058
-1.563717
-1.451756
-1.331023
-1.204355
Rank = 2
-0.352227
-0.949199
-1.54301
-1.436531
-1.323152
-1.204355
Rank = 2
-0.352227
-0.938043
-1.521357
-1.410672
-1.285205
-1.154623
Rank = 2
-0.296066
-0.894352
-1.490127
-1.390579
-1.276427
-1.154623
Rank = 2
В рамках каждой графы цепочки критериев выводят на ранг 2. Оба
информационных критерия (Акаике и Шварца) указывают на вариант «нет тренда
в данных, в коинтеграционное соотношение не включаются ни константа
ни тренд; ранг коинтеграции равен 2».
Приведем теперь сводку статистик для определения ранга коинтеграции
тройки рядов W2n W3t и W4t (табл. 11.53).
Таблица 11.53
Статистики для определения ранга коинтеграции
Series: WALK2 WALKS WALK4; Lags interval: No lags
Data Trend:
Rank or
No. ofCEs
None
No Intercept
No Trend
None
Intercept
No Trend
Linear
Intercept
No Trend
Linear
Intercept
Trend
Quadratic
Intercept
Trend
Akaike
0
1
2
3
-1.209358
-1.201837
-1.191311
-1.168162
-1.209358
-1.206417
-1.194747
-1.177195
T
-1.208105
-1.195348
-1.177195
■■■■
-1.209616
-1.193234
-1.171753
-1.205445
-1.206429
-1.192934
-1.171753
Schwarz
0
1
2
3
L.R.Test:
:4m$t
-1.151107
-1.089850
-1.015971
Rank = 0
t-tmrn
-1.147232
-1.076376
-0.999639
Rank = 0
-1.185951
-1.132009
-1.068523
-0.999639
Rank = 0
-1.185951
-1.125065
-1.049499
-0.968832
Rank = 0
-1.154715
-1.104968
-1.040743
-0.968832
Rank = 0

Раздел 11. Регрессионный анализ для нестационарных переменных...
599
Здесь в рамках каждой графы цепочки критериев выводят на ранг 0, что
соответствует DGP. Критерий Акаике указывает на варианты с трендом
в данных, тогда как критерий Шварца останавливается на вариантах без
тренда в данных, что и соответствует DGP.B
Оценивание модели коррекции ошибок
После оценивания ранга коинтеграции в рамках процедуры Йохансена можно
получить (при выбранном ранге коинтеграции г) оценки максимального
правдоподобия для г линейно независимых коинтегрирующих векторов.
Реализация такого оценивания в пакете Е Views для группы из 5 рядов,
рассмотренной в предыдущем примере (г = 2), дает следующие результаты (табл. 11.54).
Каждая строка этой таблицы содержит компоненты одного из возможных
коинтегрирующих векторов. Всего, таким образом, предлагается к
рассмотрению 5 вариантов коинтегрирующих векторов, причем эти 5 векторов
являются линейно независимыми. Первая из 5 строк содержит коэффициенты
линейной комбинации указанных рядов, «наиболее похожей на
стационарную». Вторая строка соответствует линейной комбинации, занимающей в этом
отношении второе место, и т.д.
Таблица 11.54
Оценки коинтегрирующих векторов в процедуре Йохансена
Test assumption: No deterministic trend in the data;
Series: L234 L23 WALK2 WALK3 WALK4, Lags interval: No lags
Unnormalized Cointegrating Coefficients'.
1234
-0.079261
-0.202709
0.001194
-0.002101
-0.000206
123
-0.198108
0.079211
0.000453
0.001543
0.000771
WALK!
0.236127
0.022787
-0.014625
0.019423
0.011197
WALKS
0.178603
0.161363
-0.034465
-0.024621
-0.009764
WALK4
0.159704
0.406370
0.037834
0.007077
-0.012244
Если бы мы ранг коинтеграции оценили как г- 1, то в качестве оценки ко-
интегрирующего вектора можно было взять вектор с компонентами,
приведенными в первой строке, т.е. вектор
(-0.079261, -0.198108, 0.236127, 0.178603, 0.159704)г,
или любой пропорциональный ему вектор. Выбрав из этого множества
вектор, нормализованный на первую компоненту, т.е. вектор, полученный

600
Часть 2. Регрессионный анализ временных рядов
из указанного делением всех его компонент на первую компоненту,
получим вектор
A, 2.499451, -2.979119, -2.25363, -2.014916)г.
Поскольку ранг коинтеграции был оценен как г = 2, то в качестве оценок
двух линейно независимых коинтегрирующих векторов можно взять векторы
с компонентами, приведенными в первых двух строках, т.е. векторы:
р\х) = (-0.079261, -0.198108, 0.236127, 0.178603, 0.159704)г;
Р[2) = (-0.202709, 0.079211, 0.022787, 0.161363, 0.406370)г.
Дело, однако, в том, что помимо этих двух векторов в качестве
коинтегрирующих с тем же успехом могут выступать также любые их линейные
комбинации. И в реальных экономических задачах важно, чтобы выбранная в итоге
из этого множества пара векторов выражала осмысленные с экономической
точки зрения (экономической теории) долговременные связи между
рассматриваемыми переменными (например, паритет покупательной способности,
спрос на деньги и т.п.). Это, в свою очередь, требует наложения на коин-
тегрирующие векторы соответствующих идентифицирующих ограничений,
которые позволяют различать эти векторы, выделяя их из всего множества
линейных комбинаций базисных векторов.
Если ранг коинтеграции г > 1, то для различения коинтегрирующих
векторов достаточно наложить на каждый из коинтегрирующих векторов q = г - 1
линейных ограничений (причем эти линейные ограничения сами должны
быть линейно независимыми, иначе различения не получится). Это дает
возможность определить каждый из коинтегрирующих векторов с точностью
до коэффициента пропорциональности, а затем получить единственный набор
коинтегрирующих векторов, нормируя компоненты каждого вектора на какую-
либо из его (ненулевых) компонент.
В нашем примере г = 2, так что на каждый из двух коинтегрирующих
векторов достаточно наложить по одному линейному ограничению (например,
приравнять одну из компонент коинтегрирующего вектора нулю). При этом
зануляемые компоненты в двух векторах должны быть различными. Выбор
зануляемых компонент на практике определяется исходя из представлений
той или иной экономической теории.
Имитируя такой выбор, будем исходить из наличия информации о том,
что «в соответствии с некоторой экономической теорией» между
переменными L234„ Z,23„ W2n W3t и W4t должны существовать две долговременные
связи, одна из которых связывает переменные L234„ W2n W3n W4t и не
включает переменную £23,, а другая связывает переменные L23n W2n W3n W4t и
не включает переменную L234,. Если при этом из той же «экономической
теории» следует также, что в первой долговременной связи «объясняемой»
переменной является L234,, а во второй — переменная Z,23„ то, нормируя

Раздел 11. Регрессионный анализ для нестационарных переменных...
601
первый коинтегрирующии вектор на первую компоненту, а второй
коинтегрирующии вектор — на вторую компоненту, представим эти коинтегрирую-
щие векторы в виде:
Ai) = 0.o,A3.A4,As)r;
А2) = (о,1,Аз.А4,А5)г.
Таким образом, после получения двух произвольных линейно
независимых оценок двух коинтегрирующих векторов:
(-0.079261, -0.198108, 0.236127, 0.178603, 0.159704O;
(-0.202709, 0.079211, 0.022787, 0.161363, 0.406370)г
задача состоит в отыскании линейных комбинаций этих оцененных векторов,
имеющих вид:
(l909fil39fil49fll5)T и @,1 AsO.
Решение этой задачи в пакете Е Views приводит к следующему результату
(табл. 11.55).
Таблица 11.55
Линейные комбинации векторов
Normalized Cointegrating Coefficients: 2; Cointegrating Equation(s)
1,234
1.000000
0.000000
1,23
0.000000
1.000000
WALK!
-0.499995
@.005410)
-0.991867
@.005490)
WALKS
-0.993065
@.008680)
-0.504230
@.008810)
WALKA
-2.006077
@.008520)
-0.003537
@.008650)
В соответствии с этой таблицей
J3m = A,0, -0.499995, -0.993065, -2.006077O",
Д2) = @, 1, -0.991867, -0.504230, -0.003537O".
Это соответствует двум долговременным соотношениям:
L234, = 0.499995^2, + 0.993065 И^ + 2.006077 W4t,
L23, = 0.991867^2, + 0.504230 W3t + 0.003537 W4l,
которые близки к теоретическим долговременным соотношениям,
определяемым использованным DGP:
1234, = 0.5W2t + Щ, + 2WAt,
L23t = W2t + 0.5 W3r

602 Часть 2. Регрессионный анализ временных рядов
Нетрудно заметить, что оцененные векторы /?*1} и /?(*2) являются
линейными комбинациями векторов /?A) и /?B):
/?*1} = -0.079261/?A) - 0.198108/?B),
/?*2) = -0.202709/?A) + 0.079211/?B).
Приведенные в табл. 11.55 под оценками коэффициентов значения их
стандартных ошибок (числа в скобках) дают некоторую ориентацию в
отношении того, какими в действительности могут быть компоненты истинных
коинтегрирующих векторов. Следует только учитывать, что оценки
компонент коинтегрирующих векторов не являются нормально распределенными
(даже асимптотически).
После получения оценок коинтегрирующих векторов можно приступать
к оцениванию коэффициентов ЕСМ обычными методами. Однако и здесь
следует учесть, что асимптотически нормальными являются лишь оценки
кратковременной динамики, т.е. коэффициенты при запаздывающих
разностях переменных.
В нашем примере получаем результаты, приведенные в табл. 11.56.
Таблица 11.56
Оценивание коэффициентов ЕСМ
ест\
ест!
D(L234)
-0.971220
@.11006)
(-8.82480)
-0.033474
@.10788)
(-0.31028)
D(L23)
-0.051197
@.06585)
(-0.77748)
-1.015363
@.06455)
(-15.72980)
D(WALK2)
-0.040351
@.04248)
(-0.94983)
-0.001894
@.04164)
(-0.04549)
D(WALK3)
0.005400
@.04468)
@.12086)
0.010505
@.04380)
@.23985)
D(WALK4)
0.031996
@.04231)
@.75621)
-0.024292
@.04148)
(-0.58571)
Согласно этой таблице оцененная ЕСМ имеет вид:
ДA234),=
A(L23), =
Д(Ж2), =
Д(ЯЗ), =
A(W4)t =
-0.971220(ecml),_
-0.051 \91{ест\),_
-0.04035 \(ест\),_
0.005400(ecwl),_
0.031996(ecml),_
- 0.033474(ecw2),_
-1.015363(ecw2),_
-0.001894(ecw2),_
+ 0.010505(ecw2),_
- 0.024292(ecw2),_
i + e\f>
1 + e2t,
1 + еЪп
I + e4t>
+ ebf>
где (ecml), = Z-234, - 0.499995 W2, - 0.993065 W3t - 2.006077^
(ecml), = L23, - 0.991867ff2, - 0.5042300^, - 0.003537fT4r

Раздел 11. Регрессионный анализ для нестационарных переменных...
603
В рамках процедуры Йохансена имеется также возможность проверить
гипотезы о выполнении дополнительных («сверхидентифицирующих»)
ограничений на коинтегрирующие векторы, например, гипотезу
Я0: /?25=0
о занулении последней компоненты второго коинтегрирующего вектора или
гипотезу
Я0: ап = а21 = аъх - аЪ2 = а41 = а42 = а51 = а52 = О,
означающую отсутствие составляющей (ecm\)t_x во всех уравнениях,
кроме первого, и отсутствие составляющей (ecm2)t_x во всех уравнениях,
кроме второго (что соответствует использованному процессу порождения
данных).
Процедура проверки выполнения таких ограничений на коинтегрирующие
векторы, как и процедура проверки выполнения тех или иных линейных
ограничений на элементы матрицы а корректирующих коэффициентов, не была
встроена в первые версии пакета ЕViews, но имеется в последних версиях
этого пакета. (Напомним, что распределения оценок коэффициентов коинтег-
рирующих векторов и элементов матрицы а не являются асимптотически
нормальными.) Детальный коинтеграционный анализ нестационарных рядов
можно провести также с использованием макропакета CATS (Cointegration
Analysis of Time Series), оформленного в виде процедуры для пакета RATS
(Regression Analysis of Time Series). Краткое описание соответствующих
процедур с подробными примерами анализа экономических данных можно найти,
например, в (Patterson, 2000).
Завершая описание процедуры Йохансена, обратим особое внимание на
следующие обстоятельства:
• процедура Йохансена исходит из предположения о гауссовости
процесса белого шума в VAR модели;
• процедура Йохансена чувствительна к выбору порядка р модели VAR;
• используемые критические значения статистик Ятах и Xtrace —
асимптотические, так что при малом количестве наблюдений к
полученным выводам следует относиться крайне осторожно.
В связи с последним обстоятельством при работе с умеренным
количеством наблюдений рекомендуется корректировать наблюдаемые значения ста-
з з T~NP i
тистик Ятах и Яп.асе путем умножения их на — (коррекция на число
степеней свободы).
Все эти обстоятельства означают, что при коинтеграционном анализе
реальных экономических (а не смоделированных) данных интерпретация
полученных результатов может оказаться довольно затруднительной.

604
Часть 2. Регрессионный анализ временных рядов
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каковы предположения, лежащие в основе процедуры Иохансена? Как на
практике определяется порядок векторной авторегрессии, в рамках которой эта
процедура рассматривается?
2. Как в процедуре Иохансена решается вопрос о ранге коинтеграции? Какие
проблемы возникают при этом?
3. Какие проблемы возникают при оценивании коинтегрирующих векторов при
выбранном ранге коинтеграции? Как после оценивания коинтегрирующих векторов
оценивается модель коррекции ошибок?

Задания для семинарских занятий,
работы в компьютерном классе
и для самостоятельной работы
К разделу 7
Задание 1. Проверка гипотезы случайности: непараметрические критерии
Ниже приведены данные о значениях индекса Доу — Джонса за период с 1897 по
1913 г. Проверьте гипотезу случайности для ряда этих значений, используя
критерий поворотных точек и критерий Кендалла. Проведите аналогичное
исследование для логарифмической доходности индекса, определяемой как изменение
логарифма индекса от года к году.
Год
#'
1897
45.5
1898
52.8
1899
71.6
1900
61.4
1901
69.9
1902
65.4
1903
55.5
1904
55.1
1905
80.3
1906
93.9
1907
74.9
1908
75.6
1909
92.8
1910
84.3
1911
82.4
1912
88.7
1913
79.2
Методические указания. Описание указанных критериев приведено в
Приложении П-1 к разд. 7. Проведите вычисления непосредственно, не используя пакеты
программ эконометрического анализа.
Задание 2. Проверка гипотезы случайности и гипотезы нормальности
В пакете Е Views создайте новый рабочий файл с названием dj_1984_daily.wfl.
На сайте http://www.measuringworth.org возьмите дневные данные по индексу
Доу — Джонса (на момент закрытия) за период с 28 февраля по 31 декабря 1984 г.
Поместите их в форме ряда (Series) с названием dj (ряд Index) в созданный
рабочий файл.
1. Сначала рассмотрите период с 28 февраля по 7 июня (наблюдения с
номерами 1—71). Проверьте гипотезу случайности для ряда значений индекса
на этом периоде, используя критерий серий.
2. Проведите на этом же периоде аналогичный анализ для логарифмической
доходности индекса (ряд Return), определяемой как изменение логарифма
индекса от сессии к сессии, используя критерий поворотных точек,
критерий Кендалла и критерий серий. После этого проверьте гипотезу о том, что
значения ряда логарифмических доходностей на этом периоде образуют

606
Часть 2. Регрессионный анализ временных рядов
случайную выборку из нормального распределения, используя критерии
согласия, включенные в версии пакета EViews выше 4.0 (Kolmogorov—
Smirnov, Lilliefors, Cramer—von Mises, Anderson—Darling, Watson), а
также критерий Харке — Бера.
3. Проведите аналогичный анализ ряда логарифмических доходностей на
всем периоде 28 февраля по 31 декабря (наблюдения с номерами 1—214).
Методические указания. В этом и в следующем заданиях для вычисления
значений статистик критерия поворотных точек, критерия Кендалла и критерия
серий составьте соответствующие программы в пакете EViews. Для создания новой
программы используйте в главном меню опции: File/New/Program. В
открывшемся окне наберите текст программы, по окончании набора пошлите программу
на исполнение, нажав виртуальную кнопку Run. Ниже приведены примеры
программ, которые можно приспособить для каждого конкретного случая.
Апострофом отделяется комментарий к соответствующей строке программы (команда,
стоящая в строке после апострофа, не исполняется). (При копировании текста
программы, набранного не в окне программного файла EViews, в это окно символ
апострофа воспринимается программой неправильно; в EViews6 при
правильном восприятии апострофа соответствующий ему комментарий выделяется
зеленым цветом. Если окрашивание отсутствует, в окне программы надо удалить
из текста соответствующий апостроф и набрать его непосредственно в окне
программы.)
Программа, реализующая критерий серий
loaddj_1984_daily.wfl Здесь указывается название рабочего файла, в котором
содержатся статистические данные и в который будут
записываться результаты. Если этот файл находится не в главной
директории пакета, следует указать путь к нему, например,
load «C:\program files\eviews6\econometrica\dj_1984_daily.wfl».
smpl 171 'Рассматриваются первые 71 наблюдение.
!п=71 'Количество используемых наблюдений.
series x=dj 'Процедура использует ряд dj из рабочего файла. Если
анализируется ряд логарифмических доходностей, то
полагается: series x = d(log(dj)).
series m=@median(x) 'Строится ряд т, все значения которого равны медиане
ряда х.
series sign 'Декларируется создание нового ряда sign, элементы
которого равны 1 или -1 в зависимости от того, какой знак
имеет отклонение значения ряда х от его медианы в
данном наблюдении.
'Далее производится построение ряда sign.
'Вычисляются количество плюсов и количество минусов в последовательности
отклонений от медианы.
scalar n 1=0
scalar n2=0
for !i=l to !n 'Здесь !i = 1 для ряда Index и !i = 2 для ряда Return.

Задания для семинарских занятий... и для самостоятельной работы
607
ifx(!i)>m(!i)then
nl=nl+l
sign(!i)=l
endif
next
for !i=l to !n
ifx(!i)<=m(!i)then
n2=n2+l
sign(!i)=-l
endif
next
'Вычисляются количество серий, состоящих из плюсов, и количество серий,
состоящих из минусов,
scalar z 1=0
scalar z2=0
!i=l
if sign(!i)>0 then 'Рассматривается ситуация, когда на первом месте стоит
плюс.
zl=l
for !i=2 to !n
if sign(!i)<sign(!i-l) then
z2=z2+l
endif
if sign(!i)>sign(!i-l) then
zl=zl+l
endif
next
else 'Рассматривается ситуация, когда на первом месте стоит
минус.
22=1
for !i=2 to !n
if sign(! i)<sign(! i-1) then
z2=z2+l
endif
if sign(! i)>sign(! i-1) then
zl=zl+l
endif
next
endif
scalar z=zl+z2 'Вычисляется общее количество серий z.
'!n=!n-l 'Если рассматривается ряд Return, то !п уменьшаем на 1.
scalar exp_z=B*nl *n2/!n)+l 'Вычисляется математическое ожидание Z
scalar var_z=2*nl*n2*B*nl*n2-!n)/(!nA2*(!n-l)) 'Вычисляется дисперсия Z.
scalar z_star=(z-exp_z)/@sqrt(var_z) 'Вычисляется значение статистики z*.

608
Часть 2. Регрессионный анализ временных рядов
Программа, реализующая критерий поворотных точек
load dj_1984_daily.wfl 'См. комментарий к предыдущей программе.
! start= 1 'Начало выборки.
!end=71 'Конец выборки.
!n=!end-!start+l 'Количество наблюдений.
series x=d(log(dj)) 'Если анализируется ряд индексов, полагается series х = dj\
если анализируется ряд доходностей, полагается
series x = d(log(dj)).
series z=na 'Декларируется создание ряда z.
scalar с 1=0
scalar c2=0
for !i=2 to !n-2 '!i = 2 — для Return, !i = 1 — для Index.
ifx(!i+l)>x(!i)thencl=l
endif
ifx(!i+l)>x(!i+2)thenc2=l
endif
ifx(!i+l)<x(!i)thencl=0
endif
if x(!i+l)<x(!i+2) then c2=0
endif
ifcl-c2=0thenz(!i)=l
else z(!i)=0
endif
next
scalar s=@sum(z)
'Если анализируются л or-доходности, то !п уменьшается на 1.
!n=!n-l
scalar exp_s=2*(!n-2)/3
scalar var_s=A6*!n-29)/90
scalar s_star=(s-exp_s)/@sqrt(var_s) 'Значение статистики S*.
Программа, вычисляющая статистику критерия Кендалла
Программа для вычисления статистики «тау Кендалла»
'Вычисляются нижняя и верхняя границы.
loaddj_1984_daily.wfl
smpl l 71
!n=71
series x=na 'очистка.
series x=d(log(dj)) '— для Return, dj — для Index.
scalar Q
Q=0

Задания для семинарских занятий... и для самостоятельной работы
609
for!i=lto(!n-l)
for !j=!i+l to !n
if x(!i)>x(!j) then Q=Q+1 'В этом блоке при равенстве значений
ставится 0.
endif
next
next
scalar Q_low=Q
Q=0
for!i=lto(!n-l)
for !j=!i+l to !n
if (x(!i)>x(!j) or x(!i)=x(!j)) then Q=Q+1 'В этом блоке при равенстве значений
ставится 1.
endif
next
next
scalar Q_up=Q
'Если dlog(dj), надо уменьшить п на единицу:
!n=!n-l
scalar tau_up= 1 -(D*Q_low)/(!n*(!n-1)))
scalar tau_low=l-(D*Q_up)/(!n*(!n-l)))
scalar var_tau=B*B*!n+5))/(9*(!n*(!n-l)))
scalar taustar_low=tau_low/@sqrt(var_tau) 'Нижняя граница для тау Кендалла.
scalar taustar_up=tau_up/@sqrt(var_tau) 'Верхняя граница для тау Кендалла.
Задание 3. Проверка гипотезы случайности
На сайте http://www.rts.ru возьмите дневные данные по индексу РТС-1 (на
момент закрытия) за период с 9 октября 1998 г. по 10 октября 2000 г.
Проверьте гипотезу случайности для ряда значений логарифмической
доходности индекса, определяемой как изменение логарифма индекса от сессии к сессии,
используя критерий поворотных точек, критерий Кендалла и критерий серий.
Задание 4. Построение реализаций процесса белого шума
Смоделируйте 4 реализации процесса гауссовского белого шума с единичной
дисперсией. Постройте раздельные графики этих реализаций и объединенный
график для всех 4 реализаций. Для каждой реализации проведите обычную
диагностику остатков от оцененной регрессии реализации на константу.
Методические указания. Образуйте новый рабочий файл white_noise.wfl,
рассчитанный на 100 наблюдений, и в меню этого файла выберите опцию Genr.
В открывшемся окне укажите формулу порождения ряда eps\:
epsl=@nrnd.
Снова выберите Genr, и в открывшемся окне укажите формулу порождения
рядае/л?2:
eps2=@nrnd.

610
Часть 2. Регрессионный анализ временных рядов
Проделайте аналогичные действия для получения рядов eps3 и eps4.
Образуйте новый объект Group —> GroupOl — группу, включающую все
полученные ряды. В меню этой группы выберите View -> Multiple Graph -> Line —
это дает раздельные графики полученных рядов. В меню той же группы GroupOl
выберите View —> Graph —> Line — это объединенный график для полученных
рядов.
Задание 5. Проверка ряда на независимость и одинаковую распределенность
с использованием критериев согласия
Проверьте гипотезы о том, что полученные в задании 4 ряды являются
реализациями гауссовских процессов белого шума, используя критерии согласия,
включенные в версии пакета EViews выше 4.0 {Kolmogorov—Smirnov, Lilliefors,
Cramer—von Mises, Anderson—Darling, Watson).
Согласуются ли результаты применения критериев согласия с результатами
диагностики, проведенной в задании 4?
Задание 6. Построение реализаций процесса авторегрессии
Смоделируйте реализации (длины 100) процессов авторегрессии
Xt = а0 + axXt_ j + st
с одной и той же реализацией процесса гауссовского белого шума, полагая
1) а0 = 0,
2) а0 = 0,
3) я0 = 0,
4) а0 = 5,
5) а0=5,
6) а0 = 5,
7) а0 = 0,
8) й0 = 0,
9) а0 = 5,
<*\
«1
°\
<*\
«1
<*\
«1
«i
«1
= 0.1,
= 0.5,
= -0.5,
= 0.5,
= 0.5,
= 0.5,
= 0.8,
= 0.8,
= 0.8,
Х0 = 0;
Х0 = 0;
Х0 = 0;
*о=Ю;
Х0 = 5;
Х0 = 0;
^о=Ю;
Х0 = 5;
х0 = о.
Проследите за особенностями полученных реализаций. Сравните гладкость
реализаций, полученных в пп. 1—3. Вокруг каких уровней происходят
флуктуации построенных реализаций? Вокруг каких уровней должны происходить
флуктуации в теоретических моделях? Объясните различие в поведении
реализации, полученной в п. 4, и реализаций, полученных в пп. 5 и 6. Сравните скорости
выхода на стационарный режим реализаций, полученных в пп. 4 и 7, 5 и 8, 6 и 9.
Методические указания. Постройте базовую реализацию процесса
гауссовского белого шума под именем eps.
1. Создайте объект Series с именем xl, используя клавишу Genr в меню
рабочего файла: Enter equation —> xl=0. Создайте объект Model с именем Ml
и специфицируйте его следующим образом: xl=0.1*xl(-l)+eps. В меню
модели Ml выберите клавишу Solve. В открывшемся меню отключите Stop

Задания для семинарских занятий... и для самостоятельной работы
611
on missing data в Iteration control и нажмите клавишу ОК. В результате
ряд х\ становится реализацией модели 1. В меню этого ряда выберите:
View: Descriptive Statistics -> Histogram and Stats.
В строке Mean указано среднее значение ряда xl, а в строке Std. Dev. —
стандартное отклонение этого ряда.
2. Создайте объект Series с именем х2, используя клавишу Genr в меню
рабочего файла: Enter equation —» х2=0. Создайте объект Model с именем М2
и специфицируйте его следующим образом: x2=0.5*x2(-l)+eps. В меню
модели Ml выберите клавишу Solve. В открывшемся меню отключите Stop
on missing data в Iteration control и нажмите клавишу ОК. В результате
ряд х2 становится реализацией модели 2. В меню этого ряда выберите:
View: Descriptive Statistics —» Histogram and Stats.
В строке Mean указано среднее значение ряда х2, а в строке Std. Dev. —
стандартное отклонение этого ряда.
3. Создайте объект Series с именем хЗ, Enter equation -> х3=0. Создайте
объект Model с именем МЗ и специфицируйте его следующим образом:
x3=-0.5*x3(-l)+eps. В результате ряд хЗ становится реализацией модели 3.
4. Создайте объект Series с именем х4, Enter equation -» x4=10. Создайте
объект Model с именем М4 и специфицируйте его следующим образом:
x4=5+0.5*x4(-l)+eps. В результате ряд х4 становится реализацией модели 4.
5. Создайте объект Series с именем х5, Enter equation -> x5=5. Создайте
объект Model с именем М5 и специфицируйте его следующим образом:
x5=5+0.5*x5(-l)+eps. В результате ряд х5 становится реализацией модели 5.
6. Создайте объект Series с именем хб, Enter equation -» х6=0. Создайте
объект Model с именем Мб и специфицируйте его следующим образом:
x6=5+0.5*x6(-l)+eps. В результате ряд хб становится реализацией модели 6.
Задание 7. Одно свойство коррелограммы стационарного временного ряда
Докажите, что если xt — стационарный временной ряд и с — некоторая
постоянная, то временные ряды xt и (xt + с) имеют одинаковые коррелограммы.
Задание 8. Свойства оператора запаздывания
Оператор запаздывания (обратного сдвига) действует на последовательность Xt
следующим образом: LXt = Xt_x. Если оператор запаздывания применяется к раз,
это обозначается как Lk;
L Xt-Xt_kL .
Единичный оператор при этом выражается как Z,0, так что
Li Ji.f = 1 Л.^ = si.*,
а обратный к L оператор — как L'1 (оператор опережения — lead operator),
L Xt = Xt+l.

612
Часть 2. Регрессионный анализ временных рядов
Докажите следующие свойства оператора запаздывания:
1) LkC=C;
2) Lk(CXt) = CXt_k;
3) (Lk+Lm)Xt = LkXt + LmXt = Xt_k+Xt_m;
4) LkLmXt = Xt_m_k = LmXt_k = Lm+k Xt = LmLkXt;
5) для£>0 L~kXt = Xt+k;
6) если \a\< 1,то A - aL){\ +aL + a2L2 + ...)Xt = Xt, так что оператор
A + aL + a2!} + ...) является обратным для оператора A - aL). Это соответ-
X
ствует записи: — = A + aL + a2L2 +.. .)Х,;
7) если \а\ > 1, то A - я£)A + (я£)-1 + (aL)~2 + ...)Xt = - aLXt. Это
соответствует записи: -£*— = -{aL)~l A + (aL)~l + (я!) +.. .)Xr
1-aL
Методические указания. Свойства 1—5 проверяются непосредственно. Для
доказательства свойства 6 следует рассмотреть разность
Xt-(\-aL)(\ + aL + a2L2+... + anLn)Xt,
а для доказательства свойства 7 — разность
(-aL)Xt - A - aL)(\ + (aL)'1 + (я!)-2 +... + (aLyn )Xt
и проверить, что обе они сходятся к нулю в среднем квадратическом при п ->оо.
Задание 9. Стационарные решения ARA) уравнения
При определении модели ARA) Xt = aXt_l + st предполагалось, что случайные
величины st образуют инновационную последовательность, так что st — процесс
белого шума с D(et) = а2 и Cov(Xt_s, st) = 0 для всех s > 0. При этом было
показано, что если \а\ < 1, то стационарное решение уравнения Xt = aXt_x + £, имеет
00
вид Xt = ^ak£t_k.
к = 0
Покажите, что если снять условие Cov{Xt_s, st) - О для всех s > О, то
уравнение Xt = aXt_l + £, имеет стационарное решение и при |я| > 1. Найдите это
решение.
Методические указания. В случае | а \ < 1 используйте последовательность
итераций:
Xt = aXt_ j + st = a(aXt_2 + £t_{)= ...
Для случая | a \ > 1 начните итерации с соотношения
X-lx --в
a a

Задания для семинарских занятий... и для самостоятельной работы
613
В результате получим:
оо / 1 \к оо / 1 \к оо ( ! \к+1
k=AaJ
k = o\aJ
k = Q\aJ
~t+k •
oo / i \*-l+l oo / i
Так как JTM = -£ - s,+iM = - £ -
k = AaJ m = 0\Q.
s,+m, отсюда:
Остается заметить, что E(Xt) = 0, и показать, что D(Xt) = const и Cov(Zp A^+it)
зависит только от к.
Задание 10. Использование оператора запаздывания
1. Найдите значение выражения .
F 1-0.5I
2. Запишите случайный процесс xt = 0Axt_l + 0.2х,_2 + £, с использованием
оператора запаздывания.
5 приводимых ниже заданиях под стационарностью случайного процесса
подразумевается стационарность в широком смысле. Соотношение £t ~ WN@, cr^)
означает, что случайный процесс st является процессом белого шума с нулевым
математическим оэюиданием и дисперсией &£. Предполагается, что в моделях
AR последовательность значений процесса st образует инновационную
последовательность.
Задание 11. Условие стационарности процесса авторегрессии. Вычисление
характеристик стационарного процесса авторегрессии
Пусть et ~ WN@9 1), тогда
а) является ли случайный процесс xt = 1 - §.bxt_x + st стационарным? Найдите
его математическое ожидание, дисперсию и автоковариации. Вычислите
первые 5 значений автокорреляционной функции и постройте ее график.
Если возможно, представьте этот процесс в виде процесса скользящего
среднего бесконечного порядка;
б) является ли случайный процесс xt = 1 - \2xt_x - xt_2 + st стационарным?
в) является ли случайный процесс xt - 1 + §.\xt_x + 0.2x,_2 + st
стационарным? Найдите его математическое ожидание, дисперсию и
автоковариации. Если возможно, представьте этот процесс в виде процесса скользящего
среднего бесконечного порядка. Вычислите первые 5 значений
автокорреляционной функции и постройте ее график.
Методические указания. Для случая в) чтобы вычислить автокорреляции,
используйте уравнения Юла — Уокера и найдите дисперсию, применяя выражение

614
Часть 2. Регрессионный анализ временных рядов
для у@). Для получения МА(оо)-представления используйте соотношение:
1 1
X. = + £,.
a(L) a{L)
Задание 12. Вычисление характеристик процесса скользящего среднего
Пусть st ~ WN@, 1), тогда
а) является ли случайный процесс xt = -5 + st - 0.8^_ j стационарным?
Найдите его математическое ожидание, дисперсию и автоковариации.
Вычислите первые 5 значений автокорреляционной функции и постройте ее график.
Если возможно, представьте этот процесс в виде процесса авторегрессии
бесконечного порядка;
б) является ли случайный процесс xt = st + et_x стационарным? Найдите его
математическое ожидание, дисперсию и автоковариации. Вычислите
первые 5 значений автокорреляционной функции и постройте ее график. Если
возможно, представьте этот процесс в виде процесса авторегрессии
бесконечного порядка;
в) является ли случайный процесс х, = -1 + st - §.\st_x - Q2st_2
стационарным? Найдите его математическое ожидание, дисперсию и автоковариации.
Вычислите первые 5 значений автокорреляционной функции и постройте
ее график. Если возможно, представьте этот процесс в виде процесса
авторегрессии бесконечного порядка.
Задание 13. Частная автокорреляционная функция процесса авторегрессии
Докажите, что если Xt — процесс типа АК(р)9 то ppart(k) = 0 для к >р.
Задание 14. Вычисление частной автокорреляционной функции
1. Для каждого из стационарных процессов, рассмотренных в заданиях 11 и 12,
вычислите значения частной автокорреляционной функции ppart{k) для
значений к = 1, 2 и 3.
2. Используя пакет EViews, смоделируйте реализации стационарных
процессов, рассмотренных в заданиях 11 и 12, сравните средние значения
полученных реализаций и их коррелограммы с теоретическими значениями.
Задание 15. Вычисление характеристик процесса ARMA
Пусть st ~ WN@9 1), рассмотрите случайный процесс xt = 1 + 0Axt_Y + st - §.%xt_v
1. Является ли он стационарным?
2. Найдите его математическое ожидание, дисперсию, автокорреляции и
частные автокорреляции до 3-го порядка включительно;
3. Если возможно, представьте его в виде процесса авторегрессии
бесконечного порядка и в виде процесса скользящего среднего бесконечного порядка;
4. Смоделируйте его реализацию (длины 100), сравните оцененную коррело-
грамму с теоретической.

Задания для семинарских занятий... и для самостоятельной работы
615
Задание 16. Вычисление значений автокорреляционной функции
по известным значениям частной автокорреляционной функции
По известным значениям частной автокорреляционной функции ppart{\) = 0.4
и ppartB) = 0.6 случайного процесса найдите значения р(\) и р{2) его
автокорреляционной функции.
Задание 17. Идентификация стационарной модели ARMA(p, q) no значениям
ее частной автокорреляционной функции
Найдите параметры р, q стационарной модели ARMA(/?, q) и коэффициенты
аи ..., ар и bl9 ..., bq соответствующей модели, если /0^,A) = 0.5, ppartB) = 0.5,
Ррап(к) = 0дляк>3.
Задание 18. Идентификация обратимой модели ARMA(p, q) no значениям
ее автокорреляционной функции
Найдите параметры/?, q обратимой модели ARMA(/?, q)9 коэффициенты аи ..., ар
и Ьи ..., bq соответствующей модели, если рх = 0.4, pk = 0 для к > 2.
Задание 19. Вычисление коэффициентов процесса авторегрессии
по значениям его автокорреляционной функции
Найдите коэффициенты стационарного процесса ARB), если известно, что рх= —
и р2 = 0.
Задание 20. Идентификация модели ARMA(p, q) no значениям
ее автокорреляционной функции
Найдите параметры/?, q модели ARMA(p, q\ коэффициенты al9 ..., ар и Ьь ..., bq
соответствующей модели, если рх = -0.5 и pk = 0 для к > 2. Является ли эта
модель обратимой?
Задание 21. Вычисление коэффициентов обратимой модели ARMA(p, q)
по значениям ее автокорреляционной функции
Найдите коэффициенты обратимой модели ARMAA, 1), для которой рх- р2 = 0.5.
Задание 22. Идентификация параметровр и q модели ARMA(p, q)
В таблице заданы первые 10 значений выборочных автокорреляционной
функции гк и выборочной частной автокорреляционной функции rpart{k) временного
ряда хг Известно, что ряд содержит Г= 100 наблюдений. Идентифицируйте
параметры/? и q модели ARMA(p, q).
к
ACF
PACF
1
0.718
0.718
2
0.453
-0.130
3
0.284
0.021
4
0.185
0.010
5
0.114
-0.016
6
0.099
0.064
7
0.041
-0.103
8
-0.025
-0.044
9
-0.067
-0.019
10
-0.091
-0.030

616
Часть 2. Регрессионный анализ временных рядов
Задание 23. Идентификация параметровр и q модели ARMA(p, q)
В таблице заданы первые 10 значений выборочных автокорреляционной
функции rk и частной автокорреляционной функции rpart(k) временного ряда хг
Известно, что ряд содержит Т = 100 наблюдений. Идентифицируйте параметры/?
и q модели ARMA(/?, q).
к
ACF
PACF
1
0.497
0.497
2
0.034
-0.283
3
0.025
0.207
4
-0.005
-0.168
5
0.024
0.175
6
0.038
-0.112
7
0.056
0.159
8
0.040
-0.126
9
-0.068
-0.018
10
-0.070
-0.010
Задание 24. Идентификация параметровр и q модели ARMA(p, q)
В таблице заданы первые 10 значений выборочных автокорреляционной
функции гк и частной автокорреляционной функции rpart(k) временного ряда хг
Известно, что ряд содержит Т = 100 наблюдений. Идентифицируйте параметры/?
и q модели ARMA(/?, q).
к
ACF
PACF
1
0.519
0.519
2
0.047
-0.304
3
-0.066
0.091
4
-0.069
-0.080
5
0.001
0.087
6
0.075
0.031
7
0.149
0.123
8
0.135
-0.008
9
0.026
-0.033
10
-0.099
-0.093
Задание 25. Построение реализаций смешанного процесса авторегрессии —
скользящего среднего. Проблема общих множителей
1. Постройте реализации (длины 100) процессов
Xt = \3Xt_x - 0AXt_2 + et- 0.3s,_! - 0.4£,_2,
Yt = 0.5Yt_2 + £t + 0.5£t_l9
используя одну и ту же реализацию процесса белого шума.
2. Сравните полученные реализации процессов Xt и Yt. Объясните результаты
этого сравнения.
Методические указания.
1. Сначала постройте реализацию процесса гауссовского белого шума eps.
Для построения реализации процесса Xt создайте ряд X, полагая х = 0,
а затем модель mod_x со спецификацией
x=1.3*x(-l)-0.4*x(-2)+eps-0.3*eps(-l)-0.4*eps(-2).
Для построения реализации процесса Yt создайте ряд Г, полагая у = 0,
а затем модель mod_y со спецификацией
y=0.5*y(-l)+eps+0.5*eps(-l).
2. Сравните полученные реализации процессов Xt и Yt в рамках объекта
Group. Для объяснения результатов сравнения запишите обе модели с
использованием оператора запаздывания.

Задания для семинарских занятий... и для самостоятельной работы
617
Задание 26. Подбор стационарной модели ARMA для ряда наблюдений —
объем продукции фирмы General Motors.
Рассмотрите данные о количестве произведенных всеми отделениями фирмы
General Motors Corp транспортных средств (грузовики, легковые машины и
автобусы), приведенные в табл. П-1 Приложения.
1. Ограничьте анализ ряда периодом с 1970 по 1990 г. Постройте график ряда.
Похож ли он на график стационарного ряда?
2. Можно ли для описания ряда использовать модель авторегрессии? Если
можно, то какого порядка должна быть модель?
3. Оцените соответствующую AR модель. Является ли оцененная модель
стационарной?
4. Продиагностируйте оцененную модель. Обнаруживаются ли нарушения
стандартных предположений об ошибках?
5. Можно ли упростить модель, отказавшись от включения в правую часть
уравнения некоторых запаздываний? Не приводит ли такое упрощение
к нарушению стандартных предположений об ошибках или к нарушению
стационарности модели?
6. Если представляются подходящими более одной модели, сравните
альтернативные модели, используя информационные критерии, выберите
наилучшую модель.
Методические указания.
1. В меню рабочего файла выберите: Sample -> 1970 1990. В меню объекта
Series X выберите: View —> Line Graph.
2. Проанализируйте коррелограмму ряда. Для этого в меню объекта Series X
выберите: View -> Correlogram —> Correlogram of: Level. Что касается окна
Lags to include, то можно оставить количество лагов (запаздываний),
предлагаемое программой. Обратите внимание на поведение (выборочной)
частной автокорреляционной функции.
3. Создайте новый объект — уравнение для оценивания коэффициентов
соответствующей AR модели. В главном меню выберите: Object —> New
Object -> Equation -» eql. Специфицировать уравнение можно двумя
способами.
Первый способ: X С Х(-1) Х(-2) Х(-3). Этот способ соответствует
стандартной записи процесса авторегрессии третьего порядка в виде:
Xt = а0 + axXt_x + a2Xt_2 + a3Xt_3 + sn
константа С в такой спецификации представляет коэффициент а0. Матема-
ао
тическое ожидание процесса равно: .
1 - ах -а2 — а3
Второй способ: X С ARA) ARB) ARC). Этот способ соответствует
записи процесса авторегрессии третьего порядка в отклонениях от
математического ожидания:
(Xt-Ju) = al(Xt_l-ju) + a2(Xt_2-ju) + a3(Xt_3-ju) + £t,

618
Часть 2. Регрессионный анализ временных рядов
константа С в такой спецификации представляет само математическое
ожидание.
При использовании второго способа в протоколе оценивания
указываются числа, обратные корням уравнения a(z) = О (Inverted AR Roots). Если
все эти числа по модулю меньше 1, то оцененная модель стационарна.
4. Используйте диагностические процедуры, изученные в первой части
учебника.
5. Ориентируйтесь на Р-значения для оценок коэффициентов и результаты
применения диагностических процедур.
6. Используйте для сравнения критерии Акаике и Шварца.
Задание 27. Проблемы, связанные с оцениванием
моделей скользящего среднего, близких к необратимым,
и необратимых моделей скользящего среднего
1. Смоделируйте несколько реализаций модели
Xt= st- 0.975 st_u
используя различные реализации гауссовского белого шума st, t= 1,2, ..., 50,
s0 = 0. По каждой реализации оцените статистическую модель Xt = et + Ъх st_ x.
2. Смоделируйте реализацию необратимой модели
Xt = st - \.25st_x.
По этой реализации оцените статистическую модель Xt = st + bxet_x.
Прокомментируйте полученный результат.
Методические указания.
1. Проведите оценивание без использования и с использованием опции Back-
cast MA terms. Обратите внимание на возможность получения
необратимой оцененной модели. В случае получения обратимой оцененной
модели проанализируйте влияние на результаты оценивания выбора
стартового значения коэффициента в опции ARMA options: starting
coefficient values.
2. Проведите оценивание без использования и с использованием опции Back-
cast MA terms.
Задание 28. Подбор стационарной модели ARMA для ряда наблюдений
с выраженной сезонностью
1. Для квартальных данных чисто сезонными являются стационарные модели
сезонной авторегрессии первого порядка (SAR(l) —first order seasonal
auto regression):
Xt = a4Xt_4 + £n \a4\< 1,
и сезонного скользящего среднего первого порядка (SMA(l) —first order
seasonal moving average):
Xf = £f + ^4^_4«

Задания для семинарских занятий... и для самостоятельной работы
619
В первой модели:
p(k) = akJA для k = Am, m = 0,1,2,...,
р(к) - 0 для остальных к > 0.
Во второй модели
р@) = 1, рD) = Ь49
р(к) = 0 для остальных к > 0.
Смоделируйте реализации моделей SAR(l) с а4 = 0.8 и SMA(l) с Z>4 = 0.8.
Используя эти реализации, проведите процедуру подбора подходящей
модели ряда.
Смоделируйте стационарные мультипликативные спецификации
A - axL)Xt = A + bxL){\ + bALA)sn
Xt-axXt_x + £, + hxst_x +bA£t_A + bxbA£t_5,
(l-axL)(l-a4L4)Xt = (l+bxL)£t,
Xt-axXt_x +aAXt_A- axa4Xt_5 + st + bxst_x.
Используя эти реализации, проведите процедуру подбора подходящей
модели ряда.
2. Проанализируйте данные об объемах производства водки и ликероводочных
изделий в России, приведенные в табл. П-2 Приложения. Подберите
подходящую модель порождения этого ряда данных на периоде с 1999:01 по 2003:12.
Методические указания. Постройте график ряда на периоде с 1999:01
по 2003:12. Обратите внимание на возможное наличие сезонности в
поведении этого ряда. Рассмотрите коррелограмму ряда. Обратите внимание на пики
частной автокорреляционной функции — наличие значимых пиков на лагах
1 и 12. Попробуйте использовать мультипликативную модель
(l-axL)(l-aX2Ll2)Xt=£t,
которая специфицируется в рамках объекта Equation следующим образом:
XCARA)SARA2).
К разделу 8
Задание 29. Построение реализаций динамических моделей
и оценивание динамических моделей
1. Постройте реализацию (длины 100) динамической модели
Yt = 5 + 0.5У,.! + 0.2А", + 0.3^.! + еп
meXt = Q.5Xt_x+vt, Xx = 0, Yx = 0,
stnvt — порождаемые независимо друг от друга процессы гауссов-
ского белого шума, для которых D(et) = 0.01, Z)(v,) = 0.25.

620
Часть 2. Регрессионный анализ временных рядов
Является ли эта модель стабильной? Каково теоретическое
долговременное соотношение между переменными^ и У,?
2. На основании полученного ряда значений У, идентифицируйте модель,
произведите оценивание идентифицированной модели. Является ли
оцененная модель стабильной? Если является, то каково соответствующее ей
долговременное соотношение между переменными Xt и У,? Сопоставьте
полученные результаты с результатами, полученными в п. 1.
3. Подберите по данным табл. П-3 динамические модели связи переменных:
YI иХ, ПиХ9 УЗ иХ, У4 иХ, Y5 иХ.
Методические указания.
1. Создайте объекты Series с именами X и У, полагая X = 0 и У = 0. Создайте
объект Model с именем modi и следующей спецификацией:
x=0.5*x(-l)+0.5*nu
y=5+0.5*y(-l)+0.2*x++0.3*x(-l)+0.1*eps
Реализуйте эту спецификацию. Рассмотрите графики полученных рядов.
2. Оцените статическое уравнение
У, = // + ДД, + и,.
Похожи ли оцененные значения ju и Д, на значения параметров
теоретического долговременного соотношения между переменными X, и Ytl
Проведите анализ коррелограммы ряда остатков. Если этот ряд
идентифицируется как ARA), то можно остановиться на модели ADLA, 1,1)
и оценивать коэффициенты этой модели.
3. Оцените модели линейной регрессии переменных Г1, У2, УЗ, У4, У5 на
константу и переменную X. Проведите диагностику оцененных моделей. По кор-
релограммам остатков определите порядки соответствующих динамических
моделей. Оцените динамические модели соответствующих порядков,
проведите их диагностику, освободитесь от несущественных переменных в
правой части уравнения. При необходимости проверьте гипотезу о выполнении
нелинейного ограничения на коэффициенты, при котором модель
принимает форму модели статической регрессии с ARA) ошибками.
Задание 30. Построение реализаций векторных процессов авторегрессии
и оценивание таких процессов
1. Постройте реализацию модели VAR( 1) для двух рядов:
Yu = 0.6 + 0.7^ ,_! + 0.2У2,_! + еи,
^, = 0.4 + 0.2^,^+0.7^^ + ^,,
полагая^, = У2, = 0 и D{su) = D(£2t) = 0.01. Объясните поведение
полученных реализаций.
2. По полученным реализациям оцените модель VAR(l) для двух рядов.
Сравните оценки коэффициентов со значениями, использованными при
моделировании.

Задания для семинарских занятий... и для самостоятельной работы
621
Методические указания.
1. Создайте объекты Series с именами 71 и 72, полагая 71 = 0 и 72 = 0.
Создайте объект Model с именем modi и следующей спецификацией:
yl=0.6+0.7*yl(-l)+0.2*y2(-l)+0.1*noise-yl
у2=0.4+0.2*у 1 (-1 )+0.7*у2(-1 )+0.1 *noise_y2.
Проверьте модель на стабильность и найдите долгосрочное поведение
системы.
В компактной форме эта система имеет вид:
yt = fi + Tlxyt_x + £r
где yt =
или
V
КУг
М =
tj
0.6^
0.4
П,=
'0.7 0.2^
0.2 0.7
A{L)yt = M + £,-
где АЩ = 12-ПХЬ =
так что
ЛA) =
(\ 0
0 1
0.71 0.2Z,
0.21 0.7/,
/
0.3
-0.2
-0.2Л
0.3
А-\Х)
\£2tJ
1-0.7/, -0.2/Л
-0.2Z, 1-0.7Z,
^6 4
4 6
Уравнение det A{z) - 0 принимает здесь вид:
O-0.7z -0.2гЛ
det A{z)--
-0.2 z l-0.7z
= 0,
т.е. A - 0.7zJ - @.2zJ = 0, или A - 0.9z)(l - 0.5z) = 0. Оба корня z, = —
и z2 =^L больше ,, т.е. условие стабильности выполняется.
Долгосрочное (стабильное) состояние системы находим по формуле
yt=A-\l)M =
6 4
4 6
0.6^
v0.4j
5.2
4.8
J
Таким образом, стабильное состояние системы определяется здесь
следующими значениями:
уи =5.2, ^й = 4.8,
так что стабильное состояние разности уи -у2, есть
Ух -уг = 0А.
Соответственно с течением времени независимо от начальных условий
ряд уи начинает осциллировать вокруг уровня 5.2, а ряд у2, — вокруг
уровня 4.8; разность (уи -у2,) осциллирует вокруг уровня 0.4.

622
Часть 2. Регрессионный анализ временных рядов
2. Откройте пару рядов 71 и 72 в виде VAR (Open as VAR...). В
открывшемся меню укажите следующее (остальное — по умолчанию):
VAR specification: Unrestricted VAR (VAR без ограничений на коэффициенты),
Lag intervals: l 1 (в модели учитываются запаздывания только на один шаг)
При этом автоматически создается объект VAR без имени (UNTITLED),
в котором приведены результаты оценивания модели VAR.
Для подтверждения правильности выбора порядка модели можно
оценить модель большего порядка — например, модель VARB), и посмотреть
на значимость оценок коэффициентов при yl(-2) и у2(-2).
Задание 31. Построение реализаций векторных процессов авторегрессии
Постройте реализацию модели VAR(l) для двух рядов:
7к = 0.87,^+0.27^+ ^„
72, = 0.27u_1+0.872>,_1 + £2,,
полагая Yu = Y2t = 0 и D(slt) = D(s2t) = 0.01. Объясните поведение полученных
реализаций.
Методические указания. Для этой системы
<« Л '0.8/. 0.2/ЛГ" ^ f<
Уи
0.21 0.8Z,
Уи
КУ2, J
\£2t
так что
АЩ =
1-0.8Z, -0.2/,
-0.21 1-0.81
При этом АA) =
0.2 -0.2
, определитель этой матрицы равен нулю, и
ч-0.2 0.2у
матрица А"'A) не определена.
Уравнение det A(z) = 0 имеет здесь вид
A - 0.8zJ - @.2zJ = 0, т.е. A - z)(l - 0.6z) = 0.
Корни этого уравнения равны — и 1. Наличие корня, равного 1, нарушает
0.6
условие стабильности системы.
Задание 32. Построение реализаций открытых VAR
1. Постройте реализацию открытой VAR:
Yu = 0.6 + 0.7Г,,_, + 0.272 ,_, + O.lJf, ,_! + 0.2Х2 , + еи, Yu = 0,
Y2t = 0.4 + 0.2YU,_j + 0.7Г2>,_, + 0.2*1,, + 0.4Y2,,_ х + elt, Y2t = 0,
где
Xu = 0.7л! t_! + eit, л jo — 0,
X2t = 0.5л] t_, + s^t, X20 — 0,

Задания для семинарских занятий... и для самостоятельной работы
623
и в правых частях уравнений стоят независимые между собой процессы
гауссовского белого шума с D(eu) = ... = D{sAt) = 0.01.
Положите Yl0 = Y20 = 0. Объясните поведение полученных реализаций.
2. Как надо изменить при моделировании начальные значения У10 и У20,
чтобы система быстрее выходила на стабильный режим?
Методические указания.
1. Проверьте выполнение условия стабильности модели.
2. Найдите стабильное решение и на его основе вычислите необходимые
значения 710 и Г20, учитывая, что Х10 = 0, Х20 = 0.
Здесь ju и матричный полином A(L) — те же, что и ранее, а
B(L) = B0+BlL =
0
0.2 0
0.2^ @.1 0
+
0 0.4
Л @.1Z, 0.2
1 =
так что
ЯA) = Я0+*1 =
0.1 0.2
0.2 0.4 L
^0.2 0.4^
Матрица долгосрочных мультипликаторов равна:
r6 4V0.1 0.2^1 A.4 2.8
С(\) = А~\\)В(\) =
И 6
так что стабильное решение есть
0.2 0.4
1.6 3.2
V
\У2.
5.2
4.8
1.4 2.8^
1.6 3.2
/^v Л
\X2J
т.е.
^ =5.2 + 1.4*!+2.8х2,
у2 =4.8 + 1.6х1 + 3.2х2.
К разделу 9
Задание 33. Нестационарные временные ряды
Какие из приведенных ниже моделей временных рядов являются
нестационарными и почему? Смоделируйте реализации (длины 100) этих моделей.
Соответствует ли поведение смоделированных реализаций теоретическому разделению
указанных моделей на стационарные и нестационарные?
Xt = 0.08/ + €п
Yt=\£Yt_x-0£Yt_2 + £n
Zt = 03Zt_x + 0AZt_2 + £r

624
Часть 2. Регрессионный анализ временных рядов
Методические указания. Найдите математическое ожидание ряда Хг Для рядов
Yt и Zt проверьте выполнение условия стационарности.
Задание 34. Поведение реализаций процесса авторегрессии первого порядка
при различных значениях коэффициента при запаздывающей
переменной
Смоделируйте реализации (длины 100) процесса ARA)
Xt = axXt_x + et9 Г =1,2, ...,50, Х0 = 09
при ах = 0.5, ах = 0.7, ах = 0.9, ах = 1, ах = 1.05, ах = 1.1. Проследите, как
изменяется характер траектории ряда с возрастанием значений коэффициента ах от
0.5 до 1.1.
Методические указания. Подсчитайте для каждой реализации количество
пересечений нулевого уровня и среднее арифметическое значений ряда. Обратите
внимание на периоды, в течение которых значения ряда находятся по одну сторону
от нулевого уровня.
Задание 35. Поведение коррелограмм, построенных по реализациям
процесса авторегрессии первого порядка
при различных значениях коэффициента при запаздывающей
переменной
Проанализируйте изменение характера коррелограмм, построенных по
реализациям процесса авторегрессии первого порядка при возрастании значений
коэффициента ах от 0.5 до 1.1.
Задание 36. Поведение коррелограмм, построенных по реализациям
стационарных и нестационарных процессов
Постройте выборочные коррелограммы смоделированных реализаций,
полученных при выполнении задания 33.
Методические указания. Отметьте характерное поведение коррелограмм
нестационарных рядов.
Задание 37. Процесс случайного блуждания как модель
стохастического тренда
Смоделируйте реализацию процесса случайного блуждания
Xt = Xt_x + £t9 Г =1,2, ...,500, Х0 = 09
Почему о процессе случайного блуждания говорят как о модели
стохастического тренда? Поясните это на примере смоделированной реализации.
Методические указания. Обратите внимание на интервалы времени, на
протяжении которых в поведении траектории обнаруживается линейный тренд.

Задания для семинарских занятий... и для самостоятельной работы
625
Задание 38. Фундаментальное различие между временными рядами,
имеющими только детерминированный тренд, и рядами,
которые имеют (возможно, наряду с детерминированным)
стохастический тренд
Используя одну и ту же имитацию процесса белого шума, постройте реализации
процессов:
Xt = 0.05/ +еп /=1,2,..., 500, Х0 = 0 (процесс
с детерминированным трендом),
Wt=0.05 + Wt_x + et9 t= 1,2,..., 100, W0 = 0 (процесс
со стохастическим и детерминированным трендами —
случайное блуждание со сносом).
Обратите внимание на поведение построенных реализаций. Как ведут себя
построенные реализации относительно детерминированного тренда?
Методические указания. Создайте новый рабочий файл длины 100. Образуйте
переменную t=@trend+l. Постройте реализацию процесса белого шума: eps=@nrnd.
Постройте реализацию первого ряда: x=0.05*t+eps. Для построения реализации
второго ряда образуйте ряд w=0, создайте новый объект Model и
специфицируйте его следующим образом: w=0.05+w(-l)+eps. Затем в меню этого объекта
выберите: Solve -> ОК.
Задание 39. Последствия неправильного выбора метода очистки ряда
от тренда (ложная периодичность, эффект Слуцкого,
необратимость МЛ-составляющей)
Для построенных реализаций процессов^ nWtB задании 38:
а) произведите очистку от тренда, оценив регрессию переменных Xt и Wt на
константу и переменную t и получив ряды остатков x_res, w_res;
б) произведите очистку от тренда переходом к рядам разностей AXt nAWr
Проявляются ли в полученных рядах указанные последствия неправильного
выбора метода очистки ряда от тренда?
Методические указания. Построение рядов разностей: Generate —> x_dif=d(x),
Generate —> w_dif=d(w). Коррелограмма ряда wdif соответствует тому, что ряд
AWt является процессом белого шума. Коррелограмма ряда x_dif указывает на
коррелированность соседних значений ряда AXt (эффект Слуцкого) и на то, что
моделью для этого ряда является скользящее среднее первого порядка. Результаты
оценивания такой модели указывают на наличие единичного корня у МА-состав-
ляющей, т.е. на необратимость МА-составляющей — проявление передифферен-
цированности процесса АХГ
Коррелограмма ряда x_res характерна для выборочной коррелограммы
процесса белого шума. Коррелограмма ряда w_res характерна для
нестационарного ряда. В поведении траектории ряда w_res имеется некоторое подобие
периодичности.

626
Часть 2. Регрессионный анализ временных рядов
Задание 40. TS- и DS- ряды в классе моделей ARIMA
Рассмотрите следующие ARC) модели:
Yt = Yt_x - 0.25У,_2 + 0.25У,_з + еп
Zt = 0.5Z,_! - 0.25Zt_2 + 0.125Z7,_3 + st.
Какая из этих моделей является ГЯ-моделью, а какая — /^-моделью? Как
обозначаются эти модели в классе моделей ARIMA(/?, d, q)l Смоделируйте реализации
этих моделей и отметьте различие в их поведении. Оцените по смоделированным
реализациям коэффициенты моделей, породивших эти реализации. Сравните
полученные оценки с истинными значениями коэффициентов.
Методические указания. Используйте для обеих моделей одну и ту же
реализацию белого шума.
К разделу 10
Задание 41. Применение расширенного критерия Дики — Фуллера
для ряда наблюдений — объем продукции фирмы General Motors
В задании 26 подбиралась подходящая модель для ряда данных о количестве
произведенных всеми отделениями фирмы General Motors Corp транспортных
средств (грузовики, легковые машины и автобусы) за период с 1970 по 1990 г.,
исходя из предположения о стационарности этого ряда. Проверьте гипотезу
единичного корня для этого ряда, используя подходящий вариант критерия Дики —
Фуллера.
Методические указания. График этого ряда похож, скорее, на график
стационарного ряда, флуктуирующего вокруг ненулевого уровня. Поэтому для
проверки гипотезы единичного корня используем уравнение Дики — Фуллера в
следующей форме:
Р-\
Axt = а + (pxt_x + ^Oj Axt_j + st, t = p +1,..., T.
y = i
Поскольку имеем дело с годовыми данными, проводить предварительную
десезонизацию ряда не надо. Однако необходимо установить, сколько
запаздывающих разностей следует включить в правую часть уравнения. С этой целью надо
посмотреть на коррелограмму ряда.
По форме коррелограммы предполагаем возможность описания ряда моделью
ARC) (по графику частных автокорреляций), так что /? = 3,/?-1=2,и поэтому
в правой части уравнения Дики — Фуллера берем две запаздывающие разности:
2
Axt =(pxt_x + ^ej^xt-j +£t> t = 3,...,T.
В меню объекта Series x выбираем:
View -> Unit Root Test ->
Test Type: Augmented Dickey-Fuller

Задания для семинарских занятий... и для самостоятельной работы
627
Test for unit root in: Level (проверяем наличие единичного корня у самого ряда)
Include in test equation: Intercept (в правую часть уравнения включена
константа)
Lagged differences'. 2 (в правой части уравнения две запаздывающие разности).
После этого нажимаем виртуальную клавишу ОК, получаем таблицу, верхняя
часть которой выглядит следующим образом:
ADF Test Statistic -3.912621 1% Critical Value* -3.8572
5% Critical Value -3.0400
10% Critical Value -2.6608
MacKinnon critical values for rejection of hypothesis of a unit root
Значение статистики f для проверки гипотезы Я0: ср = 0 равно -3.9726;
критическое значение, соответствующее уровню значимости 0.05 E% Critical Value),
равно -3.0400. Поскольку здесь t < tcrin гипотеза единичного корня отвергается,
и это подтверждает наше первоначальное предположение о том, что
рассматриваемый ряд стационарный.
Таким образом, нет необходимости в дифференцировании ряда, и можно
оценивать его как ARC), что уже сделано в задании 26.
Задание 42. Применение критерия Дики—Фуллера кряду наблюдений
с выраженной сезонностью —уровни безработицы в США
в период 1987—1990 г. (месячные данные)
В табл. П-4 приведены данные об уровнях безработицы в США (X) в период
1987—1991 г. (месячные данные). Проверьте гипотезу единичного корня для
этого ряда по данным за период с января 1987 г. по декабрь 1990 г., используя
подходящий вариант критерия Дики — Фуллера.
Методические указания. Критерий Дики — Фуллера здесь следует применить
к ряду, очищенному от сезонности. Для этого следует оценить уравнение
регрессии ряда на 12 сезонных переменных и образовать ряд остатков. Это и будет ряд,
очищенный от сезонности. Создайте новый объект Equation и специфицируйте
его следующим образом:
X @SEAS( 1) @SEASB) @SEASC) @SEASD) @SEASE) @SEASF)
@SEASG) @SEAS(8) @SEAS(9) @SEASA0) @SEASA1) @SEASA2)
Затем в меню этого объекта выберите: Procs —> Make residual series —» x_des\
при этом создается объект Series с именем x_des — это и есть ряд, очищенный от
сезонности.
Рассмотрите коррелограмму ряда разностей d(x_des), построенного по ряду
x_des. Для этого достаточно в меню объекта х_des выбрать:
View —> Correlogram —> Correlogram of. 1st difference —> OK.
По полученной коррелограмме определите, каким должен быть порядок AR-пред-
ставления ряда d(x_des). Именно столько запаздывающих разностей следует

628
Часть 2. Регрессионный анализ временных рядов
включить в правую часть уравнения Дики — Фуллера при проверке гипотезы
единичного корня для ряда xdes.
В меню объекта x_des выберите:
View -> Unit Root Test ->
Test Type: Augmented Dickey-Fuller
Test for unit root in: Level (проверяем наличие единичного корня у самого ряда)
Include in test equation: Intercept (в правую часть уравнения включена
константа)
Lagged differences: укажите порядок AR-представления ряда d{x_des).
После этого нажимаем виртуальную клавишу ОК.
Если значение статистики Дики — Фуллера оказывается выше 5%-го
критического уровня (соответствующего данной ситуации), так что гипотеза
единичного корня не отвергается, то (имея в виду низкую мощность критериев Дики —
Фуллера) создайте новый объект Equation, специфицируя его как
соответствующее уравнение Дики — Фуллера для ряда x_des, и оцените полученное уравнение.
Для контроля сравните результаты оценивания с протоколом, полученным при
применении процедуры Unit Root Test. Результаты должны быть одинаковыми.
Значение статистики Дики — Фуллера появляется здесь как значение
^-статистики в строке, соответствующей переменной x_des(-l).
Продиагностируйте оцененное уравнение Дики — Фуллера на нормальность
и отсутствие автокоррелированности. Если диагностика дает
удовлетворительные результаты, обратите внимание на Р-значения, соответствующие оценкам
коэффициентов при запаздывающих разностях. Для повышения мощности
критерия исключите из правой части уравнения запаздывающие разности, у которых
оценки коэффициентов статистически незначимы. Сравните значение
^-статистики в строке, соответствующей переменной x_des(-l), которое получено в
редуцированном уравнении, с тем же 5%-м критическим значением.
Если в итоге гипотеза единичного корня отвергается, следует производить
подбор подходящей модели к ряду уровней, т.е. к самому ряду Хг Если же
гипотеза единичного корня не отвергается, следует производить подбор подходящей
модели к ряду разностей АХГ
Задание 43. Многовариантная процедура проверки гипотезы единичного корня
Примените многовариантную процедуру проверки гипотезы единичного корня
к ряду DPI, представляющему значения совокупного располагаемого дохода в США
(в млрд долл., в ценах 1982 г.).
Методические указания. Воспользуйтесь данными примера 10.1.6 (разд. 10).
Значения ряда представлены в табл. П-5.
Задание 44. Ряды с квадратичным трендом
Проанализируйте графики рядов ST4 и WALK3, описанных в теме 10.1 (разд. 10).
Проверьте для каждого из этих рядов гипотезу о наличии единичного корня.
Методические указания. Значения указанных рядов представлены в табл. П-6.

Задания для семинарских занятий... и для самостоятельной работы
629
Задание 45. Критерий Перрона
В табл. П-7 приведен ряд значений реального валового внутреннего продукта
США за период с 1959 по 2006 г. Сравните наклон линии тренда на периоде
1959—1982 гг. и на периоде 1983—2006 гг. Имея в виду заметное изменение
наклона тренда при переходе от первого периода ко второму, проверьте гипотезу
единичного корня в рамках моделей, предусматривающих такое изменение.
Методические указания. Наблюдаемое изменение наклона линии тренда
можно связать с выходом из экономического кризиса 1980—1982 гг. Поэтому в
качестве момента Тв, после которого происходит излом тренда, можно взять 1982 г.,
т.е. Тв - 24, и такой выбор считать экзогенным. Примените процедуру Перрона,
соответствующую модели сегментированного тренда. Сначала оцените
статистическую модель
rgdpt =a + Ct + yDTSt + ип
где DTSt = 0jymt<TB и DTSt = t-TBwi*t> TB.
Получите ряд остатков
et=rgdpt-a-pt-yDTSr
Затем оцените модель
et = ocet_x + дх Aet_{ +... + SkAet_k + £t
с достаточным количеством запаздывающих разностей и вычислите значение
^-статистики для проверки гипотезы а = 1. Сравните это значение с критическим,
которое можно определить из табл. П-8.
К разделу 11
Задание 46. Проблема ложной регрессии
1. Смоделируйте в пакете EViews реализации длины 100 двух случайных
блужданий
Xt — Xt_ j + £^п t = 1, z, ..., i, Xj = U,
yt = yt-i + £2t> t=l,2,...9T9 y{ = 09
где sXn s2t — два не коррелированных между собой процесса гауссовского
белого шума с единичной дисперсией.
Коррелированы ли между собой процессы ytnxtl Оцените модель
регрессии j>, на константу и хг Имеются ли в протоколе оценивания признаки
ложной регрессии? Оцените ту же модель регрессии: а) по первым 50
наблюдениям; б) по последним 50 наблюдениям. Сравните результаты
оценивания.
2. Смоделируйте реализацию длины 100 случайного процесса
zt = zt_i + £3р t = 2,..., 7, Z\=\J9
где еЪг = 0.5£u + 0.5%.

630
Часть 2. Регрессионный анализ временных рядов
Является ли процесс zt случайным блужданием? Коррелированы ли
между собой процессы еЪ1 и sXtl Коррелированы ли между собой процессы zt
и xtl Оцените модель регрессии zt на константу и хг Имеются ли в
протоколе оценивания признаки ложной регрессии? Оцените ту же модель
регрессии: а) по первым 50 наблюдениям; б) по последним 50 наблюдениям.
Сравните результаты оценивания.
3. Примените критерий Дики — Фуллера для проверки: а) гипотезы о некоин-
тегрированности рядов xt и yt\ б) гипотезы о некоинтегрированности
рядов xt и zt. В уравнение Дики — Фуллера для ряда остатков не
включайте ни константу, ни тренд. Полученные значения тестовой статистики
сравните с 5%-м критическим значением -3.396.
Методические указания.
1. В пакете Е Views создайте рабочий файл длины 100 и смоделируйте две
независимые реализации гауссовского белого шума — пусть это будут
ряды eps\ и eps2. Образуйте ряды X и У, полагая сначала Х=0 и Y=0.
Создайте два объекта Model:
modx -> X=X(-l)+epsl -> Solve,
mod_y -> Y=Y(-l)+eps2 -> Solve.
При этом создаются искомые реализации двух случайных блужданий.
Создайте объект Equation со спецификацией: Y С X и оцените это
уравнение. Обратите внимание на значение ^-статистики, соответствующей
оценке коэффициента при переменной X, и на значение статистики Дарби-
на — Уотсона. Обратите внимание на коррелограмму ряда остатков. Для
выполнения п. 3 создайте ряд остатков как отдельный объект Series, дав
ему имя residjy_x.
2. Постройте ряд eps3=0.5*epsl+0.5*eps2. Образуйте ряд Z, сначала полагая
Z=0, а затем реализуя модель mod_z -> Z=Z(-l)+eps3 -> Solve.
Создайте объект Equation со спецификацией: Z С X и оцените это
уравнение. Обратите внимание на значение ^-статистики, соответствующей
оценке коэффициента при переменной Х9 и на значение статистики Дарби-
на — Уотсона. Обратите внимание на коррелограмму ряда остатков. Для
выполнения п. 3 создайте ряд остатков как отдельный объект Series, дав
ему имя resid_z_x.
За. В меню объекта resid_y_x выберите:
View -> Unit Root Test —>
None; Lagged differences 0 —> OK.
Полученное значение тестовой статистики сравните с критическим
значением -3.396, соответствующим уровню значимости 5%. Заметьте, что это
критическое значение отличается от критического значения, указанного
в протоколе (-2.8906) и соответствующего проверке гипотезы единичного
корня для «сырого» ряда.

Задания для семинарских занятий... и для самостоятельной работы
631
36. В меню объекта resid_z_x выберите:
View -> Unit Root Test ->
None; Lagged differences 0 —> OK.
Задание 47. Коинтегрированные временные ряды. Модели коррекции ошибок
Рассмотрите векторный процесс (xnyt)T:
xt = 1.5xt_! - 0.5xr_2 + £,, ^! = 0,
>>, = 2x,+ v„
где £tnvt — порождаемые независимо друг от друга последовательности
независимых, одинаково распределенных случайных величин,
имеющих стандартное нормальное распределение N@, 1).
1. Покажите, что этот процесс представим в форме VAR. Являются ли ряды xt
и yt коинтегрированными? Если являются, то постройте представление
этого векторного процесса в форме модели коррекции ошибок.
2. Смоделируйте реализацию процесса (xt, yt)T длины 100. Примените дву-
ступенчатую процедуру Энгла — Грейнджера для построения по
полученной реализации модели коррекции ошибок. После первого шага
оценивания примените критерий Дики — Фуллера для проверки гипотезы о неко-
интегрированности рядов xt и уп следуя указаниям к заданию 46. Сравните
оценки коэффициентов, полученные на первом и втором шагах процедуры,
со значениями коэффициентов в теоретической модели.
3. Сравните результаты оценивания линейной модели регрессии yt на xt по
первым 50 наблюдениям и по последним 100 наблюдениям. Отличается ли
характер этих результатов от аналогичных результатов в задании 46? Чем
объясняется это отличие?
Методические указания. При проверке гипотезы о некоинтегрированности
рядов обратите внимание на получаемые при оценивании уравнения Дики —
Фуллера остатки, проведите диагностику ряда остатков. Полученное значение
тестовой статистики сравните с критическим значением -3.396. На основании
результатов второго шага процедуры объясните, как действует механизм
коррекции ошибок в оцененной модели.
Задание 48. Коинтегрированная VAR
Смоделируйте реализацию следующей модели VAR:
xt - 0.8хг_! + 0.2yr_ I + £t,
;y, = 0.2x,_1+0.8y,_1+v,,
где £tnvt — порождаемые независимо друг от друга последовательности
независимых, одинаково распределенных случайных величин, имеющих
стандартное нормальное распределение N@, 1), полагая х0 =у0 = 0.

632
Часть 2. Регрессионный анализ временных рядов
1. Объясните поведение полученной пары рядов xt и уг
2. Используя двухшаговую процедуру Энгла — Грейнджера, постройте на
основе смоделированной реализации модель коррекции ошибок. После
первого шага оценивания примените критерий Дики — Фуллера для
проверки гипотезы о некоинтегрированности рядов xt и yt, следуя указаниям
к заданию 46. На основании результатов второго шага процедуры объясните,
как действует механизм коррекции ошибок в оцененной модели. Сравните
оцененную ЕСМ с теоретической.
3. Сравните результаты оценивания линейной модели регрессии yt на xt по
первым 50 наблюдениям и по последним 100 наблюдениям. Отличается ли
характер этих результатов от аналогичных результатов в задании 46? Чем
объясняется это отличие?
Методические указания.
1. Представьте модель в форме A(L)
f~ Л f^\
где A(L) — матричный по-
\yt) ' '
лином от оператора запаздывания. Проверьте выполнение условия
стабильности модели. Для проверки системы на коинтегрированность вычислите
ранг матрицы А{\).
2. При проверке гипотезы о некоинтегрированности рядов обратите
внимание на получаемые при оценивании уравнения Дики — Фуллера остатки:
проведите диагностику ряда остатков. Полученное значение тестовой
статистики сравните с 5%-м критическим значением -3.396.
Задание 49. Проверка нескольких рядов на коинтегрированность в случае,
когда возможный коинтегрирующий вектор не определен заранее
Смоделируйте реализации 4 рядов уи, у2п у3п уАп следуя процессу порождения
данных
DGP: yu = 5+y29t+y3tt + eu,
У It ~yi,t-\ + s2v
У it ~ З^з, г-1 + £3t>
У At =y4,t-l + £4t>
где у20=У3о = Уао = 0>
sXn sln £3t, sAt — независимые друг от друга процессы гауссовского белого шума
с дисперсиями, равными 1 для £2п £Ъп £4t и равной 2 для еи.
Рассматривайте полученные реализации как статистические данные.
1. Используя критерий Дики — Фуллера, проверьте для каждого ряда
гипотезу о том, что этот ряд является интегрированным порядка 1.
2. Используя статистику Дики — Фуллера, проверьте на
коинтегрированность: а) пару рядов уи, ylt\ б) тройку рядов уи, y2t, y3t; в) четверку рядов
УхпУшУъпУаг

Задания для семинарских занятий... и для самостоятельной работы
633
Методические указания. При проверке на коинтегрированность исследуйте
ряды остатков, получаемые при оценивании соответствующих уравнений.
Необходимые критические значения вычислите, используя табл. П-9.
Задание 50. Стохастическая и детерминистская коинтеграции
1. В условиях задания 46, замените уравнение y2t = y2t,_ i + s2t уравнением
y2t = 0J5+y2^_l + s2t,
так что ряды уи и y2t имеют не только стохастический, но и
детерминированный тренд.
Используя статистику Дики — Фуллера, проверьте на
коинтегрированность четверку рядовуи,y2t,y3t, JV
2. В условиях задания 46 замените уравнение уи = 5 + >>2, t +Уз,( +Ул, t + £\t->
уравнением
уи = 5 + 0.15t+y2,t +yXt +y4,t + eln
так что рящлу2пу3пу4г имеют только стохастический тренд, а ряцуи имеет
не только стохастический, но и детерминированный тренд.
Используя статистику Дики — Фуллера, проверьте на
коинтегрированность четверку рядовуи, y2t, y3n yAt:
а) не включая трендовую составляющую в правую часть оцениваемой
статистической модели;
б) включая трендовую составляющую в правую часть оцениваемой
статистической модели.
В каком случае имеет место детерминистская коинтеграция, а в каком —
только стохастическая коинтеграция?
Методические указания. При проверке на коинтегрированность исследуйте
ряды остатков, получаемые при оценивании соответствующих уравнений.
Необходимые критические значения вычислите, используя табл. П-9.
1. Используйте строку таблицы с N=4, случай «с константой и трендом».
2а. Используйте строку таблицы с N=4, случай «с константой и трендом».
26. Используйте строку таблицы с N=5, случай «с константой и трендом».
Задание 51. Пара коинтегрированных рядов, не образующая
треугольную систему Филлипса
Выполните задание 47 в ситуации, когда во втором уравнении вместо ряда vt
берется ряд
£ = 0.5s,+0.5vr
Сравните полученные в этом случае оценки коэффициентов модели
коррекции ошибок с оценками, полученными в задании 47.
Методические указания. Обратите внимание, что в отличие от задания 47
здесь пара рядов xt nyt не образует треугольную систему Филлипса. Почему?

634
Часть 2. Регрессионный анализ временных рядов
Задание 52. Оценивание модели парной регрессии для некоинтегрированных
рядов, имеющих стохастический и детерминированный тренды
Смоделируйте в пакете EViews реализации длины 100 двух случайных
блужданий со сносом:
xt = 0.5 +xt_r + £и, t = 2,..., 100, хх = 0,
Л=1+;у,-1 + *2г> ' = 2, ...,100, ^ = 0,
где £и, £2t— не коррелированные между собой процессы гауссовского белого
шума с единичной дисперсией.
Оцените по полученным реализациям:
а) статистическую модель yt - а + /5xt + £t;
б) статистическую модель yt = а + f5xt + yt + £r
Как интерпретируются получаемые при этом оценки коэффициента /??
Методические указания.
DGP: xt = /лх + xt_! + £и,
где £и, £2t— не коррелированные между собой процессы белого шума, причем
jux *0,;uy* 0.
Тогда при оценивании статистической модели
SM: yt = а + fixt + щ
оценка аТ для а, вычисляемая по Т наблюдениям, при Т —> оо расходится,
Иу
а оценка J3T для J3сходится по вероятности при Г—> оо к отношению —.
Если при тех же условиях оценивать статистическую модель
SM: yt = а + fixt + yt + un
то (при Т -» оо) ут сходится по вероятности к /лу, а рт сходится по
распределению к некоторой случайной величине, как и в случае ложной регрессии для
случайных блужданий без сносов.
Задание 53. Оценивание модели парной регрессии для коинтегрированных рядов,
имеющих стохастический и детерминированный тренды
1. Смоделируйте в пакете EViews реализации длины 50 треугольной системы:
xt= 1 +xt_x +vt, xx =0,
yt = 2xt + ut,
где ut = 0Aut_{ + 0.2ut_2 + £t — стационарный ARB)ряд;
£tnvt — два процесса гауссовского белого шума с единичной дисперсией,
коррелированные между собой в совпадающие моменты времени.

Задания для семинарских занятий... и для самостоятельной работы
635
2. Оцените статистическую модель
yt = a + fixt + et,
используя стандартную процедуру наименьших квадратов. Вычислите
стандартные значения /-статистик для проверки гипотез о нулевых
значениях коэффициентов. Вычислите скорректированные значения этих
статистик, учитывающие отличие процесса ut от процесса белого шума.
Сравните Р-значения для оценок коэффициентов, полученных в обоих
случаях.
Методические указания.
1. В качестве st возьмите процесс
£, = 0.5£, + 0.5v„
где %t — процесс гауссовского белого шума с единичной дисперсией, не
коррелированный с процессом vr
2. Осуществить необходимую коррекцию можно в рамках объекта Equation,
заказав опцию Heteroscedasticity —> Newey-West.
Задание 54. Оценивание единственной долговременной связи
между несколькими 1A) рядами
Смоделируйте реализации рядов yt и хп следуя процессу порождения данных
yt= 5 +xt + un
X* — X* 1 i V*, Хл — U,
где щ = 0.1vt_2 + 0.7v,+ 1 + st\
vt и et — независимые друг от друга процессы гауссовского белого шума с
дисперсиями, равными 1.
Оцените на основании полученных реализаций рядов yt и xt статистическую
модель
yt = a + fixt + l;r
Можно ли непосредственно в рамках оцененного уравнения проверить гипотезу
Н0: Р = 1? Если нельзя — что этому препятствует? Как надо изменить
спецификацию оцениваемого уравнения, чтобы проверить указанную гипотезу на
законных основаниях?
Методические указания. Произведите оценивание указанной статистической
модели и образуйте ряд остатков в форме объекта Series. Образуйте объект
Group, объединяющий этот ряд остатков и ряд Axt = xt-xt_x.B меню этой группы
выберите: Cross Correlation B)... На основании анализа сделанной коррелограммы
определите необходимое количество запаздывающих и опережающих разностей
переменной хп которое вместе с Axt следует дополнительно включить в правую
часть статистической модели.

636
Часть 2. Регрессионный анализ временных рядов
Задание 55. Оценивание ранга коинтеграции и модели коррекции ошибок
методом Иохансена
Смоделируйте реализации 5 рядов хп zn xu, x2t, x3t, следуя процессу порождения
данных:
X^f — l.JXj f_j U.jXj 1—2. ^\t>
Xo/ — 1 .ЭХ2 *_ 1 \J.jX2 t—2 ' ^2f>
x3t ~ 1 '^X3, t-1 — ®.->Хъ r-2 + 83f>
yt = 1 .JXlr + X2r 4- X3r 4- £4t,
Zf—~ Y\) \ Хл* 4~ Х21 4~ £/,
где £lp £2r, £3r, 6:4r, s5t— независимые друг от друга процессы гауссовского белого
шума с дисперсиями, равными 1 для eu, slt, s^t и Рав"
ными 2 для s4t и s5t.
Рассматривайте полученные реализации как статистические данные и
используя процедуру Иохансена в пакете ЕViews:
1) оцените ранг коинтеграции системы 5 рядов. Соответствует ли оцененное
значение теоретическому значению?
2) оцените модель коррекции ошибок, соответствующую оцененному рангу
коинтеграции. Сравните оцененную модель с теоретической.
Методические указания. Тест Иохансена на коинтеграцию позволяет выявлять
наличие стационарных линейных комбинаций временных рядов, являющихся
интегрированными рядами первого порядка, и представляет собой один из
методов оценки систем, который использует метод максимального правдоподобия
применительно к моделям векторных авторегрессий. Отметим, что основные
предположения данного теста в пакете Е Views — допущения о том, что
переменные, входящие в модель VAR, являются интегрированными процессами первого
порядка, а ошибки независимы и нормально распределены.
Чтобы провести тест Иохансена на коинтеграцию, выберите View I Cointegration
Test... в окне группы или в окне, появляющемся при оценивании векторной
авторегрессии. В первом случае появится окно, в котором в соответствии с тестом
Иохансена представлены различные опции, касающиеся спецификации
многомерного временного ряда и коинтеграционного соотношения. Поскольку
асимптотическое распределение соответствующей Lft-статистики (статистики критерия
отношения правдоподобий) зависит от спецификации коинтеграционного соотношения
и векторной авторегрессии, в ЕViews предусмотрены следующие опции:
1) No intercept or trend in СЕ or test VAR — в рядах нет детерминированных
трендов, в коинтеграционное соотношение не включены ни константа, ни тренд;
2) Intercept (no trend) in СЕ — по intercept in VAR — в рядах нет
детерминированных трендов, в коинтеграционное соотношение включена константа,
но не включен тренд;
3) Intercept (no trend) in СЕ and test VAR — допускается наличие у рядов
детерминированного линейного тренда, в коинтеграционное соотношение
включена только константа;
*11 = Х\2 = О»
Х2\ = Х22 — О'
ХЪ\ =ХЪ2 = ">

Задания для семинарских занятий... и для самостоятельной работы
637
4) Intercept and trend in СЕ — no trend in VAR — допускается наличие у рядов
детерминированного линейного тренда, в коинтеграционное соотношение
включены константа и тренд;
5) Intercept and trend in СЕ — linear trend in VAR — допускается наличие
у рядов детерминированного квадратичного тренда, в коинтеграционное
соотношение включены константа и тренд.
Если нет уверенности в том, какая из этих 5 спецификаций подходит к
имеющимся данным, можно воспользоваться опцией, позволяющей получить таблицу
со сравнительными характеристиками всех 5 возможных спецификаций;
6) Summarize all 5 sets of assumptions.
Поскольку в процессе порождения рядов для этого задания используются
только запаздывания на один и два шага, в модель для приращений
задействованных переменных входят запаздывания приращений только на один шаг.
Поэтому при выборе опции укажите:
Summarize all 5 sets of assumption; Lag intervals (pairs) in VAR: 1 1.
В результате выдается таблица, структура которой рассмотрена при
изложении темы 11.1 (разд. 11). Выберите ранг коинтеграции, ориентируясь на значения
критерия Шварца.
После этого создайте объект VAR и специфицируйте выбранную модель. Для
этого выберите в меню Basics: Vector Error Correction (это означает, что будет
оцениваться модель коррекции ошибок), в окне Endogenous Variables
перечислите эндогенные переменные в следующем порядке: Y Z XI Х2 ХЗ; в окне Lag
Intervals for D укажите: 1 1 (используются только запаздывающие на один шаг
приращения переменных). В меню Cointegration укажите выбранную ранее
спецификацию многомерного временного ряда и коинтеграционного соотношения
(один из 5 вариантов).
В результате выдается таблица, в которой приводятся результаты оценивания
коинтегрирующего вектора и модели коррекции ошибок.
Приложение
ТАБЛИЦЫ СТАТИСТИЧЕСКИХ ДАННЫХ К ЗАДАНИЯМ
Таблица П-1
Производство транспортных средств
всеми отделениями фирмы General Motors Corp, млн ед.
Год
1970
1971
1972
1973
1974
1975
Выпуск
5.3
7.8
7.8
8.7
6.7
6.6
Год
1976
1977
1978
1979
1980
1981
Выпуск
8.6
9.1
9.5
9.0
7.1
6.8
Год
1982
1983
1984
1985
1986
1987
Выпуск
6.2
7.8
8.3
9.3
8.6
7.8
Год
1988
1989
1990
1991
1992
1992
Выпуск
8.1
7.9
7.5
7.0
7.2
7.2

638 Часть 2. Регрессионный анализ временных рядов
ТаблицаП-2
Производство водки и ликероводочных изделий
в России, млн дкл
Год,
месяц
1999:01
1999:02
1999:03
1999:04
1999:05
1999:06
1999:07
1999:08
1999:09
1999:10
1999:11
1999:12
2000:01
2000:02
2000:03
2000:04
2000:05
2000:06
2000:07
2000:08
2000:09
2000:10
2000:11
2000:12
Выпуск
9.2
9.9
11.2
11.0
9.9
10.6
9.8
10.3
11.2
11.6
12.9
16.8
8.9
9.1
9.3
8.5
8.7
9.2
8.8
9.8
10.9
12.1
12.2
15.1
Год,
месяц
2001:01
2001:02
2001:03
2001:04
2001:05
2001:06
2001:07
2001:08
2001:09
2001:10
2001:11
2001:12
2002:01
2002:02
2002:03
2002:04
2002:05
2002:06
2002:07
2002:08
2002:09
2002:10
2002:11
2002:12
Выпуск
8.9
9.2
10.7
9.6
11.2
7.7
8.6
9.8
11.9
14.1
13.7
16.1
10.4
8.9
10.8
11.6
10.5
10.3
10.3
10.9
11.7
13.0
13.2
17.6
Год,
месяц
2003:01
2003:02
2003:03
2003:04
2003:05
2003:06
2003:07
2003:08
2003:09
2003:10
2003:11
2003:12
2004:01
2004:02
2004:03
2004:04
2004:05
2004:06
2004:07
2004:08
2004:09
2004:10
2004:11
2004:12
Выпуск
9.5
9.1
11.5
11.3
10.4
10.1
10.3
11.2
11.0
12.5
12.1
16.2
9.5
9.7
11.6
11.4
10.1
10.9
9.6
10.3
11.4
12.1
13.3
15.6
Год,
месяц
2005:01
2005:02
2005:03
2005:04
2005:05
2005:06
2005:07
2005:08
2005:09
2005:10
2005:11
2005:12
2006:01
2006:02
2006:03
2006:04
2006:05
2006:06
2006:07
2006:08
2006:09
2006:10
Выпуск
7.9
8.3
10.8
10.5
9.8
9.1
9.3
10.4
11.6
12.1
13.7
18.8
0.3
6.4
9.7
10.2
10.0
10.6
6.60
11.1
12.2
13.1

Задания для семинарских занятий... и для самостоятельной работы
639
ТаблицаП-3
Смоделированные данные, порожденные динамическими моделями
/
1 1
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
1 10
1 п
1 12
1 13
1 14
1 15
1 16
1 17
1 18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
X
8.000000
7.746844
7.963056
7.621878
7.667089
7.994070
8.098424
7.947546
8.123692
7.773530
8.054959
7.996305
7.755318
8.115087
7.918306
8.006121
8.140740
7.963118
7.773652
7.735924
7.593576
7.658618
7.922038
8.100324
8.180901
7.910580
8.227158
8.333015
8.626765
8.576380
8.076016
8.045565
Y\
4.778654
4.647211
4.658651
4.812711
4.890967
4.805793
4.662272
4.799026
4.901799
4.820392
4.627901
4.749784
4.689044
4.676003
4.807234
4.905622
4.851833
4.769343
4.972667
4.927739
4.978830
4.741847
4.677019
4.775965
4.815660
4.686780
4.682224
4.786983
4.621388
5.032208
5.063440
4.980322
Y1
1.600456
1.478539
1.562692
1.556651
1.648580
1.686486
1.594098
1.595897
1.686944
1.552001
1.552463
1.579669
1.498898
1.599377
1.589194
1.667248
1.659752
1.559028
1.637463
1.643206
1.663817
1.591454
1.618528
1.667547
1.658712
1.505721
1.590064
1.627781
1.569938
1.704311
1.596932
1.612876
КЗ
8.046243
7.881005
7.951495
8.070217
8.233157
8.176761
7.949535
8.013130
8.124588
7.994678
7.882986
7.960839
7.895680
7.952725
8.011069
8.132048
8.063209
7.932809
8.165465
8.192043
8.290204
8.119461
8.068240
8.094964
8.045063
7.847210
7.889265
7.922357
7.689170
7.978070
7.963457
8.007525
F4
3.387690
3.229002
3.208212
3.137928
3.122187
3.165926
3.188763
3.187727
3.230404
3.163146
3.181130
3.191761
3.138470
3.192741
3.183502
3.205627
3.230680
3.198084
3.173678
3.144955
3.110611
3.084465
3.127491
3.189895
3.230886
3.180027
3.232011
3.280381
3.338343
3.397796
3.311543
3.267464
F5
4.098754
3.935157
3.917764
3.922739
3.839786
3.904959
4.004021
4.022873
4.020804
3.985052
3.931615
4.017683
3.941481
3.950101
4.021658
3.989367
4.029703
4.024966
3.963572
3.890211
3.858911 1
3.807233 1
3.882844 |
4.002761 |
4.066036 |
4.018854 |
4.015172 |
4.132523 1
4.198057 J
4.316654 1
4.185560 |
4.034497

640
Часть 2. Регрессионный анализ временных рядов
Окончание табл. П-3
i
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
X
7.852746
7.975418
7.787466
7.624511
7.686645
7.650725
8.220778
8.094610
7.820000
7.648600
7.899919
8.085734
7.977923
7.868369
8.027590
8.036176
7.947856
7.987747
П
4.906008
4.873299
4.765737
4.793970
4.733794
4.635608
4.514412
4.860347
4.907596
4.912713
4.963546
4.755750
4.687967
4.678172
4.677120
4.598592
4.719238
4.839404
Y2
1.573519
1.628804
1.542585
1.554879
1.577045
1.531362
1.595459
1.663028
1.610573
1.609464
1.726160
1.642236
1.550315
1.521445
1.568165
1.514436
1.547716
1.624336
F3
8.005940
8.067441
7.970183
8.059954
8.079432
8.002434
7.902608
8.088211
8.093145
8.159487
8.292353
8.050178
7.909461
7.895542
7.925294
7.814402
7.916290
8.053573
F4
3.204499
3.203780
3.153030
3.108903
3.096726
3.074780
3.171685
3.218455
3.178132
3.130077
3.166283
3.190689
3.179366
3.157438
3.181989
3.183405
3.182183
3.198184
F5
3.984436
3.957354
3.943765
3.868628
3.829628
3.832410
3.929512
4.098846
3.997287
3.887012
3.895825
3.977523
4.009742
3.961132
3.963781
4.000688
4.001333
3.991449
Таблица П-4
Уровни безработицы в США
Год,
месяц
1987:01
1987:02
1987:03
1987:04
1987:05
1987:06
1987:07
1987:08
1987:09
1987:10
1987:11
1987:12
X
6.5
6.5
6.5
6.2
6.2
6.1
6.0
6.0
5.8
5.9
5.7
5.6
Год,
месяц
1988:01
1988:02
1988:03
1988:04
1988:05
1988:06
1988:07
1988:08
1988:09
1988:10
1988:11
1988:12
X
5.6
5.6
5.6
5.4
5.5
5.4
5.4
5.5
5.3
5.3
5.2
5.2
Год,
месяц
1989:01
1989:02
1989:03
1989:04
1989:05
1989:06
1989:07
1989:08
1989:09
1989:10
1989:11
1989:12
X
5.3
5.1
5.0
5.2
5.1
5.3
5.2
5.2
5.2
5.2
5.2
5.2
Год,
месяц
1990:01
1990:02
1990:03
1990:04
1990:05
1990:06
1990:07
1990:08
1990:09
1990:10
1990:11
1990:12
X
5.2
5.2
5.2
5.3
5.3
5.2
5.4
5.6
5.6
5.6
5.8
6.0
Год,
месяц
1991:01
1991:02
1991:03
1991:04
1991:05
1991:06
1991:07
1991:08
1991:09
1991:10
X
6.1
6.4
6.8
6.5
6.8
6.9
6.7
6.7
6.6
6.7

Задания для семинарских занятий... и для самостоятельной работы
641
ТаблицаП-5
Совокупный располагаемый личный доход в США,
млрд долл., в ценах 1982 г.
Год
1959
1960
1961
1962
1963
1964
1965
DPI
1066.9
1090.9
1122.5
1168.7
1208.7
1289.7
1367.4
Год
1966
1967
1968
1969
1970
1971
1972
DPI
1433.0
1494.9
1551.1
1601.7
1668.1
1730.1
1797.9
Год
1973
1974
1975
1976
1977
1978
1979
DPI
1914.9
1894.9
1930.4
2001.0
2067.9
2166.5
2211.4
Год
1980
1981
1982
1983
1984
1985
DPI
2214.8
2249.0
2261.4
2332.5
2470.5
2527.3
ТаблицаП-6
Смоделированные реализации стационарных и нестационарных процессов
/
1
?
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
ST 1
0.000000
0.609601
1.063659
0.214556
-0.546113
-2.271716
-3.064278
-2.304551
-2.312949
-2.272488
-3.370321
-1.520106
-1.948093
-4.001587
-1.913173
-1.882648
-1.565388
-2.706458
-1.107849
-0.735072
0.293338
2.875908
ST 2
0.000000
0.809601
1.423659
0.702556
0.044287
-1.599396
-2.326422
-1.514266
-1.480721
-1.406705
-2.477695
-0.606005
-1.016813
-3.056562
-0.957154
-0.917832
-0.593535
-1.728976
-0.125864
0.250516
1.281809
3.866685
ST 3
0.000000
1 0.849601
1.535659
0.912156
0.371967
-1.137252
-1.716707
-0.746494
-0.546504
-0.299331
-1.191796
0.862715
0.638163
-1.212582
1.078031
1.310315
1.828983
0.889039
2.688548
3.262045
4.491032
7.274064
ST 4
0.000000
1.029601
1.999659
1.763356
1.712927
0.795516
0.909508
2.674478
3.770274
5.014090
5.218942
8.471304
9.545035
9.092916
12.882430
14.713830
16.931800
17.791290
21.490350
24.063490
27.392190
32.374990
WALKJ
0.000000
0.609601
1.185579
0.549208
-0.168549
-2.003376
-3.250280
-3.103409
-3.572717
-3.994846
-5.547176
-4.371025
-5.103034
-7.546146
-6.258050
-6.610160
-6.669429
-8.123576
-7.066260
-6.915053
-6.033657
-3.392419
WALKJL
0.000000
0.809601
1.585579
1.149208
0.631451
-1.003376
-2.050280
-1.703409
-1.972717
-2.194846
-3.547176
-2.171025
-2.703034
-4.946146
-3.458050
-3.610160
-3.469429
-4.723576
-3.466260
-3.115053
-2.033657
0.807581
WALKJ>
0.000000
1.009601
2.085579
2.049208
2.031451
0.996624
0.649720
1.796591
2.427283
3.205154
2.952824
5.528975 |
6.296966
5.453854 |
8.441950 |
9.889840 1
11.730570 |
12.276420 1
15.433740 1
17.784950 1
20.966340 |
26.007580 |

642
Часть 2. Регрессионный анализ временных рядов
Продолжение табл. П-б
i
73
1 24
75
76
77
78
79
30
31
37
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
ST 1
2.373763
2.564043
1.488571
0.659608
1.378541
0.900088
-0.195560
-0.500432
0.339263
-1.221197
0.433163
1.124709
1.370190
1.780155
0.920089
1.345971
-0.294878
-1.064392
-0.241155
1.000602
0.158635
0.511194
-1.493654
-2.163930
-0.958555
1.301504
0.858898
1.559760
2.445310
2.127578
3.680289
3.941190
3.112465
0.174149
-1.511211
ST 2
3.366384
3.558140
2.483848
1.655830
2.375518
1.897670
0.802506
0.498021
0.659499
0.222188
1.432371
2.124076
2.369683
2.779750
1.919765
2.345711
0.704914
-0.064558
0.758713
2.000496
1.158550
1.511125
-0.493708
-1.163974
0.041410
2.301476
1.858876
2.559742
3.445296
3.127566
4.680280
4.941182
4.112459
1.174144
-0.511215
ST 3
6.972287
7.362863
6.487626
5.858853
6.777936
6.499604
5.604053
5.499259
5.860489
5.178605
7.033005
7.924583
8.370088
8.980074
8.320024
8.945919
7.505081
6.935575
7.958819
9.400581
8.758618
9.311180
7.506336
7.036061
8.441438
10.901500
10.658890
11.559760
12.645310
12.527580
14.280290
14.741190
14.112460
11.374150
9.888788
ST 4
34.373030
37.163450
38.788100
40.759230
44.378240
46.899850
48.904250
51.799410
55.260610
57.778700
2.933080
67.224650
71.170140
75.380110
78.420060
82.845940
85.305100
88.735590
93.858830
99.500590
103.158600
108.111200
110.806300
114.936100
121.041400
128.301500
132.958900
138.859800
145.045300
150.127600
157.180300
163.041200
167.912500
170.774100
174.988800
WALKJ
-3.319382
-2.654349
-3.217014
-3.748262
-2.897408
-3.100152
-4.015782
-4.359766
-4.298684
-5.248471
-3.838350
-3.060171
-2.589749
-1.905745
-2.409780
-1.799881
-3.171535
-4.000024
-3.389666
-2.196140
-2.837987
-2.453701
-4.356310
-5.325317
-4.552728
-2.484380
-2.666685
-1.794044
-0.596542
-0.425212
1.553015
2.549973
2.509486
0.193663
-1.456867
WALK_2
1.080618
1.945651
1.582986
1.251738
2.302592
2.299848
1.584218
1.440234
1.701316
0.951529
2.561650
3.539829
4.210251
5.094255
4.790220
5.600119
4.428465
3.799976
4.610334
6.003860
5.562013
6.146299
4.443690
3.674683
4.647272
6.915620
6.933315
8.005956
9.403458
9.774788
11.953010
13.149970
13.309490
11.193660
9.743133
WALKJ
28.580620
31.845650
33.982990
36.251740
40.002590
42.799850
44.984220
47.840230
51.201320
53.651530
58.561650
62.939830
67.110250
71.594250
74.990220
79.600120
82.328460
85.699980
90.610330
96.203860
100.062000
105.046300
107.843700
111.674700
117.347300
124.415600
129.333300
135.406000 1
141.903500 1
147.474800 |
154.953000 1
161.550000 1
167.209500 1
170.693700 |
174.943100 1

Задания для семинарских занятий... и для самостоятельной работы
643
Продолжение табл. П-6
i
58
59
60
61
6?
61
64
65
66
67
68
69
70
71
7?
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
ST 1
-0.926922
-0.019851
-0.239447
-0.966797
-0.792959
-0.404901
-1.437120
-2.589922
-1.184149
-1.108750
-1.360083
-2.043427
-2.013563
-2.344915
-2.114172
-1.577519
-1.181456
-0.360290
-0.038007
-1.336223
-0.474682
-0.782948
-1.922455
-0.744953
-1.784624
-0.358302
-0.264257
-1.123699
-1.863978
-1.254249
-0.580441
-0.832656
-1.253761
0.147474
1.855942
ST 2
0.073075
0.980147
0.760551
0.033201
0.207040
0.595098
-0.437121
-1.589923
0.184149
0.108751
-0.360084
-1.043427
1.013563
-1.344915
-1.114172
-0.577519
-0.181456
0.639710
0.961993
-0.336223
0.525318
0.217052
-0.922455
0.255047
-0.784624
0.641698
0.735743
-0.123699
-0.863978
-0.254249
0.419559
0.167344
-0.253761
1.147474
2.855942
ST Ъ
1 10.673080
1 11.780150
| 11.760550
1 11.233200
| 11.607040
1 12.195100
11.362880
10.410080
12.015850
12.291250
12.239920
11.756570
11.986440
11.855090
12.285830
13.022480
13.618540
14.639710
15.161990
14.063780
15.125320
15.017050
14.077550
15.455050
14.615380
16.241700
16.535740
15.876300
15.336020
16.145750
17.019560
16.967340
16.746240
18.347470 |
20.255940 |
ST 4
181.573100
188.580100
194.560600
200.133200
206.707000
213.595100
219.162900
224.710100
232.915900
239.891200
246.639900
253.056600
260.286400
267.255100
274.885800
282.922500
290.918500
299.439700
307.562000
314.163800
323.025300
330.817100
337.877500
347.355000
354.715400
364.641700
373.335700
381.176300
389.236000
398.745800
408.419600
417.267300
426.046200
436.747500
447.855900
WALKJ
-1.174820
-0.453133
-0.676700
-1.451939
-1.471460
-1.241995
-2.355193
-3.795420
-2.907631
-3.069062
-3.542145
-4.497506
-4.876326
-5.610391
-5.848631
-5.734813
-5.654253
-5.069378
-4.819153
-6.124970
-5.530674
-5.933877
-7.229973
-6.436962
-7.625624
-6.556226
-6.533842
-7.446135
-8.411154
-8.174221
-7.751262
-8.119565
-8.707201
-7.556719
-5.818756 1
WALKJ
10.225180
11.146870
11.123300
10.548060
10.728540
11.158010
10.244810
9.004580
10.092370
10.130940
9.857855
9.102494
8.923674
8.389609
8.351369
8.665187
8.945747
9.730622
10.180850
9.075030
9.869326
9.666123
8.570027
9.563038
8.574376
9.843774
10.066160
9.353865
8.588846
9.025779
9.648738
9.480435
9.092799
10.443280
12.381240
1 WALKJ
1 181.225200
1 188.046900
194.023300
199.548100
205.928500
212.658000
218.144800
223.404600
231.092400
237.830900
244.357900
250.502500
257.323700
263.889600
271.051400
278.665200 |
286.345700 1
294.630600 1
302.680800 |
309.275000 1
317.869300 1
325.566100 |
332.470000 1
341.563000 1
348.774400 |
358.343800 1
366.966200 1
374.753900 |
382.588800 |
391.725800 J
401.148700 |
409.880400 |
418.492800 |
428.943300 |
440.081200 1

644
Часть 2. Регрессионный анализ временных рядов
Окончание табл. П-в
i
93
94
95
96
97
98
99
100
ST 1
2.637576
2.245996
0.817129
0.811771
-0.248490
-0.689955
-1.837949
-1.752837
ST 2
3.637576
3.245996
1.817129
1.811771
0.751510
0.310045
-0.837949
-0.752837
STJ
21.237580
21.046000
19.817130
20.011770
19.151510
18.910050
17.962050
18.247160
ST_4
458.137600
467.346000
475.617100
485.411800
494.251500
503.810000
512.762100
523.047200
WALKJ
-4.665934
-4.529999
-5.509666
-5.351598
-6.249505
-6.740668
-8.026653
-8.309131
WALKJ.
13.734070
14.070000
13.290330
13.648400
12.950490
12.659330
11.573350
11.490870
WALKJ
450.734100
460.470000
469.190300
479.148400
488.150500
497.659300
506.473300
516.390900
Таблица П-7
Значения реального валового внутреннего продукта США
за период с 1959 по 2006 г., млрд долл., в ценах 2000 г.
Год
1959
1960
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
1972
1973
1974
RGDP
2441.300
2501.800
2560.000
2715.200
2834.000
2998.600
3191.100
3399.100
3484.600
3652.700
3765.400
3771.900
3898.600
4105.000
4341.500
4319.600
Год
1975
1976
1977
1978
1979
1980
1981
1982
1983
1984
1985
1986
1987
1988
1989
1990
RGDP
4311.200
4540.900
4750.500
5015.000
5173.400
5161.700
5291.700
5189.300
5423.800
5813.600
6053.700
6263.600
6475.100
6742.700
6981.400
7112.500
Год
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
RGDP
7100.500
7336.600
7532.700
7835.500
8031.700
8328.900
8703.500
9066.900
9470.300
9817.000
9890.700
10048.800
10301.000
10675.800
11003.400
11319.400
ТаблицаП-8
Асимптотические 5%-е критические значения f-статистики
критерия Перрона с экзогенным выбором даты структурного изменения
(сегментированный тренд, модель с аддитивным выбросом)
Л=ТВ/Т
t
0.1
-3.52
0.2
-3.72
0.3
-3.85
0.4
-3.91
0.5
-3.93
0.6
-3.94
0.7
-3.89
0.8
-3.83
0.9
-3.72

Задания для семинарских занятий... и для самостоятельной работы
645
ТаблицаП-9
Таблица для вычисления критических значений статистики Дики — Фуллера
при проверке на коинтегрированность нескольких рядов
N
1
2
3
4
5
Вариант
Без константы
и тренда
С константой,
без тренда
С константой
и трендом
С константой,
без тренда
С константой
и трендом
С константой,
без тренда
С константой
и трендом
С константой,
без тренда
С константой
и трендом
С константой,
без тренда
С константой
и трендом [
Уровень
значимости, %
1
5
10
1
5
10
1
5
10
1
5
10
1
5
10
1
5
10
1
5
10
1
5
10
1
5
10
1
5
10
1
5
10
*°°
-2.5658
-1.9393
-1.6156
-3.4335
-2.8621
-2.5671
-3.9638
-3.4126
-3.1279
-3.9001
-3.3377
-3.0462
-4.3266
-3.7809
-3.4959
-4.2981
-3.7429
-3.4518
-4.6676
-4.1193
-3.8344
-4.6493
-4.1000
-3.8110
-4.9695
-4.4294
-4.1474
-4.9587
-4.4185
-4.1327
-5.2497
-4.7154
-4.4345
к\
-1.960
-0.398
-0.181
-5.999
-2.738
-1.438
-8.353
-4.039
-2.418
-10.534
-5.967
-4.069
-15.531
-9.421
-7.203
-13.790
-8.352
-6.241
-18.492
-12.024
-9.188
-17.188
-10.745
-8.317
-22.504
-14.501
-11.165
-22.140
-13.641
-10.638
-26.606
-17.432
-13.654
*2
-10.04
0.00
1 о.оо
-29.25
| -8.36
1 -4.48
1 -47.44
-17.83
1 -7.58
-30.03
-8.98
-5.73
-34.03
-15.06
-4.01
-46.37
-13.41
-2.79 1
-49.35
-13.13
-4.85
-59.20 1
-21.57
-5.19
-50.22 1
-19.54
-9.88
-37.29 1
-21.16
-5.48
-49.56
-16.50 |
-5.77

646 Часть 2. Регрессионный анализ временных рядов
Окончание табл. П-9
N
6
Вариант
С константой,
без тренда
С константой
и трендом
Уровень
значимости, %
1
5
10
1
5
10
*оо
-5.2400
-4.7048
-4.4242
-5.5127
-4.9767
-4.6999
к\
-26.278
-17.120
-13.347
-30.735
-20.883
-16.445
*2
-41.65
-11.17
0.0
-52.50
-9.05
0.0
Примечание.
N = k + 1 — общее количество переменных;
к — количество регрессоров без учета константы.
Данные, содержащиеся в ячейках таблицы, соответствующих N = 1, можно использовать для
проверки на наличие единичного корня или для проверки на коинтегрированность нескольких
рядов при известном коинтегрирующем векторе.
Данные, содержащиеся в ячейках таблицы, соответствующих N > 1, можно использовать для
проверки на коинтегрированность группы рядов на основании ряда остатков от оцененной
(обычным) методом наименьших квадратов модели регрессии.
Асимптотические односторонние критические значения приведены в графе к^. Для конечного
количества наблюдений (Г) критические значения, соответствующие уровню значимости or,
корректируются в соответствии с формулой:
С(а,Г) = *.+|-+^,
где аг^, ATj и к2 берутся из строки, соответствующей общему количеству переменных N,
выбранному варианту (без константы и тренда; с константой, без тренда; с константой и трендом) и
выбранному уровню значимости.
Нулевая гипотеза некоинтегрированности отвергается при значениях статистики критерия,
меньших критического.

Литература
1. Андерсон Т. A976). Статистический анализ временных рядов. М.: Мир.
2. Бокс Дж., Дженкинс Г. A974). Анализ временных рядов. Прогноз и управление.
Вып. 1, 2. М.: Мир.
3. Канторович Г.Г. B002) Лекции: Анализ временных рядов // Экономический
журнал ВШЭ. Т. 6. № 1—4; Т. 7. 2003. № 1. Материал выложен на сайте: http://www.
ecsocman.edu.ru/db/msg/48941 .html
4. Кендалл М. Дж., Стьюарт А. A976). Многомерный статистический анализ и
временные ряды. М.: Наука.
5. Магнус Я.Р., Катышев П.К, Пересецкий А.А. B005). Эконометрика. Начальный
курс: Учебник. 7-е изд., испр. М.: Дело.
6. Носко В.П. B004). Эконометрика. Элементарные методы и введение в
регрессионный анализ временных рядов. М.: ИЭПП.
7. Носко В.П. B004) Эконометрика: введение в регрессионный анализ временных
рядов. М.: Логос.
8. Хеннан Э. A974). Многомерные временные ряды / пер. с англ. М.: Мир.
9. Эконометрический анализ динамических рядов основных макроэкономических
показателей B001). Научные труды ИЭПП № 34Р. М.: ИЭПП.
10. Akaike Н A973). Information Theory and an Extension of the Maximum Likelihood
Principle // Petrov B.N. and Csaki F. (eds.). Proceedings, 2nd International Symposium
on Information Theory. P. 267—281. Budapest: Akademia Kiado.
11. Akaike H A974). A new look at the statistical model identification // IEEE
Transactions on Automatic Control. Vol. 19. P. 716—723.
12. Bartlett M.S. A946). On the Theoretical Specification of sampling properties of Auto-
correlated Time Series // Journal of the Royal Statistical Society. Series B. Vol. 8.
P. 27—41.
13. Bierens H.J. A997). Testing the Unit Root with Drift Hypothesis Against Nonlinear
Trend Stationarity, with an Application to the US Price Level and Interest Rate //
Journal of Econometrics. Vol. 81. P. 29—64.
14. Box G.E.P., Pierce D.A. A970). Distribution of Residual Autocorrelations in Autore-
gressive Integrated Moving Average Time Series Models // Journal of the American
Statistical Association. Vol. 65. P. 1509—1526.
15. Chan K.H, Hayya JC, OrdJ.K. A977). A Note on Trend Removal Methods: The Case
of polynomial versus variate differencing // Econometrica. Vol. 45. P. 737—744.

648
Часть 2. Регрессионный анализ временных рядов
16. Cheung Y.-W., Lay K.S. A995). Lag Order and Critical Values of a Modified Dickey-
Fuller Test // Oxford Bulletin of Economics and Statistics. 1995. Vol. 57. № 3.
P. 411—419.
17. Cochrane J.К A998). How Big is the Random Walk in GNP? // Journal of Political
Economy. Vol. 96. P. 893—920.
18. Davidson R., MacKinnon J.G. A993). Estimation and Inference in Econometrics. New
York: Oxford University Press.
19. Dickey DA. A976). Estimation and Hypothesis Testing for Nonstationary Time Series.
Ph.D. dissertation. Iowa State University.
20. Dickey DA., Bell W.R., Miller R.B. A986). Unit Roots in Time Series Models: Tests
and Implications // American Statistican. Vol. 40. P. 12—26.
21. Dickey DA., Fuller WA. A981). Likelihood Ratio Statistics for Autoregressive Time
Series With a Unit Root // Econometrica. Vol. 49. P. 1057—1072.
22. Dickey DA., Pantula S. A987). Determining the Order of Differencing in
Autoregressive Processes // Journal of Business and Economic Statistics. Vol. 15. P. 455—461
23. Dolado #., Jenkinson Т., Sosvilla-Rivero S. A990). Cointegration and Unit Roots //
Journal of Economic Surveys. Vol. 4. P.243—273.
24. Elliott G., Rothenberg T.J., Stock J.H. A996). Efficient Tests for an Autoregressive
Unit Root // Econometrica. Vol. 64. P. 813—836
25. Enders W. A995). Applied Econometric Time Series. New York: Wiley.
26. Engle R.F., Granger C.W.J. A987). Co-integration and Error Correction:
Representation, Estimation, and Testing // Econometrica. Vol. 55. P. 251—276.
27. Engle R.F., Granger С W.J. A991). Cointegrated Economic Time Series: An Overview
with New Results // R.F. Engle and C.W.J. Granger (eds.), Long-Run Economic
Relationships, Readings in Cointegration. New York: Oxford University Press. P. 237—26.
28. EntorfH. A992). Random Walk with Drift, Simultaneous Errors, and Small Samples:
Simulating the Bird's Eye View, Institut National de la Statistique et des Etudes
Economiques.
29. Fuller WA. A976). Introduction to Statistical Time Series. New York: Wiley.
30. Fuller WA. A996). Introduction to Statistical Time Series. 2nd ed. New York: Wiley.
31. Ghysels E., Osborn D.R. A991). The Econometric Analysis of Seasonal Time Series.
Cambridge: Cambridge University Press.
32. Ghysels E., Perron P. A992). The Effect of Seasonal Adjustment Filters on Tests for a
Unit Root // Journal of Econometrics. Vol. 55. P. 57—98.
33. Granger С W.J. A983). UCSD Discussion Paper, 83—13.
34. Hall A. A994). Testing for a Unit Root in Time Series with Pretest Data-Based Model
Selection // Journal of Business and Economic Statistics. Vol. 12. P. 451 —470.
35. Hamilton JD. A994). Time Series Analysis. Princeton: Princeton University Press.
36. Hannan E.J, Quinn B.G. A979). The Determination of the Order of an Autoregression
// Journal of the Royal Statistical Society. Series B. Vol. 41. P. 190—195.
37. Holden D., Perman R. A994). Unit Roots and Cointegration for Economist //
Cointegration for the Applied Economists (ed. by Rao B.B.). Basingstoke: Macmillan.
38. Jarque C, Bera A. A980). Efficient Tests for Normality, Homoskedasticity, and Serial
Independence of Regression Residuals. Economics Letters. 1980. Vol. 6. P. 255—259.
39. Johansen S. A988). Statistical Analysis of Cointegration Vectors // Journal of
Economic Dynamics and Control. Vol. 12. P. 231—254.
40. Johansen S. A991). Estimation and Hypothesis Testing of Cointegration Vectors in
Gaussian Vector Autoregressive models // Econometrica. Vol. 59. P. 1551 —1580.
41. Johnston J, DiNardo J A997). Econometric Methods. 4th ed. N.Y., McGraw-Hill.

Литература
649
42. Kavalieris L. A991). A Note on Estimating Autoregressive-Moving Average Order //
Biometrika. 1991. Vol. 78. P. 920—922.
43. Kwan A.C.C. A996). A Comparative Study of the Finite-sample Distribution of some
Portmanteau Tests for Univariate Time Series Models // Commun. Statist-Simula. Vol. 25.
№4. P. 867—904.
44. Kwan A.C.C., Sim A.-B. A996). On the Finite-Sample Distribution of Modified
Portmanteau Tests for Randomness of a Gaussian Time Series // Biometrika. Vol. 83. № 4.
P. 938—943.
45. Kwiatkowski D., Phillips P.C.B., Schmidt P., Shin Y. A992). Testing of the Null
Hypothesis of Stationary against the Alternative of a Unit Root // Journal of Econometrics.
Vol. 54. P. 159—178.
46. Leybourne SJ. A995). Testing for Unit Roots Using Forward and Reverse Dickey-
Fuller Regressions // Oxford Bulletin of Economics and Statistics. Vol. 57. P. 559—
571.
47. Ljung G., Box G.E.P. A979). On a Measure of Lack of Fit in Time Series Models //
Biometrika. Vol. 66. P. 255—270.
48. Lomnicki Z.A. A961). Tests for Departure from Normality in the Case of Linear
Stochastic Processes // Metrika. №4. P. 37—62.
49. MacKinnon J.G. A991). Critical Values for Cointegration Tests. Chapter 13 // Long-
run Economic Relationships: Readings in Cointegration / eds. by R.F. Engle and
Granger C.WJ. Oxford University Press.
50. Maddala G.S., In-Moo Kim A998). Unit Roots, Cointegration and Structural Change.
Cambridge: Cambridge University Press.
51. Mann КВ., WaldA. A943). On Stochastic Limit and Order Relationships // Annals of
Mathematical Statistics. Vol. 14. P. 217—277.
52. Mills T. A999). The Econometric Modeling of Financial Time Series. 2nd ed.
Cambridge: Cambridge University Press.
53. Murray C.J., Nelson C.R. B000). The Uncertain Trend in U.S. GDP // Journal of Monetary
Economics. Vol. 46. P. 79—95.
54. Nelson C.R., Plosser C.I. A982). Trends and Random Walks in Macroeconomic Time
Series // Journal of Monetary Economics. Vol. 10. P. 139—162.
55. Newey W., West К A994). Automatic Lag Selection in Covariance Matrix Estimation
// Review of Economic Studies. Vol. 61. P. 631—653.
56. Ng S., Perron P. A995). Unit Root Tests in ARMA models With Data-Dependent
Methods for the Selection of the Truncation Lag // Journal of American Statistical
Association. Vol. 90. P. 268—281.
57. Nunes L.S., NewboldP., Kuan C.-M. A997). Testing for Unit Roots with Breaks. Evidence
on the Great Crash and the Unit Root Hypothesis Reconsidered // Oxford Bulletin
of Economics and Statistics. 1997. Vol. 59. № 4. P. 435—448.
58. Patterson К B000). An Introduction to Applied Econometrics: A Time Series Approach.
New York: St's Martin Press.
59. Perron P. A988). Trends and Random Walks in Macroeconomic Time Series: Further
Evidence from a New Approach // Journal of Economic Dynamic and Control. 1988.
Vol. 12. P. 297—332.
60. Perron P. A989a). The Great Crash, the Oil Price Shock, and the Unit Root Hypothesis //
Econometrica. Vol. 57. P. 1361 — 1401.
61. Perron P. A9896). Testing for a Random Walk: A Simulation Experiment When the
Sampling Interval Is Varied // Advances in Econometrics and Modelling (ed. by B. Ray).
Dordrecht and Boston: Kluwer Academic Publishers.

650
Часть 2. Регрессионный анализ временных рядов
62. Perron P. A997). Further evidence on breaking trend functions in macroeconomic
variables // Journal of Econometrics. Vol. 80. №2. P. 355—385.
63. Perron P., Vogelsang T.J. A993). Erratum // Econometrica. Vol. 61. № 1. P. 248—249.
64. Phillips P.C.B. A987). Time Series Regression with a Unit Root // Econometrica. Vol. 55.
P. 277—301.
65. Phillips P.C.B., Perron P. A988). Testing for a Unit Root in Time Series Regression //
Biometrika. Vol. 75. P. 335—346.
66. Pollock D.S.G. A999). Handbook of Time Series Analysis, Signal Processing, and
Dynamics (Signal Processing and its Applications). New York: Academic Press.
67. Said E., Dickey D.A. A984). Testing for Unit Roots in Autoregressive Moving Average
Models of Unknown Order // Biometrika. Vol. 71. P. 599—607.
68. Saikonnen P. A991). Asymptotically Efficient Estimation of Cointegrated Regressions //
Econometric Theory. Vol. 7. P. 1—21.
69. SarganJ.D., Bhargava A. A983).Testing Residuals from Least Squares Regression
for Being Generated by the Gaussian Random Walk // Economertica. Vol. 51.
P. 153 — 174.
70. Schmidt P., Phillips P.C.B. A992). LM Tests for a Unit Root in the Presence of
Deterministic Trends // Oxford Bulletin of Economics and Statistics. Vol. 54. P. 257—287.
71. Schwarz G. A978). Estimating the Dimension of a Model // The Annals of Statistics.
Vol. 16. P. 461—464.
72. Schwert G.W. A989). Tests for Unit Roots: A Monte Carlo Investigation // Journal
of Business and Economic Statistics. Vol. 7. P. 147—159.
73. Shiller R.J., Perron P. A985). Testing the Random Walk Hypothesis: Power versus
Frequency of Observation // Economic Letters. Vol. 18. P. 381—386.
74. Sims C.A., Stock J.K, Watson M.W. A990). Inference in Linear Time Series Models
with Some Unit Roots // Econometrica. Vol. 58. P. 113—144.
75. Slutzki E. A937). The Summation of Random Causes as the Source of Cyclic Processes //
Econometrica. Vol. 5. P. 105.
76. Stock J.H., Watson M. W. A993). A Simple Estimator of Cointegrating Vectors in Higher
Order Integrated Systems // Econometrica. Vol. 61. P. 783—820.
77. Taylor A.M.R. B000). The Finite Sample Effects of Deterministic Variables on
Conventional Methods of Lag-Selection in Unit-Root Tests // Oxford Bulletin of Economics
and Statistics. Vol. 62. P. 293—304.
78. Kwiatkowski D., Schmidt P. A990). Dickey-Fuller Tests with Trend, Commun // Statist-
Theory Meth. Vol. 19. № 10. P. 3645—3656.
79. West K.D. A988). Asymptotic Normality, When Regressors Have a Unit Root //
Econometrica. Vol. 56. P. 1397—1417.
80. White J.S. A958). The Limiting Distribution of the Serial Correlation Coefficient in the
Explosive Case // Annals of Mathematical Statistics. Vol. 29. 1188—1197.
81. Wold H. A938). A study in the analysis of stationary time series. Stockholm: Almqvist
and Wiksell.
82. Yu H. B007). High moment partial sum processes of residuals in ARMA models and
their applications // Journal of Time Series Analysis. Vol. 28. No. 1. P. 72—91.
83. Zivot E., Donald Andrews A992). Further Evidence on the Great Crash, the Oil-Price
Shocks, and the Unit Root hypothesis // Journal of Business and Economic Statistics.
Vol. 10.251—272.

Глоссарий
К разделу 7
Автоковариация (autocovariance) — для стационарного ряда Xt ковариация
случайных величинXt, Xt+T, у(т) - Cov(Xt, Xt+T).
Автокорреляционная функция (autocorrelation Junction —ACF) — для
стационарного рядаXt — последовательность его автокорреляций р(т) = Corr(Xt, Xt+ т),
т = 0,1,2,...
Автокорреляция (autocorrelation), коэффициент автокорреляции
(autocorrelation coefficient) — для стационарного ряда Xt коэффициент корреляции
случайных величин Xt, Xt+T, р(т) = Corr(Xt, Xt+T).
Белый шум (white noise), процесс белого шума (white noise process) —
стационарный случайный процесс Xt с нулевым средним и ненулевой дисперсией,
для которого Corr(Xt, Xs) = 0 при t Ф s.
«Более экономные» модели (more parsimonious models) — среди некоторой
совокупности альтернативных моделей временного ряда модели с
наименьшим количеством коэффициентов, подлежащих оцениванию.
Временной ряд (time series) — ряд значений некоторой переменной, измеренных
в последовательные моменты времени. Под временным рядом понимается
также случайный процесс с дискретным временем (случайная
последовательность), реализацией которого является наблюдаемый ряд значений.
Выборочная автокорреляционная функция (SACF — sample ACF) —
последовательность выборочных автокорреляций г (к), к = 0, 1,2,..., строящихся по
имеющейся реализации временного ряда. Анализ этой последовательности
помогает идентифицировать процесс скользящего среднего и его порядок.
Выборочная частная автокорреляционная функция (SPACF—sample PACF) —
последовательность выборочных частных автокорреляций rpart(k), к = 0,
1, 2, ..., строящихся по имеющейся реализации временного ряда. Анализ
этой последовательности помогает идентифицировать процесс скользящего
среднего и его порядок.

652
Часть 2. Регрессионный анализ временных рядов
Выборочные автокорреляции {sample autocorrelations) — оценки
автокорреляций р{к) случайного процесса, построенные по имеющейся реализации
временного ряда. Один из вариантов оценки автокорреляции р(к) имеет
вид:
1 Т~к
—-^(х,-м)(х1+к-м)
Пк)=Т-^-т >Ж * = U..r-i.
1 t = \
1 т
где ju = x = — ^xt — оценка для ju = E(Xt),
T t=\
1 т~к
у (к) = ^(xt ~ fi)(xt+k ~fi) — оценка для автоковариации у(к).
Т-к г=1
Выборочные частные автокорреляции (sample partial autocorrelations) —
оценки частных автокорреляций ppart(T) случайного процесса,
построенные по имеющейся реализации временного ряда.
Гауссовский белый шум (Gaussian white noise process) — процесс белого шума,
одномерные распределения которого являются нормальными
распределениями с нулевым математическим ожиданием.
Гауссовский случайный процесс (Gaussian process) — случайный процесс,
у которого для любого целого m > О и любого набора моментов времени
tx < t2 < ... < tm совместные распределения случайных величин Xt 9 ..., Xt
являются m-мерными нормальными распределениями.
Инновация (innovation) — текущее значение случайной ошибки в правой части
соотношения, определяющего процесс авторегрессии Хг Инновация не
коррелирована с запаздывающими значениямиXt_k9 к- 1, 2, ...
Последовательные значения инноваций (инновационная последовательность)
образуют процесс белого шума.
Информационный критерий Акаике (Akaike information criterion — AIC) —
один из критериев выбора «наилучшей» модели среди нескольких
альтернативных моделей. Среди альтернативных значений порядка модели
авторегрессии выбирается значение, которое минимизирует величину
1к
А1С(£) = 1п^2+ —,
где Т — количество наблюдений;
ак — оценка дисперсии инноваций st в AR модели &-го порядка.
Критерий Акаике асимптотически переоценивает (завышает) истинное
значение к0 с ненулевой вероятностью.

Глоссарий
653
Информационный критерий Хеннана — Куинна (Hannan-Quinn information
criterion — HQC) — один из критериев выбора «наилучшей» модели среди
нескольких альтернативных моделей. Среди альтернативных значений
порядка модели авторегрессии выбирается значение, которое минимизирует
величину
HQ{k) = lna2k+k ,
где Т — количество наблюдений;
а? — оценка дисперсии инноваций st в AR модели А>го порядка.
Критерий обладает достаточно быстрой сходимостью к истинному
значению к0 при Т -> оо. Однако при небольших значениях Т этот критерий
недооценивает порядок авторегрессии.
Информационный критерий Шварца (Schwarz information criterion — SIC) —
один из критериев выбора «наилучшей» модели среди нескольких
альтернативных моделей. Среди альтернативных значений порядка модели
авторегрессии выбирается значение, которое минимизирует величину
1 Т
SIC(Ar) = lno>2+Ar ,
где Т — количество наблюдений;
&1 — оценка дисперсии инноваций st в AR модели А:-го порядка.
Коррелограмма {correlogram) — для стационарного ряда: график зависимости
значений автокорреляций р{т) стационарного ряда от т. Коррелограммой
называют также пару графиков, приводящихся в протоколах анализа
данных в различных пакетах статистического анализа: графика выборочной
автокорреляционной функции и графика выборочной частной
автокорреляционной функции. Наличие этих двух графиков помогает
идентифицировать модель ARMA, порождающую имеющийся ряд наблюдений.
Обратный прогноз {backcasting) — прием получения более точной
аппроксимации условной функции правдоподобия при оценивании модели скользящего
среднего МА(#):
Xt = et + bxst_x + b2st_2 + ... + bqst_q9 bq Ф0,
по наблюдениямxl9 ...9хт. Результат максимизации (по bl9 b2, ..., bq)
условной функции правдоподобия, соответствующей наблюдаемым значениям
xl9x2, ..., хт при фиксированных значениях е09 s_X9 ..., €,q+u зависит от
выбранных значений е0, s_X9..., s_q+l. Если процесс MA{q) обратим, то можно
положить 6*0 = £_! = ... = £-q+\ = 0. Но для улучшения качества оценивания
можно методом обратного прогноза «оценить» значения s09 е_Х9 ..., s_q+x
и использовать оцененные значения в условной функции правдоподобия.
Оператор запаздывания {lag operator — L)9 оператор обратного сдвига {back-
shift operator) — оператор, определяемый соотношением: LXt = Xt_x. Удобен

654
Часть 2. Регрессионный анализ временных рядов
для компактной записи моделей временных рядов и для формулирования
условий, обеспечивающих те или иные свойства ряда. Например, с помощью
этого оператора уравнение, определяющее модель ARMA(p, q)
р я
Xt=H ajXt-j + Z bJ£t-j > ар*%\Ф О,
7=1 7=0
может быть записано в виде: a{L) Xt = b{L)sn где
a{L) = 1 - {axL + a2L2 + ... + apIf\
b{L)=l+blL + b2L2 + ...+bqLq.
Проблема общих множителей {common factors) — наличие общих множителей
у многочленов a{L) и b{L)9 соответствующих AR и МА составляющим
модели ARM А:
a(L)Xt = b(L)er
Наличие общих множителей в спецификации модели ARMA затрудняет
практическую идентификацию модели по ряду наблюдений.
Процесс авторегрессии первого порядка (first-order autoregressive process,
ARA)) — случайный процесс, текущее значение которого является суммой
линейной функции от запаздывающего на один шаг значения процесса
и случайной ошибки, не коррелированной с прошлыми значениями
процесса. При этом последовательность случайных ошибок образует процесс
белого шума.
Процесс авторегрессии порядка р (pth-order autoregressive process — AR(p)) —
случайный процесс, текущее значение которого является суммой линейной
функции от запаздывающих на р шагов и менее значений процесса и
случайной ошибки, не коррелированной с прошлыми значениями процесса.
При этом последовательность случайных ошибок образует процесс белого
шума.
Процесс скользящего среднего порядка q {qth-order moving average process —
MA(g)) — случайный процесс, текущее значение которого является
линейной функцией от текущего значения некоторого процесса белого шума
и запаздывающих нар шагов и менее значений этого процесса белого шума.
Разложение Вольда {Wold's decomposition) — представление стационарного
в широком смысле процесса с нулевым математическим ожиданием в виде
суммы процесса скользящего среднего бесконечного порядка и линейно
детерминированного процесса.
Сезонная авторегрессия первого порядка (SAR(l) —first order seasonal auto-
regression) — случайный процесс, текущее значение которого является
линейной функцией от запаздывающего на S шагов значения этого
процесса и случайной ошибки, не коррелированной с прошлыми значениями
процесса. При этом последовательность случайных ошибок образует процесс
белого шума. Здесь S = 4 для квартальных данных, S = 12 для месячных
данных.

Глоссарий
655
Сезонное скользящее среднее первого порядка (SMA(l) —first order seasonal
moving average) — случайный процесс, текущее значение которого равно
сумме линейной функции от текущего значения некоторого процесса белого
шума и запаздывающего на S шагов значения этого процесса белого шума.
При этом последовательность случайных ошибок образует процесс белого
шума. Здесь 5 = 4 для квартальных данных, 5=12 для месячных данных.
Система уравнений Юла — Уокера {Yule — Walker equations) — система
уравнений, связывающая автокорреляции стационарного процесса
авторегрессии порядка р с его коэффициентами. Система позволяет последовательно
находить значения автокорреляций и дает возможность, используя первые
р уравнений, выразить коэффициенты стационарного процесса
авторегрессии через значения первых р автокорреляций, что можно непосредственно
использовать при подборе модели авторегрессии к реальным
статистическим данным.
Случайный процесс с дискретным временем {discrete-time stochastic process,
discrete-time random process) — последовательность случайных величин,
соответствующих наблюдениям, произведенным в последовательные
моменты времени, имеющая определенную вероятностную структуру.
Смешанный процесс авторегрессии — скользящего среднего, процесс
авторегрессии с остатками в виде скользящего среднего {autoregressive moving
average, mixed autoregressive moving average — ARMA(p, q)) — случайный
процесс, текущее значение которого является суммой линейной функции
от запаздывающих на р шагов и менее значений процесса и линейной
функции от текущего значения некоторого процесса белого шума и
запаздывающих на q шагов и менее значений этого процесса белого шума.
Статистика Бокса — Пирса {Box-Pierce Q-statistic) — один из вариантов g-ста-
тистик:
м
* = 1
где Т — количество наблюдений;
г {к)— выборочные автокорреляции.
Используется для проверки гипотезы о том, что наблюдаемые данные
являются реализацией процесса белого шума.
Статистика Люнга — Бокса {Ljung-Box Q-statistic) — один из вариантов g-ста-
тистик, более предпочтительный по сравнению со статистикой Бокса —
Пирса:
к = \ L ~K
где Т — количество наблюдений;
г {к)— выборочные автокорреляции.
Используется для проверки гипотезы о том, что наблюдаемые данные
являются реализацией процесса белого шума.

656
Часть 2. Регрессионный анализ временных рядов
Стационарный в широком смысле (wide-sense stationary), слабо
стационарный (weak-sense stationary, weakly stationary), стационарный второго
порядка (second-order stationary), ковариационно стационарный (covari-
ance-stationary) случайный процесс (stochastic process) — случайный
процесс с постоянным математическим ожиданием, постоянной
дисперсией и инвариантными по гковариациями случайных величин^,Xt+T:
Cov(Xt9Xt+T) = r(r).
Строго стационарный, стационарный в узком смысле (strictly stationary, strict-
sense stationary) случайный процесс (stochastic process) — случайный
процесс с инвариантными по т совместными распределениями случайных
величин Xti+T,...,Xtm+T.
Условие обратимости процессов MA(q) и ARMA(p, q) (invertibility condition) —
для процессов Xt вида MA(g): Xt = b(L)st или ARMA(p, q): a(L)(Xt - ju) =
= b(L)st — условие на корни уравнения b(z) = О, обеспечивающее
существование эквивалентного представления процесса Xt в виде процесса
авторегрессии бесконечного порядка AR(oo):
00
Xt-fi = ^dj(Xt4-fi) + £r
7=1
Условие обратимости: все корни уравнения b(z) = О лежат вне единичного
круга \z\ < 1.
Условие стационарности процессов AR(p) и ARMA(p, q) (stationarity condition) —
для процессов Xt вида AR(p): a(L)(Xt - ju) = et или ARMA(p, q)\ a(L)(Xt - ju) =
= b(L)st — условие на корни уравнения a(z) = 0, обеспечивающее
стационарность процесса Хг Условие стационарности: все корни уравнения b(z) = О
лежат вне единичного круга \z\ < 1. Если многочлены a(z) и b(L) не имеют
общих корней, то это условие является необходимым и достаточным
условием стационарности процесса Хг
Частная автокорреляционная функция (PACF — partial autocorrelation
function) — для стационарного ряда последовательность частных
автокорреляций ррап(т\ г = 0, 1,2,...
Частная автокорреляция (РАС — partial autocorrelation) — для стационарного
ряда значение ppart(r) коэффициента корреляции между случайными
величинами Xt nXt+k, очищенными от влияния промежуточных случайных
величин Xt+l9...9Xt+k_Y.
Этап диагностики модели (diagnostic checking stage) — диагностика оцененной
модели ARMA, выбранной на основании имеющегося ряда наблюдений.
Этап идентификации модели (identification stage) — выбор модели порождения
ряда на основании имеющегося ряда наблюдений, определение порядков
р и q модели ARMA.

Глоссарий
657
Этап оценивания модели {estimation stage) — оценивание коэффициентов
модели ARMA, подобранной на основании имеющегося ряда наблюдений.
G-статистики {Q-statistics) — статистики критериев, используемых для проверки
гипотезы о том, что наблюдаемые данные являются реализацией процесса
белого шума.
К разделу 8
Векторная авторегрессия порядка р {pth-order vector autoregression — VAR(p)) —
модель порождения группы временных рядов, в которой текущее значение
каждого ряда складывается из постоянной составляющей, линейных
комбинаций запаздывающих (до порядка р) значений данного ряда и
остальных рядов и случайной ошибки. Случайные ошибки в каждом уравнении
не коррелированы с запаздывающими значениями всех рассматриваемых
рядов. Случайные векторы, образованные ошибками в разных рядах в один
и тот же момент времени, являются независимыми, одинаково
распределенными случайными векторами, имеющими нулевые средние.
Долговременная {long-run) связь — устанавливающаяся с течением времени
определенная связь между переменными, по отношению к которой
происходят достаточно быстрые осцилляции.
Долгосрочные мультипликаторы {long-run multipliers, equilibrum multipliers) —
в динамической модели с авторегрессионно распределенными
запаздываниями — коэффициенты сх,..., cs долгосрочной зависимости переменной j,
от экзогенных переменных хи, ..., xst. Коэффициент Cj отражает изменение
значения yt при изменении на единицу текущего и всех предыдущих
значений переменной xjt.
Импульсные мультипликаторы {impact multiplier, short-run multiplier) — в
динамической модели с авторегрессионно распределенными запаздываниями —
величины, показывающие влияние единовременных (импульсных) изменений
значений экзогенных переменных хи, ..., xst на текущее и последующие
значения переменной jr
Кросс-ковариации {cross-covariances) — коэффициенты корреляции между
значениями разных компонент векторного ряда в совпадающие или
несовпадающие моменты времени.
Кросс-ковариационная функция {cross-covariance function) —
последовательность кросс-корреляций двух компонент стационарного
векторного ряда.
Модели с авторегрессионно распределенными запаздываниями {autoregres-
sive distributed lag models — ADL) — модели, в которых текущее значение
объясняемой переменной является суммой линейной функции от
нескольких запаздывающих значений этой переменной, линейных комбинаций
текущих и нескольких запаздывающих значений объясняющих переменных
и случайной ошибки.

658
Часть 2. Регрессионный анализ временных рядов
Передаточная функция {transfer function) — матричная функция,
устанавливающая влияние единичных изменений в экзогенных переменных на
эндогенные переменные.
Процесс порождения данных {data generating process — DGP) — вероятностная
модель, в соответствии с которой порождаются наблюдаемые
статистические данные. Процесс порождения данных, как правило, неизвестен
исследователю, анализирующему данные. Исключением являются ситуации,
когда исследователь сам выбирает процесс порождения данных и получает
искусственные статистические данные, имитируя выбранный процесс
порождения данных.
Статистическая модель {statistical model — SM) — выбранная для оценивания
модель, структура которой предположительно соответствует процессу
порождения данных. Выбор статистической модели производится на
основании имеющейся экономической теории, анализа имеющихся в
распоряжении статистических данных, анализа результатов более ранних
исследований.
Стационарный векторный (АГ-мерный) ряд {K-dimensional stationary time
series) — последовательность случайных векторов размерности К, имеющих
одинаковые векторы математических ожиданий и одинаковые
ковариационные матрицы, для которой перекрестные корреляции (кросс-корреляции)
между значением к-й компоненты ряда в момент t и значением 1-й
компоненты ряда в момент {t + s) зависят только от s.
К разделу 9
Гипотеза единичного корня {UR — unit root hypothesis) — гипотеза,
формулируемая в рамках модели ARMA(/?, q): a{L)Xt = b{L)st. Гипотеза о наличии
у авторегрессионного полинома a{L) модели ARMA хотя бы одного корня,
равного 1. При этом обычно предполагается, что у полинома a{L)
отсутствуют корни, по модулю меньшие 1.
Дифференцирование {differencing) — переход от ряда уровней Xt к ряду
разностей Xt - Xt_x. Последовательное дифференцирование ряда дает возможность
устранить стохастический тренд, имеющийся в исходном ряде.
Интегрированный порядка к {integrated of order к) ряд — ряд Хп который не
является стационарным или стационарным относительно
детерминированного тренда (т.е. не является TS-рядом) и для которого ряд, полученный в
результате ^-кратного дифференцирования ряда Xt, является
стационарным, но ряд, полученный в результате (к- 1)-кратного
дифференцирования рядаХг, не является TS-рядом.
Коинтеграционная связь {cointegration) — долгосрочная связь между
несколькими интегрированными рядами, характеризующая равновесное состояние
системы этих рядов.

Глоссарий
659
Модель коррекции ошибок (error-correction model) — комбинация
краткосрочной и долгосрочной динамических регрессионных моделей при наличии
коинтеграционной связи между интегрированными рядами.
Оператор дифференцирования (difference operator) — оператор А,
переводящий ряд уровней Xt в ряд разностей:
bXt=Xt-Xt_v
Передифференцированный ряд (overdifferenced time series) — ряд, полученный
в результате дифференцирования Г5-ряда. Последовательное
дифференцирование ГО-ряда помогает устранить детерминированный полиномиальный
тренд. Однако дифференцирование TS-рядз, имеет некоторые нежелательные
последствия при подборе модели по статистическим данным и использовании
подобранной модели для целей прогнозирования будущих значений ряда.
Разностно стационарные, ЛУ-ряды (DS — difference stationary time series) —
интегрированные ряды различных порядков к = 1, 2, ... Приводятся к
стационарному ряду однократным или многократным дифференцированием,
но не могут приводиться к стационарному ряду вычитанием
детерминированного тренда.
Ряд типа ARIMA(p, Л, q) (ARIMA — autoregressive integrated moving average) —
временной ряд, который в результате ^-кратного дифференцирования
приводится к стационарному ряду ARMA(p, q).
Ряды, стационарные относительно детерминированного тренда, Г5-ряды
(TS — trend-stationary time series) — ряды, становящиеся стационарными
после вычитания из них детерминированного тренда. В класс таких рядов
включаются и стационарные ряды без детерминированного тренда.
Случайное блуждание, процесс случайного блуждания (random walk) —
случайный процесс, приращения которого образуют процесс белого шума:
AXt = sn так что Xt = Xt_ х + sr
Случайное блуждание со сносом, случайное блуждание с дрейфом (random
walk with drift) — случайный процесс, приращения которого являются
суммой константы и процесса белого шума: AXt -Xt- Xt_ х = а+ sn так что
Xt -Xt_x + a+ et. Константа а характеризует постоянно присутствующий
при переходе к следующему моменту времени снос траекторий случайного
блуждания, на который накладывается случайная составляющая.
Стохастический тренд (stochastic trend) — временной ряд Zn для которого
Zt - ех + 6*2 + ... + sv Значение случайного блуждания в момент t равно
t
Xt = Х0 + ^ ss, так что Xt - Х0 = ех + е2 + ... + sr Иными словами, модель
5 = 1
стохастического тренда — процесс случайного блуждания, «выходящего
из начала координат» (для него Х0 = 0).
Шок инновации (shock innovation) — единовременное (импульсное) изменение
инновации.

660
Часть 2. Регрессионный анализ временных рядов
Эффект Слуцкого (Slutsky effect) — эффект образования ложной периодичности
при дифференцировании ряда, стационарного относительно
детерминированного тренда. Например, если исходный ряд представляет собой сумму
детерминированного линейного тренда и белого шума, то
продифференцированный ряд не имеет детерминированного тренда, но оказывается
автокоррелированным.
^-гипотеза (TS hypothesis) — гипотеза о том, что рассматриваемый временной
ряд является стационарным или рядом, стационарным относительно
детерминированного тренда.
К разделу 10
Долговременная дисперсия (long-run varance) — для ряда щ с нулевым
математическим ожиданием определяется как предел
Л =lim v l '" 1—= \imTE\
T-+ao T Г-юо
ux +... + uT
Критерии Дики — Фуллера (Dickey-Fuller tests) — группа статистических
критериев для проверки гипотезы единичного корня в рамках моделей,
предполагающих нулевое или ненулевое математическое ожидание временного
ряда, а также возможное наличие у ряда детерминированного тренда.
При применении критериев Дики — Фуллера чаще всего оцениваются
статистические модели
Р-\
Ах, =a + j3t + (pxt_{ + ^0j&xt-j +£t, t = p + l,...,T,
7 = 1
Ax, = a + q>xt_x + £0; Ax,., +*„ t = p + l,...9T,
7 = 1
p-\
Ax, = cpxt_x + ]T 0,: Ax,_y +et9 t = p + l,...9T.
7 = 1
Полученные при оценивании этих статистических моделей значения г-ста-
тистик t9 для проверки гипотезы Я0: ср = О сравниваются с критическими
значениями /крит, зависящими от выбора статистической модели. Гипотеза
единичного корня отвергается, если t9 < /крит.
Критерий Квятковского — Филлипса — Шмидта — Шина (KPSS test) —
критерий для различения DS- и Г^-рядов, в котором в качестве нулевой
берется га-гипотеза.
Критерий Лейбурна (Leybourne test) — критерий для проверки гипотезы
единичного корня, статистика которого равна максимальному из двух
значений статистики Дики — Фуллера, полученных по исходному ряду и по ряду
с обращенным временем.

Глоссарий
661
Критерий Перрона {Perron test) — критерий для проверки нулевой гипотезы
о принадлежности ряда классу DS, обобщающий процедуру Дики — Фул-
лера на ситуации, когда на периоде наблюдений имеются структурные
изменения модели в некоторый момент времени Тв в форме либо сдвига
уровня (модель «краха»), либо изменения наклона тренда (модель
«изменения роста»), либо сочетания этих двух изменений. При этом
предполагается, что момент Тв определяется экзогенным образом — в том смысле,
что он не выбирается на основании визуального исследования графика
ряда, а связывается с моментом известного масштабного изменения
экономической обстановки, существенно отражающегося на поведении
рассматриваемого ряда.
Гипотеза единичного корня отвергается, если наблюдаемое значение
статистики ta критерия оказывается ниже критического уровня, т.е. если
*а ^ *крит*
Асимптотические распределения и критические значения для статистик
ta, первоначально приведенные Перроном, верны для моделей с
инновационными выбросами.
Критерий Филлипса — Перрона {Phillips-Perron test) — критерий, сводящий
проверку гипотезы о принадлежности ряда xt классу DS-рядоъ к проверке
гипотезы #0: <р = 0 в рамках статистической модели
SM: Axt = а + fit + (pxt_x + un t = 2,...,T9
где, как и в критерии Дики — Фуллера, параметры аи JB могут быть взяты
равными нулю.
Однако в отличие от критерия Дики — Фуллера к рассмотрению
допускается более широкий класс временных рядов.
Критерий основывается на Г-статистике для проверки гипотезы Я0: ср = 0,
но использует вариант этой статистики Z„ скорректированный на
возможную автокоррелированность и гетероскедастичность ряда ur
Критерий Шмидта — Филлипса {Schmidt-Phillips test) — критерий для проверки
гипотезы единичного корня в рамках модели
xt = у/+ gt + wn
где wt = jSwt_{ + st\ t = 2,..., T;
у/ — параметр, представляющий уровень;
t; — параметр, представляющий тренд.
Критерий DF-GLS {DF-GLS test) — критерий, асимптотически более мощный,
чем критерий Дики — Фуллера.
Куртозис {kurtosis) — коэффициент пикообразности распределения.
Модель аддитивного выброса {additive outlier) — модель, в которой при
переходе через дату излома Тв ряд yt сразу начинает осциллировать вокруг
нового уровня (или новой линии тренда).

662
Часть 2. Регрессионный анализ временных рядов
Модель инновационного выброса (innovation outlier) — модель, в которой
после перехода через дату излома Тв процесс yt лишь постепенно выходит
на новый уровень (или к новой линии тренда), вокруг которого начинает
происходить осцилляция траектории ряда.
Многовариантная процедура проверки гипотезы единичного корня (Dolado,
Jenkinson, Sosvilla-Rivero) — формализованная процедура использования
критериев Дики — Фуллера с последовательной проверкой возможности
редукции исходной статистической модели, в качестве которой
рассматривается модель
р-\
Axt = а + fit + (pxt_x + ^Oj^Xf-j +'€t> t = p + l,...,T.
У = 1
Предпосылкой для использования формализованной многовариантной
процедуры является низкая мощность критериев единичного корня. В связи
с этим в многовариантной процедуре предусмотрены повторные проверки
гипотезы единичного корня в более простых моделях с меньшим числом
оцениваемых параметров. Это увеличивает вероятность правильного
отвержения гипотезы единичного корня, но сопровождается потерей контроля
над уровнем значимости процедуры.
Обобщенный критерий Перрона (generalized Perron test) — предложенный Зиво-
том и Эндрюсом (относящийся к инновационным выбросам) безусловный
критерий, в котором датировка точки смены режима производится в
«автоматическом режиме», путем перебора всех возможных вариантов
датировки и вычисления для каждого варианта датировки /-статистики ta для
проверки гипотезы единичного корня; в качестве оцененной даты берется такая,
для которой значение ta оказывается минимальным.
Процедура Кохрейна, отношение дисперсий (variance ratio test) — процедура
различения TS- и DS-рядов, основанная на специфике поведения для этих
рядов отношения VRk = —, где Vk = —D(Xt -Xt_k).
Vx к
Стандартное броуновское движение (standard Brownian motion) — случайный
процесс W(r) с непрерывным временем, являющийся непрерывным
аналогом дискретного случайного блуждания. Это процесс, для которого:
• FF@) = 0;
• приращения (W(r2) - Щгх)),..., (W(rk) - W(rk_x)) независимы в
совокупности, если 0 <гх <г2 < ... <гк и W(s) - W(r)-N@, s-г) приs>r;
• реализации процесса W(r) непрерывны с вероятностью 1.
Ширина окна (window size) — количество выборочных автоковариаций ряда,
используемых в оценке Ньюи — Веста для долговременной дисперсии ряда.
Недостаточная ширина окна ведет к отклонениям от номинального размера
критерия (уровня значимости). В то же время увеличение ширины окна,
для того чтобы избежать отклонений от номинального размера критерия,
ведет к падению мощности критерия.

Глоссарий
663
К разделу 11
Векторная авторегрессия пониженного ранга (reduced rank VAR) — VAR-пред-
ставление векторного ряда в случае коинтегрированности его компонент.
Двумерный гауссовский белый шум (two-dimentional Gaussian white noise) —
последовательность независимых, одинаково распределенных случайных
векторов, имеющих двумерное нормальное распределение с нулевым
математическим ожиданием.
Детерминистская коинтеграция (stochastic cointegration) — существование для
группы интегрированных рядов их линейной комбинации, аннулирующей
стохастический и детерминированный тренды. Ряд, представляемый этой
линейной комбинацией, является стационарным.
Идентификация коинтегрирующих векторов (identification of the cointegrating
vectors) — выбор базиса коинтеграционного пространства, состоящего из
коинтегрирующих векторов, имеющих разумную экономическую
интерпретацию.
Коинтеграционное пространство (cointegrating space) — совокупность всех
возможных коинтегрирующих векторов для коинтегрированной системы
рядов.
Коинтегрированные временные ряды, коинтегрированные в узком смысле
временные ряды (cointegrated time series) — группа временных рядов, для
которой существует нетривиальная линейная комбинация этих рядов,
являющаяся стационарным рядом.
Коинтегрирующий вектор (cointegrating vector) — вектор коэффициентов
нетривиальной линейной комбинации нескольких рядов, являющейся
стационарным рядом.
Критерий максимального собственного значения (maximum eigenvalue test) —
критерий, который в процедуре Йохансена оценивания ранга коинтеграции
г системы интегрированных (порядка 1) рядов используется для проверки
гипотезы Н0:г = г* против альтернативной гипотезы НА: г = г* + 1.
Критерий следа (trace test) — критерий, который в процедуре Йохансена
оценивания ранга коинтеграции г системы интегрированных (порядка 1) рядов
используется для проверки гипотезы Н0: г = г* против альтернативной
гипотезы НА:г> г*.
Ложная, фиктивная, паразитная регрессия (spurious regression) — оцененная
регрессионная связь между временными рядами с высоким
коэффициентом детерминации, которая является лишь следствием наличия у рядов
детерминированного или стохастического тренда.
Общие тренды (common trends) — группа рядов, управляющих стохастической
нестационарностью системы коинтегрированных рядов.
Причинность по Грейнджеру (Granger causality) — факт улучшения качества
прогноза значения yt переменной Y в момент t по совокупности всех про-

664
Часть 2. Регрессионный анализ временных рядов
шлых значений этой переменной при учете прошлых значений некоторой
другой переменной.
Пять ситуаций в процедуре Иохансена — пять ситуаций, от которых зависят
критические значения статистик критериев отношения правдоподобий,
используемых в процедуре Иохансена оценивания ранга коинтеграции
системы интегрированных (порядка 1) рядов:
• Н2{г): в данных нет детерминированных трендов,
в СЕ не включаются ни константа, ни тренд;
• Н*{г): в данных нет детерминированных трендов,
в СЕ включается константа, но не включается тренд;
• Нх {г): в данных есть детерминированный линейный тренд,
в СЕ включается константа, но не включается тренд;
• Н*{г): в данных есть детерминированный линейный тренд,
в СЕ включаются константа и линейный тренд;
• Щг): в данных есть детерминированный квадратичный тренд,
в СЕ включаются константа и линейный тренд.
(Здесь СЕ — коинтеграционное уравнение.)
При фиксированном ранге г перечисленные 5 ситуаций образуют
цепочку вложенных гипотез:
Н2(г) с #,*(/■) с Я, (г) с Н\г) с Н{г).
Это дает возможность, используя критерий отношения правдоподобий,
проверять выполнение гипотезы, стоящей левее в этой цепочке, в рамках
гипотезы, расположенной непосредственно справа.
Ранг коинтеграции {cointegrating rank) — максимальное количество линейно
независимых коинтегрирующих векторов для заданной группы рядов, ранг
коинтеграционного пространства.
Стохастическая коинтеграция {stochastic cointegration) — существование для
группы интегрированных рядов линейной комбинации, аннулирующей
стохастический тренд. Ряд, представляемый этой линейной комбинацией,
не содержит стохастического тренда, но может иметь детерминированный
тренд.
Треугольная система Филлипса {Phillips's triangular system) — представление
системы TV коинтегрированных рядов с рангом коинтеграции г в виде
системы уравнений, первые г из которых описывают зависимость г
выделенных переменных от остальных {N - г) переменных (общих трендов), а
остальные уравнения описывают модели порождения общих трендов.
TV-мерный гауссовский белый шум {N-dimentional Gaussian white noise) —
последовательность независимых, одинаково распределенных случайных
векторов, имеющих TV-мерное нормальное распределение с нулевым
математическим ожиданием.

Предметный указатель
^-статистики 348
Бокса — Пирса 348, 361
Люнга — Бокса 349, 361
Автоковариация 312
Автокоррелированность
критерий Бройша — Годфри 188, 385
критерий Дарбина — Уотсона 185, 385
смещение 385
Автокорреляционная функция 312, 341
Автокорреляция 312
выборочная 343
частная 341
Автономное потребление 13
Авторегрессионные ошибки
преобразование Кохрейна — Оркатта 225,
400
преобразование Прайса — Уинстена 242
Адекватность подобранной модели 171
анализ остатков 174-175
графические методы 175-183
диаграмма квантиль-квантиль 179
диаграмма плотности 180
рекурсивные коэффициенты 181
рекурсивные остатки 181 -182
диагностика 173
использование статистических критериев
184
критерий Бройша — Годфри 188
критерий Голдфелда — Квандта 184
критерий Дарбина — Уотсона 185
критерий Уайта 189
критерий Харке — Бера 186, 363
критерий Чоу на качество прогноза 191
критерий Чоу на структурный сдвиг
199
ядерная оценка плотности 180
Белый шум 313
JV-мерный гауссовский 568, 605
векторный 537
гауссовский 313
двумерный гауссовский 547
Броуновское движение 458
Вариационный ряд 370
Векторная авторегрессия 389
замкнутая модель 393
модель коррекции ошибок (ЕСМ) 559,
581
оценивание 599
открытая модель 393
матрица долгосрочных
мультипликаторов 394
пониженного ранга 538
порядок 390
ранг коинтеграции 580
оценивание 579, 595
условие стабильности 392
Взвешенный метод наименьших квадратов
218,241
взвешенная сумма квадратов 218
взвешенные статистики 219
невзвешенные статистики 219
Временной ряд 307
гауссовский 312
векторный 381
дифференцирование 437
двукратное 438
долговременная дисперсия 490
оценивание 490
интегрированный порядка А: 439
остационаривание 440
передифференцированный 440
стационарный в разностях (DS-ряд) 440

666
Предметный указатель
стационарный в широком смысле 311
стационарный векторный 381
гауссовский 569
кросс-ковариационная функция 382
кросс-ковариация 381
разложение Вольда 336
линейно детерминированная
компонента 336
линейно недетерминированная
компонента 336
чисто линейно
недетерминированный стационарный процесс 336
стационарный относительно
детерминированного тренда (Г^-ряд) 438
строго стационарный 309
типа ARIMA(p, k, q) 440
Временные ряды коинтегрированные 528,
537
в узком смысле 548, 555, 558
векторное ARM А представление 538
движение по направлению к среднему 539
долговременная связь 540
коинтеграционное пространство 558
базис 558
коинтегрирующий вектор 537, 548
краткосрочная динамика 540
модель коррекции ошибок 538
общие тренды 596
оценивание
ряды с линейным трендом 564
треугольная система Филлипса 547, 560,
563,568
ранг коинтеграции 558
Временные ряды некоинтегрированные 528
Выбор между негнездовыми моделями
использование F-критерия 161
Выбор между моделями с разной
функциональной формой связи 163
Выборочный коэффициент асимметрии 187
Выборочный куртозис 187
Гипотеза единичного корня 453
Гипотеза значимости коэффициента 118
регрессии в целом 130
/меритерий 125, 130
использование коэффициента
детерминации 150
Гипотеза случайности 309
проверка
критерии согласия 373
критерий Андерсона — Дарлинга 375
критерий Ватсона 375
критерий Кендалла 371
критерий Колмогорова 373
критерий Крамера — фон Мизеса
(омега-квадрат) 375
критерий Купера 374
критерий Лиллиефорса 374
критерий поворотных точек 370
критерий серий 369
Дамми-переменные 203
взаимодействие переменных 209
дамми-ловушка 209
дифференциальный эффект 209
Динамические модели
авторегрессионные ошибки 399
модель коррекции ошибок 400
модель опережающего показателя 398
модель распределенных запаздываний 398
модель скорости роста 398
модель частичной корректировки 399
приведенная форма 399
процесс авторегрессии 398
Динамические модели, типы моделей 397
Дисперсия выборочная 19
Доверительные интервалы для
коэффициентов нормальной линейной модели
при известной дисперсии ошибок 100
при неизвестной дисперсии ошибок 105
Доверительный интервал 100
вероятность одновременного накрытия 106
уровень доверия (доверительная
вероятность) 100
Доверительный эллипс 126
Доверительный эллипсоид 126
Долговременная дисперсия 490, 530, 561, 564
оценка Ньюи — Веста 490, 565
ширина окна 490
Долговременная связь 394
Долговременное положение равновесия
системы 548, 558
отклонение от положения равновесия 548,
558
Доход располагаемый 12, 47
Идентифицируемости условие 30
Инновационная последовательность 320
Инновация 320, 390
вектор инноваций 390
шок инновации 447

Предметный указатель
667
Информационные критерии
Акаике (Akaike) 154, 350
Хеннана — Куинна (Наппап, Quinri) 351
Шварца (Schwarz) 155, 351
Итерационные методы 354
выбор стартового значения 354
Квантиль распределения 98
Ковариационная матрица случайного
вектора ПО
Ковариация выборочная 22
Ковариация случайных величин 110
Коинтеграция (коинтеграционная связь)
детерминистская 537, 556, 575
проверка гипотезы коинтегрированности
548
заданный коинтегрирующий вектор
548
мощность критериев 550
неизвестный коинтегрирующий
вектор
ряды без тренда 548
ряды с трендом 549
стохастическая 555, 578
Коинтегрированная VAR 559
модель коррекции ошибок (ЕСМ) 539
оценивание коэффициентов ЕСМ 602
сверхидентифицирующие ограничения
603
ранг коинтеграции 559
оценивание 579
Коинтегрированные ряды 528
Коинтегрирующие векторы 537, 548
нормализованные 599
оценивание 540, 561
двухшаговая процедура 540
идентифицирующие ограничения 600
метод Иохансена 599
сверхидентифицирующие ограничения
603
Коррелограмма 312, 362
Корреляционная связь
отрицательная 24
положительная 24
Корреляционное поле 20
Коэффициент автокорреляции 312
Коэффициент детерминации 34, 105
как статистика 149
нецентрированный 59
скорректированный 153
Коэффициент корреляции
выборочный 22
инвариантность 23
множественный 38, 77
инвариантность 38
Критерий Вальда 125
Критерий Дики — Фуллера 458, 474
для процессов ARMA(p, q) 474
критерий DF-GLS 495
мощность критериев 470, 473
расширенный 471
Критерий информационный
Акаике 154, 350
Хеннана — Куинна 351
Шварца 155, 351
Критерий Квятковского — Филлипса —
Шмидта — Шина (KPSS) 495
Критерий Лейбурна 494
Критерий Перрона 502
датировка точки излома 508
обобщенный 513
Критерий Филлипса — Перрона 489
мощность 491
Критерий Харке — Бера {Jarque-Bera)
проверка нормальности инноваций 364
Критерий Шмидта — Филлипса 494
Куртозис
выборочный 187
Линейная гипотеза 122
проверка 125
Линейная модель наблюдений 20, 75
классическая нормальная 88, 234
Линейная регрессия
дисперсионный анализ 36
интерпретация оценок коэффициентов
76,83
множественная 93
парная (простая) 94
Ложная периодичность 442, 450
Ложная регрессия 520, 526
Ложная (фиктивная, паразитная) линейная
связь 49, 520
Метод инструментальных переменных 254
Метод наименьших квадратов 28, 76
нормальные уравнения 39, 78
векторно-матричная форма 78
Методология Лондонской школы экономики
173

668
Предметный указатель
Модели
ARX382
стабильность 382
динамические (ADL) 383
мультипликаторы
долгосрочные 384
импульсные 384
передаточная функция 394
коррекции ошибок (ЕСМ) 538
с ошибками в измерении объясняющих
переменных 248
с пропущенными переменными 247
Модель математическая 20
Модель наблюдений
линейная 14, 20, 75
векторно-матричная форма 88
постоянная составляющая 74
с переключением 201
стандартные предположения 88
стандартные предположения об
ошибках 89
вектор остатков 79
вектор подобранных значений 79
ортогональная структура матрицы
значений объясняющих
переменных 86
линейная в логарифмах 67
случайная выборка 102, 109, 307
Модель связи
Michaeli-Menton 70
адекватность статистическим данным 170
истинная 27
линейная 13, 20
линейная в логарифмах 62, 64, 74
нелинейная 61
неправильно специфицированная 16
обратная 54
подобранная 16
остатки 28, 77
прогнозное значение 28, 77
пропорциональная 33
степенная 62
Мультиколлинеарность 157
коэффициент возрастания дисперсии 157
полная 156
проявления 157
Мультипликатор
долгосрочный 384
импульсный 447
Наименьших квадратов оценки 29
использование итерационных методов 68
формулы для вычисления 29,79
Наименьших квадратов принцип 28
Нарушение стандартных предположений о
модели наблюдений
автокоррелированность ошибок 224
влияние на статистические выводы 224,
229
коррекция статистических выводов
авторегрессионное преобразование
225
процедура Кохрейна — Оркатта
(Cochrane-Orcutf) 225
скорректированные оценки
стандартных ошибок
оценка Ньюи — Веста 232
ненулевое математическое ожидание
ошибок
выделяющиеся наблюдения 176
выявление, критерий RESET 190
неоднородность дисперсий ошибок (гете-
роскедастичность) 177, 215
влияние на статистические выводы
215
коррекция статистических выводов
взвешенный метод наименьших
квадратов, См. Взвешенный метод
наименьших квадратов 218
переход к логарифмам 223
скорректированные оценки
стандартных ошибок 221
оценка Уайта 221
нестабильная модель
проверка стабильности
критерии Чоу
на качество прогнозов 191
на структурный сдвиг 199
сезонность 204
коррекция модели 207
двухфазная линейная модель 201
фиктивные переменные, дамми-пе-
ременные 204
Нормальная линейная модель 88, 234
Обобщенный метод наименьших квадратов
241
доступный вариант 243
Обратимости условие 329, 332
Объясняемая переменная 36
подобранные значения 77

Предметный указатель
669
Объясняющие переменные 36
детерминированные 234
несущественные 116
стохастические 236
Оператор запаздывания 320
Остатки
стандартизованные 175
стьюдентизированные 175
Остаток в /-м наблюдении 28, 77
Оценка наименьших квадратов
обобщенная 241
суперсостоятельная 541
Оценки наименьших квадратов для
коэффициентов линейной модели
в модели с линейными ограничениями 127
в модели парной регрессии 41
дисперсия 91, 161
несмещенность 91
нормальность 90
формула для вычисления 79
эффективность 95
Гаусса — Маркова теорема 95
Гаусса — Маркова условия 96
Очистка переменных 53, 84
Фриша-Во-Ловелла теорема 83, 84
Ошибка в /-м наблюдении 14
Ошибки
аддитивные 68
мультипликативные 67
стандартные предположения 89
Переменная
зависимая 20
инструментальная 254
слабые инструменты 260
независимая 20
объясняемая 36
объясняющая 36
стохастическая 236
очищенная 53, 84
стандартизованная 31
фиктивная (дамми) 203
центрированная 86
экзогенная 393
эндогенная 393
Подбор модели
использование информационных
критериев 154
использование скорректированного
коэффициента детерминации 153
метод от общего к частному 17
Подбор стационарной модели ARMA
диагностика модели 360
идентификация модели 341
оценивание модели 353
метод максимального правдоподобия
354
Полуэластичность 67
Правило «при прочих равных» 76
Применимость стандартных статистических
выводов
ситуация А 237
ситуация^' 238
ситуация В 238
ситуация С 239
ситуация D 378
ситуация Е 379
ситуация F 381
теорема Манна — Вальда 380
Принцип охвата 17
Принцип экономности модели 17, 339
Причинность по Грейнджеру 540
Проблема выбора между полной и
редуцированной моделями
выбор наилучшей модели 151
последствия ошибочных решений 152
Прогнозирование по оцененной модели
регрессии
дисперсия ошибки прогноза 165
интервальный прогноз 165
ошибка прогноза 165
точечный прогноз 166
улучшенная модель 230
Процесс авторегрессии 314, 320, 321
векторный 389
взрывной 433
первого порядка 225, 241, 314
порядка/? 320
стационарный 316, 320, 321
Процесс порождения данных 12, 400, 458
Различение TS- и DS-рядов 451
rS-гипотеза 453
влияние протяженности ряда 498
гипотеза единичного корня 453
количество единичных корней 499
коррекция сезонности 497
многовариантная процедура 478
процедура Кохрейна 496
согласованность статистических выводов
498
структурные изменения модели 502

670
Предметный указатель
Распределение
«-мерное нормальное 111
плотность распределения 111
свойства 112
Коши 311
стандартное нормальное 98
Стьюдента (/-распределение) 103
тяжелые хвосты 362
Фишера F-распределение 124
хи-квадрат 102
Рассеяния диаграмма 13, 20
Рассеяния облако 13
Расходы наличное потребление 12, 47
Регрессионная модель 91
Регрессионный анализ 92
Регрессия
интерпретация термина 93
линейная 92
множественная 93
нелинейная 92
непараметрическая 92
одной переменной на другие переменные
92
параметрическая 92
парная линейная 94
простая линейная 94
прямолинейная 94
регрессор 92
уравнение регрессии 92
функция регрессии 92
Сезонные модели
авторегрессии 337
аддитивные 339
мультипликативные 339
скользящего среднего 311
Система одновременных уравнений 249
оценивание
двухшаговый метод наименьших
квадратов 258
косвенный метод наименьших
квадратов 257
приведенная форма 250
структурная форма 249
точно идентифицируемое уравнение 257
Склонность к потреблению 13
предельная 13, 62
Скользящее среднее порядка q 325
оценивание 354
backcasting 355
условие обратимости 329
Случайное блуждание 432
со сносом 436
Случайный вектор 109
ковариационная матрица ПО
математическое ожидание 109
совместная плотность распределения 109
функция распределения 109
Случайный процесс
стационарный в узком смысле (строго
стационарный) 309
стационарный в широком смысле (слабо
стационарный, стационарный второго
порядка, ковариационно
стационарный) 311
Смешанный процесс авторегрессии —
скользящего среднего (ARMА) 331
проблема общих множителей 333
сезонные модели 337
условие стационарности 331
экономность модели ARMA 333
Среднее значение 19
Стабильности условие 318, 382, 400
Стандартное отклонение 19
Статистика 101, 131
F-статистика 124, 127, 130, 134, 136
Р-значение (P-value) 117, 131
sMoi
как несмещенная оценка дисперсии
ошибок 102
Бокса — Пирса 348, 361
Вальда 125
Дарбина — Уотсона 185, 529
Люнга — Бокса 349, 361
отношения дисперсий 496
Статистическая гипотеза 113
двусторонняя альтернатива 139
нулевая 114
односторонняя альтернатива 139
простая 139
сложная 139
частная 139
Статистическая модель 15, 400
Статическая регрессия 397
Статистически значимая оценка 118
Статистически незначимая оценка 118
Статистические данные 75
вариабельность 19
временные ряды 211
панельные 211
перекрестные (одномоментные) 211

Предметный указатель
671
Статистический критерий 115
F-критерий 125, 131
/-критерий 115
асимптотический 125, 187
конфликт критериев 143
критическое множество 115
мощность 115, 146
наиболее мощный 116
неасимптотический 125, 187
ошибка 1-го рода 114, 149
предпочтительность одностороннего
критерия при односторонней
альтернативе 146
согласия 195
эмпирическая функция распределения
373
статистика критерия 115
структура 116
точный 187
уровень значимости 115, 141
Сумма квадратов
объясненная моделью 33, 77
остаточная 34, 76
полная 33
разложение 34
Сходимость по распределению 239
Тренд
аддитивный выброс 505
детерминированный 436
имеющий излом 503
квадратичный 487
детрендирование 436
изменение наклона 505
изменение наклона и уровня 505
изменение уровня 505
инновационный выброс 505
стохастический 435, 556
Условие идентифицируемости модели 20
Уточнение спецификации модели
использование F- критериев 134
редуцированная модель 130
Фиктивная линейная связь 49
Функция
автокорреляционная 312, 341, 345
выборочная 343
частная автокорреляционная 341
выборочная 343
Частный коэффициент корреляции 54
Экзогенные переменные 393
Эконометрика 11
Эконометрическая модель 15
спецификация 15
Эластичности функция 63
Эластичность (неэластичность) одного
экономического фактора по отношению
к другому 63
Эндогенные переменные 393
Юла — Уокера уравнения 324
использование
при выборе стартовых значений 354
при вычислении частных
автокорреляций 342

Учебник
Владимир Петрович НОСКО
ЭКОНОМЕТРИКА
Книга 1
Гл. редактор Ю.В. Луизо
Редактор Н.В. Андрианова
Художник В.П. Коршунов
Компьютерная подготовка оригинал-макета О.Ю. Гудкова
Корректоры Т.А. Смирнова, Н.Н. Цыркова
Подписано в печать 22.03.2011. Формат 70 х 100 Vi6.
Бумага офсетная. Гарнитура Тайме. Печать офсетная.
Усл. печ. л. 54,6. Тираж 3000 экз. Заказ 5873. Изд. № 218.
Издательский дом «Дело» РАНХиГС
119571, Москва, пр-т Вернадского, 82
Коммерческий отдел —тел.: D95L33-2510, D95L33-2502
com@anx.ru
www.delo.ane.ru
Отпечатано в ОАО «Можайский полиграфический комбинат»
143200, г. Можайск, ул. Мира, 93
www.oaompk.ru, www.oaoMnK^ тел.: D95) 745-84-28, D9638) 20-685
ISBN 978-5-7749-0654-3
9 »785774»906543