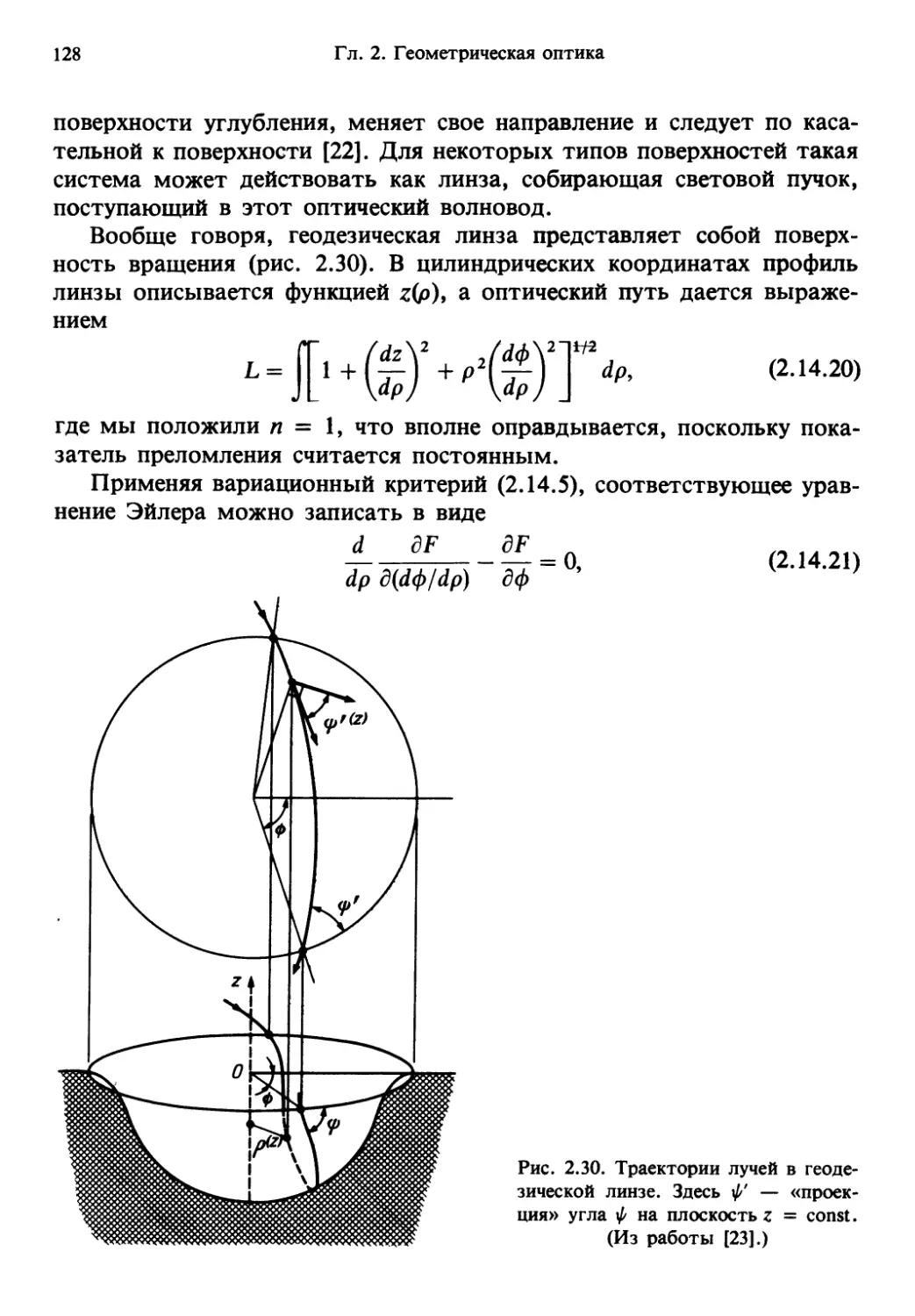
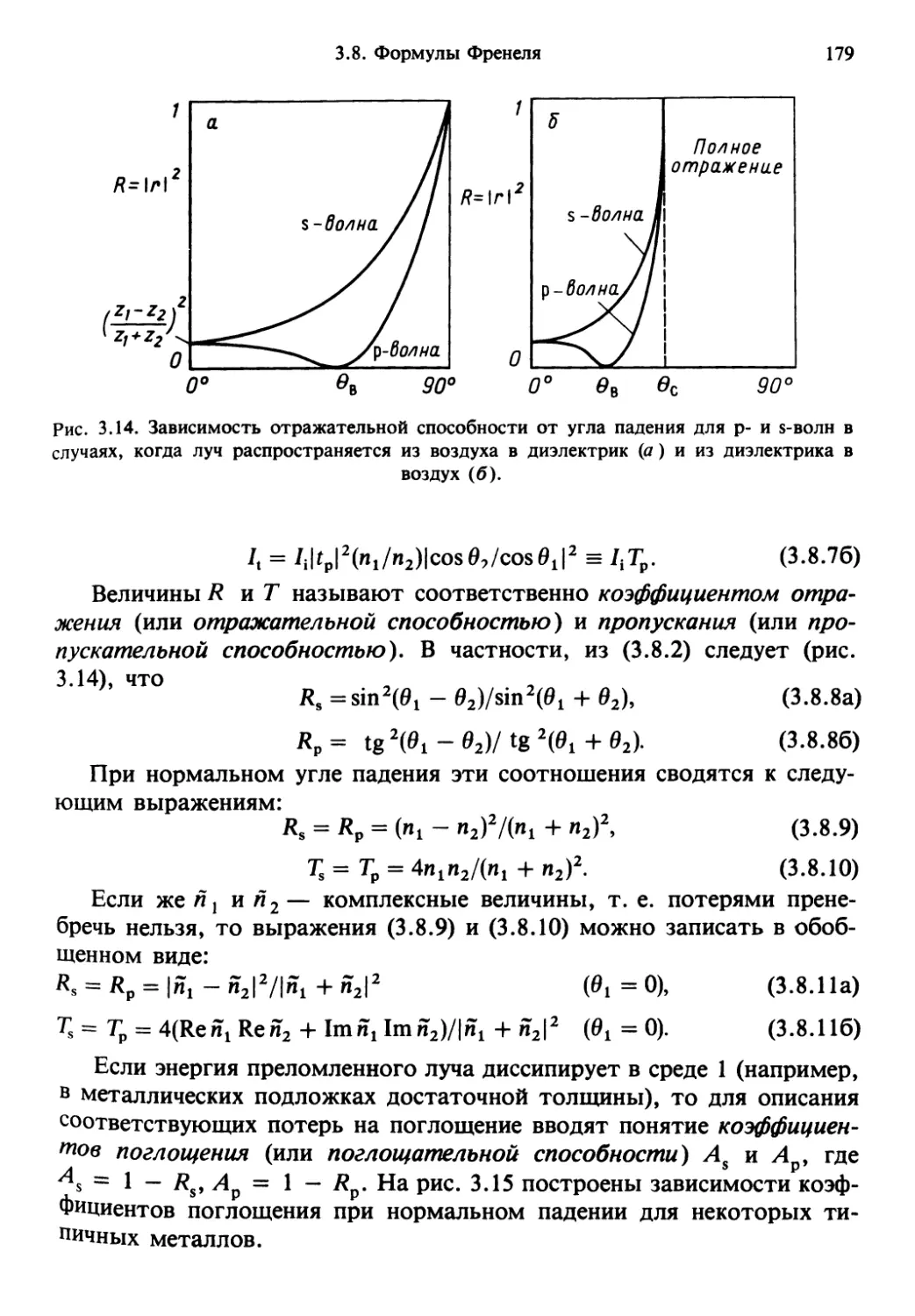
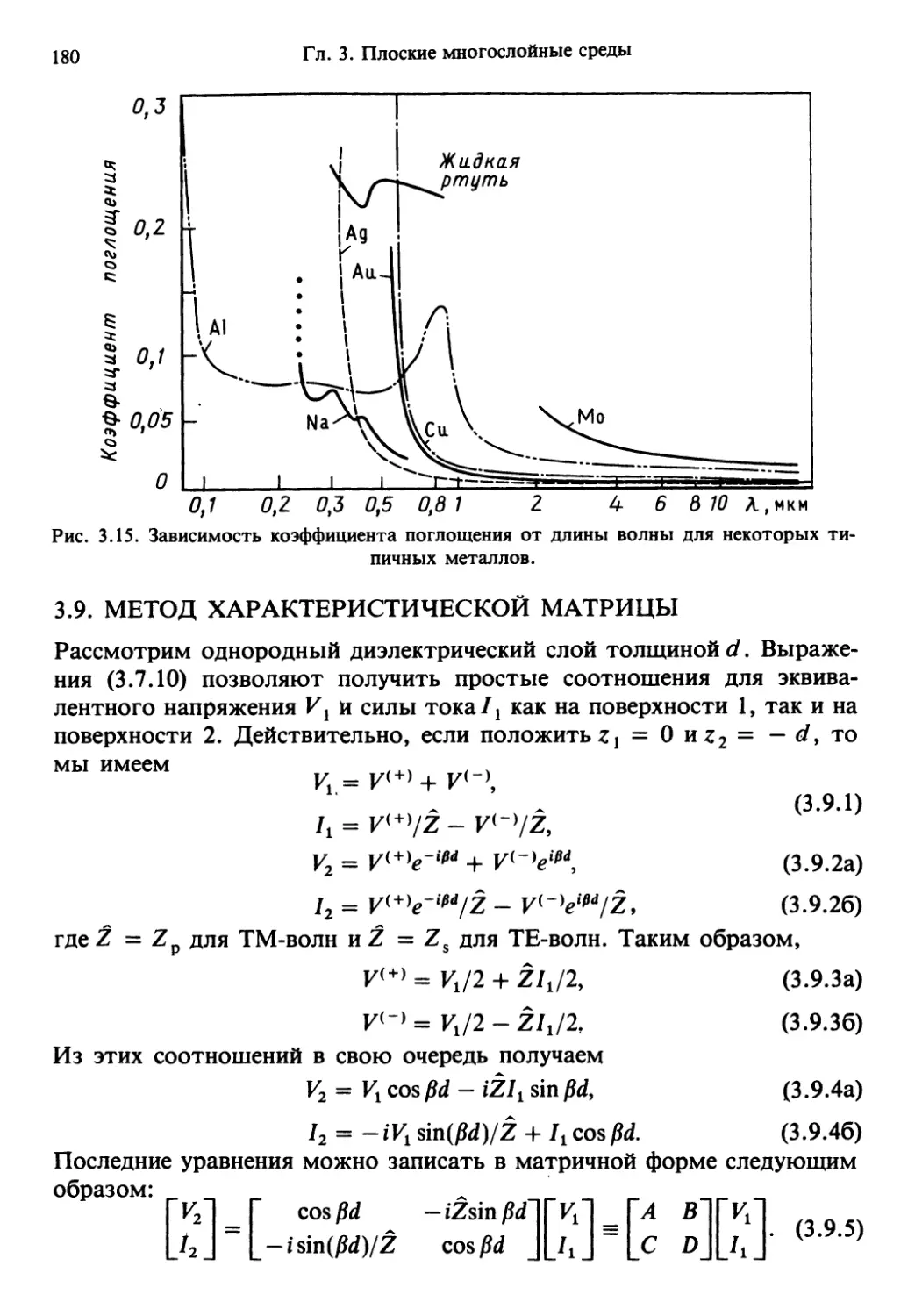
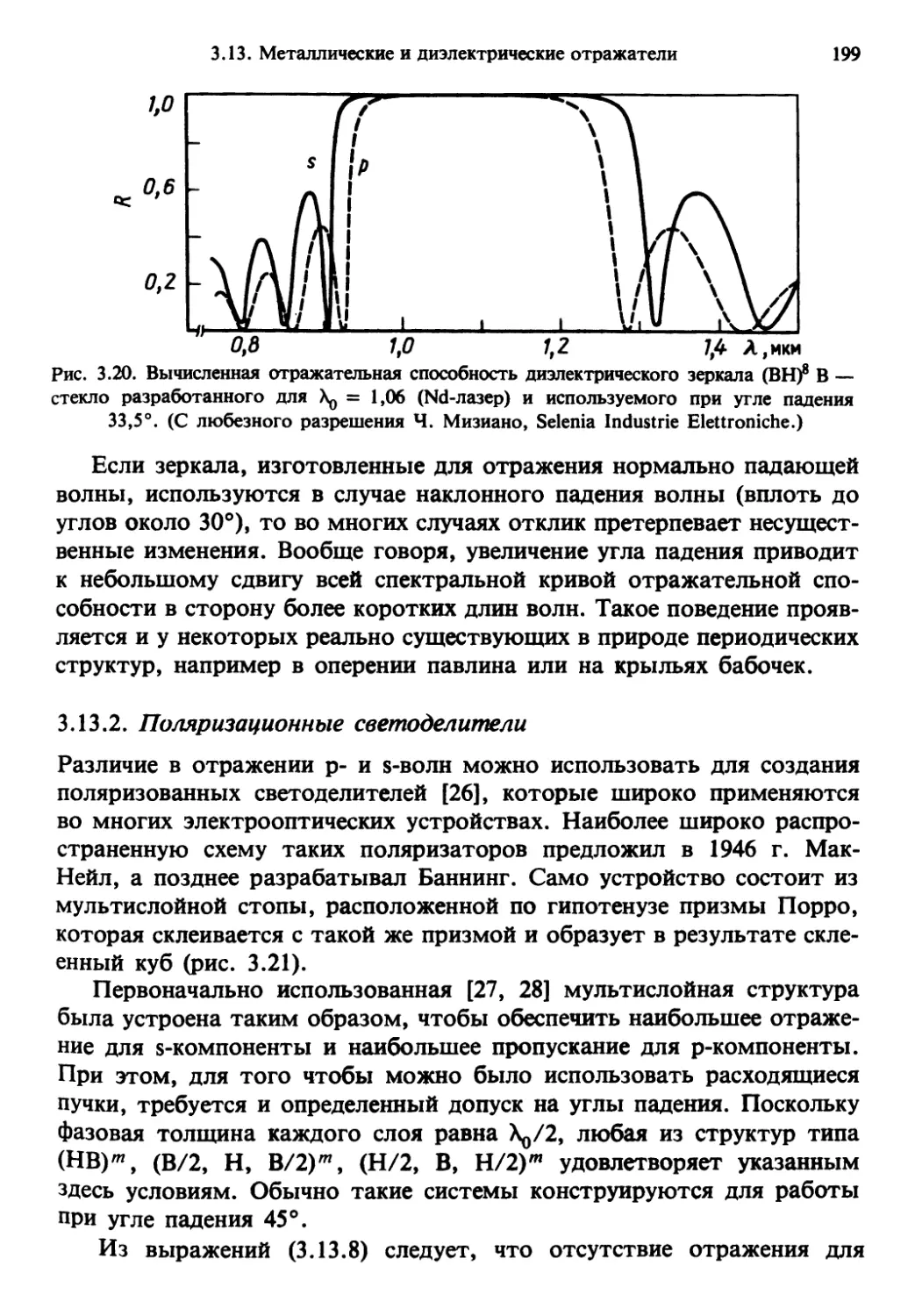
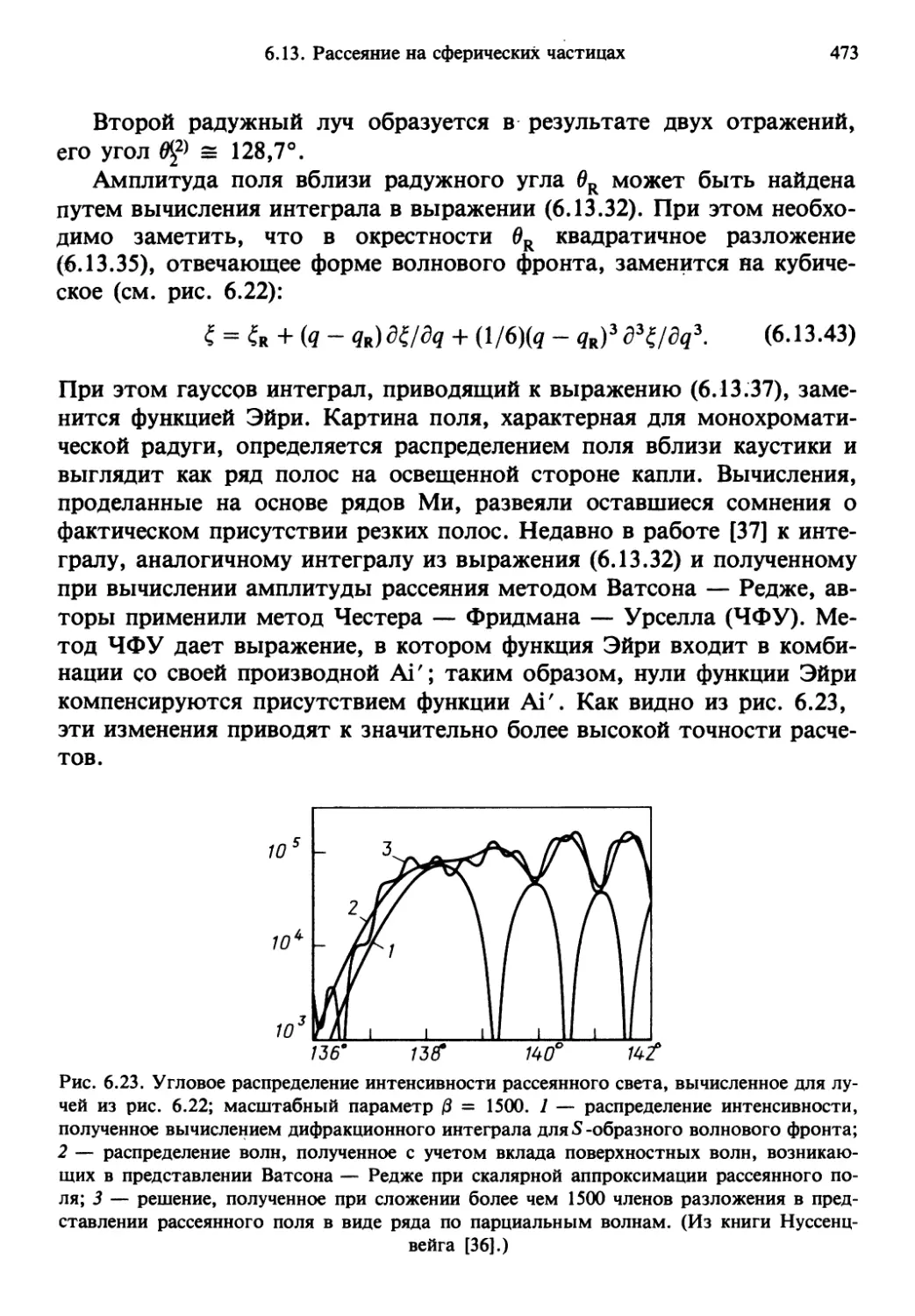
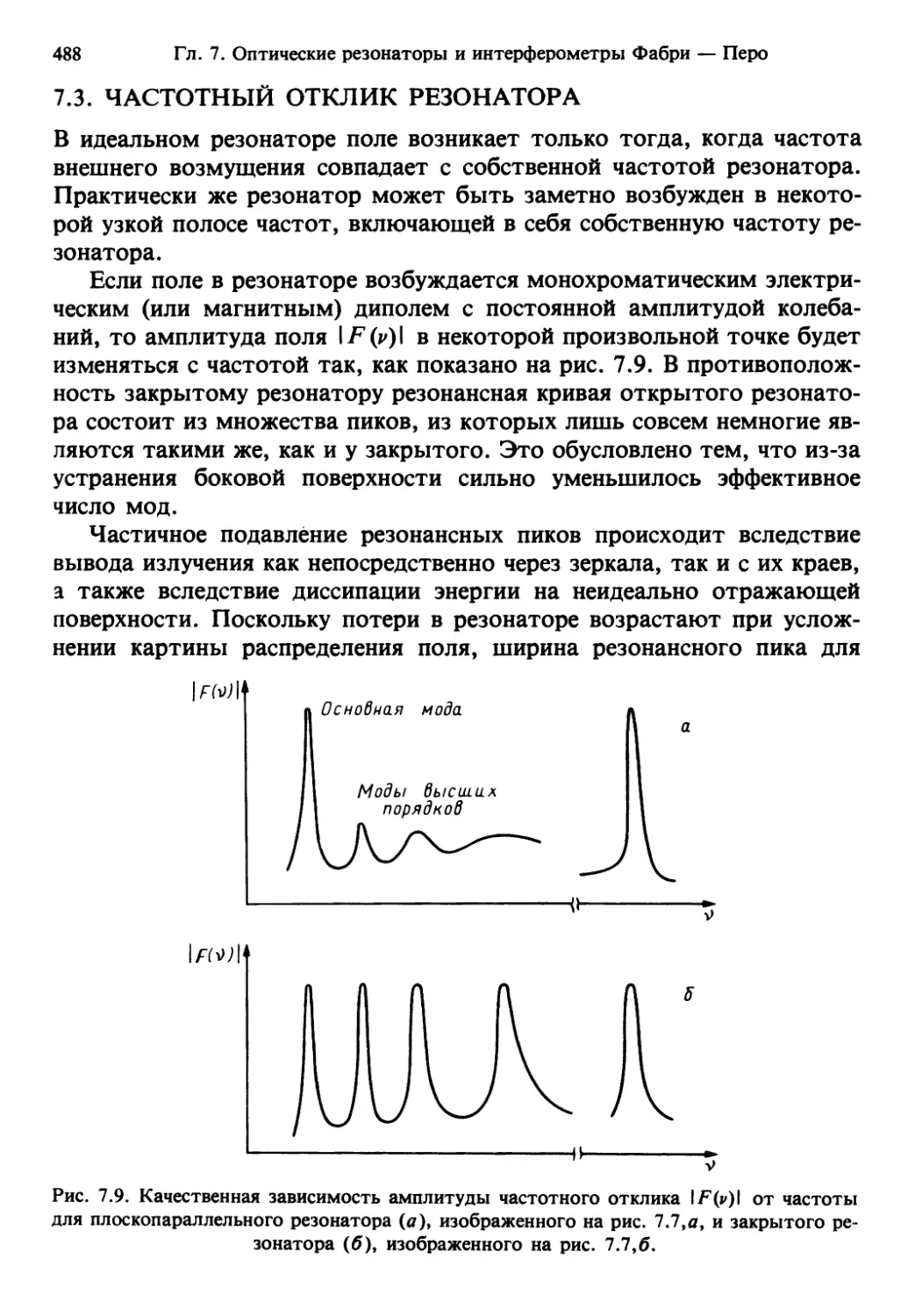
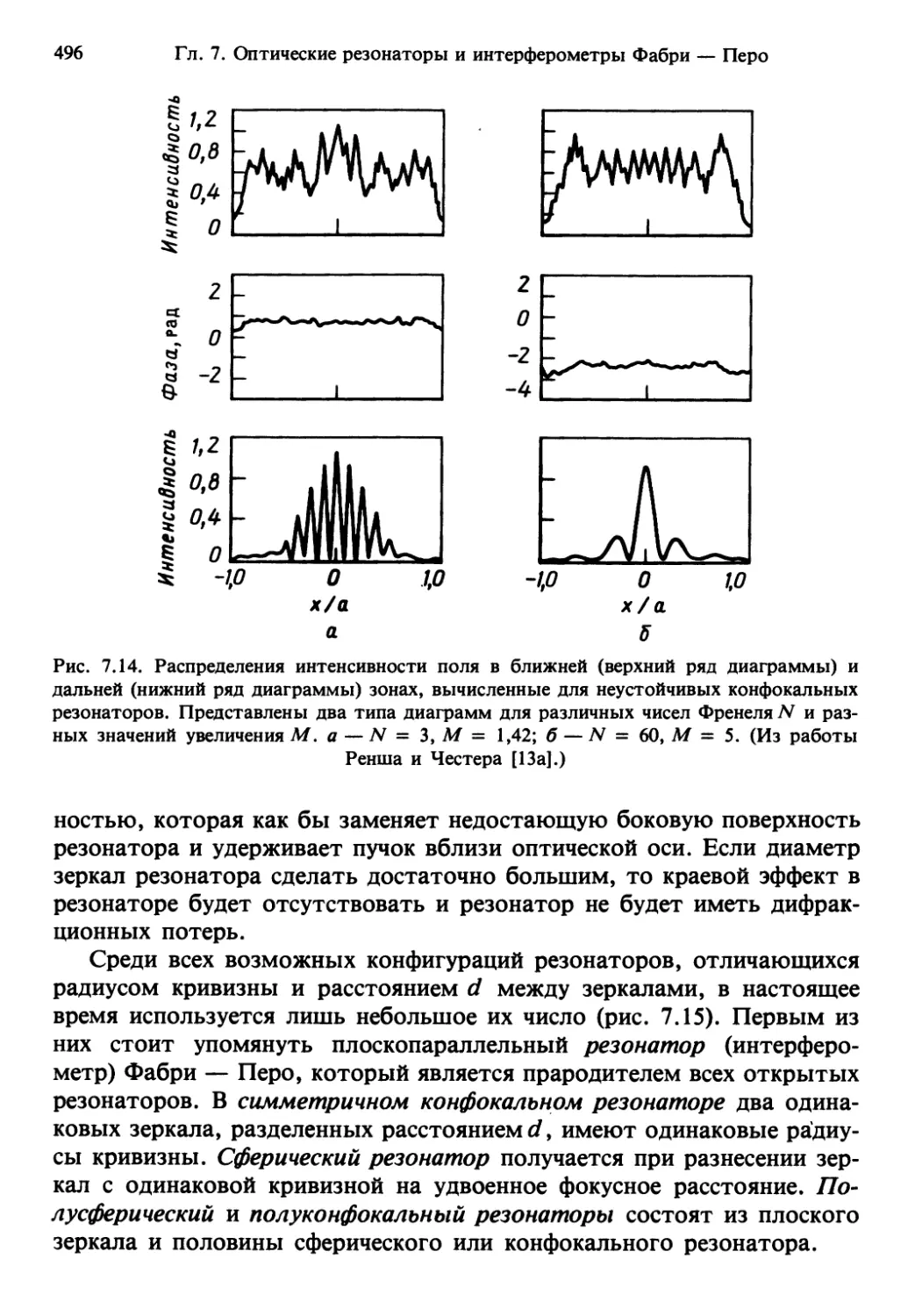
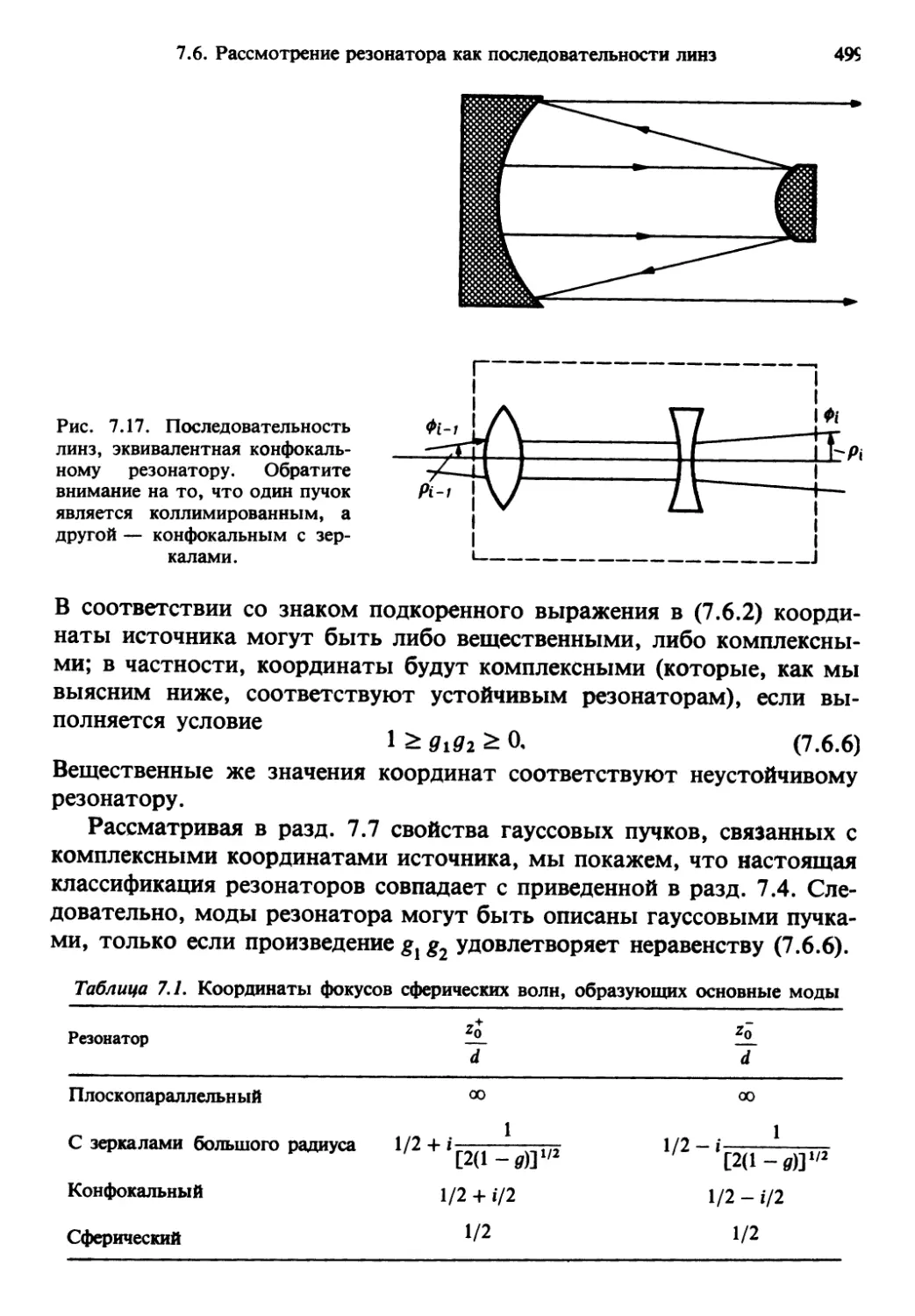
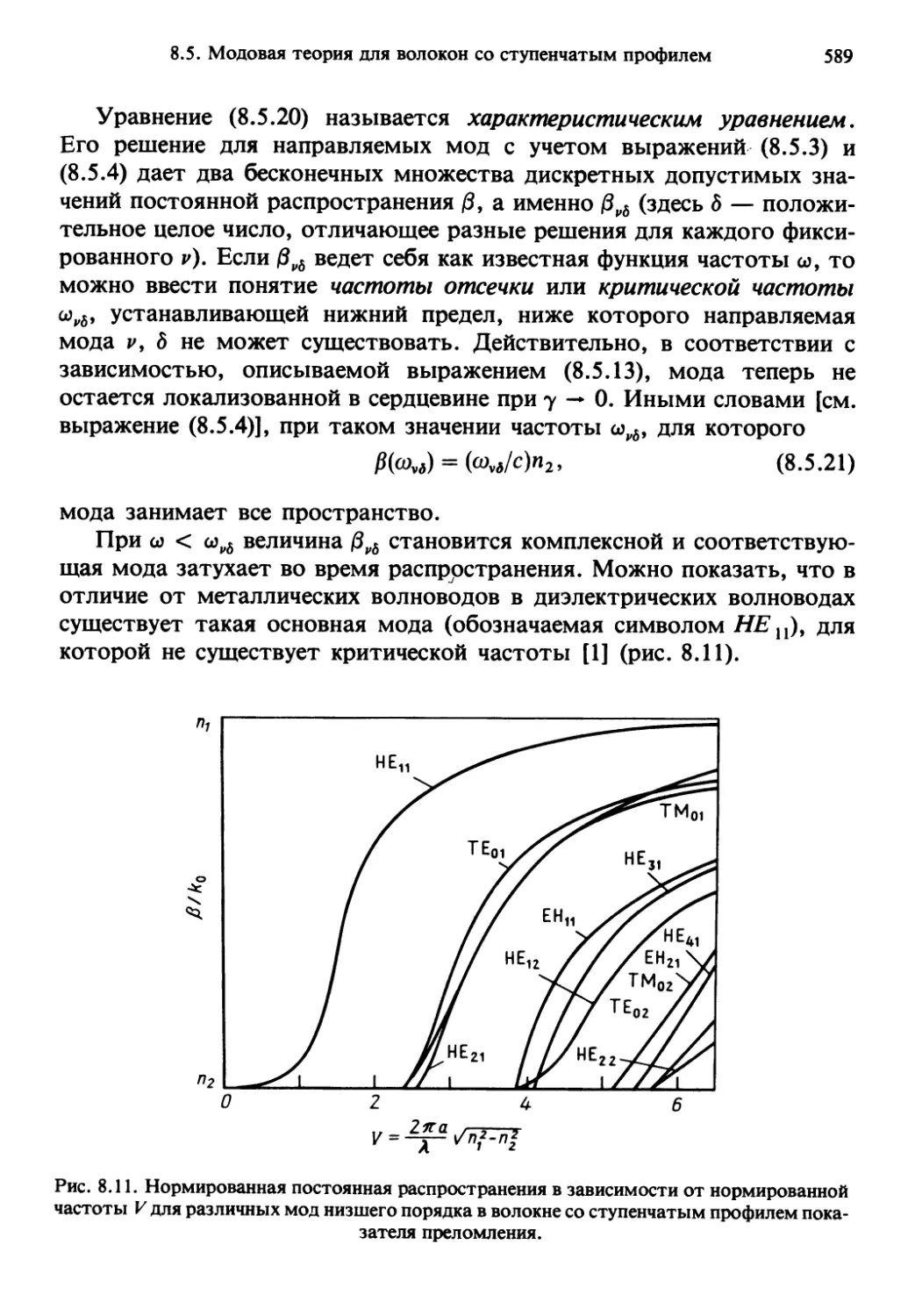
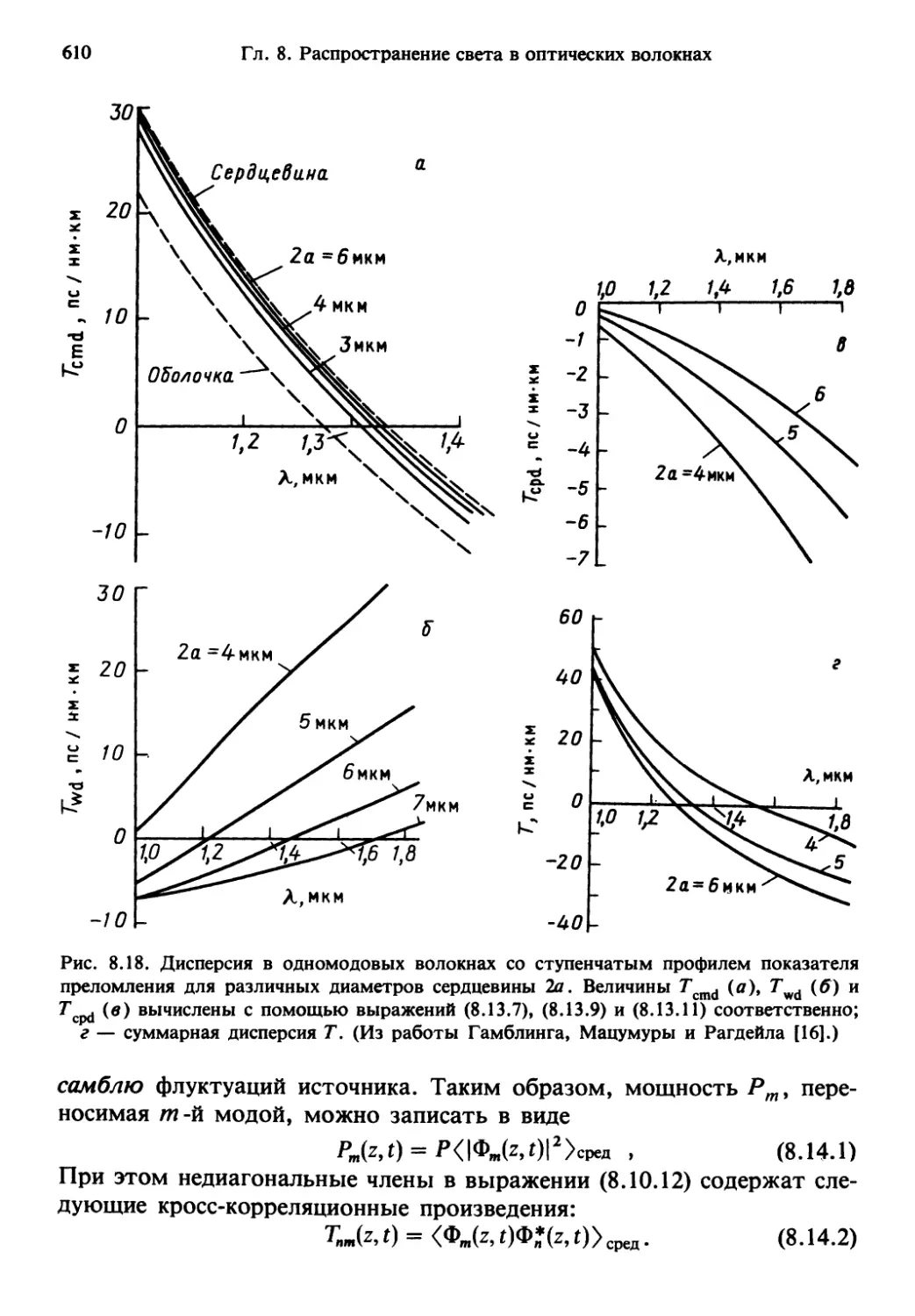
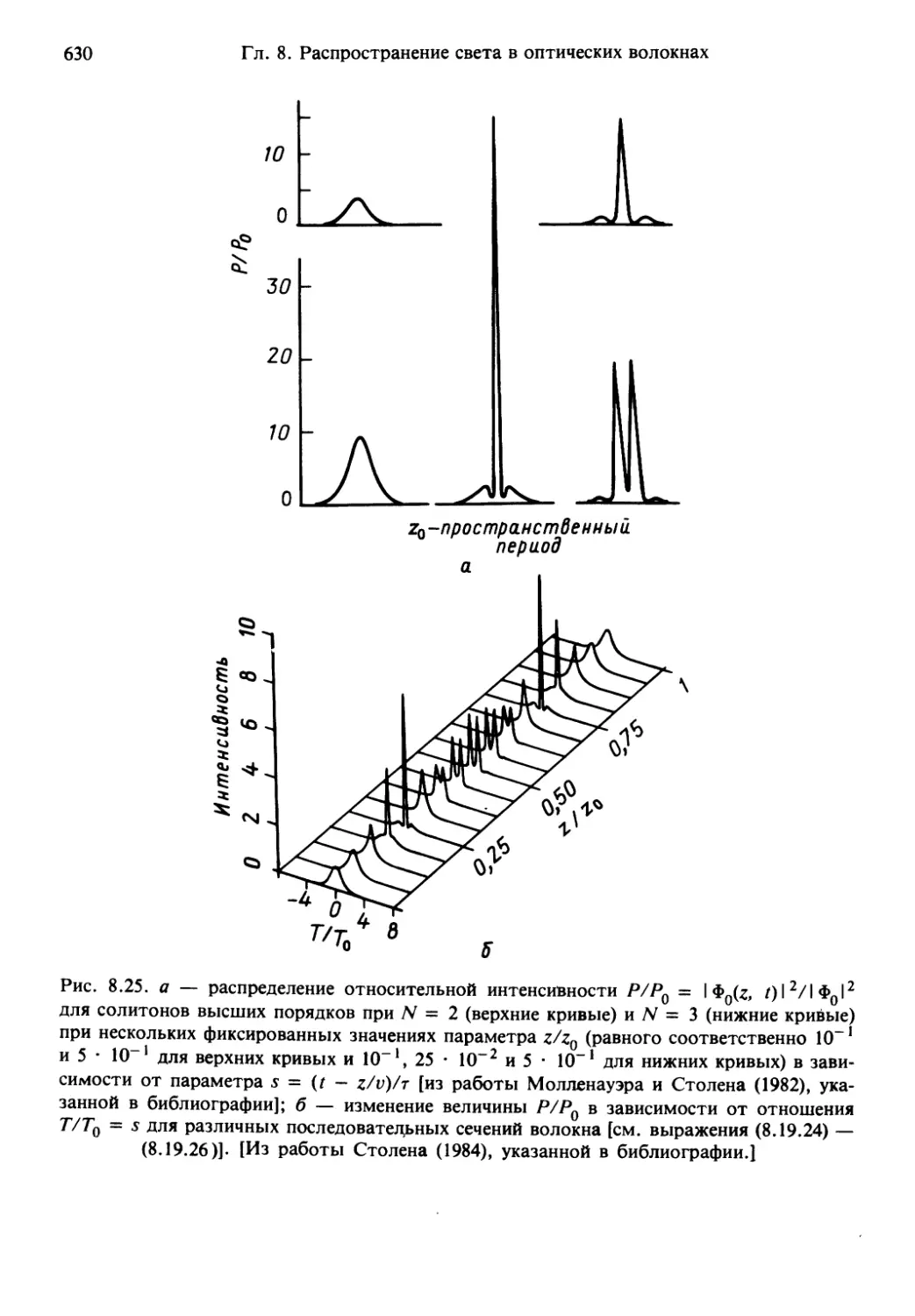
Author: Солимено С. Крозиньяни Б. Ди Порто П.
Tags: распространение световых лучей отражение преломление поглощение излучение физика инженерия оптика монография
ISBN: 5-03-001021-1
Year: 1989
Guiding, Diffraction,
and Confinement
of Optical Radiation
Salvatore Solimeno
UNIVERSITY OF NAPLES
NAPLES, ITALY
Bruno Crosignani
UNIVERSITY OF ROME, "LA SAPIENZA"
ROME, ITALY
Paolo Di Porto
UNIVERSITY OF L'AQUILA
L'AQUILA, ITALY
1986
ACADEMIC PRESS, INC.
Harcourt Brace Jovanovich, Publishers
Orlando San Diego New York Austin
London Montreal Sydney Tokyo Toronto
С.Солимено, Б. Крозиньяни,
П.Ди Порто
ДИФРАКЦИЯ
И ВОЛНОВОДНОЕ
РАСПРОСТРАНЕНИЕ
ОПТИЧЕСКОГО
ИЗЛУЧЕНИЯ
Перевод с английского
канд-тов физ.-мат. наук ЕВ. Московца и В.В. Тяхта
под редакцией
д-ра физ.-мат. наук, проф. B.C. Летохова
Москва «Мир» 1989
ББК 22.34
С60
УДК 535.3
Солимено С, Крозиньяни Б., Ди Порто П.
С60 Дифракция и волноводное распространение оптического
излучения: Пер. с англ. — М.: Мир, 1989. — 664 с, ил.
ISBN 5-03-001021-1
Монография известных итальянских специалистов посвящена актуальной
проблеме дифракции и распространения света. Вопросы классической оптики (лу-
(лучевая оптика, основы дифракции и т. д.) и современные разделы (свет в плоско-
плоскослоистой среде, оптические резонаторы, оптические волокна и т. д.) освещаются
с единой точки зрения.
Рассматриваются общие свойства распространения электромагнитного излу-
излучения и его взаимодействие с веществом, представлены асимптотические методы
решения волнового уравнения. Большое внимание уделено анализу распростране-
распространения света в слоистых периодических структурах (многослойных пленках, метал-
металлических и диэлектрических отражателях и интерференционных фильтрах). Изу-
Изучаются дифракция при распространении света, а также рассеяние света на раз-
различных предметах, резонаторы и распространение света в оптических волокнах.
Каждая глава книги снабжена задачами. Она содержит много полезных фор-
формул и сведений по обсуждаемым вопросам. Может служить учебным пособием
или справочником.
Для студентов, аспирантов, инженеров и научных работников, работающих
в области оптики и в смежных с ней областях.
1604060000-171 ББК 22.34
^ 041 @1) — 89 " "~ вУ
Редакция литературы по физике и астрономии
ISBN 5-03-001021-1 (русск.) © 1986 by Academic Press, Inc.
ISBN 0-12-654340-2 (англ.) © перевод на русский язык, «Мир», 1989
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
За последние почти тридцать лет, прошедшие со времени изобретения
лазера и повсеместного применения лазерного излучения, наши пред-
представления о распространении света, особенно в пространственно неод-
неоднородных средах, существенно расширились. Достаточно упомянуть
такие крупные разделы современной оптики, как голография, лазерная
оптика, волоконная или градиентная оптика, интегральная оптика,
компьютерная оптика, чтобы представить себе, как далеко продвину-
продвинулись оптическая наука и техника в своих возможностях управлять рас-
распространением светового пучка.
Естественно, что современное состояние проблемы дифракции и
распространения света должно быть отражено в монографической ли-
литературе. Представляемая читателю монография известных итальян-
итальянских специалистов как раз удачно служит этой цели. Опубликованные
до сих пор книги по современной оптике обычно рассматривали
какой-либо один из упомянутых разделов. В настоящей же моногра-
монографии изложение всех современных разделов оптики ведется с единой
точки зрения.
Среди многих достоинств книги следует выделить следующие. Во-
первых, она будет полезна не только научным работникам в качестве
настольного справочного пособия, содержащего множество необходи-
необходимых формул, но и студентам старших курсов и аспирантам в качестве
глубокого и продуманного учебника. В конце каждой главы помещено
несколько десятков задач, сгруппированных по разделам (всего в кни-
книге 205 задач), часто с указанием ссылок на оригинальную работу, в
которой имеется решение задачи. Во-вторых, авторы хорошо знако-
знакомы с достижениями не только зарубежных, но и советских ученых и
объективно отражают их вклад в развитие современной оптики.
Перевод книги выполнили Е.В. Московец (гл. 6—8 и приложения)
и В.В. Тяхт (гл. 1—5).
Проф. B.C. Летохов
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
В этой книге рассмотрены свойства оптического электромагнитного
излучения и те разделы прикладной математики, которые использу-
используются для его описания. Одна из задач, которую мы здесь
ставим, — провести читателя по долгому, но замечательному пути:
от первого знакомства с уравнениями Максвелла до таких достижений
современной оптики, как «геометрическая теория дифракции», асимп-
асимптотические решения волнового уравнения, теория оптических резона-
резонаторов, волоконная оптика и многослойные структуры.
«Новые физические понятия создаются не только в процессе обоб-
обобщения физических теорий, но и обратным путем: они могут возник-
возникнуть в результате применения приближенных методов к более точной
физической теории... . Так, понятие луча, а равно и вся геометричес-
геометрическая оптика могут быть выведены из волновой теории света как идеа-
идеализации, пригодные в предельном случае весьма малой длины волны
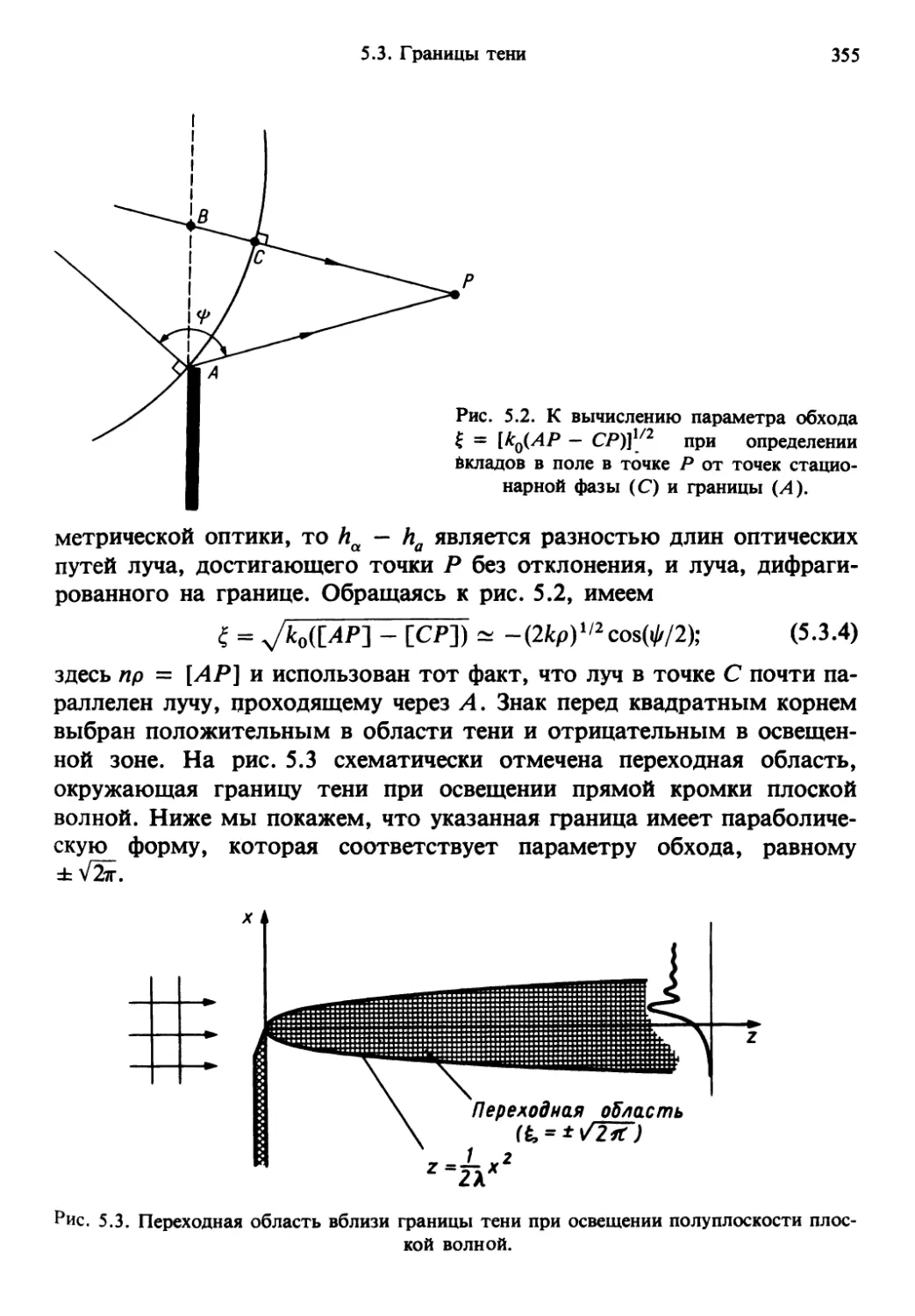
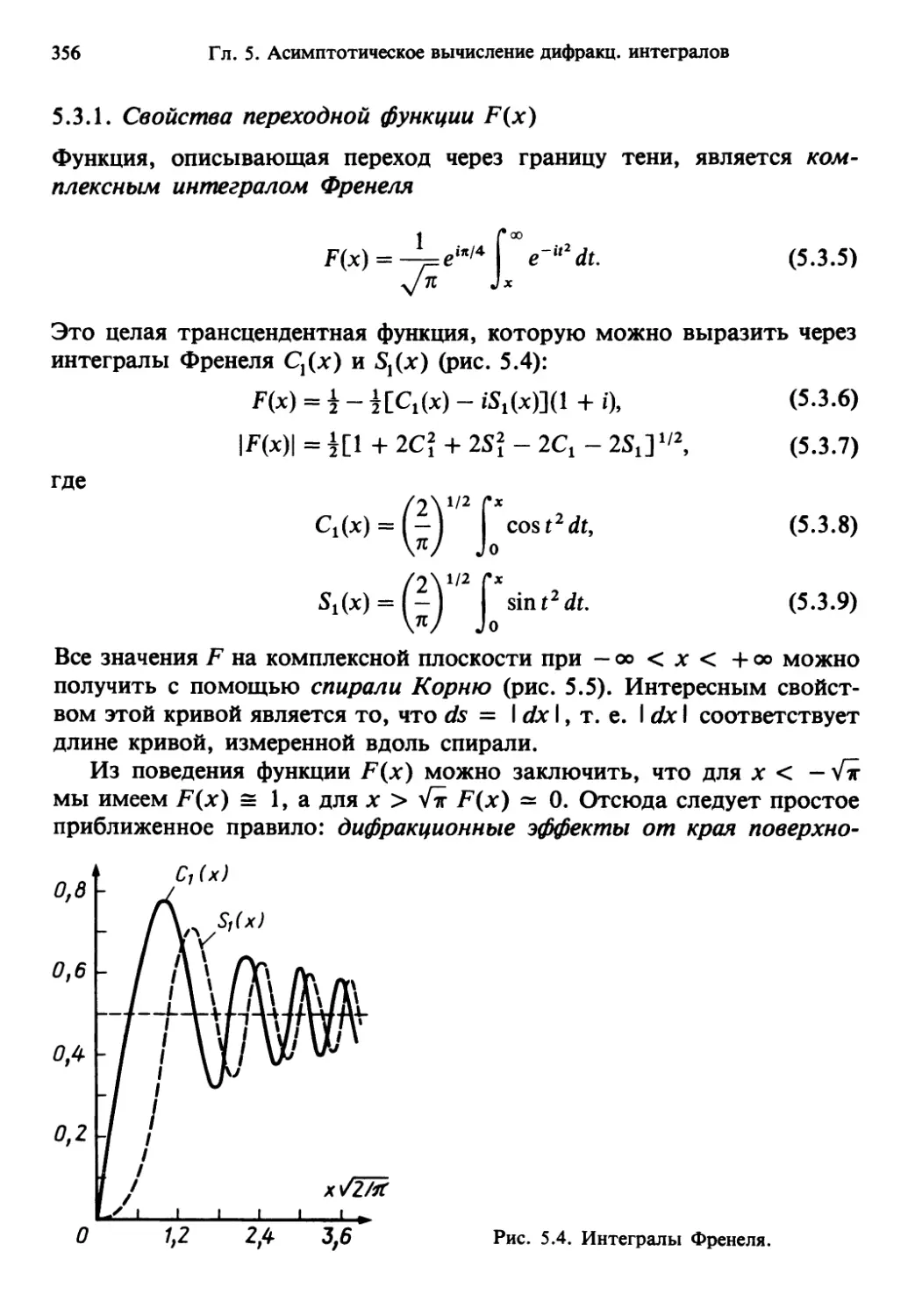
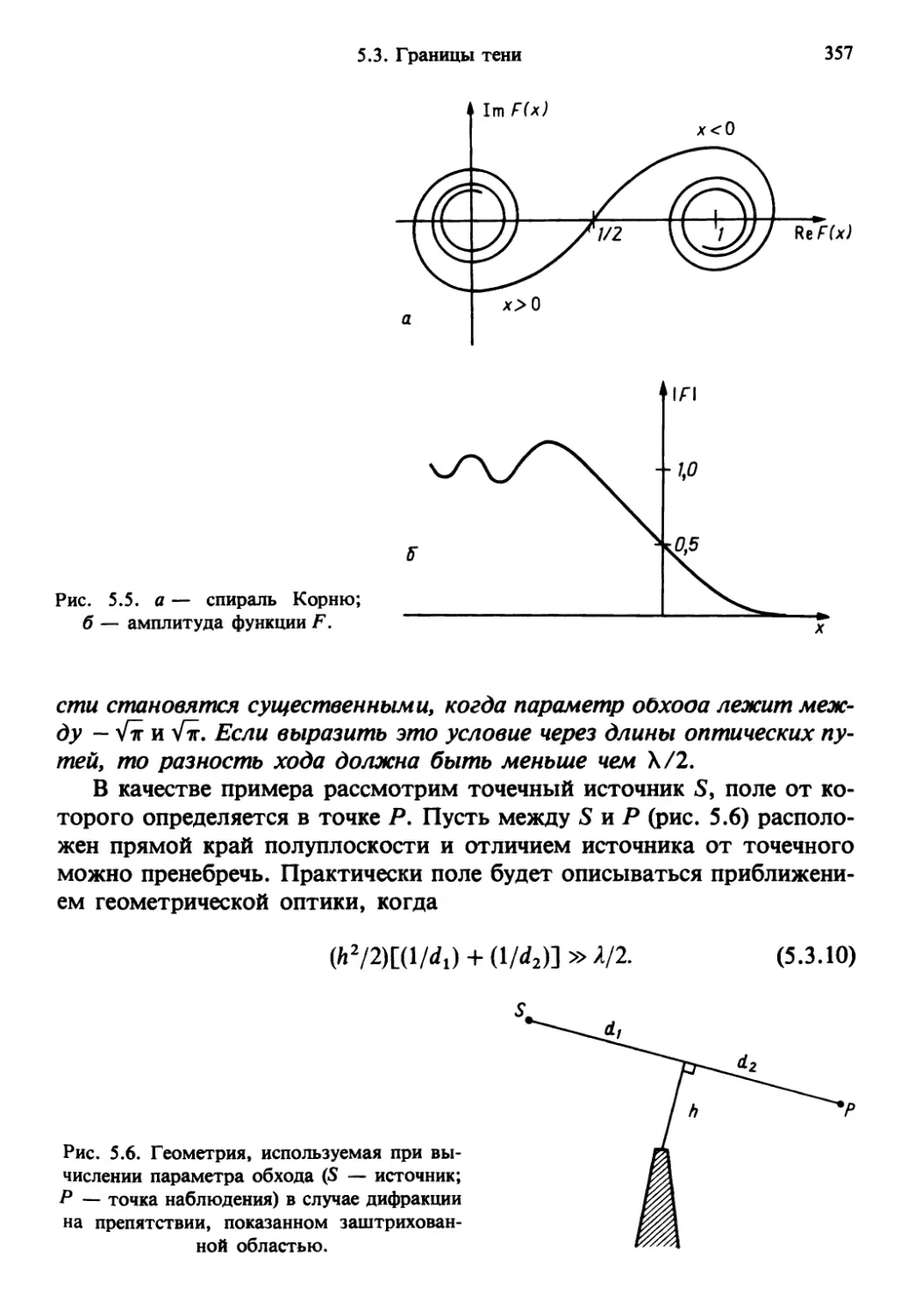
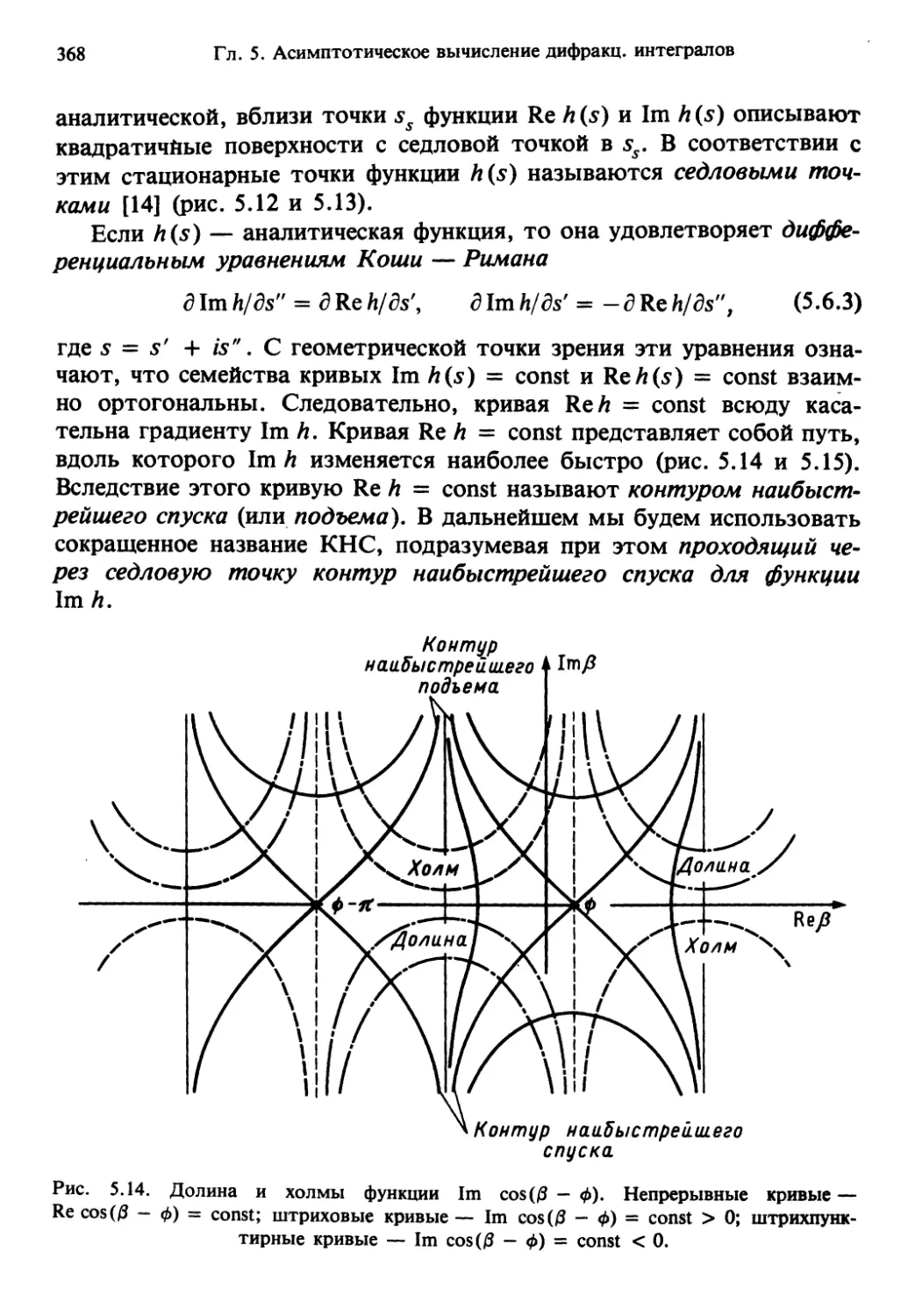
(в области вблизи границы света и тени эти идеализации уже непри-
непригодны). При менее полной идеализации учитываются и отклонения от
геометрической оптики, иначе говоря, учитывается дифракция, како-
каковая также является новым физическим понятием (дифракционные яв-
явления наиболее ярко проявляются как раз вблизи границы между све-
светом и тенью)». Этими словами академик В.А. Фок определил основ-
основные концепции геометрической оптики и теории дифракции в своей
знаменитой книге «Проблемы дифракции и распространения электро-
электромагнитных волн», ставшей одной из настольных книг целого поколе-
поколения физиков. Кроме того, следует отметить также такие классические
труды, как «Оптика» А. Зоммерфельда, «Основы оптики» М. Борна и
Е. Вольфа, «Оптика» Г.С. Ландсберга.
Канонические задачи теории дифракции были решены в нашем сто-
столетии Зоммерфельдом (дифракция на полуплоскости), Малюжинцом
(дифракция на клине), Фоком (поле на границе тени от гладкого пре-
препятствия) и Вайнштейном (дифракция на открытом конце волновода).
Специальные методы решения таких задач были развиты Вайнштей-
Вайнштейном (метод Винера — Хопфа), Уфимцевым и некоторыми другими
учеными. Особо следует отметить теорию граничного слоя.
В нашей книге мы подробно рассматриваем основы теории ди-
дифракции, уделяя особое внимание асимптотическим методам, широко
используемым в настоящее время. Из всех многочисленных приложе-
приложений для более подробного рассмотрения мы выбрали оптические резо-
резонаторы и многослойные среды, учитывая их важность в лазерной фи-
физике и оптической технологии.
Хорошо известно, что открытые резонаторы применяются в лазе-
лазерах для генерации излучения — это их первое, но далеко не последнее
приложение. Характерное свойство открытых резонаторов в том, что
их размеры гораздо больше длины волны.
Предисловие к русскому изданию 7
Если говорить только о главных приложениях многослойных систем
(мультислоев), то следует отметить отражатели сйета, лазерные зерка-
зеркала, светоделители, оптические фильтры. Современная технология по-
позволяет без особых трудностей получать мультислои для рент-
рентгеновского излучения, и уже в нескольких лабораториях были получены
зеркала с отражательной способностью порядка 60%. В будущем эти
исследования должны оказать влияние на развитие астрономии, ис-
источников синхротронного излучения и рентгеновской микроскопии.
Хотя наша книга и посвящена оптическому диапазону частот, анализ
многослойных систем без больших изменений можно приложить и к
рентгеновскому диапазону.
Последняя глава книги посвящена волоконной оптике — предмету,
который не нуждается в каком-либо дополнительном представлении.
Различные математические методы вводятся и обсуждаются в кни-
книге по мере возникновения в них надобности. Они не выделены в от-
отдельную главу. По нашему мнению, читатель гораздо эффективнее ов-
овладеет математическим аппаратом, если будет применять его к кон-
конкретным возникающим задачам. Исключение сделано лишь для фор-
формул, касающихся специальных функций. Их можно найти в приложе-
приложениях к книге.
В конце каждой главы помещен набор задач. Это связано с тем,
что, как правило, читатель изучает теорию, применяя ее к конкрет-
конкретным примерам. Мы надеемся, что возможностей для этого будет
вполне достаточно. Среди задач есть и такие, которые расширяют со-
содержание глав или вводят понятия, которым по тем или иным причи-
причинам не нашлось места в основном тексте.
В заключение мы пользуемся возможностью выразить свою глубо-
глубокую благодарность переводчикам Е.В. Московцу и В.В. Тяхту из Ин-
Института спектроскопии АН СССР за подготовку русского издания
книги. Наша признательность редактору перевода проф. B.C. Летохо-
ву чересчур велика, чтобы ее можно было измерить.
Переводчикам был предоставлен список ошибок и опечаток, попав-
попавших в оригинальное английское издание. Необходимые поправки были
внесены при переводе.
И наконец, нам хотелось бы выразить глубокую признательность
издательству «Мир» и его персоналу за внимание и тщательность, с
которыми они отнеслись к переводу, редактированию и печати этой
книги.
С. Солимено, Университет г. Неаполя
Б. Крозиньяни, Университет г. Акуила
П. Ди Порто, Университет г. Акуила
Нашим любимым родителям
ПРЕДИСЛОВИЕ
В течение последующих двадцати лет после появления в начале 1960
годов лазера было разработано множество приборов и устройств, по-
позволяющих управлять электромагнитным излучением в оптическом
диапазоне. К настоящему времени опубликовано немало превосход-
превосходных книг, в которых более или менее подробно описываются конкрет-
конкретные классы этих оптических приборов (например, оптические резона-
резонаторы и оптические волокна). Однако мы понимали, что назрела необ-
необходимость в написании руководства, которое познакомило бы читате-
читателя с общими принципами, лежащими в основе таких приборов, и про-
проиллюстрировало бы общие идеи на большом числе примеров, разбро-
разбросанных, как правило, по отдельным книгам. При таком подходе чита-
читатель ознакомится с рядом аналитических методов (многие из которых
развиты, вообще говоря, специалистами в области классического элек-
электромагнетизма, а не собственно оптики), которые дают основу для
полного понимания отдельного предмета.
Настоящая книга появилась благодаря научному опыту, накоплен-
накопленному авторами, которые работали в областях, тесно связанных со
многими рассматриваемыми здесь вопросами, а также благодаря их
преподавательской деятельности в университетах г. Акуила (Ди По-
Порто, физика твердого тела), г. Рима (Крозиньяни, оптоэлектроника) и
г. Неаполя (Солимено, электромагнитные поля и оптика). В результа-
результате возникла книга, которую можно использовать как учебник и как
монографию, посвященную современному состоянию исследований в
данной области, причем благодаря большому числу помещенных в
ней задач ее предпочтительнее отнести к учебнику.
В гл. 1 рассмотрены общие свойства распространения электромаг-
электромагнитного излучения и вводятся основные понятия, касающиеся описа-
описания электромагнитного поля и его взаимодействия с веществом.
Глава 2 посвящена главным образом асимптотическим методам
решения волнового уравнения, причем особое внимание уделено
асимптотическому представлению поля в виде ряда Лунебер-
га — Клейна (для которого геометрическая оптика является прибли-
приближением низшего порядка). В частности, с помощью уравнения эйкона-
эйконала исследуются многие оптические системы с различными распределе-
распределениями показателя преломления.
В гл. 3 изучаются слоистые среды (например, многослойные тон-
тонкие пленки, металлические и диэлектрические отражатели, интерфе-
интерференционные фильтры), которые играют весьма важную роль в инте-
Предисловие у
тральной оптике, а также распространение волн в периодических
структурах.
В гл. 4 задача о распространении волн рассматривается с позиций
теории дифракции и состоит главным образом в вычислении поля в
некоторой области с учетом вкладов от самого поля на опорной по-
поверхности. Этот метод, который можно считать прямым следствием
принципа Гюйгенса, связан с вычислением дифракционных интегра-
интегралов. Данная задача и различные систематические способы ее решения
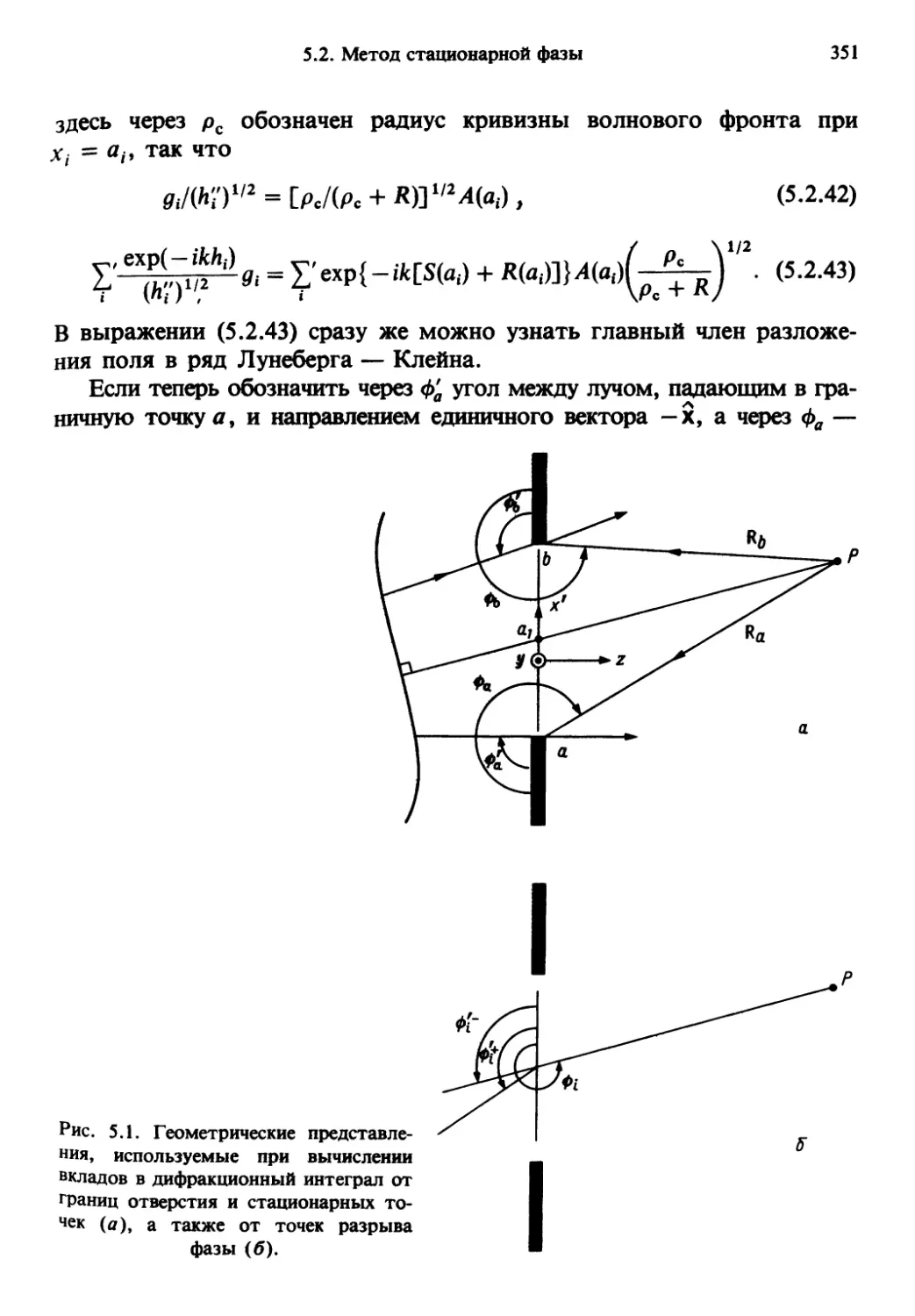
рассматриваются в гл. 5.
В гл. 6 изучается по существу рассеяние электромагнитных волн на
различных препятствиях. Она включает в себя также описание метал-
металлических и диэлектрических дифракционных решеток. Кроме того, в
этой главе довольно подробно излагается теория дифракционных мат-
матриц и 5-матриц рассеяния, обсуждение которой нечасто встретишь в
других учебниках по оптике.
В последних двух главах рассматривается концентрация поля в не-
некоторых ограниченных областях пространства, в которых имеют ме-
место определенные комбинации длин волн и неоднородностей среды;
это приводит к эффекту, который можно назвать своего рода удержа-
удержанием излучения. В частности, в гл. 7 мы рассмотрим пассивные и ак-
активные резонаторы, используемые в лазерных устройствах и предна-
предназначенные для удержания излучения вблизи оси оптических резонато-
резонаторов и интерферометров Фабри — Перо. При этом мы будем прово-
проводить изучение главным образом на основе теории дифракции. В гл. 8
для исследования удержания излучения в поперечном направлении
вблизи оси диэлектрического световода задача решается аналитически
с использованием модовых решений волнового уравнения. Это позво-
позволяет рассмотреть единым образом самые современные вопросы, свя-
связанные с такими нелинейными оптическими явлениями, как фазовая
самомодуляция и солитоны.
Настоящая книга предназначена в первую очередь аспирантам,
специализирующимся по оптике и электромагнетизму, и исследовате-
исследователям, интересующимся вопросами распространения и удержания опти-
оптического излучения. От читателя требуется предварительное знаком-
знакомство с основами теории электромагнитного поля на уровне хорошего
аспирантского курса. Что касается математического аппарата, то не-
необходимо предварительное знакомство со специальными функциями,
рядами Фурье и дифференциальными уравнениями. Мы думаем, что
широкий спектр рассматриваемых задач, а также строгость аналити-
аналитического описания сделают нашу книгу полезным справочником для
физиков и инженеров, работающих в области квантовой электроники.
10 Предисловие
Мы благодарим г-жу К. Кутилло за квалифицированную перепе-
перепечатку рукописи, М. Сансоне за подготовку оригиналов рисунков и
А. Торре за внимательное прочтение рукописи. Двое из авторов (Кро-
зиньяни и Ди Порто) признательны фонду Уго Бордони (Высший ин-
институт почты и телекоммуникаций, Рим) за гостеприимство во время
написания части этой книги. Бруно Крозиньяни глубоко признателен
своей жене Марии и дочерям Джиневре и Вере за их поддержку при
подготовке настоящей монографии. Сальваторе Солимено благодарит
Национальный совет исследований и Национальный институт ядерной
физики за поддержку, а также Р. Бруццезе за полезные советы.
ГЛАВА 1
ОСНОВНЫЕ СВОЙСТВА РАСПРОСТРАНЕНИЯ
ЭЛЕКТРОМАГНИТНЫХ ВОЛН
1.1. УРАВНЕНИЯ МАКСВЕЛЛА
Электромагнитное, поле в среде с непрерывно изменяющимися физиче-
физическими параметрами характеризуется четырьмя векторными
величинами — Е(г, /)> В(г, t), D(r, t), Н(г, t)9 которые удовлетворяют
уравнениям Максвелла:
), (l.l.l)
V х Н(г, t) = J(r, t) + C/3t)D(r, t), A.1.2)
F-B(r,f) = O, A.1.3)
F.D(r,t) = p(r,t). A.1.4)
В данной книге мы будем использовать систему единиц МКСА, по-
поэтому электрическое поле Е измеряется в вольтах на метр, магнит-
магнитная индукция В — в веберах на квадратный метр, электрическая ин-
индукция D — в кулонах на квадратный метр, магнитное поле Н — в
амперах на метр. В уравнения Максвелла входят также объемная
плотность заряда р, измеряемая в кулонах на кубический метр, и
плотность тока J' — в амперах на квадратный метр.
Наличие плотности тока J в уравнении A.1.2) может быть связано
с присутствием в среде проводящих материалов (например, металлов
или полупроводников) или внешних источников (таких, как магнитные
и электрические диполи, движущийся электрон). В некоторых случаях
вектор J заранее не известен; например, электрический ток, циркули-
циркулирующий на поверхности металлического объекта при рассеянии на нем
электромагнитной волны, сложным образом зависит от падающего и
рассеянного излучений. Поскольку решение этих задач не является
предметом изучения в данной книге, посвященной рассмотрению во-
вопросов оптики, плотность тока J мы будем считать, как правило, из-
известной величиной. При этом объемная плотность заряда возникнет
только за счет ненулевой дивергенции вектора J в соответствии с со-
соотношением
dp/df = -FJ, A.1.5)
которое непосредственно следует из уравнений A.1.2) и A.1.4).
12 1. Основные свойства распространения электромагнитных волн
Поскольку в оптическом диапазоне частот магнитная проницае-
проницаемость среды IX мало отличается от магнитной проницаемости ваку-
вакуума (магнитной постоянной) ^ = 4т ¦ 10~7 Гн/м, можно записать
следующее простое соотношение:
B(r,r) = jioH(M) A.1.6)
(случаи, когда это соотношение не выполняется, имеют место при
рассмотрении систем отсчета, связанных с движущейся средой; с эти-
этими случаями читатель может ознакомиться в разд. 1.7).
Векторы же Е(г, t) и D(r, t) связаны друг с другом, вообще говоря,
более сложным соотношением (см. следующий раздел). Однако если
ограничиться рассмотрением монохроматического поля, осциллирующе-
осциллирующего с угловой частотой со, т. е. Е(г, t) = e(r)cos[cof + Ф(г)] и D(r, i) =
= d(r)cos[co? + Щт)]9 то^ля амплитуд поля в комплексном представ-
представлении (см. разд. 1.8) Е(г, /) = е(г)ехр[/Ф(г) + iwt] ш E(r)exp(/a>0 и
D(r, t) = d(r)exp[/?(r) + /со/] s D(r)expOW) можно записать следую-
следующее соотношение, аналогичное A.1.6):
D(r,t) = fi0(l + zJE(M), A.1.7)
где е0 « 8,85 • 102 Ф/м — электрическая постоянная, ахы-в об-
общем случае комплексная диэлектрическая восприимчивость среды.
Хотя соотношение A.1.7) верно лишь для однородной изотропной
среды, его можно обобщить и на случай анизотропной среды (см.
разд. 1.4), считая величину \ш зависящей от направления распростра-
распространения электромагнитного излучения (если предположить, что поле
представляет собой плоскую волну).
Ограничившись рассмотрением изотропной среды и используя
уравнения Максвелла и соотношение A.1.7), можно получить уравне-
уравнение лишь для поля Е(г). Таким образом, полагая J = р = 0, имеем
V2E(r) + kl(\ + xJE(r) = 0, A.1.8)
где k0 = со/с, а с = 1/(ео/хоI/2 — скорость света в вакууме. Это же
уравнение A.1.8) можн$ переписать в другом виде:
V2E(r) + ЦпЦфЩт) = 0, П. 1.9)
где л(со) = A + xJVl — в общем случае комплексный показатель пре-
преломления среды. Уравнение AД.9) нетрудно получить, применяя опе-
оператор V х к обеим частям уравнений A.1.1) и A.1.2), записанных в
комплексном представлении, и используя соотношение (А. 13) (см.
приложение А в конце книги) и уравнение A.1.4).
Диэлектрическая восприимчивость изотропной неоднородной сре-
среды является функцией координаты; при этом уравнение A.1.7) прини-
принимает вид
D@ [lJ)]E(). A.1.10)
1.1. Уравнение Максвелла 13
В этом случае уравнение для Е(г) запишется в виде
V2E(r) - VV • Е(г) + к1п2(т,со)Е(т) = 0, A.1.11)
где коэффициент преломления л (г, о>) + VI + xw@ также является
функцией координаты г. Используя уравнение A.1.4) и соотношение
(А.7), можно записать
р . D = Р • (еои2Е) = <ч>Е • Уп2 + eon2V • Е = О,
откуда следует, что V • Е(г) = — 2Е(г) ¦ Vtf//?, а это, в случае когда
я(г, о)) представляет собой медленноменяющуюся функцию расстояния
г и(или) поле Е перпендикулярно вектору Vtf, позволяет в свою оче-
очередь пренебречь вторым членом в уравнении A.1.11). В этом случае
любая составляющая вектора Е(г) [обозначим ее как м(г)] в декартовой
системе координат удовлетворяет скалярному волновому уравнению
Р2м(г) + Цп2(г9(о)и(г) = 0. A.1.12)
Большая часть математических методов, представленных в данной
книге, посвящена решению уравнения A.1.12). В связи с этим еще раз
подчеркнем, что в тех областях пространства, где свойства среды рез-
резко изменяются (см., например, гл. 3 и 4), уравнения Максвелла и сле-
следующие из них волновые уравнения должны быть дополнены соотно-
соотношениями, связывающими векторы Е, Н, В и D по обе стороны по-
поверхности разрыва. Для диэлектрической среды без внешних источни-
источников (зарядов и токов) эти условия состоят в том, что при пересечении
поверхностей разрыва нормальные составляющие векторов В и D и
тангенциальные составляющие векторов Н и Е изменяются непрерыв-
непрерывно [1].
1.1.1. Векторный и скалярный потенциалы
В качестве неизвестных уравнения Максвелла содержат шесть скаляр-
скалярных функций [Ei9 Bf; (/ = х, у, z)]9 но их число можно уменьшить до
четырех, если выразить Е и В через векторный потенциал A(r, t) и
скалярный потенциал Ф(г, t):
В = Рх А, Е= -РФ-ЗА/Й, A.1.13)
Первое из этих соотношений следует непосредственно из A.1.3) и век-
векторного тождества (А. 15), а второе — из A.1.1) и (А. 14).
Для стационарной, однородной и анизотропной среды с
пространственно-временной дисперсией имеем (см. разд. 1.5)
+ 00
D(r,t)= ПТа'Г dt'x(r-r',t-t')-E(r',t') = z.E; A.1.14)
14 1. Основные свойства распространения электромагнитных волн
здесь тензор г является линейным оператором, a df s dx' dy' dz''.
Учитывая при этом независимость Г от времени [(d/dt)e'= Z(d/dt)] и
используя соотношение A.1.6) и векторное тождество (А. 13), можно
показать, что потенциалы АиФ удовлетворяют системе уравнений
Р • (г • РФ) + |- Р • (г • А) = -р, A.1.15а)
ot
V2A - Mo&V^А = -/x0J + PP. A + MofeV РФ, A.1.156)
которая эквивалентна уравнениям Максвелла.
Следует заметить, что АиФ определены с точностью до произ-
произвольной функции ¦(г, t)y так как при одновременной замене
А' = А + V* и Ф' = Ф - дЪ/dt векторные поля Е и В, связанные с
потенциалами соотношениями A.1.13), не изменяются. Это свойство
можно использовать для выбора такого потенциала А', чтобы он
удовлетворял условию кулоновской калибровки:
Р.(?.А') = 0, A.1.16)
которое эквивалентно выбору функции ¦ такой, что
P.(?.PV)= -P.(e-A)= -g(r9t). A.1.17)
Здесь g(r, t) — произвольная функция. Уравнение A.1.17) нетрудно ре-
решить, используя его пространственно-временное преобразование
Фурье, которое дает
(q-?q,«-q)*Fq,o = 0q,o> A.1.18)
где мы определили
-со
Из уравнения A.1.18) находим ?q a$ а затем, используя обратное пре-
преобразование Фурье, и искомое решение ¦(г, t).
При кулоновской калибровке A.1.16) система уравнений A.1.15)
упрощается и может быть записана в виде
Р.(?. РФ)= -р, A.1.20а)
Первое из этих уравнений описывает изменение скалярного потенциа-
потенциала Ф(г, /) за счет плотности заряда p(r, t). Точнее говоря, проводя пре-
преобразование Фурье по времени, сразу получаем, что Фы(г) линейно за-
1.1. Уравнение Максвелла 15
висит от pjj) (см. задачи 2 и 3):
+ 00
е0Фш(г) = J J1 *'Gc(r - г',ф.Ю, A.1.21)
— оо
где функция Грина Gc дается выражением
+ 00
-оо
Аналогично, используя преобразование Фурье уравнения A.1.206),
получаем
+ qq - <?21) • А„>ш = -
H • Cq,o * 4
» A.1.23)
где использовано также условие сохранения заряда [выражение
A.1.5)], которое в фурье-представлении эквивалентно соотношению
4-Jq.o^/W A.1.24)
Заметим, что, поскольку J^>w • q = 0, J^ представляет собой по-
поперечную компоненту вектора Jq w.
В случае изотропной и однородной среды для потенциалов АиФ
можно потребовать выполнения так называемой лоренцевой кали-
калибровки, а именно условия
Р-А + и^-О. A.1.25)
При этом АиФ удовлетворяют неоднородным уравнениям Гельм-
гольца
У2Ф - 1лог(д21дг2)Ф = - р/1 A.1.26а)
V2A - tioe(d2/dt2)A = —/ioJ, A.1.266)
в правые части которых входят соответственно р и J.
Наконец, для однородной анизотропной среды фурье-компоненту
Ew(r) можно представить в виде свертки
+ 00
,JJj*T(,-,"
Е„(г). -код, |||*Т(г-г')- JJr'), A.1.27)
— оо
где Г(г) — функция Грина в диадном представлении (см. задачи 4, 5
и 7).
16 1. Основные свойства распространения электромагнитных волн
1.2. РАСПРОСТРАНЕНИЕ ИЗЛУЧЕНИЯ В СРЕДЕ С ЧАСТОТНОЙ
ДИСПЕРСИЕЙ
В предыдущем разделе основная временная зависимость амплитуды
поля в комплексном представлении учитывалась множителем ехр(/со/)-
Для статической и слабодиспергирующей (в пределах ширины линии
излучения) среды это предположение не ограничивало общности рас-
рассмотрения, поскольку общее решение могло быть представлено в виде
суперпозиции монохроматических решений. Принцип суперпозиции
применим даже для дисперсной, но линейной среды, однако он нару-
нарушается, как только становятся существенными нелинейные эффекты.
Следует заметить, что благодаря обычно выполняющемуся соотноше-
соотношению 6а>/а>0 < 1, связывающему спектральную ширину до) поля и его
среднюю частоту со0, во многих случаях выражение для поля удается
факторизовать, т. е. представить его в виде произведения ехр (ко00 на
медленно меняющуюся во времени амплитуду. Иногда подобный при-
прием оказывается допустим и в координатном пространстве, если поле
можно приближенно представить плоской волной (см., например,
разд. 2.1).
Взаимодействие излучения с материальной средой обычно описы-
описывают вектором индуцированной поляризации Р, определяемым как
дипольный момент единицы объема вещества, возникающий под дей-
действием электрического поля Е [1]. Учет поляризации приводит к соот-
соотношению
P, A.2.1)
где Р — в общем случае сложная функция электрического поля Е. По-
Почти во всех случаях, которые мы будем рассматривать, соотношение
между Р и Е можно записать в простом виде (для удобства обозначе-
обозначений мы не выписываем в явном виде зависимости всех рассматривае-
рассматриваемых величин от пространственных координат):
г
+ 00
-t')dt\ A.2.2)
где функция \(t'), которая зависит лишь от параметров среды, в силу
принципа причинности должна обращаться в нуль при f < 0. Под-
Подставляя A.2.2) в A.2.1) и применяя преобразование Фурье по времени
к обеим частям получаемого выражения, находим материальное со-
соотношение
Е>„ = 6ОA + Хсо)*» = еМЕ„. A.2.3)
Фурье-образ произвольной функции/(О обозначим через /w и опреде-
1.2. Распространение излучения в среде с частотной дисперсией
17
лим его следующим выражением:
/. = Г V'-'/W*. A.2.4)
J -оо
Выражение A.2.3) позволяет выразить диэлектрическую проницае-
проницаемость г(со) через диэлектрическую восприимчивость хш = хш - Ы'ш и
показатель преломления л(со):
е(со)/ео = 1 + Хю = и2(со). A.2.5)
Зависимость ? от со обычно называют законом дисперсии.
Простое линейное Соотношение A.2.2) применимо в случае малых
интенсивностей поля и веществ с низкой плотностью и является пер-
первым приближением общего выражения, связывающего Е и Р [2]. В
тех случаях, когда в среде присутствуют временные флуктуации, мед-
медленные по сравнению с характерным временем изменения функции
х(О> выражение A.2.3) можно обобщить, включая в него параметри-
параметрическую зависимость \ш от времени [3], т. е. вместо xw нужно использо-
использовать медденно меняющуюся во времени восприимчивость хш(О- (В
частности, это приводит к уширению спектра первоначально монохро-
монохроматического излучения, распространяющегося во флуктуирующей сре-
среде.) Подобное рассмотрение применимо для описания оптического эф-
эффекта Керра (разд. 8.19).
Зависимость диэлектрической восприимчивости и, следователно,
показателя преломления п от частоты со называют дисперсией среды
(рис. 1.1). Она ответственна за искажение сигнала в прозрачных сре-
средах [в которых п (со) можно рассматривать как вещественную величи-
величину; см. разд. 1.3]. Мы детально рассмотрим этот эффект в гл. 8 в свя-
связи с изучением распространения света в оптических волокнах. Диспер-
Дисперсия приводит к различию групповых скоростей
A.2.6)
где п (со) — вещественный показатель преломления прозрачной среды,
в которой распространяются различные частотные компоненты элек-
Рис. 1.1. Качественная зависимость показа-
показателя преломления от частоты. Заштрихо-
Заштрихованные области соответствуют резонансам.
18 1. Основные свойства распространения электромагнитных волн
тромагнитного поля. Следует заметить, что, хотя в оптике удобно
выделить частотные области нормальной и аномальной дисперсии, в
которых показатель преломления увеличивается или уменьшается со-
соответственно с частотой (dn/do) > О или dn/dw < 0), в современной
литературе по оптическим волокнам эти области нередко определяют
как такие, в которых (d/du>) [\/v(o))] > 0 или (d/do))[\/v(o))] < 0, т. е.
области, в которых и(ш) является соответственно убывающей или воз-
возрастающей функцией частоты о> (см. разд. 8.19).
Как показано на рис. 1.1, область аномальной дисперсии заключе-
заключена между максимумом и минимумом функции х'(«). В небольшом ча-
частотном интервале, центр которого со0 совпадает с резонансной ча-
частотой элементарных систем, составляющих среду, среда оказывает-
оказывается сильно поглощающей, т. е. возникает очень большая мнимая вос-
восприимчивость х"И. Исследование этой частотной области требует
микроскопического описания. Пример такого подхода приведен в
разд. 1.2.2 в связи с рассмотрением распространения волн в среде ре-
резонансных двухуровневых систем.
В случае когда электрическое поле становится настолько сильным,
что нельзя пренебрегать вкладом нелинейности, простое соотношение
A.2.2) необходимо модифицировать. При этом в большинстве случаев
понятие показателя преломления становится бессмысленным. Как
следствие, функциональная зависимость Р от Е должна определяться
отдельно для каждого конкретного нелинейного процесса, и подстав-
подставлять ее в уравнения Максвелла необходимо с помощью соотношения
A.2.1). Примеры этого мы рассмотрим в следующем разделе, однако
сразу заметим, что, несмотря на явно нелинейную природу оптиче-
оптического эффекта Керра (см. разд. 8.19), понятие коэффициента прелом-
преломления сохраняет свою применимость и в этом случае.
1.2.1. Нелинейное распространение волн
Рссмотрим уравнения Максвелла A.1.1) и A.1.2), дополненные соот-
соотношением A.2.1) и законом Ома в дифференциальной форме:
J = <xE, A.2.7)
Здесь а — электропроводность среды. Для проводников уравнение
A.2.7) остается справедливым в пределе малых частот а> — 0. Строго
говоря, соотношение A.2.7) справедливо для почти монохроматичес-
монохроматического поля, центральная частота которого равна w0. При этом величи-
величина о ш а(о>0) не имеет очевидного физического смысла и введена лишь
для учета потерь, связанных с мнимой частью диэлектрической вос-
восприимчивости. С помощью метода, аналогичного использованному
1.2. Распространение излучения в среде с частотной дисперсией 19
при выводе уравнения A.1.8), нетрудно получить следующее уравне-
уравнение:
V2E - /*0<7^ - \^ = 0о^г?, A.2.8)
dt cz dt dt
где при записи члена VV-E [см. A.1.11)] мы воспользовались прибли-
приближенным соотношением V • Е = 0 (которое строго справедливо лишь в
тех случаях, когда среду можно считать идеально однородной).
Если записать теперь вектор индуцированной поляризации Р как
сумму линейной части P(L), удовлетворяющей соотношению A.2.2) и
нелинейной части P<NL), т. е. 6 виде Р = P(L) + P<NL>, то уравнение
A.2.8) принимает вид
Теперь, прежде чем приступить к исследованию и решению уравне-
уравнения A.2.9), необходимо получить выражение, определяющее P<NL) для
рассматриваемого нелинейного процесса. Эту задачу можно решать,
пользуясь совершенно разными методами описания — начиная от точ-
точного квантовомеханического микроскопического метода и кончая чис-
чисто феноменологическим подходом. В следующем разделе мы приве-
приведем пример первого метода описания; здесь же рассмотрим кратко
феноменологический подход.
Запишем /-ю компоненту вектора поляризации Р(/) как сумму по-
ляризуемостей первого, второго, третьего и т. д. порядков [4] (мы
воспользуемся здесь для простоты соглашением о суммировании по
повторяющимся индексам):
+ 00
\;(( ~ t')Ej(t')dt' + е0 IT xiJk(t - f,t - t")Ej(t')Ek(t")dt'dt"+
и(* -t',t- t",t - t'")Ej(t')Ek(t")El(t'")dt''dt"dt'"+--,
ij,kj = x9y,z, A.2.10)
Здесь тензорный характер xtj позволяет обобщить соотношение A.2.2)
на случай анизотропных сред.
В некоторых конкретных случаях общее выражение A.2.10) можно
существенно упростить, учитывая либо симметричные свойства сре-
среды, либо характер временного отклика. Например, второе слагаемое
в сумме A.2.10) равно нулю в средах, симметричных относительно ин-
20 1. Основные свойства распространения электромагнитных волн
версии. Другой пример — при определенной частоте и ширине спектра
излучения отклик среды можно считать мгновенным, т. е. величины х
зависят от времени в виде 6-функции (см., например, разд. 8.19).
Рассмотрение большинства задач нелинейной оптики основано на
предположении о том, что поле является суперпозицией нескольких
монохроматических волн. Этот подход является самосогласованным,
так как сам вид разложения A.2.10) подразумевает возможность гене-
генерации волн в виде дискретной суперпозиции монохроматических по-
полей. В соответствии с этим электрическое поле нередко записывают в
виде п
Е(г) = t (^е1т1 + E*,e-fn A.2.11)
Пример: генерация второй гармоники. Рассмотрим в качестве при-
примера процесс, связанный с поляризуемостью второго порядка, — гене-
генерацию второй гармоники (ГВГ). Чтобы описать этот процесс, пред-
предполагают, что поле состоит из двух частотных слагаемых, одно из
которых осциллирует с круговой частотой wj, а другое — с со2 = 2ил
[см. выражение A.2.11)].
После подстановки выражения A.2.11) во второе слагаемое в пра-
правой части суммы A.2.10) необходимо прежде всего выделить члены,
осциллирующие с частотами о){ и 2и19 т. е.
^!NL)@ = Peii*to1' + q2(aiiei2<ait + к. с. A.2.12)
(здесь к.с. означает «комплексно-сопряженные члены») и
P<oii ~ eoX-(oit2(oiijk^onj^2<oik + eoX2o>u-(oiijk^lau^wik^ A.2.13)
Qltoti = e0X<oit<Oiijk^<oxfi(Oik , A.2.14) ^
причем символ хш, wf /y- k означает двойное временное преобразование
Фурье величины XijA*''»*")• Подставляя выражение A.2.12) в уравне-
уравнение A.2.9), получаем
De ,, A.2.15a)
4lOlj
с е0
<?^!*21Й?2ши = -4fi0colq2(Ol, A.2.156)
с е0
Входящий в эти уравнения тензор диэлектрической проницаемости
определяется следующим образом:
*W = eo($ij + Xoij)- A.2.16)
Система уравнений A.2.15) обеспечивает аналитическое описание
ГВГ, и ее решение (которое читатель может найти в более специали-
1.2. Распространение излучения в среде с частотной дисперсией
,234
21
Рис. 1.2. Экспериментальная установка для демонстрации генерации второй гармоники
света. 1 — рубиновый лазер; 2 — пропускающий фильтр; 3 — нелинейный кристалл;
4 — призма; 5 — фотопленка.
зированных книгах, например [5]) позволяет сделать общие выводы
относительно эффективности и характеристик процесса. В частности,
эффективность ГВГ существенно зависит от разности фазовых скорос-
скоростей волны накачки (wj) и второй гармоники Bих) (рис. 1.2). Их совпа-
совпадения (условия фазового синхронизма) можно достичь в одноосном
кристалле, используя различие скоростей обыкновенной и необыкно-
необыкновенной волн (см. разд. 1.4).
1.2.2. Распространение импульса в двухуровневой резонансной среде
В этом разделе мы приведем пример того, как микроскопический под-
подход позволяет вычислить точное значение вектора поляризации Р.
Рассматриваемый случай взаимодействия электромагнитного поля с
двухуровневой системой является довольно общей моделью, описыва-
описывающей физические ситуации, в которых происходит когерентное взаи-
взаимодействие излучения с веществом.
Задача состоит в нахождении функциональной зависимости поля-
поляризации Р от Е — амплитуды квазимонохроматической плоской во-
волны, средняя частота которой совпадает с частотой перехода системы
со0 = (Еа - Eb)/h в отсутствие поля (рис. 1.3). Это требует решения
уравнения Шрёдингера при наличии внешнего возмущения. Будем сле-
следовать полуклассическому подходу, когда электрическое поле считает-
считается классической величиной (это соответствует пренебрежению вкла-
Рис. 1.3. Двухуровневая система.
22 1. Основные свойства распространения электромагнитных волн
дом в электромагнитное поле от фотонов спонтанного излучения), а
атомная система рассматривается в рамках квантовой механики, т. е.
ее состояние !¦> представляется в виде суперпозиции собственных
энергетических состояний \иа) и \иь)> соответствующих собственным
значениям Еа и Еь\ таким образом,
PF> = a(t)\ua> + b(t)\ub>. A.2.17)
Вектор состояния 1*> должен удовлетворять временнбму уравне-
уравнению Шрёдингера
Я|?> = (Но + V)\4> = ihdm/dt, A.2.18)
где Но — гамильтониан невозмущенной системы, а V — внешнее воз-
возмущение, которое описывает взаимодействие поля излучения и ато-
атомов. В дыпольном приближении, т. е. в случае когда длина волны зна-
значительно больше размеров атомной системы, это взаимодействие да-
дается выражением V = - ех • Е. Решив уравнение A.2.8), т. е. опреде-
определив зависящие от времени амплитуды a(t) и b(t\выраженные через Е,
дипольный момент р элементарной системы можно записать в виде
+ a*b), A.2.19)
Ро= -е(иа\х\щУ A.2.20)
— электрический дипольный матричный элемент. Вектор поляризации
Р получается суммированием вкладов от всех систем, находящихся в
единичном объеме.
Предположим теперь, что в начальный момент времени t = 0 каж-
каждый из атомов находится в состоянии либо а, либо Ь, и обозначим че-
через vz скорость атома в направлении z, в котором распространяется
электромагнитное поле. При этом частота его перехода в лаборатор-
лабораторной системе координат будет равна со = а>0 4- kovz. Если теперь обо-
обозначить через g(co) функцию распределения частот со, обусловленную
движением атомов в газе или наличием локальных кристаллических
неоднородностей в твердом теле, то можно написать следующее вы-
выражение:
= ^f + OCd(og(a>) X AU[fl(z,t,a),a)fr*(z,r,co,a)+K. с], A.2.21)
3-ao a = a,b
где N^ и Nb0 — число атомов в единице объема соответственно на
верхнем и нижнем уровнях при t = 0, а амплитуды a(z, t, со, а) и
b(z> t, со, а) относятся к атому со средней частотой перехода со, имею-
имеющему координату z в момент времени t и находившемуся при / = Ов
состоянии lwa>. Множитель 1/V5 возникает вследствие усреднения по
возможным ориентациям атомных систем, которые предполагаются
изотропно поляризуемыми.
1.2. Распространение излучения в среде с частотной дисперсией 23
Случайные столкновения между атомами приводят к статистичес-
статистической неопределенности фаз у a(t) и b(t). Это означает, что для опреде-
определения поляризации Р в макроскопических уравнениях Максвелла,
[в частности, в A.2.8)] необходимо провести усреднение по времени в
выражении A.2.21). Таким образом, необходимо найти (ab*) и (а*Ь)
(здесь скобки <...> означают усреднение по ансамблю), т. е. недиаго-
недиагональные элементы матрицы плотности [6]:
<|а|2> <аЬ*У\_Грт РаЬ1
Временная эволюция матрицы плотности может быть описана, исхо-
исходя из уравнения Шрёдингера, с учетом феноменологических членов
распада. Таким образом получают уравнения Блоха
РаЬ= ~ ШРаЪ - УаЬРаЬ + ^ V{Z, t)(paa - pbb),
Раа = -Уа(Раа ~ РЩаа) + \ V(z,t)(Pab ~ Pba\ (L2.23)
Рьь = ~Уъ(Рьь ~ Рщьь) - jT V(z9 t)(pab - рЬа\
Здесь точкой обозначено дифференцирование по времени, а
Уаь = A//2)(Тя + 7^) + l/^c В уравнения A.2.23) были феноменологи-
феноменологически введены времена жизни состояний а и Ъ (\/уа и 1/уь), а также
характерное время атомных столкновений Гс. Уравнения A.2.23) мож-
можно переписать таким образом, что они будут описывать прецессию
магнитного диполя в магнитном поле, что и было первоначально сде-
сделано Фейнманом, Верноном и Хеллуортом (см. также работы [5, 6]).
Поскольку мы ищем решение уравнений Максвелла, соответствую-
соответствующее линейно-поляризованной (см. разд. 1.3) узкополосной плоской во-
волне с центральной частотой вблизи а>0, справедливы следующие выра-
выражения для E(z, t) и P(z, t):
E(z, t) = |*(z, 01 cos[w0r - kz + 4>(z, t)], A.2.24)
- kz + Ф(г,0] + C(z,0cos[co0t - kz + O(z,0]fc
= (^7=) E ^o f +%M[pflb(z,r,o;,a) + к. с] dco A.2.25)
Здесь <f = I #\е1ф — огибающая поля, а вещественные функции S и С
предполагаются медленно меняющимися по сравнению с временным
1/со0 и пространственным \/к0 интервалами. Необходимо также заме-
заметить, что в электрическом дипольном приближении, как это следует
24 1. Основные свойства распространения электромагнитных волн
из A.2.24), возмущение V равно - AЛ)р0^еКш ~ n)'/V3. Подставляя со-
соотношения A.2.24) и A.2.25) в уравнение A.2.8) и используя перечис-
перечисленные выше условия и обозначения, имеем
<'""
где а = iiQ(p/2nv) — потери на единицу длины, а пх = Ve/^o ~~" пока-
показатель преломления инертной среды, окружающей активные атомы.
Теперь необходимо добавить уравнения, описывающие эволюцию
переменных S(z, t) nC(z, t); их можно вывести из уравнений A.2.23).
После несколько утомительных расчетов (для более подробного озна-
ознакомления с ними мы отсылаем читателя к статье [7]) можно пока-
показать, что для симметричной относительно соо функции g (со) справедли-
справедливо равенство С = Ф = 0. Если предположить, что вклад в электриче-
электрическое поле от спонтанного излучения пренебрежимо мал, то распреде-
распределение поля полностью описывается двумя величинами, а именно функ-
функцией (f(z, О и интегральной комплексной восприимчивостью
X(z, Т, 0 = —1— X Ng0 f + 0° 0(а>)со8[(ш - а>0)Г| X
х [pflfl(z, Г, а>3 а) - pbb(z, г,а>, а)] dco, A.2.28)
где элементы матрицы плотности раа Ъ pbb относятся к атому, имею-
имеющему частоту перехода со0, находящемуся в момент времени t в точке
с координатой z и имевшему при t = 0 состояние иа. Для медленно
меняющихся амплитуд S(z, t) и <?(z, t) величина exp (- yabt') x
x x(z, tf, t - /') играет ту же роль, что и х(О в соотношении A.2.2).
Это подтверждается следующим соотношением:
S(z,t) = -^d Г"e-"->x(z,t'9t - f)S\z,t - t')dt\ A.2.29)
^o Jo
где d = Г/з^со^Л^ - Nb0)Trg(o)Q)/(cnxe0h). Точнее говоря, распро-
распространение сигнала в двухуровневой среде описывается системой двух
интегродифференциальных уравнений:
dz с dt J.
- t\t')*(z,t')dt', A.2.30)
1.2. Распространение излучения в среде с частотной дисперсией 25
^ X(z, T91) = ?*- Z(z, T, - оо) - yabX(z, Т, 0 -
3* УаЪ
6« J-
f)dt' A.2.31)
с граничным условием (f(z = 0, t) = ^ для электрического поля и на-
начальным условием
1 Г+со
x(z,T,t= -оо) = ——— flf(o)cos[(G) - wo)T]da). A.2.32)
Рассмотрим теперь некоторые предельные случаи, когда эта систе-
система уравнений принимает значительно более простой вид и становится
аналитически разрешимой.
1.2.2.а. Режим скоростных уравнений для длинных импульсов
Пусть Гс пренебрежимо мало по сравнению со всеми остальными ха-
характерными временами системы, т. е. по сравнению с l/ya, l/yb9
Т2 — обратной шириной полосы функции #(<*>) и Тр — длительностью
импульса. При этом уравнения A.2.30) и A.2.31) принимают соот-
соответственно вид
d-f + — d4r + *s= -dT2Z(z,0,t)*(z,t), A.2.33)
oz с ot
_(•? о t\ = т* y(V q t\S^(z t\ (\ 2 34)
в то время как выражение A.2.28) можно записать следующим обра-
образом:
2ng(co0) Na0 - Nb0,
Здесь Na(z, t) и N^(z, 0 — плотности атомов на верхнем и нижнем
уровнях [в частности, Na(z, - оо) = Na0, Nb(z, - оо) = Nb(?. Таким
образом, система уравнений A.2.33) и A.2.34) связывает между собой
мгновенные значения интенсивности поля [которая пропорциональна
<?2(z9t); см. разд. 1.8] и плотности инверсии населенносгпей AN =
= Na - Nb. Эти уравнения обычно используют для описания лазер-
лазерной генерации в стационарном режиме [8] (см. разд. 7.19). Вообще го-
говоря, эти скоростные уравнения хороши в тех случаях, когда ампли-
амплитуда поля заметно изменяется на временах, больших по сравнению с
26
1. Основные свойства распространения электромагнитных волн
Т2. В следующем подразделе мы опишем противоположную ситуа-
ситуацию, которую называют когерентным распространением,
В пределе а = О, что соответствует отсутствию потерь, система,
уравнений A.2.33) и A.2.34) имеет аналитическое решение [9], особен-
особенно полезное при исследовании распространения импульса в каскаде ла-
лазерных усилителей.
1.2.2.6. Самоиндуцированная прозрачность
Можно показать, что для узкой линии при резонансе (а>0 = Q) и в от-
отсутствие диссипации
Ро
A.2.36)
Тогда если величину в фигурных скобках, пропорциональную оги-
огибающей поля, обозначить через 0(z), то мы можем написать следую-
следующее уравнение:
d®/dz + а© = \d sin 0. A.2.37)
В пределе а = О это уравнение имеет общее решение
O(z) = 2 arctg[^/2tg (Go/2)], A.2.38)
которое приводит к так называемой теореме площадей [10]; согласно
этой теореме, величины Q(z) = Bт 4- 1)тг и 9(z) = 2тж (где т —
целое) являются устойчивыми решениями в усиливающей (d > 0,
N^ > Nb0) и поглощающей (d < 0) среде соответственно (рис. 1.4). В
* Л *
1 Zz
в
Рис. 1.4. Компьютерные графики. Эволюция импульсов с различными начальными пло-
площадями 0О, полученная из расчетов на ЭВМ. (Из работы [10].) а — 90 = 0,9тг; б —
90 = 1,1т; в — 0О = 4ir для положительного параметра ослабления а. Расстояние ш из-
измеряется в единицах длин поглощения к/а. Заметим, что для0о = 4тг импульс разбива-
разбивается на два 2т-импульса; г — эволюция площади импульса, описываемая уравнением
A.2.37).
1.2. Распространение излучения в среде с частотной дисперсией 27
частности, для данного начального значения 0О величина 0(z) стре-
стремится к ближайшему четному (для усилителя) или нечетному (для по-
поглотителя) кратному числа х.
Из уравнения A.2.30) следует, что при а = 0 импульс в форме ги-
гиперболического секанса [10]
при Т < Т2 распространяется без изменения формы с групповой ско-
скоростью:
!Ь ^ 0.2.40,
v с
Это явление, когда короткий импульс, интенсивность которого
имеет оптимальную величину, может распространяться в среде двуху-
двухуровневых систем с аномально низкими потерями энергии, называют
самоиндуцированной прозрачностью [10].
1.2.2.В. Общий случай
Для получения решения в общем случае, описываемом интегродиффе-
ренциальными уравнениями A.2.30) и A.2.31), приходится, как прави-
правило, использовать численные методы. С этой целью уравнения удобно
представить в дифференциальной форме. Точнее говоря, с помощью
определяющих выражений A.2.28) и A.2.29) можно показать, что при
Т2 > у~^ (см. разд. 1.2.2.а) эти уравнения эквивалентны системе урав-
уравнений, одним из которых является A.2.26), а два других имеют соот-
соответственно вид
*тМ - ^) = -<*s- A.2.416)
at
Эту систему необходимо дополнить условиями Na(z9 t = 0) —
- Nb(z, t = 0) = Afo - N^ c?(z = 0, /) - 4@, S(z9 t = 0) = 0.
Такая система уравнений описывает распространение очень корот-
коротких импульсов (Тр s 1 не) в лазерах высокой мощности, используемых
в экспериментах по инерциональному удержанию плазмы.
1.2.3. Соотношение Крамерса — Кронига и монохроматические волны
Аналитические свойства функции хш определяются принципом причин-
причинности, согласно которому вектор поляризации среды Р в некоторый
2g 1 Основные свойства распространения электромагнитных волн
момент времени определяется значениями электрического поля только
в предшествующие моменты времени. Действительно, равенство ну-
нулю х@ ПРИ отрицательных значениях аргумента позволяет написать
выражение -
Х« = e-i(atX(t)dL A.2.42)
Jo
Отсюда сразу следует, что если рассматривать со как комплексную пе-
переменную (w = w' + /w"), то в случае пассивной среды величина хш
является аналитической функцией в нижней полуплоскости комплекс-
комплексного со (со" < 0), а в случае активной среды (т. е. в лазерах) она ана-
аналитическая в верхней полуплоскости. На этом основывается вывод
(см., например, [8]) так называемых соотношений Крамерса — Кро-
нига между вещественной и мнимой частями xw = хы - Ь&
'1 A-2-43а)
где Р обозначает главное значение интеграла в смысле Коши.
Если диспергирующая среда находится в тепловом равновесии, то
можно показать (см. § 82 в книге [1]), что величина хы всегда положи-
положительна при со > 0, отрицательна при со < 0 и равна нулю при со = 0.
Последнее утверждение следует непосредственно из равенства
Хш = *-«, A.2.44)
которое сразу следует из A.2.42). Это, разумеется, не противоречит
тому, что х'ш может принимать очень небольшие значения в некото-
некотором интервале частот; при этом о диэлектриках говорят, что они про-
прозрачны в области частот, в которой \\ш\ < 'xw'«
Используя тот факт, что хш является нечетной функцией частоты
со [следствие соотношения A.2,44)], выражение A.2.43а) можно пере-
переписать в виде
2
со'2 - а2
2 Лоо-ie т'у",
е-*п71 In-ip О) — СО
0.2.45)
где е > 0. Справедливость этого выражения нетрудно проверить, за-
заменяя контур интегрирования @, со — е) kj (со + г, оо), по которому
вычисляется главное значение интеграла в смысле Коши, на луч
@ - /г, оо - is) и отдельно вычисляя интеграл по полуокружности
радиусом е с центром в со. Для того чтобы между старым и новым
1.2. Распространение излучения в среде с частотной дисперсией
29
контурами интегрирования не оказалось полюсов функции х"ш» величи-
величина е должна быть достаточно мала.
Дифференцируя выражение A.2.45) по со, получаем
/ a 2Mdc°f ~ '2T^- A2-46)
В случае когда производная tf xl /dw пренебрежимо мала, правая часть
выражения A.2.46) является положительной величиной, если \" > О
(пассивная среда), т. е. х'« представляет собой монотонно возрастаю-
возрастающую функцию частоты w так же, как и вещественная часть пш показате-
показателя преломления \пш = A -I- xJVl] и диэлектрическая проницаемость
еш = еоA + x'j. Вспоминая определение, данное в разд. 1.2, можно сде-
сделать заключение, что спектральная область, в которой потери пос-
постоянны, является областью нормальной дисперсии.
Проведенное выше рассмотрение одинаково справедливо при высо-
высоких частотах как для диэлектриков, так и для металлов. При очень
высоких частотах не существует даже количественного различия меж-
между этими двумя случаями, причем диэлектрическая проницаемость,
как правило, имеет вид (см., например, § 84 в книге [1])
Ne2
meoco'
A.2.47)
где <ар — плазменная частота, е и т — соответственно заряд и масса
электрона, а N — полное число электронов в единице объема среды
(рис. 1.5).
Рис. 1.5. Спектральная зависимость вещест-
вещественной (л) и мнимой (к) частей комплексно-
комплексного показателя преломления п — п — Ы ме-
металла, диэлектрическая проницаемость ко-
которого описывается зависимостью, анало-
аналогичной A.2.47), причем плазменная частота
*wp= /HM?VmeoI/2 = 4,7 эВ. Для учета за-
затухания, определяемого коэффициентом у,
член со2 заменен на со(ы — iy), причем в дан-
данном случае у = 4 • Юыр. Кривая R(w)
изображает коэффициент отражения, вы-
вычисленный по формулам Френеля в гл. 3.
(Согласно работе [10а].)
с
5
4
3
2
7
2 4
H
V
\
6 8 10
-
R
I
-
-60
40
20
0
30 1. Основные свойства распространения электромагнитных волн
1.2.3.а. Диэлектрическая восприимчивость в резонансной
двухуровневой среде
Представленные в разд. 1.2 выражения позволяют нам, основываясь
на простой, но реалистической модели, точно вычислить веществен-
вещественную и мнимую части диэлектрической восприимчивости хш вблизи ре-
резонансной частоты со0. Заметим, что, используя соотношения A.2.24)
и A.2.25), а также определение аналитического сигнала (см. разд. 1.8),
можно записать
E(z91) s ei(O0t~ikzS{z, t), P(z, t) s - iei<O0t' ikzS(z, t). A.2.48)
Тогда из выражения A.2.29) следует, что
P(z,t) = -i Г*dt'?(z,t',t - t')E(z9t - t')dt'; A.2.49)
J
здесь использовано определение
f (z,t\t - О = -Bced/o)o)e~yabtt+lfiH'x(z,*',t - t'). A.2.50)
Рассмотрим случай, когда интенсивность сигнала достаточно ма-
мала, так что распределение населенностей в двухуровневой атомной си-
системе не меняется, т. е. среда находится практически в термодинами-
термодинамическом равновесий. При этом имеем x(z, t', t - t') « x(z, t', -oo),
так что, применяя преобразование Фурье к обеим частям выражения
A.2.49), получаем
PJz)= -ИМ*), A.2.51)
где ?ы — фурье-образ функции %(z, tr, 0). В то же время из определе-
определения функции х(О [см. A.2.2)] следует, что при со > 0
PJz) = SoxJM). A.2.52)
Таким образом, сравнивая два последних выражения, имеем
*<*= -(i/e0K«> A.2.53)
или
z9t9-ao)tf. A.2.54)
2icn2d C+a
=
wo Jo
Учитывая соотношение A.2.32), окончательно находим
55)
ы еот2а)<
где
i f + °° J^1 -dco\ A.2.
J _л yab -h i(co - со')
= Ntt0-Nb0, A.2.56)
1.2. Распространение излучения в среде с частотной дисперсией
31
т — масса электрона, AN0 — инверсия населенностей в единице объе-
объема, а / — так называемая сила осциллятора. Если g =
ANoe2 (o-coo „ ,AJV2 yab
X" __ .
,. A.2.57)
Xo> 2e0mco0 y2ab + (со - aHJ' Лй> J 2e0m<o0 y2b + (со - co0J'
Используя параметр расстройки f = (со — оз0)/уаЬ и лоренцеву функ-
функцию -/= A + f2), выражения A.2.57) можно переписать в виде
у' у"
—77~ — —ъ^» —^~" — -*¦ > ll.Z.Jo)
у" У
АСОО Л й>0
Соответствующие этим выражениям кривые показаны на рис. 1.6.
Для более подробного ознакомления с этими вопросами мы отсылаем
читателя к разд. 7.19.
Рис. 1.6. Вещественная х„ и мнимая xj части
восприимчивости в зависимости от параметра
расстройки $ для лоренцевой линии.
1.2.3.6. Распространение монохроматической волны в однородной
среде
В области оптических частот уравнения Максвелла, достаточные для
описания распространения волны на одной частоте в диспергирующей
среде в отсутствие внешних зарядов и токов, записываются в виде
V х Е(г) = -tojioH(r), A.2.59а)
V х Н(г) = 1(О8пП2(со)Щг). A.2.596)
Если предположить, что пространственная зависимость векторов
Е(г) и Н(г) имеет вид ехр(- /к • г), где к = к' - /к" может быть
комплексной величиной, то из уравнений A.2.59) можно сразу полу-
получить следующие соотношения:
к х Е = co/ioH, к х Н = -со80п2(со)Е. A.2.60)
Умножая скалярно эти уравнения на к, имеем
к-Е = к.Н = 0, A.2.61)
32 1. Основные свойства распространения электромагнитных волн
а исключая из тех же уравнений Е (или Н) и используя векторное тож-
тождество (А.2), приходим к соотношению
к2 =± к'2 - к - 2ik' • k" = jfcgnj.
Если к' и к" параллельны друг другу (скажем, они направлены
вдоль оси z), то пространственная зависимость векторов Е и Н имеет
вид плоской затухающей волны (поверхности постоянного поля орто-
ортогональны направлению распространения, вдоль которого волна зату-
затухает); иными словами,
E,Hoceikzk 2; A.2.62)
здесь
W - ik" = kon = ko(n - 1к\ A.2.63)
где величина к называется коэффициентом поглощения (или экстинк-
ции).
1.3. СОСТОЯНИЕ ПОЛЯРИЗАЦИИ ЭЛЕКТРОМАГНИТНОГО
ПОЛЯ
В этом разделе мы напомним некоторые основные понятия, касающи-
касающиеся поляризации электромагнитного излучения. Исторически первые
интуитивные предположения о возможности описать особые свойства
света, связанные с их состоянием поляризации, принадлежат Ньюто-
Ньютону. Этой задачей Ньютон занялся в связи с интерпретацией результа-
результатов экспериментов, выполненных Гюйгенсом. Гюйгенс наблюдал, что
при падении луча света на двоякопреломляющий кристалл (см. разд.
1.4) возникают два луча {обыкновенный и необыкновенный), которые
при прохождении второго двоякопреломляющего кристалла ведут се- *
бя иначе, чем контрольный луч, не испытавший предварительного
двойного лучепреломления.
Рассмотрим прежде всего распространение света в однородной сре-
среде, когда вектор электромагнитной волны лежит в плоскости, перпен-
перпендикулярной направлению распространения волны z. Пусть электричес-
электрический вектор Е = (Ех, Еу9 0) соответствует волне, которая в комплекс-
комплексном представлении описывается следующим аналитическим выраже-
выражением:
t(x9y9z9t) = al(x,y)eitat-ikzx + a2(x,y)ei(Ot-ikzy . A.3.1)
Тогда в каждой фиксированной точке пространства конец вектора Е
описывает замкнутую кривую. Исключая параметр / из выражений
для компонент^ иЕу, нетрудно показать, что эта кривая является
1.3. Состояние поляризации электромагнитного поля 33
эллипсом, уравнение которого имеет вид
Е2 Е2 ЕЕ
2 - _v«v = sin <5,* A.3.2)
Wl\~ \a2\ lalfl2l
здесь мы положили ах = ItfJexpO'fi,), a2 = \a2\&vp(ib^) и b = b2 - bx.
Если Itfjl = \a2\ и 5 = d= ir/2, то эллипс вырождается в окружность
(круговая поляризация), а если b = 0, ± тг, он вырождается в прямую
линию (линейная поляризация).
Это рассмотрение можно обобщить [11] на произвольное поле
Е = (Ex,Ey9Ez), которое в комплексном представлении имеет вид
где р(г) и q(r) — два вещественных вектора. При любом фиксирован-
фиксированном г конец вектора Е описывает замкнутую кривую [вследствие пери-
периодичности Е(О1, которая лежит в плоскости, определяемой векторами
р(г) и q(r). Поскольку в любой такой плоскости всегда можно вы-
выбрать пару взаимно ортогональных векторов а и b таким образом,
чтобы выполнялось соотношение
р + iq = (а + гЪ)е~1\ A.3.4)
где г) — вещественная величина, определяемая выражением
tg 2у/= 2Р q2, A.3.5)
выражение A.3.3) можно переписать в виде
Ё(м) = aexp(fcot — irj) + ihexp(icot — irj).
Отсюда сразу видно, что, если векторы а и b направлены соответст-
соответственно вдоль х и у, мы приходим к зависимости поля, аналогичной
A.3.1). Следовательно, в рассматриваемой нами плоскости конец век-
вектора Е описывает эллипс, уравнение которого следует из A.3.2) при
6 =
1.3.1. Параметры Стокса и матрица Джонса
Как мы уже показали, вектор электрического поля монохроматичес-
монохроматической волны в данной точке г изменяется во времени, оставаясь парал-
параллельным одной плоскости. Если выбрать в качестве этой плоскости
плоскость ху, то общее выражение для поля имеет вид
E(t) = axcos(cot + Фх)х + aycos(cot + Фу)у, A.3.7)
34
1. Основные свойства распространения электромагнитных волн
или, в комплексном представлении,
ауешу,
^ л A.3.8)
где ах = ахехрAФх), ay = я^ехрОФ^). Конец вектора Е описывает эл-
эллипс, главная ось которого образует угол ф с осьюх:
ф = -arctg
A.3.9)
где Ь = Фх — Фу. Кроме того, отношение b /а меньшей полуоси эл-
эллипса к большей можно выразить как функцию вспомогательного
угла х» так что b /a = tgx, где
. / 2ахау . \
arcsinl —J—~2 sin о I.
A.3.10)
Таким образом, поле в точке г однозначно характеризуется плос-
плоскостью, в которой лежит его эллипс поляризации, а также углами х и
фу определенными выше, и своей интенсивностью. Столь же полно
поле можно характеризовать так называемыми параметрами Стокса
sojsus2 и5з> определяемыми следующим образом:
so = al
+ ai
A.3.11)
st = al — a] — s0cos2xcos2^,
s2 = 2ахаусо8^ = s0 cos 2x sin 2i/r = 2Re(axa*),
s3 = 2axaysin5 = sosin2x = 2 Im(axa*).
Очевидно, что параметр s0 пропорционален интенсивности, asl9s2y
s 3.можно интерпретировать [И] как де!Йартовы координаты точки на
сфере радиусом s0 (рис. 1.7), известной как сфера Пуанкаре. Долгота и
широта этой точки равны соответственно 2ф и 2\. В частности, север-
северней полюс соответствует левой, южный полюс — правой круговой
Рис. 1.7. Сфера Пуанкаре.
1.3. Состояние поляризации электромагнитного поля 35
поляризации, в то время как линейно-поляризованным полям соот-
соответствуют точки на экваторе.
Для квазимонохроматических волн, когда амплитуды ах и ау> а
также фаза являются зависящими от времени случайными величина-
величинами, параметры Стокса нужно заменить на средние по ансамблю (см.
разд. 1.8):
so = <<>2ЛФ + <а2у(ф,
A.3.12)
s2 = 2(ax(t)ay(t)cosS(t)>9
s3 = 2<ax(t)ay(t)sm5(t)}.
В частности, если электромагнитное поле представляет собой су-
суперпозицию нескольких статистически независимых волн, параметры
Стокса суммарного поля равны сумме параметров Стокса всех состав-
составляющих волн. Исходя из этого, ван де Хюлст сформулировал следую-
следующий принцип оптической эквивалентности [12]: «Ни один прибор не
может отличить две различные некогерентные суммы простых волн,
если результирующие пучки имеют одинаковые параметры Стокса».
Волна, для которой s 0 ^ 0, но Sj =s2 = s3= 0» называется непо-
ляризованной. Данную квазимонохроматическую волну можно одно-
однозначно разложить на сумму поляризованной и неполяризованной со-
составляющих. Действительно, используя аддитивность параметров
Стокса, можно записать
Sq == Sq t" Sq , St- = Si \1 == 1,-Z, Jj, A.3.13)
где верхний индекс A) обозначает вклад поляризованной волны, а
B) — неполяризованной. Поскольку [см. выражение A.3.11)]
(s^2)J = E(j2)J + s^2)J + (sf*J, можно определить степень поляриза-
поляризации т как отношение интенсивности sff поляризованной компоненты
к полной интенсивности s0 волны:
т = [(s^J + (sB2)J + (sC2)J]1/2/50. A.3.14)
В некоторых случаях необходимо знать, как изменяются парамет-
параметры Стокса оптического пучка, распространяющегося в данной среде
или рассеянного на каком-либо препятствии. При этом результирую-
результирующее поле Ёх,, Ёу., заданное в некоторых выбранных декартовых коор-
координатах х' уу', связано с начальным полем Ех, Еу следующим линей-
линейным преобразованием [13]:
Аъх '~X| A.3.15)
36
1. Основные свойства распространения электромагнитных волн
Здесь А — так называемая матрица Джонса. Если определить вещест-
вещественные величины
Mt = АъА?~ Sv; = Sik = Re(y4.-i4?)
O,fe = 1,2,3,4), A.3.16)
Dik=-Dki=-Im(^A*)
то с помощью простых преобразований можно показать, что
= F
s2
A.3.17)
где
М2 М3 S23 -^23
М4 Мх S41 -D41
2S24 2S3i S2i+ S34 ""^21+ ^34
:i + ^34 ^21 ~ S34
A.3.18)
2D24 2D31 D21+D
Более подробно свойства матрицы F будут рассмотрены в разд. 6.13.
1.3.2. Поляризация затухающих волн
Рассмотрим затухающую волну в виде, в котором мы ее записали в
разд. 1.2. С помощью A.2.61) и с учетом комплексного характера век-
вектора к можно показать, что поле является эллиптически поляризован-
поляризованным. Для доказательства этого рассмотрим поперечную магнитную
(ТМ) волну (см. разд. 3.7), составляющие электрического поля кото-
которой запишутся в виде
Ех(т) = E0cosde Ikr, A.3.19a)
A.3.196)
-Лт
?z(r) = ?osin0e
где в = в' — /0" — комплексный угол между к и единичным векто-
вектором z. При записи этих выражений мы учли, что Е • к = 0, а также
то, что для ТМ-волны Нх = Hz = 0.
Без потери общности можно предположить, что^о = 1, и преце-
бречь несущественным общим фазовым множителем ехр(-/к • г).
Тогда зависимость составляющих электрического поля от времени за-
запишется в виде
Ex(t) = Re(cos веш) = cos в' ch 0" cos ot - sin в' sh в" sin cot A.3.20a)
Ez(t) = Re(sin 9еш) = sin в' ch 0" cos cot+ cos 0' sh в" sin coU A.3.206)
1.4. Распространение волн в анизотропной среде
37
Рис. 1.8. а — поляризационный эллипс, описываемый электрическим вектором неодно-
неоднородной плоской волны, распространяющейся в среде без потерь. Комплексный волно-
волновой вектор к = к' - /к" образует угол в = 0' - /0" с осью*. Оси эллипса пропор-
пропорциональны с ch0' и I sh0'' I. Малая ось образует угол в' с осью z; б — силовые линии
электрического поля в данный момент времени; с течением времени распределение сдви-
сдвигается вдоль направления вектора к'.
Исключая отсюда /, получаем
E2(sin2 0' + sh2fl") + E2(cos2 0' + sh2 0")
-ExEzsm29' = $sh22e". A.3.21)
Следовательно, вектор Ex(t)x + Ey(t)y описывает эллипс, большая
ось которого составляет с осью х угол б', а длины двух осей пропор-
пропорциональны ch0" и Ish0" 1. Таким образом, у ТМ-волны электриче-
электрическое поле эллиптически поляризовано в плоскости xz (рис. 1.8), а маг-
магнитное поле направлено вдоль оси у. При в =0 (распространяющие-
(распространяющиеся волны) эллипс вырождается в прямую линию. Для поперечных
электрических (ТЕ) волн вектор Н оказывается эллиптически поляри-
поляризованным, а вектор Е перпендикулярен плоскости падения.
1.4. РАСПРОСТРАНЕНИЕ ВОЛН В АНИЗОТРОПНОЙ СРЕДЕ
Многие макроскопические среды анизотропны. Поэтому в таких слу-
случаях при решении задачи о распространении волн необходимо выде-
выделить геометрически некоторое направление и обобщить введенные до
сих пор понятия [13]. В частности, заранее очевидно, что с макроско-
макроскопической точки зрения среда не может описываться теперь скалярной
диэлектрической или магнитной проницаемостью (е или yi). Очевид-
Очевидные обобщения материальных соотношений, связывающих Etf и Нш с
D* и Bw [см. соотношение A.2.3)], запишутся в виде
Ki
A.4.1а)
38 1. Основные свойства распространения электромагнитных волн
где e^j и Д^у — элементы тензора второго ранга.
В соотношениях A.4.1), применяемых для описания распростране-
распространения оптического излучения в кристаллах, \i обычно можно считать
скалярной величиной, равной примерно /г0. Это справедливо для боль-
большинства представляющих интерес частот излучения. Таким образом,
среда описывается тензором диэлектрической проницаемости ?w, эле-
элементы которого определяются выражением A.2.16); отсюда следует,
что среда по-разному откликается на приложенное в разных направле-
направлениях поле (вектор D не обязательно параллелен Е). Это в свою оче-
очередь означает, что характеристики распространения волн зависят от
направления распространения и поляризации волны (двойное лучепре-
лучепреломление).
1.4.1. Двойное лучепреломление
Рассмотрим распространение плоских монохроматических волн в про-
прозрачном кристалле (при этом тензор %ш равен вещественному тензору
диэлектрических проницаемостей ej. Предположим, что векторы Е,
D, Н и В пропорциональны общему множителю exp(/atf - /к • г), где
к — вещественный вектор. Тогда уравнения Максвелла A.2.60) прини-
принимают вид
kE H A.4.2а)
кхН= -wD. A.4.26)
Подставляя уравнение A.4.2а) в A.4.26) и используя векторное
тождество (А.2), чтобы вычислить возникающее при этом тройное
векторное произведение, получаем
/x0ftJD = к2Е - (к • Е)к; A.4.3)
здесь мы учли, что произведение к ¦ Е отлично от нуля. Таким обра*
зом, вектор к не перпендикулярен Е. В то же время из уравнений
A.4.2) непосредственно следует, что к ортогонален векторам D и Н.
Это демонстрируется на рис. 1.9, который, в частности, показывает,
что к и вектор Пойнтинга S (см. разд. 1.6), .вообще говоря, не парал-
параллельны друг другу, т. е. поток энергии не обязательно направлен
вдоль нормали к волновому фронту.
Предположим далее, что задан единичный вектор в направлении
распространения пучка S = к/к. При этом можно показать, что си-
системе уравнений A.4.2) удовлетворяют две возможные величины к и,
следовательно, два различных показателя преломления я = к /к0. Для
этого удобно ввести систему декартовых координат, совпадающих с
главными осями (х, у, ?) тензора диэлектрических проницаемостей еш.
1.4. Распространение волн в анизотропной среде
aD
39
Рис. 1.9. Взаимное расположение вектора в за-
задаче о распространении нормальных мод в
анизатропной среде.
При этом соотношение A.4.1а) приобретает диагональную форму
А* = выЕы , A.4.4)
причем величины eai называют главными диэлектрическими проница-
емостями. В этой системе отсчета после подстановки A.4.4) в A.4.3)
нетрудно получить: . Л _.
nl s • Е
-V A.4.5)
Е - "U
Умножая обе части этого уравнения на si и суммируя по /, имеем
3 2 2
nl . -
Отсюда следует уравнение Френеля
+
1
A.4.6)
A.4.7)
Это биквадратное уравнение относительно неизвестной пф §; сле-
следовательно, оно имеет две пары решений ± пх и ± п2. Вырождение
по знаку (±) тривиально и является следствием возможности распро-
распространения волны в противоположных направлениях. Существование
же двух, не равных по модулю, решений означает, что в одном и том
же направлении S могут распространяться две различные плоские во-
волны с разными фазовыми скоростями с /п j ис/л2. Можно показать,
что обе эти волны линейно-поляризованы и их направления поляриза-
поляризации (т. е. направления вектора Е) взаимно перпендикулярны. Таким
образом, для любого направления s в анизотропной среде две плоские
волны (нормальные моды) могут распространяться, «чувствуя» каж-
каждая свой показатель преломления п г или п 2. А
Если отложить из начала координат в направлении t вектора
Пойнтинга плоской волны с волновым вектором A:s отрезок длиной
п ~ \ то получим так называемую лучевую поверхность или волновую
поверхность Френеля. Она дает полную картину распределения луче-
лучевых скоростей tfj 2 = c/zjj 2 во всех направлениях. В общем случае
мы получаем двулистную поверхность — один лист соответствует
*!, а другой 1/л2. Эти два листа пересекаются в двух (одноосный
40 1. Основные свойства распространения электромагнитных волн
кристалл) или четырех (двухосный кристалл) точках, которые опре-
определяют оптические оси кристалла.
Когда мы откладываем на графике величины п~\2 как радиус-
векторы в направлении s из начала координат, то получаем двулист-
двулистную поверхность нормалей. В частности, для одноосного кристалла
один из листов является сферой (соответствует обыкновенной волне),
а другой — овалоидом (поверхность вращения четвертого порядка со-
соответствует необыкновенной волне). Эти две поверхности касаются
друг друга в двух точках, соответствующих оптической оси.
Следует заметить здесь, что реализовать в эксперименте такую си-
ситуацию, когда две волны имеют в кристалле один и тот же вектор к,
довольно сложно. Дело в том, что, попадая в кристалл извне, эти во-
волны преломляются на разный угол (см. гл. XIV в книге [11]).
В любом одноосном кристалле одна из главных диэлектрических
осей совпадает с осью симметрии (вдоль этой оптической оси обычно
направляют ось z). Две же другие оси перпендикулярны ей и произ-
произвольны (обычно используют ех = ех = J2 = еу).
Для решения многих задач по распространению волн удобно обра-
обратиться к геометрическим построениям, использующим эллипсоид по-
показателей преломления (см. гл. XIV в книге [И]), определяемый урав-
уравнением
(х2/п2х) + (у2/п2у) + (z2/n2) = 1. A.4.8)
Здесь пх yz — главные показатели преломления. Эллипсоид показате-
показателей преломления, называемый также оптической индикатрисой^\
можно использовать для определения двух показателей преломления
(п{ип2), связанных с двумя независимыми линейно поляризованными
плоскими волнами, которые могут распространяться вдоль произ-
произвольного направления s в кристалле. Для этого нужно найти эллипс,
образующийся при пересечении плоскости, перпендикулярной s и про-
проходящей через начало координат, с эллипсоидом индексов. Две полу-
полуоси построенного таким образом эллипса равны показателям прелом-
преломления пх и п2 двух нормальных мод. Эти же оси оказываются также
параллельными направлению векторов Dx 2 двух мод. Электрические
поля Е, 2 параллельны нормалям к эллипсоиду показателей
преломления — в точках его пересечения с осями эллипса.
Оказывается, что для одноосного кристалла лишь одно из решений
уравнения Френеля зависит от угла между вектором ? и осью z. При
этом одна из волн (обыкновенная) имеет эффективный показатель
преломления, который не зависит от в и равен пх = п0 = V^/e0. Дру-
Другая же волна (необыкновенная) имеет показатель преломления
!>В книге Борна и Вольфа [11] поверхность, описываемая уравнением A.4.8), назы-
называется эллипсоидом волновых нормалей. — Прим. перев.
1.4. Распространение волн в анизотропной среде
41
Оптическая
ось
Необыкновенный, луч
Обыкновенный луч
Рис. 1.10. Двойное лучепреломление обыкновенного и необыкновенного лучей.
п2 = п2(в), зависящий от 0. Величинап2 изменяется в диапазоне отя0
до Vez/?0 s ne (см. задачу 1.13).
Различие между эффективными показателями преломления для
обыкновенного и необыкновенного лучей имеет одно очевидное
следствие. Падая на поверхность кристалла, эти два луча преломля-
преломляются по-разному (рис. 1.10), чем и оправдывается название «двойное
лучепреломление» рассматриваемого в данном разделе явления.
Следует заметить, что в общем случае вектор Пойнтинга
(Vi) Е х Н составляет некоторый угол с волновым вектором нор-
нормальной моды. Если рассматривать распространение пучка лучей, на-
например гауссова лазерного пучка, то его направление не совпадает с
вектором распространения центральной компоненты плоских волн,
составляющих пучок. СМ. Рытов показал, что пучок лучей распро-
распространяется вдоль направления вектора Пойнтинга, вычисленного для
центральной компоненты волнового пакета плоских волн. Этот ре-
результат довольно легко получить, если представить поле в виде ди-
дифракционного интеграла (см. гл. 4), который можно вычислить с по-
помощью метода стационарной фазы, рассматриваемого в гл. 5.
1.4.1.а. Электрооптический эффект
Если вдоль некоторого направления в кристалле приложить электри-
электрическое поле Е@), то при этом элементы в/у тензора диэлектрических
проницаемостей изменятся. Новые компоненты еи можно выразить
42
1. Основные свойства распространения электромагнитных волн
через прежние с помощью следующих соотношений:
eij = ^ + tijkE™ + ТШЕП°\ A.4.8а)
Здесь tiJk и TiJkl — тензоры третьего и четвертого рангов, которые ха-
характеризуют соответственно линейный электрооптический эффект
(называемый также эффектом Поккельса) и квадратичный электро-
электрооптический эффект (эффект Керра). Эффект Поккельса возможен
лишь в кристаллах, не имеющих центра симметрии (т. е. не симмет-
симметричных относительно инверсии), а эффект Керра наблюдается в
центрально-симметричных кристаллах.
Из соотношения A.4.8а) мы видим, что под действием внешнего
поля Е@) изменяются как главные оси, так и главные диэлектрические
проницаемости кристалла, причем эти изменения зависят от направле-
направления и силы внешнего поля. Следовательно, изменяя к примеру лишь
амплитуду поля &°\ можно управлять параметрами распространения
электромагнитного поля ЕA), падающего на кристалл. По такому при-
принципу построена, например, ячейка Поккельса. Она состоит из распо-
расположенной между взаимно ортогональными поляризаторами кристал-
кристаллической пластинки с проводящими электродами на рабочих поверх-
поверхностях (рис. 1.11). Прикладывая к кристаллу напряжение F, можно
менять на необходимую величину разность фаз Г двух распространяю-
распространяющихся через кристалл лучей.
Рассмотрим, в частности, одноосный кристалл дигидрофосфата
калия (КН2РО4; обычно его называют KDP), вырезанный в форме
пластинки, с двумя поверхностями, перпендикулярными оси симмет-
симметрии четвертого порядка (оптической оси z), и двумя электродами, ко-
которыми служат покрытия из прозрачного оксида металла. Если внеш-
внешнее напряжение отсутствует, то одна из главных осей совпадает с оп-
оптической осью z, а две другие могут быть выбраны произвольно в
плоскости, перпендикулярной оси z. Прикладывая внешнее напряже-
напряжение V, мы снимаем это вырождение, и в то время как одна из глав-
4
Рис. 1.11. Ячейка Поккельса. 1 — по-
поляризатор; 2 — прозрачный элек-
электрод; 3 — кристалл; 4 — поляриза-
поляризатор; 5 — модулирующее напряже-
напряжение.
1.5. Распространение волн в средах с дисперсией 43
ных осей по-прежнему совпадает с осью z, две другие совпадают с
двумя осями симметрии второго порядка кристалла, повернутыми на
угол тг/4 [13]. Соответствующие главные диэлектрические проницае-
проницаемости ех и еу можно выразить через обыкновенный показатель пре-
преломления по, который имеет место в отсутствие напряжения, и ам-
амплитуду внешнего поля ?<0):
eo/fi» = A/"о) + г?@\ A.4.9а)
ео/еу = A/и02) - г?<0), A.4.96)
где г — постоянная, свойственная конкретному кристаллу. Из соотно-
соотношений A.4.9) следует, что эффективные значения показателей прелом-
преломления даются следующими приближенными выражениями (с учетом
того, что выполняется неравенство г?*0) <^ 1):
= "о ~ ?™3oEi0\ п2 = по + irno3?@). A.4.10)
Таким образом, две составляющие линейно поляризованного поля
ЕA\ распространяющегося вдоль оси z на расстояние L (длина крис-
кристалла), приобретают разность фаз Г:
Г = ко(п2 - П1)Ь = n30k0rLEi0) = konlrV, A.4.11)
где V = LE®\
Во многих случаях удобно пользоваться величиной
Кя = Я/2по3г, A.4.12)
которая равна напряжению, приводящему к задержке фазы на тт. При
X = 0,54 мкм в кристалле KDP мы имеем V\ = 7,9 кВ, а в KD*P (во-
(водород замещен на дейтерий) Vv =. 3,4 кВ. Если ^поляризованный ана-
анализатор на входе ориентирован так, что Ех^ = ЕуA\ а на выходе ана-
анализатор повернут на тг/2, то выходная интенсивность равна (без учета
размерного множителя)
W=il^%lT~l)l2^ A-4.13)
Зависимость коэффициента пропускания Т ячейки Поккельса от прило-
приложенного напряжения V дается выражением
Т = /вых/'вх = sin2(r/2) = sin2(nV/2Vn). A.4.14)
15. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ
С ПРОСТРАНСТВЕННОЙ ДИСПЕРСИЕЙ
В разд. 1.2 [см. A.2.1) и A.2.2)] мы привели соотношение между зек-
торами электрической индукции D и напряженности электрического
поля Е. В этом соотношении вектор D в момент времени / определя-
определяется значениями поля Е в момент времени /ив более ранние момен-
моменты времени/' < /. Такая нелокальность во времени неразрывно связа-
44 1. Основные свойства распространения электромагнитных волн
на с нелокальностью в пространстве [в соотношении A.2.2) этой нело-
нелокальностью мы полностью пренебрегли, считая, что Р в точке г зави-
зависит лишь от Е в той же самой точке]. Действительно, если вектор по-
поляризации Р в данный момент времени /ив данной точке г определя-
ся значением вектора Е в той же точке в момент времени / — At, то
за время At возмущение переместится на расстояние vAt (p — харак-
характерная скорость возмущения). Как следствие, на поляризацию Р в
точке г будет оказывать влияние также электрическое поле в момент
времени/ в соседних точках г', таких, что 1г' — rl = vAt. Таким об-
образом, если величина vAt (что представляет собой характерную длину
/ среды, например молекулярный размер, постоянную решетки или де-
баевский радиус экранирования) становится сравнимой с длиной вол-
волны X, то необходимо учитывать пространственную дисперсию. На-
Например, это может оказаться существенным вблизи резонансной ча-
частоты, когда показатель преломлениям может быть очень большим и
длина волны в среде X = Х0/л может соответственно измениться (см.,
например, разд. 1.2.2).
Эти соображения приводят к необходимости замены обычного со-
соотношения между Р и Е [см. A.2.2)] на более общее:
+ оо
Р(г,t) = е0 JjLr' Г df x(t -t',t- (')E(r',П A.5.1)
-оо
Используя пространственно-временное преобразование Фурье [см.
A.1.19)], материальное соотношение A.2.3) между Dq ш и Eq w запи-
запишется в виде
D,.» = eo(l + XqJK» = Ч«Л.«> (Ь5.2)
где q и со — независимые переменные. Как следствие пространствен-
пространственной дисперсии, диэлектрическая проницаемость Fq ш в общем случае
имеет тензорный характер, так что соотношение A.5.2) принимает
вид
Dq.o^^-E^, A.5.3)
где ^ ы — тензор второго ранга. Такой тензорный подход необходим
даже для среды, обычно рассматриваемой как изотропная (в нулевом
приближении по //X). Кроме того, если среда помимо макроскопичес-
макроскопической неоднородности обладает пространственной дисперсией, то ? ш
параметрически зависит от г (в полной аналогии со случаем временной
дисперсии; см. разд. 1.2).
Главные различия между распространением волн в обычной среде
и в среде с пространственной дисперсией могут быть выявлены на
примере решений уравнений Максвелла A.1.1) и A.1.2) в виде плоских
1.5. Распространение волн в средах с дисперсией 45
монохроматических волн. Для случая J = 0 с помощью соотношения
A.1.6) можно получить уравнение
V х (F х Е) + ц0—jD = 0. A.5.4)
Будем искать решения этого уравнения в виде нормальных мод, т. е.
Е'(М) = Е^'»'-*', D'(M) = Вч,пеш-**'\ A.5.5)
Используя соотношение A.5.3) и уравнение A.1.4), записанное для слу-
случая р = 0, получаем
q х (q x Eq,J + fi0co2tq^ • Eq>co= 0 A.5.6)
и
q.?qfft,.Eq>o, = 0. A.5.7)
При этом необходимо сделать различие между двумя возможно-
возможностями: ?q, о, *= 0 и ?q w = 0. В первом случае q ¦ Dq ы = 0 (попереч-
(поперечные волны), и из уравнения A.5.6) [после использования векторного
тождества (А.2)] получаем
D(q,co) = det(/ioco2cqco -f qq — q2\) = 0, A.5.8)
Это соотношение (дисперсионное уравнение) позволяет выразить q
через со (или наоборот) с помощью дисперсионной функции D(q, со). В
частности, в среде, не имеющей пространственной дисперсии, ?q w не
зависит от q и уравнение A.5.8) квадратично по q2. В дальнейшем мы
будем обозначать через k = q(w) значение q, которое удовлетворяет
приведенному дисперсионному уравнению для данного со. В частности,
если положить q = w/TqS, то можно показать, что в случае когда вели-
величина? не зависит от q, уравнение A.5.8) эквивалентно уравнению Фре-
Френеля A.4.7).
Во втором случае ?q ш = 0) из уравнения A.5.6) следует, что
qxEqft) = 0, A.5.9)
т. е. волны являются продольными.
1.5.1. Естественная оптическая активность
Пространственная дисперсия приводит к естественной оптической
активности, а именно к повороту плоскости поляризации линейно-
поляризованного света, распространяющегося через определенную
среду. Можно ожидать, что пространственная дисперсия будет играть
значительную роль только при очень малой длине волны X, которая
сравнима с характерной длиной среды /. (Заметим, что теория, не учи-
учитывающая дисперсии, является нулевым приближением по /А.) Век-
46 1. Основные свойства распространения электромагнитных волн
тор индукции D можно записать в виде следующего разложения:
Уда^Зк, A.5.10)
где для простоты мы опустили нижний индекс а>. В этом уравнении
Щ — тензор диэлектрической проницаемости в пределе q — 0, a yijk —
антисимметричный тензор. Для плоской волны с волновым вектором
q = ко§ имеем VEW = - /&JsEw, так что тензор Т можно переписать
как
Теперь удобно ввести вектор гирации д, определяемый соотноше-
соотношением
koyijkh = е&вк, A.5.12)
где е,-^ — антисимметричный единичный тензор третьего ранга
(тензор Леви — Чивита) (eijk Ф 0 для / Ф j Ф к, eijk = - eJik =
= - eijk = - e^/f ex 23 = 1). В соответствии с этим имеем
A.5.13)
Подставляя это соотношение в A.5.3), приходим к выражению
Ц,,о> = «• ' Е,,ш + ig х Eq>fi), A.5.14)
В частности, для изотропной среды тензор STw диагоналей и
g = gs, т. е. вектор гирации параллелен направлению распростране-
распространения волны. Из соотношения A.5.14) сразу следует, что, поскольку
Dq а - 3 = 0 (поперечные водны), должно выполняться и условие
Eq w ¦ s = 0. Используя его в уравнении A.5.4) и выбирая направле-
направление распространения вдоль осия, получаем следующее решение [1]:
Ex(z9t) = Е0е*'-шсо*х*>
E() Eikz-i(Ot
где к = (Уг)ко(п+ - п_), х = A^)к0(п+ - п_), а п+ и п_ можно по-
получить из уравнения
п± =nl±gn0. A.5.16)
Здесь п 0— показатель преломления изотропной среды, не имеющей
пространственной дисперсии. Говорят, что материалы, у которых
g # 0, обладают естественной оптической активностью.
Из выражений A.5.15) следует, что после прохождения волной рас-
расстояния L в среде отношение Ёу/Ёх = tg(x^ ) по-прежнему является
вещественным, т. е. поле линейно поляризовано, но направление по-
поляризации меняется. Именно это явление открыли в 1811 г. Араго в
кристаллах кварца и в 1815 г. Био в жидкостях (таких, как скипидар и
1.6. Энергетические соотношения 47
водные растворы винной кислоты). В 1810 г. Френель объяснил опти-
оптическую активнсть циркулярным двойным лучепреломлением, т. е. раз-
различием в среде скоростей распространения лево- и правополяризован-
ных по кругу волн. Позднее, в 1848 г. Пастер связал это понятие с
энантиоморфизмом (существованием зеркальных разновидностей мо-
молекул), положив таким образом начало новой области химии, называ-
называемой теперь стереохимией.
1.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
Мгновенный вектор Пойнтинга определяется как
S(M) = E(M)xH(r,t). A.6.1)
Применяя оператор V • к обеим частям этого равенства, исполь-
используя векторное тождество (А.9), а также уравнения Максвелла A.1.1) и
A.1.2), сразу получаем
с д д
Интегрируя обе части этого уравнения по произвольному объему У
и с помощью теоремы Гаусса преобразуя интеграл в левой части к ин-
интегралу по окружающей объем поверхности дУ, получаем
-CbS • ndS = I I I ( J • E + H • jB + E • jv\dV. A.6.3)
dV V
Здесь n — единичный вектор внешней нормали. Используя уравнения
A.1.6) и A.2.1), приходим к следующему интегральному соотноше-
соотношению:
ndS = J 11 (^w0 + J • E + E • ^pW A.6.4)
dV V
где
H. A.6.5)
Уравнение A.6.4) можно интерпретировать как закон сохранения
энергии электромагнитного поля. При этом взятый с обратным зна-
знаком поток вектора Пойнтинга представляет собой полную энергию,
втекающую в объем V за единицу времени; w0 — плотность запасен-
запасенной в вакууме электромагнитной энергии; - J ¦ Е — мощность, пере-
передаваемая от источников полю (при J • Е < 0) [или от поля источни-
источникам (при J • Е > 0)] в единице объема. И наконец, Е • (ЭР/*) — из-
изменение в единице объема за единицу времени внутренней энергии
электрических диполей за счет работы поля.
48 1. Основные свойства распространения электромагнитных волн
1.6.1. Соотношения Пойнтинга для квазимонохроматического пучка
в среде с пространственной дисперсией
В случае когда среда обладает пространственной и частотной диспер-
дисперсией, член Е ¦ (dD/ЗО нельзя интерпретировать как производную по
времени от плотности энергии. Действительно, эта величина по свое-
своему должна определяться локальным мгновенным значением поля. Од-
Однако если рассматривать линейную среду и квазимонохроматический
свет с пространственным распределением, аналогичным плоской вол-
волне, то первые два члена в правой части уравнения A.6.2) можно пре-
преобразовать к сумме двух вкладов, представляющих обратимый и не-
необратимый переход энергии в среду (или из среды). Покажем это на
примере узкого пучка, направленного вдоль волнового вектора к, ко-
который в общем случае является комплексным. Этот узкий пучок мож-
можно записать в виде
Е(м) = Re[*(r, *)**"-*"] = ReE(M), A.6.6)
где о) и к удовлетворяют дисперсионному уравнению A.5.8), а
'4'-'. A.6.7)
Будем считать, что Е,^ + q/ а + ы, существенно отлично от нуля, когда
а/ и вещественный вектор q' достаточно малы (пучок лучей). При
этом электрическую индукцию можно записать в том же виде, что и
A.6.6), а именно
D(r,r) = Ке[0(г,Ое|в*-Л#г] = ReD(r,t), A.6.8)
где
'J .
•^ + q',co + c^'Vr~iqr ' A.6.9)
что эквивалентно выражению
Предположим теперь, что мы провели усреднение по времени (обо-
(обозначим его как <...>,) за период, много больший, чем 27г/со. Тогда
можно написать следующее приближенное выражение (см. разд. 1.8):
1.6. Энергетические соотношения 49
Однако в соответствии с выражениями A.6.8) и A.6.10) мы имеем
A(<U?k j. ^1A.6.12)
s e
так что, используя обозначение Тк ш = e'kiW — ie'\ ш, где обе диады
е'к а и s"k. ш эрмитовы, получаем
i
2
2 д(о : dt
Закон сохранения энергии принимает вид
<J-E>,, A.6.14)
>, =~(a«U!« + ^oW, A-6.15)
S0) = iRe(<?x JT*), A.6.16)
&» =-j\ke'k,a:S&*. A.6.17)
Для рассматриваемого нами волнового пакета вектор Пойнтинга
S@> + SA) должен быть равен произведению плотности энергии < w>,
на групповую скорость, т. е.
A.6.18)
50 1. Основные свойства распространения электромагнитных волн
В частности, для анизотропной среды без пространственной дис-
дисперсии групповая скорость дается следующим выражением:
К }
1.7. РАСПРОСТРАНЕНИЕ ВОЛН В ДВИЖУЩЕЙСЯ СРЕДЕ
Если однородная изотропная среда без дисперсии как целое движется
с постоянной скоростью v = ср относительно системы отсчета F, то
векторы D и В связаны с Е и Н материальными соотношениями
Минковского [15]:
D = ?AE + bxH, B = //AH-bxE, A.7.1)
где А — диада, определяемая как
A = a(l-V) + V, A.7.2)
I — единичная диада, V = vv, а
__ 1-р2 _ ^_Р п2-\ ^
Вместо того чтобы рассматривать реальное электромагнитное по-
поле, описываемое сложными материальными соотношениями A.7.1),
можно ввести фиктивные поля Е' и ЬГ , порожденные источниками р
и J' в области пространства, характеризуемой координатой г'. Связь
с реальными физическими величинами устанавливается следующими
соотношениями [16]:
Т Т
г = А1/2 • г', р(г) = -p'(r'), J(') = - А12 • J'(r'),
а а
Е(г) = ТА'112 • Е;(г'), Н(г) = ГА/2 • Н'(г'), A.7.4)
где Т— линейный оператор expFv • r'd/dt)9 переводящий всякую
функцию/(г', О в/(г', / + Ьу - г'). При а > 0 пространство, описы-
описываемое координатой г', соответствует физическому пространству, у
которого перпендикулярные вектору v координаты сжаты в l/y/а раз.
При а < 0 координаты пространства [ г') комплексные, поэтому тре-
требуется определенная осторожность при рассмотрении соответствую-
соответствующих полей Е' иН'. Можно показать [16], что эти поля удовлетворя-
удовлетворяют следующим уравнениям:
F.E' = -(p' + b-J'),
еа
Р-Н' = 0,
1.7. Распространение волн в движущейся среде 51
FKH--J-+ .i«'. 0Л-5)
ot
РхЕ'= -/ш|-Н'.
ot
Следовательно, поля Е' иН' можно рассматривать как решения урав-
уравнений Максвелла в неподвижной среде, характеризуемой диэлектри-
диэлектрической и магнитной проницаемостями еа и fia соответственно, в то
время как плотность заряда оказывается равной р' + b • J'.
В отсутствие источников уравнения A.7.5) имеют решения в виде
набора плоских волн
Е'(ж'91) = Е'оёш-*''г\ A.7.6)
причем Ео • к' = 0 и к' = waVeju, так что истинное поле Е запишется
в виде
Е(г) = А/2.Е^"Л"Г, A.7.7)
где
k = A~ll2-k'-cobv. A.7.8)
В частности, если в — угол между к и v, то величина вектора к да-
дается выражением [17]
+ у2(п2 - 1)A - /?2cos2fl)]1/2 - py2(n2 - l)cosfl
0
l-y2(n2-l)/?2cos20
О)
= V A.7.9)
где у2 = A — /З2). В случае /3 < 1 выражение A.7.9). принимает про-
простой вид
к = ко[п - (п2 - l)j?cos0]. A.7.10)
Строго говоря, это выражение справедливо лишь в том случае,
когда среда движется с одной и той же скоростью во всем про-
пространстве. Однако это требование можно существенно ослабить и
ограничиться лишь условием постоянства скорости на размерах по-
порядка нескольких длин волн [18], и, следовательно, выражение A.7.10)
можно также использовать для вращающейся среды. В самом общем
случае фазовая скорость уф в движущейся и неподвижной среде разли-
различается на величину, пропорциональную проекции v на направление
распространения, т. е.
Это известная формула Френеля, экспериментально проверенная Фи-
зо. Множитель 1 — \/п2 называют френелевским коэффициентом ув-
увлечения.
52 1. Основные свойства распространения электромагнитных волн
1.8. СВОЙСТВА КОГЕРЕНТНОСТИ ЭЛЕКТРОМАГНИТНОГО
ПОЛЯ
Развитая в предыдущих разделах теория была основана главным об-
образом на детерминистическом описании электомагнитного поля, т. е.
предполагалось, что поле имеет вполне определенное значение даже
при конечной ширине частотной полосы излучения (что можно припи-
приписать амплитудной или фазовой модуляции). На самом же деле всегда
есть некоторая статистическая неопределенность, связанная с любым
электромагнитным полем (это касается даже излучения лучших стаби-
стабилизированных по амплитуде одномодовых лазеров). Эту неопределен-
неопределенность можно учесть, пользуясь методами статистической теории, т. е.
определив подходящим образом средние (по времени или ансамблю)
от ненаблюдаемых в эксперименте величин. Именно эта программа —
определение средних и нахождение их связи с наблюдаемыми — и яв-
является содержанием теории когерентности электромагнитного излу-
излучения. Почти всюду в этой книге мы будем иметь дело с детермини-
детерминированными полями (за исключением задач, связанных с некогерент-
некогерентным изображением; см. разд. 4.15). Однако читателя необходимо оз-
ознакомить с некоторыми основными элементами теории когерентно-
когерентности, чтобы понять, каким образом по одной определенной реализации
поля можно вычислить его значимые статистические средние.
Прежде всего введем понятие аналитического сигнала f(t) для дан-
данной зависящей от времени величины/(/) [11]. Это понятие оказывает-
оказывается весьма полезным для рассматриваемой теории. Если вещественный
сигнал f(t) допускает фурье-разложение
A.8.1)
то аналитический сигнал/(/) определяется соотношением
A.8.2)
Jo
откуда сразу следует, что/(О = Re/(O- Если сигнал монохроматиче-
монохроматический, т. е. ДО = /Ocos(o>/ + Ф), то имеем выражение
(<o>0), A.8.3)
которое называют также комплексным представлением.
Практическая важность аналитического сигнала связана со спосо-
способом измерения мгновенной интенсивности оптического сигнала
быстрым детектором. Действительно, рассмотрим реальный детек-
детектор, имеющий время отклика Td, малое по сравнению с обратной ши-
1.8. Свойства когерентности электромагнитного поля 53
риной полосы поля до), но большое по отношению к обратной средней
частоте о>0. В этом случае отклик оказывается пропорциональным сле-
следующей величине [19]:
1 Г* + ГЛ2
*d Jt-Tdl2
E\t')dt\ A.8.4)
Tdl2
причем выполнение условий
l/(o0«Td«l/dco A.8.5)
оправдывает то, что записанный выше интеграл называют мгновен-
мгновенной интенсивностью. Запишем теперь выражение
E(t) = -Re( ei(O0t \ ЕУ^-^ЧоЛ = Re[elW<?@], A.8.6)
п \ Jo /
где, как можно предполагать, величина <f(f) = e~iu3<fE(t) изменяется
медленно на временном интервале Td. Тогда получаем, что с доста-
достаточной степенью точности мгновенная интенсивность равна квадрату
модуля аналитического сигнала:
Щ = |?(t)|2 = W2. A.8.7)
Точно так же можно показать, что поток мгновенного вектора
Пойнтинга (см. разд. 1.6), усредненный по нескольким периодам элек-
электромагнитного поля, удобнее всего выразить как поток вещественной
части комплексного вектора Пойнтинга
S = iExH*. A.8.8)
Модуль вектора Пойнтинга одиночной плоской волны можно
определить как
|5| = ilS7Aior/a|E|a = i»ri/. П.8.9)
Таким образом, в этом случае модуль вектора Пойнтинга^пропоршю-
нален мгновенной интенсивности / (о сравнении величин ISI и Е • с*
см., например, работу [19]). Коэффициент пропорциональности в
A.8.9) равен произведению обратного волнового сопротивления ваку-
вакуума f0 и показателя преломления п. Вообще говоря, мгновенная ин-
интенсивность оптического сигнала имеет флуктуационный характер,
т. е. /(О является отдельной реализацией статистического ансамбля.
В соответствии с этим полное описание требует в принципе определе-
определения иерархии средних по ансамблю следующего вида:
</(ф,</2(ф,...,</я@> A.8.10)
и
</(r)/(O>,...,</('i) -/(*„)>. A.8.11)
В стационарных случаях усреднение но ансамблю эквивалентно усред-
усреднению по интервалу времени, который больше по сравнению с 1/ба>.
54
1. Основные свойства распространения электромагнитных волн
Заметим, что до появления лазеров (в начале 1960-х годов) об опреде-
определении средних и высших порядков особенно не задумывались, так как
не существовало источников излучения, время когерентности кото-
которых Тс = Ък/Ььз было бы больше, чем время отклика имеющихся де-
детекторов Td. Действительно, как видно из выражения A.8.4), если
Td > Гс, то для всех практических применений интенсивность /(/) ста-
становится детерминированной величиной, а все средние факторизуются,
т. е. их можно представить в виде произведения средних низшего по-
порядка.
Если же теперь рассмотреть более общие случаи, когда происходит
интерференция двух или более пучков (например, в экспериментах Юн-
Юнга и Майкельсона; рис. 1.12), то естественно определить корреляцион-
корреляционную функцию [20], известную также как функция взаимной когерент-
когерентности (см. разд. 4.15):
СAЛ)(г,г; г',0 = <?*(М)?(г',О>. A-8.12)
Эта функция так же, как и средние более высокого порядка, а именно
G"'m(fi,t1,...,rn,fB,...,rB+m,(n+m) _
= <?*(г1,г1)--Е*(гл,Ги)?(ги+1,Ги+1)-Ё(жя+я91я+т)>,
определяет вклад интерференционного члена в сигнал, регистрируе-
регистрируемый детектором.
С аналитической точки зрения введенное выше статистическое опи-
описание полностью характеризует стохастическое электромагнитное по-
поле. На практике средние электромагнитного поля порядка п + т (вы-
(выше второго) связаны либо с интерференционными экспериментами
высшего порядка (как в звездном интерферометре Хэнбери — Брауна
и Твисса), либо с экспериментами по счету фотонов [21].
Экран
Полупрозрачное
зеркало
М,
Экран
а 6
Рис. 1.12. Схемы интерферометров Юнга (а) и Майкельсона (б). М, и М2 — зеркала.
Задачи 55
ЗАДАЧИ
Раздел 1.1.
1. Покажите, что для однородной стационарной среды фурье-образы потенциалов
А ы, Ф w удовлетворяют соотношению
D21 - ЧЧ - К
2. Покажите, что пространственно-временное преобразование Фурье скалярного по-
потенциала Ф в кулоновской калибровке [см. выражение A.1.20а)] связано cpq w соотно-
соотношением
фч,*> = Pq.co/q • sq,a • q.
3. Покажите, что в анизотропной среде функция Сс(г, ш) [см. выражение A.1.22)]
записывается в виде
Gc(r,co) = So/^x2 + ё2у2 + 83z2I/2,
где Cj 2 3 — компоненты диэлектрического тензора относительно главных осей
(см. разд. 1.4).
4. Покажите, что пространственно-временное преобразование Фурье функции Грина
в диадном представлении в анизотропной среде имеет вид
Гч,ю = (eo2/i<>eq,a, + ЧЧ - Я2)'1 = A'/D(q,co),
где компоненты тензора А' являются алгебраическими дополнениями тензора
А = о?цо?ц ш + qq - ^1, a Z)(q, w) = detA [см. выражение A.5.9)].
5. Покажите, что для однородной и изотропной среды функция Грина в диадном
представлении дается выражением
где G(r) — скалярная функция Грина.
6. Используя интегральное фурье-представление скалярной функции Грина из предыду-
предыдущей задачи, покажите, что
+ 00
— оо
7. Используя асимптотическое выражение для величины Г
Г(г) ~ A - ff)G(r),
покажите, что поле в дальней от источников области равно
+ 00
Е(г) - - to/ioG(r) ПТA - пп) • J(r')e"*-'' dV,
-00
где й — единичный вектор, параллельный вектору г - г'.
56 1. Основные свойства распространения электромагнитных волн
8. Рассмотрим временное преобразование Фурье (Ej, И{ и Е2, Н2) полей, излучае-
излучаемых двумя монохроматическими источниками
Jx(r, t) = S^e*, J2(r, t) = J2(r)eitM.
Используя уравнения Максвелла и векторное тождество (А.9), докажите следующее со-
соотношение, справедливое для анизотропной среды:
(E2-J, -E1-J2)dK=(tt)(E1 хН2-Е2
ico lll
Покажите, что в частном случае, когда еу = eJj и объем ограничен металлической по-
поверхностью, имеет место следующее соотношение:
V V
которое называют теоремой взаимности.
Раздел 1.2.
9. Покажите, что п{оз) и к(ш) связаны следующими соотношениями Крамерса —
Кронига:
2 Л f °° со'к(сог) , , , ч 2со п f °° л(со') -1 , ,
П(СО) — 1 = —Р —75 ТИСУ , KiCO) = Р —75 ЧUCO .
я Jo со — со2 п Jo со — со2
Для этого используйте свойство л *(ы) = л(-ы) и преобразуйте контуры интегрирова-
интегрирования к положительным осям. Кроме того, запишите диэлектрическую проницаемость в
виде
еи(со) = ео[ди - ioij(co)l{coE0)']
и выведите следующие соотношения Крамерса — Кронига:
>+0° 1тст„ 1 , .
со — со са
1 2 Г
— Reao= Р
со п Jo
1 2 Г+о° Red. J
a; J n Jo со2 —со2
10. Вычислите восприимчивость xw ансамбля двухуровневых систем, используя фор-
формулы A.2.57) и считая, что частоты перехода w0 + 5 имеют гауссово распределение:
-if
— оо tab
11. Покажите, что при а > 7а^, снимая часть х'' рассмотренной в предыдущей за-
задаче восприимчивости записывается в виде
Задачи 57
Затем, воспользовавшись соотношениями Крамерса — Кронига из задачи 8, найди-
и покажите, что х' можно выразить через интеграл Даусона [см. выражение G.19.9)].
Раздел 1.4.
12. Нормальные моды анизотропной среды характеризуются показателем прелом-
преломления п, определяемым выражением
q = (o)/c)n(co,q)s9
где ы и q связаны дисперсионным уравнением A.5.8). Покажите, что п удовлетворяет
уравнению Френеля
effieySiSj -w2fi0(ViSjfin - WijSiSj) + deU4te> = 0.
13. Покажите, что в одноосном кристалле показатель преломления необыкновенной
волны дается выражением
пё(в) = (cos2 в/nl + sin2 0/nJr1'2
(см. определение одноосного кристалла в задаче 15).
14. Если величины п откладывать из начала координат в направлении s, то полу-
полученная двулистная поверхность называется поверхностью волновых векторов. Один ее
лист соответствует л v второй —п~2. Используя второе уравнение из задачи 12, докажи-
докажите, что пересечение поверхности волновых векторов с плоскостью, перпендикулярной
главной (направленной, скажем, вдоль оси z), определяется точками
й, = (?2/воI/2, Яг = [e*y?o(?*S* + V?)] Ш.
15. Те направления в кристаллах, для которых пх = л2, называются оптическими
осями. Используя второе уравнение из задачи 12, докажите, что в кристаллах может
быть не более двух таких направлений (двухосные кристаллы). Если же они совпада-
совпадают, то кристаллы называют одноосными. В частности, для случая ez > е > ех дока-
докажите, что две оптические оси лежат в плоскости xz (рис. 1.13) и образуют с осью* угол
у такой, что
Рис. 1.13. Поверхность волновых векторов
для двухосного кристалла.
Оптическая
ось
58 1. Основные свойства распространения электромагнитных волн
16. Докажите, что для одноосного кристалла поверхность волновых векторов со-
состоит из сферы (обыкновенный луч) и эллипсоида (необыкновенный луч). Приле > по
сфера лежит внутри эллипсоида и кристалл называется положительным одноосным.
Еслияо > яе, то кристалл называют отрицательным одноосным.
Раздел 1.5.
17. Исследуйте распространение нормальных мод через плазму, находящуюся в
магнитном поле, тензор диэлектрических приницаемостей которой записывается следу-
следующим образом
__ ~ _ f col(co — iv) }
[ СО[((О - IVJ - COfij
а остальные его компоненты равны нулю. Здесь ш = (е/т)В0— гирочастота элек-
электронов, Во — внешнее поле, приложенное вдоль осиг, а а>р и р — соответственно плаз-
плазменная частота и частота столкновений.
18. Рассмотрите распространение волн через полярный кристалл, характеризую-
характеризующийся скалярной диэлектрической проницаемостью
где еь(со) — вклад от электронной поляризуемости атомов, и^ — поперечная резонанс-
резонансная частота ансамбля осцилляторов, О2 = AfeVtm^e^w)], N — плотность ионов, да-
дающих вклад в поляризуемость, т^ — характеристическая масса, а постоянная у учи-
учитывает затухание. Частота, при которой е'(ш) = 0, называется продольной резонанс-
резонансной частотой; частоты a>L и о^ связаны с es = е@) и е ^ = е(со) соотношением
Лиддана — Сакса — Теллера а?ъ/ьJт = fig/e^.
19. Рассмотрите гиротропную среду, диэлектрический тензор которой
?i ig О
-ig et О
О 0 е3
Найдите нормальные моды и покажите, что те из них, которые распространяются
вдоль оси z, имеют круговую поляризацию.
20. Волновой пакет распространяется с групповой скоростью V = дш/дкх, до)/дку9
dco/dkz. Покажите, что vg можно записать через дисперсионную функцию D(q, w) с по-
помощью соотношения
г=
В частности, покажите, что для одноосного кристалла без дисперсии групповая ско-
Литература 59
рость необыкновенного луча равна
v, = (в&роУЧЦг :qqI/2e • q
и образует с вектором q угол 8:
_ (ne2-ng)sinflcos0
&n2tcos2e + n2osin20'
где $ — угол, образуемый вектором q и оптической осью.
21. Покажите, что в случае анизотропного кристалла дисперсионная функция
?>(q, о?) имеет вид
D(q9o) = (otnoSySiSjiq2 - kln\){q2 - fegnf),
где Я, и п2 — показатели преломления для нормальных мод, распространяющихся
вдоль направления S.
ЛИТЕРАТУРА
1. Ландау Л, Д., Лифшиц Е. М. Электродинамика сплошных сред. — 2-е изд., пе-
рераб. и доп. — М.: Наука, 1982.
2. Van Kranendonk /., Sipe 1 К, Prog. Opt., 15, 245—350 A977).
3. Mandel L.t Wolf E. Opt. Commun., 8, 95 A973).
4. Owyoung A., Ph.D. Thesis, California Inst. Technol., Pasadena, 1971 (Clearing House
Fed. Sci. lech. Inf. Rep. AFOSR-TR-71-3132).
5. Shen Y. R., Principles of Nonlinear Optics, Wiley, New York, 1984.
6. Sargent M, Scully M. O.t Lamb W. E.t Laser Physics, Addison-Wesley, Reading, Mas-
Massachusetts, 1974.
7. Hopf E A., Scully M. O., Phys. Rev., 179, 399 A969).
8. Yariv A.t Quantum Electronics, 2nd ed., Wiley, New York, 1975. [Имеется перевод:
Ярив А. Квантовая электроника. — М.: Сов. радио, 1980.]
9. Frantz L. M., Nodvik J. S., J. Appl. Phys., 34, 2346 A963).
10. McCall 5. L., Hahn E. L., Phys. Rev., 183, 457 A969).
10a. Wooten E, Optical Properties of Solids, Academic Press, New York, 1972.
11. Born M, Wolf E., Principles of Optics, Pergamon, Oxford, 1970. [Имеется перевод:
Борн М., Вольф Э. Основы оптики. — М.: Наука, 1973.]
12. van de Hulst H. С, Light Scattering by Small Particles, Wiley, New York, 1957. [Име-
[Имеется перевод: Ван де Хюлст. Рассеяние света малыми частицами. — М.: ИЛ,
1961.]
13. Yariv A.t Yen Я, Optical Waves in Crystals, Wiley, New York, 1983. [Имеется пере-
перевод: Ярив А., Юх П. Оптические волны в кристаллах. М.: Мир, 1987.]
14. Агранович В, М, Гинзбург Я Л. Кристаллооптика с учетом пространственной
дисперсии и теория экситонов. — 2-е изд., перераб. и доп. — М.: Наука, 1979.
15. Sommerfeld A.t Electrodynamics, Academic Press, New York, 1952. [Имеется
перевод: Зоммерфелъд А. Электродинамика. — М.: ИЛ, 1958.]
16. Solimeno S., Alta Freq., 43, 1005 A974); J. Math. Phys., 16, 218 A975).
17. Papas C. #., Theory of Electromagnetic Wave Propagation, McGraw-Hill, New York,
1965.
18. Censor D. IEEE Trans. Microwave Theory Tech., MTT-16, 565 A968).
19. Marathay A. S., Elements of Optical Coherence Theory, Wiley, New York, 1982.
20. Mandel L., Wolf E, Rev. Mod. Phys., 37, 231 A965).
60 Библиография
21. Pefina J., Quantum Statistics of Linear and Nonlinear Optical Phenomena, Reidel
PubL, Dordrecht, Netherlands, 1984. [Имеется перевод: Перина Я. Квантовая ста-
статистика линейных и нелинейных оптических явлений. — М.: Мир, 1987.]
БИБЛИОГРАФИЯ
Akhmanov 5. A.t Khokhlov R. К, Problems of Nonlinear Optics, Gordon and Breach,
New York, 1972. См. также: Ахманов С. А., Хохлов Р В. Проблемы нелинейной
оптики. — М.: ВИНИТИ, 1964.
Allen L., Eberly J. #., Optical Resonances and Two-Level Atoms, Wiley, New York,
1975. [Имеется перевод: Аллен Л., Эберди Дж. Оптический резонанс и двух-
двухуровневые атомы. — М.: Мир, 1978.)
Bloembergen N., Nonlinear Optics, Benjamin-Cummings, Menlo Park, California,
1965. [Имеется первод: Бломберген Н. Нелинейная оптика. — М.: Мир, 1966.]
Brewer R. G., Phys. Today, 30, 50 A977).
Chow W. W.t Gea-Banacloche J., Pedrotti L. A/., Sanders V. R, Schleich W.t
Scully M. a, Rev. Mod. Phys., 57, 61 A985).
Clarke D.t Grainger J. E, Polarised Light and Optical Measurement, Pergamon, Ox-
Oxford, 1971.
Feynman R. P., Vernon E L., Hellwarth R. W., J. Appl. Phys., 28, 49 A957).
Haken #., Light, v. 1 and 2. North-Holland PubL, Amsterdam, 1981 and 1985.
Hange P S., Muller R. H.t Smith С G., Surf. Sci., 96, 81 A980).
Hecht E., Zajac A., Optics, Addison-Wesley, Reading, Massachusetts, 1969.
Loudon R., The quantum Theory of Light, Oxford Univ. Press (Clarendon), London,
New York, 1978. [Имеется перевод: Лоудон Р., Квантовая теория света. — М.:
Мир, 1976.].
Мо Т. С, /. Math. Phys., 11, 2589 A970).
Nussenzveig H. M., Causality and Dispersion Relations, Academic Press, New York,
1972.
Pekar S. I., Cristal Optics and Additional Light Waves, Benjamin-Cummings, Menlo
Park, California, 1983.
Quantum Electronics (eds. H. Rabin, С L. lang), v. 1, Parts A and B, Academic
Press, New York, 1975.
Ramachandran G. N., Ramasehan S. — In: Handbuch der Physik (ed. S. Flugge),
v. 25, Part 1, Springer-Verlag, Berlin, 1961, p. 1—217.
Toraldo di Francia G.t Electromagnetic Waves, Wiley (Interscience), New York, 1955.
Van Bladel /., Proc. IEEE, 64, 301 A976). [Имеется перевод: ван Бладелъ Дж. —
ТИИЭР, 1972, т. 64, № 3, с. 14.]
Whitham G. В, Linear and Nonlinear Waves, Wiley, New York, 1973.
ГЛАВА 2
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
2.1. ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ
ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
В среде с однородным показателем преломления л(а>) решениями урав-
уравнений Максвелла являются плоские волны, которые в комплексном
представлении имеют вид Е(г, t) = Еоехр(-/?оя§ • г + tot). В случае
когда п зависит от г, таких решений в виде плоских волн не существу-
существует (всюду, кроме специальных случаев, мы не будем явно указывать
зависимость л от w). Рассмотрим возможность описания поля в пер-
первом приближении «локальными» плоскими волнами вида
Е(г, г) = Е0(г) ехр[ - ik0S(r) + icot], B.1.1)
где Е^г) — медленно меняющаяся, a S(r) — произвольная функция ко-
координаты г. Для однородной среды Eq = const, S = ns • г. Подстав-
Подставляя выражение B.1.1) в уравнения Максвелла, записанные для случая
J = 0, р = О, В = д0Н, и используя векторные тождества (А.7) и
(А.8), сразу же получаем
FS х Ео - СоНо + (i/fco) V х Ео = 0, B.1.2а)
FS х Но + (п2/Со)Ео + (i/fco) F х Но = 0, B.1.26)
FS • Но + (i/k0) F • Но = 0, B.1.2в)
FS • Ео + V/(kon2) V • (и2Е0) = 0, B.1.2г)
где f0 = 0*(/еоI/2 ( ~ 371 Ом) — волновое сопротивление вакуума
(вакуумный импеданс). В дальнейшем импеданс произвольной среды с
показателем преломления п мы будем обозначать как f = fo//z.
Если k0 -» оо, то в уравнениях B.1.2) членами, в которые входит
1/?0, можно пренебречь, выбирая как Eq, так и S не зависящими от к0.
Умножая затем векторно обе части уравнения B.1.2а) на VS и исполь-
используя уравнения B.1.26) и B.1.2г), а также тождество (А.2), имеем
FS х (FS х Ео) + п2Е0 = VS(FS. Ео) - E0(FSJ
= In2 - (FSJ]E0 = 0. B.1.3)
62 Гл. 2. Геометрическая оптика
Функция 5(г), называемая эйконалом, должна быть выбрана таким
образом, чтобы удовлетворять уравнению эйконала
(FSJ = *2(r). B.1.4)
В уравнениях B.1.2) при конечных значениях с*> пренебречь a priori
членами с l/k0 нельзя, поскольку мы не можем заранее знать погреш-
погрешность, связанную с таким приближением при выборе поля в виде
B.1.1). Обратимся поэтому к более строгому представлению поля в
виде асимптотического ряда; этому вопросу мы и посвятим следую-
следующий раздел.
2.2. АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ СКАЛЯРНОГО
ВОЛНОВОГО УРАВНЕНИЯ
Будем искать такое приближенное решение волнового уравнения для
произвольной компоненты электрического поля в комплексном пред-
представлении (м), которое локально удовлетворяет соотношению, спра-
справедливому для плоских волн:
u{x + dT)~A{r)e-*-dt. B.2.1)
Это соотношение означает, что при произвольном смещении dx фа-
фаза поля изменяется на величину - k(r) • rfr, где k(r) — локальный вол-
волновой вектор, зависящий от координаты г. При этом решение имеет
вид обобщенной плоской волны, направление и скорость которой из-
изменяются по мере распространения, а комплексная амплитуда
А(г) = |м(г)|е<*(г) B.2.2)
слабо меняется на расстоянии порядка длины волны. Символ ~ мы
будем использовать для обозначения асимптотического равенства:
lim [м(г + Лг) - Л(г)*-*-*] - 0, B.2.3)
так что функцию и можно заменить ее асимптотическим представле-
представлением лишь при к0 — оо.
Наиболее общее асимптотическое решение для поля можно пред-
представить как суперпозицию всевозможных частных решений вида
B.2.1):
и(г + Aг)~%Ап(г)е-1к»'<\ B.2.4)
п
Такое суммирование описывает случай, когда через данную точку г
проходят различные волны, возникающие при их отражении, прелом-
2.2. Асимптот, решение скалярного волнового уравнения 63
лении или дифракции на поверхностях разрыва и интерференции с ис-
исходной волной.
Применимость разложения B.2.1) ограничена малой окрестностью
точки г. Размер такой окрестности зависит от самой точки г, а в неко-
некоторых зонах (каустиках) он может обратиться в нуль. Очевидно, что
при этом понятие локальных плоских волн и, в частности, выражение
B.2.1) теряют смысл. Другим предельным случаем является идеаль-
идеальная плоская волна, которая в любой точке пространства описывается
выражением B.2.1), причем знак асимптотического равенства заменя-
заменяется в нем на точное равенство.
Для более строгого обоснования интуитивных предположений,
приводящих к представлению B.2.1), рассмотрим асимптотический
ряд Лунеберга — Клейна [1, 2]:
И(г)~*-™?-^> B.2.5)
в котором знак ~ теперь означает, что для любого целого N
ы(г) = в—•» f -Щ, + o(fc Л B.2.6)
где o(JcqN) — символ Ландау, обозначающий любую функцию, стре-
стремящуюся к нулю быстрее чем k^N, в то время как
k(r) = k0VS. B.2.7)
Асимптотический ряд B.2.5) называют также представлением гео-
геометрической оптики, поскольку эйконал 5(г) (введенный Бернсом в
1895 г.) приводит к интуитивному понятию о луче (см. разд. 2.4). По
сравнению с традиционной геометрической оптикой формула B.2.5)
дает более полное описание распространения электромагнитных волн.
Мы покажем это в разд. 2.7 на конкретном примере, связанном с вве-
введением комплексного эйконала.
Для того чтобы найти S(r) и коэффициенты Ат, подставим разло-
разложение B.2.6) в волновое уравнение [A.1.12)]. При этом мы получим
выражение N
где
Q0(r) = (VSJ - n2(r), B.2.86)
= (V2S + 2VS • F)A0, B.2.8b)
= (V2S + 2VS - V)Am., + V4,_2 (m = 2,3,4,...). B.2.8r)
64 Гл. 2. Геометрическая оптика
Уравнение B.2.8а) справедливо при любых N, только если
Qm(r) = O (m = 0,1,2,...), B.2.9)
откуда и следует искомая система уравнений для 5(г) и Ат.
Пример: разложение функции Ханкеля ЩК Смысл асимптотиче-
асимптотического разложения можно пояснить на конкретном примере. Рассмот-
Рассмотрим поле, излучаемое в вакууме линейным током. Для этого случая
известно точное решение:
мосЯ<о2)(/сор), B.2.10)
где р — расстояние от источника, а Н$> — функция Ханкеля второго
рода нулевого порядка, асимптотическое разложение которой записы-
записывается в виде [4]
^^\ B.2.11)
Чтобы улучшить точность асимптотического представления поля,
функцию Щр можно разложить в асимптотический ряд, в котором
главный член совпадает с правой частью выражения B.2.11). Члены
высшего порядка можно найти, используя B.2.9). При этом мы полу-
получим следующее разложение:
где
@,ю) = [Bm)!/Bmm!)]2/22wmL B.2.13)
Таким образом, этот результат, как и следовало ожидать, совпадает с
известным асимптотическим разложением функции Ханкеля.
Если ряд B.2.5) сходится при больших к0, то он представляет со-
собой разложение в ряд Тейлора по волновому числу и является точным
решением уравнения A.1.12), так что использование асимптотического
ряда не дает ничего нового. Однако в большинстве случаев асимпто-
асимптотические ряды расходятся, причем они имеют следующие свойства:
1) при ограничении ряда я-м членом ошибка оказывается не больше
(л + 1)-го члена;
2) с увеличением номера члены ряда сначала убывают, а затем возрас-
возрастают;
3) для данного к0 существует такой член ряда, суммирование до кото-
которого позволяет получить наилучшее приближение.
В соответствии с этим, в то время как бесконечное число членов ря-
ряда может привести к расходимости поля и, конечная частичная сумма
может дать хорошее приближение. Поскольку ошибка имеет порядок
2.3. Уравнение эйконала 65
величины первого из отброшенных слагаемых, наилучшую точность
дает сумма, полученная обрезанием ряда при таком значении N, при
котором последующий член является минимальным. Удивительная
особенность этих разложений состоит в их почти неожиданной приме-
применимости даже для не очень больших к0.
Прежде чем двигаться дальше, заметим, что приведенное выше
асимптотическое разложение поля B.2.5) неоднозначно. Некоторые
авторы считают более удобным разложение
и = е-а*нг)9 B.2.14)
где
Ф(т) ~ S(t) + ? (-*7с0Г ~Ч(г). B.2.15)
л = 0
Определив основные понятия геометрической оптики, в следующих
разделах мы используем их для описания распространения света в раз-
различных физических системах.
2.3. УРАВНЕНИЕ ЭЙКОНАЛА
Нетрудно показать, что S и Ат можно получить, последовательно ис-
используя уравнения B.2.9). В частности, соотношение бо(г) = 0, кото-
которое в декартовых координатах имеет вид
(dS/dxJ + (dS/дуJ + (dS/dzJ = n2(r), B.3.1)
называется уравнением эйконала или уравнением Гамильтона — Яко-
би. Поверхности, на которых эйконал 5 является постоянным, назы-
называют волновыми фронтами. Если эйконал S задан на произвольной
поверхности Е, то его значения на близкой поверхности Е' можно по-
получить, используя соотношение (рис. 2.1)
dS/дх = [п2(г) - (dS/daJY/29 B.3.2)
где д/дт и д/да — соответственно нормальная и тангенциальная по
отношению к Е производные (разумеется, dS/da = 0, если Е является
волновым фронтом). Таким образом, если S (а следовательно, и ее
производная dS/da) заданы на некоторой поверхности Е, то можно
вычислить (с точностью до знака) и изменение S при переходе к Е\
Следовательно, для решения уравнения B.3.1) достаточно знать значе-
значения функции S на некоторой поверхности и направление ее возраста-
возрастания.
Рассмотрим среду без дисперсии (показатель преломления не зави-
зависит от ы) и определим функцию Ф(г, /):
Ф(г,г) = ЗД-сГ. B.3.3)
66
Гл. 2. Геометрическая оптика
Рис. 2.1. Сетка точек, используе-
используемая для интегрирования уравне-
уравнения эйконала методом конечных
разностей.
Из B.3.1) следует, что Ф является решением уравнения
(РФJ - (п2(т)/с2)(дФ/д1J = 0.
B.3.4)
Если вспомнить, что характеристическое уравнение дифференци-
дифференциального уравнения в частных производных второго порядка [5] полу-
получается при замене вторых производных произведением соответствую-
соответствующих первых производных, то сразу видно, что уравнение B.3.4) явля-
является характеристическим для зависящего от времени волнового урав-
уравнения
V2u(r, t) - (п2(г)/с2)(д2и(т, t)/dt2) = 0. B.3.5)
Поскольку функция Ф постоянна на поверхностях разрыва поля м(г, /),
с помощью Ф(г, t) можно изучать эволюцию фронтов разрыва (напри-
(например, тех, на которых поле резко обрывается до нуля). Если Ф = 0 на
некотором фронте разрыва, то положение этого фронта в момент
времени t равно [см. B.3.3)] S(r) = ct.
Приведенные выше рассуждения дают физическую интерпретацию
понятия эйконала и показывают, какую роль он играет в соответству-
соответствующих расчетах. Теперь полезно определить условие, при выполнении
которого некоторое семейство поверхностей
F(r,c) = 0 B.3.6)
представляет собой множество волновых фронтов для данного рас-
распределения показателя преломления п(г). Здесь с — непрерывный па-
параметр, каждое значение которого связано с определенной поверхнос-
поверхностью. Таким образом, дифференцируя B.3.6), получаем следующее
уравнение:
VF*dr + (dF/dc)dc = 0, B.3.7)
2.4. Уравнение для лучей
67
где V обозначает градиент по переменным jc, y9 z. Для малого смеще-
смещения rfr, перпендикулярного поверхности, проходящей через точку г
(т. е. rfri VF), с помощью уравнения B.3.2) получаем
Ar = (VF/\VF\)ldS/n(r)l B.3.8)
Подставляя дифференциал B.3.8) в уравнение B.3.7), можно напи-
написать
dS/dc = -n(r)(dF/dc)/\VF\. B.3.9)
Таким образом, поскольку S зависит только от с, выражение в
правой части этого уравнения также должно быть функцией только
величины с. Иными словами, уравнение B.3.6) описывает семейство
волновых фронтов только в том случае, когда правая часть выраже-
выражения B.3.9) сохраняется постоянной на каждой поверхности этого се-
семейства.
2.4. УРАВНЕНИЕ ДЛЯ ЛУЧЕЙ
Рассмотрим эйконал S(r), представляющий собой однозначную функ-
функцию координаты, и определим единичный вектор (рис. 2.2)
s(r) = PS/|FS| = FS/n(r), B.4.1)
который перпендикулярен волновому фронту и указывает направление
распространения. Определим лучи как траектории r(s), касательные к
Луч Jl^^^ Цг)
Начало
криволинейной
координаты s
а 6
Рис. 2.2. а — семейство волновых фронтов; б — криволинейная координата 5 и направ-
направление S вдоль некоторой траектории (луча), перпендикулярной семейству волновых
фронтов.
68 Гл. 2. Геометрическая оптика
s(r) в каждой точке г. В случае когда S — неоднозначная функция,
пространство заполняется множеством лучевых семейств. Если s —
криволинейная абсцисса вдоль луча, то можно написать следующее
соотношение:
n(r) dr/ds = n(r)s(r) =VS = k/fc0 B.4.2)
[см. выражение B.2.7)], и, дифференцируя обе части по s9 мы имеем
F)VS <2A3>
Однако из уравнения B.3.1) с учетом векторных тождеств (А. 11) и
(А. 14) следует, что
2n(r) Vn = V{VS • PS) = 2(VS . V) VS, B.4.4)
Подставляя B.4.4) в B.4.3), окончательно получаем
ds|_ ds_\ ds \ds ) п(т)
*[<]-»¦
B.4.5)
или, в эквивалентном виде,
[s(r) • F][n(r)s(r)] = Vn^ B.4.6)
Полученное уравнение называют векторным уравнением для лучей.
Частный случай анизотропной среды (одноосный кристалл) рассмот-
рассмотрен в работе [6] и разд. 2.14.1. Интересно, что при переходе к новой
переменной
- Г* ds'
~J ФУ
уравнение для лучей можно переписать в виде
d2r/dT2 = V{W\ B.4.8)
Таким образом, отсюда следует, что лучи формально эквивалентны
траекториям частицы единичной массы, движущейся в поле с потен-
потенциалом V = -п2/2.
2.4.1. Теорема Малюса — Дюпина
Выполнение равенства B.4.5) является необходимым условием орто-
ортогональности пучка лучей к семейству волновых фронтов, однако оно
не всегда означает, что существует эйконал. Из B.4.2) и (А. 14) следу-
следует, что эйконал существует, только если
V х [и(г)з(г)] = 0. B.4.9)
2.4. Уравнение для лучей 69
В этом случае пучок лучей называют нормальной конгруэнцией, и ее
свойства можно описать с помощью уравнения эйконала.
Докажем теперь, что уравнение B.4.9) справедливо всюду, если
только оно выполняется в одной точке. Действительно, равенство ну-
нулю ротора вектора пй в некоторой точке означает, что диада V(/?s) —
симметричная. Покажем, что и все производные от V(/*s) симметрич-
симметричны. Действительно, используя уравнение B.4.6), можно получить сле-
следующие соотношения:
i*2) = V[(aiS • V)*S] = \У(пй)]2 + (пй - V)[V(/*S)j B.4.10)
и в более общем виде
(пй ¦ vnv(Azs)] = (пй • vr-4w(in2)] - (*s • vr - 4V(ais)]2.
B.4.11)
Видно, что в правой части соотношения B.4.11) первая диада сим-
симметрична; симметрична также и вторая диада, если только симмет-
симметричны производные от V(«s) до (т - 1)-го порядка включительно.
При этом симметрична и левая часть соотношения B.4.1). Таким об-
образом, используя метод индукции, мы показали, что все производные
от V(nu) симметричны в рассматриваемой точке. Это означает, что
V(/is) симметрична вдоль всего луча (если п является аналитической
функцией координаты г) и всюду выполняется равенство
V х (пй) = 0.
Можно показать, что если соотношение B.4.9) справедливо в
единственной точке, то оно выполняется и вдоль всего луча даже в
том случае, когда показатель преломления имеет разрывы на грани-
границах отражения или преломления. Этот результат известен как теоре-
теорема Малюса — Дюпина (см. книгу [11] в гл. 1). Интуитивно этот вы-
вывод можно понять, если представить себе лучи как предельные траек-
траектории при плавном переходе от среды с непрерывно изменяющимся
распределением л (г) к среде с резким разрывом показателя преломле-
преломления. Поскольку равенство V х (пй) = 0 выполняется для всех лучей в
области с регулярным распределением показателя преломления, это
равенство должно оставаться справедливым и при достижении грани-
границы разрыва.
2.4.2. Кривизна и закручивание лучей
Геометрически луч удобно описывать с помощью трех ортогональных
единичных векторов S, n и b = S х п, направленных соответственно
70
Гл. 2. Геометрическая оптика
Касательная
плоскость
Рис. 2.3. Тангенциальный, нормальный и
бинормальный единичные векторы и каса-
касательная плоскость, связанная с пространст-
пространственной кривой.
тангенциально у нормально и бинормально к траектории r(s) (рис. 2.3).
С помощью этих обозначений для произвольной кривой можно запи-
записать уравнения Френе [7]:
(d/ds)% = A/psK, B.4.12a)
(d/ds)& = -S/p + Ь/f,
{d/ds)b = -n/f,
B.4.126)
B.4.12b)
где р и f — соответственно радиус кривизны и закручивание кривой.
Закручивание является мерой отличия реальной кривой от плоской. Из
уравнений B.4.5) и B.4.12а) имеем
Vn = {d/ds)(ns) = (dn/ds)s + nK, B.14.13)
Отсюда следует, что лучи располагаются в касательной плоскости,
содержащей векторы S и V/*. Из уравнений B.4.12а) и B.4.13) следует
также, что кривизна К = 1/р связана с показателем преломления со-
соотношением
К = п • V(lnw). B.4.14)
Это означает, что луч изгибается таким образом, чтобы вектор Vn
указывал в сторону центра кривизны (рис. 2.4). В частности, рассмот-
рассмотрим падение луча на преломляющую поверхность. Луч будет откло-
2.5. Транспортное уравнение для AQ 71
Рис. 2.4. Искривление лучей за счет градиента показателя преломления.
няться «вверх» или «вниз» от своего первоначального направления,
если соответственно ц = п/п' < 1 или \i > 1, где п' — показатель
преломления преломляющей среды.
2.4.3. Построение луча
Простейшая вычислительная схема для построения луча [8] непо-
непосредственно основана на соотношении s = dx/ds и уравнении B.4.12а).
Действительно,
r(Sl) = ф0) + s(so)As + (l/2!)K(so)(AsJ + • • •; B.4.15)
здесь As = 5, — s0 — конечная разность. При дифференциировании
имеем
8E,) = U(SQ) + КE0)А5 + ... . B.4.16)
Далее вычисления проводятся следующим образом. Для данной
начальной точки г0 и нормали к лучу п($0) с помощью соотношения
B.4.14) вычисляют начальный вектор кривизны K(s0). Таким образом,
если известен вектор 3(s0), то с помощью выражений B.4.15) и B.4.16)
можно вычислить г($,) и 8E,) с любой заданной степенью точности.
Затем, используя B.4.14), мы получаем новый вектор КE,), причем
пE,) определяется на касательной плоскости, содержащей единичные
векторы sE0) и 6E,); после этого процесс экстраполяции продолжается.
2.5. ТРАНСПОРТНОЕ УРАВНЕНИЕ ДЛЯ Ао
Рассмотрим теперь более детально эволюцию амплитуды поля Ао.
Умножая уравнение B.2.9) (при т = 1) на Ао, получаем транспор-
транспортное уравнение
A20V2S + 2А0 VS • FA0 = 0, B.5.1)
72 Гл. 2. Геометрическая оптика
0 ^ J Рис. 2.5. Геометрическое представление трубки лучей.
которое с помощью векторного соотношения (А.7) и соотношения
B.4.2) можно переписать в виде
V - (А\п&) = 0.. B.5.2)
Рассматривая величину А\п% как аналог вектора Пойнтинга для
скалярного поля >10(г)ехр[—ik0S(t)]f уравнение B.5.2) можно интерпре-
интерпретировать как закон сохранения потока энергии. Если же, применяя те-
теорему Гаусса к малому объему, создаваемому лучами, близкими к
траектории r(s) (рис. 2.5), переписать B.5.2) в интегральной форме, то
можно получить закон изменения A0(s) вдоль произвольного луча:
[n(s )da(s I1/2
где d(j(s0) и do(s) представляют собой сечения трубки лучей в точках s0
и s.
Заметим, что с помощью B.4.1) уравнение B.5.1) можно перепи-
переписать в виде
Решение этого уравнения записывается следующим образом:
с \ Cs V2S I
A0(s) = A0(s0)exp< -- ——ds'y B.5.5)
Таким образом, выражение B.5.3) можно переписать в виде
n(so)da(so) (A0(s) V Г Cs V2S .1 „ - ~
—/ \л / ч = \ а < ч =ехр - -—-ds' I B.5.6)
n(s)da(s) \A0(s0)J [ JSon(s) J
Следовательно, в случае когда da — 0, мы имеем V2S — - оо. Этот
факт непосредственно связан с понятием каустики (см. разд. 2.10.16)
2.6. Транспортные уравнения для А„
73
Каустика
Поверхность Земли
f—О
v2s-
Волновые Волновые
фронты фронты
Рис. 2.6. а — отражение радиоволн, образующих каустику в F-слое ионосферы [слева
показан профиль показателя преломления, уменьшающегося в области ионосферной
плазмы в соответствии с выражением A.2.47)]; б — конгруэнция падающих лучей; в —
конгруэнция отраженных лучей; на каустике падающий и отраженный волновые фрон-
фронты образуют точки возврата.
как геометрического места точек, в котором лапласиан эйконала рас-
расходится (рис. 2.6).
В соответствии с полученными выше результатами амплитуда по-
поля вдоль луча зависит от того, как изменяется da или, что эквивалент-
эквивалентно, V2S. Таким образом, знания траектории отдельного луча еще не
достаточно для того, чтобы можно было вычислить амплитуду Ао;
для этого необходимо найти все лучи, расположенные вблизи этой
траектории.
2.6. ТРАНСПОРТНЫЕ УРАВНЕНИЯ ДЛЯ Ат
Рассмотрим теперь поведение коэффициентов Am(s) при т > 0. Для
этого удобно определить новые величины А', связанные с А соотно-
соотношениями
AJi) =
B-бл)
74 Гл. 2. Геометрическая оптика
При этом, используя соотношение VS • V = nd/ds, уравнение B.2.9)
можно переписать в виде
Отсюда следует транспортное уравнение
Интегрируя его вдоль луча и используя выражения B.5.5) и B.6.1), по-
получаем
Это выражение определяет изменение величины Ат вдоль произволь-
произвольного луча через амплитуды Ао и Am_v
Если 50 = 0 и Ат@) = 0. то
Л«00 = -хЛ(«) л Л/,, ds\ B.6.5)
Это означает, что с ростом т становится существенным вклад членов
высшего порядка, как если бы они возникали из-за «многократного
рассеяния», связанного с изменением амплитуды Ат на волновых
фронтах (рис. 2.7). Фактически V2Am s V2/lw, где V2 = V2 + d2/ds2.
Подводя итог предыдущим вычислениям, удобно ввести оператор
L= -A0(s) 2а1^Ш)Л$' B*6'6)
таким образом, чтобы выражение B.6.5) можно было записать в виде
/4 is) — LA (s\ = d*A (s) C2, 6 7)
Наконец, с помощью выражений B.6.7) и B.2.5), последнее из ко-
которых записывается в виде u(s) - ,4(s)exp[-/A:0S(s)], получаем
A(s) = iLA(s)/k0 + A0(s), B.6.8)
откуда, используя определение оператора ? B.6.6), имеем
2.6. Транспортные уравнения для А
75
Вклад от Vt A1
Вклад от
Исходный
волновой
фронт
Рис. 2.7. Генерация членов высшего порядка.
Дифференцируя обе части этого выражения, приходим к равенству
d A(s) -i V2A(s)
dsA0{s) k0 2A0{s)n(s)'
B.6.10)
2.6.1. Параболическое волновое уравнение Фока — Леонтовича
В тех случаях когда распространяющуюся в вакууме (п = 1) волну
можно приближенно описать идеальной конгруэнцией параллельных
лучей, из выражения B.5.3) следует, что Ао не зависит от 5, т.е. урав-
уравнение B.6.10) можно записать в виде
(d/dz)A(r) = (- i/2*o) V2A(r). B.6.11)
Здесь мы приняли соглашение о том, что общее направление лучей
совпадает с осью z. Если пренебречь вкладом продольных составляю-
составляющих в V2, то в этом приближении уравнение B.6.11) совпадает с пара-
параболическим волновым уравнением Фока — Леонтовича
(д/дг)А(т) = (- i/2k0) V? Л(г), B.6.12)
Таким образом, распространение электромагнитного поля можно рас-
рассматривать как необратимый диффузионный процесс, аналогичный
термодиффузии или квантовомеханической эволюции волновой функ-
функции.
Доказательство того факта, что асимптотические решения уравне-
уравнений B.6.12) и B.6.11) совпадают вплоть до членов порядка к^29 мы
оставляем в качестве задачи (см. задачу 2.5).
76 Гл. 2. Геометрическая оптика
2.7. ЗАТУХАЮЩИЕ ВОЛНЫ И КОМПЛЕКСНЫЕ ЭЙКОНАЛЫ
В предыдущих разделах мы неявно предполагали, что связанная с
(действительными) лучами функция S является вещественной. Однако
для описания полей, амплитуда которых существенно меняется даже
на расстояниях порядка X, мы по-прежнему можем опираться на фор-
формализм геометрической оптики. Для этого нужно ввести комплексный
эйконал. Рассмотрим прежде всего простой случай плоской затухаю-
затухающей волны, распространяющейся в свободном пространстве (рис. 2.8):
и ос e~ik'T-k"'r = e-ikoS(r\ B.7.1)
где к'2 - А: = к2 и к' ¦ к" = 0.
Основываясь на этом примере, Фелсен [3] предложил искать в об-
общем случае комплексные решения уравнения эйконала B.3.1) в виде
S(r) = Я(г) - i/(r) , B.7.2)
где R(x) и /(г) удовлетворяют уравнению
(VRJ - (VIJ = В2 - а2 = и2(г), B.7.3)
причем 4R ¦ V/ = 0 (взаимно-ортогональные поверхности равных
фаз и равных амплитуд). Волны, описываемые комплексными эйко-
эйконалами, называют обычно однородными волнами. Аналогично, если
ввести величину
A0(r) = ewiT)-iv(T\ B.1 А)
то транспортное уравнение B.5.1) приводит к следующей паре уравне-
уравнений:
iV2K + VR-Vw-FI-Vv = 09 iV2/ + VR . Fv + VI • Vw = 0. B.7.5)
Рассмотрим теперь две конгруэнции лучей, которые перпендику-
перпендикулярны поверхностям R(r) = const и /(г) = const. В первом случае тра-
траектории конгруэнции, нормальной фазовым фронтам (поверхностям
равной фазы), называются фазовыми траекториями. На них величи-
величина / постоянна. Во втором случае траектории семейства (траектории
Рис. 2.8. Плоская затухающая волна. Заштрихованная
область соответствует экспоненциально затухающему
распределению амплитуды.
2.7. Затухающие волны и комплексные эйконалы
77
затухания или контуры равной фазы), нормального поверхностям
равной амплитуды /(г) = const, лежат на фазовых фронтах. Анало-
Аналогично тому, как было получено уравнение B.4.5), можно вывести
уравнения траекторий
(d/ds)(ps) = Fft (d/dtM) = Р* B.7.6)
где ds и dt — элементы длины соответственно на фазовой траектории
и на траектории затухания (рис. 2.9). Единичные векторы s и t опре-
определяют соответствующие направления. Из уравнений B.7.6) следует,
что параметры а и /3 формально можно рассматривать как показате-
показатели преломления.
Используя дифференциальные соотношения VI? ¦ V = Pd/ds и
V/ • V = <xd/dt9 транспортные уравнения B.7.5) можно переписать в
виде
\V • (Ps) + P(dw/ds) - a(dv/dt) = О,
\V • (af) + p(dv/ds) + a(dw/dt) = 0. BЛЛ)
Повторяя вывод соотношения B.4.14), можно получить две кри-
кривизны Ks и Kt\
Ks = f • V(lnP) = (i/P)(dp/dt), Kt = s • F(lna) = (l/a)(<fa/<fe). B.7.8)
Из представленного выше рассмотрения следует, что выбор соот-
соответствующего комплексного эйконала позволяет обобщить асимпто-
асимптотический ряд Лунеберга — Клейна на поля, не описываемые вещест-
вещественной функцией 5.
Фазовые
траектории
Фазовые
фронты
Рис. 2.9. Геометрическое представление взаимно ортогональных фазовых фронтов (/? =
= const) и фазовых траекторий (/= const).
78
Гл. 2. Геометрическая оптика
2.7.1. Двумерные затухающие поля
Простые примеры затухающих волн можно получить, рассматривая
двумерные поля. Если задать семейство фазовых траекторий, то ор-
ортогональные траектории затухания определяются однозначно. Ис-
Используя соответствующие ортогональные криволинейные координаты
ц и v для обозначения двух семейств, имеем R = R(ja) и / = /(у). При
этом уравнение B.7.3) запишется в виде
(dR/d»J(l/h2u) - (dl/dvJ(l/h2) - л2(/1, v), B.7.9)
где hv и Л^ — масштабные множители выбранных координат.
Рассмотрим интересный частный случай, когда фазовыми траекто-
траекториями являются конфокальные гиперболы, а траекториями затуха-
затухания — эллипсы (рис. 2.10). Здесь удобно выбрать эллиптические коор-
координаты, определяемые равенствами
х = b sin v ch \i
@^у^2я, @g/^oo),
z = fecosv sh ц
причем h^ = hv = b(ch2fi - sin2i>I/2. В этих координатах уравнение
B.7.9) для поля в вакууме принимает вид
(dR/dpiy - (dl/dvJ = Ь2( ch 2 fi - sin2 v). B.7.11)
Рассмотрим полуплоскость z > 0 (cosy > 0) и решение уравнения
B.7.11): 1{у) = Ь(\ - cosy), R(n) = bshfi = z/cosv. В области
z > \х I (cosy « 1) имеем
B.7.12)
B.7.10)
Рис. 2.10. Геометрическое представление затухающего поля, фазовые траектории кото-
которого образуют семейство конфокальных гипербол. Амплитуда поля изменяется вдоль
осидг в соответствии с законом Гаусса.
2.8. Максвелловские поля 79
т. е. [см. выражение B.7.2)]:
e-ikoS _ e-x2!w*-ik0[z + x*H2p)]^ B.7.13)
где
w2{z) = 2(z2 + Ь2)/Ьк09 p(z) = z + b2/z. B.7.14)
Эти поля имеют гауссово распределение с шириной w(z), причем
радиус кривизны волновых фронтов равен p(z). Такие поля образуют
так называемые гауссовы пучки, поскольку поле в этом случае скон-
сконцентрировано в очень узкой трубке (см. разд. 7.7).
2.8. ГЕОМЕТРИЧЕСКАЯ ОПТИКА МАКСВЕЛЛОВСКИХ
ВЕКТОРНЫХ ПОЛЕЙ
2.8.1. Асимптотическое разложение электрического поля
Электрическое поле Е в диэлектрической неоднородной среде удовлет-
удовлетворяет векторному волновому уравнению A.1.11), записанному в виде
V2E + kln2E + 2F[E • F(lnw)] = 0. B.8.1)
В полной аналогии со скалярным случаем будем искать представ-
представление геометрической оптики электрического поля, заменив в разло-
разложении B.2.5) Ат(х) на Em(r).
Подставляя правую часть выражения B.2.5) в уравнение B.8.1) и
приравнивая нулю коэффициенты при всех степенях к0, получаем сле-
следующую рекурсивную систему уравнений:
(VSJ - п2(г) = 0, B.8.2а)
(V2S + 2VS • Р)Е0 + 2[Е0 • F(ln n)] VS = 0, B.8.26)
[V2S + 2VS-V + 2VSF{lnn) -]ЕЖ + V2Elil_1 + 2V\bm.x • F(lnn)] » 0,
B.8.2b)
в которой последнее уравнение справедливо лишь при т > 0. Сравни-
Сравнивая уравнения B.8.2) и B.2.9), можно заключить, что векторная те-
теория сводится к скалярной лишь в том случае, когда Ет перпендику-
перпендикулярны градиенту показателя преломления. Вообще говоря, компонен-
компоненты Ех, Еу и Ez перемешиваются за счет членов, содержащих V0n/i),
поэтому первоначально линейно-поляризованное поле при распростра-
распространении не сохраняет своего состояния поляризации.
Для изучения низших порядков асимптотического ряда удобно за-
заменить Е^г) на новую величину Е'(г)> определяемую выражением [ср.
С<2-61)|
80 Гл. 2. Геометрическая оптика
С учетом определения единичного вектора S B.4.1) уравнение B.8.26)
можно переписать в виде
n(d/ds)E' + s(E' • Vn) = 0. B.8.4)
Умножая скалярно это равенство на $ и используя B.4.6), получаем
ns-(d/ds)E' + Е' • Vn = ns • (d/ds)Ef + Е' • (d/ds)(ns) = 0, B.8.5)
Отсюда следует, что скалярное произведение п% • Е' постоянно вдоль
луча.
В частности, если вектор Е' перпендикулярен S в некоторой точке,
то перпендикулярность сохраняется и вдоль всей траектории луча.
Кроме того, если § • Е = 0, то, умножив скалярно B.8.4) на Е\ имеем
иЕ' • (d/ds)Ef = in(d/ds)(E'. E') = 0. B.8.6)
Таким образом, амплитуда ортогонального к S вектора Е' также по-
постоянна вдоль луча.
2.8.2. Асимптотическое разложение магнитного поля
Для того чтобы дать полное описание векторного поля, необходимо
найти асимптотическое разложение магнитного поля Н. Заметим, что,
используя выражение B.4.1) и векторное соотношение (А.8), можно
получить асимптотическое представление векторного произведения
V х Е:
V х Е ~ *"** ? (П?ХЕГ-ЛГХЕ>>|)> E-i - °> B-8-7)
m=-l ( —1*0)
так что при \х — ix0 из уравнения A.1.1) следует
н _ f у пзх ьт + г х ът_1 ikoSiT)
В частности, fH0 = s x ^(f s Sq/п). Поэтому, если Eq ортогонален
вектору 3, то тройка векторов S, Eq и Но взаимно ортогональна и в
нулевом порядке по к$ 1 поле представляет собой поперечную электро-
электромагнитную (ТЕМ) волну.
2.8.3. Асимптотическое разложение вектора Пойнтинга
Используя представленные выше разложения, асимптотическое пред-
представление комплексного вектора Пойнтинга S = A/2)Е х Н*
[см. A.6.8)] можно записать в виде
S - ? Smfcom, B.8.9)
0
2.8. Максвелловские поля 81
sm = ¦= Е е„. х н;.и.(-о-"'(О"'-" =
= wt (-1)™^ х (ns х E*_m, + V x Е:_и,_,). B.8.10)
В частности, если Eq • § = 0, то за счет векторного тождества
(А.2) получаем
B.8.11а)
о Ф')
*)]. B.8.116)
Из выражения B.8.11а) следует, что So является вещественным
вектором. Кроме того, из ортогональности векторов Eq и s имеем
A/2N^ ¦ Е? = A/2)д0Н0 • Hq. Таким образом, то, что в нулевом
порядке электрическая и магнитная плотности энергии равны друг
другу и что вектор So является вещественным, представляют собой
взаимосвязанные факты.
Все проведенные выше рассмотрения справедливы для локальной
плоской волны в нулевом порядке по Arjj, но уже в первом порядке
полученные выше выводы оказываются неверными. Действительно,
если в выражении B.8.116) пренебречь членами с Е1э то оно принима-
принимает вид 2/f0Sj = Eq х (V х Ео*), так что с помощью соотношений
B.8.3), (А.8) и (А.2), а также с учетом постоянства величины 1ЕЧ
имеем
Si ^гк1^'2^ ?=i(v2s)S°; B>8Л2)
здесь в первом приближении мы рассматриваем изменение Eq только
вдоль луча. Тот факт, что Sj — чисто мнимая величина, указывает на
то, что электрическая и магнитная энергии не равны друг другу
(см. работу [17] в гл. 1 настоящей книги).
82 Гл. 2. Геометрическая оптика
2.8.4. Ряд Лунеберга — Клейна на поверхности раздела двух сред
В средах с разрывами показателя преломления у плоской волны Ео
возникает некоторое свойство. Чтобы выявить его, рассмотрим вол-
волну, распространяющуюся в слоистой среде в направлении z, парал-
параллельном Vai . При этом как Ео, так и Но перпендикулярны Чп. Если
показатель преломления разрывен на некоторой плоскости z = const,
то оба вектора (Ео и Но) не могут одновременно быть непрерывными
функциями z. Этот факт противоречит уравнениям Максвелла, соглас-
согласно которым составляющие векторов Е и Н, параллельные поверхно-
поверхности разрыва показателя преломления, должны быть непрерывными.
Для адекватного описания возникающей особенности необходимо рас-
рассмотреть вторую волну, распространяющуюся от поверхности разры-
разрыва в направлении —2. В гл. 3 мы вычислим амплитуды отраженной и
прошедшей волн, а также дадим подробный анализ распространения
излучения в плоских многослойных средах.
2.9. ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА
ВОЛНОВЫХ ФРОНТОВ
Рассмотрим некоторые важные дифференциальные свойства волновых
фронтов в однородной среде. Разложение функции S вблизи точки г0
приводит к ряду
S(r0 + Аг) = S(r0) + Аг • VS + iArAr:Q + —, B.9.1)
где тензор Q = VVS, как будет видно в дальнейшем, описывает кри-
кривизну волнового фронта, а символ «произведения» (:) обозначает опе-
операцию, приводящую к скалярной величине LyA^ATjid/dx^id/dx^S. Так
как в однородной среде VS • VS = п2 = const, из векторных тож-
тождеств (А. 11) и (А.4) следует, что
О = V(VS • VS) = 2(VS .V)VS + 2FS x (F x PS) = 2s • О B.9.2)
(без потери общности мы предположили, что п = 1).
Равенство нулю произведения V • А ненулевого вектора V и нену-
ненулевого тензора А, что дает по определению вектор В{ = Ъ}У}А}[
(ij = 1, 2, 3), означает справедливость следующих утверждений, ко-
которые нетрудно проверить: по крайней мере одна из трех компонент
тензора А в диагональном представлении равна нулю, равны нулю
также и компоненты V вдоль главных осей тензора А, соответствую-
соответствующих ненулевым собственным значениям. Это означает, что тензор Q
можно представить в виде [см. уравнение B.9.2)]
Д *&2, B.9.3)
2.9. Дифференциальные свойства волновых фронтов 83
где t, и t2 {главные направления) перпендикулярны VS. Покажем, что
Q описывает кривизну волнового фронта в точке г0 [9]. (В частности,
если Q = 0, то волна является локально плоской; если же
qx = q2 = 0, то она сферическая, а если qx = 0, q2 Ф 0, то волна ци-
цилиндрическая.) Подставим представление B.9.3) в разложение B.9.1).
Тогда с помощью B.4.2) получим
S(r0 + Дг) = So + Аг • 50 + |(Аг • h)\i + i(Ar • t2Jq2 + • • •, B.9.4)
где все величины в правой части вычисляются в точке г0. Дифференци-
Дифференцируя, имеем
S(r0 + Дг) = So +ДГ • \l\tq{ + Дг • i2t2q2+ .... B.9.5)
Если использовать разложение B.9.4) для векторов Дг, лежащих в
пересечении волнового фронта S = S(r0) ж const с плоскостью, прохо-
проходящей через г0 и параллельной 10 и t,, а также с плоскостью, парал-
параллельной s0 и 12, то получим соответственно (рис. 2.11)
So- ДГ + ^(Дг- tjJ+ ... = О,
2 B.9.6)
й0 • ДГ + 1<72(АГ ¦ t2J + - = 0.
Таким образом, локально сечения являются параболами с кривиз-
кривизной <7j и q2 соответственно. Кроме того, кривизна считается положи-
2
Рис. 2.11. Дифференциальные характеристики волнового фронта. Индикатриса
Дюпина — геометрическое место точек, лежащих на касательной плоскости на расстоя-
расстоянии от точки касания, пропорциональном \р\ Уг, р — радиус кривизны сечения поверхно-
поверхности плоскостью, перпендикулярной этой поверхности и проходящей через точку инди-
индикатрисы. 1 — индикатриса Дюпина; 2 — плоскость, касательная к волновому фронту;
3 — волновой фронт; 4 — главные центры кривизны волнового фронта.
84 Гл. 2. Геометрическая оптика
тельной, если соответствующий центр кривизны лежит на противопо-
противоположной стороне по отношению к направлению луча s0. Поэтому оба
главных радиуса кривизны
рх - gf1 и р2 - q^ B.9.7)
положительны, если волновой фронт является вогнутым для наблю-
наблюдателя при приближении к волновому фронту вдоль направления s0.
Обратная ситуация имеет место для выпуклых волновых фронтов. В
заключение можно сказать, что, согласно принятому нами соглаше-
соглашению, pj и р2 положительны для расходящейся волны и отрицательны
для сходящейся.
Теперь уже можно получить точное выражение для Q. Для этого
заметим, что при бесконечно малом сдвиге dx уравнения B.9.4) и
B.9.5) принимают вид соответственно
S(r0 + dx) + So + dx • s0, B.9.8)
s(r0 + dx) = i0 + dx • (xXqi + Ma?,). B.9.9)
В частности, последнее равенство означает, что векторы s0, dx и
s(r0 + dx) компланарны, если dx параллелен t{ или t2. Используя про-
простое геометрическое построение, докажем теперь, что единичные век-
векторы tj и t2 постоянны вдоль луча (рис. 2.12). Рассмотрим две точки
г0 и г0' = г0 + sods, вектор rfr0, параллельный tp и луч, проходящий
через точку г ж г0 + dx0. Так как dx0 параллелен fp то вектор S ¦ s(r)
компланарен с векторами s0 и dx0. Рассмотрим теперь точку
г' = г + sds и вектор rfr0' = dx0 + ids - sods. Поскольку г0' и xf эк-
эквидистантны (ds) по отношению к волновому фронту, проходящему
через г0 и г, они лежат на одном и том же волновом фронте. Кроме
s'=S+ds
Рис. 2.12. Главное сечение волнового фронта, проходящего через точку rQ. Вектор drQ
параллелен drQ и компланарен с векторами ? и s0, т. е. параллелен главному направле-
направлению волнового фронта, проходящего через точку г'о.
2.9. Дифференциальные свойства волновых фронтов
85
того, cITq параллелен dr0, так как dx^ х dx0 = ds(s - s0) x dr0 = О
[следствие соотношения B.9.9) и параллельности векторов dr0 и tj].
Кроме того, компланарность векторов s, й0 и dxQ означает, что dr0', S
и й0 также компланарны, т. е. вектор dx^ направлен вдоль \г(х^). Сле-
Следовательно, поскольку tfr0' параллелен rfr0, а значит, и tj(r0), мы имеем
t^) = tj(r0). Таким образом, вектор \х является постоянным вдоль
луча, распространяющегося в однородной среде; очевидно, что это же
справедливо й для t2. Отсюда, учитывая постоянство s0 и s вдоль со-
соответствующих лучей, из уравнения B.9.9) имеем
откуда следует
dp =
B-9Л0)
B.9.11)
Аналогичные выкладки можно повторить и для направления t^;
для тензора Q(r) мы получим следующую простую матричную запись
(в системе координат с ортами f,, \2 и S):
О(г) =
1
Pi@)
О
О
1
р2@)
B.9.12)
Здесь рДО) и р2@) — главные радиусы кривизны волнового фронта,
проходящего через начало координат 0 (рис. 2.13), где 5=0. Соот-
Соответствующие центры кривизны (главные центры кривизны) лежат
при s = -р,@) и s = -р2@).
/
Рис. 2.13. Главные плоскости и центры кривизны волнового фронта трубки лучей, рас-
распространяющегося в однородной среде. 1 — центры кривизны; 2 — главные сечения;
3 — главные плоскости.
86 Гл. 2. Геометрическая оптика
Теперь можно получить замечательное выражение, описывающее
эволюцию амплитуды Ао вдоль луча. Действительно, поскольку
+ +
Pi(s) P2(s) Pi@) + s p2(O)
выражение B.5.5) принимает вид
B.9.13)
V
/2Г Р2@) Т/2
где квадратные корни нужно выбирать вещественными положитель-
положительными или чисто мнимыми с положительной мнимой частью. Для сфе-
сферической волны (Pj = р2) Фаза вдоль луча при прохождении через фо-
фокус претерпевает скачок, равный тг. Этот эффект наблюдал Гуи еще в
прошлом веке, и с тех пор он называется фазовой аномалией. Как
будет строго показано в гл. 4, сферическая волна с конечной аперту-
апертурой испытывает быстрое, но непрерывное изменение фазы на тт.
Вдоль оси фазовые аномалии периодически изменяются между — тг/2
и -Зтг/2 (см. рис. 4.23).
Можно привести следующие качественные соображения, объясняю-
объясняющие скачок фазы. Вдоль луча фаза описывается приближенно выраже-
выражением s
B.9.15)
= -\ K(s')ds',
где k(s') — «эффективная» компонента волнового вектора вдоль на-
направления распространения. Если амплитудное распределение волны
почти однородно на плоскости, перпендикулярной §, то к = к0. Вбли-
Вблизи центра кривизны волна сильно неоднородна и к = (к% —
— kj)l/2 < k0, где kt — эффективный поперечный волновой вектор.
Таким образом, когда луч пересекает центр кривизны, фаза ф(э) полу-
получает положительное приращение. Точнее говоря, ф($) больше, чем
ф@), на лтг/2, где п — число центров кривизны, заключенных между О
и s. Все это остается справедливым лишь в том случае, если в цецтрах
кривизны не имеется источников; в противном случае пришлось бы
рассматривать два физических луча, распространяющихся вдоль каж-
каждой прямой, пересекающей центры кривизны.
2.10. КАУСТИКИ И ВОЛНОВЫЕ ФРОНТЫ
Амплитуда поля, вычисленная в приближении геометрической оптики,
оказывается бесконечной на некоторых поверхностях, называемых ка-
каустиками, где V2S = -оо [см. соотношение B.5.6)]. Кроме того, в не-
2.10. Каустики и волновые фронты
87
которых особых точках каустики (точках возврата) поле расходится
иначе, чем на всей остальной поверхности каустики. Как видно из вы-
выражения B.9.14), в однородной среде каустика является геометриче-
геометрическим местом главных центров кривизны (фокусов) волнового фронта.
Поскольку в большинстве случаев каждой точке волнового фронта со-
соответствуют два главных центра кривизны, каустику можно рассмат-
рассматривать как двулистную поверхность. В неоднородной среде понятие о
центре кривизны не имеет смысла, и каустикой является огибающая
конгруэнции лучей. При этом каждый из лучей касается поверхности
каустики в некоторой точке, а это в свою очередь означает, что эле-
элементарный пучок лучей стягивается в отрезок на каустике, что и при-
приводит к сингулярности поля [выражение B.5.3)].
Для более строгого описания рассмотрим двумерную конгруэнцию
лучей и треугольный контур, состоящий из элемента луча 6, участка
каустики и отрезка на волновом фронте А. Очевидно, что поток век-
вектора § через этот контур равен -Д. Площадь, ограниченная конту-
контуром, стремится к нулю приблизительно как 6А. Поэтому отношение
потока к площади расходится как —1/6. Используя теорему Гаусса,
получаем, что на каустике V ¦ & стремится к — оо. Так как
V2S = Vaz • § + nV • S B.4.1), величина V25 также стремится к -оо,
следствием чего является расходимость амплитуды Ао [см. B.5.6)].
В однородной среде огибающая поверхность совпадает с геометри-
п'<п
Рис. 2.14. Примеры каустик, а — у сферической волны каустика представляет собой
точку; обратите внимание на отличие случая, когда точечный источник испускает лучи
во всех направлениях; в первом случае поле в фокусе конечно, а во втором нет; б — кау-
каустика, образующаяся в случае, когда сферическая волна входит в более плотную диэлек-
диэлектрическую линзу через плоскую границу раздела. 1 — фокус; 2 — сферический волновой
фронт; 3 — конгруэнция лучей с каустикой; 4 — каустика.
88
Гл. 2. Геометрическая оптика
Волновой фронт
Каустика
Сечение каустики
с точкой Возврата
Рис. 2.15. а — двулистная поверхность каустики, связанная с волновым фронтом, име-
имеющим вращательную симметрию; б — сечения показанной на рис. а каустики плоскос-
плоскостью, проходящей через ось вращательной симметрии; сечения с точкой возврата могут
быть ориентированы в разные стороны в зависимости от вида волновых фронтов.
ческим местом главных центров кривизны и для сферической волны
сводится в одну точку (рис. 2.14). Если волновые фронты имеют вид
цилиндрических поверхностей, то одним из листов каустики является
цилиндр, а другой лист расположен на бесконечности. Другой при-
пример — волновые фронты в однородной среде, симметричной относи-
относительно поворота вокруг некоторой оси; главные центры кривизны от-
относительно меридиональных сечений в общем случае отделены от
центров кривизны, которые расположены на самой оси вращения (фо-
(фокальная линия). В этом случае каустика состоит из поверхности вра-
вращения (имеющей точку возврата на оси) и отрезка самой оси (рис.
2.15). В обоих рассмотренных случаях каустики полностью определя-
определяются кривыми, которые представляют собой сечения каустик соот-
соответственно плоскостью, ортогональной цилиндрическим волновым
фронтам, и плоскостью, содержащей ось вращения.
Рассмотрим двумерную задачу. На рис. 2.16 изображены близкая к
каустике точка Р и два луча, проходящие через эту точку (здесь и да-
далее мы будем рассматривать однородную среду). Через каждую из то-
2.10. Каустики и волновые фронты
89
Рис. 2.16. а — пересечение лучей вблизи регулярной точки каустики; б — волновые
фронты, соответствующие случаю на рис. а; в — точка возврата, образуемая на каусти-
каустике волновыми фронтами; г — пересечение лучей вблизи точки возврата; в этом случае
более двух лучей могут пересекаться в одной точке и приводить к образованию слож-
сложной интерференционной картины; отмечена также точка Q, лежащая в темной зоне од-
одной ветви каустики и в светлой зоне другой ветви.
чек вблизи каустики проходят два луча, один из которых покидает ка-
каустику (в точке с координатой, соответствующей длине дуги t{ вдоль
каустики, на расстоянии s{ по касательной от точки Р), а другой вхо-
входит в каустику (соответственно в точке t2 на расстоянии s2 по каса-
касательной от точки Р). Таким образом, поле в точке Р является супер-
суперпозицией полей двух лучей, эйконалы которых равны соответственно
S+ и S~. Это приводит к осцилляциям амплитуды поля вблизи кау-
каустики за счет интерференции волн.
Волновые фронты S± = const можно построить как множество то-
точек, в которых оказывается конец нити, разматывающейся с каусти-
каустики. Действительно, мгновенный центр вращения прямого отрезка ни-
нити совпадает с точкой касания нити с каустикой, поэтому конец нити
движется при разматывании перпендикулярно самому лучу, т. е. тан-
тангенциально волновому фронту. Иными словами, если рассмотреть не-
некоторую опорную точку Q на каустике, то можно представить себе,
что поле порождается источником, расположенным в точке Q. Лучи
90
Гл. 2. Геометрическая оптика
первоначально движутся по криволинейной траектории вдоль каусти-
каустики, а затем покидают ее по касательной к ней. Длина оптического пу-
пути, вычисленная вдоль этой траектории, оказывается постоянной, ес-
если сдвигать точку Р по волновому фронту. Такая инерпретация позво-
позволяет легко обобщить метод построения каустики для трехмерной кон-
конгруэнции лучей. В этом случае можно показать [10], что волновые
фронты образуются при разматывании пучка нитей, протянутых
вдоль геодезических линий на поверхности каустики. Такая процедура
является непосредственным обобщением разобранного выше построе-
построения для плоской геометрии и позволяет построить волновые фронты
при известной каустике, т. е. решает задачу, обратную нахождению
каустики при заданных волновых фронтах.
Волновые фронты, проходящие через две точки, расположенные на
одном и том же луче по обе стороны относительно точки касания лу-
луча с каустикой, имеют противоположные значения кривизны, посколь-
поскольку эти фронты отвечают приходящей и уходящей волне (рис, 2.17).
Вообще говоря, фаза волны увеличивается на тг/2, когда соответству-
соответствующий луч касается каустики (см. заключительную часть разд. 2.9).
2.10.1. Аналитические свойства конгруэнции лучей, волновых
фронтов и каустик
Рассмотрим теперь соотношения между конгруэнциями лучей, волно-
волновыми фронтами и каустиками с аналитической точки зрения. Конгру-
Конгруэнция прямых лучей, например распространяющихся в однородной
среде, может быть определена следующей парой параметрических
Скачок
фазы на %
Рис. 2.17. Волновой фронт вблизи точки ка-
касания луча с каустикой.
2.10. Каустики и волновые фронты
91
уравнений:
х = olz + /(о,/*), у = /?z + <?(a,j?). B.10.1)
Соответствующий касательный единичный вектор й дается выра-
выражением
5 =
Р
1
A + а2 +
A + а2 +
A + «2 +
= рх + ^ + A - р2 -
B.10.2)
В соответствии с условием B.4.9) конгруэнция является нормаль-
нормальной, т.е. определяет семейство волновых фронтов, если
V х S = 0. B.10.3)
Произведем теперь замену переменных (х, у, z) — (а, #, z):
дх
ду
dp) да да dp
да dp) да dfi dp да]'
да)др dpda
d_
Tz
da dp) da dp dp da]'
d_ d_
Х.У
Z2+Z
B.10.4)
aa a/?J 5a dp dp da
Используя равенство V x S = 0, получаем
или, в эквивалентном виде, — dg/dp = df/dq.
B.10.5)
2.10.1.а. Волновые фронты
Для того чтобы получить волновые фронты, связанные с распростране-
распространением нормальной лучевой конгруэнции, обозначим через z = z(cc, /8, с)
координату z волнового фронта, определяемую параметром с. При
этом две другие координаты точек волнового фронта определяются
выражениями
х = az(a, ft с) + /(а, Р), у = /?z(o, ft с) + 0(а, /?). B.10.6)
Если использовать теперь ортогональность вектора смещения точ-
точки на волновом фронте (с = const) к направлению луча S, то с по-
92 Гл. 2. Геометрическая оптика
мощью B.10.2) получаем
dz df\ / dz dg\o dz Л
dot да/ V ^а 5а/ 5а
B.10.7)
&г 3/\ / Л5г дд\л dz
а-
т. e.
az + (a2 + p2 + l)(dz/da) = -a{df/da) - 0{dg/da),
B< 10'8)
Определив величину
С = z(l + a2 + Д2I/2, B.10.9)
имеем
doc docj
B.10.10)
Эти уравнения можно проинтегрировать, так как за счет равенства
dg/dp = df/dq имеем
Таким образом можно найти функцию
z = z(a,j?,c), B.10.12)
с помощью которой вместе с соотношениями B.10.6) можно ис-
исключить параметры а и /3 и получить уравнение волновых фронтов
F(x, у, z, с) = 0. Различные значения параметра с отвечают разным
решениям уравнений B.10.10); поэтому наиболее общее их решение
связано с наиболее общим волновым фронтом.
2.10.1.6. Каустики
Найдем теперь каустики, связанные с рассматриваемой конгруэнцией.
Удобно рассмотреть подмножество прямых, определяемых как
х - (xz - /[<х,/*(а)] = 0, у - Р(ф - 0[а,0(а)] = 0, B.10.13)
где /3(а) — функция, связанная с огибающей кривой Г подмножества.
Точка (хс, ус, zc), в которой рассматриваемый луч (имеющий данное
2.10. Каустики и волновые фронты 93
значение параметра а) касается кривой Г, определяется уравнениями
да dp da da да dft da
Эти уравнения подтверждают интуитивное представление о том,
что каждая точка на огибающей является точкой скопления лучей, что
означает равенство нулю производных dxc/da и dyjda при фиксиро-
фиксированном zc. Как следствие уравнений B.10.14), получаем
dfi (dg/dfi - (Sf/da) ± Щ/да) - (dg№]2 + 4(df/dp)(dg/da)}^2
_
da 28f/dp
B.10.15)
Решением этого дифференциального уравнения является функция
jS(a), для которой рассматриваемое подмножество прямых лучей опре-
определяет некоторую огибающую Г. В общем случае функция /3(а) зави-
зависит еще и от некоторого параметра у, так что Г зависит от 7 и это
можно отметить символом Г7. Если у изменяется непрерывно, то Г
будет описывать каустику. Поскольку уравнение B.10.15) имеет два
решения, в общем случае существует две несвязанные поверхности
(двулистные каустики). Можно показать [10], что кривые Г являются
геодезическими линиями каустики.
Пример. Построение каустики конгруэнции лучей. Рассмотрим
случай, когда П1П1.
/ = Р, 0 = 4 B.10.16)
(в правых частях этих соотношений неявно подразумевается наличие
общего множителя, имеющего размерность длины). В соотношениях
B.10.16) величины р и q определены с помощью B.10.2). Здесь мы
рассматриваем конгруэнцию лучей, которая обладает вращательной
симметрией, поскольку любой луч описывает поверхность вращения
вокруг оси z9 когда а и /3 принимают все возможные значения, причем
ос2 + 02 = const.
Из уравнений B.10.15) и B.10.16) имеем
dp/da = - a/jS, dp/da = 0/a, B.10.17)
или соответственно
P = (y2 _ 0,2I/2^ p = y(X B.10.18)
Если использовать теперь уравнения B.10.13) и B.10.14), то полу-
получим выражения
94
Гл. 2. Геометрическая оптика
i, X
Поверхность разрыва
волнового фронта
Рис. 2.18. Каустика и волновые фронты конгруэнции лучей B.10.16). Эйконал имеет
разрыв на осих (волнистая линия), а волновые фронты пересекают осиz их перпенди-
перпендикулярно им. Каустика, показанная жирной линией, соединяет точки @, ± 1) с точкой
(-1, 0).
которые описывают каустику [отрезок (— 1, 0) на оси симметрии и по-
поверхность вращения], соответствующую случаю вращательной сим-
симметрии (рис. 2.18). Поверхность вращения имеет вид рупора с верши-
вершиной в точке @, 0, -1), край которой касается плоскости z = 0 по
окружности z2 + у2 = 1. Заметим, что в этом случае каустика заклю-
заключена в конечном объеме, хотя лучи занимают все пространство.
Для того чтобы найти волновые фронты, заметим, что уравнения
B.10.10) при выполнении условий B.10.16) дают следующее уравне-
уравнение:
дС/д<х = -аA + а2 + J?2), B.10.20)
решение которого записывается в виде [см. B.10.9)]
ф,Дс) = ±A + а2 + 02Г3'2 + с{\ + а2 + 0Т1/2, B.10.21)
где параметр с, определяющий конкретный волновой фронт, дается
выражением
2'
B.10.22)
Наконец, используя выражения B.10.6), B.10.16) и B.10.21), полу-
получаем
(х2 + v*I" = -—^ ' г ' 4- (с
2 A + а2 + /?2K'2
+ а2 + /?2)*/2
B.10.23)
2.11. Отражение и преломление на неплоской границе раздела 95
Выражения B.10.21) и B.10.23) являются параметрическими (пара-
(параметр а2 + 02) уравнениями волновых фронтов, связанных с конгруэн-
конгруэнцией лучей B.10.16). Следует также заметить, что благодаря B.10.22)
и взаимной ортогональности волновых фронтов и оси z параметр с с
точностью до аддитивной постоянной совпадает с эйконалом.
2.11. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛНОВОГО ФРОНТА
НА НЕПЛОСКОЙ ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД
Одна из наиболее важных задач в оптике состоит в определении изме-
изменения волнового фронта при прохождении через последовательность
линз. Это требует решения канонической задачи о преломлении кон-
конгруэнции лучей на неплоской поверхности раздела между двумя одно-
однородными средами, имеющими показатели преломления соответствен-
соответственно л и л'. Вопросы, на которые при этом нужно ответить, связаны с
отклонением направления падающего луча и с изменением локального
волнового фронта, где под «локальным» мы понимаем небольшой
участок волнового фронта, через который проходит луч. Благодаря
своей малой протяженности этот участок можно представить как по-
поверхность второго порядка, характеризуемую своими главными ради-
радиусами кривизны. Поэтому задачу можно сформулировать иначе — не-
необходимо установить связь между радиусами кривизны непосред-
непосредственно до и после пересечения границы раздела. Нейсли [11] получил
простые соотношения, которые мы проиллюстрируем в следующем
разделе, где также кратко рассмотрим дифференциальные свойства
поверхности.
2.11.1. Локальная сшивка падающего и преломленного полей вдоль
неплоской границы раздела
Рассмотрим поле, падающее на искривленную поверхность разрыва
[/(г) = 0] показателя преломления. Для обеспечения непрерывности
тангенциальных к поверхности электрических и магнитных компонент
(что и следует из уравнений Максвелла) необходимо рассмотреть как
отраженные, так и преломленные поля. Мы будем обозначать их со-
соответственно двумя и одним штрихами (рис. 2.19). В приближении лу-
лучевого поля Е^г) exp [~ik0S(r)] на границе раздела/(г) = 0 можно на-
написать следующие условия сшивки:
A - пп) • Е0(г) + A - пп) • E^rje**015 "(r)"S(rI =
= A - пп) • E'0(r)^-|fcols'(r)-S(rI, B.11.1)
96
Гл. 2. Геометрическая оптика
Поверхность
ыва 4=0
Рис. 2.19. Отражение и преломление на по-
поверхности разрыва показателя преломле-
преломления. Единичные векторы v, v' и v5 лежат в
плоскости падения и перпендикулярны и.
A - ни) • [к х Е0(г)] + A - пп) • [к" х Eftr)]
= A - ии) • [к' х E'0(r)-]e-ik°ls'ir)-S(T)\ BЛ1.2)
которые обеспечивают соответственно непрерывность электрической
и магнитной тангенциальных компонент (см. разд. 2.8.2). Действи-
Действительно, символом 1 мы обозначаем единичный тензор, an — единич-
единичный вектор, ортогональный поверхности, так что A — пп) ¦ V пред-
представляет собой проекцию вектора V на поверхность.
В то время как амплитуды Eq, Е^ и EJ' — это медленно меняющие-
меняющиеся функции, фазовый множитель exp (ik0S) таковым не является. По-
Поэтому приведенные векторные соотношения могут выполняться, толь-
только если приращения A(S"-S)hA(S' - S) тождественно равны ну-
нулю на поверхности разрыва. Пусть п' — показатель преломления в
области преломленного луча, а я— в области падающего и отражен-
отраженного лучей. Используя B.4.1) и B.9.1), эти условия можно записать в
виде
A(S" - S) = nДг • ($" -s) + ?ДгАг: PF(S" - S) + • • = 0, B.11.3a)
A(S' - S) = Дг • (иТ - ns) + ^АгДг: VF(S' - S) + ••• = 0. B.11.36)
При этом должно быть выполнено дополнительное условие, заключа-
заключающееся в том, что точка г должна принадлежать поверхности / = 0,
т. е.
Дг-й + ±ДгДг:в + --- = 0, B.11.4)
где
s=PF//|F/|. B.11.5)
Если домножить уравнение B.11.4) на произвольное число —п'у и
сложить его с B.11.36), то получим уравнение
Аг • (иТ - И5 - л'уи) + |Дг Дг: [PF(S; - S) - n'ys] + • • • = 0, B.11.6)
2.11. Отражение и преломление на неплоской границе раздела 97
которое для бесконечно малых приращений г сводится к уравнению
dx • (n'i' - ni - n'yh) = 0. B.11.7)
Для того чтобы соотношение B.11.7) выполнялось при любом dx,
тангенциальном поверхности, т. е. ортогональном вектору п, вектор
n's' — п& должен быть параллелен п. Это условие эквивалентно за-
закону Снеллиуса
risinO' = nsinO, B.11.8)
связывающему углы падения и преломления в и 0', определяемые со-
соответственно как угол между п и -s и угол между п и -s'. При
этом направление вектора п таково, что в < ж/2 и 0' < 7г/2. Кроме
того, параллельность векторов ft и n'&f - /is означает, что существу-
существует такое число у, что
S = /х§ + 7П, B.11.9)
причем
ц = п/п\ B.11.10)
Отсюда следует, что плоскость падения пй совпадает с плоскостью
преломления fas'. Это утверждение вместе с соотношением B.11.8)
составляет содержание хорошо известного закона преломления (за-
(закона Снеллиуса), установленного в 1621 г. голландским математиком
из Лейденского университета Виллебрордом Снеллиусом и независимо
французским философом и математиком Рене Декартом (см., напри-
например, работу [12]).
Умножая скалярно выражение B.11.9) на п, получаем
f=/icos0-cos0/. B.11.11)
При 7 = 7 первый член в уравнении B.11.6) обращается в нуль, и
мы имеем
dtdr:lVF(S' - S) - riys] = 0, B.11.12)
Это означает, что если тензор в квадратных скобках не равен нулю,
то элемент поверхности разрыва (х9 у, z — х + dx, у + dy, z + dz)
лежит на конусе с вершиной в точке г. Поскольку мы рассматриваем
регулярную точку г поверхности, необходимо заключить, что
VVS' = VVS + riy*. B.11.13)
В частности, мы имеем следующие соотношения:
к' = Sp (VVS')/V = Sp (VVS)//i' + Sp CyS) ¦ /i* + Sp GS),
B.11.14)
к' = det(VVS')/fi/2 = det(VVS + n'yS)/n'2,
98
Гл. 2. Геометрическая оптика
где к'(и к) и к' — соответственно средняя и гауссова кривизна соот-
соответствующего волнового фронта, символом Sp обозначается след, а
det — определитель двумерных матриц, образованных первыми двумя
строками трехмерных матриц из B.11.13), где третью координатную
ось мы выбрали ортогональной главным ^>сям \[ и \'г [относительно
множителей при определении величин к', к и к' см. обсуждение после
формул B.11.23)].
2.11.2. Главные направления и радиусы кривизны преломленного
волнового фронта
Для вычисления радиусов кривизны преломленного волнового фронта
введем единичный вектор и, перпендикулярный плоскости падения ns
(см. рис. 2.19, 2.20). Так как из B.9.3) следует, что главные направле-
направления VV5 ортогональны к VS, т.е. и к s, можно записать
VVS
/UU VV
= (— + —
где
V = U
А
X S
B.11.16)
Рис. 2.20. Взаимная ориентация главных направлений падающего, отраженного и пре-
преломленного волновых фронтов. / — падающий волновой фронт; 2 — отраженный вол-
волновой фронт; 3 — преломленный волновой фронт; 4 — поверхность разрыва.
2.11. Отражение и преломление на неплоской границе раздела 99
представляет собой единичный вектор, параллельный плоскости паде-
падения. Параметр а стремится к бесконечности, если и и if совпадают с
главными направлениями падающего луча.
Заметим теперь, что функцию /, равенство нулю которой опреде-
определяет границу разрыва, всегда можно выбрать таким образом, что
V/ • V/ = const. Отсюда следует «ортогональность» между V/и VV/
[см. уравнение B.9.2)], что позволяет, используя определение B.11.5),
написать следующее выражение:
s = Ы + *А + JLtfW, + *,й). B.11.17)
Ры Pv °s
где Vj = u х п в полной аналогии с B.11.15). Окончательно получаем
: B.11.18)
Pv
причем
v' = u x s'. B.11.19)
Таким образом, соотношение B.11.13) можно записать в виде
йй . 0'v' . uv' + v и л
К P'v о> ^ Ри Р"и
j - "Л . /uv + vu
B.11.20)
Кроме того, векторное умножение B.11.9) на и дает выражение
V' = /xv + 7V,, B.11.21)
с помощью которого нетрудно доказать [11, 13], что соотношение
B.11.13) удовлетворяется, только если
I/Pi = Р/Р, + У/Pi* B.11.22а)
(cos 0')/(т[ = (fi cos 0)/а + у/аж> B.11.226)
(cos2 0')/р; = (/i cos2 в)/рр + y/pj. B.11.22в)
Отсюда можно определить величины pw', pj и а'. Для определения
главных направлений t/ и tj' преломленного луча необходимо диагона-
лизовать WS', т.е. начать вычисление с соотношения B.11.18) и
представить этот тензор в виде Щ\[/р[ + ЦЦ/р^п'. Таким образом
100 Гл. 2. Геометрическая оптика
[13], получаем следующие соотношения:
1/pi = (cos2 ф')/р\ + (sin2 ф'Iр'2> B.11.23а)
1/р; = (sin2 <?')/p'i + (cos2 ф')/р'29 B.11.236)
2/G' = (l/p\ - 1/р'2)*тBф% B.11.23b)
где ф' — угол, на который необходимо повернуть векторы ии(' в
плоскости uv' таким образом, чтобы они совпадали с векторами со-
соответственно \[ и t2'. Главными радиусами кривизны преломленного
луча являются р[ и р2. Мы показали (см. разд. 2.9), что понятие ра-
радиуса кривизны связано с соотношением VS • V5 = 1, в то время как
здесь мы имеем VS • VS = п1 и VS' • VS' = л'2. Это расхождение
учитывается множителями п и п' в соотношениях B.11.15) и B.11.18).
Подводя итог, можно заключить, что главные направления и ра-
радиусы кривизны волнового фронта сразу за границей, на которой про-
происходит преломление, можно найти, применяя последовательно следу-
следующие три операции:
1) преобразование величин рр р2 к ри, pv, а с помощью B.11.15);
2) использование формул НеЙсли B.11.22);
3) преобразование величин р'и, pj, о' к р[, р2 с помощью соотноше-
соотношений B.11.23).
Все выкладки можно повторить и для отраженного волнового
фронта. В частности, поскольку /х = п/п" = 1, имеем б" = ж — в и
7 = 2cos0. Кроме того, плоскость падения совпадает с плоскостью
отражения ns". Первое и третье утверждения составляют закон пре-
преломления.
2.11.3. Сферические преломляющие поверхности
Рассмотрим в качестве примера сферическую поверхность разрыва
(например, переднюю поверхность сферической линзы) радиусом
Rs = р? = р?. в этом случае любая пара взаимно ортогональных осей
(ортогональных также и вектору п) диагонализует матрицу B.11.17),
т. е. 1/(г = 0 и
l/p'u = fi/ptt + y/R\
I/a' = O*cos0)/(Gcos0'), B.11.24)
1/р; = (/icos20)/(pt;cos2^) + y/(Rs cos2 в').
Если падающий волновой фронт также сферический, то из второго
уравнения B.11.24) имеем \/о = 0, так что ф' = 0 [см. B.11.23в)] и,
как следствие, и и v' являются главными направлениями отраженного
2.11. Отражение и преломление на неплоской границе раздела
101
B.11.25)
B.11.26а)
B.11.266)
луча (рис. 2.21). Таким образом, имеем
Pi = PL> Pi = Р*>
или
I/Pi = fi/R + y/R\
l/p'2 = (/xcos20)/(Kcos20') + у/(Я8 cos2 0');
здесь R — радиус кривизны падающего волнового фронта. Следова-
Следовательно, радиусы кривизны р[ и р2' преломленного волнового фронта в
общем случае различны, а совпадают лишь при в = в' = 0 {нормаль-
{нормальное падение). С этим связан определенный астигматизм пучка пре-
преломленных лучей, который тем больше, чем сильнее угол падения от-
отличается от нормального.
T)r>n(pL<1)
Се чение сфер и ческой
поверхности разрыва
Сферический
фронт
падающей
волны
афронт
преломленной
волны
рис. 2.21. Изменение главных радиусов кривизны начального сферического волнового
Фронта, проходящего через сферическую поверхность разрыва, а — сечение, перпенди-
перпендикулярное плоскости падения; б — сечение, параллельное плоскости падения.
102
Гл. 2. Геометрическая оптика
2.11.4 Параксиальное приближение
При нормальном падении, как следует из соотношения B.11.11), мы
имеем у = М - *• Таким образом, если положить р[ = р{ = - rf',
то B.11.26а) сводится к хорошо известному соотношению
n'/d' + n/d = (n' - n)/Ks = n/f = п7/' B.11.27)
(рис. 2.22). Здесь d ¦ /?, а/и/' — фокусные расстояния. Соотноше-
Соотношение B.11.27) позволяет связать расстояние </' между точкой изображе-
Рис. 2.22. Изменение преломленного волнового фронта в зависимости от положения ис-
источника, а — р\ = р'2 < 0; б — р\ = р'г = оо; в — р\ = р'2 > 0.
2.12. Решение уравнения эйконала 103
ния О' и вершиной К сферической поверхности разрыва с расстоянием
d между точкой предмета О и вершиной V. Следует заметить, что в
примерах на рис. 2.22 величину R1 нужно выбрать положительной.
Действительно, из уравнения B.11.4) получаем, что вектор V/направ-
V/направлен по нормали п, которая в свою очередь ориентирована в противо-
противоположном направлении по отношению к центру кривизны поверхно-
поверхности. Отсюда следует, что величина Rs положительна. Точно так же
ранее мы считали, что расходящийся сферический волновой фронт
имеет положительный радиус кривизны (см. разд. 2.9).
На рис. 2.22 представлены следующие частные случаи: на
рис. 2.22 ,а — случай, когда р\ = р\< 0, на рис. 2.22,6 мы имеем
Р\ = Рг = °°> а на Рис- 2.22,в — случай, когда р[ = р2' > 0- Действи-
Действительно, на рис. 2.22,а изображена сходящаяся преломленная волна, на
рис. 2.22,6 — плоская преломленная волна, а на рис. 2.22,в — расхо-
расходящаяся преломленная волна, так что знаки радиусов кривизны согла-
согласуются с результатами, полученными в разд. 2.9.
2.11.5. Сферические отражающие поверхности
Рассмотрим другой пример — сферическую волну, отраженную сфери-
сферической поверхностью. В этом случае, делая в соотношении B.11.11)
замену 0' — 0", получаем
y = 2cos0, B.11.28)
где мы учли, что д = п/п" = 1и0" = тг-0. Таким образом, по
аналогии с B.11.26) имеем
1/р'2' = 1/р'; + B tg в sin 0)/R\ B.11.29)
Отсюда можно оценить степень астигматизма пучка отраженных лу-
лучей по сравнению со случаем нормального падения (р% = р^).
В заключение заметим, что геометрическая оптика не позволяет
определить коэффициенты пропускания (или отражения), т. е. связать
амплитуды падающих и преломленных (или отраженных) электромаг-
электромагнитных полей. Этой цели можно достичь, используя формулы Френе-
Френеля (см. разд. 3.8), применимость которых строго обоснована лишь
для плоских границ раздела.
2.12. РЕШЕНИЕ УРАВНЕНИЯ ЭЙКОНАЛА МЕТОДОМ
РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
Наиболее мощный метод решения волнового уравнения Гельмгольца
состоит в отыскании подходящей системы ортогональных координат
104 Гл. 2. Геометрическая оптика
xl9 x2, х3, для которых поле можно представить в виде произведения
функций одной координаты xi9 т. е. и = и1(х1)и2(х2)и3(х3). Этот метод
(разделение переменных) можно использовать и для решения уравне-
уравнения эйконала, но в этом случае S нужно представить в виде суммы
функций одного аргумента xt. Существование таких координат связано
с функциональной зависимостью л2(г). Ниже мы рассмотрим несколь-
несколько практически важных случаев.
2.12.1. Декартовы координаты
Во многих практически важных случаях выбор соответствующей си-
системы координат позволяет разложить квадрат показателя преломле-
преломления на простые слагаемые [14]. В качестве предварительного примера
рассмотрим случай, когда функция п1 разделяется в декартовых коор-
координатах, т. е<
«2(Г) = /М + ^(У) + М4 B.12.1)
Бели искать эйконал в виде
S(r) = Х(х) + Y(y) + Z(z), B.12.2)
то уравнение B.3.1) разделится на три следующих уравнения:
(dX/dxJ = a + f(x),
(dY/dyJ = b + g(y), BЛ2.3)
(dZ/dzJ = с + h(z),
где a, b и с — три постоянные, удовлетворяющие соотношению
а + Ь + с = 0. B.12.4)
Таким образом, можно написать
' + [\g(y') + bV'2dy' + |*W
B.12.5)
что дает
2 l Г"? + \ЫУ) + Ы1/2| + \lW + сУ fz.B.l2.6)
FS = [/(x) + aVl2x + lg(y) + ЬУ12у + [A(z) + c]ll2z =
= (f+g + hI/2s. B.12.7)
2.12. Решение уравнения эйконала 105
Последнее равенство является следствием выражений B.4.1) и B.12.1).
Поскольку S • х ds = dx и
ns-x = dS/dx = [/(*) + а]112, B.12.8)
мы имеем
d^(s) = dx/lf(xHa21J2 = dy/[g(yHb^2 = dz/lh(z)^cV^ B.12.9)
откуда (^помощью выражения B.12.6) получаем
S 1
-ds' = -ln[(/ -h a)(g + Ь)(й + c)] + const, B.12.10)
L 2J Ф) J
[1 fV5 1
J W)dS J Х{/ + а)/4(^ + Ь)/4(А + C)/4> BЛ2Л1)
Из соотношения B.5.5) следует, что лучевое поле можно записать в
виде
х
\g{y') +
х ехр|-*0Г \\fix') + аУ'2*х' 4- i\g{y'
B.12.12)
где функция F(r) сохраняет постоянным свое значение вдоль каждого
луча. Таким образом, поле полностью определяется геометрией кон-
конгруэнции лучей и своим распределением на волновом фронте или
(в более общем случае) на поверхности, пересекающей все лучи.
Заметим, что выражение для поля B.12.12) расходится, когда
какой-либо из множителей/ 4- a, g + Ъ или Л + с обращается в нуль.
Таким образом, соотношения
f(xc) = -а, д(ус) = -Ь, h(zc) =-c = a + b B.12.13)
определяют все возможные плоские поверхности каустик х = хс,
y = yc,z = zc.
2.12.1.а. Аксиально-симметричное распределение показателя прелом-
преломления
Важным частным случаем является аксиально-симметричный про-
профиль квадрата показателя преломления п2(г):
п2(т) = -а(х2 + у2) + п2, B.12.14)
106 Гл. 2. Геометрическая оптика
откуда следует, что
/(х) = -ах2. д(у) = -ау\ h(z) = п2. B.12.15)
Соответствующий эйконал запишется в виде
S(r) = ?х(-ах2 + aI/2 - (ш/2а1/2Iп[/х(а/яI/2 + A - х2а/аI/2] +
+ Ы-*У2 + ЬI/2 - 0*b/2a1/2)ln[i>(a/bI/2 + A - у2а/ЬI/2] +
+ («о + c)il2z + const. B.12.16)
В частности, в случае когда х2 > \а\/а и у2 > I b I/a, т. е. вдали
от оптической оси, из B.12.12) получаем
м(г) = F(r)(-ax2 + аГ114(-ау2 + b)/4(ng + с)/4 х
х exp[-fcoa1/2(x2 + >>2)/2 - iko(n2o + cI/2z] x
х x*oa/Bai/2yob/B«^2)e B.12.17)
Следовательно, при а > 0 поле затухает в радиальном направлении
по закону Гаусса. Поле B.12.17) описывает волноводную моду, рас-
распространяющуюся вдоль оси z с постоянной распространения
Р = ко(п2о + сI12. B.12.18)
2.12.1.6. Линзоподобные среды
В случае когда показатель преломления является убывающей функци-
функцией расстояния от оптической оси, такие среды называют линзоподоб-
ными. Для того чтобы исключить нефизичные сингулярности на кау-
каустике, необходимо наложить следующие дополнительные условия (см.
разд. 3.3.4, в котором рассматривается распространение излучения
вдоль оси я:):
fco[X(|xc|) - Х(-|хс|)] = (р + iK
B 12 19)
При этом с помощью B.12.16) и соотношений х\ = а/а и у% = Ь/а
можно написать следующие выражения:
fcoa/2aI/2 - 1/2 = р, ^Ь/га1/2 - 1/2 = q, B.12.20)
которые определяют дискретный набор значений а, Ъ и, следователь-
следовательно, /3. Точнее говоря, соотношения B.12.8) и B.12.4) дают
Р = /Ь = *о[п2 - 2a1/2(p + i)/*o - 2а^2(в + i)/fco]1/2 =
S fco«o - a1/2(p + q + l)/n0. B.12.21)
Если сравнить данное выражение с результатом волнового анализа
параболического профиля в многомодовых оптических волокнах, то
2.12. Решение уравнения эйконала 107
мы обнаружим полное согласие, которое свидетельствует о больших
потенциальных возможностях метода геометрической оптики [см. вы-
выражение (8.7.19)].
2.12.1.в. Физические свойства комплексных эйконалов
Необходимо сделать несколько замечаний, чтобы прояснить физиче-
физический смысл комплексного эйконала. Простое исследование выражения
B.12.16) показывает, что 5(г) имеет ненулевую мнимую часть, если
хотя бы одна из величин а — ах2 или Ъ — ау2 отрицательна. Это по-
позволяет разделить'все пространство на две области — освещенную
сторону каустики, для которой
а - ах2 > 0, Ь - <ху2 > 0,
и темную сторону, для которой хотя бы одно из этих условий не вы-
выполняется.
Освещенная обалсть характеризуется вещественным эйконалом,
темная же область — комплексным эйконалом, приводящим к экспо-
экспоненциальному затуханию электрического поля с увеличением расстоя-
расстояния от каустики [см. выражение B.12.17) и пример в разд. 2.7]. В со-
соответствии с этим луч, приходящий из светлой зоны, подходит к кау-
каустике по касательной и приводит к появлению отраженного назад дей-
действительного луча и комплексного луча, проникающего в темную зону.
В темной области единичный вектор S принимает комплексные
значения. Точнее говоря, компонента вектора s(r), перпендикулярная
каустике, является чисто мнимой при г, принадлежащих самой каусти-
каустике. Это означает, что в соответствующем направлении нет потока
энергии и прошедшему полю вообще не передается энергия падающе-
падающего поля. Однако неравенство нулю поля означает, что в темной зоне
аккумулируется реактивная энергия, которая связана со скачком фазы
на тг/2 при пересечении каустики, как показано в разд. 2.10 для случая
однородных сред (см. 2.17).
В освещенной области единичный вектор S является веществен-
вещественным. Ниже при рассмотрении теории дифракции мы покажем, что по-
поле вблизи каустики хорошо описывается функциями Эйри, асимптотика
которых в освещенной области вдали от каустики имеет вид двух бегу-
бегущих волн в соответствии с представлением геометрической оптики.
Полученные выше результаты справедливы для произвольного
распределения показателя преломления л (г). Однако в любом случае
геометрическая оптика сама по себе не позволяет вычислить коэффи-
коэффициенты отражения и пропускания для волны, касающейся каустики.
108 Гл. 2. Геометрическая оптика
Эту задачу можно решить лишь при введении определенных переход-
переходных функций, обеспечивающих сшивку поля по обе стороны от кау-
каустики (разд. 3.3).
2.12.2. Цилиндрические координаты
Рассмотрим теперь случай, когда переменные разделяются в цилинд-
цилиндрических координатах, т. е.
п2(г) = f(p) + д(ф)/р2 + h(z). B.12.23)
При этом эйконал имеет вид
S(t) = R(p) + ф(ф) + Z(z). B.12.24)
и является решением уравнения B.3.1), если
(dR/dpJ +(l/p2X<«WJ + (dZ/dzJ = f(p) + д(ф)/р2 + fc(z), B.12.25)
Отсюда следуют соотношения
= \\д(Ф') + Ь]1/2#', B.12.26)
где Ь и с — постоянные, а Ф удовлетворяет условию периодичности
Ф(ф + 2п) = Ф(ф) + 2тп/к0 (т — целое). B.12.27)
При этом функция ехр[-/А:05(г)] определена однозначно. Таким обра-
образом, если g = 0, то
Ф(ф) = тф/к0 + const, B.12.28)
b = m2/kl B.12.29)
Действуя далее так же, как и в случае декартовых координат, мож-
можно показать, что
м(г)=Щт _ с _
bI12 d<f>' + f \h{z') + сI12 «fa'lj, B.12.30)
причем функция F(r) постоянна вдоль луча.
2.12. Решение уравнения эйконала 109
2.12.2.а. Аксиально-симметричный профиль показателя преломления
При g = 0 и Л = const профиль показателя преломления является
аксиально-симметричным и выражение B.12.30) принимает вид
Г fPf g2 2 -11/2 )
expj -ik0 J ^i! V) " ^у " ^72)J <*P' - № - M|, B.12.31)
где мы использовали соотношения B.12.23) и B.12.29), а также опре-
определение
p = ko{h + c)U2 B.12.32)
Каустикой является двулистный круговой цилиндр с радиусами
ртах и pmin, определяемыми двумя последовательными нулями множи-
множителя [п2(р) — Р2/к1 — m2/(fc§p2)] в выражении B.12.31). В полной ана-
аналогии со случаем декартовых координат можно наложить следующее
условие:
ЬоЕЖртах) - Д(р«1пИ = (» + *)я (^ — Целое), B.12.33)
которое позволяет определить дискретный набор возможных постоян-
постоянных распространения /3^. При этом выражение B.12.31) описывает
волноводные моды оптического волокна с профилем показателя пре-
преломления п(р). Параболический профиль п(р)у определяемый выраже-
выражением B.12.14), получается в случае, когда
л2(р)=-ар2 + и2. B.12.34)
2.12.3. Сферические координаты
Если переменные для п2 разделяются в сферических координатах и
распределение п2 симметрично относительно оси z, т. е.
п2(т) = h(r) + д(в)/г2, B.12.35)
то эйконал имеет вид S(r) = R(r) + 0@) 4- Ф(ф), и нетрудно пока-
показать, что имеют место следующие соотношения:
if2d6'
•(¦)==*¦¦
ПО Гл. 2. Геометрическая оптика
если записать уравнение B.3.1) в сферических координатах. Затем
обычным образом можно получить
„(г) =
j-ifc
х expjJ( ^J
Н^I/2]Ц Bл2-з7)
где функция F(r) постоянна вдоль луча.
Пример. Рассеяние на теле конечных размеров. Если выбрать па-
параметры с = т = 0, то выражение B.12.37) для случая однородной
среды вне сферы радиусом R сводится к сферической волне (сфериче-
(сферические волновые фронты)
)е'1к0Г/г, B.12.38)
где без потери общности мы выбрали А = 1. Исходя из этого выра-
выражения, можно построить ряд Лунеберга — Клейна. Для этого заме-
заметим, что, выражая оператор V2 в сферических координатах и исполь-
используя зависимость A0(s) = A0(r)<xl/r> оператор L в B.6.6) можно запи-
записать в виде
- - 1 Г
?2 \Г
Ui4m
где
Нижний предел интеграла в B.12.39) равен оо, поскольку мы пред-
предположили, что Ат(оо) = 0 при т Ф 0 [см. вывод выражения B.6.6)].
Отсюда следует, что B.12.38) является точным выражением для поля
при г — оо. Если теперь положить
ф)/г = /„@, ф)/г«+ \ B.12.41)
то выражение
)/г B.12.42)
2.12. Решение уравнения эйконала 111
вместе с рекуррентными соотношениями B.6.7) и разложением B.2.5)
приводит к тому, что поле можно записать в виде
Коэффициенты fn удовлетворяют рекуррентным соотношениям
-2iko(n + l)fn+1 = [и(и + 1) + D2]/n, B.12.44)
где /0 ш /. Это легко доказать, раскладывая /л в ряд по сферическим
гармоникам Тр{ву </>)¦ которые являются собственными функциями
оператора D2. Таким образом, ряд B.12.43) оказывается суммой чле-
членов, каждый из которых является произведением Yf и сферических
функций Ханкеля hn(ktf) (см. разд. 6.12).
С интуитивной точки зрения из выполненных выше расчетов сле-
следует, что поле можно вычислить в любой точке (по крайней мере в
смысле Лунеберга — Клейна), если известно его распределение /@, ф)
в дальней зоне. Это свойство тесно связано с возможностью инте-
интегрального представления поля с учетом его значений на поверхности
(см. разд. 4.2.2).
Рассмотрим поток вектора I и 12г через сферу:
f
J4
B.12.45)
4*
Отсюда следует, что величина l/l2rf0 пропорциональна мощности,
излучаемой в телесный угол dQf а весь интеграл пропорционален пол-
полной мощности, излучаемой в бесконечность.
Можно рассмотреть также случай среды, неоднородной при г < R
и освещаемой плоской волной единичной амплитуды. В этом случае
величина ехр(-/?ог)/@, ф)/г представляет собой поле рассеяния на
бесконечности. Амплитуда рассеяния [3] равна/(см. разд. 6.11), а ве-
величина
\П2 = а(в,ф) B.12.46)
является дифференциальным сечением, которое зависит от структуры
рассеивающей среды. Как будет видно в следующем разделе, величину
о можно вычислить, прослеживая изменение поля и вдоль каждого лу-
луча коллимированной конгруэнции, описывающей изначально плоскую
волну. Эти вычисления существенно упрощаются, если неоднородная
среда имеет центр симметрии.
112 Гл. 2. Геометрическая оптика
2.13. ВЫЧИСЛЕНИЕ ТРАЕКТОРИЙ ЛУЧЕЙ МЕТОДОМ
РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
Во многих случаях метод разделения переменных позволяет получить
параметрическое представление траекторий лучей. Пусть ц, р, о — ор-
ортогональные криволинейные координаты, а Лм, hv, ha — соответству-
соответствующие масштабные множители. Тогда
(dxJ + (dyJ + (dzJ = h2(diiJ + h2(dvJ + hl(daJ. B.13.1)
Если обозначить через ц9 р, а координаты точек на данном луче,
то, проецируя векторное соотношение B.4.1) на координатную ось д,
получаем
где р и а можно рассматривать на луче как функции координаты д.
Аналогичные соотношения справедливы при замене \i на р или а.
2.13.1. Аксиально-симметричные среды
Если
и2(г) = f(p) + h(z)9 B.13.3)
то соотношение B.13.2) можно переписать в виде [см. выражение для
5 в формуле B.12.31I
fdz \2
А 1 ¦ i:r = 2,2 2 о2/\ 2 2> B.13.4)
dp/ \dp/ n2kop2 — Р (z)p2 — mz
где выбраны цилиндрические координаты (р, ф, z) = (м, р, о). Если И
зависит от z, то /3 представляет собой также функцию от z и эту
функцию можно определить, используя B.12.33) в каждом сечении
z = const. Используя теперь B.13.2) для р вместо z, получаем
1 + p2(#/dzJ + (dp/dzJ = n2kl/P2(z). B.13.5)
Из системы уравнений B.13.4) и B.13.5) следует, что
pd(pfdp = m/[n2kop2 — P2(z)p2 — m2]1/2, B.13.6)
dz/dp = $pl\n2k\p2 — P2(z)p2 — m2]1/2. B.13.7)
Разделив первое из этих уравнений на второе, имеем
= m/p(z)p2. B.I3.8)
Заметим, что эти уравнения можно получить непосредственно из
уравнения для лучей. При этом величина т не обязательно является
m
2.13. Вычисление траекторий лучей 113
целой. Здесь мы рассматриваем конгруэнцию лучей, волновые фронты
которых распространяются по всему пространству. Этот частный
случай соответствует эйконалу типа B.12.24), для которого величина
т должна быть целой. С другой стороны, пытаясь покрыть все про-
пространство множеством лучей с нецелым т, мы не можем определить
однозначный эйконал. Поэтому мы будем рассматривать нецелые т
только для лучей, образующих трубку с малым поперечным сечением.
Величину т называют, как правило, инвариантом наклона, так
как она связана с поперечными направляющими косинусами р' и q'
соотношением
= k0Jj = ko[x- - y-j = kon(xq' - yp'). B.13.9)
Ксли п не зависит от z, то /3 является интегралом движения и
Р = kodS/dz = k0n(p)cosy, B.13.10)
где cos 7 — направляющий косинус относительно оси z.
Меридиональные лучи (т = 0) лежат в плоскостях, содержащих
ось z [см. B.13.8)]. Для них из уравнения B.13.7) следует, что
d2p/dz2 = ±(ko/pJd(n2)/dp. B.13.11)
Общее решение этого уравнения определяет все возможные меридио-
меридиональные траектории.
Пример 1: меридиональные лучи в градиентных волокнах. Рас-
Рассмотрим в качестве примера среду с показателем преломления, рас-
распределенным следующим образом:
п\р) = п2[\ - 5(р/р0J + а2<52(р/р0L + а3^3(р/РоN + -], B.13.12)
где аД/ = 1, 2, 3,...), 5, р0 — произвольные постоянные. Используя
нормализованные координаты
Д = Р/Ро> B.13.13)
Z = z5ll2noko/(ppo)9 B.13.14)
уравнение B.13.11) можно переписать в виде
К + R = RfiJajS^R2"-», B.13.15)
7 = 2
где две точки над R обозначают вторую производную по Z. Это нели-
нелинейное дифференциальное уравнение, сводящееся при а. = 0 к уравне-
уравнению гармонического осциллятора. При этом лучи описывают синусо-
синусоидальные траектории с пространственным периодом
Л = 2прор/(д1/2поко), B.13.16)
114 Гл. 2. Геометрическая оптика
который через величину /3 зависит как от начального (Z = 0) радиаль-
радиального положения pin, так и от угла 7*п относительно оси z. В общем
случае решением уравнения B.13.15) является периодическая функция
R(Z + 2tt/Q) = R(Z), где П — угловая частота, которая зависит от
параметра нелинейности 5, набора коэффициентов ctj и начальных ус-
условий Ro и Ro. Следовательно, функцию R(Z) можно представить в
виде ряда Фурье (метод Линштедта [15], см. также метод Крылова,
Боголюбова, Митрополъского [16]):
? a2j+ldj
R(Z) = acos(QZ + ^in) + ? Al2k + l x
j>k
x cos[Bfc + 1)(QZ + ф-Л B.13.17)
Постоянные а, Я и ф[п удобно записать в виде степенных рядов
по 8:
а= Zaj6>9 B.13.18)
j=o
» 5ja2j
П=1- Z^F2^ B.13.19)
i L
Фы = t W- B.13.20)
Если подставить эти разложения в ряд Фурье B.13.17), то из урав-
уравнения B.13.15) следует, что
^1,3 = -«2. #i = За2, B.13.21)
, B.13.22)
B.13.23)
где я0 и ^0 определяется через начальные условия
Rin = aQ cos ^о, ^in = - а0 sin ф0. B.13.24)
Кроме того, коэффициенты Су2А:, Sy2A: зависят от ау. В частности,
Q,o = 6a2, C1>2 = — 4a2, C1>4 = —«2»
S1>2 = 8a2, Sli4 = a2. B.13.25)
Если оборвать ряд B.13.17) на члене у = 1, то рассмотренный вы-
выше метод позволяет написать следующее выражение:
2.13. Вычисление траекторий лучей 115
а3
R(Z) s acosi^Z) + ЬА1 3—cos[3ip(Z)] =
' 16
= acos^(Z) - <5a2—cos[3i/KZ)], B.13.26)
16
j5«2[6 4cosB^0) cosD*0)], B.13.27)
lo
«z,-(, _*?b)z + Фо + ^^**М, B.„.28)
Сравнивая B.13.28) и B.13.19), с помощью выражения B.13.14), в
котором величина /3 представлена в виде B.13.10) для конкретных на-
начальных условий, можно записать следующее соотношение:
где были использованы также выражения B.13.17) и B.13.10) с учетом
начальных значений. В свою очередь из B.13.24) следует
UZ = 1 + -A —-^ )(Я?П + Rfn) h члены высшего порядка по 6.
L 2\ 2 / J Ро
B.13.30)
Отсюда видно, что фаза QZ не зависит от начальных условий при
а2 = 2/3.
Пример 2: самофокусирующие волокна. Рассмотрим среду, показа-
показатель преломления которой распределен в виде функции гиперболиче-
гиперболического секанса (sch-профилъУ.
n\p)lnl = sch2(E1/2p/Po) = 1 - Чр/РоJ + B<52/3)(р/РоL + •"• B.13.31)
Можно получить следующее точное решение уравнения B.13.11):
sh (д 1/2р/р0) = sh (д 1/2pin/Po) cos(<5 v2z/p0) +
+ tg yin ch Elf2pjpo)sinEll2z/po), B.13.32)
откуда приближенно (для малых аргументов д1/2р/р0) получаем
р = Pincos(<51/2z/Po) + tg yinsin^1/2z/po)Po/^1/2. B.13.33)
Таким образом, период не зависит от начального положения и накло-
наклона луча.
116
Гл. 2. Геометрическая оптика
2.13.2. Сферически-симметричные среды
Если показатель преломления л (г) имеет сферически-симметрич-
сферически-симметричное распределение, то удобно использовать сферические координаты
(г, 0, ф) = (/а, vy а). При этом простые соображения симметрии пока-
показывают, что каждый луч описывает плоскую траекторию, которая ле-
лежит в плоскости, определяемой начальным направлением луча sin и
начальной координатой rin.
Используя уравнение B,13.2) для переменных г и 0, с помощью
первых двух выражений B.12.36) получаем
1
7" + r sin вhr) = 2 , / 2> B.13.34)
\dr) \dr) п2 + c/r2
Udr
B.13.35)
Отсюда можно написать следующие выражения для (dd/drJ и
fde\2 -скЫп2в-т2
Ы =(c + HV)fcgrW0' ^2ЛЗ-36)
%. . ..г^.2.^п- B-13.37)
Следовательно, если ф — это угол между касательной к лучу и
радиус-вектором из начала координат (рис. 2.23), то
cos2 ф = I — I = •
dr\2 n2r
)
2r2
Заметим теперь, что для любого отдельного луча всегда можно
выбрать систему координат таким образом, чтобы плоскость траек-
траектории содержала ось z. Это соответствует случаю m = О
Рис. 2.23. Траектории лучей в
среде со сферически-симмет-
сферически-симметричным распределением пока-
показателя преломления.
2.13. Вычисление траекторий лучей 117
[см. B.13.37)]. При этом выражения B.13.36) и B.13.38) дают
^V = n2r4^~\2cos2ф = -с (с < 0). B.13.39)
В частности, прямолинейному лучу, проходящему через начало ко-
координат, соответствует параметр с = 0. Поскольку sin^cfe = rdd, со-
соотношение B.13.39) эквивалентно следующему:
nr sin ф = (—сI/2 = const (вдоль любой траектории). B.13.40)
Это выражение представляет собой обобщение закона Снеллиуса
для сред со сферически-симметричным профилем показателя прелом-
преломления. Оно известно также как теорема Боугера, которую можно ин-
интерпретировать как закон сохранения углового момента фотонов, дви-
движущихся через среду.
Следует заметить, что конгруэнция лучей относится к эйконалу ви-
вида S(r) = R(r) + 0@) + Ф(ф), только если все лучи имеют одинако-
одинаковые параметры сит. Если это условие не выполнено, то эйконал
нельзя представить в виде суммы функций отдельных переменных.
При т = 0 уравнение B.13.36) принимает более простой вид:
(dO/drJ = -с/{с + п2г2)г2. B.13.41)
Мы видим, что оно является сингулярным, когда
с + п2г2 = 0. B.13.42)
Условие B.13.42) определяет каустику лучевого поля, составленно-
составленного из лучей с т = 0 и общим параметром с. Таким образом, каустика
состоит из набора сферических поверхностей с центром в начале коор-
координат. Освещенная зона, т. е. часть пространства, в которой траекто-
траектории являются вещественными, определяется условием [получаемым
сразу из B.13.41)]
с + n2r2 ^ 0.
Круговые траектории с центром в начале координат могут сущест-
существовать лишь для некоторых г = 7. При этом радиус кривизны луча
совпадает с г, т. е. [см. B.4.14)]:
1 dlnn
f dr
B.13.44)
г = г
Кроме того, поскольку в этом случае dO/dr = оо, из уравнения
B.13.41) имеем
с= -п2г2. B.13.45)
118
Гл. 2. Геометрическая оптика
Другой важный класс траекторий существует для распределений
п(г), таких, что функция п(г)г имеет относительный максимум. В
этом случае для некоторых параметров с уравнение B.13.42) имеет
два корня: г{ и г2, а луч движется по траектории, ограниченной двумя
окружностями, компланарными с лучом и имеющими радиусы г] и г2
(рис. 2.24). В частности, конгруэнции, состоящие из замкнутых траек-
траекторий, описывают колебательные моды (типы колебаний) среды.
Рассмотрим пучок лучей, распространяющихся из z = +oo под
углом в = 0, т. е. первоначально параллельно оси z. Для данного луча
из уравнения B.13.40) мы имеем
c=-n2j\ B.13.46)
где / — первоначальное расстояние от оси z (прицельный параметр в
теории рассеяния или высота в теории линз). Достигнув расстояния
максимального сближения г*, которое, как можно вычислить с по-
помощью B.13.40) и B.13.46), определяется уравнением
пН2 = п2(г*)г*2, B.13.47)
луч возвращается на бесконечность, описывая траекторию, симмет-
симметричную относительно начальной и асимптотически образующую угол
0S с отрицательным направлением оси z. Угол 0S можно вычислить,
интегрируя уравнение B.13.41):
nj
(n2r2 - ni
-dr.
B.13.48)
пг
пг
Рис. 2.24. Траектории лучей в среде с радиальной симметрией, а — зависимость пг от г;
б — луч, отражающийся между двумя сферическими каустиками.
2.13. Вычисление траекторий лучей 119
Вообще говоря, угол рассеяния 0s(l) — это сложная функция при-
прицельного параметра /. Если функция п(г) непрерывна вместе со свои-
своими производными, то 0S -> 0 при / — 0 и / — оо. В других случаях, на-
например когда п сингулярна в начале координат, 0S — тг при / —> 0. Это
означает, что лучи с малым прицельным параметром отражаются в
обратном направлении.
В случае когда функция п{г) непрерывна при г = R и среда одно-
однородна (п не зависит от г при г > R), прямой луч с прицельным пара-
параметром / = R может быть захвачен в градиентную область показате-
показателя преломления. Точнее говоря, если
1/К> -d\nn/dr9 B.13.49)
то прямая траектория не возмущается, а если
1/R< -dlnn/dr, B.13.50)
то радиус кривизны луча меньше чем R, так что луч попадает в об-
область г < R9 достигает минимального расстояния до центра и вновь
уходит на бесконечность.
Для падающей плоской волны пучок лучей с прицельным парамет-
параметром / и кольцевым сечением 2тг/ dl уходит из неоднородной области
г < R в пределах телесного угла
da = 2п sin es\dejdl\dl. B.13.51)
При этом нетрудно показать (см. разд. 2.12.3), что
B.13.52)
Данное соотношение верно, если существует однозначное соответ-
соответствие между 0S и /.
2.13.3. Градиентные оптические элементы
Еще одно приложение рассматриваемого в этом разделе формализма
связано с возможностью изготовления линзовых элементов, в кото-
которых показатель преломления изменяется непрерывно в составляющем
линзу материале. Такие градиентные элементы [17, 18] эффективно
используются для уменьшения аберраций и для решения некоторых
других специальных задач. Примером градиентной линзы является
хрусталик человеческого глаза. Измерения, выполненные Войноу, по-
показывают, что у взрослого мужчины показатель преломления хруста-
хрусталика изменяется от 1,4387 на внутренней поверхности до 1,4005 на ме-
менее плотной внешней поверхности. Интерес к линзам со сферически-
симметричным градиентом показателя преломления первоначально
120
Гл. 2. Геометрическая оптика
Источник
Фазовые
фронты
Рис. 2.25. Траектории лучей в линзе Максвелла (рыбий глаз).
' Огибающая
эллиптических
лучей
Рис. 2.26. Траектории лучей в линзе Лунеберга [18].
2.13. Вычисление траекторий лучей 121
возник в технике СВЧ. В частности, в случае когда
п = а/(Ь + г2), а > Ь > О, B.13.53)
среда, называемая максвелловским рыбьим глазом, имеет одно важ-
важное свойство, а именно то, что она обладает способностью фокусиро-
фокусировать в единственную точку все лучи, выходящие из произвольной точ-
точки пространства. Действительно, можно показать, что все лучи, вы-
выходящие из некоторого источника, пересекаются во втором фокусе,
лежащем на прямой, соединяющей источник с началом координат
(/• = 0) [13]. Лучи образуют систему окружностей с центрами на пло-
плоскости, перпендикулярной прямой, соединяющей источник с фокусом.
Плоскость расположена точно посередине между источником и фоку-
фокусом (рис. 2.25). Расстояния от начала координат до источника и фоку-
фокуса связаны соотношением
rsrf = b. B.13.54)
Очевидно, что источник и фокус здесь можно поменять местами.
При этом их называют сопряженными точками.
Другой интересной оптической системой является линза Лунеберга,
показатель преломления которой внутри сферы радиусом R изменяет-
изменяется по закону
n2 = 2-r2/R29 B.13.55)
Если источник расположен на поверхности сферы, то лучи описывают
эллипсы [18], определяемые уравнением
х2 + уг{\ + 2ctg2a) - Ixyctgoi = R2. B.13.56)
Здесь а — угол между лучом, покидающим источник, и диаметром,
проходящим через этот же источник (рис. 2.26). Можно показать, что
все касательные к эллипсам на поверхности сферы параллельны оси х.
Это означает, что в случае постоянства показателя преломления окру-
Рис. 2.27. Использование линзы Лунеберга для получения коллимированного пучка от
точечного Источника, расположенного на поверхности линзы.
122 Гл. 2. Геометрическая оптика
жацэщей сферу среды (г > R) система выходящих наружу лучей па-
параллельна оси х, т. е. диаметру, проходящему через точечный источ-
источник (рис. 2.27).
Доказательства этих свойств максвелловского рыбьего глаза и
линзы Лунеберга мы оставляем в качестве задач.
2.14. СКАЛЯРНЫЕ УРАВНЕНИЯ ДЛЯ ЛУЧЕЙ
В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ;
ПРИНЦИП ФЕРМА
Метод разделения переменных можно с успехом использовать для
определения траекторий лучей, если распределение показателя пре-
преломления я (г) обладает некоторой симметрией по отношению к кри-
криволинейной системе координат. Здесь мы хотим доказать важное
следствие уравнения B.4.6), позволяющее определить траектории для
произвольного распределения я (г).
Для этого напомним, что геодезической линией метрического про-
пространства называется траектория, длина которой стационарна при
бесконечно малых изменениях траектории с фиксированными конеч-
конечными точками. Рассмотрим метрическое пространство, точки которо-
которого совпадают с точками обычного пространства, но метрика изменя-
изменяется в соответствии с функцией л (г), так что длина произвольной кри-
кривой между точками А и В определяется как
[АЯ] = Г n(r)ds. B.14.1)
JA
Величину [АВ] обычно называют оптической длиной. Докажем те-
теперь, что кривые, для которых величина [АВ] стационарна при фикси-
фиксированных точках А и В, или (что эквивалентно) геодезические линии
рассматриваемого пространства совпадают со всеми возможными ре-
решениями уравнения B.4.6), т. е. со всеми возможными лучами. Если
через А и В (сопряженные точки) проходит большее число лучей, то в
большинстве случаев эти лучи имеют одинаковую оптическую длину
[АВ], так что мы можем определить функцию V(A9 В), совпадающую
с оптической длиной лучей. Эту функцию называют точечной харак-
характеристикой среды, и ее свойства мы рассмотрим более подробно в
разд. 2.15.
На языке вариационного исчисления сформулированное выше свой-
свойство означает, что оптический путь является экстремальным по отно-
отношению ко всем другим кривым, которые не удовлетворяют законам
2.14. Скалярные уравнения для лучей 123
оптики. Для доказательства этого вычислим вариацию 8 величины
[АВ], используя для простоты математических выкладок в качестве
переменной интегрирования декартову координату (например, z):
гв гв
5 n(x9y9z)(l + х2 + y2)lf2dz = д F(x,x,y,y,z)dz, B.14.2)
JA JA
Здесь точки над буквами означают дифференцирование по z. Любая
кривая, соединяющая две фиксированные точки А и В, соответствует
одной из возможных выборок пар непрерывных функций x(z) и y(z),
принимающих определенные значения на концах интервала (zA> zB).
Вариация длин соответствует следующему изменению этих функций:
x(z) - x(z) + 8x(z)9 y(z) - y(z) + 8y(z), так что
5[АВЛ = (—дх + —дх + —ду + —dy)dz. B.14.3)
]А\дх дх ду ду )
Интегрируя по частям второй и четвертый члены в правой части
этого выражения и учитывая возможную разрывность показателя
преломления я(г), получаем
В / ^
дХ:
А
дх
„ CAs d 8F BF
sJas-X^Sxj dx
dz' B.14.4)
В правой части уравнения B.14.4) второй член является суммой по
поверхности S разрывов функции п(т), А связано с резкими изменения-
изменениями п при увеличении s, а третий член является суммой вкладов от об-
областей, в которых п(т) непрерывна. Одинаковыми индексами в каж-
каждом из членов обозначено суммирование по л: и >>. Так как А и В фик-
фиксированы, 8х(А) = 8х(В) = Ьу{А) = 8у(В) = 0. Поэтому первый
член в правой части B.14.4) равен нулю. Однако мы ищем геодезиче-
геодезические линии, удовлетворяющие условию
д[АВ~] = д n(r)ds = 0 (Л, В фиксированы) B.14.5)
при любых &с и Ьу. Из уравнения B.14.4) следует, что это возможно,
только если удовлетворяются следующие уравнения:
'"_„, |-^-^ = 0 B.Ы.6,
dz дх дх dz ду ду
124 Гл. 2. Геометрическая оптика
{уравнения Эйлера), дополненные условиями скачка на каждой по-
поверхности разрыва:
A(dF/dx) = A(dF/dy) = 0. B.14.7)
Если использовать соотношения ds = dz{\ + х1 + У1I'2,
sx = */A + i2 + j^I/2, sy = .у/A + jc2 + .у2I72, то сразу выяснится,
что уравнения B.14.6) совпадают со скалярными компонентами урав-
уравнения лучей B.4.5) вдоль осей х и у. Очевидно, что то же самое верно
и для оси z. Доказательство совпадения лучей с геодезическими линия-
линиями можно считать завершенным, если заметить, что уравнение
B.14.7) эквивалентно закону Снеллиуса. Это легко показать, выбирая,
например, ось z перпендикулярно поверхности разрыва, а плоскость
xz в качестве плоскости падения. Более строгий вывод закона Снелли-
Снеллиуса из вариационных принципов содержится в работе Зацкиса [19].
Обычно соотношения B.14.5) называют принципом Ферма. Со-
Согласно этому принципу, оптическая длина луча, соединяющего точки
А и В, меньше оптической длины любой другой кривой, соединяющей
эти точки и расположенной вблизи луча. Строго говоря, принцип
Ферма справедлив лишь в том случае, когда точки А и В расположе-
расположены достаточно близко друг от друга. Покажем это на примере вогну-
вогнутого сферического зеркала [1] (рис. 2.28). Пусть луч AQB соединяет
точки А и В, расположенные симметрично на прямой, проходящей че-
через центр О сферического зеркала у. Эллипс е с фокусами в точках А
и В лежит правее у, поэтому [AQB] = [AQ'B] > [AQ"B]. Следова-
Следовательно, длина [AQB] является относительным максимумом при сме-
смещении точки Q по поверхности зеркала. Обратная ситуация возника-
возникает, если рассматриваемые две точки А' и В' располагаются достаточ-
достаточно близко к точке Q. Из-за своей ограниченной применимости прин-
Рис. 2.28. Иллюстрация к формулировке
Каратеодори принципа Ферма [1].
2.14. Скалярные уравнения для лучей
125
цип Ферма нуждается в уточнении. Каратеодори сформулировал его
следующим образом: для каждой точки светового луча существует
конечная окрестность, в которой принцип Ферма справедлив. (Обоб-
(Обобщение принципа Ферма для дифрагированных лучей см. в разд. 6.7.)
2.14.1. Анизотропные среды
Проведенное рассмотрение можно обобщить и на тот случай, когда п
зависит как от г, так и от §, т. е. когда диэлектрическая проницае-
проницаемость является тензором [20, 21] (см. разд. 1.4). Если определить
функцию „ . «,„
eyy у v v 7^ — nlv v 7 г vVI -4- х2 4- v2\112 СУ 14 9Л
r\X,X,y,yiL) — П\Х, у, Z, Л, У )yi ^Г Л Т у ) 9 lZr.lt.OJ
то с ее помощью можно найти подходящее обобщение уравнения
B.4.6). Действительно, из B.14.6) следует, что
d dF dF ,Л .2 .2ч1/2Яйин ,2 ,2ч1/2
— —- — = A+х2 + У2I/2Т\ тгтA + х + У) +
dz dx dx ds\jdx
_l_ n * _ —(i + v2 + v2I/2 =0 B 14 9)
+ nA + x2 + y2I/2 I dx( + X + У ] ' ( Э)
или
B.14.10)
Поскольку
д _8sx д dsy д _
дх дх dsx дх dsy
l+у2 д
ху
A-f x2 + j>2K/2 dsx A + x2
уравнение B.14.10) можно привести к виду
d_\dn_ ( dn
dn
«Г. B-14.11)
B.14.12)
Это уравнение выведено в предположении, что п является функци-
функцией величин г, sx и sy9 причем sz = A - s? - фи2. Можно также пред-
представить п в виде явной функции величин sx, s и sz, если учесть следую-
B.14.13)
щие соотношения:
д
dsx
д7у
sy = const
sx = const
--I
QSX \Sy s const, 5Z = COnSt
-M
У \sx = const, Sz — const
sx d
sz dsz
Sy d
s2 ds2
sx = const, Sy = const
sx — const, Sy = const
126 Гл. 2. Геометрическая оптика
При этом уравнение B.14.12), а также аналогичные уравнения для
осей у и z относительно поверхности с нормалью п0 можно перепи-
переписать в виде
г я™ / д-\п л-
B.14.14а)
Д[{(л - s • \sn)s + \sn} • A - попоу] = 0. B.14.146)
Уравнения B.14.14) являются искомыми обобщениями уравнения
B.4.6) для анизотропной среды, в которой показатель преломления
зависит от направления распространения.
Заметим, что полученные выше соотношения описывают траекто-
траектории в виде узкого пучка лучей. В анизотропной среде такой узкий пу-
пучок распространяется параллельно вектору Пойнтинга (см. разд. 1.6),
который оказывается направленным под некоторым углом к нормали
к волновому фронту. Это указывает на различие между рассматривае-
рассматриваемым случаем и изотропной средой, в которой лучи совпадают с тра-
траекториями, перпендикулярными волновым фронтам.
Заметим также для большей ясности, что в однородной анизотроп-
анизотропной среде, согласно уравнениям B.14.14), лучи представляют собой
прямые линии. Напротив, волновые фронты, создаваемые точечным
источником в той же среде, являются сфероидами, а линии, нормаль-
нормальные к волновым фронтам, в общем случае криволинейны.
Пример 1. Приложение к электронной оптике. Интересна анало-
аналогия геометрической оптики с движением электрона в области постоян-
постоянных электрических и магнитных полей. Траекторию электрона можно
определить с помощью эквивалентного показателя преломления лэкв,
определяемого выражением
_ mv д # - (с точностью до произвольного
экв~ A — /?2I/2 * постоянного множителя), B.14.15)
где е — заряд электрона, т — его масса покоя, А — векторный по-
потенциал и /3 = v/c. Скорость электрона v связана со скалярным по-
потенциалом релятивистским законом сохранения энергии:
тс2
A _ ЩЩ -еФ = const. B.14.16)
Выражение B.14.15) называют основным уравнением электронной оп-
оптики.
Если подставить выражение B.14.15) для пэкв в уравнение
B.14.14а), то получим
d Г mvst ~| дпэкв
l^ + ^ BЛ4Л7)
2.14. Скалярные уравнения для лучей 127
Пример 2. Преломление необыкновенного луча в одноосном кри-
кристалле. К выводу правильного соотношения между п и § нужно отне-
отнестись с определенным вниманием. Поскольку единичный вектор S ка-
сателен к траектории луча, необходимо использовать уравнение луче-
лучевой поверхности (см. разд. 1.4.1). В частности, для одноосного кри-
кристалла
л2(§) = (S ¦ сЯп2о - гф + п],
где С и S — направления оптической оси (образующей угол ос с нор-
нормалью п0 к поверхности) и луча (параллельного вектору Пойнтинга)
соответственно. Следовательно,
VgAi = п-\п\ - nl)(S • С)С, B.14.18)
и для нормального падения луча из уравнения B.14.146) мы имеем
2.14.2. Геодезические линзы
Интересным приложением принципа Ферма является геодезическая
линза, которая состоит из тонкого диэлектрического слоя с постоян-
постоянным показателем преломления п, нанесенного на подложку с неболь-
небольшим углублением (рис. 2.29). Такие двумерные структуры обладают
волноводными свойствами, т. е. луч, первоначально касательный к
волновод
Рис. 2.29. Геодезическая линза, образованная углублением в планарном волноводе. (Из
работы [23].)
128
Гл. 2. Геометрическая оптика
поверхности углубления, меняет свое направление и следует по каса-
касательной к поверхности [22]. Для некоторых типов поверхностей такая
система может действовать как линза, собирающая световой пучок,
поступающий в этот оптический волновод.
Вообще говоря, геодезическая линза представляет собой поверх-
поверхность вращения (рис. 2.30). В цилиндрических координатах профиль
линзы описывается функцией zip), а оптический путь дается выраже-
выражением
где мы положили п = 1, что вполне оправдывается, поскольку пока-
показатель преломления считается постоянным.
Применяя вариационный критерий B.14.5), соответствующее урав-
уравнение Эйлера можно записать в виде
dp д(Aф/с1р) дф
Рис. 2.30. Траектории лучей в геоде-
геодезической линзе. Здесь ф' — «проек-
«проекция» угла ф на плоскостью = const.
(Из работы [23].)
2.14. Скалярные уравнения для лучей 129
где F — подынтегральное выражение в формуле B.14.20). Учитывая
затем соотношение dF/дФ = 0, получаем
[1 + (dz/dpJ
о ы
здесь С — величина, постоянная вдоль луча. Полученное отсюда вы-
выражение для ф дает дифференциальное уравнение геодезической линии:
ф = СП + z2I/2/p(p2 - C2I/2, B.14.23)
где точка над буквой обозначает производную по р.
Если обозначить через тг/2 — ф угол между лучом и меридиональ-
меридиональной линией (ф = const) на поверхности, а через dL — длину дуги, то
B.14.20) и B.14.22) сводятся к уравнению
pcosi^ = p2|d</>/dL| = \C\. B.14.24)
Это уравнение называется теоремой Клэро, которую можно рас-
рассматривать как обобщение закона Снеллиуса [см. также теорему Боу-
гера B.13.40)] применительно к однородной среде.
2.14.3. Метод ковариантного дифференцирования
Эквивалентность лучей и геодезических линий позволяет использо-
использовать стандартный формализм ковариантного дифференцирования,
обычно используемый в общей теории относительности. При этом
мы можем получать дифференциальные уравнения, описывающие оп-
оптические траектории в произвольной системе координат.
Как мы уже отмечали, метрику трехмерного пространства можно
определить с помощью соотношения
#2 = n2ds2 = giidxidxi B.14.25)
[символ d\l/, используемый здесь и в дальнейшем, не имеет ничего об-
общего с углом ф в B.14.24)], где предполагается суммирование по пов-
повторяющимся индексам (правило Эйнштейна). Тензор gtj зависит от
выбранной системы координат. Например, в ортогональных коорди-
координатах имеем
V*? 0 0 "
B.14.26)
~n2h\
0
0
0
n2h\
0
0 "
0
n2h2
где Л. — соответствующие масштабные множители.
Геодезические линии, соответствующие метрике B.14.25), описыва-
130 Гл. 2. Геометрическая оптика
ются уравнениями [24]
d х. Их-J /7v
ii? + Fjk — — = 0, B.14.27)
где r'Jk (символы Кристофеля второго рода) определяются следую-
следующим образом:
Г» — ±nim(n 4- п — а \ B 14 28^
1 :к — 2?/ \Ут] к ' Утк.] У]к,т/* у**ш i~t»**\jj
Правый нижний индекс ", Г обозначает частную производную по х'.
Тензор gim является дуальным к gim и его компоненты удовлетворяют
соотношению
gimgmj = 5), B.14.29)
где
<5}=1 (/=;), 5) = 0 (i#;) B.14.30)
есть тензор Кронекера. Для ортогональных координат, соответству-
соответствующих тензору B.14.26), сразу получаем
~\/(n2hi) 0 0
0 l/(n2h22) 0 . B.14.31)
0 0 l/(n2h32)
Несмотря на формальную элегантность скалярных уравнений лу-
лучей в криволинейных координатах [уравнения B.14.27)], их не столь
просто использовать из-за зависимости коэффициентов Т1]к от распре-
распределения показателя преломления. Чтобы придать этим уравнениям
более простую форму, введем величины gij9 определяемые следующим
образом:
ди = д»/п2, B.14.32)
которые зависят только от выбора системы координат. Используя в
B.14.28) обозначения B.14.32), мы имеем
Г)к = Г)к + (l/n)gim(nkgmj + njmk - nmgjk), B.14.33)
так что с помощью соотношений дуальности, определяющих g*J, мож-
можно записать следующее выражение:
Г}к = Г)к + A/п)E)пк 4- Sfrj - njimgjk). B.14.34)
УЧ.
Символ PJk обозначает ту же величину, что и Г^, но выраженную
через g, а не через g. Таким образом, мы имеем следующие уравнения:
d2xl I d/ldxl\ I d2xl 1 dndx1
_ 1 d /1 dxl\ _ 1 d2xl
nds\n ds J n2 ds2
dip2 nds\n dsj n2 ds2 n3 ds ds
2.15. Элементы гамильтоновой оптики 131
d2xl 1 дп dxj dxl
'dsr~ni'dx~'lblb- BЛ4'35)
Заметим также, что из B.14.25) и B.14.32) следует равенство
= 1. B.14.36)
Эти соотношения позволяют переписать уравнения B.14.27) в виде
as as as as as /i dxJ
Здесь второй член связан непосредственно с выбранной системой
координат, а третий и четвертый — с неоднородностью среды.
Пример. Цилиндрические координаты. Запишем уравнения
B.14.37) в цилиндрических координатах я1 = р, х2 = </>, х3 = z. Не-
Нетрудно доказать (мы оставляем это доказательство в качестве
задачи), что
Г\2 = -Л Т\2 = Г221 = 1/р, B.14.38)
а все остальные Г обращаются в нуль. Отсюда следует, что уравнения
B.14.37) можно переписать в виде
d2p [d(l)\2 dinn dp I дп
ds2 \ds J ds ds ndp'
d2<t> Idpdfy dlnnd<t> 1 дп
—T -I ^ z_ — — — Г2 14 39)
ds p ds ds ds ds np дф \*.i-r.j7)
d2z dlnn dz _ 1 дп
ds2 ds ds n dz
2.15. ЭЛЕМЕНТЫ ГАМИЛЬТОНОВОЙ ОПТИКИ
Любой оптический прибор К можно рассматривать как среду, показа-
показатель преломления которой описывается определенной функцией коор-
координат. Вообще говоря, прибор предназначается для создания по воз-
возможности наилучшего изображения предмета с заданными характери-
характеристиками. Ту область, в которой находится предмет, принято назы-
называть пространством предмета. В свою очередь термин простран-
пространство изображения используют для обозначения области, в которую
попадают лучи от предмета после прохождения через прибор К. Су-
Существенное упрощение построения изображения возможно в том слу-
132 Гл. 2. Геометрическая оптика
чае, когда среда однородна как в пространстве предмета, так и в про-
пространстве изображения. При этом начальные и конечные участки луча
являются прямыми линиями.
Чаще всего от оптического прибора требуется, чтобы он давал
резкое изображение плоского предмета, которое геометрически подоб-
подобно самому предмету. В некоторых случаях от прибора К требуют,
чтобы он давал квадратное изображение прямоугольного предмета.
Это бывает необходимо, например, для съемок широкоформатных
фильмов, когда очень большое горизонтальное поле зрения требуется
спроецировать на кинопленку обычного формата. В других случаях
может потребоваться создание резкого изображения плоского предме-
предмета на неплоской поверхности.
Идеальным было бы такое изображение, когда все лучи, исходя-
исходящие из некоторой точки О предмета, проходили бы через соответ-
соответствующую точку изображения О'. В реальных же системах лучи из
точки О, вообще говоря, не пересекаются в одной точке О' про-
пространства изображения. Если система отображает плоский предмет,
расположенный в плоскости Г^, в плоское изображение на Ц и если
некоторый луч из О пересекает Ц в точке О[% то вектор О'О[Ь соеди-
соединяющий искомое изображение О' с О/, является мерой Лучевой абер-
аберрации.
Если пространства предмета и изображения однородны, то узкий
гомоцентрический пучок лучей с фокусом в точке О, собранный вокруг
центрального луча Ry преобразуется оптическим прибором К в астиг-
астигматический пучок, характеризующийся двумя фокальными линиями,
расстояние между которыми называют астигматической разностью
пучка. Из простых геометрических построений следует, что если фо-
фокальные отрезки имеют одинаковую длину а, то лучи пучка пересека-
пересекают круговой контур диаметром а/2. При этом точка наилучшего изо-
изображения О' располагается точно посередине между фокальными ли-
линиями, в центре диска наименьшего искажения.
Вообще говоря, различная ориентация центрального луча пучка не
позволяет свести до нуля астигматическую разность пучка. Исключе-
Исключения возможны лишь для некоторых частных поверхностей, создава-
создаваемых полем предмета. При этом резкое изображение определенных
точек можно получить путем ограничения апертуры пучка лучей. Од-
Однако в некоторых специальных системах существуют поверхности,
идеальное изображение которых можно получить и с помощью
широкоугольных лучей. Например, для однородной сферы радиусом г
с показателем преломления л, помещенной в среду с показателем пре-
2.15. Элементы гамильтоновой оптики 133
ломления л', идеально отображаются друг в друга сферические по-
поверхности радиусами rn/ri и гп'/п (предлагаем доказать это читате-
читателю самостоятельно). Учитывая это свойство, Амичи в 1840—1850 го-
годах использовал сферические линзы для объективов микроскопа (см.
задачу 13 в данной главе).
Для большей конкретности рассмотрим осесимметрическую си-
систему К, состоящую из поверхностей вращения с общей оптической
осью. Точка предмета О и оптическая ось определяют меридиональ-
меридиональную плоскость. Луч, касательный к этой плоскости, должен лежать в
ней полностью. Немеридиональный луч называется косым и нигде не
пересекает оптическую ось. Как следует из соотношений B.11.22), в
пространстве изображения фокальные линии меридионального луча
соответственно параллельны и перпендикулярны меридиональной
плоскости. Поэтому их называют сагиттальной и тангенциальной
фокальными линиями. Для косых лучей это свойство несправедливо.
В частности, если точка О лежит на оптической оси, то каждый про-
проходящий через нее луч является меридиональным. При этом каустика
широкоугольного пучка лучей состоит из сагиттальной поверхности
вращения вокруг оптической оси и тангенциальной фокальной поверх-
поверхности, представляющей собой отрезок оптической оси (см. пример в
разд. 2.10.1.6). Для небольших апертур эта поверхность стягивается в
точку, если О совпадает с апланатической точкой линзы. На языке
теории аберраций конечные размеры каустики аксиального точечного
источника обусловлены главным образом сферической аберрацией, ко-
которая минимальна для некоторого определенного положения предмета.
2.15.1. Точечные, угловые и смешанные характеристики
Для анализа качества изображения, создаваемого в системе последо-
последовательных искривленных преломляющих поверхностей, необходимо
проследить за достаточно большим числом лучей, интегрируя уравне-
уравнения лучей в наиболее удобной системе координат. Кроме того, может
потребоваться последовательное вычисление с помощью B.11.22)
центров кривизны пучков лучей в отдельных однородных областях
пространства. Эти расчеты можно выполнить очень быстро с по-
помощью специальных компьютерных программ. Однако для предвари-
предварительного выбора параметров линзы необходимо провести приближен-
приближенный аналитический расчет аберраций. Этому существенно поможет
применение изящной теории аберраций, предложенной Гамильтоном.
Преимущества этого метода основаны на возможности получения
точных результатов исходя лишь из симметрии системы.
134
Гл. 2. Геометрическая оптика
R(x,y,z)
Рис. 2.31. Оптический путь между двумя точками (PQ и Pj), расположенными соот-
соответственно в пространстве предмета и изображения.
Главным параметром в методе Гамильтона, называемом гамиль-
тоновой оптикой, является длина оптического пути [Ро, Рх] между
двумя произвольными точками Ро и Рх системы К (рис. 2.31). Это рас-
расстояние называют точечной характеристикой и обозначают как
V(P0, Рх). Она совпадает с эйконалом в точке Рх лучевого поля от ис-
источника, расположенного в Ро (или наоборот). Непосредственно из
уравнения эйконала B.3.1) следует, что градиентом величины К по ко-
координате РО(РХ) является вектор, направленный по лучу R через точку
Р0(Р{) и имеющий модуль п(Р0)[п(Рх)]. Градцент направлен вдоль лу-
луча R для точек, лежащих в пространстве изображения, и противопо-
противоположно ему для точек в пространстве предмета. В дальнейшем мы бу-
будем считать, что Ро располагается в пространстве предмета, а Рх — в
пространстве изображения, так что
Го V(P0,Pi) = -nos(Po), V, V(PO9PX) = пМ). B.15.1)
Теперь удобно определить оптические направляющие косинусы1^
р = nsx, q = nsy и г = nsz, с помощью которых уравнения B.15.1)
можно переписать в скалярной форме:
Ро = -dV/dx0, q0 = -dV/dy0, r0 = -dV/dz0,
Pl = dV/dxl9 q1 = dV/dyl9 rv = dV/dzx. BЛ5-2>
Здесь ^о,^,^ — декартовы координаты точки Ро в системе коорди-
координат Со, a xv yv zx — координаты точки Р]9 относящиеся, вообще го-
говоря, к другой системе. Обозначая буквами с точкой производные по
z0, из уравнения лучей B.4.6) имеем
Ро = дго/дхО9 q0 = дго/дуо,
х0 = -дго/дро, у0 = -dro/dqo.
!) Эти же величины называют лучевыми компонентами. См. книгу [11] в гл. 1,
с. 139 русского издания. — Прим. перев.
2.15. Элементы гамильтоновой оптики 13 5
Величины ро> q0 и х0, у0 являются сопряженными переменными в
функции Гамильтона #(*<,, х0, у0, /?0, д0) = г0 = [л2(*0> >>0, ^) - /т§ -
— ^о!12' К0Т°Рая в общем случае представляет собой явную функцию
координаты z0. В соответствии с этим луч ведет себя так же, как зави-
зависящая от времени система с двумя степенями свободы. Следователь-
Следовательно, мы можем ввести фазовое пространство, образуемое точками с
координатами р0, q0, х0 и у0. Для систем, описываемых гамильтониа-
гамильтонианом, справедлива теорема Лиувилля [25, 26], которая гласит, что
объем элемента фазового пространства сохраняется постоянным за
время его эволюции. В нашем случае объем dx0 dy0 dp0 dq0 постоянен
вдоль луча. В соответствии с этим определитель лучевой матрицы,
которую мы рассмотрим в разд. 2.15.3, должен быть равен единице.
Таким образом, форма области, занимаемой пучком лучей в фазовом
пространстве, при прохождении через оптический прибор изменяется,
но объем ее сохраняется постоянным. Следует заметить, что в парак-
параксиальном приближении это свойство позволяет определить инвариант
Лагранжа [см. B.15.27)].
Анализ распространения в фазовом пространстве является весьма
общим методом при проектировании систем, связанных с транспорти-
транспортировкой пучков частиц. Каждый элемент (например, квадруполь) таких
систем характеризуется областью захвата. Только те пучки, объем фа-
фазового пространства которых попадает в области захвата отдельных
элементов, могут пропускаться системой [27].
Если не рассматривать афокальных систем, используемых, напри-
например, в качестве расширителей пучков, то для определения луча R до-
достаточно шести координат: х0, у0, z0, xv yv zx или же величин направ-
направляющих косинусов р0, q0, pv qv заданных вместе с Zq и zv Вообще го-
говоря, можно установить взаимно-однозначное соответствие между
двумя наборами переменных: (х0, у0, z0, xv yv zx) ~ Uo, zvp0>q0,pvqx).
Чтобы можно было использовать второй комплект переменных, не-
необходимо ввести другую характеристическую функцию, а именно
функцию Г, называемую угловой характеристикой, которая связана с
У соотношением
B.15.4)
При малых сдвигах точек Ро и Рх с помощью выражений B.15.2) мож-
можно записать дифференциал функции Т в виде
dT = xodpo + yodqo + zodro -х^рх -y^dqx -zxdrx. B.15.5)
Учитывая.затем соотношение между г0, гх и р0, q0, pv qv мы
136 Гл. 2. Геометрическая оптика
имеем
х0 = дТ/др0 + to(pjro\ Уо = ST/dq0 + zo(qo/ro),
xt = -дТ/др% - z.ipjr.l у, = -dt/dqt - z^qjrj. BЛ5^
Из простого геометрического рассмотрения следует, что Т являет-
является оптической длиной луча между основаниями Qo и Qx перпендикуля-
перпендикуляров, опущенных на луч из начал систем координат, заданных соот-
соответственно в пространстве предмета и изображения. В частности, для
осесимметричных систем и систем координат Со и Сх (см. рис. 2.31), у
которых оси z совпадают с оптической осью, Т зависит только от сле-
следующих комбинаций направляющих косинусов:
" = Ро + 4о> v = P2i+Ql> w = 2(p0Pi + 9o9i)- B.15.7)
В некоторых задачах, встречающихся, например, в связи с дифрак-
дифракционным анализом оптических приборов (разд. 4.13), удобно исполь-
использовать смешанную характеристику W, определяемую следующим об-
образом:
W{xO9yO9zo; zupuqx) = К(Р0,Л) - *iPi - У1Я1 - zir\* B.15.8a)
Для этой характеристики мы имеем
р0 = -dW/дХо, q0 = -dW/dy09
B.15.ОО)
хх = -dWldpx - ZiipJrJ, yx = -dW/dqx - z^qjr^.
2.15.2. Угловая характеристика поверхности вращения
Последовательность поверхностей вращения, разделяющих однород-
однородные среды, образует составные линзы. В общем случае, если записать
уравнение отдельной поверхности в виде z = f(x, у), то непосред-
непосредственно из принципа Ферма (разд. 2.14) получаем выражение
для V:
V(xo,yo,zo; xi9yl9zt) = g(P0,Pi\ x9y,z) m
= *o[(x " xoJ + (У - >>oJ + (z - zoJV12 +
+ «i[(^i - *J + (Ух - УJ + (*i - ^J]1/2> B.15.9)
причем мы имеем следующие условия:
|*+§?f = 0, l^ + ^-a B.15.10)'
дх dz дх ду dz ду
Вследствие этого, если в качестве системы координат для плоско-
плоскостей предмета и изображения использовать плоскость, проходящую
2.15. Элементы гамильтоновой оптики
137
Рис. 2.32. Распространение луча через
две однородные среды, разделенные по-
поверхностью вращения вокруг оси z.
через вершину поверхности z0 = z{ = zv = ДО, 0), то относительная
угловая характеристика То (см. соответствующее геометрическое по-
построение на рис. 2.32) запишется в виде
То - (Ро ~ Pi)x + (во " <Lib + (г0 - rj/fey), B.15.11)
где Р{х9 у, f(x, у)) — точка пересечения преломляющей поверхности
лучом R. Кроме того, из закона Снеллиуса следует, что
Ро ~ Pi = -{г0 - rx)df/dx9 q0 - qx = -(г0 - rjdf/ду. B.15.12)
Учитывая это, относительйую угловую характеристику можно запи-
записать в виде
То = (г, - ro)lx(df/dx) + y(df/dy) - /]. B.15.13)
Далее, следуя Лунебергу [1], введем переменные а = df/dx и
/? = df/dy, а также функцию Й(а, ]8), определяемую следующим обра-
образом:
П(а,/») = х^ + у~ - / = х(а,j?) + y(<xj) -
p). B.15.14)
Учитывая выражения B.15.12)—B.15.14), окончательно получаем
B.15.15)
ro ~~ ri
ro ri
Нетрудно проверить, что для поверхности вращения z = /(p) при
О = pdf/dp - /, соотношение B.15.15) принимает вид
-J—^-j \ B.15.16)
где аргументы и, v и w определены выражениями B.15.7). Для сфери-
сферической поверхности радиусом R выражение B.15.16) имеет простой
138 Гл. 2. Геометрическая оптика
вид:
То = jRsgn^ - no)(nl + п\ - w - 2гхг0I/2 + Я(г0 - гг) =
= Ksgn^ - no)\noso - n&l + Я(г0 - rj. Г2.15.17)
Здесь учтено, что R > О для выпуклой поверхности и Я < 0 в обрат-
обратном случае.
Теперь нетрудно найти угловую характеристику при z0 Ф zx Ф zv,
поскольку в общем случае Т линейно зависит от z0 и z{, причем коэф-
коэффициенты пропорциональности равны соответственно — г0 и гх. Таким
образом,
T(z^zx\ po,qo>Pu<li) = ^sgn(n! - no)(n% + n2t - w - Ir^I12 +
+ (zx -zv- R)r, - (z0 - zp - R)r0. B.15.18)
В частности, если u9 v9 w < l9 то для zy = 0 и Д = nl - л0 полу-
получаем
If A A 1
Т~ nlzl - nozo + — —Rw + Ru-\ zou + Rv z^v +
2AL "o *i J
\2
2.15.3. Лучевая матрица
Определим для осесимметрической системы поперечные векторы
р0 = хх0 4- уу0 и pj = &J + $yv При этом выражения B.15.6) можно
переписать в векторной форме:
= 2родТ/ди + 2рх 3T/5w,
B.15.20)
= -2р0 3T/3 2 5T/3
где р0 = хр0 4- у<70, pj = xpj + y^j. Из этих соотношений, в частно-
частности, следует, что вектор р х р остается постоянным вдоль луча, рас-
распространяющегося через осесимметрическую систему. Модуль m это-
этого вектора, называемый наклоном (см. также инвариант наклона;
разд. 2.13.1), можно использовать для того, чтобы сделать проще по-
построение хода луча в центрированной системе, как это было первона-
первоначально сделано Смитом в 1821 г. Например, инвариантность наклона
приводит к оптической теореме синусов [28]. В общем случае выра-
2.15. Элементы гамильтоновой оптики 139
жения B.15.20) удобно переписать в матричной форме:
Г Pi I [А Bl Гр0 | ^ s ^ Гро1 B.15.21)
где
дТ/dv = gT/3n 1
dT/d' 5T/a' 2(dT/d)9
2(dT/dw)9 С '
B.15.22)
Из написанных выше выражений следует, что определитель луче-
вой матрицы S равен единице. В частности, для сферической поверх-
поверхности, описываемой угловой характеристикой B.15.16), можно напи-
написать
Л = го/гх -(zx -zv-R)KJru
B = (zt-zv-R)/r0-(zv + R-zo)/rl + Kx(zx -zv-R)(zv + R-
C=-tnoso-n1s1|/[Rsgn(n1-no)]=-/C1, B.15.23)
где Кх называется степенью наклона поверхности. В общем случае Кх
является функцией переменных и, v и w.
При достаточно малых р0 и р0 коэффициенты А, В, С и D не зави-
зависят от р0 и рг Это область гауссовой оптики, в которой оптические
приборы описываются системной матрицей Sj 0, образованной гаус-
гауссовыми постоянными А, В, С и D. (Свое название этот раздел оптики
получил в честь К. Гаусса, который в своей известной статье «Диоп-
«Диоптрические исследования», опубликованной в Гёттингене в 1841 г., пер-
первым провел анализ преломляющей сферы, используя разложения в
степенные ряды.) Например, для сферической преломляющей поверх-
поверхности соотношения B.15.23) при нулевых р0 и рх приводят к матрице
1"-vi "v/ '
w0 n1
-к и.
B.15.24)
где К = (пх — no)/R — предельное значение степени наклона К{ при
малых углах, называемое преломляющей способностью.
Если сдвинуть плоскости z = z0 и z = zv то новую матрицу мож-
можно построить, используя линейную связь между угловой характери-
характеристикой Т и Zq, z}:
140 Гл. 2. Геометрическая оптика
= T(z\9zx) • S(zo,*i) • T(zo,z'o)9 B.15.25)
где матрицы перехода Т учитывают сдвиг опорных плоскостей.
В общем случае, если коэффициент В равен нулю, то все лучи, вы-
выходящие из Ро, проходят через Рх независимо от начального направле-
направления. Это означает, что Рх является параксиальным изображением точ-
точки Ро. Если это свойство выполняется в параксиальном приближении
для всех точек плоскостей z = z$ и z = zx, то эти плоскости называ-
называются сопряженными плоскостями. Таким образом, условием сопря-
сопряженности двух плоскостей является равенство нулю коэффициента В.
Для двух произвольных величин z = Zq, z = zx плоскость, сопряжен-
сопряженную к z = Zq, можно найти, сдвигая опорную плоскость в простран-
пространстве изображения, т. е. изменяя величину z[ в B.15.25) до тех пор, по-
пока коэффициент В не станет равным нулю.
Аналогично если система освещается коллимированным пучком,
то вектор рх не будет зависеть от р0, при условии, что плоскость
z = zx совпадает с фокальной плоскостью прибора. Ее положение
можно найти, сдвигая плоскость z = z[ до тех пор» пока не станет
равным нулю коэффициент А. Каждая система имеет две главные
(или единичные) плоскости, такие, что изображением любой точки р0
является pj = р0. Положение этих плоскостей можно найти, потребо-
потребовав выполнения условий А = 1 и В = 0. Точка на оси такая, что исхо-
исходящий из этой точки исходный луч составляет с оптической осью
угол, равный углу, образуемому выходящим пучком, называется узло-
узловой точкой; для нее В = 0, D = пх/п0. Если пх = п0, то узловые точ-
точки (в пространстве предмета и изображения) лежат на главных пло-
плоскостях.
В общем случае оптическая система характеризуется своими фо-
фокальными и главными плоскостями. Изображение предмета О можно
получить с помощью геометрического построения, иллюстрируемого
на рис. 2.33 и 2.34. Соответствующая лучевая матрица записывается в
виде
где М — поперечное увеличение предмета, a fx — расстояние от фо-
фокальной плоскости в пространстве изображения до соответствующей
главной плоскости; величина fx положительна, если П^ лежит справа
от Пм1. Обозначим теперь через ф0 и ф{ начальный и конечный углы,
2.15. Элементы гамильтоновой оптики
141
Рис. 2.33. Положение единичных (главных) плоскостей Пм0, Пм1 и фокальных плоскостей
Пу0, Пу-j линзы, лучевая матрица которой построена относительно произвольных пло-
плоскостей По и Пг
образованные с оптической осью параксиальным лучом, проходящим
через точки Р и Р'. Используя приведенное выражение для S, имеем:
фх = фопх/(Мпо). Кроме того, рх = Мр0. Объединяя эти два соотноше-
соотношения, получаем так называемый инвариант Смита — Гелъмголъца или
Лагранжа (см. книгу [11] в гл. 1):
noPo<t>o = niPi<t>i- B.15.27)
Чаще всего оптическая система ограничивает возможный размер
пучков, которые могут проходить через К. Такими ограничителями
могут быть оправы линз или другие препятствия, наличие которых
называют виньетированием (рис. 2.35). Параксиальные изображения
передним и задним элементами системы К образуют соответственно
входной и выходной зрачки. Лучи, касающиеся границ зрачков, назы-
называются боковыми, а луч, проходящий через предмет и центр выходно-
выходного зрачка, называют главным лучом. Эти лучи играют важную роль
при анализе аберраций.
(
р
¦ojf
По
« о]
Рис. 2.34. Лучевая матрица относительно двух сопряженных плоскостей (Пр и Ilj); M — ли-
линейное увеличение предмета в плоскости Г^; fx — расстояние от фокальной плоскости ГЬ,
до главной плоскости Пм1; fx положительно, если плоскость П^ лежит справа от Т\иХ •
142
Гл. 2. Геометрическая оптика
Рис. 2.35. Входной и выходной зрачки оптической системы. Луч, проходящий через О'
и Е', называется главным. Апертура А не отделяет пучка лучей от аксиальных точек.
Если предмет О расположен достаточно далеко от оси, то выходной зрачок выглядит
частично освещенным, что показано на врезке (на рисунке справа вверху). Такое частич-
частичное освещение называют виньетированием. I — плоскость предмета; 2 — входной зра-
зрачок; 3 — первая поверхность; 4 — последняя поверхность; 5 — выходной зрачок; б —
плоскость изображения; 7 — ограничитель; 8 — прошедший пучок.
Для оценки световой энергии, проходящей через систему, часто ис-
используют числовую апертуру (ЧА). В параксиальном приближении
она равна показателю преломления л0, умноженному на половину
угла конуса лучей, собираемых входным зрачком от точки О аксиаль-
аксиального предмета. Аналогичную величину можно определить и в про-
пространстве изображения. Используя значения волнового вектора, чис-
числовой апертуры и координат предмета Р0(х0, у0, z0), положение точки
Ро можно охарактеризовать с помощью безразмерных величин, назы-
называемых оптическими координатами:
vx = feoxoNAo, vy = /co.yoNAo, п = feoz0NAg. B.15.28)
Аналогичные определения можно ввести и для пространства изо-
изображения, в котором числовую апертуру 4Aq необходимо заменить на
на 4Aj = (no/n{LAo/ IMI, где М —- поперечное увеличение. Если
плоскости z0 = 0 и zx = 0 являются сопряженными, то легко пока-
показать, что модули оптических координат двух сопряженных точек,
близких соответственно О и О', равны друг другу.
Оптический прибор можно также характеризовать размером пред-
предмета, изображение которого воспроизводится более или менее правдо-
правдоподобно. Если обозначить через Л площадь области предмета, а через
Q — инструментальный угол, то величину
U = ACl B.15.29)
называют светосилой или светособирающей способностью. Этот па-
параметр имеет большое значение для спектроскопических приборов
2.15. Элементы гамильтоновой оптики 143
(см. разд. 7.21.2). Кроме того, величина U/X2 определяет число точек
предмета, которые можно разрешить на изображении предмета, фор-
формируемом прибором с данной светосилой (см. разд. 4.15.5).
Показав, какими богатыми возможностями обладает гауссова оп-
оптика для анализа оптических систем, в заключение напомним читате-
читателю, что лучевую матрицу системы можно построить, заменяя линзу
набором плоскостей, касательных к вершинам преломляющих поверх-
поверхностей. Последовательно перемножая матрицы, относящиеся к пре-
преломляющим поверхностям, и матрицы перехода между соседними
плоскостями, можно вычислить результирующую матрицу системы.
Этот метод не является новым, он давно используется для конструи-
конструирования и анализа систем, применяемых в технике ускорителей для
транспортировки заряженных частиц. Интересное описание этого при-
приложения содержится в книге Стеффена [27].
2.15.4. Аберрации волнового фронта
В анализе аберраций, начатом в 1856 г. Зайделем, удобно использо-
использовать специальные координаты для плоскостей предмета и изображе-
изображения и для входного и выходного зрачков. Их выбирают из тех сообра-
соображений, чтобы в параксиальном приближении все координаты точек
пересечения луча с указанными плоскостями совпадали. При этом из-
изменения этих координат (координат Зайделя) для конечного луча яв-
являются мерой отклонения от идеальной параксиальной траектории.
Мы уже определили аберрацию оптической системы К как ее не-
неспособность пропустить луч из точки предмета О точно через точку
изображения О'. При рассмотрении дифракционных явлений, приво-
приводящих к отличию К от идеального прибора, удобно описывать абер-
аберрации как отклонения волновых фронтов от некоторых идеальных по-
поверхностей. В частности, если рассматривать изображение точки О
осесимметричной системой К, то ее гауссово изображение О' находит-
находится в точке пересечения главного луча, выходящего из точки О, с пло-
плоскостью, сопряженной с плоскостью предмета. Рассмотрим теперь
волновой фронт W, проходящий через центр выходного зрачка ?" и
гауссову опорную сферу Ws радиусом R, также проходящую через Е'
и имеющую центр в точке О' (рис. 2.36). Луч R, выходящий из точки
О, будет пересекать W и Ws в двух точках, например соответственно в
точках А и В. Расстояние между этими точками с учетом знака
[АВ] = wo принимается в качестве меры деформации волнового
Фронта W и называется функцией аберраций или запаздыванием вол-
волнового фронта (см. книгу [29], с. 106).
144
Гл. 2. Геометрическая оптика
О'(х,у,О)
Рис. 2.36. Сечения истинного и опорного сферических волновых фронтов (радиусом R).
Функция аберраций JVQ равна расстоянию [АВ] между двумя поверхностями. Выходной
зрачок задает область определения функции WQt которая для главного луча обращается в
нуль. 1 — опорная сфера; 2 — центральная точка луча; 3 — истинный волновой фронт; 4 —
отрицательная функция аберраций WQ; ^ -— положительная WQ; 6 — главный луч; 7 — фо-
фокальная плоскость WQ; O'(x, yt 0) — параксиальное изображение.
Здесь мы сталкиваемся с задачей вычисления Wo при помощи ха-
характеристических функций прибора К. Для того чтобы упростить вы-
вычисления, полезно сравнить с параметрами р и q луча R отдельные ве-
величины, входящие в выражение для Wo. В частности, если разложить
смешанную характеристику прибора К по степеням р и q, то получим
ряд W = Ц№ + jpB) + j04)s где j02n) — полином степени 2л относи-
относительно р и q. Из-за аксиальной симметрии в разложении отсутствуют
нечетные члены. Слагаемое W^ соответствует параксиальной оптике,
а аберрации оказываются членами не менее чем четвертого порядка.
Этот факт можно сформулировать так: в аберрации вносят вклад чле-
члены W порядка ОD). Аналогично говорят, что \SXO'\ имеет порядок
ОC) и т. д. (рис. 2.36).
После этих предварительных замечаний запишем следующее соот-
соотношение:
Задачи 145
[AQ] -R + px + qy = [ASJ - R - pdx - qdy =
= [^SJ - [ВД + 0F) = Wo + 0F). B.15.30)
Действительно, p bx -h q by = О D), а Л = [#Sj] - p bx - q by +
-h О Eл:2 + by1). Следовательно, в качестве функции WQ для вычисле-
вычисления аберраций третьего и пятого порядка можно выбрать левую часть
выражения B.15.30), т. е.
W0(X, У) = W(z09Zl; xo,yQ,p9q) + px + qy - R - V(O,E') =
= T{zo,z1;po,qOip9q)-poxo-qoyo +
+ P* + 9У- R - V(O9E% B.15.31)
где X и Y — координаты выходного зрачка, равные соответственно
X = Rp/r и У = Rq/r.
Теперь можно разложить Т в степенной ряд по s0 ж и, s{ ¦ v,
s2 ж w. Мы уже отмечали, что функция Wo должна быть по крайней
мере четвертого порядка, т. е. WQ = Wtf> + W$ + ... , где в соот-
соответствии с B.15.31) Wff = Г<4>. Таким образом,
B.15.32)
Z
Определяя новые переменные и = х% + у%, v = р* + q* и
w = 2(х0р{ + Jo^i)» Формулу B.15.32) можно переписать в виде
+ i?wvv + ±Fvw, B.15.33)
где В, С, D, E, F — коэффициенты первичных аберраций (или аберра-
аберраций Зайделя) [30, 31]. Они связаны с такими дефектами изображения,
как сферическая аберрация (В), кома (F), астигматизм (С), кривизна
поля (D) и дисторсия (Е).
ЗАДАЧИ
Раздел 2.2
1. Покажите, что члены асимптотического ряда Ханкеля для функции tf2\kQp)
[B.12.12)] удовлетворяют рекуррентным соотношениям B.2.9). Подсказка:
V2 = d2/dP2 + p~ld/dp.
Раздел 2.4
2. Покажите, что в параксиальном приближении (малое отклонение пучка лучей от
аксиального направления) уравнения для лучей принимают вид
d2x dlnn dx д
dz oz dz ox
146 Гл. 2. Геометрическая оптика
d2y dinn dy д
dzz dz dz dy
3. Покажите, что в параксиальном приближении лучи в линзоподобной среде с по-
показателем преломления
п2 = п20- а(х2 + у2)
описывают синусоидальные траектории.
Раздел 2.6
4. Покажите, что асимптотическое решение параболического волнового уравнения
B.6.12) можно получить в виде
где коэффициенты Лт удовлетворяют рекуррентным соотношениям
5. Докажите, что асимптотические решения уравнений B.6.11) и B.6.12) совпадают
с точностью до членов второго порядка по к~ 10. Подсказка: см. задачу 2.4.
Раздел 2.8
6. Рассмотрите линейный ток J(p, () = e*w/[S(/>)/2*y>]z, текущий вдоль оси z. Соот-
Соответствующий векторный потенциал А пропорционален 1Н0^2\к0р). Вычислите векторы
Е, Н и S и с помощью B.12.12) найдите их асимптотические разложения в ряд.
Раздел 2.9
7. Пусть распределение показателя преломления таково, что прямой луч может
распространяться вдоль оси г. В небольшой окрестности около этой оси распределение
показателя преломления можно приблизительно записать в виде
n2(t) = n2o(z) + f(z)x2 + g(z)y2.
Покажите, что эйконал можно разложить в следующий степенной ряд:
S(r) = So(z) + ja(z)x2 + jb(z)y2 -f c(z)xy + высшие степени похи^
где
dS<> I X dC < 1 1Л C
— = no(z), — = -(a + b)—,
dz dz n0
da a2 f-c2 db b2 g-'c2
—- = 1 (уравнение Риккати), — = 1 .
dz n0 n0 dz n0 n0
8. Используя уравнения из задачи 7, получите закон изменения главных радиусов
кривизны в вакууме B.9.12).
Раздел 2.10
9. Рассмотрите точечный источник в среде с показателем преломления л, находя-
находящийся на расстоянии t от плоской границы раздела со средой, в которой показатель
Задачи
147
преломления равен ri. Покажите, что каустика преломленных лучей описывается урав-
уравнением
H2l3z2'3 + (ii2 - 1I/3р2/3 = t213 (ц = и/и'),
где z и р = С*2 + Л'72 — координаты в системе отсчета, начало которой расположено
в плоскости раздела, а ось z совпадает с перпендикуляром, опущенным из источника на
эту плоскость. Покажите, что при р ^ 1 каустика является эволютой эллипса. Иссле-
Исследуйте форму волновых фронтов. Подсказка. См. разд. Х.4 в книге [13].
Раздел 2.11
10. Вычислите поле, отраженное металлической сферой при ее облучении плоской
волной. Считайте, что коэффициент отражения для скалярного поля равен -1, что оз-
означает равенство нулю полного поля на поверхности.
11. Пусть точечный источник расположен внутри сферы радиусом R, показатель
преломления внутри которой равен лр а снаружи — ло(< я,). Докажите, что если рас-
расстояние от источника S до центра сферы О равно Rno/nv то лучи, образующие с на-
направлением SO угол ^ т/2, преломляются таким образом, что имеют мнимый фокус в
точке S' на расстоянии Rn{/n0 от точки О. Идеальные точки S и S' называют аплана-
тическими точками сферы. Подсказка. Используйте соотношения B.11.22) и закон
Снеллиуса.
12. Рассмотрите точечный источник и пучок лучей, перпендикулярный плоскому
«окну» или цилиндрической линзе с заданными размерами и показателем преломления
(рис. 2.37). Вычислите главные радиусы кривизны вдоль пучка лучей при пересечении
линзы и после выхода из нее.
13. Рассмотрите мениск Амичи (рис. 2.38), получаемый из диэлектрической сферы
радиусом R с показателем преломления лр часть которой выбрана в форме другой сфе-
сферы с центром в апланатической точке S (см. задачу 11). Вся система помещена в среду с
Рис. 2.37. Обозначения для задачи 12.
148
Гл. 2. Геометрическая оптика
Рис. 2.38. Мениск Амичи.
показателем преломления ло(< п{). Вычислите отношение числовых апертур падающей
и преломленной после выхода из мениска конгруэнции, если источник находится в точке
5. Числовая апертура (ЧА) определяется как п sin0MaKC, где 0макс — угол между оптичес-
оптической осью линзы и наиболее отклоненным лучом конгруэнции.
. 14. Рассмотрите объектив микроскопа с масляной иммерсией (рис. 2.39). В этом
случае предмет погружен в жидкость, показатель преломления которой лмасл близок к
показателю преломления первого сферического элемента. Источник расположен в апла-
натической точке этой сферы, причем его изображение находится в центре кривизны
первой поверхности R2 дополнительного мениска, являющемся также апланатической
точкой второй поверхности мениска радиусом Ry Вычислите ЧА конгруэнции лучей,
покидающих мениск Амичи (см. задачу 13), как функцию входной ЧА = nbAacnsm6.
Раздел 2.12
15. Запишите уравнение для лучей в эллиптических цилиндрических координатах
Су> Д» v) [см. выражения B.7.10)], предполагая, что показатель преломления является
постоянным на каждом эллипсе из координатного семейства и не зависит от у. Найдите
интеграл движения, соответствующий наклону данного луча в волокнах с вращательной
симметрией относительно поворота волокна. Проанализируйте моды, распространяю-
Плоскость
предмета
Рис. 2.39. Объектив микроскопа
с масляной иммерсией.
Задачи 149
щиеся вдоль оси у этого эллиптически градиентного волокна. Для этого исследуйте от-
относительные каустики и зависимость постоянной распространения /3 от модовых индек-
индексов.
раздел 2.13
16. Используя соотношение B.13.45), найдите круговые траектории с центром в на-
начале координат максвелловского рыбьего глаза [выражение B.13.53)] и линзы Лунебер-
га [выражение B.13.55)]. Покажите, что радиусы этих траекторий равны соответствен-
соответственно bVl и R.
17. Пусть в линзе Лунеберга луч распространяется вдоль оси х. Используя тран-
транспортные уравнения из задачи 2.7, покажите, что изменение радиуса кривизны
вращательно-симметричного волнового фронта вдоль оси х описывается уравнением
т=l[2-(*/*J]i/2tg (~ *"** wr+¦>•
где ф — угол для начального значения р, а координата х измеряется относительно цент-
центра линзы.
18. Докажите, что начальный и конечный радиусы кривизны вращательно-
симметричного волнового фронта, распространяющегося вдоль диаметра линзы Луне-
Лунеберга, связаны соотношением
2
Раздел 2.14
19. Решите уравнение B.14.19) при наличии однородного магнитного поля (потен-
(потенциал А неоднороден!). Покажите, что траекторией является спираль с осью, параллель-
параллельной вектору Н. Найдите частоту вращения вокруг Н (циклотронную частоту).
20. Рассмотрите периодически наклонный нематический жидкий кристалл, компо-
компоненты диэлектрического тензора которого зависят только от координаты г:
~l+5cos(pz) 0 dsin(pz)
0 1 +<5 0
ф) = в
<5sin(j?z) 0 l-«cos(jfe)
здесь I д I <1, 0 = 2ic/L, a L — пространственный период дисторсии. Докажите, что
тензор е описывает одноосный кристалл, и вычислите направление оптической оси как
Функцию z. Предполагая, что L > X и используя уравнение B.14.14а), вычислите траек-
траекторию необыкновенного луча. Подсказка: см. пример 2 в разд. 2.14.1 и работу Онга и
Мейера в библиографии к данной главе.
21. Рассмотрите луч, падающий в однородный одноосный кристалл и распростра-
распространяющийся как необыкновенный луч. Предполагая, что оптическая ось компланарна с
плоскостью падения, и используя соотношение B.14.19), определите угол преломления
150
Гл. 2. Геометрическая оптика
как функцию угла падения. Подсказка. Покажите, что обобщенное соотношение
B.14.19) имеет вид
tg в' = -С/В + (sin е/В){(АВ - С2)/(В - sin2 0)}1/2,
где
А = п2 sin2 a + no2 cos2 а, В = п2 sin2 а + w2 cos2 а, С = sin а cos а(и2 — и2).
22. Используя символы Кристоффеля для сферических координат, определите тра-
траектории в диэлектрике с зависящим от г показателем преломления. Примените получен-
полученный результат для максвелловского рыбьего глаза.
23. Используя сферические координаты г, 0, ф> исследуйте траектории, соответству-
соответствуйте плоской волне, отклоняемой статическим гравитационным полем звезды. Подсказ-
Подсказка. Пространственно-временная траектория фотона является нулевой геодезической
для метрики
ds2 = eMr)dr2 + r2d92 + r2sm29d<lJ - ev{r)c2dt29
где функции X и v описывают влияние гравитационного поля [32] (X = v = 0 в плоском
пространстве-времени). Как следствие, пространственные траектории можно полу-
получить, рассматривая эквивалентную среду с показателем преломления
и метрическим тензором с компонентами
дм = гге~*\
дфф = г2 sin2
9„ = «*>-*>
24. Используя результаты задачи 27, вычислите траекторию луча, отклоняемого
черной дырой с массой М. Считайте, что
9гг = A - rjry\ двв = ^sin-2 в = r2(l - rjry\
где rg = 2GM/c2, a G — гравитационная постоянная. Покажите, что при
/ > 33/2 г/2 = / лучи отклоняются массой Л/, а при / < Г захватываются грави-
? кри1 кри г
тационным полем [32] (рис. 2.40).
Раздел 2.15
25. Вычислите угловую характеристику сферической линзы во втором порядке по м,
v, w. Подсказка. Выберите опорные плоскости Tl^z = 0) и П^г = </), которые являют-
являются касательными к сфере, и определите вспомогательную плоскость П', совпадающую,
Черная дыра
Рис. 2.40. Траектории лучей
вблизи черной дыры.
Литература 151
к примеру, с Пг После этого представьте Глинза в виде
Тпшза= T@J;pO9qo,p\q')+ T0(d,d;p',4',Pi,4i).
Поскольку точка пересечения плоскости П' лучом, приходящим слева, совпадает с точ-
точкой пересечения той же плоскости лучом справа, характеристика Глинза стационарна по
отношению кр' и q'. Это позволяет исключить р' и q' и, таким образом, с помощью
формулы B.15.17) записать 7"линза как явную функцию величин/^, q0, pv qv
ЛИТЕРАТУРА
1. Luneburg L. К,, Mathematical Theory of Optics, Univ. of California Press, Berkeley,
1964.
2. Kline M., Kay I. W., Electromagnetic Theory and Geometrical Optics, Wiley (Inter-
science), New York, 1%5.
3. Felsen L. R, Marcuvitz M, Radiation and Scattering of Waves, Prentice-Hall, Engle-
wood Cliffs, New Jersey, 1973.
4. Abramowitz M., Stegun I. A., Handbook of Mathematical Functions, Dover, New
York, 1965. [Имеется перевод: Абрамович М., Стпиган И. Справочник по спе-
специальным функциям. — М.: Наука, 1979.]
5. Courant R.t HUbert D., Methods of Mathematical Physics, v. 2., Wiley (Interscience),
New York, 1962. [Имеется перевод 1-го изд.: Курант Р., Гильберт Д. Методы
математической физики. Т. 2. — М. —Л.: Гостехиздат, 1951.]
6. Stavroudis О. К, J. Opt. Soc Am., 52, 187 A962).
7. Laugmtz D., Differential and Riemannian Geometry, Academic Press, New York,
1965.
8. Montagnino L., J. Opt. Soc Am., 58, 1667 A968).
9. Deschamps G A.t Proc. IEEE, 60, 1022 A972). [Имеется перевод: ТИИЭР, 1972,
т. 60, № 9, с. 5.]
10. Ludwig D., Commun. Pure. Appl. Math., 19, 215 A966).
11. Kneisly J. A., //, J. Opt. Soc. Am., 54, 229 A964).
12. Herzberger M, Appl. Opt., 5, 1383 A966).
13. Stavroudis O. TV., The Optics of Rays, Wavefronts and Caustics, Academic Press, New
York, 1972.
14. Buchdahl H. A., J. Opt. Soc. Am., 63, 46 A973).
15. Streifer W., Paxton К. В., Appl. Opt., 10, 769 A971); 10, 1164 A971).
16. Bogoliubov N. N., Mitropolsky Yu. A., Samoilenko A. M, Methods of Accelerated
Convergence in Nonlinear Mechanics, Springer-Verlag, Berlin and New York, 1976.
17. Marchand E. W.t Gradient Index Optics, Academic Press, New York, 1978.
18. Cornbleet S., Microwave Optics, Academic Press, New York, 1976.
19. Zatzkis H., J. Opt. Soc Am., 55, 59 A965).
20. Budden K. G., Radio Waves in Ionosphere, Cambridge Univ. Press, London and New
York, 1961.
21. Brandstatter J. J., An Introduction to Waves, Rays and Radiation in Plasma Media,
McGraw-Hill, New York, 1963.
22. Righini G. C, Russo K, Sottini S., Toraldo di Francia G.t Appl. Opt., 12, 1477 A973).
23. Sottini S., Russo K, Righini G. C, J. Opt. Soc. Am., 69, 1248 A979).
24. Moller C, The Theory of Relativity, Oxford Univ. Press, London and New York,
152 Гл. 2. Геометрическая оптика
1972. [Имеется перевод: Меллер К. Теория относительности. — М.: Атомиздат,
1973.]
25. Goldstein #., Classical Mechanics, Addison-Wesley, Reading, Massachusetts, 1980.
[Имеется перевод 1-го изд.: Голдстейн Г. Классическая механика. — М.: Наука,
1975.]
26. Marcuse D., Light Transmission Optics, Van Nostrand-Reinhold, Princeton, New
Jersey, 1972.
27. Steffen K. G., High Energy Beam Optics, Wiley (Interscience), New York, 1965.
28. Welford W. T.t Aberrations of the Symmetrical Optical Systems, Academic Press, New
York, 1974.
29. Buchdahl К A, An Introduction to Hamiltonian Optics, Cambridge Univ. Press,
London and New York, 1970.
30. Kingslake R., Lens Design Fundamentals, Academic Press, New York, 1978.
31. Cagnet M., Frangon M.t Thrierr J. C, Atlas of Optical Phenomena, Springer-Verlag,
Berlin and New York, 1962.
32. Zeldovich Y. R, Novikov L. D., Relativistic Astrophysics, v. 1, Chicago Univ. Press,
Chicago, Illinois, 1971.
БИБЛИОГРАФИЯ
Brouwer W.t Matrix Methods in Optical Instruments Design, Benjamin, New York,
1964.
Chretien #., Calcul des Combinaisons Optiques, Masson, Paris, 1980.
Cornbleet S. Microwave and Optical Ray Geometry, Wiley, New York, 1984.
Handbuch der Physik, v. 24, (ed. S. Flugge), Springer-Verlag, Berlin, 1967.
Focke J., Prog? Opt., 4, 1—36 A965).
Gerrard A., Burch J. M.t Introduction to Matrix Methods in Optics, Wiley, New York.
[Имеется перевод: Джерард А., Берн Дж. Введение в матричную оптику. — М.:
Мир, 1981.]
Herzberger М. Modern Geometrical Optics, Wiley (Interscience), New York, 1958.
[Имеется перевод Герцбергер M. Современная геометрическая оптика. — М.:
ИЛ, 1962.]
Кравцов Ю. А., Орлов Ю. И. — УФН, 1983, т. 141, с. 591.
Ми G., Zhan Y., Optics, The People's Education Publishing House, Peking, 1978
(китайск.).
Ong H. L.t Meyer R. A, J. Opt. Soc. Am., A2, 198 A985).
Shaomin W.t Opt. Quantum Electron., 17, 1 A985).
Slyusarev G. G., Aberration and Optical Design Theory, Adam Hilger, Bristol 1984.
[См. также: Слюсарев Г. Г. Методы расчета оптических систем. — Л.: Маши-
Машиностроение, 1969; Расчет оптических систем. — Л.: Машиностроение, 1975.]
Smith W. /., Modern Optical Engineering, McGraw-Hill, New York, 1966.
Welford W. T.t Winston R., The Optics of Nonimaging Concentrators, Academic
Press, New York, 1980.
ГЛАВА 3
ПЛОСКИЕ МНОГОСЛОЙНЫЕ СРЕДЫ
3.1. ВВЕДЕНИЕ
Из всех возможных неоднородностей в оптике чаще всего встречают-
встречаются разрывы показателя преломления. Они приводят к возникновению
отраженных волн, которые интерферируют с падающей волной и об-
образуют весьма сложную интерференционную картину. В большинстве
случаев для вычисления амплитуды волн, отраженных или пропущен-
пропущенных оптической системой, обычно необходимо учесть бесконечное
число многократных отражений, испытываемых падающим пучком.
На языке геометрической оптики это соответствует бесконечной по-
последовательности лучей, суперпозиция которых определяет полное по-
поле. Это обстоятельство определяет главное отличие рассматриваемых
здесь задач от тех, которые мы изучали до этого. В частности, необ-
необходимы новые методы, которые позволили бы в случае бесконечного
множества лучей получить ответ на главный вопрос, а именно на во-
вопрос об амплитудах при отражении и пропускании оптических пучков.
Для того чтобы подчеркнуть практическое значение таких методов,
мы приведем ниже несколько^примеров реально существующих прило-
приложений, в которых модулированная диэлектрическая проницаемость
приводит к тому, что амплитуды отраженных или прошедших волн
зависят от частоты самого поля.
В оптических приборах для улучшения их характеристик, а именно
для увеличения прозрачности и ослабления паразитных изображений,
используют покрытия стеклянных поверхностей тонкими диэлектри-
диэлектрическими пленками [1]. Преимущества такого метода борьбы с отраже-
отражением становятся еще более явными при увеличении числа покрытий.
Полупрозрачные тонкие пленки используются и для увеличения отра-
отражения света от стеклянной поверхности [2]. Такие диэлектрические
зеркала особенно важны в лазерных резонаторах и интерферометрах.
В частности, с их помощью создаются оптические фильтры, ограни-
ограничивающие полосу пропускания узким частотным интервалом.
В последние годы с развитием источников синхротронного излуче-
излучения потребовались зеркала для далекого УФ-диапазона [3]. Известно,
что при длинах волн меньше 300 А ни один из материалов не имеет
154 Гл. 3. Плоские многослойные среды
достаточно высокого коэффициента отражения, если только не ис-
используется скользящее падение света. В этом случае в качестве отра-
отражателя можно использовать лишь набор тонких пленок. Уже созданы
диэлектрические зеркала для длин волн вплоть до нескольких ангст-
ангстрем, причем цх отражательная способность превышает 50% [4].
Для создания периодических структур можно применять фотомате-
фотоматериалы. Для этого они экспонируются в поле двух (или более) интерфе-
интерферирующих монохроматических пучков и после этого закрепляются,
так что фотопленка оказывается периодической, причем пространст-
пространственный период зависит как от длины волны, так и от угла, образуе-
образуемого падающими пучками [5]. Эти системы обеспечивают резонанс-
резонансное отражение или пропускание и благодаря своей более высокой эф-
эффективности и лучшему разрешению могут заменить традиционные
решетки [6] (см. обсуждение голографических решеток в разд. 6.10).
Описанный метод можно использовать для записи трехмерных
изображений в толстослойных голограммах^. Для этого толстый
слой эмульсии на фотопластинке высокого разрешения экспонируют в
поле опорной сферической волны, интерферирующей с когерентным
полем, рассеянным предметом, восстановленное изображение которо-
которого и должно быть получено.
Простейший пример неоднородной среды — это такая среда, в ко-
которой показатель преломления п изменяется только вдоль одного на-
направления [7, 8]. В этом случае среда называется слоистой, причем ее
диэлектрические свойства постоянны на каждой плоскости, перпенди-
перпендикулярной оси расслоения. Более сложным примером является семей-
семейство коаксиальных цилиндров, на поверхностях которых показатель
преломления постоянен. Такая геометрия встречается в градиентных
волокнах (см. гл. 8). Однако к настоящему времени наибольшее рас-
распространение получили плоскослоистые среды. Поэтому данную гла-
главу мы посвятили исключительно этим структурам. В частности, в по-
последующих разделах мы рассмотрим среды с медленной, ступенча-
ступенчатой и синусоидальной модуляциями показателя преломления.
Хотя основное внимание в этой главе будет сконцентрировано на
распространении света в направлении расслоения z, мы рассмотрим и
задачу о боковых волнах, которые распространяются параллельно
тонкой пленке (в направлениих или.у; рис. 3.1). Существование таких
поверхностных волн или волн утечки показывает, что можно создать
структуры, которые удерживают распространяющиеся волны в преде-
пределах ограниченной области, которая может иметь толщину, равную
*) Толстослойные (трехмерные) голограммы были предложены Ю.Н. Денисюком в
1962 г. (см. работу [13], указанную в литературе к гл. 6). — Прим. ред.
3.2. Геометрическая оптика в слоистых средах
155
Окружающая
среда
Тонкая
пленка
Подложка
Рис. 3.1. Структура планарного пленочного световода.
всего лишь нескольким длинам волны. В настоящее время это свой-
свойство используют для создания оптических планарных волноводов и
других устройств интегральной оптики [9].
Распространение поверхностных волн можно использовать также
для исследования физических свойств тонких пленок. В частности, в
металлах возбуждение и анализ поверхностных волн, удерживаемых
тонкими пленками, позволяет изучать параметры поверхностных
плазмонов [10].
Данная глава состоит из двух частей. Первая, более короткая, по-
посвящена средам, в которых изменение показателя преломления п про-
происходит на характерных размерах, существенно превышающих длину
волны, в то время как во второй, боЛее длинной, части мы рассмат-
рассматриваем противоположную ситуацию. В первой части завершается ана-
анализ градиентных сред, начатый в гл. 2 изучением представления поля
вблизи критических областей {каустик или точек поворота). Рас-
Рассмотренные практические примеры касаются распространения опти-
оптического излучения в градиентных многомодовых оптических волокнах.
Вторая часть в основном посвящена анализу сред с кусочно-
постоянными профилями показателя преломления.
Мы очень кратко остановимся на задаче о создании оптических
фильтров, так как здесь требуется сложный математический аппарат,
для изложения которого объем данной главы явно недостаточен. За-
Заинтересованный читатель должен обратиться к более специализиро-
специализированным книгам, часть которых мы привели в списке литературы в
конце панной главы.
32. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СЛОИСТЫХ СРЕДАХ
Рассмотрим случай, когда показатель преломления не зависит от х
и.У, что соответствует неограниченной слоистой среде. Пусть показа-
156
Гл. 3. Плоские многослойные среды
n(z)
Веи^естден -
ныи луч
Рис. 3.2. Отражение и пропускание плоской волны на каустике плоскослоистой среды.
а — профиль показателя преломления и распределение поля вблизи каустики z = za;
б — траектория комплексного луча; в — траектории лучей в плоскости xz.
тель преломления п (z ) принимает постоянные значения п 0 и п х соот-
соответственно приг — -оои?— + оо (рис. 3.2, а). Предположим, что
поле приг = - оо имеет вид плоской волны ui9 распространяющейся
под углом в к оси z:
и _ e-ikon0(zcose + xsine)^ C.2.1)
Без потери общности в дальнейшем будем считать, что амплитуда на-
начального поля равна единице.
3.2. Геометрическая оптика в слоистых средах 157
Стандартный путь исследования задачи о распространении волн
состоит в поиске подходящего приближенного метода решения волно-
волнового уравнения. Точные аналитические рашения получаются только
для некоторых частных случаев профиля п (г). Например, в методе
Венцеля— Крамерса— Бриллюэна (ВКБ) [11] ищется приближенное
решение, которое является асимптотическим по параметру
е = (dn /dz )/(ko/n ). Малость е означает, что показатель преломления
слабо изменяется на размерах порядка длины волны. В данном разде-
разделе мы используем развитый в гл. 2 формализм геометрической опти-
оптики, который в низшем порядке по 1/&0 приводит к тем же результа-
результатам, что и ВКБ-метод.
Записанное в виде B.4.10) уравнение для лучей можно решить, ис-
используя декартовы координаты. При этом получаем
d2z/dx2 = (d/dz)$n2), d2x/dx2 = d2y/dx2 = 0. C.2.2)
Таким образом, п dx /ds и п dy /ds являются интегралами движе-
движения. Для удобства можно выбрать направление оси* таким, чтобы
все лучи начальной плоской волны были ортогональны оси>>. Это уже
неявно предполагалось при записи выражения C.2.1). Следовательно,
dy = ° И dx == ds/n = (dx2 + dz2I/2/n. C.2.3)
Кроме того, из C.2.2) мы имеем tf r = dx /а (а — постоянная), так
что можно записать следующее уравнение:
dx/dz = а/(п2 - а2I12. C.2.4)
При z — — оо из этого уравнения и C.2.1) следует, что
tg0 = а(п% - а2)~1/2 и, таким образом,
a = noSin0. C.2.5)
Используя уравнение C.2.4), траекторию любого луча можно запи-
записать в виде
Х =
гдел*0 и?0 — координаты произвольной точки траектории.
В нашем случае эйконал запишется в виде
S = So + а(х - х0) + f V - *2)llldz\ C.2.7)
где So — постоянная. Действительно, это выражение является част-
частным случаем формулы B.12.5) и описывает волну, направление рас-
распространения которой прия = — оо образует угол в с осью z. В соот-
соответствии с C.2.7) имеем
W4(H C-2-8)
158 Гл. 3. Плоские многослойные среды
Кроме того, поскольку ds/n dz = (п2 - а2I/2 [см. уравнения
C.2.3), C.2.4) и B.5.6I, можно записать Уравнения
[1 С2 1 / d \ 1 (и cos0I/2
— - —2 *\\~T~'n2)^z' "Г"! 2U74- C.2.9)
Здесь мы положили z 0 = -оо.
Окончательно, используя выражение C.2.7), нетрудно получить ис-
искомое лучевое поле в виде ¦
»(г) = A0(x)e-w = ^^1I/4 ^^"^ C2Л0)
гдемДг) представляет собой плоскую волну C.2.1), распространяющу-
распространяющуюся без возмущения в однородной среде с показателем преломления
/г0, a 8j — связанная с изменением показателя преломления задержка
фазы волны и по сравнению с и{:
biz) = к0 Г [in2 - а2I12 - n0cos6]dz'. C.2.11)
J -оо
Полученное выражение для поля и (г) имеет сингулярность при
п2 — а2 = 0. Соответствующее значение zfl, при котором n2(za) =
= а2 = w§sin20, является точкой поворота для волнового уравнения.
Плоскостью = zay если она вообще существует, представляет собой кау-
каустику, связанную с конгруэнцией всех лучей, имеющих одинаковое
значение sinfl.
Чтобы вычислить поле вблизи za, рассмотрим снова волновое
уравнение. Начальные условия позволяют искать решение уравнения
A.1.12) в виде
u-e ° J(z). C.2.12)
Подстановка этого выражения в уравнение A.1.12) дает
d2u/dz2 + k2Q(n2 - а2)и = 0. C.2.13)
Для наших целей удобно искать решение уравнения C.2.13) в виде
и = м+ exp —ik0 (п2 — a2I12 dz' — ikonoxsin6 +
+ м_ exp ik0 I (n2 - a2I12 dz' - ikonox sin в L C.2.14)
Здесь м+им_- две функции координаты z, удовлетворяющие урав-
уравнению
которое нетрудно получить, подставив выражение C.2.14) в уравнение
3.3. Сшивка асимптотических разложений 159
C.2.13). При&0 — оо получаем
2(„2 _ а2I'2^ + иЛ{п2 - а2I12 = 0, C.2.16)
dz dz
так что и+ и м _ являются медленно меняющимися функциями коор-
координаты z типам^ ~ (л2 - а2)~у* [все быстро меняющиеся множители
включены в экспоненту C.2.14)].
Таким образом, мы показали, что в выражении C.2.14) предел
к0 — оо соответствует лучевому полю, если считать, что членм_ опи-
описывает волну, распространяющуюся в отрицательном направлении
оси z (ВКБ-решение).
3.3. СШИВКА АСИМПТОТИЧЕСКИХ РАЗЛОЖЕНИЙ; МЕТОД
ЛАНГЕРА
Для того чтобы исключить область нефизического поведения поля
при z = za, можно обратиться к методу сшивки асимпотических ре-
шений [11], позволяющему построить полное приближенное решение
дифференциального уравнения, имеющего точки поворота. Этот ме-
метод состоит в объединении различных приближенных решений (ВКБ
или геометрической оптики), которые справедливы лишь в соответст-
соответствующих областях применимости. Аналогичный подход для вычисле-
вычисления дифракционных интегралов в переходных областях мы рассмот-
рассмотрим в гл. 5.
Для начала заменим в уравнении C.2.13) величину k^in2 — а1) ее
линейным разложением , -
-y(z - za) = k&z - za)—-
C.3.D
dz
При этом уравнение C.2.13) в окрестности точкига сводится к уравне-
уравнению Эйри (см. работу [4] в гл. 2)
d2u/dz2 - y(z - z> = 0. C.3.2)
Это частный случай уравнения более общего вида с точками пово-
поворота т -го порядка:
d2u/dz2 - y(z - za)mu = 0, C.3.3)
решение которого можно записать в виде
-I:
u(z) ос ^2y(z - zaymJ±n(Z\ i = [ У1;V - *аГ/2 &\ C.3.4)
где Jn — функция Бесселя дробного порядка п = \/{т + 2). При
т = 1 C.3.4) сводится к уравнению C.3.2) и его решение, если исполь-
использовать разложение C.2.14), имеет вид
и = ^-"ополет* Ai[fco*/1/3(z - г.)] + c2e-fko^sineBi[M1/3(^ - *.)], C.3.5)
160 Гл. 3. Плоские многослойные среды
raecj ис2 — постоянные, rj = у/ко~г — безразмерный параметр, a Ai
и Bi — функции Эйри.
Теперь видно, что наше начальное предположение о виде волны
при z —• - о© означает, что полупространство z < za представляет со-
собой освещенную зону, в которой эйконал является вещественным.
Следовательно, при* < za мы имеемn2(z) > а2 = п2(ра), так что 7 и
у) — положительные величины.
Переходные функции Ai и Bi осциллируют при отрицательных зна-
значениях аргумента, при положительных Ai монотонно спадает, a Bi
монотонно возрастает. Из физических соображений можно сделать
вывод, что с2 = 0, т. е. зависимость функции и orz можно предста-
представить кривой, изображенной на верхнем графике рис. 3.2.
Сравним теперь два выражения C.2.14) и C.3.5) для и. Первое из
них представляет собой лучевое поле и является хорошим приближе-
приближением на достаточно большом расстоянии от каустикиz = za. Второе
выражение является решением волнового уравнения, справедливым
при достаточно малых \z — za I [так, чтобы выполнялось приближе-
приближение C.3.1)]. Если области применимости обоих приближений перекры-
перекрываются, что обычно и имеет место для реальных распределений п (г ),
то оба этих решения можно сшить и получить полную информацию о
поле. Точнее говоря, если использовать асимптотические выражения
для функции Ai при больших аргументах (см. книгу [4], цитируемую в
гл. 2)
^KB/3K3/2 C-3'6а)
2^ J2sin[B/3)|C|3/2 + я/4] (С < 0), C.3.66)
то из уравнения C.3.5) получаем выражения
fcg/2Hz-zeK/2 (z > za), C.3.7a)
p-ikonox sin в
I-/Я/4Г iB/3)lfl/2[*0(Za-z)]3/2 +
Ы*а-ж)]*'2еЫ/2Л (z<z),
C.3.76)
для поля в области, где оба используемых приближения приводят к
одному и тому же результату. В соответствии с этим, когда волна
подходит к точке поворота, всегда существует отраженная волна [см.
второй член в правой части выражения C.3.76)]. Она имеет ту же ам-
амплитуду, что и падающая, и задержана по времени на ж/2ш (см. разд.
2.10 и рис. 2.17).
3.3.1. Прошедшие и отраженные волны
В соответствии с проведенным выше рассмотрением поля отраженной
и прошедшей волн можно найти, используя следующие правила: когда
3.3. Сшивка асимптотических разложений 161
действительный луч подходит к каустике, он становится касательным
к плоскости z = za и расщепляется на два, один из которых является
действительным и отражается от каустики, а другой, комплексный
луч, проникает в неосвещенную область z > za и соответствует зату-
затухающей волне (рис. 3.2,6). Амплитуда поля отраженного луча умно-
умножается на eir/2, а прошедшего — на е/т/4. Видно, что падающий и от-
отраженный лучи симметричны относительно оси z, и по аналогии с
разложением C.2.10) поле отраженного луча можно записать в виде
*».-*. C.3.8)
где иг — однородная волна, которая является «зеркально-
симметричной» к и{ относительно плоскости каустики и имеет такую
же величину амплитуды и фазы, как и иг Параметр г = eiv/1 играет
роль коэффициента отражения (см. рис. 3.2.6), а 8Г — фазовый сдвиг
по отношению к иг и ип набранный волной при проходе от — оо до
каустики и обратно дог. Для Ьг по аналогии с C.2.11) имеем
«rW = ^о Г Е(и2 - а2L1 - п0cos 0] dz' +
J -оо
+ 2fe0 I \(n2 - a2I'2 - nocos0]dz' =
= ад + 2kS\{n2 - a2I12 - n0cos6T|dz'. C.3.9)
Из тех же соображений поле затухающей прошедшей волны ип ко-
которое при z > za в области перекрытия описывается выражением
C.3.7а), имеет вид
где t = е/7Г/4, а фазовый сдвиг б, = 5^ — /6/ определяется выражени-
выражением, аналогичным выражению для Ьг. Величина 5," соответствует экс-
экспоненциальному затуханию поля в неосвещенной области (см. также
[12]).
3.3.2. Переход из запрещенной зоны в разрешенную
Рассмотрим теперь противоположный случай — переход из запрещенной
зоны в разрешенную. Точнее говоря, пусть полупространством >za яв-
является освещенной областью, а затухающая волна возникает прим < za.
Так как при z > za существует лишь одна бегущая волна, то решение
Уравнения Эйри необходимо выразить в виде подходящей комбинации
162
Гл. 3. Плоские многослойные среды
функций Ai и Bi. Используем тот факт, что при больших значениях аргу-
аргумента Bi(f) имеет вид (см. книгу [4], цитируемую в гл. 2)
Bi(C) - A/тг^2)|СГ1/4со8[B/3)|С|3/2 + тг/4] (С < 0). C.3.11)
При этом непосредственно из выражений C.3.5) и A.3.6а) следует, что
правильная комбинация, представляющая собой переходную функцию,
имеет вид и^ ..д.^^ _ zJ] + щ^т^ _ zJ]e C.3.12)
(В данном случае параметр у отрицательный, т. е. f < 0 соответст-
соответствует освещенной зонег > zai) Используя выражения CJ.12), C.3.6а) и
C.3.11), получаем начальный фазовый множитель е ~|>/4 для прошед-
прошедшей бегущей волны. Кроме того, при больших значениях аргумента
мы имеем ^ ^ A/wi/2)|Cri/V2/3^ (С > 0). C.3.13)
Поскольку волна, возникающая в неосвещенной области, представ-
представляется в переходной области функцией Bi, из уравнения C.3.12) следу-
следует, что второй комплексный луч возникает за счет отражения. При
этом его начальная амплитуда имеет множитель (Уг)е~*ж/1 по сравне-
сравнению с амплитудой затухающего поля Bi (см. рис. 3.3, на котором ос-
освещенная область находится при z < za).
n(zI
Отраженный
вещественный
луч
Вещественный
луч
Прошедший
вещественный
луч
Комплексный
прошедший
луч
Комплексный
отраженный
луч
r=±e-i*/2
Комплексный
луч
Рис. 3.3. Схематическое представление распределения поля в области уменьшающегося
показателя преломления. Средний график иллюстрирует полное отражение.
3.3. Сшивка асимптотических разложений
163
3.3.3. Темный барьер
Рассмотрим случай, когда существуют две точки поворота — za и
z'a > za. Темным барьером является интервалza < z < za, гдея(*) име-
имеет провал. Полученные выше результаты позволяют искать лучевое по-
поле в виде (рис. 3.4)
/ч (п0 cos в)
(„*_ „2)
2I/4
za),
(za<z<
C.3.14a)
C.3.146)
C.3.14b)
причем
Предположение об отсутствии волны, приходящей из z — + оо, что
позволяет использовать формулу C.3.146), означает, что лучевое поле в
темной области описывается выражением C.3.14в), поскольку это пове-
поведение поля согласуется с результатами, полученными для перехода из
запрещенной в разрешенную зону. Для того чтобы определить лучевое
поле при - оо <z <za, заметим, что в выражении C.3.14в) член
?/*/4 + а - $ _|_ (i/2) ?-/ir/4 - « + 4 ] у первой точки поворота должен
быть заменен на член, содержащий переходную функцию
eir/4 + «д| _|_ (i4)e-'*/4 - «Bi. Это следует из выражений для Ai и Bi при
больших значениях аргумента [C.3.6а) и C.3.13)]. Следуя тому же ме-
методу, который мы уже использовали в этом разделе, будем рассматри-
рассматривать непрерывное движение налево от точки za. Далее, вновь выражая
Ai и Bi с помощью соотношений C.3.66) и C.3.11), используем совпаде-
совпадение полученного асимптотического приближения с C.3.14а). Действуя
таким образом, коэффициенты отражения гь и пропускания tb можно
записать следующим образом:
гь =
- е
~2а
)/D
е~2л
\
tb =
C.3.15)
рис. 3.4. Распределение интенсивности (нижняя кривая) вблизи ямы показателя прелом-
преломления (верхняя кривая) при падении плоской волны слева направо.
164
Гл. 3. Плоские многослойные среды
nlz).
Im z
-2агг,
Рис. 3.5. Схематическое представление изменений в распределении амплитуды поля при
наличии ямы (барьера) в профиле показателя преломления. На нижней диаграмме пока-
показаны многократные отражения луча, приходящего из освещенной области. Амплитуды
прошедшего и отраженного полей можно вычислить, суммируя бесконечную последова-
последовательность полей, помеченных индексом т. Индексы г и / относятся к точкам za и z^
Они удовлетворяют соотношению I rb 12 4- I tb 12 = 1, которое выра-
выражает закон сохранения потока энергии вдоль направления распростра-
распространения z.
Для полноты картины заметим, что тот же результат можно поду-
подучить, если рассматривать отраженные и прошедшие пучки как суммы
бесконечного числа вкладов от «захваченной в ловушку» барьера зату-
затухающей волны, отражающейся между плоскостями za nza (рис. 3.5).
Разумеется, если z'a -+ оо, то а — оо, т. е. tb = 0 и гь = ехр(/х/2),
что согласуется с выражением C.3.8). В общем случае^ не равно ну-
нулю, что связано с частичным просачиванием энергии через темную
область — явление, аналогичное эффекту туннелирования в кванто-
квантовой механике. Величина этого просачивания зависит от параметра а,
который служит мерой величины провала между двумя листами кау-
каустики z = za nz = za. Такое просачивание приводит к эффекту, назы-
называемому нарушенным полным отражением, который применяется в
интегральной оптике для возбуждения волн в тонкопленочных волно-
3.3. Сшивка асимптотических разложений
165
Воздушная
прослойка
Подложка
Рис. 3.6. Призменный элемент связи, использующий эффект нарушенного полного отра-
отражения для возбуждения удерживаемой волны в пленке на подложке.
водах при помощи призменного элемента связи (см. рис. 3.6 и разд.
3.20.1).
Заметим, что при а = 0 мы должны получить гь = 0 и tb = 1, но
это противоречит выражениям C.3.15). Такое расхождение связано с
неприменимостью процедуры сшивки в тех случаях, когда темный
барьер недостаточно велик.
Точная зависимость величин гь и tb от волнового числа связана с
особенностями среды вблизи точек поворота и определяется вкладом
функций Ai и Bi в разложение поля.
В заключение рассмотрим случай затухающей волны м(е), возника-
возникающей при z = -оо. Затухание можно учесть подстановкой
в -* тг/2 + /0', и сам читатель может получить выражение
() ' ( 6)
ц(е)/-л _
ch
гдег7/е)(г) = ехр( -
сывается в виде
"), а фазовый сдвиг 5(е) запи-
запи[(а(еJ - и2)
1'2 -
3.1.7)
гдеа<е> = ffi
При приближении комплексного луча к точке поворота za он рас-
расщепляется на комплексный отраженный и действительный прошед-
прошедший лучи.
166 Гл. 3. Плоские многослойные среды
3.3.4. Канал
В тех случаях, когда две точки поворота za и za ограничивают некото-
некоторый канал, т. е. область, в которой показатель преломления п (z) име-
имеет максимум, возникает ситуация, сходная с рассмотренной выше. В
частности, операция сшивки позволяет получить коэффициент отраже-
нияг.ввиде Wl .„ ,
Ц* CЗЛ8)
где ф — сдвиг фазы (действительного) луча при проходе oiza jyoza\
ф = к0 [Z\n2 - п2 ch29"I12dz'. C.3.19)
ha
Мы видим, что rd расходится при ф = (п + 1/2)тг. Из интуитив-
интуитивных соображений это означает, что слабая падающая волна может
возбудить очень сильное поле внутри канала. Иными словами, ситуа-
ситуация, при которой ф = (п + 1/2)тг, соответствует резонансу системы,
в которой возникает поле бесконечно большой амплитуды при конеч-
конечной амплитуде возбуждения. Создаваемое таким образом в системе
поле называют модой, распространяющейся в направлении х. При
этом соотношение C.3.19) определяет значения-0, при которых воз-
возможно возбуждение мод. Так как величина/:, s rif/coch в" однозначно
определяется при данной величине 0 , одновременно с 0 можно най-
найти и дискретный набор разрешенных значений кг Каждая из мод в
большей или меньшей степени сконцентрирована внутри освещенной
области za < z <za. При этом система ведет себя как диэлектриче-
диэлектрический волновод, передающий возмущение вдоль оси х с возможными
волновыми числами kt.
3.4. ОТРАЖЕНИЕ И ПРОПУСКАНИЕ
ПРОИЗВОЛЬНОЙ НЕОДНОРОДНОЙ СРЕДОЙ
Как следует из предыдущего раздела, отражение возможно только
при наличии точек поворота. Казалось бы, это явно неверное утверж-
утверждение, ведь, как хорошо известно, разрывность показателя преломле-
преломления в любом случае приводит к появлению отраженного луча. Проти-
Противоречие это обусловлено тем, что метод сшивки асимптотических ре-
решений учитывает правильно распределение поля в непосредственной
близости от точки поворота. Однако этот метод неприменим в тех
случаях, когда показатель преломления существенно изменяется на
масштабах порядка длины волны. Здесь мы рассмотрим приближе-
приближение, основанное на решении волнового уравнения методом ВКБ [13].
3.4. Отражение и пропускание 167
Как будет видно ниже, отражение зависит от поляризации поля, т. е.
с самого начала надо рассматривать векторную задачу.
Следуя работе [13], рассмотрим плоскую волну
Е, = [ — sin@) cos(/?)z + sin(P)y + cos@)cos(fi)x]e~ikoixsine+zcose\ C.4.1)
распространяющуюся в свободном полупространстве z < О и падаю-
падающую на плоскость z = 0, отделяющую пустую область от неоднород-
неоднородного полупространства z > 0. Пусть при z > 0 диэлектрическая про-
проницаемость является некоторой функцией нормализованной координа-
координаты ? = z/a, где а — произвольная единица длины. В выражении
C.4.1) /S — угол поляризации, а в — угол падения.
Поле, отраженное средой при z < 0, и поле, прошедшее в полу-
полупространство z > 0, даются соответственно выражениями
Er = [-sin@)cosO5)rpz + sin(j8)rsy - cos(e)cos(P)rpx2e~iko(xsine~zc08$\
C.4.2)
Et = [ — sir
где штрих означает производную по переменной ?, Л = коа, агр и
rs — коэффициенты отражения при поляризации, соответственно па-
параллельной 08 = 0) и перпендикулярной 08 = 7г/2) плоскости падения.
В частности, функция д (?) является решением дифференциального
уравнения
Из непрерывности составляющих векторов Е и Н, тангенциальных
к поверхности z = 0, следует, что
An2(O)cos0~^J/L + Лп2@) cos 0 0@)
Определив величины
= | 1 * vv/ I/I I I ^Ц о 4^
= Гп2ЮК\
C.4.5)
уравнение C.4.3) можно переписать в виде
d2g/drj2 + A2Q(ri)g = 0. C.4.6)
Можно получить асимптотическое решение этого уравнения для
больших Л, раскладывая функцию д по аналогии с разложением
B.2.5). Таким образом, если положить
g(fl) - СехрГ-iA ? (iA)-nSn(rj)\ C.4.7)
L »=° J
и повторить выкладки, приведшие к уравнению B.2.8), то можно по-
168 Гл. 3. Плоские многослойные среды
казать, что
C.4.8а)
C.4.86)
(ЗА8в)
где штрихи у Q означают производные по t\ (выражения для54 и«55
можно найти в работе [11]).
Если неоднородная среда не обладает существенным отражением,
то в качестве 9 можно выбрать решение уравнения C.4.7), связанное с
волной, распространяющейся слева направо. Это отвечает положи-
положительной определенности величин So, S2 и т. д. Получив таким образом
выражение цпяд, с помощью соотношения C.4.4) можно вычислить
Гр1 _ l-(i/Acose)dlng/dri cosfl -
Гр ~ 1 +(i/Acose)dlng/dv ~ cos0 +
= r<P - (i/A)r™ - A/A2)r<,2> + • • •, C.4.9)
где
r(F)=limr _ ^^2^2
Здесь n0 = n @). Остальные члены можно вычислить методом итера-
итераций, используя следующее выражение:
= lim(iA)«|rp - ^ (iA)--r«l C.4.11)
Главный член в асимптотическом разложении г р(Л) мы обозначили
через г?\ так как он совпадает с коэффициентом отражения Френеля
[см. ниже выражение C.8.1)]. В то время какг^* зависит от разрыва
показателя преломления на границе раздела, величина г^{) пропорцио-
пропорциональна первой производной от п2. Продолжая разложение, нетрудно
показать, что произвольный член г (^г) содержит m-ю производную от
п2. Коэффициент отраженияrs вычисляется аналогичным образом.
Важно заметить, что в соответствии с полученными выше резуль-
результатами возникновение отраженной волны обусловлено разрывностью
производной от функции п (z). Казалось бы, отсюда можно сделать
вывод, что отражения не может быть, если л (z) является аналитичес-
аналитической функцией. Ошибочность этого заключения можно показать на
следующем контрпримере, разобранном Эпштейном, который вычис-
вычислил коэффициент отражения I r I при нормальном падении на гладкую
границу раздела между двумя средами с показателями преломления
r(q)
3.5. Точное решение для слоя 169
соответственнопх ил2. Эпштейн рассмотрел следующий профильп(z)
(см. [1], с. 446):
(z) = l("i + nf) + i(n| - и?) th(z/e) C.4.12)
и получил для коэффициента отражения
|r| = sh 1п2(а/Щп2 - пх\]/ sh [n\alk){n2 + nj]. C.4.13)
В частности, мы видим, что при а /X — 0 справедливо соотношение
|г | = |л2 — /*j |/(л2 + /ij), которое совпадает с величиной френелев-
ского коэффициента отражения от резкой границы между средами
[см. ниже выражение C.8.9)].
Неудача асимптотического метода не вызывает удивления. Она
связана с тем известным фактом, что во всех порядках по к ~1 асимп-
асимптотическое разложение функции е~кх обращается тождественно в
нуль. Как мы покажем в разд. 3.12.4, эту трудность можно преодо-
преодолеть, используя метод характеристической матрицы.
3.5. ТОЧНОЕ РЕШЕНИЕ ДЛЯ СЛОЯ
С ЛИНЕЙНО УВЕЛИЧИВАЮЩИМСЯ ПОКАЗАТЕЛЕМ
ПРЕЛОМЛЕНИЯ
Рассмотрим переходный слой толщиной я, связывающий два одно-
однородных полупространства с показателями преломления соответствен-
соответственно л = 1 и л > 1. Предположим, что s -волна падает на переходный
слой под углом в. Если n2(z) изменяется линейно в переходной облас-
области 0 < z ^ а, то уравнение C.4.3) принимает вид
d2f/d?2 + A2[cos20 + (n2 - 1)<П/ = 0. C.5.1)
Преобразуя переменную ? — [А/(п2 - l)]2/3[cos20 + (л2 — 1)?], по-
получаем уравнение Эйри, решение которого можно выразить через
функцию Бесселя порядка 1/3 [см. выражение C.3.4)]. Используя за-
затем непрерывность тангенциальных составляющих электрического и
магнитного поля при z = 0 и z = а, получаем после некоторых алге-
алгебраических выкладок коэффициент отражения rs (см. [14], с. 70):
Здесь w0 = B/3)[A/(/i2 - l)]cos30, w, = B/3)[Л/л2 - 1)](л2 - sin^K72
и/rU.2) = fj^,i) + /Я^'32). Таким образом, коэффициент отражения
зависит от нескольких факторов, а именно от характера изменения
Функции п 2(z) между двумя однородными средами, толщины переход-
переходного слоя, длины волны и угла падения. Поэтому, измеряя rs для раз-
различных длин волн и угла падения, можно в принципе определить па-
параметры переходного слоя.
170 Гл. 3. Плоские многослойные среды
3.6. МНОГОСЛОЙНЫЕ СРЕДЫ С КУСОЧНО-ПОСТОЯННЫМ
ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
В качестве простейшего примера неоднородной среды рассмотрим
многослойную область (мультислой) с кусочно-постоянным (ступенча-
(ступенчатым) законом изменения показателя преломления. В разд. 3.2 мы
уже обсуждали обобщение метода геометрической оптики на неодно-
неоднородный диэлектрик с непрерывным профилем показателя преломле-
преломления; сущностью этого анализа была основанная на свойствах функций
Эйри возможность сшивки асимптотических решений. При наличии у
показателя преломления разрывов непрерывности можно также при-
применить этот метод, учитывая, однако, некоторые небольшие измене-
изменения в выражениях для коэффициентов отражения и пропускания. Если
же в задаче возникает большое число разрывов функции п (z), то опи-
описание многократного отражения проходящей через среду волны стано-
становится очень сложным. Для этого требуется систематическое изучение
зависимости коэффициентов отражения и пропускания от числа раз-
разрывов, их характера и относительных положений разрывов непрерыв-
непрерывности п (z).
Многослойная среда с кусочно-постоянным показателем преломле-
преломления оказывается удобной моделью для анализа эффектов распростра-
распространения, присущих средам с многочисленными разрывами. В частности,
в слоистых средах с эквидистантным расположением поверхностей
разрыва непрерывности возникает полоса непрозрачности, которая
свойственна всем средам с периодическим изменением показателя пре-
преломления [15], так что для некоторых частотных интервалов волна
вообще не может распространяться без существенного затухания.
Благодаря наличию у многослойных сред полос непрозрачности их
можно использовать в качестве селективных зеркал, которые нетруд-
нетрудно изготовить методами последовательного нанесения тонких пленок.
Диэлектрические мультислой широко применяются в электроопти-
электрооптических устройствах для уменьшения отражения от поверхности, полу-
получения полосовых фильтров или увеличения отражательной способно-
способности при определенных длинах волн [16, 17]. Создание таких сред при
помощи испарения или напыления возможно на многих подложках
(стекла, полимеры, металлы, композитные материалы) [18] (рис. 3.7).
Простейший мультислой представляет собой стопу четвертьволно-
четвертьволновых пластинок, каждая из которых имеет оптическую толщину
nd = Xq/4. В современных системах вместо одинаковых четвертьвол-
четвертьволновых пластинок используют слои со слабо изменяющейся толщиной,
поскольку это позволяет обеспечить лучшее управление пропускатель-
ной способностью в широком частотном диапазоне. При изготовле-
3.6. Многослойные среды с кусочно-постоянным профилем 171
Окружающая среда
Рис. 3.7. Схематическое ^\\\\\\\\\\\\\\\\\\\\\\\\
представление мультислоя Подложка
нии многослойных покрытий их рассчитывают, вообще говоря, для
определенных углов падения волны, причем наиболее часто использу-
используются углы 0 и тг/4.
Конкретную стопу четвертьволновых пластинок обозначают по-
последовательностью символов; так, например, пишут «воздух ВН
ВН...ВН стекло» или «в(ВН)тст». Здесь содержится информация о
том, что главный период мультислоя ВН (В — высокий показатель
преломления п, Н — низкий) повторяется т раз, в то время как под-
подложка сделана из стекла и вся структура находится в воздухе (в и
ст — начальные буквы слов воздух и стекло). Более сложные структу-
структуры типа в(ВН)тВст используются как зеркала с высоким отражением.
Иногда оптическая толщина основной ячейки ВН слабо и монотонно
увеличивается при переходе от первой ячейки к последней,
граничащей с подложкой. Если показатели преломления в четверть-
четвертьволновой стопе (BH)W выбирают таким образом, чтобы
(«в//гнJт = ns/nl9 гдел8 ип{ — показатели преломления соответст-
соответственно подложки и окружающей среды, то при длине волны в вакууме
Хо, равной учетверенной оптической толщине одного слоя из стопы,
отражение равно нулю. Это свойство используется для создания мно-
многослойных просветляющих покрытий, называемых из-за характерной
зависимости г от частоты также V-покрыпшями. При т = 1 и nL = 1
условие, приведенное выше, принимает видл| = ns/n{. Это означает,
что для уменьшения коэффициента отражения от подложки на нее
нужно нанести покрытие толщиной, равной примерно четверти длины
волны, с показателем преломления = (ns/ny/2. Чаще всего для сте-
стеклянных подложек в воздухе используют однослойные просветляю-
просветляющие покрытия из MgF2. У этого материала показатель преломления (в
зависимости от поляризации волны) равен 1,37 — 1,38, т. е. не сильно
отличается от значения 1,22 = VT3, которое представляет собой ко-
Рень квадратный из показателя преломления, характерного для боль-
большинства оптических стекол.
172
Гл. 3. Плоские многослойные среды
3.7. ПРИМЕНЕНИЕ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Как мы уже отмечали во введении, многослойные диэлектрические по-
покрытия широко используются в настоящее время в оптических прибо-
приборах. Типичный пример — диэлектрические зеркала в лазерных резона-
резонаторах, полностью отражающие или обеспечивающие вывод части из-
излучения. Все такие устройства принадлежат к классу мультислоев. Но
все же главной их особенностью является то, что размер неоднород-
неоднородности в них сравним с длиной волны. Вследствие этого их нельзя ис-
исследовать развитым выше методом, основанным на переходных функ-
функциях. Требуется развитие нового подхода, который позволил бы
учесть эффекты многократного отражения на последовательности по-
поверхностей разрыва, разделяющих отдельные диэлектрические слои
стопы. Задачу можно упростить, если пренебречь конечностью попе-
поперечных размеров. В частности, пропускание мультислоя можно вы-
вычислить, считая радиус зеркала бесконечным. Возникающая при этом
ошибка невелика. Кроме того, можно предположить, что показатель
преломления постоянен по всей толщине каждого из слоев и резко из-
изменяется лишь при переходе через границы раздела. Более общая си-
ситуация рассмотрена в книге Бекмана и Спицичино и в статье Хандери,
полные ссылки на которые приведены в библиографии в конце главы.
Таким образом, мы будем рассматривать модель мультислоя, а имен-
именно последовательность пластин с неограниченными поперечными раз-
размерами, разделенных идеальными плоскопараллельными поверхностя-
поверхностями. Показатель преломления каждой из пластин постоянен (рис. 3.8).
Будем нумеровать пластины последовательно справа налево, причем
индексом 1 отметим среду, наиболее удаленную от источника падаю-
падающей волны. Предположим, что ось z направлена поперек слоев, а
xz — плоскость падения плоской волны, приходящей из? = — оо. Не-
4-2
Рис. 3.8. Обозначения и система координат для описания мультислоя.
3.7. Применение теории электрических цепей
173
трудно показать, что любая составляющая поля и (х, z) запишется в
ВИДС Щх,г)-в-**/(х), C.7.1)
где кх — постоянная, зависящая от направления распространения
плоской волны, освещающей первую из пластин. Для решения рас-
рассматриваемой задачи удобно использовать теорию электрических це-
цепей (см. гл. 2 и 5 в книге [3], цитируемой в гл. 2 настоящей книги).
Для этого используем следующие обозначения:
K(z) = Ех@, z), Vh(z) = - ?,@, z),
Je(z) = #y@,z), /h(z) = #x@,z).
Выражения C.7.1) и C.7.2) с учетом A.1.1) —- A.1.4.) позволяют полу-
получить следующие уравнения для q -го слоя, характеризуемого показате-
показателем преломления л •
-dVJdz = ;Д^е)/е, C.7.3а)
C.7.36)
C.7.4)
Здесь f0 — волновое сопротивление вакуума, пд (в общем случае
комплексный) — показатель преломления q-й среды, а
Для вещественных nq угол вя (рис. 3.9) есть угол между направле-
направлением распространения волны в q -м слое и осью z, перпендикулярной
поверхностям раздела слоев. Среды с потерями будут рассмотрены в
разд. 3.21. Множитель (Зд в уравнениях C.7.3) определяется выражени-
Окружающая
среда
где
Рис. 3.9. Направления распространения плоских волн, интерферирующих в многослой-
многослойной системе.
174 Гл. 3. Плоские многослойные среды
™еМ Д, = {п\к20 - к2хI'2 = nqk0cos в„, C.7.6)
так что соотношение C.7.4) можно переписать в виде
Z? = Z, cos вч = /У(<ое0п,2), C.7.7)
ГДе Z, = Со/", C-7.8)
есть характеристический волновой импеданс q-ro слоя. Индекс «е»
(или ТМ) означает поперечную магнитную волну, для которой маг-
магнитное поле перпендикулярно оси* (Hz = 0), т. е. параллельно плос-
плоскости раздела между последовательными пластинами (рис. 3.10,а).
При этом Нх = 0 и Еу = 0.
Дополнительный случай имеет место, если положить Ег = 0
(ТЕ-волныу отмечаемые индексом «h»). Для этих поперечных
электрических волн (рис. 3.10,6) Ну = 0, Ех = 0 и справедлива систе-
система уравнений, аналогичная C.7.3), причем необходимо сделать замену
-* Zih) гле
q q Z<h> = Co/(^cos0,) = ^o/ft. C.7.9)
В оптике ТМ-поля отмечают, как правило, индексом «р», указывая
на то, что вектор Е параллелен плоскости падения, ТЕ-поле — индек-
индексом s, указывая на то, что электрическое поле перпендикулярно (от
немецкого слова senkrecht) плоскости падения.
Система уравнений C.7.3) позволяет изучать распространение ТМ-
или ТЕ-волн, используя аналогию с электрической линией передачи,
состоящей из однородных секций (рис. 3.11) с соответствующими им-
педансами. Для каждой секции общее решение уравнений C.7.3) запи-
записывается следущим образом:
V(z) = К<+V«2 + К<" V<4 C.7.10а)
C.7.106)
рн
а
Рис. 3.10. а — поперечные магнитные (ТМ) и б — поперечные электрические (ТЕ)
волны.
3.7. Применение теории электрических цепей 175
Рис. 3.11. Эквивалентная линия передачи для мультислоя на рис. 3.8. Каждая из секций
имеет длину, равную толщине соответствующего слоя.
где V* + ) и Kj"}— постоянные, а импеданс Z совпадает с Z^e) для ТМ-
волн или ZW для ТЕ-волн. Величины V(z) и I(z) [равные Vt (z),
/е (z) для ТМ-волн и Vh(z), Ih(z) для ТЕ-волн] формально можно рас-
рассматривать как напряжение и силу тока в электрической цепи. Как
принято в теории линий передачи, ток в верхней цепи считается поло-
положительным, если он направлен в положительном направлении оси z.
При рассмотрении многослойных сред поставим в соответствие каж-
каждому из однородных слоев диэлектрика (обозначаемому нижним ин-
индексом д) элемент линии передачи с характеристическим импедансом
Za и длиной dQ.
Указанная выше аналогия становится полной, если ввести понятие
«окольного импеданса ^ = ^^ (з ?л 1}
для которого с помощью соотношений C.7.10) можно получить выра-
ЖеНИе
e
eq_vUeieq*' C.7.12)
Пусть рассматриваемый q-ft слой находится в сечении z = 0. Тогда
4- V{~)
H->' C'7ЛЗ)
v q
/ (ЗЛЛ4)
Сравнивая выражения C.7.12) и C.7.13), получаем
2>(z).Z,f|0)--'V8(ft". C.7..5)
qZq-iZ@) tg (Pqz)
Величина ?(z) представляет собой измеряемое отношение разно-
разности потенциалов и тока в сечении z в том случае, когда часть линии
левее z удалена и заменена на генератор электрического напряжения
(рис. 3.12). Выражение C.7.15) можно интерпретировать как соотно-
соотношение, связывающее локальный импеданс в произвольной точке z с
его известным значением в некоторой точке z, той же пластины. На
176 Гл. 3. Плоские многослойные среды
Рис. 3.12. Схематическое представле-
представление измерения импедансов в произ-
произвольном сечении линии передачи на
рис. 3.11.
самом деле произвол в выборе начала отсчета z = 0 позволяет обоб-
обобщить соотношение C.7.15) следующим образом:
Z(z) = Zg?Zl):^tg№"Zl)^ C.7.16)
qZq-iZ(Zl) tgE/^z-z,)]
Рассмотрим теперь амплитудный коэффициент отражения г,
определяемый как отношение обратной и прямой составляющих на-
напряжения V(z), а именно
r(z) = e2i^2Vq-)/Vq+\ C.7.17)
С помощью соотношений C.7.10) и C.7.11) это выражение можно
переписать в виде ^
r(z) = tZ(z) - ZqVlZ(z) + ZJ. C.7.18)
Заметим, что, в то время как Z(z) наряду с величинами V(z) и I(z)
являются непрерывными функциями координаты z, импеданс Zq пред-
представляет собой кусочно-непрерывную функцию, так что функция г (z)
разрывна приг = zq9 где^ — левая граница q-го слоя.
На каждой из границ разрыва z = zq можно определить также ам-
амплитудный коэффициент пропускания tq:
U = УBя)/1Уч++\е-^^\ C.7.19)
который есть не что иное, как отношение V(zg) к прямой составляю-
составляющей V(z) непосредственно перед zq. Отметим здесь, в чем состоит
различие между ТМ- и ТЕ-волнами. Если мы ищем комплексную ам-
амплитуду полного электрического поля Е = хЕх + 2EZ сразу за поверх-
поверхностью z = zg, то удобно определить новый коэффициент ^полн), полу-
получаемый из tq подстановкой в выражение C.7.19) соответствующих
суммарных амплитуд электрического поля вместо V(zq) и
^X\e~i0q+lZq- ПРИ этом Ддя ТМ(р)- и ТЕ(8)-волн нетрудно полу-
получить следующие выражения:
= tqtP(n2q+1 - n2q+x sin2 eqY'2/(n2q+1 - n\ sin2 О,I'2, C.7.20)
(полн)_
lq,S
так как в этом случае V представляет собой полное электрическое по-
поле. Формальное описание распространения волн в последовательности
3.8. Формулы Френеля 177
слоев можно завершить, замечая, что из условия непрерывности тан-
генциальные составляющие поля связывают И+i и Ит*, с И+) и И~
q+l q+l q q
следующими выражениями:
y( ) g-ifiq+lZq y(~) gtfq+lZq
3.8. ФОРМУЛЫ ФРЕНЕЛЯ
Рассмотрим простейший случай двух диэлектрических сред с показате-
показателями преломления соответственно п1 и л2, разделенных плоскостью
z = 0. Согласно принятому нами соглашению п2 — это показатель
преломления той среды, куда волны поступают прежде всего. Мы бу-
будем следовать этому несколько неестественному выбору, поскольку он
согласуется с тем, что мы приняли уже при рассмотрении мультисло-
ев (см. рис. 3.8), когда, грубо говоря, отражение начинается с подлож-
подложки.
Коэффициент отражения гр для ТМ-волны на поверхности раздела
(а точнее, сразу перед границей раздела 2 —> 1) определяется выраже-
выражением [см. C.7.18)]
= Z2cos92-Zlcosei
где мы использовали соотношение C.7.7), а также учли то, что ()
совпадает с Z^e) [поскольку среда 1 расположена между z = 0 и
z = + оо и в ней нет волны, бегущей в обратном направлении, т. е.
из C.7.12) следует, что при z > 0 Z(z) = ZJ. Закон Снеллиуса и вы-
выражение C.7.8) позволяют переписать выражение C.8.1) и аналогич-
аналогичные выражения для rs, t и fs в виде
sin(fl2 - вх)
*8@1 + 02)' Г§ sin(ei+e2Y
C.8.2)
2 sin 0t cos вх 2 sin 0X cos в2
tp = sin@1 + 02)cQ&@l-02)9 ts = Ш1(в1 + 02) '
Здесь 6Х и в2 — соответственно углы преломления и падения.
Соотношения C.8.2) известны как формулы Френели. Они справед-
справедливы лишь для идеально плоских поверхностей раздела. Наличие не-
неровностей, шероховатостей или царапин приводит к рассеянию пада-
падающего излучения, что сказывается на действительной отражательной
способности. Заметим, что гр = 0, если вг + 02 = тг/2. Угол падения
0В, для которого верно это равенство, называют углом Брюстера, ко-
178 Гл. 3. Плоские многослойные среды
^
Рис. 3.13. Используемая в качестве по-
поляризатора стопа стеклянных пластин,
У/////////////////////////////////////////////////////////////Л расположенных под углом Брюстера.
торый в соответствии с законом Снеллиуса определяется выражением
*g 0B = nJn2. C.8.3)
Равенство rp@B) нулю широко используется в светоделительных
поляризаторах (рис. 3.13). В трубках газовых лазеров для улучшения
пропускания р-компоненты поля окна располагают под углом Брюсте-
Брюстера к оси трубки.
С физической точки зрения источником отраженного поля являют-
являются диполи, возбуждаемые во второй среде преломленным полем Е и
направленные параллельно самому вектору Е. Однако в направлении
своей ориентации диполь не излучает. Следовательно, если отражен-
отраженные лучи параллельны возникающим во второй среде диполям, то
связанное с ними поле должно быть равно нулю. Именно такая ситуа-
ситуация реализуется при в = 0В.
В случае когда гр@в) = 0 и гр@>в) = 1, выражения C.8.2) и C.8.3)
приводят к следующим равенствам:
Фъ) = {п1-п\)/{п\ + п\\ C.8.4а)
Фъ) = 2ni/(n? + п\\ C.8.46)
Необходимо также подчеркнуть, что для любого угла падения ко-
коэффициенты гр, rs, /p и rs, определяемые выражениями C.7.17) и
C.7.19), удовлетворяют в соответствии с C.7.10а) следующим соотно-
соотношениям: , 4 /1 о с\
's - г% = Гр - гр = 1. C.8.5)
Выразим теперь коэффициенты отражения и пропускания через со-
соответствующие оптические интенсивности (измеряемые в ваттах на
квадратный метр) /г и /t. Если интенсивность падающей волны обо-
обозначить через /j, то можно записать следующую цепочку соотноше-
соотношений, справедливых для s-волн:
/, = ВД*/2 = и2|?,|2/BСо), C.8.6а)
Л = h\r*\2 = ДЯ8, C.8.66)
It = Ii\ts\2nl/n2 = IiTs, C.8.6b)
в то время как для р-волн мы имеем
/г = Ц\гр\2 = LtRv, C.8.7а)
3.8. Формулы Френеля
179
Я=1Н2
,z,-z2f
0
а
л
%-волна / /
^^_ ^А-волна
еа
R=\r\2
0
6
s -волна
р-вол на/ 1
Полное
отражение
90°
9*
0с
90°
Рис. 3.14. Зависимость отражательной способности от угла падения для р- и s-волн в
случаях, когда луч распространяется из воздуха в диэлектрик {а) и из диэлектрика в
воздух (б).
2 = 1{ТР. C.8.76)
Величины R и Т называют соответственно коэффициентом отра-
отражения (или отражательной способностью) и пропускания (или про-
пускательной способностью). В частности, из C.8.2) следует (рис.
3.14), что о
Rs =sin2@1 - fl^/sin2^ + 02), C.8.8a)
^р = tg \в1 - 02)/ tg 2@Х + в2). C.8.86)
При нормальном угле падения эти соотношения сводятся к следу-
следующим выражениям:
jRs = Rp = (jti — п2) l\Yi\ + п2) , C.8.9)
Ts = Tp = 4nln2/(nl + n2J. C.8.10)
Если же л, и Л2 — комплексные величины, т. е. потерями прене-
пренебречь нельзя, то выражения C.8.9) и C.8.10) можно записать в обоб-
обобщенном виде:
Rs = Rp = \пг - п2\2/\пг + Я2|2 @! = 0), C.8.11а)
Ts= Tp = 4(Ren1 Ren2 + lmnllmn2)/\nl + п2|2 (в1 = 0). C.8.116)
Если энергия преломленного луча диссипирует в среде 1 (например,
в металлических подложках достаточной толщины), то для описания
соответствующих потерь на поглощение вводят понятие коэффициен-
коэффициентов поглощения (или поглощательной способности) As и А , где
^s = 1 - /?s, Ap = 1 - /?р. На рис. 3.15 построены зависимости коэф-
коэффициентов поглощения при нормальном падении для некоторых ти-
типичных металлов.
180
Гл. 3. Плоские многослойные среды
0,1 0,1 0,3 0,5 0,8 1 1 4 6 5 10 Л,мкм
Рис. 3.15. Зависимость коэффициента поглощения от длины волны для некоторых ти-
типичных металлов.
3.9. МЕТОД ХАРАКТЕРИСТИЧЕСКОЙ МАТРИЦЫ
Рассмотрим однородный диэлектрический слой толщиной d. Выраже-
Выражения C.7.10) позволяют получить простые соотношения для эквива-
эквивалентного напряжения V{ и силы тока/j как на поверхности 1, так и на
поверхности 2. Действительно, если положить zx = 0и?2=— d, то
мы имеем ^
V2 =
C.9.2a)
C.9.26)
где Z = Z для ТМ-волн и Z = Zs для ТЕ-волн. Таким образом,
= VJ2 + ZIJ2,
F<-> = VJ2 - ZIJ2,
Из этих соотношений в свою очередь получаем
V2 = Vj, cos fid - iZ^ sin 0d,
C.9.3a)
C.9.36)
C.9.4a)
C.9.46)
I2 = - ,Tj sin(Pd)/Z + h cos Ц.
Последние уравнения можно записать в матричной форме следующим
образом:
WJ c
/2J l-iSi
cospd -iZsinpd
iSin(f}d)/Z cospd
J
A BjV.
3.9. Метод характеристической матрицы 181
Входящая сюда матрица 2x2 называется характеристической
матрицей у или матрицей пропускания слоя [19]. В оптике эти матри-
матрицы впервые использовали Херпин и Мачмор при рассмотрении прос-
простых сред. Позднее они были обобщены на анизотропные кристаллы
[20]. Элементы характеристической матрицы зависят от оптической
толщины /3rf и импеданса Z однородного слоя, а ее детерминант равен
единице.
Когда рассматривается стопа пластин, пронумерованных, как
обычно, справа налево, пара величин Vn,In может быть выражена че-
через К/1э если (п - 1) раз использовать умножение вектора на матри-
матрицу аналогично тому, как это сделано в C.9.5). Точнее говоря, если
обозначить через М, ,_! матрицу, относящуюся к /-й пластине, то
можно написать следующее выражение:
[Я =
C.9.6)
где Мл j — произведение матриц Мл п_{ ••• М2 г Заметим, что произ-
произведение матриц требуется вычислять именно в указанном порядке, так
как в общем случае матрицы не коммутируют, исключение составляет
лишь случай пластин с одинаковыми характеристиками. Таким обра-
образом, можно сказать, что для любого мультислоя, используя соот-
соответствующую характеристическую матрицу, можно получить одну из
другой пары V, /, относящиеся к произвольным поверхностям разде-
раздела.
Проведенное выше рассмотрение применимо для границ раздела
мультислоя. Однако это ограничение можно обойти для произвольно-
произвольного сечения с абсциссой z. Поскольку нам ничто не мешает рассматри-
рассматривать это сечение как поверхность раздела между двумя средами, су-
существует матрица M(z, z'), такая, что в общем случае мы можем за-
записать г- ,-
Пг)Л _ м,_ _,ч №Л C.9.7)
В качестве следующего шага можно отказаться и от предположе-
предположения о постоянстве показателя преломления в каждом слое. Действи-
Действительно, каждый непрерывный профиль можно аппроксимировать
мультислоем, состоящим из бесконечно тонких пластин. Отсюда
можно заключить, что метод характеристической матрицы применим
и для общего случая произвольной плоскослоистой среды. В частно-
частности, для любой такой среды det M(z, z' ) = 1, так как для каждой
матрицы М детерминант равен единице, а детерминант произведения
матриц равен произведению детерминантов.
В следующем разделе мы рассмотрим сначала случай пластины с
182 Гл. 3. Плоские многослойные среды
произвольным профилем п (z), а затем дадим последовательный ана-
анализ периодической стопы, состоящей из одинаковых пластин, каждая
из которых характеризуется одной и той же матрицей М.
3.9.1. Уравнение для ЪЛ-матрицы
Для среды с изменяющимся п с помощью соотношения C.9.5) по-
получаем
M(z + dz,z') = M(z + dz9z) • M(z,z') = M(z,z') + idzl °~ ^1 • M(z,z'),
Следовательно, C.9.8)
м>.А Г» f
dz \_P/Z O
Если теперь обозначить элементы матрицы M(z, г' ) как Л = Mul,
= Mj 2, С = М2 j и D = М2 2, то из уравнения C.9.9) мы имеем
C.9.10а)
C.9.106)
C.9.10b)
p C.9.10г)
где как /3, так и Z являются функциями координаты z. Если п — не-
непрерывная функция otz, то уравнения C.9.10а) и C.9.10в) дают
здесь ф = \0 dz — фазовая толщина. Это уравнение необходимо ре-
решать вместе с дополнительными условиями A(z', z')= 1 и
dA/dz = 0 при z = z' [последнее соотношение следует из того, что
C(z', z') = 0]. Если в среде нет потерь, то /3 и Z вещественны и
из уравнения C.9.11) при начальном условии А = 1 следует, что
A(z, z') — тоже вещественная функция. В свою очередь из уравнения
C.9.10в) следует, что С— мнимая величина. Аналогичные выкладки
можно повторить для В и ?>. Поэтому можно заключить, что для сре-
среды без потерь диагональные элементы М -матрицы являются вещест-
вещественными, а недиагональные — мнимыми.
Заметим, что 0(z) = ko[n2(z) - кгх/кг$ау т. е. уравнение C.9.11)
содержит большой параметр к\. Поэтому его можно переписать по
аналогии с C.4.6), используя следующие подстановки: d-ц =
= Z(n2 - k2x/kl)V2dz, Л = к09 Q(n) = 1/Z2. Таким образом, если n(z)
мало изменяется на расстоянии порядка длины волны, то функцию А
3.9. Метод характеристической матрицы 183
можно разложить в асимптотический ряд C.4.7). Таким образом, ис-
используя начальные условия, нетрудно получить
A(z9z')~[Z(zyZ(z)r1i2CQslk0(S0-S2/kl + --% C.9.12)
где
4J dz"> C-9ЛЗа)
Ь2\1/2
-4) " °-9136)
здесь Z' и Z" — производные импеданса Z первого и второго поряд-
порядков по фазовой переменной \(п2 - ?2/?2I/2 dz". Аналогичные разло-
разложения можно получить и для остальных компонент М-матрицы.
3.9.2. Вычисление lh-матрицы для мулыпислоя
Рассмотрим теперь мультислой из т слоев, каждый из которых ха-
характеризуется одинаковой М-матрицей, а чтобы получить матрицу
для всего мультислоя, матрицу М нужно повторить т раз, т. е. вы-
вычислить m-ю степень матрицы М. Для этого М удобно представить в
виде двух матриц О<+> и О(-\ таких, что О(+J = О(+>, О(~J = О(~> и
(У+> ¦ О(-) = 0. Для того чтобы найти это представление, будем дей-
действовать в три этапа. Во-первых, найдем два собственных значения
у± матрицы М (для простоты будем считать, что они различны);
во-вторых, вычислим правые и левые собственные векторы матрицы
М, соответствующие у+ и у_9 и, в-третьих, построим О(+) и (У"\ ис-
используя эти собственные векторы. Для нахождения собственных зна-
значений нужно решить уравнение
из которого с учетом равенства detM = 1 получаем
у± = \{А + D) Т /[1 - (А + DJ/4]1/2 = eTid. C.9.15)
д = arccos[(>l + D)/2]. C.9.16)
Вычислим затем правый собственный вектор V(+) ж (К(+), /(+)),
соответствующий y+- Для этого нужно решить однородную систему
уравнений
(А-у+)К(+) + В/(+) = 0, C.9.17а)
СК(+) + (D - у+)/(+) = 0. C.9.176)
Аналогично для нахождения левого собственного вектора
184 Гл. 3. Плоские многослойные среды
}/(+) = [к(+)э/(+)] решаем систему уравнений
(А - у+)К(+) + с7(+) = 0, C.9.18а)
(D-y+)Ii+) = O< C.9.186)
При этом все собственные векторы определяются с точностью до
призвольного постоянного множителя. Очевидно, что те же уравнения
справедливы при замене 7 + , V(+), V(+)-* y_, V(~}, V(~\
Теперь нетрудно построить матрицу О(>) (О(~}), комбинируя со-
составляющие векторов V(+) и V(+) следующим образом:
С D-
Матрица О(~} определяется аналогично. Таким образом, мы имеем
1 V(+)V(+) = O(+), C.9.20)
• *-№-> - 0. C.9.21)
Равенство нулю последнего произведения следует из соотношения
у<+>. V(-> = — V(+). М . V("> = — V(+) • M . V(">, C.9.22)
У- У+
которое при 7+ Ф 7- верно лишь в том случае, если V*+)- V(~) = 0.
Теперь можно выразить М через О(+) и О(~}:
М = С+О(+) + С_О(). C.9.23)
Умножая обе части этого равенства на О(+), получаем
М . О(+) = С,О(+) = у+О(+) - С+ = у+. C.9.24)
Поскольку аналогичное равенство справедливо и для С_ , окончатель-
но имеем М = У+О<+> + г_О«->. " C.9.25)
Кроме того, с использованием условия ортогональности ((У+)-(У~) =
= 0) и идемпотентности (О<±J = О(±)) нетрудно получить (другое
выражение для М" приведено в задаче 7)
М" =7 + О(+) + /.О^^ C.9.26)
Пример: fli-матрица мулыпислоя с попеременно изменяющимся
показателем преломления. Соотношение C.9.26) полезно применять,
в частности, для вычисления матрицы мультислоя, состоящего из 2т
3.10. Блоховские волны 185
чередующихся слоев с показателями преломления соответственно па,
пь и толщинами da, db. В этом случае, если обозначить через Мо и
Mj, матрицы отдельных слоев, то из уравнения C*9.5) для матрицы
М^ двойного слоя получаем
z ~ ^
cos фа cos фь — -^ sin фа sin фь — iZa sin фа cos фь — iZb cos фа sin фь
-3- cos фа sin фъ — ^г sin фа cos фь —^ sin <?fl sin фъ + cos </>a cos фъ
Л za zb
C.9.27)
где фа = Eada и фь = j8ft d^ — фазовые толщины слоев соответственно
а и b. Для того чтобы представить матрицу ЬЛЬа в виде, аналогичном
C.9.25), нужно с помощью выражения C.9.16) вычислить 6 и решить
уравнения C.9.17) и C.9.18).
Следует заметить, что для любой слоистой среды матрица М при
данной длине волны равна характеристической матрице некоторой
двухпленочной комбинации (теорема Херпина). Математически это
утверждение эквивалентно тому, что можно найти четыре таких пара-
параметра: Za, Zb, фа и фь, при которых матричные элементы в C.9.27)
будут совпадать с величинами А, В, С и D.
3.10. БЛОХОВСКИЕ ВОЛНЫ
Продолжим анализ структур, состоящих из т одинаковых слоев тол-
толщиной Л, причем каждый элементарный слой характеризуется матри-
матрицей М. Периодичность слоев приводит к хорошо известному явлению
частичной непрозрачности. Это означает, что в среде могут распро-
распространяться лишь волны, частоты которых лежат в определенных ин-
интервалах, называемых полосами пропускания. Вне этих полос поле за-
затухает экспоненциально, аналогично тому, как затухают волны в сре-
средах с потерями. Изучение свойств полос непрозрачности возможно с
помощью теоремы Флоке. Этим мы займемся в разд. 3.17. Положе-
Положение различных полос и их ширина зависят от характеристик элемен-
элементарного слоя (толщин и показателей преломления составляющих их
тонких пленок). С математической точки зрения полосы непрозрачно-
непрозрачности соответствуют тем частотным интервалам, для которых модули
собственных значений у± характеристической матрицы элементарного
слоя отличны от единицы, т. е. IA + D I > 2.
Собственные векторы V(+) и V(~> матрицы М являются также
собственными векторами для матрицы степени Мя, где п — произ-
186 Гл. 3. Плоские многослойные среды
вольная степень. Это позволяет найти значения вектора V(^) на лю-
любой поверхности раздела между соседними элементарными слоями, а
именно при z = zq = -#Л, где q — целое. Правая поверхность пер-
первого элементарного слоя расположена в начале оси z. Если V@) совпа-
совпадает с У(+) или V*-), то
V(zf) = e±iqd\{±). C.10.1)
Для полного описания поля требуется рассмотреть поведение век-
вектора V в произвольной точке z. Для этого воспользуемся теоремой
Флоке (разд. 3.17.1), в соответствии с которой V(z) можно предста-
вить в виде v<±»(z) = f<±>(z)^'^, C.10.2)
где ft^iz)— периодическая функция с периодом Л, зависящим от
профиля n(z) в элементарном слое. В частности, если элементарный
слой имеет плоскость симметрии, то fl+)(z - Л/2) <х H'^-z- Л/2).
Зависимость V(±)(z) в виде C.10.2) можно рассматривать как элек-
электромагнитный аналог квантовомеханических электронных волн, рас-
распространяющихся в кристалле с постоянной решетки Л. Благодаря
этой аналогии векторы V(+)(z) и V<~)(z) называют блоховскими
волнами [21].
Заметим, что V(+)(z) и V<~)(z) только в том случае описывают
волны, распространяющиеся соответственно в прямом и обратном на-
направлениях, когда S является вещественной величиной, т. е. [см. выра-
выражение C.9.16)]
\A + D\?2. C.10.3)
Для элементарного слоя, состоящего из двух пластин, выражения
C.9.27) и C.9.16) приводят к следующему соотношению:
cos<5 = cos</>ecos0b - (l/2)(ZJZb + Zb/Za)sinфаsinфь. C.10.4)
Если фа = фь = ф, то выражение C.10.4) принимает вид
cosд = cos2 ф - - Zfl2AZ*2 sin2 ф. C.10.5)
2 ZaZb
Таким образом, 5 вещественно, если
cos2 ф ^(Za - ZbJ/(Za + ZbJ = cos2 фг. C.10.6)
Поскольку V<+) и V(") определены с точностью до произвольного
постоянного множителя, блоховские волны удобно характеризовать
импедансами Z<+) и Z(">, определяемыми следующими выражения-
выражениями:
Z<+> = K<+>(zq)//<+>(z,), Z<"> = V<-\zq)/I<-\zq). C.10.7)
Если учесть уравнения C.9.17), то сразу получаем
= -В/(А - e~id), Z{~} = -B/(A - eid). C.10.8)
3.11. Полосы пропускания и непрозрачности
187
Заметим, что для вычисления /<+) и /("> используется одно и то
же определение положительного направления тока. Поэтому для
волн, распространяющихся в однородной среде справа налево, /(-) и
Z(-) отрицательны.
3.11. ПОЛОСЫ ПРОПУСКАНИЯ И НЕПРОЗРАЧНОСТИ
СТОПЫ ЧЕТВЕРТЬВОЛНОВЫХ ПЛАСТИНОК
В случае когда характеристическая экспонента 5 вещественна, блохов-
ские волны распространяются через мультислой без затухания и стопа
ведет себя как прозрачный диэлектрик. Если же 1тб Ф О, то амплиту-
амплитуда одной блоховской волны экспоненциально затухает, а другой экс-
экспоненциально возрастает. Это означает, что падающая извне волна не
может проникнуть в среду. В данном случае стопа действует как отра-
отражатель.
Благодаря этим свойствам те частотные интервалы, в которых
Im6 = 0, называют полосами прозрачности (или пропускания), а все
остальные части спектра — полосами непрозрачности. Полосы про-
пропускания для мультислоя с однородной фазовой толщиной (фа = фь)
непосредственно определяются из уравнения C.10.6). Каждая полоса
пропускания простирается от Ят — ДО до fim + АИ, где пт — цент-
центральная угловая частота (рис. 3.16). Величины Qw и ДО можно сразу
вычислить, заметив, что при w = Йт мы имеем cos20fl = 1, а при
со = пт ± AQ, соь2фа = cos2</>,. В соответствии с C.10.6) получаем
Qm = mnc/(nadacosea) (m — целое) C.11.1)
Zb)\:
C.11.2)
Рис. 3.16. Схематическое представление дис-
дисперсионной кривой /3 = 0(ш) (сплошная кривая)
и постоянной затухания а = а(ш) для периоди-
ческой структуры (штриховые кривые). Поло-
Полосы непрозрачности отмечены толстыми отрез-
отрезками.
188 Гл. 3. Плоские многослойные среды
В частности, если пь = па, то из выражения C.11.2) следует, что
2Д0 = Пт + 1 - пт\ это отражает тот очевидный факт, что однород-
однородная диэлектрическая среда пропускает все частоты. Центральные
угловые частоты пт полос непрозрачности определяются выражением
пт = (т + l/2)nc/(nadacosea), C.11.3)
а ДО (полуширина полосы непрозрачности) записывается в виде
ДП = . ° а arcsin|(Za - Zb)/(Za + Zb)\. C.11.4)
nadacosda
В частности,
ДЯ/Qo = B/7i)arcsin|(Zfl - Zb)/(Za + Zb)\, C.11.5)
в то время как длина волны в вакууме Aq, соответствующая первой
полосе непрозрачности По, определяется выражением
nada cos ва = nbdb cos вь = Ао/4. C.11.6)
Следует заметить, что Ц^ и fiw не зависят от поляризации, а ДП и
ДЯ зависят от нее всегда, за исключением случая нормального паде-
падения.
Из выражений C.11.1) и C.9.27) следует, что в центре любой поло-
полосы пропускания матрица МЬа сводится к единичной матрице, так что
7+ = 7- = 1-
Аналогично, в центре любой полосы непрозрачности матрица ЬЛЬа
принимает вид
Г7 17 П "I
C.11//
так что 7+ = -Za/4> 7- = -^/^аи z(+) = «, Z~ = 0.
В случае когда фа = фь, можно показать [используя выражения
C.10.8) и C.9.27)], что импедансы блоховских волн записываются в
виде
z(±)= i(Za
;;„.8)
Используя затем выражение C.10.6), получаем Za/Zb =
= A + со8ф^)/A - cos^), так что Z(±) можно записать в виде
Z(±) _ ? *тфсо*ф
~ IZcbcos^
где 2сЪ — это блоховский импеданс Z(+) = ~Z(") в центре полосы
пропускания, причем
Zcb = (Ze + Zb)/B + ZJZb + Zb/ZJ1/2. C.11.10)
3.12. Коэффициент отражения мультислоя 189
В соответствии с этими выражениями произведение
= - Z\b является постоянной величиной. К тому же внутри полосы
непрозрачности arg(Z(+)) = arg(Z~1) = тг/2. Кроме того, в центре
полосы непрозрачности cos#a = 0, а это означает, что Z(+) — оо и
Z(-) = 0, как мы уже отмечали. Внутри полосы пропускания ампли-
амплитуда IZ(+)I = Zcb постоянна и arg(Z(+)) + arg(Z<~>) = тг. Кроме
того, при изменении частоты от центра к границе полосы arg(Z(+))
монотонно увеличивается от 0 до 7г/2.
3.12. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ МУЛЬТИСЛОЯ
Одной из важных задач является определение соотношений между
амплитудами блоховских волн, распространяющихся в прямом и об-
обратном направлениях по стопе, расположенной на некоторой подлож-
подложке S, имеющей импеданс Zs. Для решения этой задачи заметим, что
отношение V = К<+> + К(~> к / = /<+) + /<-> на поверхности под-
подложки равно Zs, т. е. в соответствии с выражениями C.10.7) имеем
(~)
(~)/Z(~) = C.12.1)
Таким образом, если ввести обозначение rs = K(~V K(+)), то по-
получим
_7<~> 7 — 7< + >
В центре полосы непрозрачности Z<+> = oo, Z(~> = 0 (см.
разд. 3.11), поэтому вне зависимости от подложки rs = 0. Однако ра-
равенство нулю амплитуды отраженной волны вовсе не означает, что
падающая волна поглощается в нагрузке. На самом деле внутри поло-
полосы непрозрачности F<+> представляет собой стационарную волну
(вновь обратите внимание на аналогию с электронными волнами в
кристалле). При этом обычное представление о полях, распространя-
распространяющихся в прямом и обратном направлении, уже теряет смысл. В со-
соответствии с выражением C.10.2) коэффициент отражения г_+1 на ле-
левой границе q-ro слоя имеет вид
rq+l = rse-2i«d (q = 1,2,...,m). C.12.3)
Необходимо отдельно остановиться на различии между определе-
определением коэффициента отражения, которое мы дали здесь, и тем, кото-
которое было дано в разд. 3.3.3. Здесь мы определили коэффициент отра-
отражения по отношению к блоховским волнам. Для них понятие о пря-
прямом или обратном распространении возможно лишь в приближенном
смысле, поскольку такая интерпретация не годится при приближении
190 Гл. 3. Плоские многослойные среды
к центру полосы непрозрачности. В то же время в разд. 3.3.3 эти по-
понятия совершенно строгие, так как относятся к бегущим волнам.
Естественно, что оба используемых определения совпадают при рас-
рассмотрении практически однородной среды.
Вычислим теперь коэффициент отражения г на поверхности разде-
раздела между мультислоем и окружающей средой. При этом будем рас-
рассматривать структуру типа «окружающая среда — (BH)W — подлож-
подложка». Заметим, что Z (локальный импеданс q-то элементарного слоя)
связан с коэффициентом отражения rq и величинами Z(+), Z(-) следу-
следующим соотношением:
1 -4- г_
у C.12.4)
При этом Z(+) и Z(~\ как уже отмечалось, представляют из себя
локальные импедансы прямой и обратной блоховских волн. Вследст-
Вследствие этого входной импеданс стопы равен величине
1 4- л~2»тЛ,.
7 - 7{ + ) s П 12 5
которую с помощью C.9.5) можно выразить через Zs и матричные
элементы А, В, С и D> характеризующие стопу. Коэффициент отра-
отражения г можно теперь получить, используя соотношение C.7.18) для
случая i?(z) = Z-jX, Zq = Zj, где ZY — импеданс окружающей сре-
среды. При этом
2id
г = я
Z< + )Z<~) -f_ ZZ*~* + Z* + *Z*~*
AZS + B- CZsZt - DZi .
= t: >s x зч-. (jAZ.O)
AZS + В + CZSZY + DZX
Определим следующий набор вещественных параметров X, Y, W, V:
Х =
Ж = Re(D/Zs),
V = Im(C + D/Zs).
Теперь с помощью соотношения C.12.6) нетрудно получить отража-
отражательную способность R = I r 12:
Я = [(X - WI + (У - КJ]/[(ЛГ 4- WJ + (У + КJ]. C.12.8)
Кроме того, если arg(r) = ф, мы имеем
JX+W)(Y-V)-(X-W)(Y+V)
*W (X + W)(X - W) + (Y + V)(Y - V)' K '
3.12. Коэффициент отражения мультислоя 191
Следует заметить, что слоистая среда без потерь имеет ту же са-
самую отражательную способность как со стороны окружающей среды,
так и со стороны подложки. Это утверждение можно доказать, ис-
используя теорему взаимности или простые трансформационные
свойства М-матрицы при инверсии положительной оси распростране-
распространения (см. задачу 3.8). В соответствии с этим отражательную способ-
способность и пропускание Т = 1 - R можно считать характеристиками са-
самой многослойной среды независимо от того, с какой стороны падает
на нее излучение.
3.12.1. Формула Эйри
В некоторых случаях пропускание системы удобно представить в виде
функции от отражательной способности отдельных составляющих
подсистем. Рассмотрим для примера среду, изображенную на
рис. 3.17. Пусть известен коэффициент отражения двух смежных по-
поверхностей, вычисленный в предположении, что окружающей средой
является соответствующий прилегающий слой, который будем счи-
считать бесконечно толстым. При этом пропускание Т промежуточного
слоя, окруженного двумя мультислоями, определяется формулой сум-
суммы Эйри:
Т Т Г 4Д 1 ~\~1
Здесь Тх и Т2 — коэффициенты пропускания соответственно первой и
второй подсистем, Rg = V/?j R2, Фх и ф2 — фазы коэффициентов от-
отражения гг и г2, а ф — фазовая толщина слоя между двумя выделен-
выделенными поверхностями. Доказательство этой формулы оставляем чита-
читателю в качестве упражнения (см., например, книгу Стоуна [22]).
Из структуры выражения C.12.10) видно, что пропускание всей си-
системы может быть равно единице только при выполнении условий
Окружающая
среда
Подсистема 7
' Г; Промежуточный
| Г2 слой
L Подсистема 2
Рис. 3.17. Система, для которой вычисляется ШЩЩШ Подложка
сумма Эйри.
192 Гл. 3. Плоские многослойные среды
R{ = R2 и sin (фх + ф2 - 2<?)/2 = 0. Отсюда следует, что для муль-
тислоев, симметричных относительно центрального слоя, можно до^
стичь высокой прозрачности, если добиться выполнения этого усло-
условия за счет изменения относительной фазовой толщины. Эти системы
ведут себя аналогично интерферометрам Фабри — Перо. Изменение
расстояния между симметричными мультислоями позволяет управ-
управлять частотами, при которых достигаются максимумы пропускан»
(см. разд. 7.21).
Применительно к интерферометрам формулу Эйри обычно записы-
записывают в виде
Т = 7макс{1 + ^/T^sin2^ +ф2- 2ф)}}~\ C.12.11)
где
— максимальное пропускание, называемое также пропускной способ*-
ностью, а величина ^
- R ) (Ъ 12 HY
— резкость интерферометра. Более подробно эти вопросы будут об-
обсуждаться в разд. 7.21.
3.12.2. Четвертьволновые стопы
В пределах полосы пропускания четвертьволновой стопы без по-
потерь (фа = фь) выражение C.12.6) принимает более простой вид:
7( + ) z — Z*~* г — г p~2imS
r = ^FO'^7( + >1 ' *S -2,m*' C.12.14)
?, ^\ -r Z/ i — jj rsef
где Tj — коэффициент отражения по отношению к окружающей среде
(без потерь). С учетом равенства Z(~> = - Z(+)*, которое справедли-
справедливо для диэлектрических пленок без потерь, имеем
г, = -(Z(-yz(+))(Z, - Z(+))/(Z, - Z(->). C.12.15)
Вычисляя квадрат модуля выражения C.12.14) для г, получаем
1 + |r,rs|2 + 2|r,rs|cosBm<5 + ф) '
здесь </> = 7г + arg(rs) - arg(/*j). Рэлей и другие авторы исследовали
поведение мультислоев при т — оо. В этом случае для отражатель-
отражательной способности выполнено одно из двух условий: 1) R стремится к
единице или 2) R принимает значение между Ruim и #макс, которые
определяют огибающую функцию /?(Х). Если рассматривать R как
функцию непрерывного параметра т, то сразу получаем
3.12. Коэффициент отражения мулътислоя
193
10,8
О 0,2 0,6 1,0 t,4 Ло/А
Рис. 3.18. Вычисленные спектры отражения диэлектрического зеркала «стекло —
(BHf». Здесь п s = 1,51, /*в = 2,3 (ZnS), 4nBdn = Хо; лн = 1,38 (MgF2);
<—-> Р - * (-) Р - 5. (Из [22а].)
На рис. 3.18 построены зависимости R(\) для мультислоев, состоя-
состоящих из двух и пяти элементарных составляющих структур. Эти зави-
зависимости нормированы на центр полосы непрозрачности. Из рисунка
видно, что величина R осциллирует между огибающими #макс и R^^
(вычисление /?макс и Rum из уравнения C.12.8) см. в работе [23]).
3.12.3. Однослойные покрытия
В случае когда покрытие состоит из одного слоя, выражение C.12.5)
определяет входной импеданс:
Z ,z/ + '(f/f)tg»«, C.12.18)
вх 1 + i(Zs/Zc) tg фс
где индекс «с» указывает на принадлежность вычисляемых величин
покрытию. Отсюда, используя C.7.8), получаем коэффициент отраже-
отражения для р-волн:
— ZSZX) tg фс _
+ ZSZX) tg фс "
cos 0S cos 0i
ZX)ZC
COS 0S COS 0i /COS0C COS 0c COS 0i Hc \
5 ! + i( ? ^—- — tg фс
ns щ \ nc cos0c nsnj
COS 0c COS 0| ./COS 0C COS 0c COS 0| И
————— -^. ——— -^- 11 ———^— ~l- -^—————— —i—
ws щ \ nc cos0c ns
. C.12.19)
Для данного направления падающей волны коэффициент отраже-
отражения гр является периодической функцией угловой частоты и: гр(со) =
= гр(о> + О). При этом период О дается выражением
П= ?** C.12.20)
ncdccos0c
Экстремальными значениями величины I г (со) I являются
|(ZS - Zy)l{Zs + Z,)|, . |(ZC2 - ZsZt)/(Z2c + ZSZ,)|, C.12.21)
194 Гл. 3. Плоские многослойные среды
что соответствует угловым частотам
со = [с/Мссо8 0сШтг, со = [c/(Mccos0c)]B<? + 1)я/2 C.12.22)
для любого целого д. Если Zc = (ZsZjI/2, то минимум величины гр
равен нулю, т. е. покрытие «преобразует» импеданс подложки в импе-
импеданс окружающей среды в полной аналогии с четвертьволновыми пре-
преобразователями, используемыми для синхронизации двух линий пере-
передачи. Аналогичное рассмотрение можно провести и для rs.
3.12.4. Отражение от слоя со слабо изменяющимся профилем п
В случае когда п является медленно меняющейся функцией координа-
координаты z9 мы можем получить асимптотические решения уравнений
C.9.10), которые описывают эволюцию компонент М-матрицы. Точ-
Точнее говоря, асимптотическое представление компоненты А, даваемое
выражением C.9.12), нетрудно обобщить и на остальные компоне-
компоненты. Таким образом, мы имеем
A(z,z') ~ [Z(z')/Z(z)]/2cosfe0(So - S2/k20 + •••),
B(z,z') ~ -iiZ{z')Z{z)V12 sin ko(So - S'2/k2 + ••),
), 12 23)
C(z,z') ~ -/[Z(z)Z(z')r1/2sinfco(So - S2/k20 + •••),
D(z,z') - [Z(z)/Z(z')]/2cosfeo(So - S'2/k20 + •••),
где величины So и S2 определяются выражениями C.9.13), a S2 полу-
получается заменой Z на 1/Z в выражении C.9.136). Если рассмотреть те-
теперь среду без потерь, подставить выражение C.12.23) в C.12.8) и ис-
использовать равенства Z(z) = 2l9 Z(z') = ?s,to получим
*= tg 2[(S2 - S'2)/2kol C.12.24)
3.13. МЕТАЛЛИЧЕСКИЕ И ДИЭЛЕКТРИЧЕСКИЕ ОТРАЖАТЕЛИ
Большинство отражателей, используемых для ультрафиолетового, ин-
инфракрасного и видимого излучения, изготавливают, используя метод
напыления металлов на полированную поверхность [24]. На рис. 3.15
приведены спектры поглощательной способности некоторых металли-
металлических пленок. Почти все такие пленки, за исключением родиевых,
плохо пригодны для практического использования из-за их окисления
и потускнения. Эти же свойства ограничивают использование в ка-
качестве второго слоя зеркал серебро, хотя для него отражение в види-
видимом и ИК-диапазонах максимально. В подавляющем большинстве
приложений предпочтительным покрытием является алюминий, име-
имеющий высокую отражательную способность в широкой спектральной
3.13. Металлические и диэлектрические отражатели 195
полосе и приемлемую долговечность. В спектре отражательной спо-
способности А1 существует за счет слабого внутризонного перехода не-
небольшой провал вблизи 0,825 мкм A,4 эВ). Алюминиевые зеркала для
их защиты, а также для увеличения отражательной способности в
УФ-диапазоне нередко дополнительно покрывают тонким слоем фто-
фторида магния или монооксида кремния.
Большинство металлических отражателей имеют отражательную
способность менее 99%. Если же требуется более высокая отража-
отражательная способность, необходимо использовать диэлектрические зер-
зеркала. Такие зеркала применяются для достижения полного отражения
в лазерах с малым усилением, а также в интерферометрических систе-
системах. Многослойные диэлектрические покрытия очень слабо поглоща-
поглощают, так что нетрудно изготовить частично пропускающие зеркала.
Они широко используются в качестве устройств вывода в стабильных
оптических резонаторах.
Простейшие диэлектрические зеркала имеют структуру «стекло —
(ВН)т». Используя выражения C.12.2) и C.12.5), а также равенства
eid ._ _ пв/пн, Z(+) = оо и Z(-) = 0, нетрудно показать, что в
центре полосы непрозрачности импеданс системы определяется следу-
следующим образом:
г« = V2/m5 = zs( VV2- C131>
Отсюда с помощью соотношения C.7.18) находим
zs( VHJm + ^i
Для данной комбинации показателей преломления отражательную
способность подложки можно увеличить за счет установки достаточ-
достаточного большого числа двойных слоев, для которых частота излучения
попадает в центр полосы непрозрачности. При этом удобно предста-
представить отражательную способность R диэлектрического зеркала как
функцию параметра, называемого отношением стоячей водны V и
учитывающего распределение поля, локализованного у передней по-
поверхности всей системы [25]. Этот параметр широко используется в
микроволновой технике [21] для характеристики импедансного рассо-
рассогласования в волноводе. В нашем случае V является отношением мак-
максимума и минимума амплитуды поля, образующегося в результате
интерференции с усилением и ослаблением между начальной и отра-
отраженной плоской волной. В отсутствие отражения амплитуда поля
вдоль направления распространения постоянна. Если же существует и
отраженная волна, то интерференция приводит к появлению стоячей
волны и амплитуда поля записывается в виде
196 Гл. 3. Плоские многослойные среды
Ex(z, t) = Re[(<r'*kz + reikz)ei<ot E+l C.13.3)
где г — коэффициент отражения. В соответствии с этим Ex(z, t) из-
изменяется в промежутке между максимальным значением I Е + I A +
+ I г I) при z, таких, что 1 + re2Ucz = 1 + I г I, и минимальным зна-
значением I Е+ 1A - I г I), когда 1 + e2ikz = 1 - I г I. При X = \ от-
отношение максимального и минимального значений записывается в ви-
. C.13.4)
у = 1 + 1г1 = lgBx' = Jh_ /4
1 - \r\ Z, ns \пи
Для тех структур, у которых I 2ЪХI < ZY, имеем К = Z,/l 2BXI и, как
следствие,
4F
Г = (*4/ К для высокоотражательного зеркала).C.13.5)
Определим теперь безразмерную частоту д = \/\, где Xq — центр
первой полосы непрозрачности. Тогда полуширина полосы Д#, т. е.
расстояние от центра первой полосы непрозрачности (д = 1) до ее
границы [см. выражения C.9.15), C.11.5) и C.11.7)], запишется в виде
Ад = B/я)агс8ш[(пв/пн~ 1)/(пв/пн+ 1)]. C.13.6)
В соответствии с выражением C.13.4) чем больше число двойных
слоев, тем больше величина V. Однако практически V не превышает
103—10* вне зависимости от того, как много слоев используется. Дело
в том, что в тонких пленках потери за счет поглощения и рассеяния
увеличиваются с ростом т, что и ограничивает максимально дости-
достижимую отражательную способность. Аналогичное рассмотрение мож-
можно провести и для поля внутри мультислоя (см. задачу 13).
Отражательная способность R периодической структуры типа
«стекло — (ВН)т» может быть увеличена добавлением еще одного
В-слоя, так что мультислой имеет теперь структуру «стекло—
(ВН)"В». В этом случае V = [nl/in^n^in^/nHfm .
Располагая одну или более стоп на соответствующей подложке и
устанавливая центры полос непрозрачности на тех длинах волн, кото-
которые должны быть подавлены, можно создать либо длинноволновые,
либо коротковолновые фильтры (рис. 3.19). Коротковолновые
фильтры с границей при 0,7 мкм применяются в кинопроекторах и
других оптических приборах, у которых основная часть излучаемой
лампой или угольной дугой энергии сосредоточена в ИК-области
спектра. Так называемые тепловые отражатели или холодные
3.13. Металлические и диэлектрические отражатели
197
80
Рис. 3.19. Спектр пропускания коротковол-
коротковолнового фильтра (Optical Coating Laboratory).
Г
2,0
3,0
зеркалаХ) эффективно предохраняют оптические элементы от тепло-
тепловых нагрузок.
Пример. Вычисление спектра отражения диэлектрического зерка-
зеркала. Вычислим спектр отражения при нормальном падении излучения
на диэлектрическое зеркало, состоящее из 22 четвертьволновых
пластинок на стеклянной подложке [структура «стекло — (ВНI1»].
Пусть в максимуме отражения \ = 660 нм, а диэлектрическими мате-
материалами с высоким и низким показателями преломления являются
ТЮ2 (лв = 2,3) и SiO2 (лн = 1,45) соответственно.
При этих параметрах сразу можно вычислить требуемые величины
cos0, = (лв - пя)/(пъ + пн) = 0,226 и Zcb = 0,548 f0 [см. выраже-
выражение C.10.6) и C.11.10)]. В дальнейшем будет удобно нормировать им-
импеданс на 2Qb. Для простоты мы будем использовать одинаковые
символы как для нормированных, так и ненормированных величин.
Теперь с помощью выражений C.10.5) и C.10.6) можно вычислить
угол расфазировки 5: cosS = 1 - 2sin20/sin20, = 1 - 2,108sin2</>, где
Ф = 2irnd/\ есть фазовая толщина одного слоя. Таким образом, б яв-
является вещественной величиной при 0 < ф < 1,34 и 1,80 < ф < 4,48.
Если же 1,34 < ф < 1,80, то угол 6 комплексный: 8 = ж + i6" . Сле-
Следовательно, полоса непрозрачности, центрированная при Xq = 660 нм
(Ф = тг/2), имеет границы Х^ = ^/(гКЬвО) = 576 нм, Х,^ =
= tXq/BX1»34) = 779 нм. Импедансы Z(±) внутри полосы про-
пропускания равны Z<+> = /exp(-/^) и Z("> = /exp(/», где
Ф = arctgKtg^/sin2^ ~ 1/cos2^)]172 [см. выражение C.11.9)], а в по-
полосе непрозрачности Z<+> = /Z, a Z<~> = j'/Z, причем Z =
Используя эти результаты, соответствующий коэффициент отра-
]) Зеркала с высоким отражением в видимом диапазоне и высоким пропусканием в
ИК-диапазоне. — Прим. перев.
198 Гл. 3. Плоские многослойные среды
жения rs [выражение C.12.2)] можно записать в виде
s2)] sin ф\1/2 Л , sin
exp/[arctg 1/(ZSZ) - arctg (Z/Zs)] C.13.7)
(в полосе непрозрачности),
где Zs = 1/@,548ns) = 1,2 для ns = 1,52. Величина rY дается анало-
аналогичным выражением, нужно лишь Zs заменить на Z, = 1,82 при
Отражательную способность R можно вычислить с помощью
C.12.16). В частности, в центре полосы непрозрачности коэффициент
отражения г определяется выражением C.13.2), откуда получаем г =
= 1 - 4,66-10~5, R = \г\2 = 1 - 0,93-10. С помощью формул
C.12.17) нетрудно найти огибающие спектра отражения.
3.13.1. Отражение при наклонном падении
В некоторых случаях, например в кольцевых лазерах или системах с
многопроходными кюветами (лазеры на красителях, системы полного
вывода из резонаторов и др.), диэлектрические зеркала располагаются
под наклонным углом падения. При этом покрытия изготовляются
несколько более толстыми, чем для обычных лазерных зеркал. Это
нужно для того, чтобы компенсировать множитель cos0, входящий в
условие резонанса 4/w/cos 0 = Xq. Из-за различия величин Z(h) и Z(e)
отражение волн с s- и р-поляризацией различно. При этом у стоп с
одинаковой фазовой толщиной величины Vs и Кр в центре полосы не-
непрозрачности даются соответственно выражениями
где в — угол падения. Следовательно Vs > 1(лв > лн) и Vs > Кр,
Rs > Rp. Этим и объясняется тот факт, что для большинства кольце-
кольцевых лазеров излучение имеет s-поляризацию. Аналогично, из уравне-
уравнения C.14.4) мы имеем A0s > А0р. На рис. 3.20 показаны спектры от-
отражения для зеркала при угле падения 33,5°. Различие между полоса-
полосами непрозрачности для двух поляризаций очевидно. В то же время
различие пиковой отражательной способности нельзя заметить, не из-
изменив шкалы R. г
3.13. Металлические и диэлектрические отражатели
199
0,8 1,0 1,1 7,4 А,мкм
Рис. 3.20. Вычисленная отражательная способность диэлектрического зеркала (ВН)8 В —-
стекло разработанного для \ = 1,06 (Nd-лазер) и используемого при угле падения
33,5°. (С любезного разрешения Ч. Мизиано, Selenia Industrie Elettroniche.)
Если зеркала, изготовленные для отражения нормально падающей
волны, используются в случае наклонного падения волны (вплоть до
углов около 30°), то во многих случаях отклик претерпевает несущест-
несущественные изменения. Вообще говоря, увеличение угла падения приводит
к небольшому сдвигу всей спектральной кривой отражательной спо-
способности в сторону более коротких длин волн. Такое поведение прояв-
проявляется и у некоторых реально существующих в природе периодических
структур, например в оперении павлина или на крыльях бабочек.
3.13.2. Поляризационные светоделители
Различие в отражении р- и s-волн можно использовать для создания
поляризованных светоделителей [26], которые широко применяются
во многих электрооптических устройствах. Наиболее широко распро-
распространенную схему таких поляризаторов предложил в 1946 г. Мак-
Нейл, а позднее разрабатывал Баннинг. Само устройство состоит из
мультислойной стопы, расположенной по гипотенузе призмы Порро,
которая склеивается с такой же призмой и образует в результате скле-
склеенный куб (рис. 3.21).
Первоначально использованная [27, 28] мультислойная структура
была устроена таким образом, чтобы обеспечить наибольшее отраже-
отражение для s-компоненты и наибольшее пропускание для р-компоненты.
При этом, для того чтобы можно было использовать расходящиеся
пучки, требуется и определенный допуск на углы падения. Поскольку
фазовая толщина каждого слоя равна \/2, любая из структур типа
(НВ)™, (В/2, Н, B/2)m, (H/2, В, Н/2)т удовлетворяет указанным
здесь условиям. Обычно такие системы конструируются для работы
при угле падения 45°.
Из выражений C.13.8) следует, что отсутствие отражения для
200
Гл. 3. Плоские многослойные среды
Рис. 3.21. Схема поляризационного делителя Мак-Нейла. Многослойную прокладку
можно рассматривать как предельный случай поляризатора из пластин, показанного
на рис. 3.13.
компоненты при в = тг/4[ Кр(тг/4) = 1] требует выполнения условия
Fs(?r/4) = vf(O). Используя формулу C.13.8а) при в = тг/4 и положив
\ = ns = "стекло s nG> мы получаем
[Bп* - п2о)/Bп2п - nl)T = (пв/пнLт. C.13.9)
Нетрудно показать, что выражение C.13.9) выполняется при лю-
любых m только в том случае, если показатель преломления стекла свя-
связан с пв и пн соотношением
4 = 2п^/(п? + 4)- C.13.10)
В первой такой системе, созданной Баннингом, использовалась
комбинация сульфида цинка (лв = 2,3) и криолита (пн = 1,25). При
этом показатель преломления стеклянной призмы, удовлетворяющий
выражению C.3.10), должен быть равен 1,55, что очень близко к пока-
показателю преломления большинства оптических стекол. Для улучшения
физических свойств таких устройств и увеличения ширины спектраль-
спектральной полосы Шредер и Шлафер [29] разработали более сложные кон-
конструкции.
Если условие C.13.10) выполняется точно, то пропускание s-волны
может быть сделано крайне малым за счет увеличения m в соответст-
вин с выражением ^ = ^„^ (ЗЛЗЛ1)
3.14. ПРОСВЕТЛЯЮЩИЕ ПОКРЫТИЯ
В начале 20-го века английский оптик Дэннис Тэйлор случайно обнару-
обнаружил возможность искусственного старения оптического стекла при
травлении линз, приводящего к уменьшению нежелательного отраже-
отражения. Этот эффект был объяснен образованием переходного слоя, в ко-
Э.14. Просветляющие покрытия
201
тором показатель преломления плавно изменяется от псккпо до
^воздух- ^ середине 1930-х годов с развитием процесса вакуумного на-
напыления тонких пленок Смакула в Германии и Стронг в США откры-
открыли антиотражающие свойства напыленного диэлектрического слоя.
Позднее в 1944 г. Вальтер Геффкен запатентовал процесс просветляю-
просветляющего покрытия с тремя диэлектрическими слоями. С тех пор было ис-
исследовано множество просветляющих покрытий [30, 31]. Были разви-
развиты конкретные методики изготовления покрытий с необходимыми ха-
характеристиками [32—34]. Некоторые из них мы обсудим ниже.
Как мы уже показали, отражение от диэлектрика можно свести к
нулю, а относительное пропускание увеличить до единицы, если ис-
пользовать пленку толщиной Xq/4 с показателем преломления V ns nY.
К сожалению, в большинстве практических случаев этому условию
трудно удовлетворить. Например, при нанесении наиболее широко
распространенного покрытия из MgF2 не удается достичь отражатель-
отражательной способности меньше, чем 1,26%, если окружающая среда — это
воздух (рис. 3.22, а). Для исключения потерь на отражение необходи-
необходимо использовать по крайней мере двухслойное покрытие. Действи-
Действительно, если показатели преломления двух выбранных для покрытия
материалов заданы, то нулевое отражение можно получить, выбирая
фазовые толщины в соответствии со следующими соотношениями
1 fas"? -
i-nlY
0,02
0,01
а
ч
**-
-"
0,4
0,2
400 500 600 Гни;
Рис. 3.22. Отражательная способность стеклянной
подложки (/?s = 1,51) для различных просветляю-
просветляющих покрытий, а — однослойное покрытие из
MgF2 (n = 1,38) с оптической толщиной
4лсаГс - 555,4 нм; б— двухслойное V-покрытие:
1,38 (MgF2), 4л, rfj = 633 нм, п2 = 2,3 (ТЮ2),
= 633 нМ (линия Не—Ne-лазера); в — двух-
S
¦
У
IV
/
/
/
500
2
слойное W-покрытие: л, = 1,38 (MgF2),
*nxdx = 510 нм, л2 = l,6(CeF3), 4n2d2 = 1020 нм.
(Из работы [301).
600
•7 1
0 1
700 (им)
—*^
у
400 500 600 700Ы*)
202 Гл. 3. Плоские многослойные среды
»i) C.14.1)
В частности, если п\ л8 = /i| /jj, то фх = 02 = тг/2. Такое покрытие
называют двойным четвертьволновым. Заметим, что в такой систе-
системе изменение R с частотой (рис. 3.22, б) имеет вид типичной
V-образной зависимости, что и привело к появлению названия
«V-покрытие».
В случае когда необходимо иметь слабое отражение в более широ-
широком частотном интервале, предпочтительно использовать так называ-
называемые четвертьполуволновые покрытия, состоящие из полуволновой
(прилегающей к подложке) и четвертьволновой пленок. Используя вы-
выражение C.12.8) и C.9.8) и соотношение R = X /(I + X), нетрудно
показать, что для произвольной частоты, для которой ф = фх =
= Ф7/2, имеем
>.
C.14.2)
Здесь А4и А6 — коэффициенты, которые зависят от показателей пре-
преломления [30]. Для ф = тг/2 получаем
R = [(n,ns - иМил + nJJ2. C.14.3)
Спектральные зависимости отражательной способности имеют
при этом типичный вид с двумя минимумами. Поэтому такие покры-
покрытия называют «W-покрытиями» (рис. 3.22, в).
Другие двухслойные просветляющие покрытия используются для
подложек с большим показателем преломления [например, nsi = 3,45
» nGc = 4]. При этом должны быть выполнены условия фг = ф2 и
п2 = aIjVais//2j (так называемые покрытия 1-типа) или </>j = ф2 и
я2 = nsnl/nl (покрытия Н-типа). В первом случае R имеет единст-
единственный широкий минимум, причем R = 0 при ф = тг/2 (рис. 3.23). Во
втором случае отражательная способность характеризуется неболь-
небольшим максимумом Ro при ф = ж/2 и достигает нулевого значения в
двух точках, в которых ф = arctg( Лбп/ Д0I/4, где Лбп — отражатель-
отражательная способность образца без покрытия.
Используются и трехслойные покрытия. При этом также выделя-
выделяют покрытия типа I и II, причем фазы ф19 ф2 и фъ выбирают оди-
3.15. Интерференционные фильтры
203
Рис. 3.23. Отражательная способность двухслой-
двухслойных покрытий типа I (один минимум) и типа II
(два минимума) на кремниевой подложке
(ns = 3,45), Wj = 1,56, п2 = 2,896 (один мини-
минимум), 2,21 (два минимума) {nxdx = n2d^. (Из ра-
работы [30]).
20
\
\
1
У/
1
0,8
1,6
наковыми, а показатели преломления находят из следующих соотно-
соотношений: п2 = V ns пх, п3 = л, V ns / пх для типа I и п2 = V ns п{, л3 =
= nsnl/nl для типа II. Частотные зависимости отражательной спо-
способности таких покрытий имеют соответственно 2 и 3 нулевых мини-
минимума.
Из-за отсутствия материалов с достаточно малым показателем
преломления такие покрытия нельзя использовать на стеклянных под-
подложках. Однако при этом можно использовать комбинацию п2 =
= /ijVnD/nl9 пъ = VnDns, где nD — показатель преломления произ-
произвольного очень тонкого фиктивного слоя, расположенного между
пленками 2 и 3. Такая комбинация показателей преломления позволя-
позволяет достичь 100%-ного пропускания в подсистемах «воздух — слой 1 —
слой 2— фиктивный слой» и «фиктивный слой — слой 3—под-
3—подложка». Приведенные соотношения показателей преломления получа-
получаются из условий, что первая подсистема является двухслойным по-
покрытием типа I, а вторая удовлетворяет Xq/4-условию.
Операцию, аналогичную описанной выше, можно обобщить на че-
тырехслойные покрытия, которые можно изготовить из двух покры-
покрытий типа П. При этом показатели преломления должны быть выбра-
выбраны так, чтобы пх п2 = пгпии пъ пА = nD ns. Если же потребовать ра-
равенства нулю отражательной способности при некоторой длине волны
Xq, to эти соотношения необходимо дополнить еще одним, а именно
V
Читателя, интересующегося более сложными структурами, мы от-
отсылаем к работам Ниттла [1], Мак-Леода [16], Массета и Телена [30],
Кокса и Хасса [31], а также Добровольского [35].
3.15. ИНТЕРФЕРЕНЦИОННЫЕ ФИЛЬТРЫ
Свойства интерференционных фильтров определяются их действием
на интерференцию оптических пучков, многократно отраженных в
204
Гл. 3. Плоские многослойные среды
Область
свободной дисперсии
0,3 0,4- 0,5 Ofi Л,мкм
Рис. 3.24. Типичный спектр пропускания узкополосного фильтра Фабри—Перо. 1 —
четвертый порядок; 2 — третий порядок; 3 — второй порядок.
многослойной системе. Простейший фильтр, изобретенный Геффеке-
ном в Германии в 1939 г., представляет собой трехслойное покрытие,
которое состоит из диэлектрического промежуточного слоя (показа-
(показатель преломления /?sp), окруженного двумя полупрозрачными метал-
металлическими пленками. Заменяя металлическую пленку диэлектрическим
мультислоем, можно (приближенно) получить любые необходимые
спектральные характеристики пропускания [35].
Типичный спектр пропускания интерференционного фильтра изо-
изображен на рис. 3.24. Почти во всем диапазоне, за исключением неко-
некоторых выделенных длин волн, пропускание Т очень мало. Значения X,
для которых пропусканиемаксимально, образуют последовательность
\/q> где 4=1,2,..., a Xq = 2cos б dnsp (здесь в — угол преломления
внутри промежуточного слоя толщиной d).
В соответствии с этим, изменяя угол падения, можно сдвигать и
максимум пропускания. Величина qir — это фазовая толщина, соот-
соответствующая <7-му максимуму пропускания, и q называют порядком
промежуточного слоя. При очень больших q ( > 103) отношение по-
поперечного размера к толщине пленки является важным параметром,
которым определяется пропускание. Принцип действия таких уст-
устройств легче всего понять, рассматривая их как оптические резонато-
резонаторы; соответствующая теория будет рассмотрена в гл. 7. При малых q
влияние апертуры несущественно и всю систему можно считать беско-
бесконечной в направлении, перпендикулярном оси расслоения. В дальней-
дальнейшем нашем рассмотрении мы будем пользоваться именно этим пред-
предположением.
Спектр пропускания можно характеризовать величинами Гмакс,
Тмш, \, А\5 и областью свободной дисперсии. Здесь Гмакс — пропу-
пропускание в максимуме полосы прозрачности, 7^ — пропускание в об-
области подавления, а А\5 — полуширина линии пропускания с цент-
центром в Xq . Расстояние между соседними с главным максимумами про-
пропускания называют областью свободной дисперсии. Как будет видно
ниже, все эти величины связаны между собой.
3.15. Интерференционные фильтры 205
В разд. 3.12 мы уже приводили формулу суммирования Эйри [вы-
[выражение C.12.10)], позволяющую вычислять пропускание системы
Fj DF2, где Fj и F2 — покрытия с двух сторон диэлектрического слоя
D. Пленки покрытия могут быть как металлическими, так и диэлект-
диэлектрическими, а в некоторых особых случаях — просто окружающей сре-
средой. Если Rx и R2 — отражающие способности на границах раздела
Fj - D и F2 ~ D, то выражение C.12.10) дает
T=T^J(l + F2*in20). (ЗЛ5.1)
Здесь F {резкость) определяется выражением
F = 2(R1R2I'4/A - VSDQ, C.15.2)
6 = $(Ф1 + Ф2-2Ф). C.15.3)
Для фильтров Фабри — Перо весьма существенную роль играют
малые потери А на поглощение. Симметричная структура характери-
характеризуется максимальным пропусканием Гмакс = 1/A + А /ГJ, где Т =
= Тх = Г2. Поскольку Т обычно весьма мало, отношение А/Т
практически равно единице и при этом Гмакс ~ 25%.
Если \ — длина волны, для которой Г = Гмакс, а именно
^i(Ao) + Фг(К) - 2ф(Л0) = -2тсд, C.15.4)
то с учетом равенства ф(К) = Ъкйп^ cos0/X при X s \ мы имеем
ФА») + *W WV 2 +
Я-Я0) C.15.5)
<ЗЛ56>
ГДе 1 4
F
Величина Д\^ есть полуширина полосы пропускания, a F=irJ?J/2/(l—/?.)
— резкость интерференционного фильтра [см. выражение C.15.2)].
В соответствии с выражением C.15.6) фильтр Фабри — Перо имеет
лоренцеву форму линии. В частности, ширина на уровне 1/100 (так на-
называемая ширина по основанию) АХ001 равна приблизительно IOAXq5.
Отношение A\),oi ^\s называют фактором формы. Он показывает,
насколько полоса пропускания близка к прямоугольной. Для фильтра
Фабри — Перо (лоренцева форма линии) этот фактор равен 10, а для
гауссовой формы линии он равен 2,57.
При больших отклонениях от \ отклик фильтра Фабри — Перо
определяется спектрами отражательных способностей Rx и R2. Зна-
206 Гл. 3. Плоские многослойные среды
чения Rx и R2 промежуточного слоя, окруженного металлическими
пленками, практически не изменяются с частотой в видимом и ИК-
диапазонах. При этом, как мы уже указывали, ^опускание является
периодической функцией величины Х~*. Когда \ соответствует тол-
толщине промежутка ф = тг + (^ + Ф2)/2, спектральные максимумы Т
расположены при X = \ [q + (&х + ф^/!*]'1, где q — порядок мак-
максимума пропускания. Поэтому область свободной дисперсии, т. е.
максимальная возможная спектральная ширина пучка, из которого
еще можно выделить узкую линию данного порядка, равна 2А^~{.
Обычно используется первый или второй интерференционный порядки
полосы пропускания. При этом максимальное пропускание имеет зна-
значения в интервале 20—40%. Поскольку фазовая дисперсия коэффици-
коэффициента отражения металлических пленок пренебрежимо мала, полуши-
полуширина А\5 при (ф1 + ф2)/2ж < 1 определяется выражением
ДЯ0>5 = B/F)(X0/qn) = [A - Rg)/Rlgl2№0/qn), C.15.8)
в то время как Тмян/Тмакс связано с полушириной AXq5 соотноше-
соотношением: '
МИН /^ 1 < Q4
Последние две величины зависят как от порядка промежуточного
слоя, так и от отражательной способности покрытия. Обычно
5/\ = A - 8)% при q = 1.
Если необходимо уменьшить ширину линии фильтра, мы должны
увеличить отражательную способность металлической пленки. Это
можно сделать, увеличивая ее толщину. К сожалению, это приводит
также к возрастанию потерь за счет поглощения, т. е. за счет умень-
уменьшения Гмакс. Для создания фильтров с полуширинами меньше чем 1%
необходимо использовать диэлектрические зеркала, покрывая обе по-
поверхности промежуточного слоя соответствующими мультислоями.
При этом за счет резонансных свойств таких структур коэффициенты
отражения ^и R2 сильно зависят от частоты [36], за счет чего ре-
результирующее пропускание фильтра с высокочастотной стороны от
пика первого порядка сильно отличается от простого профиля Эйри
[37] (рис. 3.25). Несмотря на потерю периодичности, диэлектрические
мультислои часто используются в УФ-диапазоне, в котором металлы
практически прозрачны. Примером таких структур может быть
(BH)mBB(HB)w = [(BH)mB]2.
Если в одну и ту же многослойную структуру ввести два фильтра
Фабри — Перо, то полученная структура будет иметь вид
(BH)mBB(HB)mC(BH)wBB(HB)m, где С — связующий слой [37]. При
этом связь между двумя резонансами приведет к расщеплению двух
3.16. Анизотропные слоистые среды
Т
207
рис. 3.25. Форма полосы интерферо-
интерферометра Фабри—Перо, полученная из
формулы сумм Эйри (штриховая кри-
кривая), и пропускание, вычисленное для
фильтра ВНВВНВ (сплошная кривая).
(Из работы [37].) 2,0 1,6 1,1 Ло/Л
пиков, так что на кривой относительного пропускания появится не-
небольшой провал при X = Xq. Если увеличивать количество фильтров
Фабри — Перо, то можно получить более резкий переход от полосы
непрозрачности к полосе пропускания и более гладкий максимум. При
этом для систем из двух, трех и четырех резонаторов факторы формы
AXqoj/AXq^ приблизительно равны 3,5: 2 и 1,5 соответственно. Кроме
того, можно независимо варьировать полуширину и отношение
Гмин / Гмакс. В общем такие структуры более предпочтительны по
сравнению с металлическими фильтрами Фабри — Перо, так как обес-
обеспечивают более высокое пропускание и более резкие границы полосы
пропускания.
3.16. АНИЗОТРОПНЫЕ СЛОИСТЫЕ СРЕДЫ
Если многослойная среда характеризуется тензорной диэлектрической
проницаемостью, то вычисление поля, образуемого при падении плос-
плоской волны, становится невероятно громоздким. Причину этой трудно-
трудности нетрудно понять, если вспомнить, что в каждом направлении пло-
плоская волна может распространяться только с вполне определенной
ориентацией вектора электрического поля. Кроме того, если фиксиро-
фиксировать два из четырех параметров о>, к, от которых зависят нормальные
моды, то два других параметра должны определяться из дисперсион-
дисперсионного уровня D(w, к) = 0.
Для того чтобы пояснить сделанные замечения, рассмотрим мно-
многослойную среду, изображенную на рис. 3.8. Предположим, что реше-
решение для поля зависит от поперечных координат х, у в виде простой
экспоненты ехр(— ikx). Это означает, что для каждого слоя могут су-
существовать две различные нормальные волны, для которых волновой
вектор kz{o)\ кх) принимает одно из двух значений, определяемых
дисперсионным уравнением.
3.16.1. Метод характеристической матрицы 4x4
В разд. 3.7 мы показали, что уравнения для ТЕ- и ТМ-волн в изотроп-
изотропной среде разделяются. Для анизотропных сред это не выполняется, и
208
Гл. 3. Плоские многослойные среды
причины такого различия мы уже обсудили. Для однородного ело*
уравнение C:7.3) нужно заменить следующим векторным уравнением
[20]:
C.16.1:
л.
где Чг — четырехкомпонентный вектор-столбец, а А —
рая в среде со скалярной проницаемостью f0 имеет ви -
здесь
0
0
A13
A13
A23/Co
0
A43/C0
C.16.
А13 =
^21 = focxAo) - ?
A23 = -
C.16..
Компоненты матрицы Д,у для сред более общего вида приведены в ра
боте [20]. Обозначим через kz(J) четыре собственных значения матрн
цы ?0Д. Их можно получить, решая алгебраическое уравнение 4-го по-
порядка det(?0A — kz) = 0. С физической точки зрения величины kz{J
соответствуют z-составляющим четырех нормальных волн, которы
могут распространяться в кристалле при равных нулю величинах кх г
ку. Для одноосного кристалла это соответствует двум обыкновенные
волнам и двум необыкновенным, и мы имеем следующие выражения
"" Кх) =
C.1О.4
где по — показатель преломления обыкновенной волны, а пе1 и ле2 —
показатели преломления необыкновенных волн, для которых величина
кг соответственно положительна и отрицательна. Кроме того, не-
нетрудно показать, что ?zC) и kz{4) являются корнями квадратного ура*
НеНИЯ fc*[l + cl(n2t - n2)/nft + 2к2кхсхс2(п2 - nD/nl +
c2x(nl
= 0,
C.16.5:
3.16. Анизотропные слоистые среды 209
где сх и cz — направляющие косинусы оптической оси. В большинстве
практических важных случаев ле мало отличается от по.
Определив четыре собственных значения, kz(J), можно вычислить
правые и левые собственные векторы ¦. и ¦,. матрицы А:
А = fczC/)?y, C.16.6)
где 4fj = (fj9i9 ¦/J» */,з» */,4) — это четырехкомпонентный вектор-
столбец. Следуя затем стандартной процедуре (см. разд. 3.9), можно
представить к0А в виде следующего разложения:
*°А = ?^г*'*'э?**»0'' (ЗЛ6-7>
где Оу — проекционные операторы (т. е. О? = Оу,; -Oj'Qj, = 0 при
j * j'). Для однородного слоя, используя представление А в виде
C.16.7), уравнение C.16.1) можно проинтегрировать. При этом полу-
Г 4 П
*(*) = I Д е-а-«с-''>ОА • f(z') s M(z - z') • !P(z'); C.16.8)
здесь М представляет собой 4х4-аналог характеристической матрицы
слоя. Ее используют таким же образом, как и рассмотренную выше
матрицу 2x2.
3.16.2. Коэффициенты отражения и пропускания мультислоя
Рассмотрим мультислой, расположенный между некоторой подлож-
подложкой (справа от мультислоя) и бесконечно протяженной окружающей
средой (слева). Пусть мультислой описывается характеристической
М-матрицей 4x4, а падающая на границу раздела 2*> волна — четы-
четырехмерным вектором ¦(i). Тогда обратно в окружающую среду отра-
отражается волна *(г), а волна ?(t) проникает в подложку. При этом Ф<г)
является суперпозицией двух собственных векторов среды, описываю-
описывающих волны, бегущие справа налево. В соответствии с уже принятыми
обозначениями C.16.4) эти волны будем отмечать индексами 2 и 4, а
бегущие слева направо — индексами 1 и 3. Это упорядочение остается
справедливым не только для одноосных кристаллов, но и для двухос-
двухосных. Поэтому векторы ¦<*), 4*г) и ¦&> можно записать в виде
См. порядок нумерации границ в разд. 3.7. — Прим. перев.
210 Гл. 3. Плоские многослойные среды
+ А$Г$, C.16.9)
где векторы ^ и i^ относятся соответственно к окружающей среде,
из которой приходит волна, и к подложке.
Используя М-матрицу, напишем соотношение между *(t), ¦W и
ус» + у (г) = м . v « C.16.10)
Учитывая ортогональность собственных векторов, легко получить
следующие соотношения:
TxlAf +T13Af = Fl9
F3,
F (ЗЛ6Л1)
и F24 =
= ¦^•M~1-*(i). Решение системы уравнений C.16.11) позволяет
вычислить отраженную и прошедшую волны.
Интересна ситуация, когда слой имеет бесконечно малую толщину
и подложка непосредственно граничит с окружающей средой. При
этом М сводится к единичной матрице, а коэффициенты в системе
уравнений C.16.11) имеют^ вид Ти = *f>-*js>; Rtj = *Р>-*};
Fj з = Ф[1\ ¦ir(i), F24 = -*fl -Яг®. В частности, если среда, из кото-
которой приходит волна, изотропна, то в качестве векторов ^ и Ягф
можно выбрать ¦<+> (р-волна) и ^+) (s-волна). Аналогично можно по-
поступить и с векторами ¦21)(= *р"}) и ¦41)(= ¦?~))- Тогда для падаю-
падающей р-волны Ч№ = ¦[)+) получаем
Поскольку в общем случае коэффициент A['^ не равен нулю, отра-
отраженная волна является суперпозицией р- и s-волн, хотя падающее поле
имеет вид чистой р-волны. Аналогичный результат нетрудно полу-
получить и для случая падения s-волны.
Если определить векторы ir^±> и ¦<*> таким образом, чтобы соот-
соответствующие электрические поля имели единичные амплитуды, то ко*
эффициенты A(-J в приведенной выше системе уравнений будут равны
коэффициентам отражения анизотропной среды. Систему уравнений
C.16.12) и уравнение C.16.5) можно использовать для вычисления сле-
следующих коэффициентов отражения одноосных кристаллов, которые-
3.17. Распространение волн в периодической среде 211
первоначально были получены Друде для случая, когда оптическая ось
кристалла перпендикулярна плоскости падения:
ncos0-(ne2-n2sin20I/2
Г* " ncos0 + (n2 - n2sin20I/2'
_n2cosfl-n(n2-K2sin2flI/2 " ' 3)
Гр " n2 cos 0 + n{nl - n2 sin2 вI11'
Если же оптическая ось параллельна плоскости падения и образует
угол а с нормалью к поверхности, то мы имеем следующие выраже-
выражения:
_/icos0-(no2-n2sin20I/2
'с
ncos0 + (nl-n2 sin20I/2'
C.16.14)
попе cos 0 — п(п2 cos2 а + л2 sin2 а — п2 sin2 0I/2
р попе cos 0 + п(и2 cos2 а + п2 sin2 а — п2 sin2 0I/2*
Здесь яо и яе — показатели преломления обыкновенной и необыкно-
необыкновенной волн в подложке, а л — показатель преломления окружающей
среды, б — угол падения.
3.17. РАСПРОСТРАНЕНИЕ ВОЛН В ПЕРИОДИЧЕСКОЙ СРЕДЕ
В голографии [38], интегральной оптике [39] и полупроводниковых ла-
лазерах часто приходится сталкиваться с примерами распространения
волн через среды, показатель преломления которых имеет вид
n2(z)
= nl I + 2 f Xmcos(-?-mz) . C.17.1)
Например, если толщина материала, используемого для записи голо-
голограмм, превышает размеры записываемой дифракционной картины,
то голограмма приобретает свойства трехмерной дифракционной ре-
решетки. При этом дифракцию следует описывать через брэгговские
углы отражения, аналогично дифракции рентгеновских лучей на кри-
кристаллах. Свойства этих систем, т. е. чувствительность реконструиро-
реконструированного изображения к углу падения и длине волны считывающего го-
голограмму пучка, можно исследовать на примере синусоидальной про-
пространственной решетки, типа решетки, получаемой при экспонирова-
экспонировании эмульсии в интерференционном поле от двух произвольных пло-
плоских волн. В этом случае профиль показателя преломления определя-
определяется выражением C.17.1), причем ось z параллельна разности векто-
векторов kj - k2, где kj и kj — волновые векторы двух плоских волн.
Успехи микроэлектроники и тонкопленочной технологии позволили
создать гофрированные тонкопленочные волноводы. Они широко ис-
212
Гл. 3. Плоские многослойные среды
пользуются в различных оптических устройствах интегральной оптики
и в полупроводниковых лазерах. В качестве примеров можно назвать
лазеры с распределенной обратной связью, в частности с распределен-
распределенной обратной связью на брэгговском отражении, частотные фильтры,
устройства ввода — вывода пучков и направленные ответвители. Об-
Общим для всех таких систем является распространение волны по тон-
тонкой диэлектрической пленке, толщина которой изменяется периодиче-
периодически. Это приводит примерно к такой же периодической модуляции по-
поперечной компоненты волнового вектора к
компонента к, связана с
,х. Поскольку продольная
соотношением к\ + к\ = к\п\>
Воздух п0
Верхний
слой
Воздух п0
Пленка
Верхний
Подложка ns
Воздух п0 $
Подложка п$
уть
1
Воздух п0
Пленка
Подложка ns Подложка /?s
Рис. 3.26. Периодические волноводы для лазеров с распределенной обратной связью.
а иб — периодическое изменение толщины верхнего диэлектрического слоя; в и г — пе-
периодические изменения толщины пленки. (Из работы [39а] © 1974 IEEE)
А ктибнып. полос коды п.
элемент Ga As
Омический контакт
Гофрированная
/ периодическая
структура
N-A1O>15 GaOt85
N"A10,36 Ga0,64
n-GaAs
Омический контакт
Рис. 3.27. Схематическое представление полоскового гетероструктурного лазера с двух-
двухсторонней распределенной обратной связью на брэгговских отражателях. (Из работы
[396] © 1979 IEEE.)
3.17. Распространение волн в периодической среде 213
где nf — показатель преломления пленки, периодическое изменение кх
приводит к такой же вариации kz. Поэтому распространение волны в
продольном направлении практически происходит в периодической
многослойной вдоль z среде (рис. 3.26 и 3.27).
Амплитуда ТЕ-волны, распространяющейся в среде, показатель
преломления которой определяется выражением C.17.1), удовлетворя-
удовлетворяет уравнению Хидда [401:
Sf + (во + 2 ? emcos2mt)u = 0, C.17.2)
где Г = ttz/A, в0 = BЛ/ХJ, вт = Хтв0.
3.17.1. Теорема Флоке
Обозначим через их(?) и w2(f) два линейно-независимых решения
уравнения C.17.2). Тогда за счет периодичности функции, входящей в
это уравнение сомножителем перед м, функции t/j(f + тг) и w2(f + ж)
также должны быть решениями. Это означает, что можно найти че-
четыре таких коэффициента а^, что
C.17.3)
Найдем теперь два частных решения F(+) и К(~) уравнения
C.17.2), имеющие следующее свойство:
К(±>({ + тг) = Я±К(±>@. C.17.4)
Если переписать их в виде К(±> = И±>1/1 + Hd=)w2 и учесть разло-
разложения C.17.3), то K(±)(f -h ж) совпадает с Х± F(±)(f), если выполне-
"ыравик™ ((,„-А1)П*' + <.12П'> = о,
В соответствии с этим два собственных значения Х+ и Х_ можно вы-
вычислить, потребовав равенства нулю детерминанта однородной систе-
системы уравнений C.17.5).
Рассмотрим вронскиан W функций И+> и К(~)#.
ЩС) = v<+\t)dv<->/dt; - v^iQdv^/dt;. C.n.6)
С помощью соотношения C.17.4) нетрудно показать, что W(? 4- тг) =
= Х+Х_ H^(f). Так как вронскиан двух решений волнового уравнения
C.17.2) не зависит от f, мы имеем
Я+А_ = 1. C.17.7)
Для завершения доказательства теоремы Флоке представим Х+ как
214 Гл. 3. Плоские многослойные среды
e~ib. Тогда два линейно-независимых решения И*) запишутся в виде
a <ЗЛ7'8)
где /(±) — периодические функции.
В частности, поскольку в рассматриваемом нами случае л(?) =
= я(—f)f TO Функция /<+)(—0е/д*"/т является линейно-независимым
по отношению к К<+)({) решением уравнения C.17.2) и удовлетворяет
условию периодичности C.17.4). Следовательно, она должна совпа-
совпадать с К<~)({). Таким образом доказана теорема Флоке: любое реше-
решение уравнения C.17.2) можно представить в виде
м(С) = Ae-w*№ + Ве«/(-О. C.17.9)
где 6 — некоторая постоянная.
3.17.2. Детерминант Хилла
Функция /(f), входящая в разложение C.17.9), является периодичес-
периодической с периодом тг и, следовательно, ее можно разложить в ряд Фурье:
uiQ^Ae-w* ? /we2m* + Be*** ? fme~2mK. C.17.10)
m= —oo m— — oo
Подставляя выражение из правой части C.17.10) в уравнение C.17.2),
получаем тригонометрический ряд, который должен быть тождест-
тождественно равен нулю. В соответствии с этим мы имеем
й\2 °° +00
--)/.- ? ftJi- - I ^/- = 0, C.17.11)
7Г/ m = -oo J т=-оо
= вт. Если обозначить через А(б) детерминант этой системы
уравнений (называемый также детерминантом Хилла), то характери-
характеристический показатель экспоненты 8 определяется соотношением
Д(<5) = 0. C.17.12)
Хилл доказал, что корни этого уравнения являются и корнями уравне-
уравнения . t
sin(<5/2) = ±v/A^siii[(W/2)v^], C.17.13)
которое представляет собой обобщение уравнения C.9.15), полученно-
полученного ранее для кусочно-постоянной периодической среды, на случай про-
произвольного профиля показателя преломления, симметричного относи-
относительно начала координат.
Если модуль правой части C.17.13) меньше единицы, то 5 — ве-
вещественное число. В противном случае 6 = Bq + 1)тг + /ImS.
В важном частном случае первого брэгговского резонанса q = 0.
В общем случае мы сталкиваемся с необходимостью вычисления при
3.17. Распространение волн в периодической среде
5 = 0 детерминанта матрицы бесконечной размерности:
[0/к + 2J - в0] -0,
215
D - в0)
во
-02
D - во)
D - в0)
(во-W
0о
-0х
D - в0)
0о
Щп - 2J - 0О]
D - во)
. C.17.14)
При в0 = 1 уравнение C.17.13) можно записать приближенно в виде
ch ImS/2 = [Ao(O)]1/2sin@o/27t/2), C.17.15)
где Др(О) вычисляется при в0 — 1. В соответствии с этим если \@)
чуть больше единицы, то ImS Ф 0 при 10О/2 - II < 2[[Д,@)]1/2 - \}/-к;
иными словами, периодическая среда ведет себя как брэгговский от-
отражатель при IX - \\ < {[\@)]in- l)Xo2/ir.
3.17.3. Теория связанных мод
Если найдено 5, то коэффициенты fm ряда Фурье для /(f) можно вы-
вычислить, решив однородную систему уравнений C.17.11). Если 0О = 1
и '^1,...' ^ Ь то можно показать, что все коэффициенты /т прене-
пренебрежимо малы по сравнению с /0 и f{. В качестве упражнения чита-
читатель может проверить это на примере выражения для /(f) в среде с
кусочно-постоянным показателем преломления (задача 14) или ап-
аппроксимировать бесконечную матрицу C.17.14) матрицей 3x3. Вместе
с равенством 5 = тг + / Im 6, справедливым вблизи брэгговского резо-
резонанса, это позволяет записать разложение C.17.10) в виде
Bfoelmd«*) =
C.17.16)
Использование предположения llmSI < 1 означает, что /?(f) и
являются медленно меняющимися функциями от f.
Хотя мы получили разложение C.17.16), исходя из свойств реше-
решений Флоке, его можно использовать лишь вблизи брэгговского резо-
резонанса. Если подставить последнее выражение из C.17.16) в уравнение
C.17.2), пренебречь вторыми производными величин S и R и удер-
удержать лишь члены 0О и 0{9 то можно получить следующую систему
216
Гл. 3. Плоские многослойные среды
уравнений:
dR/dt; -Wo - l)R = -ВД dS/dC + 1(в0 - l)S = iOxR. C.17.17)
Этот метод называют теорией связанных мод и его нетрудно обоб-
обобщить на случаи, когда среда характеризуется поглощением или усиле-
усилением. Важные приложения этой теории мы рассмотрим в гл. 8.
3.18. АНАЛИТИЧЕСКИЕ СВОЙСТВА КОЭФФИЦИЕНТА
ОТРАЖЕНИЯ
Для многослойной области с кусочно-постоянным показателем пре-
преломления коэффициент отражения r(z) в любом сечении определяет-
определяется различными постоянными распространения /3 = (п*к% — к*I/29
зависящими от конкретного слоя [см. выражение C.7.1/)]. Каждая ве-
величина &q, если ее рассматривать как функцию комплексной перемен-
переменной кх, имеет две точки ветвления кх = ± пдк0, где d(ig/dkx и все
производные высших порядков сингулярны.
Двузначная функция 0 = (л2 к\ - ?2I/2может быть определена
как однозначная, если в комплексной плоскости кх провести разрезы,
такие, что (рис. 3.28,6):
lm(fi2kl - к2х) = -2к%ш - 2ImfcxRefcx = О,
C.18.1)
Re(n2fc2 - k2x) й 0.
Две кривые, определяемые уравнениями C.18.1), являются участками
гиперболы, проходящей из точек ветвления к вещественной оси в
Л^-плоскости. При к = 0 они вырождаются в две полупрямые, как по-
пк0 вещественное
Im kx
пк0
Re/rx
пк0 комплексное
Im/fv
Рис. 3.28. Разрезы в комплексной плоскости^, используемые для однозначного опреде-
определения зависимости коэффициента отражение от кх для вещественного {а) и комплексно-
комплексного (б) показателей преломления.
3.18. Аналитические свойства коэффициента отражения 217
казано на рис. 3.28, а. Поскольку выполненные разрезы определяют
все точки, для которых п2к\ - к2х является неположительной ве-
вещественной величиной, функция Re[(n2kl - /г*I/2] всегда положи-
положительна (или отрицательна) на всей остальной части плоскости. Это
свойство весьма полезно для качественной интерпретации происходя-
происходящих физических процессов. Действительно, так как падающая волна,
для которой справедливо выражение C.7.17), проходит слева (z =
= -оо) направо (z = +<»), величина Re /3 = Rt[(n2kl - k2)x/1]
должна быть положительной. Таким образом, мы установили взаим-
взаимно-однозначное соответствие между распространяющимися в прямом
направлении волнами и теми величинами /3, которые определяются на
римановом листе, задаваемом указанными выше разрезами. Если рас-
рассмотреть всю гиперболу, определяемую первым выражением C.18.1),
то нетрудно показать, что положительность Rej3 означает выполне-
выполнение неравенства 1т[(п2к1 - kl)vl\ < 0 в незаштрихованных обла-
областях и lm[(n2kl - А:2I72] > 0 в заштрихованных областях на
рис. 3.28. Более кратко это можно записать следующим образом:
sgnlm(n2k2 - fc2I'2 = sgnlm(n2fc2 - к2х). C.18.2)
Рассмотрим коэффициент отражения г(кх) в данном сечении муль-
тислоя как функцию поперечной компоненты кх волнового вектора
падающей волны и воспользуемся выражением C.7.18). При этом мы
видим, что^функция г(кх) имеет полюсные сингулярности в нулях
функции (Z +^Z) и точки ветвления, совпадающие^ точками ветвле-
ветвления функций ZhZ[7]. Точки ветвления фуню^ии Z?(z) удобно иссле-
исследовать, переписав выражение C.17.16) в виде
1 - tZ(Zl) tg tfi(z2 - )]/Z
Поскольку как Ztg[/3(z2 - zx)], так и tg[j3(z2 - zx)]/Z являются
нечетными функциями величины /3, они же являются регулярными
функциями постоянной распространения кх при /3 = 0. Следователь-
Следовательно, точками ветвления функции Z(z2) являются только точки ветвле-
ветвления функции Z(Zi). Применяя последовательно выражение C.18.3)
для различных слоев, можно сделать вывод о том, что точки ветвле-
ветвления импеданса в данном направлении не зависят от локального поло-
положения оси расслоения. В частности, эти особые точки совпадают с
точками ветвления в последней справа среде (при ориентации импе-
импеданса слева направо) или в последней слева среде (в противоположном
случае). Следовательно, функция г(кх) для подложки, покрытой неко-
некоторым диэлектрическим мультислоем, имеет четыре точки ветвления
218 Гл. 3. Плоские многослойные среды
при кх = ± nsk0 и кх = ± пгк09 где nY — показатель преломления
окружающей среды.
В частности, в ограниченной области комплексной Л^-плоскости
коэффициент отражения г(кх) можно записать в виде рациональной
При этом выполняется очевидное условие четности функции г(кх).
Полюсы коэффициента рассеяния г многослойной системы совпадают
с резонансными поперечными волновыми числами и дают все воз-
возможные решения уравнений Максвелла в пространстве без источни-
источников. С интуитивной точки зрения поскольку I r I — оо при приближе-
приближении к полюсу, амплитуда падающей волны может стремиться к нулю,
но по-прежнему она будет возбуждать отраженную волну конечной
амплитуды.
Можно ожидать, чтб рассматриваемые полюсы будут соответст-
соответствовать векторам к, имеющим и мнимую составляющую, когда мы
имеем дело с волнами, распространяющимися по волноводу (свето-
водные моды). Действительно, как станет ясно при рассмотрении за-
задачи о распространении болн в оптических волокнах, передающиеся
вдоль диэлектрической структуры моды затухают в направлении, по-
перечном направлению распространения волны. Подчеркнем тот
факт, что в плоскослоистой среде моды будут распространяться па-
параллельно поверхности слоев и экспоненциально затухать в направле-
направлении расслоения z.
В среде без потерь корни уравнения
ZBX(kx) + Z,(fcJ = 0 C.18.5)
являются полюсами коэффициента отражения, соответствующими
распространяющимся модам (вдоль оси л:) структуры. Остальные
комплексные корни соответствуют дискретному набору немодовых
решений уравнений Максвелла в пространстве без источников. Строго
говоря, эти решения нельзя назвать «модами», так как по определе-
определению модового решения величины 1Е(гI2 не должны зависеть от х.
Такая независимость имеет место лишь при вещественных кх [см.
A3.7.1)]. Поэтому о решениях с мнимыми кх говорят как о «волнах
утечки», или «затухающих резонансах». Несмотря на их физически
неприемлемое поведение в далекой области (где амплитуда стремится
к бесконечности), такие решения можно использовать как хорошее
приближение для истинных полей, передающихся вдоль оси х с одно-
одновременной сильной утечкой энергии в направлении оси z. j
Из проведенного выше рассмотрения следует, что полюсами функ-
3.18. Аналитические свойства коэффициента отражения
219
Рис. 3.29. а — профиль поверхностной волны, распространяющейся перпендикулярно
оси расслоения в отражателе Брэгга; б — поверхностная волна в щели между двумя от-
отражателями Брэгга. (Из работы [41].)
ции г(кх) являются комплексные значения /3 — /а величины кх. В
дальнейшем мы покажем, что этим полюсам соответствует либо по-
поверхностная волна (а —> 0, оставаясь отрицательной величиной), либо
волна утечки (а > 0), которые могут передаваться в плоском слое.
В гл. 8 мы увидим, что для цилиндрических оптических волокон
(у которых ось симметрии совпадает с осью z) поверхностная волна со-
соответствует световодным модам, а волны утечки — затухающим мо-
модам. Аналитическое описание здесь и в гл. 8 различно. Однако заме-
заметим, что для случая цилиндрического волновода нужно рассматривать
волны, попадающие в волокно при z = — о° и распространяющиеся в
положительном направлении оси z. В планарных же волноводах волна
входит ортогонально оси z и распространяется как поверхностная или
затухающая волна вдоль самой оси z.
Используя аналогию между оптикой тонких пленок и электронной
зонной теорией твердого тела, нетрудно показать существование мод,
локализованных вблизи границ раздела многослойной и однородной
сред. Аналогично тому, как поверхностные состояния описывают при-
примеси вблизи границ твердого тела, особые волны могут быть возбуж-
возбуждены и вблизи границ раздела мультислоя. Свойства этих волн можно
изучать [41], отыскивая вещественные корни уравнения C.18.5) и по-
получая распределение поля с помощью рассмотренной выше теории
электрических цепей. На рис. 3.29, а показано поперечное распределе-
распределение поля для типичной основной поверхностной моды, направляемой
периодической структурой.
3.18.1. Условие поперечного резонанса
Условие резонанса C.18.5) было получено для мультислоя, граничаще-
граничащего с однородной бесконечной окружающей средой (при наших обозна-
220 Гл. 3. Плоские многослойные среды
чениях — неограниченной в направлении z = - <»). Обозначим теперь
через Z(z) и 2(z) импедансы, вычисленные относительно произ-
произвольного сечения мультислоя для левого и правого направления соот-
соответственно. Тогда, последовательно преобразуя с помощью C.7.15) Z
и ^, нетрудно доказать, что условие C.18.5) справедливо и для любо-
любого сечения многослойной среды, а именно
Z(z,kx9k0) + Z(z,kx,k0) = 0. C.18.6)
Это соотношение, называемое условием поперечного резонанса, поз-
позволяет найти величины кх и к0, соответствующие свободным колеба-
колебаниям системы. При этом импедансы 5 и 2 можно вычислить в
наиболее удобных сечениях мультислоя. Например, для симметрич-
симметричной относительно начала координат системы на рис. 3.29,6 имеем
2Г@, кх, к0) = Z@, kx, к0). Поэтому распространяющиеся моды
легко найти, определив нули функции ^@, кх, к0).
3.19. РАСПРОСТРАНЕНИЕ ПОВЕРХНОСТНЫХ
' И ЗАТУХАЮЩИХ ВОЛН ПО ТОНКИМ ПЛЕНКАМ
Во введении мы уже отмечали, что многослойные структуры могут
обеспечивать возможность распространения определенных волн, а
именно поверхностных волн и волн утечки. В качестве простейшего
примера рассмотрим идеальную металлическую подложку (ks > 1),
покрытую единичным диэлектрическим слоем (заземленный диэлект-
диэлектрический экран; рис. 3.30). В этом случае коэффициент отражения гр,
определяемый выражением C.12.19), принимает простой вид:
= -cosfl1 + (i cos djn) tg J[concdc(cosec)/c2
p cos0, + (icosejn) tg [wnc
где n = nc/ nl9 д индекс «с» используется для величин, относящихся
к покрытию. Пусть в выражении C.19.1) пг = 1 и cos0c =
= Vl ~ k^/o^n2. Тогда сразу получаем, что полюсы и нули
функции rp(kx) можно определить из следующего уравнения на соб-
собственные значения (случай ТЕ-волн рассмотрен в [41]):
(k20n2 - klI'2 tg [dc(k2n2 - ^I/2] = ±in2(k2 - k2x)l/\ C.19.2)
Диэлектрик
Рис. 3.30. Заземленный диэлектрический
Металл волновод.
3.19. Распространение поверхностных волн по тонким пленкам 221
в котором знаки плюс и минус относятся к полюсам и нулям соот-
соответственно. При этом для каждой частоты коэффициент отражения гр
обращается в нуль или расходится, когда поперечный волновой век-
вектор кх удовлетворяет уравнению C.19.2). При фиксированных значе-
значениях к, п и rfc, если к®* — корень уравнения C.19.2) со знаком +, то
Л<р>* — корень того же уравнения со знаком -. Этот факт является
следствием того, что при вещественных п изменение к№ на kS&* озна-
означает и замену функций {к\п2 — ?2I/2 и (/rg ~ ?2I/2 на их комплек-
комплексно-сопряженные. Таким образом, нули функции гр(кх) совпадают с
комплексно-сопряженными значениями полюсов.
Для нахождения полюсов перепишем уравнение C.19.2) в виде
wtgM = n2t>, u2 + v2 = V2, C.19.3)
где V (в теории оптических волокон — нормированная частота), v и
и определяются следующим образом:
V = (п2 - 1I/2Мс, v = idc(k20 - fc2I'2, и = dc(k2n2 - hiI'2. C.19.4)
Поскольку sgnlm(?§ - ?2I/2 = -sgnlm/^, то для вещественных
п и при Rekx > 0 имеем sgnRet; = sgnlm?x.
Заметим между прочим, что магнитное поле падающей и отражен-
отраженной волн можно выразить через v:
Hyi ос e-ikxX~vzld% Hyt ос e-ik*x+vz/dc. C.19.5)
Уравнения C.19.3) имеют бесконечно много комплексных корней,
каждый из которых можно рассматривать как функцию от V. В част-
частности, для Y — оо сразу получаем, что u(V) -- (q - 1/2)тг, где q —
целое число. Поэтому каждый корень можно пометить индексом q,
соответствующим его асимптотическому значению, т. е. и — и .
В случае когда и и v вещественны, уравнения C.19.3) можно ре-
решить графически, как показано на рис. 3.31,а. При этом корень и
определяется пересечением кривой (utgu)/n2 с окружностью радиу-
радиусом V. Если мы уменьшим величину К, то и и v сдвинутся влево от-
относительно соответствующих вещественных осей, в то время как кх
(рис. 3.31, б) сначала сдвинется влево от точки пк (мы предположили,
что п > 1), а затем, достигнув точки ветвления к, возвратится напра-
направо, в нижний квадрант правой комплексной полуплоскости кх. Если
V станет меньше критической величины Vm, при которой окруж-
окружность касается кривой (и tg и)/ п2, то корень uq становится комплекс-
комплексным.
Для вычисления вещественной и мнимой частей корня uq - u'q +
+ ш? возведем уравнения C.19.3) в квадрат. Затем после простых
алгебраических выкладок получим
222
Гл. 3. Плоские многослойные среды
\тк.
Imu
КО
0,5
V+0
У+0
-1.21
Re V
Рис. 3.31. а — графическое определение собственных значений уравнения C.19.3); тол-
толстые кривые — график функции v = wtg(w)//?2, окружность — у2 = м2 + А Геометри-
Геометрические места точек решений для ТМ^-моды заземленного диэлектрического световода
на комплексной плоскости кх (б); на плоскости и (в); на плоскости v <г). Волнистая ли-
линия на рис. б — разрез функции (** - фу\ Значения kx{Vm) лежат на нижнем берегу
разреза справа от kQ. Геометрическое место точек кх имеет точку возврата при kx(Vm) и
при V < Vm изменяется по верхнему берегу разреза, достигая минимального значения
меньшего, чем kQ.
[sin2BiQ- sh
sh
+ chBM")]2
shB«")
,2 _ „2 =
[cosBm')+
C.19.6a)
= 0
ch Bм") и'2 - и
C.19.66)
Уравнение C.19.66) устанавливает связь между и" и и', а уравне-
уравнение C.19.6а) позволяет определить соответствующее значение V. При
и" = 0 для V имеем следующее уравнение:
и'2 tg V + nV2 = п4К2. C.19.7)
Минимально возможное значение К, совпадающее с критической
3.19. Распространение поверхностных волн по тонким пленкам
223
величиной Vm, определенной выше, достигается при и ж ит, где
1« 2 "т + (Цп tg uj/cos2 wm = - и4. C.19.8)
При V < Vm величина и становится комплексной. На рис. 3.31, в
изображена зависимость м" от и' для случая q = 2. Используя урав-
уравнение C.19.3а), можно построить график зависимости v" от v'
(рис. 3.31,г). Из физических соображений величина v" должна быть
положительной, если Ну{ в выражении C.19.5) представляет собой
волну, падающую на диэлектрик и распространяющуюся от z = - »
kz= +оо. В частности, из рис. 3.31, в видно, что значение и2" тож-
тождественно равно нулю при Зтт/2 > и'г > ит = 2,52, а при меньших
Re и быстро растет и достигает максимума при KsO. Такое поведе-
поведение легко подтвердить, используя уравнение C.19.3а) и условие v =
= ±т. Отсюда следует, что ид( V = 0) можно получить, решая
уравнение tg uq = ± in2. Таким образом, если записать uq @) =
= (q - 3/2Oг + Шд@), то сразу находим, что «^@) не зависит от мо-
дового индекса q и определяется выражением
м"@) = 1п[(п2 - 1I/2/(п2 + 1I/2]. C.19.9)
На рис. 3.32 показано, как изменяются величины ft и а (кх ж /3 —
- /а) с ростом V от нуля до оо. В тех случаях когда кх лежит в пер-
первом квадранте комплексной ^-плоскости непосредственно над разре-
разрезом, волна в окружающей среде бежит параллельно поверхности раз-
раздела и затухает в перпендикулярном ей направлении (поверхностная
волна; рис. 3.33, а).
Интересен случай, когда кх лежит в четвертом квадранте. При
этом внешнее поле представляет собой неоднородную волну, движу-
Незатухающая
волна утечка
Поверхностная
волна
Рис. 3.32. Постоянные затухания (а) и распространения ф) для ТМ02-моды, распростра-
распространяющейся по тонкой пленке (л 2 = 1,5) на металлической подложке. Если нормализован-
нормализованная частота V больше, чем т, то распространяется поверхностная волна. При
Ут < V < т ТМ02-модой является незатухающая волна утечки. При V < Vm постоян-
постоянная затухания а волны утечки быстро становится сравнимой с /с. При V — оо имеем
/3 -*лЛ:0 (см. рис. 8.11).
224
Гл. 3. Плоские многослойные среды
ОУ////////////^
Рис. 3.33. Схематическое изображение сило-
силовых линий электрического поля, а — для по-
верхостной волны; б — для незатухающей
волны утечки (Im кх = 0); в — для излучц-
ющей волны утечки (Im кх < 0).
щуюся от плоскопараллельного слоя. Вследствие этого энергия, пере-
переносимая распространяющейся внутри слоя модой, постепенно теряет-
теряется за счет непрерывной утечки на излучение во внешнюю среду. Это в
свою очередь приводит к экспоненциальному затуханию амплитуды
моды в направлении распространения (т. е. параллельно слою). Имен-
Именно этот эффект утечки используется в диэлектрических антеннах, в ко-
которых распространяющаяся внутри диэлектрического стержня волна
приводит к появлению поля излучения во внешней области.
Казалось бы, что растущая амплитуда волн утечки вне слоя
должна привести к физическому парадоксу, а именно к бесконечной
амплитуде поля на бесконечном расстоянии от слоя. Этот парадокс
легко объяснить, замечая, что мы рассматривали слой бесконечной
протяженности. Это означает, что амплитуда поля должна быть бес-
бесконечной в той области, откуда приходит волна. Поскольку внешне
поле на бесконечном расстоянии от слоя вызвано этими удаленным
источниками, оно должно обращаться в бесконечность.
Поверхностные волны и волны утечки, распространяющиеся mi
диэлектрическому слою, окруженному средой с иным показателе^
преломления, исследовали Су и Тамир (см. библиографию к данной
главе).
3.20. ОСВЕЩЕНИЕ ПОД УГЛОМ, БОЛЬШИМ КРИТИЧЕСКОГО
При д = n/ri < 1 закон Снеллиуса определяет действительный угол
преломления, меньший 7г/2. Если \i > 1 и угол падения в больше кри-
критического угла
вс = arcsind///), C.20.1)
то sin0' больше единицы и угол преломления в' = тг/2 + /0'f явля-
является комплексным. Его мнимая часть определяется соотношением
r) C.20.2)
3.20. Освещение под углом, большим критического
225
Таким образом, поле, возникающее в результате преломления,
можно связать с комплексным преломленным лучом, направление
распространения которого §' можно получить из выражений B.11.9) и
B.11.11):
$'=(? + ncos0) + /nsh0'<"> = /*nxsxn + iAsh0'<*>. C.20.3)
Здесь s и А — соответственно направление падающего луча и нормаль
к границе раздела (ориентированная в сторону среды, из которой при-
приходит луч). Благодаря комплексности величины S' преломленное поле
представляет собой затухающую волну
w(r) а ехр[- ikon(Axuxfi)r + п' fcon-fshe/(//)], C.20.4)
амплитуда которой экспоненциально убывает по нормали к границе.
Рассмотрим векторную составляющую Н затухающего ТЕ-поля. Для
нее выполнено общее свойство затухающих волн (разд. 2.7), а именно
то, что магнитные линии в менее плотной среде начинаются от по-
поверхности и заканчиваются на ней, в то время как в более плотной
среде магнитные линии могут быть замкнутыми или соединять две
точки на поверхности (рис. 3.34).
Используя выражения C.8.2) и C.20.2), получаем
/icos0 + ish 0'Г) 2иь
Здесь (рис. 3.35)
(.
-г sh в'п
в'П\
ф& = arctg . = arctg [(/i2 sin2 в - l)/(/i2 cos2
V ficosu )
1/2
ГР =
_ р21фр
Магнитные
силовые линии
C.20.5)
C.20.6)
C.20.7)
Рис. 3.34. Слева показана амплитуда электрического поля по нормали к границе раздела
Двух сред, освещаемых плоской волной под углом падения, большим критического.
Справа — магнитные силовые линии.
226
lrsl
0,5
a
j
r
v ,
/
/
i
Гл. 3. Плоские многослойные среды
80°
-60°
- 20°
О
l/yl
0.5
S
I
/ 0,-90°
С 1 1
- 80°
60°
40°
20°
0 20° 40° 60° 80°6 0 20° 40° 60° 80° 9
Рис. 3.35. Коэффициент отражения и фазовый сдвиг в зависимости от угла падения.
а — s-волна; б — р-волна; л, = 1,5; п2 = 1,0; ф5 = -90° при в < вс и фр = -90° при
в 0 0° 0 $ в
, 2 5
в < 0В; фр = 0° при 0В < $ < вс.
2ф(в) = ж + 2 arctg
~cos0(/i2sin20-
C.20.8)
Отсюда имеем I г I = I rs I = 1, что является очевидным следст-
следствием закона сохранения энергии, так как преломленная затухающая
волна энергии не переносит.
Разность 2ф(в) между изменениями фазы ТМ- и ТЕ-волн можно ис-
использовать для преобразования состояния поляризации поля. Точнее
говоря, ф = ж/2 для скользящего падения @ = тг/2) и для падения под
критическим углом, а максимальное значение Фмакс достигается, когда
sin20 = 2/(l + /i2) C.20.9)
И РаВН° Фмакс = arctg [(/г2 - l)/2/z] + я/2. C.20.10)
Например, если использовать стекло с показателем преломления
1,51 (окружающая среда — вакуум), то значение <Дмакс = 45°16' дости-
достигается при угле падения в = 51°20\ Таким образом, после одного
полного отражения разность фаз равна приблизительно 90°, что соотн
ветствует преобразованию линейной поляризации в круговую. После
двух полных отражений результирующая поляризация совпадает с на-
начальной. Этот эффект используется в так называемом ромбе Френеля,
который аналогично четвертьволновым пластинкам преобразует ли-
линейную поляризацию волны в круговую.
Рассмотрим теперь волну, проходящую из среды с определенной
плотностью в более плотную среду. При этом д < 1 и соотношение
C.20.1), определяющее критический угол, выполняется при комплекс-
ном значении^: в. - «/2 -».», (ЗЖЩ
причем ch0c" = l/[i. В соответствии с этим полное отражение может
быть получено только для затухающих волн, распространяющихся па-
3.20. Освещение под углом, большим критического 227
раллельно поверхности. Для более точного описания этого случая
применим формальное определение полного отражения, считая пол-
полностью отраженными затухающие волны, распространяющиеся под
углом падения 0 = ж/2 - /0" , где 0" < 0С" . При этом с помощью за-
закона Снеллиуса сразу получаем угол преломления
0' = arcsin(ch0"/ch0c"), C.20.12)
который является вещественной величиной и соответствует вещест-
вещественному преломленному лучу. Тгрсим образом, мы имеем два возмож-
возможных случая: если п/п' > 1, то полное отражение соответствует ве-
вещественным падающим и отраженным волнам и затухающей прелом-
преломленной волне, а если п/п' < 1, то полное отражение имеет место
для затухающих падающих и отраженных волн и вещественных пре-
преломленных.
3.20.1. Нарушенное полное отражение
Для контроля мощности, передаваемой между двумя элементами в
устройствах интегральной оптики, стало привычным вводить в ка-
качестве темного барьера между элементами менее плотную среду
(разд. 3.3.3). Оптическая толщина щели, разделяющей два связанных
между собой элемента, представляет собой параметр, который позво-
позволяет управлять связью. Точнее говоря (рис. 3.6), волна попадает на
границу раздела между первой средой (п = п{) и щелью (п = п <
< пх) под углом 0, бблыыим критического угла 0С = arcsin(wg//Zj).
Ширина щели до подложки (л = ns > ng) равна rfg.
Если пренебречь наличием подложки, то поле, проникающее в
щель, в ней же и затухает. На самом же деле из-за конечности толщи-
толщины щели d между средой, на которую падает волна, и подложкой
хвост затухающей волны может достичь подложки и привести к тун-
нелированию энергии через щель. При этом наличие второй границы
раздела приводит к появлению второй затухающей волны, распро-
распространяющейся уже в обратном направлении, к первой границе раздела
и т. д. Эта бесконечная последовательность отражений порождает ре-
результирующее распределение поля, состоящее из двух затухающих
волн в щели, прошедшей волны в подложке и отраженной волны в
первой среде. Амплитуды соответствующих полей можно найти с по-
помощью характеристических М-матриц. Нужно лишь при определении
импеданса и фазовой толщины учитывать тот факт, что угол 0 явля-
является комплексным: 0g = -к/2 + /0g", т.е. ф% = /*grfgA:ocos0g =
= - ingdgkosh0? . Применим, например, выражение C.12.19) для вы-
22g Гл. 3. Плоские многослойные среды
числения коэффициента отражения р-волны. Для простоты предполо-
предположим, что показатели преломления подложки и первой среды одинако-
одинаковы. Тогда из C.12.19) имеем
б
Гр " /г2 + 1 - (И4 + l)sin20 - Ицсоьв sh 0g cth (dgngko sh 0;')' K ' J
где fi = ^s/^g и» как того тРебует закон Снеллиуса, sh0g' =
= (и2sin2в — 1)^2.При d — оо коэффициент отражения г становится
равным коэффициенту Френеля ехрB/>р) [см. выражение C.20.7)], а
при d — О величина гр обращается в нуль. В общем случае I rp I <
< 1 (нарушенное полное отражение). При этом следствием закона
сохранения энергии для щели без потерь является равенство 17 I =
3.21. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ГРАНИЦЕ РАЗДЕЛА
МЕЖДУ ДИЭЛЕКТРИКОМ И СРЕДОЙ С ПОТЕРЯМИ
Угол преломления для волны, падающей из вакуума на среду с поте-
потерями, является комплексной величиной, которую легко определить,
используя закон Снеллиуса:
0' = 0'п + i0'r) = arcsin[sin в/(п - ikf], C.21.1)
(В дальнейшем все соотношения нетрудно обобщить на случай, когда
волна приходит из диэлектрической среды без потерь, а не из вакуу-
вакуума.) Если выразить cos в' через вещественные параметры q и
7 (cos Of = qe~iy) и предположить, что волна распространяется в пло-
плоскости xz, причем ось z перпендикулярна плоской границе раздела, то
волновой вектор преломленной волны к' можно записать в виде
к' = fco[*sin0 + z(n - iK)qe-*-\ = к'<> - &'<">, C.21.2)
где мы использовали постоянство величины кх после преломления
[см. C.7.1)] и обозначили угол падения через в. Вещественная и мни-
мнимая части вектора к' записываются соответственно в виде
к'° = fco[xsin0 +zq(ncosy — /csiny)],
k'r) = k0zq(KCOsy + nsiny).
Из этих соотношений видно, что плоскости равной фазы (перпен-
(перпендикулярные вектору к'(")) и плоскости равной амплитуды (перпенди-
(перпендикулярные вектору к'("), т. е. вектору z) не являются взаимно ортого-
ортогональными. В этом состоит отличительная особенность рассматривае-
рассматриваемого здесь случая по сравнению с затухающими полями в средах с ве-
вещественным показателем преломления (см. разд. 2.7).
Для комплексного показателя преломления можно определить и
3.21. Отражение и преломление на границе раздела 229
комплексный угол Брюстера. Действительно, из C.8.3) следует, что
tg 0В = tg @В - id'i) = n - Ы. C.21.4)
Для хорошего проводника (к > п) это условие удовлетворяется
при значении угла 0В, равном
0В ? я/2 - i arcth A/к) s я/2 - i/к s я/2. C.21.5)
Вблизи плазменной частоты металла неравенство к > п уже не
выполнено, так что в этом случае величиной п нельзя пренебрегать по
сравнению с / к и угол Брюстера существенно отличен от тг/2 (т. е. от
угла скользящего падения).
Выясним теперь основные особенности отражения на плоской гра-
границе раздела между диэлектриком и средой с потерями. Для этого
воспользуемся формулами Френеля [43, 44] и заметим, что выражения
C.8.2а) и C.8.26), а также закон Снеллиуса приводят к следующему
соотношению: . л
гр - rs _ -sin0 tg 0 -sin0 tg 0
где мы пренебрегли величиной sin20 по сравнению с п2. Предполо-
Предположим, что , 4 /S4 _lis
rjrp= tg (д)е 21ф, C.21.7)
Тогда мы получим
-sin0 tg0cosB<5) ,_ _
M=
l-sinB<5)cosB0)'
к = tg B<5)sinB<?)n. C.21.86)
С помощью C.21.8) вычисляют значения ликпо результатам по-
поляризационных измерений. В частности, при 6 = 0 имеем 8 = т/4,
ф = 0 и г/гр = 1, а это означает, что при нормальном падении ТЕ- и
ТМ-волны эквиваленты друг другу. _
Определим теперь вещественный угол падения в, для которого от-
отношение I rs/rp I принимает максимальное значение. Из C.21.86) полу-
K/]
K/n -J—> C.21.9)
т. е.
I4.fi J. K2/n2I/2
при 2ф = -тг/2. Теперь угол б нетрудно вычислить из соотношений
C.21.8а) и C.21.10): _ _
sin0tg 0 = (и2 + к2I/2 = 1"|. C.21.11)
Благодаря тому обстоятельству, что максимальное значение (<оо)
отношения \rs/r \ при вещественных углах падения достигается при
в = ^, угол б* называют псевдобрюстеровским углом. Этот угол иног-
230
1,0
R
0,9
0,8
0,7
0,6
0,5
- R
—^
Ag
s
CV /
R J I
Гл. З. Плоские многослойные среды
Ф
100°-
50° 90°в
90°в
50°
а б
Рис. 3.36. а — коэффициент отражения Ag (л = 0,055; к = 3,32) и Си (л = 0,76;
к = 2,42) в зависимости от угла падения для зеленой линии ртути (X = 5450 А). Вели-
Величина/? = (Rp + Rs)/2 относится к неполяризованному свету; б — фазовый сдвиг коэф-
коэффициента отражения г = /?1/2ехр (Иф) в зависимости от угла падения для тех же метал-
металлов. 0Си и 0Ag — псевдобрюстеровские углы, соответствующие 2ф8 - 2фр = 7г/2. (Из
работы [43], © North-Holland Physics Publishing, Amsterdam, 1972.)
да называют также главным углом падения. При падении под углом в
фазовый сдвиг отраженной волны равен 90° (рис. 3.36).
3.21.1. Отражение и преломление при скользящем падении
Поскольку 0В = тг/2, интенсивность отраженной волны, получаемой
при скользящем падении, сильно зависит от поляризации падающего
поля. Действительно, из выражений C.8.2) имеем
-1 + cosв/{п2 - sin2в}1/2 2cos0 C 2112)
Г$~ l+cos0/{n2-sin20}1/2 =~l+(n2-l)V2'
Отсюда находим следующее выражение для коэффициента поглоще-
поглощения As = 1 - Rs:
As s 4cos0Re[l/(n2 - 1I/2] s 4ncos0/(n2 + к2\ C.21.13)
которое справедливо при I п I > 1. Аналогично получаем
Ар s 4cos0Re[n2/(n2 - 1I/2] s 4ncos0. C.21.14)
Таким образом, при скользящем падении на металлическую поверх-
поверхность коэффициент поглощения для ТМ (р)-волны примерно в
I /? 12 A03 - 104) раз больше, чем коэффициент поглощения для ТЕ
3.21. Отражение и преломление на границе раздела 231
($)-волны. Очевидно, что этот эффект непосредственно связан с су-
существованием брюстеровского угла падения.
3.21.2. Отражение и преломление при нормальном падений
При нормальном падении R = Rs = Rp и коэффициент поглощения
А = As = Ар = 1 - R дается выражением
А = -г 24" fl „ . C.21.15)
п2 + к2 + 1 + 2и
Как Ry так и Л сильно зависят от длины волны в видимой обла-
области спектра (рис. 3.14 и 3.15).
Амплитудный коэффициент отражения rs@ = 0) = гр@ = 0) = г
легко получить, используя выражения C.8.2) и закон Снеллиуса:
г = RWe* = A - и)/A + Я). C.21.16)
Величины л и к и, следовательно, Лиф зависят от угловой часто-
частоты о). В частности, с помощью дисперсионных уравнений
Крамерса—Кронига можно показать, что угол 0(о>) связан с R (с*>) ин-
интегральным соотношением
ф(со) = Р —= -prdco' + const. C.21.17)
п Jo ^ -«
Это соотношение используется в методе Робинсона—Прайса, ко-
который позволяет измерить зависимость показателя преломления ве-
вещества от частоты в области сильного поглощения. В этом методе
прежде всего измеряют отражательную способность в возможно бо-
более широком диапазоне частот, а затем, используя C.12.17), вычисля-
вычисляют фазу ф(и) амплитудного коэффициента отражения. Если R (о>) и
ф(о)) известны, то с помощью выражения C.12.16) нетрудно вычис-
вычислить п (и) и к(а>). Полное описание различных методов определения
оптических констант см. в книге Белла [45].
3.21.3. Отражение при произвольном угле падения
Для произвольного угла падения коэффициенты отражения Rp и Rs
легко вычисляются с помощью выражений C.8.2) и закона Снеллиуса.
Если \ п\ > 1, то
1 Ч~~ П ~™ C.21.18)
Заменяя в этом выражении cost? на l/cos0, получаем аналогичное вы-
выражение для Rs.
232 Гл. 3. Плоские многослойные среды
3.22. ПОВЕРХНОСТНЫЕ ВОЛНЫ
НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД
Изучим теперь поверхностные волны, возникающие на границе разде-
раздела между диэлектриком и средой с комплексным показателем прелом-
преломления, когда падающая волна распространяется под углом Брюстера.
Для этого сделаем несколько предварительных замечаний о связи
между углом Брюстера и положением нулей и полюсов функции
гр(кх). Действительно, если мы имеем дело со средой, у которой по-
показатель преломления комплексный, и пытаемся продолжить коэффи-
коэффициент отражения гр, определяемый выражением C.8.1), в комплекс-
комплексную область, мы сразу обнаруживаем, что функция гр(кх) может
иметь два определения, т. е. угол Брюстера может быть неоднознач-
неоднозначной величиной. Заметим прежде всего, что при замене в C.8.1) на-
направления распространения падающей волны на направление отражен-
отраженной величина гр преобразуется в обратную ей величину. Это легко до-
доказать, заменяя к&) на — к^ (напомним, что индекс «2» относится к
первой среде). Таким образом, при брюстеровском угле падения гр
может быть либо нулем, либо бесконечностью в зависимости от того,
как мы определили к&. В соответствии с нашей договоренностью
I гр I =0, если Re*<2) > 0, и I гр I = оо, если Re*<2> < 0. Однако во
многих задачах удобнее выразить гр как функцию величины кх. При
этом гр является двузначной функцией от кх, причем эти значения яв-
являются взаимно обратными. Действительно, если предположить для
простоты, что среда 2 — это вакуум, и использовать выражение
C.8.1) и закон Снеллиуса, то мы можем записать
\1/2 -2/1
Квадратные корни можно вычислить однозначно, если провести
разрезы в комплексной /^-плоскости. При этом когда мы находим
угол Брюстера, необходимо иметь в виду, что он соответствует либо
нулю, либо полюсу функции гр(кх)9 в зависимости от того, как мы
определяем сам коэффициент отражения гр. Таким образом, если при
некотором кх величина гр равна нулю, то определенная другим обра-
образом функция гр(кх) в этой же точке расходится. Следовательно, нули
я полюсы двузначной функции гр(кх) совпадают. С физической точки
зрения это связано с тем, что угол Брюстера, соответствующий «от-
«отсутствию отражения», при замене падающей волны на отраженную и
обратно может быть, очевидно, обусловлен бесконечным отликом на
исчезающе малое возмущение. Следовательно, мы можем ограничить-
ограничиться рассмотрением лишь случая гр(кх) = 0, что соответствует погло-
3.22. Поверхностные волны на границе раздела двух сред 233
щению излучения во второй среде, которая в общем случае является
многослойной.
В случае когда волны в подложке (т. е. в крайнем полупространст-
полупространстве многослойной среды) уходят в направлении оси z, перпендикуляр-
перпендикулярном границе раздела первой и второй сред, без ослабления (кх в под-
подложке вещественно), вся падающая энергия переносится к точке
z = +оо. В противном случае возмущение поля удерживается у пло-
плоскости раздела, образуя поверхностную волну адш волну утечки (см.
также разд. 3.18). Точнее говоря, если мнимая часть волнового числа
кх не равна нулю, то возникает волна утечки, а если величина кх ве-
вещественна, то мы имеем дело с поверхностной волной. В то время
как в последнем случае поле распространяется вдоль границы раздела
в направлении х без затухания, волна утечки теряет свою энергию при
распространении вдоль оси х. Различие между этими двумя случаями
(волны утечки и поверхностные волны) особенно важно в случае, ког-
когда на границу раздела падает пучок конечного сечения. При этом
только поверхностная волна обеспечивает эффективный перенос энер-
энергии на большие расстояния в направлении, перпендикулярном оси рас-
расслоения.
Выберем обычную систему координат, когда ось z направлена пер-
перпендикулярно плоской границе раздела, а ось х располагается в пло-
плоскости падения луча. Пусть для простоты первой средой (индекс 2) яв-
является вакуум. Тогда составляющая kz волнового вектора ТМ-волны,
распространяющейся под углом Брюстера [выражение C.8.3)], запи-
запишется в виде
,3.22.2,
где е = е0п2 — диэлектрическая проницаемость второй среды. После
преломления по закону Снеллиуса имеем
К2 _ Кг 1К2 - К0A + я2I/2 - с (gQ + ?)i/2gi/2 > C.22.3)
а компонента кх остается без изменения.
3.22.1. Поверхностные волны в металлах
В хороших проводниках при частотах, много меньших плазменной
(видимый или ИК-диапазон), коэффициент экстинкции к значительно
больше единицы и приведенные выше выражения в хорошем прибли-
приближении можно записать следующим образом:
42) ? ко(п/к2 + г/к\ kzl) s ko(n - 1к). C.22.4)
234 Гл. 3. Плоские многослойные среды
Здесь мы ограничились как для вещественной, так и для мнимой ча-
частей лишь главными членами разложения по параметру малости 1/к.
Таким образом, хотя в первой среде плоскости постоянной фазы и ам-
амплитуды ортогональны друг другу (k'<2>'k"B) = к'хк* + к?2)к^2) =
= 0), во второй среде это уже не так, что обусловлено комплекснос-
комплексностью показателя преломления.
Волновые векторы C.22.4) соответствуют полю, достигающему
максимального значения на границе раздела и затухающему по обе
стороны от нее. Затухание вдоль направления х (параллельно границе)
гораздо слабее, чем в перпендикулярном направлении. Действительно,
нетрудно показать, что
-К™1К = к2In » 1, KKl)IK = к*In » 1- C.22.5)
Поскольку длина затухания вдоль поверхности значительно боль-
больше оптической длины волны, поле распространяется как поверхност-
поверхностная волна, обусловленная собственными колебательными модами
электронного газа металла {поверхностные плазмоны) [10, 46]. Одна-
Однако длина проникновения внутрь металла {кок)~1 достаточно велика,
т. е. характеристики поверхностной волны определяются главным об-
образом диэлектрической проницаемостью металла в целом. Но вместе
с тем существенное влияние на поверхностную волну могут оказать и
возмущения на поверхности, например слои адсорбированного газа.
При е = eL [1 - со?/со(со - /Г)] [см. выражение A.2.47) и подпись к
рис. 1.5] соотношение C.22.2) позволяет представить вещественную
часть величины кх в виде
. / j \ v • -*-/ \-- -L. — р/ \~и • ~l.// L Р \ О ' L
о
C.22.6)
где мы пренебрегли частотой столкновений Г. В соответствии с этим
результатом поверхностная волна не может распространяться
при частотах со, лежащих в диапазоне между о>рг?2/(е0 + eL)l/2 и сор.
Это обстоятельство обычно связывают с существованием запрещен-
запрещенной зоны (рис. 3.37). Для конечных значений Г дисперсионная кривая
непрерывна. При этом функция к'х уже не расходится при со =
= соре?2/(е0 + ?LI/2, но достигает при этом своего максимума, а при
больших со резко уменьшается и принимает минимальное значение при
некотором со/сор, зависящем от Г. Таким образом, с ростом Г запре-
запрещенная зона исчезает. Заметим, что при со > сор среда становится про-
3.22. Поверхностные волны на границе раздела двух сред
J/2
235
Рис. 3.37. Схематическое представление дисперсионной кривой поверхностной волны,
распространяющейся на границе металл — диэлектрик. Штриховые кривые — идеаль-
идеальный металл без затухания, диэлектрическая функция которого та же, что для бесстолк-
новительной плазмы. о?р — плазменная частота металла.
зрачной, так что поле, соответствующее C.22.6а), не связано уже с
поверхностными плазмонами.
Поскольку поверхностная электромагнитная волна удерживается
вблизи границы раздела, она будет преобразовываться в излучатель-
ную волну утечки лишь при наличии возмущений или неоднородности
на поверхности. Кроме того, поверхностную волну невозможно и воз-
возбудить, освещая непосредственно гладкую поверхность световым пуч-
пучком. Для изучения свойств поверхностных волн были разработаны
различные методы их возбуждения и регистрации, а именно методы
линейного или нелинейного оптического возбуждения и регистрации
на неоднородностях поверхности. Кроме того, используются призмы,
расположенные с небольшим (порядка длины волны) зазором над по-
поверхностью (см. рис. 3.6 и разд. 3.3.3). Последний метод известен как
ослабленное полное отражение. При этом для возбуждения поверх-
поверхностной волны используется затухающая волна, возникающая на гра-
границе раздела «среда — воздух» в том случае, когда луч света в среде
испытывает полное внутреннее отражение. Поглощение отраженной
волны и приводит к ослабленному полному отражению. Первая из та-
таких систем была предложена Отто. Она состоит из призмы (Р), отде-
отделенной от толстого образца среды (М) небольшим воздушным или ва-
вакуумным слоем (А) [так называемая конфигурация РАМ ATR, пока-
показанная на рис. 3.38,а]. Если воздушный слой достаточно тонкий, то
затухающая в этом слое волна, вызванная полным внутренним отра-
236 Гл. 3. Плоские многослойные среды
Воздух
Рис. 3.38. Применение цилиндрических призм для возбуждения поверхностных плазмо-
нов. Конфигурации а и б называются системами соответственно Отто и Кретчманна.
жением в призме, может достигнуть границы раздела «воздух — сре-
среда» и возбудить поверхностный плазмон.
В системе «призма — среда — воздух» (конфигурация РМА, метод
Кретчманна) слой активного вещества нанесен непосредственно на ос-
основание призмы. При этом затухающая волна образуется на границе
раздела «призма — среда», проникает внутрь слоя активного вещест-
вещества и возбуждает поверхностную волну на границе «среда — воздух»
(рис. 3.38,6).
Возбуждение поверхностной волны можно зафиксировать по резко-
резкому ослаблению интенсивности отраженной ТМ-волны. Измеряя угол,
при котором такой минимум наблюдается, можно сразу определить
компоненту волнового вектора к'х возбужденной поверхностной вол-
волны. Изменяя частоту, можно последовательно восстановить вид дис-
дисперсионной кривой, схематически представленной на рис. 3.37.
3.23. ИМПЕДАНСНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
Учитывая затухание поля вдали от границы раздела, можно опреде-
определить граничные условия на поверхности металла. Рассмотрим пло-
плоскую ТЕ-волну, падающую из вакуума на металл. Амплитуду прошед-
прошедшего поля можно записать в виде
u'(x9z) = exp[-ifcon(zcos0' + xsin0')]> C.23.1)
где ось z перпендикулярна плоской границе раздела и направлена
внутрь металла, a xz — плоскость падения. Поскольку для металла
I п I > 1, из закона Снеллиуса получаем, что угол преломления 0' г 0 и
U'(X9 Z) ? e-*oinz + xsm0)e-koKz C.23.2)
В соответствии с этим глубина проникновения волны в металл при-
примерно равна (кок)~1. Если и — это компонента электрического векто-
вектора Еу> параллельная поверхности, то и(х, z) непрерывна на границе
раздела. Кроме того, производная du/dz пропорциональна магнит-
магнитной компоненте Нх, которая является также непрерывной. Поэтому в
3.23. Импедансные граничные условия 237
вакууме вблизи границы раздела справедливо соотношение
П-Vms iukon (ТЕ-волны), C.23.3)
где п — нормаль к поверхности, направленная в сторону от металла.
Выражение C.23.3) представляет собой следствие формулы C.23.2) и
непрерывности составляющих Еу и Нх.
Те же рассуждения, что и выше, можно повторить для ТМ-волн,
если и совпадает с Ну. В этом случае непрерывными величинами на
границе раздела являются величины и и (l/n2)du/dz (пропорцио-
(пропорциональная Ех), а выражение C.23.3) принимает вид
n-Vw = iuko/n (ТМ-волны). C.23.4)
Приведенные выше формулы, связывающие и и du/dz непо-
непосредственно над поверхностью металла, называют импедансными
граничными условиями Леонтовича {47} для неидеально проводящих
поверхностей. Используя выражения C.23.3) и C.23.4), поверхности
можно охарактеризовать величиной
Zs = (iCo/kou)(du/dz)9 C.23.5)
где Z~ _ = fnw для ТЕ-волн и ZQ n = tn/n для ТМ-волн.
ЗАДАЧИ
Раздел 3.3
1. Покажите, что формулы C.3.9) и C.3.11), пригодные в окрестности или вдали от
точки поворота, можно заменить универсальной формулой Лангера, которая справед-
справедлива при любых z:
u(z) ос Sj/6(z)[>2(z)-
Здесь
2. Вычислите коэффициент пропускания канала /d.
Раздел 3.8
3. Докажите, что для угла падения 45° коэффициенты отражения Френеля удовлет-
удовлетворяют так называемому соотношению Абеля: /?2 = Rp и 2^s = фр, где ^s и фр — аб-
абсолютные изменения фазы при отражении для s- и р-волн.
4. Пусть в пластине, на которую падает пучок, нет потерь, и волна в ней много-
многократно некогерентно отражается. Покажите, что пропускание такой пластины можно
вычислить по формуле 7"s = A — R$ _)/A + Rs p). Вычислите отношение экстинк-
ции TJT как функцию угла падения/
5. Рассмотрите поляризатор, состоящий из стопы пропускающих пластинок
(рис. 3.13). Вычислите полное пропускание р- и s-волн, предполагая, что внутри каждой
из пластин происходит многократное некогерентное отражение, а между пластинами
238 Гл. 3. Плоские многослойные среды
свет не отражается. Покажите, что
Т,,р = [A - «s,pJl"e-—]/[(l + Rs2,pe~2aT]>
где m — число пластин, а = 4tk/(Acos0'), к — коэффициент экстинкции (см. разд.
3.17), 0' — угол преломления и d — толщина пластины.
6. Используя формулу из задачи 3.5, покажите, что достижимая в поляризаторе
(рис. 3.13) степень поляризации записывается в виде
Гр - Ts _ 1 - cos4w(fl - fl'Xl - Jfo-2T/A - R2e~2ad)m
Tp + Ts ~ 1 4- cos4m@ - 0')(l - Rle'2ad)m/(l - R2e~2ad)m'
где в и 0' — углы падения и преломления соответственно.
Раздел 3.9
7. Представьте характеристическую матрицу М^ двойного слоя в виде следующей
суммы: шя _ _
МЬа = а<*0 + b<Si + СО2 +do3,
где
п о
п о~| Го п го -л
= |_o ij' °l = b о) *2 = b о)
— спиновые матрицы Паули иа2 — Ь2 — с2— d2 = 1. Затем, используя соотношение
А + D = 2 cos 6 и свойства матрицы Пауля, покажите, что
— sin[(w — 1)<5] Bsin(mS)
_
ba = shi^L csin(m^) D sin(md)
sin(mS) I
- sin[(m - 1M] J.
8. Покажите, чтс
Мь • Мв - Мв • Mb = [-(Zb/Za) -f {ZJZb)~\ sin^sin
где _
П о
ff3 = Lo -i
9. Используя М-матрицу для системы (ВН)^ (задача 7), вычислите матрицу для
симметризованной системы (ВН)Р В. Кроме того, вычислите показатель преломления и
фазовую толщину эквивалентного единичного слоя (см. задачу 10).
10. Покажите, что любая комбинация тонких пленок при некоторой длине волны
эквивалентна определенной двухпленочной системе (теорема Херпина). Подсказка. По-
Покажите, что представление C.9.27) возможно для М-матриц более общего вида.
11. Рассмотрите трехпленочную систему aba, у которой внешние слои имеют оди-
одинаковую толщину и показатель преломления. Покажите, что
А = D = cos 2</>а cos 0b — (l/2)(na/nb + wb/na)sin2<?asin$b,
В = (*7na)[sin2<?acos<?b + (l/2)(na/nb + пь/пл) cos 2фл sin фъ +
+ A/2)(пъ/па - wa/nb) sin фъ].
12. Исследуйте изменение матрицы М^ в зависимости от угла падения. Вычислите,
в частности, дЪЛ/дд при 0 = 0. Подсказка. Используйте представление C.9.27) и равен-
равенство дфь/дфа = (db/da?4>a/4>b.
Раздел 3.10
13. Рассмотрите четвертьволновую стопу (ВН)т. Покажите, что при выполнении
условия брэгговского резонанса (т. е. при X = \) напряжение в эквивалентной линии
Задачи 239
передачи пропорционально величине
cos
l
\4
Здесь <?(z) — функция, принимающая целочисленные значения, равные номеру двойно-
двойного слоя, в котором лежит точка z; ? = 0 или 1, если z принадлежит соответственно
Z
слою В или Н; ф ш к0 f n(z' )dzf. Начало координат принадлежит плоскости, проходя-
о
щей через середину слоя с более высоким показателем преломления [ Vo — V(— dB),
V^ = dV/dz]. 2
14. Для системы, рассмотренной в предыдущей задаче, покажите, что блоховская
функция И+)(г) записывается в виде /(z)exp(-/dz/A), где Л = dB + dH и
f(z) = |cos[(tt/4) - фЖпнМ2/Ае^ (-dH/2 < z < (dH/2) + dL).
Кроме того,покажите, что K(~*(z) «
15. Рассмотрите среду, состоящую из бесконечного числа чередующихся диэлектри-
диэлектрических слоев а и b без потерь. Вычислите фазовый множитель 5 при X > da, db. Пока-
Покажите, что для s- и р-волн имеют место следующие выражения:
Ь2 + (d. + dbJ(P2x + P2) = nidi + n2dl + (na2 + nl)djb (s-волна),
52 + (da + dbJ + (na/nb + nb/na - 2)dadb(^ + /JJ) =
= n2d2 + wbdb + («a + «b)^adb (р-волна).
Обратите внимание на то, что поле можно сравнить с плоской волной, волновой вектор
которой имеет составляющие (Зхивс фазовым множителем 6/(da + db). Таким обра-
образом, многослойная среда в пределе больших длин волн аналогична однородной одноос-
одноосной анизотропной среде, у которой показатели преломления обыкновенной и необыкно-
необыкновенной волн записываются соответственно в виде
Иа<*а + n^dl + (И2 + nb)dadb
n\d\ + nidi + (n2 + nl)djb
Пе —~T2 T2 2 2 2 2\л Л '
Подсказка. Используя приближение cos<? = 1 - ф2/2, вычислите характеристическую
матрицу. Кроме того, примените подстановку cos0a b = (лаЬ^о "" @х
~ /3j)/2/(wa bA:Q). (См. книгу [48].)
16. Покажите, что в центре полосы пропускания (8 = 2п-куф = пъ) имеет место ра-
равенство: дд/дф = B + п в/п н + п^/п^2.
Раздел 3.11
17. Получите выражение C.11.9). Подсказка. Используйте для этого выражения
240 Гл. 3. Плоские многослойные среды
C.10.8) и C.9.27), положив фа = фь, и вспомните определение угла <j>t с помощью
C.10.6).
18. Покажите, что на краях полосы пропускания мультислоя с чередующимися пока-
показателями преломления фаза величины Z + становится равной т/2, а амплитуда дается
выражением
Раздел 3.12
19. Докажите, что входной импеданс Zbx подложки с многослойным покрытием
можно записать в виде
ZBX = (AZS + B)/(CZS + D),
где параметры А, В, С и D относятся к мультислою.
20. Покажите, что входной импеданс системы "(ВН)р — стекло" можно записать в
виде
Zg[>4 sinp<5 — sin(p — 1)<5] + Bsinpd
вх "" Z%C sin рд + Dsinpd - sin(p - 1M
Подсказка. См. задачу 7.
21. Используя соотношение C.12.6) и определения C.12.7), выведите выражение
C.12.8).
22. Пусть два объема, в которых не происходит потерь энергии, разделены мульти-
слоем. Используя второй закон термодинамики, докажите, что пропускание мультислоя
одинаково для любого направления распространения плоской волны. Обратите внима-
внимание на то, что отражательные способности каждого слоя одинаковы только в том слу-
случае, когда на диафрагме нет потерь.
23. Используя выражение C.12.16), покажите, что отражательная способность од-
однослойного покрытия дается выражением
_ RY + Д8 4 2y/RjR* cosBncdgfc0 cos gc)
1 + K,jRs + 2y^Ks cosBncdck0 cos 0C)'
где/? j и/?5 — френелевские коэффициенты отражения для границ раздела "окружающая
среда — покрытие" и "покрытие — подложка" соответственно [см. выражение C.8.8I.
Раздел 3.13
24. Рассмотрите тонкую пленку без потерь, нанесенную на металлическую подлож-
подложку, оптические постоянные которой равны п s и к§. Докажите, что отражательная спо-
способность/? дается выражением
1 + Ук|(а! cos 2фс + Ъх sin 2фс) + Л,(а| + Ъ\)
К = -==. ,
Я, + 2jRx(ax cos2<?c + Ъх sin2</>c) + а\ + Ъ\
где/^j — френелевский коэффициент отражения на границе "пленка — окружающая сре-
среда", фс — ncdQk0 — фазовая толщина покрытия и
01 =
25. Рассмотрите нормальное падение волны на диэлектрическую пластину без по-
потерь. Считая, что между двумя поверхностями пластины луч претерпевает некогерент-
Задачи 241
ное отражение, покажите, что амплитуда электрического поля вблизи поверхности в
2/(л + 1) раз меньше, чем амплитуда исходного поля. И наоборот, интерференция
между падающей и отраженной от выходной поверхности волны приводит к увеличе-
увеличению Е на границе в Ъг/(п + 1) раз. Обратите внимание на то, что различное измене-
изменение Е объясняет, почему именно выходная поверхность пластинки более часто подвер-
подвергается оптическому разрушению.
26. Рассмотрите металлическую подложку с нанесенным двойным покрытиемLjL2,
каждое из которых имеет одинаковую фазовую толщину ф. Покажите, что отражатель-
отражательная способность дается выражением
К = . ,
1 + R$R\ — 2y/RsRi cosB<? — S)
где Rs — френелевский коэффициент для поверхности раздела "металл — диэлектрик 2",
5 — относительный фазовый сдвиг:
д = arctg [2п2к3/(п2 - nf - к|Д,
/?j — френелевский коэффициент для системы "окружающая среда — диэлектрик 1", аи§ и
к8 — вещественная и мнимая части показателя преломления металла.
27. Рассмотрим четвертьволновой диэлектрический отражатель типа "стекло — (ВН)Р".
Обозначим через пв - /кв илн — /кн комплексные показатели преломления чередующихся
слоев. Докажите, что при р — оо отражательная способность имеет предел
(см. работу [49]).
28. Покажите, что спектр отражения однослойного просветляющего покрытия
(/j2 = /ijWg) имеет вид
Щл, и) =
1 + ЩвШОс) + 2 у/1Щ^вс) cos[7t(A0/A) cos 0e]
Здесь в — угол падения, вс — угол отражения в покрытии и \ - A/4) пс dc (индекс "с"
относится к покрытию).
29. Постройте зависимости отражательной способности от X и В для s- и р-волн в систе-
системе "стекло (п = 1,51) — покрытие из MgF2 (л = 1,38)".
30. Представьте отражательную способность в виде/? = Л7A -I- X) и вычислите X для
двухслойных просветляющих покрытий типа I и II (см. выражения A8) и A9) в работе [30]).
31. Вычислите отражательную способность трехслойного просветляющего покрытия
типа I при ф1 = ф2 = фъ,п2 = Vflgflj, n3 = WjVwg/zij. Покажите, что у этого покрытия
есть две точки нулевого отражения, а отражательная способность в центре (ф = тг/2)
Подсказка. Используйте выражение C.12.10). См. также выражение B5) в работе [30].
32. Вычислите отражательную способность трехслойного просветляющего покрытия
типа II (ф, = ф2 = ф3 = ф, п2 = V/ig/ij, /i3 = ns «j/zij). Покажите, что у этого покры-
покрытия имеются три точки нулевого отражения, одна из которых расположена в центре
@ = тг/2). Подсказка. Используйте C.12.10). См. также выражение B8) в работе [30].
Раздел 3.15
33. Вычислите эквивалентный показатель преломления и фазовую толщину симме
242 Гл. 3. Плоские многослойные среды
тричной системы aba. Определите интервал частот, в котором 0ЭКВ — комплексная
величина. Подсказка. См. задачу 11.
34. Вычислите пропускание двойного полуволнового фильтра (BHf ВВ(НВУ" В(ВНУ°
ВВСНВ/*. Подсказка. Используйте соотношения C.12.8) — C.12.10), а также результаты
предыдущей задачи.
35. Постройте график зависимости эквивалентного показателя преломления и фазовой
толщины симметричной тонкопленочной системы pqp от величины 20р + <?q. (См рабо-
работу [50]).
36. Рассмотрите два симметричных мультислоя, таких, что показатель преломления
каждого слоя в первой системе является обратной величиной к показателю преломления
соответствующего слоя во второй системе. Кроме того, предположите, что фазовые тол-
толщины соответствующих друг другу слоев у двух систем одинаковы. Покажите, что экви-
эквивалентный показатель преломления первой системы равен обратному эквивалентному по-
показателю преломления второй системы. (См. работу [51].)
Раздел 3.19
37. Вычислите постоянную затухания а поверхностной волны, распространяющейся
вблизи тонкой пленки без потерь, нанесенной на металл, в котором потери велики. Под-
Подсказка. Вычислите входной импеданс подсистемы "тонкая пленка — металл" в мульти-
слое "вакуум — тонкая пленка — металл" и найдите комплексный волновой вектор
кх = /3 - /а, для которого вещественная и мнимая части импеданса удовлетворяют усло-
условию резонанса.
Раздел 3.20
38. Рассмотрите полый волновод, состоящий из двух диэлектрических пластин без по-
потерь, расстояние между которыми d > К. Вычислите постоянную распространения и ко-
коэффициент затухания а для распространяющейся в волноводе моды. Покажите, что для
ТЕ- и ТМ-волн относительно диэлектрических поверхностей величина а дается прибли-
приблизительно выражениями
аТЕ = Л2/ЫЪу/п2- 1, атм = /
где л — показатель преломления диэлектрика. Подсказка. Представьте моду в промежут-
промежутке между диэлектриками в виде суперпозиции двух затухающих плоских волн, претерпева-
претерпевающих полное отражение на диэлектрических поверхностях и преобразующихся одна в дру-
другую за счет таких отражений. (См. книгу [52]).
39. Пусть диэлектрическая пластина без потерь покрыта тонким слоем вещества, по-
показатель преломления которого меньше единицы (например, металлом вблизи плазмен-
плазменной частоты шр или диэлектриком в окрестности узкого и ярко выраженного
резонанса), а коэффициент экстинкции мал. Вычислите отражательную способность как
функцию угла падения и длины волны. Покажите, что критический угол покрытия
0С = arcsin n с хорошей точностью совпадает с углом 6т, при котором зависимость/? (в)
имеет максимальный наклон. Кроме того, рассмотрите эффекты, возникающие при
многократных отражениях внутри покрытия. (См. работу [53]).
40. Покажите, что магнитные силовые линии поля s-волны, падающей под углом,
который больше критического, описываются в более плотной среде уравнением
sin(cot + kx sin в) sin(ky cos в) = const.
Раздел 3.21
41. Вычислите постоянную затухания а ТЕ- и ТМ-волн, распространяющихся по
планарному волноводу с боковыми стенками, изготовленными из металла с большими
Литература 243
потерями. Предполагая, что расстояние между стенками d гораздо больше X, пока-
покажите, что _
а = тЛА(в)/2A2,
где в = т/2 - т\/2с/ — угол падения плоских волн, представляющих собой т-ю моду.
Используя выражения C.21.14) и C.21.15), докажите, что
атн = (w2^2/rf3)Re(l/n), а™ = (m42/d3)Rcn.
(См. работу [54].)
42. Нарисуйте график зависимости псевдобрюстеровского угла от величины
(л2 + к2)у\
43. Вычислите комплексный показатель преломления металла, если известны его от-
отражательная способность при нормальном падении и псевдобрюстеровский угол в.
ЛИТЕРАТУРА
1. Knittl Z, Optics of Thin Films, Wiley, New York, 1976.
2. Hass G., J. Opt. Soc. Am., 72, 27 A982).
3. Spiller E.y Appl. Opt., 15, 2333 A976).
4. Rosenbluth A. E., Foresyth J. M.t Reflecting Properties of X-Ray Multilayer
Devices, Inst. Opt., Univ. of Rochester, New York, 1982.
5. Leith E. #., Kozma A., Upatnieks J., Marks J., Maney N., Appl. Opt., 5, 1303
A966).
6. George N., Matheus J. W., Appl. Phys. Lett., 9, 212 A966).
7. Brekovskikh L. M.t Waves in Layered Media, Academic Press, New York, 1960.
8. Wait J. R., Electromagnetic Waves in Stratified Media, Macmillan, New York, 1962.
9. Tien R, Rev. Mod. Phys., 19, 361 A977).
10. Agranovich V. M.t Mills D. L.t Surface polaritons, North-Holland Publ., Amster-
Amsterdam, 1982.
11. Bender С M, Orszag S. A., Advanced Mathematical Methods for Scientists and
Engineers, McGraw-Hill, New York, 1978.
12. Jacobsson R., Prog. Opt., 5, 247 — 286 A966).
13. Alexopulos N. G, Uslenghi P. L., J. Opt. Soc. Am., 71, 1508 A981).
14. 7)>ras G., Radiation and Propagation of Electromagnetic Waves, Academic Press,
New York, 1969.
15. Brillouin L., Wave Propagation in Periodic Structures, 2nd ed., Dover, New York,
1953.
16. MacLeod H. A., Thin Film Optical Filters, Am. Elsevier, New York, 1969.
17. Vasicek A., Optics of Thin Films, North-Holland Publ., Amsterdam, 1960.
18. Physics of Thin Films, v. 1, (ed. G. Hass), Academic Press, New York, 1963.
19. Abeles A., Ann. Phys. (Paris), 5, 596; 706 A950).
20. Berreman D. W.t J. Opt. Soc. Am., 65, 502 A972).
21. Collin R. E., Foundations for Microwave Engineering, McGraw-Hill, New York,
1965.
22. Stone J. M., Radiation and Optics, McGraw-Hill, New York, 1963.
22a. Baumeister P., A Survey of Optical Interference Coatings, Inst. Opt., Univ. of
Rochester, Roshester, New York, 1977.
23. Arndt J., Baumeister P., J. Opt. Soc Am., 56, 1760 A966).
24. Hass G.t J. Opt. Soc. Am., 45, 945 A955).
25. Baumeister R.s Arnon O., Appl. Opt., 16, 439 A977).
244 Гл. 3. Плоские многослойные среды
26. Thelen A., J. Opt. Soc Am., 61, 365 A971).
27. Clapham P. В., Downs M. J., King R. J., Appl. Opt., 8, 1965 A969).
28. Bennet J. M, Bennet H. E.t — In: Handbook of Optics (eds. W.G.Driscoll, WYau-
ghan), McGraw-Hill, New York, 1978, p. 10. 1—10. 100.
29. Schroder Я., Schlafer R.t Zs. Naturforsch., 49, 576 A949).
30. Musset A, Thelen A., Prog. Opt., 8, 201 — 237 A970).
31. Cox J. Т., Hass G. — In: Physics of Thin Films (eds. G.Hass, R.E. Thun), v. 2,
Academic Press, New York, 1964, p. 239—303.
32. Кард 77. Анализ и синтез многослойных интерференционных покрытий. —
Таллин: Валгус, 1971, с. 79—91.
33. Delano E., Pegis R. J., Prog. Opt., 7, 67 —137 A969).
34. Baumeister P., Moore Л, Walsh K., J. Opt. Soc. Am., 67, 1039 A977).
35. Dobrowolski J, A. — In: Handbook of Optics (eds. W.G. Driscoll, W. Vaughan),
McGraw-Hill, New Tjbrk, 1978, p. 8.1 — 8.117.
36. Seeley J. S., J. Opt. Soc Am., 54, 342 A964).
37. Smith S. D, J. Opt. Soc. Am., 48, 43 A958).
38. Kogelnik #., Befl Syst. Tech. J., 48, 2909 A969).
39. Integrated Optics (ed. T. Tamir), Springer-Verlag, Berlin, New York, 1975. [Имеется
перевод: Интегральная оптика/Под ред. Т.Тамира.— М.: Мир, 1978.]
39а. Wang S., IEEE J. Quantum Electron., QE-10, 413 A974).
39b. Tsang W. T, Logan R. A., Johnson L. E J.t Hartman R. L., Koszi L. A., J.
Quantum Electron., QE-15, 1091 A979).
40. Magnus W.t Winkler S., Hill's Equation, Wiley, New York, 1966.
41. Yen P., Yariv A., Hong C-S., J. Opt. Soc. Am., 67, 423 A977).
42. Collin R. E, Field Theory of Guided Waves, McGraw-Hill, New York, 1960.
43. Optical Properties of Solids (ed. RAbeles), North-Holland Publ., Amsterdam, 1972.
44. Abelbs F. — In: Advanced Optical Techniques (ed. A.C.S. van Heel), North-Holland
Publ., Amsterdam, 1963, p. 143—188.
45. Bell E. E. — In: Handbuch der Physik, v. XXV-2A (ed. S.Flugge), Springer-Verlag,
Berlin, New York, 1967, p. 1—57.
46. Polaritons, (eds. E.Burstein, F. De Martini), Pergamon, New York, 1974.
47. Senior R A., Appl. Sci. Res., Sect.B, 8, 437 A960).
48. Yariv A., Yeh P., J. Opt. Soc Am., 67, 438 A977).
49. Koppelmann G., Ann. Phys. (Paris), 5, 388 A950).
50. Epstein I. I., J. Opt. Soc Am., 42, 806 A952).
51. Thelen A., J. Opt. Soc Am., 56, 1533 A966).
52. Marcuse D, IEEE J. Quantum Electron., QE-8, 661 A972).
53. Hunter W R., J. Opt. Soc Am., 54, 15 A964).
• 54. Carmire E., McMahon T. M, Bass M, IEEE J. Quantum Electron., QE-16, 23
A980).
БИБЛИОГРАФИЯ
Surface Excitations (eds. V.M. Agranovich, R. Loudon), North-Holland Publ.,
Amsterdam, 1984.
Azzam R. M A., Bashara N. M.t Ellipsometry and Polarized Light, North-Holland
Publ., Amsterdam, 1977. [Имеется перевод: Аззам Р., Башара Н. Эллипсо-
метрия и поляризованный свет. — М.: Мир, 1981.]
Весктап P., Spizzichino A.t The Scattering of Electromagnetic Waves from Rough
Surfaces, Pergamon, Oxford, 1963.
Библиография 245
Hsue С. Ж, Tamir Т., J. Opt. Soc. Am., A2, 923 A985).
Hunderi О., Surf. Sci., 96, 1 A980).
Jacobsen R. Т., J. Opt. Soc. Am., 54, 1170 A964).
Handbook of Synchrotron Radiation, v. 1. (ed. E.E. Koch), North-Holland Publ.,
Amsterdam, 1983.
Kortum G. F.t Reflectance Spectroscopy, Springer-Verlag, Berlin, New York, 1969.
Rovard P., Bousquet P. — In: Progress in Optics, v. IV (ed. E. Wolf), North-
Holland Publ., Amsterdam, 1965, p. 145—197.
Tamir Т., Wang H. C, Oliver A. A., IEEE Trans. Microwave Theory Tech., MTT-12,
323 A964).
Yeh P., J. Opt. Soc Am., 69, 742 A979).
Yeh P., Surf. Sci., 96, 41 A980).
ГЛАВА 4
ОСНОВЫ ТЕОРИИ ДИФРАКЦИИ
4.1. ВВЕДЕНИЕ
4.1.1. История вопроса
Волновая теория в том виде, в котором она теперь существует, явля-
является результатом длительной и интересной эволюции взглядов, беру-
берущих свое начало в идеях, высказанных в 1690 г. Христианом Гюйген-
Гюйгенсом в знаменитом "Трактате о свете" 1К В первой главе своей книги
Гюйгенс написал, что он был поражен тем фактом, что
"...волнообразное движение, производимое столь малыми дви-
движениями и тельцами, может распространяться на огромные рас-
расстояния, как, например, расстояния от Солнца или от звезд до
нас. Действительно, сила этих волн должна ослабевать по мере
их удаления от своего источника, так что каждая из них в от-
отдельности, несомненно, теряет способность воздействовать на
наше зрение. Но это перестает быть удивительным, если при-
принять во внимание, что бесконечное число волн, исходящих, прав-
правда, из различных точек светящегося тела, на большом расстоя-
расстоянии от него соединяются для нашего ощущения только в одну
волну, которая, следовательно, и должна обладать достаточной
силой, чтобы быть воспринятой. Таким образом, то бесконечное
число волн, которые одновременно нарождаются во всех точках
неподвижной звезды, быть может такой же большой, как и Солн-
Солнце, для ощущения представляется только одной волной, которая
вполне может быть достаточно сильной, чтобы вызвать впечат-
впечатление в наших глазах..."
Это описание волнового распространения известно как принцип
Гюйгенса.
Большая заслуга Томаса Юнга состоит в том, что он, следуя Нью-
Ньютону, снова привлек идеи волнового распространения для объяснения
корпускулярной теории оптических явлений. Действительно, в трех
бейкеровских лекциях, прочитанных им в Королевском Обществе в
1801—1803 годах, он ввел принцип интерференции, который примени-
применительно к волнам, сопутствующим постулированным Ньютоном кор-
1) Есть русское издание этого труда: Христиан Гюйгенс. Трактат о свете. —
М.—Л.: Объединенное научно-техническое изд-во НКПТ СССР, 1935. — Прим. перев.
4.1. Введение 247
пускулам света, позволил объяснить появление колец, наблюдаемых
при соединении изогнутой стороны выпуклой линзы с плоской опти-
оптической поверхностью.
Благодаря этому принципу Юнг смог впервые вычислить длины
волн для разного цвета. К сожалению, из-за господства корпускуляр-
корпускулярной теории остальные ученые не приняли его идеи.
Позднее, 15 октября 1815 г., Огюстен Жан Френель представил
Французской академии знаменитый трактат "Дифракция света", в ко-
котором, развивая идеи Гюйгенса и Юнга, изложил систематическое
описание интерференционных полос, наблюдаемых на темной стороне
препятствия, освещаемого небольшим источником света. Френель
смог показать, что измеренные расстояния между полосами совпада-
совпадают с результатами вычислений, основанных на волновой теории. Кро-
Кроме того, Френель придал более строгую форму принципу Гюйгенса,
подчеркнув важную роль фаз отдельных вкладов от излучателей. Дей-
Действительно, Гюйгенс еще не знал ни о поперечных колебаниях, ни о
принципе интерференции, ни о существовании упорядоченной последо-
последовательности волн в цуге. В июле 1819 г. Французская академия награ-
наградила Френеля специальной премией, отметив таким образом оконча-
окончательную победу волновой теории над корпускулярными представлени-
представлениями Ньютона.
Другой выдающийся успех волновой теории был зафиксирован в
1835 г. в связи с публикацией в "Трудах Кэмбриджского Философско-
Философского общества" фундаментальной статьи сэра Джорджа Биддела Эйри
(директора Кэмбриджской обсерватории), в которой он вывел свое
знаменитое выражение, описывающее изображение звезды, видимой
через хорошо скорректированный телескоп. Изображение состоит из
яркого ядра (называемого с тех пор диском Эйри), окруженного сла-
слабосветящимися кольцами, из которых только первое глаз ощущает
как достаточно яркое.
Вплоть до публикации Максвеллом в 1873 г. "Трактата об электри-
электричестве и магнетизме" успешное применение идей Френеля для решения
большого числа задач рассеяния и дифракции основывалось на физи-
физической модели распространения через упругую среду. В частности, в
1861 г. Клебш описал дифракцию плоской волны на сферическом пре-
препятствии. Удивительно, что большинство из этих решений было под-
подтверждено электромагнитной теорией уже в рамках уравнений Макс-
Максвелла. Типичным примером являются решения Клебша для сферы.
Такой успех обусловлен тем, что и электромагнитные, и упругие поля
могут быть в принципе описаны скалярными функциями, удовлетво-
удовлетворяющими скалярному волновому уравнению. Таким образом, это
248 Гл. 4. Основы теории дифракции
уравнение можно рассматривать как единую основу для многих полей,
существующих в природе. Оно же объясняет тот удивительный факт,
что малое возмущение, рожденное в конечном объеме, может распро-
распространяться в физическом пространстве и восприниматься даже на ас-
астрономических расстояниях. Эта восхитительная история оптических
теорий повторяется в современных попытках описать более сложные
поля, которые управляют внутриядерным миром, что является облас-
областью физики высоких энергий.
Начиная с первого успеха формулы Эйри, теория дифракции при-
приобретала все большую популярность, обеспечивая исследователей
фундаментальными методами количественной оценки качества изо-
изображений и возможностей оптических систем формировать хорошо
разрешенные изображения. Этот успех можно объяснить на извест-
известном примере. Размер центрального дифракционного диска в изобра-
изображении точечного предмета не сильно зависит от точности установки
плоскости наблюдения или от существования сферической аберрации.
Например, вычисления показывают, что при дефокусировке на чет-
четверть длины волны размер диска ^охраняется практически неизмен-
неизменным. Это означает, что в данном случае прибор может разрешить две
соседние точки так же, как и в идеальной оптической системе без
аберраций. Интересно, что ситуация изменяется при наблюдении про-
протяженных предметов. В частности, для тех же отклонений системы от
идеальной наблюдается уже заметная потеря контраста в тонких де-
деталях изображения протяженного предмета. Объяснение этому следу-
следует искать в изменении всей дифракционной картины изображения. Дейст-
Действительно, хотя размер центрального диска остается прежним, аберра-
аберрации изменяют распределение интенсивности между центральным дис-
диском и концентрическими кольцами. Вычисления показывают, что при
тех же аберрациях интенсивность колец увеличивается на 17% и соот-
соответственно уменьшается яркость центрального диска.
Для того чтобы разобраться в этой сложной ситуации, в 1946 г.
Дюффо предложил исследовать изображение как функцию периода
при синусоидальном распределении интенсивности. В результате ин-
информация об оптической системе содержится в оптической переда-
передаточной функции (ОПФ), которая определяет отклик системы в зави-
зависимости от числа линий предмета на единице длины. Эту функцию
можно вычислить, используя интегралы теории дифракции, в то вре-
время как функция аберраций Wo системы (см. разд. 2.15) определяется с
использованием формализма геометрической оптики.
Уже в наше время с развитием идей Габора и Торальдо ди Фран-
чиа оптические системы стали характеризоваться с помощью счетного
4.1. Введение 249
множества полей предмета, которые достоверно воспроизводятся
(в том числе и для конечных зрачков, и в присутствии аберраций). Этот
подход, основанный на решении интегральных уравнений Фредголь-
ма, получаемых из стандартных дифракционных интегралов, позволя-
позволяет использовать идеи теории информации для описания оптических
приборов. Таким образом, квантуя информацию, заложенную в изо-
изображении, и измеряя информационную емкость оптического прибора,
можно непосредственно определить пропускную способность элек-
электронных каналов связи, необходимых для передачи изображения.
4.1.2. Математический аппарат
Волновая оптика рассматривает, чем отличается истинное поведение
электромагнитных полей от того, что предсказывает геометрическая
оптика. Результаты геометрической оптики основываются на прибли-
приближении, в котором волны распространяются вдоль определенных тра-
траекторий (лучей). В действительности же электромагнитные поля под-
подчиняются волновым уравнениям Гельмгольца, дополненным соот-
соответствующими граничными условиями. Решения краевых задач в тео-
теории электромагнитного поля ограничены и непрерывны, в то время
как в геометрической оптике поля сингулярны на каустиках и разрыв-
разрывны при пересечении границ тени, образуемых препятствиями, разру-
разрушающими пучки лучей.
К сожалению, сингулярности геометрической оптики не устраняют-
устраняются и при рассмотрении высших порядков в рядах Лунеберга— Клейна
(ЛК) [выражение B.2.5)]. Действительно, два последовательных члена
этого ряда связаны рекурсивными соотношениями B.6.2); поэтому,
если первый член расходится, то последующие члены вычислить уже
невозможно. Таким образом, приходится выискивать различные пред-
представления для полей, по крайней мере вблизи этих критических обла-
областей. Целью волновой оптики является устранение нефизических осо-
особенностей полей, вычисленных методами геометрической оптики, и
улучшение методов вычисления полей при распространении их на
очень большие расстояния.
Анализируя доступные аналитические решения уравнении Максвел-
Максвелла, которые в пределе X = 0 приводят к каустикам или границам те-
тени, можно заметить, что вблизи критических областей амплитуда по-
поля испытывает систематические колебания в пространстве. Иными
словами, каустики и границы тени окружены чем-то вроде пригранич-
приграничного слоя аналогично тому, что происходит при обтекании поверхно-
поверхности жидкостью (рис. 4.1). Толщина и скорость изменения поля внутри
250
Гл. 4. Основы теории дифракции
Падающий
Волновой
фронт
Параксиальный
фокус
Рис. 4.1. Отверстие в плоском экране, освещаемое сферической волной с аберрациями.
Заштрихованные области представляют собой граничный слой, окружающий границу
тени и каустику.
этого слоя зависит от волнового числа к. При к — оо толщина слоя
стремится к нулю, а решение волнового уравнения стремится к своему
предельному виду [1].
Вообще говоря, отличие истинных полей от полей, полученных в
приближении геометрической оптики, тем больше, чем дальше мы
отодвигаемся от источников и от препятствий, мешающих свободно-
свободному распространению света. Рассмотрим в качестве примера отверстие
в металлическом экране, на которое падает плоская волна. В прибли-
приближении геометрической оптики распределения поля на любой плоско-
плоскости, параллельной экрану, имеют одни и те же размеры и форму. Ис-
Истинное же распределение интенсивностей, называемое дифракционной
картиной, при удалении от экрана с каждым шагом все заметнее из-
изменяется по форме и размерам. В конечном счете достигается область
далекого поля, в которой с увеличением расстояния изменяются лишь
размеры картины, форма же сохраняется постоянная.
Другая ситуация возникает при неоднородном распределении по-
показателя преломления. В этом случае необходимо ввести в рассмот-
рассмотрение несколько волн, распространяющихся в различных направлени-
направлениях, причем связь между этими полями определяется неоднородностя-
ми среды. Физически это можно интерпретировать как процесс рассе-
рассеяния: падающая волна порождает рассеянную волну, распространяю-
распространяющуюся в разных направлениях.
Задачи, которые решает волновая теория, можно условно разде-
разделить на три класса:
1) изучение распространения волн через неоднородную среду
(см. гл. 3);
4.1. Введение 251
2) вопросы дифракции (см. данную главу) и
3) изучение рассеяния на препятствиях (см. гл. 6).
В частности, теория дифракции занимается главным образом изу-
изучением полей вблизи каустик, фокусов и границ тени, связанных с вол-
волновыми фронтами, ограниченными отверстиями (или препятствиями).
В строгом смысле слова всякое препятствие можно рассматривать как
область, в которой показатель преломления отличается от его величи-
величины в окружающей среде; поэтому дифракцию на отверстиях или рас-
рассеяние на препятствиях можно рассматривать как распространение че-
через неоднородную среду. Таким образом, приведенная классификация
определяется главным образом соображениями удобства.
Волновая теория использует большое число различных аналитиче-
аналитических методов [2, 3]:
1) спектральное представление полей (разложение по плоским, ци-
цилиндрическим и сферическим волнам; пучки Эрмита — Гаусса; вытя-
вытянутые сфероидальные гармоники) (см., например, гл. 4, 5 и 7);
2) дифракционные интегралы (см. данную главу);
3) интегральные уравнения (см., например, гл. 7);
4) интегральные преобразования (преобразования Лебедева —
Канторовича, преобразование Ватсона) [4] (см., например,
гл. 5);
5) разделение переменных (см., например, гл. 8);
6) функциональный метод Винера — Хопфа — Фока [5];
7) асимптотические ВКБ-решения волнового уравнения для неод-
неоднородных сред (см., например, гл. 3);
8) вариационные методы [6, 7];
9) решения уравнений Максвелла с помощью теории возмущений
[8] для слабо неоднородных сред {разреженная среда) (см., на-
например, гл. 6).
Во многих случаях решения можно выразить в виде комплексных
интегралов и рядов, которые можно вычислить либо асимптотически,
либо численными методами, используя
1) методы перевала и стационарной фазы (см., например, гл. 5);
2) теорию приграничного слоя;
3) алгоритм двумерного быстрого преобразования Фурье (БПФ) [9].
Метод перевала, который в общем случае более точен, чем метод
стационарной фазы, состоит в деформации контура интегрирования в
комплексной плоскости и последующего вычисления интеграла с по-
помощью асимптотического ряда. Можно показать, что этот ряд в це-
252 Гл. 4. Основы теории дифракции
лом совпадает с модифицированным ЛК-представлением поля, в ко-
котором главный член пропорционален дробной степени величины/г.
Аномалии на каустиках или на границе тени можно в принципе ис-
исключить, используя "растянутую" соответствующим образом систему,
координат, которая в хорошем приближении позволяет описать быст-
рые изменения поля. Такой подход обычно называют приграничной?
теорией дифракции [1].
Напомним здесь, что полное знание электромагнитного поля озна-
означает определение всех скалярных компонент полей Е и Н. В общем]
случае три компоненты поля (например, Е) колеблются с общей ча-
частотой со и различными фазами. Как следствие, конец вектора Е(г, t)
при данном г описывает за период Т = 27г/со плоскую фигуру, имею-
имеющую форму эллипса. Когда эллипс вырождается в отрезок, поле ока-
оказывается линейно поляризованным. Во многих случаях при изменении
г поляризация также изменяется. Например, если сфокусировать лин-
линзой линейно поляризованный пучок света, то с приближением к фоку-
фокусу степень его линейной поляризации становится все меньше. Эти про-
процессы можно удовлетворительно описать лишь с помощью векторной
волновой теории (см. разд. 4.13).
Важной особенностью интегрального представления поля является
тот факт, что во многих случаях резонансы системы можно изучать,
отыскивая полюсы подынтегрального выражения. В частности, полю-
полюсы, соответствующие вещественным значениям частоты, приводят к
колебательным или распространяющимся модам системы, а ком-
комплексные частоты соответствуют модам утечки (см. разд. 3.19). Кро-
Кроме того, наличие разрезов в плоскости определения подынтегрального
выражения связано с существованием некоторых специальных волн
(например, поверхностных и боковых волн). В общем случае сущест-
существенную информацию можно получить, исследуя области аналитично-
аналитичности подынтегрального выражения.
4.2. МЕТОД ФУНКЦИИ ГРИНА
4.2.1. Интегральная теорема Гельмгольца — Кирхгофа
Рассмотрим объем V, ограниченный замкнутой поверхностью 5 (в об-
общем случае многолистной), и две произвольные функции и(т) и /(г, г'),
где г и г' — координаты точек внутри этого объема (рис. 4.2). Если
обозначить производную по внешней нормали п0 к поверхности S че-
через д/дп0, то с помощью теоремы Гаусса можно записать следующее
выражение:
4.2. Метод функции Грина 253
Источника
ис. 4.2. Область поля, ограниченная
двумя замкнутыми поверхностями.
ПТ[/(г,г')У2«(г) -
V
= J(Tf • [/(г,г') F«(r) - «(г) Р/(г, г')] dV =
где оператор V действует на координату г.
Для наших целей удобно ввести функцию G(r, г'), удовлетворяю-
удовлетворяющую неоднородному волновому уравнению
[V2 + n2(r)fc2]G(r,r') = -<5(г - г'), D.2.2)
где 6(г) — трехмерная б-функция. Любая функция G, удовлетворяю-
удовлетворяющая линейному дифференциальному уравнению, правая часть которо-
которого записывается так, как в D.2.2), называется функцией Грина опера-
оператора, стоящего в левой части того же уравнения. Из уравнений Макс-
Максвелла получаем следующее уравнение:
V2E + k2on2(r)E + 2 F[E. P(ln n)] = iojfi0J - (i/coe0) F[P • J/n2(r)], D.2.3)
которое при J = О сводится к B.8.1). Используя приближение скаляр-
скалярной теории, т. е. пренебрегая третьим членом в левой части уравнения
D.2.3), имеем
V2M + fcgn2(r)u = -/i(r), D.2.4)
здесь и — любая из декартовых компонент вектора Е, а функция
А — соответствующая компонента вектора в правой части уравнения
D.2.3). Поскольку и линейно зависит от А, можно использовать прин-
принцип суперпозиции и записать следующее выражение:
«(г)= (TfG(r,rW)A-', D.2.5)
254 Гл. 4. Основы теории дифракции
где G — решение уравнения D.2.2). В частном случае, когда
А(г') = 5(г' - г0), из D.2.5) следует
u(r) = G(r,r0), D.2.6)
т. е. любое решение w(r), порождаемое 6-источником, расположенным
в точке г', является функцией Грина G(r, г'). Уравнение D.2.2) имеет
бесконечное множество решений, каждое из которых определяется
своими значениями на поверхности S. Во многих случаях, используя
формальную идентичность уравнений D.2.2) и D.2.4), удобно рассмат-
рассматривать только те решения, которые связаны с источниками внутри
объема V, а не вне поверхности S. Другой тип функций Грина можно
получить, рассматривая внешние по отношению к V источники так,
чтобы удовлетворялись соответствующие граничные условия.
Для неограниченной однородной среды (показатель преломления
не зависит от г) функция Грина уравнения D.2.2) записывается в виде
(см. задачи 5 и 6 в гл. 1):
G(r,r') = G(r',r) = G(|r - r'|) = еХр(~^|Г~г1). D.2.7)
Рассмотрим теперь компоненту и поля, удовлетворяющую одно-
однородному волновому уравнению
[V2 + fc2n2(r)]u(r) = 0. D.2.8)
Умножая D.2.8) и D.2.2) соответственно на G и и и вычитая получен-
полученные уравнения одно из другого, находим простое соотношение:
G(r,r')V2u(r) - М(г)V2G(r,r') = и(т)8(т - г'). D.2.9)
Полагая G * f и используя уравнение D.2.9) в соотношении D.2.1),
получаем интегральную теорему Гельмгольца — Кирхгофа (которую
называют также теоремой Грина):
ii(r) =
дп0 дп0
= <fl>[G(r',r) V'ti(r') - и(г') V'G(r'.r)] . nodS' =
v(r,r')- nodS'. D.2.10)
Функция v(r, г'), называемая векторным полем Гельмгольца, опреде-
определяется выражением
v(r,r') = G(r',r)P'W(r') - w(r')P'G(r',r). D.2.11)
При написании выражения D.2.10) мы поменяли ролями гиг', так
4.2. Метод функции Грина 255
что интеграл и производные должны вычисляться относительно коор-
координаты г', как это указывается символом V.
Следует заметить, что из D.2.9) вытекает соотношение
Р'.у(г,г') = О, D.2.12)
справедливое всюду, кроме точки г = г'. Таким образом, согласно те-
теореме Гаусса, интеграл в правой части равенства D.2.10), а тем са-
самым и w(r) не зависят от выбора поверхности S, ограничивающей объ-
объем, включающий в себя точку наблюдения г.
Если интеграл Гельмгольца — Кирхгофа берется по поверхности
S, характеризуемой поверхностным импедансом Zs, то величину
ди/дп0 можно представить как функцию только от и [см. уравнение
C.23.5)], так что уравнение D.2.10) принимает вид
T')dS\ D.2.13)
S
коп и f = fo//i.
Соотношение D.2.13) особенно полезно при рассмотрении дифрак-
дифракции от металлических предметов с конечной проводимостью. В этом
случае Z5/f0 совпадает или с комплексным показателем преломления
п - /к, или с обратной ему величиной в зависимости от поляризации
поля, перпендикулярной или параллельной плоскости падения [см. вы-
выражения сразу за C.23.5)]. Для однородной среды, ограниченной по-
поверхностью S, функция Грина определяется выражением D.2.7), так
что из D.2.13) имеем
s
здесь 6 = (г' - r)/lr' - rl.
В соответствии с выражением D.2.10) поле м(г) полностью опреде-
определено, если оно задано вместе с производной по нормали на замкнутой
поверхности, ограничивающей интересующий нас объем. Однако при
этом мы еще не можем получить распределение поля. Действительно,
чтобы воспользоваться выражением D.2.10), должна быть известна
функция Грина для конкретного закона изменения показателя прелом-
преломления и конкретных граничных условий, определяемых рассеивающи-
рассеивающими объектами, диафрагмами и т. д. Формально мы можем рассмат-
рассматривать и и ди/дп0 на поверхности S как входные данные линейной си-
системы, отклик которой м(г) дается интегралом D.2.10). Следователь-
Следовательно, оптическую систему можно сравнить с черным ящиком, входными
параметрами которого являются и и ди/дп0, заданные на S, хотя, как
мы покажем ниже, их нельзя варьировать независимо. При этом
256
Гл. 4. Основы теории дифракции
функция Грина представляет собой аналог импульсного отклика элек-
электронного устройства.
Первый из способов определения поля, создаваемого точечным ис-
источником, т. е. функции G(r, г'), основывается на методах геометри-
геометрической оптики. Если источник расположен в точке г', то можно опре-
определить траектории лучей, выходящих из г', и соответствующие вол-
волновые фронты. В общем случае из-за неоднородности среды траекто-
траектории лучей являются криволинейными. Если внутри объема можно вы-
выделить поверхность, на которой показатель преломления меняется
скачком, то электромагнитная волна испытывает частичное отраже-
отражение и преломление. В некоторых случаях конгруэнции отраженных и
падающих лучей перекрываются, что приводит к сложной дифракци-
дифракционной картине (рис. 4.3). Кроме того, преломленные лучи могут поки-
покинуть диэлектрик лишь в том случае, когда они попадают на ограничи-
ограничивающую его поверхность под углом, который меньше критического.
Чтобы учесть это, нужно использовать формулы Френеля (гл. 3) для
коэффициентов пропускания и отражения волн, падающих на поверх-
поверхности разрыва показателя преломления п(г). Как только определены
траектории лучей, можно в принципе вычислить амплитуды поля
Ат(г), используя транспортные уравнения [см. B.6.4)]. Структура этих
уравнений такова, что пренебречь высшими членами разложения
Ат(т > 1) в рядах Лунеберга — Клейна нельзя, если Ао быстро изме-
изменяется в пространстве. Например, изображенные на рис. 4.3 лучи рез-
резко изменяют направление своего распространения, пересекая диэлект-
Рис. 4.3. Схематическое представление поля, дифрагированного на прямоульном диэлек-
диэлектрическом клине. Прошедшие, отраженные и преломленные лучи, отходящие от клина,
окружены критическими областями, где поле существенно отличается от предсказаний гео-
геометрической оптики.
4.2. Метод функции Грина 257
рик. Дважды применяя закон Снеллиуса B.11.8), легко показать, что
угловое отклонение луча после попадания из вакуума на кромку диэ-
диэлектрического клина с показателем преломления п и углом тг/2 дается
выражением 0 = 0 - arcsin A + sin20 - л2I72, где 0 — угол паде-
падения. Та^им образом, поле в заштрихованных на рис. 4.3 участках ис-
испытывает быстрые изменения и необходимо учитывать все амплиту-
амплитуды высших порядков Ат.
Функцию Грина неоднородной среды можно также вычислить, ис-
используя совсем иной метод. Он применим, например, если распределе-
распределение показателя преломления обладает аксиальной симметрией и ха-
характеризуется дискретным набором волноводных мод [выражение
B.12.17)]. Как мы покажем, в этом случае функция Грина представи-
ма в виде разложения в ряд по соответствующим модам.
В общем случае построение функции Грина основывается на после-
последовательном переборе и учете всевозможных факторов — свободного
распространения, дифракции на канонических (диафрагмы, клинья и
т. п.) и других гладких препятствиях общего вида, отражения и пре-
преломления на границах разрыва п(г). Во многих случаях вычисление
функции Грина упрощается тем, что источник находится на бесконеч-
бесконечности и, следовательно, поле от него можно представить плоскими
волнами.
4.2.2. Принцип Гюйгенса
Рассмотрим поле, распространяющееся в однородной среде. Объе-
Объединяя уравнения D.2.10) и D.2.7), получаем
** dulr') д e~ikR~
s
где R = г - г'. Следовательно, поле можно представить в виде су-
суперпозиции элементарных возбуждений
-ikR Гди(т) ( 1М
Ы) D>2Л6)
В случае когда Rk > 1, что обычно имеет место для оптического
диапазона, уравнение D.2.16) принимает вид
du(r) = ^Г^ + Мо ¦ Ru(r<)~U'. D-2.17)
Для тех полей м, которые допускают представление геометрической
258
Гл. 4. Основы теории дифракции
Рис. 4.4. Обозначения, используе-
используемые при рассмотрении принципа
Гюйгенса.
оптики и = A(r)e~iks(T\ можно написать следующее выражение:
e~ikRd(S-R)
du(r)= -ik
-dS\
D.2.18)
4nR dn0
где мы пренебрегли медленным изменением амплитуды А (г). Таким
образом, величина du{x) пропорциональна и (г') и каждая элементар-
элементарная поверхность dS' дает дифрагированное поле, амплитуда которого
убывает как \/R и характеризуется следующей диаграммой направ-
направленности излучения:
-d(S - R)/dn0 = -n0- s+ n0- R = cos0i + cos0d =
= 2со8[(^ -»- 0d)/2] cosC^ - 0d)/2], D.2.19)
где 0j — угол между падающим лучом, проходящим через точку г',ли
внутренней нормалью -й0 к S, a 0d — угол между направлением - R,
вдоль которого вычисляется дифрагированное поле, и вектором -ri0
(рис. 4.4). При этом дифракционный интеграл D.2.15) принимает вид
М(Г) = i
D.2.20)
(здесь не следует путать эйконал S в экспоненте с обозначением по-
поверхности 5). В частности, когда поверхность 5 совпадает с волновым
фронтом (в{ = 0), выражение cos в{ + cos 0d преобразуется в коэффи-
коэффициент наклона 1 + cos0d^. Представление поля в виде суперпозиции
многих элементарных волн B.2.17) называется принципом Гюйгенса.
Рэлей в своей статье для Британской энциклопедии в 1889 г. сформу-
сформулировал его следующим образом:
"Если изобразить вокруг источника волн идеальную замкнутую
поверхность, то результирующее воздействие волн во внешней
области можно представить как сложение волн от всех элемен-
элементов этой поверхности. Волновое движение от каждого из элемен-
элементов поверхности называется "вторичной волной", а для нахожде-
Угол 0d при этом называют углом дифракции. — Прим. перев.
4.2. Метод функции Грина
On
259
Рис. 4.5. Кольца Френеля при наблюдении из точки г, в которой определяется поле.
ния суммарного воздействия в каждой точке нужно учитывать
как амплитуды, так и фазы всех компонент...".
На самом деле можно показать, что для нахождения искомого по-
поля нужно учитывать лишь вклады du(r) от вполне определенных
участков фиксированного волнового фронта. Для иллюстрации этого
утверждения рассмотрим сферический волновой фронт А с радиусом
кривизны R. Его можно разбить на элементарные кольца, называе-
называемые зонами Френеля (или Гюйгенса), которые вырезаются из волно-
волнового фронта сферами с центром в точке г (рис. 4.5), в которой требу-
требуется определить поле н(г). Пусть первая из этих сфер радиусом Ro ка-
сательна к поверхности А, а последующие сферы радиусами
Rm = Ro + тХ/2 пересекают волновой фронт А по окружности ради-
радиусом Rm = [m\R0R/(R - R0)]l/2> где X = 2ir/k — длина волны. Та-
Таким образом, волновой фронт А будет разделен последовательностью
колец одинаковой площади, равной приблизительно тг\\ R0R/
/(R - Rq)\. Если um(t) — поле от m-го кольца, то м(г) можно полу-
получить, просуммировав все ит. Два последовательных члена этой сум-
суммы имеют примерно равные амплитуды, но разные знаки, так как
iL-D ikR
е т = — е m+l. Из-за такой нейтрализации последовательных
членов результирующее поле определяется главным образом слагае-
слагаемыми низших порядков (малые т). Следовательно, лишь участок вол-
волнового фронта А площадью около ir\\RR0/(R - Ro)\ определяет по-
поле в точке г. Ниже эти интуитивные соображения будут сформулиро-
сформулированы более строго в связи с асимптотическими вычислениями дифрак-
дифракционных интегралов. Мы покажем также, что тот же результат имеет
место и для волновых фронтов более общего вида.
В заключение можно сформулировать качественный вывод о том,
что поле и(х) представимо в виде суперпозиции вторичных волн, при-
приходящих из некоторых участков А волнового фронта, которые окру-
260
Гл. 4. Основы теории дифракции
Рис. 4.6. Точки стационарной фазы волнового фронта, дающие вклад в поле. Семейства
колец представляют соответствующие зоны Френеля. Конечный размер апертуры приво-
приводит либо к нейтрализации, либо к уменьшению вкладов от точек, лежащих у границы.
жают точки стационарной фазы г*. Эти точки получаются при пере-
пересечении волнового фронта лучами, проходящими через точку г (рис.
4.6). При X — 0 каждый участок Ад стягивается к соответствующей
стационарной точке, так что ее вклад в и(г) в полном соответствии с
геометрической оптикой оказывается пропорциональным u(r*Q). При
конечных значениях X вклад в и{х) от А по-прежнему пропорционален
и(гд) при условий, что м(г') не сильно изменяется на площади, равной
приблизительно тгХ1г' - r*q\. Это и есть точный критерий примени-
применимости приближения геометрической оптики.
4.3. ПРИНЦИП ГЮЙГЕНСА
В ФОРМУЛИРОВКЕ КИРХГОФА — КОТТЛЕРА
В областях с постоянным показателем преломления интеграл
Гельмгольца — Кирхгофа может быть представлен в виде D.2.15).
Поскольку это соотношение верно для любой декартовой компоненты
поля Е, в области без источников, окруженной замкнутой поверхнос-
поверхностью S, мы имеем
4.3. Принцип Гюйгенса в формулировке Кирхгофа — Коттлера 261
Этот интеграл можно записать в другом эквивалентном виде, выра-
выразив подынтегральное выражение только через величины полей Е и Н.
А именно, используя уравнения Максвелла и простые векторные соот-
соотношения, можно показать, что для замкнутой поверхности
E(r) = - Q?-i?k(h0 x H)G(r,r') + (h0 x E) x P'G(r,r') +
K*,T')]dS'. D.3.2)
Аналогично для магнитного поля получаем
Н(г) = -&\j(п0 х E)G(r,r') + (п0 х Н) х PG(r,r')+ (п0 . Н) P'G(r,r')l dS'
5 D.3.3)
Эти соотношения остаются справедливыми и для многосвязных обла-
областей. Например, S может состоять из двух или более замкнутых по-
поверхностей, расположенных внутри некоторой общей внешней поверх-
поверхности (рис. 4.2).
Для вычисления поля, дифрагированного на экране, можно предпо-
предположить (по аналогии с принципом Кирхгофа в скалярной теории ди-
дифракции), что истинное поле на диафрагме (отверстии) совпадает с не-
невозмущенным падающим полем, а непосредственно за экраном поле
равно нулю. В соответствии с этим можно попытаться выразить ди-
дифрагированное поле с помощью интегральных представлений D.3.2) и
D.3.3), ограничивая область интегрирования поверхностью апертуры
А и используя в подынтегральном выражении лишь поля Е{ и Hj пада-
падающих лучей. К сожалению, когда точка наблюдения близка к диа-
диафрагме, результат, полученный таким образом, существенно отлича-
отличается от истинного дифрагированного поля. Эту несогласованность
можно преодолеть, добавляя к поверхностному интегралу контурный,
т. е. записывая интегралы следующим образом [10]:
ГС
Е= - Г-*.
kJdA
H= - fjГф
rlV'Gdl9 D.3.4)
E,)G + (n0 x Щ x P'G + (JvHJP'
f D.3.5)
sa
262 Гл. 4. Основы теории дифракции
где I — единичный вектор, касательный^ к элементу контура диафраг-
диафрагмы dl (край диафрагмы обозначается дА). Обход контура диафрагмы
осуществляется против часовой стрелки, если смотреть из точки, в ко-
которой определяется поле. Как видно из полученных соотношений, ска-
скалярная теория Кирхгофа для нахождения декартовых компонент по-
полей Е и Н, вообще говоря, неприменима. Однако, как мы покажем в
разд. 4.13, контурным интегралом можно пренебречь, если точка на-
наблюдения находится на расстоянии многих длин волн от края диаф-
диафрагмы.
4.4. УСЛОВИЕ ЗОММЕРФЕЛЬДА НА ПОЛЕ ИЗЛУЧЕНИЯ
Формулируя после вывода соотношения D.2.20) принцип Гюйгенса,
мы неявно использовали одно предположение. А именно, предполага-
предполагалось, что поле в точке наблюдения образуется вторичными волнами,
исходящими лишь с поверхности волнового фронта. При этом мы
пренебрегли вторичными источниками на бесконечно удаленной по-
поверхности, которая вместе с волновым фронтом должна образовы-
образовывать замкнутую поверхность, фигурирующую в интегральной теореме
Гельмгольца — Кирхгофа. Теперь мы покажем, что для весьма обще-
общего класса полей поверхностью на бесконечности действительно можно
пренебречь. С этой целью рассмотрим замкнутую поверхность, состо-
состоящую из ограниченного почти плоского участка (не обязательно со-
совпадающего с волновым фронтом) и части сферы А$ с центром в точ-
точке наблюдения г и радиусом R > X (рис. 4.7). Учет поверхности As
приводит к следующему вкладу в и(т) [выражение D.2.16)]:
As As
где dQ = dS' /DirR2) — элемент телесного угла.
_Если источники поля находятся с противоположной по отношению
к As стороны плоского участка, то пределы интегрирования на по-
Источники
Рис. 4.7. К выводу излучательного усло-
условия Зоммерфельда.
4.5. Дифракционные интегралы Рэлея 263
верхности As можно устремить к бесконечности. Поэтому остается
оценить асимптотическое поведение интеграла D.4.1) при R — оо.
Этот интеграл стремится к нулю, если выполнено условие
lim R[(du/dR) + iku] = 0, D.4.2)
R-* оо
которое называется излучательным условием, или условием Зоммер-
фелъда на поле излучения [11].
Поля, удовлетворяющие условию D.4.2), называются полями излу-
излучения. Для них интеграл Гельмгольца — Кирхгофа можно вычислять
по бесконечной незамкнутой поверхности S, отделяющей точки наб-
наблюдения от источников. Условие D.4.2) выполняется для полей, име-
имеющих следующее асимптотическое поведение:
- e~ikR
и(г)ос/(Я)—, R -оо, D.4.3)
которое соответствует расходящейся сферической волне с диаграммой
направленности /(R). Однако во многих случаях довольно трудно
определить из интегрального выражения, удовлетворяет ли поле усло-
условию Зоммерфельда. Можно предложить следующий практический со-
совет, основанный на приведенном выше условии для расходящейся сфе-
сферической волны. Будем считать, что поле удовлетворяет соотноше-
соотношению D.4.2) при условии, что замена к — к - /в, где е — бесконечно
малая положительная величина, приводит к равенству нулю интеграла
при R — оо.
4.5. ДИФРАКЦИОННЫЕ ИНТЕГРАЛЫ РЭЛЕЯ
ДЛЯ ПЛОСКИХ ЭКРАНОВ
Рассмотрим теперь случай, когда плоскость П отделяет область I, со-
содержащую источники, от однородной области II, в которой вычисля-
вычисляется поле. В этом случае функцию Грина G удобно выбирать в таком
виде, чтобы либо G, либо dG/dn0 были равны нулю в плоскости П.
При этом интеграл Гельмгольца — Кирхгофа принимает более про-
простой вид, поскольку одно из двух слагаемых подынтегрального выра-
выражения исчезает. Нетрудно построить необходимую функцию Грина,
если к мнимому источнику в точке г добавить другой мнимый источ-
источник той же интенсивности с тем же или с противоположным знаком,
расположенный в точке rs, представляющей собой зеркальное изобра-
изображение точки г относительно плоскости П:
exp(-ifc[r - г'|) л exp(-/fclrs - r'|)
С±(Г'Г) = 4*|гг'| ± D5Л)
4*|rs-r'|
264 Гл. 4. Основы теории дифракции
Нетрудно показать, что при г' на поверхности П
dG+(r, т')/дп0 = G_(r, г') = 0. D.5.2)
Используя функцию G+, дифракционный интеграл D.2.10) можно за-
записать в виде
п п
где ось z' перпендикулярна П и направлена внутрь области II, а
R = [(х — х'J + (у - у'J + (z — z'J]1/2. Аналогично если исполь-
использовать функцию G_, то
D.5.4)
где 0(< тг/2) — угол между векторами R = г' - г и п0. Обычно быва-
бывает удобно заменить общее выражение для и D.2.14) либо выражением
D.5.3), либо D.5.4).
Пример. Отверстие в плоском экране. В приближении геометри-
геометрической оптики поле, отличное от нуля на части плоскости (на отвер-
отверстии), с помощью выражения D.5.4) можно записать в виде
Т UU
и(г) = 2 JT \р{х\ у')А(х\ у', z')(ik + j
D.5.5)
где Р(х', у') (функция зрачка) равна единице на поверхности отвер-
отверстия и нулю для всех остальных х', у'. Можно показать, что главный
вклад в этот интеграл дают точка Р*, в которой производная
\d(S - R)/dno\ максимальна [см. уравнение D.2.18)], и края отвер-
отверстия.
В параксиальном приближении (cos0 « 1) из D.5.5) следует, что
поле на плоскости z = const можно сравнить с выходным сигналом
линейной системы, характеризуемой импульсным откликом К(х', у';
х, у, z) [поле в плоскости z = const, соответствующее полю
6-источника 5(д: - х'Щу - у') на поверхности отверстия (ср. с разд.
4.15)]. Таким образом, мы имеем следующее выражение:
К(х'9у'; x,y9z) = iP(x',/)exp{-ifc[(x - *'J + {у- /J]/Bd) - ikd}/(Xdl
где*/ - \z - z'l > l/k D'5-6)
4.7. Дифракционные интегралы для двумерных полей 265
4.6. ПРИНЦИП БАБИНЕ
Рассмотрим два случая дифракции на плоских экранах. Пусть задан
некоторый экран. Заменой отверстий на непроницаемые участки и на-
наоборот можно получить так называемый дополнительный экран. Ес-
Если и} и и2 — дифрагированные поля на этих двух экранах, то имеет
место, следующее соотношение (принцип Бабине) [12]:
«iW + u2(w) = м(г), D.6.1)
где м(г) — поле в отсутствие экрана. Соотношение D.6.1) непосредст-
непосредственно следует из D.5.4), если интегрирование в этом соотношении вы-
выполнить по всей плоскости. Остается лишь предположить, что поля
их(х') и м2(г') на отверстиях первого и второго экрана совпадают с по-
полем м(г'), которое имеет место в отсутствие экрана. Вообще гозоря,
принцип Бабине выполняется лишь приближенно, так как их(х') и
и2(г') не равны м(г'), но нарушение D.6.1) существенно лишь вблизи
границ диафрагм. Тем не менее точное доказательство принципа
Бабине может быть получено для идеально проводящего плоского
экрана (см. с. 559 в книге Борна и Вольфа [11], указанной в литерату-
литературе к гл. 1).
4.7. ДИФРАКЦИОННЫЕ ИНТЕГРАЛЫ ДЛЯ ДВУМЕРНЫХ
ПОЛЕЙ
В некоторых случаях электромагнитное поле можно записать в виде
u(x9y,z) = exp[-i(fc2 - X2)li2y]u(x,z)- D.7.1)
При этом функция и удовлетворяет двумерному уравнению Гельм-
гольца
д2и/дх2 + d2u/dz2 + г2и = О, D.7.2)
что следует из уравнения A.1.12). Поля и(х9 у, z) принято называть
цилиндрическими волнами.
Повторяя те же выкладки, что и при выводе D.2.10), нетрудно по-
показать, что
и(Р) = ?|W.^ - и(Р')^У', D.7.3)
где С — замкнутая кривая, охватывающая не содержащий источников
участок плоскости у = const, a p s xx + zz. При этом двумерная
функция Грина удовлетворяет уравнению
(д2/дх'2 + d2/dz'2 + x2)G(p\p) = -д(х - x')d(z - z'\ D.7.4)
В наиболее простом виде функция Грина, удовлетворяющая условию
излучения на бесконечности и имеющая сингулярность только при
266 Гл. 4. Основы теории дифракции
р' = р, записывается следующим образом:
G(p, р) = G(p\ p) = (//4)Я<02)(хЯ), R = P'-P, D.7.5);
где /^2) — функция Ханкеля второго рода нулевого порядка. Она имеет
следующее асимптотическое представление:
Я@2)(*Д) ^ l2/GixRy]1/2e-i{xR-n/*\ Rx -> oo. D.7.6)
Если цилиндрическая волна удовлетворяет условию Зоммерфельда
D.4.2), то для рассматриваемого плоского случая применимы те же
рассуждения, что и в разд. 4.4. При этом мы имеем
здесь Сда — бесконечно удаленный контур, отделяющий точку наблю-
наблюдения р от источников. Аналогами соотношений D.5.3) и D.5.4) здесь
являются следующие:
и(р)
щ
2J-o
D.7.8)
где Р(х') — аналог функции зрачка (см. разд. 4.5), а 0( < тг/2) — угол
между векторами — R и z'. Здесь z' — нормаль к прямой z' = 0, от-
отделяющей область наблюдения z' ^ 0 от источников, расположенных
при z' < 0. При /? > 1/х можно использовать приближение D.7.6)
для функции Hfi\ При этом получаем
у/2 ?
| D.7.9)
4.8. РАЗЛОЖЕНИЕ ПОЛЯ ПО ПЛОСКИМ ВОЛНАМ
Рассмотрим теперь задачу о разложении поля по плоским волнам в
однородном полупространстве, ограниченном плоскостью, на которой
это поле задано [13].
Вычислим сначала двумерное фурье-преобразование функции
G(r, г'), рассматриваемой как функция от *' и у' при фиксированных
значениях z\ х, у и z при z > z' - Заметим для этого, что выражение
D.5.3) можно переписать в эквивалентном виде
и(г) = -2 JJW " r'\)8u(X'?>Zl)dx'dy\ D.8.1)
п
где П — это плоскость z' = const, а область пространства без источ-
4.8. Разложение поля по плоским волнам 267
ников расположена при z > z'. Применим теперь выражение D.8.1) к
плоской волне
ехр(- ikxx - ikyy - \kzz\ D.8.2)
где кх и к у — вещественные величины. При этом удовлетворяется сле-
следующее соотношение:
кя = (к2 -к2х- к2I12 D.8.3)
(kz — вещественная положительная или мнимая отрицательная велиг
чина). Соотношение D.8.3) означает, что плоская волна D.8.2) распро-
распространяется в сторону увеличения z, что требуется для выполнения
D.8.1) (см. разд. Л А). Следовательно, мы можем написать следующее
выражение:
ехр( — ikxx — ikyy — ikzz) = 2i7czexp( — ikzzf) x
-boo
x 11 exp(- ikxx' - ikvy')G{[{x - x'J +
+ (У - У'J + (z - z'J]1/2} dx' dy' =
= 2ik2txp(-ikzz')FlG(x',y'); -kx, -ky], D.8.4)
где F — фурье-образ функции G:
+00
FlG(x',y'); kx,kyl = H G(x',y')cxp(ikxx' + ikyy')dx'dy'; D.8.5)
-00
здесь для простоты мы не стали писать переменные х, у, z и z', кото-
которые не меняют своих значений при преобразованиях. Таким образом,
имеем
FlG(x\y); кх9к,] = -^-ехр[^х + ikyy - ikz(z - z')]. D.8.6)
Поскольку операции фурье-преобразования по переменным х' п у'
и дифференцирования по z' независимы друг от друга, можно сразу
написать соотношение для фурье-образа производной dG/dz':
+ гкуу - ikz(z - z')]. D.8.7)
Используя теперь обратное преобразование Фурье, мы имеем
+ 00
dG 1
И* ехр[ - ikx(x' -x)- iky(y' -y) + ik,(z' - z)] dkx dky. D.8.8)
dz' 2BяJ
Отсюда с помощью соотношения D.5.4) приходим к следующему вы-
268 Гл. 4. Основы теории дифракции
ражению: +а0
M(X>>;'Z) = ШI JIII ехР[-Л*(х' " *) - 'W ~ У) + *кж(г' - zj] х
— оо
х u(x',y',z')dx'dy'dkxdky. D.8.9)
Определив фурье-образ функции и(х9 у, z')
+ 00
F'[u(x',y',z')\ кх, ку] = IT M(x;^z')exp(iM'+ ik,f)dxdy', D.8.10)
— оо
выражение D.8.9) можно переписать в виде
+ 00
u(x,y,z) = t^ti 11 exp[ + ifcxx + ikyy - ikz(z - z')] x
— oo
x Flu(x',y',z'); -kx,-ky-\dkxdky =
+ 00
= Щ2 JJ e\p(-ikxx - ikyy)F[u(x',y',zy, -kx,-ky1dkxdky, D.8.11)
— oo
откуда в свою очередь следует, что
Flu(x\y\z); fex,fcj = ехр[-Лж(г - z')]F[!i(x'f/,z'); fc,,fc,]. D.8.12)
Соотношение D.8.11) и есть конечное представление в виде разло-
разложения по плоским волнам полей излучения наиболее общего вида в
полупространстве z > z'. Заметим, что существование затухающих
волн учитывают с помощью мнимых отрицательных значений kv ког-
когда к% + к* > к2. Соответствующие волны распространяются перпен-
перпендикулярно оси z и затухают в направлении положительных z.
4.9. УГЛОВОЙ СПЕКТР
Во многих случаях удобно записать компоненты kY, kv и к- в виде
кх = к cos f} sin у, D.9. la)
D.9.16)
D.9.1b)
где /3 изменяется от 0 — /oo до тг + /оо {контур Зоммерфельда), а угол
у от 0 до 7г (рис. 4.8). Используя эти определения, выражение D.8.11)
можно переписать в виде
u(x,y,z)= Г*1" dpi* dyS(p9y)cxp(-ikrcose), D.9.2)
JO-ioo JO
4.9. Угловой спектр
269
Imp
Рис. 4.8. Контур интегрирования Зоммер-
фельда.
Re/J
О-Zoo
где г = (х2 + у2 + z2)l/2, a 0 — угол (возможно, комплексный) между
векторами г ш (х9 у, z) и k s (?х, & ^). Если 6 и ф — углы
соответственно между г и z и между х и лгх + уу9 то cos 0 =
= cos /? sin б cosW> - 7) + sin /3 cos 6 и мы имеем
S(fty) = e*-*'F[ii(x',y',z'); fcx,fcy] sinBj8)/2A2. D.9.3)
Функция S(/8, 7) называется угловым спектром и обладает важным
свойством, а именно независимостью от выбора опорной плоскости
z = z' [см. D.8.12)]. Для мнимых значений /3 функция S определяет
затухающую часть излучения. Мы увидим, что при кг — оо интеграл в
D.9.2) можна вычислить методом стационарной фазы [см. разд. 5.11
и уравнение E.11.7)], что приводит к следующему асимптотическому
выражению:
u(x,y,z) ос —2711-
fcr->oo
г,—ikr
кг
D.9.4)
Отсюда следует, что при движении точки наблюдения по сфере
большого радиуса г с центром в начале координат величина поля про-
пропорциональна S(j3, 7)» если вектор к(/3, 7) направлен вдоль радиус-
вектора г. Именно поэтому функцию S называют угловым спектром.
В частности, для полей, инвариантных относительно вращения во-
вокруг оси z, угловой спектр S(fi9 7) не зависит от угла 7 и не меняется
при замене угла /3 на 7г - /3. Поэтому S(/3, 7) s S(j3) = S(tt - ]S). Как
следствие, выражение D.9.2) можно записать в виде
и{г98)
Гп/2
= 2
J O-ia
J O-ia
S(p) dp exp{ — ifcr[cos j? sin д cos((f> — y) + sin ft cos <5]} dy =
J 0
S(p)J0{kr cos J? sin E)exp( - ifcr sin p cos <5) dj?.
D.9.5)
270 Гл. 4. Основы теории дифракции
4.9.1. Угловой спектр двумерных волн
Рассматривая двумерные волны, определяемые выражением D.7.1),
нетрудно показать, что из соотношений D.8.11), D.9.2) и D.9.3) следу-
следует, что
u(x9z) = — exp[-i*,x - ikz(z - z')]F[ii(x\z'); fcjdkx =
exp[-iXpcos(j? - 0]S(j8)dft D.9.6)
/0-ioo
где* = pcos<?, z = psin^,
F[tt(x',z');kJ = f+%xp(ifcx;c>(x',z')<*x', D.9.7)
J-oo
S(P) = exp(iZz'sin/J)F[ii(x',z');fcJ^-sin7J. D.9.8)
-г
Jo
При выводе соотношения D.9.6) мы положили kx = \ cos /3,
fcz = x sin /3, а затухание излучения (вдоль оси z) учли с помощью
мнимых значений 0.
Пример. Гауссов угловой спектр. Рассмотрим случай, когда
S(i?) = exp[-(i8-0)>2]. D.9.9)
При этом получаем
In Г (р-9J \
exP[ 'Zz'sin^J D.9.10)
11)
Ля + too Г /о 0^2~|
и(р9ф) = exp -ixpcos(p -ф)- {-E-^L Ш. D.9.
JO-ioo L G J
Этот интеграл нельзя вычислить в замкнутой форме. Однако метод
наибыстрейшего спуска (см. разд. 5.6) позволяет оценить его в преде-
пределе хр — °°.
4.9.2. Угловой спектр в комплексной области
Разложение с помощью углового спектра не ограничивается лишь слу-
случаем, когда поле сосредоточено в полупространстве. В разд. 6.2 мы
покажем [выражениеF.2.2)], что при дифракции на клине поле может
быть представлено двумя интегралами по угловому спектру, контуры
интегрирования которых представляют из себя два контура Зоммер-
фельда, сдвинутых относительно друг друга на 2тг. Следовательно,
рассмотренные выше соотношения можно обобщить, используя инте-
интеграл /.
/ = I S(jJ)exp[-iZpcos(jB - ФУ] dp, D.9.12)
4.9. Угловой спектр
271
где Г — произвольный и в общем случае комплексный контур инте-
интегрирования. Выражение D.9.12) описывает цилиндрическую волну в
виде суперпозиции плоских волн с амплитудой S(fi) и волновым векто-
вектором k = txcos/8, (к2 - х2)/2> Xsin/З]. У функции S(fi) могут быть по-
полюсы и точки ветвления, а в тех случаях, когда она периодична и ее
период кратен 2тг, контур интегрирования Г может быть сдвинут на
величину периода без изменения значения интеграла.
Можно найти такие контуры интегрирования, для которых выра-
выражение D.9.12) описывает физически возможные поля, не имеющие
расходимости при р — оо. Для этого запишем величину 0 в виде
<8 = /3' 4- //3". При этом зависимость от р показателя экспоненты в
подынтегральном выражении D.9.2) запишется следующим образом:
-ixpcos(p' + IP" - ф) = -ixpcos(P' - ф) ch p" - #psin(/?' - ф) sh /Г.
D.9.13)
Следовательно, интеграл / остается конечным при условии, что Г
включает в себя лишь те комплексные значения /3, которые принадле-
принадлежат заштрихованным на рис. 4.9 областям, определяемым неравенст-
неравенствами
Р" < О, 2л + 2пп > Р' - ф > и + 2пп (п = 0, ±1, ±2,...), ,4 9 14ч
Р" > 0, п + 2пп>р'-ф> 2пп (п = 0, ±1, ±2,...). * • • '
Вообще говоря, выбранный контур удовлетворяет этим неравенст-
неравенствам лишь для некоторой области значений углов наблюдения ф, по-
поскольку границы описываемых физических областей сами зависят от
ф. Например, контур Зоммерфельда @ — /оо, тг + /оо) удовлетворяет
неравенствам D.9.14) в области 0 < ф ^ тг и, следовательно, его мож-
можно использовать для определения поля в области z = p sin ф ^ 0.
-яг+Ф
*+<!>
~ReT
Рис. 4.9. Области комплексной ^-плоскости, в которых функция ехр [- /xpcos@ - ф))
остается ограниченной при хр —¦ °° • Сплошные кривые — контуры наибыстрейшего
спуска (см. разд. 5.6 в гл. 5).
272 Гл. 4. Основы теории дифракции
Для вычисления интегралов типа D.9.12) часто используется метод
наибыстрейшего спуска (см. разд. 5.6). Для этого интегрирование не-
необходимо проводить вдоль контура наибыстрейшего спуска (КНС),
который получают посредством непрерывного преобразования перво-
первоначально выбранного контура (например, контура Зоммерфельда) в
КНС. Точнее говоря, мы имеем [см. выражение E.^.4)]
VJkhc Jw
S(P)expl-i(k2 - х2I12У - iXPcos(/? - 4>)]dfl
-i(fc2 - Х2I12У ~ ЧР cos(j8, - </>)]. D.9.15)
q
Здесь Гв — контур, окружающий точки ветвления (если таковые име-
имеются) функции S, расположенные между Г и КНС, а гд — значение
<7-го вычета функции S (см. рис. 5.16):
rq = 2ni lim S(p)(p - pq), D.9.16)
где Cq — q-ft полюс функции S в области между Г и КНС. Суммирова-
Суммирование в D.9.15) проводится по всем полюсам, расположенным также
между Г и КНС.
В следующей главе мы покажем, что интеграл по КНС в общем
случае убывает как 1/р1/2, т. е. описывает цилиндрическую волну с за-
зависящим от ф распределением интенсивности поля в дальней зоне [см.
E.68)].
4.9.3. Полюсные сингулярности
Предположим, что плоскость z = 0 частично освещается излучением,
которое записывается в виде
u(x,y,z = 0) = C/(x)exp(-/fcxcos</>0), D.9.17)
где U(x) — ступенчатая функция [U(x) = 0 при х < 0, U(x) = 1 при
х > 0], а ф0 — угол с малой мнимой частью (Im cos ф0 < 0). В этом
случае поле не зависит от у\ т. е. к = х- Из выражений D.9.7) и
D.9.8) получаем соответственно
Г00
=
Jo
Г
F[u{x\ 0); кх~] = exp[i(kx — к cos фо)х'] dx' =
J
_ 1
kx - fecos^o " к cosjS - cos(/>0' D.9.18)
4.9. Угловой спектр
273
Рис. 4.10. Контуры наибыстрейшего спуска (КНС) в
присутствии комплексного полюса в точке ф0 [см. вы-
выражение D.9.20)].
В свою очередь из D.9.12) и D.9.15) имеем
ioo_sin/?
Rep
sin/?
— ikpcos(p —
L
Ф + <?o), D.9.20)
где КНС обозначен на рис. 4.10 толстой линией, а ?0 — точка пересе-
пересечения КНС с осью Re/З, причем КНС проходит через точку ф0 в ком-
комплексной плоскости. Последний член в выражении D.9.20) представля-
представляет собой плоскую волну в угловом секторе, границы которого заданы
ступенчатой функцией ?/(#), т^е. определяются условием 0 ^ ф < $0.
Эта волна разрывна при ф = ф0, что указывает на существование гра-
границы раздела между освещенной зоной (см. разд. 2.12.}в) и тенью.
Полупрямая ф = ф0 представляет собой типичный пример границы
тени. Рассмотренный случай доказывает существование соответствия
между полюсами углового спектра и границей тени в произвольном
поле (см. разд. 5.6.1).
4.9.4. Точки ветвления
Рассмотрим теперь случай, когда не зависящая от координаты у вол-
волна отражается от плоскости z = 0, разделяющей две диэлектрические
среды, в которых нет потерь (рис. 4.11). Пусть единичный линейный
источник света параллелен оси у и расположен вдоль линии с коорди-
координатами х = xs и z = z$ > 0. В этом случае начальное поле uty)
совпадает с функцией Грина G(p9 ps) [ps = (xs, zs)], так что по анало-
аналогии с выражением D.8.6) для двумерного случая можно написать еле-
274
Гл. 4. Основы теории дифракции
(р,ф)
Рис. 4.11. К задаче об отражении плоской вол-
волны на границе раздела двух диэлектрических
сред.
дующее выражение:
F[n(x',0);*J = (-i/2kz)Qxp(ikxxs - ikzzs =
= (-i/2fcsin0)exp[-ifc(-xscosj8 + zssin j?)], D.9.21)
где использовано соотношение D.9.8) и равенство к = х-
Заметим теперь, что отраженная волна, распространяющаяся с
данным значением кх, может быть получена, если выражение для на-
начальной падающей волны умножить на коэффициент отражения г(кх).
Следовательно, используя выражение D.9.5), полное отраженное поле
ur(x, z) можно записать в виде
1 f+G
ur(x,z) = —
27Г J-oc
Л
ехр( - ikxx - ikzz)r(kx)F[Ui(x9 0); fcj dkx =
exp[-i*pcos@ - ФЖМкМ D.9.22)
где kx = к cos j8, a S, относится к падающей волне, т. е.
$(/0 = *ТИ|(*, 0); fex](k/27i) sin fi. D.9.23)
Если источником поля является электрический ток, текущий парал-
параллельно оси у, то электрическое поле направлено также вдоль у, так
что можно положить и(х, z) = Ey(x, z), а коэффициент отражения в
выражении D.9.22) относится к ТЕ-волне [см. уравнение C.8.2)]. Та-
Таким образом, коэффициент отражения rs запишется в виде
rs = [cos в - (п2 - sin2 0I/2]/[cos в + (nz - sin2 0I/2], D.9.24)
где в — угол падения компоненты плоской волны, направленной
вдоль Хкх + zkv a n равно отношению показателя преломления п2 в
полупространстве z < 0 к показателю преломления п} в полупрост-
полупространстве z > 0. Подставляя выражения D.9.23) и D.9.24) в D.9.22) и
Рис. 4.12. а и б — разрезы и контуры Зоммерфельда в случае, когда поле, отраженное от разделяющей два диэлектрика плоской
границы, освещаемой цилиндрической волной, представляется в виде углового спектра; в — контур наибыстрейшего спуска, полу-
полученный изменением контура Зоммерфельда (рис. 4.8) и частично окружающий (Гв) разрез, изображенный волнистой линией.
276 Гл. 4. Основы теории дифракции
используя D.9.21), нетрудно получить следующее выражение:
-i fn+ioosinp-(n2 -cos2pI/2
'-ioo
(n2-cos2/?I/2
x exp{-ffc[-xscos)? + zssinp + pcos(j? - <t>)]}dp, D.9.25)
где мы использовали соотношения cos в = sin/3 и sin20 = cos2j3.
Подынтегральное выражение в D.9.25) имеет точки ветвления,
определяемые из уравнения cos/З = ± п, причем при п > 1 существу-
существует одна точка ветвления на мнимой оси, а при п < 1 две точки на ве-
вещественной оси (рис. 4.12, я, б). Таким образом, если требуется пре-
преобразовать контур Зоммерфельда к КНС, то необходимо учесть вкла-
вклады от обхода разрезов, выходящих из точек ветвления (волнистые ли-
линии на рис. 4.12). На рис 4.12, в представлена одна из возможных мо-
модификаций контура Зоммерфельда, который включает в себя контур
Гв, частично окружающий разрез (см. разд. 5.6.2).
Два примера, рассмотренных выше, позволяют сделать интерес-
интересные выводы. Во-первых, если поле состоит из плоских волн в некото-
некоторых ограниченных областях пространства, то угловой спектр S(fi)
имеет ряд полюсов на /3-плоскости. Во-вторых, наличие поверхностей
разрыва в среде приводит к появлению точек ветвления и полюсов у
функции S(j8), которые можно связать с существованием боковых волн
и волн утечки, как мы покажем в разд. 5.7.1.
4.10. ДИФРАКЦИОННЫЕ ФОРМУЛЫ ФРЕНЕЛЯ
И ФРАУНГОФЕРА
4.10.1. Формула Френеля
Рассмотрим случай, когда угловой спектр поля имеет ограниченную
полосу. Точнее говоря, предположим, что F(u\— kx, - ky) = 0, если
k% + Щ > k\ < к2. При этом выражение D.8.11), в котором kz мож-
можно заменить на к - AЛ)(к2 + к2)/к у принимает вид
x F[u(x,y9 z')\ kx, ky] dkxdky =
u(x,y9z'),
D.10.1)
4.10. Дифракционные формулы Френеля и Фраунгофера 277
где с помощью * мы обозначили операцию свертки и использовали
теорему свертки об обратном преобразовании Фурье (обозначаемом
символом F) произведения двух функций. Выражение D.10.1) не-
нетрудно переписать следующим образом:
/ * *exp{-ik(z - z') - ik(x2 + y2)/[2(z - z')]} ^
ф, **) = ¦ j^r^ x
ky \
Таким образом, дифракционный интеграл эквивалентен фурье-
образу поля в опорной плоскости z' = const < z, умноженному на со-
соответствующий фазовый множитель. Практическая ценность этого
результата состоит в том, что он позволяет выполнить численный
расчет поля с помощью алгоритма быстрого преобразования Фурье
(БПФ). Выражение D.10.2) представляет собой одну из возможных за-
записей дифракционной формулы Френеля.
Ошибкой, возникающей при замене kz на к - (Уг)(к\ + kj)/k,
можно пренебречь только, если I kz - к + (й)(Д? + kj)/k\ \z - z'\<
< 2тг. Это означает, что формула D.10.2) может быть использована
только для точек, расстояние которых от поверхности интегрирова-
интегрирования не превосходит некоторой величины zk. Это расстояние zk можно
определить из следующего приближенного соотношения:
\К - k + i(k2/k)\zk s UKЧ1къ) = а, D.10.3)
где а — малая величина (например, 10"). Следовательно, дифракци-
дифракционная формула Френеля для пдлей с ограниченной полосой углового
спектра может быть использована лишь для вычисления полей в огра-
ограниченной координатной zk области.
Рассмотрим теперь поле, отличное от нуля лишь на некотором
конечном отверстии в плоском экране. Обозначим через а радиус наи-
наименьшей минимальной окружности, охватывающей отверстие, и пред-
предположим, что \z — z' I > а. При этом величину R можно считать при-
приблизительно равной \z ~ z'\ + (Уг)[(х - л:'J + (у - yf>p\/\z - z'\.
Таким образом, дифракционный интеграл D.5.5) можно переписать в
виде
- y')*V>
- x'f + (y- y')*V>dx'dy'. D.10.4)
278 Гл. 4. Основы теории дифракции
Заметим сразу, что это выражение по виду совпадает с выражением
D.10.2), хотя они были получены при существенно разных предположе-
предположениях. В действительности последнюю формулу можно использовать
лишь при I z - z'\ > zR, где zR определяется из соотношения, аналогич-
аналогичного D.10.3):
г - г'\ - \z - z'\ + \ <*-*) +(У-У) s l(fcfl^/z3) = a> D.10.5)
2 \z-z\
Если zR < zk, то формула Френеля применима при любых U - zf I
для полей, ограниченных в пространстве и по спектру. Из соотношений
D.10.3) и D.10.5) можно сразу получить простое условие, позволяющее
использовать приближение Френеля во всем пространстве. Это условие
имеет вид
akt < 8a(fc/fctJ D.10.6)
и определяет верхний предел произведения "размер х ширина спектра".
Для однородно освещаемой щели спектр плоской волны пропор-
пропорционален sin(kta)/(kta), так что произведение kta равно приблизитель-
приблизительно 2тг и неравенство D.10.6) принимает вид
In < Ы{ка/2пJ. D.10.7)
Поэтому для достаточно больших отверстий, таких, что ка > 2тг, и ос-
освещаемых однородно (как по амплитуде, так и по фазе), интеграл Френе-
Френеля можно использовать для нахождения поля на произвольном расстоя-
расстоянии от плоскости интегрирования.
Рассмотрим теперь влияние неоднородности фазового распределе-
распределения. Как мы покажем ниже, в пределе к — оо можно использовать ра-
равенство kt = &[sin0MaKC + 2ir/(ak)], где 0макс — максимальный угол с
осью z9 который могут образовывать лучи, проходящие через отвер-
отверстие. В соответствии с этим условие D.10.6) запишется в виде
afc[sin 0макс+ {2п/ак)]3 < 8а. D.10.8)
Отсюда следует, что формулу Френеля во всем полупространстве
можно применять лишь при выполнении определенного условия. В
частности, для луча с числовой апертурой ЧА = sin 0макс = 10~2 и
а = 0,1 размер отверстия должен быть меньше, чем Ш^Х. При этом
формулу Френеля можно использовать без ограничений. Это в свою
очередь означает, что для света с длиной волны 1 мкм максимальный
допустимый размер освещаемой зоны в плоскости интегрирования ра-
равен примерно 10 см. Если же числовая апертура увеличивается до
10" ^ то допустимый размер резко уменьшается и составляет всего
лишь 100 мкм.
В заключение заметим, что поля, определяемые выражением
D.10.4), удовлетворяют параболическому волновому уравнению, кото-
4.10. Дифракционные формулы Френеля и Фраунгофера 279
рое рассматривалось в разд. 2.6. [см. уравнение B.6.12)]. Поэтому не-
некоторые авторы, в частности советские ученые, называют приближе-
приближение Френеля параболическим приближением.
4.10.2. формула Фраунгофера
Возвращаясь к общему выражению D.10.2), заметим, что если
z — z' > D2ir/\, где D — характерное расстояние от точки @, 0, z'),
в которой поле и(х', у\ z') можно считать равным нулю, то в подын-
подынтегральном выражении D.10.4) экспоненциальным членом с показателем
х*г + у>2 Можно пренебречь, так что мы имеем
+ 00
iexp( — ikR0) CC (' хх' + уу , ,Л , , , ,
JJ QXV[lk^)u(x'y'z')dx'dy' D.10.9)
JJ
где
*о = \z - z'\ + i(x2 + y2)l\z - z'\ ? [(z - z'J + x2 + д,2]1'2. D.10.10)
Это выражение, называемое дифракционной формулой Фраунгофера,
позволяет представить дифракционное поле в дальней зоне через двумер-
двумерное преобразование Фурье для переменных kx = kx/\z - z'l,
ку = ky/\z - z'\ от функции и на опорной поверхности. На рис. 4.13
приведены поля Фраунгофера для некоторых типичных диафрагм, облу-
облучаемых плоскими волнами.
Поле дальней области можно измерить и на конечном расстоянии.
Для этого перед диафрагмой помещают линзу, а результирующее поле
измеряют в ее фокальной плоскости. Таким образом, применение линзы
позволяет вместо распределения самого поля на плоскости получить его
фурье-образ. Это свойство линз широко используется в когерентной оп-
оптике для создания оптических корреляторов и оптических согласующих
фильтров. С их помощью производится распознавание образов и фильт-
фильтрация изображений.
4.10.3. Обобщение на двумерные поля
Все предыдущие выводы нетрудно обобщить на двумерные поля типа
D.7.1). Точнее говоря, легко показать, что выражения D.10.4) и D.10.9)
можно записать следующим образом:
1,38 4,45 7,73 v
Yb
1 2 N
2a
1 2 N
ч
\
\
4
122/a
4.10. Дифракционные формулы Френеля и Фраунгофера 281
ГДС Ро ? [(z - z'J + х2]1/2. D.10.13)
4.10.4. Дифракция периодических полей
Среди немногих случаев, для которых дифракционные поля могут
быть вычислены аналитически, особую важность представляют поля,
имеющие вид периодических функций. Рассмотрим такие поля более
подробно, поскольку их дифракция имеет интересные приложения для
теории решеток [14] (см. разд. 6.10).
Пусть цилиндрическое поле и(х9 z), фаза которого не зависит от
координаты>> [см. выражение D.7.1)], в плоскости z1 = 0 записывает-
записывается в виде
+N / х'\
и (х',0) = f(x') = ?jaexp\Ulnj\9 D.10.14)
где/С*') = f(x' + d) — периодическая функция координаты х', содер-
содержащая столько гармоник N9 что N\/d < 1. Тогда при kz < 4ot(d/N\L
[см. неравенство D.10.3)] можно использовать дифракционную форму-
формулу Френеля D.10.4), и мы имеем
Следует заметить, что в частном случае z = zq = gd2/\ мы имеем
%] = ехр(ш2тг<7) = ехр(Ш7г<зО, так что
u(x9zq) = exp(-*'fc zg)f(x + iqd). D.10.16)
Отсюда следует, что во всех плоскостях^ распределение интенсивно-
интенсивности поля одинаково. Это свойство называют эффектом Талбота, или
эффектом самовоспроизведения. Оно было впервые замечено Талбо-
том в 1836 г. и имеет весьма важные приложения в фурье-спектроскопии
и интерферометрии.
Рис. 4.13. Дифракционные картины от типичных апертур. Функции распределения
\G(et<f>')\2 пропорциональны: а — [sin(v)/v]2, v = kasin6cos<j>; б— {[sin (у )/у ] x
x [sin (vb)/vb]\2, va = A»zsin0cos4, vb = Ar6sin0cos& в— {[sin(y)/yj [sin(^)/sin vb]J,
va = A:flrsin(9cos0, vb = Arbcos(9cos0, г — BJx(v)/vf,v = kasmB; д — {[2Jx(va)/va] x
x [s\n{Nv)/]J Ai^ A#i0
282 Гл. 4. Основы теории дифракции
4.11. РАЗЛОЖЕНИЕ ПОЛЯ ПО ЦИЛИНДРИЧЕСКИМ ВОЛНАМ
В этом разделе мы покажем, что в наиболее общем случае поле, удов-
удовлетворяющее условию Зоммерфельда, можно представить в виде су-
суперпозиции цилиндрических мод. Это представление можно использо-
использовать как альтернативный метод разложения по плоским волнам вме-
вместо рассмотренного в разд. 4.8. Оказывается, что он особенно полезен
для полей, симметричных относительно вращения вокруг некоторой
оси (например, оси z). Рассмотрим сначала разложение функции Грина
exp(-ifc|r-r'|) -I + ?
4я|г-г'| ь?
х exp[-f(fe2 - X2)ll2\z - z'Uxdx, D.11.1)
которое следует из представления Зоммерфельда — Отта для функ-
функции Грина G и из теоремы сложения Графа для функций Бесселя (см.
задачу 8). В разложении D.11.1) Jm представляет собой функцию
Бесселя первого рода т -го порядка, и мы используем цилиндрические
координаты р, ф, z.
Если полученный ряд D.11.1) подставить в разложение D.5.4), при-
причем в качестве поверхности интегрирования выбрать плоскость, пер-
перпендикулярную оси z, то поле в точке г запишется в виде
j Гсо Г2п +оо
u(x, y9 z) = и{р, ф9 z) = — р' dp' и(р\ ф\ z') X exp[im(</> - ф')~] #'
*-n JO JO m=-oo
Jm(XP)Jm(XP')™Vt-i(k2 - X2)ll2\z -z'Wxdx. D.11.2)
Jo
o
Кроме того, поле на поверхности интегрирования можно разложить в
ряд Фурье по ф': +оо
и(р\ф\2')= f Cm(p\z')eim*' D.11.3)
т— — оо
(здесь т принимает все целые значения, aw— однозначная функция
своих параметров). Таким образом, мы имеем
[™p'dp' [
Jo Jo
= 2neim+\ Cm(p',z')Jm(XP')p'dp' =
Jo
= 2ne"+HmlCm(p'9 z'); ZJ; D.11.4)
здесь черезHm\f(p')\ \] обозначено преобразование Ханкелят-то по-
порядка с аргументом \ (см. книгу [15] и приложение Д в нашей книге).
Теперь можно вычислить коэффициенты Cm(p9 z) фурье-разложения
4.11. Разложение поля по цилиндрическим волнам 283
поля (по Ф) на плоскости с координатой z, используя выражения
D.10.2) — D.10.4):
Cm(p,z) = ГHm[Cm(p',z'); х]exp[-i(fc2 - X2)l'2\z - г'
Jo
= HmlHm{Cm(p',z'); x}exp[-f(fe2 - X2I/2|z - z'|]; p] =
= Cm(p,z') * Hm{expl-i(k2 - X2)il2\2 - z'|]; p}. D.11.5)
При получении этого результата мы использовали свойство сверт-
свертки преобразования Ханкеля и тождество двойного преобразования
Hm\Hm[f}} = /. В частности, легко проверить, что при z = z' мы
имеем Ст(р9 z) = Cm(p9z'). Наконец, поле можно записать в виде
M(p,0,z)=f +f eim*Cm(p,z')= +f Cm(p9z)eim+, D.11.6)
m=-co m=-oo
где f — линейный оператор, который преобразует Ст(р, z')BCm(p9z)
в соответствии с D.11.5).
Если в используемом выше ряде оставить какой-либо т -й член, то
его можно рассматривать как суперпозицию цилиндрических мод сле-
следующего вида:
l D.11.7)
Разложения по плоским и цилиндрическим волнам взаимозаменяе-
взаимозаменяемы, так как они применимы к одному и тому же классу полей. При
этом представление поля через плоские волны требует трех непрерыв-
непрерывных параметров kx9 ky9 kz, связанных соотношением к\ + к^ +
4- к% = к2, в то время как для цилиндрических волн необходим один
дискретный параметр т, указывающий на угловую зависимость
ехр(/тф), и непрерывный параметр *, определяющий зависимость от
координаты z, а именно ехр[-/(^2 - -)i2)Vl\z - z' I]. Радиальная
функция Jm(xp) зависит как отт, так и от х-
4.11.1. Приближение Френеля
В тех случаях, когда спектр Ат(х) каждой из цилиндрических мод об-
обращается в нуль при х > Хмакс (причем хмаКс * *)» выражение D.11.5)
можно упростить, если экспоненту, описывающую распространение,
записать в следующем приближенном виде:
-*|z - z'\ + iX2\z - z'|/B*)], D.11.8)
284 Гл. 4. Основы теории дифракции
так что после тождественных преобразований получаем
c-{p'z) = 17Г7| B|rr7[)
х Hm{cra(,',z')exp(-,fc^);I7^[}. D.11.9)
Здесь было использовано интегральное тождество
Выражение D.11.9) эквивалентно формуле Френеля D.10.2), полу-
полученной в декартовых координатах.
4.11.2. Разложение плоской волны по цилиндрическим волнам
Мы уже видели, что всякое поле, которое можно представить в виде
разложения по плоским волнам, может быть в то же время выражено
и в виде суперпозиции цилиндрических мод. Наиболее естественный
метод перехода от одного представления к другому состоит в разло-
разложении по цилиндрическим модам каждой отдельной плоской волны.
Для этого заметим, что на плоскости z = z' плоская волна может
быть записана в виде
и(р',ф',г') = exp[-iVcos@' - <?'o)sin0], D.11.11)
где в — угол между волновым вектором к0 и осью z. Если разложить
правую часть выражения D.11.11) в ряд, то получим
и(р\ф',г') = +? (-1)тикр'*те)ыр1Щф'-ф'0П. D.11.12)
т= —оо
Сравнивая это выражение с D.11.3), имеем
СЛМ = (-i)me-im*'°Jm(kp'sme). D.11.13)
Таким образом, преобразование Ханкеля можно записать в виде
HmlCM(p\z');x] =(-i)me-im*'° [™ Jm(kp'sine)Jm(XP')p'dp'=
Jo
= (-i)me-im+'°x~lS(x-ksin6)9 D.11.14)
и выражение D.11.5) принимает окончательный вид:
Cm(p,z) = Cm(p,z')exp(-ik0\z - z'| cos в). D.11.15)
В результате представленного выше рассмотрения мы нашли, что
разложение по цилиндрическим волнам плоской волны с начальным
4.11. Разложение поля по цилиндрическим волнам 285
распределением D.11.11) на опорной плоскости имеет вид
u(p,<M = exp(-ifc|z-z'|cos0) ~? (-i)mJm(kpsme)eimi+-+'<>K D.11.16)
m=+oo
4.11.3. Лпертурно ограниченные вращательно-симметричные поля
Продемонстрируем теперь использование приближения Френеля в ци-
цилиндрических координатах на конкретном примере. А именно, рас-
рассмотрим поле, которое отлично от нуля лишь на диске радиусом а,
принадлежащем плоскости z = z', и не зависит от угла ф. Такая вра-
вращательная симметрия означает, в частности, что для т Ф 0 все
Ст = 0, и разложение D.11.6) принимает простой вид:
M(p,z) = C0(p,z). D.11.17)
Предположим теперь, что на начальной плоскости z = z' для поля
применимо представление геометрической оптики, т. е.
u(p\z') = A{p')e-ikS^ = C0(p',z'), D.11.18)
если р' <я, и и(р', я')= 0, если р' >а. Объединяя формулы
D.11.5), D.11.7) и D.11.18), можно записать следующее выражение:
Г00 Г1
u(p,z) = a2 xdx xA(ax)expt-ikS(ax) - i{k2 -
Jo Jo
x Jo(x<*x)MXP)db D.11.19)
которое в приближении Френеля [см. D.11.9)] принимает вид
u(p,z) = -ШАкаехрН-ik\z - z'\ - ik^—
х Г A{ax)J0^kaXP]exp\ -ika4A?r- - ikS(ax) \xdx\. D.11.20)
Jo \z-z\ I 2 J J
Здесь ЧА = a/\z - z' I — числовая апертура диска, если смотреть на
него с расстояния \z - z' I.
На больших расстояниях, когда ехр(— ika ЧАх2/2) = 1, выраже-
выражение D.11.20) принимает более простой вид:
u(p,z) = -iHAkaexpt -ik\z - z'| - ik® |Z~Z|
x Г A(ax)J0(kaex)exp[-ikS(axy]xdx, D.11.21)
где в = p/\z - z' I. Таким образом, мы получили результирующее
выражение, которое называют дифракционной формулой Фраунгофе-
ра для вращателъно-симметричных полей.
286 Гл. 4. Основы теории дифракции
4.11.3.а. Разложение в ряды Буавена
Полагая A (ax)exp(-ikS - ika ЧАх2/2) =/(х2), мы следуем Буавену
[16], вводя множество функций Ар(?), определяемых выражением
АД) [ хЫе)ъ D.11.22)
+ * Jo
которое есть не что иное, как преобразование Ханкеля нулевого по-
порядка для функцииg(x), такой, что?(х) = Bр + \)х^ при* < 1 и
g(x) = 0 при всех других аргументах. Раскладывая теперь/(л:2) в сте-
степенной ряд, поле можно записать в виде следующего ряда:
D-ПИ)
где С — множитель, стоящий перед интегралом в D.11.20). Последо-
Последовательность коэффициентов Ар легко вычисляется с помощью рекур-
рекуррентного соотношения [16]
АД) + tfVWP + 1)]AF+1«) = МО + КЛ«)/2р], D.11.24)
а также выражения ,Л ,. -.ч
Л1==2Л(^. DЛ1.25)
Буавен получил следующее разложение в ряд [16]:
^ D.11.26)
где ? = &tfp/U - z'l. В частности, если /= exp{/(wjA:2 + о^
a = -о?! - 2co2 и р = -2оJ. Нетрудно показать, например, что усло-
условие а = О соответствует краевому фокусу, а = /J — параксиальному
фокусу, а а = /8/2 — окружности наименьшего искажения, т. е. мини-
минимальному размеру изображения на экране, перпендикулярном оптичес-
оптической оси.
4.12. ЦИЛИНДРИЧЕСКИЕ ВОЛНЫ КОМПЛЕКСНОГО ПОРЯДКА
И ПРЕОБРАЗОВАНИЕ ВАТСОНА
Разложения по цилиндрическим волнам являются нередко лишь про-
промежуточным этапом в поиске простых аналитических представлений
поля. Действительно, во многих случаях эти ряды сходятся столь
медленно, что для получения удовлетворительной точности необходи-
необходимо учитывать очень большое число членов суммы. Типичным приме-
примером является задача о рассеянии плоской волны на цилиндрическом
препятствии. Несмотря на простоту решения в приближении геомет-
геометрической оптики, по виду разложения в ряды Фурье и Бесселя совсем
4.12. Цилиндрические волны комплексного порядка 287
не просто предсказать существование области тени. Путь к преодоле-
преодолению этой сложности был предложен Ватсоном, который преобразо-
преобразовал начальное разложение в другое, сходящееся гораздо быстрее к
пределу геометрической оптики при X -* 0. Проиллюстрируем теперь
на частном примере главные этапы метода Ватсона, ведущего к полу-
получению быстро сходящихся рядов. Рассмотрение преобразования Ват-
Ватсона для случая рассеяния на диэлектрическом цилиндре мы отложим
до разд. 6.5.
Из общих соображений можно предположить, что при дифракции
плоской волны на круговом цилиндре поле на поверхности цилиндра в
области геометрической тени должно затухать, так что
и(а,ф) ос ехр[- у(ф - ф$ъ)У, D.12.1)
здесь </>SB — угол, связанный с границей тени, a v — комплексное чис-
число, причем Re*> > 0. С формальной точки зрения решение соответст-
соответствует цилиндрической волне, «вращающейся» вокруг цилиндра и имею-
имеющей комплексную постоянную распространения р/а, где а — радиус
цилиндра. Таким образом, в освещаемой области поле представляет
собой комбинацию цилиндрических волн вещественного порядка т, а
в области тени в разложении участвуют компоненты комплексного
порядка v.
Чтобы показать применимость выражения D.12.1) при X — 0, не-
необходимо прежде всего преобразовать разложение D.11.3) для того,
чтобы учесть в нем вклад от волн общего вида Jp(xp) ехр (/>ф) с ком-
комплексным v. С этой целью заметим, что выражение D.11.6) для поля,
не зависящего от z, принимает вид
и{р,ф) = ? Ая
= \ ? АтН^(кр)е^+1- ? АтН%\кр)е**, D.12.2)
— оо
где Н$ — функция Ханкеля первого рода, а Н$ — та же функция
второго рода. Их можно определить для любого комплексного v, при-
причем при фиксированной вещественной части v и 1x1 — оо они имеют
следующее асимптотическое представление:
(x-iv^-ij\ D.12.3)
откуда следует, что Н^ описывает волну, уходящую на бесконеч-
бесконечность, в то время как Н^ — притивоположно направленную. Таким
образом, если нас интересует лишь компонента поля, уходящая на
288 Гл. 4. Основы теории дифракции
бесконечность, то и(р, ф) можно записать в следующем простом виде:
+ 00
и(р,ф)= ? АЖЧкрУ"*. D.12.4)
т= —оо
Если и(р, ф) задана на круге радиусом а, ряд D.12.4) можно пере-
переписать в виде
, Ф) = т ?в <«(*> Ф')е-1тф>Ф^^е^, D.12.5)
где 0 = ка — так называемый масштабный параметру а
<||(а,0>-*"*'V = Т- Ги(а,Ф')е-*тф'<1ф'. D.12.6)
^я Jo
В выражении D.12.5) мы учли тот факт, что при р = а выражение
D.12.4) является разложением в ряд Фурье периодической функции
ЯФ) = /(Ф + 2тг) = и(р, 0).
Когда оба параметра C и кр очень велики, в сумме D.12.5) функции
Ханкеля можно заменить их асимптотическим представлением
D.12.3), и тогда выражение D.12.5) можно записать приближенно в
следующем виде:
1/2 +оо
1/2
е~щр~а)и(а9ф\ D.12.7)
что представляет собой точное выражение для поля в пределе геомет-
геометрической оптики. Асимптотическое приближение для Н?> D.12.3) не-
непригодно в тех случаях, когда нельзя пренебречь вкладом членов с
большим индексом т. На самом деле асимптотическое разложение не-
неприменимо, если величина I л: I по порядку величины равна или мень-
меньше, чем Ы. В этих случаях, для постоянного отношения x/v при
Ы — оо асимптотическое поведение функции ЯB) имеет вид (см. кни-
книгу [4], с. 71)
п> argv>0- D.12.8)
Аналогичное выражение может быть получено для Щ1\ если исполь-
использовать соотношение Щ1\х) = ехр(-утг/)//р[ехр(-7г/л:)]. Таким обра-
образом, мы имеем
Н[2\кр)/Н[2\Р) ~ (а/р)\ 7c/2>argv>0, D.12.9а)
|v|-*oo
Н[2)(кр)/Н[2\р) ~ (р/а)\ 7i>argv>7c/2. D.12.96)
М-оо
Отсюда следует, в частности, что в данном случае члены высшего по-
4.12. Цилиндрические волны комплексного порядка
289
Область
ползущих
доли
ф-фт-&гссо$(а/р)
]Рис. 4.14. Возбуждение ползущих волн в области тени при освещении отверстия в ме-
металлическом цилиндре.
рядка в ряде D.12.5) убывают как (а/р)т в отличие от зависимости,
описываемой выражением D.12.7). Такое существенное уменьшение
членов высшего порядка означает сильное сглаживание дифракцион-
дифракционной картины в дальней зоне по сравнению с тем, что мы имеем в
приближении геометрической оптики.
Рассмотрим конкретную задачу. Пусть в металлическом круговом
цилиндре радиусом а имеется отверстие, простирающееся от
ф = - фт до ф = фт, как показано на рис. 4.14. Предположим также,
что источники находятся внутри цилиндра и создают на отверстии
распределение поля и(а, ф). В приближении геометрической оптики
волна будет распространяться наружу лишь внутри угла \ф\ < \фт\ и
резко спадать до нуля вне этого сектора. Однако благодаря быстрому
убыванию амплитуды высших гармоник ~ (а/р)т переход от освещен-
освещенной области к области тени будет тем менее резким, чем в более
дальней зоне находится точка наблюдения.
Этим качественным рассуждениям можно сопоставить вполне
определенные количественные выражения, если ряд D.12.5) преобразо-
преобразовать к контурному интегралу (рис. 4.15)
еЫФ-п)
/ф rW2W m uv>
D.12.10)
где контур С, обход по которому производится против часовой стрел-
стрелки, охватывает все нули функции sin*>?r и оставляет во внешней облас-
области все полюсы отношения Н&\кр)/Н^ф). Справедливость этого ин-
интеграла можно проверить сразу, если заметить, что его подынте-
подынтегральное выражение имеет внутри С лишь простые полюсы, совпада-
совпадающие с нулями функции sim>7r, т. е. лежащими при v = т. Следова-
290
Гл. 4. Основы теории дифракции
\ Нули {г)
l#\ функции //у (x)
Нули
функции
Im V
+х
Нули
функции
н\2)
Рис. 4.15. Распределение нулей функций tif\X)n sin (pit). Контур интегрирвания Сзамыка-
ется вокруг нулей sin(?n>) и оставляет во внешней области нули функции Н® (х).
тельно, вычисляя интеграл D.12.10) с помощью теоремы о вычетах,
мы вновь получаем ряд D.12.5). Если принять теперь во внимание со-
соотношение H@l(x) = e~ivTH^\x) и тот факт, что функция Н^ не име-
имеет ни нулей, ни полюсов при Im*> = 0, то контур С можно преобразо-
преобразовать к прямой - оо + /г, ie + оо, причем е > 0. Таким образом,
D.12.И,
Учитывая асимптотические выражения D.12.9), получаем, что подын-
подынтегральное выражение в D.12.11) обращается в нуль при Ы — оо для
I -л- - ф + ф' I < 1г и т > argy > 0. Следовательно, контур интегри-
интегрирования можно замкнуть полуокружностью в верхней полуплоскости.
Так как функции Н^(х) можно представить в виде комбинации функ-
функD.12.12)
D.12.13)
где T(z) — гамма-функция Гаусса, то можно написать следующее вы-
выражение:
ций Бесселя Jv и J_y:
Я<2>(х) = i{[J-v(x) - Jv(x)eiv*]/sinv7r},
a Jv(x) можно разложить в ряд
(jY+2W + 1 + т))-\
-v)]-,
lf DЛ2Л4)
4.12. Цилиндрические волны комплексного порядка 291
Заметим теперь, что Г~!(^) — целая функция аргумента v (т. е. она ре-
регулярна во всей комплексной плоскости *>), а Н^(х) стремится к ко-
конечному пределу при р = т(т — целое число, положительное или от-
отрицательное). Отсюда следует, что Н^2\х) также является целой функ-
функцией аргумента v.
Возвращаясь теперь к интегралу D.12.11), контур которого зам-
замкнут в верхней полуплоскости; приходим к выводу, что подынте-
подынтегральное выражение содержит только полюсные особенности, соот-
соответствующие нулям рп (л = 1,..., оо) функции Н®){&). Применяя тео-
теорему о вычетах, окончательно получаем
«=i sin(v^) dH(v2)(P)/dv\v=Vn
Таким образом, в результате долгих выкладок мы заменили на-
начальный ряд D.12.5) на новый, содержащий функции комплексного
индекса vn. Это преобразование впервые предложил Ватсон в 1918 г.
для улучшения сходимости разложения по сферическим волнам поля в
зоне тени, рассеянного сферическим препятствием. При этом он дока-
доказал, что в полученном ряде можно оставить только первый член, и
объяснил таким образом экспоненциальное затухание поля, излучае-
излучаемого передатчиком, находящимся за линией прямой видимости, в об-
области геометрической тени Земли. Значительно позднее, а именно в
1958 г. Редже вновь открыл этот метод для решения задачи о рассея-
рассеянии шрёдингеровской волновой функции частицы на центральном по-
потенциале. В этом случае индекс т с точностью до постоянной Планка
А совпадает с квантовомеханическим угловым моментом частицы.
Аналитическое продолжение в область комплексных v можно при
этом интерпретировать так, что частицы в области тени имеют ком-
комплексный угловой момент [17].
Теперь остается исследовать распределение нулей и сами выраже-
выражения для слагаемых в рядах Ватсона D.12.15).
4.12.1. Нули функции Н&> (/3) в верхней полуплоскости
Нули функции Н^ЦЗ) (а также Н^\ Н^' и Н^у) исследовали несколько
авторов [18—21]. В частности, Шёбе [19] получил следующее разложе-
разложение для /^2H8), справедливое при \v + j8l = О(х1/з), 1/31 > 1:
(Ш mZjeiK/\-p) Ai(-?)> D.12.16)
292 -Гл. 4. Основы теории дифракции
где Ai(z) — функция Эйри, a Ai'(z) — ее производная и
? = -еЫ13B/рI/3(у + р). D.12.17)
Для первых нескольких коэффициентов Рп и Qn имеем
--^+1й- DЛ2Л8)
Используя приведенное разложение D.12.16) и применяя формулу
Стрейфера и Кодиса [18], можно показать, что первые нули vn функ-
функции /^2H8) с хорошей точностью можно аппроксимировать следующей
функцией [см. также F.6.3) и выражение (А.8) у Нуссенцвейга [22]]:
%1 -р - e-™(P/2)ll3x., D.12.19)
где хп — нули функции Ai(—л:), а
( а!'? 29х„ \/2У
14,536,000 \im)\fi) ' ( }
Первые пять коэффициентов д:Л имеют следующие значения:
хх = 2,338, jc2 == 4,088, х3 = 5,521, D.12.21)
х4 = 6,787, л:5 = 7,944,
а при больших п (но меньших, чем /8) хп определяется асимптотичес-
асимптотической формулой
хп - {C/2)тс[п + C/4)]}2'3. D.12.22)
Кроме того, при п — оо мы имеем (см. [21])
Распределение нулей *>Л схематически иллюстрируется на рис. 4.15, из
которого ясно видно, что Imi^ является возрастающей функцией чис-
числа п. Кроме того, при достаточно больших х первые нули расположе-
расположены на линии, составляющей угол 60° с вещественной осью.
Функцию /ДО для первых нулей, как видно из разложения D.12.16),
можно заменить на функцию Эйри Ai(-?). Таким .образом, мы мо-
4.12. Цилиндрические волны комплексного порядка
293
жем написать
dv
2/3
D.12.24)
В то же время для нулей высокого порядка (\vn\ > /3) можно исполь-
использовать разложение D.12.8), и мы имеем
Таким образом, с учетом D.12.23а) получаем
4.12.2. Ползущие волны
Быстрое убывание слагаемых в ряде Ватсона при п — оо, подтвержда-
подтверждаемое выражением D.12.26), позволяет нам рассмотреть только члены
малого порядка, для которых \vn + /31 = О(/31/з). При этом можно ис-
использовать приближение D.12.24) и записать
Если необходимо рассмотреть поле при всех р, таких, что а < р < оо,
то должно быть известно выражение для Н^(кр)9 которое примени-
применимо для значений кр как очень больших, так и сравнимых с \рп\. Де-
бай, а затем Ватсон получили асимптотические выражения при очень
больших х и Ы, когда \х + И >О(х1/з). Используя их результаты,
можно записать (см. [4], с. 262)
• Н[2\х) - [2/я(х2 + v2I/2]1/2exp(-i{(x2 - v2I/2 +
+ v[n — arccos(v/x)] — л/4}), п > argv > я/2. D.12.28)
Если, учитывая D.12.19), использовать приближение (к2р2 — р%I/2 s
s А:(р2 - а2I/2 и тг - arccos(^/A:p) s arccos(a/p), то
D.12.29)
Однако, поскольку 1пфЛ)>1 [см. D.12.236)], можно использовать
следующее приближенное равенство: cos[^(tt — 0 + Ф')]/ьш(жрп) s
s - &уп\к - Jtt + ф1 - ф1] при этом мы имеем
<u(a,0')cos[vnGr - ф + 0'] V nfc*J е^-« D.12.30)
294 Гл. Л. Основы теории дифракции
Следовательно, разложение Ватсона принимает вид
х
еы/2
1 «> 1 ( а2 V
mhx Ai'(-*J V2 - а2)
{-ifc[7p2 - а2I12
х ехр< -ik\ р2 - а2I12 + а[ф-фт- arccosl - 11 -
D.12.31)
Каждый член этой суммы можно интерпретировать как амплитуду
поля вдоль луча, начинающегося от края отверстия, следующего сна-
сначала по поверхности цилиндра р = а до тех пор, пока не будет до-
достигнут угол ф — фт - arccos(tf/p), и идущего затем по прямой, каса-
касательной к поверхности цилиндра, до точки наблюдения (р, 0)
(рис. 4.14). Множитель ат/(р2 - о2I4 учитывает затухание амплиту-
амплитуды вдоль прямого отрезка траектории. Фаза состоит из двух слагае-
слагаемых, первое из которых (в квадратных скобках) представляет собой
задержку луча при движении его по искривленной траектории от края
отверстия до точки наблюдения, а второе учитывает отклонение от
закона геометрической оптики, возникающее из-за кривизны части
траектории. Именно этот фактор объясняет характерную особенность
рассматриваемых волн — они экспоненциально затухают при распро-
распространении вдоль поверхности цилиндра, причем чем больше я, тем
сильнее это затухание в соответствии со значениями хп [ср. с
D.12.21)]. В литературе эти волны называют ползущими, или
стелющимися^). Их свойства мы рассмотрим снова в разд. 6.5 в связи
с задачей о рассеянии волн на диэлектрическом цилиндре.
Необходимо заметить, что разложение D.12.31) справедливо при
I кр - /31 > /31/з. Для вычисления поля в более близкой к цилиндру
области для Щ\кр) можно использовать асимптотическое выражение
D.12.16). Кроме того, при не очень больших 0 нули vn даются выра-
выражениями D.12.19) и D.19.20). Этот случай имеет место, когда размер
рассеивателя сравним с длиной волны света (см. разд. 6.5).
4.13.РАСПРЕДЕЛЕНИЕ ПОЛЯ В ОКРЕСТНОСТИ ФОКУСА
Системы изображения конструируются для переноса конической кон-
конгруэнции лучей, создаваемой точечным источником в плоскости пред-
предмета, в фокальную точку в плоскости изображения (см. гл. 2). В боль-
!> Соответствующие английский и немецкий термины "creeping waves" и "Kriechwel-
len". Обсуждение свойств ползущих волн см. также в книге: Хёрл X., Мауэ А., Вест-
пфаль К. Теория дифракции: Пер. с нем./Под ред. Г. Д. Малюжинца. -— М.: Мир,
1964. — Прим. перев.
4.13. Распределение поля в окрестности фокуса 295
шинстве случаев распределение поля в области между источником и
выходным зрачком можно найти, используя методы геометрической
оптики, а именно определяя траектории лучей, распространяющихся
через последовательность преломляющих поверхностей, и вычисляя
затем амплитуду А вдоль каждого луча. Однако при попытке приме-
применить тот же подход в пространстве изображения (за выходным зрач-
зрачком) мы сталкиваемся с физически бессмысленным результатом, по-
поскольку вычисленное таким образом поле оказывается равным нулю
сразу при переходе границы геометрической тени, образуемой огибаю-
огибающей поверхностью, т. е. лучами, проходящими через край выходного
зрачка. Для устранения этого противоречия, связанного с использова-
использованием приближения геометрической оптики, необходимо обратиться к
представлению через дифракционный интеграл. В частности, можно
предположить, что поле на поверхности выходного отверстия совпа-
совпадает с полем, которое существовало бы на той же поверхности в от-
отсутствие апертуры. Это приближение, известное как принцип Кирхго-
Кирхгофа, эквивалентно предположению о том, что конечность размеров вы-
выходного зрачка не влияет на поле в плоскости зрачка. Поскольку в дей-
действительности возмущение поля значительно лишь вблизи границы
зрачка, можно ожидать, что ошибка, связанная с применением прин-
принципа Кирхгофа, пренебрежимо мала, если апертура достаточно велика.
Точный анализ (см. гл. 6) решений для простых апертур (напри-
(например, полуплоскость, щель) подтверждает то, что гипотезу Кирхгофа
можно применять с целью вычисления поля вблизи границы тени.
Ошибки становятся существенными лишь при вычислении поля в ос-
освещенной или темной областях. Но именно здесь хорошо работает
приближение геометрической оптики.
Проведенное выше рассмотрение объясняет, почему применение
принципа Кирхгофа в оптическом диапазоне общепринято и не вызы-
вызывает критики, хотя в физике радиоволн делались многочисленные по-
попытки создать более общую теорию. При этом слабое поле в области
тени необходимо вычислять точно, например при рассмотрении излу-
излучения на задней стороне отражательной антенны. В других задачах
бывает необходимо вычислить точное значение поля на апертуре,
определяя его самосогласованно, исходя из выражения для поля, излу-
излучаемого произвольной точкой самой апертуры. Всякий раз, когда как
геометрическая оптика, так и теория дифракции приводят при исполь-
использовании принципа Кирхгофа к нефизичным результатам, можно при-
применить альтернативный подход, а именно геометрическую теорию
дифракции (которую мы рассмотрим в последующих главах).
Во всех этих рассуждениях неявно предполагается возможность ис-
использования скалярного описания поля. Однако в тех случаях, когда
296 Гл. 4. Основы теории дифракции
числовая апертура пучка, падающего или выходящего из линзы, до-
достаточно велика, необходимо учитывать векторный характер полей Е
и Н. Это существенно, например, для теории изображения в микроско-
микроскопе, когда апертура падающего пучка может быть очень большой. Ана-
Анализ результатов показывает существенное отклонение от предсказаний
параксиальной теории (даже в отсутствие аберраций). В частности, да-
даже для линз с вращательной симметрией пятно в фокальной плоскости
не будет радиально-симметричным, если падающее излучение линейно-
поляризовано. Это обстоятельство в свою очередь влияет на разреша-
разрешающую способность оптического прибора. Кроме того, электрическое
поле имеет как поперечную, так и аксиальную компоненту.
Так как изменение поля в. фокальной области оптических систем с
малой числовой апертурой обсуждается во многих учебниках (см., на-
например, книгу Борна и Вольфа [11], цитируемую в гл. 1), в последую-
последующем рассмотрении мы сосредоточим внимание на главных особенно-
особенностях векторного поля, а результаты скалярной теории получим как
частный случай векторного интеграла Лунеберга — Дебая [23, 24].
4.13.1. Точечные источники электромагнитного поля
Укажем на некоторые свойства точечных источников, излучающих век-
векторные поля. Напомним, что в скалярной теории точечный источник,
создающий поле, пропорционален трехмерной б-функции, появляющей-
появляющейся в виде возмущающего члена в волновом уравнении [см. D.2.2)]. В
векторном случае мы должны представить себе поле излучения как со-
соответствующую комбинацию полей элементарных электрических и
магнитных мультиполей. В простейшем случае мы имеем дело с
электрическим диполем р и магнитным диполем т, локализованными
в точке rs ж (*0, у0, z0). Если источник находится в однородной среде,
то поле, излучаемое диполями р и т, дается выражением (см. книгу
[17], гл. I, с. $0—93)
1 e~ikR
Е(г) = -[(р • V) VG + k2pG] - ia)/i0ni x VG -> -—Е'(п), D.13.1)
g kK-*oo /{
где Е' — вектор, не зависящий от R [см. выражение B.8.3)]:
E'(n) = (-c*V47r)[n x (n x p) + (n/c)m x n] D.13.2)
и fi = (r - rs)/lr - rsl ж R/R, n = y/e/e0. Функция Грина G(r, rs) =
= G(R) совпадает в этом случае с выражением D.2.7), где г' = rs.
Во многих приложениях точечные источники получают при облуче-
облучении маленького круглого отверстия диаметром 10—100 мкм, располо-
расположенного в фокальной плоскости объектива микроскопа, лазерным пуч-
4.13. Распределение поля в окрестности фокуса 297
Объектив
макроснопа
Малое
отверстие
Рис. 4.16. Устройство, состоящее из рассеивающей линзы, объектива микроскопа и ма-
малого отверстия, для получения из начального лазерного пучка сферической волны боль-
большой апертуры.
ком, сфокусированным этим объективом (рис. 4.16). В этом случае ес-
если пренебречь вкладом края отверстия в дифракционную формулу
Коттлера [выражения D.3.4) и D.3.5)], то отверстие можно рассмат-
рассматривать как электрический и магнитный диполи, величина которых
пропорциональна электрическому и магнитному полю, проинтегриро-
проинтегрированному по апертуре.
В оптических системах, использующих синхротронное излучение,
источник представляет собой ток электронов, движущихся на расстоя-
расстоянии R от наблюдателя. Фурье-компонента поля, излучаемого этим ис-
источником, дается выражением (с точностью до несущественного фазо-
фазового множителя)
¦» ¦ й1- И- - «-
п
Здесь п — направление из малой конечной области, которую пролета-
пролетает электрон, к точке наблюдения; ге(/')— траектория электрона,
0 = (\/c)dxe/dt', $ = dfi/dt' и -ef0 — произведение заряда электро-
электрона на волновое сопротивление вакуума. В других случаях источником
является электрический диполь rfp, индуцированный полем Ej, падаю-
падающим на элементарный объем dV среды с диэлектрической проницае-
проницаемостью е. Таким образом, мы имеем следующее выражение:
Ф(г') = O(r') - eo]Et(*')dV9 D.13.4)
где dV включает в себя точку г'. Если падающее поле создается теп-
тепловым источником, как в случае облучения коденсора микроскопа
светом от лампы, необходимо учитывать флуктуирующую фазу век-
вектора Ej, которая воздействует на фазу электрического диполя р и в
конечном счете на поле в области изображения.
4.13.2. Перенос векторных полей из пространства предмета
к выходному зрачку
Обратимся теперь к наиболее важным свойствам, проявляющимся
при переносе векторных полей из пространства предмета в простран-
298 Гл. 4. Основы теории дифракции
ство изображения. Для простоты рассмотрим источник, расположен-
расположенный на оптической оси центрированной системы. Выберем для про-
пространства предмета сферическую систему координат г', 0', ф с нача-
началом в точке расположения источника rs, причем 0' = О соответствует
оптической оси в направлении z = + <». Для пространства изображе-
изображения введем аналогичную систему координат г, 0, ф таким образом,
чтобы оптическая ось была направлена в сторону z = — оо. В тех
случаях, когда на пути луча не происходит потерь на отражение за
счет поверхностей разрыва, можно получить простое соотношение,
связывающее амплитуды поля в пространстве предмета и изображе-
изображения для произвольного луча, выходящего из источника в направлении
0', ф и попадающего в точку выходного зрачка с координатами 0, ф.
Это соотношение имеет вид
\Е'(в,ф)\ = \Щ0\ф)\((Ш'/<ЮI/2 =
^\Щв\ф)\д(в) D.13.5)
и выражает собой постоянство потока энергии вдоль узкого пучка лучей.
(Здесь du = sine dd йф и dO' = sin0' d&' с!ф — телесные углы пучка лучей
в пространствах соответственно изображения и предмета.)
Для линзы, удовлетворяющей условию синусов Аббе (см. в книге [11,
с. 166 русского издания], цитируемой в гл. 1), можно положить
sin0'/sin0 = М, где М — линейное увеличение, так что g@) =
= Af(cos0/cos0')l/2. Если источник расположен на бесконечности, то
соотношение D.13.5) принимает вид
\Щв9ф)\ =
= \ЩЬ cos ф9 h sin ф)\/до@)> D.13.6)
где Л@) — высота луча в пространстве предмета, а/— постоянная, кото-
которая играет роль фокусного расстояния. Для системы, удовлетворяющей
условию синусов, мы имеем A/sin0 = frgo(ff) + (cos0I/2. Это приближение
основано на предположении о том, что падающая плоская волна не изме-
изменяется до тех пор, пока на ее пути не окажется сферическая поверхность,
на которой волна преломляется непосредственно в волну со сходящимся
сферическим фронтом, имеющим тот же радиус кривизны, что и сфера
(рис. 4.17).
Рассмотрим другой пример, когда преобразование плоской волны
в сферическую происходит таким образом, что одинаковые радиаль-
радиальные расстояния от оптической оси преобразуются в равные углы на
сфере (однородная сферическая проекция). При этом А@) = /@) и
go@) = @/sin0)l/2. По сравнению с апланатической эта проекция позво-
позволяет более точно описать свойства системы, состоящей из последова-
последовательности тонких линз, когда полная длина оптической системы боль-
4.13. Распределение поля в окрестности фокуса
299
Рис. 4.17. Зависимость от угла в измеряемой относительно оптической оси высоты луча
h (в) для апланатической (я), однородной (б) и параболической (в) фокусирующих
ше, чем результирующее фокусное расстояние. Для плоской волны,
падающей на параболическое зеркало с фокусным расстоянием /, не-
нетрудно показать, что й@) = 2/A — cos0) и, следовательно,
go«f) = 2/A + cos0).
Уравнение D.13.5) можно переписать в векторной форме (рис. 4.18):
що9ф) = дШФФ + 00') • Щ0\ФУ D.13.7)
В случае локализованного на бесконечности источника (R -* оо, п — ?)
это уравнение принимает вид
Е'@,ф) = /доШФФ + в(? х ф)] • E(/icos</>, Asin<?). D.13.8)
Рис. 4.18. Взаимная ориентация сферических систем координат, относящихся к источни-
источнику и изображению, образуемому линзой.
300 Гл. 4. Основы теории дифракции
Если поле Е'@\ ф) излучается диполями р и m [см. D.13.2)], то
для вакуума уравнение D.13.7) запишется следующим образом:
Е'@, ф) = (со2Ио/4п)д(в){[9 -их (т/с)] . фф +
+ (т/с + йхр)-^}. D.13.9)
Аналогичные рассмотрения справедливы и для магнитного поля,
которое приближенно выражается через электрическое соотношением
[см. B.8.12)] foH'@, ф) = S х Е'(в, ф), где S — направление распро-
распространения поля изображения.
4.13.3. Дифракционный интеграл Лунеберга — Дебая
В случае когда поля Е и Н можно представить лучевыми полями, ди-
дифракционная формула Коттлера — Кирхгофа D.3.4) принимает вид
Е(г) s j ГLr*<*+S)E'(n0)<to + j I \e-ikiR+S)(R - п0) х (Е' х nQ)du +
(noLe Sidl, D.13.10)
JdA K
где E'(n0) = EqR — вектор, зависящий только от направления луча
-_р0, a du = dA /R2 — телесный угол, которым элемент поверхности
dA стягивается к фокусу. При выводе этого выражения из D.3.4) мы
использовали соотношения VG = — ikRG и H'f = Е' х г^, кото-
которые следуют из уравнения B.8.12). При R/X — оо последним контур-
контурным интегралом можно пренебречь. Аналогично, если волновой
фронт, проходящий через центр Е' выходного зрачка А, слабо отли-
отличается от опорной сферы, также включающей точку Е' и имеющей
центр в гауссовом изображении х, у, 0 источника (см. разд. 2.15.4), то
разность п — п0 становится пренебрежимо малой и приведенное инте-
интегральное представление принимает вид
D.13.11)
Выберем декартову систему координат с осью z, параллельной оп-
оптической оси, и пусть плоскость z = 0 совпадает с гауссовым изобра-
изображением плоскости z = Zq(< 0). Координаты источника равны х0, у0,
z0. Для определения величины R + S, стоящей в фазовом множителе
интеграла D.13.11), можно воспользоваться гамильтоновой смешан-
смешанной характеристикой W(x0, y0, z0; p, q), построенной с использовани-
использованием координат источника х0, у0, z0 и направляющих косинусов р и q лу-
4.13. Распределение поля в окрестности фокуса
301
Рис. 4.19. Используемые в разд. 4.13.3 обозначения: Р(х, у, z)— точка, в которой
определяется поле; Q(?, ч, f) — волновой фронт; (/с, у, 0) — гауссово изображение.
ча в пространстве изображения (см. гл. 2). Обозначим через ?, ч, К ко-
координаты точки волнового фронта Q, а через х, у, z — координаты
точки Р, в которой определяется поле. При этом мы можем написать
следующее выражение (рис. 4.19):
S + R = S - (р? + qr\ + rQ + (p? + qti + rQ +
+ Ш - хJ + (г,- уJ + (С - zJ]1'2, D.13.12)
где р = - пОх, д = - пОу, г = — nOz — направляющие косинусы луча,
проходящего через точку ?, ij, f. Поскольку волновой фронт образуется
точечным источником с координатами х0, yQ, Zq, эйконал S(?, ц, f) сов-
совпадает с точечной характеристикой V(x0, y0, z0; ?, ч, f), и мы имеем
S - (Pi + <т + К) = V(Xo,yo,zo;t,ti,Q - (р^ + qri + r?)
^x^y^q); D.13.13)
здесь W не зависит от конкретного выбора волнового фронта (напо-
(напомним, что W представляет собой длину оптического пути между то-
точечным объектом и основанием перпендикуляра, опущенного из точки
х = ^ = г = 0на луч).
Для точек наблюдения Р(х, у, z), близких к гауссовому изображе-
изображению (х, у, 0) источника, имеем (рис. 4.19)
1-P2
- уJ + С2]1/2 + р(х -x) + q(y-y)
(х - хJ +
1-д2
2R v ' 2R
= p(x - ?) + q(y -n) + r(z - C)
i Л 1 _ q2
(У ~ УJ +
1-г2
2R
,2 ~
2R
(X -XJ +
2R
(j-tf + ^H.
D.13.14)
302 Гл. 4. Основы теории дифракции
Отсюда с помощью D.13.12) и D.13.13) получаем
h'>xo,yo>P>q) + px + qy + rz
+l-if{x-^J+1-if{y-yJ+l-ifz2-DЛЗЛ5)
Используя введенную ранее функцию аберраций Wo [см. выражение
B.15.31)], можно записать
W(zO9zl;xO9yO9p9q)=V(xO9yO9zo-9x9y90)-px-qy^Wo(xO9yO9zo;p9q9r)9
что позволяет представить сумму D.13.15) в виде ( • • )
S + R = Ко + р(х - х) + q(y - у) + rz + Wo +
где Ко = F(x0, у0, ZqI х, у, 0).
Следует заметить, что
i_[(l _ р2){х _ jga + A _ 42Ху . Я2-| ^ ^|«= яДи&^ D.13.18)
здесь рмакс — радиус круговой области, в которой содержится практи-
практически все фокальное изображение, a NMagc — относительное число Фре-
Френеля, равное видимому из выходного зрачка числу колец Френеля, со-
дерокащихся в круге площадью тгр^|акс. Можно показать, что NMJiKC по
порядку величины равно обратному числу Френеля Nc, вычисленному
для выходного зрачка при наблюдении из фокуса. Поэтому в случае
Ne > 1 при вычислении экспоненты в D.13.11) можно пренебречь ле-
левой частью в D.13.18). Аналогично можно написать, что
kip1 + q2)z2/BR) < u21ABXC/Ne9 где wMaKC = k\zMaKC\ ЧА2 [см. ниже вы-
выражения D.13.21)], а кмакс1 — максимальное рассматриваемое рассто-
расстояние от фокуса. Так как ммакс имеет порядок величины 102, в записан-
записанном выше неравенстве можно также пренебречь левой частью. Однако
в случае когда Ne - 1, наличие в D.13.17) слагаемого, пропорцио-
пропорционального z2, приводит к сдвигу фокуса по сравнению с построением
геометрической оптики [см. ниже выражение D.13.37)]. Если поле
определяется в точке, столь близко расположенной к гауссову изобра-
изображению, что в D.13.17) можно пренебречь тремя последними членами,
то выражение D.13.11) преобразуется в интеграл Лунеберга —' Дебая:
— ikV Г /*
Е(г) = ^-^ E'(tfo)exp[-ifcWo - ik(p(x -x) + q(y - у) + rz)] <to.
А D.13.19)
Эквивалентное выражение для Н получается заменой
Е' - Е' х V
4.13. Распределение поля в окрестности фокуса 303
Если точка наблюдения г достаточно близка к началу координат,
то телесный угол rfO, которым элемент волнового фронта стягивается
к фокусу (х, у, 0), можно заменить телесным углом, которым этот
элемент стягивается к началу координат @, 0, 0). В этом случае, если
выбрать систему координат такой, чтобы углу в = 0 соответствовало
направление z = — оо, то последний интеграл можно преобразовать к
виду
Ie-ikV0 Г Г
Е(г) = -у- РF,ф)Е'(е,ф)ехр1-Ис\У0 + ifcpsin@)cos@ - ф)] х
х exp[-*fccos@)z]sin@)rf0#, D.13.20)
где функция зрачка Р равна единице на апертуре и нулю при всех дру-
других углах (см. разд. 4.5) и, кроме того, х - х = pcos^,
У - У = psin^, р = - sin0cos0, q = - sin0sin<?, r = cos0 (не следует
путать обозначения направляющих косинусов г со сферической коор-
координатой).
Теперь удобно ввести оптические координаты v, и, определяемые
выражениями [см. B.15.28)]
v = kp ЧА, п = kz ЧА2, D.13.21)
где ЧА = sin0MaKC — числовая апертура, причем 0макс — половина
апертурного угла в пространстве изображения (в гл. 8 мы покажем,
что координата v играет важную роль в теории распространения элек-
электромагнитных волн в оптическом волокне; в связи с этим ее называ-
называют нормализованной частотой и обозначают через V). При этом ин-
интеграл Лунеберга — Дебая можно переписать таким образом, что он
не будет зависеть от z и р:
E(r) = texp(~l7cKo) ffP@,ф)Щв9ф). X
[1 иг • sin@)cos(<? - ф) ._cos@)~l . м м ^^ч
- ifcWo + w —v —— - ш -rrfy^ sm@) d0 ^ф. D.13.22)
ЧА HA J
При достаточно малых числовых апертурах это выражение принима-
принимает вид
Г 021
х exp -ikW0 + №0cos(</> - ф) + ш—
304
Гл. 4. Основы теории дифракции
где 9 ш 0/ЧА. Если линза не имеет аберраций (Wo = 0), то поле в
фокальной плоскости Щи = 0) имеет вид преобразования Фурье:
00
Е(х9у,0) = -jjj- JJ
fe~*Ko Г х vl
= -Т72-F\ P(x',y'W(x',y'9 -Л); *Т»*Т • D.13.24)
Здесь при переходе от D.13.22) к D.13.24) мы использовали соотноше-
соотношение sin0 с1вс1ф = dx' dy' /f2l, где фокусное расстояние fx совпадает с
расстоянием от выходного зрачка до фокуса.
В том же параксиальном приближении поле Е^ во входной плоско-
плоскости еще одной линзы, у которой передняя фокальная плоскость совпа-
совпадает с П (рис. 4.20), является в свою очередь фурье-преобразованием
распределения поля в плоскости П и, таким образом, воспроизводит
распределения поля Е/ на выходном зрачке первой линзы. Однако ес-
если в плоскости П расположен транспарант, изменяющий амплитудное
и фазовое распределение, то поле в этой плоскости умножается на со-
соответствующую функцию t(x, у) и поля Е, и Е' не совпадают друг с
другом. При этом поле Щ пропорционально свертке Е' с фурье-
образом функции t(x, у) и записывается в виде
+ 00
= [Т к{^ - х'? -
D.13.25)
где М = /2//j — увеличение (см. гл. 2) афокальной системы (у фо.
кусное расстояние второй линзы; рис. 4.20) (см. гл. 2), а
D.13.26)
Входная
плоскость
Транспарант
Выходная
плоскость
Рис. 4.20. Схематическое представление афокальной оптической системы, включающей
в себя транспарант. Изображение точких'> у' во входной плоскости описывается функ-
функцией К (х/М - х'', у /М - у' ) [см. выражение D.13.25)]. В этой системеМ =f2/fv
4.13. Распределение поля в окрестности фокуса 305
Следовательно, каждый транспарант соответствует вполне опреде-
определенному линейному интегральному преобразованию поля Е\ Это
свойство используется, в частности, для преобразования полей Е' с
однородной интенсивностью и неоднородной фазой в поля Е" с неод-
неоднородной интенсивностью. Таким образом, возможна визуализация
фазовых изменений. Этот метод впервые был предложен Цернике
(метод фазового контраста, метод полос или метод теневого изобра-
изображения). Высокой степени развития достигли другие методы, служа-
служащие улучшению качества изображения и использующие корреляцию
оптического сигнала, которые привели к возникновению новой облас-
области когерентной оптики [25, 26]. (Дополнительные подробности по
этому вопросу изложены в разд. 4.15.)
4.13.4. Фокусировка линейно-поляризованных плоских волн
На основе полученных выше результатов мы изучим здесь поведение
поля Е(г) в фокальной области апланатической линзы (см. гл. 2) в тех
случаях, когда источник излучает линейно-поляризованное поле Е{ [24,
27, 28]. Для этого подставим правую часть выражения D.13.8) в
D.13.22) и, таким образом, для круглого зрачка с полуапертурой 0макс
получим
Е(г) = ^ йф | ьтвдо(в) х
Jo
• sin0cos@ - ф)
*«^J Х
x 1фф + §(z x фу] • E{d9. D.13.27)
Здесь мы опустили несущественный фазовый множитель ехр(— ikV0).
Если вектор Е} параллелен оси х, то мы имеем
1фф + 0(? х </>)] • Е, = {[cos0 + A - cos 0)sin2 ф]х +
+ A - cos0)sin0cos<?>> + sin0cos<?z}?i. D.13.28)
Подставляя выражение D.13.28) в D.13.27) и предполагая, что ам-
амплитуда излучаемого поля зависит только от расстояния й, т. е.
Е{ = EiifsinO), можно показать, что поле Е удовлетворяет соотноше-
соотношению
Е = М{[/0 + /2 cosB^)]x + /2 ьтBф)у + 2\lx cos ф ?}, D.13.29)
где А = тг/Е;(О)/Х и
Гвмакс /vsin9\ ( cos0 \
/i№«»;flUc)= яМтътзА-^-к- ехр -Ш-t-j- &W0 )de.
Jo \slntW/ \ Sln Рмакс /
D.13.30)
306 Гл. 4. Основы теории дифракции
Здесь предполагается, что величины /@) = Е{(в)/Е{@)9 Ьо =
= sin0(l + cos0), bx = sin20, b2 = sin0 A - cos0) и WO зависят только
от 0. В частности, для и = 0, т. е. в фокальной плоскости z = 0, и
для Wo = 0 (линз без аберраций) все три интеграла /0, IY и /2 вещест-
вещественны, а компонента ?*г сдвинута по фазе на 90° по сравнению с Ех и
2?г Следовательно, поле является эллиптически-поляризованным в
плоскости, перпендикулярной фокальной. Кроме того, вдоль оси у
(при ф = тг/2), т. е. в направлении, перпендикулярном поляризации
падающего пучка, поле в фокальной плоскости поляризовано линейно.
На оси системы v = 0 и, как следствие, 1Х = /2 = 0 из-за равенства
нулю величин /j(O) и J2@). Поэтому на оси вращения в пространстве
изображения поле поляризовано в том же направлении, что и падаю-
падающий пучок.
В соответствии с выражением D.13.29) усредненные по времени
плотности энергии электрического we и магнитного wm полей записы-
записываются в виде
2|/о|2 + 4|/1|2cos2iA + \12\2 + 2cosB^)Re(/0/f)] =
= wm(*,t^ + 7r/2). D.13.31)
Буавен и др. [27] вычислили /0, /р /2 для случая/@) = 1 (однород-
(однородно облучаемый выходной зрачок), go@) = (sin0I/2 (апланатическая лин-
линза) и 0макс = 45°. Они обнаружили, что распределение энергии электри-
электрического поля в фокальной плоскости несимметрично относительно по-
поворота. Контуры равной энергии при v >-4 приближенно совпадают с
эллипсами, главные оси которых направлены вдоль электрического
вектора падающей волны. Плотность энергии равна нулю только
вдоль меридиональной линии ф = тг/2 (т. е. вдоль оси у), а в направ-
направлении ф = 0 (ось х) имеет последовательность отличных от нуля ми-
минимумов. На рис. 4.21 изображены контуры энергии электрического
поля в меридиональной плоскости ф = 0. Хотя можно показать, что
минимумы вдоль оптической оси и = 0 равны нулю при ф = 7г/2, в
случае ф = 0 это не так. В фокусе мы имеем Еу = Ez = 0 и
хмакс= Шо@,0; 0макс) = (inflk)E& [I -(cos
1
D.13.32)
Из других результатов можно отметить тот, что при 0макс = 45°
величина Ez достигает максимального значения 0,28 Е*?шс в азиму-
азимутальном направлении 0, тг в точке v г 2,25 (примерно половина дли-
длины волны от оси). Это означает, что для больших апертур амплиту-
амплитуды продольных составляющих поля почти такие же, как и у попереч-
поперечных. На рис. 4.21 представлены линии тока усредненного по времени
4.13. Распределение поля в окрестности фокура
307
Фокальная
плоскость
Оптическа*
ось
Рис. 4.21. Линии тока вектора Пойнтинга вблизи фокуса апланатической системы с
угловой полуапертурой 45°. (Из работы [27].)
вектора Пойнтинга (см. разд. 1.8) для условий освещения, рассмот-
рассмотренных выше. В частности, видно, что вблизи фокальной плоскости
эти линии образуют серию завихрений* формирующихся вокруг самой
фокальной плоскости.
4.13.5. Фокусировка пучков с малой апертурой
В случае когда углы 0макс достаточно малы @макс < 5°), интегралы 1Х
и /2 становятся пренебрежимо малыми, так что поле Е s iAIox ока-
оказывается линейно-поляризованным, и скалярная теория дает описание
в хорошем приближении. Точнее говоря, если для общности отказать-
отказаться от предположения о независимости Wo от ф, то выражение
D.13.29) остается в силе при 1г = /2 = 0 и использовании вместо /0 ве-
308 Гл. 4. Основы теории дифракции
ЛИЧИНЫ
I{U, V, в^
о2 Г2
Jo
х 0/@,<?)ехр ii^cos(<? - ф) - ikW0 + ю-^- \d&,
J° L 2 JD.13.33)
где 0 ш 0/0макс, /(9, ф) ш ?".(9, Ф)/Е{@, 0). Таким образом можно
учесть возможную несимметричность относительно вращения началь-
начального распределения амплитуды поля. Существенным является вывод
о том, что / оказывается не зависящим от ф, если /и Wo не зависят
от ф. Это означает, что начальная симметрия поля сохраняется в фо-
фокальной области. Для.больших 0макс это неверно, на что указывают
стоящие в выражении D.13.29) множители перед 1Х и /2, зависящие от
угла.
Для малых чисел Френеля (Ne ^ 1) выражение D.13.33) уже непри-
неприменимо. Ли и Вольф в 1984 г. показали, что несмотря на это симмет-
симметричные относительно вращения поля все же могут быть представлены
в виде интегралов, аналогичных D.13.33). Для этого оптические коор-
координаты и и v нужно заменить на новые величины
wN = u/[l +* г//BтгЛГе)} и vN = v/{\ + м/BтгЛГе)}.
Как мы уже показали в разд. 2.15, для малых круглых апертур
функция аберраций сводится к первичным аберрациям Зайделя, и мы
"Т ) - -Sffl+y
Т* -
D.13.34)
причем оси х и у мы сориентировали таким образом, чтобы х0 = 0.
Здесь функции №пт)@) представляют собой полиномы Цернике (см. гл. I
в книге [11], цитируемой в гл. 1 настоящей книги), нормированные
условием /^w)(l) = 1. Как следствие, коэффициенты В, С, D, Е и F яв-
являются мерой отклонения фазы боковых лучей относительно фазы
главного луча. В частности, эти пять коэффициентов описывают соот-
соответственно сферическую аберрацию, астигматизм, кривизну поля,
дисторсию и кому.
Интеграл I(u, v, ф, 0макс) вычислял Ниджбоер для различных типов
малых первичных аберраций. Для сферических аберраций фокальное
распределение двумерного поля может быть выражено через функции,
исследованные Перси (разд. 5.5). В гл. IX книги Борна и Вольфа [11]
(см. гл. 1 настоящей книги) можно найти строгое описание аналитиче-
4.13. Распределение поля в окрестности фокуса
309
Рис. 4.22. Дифракционная картина при падении плоской волны на кольцевое отверстие,
получаемая на расстоянии, соответствующем числу Френеля, равному 15. Отношение
внутреннего диаметра к внешнему равно 0,8. Трехмерный график был построен при ис-
использовании улучшенного алгоритма быстрого преобразователя Фурье. (Из работы
[28а].) © North-Holland, Amsterdam, 1984.
ских методов и специальных функций, используемых для вычисления
интеграла /. Здесь мы хотим лишь подчеркнуть, что в ряде случаев /
можно вычислить с использованием асимптотических формул, рас-
рассматриваемых в разд. 5.2 и 5.8. Результат численного расчета рас-
распределения интенсивности вблизи фокальной плоскости методом
быстрого преобразования Фурье представлен на рис. 4.22.
4.13.6. Распределение поля вдоль оптической оси
для гауссова пучка с ограниченной апертурой
Для гауссова пучка {/(в) = ехр[-02/B52)]), обрезанного при в = 0макс в
случае Wo = 0, можно показать, что на оптической оси /? = у = 0
/(п,О;0макс) = |/|ехрГ-ш/Й«- Щи) - т/Т\, A4.13.35а)
310
где
Гл. 4. Основы теории дифракции
Q4 ехр(-03ме/Д2)+ 1 -
= ^макс"
A4.13.356)
макс /"
ф(п)= -я/2 + arctg __
Поведение фазового фактора Ф(м) вблизи фокуса и = 0 связано с
фазовой аномалией поля Гуи, о которой мы уже упоминали в конце
разд. 2.9. На рис. 4.23 изображены функции Ф(и) для разных значений
параметра 0^/S2. Для 5 > 0макс (однородное освещение) Ф(«) пред-
представляет собой ступенчатую зависимость с амплитудой скачков тг/2
около средних значений 0 (при и < 0) и - тг (при и > 0). В противопо-
противоположном случае @макс > 6) осцилляции исчезают и переход от 0 к — тг
становится гладким. Это позволяет заключить, что фазовые осцилля-
осцилляции связаны с освещением границы апертуры. В общем случае они
становятся несущественными, если поле на выходном зрачке доста-
достаточно «сужено» по сравнению с размером зрачка. Во всяком случае
убывание Ф(и) на тг при переходе через фокус соответствует скачку на
тг, полученному ранее в разд. 2.9 в рамках геометрической оптики.
Интенсивность, пропорциональная I/I2 в выражении D.13.356),
сводится к зависимостям 1/(й_= 0)l2 [sin(w/4)/(w/4)]2 при 5/0макс -* оо
(однородное освещение) и \1(п = 0I2/A -h uty/O^J при 5/0макс — о
(большая по сравнению с размером гауссова пятна апертура). Поэто-
Поэтому если мы ограничим максимгшьно допустимую потерю интенсивно-
интенсивности при острой фокусировке величиной 20%, то нормированная глуби-
глубина резкости нмакс окажется равной 3,2 для однородного случая и при-
примерно 0,50^/S2 при освещении гауссовым пучком, слабо возмущен-
возмущенным выходным зрачком. Если обозначить через N = ^/(Х/) число
Рис. 4.23. Фазовые аномалии для гауссова пучка вблизи фокуса. Сплошная кривая —
однородная волна; штриховая кривая — 0^ = 2б2; штрихпунктирная кривая —
0^ = бб2; здесь вт — апертура пучка, ограниченного круглым отверстием, a V2 8 — эф-
эффективная апертура гауссова пучка.
4.13. Распределение поля в окрестности фокуса 311
Френеля для видимой из фокуса круглой апертуры радиусом а, то для
однородно освещаемого зрачка глубина резкости запишется в виде
'*макс I = %кс/(*ЧА2) = "максХ/B^Г«П2вмакс) =
= «максМгтго2//2) = O,51//7Va. D.13.36)
Если Ne мало, то глубина резкости сравнима с/, что противоречит
нашему неявному начальному предположению о локализации фокаль-
фокальной области вдали от волнового фронта. Ли и Вольф [29] [см. также
работы Эрккилы A981) и Ли и Вольфа A984), приведенные в библио-
библиографии к данной главе] тщательно исследовали эту задачу и показали,
что максимум интенсивности достигается на расстоянии z от гауссова
изображения, причем
z = -//A + 0t82N2). D.13.37)
4.13.7. Распределение поля в фокальной плоскости
для гауссова пучка с ограниченной апертурой
В оптической системе без аберраций (Wo = 0), освещаемой гауссовым
пучком, обрезанным при в = 0макс, в случае малых бмакс, для которых
были получены все результаты предыдущего раздела, изображение в
фокальной плоскости (и = 0) записывается в виде
м
f(®)J0(v®)®d®, D.13.38)
Jo
что нетрудно получить с помощью выражения D.13.30). Для гауссова
пучка (см. работу Федорова и др. A984), приведенную в библиографии
к данной главе), имеющего вид
2 Г
MaKCJo
можно использовать разложение A0.2.37) из гл. II справочника Стега-
Стегана и Абрамовица [4] (см. литературу к гл. 2 настоящей книги) и запи-
записать следующее выражение:
D-13.39)
где 1п + 1/2 — модифицированные функции Бесселя порядка п + 1/2;
здесь мы использовали соотношение между полиномами Цернике и
Лежандра, а именно R$(O) = РпB92 - 1). Подставляя разложение
312 Гл. 4. Основы теории дифракции
D.13.39) в выражение D.13.38) и используя результат задачи 27, имеем
**ы -21p.¦oVl'^/fff'":'M: D13Ж|>
ы
i(U,U, c/MaKJ
здесь #(*;) — импульсный отклик, который мы обсудим ниже в
разд. 4.15. В частности, для 0макс/б = 0 можем написать
K(v) = 2Jx(v)/v. D.13.41)
Квадрат величины K(v) дает известное распределение Эпри. Таким
образом, распределение интенсивности в фокальной плоскости одно-
однородно освещаемой идеальной оптической системы имеет центральное
пятно, нормализованный радиус которого v0 = 3,8 совпадает с пер-
первым нулем функции Jx(v)\ это пятно содержит около 84% всей сфоку-
сфокусированной энергии и называется диском Эйри.
4.13.8. Разрешающая способность
Пусть две плоские волны распространяются под углом в друг к другу
и образуют дифракционную картину. Если нормализованное расстоя-
расстояние между соответствующими дисками Эйри равно v, то легко пока-
показать, что в параксиальном приближении выполняется соотношение
v = irDd/\9 где D — диаметр выходного зрачка. Общепринято опре-
определять предел разрешения как расстояние t>, при котором центр диска
Эйри от одного источника совпадает с первым темным кольцом от
другого (критерий разрешения Рэлея). Это соответствует угловому
разрешению
вМИН = 1.22Х/Л. D.13.42)
[Полезно заметить, что оптическая координата v дается выражени-
выражением v = 2Tr(NeNv)l/29 где Ne — число Френеля выходного зрачка, опре-
определенное в разд. 4.13.6, a Nv — число Френеля, относящееся к диску в
фокальной плоскости с нормализованным радиусом v, который наб-
наблюдается с выходного зрачка. Число Френеля диска Эйри примерно
равно А^Эйри = O,36/7Ve.] Выражение, аналогичное D.13.42), можно по-
получить и для микроскопа, применяя рассмотренный выше метод к ин-
интегральному представлению [выражение D.15.6)] изображения предме-
предмета, создаваемого на конечном расстоянии изопланатической оптичес-
оптической системой. Оставляя этот вывод читателю, который может вос-
воспользоваться несколькими учебниками, мы приведем лишь конечное
выражение для предела разрешения микроскопа в плоскости предме-
предмета:
4иин = 0,6U0/(h sina), D.13.43)
где а — половинный угол конуса лучей, собираемых линзой из акси-
4.14. Преобразование дифракционных интегралов к контурным 313
альной точки предмета, \ — длина волны в вакууме, п — показатель
преломления среды, в которую помещен объектив (воздух или масло).
При выводе критерия Рэлея использовалось существенное предпо-
предположение о том, что распределение интенсивности изображения двух
точек йвлялось суперпозицией двух соответствующих распределений
интенсивности. Это означает, что фазы излучения от двух предметов
преполагаются некоррелированными. Хотя для телескопов это усло-
условие, как правило, выполняется, в микроскопии оно, вообще говоря,
неверно. Эта проблема была продробно рассмотрена с учетом частич-
частичной когерентности освещающего предметы излучения, что привело к
различным критериям разрешения [30].
4.14. ПРЕОБРАЗОВАНИЕ ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ
К КОНТУРНЫМ
В тех случаях, когда область поля ограничена апертурой, для удобст-
удобства вычислений и для более ясного интуитивного представления дифра-
дифрагированной волны удобно выразить двумерные дифракционные инте-
интегралы через интеграл по соответствующим контурам, ограничиваю-
ограничивающим апертуры. Для этого можно использовать свойства вектора
Гельмгольца [выражение D.2.11)], рассматриваемого в виде функции
координаты г', для заданной координаты г точки, в которой опреде-
ЛЯвТСЯ TTOJTG
у(г') = G(r'jr) rw(r,) _ й(г>)p'G(r',r)v D.14.1)
Этот вектор удовлетворяет соотношению V ¦ v = 0 [выражение
D.2.12)] в области, не содержащей точки г и сингулярностей (источников)
поля. Это позволяет ввести векторный потенциал w(r') так, чтобы
v(r') = Г х w(r') + F'/(r'), D.14.2)
где /— функция, удовлетворяющая уравнению Пуассона V2/(r') = 0
в области, в которой функция v регулярна, так что функция / учиты-
учитывает сингулярности V.
Вектор w, разумеется, нельзя определить однозначно. Если доба
вить к данному w градиент произвольной скалярной функции Л (г7), то
ротор нового потенциала w' = w 4- V h будет вновь равен V х w.
Как будет ясно в дальнейшем, эта неоднозначность не мешает исполь-
использовать w для определения поля, дифрагированного на апертуре. С по-
помощью D.14.2) дифракционный интеграл D.2.10) можно теперь пере-
переписать в виде
"(г) = JJv(r') ¦ Й0А4 = jJ[V' х w(r')] - Й0Л4 =
Л Л
= HV/(r') • nodA = $ w(r') • d\ + и'(г), D.14.3)
А дА
314 Гл. 4. Основы теории дифракции
где использовано предположение о равенстве нулю поля на некоторой
поверхности, удаленной от апертуры А. В этом выражении ЪА пред-
представляет собой границу апертуры А, ориентированную таким обра-
образом, что положительным направлением движения по контуру считает-
считается то, при котором обход совершается против часовой стрелки при
наблюдении со стороны внешней (по отношению к г) нормали п0.
Функция w(r') зависит от сингулярностей функции w(r') на А. Таким
образом, поле и (г) можно рассматривать как суперпозицию волны,
приходящей от границы апертуры, с волной, которая зависит только
от поля во внутренней области.
4.14.1. Историческое отступление
Представление поля в виде контурного интеграла основывается на на-
наших интуитивных знаниях о том, какое влияние оказывают границы
апертуры. Из эксперимента известно, что при наблюдении из области
тени границы освещаемой апертуры кажутся светящимися. Это наб-
наблюдение обсуждалось уже Ньютоном, который объяснил его отталки-
отталкиванием корпускул света границами [И. Ньютон, «Оптика», кн. 3, наб-
наблюдение I, рис. 1 и 2]..Позднее Юнг сформулировал волновую тео-
теорию, согласно которой дифрагированная волна образуется при отра-
отражении падающей волны на элементах границы, вызывающей дифрак-
дифракцию. Френель же объяснял дифракционные эффекты на основе прин-
принципа Гюйгенса; если поле определяется в столь далекой области от ге-
геометрической тени, что открыты фактически все зоны Френеля
(см. разд. 4.2.2), то освещенность остается той же самой, что и в от-
отсутствие препятствий. И наоборот, если поле определяется в точке,
лежащей глубоко в области геометрической тени, то вклад от колец
низкого порядка отсутствует. Как следствие, сумма вкладов от ча-
частично освещенных колец равна приблизительно нулю, поскольку по-
поле каждого из них компенсируется входящими с другим знаком поля-
полями от половинок ближайших соседей. В промежуточной области меж-
между светом и тенью из-за суперпозиции полей от разных колец можно
ожидать осциллирующего поведения интенсивности.
В 1896 г. Зоммерфельд [31] получил строгое решение задачи о диф-
дифракции на полуплоскости. Используя его результат, можно показать,
что суммарное поле состоит из волны, полученной в приближении
геометрической оптики, и волны, дифрагированной на границе. Впос-
Впоследствии, в 1917 г., Рабинович заново рассчитал скалярный дифракци-
дифракционный интеграл для произвольной апертуры, освещенной сферической
волной, а также показал, что его можно представить в виде интеграла
4.14. Преобразование дифракционных интегралов к контурным 315
по контуру и поля, полученного в приближении геометрической опти-
оптики.
Параллельно этим исследованиям Келлер с успехом обобщил поня-
понятие луча, включив в рассмотрение и лучи, дифрагированные на грани-
границе апертуры. Келлер вывел свои результаты, исходя из обобщенного
принципа Ферма, применимого для лучей, попадающих в точку наб-
наблюдения с границы апертуры, и, подчеркивая геометрическую основу
такого подхода, назвал его геометрической теорией дифракции
(см. гл. 6). Эта теория оказала значительное влияние на современную
теорию дифракции, позволив, в частности, выйти за пределы скаляр-
скалярной теории и отказаться от приближения Кирхгофа, состоящего в
предположении о том, что поле на апертуре равно своему значению в
отсутствие экрана при наличии тех же источников. Кроме того, гео-
геометрическая теория дифракции позволяет учесть различные возмож-
возможные формы и электрические свойства клиньев (кромок), ограничиваю-
ограничивающих апертуру. Эта теория применима также для описания дифракции
на гладких препятствиях, освещаемых скользящим пучком, т. е. она
применима в случаях, когда возбуждаются поверхностные волны.
4.14.2. Векторный потенциал сферических волн
Рассмотрим векторное поле Гельмгольца v(r') и расположим начало
координат в точке наблюдения Р. Нетрудно доказать, что [33]
v(r') = Г х w(r') + u@) V'(-ЦY D.14.4)
w(r') = - (*' tr'
x\(tr')dt. D.14.5)
Действительно, вычисляя ротор вектора w, получаем следующее вы-
выражение:
V х w = - t F' х [г' х v(rr')] dt=\ t\ 2v(tr') + t—v(rr') \dt =
Jo+ Jo+ L dt J
= f2
= у(г') - 0+2v(r'0+) = v(r') - m@) ^(^l D.14.6)
= f2v(rr')
где использовано определение D.14.1) и векторное тождество
V х [г х v(fr)] = [v(*r) • F]r - y(tr) F • г - (г • V)\(tr) + r[F • v(tr)] =
= v(tr) - 3v(rr) - tjtv(tr) = -2v(tr) - r^v(rr). D.14.7)
316 Гл. 4. Основы теории дифракции
Применяя затем выражение D.14.1), т. е. записывая
v(r') = -w(r') V'le-ikr>/Dnr')] + le~ikr'/Dnr')] P'u(r'), D.14.8)
с помощью подстановки этого выражения в D.14.5) нетрудно пока-
показать, что
w(r')=-^x Г e~iktr'Vu{trf)dL D.14.9)
4л Jo
В случае когда поле создается сферической волной, выходящей из
точки Rs, u(tr') = ехр(- /&5)/Dто), где S = tx' - Rs и s = I si явля-
является функцией величины t. Поскольку г' х S = (Rs x r')/(sr'), выра-
выражение D.14.9) преобразуется к виду
(л e~\
Далее можно показать, что подынтегральное выражение в этой фор-
формуле является полным дифференциалом (см. гл. I в книге Борна и
Вольфа [11], с. 410 русского издания, цитируемой в литературе к гл. 1
настоящей книги):
где $ __ уГ0Л между векторами виг' (рис. 4.24). Отсюда следует, что
г' х s' ?>-*<''+в#> г' х Rs u@)
w(r)= — —,-^г-т-, тъ rVr^' D.14.12)
r's' + r' • s' 4nr's' r'Rs - r' • R Anr' v
где s' = r' — Rs. Векторный потенциал становится сингулярным, ес-
если точка г' лежит на векторе Rs, соединяющем источник с точкой наб-
наблюдения Р. Таким образом, функция w сингулярна только в тех случа-
случаях, когда г лежит в области, достижимой лучами, выходящими из ис-
источника и проходящими сквозь апертуру.
Используя затем простые векторные преобразования, можно пока-
показать, что
так что выражение D.14.4) можно заменить на v(r') = V х w0, где
w0 = - (г' х e')e-*<''+*'>[4TrV(rV + г' - s')]-1. Используя ци-
цилиндрическую систему координат, у которой ось z параллельна векто-
вектору -Rs, мы имеем (рис. 4.24,6)
v(r') = Г х lwo(p,z)j>] = -(дщ/дг)р - A/р)(д/др){рщ)п0, D.14.14)
где $ = z х р — единичный вектор, перпендикулярный оси z и векто-
вектору р, a ft0 = - Rs. Кроме того, рассмотрим диск Д, имеющий радиус
р*, перпендикулярный вектору Rs и расположенный в точке пересече-
4.14. Преобразование дифракционных интегралов к контурным
317
в
Рис. 4.24. Геометрические представления, связанные с преобразованием поверхностного
дифракционного интеграла к интегралу по контуру.
ния Rs с апертурой. Тогда с помощью D.14.14) можно написать инте-
грал
v • nodS = 2np*wo(p*,z) - Inlimpw0(p,z), D.14.15)
JJ p-o
Л
который стремится к нулю при р* —• 0. С учетом этих результатов
мы имеем [см. D.14.4)]
vno<*S= vnodS+
А-А
= (J)wo-tfl-d)wo-<fl+
ъа ед
D.14.16)
318 Гл. 4. Основы теории дифракции
Здесь при наблюдении _из точки Р обход по замкнутым контурам дА
(граница апертуры) и дА (граница диска) производится против часовой
стрелки. Если р* — 0, то
• n0 dS = ф w0 • d\ — lim ф w0 • Л = ф w0 • <fl + 2n lim p*wo(p*, z).
e*!* ^°L I "*"° D.14.17)
Последнее выражение следует из определения w0, использованного в
D.14.14).
Кроме того, для вектора г', соединяющего точку Р с границей дис-
диска ЗА, имеем Ir' x s'l = R.p*, так что можно написать
s
s] e
2пр*щ = J-]rxs] e _> T^e~ikRs- D.14.18)
Наконец, переходя к сферическим координатам, получаем окончатель-
окончательное выражение:
# +с,Ub,P)^p,^
где ф — угловая координата, соответствующая вращению против ча-
часовой стрелки вектора г', соединяющего точку наблюдения Р с грани-
границей апертуры, а в' — угол, образуемый векторами г' ив'. Множи-
Множитель С равен единице в освещенной в приближении геометрической
оптики зоне и нулю в области тени и определяет таким образом поле
ug. Мы показали, что результирующее выражение D.14.19) получается
из выражения D.14.17), причем
(г' х s') х d\f Rsp'2 d(p 1 - cos в''.
r'sVs' + г'. 8')=->УJA+ cos V) = *T~#' DЛ4'20)
где все переменные со штрихом относятся к границе апертуры. Поле
иъ(Р) представляет собой вклад волны, дифрагированной на границе.
В тех случаях, когда сферическая волна сводится к плоской
[ехр(— /к ¦ г')], можно показать, что выражение D.14.19) принимает
вид
1 С2п
= Ce-ikr-i-\ A-
47tjo
м(г) = Ceikr - — A - cos0>-'krA+cose)# = ug + мь. D.14.21)
С физической точки зрения поле в г представляет собой суперпози-
суперпозицию поля и% в отсутствие экрана и поля граничной дифрагированной
волны (ГДВ), распространяющейся от краев апертуры. В области те-
4.15. Изображение при когерентном и некогерентом освещении 319
ни первое слагаемое в D.14.21) исчезает, так что полное поле совпада-
совпадает с иъ.
Применимость данных выше выражений строго доказана для сфе-
сферических волн. Однако можно показать [32], что они могут быть ис-
использованы для оптических лучей в пределе малых длин волн.
В разд. 5.10 мы будем пользоваться ГДВ-представлением полей, ди-
дифрагированных на апертуре, для получения асимптотического разло-
разложения в пределе малых длин волн.
4.15. ИЗОБРАЖЕНИЕ ПРИ КОГЕРЕНТНОМ
И НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
Идеальную систему формирования изображения математически мож-
можно описать как отображение точек из плоскости предмета По, распо-
расположенной в пространстве предмета Ео, в точки плоскости IIj в про-
пространстве изображения L{. В присутствии аберраций для конечных
длин волн и ограниченного зрачка одиночный точечный источник,
расположенный в точке (*0, у0), образует распределение поля К(х, у;
х0, у0), называемое импульсным откликомх\ который отличается от
дельта-функции 5B>(лг - х, у — у), имеющей ненулевое значение в точ-
точке (х, у) гауссова изображения предмета. Это означает, что аберрации
и дифракция нарушают взаимно-однозначное соответствие между Ео и
Ej. Если же с помощью высококачественных составных линз и умень-
уменьшения апертуры инструментального зрачка удается исключить абер-
аберрации, то импульсный отклик определяется лишь дифракционными
эффектами; в этом случае говорят, что оптическая система является
дифракционно-ограниченной.
Отличие К от дельта-функции приводит к определенной неодно-
неоднозначности при восстановлении предмета по изображению. На это ука-
указывает, например, тот факт, что два точечных источника при наблю-
наблюдении через один оптический прибор различимы по отдельности толь-
только в том случае, когда расстояние между ними больше некоторой ве-
величины W. При этом W можно оценить как поделенный на увеличе-
увеличение размер области в плоскости Ц, в которой К существенно отлична
от нуля. Как мы увидим ниже, параметр W, определяющий мини-
минимальное разрешимое прибором расстояние, линейно уменьшается с
уменьшением длины волны. Таким образом, чем выше частота, тем
лучше разрешающая способность. Этим объясняется популярность
синхротронных источников, с помощью которых получают высокие
*) Функцию К{х, у; xQy у0) называют также функцией пропускания (см. книгу Борна
и Вольфа [41 , с. 442 русского издания], приведенную в литературе гл. 1 настоящей кни-
книги). — Прим. перев.
320 Гл. 4. Основы теории дифракции
потоки энергии в диапазоне УФ, ВУФ и мягких рентгеновских лучей.
Это позволило создать системы для получения изображения с разре-
разрешением лучше чем 0,1 мкм, т. е. с характерным размером, используе-
используемым в микроэлектронике для фотолитографического производства
сверхбольших интегральных схем (СБИС), имеющих расстояния меж-
между смежными элементами всего лишь ~ 0,2 мкм.
Изображение регистрируется прибором (например, человеческим
глазом, фотографической эмульсией, мозаичными твердотельными
детекторами микроскопа), который реагирует только на интенсив-
интенсивность. Кроме того, фазы точечных источников, образующих «пред-
«предмет», в некоторых случаях оказываются пространственно-некоррели-
пространственно-некоррелированными. В этих случаях линза служит лишь для установления со-
соответствия между распределениями интенсивности в двух сопряжен-
сопряженных плоскостях. Отличая случаи фазово-коррелированных и некорре-
некоррелированных источников, мы будем говорить соответственно о коге-
когерентном и некогерентном изображении, В реальной жизни мы часто
имеем дело с оптическими полями, которые являются частично кор-
коррелированными. Например, в микроскопах обычно используется облу-
облучение светом, который не полностью когерентен. При этом требуется
применение точного анализа, связанного с преобразованием корреля-
корреляционных функций [34] (см. разд. 1.8).
Анализ корреляционных функций стал предметом современной ра-
радиометрии, значительное развитие которой за последние 20 лет связа-
связано с космическими программами, где необходимы точные радиомет-
радиометрические измерения. В то время как классическая радиометрия осно-
основывалась главным образом на измерении средней спектральной плот-
плотности излученной энергии, эксперименты по измерению когерентно-
когерентности первого и второго порядка (разд. 1.8) открыли новые перспекти-
перспективы, связанные с разработкой систем, в которых используются лазеры.
В настоящее время мы находимся на той стадии, когда радиометрия
вовлекает в себя квантовую теорию когерентности. Это основано на
развивающемся начиная с 1963 г. (работы Глаубера [35] и Сударшана
[36]) квантовостатистическом описании полей излучения. Глаубер ввел
в квантовую электродинамику так называемые когерентные состоя-
состояния поля, переходящие при «обращении в нуль» постоянной Планка
(что соответствует большому числу фотонов в поле) в классические
синусоидальные колебания вектора поля с данной амплитудой и фа-
фазой, которые записываются в виде E(r, t) = ?"оехр( — /к • r)exp(/w/.).
Полезным аналитическим методом статистического описания кванто-
квантованного поля является Р-представление, которое в классическом пре-
пределе соответствует распределению плотности вероятности для ком-
4.15. Изображение при когерентном и некогерентом освещении 321
плексной амплитуды а = li?0Jexp(/<?). Детальное обсуждение теории
квантовой когерентности не входит в задачу этой книги. Заинтересо-
Заинтересованному читателю мы рекомендуем обратиться к соответствующим
монографиям и обзорным статьям (см., например, [37—39] и др.).
4.15.1. Импульсный отклик и передаточная функция точки
Пусть единичный точечный источник (д^, yQ9 Zq) создает сферический вол-
волновой фронт, который преобразуется составной линзой в волну, сходя-
сходящуюся к точке параксиального изображения (х, у, z). Используя инте-
интеграл Лунеберга — Дебая D.13.19), импульсный отклик К(х, у; д^, у0) в
плоскости Ц можно записать через интеграл по поверхности волнового
фронта сходящейся волны следующим образом:
К(х,у; хо,уо) = ехр(-ВД II P(p,q)A(p,q) X
х e\p[i(vxp + vyq) - ikW0(p,q; xo,yo)] dpdq, D.15.1)
где vx = k(x - х)ЧА и vy = k{y - у)ЧА — оптические ^еоординаты
точки (х, у) относительно параксиального изображения (х, у), ЧА —
числовая апертура линзы в пространстве изображения, Р — функция
зрачка, а р и q пропорциональны направляющим косинусам нормали
к сходящемуся волновому фронту в пространстве изображения, при-
причем /т2 + ф = 1 на окружности наибольшего диаметра, содержащейся
в выходном зрачке. Функция аберраций Wo равна расстоянию от ис-
истинного волнового фронта на выходном зрачке до гауссовой опорной
сферы (см. разд. 2.15.4), выбранной таким образом, чтобы Wo = б
для лучей, проходящих через параксиальное изображение. Vo =
= V(xo> Уо> х> У) ~~ оптическая длина между точкой (х0, у0) и ее гаус-
гауссовым изображением. В параксиальном пределе Ко можно приближен-
приближенно записать в виде
V0(x09y0; х,у) = F0@,0; 0,0) + (х20 + y20)/Bd0) + (х2 + y2)/Bd) =
= Fo@,0;0,0) + [l/Bte)](»k + v2Oy + v2x + v% D.15.2)
где d0 и d — расстояния от предмета и изображения до соответствую-
соответствующих главных плоскостей. Величины (vOx, vOy), (vx, ^)ий = й0 явля-
являются оптическими координатами соответственно точек (х0, у0), (х, у)
и главных плоскостей. Определим функцию А (р9 q) следующим об-
образом:
A(p9q) = Rn\U(p9q)k D.15.3)
здесь R -— радиус опорной сферы, Q — телесный угол линзы в про-
пространстве изображения, a I UI — амплитуда поля на опорной сфере.
322 Гл. 4. Основы теории дифракции
Воспользуемся теперь тем, что в пространстве предмета R I U\ = 1/4тг
для единичного источника, а при переходе в пространство изображе-
изображения R I UI испытывает скачок и должно быть умножено на амплитуду
пропускания оптического прибора ТУ2(р, <7>.Таким образом,
А{р, q) = [П/Dя)] Г1'2^, q\ D.15.4)
Функция аберраций оптически центрированной системы зависит
только от трех вращательных инвариантов: ? = х% + у$, у = р2 + q2,
f = хор + yoq. Рассматривая зависимость Wo от положения точечно-
точечного источника, можно ввести несколько определений. В частности, со-
согласно Велфорду [40], «произвольная оптическая система, симметрич-
симметричная или несимметричная, называется изопланатической, если ее абер-
аберрации стационарны при малых смещениях точечного предмета». Это
означает, что в достаточно малой окрестности центра поля нет асим-
асимметрии изображения. Следовательно, должна отсутствовать круговая
кома. Можно также показать, что в осесимметричных системах от-
отсутствие комы приводит и к отсутствию сферических аберраций на
оптической оси. По аналогии с нелинейными электрическими цепями,
отклики которых зависят от уровня смещающего сигнала, нарушение
изопланатизма можно рассматривать как нелинейное поведение опти-
оптических систем. Если система является изопланатической, то ее функ-
функция аберраций Wo удовлетворяет соотношению
Woip9q;xO9yo)=Wo(P-p;<l-9)> D.15.5)
где через р и q мы^ обозначили направляющие косинусы главного лу-
луча. Подставляя Wo в интеграл D.15.1) и используя разложение
D.15.2), для прозрачного зрачка (Г = 1) получаем
К(х,у; хо,уо) = expf -ik 0^ ° - ik——— 4- ivxp + ivyqj X
Qff
4тг P^'
y9 ~ ikW0(p,q)]dpdq
-х;у-у); D.15.6)
здесь ф = A^ + 1^ + 1^ + v^)/Bu)±(vxvOx + vyvOy)/uMaKC и исполь-
использовано совпадение оптических координат сопряженных точек с точнос-
точностью до знака (см. разд. 2.15). В этом выражении vMaKC — оптическая
координата, соответствующая радиусу самой большой окружности,
содержащейся в выходном зрачке.
С физической точки зрения нас интересует интенсивность поля, по-
поэтому удобно определить так называемую передаточную функцию
точки t(x, у; х0, у0) или нормированное распределение интенсивности
4.15. Изображение при когерентном и некогерентом освещении 323
от точечного источника:
t(x,y; хо,уо) = \К(х9у; хо,уо)/К(х,у; xo,7o)l2- D.15.7)
В случае когда система является изопланатической, импульсный от-
отклик становится стационарным, т. е. он зависит лишь от расстояния
между точкой наблюдения и гауссовым изображением источника
[А: ш К(х - х, у - у)]. В частности, для дифракционно-ограниченных
приборов с прозрачным круглым и квадратным зрачком функция К
определяется соответственно следующими выражениями:
К ос 2JM/V, К ос (wLvJvJitmvJv,), D.15.8а)
где
vx = /сЧА(х + Мх0), vy = кЧА(у + Муо\ v = (vl + v*)lt2. D.15.86)
Мы видим, что К линейно убывает с уменьшением длины волны,
как уже отмечалось. Однако для систем, у которых каким-либо обра-
образом коррекция аберраций доведена до дифракционного предела,_увели-
чение частоты приводит к увеличению фазового множителя kW0, что
существенно изменяет форму импульсного отклика.
Для круглого зрачка импульсный отклик, а именно интеграл в
D.15.6), можно вычислить, используя полиномы Цернике [см., напри-
например, выражение D.13.34)]. В частности, при простой дефокусировке
этот интеграл можно выразить через функции Ломмеля (см. задачу 23).
Для квадратного зрачка при дефокусировке и наличии сферической
аберрации К можно выразить через функцию I(u, v), вычисленную
Перси (см. обсуждение в разд. 5.5). При малых аберрациях наблюда-
наблюдается уменьшение интенсивности в центральном пятне, в то время как
внешние кольца становятся более яркими. При этом размер централь-
центрального пятна существенно не изменяется. Основываясь на этом наблю-
наблюдении, Стрел в 1902 г. предложил для измерения аберраций использо-
использовать отношение максимального значения интенсивности в централь-
центральной зоне изображения точечного источника реальной системы к соот-
соответствующей величине в оптической системе без аберраций, имеющей
ту же апертуру и фокусное расстояние. Это отношение V, называемое
отношением интенсивности Стрела, фактически определяет долю
света, приходящуюся на центральное пятно. Отношение Стрела не-
нетрудно вычислить с помощью выражения D.15.6), если положить
х = у = х = у = 0, вычесть из величины WQ ее среднее значение по
апертуре _ и _ использовать для фазового множителя
ехр[- ik(W0 - (Woy)\ разложение 1 - ik(W0 - <W0))9 что допусти-
допустимо из-за малости k(W0 - <W0». Таким образом, мы получаем
= 1 - к2\ [[
DЛ5.9)
324 Гл. 4. Основы теории дифракции
В прекрасном «Атласе оптических явлений» (см. книгу [31] в литера-
литературе к гл. 2) приведены фотографии, показывающие распределения
интенсивности света при наличии различных аберраций.
4.15.2. Когерентное изображение протяженных источников
Теперь можно, используя принцип суперпозиции, вычислить поле изо-
изображения i(x, у, z), соответствующее полю протяженного предмета
о(х0, у0, Zq). При этом мы имеем
i(x,y,z) = X(x,y,z; X0,y0,z0)o(x09y0,z0)dx0dy0. D.15.10)
So
Заметим, что мы указали в явном виде зависимость /, о, К от z и
Zq для того, чтобы отметить применимость линейного соотношения
D.15.10) между полями в точках Zq и z и в тех случаях, когда плос-
плоскость z = const не совпадает с плоскостью изображения Zq = const.
Очевидно, что в этом случае функция К не представима более в виде
интеграла Лунеберга — Дебая. Вообще говоря, поскольку /(г) является
решением скалярного уравнения Гельмгольца, функция К (г; г0) должна
.удовлетворять тому же уравнению, в котором переменной является г.
Интересуясь лишь распределением интенсивностей, из выражения
D.15.10) получаем
9y,z)\2 = Ыхо4уо \dxo
l'(x,
x o(x0,y09z0)o*(x'0,y'0,z'0). D.15.11)
4.15.3. Распространение взаимной интенсивности;
теорема Ван-Циттерта — Цернике
Рассмотрим случай, когда амплитуда и фаза поля o(Xq9 yQ9 Zq) неизвест-
неизвестны точно, т. е. o(xQ9 yo> Zq) и i(x, у, z) можно рассматривать как стоха-
стохастические процессы, задаваемые своими моментами (см. разд. 1.8).
При этом важная информация связана со взаимной интенсивностью
О(х, у, z)i*(x', у', z)>, вычисляемой в плоскости z = const. Эту ве-
величину можно найти с помощью выражения D.15.10) через аналогич-
аналогичную величину в плоскости Zq = const [ср. с A.8.12)]. Таким образом,
мы можем написать
гг гг
dx'o dy'o К(х, у, z; х0, у0, z0) х
4.15. Изображение при когерентном и некогерентом освещении 325
х K*(x\y\z;xo9yo9zQ)io{x09y09z0)om(xo9y'09z0)y s
= \\dxody0K{x9y9z;xO9yO9zo)F(xO9yO9zo;xt9y'9z). D.15.12)
Если зафиксировать теперь плоскость х', у', то левая сторона это-
этого равенства становится функцией координат х, у, z9 выраженной че-
через интеграл, аналогичный интегралу D.15.10). Поскольку функция,
определяемая выражением D.15.10), представляет собой поле, удов-
удовлетворяющее уравнению Гельмгольца, мы приходим к следующему
уравнению
(д2/дх2 + д2/ду2 + d2/dz2 + fc2)<i(x,^z)i*(x',/,z)> = 0. D.15.13)
Благодаря симметрии взаимной интенсивности по отношению к
координатам гиг' аналогичное уравнение справедливо и для зависи-
зависимости </(*, у, z)/*(x', у', z)> от х', у' и z.
Важным частным случаем является случай, когда взаимная интен-
интенсивность <о(х0, уо> Zo)o*(*o> Л>> *о)> отлична от нуля лишь в столь ма-
малой окрестности точки (х0, у09 Zq)9 в которой К(х, у, z; xQ9 /Q9 Zq) изме-
изменяется очень слабо. При этом выражение D.15.12) можно приближен-
приближенно записать следующим образом:
<i(x,;y,z)j*(x',/,z)>=
оФо(,у,;о>Уо.о) X
х X*(x',/,z; xo,yOyzo)Io(xO9yo,zQ), D.15.14)
где
I0(x0,y0,z0) = <o{xo,yo9z0)o*(x'09y'o9z0)ydx'0dy'0. D.15.15)
So
Величину /0 с некоторой осторожностью можно интерпретировать
как интенсивность. Чтобы показать это, заметим, что корреляцион-
корреляционная длина взаимной интенсивности зависит от расстояний между дей-
действительными или мнимыми источниками и плоскостью предмета.
Для источников, близких к IIq, корреляционная длина существенно
уменьшается. Это имеет важные следствия: амплитуда о(х, у, z) дол-
должна стать очень большой, и поле даже локально нельзя рассматри-
рассматривать как плоскую волну, так что квадрат модуля амплитуды о(х, у, z)
не является модулем вектора Пойнтинга. В тех случаях, когда всеми
этими фактами можно пренебречь, величину /0 можно рассматривать
как интенсивность.
В качестве примера рассмотрим оптическую систему, представляю-
представляющую собой круглое отверстие в плоскости предмета. При этом К
326 Гл. 4. Основы теории дифракции
определяется выражением D.5.6), так что с точностью до несущест-
несущественного фазового множителя имеем
x Io(xO9yo,zo)dxodyo. D.15.16)
Из этого выражения следует, что корреляционная функция поля на
расстоянии d от некогерентно освещаемого отверстия совпадает с
фурье-образом освещенности этого отверстия. Этот результат, пер-
первоначально полученный Ван-Циттером и Цернике, лежит в основе
знаменитой теоремы, носящей их имя (см., например, книгу Борна и
Вольфа [11], приведенную в литературе к гл. 1 настоящей книги).
4.15.4. Исследование оптических систем
с помощью оптической передаточной функции (ОПФ)
В тех случаях, когда нужно найти распределение интенсивности
1(х, у) а </(*, y)i*(x, у)), выражения D.15.7) и D.15.14) дают
1(х> У) = ' о(*о > У о М*> У> *о»У о) dx0 dy0. D.15.17)
Для изопланатической системы этот интеграл имеет вид свертки
D.15.18)
\ 1V1 1У1 I
?6
где Eq = A^Dq. Фурье-преобразование выражения D.15.18) приводит к
соотношению
/(a,j8)ocT(a,jS)/o(a,j8), D.15.19)
где Т(а, 0) — оптическая передаточная функция (ОПФ) системы
(см., например, рис. 4.25), которая пропорциональна фурье-образу
введенной в D.15.7) передаточной функции точки t изопланатической
системы:
Т( В) = Я-^г(^^у)схр0«^ + iPvy)dvxdvy _
U"J()dd
0 + i
D.15.20)
4.15. Изображение при когерентном и некогерентом освещении
2 Я
327
Рис. 4.25. Оптические передаточные функции, связанные с некогерентным освещением
квадратного (слева) и круглого (справа) зрачков.
Этот результат получается как следствие выражения D.15.7), теорем
Парсеваля и свойств свертки. Знаменатель здесь равен площади апер-
апертуры. Для систем без аберраций интеграл в числителе связан с пло-
площадью перекрытия двух функций зрачка Р9 сдвинутых относительно
друг друга на а и /J вдоль осей х и у соответственно. Можно показать,
что наличие аберраций уменьшает ОПФ, хотя при а = ]8 = О ОПФ
всегда равна единице. Поскольку Т является фурье-образом вещест-
вещественной функции, ее вещественная часть Т является четной, а
мнимая — нечетной функцией величин а и /3. Модуль функции Т назы-
называют модуляционной передаточной функцией (МПФ). Следует заме-
заметить, что ОПФ можно определить также для фотоэмульсий, телеви-
телевизионных камер и других электрооптических приборов. Это особенно
важно при конструировании сложных электрооптических систем фор-
формирования изображения. Если любую из компонент оптической систе-
системы можно описать соответствующей ей ОПФ, то создание сложной
электрооптической системы возможно по принципу построения каска-
каскада электронных усилителей.
Нетрудно вычислить оптическую передаточную функцию круглого
зрачка в отсутствие аберраций (рис. 4.25, правая сторона):
= |B/тг)[агссо8(ш/2) - о>A - со2/4)^21 О й <о й 2,
(О в других случаях; D.15.21)
здесь со = (а2 + /?2I/2. Таким образом, для круглого зрачка про-
пространственная частота со ограничена интервалом @, 2). Безразмерная
частота со, сопряженная оптической координате v, связана с про-
пространственной частотой /, определяемой числом циклов на единич-
328
Гл. 4. Основы теории дифракции
2,0 а
Рис. 4.26. а — оптическая передаточная функция для круглого зрачка при полной разно-
разности хода за счет сферических аберраций IX; различные кривые построены для разного
положения приемной плоскости, сдвинутой на Х/4; 0; — 1,5Х; — X; — 0,5Х относительно
параксиального фокуса (из работы [41]); б — сечение ОПФ для квадратного зрачка при
расфокусировке Х/4, Х/2, ЗХ/4 и X.
ной длине, соотношением/= ?соЧА. Выражение D.15.21) указывает
на то, что дифракция света в оптической системе устанавливает верх-
верхний предел на способность системы разрешить отдельные элементы
юстировочной таблицы с нормализованной пространственной часто-
частотой более 2.
Как видно из рис. 4.26, заимствованного из работы Блэка и Линфу-
та [41], наличие аберраций существенно изменяет ОПФ. На рис. 4.26,я
штриховой кривой представлена зависимость Г(со) для линзы без абер-
аберраций. Остальные кривые соответствуют возникающей за счет
сферических аберраций разности хода IX для различных положений
приемной плоскости относительно гауссова фокуса. Следует Заме-
Заметить, что наилучшее приближение ОПФ к идеальному случаю? воз-
возможно при дефокусировке на —X. Существенной особенностью* кри-
кривых на рис. 4.26,6 является реверсия фазы изображения, т. е. отрица-
отрицательный знак ОПФ при большой дефокусировке. Более подробно ме-
метод Фурье в анализе изображений рассмотрен в работах [25, 26, 42,
43], а также к книге Мураты A966), приведенной в библиографии к
данной главе.
4.15.5, Степени свободы изоЬражения
Рассмотрим оптическую систему К без аберраций, имеющую квадрат-
квадратный зрачок и образующую прямое изображение. Для нее из выраже-
выражений D.15.8) и D.15.10) получаем
.(х rfsin^-^sin^-^ x
JJ *-*о У-Уо
-а
4.15. Изображение при когерентном и некогерентом освещении 329
,^o(x0),0)dx0^0; D.15.22)
2w "макс /
здесь ради простоты мы использовали для оптических координат обо-
обозначения обычных декартовых координат; 2 а— это выраженный в
оптических координатах боковой размер области поля предмета. Зада-
Зададимся теперь вопросом, может ли система К полностью и без искаже-
искажений воспроизвести истинное изображение предметов [44]. Для получе-
получения ответа нам необходимо найти решения записанных выше уравне-
уравнений, в которых интенсивность /(х, у) пропорциональна о(х, у). При
этом мы получим интегральное уравнение Фредгольма с симметрич-
симметричным ядром, в общем случае комплексным. Поскольку ядро факторй-
зуется в виде произведения двух функций, зависящих лишь от х и у со-
соответственно, собственные функции полученного уравнения можно
представить в виде о(х, у) = Фп(х)Фт(у), где Фл — это соответствую-
соответствующая собственному значению уп собственная функция интегрального
уравнения
В частности, для поля малого предмета, когда п > о2 и умакс > о2,
можно пренебречь фазовым множителем в приведенном ядре. Соот-
Соответствующее уравнение имеет полный набор собственных функций,
которые являются аналогом вытянутых угловых сфероидальных
функций [45] [ср. с уравнением G.16.7) в гл. 7]. Как отмечалось в ра-
работах [44, 45], для п < 2а/ж модули србственных значений почти по-
постоянны и равны тг, а для п > 2а/ж собственные значения уп резко па-
падают до нуля. Это свойство имеет существенные физические следст-
следствия. Раскладывая с использованием набора функций Фл произвольную
функцию о, имеем
o(x0Jo)= ? О...Ф.(*о)Ф.Ы. ^4Л5'24)
и,т = О
причем поле изображения i(x, у) дается выражением
*(*,}>)= I УпУтОптФп(х)Фт(у) * ? упут0птФп(х)Фт{у). D.15.25)
л,т = О л,т = О
Таким образом, можно сказать, что система К «пропускает» не боль-
больше чем Bа/*I членов из суммы D.15.24), так что вся информация, со-
содержащаяся в остальных членах, теряется. Ряд D.15.24) можно интер-
интерпретировать как разложение функции о(х0, у0) по ее составляющим в
бесконечномерном гильбертовом пространстве, в котором функции Фл
образуют базис. При этом каждый из членов ряда представляет собой
одну степень свободы предмета. Из выражения D.15.25) следует, что
330 Гл. 4. Основы теории дифракции
число степеней свободы изображения (N) не превышает (la/жI. Пре-
Преобразуя а к физическим координатам, имеем
N = Bа/жУ = С/Л? = WW* " WW** D-15.26)
здесь S — протяженность предмета (изображения), а О — телесный
угол апертуры системы [соответствующий входному (выходному)
зрачку, как его видно из плоскости предмета (изображения)]. Выраже-
Выражение D.15.26) показывает, что пропускная способность оптического
прибора увеличивается по квадратичному закону с ростом частоты из-
излучения, если только в системе нет аберраций.
Можно также показать, что величина N соответствует тому ко-
количеству элементов предмета, выбранных через одинаковые интер-
интервалы, которых достаточно для определения изображения. Следова-
Следовательно, если изображение нужно «прочесть» с помощью мозаики из Nd
микроскопических детекторов, то пропускная способность U
[см. разд. 2.15.3 и выражение B.15.29)] оптического прибора, исполь-
используемого для построения изображения, должна быть больше, чем
X2Nd. Можно показать, что проведенное в данном разделе рассмотре-
рассмотрение качественно справедливо для любой формы предмета и зрачков.
Более подробно со всеми этими вопросами читатель может позна-
познакомиться в статьях Гори и Гуаттари [46], а также Гори и Рончи [47].
ЗАДАЧИ
Раздел 4.10
1. Пусть плоский экран с прямоугольным отверстием, стороны которого а и Ь, ос-
освещается сферической волной, излучаемой точечным источником в точке 5. Докажите,
что поле вдоль нормали от S к экрану дается выражением
и(г) = и,(гХЧ0|Т«2) - FfaWfc) - F(rii)l
где t/g — поле в отсутствие экрана, F(x) — комплексный интеграл Френеля, определяе-
определяемый выражением E.3.5), и
Ъл = *2,i[2(<*s + dP)/(MsdP)y'2, ц2л = y2tll2(ds + dP)/(MsdP)V'2.
Здесь ds и dp — расстояния от точек соответственно S и Р до плоскости отверстия, а
*i, 2 и У\, 2 ~~ координаты вершин отверстия в декартовой системе координат с центром
на нормали, опущенной из S на экран.
2. Используя результаты задачи 1, покажите, что дифракционная картина в плос-
плоскости, параллельной экрану, останется неизменной, если экран сдвинуть таким обра-
образом, что его новое расстояние ds от источника равно первоначальному расстоянию dp
от плоскости наблюдения.
3. Рассмотрите плоское отверстие, облучаемое перпендикулярно плоской волной.
Пусть О — проекция из точки наблюдения на экран, а р и ф — полярные координаты с
центром в точке О. Йусть в этой системе граница отверстия задается выражением
Ф = Ф(р), где ф(р) — неоднозначная в общем случае функция координаты р, ар изменя-
изменяется от рмин до рмакс. Покажите, что дифракционный интеграл Френеля можно перепи-
Задачи 331
сать в виде одномерного интеграла по неременной р, а именно как
х /(р)ехр —-?- )pdp;
J^mhh. \Z'Z Z I/
здесь /(p) — длина дуги, полностью содержащейся в отверстии и имеющей радиус р и
центр в точке О. Найдите аналитическое выражение для/(р) в случае круглого и прямо-
прямоугольного отверстий (см. также задачу 1 в гл. 5).
4. Пусть поле, пропорциональное ехр(- 2Ьр2), освещает круглое отверстие радиу-
радиусом а. Покажите, что поле в дальней зоне G@), где в — угол между направлением наб-
наблюдения и нормалью к экрану, представимо в виде разложения Неймана [см. разд.
4.11.3а и выражение D.11.23) и уравнение D.11.24)]:
G(V)cc 2, C^s+
s = 0
где v = kasinB и
G2s-1
2s+1 e2b 2s-3
(см. работу Корнблита [18], с. 215, указанную в литературе к гл. 2 настоящей книги).
5. Пусть амплитуда освещающего круглое отверстие пучка пропорциональна
f{x) = 0,076 - 0,0441A - х2) + 0,528A - х2? + 0,44, причем х = р/а, где а — радиус
отверстия. Нарисуйте распределение поля в дальней зоне и покажите, что величина бо-
боковых лепестков диаграммы направленности составляет менее чем 4 • 10~3 величины
центрального пика (в = 0), в то время как ширина пучка почти та же, что и при одно-
однородном освещении апертуры. Приведенное здесь распределение амплитуды является
примером плавно изменяющегося освещения, используемого для ослабления боковых
максимумов дифракционной картины, т. е. для увеличения разрешения оптических при-
приборов (особенно микроскопов и телескопов), а также отражательных антенн. В оптике
изменение амплитуды освещения достигается с помощью транспарантов, расположен-
расположенных или в самой апертуре, или в фокальных плоскостях. Этот процесс называют аподи-
зацией. (См. работу Корнблита [48], в которой рассматриваются свойства заданного
здесь освещения, а также статью Жакино и» Руазен-Досье [49], в которой приведен об-
обзор по исследованию аподизации.)
6. Пусть круглое отверстие имеет в центре препятствие в виде диска. Исследуйте
свойства поля в дальней зоне, обратив особое внимание на зависимость ширины глав-
главного максимума и амплитуды первого бокового максимума от относительных размеров
препятствия. На этом примере определите накладываемые на поле освещения условия,
позволяющие уменьшить ширину пучка до сколь угодно малого значения (см. статью
Торальдо ди Франчиа [50]).
Раздел 4.11
7. Покажите, что функция Грина G в свободном пространстве может быть пред-
представлена интегралом Зоммерфельда — Отта
<Г'Г)-
~ 4п]0
4я|г-г'| ~ 4п]0 (к2-Х2I12
332 Гл. 4. Основы теории дифракции
гдей? = [р2 + р'2 - 2рр' cos(<? - ф' )]1/2, a p,z, Ф — цилиндрические координаты точки
г. Подсказка. Запишите решение неоднородного волнового уравнения в цилиндрических
координатах.
8. Используя интеграл Зоммерфельда — Огта из предыдущей задачи и разложение,
следующее из теоремы Графа о сложении функций Бесселя,
2 + р'2 - 2рр'сов(ф -<*>')]= I
т= —ао
докажите соотношение D.11.1).
9. Покажите, что в тех случаях, когда z -компоненты произвольного поля/?г h#z за-
зависят от z как е "'**, в области свободного пространства справедливы следующие соот-
ношения*
Н, = - i(o>2/c2 - XTl 1х ЪИг + (o/(C0c)z х VtEJ,
Е, = i(a,2/c2 - Х2УЧ-Х № + Мег х VtHz),
где Et = pEp 4- $Еф и Ht = рНр + $Нф — поперечные компоненты полей Е и Н в ци-
цилиндрической системе координат. Здесь Vt = рд/др + $р~1д/дф.
10. Покажите, что при х > kQi цилиндрическая волна, расширяющаяся в пустом про-
пространстве до бесконечно большого размера (р — »), может быть записана в виде
exp(-iXz + тф)Кт[(Х2 - **I/2р].
тцеКт(х) — модифицированные функции Бесселя второго рода, убывающие на беско-
бесконечности как е ~х (см. гл. 8).
11. Решите скалярное волновое уравнение в сферических координатах и покажите,
что в однородной области поле можно разложить в ряд по сферическим модам (см. в
настоящей книге гл. 2, пример в разд. 2.12.3 и раздел 6.12):
1 t
11 = 0 т=-я
Здесь Л^2) и Л^ = л?2)* — сферические функции Ханкеля второго и первого рода соот-
соответственно. Подсказка. См. гл. 6 настоящей книги.
12. Покажите, что электромагнитное поле в пустом пространстве можно предста-
представить в виде
Е = V х V х (п?) - ia>Ho V x (гм),
Н = V х V х (гм) - icos0 У х (rv),
где и и v — два решения однородного волнового уравнения, известные как потенциалы
Дебая (см. статью Паласа [17], указанную в литературе к гл. 1).
13. Используя потенциалы Дебая и асимптотическое разложение сферических функ-
функций Ханкеля, докажите, что в дальней зоне поле от источников, находящихся в ограни-
ограниченной области, можно представить в виде
е^ f t х (г х
Подсказка. Выразите поле Е через потенциалы Дебая из предыдущей задачи, а затем
разложите и и v по сферическим гармоникам ( см. уравнение A68) в работе Паласа [17],
указанной в литературе к гл. 1, а также выражения B.12.43) и F.12.26) в настоящей
книге).
14. Пусть электрический диполь J(r) = d(x)8(yN(z)z ориентирован параллельно
Задачи 333
оси z. Используя интегральное соотношение
А(г) = мо [If J(r')G(|r - r'\)dV,
связывающее векторный потенциал А с распределением тока J, и подставляя электриче-
электрическое и магнитное поля в виде функций векторного потенциала А [например,
Н = A//*) V х А], с помощью соотношения D.11.1) напишите разложение поля Н по
цилиндрическим волнам.
Раздел 4.12
15. Рассеянное на сфере поле можно представить в виде суперпозиции сферических
гармоник. С математической точки зрения выражение для поля есть ряд сферических
функций Ханкеля, умноженных на сферические гармоники Y%(в, ф). Для скалярной зада-
задачи рассеяния волновая функция может быть найдена, если наложить на полную водно*
вую функцию и (г, 0, ф) = w.(r, 0, ф) + wd(r, 0, ф) граничные условия на поверхности
сферы. Если падающая волна является плоской и распространяется вдоль оси*, а пол-
полное поле на сфере равно нулю, то покажите, что рассеянное поле можно разложить по
сферическим гармоникам следующим образом:
п-0
Раздел 4.13
16. Рассмотрите изотропный точечный источник, расположенный в фокусе аксиаль-
аксиально-симметричного параболоида с конечной апертурой. Исключая вклад лучей, покидаю-
покидающих источники и не попадающих в параболоид, вычислите в дальней зоне поле, излу-
излученное вдоль направления, образующего угол ф с осью отражателя. Подсказка. Прове-
Проведите вычисления с использованием дифракционного интеграла на апертуре параболоида
с распределением поля, которое можно найти, используя законы геометрической опти-
оптики для распространяющихся из источника сферических волн. После этого, учитывая со-
соотношение между отклонением h луча от оси и углом 0 между лучом и осью параболо-
параболоида [Л@) = 2Д1 -. cos0); см. рис. 4.17], поле в дальней зоне может быть получено из
интеграла Фраунгофера
Г
Jo
u(v) ос A + cosO)J0(vx)xdx,
где* = Л/Лмакс и у
17. Пусть осьдг декартовой системы координат направлена по краю металлической
полуплоскости (лезвие ножа), а осьг совпадает с оптической осью тонкой линзы L { без
аберраций. Предполагая, что экран расположен в задней фокальной плоскости L v кото-
которая в свою очередь совпадает с передней фокальной плоскостью второй тонкой линзы
^2 без аберраций, покажите, что поле /(*, у) в выходной плоскостиL2 связано с рас-
распределением амплитуды поля предмета ыо(х, у) во входной плоскости L, следующим
интегральным соотношением:
где М =f2/f{ — линейное увеличение афокальной системы, а/. — фокусное расстояние
линзы L.. Это преобразование используется в шлирен-методе для анализа конвектив-
конвективных потоков в аэродинамических трубах.
334 Гл. 4. Основы теории дифракции
18. Пусть решетка, характеризуемая функцией пропускания t(x,y) =
= E^J^LaT^exp (inxlir/ci), расположена в задней фокальной плоскости линзы, освещае-
освещаемой плоской волной вдоль оптической оси. Покажите, что вдали от решетки поле про-
пропорционально выражению
и{х,у) ос
наблюдения до фокальной плоскости,/ — фокусное расстояние линзы. Функция К дает-
дается выражением
+ 00
Щ,г,) ос [[ t(x",y")exp(-ikox4 + У"Лйх"<1у" =
= <5(f) I '
n— — oo
Эта система известна как интерферометр Рончи и используется для определения абер-
аберраций в оптических системах (см. статью Рончи [51]).
19. Рассмотрите тот же, что и в предыдущей задаче, интерферометр Рончи. Предпо-
Предполагая период решетки d таким, что только два последовательных порядка [например,
л-й и (п +. 1)-й] дают вклад в распределение интенсивности, измеряемое в плоскости на
расстоянии d, покажите, что распределение интенсивности дифрагированного поля да-
дается выражением
l«W)|oc
-Wn±--f(n)±
Здесь обозначения те же, что и в предыдущей задаче.
20. Определите форму интерференционных полос в интерферометре Рончи для пер*
вичных аберраций Зайделя. Подсказка. Используйте выражение для интенсивности,
приведенное в предыдущей задаче, и следующее приближенное выражение:
ИЬК - (и + l)o,ij] - Wo(? - ш,П) 2 -x-^W0(Z - по,*)
(см. работу Торальдо ди Франчиа [52]).
21. Рассмотрите поле в дальней области от освещаемой плоской волной собирающей
линзы без аберраций. Вычислите двумя разными способами поле Фраунгофера G(v)
вдоль направления, образующего угол ф с оптической осью. Во-первых, запишите G в
виде преобразования Ханкеля поля на выходной плоскости линзы:
Г
Jo
G(v)oc J0(vx)elux xdx,
Jo
где v = AQflsinVs и = k^/{2f)t а и /' — это радиус апертуры и фокусное расстояние
линзы. Во-вторых, вычислите поле в фокальной плоскости линзы и затем найдите его
преобразование Ханкеля. Поскольку поле в фокальной плоскости определяется распре-
Задачи 335
делением Эйри Jx(v')/v\ для которого преобразование Ханкеля пропорционально
circ(i///tf), найденное таким образом поле быстро спадает до нуля за границей тени.
Этот результат противоречит общим выводам теории дифракции. Следовательно, для
правильного вычисления поля в дальней области необходимо использовать приведен-
приведенный выше интеграл. Покажите, что возникшее противоречие объясняется тем фактом,
что формула Эйри правильно описывает поле лишь вблизи оптической оси (параксиаль-
(параксиальное приближение).
22. Покажите, что поле, создаваемое на большом расстоянии объективом, освещае-
освещаемым сферической волной, пропорционально полю, вычисленному в плоскости вблизи
фокуса на расстоянии и = k^/ild) он него, где d — расстояние между выходным зрач-
зрачком и изображением, формируемым плоской волной, и а — диаметр зрачка. Рассмот-
Рассмотрите изменения в распределении поля в дальней области, вызываемые как сдвигом ис-
источника относительно объектива, так и изменением диаметра зрачка. При каких соот-
соотношениях между я, d и А центральное светлое пятно Эйри заменяется темным? Для от-
ответа используйте фотографии из гл. 9 книги Борна и Вольфа [11], указанной в литерату-
литературе к гл. 1 настоящей книги.
Раздел 4.13.5
23. Покажите, что амплитуда поля сферической волны вблизи фокуса малой аперту-
апертуры без аберраций может быть представлена в виде (см. приложения В и Д)
2 =
u(u9v) = 2\ J0(vp)eiufi2l2pdp = Ieiu/2UX + ile~iu/2U
Jo и и
и и и
где f/n иКл — функции Ломмеля, определяемые выражениями (В.21) из работы Декано-
сидзе [53].
24. Покажите, что вдоль границы тени (м = v) апертуры без аберраций, освещае-
освещаемой сферической волной, интенсивность поля I (v, v) дается выражением
jUv) 1@,0).
25. Выведите формулу Рэлея для мощности, проходящей через расположенный в фо-
фокальной плоскости сферической линзы без аберраций диск с нормализованным радиу-
радиусом vQ (так называемая кумулятивная передаточная функция точки):
г
Jo
I@,v)vdv = 2/@,0)[1 - Jl(v0) - J?(i?o)].
)о
26. Покажите, что при малых аберрациях изображение сферической волны для
Уо = 1 дается приближенно выражением
= п Г
Г2п Г1
i\ йф\
Jo Jo
4- i\ йф\ d00exp[>0cos(</> -
J J
х ~ RB2)@)cos2(/> + Е^Щ cos ф + jj
[см. выражения D.13.33) и D.13.34)].
336 Гл. 4. Основы теории дифракции
27. Используя следующее из книги Борна и Вольфа (см. ссылку [11, с. 727], в литера-
литературе к гл. 1):
Jo
вычислите интеграл в предыдущей задаче.
28. Интенсивность/(к, v ) удобно выразить в виде отношения к/*, т. е. к интенсивно-
интенсивности, которая получалась бы в точке гауссова изображения в отсутствие аберраций, т. е.
= *-^ = р-1 Г* вйв fd0exp|>0cos(tf> -ф)- ikWo
Покажите, что в пределе малых аберраций вычисленная в точке гауссова изображения
нормализованная интенсивность/' @, 0) пропорциональна среднеквадратичной деформа-
деформации волнового фронта:
где
- Г1 в<ю [2n
я Jo Jo
Раздел 4.14
29. Пусть отверстие в плоском экране освещается гауссовым пучком. Найдите ди-
дифрагированное поле, используя теорию дифракции волны на границе. Рассматривая
гауссов пучок как сферическую волну, выходящую из точки на комплексной плоскости,
положение которой связано как с размером, так и с координатой перетяжки пучка, а
также с направлением пучка уравнениями E.7.9), вычислите векторный потенциал w. В
частности, для освещения круглого отверстия под прямым углом найдите поле вдоль
оси (см. статью Отиса [54]).
ЛИТЕРАТУРА
7. ВаЫс К М„ Kirpicnikova К Y., The Boundary Layer Method in Diffraction
Problems, Springer-Verlag, Berlin and New York, 1979.
2. Baker R R, Copson E. Т., The Mathematical Theory of Huygens' Principle, Oxford
Univ. Press (Clarendon), London and New York, 1950.
3. Bowman S. /., Senior T. R A., Uslenghi P. L. R, Electromagnetic and Acoustic Scat-
Scattering by Simple Shapes, North-Holland Publ., Amsterdam, 1969.
4. Watson G. N., Theory of Bessel Functions, Cambridge Univ. Press, London and New
York, 1962. [Имеется перевод: Ватпсон Г. Теория бесселевых функций. — М.: Нау-
Наука, 1964.]
5. Вайнштпейн JI. А. Теория дифракции и метод факторизации. — М.: Сов. радио,
1966.
6. Mittra R., Lee S. Ж, Analitical Techniques in the Theory of Guided Waves, Macmil-
lan, New York, 1971.
7. Borgnis R ?., Papas С H. — In: Handbuch der Physik, v. XVI (ed. S. Fhlgge),
Springer-Verlag, Berlin and New York, 1958, p. 285—422.
8. Van Bladel /., Electromagnetic Fields, McGraw-Hill, New York, 1964.
9. Nussbaumer К J* Fast Fourier Transform and Convolution Algorithm, Springer-
Verlag, Berlin and New York. 1981.
10. Stratton X A., Electromagnetic Theory, McGraw-Hill, New York, 194L [Имеется
Литература 337
перевод: Стрэттон Дж. А. Теория электромагнетизма. — М.—Л.: Гостехиздат,
1948,1
11. Mutter С, Grundprobleme der Matematischen Theorie Elektromagnetischer Schwin-
gungen, Springer-Verlag, Berlin and New York. 1957.
12. Smythe W. R., Static and Dynamic Electricity, 2nd ed., McGraw-Hill, New York, 1941.
13. Clemmow P. G, The Plane Wave Spectrum Representation of Electromagnetic Fields,
Pergamon, Oxford, 1966.
14. ДенЫсюк Ю. Н„ Рамишвили H. M., Чавчанидзе В. В. Опт. и спектр., 1971,
т. 30, с. ИЗО; см. также:
Lohmann A. W., Silva D. A, J. Opt. Soc Am., 61, 687 A971);
Silva D. A., Appl. Opt., 11, 2613 A972).
15. Sneddon I. N., The Use of Integral Thmsfonns, McGraw-Hill, New Yord, 1972.
16. Boivin A,, Theorie at Calcul des Figures de Diffraction de Revolution, Presses Univer-
site Laval, Quebec 1964.
17. Newton R. G., The Complex j-Plane, Benjamin, New York, 1964.
18. Streifer W.t Kodis R. D., Q. Appl. Math., 21, 285 A964).
19. Schobe W, Acta Math., 92, 265 A954).
20. Bremmer A., Terristrial Radio Waves, Elsevier, Amsterdam, 1949; см. также:
Franz Ж, Zs.Naturforsch., 9A, 705 A954).
21. Magnus W, Kotin L., Numer. Math., 2, 228 A960); см. также:
Keller J. A, Rubinow S. L, Goldstein At, J. Math. Phys., 4, 829 A963).
22. Nussenzveig H. M, J. Math. Phys., 10, 82 A969); 10, 125 A969).
23. Wolf E., Proc. R. Soc. London, Ser. A, 253, 349 A959).
24. Richards R, Wolf E., Proc. R. Soc. London, Ser. A, 253, 358 A959).
25. Goodman J. W., Introduction to Fourier Optics, McGraw-Hill, New York, 1968.
[Имеется перевод: Гудмен Дж. Введение в фурье-оптику. — М.: Мир, 1970.]
26. Gaskill J. D., Linear Systems, Fourier Transforms and Optics, Wiley, New York, 1978.
27. Boivin A., Dow /., Wolf E, J. Opt. Soc. Am., 57, 1171 A977).
28. Linfoot E. H.t Recent Advances in Optics, Oxford Univ. Press, London and New York,
1955.
2Ы.ЬисМт Р., Comput. Phys. Commun., 31, 303 A984).
29. Li Y., Wolf E., Opt. Commun., 39, 211 A981).
30. Thompson R /., Prog. Opt., 7, 169 —230 A969).
31. Sommerfeld A., Optics, Academic Press, New York, 1954. [Имеется перевод:
Зоммерфельд А. Оптика. — M.: ИЛ, 1953.1
32. Rubinnowicz A., Prog. Opt., 4, 199 — 240 A965).
33. Gordon Ж R, J. Math Phys., 16, 448 A975).
34. Beran M. J., Parrent G. A, Theory of Partial Coherence, Prentice-Hall, Englewood
Cliffs, New Jersey, 1964;
Glauber R. J. — In: Quantum Optics and Electronics (eds. С De Witt, A.Blandin,
CCohen-Tannoudji), Gordon and Breach, New York, 1965, p. 63—185. [Имеется
перевод в кн.: Квантовая оптика и квантовая радиофизика. — М.: Мир, 1970,
с. 91—280.]
Mandel L., Wo(f E., Rev. Mod. Phys., 37, 231 A965);
Klauder J. R., Sudarshan E. C. G.M Fundamentals of Quantum Optics, Benjamin, New
York, 1968. [Имеется перевод: Клаудер Дж., Сударшан Э. Основы квантовой
оптики. — М.: Мир, 1970.]
35. Glauber R. 7., Phys. Rev., 130, 2529 A963); Phys. Rev., 131, 2766 A963).
36. Sudarshan E. C. G., Phys. Rev. Lett., 10, 277 A963).
37. Pike E. R. — In: Quantum Optics (eds. S. M. Kay, A.Maitland), Academic Press,
New York, 1970, p. 127.
338 Гл. 4. Основы теории дифракции
38. Arecchi Е Г, De Giorgio К — In: Laser Handbook (eds. F. T. Arecchi, E. O. Schulz-
Dubois), v. 1, North-Holland PubL, Amsterdam, 1972, p. 191—264.
39. Crosignani R, Di Porto P., Bertolotti M, Statistical Properties of Scattered Light,
Academic Press, New York, 1975.
40. Welford W. T.t Prog. Opt., 13, 267—292 A976).
41. Black Gn Linfoot E. H., Proa R. Soc London, Ser. A, 239, 522 A957).
42. Duffleux P. A/., The Fourier Transform and its Application to Optics, Wiley, New
York, 1983.
43. Linfoot E. H., Fourier Methods in Optical Image Evaluation, Focal Press, London,
1960.
44. Toraldo di Francia G.t J. Opt. Soc Am., 59, 799 A969).
45. Landau H. /., Pollack К О., Bell Syst. Tech. J., 41,. 1295 A962).
46. Gori E, Guattari G., Opt. Commun., 7, 163 A973).
47. Gori E, Ronchi L.t J. Opt. Soc Am., 71, 150 A981).
48. Cornbleet S., Electron.Lett., 2, 79 A966).
49. Jacquinot R, Roizen-Dossier R, Prog. Opt., 3, 29—186 A964).
50. Toraldo di Francia G., Nuovo Cimento Suppl., 9, 426 A952).
51. Ronchi K, Appl. Opt., 3, 437 A964).
52. Tbraldo di Francia G., Optical Image Evaluation, Nat. Bur. Stand., Washington, D. C,
1954.
53. Dekanosidze & N. lables of Lommel's Functions of Two Variables, Pergamon, Ox-
Oxford, 1960.
54. Otis G., Opt. Soc Am., 64, 1545 A974).
БИБЛИОГРАФИЯ
Cowley J. M, Diffraction Physics, North-Holland PubL, Amsterdam, 1984.
Erkkila J. #., J. Opt. Soc Am., 71, 197 A981).
Федоров В. Б., Митяков А Г., Опт. и спектр., 1984, т. 56, с. 878.
Li Y., Wolf E, J. Opt. Soc Am., 1A, 801 A984).
Murata К. — In: Progress in Optics, v. 5, (ed. E. Wolt), North-Holland Publ., Amster-
Amsterdam, 1966, p. 199—245.
Northover E #., Applied Diffraction Theory, Amer. Elsevier, New York, 1971.
Yu E T. 5., Optics and Information Theory, Wiley, New York, 1976.
ГЛАВА 5
АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ
ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ
5.1. ВВЕДЕНИЕ
Несмотря на видимую простоту, интегралы Гельмгольца — Кирхгофа
и Гюйгенса — Френеля можно вычислить аналитически только в огра-
ограниченном числе случаев; вообще же необходимо привлекать численные
методы.
Применимость всех численных методов ограничена тем, что при
вычислениях можно использовать лишь конечный набор значений по-
поля на опорной плоскости. Это приводит к появлению ошибок, особен-
особенно существенных в тех случаях, когда подынтегральные функции явля-
являются быстроменяющимися. К сожалению, в большинстве случаев ди-
дифракционная картина в дальней области при рассеянии света на пре-
препятствиях состоит из контрастных и узких пиков. При этом числен-
численный подход становится крайне трудоемким из-за необходимости ис-
использования множества конкретных значений поля.
Альтернативой численным методам стала очень популярная техни-
техника, основанная на асимптотическом вычислении интегралов [1]. Есть
несколько причин такого успеха. Это и простота выражений, и высо-
высокая степень точности, достигаемая за счет удержания необходимого
числа членов асимптотического ряда, и возможность разделения обла-
области поля на участки, в которых предсказывается конкретное поведе-
поведение поля. Но наиболее важна возможность использования более точ-
точного представления поля на опорной апертуре.
Из всех перечисленных преимуществ последнее нуждается в допол-
дополнительных комментариях. Обычно наиболее важной задачей является
вычисление истинного распределения поля на опорной поверхности,
поскольку, если поле здесь известно, то мы можем его определить и
во всем пространстве. Вообще говоря, эту задачу нельзя решить точ-
точно, и поэтому в большинстве случаев используется приближенное рас-
распределение поля, вычисленное или в отсутствие препятствий, если
апертура достаточно велика по сравнению с длиной волны (приближе-
(приближение Кирхгофа)у или в других случаях без учета апертуры {приближе-
{приближение Бете). При использовании приближения Кирхгофа поле считается
340 Гл. 5. Асимптотическое вычисление дифракц. интегралов
равным нулю на непрозрачных участках экрана и равным невозму-
невозмущенному значению на самой апертуре. Это распределение в дальней-
дальнейшем можно улучшить, используя итерационную процедуру, состоя-
состоящую в вычислении поля с использованием на каждом шаге значения
поля на предыдущем шаге. С практической точки зрения такая страте-
стратегия требует для полей изучения простых выражений, допускающих
асимптотические представления. С некоторыми приближениями
ad hoc данный метод применяется, например, для вычисления дифрак-
дифракции на щели. Этот и аналогичные случаи привели к новому направле-
направлению, в котором, по сути дела, асимптотические представления явля-
являются составными блоками выражений для электромагнитных полей.
Все асимптотические методы, которые мы обсудим, можно счи-
считать модификациями методов Вентцеля — Крамерса — Бриллюэна
(ВКБ) и стационарной фазы (СФ). Первый из них (ВКБ) более приме-
применим к дифференциальным уравнениям, а во втором (СФ) рассматрива-
рассматриваются интегралы, содержащие быстро осциллирующие функции. В не-
некоторых случаях метод стационарной фазы удобнее заменить мето-
методом наибыстрейшего спуска (НС), который позволяет точно учесть
локализацию на комплексной плоскости стационарных точек фазового
множителя.
В простейшем случае дифракционный интеграл сводится к фурье-
преобразованию следующего вида:
/(*)= \bg(s)e-iksds. E.1.1)
Если g (s) — функция, непрерывная вместе со своими производны-
производными порядка меньше, чем ЛГ, то при больших к можно определить
функцию 1(к), последовательно, применяя интегрирование по частям:
n—iks
b
1 dg _
iks
(-ikJ ds
ь
„-iks
(-ikf ds
N-l
b
E.1.2)
Последний интеграл в правой части этого выражения можно оце-
оценить, используя теорему Римана — Лебега, согласно которой если
%\dNg/dsN \ds < 00, то мы имеем
1*Ь jN
lim -4
*->оо Ja "s
E.1.3)
5.1. Введение 341
Следовательно, процедура интегрирования по частям позволяет
вычислить фурье-преобразование вплоть до членов O(k~N)> гдеЛГ —
максимальное целое число, для которого интеграл от I dNg/dsN I коне-
конечен. Это, разумеется, приводит к сильным ограничениям класса рас-
рассматриваемых функций. Например, для функции g (s) = VF такое вы-
вычисление при а = 0 и Ъ > О возможно лишь до N = 1, и самое луч-
лучшее, что можно сделать, так это записать функцию / (к) в виде
* „1/2 „-iks
-ik
Ъ
О
1 1
В дальнейшем мы покажем, что 1{к) можно представить в виде
асимптотического ряда по большому параметру к, так что члены выс-
высшего по сравнению с \/к порядка можно получить путем обобщения
процедуры интегрирования по частям.
В некоторых случаях встречаются дифракционные интегралы вида
1(к)= Г°° e-ikas2g(s)ds. E.1.5)
При к — оо можно получить точную оценку этого интеграла, если
предположить, что# (s) является постоянной в окрестности нуля. При
этом мы имеем
Видно, что эта формула получена методом стационарной фазы.
Интегралы в теории углового спектра могут иметь различный вид
[см., например, выражения D.9.2), D.9.5) и D.9.6)]. В общем случае их
можно записать следующим образом:
= Г
E.1.7)
где5(/3)— некоторая функция величины 0, характеризуемая полюс-
полюсными сингулярностями и разрезами. Для вычисления I(к) при боль-
больших к удобно преобразовать контур Г аналогично тому, как это было
сделано в выражении D.9.15). При этом в1(к) дают вклад полюсы
5@), а также интегралы типа E.1.7), у которых контур Г заменяется
на контур наибыстрейшего спуска (КНС), и интегралы по контуру Гв,
окружающему точки ветвления функции S A3), если они есть. КНС
определяется как контур, который проходит через ту точку на ком-
комплексной /З-плоскости, где фаза kpcos(C - ф) стационарна, и затем
342 Гл. 5. Асимптотическое вычисление дифракц. интегралов
следует по траектории наибыстрейшего уменьшения мнимой части
cos(/3 - ф). Вдоль КНС фазовый множитель можно записать как
exp[-/A:pcos(/3 - ф)] ос ехр(-м2), где и — вещественная функция ве-
величины s вдоль КНС. Таким образом, используя замену переменных
s — w, интеграл можно свести к виду E.1.6).
Вблизи каустик или фокуса методы ВКБ, СФ и НС приводят к син-
сингулярным полям. Средством устранения этих сингулярностей являют-
являются сравнительные интегралы, из которых наиболее известны функции
Эйри, они же — интегралы радуги, получившие свое название при
объяснении Эйри образования радуги. Умножая эти интегралы срав-
сравнения на асимптотический ряд, можно получить полное представление
поля, которое справедливо как вблизи, так и вдали от критических
участков. Такой подход, имеющий много общего с методом Лангера
(разд. 3.3), называют теорией однородного асимптотического пред-
представления [2—б].
5.2. МЕТОД СТАЦИОНАРНОЙ ФАЗЫ
Подынтегральное выражение в дифракционных интегралах содержит
фазовый множитель, который может осциллировать почти всюду
сколь угодно быстро, если устремить к к бесконечности. Это верно
всегда, за исключением тех значений переменной интегрирования, при
которых обращается в нуль производная фазы. Удобно разделить
весь интервал интегрирования на два множества, одно из которых со-
состоит из окрестностей стационарных точек фазы. При этом можно
ожидать, что при достаточно больших/: вклад от тех областей, в ко-
которых фазовый множитель быстро осциллирует, становится прене-
пренебрежимо мал. Действительно, если подынтегральное выражение име-
имеет вид g(s)zxp[-ikh(s)], то фаза изменяется на 2тг при As =
= 2ir/[h'(s)k] = О(\/к). Полагая к —• оо при Л' Ф О, приращение As
можно сделать сколь угодно малым, так что изменением * функции
g(s) на интервале s, s + As можно пренебречь и соответствующий
интеграл обратится в нуль. Таким образом, весь интеграл сводится к
вкладам от окрестностей точек, в которых Л' = О (стационарные
точки). Так как вблизи этих точек фаза приблизительно равна
k(h0 + -HqS2), соответствующий интеграл вычисляется в явном виде
(метод стационарной фазы).
Считается, что Стоке [7] был первым, кто еще в 1856 г. использо-
использовал преимущества предлагаемого метода и получил приближенное вы-
5.2. Метод стационарной фазы 343
ражение для интеграла Эйри. Общий метод был предложен лордом
Кельвином [8] в 1887 г., а строгое его обоснование было дано Ватсо-
ном [9] в 1918 г. Строгость нашего изложения будет ограничена упро-
упрощенным подходом Эрдейи [10, 11], базирующимся на использовании
последовательного интегрирования по частям [12]. Прежде всего рас-
рассмотрим случай, когда стационарные точки, если они есть, совпадают
с конечными точками интервала интегрирования. Затем мы обобщим
анализ на интегралы с произвольным числом стационарных точек,
расположенных внутри интервала.
Для того чтобы рассмотреть отдельно вклад каждой из критиче-
критических точек, применим математический метод ван дер Корпута [12,
13]. В этом методе используется специальный класс функций так назы-
называемых нейтрализаторов у которые равны единице вблизи одного из
концов интервала и нулю вблизи другого. Кроме того, производные
любого порядка от этих функций равны нулю на обоих концах интерва-
интервала.
5.2.1. Асимптотическое разложение интегралов типа
преобразования Фурье с монотонной фазой
В качестве предварительного шага рассмотрим асимптотическое раз-
разложение интеграла типа Фурье [14, 15]:
/(*) = Гe-ikh^v(s)g(s)ds9 E.2.1)
Jo
где h (s) — монотонная функция аргумента s на интервале @, а) и
— функция, введенная Ван дер Корпутом [13], которая называется
нейтрализатором, причем
v@) = 1, v(a) = 0. E.2.3)
Функция v(s) обладает также тем свойством, что при приближении
s е @, а) к концам интервала все производные функции v (s) обраща-
обращаются в нуль. Предположим, кроме того, что в интервале @, а) функ-
функции Л и g можно записать в виде
h(s) = h0 + spu(s\ E.2.4a)
0E) = *Ч4 E.2.46)
344
Гл. 5. Асимптотическое вычисление дифракц. интегралов
где и и v — аналитические функции переменной s, отличные от нуля
при 5 = 0. Пусть, кроме того, 0 > Re7 > -1 и р > 0. Поскольку
splt/(s)l — возрастающая функция переменной 5, можно перейти к
другой переменной, определяемой следующим образом:
х' = s>(s)|,
E.2.5)
где выбирается та ветвь, для которой х — возрастающая функция пе-
переменной s. Заменяя в E.2.1M нал:, получаем
Гх(а)
)
Jo
= exp(-i7cft0) Qxp(-ikexp)xyf(x)v(x)dx9
J
где х > 0, е = sgn w@) и
f(x) = (g(s)/\Hs) - ho\*">)ds/dx.
E.2.6)
E.2.7)
Если/(*) можно продифференцировать N раз, то, на что первона-
первоначально указал Эрдейи (см. работу Блейстейна и Хандельсмана [14],
разд. 3.4), интеграл в E.2.6) можно записать в виде полинома относи-
относительно \/к с помощью последовательного интегрирования по частям:
I(k)cxp(ikho)= -
и = 0
i>(x;/с)—
X
x(a)
где
RN = (-
+ RN, E.2.8)
E.2.9)
(;)
rx+aoi-iEI"* Г xn+oo(- isI /p f*i + «(-ieI^
dxn\ dxn _ l • • dx0 xy0 exp( - ifeexg) =
jx Jxn Jxi
i Лх + оо(-»еI/р
= - Л (xo - x)W0 exp( - ifcexg) dx0. E.2.10)
Последнее тождество нетрудно доказать, изменяя порядок интегриро-
интегрирования. В частности,
й<-"-1»@Д)= -- Г* U)'Pxl+^xp(-i
n'J о
5.2. Метод стационарной фа^ы 345
Здесь Г (х) — гаммагфункция Гаусса. Наличие функции-нейтрализато-
функции-нейтрализатора приводит к тому, что дклад граничной точки х = х (а) тождествен-
тождественно равен нулю и разложение E.2.8) с помощью соотношения E.2.11)
можно переписать в виде
I(k)exp(ikh0) =
1 w-i 1 Г?(и + У + 1)/р]ехр[-1(я/2)в(п + у + 1I р] d»f(x)
^/ цгЦ П, /V (XX
E.2.12)
Можно показать (см. работу [14, с. 99, выражение C.5.46)]), что
хТ[(и + 1)/р]
E.2.13)
Таким образом.
1 _/N + v+l\ / -л ^ + 7 +
ехр -1-е —
E.2.14)
откуда находим
KN = O(r(N+y+1)/p). E.2.15)
Если/ можно продифференцировать бесконечное число раз, то TV
можно выбрать сколь угодно большим. Следовательно, в E.2.12)
можно формально заменить TV на оо, опустив RN и заменив знак ра-
равенства знаком асимптотического равенства (т. е. знак = переходит
в ~). Если теперь ввести функцию
a(s) = (dx/ds)-\ E.2.16)
то мы можем написать следующее выражение:
(dn/dxn)f(x) = la(s)d/dsYa(s)g(s)\h(s) - ЙОП/Р> E.2.17)
подстановка которого в E.2.12) окончательно дает
I(k)~exp(-ikh0)-^-___exp^-i-e j х
E*2Л8)
Последнее разложение можно использовать в интеграле E.2.1), ес-
если в подынтегральное выражение ввести функцию-нейтрализатор.
Для этого нужно воспользоваться следующим тождеством:
346 Гл. 5. Асимптотическое вычисление дифракц. интегралов
/(?) = | V'**(sH(s)<fe= Г e~ikh(s)v(s)g(s)ds + \ae-ikhi5)[l-v(s)Ms)ds =
Jo Jo Jo
= /0(fc) + IM E.2.19)
В частности, 1а(к) можно переписать в виде
Ш = ехр( —Л*.) Г Qxp(-ikeax^)x"fa(x)v(x)dx, E.2.20)
Jx(O)
гдел-(О) < 0, еа = sgnw(a), а показатели степени 7в» Рв и^а определя-
определяются выражениями
h(s) = К + E - <вмЛD E.2.21а)
9E) = (s - af*vM E.2.216)
в то время как
х = E - a)\ua(s)\1/pa, E.2.21b)
/.W = Ш/\Цз) - К\у^ (ds/dx). E.2.21r)
Теперь в выражении E.2.20) можно сделать замену х — —х и исполь-
использовать разложение E.2.18). Таким образом, мы получаем следующее
выражение:
Г-х@)
Ia(k) = cxp(-ikha)(- 1)Ув exp[-ifc(-iy^x^ea]xyafa(-x)v(x)dx ~
Pa
где (-1O* = e'*7* и (— Г
E.2.22)
5.2.2. Обобщение метода СФ на дифракционные интегралы
с несколькими стационарными и сингулярными точками
Рассмотрим одномерный дифракционный интеграл вида
/ь\1/2 ГЪ -ikR
w(r) = f—J e'*/4| uix'^—^z-Rdx'. E.2.23)
5.2. Метод стационарной фазы 347
Если и(х'у z) — лучевое поле вида Лехр(—ikS)9 то м(г) можно запи-
записать в виде
/ h \l/2 ГЬ
где через s мы обозначили х', g(xf ) = А (х' )R~Vlz -R, а А(*') =
= R(x') + S(xf ). Если Л — ограниченная функция переменнойs, a g
и ее производные имеют конечное число разрывов, то интервал (а, Ь)
можно разбить на конечное число меньших интервалов, отделенных
друг от друга критическими точками подынтегрального выражения
(т. е. точками разрыва функций Л и g и их производных, граничными
точками а и 6, а также стационарными точками функции Л). Пусть
критические точки можно упорядочить следующим образом:
а = а0 < ах < а2 < • • • < ат = Ь. E.2.25)
В каждом из интервалов Л (у) является монотонной функцией перемен-
переменной 5, непрерывной вместе со всеми своими производными. Те точки
s, для которых Л'(^) = 0, называются стационарными точками
функции h (s). Теперь для каждого из интервалов можно использовать
асимптотические разложения E.2.18) и E.2.22), чтобы вычислить
вклады If и If от правой и левой окрестностей каждой из критических
точек ai9 так что
+Т). E-2.26)
Заметим, что в граничных точках 1а и 1? опускаются.
В общем случае, используя E.2.18) и E.2.22), имеем
1
-( ]
Здесь р и у — индексы критических точек а, при подходе слева (—) или
справа (+), в то время как
С = ехр[-/(тс/2)е(и + у + 1)/р], E.2.28а)
С; = (- 1)и+уехр[-1(тг/2)г(- 1)^(и + у + 1)/р]. E.2.286)
В частности, если A ng непрерывны в точке ai9 то функция a (s),
определяемая выражением E.2.16), также непрерывна и
348 Гл. 5. Асимптотическое вычисление дифракц. интегралов
/ — /+ _|_ 1- ~ иИ2-а+у)/р
*Иру) - Л<ру) + Ч{р,У) ~ к (
B
с- {
пI/2р I 4у
n\knlp
E.2.29)
5.2.3. Вклады стационарных точек
В случае когда в точке а, функция/г (s) непрерывна, а ее производные
порядка меньше чем р равны нулю, точка а, называется стационарной
точкой порядка р. В частности, для р — 2 и у = 0 выражение E.2.29)
дает
exp[i(l - е)я/4 - ifc/»] ^ Г(п + 1/2)
iB-0) ~ Щ& ~?о Bn)!*- x
—J [a(s)gr(s)]
[.., Лл ..,,. f exp[ —i(n/2)e]
i(l - е)- 2 A/2)ехр(-/ЛЛ)^ + 4k x
х [(aa'2 + a2a")g + 3a2aV + a39"] + О(к~2)\ E.2.30)
где для простоты обозначений мы опустили аргумент а, и отметили
штрихом производную по 5. Следующие члены разложения читатель
сможет найти в книге Дингла [16].
Теперь нетрудно показать, что
а(а,) =-[2№(а,)У'2, E.2.31а)
a'(a,)=-4(/r/ft")a(aA E.2.316)
*"J]^^). E.2.31в)
Подставляя эти выражения вновь в E.2.30), окончательно получаем
5.2. Метод стационарной фазы 349
ikh] \
exp[i(l - е)я/4 - ikh] \ ж exp[-iGt/2)e]
где все величины вычислены при 5 = аг Заметим, что главный член
асимптотического ряда не зависит от к [см. выражение (Е1) в прило-
приложении].
Выполняя аналогичные преобразования, получаем для/C§0):
fc1/6exp(i7c/4 — isn/6 — ikh) * Г[(и т x;/^j # .«, \
ъп„\И2 L ZJlMb exP\ ~*Геи J x
^ _ . E.2.33)
В этом случае
3, E.2.34)
так что
к 1/6ехр(*тг/4 - ien/6 - ikh)
х
хГ-
5.2.4. Вклады граничных точек
В граничных точках а и Ь, если g не равна нулю, мы имеем 7 = 0,
р = 1 и [см. выражение (Е1) в приложении Е]
E.2.36а)
-а
1
Bтг-
ех
Jb(l,0)
exp(-m/4~ifcftfl) « _l_/j__u_» y_
ехр( —jtt/4 — /fcft
ехр(—in/4 — ik
L
В случае же когда g обращается в нуль, скажем в точке а, мы име-
имеем 7 = 1 и
350 Гл. 5. Асимптотическое вычисление дифракц. интегралов
ехр( — i3n/4 —
I
ikha) • « + 1/1 <Л"Г д
я% (ik)"\h' ds) \h'{h -
0A •» Bn)l'2k312 J?o (ifc)" V»' ds) [h'{h - ha)
exp(-i3*/4 - iWiJf g'a_ 2_ g"aKa - Ъд'Х + 0(fe-2)] E 2 3?)
Следует отметить, что пренебречь вкладом граничных точек нельзя
даже в том случае, когда поле в них равно нулю.
5.2.5. Вклады точек разрыва
Для точек разрыва функций g или h при р = 1 и у = 0 первые два
слагаемых асимптотического разложения записываются в виде
_ехр(-/тг/4-
(ит + 7Г—S h'+з ) -
\П 1К П )
ехр( — in/4 — ikh )
1/2
Bnk)
5.2.6 Асимптотическое выражение для дифракционных интегралов
Если собрать все главные члены в полученных интегралах, то для
р = 1 можно записать
^ e
m = Vw
где сумма ? ' включает в себя все стационарные точки, а ? " — все
точки разрыва.
Учитывая равенство Л = S -f- R [ср. с выражениями* E.2.23) и
E.2.24)], непосредственно получаем, что стационарные точки соот-
соответствуют корням уравнения
W = (VS 4- VR) • х,= (в"' + ft) • X = 0. E.2.40)
Поскольку векторы §' и — R направлены вдоль х, уравнение E.2.40)
может быть удовлетворено лишь при 3' = — R. Следовательно,
Н" = S" + (z - z'J/K3 = [A/рс) + A/R)](z- ftJ, E.2.41)
5.2. Метод стационарной фазы
351
здесь через рс обозначен радиус кривизны волнового фронта при
х, = ait так что
= [Р«/(Рс + ЮУ/2А(а(), E.2.42)
- E-2-43)
В выражении E.2.43) сразу же можно узнать главный член разложе-
разложения поля в ряд Лунеберга — Клейна.
Если теперь обозначить через ф'а угол между лучом, падающим в гра-
граничную точку а, и направлением единичного вектора -х, а через фа —
Рис. 5.1. Геометрические представле-
представления, используемые при вычислении
вкладов в дифракционный интеграл от
границ отверстия и стационарных то-
точек (а)> а также от точек разрыва
фазы (б).
352 Гл. 5. Асимптотическое вычисление дифракц. интегралов
угол (больший чем тг) между векторами -Ra и -х (см. рис. 5.1, а), то
мы имеем
E.2.44)
Следовательно, вклад от граничной точки а можно записать в виде
Аналогично, рассматривая точку Ъ и точку разрыва функций h и g,
окончательно получаем (см. рис. 5.1, б> на котором определены все
углы)
12
ехр( —17Г/4)
^ cos
,ехр(-пг/4)Г
Здесь«f относится к стационарным точкам, аиь ииА — соответствен-
соответственно к граничным точкам и точкам разрыва. Член ug совпадает с пред-
представлением поля в рамках геометрической оптики, в то время как
остальные члены учитывают дифракционные эффекты, связанные с
конечностью волнового фронта и с разрывами фазы и амплитуды.
Теперь следует переписать иь в виде функции падающего поля и%:
^1/2, E.2.47)
где введен дифракционный коэффициент D v определяемый следую-
следующим образом (см. уравнение B7) в статье Келлера [1]):
ОЛФ,ф') = [e-^/4/(87rfeI/2](-2sin0)/(cos</) + со&ф'). E.2.48)
Согласно этому выражению, граница апертуры полностью описыва-
описывается своими дифракционными коэффициентами. Однако выражение
E.2.47) получено в приближении Кирхгофа, поскольку поле^ определя-
определяется как падающее поле, вычисленное в отсутствие экрана. В следую-
5.3. Границы тени 353
щей главе мы увидим, что можно учесть и изменение падающего поля
за счет самого экрана. При. этом выражение E.2.47) остается справед-
справедливым и при использовании невозмущенного падающего поля. Доста-
Достаточно применить лишь другие выражения для дифракционных коэф-
коэффициентов, как это было предложено Зоммерфельдом при решении
канонической задачи о дифракции плоской волны на полуплоскости.
5.2.7. Устранение СФ-сингулярностей
с помощью сравнительных интегралов
Асимптотические выражения, рассмотренные выше, становятся сингу-
сингулярными, когда Л" (Sj) = 0 или стационарная точка подходит близко к
граничной. Для того чтобы избавиться от этих сингулярностей и по-
получить асимптотически правильное представление дифракционного ин-
интеграла, мы можем заменить его сравнительным интегралом, кото-
который в асимптотическом представлении, приведенном в предыдущем
разделе, имеет те же самые сингулярности. Этот интеграл обычно
выбирают из класса известных специальных функций, таких, как ком-
комплексный интеграл Френеля F (рс), функция Эйри Ai(x) или функция
параболического цилиндра D_V2(eiT/\). В окрестности тех значений
параметров, для которых обычное разложение расходится, дифракци-
дифракционный интеграл нужно представить в виде произведения сравнитель-
сравнительного интеграла на асимптотический ряд, который принимает конечное
значение при выполнении условия сингулярности. В большинстве слу-
случаев точное вычисление суммы ряда не требуется, так как сравнитель-
сравнительный интеграл с достаточной степенью точности равен искомому по-
полю, что, однако, верно лишь до тех пор, пока мы находимся доста-
достаточно далеко от критических областей, так что обычные разложения
справедливы. Иными словами, выражение, полученное с помощью
сравнительных интегралов, постепенно и непрерывно переходит в ряд
Лунеберга —- Клейна. Поэтому представление, основанное на сравни-
сравнительных интегралах, называют однородным, а соответствующий
подход — однородной асимптотической теорией. В следующих раз-
разделах мы рассмотрим наиболее интересные частные случаи.
5.3. ГРАНИЦЫ ТЕНИ;
СТАЦИОНАРНАЯ ТОЧКА ВБЛИЗИ ГРАНИЧНОЙ
Полученное в разд. 5.2.6 выражение для вклада в дифракционный ин-
интеграл от граничных точек сингулярно при фа - ф'а = тг, т. е. в тех
случаях, когда дифрагированный луч параллелен лучу, падающему на
35/ Гл. 5. Асимптотическое вычисление дифракц. интегралов
границу а (рис. 5.1, а). С геометрической точки зрения продолженный
падающий луч разделяет области света и тени, т. е. определяет грани-
границы тени, проецируемой апертурой. Поэтому поверхность, образуемая
лучами, касающимися края апертуры, называется границей тени. При
освещении щели цилиндрической волной граница тени сводится к двум
полуплоскостям. Если ограничиться в случае цилиндрического поля
лишь анализом его распределения на плоскости, то границей тени
естественно и удобно называть две полупрямые, получаемые в сече-
сечении истинной границы тени плоскостью.
Мы уже неоднократно обращали внимание читателя на сингуляр-
сингулярное поведение поля вблизи границы тени. Благодаря совпадению гра-
граничной точки интеграла и его стационарной точки такое поведение
аналогично сингулярности вклада в дифракционный интеграл от гра-
граничных точек. В принципе эту аномалию можно исключить при более
точном асимптотическом вычислении интеграла.
В качестве предварительного шага заметим, что главный член в
асимптотическом ряде, представляющем вклад стационарной точки а,
дается выражением
ехр(-го/4 - ikha) ^ч f °° _, л^.и^ E 3 1}
j:
где и ° = uJQ) = A" (a)/2 nsa = 0. В случае когда вблизи а находится
и граничная точка, этот интеграл принимает вид
1/2
/ Ь \1
4 ~\гп)
E.3.2)
гдем^Р) — падающее поле в точке наблюдения Р, aF(?) — комплекс-
комплексный интеграл Френеля, учитывающий переход от освещенной области
к темной. Здесь ? — так называемый параметр обхода, определяемый
выражением
? = JW^K) = УЬ? sa. E.3.3)
Напомним, что kh — это фаза поля в точке Р, создаваемого цугами
волн, выходящих из точки апертуры Р' (у). Следовательно,
k(h - ha) = ?2 представляет собой разность между фазой поля, свя-
связанного с идущим без возмущения лучом, и фазой поля, дифрагиро-
дифрагированного на границе апертуры. Если использовать терминологию гео-
5.3. Границы тени
355
Рис. 5.2. К вычислению параметра обхода
{ = [ко(АР - СР)]т при определении
вкладов в поле в точке Р от точек стацио-
стационарной фазы (С) и границы (А).
метрической оптики, то Аа - На является разностью длин оптических
путей луча, достигающего точки Р без отклонения, и луча, дифраги-
дифрагированного на границе. Обращаясь к рис. 5.2, имеем
- 1СР-]) <* -BfcpI/2cos(iA/2); E.3.4)
здесь пр = [АР] и использован тот факт, что луч в точке С почти па-
параллелен лучу, проходящему через А. Знак перед квадратным корнем
выбран положительным в области тени и отрицательным в освещен-
освещенной зоне. На рис. 5.3 схематически отмечена переходная область,
окружающая границу тени при освещении прямой кромки плоской
волной. Ниже мы покажем, что указанная граница имеет параболиче-
параболическую форму, которая соответствует параметру обхода, равному
рис. 5.3. Переходная область вблизи границы тени при освещении полуплоскости плос-
плоской волной.
356 Гл. 5. Асимптотическое вычисление дифракц. интегралов
5.3.1. Свойства переходной функции F(x)
Функция, описывающая переход через границу тени, является ком-
комплексным интегралом Френеля
F(x) = -1=еы/* \ e-it2dt. E.3.5)
j J
Это целая трансцендентная функция, которую можно выразить через
интегралы Френеля Сх(х) и Sj(jc) (рис. 5.4):
F(x) = \ - КСЛх) - «i(x)](l + 0, E.3.6)
\F(x)\ = |[1 + 1С\ + 2S? - 2СХ - 2SJ1/2, E.3.7)
где
Ci(x) = M I cost2dt, E.3.8)
/2\1/2 Лх
S^x)^!-) sin t2dt. E.3.9)
Все значения F на комплексной плоскости при - оо < х < + оо можно
получить с помощью спирали Корню (рис. 5.5). Интересным свойст-
свойством этой кривой является то, что ds = I dx I, т. е. I dx I соответствует
длине кривой, измеренной вдоль спирали.
Из поведения функции F(x) можно заключить, что для х < - Vx
мы имеем F(x) s 1, а для х > Vr F(x) » 0. Отсюда следует простое
приближенное правило: дифракционные эффекты от края поверхно-
0,2
/,2 2,4 3;6 Рис. 5.4. Интегралы Френеля.
5.3. Границы тени
4 Im Fix)
357
х<0
ReF(x)
Рис. 5.5. а — спираль Корню;
б — амплитуда функции F.
сти становятся существенными, когда параметр оОхооа лежит меж-
между — Vw и у[ж. Если выразить это условие через длины оптических пу-
путей, то разность хода должна быть меньше чем Х/2.
В качестве примера рассмотрим точечный источник S, поле от ко-
которого определяется в точке Р. Пусть между S и Р (рис. 5.6) располо-
расположен прямой край полуплоскости и отличием источника от точечного
можно пренебречь. Практически поле будет описываться приближени-
приближением геометрической оптики, когда
E.3.10)
Рис. 5.6. Геометрия, используемая при вы-
вычислении параметра обхода E — источник;
Р — точка наблюдения) в случае дифракции
на препятствии, показанном заштрихован-
заштрихованной областью.
358
Гл. 5. Асимптотическое вычисление дифракц. интегралов
Эллипс Френеля
Рис. 5.7. Различное по отношению к
эллипсу Френеля положение дифрак-
дифракционных препятствий (Р — ¦ точка
наблюдения; S — источник). Поле в
точке Р существенно изменяется
только за счет препятствия, оказав-
оказавшегося внутри эллипса Френеля.
Если рассмотреть эллипс Френеля с фокусами в точках S и Р и полу-
полуосью а = Х/4 + SP/2 (рис.5.7), то можно сказать, что препятствие,
если оно лежит вне эллипса, не изменит наблюдаемого поля. Этот ре-
результат был обобщен Кравцовым и Орловым на случаи более слож-
сложных полей fl8].
5.3.2. Асимптотическое поведение функции F(x)
При изучении асимптотического поведения дифрагированного поля
полезно рассмотреть вспомогательную функцию
G(x) = -хе-й*1*-*2± 2 . 2dt - resf * , 2 ) =
2ти J t2 + ix2 \t2 + ix2/
1 f+
2J
_„ t2 + ix2
dt.
E.3.11)
Здесь res — вычет в верхней полуплоскости комплексной переменной t
(т. е. Imf > 0). В первом случае контур интегрирования связывает
x=-oocx=+oo, оставляя справа полюсы подынтегрального вы-
выражения. Функция G является аналитической на всей комплексной
плоскости, за исключением прямой линиих = ±\х \е!*м, которая яв-
является разрезом. Функция G разрывна при переходе через разрез, и
разность ее значений на двух берегах разреза равна 1. Это легко про-
проверить, используя приведенное интегральное представление функции G
и замечая, что скачок связан лишь с изменением res( ).
Теперь заметим, что для положительных вещественных х функция
G (рс) сводится kF(x). Таким образом, в общем виде имеем
E.3.12)
5.3. Границы тени 359
где UF(-x) равна 0 на нижней стороне разреза [т.е. при
Im(ve~iT/4)< 0] и единице в противном случае. Введение функции UF
позволяет компенсировать разрывность функции G.
Можно показать, что при интегрировании по частям последнего
интеграла в E.3.11) функция G(x) допускает следующее асимптотиче-
асимптотическое представление:
G(x) ~ F(x)[l + l/3^^,1^ E.3.13)
где
F(x) = A/2^)A/х)е-«*2+я/4). E.3.14)
Поскольку это разложение применимо для любых значений фазы ве-
величины х, окончательно получаем
F(x) ~ UF(-x) + F(x) + ОA/х2), |х| » 1. E.3.15)
5.3.3. Асимптотическое представление поля
Используя представление дляF E.3.15), получаем
4~И|[ЬИ-0 + Р(«|, E.3.16)
если величина I ? I достаточно большая. В соответствии с этим в слу-
случае когда стационарная точка приближается к граничной, мы можем
пренебречь изолированным вкладом от последней и просто умножить
падающее оптическое поле«1 на переходную функцию F. Таким обра-
образом,
и(Р) = щЩ-t) + tt,G«) = Mi[/F[BfepI/2cos(^/2)] +
+ M?G[-BfcpI/2cosWr/2)] s ug + ud\ E.3.17)
здесь ud s up.
4.3.4. F(x) при малых аргументах
При малых х функцию F можно аппроксимировать первыми членами
ее разложения в степенной ряд:
|_ + ...|. E.3.18)
В частности, F@) = 1/2, F(l, 6) = -0,16, F(-l, 6) = 1,16.
360
Гл. 5. Асимптотическое вычисление дифракц. интегралов
5.4. КАУСТИКИ ЦИЛИНДРИЧЕСКИХ ПОЛЕЙ;
ДВЕ СОСЕДНИЕ СТАЦИОНАРНЫЕ ТОЧКИ
С приближением точки наблюдения Р к каустике два или более лучей
проходят через Р почти в одном и том же направлении. Математиче-
Математически это означает (рис. 5.8), что у функции h(s) две или более стацио-
стационарных точек весьма близки друг к другу. Для определенности пред-
предположим, что имеются две такие точки, например sx и %. Поскольку
h'(s)=O в точках ^ и %, между ними должна быть точка, скажем %, в
которой Л" Ц,)=0. Если поместить теперь начало координат в %, то
главный член асимптотического приближения для дифракционного ин-
геграла можно получить, записывая
- ikhj f t ,
9 J exPC*(tt + Ul*y\d E.4.1)
Д
ыва
J
где мы обозначили через а точку50=0, а обозначениям^ им^ исполь-
использовали соответственно для первой и третьей производных функции Л в
точке Sq. Необходимо заметить, что % не является стационарной точ-
точкой и поэтому производная и1а отлична от нуля. В случае когда sx
очень близка к ^, мы имеем
"i+K3*i=0, E.4.2а)
-/!"^), E.4.26)
Pi
Рис. 5.8. Геометрия, используемая при вычислении поля вблизи каустики.
5.4. Каустики цилиндрических полей
361
так что
«i = -Tft"Ei)si=i^A, E.4.3а)
и^к'^Уз^-Щ/А, E.4.36)
st = -iA. E.4.3b)
Здесь Д — расстояние между двумя стационарными точками. Инте-
Интеграл в правой части выражения E.4.1)— это функция Эйри
Ai (см. разд. 3.3. и рис. 5.9). Таким образом, мы можем написать
ехр(ш/4 — ik
2
1/3
]. E.4.4)
Однако известно, что [см. разд. 5.2.6, уравнение E.2.41)]
К = [(* + Р)/ВД* • КJ ^ -(P7^2)(z • RJ, E.4.5)
А2 =(Д2 sin2 0)/(f. ЯJ, E.4.6)
где знакопеременная величина р' = I р I -Л равна расстоянию, изме-
измеренному вдоль луча, от Р до каустики (величина р' положительна,
когда Р лежит между центром кривизны Q и апертурой, и отрица-
отрицательна в противном случае), а ф — угол, образованный двумя лучами,
проходящими через Р. Используя выражения E.4.5) и E.4.6), получа-
получаем соотношение
_-АУ/3 = [*/(?. R)][sin0/(fcp')]1/3. E.4.7)
Из простого геометрического рассмотрения можно показать, что при
малых ф величины р', ф и радиус кривизны каустики рс связаны про-
простым соотношением (рис. 5.8)
Ф*2\р'\/рс. E.4.8)
Ai(-x)
Рис. 5.9. График функции Эйри Ai(jc)
для - 10 < х ^ 6. Функция Ai(x) ос-
осциллирует при отрицательных значениях
х и экспоненциально затухает при
х — оо.
362 Гл. 5. Асимптотическое вычисление дифракц. интегралов
Каустика \
Каустика
а
Рис. 5.10. дг — интерференционные полосы вблизи каустики; б — изменение амплитуды
поля вдоль луча; в — изменение амплитуды поля в перпендикулярном каустике направ-
направлении.
Поэтому, заменив ga mAR~U2 и положив Z-R = 1, окончательно по-
получаем
/л ikh \AR^^2l I Ail I j I E.4.9)
Поскольку произведение ARW2 постоянно вдоль луча, правая часть
выражения E.4.9) не зависит от положения опорной плоскости ? = 0.
Функция 7(р' ) схематически показана на рис. 5.10, в. На каустике
имеем
/ 9 V/3
4@) - 0355B7tk)l/2ARi/2( — ехр(йс/4 - ikha\ E.4.10)
\kPc/
в то время как на некотором расстоянии от нее функцию Эйри можно
заменить ее асимптотическим выражением [см. C.3.6)], так что мож-
можно написать следующее выражение:
,1/2
) ехр(—ifcfca){exp[*7cp'3/Cpc)] — *'ехр[ — ifcp'3/Cpc)]} =
JP'I/
где ug(P, е/)=Л(/?/1р/1I/2ехр[-/А:(Ла - p'3/Cp2))] представляет со-
собой поле вдоль луча, проходящего через точки Р и Qt\ величина р' по-
положительна, если Qi лежит вне отрезка РР(9 где Р. — точка пересече-
пересечения с волновым фронтом. Два луча интерферируют, что приводит к
типичной осциллирующей картине (рис. 5.10, б). Следует заметить,
что каждое из полей при прохождении по касательной к каустике пре-
претерпевает сдвиг фазы тг/2. Кроме того, эффективное волновое число
изменяется как k(p')=k(l - р'2/р^). Это позволяет говорить, что
вблизи каустики волна «замедляется».
Возвращаясь вновь к выражению E.4.9), заметим, что р'2 = 2рср,
5.5. Поле вблизи двумерного острия каустики 363
где р — расстояние по нормали от точки Р до каустики. Следователь-
Следовательно, выражение E.4.9) можно переписать в виде
ф) ~ Bnk)^R^(j-y\xp(^- - ikh^j Ai[-2^ypcp]. E.4.12)
В этом выражении р можно считать положительной или отрицатель-
отрицательной величиной в зависимости от того, в тени или в светлой области
лежит точка Р. На рис. 5.10, в приведено распределение поля вдоль
нормали к каустике.
5.5. ПОЛЕ ВБЛИЗИ ДВУМЕРНОГО ОСТРИЯ КАУСТИКИ;
модаль для импульсного отклика при наличии
ДЕФОКУСИРОВКИ И АБЕРРАЦИЙ ТРЕТЬЕГО ПОРЯДКА
В предыдущем разделе мы показали, что структура поля вблизи про-
простой каустики, создаваемая распространяющейся цилиндрической вол-
волной, имеющей сферические аберрации, зависит от кривизны каустики.
При этом изменение поля в перпендикулярном каустике направлении
выражается через интеграл Эйри. Вблизи острия (точки возврата) кау-
каустики (см. рис. 2.15 и 2.16 в гл. 2) из-за интерференции трех или более
лучей распределение поля становится значительно более сложным.
Эту ситуацию можно описать, рассматривая дифракционный инте-
интеграл, у которого три стационарные точки функции h (s) близки друг к
другу. В соответствии с этим мы можем изучить поле, анализируя
сравнительный интеграл
Ja
^ !\Xpl-i(as + bs2 + cs4)]ds. E.5.1)
у/к
Заметим, что отсутствие в данном выражении члена cs3 не ограничи-
ограничивает общности рассмотрения, поскольку этот член всегда может быть
исключен простым сдвигом координаты s.
Для того чтобы найти физическую модель, приводящую к интегра-
интегралу E.5.1), рассмотрим щель шириной и>= \Ь—а I, освещаемую одно-
однородным полем с фазой — kS(s)=ks2/Bf) - (В/4)(s/wL9 где/ — рас-
расстояние от фокуса до апертуры, а В служит мерой сферических абер-
аберраций [см. разд. 2.15 и 4.13, а также выражение D.13.34)]. При этом
дифрагированное поле записывается в виде
кх /с/1 1\ 2 Bsl] J /с с^
+К + M <5-5-2)
364 Гл. 5. Асимптотическое вычисление дифракц. интегралов
Вблизи фокуса (х » 0, z ~ f) три стационарные точки фазового мно-
множителя стремятся слиться в одну точку, а именно с самим фокусом.
Это означает, что каустика поля имеет вершину в параксиальном фо-
фокусе. Однако мы можем сразу получить уравнение каустики в случае,
когда совпадают две стационарные точки. А именно, проанализируем
кубическое уравнение Л' (s) = 0, которое при z ~ f имеет вид
s3 + [(ww2s)/B] + [(w3r)/BB)] = 0, E.5.3)
где v = кЧА х и и = ^(ЧАJ^ - /) — оптические координаты точки,
в которой определяется поле. Отсюда мы видим, что два корня совпа-
совпадают при условии, когда
пъ = -B7/16)BtA E.5.4)
Если пренебречь вкладом граничных точек, то выражение E.5.2) мож-
можно переписать в виде [19]
1(к) ос Г Qxpi-i(Vt + Ut2 + r4)]dt = /(V, [/), E.5.5)
J -оо
где U и V — безразмерные координаты, связанные с и и v соотноше-
соотношением
U = п/В1/29 V = v/B1/2B1/4). E.5.6)
Несобственный интеграл I(V, U) был вычислен Перси, и на рис. 5.11
представлены построенные им линии уровня модуля величины 1. За-
Заметим, что главный фокус образуется на оси U при U s - 1,8. Слева
от острия каустики имеется система трех лучей, лежащих между дву-
двумя ветвями каустики. Интерференция этих лучей приводит к образова-
образованию сложной системы максимумов и минимумов, хорошо видных на
рис. 5.11. В то же время справа существует лишь одно семейство лу-
лучей, так что / убывает монотонно.
Вдоль оси U функцию / (U, 0) можно выразить через функцию па-
параболического цилиндра D _ 1/2 (см. справочник Абрамовича и Стегана
[4], указанный в литературе к гл. 2 настоящей книги):
7A7,0) = 2 f °°exp[-/(l/*2 + t*y]dt ос D.1/2(Qxp(in/4J'l/2U). E.5.7)
Jo
Вспоминая, что D_х/г{х) удовлетворяет дифференциальному уравне-
уравнению
(d2/dx2)D.lB(x) - ix2D_i/2\x) = 0, E.5.8)
0,656 0,625
-7 -5 -5 -4 -3 -2 -/
I+OO
Рис. 5.11. Линии уровня функции I{V, U) = J ехр[ — /(К/ + С//2 + tA)\dt, вычисленные Перси. (Из работы [19].)
8 U
366 Гл. 5. Асимптотическое вычисление дифракц. интегралов
можно сразу показать, что
(d2/du2)I(V,0) + ^U2I(U,0) = 0. E.5.9
Это уравнение можно сравнить с уравнением Эйри C.3.2); оба имеют
точку поворота в начале координат, но разного порядка. В то время
как функция Эйри Ai убывает экспоненциально при х — оо, в нашем
случае при U > 1 мы имеем
/@,17) - 04±/|l/|1/2)sin(t/2/8 + ф). E.5.10)
5.6. МЕТОД НАИБЫСТРЕЙШЕГО СПУСКА
В некоторых случаях из-за медленной сходимости асимптотического
ряда, представляющего дифракционный интеграл, метод стационар-
стационарной фазы применять нельзя. Это особенно явно проявляется в одном
важном частном случае, когда распределение поля на опорной плоско-
плоскости является гауссовым. Рассмотрим следующий дифракционный ин-
интеграл:
ехр(^/4)
J -о
ехр(-ikas2 - bs2 - ikcs)ds =
(la-Hb/kI'2 ' (Э'бЛ)
где а иЬ — вещественные числа. Если положить g (s) = exp(-te2) и
h is) = as2 + cs9 то используя выражение E.2.32), получаем
^ - b/a2)]. E.6.2)
Это выражение отличается от точного результата E.6.1), особенно в
тех случаях, когда с2 к2 и Ъ сравнимы с ка. С физической точки Зрения
1(к) представляет собой поле с гауссовым распределением
и (х, 0) ос ехр( — Ьх2) в направлении в = arcsin с на расстоянии
z = 1/Bа). В дальней зоне при а — 0 (z — оо), точное выражение
E.6.1) имеет асимптотику ехр(- kW/Ab), в то время как разложение
E.6.2) приводит к ехр( — Ьх2). Отсюда следует, что метод стационар-
стационарной фазы не может правильно описать расходимость пучка при его
распространении.
Улучшить метод стационарной фазы можно за счет введения ком-
комплексной функции h(s) = as2 + cs - ibst/k. Обобщение фазовой
функции на комплексные значения аргумента приводит к некоторым
5.6. Метод наибыстрейшего спуска
367
\mh(s)
[ms
в
Рис. 5.12. Примеры поверхностей вблизи простой седловой точки (д), седловой точки
второго порядка (называемой также «обезьяньим седлом») (б) и двух седловых точек
(в). Заштрихованные области представляют проекции соответствующих долин на плос-
плоскость ху.
проблемам, связанным с решением уравнения h'(s) = 0, которое в об-
общем случае будет иметь комплексные корни. Если эти корни не явля-
являются вещественными, то не будет и точек на вещественной оси, где
вещественная и мнимая части величины h' одновременно обращаются
в нуль. Эту трудность можно преодолеть, изменяя контур интегриро-
интегрирования таким образом, чтобы он проходил через комплексные корни ss
уравнения h' = 0. Вследствие того, что функция h(s) предполагается
sin (Re/J sh(Im^)
Контур
наибыстрейшего
спуска
Рис. 5.13. Трехмерный график функции sin (Re/3) sh(Im|C) = Im sin(/3) (с любезного раз-
разрешения П. Л учини).
368
Гл. 5. Асимптотическое вычисление дифракц. интегралов
аналитической, вблизи точки ss функции Re h (s) и Im h (s) описывают
квадратичйые поверхности с седловой точкой В55. В соответствии с
этим стационарные точки функции h (s) называются седловыми точ-
точками [14] (рис. 5.12 и 5.13).
Если h (s) — аналитическая функция, то она удовлетворяет диффе-
дифференциальным уравнениям Коти — Римана
dlmhlds" = dRth/ds\ dim h/ds' = -dReh/ds", E.6.3)
где s = s' + is". С геометрической точки зрения эти уравнения озна-
означают, что семейства кривых Im h(s) = const и Re h (s) = const взаим-
взаимно ортогональны. Следовательно, кривая Re A = const всюду каса-
тельна градиенту Im h. Кривая Re h = const представляет собой путь,
вдоль которого Im Л изменяется наиболее быстро (рис. 5.14 и 5.15).
Вследствие этого кривую Re Л = const называют контуром наибыст-
наибыстрейшего спуска (или подъема). В дальнейшем мы будем использовать
сокращенное название КНС, подразумевая при этом проходящий че-
через седловую точку контур наибыстрейшего спуска для функции
ImA.
Контур
наибыстрейшего f
подъема
\
\ V__
Контур наибыстрейшего
спуска
Рис. 5.14. Долина и холмы функции Im cos@ - ф). Непрерывные кривые —
Re cos(/3 - ф) = const; штриховые кривые — Im cos(/3 - ф) = const > 0; штрихпунк-
тирные кривые — Im cos@ - ф) = const < 0.
5.6. Метод наибыстрейшего спуска
369
Рис. 5.15. Контуры наибыстрейшего спуска функции cos(jC - ф).
Предположим на время, что седловая точка единственная и
Im h(ss) > Im h(s). Тогда сделанные нами предварительные замеча-
замечания свидетельствуют о необходимости изменить путь интегрирова-
интегрирования, проходящий вдоль вещественной оси, на КНС. Таким образом,
можно написать следующее выражение:
Jr
*КНС+ г»
КНС ^гв
V
-ikh(sq)
E.6.4)
где Гв — набор контуров, окружающих разрезы функции g(s)9 если
таковые есть, a rq — q-й вычет в полюсе функции g, лежащем между
первоначальным контуром и КНС + Гв. Преимущество разделения
интеграла на две части, одна из которых вычисляется вдоль КНС,
связано с тем, что вдоль КНС функцию h (s) можно записать в виде
h (s) = Rth(ss) + /1тЛ($). Следовательно, замечая, что вдоль КНС
функция 1тЛ имеет единственный максимум в точке ss и при отходе
от него монотонно уменьшается, можно выполнить следующее преоб-
преобразование:
и = +
ss) — Im h(s),
E.6.5)
370 Гл. 5. Асимптотическое вычисление дифракц. интегралов
где s е КНС. Следовательно, в выражении E.6.4) интеграл, вычисляе-
вычисляемый вдоль КНС, можно преобразовать к виду
W = e-ikh^e-^ Г gls(uy]e-ku2fdu. E.6.6)
jA J -00
При к — оо множитель е~ки2 быстро убывает при удалении от точки
и = О л главный вклад в интеграл дают значения g вблизи седловой
точки. Таким образом,
Лснс = e-ik«°MsMh"(ss)V12. E.6.7)
В частности, интеграл углового спектра в выражении D.9.12) запи-
запишется в виде
W = i S{p)e-ik^cos^-^dp = SD>)(pX/2eiK'4-ik'u E.6.8)
кнс \kpj
Последнее выражение подтверждает, что интеграл углового спектра
при вычислении его по КНС можно рассматривать как цилиндриче-
цилиндрическую волну с угловым распределением S@) (ср. с разд. 4.9.2).
5.6.1. Полюс вблизи седловой точки
В некоторых случаях седловая точка лежит вблизи полюса подынте-
подынтегрального выражения. Это особенно часто имеет место, когда поле
рассматривается в представлении углового спектра. В этих случаях
можно записать интеграл в следующем конкретном виде:
-lW-e-ks2ds9 E.6.9)
где sp — полюс вблизи седловой точки ss = 0. Если $р « о, а/E) яв-
является практически постоянной в интервале \s\ < k~1/29 то интеграл
в E.6.9) можно переписать следующим образом:
)
E.6.10)
5.6. Метод наибыстрейшего спуска 371
где G(x) определяется выражением E.3.11). В частности, интеграл
E.6.11)
кнс Р Рр
вычисляемый вдоль контура наибыстрейшего спуска, проходящего че-
через /3 = ф, можно привести к виду E.6.9), если использовать подста-
подстановку /pcos(j3 - ф) = s2 + /р и учесть тот факт, что для /3 - </> имеем
j3 - ф в е*ж/* sB/p)l/2. Поступая таким образом [см. выражение (Е.2)
в приложении Е], имеем
-.S-(^-
* -27tiexp[-ifcpcos(/?p - <?)] сГ(/?р - 0)teYl/@). E.6.12)
5.6.2. Гоч/fa ветвления вблизи седловой точки
Рассмотрим интеграл
¦я/4 Лоо -ilu -1%1А
E-6.13)
Для него все члены асимптотического разложения по степеням \/к
тождественно равны нулю, так как lim^ _ ^кРЦк) = 0 при всех поло-
положительных целых п. Преодолеть эту трудность можно, опираясь на
то, что в знаменателе стоит величина Va2 + si1, имеющая две точки
ветвления при sb = ± ia. Если в предыдущем разделе мы рассматри-
рассматривали полюсные сингулярности подынтегрального выражения, то те-
теперь необходимо сделать следующий шаг, а именно учесть близкое
расположение к контуру интегрирования точек ветвления.
Задача, к которой мы здесь обращаемся, связана с получением точ-
точного представления следующего класса интегралов [см. выражения
(ЕЗ) и (Е4) в приложении Е]
I±(k) = -fi\(s ~ sb)±il2g(s)e-ik«s)ds, E.6.14)
где Г — произвольный контур в комплексной 5-плоскости (рис. 5.16).
Квадратный корень в подынтегральном выражении предполагается
однозначно определенным, по крайней мере при движении s вдоль F.
372
Гл. 5. Асимптотическое вычисление дифракц. интегралов
Начальная
долина
Полюс
s-плоскость
Л»
Res
КНС
Разрез
Конечная
долина
Рис. 5.16. Контур наибыстрейшего спуска, проходящий вблизи полюса и разреза.
Это означает, что разрез в плоскости s сделан в точке sb и идет парал-
параллельно вещественной оси в направлении к s = — оо.
Если преобразовать контур интегрирования к суммарному конту-
контуру, включающему в себя контур Гь, окружающий точку ветвления и
соответствующий разрез, то можно рассмотреть отдельно вклад в
I(k) одного лишь интеграла по Гь. При этом заметим, что для Гь,
близкого к полупрямой s = sb - х9 х > О, можно использовать следу-
следующее приближение: 1/2 ,.,,..
(s - sbI/2 = iw, E.6.15)
где w > О для s на верхнем берегу контура Гь и w < 0 на нижнем. В
соответствии с этим при и>, изменяющемся от - оо до + оо, s будет
описывать обход по контуру Гь. Таким образом, если мы заменим пе-
переменную интегрирования s на и>, то контур Гь преобразуется в пря-
прямую (-оо, + оо). В частности, для I_(k) [см. E.6.14)] имеем
t.exp(fa/4)
Л1'2
0[s(w)]exp{-ifcft[s(w)]}dw. E.6.16)
Функция h [s(w)] имеет седловую точку при w = 0, которая дает
вклад в /_(А:), а именно
/_Sb(fc)~-2
exp[ — ik
[2*4
E.6.17)
здесь функции с необозначенным аргументом вычисляются при s = sh.
Поступая аналогичным образом, получаем следующее выражение
5.7. Дифракционные эффекты на границе раздела 373
для 1+(к):
v)] ехр {— ikh [.siw)]} dw ~
J-
txpl-ikh(sby]g(sb)
ТЩ JT" E.6.18)
\fl [*'(sb)]
Здесь в отличие от выражения E.6.17) главный член содержит множи-
множитель к~19 так что вклад от точки ветвления стремится к нулю при
к — оо. Следует заметить, что каждый из этих двух асимптотических
вкладов стремится к бесконечности при приближении точки ветвления
к стационарной точке, так как в знаменателях выражений E.6.17) и
E.6.18) содержится А'.
Возвращаясь к тому интегралу, с которого начинался этот раздел,
заметим, что его можно переписать в виде
exp(i7r/4) Г 1 ч_
*V g(s)exp[-!fe/i(s)] ds, E.6.19)
где g(s) = (s - ia)~l/2 и h (s) = s. Таким образом, используя выраже-
выражение E.6.17), получаем непосредственно правую часть выражения
E.6.13).
5.7. ДИФРАКЦИОННЫЕ ЭФФЕКТЫ
НА ГРАНИЦЕ РАЗДЕЛА ДВУХ ДИЭЛЕКТРИКОВ
В разд. 4.9 мы показали, что поле отраженной от плоскости раздела
двух диэлектриков цилиндрической ТЕ-волны представляется интегра-
интегралом Зоммерфельда [см. выражение D.9.25)], подынтегральное выра-
выражение которого имеет точки ветвления. Следовательно, используя
угловой спектр, этот интеграл можно записать в виде (см. задачу 13)
100 cos20 + 2(п2 - cos2 P)l/2 sin0 - п2
1-й2
X
+ pcos(j3 - фу]} dp m /KHC + /Гь, E.7.1)
где кх относится к среде 1, содержащей источник, и пг — показатель
преломления среды 2, п = пг/пх. Слагаемое /кнс представляет собой
вклад седловой точки, а /Гь — вклад контура Гь, окружающего часть
374 Гл. 5. Асимптотическое вычисление дифракц. интегралов
разреза, возникновение которого связано с функцией (л2 - cos2j8I/2,
причем Гь расположен между точкой ветвления
А> = Чп — arccosn
и точкой пересечения с КНС (см. рис. 4.12, в). Координаты xs и zs —
это координаты источника, а х = pcos<? и z = psin<? — координаты
точки наблюдения (рис. 4.11).
Для вычисления /кнс заметим прежде всего, что седловая точка /3S
является корнем уравнения
tg ft = (z + z,)/(x - xs), E.7.2)
что позволяет дать геометрическую интерпретацию точки Д,. А имен-
именно, j3s представляет собой угол, образованный осью х и вектором, свя-
связывающим зеркальное изображение источника, расположенного в точ-
точке л^, — zs, с точкой наблюдения.
Используя затем выражение E.6.8) (см. задачу 14), нетрудно полу-
получить
- -[exp(-i*/4 - iktpWnktpmrJLflti E.7.3)
здесь р = [(х — л^J + (z + ZgJ]172 — расстояние между изображени-
изображением источника и точкой, где определяется поле, a rs — коэффициент от-
отражения Френеля. Таким образом, /кнс-представляет конгруэнцию лу-
лучей, выходящих из источника, достигающих поверхности раздела и
отраженных по законам Снеллиуса и Френеля.
5.7.1. Боковые волны
В случае когда среда, содержащая источник и точку наблюдения, яв-
является оптически более плотной по сравнению с граничащей с ней сре-
средой, мы имеем п < 1. Следовательно, в этом случае точки ветрления
вещественны и контур наибыстрейшего спуска пересекает разрез толь-
только тогда, когда /3S > тг — arccos n или arccos/? > /3S. Предположим,
что выполнено первое неравенство. При этом мы имеем
\
Jr
E.7.4)
здесь
fi(cos Р) = - xs cos p + zs sin p + р cos(p - ф),
g(cosP) = -[Я11/2/Bя)] ехр(т/4)(и + cos0I/2/A - п2). E.7.5)
5.7. Дифракционные эффекты на границе раздела
375
Используя затем результат интегрирования E.6.8), где s^ = п, полу-
получаем
. ехр(ш/4)
Bя)
1/2
-п1/2A-л2Г1/4х
- и2I'2
и2I'2]}
E.7.6)
{*i[-(* + *.)* + (х - х.)A - и2I'2]}3'2 *
Если переписать теперь выражение для фазы в виде
пк.Цх - х.) - (z + zs)n(l - и2)'2] + М*. + «XI " "Т1/2,
то можно считать, что эта фаза связана с лучом, который распро-
распространяется от источника до границы раздела под критическим углом
0С = arcsin я, затем после преломления во второй среде распространя-
распространяется параллельно границе и, наконец, покидает ее, преломляясь под
углом вс и попадая в точку наблюдения (рис. 5.17). Если обозначить
через Lj, L2 и L3 расстояния, пройденные по этим трем отрезкам, то
выражение E.7.6) можно переписать следующим образом:
ехр(ш/4) n
1/2
Bтг)
1/2 A-
E.7.7)
Из-за приграничного характера распространения этой волны ее и
назвали боковой водной. Ее амплитуда убывает пропорционально рас-
расстоянию, пройденному вдоль границы раздела, в степени 3/2. То что
эта волна затухает более сильно, чем цилиндрическая волна (т. е.
-L~1/2), обусловлено утечкой энергии при распространении вдоль бо-
бокового пути (см. книгу Бреховских [7], указанную в литературе к гл. 3
настоящей книги).
Проведенное выше рассмотрение основывалось на предположении
l2 ;
Рис. 5.17. Геометрическое
рассмотрение задачи о воз-
возбуждении боковой волны.
(x,z)
Фронт
боковой
волны
Источник
(O,rsJ
376 Гл. 5. Асимптотическое вычисление дифракц. интегралов
о том, что в обеих средах волна распространяется без потерь. Легко
доказать, что с небольшими изменениями выражение E.7.6) остается
справедливым и для сред при наличии потерь. В частности, если поте-
потери есть только в среде, содержащей источник, то при смещении точки
наблюдения параллельно границе раздела величина /г с расстоянием
х убывает в соответствии со степенным законом, в то время как вели-
величина /кнс убывает по экспоненциальному закону. Это приводит к то-
тому, что вклад от боковых волн становится преобладающим по сравне-
сравнению с вкладом, определяемым в приближении геометрической опти-
оптики. Качественно можно представить себе, что в этих случаях лучи
стремятся распространяться вдоль поверхности, чтобы избежать по-
потерь в объеме среды, однако эти волны не следует путать с поверх-
поверхностными волнами, рассматриваемыми в разд. 3.21 и 3.22 (см. гл. 3
настоящей книги). Действительно, в то время как амплитуда поверх-
поверхностной волны убывает экспоненциально в перпендикулярном границе
раздела направлении, боковые волны сравнительно глубоко проника-
проникают в обе среды.
Боковые волны существуют также и при освещении границы раз-
раздела точечными источниками. При этом основные свойства этих волн
сохраняются без изменения, единственное отличие связано с возникно-
возникновением в выражении E.7.6) дополнительного множителя р~1/2 =
= [(х — Xj,J + (у — д^J]74 (см. [книгу 3, с. 514], указанную в литера-
литературе к гл. 2). Таким образом, в случае когда граница раздела освеща-
освещается волной, излучаемой точечным источником, мы имеем
/Гь ос exp[-/(fe1L1 + k2L2 + к^3)]/[р1/2(*1^2K/2]. E.7.8)
Возникновение этого дополнительного множителя можно объяснить
эвристически, считая, что полная мощность, переносимая боковой
волной, сохраняется постоянной.
Наконец, следует заметить, что записанные выше асимптотические
выражения применимы лишь в том случае, когда седловая точка не
очень близка к точке ветвления. Нетрудно показать, что при /3S — (Jc
имеем L2 — 0 и выражение E.7.7) становится сингулярным. В этом
случае более точно интеграл можно вычислить с помощью найденной
Фоком переходной функции, связанной с функцией параболического
цилиндра порядка 1/3 (см. книгу Бреховских [7], указанную в литера-
литературе к гл. 3 настоящей книги).
5.7. Дифракционные эффекты на границе раздела
377
5.7.2. Эффект Гуса — Хенхена
Рассмотренные выше интегралы /кнс и /г являются аналитическими
функциями координат источника л^ и zs. Поэтому выражения E.7.3) и
E.7.6) можно использовать и в том случае, когда и xs и zs — ком-
комплексные величины:
xs = Re xs — ib sin ф,
zs = Re zs + ib cos ф;
E.7.9a)
E.7.96)
здесь Ь и ф — произвольные вещественные величины. Если ввести но-
новую систему декартовых координат ?, f (рис. 5.18) с центром в точке
ReJ^, — Rezs, повернутую на угол ф относительно системы координат
х, z, то легко показать, что ? = 0 и ? = - ib. Следовательно, рассто-
расстояние р от точки наблюдения до изображения источника можно запи-
записать в виде
9 = ie + (С + ibJV12 = С + й>"+ К2/(С + ib\ E.7.10)
справедливом для точек, близких к оси f. Подставляя это выражение
для р в выражение E.7.3), получаем поле с комплексным эйконалом
(см. разд. 2.7):
exP(-i7t/4)A}'2 1
'кнс
E.7.11)
Рис. 5.18. Отражение гауссова пучка.
Показано, что при учете эффекта
Гуса — Хенхена отраженный пучок
испытывает смещение на расстояние
378 Гл. 5. Асимптотическое вычисление дифракц. интегралов
Таким образом, вдоль направления ? (см. разд. 2.7.1) поле имеет гаус-
гауссово распределение с шириной w2 = 2(?2 + Ь2)/(к 1? Ъ). Однако нельзя
пренебрегать и множителем rs(Ji^, который в общем случае является
функцией точки наблюдения [см. выражение E.7.2)].
Рассмотрим важный частный случай, когда гауссов пучок претер-
претерпевает полное отражение. При этом модуль коэффициента отражения
равен единице, а его фаза 2ф$ определяется выражением C.20.6). Если
точка наблюдения находится от оси f на небольшом расстоянии (что
имеет место для достаточно узкого) гауссова пучка, то можно запи-
записать следующее выражение:
г(Д) = ехр[2#.(&)] = ехр[2#§(Д.) + ШФМ) <%], E.7Л2)
где величина rf/Js связана со смещением виртуального источника отра-
отраженного пучка соотношением E.7.2), которое можно переписать в виде
Д. + dp% = in + ф + arctg [{/(С + ib)] ? iTr + ф + {/(С + ib\ E.7.13)
где ^ — угол между аксиальным направлением гауссова пучка (ось f)
и осьюг. Однако из выражения C.20.6) (см. гл. 3 настоящей книги)
после подстановки 0 = /3S — — 7г = ^ получаем
2
cos Д8 sin ф
dps (cos2 /?, - n2I/2 (sin2 ф - sin2 0СI/2
Ml,
где вс = arcsin(w) — критический угол для поверхности раздела.
Подставляя выражения E.7.13) и E.7.14) в E.7.12), выражение
E.7.11) можно переписать в виде
, ехр(-1я/4)/11/2 1
'к„с 4,
ib fcx Jj
где 5S = ^g/Arj. Отсюда следует, что при полном отражении диспер-
дисперсия фазы коэффициента отражения Френеля приводит к смещению
пучка в направлении, перпендикулярном его оси. В частности, для
s -волны (см. задачу 19) это смещение запишется в виде
3S = B/k1)[sin^/(sin2^ - sin20cI/2]. E.7.16)
В выражение E.7.15) входит лишь главный член асимптотического
разложения интеграла. Можно показать, что при ф -* тг/2 следующий
член разложения становится сравнимым с первым. В частности, при
5.7. Дифракционные эффекты на границе раздела 379
падении пучка под углом скольжения выражение E.7.16) дает конеч-
конечное смещение, которое не имеет физического смысла. В действитель-
действительности 8S — О при ^ —¦ тг/2 (см. книгу Бреховских [7], указанную в лите-
литературе к гл. 3 настоящей книги).
Из-за малости множителя А: смещение 5S можно достоверно оце-
оценить только в том случае, когда угол падения близок к критическому.
Однако для ф, близких к 0С, седловая точка /3S приближается к точке
ветвления настолько, что асимптотические вклады величин /КНс и ^г
уже нельзя разделить. В этом случае необходимо использовать соот-
соответствующую переходную функцию.
Боковое смещение оптического пучка наблюдали Гус и Хенхен в
1947 г. [20], подтвердив таким образом то, что электромагнитные
волны [21] испытывают такие же смещения, какие ранее наблюдались
у ультразвуковых волн. Совсем недавно [22] наблюдались смещения
на нескольких длинах волн пучка, падающего на плоскую четырех-
слойную структуру. Большое смещение присходит вследствие зависи-
зависимости коэффициента отражения от угла падения. Действительно, как
мы уже отмечали в разд. 3.18, функция г (кх) имеет, вообще говоря,
несколько полюсов в комплексной кх-плоскости. Отраженное поле
можно представить в виде, аналогичном E.7.1), в котором подынте-
подынтегральное выражение заменяется на
Ля + ioo
иЛр'Ф)аС\0 „(cosZ-^s^) X
i/CiC-XjCos^ + zssin/f + cos(j? - 4>)~]}dfl, E.7.17)
где f(C) = r(j3)(cosi3 - cos/Jj), а (Зг — ближайший к КНС полюс коэф-
коэффициента отражения. Асимптотическое вычисление этого интеграла
показывает, что отраженный пучок смещается относительно зеркаль-
зеркальной траектории в том случае, когда комплексный полюс jSj близок к
КНС. Так как /3| связан с модой утечки многослойной структуры (см.
разд. 3.18), большое боковое смещение можно объяснить тем [23], что
падающий луч возбуждает волну утечки, которая распространяется на
некоторое расстояние параллельно плоским границам раздела муль-
тислоя, а затем переизлучается в полупространство, содержащее ис-
источник. Тщательный выбор параметров многослойной структуры по-
позволяет получить очень большое смещение. Этот эффект можно ис-
использовать для создания устройств связи в системах интегральной оп-
оптики.
380 Гл. 5. Асимптотическое вычисление дифракц. интегралов
5.8. АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ДИФРАКЦИОННЫХ
ИНТЕГРАЛОВ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
Займемся теперь вычислением интеграла 1(к)9 возникающего в связи с
использованием цилиндрических координат. Обычно такой интеграл
записывается в следующем виде:
E.8.1)
[см., например, выражение D.11.4)], где/(?) и Г (у) зависят от величи-
величины на опорной плоскости z = z'. В частности, для опорного поля с
вращательной симметрией, обращающегося в нуль вне границ круглой
апертуры радиусом a,f(s) nT(s) равны соответственно произведе-
произведению амплитуды Л (s) на фазовый множитель —iexp(—ikL) и эйконалу
S (у ). Действительно, в этом случае правые части выражений E.8.1) и
D.11.19) совпадают, если/т = Jo и \z - zf I = L.
Если записать Jm следующим образом (см. справочник Абрамови-
ца и Стегана [4, с. 364], указанный в литературе к гл. 2 настоящей
книги):
¦Ш = [2/W]1/2i№,C) + *e(m,C)]exp{i[C - (m/2
+ 12/(пОУ!2ЦР(тЛ) - ie(m,C)]exp{-i[C " (т/2 + 1/4)тг]},E.8.2)
гдеР и б — медленноменяющиеся функции перменной ?*, которые при
больших f равны соответственно единице и нулю, то1(к) можно пе-
переписать в виде [см. статью Саусуэлла A978) в библиографии]:
:)]ds +
E.8.3)
причем для вращательно-симметричных полей мы имеем
9i(s) = [-i/(LpI/2]e-*M(s)s1'2[P@,fcsp/L) + iQ(O,ksp/L)l E.8.4a)
/i,(s) = (s - pJ/BL) + S(s), E.8.46)
= _e-2'^r(S), E.8.4b)
= (s + pJ/BL) + S(s). E.8.4Г)
5.8. Асимптотическое вычисление в цилиндрических координатах 381
Главные члены разложения интегралов можно вычислить с по-
помощью выражений E.2.32) и E.2.36), и при использовании соотноше-
соотношения sVl(P + iQ) -+sVl (при к —> оо) получаем
[с ~|
рA + LS"(sp))\
[с
p(i+lVM
Bккр)
1/2
172 Л^Щ I * л _,_ Т С7^ I X
1/2
X
Г -IL/V. Г а
х ехр[ — гкп^а)] + г
х exp[-ii№2(fl)]j, E.8.5)
где s и sq — точки стационарной фазы функций соответственно И^ и
Л2, а третий член представляет собой вклад от граничной точки
s = а. Другая граница (s = 0) не дает вклада в /(?), поскольку
sU2(P + iQ) = 0 при 5 = 0. Записанные выше выражения будут ис-
использованы в разд. 7.18 при вычислении поля в неустойчивых резона-
резонаторах.
Как видно из выражения E.8.5), уменьшение амплитуды поля с
расстоянием/, до апертуры определяется по существу множителем
| 1/2
E.8.6)
который отличается от аналогичной величины [см. выражение
E.2.43)], полученной для цилиндрических полей, дополнительным
множителем (sp/pVl). Это обусловлено тем, что в рассматриваемом
случае волновые фронты в отличие от цилиндрических волновых
фронтов имеют два различных конечных радиуса кривизны.
Если точка наблюдения лежит на оптической оси (р = 0), то удоб-
удобнее обратиться непосредственно к интегралу E.8.1), который прини-
принимает вид
-idji + S(s)lj
sds, E.8.7)
382 Гл. 5. Асимптотическое вычисление дифракц. интегралов
где волна предполагается вращательно-симметричной. Если A(s) = 1
и S(s) = -^/(If) + Bs(*/Dtfk) (см. разд. 5.5), причем w = 2а, то
выражение E.8.7) можно переписать следующим образом:
Здесь N = a2/(LX) — число Френеля апертуры, a F(f) — комплексный
интеграл Френеля [выражение E.3.5)], причем для простоты мы пред-
предположили, что В > 0.
Этот результат позволяет сделать некоторые важные заключения
о свойствах поля. Если расстояние от точки наблюдения до фокуса та-
таково, что
- l/f\Sa2k > 10В1/2, E.8.9)
то интеграл Френеля можно аппроксимировать его асимптотическим
значением [выражение E.3.15)] и таким образом получить выражение,
совпадающее с полем, вычисленным в приближении геометрической
оптики. И наоборот, отрезок оптической оси, на котором нарушается
приближение геометрической оптики, имеет длину \L —/I, определя-
определяемую выражением
\L - /| ? (Bll2/l,6nNA2)± E.8.10)
При В = 0, используя первый интеграл в E.8.8), нетрудно вычис-
вычислить поле, амплитуда которого дается выражением
Si*«1/DL)- E.8.,1,
L[1/BL) ~ 1/B/)]
5.8. Асимптотическое вычисление в цилиндрических координатах 383
В частности, если отверстие освещается плоской волной (l/f = 0),
выражение E.8.11) принимает вид
\и(р = 0,L)| = 2|sin[fca2/DL)]|. E.8.12)
Это означает, что интенсивность поля осциллирует, уменьшаясь
до нуля при Lq = cP/QqX), а при больших расстояниях (L -> оо) стре-
стремится к нулю как 1/L2. Отсюда следует, что дифрагированное на от-
отверстии поле ведет себя практически как сферическая волна, только ес-
если расстояние L до точки наблюдения много больше, чем а2/\. Таким
образом, если N — число Френеля отверстия относительно точки наб-
наблюдения, то поле на оси равно нулю при N(L) = 2q и описывается
сферической волной лишь при N < \.
Можно рассмотреть также и комплексные/:
l/f = (l//r) + i/(kw2l E.8.13)
Этот случай соответствует освещению апертуры гауссовым полем
при наличии сферических аберраций. При этом поле на оси не являет-
является более осциллирующей функцией расстояния/, и может быть вычис-
вычислено непосредственной подстановкой комплексного аргумента в инте-
интегралы Френеля.
Аналогичные осцилляции можно наблюдать вдоль оптической оси,
когда волна, возмущенная сферическими аберрациями третьего и пято-
пятого порядка, подходит к фокусу линзы Тессара, как показано на рис. 5.19
(заимствованном из работы Фоке [24]).
0,Щ -
°'wL/\
/\Л/\Л
-0,6А 0 z
Рис. 5.19. Интенсивность поля на оптической оси вблизи фокуса линзы Тессара, вычис-
вычисленная Фоке [24а] для трех апертур A:2,8; 1:4; 1:5,6). Безразмерный параметр А соот-
соответствует определенной в D.13.21) оптической координате м, относящейся к расстоянию
между фокусом бокового луча и параксиальным фокусом: Д = (l/2)A:04A2zaj), где z^ —
продольная сферическая аберрация бокового луча с отклонением от оси на высоту р0. Рас-
Распределение поля вычислялось с учетом первичных и вторичных сферических аберраций в
предположении, что zc$ зависит от р0 в виде гсф= -(l/2)/2(/pf + I*Pq). Остальные пара-
параметры: / = 52,5 мм, р0 = 9,15 мм, z^ = 0,42 мм и Д = -75 при X = 546 нм.
384 Гл. 5. Асимптотическое вычисление дифракц. интегралов
5.9 ВЫВОД АСИМПТОТИЧЕСКИХ РЯДОВ
ИЗ СРАВНИТЕЛЬНЫХ ИНТЕГРАЛОВ;
МЕТОД ЧЕСТЕРА— ФРИДМАНА— УРСЕЛЛА (ЧФУ)
В разд. 5.4 мы получили главные члены асимптотического ряда, к ко-
которому можно прийти с помощью метода, предложенного в 1956 г.
Честером и др. [25]. Он основан на замене переменнойs — и, опреде-
определяемой неявным соотношением
E.9.1)
где f — параметр, учитывающий взаимное положение двух седловых
точек функции А. Можно показать, что это преобразование однородно
регулярно вблизи s = 0. Если разложить теперь gds/du в степенной
ряд .
9(s)f- = 1Рт(и2 - 0т + lqmu(u2 - 0м E.9.2)
пи
и подставить этот ряд в дифракционный интеграл E.2.24),го получим
/*ioo
+ Z<7m u{u2 - ()mexp| k[ \ - Си ) \du\e~ikh*. E.9.3)
m J -ioo
Введем теперь следующие функции:
Г
Г*/у - Cuj\
= ^ Г < ~ ОиехрГ*/у - Cuj\du, E.9.4а)
GJC, *:) = 2^т Г" и(и2 - 0т ехрГкГу - Cuj\ du, E.9.46)
которые связаны между собой рекуррентными соотношениями
Fm = -B/Щт - l)Gra_2, E.9.5а)
Gm = -A/Jfc)Bm - l)Fm_1 - B/Щт - l)CFm-2. E.9.56)
Эти соотношения легко получить, проводя в E.9.4) интегрирование по
частям. В частности,
Fo = Г1/3 АЦ?к213), Go = -к'213 АЩк2/3). E.9.6)
Если эти функции подставить в ряд E!9.3), то получим
Цк) . 2
5.10. Асимптотическое вычисление поля 385
Ро'-^^ + 4р + --., E.9.8а)
E.9.86)
5.10. АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ПОЛЯ,
ДИФРАГИРОВАННОГО НА ОТВЕРСТИИ
В разд. 4.14 мы показали, что возбуждение в точке Р, производимое
сферической волной от источника S, дифрагированной на отверстии
А, можно представить в виде суммы лучевого поля ug и поля иь, воз-
возникающего на границе отверстия [граничной дифрагированной волны
(ГВД)].
С математической точки зрения введение граничной дифрагирован-
дифрагированной волны позволяет свести двумерный дифракционный интеграл к
интегралу по контуру. Это преобразование облегчает асимптотиче-
асимптотическое вычисление поля. Действительно, мы уже научились получать
асимптотические ряды для одномерных определенных интегралов,
имеющих разрывы в подынтегральных выражениях. Теперь осталось
применить полученные формулы к интегралу вида [см. D.14.19)]
«ь = -7ГЩ- f'V - cos0>-ffc<''+s'># = иьл + иълъ E.10.1)
где иъ j включает в себя все вклады от точек стационарной фазы
[т. е. д(г' + 5')/Эф = 0], а иъ и связано с точками разрыва произво-
производных в' (ф) и г' (</>) + s'(ф). Последние локализовны в вершинах грани-
границы отверстия.
Что касается точек стационарной фазы, то они имеют очень про-
простую геометрическую интерпретацию. Действительно, если обозна-
обозначить через s криволинейную координату границы отверстия, а через
е — единичный вектор, касательный к границе, то (см. рис. 5.20)
(д/дф)(г' + s') = 0 -> (d/ds)(r' + s') = ё• V(r' + s') = е • (Р + Г) = 0. E.10.2)
Как следствие, в стационарной точке падающий луч образует с тан-
тангенциальным вектором 3 угол C, равный углу между вектором е и лу-
лучом, дифрагированным вдоль г'. Это свойство позволяет сделать вы-
вывод о том, что все лучи, дифрагированные в точке границы Qe, обра-
образуют полуконус, ось которого параллельна касательному к границе
вектору, а угол /3 равен углу между падающим лучом и границей.
386
Гл. 5. Асимптотическое вычисление дифракц. интегралов
Конус
дифрагирован-
дифрагированных лучей
Падающий
луч
Рис. 5.20. Конус лучей, дифрагированных
в точке Qe на границе отверстия.
Благодаря этому геометрическому представлению дифракцию на реб-
ребре отверстия можно рассматривать как локальное образование кони-
конической конгруэнции лучей. Таким образом, дифракция сферической во-
волны на отверстии есть образование конических конгруэнции вдоль
границы отверстия. При этом граничная дифрагированная волна в
точке Р будет определяться вкладом дифрагированных лучей, выходя-
выходящих из различных точек границы отверстия и проходящих через Р
(рис. 5.21). Такая картина более или менее эквивалентна объяснению
Т. Юнга, согласно которому падающий луч претерпевает отражение
Лучи, дифрагированные
от угла
Лучи Лучи,
геометри - дифрагированные
ческой оптики на границе
Рис. 5.21. Схематическое представления поля в точке Р, создаваемого за счет суммиро-
суммирования лучей геометрической оптики и лучей, дифрагированных на границе и в углах от-
отверстия.
5.10. Асимптотическое вычисление поля
387
на границе, в результате чего возникают распределенные по конусу
отраженные лучи.
5.10.1. Каустика дифрагированных лучей
Конгруэнция лучей, дифрагированных на границе отверстия, полнос-
полностью аналогична конгурэнциям, рассмотренным в гл. 2. Заметим пре-
прежде всего, что граница сама по себе является каустикой дифрагиро-
дифрагированных лучей. Действительно, по определению каустикой называют
геметрическое место точек, где сечение элементарной лучевой трубки
стягивается в отрезок. Именно это имеет место на кромке отверстия.
Следовательно, отличительной особенностью таких конгруэнции явля-
является, то что одна из поверхностей каустики сводится к криволинейно-
криволинейному контуру. Форма и положение второй поверхности каустики опреде-
определяется конкретной геометрией задачи дифракции (рис. 5.22) [26].
Рассмотрим для примера прямолинейную кромку, освещаемую из
точечного источника 5. Построив дифрагированные лучи, нетрудно
убедиться в том, что второй каустикой (рис. 5.23) является окруж-
окружность, проходящая через S. Эта окружность лежит в плоскости, пер-
перпендикулярной кромке, а ее центр — на самой кромке. Следователь-
Следовательно, на каждом дифрагированном луче будет два фокуса. Один из них
(F{) совпадает с точкой пересечения с кромкой, а другой (F2) лежит на
том же расстоянии otFj, что hFj от источника. С геометрической
Каустика
Дифрагиро-
Дифрагированные лучи
Падающие
лучи
Граница
Рис. 5.22. Геометрия в задаче о дифрак-
дифракции пучка лучей на краю отверстия. (Из
работы [1]).
Рис. 5.23. Круговая каустика лучей, ди-
дифрагированных на прямолинейном крае,
освещаемом точечным источником.
388 Гл. 5. Асимптотическое вычисление дифракц. интегралов
точки зрения присутствие кромки эквивалентно преобразованию на-
начальной конгурэнции, имеющей центр в точкеS, в конгруэнцию, кау-
каустики которой представляют собой прямую линию и окружность*
Для криволинейной границы вторая каустика определяется огиба-
огибающей конгруэнции дифрагированных лучей, которая задается пара-
параметрически выражением (см.приложение I в статье Келлера [26])
[г - геE)] • e(s) = |г - re(s)\cosp(s); E.10.3)
здесь s — длина дуги границы, § — единичный вектор, касательный к
границе в точке s, a re — координата точки (?е на границе. Дифферен-
Дифференцируя это уравнение по s, получаем второе уравнение, которое вместе
с E.10.3) определяет векторы fc каустики, т. е.
(г. - О. ^ - 1 + flr. - r.| sin р + (Г' - ^ 7S * = 0; E.10.4)
здесь точка сверху буквы означает производную по s, р — радиус
кривизны границы, an — главная нормаль границы (см. разд. 2.4.2),
направленная от центра кривизны. Теперь, используя E.10.3), можно
заменить (гс - ге) ¦ е на I гс - ге1 cos/З, так что уравнение E.10.4)
приобретает вид
|rc - re|(cos<5 + p/JsinjS) = psin2 j8, E.10.5)
где cos 6 = (rc — гс) ¦ fi/lrc — ге1. Таким образом, расстояние (с уче-
учетом знака) р{ = - I rc - ге I от границы до каустики запишется в виде
Pi = - р sin2 p/(pP sin P + cos 5). E.10.6)
Следуя нашему первоначальному определению, величина рх должна
быть отрицательной. Однако в последнем выражении рх может быть
как отрицательной, так и положительной. Неравенство р{ > 0 означа-
означает, что каустика является виртуальной и лежит на противоположной
стороне от дифрагированного луча. Следовательно, вычисление необ-
необходимо начинать с выражения для дифрагированных лучей, аналогич-
аналогично E.10.3), с той лишь разницей, что знак минус перед величиной
Ir - rel нужно заменить на плюс.
Для прямой кромки имеем
Pl = -sinp/p (>0). E.10.7)
В этом случае величина р{ одна и та же для всех лучей, выходящих из
одной и той же точки Qe. Нетрудно проверить, что для точечного ис-
источника S величина рх совпадает с расстоянием от(?е JloS, так что ка-
каустикой является окружность, проходящая через S и лежащая в пло-
плоскости, перпендикулярной кромке, причем центр этой окружности рас-
располагается на кромке (рис. 5.23).
5.10. Асимптотическое вычисление поля
389
В случае когда /3 = 0, имеем
/>! = -psin2j8/cos<5, E.10.8)
так что величина рх положительна при cos 5 < 0; иными словами, рх
положительна, когда проекция дифрагированных лучей на п является
отрицательной. В частности, для плоского отверстия, освещаемого в
перпендикулярном к нему направлении, мы имеем р = тг/2, так что
р = -pjeosS. Это означает, что перпендикулярная проекция каустики
на плоскость апертуры совпадает с центром кривизны самой аперту-
апертуры. Таким образом, каустикой является цилиндр, перпендикулярный
апертуре и в сечении совпадающий с эволютой границы отверстия
(рис. 5.24). Для круглого отверстия каустика стягивается в прямую
линию, проходящую через центр круга. Цилиндр, продолженный за
плоскость апертуры, представляет собой виртуальную каустику ди-
дифрагированных лучей, образующих угол больше чем тг/2 с нормалью
й к границе. В общем случае наличие вещественной каустики обуслов-
обусловлено сильным дифрагированным полем. В разд. 5.8 мы уже приводи-
приводили пример, когда поле дифрагирует на круглом отверстии.
В случае когда апертура не состоит из прямолинейных отрезков,
каустики существуют лишь в ограниченных областях. Таким образом,
соответствующие усиления или ослабления поля можно заметить
лишь для отверстий, границы которых криволинейны. В определен-
Каустика
Рис. 5.24. Цилиндрические каустики, образуемые лучами, дифрагированными на отвер-
отверстии в плоском экране, освещаемом плоской волной. Сечение цилиндра является эволю-
эволютой границы отверстия, а — общий случай; б — круговое отверстие. Каустика сводится
к нормали, проходящей через центр.
390 Гл. 5. Асимптотическое вычисление дифракц. интегралов
ном смысле можно сказать, что они оказывают фокусирующее влия-
влияние на дифрагированные лучи.
В заключение следует подчеркнуть, что проведенное нами рассмот-
рассмотрение каустик не зависит от способа возбуждения дифрагированных
лучей. Если даже лучи, попадающие на границу, вышли не из одного
источника, выводы данного раздела остаются справедливыми.
5.10.2. Дифракция на острие
Для того чтобы вычислить иь j, можно применить формулы разд. 5.2,
положив ЛE) = r'(s) + s'(s) и g(s) = Х1/2ехр(- /V/4)(l - cos0')/
/[Dt?Rs]. При этом получаем
"b,I
DnJR
s
д2(г' + s')
дф2
-1/2
; E.10.9)
здесь е = sgn[32(r' + s' УдФ2]> a rs, ss и в'$ — координаты стационар-
стационарной точки. Производная Э2(г' 4- s' )/дф2 вычисляется следующим об-
образом. Во-первых, заметим, что
ds'/ds = cos ft E.10.10)
и поэтому
d2s'/ds2= -jSJsmft E.10.11)
Кроме того, для вектора г' = TG(s) — г(Р) имеем
r'(s + ds) = r'(s) + e(s)ds + n(s)ds2/[2p(s)]9 E.10.12)
где пир — соответственно нормаль и радиус кривизны отверстия.
Следовательно,
r'(s + ds) = r'(s) + f • eds + if— + 1""(r)'
2L P r
= r'(s) - sin(P)ds + IГ^^ + ^l^2; E.10.13)
2L p r J
здесь cos б совпадает с величиной, введенной в E.10.5). Окончательно
уравнения E.10.11) и E.10.13) сводятся к виду
где мы заменили cos 5 на - р/3sin /3 - psm20/px [см. выражение
E.10.6)]. Используя выражение D.14.20), получаем
йз/йф = [A - cos0')/Ks][r's'(l + cos0')]/[?-(?' x s')]. E.10.15)
5.10. Асимптотическое вычисление поля
391
Конус
дифрагированных
лучей
Падающий
луч
Плоскость
падения
Рис. 5.25. Геометрия, используемая при вычислении поля, дифрагированного на острие.
Для того чтобы вычислить cos 0' и % • (г' х §'), разложим векто-
векторы г' и s' на составляющие вдоль вектора $ и в плоскости, перпенди-
перпендикулярной ё. Если обозначить через фе и ф^ углы, образованные проек-
проекциями векторов — г' и s' и касательными к поверхности экрана векто-
векторами t (рис. 5.25), то можно показать, что
1 + cos0' = 1+ г' • s' = 1 - cos2)? + ьт2рсоь(фе - ф'е) =
E.10.16)
E.10.17)
ё-(г' х Г) = -si
так что
ds|dф = -[A - cos0')/Ks]ctg[(</>e - </>;)/2]rV. E.10.18)
Как следствие, объединяя уравнения E.10.14) и E.10.18), получаем
ds
5/) d ds (ds\2d2(r'
+ )
• 2of
ds ds dф + \d4>) ds2
l
ct8
У^ EЛ0Л9)
поскольку условие d(rf + sf )/ds - 0 соответствует стационарной
точке.
392 Гл. 5. Асимптотическое вычисление дифракц. интегралов
Окончательно выражение E.10.9) с учетом E.10.19) запишется в
виде
1/2
E.10.20)
где Wi(<2e) = ехр(—/*s')/Dirs')— амплитуда волны, падающей на гра-
граничную точку Qe, aDK — коэффициент дифракции, аналогичный вели-
величине Dp введенной в разд. 5.2.6, и совпадающий с выражением B9) из
работы Келлера и др. [27], причем
Ок(фе,ф'е;Р) = [e~IJt/4/(87rfeI/2](l/sinj?) tg [(фе — Фс)/2]- E.10.21)
Миамото и Вольф (см. книгу Рабиновича [32], указанную в литера-
литературе к гл. 4 настоящей книги) показали, что при освещении апертуры
произвольным лучевым полем дифрагированную волну в пределе ма-
малых длин волн можно представить с помощью ГДВ. Поэтому если
проследить снова за всеми выполненными выше преобразованиями,
то нетрудно прийти к заключению, что выражения E.10.20) и E.10.21)
остаются справедливыми для любых падающих лучевых полей и{.
Келлер и др. [27] получили выражение E.10.20), используя асимптоти-
асимптотическое разложение дифракционного интреграла. При этом они нашли
такое же выражение для коэффициента DK (индекс К означает, что ди-
дифракционное поле вычислялось с использованием замкнутой инте-
интегральной формулы Гельмгольца — Кирхгофа). Заметим здесь, что DK
отличается от коэффициента Dx в выражении E.2.48), за исключением
случая, когда фе - фе' s тг. В разд. 6.2 мы еще вернемся к обсужде-
обсуждению этого расхождения.
5.10.3. Дифракция от угла
На угловой части апертуры производная г'(ф) + s'W>) терпит разрыв.
Поэтому для вычисления вклада иъ п дифракции от угла можно ис-
использовать формулу E.2.38), которая дает
1/2 1 -ik(r'+s') 1
E.10.22)
здесь 5(...) указывает на наличие разрыва функции в правой части вы-
выражения.
Далее, используя соотношение
5.10. Асимптотическое вычисление поля
393
— (г' + S') = ——Г S' . 7Г7^г(г + s ) * е =
йф R sin [(</>' - </>)/2]
1 -COS0' , , 1 +COS0' _ _ Л
"—к—^^Т>?(г+я)-в' EЛ0'23)
после простых алгебраических преобразований получаем
"*' 4nr' [(?' + f')«
л -ikr'
' 4- r'). e_
E.10.24)
здесь e+ и8, - единичные векторы, касательные к границе на двух
сторонах углового препятствия. Таким образом, угол апертуры при-
приводит к образованию сферической волны, характеризуемой коэффици-
коэффициентом угловой дифракции
,*, ^ *\г,* , Д . V E.10.25)
который можно выразить через углы, указанные на рис. 5.26.
В заключение заметим, что при преобразовании с помощью этой
формулы Мэгги — Рабиновича интеграла Гельмгольца — Кирхгофа в
контурный интеграл отверстие, освещаемое сферической волной, дает
поле, которое представляет собой суперпозицию вкладов поля геомет-
геометрической оптики (Mg), стационарных граничных точек (иь {) и углов
(если таковые имеются) (иъ п):
и(Р) = и% -h iibtI + wb,n = С
1/2
E.10.26)
здесь С = 1 в геометрически освещенной области.
i-xi.
Рис. 5.26. Геометрия
для вычисления коэф-
коэффициента угловой ди-
дифракции.
394 Гл. 5. Асимптотическое вычисление дифракц. интегралов
Лучи, дающие вклад вмЬ1, образуют конус вокруг касательной к
границе, причем угол раствора конуса равен углу /J, образуемому пада-
падающим лучом и границей отверстия. Вершинная (угловая) точка дей-
действует как точечный источник с диаграммой направленности Ск, кото-
которая сингулярна на конусах (s' + г') ¦ е+ = 0 и (s' + г') • 6_ = О,
что аналогично появлению границы тени.
То, что мы показали на примере облучения препятствия сферичес-
сферической волной, остается справедливым и для более общих лучевых по-
полей. Это легко доказать непосредственным вычислением интеграла
Гельмгольца — Кирхгофа [27] с использованием хорошо известных
формул [24, 28].
5.11. АСИМПТОТИЧЕСКАЯ ФОРМА РАЗЛОЖЕНИЯ ПОЛЕЙ
ПО ПЛОСКИМ ВОЛНАМ
В гл. 1 и 4 мы показали, что при весьма общих условиях гармониче-
гармонически зависящее от времени поле Е(г), распространяющееся в изотроп-
изотропной или анизотропной среде, можно представить в однородном полу-
полупространстве z > О с помощью его разложения по плоским волнам.
+ 00
вд-ff
Е0(к)ехр[-*Ф(к) - i(kxx + kyy + k,z)] dkxdky, E.11.1)
где kz = kz(kx, ky) — функция величин кх и ку, определяемая из дис-
дисперсионного уравнения ?>(о>, к) = 0 (см. гл. 1), a Eq и Ф — соответст-
соответственно амплитуда и фаза нормальной волны, распространяющейся
вдоль волнового вектора к. Если кх и ку лежат внутри некоторой об-
области Z>H, имеющей в общем случае форму эллипса, то kz является ве-
вещественным и положительным, в то время как вне области ?>н вели-
величина kz = —i\kz\ является мнимой.
В большинстве случаев приведенный выше интеграл невозможно
вычислить аналитически и приходится находить его асимптотическое
выражение, отыскивая стационарные точки [24, 29—33]. В частности,
если Ео — достаточно гладкая функция величин кх ику, то можно за-
записать следующее приближенное выражение:
^ + Еп(г), E.11.2)
где суммирование распространяется на стационарные векторы к„,
х + (dkz/dkx)z + дФ/дкх = 0, E.11.3а)
5.11. Асимптотическая форма разложения полей 395
у + (дкг/дку)г + дФ/дку = О E.11.36)
[здесь частные производные по кх(ку) вычисляются при фиксирован-
фиксированных ку{кх)], а Д дается выражением
d2kz д2Ф\{ дгкг д2Ф\ ( d2kz д2Ф V
^+щ){2114+щ)-щжУ2+жд;) EЛЫ)
Кроме того, Фл = Ф(к„) и
+ 1, если д>0 и zd2kJdk2x + d2<l>/dk2x>0,
8=<-1, если Д>0 и гд2к2/дк2х + д2Ф/дк1<0, E.11.5)
i, если Д < 0.
Наконец, вектор Еп(г) учитывает вклады сингулярных точек фазы
Ф(к) + к • г.
5.11.1. Анизотропная среда
Седловую точку кп можно определить, используя уравнение Ф = const
и для каждого направления к откладывая из начала прямоугольной
системы координат два волновых числа (кх и к2) распространяющихся
в этом направлении волн. Таким образом, можно получить двулист-
двулистную поверхность волновых векторов, один лист которой соответству-
соответствует значениям к1э а другой — к2 (см. задачу 14). При этом в соответст-
соответствии с уравнениями E.11.3) нормаль к поверхности в точке кп является
параллельной вектору г.
В кристаллооптике принято представлять зависимость фазовых
скоростей v{ и v2 от направлений вектора к или вектора Пойнтинга,
используя соответственно нормальную и лучевую поверхности
(см. разд. 1.4.1). Расстояние от точки на этих поверхностях до центра
пропорционально либо vv либо v2. Эти два метода различаются тем,
что на нормальной поверхности значения vx 2 откладывают вдоль на-
направления ft, в то время как на лучевой поверхности — вдоль вектора
Пойнтинга, связанного с вектором к. Можно показать, что нормаль-
нормальная и лучевая поверхности связаны между собой простым геометриче-
геометрическим соотношением (см. книгу Зоммерфельда [31], указанную в лите-
литературе к гл. 4 настоящей книги): лучевая поверхность является огиба-
огибающей плоскостей, проходящих через вершину вектора kvx 2 и перпен-
перпендикулярных (с.
Когда среда изотропна и Ф = 0, уравнение E.11.4) принимает бо-
более простой вид:
A 2k2/k$ E.11.6)
396 Гл. 5. Асимптотическое вычисление дифракц. интегралов
При этом вектор кл параллелен г, так что представление E.11.2) дает
Е(г) = 2ni(ke-ikr/r)(z/r)E0(k ?). E.11.7)
Выражение E.11.7) можно использовать для асимптотического вы-
вычисления интеграла углового спектра, причем необходимо положить
dydC = -dkxdky/(khin0).
5.12. ФОРМУЛА УИЛЛИСА
Вычисление дифракционных интегралов может быть основано на раз-
разложении в ряд неосциллирующих частей подынтегрального выраже-
выражения вблизи краевых точек интервала интегрирования. Следуя методу
У ил лиса (рассмотренному Барака [34]), запишем следующее разложе-
разложение в ряд:
g(x)G(k>x)e-'xdx = ? —^
Jo " = 0 "! JO
(*)(Г)\ Г0
= ? ^ ->* -ф<">(«), E.12.1)
л = 0 п-
где мы предположили, что функцию g (v ) можно разложть в ряд Тей-
Тейлора вблизи точки z = 0. Полагая а — 0, получаем
^(x)G(Jk,x)djc = У (-1)Уя)@)ф(И)@) E.12.2)
и=о п!
Например, полагая G (А:, х) = sin(fcx)/x, имеем
^inCfcx) __axJ_ it ос , а3 а5 .
Г0
= Ф@) + ФA)@)а + |ФB)@)а2 + • • •,
и поэтому
/0 8Ш/ " ^. " а Т \!0) EЛ2.4)
Аналогичное выражение приведено в приложении Е, формула (Е5).
ЗАДАЧИ
Раздел 5.2.
1. Вычислите поле, дифрагированное на отверстии в плоском экране, освещаемом в
перпендикулярном к нему направлении плоской волной. Представьте дифракционный
интеграл в том же виде, что в задаче 3 из гл. 4 настоящей книги и сделайте замену пе-
переменных* = р2. Покажите, что поле определяется только вкладом от граничных то-
точек. Поскольку/(р) обращается в нуль при р = /омакс, можно использовать выражение
Задачи 397
E.2.37). Кроме того, рассмотрите случай, когда любая граничная точка соответствует
углу апертуры. При этом учтите, что при использовании переменной х соответствую-
соответствующие индексы дифракционного интеграла равны: р = 1 и у = 1/2.
2. Используя следующее интегральное представление функции Бесселя для вещест-
вещественных v и /3 Ф О, тг:
1 Г00
Jv(v sec j8) = - cos v@ - sec Д sin 0) d0 -
rcjo
докажите формулу Дебая
ЫГ{/?~ tg
при v — oo. Подсказка. Используйте метод стационарной фазы, учитывая, что
Г00 Г00 _ 1
О < e~v(r+sec/? sh ° Л < е vtdt = -,
Jo Jo v
а также то, что функция /@) = 0 - sec/? sin0 является стационарной при 0 = C и
/3) = tg/3.
3. Покажите, что
Jv(v) = (l/7r)rD/3)F/vI/331/6/2 + O(v~2/3).
Подсказка. Используйте метод стационарной фазы, учитывая то, что Jp{y) = У (*>sec0)
при /3 = 0. В этом случае фаза/@) = 0 - sec 0 sin0, введенная в предыдущей задаче, яв-
является стационарной в граничной точке 0 = 0 интегрального представления функции
Бесселя. Кроме того, /" @) = 0 и /'"@) = 1. В соответствии с этим используйте выра-
выражение E.2.18) при р = 3 и у = 0.
Раздел 5.6
4. Рассмотрите холмы, долины и контуры наибыстрейшего спуска и подъема функ-
функции cos z (рис. 5.14), которая входит в подынтегральное выражение углового представ-
представления поля. Докажите, что КНС можно записать в виде
Rez = nn + (- l)"gd(Imz),
где п - 0, =fcl, ±2, ... — целые числа, a gd(x) — так называемый гудерманиан
[см. уравнение D.3.117) в справочнике Абрамовица и Стегана [4], указанного в литера-
литературе к гл. 4 настоящей книги]:
gd(x) = 2 arctg e* - тг/2.
5. Найдите холмы, долины и контуры наибыстрейшего спуска и подъема функции
Re(z - zV3), входящей в интегральное представление функции Эйри.
6. Исследуйте холмы, долины, а также контуры наибыстрейшего спуска и подъема
функции cos z + b(z - тг/2), входящей в интегральное представление функций Бесселя и
Ханкеля при b > 1 и b < 1.
7. Найдите главный член асимптотического представления функции Ханкеля
), используя интегральное представление, которое можно получить, основываясь
398
Гл. 5. Асимптотическое вычисление дифракц. интегралов
на фурье-преобразовании D.8.6) двумерной функции Грина [выражение D.7.5)] при
*,-0.
8. Покажите, что седловыми точками функции cosz + z — т/2 являются точки второ-
второго порядка zs = т/2 + 2т л (обезьяньи седла), в то время как КНС имеют направления
0 = -т/6, -5т/6, +х/2 и определяются уравнением sin(s'-zs)chz" = z' — zs.
9. Используя результаты двух предыдущих задач, покажите, что главный член
асимптотического разложения функции Hf\n) при п — оо имеет вид
10. Рассмотрите функцию Эйри Ai(x), определяемую интегралами
1 Лоо /t3 \ I f+ioo
Ai(x) = - cos(V + xt)dt = —\
Проведя замену переменных т = х?А z, где выбрана главная ветвь квадратного корня,
можно записать
1/2
AiM "
Если же выбрать контур интегрирования L0 в комплексной z-плоскости (рис. 5.27), то
функция Эйри запишется в виде
Рис. 5.27. Контуры дли вы-
вычисления функций Эйри
Ai и Bi.
Задачи 399
Наконец, метод стационарной фазы дает
Ai(x) ~ sinB|x|3/2/3 + я/4)/(я1/2|х|1/4) (х < 0).
Докажите записанные выше соотношения.
11. Используя результаты задачи 10, покажите, что при х > 0 замена контура /^
на КНС, проходящий через седловую точку z = — 1, приводит к следующему инте-
интегральному представлению:
*1/2ехр
/ хз/2\
hZJO
2я1
где z + (s) и z_(s) = z + (s) являются решениями уравнения s = (l/3)z3 — z — 2/3 =
= (l/3)(z — 2)(z + lJ. Учитывая затем соотношение
1/D - 1) - 1/B- - 1) = BJA1/2) - A5/72)й1/2 + ¦ • •,
покажите, что
' expf -2^— J /Bя1/2х1/4) (х > 0).
12. Функция Эйри Bi(x) имеет такое же интегральное представление, как и Ai(x), за
исключением лишь того, что контур интегрирования L 0 нужно заменить на L + - L _
(рис. 5.27). Покажите, что при л: > 0 функция Bi(A") асимптотически стремится к следу-
следующему выражению:
Bi(x) - ехрBх3/2/3)/(тс1/2х1/4).
Раздел 5.7
13. Вычислите поле, дифрагированное на плоской границе раздела между двумя ди-
диэлектриками, освещаемой цилиндрической р-волной. Подсказка. Используйте выраже-
выражение E.7.1), изменив в нем подынтегральное выражение с учетом р-поляризации волны.
14. Вычислите следующий за главным член асимптотического разложения интегра-
ла/кнс, определяемого выражением E.7.1), если главный член разложения дается вы-
выражением E.7.3). Подсказка. Для вычисления члена второго порядка используйте пред-
представление E.2.32).
15. Вычислите боковое смещение гауссова пучка, имеющего р-поляризацию волны,
когда он полностью отражается плоской границей раздела двух сред.
16. Вычислите асимптотическое поле, дифрагированное на многослойной структу-
структуре, в которой возбуждаются волны утечки. Для этого, воспользовавшись однородным
асимптотическим выражением E.6.12), выразите интеграл типа Зоммерфельда E.7.17)
через комлексный интеграл Френеля (см. статью Тамира и Бертони [23]).
17. Сравните вклад от боковой волны и поля, вычисленного в приближении геомет-
геометрической оптики, на границе раздела двух сред. Покажите, что, когда угол падения га-
гауссова пучка почти равен критическому, амплитуда боковой волны становится стравни-
мой с амплитудой лучевого поля.
18. Вычислите поле, пропускаемое плоской границей раздела между двумя средами,
освещаемой гауссовым пучком. Покажите, что прошедшее поле можно разделить на
боковую волну и лучевое поле.
400 Гл. 5. Асимптотическое вычисление дифракц. интегралов
19. Покажите, что боковое смещение Гуса — Хенхена пучка, отражаемого от плос-
плоской границы раздела между двумя диэлектриками, можно рассматривать как результат
небольшого смещения плоскости отражения внутрь второй среды. Вычислите расстоя-
расстояние от этой виртуальной плоскости до границы раздела как функцию угла падения.
20. Рассмотрите две диэлектрические среды (скажем, 1 и 2), разделенные цилиндри-
цилиндрической поверхностью радиусом а. Пусть коллимированный гауссов пучок освещает по-
поверхность раздела под углом падения (относительно оси пучка), который больше крити-
критического. Вычислите в дальней зоне поле, прошедшее во вторую среду в случае р- и s-
волн как функцию угла падения. Кроме того, вычислите, какую часть энергии потерял
падающий пучок при отражении за счет частичного пропускания. Подсказка. Вычисляя
поле на поверхности раздела, используйте коэффициент пропускания Френеля для лу-
лучей, направленных по оси пучка. Затем найдите асимптотическое представление дифрак-
дифракционного интеграла Фраунгофера, используя метод наибыстрейшего спуска, чтобы пра-
правильно учесть гауссово распределение освещенности. (См книгу [35].)
Раздел 5.9
21. Рассмотрите дифракционный интеграл
= Г"ехр(-Ьв2)ехрГ-й/& + Jj\
\ds-
С помощью выражения E.9.7) найдите асимптотическое разложение /(к). Подсказка.
Для вычисления параметровg0 ngl в выражениях E.9.2) и E.9.8) используйте подста-
подстановку и = is и разложение
= ? ^«2« = ? («2 - С)" ? С«Ьт+*-^7
„=оп\ т = о q=o miql
[ср. с E.9.2)].
ЛИТЕРАТУРА
1. Keller J. В., J. Opt. Soc. Am., 52, 116 A962).
2. Ludwig D.t Commun. Pure Applr Math. Phys., 19, 215 A966).
3. Lewis R. M, Boersma J., J. Math. Phys., 10, 2291 A969).
4. Ufimtsev P. K, transl. by Air Force Syst. Command, Foreign Tech. Div., Doc. ID
No. FTD-HC-23-259-71 A971).
5. Ufimtsev P. Y., Proc. IEEE, 63, 1734 A975). [Имеется перевод: Уфимцев П. Я. —
ТИИЭР, 1975. т. 63. № 12, с. 115.]
6. Kouyoumjan R. G., Pathak R К, Proc. IEEE, 62, 1448 A974). [Имеется перевод:
Куюмджан Р., Патхак П. — ТИИЭР, 1974, т. 62, № 11, с. 40.]
7. Stokes G. G.t Cambridge Philos. Trans., 9, 166 A856).
8. Kelvin Lord (Thompson W.), Philos. Mag., 23, 252 A887).
9. Watson G. N., Proc Cambridge Philos. Soc, 19, 49 A918).
10. Erdelyi A., SIAM J. Appl. Math., 3, 17 A955).
11. Erdelyi A., Asymptotic Expansions, Dover, New York, 1956.
12. Van der Corput J. G., Proc. Anst. Akad. Wet., 51, 650 A948).
13. Van der Corput J. G., Asymptotic Expansions I—III, lech. Rep. Dep. Math., Univ.
of California, Berkeley, 1954—1955.
Литература 401
14. Bleistein N.. Handelsman R. Л. Asymptotic Expansions of Integrals, Holt, New York,
1975.
15. Sirovich L., Techniques of Asymptotic Analysis, Springer-Verlag, Berlin, New York,
1971.
16. Dingle R. Я, Asymptotic Expansions: Their Derivation and Interpretation, Academic
Press, New York, 1973.
17. Lee S-Wi, Deschamps G., IEEE Trans. Antennas Propag., AP-24, 25 A976).
18. Кравцов Ю. А., Орлов Ю. И. — УФЫ, 1980, т. 132, № 3, с. 475.
19. Pearcey Т., Philos. Mag., 37, 311 A946).
20. Goos E, Haenchen H. H., Ann. Phys. (Leipzig), 1, 333 A947).
21. Lotsch H. K, J. Opt. Soc Am., 58, 551 A968).
22. Midwinter J. E., Zernike E, Appl. Phys. Lett., 16, 198 A970).
23. Tamir Г, Bertoni H. L., J. Opt. Soc Am., 61, 1397 A974).
24. Focke /., Ber. Saech. Akad. Wiss. Leipzig, 101C), 1 A954).
24a. Focke /.. Opt. Acta, 3, 110 A956).
25. Chester C, Friedman R, Ursell E, Proa Cambridge Philos. Soc, 53, 599 A957).
26. Keller J. R, J. Appl. Phys., 28, 426 A957).
27. Keller J. R, Lewis R. M., Seckler R D.t J. Opt. Soc. Am., 28, 570 A957).
28. Geometric Theory of Diffraction (ed. R. C. Hansen), IEEE Press, New York, 1981.
29. Braun G., Acta Phys. Austriaca, 10, 8 A956).
30. Jones D. 5., Kline M, J. Math. Phys., 37, 1 A958).
31. Chako N., J. Inst. Math. Its Appl., 1, 372 A965).
32. Lalor E.t J. Opt. Soc. Am., 58, 1235 A968).
33. Sherman G. C, Stamnes J. /., Lalor E., J. Math. Phys., 17, 760 A976).
34. Barakat R. — In: The Computer in Optical Research (ed. B. R. Frieden), Springer-
Verlag, BerUn, New York, 1980, p. 35—80.
35. Unger H. G., Planar Optical Waveguides and Fibers, Sect. 2.8., Oxford Univ. (Claren-
(Clarendon), London, New York, 1977.
БИБЛИОГРАФИЯ
Bleistein I. N. Mathematical Methods for Wave Phenomena, Academic Press, Orlando,
Florida, 1984.
Southwell W. #., Opt. Lett., 3, 100 A978).
ГЛАВА 6
ДИФРАКЦИЯ СВЕТА НА ОТВЕРСТИИ
И РАССЕЯНИЕ НА МЕТАЛЛИЧЕСКИХ И
ДИЭЛЕКТРИЧЕСКИХ ПРЕДМЕТАХ
6.1. ВВЕДЕНИЕ
В большинстве практических случаев дифракционные задачи [1, 2]
(см. также работу Боумана и др. [3], указанную в литературе к гл. 4
настоящей книги) не имеют замкнутых аналитических решений. В свя-
связи с этим еще с прошлого века усилия исследователей были направле-
направлены на поиск приближенных решений. Исходной точкой для многих ав-
авторов явился принцип Кирхгофа, особенно часто с его помощью рас-
рассматривалась задача о дифракции на отверстии. Как уже упомина-
упоминалось, сущность этого принципа заключается в том, что поле на отвер-
отверстии полагается равным полю, создаваемому теми же источниками,
что и в отсутствие экрана, ограничивающего данное отверстие. С фи-
физической точки зрения данное утверждение эквивалентно тому, что на-
наличие экрана не влияет на поле в области отверстия и лишь вблизи
границы отверстия это влияние становится существенным. Следова-
Следовательно, если отверстие достаточно велико, то ошибкой, возникающей
вследствие изменения поля вблизи краев, можно пренебречь. Однако
для малых отверстий применение принципа Кирхгофа приводит к зна-
значительным погрешностям. Поэтому для того, чтобы оценить ошибку,
которая возникает из-за неверного представления поля в некоторой
области вблизи границы отверстия, необходимо прежде всего выяс-
выяснить размеры этой области. Для ответа на последний вопрос требует-
требуется знание точных решений, которые можно получить лишь в весьма
ограниченном числе случаев и для отверстий специальной формы.
К настоящему времени хорошо развиты различные приближенные
методы решения задач дифракции на металлических препятствиях
(геометрическая теория дифракции и теория однородных асимптоти-
асимптотических разложений), в то время как для дифракции на диэлектриках
полной ясности пока нет. Причиной этого является отсутствие анали-
аналитического решения для основной задачи дифракции, а именно для ди-
дифракции плоской волны на диэлектрическом клине.
За последние десятилетия развиты асимптотические методы реше-
решения задач дифракции (см. литературу [1, 6, 27, 28], указанную в гл. 5
настоящей книги), а также разработаны методы, в которых дифраги-
6.1. Введение 403
рованные поля строятся с учетом модификации этих полей на пре-
препятствиях и отверстиях. Постоянно развиваясь, теория продвинулась
столь далёко, что в пределе/: — оо позволяет описывать распределе-
распределения полей для объектов любой сложной формы с более или менее до-
достаточной степенью точности.
Методы асимптотического построения дифрагированных полей
можно проиллюстрировать на простых классических примерах, таких,
как клин с конечным поверхностным импедансом, круговой цилиндр и
сфера. Дифракция на клине представляет особый интерес, поскольку
1) для клина можно получить коэффициенты дифракционной матри-
матрицы D, которая является основным математическим инструментом при
вычислении поля, дифрагированного на искривленном клине, ограни-
ограничивающем физическое отверстие, и 2) дифрагированное поле включает
в себя две поверхностные волны, которые своим появлением обязаны
конечному поверхностному импедансу двух граней клина. Свойства
таких поверхностных волн мы проиллюстрируем на примере дифрак-
дифракции плоской волны на металлическом круговом цилиндре. Если разло-
разложение для дифрагированной волны получено с помощью преобразова-
преобразования Ватсона (см. гл. 4), то поле в области тени принимает вид поверх-
поверхностной волны. Наконец, дифракция на сфере используется для уста-
установления некоторых общих теорем для поля, рассеиваемого на произ-
произвольных препятствиях конечных размеров, и для обобщения теории
поверхностных волн, возбуждаемых лучами, идущими по касательной
к поверхности рассеивающего тела и распространяющимися вдоль
геодезических линий этой поверхности.
Основной особенностью любых дифракционных полей является их
зависимость от длины волны. Это свойство используется в различно-
различного рода оптических устройствах для спектрального анализа излучения.
Примером такого устройства служит дифракционная решетка, кото-
которая состоит из большого числа клиньев (штрихов). Поле, дифрагиро-
дифрагированное на одном штрихе, интерферирует с полями от других штрихов,
в результате чего получается картина, состоящая из узких линий, со-
соответствующих интерференционным порядкам дифракционной решет-
решетки. Угол отражения каждого луча зависит от частоты падающего из-
излучения. Поэтому если на пути этого луча поставить щель, а за ней
поместить фотодиод, то для известного интерференционного порядка
и при известной ширине линии можно узнать, какая доля интенсивно-
интенсивности излучения попадает в данный спектральный интервал. Такой
принцип работы лежит в основе устройства современных спектромет-
спектрометров на дифракционных решетках, которые практически вытеснили спект-
спектрометры, использующие в качестве диспергирующего элемента призму.
404 Гл. 6. Дифракция света на отверстии
6.2. ДИФРАКЦИЯ НА КЛИНЕ
Рассмотрим в качестве первого случая клинообразную область (р > 0,
2ф > ф ^ 0) (рис. 6.1), освещаемую плоской s-волной (т. е. волной,
вектор напряженности магнитного поля которой параллелен кромке
клина), распространяющейся вдоль направления ф = ф' перпендику-
перпендикулярно границе препятствия, которое считается идеальным проводни-
проводником:
Щ{Р,Ф) = exp[i7cpcos(<? - ф']}. F.2.1)
В этом выражении знак плюс у показателя экспоненты соответствует
распространению волны под углом ф = ф' в направлении к клину.
Следуя Зоммерфельду (см. работу [31], указанную в литературе к
гл. 4 настоящей книги), суммарное поле (т. е. сумму падающего, отра-
отраженного и дифрагированного полей) можно записать в виде интеграла
F.2.2)
г
вычисляемого по комплексному контуру Г (рис. 6.2). Угловой спектр
S имеет простые полюсные сингулярности и определяется из условия
равенства нулю производной ди /дф на гранях клина:
dp = 0. F.2.3)
дф
Поскольку dS /дф = dS /Э/3, этот интеграл можно взять по частям.
Таким образом, получаем
Этому уравнению удовлетворяет любая функция S Q3), такая, что для
любых /3 выполняются следующие условия: S(/3 + тг) = -S(-/J + тг)
и 5(j3 + 2Ф + тт) = — S(—(j + 2Ф + тг). Одним из возможных реше-
Рис. 6.1. Рассеяние падающей ТМ-волны на клине.
6.2. Дифракция на клине
405
к-нс,
-яг/2
Рис. 6.2. Комплексный контур интегри-
интегрирования при интегральном представле-
представлении поля в области клина [см. выраже-
выражение F.2.2)].
Imft
К НС,
я/2
Re/M
ний является
S(OL-T) =
sin(a/N)
= —. F.2.5)
2nN cos(<x/N) — cos@'/N)' n
Мы видим, что функция/7(а) имеет бесконечное число простых полю-
полюсов, расположенных в точках а = @д9 причем
ft = (_Щф' _ ф) + Bq + 1)Ф + тг, q = 0, ± 1, ±2,.... F.2.6)
Если заменить контур интегрирования Г двумя контурами наибыст-
наибыстрейшего спуска KHCj и КНС2, проходящими из-за наличия множителя
exp(-//:pcosiS) через точки 0 и 2тг соответственно, то выражение
F.2.2) можно переписать в виде
и(р,ф) = ( Г dp + | dp)exp(-ikpcosP)S(p + ф) +
VJkHCj J'KHC'2 /
Wl F.2.7)
ч
где rq — вычеты функции S (J3 + ф) в полюсах, расположенных между
КНС, и КНС2:
1* *-•*"*¦ ^4//ll-0-ft)=l. F.2.8)
г = lim
Если угол 0' является вещественным, то из выражения F.2.6) следу-
следует, что полюсы (Зд лежат на вещественной оси. Таким образом, для
полюсов /3^, расположенных между KHCj и КНС2, справедливо нера-
неравенство 2тг ^ 0д - ф s 0. С учетом этого разложение F.2.7) можно
представить в виде
э, 0) = dj?[S(j8 + ф)- S(P + ф- 2тг)] ехр( - ikp cos /?) +
Jkhc2
+ Zexp[-l7cPcosD> - РЖи(Ф - ft +2я) - W - ДД F-2-9)
406 Гл. 6. Дифракция света на отверстии
где через U(x) обозначена ступенчатая функция Хевисайда. В соот-
соответствии с F.2.9) поле включает в себя только те плоские волны, на-
направление распространения которых ограничено углами в секторе
max(j8^ - 2тг, 0) < ф ^ min(/3^, 2Ф). Однако в пределе к - оо поле
должно сводиться к суперпозиции лучевых конгруэнции, каждая из ко-
которых своим появлением обязана отражениям падающей волны. Лег-
Легко проверить, что поле, вычисленное в приближении геометрической
оптики, совпадает с F.2.9).
Поскольку выражение F.2.9) для м(р, ф) удовлетворяет граничным
условиям и сводится к правильному виду в пределе к — оо, естествен-
естественно предположить, что это выражение правильно описывает поле и
при конечных значениях к.
При кр — оо интегралы по обоим контурам KHCj и КНС2 могут
быть заменены соответствующими вкладами от седловых точек. В ре-
результате мы имеем
+ ?exp[-ifcpcosD> - ф'Ш(Ф - & + 2я) - Щф - Д,)]; F.2.10)
q
здесь
NBnk)l/2
1 1
[cosGc/iV) — cos[@ — </>')/iV] cos(n/N) — cos[@ + ф
F.2.11)
представляет собой дифракционный коэффициент, вычисленный для
случая, когда на клин падает s-волна. Для р-волны (т. е. волны, поля-
поляризованной параллельно кромке) соответствующий коэффициент D
можно получить из Ds заменой минуса на плюс перед вторым членом
в правой части выражения F.2.11)
В случае когда полюс близок к какой-либо седловой точке, можно
получить более точное представление поля, используя переходную
функцию, рассмотренную в разд. 5.6.
6.2.1. Клин с конечным импедансом
Разница в проводимости реальных металлов и идеальных проводни-
проводников в оптическом диапазоне проявляется особенно сильно. Как мы
уже показали в конце гл. 3, это можно учесть, представляя поверх-
6.2. Дифракция на клине 407
ность металла поверхностным импедансом. Разумеется, такое пред-
представление оказывается неверным, если частота слишком близко приб-
приближается к плазменной частоте. Характеризуя реальную поверхность
импедансом, можно получить аналитическое решение многих задач
дифракции, например задачу дифракции на клине с конечным импе-
импедансом. Аналогичный подход можно применить и для анализа ди-
дифракции на металлических телах с диэлектрическими покрытиями. В
этом случае некоторую информацию о дифракции можно получить,
выполняя вычисления для клина с импедансной поверхностью.
В частности, препятствия с мнимыми поверхностными импеданса-
ми возбуждают поверхностные волны. В гл. 3 мы показали, что угол
Брюстера для этих поверхностей дается формулой 0В = Z/f. Для хо-
хорошего металлического проводника вв = тг/2 — i/k9 так что на его
поверхности может распространяться поверхностная волна, которая
проникает на некоторую конечную глубину в металл. При рассмотре-
рассмотрении дифракции на клиньях, отверстиях и других объектах с поверх-
поверхностным импедансом необходимо учитывать, что поверхностные вол-
волны могут вносить изменения как в интенсивность, так и в фазу сум-
суммарного дифрагированного поля.
Для того, чтобы учесть влияние конечной проводимости на дифра-
дифрагированное поле, полезно обобщить проведенный выше анализ на слу-
случай клина, характеризуемого поверхностным импедансом Zs, соот-
соответствующим углу Брюстера 0В. В этом случае s-волна, у которой век-
вектор магнитного поля параллелен оси z, на поверхности клина удовлет-
удовлетворяет граничному условию
(\/р)(ди/дф)+ ik cos вви = О для <? = 0,2Ф. F.2.12)
Здесь и(р9 ф) = Н(р, ф), а знаки плюс и минус относятся соответст-
соответственно к верхней и нижней граням клина (рис. 6.1). Малюжинец [3] по-
получил в представлении углового спектра выражение для и в виде обоб-
обобщенного интеграла Зоммерфельда, аналогичного интегралу из соотно-
соотношения F.2.2):
и{р,ф) =
где S ф) — функция, определяемая выражением F.2.5), а дф + ф) —
функция, учитывающая конечный поверхностный импеданс:
М(а - 0в)М(а + 0в - 2Ф)
Х
М(а - л + 0в)М(а - 0в - 2Ф + л)
х cos[(l/2iV)(a + flB - я/2)] sin[(l/2AQ(a - 0В + я/2)] ^
sin(a/N)
408 Гл. 6. Дифракция света на отверстии
Функция М (а), введенная Малюжинцом, представляет собой бесконеч-
бесконечное произведение:
ММ " J3.L1 - U-l) + —I/O J ¦ »*">
Асимптотическое значение интеграла в F.2.13) при кр — оо можно
вычислить тем же способом, с помощью которого было получено вы-
выражение F.2.10). Таким образом, проделав необходимые вычисления,
получим
и(р9ф) ~ й8(ф,ф') щ Ь S+ ехр[ — гкр$т{ф + 0В)] +
+ 5_ ехр[ — ikp sin( — ф + 2Ф + 0В)] +
+ 1г,ехр[-*7срсо8(ф - Д)]. F.2.16)
Это выражение отличается от F.2.10) в трех отношениях. Во-
первых, коэффициент дифракции Ds зависит от угла Брюстера. Во-
вторых, в угловых секторах, примыкающих к граням клина, могут су-
существовать две поверхностные волны с амплитудами S + и S _ соот-
соответственно, которые ограничены углами ф, такими, что
2Ф > ф > 2Ф - Archf- 1/0JJ) + я/2 - 0В,
F.2.17)
0 < ф < Arch(— 1/0в) — 7г/2 + 0В.
Эти волны существуют, только если выполняется неравенство
0В + Arch(-l/0 g) > тг/2. И в-третьих, дополнительные амплитуды
отраженных клином волн и распространяющихся в направлении
ф = /3^, не равны единице. Эти амплитуды можно вычислить, исполь-
используя для граней клина формулу Френеля. Можно показать, что в дан-
данном случае коэффициент дифракции Ds записывается в виде
e"I1t/4sinGc/N)r 1 д(ф)
Я8(Ф>Ф)= Щ2пкI12 [cos(n/N) - соэДф - ф^/N] д(ф' + п) +
+. 1 ; я(Ф + Щ F218)
cos(n/N) — со8|](ф + ф')/^] ^(ф' + я) J
В свою очередь амплитуда rq q-ft отраженной волны дается выраже-
И), F.2.19)
что нетрудно показать, используя выражение F.2.8) и замечая, что
вычет функции S 08 + ф\9{& + Ф) при ф + /3 = /39 равен й' (/3^). Из это-
этого выражения следует, что амплитуда пучка, дифрагированного в на-
6.2. Дифракция на клине
409
правлении Рд ± тг, с точностью до коэффициента отражения гя совпа-
совпадает с амплитудой пучка, дифрагированного на идеальном проводнике
@В = 7г/2). Поскольку rq не зависит от частоты, эту величину можно
вычислить с помощью формулы Френеля (см. гл. 3 для среды с пока-
показателем преломления п = tg0B).
Амплитуды S ± двух поверхностных волн равны вычетам в полю-
полюсах функции g (J3 + 0), входящей в подынтегральное выражение инте-
интеграла F.2.13), которые лежат между КНС^ и КНС2. Из выражений
F.2.14) и F.2.15) следует, что эти два полюса находятся в точках
/3± + ф - Ф = ±(Зтг/2 +Ф- 0В) + тг.
6.2.2. Дифракционная матрица для искривленной кромки
Полученные выше результаты можно обобщить на случай дифракции
на искривленной металлической кромке (рис. 6.3), освещаемой лучами,
образующими угол /3 с касательным к кромке вектором $ в точке Qe
(ср. с разд. 5.10 и рис. 5.25). Если рассмотреть проекцию падающего и
дифрагированного лучей на плоскость, перпендикулярную вектору ё,
касательному к кромке в точке Qe, и направить падающий луч под
углом Ф', то положение дифрагированных лучей, образующих кониче-
коническую поверхность, будет задаваться углом ф (рис. 6.4). Напряжен-
Напряженность электрического поля дифрагированного на кромке луча можно
записать в виде
Ed(r) = [pi/MPi + ')]] 112е-ШгО(ф, 0'; J?) • Е<Ш F.2.20)
где вектор г совпадает с г' из разд. 5.10, а параметр р{ имеет то же
значение, что и в E.10.20). Входящую в выражение F.2.20) дифракцион-
Рис. 6.3. Геометрическое представление
дифракции на крае.
Рис. 6.4. Дифракция на полуплоскости.
Плоскость рисунка перпендикулярна век-
вектору 6 в точке Qe.
4Ю Гл. 6. Дифракция света на отверстии
ную матрицу D получили Коуюмьян и Патак [4] и записали ее в виде
О(ф9 ф'; Р) = Д»Д/>Р + ФФ'ОЯ9 (б-2-21")
где $d = ф х г, Д = $ х s', а ?>р и Д, являются обобщением дифрак-
дифракционного коэффициента F.2.11) на случай /3 * тг/2 и определяются
выражением
_ g
p's"iVB7rfcI/2sin/?
11
±
1
cos(n/N) — cos[(</> — </>')/N] cos(k/N) — <
F.2.22)
где N = 2Ф/тг. В частности, для полуплоскости мы имеем N = 2 и
выражение F.2.22) принимает вид
1 " - * ' F.2.23)
J"
Сравнивая дифракционные коэффициенты Dp s с полученными ра-
ранее коэффициентами Dг [см. E.2.48)] nDk [см. E.10.21)], можно заме-
заметить, что они отличаются только множителем, стоящим в квадрат-
квадратных скобках. Кроме того, коэффициенты Dp s становятся сингулярны-
сингулярными в случае, когда ф = тг + ф', т. е. когда мы рассматриваем лучи,
лежащие в плоскости, проходящей через падающий луч и точку Qe.
С точки зрения геометрической оптики эта плоскость отделяет осве-
освещаемую область от области тени, отсюда и ее название — граница
тени. В то время как при ф + ф' = тг коэффициенты D{ uDp s стано-
становятся сингулярными, коэффициенты Dk остаются конечными. Легко
показать, что данному направлению в геометрической оптике соот-
соответствует направление отраженных лучей. Поэтому полуплоскость,
проходящая через точку Qt и включающая в себя отраженный луч, на-
называется границей отражения. В заключение заметим, что все упомя-
упомянутые дифракционные коэффициенты, вычисленные для направлений,
лежащих вблизи границы тени, практически совпадают, в то время
как для других направлений их различие становится существенным.
Таким образом, можно сделать вывод, что вычисления, проведенные
на основе скалярного представления и приближения Кирхгофа, совпа-
совпадают с расчетом на основе точной теории только тогда, когда мы
рассматриваем лучи, дифрагированные в прямом направлении и от-
отклоняемые лишь ненамного от границы тени. Фактически же данное
утверждение означает, что приближение Кирхгофа неверно как в глу-
глубине области тени, так и в глубине освещенной области.
6.2. Дифракция на клине
411
Вблизи границы тени выражение F.2.20) для поля и(р, ф) стано-
становится сингулярным. В этом случае, как было показано в разд. 5.3, для
получения выражения, аналогичного F.2.20), необходимо воспользо-
воспользоваться выражением для комплексного интеграла Френеля F и пара-
параметра обхода ?, причем коэффициенты D s заменяются величиной
s
в - -
где параметр обхода определяется выражением
> <6-2-24>
здесь pit 2 — главные радиусы кривизны падающего волнового фронта
[ср. с разд. 2.9], а р\ — радиус кривизны кромки в плоскости падения.
Можно показать, что для падающей плоской волны параметр ? ра-
равен B&rI/2sin/3 cos[(l/2)@ — Ф')]. Подставляя это выражение в фор-
формулу F.2.24) и учитывая, что для прямой кромки р[е = оо, в итоге по-
получим выражение для поля, совпадающее с выражением E.3.2).
6.2.3. Дифракция на диэлектрическом клине
Как уже отмечалось во введении, задача дифракции на диэлектричес-
диэлектрическом клине не имеет аналитических решений. Поэтому ограничимся
рассмотрением той области, где задача может быть решена с по-
помощью двух интегралов Зоммерфельда, содержащих неизвестную
Рис. 6.5. Дифракция плоской волны на прямоугольном диэлектрическом клине при
п — 2 и оо. Заметьте убывание дифрагированного поля вдоль граней клина. (Из работы
Джу и др. [5].)
412 Гл. 6. Дифракция света на отверстии
угловую функцию, с последующей сшивкой выражений для полей на
противоположных гранях клина. Этот метод [5] применялся для полу-
получения картины, изображенной на рис. 6.5. Вкратце он состоит в следу-
следующем.
В качестве исходного распределения берется поле, вычисленное в
приближении геометрической оптики. Затем дифрагированное на
кромке поле представляется в виде комбинации полей, излучаемых
мультиполями. Далее ограничиваются лишь теми из этого набора,
аналитическое продолжение которых внутрь диэлектрика представля-
представляет собой убывающую функцию, и амплитуды этих мультипольных
полей получают при решении системы линейных уравнений.
6.3. ДИФРАКЦИЯ НА ЩЕЛИ
Метод, рассмотренный в предыдущем разделе, можно с успехом при-
применить и к вычислению дифракции на бесконечной щели шириной 2 а
(рис. 6.6). Для простоты предположим, что поле, падающее на щель
перпендикулярно ее плоскости, представляет собой плоскую волну. В
первом приближении будем считать, что поле на апертуре равно полю
падающей волны (приближение Кирхгофа). В этом случае поле в точ-
точке Р определяется двумя лучами, отходящими от двух границ щели, и
геометрическим лучом, если таковой имеется. Вклад дифрагирован-
дифрагированных лучей можно вычислить, используя формулу F.2.21), в которой
матрица D определяется границами апертуры щели:
Если точка/3 находится в области тени, то поле, соответствующее ге-
геометрическому лучу, отсутствует. Следовательно, в дальней зоне при
любом угле дифракции 0 =? 0 выражение F.3.1) можно переписать в
виде
где дифракционная матрица D зависит от апертурного угла краев,
ограничивающих щель. Поскольку это распределение является непре-
непрерывной функцией угла 0, выражение F.3.2) остается справедливым и
при 0 = 0, т. е. для дифракции вперед.
На конечном расстоянии от щели разделение на дифрагированные
и геометрические лучи не является однородным. Действительно, если
мы представим поле через дифракционный интеграл, то, как следует
6.3. Дифракция на щели
413
Граница тени
SB~
Дифрагированные
лучи
Рис. 6.6. а — дифракция на щели
шириной 2а; б — распределение
интенсивности в дальней зоне для
р-волны при ка= 8; сплошная кри-
кривая получена с учетом однократной
дифракции, в то время как штрихо-
штриховая кривая получена с учетом эф-
эффектов многократной дифракции;
точки соответствуют точному ре-
решению. (Из работы Келлера [5а].)
9
из предыдущей главы, вклад в общее выражение от граничных точек
интеграла можно рассматривать отдельно от вклада точек стационар-
стационарной фазы, только если первые и вторые достаточно удалены друг от
друга. В частности, когда точка стационарной фазы близка к гранич-
граничной (например, у границы тени), поле необходимо описывать с по-
помощью комплексного интеграла Френеля.
Рассмотрим еще один вопрос, а именно о границах применимости
принципа Кирхгофа. Считается, что приближение, основанное на этом
принципе, применимо в условиях, когда длина волны падающего излу-
излучения намного меньше ширины щели. Если это не так, то в следую-
следующем приближении необходимо учитывать многократную дифракцию,
которую претерпевают лучи последовательно сначала на одном краю
щели, затем на противоположном и т. д. При умеренных значениях
414 Гл. 6. Дифракция света на отверстии
масштабного параметра ка ( ^ 4) мы можем рассмотреть один цикл
такой дифракции и получить таким образом распределение, изобра-
изображенное на рис. 6.6,6 (этот рисунок заимствован из статьи Келлера
[26], указанной в литературе к гл. 5 настоящей книги).
6.4. ДИФРАКЦИЯ НА ДИЭЛЕКТРИЧЕСКОМ ЦИЛИНДРЕ
Для иллюстративных целей начнем рассмотрение с двумерной ди-
дифракционной задачи на примере однородного диэлектрического ци-
цилиндра, протяженного на бесконечно большое расстояние вдоль оси у.
Будем считать, что поле и не зависит от координаты у. В этом случае
для компоненты поля, параллельной оси цилиндра, и(х, z) (= Еу для
ТЕ-волны и Ну для ТМ-волны) мы имеем уравнение
д2и/дх2 + d2u/dz2 + к20и = -к2(п2 - 1)Р(х,ф, F.4.1)
где функцияР(х, z) = 1, когда точка (х, z) лежит внутри цилиндра, и
Р(х, z) = 0 в противном случае, а п — показатель преломления, не
зависящий от поперечных координат.
На границе цилиндра С в случае ТЕ-волны функция и и ее градиент
Vw непрерывны, в то время как в случае ТМ-волны непрерывными яв-
являются тангенциальные составляющие поля и его нормальная произ-
производная, деленная на квадрат показателя преломления.
Выведем выражение для поля и внутри и снаружи цилиндра при
падении на него плоской волны и{. Для этого приведем уравнение
F.4.1) к интегральному виду, рассматривая его правую часть в качест-
качестве источника:
u(x,z) = щ(х,г) + к2(п2 - 1) | ГG(x -x';z- z')u(x\z')dx'dz\ F.4.2)
sd
raeSd — поперечное сечение диэлектрического цилиндра, a G — дву-
двумерная функция Грина для случаях = к0 [см. уравнение D.7.5)]. Для
решения интегрального уравнения F.4.2) в задачах рассеяния на ди-
диэлектриках разработан метод итераций [6]. В первом порядке этого
приближения сначала вычисляется поле внутри цилиндра, а рассеян-
рассеянное поле затем находят с помощью эквивалентных объемных токов в
диэлектрической области в предположении, что излучение происходит
в неограниченном пространстве [см. разд. 6.8, уравнение F.8.2)].
Если положить е = kl(n2 — 1)и обозначить через G* оператор ли-
линейной свертки, определяемой выражением
G*/ = [fax - x\z - z')f(x\z')dx'dz\ F.4.3)
sd
6.4. Дифракция на диэлектрическом цилиндре 415
то уравнение F.4.2) можно переписать в операторном виде
и = щ + eG*w. F.4.4)
Это интегральное уравнение Фредгольма (см. работу Трикоми
[26], указанную в литературе к гл. 7), определяемое в области Sd и
имеющее в качестве ядра следующую функцию:
G = W)H™[k0J(x - х'J + (z - z'J],
которая является сингулярной в точках х = х' , z = z' или &0 = 0.
Решения уравнения F.4.2) существуют почти всегда, за исключени-
исключением случаев с конкретными значениями к0, соответствующими колеба-
колебательным модам диэлектрического цилиндра. В этих случаях уравнение
F.4.2) имеет ненулевое решение щ>ии{ = 0.
Если показатель преломления диэлектрического препятствия слабо
отличается от показателя преломления окружающей среды, т. е.
п яг 1, то уравнение F.4.4) можно переписать в виде
и = щ + eG*Ui. F.4.5)
Это приближенное соотношение известно как формула Рэлея —
Ганса. Иногда ее называют формулой Борна, который широко приме-
применял это уравнение для решения задач о рассеянии частиц на централь-
центральном потенциале. Если е не является малым параметром, то член G*u{
в уравнении F.4.5) должен быть заменен на G*u , где и — поле, най-
найденное в приближении геометрической оптики.
6.4.1. Дифракция на круговом диэлектрическом цилиндре
Покажем теперь, как можно решить интегральное уравнение F.4.2)
для кругового диэлектрического цилиндра, освещаемого р-волной
(т. е. поляризованной параллельно оси цилиндра). В этом случае поле
удобно представить в виде совокупности цилиндрических волн (см.
разд. 4.11). Предположим без потери общности, что падающее поле и{
имеет вид плоской волны, распространяющейся в направлении
Ф' = 0, т. е. перпендикулярно оси у. Полученные результаты можно
обобщить на случай наклонного падения, заменяя волновое число к0
вне цилиндра на к0 sin б, а внутри цилиндра — на ko(fp- — cos20I/2, где
В — угол между осью у и направлением распространения волны, а
получаемые результаты справедливы для НЕ(ЕН)-полей [вместо
ТЕ(ТМ)-полей] (см. гл. 8 настоящей книги).
В рассматриваемом случае поле внутри цилиндра можно записать
в виде (см. разд. 4.11)
416 Гл. 6. Дифракция света на отверстии
и(р',Ф')= Е CmJm(konp')eim>- (р'<а\ F.4.6)
т= —оо
где п — обобщенный комплексный показатель преломления.
Используя теорему сложения Графа для цилиндрических функций
(см. задачу 4.8) при р > р , разложим ядро G интегрального уравне-
уравнения в ряд по цилиндрическим функциям
- ф')) =
= 7 Z Н%\кор)икор')е™«-*\ F.4.7)
^т= -оо
После подстановки правых частей выражений F.4.6) и F.4.7) в урав-
уравнение F.4.2) мы имеем
и(р,Ф)= I (-i)mJm(koP)eim+ + ?k2o(fi2-l) +f
т= -со
х ('jm(koPVm(koHp')p'dp'= I (-i)meim+x
Jo m= —оо
x ШкоР) + г* Я<.а)(*ор)], F.4.8)
где ряд Ет(—1)те""^т представляет падающую плоскую волну [см.
выражение D.11.12)], а
rHm = im+lj(n2 - l)cmj\(nx)JJx)xdx. F.4.9)
Учитывая соотношение
= (л2 - l)Jm(x)Jm(nx)x9 F.4.10)
ил jj
нетрудно получить, что
rm = -^m+1(^/2)Cmj8[Jm(j8)J/w(a)n - Jm(P)Jm(a)]> F.4.11)
где C = коа — масштабный параметр, а а = л]3.
В соответствии с F.4.8) поле снаружи диэлектрика представляет
собой суперпозицию цилиндрических волн с весовыми коэффициента-
коэффициентами г^, которые в данном случае можно рассматривать как коэффици-
коэффициенты отражения от цилиндра m-й парциальной волны. Коэффициенты
г^т нетрудно вычислить в предположении о непрерывности функции
при переходе через границу цилиндра. При этом мы имеем
= CwJm(a). F.4.12)
6.4. Дифракция на диэлектрическом цилиндре 417
Таким образом, выражая коэффициенты Ст в виде функции от rjj и
учитывая соотношение 2/7тг0 = /тф)Н${Р) - Jm(P)H%y (P), получаем
следующее выражение:.
к Jm@) \n'Jm(P)
где In' — логарифмическая производная, а
В частности, для вещественных п абсолютное значение функции S (т, /3)
равно единице. Заметим далее, что выражение F.4.14) определяет S как
функцию в общем случае комплексного параметра т. В результате та-
такого искусственного расширения появляется возможность использо-
использовать преобразование Ватсона, если рассеянное поле при этом предста-
представить в виде парциальных волн (см. работу Ньютона [17], указанную в
литературе к гл. 4).
Приведенное выше рассмотрение можно обобщить на случай
s-волны. При этом получаем следующее выражение:
' A SJ FA15)
ЛЯ ^(P) - In'
где
In' Jm(a) - nIn' НЧЩ' ®ЛЛ®
Предельный случай, соответствующий металлическому цилиндру,
можно получить, положив п — оо. При этом выражения для гт прини-
принимают более простой вид:
г* = -иР)/Н%Ш < = -J'JMHWm F.4.17)
где функция /т (лГ/S) заменена ее асимптотическим выражением.
Из приведенных выражений следует, что коэффициент отражения
для m-й цилиндрической волны сильно зависит от поляризации. Дей-
Действительно, когда значение функции/т 08) достигает максимума, гр
становится очень большим, аг8 незначительным, и наоборот, при ми-
минимальном гр достигает максимального значения rs. Это свойство
можно использовать для создания поляризатора. Например, поляри-
поляризующими свойствами будет обладать система, состоящая из большо-
большого числа равноотстоящих параллельных проволочек. Пеоиодическая
418 Гл. 6. Дифракция света на отверстии
структура в данном случае как бы усиливает поляризационные свойст-
свойства каждой проволочки. Такие поляризаторы успешно применяются в
дальнем ИК-диапазоне.
6.5. 5-МАТРИЦА И ПРЕДСТАВЛЕНИЕ ВАТСОНА — РЕДЖЕ
Если за направление распространения падающей волны выбрать ось z,
то выражение F.4.8) можно переписать в следующем эквивалентном
виде:
-z) + [ий(р,ф) + e-ik°'U(z)] m
&e-*°4J(-z) + ut(p,4>). F.5.1)
Поле wd можно представить как результат действия оператора § на
претерпевающую дифракцию плоскую волну е~ ikozU(z), а именно
\ +f F.5.2)
При отсутствии препятствия оператор S сводится к единице.
Если в качестве базисных функций взять набор цилиндрических
мод(- i)meim4>H^ , то коэффициенты 5Ш будут представлять собой
диагональные матричные элементы оператора ?(/3). Из коэффициентов
Sm в свою очередь можно составить так называемую S -матрицу, ко-
которая в базисе Н$ е'тф будет диагональной. Следует заметить, что
при дифракции на рассеивающем теле без потерь мы имеем I Sm I = 1.
Для матриц S (/?) и^(—C) [сопряженной к транспонированной матри-
матрице ?(/3)] справедливо соотношение
Таким образом, 5-матрица является унитарной, а соответствующий
оператор § называется унитарным оператором.
Если параметр /3 в S -матрице является комплексным, то точки син-
сингулярности этой матрицы могут дать информацию о параметрах и
радиальной структуре препятствия. Рассмотрим теперь круговой ци-
цилиндр, показатель преломления которого зависит от радиальной ко-
координаты р. В этом случае, комплексные значения /3, при которых
собственные значения § становятся бесконечными (эти значения /3 на-
называются резонансами рассеивающего тела), можно использовать для
нахождения профиля п (р).
Резонансы, соответствующие вещественным значениям 13, пред-
6.5. 5-матрица и представление Ватсона — Редже 419
ставляют собой различные связанные состояния электромагнитного
поля, которые как бы захватываются рассеивающим телом. Этим ре-
зонансам соответствуют собственные функции уравнения F.4.4), если
таковые имеются. Комплексные значения Eq, отвечающие разонансам,
«представляют» поле, временно захваченное рассеивающим телом,
причем время этого захвата обратно пропорционально мнимой части
6.5.1. Дебаевское разложение
Дебай [7] показал, что S -матрицу можно разложить в следующий сте-
степенной ряд:
пенной ряд:
где
_ 1п'Н[2\р)-п1п'Щ2\<х)
q In'Я<2)@) - nln'H™(a)9
Т2 = п[1п'Я^2)(а) - In'Я^(а)][1п' Щ2)(Р) - \ri ЩХ)(РУ) х
х [}п'Щ2)(р) - nln'H^a)], F.5.56)
Щ2\хIп'Щ2\р)-п1п'Н?\<х)
Pq Я^(аIп'Я<2>()?)-и1п'Я^(а)- 1"' '
Здесь R — коэффициенты отражения q-ft парциальной волны от по-
поверхности, член Т2 — учитывает прохождение парциальной волны
внутрь и затем наружу рассеивающего тела, а рР~~1 — коэффициенты,
учитывающие р - 1-кратные внутренние отражения от поверхности.
В частности, если а, /3 > 1, то ln'i/<2> ^ - /, и мы имеем Rq =
~ __(„ _ !)/(« + 1), Т2 = Ап/(п + 1)*2 и рд =¦ pitq(n - \)/(п + 1).
Таким образом, если показатель преломления п близок к единице, то
Ip I < 1 и ряд быстро сходится.
ud = w<i0) + ••• + п^ + •••, F.5.6а)
где
"" - ' ¦ ,) F.5.66)
p-leiq+H(q2)(k0p). F.5.6b)
420
Гл. 6. Дифракция света на отверстии
Рис. 6.7. а — области тени, соответствующие полям нулевого порядка (вверху) и перво-
первого порядка (внизу); б — многократное отражение лучей, полученное из дебаевского раз-
разложения S-матрицы кругового цилиндра.
Компонента с индексом /?- и д-й парциальной волны соответствует
волне, проникающей внутрь рассеивателя G^), претерпевшей/? отра-
отражений от внутренней поверхности (р~*) и вышедшей наружу (Тд). Ес-
Если 0 взять достаточно большим и положить1) п ^ 1, то вкладом от
uW можно пренебречь. В этом случае выражение для ud сведется к
выражению для ufK На рис. 6.7, а показаны заштрихованные обла-
области, соответствующие значениям р = 0, 1.
Ряд Дебая сходится со скоростью, которая зависит от коэффициен-
коэффициента затухания парциальной волны при каждом внутреннем отражении.
Если среда рассеивающего цилиндра не является абсолютно прозрач-
прозрачной, то возникает дополнительное затухание вследствие поглощения
излучения. В частности, в таком важном случае, как дифракция на
водном препятствии (л = 1,33), более чем 98,5% всей интенсивности
идет на последовательную рефракцию трех первых преломленных лу-
лучей, сооветствующих трем первым членам в дебаевском разложении.
^Рассеиватели, которые имеют показатель преломления, близкий к показателю
преломления среды, обычно называют слабо рассеивающими или мягкими, — Прим.
перев.
6.5. 5-матрица и представление Ватсона — Редже 421
6.5.2. Представление Ватсона — Редже
Вычисление амплитуды рассеянной волны и$\ представляющей /7-й
член в дебаевском разложении, сводится к суммированию парциаль-
парциальных волн [см. выражение F.5.6в)]. Суммирование можно заменить
интегрированием, как это было сделано при выводе выражения
D.12.10), только в данном случае коэффициент <м (я, ф')е~Ьф') должен
быть заменен на (\/2)en*v/2S^Hf\ что дает
F.5.7)
Учитывая теперь соотношение Я <?> = е ~iTVH^2) для соответствующего
члена из разложения F.5.4), мы имеем S(f> = S^expIi'O — рJт>]9
так что контур С [см. выражение D.12.10)] можно свести к линии, па-
параллельной вещественной оси v и отстоящей от нее на малое расстоя-
расстояние е > 0. Отсюда для поля и jf ^получим
^ F.5.8)
Чтобы применить преобразование Ватсона, нужно найти положения
полюсов функций Sjp\ даваемых выражениями
siP) =
v
Если известны функции/?^, Т* и pq9 то полюсы функции Sf} совпада-
совпадают с корнями уравнения (см. работу Нуссенцвейга [22], указанную в
литературе к гл. 4)
In' Н[2)(р) = win' Я(Ла). F.5.10)
В случае металлической поверхности полюсы функции Sj/?) совпадают
с нулями функции #2@) (см. разд. 4.12).
Сразу же заметим, что полюсы функции Sf) в комплексной пло-
плоскости v одни и те же для всех членов разложения, причем для/?-го
члена их порядок равен р + 1. Полюсы расположены либо вблизи ну-
нулей функции #$2)(/3), либо вблизи нулей Н^\а). В частности, можно
показать (ср. с разд. 4.12), что полюсы первого типа даются выраже-
выражением [ср. с D.12.19)]
у„ - -р - e-in/3(P/2)l/3xn - i/(n2 - 1I/2, F.5.11)
422
Гл. 6. Дифракция света на отверстии
где хп — л-й нуль функции Ai(-x). Последний член в правой части
этого выражения учитывает разницу граничных условий на диэлектри-
диэлектрической и металлической поверхностях.
Аналогично, в верхней полуплоскости полюсы второго типа дают-
даются выражением
v; ~ а + еЫ13(фI/3хп + п/(п2 - 1I/2. F.5.12)
С учетом распределения этих полюсов в комплексной плоскости
(см. работу Нуссенцвейга [22], указанную в литературе к гл. 4) введем
переменные rjl9 ri2 и ту (рис. 6.8):
= <51п
2v
ecu
<51п
г\ = <51п
2v
F.5.13)
где 5 = arg(i>) - (*72)sgn arg(*>). Из выражений D.12.22) и D.12.23)
можно найти положения нулей хп при л — оо и соответственно полу-
получить, что полюса рп в асимптотике располагаются на кривой
т|2 = тг/2, а полюса v'n — на кривой г\х = -тг/2.
6.5.3. Первый член дебаевского разложения
При р = 0 уравнение F.5.8) сводится к следующему
F.5.14)
AlmV
\ \
=-? /
Рис. 6.8. Комплексная плоскость v, на которой показаны переменные г\х итJ, определяе-
определяемые выражениями F.5.13); крестиками обозначены полюсы vn, а крестиками в
кружках — полюсы v'n. Контур интегрирования для интеграла из выражения F.5.14)
обозначен жирной линией, параллельной вещественной оси.
6.5. 5-матрица и представление Ватсона — Редже 423
р) = Н?\коР)Н?>AП + *v(o, ПН?\кор)Н?Ш F.5.15)
Поскольку интеграл в F.5.14) представляет поле — С/(—z) e~lk°z, в
дальнейшем мы будем его опускать, а й0) заменим на
й@) s 駻 + (/(-z) e"/Ar°z- Кроме того, Rv - 1 при Ы — оо во всей
комплексной плоскости, за исключением области между г?2 = тг/2 и
г/2 = -я72, в которой/?„ — 0 как /32(п2 - 1)/4р2. Используя асимпто-
асимптотическое представление D.12.8) для функций Н^2\ можно установить,
что подынтегральное выражение первого интеграла в F.5.14) в пер-
первом квадранте комплексной плоскости равно нулю. Таким образом,
путь интегрирования (/в, оо + ie) можно сдвинуть в сторону положи-
положительной мнимой оси (/с, /оо) с охватом полюсов v'n, что в итоге дает
Uco)_l
у
F.5.16)
Здесь r^ — вычеты функции gJHf* в полюсах v = v'n.
Теперь можно использовать представление
sin vn m=о
и переписать интегралы в F.5.16) в виде
= -2ie'"v У e'2"mv F.5.17)
о
m = O\J-o
+ fV'<3/2)*v+'*MVcosW)-S(radv- <6-5Л8>
J Pi
Вычисление этих интегралов можно еще более упростить, исполь-
используя то обстоятельство, что подынтегральное выражение во втором
квадранте обращается в нуль при i/-oo и/w ^ 1. Следовательно,
путь интегрирования (/?, /оо) для всех членов с т ^ 1 можно сдви-
сдвинуть в положение (/е, -оо + /е) с охватом полюсов vm. В итоге полу-
получим следующее выражение:
и{0)(р,Ф) = и4р,ф) + *Е Е
l
? ? e«"a>"+2-"Wcoe(v^)r;, F.5.19)
л т = 0
где гл — вычеты функции g/H^ в полюсах рл, a wg — член ряда
F.5.18) cm = 0. Можно показать что при я > 1 значения вычетов г'п
пренебрежимо малы (см. работу Нуссенцвейга [22, Sect. 3D], указан-
указанную в литературе к гл. 4 настоящей книги).
Подынтегральная функция в интеграле, представляющему, стре-
424
Гл. 6. Дифракция света на отверстии
мится к нулю на бесконечности при всех значениях у\ > Ф, а для
ф < ж/2 контур интегрирования (—оо + ie) сдвигается к г\ = тг/2. Та-
Таким образом, мы имеем следующее выражение:
Tn)<JHdv, F.5.20)
где Г — контур интегрирования, охватывающий полюсы Rv и пересе-
пересекающий дважды вещественную ось, первый раз между точками 0 и
-/3 и второй раз между ~/3 и -кор. Подынтегральное выражение в
интеграле F.5.20) в каждом из этих интервалов имеет по одной седло-
вой точке (рис. 6.9), а именно
v<2> = -fcop sin ф. F.5.21)
Седловые точки р^ и р® относятся к лучам, падающим на цилиндр с
прицельными параметрами р (не путать с индексом/?) и psin</>. В
частности, прицельный параметрр относится к тем падающим лучам,
которые испытывают геометрическое отражение от цилиндра и про-
проходят через точкуР (рис. 6.10) [например, прир — оо,/? = a cos(</>/2)],
в то время как параметр р sin ф соответствует лучам, которые до-
достигают точки Р, не испытав влияния препятствия.
Если контур Г изменить таким образом, чтобы он проходил через
седловые точки, то получим асимптотическую оценку интеграла
F.5.20). Таким образом, в геометрической оптике функциюwg(p, ф) не-
нетрудно найти, умножая поле соответствующего луча на френелевский
коэффициент отражения.
Прямой луч
Р(р,ф)
Рис. 6.9. Путь интегрирования Г для вы-
вычисления геометрооптического вклада в
поле, дифрагированное на цилиндре.
Рис. 6.10. Вклад седловой точки в поле
w@) c точки зрения геометрической
оптики; р — прицельный параметр для
луча, достигающего точки Р после отра-
отражения его от цилиндра в точке Q.
6.6. Поверхностные дифракционные волны 425
Если зафиксировать значение угла ф и начать уменьшать р, то рассто-
расстояние между двумя седловыми точками будет уменьшаться до тех пор,
пока они не сольются в одну; последнее произойдет в том случае, когда
точка Р располагается на границе тени. По мере дальнейшего продвиже-
продвижения в область тени вклад от и% стремится к нулю (см. работу Нуссен-
цвейга [22], указанную в литературе к гл. 4 настоящей книги).
6.6. ПОВЕРХНОСТНЫЕ ДИФРАКЦИОННЫЕ ВОЛНЫ
Выражения для амплитуд рассеяния, полученные в предыдущем разде-
разделе, позволяют записать полное поле и(р, ф) вокруг металлического
кругового цилиндра, освещаемого р-волной единичной амплитуды
перпендикулярно его оси, в виде суммы парциальных волн:
+ 00 Г J
IJi)mi^W)^H™(k)^ F.6.1)
где /3 ш коа. Опыт численных расчетов показывает, что минимальное
число членов разложения, необходимых для получения хорошего
приближения, однозначно связано с величиной параметра /3. При
/3 > 1 многочисленные парциальные волны дают в сумме крайне нере-
нерегулярную картину дифракции. При 0 — оо можно использовать при-
приближение геометрической оптики, которое приводит к картине с тем-
темными и светлыми областями, разделенными двумя границами тени.
Светлые области образуются там, где перекрываются падающий луч
и лучи, отраженные но правилам геометрической оптики. Эти лучи
можно взять в качестве главных членов в разложении Лунеберга —
Клейна для поля с конечным к0. Однако поле в темной области в
обычном приближении геометрической оптики получить нельзя, по-
поскольку при?0 —> оо соответствующее выражение стремится к нулю. В
этом случае приближенное выражение для поля можно получить, ис-
используя преобразование Ватсона, о котором шла речь в предыдущем
разделе. Суть этого преобразования заключается в замене парциаль-
парциальных волн из разложения F.6.1) на волны с комплексными индексами
vn, поскольку в случае металлического тела вкладами вычетов в полю-
полюсах v'n можно пренебречь. Такие волны представляют собой особые
моды, которые «ползут» по искривленной поверхности цилиндра, но
при этом не проникают в него, отсюда их название — ползущие вол-
волны. В частности, для р-волны с единичной амплитудой с помощью
формул, приведенных в разд. 4.12 и 6.S, получаем
426
Гл. 6. Дифракция света на отверстии
F.6.3)
+ exp< — jvj ф- — - arccosf -I- 2nm > 1, F.6*2)
где.? = (p2 - a2)l/2 — расстояние от точки Q2 доР (рис. 6.11 и 6.12).
Коэффициенты vn определяются выражением D.12.19) [см. также вы-
выражение F.5.11) при Я — оо] и записываются следующим образом:
1,856 (к = 1),
Р Р 4,381 (п = 3),
5,387 (п = 4).
Параметры D2 р играют роль поверхностных дифракционных ко-
коэффициентов и равны Ьычетамгя, о которых речь шла в предыдущем
разделе:
Ъ\р = rn = 0?/2I/3e"in/12/[Ai/2(-xn)]; F.6.4)
здесь хп — нули функции Эйри Ai(- x), a Ai' — соответствующая
производная.
В соответствии с выполненным выше рассмотрением результирую-
результирующее поле является суммой вкладов лучей, которые возникают в точ-
,(a, f.
Освещенная
область
Граница тени
Область
тени
Р(р,ф)
Граница тени
Освещенная
область
Рис. 6.11. Геометрическое рассмотре-
рассмотрение ползущих волн, распространяю-
распространяющихся в области тени металлического
цилиндра, освещаемого плоской
волной.
Рис. 6.12. Геометрическое рассмот-
рассмотрение поверхностных волн при ди-
дифракции на цилиндре, освещаемом
конгруэнцией лучей с началом
в точке S.
6.7. Обобщенный принцип Ферма 427
ках скользящего падения Q ,(ф = 7г/2) и Q 3(Ф = Зт/2), а затем некото-
некоторое время распространяются по поверхности, проходя при этом
расстояния а[ф - т/2 - arccos (а/р) + 2xmJ и а[Зт/2 -ф- arccos (а/р) +
+ 2яти], где т — число обходов цилиндра, совершенных лучом с ком-
комплексной постоянной распространения кп:
kn=-(vn/a) = k0-iantP9 F.6.5)
где ап = (\/а)хпф/2)уге ™/ь — комплексный коэффициент ослабления.
6.7. ОБОБЩЕННЫЙ ПРИНЦИП ФЕРМА
И ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ДИФРАКЦИИ
Следует заметить, что траектории ползущих волн представляют со-
собой наикратчайшие пути, соединяющие источник с точкой наблюде-
наблюдения при условии, что поле данной волны не проникает в цилиндр. Та-
Таким образом, используя аналогию с лучами, распространяющимися в
трехмерном пространстве, или с лучами, дифрагированными на крае,
можно вывести обобщенный принцип Ферма. Эти три класса лучей
описывают траектории, которые являются стационарными относи-
относительно небольших изменений траектории при условии выполнения со-
соответствующих ограничений. Для лучей, дифрагированных на крае,
эти ограничения состоят в том, чтобы эти лучи касались края по
крайней мере в одной точке, в то время как ползущие волны должны
обязательно касаться гладкой поверхности.
Обобщенный принцип Ферма был впервые сформулирован Келле-
Келлером (см. работу [26], указанную в литературе к гл. 5) при получении
асимптотических выражений для лучей, дифрагированных на пре-
препятствиях произвольной формы. Ценность этого принципа состоит в
том, что он сразу позволяет обобщить формулы, полученные выше
для кругового цилиндра, на случай излучения произвольного вида.
При этом мы по-прежнему можем считать что поле в темных обла-
областях является суммой вкладов ползущих волн, которые на поверхно-
поверхности цилиндра распространяются по кривым, удовлетворяющим при-
принципу Ферма. Следовательно, каждый луч из конгруэнции, падающий
по касательной на поверхность цилиндра, должен описывать на ней
геодезическую линию, а именно спираль. Ползущая волна на поверх-
поверхности цилиндра полностью определяется семейством спиральных тра-
траекторий, образованных поверхностными волнами, распространяющи-
распространяющимися с комплексным показателем преломления, определяемым выра-
выражением F.6.5):
кп = к0 - И„ = к0- i(xJp№oPj2)ll3elM/69 F.7.1)
428 Гл. 6. Дифракция света на отверстии
где параметр pg — радиус кривизны поверхностного луча. Для спи-
спиральной траектории pg = const; таким образом, икп = const.
Данное рассмотрение можно обобщить и на произвольную глад-
гладкую поверхность. В этом случае поле представляется в виде суперпо-
суперпозиции бесконечного числа вкладов вида
х exp -ikos - ikot - аи,рЛ' I. F.7.2)
Здесь множитель \pc/s (pc + s )]1/2 учитывает расходимость дифрагиро-
дифрагированных лучей, покидающих поверхность в точке Q2 и фокусирующихся
на расстоянии рс отб2» множитель dy\x/dt\2 представляет собой отно-
отношение расстояний между двумя соседними лучами в точках Qx hQ2, и,
таким образом, (drjl/dfq2)l/2 учитывает расходимость поверхностных
лучей. В выражении F.7.2) дифракционный коэффициент^ р записан
в виде произведения двух коэффициентов?>„9P(Q\) viDn p(Q^, посколь-
поскольку радиусы кривизны траекторий (и, следовательно, 0), в точках Q} и
?? 2 в общем случае являются различными. Наконец, 5 — это расстоя-
расстояние от точкиР до точкиQ2, at — длина дуги траектории между точ-
точками Q{ nQ2.
В качестве заключительного этапа приведенные выше выражения
можно обобщить на случай s-волны, заменяя дифракционный коэффи-
коэффициент ?>„ р naDn s, определяемый выражением
Dl = -№12У1Ъе-Ы112Жх'п Ai2(-x;)], F.7.3)
гдел:^ — значения нулейфункции Ai'(-x). Кроме того, необходимо
заменить vn на величину рп9 определяемую следующим образом [ср. с
выражением F.7.3)]:
0,809 (л = 1),
{П = 2)' F.7.4)
3,826 (и = ЗХ
4,892 (п = 4),
Указанные скалярные дифракционные формулы можно записать в
виде одного векторного соотношения [6.4]:
+ b2bxG)
где Ed(P) — поле в точке Р, дифрагированное на гладкой поверхно-
поверхности, освещаемой падающей волной Е^ п и 6 — соответственно глав-
6.7. Обобщенный принцип Ферма
429
ная нормаль и бинормаль к траектории поверхностного луча в точках
Q{ nQ2; величина F определяется выражением
-*М - i^j, F.7.6)
а величину G можно вычислить из приведенного выше соотношения,
заменяя индекс s нар.
В заключение заметим, что как и в случае дифракции на крае, ди-
дифрагированное на гладкой поверхности поле может быть представле-
представлено в виде суперпозиции мод, каждая из которых является резуль-
результатом умножения падающего поля на дифракционную матрицу
Геометрическая теория дифракции посвящена изучению дифракции
лучей на предметах любого сорта (рис. 6.13). Название данной теории
предложил Дж. Келлер, который заложил ее основы. В настоящее
время геометрическая теория дифракции развилась в довольно слож-
сложный аппарат, который включает в себя систематическое использова-
использование дифракционных матриц и однородных представлений для специ-
специальных областей (например, на границе тени и в каустике), рассмот-
рассмотренных в предыдущей главе. В некотором смысле геометрическую те-
Верашна
Геометрические
лучи
Отверстие
^Касательная
а
Отверстие
Выпуклая
цилиндр,
поверхность
Дифраги-
Дифрагированные
лучи
Ползущие
лучи
Рис. 6.13. Лучи, дифрагированные на различных препятствиях. Заметьте, что на рис. г
имеются дважды дифрагированные лучи, а на рис. в — прошедшие лучи.
430 Гл. 6. Дифракция света на отверстии
орию дифракции можно рассматривать как электромагнитный аналог
фейнмановских диаграмм, применяемых в квантовой теории поля.
Действительно, они имеют общее свойство, заключающееся в том, что
устанавливаемые ими правила позволяют представить сложные конфигу-
конфигурации поля в виде суперпозиции стандартных полей, которые в случае
геометрической теории дифракции описываются дифрагированными лу-
лучами, а в фейнмановских диаграммах — графиками. Заинтересованный
читатель может найти сведения о некоторых применениях и разработках
геометрической теории дифракции в книге под редакцией Хансена [28],
указанной в литературе к гл. 5 настоящей книги.
6.8. РАССЕЯНИЕ СВЕТА ДИЭЛЕКТРИЧЕСКИМИ ТЕЛАМИ
При рассмотрении рассеяния света диэлектрическими телами можно
использовать два различных подхода. Один из них основывается на
решении поверхностного, а другой — объемного интегрального урав-
уравнения [8]. Для того чтобы получить интегральное представление поля
снаружи и внутри рассеивающего тела, рассмотрим сначала интег-
интегральное представление поля в виде D.3.1) в однородной рассеивающей
среде как функцию поля на поверхности. Затем, учитывая, что на ди-
диэлектрической поверхности нормальные составляющие вектора D и
тангенциальные составляющие векторов Е и Н непрерывны, произве-
произведем необходимые преобразования уравнений D.3.2) и D.3.3), в резуль-
результате чего получим следующие выражения для полей на внешней сто-
стороне поверхности S рассеиваюшего тела:
п0 х Ei(r) = п0 х &Ъ < 1(оц{п'0 х H)(Gl + G2) - (п'0 х Е) х V'(GX + G2) -
S'o, F.8.1a)
^
S
+ n'0-HF(G1 + G2)idS\ F.8.16)
где индексы 1 и 2 относятся соответственно к внутренней и внешней
областям рассеивающего тела: G{ 2 = G(n 12г); Е и Н — поля на внеш-
6.9. Приближение физической оптики 431
ней части поверхности S, п0 — внешняя нормаль. Уравнения F.8.1),
если в них рассматривать Е и Н как неизвестные функции, представля-
представляют собой систему интегральных уравнений Фредгольма, у которых
неоднородный член выражается через поле Ej(r) или Hj(r) падающего
излучения. Эти уравнения, как правило, имеют единственное решение,
за исключением особых значений к0 (в общем случае комплексных),
для которых при нулевом падающем поле уравнения F.8.1) допускают
ненулевые решения. Эти особые значения к0 соответствуют резонанс-
резонансным частотам диэлектрического тела, примером которых служат рас-
рассматриваемые в разд. 6.13 резонансы диэлектрической сферы. Разби-
Разбивая поверхность рассматриваемого тела на большое число достаточно
малых участков, таких, что на этих участках значения всех функций,
входящих в подынтегральное выражение, являются практически по-
постоянными, систему уравнений F.8.1) можно записать в матричном
виде. Данная процедура лежит в основе метода моментов (см. рабо-
работу Харингтона [9]). Предложенный Харингтоном метод моментов
был в значительной степени дополнен и расширен другими авторами.
Не будем останавливаться на всех вариантах данного метода, упомя-
упомянем лишь метод сингулярных разложений, позволяющий сформули-
сформулировать временную задачу рассеяния [10].
Другой метод решения рассматриваемой задачи состоит в приме-
применении следующего интегрального представления поля внутри рассеи-
рассеивающего тела:
Е(г) = Ei(r) + ^^i f [(Wai^E + Г • Е F'GJ dV, F.8.2)
v
которое нетрудно получить, если в уравнениях Максвелла в качестве
источника рассматривать величину (е2 — ?i)E.
6.9. ПРИБЛИЖЕНИЕ ФИЗИЧЕСКОЙ ОПТИКИ
ДЛЯ ИДЕАЛЬНО ПРОВОДЯЩЕГО ТЕЛА
Если длина волны падающего на металлическое препятствие излуче-
излучения короче характерного радиуса кривизны его поверхности, то по-
последняя в некотором приближении может быть разделена на освещае-
освещаемую (Sqcb) и теневую (STeH) области. Исходя из точного решения инте-
интегрального уравнения для возбуждаемых поверхностных токов, Фок
(см. работу [3], указанную в литературе к гл. 4 настоящей книги) оце-
оценил ширину переходного участка между этими двумя областями и на-
432 Гл. 6. Дифракция света на отверстии
шел, что она составляет величину порядка [2/(?pg)]1/3pg, где pg — ло-
локальный радиус кривизны поверхности.
Сделанные выше допущения позволяют при вычислении дифраги-
дифрагированного поля использовать так называемое приближение физичес-
физической оптики. Это приближение состоит из двух последовательных ша-
шагов. На первом шаге предполагается, что в каждой точке освещаемой
области SOCB отраженное поле вычисляется так же, как и в случае па-
падения плоской волны по касательной к бесконечной плоскости; при
этом поле на теневой стороне поверхности считается равным нулю.
Таким образом, принимается, что Ed + Е{ = 2fto(no ¦ Е{) и
^d + ^ = -2А0 х (п0 х Н^ в области S^g, где п0 — внутренняя нор-
нормаль к поверхности S. На втором шаге, рассеянное поле получается
интегрированием на поверхности S0CB.
Выполнив эти операции и воспользовавшись соотношением D.3.3),
нетрудно получить следующее выражение для рассеянного поля:
Hd(r) = f j[(H, + Hd) x no] x YGdS'. F.9.1)
Socb
В дальней зоне V'G = ikGn9 где А = f, и мы имеем
Hd(r) s 2ik (Hj x iio) x n0G dS'==
Socb
? 2ikG(r)n x n0 x Н{ет'г' dS' ж
Socb
E'Jn). F.9.2)
- iixEi(n).
ПриАгг — oo, Hd = f ~'A x Ed и из соотношения F.9.2) получаем
Eu(r)Si(e-ik'/r)Vd{f). F.9.3)
Если падающее поле представляет собой плоскую волну,
Hj = H,fi~ ' ', то выражение для.Еа(п) сводится к виду
f| no(r
Socb
.-B,.fio).EorfS'sS.Eo, F.9.4)
6.9. Приближение физической оптики 433
где S — матрица рассеяния, которую мы рассмотрим в разд. 6.11. В
соответствии с последним выражением вектор Ed пропорционален
фурье-образу вектора flo(r'), причем фурье-преобразование вычисляет-
вычисляется по освещаемой области металлического препятствия. Это фурье-
преобразование можно вычислить асимптотически, используя метод
стационарной фазы, рассматриваемый в гл. 5. Нетрудно показать,
что станционарные точки, если они существуют, удовлетворяют усло-
условию п0 • (fi + ftj) = 0; иными словами, они совпадают с точками от-
отражения падающих лучей, рассеянных поверхностью в направлении п.
Как уже отмечалось, члены асимптотического разложения для каждой
стационарной точки совпадают с соответствующими членами разло-
разложения Лунеберга — Клейна. Поэтому мы можем опустить здесь де-
детальное рассмотрение вкладов в рассеяние от каждой точки, а чита-
читатель может обратиться^ к соответствующим методам, иллюстрируе-
иллюстрируемым в гл. 2. К сожалению, в рамках геометрической оптики не удает-
удается определить вклад в рассеяние от границы области интегрирования
S^g. Для того чтобы найти дифрагированные поля от периферии осве-
освещаемой области SOCB, необходимо непосредственно вычислить дифрак-
дифракционный интеграл. С целью упрощения расчетов главных членов в
выражениях для дифрагированных полей можно использовать геомет-
геометрическую теорию дифракции.
Интегральное представление векторной величины E'd значительно
упрощается, если рассматривать его в направлении вперед. В частно-
частности, при п = flj s z интегральное уравнение F.9.4) принимает вид
= - / X н0 х [[ n0 dS = -I -?¦ Но х
Socb
X
(x jj dSx + y\\dSy + z \\dSz), F.9.5)
^OCB OCB OCB
где dSxf dSy и dSz — проекции ориентированной площадки dS с нор-
нормалью fl0 на координатные плоскости yz, xz и ху. Для простых по-
поверхностей нетрудно показать, что J(c dSx = JL rfSv = 0. Отсюда
находим, что Ed(z) = z x n^^g z. Иными словами, величина Ed про-
пропорциональна произведению падающего электрического поля и проек-
проекции освещаемой площадки на плоскость, перпендикулярную направле-
направлению падающей волны.
Если направления векторов п и х\{ не совпадают, но близки друг к
другу, то в качестве вектора, перпендикулярного вектору п — п{9 мож-
можно взять вектор n — ni9 и тогда соотношение F.9.4) принимает следу-
434 Гл. 6. Дифракция света на отверстии
ющий вид:
Ei(n) = -*j(Ho х щ) J I dx'dy'cipl1k*± • (х'х + /у)],- F.9.6)
Socb
где х'х + .у'9 = г" - (г' ¦ fiiJtij. Интеграл в этом выражении пред-
представляет собой фурье-образ отверстия, расположенного в плоскости
ху, полученного проецированием вдоль п{ освещаемой части препятст-
препятствия. С физической точки зрения это означает, что рассеяние вперед в
некотором приближении эквивалентно дифракции на отверстии, кон-
контуры которого определяются проекцией препятствия на плоскость,
перпендикулярную направлению падающей волны.
Пример. Дифракция на сфере. Рассмотрим сферу радиусом а>
центр которой расположен в точке О. Пусть эта сфера освещается
плоской волной, поляризованной вдоль оси .у и распространяющейся
вдоль оси z. В этом случае амплитуда E'd рассеянного поля при п » щ
дается выражением
2к J (kaln \)
= ~ika fcll °' F'9e?)
При рассеянии вперед данное выражение совпадает с выражением для
поля рассеяния на диске, радиус которого равен радиусу рассматрива-
рассматриваемой сферы.
6.10. ЭЛЕКТРОМАГНИТНАЯ ТЕОРИЯ ДИФРАКЦИИ
НА ИДЕАЛЬНО ПРОВОДЯЩИХ И ДИЭЛЕКТРИЧЕСКИХ
ДИФРАКЦИОННЫХ РЕШЕТКАХ
В истории физики дифракционные решетки выступают как одни из са-
самых незаменимых инструментов. До 1891 г., когда Майкельсон изо-
изобрел интерферометр, названный его именем, дифракционные решетки
были единственным инструментом, с помощью которого измерялись
характеристические длины волн атомных спектров.
Дифракционные решетки, как известно, были изобретены амери-
американским астрономом Дэвидом Риттенхаузом примерно в 1785 г. и не-
несколькими годами позже независимо Йозефом фон Фраунгофером, ко-
который опубликовал свои оригинальные исследования лишь в 1819 г. В
ранних конструкциях дифракционная решетка представляла собой ряд
очень тонких проволочек или нитей, навитых на два параллельных
винта, которые выполняли роль рдспорок. Эта конструкция представ-
представляла собой как бы многократно повторенную в пространстве щель, на
6.10. Электромагнитная теория дифракции 435
которой модуляция падающего волнового фронта осуществляется при
помощи чередующихся прозрачных и непрозрачных участков.
Более распространенными являются решетки, выполненные путем
нанесения алмазным резцом тончайших канавок на поверхность сте-
стекла для пропускающих решеток или на зеркальные металлические по-
поверхности для отражательных решеток. В недалеком прошлом отра-
отражательные решетки изготовлялись на зеркальном металле, представ-
представляющем собой очень твердый сплав меди и олова. В настоящее время
их изготавливают путем напыления слоя алюминия, который лучше
отражает в УФ-области.
Большой прогресс в производстве дифракционных решеток произо-
произошел после изобретения Роуландом в 1882 г. специальной гравироваль-
гравировальной машины, которая наносила периодические штрихи с ошибкой, не
превышающей одной трехсоттысячной доли дюйма. В настоящее вре-
время после работ Стронга и Бэбкока, а впоследствии Харрисона [11] и
Строука [12] из Массачусетского технологического института (МТИ) в
технологии производства дифракционных решеток достигнуты значи-
значительные успехи. Так, например, Харрисон в МТИ изготовлял решетки
длиной до 26 см и полезной площадью до 360 см2.
Производство гравированных решеток достаточно сложно и требу-
требует значительных затрат времени. В действительности большинство
решеток представляет собой реплики, отлитые с матрицы оригиналь-
оригинальных гравированных решеток (шаблонов). При освещении интенсив-
интенсивным светом реплики и шаблоны ведут себя по-разному. Например, в
резонаторах мощных лазеров должны использоваться шаблоны, по-
поскольку они могут выдерживать огромные интенсивности излучения.
В поисках дальнейшей информации об истории и производстве ди-
дифракционных решеток мы рекомендуем читателю обратиться к книге
Строука [12].
Из-за трудностей, связанных с механическим изготовлением решеток,
рассматривалось много других методов их изготовления. В 1927 г. Май-
кельсон впервые предложил использовать в производстве дифракцион-
дифракционных решеток фотографический метод. В 1962 г. Денисюк [13] рассмотрел
возможность получения дифракционных решеток с помощью записи ин-
интерференционных полос. Современная технология позволяет получать
периодическое гофрирование с помощью так называемого голографиче-
ского метода. Рельеф решетки в этом методе создается путем интерфе-
рометрической экспозиции и обработки фоторезиста. Затем с помощью
ионной бомбардировки или химического травления решетка переносится
на подложку. Первые голографические решетки для спектроскопических
исследований были изготовлены в 1967 г. Шмалем и Рудольфом [14] в
436 Гл. 6. Дифракция света на отверстии
оптической лаборатории Гёттингенской обсерватории и в 1968 г. Лабей-
ри и Фламаном [15] в Париже. С тех пор созданы решетки для видимо-
видимого, УФ и мягкого рентгеновского диапазонов. В настоящее время су-
существует возможность изготовления решеток шириной более чем 600 мм
с плотностью линий более чем 10 000 штрихов на миллиметр. Эти ре-
решетки практически не имеют «духов» и характеризуются минимальным
рассеянием падающего света. Голографические решетки могут быть из-
изготовлены на искривленной поверхности. Кроме того, в принципе можно
создать решетки, период которых будет изменяться по поверхности и
таким образом обеспечивать возможность фокусировки дифрагирован-
дифрагированных пучков. Отражательная способность голофафических решеток мень-
меньше, чем у гравированной, и сильно зависит от поляризации падающей
волны.
Прежде чем завершить данное введение, следует заметить, что в
природе существуют некоторые системы, которые, с одной стороны,
обладают достаточными размерами, а с другой, — высокой степенью
упорядочения, так что их можно рассматривать как дифракционные
решетки оптического диапазона. Например, свойствами дифракцион-
дифракционных решеток обладают жидкие кристаллы, молекулы которых распо-
расположены с достаточной регулярностью. В жидких кристаллах расстоя-
расстояние между соседними молекулами зависит от температуры, так что
спектр дифрагированного на этих кристаллах оптического поли также
изменяется с температурой, и, следовательно, жидкие кристаллы
можно использовать как температурные датчики. Превосходной ди-
дифракционной решеткой является опал. Опал состоит из двуокиси
кремния, в которую вкраплены маленькие водяные пузырьки. Эти пу-
пузырьки образуют плотноупакованную трехмерную решетку с расстоя-
расстоянием между штрихами около 0,25 мкм. Показатель преломления про-
прозрачного вещества матрицы, которая окружает водяные пузырьки, не-
немного отличается от показателя преломления вещества пузырьков.
Именно трехмерная дифракционная решетка опала, впервые разре-
разрешенная в 1964 г. с помощью электронного микроскопа, делает этот
драгоценный камень окрашенным при освещении его белым светом,
причем цвет опала меняется как при изменении угла зрения, так и при
повороте самого камня.
6.10.1. Применения дифракционных решеток
При освещении отражательной (или пропускающей) дифракционной
решетки плоской волной с известной длиной волны в пространстве
возникает несколько лучей, которые обозначаются целыми числами
6.10. Электромагнитная теория дифракции 437
т @, ±1, ±2...) и определяют интерференционный порядок. Если че-
через 0 обозначить угол падения, а через d — период решетки, то, как
мы покажем ниже, m-му отраженному (прошедшему) лучу будет соот-
соответствовать угол 0т, который удовлетворяет соотношению
sin вт - sin в = m(A/d). F.10.1)
Это соотношение известно как формула дифракционной решетки.
Прит = 0 мы имеем 0 = 0О; иными словами, нулевой порядок со-
соответствует зеркальному отражению, и решетка выступает в роли
обычного зеркала. Если т достаточно велико, то соотношению
F.10.1) удовлетворяет комплексное значение угла Вт = /0^ +
+ sgn(w)?r/2. Это означает, что отраженные решеткой лучи пред-
представляют собой затухающую волну. В случае когда луч падает прак-
практически параллельно плоскости решетки @ = тг/2), дифрагированные
лучи в зависимости от знака т состоят из лучей, отраженных назад, и
преломленных лучей.
В диэлектрическом волноводе простым способом вывода части
мощности волноводной моды является гофрирование поверхности. В
этом случае мода действует как луч, падающий под скользящим
углом к рифленой поверхности, который в результате дифракции ча-
частично рассеивается в окружающее пространство. Гофрирование ис-
используется для селективного ввода и вывода в волновод мод соот-
соответствующей пространственной структуры. На основе гофрированных
поверхностей изготавливаются узкополосные фильтры, детекторы
света и фазочувствительные элементы. Принципы работы этих прибо-
приборов рассмотрены в книге [16]. Кроме того, гофрирование применяется
для брэгговских отражателей, используемых в полупроводниковых ла-
лазерах.
Основное свое применение решетки нашли в спектроскопии, где
они заменили дисперсионные призмы, поскольку по сравнению с приз-
призмами имеют значительно более высокую разрешающую способность.
При замене призмы решеткой в спектрометре можно добиться деся-
десятикратного увеличения светового потока, так как в спектрометре с ре-
решеткой ширина входной щели может быть значительно увеличена по
сравнению с призменным спектрометром, имеющим такое же разре-
разрешение. Кроме того, решетка как диспергирующий элемент может об-
обладать большей площадью, что еще более увеличивает ее разрешаю-
разрешающую способность. Однако по сравнению с призменными спектромет-
спектрометрами спектрометры с дифракционными решетками имеют один недо-
недостаток, который состоит в необходимости устранения нежелательных
порядков интерференции.
438
Гл. 6. Дифракция света на отверстии
В спектрометрах в основном применяются решетки отражательно-
отражательного типа, когда источник излучения и точка наблюдения лежат по одну
сторону от плоскости решетки. Штрихи решетки могут иметь различ-
различную форму. Однако обычно им придают пилообразный профиль с оп-
оптически гладкими сторонами. Такой профиль решетки, предложенный
Вудом, позволяет увеличивать интенсивность отражения в определен-
определенном порядке и тем самым улучшать эффективность спектрометра.
Для характеристики дифракционной решетки широко используют
понятие эффективности, которую определяют как отношение потока
излучения в каком-либо порядке к падающему потоку монохроматиче-
монохроматического излучения. Эффективность зависит от профиля решетки и от
плотности штрихов. На рис. 6.14 показана спектральная зависимость
эффективности типичной дифракционной решетки с плотностью 1200
штрихов на миллиметр и углом блеска а = 17°27' для р- и s-волн,
причем у р-волны вектор поляризации направлен параллельно штри-
штрихам решетки, а у s-волны — перпендикулярно им.
Решетки, используемые в монохроматорах, характеризуются по-
постоянным значением угла между падающим и отраженным лучами
(рис. 6.15). В этом случае в + вт = а и соотношение F.10.1) принима-
принимает вид
sin[0 _ (i/2)a] = - [(шЯ)/Bй)ЗЕ1/со8(а/2)]. F.10.2)
В частности, когда угол отражения а равен нулю, говорят, что решет-
решетка работает в схеме Литтроу (рис. 6.16). В соответствии с соотноше-
соотношением F.10.2) длина волны излучения, прошедшего через выходную
щель монохроматора, изменяется пропорционально синусу угла пово-
поворота решетки 0. Для того чтобы получить линейную развертку во вре-
времени, необходимо использовать синусный механизм поворота решетки.
100 -
~ 60 -
Рис. 6.14. Типичная кривая зависимости эффек-
эффективности Е от X для решетки с углом блеска
а = 17°27' и количеством штрихов 1200 на
миллиметр (из каталога фирмы Jobin — Yvon).
0,3 0,4 0,5 0,6
Л,мкм
6.10. Электромагнитная теория дифракции
439
М
Рис. 6.15, Схемы Черны — Тернера (а) и Эберта — Фасти (б), используемые в скани-
сканирующих спектрометрах. Спектральный состав излучения на входе спектрометра анали-
анализируется путем наблюдения интенсивности на выходной щели с помощью ФЭУ в зави-
зависимости от угла поворота плоскости решетки. Основной особенностью данных схем яв-
является то, что угол а между падающим и дифрагированным на решетке лучами сохра-
сохраняется постоянным.
С помощью решетки можно в принципе исследовать любой спект-
спектральный диапазон. Действительно, соотношение F.10.2) может удов-
удовлетворяться при любом значении \/d, если имеет место соответству-
соответствующее сочетание угла падения в и рабочего порядка т решетки. Одна-
Однако общим правилом является то, что интенсивность дифрагированно-
Решетка
в схеме
Литтроу
Рис. 6.16. Схематическое пред-
представление решетки в схеме
Литтроу.
Остальные
линии
440
Гл. 6. Дифракция света на отверстии
Входная /цель
Третий
порядок
Второй
порядок
Первый
порядок
Центральное
изображение
Рис. 6.17. Вогнутая решетка; показан
круг Роуланда. На входную щель по-
подается пучок с исследуемым спект-
спектром. Угловые секторы соответству-
соответствуют различным порядкам дифракции.
Благодаря фокусирующим свойствам
решетки излучение, соответствующее
различным участкам спектра, соби-
собирается в различных точках окружно-
окружности Роуланда.
го пучка сильно уменьшается с увеличением порядка т. Кроме того,
эффективность решетки в данном порядке дифракции велика только в
некотором небольшом интервале с центром на длине волны
X/[2rfcos(a/2)] (см. рис. 6.14). Если увеличить порядок т, то решетку
можно использовать для длин водн \/т. С точки зрения электромаг-
электромагнитной теории решетка будет иметь ту же эффективность, однако в
этом случае необходимо еще учитывать уменьшение коэффициента от-
отражения материала решетки при изменении длины волны.
В УФ-диапазоне используются в основном вогнутые решетки [17].
Основной принцип здесь следующий — изображение источника, полу-
получающееся в результате дифракции излучения на вогнутой решетке,
должно фокусироваться в точку окружности, которая является грани-
границей круга Роуланда. Диаметр этой окружности равен радиусу кривиз-
кривизны данной решетки, так что поверхность решетки касается круга Роу-
Роуланда. Штрихи решетки расположены перпендикулярно плоскости
круга, а входная щель располагается на границе круга Роуланда и па-
параллельна штрихам решетки. На рис. 6.17 показан оптический путь
лучей в спектрографе. Существуют два основных типа УФ-
спектрометров; спектрометр с нормальным падением для длин волн
300—2000 А и спектрометр со скользящим падением для длин волн
короче 300 А. Если угол падения меньше примерно 10°, то считается,
что излучение падает нормально на решетку. Для разложения в
спектр излучения с длиной волны короче 300 А используется схема со
скользящим падением, поскольку в этом случае уменьшение коэффи-
коэффициента отражения материала решетки компенсируется общим возрас-
возрастанием отражения при скользящих углах падения. Различные типы
профилей решеток показаны на рис. 6.18.
6.10. Электромагнитная теория дифракции
441
<
i
Рис. 6.18. Профили штрихов ре-
решетки прямоугольной (сг), синусо-
синусоидальной (б), в форме эшелона
(б) и эшелетта (г). Угол раствора
кромки штриха на рис. г состав-
составляет 90°.
6.10.2. Поле, дифрагированное на решетке
Рассмотрим периодическую цилиндрическую поверхность (дифракци-
(дифракционную решетку), задаваемую функцией z =/(*)> образующие которой
параллельны ochj. Функция fix) является периодической с периодом
d, т.е./(v +tf) =/(#), и характеризуется максимальным и мини-
минимальным значениями/макс и/мин. Представим себе, что функция/(л:)
описывает границу раздела двух сред 1 и 2 с различными показателя-
показателями преломления п ^ >/(*)] nn2[z <fty)]. Предположим, что нор-
нормаль z к решетке направлена в ту среду, откуда приходит падающее
излучение. Заметим, что данное направление противоположно тому,
которое было принято выше при рассмотрении многослойных струк-
структур. Тем не менее именно такой выбор оказывается наиболее удоб-
удобным, поскольку далее речь пойдет только об отражательных решет-
решетках, имеющих наибольшее распространение. Среда 2 характеризуется
комплексным показателем преломления п = п — /к, который для иде-
идеально проводящих металлов становится чисто мнимой величиной. Ес-
Если влиянием конечной проводимости материала решетки на длинах
волн больше 4 мкм можно пренебречь, то при длинах волн короче
1 мкм это влияние оказывается существенным, причем область 1—4 мкм
считается переходной. В УФ-диапазоне @,1—0,2 мкм) вместо малоэф-
малоэффективного алюминиевого используются диэлектрические покрытия.
Кроме того, решетки с диэлектрическим покрытием как спектральные
селекторы используются в лазерах, на красителях для увеличения их
КПД. Предположим, что из среды 1 на решетку под углом в падает
плоская монохроматическая волна. Вектор напряженности электриче-
442 Гл. 6. Дифракция света на отверстии
ского поля в такой волне может быть направлен как вдоль (р-волна)э
так и поперек (s-волна) штрихов решетки (оси у).
Пусть Wj(r) = ехр(— /к| - г) — произвольная скалярная составляю-
составляющая падаюШего пучка с единичной амплитудой, awd(r) — соответству-
соответствующая компонента дифрагированного поля. Если сместить начало ко-
координат вдоль оси х на величину d (период решетки), то в новой си-
системе координат падающий и дифрагированный лучи запишутся как
>с, у, z) = wicTap(x + d, у, z) = uiCT&p(x, У, z) exp( - ikixd\ F.10.3a)
И<Инов)(*> У, z) = UdCT^X + d, У, z). F.10.36)
Здесь индексы «нов» и «стар» относятся к выражениям для поля
соответственно в новой и старой системе координат. Поскольку в но-
новой системе координат профиль решетки остается таким же
1/(нов)(*) = /стаР(* + <0 = /СтаР(*)]> падающие поля в новой и ста-
старой системе координат будут различаться фазовым множителем
expi—ikj/l). Таким образом,
и*(иав)(*>Л*) = udCTat?x9y9z)exp(-ikixd). (б.Ю.Зв)
Сравнивая выражения F.10.36) и (б.Ю.Зв), получаем
ud(x + d9 у, z) explikix(d + х)] = и6(х9 у, z)exp(ifciJCx), F.10.4)
откуда следует, 4TOWdexp(/?/J(x) является периодической функцией ко-
координаты х с периодом rf.
Прежде чем перейти к фурье-разложению поля «d, остановимся на
вопросе о граничных условиях на поверхности решетки. По аналогии с
плоской границей раздела между двумя поверхностями (см. разд. 3.6)
положим wd = и - и{ в среде 1 и wd = и в среде 2. Далее, если пред-
предположить, что плоскость падения перпендикулярна решетке (т.е.
kiy = 0) — условие, которое имеет место для решеток, используемых
в монохроматорах, то мы можем выбрать и = Еу для р-волн и
и = Ну для s-волн.
Приняв указанное выше соглашение, нетрудно доказать, что непре-
непрерывность тангенциальных составляющих поля дает следующие гра-
граничные условия для и:
Щ + wdl = Md2 ' Р" И S-ВОЛНЫ,
8х
dud2 „ dUdl р.ВОлна,
дх J dz
ir_*b?\* 8-волна.
dz In2*
F.10.5)
6.10. Электромагнитная теория дифракции 443
В этих выражениях производные/' = df/dx берутся в точках поверх-
поверхности решетки г = [*,.У,/(*)]. В частности, если среда 2 представляет
собой идеальный проводник, то записанные выше условия принимают
более простой вид:
щ + udl = 0, р-волна,
(dudl/dx)f - dudl/dz = i(kixf - ki2)u{, s-волна.
Вернемся к рассмотрению функции udexp(ikjxx), учитывая, что
и{ехр(Исих) и, следовательно, и txpiik^) являются периодическими
функциями координаты х. Если проделать для оси у то же, что для
оси х, то нетрудно показать, что функция и expiik^x + ikiyy) не зави-
зависит от у. Здесь можно заметить, что если функция и представляет со-
собой р-волну, то результирующее поле непрерывно вместе со своими
производными, взятыми по поверхности решетки, откуда следует, что
поле и можно разложить в ряд Фурье по координате х:
+ 00
u(x,y,z) = exp(-ikixx-ikiyy) ? exp(-i2nmx)Vm(z), F.10.7)
m= -oo
где Vm(?) — искомые непрерывные функции. После подстановки дан-
данного разложения в волновое уравнение получаем
XJffi ^(т)°' FЛ0-8)
где
jBi(x,z) = k2on2(x,z) - lkix + Bn/d)m? - kfy. F.10.9)
Умножая каждое из этих уравнений на exp[iBir/d)qx]9 где<7 — целое
число, и интегрируя их по периоду rf, находим следующее уравнение:
^ + k20Vq(z)g0(z) = -kgjg Vm(z)gq.m(z), F.10.10)
где
Hgq-m(z) = j Г fil(x9z)apli~j-{q - m)x\dx. F.10.11)
В частности, для косинусоидального профиля z = A/2)Л cosB7cc/rf)
имеем
Gl{z) = g_x(z) = i(n\ - nD/id] sin[Bn/d)lx) + п\дг. F.10.12)
Таким образом, возникают три области А , В и С, определяемые
соответственно условиями z > /макс (область А ), /MaKC(z ) > z >
>/MHH(z) (область В) и/мин(г) > z (область С). В областях А и С
444
Гл. 6. Дифракция света на отверстии
функции g,(z) тождественно равны нулю при / Ф 0, так что для Vm
можно получить следующие выражения:
z) + 5т exp(ifc/2z),
/м
где Re/?m > 0 и j8w > 0. Комплексные коэффициентыRт1 пТт2 можно
найти, если сшить функции Vm(z) на границах области В. Методы, ис-
используемые для решения приведенной выше системы дифференциаль-
дифференциальных уравнений, достаточно сложны и во всяком случае трудоемки.
Подставим теперь полученные выражения для Vm в фурье-разложение
F.10.7) и убедимся, что поле плоской волны, претерпевшей дифракцию
на решетке, представляет собой бесконечный набор плоских волн, соот-
соответствующих различным порядкам дифракции. Конечный размер решет-
решетки приводит к уширению пика в каждом порядке, как показано схемати-
схематически на рис. 6.19.
6.10.3. Представление Рэлея для металлической решетки
В 1897 г. Рэлей предложил свой метод вычисления рассеянного от пе-
периодической решетки поля, основанный на предположении о том, что
представление поля в области перед решеткой в соответствии с при-
принятым выше соглашением (область А ) должно быть также справед-
справедливо и для области, непосредственно примыкающей к поверхности
решетки {гипотеза Рэлея). Из этого следует, что на границе решетки
падающую р-волну с kiy = 0 можно записать в виде
^]^.г/B)]. F.10.14)
sbf\J V^N-л.
Рис. 6.19. Схематическое представление поля в дальней зоне при дифракции на решетке.
Угол рассеяния отсчитывается от внешней нормали к поверхности решетки; знак угла в
зависит от выбора направления отражения от решетки. Уширение линий отдельных по-
порядков происходит благодаря конечному размеру решетки.
6.10. Электромагнитная теория дифракции 445
В справедливости гипотезы Рэлея никто не сомневался до тех пор,
пока не так давно Дерюгин A952) и Липман A953) не высказали сооб-
соображения по поводу ее обоснованности, указав на то, что на гофриро-
гофрированной поверхности существуют приходящие и уходящие вторичные
волны, а вместе с ними можно предположить и существование экспо-
экспоненциально нарастающих и затухающих волн (см. в книге [18] главу,
написанную М. Кадильяком). В 1969 г. Миллар показал, что для вы-
выполнения гипотезы Рэлея необходимо и достаточно, чтобы соответст-
соответствующее разложение являлось аналитической функцией координат х и
z. В результате тщательного анализа области аналитичности несколь-
несколькими авторами установлена предельная ширина штриха. В частности,
Пти, Кадильяк и Миллар показали, что для косинусоидального про-
профиля (l/2)AcosB7rx:/rf) гипотеза справедлива при всех значениях
h/d < 0. Однако для треугольного профиля гипотеза Рэлея никогда
не выполняется. Ван ден Берг и Фоккема доказали некоторые допо-
дополнительные теоремы, позволяющие подтвердить или опровергнуть
гипотезу Рэлея.
Несмотря на то что гипотеза Рэлея не всегда верна, воспользуемся
все же разложением и(х9 z) в ряд по плоским волнам
ww(x,z) = exp(-ij3wz - iymx)9 F.10.15)
где 7m = к* + B7r/tf )m. Действительно, Ясуура показал, что приве-
приведенный выше набор уходящих и затухающих волн является полным и
может быть использован для вычисления соответствующих коэффици-
коэффициентов. Для этого необходимо решить следующую замкнутую систему
уравнений:
-г
Jo
+ г2учх, F.Ю.16)
где п = 0, ±1, ... ±N. В 1973 г. Икуно и Ясуура доказали, что
lim R1! = Rm. В этом подходе, который обычно называют методом
N — оо
наименьших квадратов, коэффициент отражения Rm, относящийся к
т -й дифрагированной волне, получается решением системы уравнений
F.10.16) при достаточно большом выбранном значении ЛГ. Коэффици-
Коэффициенты отражения R т вычисляются путем интегрирования по профилю
решетки произведения амплитуды падающей волны на т -ю рэлеев-
скую волну ww. В другом варианте метода наименьших квадратов
446 Гл. 6. Дифракция света на отверстии
wm(* >/(*))(! +/'2) заменяется наиДк, 0). Метод, в котором исполь-
используется данная замена, называется методом разложения в ряд Фурье.
6.10.4. Интегральный метод
Рассмотрим теперь другой метод, который не содержит ограничений,
характерных для рэлеевского приближения (см. в книге [18] главу, на-
написанную Мэйстром). Из интегрального уравнения F.9.1) в общем
случае следует, что
Н(г) - Щг) = - <Н> (и0 х Н) х P'G0(r - Tf)dS\ F.10.17)
преп
здесь п0 — нормаль к решетке, направленная в среду 2. Если г е S преп,
то F.10.17) становится неоднородным интегральным уравнением для
неизвестной функции Нпреп(г).
В случае когда препятствием является дифракционная решетка,
данное уравнение становится двумерным, если мы заменяем функцию
Грина G на двумерную функцию Грина, определяемую выражением
D.7.5). Интеграл по поверхности вырождается в линейный интеграл
по профилю решетки. Кроме того, учитывая периодичность функции
НехрЦк^х) по оси л:, интеграл можно вычислить в пределах одного
периода этой функции @, d). Таким образом, получаем
H(x,z) - Щх,2) = - Г (п0 х Н) х V'Gperlx - x',z - /(x')] x
Jo
*(\+f'2II2dx'; F.10.18)
здесь
Gper(x-x',z-z') = +f exp(-ikixdn)Gi2)(x-x'-nd,z-z'). F.10.19)
*
п= -оо
Функция G^e lx* является периодической относительно координаты
х, причем ее йериод равен d. Эта функция удовлетворяет излучатель-
ному условию на бесконечности (приг — оо) и неоднородному волно-
волновому уравнению
с1 *!)?* fco)GPcr = ~ % exp(-ifclxmdM(x - mdM{z\ F.10.20)
Ее можно записать в виде
i +0° 1
Gper(x,2) = — X ^ехр[-*(ушх + АЛ]. F.10.21)
?Q т = - оо Р
т = - оо
6.10. Электромагнитная теория дифракции 447
Для s-волны вектор Н = уи параллелен штрихам решетки и инте-
интегральное уравнение F.10.18) принимает следующий вид:
ul(x,z) - u{xtz) = [\{x\z')(f^-t - ^т)срег(х - x\z - z')dx'9 F.10.22)
гдег =/(*) hz' = /(*'). Данное уравнение можно решить, если его
свести к матричному и затем воспользоваться методом моментов.
При г = f функция Грина G^ является сингулярной, поэтому не-
необходимо аккуратно вычислить вклад этой сингулярности. Подробно-
Подробности читатель может найти в работе Заки и Нерентера [19]. Интеграль-
Интегральный метод можно обобщить и на диэлектрические решетки как для р-,
так и для s-волн.
6.10.5. Разрешающая способность
В разд. 6.10.1 мы привели общую формулу дифракции на решетке, ко-
которая справедлива для произвольной решетки (т.е. независимо от ее
профиля). Знак дифракционных углов выбирался таким образом, что-
чтобы для нулевого порядка (зеркальное отражение) мы имели &0 > 0.
Амплитуда поля в различных порядках вычисляется с помощью коэф-
коэффициентов отражения/?т, которые определяются профилем решетки,
поляризацией, длиной волны и углом падения. Эти коэффициенты от-
отражения можно вычислить, используя либо методы с разложением по
плоским волнам (скажем, метод наименьших квадратов или метод
Фурье), либо рассмотренный в предыдущем разделе интегральный ме-
метод. Вообще говоря, дифракционные решетки применяют в качестве
диспергирующих элементов. Следовательно, для них наиболее важны-
важными параметрами являются те, которые связаны с их способностью
разделять различные длины волн, скажем X и X + rfX. Эта способ-
способность зависит от расстояния d между штрихами, от порядка т, в ко-
котором наблюдается дифракция, от расстояния между решеткой и точ-
точкой наблюдения и от размера всей решетки. Рассматривая параметры
решетки rf/X и/я, мы видим, что при фиксированном угле падения
формула решетки дает дисперсионное уравнение
dQJdk = m/(d cos 0J. F.10.23)
В случае когда используются низкие порядки решетки т = ±1,
±2, ..., высокая угловая дисперсия получается лишь при достаточно ма-
малых dy т. е. необходимо использовать решетку с высокой плотностью
штрихов. Однако значительную угловую дисперсию можно получить и
448 Гл. 6. Дифракция света на отверстии
ных порядках и использовать скользящие углы падения. В некоторых
случаях для выбранных 0, X и d существует порядок интерференции,
скажемmL, в котором направление дифрагированного пучка практиче-
практически совпадает с направлением падающего. В таком случае говорят,
что решетка работает в обратном отражении в порядке т . Данный
режим называют условием Литтроу, а про решетку говорят, что она
работает в схеме Литтроу. Из формулы решетки можно сразу же
найти номер mL такого порядка, в котором вт ~ -0, и мы имеем
следующее соотношение:
mL^-2(rf/A)sin0, F.10.24)
гдет, — отрицательное целое число. При выполнении условия Литт-
Литтроу угловая дисперсия становится равной
demJdk ~ -Btan0)/l F.10.25)
Отсюда следует, что угловая дисперсия решетки, работающей в схеме
Литтроу, не зависит от числа штрихов решетки. Кроме того, заме-
заметим, что угловую дисперсию можно сделать очень высокой, если па-
падающее излучение направить под углом, близким к 90°.
В принципе любая решетка могла бы работать в схеме Литтроу
при больших углах падения. Однако на практике это требует того,
чтобы дифрагированный пучок имел достаточно большую интенсив-
интенсивность. Для этой цели используются эшелетты, которые имеют треу-
треугольный профиль штриха и угол блеска а = 0, приблизительно совпа-
совпадающий с углом падения (рис. 6.18, г). В случае когда длина волны
падающего света удовлетворяет условию Литтроу, эффективность ре-
решетки EmL = \RmL\2 равна единице для падающей s-волны. Как пра-
правило, эшелетты Литтроу используются cm = — 1. Относительная эф-
эффективность Е _ j таких эшелеттов является функцией угла падения или,
что то же самое, отношения \/d = 2sin0, величина которого может ме-
меняться от нуля до двойки. На рис. 6.14 показана типичная спектральная
зависимость эффективности для s- и р-волн.
До сих пор мы це учитывали конечный размер решетки, что позво-
позволяло нам представлять дифрагированное поле в виде дискретного на-
набора плоских волн. Конечную ширину W решетки можно учесть, если
каждую плоскую волну ограничить апертурой, соответствующей про-
проекции решетки на направление луча т -го порядка. При этом поле, ди-
дифрагированное в дальней зоне, можно записать в виде
, У, г) = ехр( - ikiyy) ? Rm exp( - iymx - ipmz)
т= -оо
тФО
х sinc[fc0Wcos2 0d( tg вт - tg 0d)], F.10.26)
6.10. Электромагнитная теория дифракции 449
где 0d = arctg(x/fe) представляет собой угол рассеяния, измеренный
относительно нормали решетки. Выражение F.10.26) отличается от
F.10.16) только множителем sine ( ), который учитывает конечность
ширины решетки W в направлении оси*. Для простоты мы прене-
пренебрегли аналогичным множителем, учитывающим конечный размер
решетки по оси .у. В частности, при 0d - вт интенсивность /@d) поля в
т-м порядке записывается в виде
U0d) * \RJ2&nc2[koWcas0M@d - 0J]. F.10.27)
Соответственно выражение для угловой дисперсии вт-м порядке ди-
дифракции запишется в виде ddm ~ 27r/(?oWcos0m). Далее, используя
дисперсионное уравнение F.10.23), решетку можно применить для из-
измерения длины волны монохроматического излучения с точностью
d\f которая определяется выражением
dl ~ (d cos вт/т) d9m = XI(mN\ F.10.28)
В этом выражении N — полное число штрихов решетки. Разделив X
на rf\, мы получим выражение для разрешающей силы & решетки:
M = mN. F.10.29)
Таким образом, ш равна произведению порядка дифракции на число
освещаемых штрихов. Однако из формулы решетки F.10.2) для спект-
спектрометров с фиксированной разностью между углом падения и отраже-
отражения можно получить зависимость порядка т от угла падения 0. Таким
образом, мы имеем
® = BW/X)cos(a/2)&n[6 - (а/2)] < 2W/X = ^мак.. F.10.30)
Мы видим, что максимальная разрешающая способность спектромет-
спектрометра пропорциональна ширине освещаемой части решетки и не зависит
от числа штрихов. Поэтому, чтобы получить близкое к максимально-
максимальному ^макс разрешение, необходимо уменьшить разность между углом
падения и отражения и использовать скользящее падение на решетку.
Это означает, что решетка в спектрометре должна работать в схеме
Литтроу (а = 0) при скользящем падении излучения. Для решеток с
углом блеска можно показать, что максимальную энергию имеет та
дифрагированная волна, длина волны которой позволяет ей отра-
отражаться от граней штрихов зеркальным образом. Следовательно, что-
чтобы получить максимальную разрешающую силу, необходимо рабо-
работать при достаточно малых углах блеска. При выполнении этих усло-
условий была достигнута разрешающая способность 1 млн. При длине
волны 5000 А это означает разрешение полосы 600 МГц, что не до-
достаточно для разрешения спектра генерации лазера или изучения ли-
линий сверхтонкой структуры. В этих случаях существенно улучшает де-
450 Гл. 6. Дифракция света на отверстии
ло совместное применение спектрометра с дифракционной решеткой и
интерферометра Фабри — Перо; такое комбинированное устройство
мы рассмотрим в конце следующей главы.
6.10.6. Эффективность решетки и аномалии Вуда
Мы показали, что комплексные амплитуды Rm парциальных волн,
претерпевших дифракцию на решетке, очень сложным образом зави-
зависят от поляризации падающего излучения, угла падения, длины волны
и профиля штриха. Если дифракционная решетка применяется в спект-
спектрометрах и лазерных резонаторах только для селекции линий или же
частотной настройки (см. разд. 7.20), то интерес здесь представляют
лишь затухающие волны. В других случаях, встречающихся довольно
редко, необходимо знать поле вблизи штрихов. Хотя первый случай и
кажется более простым, поскольку для вычисления эффективности
Еп = \Rn\2 требуется небольшое число распространяющихся мод,
аналитический расчет здесь в принципе столь же труден, как во вто-
втором случае. Действительно, эффективности этих распространяющихся
мод приходится вычислять посредством включения в усеченные разло-
разложения поля некоторого числа как распространяющихся, так и затуха-
затухающих волн. Однако существуют случаи, когда относительно эффек-
эффективности можно сделать определенные предположения. Особый инте-
интерес представляет случай решетки в схеме Литтроу с углом падения,
совпадающим с углом блеска или дополнительным к нему, когда эф-
эффективность равна единице для s-волны.
В 1902 г., исследуя отражение от решетки различных s-волн, Вуд
обнаружил быстрое изменение эффективности в различных интерфе-
интерференционных порядках в некоторых узких частотных областях. Они
наблюдаются в виде ранее неизвестных узких темных и светлых полос
в спектре отражения решетки при ее освещении источником света,
спектр излучения которого медленно изменяется. В 1907 г. Рэлей объ-
объяснил это аномальное поведение тем, что рассеянное поле становится
сингулярным при длинах волн, на которых один из интерференцион-
интерференционных порядков направлен под скользящим углом. Он обнаружил, что
аномалиям Вуда соответствуют определенные длины волн XR, кото-
которые были названы рэлеевскими длинами волн; для этих волн сущест-
существует порядок спектра т, такой, что выполняется равенство /3 = 0.
Возможные значения XR можно найти из выражения F.10.9), а именно
AR = d{\ — cos0)/w (n — целое число). F.10.31)
6.11. Рассеяние на телах конечных размеров 451
Первым, кто предположил, что аномалии Вуда соответствуют воз-
возбуждению поверхностных волн на решетке, был Фано. Исследовате-
Исследователи, занимавшиеся поверхностными плазмонами (см. конец гл. 3), раз-
разработали другой подход к решению этой задачи. В качестве нулевого
приближения ими рассматривались плазмоны на плоской поверхно-
поверхности, затем при вычислении вероятности возбуждения поверхностных
плазмонов они включали возмущение, обусловленное штрихами ре-
решетки. Подробное рассмотрение различных походов можно найти в
книге под редакцией Пти [18] и в статье Хесселя и Олинера [20]. В по-
последней работе дифракционная решетка рассматривалась как плоская
поверхность с периодическим поверхностным импедансом.
6.11. РАССЕЯНИЕ НА ТЕЛАХ КОНЕЧНЫХ РАЗМЕРОВ
В данном разделе мы рассмотрим рассеяние на некотором препятст-
препятствии волны, распространяющейся в вакууме. На определенном расстоя-
расстоянии, которое должно быть намного больше как длины волны, так и
характерных размеров препятствия, поле состоит из плоской и сфери-
сферической волн, причем последняя представляет собой дифрагированную
волну. Обозначим через к0 волновой вектор падающего лучаАи через
к'о волновой вектор луча, рассеянного в направлении вектора к' . Пло-
Плоскость, определяемую этими двумя векторами, будем считать базис-
базисной плоскостью и в дальнейшем называть плоскостью рассеяния. Та-
Таким образом, поляризация падающего луча и соответствующие векто-
векторы Джонса (см. разд. 1.3) будут направлены вдоль перпендикулярных
к0 векторов г и Г, из которых первый перпендикулярен, а второй па-
параллелен плоскости рассеяния. Буквы г и / были введенЭы Чандрасека-
ром и соответствуют последним буквам в английских словах «per-
«perpendicular» и «parallel». Векторы ?' иТ' для рассеянной волны пер-
перпендикулярны вектору к0 и плоскости рассеяния.
Поскольку рассеянная волна асимптотически ведет себя как сфери-
сферическая, удобно сразу же ввести радиальную зависимость вида e~lk°r/r,
где г — расстояние от начала координат, расположенного в окрестно-
окрестности рассеивающего тела, до точки наблюдения. Таким образом, мож-
можно записать следующее соотношение:
где Еи и Eir представляют собой амплитуды каждой из двух составля-
составляющих в падающей волне, изменяющейся по закону ехр(-/?ог). Пусть
452 Гл. 6. Дифракция света на отверстии
начало О лучевого вектора г совпадает с началом сферических коорди-
координат, в которых было записано выражение для рассеянной волны. Для
удобства выберем направление полярной оси таким образом, чтобы
оно совпадало с направлением вектора к0. Матрица S описывает рас-
рассеяние на препятствии и зависит от того, как данное препятствие ори-
ориентировано относительно векторов к0 и kj,. В отличие от матрицы,
введенной ван де Хюлетом, в данной матрице отсутствует множи-
множитель ik0.
При данных к0 и к^ существуют в общем случае три разных поло-
положения, в которых матрица рассеяния может быть выражена через
компоненты исходной матрицы. Из теоремы взаимности (см. задачу 8
в гл. 1 настоящей книги) следует инвариантность процесса рассеяния
по отношению к преобразованиям к0 — -к^, к'о — -к0 [21]. Эти пре-
преобразования можно представить себе, как если бы падающий луч на-
начал распространяться в направлении, обратном тому, в котором пер-
первоначально распространялся рассеянный луч. После выполнения дан-
данных преобразований матрица S принимает вид
s = l ~~ ~ I- F.11.2)
Кроме того, можно показать (см. книгу ван де Хюлста [12], ука-
указанную в литературе к гл. 1 настоящей книги), что при зеркальном
отражении рассеивающего тела относительно плоскости рассеяния
матрица S преобразуется к виду
а
Объединяя эти преобразования, мы получаем картину, представляю-
представляющую собой зеркальное отражение препятствия относительно плоско-
плоскости, перпендикулярной плоскости рассеяния и делящей пополам угол
между векторами к0 и к'о. Таким образом, окончательно имеем
S = PC2 H F.11.4)
В частности, для сферического рассеивающего тела матрица S при
рассмотренных выше преобразованиях не изменяется. Следовательно,
компоненты 5з nS4 должны быть равны нулю.
6.11.1. Сечение экстинкции и оптическая теорема
Важным параметром при описании рассеяния на различных телах яв-
является сечение экстинкции аэкст, определяемое как отношение мощно-
6.11. Рассеяние на телах конечных размеров 453
сти, теряемой в результате рассеяния (^расс) и диссипации (Рдисс), к ве-
величине вектора Пойнтинга падающей плоской волны:
(тэкст= 2Co(ip-acc+ PJIEl F.11.5)
Рассеянную мощность можно вычислить, интегрируя вектор Пойн-
Пойнтинга рассеянной волны по сфере достаточно большого радиуса. При
этом с учетом выражения F.11.1) получим
Ррасс= 2^§ 2^
На границе сферы полная мощность (падающая, потерянная на дисси-
диссипацию и унесенная в рассеянной волне) должна сохраняться. Таким
образом, мы имеем
RecfW + Ed) x (Hf + HJ)] • rdil =
4*
4тг
а поскольку
получаем
+ Rec
•
2РдИ
г2
Й(Е, х Hf)
4я
/?исс= —2Reli
г-
таЕ, х Н
)J
Хп
tec..
. f ДО = A
im г2сгЬ(Е
"*°° JJ
4я
* + Ed
Ej x Hf
=. x Hd*
x
!)
4
Hf
•<rt
¦E,
¦) • f da
,rd?l =
X Hi )
=
F.11.7)
F.11.8)
Q. F.11.9)
Однако, поскольку Hd = — fo~!Ed x t приг — oo, можно написать
exp( - iko • г + ikor)E{ • S * • Ef +
+ exp(ik0 • r-ikor)k • fEf • S • Ej-
-exp(ik0 • r-ifcor)Ef • fk • S • E{. F.11.10)
454 Гл. 6. Дифракция света на отверстии
Наконец, воспользуемся методом стационарной фазы. Это даст
lim г(КехрAк0 • г - ikor)f&r)du = _,^[/(??) -
4*
-Qxp(-2ikor)f(k,-k)l F.11.11)
Подставим правую часть выражения F.11.10) в F.11.9) и воспользуем-
воспользуемся результатом F.11.11). В итоге находим следующие выражения:
рРасс+ рдисс= -W2C0)Re[ffi,. S*(U) • Ef - te^E, • S*(fc, -*) • Ef-
-Ж? • S(fc,fc) • E, - iEf • S(fc, -fc) • E,e-2ttor] =
= -WC0)Im[Ef .S&fcJ-E,], F.11.12)
Gext = -2A{Im[Ef • S(U) • EJ}/!^!2. F.11.13)
Последнее выражение означает, что сечение экстинкции зависит от
значения элементов S-матрицы для рассеяния вперед. В частности,
для сферических частиц при рассеянии вперед оба диагональных эле-
элемента в матрице рассеяния равны друг другу, и выражение F.11.13)
принимает более простой вид:
^сфера) = _ 2Я Im S(k, к). F Л1.14)
Это выражение представляет собой так называемую оптическую тео-
теорему.
6.12. РАЗЛОЖЕНИЕ РАССЕЯННОГО ПОЛЯ
ПО СФЕРИЧЕСКИМ ГАРМОНИКАМ
В качестве первого шага рассмотрим некоторую скалярную функцию
/(г), которая представляет собой решение волнового уравнения
Гельмгольца в определенной области:
(??'*!:+?+ »')№.*¦>-а «-12Л)
где оператор
д\ 1 д2
д ( . д\ 1 д
— sin0— +-T-2--—у F.12.2)
d9\ дв) ып2вдф2 v '
называется оператором Бельтрами для сферы [ср. с выражением
B.12.40)]. Оператору 252 соответствует дискретный набор собственных
функций Y™у называемых сферическими гармониками:
6.12. Разложение рассеянного поля по сферическим гармоникам 455
причем
??@>Ф) = ; tj " PJT(cos в)е(тф9 F.12.4)
а через P%(cos6) обозначены присоединенные функции Лежандра пер-
первого рода, определяемые выражением
P™(cos0) = sinM0(d/dcos0)wPn(cos0), 0 < т < п. F.12.5)
Функции Pn(cos6) представляют собой полиномы Лежандра, определя-
определяемые формулой Родрига
Pn(cos 0) = [(- 1OBйп \y]{d/dcos в)"яп2" 0. F.12.6)
Четность полиномов Лежандра определяется четностью числа л, т.е.
Рп(—х) = (—\уРп(х). Кроме того, для полиномов Лежандра оказы-
оказываются справедливыми следующие рекуррентные соотношения:
nPn.l = wcos0Pn + sin20P;, F.12.7)
где штрих означает производную по cos0.
Поскольку на поверхности сферы сферические гармоники образуют
полный ортогональный набор, а именно
1 ГГ
11 ™-™ ,~ с о F.12.8)
скалярная волновая функция/(г, в, ф) может быть разложена по этим
функциям: да п
ЯЛФI Z Я(твф), F.12.9)
и = 0 т= -п
где
KJr) = ^ [2Я# [d0sinв?:*@,ф)ЯгЛФ). F.12.10)
47rJo Jo
Пример. Скалярная плоская волна. Для скалярной волны
exp(-/Arcos0), распространяющейся вдоль полярной оси, выражение
F.12.10) дает
Rnm(r) = Bи 4- 1I/2Рл[-Hd/dxmsinx/xMm(x =
= Bп + 1I'\-1)ШЬ)/(кг)]6я0; F.12.11)
здесь л* = /:г, diPn(—id/dx) — дифференциальный оператор, получае-
получаемый подстановкой -id/dw вместо аргумента и> в выражение для
pn(w). В выражении F.2.11) функция \//п(кг) записывается в виде
фп(х) = ГхРп[ - i(d/dx)] sin x/x F.12.12)
456 Гл. 6. Дифракция света на отверстии
и называется функцией Риккати — Бесселя. Она обладает свойством
регулярности в точке х = 0, а прил: — оо асимптотически стремится к
sin(v — ятг/2). После подстановки правой части выражения F.12.11) в
разложение F.12.9) получаем формулу Бауэра:
e-ikrcose = J_ g (_lTBn + l)^(fcr)Pn(cos0). F.12.13)
6.12.1. Радиальное волновое уравнение
Поскольку каждый член разложения в правой части выражения
F.12.9) должен удовлетворять уравнению F.12.1), то функция
fnm(kr) = Bkr/ir)l/2Rnm(r) должна в свою очередь являться решением
уравнения Бесселя полуцелого порядка
d2fnm/dx2 + (l/x)(dfnm/dx) + [1 - (п + l/2J/*2]/nm = 0. F.12.14)
Этсюда следует, что значения функции fnm не зависят от индекса т,
который в дальнейшем мы будем опускать. Если использовать опре-
целение сферических функций Ханкеля h n, а именно
1/2 pix n iq~n~1(n -J- аI 1
ид ';<61215»
то в общем случае можно записать, что
RJT) = AmhP(b) + ВЛ2)(кг) = [я/B/сг)]1/2/„(И. F.12.16)
Используя функции Ханкеля hn, можно определить сферические
функции Бесселя jn(x) = Re/i^. Функции jn регулярны в точке а: = 0 и
связаны с функциями Риккати — Ханкеля простым соотношением
фп =xjn. Аналогично можно образовать функции Риккати — Ханкеля
f<'>' <2>, полагая f?> = xh«\
Из выражения F.12.13) следует, что плоскую волну можно разло-
разложить в ряд, используя в качестве базисных функций приходящие и
уходящие волны:
* g (-i)nBn ?
' л = 0
+ ^ I (-0"Bп + 1)й<ЛВД(со80). F.12.17)
6.12.2. Векторные сферические гармоники
Применим к обычным гармоническим функциям YJJ1 векторный опера-
оператор L, такой, что [22]
L = г х V = ф(д/дв) - ?(l/sin в)(д/дф). F.12.18)
6.12. Разложение рассеянного поля по сферическим гармоникам 457
В результате получим так называемые векторные сферические гармо-
гармоники. Прежде чем рассмотреть свойства этих функций, сделаем не-
несколько замечаний относительно свойств скалярных компонент ?x,Ly
и Lz^оператора L. Оказывается, что существуют удобные комбинации
Lx,Ly n?z, такие, что
L+=L*-=LX + ily = е1ф[г(д/дв) - ctgв(д/дфI L2 = д/дф. F.12.19)
Отсюда, например, следует, что оператор/52, определенный выраже-
выражением F.12.2), можно представить в виде суммы L+L_ + L\. Кроме
того, нетрудно показать, что выполняются следующие коммутацион-
коммутационные свойства операторов L, /52 и V2:
D2L = LD2, L х L = -L, L,V2 = V2L,, F.12.20)
а также соотношения
L2Y™ = imlT, L+Y™ = i[(n - m)(n + m +• 1)]1/2У?+1. F.12.21)
Таким образом, скалярные сферические гармоники Y% являются соб-
собственными функциями операторов Lz и D2. Читатели, знакомые с
квантовой механикой, заметят совпадение этих операторов с операто-
операторами углового момента.
Теперь можно получить векторные сферические гармоники, воздей-
воздействуя оператором 1 на функции Y™:
Y ™ = Ly? = i(m/sin0)y™0 + (mcotflY? + e'*Y~+1)<?. F.12.22)
Из определения оператора 1 ясно, что ? ¦ L = 0, а следовательно, и
г • Y- = 0.
Векторные сферические гармоники можно использовать для описа-
описания векторных полей, направленных по касательной к сфере. В част-
частности, с их помощью можно составить так называемые электриче-
электрические мультипольные поля
B?(r) = Rn(kr)Y:@,ф\ ЕЦ(г) = -[0/(^ое)] F х В«. F.12.23)
Отсюда следует, что радиальную компоненту вектора Е^ можно
записать в виде
г • Ей = (l/fe)r • [Г х (Rmr х VYW = ~(RJk)t • [F x (r x FYD] =
:, F.12.24)
где мы использовали векторные тождества (А8) и (А10) (см. приложе-
приложение А к настоящей книге). Аналогичным образом можно найти выра-
выражения для мультипольных полей с поперечными электрическими поля-
полями:
К(кг)\:, В<ь„> = (I/O») V х Ей. F.12.25)
458 Гл. 6. Дифракция света на отверстии
Наконец, более общее выражение для электромагнитного поля может
быть записано в виде суперпозиции TE(h) и ТМ(е) сферических муль-
мультипольных полей:
Е(г) = ? I [а„тЕЙ(г) + Ь„ИЕ<Ь»], F.12.26)
л=1т= —я
где коэффициенты а пт можно вычислить, если скалярно умножить вы-
выражение для Е(г) на г, а затем использовать соотношение F.12.24) с
учетом взаимной ортогональности функций Y%. Исходя из взаимной
ортогональности мультипольных полей и следуя тем же путем, кото-
который привел нас выше к разложению скалярной плоской волны
F.12.17), нетрудно получить формулу Бауэра для векторной плоской
волны:
хе-** = 1 У (-i)"l/.(Y2 +Y:1) + rF x n.(Yi - Y;1)]!. F.12.27)
6.13. РАССЕЯНИЕ НА СФЕРИЧЕСКИХ ЧАСТИЦАХ
В качестве примера рассеяния на телах с конечными размерами лучше
всего рассмотреть рассеяние на сферических частицах. Интерес к этой за-
задаче привлек внимание физиков благодаря работам Рэлея, который объ-
объяснил голубой цвет неба и появление синеватого оттенка у аэрозолей.
В 19 в., как описывается у Керкера [23], эта проблема была объек-
объектом тщательного экспериментального изучения. Брюкке A853) и Гови
A860) наблюдали голубой оттенок у спиртового раствора смолы мас-
мастикового дерева, паров спирта и табачного дыма. Почти в то же вре-
время к такого же рода экспериментам обратился и Тиндаль A869), ди-
директор Королевского института, интерес к ним ему внушил Джон
Гершель, сын великого астронома Вильгельма Гершеля. В своих экс-
экспериментах Тиндаль использовал аэрозоли, полученные р результате
конденсации продуктов газофазных реакций. Эксперименты, проведен-
проведенные Гови и Тиндалем, показали, что 1) малые частицы рассеивают го-
голубой цвет и 2) свет, рассеянный под прямыми углами к падающему,
является линейно поляризованным.
В 1871 г. лорд Рэлей [24] опубликовал свою первую статью по рас-
рассеянию света малыми частицами в земной атмосфере, причем для
простоты он принял форму частиц сферической. С помощью такого
приближения Рэлей показал, что для частиц, размеры которых мень-
меньше длины волны падающего света, интенсивность рассеянной волны
пропорциональна 1/Х4.
В своих первоначальных исследованиях Рэлей рассматривал только
6.13. Рассеяние на сферических частицах 459
те рассеивающие тела, показатели преломления которых слабо отли-
отличались от показателя преломления окружающей среды. Такое пред-
предположение, называемое сейчас приближением Рэлея — Ганса (см.
разд. 6.4), фактически состоит в замене внутренних полей в рассеива-
рассеивающей частице соответствующими полями падающей волны.
Когда размеры частицы становятся сравнимыми с длиной волны,
частицу можно представить в виде совокупности мультиполей (дипо-
(диполя, квадруполя, октуполя и т. д.), а рассеянное поле разложить в ряд
по к 0 (ряд Рэлея), а именно Ed = E^E^. Каждый член Е(л) может
быть получен из члена ряда Е(л " 1}, если рассеянное поле представить
в виде интеграла, взятого по поверхности частицы. Полное описание
этого метода можно найти у Нобля [25] и Клейнмана [26].
В 1881 г. Лэмб решил задачу о рассеянии электромагнитной волны
на сфере. Метод, который он использовал при этом, тесно связан с
методом разделения переменных, примененным Клебшем в 1861 г.
при решении класса граничных задач с целью изучения взаимодейст-
взаимодействия волн в упругой среде на сферической поверхности.
В 1908 г. Густав Ми объяснил окраску, возникающую при освеще-
освещении коллоидного раствора металлических частиц, рассмотрев рассея-
рассеяние волны на сферической частице, имеющей комплексный показатель
преломления, в среде с потерями. Рассчеты Ми включали в себя сум-
суммирование нескольких первых парциальных волн в разложении поля
по этим волнам [27].
Через год после статьи Ми опубликовал свои исследования Дебай
[28] о давлении света на проводящую сферу. Дальнейший вклад в рас-
рассматриваемую задачу внесли Бромвич A899) и его сотрудники из Кэм-
бриджского университета.
В частности, студенту Бромвича Уайту принадлежит представле-
представление решения Ватсона в виде контурного интеграла, состоящего из от-
отраженной волны и ряда вычетов. Этот метод мы рассмотрели в
разд. 6.5 для случая рассеяния на цилиндре. Важный вклад в решение
рассматриваемой задачи внесли голландские физики ван дер Поль,
Бреммер и советский физик Фок, которому удалось получить инте-
интегральное представление поля в промежуточной области, а также ван
де Хюлст (см. книгу ван де Хюлста [12], указанную в литературе к
гл. 1 настоящей книги).
6.13.1. Разложение рассеянного поля по парциальным волнам
Рассмотрим диэлектрическую сферу радиусом а и с показателем пре-
преломления п, которая освещается плоской волной, распространяющей-
460 Гл. 6. Дифракция света на отверстии
ся вдоль положительного направления оси z и поляризованной вдоль
оси л:. В соответствии с формулой Бауэра F.12.27) падающая волна
вне сферы может быть представлена линейной комбинацией бесконеч-
бесконечного числа поперечных электрических (Ел ^j) и поперечных магнит-
магнитных (Е^^) мод. Кроме того, из разложения радиальной функции
2jn = л?> + й<2) следует, что каждая угловая мода может быть пред-
представлена в виде волны, уходящей на бесконечность, и волны, сходя-
сходящейся к центру сферы. Каждая парциальная волна, из которых со-
составлено поле падающего излучения, порождает отраженную и про-
прошедшую волну с одинаковой угловой зависимостью. Иными словами,
падающая волна (скажем, Е^\) порождает отраженнуюr^Y^h^2)(kor) и
прошедшую t" y\inJn^or) волны.
Коэффициенты отражения и пропускания можно найти из условия
непрерывности электрической и магнитной составляющих на поверх-
поверхности сферы. В частности, из условия непрерывности Е^ следует,
что Ш) + Г*К2)(Р) = thJ№ F.13.D
где а = /2j3. Аналогичным образом условие непрерывности тангенци-
тангенциальной составляющей В$[ = iw~ V x Е$( дает
W) + r*X4l}) = Kf№ (блз.2)
Решая эти уравнения относительно коэффициента отражения г* (на-
(называемого также коэффициентом Ми), имеем [ср. с F.4.13)]
Г" ~ In'?<2>(/?) - «In'ф(а) #>(/?) ~ 2К ч (Р))' {ЬЛЗ-3
здесь фд и f^2) — соответственно функции Рцккати — Бесселя и Рикка-
ти — Ханкеля. Функции S^(j3) даются выражением
e ехр(-«2а-) F 13 4)
^)~ P( Д FЛЗ'4)
где 0$ — фазовый сдвиг q-u парциальной волны, который определяет-
определяется соотношением
ь'пЧ(/0-"~1п'Л(«)Щ.
»«^)' FЛЗ'5)
здесь пдф) — сферическая функция Неймана (fi^ = jq - inq). В част-
частности, при вещественных п абсолютное значение функции S? равно
единице и угол ад является вещественным.
Коэффициент отражения r*q для электрической компоненты может
быть получен из указанных формул простой заменой п на \/п.
В частностиу для металлической сферы коэффициенты отражения
6.13. Рассеяние на сферических частицах 461
принимают вид [ср. с выражением F.14.17)]
< = -w)/h™№ ^ =-да/о/о- F.13.6)
6.13.2. Амплитуды рассеяния S и фактор эффективности Q
Если на сферу падает линейно поляризованная плоская волна, то вы-
выражение для рассеянного сферой поля можно представить в виде ряда,
состоящего из парциальных волн, который при г —¦ оо сводится к сле-
следующему:
ik Г «с
1
1/ *
~ Y«">J ¦
g-ikor
[cos0S2@H + sin^S^e)^], F.13.7)
где Sj и S2 — амплитуды рассеяния соответственно магнитной и
электрической составляющих:
29+1 г_.
5i=i Д
Д
f 5ттт F.13.86)
В этих выражениях функции irq и т^ определяются через первую и вто-
вторую производные обычных функций Лежандра:
тг„(со$0) = P,1(cos0)/sin0, t9(cos0) = (d/d6)Plq(cose). F.13.9)
Будем считать, что единичные векторы в и ф совпадают с вектора-
векторами f' иг', связанными с плоскостью рассеяния в соответствии с опре-
определениями, данными в разд. 6.11. Сравнивая затем выражение для по-
поля в дальней зоне F.13.7) с выражением F.11.1), нетрудно заметить,
что амплитуды рассеяния S { и S 2 совпадают с элементами матрицы
рассеяния S. Вычисленные таким образом интенсивности
ij = ISyl2(y = 1,2) и соответствующий фазовый сдвиг 8 = argSj-
— argS2 полностью характеризуют процесс рассеяния.
Определив элементы матрицы рассеяния и воспользовавшись опти-
оптической теоремой F.11.14), можно написать выражение для сечения
экстинкции аэкст:
Т s <4СТ(М) т^Ьпад = -4 ? Bq + l)Re(rJ + rj). F.13.10)
При выводе этого выражения было использовано соотношение
7глA) = тлA) = A/2)л(я + 1), а через Q3KCT(n, /3) обозначен фактор
462 Гл. 6. Дифракция света на отверстии
эффективности, который представляет собой отношение сечения экс-
экстинкции к геометрическому поперечному сечению сферы. Ми также
получил простое выражение для полной рассеянной интенсивности,
проинтегрировав вектор Пойнтинга рассеянного поля по поверхности
сферы бесконечного радиуса:
-U5PL Q (nj) = i f\н(в) + i2№ sinвс1в = -^
тса p*** p Jo P
F.13.11)
где apacc = 2?Ppacc/Ef. Разность между этими двумя сечениями опре-
определяет часть интенсивности падающей волны, поглощенной в объеме
сферической части. В частности, для сферы, не имеющей потерь,
арасс = (тэкст, так что ряды F.13.10) и F.13.11) должны совпадать.
Действительно, если показатель преломления п вещественный, то
углы ад и а* являются также вещественными, и, следовательно,
-Re(r? + г|) = lr?l2 + lr|l2 =sin2a? + sin2a^. Исчерпывающую ин-
информацию о сечениях рассеяния и экстинкции можно найти в работе
[29].
Процесс рассеяния можно характеризовать также с помощью еще
одного параметра, а именно полного импульса ррасс, перешедшего в
рассеянное поле из поля падающей волны единичной амплитуды:
J ^ F.13.12)
где р; = hk0z(cos8)e представляет собой так называемый фактор
асимметрии, который определяет относительный вклад интенсивно-
стей излучения, рассеянного вперед и назад. В частности, Дебай полу-
получил следующее важное соотношение:
• F.13.13)
С одной стороны, импульс, ушедший из падающего пучка, пропорци-
пропорционален аэкст, а с другой стороны, как было показано выше, арасс содер-
содержит в себе член < cos 0> ^арасс, пропорциональный импульсу, соответст-
соответствующему рассеянию вперед. Отсюда мы находим, что полный им-
импульс, потерянный в результате рассеяния, с учетом дополнительного
вклада из-за рассеяния вперед, пропорционален величине
c = Gабс + A - < COS0> ,)<7расс ¦ M2Qдавл,
F.13.14)
гдевДавл — фактор эффективности светового давления (рис. 6.20).
6.13. Рассеяние на сферических частицах
463
Рис. 6.20. Зависимость эффективности
экстинкции (Q) и давления (бдаш1) от
масштабного параметра C для метал-
металлической сферы.
0
Следствием потери импульса при взаимодействии излучения с рас-
рассеивающей частицей является появление силы F, которая действует на
частицу в направлении распространения падающей волны:
здесь S — вектор Пойнтинга падающей волны. Явление светового
давления хорошо известно астрофизикам. Оно было открыто и изме-
измерено в 1899 г. П.Н. Лебедевым в Москве [30]. Сила светового давле-
давления — наиболее существенная внешняя сила, действующая на атомы и
пыль в межзвездном пространстве [31].
Когда частота падающего света совпадает с линией поглощения
рассеивателя, сечение аабс может стать очень большим и величина све-
светового давления также увеличится. В последние годы явление светово-
светового давления было использовано в задаче охлаждения частиц газа, при
этом были достигнуты температуры порядка нескольких градусов
Кельвина (см. работу Миногина и Летохова [32] и статью Шена [5],
указанную в литературе к гл. 1 настоящей книгиI*.
Фактор асимметрии и фактор эффективности бдавл детально иссле-
исследовались Ирвайном [33]. Точный численный расчет выявил наличие
регулярной последовательности узких оптических резонансов. Ашкин
и Дзидзик тщательно измерили зависимость силы светового давления
от длины волны [34]. В частности, используя лазер на красителе с вы-
высокой спектральной однородностью выходного излучения, эти авторы
исследовали силу светового давления, действующую на прозрачную
масляную каплю, и обнаружили ряд узких резонансов, тем самым
подтвердив результат численного расчета Ирвайна. Они показали так-
также, что если сфокусировать луч на каплю таким образом, чтобы при
этом не задевать края капли, то резонансы исчезнут.
** В настоящее время достигнуты температуры порядка тысячных градуса Кель-
Кельвина. — Прим. ред.
464
Гл. 6. Дифракция света на отверстии
6.13.3. Параметры Стокса для рассеянного поля
Матрица рассеяния, определяемая выражением F.11.1), эквивалентна
матрице Джонса А, введенной в гл. 1 настоящей книги [см. выраже-
выражение A.3.15)]. Таким образом, можно воспользоваться соответствую-
соответствующим формализмом, который был применен в разд. 1.3 при вычисле-
вычислении параметров Стокса рассеянного поля. Например, для рассеиваю-
рассеивающей среды в матрице Джонса не равны нулю всего два элемента, а
именно S j =AlnS2=A2, так что матрица F, определяемая выраже-
выражением A.3.18), принимает совсем простой вид:
"сфера "~
о
»1
о
о
о
о
D
21
О
о
-D2l
s2l
F.13.16)
aD2i =
2i
где/, = IS7I2 — интенсивности, S21 =
Отсюда можно определить степень поляризации т (в) оптического
излучения, рассеянного в направлении в [см. выражение A.3.14)]:
[('1 + '2J(«о + *?) + 201 - il)sosi + 2i! /2(sf - si) +
где s{ — параметры Стокса для падающего излучения.
6.13.4. Малые сферы
При а, /3 < 0,8 возбуждаются лишь первые две электрические моды и
первая магнитная мода, так что с хорошей точностью амплитуду рас-
рассеяния S, можно записать в виде
SA6) ^- =—-В3\ 1 + \--y-—- Н гг—cos0 + 771—rcosfl
1 w к0 п2 + 2н |_ \5п2 -2 30 6 2п2 + 3
я)/?2-
-'1^4
F.13.18)
Аналогичное выражение можно записать и для52.
Подставим полученные выражения для S, и S 2 в формулу для эф-
эффективности рассеяния F.3.11):
В частности, при C < 1 выражение для интенсивности рассеяния
сводится к выражению, полученному в 1871 г. Рэлеем, а именно
6.13. Рассеяние на сферических частицах 465
Подставляя выражения для интенсивностей в F.13.17), находим
т(в) = sin2 0/A + cos2 в). F.13.21)
В 'То время как для малых сфер рассеянный под прямым углом свет
является линейно поляризованным, для сфер большего радиуса в раз-
разложениях дляЯ 1 hS2 уже нельзя пренебрегать членами более высокого
порядка, чем C. В этом случае \S2\ принимает минимальное (почти
нулевое) значение при углах 0^,,, отличных от прямого и определяем
мых выражением (см. книгу ван де Хюлста [12, с. 146], указанную в
литературе к гл. 1 настоящей книги)
cos0MHH= -02[(n2 - 1)(п2 + 2)]/[15Bи2 + 3)]. F.13.22)
Если п — известная величина, то, измерив угол 0МИН, для которого
свет является линейно поляризованным, можно найти размер час-
частицы.
Другим параметром, который характеризует отклонение рассеяния
от рэлеевского [см. выражение F.13.20)], является отношение интен-
интенсивностей рассеяния вперед и назад:
|Si(O)|2/|Si(*)l2 = 1 + D/15)j?2[(n2 + 4)(n2 + 2)]/Bn2 + 3). F.13.23)
При рассеянии на прозрачных частицах с п/3 < 0,8 вперед рассеи-
рассеивается всегда больше излучения чем назад.
6.13.5. Собственные моды диэлектрической сферы
Полюсы матрицы рассеяния соответствуют собственным модам ди-
диэлектрической сферы. Эти моды нетрудно найти для вещественных п.
Для этого необходимо вычислить значения параметра /3 = /соа =
= (а/с )(и +/с/), при которых знаменатель в выражении F.13.3)
обращается в нуль. Таким образом, мы можем записать следующие
уравнения соответственно для h- и е-мод собственных колебаний рас-
сеивателя: ^2)/(ДЩа) - пф'я№?\Р) = 0,
В предельном случае п — оо уравнения F.13.24) сводятся кИ^ЦЗ) = 0
и hf)f 03) = 0. В случае q = 1 мы имеем (см. книгу ван де Хюлста
[12, Sect. 10.51] в литературе к гл. 1 настоящей книги)
C = ±0,86 + /0,5 для е-мод и /3 = / для h-мод. Действительно, эти
моды и моды с ббльшими значениями q оказывают сильное влияние
466 Гл. 6. Дифракция света на отверстии
на рассеяние на сфере, хотя последние и не дают типичную резонанс-
резонансную картину. К резонансам же, которые играют весьма важную роль,
приводят волны, которые удерживаются внутри сферы благодаря
внутреннему отражению от ее границы. Затухание этих мод при боль-
больших 0 и п достаточно малб, поэтому они представляют собой свобод-
свободные моды колебаний диэлектрической сферы. Эти моды первоначаль-
первоначально были обнаружены в 1909 г. Дебаем при вычислении параметров а,
близких к q + 1/2.
Если $2)/ 03) приближенно записать как - (q/&)$2)(Р), то можно по-
показать, что мнимая компонента а>" частоты этих резонансов дается
выражениями (см. монографию Вайнштейна [2] в литературе к гл. 7
настоящей книги)
(магнитные моды),
(электрические моды),
F.13.25)
где
\ */ \ V " / L * J V "
F.13.26)
здесьхт(<0) —т-й корень уравнения
«2-1)ехрBГ,м){1/и
I п
Заметим, что добротностьQgm(=z' /2c/ ) (ср. с разд. 7.3) увеличивает-
увеличивается с ростом q и падает при увеличении m .
Резонансные частоты определяются выражением
В следующей главе мы рассмотрим оптические приборы, которые ге-
генерируют излучение на некоторых дискретных частотах с*/^, опреде-
определяемых выражениями, аналогичными записанному выше [см., напри-
например, выражение G.11.5)]. Точнее говоря, частота со^ обратно пропор-
пропорциональна размеру резонатора и прямо пропорциональна сумме цело-
целого индекса (в рассмотренном здесь случае — это q, а в случае резона-
резонатора Фабри — Перо — это номер продольной моды) и некоторой до-
дополнительной величины (в рассмотренном случае — этол:т, а в случае
резонатора Фабри — Перо — фаза поперечной гауссовой моды).
6.13.6. Теория ван де Хюлста для сферы очень большого размера
В пределе 0 — оо рассеяние плоской волны на сфере можно описать в
рамках геометрической оптики. Связь между этим асимптотическим
6.13. Рассеяние на сферических частицах 467
приближением и рядами Ми устанавливается при помощи принципа
локализации у согласно которому парциальная волна q-то порядка
при /3 — оо соответствует семейству лучей, падающих на сферу на
расстоянии (<7 + l/2)/fc0 от ее центра. Таким образом, будем считать,
что моды с индексом q падают на сферу под углом 9Х Q =
= arcsin[(<7 4- 1/2)//3], в то время как другие моды проходят не рассе-
рассеиваясь и не отражаясь. Эти последние моды образуют плоский фронт,
в котором, однако, отсутствует часть его в виде центрального диска
радиусом, равным радиусу сферы. В дальней зоне этот неполный вол-
волновой фронт представляет собой поле плоской волны, из которого
нужно вычесть компоненту, соответствующую дифракции Фраунгофе-
ра на круглом отверстии. Лучи, захваченные сферой, могут затем по-
покинуть ее, претерпев некоторое число внутренних отражений, внося
таким образом свой вклад в общую картину рассеяния (часть энергии
волна теряет из-за поглощения ее в сфере). В заключение заметим,
что рассеянное поле можно представить себе состоящим из двух ча-
частей, одна из которых обусловлена отражением и преломлением на
сфере, а другая — дифракцией волнового фронта на внешней границе
рассеивающей сферы.
Разделение поля на две составляющие проявляется в записи коэф-
коэффициентов Ми. Действительно, каждый из этих коэффициентов со-
содержит два члена, один из которых равен --1/2 и не зависит от вида
рассеивающего тела, а другой равен A/2)е '^ и существенно зависит
от рассеивателя через фазу с^. Первый член определяет дифракцию
Фраунгофера, в то время как второй связан с отражением и преломле-
преломлением света на сфере.
Интерференция между различными составляющими приводит к по-
появлению быстрых осцилляции интенсивности при изменении направле-
направления наблюдения рассеяния.
В дальнейшем мы рассмотрим теорию дифракции на сферах боль-
больших размеров лишь в общих чертах, более подробно эта теория пред-
представлена в книге ван де Хюлста. Например, основное внимание мы
обратим на вычисление сумм, содержащих фазовые сдвиги. При этом
будем полагать, что оставшиеся члены, пропорциональные постоян-
постоянному множителю 1/2, дают картину, характерную для дифракции на
диске.
С учетом принципа локализации поставим в соответствие q-ft пар-
парциальной волне луч, падающий под углом вх д. Используя асимптоти-
асимптотические выражения для цилиндрических функций, сначала Дебай, а за-
затем ван де Хюлст получили следующие соотношения:
468 Гл. 6. Дифракция света на отверстии
У e?[iexp( — i2(xfq)Y9 F.13.27)
p — O
в которых коэффициенты е^ определяются следующим образом:
'-1, р= 1,2,...; F.13.28)
здесь гЧв{) — коэффициенты Френеля для h-волны, падающей под
углом вг д9 а величина/ определяется выражениями
fq = cos0! f + («!, - я/2)япв1§€, /; = cos02,, + @2), ~ 7r/2)sin02,,,
F.13.29)
где 02 q — угол преломления. Заменяя rh на ге9 можно получить ана-
аналогичное выражение для ехр(—/2о§). Используя затем асимптотиче-
асимптотические выражения для тг и г при больших q и конечных 0, а именно
я<? ~ [1/fe + l)][2/(rcgsin30)]1/2sin[(# + 1/2H — тс/4],
+ lD^Hrtsin^^^os^ + 1/2H - я/4], F.13.30)
мы получаем (см. работу [22, Sect. 3.5.2])
Si@)= f
= -i.i
7Г Я
; - fq) --p--t + tp9smeiq + 2тгт; F.13.31)
здесь /и — произвольное целое число. Поскольку сумма по д в выра-
выражении njinSffl) содержит большое число относительно медленно ме-
меняющихся членов, ее можно заменить интегралом. Таким образом,
г= —1,1
Вычислим этот интеграл методом стационарной фазы. Это означает,
что при больших /3 основной вклад в интеграл дает то значение вх
угла 0j, для которого d%/dBx = 0. Таким образом, мы имеем
0-М0-2тгт = О, F.13.33)
где
0 = 2р(в2 - ±я) + п - 20J. F.13.34)
В окрестности угла вх функцию ^ можно разложить в ряд по q - q\
? = Z + b(q-qJ + '-', F.13.35)
6.13. Рассеяние на сферических частицах 469
причем 0j и q связаны между собой соотношением sin0j =
= (q + 1/2H-*, а коэффициент Ъ дается выражением
Ь = (l/2)(d2$/dq2)\q=< = [1/BM cos вШ®1*ё,\ F.13.36)
Таким образом, окончательно получаем следующее асимптотическое
выражение:
- Р- - \ - т)
4 2 4 /
F.13.37)
где s = sgnrf9/rf0j и д ш 2&(pncoslJ - cos0j). Наконец, заменяя в
выражении F.13.37) е^ на е®, находим S2@).
Выполненные выше расчеты можно провести более строго, если
рассеянное поле представить в виде ряда Ми и затем применить к это-
ЫУ ряду метод Ватсона—Редже. Основная трудность, которую придет-
придется преодолеть при таком подходе, заключается в векторном характере
процесса рассеяния. Если использовать скалярное представление поля, то
в случае сферы можно шаг за шагом повторить выкладки, описанные в
разд. 6.5 для кругового цилиндра (подробнее об этом см. в книге Нус-
сенцвейга [22], указанной в литературе к гл. 4 настоящей книги).
6.13.7. Теория глории и радуги в приближении геометрической оптики
Если радиус сферы гораздо больше длины волны, то поле рассеяния
такой сферы можно найти, используя приближение геометрической
оптики (см. гл. 2) или подход, развитый в разд. 6.13.6. В частности,
используя соотношения F.13.33) и F.13.34), легко показать, что угол
рассеяния 0, измеренный относительно направления z падающей вол-
волны, связан с углом падения вх простым соотношением (рис. 6.7, б):
в = (р - \)п + 20Х - 2рв2, F.13.38)
где р — 1 — число внутренних отражений, а 02 — угол преломления.
Если на сферу радиусом а падает плоская волна, то поле отражен-
отраженного луча /@) [см. выражение B.12.42)] пропорционально величине
(р{р2У/2, где р[ и р2 — радиусы кривизны волнового фронта, отра-
отраженного от поверхности сферы. Учитывая затем соотношение
B.11.26), мы находим, что/@) ос а/2. Таким образом, сфера, у кото-
которой радиус больше длины волны, рассеивает свет изотропно.
В более общем случае, т. е. когда лучи проникают в диэлектриче-
диэлектрическую сферу и испытывают р - 1 внутренних отражений, интенсив-
интенсивность рассеяния /@) в дальней зоне, как следует из выражения
F.13.37), записывается в следующем виде:
470 Гл. 6. Дифракция света на отверстии
" 4sin0[l - (p/n)(cosejcose2)-]
где D — так называемый коэффициент расходимости [ср. с выраже-
выражением B.13.52)].
В соответствии с выражением F.13.39) интенсивность рассеяния
становится бесконечной при sin в = 0 или при d0/ddl = 0. В случае
sin0 = 0 при sin20j * 0 интенсивность оказывается бесконечно боль-
большой для прямого рассеяния назад (явление глории) или для прямого
рассеяния вперед, в то время как в случае de/d0l = 0 мы имеем явле-
явление радуги.
Глория возникает, когда угол рассеяния отличается от угла паде-
падения 0j Ф 0, 7г/2 на число, кратное ж. Распределение интенсивности по-
поля в дальней зоне при рассеянии сферической частицей назад, соот-
соответствующее лучам глории, совпадает с распределением, которое дает
кольцевой волновой фронт. Таким образом, в дальней зоне образуется
центральное пятно с максимальной яркостью, окруженное кольцами с
постепенно убывающей интенсивностью.
Явление глории хорошо известно в метеорологии. Глория имеет
вид окрашенных концентрических колец, красных в наружной части и
фиолетовых во внутренней, с яркой областью в центре. Вся картина
при этом наблюдается в направлении, противоположном направле-
направлению на Солнце. Глорию не нужно путать с дифракционной короной,
которая окружает закрытое пеленой или облаками Солнце. Глорию
можно наблюдать, если встать на холм и посмотреть на свою соб-
собственную тень. Можно увидеть глорию во время полета на самолете,
наблюдая за его тенью на окружающих легких облаках или дымке.
При благоприятных условиях наблюдатель увидит, что тень от голо-
головы или самолета окружена ярким гало.
Из истории физики известно, что в 1895 г. Ч.Т.Р. Вильсон построил
первую свою камеру с целью экспериментального изучения глории.
Угол падения луча глории (рис. 6.21) нетрудно вычислить по фор-
формуле F.13.38) с учетом, что sin0 = 0. Учитывая при этом, что любой
из углов 0 и 0j меньше чем тг/2, для луча глории, испытывающего
/7—1 отражений, находим
0i = pOi + B - р)(я/2). F.13.40)
Используя закон Снеллиуса для однократно отраженного луча р = 2,
это соотношение можно записать в виде cos02 = л/2. Поскольку угол
02 принимает значение между 0 и и74, показатель преломления п
должен быть заключен в интервале между 2 и V2. Аналогичные огра-
ограничения можно получить и для р > 2. Здесь необходимо указать, что,
6.13. Рассеяние на сферических частицах 471
Луч глории ЛУЧ г/1°Рии
Падающий / _ ——•—т-
лцч / Падающий /
луч I
а 5
Рис. 6.21. Лучи глории в случае одного (а) и двух отражений (б).
согласно геометрической оптике, глория на водяных каплях (п = 1,33)
вообще не может наблюдаться! Учитывая невозможность объяснения
данного эффекта в рамках геометрического приближения — случай
сам по себе довольно значительный с точки зрения физики, — ван де
Хюлст пришел к предположению, что поворот лучей глории происхо-
происходит как вследствие нескольких отражений внутри капли, так и частич-
частично из-за пробега по поверхности капли в виде поверхностной волны.
Красивое явление радуги с древнейших времен привлекало внима-
внимание натуралистов [35]. Она часто возникает после грозы, когда лучи
солнца освещают облака. Аристотель предполагал, что радуга — это
необычный тип отражения солнечных лучей от облаков, возникающий
при определенных углах падения и приводящий к возникновению ра-
радужных лучей, образующих круговой конус. Английский философ и
естествоиспытатель Роджер Бэкон [36] впервые в 1266 г. измерил угол
A38°) между лучами радуги и падающим светом. В 1304 г. немецкий
монах Теодорик из Фрейберга предположил, что радуга возникает в
каждой капельке облака. Ту же идею высказал впоследствии Антонио
Доминиканский (архиепископ из Спалато) в своей книге "De Radiis
Visus et Lucis" A611). Исаак Ньютон приводит следующий отрывок из
этой книги: «... ибо он учит там, что внутренняя дуга образуется в
круглых каплях дождя посредством двух преломлений солнечного све-
света и одного отражения между ними в каждой капле воды; он доказы-
доказывает свои объяснения при помощи опытов, произведенных с фиалом,
наполненным водой, и со стеклянными шарами, наполненными водой
и помещенными на солнце так, чтобы были видны цвета обеих дуг.
То же объяснение приводил Декарт в своих Метеорах, исправив объяс-
нение внешней дуги...»1).
1) Ньютон И. Оптика. Книга I, ч. 2, предложение 9, задача 4. — М.—Л.: 1927. —
Прим. перев.
472
Гл. 6. Дифракция света на отверстии
Ньютон дополнил геометрическую теорию радуги объяснением ее на-
наиболее загадочного свойства — окрашиваться в разные цвета. Осно-
Основываясь на результатах своих исследований по разложению белого
света в призмах, он объяснил, что наблюдаемая картина является на-
набором монохроматических радуг, каждая из которых немного смеще-
смещена относительно предыдущей. На основе тщательных измерений
Ньютон вычислил радужный угол для красного 137°58' и для фиоле-
фиолетового 139°43' цветов.
В 1835 г. Р. Поттер указал, что пересечение различных групп све-
световых лучей в капле приводит к образованию каустики. На основе
этих данных Эйри в 1838 г. удалось найти распределение интенсивно-
интенсивности в монохроматической радуге, причем в своих расчетах он исполь-
использовал знаменитый интеграл радуги, известный теперь как функция Эй-
Эйри. Метод, которым воспользовался Эйри (рис. 6.22), состоял в при-
применении принципа Гюйгенса к волновому фронту, огибающая которо-
которого описывается кубической функцией.
В соответствии с формулой F.13.39) радуга возникает при условии,
что de/dex = 0. Таким образом, с учетом выражения F.13.38) углы
падения вх R определяются выражением
в1Л = arcsin[(p2 - п2)/(р2 - 1)]1/2. F.13.41)
Поскольку аргумент функции arcsin x должен быть меньше единицы,
радужный луч должен претерпеть более чем п — 1 внутренних отра-
отражений (п — показатель преломления капли). Например, для капель
воды (п = 4/3) первый радужный луч возникает при р = 2 и рассеи-
рассеивается под углом в$:
в{" = п + 2arcsin[D - л2)/3]1/2 - 4arcsin[D - n2)/Cn2)]1/2 s 138°.
F.13.42)
Рис. 6.22. Слияние лучей, рассеянных
на капле, приводящее к конгруэнции
обратно рассеянных лучей с S-образ-
ным волновым фронтом.
6.13. Рассеяние на сферических частицах
473
Второй радужный луч образуется в результате двух отражений,
его угол &р = 128,7°.
Амплитуда поля вблизи радужного угла 0R может быть найдена
путем вычисления интеграла в выражении F.13.32). При этом необхо-
необходимо заметить, что в окрестности 0R квадратичное разложение
(i6.13.35), отвечающее форме волнового фронта, заменится на кубиче-
кубическое (см. рис. 6.22):
Z = U + (9 " q*W/dq + A/б)D - qRK d3?/dq3. F.13.43)
При этом гауссов интеграл, приводящий к выражению F.13.37), заме-
заменится функцией Эйри. Картина поля, характерная для монохромати-
монохроматической радуги, определяется распределением поля вблизи каустики и
выглядит как ряд полос на освещенной стороне капли. Вычисления,
проделанные на основе рядов Ми, развеяли оставшиеся сомнения о
фактическом присутствии резких полос. Недавно в работе [37] к инте-
интегралу, аналогичному интегралу из выражения F.13.32) и полученному
при вычислении амплитуды рассеяния методом Ватсона — Редже, ав-
авторы применили метод Честера — Фридмана — Урселла (ЧФУ). Ме-
Метод ЧФУ дает выражение, в котором функция Эйри входит в комби-
комбинации со своей производной Ai'; таким образом, нули функции Эйри
компенсируются присутствием функции Ai'. Как видно из рис. 6.23,
эти изменения приводят к значительно более высокой точности расче-
расчетов.
136" /35е Ш0° /4/
Рис. 6.23. Угловое распределение интенсивности рассеянного света, вычисленное для лу-
лучей из рис. 6.22; масштабный параметр 0 = 1500. 1 — распределение интенсивности,
полученное вычислением дифракционного интеграла для S -образного волнового фронта;
2 — распределение волн, полученное с учетом вклада поверхностных волн, возникаю-
возникающих в представлении Ватсона — Редже при скалярной аппроксимации рассеянного по-
поля; 3 — решение, полученное при сложении более чем 1500 членов разложения в пред-
представлении рассеянного поля в виде ряда по парциальным волнам. (Из книги Нуссенц-
вейга [36].)
474 Гл. 6. Дифракция света на отверстии
ЗАДАЧИ
Раздел 6.2
1. Покажите, что для металлической полуплоскости интеграл из F.2.2) при ф' > ж
записывается в виде
72) F
471
(*'/2)J"
2. Учитывая приведенное в задаче 1 интегральное представление, получите соотно-
соотношения Зоммерфельда для поля при дифракции р- или s-волны на металлической полу-
полуплоскости, а именно
=F e^cos(^+^F{-BM1/2cos[@ + ф')/2]}9
где F — комплексный интеграл Френеля, а знаки минус и плюс относятся соответствен-
соответственно к р- и s-поляризациям.
3. Вычислите распределение токов на металлической полуплоскости при освещении
ее s-волной с углом падения ф' = ж/2.
4. Покажите, что функция Малюжинца Л/, определяемая выражением F.2.15), мо-
может быть представлена следующим интегралом:
-J- fV Г™ tg (^)—Л -dv\
8<l> Jo J-ico \4ф/с°Ф-м) J
Подсказка. Найдите выражение для функции dlnM/da.
5. Используя приведенное в задаче 4 представление функции Л/(а), докажите следу-
следующие соотношения:
М(а + 2Ф)/М(а - 2Ф) = ctg [A/2)(а + тс/2)],
М(а.+ я/2)М(а - я/2) = M2Gc/2)cos[Gca)/DO)],
М(а + Ф)М(а - Ф) = М2(Ф)М'(а),
где М' — функция Малюжинца при Ф' = Ф/2.
6. Покажите, что при Ф = ж функция Л/ из предыдущей задачи принимает вид
Г ! fe*sm(ii) - 23/27rsin(w/2) - 2и J 1
M(a) = exp — i-J Li_! ^M I
L8teJ0 cosm J
7. Покажите, что при Ф = ж функцию Малюжинца М можно записать следующим
образом:
Литература 475
здесь Еъ — числа Эйлера.
8. Вычислите функцию g(a) при Ф = т и (( = т/2, аппроксимировав функцию
М(а + вв) выражением
М(а + 0В) s М(а + я/2) + @В - n/2)dM/da =
= М(а + я/2) - @В - л/2)М(а + я/2) х
х [cos(a) - 23/2 sin(a/2 + я/4) - 2а/я - l]/(8cosa) .
Подсказка. См. задачу 6.6.
9. Покажите, что при Ф = Зэт/4 функция Малюжинца М определяется выражением
M(a) = cos[(a - 7r)/6]cos[(a + 7r)/6]/[cos2(rc/6)cos(a/6)].
10. Выведите выражение F.2.11) с помощью тождества (Е2) из приложения, учиты-
учитывая следующее соотношение:
@ + ф) - S(j? + ф - 2л)]е-'*"сов
'кнс2
24 + ф) -
0ТН(
L
11. Вычислите коэффициенты дифракции Ds для прямоугольного клина с помощью
выражения F.2.18). Обсудите, в частности, зависимость ?>s от 0В.
12. Вычислите амплитуду S+ поверхностной волны, которая возбуждается s-волной
единичной амплитуды, падающей на прямоугольный клин (Ф = Зя-/4). Подсказка. Исполь-
Используйте выражение, полученное в задаче 9.
ЛИТЕРАТУРА
1. King R. Ж P., Wu Т. Т., The Scattering and Difraction of Waves, Harvard Univ.
Press. Cambridge^ Massachusetts, 1959.
2. Electromagnetic Scattering, (ed. P.L.E. Uslenghi), Academic Press, New York, 1978.
3. Малюжинец Г. Д. — ДАН СССР, 1958, т. 121, № 3, с. 436—439.
4. Kouyoumjian R. G. — In: Numerical and Asymptotic Techniques in Electromagnetics
(ed. R. Mittra), Springer-Verlag, Berlin and New York, 1975, p. 166—215.
5. Joo GS., Ra J.-W., Shin S.-K, Electron. Lett., 16, 934, 1980.
5a. Keller J. R, J. Appl. Phys., 28, 426, A957).
6. Rhodes D. R., On the Theory of Scattering by Dielectric Bodies, Rep. 475-1, Antenna
Lab., Ohio State Univ., Columbus, 1953.
7. Debye P. J., Phys. Zs., 9, 775 A908).
8. Poggio A. J., Miller E. K. — In: Computer Techniques for Electromagnetics (ed.
R. Mittra), Pergamon, New York, 197°, Ch. 4.
9. Harrington R. E, Field Computation by Moment Method, Macmillan, New York,
1968.
10. Байт С. E.t Proc. IEEE, 64, 1598 A976). [Имеется перевод: Баум К. Э. —
ТИИЭР, 1976, т. 64, № 11, с. 53.]
11. Harrison G. R., Appl. Opt., 4, 1275 A965).
476 Гл. 6. Дифракция света на отверстии
12. Stroke G. W. — In: Handbuch der Physik, v. 29 (ed. S. Flugge), Springer-Verlag,
Berlin and New York, 1967, p. 426—754.
13. Денисюк Ю. H. — ДАН СССР, 1962, т. 144, № 6, с. 789—791.
14. Schmahl G., Rudolf D. R., Progr. Opt., 14, 195 - 244, A976).
15. Labeyrie A., Flamand /., Opt. Commun., 1, 5, A969).
16. Tamir Т., Integrated Optics, Springer-Verlag, Berlin and New York, 1975. [Имеется
перевод: Тамир Т. Интегральная оптика. — М.: Мир, 1978.]
17. Samson J. A. R., Techniques of Vacuum Ultraviolet Spectroscopy, Wiley, New York,
1967.
18. Electromagnetic Theory of Gratings (ed. R. Petit), Springer-Verlag, Berlin and New
York, 1980.
19. Zaki K. A., Neurenther A. R.t IEEE Trans. Antennas Propag., AP-19, 208 A971).
20. Hessel A.t Oliner A. A., Appl. Opt., 4, 1275 A965).
21. Microwave Antenna Theory and Design (ed. S. Silver), MIT Radiat. Lab. Sen,
v. 12, Cambridge, Massachusetts, 1949, Ch. 2.
22. Newton R. G., Scattering Theory of Waves and Particles, McGraw-Hill, New York,
1966. [Имеется перевод: Ньютон P. Теория рассеяния волн и частиц. — М.:
Мир, 1969.]
23. Kerker M, The Scattering of Light, Academic Press, New York, 1969.
24. Twersky K, Appl. Opt., 3, 1150 A964).
25. Noble Я — In: Electromagnetics Waves (ed. R. Langer), Univ. of Wisconsin Press,
Madison, 1962, p. 323—360.
26. Kleinman R. E.t Proc. IEEE, 53, 848 A965). [Имеется перевод: Клейнман RE.
— ТИИЭР, 1965, т. 53, № 8, с. 975.] См. также ссылку [2] из гл. 1 настоящей
книги.
27. Mie G., Ann. Phys. (Leipzig), 25, 377 A908).
28. Debye P., Ann. Phys. (Leipzig), 30, 57 A909).
29. Wickramasinghe N. С Light Scattering Functions for Small Particles, Wiley, New
York, 1973.
30. Ландсберг ПС. Оптика. — M.: Наука, 1976.
31. Vauclair S. —In: Astrophisical Processes in Upper Main Sequence Stars (eds.
B. Hauck., A. Maeder), Geneva Observ., CH-1290, Sauverny, Switzerland, 1983,
p. 167.
32. Minogin V. G., Letokhov V. S., J. Opt. Soc. Am., 69,* 413 A979).
33. Irvine W. M, J. Opt. Soc. Am., 55, 16 A965).
34. Ashkin A.t Dziedzic J. M., Phys. Rev. Lett., 38, 1351, 1977.
35. Thicker R. A. R., Introduction to Meteorological Optics, Am. Elsevier, New York,
1970.
36. Nussenzveig H. M. — In: Light from the Sky (ed. J. Walker), Freeman, San Fracisco,
California, 1980, p. 54—65.
37. Khare K, Nussenzveig H. M, Phys. Rev. Lett., 33, 976, 1974.
БИБЛИОГРАФИЯ
Bohren С. Е, Huffman D. R., Absorption and Scattering of Light by Small Particles,
WUey, New York, 1983.
Фабелинский И.Л. Молекулярное рассеяние света. — М.: Наука, 1976.
Ishimaru A., Wave Propagation and Scattering in Random Media, Academic Press,
New York, 1978. [Имеется перевод: Исимару А. Распространение и рассеяние
волн в случайно-неоднородных средах. — В 2-х т. — М.: Мир, 1981.]
Библиография 477
Казанцев А. П. — УФН, 1978, т. 124, вып. 1, с. 113 — 145.
Lax P. D., Phillips R. S. Scattering Theory, Academic Press, New York, 1967.
Maystre D., Prog. Opt., 21, 3 — 57 A984).
Reed M, Simon A, Methods of Modern Mathematical Physics, v. 3, Academic Press,
New York, 1979.
Stenholm S., Minogin V. G., Letokhov V. S.t Opt. Commun., 25, 107 A978).
Stroke G. W., Prog. Opt., 2, 1—72 A963).
van de Hulst H. C, Multiple Light Scattering, Academic Press, New York, 1980.
Wilcox С Я., Scattering Theory for Diffraction Gratings, Springer-Verlag, Berlin and
New York, 1984.
Welford W. Т., Prog. Opt., 4, 241—280, 1965.
ГЛАВА 7
ОПТИЧЕСКИЕ РЕЗОНАТОРЫ И ИНТЕРФЕРОМЕТРЫ
ФАБРИ - ПЕРО
7.1. ОБЩИЕ СВОЙСТВА РЕЗОНАТОРОВ
ДЛЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
7.1.1. Обычные колебательные системы
Физическая система, выведенная из состояния равновесия импульсным
воздействием, через некоторое время возвращается в исходное состоя-
состояние, совершая при этом ряд затухающих колебаний. Данное свойство
имеет общую природу и присуще как небоскребам, раскачивающимся
под действием ветра, так и атомам, взаимодействующим с импульс-
импульсным электромагнитным полем. Единственным различием в поведении
этих систем является скорость затухания колебаний. В некоторых слу-
случаях, когда основную роль играют процессы затухания, колебания
вообще не возникают, в других случаях колебания могут длиться
столь долго, что систему можно рассматривать как идеальный осцил-
осциллятор.
Читатели, владеющие элементарными навыками в области электро-
электроники, знают, что возбуждение системы из параллельно соединенных
катушки индуктивности L и конденсатора емкостью С приведет к то-
тому, что в ней возникает переменный ток, угловая частота колеба-
колебаний которого дается выражением с^ = 1/VlC, причем этот ток будет
течь бесконечно долго. Однако как катушка индуктивности, так и кон-
конденсатор имеют омические потери, которые можно учесть, если в со-
соответствующие эквивалентные цепи ввести активные сопротивления
Rl и Яс (см. врезку на рис. 7.1), что приведет к затуханиям колеба-
колебаний в рассматриваемой системе. Если через / (/) обозначить ток, про-
протекающий через контур, сформированный из L и С, то можно запи-
записать следующее выражение:
^t + ф}9 G.1.1)
где RL + Rc = /?, а /0 и ф — соответственно начальный ток и фаза
колебаний. Удобно характеризовать затухание этих колебаний до-
добротностью Q:
Q = пх/Т = IL/(CR2) - i]1'2 ~ (L/CY'4/R, G.1.2)
где т - 2L/R — постоянная затухания и Т = 2тг/соо—- период колеба-
колебаний [см. выражение G.1.1)]. Добротность Q является мерой отклоне-
отклонения данной системы от идеальной, т. е. от системы, колеблющейся
7.1. Общие свойства резонаторов для электромаг. волн
479
\ Бесконечная
г добротность
Высокая
добротность
Низкая
добротность
Рис*. 7.1. Зависимость импеданса
резонансной цепи от частоты при
различных Q. Частота
бесконечно долго. Чем больше Q, тем более близка данная система к
идеальной. С помощью выражения G.1.1) нетрудно показать, что
Q = (l/2)coo[L/2 + (l/C)(\i dtJ]/Ri = 2тг; иными словами, с точнос-
точностью до множителя 2тг величина Q равна отношению энергии, запасен-
запасенной в LC-контуре, к энергии, теряемой за один период колебаний.
Найдем теперь импеданс Z (со) LC -контура, выразив его через
L и С. Для случая R2 < L/C вблизи резонансной частоты соо =
= \/(LC)xri импеданс Z (со) дается выражением
Z(co) = (L/CI/2Q/[1 + i2Q(co - а>о)/юо] = №)И(<0). G.1.3)
(В данном разделе мы будем использовать круговую частоту со; в сле-
следующем разделе мы перейдем к частоте v.)
В соответствии с выражением G.1.3) при Q > 1 зависимость мо-
модуля величины Z от расстройки Асо = со - соо имеет очень острый ре-
резонансный характер (рис. 7.1), в то время как фаза j3(co) при прохожде-
прохождении со через соо претерпевает резкий скачок.
Кроме того, из выражения G.1.3) нетрудно показать, что полоса
частот по уровню 0,71 от максимального значения (или по уровню
3 дБ от резонансной амплитуды) равна В = coq/Q .
Выражение G.1.1) для тока i (t) остается справедливым, даже если
сопротивления RL и Rc отрицательны, причем величина R также от-
отрицательна. Это означает, что ток в системе будет совершать колеба-
колебания с экспоненциально нарастающей амплитудой.
Если параллельно соединить два контура с одной и той же резо-
резонансной частотой, но с разными Q и разными импедансами Z (соо), то
результирующий импеданс запишется в виде
Zpe3(co) = Z3KB/[1 + i2Q3KB((o - соо)/со], G.1.4)
где
Z3KB= Z.ZJiZ, + Z2), еэкв= (QXZ2 + Q1Zl)l{Zl + Z2), G.1.5)
480
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
J *
z
I
Рис. 7.2. а — цепь с обратной связью; б — эквивалентная схема для определения тока/
в зависимости от величины напряжениям, создаваемого генератором.
причемZj = Z{(oH) hZ2 = Z2(o>0). Таким образом, когдаZj + Z2 = 0,
величина Z3KB может быть очень большой. Следовательно, чтобы по-
получить резонансную цепь с бесконечно большим импедансом, к имею-
имеющейся резонансной цепи необходимо подключить другую цепь, импе-
импеданс которой противоположен по знаку и равен по абсолютной вели-
величине импедансу первой цепи. Отрицательное значение Z2(a>0) является
лишь необходимым условием для достижения этой цели.
Любой генератор может быть представлен в виде генератора шу-
шума с комплексной амплитудой е, включенного в цепь из элементов Z,
hZ2 (рис. 7.2, a), raeZj представляет собой пассивный, aZ2 — актив-
активный элемент. В теории систем связь между амплитудойе и током/,
протекающим через цепь, есть не что иное, как связь типа замкнутой
петли, показанной на рис. 7.2,5. ОткликZj(co) фильтра обратной связи
может сильно зависеть от частоты, определяя таким образом частоту
генератора, в то время KaKZ2(co) может практически не зависеть от ча-
частоты вблизи резонанса. Кроме того, eoraZj соответствует обычно
линейному отклику, toZ2 нелинейно зависит от прикладываемого на-
напряжения и, таким образом, определяет амплитуду генерации.
В качестве альтернативы цепи, изображенной на рис. 7.2, можно
представить себе цепь (рис. 7.3), состоящую из генератора с нелиней-
нелинейной обратной связью, насыщаемого усилителя с усилением А (К), по-
почти не зависящим от частоты со вблизи со0 и уменьшающимся с увели-
увеличением К, и фазосдвигающей цепи, имеющей частотный отклик
F(co) = |F|e-"<e) = [1 + i2Q(co - а>0)/сооу\ G.1.6)
где 0 — фазовый сдвиг входного сигнала после полного обхода петли
обратной связи. Иными словами, в цепь насыщаемого усилителя мы
включили все частотно-независимые члены, для того чтобы ornmaF в
цепи обратной связи при со = соо был в точности равен единице. Стро-
Строго говоря, с целью учета нелинейного вклада активных элементов в
фазовый множитель к этому необходимо добавить еще и условие за-
зависимости амплитуды V от добротности Q.
7.1. Общие свойства резонаторов для электромаг. волн
481
Спонтанное
излучение
Рис. 7.3. Цепь с обратной связью, представляющая нелинейный генератор, который
включает в себя насыщаемый усилитель G) с характеристической кривой зависимости
А {У) усиления от входного напряжения, изображенной на врезке, и насыщаемую
фазосдвигающую цепочку с F( w) = el^w) B).
7.1.2. Микроволновые {СВЧ) и оптические генераторы
В отличие от низкочастотных генераторов, для которых параметры
резонансной цепи определяются легко и однозначно, микроволновые
[1] и оптические [2—6] генераторы требуют более глубокого матема-
математического и физического анализа. Для определенности рассмотрим ге-
генератор, в резонатор которого помещен лавинный диод с обратносме-
щенньЫ переходом (рис. 7.4). Диод можно характеризовать поляриза-
поляризацией Р, действующей как источник электрического поля в соответст-
соответствии с выражением A.2.8). Таким образом, электрическое поле Е(г, /)
можно интерпретировать как отклик резонатора на излучение дипо-
диполей, распределенных в области диодного перехода:
Е(М)
¦г..* я/
T(r,r';t-t')-P(r',t')dV
G.1.7)
Переход
где Г — диадное представление отклика на излучение диполя, распо-
расположенного в точке f и включенного в момент времени Г на очень ко-
Рис. 7.4. Схематическое представле-
представление микроволнового генератора с от-
отрицательным сопротивлением. 1 — к
источнику смещающего напряжения;
2 — настройка; 3 — устройство; 4 —
нагрузка.
482 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
роткий промежуток времени, т. е. представляет собой пространствен-
пространственно-временную функцию Грина резонатора.
Поскольку Р является нелинейной функцией вектора Е, для вычис-
вычисления амплитуды и частоты генерации можно в принципе воспользо-
воспользоваться уравнением G.1.7) [или эквивалентным ему уравнением A.2.9) с
граничными условиями]. Эти расчеты можно значительно упростить,
если Е и Р представить в виде комбинации мод резонатора. Согласно
этому представлению, которое мы рассмотрим ниже более детально,
резонатор и, следовательно, весь генератор можно промоделировать
бесконечной дискретной последовательностью простых генераторов
со свойствами LC-контуров. Отсюда в свою очередь следует, что си-
система может генерировать на нескольких частотах, так что в одних
случаях имеет место генерация на одной частоте, в других — на не-
нескольких частотах одновременно. Таким образом возникает совершен-
совершенно новая ситуация, которая не может быть описана в рамках традици-
традиционного анализа LC -цепей; она и определяет коренное различие между
генераторами радиочастотного и микроволнового диапазона.
Третий класс генераторов — это мазеры и лазеры, которые обыч-
обычно объединяют в класс квантовых генераторов. Их работа основыва-
основывается на одноквантовом- обмене энергией между лазерным полем и ак-
активной средой, что, как показали Шавлов и Таунс, позволяет снять
термодинамические ограничения на ширину линии, характерные для
стандартных источников излучения.
Одним из наиболее существенных различий между оптическими и
микроволновыми генераторами является то, что в последнем случае
активная область имеет, как правило, малые размеры по сравнению с
длиной излучаемой волны X, и поэтому такой генератор можно рас-
рассматривать как точечный диполь. В лазерном же генераторе, наобо-
наоборот, размеры активной области велики по сравнению с длиной волны
X, поэтому здесь сразу же возникает проблема, связанная с необходи-
необходимостью учета взаимодействия поля и распределенных диполей.
Замкнутые резонаторы можно применять только в микроволновых
генераторах. Известно, что частоты прямоугольного резонатора опре-
определяются выражением
<*>** = netif/aJ + (т/ЬJ + (пД/J]1'2, G.1.8)
где а, Ъ vi d — размеры прямоугольной области резонатора, а/, /и и
п — неотрицательные целые числа, такие, что / + т + п > 2. Если
учесть, что, исходя из практических соображений, размеры резонато-
резонатора должны превышать 1 мм, то очевидно, что такой резонатор уже
невозможно использовать для генерации волн субмиллиметрового
диапазона (< 1 мм).
7.1. Общие свойства резонаторов для электромаг. волн
483
Рис. 7.5. Схематическое представление
лазерного генератора.
м,
I
М2
Для того чтобы преодолеть эту трудность, Прохоров, Шавлов и
Таунс предложили использовать (открытый) резонатор Фабри — Пе-
Перо. Таким образом, лазерный генератор имеет вид, показанный на
рис. 7.5, в котором плоская волна со средней интенсивностью/ совер-
совершает много проходов в прямом и обратном направлениях между зер-
зеркалами М, иМ2 (с коэффициентами отражения/?, и/?2 соответствен-
соответственно), усиливаясь активной средой.
Представление пучка плоской волной на самом деле прямо связано
с предположением о стационарном режиме генерации лазера, когда
потери и усиление взаимно компенсируются (надпороговый режим).
При работе ниже порога каждый элементарный объем излучает неко-
некогерентно с соседними, так что результирующее поле представляет со-
собой суперпозицию полей, распространяющихся во всех направлениях.
Используя условия обратной связи, можно записать,
где G — усиление за полный проход. Кроме того, если потребовать,
чтобы при со = соо фазовый набег плоской волны за полный проход
был равен 2 ттт, где т — целое число, то в общем случае G.1.6) мы
получаем выражение
fijco) = 2тп + arctg [2Q((o - ео0)М)], G.1.10)
которое в последующих разделах выведем с помощью более строгого
рассмотрения.
В некоторых случаях важно учесть расстройку частоты генерации
резонатора относительно частоты coL, соответствующей максимуму
кривой коэффициента усиления активной среды. Соответственно необ-
необходимо также учитывать спектральную зависимость коэффициента
усиления G и полного усиления А, так что в общем случае мы имеем
А = А (/, со, coL). Кроме того, не всегда можно пренебречь и набегом
фазы, обусловленным активной средой. В этом случае обычно вводит-
вводится фазосдвигающая цепочка с функцией отклика FL(I, со, coL) =
= exp[-/j3L(/, со, o)L)] (где 0L(I, со, wL) — нелинейная функция, зави-
зависящая от интенсивности /) в цепи обратной связи, показанной на
рис. 7.3.
484
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Грез
Насыщаемый
усилитель
FL
Рис. 7.6. Цепь с нелинейной обратной
связью, эквивалентная лазерному гене-
генератору.
Таким образом, исходя из проведенного выше рассмотрения, мы
можем связать в цепи обратной связи на рис. 7.6 выход V (со)
(I v I2 = / — средняя интенсивность оптического излучения внутри ла-
лазера) с входом е (со); это — эквивалентная схема лазерного генератора,
изображенного на рис. 7.5. Соответствующее соотношение записыва-
записывается следующим образом:
V(co) = е(со) АA, со, wL)/[l - АA, со, coL)Fpe3(co)FL(I, со, coL)l G.1.11)
В отсутствие входного сигнала е (со) система будет находиться в ре-
режиме свободной генерации, если выполняется следующее условие ре-
резонанса:
Это условие можно записать в виде системы двух нелинейных уравне-
Ppjco) + j8L(/,o>,caL) = 2mn, A(I,co,coL)\Fpe3(co)\ = 1, G.1.13)
из которых можно найти частоту со и интенсивность / генерируемого
пучка.
В принципе лазер должен генерировать линейчатый спектр. Однако
в рассматриваемой модели совершенно пренебрегалось наличием у ла-
лазера шума. Шавлов и Таунс, привлекая статистические методы, пока-
показали, что уширение линии вследствие квантового шума (см. книгу
Ярива [8], указанную в литературе к гл. 1 нашей книги) дается выра-
выражением
Дшген = [(M/P](Acope3)V G-! •14)
где Асорез — полуширина резонанса по полувысоте, Р — излучаемая
лазером мощность, а параметр д = Na/\Na - Nb(ga/gb)]nop учитывает
тот факт, что в условиях порога, чтобы сохранялось равенство усиле-
усиления и потерь, конечное увеличение населенности нижнего лазерного
состояния Nb должно сопровождаться увеличением населенности Na
верхнего лазерного состояния. Поскольку на генерируемое излучение
оказывают сильное влияние флуктуации параметров лазерной среды и
вибрация выходных зеркал, практически невозможно достичь узкой
ширины линии, определяемой выражением G.1.14).
7.2. Общие свойства оптических резонаторов 485
7.2. ОБЩИЕ СВОЙСТВА ОПТИЧЕСКИХ РЕЗОНАТОРОВ
Микроволновые объемные резонаторы были разработаны главным
образом для сантиметрового диапазона волн. Увеличение длины вол-
волны X приводит к необходимости увеличивать линейные размеры резо-
резонатора; в предельном случае он сводится к обычному LC-контуру.
Уменьшение же X требует и уменьшения размеров резонатора, что со-
соответственно приведет к понижению его добротности Q. Вообще го-
говоря, в миллиметровом диапазоне Q уменьшается обратно пропорцио-
пропорционально квадратному корню из частоты. Для генерации коротких длин
волн, скажем субмиллиметрового диапазона, уже невозможно сконст-
сконструировать объемный резонатор для генерации отдельной моды низ-
низшего порядка (например, моды ТЕ011), поскольку потребовались бы
практически неосуществимые малые размеры резонатора. Поэтому
приходится иметь дело с генерацией мод очень высокого порядка,
причем режим одномодовой генерации оказывается принципиально
недостижимым. При возрастании порядка моды частотный сдвиг
между соседними модами сравнивается с шириной отдельной моды,
что приводит к уменьшению селективности. Пользоваться такими ре-
резонаторами крайне неудобно, поскольку заранее не известно, на какой
частоте они будут возбуждаться. Фактически же они генерируют од-
одновременно несколько мод с почти непрерывным спектром, характе-
характеризующимся некоторой средней частотой.
Согласно формуле Рэлея — Джинса, в случае очень высоких частот
число мод в интервале Av для закрытого резонатора объемом V про-
произвольной формы записывается в виде [7]
ANm = [(8;r)/c3]v2 Av К, G.2.1)
где с — скорость света. Отсюда следует, что с возрастанием частоты
плотность мод в спектре увеличивается. Для v = 5-1014 Гц (частота
генерации Не—Ne-лазера) иД^= 1,5 ГГц формула G.2.1) дает около
1,7-108 мод на кубический сантиметр. Отсюда с очевидностью следу-
следует, что резонатор объемом 10 см3, представляющий собой замкнутую
цилиндрическую полость с металлическими стенками, к которой и
применима формула G.2.1), не в состоянии выделить какую-либо
определенную частоту из спектра излучения гелий-неоновой плазмы.
В данном случае в спектре генерации будут наблюдаться миллиарды
линий, отстоящих друг от друга по частоте на 1 Гц.
Рассуждая таким же образом, Шавлов, Таунс [8] и Прохоров [9]
пришли к идее использования резонаторов другого типа, которые вы-
выделяли бы из всех остальных мод лишь некоторые, так называемые
основные моды. Эти авторы рассмотрели такую конфигурацию резо-
резонатора, которая обеспечивает очень высокую добротность для основ-
486 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Рис. 7.7. Плоскопараллельный открытый
резонатор (а), полученный устранением бо-
боковых стенок цилиндрического закрытого
резонатора (б).
ных мод, в то время как для остальных (весьма многочисленных) мод
потери должны быть столь велики, чтобы при заполнении резонатора
активной средой их генерация была бы невозможна.
Простейшим примером резонатора, который удовлетворяет ука-
указанным требованиям, является интерферометр Фабри — Перо [10] с
парой плоскопараллельных зеркал (рис. 7.7). Этот резонатор можно
представить себе как обычный резонатор, имеющий форму замкнутой
цилиндрической поверхности, у которой устранены боковые стенки,
так что модам с высокой добротностью, соответствуют лишь две ква-
квазиплоские волны, бегущие в противоположных направлениях перпен-
перпендикулярно плоскости зеркал. Условия распространения этих волн бо-
более благоприятны, чем любых других волн, распространяющихся под
косыми углами к оптической оси интерферометра Фабри — Перо. То,
что некоторая часть мощности теряется вне резонатора за счет плос-
плоской коллимированности лучей в пучке, приводит к снижению относи-
относительной добротности Q.
Предполагая, что в резонаторах Фабри — Перо основные моды
адекватно представляются плоскими волнами, распространяющимися
между зеркалами в прямом и обратном направлениях (расстояние
между зеркалами равно d), для частот vn этих мод можно написать
простое соотношение: vn = ро(\ + п), где р0 = с /Id — частотный ин-
интервал между двумя соседними модами. Заметим, что в случае когда
в качестве резонатора используется интерферометр Фабри — Перо,
частоту v можно измерить с точностью до величины, кратной v0. По-
Поэтому р0 называют областью свободной дисперсии.
Характерной особенностью этих резонаторов является то, что
каждой его моде соответствует определенное распределение узлов и
пучностей стоячих волн. Однако в некоторых случаях удобно исполь-
использовать резонаторы, моды которых представляют собой бегущие вол-
волны. Например, в кольцевом резонаторе, предложенном Мацеком и
7.2. Общие свойства оптических резонаторов 487
Полупрозрачное
зеркало
Рис. 7.8. Схематическое представление кольцевого резонатора с квадратным располо-
расположением зеркал. Другим типичным расположением зеркал является треугольное. Зеркала
могут быть заменены призмами полного внутреннего отражения, которые имеют более
высокий порог оптического разрушения.
Дэвисом [11], волны распространяются как по часовой, так и против
часовой стрелки (рис. 7.8). Если одну из этих волн удается устранить,
то поле в резонаторе будет представлять собой одну бегущую волну.
Вращение кольцевого резонатора вокруг оси, перпендикулярной его
плоскости, приводит к расщеплению частот этих двух противополож-
противоположно направленных волн. Измеряя их частоту биений, можно опреде-
определить скорость вращения системы. Этот принцип применяется в лазер-
лазерных гироскопах.
Если уширение резонансов, обусловленное потерями резонатора,
становится много больше межмодового интервала, то спектр соб-
собственных значений мод такого резонатора превращается в почти не-
непрерывный. Такого же эффекта можно добиться, если одно из зеркал
резонатора заменить рассеивающей поверхностью. Аналогично, если
в активную среду поместить достаточное количество рассеивающих
частиц, то возникает обратная связь и система может действовать как
лазер. Вообще говоря, резонаторы, имеющие большое число вырож-
вырожденных мод, могут использоваться для создания нерезонансной обрат-
обратной связи [12]. Важное преимущество этих резонаторов перед резона-
резонаторами типа Фабри — Перо заключается в том, что их частота гене-
генерации не зависит от геометрических размеров лазера. Это позволяет
использовать лазеры с такими резонаторами в качестве стандартов
частоты, которые, однако, не имеют преимуществ, связанных с вре-
временной и пространственной когерентностью обычных лазеров.
Для полноты рассмотрения нельзя обойтись без того, чтобы не
упомянуть о распределенной обратной связи, которая позволяет обой-
обойтись без зеркал резонатора. Для сужения спектра излучения инжекци-
онных лазеров Когельник и Шанк [13] впервые предложили использо-
использовать брэгговское отражение двух волн, бегущих в противоположных
направлениях через периодическую среду (см. рис. 3.27), что позволи-
позволило совместить эти лазеры с интегрально-оптической технологией.
488 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
7.3. ЧАСТОТНЫЙ ОТКЛИК РЕЗОНАТОРА
В идеальном резонаторе поле возникает только тогда, когда частота
внешнего возмущения совпадает с собственной частотой резонатора.
Практически же резонатор может быть заметно возбужден в некото-
некоторой узкой полосе частот, включающей в себя собственную частоту ре-
резонатора.
Если поле в резонаторе возбуждается монохроматическим электри-
электрическим (или магнитным) диполем с постоянной амплитудой колеба-
колебаний, то амплитуда поля \F(v)\ в некоторой произвольной точке будет
изменяться с частотой так, как показано на рис. 7.9. В противополож-
противоположность закрытому резонатору резонансная кривая открытого резонато-
резонатора состоит из множества пиков, из которых лишь совсем немногие яв-
являются такими же, как и у закрытого. Это обусловлено тем, что из-за
устранения боковой поверхности сильно уменьшилось эффективное
число мод.
Частичное подавление резонансных пиков происходит вследствие
вывода излучения как непосредственно через зеркала, так и с их краев,
а также вследствие диссипации энергии на неидеально отражающей
поверхности. Поскольку потери в резонаторе возрастают при услож-
усложнении картины распределения поля, ширина резонансного пика для
If И
Основная мода
Рис. 7.9. Качественная зависимость амплитуды частотного отклика \F(p)\ от частоты
для плоскопараллельного резонатора (а), изображенного на рис. 7.7,а, и закрытого ре-
резонатора (б), изображенного на рис. 7.7,6.
7.3. Частотный отклик резонатора 489
данной моды становится тем больше, чем больше ее расстояние от
основной моды.
Рассматривая резонатор как набор резонансных LC-контуров с со-
сосредоточенными параметрами, комплексный частотный отклик F {у)
резонатора можно написать в виде
где рп — собственная частота л-й моды, Q — добротность, определя-
определяющая ширину л-го резонанса, a Fn — весовой коэффициент, зависящий
от геометрических параметров резонатора. Интеграл в правой части
выражения G.3.1) представляет собой вклад непрерывной части спект-
спектра, которая всегда существует в открытых системах. Во многих слу-
случаях удобно использовать комплексную частоту уп = vn + ipn/BQn)9
что позволяет записать знаменатель в резонансном члене выражения
G.3.1) в виде Цу - vnJQn/vn.
Спектр резонатора можно считать дискретным в той степени, в
которой ширина
Av.-v.e;1 G.3.2)
л -й моды меньше расстояния между двумя соседними невырожденны-
невырожденными модами.
В соответствии с выражением G.3.1), если излучение в резонаторе
возбуждается полем, имеющим вид временной б-функции, то генери-
генерируется поле, пропорциональное функции f(t), определяемой выраже-
выражением (если пренебречь вкладом от непрерывной части спектра)
/(f) = I^exp^-m^ + ilnvA G.3.3)
Отсюда следует, что параметр Qn/vn-K представляет собой постоян-
постоянную затухания л-й моды. Предполагая, что возбуждается лишь л-я
мода, Qn можно записать в виде
^ - Запасенная энергия <н i л\
Qn = 2тг— = 2тг^/фотон, G.3.4)
Потери энергии за период
где ^фОТОН — время жизни фотона в резонаторе. В интерферометре
Фабри — Перо моды состоят из двух плоских волн, и поэтому потери
за период колебаний для них эквивалентны потерям энергии за про-
проходу поделенным на соответствующее число совершенных за проход
колебаний. Следовательно, если через ап обозначить потери за про-
проход, то Qn можно записать в виде
Qn = MM.. G.3.5)
где?л = 2irvn/c — волновое число л-й моды и d — длина резонатора.
С добротностью б тесно связан параметр, называемый резкостью
490
Гл. 7. Оптические резонаторы и интерферометры Фабри —« Перо
tn резонатора: ^ = ^ _ ^^ (? 3 6)
Резкость резонатора является мерой ширины резонансов по сравне-
сравнению с областью свободной дисперсии. Таким образом, все величины
Q> F> t фОТон» ОСД и а связаны между собой. Например, Q = Fv/OCJX
и ^
фотон =
= 1/аОСД.
7.4. РАССМОТРЕНИЕ ЗАКРЫТОГО ЭЛЛИПТИЧЕСКОГО
РЕЗОНАТОРА В РАМКАХ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
Для того чтобы ознакомиться с основными особенностями распреде-
распределения полей в резонаторе, рассмотрим точно решаемую (в рамках гео-
геометрической оптики) модель оптического резонатора, состоящего из
цилиндрической полости с эллиптическим сечением, полуоси которого
равны a nrf/2 (рис. 7.10). Чтобы не загромождать рассуждения мате-
математическими выкладками, ограничимся рассмотрением двумерной
конфигурации мод, поле которых и (х, z) не зависит от координа-
координаты .у. В рамках лучевой оптики полем, как показано в гл. 2, можно
записать в виде линейной суперпозиции полей Л exp(-ikS):
u(x,z) = Aie-ikS> + A2e-ikS> + • • • + Ame-ikS». G.4.1)
Разложение поля и по т каноническим функциям, каждая из которых
описывает конгруэнцию лучей, в общем случае зависит от формы гра-
границ. В рассматриваемом случае из симметрии эллипса следует, что и
Рис. 7.10. Сечение цилиндрического эллиптического резонатора. Кривые /* = const и
v = const представляют собой соответственно семейства конфокальных гипербол и эл-
эллипсов. Ось х определяется выражениями v = ± т/2, 0^/*<оо и д = 0,
- х < v < т.
7.4. Рассмотрение закрытого эллиптического резонатора 491
может быть представлена суммой двух функций (например, для коль-
кольцевого резонатора, изображенного на рис. 7.8, требуется восемь функ-
функций, по две на каждое плечо).
Функция S может быть решением уравнения эйконала. В рассмат-
рассматриваемом случае удобно ввести систему эллиптических координат,
определяемую выражениями B.7.10), с ограниченными переменными
/х>Ои~тг<^<^г. Условию /г = const соответствуют эллипсы с
фокусами в точках х = ±Ь, в то время как граница резонатора опре-
определяется кривой pi = /I. При этом простой способ решения уравнения
эйконала состоит в поиске решений вида (см. разд. 2.12; координату v
не надо путать с частотой v)
S(ftv) = Af(/i) + E(v). G.4.2a)
В результате этого мы получаем (см. задачу 1)
["(shV + cos2vc)ll2dfi' + М@), G.4.26)
М(ц) = ±b Г
Jo
?(v)=±b|
J(
(cos2 v' - cos2 vcI/2 dvr + ?@). G.4.2b)
о
Поскольку подынтегральное выражение в интеграле G.4.2в) становит-
становится мнимым при Ы > \рс I, продольное сечение каустики представляет
собой гиперболу v = ±vc (рис. 7.11,в); при этом пространственная
структура мод описывается параметром cosi>c. Распределение для
каждого значения vc в интервале @, я72) зависит, как мы покажем ни-
ниже, от дискретного индекса п, поэтому произвольная мода обознача-
обозначается двумя индексами, учитывающими непрерывный параметр vc и
дискретный параметр п.
В случаях когда рс = ±тг/2, каустика вырождается в прямые ли-
линии, выходящие из фокусов и уходящие в бесконечность (рис. 7.11, а),
в то время как волновые фронты (S = const) вырождаются в окруж-
окружности с центрами в точках х = ±Ь. Лучи с фокусами при х = —6 и
направленные к точке z = + оо описываются уравнением эйконала
S_(/z, v) = S_@, - я/2) - sgn(z)M ch \i + sin v), G.4.3)
где sgn( ) — знаковая функция, принимающая значение + 1 или - 1 в
зависимости от знака аргумента и учитывающая то, что при z < 0
волновые фронты сходятся в направлении к фокусу и расходятся от
него при z > 0. Аналогично, лучи, проходящие через фокус х = Ь и
направленные в точку z = - оо, описываются уравнением эйконала
S+(fr v) = S+@, я/2) + sgn(z)b( ch \i - sin v), G.4.4)
так что окончательно мы можем написать
и = A+e~ikS+ + A-e-ikS~ = u+ + w_. G.4.5)
492
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
8
Рис. 7.11. Моды эллиптического резонатора, полученные суперпозицией двух лучевых
конгруэнции, движущихся соответственно вверх и вниз и описываемых гиперболически-
гиперболическими каустиками с фокусами в точках х = ± Ъ; когда обе каустики вырождаются в ли-
линию, лежащую на оси*, возникают два мнимых фокуса в точкахz = ± ib и мода ста-
становится гауссовой, а — каустики вырождены в линию, лежащую на ochz; б — каустики
с фокусами в точках х = ± b; в — каустики с фокусами в точках z = =fc ib.
Поскольку функция и должна удовлетворять граничному условию,
волновое число к, соответствующее незатухающим колебаниям резо-
резонатора, должно принимать дискретные значения, которые в дальней-
дальнейшем мы будем обозначать через к^ъ. Используя соотношение G.4.5) и
7.4. Рассмотрение закрытого эллиптического резонатора 493
считая поле и на границе резонатора (ji = p) равным нулю, получаем
G.4.6а)
?> V) - Я_(Д, v)] = fcpe3[S+@,7r/2) - S_@, -7Г/2)] ±
± Ik^b ch Д = Bn± + l)n; G.4.66)
в этом выражении знаки плюс и минус относятся к частям границы
соответственно с положительным и отрицательным значением z> Да-
Далее, вычитая выражение G.4.66), записанное для л_ , из такого же вы-
выражения, записанного для п+ , получаем
2*pe3(n,7r/2)bcosД = (и+ - п.)п -> Лрез = пя/Bа), G.4.7)
причем л = л+ — л_ = 1, 2, ....
Рассмотрим теперь случай vc = О (см. рис. 7.11,в). Используя вы-
выражения G.4.2), нетрудно проверить, что формулы G.4.3) и G.4.4)
принимают вид
S±(/x,v) = S±(+irc/2,0) + sgn(z)b( + sh/z + icosv). G.4.8)
Эти эйконалы описывают поля с фокусами в точках с эллиптическими
координатами \kf — ^i/2nvf= 0, которые в прямоугольных коорди-
координатах соответствуют точкам хf = 0 и Z/ = ±ib. Соответствующие
поля запишутся в виде
M±(^v) = exp[-ifcS±(Tni/2,0) + isgn(z)kbshfi -h sgn(z)kbcosv] г
S exp[-ifcS±( + i7c/2,O) + i/cz + fcb - $kbx2/(b2 + z2)], G.4.9)
где cos v мы заменили его приближенным выражением 1 — v2/2. В то
время как для действительных фокусов поле и± имеет однородный
волновой фронт, в случае мнимых фокусов его волновой фронт прини-
принимает гауссову форму, т. е. амплитуда поля экспоненциально спадает с
квадратом расстояния х2 от оси z. Обе моды, определяемые выраже-
выражением G.4.9), можно объединить, чтобы получить моду колебаний, ко-
которая удовлетворяет следующему резонансному условию, аналогично-
аналогичному G.4.7):
nnld> «=1,2,.... G.4.10)
Вообще говоря, каждая мода, соответствующая определенному
значению рс, описывается гиперболической каустикой. При рс = 0 обе
ветви гиперболы стремятся прижаться к оси z и поле сосредоточива-
сосредоточивается вдоль малой оси эллиптического резонатора. Моды с vc > 0 за-
занимают большую часть объема резонатора и называется неустойчи-
неустойчивыми, в то время как моды с vc = 0 называются устойчивыми. Если
удалить значительную часть стенок эллиптического резонатора, то
это никак не отразится на распределении поля в устойчивых модах
(рис. 7.12,а), но сильно повлияет на распределение поля в неустойчи-
494 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Hay с тина
Рис. 7.12. а — устойчивый резонатор с зеркалами в виде бесконечных полос, получен-
полученный устранением части поверхности закрытого эллиптического резонатора вблизи вер-
вершин большой оси; при удалении от оси резонатора поле быстро уменьшается и может
быть представлено затухающей волной с чисто мнимым волновым вектором
к( = /1 kt I; на отражающие поверхности падает излучение с почти гауссовым профилем
интенсивности; б — неустойчивый резонатор с зеркалами в виде бесконечных полос, по-
полученный удалением части поверхности вблизи вершин малой оси; следует обратить
внимание на постепенное расхождение лучей после каждого отражения, вследствие чего
отражатели освещаются почти однородно.
вых модах (рис. 7.12,6), а именно приведет к так называемым радиа-
радиационным потерям.
7.5. ЛИНЕЙНЫЕ РЕЗОНАТОРЫ
Математические выражения, полученные нами для эллиптических ре-
резонаторов, качественно справедливы и для большинства открытых ре-
резонаторов, которые представляют собой обычно конструкцию из двух
зеркал, обращенных друг к другу отражающими поверхностями. Это
7.5. Линейные резонаторы
495
Рис. 7.13. Простой линейный оптический резонатор. Излучение из резонатора выво-
выводится различными способами: с помощью частично просветленного зеркала, с по-
помощью отверстия, высверленного в одном из глухих зеркал, или с использованием лу-
лучей, претерпевших дифракцию на краях зеркала (в неустойчивых резонаторах).
так называемый линейный резонатор, показанный на рис. 7.13. Попе-
Поперечными размерами линейного резонатора можно пренебречь и, сле-
следовательно, считать, что он имеет одну размерность, которая опреде-
определяет оптическую ось. Поле в таком резонаторе можно рассматривать
в геометрическом приближении в виде exp(-/?S), представляющем
собой поперечные электромагнитные (ТЕМ) волны. Эти предположе-
предположения позволят нам в последующих разделах применить приближение
параксиальной оптики, для которой построен метод лучевых матриц.
Кроме того, моды линейного резонатора можно подразделить на
устойчивые и неустойчивые. В то время как в замкнутых эллиптиче-
эллиптических резонаторах могут существовать моды обоих этих типов, в от-
открытых резонаторах может быть лишь один тип колебаний, и поэто-
поэтому резонаторы подразделяются на устойчивые и неустойчивые. Мо-
Моды устойчивого резонатора концентрируются вблизи оптической оси,
и, вообще говоря, на них не влияют размеры зеркал. Моды неустой-
неустойчивого резонатора заполняют весь объем резонатора и сильно зависят
от формы и размеров зеркал. Неустойчивые резонаторы применяют в
тех лазерах, в которых необходимо возбуждать генерацию в больших
объемах активной среды (как, например, в лазерах высокой мощно-
мощности). Характерной особенностью неустойчивых резонаторов является
то, что излучение на выходе лазеров с такими резонаторами является
пульсирующим (рис. 7.14).
В устойчивом резонаторе компонента к, волнового вектора, пер-
перпендикулярного оптической оси, является мнимой; действительно, ве-
вещественная величина к, означала бы, что сечение пучка изменяется
при его отражении (рис. 7.12).
Устойчивые моды, как известно, ограничены каустической поверх-
496
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Рис. 7.14. Распределения интенсивности поля в ближней (верхний ряд диаграммы) и
дальней (нижний ряд диаграммы) зонах, вычисленные для неустойчивых конфокальных
резонаторов. Представлены два типа диаграмм для различных чисел Френеля N и раз-
разных значений увеличения М. а — N = 3, М = 1,42; б — N = 60, М = 5. (Из работы
Ренша и Честера [13а].)
ностью, которая как бы заменяет недостающую боковую поверхность
резонатора и удерживает пучок вблизи оптической оси. Если диаметр
зеркал резонатора сделать достаточно большим, то краевой эффект в
резонаторе будет отсутствовать и резонатор не будет иметь дифрак-
дифракционных потерь.
Среди всех возможных конфигураций резонаторов, отличающихся
радиусом кривизны и расстоянием d между зеркалами, в настоящее
время используется лишь небольшое их число (рис. 7.15). Первым из
них стоит упомянуть плоскопараллельный резонатор (интерферо-
(интерферометр) Фабри —Перо, который является прародителем всех открытых
резонаторов. В симметричном конфокальном резонаторе два одина-
одинаковых зеркала, разделенных расстоянием rf, имеют одинаковые радиу-
радиусы кривизны. Сферический резонатор получается при разнесении зер-
зеркал с одинаковой кривизной на удвоенное фокусное расстояние. По-
Полусферический и полуконфокальный резонаторы состоят из плоского
зеркала и половины сферического или конфокального резонатора.
7.6. Рассмотрение резонатора как последовательности линз
497
Рис. 7.15. Распределение интенсивности излучения внутри резонатора для различных
конфигураций резонаторов, а — плоскопараллельный резонатор; б — с зеркалами боль-
большого радиуса кривизны; в — конфокальный; г — сферический; д — вогнутовыпуклый;
е — полусферический. (Из работы Блума [136].)
Особенность плоского и сферического резонаторов состоит в том,
что они слабо устойчивы, т. е. любое небольшое отклонение их гео-
геометрии от идеальной сразу же делает их неустойчивыми.
7.6. РАССМОТРЕНИЕ РЕЗОНАТОРА
КАК ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЗ
С целью ограничения числа параметров, определяющих положение и
размеры зеркал, любой резонатор можно рассматривать как периоди-
периодическую фокусирующую систему, в которой траекториям световых лу-
лучей, распространяющихся в прямом и обратном направлениях между
зеркалами, поставлены в соответствие траектории лучей, периодиче-
периодически меняющих свое направление при попадании на искривленные по-
поверхности линз. В параксиальном приближении тонкая линза эквива-
эквивалентна зеркалу с таким же фокусным расстоянием, так что резонатор
можно рассматривать как бесконечную последовательность линз, фо-
фокусные расстояния которых равны фокусному расстоянию соответст-
соответствующих зеркал, а расстояние d между линзами равно длине резонато-
резонатора (рис. 7.16) (принято считать, что радиус кривизны вогнутого зерка-
зеркала положителен, а выпуклого — отрицателен). Таким образом, пове-
поведение волнового фронта в резонаторе можно изучать, рассматривая
498
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Рис. 7.16. Последовательность линз, эквивалентная резонатору, изображенному на рис.
7.13. Расстояние zt берется с положительным знаком, если соответствующий фокус рас-
располагается с левой стороны линзы L..
его распространение в оптической линии передачи (состоящей из бес-
бесконечной последовательности линз Lt, таких, что линза L{ имеет такие
же характеристики, как и линза Li+2), моды которой взаимно одно-
однозначно соответствуют модам резонатора.
Характеристики этих мод можно найти по изображению точечного
источника, расположенного в произвольной точке оптической оси лин-
линзового волновода. Предположим, что при прохождении луча через
линзу L, он пересекает оптическую ось на расстоянии z/41 от плоско-
плоскости линзыLl + 1. Заметим, что в общем случае как*,, так иг/+, отли-
отличаются otz0 (расстояние от точечного источника до линзы Lo), если
только z0 не принимают некоторых конкретных значений. Действи-
Действительно, распределение изображения получается периодическим, когда
Z2 = ^о» так что в соответствии с формулой тонкой линзы условие
взаимного отображения можно записать следующим образом:
1/zo + W - гг) = 1/Л, 1/z, + l/(d - z0) = 1//2. G.6.1)
Отсюда мы получаем два решения дляг0, каждое из которых пред-
представляет собой расстояние от двух фокусов пучка до зеркала 1:
z<±> = d{l/2 + [дх -в2± 2(д\д\ - gig2)lf2Vl2(gt +g2- 2д1в2)]}; G.6.2)
здесь мы ввели параметры g, определяемые выражением
01.2 = 1 - d/Bfia). G.6.3)
В конфокальной конфигурации фокусы двух зеркал совпадают (rf =
= /i + fi)- Это условие, записанное через параметры g, имеет следу-
следующий вид:
01 + 02 = 20102- G.6.4)
Следовательно, если g2xg\ > gxg2> то в соответствии с G.6.2) один пу-
пучок является коллимированным, а другой имеет общий фокус с одним
из зеркал (рис. 7.17), и мы имеем
4+) = оо и z<0"> = d/[2(l - дЛ. G.6.5)
7.6. Рассмотрение резонатора как последовательности линз
499
Рис. 7.17. Последовательность
линз, эквивалентная конфокаль-
конфокальному резонатору. Обратите
внимание на то, что один пучок
является коллимированным, а
другой — конфокальным с зер-
зеркалами.
В соответствии со знаком подкоренного выражения в G.6.2) коорди-
координаты источника могут быть либо вещественными, либо комплексны-
комплексными; в частности, координаты будут комплексными (которые, как мы
выясним ниже, соответствуют устойчивым резонаторам), если вы-
выполняется условие
1 >: дхд2 > 0, G.6.6)
Вещественные же значения координат соответствуют неустойчивому
резонатору.
Рассматривая в разд. 7.7 свойства гауссовых пучков, связанных с
комплексными координатами источника, мы покажем, что настоящая
классификация резонаторов совпадает с приведенной в разд. 7.4. Сле-
Следовательно, моды резонатора могут быть описаны гауссовыми пучка-
пучками, только если произведение gx g2 удовлетворяет неравенству G.6.6).
Таблица 7.1. Координаты фокусов сферических волн, образующих основные моды
+ —
Резонатор — —
Плоскопараллельный
С зеркалами большого радиуса
Конфокальный
Сферический
1/2 + i
1
[2A -д)У12
1/2 + i/1
1/2
1/2 -I-
1
1/2 - цг
1/2
500 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
В табл. 7.1. перечислены комплексные координаты фокусов для наи-
наиболее распространенных резонаторов. Обратите внимание на то, что
плоские и сферические резонаторы имеют действительные фокусы в
соответствии с их определением как слабоустойчивых резонаторов
(см. конец разд. 7.5).
В параксиальном приближении любое распределение поля и в пло-
плоскости z = z0 является периодически повторяющимся. Таким образом,
распределение поля будем искать в виде
u(p,z) = 2ik u(po,zo)G(p - po,z - zo)dxodyo =
m(p,z-z0\ G.6.7a)
где G — функция Грина для однородной области, а функции//m(z0)
определяются выражением
00
/Im(z0)= \\u(po,zo)xloyZdxodyo. G.6.76)
— оо
Функция Грина G может быть разложена в ряд по степеням х {> у g7, ко-
коэффициентами которого являются функции
ulm(p,z) = (д1/дх10)(дт/ду%)С(р - p0,z)L=yo = o , G.6.7b)
которые описывают поле, излучаемое мультиполем, расположенным
в точке z 0 и имеющим порядок /в направлении оси л: ит — в направ-
направлении оси>>. Таким образом, любое поле и можно представить в виде
суперпозиции мод uim, имеющих фокус в точке z = z0 на оптической
оси.
7.7. ПОЛЯ ОТ ИСТОЧНИКОВ,
РАСПОЛОЖЕННЫХ В КОМПЛЕКСНОЙ ПЛОСКОСТИ
Выше мы показали, что если источник расположен в точке с вещест-
вещественной координатой z0, to поле, обусловленное этим источником и
распространяющееся вдоль цепочки линз, полностью описывается по-
последовательностью фокальных точек, определяемых выражением
G.6.2) (см. пример, иллюстрируемый на рис. 7.16). Менее наглядна
физическая интерпретация другого случая, а именно когда положение
источника определяется комплексной координатойz0. Вообще говоря,
в этой ситуации легче было бы отбросить саму возможность распро-
распространения излучения и по аналогии с электромагнитными волнами в
7.7. Поля от источников, расположенных в комплексной плоскости 501
металлических волноводах с частотами ниже частоты отсечки сделать
вывод о том, что при комплексных z 0 излучение вдоль цепочки линз
распространяться не может. Однако известно, что в структурах, по-
подобных волноводной, существует стационарное поле, амплитуда кото-
которого вдоль оси волновода экспоненциально убывает. Отсюда можно
предположить, что в рассматриваемом случае поле также будет зату-
затухать в направлениях, перпендикулярных оптической оси.
С учетом этих предварительных замечаний рассмотрим источник
5' , расположенный в точке Р с координатами @, 0, —/6). Излучаемое
им поле пропорционально скалярной функции Грина G, которая в
предположении, что величина р = (к2 + у 2I/2 много меньше
Iz + ib I, определяется формулой Френеля (см. разд. 4.10)
G = 1/[4tc(z + ib)]exp[-ifc(z 4- ib + (l/2)p2/(z + Щ]. G.7.1)
Согласно этому определению, G описывает волну, распространяю-
распространяющуюся из точки z = — оо в точку источника и из точки источника в
точку z = +оо; следовательно^ не удовлетворяет однородным об-
образом излучательному условию Зоммерфельда и не может рассматри-
рассматриваться как уходящая функция Грина.
Записывая тождества
l/q(z) ss l/(z + ib) = z/(z2 + b2) - ib/(z2 + b2) = l/R{z) - iA/[*w2(z)], G.7.2a)
ф ж arctg(z/b ), G 7 26)
мы имеем y/.t.wj
l/(z + ib) = -(i/6)[w0Mz)]e^, G.7.2b)
где w0 = w @) = (ХЬ /тгI/2. Выбрав значения b положительными и та-
таким образом обеспечив затухание функции G в направлениях от опти-
оптической оси, получим
w(z)
ехр
^ехрГ-Zfcz + ?Л + Ы>\ G.7.3)
В соответствии с выражением G.7.3) функция w (z) соответствует
радиальному расстоянию, на котором амплитуда поля уменьшается в
е раз относительно своего максимального значения. В противополож-
противоположность сферической волне поле, излучаемое источниками, расположен-
расположенными в комплексных точках, на сферической поверхности постоянной
фазы имеет гауссово распределение амплитуды, и излучение, распро-
распространяющееся вдоль ochz, по существу ограничено сечением радиусом
н> (z) в плоскости ху. Если величина w очень мала, то поле можно
представить пучком лучей, распространяющихся параллельно оси z.
Таким образом, переход от вещественных координат z0 к комплекс-
502
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Рис. 7.18. Вид сбоку на гауссов пучок. Показаны волновые фронты, перетяжка, рэлеев-
ская длина Ь и угол дифракции в.
ным преобразует сферическую волну в пучки более или менее хорошо
коллимированных лучей.
Ширина w (z) пятна гауссова пучка изменяется с расстоянием z в
соответствии с выражением
w2(z) = wg(l + z2/b2) G.7.4)
и имеет минимальное значение при z = 0, что согласуется с определе-
определением перетяжки гауссова пучка w0 как характерного параметра. Пу-
Пучок ограничен поверхностью гиперболоида, пересечения которого с
плоскостями, перпендикулярными оси z, представляют собой окруж-
окружности радиусом w(z) (рис. 7.18). Величину Ь можно рассматривать
как расстояние от перетяжки, на котором пучок еще можно считать
хорошо коллимированным. Вне участка z = Ъ (обозначаемого также
zR), который называют, как правило, рэлеевской длиной, из-за ди-
дифракционных эффектов пучок начинает расходиться.
По мере удаления от перетяжки гиперболоид w (z), ограничиваю-
ограничивающий контур пучка, все больше принимает форму конуса, угол полу-
полураствора которого равен полууглу расходимости 0пучок в дальней зоне,
определяемому выражением
Япучок = atctg [A/Grw0)] s A/(tcw0) = [Я/(яЬ)]1/2. G.7.5)
В соответствии с выражением G.7.5) чем уже перетяжка, тем боль-
больше апертура пучка; это согласуется с представлением о том, что поле
в дальней зоне является фурье-образом поля в перетяжке. Здесь мож-
можно провести аналогию с ситуацией, которая имеет место в случае ще-
щелевой антенны для главного лепестка ее диаграммы излучения.
Из выражения G.7.2а) непосредственно следует, что радиус кривиз-
кривизны волнового фронтаR (z) = z + b2/z в перетяжке становится очень
большим. При удалении от перетяжки величина/? сначала уменьшает-
уменьшается и достигает минимального значения 2 Ъ на расстоянии Ь, а затем
вновь увеличивается и в конечном счете становится равной z.
Проведенное выше рассмотрение предполагает, что векторы Е и Н
строго и полностью определяются функцией Грина G. Здесь стоит на-
7.8. Эомит-гауссовы и лагерр-гауссовы пучки 503
помнить, не вдаваясь в подробности, некоторые выводы из векторно-
векторного анализа волновых пучков, полученные Губау и Шверингом [14]. Ис-
Используя подход, основанный на решении уравнений Максвелла, эти ав-
авторы показали, что волновые пучки только тогда адекватно описыва-
описываются выражениями, аналогичными G.7.3), когда они немного расхо-
расходятся (на несколько градусов). Этот результат согласуется с тем фак-
фактом, что только хорошо коллимированные пучки могут быть пред-
представлены ТЕМ-волнами, к которым применение скалярной теории яв-
является корректным.
7.8. ЭРМИТ-ГАУССОВЫ И ЛАГЕРР-ГАУССОВЫ ПУЧКИ
При выводе выражений для полей, описывающих оптические пучки,
можно использовать аналогию между гауссовыми пучками и сфериче-
сферическими волнами. Действительно, сферические волны принадлежат об-
обширному семейству мультипольных полей, в котором они представля-
представляют мультиполь нулевого порядка. Можно предположить, что то же
самое справедливо и для гауссовых пучков, определяемых формулами
G.6,7а)—G.6.7b).
Поскольку мультипольные поля, определяемые выражением
G.6.7в), не являются взаимно ортогональными в поперечной пло-
плоскости, найдем другое (более удобное) семейство мультиполей,
называемых модами, которые затем используем в качестве базиса при
разложении поля. Для этого запишем поле в виде и (рс, у, z) =
= А (х, у, z)eikz, где к = kf + ik" — в общем случае комплексная по-
постоянная распространения. Нетрудно показать, что в рамках паракси-
параксиального приближения для и амплитуда Л удовлетворяет параболиче-
параболическому волновому уравнению, рассмотренному в разд. 2.6 гл. 2 настоя-
настоящей книги. Будем искать решение этого уравнения в виде
u(p,z) = [l/w(z)]/[21/2p/wW]exp{-i[jJW + WBq)lp2 + Ь]} =
= >l(p,z)exp(-ifcz), G.8.1)
гдер = ybc + $У, a w (z) и # (z) — соответственно размер перетяжки и
комплексная кривизна волнового фронта гауссова пучка, определяе-
определяемые формулами G.7.2), в которых длина волны X = 2-к/к' и фазовый
множитель j3(z) (не путать /3 с волновым вектором) должны быть
определены вместе с неизвестной функцией /. Подстановка выражения
G.8.1) в B.6.12) дает следующее уравнение:
[V,2 - D/w2)p • РJ/ = D/w2 + 2к dfi/dz)f = |iW/, G.8.2)
где V, = х д/дх + 9 д/ду. Предположим, что/ — квадратично-
интегрируемая функция в плоскости ху. Тогда уравнение G.8.2) одно-
504 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
значно определяет/ (х, у) как собственную функцию дифференциаль-
дифференциального оператора, стоящего в левой части уравнения, с собственным
значением /x(w). Вспоминая, что дифференциальное уравнение, кото-
которому удовлетворяют полиномы Эрмита, записывается в виде
d2HJt)ldt2 - It dHm(t)/dt = -2mHJt\ G.8.3)
можно сразу показать, что в прямоугольной декартовой системе коор-
координат нормализованные собственные функции уравнения G.8.2) запи-
запишутся в виде
fm(x,y) = Gc2/+m-1/!m!)-1/2H/B1/2x/vv)HwB1/2y/w), G.8.4)
причем соответствующие им собственные значения даются выраже-
А**» = -D/w2)(J + m). G.8.5)
Сравнивая последнее выражение с выражением для /x(w) из G.8.2),
получаем следующее дифференциальное уравнение:
A + ik"/k')dpjdz = -2(т + / + l)/[fc'w2(z)] = -(т + I + l)b/(z2 + Ь2\
G.8.6)
решение которого для /3/m = fi'lm - iC'/m записывается в комплексном
виде следующим образом:
(/ + т + 1) Xz (I + т + 1) . . . п о 7ч
^ = ITlkW arctg ^ = TTTFvF^2^ G-8Л)
здесь \f/(z) определяется выражением G.7.26).
Следует заметить, что, согласно G.8.1), кривизна фазового фронта
не зависит от порядка моды / й т, в то время как фазовая скорость
vlm уменьшается с ростом порядка моды и увеличивается с расстояни-
расстоянием от перетяжки пучка:
о
(d/dzWlm
= ^ „)
1 + [(/ + т + t)/(bfe')]{l/[l + (z/bJ]}{l/[l + (к"/к'П} ¦ К • • '
Из табл. 7.2 можно определить некоторые моды низших порядков
= Л ffi exp(-ikz), используя выражение
Для данного к функции и ffi 9 являющиеся собственными функция-
функциями лапласиана V2 и имеющие собственные значения к2, образуют
полный и ортонормированный набор мод, который заменяет мульти-
польные поля, определяемые выражением G.6.7в). Верхний индекс (Н)
7.8. Эрмит-гауссбвы и лагерр-гауссовы пучки 505
Таблица 7.2. Полиномы Эрмита (в колонке слева) и обобщенные полиномы Лагерра
(в колонке справа) низших порядков
яо@ = 1 ~~~ 4@ = 1
ЯДГ) = 2t L[(t) = I + 1 - t
H2(t) -At1 —2 Ll2(t) = (/ + 2)f + —
H3(t) = St3 - 12t L'3(f) =
HH+l = 2tHH-2nHH-1
W +
2 v ' 2
(/ + 1)(/ + 2)(/ +3) (/ + 2)(/ + 3)
6 2
/_+3 2_^
+ 2 ^ ~6~
n — m/ m!
употребляется для того, чтобы отличить пучки, записанные в прямо-
прямоугольных координатах, для которых естественным выбором являются
полиномы Эрмита, от пучков в полярных координатах, где удобнее
использовать полиномы Лагерра. Действительно, уравнение G.8.2)
допускает также следующий набор решений, представляемых в виде
комбинации полиномов Лагерра и тригонометрических функций:
G.8.10)
TjytLlp — полиномы Лагерра с радиальным индексом р и угловым ин-
индексом /.Это нетрудно доказать, используя те же рассуждения, с по-
помощью которых было получено выше выражение G.8.4). Замена по-
полиномов эрмита полиномами Лагерра приводит к следующему выра-
выражению для фазового множителя Рр1:
/W = СBр + / + 1)/A + 1кк'Ш*\ G.8.11)
так что и <{;> можно теперь записать в виде
м„г =
VлA + р)! \ w) \ w2j\cosЩ
G.8.9а)
506
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Таблица 7.3. Гауссовы пучки в прямоугольной [и^(х, у, z)] и цилиндрической
[u^f(pt z)] системах координат
) = wo(l+z2/b2I/2,
«H—(p/wXl -Pa/w V-3*f" * }uoo
2 (cos<pj
:B1/2p/w)'
- 2p2w2) x
В табл. 7.3 приведены некоторые моды uty низших порядков.
Легко проверить, что любую моду и$ можно представить в виде
линейной комбинации мод uffi [например, м<$ = (м<Ц> + и<$)/4].
На рис. 7.19 показаны распределения интенсивностей для нескольких
мод
ТЕМП
* I 1,6 \ \ 0,6 0 0,8 1,6 p/w00
10 01 00
Рис. 7.19. Распределение интенсивности некоторых мод в цилиндрических координатах.
7.8. Эрмит-гауссовы и лагерр-гауссовы пучки
507
На рис. 7.19 приведено также распределение интенсивности
ТЕМ01.-моды, которая представляет собой гибридную моду с угло-
угловым распределением, возникающим в результате некогерентной супер-
суперпозиции двух ТЕМ01-мод, каждая из которых пропорциональна либо
соьф, либо sin0:
иол»(х,у) ос (ajsintf» + 6cos<?)pexp(-p2/w2); G.8.12)
Рис. 7.20. Распределение ин-
интенсивности основной моды
(я) и гибридной моды
ТЕМ01. (б).
508
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
00
ТЕМ
20
ТЕМ
21
ТЕМ
22
Рис. 7.21. Пространственная структура и конфигурация поля для некоторых мод гауссо-
гауссовых пучков. Длина стрелки и ее направление соответствуют амплитуде и поляризации
лагерр-гауссовой моды.
здесь а и Ь флуктуируют независимо друг от друга (например,
вследствие нестабильной работы лазера). В случае когда <а2> =
= (Ь 2>, средняя интенсивность /01„ моды ТЕМ01* записывается в виде
(рис. 7.19 и 7.20)
/01<ос<я2>р2ехр(-2р2). G.8.13)
Моды Лагерра — Гаусса в случае / = 0 являются аксиально-
симметричными и соответствуют набору темных колец, число кото-
которых равно/7. Прир = 0 поле и§) имеет 2/ радиальных темных полос.
С ростом радиальных и угловых индексов растет и секционирование
мод. В случае эрмит-гауссовых мод темные кольца заменяются поло-
полосами, параллельными осям симметрии. Число полос совпадает с но-
номером соответствующего индекса. На рис. 7.21 показана пространст-
пространственная структура мод и конфигурации мод для линейно-
поляризованных мод Лагерра —- Гаусса (обратите внимание на торои-
тороидальную форму моды
7.9. ПРИМЕНЕНИЕ ЛУЧЕВЫХ МАТРИЦ
ДЛЯ ОПИСАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЗ,
ЭКВИВАЛЕНТНОЙ РЕЗОНАТОРУ
Альтернативным методом решения систем уравнений, описывающих
последовательное построение изображения осевого источника [см. вы-
выражение G.6.1)], является использование формализма лучевых матриц
(см. разд. 2.15). Этот метод представляет собой по существу метод,
разработанный Пирсом для анализа прохождения электронного пучка
7.9. Применение лучевых матриц
509
По
Рис. 7.22. Элементы последовательности линз. Плоскости По и Пр касательные к по-
поверхностям линз, являются соответственно входными и выходными плоскостями блока
(см. на рис. 7.16 прямоугольную область, очерченную штриховой линией).
через последовательность электронных линз (см., например, работу
Стеффена [27], указанную в литературе к гл. 2 настоящей книги).
Группируя эквивалентную резонатору последовательность линз в
блоки, образуемые наименьшим числом элементов (рис. 7.22), мы мо-
можем записать соотношение ,_.„
Ўi+i=y*i> G.9.1)
где вектор V, (рис. 7.23) зависит от пространственной р, и угловой ф,
координат меридионального луча на входе/-го блока, в то время как
у зависит от фазового сдвига и ослабления вектора V, при прохожде-
прохождении через блок.
7.9.1. Увеличение
Вводя лучевую матрицу S блоков, соотношение G.9.1) можно перепи-
переписать в виде (п Q
S • v = yv. G.9.2)
Это соотношение определяет величину у как собственное значение
матрицы S. Из вида этой матрицы [см. выражение B.15.21)] с учетом
того, что detlSt = 1, следует
у± = (А + D)/2 ± /{1 - [(А + D)/2]2}1/2 ^ e±id; G.9.3)
i
Рис. 7.23. Цепочка четырехполюсников, эквивалентная бесконечной последовательности
линз. vf. = Ц, ф}) — двухкомпонентный вектор, составленный из пространственной р{ и
угловой ф1 координат луча на входе /-го блока.
510 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
здесь 5 = arccos[(l/2)(/l +?>)]. В соответствии с комплексным или
вещественным значением 5 величина вектора v либо изменяется, либо
остается постоянной вдоль цепочки четырехполюсников. Обобщая не-
неравенство G.6.6), можно получить следующее условие устойчивости
резонатора: \A + D\<2. G.9.4)
Если величина у вещественна и больше единицы, то при прохождении
пучка через один блок она соответствует увеличению М пучка. Из
рис. 7.17 и 7.23 мы видим, что величинам совпадает с отношением
Pi + i/Pj высот луча на выходной и входной плоскостях блока. Таким
образом, для последовательности линз, изображенной на рис. 7.16,
имеем
у = М = Pt+Jpi = [zj(d - ZxW^ilid - z2)]. G.9.5)
Отсюда, используя выражение G.6.2), можно определить увеличение
М за полный обход резонатора с параметрами g x ng2:
АГ= [1 + A - дТ1Я21IBУИ - A - Л1*!1I72]. G.9.6)
7.9.2. Комплексная кривизна волнового фронта
Вектор v при известном у можно записать через собственные векторы
v± матрицы S в виде
G.9.7)
Отсюда следует, что углы наклона ф± лучей, входящие в выражение
для У±, связаны с их высотами соотношением
Р±/Ф±**~В/(А-у±). G.9.8)
Поскольку, согласно геометрической оптике, поле и (х, у) пропорцио-
пропорционально величине exp[—ikS(x, у)] и угол наклона ф луча связан cS со-
соотношением ф = dS/ dp, из G.9.8) можно получить следующее выра-
выражение:
S±(P) - У\У± - А)/В = ip2/q±9 G.9.9)
где q ± — комплексная кривизна волнового фронта, удовлетворяющая
соотношению
1/9± = -A/2B){U-I»±i[4-M + DJ]1/2}, G.9.10)
которое согласуется с условием G.9.4) устойчивости резонатора с га-
гауссовыми модами.
Комплексную кривизну волнового фронта на выходе каждого бло-
блока можно получить, используй простое соотношение
4вых= (А1вх + B)/(Cqn + D\ G.9.11)
известное как закон ABCD и которое нетрудно проверить подстанов-
7.9. Применение лучевых матриц 511
койд = р/ф. Если полдвх понимается величина, определяемая выра-
выражением G.9.10), то как следствие самосопряженности лучков, образуе-
образуемых лучами, удовлетворяющими G.9.10), мы имеемдвых = двх.
В заключение можно показать, что для резонаторов, описываемых
параметрами g{ и#2, матрица S = S12-S21 записывается следующим
образом:
202 - 1 2g2d
;jB0i02 -01 ~9г) *"-<*--i*--* ' G.9.12)
Заменой индексов можно получить аналогичное выражение для
S21S12. Выражение G.9.10) для^ и<72 относительно двух зеркал дает
l'/qx = l/Rt - i(\ld)\_{gjg2)(\ - gxg2)Yl2\ G.9.13a)
I/ft = l/«2 - Ч№Иаг1Я1*\ " 9i92)V12. G.9.136)
В устойчивых резонаторах коэффициенты при мнимой единице в пра-
правых частях выражений G.9.13) определяют размер пятна и>,:
w2/(Xd) » Nx = A/пШд1/д2)A - 0102)]/2, G.9.14а)
w22/(M) = N2 = (l/rt)[@2/01)(l ^ g^JY112 G.9.146)
(где NA и N2 — число Френеля для первого и второго зеркал). Для
симметричного резонатора числа Френеля одинаковы и равны N =
= ж~1A — ?2)~1/2, а размер пятна соответственно равен w =
= (kR/*)l/2[d/BR -
7.9.3. Диаграмма устойчивости Бойда — Когельника
Предыдущее обсуждение выявило связь между условием устойчивости
G.6.6) и поперечным распределением мод внутри резонатора (эквива-
(эквивалентной последовательности линз). Диаграмма устойчивости Бой-
да — Когельника [15], построенная в соответствии с неравенством
[7.6.6] (рис. 7.24), обобщает модовые свойства как оптических резона-
резонаторов, так и периодических фокусирующих систем. Любой резонатор
представляется отдельной точкой в плоскости gxg2. Резонаторы, рас-
расположенные в незаштрихованных областях, устойчивы в том смысле,
что любая осциллирующая лучевая траектория всегда остается огра-
ограниченной их пределами. Наоборот, для систем, расположенных в за-
заштрихованных областях, решения уравнения vl + 1S-v, = (S)' -v0 явля-
являются расходящимися, а соответствующие им лучевые траектории —
пространственно неограниченными. Если параметры g резонатора та-
таковы, что соответствующие им точка лежат достаточно глубоко в об-
области устойчивости, то основная мода этого резонатора будет огра-
512
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Рис. 7.24. Диаграмма Бойда — Когельника. Незаштрихованные области на плоскости
gjg 2 (g j 2 — параметры, определяемые значениями радиусов зеркал и расстояний d
между ними) соответствуют устойчивым конфигурациям резонаторов (низким
потерям), а заштрихованные — неустойчивым конфигурациям (высоким потерям).
ничена небольшим пространством в окрестности оптической оси, а
энергетические потери в этой моде, связанные с дифракцией пучка на
краях зеркал, будут минимальны. Наоборот, в неустойчивых резона-
резонаторах потери значительно выше — недостаток, который вполне ком-
компенсируется большим модовым объемом и более эффективной ди-
дифракционной связью, которая устраняет недостатки частично пропу-
пропускающих зеркал.
Анализ в рамках волновой оптики, представленный в разд.
7.14—7.19, показывает, что в устойчивом резонаторе поперечные раз-
размеры мод увеличиваются при приближении к границам областей
устойчивости. В частности, слабо устойчивые резонаторы (т. е. нахо-
находящиеся очень близко к границе устойчивости) ведут себя аналогично
открытому волноводу, у которого стенками являются зеркала резона-
резонатора и распространение излучения происходит в перпендикулярном
оптической оси направлении [2]. Эти волноводы работают в области
7.10. Модовое представление поля 513
критических углов, что обеспечивает близкие к единице коэффициенты
отражения на открытых концах.
7.10. МОДОВОЕ ПРЕДСТАВЛЕНИЕ ПОЛЯ
ВНУТРИ УСТОЙЧИВОГО РЕЗОНАТОРА,
НЕ ИМЕЮЩЕГО ДИФРАКЦИОННЫХ ПОТЕРЬ
Рассмотрим линейный резонатор, ограниченный двумя бесконечно
протяженными сферическими зеркалами с коэффициентами отражения
по амплитуде г j иг2. Для того чтобы найти поле и, возбуждаемое ис-
источником гармонических колебаний, расположенным внутри резона-
резонатора, удобно представить и как сумму собственных функций Ф1тп (то>
что у Ф!тп используются три индекса, мы объясним ниже) лапласиана
V2 (см. работу ван Бладеля [8], указанную в литературе к гл. 4 насто-
настоящей книги):
У2Ф1тп=~к1пФ1тп, G.10.1)
удовлетворяющих следующему условию ортогональности (см. зада-
чу 7):
(fcfw - *•?-) I j I Virtn^ndV = 0, G.10.2)
Резонатор
и граничному условию на поверхности зеркал (ср. с разд. 3.23):
дФ!тп/дп0 = (-'Vfo)^^' G.10.3)
где импеданс на поверхности зависит от коэффициента отражения,
т. е. Zs = (г - \)/(г + 1).
Поле Е(г, О» наведенное полем поляризации Р(г, t), присутствую-
присутствующим внутри резонатора, удовлетворяет неоднородному уравнению
Гельмгольца и граничному условию G.10.3) на зеркалах. Если Р и Е
являются линейно-поляризованными и ортогональными оптической
оси и VP = 0, то уравнение A.1.11) сводится к неоднородному ска-
скалярному уравнению Гельмгольца:
V2E(r) + (о2/с2)Е = -ti0co2P(r). G.10.4)
Разложим вектор электрического поля Е в ряд по модам резонатора:
Е(г) = ?Е„Фи(г), GШ5)
л
где три индекса 1тп мы суммировали в один. При этом уравнение
G.10.4) принимает вид
?Е„(*2 - /с2)Ф„ = -co2/ioP. GЛ0.б)
Отсюда находим следующее выражение для коэффициентов Е„:
Е1^-Щу-к^?р- GЛ0-7)
514 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
При выводе этого выражения мы использовали условие G.10.2), при-
причем было сделано дополнительное предположение о том, что различ-
различные ортогональные собственные функции могут иметь одно и то же
собственное значение. Таким образом, разложение G.10.5) можно пе-
переписать в виде
Е(г) = со2/1о1рзрФи(г). GЛ0-8>
В частности, когда Р описывается дельта-функцией [Р — 6(г — го)],м
представляет собой отклик резонатора на электромагнитное излуче-
излучение точечного источника и, таким образом, совпадает с функцией
Грина резонатора Gpe3, которая в соответствии с G.10.8) запишется в
виде
Читатель должен обратить особое внимание на то, что поле в ре-
резонаторе в общем случае состоит из набора мод Ф/тя даже тогда, ког-
когда в резонаторе возбуждается всего одна частота. В частности, когда
говорят, что лазер работает в одномодовом режиме, подразумевается
то, что поле в резонаторе имеет одну частоту, при этом оно необяза-
необязательно представлено одной собственной функцией Ф1тп.
Оставим пока проблему определения собственных функций Ф/т/?.
Предположим, что зеркала достаточно велики и отражают гауссовы
пучки любого порядка. Тогда мы можем записать следующее выраже-
выражение:
<bbm*u№ + Cbjitt, G.10.10)
где uj?> и и\~1 представляют либо эрмит-гауссовы, либо лагерр-
гауссовы пучки, распространяющиеся соответственно справа налево и
слева направо, волновые фронты которых на выходе резонатора сов-
совпадают с поверхностями зеркал.
Коэффициенты Cimn определяются из граничных условий G.10.3),
которые можно записать в следующем эквивалентном виде:
C\}() №(x9y9z2)9 G.10.11а)
u№(x9y9z1}. G.10.116)
Поскольку эта система уравнений может быть решена, только если
"У {х, у, z2)u<i+}(x, у, zx) = rxr2u\+l(x, у, Z2)u\-l(xf у, zx), граничные
условия можно преобразовать в следующее уравнение для волнового
вектора к1тп эрмит-гауссовой моды:
exp{-2ilklmnd - (/ + т + l)|>(z2) - *(*!)]]} = 1/(Г1г2),
7.10. Модовое представление поля 515
которое удобно разделить на два уравнения
2кЧ - 2(fc'7*')/[l + (fc"/fc'J]C + m + 1) х
х [arctg {z2/b) - arctg {zjb]\ = -lnlr^l, G.10.13a)
2k'& - 2A + m + 1)/[1 + (fc"/fc'J] x
x [ arctg (z2/b) - acrtg (zjb)] = 2nn + argfr^), G.10.136)
где в выражениях для ?' = Re klmn и ?" = Im /:/тл индексы 1тп для
простоты опущены.
Здесь удобно заметить, что моды, возбуждаемые источником с ча-
частотой со, имеют собственные значения кПУ близкие к со/с. В этом
можно убедиться, исследуя выражение для функции Грина G.10.9).
Кроме того, поскольку коэффициенты отражения зеркал резонатора
обычно очень близки к единице, с учетом выражения G.10.13а) мы
имеем/:" = O(\/d) и аналогично/:' = О A/Х); так как^А > 1, то
\к" /к' I < 1. Таким образом, уравнения G.10.13а) и G.10.136) прини-
принимают вид
2*^=-1п|гЛ|, G.10.14а)
Kmnd - (/ + m + 1)[ arctg (z2/b) - arctg (zjb)] = пл + iargfr^). G.10.146)
В соответствии с G.10.14а) мнимая величина к"тп = A - I rx r2 l)/Brf)
не зависит от порядка рассматриваемой моды, в то время как вещест-
вещественная часть величины к1тп зависит от продольного индекса п и по-
поперечных индексов / и т. Для лагерр-гауссовой моды уравнение
G.10.146) необходимо заменить на следующее:
k'lpnd - Bр + / + 1)[arctg (z2/b) - arctg (zjb)] = nn + iarg(rxr2). G.10.14b)
Наконец, для симметричного резонатора в случае г} = г2 совмест-
совместное решение уравнений G.10.10) и G.10.11) дает
Ф1тп ос^ЯД^хр^-**^ - ?\ sin[klmnz -{l + m+ \Щх) + n
G.10.15)
7.10.1. Приближение медленноменяющейся амплитуды
Несмотря на внешнюю простоту, модовое представление поля и с по-
помощью разложения G.10.5) само по себе не дает простого описания
поля. Если подставить выражение G.10.15) в разложение G.10.5) а
обозначить через п значение индекса л, при котором разность
I к1тп - о)/с I принимает минимальное значение, то можно записать
следующее выражение:
516 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Если число возбуждаемых мод ограничено условием \п - п I < d A,
то ? ^ (г) является медленноменяющейся функцией координаты z на
длине X, а именно Iг/2 Effi/dz2 \ < к\dEffi/dzI.
Поскольку поляризация Р представляет собой функцию отклика
среды на действие поля Е, разумно предположить, что Р определяется
выражением, аналогичным G.10.16), в котором медленноменяющиеся
функции Е \$ (z) заменены аналогичными функциями Р ffi (z). Таким
образом, подставляя соответствующие выражения для Е и Р в уравне-
уравнение G.10.4) и пренебрегая вторыми производными, мы имеем следую-
следующее уравнение:
IJ - Ц) - Ш
lm\
= °' C7.1O.17)
которое с учетом условия ортогональности между различными мода-
модами и1тп можно записать в виде системы дифференциальных уравне-
уравнений, связывающих амплитуды Е \$ (г) двух пространственно неодно-
неоднородных волн, а именно ТЕМ-мод резонатора, с аналогичными величи-
величинами, связанными с поляризацией. Решения этих уравнений мы рас-
рассмотрим в разд. 7.19.
7.11. УСТОЙЧИВЫЕ РЕЗОНАТОРЫ
Согласно представленному выше рассмотрению, в устойчивых резона-
резонаторах собственными модами являются гауссовы пучки. Это впервые
экспериментально подтвердили Когельник и Ригрод [16], получив-
получившие с помощью ЭОП фотоснимки отдельных мод Не—Ne-лазера
(X = 1,15 мкм), который имел концентрический резонатор длиной 230
см. Из-за трудностей, связанных с получением высокой точности из-
измерений распределения интенсивности эти авторы ограничились изме-
измерениями расстояний между узлами и обнаружили хорошее согласие со
значениями, полученными в предыдущем разделе. Отсутствие часто-
частоты модуляции в спектре интенсивности излучения явилось подтверж-
подтверждением того, что в распределении отсутствуют другие моды [17, 18].
После этого короткого отступления вернемся теперь к определе-
определению параметров моды (размера пятна и положения перетяжки). Эти
параметры можно получить двумя различными способами. С одной
7.11. Устойчивые резонаторы 517
стороны, используя выражение G.6.2), можно определить комплекс-
комплексную абсциссу z0, а затем из соотношения G.7.2а) вычислить w и Л на
зеркалах. С другой стороны, можно определить величину комплекс-
комплексной кривизны на зеркалах, используя матрицу ABCD [см. выражение
G.9.10)].
Диаметр перетяжки w0 для симметричного резонатора можно вы-
вычислить по формуле
Щ = (W2(d/2)li*{R - d/2I'* = \_{Щ1{2п)Т\(\ + g)l(\ - д)Г\ G.11.1)
а размер пятна за зеркалах дается выражением
w = wo[2/(l+^)]1/2. G.11.2)
Можно показать, что диаметр перетяжки в асимметричном резона-
резонаторе записывается в виде
wo = (A/*I/2{W(*i " d){R2 - d)(Rx + R2 - d)y(Rx +R2- 2dJ}1/4,
G.11.3)
где/?! и Л 2 положительны, если зеркала вогнутые, и отрицательны,
если зеркала выпуклые. Кроме того, мы имеем следующее выражение
для расстояний d{ nd2 от перетяжки до зеркал:
<*i.2 = «1.2/2 + (l/2)(*b - 4b2I/2. G.11.4)
Резонансные частоты можно найти, если потребовать, чтобы фа-
фаза гауссовой моды при смещении волнового фронта от одного зеркала
к другому изменялась на число, кратное -к [см. выражения G.10.146) и
G.10.14в)]. Таким образом, мы имеем для резонаторов прямоуголь-
прямоугольной и цилиндрической геометрии соответственно
Ьтп = vo{" + [(/ + m + l)/7c]arccos(^^2I/2}, G.11.5a)
ЬРп =vo{n + [Bp + /+ lyiflaiccoste^I'2}. G.11.56)
Для конфокального резонатора модовые множители / + /и + 1 и
2р + / ¦+ 1 заменяются множителем 1/2, так что в этом случае мы
имеем сильное вырождение мод. Точные выражения для резонансных
частот в резонаторах с зеркалами конечных размеров мы рассмотрим
ниже (см. разд. 7.14), а пока, за исключением резонаторов с плоскопа-
плоскопараллельной и концентрической конфигурациями (которые, как уже
указывалось, являются слабоустойчивыми и у которых моды отлича-
отличаются от гауссовых), будем пользоваться выражениями G.11.5).
Выражения для резонансных частот, записанные выше, справедли-
справедливы лишь для пустых резонаторов. В случае когда резонатор заполнен
усиливающей средой, аномальная дисперсия приводит к изменению
показателя преломления с частотой вблизи центральной частоты ла-
лазерного перехода. Вследствие этого частоты продольных мод уже не
будут отделены друг от друга одинаковыми интервалами. Однако в
518 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
газовых лазерах эти частотные сдвиги составляют величину всего
лишь порядка 10.
7.11.1. Дифракционные потери и расходимость
Потери в резонаторе можно вычислить, учитывая дифракционные эф-
эффекты, обусловленные конечным размером зеркал. В разд. 7.14 мы
покажем, что дифракционные эффекты эквивалентны ослаблению, ко-
которому подвергается излучение, распространяющееся от одного зерка-
зеркала к другому в среде с мнимой компонентой ?" волнового вектора к.
Определим потери /?/-Й моды за один проход ар{:
u.pl = 2k"pld. G.11.6)
Ниже мы покажем, что api зависит от параметров резонатора g и
числа Френеля N = a2/\d, где а — радиус зеркала. В общем случае
величину ар1 приходится вычислять путем решения интегральных
уравнений Фокса — Ли (см. разд. 7.14), поскольку она связана с
собственными значениями ух и 72 этих уравнений соотношением
«pi = 1 - \УиРУ21р1 G.11.7)
Вайнштейн [2] получил некоторые асимптотические выражения для
коэффициента потерь и фазового сдвига /3 за один проход для мод
плоскопараллельного резонатора с круглыми зеркалами. Таким обра-
образом, при больших числах Френеля мы имеем
olp1 = ZklpS(m + <5)/[(m + дJ + <52]2, plp = [m/D5)]a/p; G.11.8)
здесь 5 = 0,824 [см. разд. 7.16 и, в частности, выражение G.16.23)],
klp —р-й нуль функции Бесселя /,, am = (StNI/2. Для конфокаль-
конфокальных резонаторов Слепян [19] нашел, что при N > 1
Д, = Bр + / + 1)я/2. G.11.9)
Таблица 7.4. Отношение а^/а^ потерь для моды высоких порядков к потерям для
основной моды
ТЕМр/
01
02
10
03
11
04
12
Плоскопараллельный
резонатор
1,59
2,13
2,29
2,65
2,92
3,15
3,50
Конфокальный
резонатор
AN
\0N2
16N2
21N3
S5N3
327V4
1607V4
7.11. Устойчивые резонаторы
519
Из этих выражений видно, что потери в конфокальных резонато-
резонаторах сильнее зависят от модовых индексов / и р, чем в плоскопарал-
плоскопараллельных. В табл. 7.4 приводятся величины отношений ос^/а^ потерь
за один проход для плоского и конфокального резонаторов. В частно-
частности, upnN = 1, т. е. когда диаметр моды такой же, как и у зеркала,
для конфокального резонатора а]0/а00 = 16. Таким образом, стано-
становится понятным, почему по сравнению с другими резонаторами в пло-
плоскопараллельном резонаторе основная мода легче распадается на мо-
моды высоких порядков в результате рассеяния на неоднородностях сре-
среды (например, на частицах пыли на зеркалах) и других препятствиях.
Если конфигурация устойчивого резонатора отличается от плоско-
плоскопараллельной, концентрической или конфокальной, то профили мод
резонатора близки к гауссовым, поэтому в первом приближении ди-
дифракционные потери в нем можно вычислить, считая, что часть мощ-
мощности излучения, падающего на зеркала, отражается назад в резона-
резонатор [20]. Таким образом, мы имеем
G.11.10)
Наиболее важным параметром резонатора является полная угло-
угловая расходимость 20 в одномодовом режиме. Для симметричного ре-
резонатора эта величина дается выражением [см. выражение G.7.5)].
20 = 2A/(;rw0) = 2[2Я/(^)]1/2[A -</)/(! + я)]1'4. G.11.11)
7.11.2. Влияние разъюстировки резонатора
До сих пор рассматривались только идеально съюстированные резо-
резонаторы. Если одно из зеркал, скажем М j, немного повернуть на угол
дф1 (рис. 7.25), то пучок будет распространяться вдоль новой оси, про-
проходящей через новый центр кривизны О\ зеркала Mj. Новые оптиче-
f/
УГ
I
6hz
\
I
1
I
Рис. 7.25. Смещение оптической оси, вызванное наклоном зеркала.
520 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
ские оси пересекут поверхности обоих зеркал в других точках, положе-
положения которых относительно прежних смещаются на расстояния bhx и
5Л2. Если оба зеркала повернуты на угол соответственно Ьфх и 8ф2, то
для смещений dh} и 5Л2 имеем
Shjd = [02/A - д1д2)]5ф1 + [1/A - g&Wi, n
5h2/d = [1/A - д1д2)']5ф1 + [в2/A - д1д2)-]дф2.
Вычитая первое уравнение из второго, угловой сдвиг Ьф новых опти-
оптических осей относительно прежних можно записать в виде
W = [A - 02)/A ~ 9i9i)~\Hi - [A - 0i)/O - ffiflf2)]^2- G.11.13)
7.12. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
Лазеры высокой мощности можно разделить на два типа. В так назы-
называемых усилителях мощности с задающим генератором (название за-
заимствовано из радиотехники) стабилизированный маломощный лазер
управляет несколькими ступенями усиления. Напротив, если процессы
генерации и стабилизации частоты излучения в генераторе идут од-
одновременно с усилением, то лазеры относят к типу мощных генерато-
генераторов. Лазеры первого типа более устойчивы, чем лазеры с самовозбуж-
самовозбуждающимся генератором. Последние чаще находят применение в тех
случаях, когда важную роль играют небольшие размеры и компакт-
компактность, а не требования к стабильности. Однако к обоим этим типам
лазерных систем должно предъявляться важное требование, а именно
работать по возможности в режиме одной поперечной моды (TEMqq);
это необходимо для получения почти однородного волнового фронта
на выходе системы, что позволяет сфокусировать лазерный пучок до
дифракционного предела, поскольку любое отклонение волнового
фронта от однородного приведет к увеличению размеров фокального
пятна и расходимости в дальнем поле. В режиме многомодовой гене-
генерации характерные нерегулярности структуры волнового фронта
флуктуируют столь быстро, что их трудно уменьшить даже специаль-
специальным образом сконструированными фазовыми корректорами на выхо-
выходе. Опуская рассмотрение свойств систем с задающими генераторами,
мы сконцентрируем свое внимание на изучении мощных генераторов.
Для получения оптически однородной моды резонатор необходимо
конструировать таким образом, чтобы все элементарные излучатели в
нем (возбужденные атомы или молекулы) сильно взаимодействовали
между собой, поскольку это обеспечивает необходимую фазовую коге-
когерентность колебаний отдельных источников. Пучок, расходящийся за
счет дифракции, возбуждает множество элементарных источников, а
7.12. Неустойчивые резонаторы
521
Рис. 7.26. Схематическое представление основной моды и мод высших порядков при
N > 1 для устойчивого (а) и неустойчивого (б) резонаторов. (Из работы Чоцко и Че-
Честера [5]. © John Wiley and Sons, Inc., 1976.)
поскольку число Френеля представляет собой главный фактор, от-
ответственный за этот эффект, можно сделать заключение, что малое
число Френеля N является необходимым условием сильного дифрак-
дифракционного взаимодействия элементарных источников в резонаторе.
Действительно, режим одномодовой генерации достигается в устойчи-
устойчивых резонаторах с числом Френеля, близким к единице. Однако это
условие не применимо к лазерам высокой мощности, которые, как из-
известно, характеризуются большим объемом активной среды (напри-
(например, при объеме активной среды 1 л, чтобы получить на длине волны
3 мкм число Френеля, равное единице, необходим резонатор длиной
15 метров). Следовательно, в данной ситуации приходится идти на
увеличение числа Френеля.
На рис. 7.26, а схематически показана конфигурация поля в устой-
устойчивом резонаторе с большим числом Френеля. Выходной пучок
(изображен перекрестными штрихами) образуется в результате
некогерентных вкладов различных мод, что является следствием не-
неэффективной дифракционной связи. В неустойчивом же резонаторе
(рис. 7.26, б) дифракционные эффекты компенсируются геометриче-
геометрическим взаимодействием между лучами, поскольку в данном случае лучи
522 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
перекрывают весь объем резонатора. Иными словами, в центральной
области резонатора, для которой число Френеля порядка единицы, су-
существует некоторое ядро моды, обеспечивающее однородное усиление
волнового фронта при каждом полном проходе; при этом излучение
выводится с краев выходного зеркала1*.
На преимущества неустойчивых резонаторов впервые указал Сиг-
мэн [21] в 1965 г., который разработал также простой метод в приб-
приближении геометрической оптики [22]. В этом методе предполагается,
что основная мода неустойчивого резонатора состоит из двух сфери-
сферических волн, распространяющихся в противоположных направлениях.
Обозначим через Г, ту часть энергии волны, которая распространяет-
распространяется в направлении зеркала 2 после отражения от зеркала 1 сферической
волны единичной интенсивности. Аналогичным образом определим и
Г2. С помощью рис. 7.16 нетрудно показать, что
Гх = {Wft* - z^]}2, Г2 = {z2a2/l(d - z2)a{]}\ G.12.1)
здесь Zj 2 — расстояния от фокусов двух сферических волн до зеркал
(см. разд. 7.6), aflj 2 — радиусы зеркал. Таким образом, относитель-
относительную интенсивность волны на любом из зеркал после полного прохода
в прямом и обратном направлениях можно записать в виде
Т
Главный результат этого геометрического рассмотрения состоит в
том, что потери за полный проход а = 1 — Г зависят лишь от уве-
увеличения М резонатора и не зависят от диаметра зеркал. На плоско-
плоскости gxg2 можно построить семейство гипербол, каждая из которых со-
соответствует различным конфигурациям резонаторов с одинаковыми
потерями (рис. 7.27).
На рис. 7.28 показаны различные типы неустойчивых резонаторов.
Из них наиболее часто применяются первые два, поскольку фокусы
зеркал располагаются вне резонатора. Действительно, если фокусы
лежат в области активной среды, то образующееся в них интенсивное
световое поле может вызвать нелинейные эффекты (даже пробой),
что, естественно, ухудшит качество оптического пучка. Отрицатель-
Отрицательная же конфигурация Неустойчивых резонаторов (рис. 7.28, г) менее
чувствительна к недостаточно точному изготовлению зеркал и их
юстировке. Положительная конфокальная (рис. 7.28, а) конфигура-
конфигурация, впервые предложенная Ананьевым [3], применяется наиболее ча-
]) Такой способ вывода излучения лазера называется дифракционным. — Прим.
перев.
-1
-2
__ Отрицательная
ветвь
.^ 75%
1остоянные потери. 50% *чч
Положительная
ветвь
(тип Ж)
i90%
Положи тельная
ветвь (muni)
90%
Область
устой чивости
I Отрицательная
I Ветвь
[96%
-2
1
Рис. 7.27. Конфигурации резонаторов с одинаковыми значениями увеличения и потерь
(90%) (гиперболы, изображенные непрерывной линией) в плоскости gxg2- Гипербола,
изображенная штриховой линией, представляет собой геометрическое место точек для
различных конфокальных конфигураций. (Из работы Чоцко и Честера [5] © John Wiley
and Sons, Inc., 1976.).
Рис. 7.28. Геометрическая картина волновых фронтов в
различных неустойчивых резонаторах, а и б — положи-
положительная ветвь (тип /), gxg2> I, gx >0; в — положительная
ветвь (тип II), glg2>\, gt<0; г — отрицательная ветвь,
#i#2 <0* №*3 работы Чоцко и Честера [5]. © John Wiley
and Sons, Inc., 1976 J.
524
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Рис. 7.29. Схематическое представление телескопического резонатора, используемого в
проточных лазерах с поперечным разрядом. 1 — входной поток; 2 — выходное зеркало;
3 — фокусирующее зеркало; 4 — катод; 5 — анод; 6 — выходной поток; 7 — глухое
зеркало.
сто, поскольку в этом случае коллимированное выходное излучение
снимается с одного конца резонатора (рис. 7.29). Своим названием эта
конфигурация обязана выпуклому выходному зеркалу и тому, что в
плоскости gj g2 она располагается в правом верхнем квадранте1*. Вы-
Выходное зеркало (меньшего размера) радиусом а 2 имеет отрицательную
кривизну радиуса/? 2, в то время как глухое зеркало радиусом а х имеет
положительную кривизну радиуса R х. Потери а за полный обход в
приближении геометрической оптики равны коэффициенту связи С,
определяемому выражением
С = 1-Г = 1-1/М2, G.12.3)
причем увеличениеМ связано сRг nR2 простым соотношением
M=-RJR2> G.12.4)
а параметрыg, и^2 записываются в виде
в1 = (М + 1)/BМ), д2 = (М + 1)/2. G.12.5)
Пучок, выходящий из этих резонаторов, в ближней зоне имеет
форму бублика, поскольку центральная область ослаблена выходным
зеркалом. В промежуточной зоне могут появиться постепенно исчеза-
1} Этот резонатор называется телескопическим. — Прим. перев.
7.13. Волновая теория пустых резонаторов
525
Интенсивность
Неустойчивый
резонатор
'Шляпа
(распределение
с плоской вершиной)
Рис. 7.30. Типичная форма пучков, используемых в лазерах высокой мощности.
ющие с расстоянием от источника кольца Френеля, модулирующие
бубликовую форму профиля пучка, в центре которого возникает ма-
маленькое пятно, имеющее чрезвычайно высокую плотность мощности
излучения и могущее потенциально приводить к разрушению оптиче-
оптических элементов. Это пятно называют пуассоновским, или пятном
Араго. В дальней зоне поперечный профиль пучка описывается функ-
функцией Эйри.
На рис. 7.30 схематически показаны профили пучков, которые наи-
наиболее часто используются в различного рода лазерных приложениях.
Промежуточной между гауссовой формой и формой с провалом явля-
является распределение с плоской вершиной, которое можно рассматри-
рассматривать как гауссиан с усеченной вершиной. Неустойчивые резонаторы
исключительно чувствительны к разъюстировке, в частности к накло-
наклону зеркал [23]. Если в телескопическом резонаторе наклонить заднее
зеркало на угол 8ф9 то выходной пучок отклонится на угол ф [ср. вы-
выражения G.11.13) и G.12.5)], определяемый выражением
ф = [2М/(М - 1)] дф. G.12.6)
Из-за наличия здесь в знаменателе разности М •— 1 величину М выби-
выбирают, как правило, больше чем 1,5.
7.13. ВОЛНОВАЯ ТЕОРИЯ ПУСТЫХ РЕЗОНАТОРОВ
Как дифракционные потери, так и преобразование гауссовых пучков
внутри резонаторов определяются конечным размером зеркал.
526 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
му окончательная пространственная конфигурация мод может значи-
значительно отличаться от гауссова распределения. Используя приближе-
приближение геометрической оптики, можно найти конфигурацию и собствен-
собственную частоту моды как в устойчивых, так и в неустойчивых резонато-
резонаторах; при этом эффектами, связанными с дифракцией на краях зеркал
или на введенных внутрь резонатора апертурах, можно, как правило,
пренебречь. Однако существуют параметры (к ним относятся поте-
потери а), которые не могут быть точно вычислены в рамках данного
приближения.
Метод, который позволит преодолеть указанную трудность, осно-
основан на рассмотрении уравнений Максвелла с граничными усло-
условиями, которым соответствуют конечные размеры выходных зеркал.
В 1893 г. Дж. Дж. Томсон в своем труде «Последние исследования по
электричеству и магнетизму» впервые проанализировал замкнутый ре-
резонатор с точки зрения теории электромагнетизма.
Для простоты предположим, что поле описывается скалярной
функцией м, нормальная производная которой на границах обращает-
обращается в нуль. Используя выражение D.2.10), поле на границе можно запи-
записать через интеграл вида
"(г) = - IT Г^-С(г - r')]n(r')iS, G.13.1)
Стенки
резонатора
где г и г' — радиусы-векторы стенок резонатора, ап0- внешняя нор-
нормаль. Выражение G.13.1) является интегральным уравнением, реше-
решения которого определяют конфигурацию мод. Собственные частоты
мод входят в это уравнение через функцию Грина G, экспонента кото-
которой содержит волновое число к.
Физически уравнение G.13.1) является следствием того, что поле в
любой точке, принадлежащей стенкам резонатора (границе), совпада-
совпадает с полем, индуцированным всей совокупностью пристеночных токов
(которые в свою очередь пропорциональны и). Взаимодействие между
полем и токами способствует установлению равновесной конфигура-
конфигурации в генерируемой моде, в то время как собственная частота моды
определяется фазовым сдвигом между вкладами отдельных элементов
тока.
Интегральное уравнение G.13.1) дает вещественные значения соб-
собственных частот только в том случае, когда стенки резонатора обра-
образуют замкнутую поверхность и омическими потерями на них можно
пренебречь.
Открытый резонатор [2, 24] можно рассматривать как замкнутую
полость, у которой часть поверхности совпадает со сферой бесконеч-
7.14. Интегральные уравнения Фокса — Ли
527
ного радиуса. Поскольку из бесконечности ничего не отражается, мо-
моды такого резонатора характеризуются комплексными собственными
частотами. В некоторых случаях в открытых резонаторах может су-
существовать набор мод с низкими потерями, образующих дискретный
спектр в данном частотном диапазоне.
7.14. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФОКСА — ЛИ
Ограничимся здесь рассмотрением линейного резонатора Фабри —
Перо. Можно считать, что если число Френеля не очень велико, то ос-
основные моды резонатора будут приблизительно ТЕМ-типа. Это пред-
предположение является необходимым для обоснования перехода к скаляр-
скалярной дифракционной теории. Кроме того, можно использовать резуль-
результаты, полученные в приближении геометрической оптики, а именно
те, что моды состоят из двух противоположно направленных волн.
Обозначим через и (+) hi/ (~} амплитуды прямой и обратной волн, от-
отраженных от зеркал Мх и Л/2. Пользуясь формулами из разд. 4.2,
можно связать поле и (~") на зеркале М{ с полем и (~> на зеркале М2.
Применив те же формулы [см. выражение D.2.14)] км (+) и предполо-
предположив, что волновые фронты совпадают с поверхностью зеркал, можно
написать следующие выражения:
ехрС-ЩЛ + И^-Ид]
Afi
«1
exp[-ik(R + W2-
R
1A+cos 0J
G.14.1)
+ cos 02)dS2,
Ml
где нижние индексы 1 и 2 относятся соответственно к зеркалам 1 и 2,
R — расстояние между точками Рх нР2 (рис. 7.31), 0, и в2 — углы
Рис. 7.31. К вычислению пространственной конфигурации мод резонатора с помощью
дифракционного интеграла Кирхгофа.
528 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
между вектором R и нормалями кМх иМ2 в точкахР{ иР2> а^ и
W2 — функции аберраций на соответствующих зеркалах. Формулы
G.14.1) справедливы также и для резонаторов лазеров высокой мощ-
мощности, вывод из которых осуществляется за счет дифракции на апер-
апертуре выходного зеркала [25].
В случае когда расстояния между зеркалами много больше их раз-
размеров, расстояние R можно записать приближенно в виде
R ? d + &gjd)(xl + у\) + \Lg2ld)(x\ + y\) - (l/d)(Xlx2 + у1Уг\ G.14.2)
где#! и#2 — параметры резонатора.
Функции аберраций Wх и W2 определяются тем, насколько сильно
отклоняются зеркала от идеальной формы. Например, если зеркало
слегка отклонено (см. разд. 7.11.2) на углы Ьфх и 8фу, то мы имеем
W = х дфх + у Ьфу. Окна Брюстера являются еще одним источником
аберраций (астигматизм и кома). Источником аберраций является и
сама активная среда, например нагрев стержней в АИГ: Nd3+-лазере
вызывает линзовый эффект. В газовых проточных лазерах основны-
основными факторами, искажающими поле в резонаторе, являются ударные
волны и турбулентность. В этом случае их влияние может быть учте-
учтено некоторыми дополнительными функциями аберраций.
Перейдем теперь к обсуждению граничных условий интегрального
уравнения G.14.1). Еслим— компонента магнитного поля, совпадаю-
совпадающая по направлению с касательной к поверхности зеркал с коэффици-
коэффициентами отражения соответственно г х иг2, то граничные условия запи-
запишутся следующим образом:
м<2-> = г2и?\ и[+) = гхи[-\ G.14.3)
Заменяя в уравнении G.14.1) и[~) на и^ и w{+> на и<~> и используя
выражение G.14.2), получим систему интегральных уравнений Фред-
гольма [26]
^S2, G.14.4a)
м2
JJf^, G.14.46)
где Mi
9y2) = K(xux2)K(yl9y2)cxplik(W2 - Wx)\ G.14.5)
/ i у/2 Г & "I
'v>> = \ы) ехр "id^1^ + Giv2uv) r
7.14. Интегральные уравнения Фокса — Ли 529
Уравнения G.14.4) были впервые выведены в 1960 г. Фоксом и Ли
[27] для плоскопараллельного и конфокального резонаторов, а затем
были обобщены на резонаторы со сферическими зеркалами.
Если размеры зеркал малы по сравнению с расстоянием между ни-
ними d, то отклонением хода лучей от прямого пути можно пренебречь
и считать, что cosflj = cos02 = 1. В этом случае, заменяя м^+) в урав-
уравнении G.14.4а) левой частью уравнения G.14.46), получаем
G.14.6)
здесь t, и t2 — поперечные векторы (t = хх + уу), а
ад*! " t2)K12(t2 - t'i)dS2, G.14.7)
Аналогичные выражения можно записать и длям^"*. В заключение за-
заметим, что урайнения Фокса — Ли G.14.4) эквивалентны двум инте-
интегральным уравнениям Фредгольма, имеющим одно и то же собствен-
собственное значение Yi72- Из этого следует, что в уравнениях G.14.4) сохра-
сохраняется постоянным только произведение 7i72» в то время как сами ве-
величины 7i и 72 изменяются.
7.14.1. Потери за полный проход
Выбрав частоту, вблизи которой будет проводиться поиск резонанс-
резонансных мод, мы можем вычислить точные значения соответствующих
волновых чисел из собственных значений уравнения G.14.6) при после-
последующей подстановке их в уравнение G.14.5а). Проделав эту процеду-
процедуру, получим
kimn = к\тп + ik'(mn = "i/Bd)ln{yUnmy2lnmr1r2); G.14.8)
здесь индексы /, т и п относятся к соответствующей моде. Вещест-
Вещественная часть к\тп = 2щтп/с волнового числа к1тп определяет резо-
резонансную частоту vlmn , а мнимая часть к"тп (> 0) определяет коэффици-
коэффициент усиления (см), необходимый для возникновения генерации в ре-
резонаторе. Вследствие малости параметра fc"rf мы можем записать с
хорошей точностью следующее выражение для потерь за полный
проход а1т [см. выражение G.11.6)]:
a/m = 2k'lmd ^ 1 - ly^j^r^l s A - |yllmy2lm|) + A - |гхг2|) = а&> + аЦ,
G.14.9)
(здесь продольный индекс п опущен, поскольку величина к"тп практи-
практически от него не зависит). В выражении G.14.9) потери а1т зависят как
530 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
от геометрических параметров разонатора (a(d)), так и от коэффициен-
коэффициентов отражений зеркал (а(г)), причем общая величина этих потерь полу-
получается сложением двух этих факторов.
7.14.2. Фазовый сдвиг
Чтобы разобраться, каким образом vlmn [ср. с выражением G.11.5)]
зависит от геометрических параметров резонатора, воспользуемся
аналогией с прямоугольным резонатором, описываемым формулой
G.1.8). При этом резонансный волновой вектор к\тп при я — оо запи-
запишется в виде
k'lmn = (n/d)n + plm/d, G.14.10)
где 0im — фазовый сдвиг данной моды относительно идеальной плос-
плоской волны, имеющей ту же частоту. Определенная таким образом ве-
величина /3/т является мерой отклонения лучевых траекторий от опти-
оптической оси. Используя выражения G.14.8) и G.14.10), можно сразу по-
показать, что Щт есть не что иное, как фаза величины 7VmT^mrir2» nPu~
нимающая значение в интервале (-7г, +*¦). В соответствии с этим
удобно ввести комплексную величину р1т, определяемую следующим
образом:
УипУ21т = ехр(-4тпр|т) s exp(-2iftw - а,т). G.14.11)
До сих пор считалось само по себе разумеющимся существование у
уравнения G.14.4) собственных функций. Доказать, что такие функции
действительно существуют, —- непростая задача. Действительно, по-
поскольку ядро К12 интегрального уравнения не является эрмитовым,
мы не можем использовать результаты хорошо развитой теории эр-
эрмитовых операторов. Эта проблема явилась своеобразным вызовом
изобретательности математиков, которым в конце концов удалось до-
доказать существование собственных значений уравнения G.14.4) [28].
7.14.3 Симметричные резонаторы
Ситуация значительно упрощается в случае, когда резонатор обладает
плоскостью симметрии, перпендикулярной оптической оси. В этом
случае моды можно разделить на две группы в соответствии с тем,
что либо и f") = и^+) (а = 1), либо w f"* = -t/^+) (<j = -1). Следова-
Следовательно, мы имеем
уи= \\uKl2dS\ G.14.12)
-Я
м
здесь 7 = (- l)a7i и и = и^ = (- 1)аи\+\ аК{2 — симметричное не-
неэрмитово ядро. Таким образом, если два решения иаии» этого урав-
7.15. Методы расчета модовы х конфигураций 5 31
нения имеют различные собственные значения уа и у$, то они взаимно
ортогональны. Условие взаимной ортогональности запишется при
этом в виде [ср. с аналогичными условиями G.10.2) для мод резонато-
u,dS = 0, G.14.13)
м
Это выражение отличается от условия для эрмитового ядра только
тем, что не содержцт комплексного сопряжения одной из собственных
функций. Поэтому, если моды «аи«^ комплексные, с точки зрения
вычисления интенсивности они не будут ортогональными, т. е. интен-
интенсивность, связанную с суммой иа +м^, уже нельзя представить в виде
суммы отдельных вкладовиа й и@.
7.14.4. Соотношения подобия
Прежде чем завершить данный раздел, воспользуемся уравнениями
G.14.4) и выведем некоторые полезные соотношения подобия для ре-
резонаторов с различными линейными размерами, но с зеркалами оди-
одинаковой формы (т. е. либо круглой, либо прямоугольной). Из уравне-
уравнений G.14.4) следует, что два резонатора с тремя одинаковыми пара-
параметрами [29]N, G{ иС2, причем
N = а^/Щ), Gt = gxaja2 G2 = g2a2/au G.14.14)
(здесьа, иа2 — типичные размеры зеркал 1 и 2), имеют одни и те же
собственные значения 7/ и соответственно одни и те же дифракцион-
дифракционные потери и фазовые сдвиги. Независимо от размеров резонаторов
распределение интенсивности в модах у них также будет одинаковым.
В частности, для симметричных резонаторов (#{ = а2) параметр N
совпадает с числом Френеля. Поэтому если параметры g и числа Фре-
Френеля для таких резонаторов одинаковы, то одинаковыми у них будут
как потери, так и фазовые сдвиги.
7.15. МЕТОДЫ РАСЧЕТА МОДОВЫХ КОНФИГУРАЦИЙ
7.15.1. Метод Фокса — Ли
Фокс и Ли впервые решили интегральное уравнение G.14.12) [27, 29],
используя метод итераций [30]. В своих расчетах они выбирали произ-
произвольное начальное распределение поля в волне, падающей на зеркало
(скажем, на зеркало 1), и затем, подставляя это распределение в инте-
интеграл G.14.12) при 7 = 1, получали распределение поля, распространя-
532
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
ющегося в прямом и обратном направлениях в резонаторе. При этом
они нашли, что моды начального распределения, за исключением ос-
основной моды, имели сильное затухание. Процесс итерации заканчи-
заканчивался, когда форма распределения поля не менялась от прохода к про-
проходу и амплитуда поля при этом экспоненциально уменьшалась. Ста-
Стационарное распределение интенсивности поля (если отбросить фактор
экспоненциального затухания) рассматривалось как нормальная мода
о ЮО
К 50
г
10
5
10
0,5
О^
: ^k TEMoo
I W&,
г \ \ \ т\\^^С
1 1 1 1 и ill 1 \ \ 111 Дм
9
i i
1
=ho
Мин
0,1 0,5 1,0 5 10 50100
N=a2Md
a
100
50
ex
TJ •
CL
u, io
3 5
GO
1 bo
1 0,5
0,1
l^>^ lG|—0
-^^^ u>b
— ^ч^»^^. 0,9
4 0,95
[ TEM«« \,,0
:
1 1 1 1 IMI 1 1 1 1 I 1 III 1 1 1 1 1 1 III
0,1 0,5 1ft 5 10 50100
N=a2Md
5
Рис. 7.32. Дифракционные потери а (а) и фазовый сдвиг 0 (б) за один проход для ос-
основной моды симметричного резонатора с круглыми зеркалами радиусом Q в зависи-
зависимости от числа Френеля при различных значениях параметра g. Следует заметить, что
для ТЕМод-моды величины а и 0 для# те же, что и для — ?.(Из работы Ли [31]. @
1965 AT and T Bell Laboratories.)
7.15. Методы расчета модовых конфигураций
1,0
О.в
533
1
ТЕМоо
N=1,0
±0,95
0,9
%
0'
Ofi
О 0,2 0,4 0,6 0, в р/а
Рис 7.33. Относительные распределения поля в основной ТЕМ^-моде симметричного
резонатора с круглыми зеркалами радиусом Q и с числом Френеля N = a2/QM) = 1.
резонатора. Таким образом, если стационарное распределение уста-
устанавливается на/-й итерации
Я.
м
G.15.1)
(коэффициент у намеренно опущен), то
u{i+1)(x,y)/u{i){x,y) = const = у. G.15.2)
Итерационный метод был успешно применен Ли [31] в 1965 г. для
исследования неконфокальных симметричных резонаторов с круглыми
зеркалами. Результаты этих вычислений, представленные на рис. 7.32
и 7.33, позволяют определить потери за проход, фазовый сдвиг и рас-
распределение поля в ТЕМ^-моде симметричных резонаторов с различ-
различными значениями параметров g и чисел Френеля. Заметим, что гори-
горизонтальные участки кривых фазового сдвига соответствуют значени-
значениям @р1 = B/? + / + l)arccosg, что согласуется с формулой G.11.56).
Чекаччи и др. [32] разработали иной подход, суть которого состо-
состоит в вычислении интеграла посредством гауссовых квадратур и преоб-
преобразовании интегрального уравнения к матричному.
7.15.2. Алгоритм быстрого фурье-преобразования
Для вычисления интегралов Фокс и Ли использовали сетку из Np зна-
значений амплитуды поля и. Для вычисления дифракционных интегралов
в одномерном случае наименьшее число точек Np ограничено условием
534 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Np > 4N9 где N — число Френеля. Чтобы вычислить двумерные инте-
интегралы, мы должны иметь Np > 16ЛГ2 точек. Следовательно,* при
больших N число точек Np будет столь велико, что потребуется ЭВМ
с большим объемЪм памяти, а время расчета резко возрастет. Другое
значительное препятствие использования уравнения G.14.12) состоит в
том, что в случаев > 1 при численных расчетах необходимо будет
запоминать ЛГ^ значений ядра#12, гдеЛГр — число разбиений на зерка-
зеркалах Мх иМ2. Эти трудности можно обойти, если переписать G.14.12)
в виде интеграла свертки [33]:
+ 00
i-t2)/(t2Mt2)</S2, G.15.3)
гдеР (t2) — функция зрачка зеркала, v = ufyl и
/(t) = Qxp(-ikt2/R), H(t) = [i/(Ad)]1/2exp[ — iht2l{2d)~§ G.15.4)
здесь R — радиус кривизны зеркал.
Для решения уравнения G.15.3) требуются два массива размерами
Np соответственно для функций Я и/. Главным достоинством этого
уравнения является то, что его правая часть представляет собой
свертку, которую можно очень быстро вычислить с помощью алго-
алгоритмов быстрого фурье-преобразования (БПФ). Таким образом, мы
можем записать
Я
P{t2)H(t2 - tJ/feMtjJdSa ^F-4F{H) ¦ F{Pfv}}. G.15.5)
Несмотря на то что в данном случае приходится делать три фурье-
преобразования, увеличение объема вычислений компенсируется быст-
быстротой алгоритма БФП. Для симметричных резонаторов с круглыми
зеркалами вышеприведенные интегралы сводятся к одномерным, если
использовать ядро, содержащее функции Бесселя Jt [ср. с уравнением
G.17.4)]. В этом случае можно обратиться к специальному алгоритму,
разработанному Сигмэном [34] с целью расчета преобразований Хан-
келя.
7.15.3. Вычисление мод высокого порядка
При расчете низших симметричных и асимметричных мод особенно
удобно применять метод итерации. Если же необходимо вычислить
моды более высоких порядков, то приходится начинать с тех распре-
распределений поля, которые исключают появление мод с потерями мень-
меньшими, чем в искомых модах. Этот метод требует выполнения значи-
7.16. Устойчивые резонаторы с прямоугольными зеркалами 535
тельного объема работы, который можно существенно сократить, ес-
если обратиться к методу разложения ядра в ряд9 предложенному
Штрейфером [35], а также Бергштейном и Маромом [36]. Он состоит
в разложении ядра и мод в ряд по ортогональным функциям таким
образом, чтобы преобразовать интегральное уравнение в бесконечную
систему линейных уравнений, собственные значения которых дадут
фазовые сдвиги и потери в резонаторе. В частности, для достижения
более высокой эффективности расчетов основных мод в неустойчивых
резонаторах Сигмэн и Миллер [37] предложили метод Прони.
7.16. УСТОЙЧИВЫЕ РЕЗОНАТОРЫ С ПРЯМОУГОЛЬНЫМИ
ЗЕРКАЛАМИ
В настоящем разделе ограничимся подробным рассмотрением сим-
симметричных резонаторов, содержащих прямоугольные зеркала цли диа-
диафрагмы. Поиск мод в этом случае значительно упростится, если поле
представить в виде произведения двух независимых функций:
u{x9y) = fx(x)ff(y). G.16.1)
Используя свойство ядраА^ факторизоваться в произведение двух
функций К и пренебрегая аберрациями, систему уравнений G.14.4)
можно привести к следующему однородному уравнению Фредгольма
второго рода с симметричным непрерывным ядром:
yf(v)= Г f(u)K(u9v)du, G.16.2)
где/ означает либоД, либо/,,, а 2а представляет собой ширину зер-
зеркала. Это уравнение определяет моды резонатора с зеркалами в виде
бесконечно протяженных полос (т. е. вытянутых на бесконечность в
одном из поперечных направлений).
Введем теперь [2] новые переменные {иг, определяемые выраже-
выражениями
{ = arccostf, т = 2w/w = Bfcsin?/dI/2w, G.16.3)
где w — размер пятна гауссова пучка на зеркалах. Тогда уравнение
G.16.2) запишется в виде
у/(т) = Г С(т, т', ?)/(т') dx' G.16.4)
где г = 2(Na/Nw)W2 = 2a/w [причем Na = a2/\d — число Френеля
резонатора и Nw = wVXd = l/(?rsin?) — число Френеля для пятна w
гауссовой моды на зеркале], а
536 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
7.16.1. Конфокальный резонатор
Уравнение G.16.4) в общем случае можно решать численными метода-
методами, хотя нередко можно получить и аналитические решения. Приме-
Примером последнего случая является конфокальный резонатор
(g=0— ? = тг/2), для которого уравнение G.16.4) принимает вид
L-
yf(t) = Nl/2e+iK/4 Г e+ictt'f{t') dt\ G.16.6)
где t = r/r и с = 2irNa. Собственные функции этого уравнения, как бы-
было первоначально показано Ландау, Слепяном и Поллаком [38, 39], а
также Бойдом и Гордоном [40], могут быть выражены через угловые
и радиальные функции вытянутого сфероида соответственно SOm(c, t)
и ROm(c, t). Они являются решениями дифференциального уравнения
A - t2)d2f/dt2 - 2tdf/dt + (/ - c2t2)f = 0, G.16.7)
которое имеет непрерывные решения в интервале t [—1, 1] лишь при
определенных вещественных положительных значениях параметра х
таких, что O<Xo(c)<Xi(c)< ...<хп(с). Каждому собственному значе-
значению хп (с) (л = 0, I, 2, ...) при f=0 соответствует только одно ограни-
ограниченное решение \п\с, t\ такое, что SOn(c, 0)=Рл@), где Рп (О —по-
—полином Лежандра степени п. Функции SOn(c, t), называемые угловыми
функциями вытянутого сфероида, на отрезке [-1, 1] образуют по-
полный набор ортогональных вещественных функций, непрерывных по с
при с>0. Функции SOn(c, t) на отрезке [-1, 1] имеют точно п нулей и
при с — оо сходятся равномерно к Pn(t), причем четность функции
50л(с, О совпадает с четностью п. Собственные значения хп(с) явля-
являются непрерывными функциями параметра с, и хл@) = п(п + 1).
Можно показать, что собственные значения уп уравнения G.16.6),
соответствующие собственным функциям SOn(c, t)f даются выра-
выражением
уп = 2N'J2R^BnNa, 1)ехр[/Gг/2)(п + 1/2)], G.16.8)
где R о„ — так называемые радиальные функции вытянутого сферо-
сфероида, которые отличаются от SOn лишь вещественным множителем
Кп (с), причем
R$(c,t) = Kn(c)SOn(cj) -+ coslct - п(п + 1I211 cL G.16.9)
f->oo
В соответствии с выражением G.16.8) в конфокальном резонаторе
с зеркалами в виде двух бесконечных полос фазовый сдвиг (Зп [см. со-
соотношение G.14.10)] кратен 7г/2, так что в том же резонаторе с пря-
прямоугольными зеркалами фазовый сдвиг 0im будет кратен ж/2* Заме-
Заметим, что данное утверждение справедливо для любых резонаторов с
конечным размером зеркал. Свойство фазы изменяться только на це-
7.16. Устойчивые резонаторы с прямоугольными зеркалами 537
лое число тг/2 позволяет использовать данные резонаторы в качестве
интерферометров, поскольку их резонансные частоты не зависят ни
от числа Френеля, ни от порядка возбуждаемой моды. Этот факт лег-
легко объясняется в рамках приближения геометрической оптики: незави-
независимо от угла падения путь произвольного луча при полном проходе
резонатора равен Id. Таким образом, если конфокальный резонатор
используется в качестве интерферометра, то положение резонансных
частот такого интерферометра не зависит от направления распростра-
распространения луча, на что впервые указал Конн (см. разд. 7.21.4).
7.16.2. Теория Вайнштейна для концентрических и плоскопараллелъ-
ных резонаторов
Особый интерес представляют плоскопараллельные (g=l) и
концентрические (g=-l) резонаторы. В этих случаях ? = 0 или ж и
ядро уравнения G.16.5) оказывается сингулярным. Подстановкой
/=т/B sin?I/2 = x(k/d)U2 уравнение G.16.4), как нетрудно показать,
принимает вид
yfit) = ^^|„p[-i(t - Г'ф')А'. G.16.10)
гдеГ=BтгЛ^I/2 = (ka2/d)U2.
Вайнштейн [2] предложил изящный метод решения интегрального
уравнения G.16.10). В этом методе используются собственные функ-
функции резонатора с бесконечно большими размерами зеркал. Здесь резо-
резонатор можно рассматривать как волновод высотой d, простирающий-
простирающийся от / = — оо до t = + оо. Аналогично, резонатор с конечными разме-
размерами зеркал можно рассматривать как волновод ограниченных разме-
размеров, в котором моды распространяются к открытым концам, где они
затем частично отражаются обратно за счет дифракции на краях. Та-
Таким образом, собственные функции резонатора при выбранных значе-
значениях t могут быть выражены комбинацией мод бесконечно длинного
волновода, претерпевающих дифракцию на открытых концах.
Если / представляет собой компоненту Нх магнитного поля Н на
зеркалах резонатора, то поле uqe=Hy внутри волновода для^-й моды
записывается в виде
uqe(x,z)occos{qnz/d)expli8sqx(k/dI/2], G.16.11)
где е = ±1, z = 0, d — координаты стенок и
Sq = (k2 - q2n2/d2I/2(d/k)lf2. G.16.12)
Волновая функция uqe представляет собой суперпозицию плоских
волн, падающих под некоторым углом к стенкам резонатора
538
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Рис. 7.34. Углы падения (ф ) и дифракции (фд,) при преобразовании д-й моды, бегущей
вверх, в q'-ю моду, бегущую вниз, за счет дифракции на краях волновода.
7.34), определяемых выражением
фч = я/2 - arctg lsq/(kdI/2l G.16.13)
Ограничимся рассмотрением случая сильного отражения мод от краев
резонатора. Согласно теории дифракции на полуплоскости, развитой
в гл. 6, поле, дифрагированное в направлении, противоположном на-
направлению падающего пучка, оказывается значительным, когда угол
падения фд близок к тг/2. Следовательно, мы можем ограничиться
изучением тех мод, для которыхsg<(kd)y2. Кроме того, если к мож-
можно записать в виде k=ic(n — 2p)/d9 причем -1/2 <р <1/2, и поло-
положить q=n — 2j, где j=0, ±1, ±2, ..., то, используя приближенное
выражение к « qir/d и заменяя q на у, имеем
s^C^tf-p)]1'2. G.16.14)
Следует добавить, что мы рассматривали лишь те моды, индекс q ко-
которых отличается от п на четное число. Это допущение обусловлено
тем фактом, что при отражении на открытых концах волновода моды
с четными q не взаимодействуют с модами, имеющими нечетные q.
Это можно доказать, учитывая то, что на зеркалах поля четных и не-
нечетных мод направлены в противоположные стороны. Кроме того,
следует заметить, что в зависимости от знака разности у-/? величина
Sj будет либо вещественной (при у —р > 0), либо мнимой (при у —р < 0).
В первом случае мода распространяется вдоль оси х, в то время как
во втором она затухает.
Для зеркал конечных размеров, следуя Вайнштейну [2], разложим
/(О в ряд:
f(t) = LFJe exp(i5,eO. G.16.15)
Подстановка этого ряда в уравнение G.16.10) дает следующее уравне-
уравнение: _ _
7.16. Устойчивые резонаторы с прямоугольными зеркалами 539
где F — комплексный интеграл Френеля, определенный в гл. 5 выра-
выражением E.3.5). В случае когда мы рассматриваем поле на некотором
расстоянии от концов волновода и t>l9 уравнение G.16.16), если по-
положить y = exp(iSj2/2) = ехр(-2тгф), сводится к тождеству. Это в
свою очередь означает, что моды, распространяющиеся в области,
достаточно удаленной от концов волновода, как и следовало ожидать,
не взаимодействуют между собой. Напротив, вблизи концов волново-
волновода, т. е. при t = t9 уравнение G.16.16) принимает вид
^j = 0, G.16.17)
поскольку F(-21/2 F)-*l при 7"-*оо.
Забудем на время, что мы исследуем резонатор, и представим се-
себе, что мода у движется к концу t= 7 волновода из t= -oo в точку 7,
где вследствие дифракции распадается на ряд отраженных мод. Оче-
Очевидно, что при этом интегральное уравнение G.16.10) остается спра-
справедливым, поскольку замена координаты — t на — оо обоснована тем,
что поля в соответствующих сечениях совпадают.
Обозначим через г у амплитуду отраженной у- й моды (е= 1), кото-
которая является результатом дифракции падающей моды с индексом
У (е=-1), и положим Fj_x = 6 приучу', FJ,_1 exp(—u?y,//)=l и
FJ1 exp (isj 7) = г.у. Тогда уравнение G.16.17) преобразуется к виду
G.16.18)
Коэффициенты г^, можно получить, решив данную систему уравне-
уравнений для всех значений У ив силу теоремы взаимности положив
rjJf = ryj. В первом приближении мы имеем
r00 s -F(so/2^2)/F(-so/21/2) = -схр[ЙA 4-1>0], G.16.19)
здесь 5 = 0,824, в то время как другие коэффициенты равны нулю. По-
Последняя формула для Гад была выведена Вайнштейном (см. книгу
Вайнштейна [5], указанную в литературе к гл. 4 нашей книги) для
предельного случая малых р из точного выражения, полученного ме-
методом факторизации Винера — Хопфа — Фока. Более точный расчет
этих коэффициентов, выполненный Вайнштейном, дает (рис. 7.35)
rjr s ^?_exp[itf(l + Щ + sr)l G.16.20)
Sy
(О другом методе приближенного расчета коэффициентов отражения
rjj и rjj' см- в Работе Лючини и Солимено [41].)
Представим теперь резонатор в виде последовательности откры-
открытых передающих линий длиной 2 t, имеющих постоянные распростра-
540 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
1
0,01
-0,5 -0,25
Рис. 7.35. Коэффициенты отражения I г~ I и ко-
коэффициенты преобразования I г~, I мод вблизи
порога в зависимости от параметра
р = -s2j/Dt) + у, где велична.уу. связана с углом
4>j г тг/2 - [4т(/ - /?)/(^>]1/2. (Из книги Вайн-
штейна [2].).
нения Sj и характеризующихся матрицей рассеяния на концах [rjr]. С
хорошим приближением все коэффициенты rjjf можно приравнять к
нулю, за исключением коэффициента г^ что позволяет записать/ в
виде
f(t) = expOV) ± exp(-*V). G.16.21)
Поскольку при /= ±t мы имеем ±ехр (-isQ t) = г^ exp (is0 t)9 подста-
подстановка сюда вместо г^ выражения G.16.19) дает
Bt + d + i5)DnPmIt2 = n(m+ I), m = 0,l,.... G.16.22)
Здесь индекс т относится к различным значениям рт, а каждому рт
соответствует своя поперечная мода. Решив уравнение G.16.22) отно-
относительно вещественной и мнимой частей комплексного параметра /7,
получим следующие выражения для фазового сдвига /Зт и потерь за
один проход ат т-й моды резонатора:
_2к2(т+1)Ч(Т+д) f,_n2(m+lJSBt + d)
*np
G.16.23)
Объединив моды двух резонаторов в виде бесконечных полос, по-
получим распределение поля в резонаторе с прямоугольными зеркалами.
При t > 1 в хорошем приближении можно записать следующее выра-
выражение:
Ых, у) ос {lSl(M){COS W G-16-24)
I МП j I Sin j
где cos или sin выбираются в зависимости от того, четным или нечет-
нечетным является / (m), a
К = (/ + 1)(тг/2а)[1 + <5A + ОДвяЛТ.I72]; G.16.25)
выражение для ку записывается аналогично, необходимо лишь заме-
заменить / на т, a Na на N^
Вайнштейн применил также этот метод к случаю резонатора с
круглыми зеркалами и показал, что в этом случае собственные функ-
7.17. Резонаторы с аксиальной симметрией 541
ции записываются в виде
J[ k]Sl<t>' <7Л6'26>
где/г/т — т-ft нуль функции Бесселя7,(к) и N=a2/\d (a — радиус зер-
зеркала). В этом случае потери определяются формулой G.11.8).
7.17. РЕЗОНАТОРЫ С АКСИАЛЬНОЙ СИММЕТРИЕЙ
Если резонатор обладает аксиальной симметрией, то выражение для
поля внутри резонатора удобно искать в виде
и(Р,Ф) = KVin/ф + Clpcosty)Rlp(p\ G.17.1)
Up
где Stp и Clp — соответствующие коэффициенты, a Rlp (р) — функция,
которую можно определить, решив интегральное уравнение Фокса —
Ли. Ядро этого интегрального уравнения нетрудно вычислить, усред-
усредняя интегральное уравнение G.15.1) по cos 1ф (или sin/ф):
2я fcos/d>l Ca С2п
W)wH '*' J ('*w *
o "'*' J. "(''-*w
Ядро К12 этого уравнения совпадает с ядром уравнения G.14.56), если
положить W{=W2=O. Таким образом, мы имеем
Кц(р, Р', Ф> *') = [- »7(М)] ехр{ - ik/Bd)lgp2 + </р'2 - 2рр' oos@ - ф'У]}.
G.17.3)
Наконец, подставляя правые части выражений G.17.1) и G.17.3) в
уравнение G.17.2), получаем
ylpR'p(p) = 2п
Г j{2nN^rAexpl-inNgt^ + г/^J Up
G.17.4)
здесь N=a2/)ri и ту=р' /а. Заметим, что если g заменить на -g, то
собственные зйачения у1р заменятся на (—1)/+17/^ Отсюда следует,
что два резонатора с одинаковыми числами Френеля N и противопо-
противоположными по знаку значениями параметров g имеют одни и те же по-
потери.
542
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
7.18. ДИФРАКЦИОННАЯ ТЕОРИЯ НЕУСТОЙЧИВЫХ
РЕЗОНАТОРОВ
В телескопических резонаторах с зеркалами М\ и М2 излучение обыч-
обычно выводится с зеркала Мх (рис. 7.17); поэтому для простоты можно
предположить, что зеркало М2 имеет бесконечный диаметр. В этом
случае уравнение Фокса — Ли принимает вид
+ ri2)]Rl(ri)rjdrj, G.18.1)
02
)]Rl
М
N{ =
где e±ll<)>Rl(p/a) — распределение поля на зеркале Ми
= агх/\ d — число Френеля на зеркале Mv a J и ч\ — радиальные ко-
координаты, нормированные на величину ах.
Легко показать, что выражение G.18.1) описывает также и сим-
симметричный резонатор (рис. 7.36) с числом Френеля #^=N/B g2) и
параметром gcim= (g{ g2)l/2' Определим эквивалентное число Френеля
N3KB, которое равно расстоянию от поверхности волнового фронта
(проходящего через центр зеркала) до края зеркала, деленному на Х/2
(рис. 7.37). Таким образом, мы можем написать
^кв= ШЯ119г*Ях9г ~ Ш1/2(ЛГ0/2) = (М - 1/М); G.18.2)
здесь М— увеличение резонатора, a N=Nx/Bg2)- При этом выраже-
выражение G.18.1) принимает вид
MyfW) =
)]f(ri)rjdrj9 G.18.3)
Дифрагированные
лучи, достигающие
•Лучи,
дифрагиродан- 4г"
ные назад
Рис. 7.36. Формирование лучей, дифрагированных на краях в неустойчивом резонаторе.
7.18. Дифракционная теория неустойчивых резонаторов
543
Рис. 7.37. К определению эквива-
эквивалентного числа Френеля в неустой-
неустойчивом резонаторе.
где * = 2тгМЛГ=47гЛГэкв М2/(М2-1) и Д^= ДЧОехр(/тгАГэкв?2). При до-
достаточно больших числах Френеля интеграл в A7.8.3) можно вычис-
вычислить асимптотически, используя выражения E.8.1) и E.8.5). Таким об-
образом, для аксиально-симметричных мод (/=0) получаем
U)f G.18.4)
представляет собой волну, возникающую за счет краевой
дифракции. Следуя процедуре, предложенной Хорвицем [42] для пря-
прямоугольных зеркал, определим последовательность волн Fn краевой
дифракции, получаемых подстановкой волны Fn_{ в правую часть
уравнения G.18.3) с последующим вычитанием вклада волны F/1_1 в
краевую дифракцию. Таким образом, мы имеем
G.18.5)
G.18.6)
Разлагая Л?) в РЯД по &# получаем
m
ПО = 1+ Е
я=1
где т выбирается достаточно большим, чтобы на отрезке
функция Fm + l (f, t) была почти постоянной. Подставляя выражение
G.18.6) в G.18.3) и используя затем уравнение G.18.5), мы окончатель-
544 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
но имеем
Му\\ + ? anFn(U)\ = 1+1 anFn+1(U) + [l + ?
L "=1 J "=1 L "=1 J G.18.7)
Учитывая то, что функция Fm + { (?, t) на отрезке 0<? < 1 почти посто-
постоянна, и приравнивая коэффициенты при Fn(%41) в правой и левой ча-
частях данного уравнения, находим ат = (у— l)/Fm+1(l, t) и ап/оп^\^
=У"*. Таким образом, _
^ = [(У - l)/Fm+l(l№m-n; G.18.8)
здесь у=М7. Окончательно, приравнивая в уравнении G.18.7) коэф-
коэффициенты при Fj(?, 0 друг другу и используя выражение G.18.8) для
7, получаем следующее уравнение относительно"^:
Г(у- 1) = Fa+1(U) + (у - 1) ? у"
и=1
Решив это уравнение, можно вычислить коэффициенты ап с помощью
выражения G.18.8).
При / — оо (см. работу Батса и Авизониса [42а]) функцию Fn(^9 t)
можно записать как функцию
F(U) = l-e-w+^liX - (J2)][/oB^) + «4Bф], G.18.10)
гд^ 70 и 7j — функции Бесселя. При получении выражения G.18.10)
мы положили mt) = Щ/М^/Мп_1}. G 18Л1)
здесь Мл — увеличение М вп-й степени, а
Мт= ? М-2*. G.18.12)
к = 0
В частности, можно показать, что
Fw@, г) = - ехр( - 147г^Экв),
Fm(l,f) = -ехр[~147г^эквA + М-2т)]У0[8тгЛГЭкв)/(Мт)], G.18.13)
где параметр Мт заменен приближенным значением М^М2/
ДЛ/2-1), а //А/^ заменено на 4tN3KB. Поскольку Fm почти постоянна
на интервале @,1), из выражения G.18.13) следует, что значение Мт
должно быть больше, чем 8тг7Уэкв . Проверка, выполненная с по-
помощью серии численных расчетов, показала, что параметр т должен
быть установлен в соответствии с критерием Корейца
Mm = 25QN3KB, G.18.14)
Кроме того, решая уравнение G.18.9), можно определить потери а
для соответствующих мод, используя стандартное выражение
а=1-|у/М|2. G.18.15)
При этом для данных М и N3KB естественно расположить собствен-
собственные значения у в порядке уменьшения их абсолютного значения. В
частности, главным будет собственное значение, соответствующее ос-
7.19. Резонаторы с активной средой
545
0 5 70 /УЭкв
Рис. 7.38. Собственные значения 7 для аксиально-симметричных мод с индексами 1, 2, 3
и 4 в симметричном неустойчивом резонаторе с М - 5 и g = 2,6. Следует заметить,
что значения I7I осциллируют около значений, полученных в приближении геометри-
геометрической оптики. (Из работы Сигмэна и Миллера [37].)
новной моде. При Af3KB—00 главное собственное значение стремится к
единице. Действительно, сферическая волна /(?), будучи основной мо-
модой резонатора с зеркалами бесконечных размеров (см. разд. 7.12),
должна сохраняться неизменной и коэффициенты ап должны быть
равны нулю. Для зеркал с конечными размерами величина у уже не
равна единице, и если для нескольких мод построить график функции
« = a(N3KB), то мы получим зависимость, характеризуемую некоторой
периодичностью (рис. 7.38). Заметим, что I7I достигает максимально-
максимального значения при полуцелых значениях Nэкв. Отсюда следует, что поте-
потери основной моды минимальны при полуцелых значениях N3KB и мак-
максимальны при целых1*. Такое поведение основной моды обусловлено
сложным интерференционным взаимодействием между невозмущен-
невозмущенной сферической волной и волнами, дифрагированными на краях зер-
зеркал [43],
7.19. РЕЗОНАТОРЫ С АКТИВНОЙ СРЕДОЙ
До сих пор мы рассматривали лишь незаполненные активной средой
резонаторы. Поэтому, исходя из представленной выше теории, мы не
можем сделать заключения об амплитуде и частоте генерации в лазе-
лазерах. Для того чтобы получить информацию об этих параметрах, мы
должны решить уравнения G.1.13), а для этого нам необходимо
1} Как показали Ананьев и Шерстобитов (см. сб. Квантовая электроника /Под
ред. Н.Г. Басова, 1971, № 3, с. 82) рассмотренный случай резонатора с зеркалами с
острым краем является гипотетическим. На практике зеркало имеет сглаженный
край и периодическая зависимость дифракционных потерь от Мэкв исчезает. Поэто-
Поэтому требование СигмэнаЛ^экв=/и/2 является неверным. —Прим. перев.
546 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
иметь аналитическую зависимость лазерного усиления AL(I, а>, wL) и
фазового множителя j3L(/, w, wL) от частот о>, o?L и интенсивности.
Кроме того, необходимо учитывать и тот факт, что поле в окрестно-
окрестности оси резонатора неоднородно, поэтому каждому сечению резонато-
резонатора придется приписывать свое значение интенсивности. Таким обра-
образом, введенный выше параметр / для определения AL и j8L теперь мож-
можно использовать лишь для учета того, что обе эти величины зависят
от общей интенсивности генерируемой моды.
Кроме того, при определении величин A LnBL мы будем предпола-
предполагать, что лазер работает в одномодовом режиме, т. е. считать, что
поле в резонаторе генерируется на одной частоте, совпадающей с ча-
частотой данной продольной моды. Это предположение более или ме-
менее верно для некоторых типов лазеров, имеющих однородную шири-
ширину линии усиления. Однако газовые лазеры, линии которых являются
неоднородно уширенными за счет эффекта Доплера, трудно заставить
работать в одномодовом режиме, и для этого, как правило, требуется
принимать дополнительные меры.
Анализ многомодового режима генерации чрезвычайно сложен, по-
поскольку он должен учитывать нелинейный характер взаимодействия
между различными модами, которое может привести к возникнове-
возникновению нежелательных эффектов, таких, как генерация периодических по-
последовательностей или пакетов коротких импульсов вследствие фазо-
фазовой когерентности между различными генерируемыми модами (см.
книгу Ярива [8], указанную в литературе к гл. 1 нашей книги). В слу-
случае когда фазовая синхронизация обусловливается нелинейным поведе-
поведением активной среды, принято говорить о самосинхронизации, чтобы
отличить это от случая, в котором синхронизация возникает за счет
включения в оптический резонатор пассивной среды, коэффициент
пропускания которой увеличивается с интенсивностью излучения (пас-
(пассивная синхронизация мод). Примерами таких сред, называемых на-
насыщаемыми поглотителями, являются газы (например, SFg), жидко-
жидкости (например, красители), а также твердые тела, линия поглощения
которых совпадает с рабочей частотой лазера. Принцип действия на-
насыщаемых поглотителей нетрудно понять, если заметить, что погло-
поглотительная способность среды понижается, когда населенности верхне-
верхнего и нижнего уровней поглотителя выравниваются. (Следовательно,
хороший насыщаемый поглотитель должен насыщаться при умерен-
умеренных значениях интенсивности света). Более надежным способом син-
синхронизации мод является введение в резонатор нелинейной среды, по-
потери в которой могут быть промодулированы переменным электриче-
электрическим полем с частотой модуляции, совпадающей с межмодовым ча-
7.19. Резонаторы с активной средой 547
стотным интервалом. Этот метод, известный под названием актив-
активной синхронизации мод, в основном используется для генерации ко-
коротких импульсов в лазерах непрерывного действия.
В остальной части этого раздела рассмотрим процесс установления
непрерывной генерации в одномодовых лазерах с однородно уширен-
уширенной линией лазерного перехода. Хотя такая ситуация встречается ред-
редко, однако в этом случае рассмотрение оказывается не столь слож-
сложным, как при неоднородном уширении линий. Тем не менее к послед-
последнему случаю мы будем иногда обращаться [44].
7.19.1 Нелинейная диэлектрическая восприимчивость лазерной среды
В приближении изолированного резонансного уровня восприимчи-
восприимчивость активной среды можно записать в простом виде [ср. с выраже-
выражением A.2.57)]:
Z(v) = Хо + *[/ЛАГ/A + ^)]Г/[Г + i(v - vj] = x' + ix". G.19.1)
Здесь Г — коэффициент затухания, имеющий размерность частоты
(обычно измеряется в обратных сантиметрах) и соответствующий ши-
ширине линии кривой усиления х'Ч*') по полувысоте, / — сила осцилля-
осциллятора и«/=<?2 >/?| — усредненный по времени квадрат напряженно-
напряженности электрического поля Е, нормированный на квадрат напряженно-
напряженности поля насыщения Es. В выражении G.19.1) величина хо учитывает
нерезонансные вклады в восприимчивость, так что вблизи централь-
центральной частоты vL лазерного перехода ее можно считать постоянной. На-
Наконец, AN = (e2AN0)/BB(/no)LT) пропорционально плотности инверсии
населенностей AN0.
Во многих случаях значение х несущественно отличается от Хо* так
что вблизи линии лазерного перехода комплексный показатель пре-
преломления среды п=п+1к можно записать в виде
n + iK^xy2 + [i/B^/2][^AN/(l+y)]r/[r + i(v-vL)] = Wo + An + ^. G.19.2)
Используя безразмерную лоренцеву функцию
2{? - vL) = Г2/[Г2 + (v - vLJ] ее 1/A + С2), G.19.3)
где f=(*>— vL)/T — параметр расстройки, получаем
An = [1/Bио)][/ДЛГД1 + </)]^С, 19
K = [l/Biio)][/AAr/(l+^)]JSr.
Для пассивных сред мы имеем к<0, а для активных к>0.
В соответствии с выражением G.19.4) постоянная распространения
k=(}+ig/2 лазерной среды дается выражением
«2 -*»(»„ + ?rT7*f) + *•? ТТ^ G'19-5)
548 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
где усиление g среды на частоте pl было выбрано таким, чтобы ин-
интенсивность плоской волны, распространяющейся в среде, увеличива-
увеличивалась с расстоянием z как e8Z.
Для доплеровски уширенной линии записанное в G.19.5) выраже-
выражение для g должно быть заменено следующей формулой (вывод этой
формулы выходит за рамки настоящей книги):
rsp ( [_ AvD
здесь rsp — радиационное время жизни, a AvD — полная ширина ли-
линии по полувысоте, зависящая от атомной массы М следующим об-
образом:
AvD = 2vL[2KT/(Mc2)ln2]^2; G.19.7)
здесь К — постоянная Больцмана, а Г — абсолютная температура.
Изменение А п показателя преломления на частоте v вблизи vL мо-
может быть вычислено из дисперсионного уравнения Крамерса — Кро-
нига (см. задачу 9 в гл. 1 настоящей книги и книгу Беннета [18]):
f
Jo
Щ Щ@, G.19.8)
СОП1'2 Jo СОП1'2
где f=2(ln2I/2(*> — p^/Apd— расстройка для доплеровской линии, а
Z(f) — интеграл Доусона Z(f) = е~*2\^ e^dx (см. справочник Абрамо-
вица и Стегуна [4, с. 319], указанный в литературе к гл. 2 нашей кни-
книги). Интеграл Z(f), который напоминает функцию f/(l + f2), имеет
максимум ZMaKC = 0,54 при f= 0,924 и точку перегиба при f= 1,5. Таким
образом, изменение An показателя преломления при p = pl равно ну-
нулю, а при f = ± 0,924 принимает соответственно максимальные поло-
положительное и отрицательное значения.
7.19.2. Одномодовый режим
Строгое рассмотрение одномодового режима работы лазеров чита-
читатель может найти у Сарджента и др. (см. ссылку [6, ch. 7] в литерату-
литературе к гл. 1 нашей книги). Мы же ограничимся рассмотрением резонато-
резонаторов, заполненных активной средой с однородно уширенной линией.
Пусть активная среда характеризуется восприимчивостью х, определя-
определяемой выражением G.19.1), а генерация происходит на одной частоте
v. В этом случае соотношение G.10.7) можно переписать в виде
, '/во
где индексы /, т и п заменены одним индексом п. Предположим те-
теперь, что величина J столь мала, что коэффициент насыщения можно
7.19. Резонаторы с активной средой 549
взять равным единице. Тогда, используя выражения G.10.5), G.10.7) и
G.19.9), мы можем написать следующее уравнение:
{к2 - к2)Е„ = №2o<bN}J{l + «Ж, G.19.10)
где
Уравнение G.19.10) имеет решение либо ?"„ = 0, либо
К - к2 = ifk2<AN>J(f + »С). G.19.11)
Это означает, что поле в резонаторе с точностью до некоторого
неопределенного множителя Ап будет совпадать с модой Ф„, соб-
собственное значение кп которой удовлетворяет уравнению G.19.11). Если
кп разделить на вещественную к'п и мнимую кЦ части, то последнее
уравнение можно привести к виду
Bп/ф - v.) = -[/feo<AN>B/Bfe)]ifC, G.19.12а)
К = [/ko<AN>n/Bk)]^. G.19.126)
Поскольку частота vn фиксирована резонансными условиями G.10.146)
и G.10.14в), выражение G.19.12а) определяет расстройку частоты ге-
генерации по отношению к частоте резонатора vn. В частности, при
A/V=0 частота генерации v совпадает с vn. С увеличением инверсии на-
селенностей< AN)n частота v стремится уйти от резонансной частоты
и принимает значения между vn и vL. Это явление известно как затя-
затягивание частоты. Выражение G.19.126) устанавливает соответствие
между потерями в резонаторе, представляемыми величиной к" , и ин-
инверсией населенностей (AN)n. Величина AiVth, удовлетворяющая это-
этому условию, называется пороговой инверсией населенностей. Если
(AN)n записать в виде < AN)n = J^ANth, где jYn —так называемый
параметр возбуждения, a AA^th отнести к случаю, когда ^L=^w, то ус-
условия ^Ж<1 и -2%Ж>1 относятся соответственно к предпороговому
или надпороговому режимам генерации.
Если пренебречь дифракционными потерями, то к% с хорошей точ-
точностью можно записать в виде [см. выражение G.10.14а)]
А^'=A- \rlr2\)/Bd)9 так что пороговая инверсия населенностей с по-
помощью соотношения G.19.126) запишется следующим образом:
ANth = [2fc/(/fcgif)](l - \rxr2\)lBd). A7.19.13a)
Для газового лазера с доплеровски уширенной линией это выраже-
выражение заменится следующим [18]:
AWo,,h = 11/(п1п2У^к2Ш - |r1r2|)/Bd)] AvDtsp^\ A7.19.136)
а выражение G.19.12а) для расстройки лазера принимает вид
G.19.14)
550 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
где параметры Z и f определяются выражением G.19.8) [см. в книге
Беннета [18] выражение B.116)].
При ^Уп > 1 амплитуда поля становится столь большой, что уже
нельзя пренебрегать эффектами насыщения. В этом случае, полагая,
что в резонаторе поле is можно представить одной модой Ф„, из вы-
выражения G.19.9) получаем
здесь мы учли в явном виде зависимость параметра насыщения
Щ=Ё\/& от параметра расстройки f. Поскольку поперечное рас-
распределение поля медленно меняется с z, а 1Ф^1 является быстроме-
быстроменяющейся функцией от z, то подынтегральные выражения в G.19.9) и
G.19.15) можно заменить их значениями, усредненными на расстоянии
в несколько длин волн по оси z. Таким образом, получим
п : /* г ЩЫГМЮиНУ G19Л6)
причем
W = (E2jEl)<t>\ufm\, G.19.17)
~l-lw+-"- GЛ9Л8)
При достаточно малых W величину А( W) можно аппроксимиро-
аппроксимировать выражением l-C/2)lV, так что G.19.16) можно записать в виде
,Е„. G.19.19)
Таким образом, выражения G.19.12а) и G.19.126) можно перепи-
переписать следующим образом:
Bп/ф - vn) = -[/<AN>,,/Bfc)]i?C(l - \El*n<e\ G.19.20a)
1 = <?JTn{\ - \E2ndnSe\ G.19.206)
причем ап здесь заменяет несколько коэффициентов при втором члене
в скобках в выражении G.19.19). Как правило, моды лазера аппрокси-
аппроксимируют плоскими волнами, а инверсию населенностей AN считают
однородной по всему объему резонатора.
Из выражения G.19.206) следует, что квадрат амплитуды Еп опре-
определяется выражением
Еп = [2/CO](J?? - 1/^I/JS?2. G.19.21)
Величину El можно определить с хорошей точностью, если положить
На рис. 7.39 показано изменение мощность генерации в зависимо-
7.19. Резонаторы с активной средой
551
-50
50
Рис. 7.39. Зависимость интенсивности излучения
в случае одномодовой генерации от расстройки
vn — ?L частоты для лазерной среды с однород-
однородно уширенной линией генерации (Г = 100 МГц)
при возрастании параметра возбуждения
^Г= 1,05; 1,Ю; 1,15; 1,2.
сти от расстройки vn - vL (например, при перемещении одного из зер-
зеркал резонатора). Как и ожидалось, мощность достигает максимума
при рп = vL и убывает до нуля при f- = Jfn -1. Отсюда следует, что
допустимая расстройка резонатора зависит от ширины лазерной ли-
линии Г и от величины, на которую инверсия населенностей превышает
пороговое значение ANth9 которое в свою очередь определяется поте-
потерями в резонаторе. Можно расширить область допустимой расстрой-
расстройки частоты резонатора относительно центральной частоты лазерной
линии, если уширить лазерную линию и сузить полосу резонатора;
при этом, вообще говоря, необходимо увеличить и инверсию населен-
населенностей. В частности, когда интервал расстройки становится больше
межмодового расстояния, интенсивность лазерного излучения практи-
практически не зависит от длины резонатора. Это достигается при выполне-
выполнении условия <Ж> [c/BdT)+ I]2.
В одномодовом лазере с доплеровски уширенной линией (напри-
(например, в He-Ne-лазере) выходная мощность по мере изменения длины
резонатора (или, что эквивалентно, частоты) достигает своего макси-
максимума на частоте, соответствующей центру лазерной линии. Данное
явление, предсказанное Лэмбом (см. книгу [6], указанную в литерату-
литературе к гл. 1), впервые наблюдали Макфарлэйн и др. [4S], а также Зоке и
Джаван [46]. Это связано с тем, что каждая частица, движущаяся с
тепловой скоростью, «видит» две бегущие волны, из которых состав-
составлена картина стоячих волн, соответствующая моде резонатора, при-
причем частоты этих волн сдвинуты вверх или вниз относительно цент-
центральной частоты vL. Ширина провала, образующегося на кривой уси-
усиления, определяется в данном случае уже не доплеровской, а естест-
естественной шириной линии. Аналогичный эффект наблюдается всякий раз,
когда стоячая световая волна взаимодействует с поглощающей или
552 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
усиливающей газообразной средой. В настоящее время для определе-
определения естественной ширины доплеровски уширенных линий применяется
спектроскопия насыщения поглощения (см., например, монографии
Летохова и Чеботаева [47] и Корни [48]).
7.19.3. Одночастотная многомодовая генерация
Когда усиление за один проход превышает пороговую величину, насы-
насыщение среды может настолько сильно изменить распределение поля в
резонаторе, что оно будет существенно отличаться от того, что мы
имеем при генерации одной моды Фл. К аналогичному эффекту может
привести и значительное пространственное изменение инверсии насе-
ленностей в объеме моды. В этом случае для вычисления поля в резо-
резонаторе полезно применить приближение медленноменяющейся ампли-
амплитуды, рассмотренное в разд. 7.10.1.
В частности, если предположить, что лазер генерирует на основ-
основной моде TEMqq, to из уравнения G.10.17) имеем
?(±)(/с2 _ k2) T 2ikudE{±)ldz + со2fi0P{±) = 0, G.19.22)
откуда после простых преобразований получаем следующее соотноше-
d\E<±)\2/dz= ±ф,Е(*\Е1~))\Е1±)\2, G.19.23)
где а — коэффициент усиления интенсивности li?(±)l2, причем
a(z,?(+»,?<-») = -Re{(i/fcn-)[fc2 - kj + со2ц0Р{±)'/'?(±)]} =
= -Re[i(fe2 - fc?)/fce] + g(z,?<+>,?<->). G.19.24)
В этом выражении коэффициент усиления лазерной среды g записыва-
записывается в виде
Я>оо ' ( }
где скобки < > означают среднее значение на интервале Az>X.
Аналогично можно показать, что фазы ф(±), соответствующие ам-
амплитудам Е(±\Е(±) = Е^Це*^), удовлетворяют следующему урав-
уравнению:
йф{±)/й i{2 - k\ + c
J(->]. G.19.26)
Используя уравнение G.10.11) и выражение G.10.16), нетрудно пока-
показать, что обобщенные комплексные амплитуды ?1(±) в осевых точках
z j и z 2, расположенных на зеркалах резонатора, удовлетворяют еле-
7.19. Резонаторы с активной средой 553
дующему условию:
Kz2)E^iz1)-} = 1. G.19.27)
Если амплитуда поля?(±) в резонаторе много меньше амплитуды по-
поля насыщения Es, то g и /3 не зависят от Е{±) и системы уравнений
G.19.23) и G.19.26) нетрудно проинтегрировать в квадратурах. Кроме
того, граничные условия G.19.27) дают
G.19.28)
Отсюда можно вывести следующее соотношение для резонансного
значения kz:
uoo\
которое заменяет аналогичное соотношение G.19.11). Если в выраже-
выражении G.19.29) интеграл в числителе слабо зависит otz, to как afc), так
и /3 fe) стремятся к нулю и поля?(±) вдоль ochz остаются постоянны-
постоянными. В физическом смысле это означает, что возбуждается только одна
мода Ф^.
7.19.4. Уравнения Ригрода
Учет эффектов насыщения затрудняет решение представленных выше
уравнений. Поэтому для получения хотя бы качественных представле-
представлений о влиянии этих эффектов будем считать, что мода и^ является
плоской волной, а величина A7V=const во всем объеме резонатора. За-
Затем в коэффициенте насыщения, стоящем под интегралом в числителе
выражения G.19.25), заменим I ?"<+> t/00+?'(->t/00l2 на 1?<+>12 +
+ 1/?(~Ч2. Используя эти допущения, Ригрод [49] проанализировал
решения уравнения G.19.23), представив при этом коэффициент усиле-
усиления в виде
9 = ffo/D + ^(+) + S{~}1 G.19.30)
где J (±)= 12?(±) ит\г/Е\у a gQ — коэффициент усиления слабого сиг-
сигнала лазерной среды. Поскольку lwoolaexp(-A:/'z), уравнение G.19.23)
можно переписать в виде
dJ{±)/dz = ±{flfo/[l + ^(+) + *{-}1}А\ G.19.31)
причем граничные условия для этого уравнения запишутся следующим
образом:
J<+\zx) = Ы2./*-)^), y(-)(Z2) = \r2\2J^(z2). G.19.32)
Из граничных условий G.19.32) следует, что J{*\z) J{~Hz) =
= const. Следовательно, мы имеем [ср. с выражением G.1.9)]
= e2G9
G.19.33)
554 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
здесь функция G=\n[S(+\z2)/ ^(+)(^i)l представляет собой допусти-
допустимые потери за один проход. Для возникновения генерации необходи-
необходимо, чтобы коэффициент усиления слабого сигнала g0 превышал вели-
величину G/d.
Чтобы найти ^i+)(z{)9 необходимо проинтегрировать уравнение
G.19.31). После соответствующих вычислений имеем
./<+>(- 1 = e°d + 1п|Г1Г21 ~ e°d ~ ^{Al + A2 + Tl) G 19 34)
1 1} \ггГ2Г1 + \пГ2 - \г2/гх\ - 1 ~ Ах + А2 + Тх '
здесь А и Т — соответственно коэффициенты поглощения и пропуска-
пропускания зеркал (Г2=0). Последнее приближенное выражение подтвержда-
подтверждается тем, что при I л-1 — 1 мы получаем 1/lrl-l + A/2)Л + A/2)!Г.
7.19.5. Выходная мощность
В резонаторах, в которых для вывода излучения используется полу-
полупрозрачное зеркало Мх с коэффициентом пропускания Ти интенсив-
интенсивность выходного излучения о^вых, нормированная на интенсивность на-
насыщения, может быть получена с помощью выражения G.19.34). Та-
Таким образом, мы имеем
SB^(Ti/\ri\2)Si+\zi) = 9odlTJ{Al+A2 +
G.19.35)
Следовательно, «/вых максимальна, когда пропускание выходного
зеркала равно величине Гопт, определяемой выражением
Гопт= (А, + A2){t2god/(A1 + A2)V12 - 1}. G.19:36)
Таким образом, максимальная мощность, которую можно выде-
выделить из плоского резонатора при условии, что 2god>Ax + A2, дается
выражением
^вых= *Ua W1 - [Mi + A2)/B9od)Y% G.19.37)
где ^MOfla=rf>v2 — объем генерируемой моды, a /s — интенсивность
насыщения (в ваттах на квадратный сантиметр) активной среды.
До сих пор мы не учитывали ни дифракционные, ни внутренние
потери, присущие лазерной среде, ни потери на отражение. Эти поте-
потери можно учесть, включив их в коэффициент А Х+А29 который мы те-
теперь будем рассматривать как меру всех внутренних потерь резонато-
резонатора. Кроме того, можно предположить, что выражение G.19.37), полу-
полученное для резонатора с плоскими зеркалами, справедливо и для более
общего случая устойчивых резонаторов, если только расходимость ге-
генерируемой моды не становится слишком большой.
Выражение G.19.35) можно также использовать и для неустойчи-
неустойчивых резонаторов с умеренным значением увеличения (Л/~1). При
7.20. Перестройка частоты 555
этом для телескопического резонатора можно получить следующее
выражение^
С7.19.
В выражении G.19.38) множитель М— 1 учитывает тот факт, что
выходная мощность снимается с площади, которая в М— 1 раз боль-
больше площади вогнутой поверхности зеркала. Коэффициент отражения
R = l—A —Ad выбирается с учетом дифракционных потерь Ad, вели-
величина которых в данном случае весьма существенна. Поскольку эти по-
потери, а следовательно, и произведение Ах А2 в значительной мере зави-
зависят от эквивалентного числа Френеля 7V3KB, мощность РВЬ1Х для данного
значения оптимизируется соответствующим выбором величины М.
7.20. ПЕРЕСТРОЙКА ЧАСТОТЫ
Поведение резонатора, заполненного активной средой, существенным
образом определяется механизмами, ответственными за уширение ли-
линии усиления [50]. Если линия усиления является однородно уширен-
уширенной, то генерация на данной частоте препятствует возникновению ге-
генерации на других частотах. Наоборот, если линия усиления имеет не-
неоднородное уширение, то резонансное поле уже не будет взаимодейст-
взаимодействовать со всеми молекулами активной среды сразу и может возник-
возникнуть генерация на других частотах. Этот механизм ответствен за мно-
гомодовую генерацию во многих лазерах, особенно в тех, которые ха-
характеризуются высоким усилением. Такой режим используется в неко-
некоторых случаях для получения генерации излучения с достаточно широ-
широкой полосой с целью модуляции излучения на высокой частоте.
7.20.1. Изменение длины резонатора
В разд. 7.19 мы показали, что в случае когда ширина полосы излуче-
излучения лазера сравнима с межмодовым расстоянием р0 и величина Л
равна приблизительно единице, выходная мощность Рвых зависит в ос-
основном от расстройки vlmn — vL. При этом оптимизация выходной
мощности лазера требует соответствующей юстировки длины резона-
резонатора d, чтобы выполнялось условие vlmn = vh. Нетрудно показать, что
изменение d на А/2 означает изменение частоты на v0; следовательно,
длина резонатора должна контролироваться с точностью, лучшей чем
X. В некоторых случаях этого можно достичь, располагая выходные
зеркала на двух пластинах, скрепленных друг с другом инваровым
стержнем, или закрепляя их на оптической скамье из гранита, что осу-
осуществить значительно проще. Кроме того, между зеркалом и поддер-
556
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
живающей пластиной вводят пьезоэлектрический преобразователь,
толщину которого в диапазоне нескольких микрометров можно регу-
регулировать подачей соответствующего напряжения.
7.20.2. Перестройка частоты с помощью призм, решеток, эталонов
и резонансных отражателей
Другим способом управления частотой является введение внутрь резо-
резонатора диспергирующего элемента [50] в виде сочетания призмы и
эталона (рис. 7.40) или замена одного из зеркал резонатора дифракци-
дифракционной решеткой или стопой эталонов высокой резкости, образующей
так называемый резонансный отражатель. Широко используется так-
также метод ввода в резонатор эталона Фабри — Перо (см. следующий
раздел), развернутого на небольшой угол. Отражательная способ-
способность составного зеркала из наклонного эталона и примыкающего к
нему глухого зеркала соответствует кривой пропускания простого ре-
резонатора Фабри — Перо с большой областью дисперсии. Максимум
отражения составного зеркала достигается изменением угла наклона
эталона. Генерация в резонаторе будет происходить на частоте, соот-
соответствующей минимуму пропускания эталона.
В молекулярных лазерах спектральные линии, на которых происхо-
происходит усиление, отстоят друг от друга на расстоянии, равном несколь-
Решетка 6 схеме
Литтроу
Эталон
7
Стайилизиро-
данный интер-
ферометр
в
Рис. 7.40. Различные способы селекции линий излучения с мощью дисперсионных эле-
элементов, вводимых внутрь резонатора СО2-лазера (а) или аргонового лазера (б) с по-
помощью решетки или сочетания призмы и эталона. На рис. в резонатор Не—Ne-лазера,
снабженный интерферометром с целью уменьшения ширины линии лазерного излучения.
7.20. Перестройка частоты
557
ким обратным сантиметрам. Передача энергии в молекулярных
столкновениях приводит к тому, что система начинает генерировать
преимущественно вд линиях с небольшим усилением {эффект конку-
конкуренции линий). Иными словами, набор лазерных линий ведет себя
как одна однородно уширенная линия усиления. Если в резонатор вве-
ввести избирательные потери на всех линиях, кроме какой-либо выбран-
выбранной, то систему можно заставить генерировать на другой линии, не
обязательно совпадающей с наиболее эффективной. Поскольку рассто-
расстояние между спектральными линиями имеет величину порядка несколь-
нескольких обратных сантиметров, приходится отказываться от использова-
использования эталона, так как его область свободной дисперсии по порядку ве-
величины совпадает с расстоянием между линиями. В этом случае более
предпочтительно применять решетку Литтроу (рис. 7.40, а и 7.41). Ес-
Если мы имеем дело с немонохроматическим пучком, то внутрь полости
резонатора отражается лишь часть спектра, длина волны которой
удовлетворяет соотношению F.10.2) при а = 0. Остальные компонен-
компоненты спектра распространяются вне направления оптической оси и по-
поэтому теряются. Вращением решетки можно изменять длину волны
излучения, отраженного в резонатор. Ширина полосы генерации твер-
твердотельных лазеров [51] может быть сужена, если одно из зеркал заме-
Эталон
Частота
Рис. 7.41. Селекция мод в лазере на красителе, а — схематическое представление резо-
резонатора с решеткой и эталоном; 1 — решетка в схеме Литтроу; 2 — эталон; 3 — теле-
телескоп (расширитель пучка); 4 — ячейка с красителем; 5 — пучок от эксимерного или N2-
лазера. б — кривые, иллюстрирующие преселекцию мод решеткой и их селекцию с по-
помощью эталона.
558
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
нить специально сконструированным резонансным отражателем с уз-
узкой (скажем, 1 А) полосой отражения.
7.20.3. Одночастотная генерация с помощью интерферометра
Фокса — Смита
Существует несколько интерферометрических методов селекции мод.
Все они основаны на принципе замены одного из зеркал дополнитель-
дополнительным вторичным резонатором, область свободной дисперсии которого
сравнима с шириной полосы генерации. Таким образом, такой допол-
дополнительный резонатор можно рассматривать как составное зеркало с
переменной отражательной способностью.
В резонаторе, в котором селекция продольной моды осуществляет-
осуществляется с помощью интерферометра Фокса — Смита [52], протяженный ла-
Пропускание
интерферометра
Усиление
лазера.
Моды
резонатора
L
Частота
Рис. 7.42. Схематическое представление стабилизированного одномодового лазера с ин-
интерферометром Фокса — Смита, а — расположение зеркал; б — зависимости усиления
лазера и пропускания интерферометра от частоты. При изменении расстоянияd3 возни-
возникает максимум интенсивности выходного лазерного излучения, когда максимум пропу-
пропускания интерферометра совпадает по частоте с модой резонатора. Зеракло М'2 играет
роль делителя пучка.
7.20. Перестройка частоты 559
зерный резонатор длиной dx + d2 при помощи разделяющего зеркала
М2 связан с относительно коротким вторичным резонатором длиной
d2 + ^3 (рис. 7.42). В этом устройстве коэффициент отражения лазер-
лазерного излучения резонатором достаточно высок для того, чтобы осу-
осуществить генерацию в небольшом интервале области свободной дис-
персии резонатора с/2(,2 + ,з), G.20.,)
которая превышает ширину полосы генерации лазера.
Потери при полном проходе резонатора даются выражением
R Т2 R
СС1 {1Ж2)
где Л, — коэффициенты отражения зеркал, аГ2 — коэффициент про-
пропускания делительного зеркала М2.
В случае когда /?,= 1, Г2 = 0,5, d2+rf3 = Xm/2 и dl+d2 = \ п/2 (где пг
и п — целые числа), а стремится к нулю и интенсивность в моде не
убывает. Это обусловлено тем, что в картине стоячих волн резонато-
резонатора на разделительном зеркале имеется узел. Иными словами, регули-
регулируя длину плеч d2 и d3 соответствующим образом, можно добиться
того, чтобы потери в резонаторе были равны нулю на данной длине
волны. При переходе к следующему резонансу величина а резко воз-
возрастает. Огибающая потерь для различных мод совпадает с кривой
пропускания интерферометра, показанной на рис. 7.42,6.
7.20.4. Стабилизация частоты с помощью инжекции внешнего
сигнала
Важную роль играет метод стабилизации частоты лазера, который
заключается во введении в резонатор внешнего сигнала от стабилизи-
стабилизированного лазера низкой мощности, генерирующего излучение той же
частоты. Этот метод, известный как внешняя стабилизация частоты
[53, 54], использует нелинейную зависимость усиления от амплитуды
усиливаемой волны. Он был впервые предложен в 1927 г. ван дер По-
Полем в работах по синхронизации частоты генераторов на триодах (см.
книгу Сарджента и др. [6, с. 52], указанную в литературе к гл. 1 на-
нашей книги).
Влияние стабилизированного монохроматического сигнала e(t) =
= esino)meuit на амплитуду V(t) поля в лазерном генераторе можно
изучить на примере цепи с обратной связью, представленной на
рис. 7.6. Предположим, что коэффициент усиления А =А (V2) подчи-
подчиняется квадратичному закону А =А 0—A 2V2, и пренебрежем зависи-
зависимостью фазового сдвига /3(/, о>, wL) от частоты со [вследствие узости
спектрального диапазона V(J) с центром на частоте совнеш]. Величина
560 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
амплитуды V(t) удовлетворяет дифференциальному уравнению вин
дер Поля
d2V/dt2 - (d/dt)(A0V - Л3К3) + co2pe3F = ?eiusinetfBHeili;, G.20.3)
где VBHeui — величина, пропорциональная амплитуде внешнего сигна-
сигнала. Если Wp^-WB,,^,, то можно применить приближение медленноме-
няющейся амплитуды. Тогда решение уравнения G.20.3) можно напи-
написать в виде
V(t) = Re{?@exp[/ft>BHeui* + *Ф@]}, G,20.4)
где?*(О иФ(/) — две медленноменяющиеся функции времени f, такие,
что их вторыми производными по времени можно пренебречь. Учи-
Учитывая это условие, подставим в уравнение G.20.3) правую часть выра-
выражения G.20.4), тогда
dE/dt = ±(А0 - А3Е2)Е - ±а>шеш Квнеш cos Ф, G.20.5а)
d<b/dt = шрез- шнеш+ iaw(FBHeui/?)sinФ. G.20.56)
Если амплитуда Ушеш достаточно мала, то в уравнении G.20.5а)
членом, пропорциональным ^внеш, можно пренебречь, положив при
этом в уравнении G.20.56) Е = (А ^А 3I/2. Интегрируя последнее урав-
уравнение, получаем [55]
Ф@ = 2 arctg {1/К - ЦК2 - II'2/*] tg [Щг - to)(K2 - II/2]}; G.20.6)
здесь L = совнешКвнеш/BБ) — коэффициент синхронизации, К =
= (^рез^^внеш/^ "~ параметр расстройки, нормированный на L, а
t0 — постоянная интегрирования. Сразу заметим, что при \К\ > 1 про-
производная d$/dt никогда не становится равной нулю, поэтому генера-
генерация никогда не достигает стационарного режима. Мгновенная частота
генерации со@ является периодической функцией времени t, а именно
^рез + L sin ф@- G.20.7)
Напротив, в случае \К\ < 1 функция tg () в выражении G.20.6) пре-
преобразуется в th () и функция Ф(О асимптотически стремится к величи-
величине Ф^, связанной с К простым соотношением:
Ф,, = arcsinX. G.20.8)
Кроме того, мгновенная частота o)(t) асимптотически стремится к ча-
частоте внешнего сигнала со скоростью, определяемой произведением
В заключение заметим, что частота лазера может быть синхрони-
синхронизована с частотой внешнего источника, только если коэффициент син-
синхронизации L больше, чем расстройка 1сорез-совнеш1 между частотой
совнеш внешнего сигнала и частотой лазерной моды сорез. Это условие
дает нижний порог для минимальной мощности инжектируемого сигна-
сигнала, когда еще можно наблюдать устойчивую синхронизацию частоты.
7.21. Интерферометры Фабри — Перо 561
7.21. ИНТЕРФЕРОМЕТРЫ ФАБРИ — ПЕРО
В 1897 г. С. Фабри и А. Перо [10] впервые использовали плоскопарал-
плоскопараллельный оптический резонатор в качестве интерферометра. С тех
пор эти резонаторы интенсивно применяются для спектрального ана-
анализа сверхтонкой структуры и в точных метрологических измерениях
[56, 57]. Изобретение лазера привело к бурному росту теоретических и
экспериментальных работ по изучению свойств и применений резона-
резонаторов. Можно встретить резонаторы, имеющие зеркала с произволь-
произвольными фокусными расстояниями и зазором между ними от нескольких
миллиметров до нескольких метров. В многочисленных разделах дан-
данной главы мы представили результаты этих работ. Однако в этом
разделе мы обсудим главные особенности плоскопараллельных резо-
резонаторов, поскольку они находят широкое применение именно как ин-
интерферометры.
Во многих случаях интерферометры Фабри — Перо имеют очень
большие числа Френеля и дифракционными эффектами в них можно
пренебречь. Поэтому, в принципе для их изучения хотя и следовало
бы применить анализ мод, обычно предпочитают более простое рас-
рассмотрение. Кроме того, дифракционный анализ излучения, прошедше-
прошедшего через интерферометр, должен включать в себя решение неоднород-
неоднородных интегральных уравнений Фокса — Ли, в которые входит функция
источника, создаваемая падающим пучком, так что задача оказывает-
оказывается очень сложной.
В простейшем виде интерферометр Фабри — Перо состоит из двух
параллельных оптических поверхностей, между которыми возникает
множество отражений. Интерферометры могут состоять из пары по-
полупрозрачных зеркал, разнесенных на малое расстояние d, при этом
зеркальные поверхности должны быть обращены друг к другу и быть
параллельными с весьма хорошей точностью (рис. 7.43, а). Обратные
поверхности зеркал обычно делаются наклонными (типичные значе-
значения угла наклона 10—30') по отношению к рабочим поверхностям.
Это делается для того, чтобы избежать интерференции между луча-
лучами, отраженными от этих поверхностей, и теми, которые испытыва-
испытывают многократное отражение. Эти вторичные отражения не могут
быть устранены простым нанесением просветляющего покрытия, по-
поскольку даже лучшие просветляющие покрытия имеют отражатель-
отражательную способность 0,1—0,2%.
Устройства с фиксированным расстоянием между зеркалами назы-
называются эталонами. В этих приборах можно регулировать пропуска-
пропускание, изменяя угол падения луча. Эталон можно также изготовить, на-
напылив многослойные диэлектрические пленки, выполняющие роль
562
Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
Полупрозрачные
зеркала
Рис. 7.43. Схематическое представление двух конструкций интерферометров
Фабри—Перо, а — два полупрозрачных зеркала разнесены друг от друга на расстоя-
расстояние d и выставлены строго параллельно друг другу; б — твердотельный эталон.
зеркал, на противоположные грани пластинки из кварца или других
каких-либо оптических материалов, прозрачных в рабочем диапазоне
интерферометра (рис. 7.43, б). Качество таких твердотельных этало-
эталонов исключительно сильно зависит от степени параллельности про-
противоположных граней (обычно требуется, чтобы она была лучше чем
0,2'), а также от того, насколько сильно показатель преломления п и
толщина d зависят от температуры. Последние два параметра обычно
стабилизируют, помещая интерферометр в термостат, в котором
температура поддерживается с высокой степенью точности (обычно
±0,01 °С).
7.21.1. Коэффициент пропускания идеального интерферометра
Фабри — Перо
Популярность интерферометра Фабри — Перо объясняется тем, что
его пропускание Т(К0, 0) периодически изменяется с частотой и пред-
представляет собой серию пиков одинаковой амплитуды и очень малой
ширины. В частности, для идеального бесконечно протяженного ин-
интерферометра Фабри — Перо, освещаемого плоской волной, пропус-
пропускание Т(\9 в) определяется функцией Эйри (см. разд. 3.12.1):
Т2 1
)
A - RJ 1 + [4R/A - KJsin2(fcowdcos0')
A -
G.21.1)
где R = (RlR2)l/2, T= (TtT2)m a A — функция пропускания Эйри
(рис. 7.44), выраженная через резкость FR, которая определяется вы-
выражением G.21.6). Здесь Т12 — коэффициенты пропускания, а
7.21. Интерферометры Фабри — Перо
563
100%
mrt
Рис. 7.44. Зависимость функции Эйри от величины 2тА при различных коэффициентах
отражения/? интерферометра Фабри — Перо. С увеличением/? (выраженного в процен-
процентах) максимумы пропускания сужаются. Штриховые кривые представляют пропускание
наклонного эталона.
R! 2 — коэффициенты отражения двух отражающих поверхностей, в
то время как п nd — соответственно показатель преломления и тол-
толщина среды, заполняющей пространство между зеркалами. Угол па-
падения в внешней плоской волны связан с углом падения двух плоских
волн 0' внутри резонатора законом Снеллиуса: sin в=п sin в'. Во мно-
многих случаях 0 и 0' столь малы, что можно положить 0' = 0/л. Коэффи-
Коэффициенты пропускания Тх 2 и отражения связаны друг с другом соотно-
соотношением _
^1,2 + ^1,2 + ^1,2 = 1, G.21.2)
где A j 2 представляет суммарные потери, связанные с поглощением
излучения в покрытии, торцов интерферометра и рассеянием излучения
на шероховатостях поверхности D = А П0ГЛ+А расс). Потери, связан-
связанные с рассеянием, определяются приближенно выражением А расс=
= 2(k0n<jw?, где ow — стандартное отклонение отражающей поверх-
поверхности от идеальной плоскости.
В соответствии с формулой Эйри кривая пропускания интерферо-
интерферометра Фабри — Перо состоит из серии эквидистантных по частоте
(или волновому числу Х~о) пиков. При нормальном падении @' = 0)
минимальному ослаблению подвергается излучение с длиной волны
T^j^Tnd/m, гдеm — целое число, называемое порядком интерферен-
интерференции. При наклонном падении длина волны, на которой имеет место
максимальное пропускание, становится равной \„ = 2nd cos в' /т. При
достаточно малых 6' положение пика, соответствующего частоте
vm = с/\и> смещается относительно его положения при v 0 — 0 на ве-
величину bvm, которая зависит от 0' квадратичным образом:
Svm = vmO0'2/2. G.21.3)
Твердотельные эталоны нуждаются в тепловой стабильности, по-
поскольку как показатель преломления п9 так и расстояние d зависят от
температуры. Действительно, при изменении температуры Г на 5Г
564 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
частота рт, соответствующая максимуму пропускания эталона, сдви-
сдвигается на
<5vw = - vm[(l/n)(dn/dT) + (l/d)(d(d)/dT)li ST ==-rjST. G.21.4)
Температурный линейный коэффициент расширения rj материала эта-
эталона составляет величину порядка B — 10) • 10~6 [58]. Поэтому, чтобы
гарантировать минимальный сдвиг частоты bvm = ± 20 МГц для этало-
эталона, работающего на длине волны 500 нм, изменение его температуры
не должно превышать ±0,01 °С. Этого добиваются, помещая эталон
в небольшую камеру с хорошо стабилизированной температурой.
Коэффициент пропускания эталона изменяется от Гмакс до 7^.
Отношение С- ^макс/^мин» называемое контрастом интерферометра,
дается выражением
с=JS4"!»1»2?!!^!. G.21.5)
Интерферометры, используемые для спектрометрических исследова-
исследований, характеризуются высокими значениями контраста С, в то время
как эталоны, применяемые в лазерных резонаторах, обычно имеют
умеренные значения С.
Если контраст достаточно высок, то эталон можно характеризо-
характеризовать резкостью F, которая определяется как отношение величины об-
области свободной дисперсии эталона vo=c cos 0' /Bnd) к полной ширине
пика пропускания по полувысоте. В случае когда пропускание эталона
описывается функцией Эйри, резкость F определяется выражением
FK = я(КхH^/VCl - (ДАI'2], G.21.6)
где нижний индекс R (приТ7) служит напоминанием того, 4toFr зави-
зависит от коэффициентов отражения зеркал.
Ниже мы представим более сложное выражение для F, в котором
учитывается влияние ограниченности апертуры светового пучка и
аберрации зеркал. Поэтому через FR мы будем обозначать величину
резкости, зависящей только от коэффициента отражения зеркал, и на-
называть ее отражательной резкостью.
Резкость интерферометра есть его способность разрешать близко
расположенные линии в спектре падающей плоской волны. Величина
резкости пропорциональна времени жизни фотона в интерферометре,
поэтому ее можно определить как эффективное число пучков, с по-
помощью которых создается интерференционная картина в интерферо-
интерферометре.
7.21.2. Применение интерферометра Фабри — Перо
Интерферометр Фабри — Перо обычно используют [59] в условиях,
когда его входная грань освещается кодлимированным пучком и ис-
7.21. Интерферометры Фабри — Перо 565
следуется прошедший луч в фокальной плоскости линзы, помещенной
со стороны выхода.
Первоначально интерферометр Фабри — Перо использовался как
спектрограф, в котором в фокальную плоскость выходной линзы по-
помещали фотопластинку. Если источник монохроматического излуче-
излучения имеет конечные размеры, то излучение, падающее на эталон,
может быть представлено суперпозицией плоских волн с волновыми
векторами, заполняющими некоторый телесный угол. Следовательно,
через эталон проходят только те компоненты излучения, углы паде-
падения 0т которых принадлежат ряду дискретных значений, таких, что
kondcos вт = тп . G.21.7)
В случае когда на интерферометр нормально его поверхности пада-
падает плоская монохроматическая волна, картина поля за ним представ-
представляет собой совокупность концентрических узких колец, центр которых
расположен на бесконечности. Угловые диаметры у-го и к-го колец
связаны соотношением 2(cos0y — cos0fc)=(fc—у')Хо/0л)=0?—0f. Угловую
ширину кольца можно измерить по точкам, соответствующим поло-
половине максимальной интенсивности, eU2 = \/(F2nd0). Таким образом,
данное кольцо наблюдается под телесным углом
П = 2пвв1/2 = nXJ(Fdn) = 2п/Я9 G.21.8)
где &= XA1/2=2Frf/X0 — теоретическое разрешение интерферомет-
интерферометра. В соответствии с выражением для & разрешение интерферометра
Фабри — Перо можно варьировать в широких пределах, изменяя рас-
расстояние rf, и в менее узких пределах, изменяя отражательную рез-
резкость.
Кольца, наблюдаемые в фокальной плоскости выходной линзы,
представляют собой совокупность тонких круговых полос равного на-
наклона и называются кольцами Хайдингера по имени австрийского фи-
физика Вильгельма Карла Хайдингера A795 — 1871). Радиусы рт этих
колец даются выражением
Рт = /вт = 2^2/[1 - mA0/Bd)]1/2, G.21.9)
где/ — фокусное расстояние выходной линзы.
Если источник излучает в узком спектральном диапазоне, то каж-
каждая линия спектра определяет свою картину полос. Обрабатывая на
микроденситометре фотографию полученной интерференционной кар-
картины, можно с соответствующим разрешением получить спектр ис-
источника. Этот метод широко применяется для изучения сверхтонкой
структуры атомов, откуда в свою очередь можно получить информа-
информацию о структуре атомного ядра. Современные интерферометры Фаб-
Фабри — Перо используются при изучении комбинационного,
566 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
мандельштам-бриллюэновского и рэлеевского рассеяния в газах, жид-
жидкостях и твердых телах.
В 1948 г. Жакино и Дюфур предложили спектрометр Фабри — Пе-
Перо, в котором фотопластинка была заменена фотоэлементом (кото-
(который в настоящее время представлял бы собой ФЭУ или фотодиод),
расположенным за системой точечных отверстий в плоскости, совме-
совмещенной с фокальной плоскостью выходной линзы. Этот метод назы-
называется сканированием центрального пятна. Изменяя линейно во вре-
времени давление газа внутри интерферометра или смещая зеркала, под-
поддерживаемые пьезоэлектрическими прокладками, с фотодетектора мы
получим сигнал, который будет пропорционален спектральной ярко-
яркости источника излучения на той частоте, на которую в данный мо-
момент настроен интерферометр. Например, если интерферометр поме-
поместить в камеру высокого давления, содержащую газ SF6 (показатель
преломления газообразного SF6 при нормальных условиях равен при-
примерно 1,00078), то можно достичь [60] скорости сканирования
3,9 А/атм. Если при сканировании давлением область свободной дис-
дисперсии не зависит от расстояния rf, то при механическом сканирова-
сканировании эта область увеличивается с уменьшением d. Чтобы просканиро-
вать всю область дисперсии, величину d необходимо изменить на Х/2.
Спектроскопические приборы характеризуются пропусканием U
(см. разд. 2.15 и 4.15), определяемым как произведение площади 5 на
телесный угол Q сбора излучения. Систематическое исследование
пропускания различных приборов впервые выполнил Жакино [56]. Для
интерферометра Фабри — Перо с учетом выражения G.21.8) можно
записать u = SQ = nJi0S/(Fd) = 2nS/®. G.21.10)
Пропускание U, которое также называется светособирающей способ-
способностью или светосилой, представляет собой способность интерферо-
интерферометра собирать максимум излучения от источника, разлагать его в
спектр и затем детектировать.
Если через L (светимость) обозначить отношение спектральной
плотности потока Ф(?о) (измеряется в эрг-см/с) излучения, попадаю-
попадающего на фотодетектор, к спектральной яркости В(к0) (измеряется в
эрг/см • ср • с) протяженного источника, то можно записать следующее
выражение:
L = Ф/Б = т1/ = r2nS/<%, G.21.11)
где г — максимальный коэффициент пропускания интерферометра.
Следует заметить, что для данного эталона произведение светимо-
светимости на разрешающую силу является постоянным и определяется толь-
только площадью эталона S и коэффициентом пропускания т. Жакино по-
показал, что у интерферометров Фабри — Перо произведение L& в
7.21. Интерферометры Фабри — Перо 567
70—350 раз превышает аналогичное произведение у спектрометров с
дифракционными решетками. Это объясняется тем, что интерферо-
интерферометр Фабри — Перо собирает свет с гораздо большего телесного
угла, чем спектрометр с дифракционной решеткой. Более полную ин-
информацию о методах записи и сканирования спектра читатель может
найти в монографии Кука [59].
7.21.3 Составные интерферометры Фабри — Перо
В некоторых случаях необходимо иметь высокое разрешение в относи-
относительно широком спектральном диапазоне. В частности, при изучении
сверхтонкой структуры расстояние между отдельными ее компонента-
компонентами может во много раз превышать ширину отдельной компоненты.
Поэтому, чтобы получить однозначную информацию о таком спек-
спектре, необходимо расширить область свободной дисперсии эталона.
Этого обычно достигают, помещая последовательно [60] с основным
эталоном дополнительный эталон, имеющий более короткую длину
d'. В общем случае области низкого пропускания короткого эталона
совпадают с максимумами пропускания длинного. Подбирая длину
d', пики короткого эталона можно совместить с любым q-м макси-
максимумом длинного. Таким образом у более длинного эталона все макси-
максимумы, за исключением д-го, подавляются, а разрешение остается
прежним.
Этот принцип может быть распространен и на большее число сое-
соединенных последовательно интерферометров. Например, для спектро-
спектроскопических исследований атмосферы планет, спектров межзвездного
газа и Солнца применяется спектрометр PEPSIOS [61], который со-
состоит из трех интерферометров и интерференционного фильтра.
7.21.4. Аппаратная функция интерферометра
В случае когда источники создают излучение в узком спектре с прак-
практически нулевой шириной, с помощью интерферометра мы наблюда-
наблюдаем спектральный профиль, который называется аппаратной функцией
W(k0). Вид функции W зависит от характеристик спектрометра и
входного светового пучка. В идеальном случае функция W совпадает с
функцией Эйри. На практике из-за того, что нельзя достичь идеальной
плоскостности, зеркала интерферометра будут иметь некоторые нере-
нерегулярности, которые вызовут уширение полос и уменьшение их макси-
максимумов. Дополнительное ограничение состоит в том, что падающее на
приемную площадку фотодиода излучение составлено из тех плоских
568 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
волн, направления распространения которых лежат внутри телесного
угла Й с углом полураствора a=a/f, где а — радиус отверстия в фо-
фокальной плоскости выходной линзы с фокусным расстоянием/.
Отклонение функции W от функции Эйри вследствие указанных
выше причин впервые исследовал Чеббол {62]. В частности, неплос-
неплоскостность зеркал можно учесть, если рассматривать интерферометр в
виде мозаики микроэталонов. Распределение длин d можно предста-
представить в виде функции распределенияD(x —d)=dS /dx, гдеой — элемент
площади, на котором толщина эталона имеет величину, лежащую в
интервале от х до х + dx, и d — средняя толщина эталона. Например,
если зеркала обладают кривизной, близкой к сферической, то функция
D (х — d) описывает прямоугольник. Если же зеркала имеют случайные
дефекты, то функция распределения является гауссовой. Очевидно,
что D представляет собой весовую функцию для толщин d в функции
Эйри. Следовательно, W(k0) можно записать в виде свертки, а именно:
Гамаке
W(k0) = т D(x - d)A{F,k0nxcosef)dx = D*A. G.21.16)
J*MHH
Учитывая конечный угловой размер а = a/f точечного отверстия,
помещенного перед фотодетектором, выражение для W можно пере-
переписать в виде
fa Г*макс
W(k0) = т d(92) D(x - d)A[F,k0nxcos(e/n)~]dx, G.21.17)
JO Jxmhh
где мы положили 0' = в/п. Последний интеграл можно найти либо
численными методами, либо с помощью разложения функции А в ря-
ряды Фурье (см. задачу 25 и монографию Кука [59]). Наконец, мы дол-
должны учесть конечный диаметр пучка, падающего на интерферометр.
Простой способ учета всех перечисленных выше эффектов состоит
в предположении о том, что функция W пропорциональна функции
Эйри, соответствующей аппаратной резкости Fl9 причем последняя
определяется выражением
1/Ff = 1/FI+ 1/Fi + \/Fl + 1/FS, G.21.18)
где FF=M/2—резкость, определяемая точностью изготовления и
юстировки, (М — приведенная к длине волны величина отклонения
поверхности зеркала от плоскости), Fp = \f2/(a2d) — резкость,
определяемая размером точечного отверстия; FD = 2?J/(X0 nd) —
дифракционная резкость (D — диаметр апертуры интерферометра).
Заметим, что FF учитывает также непараллельность зеркал. Лучшие зер-
зеркала изготовляются с неплоскостностью Х/200 на длине волны 500 нм,
поэтому их аппаратная резкость не может быть больше чем 100.
Как было показано выше, аппаратная функция интерферометра
Задачи 569
Фабри — Перо зависит от нескольких факторов. Однако при любых
обстоятельствах она является идеально симметричной в противопо-
противоположность асимметричной форме аппаратной функции спектрометров с
дифракционной решеткой. Благодаря этой симметричности интерфе-
интерферометры Фабри — Перо удобно использовать для проведения точных
измерений асимметрии линий, излучаемых астрономическими объек-
объектами, откуда можно получить данные о гидродинамических условиях
на поверхности этих объектов.
Размер поверхности интерферометра ограничивается площадью,
на которой плоскость может быть выдержана с точностью до Х/200
(типичные углы 2—3"). Однако апертурный угол Q, т. е. телесный
угол собираемого излучения, обратно пропорционален разрешающей
способнрсти ^. Это означает, что светосила интерферометров умень-
уменьшается с ростом 3?. Чтобы преодолеть эту трудность, Конн [63] в
1958 г. предложил интерферометр, состоящий из двух сферических
зеркал, расстояние между которыми равно радиусу их кривизны.
Этот интерферометр имеет такую же аппаратную функцию, область
свободной дисперсии и разрешающую силу, как и плоский интерферо-
интерферометр с удвоенным расстоянием между зеркалами. Однако у интерфе-
интерферометра Конна имеется важное свойство, а именно то, что в нем те-
телесный угол собираемого излучения пропорционален величине ^. Бла-
Благодаря этому свойству светосила интерферометра Конна может на-
намного превышать светосилу плоского интерферометра. Данное обсто-
обстоятельство становится особенно существенным при зазоре между зер-
зеркалами интерферометра, большим чем 0,1 м.
ЗАДАЧИ
Раздел 7.4
1. Покажите, что в эллиптических координатах дис, определяемых выражениями
дг= fcch/isinp, z = b shucosp, уравнение эйконала записывается в виде
|VS|2 = {l/[b2(cosh2/i - sin2 v)]}[(as/^J + (dS/dvJl
Раздел 7.9
2. Рассмотрите резонатор, заполненный линзоподобной средой с показателем пре-
преломления, который с расстоянием р от оси z изменяется как п(р)= nQ-(\/2)n2p2 на дли-
не от z=0 до z = d. Ось резонатора совпадает с осью z. Найдите параметры основной
гауссовой моды, полагая показатель преломления среды вне резонатора равным едини-
единице. Подсказка. Используйте метод матрицы ABCD. Чтобы вычислить матрицу резона-
резонатора, рассмотрите сначала тонкий слой между z и z+dz, когда матрица S (z, z+dz)
сводится к матрице тонкой линзы с фокусным расстоянием f=no/(n2dz). Таким обра-
образом, можно записать следующее уравнение:
S(z,z 4- dz) = 1 - (n2/n0)Adz,
570 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
причем
И-
Затем проинтегрируйте уравнение
S@,z + dz) - S@,z) = -(п2/и0)А • S@, z)dz.
С учетом А2 = 0 получаем
S@,z)=l-(n2/«o)zA.
3. Рассмотрите лазер, генерирующий излучение в дальнем ИК-диапазоне, в кото-
котором активной средой является HCN-плазма, излучающая на длине волны 337 мкм.
Предполагается, что профиль электронной плотности в положительной области столба
описывается функцией УоB,4О48/о/я), где а — радиус плазменной трубки и
/ — функция Бесселя нулевого порядка. Из-за наличия электронного газа частотная за-
зависимость показателя преломления описывается формулой (l-Wp/w2I/2, где
«р = (е2ле//исе0I/2=5,6-1014/?е1/2 рад/с — плазменная частота и ле — число электро-
электронов в кубическом сантиметре. Вследствие изменения показателя преломления п с рас-
расстоянием от оси трубки плазменный столб представляет собой рассеивающую линзу,
которая стремится расфокусировать излучение резонаторных мод. Полагая d= 3 м, ра-
радиусы зеркал /? = 10 м и а=5 см, вычислите максимальную электронную плотность,
при которой резонатор еще будет устойчивым. Подсказка. Используйте для линзо-
линзообразной среды с параболическим профилем показателя преломления метод лучевых
матриц, подобный тому, который был использован в предыдущей задаче (аппроксими-
(аппроксимируйте функцию Бесселя параболой) и примените условие устойчивости \A + D\ <2.
4. Выведите выражение для размера пятна и радиуса кривизны гауссова пучка, сфо-
сфокусированного тонкой линзой в среду с показателем преломления п. Найдите положе-
положение и диаметр перетяжки пучка.
5. Вычислите поля гауссова пучка, дифрагированного на апертуре с пропусканием
Плоскость апертуры перпендикулярна направлению распространения гауссова пучка.
Вычислите также с помощью закона A BCD соответствующую лучевую матрицу.
6. Имеется симметричный резонатор с гауссовым профилем коэффициента отраже-
отражения зеркал. Найдите размер пятна и радиусы кривизны ТЕМ^-моды в непосредствен-
непосредственной окрестности зеркал и вычислите поле излучения, выходящего из резонатора, а так-
также интегральные потери на отражение. Подсказка. Рассмотрите резонатор как последо-
последовательность линз, в которой каждая линза имеет гауссов профиль пропускания. Заметь-
Заметьте, что интенсивность гауссовой моды, распространяющейся слева направо, не совпада-
совпадает с интенсивностью моды, распространяющейся в противоположном направлении.
(Подробнее об этом см. в работе [64].)
Раздел 7.10
7. Докажите условие ортогональности G.10.2) для мод замкнутого резонатора с
конечным импедансом стенок. Подсказка. Ознакомьтесь с работой ван Бладеля (см. ра-
работу [8, Ch. 10], указанную в литературе к гл. 4 данной книги), а также используйте вы-
выражение D.2.1).
Раздел 7.11.
8. Вычислите диаметр входного отверстия в плоскопараллельном или конфокаль-
конфокальном резонаторе, помещенном перед выходным зеркалом с целью получения генерации
в СО2-лазере. Считайте, что показатель усиления g = 0,04 см и дли-
Задачи 571
на резонатора d = 1 м. Подсказка. Используйте ассимптотические выражения G.11.8)
и G.11.9) для вычисления потерь в резонаторе.
9. Простой способ вывода излучения из резонатора И К-лазера заключается в ис-
использовании кольцевого зеркала. Рассмотрите резонатор, состоящий из плоского и во-
вогнутого зеркал. Предположите, что диаметр отверстия в зеркале меньше размеров пят-
пятна пучка на зеркале, так что картины мод возмущаются незначительно. Вычислите:
а) коэффициенты потерь для ТЕМ^, ТЕМ10 и ТЕМ^ аксиально-симметричных мод и
б) распределение интенсивности в дальнем поле для пучка, прошедшего через отвер-
отверстие. В частности, рассмотрите случай, когда X = 3 мкм, d = 1 м, а радиус кривизны
вогнутого зеркала R = 20 м. (Подробности можно найти в статье Мак-Камбера [65].)
10. Рассмотрите криптоновый лазер, имеющий выходную мощность 0,5 Вт и вы-
выходное полупрозрачное зеркало с пропусканием 2%. Вычислите среднее число фотонов
в резонаторе, если резонатор состоит из плоского зеркала и полупрозрачного выходно-
выходного зеркала с радиусом кривизны 6 м. Зеркала находятся друг от друга на расстоянии
0,75 м, длина волны генерации равна 415 нм. Сравните число фотонов в единице объема
с плотностью частиц газа и предполагаемой плотностью числа плазменных электронов.
11. Рассмотрите резонатор, состоящий из плоского зеркала и полупрозрачного во-
вогнутого зеркала с радиусом кривизны R = 15 м. Вогнутое зеркало имеет плоскую
внешнюю поверхность, поэтому действует как плосковогнутая линза с показателем пре-
преломления п - 1,5 на длине волны X = 500 нм и толщиной d = 1 см. Вычислите с уче-
учетом этих условий расходимость выходного пучка в дальнем поле.
12. Рассчитайте конструкцию из собирающей и рассеивающей линз, которая позво-
позволяет сфокусировать гауссов пучок с известными параметрами в данную точку с задан-
заданными параметрами перетяжки. Рассмотрите пучок, у которого размер пятна равен
1,5 мм, а расходимость в дальнем поле составляет 0,7 мрад. Считайте при этом, что
длина волны излучения равна 500 нм.
13. Оптический резонатор аргонового лазера (X = 5145 А) состоит из двух зеркал с
коэффициентами отражения 99,8 и 87,8%, разнесенных на расстояние 60 см. Вычислите
спектральную ширину резонансных мод пассивного резонатора и теоретическую шири-
ширину линии генерации лазера, определяемую выражением G.1.14), при условии, что вы-
выходная мощность лазера в одномодовом режиме составляет 0,5 Вт. Затем, воспользо-
воспользовавшись выражением G.11.5), оцените изменение длины резонатора, которое привело
бы к сдвигу частоты генерации на величину, равную теоретической ширине лазерной
линии. (См. книгу Корни [48, с. 375].)
14. Вычислите дифракционные потери излучения для аксиально-симметричных мод
ТЕМод и ТЕМ01, если в симметричный резонатор вблизи одного из зеркал ввести диа-
диафрагму, диаметр которой в 3,5 раза превышает размер перетяжки гауссова пучка в ре-
резонаторе. (См. книгу Корна [48, с. 375].)
Раздел 7.14
15. Покажите, что на каждом зеркале линейного резонатора две лагерр-гауссовы
моды удовлетворяют условию ортогональности G.14.13).
Раздел 7.16
16. Покажите, что при т=оо решением уравнения G.16.4) является эрмит-гауссова
мода. Вычислите собственное значение у.
17. Вычислите для резонатора с зеркалами в виде бесконечных полос комплексный
параметр р. Для этого моду резонатора можно записать в виде
f(t) = COS So t + A COS Sjfj + В COS S-Xt.
572 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
18. Используя выражения G.16.19) и G.16.20) для коэффициентов отражения и пре-
преобразования мод на открытых концах резонатора, найдите числа Френеля резонатора,
у которого амплитудами А и В в формуле из предыдущей задачи можно пренебречь.
Раздел 7.17
19. Покажите, что прия = оо уравнению G.17.4) удовлетворяют лагерр-гауссовы
моды.
Раздел 7Л9
20. Покажите, что справедливо следующее соотношение:
\ С2п dx
]
_ A
Используя это соотношение, выведите дисперсионное уравнение G.19.8).
21. Покажите, что если инверсия населенностей AN постоянна по сечению основной
моды лазерного резонатора, то усиление лазерного резонатораg(z, ?(+), Я*"*), опреде-
определяемое выражением G.19.25), запишется в виде
где
W = ,/(+> + J»"<-> + 2[^(+>l/(-»]1/2cosBfe;z + ф),
22. Используя формулы, приведенные в предыдущей задаче, покажите, что
2 C*
л Jz
где
23. Используя выражения, приведенные в предыдущих двух задачах, покажите, что
для гауссовой моды малой интенсивности уравнение Ригрода G.19.31) можно заменить
следующим уравнением:
Затем, используя равенство J^+^J^~^ = const, запишите »/*+) в виде функции координа-
координаты z при gQ(z)=const.
Раздел 7.20
24. Рассмотрите твердотельный эталон, который наклонен на угол 0 относительно
падающего гауссова пучка. Вычислите интенсивность прошедшего пучка. В частности,
обсудите уменьшение Максимума пропускания эталона при больших значениях в. Это
явление уменьшения интенсивности обусловлено частичной суперпозицией многократно
отраженных пучков, происходящей при вФОу и является источником потерь при выводе
излучения из резонатора.
25. Покажите, что формулу Эйри для пропускания эталона можно записать в виде
ряда Фурье:
1 1-.
Задачи 573
Подсказка. Запишите 2cosB п ф) в виде е'2и* + е"-'2л* и покажите» что правая часть при-
приведенного здесь выражения представляет собой геометрическую прогрессию, сумма ко-
которой равна левой части этого выражения.
26. Покажите, что если вектор разности оптических длин Dj одного из двух интер-
интерферометров Фабри — Перо почти параллелен вектору D2 другого интерферометра, то
полосы суперпозиции в белом свете представляют собой гиперболы. (См. книгу Кука
[5% с. 132].)
27. Рассмотрите эталон, на который под прямым углом падает гауссов пучок. Най-
Найдите форму изображения, возникающего в фокальной плоскости выходной линзы ин-
интерферометра. В частности, проверьте соотношение между диаметром перетяжки гаус-
гауссова пучка, расстоянием между зеркалами эталона и числом наблюдаемых колец.
28. Определите основные параметры стеклянного эталона ^7 = 1,5), который ис-
используется для выделения одночастотного излучения с длиной волны 4880 А на выходе
ионного аргонового лазера. Считайте, что в этом случае ширина кривой усиления по-
порядка 6 ГГц, а однородная ширина линии достигает почти 500 МГц. (См. работу Хер-
шера [66].)
29. Имеется импульсный лазер на красителе, в котором для настройки использует-
используется дифракционная решетка. Рассчитайте параметры твердотельного эталона Фабри —
Перо, который сужает линию лазера до 100 МГц. Ширина полосы генерации без этало-
эталона равна 2 ГГц. Вычислите угол, на который следует повернуть эталон, чтобы проска-
нировать интервал 2 ГГц.
30. Покажите, что характеристическая матрица М (см. гл. 3) эталона, представляю-
представляющего собой плоскопараллельную пластину, на которую с противоположных сторон на-
напылены одинаковые многослойные диэлектрические покрытия, дается выражением
М
где <?=fcom/cos0', Z=(fo/rt)cos0'(l/cos0') для ТМ (ТЕ)-волн, а А, В, С и
D—соответствующие компоненты характеристической матрицы многослойного ди-
диэлектрического покрытия.
31. Покажите, что амплитудный коэффициент пропускания выходной пластины
эталона, рассмотренного в задаче 30, дается выражением
(AD + ?C)cos<? - if ACZ + — jsin<? 2АВсоьф - Ia1! + — Jsin^
2CD cos ф - i( C2Z + — J sin ф (ВС + AD) cos ф - I ACZ + ^-\ sin ф
t = {IAD + ВС+AB/Zamuf CD^J cos<? - i\_ACZ+(BD/Z) + M2Z)/BgJ+
+ B2/BZZBHem) + (l/2)C2z4,eui+ (l/2)(D2ZBHeui /Z)] sin ф}~\
где?адеш — импеданс среды на левой и правой сторонах обеих пластин эталона. Под-
Подсказка. Покажите, что / = (l+r)/(y4+2?/ZBHeui), где г — коэффициент отражения от
входной пластины, а Л и В — коэффициенты вышеупомянутой матрицы. Используйте
также соотношение C.12.6).
32. Используйте приведенное в задаче 31 выражение для / и вычислите коэффи-
коэффициент пропускания интерферометра Фабри — Перо с зеркалами, имеющими алюминие-
алюминиевое и серебряное покрытия.
574 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
ЛИТЕРАТУРА
1. Ыао S. Y., Microwave Devices and Circuits, Prentice-Hall, Englewood Cliffs, New
Jersey, 1980.
2. Вайнштейн Л. А. Открытые резонаторы и открытые волноводы. — М.: Сов.
радио, 1966.
3. Ананьев Ю. А. Оптические резонаторы и проблема расходимости лазерного
излучения. — М.: Наука, 1979.
4. Ronchi L. In: Laser Handbook, v. 1 (eds. F. T. Arecchi, E. O. Schulz-Dubois),
North-Holland Publ., Amsterdam, 1972, p. 153.
5. Chodzko R. A^ Chester A. N. — In: Handbook of Chemical Lasers (eds. R. W.
G. Gross, J. F. Bott), Wiley, New York, 1976, p. 95—203. [Имеется перевод в
кн.: Химические лазеры /Под ред. Р. Пюсса, Дж. Ботта. — М.: Мир, 1980.]
6. Steier W. Н. In: Laser Handbook, v. 3 (ed. M.L. Stitch), North-Hollland Publ.,
Amsterdam, 1979, p. 5. t
7. Courant R., Hilbert D., Methods of Matematical Physics, v. 1, Theorem 18, Wiley
(Interscience), New York, 1953, p. 442. [Имеется перевод: Курант P., Пихь-
берт Д. Методы математической физики. — М.: Мир, 1964.]
8. Schawlow A. L., Townes С. #., Phys. Rev., 112, 1940 A958).
9. Прохоров А. М. — ЖЭТГФ, 1958, т. 34, вып. 6.
10. Fabry С, Perot A., Ann. Chim. Phys., 16, 115 A899).
11. Масек W. М., Davis D. Т. M., Appl. Phys. Lett., 2, 67 A963).
12. Ambartsumyan R. V., Basov N. G., Kryukov В G., Letokhov V. S., Prog. Quantum
Electron., 1, Part 3 A970).
13. Kogelnik H., Shank С. V., Appl. Phys. Lett., 18, 152 A971).
13a. Rensch D. B, Chester A. N, Appl. Opt., 12, 997 A973).
13b. Bloom A. JL, Spectra Phys. Laser Tech. Bull., No. 2X Mountain View, California,
1963.
14. Goubau G., Schwering E, IRE Trans. Antennas Propag., AP-9, 248 A961).
15. Boyd G. D., Kogelnik H., Bell Syst. lech. J., 41, 1347 A962).
16. Kogelnik #., Rigrod W. Ж, Proc IRE, 50, 220 A962).
17. Herriott D. R., J. Opt. Soc Am., 52, 31 A962).
18. Bennett W. R., Jr., The Physics of Gas Lasers, Gordon and Breach, New York,
1977.
19. Slepian D., Bell Syst. Tech., J., 43, 3009 A964).
20. Solimeno S., Torre A., Phys. Res., A237, 298 A985).
21. Siegman A.t Proc IEEE, 53, 277 A965). [Имеется перевод: Сигмэн А. —
ТИИЭР, 1965, т. 53, Jfc 3, с. 318.]
22. Siegman A., Arrathon R. Ж, IEEE J. Quantum Electron., QE-3, 156 A967).
23. Krupke W. E, Sooy W. R.t IEEE J. Quantum Electron., QE-5, 575 A969).
24. Нефедов Е. И. Открытые коаксиальные резонансные структуры. — М.: Нау-
Наука, 1982.
25. Patel С. К. N, Appl. Phys. Lett., 7, 15 A965).
26. Jricomi E Integral Equations, Wiley (Interscience), New York, 1957. [Имеется
перевод: Трикоми Ф. Интегральные уравнения. — М.: ИЛ, I960.]
27. Fox A. G., Li Т., Bell Syst. Tech. J., 40, 453 A960).
28. Gordon E. /., White A. D., Proc. IEEE, 52, 206 A964). [Имеется перевод: Гор-
Гордон, Уайт. — ТИИЭР, 1964, т. 52, № 2, с. 218.]
29. Gordon J. P~ Kogelnik H., Bell Syst. Tech. J., 43, 2873 A964).
Литература 575
30. Wilkinson J. H., The Algebraic Eigenvalue Problem, Oxford Univ. Press (Claren-
(Clarendon), London and New York, 1965. [Имеется перевод: Уилкинсон Дж X. Ал-
Алгебраическая проблема собственных значений. — М.: Наука, 1970.]
31. U Т., Bell Syst. Tech. J., 44, 917 A965).
32. Checcacci P. F.$ Consortini A., Scheggi A., Proa IEEE, 54, 1329 A966). [Имеется
перевод: Чекаччи, Консортини. — ТИИЭР,* 1966, т. 54, № 10, с. ИЗ.]
33. Johnson М. М., Appl. Opt., 13, 2326 A974).
34. Siegman A. R, Opt. Lett., 1, 13 A977).
35. Streifer W.t J. Opt. Soc Am., 55, 868 A965).
36. Bergstein L.t Marom R, J. Opt. Soc. Am., 56, 16 A966).
37. Siegman A. R, Miller H. Y.t Appl. Opt., 9, 2729 A970).
38. Slepian D., Pollack H. О., Bell Syst. Tech. J., 40, 43 A960).
39. Landau N. J.t Pollack H. Q, Bell Syst. Tech., J., 40, 65 A960); 42, 1295 A962).
40. Boyd G. D., Gordon J. P., Bell Syst. Tech. J., 41, 489 A961).
41. Luchini P, Solimeno S., Opt. Lett., 7, 259 A982).
42. Horwitz P, J. Opt. Soc. Am., 63, 1528 A973).
42a. Butts R., Avizonis #, J. Opt. Soc. Am., 68, 1072 A978).
43. Chen L. W., Felsen L. R, IEEE J. Quantum Electron., QE-9, 1102 A973).
44. Stenholm S. — In: Progress in Quantum Electronics, v. 1, Part A (eds. J. H. San-
Sanders, K. W. H. Stevens), Pergamon, Oxford, 1970, p. 189—271.
45. McFarlane R. A., Bennett W. R., Lamb W. R, Appl. Phys. Lett., 2, 189 A963).
46. Szoke A., Javan A, Phys. Rev. Lett., 10, 521 A963).
47. Летохов В. С, Чеботаев В. П. Принципы нелинейной лазерной спектроско-
спектроскопии. — М.: Наука, 1975.
48. Corney A., Atomic and Laser Spectroscopy, Oxford Univ. Press (Clarendon), Lon-
London and New York, 1977, Ch. 13.
49. Rigrod W. Ж, J. Appl. Phys., 34, 2602 A963); 36, 2487 A965).
50. Smith P. Ж, Proc. IEEE, 60, 422 A972). [Имеется перевод: Смит П.В. —
ТИИЭР, 1972, т. 60, № 4, с. 106.]
51. Koechner W., Solid-state Laser Engineering, Springer-Verlag, Berlin and New York,
1976.
52. Smith P. W., IEEE J. Quantum Electron, QE-1, 343 A965).
53. Kurokawa K., Proc IEEE, 61, 1386 A973). {Имеется перевод: Курокаеа К. —
ТИИЭР, 1973, т. 61, № 10, с. 12.]
54. Buczek С. J., Freiberg R. J., Skolnick M. L., Proc. IEEE, 61, 1411 A973). [Имеется
перевод: Бучек Д., Фрейберг Р.Д., Сколник М.Л. — ТИИЭР, 1973, т. 61,
№ 10, с. 41.]
55. Adler R., Proc. IEEE, 61, 1380 A973). [Имеется перевод: Адлер Р — ТИИЭР,
1973, т. 61, № 10, с. 5.]
56. Jacquinot Д Rep. Prog. Phys., 23, 267 A960).
57. Girard A., Jacquinot P — In: Advanced Optical Techniques (ed. A. C. S. van
Heel), North-Holland Publ., Amsterdam, 1967, p. 71—121.
58. Danielmyer H. G., IEEE J. Quantum Electron., QE-6, 101 A970).
59. Cook A. #., Interference of Electromagnetic Waves, Oxford Univ. Press (Claren-
(Clarendon), London and New York, 1971.
60. Roesler EL.— In: Astrophysics, Part A, Optical and Infrared Astronomy (ed.
N. Carleton), Methods of Experimental Physics, v. 12, Academic Press, New York,
1974, p. 531—569.
61. Mack J. R, McNutt D. P., Roesler F. G., Chabral R.t Appl, Opt., 2, 873 A963).
576 Гл. 7. Оптические резонаторы и интерферометры Фабри — Перо
62. Chabbal R., J. Phys. Radium, 19, 295 A958).
63. Connes P, J. Phys. Radium, 19, 262 A958).
64. Zucker #., Bell Syst. Tech. J., 49, 2349 A970).
65. McCumber D. E, Bell Syst. Tech. J., 44, 333 A965).
66. Hercher M, Appl. Opt., 8, 1103 A969).
БИБЛИОГРАФИЯ
Harris S. E, Proc. IEEE, 57, 2096 A969). [Имеется перевод: Харрис. — ТИИЭР,
1969, т. 57, № 12, с. 5.]
Басов Н. Г., Крохин О. #., Попов Ю. М. — УФН, 1960, т. 72, с. 161.
Bertolotti M, Masers and Lasers: an Historical Approach, Adam-Hilgher Ltd.,
Bristol, 1983.
Siegman A. E., Belanger P. A.t Hardy A. — In: Optical Phase Conjugation (ed.
R. A. Fisher), Academic Press, New York, 1983, p. 469—528.
Sveito Q, Principles of Lasers, Plenum Press, 1976. [Имеется перевод: Звелто О.
Физика лазеров. — М.: Мир, 1979.]
ГЛАВА 8
РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ
ВОЛОКНАХ
8.1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
Электромагнитная энергия в оптическом диапазоне частот может пе-
передаваться на расстояние путем распространения электромагнитного
поля в специальных диэлектрических волноводах. Их волноводные
свойства обусловлены, главным образом, полным внутренним отра-
отражением, согласно которому световой пучок, распространяющийся в
среде с показателем преломления nl9 может полностью отразиться от
поверхности раздела между первой и второй средой, имеющей показа-
показатель преломления п2 < пх. Точнее говоря, существует угол вс [пре-
[предельный угол; см. выражение C.20.1)], определяемый выражением
вс = arcsin^/nj, (8.1.1)
такой, что полное внутреннее отражение происходит при углах
0 = 0С, (8.1.2)
где в — угол между осью пучка и нормалью fi к поверхности раздела
двух сред. При в < вс пучок частично отражается и частично про-
пропускается (рис. 8.1).
Эти процессы описываются законами геометрической оптики
(см. разд. 2.11.1), согласно которым угол падения в равен углу отра-
отражения 0" (т. е. углу между отраженным лучом и направлением - п),
0 = 0", (8.1.3)
9
Рис. 8.1. Отражение и преломление на границе раздела двух сред.
578
Гл. 8. Распространение света в оптических волокнах
а угол преломления 0' (угол между прошедшим лучом и ft) связан с в
следующим соотношением [см. закон Снеллиуса B.11.8):
nt sin в = п2 sin0'. (8.1.4)
Это предварительное рассмотрение достаточно для того, чтобы,,
качественно описать волноводные свойства простой планарнои струк-
структуры, в которой диэлектрический слой с показателем преломления п {
окружен диэлектриком с показателем преломления п2 < пх (рис. 8.2).
Световые лучи, для которых
в процессе многократных отражений распространяются в световоде, а
лучи, которые не удовлетворяют соотношению (8.1.5), ослабляются в
результате последовательных преломлений.
На практике волноводы, наиболее широко применяемые для пере-
передачи света на большие расстояния, имеют цилиндрическую симмет-
симметрию. В этом случае траектории лучей страновятся значительно более
сложными, даже если проведенное выше элементарное доказательство
объясняет их поведение. Кроме того, уменьшение показателя прелом-
преломления, обусловливающее направленное распространение, может быть
реализовано либо дискретным (волокна со ступенчатым профилем
показателя преломления), либо непрерывным (градиентные волокна)
способом. В первом случае показатель преломления имеет постоян-
постоянную величину п j в цилиндрической области радиусом а (сердцевина) и
постоянную величину п2 в концентрической кольцевой области (обо-
(оболочка). Во втором случае показатель преломления в сердцевине непре-
непрерывно уменьшается с расстоянием р от оси симметрии z, пока не до-
достигнет постоянной величины п 2 в оболочке (рис.8.3).
Рис. 8.2. Схематическое представление волноводного ме-
механизма в плоской структуре.
Рис. 8.3. Профили показателя преломления, а — ступен-
ступенчатый; б — градиентный.
8.2. Волокна со ступенчатым профилем показателя преломления
579
Понятие луча имеет строгое объяснение с помощью уравнения эй-
эйконала B.3.1), которое было подробно изучено в гл. 2 в рамках при-
приближения лучевой оптики. Область применения этого понятия сущест-
существенно ограничена длинами волн, много меньшими поперечных разме-
размеров оптического волокна.
8.2. ВОЛОКНА СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ
ПРЕЛОМЛЕНИЯ
Элементарное описание процесса распространения света в цилиндри-
цилиндрических волокнах со ступенчатым профилем применимо лишь к лучам,
введенным в волокно в плоскости, содержащей ось z {меридиональ-
{меридиональные лучи) [см., например, выражение B.13.11)]. Действительно, из со-
соображений симметрии следует, что траектории этих лучей будут все
время оставаться в этой плоскости, как показано на рис. 8.2 для дву-
двумерного случая. Это позволяет ввести параметр 0М {приемный угол),
представляющий собой наибольший угол, который может образовать
с осью z направляемый меридиональный луч. Из соотношений (8.1.1)
и (8.1.4) имеем (рис. 8.4)
nesin0M = nx sin0М = п1со^вс = {п\ - п\)т\ (8.2.1)
здесь п е — показатель преломления среды перед входом в волокно,
который, как правило, равен приблизительно единице. На практике
разница между значениями показателей преломления в сердцевине и
оболочке составляет несколько процентов:
А ее (и? - и|)/Bя?) « 1, (8.2.2)
так что
0М = sin0M = (nJnJW2. (8.2.3)
Полезно также определить числовую апертуру (ЧА) (см. разд. 2.15.3)
через соотношение
ЧА = nesin0M = (п\ - п22I12. (8.2.4)
Рис. 8.4. Приемный угол в волокне
со ступенчатым профилем показате-
показателя преломления.
580
Гл. 8. Распространение света в оптических волокнах
Рис. 8.5. Косые лучи в волокне со ступенчатым профилем показателя преломления.
Для немеридиональных лучей (косых лучей) описание становится
более сложным, поскольку плоскость, содержащая отрезок луча и две
образующие цилиндра, которые он пересекает, изменяет свое положе-
положение при каждом отражении (рис. 8.5). Однако можно показать, что
угол падения ф между произвольным отрезком луча tj и нормалью й к
поверхности раздела сердцевина — оболочка является интегралом
движения [см. инвариант наклона в разд. 2.13.1] наряду с углами 0 и
7 (рис. 8.5) и что
cosi/f = — sin в cos у. (8.2.5)
Это соотношение позволяет обобщать понятие приемного угла на
случай косых лучей. В соответствии с выражением (8.2.5) направляе-
направляемыми лучами являются те лучи, для которых
|cos^| = sin0|cosy| < cos0c = (l/n^w? - n22)ll\ (8.2.6а)
т. е.
sin0 < (и? - niI/2/(ni|cosy|), (8.2.66)
что соответствует числовой апертуре
4A = (nl-n22y2/\cosy\, (8.2.7)
большей чем числовая апертура для меридиональных лучей. Однако
строгий анализ мод показывает, что косые лучи могут испытывать
потери на границе раздела сердцевина — оболочка, обусловленные
кривизной этой границы. Используя понятия лучевой оптики, можно
выделить три класса лучей. Направляемые (волноводные) лучи (кото-
(которые могут быть либо меридиональными, либо косыми) удовлетворя-
удовлетворяют условию
sin6 uinl-nlI12/^ (8.2.8)
8.2. Волокна со ступенчатым профилем показателя преломления 581
и распространяются без ослабления. Лучи, которые не удовлетворяют
условию (8.2.8), в свою очередь подразделяются на просачивающиеся
туннелирующие лучи9 удовлетворяющие условию (8.2.6) (очевидно,
все эти лучи являются косыми) и просачивающиеся преломленные лу-
лучи, которые не удовлетворяют условию (8.2.6). Обычно туннелирую-
туннелирующие лучи ослабляются значительно слабее, чем преломленные лучи.
8.3. ГРАДИЕНТНЫЕ ВОЛОКНА
Волноводный эффект можно получить в структурах, в центральной
области которых показатель преломления непрерывно уменьшается с
расстоянием от оси z, пока не достигнет постоянного значения в обо-
оболочке (рис. 8.3). Чтобы проверить это утверждение, вспомним резуль-
результаты, полученные в рамках лучевой оптики при изучении распростра-
распространения света в среде с аналогичным радиальным профилем показателя
преломления [см., например, в гл. 2 выражения B.12.14) и B.13.31)].
Очевидно [см. выражение B.13.33)], что если электромагнитное поле
распространяется вдоль оси симметрии z, то оно стремится сосредо-
сосредоточиться вблизи этой оси, что объясняет волноводные свойства такой
структуры.
Приведем другой пример. Рассмотрим гауссов профиль показателя
преломления вида
п2(р) = п20схр(-Ьр2/п0), ОйР^а, (8.3.1)
где р2 = х2 + у2, х и у — поперечные декартовы координаты. Этот
профиль особенно интересен, поскольку обусловленные им траектории
лучей имеют очень простой вид и его можно рассматривать как при-
пример широкого класса профилей показателя преломления. Действитель-
Действительно, если (как это часто случается на практике)
Ьа2/п0 « 1, (8.3.2)
то выражение (8.3.1) с хорошей точностью описывает параболический
профиль показателя преломления:
п2(х,у) = п2-п0Ър29 (8.3.3)
который является частным случаем (д = 2) широкого класса профи-
профилей показателя преломления вида (рис. 8.6)
П(Р)-\п0A-2А), р>а. (8.3.4)
В параксиальном приближении, когда угол наклона лучей к оси z
мал, траектории лучей описываются уравнениями (см. задачу 2 в гл. 2)
d2x/dz2 = -{Ь/по)х, d2y/dz2 = -(Ь/по)у, (8.3.5)
582
Гл. 8. Распространение света в оптических волокнах
Рис. 8.6. Профили показателя преломле- Рис. 8.7. Направляемое и ненаправляемое
ния, соответствующие выражению (8.3.4). распространение лучей в градиентном
волокне.
которые имеют общее решение, определяемое выражениями
x(z) = Axsml(b/n0)V2z + фх1 y(z) = Aysinl(b/n0)l>2z + фу1 (8.3.6)
Эти выражения, полученные в параксиальном приближении, можно
сравнить с формулами B.13.33), с которыми их роднит наличие у них
пространственной периодичности, независимой от начального положе-
положения и наклона луча (рис. 8.7).
Направляемыми лучами являются те лучи, для которых справедли-
справедливо неравенство
А\ + А) < а\ (8.3.7)
в то время как лучи, не удовлетворяющие этому условию, проникают
в оболочку и пересекают ее по прямой линии (рис. 8.7). В соответст-
соответствии с условием (8.3.7) направляемые лучи подчиняются соотношению
(dx/dzJ + (dy/dzJ U{A2X + А2)Ь/п0 й Ьа2/п0, (8.3.8)
которое оправдывает a posteriori использование параксиального при-
приближения [см. выражение (8.3.2)]. Среди направляемых лучей мери-
меридиональными лучами будут те, для которых фх = фу.
ТСак для волокон со ступенчатым профилем показателя преломле-
преломления, можно ввести приемный угол и для градиентных волокон, кото-
который, как будет показано, является функцией расстояния р от оси z.
Напомним, что в соответствии с выражением B.2.5) изменение фазы
8.4. Модовая теория 583
на элементарном отрезке пути rfr дается выражением
-k0VS-dr9 (8.3.9)
что позволяет определить локальный волновой вектор [см. выражение
B.4.2)]
k(r) = k0VS. (8.3.10)
Этот вектор является интегралом движения, в чем можно сразу убе-
убедиться, записав проекцию соотношения B.4.2) на ось z и вычислив
производную по криволинейной абсциссе s от обеих частей полученно-
полученного уравнения. Если предположить, что п (г) не зависит от z, то полу-
получим следующее уравнение:
d(VS)Jds = (d/ds)[n(x,y)dz/ds], (8.3.11)
правая часть которого в соответствии с B.4.5) равна нулю, поскольку
( Vai)z = 0. При этом угол в(р) между осью z и лучом на расстоянии р
от оси z определяется соотношением
cos0(p) = fcz/[k(p) • k(p)]1/2, (8.3.12)
или в соответствии с (8.3.10) и B.3.1) соотношением
cos0(p) = fcz/[fcon(p)]. (8.3.13)
Среди множества лучей, проходящих через р при любом данном его
значении, угол в(р) достигает максимума 6м(р) для касательного луча к
поверхности раздела сердцевина — оболочка. При этом kz принимает
минимальное значение коп(а), и мы имеем
со8 0м(р) = Ф)Мр). (8.3.14)
Следовательно, числовую апертуру можно записать в виде
ЧА = n(p)sin0M(p) = [п2(р) - п2(а)Уг\ (8.3.15)
что совпадает с аналогичным выражением (8.2.4) для волокна со сту-
ступенчатым профилем показателя преломления, для которого п (р) = п {
независимо от расстояния от оси до выбранной точки на входной пло-
плоскости волокна.
Общие рассуждения, кратко изложенные нами в предыдущих раз-
разделах, более подробно рассматриваются в специальных книгах [1—8],
число которых постоянно увеличивается в связи с возрастающим ин-
интересом к данному предмету.
8.4. МОДОВАЯ ТЕОРИЯ
Изучение общего решения уравнений Максвелла для цилиндрического
волокна приводит к понятию распространяющейся моды, т. е. опре-
определенной конфигурации электромагнитного поля, зависящей от рас-
расстояния z в направлении распространения как exp (-i@z). Направляв-
584
Гл. 8. Распространение света в оптических волокнах
Рис. 8.8. Лучи, соответствующие направляемым и излучательным модам в волокне со
ступенчатым профилем показателя преломления.
мые (волноводные) моды — это такие распространяющиеся моды, у
которых электромагнитная энергия сосредоточена, главным образом,
в сердцевине на всем протяжении волокна.
Различие между волноводными и неволноводными модами, кото-
которое отсутствует в теории распространения в металлических волново-
волноводах, существенно для диэлектрических волноводов. Для того чтобы
полностью описать электромагнитное поле в волокне, кроме дискрет-
дискретного спектра волноводных мод (соответствующего в геометрической
оптике лучам, локализованным в ходе последовательных отражений
внутри сердцевины), необходимо рассмотреть и непрерывный спектр
излучательных мод (соответствующий лучам, пересекающим волокно
при последовательных отражениях; рис. 8.8).
Распространение электромагнитных волн в однородной диэлектри-
диэлектрической среде в отсутствие зарядов и токов описывается уравнениями
Максвелла A.1.1)—A.1.4) наряду с материальными уравнениями
A.1.6) и A.2.3). Обратите внимание на то, что в нестационарном слу-
случае (d/dt Ф 0) последние два уравнения Максвелла A.1.3) и A.1.4) яв-
являются следствиями первых двух, что можно сразу доказать, приме-
применяя оператор V к обеим частям уравнений A.1.1) и A.1.2) и используя
векторное тождество (А. 15) (см. приложение А в конце книги). Поэто-
Поэтому в дальнейшем достаточно будет рассматривать лишь уравнения
Рис. 8.9. Система координат, приме-
применяемая при изучении распространения
мод в цилиндрических структурах.
8.4. Модовая теория 585
A.1.1) и A.1.2) вместе с условиями непрерывности тангенциальных со-
составляющих электрического и магнитного полей на поверхности раз-
разрыва диэлектрической проницаемости е(г, oj).
Будем искать решения в виде монохроматических волн
Ё(г, t) = Е(т)еш, H(r, t) = Щт)еш. (8.4.1)
Рассмотрим наиболее общую цилиндрическую структуру, в которой
ось z параллельна образующей цилиндра, а в поперечном сечении
определим криволинейную систему координат (qx,q2) (рис. 8.9). Если
диэлектрическая проницаемость е зависит только от поперечных коор-
координат <?j ид2, то из соображений симметрии решения можно записать
в виде
Е(в1,«2,*) = Eofabfc)*-1". Щв1,42,z) = Ko(ql9q2)e'^. (8.4.2)
Дифференциальный оператор V удобно выразить в виде суммы по-
поперечной и продольной составляющих:
V = Vt + zd/dz9 (8.4.3)
Из уравнений A.1.1) и A.1.2) и материальных уравнений получаем
FtxE0- ipz х Ео = -ш>/10Н0, FtxH0- ifiz х Но = toeE0. (8.4.4)
Как станет видно в дальнейшем, постоянная /8 может принимать
толысо некоторые дискретные значения (собственные значения), зави-
зависящие от граничных условий, налагаемых волноводной структурой.
Если записать электрические и магнитные поля в виде суммы попереч-
поперечных и продольных составляющих
Ео = Et + zE2, Но = Ht + zHz, (8.4.5)
то после алгебраических преобразований можно выразить поперечные
компоненты полей через их продольные составляющие:
Ht = - [i/(a>2/ioe - Р2ЖР КН2 - сое VtEz x ?), ^
Et = - [i/(o>2jio8 - Р2ШР VXEZ + oyio VtHz x z).
Таким образом, возникает задача нахождения выражений для про-
продольных компонент Ez и Hz электрического и магнитного полей. В со-
соответствии с выражением B.8.1) продольная компонента электриче-
электрического поля подчиняется следующему уравнению:
Vt2?z + (co2fx0e - P2)EZ - ipEt. Ftlne = 0, (8.4.7)
а соответствующая магнитная компонента — уравнению
Vt2#z -h ((o2ii0e - P2)HZ + icoe Pt(ln e) x Et. z = 0. (8.4.8)
Эти уравнения можно переписать в виде
V2EZ + (со2ц0е - Р2)Е2 = 0, (8.4.9)
586 Гл. 8. Распространение света в оптических волокнах
Vt2#z + (со2»0е - р2)Н2 = 0, (8.4.10)
если предположить, что е меняется незначительно на расстояниях по-
порядка длины волны.
8.5. МОДОВАЯ ТЕОРИЯ ДЛЯ ВОЛОКОН СО СТУПЕНЧАТЫМ
ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
Основная трудность в решении краевой задачи при изучении волно-
водных мод в оптическом волокне связана с интегрированием уравне-
уравнения в частных производных методом разделения переменных. Хотя
для волокон со ступенчатым профилем показателя преломления эта
задача оказывается не столь уж сложной, удобно все-таки ввести не-
некоторые приближения, для того чтобы получить простые выражения
для интересующих нас величин. Таким образом, предположим, напри-
например, что оболочка простирается на бесконечно большое расстояние;
такое предположение правомерно благодаря экранирующей роли обо-
оболочки и экспоненциальному затуханию волноводных мод с расстояни-
расстоянием р от оси волокна. Кроме того, особое внимание уделим случаю,
когда показатели преломления сердцевины и оболочки отличаются
всего на несколько процентов (А < 1, случай слабонаправляющих во-
локон), что часто имеет место на практике, так как малость А огра-
ограничивает искажения, вносимые волокном в распространяющийся им-
импульсный сигнал, при сохранении волноводных свойств волокна.
Уравнения (8.4.9) и (8.4.10) для продольных компонент электри-
электрического и магнитного полей становятся строгими, поскольку теперь
a = const как в сердцевине, так и в оболочке, и их можно переписать в
виде
V2E2 + Х2ЕЖ = 0, V2H2 + х2Н2 = 0, р^а9 (8.5.1)
V2E2-y2E2 = 0, V2H2 - у2Н2 = 0, р>а, (8.5.2)
т2
X2 = «Vi " Р2 = (со2/с2)—п2 - Р\ (8.5.3)
с
где
X2 = «Vi " Р2 = (со2/с2)
с
У2 =Р2- co2fi0s2 = 02- (со2/с2)п1 (8.5.4)
Здесь е{ и е2 (п{ ип2) — диэлектрические проницаемости (показатели
преломления) соответственно сердцевины и оболочки. Обычно поми-
помимо величин 7 и х вводят еще один параметр V (так называемую нор-
8.5. Модовая теория для волокон со ступенчатым профилем 587
мированную частоту), определяемый выражением
= a(colc)(n\ - nlI'2 = ако(п2 - п\)^\ (8.5.5)
Для волноводной моды постоянная распространения /3 является ве-
вещественной и удовлетворяет соотношению
(со/с)п2 ^р^ (ю/Фх (8.5.6)
(положительные значения /? соответствуют модам, распространяю-
распространяющимся в положительном направлении оси z). Справедливость этого
соотношения обусловлена тем, что величины (ш/с)п1 = копг и
(о)/с)п2 = к0п2 соответствуют однородной плоской волне, распро-
распространяющейся в однородной среде с показателями преломления пх и
п2, и что волноводный случай является промежуточным. Как следст-
следствие, х и 7 являются вещественными и предполагаются положительными.
В соответствии с симметрией задачи введем полярные координаты
риф. Оператор V* при этом принимает вид
V? = д2/др2 + A/р)(В/др) + A/р2)(д2/дф2), (8.5.7)
и переменные разделяются:
ЕХ(Р, Ф) = FApW** Н*(Р> Ф) = Ыр)е**> v = 0,1,2,.... (8.5.8)
Уравнения (8.5.1) и (8.5.2) в этом случае принимают вид соответствен-
соответственно уравнения Бесселя и модифицированного уравнения Бесселя:
d2Flt2/dp2 + (l/p)/(dFia/dp) + (x2 - v2/p2)FU2 =0, р й а , (8.5.9)
d2FU2/dp2 + (l/p)/(dFU2/dp) - (у2 + v2/p2)FU2 =0, р > а, (8.5.10)
решения которых записываются в виде
FiJp) = alf2Uxp) + biaYv(Xp\ рйа, (8.5.11)
Ki(p) = cU2Kv{yp) + dU2
где Jv и Yv — функции Бесселя соответственно первого и второго ро-
рода, a Kv и /„ — модифицированные функции Ханкеля первого и второ-
второго рода (см. книгу [4, ch. II] и уравнения В. 10 в приложении В).
Функции Yv и 1Р расходятся соответственно при р — 0 и р — оо (по-
(поскольку 7 > 0), так что их нельзя использовать для описания компо-
компонент Ez и Hz (которые предполагаются конечными). Следовательно,
необходимо положить bl2 = dx 2 = 0. Наоборот, Jv ограничена при
р = 0, a Kv при р — оо дается асимптотическим выражением
Kv(yp)~e-"/(yp)l/2. (8.5.13)
588
Гл. 8. Распространение света в оптических волокнах
Рис. 8.10. Цилиндрическая система координат.
Условие непрерывности тангенциальных составляющих полей на
границе раздела сердцевина — оболочка позволяет записать следую-
следующие выражения:
Р > а,
"•"*"' - \ВШхаIКШКАур)е**, р > а; <*5Л5)
здесь А и В — произвольные постоянные, а целое v представляет со-
собой азимутальное число.
Теперь с помощью выражений (8.4.6) можно найти поперечные
компоненты полей в цилиндрической системе координат (рис. 8.10),и
затем наложить условия непрерывности
Еф(а+) = Еф(а~\ (8.5.16)
Нф(а+) = Нф{а~). (8.5.17)
Действительно, можно показать, что если ех = е2, то соотношение
t == v^l/A^O/ -^t ^о.«/.ю/
связывает поперечные компоненты электрического и магнитного по-
полей (аналогичное соотношение справедливо для однородной плоской
волны, распространяющейся в сердцевине вдоль оси z). Поэтому вме-
вместо условия (8.5.17) можно наложить эквивалентное условие
Ер{а+) = ?>"). (8.5.19)
Не вдаваясь в подробности вычислений, запишем следующее урав-
уравнение, полученное на основании выражений (8.5.16) и (8.5.19):
ру-Лха) К-i(ya)~|pv+Лх<*) , Kv+iMl
yaKv(ya)]lxaJv(xa) уаКу(уа)]
8.5. Модовая теория для волокон со ступенчатым профилем
589
Уравнение (8.5.20) называется характеристическим уравнением.
Его решение для направляемых мод с учетом выражений (8.5.3) и
(8.5.4) дает два бесконечных множества дискретных допустимых зна-
значений постоянной распространения /3, а именно f3v6 (здесь 6 — положи-
положительное целое число, отличающее разные решения для каждого фикси-
фиксированного v). Если fivb ведет себя как известная функция частоты со, то
можно ввести понятие частоты отсечки или критической частоты
о>„6, устанавливающей нижний предел, ниже которого направляемая
мода v, 8 не может существовать. Действительно, в соответствии с
зависимостью, описываемой выражением (8.5.13), мода теперь не
остается локализованной в сердцевине при у — 0. Иными словами [см.
выражение (8.5.4)], при таком значении частоты со„6, для которого
= (cojc)n2, (8.5.21)
мода занимает все пространство.
При о) < со„5 величина /3„6 становится комплексной и соответствую-
соответствующая мода затухает во время распространения. Можно показать, что в
отличие от металлических волноводов в диэлектрических волноводах
существует такая основная мода (обозначаемая символом НЕ п), для
которой не существует критической частоты [1] (рис. 8.11).
п2
Рис. 8.11. Нормированная постоянная распространения в зависимости от нормированной
частоты V для различных мод низшего порядка в волокне со ступенчатым профилем пока-
показателя преломления.
590 Гл. 8. Распространение света в оптических волокнах
8.6. СЛАБОНАПРАВЛЯЮЩИЕ ВОЛОКНА СО СТУПЕНЧАТЫМ
ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
В случае А < 1 модовая структура и характеристическое уравнение су-
существенно упрощаются. Этот случай всегда реализуется на практике в
волоконно-оптической связи. Главное преимущество при этом состоит
в том, что электромагнитное поле можно теперь представить в виде
суперпозиции линейно-поляризованных мод (ЬР)„6, продольные ком-
компоненты которых пренебрежимо малы по сравнению с поперечными
(порядка А1/2) [1, 9].
После введения единичных векторов х и у в направлении осей а: и .у
(рис. 8.10) электрические поперечные компоненты этих мод можно за-
записать в виде
где А 0 — произвольная постоянная. Запятая в квадратных скобках
([ , ]) означает, что можно выбирать либо cos, либо sin; /J, \ и у связа-
связаны с v и 8 характеристическим уравнением
-Uia)lxaJy + 1(Xa) = К&аУуаК^^уа). (8.6.3)
Поперечные составляющие магнитного поля получаются из выра-
выражений (8.6.1) и (8.6.2) с помощью соотношения (8.5.18). Каждая из
LP-мод при v ^ 1 является четырехкратно вырожденной в том смыс-
смысле, что для любых фиксированных v и 8 существуют по две моды LP^
и LPy (соответствующие решениям с sin</> и cos<?) с одним и тем же
значением /3„6. Моды с v = 0 имеют двукратное вырождение.
Для частот, значительно превышающих критическую частоту, ре-
решение уравнения (8.6.3) можно получить с хорошей точностью. Вдали
от критической частоты (уа — оо) уравнение (8.6.3) с учетом зависимо-
зависимости (8.5.13) принимает вид
(8.6.4)
а поскольку у а & К, это уравнение можно переписать в следующем
эквивалентном виде:
(8.6.5)
Вычисляя производную по V от обеих частей уравнения (8.6.5) и ре-
решая полученное уравнение относительно d(xa)/dV, получаем
8.6. Слабонаправляющие волокна со ступенчатым профилем 591
. (8.6.6)
dV -vJv
При этом были использованы следующие тождества [8]:
WOW) = НЛ-,@ - Л+2@1 (8.6.7)
(v/СШС) = iW+i(O + Л-1@]. (8.6.8)
Подставляя (8.6.5) в уравнение (8.6.6), окончательно имеем
Решение этого уравнения при v =? 0 запишется в виде
Xa = (^)ao(l-2v/FI^>, (8.6.10)
а при v = 0 — в виде
Z* = Мао*~1/К, (8.6.11)
где (хя)оо является 6-м нулем уравнения J„(х**) = 0 [см. уравнение
(8.6.5)].
В многомодовом волокне, т. е. в волокне, в котором распростра-
распространяется не одна, а множество направляемых мод, почти для всех из
них уа > 1 (за исключением нескольких мод вблизи критической ча-
частоты), поэтому решения (8.6.10) и (8.6.11) наряду с уравнением (8.5.3)
с хорошей точностью определяют постоянные распространения прак-
практически для всех мод.
В отличие от только что рассмотренной ситуации, случай, когда
мы имеем дело с отсечкой, реализуется при у а — 0. Подставляя в
уравнение (8.6.3) асимптотическое выражение для Кр(уа) при уа — 0,
находим его решения и из них определяем критические частоты о?^,
которые можно записать в виде
ovi = (с/а)[1/(и? - nimU, (8.6Л2)
где ?„5 являются решениями уравнений Jv_l(^) = 0 при v ^ 1 (за ис-
исключением решения ? = 0 при v ^ 2), а ^ являются решениями урав-
уравнения /j(f) = 0. Так как /ДО) = 0, ?01 = 0, то мода (LPH1 и только
она не имеет отсечки. Минимальная критическая частота находится
по наименьшему из ненулевых корней ?„5, которым оказывается пер-
первый нуль функции J4?)у т-е- ?ц = 2,405.... Выражения (8.5.5) и
(8.6.12) позволяют сформулировать условие одномодовости для во-
волокна со ступенчатым профилем показателя преломления в следую-
следующем виде:
V ^2,405. (8.6.13)
592 Гл. 8. Распространение света в оптических волокнах
8.7. ВОЛОКНА С ПАРАБОЛИЧЕСКИМ ПРОФИЛЕМ ПОКАЗАТЕ-
ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
Изучение распространения направляемых мод в волокне с параболиче-
параболическим профилем показателя преломления можно упростить, если пред-
предположить, что показатель преломления мало меняется на расстоянии
порядка длины волны и что его параболическая зависимость остается
справедливой для любого р (таким образом, допускаются сколь угод-
угодно большие значения р) (рис. 8.12). Последнее предположение под-
подтверждается результатами, полученными в разд. 8.3 относительно
траектории направляемых лучей, откуда можно сделать вывод, что
по крайней мере моды низших порядков локализуются вблизи оси
волокна, так что они нечувствительны к изменениям показателя пре-
преломления при больших р. Таким образом можно избежать трудно-
трудностей, связанных с необходимостью согласования тангенциальных ком-
компонент поля на границе раздела сердцевина — оболочка и перейти не-
непосредственно к скалярной теории поляризованных мод в декартовых
координатах.
Согласно уравнению A.1.9), любая декартова компонента Eft,у)
электрического поля удовлетворяет (в скалярном приближении) урав-
уравнению
82Ei/dx2 + д2Е(/ду2 + {Ц?п2 - nob(x2 + у2)] - Р2}Е( = 0, (8.7.1)
в котором мы учли параболический профиль показателя преломления
(8.3.3). В декартовых координатах этот профиль запишется в виде
п2 = c2fioe = п2- п0Ь(х2 + у2). (8.7.2)
После разделения переменных, а именно записывая Et(x, у) =
= /(*)? (У )> уравнение (8.7.1) можно записать в виде
22^2^2V2S2=0, (8.7.3)
Рис. 8.12. Реальный и идеальный профили по-
показателя преломления в виде параболы.
8.7. Волокна с параболическим профилем 593
или (что эквивалентно) в виде двух уравнений
d2f/dx2 + (п20к20 - R2 - р2 - k2nobx2)f = 0, (8.7.4)
d2g/dy2 + (R2 - k2noby2)g = 0, (8.7.5)
где R2 — постоянная разделения. После введения безразмерных пере-
переменных
t = кУ2(п0ЬI1Ах9 (8.7.6)
Ч = кУ2{п0Ъу1*у (8.7.7)
уравнения (8.7.4) и (8.7.5) принимают вид
d2f/d{2 + (а2 - ?2)/ = 0, (8.7.8)
d2g/drj2 + (ф2 - rj2)g = 0, (8.7.9)
причем
о2 = (п2к2 -R2- P2)/lko(nobI/2l (8.7.10)
ф2 = Я2/[М«оЬI/2]. (8.7.11)
Уравнение (8.7.8) [или (8.7.9)] хорошо известно: это уравнение
Шрёдингера для одномерного гармонического осциллятора, и его ре-
решение можно найти в любом учебнике по квантовой механике. Можно
показать, что уравнения (8.7.8) и (8.7.9) имеют решения, которые ко-
конечны и непрерывны во всем пространстве и стремятся к нулю при ?,
т] — ±оо тогда и только тогда, когда
(Х2 = 2р + 1, р = 0,1,2,..., (8.7.12)
iA2 = 24+l, q = 0,1,2,..., (8.7.13)
Эти решения записываются в виде
& (8.7.14)
(8.7.15)
где Нт — полином Эрмитат-го порядка (см. разд. 7.8 и табл. 7.2, а
также выражения (В.4) в приложении В).
Учитывая представленное выше рассмотрение, можно написать
следующий набор линейно-поляризованных направляемых мод:
Epq(lrj) = [(г/тгI^^^!^!)^2]^)^^-^^^, (8.7.16)
где нормировочный множитель выбран таким образом, чтобы
(8.7.17)
Л
J -
Подставляя выражения (8.7.12) и (8.7.13) в (8.7.10) и (8.7.11), получаем
постоянную распространения &pq:
594 Гл. 8. Распространение света в оптических волокнах
Ppq = [*о*о - 2ko(nob)^2(p + q+ I)]1'2. (8.7.18)
Для мод низших порядков, поскольку Ь1/2/к0 < 1 благодаря пренебре-
пренебрежимо малому изменению показателя преломления на расстоянии, рав-
равном одной длине волны, выражение (8.7.18) принимает вид
РРЯ = "(Л - (Ь/поI12(р + q + 1). (8.7.19)
Результаты этого раздела можно сравнить с теми, которые мы
получили в рамках геометрической оптики в гл. 2 (см. разд. 2.12.1а)
для параболического профиля показателя преломления в радиальном
направлении [см. выражение B.12.14)]. В частности, интересно срав-
сравнить распределение мод, определяемое выражением (8.7.16), с рас-
распределением поля, определяемым выражением B.12.17), и отметить
замечательное совпадение двух выражений для постоянных распро-
распространения Cpq [а именно B.12.21) и (8.7.18)], полученных двумя пол-
полностью различными методами.
8.8. НЕНАПРАВЛЯЕМЫЕ МОДЫ
Решения характеристического уравнения, для которых величина C ве-
вещественна и подчиняется соотношению [см. (8.5.6)]
k0n2<jS<k0n1, (8.8.1)
определяют (см. разд. 8.5) дискретный набор волноводных мод, кото-
которые распространяются без ослабления вдоль волокна и экспоненци-
экспоненциально затухают на больших расстояниях от оси. Однако для того,
чтобы полностью описать электромагнитное поле, к первоначальному
необходимо добавить непрерывный набор мод. С аналитической точ-
точки зрения такие моды получаются, когда коэффициенты d { 2 [см. вы-
выражение (8.5.12)] отличны от нуля, а это означает, что у должна быть
мнимой величиной, чтобы удовлетворить физическому условию обра-
обращения в нуль поля при р ^ оо. Действительно, можно написать следу-
следующее асимптотическое выражение:
Цур) ~ е"/(урI12, (8.8.2)
ур->оо
которое наряду с асимптотической зависимостью К v(yp) [см. выраже-
выражение (8.5.13)] показывает, что допустимым являются лишь мнимые
значения величины 7- Следовательно, из выражения (8.5.4) можно за-
заключить, что /3 принимает вещественные значения в интервале
О < Р й п2к0, (8.8.3)
а мнимые значения в интервале
-ioo<P<0. (8.8.4)
8.8. Ненаправляемые моды 595
Выбор положительных вещественных значений в (8.8.3) и отрица-
отрицательных мнимых значений в (8.8.4) определяет соответственно моды,
распространяющиеся в положительном направлении оси z, и моды,
экспоненциально затухающие в том же направлении. Благодаря доба-
добавочной степени свободы, появившейся за счет сохранения члена /„ в
(8.5.12), условию непрерывности на границе раздела сердцевина —
оболочка можно удовлетворить без обращения к характеристическому
уравнению. Таким образом, величины /8 могут теперь быть не дис-
дискретными, а принимать непрерывное множество значений в интерва-
интервалах, определяемых неравенствами (8.8.3) и (8.8.4)
В общем случае электромагнитное поле, связанное с цилиндриче-
цилиндрическим волокном, можно записать в виде суперпозиции направляемых и
непрерывных мод:
E(p,z,f) = ? ЛмЕ
f
Jo
(8 8 5)
где первый член представляет вклад направляемых мод, Е„6 обознача-
обозначают относительные модовые конфигурации (зависимости от р и о? для
простоты опущены), Avb — соответствующие амплитуды, а второй и
третий члены представляют вклады непрерывных мод, для которых
соответственно
0^y</feo, (8.8.6)
ik0n2 <y< ioo. (8.8.7)
то имеют место следующие неравенст-
неравенстТаким
ва:
образом,
если ?
= -iy
0
коп2
<
<
(8.8.8)
< оо. (8.8.9)
Непрерывные моды, удовлетворяющие условию (8.8.8), для кото-
которых величина /3 вещественна, называются радиационными модами, а
моды, удовлетворяющие условию (8.8.9), называются затухающими
модами.
Описание электромагнитного поля с помощью выражения (8.8.5)
на практике оказывается слишком сложным. Поэтому в большинстве
случаев при рассмотрении распространения волн предпочитают ис-
596 Гл. 8. Распространение света в оптических волокнах
пользовать приближенное описание, в котором радиационные моды
заменяются соответствующим набором дискретных мод (мод утечки)
[7], которые экспоненциально затухают в положительном направле-
направлении оси z. Эти моды вместе с направляемыми модами с хорошей точ-
точностью представляют электромагнитное поле в сердцевине волокна и
в ее окрестности (так что при достаточно больших z поле описывает-
описывается одними лишь направляемыми модами). Это не противоречит тому
факту, что отдельно взятая радиационная мода не затухает с расстоя-
расстоянием z, поскольку любое реальное поле, переносящее энергию по во-
волокну, представляет собой интеграл по конечной области значений ? и
именно этот интеграл стремится к нулю при достаточно больших z.
Спектр мод утечки получается естественным образом, если вы-
выбрать решения 0 характеристического уравнения с отрицательной
мнимой частью /32 и вещественной частью jSj, удовлетворяющей нера-
неравенству (8.8.3), что, как и следовало ожидать, соответствует направ-
направлениям распространения, образующим с осью z угол, больший чем
тг/2 - 0С. При этом мода будет направляемой, если частота поля
больше критической, и модой утечки в противоположном случае.
Заметим, что в соответствии с выражением (8.5.4) и условием
(8.8.3), а также с учетом того обстоятельства, что 02 отрицательна
при отрицательной вещественной части величины у, из (8.5.13) сразу
находим, что моды утечки расходятся при р —> оо. Это означает, что в
области, не слишком удаленной от границы раздела сердцевина —
оболочка, электромагнитное поле, распространяющееся вдоль волок-
волокна, может быть представлено в виде суперпозиции направляемых мод
и мод утечки (см. также разд. 3.19).
8.9. ОДНОМОДОВЫЕ ВОЛОКНА
В разд. 8.6 мы показали, каким образом волокно со ступенчатым
профилем показателя преломления может работать в одномодовом
режиме, т. е. направлять только две вырожденные ортогонально-
поляризованные волны, соответствующие моде (LP)^ при условии, что
нормированная частота V удовлетворяет неравенству (8.6.13). В обла-
области длин волн 1,2—1,6 мкм, в которой кварцевые волокна характери-
характеризуются малыми потерями и слабой хроматической дисперсией (см.
разд. 8.13 и 8.14), одномодовые волокна имеют большие потенциаль-
потенциальные возможности для ультраширокополосной оптической связи, что
побуждает заняться детальным изучением их характеристик распро-
распространения. Однако это изучение не может ограничиваться рассмотре-
рассмотрением волокон со ступенчатым профилем показателя преломления, для
8.9. Одномодовые волокна 597
которого уже имеется аналитическое решение, хотя и сложное. В
практически важном диапазоне длин волн (по крайней мере используе-
используемом в настоящее время) одномодовость достигается при малых ради-
радиусах сердцевины, что не позволяет осуществлять в процессе изготов-
изготовления точный контроль профиля показателя преломления волокна, ко-
который проявляет искажения или провалы вокруг оси волокна. К счас-
счастью, оказывается, что поле моды и постоянная распространения од-
номодового волокна практически нечувствительны к малым искажени-
искажениям профиля показателя преломления и эти параметры можно вычис-
вычислять независимо от тонкой структуры профиля [10].
В соответствии с рассмотрением, проведенным в предыдущих раз-
разделах, разумно предположить, что в слабонаправляющих волокнах с
произвольным профилем показателя преломления п(р) в сердцевине
поле любой моды можно аппроксимировать поперечной линейно-
поляризованной волной, являющейся решением скалярного волнового
уравнения. Например, направляя плоскость поляризации по оси х и
записывая приближенно (с учетом предположения о слабой направлен-
направленности
(8.9.1)
получаем следующее уравнение для амплитуды \^(р) моды с азиму-
азимутальным числом v\
d^Jdp2 + (l/p)(#v/dp) + lk2n2(p) -P2- v2/p2Wv = 0. (8.9.2)
Прямой подход к решению уравнения (8.9.2) с целью изучения ха-
характеристик распространения одномодовых оптических волокон, состоя-
состоящий в том, чтобы определить конкретный вид п(р)и найти какой-ли-
какой-либо точный численный метод расчета [11], в общем случае при произ-
произвольных профилях показателя преломления является трудным. Одна-
Однако разработан значительно более простой подход, который позволяет
получить важные характристики, исходя всего лишь из двух-трех па-
параметров, соответствующих моментам профиля показателя преломле-
преломления [12]. В этом методе обычно вводится функция профиля s(p), опре-
определяемая выражением ¦ _ , -
и2(р) = п| + (и5-и|Мр), (8.9.3)
где п 0 — максимальное значение п (р) в сердцевине, а«2 — показатель
преломления в оболочке, имеющий постоянную величину. Функция
профиля s (р), очевидно, тождественно равна нулю для р, больших чем
радиус сердцевины (р ^ а; рис. 8.13), а ее моменты Q, определяются
выражением
Nt = \\n\p) - nUpl + 1dp ее (п2 - п2)а1 + 2Пь (8.9.4)
Jo
598
Гл. 8. Распространение света в оптических волокнах
s(R)
Рис. 8.13. Типичный вид функции профиля s(R)
(R = р/а).
откуда находим
-Г
Jo
(8.9.5)
причем R = р/а. Заметим, что для полного определения функции
профиля s(R) достаточно только четных моментов, поскольку она
определяется лишь в области R ^ 0. Моменты No и п0 и эффектив-
эффективная нормированная частота волокна, определяемая выражением
(8.9.6)
связаны друг с другом следующим простым соотношением:
V2 = 2k2N0 = 2K2Q0, (8.9.7)
где
V = koa(n2 - п2I12 (8.9.8)
— нормированная частота волокна со ступенчатым профилем, имею-
имеющего тот же радиус а и показатель преломления сердцевины п 0, что и
у рассматриваемого волокна.
В остальной, части этого раздела мы будем следовать методу, ко-
который применяли Хасси и Паск [13]. Рассматривая основную моду,
для которой v = 0, перепишем уравнение (8.9.2) в виде
[-Do + \V2s{K)\y\f = Г2ф, (8.9.9)
где/? = p/a,s(R) =s(R)/Q0,
Do = -d2/dR2 - (\/R)(d/dR)
(8.9.10)
Г2 = р2а2-к2п22а2. (8.9.11)
Предполагая, что опорный профиль s и поле ф удовлетворяют
уравнению
8.9. Одномодовыв волокна 599
(-О0+Ь?2$)ф = Г2ф, (8.9.12)
в первом приближении теории возмущений получаем
Г2 f 2 у j;(s-$)ij/2RdR
+ ' (8'9ЛЗ)
В частности, если ф2 представить в виде полинома от R2 [в соот-
соответствии с уравнением (8.9.9) \j/ является четной функцией величины R]
с коэффициентами разложения ft,, то мы можем записать следующее
равенство:
Г°E - SJRdR = ? bt(U2i - Q2l), (8.9.14)
Jo « = i
где О, = 0/00.
Обычно за исходный удобно принять ступенчатый профиль показа-
показателя преломления, для которого поля ф = % и Т/а = у хорошо из-
известны (см. разд. 8.6), так что V = V, а радиус сердцевины as предпо-
предполагается a priori неизвестным опорным параметром. Вычислив коэф-
коэффициенты ft,, можно получить следующие соотношения, выраженные
через моменты низших порядков;
aja = {2U2yi2, Г2/а2 ? ?2(F)/BQ2), (8.9.15)
для х < 0 и
aja = (ЪпАУ'\ Г2/а2 s [72(K)/CQ4) ^^{l + xX2a2J^J2{XaJ]} (8.9.16)
для х > 0, где параметр
lBi]/CflI/2) (8.9.17)
определяется типом профиля. В частности, для ступенчатого профиля
х = 0, для профилей со степенной зависимостью типа?.,(К ) = \ — Rq
величина х положительна, а для зависимости типа s 2(R) =
= 1-A—/?)* (которые имеют провал на оси волокна) она отрица-
отрицательна.
Выражения (8.9.15) и (8.9.16) позволяют нам описывать одномодо-
вые оптические волокна с помощью первых трех моментов Qo, Й2 и ^4
профиля показателя преломления. Поскольку моменты являются ус-
усредненными по профилю величинами, данный метод автоматически
приводит к сглаживанию несущественнюй тонкой структуры показате-
показателя преломления п(р).
Для того чтобы описать распространение импульса и хроматиче-
хроматическую дисперсию (см. разд. 8.13), обычно вводится параметр ft, опре-
определяемый выражением [9]
(8.9.18)
600 Гл. 8. Распространение света в оптических волокнах
где Д = А(по/п2J' Параметр Ъ можно выразить через Г в виде
b(V) = Г2/У2 = 2п0Г2/У2 = 2П0Ь(П (8.9.19)
Другим важным параметром, особенно в связи с вопросом о связи
источника с волокном и потерях на микроизгибах (см. разд. 8.15), яв-
является размер пятна р0. Его можно определить, вспомнив, что для
ступенчатых профилей и профилей, изменяющихся в соответствии со
степенным законом, функция ф(р) с хорошей точностью аппроксими-
аппроксимируется гауссовой функцией
^(P)sexp(-lp2/pS) (8.9.20)
или непосредствнно выражением
Величину р0 можно вычислить в явном виде с помощью рассмот-
рассмотренного выше метода, который дает следующее выражение:
(Ро/Ф = BQ2I/2(Po/<v=k. (8.9.22)
В частности, можно показать [10], что при V > 1 с хорошей точ-
точностью мы можем записать
(ро/аJ = 1/1п V2. (8.9.23)
Остается вычислить критическую частоту для второй моды. Это
можно сделать, применяя ко второй моде v = 1 рассмотренный выше
метод и учитывая условие отсечки Г = 0, которое после некоторых
алгебраических преобразований можно записать следующим образом:
УйКо = 2,405/A - 1,1419хI/2. (8.9.24)
8.10. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ВНУТРИ ВОЛОКНА
В предыдущих разделах основные особенности процесса распростране-
распространения волн в оптических волокнах были изучены на примере мод, рас-
распространяющихся при фиксированной частоте в идеальных диэлектри-
диэлектрических волноводах. Рассмотрим теперь реальную ситуацию, когда по-
поле, представляющее собой суперпозицию различных мод и имеющее
ограниченную полосу частот, распространяется в реальном волокне,
профиль показателя преломления которого неизбежно отклоняется от
идеального, что приводит к ослаблению волн и связи между различ-
различными модами. Одновременное возбуждение многих мод и зависи-
зависимость постоянной распространения от частоты приводит к искаже-
искажению сигнала и ухудшению характеристик оптического волокна.
Обозначим пространственную конфигурацию произвольной моды,
8.10. Электромагнитное поле внутри волокна 601
определяемой индексом т (который, как было показано, на самом де-
деле означает набор индексов), через Ет(р;о)9 а постоянную распростра-
распространения этой моды (вещественную для направляемых мод и комплекс-
комплексную для мод утечки) через /3w(co). При этом аналитический сигнал (см.
гл. 1, разд. 1.8), соответствующий монохроматическому электрическо-
электрическому полю, распространяющемуся в идеальном волокне, можно запи-
записать в виде следующего разложения:
Е(ру z, t) = ? стЕт(р; со) ехр[ - ipm(co)z + tot], (8.10.1)
т
где ст — коэффициенты разложения. Если поле имеет конечную ши-
ширину полосы 6а>, то выражение (8.10.1) заменяется на
Г00
E(p,z,t) = X cm((o)Em(p;€o)apl-ipm(a>)z + icoQdco. (8.10.2)
т JO
Как уже отмечалось, поле в волокне не является строго попереч-
поперечным, причем отношение его продольной компоненты к поперечной со-
составляет величину порядка А1/2. Однако в качестве значимой величины
обычно рассматривают мощность Р(а), переносимую через элемент
поперечного сечения а волокна (рис. 8.14) и определяемую следующим
образом:
Pi<T)(z,t) = Re Г Г S • zdxdy. (8.10.3)
Здесь z — единичный вектор в положительном направлении оси z, a
§ — комплексный вектор Пойнтинга, определяемый выражением (см.
разд. 1.8) ^
S = i(ExH*>t, (8.10.4)
где скобки < >, обозначают усреднение во времени за несколько перио-
периодов 2тг/о) изменения поля. Следовательно, для вычисления вектора
Пойнтинга необходимо иметь лишь поперечною составляющую элек-
электромагнитного поля. Произведя замену Е — Н и Ет — Ит можно за-
записать выражения, аналогичные (8.10.1) и (8.10.2), для поперечной со-
составляющей магнитного поля. Коэффициенты разложения ст направ-
направляемых мод можно в принципе определить по известным граничным
Рис. 8.14. Поперечное сечение волокна.
602 Глх. 8. Распространение света в оптических волокнах
условиям E(p,z = 0, О» используя следующее соотношение ортого-
ортогональности:
•+оо
dylEm(p; со) х Н*(р; «)]•?= 2Рдтп, (8.10.5)
J -
где Р — положительный нормировочный коэффициент, а Ьтп — сим-
символ Кронекера. Соотношение ортогональности, аналогичное (8.10.5),
приближенно справедливо и для просачивающихся туннелирующих
моду соответствующих туннелирующим лучам (см. разд. 8.2), кото-
которые могут вносить заметный вклад в суммарное поле на значитель-
значительных расстояниях вдоль оси.
Если предположить, что ширина полосы 6w удовлетворяет нера-
неравенству (как это имеет место в большинстве случаев)
д(о/со0«1, (8.10.6)
где оH— характерная частота поля, то в (8.10.2) можно положить
Ew(p; о)) as Ет(р; оH). В результате мы получим более простое выра-
выражение
Г00
E(p9z9t) =XE«(P;wo) cm(co)expl-ipm(co)z + icoQdco. (8.10.7)
m JO
Заметим, что выражения (8.10.2) и (8.10.7) можно без труда обоб-
обобщить на случай реального волокна, у которого профиль показателя
преломления лишь незначительно отличается от идеального. Для это-
этого необходимо ввести зависимость коэффициентов cw(co) от z. Такая
зависимость учитывает связь между различными модами, образую-
образующимися вследствие искажения профиля показателя преломления. Сле-
Следовательно, в общем случае мы имеем
Г00
Е( р, z, t) = ?Em(p; а,) Ст(со9 z) ехр[ - фт(ф + icof] dco. (8.10.8)
w Jo
Используя выражения (8.10.5) и (8.10.7), можно сразу вычислить
коэффициенты cw(w, z = 0) при известных граничных условиях:
dyz •
. [E(p,z = 0,0 x H*(p;g>0)] (8.10.9)
[в идеальном случае cw(w, z) = cm(w, 0) ¦ cm(o))]. Выделяя в виде от-
отдельного множителя быстро меняющиеся (как в пространстве, так и
во времени) члены, выражение (8.10.8) можно переписать в виде
M (8.10.10)
л Г +00 Л +оо Л +
,z = 0) = —\ dte--"] dx\
*№* J-oo J-oo J-
8.11. Затухание 603
где Em(p) ш Em(p;w0) и Фт — медленноменяющаяся амплитуда, кото-
которая дается выражением
<bm(z9t) = cm(<D9z)exp{-ilPJp>) - А,Ю> + К<о ~ oj0)t}dco. (8.10.11)
J
Подставляя формулы (8.10.4) и (8.10.10), а также аналогичные выра-
выражения для магнитного поля в (8.10.3), имеем
х<ФтB,0Ф*(г,0>,; (8.10.12)
j I х Н*(р;со0У] • г. (8.10.13)
j I
Если элемент площади о совпадает со всем сечением волокна, то
,t), (8.10.14)
причем недиагональные члены, представляющие интерференцию раз-
различных мод, обращаются в нуль благодаря соотношению ортогональ-
ортогональности [см. (8.10.5)]. Ненулевые диагональные члены Pm(z, t) можно
интерпретировать как суммарную мощность, переносимую т -й модой
через полное сечение волокна при данном z.
8.11. ЗАТУХАНИЕ
Затухание излучения внутри оптического волокна обусловлено как по-
поглощением в материале волокна (включая рассеяние, вызванное флук-
туациями плотности на микроскопическом и атомном уровнях), так и
самим процессом распространения света в волноводе. Первый меха-
механизм затухания определяется материалом и может быть исследован
на любом образце этого материала, тогда как второй определяется
геометрической формой волновода. Потери, обусловленные поглоще-
поглощением в стекле, можно подразделить на три части: поглощение матери-
материала, поглощение на примесях, неизбежно присутствующих в материа-
материале, и поглощение на атомных дефектах. Эти потери можно описать
феноменологически через коэффициент потерь а — характеристику
рассматриваемого материала, который определяет относительное за-
затухание на единицу длины полной энергии, переносимой электромаг-
электромагнитным полем. Разумеется, необходимо ввести два коэффициента по-
потерь «j и а2, первый из которых относится к материалу сердцевины, а
604
Гл. 8. Распространение света в оптических волокнах
второй — к оболочке. При этом относительный декремент затуханий
на единицу длины полной энергии /w(z), переносимой т -й модой ft
определяемой выражением
-j:
запишется в виде
B)
m '
(8.11.1)
(8.11.2)
где/W — доля энергии т-й моды, распространяющейся в сердцевине,
a f$ — то же, но в оболочке (эти величины вычислены для идеально*
го волокна).
Еще одним источником затухания является рассеяние света на
флуктуациях плотности числа частиц на атомном уровне. Если бы
атомы и молекулы составляли идеально однородную структуру, то
поля, рассеиваемые отдельными атомами, при интерференции взаим-
взаимно компенсировались бы и рассеяние не наблюдалось. Этого не проис-
происходит из-за наличия локальных неоднородностей, зависящих от време-
времени и вызванных тепловыми флуктуациями. В волокне неоднородности
имеют статический характер и образуются при температуре Т фазово-
фазового перехода стекла; эти неоднородности остаются «замороженными»
в стекле после его затвердевания. Наличие таких неоднородностей в
стекле вызывает рассеяние (рэлеевское рассеяние) электромагнитных
волн, приводящее к их затуханию с коэффициентом a(s) (см. также
разд. 8.13.4):
a(e) = [(87e3)/CAS)](h2 - l)XBTj?c, (8.11.3)
где Хо — длина волны излучения в вакууме, п — показатель преломле-
преломления материала, АГВ —- постоянная Больцмана, а <3С — изотермический
коэффициент сжимаемости среды.
0.1
0,7 1,0 1,2 7,4 1,6
Длина Волны , мкм
Рис. 8.15. Спектральная зависимость зату-
затухания для типичного оптического волокна.
8.12. Дисперсия мод 605
На рив. 8.15 показано изменение коэффициента затухания с длиной
волны Хо. Рэлеевское рассеяние отвечает за затухание в более длинно-
длинноволновой* части, где коэффициент затухания зависит от длины волны
как 1AJ}.
Различные виды потерь в волокне связаны с его геометрической
структурой (например, уже упоминавшиеся потери мод утечки с коэф-
коэффициентом затухания а = -2/32 и потери, обусловленные конечной
кривизной волокна).
Конечный диаметр оболочки приводит к дополнительному затуха-
затуханию, обусловленному тем, что часть электромагнитной энергии рас-
распространяется в окружающем волокно покрытии, которое обладает
большими потерями. Другие виды потерь вызываются нелинейными
оптическими эффектами, вынужденным комбинационным рассеянием
и рассеянием Мандельштама — Бриллюэна, которыми в оптических
волокнах при низкой мощности света можно, как правило, пренебречь
(см. разд. 8.18).
Помимо перечисленных выше механизмов потерь, которые имеют
детерминированную природу, существуют и другие, вызванные тем,
что в любом волокне неизбежно происходят случайные деформации
сердцевины и микроизгибы его оси. Эти случайные неоднородности
приводят к возникновению связи между различными модами и взаим-
взаимной перекачки электромагнитной мощности. Увеличивающийся при
этом поток мощности от направляемых мод к модам утечки и далее к
преломленным модам является одной из причин затухания энергии,
распространяющейся в волокне.
8.12. ДИСПЕРСИЯ МОД
Исходя из выражений (8.10.10) и (8.10.11), а также учитывая неравен-
неравенство (8.10.6), можно записать следующее приближенное выражение:
00
cm(co,z) х
O
ли
Г0
JO
~Pm
x exp ~Pm{(o0){co - (O0Jz + i(co - oH)i]dco9 (8.12.1)
где«,(«о) = 0 o
Рассмотрим сначала случай, когда Sco столь мало, что в выраже-
выражении (8.12.1) членом (со — а>0J можно пренебречь. Определяя группо-
606
Гл. 8. Распространение света в оптических волокнах
вую скорость vm m -й моды
»-=1Шо>оХ (8.12.2)
для идеального волокна нетрудно получить следующее выражение:
--), (8.12.3)
из которого видно, что различные моды распространяются с различ-
различными скоростями vm. Мощность моды Pm(z,t) удовлетворяет соот*-
ношению
Pm(z,t) = PM(O,t-z/vm), (8.12.4)
так что сигнал, образованный суперпозицией различных мод, претер-
претерпевает искажение, обусловленное различными скоростями их распро-
распространения (дисперсия мод). Определяя задержку тт т-й моды
*m = L/vM (8.12.5)
(L — длина волокна), дисперсию мод можно выразить количественно
через максимальную возможную разность времен запаздывания раз-
различных мод:
Т^п) = тах|тш - tj. (8.12.6)
Для практических целей нередко приходится рассматривать форму
импульса, прошедшего определенное расстояние по волокну, при усло-
условии, что его ширина на входе пренебрежимо мала и все моды возбуж-
возбуждаются в одинаковой степени (импульсный отклик). Форма этого им-
импульса изображена на рис. 8.16 для различных профилей показатели
преломления. Можно показать, что выходной импульс имеет мини-
5
Л
0-
-
\
< 2
J
4/
/
-A/3)А 0
10
оо
1
h л
Рис. 8.16. Импульсный отклик для различных про-
профилей показателя преломления в зависимости от
нормированной задержки Д = (t — Ln Q/c )/(Ln Q/c).
8.13. Хроматическая дисперсия 607
мальную ширину А2/8 при [14]
9 = 2- 2,4 А, (8.12.7)
где q — показатель степени в представлении профиля показателя пре-
преломления в виде степенной зависимости [см. выражение (8.3.4)].
8.13. ХРОМАТИЧЕСКАЯ ДИСПЕРСИЯ
В предыдущем разделе при рассмотрении выражения (8.12.1) мы пре-
пренебрегли эффектом искажения, связанным с конечной шириной поло-
полосы бсо сигнала и учитываемым квадратичными членами по (со - соо).
Этот эффект, который оказывается пропорциональным бсо, в много-
модовых волокнах, если возбуждающий источник является достаточ-
достаточно монохроматическим, на практике пренебрежимо мал, но в идеаль-
идеальном одномодовом волокне он представляет собой единственный ис-
источник искажения. Простой метод изучения этого явления состоит в
рассмотрении зависимости групповой скорости vm от частоты (для
данной моды т) и связанной с этим задержки между самой «медлен-
«медленной» и самой «быстрой» частотами со' и со" . Точнее говоря, можно
записать следующее выражение:
J L.1 =
>') vn(co")j
которое при обычном допущении, учитываемом в (8.10.6), можно пе-
переписать в виде
Г<«> = L\d2pjdo>l=m\da>, (8-13.2)
где бсо в стандартных условиях представляет собой ширину полосы не-
несущей (как правило, эта ширина больше, чем ширина полосы, связан-
связанная с модуляцией сигнала).
При выполнении операции дифференцирования в выражении
(8.13.2) появляются различные члены, вызванные тем, что постоянная
распространения 0т помимо зависимости от со из-за дисперсионных
свойств материала волокна (дисперсия материала) проявляет зависи-
зависимость от частоты, обусловленную волноводной структурой волокна,
изготовленного даже из недисперсионного материала (волноводная
дисперсия). Кроме того, зависимость от со связана и с изменением
профиля показателя преломления с со (дисперсия профиля). В общем
случае эти три эффекта связаны между собой сложным образом и раз-
разделить их относительные вклады невозможно.
Для того чтобы вычислить/7^, предположим, что постоянную рас-
распространения мод в многомодовом волокне вдали от частоты отсечки
608
Гл. 8. Распространение света в оптических волокнах
можно записать в виде
i?«H = n1(co)w/c, (8.13.3)
где п ,(о>) — показатель преломления материала именно сердцевины,
поскольку моды стремятся быть локализованными внутри сердцеви-
сердцевины, которая считается бесконечно протяженной. Записывая выраже-
выражение (8.13.2) через длину волны (в вакууме) Хо, мы имеем
Г<сг) = AЛо/с)М2п1(Яо)/^о1 SXol (8.13.4)
здесь 6\ = Xq 8o)/oH. Отсюда мы видим, что хроматическая дисперсия
сводится к дисперсии материала. В соответствии с (8.13.4) дисперсией
материала можно пренебречь в окрестности длины волны Хо, для ко-
которой выполняется следующее условие:
РЧОоУОДа.-Д. = 0. (8.13.5)
Вообще говоря, более значимой величиной является не Т{ст\ а
T^CT)/L8X0, т. е. задержка на единицу длины волокна при единичном
интервале 5Х0. Зависимость этой величны от Хо показана на рис. 8.17.
Для одномодового волокна (или многомодового волокна, когда
рассматриваемые моды находятся либо вблизи отсечки, либо в диапа-
диапазоне длин волн Хо ^ Хо, когда уже нельзя пренебрегать волноводной
дисперсией и дисперсией профиля) выражение (8.13.4) становится не-
неточным и приходится прибегнуть к более сложному методу расчета,
указанному в работе Глоджа [15]. Этот метод использовали Гамблинг
и др. [16] для расчета одномодового волокна. Он состоит в том, что в
выражение (8.13.2) подставляется формула для /3 (8.9.18) и после неко-
некоторых алгебраических преобразований мы можем записать
где
с'> = L\Tcmd + Twd + Tcpd| <5А0,
= (Xo/c){A(V)d2nt/dX
(8.13.6)
(8.13.7)
ZOO
180
160
140
120
100
80
60
20
0
г \
i i i i i
600 800 1000
1200^J500
HM
Рис. 8.17. Дисперсия материала в зависи-
зависимости от длины волны на примере кварца.
Величина М{ соответствует Т*ст\ определяе-
определяемой выражением (8.13.4).
8.14. Модовый шум 609
A(V) = №(bV)/dV + bl
Twd = (n2 A/cX0)BVd2(bV)/dV2,
B = [l-(lo/n2)(dn2/dXo)]2,
= —(n2/c)CD(V)dA/dA0, A = A(no/n2J,
С = 1 - (Я0/п2)^2/Л0 - (Ao/4A)dA/dAo,
D(V) = Vd2(bV)/dV2 + d(bV)ldV - b
(8.13.8)
(8.13.9)
(8.13.10)
(8.13.11)
(8.13.12)
(8.13.13)
[величина b определяется выражением (8.9.18)]. Здесь Tcmd, Fwd и Tcpd
являются соответственно дисперсией материала, волноводной дис-
дисперсией и дисперсией профиля.
Классификация, приведенная выше, продиктована тем, что любой
из указаных выше вкладов обращается в нуль, когда соответствую-
соответствующий дисперсионный параметр полагается равным нулю. Например,
нетрудно заметить, что выражение для дисперсии материала в случае,
когда частоты мод находятся достаточно далеко от отсечки, т. е.
Ъ ss. 1 и V db/dV в 0, становится эквивалентным выражению (8.13.4),
в то время как вблизи отсечки дисперсионные свойства материала
оболочки становятся существенными. Для волокна со ступенчатым
профилем показателя преломления при V = 2,402 можно получить
следующее выражение:
\mJl , 2n2ldX2\. (8.13.14)
с
Следует заметить, что для любой наперед заданной длины волны вели-
личины rcmd, rwd и Гсрс1 не всегда имеют одинаковый знак, а длина
волны, при которой Г(с[> имеет пренебрежимо малое значение, в об-
общем случае отлична от Xq. Представление об относительных вкладах
трех видов дисперсии можно получить из рис. 8.18.
8.14. МОДОВЫЙ ШУМ
Рассмотрим выражение (8.10.12) для мощности P(°\z, t), проходящей
через элемент сечения о(р) с центром в точке р. Предварительно заме-
заметим, что на практике усреднение величин во времени, обозначаемое
чертой сверху, соответствует показаниям детектора за промежуток
времени TD, который обычно велик по сравнению с характерным вре-
временем флуктуации возбуждающего источника (время когерентности
Тс). При этом предположении черту над буквенным обозначением
можно заменить символом <>сред, который означает усреднение по ан-
610
Гл. 8. Распространение света в оптических волокнах
Сердцевина
бмкм
-/01-
/t^*1,6 1fi
Л,мкм
О
-1
-2
-3
-4
-5
-6
-7
0
А,мкм
1,2 /,4 /,?
2а =4мкм
1С
Л, мкм
-2^7 -
-4G -
Рис. 8.18. Дисперсия в одномодовых волокнах со ступенчатым профилем показателя
преломления для различных диаметров сердцевины 7а. Величины Tcmd (a), Twd (б) и
Fcpd (в) вычислены с помощью выражений (8.13.7), (8.13.9) и (8.13.11) соответственно;
г — суммарная дисперсия Т. (Из работы Гамблинга, Мацумуры и Рагдейла [16].)
самблю флуктуации источника. Таким образом, мощность Рт> пере-
переносимая т-й модой, можно записать в виде
Pm(z,t) = Р<|Ф,и(М)|2>сред > (8.14.1)
При этом недиагональные члены в выражении (8.10.12) содержат сле-
следующие кросс-корреляционные произведения:
Tnm(z,t) = <ФтМ)Фи*B,г)>сред. (8.14.2)
8.14. Модовый шум 611
Для того чтобы выразить Тпт в явном виде, пренебрежем взаимо-
взаимодействием мод и хроматической дисперсией; таким образом можно
положить (см. разд. 8.12), что Фш(?, О = Фш@, t - z/vm) и, следова-
следовательно,
Tm(z91) - <Фт@, г - фт)Ф*@, t - z/vn)>
= S(t - z/vm)S*(t - z/vnKF(t - z/vn)F*(t - z/n.» w s
= S(t - z/vm)S*(t - z/vn)G(\xnm\l (8.14.3)
где для простоты мы преположили, что все направляемые моды воз-
возбуждаются на входной плоскости волокна одинаковым образом и Ф(О
можно представить в виде произведения быстро колеблющегося члена
F(t) (связанного с флуктуациями источника) и относительно медлен-
медленного члена 5 (/) (связанного с внешними флуктуациями и модуляцией
сигнала).
Величина G (I тпт I) становится пренебрежимо малой, если
\xJl = L\l/vn-l/vu\»TC9 (8.14.4)
т. е. если задержка п -й моды относительно /w-й моды превышает вре-
время когерентности источника возбуждения мод. В случае, когда данное
условие выполняется для любой пары мод, все недиагональные члены
в выражении (8.10.12) обращаются в нуль и Р{а) [так же, как и интен-
интенсивность света 1{р у z, О» получающаяся при переходе к пределу Р^/а
при а — 0] представляет собой сумму одних лишь диагональных чле-
членов. В противном случае, когда имеются не равные нулю недиаго-
недиагональные члены, вклады от этих членов локально складываются с
вкладами от диагональных членов или вычитаются из них в зависимо-
зависимости от взаимных фаз, что приводит к возникновению спекловой
структуры в поперечном сечении волокна (рис. 8.19) [17].
Рис. 8.19. Типичная спекловая картина на вы-
— ходной грани оптического волокна.
612 Гл. 8. Распространение света в оптических волокнах
излучение 0о/1°"»о I Волокно П
L
Рис. 8.20. Пример возникновения потерь за счет спеклов, образующихся при несцентри-
рованном соединении волокон..
Вообще говоря, эти спекловые картины претерпевают случайные
динамические изменения благодаря тому, что S (t) помимо детерми-
детерминированной модуляции, связанной с информационным сигналом, мо-
может иметь случайную временную зависимость, связанную с вибрация-
вибрациями волокна или с небольшими изменениями длины волны излучения
лазера. Такое постоянное изменение спекловой картины может приве-
привести к флуктуациям потерь, т. е. к стохастической амплитудной моду-
модуляции передаваемого сигнала (к так называемому модовому шу-
шуму) [18]. Модовый шум присутствует в любом случае, когда в волок-
волокне имеют место потери, связанные с возникновением спекловой карти-
картины в некотором сечении волоконной линии при несцентрированной
стыковке двух волокон (рис. 8.20).
Из вышесказанного следует, что проблема модового шума связана
с наличием когерентных источников. Действительно, если волокно
возбуждается некогерентными источниками (например, светодиодом),
соотношение (8.14.4) благодаря малости Тс оказывается справедли-
справедливым для любой пары мод и практически любой длины волокна L, так
что никакой спекловой структуры не возникает.
8.15. ТЕОРИЯ СВЯЗАННЫХ МОД
В оптическом волокне взаимодействие между различными модами
[приводящее в выражении (8.10.8) к зависимости коэффициентов ст от
координаты z ] обусловлено отклонениями геометрической формы оп-
оптического волокна от идеальной цилиндрической. Такое взаимодейст-
взаимодействие приводит к взаимной передаче мощности от одной моды к дру-
другой, так что мощность в моде Рт является некоторой суммой перво-
первоначальных мощностей различных мод, а скорость распространения
моды по световоду равна некоторой величине, усредненной по ансамб-
ансамблю скоростей возбуждаемых мод, взятых с определенными весовыми
8.15. Теория связанных мод 613
коэффициентами. Как и следовало ожидать, этот эффект является
благоприятным и с точки зрения дисперсии, которая стремится к
уменьшению при взаимодействии мод. Однако взаимодействие мод
отрицательно сказывается на потерях, поскольку ведет к постоянно
нарастающей перекачке мощности от направляемых мод в радиацион-
радиационные, что в итоге приводит к уходу излучения из волокна.
В подавляющем большинстве случаев взаимодействие между мода-
модами носит случайный характер, так как неоднородности в волокнах
прямо связаны со случайными отклонениями в процессе изготовления
и сборки волноводной структуры. Именно поэтому, а также вследст-
вследствие того, что даже при известном механизме возмущения задача о
распространении взаимодействующих мод аналитически разрешима
лишь в очень небольшом числе случаев, эту задачу решают с по-
помощью статистических методов.
Прежде чем рассмотреть конкретную статистическую модель, не-
необходимо найти систему уравнений, описывающих изменение коэффи-
коэффициентов cw(<o, z) [см. выражение (8.10.8)] при наличии заданного взаи-
взаимодействия. Если выбрать, например, слабонаправляющие волокна и
пренебречь взаимодействием между модами, распространяющимися в
противоположных направлениях, то можно показать, что для ампли-
амплитуд направляемых мод, распространяющихся вперед, справедлива сле-
следующая система уравнений [1]:
(8.15.1)
fxw^z)cn(w
dz „ = i
где N — общее число направляемых мод, а
Kmn{z) = ^ [°° dx Г dy[n\p,z) - п20(р)-]Ет(р) • Ев*(р). (8.15.2)
^** J -оо J -оо
В выражении (8.15.2) через n(p,z) обозначен коэффициент прелом-
преломления реального волокна, в то время как через ло(р), Ет и Еп обозна-
обозначены соответственно показатель преломления и поперечные компоне-
компоненты aw-й ил-й мод идеального волокна. При записи уравнений (8.15.1)
пренебрегалось взаимодействием с континуумом радиационных мод,
так что в этом приближении общая мощность направляемых мод со-
сохраняется. Кроме того, предполагалось, что для любого z реальные
оптические волокна слабо отличаются от идеальных (рис. 8.21) и, сле-
следовательно, электромагнитное поле можно по-прежнему разлагать по
модам идеального волокна. В более общем случае, например когда
ось оптического волокна отклоняется от прямолинейной (так называе-
называемые микроизгибы; см. рис. 8.22), упомянутое разложение оказывается
614
Гл. 8. Распространение света в оптических волокнах
неверным. В данном случае удобно ввести набор «локальных» мод,
относящихся хотя и к идеальному случаю, но все же для любого z
сильно напоминающих реальную картину. С учетом сделанных заме-
замечаний, переписывая систему уравнений (8.15.1) и выражение (8.15.2)
для пространственных конфигураций Ew(p, z) и Hm(p, z) и соответ-
соответствующих им постоянных распространения (зависящих от координа-
координаты z), получаем соответственно
dz
*«(*) =
»
dy-
dz
[co,z) (m=l,2...,N),
(8.15.3)
^Em(p,z)-EH(p,z); (8.15.4)
здесь p и z относятся к системе координат идеального волокна.
Искажения, подобные изображенным на рис. 8.21, можно учесть,
записав расстояние О(ф, z) между границей раздела сердцевина —
оболочка и осью волокна в виде
X ^). (8.15.5)
Влияние же микроизгибов (рис. 8.22) можно учесть через величину
n2(p,z), получаемую из /Jq(p) подстановкой вместо р величины
Р' = {О - /(г)]2 + ly- g(z)?I/2, (8-15-6)
где/(г) и g(z) — функции, определяющие расстояния осей соответст-
соответственно х и у от оси реального волокна.
Рис. 8.21. Деформация волокна на границе раздела сердцевина — оболочка (качествен-
(качественное представление).
Рис. 8.22. Микроизгибы волокна.
8.15. Теория связанных мод 615
Используя соотношение
dn2(p,z)/dz = (дп20(р')/др')(др'/дг) (8.15.7)
и выражение (8.15.6), мы находим (в низшем порядке теории возму-
возмущений), что микроизгибы могут приводить к связи только тех мод,
для котрых справедливо следующее правило отбора:
v'-v= ±1, (8.15.8)
где *>' и v — соответстующие азимутальные числа. В случае когда па-
параметры возмущения определяются выражением (8.15.5), выполняется
правило отбора
v'-v=±/, (8.15.9)
где / определяется номером соответствующего члена в сумме выраже-
выражения (8.15.5), связывающего моды с азимутальными числами v и v .
Системы уравнений (8.15.1) и (8.15.3) имеют аналитические реше-
решения лишь в ограниченном числе случаев, а именно тогда, когда рас-
рассматриваются только самые простые отклонения формы волокна
от идеальной и взаимодействуют всего несколько мод. Если ввести в
рассмотрение статистическую модель, то задача о распространении
мод в оптических волокнах с учетом межмодового взаимодействия
становится аналитически разрешимой в гораздо большем числе случа-
случаев, однако при этом мы получаем лишь «усредненные» величины.
Точнее говоря, мы рассматриваем ансамбль макроскопически идентич-
идентичных волокон, отличающихся друг от друга случайными микроскопиче-
микроскопическими дефектами, и вычисляем значимые физические величины, усред-
усредненные по этому ансамблю, которые мы будем обозначать с помощью
угловых скобок < >. Если применить операцию усреднения к системам
уравнений (8.15.1) или (8.15.3), то мы получим следующую систему
уравнений для средней мощности моды (РтУ =Ж< I Фт(г,
[см. выражение (8.14.1)] [1, 19]:
(m = 1,2...fN\ (8.15.10)
где otm — феноменологически введенный общий коэффициент потерь
m-й моды, а
Г
J -ос
z, (8.15.11)
причем аналогичное выражение можно записать и для случая, когда
вместо Ктп используется Rmn.
Корреляционной длиной L стохастической переменной Kmn(z)
616 Гл. 8. Распространение света в оптических волокнах
[или Rmn(z)] называется максимальная длина отрезка волокна, на ко-
котором корреляционная функция <Kmn(z)K^n@)) не равна нулю. Таким
образом, корреляционная длина определяет средний пространствен-
пространственный период дефектов отдельного оптического волокна. При выводе сис-
системы уравнений (8.15.10) предполагалось, что значения коэффициентов
cm(z) на длине Lc существенно не меняются (гипотеза слабой связи).
Межмодовая связь приводит к возникновению потерь, которые
можно описать в рамках механизма, связывающего направляемые и
радиационные моды. Эти потери прибавляются к потерям, связанным
с поглощением и рассеянием излучения в волокне и учитываемом в
уравнениях (8.15.10) с помощью коэффициентов затухания ат. Сделав
соответствующие предположения относительно вида коэффициентов
hmn, потери 7i> обусловленные взаимодействием мод, можно найти,
если решение системы уравнений (8.15.10) для стационарного случая
искать в следующем виде:
Pm(z)ocexp[-(a + y1)z]. (8.15.12)
Как уже упоминалось выше, взаимодействие между модами нару-
нарушает дисперсию мод, что можно подтвердить, решив систему уравне-
уравнений (8.15.10). Хотя эта система уравнений в общем случае неразреши-
неразрешима, можно прийти к простому описанию, исследуя асимптотическое
поведение временной ширины o(z) импульса, имеющего пренебрежи-
пренебрежимо малую начальную ширину. Если < Р (z, t)) — общая мощность,
проходящая через данное сечение волокна, то определив величины
-г
можно записать, что
ф) = (? - Г2I'2- (8.15.15)
Для больших z можно показать, что
a{z) ос z1/2, (8.15.16)
в то время как для малых z мы имеем
(t(z)ocz. (8.15.17)
Выражения (9.15.17) и (8.15.16) описывают два различных предель-
предельных случая. В первом случае расстояния столь малы, что межмодо-
вым взаимодействием можно пренебречь, поэтому зависимость дис-
8.15. Теория связанных мод
617
= 2000
I WOO
| 800
3 600
| 400
о
I 200
^ 100
80100 200 400 600 1000 2000
Расстояние, м
Рис. 8.23. Зависимость временной шири-
ширины импульса от расстояния вдоль оси г,
пройденного им в оптическом волокне
при наличии межмодового взаимодейст-
взаимодействия. (Из книги Окоси [6].)
персии от длины волокна является линейной. Во втором случае, когда
волокно имеет большую длину, межмодовым взаимодействием прене-
пренебречь уже нельзя, отсюда появляется более слабая по сравнению с
первым случаем зависимость дисперсии от расстояния (рис. 8.23). Эта
зависимость от z в виде квадратного корня может быть эвристически
объяснена с помощью простой модели, в которой рассматриваются
всего две моды [20], связанные между собой таким образом, что веро-
вероятность того, что фотон, принадлежащий одной моде, перепрыгнет в
другую на расстоянии dz, равна h dz, причем h не зависит от z> При
этом эволюцию импульса можно описать с помощью механизма слу-
случайных блужданий, согласно которому на отрезке 1/Л фотон распро-
распространяется со скоростью vx или v2, так что среднее время его пролета
t дается выражением
v2)l (8.15.18)
а задержка относительно этого времени пролета запишется в виде
|t - t\ = (l/fc)|lM - 2/(vx + v2)\ s [l/Bfc)]|t;2 - vt\/vl (8.15.19)
Согласно общей теории диффузионных процессов, среднеквадра-
среднеквадратичное значение суммарной задержки равно квадрату задержки на от-
отдельном шаге длиной 1/Л, умноженному на число zh шагов на рассто-
расстоянии z. Таким образом, мы имеем
it2 - г2I'2 = (t - о2 s [|»2 -
Это выражение согласуется с (8.15.16)
Г8.15.20)
618 Гл. 8. Распространение света в оптических волокнах
8.16. СТАТИСТИЧЕСКАЯ ТЕОРИЯ РАСПРОСТРАНЕНИЯ
В СИСТЕМЕ ОПТИЧЕСКИХ ВОЛОКОН
Статистический метод решения задачи о распространении излучения в
оптическом волокне при наличии межмодового взаимодействия, о ко-
котором шла речь в предыдущем разделе, состоит в вычислении средней
мощности (Рт) моды. Операция усреднения по ансамблю макроско-
макроскопически идентичных волокон является довольно надуманной, посколь-
поскольку на практике обычно имеют дело с одним волокном. Статическая
природа ансамбля волокон также не позволяет в рамках какой-либо
гипотезы эргодичности получить взаимное соответствие между < Рт >
и усреднением по длительному временнбму интервалу (что часто име-
имеет место в статистической механике). Можно было бы попытаться с
целью установления хоть какой-нибудь эргодичности найти соот-
соответствие между (Рт) и пространственным усреднением по длине во-
волокна, на которой укладывается много периодов нерегулярности, од-
однако и это в конце концов оказывается невозможным.
В этих условиях остается только одно, а именно, чтобы извлечь из
величины (Рт) некоторую практическую информацию, необходимо
найти флуктуации величины Рт относительно среднего значения, тог-
тогда относительно малая величина этих флуктуации позволит надеяться
на то, что средняя величина Рт совпадает с фактической. Для того
чтобы это осуществить, необходимо записать систему дифференциаль-
дифференциальных уравнений для <Р^> и (РтРп). Считая, что оптическое волокно
не имеет потерь и возбуждается монохроматическим сигналом, для
и (РтРп) можно написать следующие уравнения [19]:
- 2<РтРк)) (т = 1,2...,ЛГ), (8.16.1)
Рп> - <РтРк» +
(8.16.2)
Теперь заметим, что система уравнений (8.15.10) в стационарном
случае (d/dt = 0) и при пренебрежимо малых потерях (ат = 0) описы-
описывает так называемое асимптотическое равнораспределение мощно-
мощности, т. е. ситуацию, когда (Pm(z — оо)> не зависит от выборат. В
случае монохроматической волны это свойство позволяет получить из
системы уравнений (8.16.1) и (8.16.2) следующее асимптотическое со-
8.17. Оптические волокна, сохраняющие поляризацию излучения 619
отношение [19]:
^2 (х-соХ (8-16.3)
из которого следует довольно разочаровывающий результат, а имен-
именно 100%-ная неопределенность фактического значения Рт при извест-
известном его среднем значении.
Ситуация меняется в случае, когда сигнал имеет конечную ширину
полосы до). Можно показать [21], что при этом нормальная дисперсия
УУ (8.16.4)
стремится к нулю при z > 4т'л)(л, ю = 1, 2, ..., N), где Жст>п) =
= Тс/ \\/vn - \/vm I — характерное расстояние, на котором пол-
полностью исчезает корреляция между m-й и л-й модами [см. выражение
(8.14.4)]. Таким образом, в этих условиях никакой статистической не-
неопределенности в определении величины Рт для отдельного волокна
не имеется.
8.17. ОПТИЧЕСКИЕ ВОЛОКНА, СОХРАНЯЮЩИЕ
ПОЛЯРИЗАЦИЮ ИЗЛУЧЕНИЯ
Аксиально-симметричные оптические волокна, работающие в одномо-
довом режиме, на самом деле являются двумодовыми световода^ш,
поскольку в них могут распространяться две ортогонально-поляризо-
ортогонально-поляризованные собственные моды [например, моды (LP^ и (LP,)^ в волок-
волокне со ступенчатым профилем показателя преломления]. Если оптиче-
оптическое волокно обладает идеальной структурой, то очевидно, что два
поляризационных состояния вырождаются, т. е. соответствующие им
постоянные распространения 0Х и 0у совпадают (главные оси ? и j> во-
волокна выбираются произвольным образом). В реальных условиях зна-
значения fix и (Зу очень близки друг к другу, что может вызвать сильное
взаимодействие двух ортогонально-поляризованных мод. В свою оче-
очередь это взаимодействие приведет к перекачке мощности (которая со-
сопровождается процессом поляризационной конкуренции мод) на очень
коротких расстояниях (от нескольких сантиметров до нескольких мет-
метров).
Для того чтобы понять, как это происходит, достаточно обра-
обратиться к теории связанных мод. Если в выражении (8.15.2) скалярное
произведение поперечных составляющих собственных мод заменить
на скалярное произведение их продольных составляющих, то это вы-
620 Гл. 8. Распространение света в оптических волокнах
ражение будет описывать, в частности, эволюцию двух поляризацион-
поляризационных состояний. В большинстве практических случаев коэффициент
связи hxy(\)[x = ll^ — jSyl; см. выражение (8.15.11)], который опре-
определяет спектр мощности случайного возмущения Kxy(z)9 обусловлива-
обусловливающего межмодовую связь, имеет вид функции пропускания низкоча-
низкочастотного фильтра с пространственной частотой отсечки хс [22]. Таким
образом, в соответствии с выражением (8.15.11) между двумя поляри-
поляризационными состояниями перекачки мощности не происходит, если
выполняется условие
\Рх-РУ\»Хс* (8.17.1)
и, наоборот, она становится существенной, если справедливо обрат-
обратное неравенство и, уж тем более, когда &х » /3'
Однако в таких устройствах, как линии оптической связи гетеро-
гетеродинного типа и волоконные датчики, выходной сигнал должен иметь
заданную и постоянную поляризацию. В соответствии с проведенным
выше рассмотрением один из методов получения постоянной поляри-
поляризации состоит в том, чтобы сделать как можно большую разность
между значениями постоянных распространения. Добиться этого
можно, либо нарушив аксиальную симметрию сечения самого волок-
волокна, либо изменив геометрию его сердцевины с круговой на эллиптиче-
эллиптическую, или же создав в сердцевине поперечное напряжение с большой
асимметрией [23].
Примем для определенности, что рх > 0у и, как это обычно дела-
делается, введем нормированную величину В, называемую двулучепре-
двулучепреломлением моды и определяемую выражением
В = 2(рх - ру)/(рх + РУ) ? (Рх - Ру)/поко. (8.17.2)
Типичные значения В лежат в интервале 10~5 — 10~7 для обычных
волокон и в интервале 10 — 10~4 для волокон, сохраняющих поля-
поляризацию. Величина В служит характеристикой способности волокна
сохранять поляризацию моды, возбуждаемой светом, поляризован-
поляризованным вдоль одной из главных осей. Если падающий свет поляризован
под углом в к оси х, то, распространяясь по волокну, он пройдет че-
через различные состояния эллиптической поляризации. Разность фаз
между лучами с разными поляризациями в волокне длиной z записы-
записывается в виде
= (Рх - Py)z = Bnokoz, (8.17.3)
Отсюда можно определить длину биений Lb:
2n = BnokoLb. (8.17.4)
8.18. Нелинейные эффекты в оптических волокнах 621
Используя определение Lb, условие (8.17.1) можно сформулировать
следующим образом: пренебрежимо малая передача мощности из од-
одного поляризационного состояния в другое имеет место только тогда,
когда длина биений намного меньше типичного пространственного пе-
периода геометрических дефектов волокна.
Очевидно, что снятие вырождения в одномодовых волокнах приво-
приводит к модовой дисперсии между двумя поляризационными модами
{поляризационная дисперсия). Согласно результатам, полученным в
разд. 8.12, величина межмодовой задержки дается выражением
тр = Щ/<ко)(Рх-ру)9 (8.17.5)
или же, если ввести эффективный показатель преломления пх = с$х/ы
(пу = cCy/w) и учесть, что обычно кварцевое стекло в ближнем ИК-
диапазоне имеет низкую дисперсию (dn/du < п/ш), мы имеем
тр = Цпх - пу)/с + (Lco/c)(dnx/do) - dny/dco) ? L(nx - пу)/с ? LB/(c/no\
(8.17.6)
8.18. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ В ОПТИЧЕСКИХ ВОЛОКНАХ
Замечательные характеристики волокон с очень низкими потерями
привели к возможности создания широкополосных передающих си-
систем дальнего действия. Необычайная протяженность этих систем по-
позволяет исследовать нелинейные явления, возникающие при распро-
распространении излучения в световодах. Кроме большой длины взаимо-
взаимодействия для проявления нелинейности оказывается существенным на-
наличие малого диаметра у сердцевины, что имеет место в одномодо-
одномодовых волоконных световодах, а также использование узкополосных од-
ночастотных лазеров. В частности, произведение длины волокна L на
интенсивность Р/(тга2), где Р — входная мощность, a a — радиус
сердцевины, может стать достаточно большим по сравнению с харак-
характерной интенсивностью при нелинейном распространении в простран-
пространственно-неограниченной среде. Таким образом, низкая нелинейная вос-
восприимчивость кварцевого стекла при относительно малой мощности
компенсируется большой протяженностью волокна.
С одной стороны, нелинейные эффекты вредны и ограничивают
передаваемую мощность в волоконных системах связи, а с другой, —
их можно с выгодой использовать при создании специальных оптиче-
оптических приборов (например, волоконных лазеров на комбинационном
622 Гл. 8. Распространение света в оптических волокнах
рассеянии [24]) или же для улучшения рабочего режима самого волок-
волокна (например, генерации солитонов).
Вспомним (см. гл. 2), что нелинейные оптические явления обычно
описываются с помощью поляризуемости Р, которую формально
можно разложить в степенной ряд по напряженности электрического
поля следующим образом (см. разд. 1.2.1):
". (8-18.1)
Первый нелинейный член Хг^2» связанный, например, с генерацией
второй гармоники, в стеклах равен нулю вследствие симметрии по от-
отношению к инверсии, поэтому практически все нелинейные эффекты,
имеющие место в стеклянных оптических волокнах, связаны с членом
Х3?. Эти эффекты можно грубо разбить на два класса, различающие-
различающиеся тем, колеблется ли наведенная поляризация с частотой падающего
поля или нет. Ко второму классу относятся вынужденное комбинаци-
комбинационное рассеяние (ВКР), вынужденное рассеяние Мандельштама —
Бриллюэна (ВРМБ) и четырехволновое смешение. К первому классу
относятся так назвыаемые самоиндуцируемые эффекты, которые
описываются, как будет показано в следующем разделе, с помощью
нелинейного показателя преломления (оптический эффект Керра\
В данном разделе мы кратко рассмотрим ВКР и ВРМБ, поскольку
именно эти явления накладывают ограничения на вводимую в волокно
максимальную мощность. В следующем разделе мы изучим более
подробно самоиндуцированные эффекты, которые можно описать с
помощью некоторой общей теории;
Как ВКР, так и ВРМБ с классической точки зрения могут быть
представлены как трехволновое взаимодействие между падающей вол-
волной (накачкой), сигнальной волной (стоксовой или мандельштам-
бриллюэновской) и соответственно либо волной, связанной с колеба-
колебательным возмущением молекул среды, либо звуковой волной [25].
В результате такого взаимодействия часть энергии, которая вначале
содержится в волне накачки, постепенно преобразуется в сигнальную
волну, распространяющуюся в случае ВКР в прямом и обратном на-
направлениях, а в случае ВРМБ только в обратном направлении. В оп-
оптических линиях связи даже в отсутствие инжектируемого сигнального
поля благодаря спонтанной эмиссии всегда существует слабый сигнал,
который может быть значительно усилен за счет мощности волны на-
накачки, несущей полезную информацию.
Оба процесса обычно характеризуются коэффициентами усиления
слабого сигнала GK(p) hGb(*>), которые представляют собой коэффр-
8.18. Нелинейные эффекты в оптических волокнах
623
циенты в экспоненте, характеризующей зависимость спектральной ин-
интенсивности сигнала на частоте v от расстояния z при условии, что
поглощением интенсивности волны накачки пренебрегается. Соот-
Соответствующие выражения для интенсивностей записываются в виде
/r(z,v) = /R@,v)exp[GR(v)z], (8.18.2)
/b(*,v) = /B@,v)exp[GB(v)z]. (8.18.3)
Оба коэффициента усиления пропорциональны интенсивности на-
накачки 70. Для ВКР мы имеем следующее выражение:
Gr(v) = 0(Av)/o, (8.18.4)
где Ар = р0 - ps — разность между частотой волны накачки v0 и
стоксовой частотой ps, a g(Ap) (рис. 8.24) дается соотношением
g(Av) = G0(Av)c2/[^s3n2(vs)], (8.18.5)
где ао(Ар) — стоксово сечение на единицу объема в единичном частот-
частотном интервале, a n(ps) — показатель преломления на частоте ps.
Коэффициент усиления в случае ВРМБ существенно зависит от то-
того, как соотносятся между собой ширина линии накачки Арр и ширина
линии спонтанного рассеяния Мандельштама — Бриллюэна Арв (зна-
(значение последней лежит в пределах 15—40 МГц для плавленого кварца
в полосе пропускания оптического волокна). Например, если
Арр > Арв, то при увеличении Арр коэффициент усиления ВРМБ сигна-
сигнала уменьшается в соответствии с отношением Арв/Арр [26]. Всякий
раз, когда выполняется это условие, ВКР (его порог, т. е. значение
мощности накачки, при которой данный эффект становится замет-
заметным, лежит в области 1 Вт и выше) становится доминирующим нели-
Рис. 8.24. Зависимость коэффициента
усиления GR для ВКР от разностной
частоты для плавленого кварца при
длине волны накачки 1,0 мкм. (Из
работы Столена [24].).
0 200 U00 600 800 1000 1200Ш00
Сдвиг частоты, см4
624 Гл. 8. Распространение света в оптических волокнах
нейным процессом. Если же в качестве источника накачки использует-
используется достаточно узкополосный лазер (Дрр < 1 МГц), то доминирующим
будет ВРМБ. В последнем случае максимальная входная мощность
[26], передаваемая многокилометровым волокном, будет в сильной
степени ограничена именно этим эффектом; в этом случае предельная
входная мощность составит несколько милливатт. При превышении
порога значительная часть интенсивности волны, распространяющей-
распространяющейся вперед и представляющей собой волну накачки, преобразуется в
распространяющуюся назад сигнальную волну.
8.19. САМОИНДУЦИРОВАННЫЕ НЕЛИНЕЙНЫЕ ЭФФЕКТЫ
Рассмотрим третий член в разложении (8.18.1), описывающий поляри-
поляризуемость третьего порядка Р^3). Допустим, что материал, из которого
изготовлено волокно, является изотропным и нелинейная характери-
характеристика волокна определяется быстро протекающими электронными
процессами. Тогда РC) можно записать в виде [27] (см. также диссер-
диссертацию Овиюнга [4], указанную в литературе к гл. 1 нашей книги)
РC) = в0ХC)Е • ЕЕ, (8.19.1)
(дисперсия здесь отсутствует), где е0 — электрическая постоянная ва-
вакуума, а л^ — нелинейная восприимчивость среды. Для того чтобы
выделить самоиндуцированные эффекты, в выражении (8.19.1) необхо-
необходимо найти члены с частотой колебаний, примерно совпадающей с ча-
частотой поля (в точности ту же частоту они будут иметь в том случае,
если поле представляет собой монохроматическую волну); тогда вы-
выражение (8.19.1) можно записать» в виде
Р<,3) = еC).Еш, (8.19,2)
где Р@> иЕш- фурье-образы величин Р<3) и Е во временной области
при угловой частоте со, а ?C) — соответствующий тензор [см., напри-
например, выражение (8.19.4)]. Пусть в слабонаправляющий световод вво-
вводится некоторый аналитический сигнал с амплитудой Е [28] [напо-
[напомним, что Е = (§ + Ё*)/2; см. разд. 1.8.]. Поскольку известно, что в
таком световоде поперечная компонента поля Ет велика по сравнению
с продольной (см. разд. 8.6.), в выражении (8.19.2) останутся лишь
поперечные компоненты, так что это выражение принимает вид [29]
Р& = 43)-Ет„, (8.19.3)
где
,C) _
fg 1
8.19. Самоиндуцированные нелинейные эффекты 625
Для волокон, сохраняющих поляризацию (см. разд.8.17), можно
положить, например, Еу = О (как потом выяснится, нелинейное взаи-
взаимодействие не смешивает ортогональные поляризации). Тогда выра-
выражение (8.19.3) сведется к
Р?> = e2\Ex\2Ejm, (8.19.5)
где е2 = C/4)вохC). Это же соотношение при условии, что е2 =
= E/4)?охC), справедливо и для регулярных волокон, в которых кон-
конкуренция поляризаций происходит на очень коротких расстояниях и
для которых в среднем ЁуЁ*х = 0. В обоих случаях в показателе пре-
преломления можно формально выделить нелинейную составляющую,
использовав для этого связь между фурье-компонентами вектора сме-
смещения DTo) и электрического поля ЕТб,:
Dw = ?l(w)Ew + ?<3)E.,, (8.19.6)
откуда в соответствии с выражением (8.19.5) получаем
. е = ех + е2\Ёх\2, (8.19.7)
так что в хорошем приближении можно написать следующее выраже-
выражение:
п{а>) = п^со) + п2\Ёх\\ (8.19.8)
где п = (е/еоI/2. Линейная часть показателя преломления представле-
представлена слагаемым пг = (е{/е0)и2, а нелинейная — слагаемым
п2 = е2/Bлг1е0). Выражение (8.19.8) дает пример зависящего от време-
времени (через \ЁХ\2) показателя преломления, шкала изменения которого
во времени велика по сравнению с 1/Дсо, где Асо представляет типич-
типичную временную шкалу изменения пх(<х>) (см. в гл. 1 разд. 1.2 и работу
[3] в литературе, указанной к этой главе). Заметим, что выражение
(8.19.8) можно также переписать через интенсивность /, а именно в
виде п = пх + J^2I, где JY2 = 2(п2/пх)$0. Для кварца пх « 102(м/ВJ
и jV2 = 5-Ю6 см2/Вт.
Присутствие квадратичного по электрическому полю нелинейного
члена в правых частях выражений (8.19.7) и (8.19.8) приводит к появ-
появлению эффекта Керра. Чтобы исследовать влияние этого члена на
процесс распространения света в волокне, можно либо воспользовать-
воспользоваться непосредственно решениями уравнений Максвелла в среде с диэ-
диэлектрической проницаемостью, определяемой выражением (8.19.7)
[30], либо (как и будет сделано в дальнейшем) применить теорию свя-
связанных мод, рассмотренную в разд. 8.15 (см. также разд. 8.17), уста-
устанавливая связь нелинейной компоненты показателя преломления с на-
нарушениями регулярности волокна.
626 Гл. 8. Распространение света в оптических волокнах
Прежде чем продолжить обсуждение, с целью обобщения рассмат-
рассматриваемого формализма на случаи, когда основную роль играют вол-
волны, распространяющиеся назад, выражение для поля внутри волокна
необходимо переписать в виде
Ex(p,z9t) = K(p^t) + E-X(p,z9t) =
z9t)}, (8.19.9)
где
Ф± - Г
Jo
exp{i(o> - co0)t + iipm(€o) - pm(co0ftz}c±(co,z)dco. (8.19.10)
Здесь Ёт{р) = Е^-х, причем х — единичный вектор, параллельный
оси*. Выражение (8.19.9) представляет собой естественное обобщение
выражения (8.10.10) на случай, когда волной, распространяющейся на-
назад, пренебречь нельзя. В соответствии с этим теорию связанных мод
необходимо модифицировать таким образом, чтобы учесть взаимо-
взаимодействие прямых и обратных волн. При этом система уравнений, опи-
описывающая изменение коэффициентов с*, запишется в виде [1]
dz
dc<T>(co,z)
^+ ехр{-|[Д,(а))
dz
+ Km<n~ exp{-/[j?w(w) - PH((o)]z\c~((o9z)]9 (8.19.11)
а коэффициенты связи в соответствии с (8.19.7) молено записать следу-
следующим образом:
•+оо Л+оо
dx dy\Ex(p,z,t)\*Em{p)En(p) =
-оо J -oo
(8.19.12)
^'¦* J -оо J -o
Из уравнений (8.19.11) можно получить следующую систему урав-
уравнений для Ф^ [31]:
H9tw
8.19. Самоиндуцированные нелинейные эффекты 627
+ 2i ? КИИФП+ФЛ-Ф:* (п,т = 1,2,-..,N), (8.19.13)
пФт
где коэффициенты связи /?тА2 записываются через интегралы перекры-
перекрывания пространственных конфигураций различных мод:
-' (81914)
а дифференциальные операторыL* определяются выражением
+ д 1 В id2 Id3 idA /o ,ft ,,„
/-=^±^^т2л:^+з!д:^±4!о:^+-' (8-19Л5)
где vm — групповая скорость [см. выражение (8.12.2)] и
Лт — групповая дисперсия второго порядка:
Ат = (d2PJdco2)~i(O0, (8.19.16)
а Вт, Ст — групповые дисперсии более высших порядков:
Вт = (d3pJd(o3)-1\(a=(O0, Ст = {d+PJd(o4)'-1\€O=mo9.... (8.19.17)
В частности, если Ёт (р) выбрать таким образом, чтобы
E2m(p)dxdy=l (8.19.18)
то выражения для Rmm можно переписать в виде
Rmm = kon2/amt (8.19.19)
где ат — эффективная площадь w-й моды [29].
Система уравнений (8.19.13) является основой для описания различ-
различного типа нелинейных эффектов, имеющих место при распростране-
распространении оптического сигнала в длинном волокне, а именно фазовой само-
самомодуляции, солитонов и вырожденного четырехволнового смешения,
о которых речь пойдет ниже.
8.19.1. Фазовая самомодуляция
Предположим, что в волокне длиной L входное поле имеет место
только при z = 0, так что никакой обратной волны не возбуждается в
628 Гл. 8. Распространение света в оптических волокнах
соответствии с системой уравнений (8.19.13), из которой следует
$m(z> 0 = 0 (для любого т), если Ф~(г = L, О = О (для любо-
любого т). В случае когда мы имеем дело с одномодовым волокном, си-
система уравнений (8.19.13) сводится к одному нелинейному дифферен-
дифференциальному уравнению
(д/dz + (l/vMd/dt) - [*/B^)]C2/^2))<I>T = -1'Кц|ФЛ2Ф1 (8.19.20)
где мы пренебрегли дисперсией более высокого порядка, чем второй.
Из структуры этого уравнения хорошо видно, что поведение распро-
распространяющегося в волокне импульса зависит от относительных вкла-
вкладов диффузионного члена [- /7B^1)]Э2/Э/2, учитывающего хромати-
хроматическую дисперсию, и нелинейного члена - /7?111Ф112Ф1. Действитель-
Действительно [за исключением тех случаев, когда этими членами можно прене-
пренебречь и уравнение (8.19.20) имеет неискаженное решение типа
$\(z, i) = ФДг = 0, t - z/vx)], если преобладает диффузионный член,
то вследствие хроматической дисперсии инжектированный (при z = 0)
импульс подвергается временному уширению, а если преобладает не-
нелинейный член, то фаза инжектированного импульса подвергается мо-
модуляции. Данное утверждение становится понятным, если вниматель-
внимательно взглянуть на решения уравнения (8.19.20), которые соответственно
для дисперсионного и нелинейного режимов записываются в виде
f (г, 0 =
Ф\ (z = 0,Г - ^)
(8.19.21)
k>f (z = 0,f - ?). (8.19.22)
Вообще говоря, уравнение (8.19.20), если в него входят как диффу-
диффузионный, так и нелинейный члены, не допускает аналитических реше-
решений. Поэтому необходимо прибегнуть к приближенным или числен-
численным расчетам, вид которых во многом определяется соотношением
между этими двумя членами. Анализируя уравнение (8.19.22), можно
показать, что мгновенная частота поля в некотором приближении да-
дается выражением
co(t) = ш0 - Rnid/dtWKz = 0,t - zM)|2z, (8.19.23)
Таким образом, на переднем фронте импульса все частоты претерпе-
претерпевают сдвиг вниз, в то время как на заднем фронте частоты сдвинуты
вверх. Отсюда следует, что в случае нормальной дисперсии (см. разд.
1.2) (Aj > 0, X ^ 1,3 мкм для плавленого кварца), т. е. когда группо-
групповая скорость vx становится меньше для более высоких частот, измене-
8.19. Самоиндуцированные нелинейные эффекты 629
ние частоты из-за нелинейной фазовой самомодуляции приведет к
уширению импульса, в то время как в случае аномальной дисперсии
(A j < О, X ^ 1,3 мкм для плавленого кварца) возникает сжатие им-
импульса [32, 33].
8.19.2. Солитоны
В разд. 8.19.1 мы показали, что в режиме с аномальной дисперсией
уширение импульса, вызванное хроматической дисперсией, может
быть скомпенсировано соответствующей наведенной нелинейностью;
когда устанавливается точный баланс между этими механизмами,
огибающая оптического импульса, как можно показать, принимает
форму солитона [34], который распространяется без искажений. Ука-
Указанное свойство подтверждается наличием у уравнения (8.19.20) точ-
точного решения вида
Ot(z,t) = OoexpC/z/^T2)] sch [(r - zM)/t],. (8.19.24)
при условии что выполняется следующее условие баланса между ам-
амплитудой 1Ф01 и временной шириной г импульса при z = 0:
-1/(>11т2) = Я11|Фо12. (8.19.25)
Огибающая указанного выше основного солитона распространяется
без изменения своей формы с групповой скоростью vv совпадающей
со скоростью рассматриваемой моды.
Помимо основного солитона, определяемого выражением (8.19.24),
существуют и другие солитоны, так называемые солитоны высших
порядков [35, 36], для которых характерно периодическое noz измене-
изменение формы импульса и которые представляют собой решения уравне-
уравнения (8.19.20), удовлетворяющие следующему граничному условию:
0>|(z = 0,0 = МФ0 sch (Г/т), (8.19.26)
rjxeN — целое число ( ^ 2), а 1Ф01 и т связаны по-прежнему соотно-
соотношением (8.19.25). Используя численные методы, можно показать, что
в процессе распространения импульса по волокну его форма сначала
сжимается, а затем начинает изменяться более сложным образом,
включающим в себя периодическую последовательность сжатий и рас-
расщеплений (рис. 8.25) с периодом z0 [33, 37], определяемым выражением
zo = (tt/2)t2M1|. (8.19.27)
Необходимо упомянуть и о важном значении солитонов в решении
такой проблемы, как увеличение скорости передачи информации по
одномодовым оптическим волокнам. Интересующиеся читатели мо-
630
Гл. 8. Распространение света в оптических волокнах
10
0
30
20
10
л
ZQ-пространственнып
период
а
Рис. 8.25. а — распределение относительной интенсивности Р/Ро = I $0(z, /) 12/1 Фо12
для солитонов высших порядков при N = 2 (верхние кривые) и N = 3 (нижние кривые)
при нескольких фиксированных значениях параметра z/z0 (равного соответственно 10
и 5 • 10 для верхних кривых и 10, 25 • 10~2 и 5 ¦ 10 для нижних кривых) в зави-
зависимости от параметра s = (t - z/v)/t [из работы Молленауэра и Столена A982), ука-
указанной в библиографии]; б — изменение величины Р/Ро в зависимости от отношения
Т/То = s для различных последовательных сечений волокна [см. выражения (8.19.24) —
(8.19.26)]. [Из работы Столена A984), указанной в библиографии. 1
8.19. Самоиндуцированные нелинейные эффекты
631
гут получить более обширную информацию в статье Хасегавы и Ко-
дамы [38].
8.19.3. Вырожденное четырехволновое смешение
Рассмотрим ситуацию, схематически представленную рис. 8.26, когда
на входе в волокно присутствуют одновременно три поля /?;-+, Е+ и
Е~ с одной и той же центральной частотой о>0, которые возбуждают
соответственно распространяющуюся вперед моду / при z = О (сиг-
(сигнальную моду) и две противоположно направленные моды р Ф I при
z = 0 и z = L (моды накачки). Общая теория, представленная в
разд. 8.19, позволяет предсказать как порог появления моды //рас-
//распространяющейся назад, так и эволюцию медленноменяющихся ам-
амплитуд Ф,+, Ф,~, Ф+ иФ~, поведение которых описывается системой
уравнений (8.19.13). Считая, что выполняется условие сильной накач-
накачки, т. е. 1Ф+ 1, 1Ф~ I > 1Ф/+ 1, 1Ф/~ I, можно написать следующую си-
систему уравнений:
L-Ф- =
(8.19.28)
Lfф,- = 2здф;|2 + |ф;|2)фг + 2«||Гф;ф
Система уравнений (8.19.28) решается независимо от системы
(8.19.29), и в случае стационарной накачки эти решения имеют вид
2|Ф;@)|2]B -
<8Л9-30>
Таким образом, член
в уравнениях (8.19.29) записывается как
г} х
(8.19.31)
Фр
Рис. 8.26. Схема четырехволнового смешения в оптическом волокне.
632 Гл. 8. Распространение света в оптических волокнах
и не зависит otz, только если 1Ф^@I2 = \Ф~(Ь)\2. Оставаясь в рам-
рамках гипотезы сильной накачки и определяя величины
slp = 2д/р[|ф;@)|2 + |0>;(L)|2], (8.19.32)
Tlp = 2Rlp<t>;(z)<b-p(zl (8.19.33)
систему уравнений (8.19.29) можно записать в виде
Ь}ф+ = iSlp<l>t - 1Т1рФ7*, ЬГФГ = iSlp<*>7 + ЩРФГ*9 (8.19.34)
Эта система уравнений описывает вырожденное четырехволновое
смешение поля внутри оптического волокна (термин "вырожденное"
применяется потому, что сигнальная волна и волна накачки имеют
одну и ту же центральную частоту соо). В частности, в стационарном
случае (L/+ = Lf = d/dz) из (8.19.34) мы получаем хорошо известные
уравнения, которые можно найти в литературе [30, 39]. Решения этих
уравнений записываются в виде
(8.19.35)
7Jp|L)
При z = 0 имеем
ФГB = 0) = &,ФГ*(* = ОХ (8.19.36)
причем
Q,P=-i(Tlp/\Tlp\)tg(\Tlp\L), (8.19.37)
Отсюда следует, что мода, распространяющаяся назад и обусловлен-
обусловленная нелинейным взаимодействием накачки со средой, в свою очередь
порождает при z = 0 сопряженную с ней по фазе моду ("реплику"),
распространяющуюся вперед, которая затем усиливается в случае
ltg(l Tlp\L)\ > 1 и ослабляется в случае ltg(l Tlp\L)\ < 1.
Представленный выше результат можно обобщить на случай, ког-
когда несущий изображение луч возбуждает определенное число мод, рас-
распространяющихся вперед, амплитуды которых связаны с амплитудами
противоположно направленных мод соотношением (8.19.36). В этом
случае осталось только проверить, в какой степени данная ситуация
похожа на ту, которая возникает при оптическом обращении волново-
волнового фронта [40] в объеме нелинейных кристаллов, где волна, распро-
распространяющаяся назад при z = 0, несет фазосопряженную картину рас-
распределения интенсивностей в падающей волне, что в случае монохро-
монохроматических волн записывается в виде
E~(p,z = 0) ос ?+*(p,z = 0). (8.19.38)
Задачи 633
Используя соотношения (8.19.9), (8.19.33) и (8.19.36), в приближе-
приближении слабого сигнала (\Tip\L < 1) можно написать следующее выра-
выражение: „ ~
EZ(p9z = 0) = -m^L^EMR^t^z = 0), (8.19.39)
которое можно сравнить с выражением
E+x (p, z = 0) = ? ?,(/>)Ф,+(z = 0). (8.19.40)
z
Из анализа выражений (8.19.39) и (8.19.40) становится понятным
тот факт, что обращение волнового фронта возникает только тогда,
когда коэффициенты/?^ (т. е. интегралы перекрывания между 1-й ир-й
модами) практически не зависят от модового индекса / для рассматри-
рассматриваемой группы мод.
Если входной сигнал зависит от времени, то необходимо решить
уравнения (8.19.29) в случае, когда Lf uLj~ определяются выражени-
выражением (8.19.15). Ограничиваясь рассмотрением дисперсий первого и вто-
второго порядков, т. е. записывая ?/*= как
L? = д/dz ± (l/v^d/dt) + [i/B^)]/(d2/5*2), (8.19.41)
мы находим аналитическое решение [41], которое, в частности, пред-
представляет собой обобщение выражения (8.19.36) и записывается в виде
фГ (Z = 0, t) = eintR(u)G(U) du, (8.19.42)
J-oo
где
G(Q) = i- I +<V«tyf+*(z = 09t)dt, (8.19.43)
27CJ-oo
d/q\ = .(ф tan Г f(?$)L~\/ii(?l/V) tg Г f(Ci)LS] /X?i)| (8.19.44)
причем /(П) = AП2 + u2/vf)Vl. Фазосопряженный отклик волокна
таким образом аналогичен отклику оптического полосового фильтра
[42]. В заключение следует заметить, что в выражения (8.19.42)
— (8.19.44) не входит параметр Ah откуда следует, что процесс обра-
обращения волнового фронта не зависит от хроматической дисперсии [41].
ЗАДАЧИ
Раздел 8.2
1. Выведите соотношение (8.2.5).
Раздел 8.3
2. Вычислите отношение потока мощности, направляемого градиентным волокном
[см. выражение (8.3.4)], к потоку мощности, направляемому эквивалентным волокном
со ступенчатым профилем показателя преломления (nQ = п{ и те же значения радиуса
634 Гл. 8. Распространение света в оптических волокнах
сердцевины и показателя преломления оболочки), при условии, что возбуждение в обо-
обоих случаях осуществляется на входе в волокно одинаковыми источниками, излучающи-
излучающими изотропно в пределах приемного угла.
Раздел 8.4
3. Получите уравнение (8.4.8).
Раздел 8.5
4. Выведите характеристическое уравнение (8.5.20).
Раздел 8.6
5. Используя свойства нулей функции Бесселя J р9 покажите, что число волноводных
мод в волокнах со ступенчатым профилем показателя преломления в пределе V > 1
равно N = V2/2.
6. Покажите, что число направляемых мод в градиентном волокне [см. выражение
(8.3.4)] равной = (V2/2)q/(Q + 2). Подсказка. См. книгу [2, с. 257].
7. Получите выражение (8.6.2). Подсказка. Используйте рекуррентные свойства и
асимптотическое поведение функций Jp иКр.
Раздел 8.9
8. Вычислите моменты 12/ для произвольного градиентного волокна [см. выражение
(8.3.4)].
9. Выведите выражение (8.9.13).
Раздел 8.10
10. Покажите, что различные моды волокна с параболическим профилем показателя
преломления [см. выражение (8.7.16)] взаимно ортогональны. Подсказка. Вспомните,
что для слабонаправляющих волокон Н s (е/д^З х Е.
11. Найдите коэффициенты сш(«, z = 0), определяемые выражением (8.10.9), для во-
волокон с параболическим профилем показателя преломления, полагая, что на вход во-
волокна подается линейно-поляризованный гауссов пучок Е(р, z = 0, t) =
= #оехр[ - р2/B/?2) + /oqT] (R < а). Подсказка. См. в предыдущей задаче.
Раздел 8.12
12. Используя решение задачи 5, покажите, что при v > 1 справедливо выражение
Р*б = *ол1 ~" »дЛ^/(8Аг0/11 а2), где М = v + 26, а также вычислите 7™°*.
13. Вычислите разность lrp+^g - t^I для волокна с параболическим профилем по-
показателя преломления при наинизшем значимом порядке по А.
Раздел 8A3
14. Получите выражение (8.13.2) при больших/,, используя выражение (8.19.21) и
полагая, что на вход волокна подается сигнал в виде гауссова импульса Ф+U =
= 0, 0 = Ф1Оехр[- А'афЬ
15. Решите задачу 14, полагая что на входе волокна сигнал описывается выражением
= 0, /) = Ф10 ехр[- /2/B7^)]F(O, где F является стохастической величиной с
корреляционной функцией <F(t')F*(t")) = ехр(- I/' - t"\2/T2).
16. Покажите, что максимальная полоса пропускания Д/, достижимая в одномодо-
вом волокне, имеющем лишь хроматическую дисперсию, пропорциональна 1/L, если
основной вклад в bw вносит ширина полосы источника возбуждения, и пропорциональна
\/Lv\ если в бы основной вклад вносит уширение, связанное с частотной модуляцией
направляемой моды. Подсказка. А/ г 1/7<СГ).
Литература 635
Раздел 8.15
17. Используя систему уравнений (8.15.10), определите стационарное (д/dt = 0) рас-
распределение мощности в двухмодовом волокне. Подсказка. Ищите частные решения ви-
вида <Р12> = АХ1 е~аг.
Раздел 8.16
18. Используя систему уравнений (8.15.10), покажите, что асимптотическое равно-
равнораспределение мощности различных волноводных мод имеет место в стационарном
случае при отсутствии потерь в волокне.
Раздел 8.17
19. Рассмотрите одномодовое волокно с эллиптическим поперечным сечением и
входное поле, линейно-поляризованное в направлении, образующем угол т/4 с главны-
главными осями. Вычислите расстояние, на котором начальная мощность полностью перерас-
перераспределится по двум взаимно ортогональным состояниям. Подсказка. См. книгу Марку-
зе [1, с. 157].
Раздел 8.19
20. Получите выражение (8.19.21).
21. Используя выражение (8.19.23), выведите приближенное соотношение
BrfPQ = 1,6 Вт пс2, которое связывает т и пиковую мощность Ро, необходимую для
возбуждения основного солитона. Считайте при этом, что п2 — 1,2-102 м2/В2,
A j = Ю^см/с2, та2 = 20 мкм2, Хо = 1,3 мкм и л0 = 1,5. Подсказка. Покажите снача-
сначала, что для нормированной на единицу пространственной конфигурации моды
R 2
n
22. Найдите наиболее общее решение уравнения (8.19-20) в виде Ф*(?> 0=
= exp[/(c,z + c2t)]f(t - z/v) при v Ф vx [38].
ЛИТЕРАТУРА
1. Marcuse ?>., Theory of Dielectric Optical Waveguides, Academic Press, New York,
1974.
2. Arnaud /., Beam and Fiber Optics, Academic Press, New York, 1976.
3. Unger H. G., Planar Optical Waveguides and Fibers, Oxford Univ. Press (Clarendon),
London and New York, 1977. [Имеется перевод: Унгер X.-T. Планарные и воло-
волоконные оптические волноводы. — М.: Мир, 1980.]
4. Midwinter I E.t Optical Fibers for Transmission, Wiley, New York, 1979.
5. Adams M. J., An Introduction to Optical Waveguides, Wiley, New York, 1981. [Имеет-
[Имеется перевод: Адаме М. Введение в теорию оптических волноводов. — М.: Мир,
1984.]
6. Okoshi Т., Optical Fibers, Academic Press, New York, 1982.
7. Snyder A. W.t Love J. D., Optical Waveguide Theory, Chapman and Hall, London,
1983. [Имеется перевод: Снайдер A.t Лав Д. Теория оптических волноводов. —
М.: Радио и связь, 1987.]
8. Jeunhomme L. A, Single-Mode Fiber Optics Principles and Applications, Dekker, New
York, 1983.
9. Gloge A, Appl. Opt., 10, 2252 A971).
10. Snyder A. W., Proc IEEE, 69, 6 A981). [Имеется перевод: Снайдер А. — ТИИЭР,
1981, т. 69, Mi 1, с. 7.]
636 Гл. 8. Распространение света в оптических волокнах
И. Gambling W. A., Matsumura #., Opt. Quantum Elect., 10, 31 A978).
12. Stewart W. J., Electron. Lett., 16, 380 A980).
13. Hussey C. D, Pask C, Proa IEEE, 129, 123 A982).
14. Gloge D, Rep. Prog. Phys., 42, 1777 A979).
15. Gloge D, Appl. Opt., 10, 2442 A971).
16. Gambling W. A., Matsumura #., Ragdale С М, IEEE Microwave Opt. Acoust., 3,
239 A979).
17. Crosignani R, Daino A, Di Porto P., J. Opt. Soc. Am., 66, 1312 A976).
18. Epworth R. E.t Laser Focus, 17, 109 A981).
19. Crosignani A, Daino A, Di Porto P., IEEE Trans. Microwave Theory Tech., MTT-23,
416 A975).
20. Kawakami S., Ikeda M, IEEE J. Quantum Electron., QE-14, 608 A978).
21. Crosignani A, Wabnitz 5., Di Porta, Opt. Lett., 9, 371 A984).
22. Kaminow I. P, IEEE J. Quantum Electron., QE-17, 15 A981).
23. Okoshi Т., IEEE J. Quantum Electron., QE-17, 879 A981).
24. Stolen R. H. — In: Fiber and Integrated Optics (ed. D.B. Ostrowsky), Plenum, New
York, 1979, p. 157—182.
25. Smith R. G., Appl. Opt., 11, 2489 A972).
26. Cotter D, J. Opt. Commun., 4, 10 A983).
27. Rloembergen N., Nonlinear Optics, Benjamin, New York, 1965. [Имеется перевод:
Бломберген Н. Нелинейная оптика.— М.: Мир, 1966.]
28. Gabor D, J. Inst. Electr. Eng., 93, 429 A946).
29. Crosignani A, Cutolo A., Di Porto P., J. Opt. Soc. Am., 72, 1136 A982).
30. Yariv A., AuYeung J.t Fekete Д, Pepper D, Appl. Phys. Lett., 32, 635 A978).
31. Crosignani A — In: New Directions in Guided Wave and Coherent Optics (eds.
D. B. Ostrowsky, E. Spitz), Nijhoff, The Hague, 1984, p. 23—41.
32. Stolen R.H. — In: Optical Fiber Telecommunications (eds. S. E. Miller,
A. G. Chynoweth), Academic Press, New York, 1979, p. 125—150.
33. Mollenauer L. E, Stolen R. #., Gordon J. P, Phys. Rev. Lett., 45, 1095 A980).
34. Hasegawa A.t Tappert E, Appl. Phys. Lett., 23, 142 A973).
35. Захаров A E, Шабат А. Б. — ЖЭТФ, 1973, т. 64, с. 1627.
36. Satsuma J., Yajima N., Suppl. Prog. Theor. Phys., No. 55, 284 A974).
37. Stolen R. #., Mollenauer L. E, Tomlinson W. J., Opt. Lett., 8, 186 A983).
38. Hasegawa A., Kodama X, Proa IEEE, 69, 1145, 1981. [Имеется перевод: А.Ха-
сэгова, Ю. Кодама. — ТИИЭР, 1981, т. 69, № 9, с. 57].
39. Hellwarth R. W., IEEE J. Quantum Electron., QE-15, 101 A979).
40. Optical Phase Conjugation (ed. R. A. Fisher), Academic Press, New York, 1983.
41. Crosignani A, Di Porto P., Opt. Lett., 7, 489 A982).
42. Pepper D. K, Abrams R. L., Opt. Lett., 3, 212 A978).
БИБЛИОГРАФИЯ
Keiser G. R, Optical Fiber Communications, McGraw-Hill, New York, 1983.
Mollenauer L. E, Stolen R. #., Laser Focus, 18, 193 A982).
Sharma A. A, Halme S. L., Butusov M. M., Optical Fiber Systems and their Compo-
Components, Springer-Verlag, Berlin and New York, 1981.
Stolen R. H. — In: New Directions in Guided Wave and Coherent Optics (eds.
D. B. Ostrowsky, E. Spitz), Nijhoff, The Hague, 1984, p. 1—22.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ А. ФОРМУЛЫ ВЕКТОРНОГО АНАЛИЗА
АВхС=АхВС = ВСхА=ВхСА = САхВ=СхАВ,
А х (В х Q = (А • С)В - (А • В)С,
А х (В х С) + В х (С х А) + С х (А х В) = О,
(А х В) • (С х D) = (А • С)(В • D) - (А • D)(B • С),
(А х В) х (С х D) = (А х В • D)C - (А х В • QD,
F х (/A) =
F • (А х В) = В • (F х А) - А • (F х В),
F х (А х В) = A(F • В) - B(F • А) + (В • Р)А - (А . Р)В,
F(A • В) = А х (F х В) + В х (F х А) + (А • Р)В + (В • Р)А,
V2/ = F • F/,
F2A = F(F • А) - F х F х А,
F х F/ = О,
F • F х А = О,
ПРИЛОЖЕНИЕ Б. ДИАДЫ И ИХ СВОЙСТВА
ab =
axbx
aybx
axby ax
ayby ay
azby az
ab = ba,
Sp(ab) =
К
К
К
a-
=
a*
ay
az
(АЛ)
(A.2)
(A.3)
(A.4)
(A.5)
(A.6)
(A.7)
(A.8)
(A.9)
(A. 10)
(A.11)
(A.12)
(A.13)
(A.14)
(A.15)
(A.16)
(Б.1)
(Б.2)
(Б.З)
638
Приложения
ab • с = a(b • с) = (Ь • с) = (b • с)
с • ab = i
ab • cd = (b • c)ad = (b • с)
axdx axdy axdz
aydx aydy ayd2
azdx a2dy a2d2
ab :cd = (b • c)(a • d) = Tr(ab • cd),
A i В = АцВц9
PA:PB= —4uh— Bu
ПРИЛОЖЕНИЕ В. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Ортогональные полиномы
Полиномы Лежандра
Присоединенные функции Лежандра
j:
j:
(и - m)!
(и + ih)!
""''
(Б.4)
(Б.5)
(Б.6)
(Б.7)
(Б.8)
(Б.9)
(Б.10)
(ВЛ)
(B.2)
¦(и-т)! ""''
Приложения 639
Полиномы Лагерра __ lid"
J. •¦¦'
—zxn + a\
(В.З)
Полиномы Эрмита
Я„(г) = (-\)nezl±-e-2\ I e-**Hn(z)Hn.(z)dz = 2"nl"nldm.t (B.4)
«Z J -00
Круговые полиномы Цернике
(l/2)(n-|m|) (П — 5V
K) k У } s![(n + m)/2 - 5]![(и - m)/2 - s]!
(n-|m|)/2
j,w)(l) = 1, «5,и)B) = zn , (B.5)
2(n + 1)
f' zR^\z)Jm{az)dz = (-1)<---»)/2^
Jo
Скалярные сферические гармонические функции
У8 = 1/DяI'2 ,
y° = C/4rcI/2cos0 ,
y±i = +C/87tI/2sin0e±1*,
Y°2 =
= E/4tiI/2C/8I'2 sin2
Y°3 = G/47tI/2(l/4I/2Bcos30 - 3cos0sin20) ,
= +G/4nI/2C/16I/2Dcos20sin0-sin30)e±'*,
= +G/47tI/2E/16I/2sin30e±3i* .
640 Приложения
Векторные сферические гармонические функции
Y?
Y71 l
П = -A'/3I/2У|в+1 + B/3)У2е0
| = A/2)^У»е +
° =
2
Y|
Y1
где
^^^Цяпв^ + (eoi0)§ + i
ё-i = (e"'*/21/2)[(sin в)р + (cos0H - ^
Функция Малюжинца
м(«)=
№ - 1) + т - 1/2
М(а-2ф)
= ctg |-(a + -
М(а + ф)М(ос -
Функции Бесселя
1 Гя sin vn Г
= - cos(zsin0-v0)d0-^—^
e
o
™e * = ~n • (B.8)
M(a-
Приложения 641
_ Jv(z) cos(vtt) - J_v(z) _
sin(v7i)
1 /•* if00
= - sin(z sin в - v0) de - - [evf + e~w cos(v7r)]e"z shtdt,
n)o nJo
. fao-Hri
i = Jv(z) + iYy(z) = ^ ЙГ"ЛЛ ,
Kj-oo
Ht2)(z) = Jv(z) - ВД = i- I °° Шez sh f-w* . (B.9)
Модифицированные функции Бесселя
/7\v oo /W>\2n
/v(z) = e-'("/2)v Jv(e'*/22) = (^;
' """"!"V"H"*" ' (B.10)
J
n
= -cscGrv)[/_v(z) - /,(z)] =
Сферические функции Бесселя
2z
Функции Риккати — Бесселя
фяB) = zjn(z)9 tt1}B) =
Функция параболического цилиндра
l/2 Z j e
jl (ВЛЗ)
Приложения
(i\l/2 Г»
М еы,л\
J 1
642
Интегралы Френеля
1/2
1/2
г'*/4 Л iz2 z* iz6
-M1~TT3-2!5 + 3-!7 + -
Примечание: для функции UF см. выражение (В.19).
^d(z) = 2 arctg ez - я/2.
Функции Эйри
1 Г00 А3 \
Ai(z) =.« Jo СОЛ^"+ Z) = Cl/(z) ~C20(z)'
3-2/3
ГШ Cft)!'
= °'35503'
-1/3
m
112
(В. 15)
Г® Cft
= 0,25882,
z z1 0
AiB) =—[/_1/3@ - /1/3@] = ^зттгK1/3(C), ? > 0, С = f г3'2 ;
.1/2
1/2
Приложения 643
Знаковая функция
sgn(x) =
1, х > О,
О, х = 0, (В. 17)
-1, х<0.
Гамма-функция
Г(г)
Г(г + 1) = zT(z\
Г00
?-*€-* dt9 (Rez>0);
Jo
гг, (В. 18)
12z ^ У (формула Стирлинга);
(эйлеровское бесконечное
1 в f / л ] ^эйлеровское оеско
-— = zeyz f] U 1 + - )e~z/n>, произведение)
1 (z) и=1 (\ п) j у = 0>57721 (константа Эйлера).
Единичная ступенчатая функция U? (х) комплексного аргумента х
) < U,
Функция sine
ев 1
), для остальных х [см. ур. E.3.12)].
sinc(x)=— • (В.20)
X
z\v+2"
Функции Ломмеля двух переменных
L/v(w,z)=I(-ir(-) Jv+2n(z) ,
/w z2 v\
(B.21)
ПРИЛОЖЕНИЕ Г. ФОРМУЛЫ РАЗЛОЖЕНИЙ В РЯД
Разложение в ряд Тейлора
-r-h ¦
где limyv_00(/ — J] ...) = 0 при достаточно малых значениях X.
544 Приложения
Асимптотическое разложение
N
где limx_0(/ - J] ...JX^ = 0 при любых N. В случае когда функция/
является решением волнового уравнения Гельмгольца [A.1.12)], коэф-
коэффициенты Лп могут быть получены интегрированием системы уравне-
уравнений B.2.8).
Разложение по сферическим гармоническим функциям
\:(о,ф). (г.з)
Тождество Якоби
g )., (Г.4)
Формула Бауэра
/тг\1/2 °°
eizcos4> = 1 — 1 Y, iSB« + l)«/s+l/2(z)^s(COS<^),
S=0 oo (Г#5)
s=o s 4
Теорема сложения полиномов Лежандра
Я 2П + 1 т=-п
здесь w —- угол, образованный направлениями (б, ф) и (ff , ф').
Произведение двух сферических гармонических функций
п+п' J^
j=\n-n'\m"=-j
здесь С — коэффициенты, называемые в различных источниках либо
коэффициентами Вигнера, либо Зу -символами, либо коэффициентами
Клебша — Гордана. Свойства, а также таблицы со значениями этих
коэффициентов можно найти, например, в книге: Weissbluth M, Atoms
and Molecules, Academic Press, New York, 1978.
Теорема сложения Графа для функций Бесселя
(Г.8)
Приложения 645
где
<^{2 + '22V@tf')}1/2, a sin i/f=
ПРИЛОЖЕНИЕ Д. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
Пространственное преобразование Фурье
F[n(x);*]= r<X>u(x)eikxdx,
J -оо
+ 00
F[n(x, у); кх, к,-] = | Г м(х, y)eik**+ikyy dx dy, (Д. 1)
-00
+ 00
F [м(г);к] = fff н(г)вл-'А = uk.
— oo
Временное преобразование Фурье
-oo
Ж s мш. (Д.2)
Пространственно-временное преобразование Фурье
+ 00
F[«(r,t);k,o] = fjJLr.Oe»-'-'*-АЛ = Mk>0). (Д.З)
-00
Обратное преобразование Фурье
F-lMk);xl=±-rC°w(k)e-ikxdk,
2nJ-oo
+ 00
"A, (Д.4)
— oo
+ 00
=^ Г f fL(k,(u)e-ikr
646 Приложения
Интегральная теорема Фурье
t\t')'Xoi\\t9t\ = u(r,t). (Д.5)
Фурье-преобразование свертки
F[u(M) ¦ t>(r,t);k,a>] = F[M(r,t);k,a>]F[t;(r,O;k,a>], (Д.6)
где через * обозначен оператор свертки
+ 00
«(г, г) * v(r, t) = ГПТ u(r - г', t - t')v(r', f) dr' dt:
-00
Преобразование Ханкеля т -го порядка
#m[u(p);x]= u(p)JJxp)pdp. (Д.7)
Jo
Интегральная теорема Ханкеля
Ят[Яж[и(р');х];р] = «(р)- (Д.8)
Соотношение между преобразованиями Фурье и Ханкеля
Пуеть функция и (х, у) зависит только от р = (х2 + д>2I/2; тогда
F[u(p); kx9 k J = 27гЯ0[ы(р); р]. (Д.9)
ПРИЛОЖЕНИЕ Е. АСИМПТОТИЧЕСКОЕ РАЗЛОЖЕНИЕ
ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ
l/2 foo
1
kBnk)il2 ft'@J
Таблица Д. 10. Преобразования Ханкеля
9(у) = f °°f(x)(xy^2Jv(xy)dx =
Jo
x1/2/(b2 + x2) У1/2К0(Ъу) (v = 0)
x1/2(aa + x2)-1/2 (-J Kl/2(ay) (v = 0)
rl/2 / \ 3/2Г 2 V2"
" *«/fu — 1 W> IT— I ^>
v(y \
\a)
e L"(ax2) ( l) a^6 У
X42elax* ±yll2e-V/M (V = 0)
2a
/9_\l/2 oo
\a) .W{
il/2
(X>1)
3 (s + 2)(s
ГДе a
1 2 Bs + 3)Bs + 1)
s(s + 1)
J = Bs + 3)Bs- 1)
3 s(s - 1)
Cs~2Bs+ l)Bs- 1)
Из книги: Oberhettinger F. Tables of Bessel Transforms, Springer-Verlag, Berlin and New York,
1972.
548 Приложения
здесь е = sgn h" @), а символами ' и " обозначены соответственно
первая и вторая производные по s, а через а — стационарная точка.
(ф = рр)
(Е.2)
К2п/ Jr
где вклад от седловой точки определяется выражением
ei(l-e)n!4-ikh(s*)
причем е = sgn Л" E*) E* — седловая точка); вклад от разреза опре-
определяется выражением
e-Uh(sb)
/4]1/2^>; (Е.4)
где
Jo
\o9{s)'
Г00
lg{s
(Е.5)
3@)
i + 7~ттт + тттт + О(к ) (а — в общем случае
v ; v ; комплексная величина),
ИМЕННОЙ УКАЗАТЕЛЬ
Ананьев Ю. А. 522
Араго (Arago) 46
Аристотель 471
Ашкин (Ashkin) 463
Баннинг (Banning) 199, 200
Бергштейн (Bergstein) 535
Берне (Bums) 63
Био (Biot) 46
Бойд (Boyd) 536
Бромвич (Bromwich) 459
Брюкке (Briicke) 458
Буавен (Boivin) 286
Бэбкок (Babcock) 435
Бэкон (Bacon) 471
Дебай (Debye) 459, 462, 466, 467
Декарт (Descartes) 97
Денисюк Ю. Н. 435
Дерюгин 445
Джаван (Javan) 551
Дзидзик (Dziedzic) 463
Дюфур (Dufour) 566
Дюффо (Duffieux) 248
Жакино (Jacquinot) 566
Зайдель (Seidel) 143
Зоке (Szoke) 551
Зоммерфельд (Sommerfeld) 314, 353
Вайнштейн Л. А. 518, 537, 538—540
Ван ден Берг (van den Berg) 445
Ван дер Корпут (van der Corput) 343
Ван дер Поль (van der Pol) 459, 555
Ван де Хюлст (van de Hulst) 35, 459,
467, 471
Ван-Циттерт (Van Cittert) 326
Ватсон (Watson) 287
Верной (Vernon) 23
Вильсон (Wilson) 470
Вольф (Wolf) 308, 311, 392
Вуд (Wood) 450
Габор (Gabor) 248
Гаусс (Gauss) 139
Геффкен (Geffcken) 201, 204
Глаубер (Glauber) 320
Гови (Govi) 458
Гордон (Gordon) 536
Гуи (Gouy) 86
Гус (Goos) 379
Гюйгенс (Huygens) 32, 246
Икуно (Ikuno) 445
Ирвайн (Irvine) 463
Кадильяк (Cadilhac) 445
Келлер (Keller) 315
Клебш (Clebsch) 247, 459
Когельник (Kogelnik) 516
Конн (Connes) 537, 569
Кравцов Ю. А. 358
Лабейри (Labeyrie) 436
Ландау Н. Дж. (Landau N. J.) 536
Лебедев П. Н. 463
Летохов В. С. 463
Ли (Li) 308, 311, 529, 531, 533
Липман (Lippmann) 445
Лэмб (Lamb) 459, 551
Мак-Нейл (MacNeille) 199
Максвелл (Maxwell) 247
650
Именной указатель
Макфарлэйн (McFarlane) 551
Маром (Магот) 535
Мачмор (Muchmore) 181
Ми (Mie) 459
Миамото (Myamoto) 392
Миллар (МШаг) 445
Миногин В. Г. 463
Нейсли (Kneisly) 95
Ниджбоер (Nijboer) 308
Ньютон (Newton) 32, 314, 472
Орлов Ю. И. 358
Отто (Otto) 235
Паск (Pask) 598
Пастер (Pasteur) 47
Перо (Perot) 561
Поллак (Pollack) 536
Поттер (Potter) 472
Прохоров А. М. 485
Пти (Petit) 445
Рабинович (Rubinowicz) 314
Ригрод (Rigrod) 516, 553
Риттенхауз (Rittenhouse) 434
Роуланд (Rowland) 435
Рудольф (Rudolph) 435
Рытов С. М. 41
Рэлей (Rayleigh) 258, 449, 450, 458, 464
Сигмэн (Siegman) 522, 534
Слепли (Slepian) 518, 536
Смакула (Smakula) 201
Смит (Smith) 138
Снеллиус (Snell) 97
Стрел (Strehl) 323
Строит (Strong) 201, 435
Су (Hsue) 224
Талбот (Talbot) 281
Тамир (Iamir) 224
Таунс (Townes) 485
Тиндаль (fyndall) 458
Томсон Дж. Дж. (Thomson J. J.) 526
Тэйлор (Taylor) 200
Уиллис (WilUs) 396
Фабри (Fabry) 561
Фано (Fano) 451
Фейнман (Feynman) 23
Физо (Fizeau) 51
Фламан (Flamand) 436
Фок В. А. 459
Фоккема (Fokkema) 445
Фокс (Fox) 529, 531, 533
Франчиа ди Торальдо (Francia di
Toraldo) 248
Фраунгофер (Fraungofer) 434
Френель (Fresnel) 47, 247
Хайдингер (Haidinger) 565
Харрисон (Harrison) 435
Хасси (Hussey) 598
Хеллоуорт (Hellwarth) 23
Хенхен (Haenchen) 379
Херпин (Herpin) 181
Хорвиц (Horvitz) 534
Цернике (Zernike) 326
Чеббол (Chabbol) 568
Честер (Chester) 384
Шавлов (Schawlow) 485
Шеи (Shen) 463
Шлафер (Schlafer) 200
Шмаль (Schmahl) 435
Шродер (Schroder) 200
Штрейфер (Streifer) 535
Эйри (Airy) 472
Эрдейи (Erdelyi) 434, 344
Юнг (Young) 246, 314, 384
Ясуура (Yasuura) 445
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аббе условие синусов 296
Абеля условие 237
Аберрации волнового фронта 143
Аберраций функция 302, 528
изопланатической системы 298
Аберрация, астигматизм 145, 308
— кома 145, 308, 322
— кривизна поля 145
— сферическая 145
Амичи мениск 147, 148
Амплитудный коэффициент отражения
176
пропускания 176
Амплитуды рассеяния 461
Аналитический сигнал 52
Анизотропная среда 125, 126, 395
слоистая 207—211
отражение и пропускание
209—211
Апланатическая система 299
Апланатические точки сферы 147
Аподизация 331
Араго пятно 525
Асимметрии фактор 462, 463
Асимптотическое представление поля 359
— разложение вектора Пойнтинга 80,
81
поля магнитного 80
электрического 79
— решение волнового уравнения 62—65
Астигматическая разность пучка 132
Бабине принцип 265
Бауэра формула 456, 458
Белътрами оператор 454
Бете приближение 339
Биений длина 621
Блеска угол 438
Блоха уравнения 23
Елоховские волны 185—188
импедансы 188
полосы пропускания 185
Бойда — Когельника диаграмма устойчи-
устойчивости 511, 512
Боковые волны 374, 375
Брэгговский отражатель 215
Брюстера угол 177, 178
Буавена разложение 286
Ван-Циттерта — Цернике теорема 324,
326
Ватсона разложение 291
Ватсона — Редзюе представление 421
Вектор гирации 46
Векторный потенциал 13, 313
сферические волны 315
Венцеля — Крамерса — Бриллюэна (ВКБ)
метод 157
Взаимная интенсивность 324
Взаимной когерентности функция 54
Взаимности теорема 56
Виньетирование 141, 142
Волновая оптика 249, 250
Волновое сопротивление вакуума 61
— уравнение 13
векторное 79
Волновой фронт 65
аналитические свойства 90—92
на неплоской границе 95
Волновых векторов поверхность 57
Волны в движущейся среде 50, 51
Восприимчивость интегральная ком-
комплексная 25
Время когерентности 54
Вуда аномалии 450
Входной зрачок 141, 142
652
Предметный указатель
Вынужденное рассеяние комбинационное
(ВКР) 622
Мандельштама — Бриллюэна
(ВРМБ) 622, 623
Выходной зрачок 141, 142
Гамильтона функция 135
Гамильтона — Якоби уравнение. См.
Эйконала уравнение
Гамильтонова оптика 133, 134
Гауссова кривизна 97, 98
— оптика 139
Гауссов пучок, дифракции угол 502, 506
отражение 377
перетяжка 502
рэлеевская длина 502
с ограниченной апертурой 309—312
Гельмгольца векторное поле 254
Гельмгольца — Кирхгофа теорема 254
— уравнение для двумерных полей 265
неоднородное 15
Генерация второй гармоники (ГВГ) 20,
21
Геодезические линзы 127—129
Геометрическая оптика 63
критерий применимости 260
— теория дифракции 295, 315, 400, 429
Гирочастота 58
Главные диэлектрические проницаемости
39
— радиусы кривизны 84
Главный луч 141
— угол падения 230
Глория 469, 470
Голографические решетки 436
Градиентные оптические элементы 119,
120
Граничная дифрагированная волна (ГДВ)
318
Граница отражения 410
— тени 273, 410
Графа теорема сложения 282
Грина функция 15, 55, 253
Групповая скорость 17
ГУса — Хенхена эффект 377
Пойгенса принцип 246, 257, 258
Кирхгофа — Коттлера формули-
формулировка 260, 300
Двулучепреломление 38, 40"
— моды 620
Двухосный кристалл 40
Дебаевское разложение 419, 422
Дебая потенциалы 332
Джонса матрица 36
Диаграмма направленности 258
Дигидрофосфат (КН2РО4) 42
Дипольное приближение 22
Дипольный момент 22
Дисперсионное уравнение 45
Дисперсия мод 605—607
— среды 17
аномальная 18
нормальная 18
— хроматическая 607—609
Дисторсия 145, 308
Дифракционная картина 250
— матрица, искривленная кромка 409
— расходимость 518, 519
— формула Фраунгофера 279, 285
Френеля 276, 277
Дифракционно-ограниченная система 319
Дифракционные потери 518
— решетки, применение 437, 441
разрешающая способность 447, 449
формула 437
эффективность 438, 450
Дифракционный коэффициент 352, 406
Дифракция на дифракционных решетках
434, 441
клине 404, 411
острие 390
сфере 434
цилиндре диэлектрическом 414, 415
Дифракция на щели 412
— от угла 392
— периодических полей 281
— приграничная теория 252
Диэлектрическая восприимчивость 12, 30
— проницаемость 29
— сфера 465
Добротность 478
Дополнительный экран 265
Дюпина индикатриса 83
Естественная оптическая активность 45,
46
Предметный указатель
653
Заземленный диэлектрический волновод
220
Зайделя аберрации 308
— координаты 143
Закон дисперсии 17
— сохранения энергии 47
Закручивание лучей 69, 70
Запрещенная зона 234
Затягивание частоты 549
Зеркало диэлектрическое 194—198
— металлическое 194—198
Зоммерфелъда — Отта интеграл 331
Зоммерфелъда условие излучения 262,
263
Иерархия средних по ансамблю 53
Изображение когерентное 319, 324
— некогерентное 2%
Изопланатическая система 322, 326
Импедансные граничные условия 236
Импульсный отклик 264, 312, 318, 321
Инвариант наклона 113, 580
Интерференционные фильтры 203—207
Интерференционный порядок 437
Ионосфера, отражение волн 73
Канал 166
Каустика 72—74, 86, 87
— аналитические свойства 90, 92—95
— гиперболическая 493
— дифрагированных лучей 387
— цилиндрических полей 360
Квазимонохроматическая волна 35
Керра эффект 42
Кирхгофа — Коттлера формула 300
Кирхгофа приближение 339
— принцип 402
Клин с конечным импедансом 408—409
Клэро теорема 129
Комплексный вектор Пойнтинга 53
Контраст 564
Контур наибыстрейшего спуска (КНС)
272
Корню спираль 356, 357
Корреляционная длина 615, 616
Коши — Римана дифференциальные урав-
уравнения 368
Коэффициент поглощения 32
Крамерса — Кронига соотношения 28, 56
Кретчманна метод 236
Кривизна лучей 69, 70
— поля 308
Кристофеля символы 130
Критическая частота (частота отсечки)
589
Круговая поляризация 33
Кулоновская калибровка, условие 14
Кумулятивная передаточная функция
точки 335
Лагерр-гауссовы пучки 503
Ландау символ 63
Лиддана — Сакса — Теллера соотношение
58
Линейная поляризация 33
Линзовый эффект 528
Линзоподобные среды 106
Литтроу схема 438, 439
Лиувилля теорема 135
Локализации принцип 467
Локальная сшивка полей 95—98
Локальный импеданс 175
Лоренцева калибровка 15
— форма линии 205
— функция 31
Лунеберга — Дебая интеграл 300, 302,
303
Лунеберга — Клейна асимптотический
ряд 63, 82
Лунеберга линза 120, 121
Лучевая аберрация 132
— матрица 138—143
— поверхность 39, 395
— скорость 39
Магнитная индукция 11
Майкельсона интерферометр 54
Максвелла линза (рыбий глаз) 120, 121
— уравнения 38
Малюжинца функция 408
Малюса—Дюпина теорема 68
Материальное соотношение 16, 37
Матрица плотности 23
Матрица пропускания слоя. См. Харак-
Характеристическая матрица
654
Предметный указатель
Медленноменяющейся амплитуды при-
приближение 515
Меридиональные лучи 113
Метод ковариантного дифференцирова-
дифференцирования 129
— характеристической матрицы 180—185
Ми коэффициент 460
Микроволновые (СВЧ) генераторы 481
Минковского материальные соотношения
50
Многослойные просветляющие покрытия
171
Модовый шум 609
Моментов метод 431
Монохроматическая волна в однородной
среде 31
Мультислой 171
— импеданс блоховских волн 188
— отражение 189
— пропускание 191
— с попеременно изменяющимся показа-
показателем преломления 184, 185
— характеристическая матрица 181, 183
Наибыстрейшего спуска контур (КНС)
368
метод 366
Насыщаемый поглотитель 546
Нарушенное полное отражение 164, 227
Нейтрализаторы 343
Ненаправляемые моды 594
Необыкновенная волна 41
Необыкновенный луч 32
Неограниченная слоистая среда 155, 156
Неполяризованная волна 35
Непрозрачности полоса 170
Нормальная конгруэнция 69
— поверхность 395
Нормальное падение 232
Нормальные моды 45
Нормированная глубина резкости 310,
311
Обыкновенная волна 41
Обыкновенный луч 32
Объектив микроскопа с масляной им-
иммерсией 148
Овалоид 40
Одноосный кристалл 39, 40
Однородные волны 76
Однослойные покрытия 193
Ома закон 13
Оптическая длина 122
— индикатриса 41
— интенсивность 178
— ось кристалла 40
— передаточная функция 248
Оптические волокна 577, 578
градиентный профиль 578, 581
затухание излучения 603
многомодовые 591
модовая теория 583, 586
нелинейные эффекты 621
одномодовые 596
параболический профиль 592
слабонаправляющие 590
сохранение поляризации излучения
619
статистическая теория 618
ступенчатый профиль 578, 579—581
электромагнитные волны внутри
600
— генераторы 481—484
— координаты 142, 303
— направляющие косинусы 134
Основное уравнение электронной оптики
126
Отражение при нормальном угле паде-
падения 231
Параболического цилиндра функция 364
Параболическое приближение 279
Параксиальное изображение 140
— приближение 102, 103
Параметр возбуждения 549
— расстройки 31
Перевала метод 251
Передаточная функция 326, 327
точки 322, 323
Перестройка частоты 555—560
дисперсионные элементы 556
изменение длины резонатора 555
Плазменная частота 29
Планарный световод 155
Плоские волны 32, 51, 61
Плотность инверсии населенностей 25
Поверхностные волны 232
Предметный указатель
655
Поверхностные волны в металлах 233
— плазмоны 234
Поверхность нормалей 40
Пойнтинга вектор 47
Показатель преломления 43
аксиально-симметричное распреде-
распределение 105, 106, 109, 112
комплексный 12
кусочно-постоянный профиль 170,
171
Поккелъса эффект 42
— ячейка 42
пропускание 43
Ползущие волны 289, 293, 294, 425
Полоса непрозрачности 187
Полюсные сингулярности 217, 272
Поляризатор 178
Поляризационные светоделители 199
Построение луча 71
Преломление необыкновенного луча в
одноосном кристалле 127
Преломленный волновой фронт 98
главные направления и радиусы
кривизны 98
Пропускная способность 192
Просветляющие покрытия 200—203
Пространственная частота 327
Пространство изображения 131
— предмета 131
Протяженного предмета поле 324
Псевдобрюстеровский угол 229
Пуанкаре сфера
Радуга 469—473
Разложение по плоским волнам 266—268
цилиндрическим волнам 282, 284
Разрешающая способность 312
Рассеяние, коэффициент 218
— света диэлектриками 430
— сферическими частицами 458
— телами конечных размеров 110,
451—454
Резкость 192
Резонансная двухуровневая среда 30
— частота 18
Резонаторы, Вайнштейна теория
537—541
— волновая теория 525
— линейные 494—497
Резонаторы неустойчивые 520—525
дифракционная теория 542—545
— потери 529
— симметричные 530, 531, 541
— соотношения подобия 531
— телескопические 524
— устойчивые 512, 513, 516—525, 535
влияние разъюстировки 519
конфокальные 517—519, 536
Ригрода уравнения 553
Робинсона — Прайса метод 231
Рончи интерферометр 334
Роуланда круг 440
Рэлеевские длины волн 450
Рэлея—Джинса формула 485
Рэлея дифракционные интегралы 263,
264
— критерий разрешения 312
Саггитальная фокальная линия 133
Самоиндуцированные нелинейные эффек-
эффекты 624
Светосила 142
Связанных мод теория 215, 216,
612—617
Седловая точка 370, 371
Сила осциллятора 31
Сингулярных разложений метод 431
Скалярный потенциал 13
Скоростные уравнения 25
Смешанная характеристика 136
Смита — Гелъмголъца инвариант 141
Снеллиуса закон 97, 100
Солитоны 629
Сопряженные плоскости 140
— точки 121
Спекловая структура 611, 612
Сравнительные интегралы 342
Средняя кривизна 97, 98
Стабилизация частоты внешним сигна-
сигналом 559
Стационарной фазы метод 340
точки 260
Степень поляризации 35
Стокса параметры 34, 35, 464
Стопа четвертьволновых пластинок 187,
192
Стоячей волны отношение 195
Стрела отношение интенсивности 323
656
Предметный указатель
Сферические гармоники 454
— — векторные 457
— координаты 109
Сферически-симметричные среды 116
Сшивка асимптотических решений 159
Талбота эффект 281
Тангенциальная фокальная линия 133
Темный барьер 163
Тензор диэлектрической проницаемости
20
Теорема площадей 26
Теория когерентности 52
Точечная характеристика 122, 134
Точки ветвления 217, 273
— возврата 87
— поворота 158
Траектории затухания 76, 77
Транспортные уравнения 71, 73
Трубка лучей 72
Угловая дифракция, коэффициент 393
— характеристика 135, 136
Угловой спектр 268—272
Узловая точка 140
Уиплиса формула 396
Унитарный оператор 418
Условие поперечного резонанса 219, 220
— сохранения заряда 15
Утечки волна 218, 219
Фабри— Перо интерферометры 561, 562
аппаратная функция 567—569
- коэффициент пропускания 562
— применения 564—567
составные 567
Фазовая аномалия 86
— самомодуляция 627
— толщина 182
Фазовые траектории 76
— фронты 76
Фазовый синхронизм, условие 21
Фазосдвигающая цепочка 483
Фактор формы 205
Ферма принцип 124, 427
Физической оптики приближение 432
Флоке теорема 185, 186, 213
Фока — Леонтовича параболическое
волновое уравнение 75
Фокальная линия 88
Фокса — Ли интегральные уравнения
527—529
метод 531—533
Фокса — Смита интерферометр 558
Фокусировка пучков с малой апертурой
307-309
Фокусирующая система 299
Френеля зоны 259
— интеграл 354, 356
— кольца 259
— коэффициент увлечения 51
— коэффициенты отражения 177
— приближение 283
— ромб 232
— формулы 177
— число 302
Френё уравнения 70
Функция профиля 597
Фурье преобразование 114, 267
Характеристическая матрица 181
Характеристический волновой импеданс
слоя 174
Характеристическое уравнение 66
Херпина теорема 185
Хилла детерминант 214
— уравнение 213
Холодные зеркала 196, 197
Хорвица критерий 544
Цилиндрическая волна 265, 266
Цилиндрические координаты 108
Черная дыра 155
Черны — Тернера схема 439
Четвертьполуволновые покрытия 202
Четырехволновое смешение 622
вырожденное 632
Числовая апертура (ЧА) 142, 579
Шлирен-метод 333
Эберта — Фасти схема 439
Предметный указатель
657
Эйконал 62
— комплексный 76, 107
— уравнение 62, 65—67
—' — интегрирование 66
Эйри диск 247, 312
— распределение 312
— суммы формула 191
— уравнение 159
— функции 160, 342
Экстинкции сечение 452, 454
Экстинкция 32
Электрическая индукция 11
— постоянная 12
Электрические мультипольные поля 457
Электрических цепей теория 173
Электрооптический эффект 41
квадратичный 42
линейный 42
Электропроводность 18
Эллипсоид показателей преломления (ин-
(индексов). См. Оптическая индикатриса
Энантиоморфизм 47
Эталон 561, 562
Эффективности фактор 461—463
Эшелетт 441
Эшелон 441
Юнга интерферометр 54
ОГЛАВЛЕНИЕ
Предисловие редактора перевода .
Предисловие к русскому изданию
Предисловие
Глава 1.
Глава 3.
Основные свойства распространения электромагнитных волн 11
.1. Уравнения Максвелла 11
.2. Распространение излучения в среде с частотной дисперсией .... 16
.3. Состояние поляризации электромагнитного поля 32
.4. Распространение волн в анизотропной среде 37
.5. Распространение волн в средах с пространственной дисперсией 43
.6. Энергетические соотношения 47
.7. Распространение волн в движущейся среде 50
.8. Свойства когерентности электромагнитного поля 52
Задачи 55
Литература 59
Библиография 60
Глава 2. Геометрическая оптика 61
2.1. Приближенное представление электромагнитного поля 61
2.2. Асимптотическое решение скалярного волнового уравнения. .. 62
2.3. Уравнение эйконала 65
2.4. Уравнение для лучей 67
2.5. Транспортное уравнение для AQ 71
2.6. Транспортные уравнения для Лт 73
2.7. Затухающие волны и комплексные эйконалы 76
2.8. Геометрическая оптика максвелловских векторных полей 79
2.9. Дифференциальные свойства волновых фронтов 82
2.10. Каустики и волновые фронты 86
2.11. Отражение и преломление волнового фронта на неплоской
границе раздела двух сред , 95
2.12. Решение уравнения эйконала методом разделения переменных 103
2.13. Вычисление траекторий лучей методом разделения перемен-
переменных 112
2.14. Скалярные уравнения для лучей в криволинейных координа-
координатах; принцип Ферма 122
2.15. Элементы гамильтоновой оптики
Задачи
Литература
Библиография
Плоские многослойные среды
3.1. Введение
131
145
151
152
153
153
Оглавление 659
3.2. Геометрическая оптика в слоистых средах 155
3.3. Сшивка асимптотических разложений; метод Лангера 159
3.4. Отражение и пропускание произвольной неоднородной средой 166
3.5. Точное решение для слоя с линейно увеличивающимся показа-
показателем преломления 169
3.6. Многослойные среды с кусочно-постоянным профилем показа-
показателя преломления 170
3.7. Применение теории электрических цепей 172
3.8. Формулы Френеля 177
3.9. Метод характеристической матрицы 180
3.10. Блоховские волны 185
3.11. Полосы пропускания и непрозрачности стопы четвертьволно-
четвертьволновых пластинок 187
3.12. Коэффициент отражения мультислоя 189
3.13. Металлические и диэлектрические отражатели 194
3.14. Просветляющие покрытия 200
3.15. Интерференционные фильтры 203
3.16. Анизотропные слоистые среды 207
3.17. Распространение волн в периодической среде 211
3.18. Аналитические свойства коэффициента отражения 216
3.19. Распространение поверхностных и затухающих волн по тон-
тонким пленкам 220
3.20. Освещение под углом, большим критического 224
3.21. Отражение и преломление на границе раздела между диэлект-
диэлектриком и средой с потерями 228
3.22. Поверхностные волны на границе раздела двух сред 232
3.23. Импедансные граничные условия 236
Задачи 237
Литература 243
Библиография 244
Глава 4. Основы теории дифракции *. 246
4.1. Введение 246
4.2. Метод функции Грина 252
4.3. Принцип Гюйгенса в формулировке Кирхгофа — Коттлера .... 260
4.4. Условие Зоммерфельда на поле излучения 262
4.5. Дифракционные интегралы Рэлея для плоских экранов 263
4.6. Принцип Бабине 265
4.7. Дифракционные интегралы для двумерных полей 265
4.8. Разложение поля по плоским волнам 266
4.9. Угловой спектр. 268
4.10. Дифракционные формулы Френеля и Фраунгофера 276
4.11. Разложение поля по цилиндрическим волнам 282
4.12. Цилиндрические волны комплексного порядка и преобра-
преобразование Ватсона 286
4.13. Распределение поля в окрестности фокуса 294
4.14. Преобразование дифракционных интегралов к контурным 313
4.15. Изображение при когерентном и некогерентном освещении .... 319
Задачи 330
Литература 336
660
Оглавление
Библиография 338
Глава 5. Асимптотическое вычисление дифракционных интегралов 339
5.1. Введение 339
5.2. Метод стационарной фазы 342
5.3. Границы тени; стационарная точка вблизи граничной 353
5.4. Каустики цилиндрических полей; две соседние стационарные
точки 360
5.5. Поле вблизи двумерного острия каустики; модель для им-
импульсного отклика, при наличии дефокусировки и аберраций
третьего порядка 363
5.6. Метод наибыстрейшего спуска 366
5.7. Дифракционные эффекты на границе раздела двух диэлектри-
диэлектриков 373
5.8. Асимптотическое вычисление дифракционных интегралов в
цилиндрических координатах 380
5.9. Вывод асимптотических рядов из сравнительных интегралов;
метод Честера — Фридмана — Урселла (ЧФУ) 384
5.10. Асимптотическое вычисление поля, дифрагированного на от-
отверстии 385
5.11. Асимптотическая форма разложения полей по плоским вол-
волнам , 394
5.12. Формула У и ллиса 396
Задачи 396
Литература 400
Библиография * 401
Глава 6. Дифракция света на отверстии и рассеяние на металлических и ди-
диэлектрических предметах ¦ 402
6.1. «Введение 402
6.2. Дифракция на клине 404
6.3. Дифракция на щели 412
6.4. Дифракция на диэлектрическом цилиндре 414
¦,'-;: 6.5. 5-матрица и представление Ватсона — Редже 418
6.6. Поверхностные дифракционные волны 425
6.7. Обобщенный принцип Ферма и геометрическая теория ди-
дифракции 427
6.8. Рассеяние света диэлектрическими телами 430
6.9. Приближение физической оптики для идеально проводящего
тела 431
6.10. Электромагнитная теория дифракции на идеально проводящих
и диэлектрических дифракционных решетках 434
6.11. Рассеяние на телах конечных размеров 451
6.12. Разложение рассеянного поля по сферическим гармоникам ..... 454
6.13. Рассеяние на сферических частицах 458
Задачи 474
Литература 475
Библиография ¦ 476
Глава 7. Оптические резонаторы и интерферометры Фабри — Перо 478
7.1. Общие свойства резонаторов для электромагнитных волн 478
7.2. Общие свойства оптических резонаторов 485
Оглавление 661
7.3. Частотный отклик резонатора 488
7.4. Рассмотрение закрытого эллиптического резонатора в рамках
геометрической оптики 490
7.5. Линейные резонаторы 494
7.6. Рассмотрение резонатора как последовательности линз 497
7.7. Поля от источников, расположенных в комплексной плоско-
плоскости .. 500
7.8. Эрмит-гауссовы и лагерр-гауссовы пучки 503
7.9. Применение лучевых матриц для описания последовательно-
последовательности линз, эквивалентной резонатору 508
7.10. Модовое представление поля внутри устойчивого резонатора,
не имеющего дифракционных потерь 513
7.11. Устойчивые резонаторы 516
7.12. Неустойчивые резонаторы 520
7.13. Волновая теория пустых резонаторов 525
7.14. Интегральные уравнения Фокса — Ли 527
7.15. Методы расчета модовых конфигураций 531
7.16. Устойчивые резонаторы с прямоугольными зеркалами 535
7.17. Резонаторы с аксиальной симметрией 541
7.18. Дифракционная теория неустойчивых резонаторов 542
7.19. Резонаторы с активной средой 545
7.20. Перестройка частоты 555
7.21. Интерферометры Фабри — Перо 561
Задачи 569
Литература 574
Библиография 576
Глава 8. Распространение света в оптических волокнах 577
8.1. Геометрическая оптика 577
8.2. Волокна со ступенчатым профилем показателя преломления. . 579
8.3. Градиентные волокна 581
8.4. Модовая теория 583
8.5. Модовая теория для волокон со ступенчатым профилем пока-
показателя преломления 586
8.6. Слабонаправляющие волокна со ступенчатым профилем пока-
показателя преломления 590
8.7. Волокна с параболическим профилем показателя преломления 592
8.8. Ненаправляемые моды 594
8.9. Одномодовые волокна 596
8.10. Электромагнитное поле внутри волокна 600
8.11. Затухание 603
8.12. Дисперсия мод 605
8.13. Хроматическая дисперсия 607
8.14. Модовый шум 609
8.15. Теория связанных мод 612
8.16. Статистическая теория распространения в системе оптических
волокон 618
8.17. Оптические волокна, сохраняющие поляризацию излучения .... 619
8.18. Нелинейные эффекты в оптических волокнах 621
8.19. Самоиндуцированные нелинейные эффекты 624
662 Оглавление
Задачи 633
Литература 635
Библиография , 636
Приложения 637
Приложение А. Формулы векторного анализа 637
Приложение Б. Диады и их свойства 637
Приложение В. Специальные функции 638
Приложение Г. Формулы разложений в ряд 643
Приложение Д. Интегральные преобразования 645
Приложение Е. Асимптотическое разложение дифракционных инте-
интегралов 646
Именной указатель 649
Предметный указатель 551